Author: Даламбер Ж.
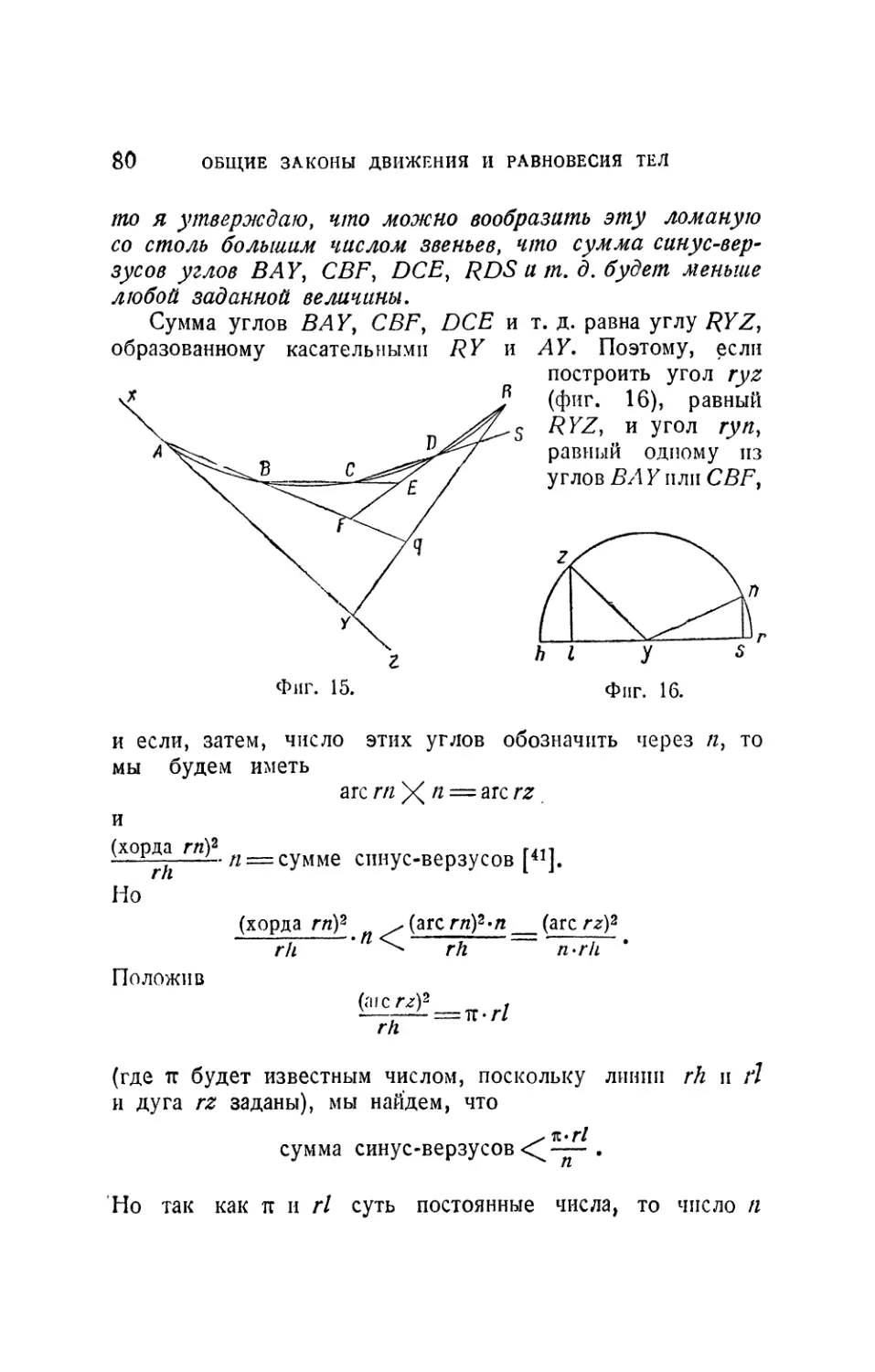
Tags: физика математика механика движение тел трактат законы равновесия
Year: 1960
Text
Ж. ДАЛАМБЕР
(1717-1783)
КЛАССИКИ
ЕСТЕСТВОЗНАНИЯ
КЛАССИКИ
ЕСТЕСТВО ЗНАНИЯ
МАТЕМАТИКА
МЕХАНИКА
ФИЗИКА
АСТРОНОМИЯ
ГОСУДАРСТВЕННОЕ ИЗДАТЕЛЬСТВО
ТЕХНИКО * ТЕОРЕТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА М950' ЛЕНИНГРАД
Ж.ДАЛАМБЕР
ДИНАМИКА
ТРАКТАТ,
В КОТОРОМ ЗАКОНЫ РАВНОВЕСИЯ
И ДВИЖЕНИЯ ТЕЛ сводятся к
возможно МЕНЬШЕМУ ЧИСЛУ И
ДОКАЗЫВАЮТСЯ НОВЫМ СПОСОБОМ.
И В КОТОРОМ ИЗЛАГАЕТСЯ ОБЩЕЕ
ПРАВИЛО ДЛЯ НАХОЖДЕНИЯ
ДВИЖЕНИЯ НЕСКОЛЬКИХ ТЕЛ,
ДЕЙСТВУЮЩИХ ДРУГ НА ДРУГА
ПРОИЗВОЛЬНЫМ ОБРАЗОМ
Jlepeeoq с французского
и прилсвтания
В.П. ЕГОРШИНА
*^%F^
ГОСУДАРСТВЕННОЕ ИЗДАТЕЛЬСТВО
ТЕХНИКО'ТЕОРЕТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА • I96 0 ' ЛЕНИНГРАД
12-5-4
ПРЕДИСЛОВИЕ
К РУССКОМУ ИЗДАНИЮ
Имя знаменитого французского ученого Жана Далам-
бера (1717—1783) знает каждый инженер, каждый физик,
механик и математик. Даламбер стоит в одном ряду
с основателями механики — Ньютоном, Эйлером и Лагран-
жем. Принадлежа к передовой группе французских
энциклопедистов, сотрудничая с материалистом Дидро, Даламбер
хотел поставить механику и математические науки на
службу хозяйственному прогрессу и техническому
обновлению, в котором так нуждалась Франция, находившаяся в то
время в тисках феодализма.
Среди работ Даламбера основное значение имеет
предлагаемая читателю в переводе на русский язык книга
«Динамика». В этой книге развивается широко известный
«принцип Даламбера». Однако, как увидит читатель,
формулировка этого принципа, принадлежащая самому Даламберу,
сильно отличается от принятой ныне в учебниках.
«Динамика» Даламбера имеет особый интерес потому,
что она вводит нас в круг методологических споров,
которыми отличалась механика первой половины XVIII в.
Даламбер был видным общественным деятелем эпохи кануна
буржуазной революции во Франции. Дыхание этой
революции чувствуется в его публицистических выступлениях, и
6
ОТ ИЗДАТЕЛЬСТВА
официальные круги феодальной Франции едва терпели
Даламбера, сотрудника Дидро и Вольтера.
До Даламбера механика развивалась в условиях
антагонизма между картезианским (декартовским) и ньютониан-
ским направлениями, а также в условиях борьбы между
картезианским и лейбницевским направлениями. Декарт в
философии механики стоял ближе к материализму, чем Ньютон,
но он не сумел или ему не удалось построить на своих
принципах все здание механики. Ньютону удалось дать
систему механической науки ценой отказа от наиболее
принципиальных вопросов и ограничения формальной стороной
дела. Даламбер был слишком математиком, чтобы соглашаться
с Декартом, и слишком философом, чтобы соглашаться
с Ньютоном. И тем не менее он не сумел синтезировать
лучшие стороны ньютонианства и картезианства путем
преодоления ограниченности того и другого. Для этого нужно
было быть материалистом-диалектиком.
Даламбер не соглашался с крайними формалистами,
желавшими растворить механику в математике, он был
близок к техническим задачам своего времени, но в споре
между картезианцами и лейбницианцами по вопросу о мере
движения Даламбер занял такую позицию, что сущность
спора оказалась у него потопленной в формальной стороне
дела. Вопроса о двух мерах движения в механике он не
решил, — он как бы снял его с очереди. Прочтя в
настоящей книге «Введение» самого Даламбера, читатель, конечно,
вспомнит замечательный анализ этого вопроса у Ф. Энгельса
в его «Диалектике природы».
Механика как наука в капиталистических странах
в методологическом отношении не только не поднялась
выше Даламбера, но шагнула далеко назад. Вопросы,
поставленные Даламбером в его «Динамике», сохраняют свой
интерес и в наши дни, причем не только для лиц, зани-
ОТ ИЗДАТЕЛЬСТВА
7
мающихся историей механики, но и для исследователей,
занимающихся разработкой обоснования механики как науки.
Эти обстоятельства и побудили издательство выпустить
книгу Даламбера в переводе на русский язык.
Только советская наука, основывающаяся на
марксистско-ленинской теории познания, сумеет правильно понять
Даламбера, усвоив у него все положительное и отсеяв его
заблуждения.
В. /7. Егоршан
TRAITE
D E
DYNJMIQUE,
DANS LEQUEL LES LOIX DE L'EOUILIBRE
& du Mouvement des Corps font rcduites au plus petit nombre pof-
fible, & demontrees d'une manicre nouvelle , dc ou Ton donne un
Principe general pour trouver к Mouvement de plufieura Corps qui
agiflent les uns fur les autres, d'une maniere quelconque.
Par M. d'AiEMBERTyde TAcadlmie Roy ale des Sciences.
Chez David I'aine, Libraire, rue Saint Jacques, a la Plume d or.
M D С С X L I I I.
AVEQ APPROBATION ET PRIVILEGE DV ROL
Ж.ААААМБЕЗР
ДИНАМИКА
JSfb
4^5?3®J§4n>
ПРЕДИСЛОВИЕ АВТОРА [*] КО ВТОРОМУ ИЗДАНИЮ *)
Настоящее второе издание увеличено более, чем на
одну треть.
Во введении добавлены некоторые соображения по
вопросу о живых силах и разбирается новый важный вопрос,
предложенный Прусской королевской академией наук:
«являются ли законы статики и механики необходимой, или
случайной истиной»? [2].
В первой части настоящего сочинения значительно
подробнее, чем это было сделано в первом издании, изложен
вопрос об измерении и сравнении ускоряющих сил и
добавлены по этому поводу некоторые замечания, которых нигде
в другом месте найти нельзя. Далее, в первую часть
включено несколько новых исследований, относящихся к законам
равновесия.
Основные добавления, сделанные во второй части,
следующие: некоторые предложения о центре тяжести
нескольких тел, действующих друг на друга; полное решение
одной динамической задачи, которая до сих пор была
решена не полностью, потому что з уравнениях не умели
разделять переменные (эта проблема разбирается в п° 97
и ел.); гораздо более простое решение задачи V о
движении нити, нагруженной несколькими грузами, — решение,
с которым связан ряд любопытных соображений; более
полное ив то же время более простое решение задачи
*) Цифры в квадратных скобках указывают на примечания
переводчика, помещенные в конце книги.
12 ПРЕДИСЛОВИЕ АВТОРА КО ВТОРОМУ ИЗДАНИЮ
о телах, качающихся на плоскости; наконец, новые
исследования и немаловажные замечания по поводу соударения
упругих тел. Я не отмечаю многих иных, менее
значительных добавлений, разбросанных по всей книге. Они, по
большей части, служат более детальному изложению того, что,
по моему мнению, нуждалось в этом.
Я не могу, однако, не отметить того, что я весьма
признателен Безу, члену королевской академии наук, который
любезно снабдил настоящее издание большим количеством
примечаний, имевших своей целью сделать книгу
доступной большему кругу читателей, чем это было в первом
издании. Эти примечания, число которых превышает
шестьдесят, помещены подстрочно.
Хотя настоящее издание и так уже сильно возросло,
я намеревался дополнить его еще различного рода статьями,
относящимися к динамике, но составленными большей частью
гораздо раньше. Эти статьи относятся к следующим
разделам.
1) Исследования движения тела, вращающегося вокруг
подвижной оси. Эта задача — того же рода, как и задача
«о предварении равноденствий», которой я посвятил
сочинение, вышедшее в свет в 1749 г. и содержащее все
необходимые принципы для решения этой задачи в общем
виде [8]; исследования, о которых я говорю здесь и
которые я хотел присоединить к настоящему трактату, суть
не что иное, как применение этих принципов.
2) Несколько добавлений к тому совершенно новому-
гидродинамическому исследованию, которое было дано
мною в главах VIII и IX моей «Теории сопротивления
жидкостей» [4], опубликованной в 1752 г. Этими добавлениями
я хотел показать, что указанное гидродинамическое
исследование при всей его краткости заключает в себе метод
настолько общий, насколько можно желать для того, чтобы
подчинить математическому анализу движение жидкостей
и в то же время- определить то небольшое число случаев,,
в которых к исследованию этого рода движения можно*
строго применять анализ.
3) Теория колебаний плавающих тел, служащая
дополнением к тому, что было намечено мною в главе VI толь-
ПРЕДИСЛОВИЕ АВТОРА КО ВТОРОМУ ИЗДАНИЮ 13
ко что указанного моего сочинения «О сопротивлении
жидкостей» [5].
4) Довольно объемистое сочинение о колебаниях струн —
в ответ на те возражения, которые были мне сделаны по
этому вопросу на страницах «Memoires de TAcademie de
Berlin» (1753) двумя крупнейшими математиками, г.г. Бер-
нулли и Эйлером. Эти авторы, кстати сказать, расходятся
между собою даже в-тех вопросах, по которым они
возражают мне: один согласен со мной в том, что другой
отрицает [6].
5) Наконец, доказательство правила сложения сил,—
правда, не столь простое, как доказательство, помещенное
в п° 28 настоящего сочинения, но, как я полагаю, не
безынтересное для математиков благодаря тому приему,
который я нашел для упрощения замечательно остроумного
доказательства этого правила, помещенного в первом томе
петербургских «Commentarii» [7].
Однако, как ни интересны все эти дополнения по их
замыслам, они сильно увеличили бы объем данной книги.
Поэтому я решил опубликовать их в другой раз, все вместе
или по отдельности.
\^!RjW4n»
ВВЕДЕНИЕ [8]
Достоверность математики является тем ее
преимуществом, которым она обязана главным образом простоте
своего предмета. Более того, нужно признать, что
поскольку не все отделы математики имеют одинаковый по
простоте предмет, постольку и достоверность в
собственном смысле слова,—достоверность, основывающаяся
на принципах, являющихся необходимо истинными и
очевидными сами по себе, — присуща различным ее
отделам не в одинаковой степени и не одинаковым образом.
Многие отделы математики, опирающиеся или на
физические принципы, т. е. на опытные истины, или же на
простые гипотезы, обладают, так сказать, лишь
достоверностью опыта или даже достоверностью чистого
допущения. Строго говоря, обладающими полной очевидностью
можно считать только те отделы математики, которые
имеют дело с исчислением величин и с общими
свойствами пространства: таковы алгебра, геометрия и
механика [9]. Даже и здесь в степени ясности, которую наш ум
находит в этих науках, можно заметить своего рода
градацию и, если можно так выразиться, те или иные оттенки.
Чем шире тот предмет, который ими обнимается, и чем
более обща и абстрактна та форма, в которой он в них
рассматривается, тем больше их принципы избавлены от
неясностей и тем более они доступны для понимания.
Именно по этой причине геометрия проще механики, а
они обе менее просты, чем алгебоа.
16
ВВЕДЕНИЕ
Этот парадокс перестает казаться парадоксом для тех,
кто изучал эти науки как философ: для них наибольшей
ясностью обладают именно те наиболее абстрактные
понятия, которые обычно считаются наиболее недоступными.
Наоборот, нашими мыслями овладевает мрак по мере того,
как мы сталкиваемся в том или ином объекте с
чувственными свойствами. Так, прибавляя к понятию протяженности
непроницаемость, мы, мне кажется, лишь увеличиваем
тайну; природа движения является загадкой для
философов; не менее скрыто от них и метафизическое начало законов
соударения. Одним словом, чем более углубляют они
образующееся у них понятие о материи и о свойствах,
ее представляющих, тем более это понятие затемняется,
как будто стремясь ускользнуть от них, и тем более они
убеждаются, что о внешних объектах наименее
несовершенным образом мы знаем лишь одно, — это их
существование, да и оно опирается на сомнительное
свидетельство наших чувств.
Из этих соображений следует, что наилучший метод
в любом отделе математики (можно даже сказать: в любой
науке) состоит в том, чтобы не только вводить туда и
максимально применять знания, полученные из более
абстрактных, а следовательно, и более простых наук, но и
самый объект данной науки рассматривать наиболее
абстрактным и наиболее простым из всех возможных способов,
ничего не предполагать и ничего не приписывать объекту
данной науки, кроме тех свойств, из которых, как из
предпосылки, исходит сама данная наука. Отсюда вытекают
два преимущества: во-первых, принципы получают всю
возможную для них ясность; во-вторых, эти принципы
оказываются сведенными к наименьшему числу, выигрывая
тем самым в своей общности, так как, поскольку
предмет науки необходимо определен, принципы этой науки
тем плодотворнее, чем меньше их число.
С давних пор намеревались, и даже не без успеха,
выполнить по отношению к математике некоторую часть
того плана, который нами только что намечен: алгебру
удачно применяли к геометрии, геометрию к механике и
каждую из этих трех наук ко всем остальным наукам,
ВВЕДЕНИЙ
17
основанием и фундаментом которых они являются. Однако
при этом не заботились ни о сведении принципов этих
наук к наименьшему числу, ни о том, чтобы придать этим
принципам всю ту ясность, которой можно было бы
желать. Особенно пренебрегав этой задачей, мне кажется,
в механике: большинство ее принципов или неясных самих
по себе, или неясно сформулированных и доказанных,
давали повод к ряду трудных вопросов. Вообще до сих
пор занимались больше увеличением здания, чем
освещением входа в него. Думали, главным образом, над тем,
как бы возвысить его, не заботясь о том, чтобы придать
необходимую прочность его основанию.
В настоящем сочинении я поставил себе двойную цель:
расширить рамки механики и сделать подход к этой
науке гладким и ровным. При этом я больше всего
заботился о том, чтобы одна задача разрешалась с помощью
другой, т. е. я стремился не только вывести принципы
механики из наиболее ясных понятий, но и расширить
область их применений. Наряду с этим я стремился
показать как бесполезность многих принципов,
употреблявшихся до сих пор в механике, так и выгоды, которые
можно получить для прогресса этой науки от объединения
остальных. Одним словом, я стремился расширить область
применения принципов, сокращая в то же время их число.
Таковы были мои намерения в настоящем сочинении. Для
того чтобы ознакомить читателя со средствами, при
помощи которых я старался осуществить эти намерения,
может быть будет не лишним заняться логическим
анализом науки, которую я взялся излагать.
Движение и его общие свойства — таков первый и
главный объект механики. Механика предполагает, что
движение существует, и поскольку в этом ни у кого из
физиков никаких сомнений нет, мы будем также исходить
из этой предпосылки. Что же касается природы движения,
то здесь, напротив, философы резко расходятся друг с
другом. Правда, нет ничего более естественного, чем
представлять себе движение как последовательное приложение
движущегося предмета к различным частям безграничного
пространства, мыслимого нами в качестве места тел. Но
2 Ж Даламбер
18
ВВЕДЕНИЕ
такое представление предполагает пространство, част
которого проницаемы и неподвижны, а между тем всякий
знает, что картезианцы (секта, которая ныне, правда, почти
уже не существует) совершенно не признают пространства,
отличного от тел, оюждествляя материю и протяженность.
Необходимо признать, что если исходить из подобного
принципа, то движение становится вещью очень трудной
для понимания: картезианцам, может быть, лучше вовсе
отрицать существование движения, чем пытаться опреде-,
лить его природу. Впрочем, хотя мнение этих философов
и представляется нам абсурдным и хотя в тех
метафизических принципах, из которых они стремятся вывести свое
учение, весьма мало ясности и строгости, мы не
собираемся здесь заниматься его опровержением. Мы ограничимся'
лишь следующим замечанием. Для того чтобы у нас было
ясное представление о движении, необходимо различать
два рода протяженности: одну, рассматриваемую как
непроницаемая и составляющую то, что называют собственно
телами, и другую, рассматриваемую просто как
протяженность— безотносительно к тому, проницаема она или нет,
и являющуюся не более как мерой расстояния одною
тела от другого: части этой последней протяженности
мыслятся нами закрепленными и неподвижными, и с
помощью их мы можем судить о покое или движении тел.
Таким образом, мы будем всегда считать себя вправе
рассматривать безграничное -пространство в качестве места
тел, реального или только воображаемого, а движение
рассматривать как перенос движущегося тела из одного
места в другое место.
Рассмотрение движения иногда встречается и в
исследованиях по чистой геометрии: так, часто представляют
линии,— прямые или кривые, — как образующиеся путем
непрерывного движения точки; поверхности—как
образующиеся путем движения линии; наконец, тела — как
образующиеся путем движения поверхности. Однако есть
разница между геометрией и механикой: эта разница
состоит не только в том, что образование тех или иных
фигур путем движения косит, так сказать, произвольный
характер и о нем говорят просто в целях изящества изло-
ВВЕДЕНИЕ
19
жения, но еще и в том, что геометрия, говоря о
движении, ограничивается рассмотрением пройденного
пространства, в то время как механика рассматривает кроме того
и время, затрачиваемое движущимся телом на
прохождение этого пространства.
Нельзя сравнивать между собой две вещи различной
природы, какими являются пространство и время, но можно
сравнивать отношение частей времени с отношением частей
пройденного пространства. Время по своей природе течет
равномерно, и механика исходит из этой равномерности.
Поскольку мы, однако, не знаем времени, как такового, и
не обладаем точной мерой времени, мы не можем
составить себе более ясного представления об отношении
частей времени иначе, чем при помощи отношения отрезков
неограниченной прямой линии. Отношение же между
частями такого рода линии может быть связано с отношением
между частями пространства, пройденного телом,
движущимся произвольным образом, при помощи некоторого
уравнения, а именно: можно представить себе кривую,
абсциссы которой будут соответствовать частям времени,
протекшего с начала движения, а ординаты —
пространствам, пройденным за эти части времени. Уравнение этой
кривой будет выражать не соотношение между
пространством и временем, а, если можно так выразиться,
соотношение между отношением частей времени к единице
времени и отношением частей пройденного пространства к
единице пространства. В самом деле, уравнение кривой
можно рассматривать • или как соотношение между
ординатами и абсциссами, или как уравнение, связывающее
отношения ординат к единице ординат с отношениями
соответствующих абсцисс к единице абсцисс.
Очевидно, что достаточно одного применения геометрии
и анализа, чтобы, без помощи каких бы то ни было иных
принципов, найти общие свойства движения, меняющегося по
какому-нибудь закону. Но каким образом получается, что
движение тела подчиняется именно тому или другому закону
в частности? Одна геометрия ничего не может сказать по
этому поводу. Это и есть то, что можно рассматривать как
первую задачу, относящуюся непосредственно к механике.
2*
20
ВВЕДЕНИЕ
Прежде всего совершенно очевидно, что никакое тело
не может сообщить движения самому себе. Оно может
быть выведено из состояния покоя только в результате
действия какой-либо внешней причины. Но будет ли оно
само по себе продолжать свое движение, или для его
движения необходимо повторное действие этой причины?
Как бы мы ни решали этот вопрос, одно несомненно: если
сделано раз предположение о существовании движения
без какого-либо другого особого допущения, то
простейшим законом, которому может следовать тело в своем
движении, будет закон равномерности; поэтому именно
такому закону тело и должно следовать, как это будет
показано ниже, в первой главе настоящего сочинения.
Движение, таким образом, является равномерным вследствие своей
природы. Правда, те доказательства, которые давались
этому принципу до сего времени, были, может быть,
недостаточно убедительными; в настоящем сочинении
указываются возникающие здесь трудности, как равно и путь,
избранный мною для того, чтобы уклониться от
обязательств их разрешить.
Мне кажется, что указанный закон равномерности,
присущий .движению, как таковому, дает нам одно из лучших
оснований, на которое может опираться измерение времени
при помощи равномерного движения. Я счел необходимым
осветить этот вопрос несколько подробнее, хотя может
показаться, что в сущности эти рассуждения выходят из
рамок механики.
Поскольку установлена «сила инерции» [10], т. е.
свойство тел неизменно пребывать в их состоянии покоя или
движения, ясно, что если для начала движения
необходима та или иная причина, то и для ускорения или
замедления этого движения также необходима внешняя
причина. Что же это за причины, способные произвести
или изменить движение в телах? К настоящему времени
нам известны только два рода этих причин: одни
проявляются для нас вместе с производимыми ими действиями
пли, вернее, с действиями, причиной которых они
являются. Эти причины имеют своим источником осязаемое
действие тел друг на друга, обусловленное их непроница-
ВВЕДЕНИЕ
21
емостыо; они сводятся к удару и к некоторым другим
производным от него действиям. Все другие причины мы
познаем лишь по их действию, природа же их самих нам
совершенно неизвестна: такова причина, заставляющая
тяжелые тела падать к центру земли, причина,
удерживающая планеты на их орбитах, и т. п.
Мы вскоре увидим, каким образом можно определить
результаты удара и те причины, которые могут сюда
относиться. Что же касается причин второго рода, то
очевидно, что поскольку вопрос заключается в действиях,
вызванных этими причинами, эти действия должны всегда
задаваться независимо от знания причины, так как их нельзя
вывести из самих причин. Так, не зная причины тяжести,
мы на опыте убеждаемся, что пути, пройденные падающим
телом, пропорциональны квадрату времени. Вообще в
неравномерных движениях, причины которых неизвестны,
действие, произведенное причиной,—пли в течение
конечного времени, или в течение одного
мгновения,—очевидно, должно быть задано при помощи уравнения,
связывающего время и пространство. Раз известно это
действие и раз мы допускаем принцип силы инерции, —■
свойства этого рода движений могут быть найдены с
помощью только одной геометрии и анализа. Для чего же
тогда нам прибегать к тому принципу, которым сейчас
все пользуются, — а именно, к принципу, что сила,
ускоряющая или замедляющая, пропорциональна элементу
скорости? 'Принцип этот опирается только на расплывчатое
и неясное положение, что действие пропорционально своей
причине. Мы не будем вдаваться в рассмотрение того,
принадлежит ли этот принцип к числу необходимых истин.
Мы отметим лишь, что дававшиеся до сих пор
доказательства этого принципа не кажутся нам безупречными; мы не
примем его, подобно некоторым геометрам, и в качестве
случайной истины: это разрушило бы достоверность
механики и сделало бы ее просто опытной наукой. Мы
ограничимся лишь замечанием, что этот принцип, —
истинный он или сомнительный, ясный или темный, — в
механике бесполезен, и потому он должен быть из нее
исключен»
22
ВВЕДЕНИЕ
До сих пор мы говорили лишь об изменениях скорости
движущегося тела под влиянием причин, могущих изменить
движение, и совершенно не исследовали, что должно
происходить, если движущая причина стремится двигать тело
в направлении, отличном от того, которое имеет тело.
Принцип силы инерции в данном случае нам говорит лишь
то, что тело будет стремиться описывать прямую линию и
притом описывать равномерно; но отсюда нельзя узнать ни
скорости тела, ни его направления [п]. Здесь необходимо
прибегнуть к другому принципу, который называют
сложением движений и при помощи которого определяют единое
движение тела, стремящегося двигаться с заданными
скоростями по различным направлениям одновременно. В
настоящем сочинении дается новое доказательство принципа
сложения движений, где я ставил себе целью избежать
всех тех трудностей, которые присущи обычным
доказательствам данного принципа, ив то же время стремился
к тому, чтобы не выводить его из большого числа
сложных предпосылок: этот принцип, один из первых принци;
пов механики, необходимо должен опираться на простые и
легкие доказательства.
Поскольку движение тела, меняющего свое направление,
можно рассматривать как движение, составленное из
первоначального движения тела и из движения вновь им
полученного, постольку и первоначальное движение тела можно
рассматривать также как движение, составленное из нового,
воспринятого телом, движения и из некоторого другого
движения, им утраченного. Отсюда следует, что законы
движения, изменяющегося благодаря тем или иным
препятствиям, зависят исключительно от законов движения,
уничтоженного этими самыми препятствиями. В самом деле,
легко видеть, что достаточно разложить движение, которым
тело обладало до встречи с препятствием, на два таких
движения, из которых одному препятствие ни в какой мере
не является помехой, а другое им уничтожается. С помощью
этого метода можно не только получить законы движения,
изменяющегося благодаря непреодолимым препятствиям (эти
законы только и были найдены данным методом), но также
определить, в каком случае этими препятствиями движение
ВВЕДЕНИЕ
23
будет уничтожено. Что касается законов движения,
изменяющегося благодаря препятствиям, которые сами по себе
непреодолимыми не являются, то по тем же основаниям
очевидно, что вообще для нахождения этих законов
необходимо лишь твердо установить законы равновесия.
Каков же должен быть общий закон равновесия тел?
Все геометры сходятся на том, чго два тела с
противоположными направлениями уравновешиваются в том случае,
когда их массы обратно пропорциональны скоростям, с
которыми они стремятся двигаться. Однако, доказать этот
закон со всей строгостью и притом так, чтобы ие
оставалось никакой неясности, повидимому, не так легко. Поэтому
большинство геометров предпочитает это положение
рассматривать в качестве аксиомы, не давая себе труда
доказывать его. Между тем, при внимательном рассмотрении
можно заметить, что имеется только один единственный
случай, когда равновесие проявляется ясно и четко: это —
тот случай, когда массы обоих тел равны, а скорости их
равны и противоположны. И мне кажется, единственный
путь, который можно избрать для доказательства
равновесия в других случаях, должен заключаться в том, чтобы,
если это возможно, привести их к указанному случаю,
простому н очевидному самому по себе. Это я также
старался осуществить в настоящем сочинении. Насколько мне
это удалось, пусть судит читатель.
Принцип равновесия вместе с принципом силы инерции
и принципом сложения движений позволяют находить
решение всех задач, относящихся к движению одного тела,—
поскольку оно может быть изменено непроницаемым и
подвижным препятствием, т. е., вообще говоря, каким-нибудь
другим телом, которому данное тело необходимо сообщает
движение, сохраняя по меньшей мере часть своего
движения. Из совокупности этих принципов можно легко
вывести и законы движения соударяющихся каким-либо
образом тел или тел, из которых одно тянет другое
посредством того или иного промежуточного тела, скрепленного
с ними.
Если принцип силы инерции, принцип сложения
движений и принцип равнрвесия существенно отличаются друг от
24
ВВЕДЕНИЕ
друга,—- a t этим нельзя не согласиться,— и если, с другой
стороны, этих трех принципов достаточно для механики, то
это и значит, что данная наука приведена к минимальному
числу принципов и что все законы движения тел при каких
угодно условиях могут быть получены из этих трех
принципов. Это я и пытался осуществить в настоящем сочинении..
Что касается доказательств самих этих принципов, то,
для тою, чтобы придать этим доказательствам всю ту
ясность и простоту, какая только в данном случае казалась
мне возможной, я старался вывести их лишь из
рассмотрения движения, причем это рассмотрение должно быть
опять-таки наиболее простым и наиболее ясным. В
движении любого тела весьма отчетливо мы видим лишь то,
что тело проходит известное расстояние и что на это
тратится известное время. Из этой одной идеи и надлежит
вывести все принципы механики, если мы хотим их
доказать с необходимой ясностью и строгостью. Поэтому
читатель не должен удивляться, если я, исходя из этих
соображений, так сказать, игнорирую «движущие причины» и
рассматриваю исключительно движение, которое
производится ими. Я полностью изгоняю присущие движущемуся
телу силы, как понятия неясные и метафизические,
способные лишь распространить мрак над ясной самой по
себе наукой.
По этой причине я считал ненужным вдаваться в
рассмотрение нашумевшего вопроса о «живых силах». Этот
вопрос, который уже тридцать лет разделяет геометров,
заключается в следующем: чему пропорциональна сила
движущегося тела — произведению массы на скорость или
же произведению массы на квадрат скорости? Например,
если одно тело в два раза больше другого [12], а скорость
его в три раза больше скорости последнего, то во сколько
раз сила первого тела больше силы второго — в
восемнадцать раз или только в шесть раз? Какие бы споры этот
вопрос ни вызывал, полнейшая бесполезность его для
механики заставила меня совершенно не упоминать о нем в
настоящем сочинении. Однако, я полагаю, нельзя совершенно
обойти молчанием мнение, которое Лейбниц считал
возможным ставить себе в заслугу, как открытие, которое затем
ВВЕДЕНИЕ
^5
столь искусно и столь удачно развил великий Бернулли *)>
которое изо всех сил старался опровергнуть Маклорен[14]
и к которому привлекли интерес широкой публики статьи
большого числа известных математиков. Не желая
обременять читателя детальным изложением всего того, что
было сказано по этому поводу, я считаю не лишним
изложить вкратце те принципы, которые могут помочь в
разрешении данного вопроса [15].
Когда говорят о силе движущихся тел, то пли с
произносимым словом вовсе не связывают никакой ясной идеи,
или под ним понимают лишь свойство движущихся тел
преодолевать встречаемые ими препятствия или
сопротивляться этим препятствиям. Поэтому силу надо
непосредственно измерять вовсе -не расстоянием, равномерно
проходимым телом, не временем, употребляемым телом на это
движение, и, наконец, не массой и скоростью тела,
взятыми в их простом, голом и абстрактном рассмотрении, а
исключительно теми препятствиями, которые тело
встречает, и тем сопротивлением, которое ему оказывают эти
препятствия. Чем значительнее то препятствие, какое тело
может преодолеть или против какого оно может устоять,
тем больше, скажем мы, его «сила». Если не желают
подразумевать под этим словом какую-то мнимую сущность,
находящуюся в теле, то пользуются им просто как
кратким выражением некоторого факта,—примерно, подобно
тому, как говорят, что у одного тела «скорость» в два
раза больше, чем у другого, вместо того, чтобы сказать,
что одно тело проходит за определенное время вдвое
больший путь, чем другое тело: никто этим не хочгт
утверждать, будто термин «скорость» представляет некоторую
сущность, содержащуюся в теле.
Если это твердо усвоить, то очевидно, что движению
тела можно противопоставить три рода препятствий: пре-
*) См. его «Рассуждение о законах передачи движения»,
заслужившее похвальный отзыв Академии в 1726 г., когда Мазьер
получил премию. Почему сочинение Бернулли не удостоилось
премии, объяснено мною в похвальном слове, посвященном этому
великому геометру вскоре после его смерти, происшедшей в
начале 1748 г. [18].
26
ВВЕДЕНИЯ
пятетвия непреодолимые, совершенно уничтожающие всякое
движение; далее, препятствия, оказывающие как раз такое
сопротивление, какое лишь необходимо для того, чтобы
уничтожить движение тела, и уничтожающие его
мгновенно,— это случай равновесия; и, наконец, препятствия,
уничтожающие движение постепенно, — это случай
замедленного движения.
Поскольку непреодолимые препятствия одинаково
уничтожают любое движение, они не могу г служить для
определения силы. Поэтому меру силы надлежит искать лишь
в равновесии или в замедленном движении.
Всеми признано, что между двумя телами существует.
равновесие, если у них одинаковы произведения масс на
виртуальные скорости, т. е. на скорости, с которыми
тела стремятся двигаться. Поэтому в случае равновесия
произведение массы на скорость, или, что то же самое,
количество движения, может служить выражением силы.
Всеми признается также и то, что в случае
замедленного движения число преодоленных препятствий
пропорционально квадрату скорости: тело при известной скорости
сжимает, например, одну пружину; при удвоенной скорости
оно может сжать, одновременно или последовательно, уже
не две, а четыре пружины, подобные первой; при
утроенной скорости—девять пружин и т. д. .Отсюда сторонники
живых сил заключают, что вообще сила тел, находящихся
в действительном движении, пропорциональна произведению
массы на квадрат скорости.
В сущности, какое неудобство могло бы произойти от
того, что мера силы в случае равновесия, с одной стороны,
и в случае замедленного движения, с другой, различна?
Ведь если мы хотим иметь дело только с отчетливыми
понятиями, то под «силой» мы не должны понимать ничего
кроме эффекта, произведенного при преодолевании
препятствия или при сопротивлении препятствию. В то же время
нужно признать, что мнение тех, которые рассматривают
силу, как произведение массы на скорость, может быть
справедливым не только в случае равновесия, но и в
случае замедленного движения, если в последнем случае
измерять силу не числом препятствий, а суммой величин их
ВВЕДЕНИЕ
27
сопротивления. И в самом деле, не подлежит никакому
сомнению, что эта сумма сопротивлений пропорциональна
количеству движения, так как всякому известно, что
количество движения, теряемое телом в каждый элемент
времени, пропорционально произведению сопротивления на
бесконечно малую продолжительность этого элемента; сумма
же этих произведений даст, очевидно, полное сопротивление.
Вся трудность, таким образом, сводится к тому, чтобы
определить, следует ли измерять силу числом препятствий,
или же суммой сопротивлений этих препятствий. Может
показаться более естественным измерять силу именно
последним способом, так как всякое препятствие является
таковым лишь постольку, поскольку оно оказывает
сопротивление, так что, собственно говоря, сумма сопротивлений
и представляет собой преодолеваемое препятствие. К тому
же при таком измерении силы мы имели бы то
преимущество, что у нас была бы одна общая мера силы как
для случая равновесия, так и для случая замедленного
движения. И тем не менее, поскольку в слове «сила» не
содержится никакого ясного и точного смысла помимо
соответствующего ей действия, я полагаю, что нужно каждому
предоставить свободу решать данный вопрос по его
усмотрению. К тому же затронутый вопрос представляет собой
не более, как совершенно бесплодный метафизический спор
или спор о словах, недостойный внимания философов.
Сказанного достаточно для того, чтобы читателю дать
почувствовать это. Но есть еще одно весьма естественное
соображение, которое убедит его окончательно. Тело может,
во-первых, обладать лишь стремлением двигаться с
известной скоростью, но это стремление уничтожается тем или
иным препятствием; во-вторых, оно может действительно
двигаться равномерно с этой скоростью; в-третьих, оно может
начать движение с этой же самой скоростью, но эта
скорость в дальнейшем постепенно может уменьшаться и
наконец уничтожиться вследствие той или иной причины. Во
всех этих случаях тело будет производить различные
действия; но тело само по себе ничего не имеет в одном случае
сверх того, что оно имеет в другом. Здесь лишь по-разному
проявляется действие причины. В первом случае действие
28
ВВЕДЕНИЕ
сводится к простому стремлению, у которого, собственно
говоря, никакой меры нет, поскольку не возникает никакого
движения. Во втором случае действием служит то
расстояние, которое проходится равномерно в течение данного
времени: этого рода действие пропорционально скорости.
В третьем случае действие выражается тем расстоянием,
которое проходится вплоть до полного поглощения
движения, и эго действие пропорционально квадрату скорости.
Но ведь все эти различного рода действия происходят,
очевидно, от одной и той же причины. Следовательно, как
те, которые утверждают, что силы пропорциональны
скорости, так и те, которые считают, что силы пропорциональны
квадрату скорости, говорят лишь о действиях различного
рода. Кстати заметим, что это различие действий,
происходящих от одной и той же причины, может служить
доказательством недостаточной правильности и точности
мнимой аксиомы, которой так часто пользуются: аксиомы о
пропорциональности причины своему действию.
Наконец, те, кто окажется не в состоянии подняться
до метафизических начал по вопросу о живых силах, легко
могут убедиться в том, что спор идет лишь о словах, если
они учтут, что оба течения нисколько не расходятся между
собой по поводу основных принципов равновесия и движения.
Предложите решить одну и ту же задачу из механики двум
геометрам, из которых один является противником живых
сил, а другой их сторонником. Решения обоих этих
геометров, если вообще они верны, совпадут друг с другом.
Следовательно, вопрос об измерении сил совершенно
бесполезен для механики, он даже не имеет реального смысла.
Если бы к данному вопросу подходили, различая в нем
ясное и темное, то он, без сомнения, не породил бы такую
огромную литературу: решение его потребовало бы всего
нескольких строк. Но мне сдается, однако, что большинство
писавших об этом вопросе словно боялись говорить о нем
в немногих словах.
Достигнутое нами сведение всех законов механики к трем
основным, а именно: к закону силы инерции, закону
сложения движений и закону равновесия, послужит нам для
решения важной метафизической проблемы,' предложенной
ВВЕДЕНИЕ
29
недавно одной из знаменитейших академий Европы, —
«являются ли законы статики и механики необходимой или
случайной истиной?». Чтобы установить наши взгляды по
этому вопросу, необходимо прежде всего придать ему тот
единственный разумный смысл, который он может содержать.
Дело здесь вовсе не в том, чтобы выяснить, мог ли бы
создатель природы дать природе другие законы, отличные
от тех, которые мы в ней наблюдаем. Как только мы
допустим наличие некоторого разумного существа, способного
воздействовать на материю, нам должно быть ясно, что это
существо сможет в любой момент по своему желанию
приводить материю в движение и останавливать ее или по
неизменным законам, или же по законам, меняющимся для
каждого мгновения и для каждого элемента материи.
Повседневные наблюдения над движениями нашего
собственного тела нам ясно показывают, что движущаяся материя,
подчиненная воле мыслящего начала, может отклоняться от
тех движений, которые она, наверное, имела бы, если бы
она была предоставлена самой себе. Следовательно,
предложенный вопрос сводится к тому, чтобы выяснить,
отличаются ли наблюдаемые в' природе законы равновесия и
движения от тех законов, которым подчинялась бы материя,
предоставленная самой себе?
Разовьем нашу мысль. Совершенно очевидно, что если
ограничиться только предположением существования
материи и движения, то из одного этого двойного
существования (материи и движения) с необходимостью должны
вытекать некоторые действия: тело, приведенное той или иной
причиной в движение, должно или остановиться по
истечении некоторого времени, или продолжать движение вечно;
тело, стремящееся двигаться одновременно по двум
сторонам параллелограмма, с необходимостью должно описывать
или диагональ, или какую-то другую линию; когда несколько
движущихся тел встречаются друг с другом и соударяются,
то вследствие взаимной непроницаемости тел с
необходимостью должно произойти ' какое-то изменение состояния у
всех этих тел или, по крайней мере, у некоторых из них.
Но • будь то движение одного изолированного тела, или
движение нескольких тел, действующих друг на друга, —
30
ВВЕДЕНИЕ
из всех возможных эффектов имеется один такой эффект,
который в каждом отдельном случае должен непременно
быть и вытекает из одного только существования
материи,— при сделанном допущении об отсутствии всякого
другого начала, могущего изменить или исказить этот
эффект.
Итак, вот путь, по которому должен следовать
философ, чтобы решить вопрос, о котором идет речь. Сначала
он должен постараться выяснить при помощи рассуждения,
каковы были бы законы статики и механики в материи,
предоставленной самой себе. Затем с помощью опыта он
должен исследовать, каковы законы во вселенной. Если
окажется, что одни отличаются от других, то он отсюда
заключит, что законы статики и механики в той форме,
как они нам даны опытом, являются истиной случайной,
так как они будут тогда вытекать из особой, специально
выраженной, воли высшего существа. Если же, наоборот,
законы, найденные в опыте, будут совпадать с теми
законами, к которым приводит чистое размышление, то он
заключит, что наблюдаемые законы являются необходимой
истиной, — не в том смысле, что творец не мог установить
совершенно иных законов, а в том смысле, что он не нашел
нужным устанавливать законов, отличных от тех, какие
вытекают из самого существования материи.
В настоящем сочинении мы, думается, доказали, что
тело, предоставленное самому себе, неизменно должно
пребывать в своем состоянии покоя или равномерного
движения. Мы, думается, доказали также, что если тело
стремится двигаться одновременно по двум сторонам какого-
нибудь параллелограмма, то направлением, которое должно
принять движение тела самого по себе, которое, если можно
так выразиться, тело выберет из всех других, будет
диагональ. Мы, наконец, доказали, что все законы передачи
движения от одного тела к другому сводятся к законам
равновесия, а законы равновесия, в свою очередь, сводятся
к законам равновесия двух равных тел, обладающих двумя
равными и противоположно направленными виртуальными
скоростями. В этом последнем случае движения обоих тел,
оче видно, уничтожат друг друга. Отсюда уже с геометрической
ВВЕДЕНИЕ
31
необходимостью будет вытекать, что равновесие будет иметь
место и в том случае, когда массы обратно пропорциональны
скоростям. Остается только выяснить, единственный ли это
случай равновесия, т. е. обязательно ли одно тело заставит
двигаться другое тело, если отношение масс не равно
обратному отношению скоростей. Легко сообразить, что
поскольку существует один возможный и необходимый
случай равновесия, никаких других случаев быть не может:
в противном случае законы удара тел, которые
необходимым образом сводятся к законам равновесия, стали бы
неопределенными, что невозможно, так как в результате удара
двух тел непременно должен возникать какой-то
единственный эффект, как необходимое следствие существования и
непроницаемости данных тел. Впрочем единственность закона
равновесия можно доказать и при помощи другого
рассуждения, но оно имеет слишком математический характер,
чтобы развивать его здесь во введении. Однако, я старался
сделать его осязательным в своем сочинении, к которому
я и отсылаю читателя *).
Из всех этих соображений следует, что законы
статики и механики, излагаемые в настоящей книге, это — те
законы, которые вытекают из существования материи и
движения. Но опыт показывает нам, что эти же законы
наблюдаются и в действительности в окружающих нас
телах. Следовательно, те законы равновесия и движения,
которые даны нам в наблюдении, являются необходимой
истиной. .Какой-нибудь метафизик для доказательства
этого положения, пожалуй-, ограничился бы ссылкой на то,
что из мудрости творца и из простоты его
взглядов вытекало то, что не установлены другие законы
равновесия и движения кроме тех, которые вытекают из
самого существования тел и из их взаимной
непроницаемости. Мы, однако, сочли необходимым воздержаться от
такого способа рассуждения, так как нам кажется, что он
опирается на слишком неясное начало. Природа
верховного существа слишком скрыта от нас, чтобы мы могли
непосредственно знать, что соответствует его мудрости
') См. п° 46, в конце третьего случая, и п° 47.
32
ВВЕДЕНИЕ
и что не соответствует. Мы можем лишь мельком видеть
результаты этой мудрости при наблюдении законов
природы, в то время как математическое рассуждение
показывает нам простоту этих законов, а опыт — их
применения и их границы.
Только что приведенные соображения, мне кажется,
могут служить для оценки тех доказательств законов
движения, которые давали некоторые философы, исходя
из принципа конечных причин, т. е. из тех целей,
которые творец мира должен был ставить' себе, устанавливая
эти самые законы. Подобные доказательства могут иметь
силу лишь в том случае, когда они опираются на
предшествующие им прямые доказательства, полученные из
принципов, более доступных нашему пониманию. В противном
случае, как это нередко бывает, они могут приводить нас к
ошибочным заключениям. Именно потому, что Декарт
следовал этому пути, именно потому, что он полагал, что
по мудрости создателя во вселенной сохраняется всегда
одно и то же количество движения, он ошибся в законах
удара. Кто будет подражать в этом Декарту, тот рискует
или впасть в такую же ошибку, или выдать за общий
принцип то, что справедливо лишь в определенных случаях,
или, наконец, счесть за первичные законы природы то,
что является лишь чисто математическим следствием из
тех или иных формул [16].
После того, как читатель получил общее
представление о цели, которую я поставил перед собой в настоящем
сочинении, мне остается сказать лишь несколько слов о
той форме, которую я считал нужным придать этому
сочинению.
В первой части я пытался изложить принципы механики
так, чтобы они были, насколько возможно, доступны для
начинающих. В теории неравномерного движения я не мог
избежать употребления дифференциального исчисления:
к этому меня принуждал самый характер предмета. В этой
первой части у меня заключено на немногих страницах
довольно большое количество вопросов, и если я не
входил при этом во все подробности, приличествующие той
или иной проблеме, то только потому, что, поставив
ВВЕДЕНИЕ
33
в центре - внимания изложение и доказательство основных
принципов механики и поставив своей целью дать в
настоящем сочинении лишь то, что может представить в той
или иной области нечто новое, я не считал возможным
увеличивать его объем множеством частных предложений,
которые легко- можно найти в другом месте*
Гораздо более значительна вторая часть сочинения,
посвященная изложению законов движения тел,
взаимодействующих друг с другом. Это и побудило меня дать
всей книге название «Динамика» [17]. Может показаться,
что это название, обозначающее буквально науку о силах,
или о причинах движения, не подходит к данной книге,
в которой я рассматриваю механику, как науку, скорее,
о действиях, чем науку о причинах. Поскольку, однако,
за последнее время слово «динамика» часто
употребляется учеными для обозначения науки о движении тел,
тем или иным образом действующих друг на друга, я счел
необходимым оставить это название, чтобы самым
названием этого трактата показать геометрам, что главной целью
своей я ставлю усовершенствование и развитие именно
этой части механики.
Эта ветвь механики столь же интересна, сколь и трудна
для исследования, и к ней относится огромное количество
задач. Весьма крупные геометры, в особенности за
последние годы, оказывали ей особенное внимание. Тем не
менее, до сих пор решено лишь весьма небольшое число
задач этого рода, и притом задачи эти относятся лишь
к частным случаям. Помимо этого, большая часть
предлагавшихся до сих пор решений опирается на такие принципы,
которые в общей форме еще не доказаны: примером
может служить принцип сохранения живых сил. Потому я и
считал необходимым подробнее остановиться на этой
проблеме и показать, каким образом все задачи динамики
можно решать одним и притом весьма простым и, прямым
методом. Этот метод состоит лишь в том сочетании
принципов равновесия и сложения движений, о котором мы
говорили выше. Применение данного метода я показываю
на небольшом числе отдельных задач, из которых одни
уже были решены раньше, другие решены только нами,
3 Ж, Даламбер
34
ВВЕДЕНИЕ
а третьи решались ошибочно даже самыми известными
математиками.
Изящество в решении какой-либо задачи достигается,
главным образом, тем, что при этом используются только
прямые принципы, и притом в очень небольшом числе [18].
Поэтому не нужно удивляться, что единообразие во всех
моих решениях, к которому я больше всего стремился,
достигается иногда тем, что решение получается более
длинное, чем в том случае, если бы оно основывалось
на менее прямых принципах. Впрочем, доказательства,
которые мне тогда пришлось бы давать этим принципам,
только удалили бы меня от той краткости, которой я с
их помощью мог бы добиться. И наиболее значительная
часть моей книги представляла бы собой тогда лишь
бесформенную груду задач, недостойную появления в свет,
несмотря на все разнообразие этих задач и несмотря на
трудность всех этих задач.
Вторая часть предназначается, главным образом, для
лиц, которые уже знают дифференциальное и интегральное
исчисление, уже освоились с принципами, установленными
нами в первой части, и имеют уже опыт в решении
обычных механических задач. Поэтому во второй части я часто
пользуюсь неясным термином «сила» и некоторыми другими
терминами, обычно употребляемыми, когда говорят о
движении тел. Предупреждая об этом во избежание
недоразумений, я должен сказать, что с этими терминами я нигде
не связываю никаких представлений, отличных от тех,
которые вытекают из принципов, установленных мною как
здесь, во введении, так и в первой части трактата.
Наконец, из того же самого принципа, который
позволяет решить любую задачу динамики, я вывожу и
некоторые свойства центра тяжести, из которых одни совершенно
новы, а другие доказывались лишь неясным образом.
Заканчиваю я свое сочинение доказательством принципа,
обычно называемого «сохранением живых силъ.
Прием, который был оказан этому первому опыту,
появившемуся в свет в 1743 г., побудил меня в 1744 г.
опубликовать другое сочинение, где тем же самым
методом рассматривается все касающееся движения и равновесия
ВВЕДЕНИЕ
35
жидкостей [19]. Но как ни трудны задачи, относящиеся
к этой области, ими, однако, не исчерпывается сфера
применения нашего принципа. Наиболее важные применения
указаны мною в сочинении «Исследования о предварении
равноденствий»}20], посвященном задаче, решения которой
долго и безуспешно добивались крупнейшие геометры и
решение которой мною найдено впервые; далее, в сочинении
«Опыт о сопротивлении жидкостей», основывающемся
целиком на нашей новой теории [21]; наконец, в сочинении
«Рассуждения о причине ветров» [22], где речь идет об
определении колебаний, которые должны вызываться в
нашей атмосфере действием Солнца и Луны, — задаче, за
которую до того никто еще не брался.
В заключение я смею сказать, что чем к большему
числу случаев я применял методы, излагаемые и
развиваемые в настоящем сочинении, тем больше я убеждался
в простоте, общности и плодотворности этих методов.
ч^?'
^j^-
з*
^^[^^J^
ПРЕДВАРИТЕЛЬНЫЕ ОПРЕДЕЛЕНИЯ И ПОНЯТИЯ.
I.
„Если две подобные и равные части пространства
непроницаемы, т. е. если нельзя представить себе их соединенными,
слившимися одна с другой так, чтобы они образовали
одну часть пространства, меньшую, чем с)мма их обеих,
то каждая из этих частей пространства есть то, что
называют телом. Непроницаемость является главным свойством,
с помощью которого мы отличаем тела от частей
безграничного пространства, в котором мы их мыслим
расположенными.
Место тела есть та часть пространства, которую это
тело занимает; другими словами,—та часть пространства,
с которой совпадает объем данного тела.
П.
Тело находится в покое, если оно остается в одном и
том же месте. Оно движется, если оно переходит из
одного места в другое, т. е. если оно последовательно, без
перерывов, занимает части пространства, непосредственно
соприкасающиеся друг с другом.
III.
Поскольку тело не может занимать одновременно
несколько мест, оно не может за одно мгновение перейти
ПРЕДВАРИТЕЛЬНЫЕ ОПРЕДЕЛЕНИЯ И ПОНЯТИЯ
из одного места в другое место. Следовательно,
движение может осуществляться лишь в течение известного
времени.
IV.
Пространство, проходимое движущимся телом, делимо
до бесконечности; следовательно, и время также делимо
до бесконечности. Если тело, движущееся прямолинейно,
не претерпевает никаких изменений, кроме перемены места,
то оно в равные промежутки времени проходит равные
пространства. В таком случае говорят, что тело движется
равномерно. Если пространства, проходимые за равные
промежутки времени, возрастают или убывают, то
движение называется ускоренным или замедленным.
♦
**^??Z$§&\
ЧАСТЬ I.
ОБЩИЕ ЗАКОНЫ ДВИЖЕНИЯ
И РАВНОВЕСИЯ ТЕЛ.
1. Все принципы механики можно свести к трем, а именно
принципу силы инерции, принципу сложения движений и
принципу равновесия. По крайней мере, я надеюсь
доказать в настоящем сочинении, что вся механика может быть
выведена из указанных трех принципов. О каждом из этих
принципов, в частности, я буду говорить отдельно в
следующих главах.
ГЛАВА I
О силе инерции
и о вытекающих из нее свойствах движения.
2. Силой инерции я вместе с Ньютоном называю
свойство тел сохранять то состояние, в котором они находятся.
Это свойство и нужно здесь доказать. Но тело необходимо
находится или в состоянии покоя, или в состоянии движения.
Поэтому необходимо доказать следующие два закона.
Первый закон.
3. Тело, находящееся в покое, будет неизменно
пребывать в покое, пока какая-нибудь внешняя причина не
выведет его из этого состояния,
О СИЛЕ ИНЕРЦИИ
39
В самом деле, тело не может само себя привести
в движение, потому что нет никакого основания к тому,
чтобы оно двигалось предпочтительнее в одну сторону,
чем в другую.
Следствие.
4. Отсюда вытекает, что если вследствие какой-либо
причины тело получило движение, оно не сможет само по
себе ни ускорить, ни з'амедлить этого движения.
5. Все то, что побуждает тело к движению, называют
вообще силой, или движущей причиной.
Второй зако и.
6. Тело, приведенное однажды какой-либо причиной
в движение, должно неизменно пребывать в состоянии
равномерного прямолинейного движения, пока на него не
подействует какая-нибудь новая причина, отличная от той,
которая привела его в движение. Другими словами, до тех
пор, пока на это тело не подействует какая-либо внешняя
причина, отличная от движущей причины, оно будет
неизменно двигаться по прямой линии и за равные промежутки
времени проходить равные расстояния.
В самом деле, или достаточно мгновенного и
неделимого действия движущей причины в начале движения для
того, чтобы заставить тело пройти определенное
расстояние, или для движения тела необходимо постоянное
действие движущей причины.
В первом случае очевидно, что пройденный путь может
быть только прямой линией, описываемой движущимся
телом равномерно. Действительно (по предположению), по
прошествии первого мгновения действие движущей причины
уже не существует, однако, движение еще происходит.
Но так как тело само по себе не может ни ускорить,
ни замедлить своего движения (п° 4), то движение
необходимо будет равномерным. Кроме того, нет никакого
основания для того, чтобы тело отклонялось вправо скорее,
чем влево. Следовательно, в этом первом случае, когда
предполагается, что тело способно двигаться в течение
40 ОБЩИЕ ЗАКОНЫ ДВИЖЕНИЯ И РАВНОВЕСИЯ ТЕЛ
известного промежутка времени само по себе, независимо
от движущей причины, оно будет двигаться в течение
этого промежутка времени равномерно и прямолинейно.
Но тело, которое может двигаться само по себе
равномерно и прямолинейно в течение известного промежутка
времени, должно продолжать двигаться таким же образом
вечно, если только ничто не будет нарушать этого
движения. В самом деле, пусть тело выходит из А (фиг. 1)
и оно способно само по себе
t пройти равномерно линию АВ.
A CD В 6 Возьмем на линии АВ две
- 1 произвольные точки С и £>,
Фиг. 1. р . D „ '
лежащие между А и В.
Находясь в D, тело пребывает
в точно таком же состоянии, в каком оно пребывало в С,
с той лишь разницей, что оно теперь находится в другом
месте. Следовательно, с этим телом здесь должно
происходить то же самое, что и в С. Но, находясь в С, тело
(по условию) можег двигаться само по себе равномерно
до В. Поэтому, и находясь в D, оно также сможет
двигаться само по себе равномерно до точки G, взятой так, что
DG = CB.
Таким же образом можно рассуждать и дальше.
Итак, если первое и мгновенное действие движущей
причины способно привести тело в движение, то тело
будет двигаться равномерно и прямолинейно, пока это
движение не будет нарушено какой-либо новой причиной*
Во втором случае предполагается, что на тело не
действует никакая внешняя причина, отличная от движущей
причины, и потому ничто не вызывает ни увеличения, ни
уменьшения движущей причины. Отсюда следует, что
непрерывное действие этой причины будет все время
одинаковым и постоянным и, таким образом, пока действует
эта движущая причина, тело будет двигаться прямолинейно
и равномерно. Но если движущая причина, действию
которой ничего не противополагается, остается в течение
данного промежутка времени равной себе и постоянной,
то на том же самом основании всегда одним и тем же
О СИЛЕ ИНЕРЦИИ
ц
будет, очевидно, оставаться и действие этой причины,
производя всегда один и тот же результат. Отсюда
следует, и т. д.
Итак, вообще, тело, приведенное в движение какой
бы то ии было причиной, будет неизменно двигаться
равномерно и прямолинейно, пока на него не подействует
какая-либо новая причина [23].
Прямая линия, которую тело описывает или стремится
описывать, называется направлением этого тела.
Замечание I.
7. Я даю несколько пространное доказательство второму
закону по той причине, что были, а может быть и до
сих пор имеются, такие философы, которые утверждали,
что движение тела само по себе должно мало-помалу
замедляться, как это, видимым образом, показывает опыт.
Впрочем, нужно признать, что все доказательства, которые до
сих пор давались сохранению движения, вовсе не обладают
той степенью очевидности, какая необходима для
убеждения разума. Почти все эти доказательства основываются
либо на приписывании материи силы, вследствие которой
материя сопротивляется всякому изменению состояния, либо
на безразличии материи к движению и покою.
Первый из этих двух принципов, помимо того, что он
предполагает в материи такую сущность, о которой никто не
имеет ясного представления, нельзя признать достаточным
для доказательства того закона, о котором здесь идет
речь. В самом деле, когда тело движется, хотя бы и
равномерно, движение, которым оно обладает в тот или иной
момент, отлично и как бы изолировано от движения,
которым оно обладало в предшествующие моменты или
которым оно будет обладать в последующие моменты. В
каждый момент тело находится в некотором смысле в новом
состоянии, которое не имеет ничего общего с предыдущим
состоянием. Тело, если можно так выразиться, только и
делает, что непрерывно начинает движение; и можно,
пожалуй, думать, что если бы та же причина, которая вы-
42 ОБЩИЕ ЗАКОНЫ ДВИЖЕНИЙ И РАВНОВЕСИЯ ТЕЛ
вела однажды его из состояния покоя, не продолжала его
каким-то образом снова приводить в движение, то тело
неуклонно стремилось бы вернуться в состояние покоя.
Что касается безразличия материи к движению и покою,
то, мне кажется, этот принцип дает нашему разуму лишь
ту отчетливую идею, что материи не присуще ни
находиться всегда в движении, ни находиться всегда в покое.
Но следует ли отсюда с очевидностью, что движущееся
тело не может стремиться неизменно к покою? Это
не значит, что телу более присущ покой, чем
движение; а можно, скажем, полагать, что для того,
чтобы находиться в состоянии покоя, телу достаточно
быть просто телом, тогда как для движения
необходимо еще нечто, так сказать, непрерывно
воспроизводящееся в нем,—до некоторой степени так мы ощущаем
движение нашего собственного тела, для движения которого
необходимы непрерывные усилия, тратящиеся и
возобновляющиеся каждое мгновение. Мы совсем не настаиваем
на правильности аналогии между телами одушевленными
и неодушевленными. Но эта параллель может, по крайней
мере, заставить думать, хотя это и неправильно, что
в движущемся теле якобы имеется нечто такое, чего нет
в теле покоящемся. Следовательно, этой параллели уже
достаточно для того, чтобы признать несостоятельным то
самое доказательство, о котором мы сейчас говорим.
Доказательство сохранения движения, данное нами выше,
имеет ту особенность, что оно сохраняет свою силу,
действует ли движущая причина на тело беспрерывно, или
пет. Это не значит, что я считаю необходимым
беспрерывное действие этой причины для движения тела, ибо чго
за эффект имело бы это действие, если бы недостаточно
было мгновенного действия? Ведь если бы мгновенное
действие не имело никакого эффекта, то каким образом могло
бы иметь тот или иной эффект непрерывное действие?
Однако, поскольку при решении какого-нибудь вопроса
нужно ограничиваться наименьшим количеством принципов,
я счел необходимым ограничиться доказательством того,
что движение сохраняется безразлично как при том, так и
При другом допущении.
О РАВНОМЕРНОМ ДВИЖЕНИЙ
43
Правда, наше доказательство предполагает, что
движение существует и тем более, что оно возможно. Но
отрицать существование движения, значит, отказываться признать
факт, который никем не подвергается сомнению.
Замечание II.
8. В согласии с лриведенными рассуждениями опыт
также подтверждает принцип силы инерции. Во-первых, мы
видим, что окружающие нас тела остаются в покое,
пока что-нибудь не выведет их из этого состояния.
И если иногда нам кажется, что тела движутся без видимой
причины, то по аналогии, а также на основании
единообразия законов природы и вследствие неспособности материи
самой по себе приходить в движение мы вправе заключить,
что причина здесь не менее реальна, хотя она и скрыта
от нас. Во-вторых, хотя и не существует таких тел,
которые бы вечно сохраняли свое движение, — всегда ведь
существуют причины, как, например, трение и
сопротивление воздуха, которые постепенно замедляют движение, —
тем не менее мы видим, что движущееся тело тем дольше
сохраняет движение, чем меньше эти причины,
замедляющие движение. Отсюда мы можем заключить, что движение
никогда бы не кончилось, если бы никаких замедляющих
причин не было*).
О равномерном движении.
9. Мы только что видели, что когда на тело не
действует никакая внешняя причина, оно будет двигаться
равномерно и прямолинейно. Отсюда следует, что то же тело
может двигаться также равномерно и в том случае, если
на него действуют одновременно две равные причины, одна
ускоряющая, а другая замедляющая движение тела. (Именно
поэтому, заметим мимоходом, падающие тела начинают
*) В «Encyclopcdie» под словом «Force» (Сила) можно найти
ряд других замечаний о принципе силы инерции. Поскольку эти
замечания выходят из рамок дайной темы, мы отсылаем читателя
туда [24].
4 4 ОБЩИЕ ЗАКОНЫ ДВИЖЕНИЯ И РАВНОВЕСИЯ ТЕЛ
двигаться равномерно, когда сопротивление той жидкости,
в которой движутся эти тела, стремится уменьшить их
движение ровно настолько, насколько вес их стремится его
увеличить.) Во всех других случаях движение может быть
только или ускоренным, или
замедленным.
10. Если две какие-либо части АВ
и АС (фиг. 2) неограниченной прямой
АО представляют. два промежутка
времени, истекшего с момента начала
движения, а линии BD и СЕ — пути,
пройденные за эти промежутки времени
равномерно движущимся телом, то
точки D и Е будут лежать на одной
прямой ADE.
В самом деле, так как равномерно
движущееся тело за равные промежутки
времени проходит равные пути, то точки D и Е должны
лежать на такой линии, что при произвольных, но равных
между собой АВ и ВС мы всегда будем иметь
BD = FE.
Фиг. 2.
А этим свойством обладает только прямая линия. Отсюда
следует, и т. д.
Следствие.
И.
BD:CE = AB:AC[**l
т. е. при равномерном движении пути относятся между
собой как промежутки времени, затраченные на их
прохождение.
Замечание по поводу измерения времени.
12. Так как отношение промежутков времени самих по
себе нам не известно, то единственный способ, который мы
можем применить, чтобы определить это отношение, это —
найти какое-то другое, более доступное нашим чувствам
и лучше нам известное отношение, с которым мы могли
ЗАМЕЧАНИЕ 110 ПОВОДУ ИЗМЕРЕНИЯ ВРЕМЕНИ 45
бы сравнить первое. Если нам удастся наиболее простым
способом сравнить отношение промежутков времени с
каким-нибудь другим отношением, известным нам лучше всего,
то мы и найдем простейшую меру времени.
Отсюда следует, что простейшей мерой времени
является равномерное движение. В самом деле, с одной
стороны, легче всего мы воспринимаем отношение отрезков
прямой линии; с другой стороны, вообще нет отношений,
которые было бы легче сравнивать друг с другом, чем
равные отношения. При равномерном же движении
отношение промежутков времени равно отношению
соответствующих частей пройденного пути. Таким образом,
равномерное движение дает нам одновременно и средство сравнить
отношение промежутков времени с таким отношением,
которое наиболее доступно нашим чувствам, и средство
осуществить это сравнение наиболее простым способом.
Следовательно, в равномерном движении мы находим наиболее
простую меру времени.
Помимо этого, я утверждаю, что измерение времени
при помощи равномерного движения, независимо от его
простоты, является и наиболее естественным, которое можно
придумать для пользования. Действительно, так как никакое
отношение не известно нам точнее, чем отношение частей
npocTpaHCTBaj и так как вообще любое движение, закон
которого нам задан, приводит к отысканию отношения
между промежутками времени, исходя из известной нам
связи э*гого отношения с отношением частей пройденного
пути, то ясно, что такое движение будет наиболее точной
мерой времени, и потому именно им и надлежит пользоваться
предпочтительно перед всеми прочими.
Поэтому если существует такой частный вид движения,
при котором связь между отношением промежутков
времени и отношением частей пройденного пути известна
независимо от каких бы то ни было допущений, а просто
в силу природы самого движения, и если этот частный
вид является единственным движением, обладающим этим
свойством, то он, очевидно, и будет наиболее
естественной мерой времени. Обоим этим условиям удовлетворяет
только равномерное движение.
46 ОБЩИЕ ЗАКОНЫ ДВИЖЕНИЙ И РАВНОВЕСИЯ ТЕЛ
В самом деле, движение тела само по себе будет
равномерным (п°6): ускоренным или замедленным оно
становится лишь при действии той или иной внешней причины,
и тогда это движение может подчиняться бесчисленному
множеству различных законов изменения. Закон
равномерности, т. е. равенство отношения между промежутками
времени и отношения между пройденными путями, является
свойством этого движения, взятого само по себе. Поэтому
равномерное движение имеет наибольшее соответствие
с длительностью, и вследствие этого оно наиболее пригодно
служить мерой этой длительности, поскольку части
последней следуют одна за другой также неизменно и равномерно.
Напротив, всякий закон ускорения или замедления
движения, так сказать, произволен и зависит от внешних
обстоятельств. Неравномерное движение не может быть, поэтому,
естественной мерой времени. Действительно, во-первых,
у нас не было бы никакого основания для того, чтобы
какой-нибудь один вид неравномерного движения взять
первичной мерой времени предпочтительно перед другим.
Во-вторых, при помощи неравномерного движения
невозможно было бы измерять время, не зная откуда-нибудь
заранее, какая связь между отношением времен и
отношением пройденных путей соответствует данному движению.
А откуда же можно знать эту связь, как не из опыта?
А не предполагает ли опыт, что уже имеется вполне
определенная мера времени?
Но, скажут, каким образом можно убедиться в том,
что данное Движение является в точности равномерным?
Прежде всего я на это отвечу, что ни у какого
неравномерного движения мы также не знаем точно закона этого
движения. Поэтому приведенное возражение доказывает
только то, что мы не можем определить со всей точностью
и строгостью отношения между промежутками времени.
Но отсюда вовсе не следует, что равномерное движение
не является по своей природе единственной первичной и
простейшей мерой времени. Если у нас нет возможности
найти точную и строгую меру времени, то мы должны
искать, по крайней мере, приближенную меру, — среди
движений примерно равномерных. Для установления того,
ЗАМЕЧАНИЕ ПО ПОВОДУ ИЗМЕРЕНИЯ ВРЕМЕНИ 47
что движение приближенно равномерно, у нас есть три
способа.
Во-первых, движение тела можно считать приближенно
равномерным в том случае, если тело проходит одинаковые
пути за такие промежутки времени, которые мы можем
считать одинаковыми. Промежутки же времени мы можем
считать одинакоэыми в том случае, если многократные
наблюдения показывают, что в течение их происходят
одинаковые события, которые можно считать длящимися
одинаково долго. Так, мы можем считать, что из одной и той
же клепсидры [26] вода вытекает всякий раз за одно и то
же время. Если, поэтому, за такие промежутки времени
тело проходит одинаковые пути, то мы можем считать, что
движение этого тела является равномерным.
Во-вторых, движение можно считать приближенно
равномерным, когда мы вправе полагать, что действие
ускоряющей или замедляющей причины,—если таковая имеется,—
может быть только неощутимым. На основании первого и
второго критерия вместе полагают, что движение Земли
вокруг ее оси является равномерным, и это
предположение не только ни в какой степени не было опровергнуто
другими небесными явлениями, но даже, повидимому,
находится с ними в полном согласии.
В-третьих, движение можно считать приближенно
равномерным, когда мы, сравнивая его с другими движениями,
замечаем, что все они управляются одним и тем же законом.
Так, есЛи несколько тел движутся таким образом, что пути,
проходимые ими за одно и то же время, всегда находятся
(точно или приближенно) в одном и том же отношении
друг к другу, то считают движение этих тел равномерным
или по меньшей мере весьма близким к равномерному.
В самом деле, пусть какое-нибудь движущееся равномерно
тело Л за произвольно взятый промежуток времени Т
проходит путь Е, а другое тело В> движущееся также
равномерно, за то же время Т проходит путь е. Тогда
независимо от того, одновременно ли начали двигаться эти два
тела или нет, отношение Е к е будет всегда одним и
тем же. И этим свойством обладает лишь равномерное
движение. Вот почему, если промежуток времени разделить
48 ОБЩИЕ ЗАКОНЫ ДВИЖЕНИЯ II РАВНОВЕСИЯ ТЕЛ
на произвольные равные или неравные части, и если при
этом окажется, что пути, проходимые обоими телами за
одну и ту же часть этого промежутка, находятся между
собой всегда в одном и том же отношении, то чем больше
будет число частей, на которые разделен данный
промежуток времени, тем с большим правом можно будет
заключить, что движение обоих тел является равномерным.
Правда, ни один из этих критериев не удовлетворяет
требованиям геометрической строгости. Однако, они
достаточны для того, чтобы сделать законное заключение, если
не об абсолютной, то по крайней мере о приближенной
равномерности движения,—в особенности если этими
критериями пользоваться по нескольку раз и в комбинации
друг с другом.
13. Говорят, что тело, движущееся равномерно,
движется тем быстрее, чем больше путь BD, проходимый им
в определенное время АВ. Так, если пути, пройденные
двумя равномерно движущимися телами за одно и то же
время АВ, равны BD и Bd, то говорят, что скорости этих
тел относятся друг к другу, как BD к Bd.
Следствие.
14. Отношение BD к Вd равно
BD9B£ BD . Се
АВ: АВ~~~ АВ' АС*
Это значит, что вообще скорости двух тел находятся друг
к другу в том же отношении, как и пути BD и Се,
проходимые этими телами за произвольные промежутки
времени, деленные на эти самые промежутки времени*).
'"'•) Поскольку путь и время являются величинами разного
рода, как это указывалось во введении, всякому ясно, что путь
нельзя делить на время. Поэтому, когда говорят, что «скорости
находятся в том же отношении, как пути, деленные на
промежутки времени», этим кратко выражают то, что скорости
пропорциональны отношениям расстояний к общей мере расстояний,
деленным на отношения времен к общей мере времен. Другими
словами, если, например, взять за общую меру расстояний фут,
а за меру времен — минуту, то скорости двух тел, движущихся
ОБ УСКОРЕННОМ ПЛИ ЗАМЕДЛЕННОМ ДВИЖЕНИИ 49
Итак, вообще скорость равномерно движущегося тела
пропорциональна пути, деленному на время. Скорость
представляет собой лишь относительное понятие, и потому она
вовсе не имеет абсолютной меры; никогда не судят о
скорости тела самой по себе, а сравнивают ее со скоростью
какого-нибудь другого тела. Поэтому, способ выражения,
столь обычный у механиков, что «скорость равна пути,
деленному на время»,-является лишь сокращенным
выражением того, что скорости двух тел, движущихся
равномерно, относятся друг к другу так, как пути, проходимые
телами, деленные на промежутки времени, затраченные на
это прохождение. При этом последнее выражение надо
понимать в том смысле, как это указывается в сноске.
Об ускоренном или замедленном движении.
15. Если концы линий BD и СЕ, представляющих пути,
пройденные за промежутки времени АВ и АС, лежат не на
F
В
С
К
D
Р
Р
N
V»
Y\ V
Qtf\^
^
а
я
л
\
е\ V4,
f\ N о
Фиг. 3. Фиг. 4.
прямой, а на кривой ADE (фиг. 3 и 4), то это значит, что
равномерно, находятся друг к другу в том же отношении, как
числа пройденных футов, деленных на числа затраченных на это
минут, а вовсе не как футы, деленные на минуты. См. по этому
поводу «Encyclopedie», конец статьи «Equation» (Уравнение) [2?].
{Примечание Безу.)
4 Ж. Даламбер
50 ОБЩИЕ ЗАКОНЫ ДВИЖЕНИЯ И РАВНОВЕСИЯ ТЕЛ
данное движение не равномерное, а ускоренное или
замедленное,— смотря по тому, будет ли кривая ADE
обращена к АС своей выпуклостыь или вогнутостью. В самом
деле, если, например, движение ускоренное, то пути DX
П*
и РЕ (фиг. 5), пройденные за равные промежутки
времени BQ и ВС, возрастают. Таким образом,
PE>DX.
Это возможно лишь в том случае, когда кривая ADE
обращена к АС своей выпуклостью. Подобное непрерывное
изменение может иметь место только при какой-нибудь
постоянно действующей внешней причине, ускоряющей или
замедляющей движение тела (п°6).
При ускоренном или замедленном движении скорость
тела меняется в каждый момент и не может измеряться
постоянной величиной, как при равномерном движении.
Однако, нетрудно понять, что для данного момента ее
выражение должно быть таково же, каким оно было бы, если
бы движение в этот момент перестало быть ускоренным
-или замедленным. Предположим, например, что тело
движется ускоренно и пусть в тот момент, когда оно прошло
ОБ УСКОРЕННОМ ИЛИ ЗАМЕДЛЕННОМ ДВИЖЕНИИ 5Г
путь BD, оно начинает двигаться равномерно с той самой
скоростью, какую оно имело в D. В таком случае ясно,
что, во-первых, линии TZ и PN (фиг. 5), представляющие
те пути, которые тело будет дальше проходить за какие-то
конечные промежутки времени ВМ и ВС, оканчивались бы
на прямой линии DN; во-вторых, эти отрезки PN и TZ
должны быть больше, чем отрезки DX и Dx, которые
тело проходило перед этим за время Вт — ВМ и за время
BQ=BC; в-третьих, те же отрезки PN и TZ должны
быть меньше отрезков РЕ и TG, которые тело прошло бы
за время ВС и за время ВМ, если бы оно продолжало
двигаться ускоренно. Но для этого необходимо, чтобы
прямая DN была касательной *). То же самое можно доказать
и для случая замедленного движения. Отсюда в общем
случае следует, что если провести касательную DN
(фиг. 3 и 4), то за время ВС тело при равномерном
движении прошло бы не отрезок РЕ, а отрезок PN. Тогда
\7Тр) бУдет выражать скорость тела (п° 14), Но
отношение PN и DP равно отношению приращения линии BD
к приращению линии АВ, так как DM является
касательной. Итак, если в общем случае через / обозначить время,
через е—пройденный телом путь, через а — скорость
в конце времени t} то мы будем иметь
Продолжим касательную DN (фиг. 3 и 4) до
пересечения с АВ в точке F. Тогда BF будет представлять
время, которое тело должно было бы затратить на то,
*) Очевидно, нельзя предположить, что тело при
равномерном движении пройдет отрезок РО, меньший чем отрезок /W,
отграниченный касательной DN: в противном случае РО было бы
меньше DX, так как
PO = Dy.
Нельзя также предположить и того, что тело пройдет отрезок Р/?>
больший чем PN, так как в противном случае всегда можно
вообразить такую точку Г, что отрезок ГО', проходимый равномерно
за время DT, будет больше отрезка ГО, оканчивающегося на
кривой, а это невозможно, (Примечание Безу*)
4*
52 ОБЩИЕ ЗАКОНЫ ДВИЖЕНИЯ II РАВНОВЕСИЯ ТЕЛ
чтобы пройти 3D, двигаясь равномерно с той скоростью,
какую оно имеет в точке D. Следовательно, если из точки А
провести Ad параллельно FD, то 3d будет тем
расстоянием, которое это тело прошло бы за время A3, двигаясь
равномерно с этой самой скоростью.
Отсюда мы получаем, что если, скажем, ADE (фиг. 3)
является параболой, т. е. если расстояния 3D и СЕ
пропорциональны квадрату времен, то
АЗ = 23Е[2*]
и
3d = 23D.
Следствие I.
16. Тело за времена ЗС и Зс (фиг. 3 и 4) проходит
расстояния большие или меньшие, чем расстояния PN
и рп, которые оно прошло бы, двигаясь равномерно с той
скоростью, которой оно
обладает в D, на отрезки NE и пе.
Если предположить промежутки
времени ЗС и Зс
бесконечно малыми, то линии NE и
пе будут относиться друг к
другу так же, как квадрат ВС
относится к квадрату Зс.
В самом деле, при
бесконечно малой величине дуги DE
эту дугу можно рассматривать
как дугу круга. Возьмем на
касательной к дуге круга
бесконечно малый отрезок DN
(фиг. 6). Через точку N и через другую произвольную
точку п, лежащую на этом отрезке, проведем какие-нибудь
параллельные прямые NQ и nq. Тогда на основании
(известных) свойств круга мы будем иметь
NE-NQ = DN2, ne>nq^ DnK
Фиг. 6.
ОБ УСКОРЕННОМ ИЛИ 3-АМЕДЛЕННОМ ДВИЖЕНИИ 53
Ввиду того, что отрезки NQ и nq следует считать равными
друг другу, мы получим
NE:ne = DN2:Dn*.
Но (см. фиг. 3 и 4)
DN:Dn=BC:Bc
и потому в общем случае
NE:ne = BC2:Bc\
Следствие II.
17. Ясно, что отрезки NE и пе представляют собой
те расстояния, которые телом проходились бы за элементы
времени ВС и Вс под действием ускоряющей причины,
если бы оно в начале этих элементов времени находилось
в покое. Отсюда следует, что пути, проходимые телом под
действием ускоряющей причины, в начале движения
пропорциональны квадрату времени.
Следствие III.
18. Считая ВС, илия#, постоянным, можно будет положить
*Ш— F
ВС2 '
где F—некоторая величина, если угодно, изменяющаяся
с изменением абсциссы АВ, но которую можно считать
постоянной при бесконечно малом изменении АВ*).
*)Из пропорции
NE:ne = BC2:Bc2
мы получаем
NE пе
ВС2 ~ Вс2 '
NE пе
Если -дг^г обозначить буквой Т7, то ^ будет также равно F.
Следовательно, величина F остается неизменной при бесконечно
малых изменениях АВ. (Примечание Безу.)
54 ОБЩИЕ ЗАКОНЫ ДВИЖЕНИЯ И РАВНОВЕСИЯ ТЕЛ
Следствие IV,
19. Если в круге RDQ (фиг, 6) провести бесконечно
малые хорды RD и DE% которые или равны между собою,
или отличаются друг от друга на величину, бесконечно
малую по сравнению с ними самими; если, далее,
продолжить хорду RD до точки О, так что DO — RD; если,
наконец, через точки О и Е провести прямую OQ, а через
точку D — касательную DN, пересекающуюся с OQ
в точке N} то по известному свойству круга мы будем
иметь
DN* = NE.NQ
и
OD • OR, или 2D02 = ОЕ- OQ.
Так как линии DN и DO должны рассматриваться как
линии, равные между собою, и точно так же должны
рассматриваться линии NQ и OQ, то мы получим
OE=2NE*).
Если, следовательно, элемент дуги DE произвольной
кривой ADE (фиг. 3 и 4) считать малой дугой круга, — а
это всегда можно предположить, не делая ошибки,—то
вторая разность ОЕ от пройденного пути [29] будет в два
раза больше действительного пути NE> который тело
проходит за элемент времени ВС под действием ускоряющей
или замедляющей силы, хотя на первый взгляд линии ОЕ
*)Если линии OD и DE равны между собою, то можно строго
доказать, что
OE=2NE.
В самом деле, треугольник DOE будет тогда равнобедренным,
угол ODE измеряется половиной дуги RDE, а угол
NDE—половиной дуги DE. Отсюда следует, что линия DN делит угол ODE
пополам; а так как
DO^DE,
то мы будем иметь
OE=2NE.
Приведенное в тексте доказательство распространяется и на тот
случай, когда OD и DE отличаются друг от друга на величину,
бесконечно малую по сравнению с ними самими, и следовательно,
не в точности равны между собою. (Примечание Безу.)
ОБ УСКОРЕННОМ ИЛИ ЗАМЕДЛЕННОМ ДВИЖЕНИИ 55
и NE кажутся равными друг другу в кривой,
рассматриваемой как ломаная: касательная DN тогда совпадает
с продолжением DO весьма малого звена RD кривой.
Следствие V.
20, Если путь BD, пройденный за время /, обозначить
через е> то на основании изложенного мы будем иметь
d*e = 2NE
и, так как
ВС* '
то
£l — 2F
Следовательно, вообще для кривой ADE можно взять
дифференциальное уравнение второго порядка в виде
где ф представляет "собой некоторую функцию от е и /,
или от е, t и их дифференциалов. При этом знак -\- будет
соответствовать ускоренному движению, т. е. тому случаю,
когда кривая ADE обращена к АС своей выпуклостью, а
знак — будет соответствовать замедленному движению,
т. е. тому случаю, когда кривая ADE обращена к АС
своей вогнутостью.
Следствие VI.
21. Так как
(п° 15), то при постоянном dt мы будем иметь
d2e = dudt.
Отсюда предыдущее уравнение
ydt* ^z^dte
принимает вид
tfdt — nb dtt,
•или
tfde — -^ru dtt,
56 ОБЩИЕ ЗАКОНЫ ДВИЖЕНИЯ И РАВНОВЕСИЯ ТЕЛ
Замечания по поводу ускоряющих сил и сравнения их
между собою.
Замечание L
22. PvaBHOMepHoe движение тела может быть изменено
лишь внешней причиной. Но из всех причин, оказывающих
влияние на движение тела, только удар, как это мы
увидим во второй части, обладает тем свойством, что его
действие мы в состоянии определить, исходя из известной
нам причины. Все остальные причины остаются совершенно
нам неизвестными; вследствие этого они проявляются для
нас только своим действием, ускоряя или замедляя
движение тел; и мы можем отличить одни причины от других
только при помощи закона и известной величины их
действия, т» е. при помощи закона и величины производимого
ими изменения движения.
Следовательно, в том случае, когда причина нам
неизвестна,— а лишь об этом случае здесь у нас и будет
итти речь,—нам должно быть непосредственно дано
уравнение кривой ADE> либо в конечной, либо в дифференциальной
форме. Если движение ускоряется или замедляется, следуя
некоторому произвольному закону, носящему характер
чистого допущения, то уравнение обыкновенно имеет
дифференциальную форму. Если же закон, связывающий пространство
и время, известен нам из опыта, то это уравнение,
напротив, обыкновенно бывает дано в конечных величинах.
Предположим, например, что ускоряющая сила такова,
что тело за одинаковые мгновения получает одинаковые
приращения скорости. Тогда, так как dt постоянно, da
также будет постоянно. Постоянной будет и величина ср.
Уравнение
(fdt = du
в данном случае вытекает непосредственно из сделанного
допущения.
Предположим теперь, что в каком-то частном случае опыт
показал, что конечные расстояния, пройденные с начала
ЗАМЕЧАНИЯ ПО ПОВОДУ УСКОРЯЮЩИХ сил 57
движения, пропорциональны квадрату затраченных времен.
Тогда уравнение кривой ADE будет иметь вид
at2
f2
е=:^>
где а — путь, пройденный за какое-то определенное время 7,
Отсюда следует, что
з __ 2adt*
а в — у,2
и
2adt
аа = - Т2 ■ f
Мы видим, что при данных предположениях приращения
скорости в каждый элемент времени одинаковы. Это
выражают иначе, говоря, что ускоряющая сила <р постоянна,
В данном случае, как и в других, ему подобных,
дифференциальные уравнения
(pdt2 = ±:d2e
и
ydt= + du
мы получаем из заданного конечного уравнения кривой
ADE.
В том случае, когда причина нам неизвестна, очевидно,
должно быть задано уравнение
-»)Мы только что видели, что каково бы ни было ускорение
или замедление движения, кривая будет иметь дифференциальное
уравнение одного и того же вида, а именно:
Однако, для того, чтобы из этого уравнения, а равно из
уравнений
ydt =3~da
и
yde = + udti
найти для данного движения то или иное соотношение между и, t
и е, нужно знать <р. Можно было бы думать, что для этого ие-
58 ОБЩИЕ ЗАКОНЫ ДВИЖЕНИЯ И РАВНОВЕСИЯ ТЕЛ
Большинство геометров рассматривает уравнение
<pdt=du,
связывающее время и скорость, с другой точки зрения.
То, что по-нашему есть лишь допущение, ими
возводится в принцип. Поскольку увеличение скорости есть
действие ускоряющей причины и поскольку, по их мнению,
действие всегда пропорционально своей причине, они
рассматривают величину ср не просто как выражение
отношения du к dt: по их мнению, она, кроме того, является
выражением ускоряющей силы, которой, как они
утверждают, при постоянном dt должно быть пропорционально
du. Отсюда они получают общую аксиому, что
произведение ускоряющей силы на элемент времени равно элементу
скорости.
Даниил Бернулли в петербургских «Commentarii» (том 1)
утверждает, что принцип этот является лишь случайной
истиной, поскольку мы не знаем природы причины и
способа ее действия и потому не можем знать, действительно
ли действие пропорционально своей причине, или же оно
обходимо знать, в чем заключается та причина, которая ускоряет
или замедляет движение. Цель настоящего замечания заключается
в том, чтобы показать, что на самом деле это не так: <р всегда
задано самим характером рассматриваемого движения. Так,
согласно этому замечанию, для того чтобы определить зависимость
между путем, скоростью и временем при заданном законе
движения, нужно воспользоваться уравнениями
ydt ~ + dti
и
yde =3ztida.
В эти уравнения достаточно подставить вместо <р ту величину,
которая выражает закон увеличения или уменьшения скорости.
Предположим, например, что уменьшение скорости за любое
мгновение пропорционально квадрату скорости. В таком случае мы
можем записать
ga4t =— da,
gtfide = — и dny
где g—постоянный коэффициент. Таким же образом нужно
поступать и в других случаях. (Примечание Безу*)
ЗАМЕЧАНИЯ ПО ПОВОДУ УСКОРЯЮЩИХ сил 59
пропорционально какой-нибудь степени, или вообще какой-
нибудь функции от своей причины [30].
Напротив, Эйлер в своей механике старается доказать,
что данный принцип представляет собой необходимую
истину ["J.
Что касается нашего мнения по вопросу о
необходимости или случайности этого принципа, то мы, не желдя
разбирать здесь этого вопроса, ограничимся тем, что
данный принцип примем за определение ускоряющей силы:
термином «ускоряющая сила» мы будем обозначать Просто
величину, пропорциональную приращению скорости. Так,
вместо того, чтобы говорить, что приращение скорости
в любое мгновение постоянно или что это приращение
пропорционально квадрату расстояния тела от некоторой
неподвижной точки и т. д., мы в целях краткости, а
также в целях согласия с принятой терминологией, будем
просто говорить, что ускоряющая сила постоянна или что
она пропорциональна квадрату расстояния и т. д. Вообще
под отношением двух сил мы всегда будем понимать
просто отношение их действий, не вдаваясь в рассмотрение
того, пропорционально ли действие своей причине или же
оно пропорционально какой-то функции от этой причины, —
рассмотрение совершенно излишнее, поскольку действие
всегда задается независимо от причины либо на основании
опыта, либо в качестве допущения.
Итак, под движущей причиной вообще мы будем
понимать произведение движущейся массы на элемент ее
скорости или, что то же самое, на малый отрезок пути,
который эта масса прошла бы в течение данного элемента
времени под действием ускоряющей или замедляющей
причины. Под ускоряющей же силой мы будем понимать
просто элемент скорости [32].
После подобных определений нетрудно видеть, что
любая задача, относящаяся к прямолинейному движению
тел, обладающих некоторыми силами [33], направленными
к* какому-нибудь центру, или тел, притягивающих друг
друга по тому или иному закону, будет задачей, по
крайней мере, столь же геометрической, сколь и механической,
II трудности, встречаемые в задачах этого рода, будут
60 ОБЩИЕ ЗАКОНЫ ДВИЖЕНИЯ И РАВНОВЕСИЯ ТЕЛ
лишь трудностями вычислительного порядка, если только
движущееся тело можно рассматривать как точку.
Можно, пожалуй, подумать, что уравнение ydt-=-^rdu,
рассматриваемое не как гипотеза, а как принцип, будет но
крайней мере необходимым для вычисления действий,
причины которых известны, как, например, удар, в
особенности когда этот удар состоит из повторяющихся маленьких
толчков. Я надеюсь, что из второй части настоящего труда
будет видно, что этот мнимый принцип не только
бесполезен и в этом случае, но что применение его будет
недостаточным и может привести даже к ошибкам.
Замечание II.
23. Небесполезно будет заметить, что в тех случаях,
когда задано уравнение между е и t в конечном виде
и когда при помощи дифференцирования из него
получается обычное уравнение
значение d2e, определяемое из этого уравнения, будет как
раз равно ОЕ} истинной второй разности от BD. На-
первый взгляд может показаться, что на основании самой
природы дифференциального исчисления можно усумниться
в том, действительно ли величина d2e, найденная при
помощи дифференцирования, представляет собой истинную
длину отрезка ОЕ или какого-либо другого отрезка,
скажем, NE. Однако, с помощью этого самого исчисления
можно убедиться в том, что найденная величина ydt2
равна ОЕ*).
*)Для того чтобы указанное сомнение возникло, достаточно
вспомнить то правило, по которому находится вторая разность.
Предположим (фиг. 8), что AM=t и MP представляет какую-то
функцию от t, которую я обозначу ср(£). Для того чтобы найти
величину ID, предположим, что t переходит в t-\-dt, и тогда,
так как
BD = v{t-{-dt)9
мы получим
ID = v(t + dt) — 4(t),
если пренебречь бесконечно малыми величинами второго и бо-
ЗАМЕЧАНИЯ ПО ПОВОДУ УСКОРЯЮЩИХ сил G1
Замечание III.
24. Выше (п° 15) мы видели, что если пройденные
пути пропорциональны квадратам соответствующих времен,
то тело, проходящее за время Т путь Е (фиг. 7),
прошло бы равномерно за то же время путь 2£, если бы
оно обладало той скоростью, какую оно имеет в конце
пути Е. Но и при любрй ускоряющей или замедляющей
силе пути пе и NE, проходимые телом под действием этой
силы в течение
элементов времени Вс и BCt м> -^
относятся между собой,
как квадраты этих
элементов времени.
Отсюда следует, что в
кривой,
рассматриваемой в качестве
ломаной [35], величину
ОЕ или d2e = 2NE,
рассматриваемую как
действие ускоряющей
или замедляющей силы,
следует представлять
как расстояние, которое
проходится телом при равномерном движении с бесконечно
малой скоростью, приобретенной телом в конце элемента
Фиг. 7.
лее высоких порядков. Затем, чтобы найти величину ЕО, нужно
в ID предположить, что t перешло в t-\-dt, и на этот раз
пренебречь бесконечно малыми величинами третьего и более высоких
порядков: мы получим тогда величину RE. За величину d2e
принимают разность между этой величиной RE и величиной /Д
найденной ранее. Однако нужно отметить, что, поскольку при
определении величины ID мы отбрасывали величины второго,
порядка, это отбрасывание может повлиять на искомую разность
' отрезков ID и RE, представляющую собой бесконечно малую
величину второго порядка. Следовательно, мы не вправе делать
заключение о том, что ОЕ равно величине d2e, если не будет пока-
зано> что то отбрасывание, о котором идет речь, дает лишь
бескънечно малую ошибку порядка выше второго.
Для того чтобы убедиться в этом, докажем одно предложе-
G2 ОБЩИЕ ЗАКОНЫ ДВИЖЕНИЯ II РАВНОВЕСИЯ ТЕЛ
времени ВС. Отсюда явствует, каким образом мгновенное
действие ускоряющей или замедляющей силы можно свести
к равномерному движению.
Замечание IV.
25. В кривой, рассматриваемой в качестве ломаной
(фиг. 8), действия ускоряющей силы в течение элементов
А времени Вс и ВС будут
представлены отрезками О'В и ОЕ.
Эти отрезки, очевидно,
пропорциональны временам Вс и ВС
вследствие подобия треуголь-.
ников DE'O' и DEO, что как
раз и подтверждает то, что мы
только что отметили, а именно,
м
/77
В
4%<
О
что расстояние ОЕ можно
рассматривать как проходимое рав-
Фиг. 8. номерно за время ВС. Ведь если
пути О'Е' и ОЕ находятся друг
к другу в том же отношении, как и затраченные времена
Вс и ВС, то движение — равномерное.
ние, приводимое нашим автором в его «Исследованиях о системе
мира».
Пусть cp(2r+?) есть некоторая функция от z + 5, где 5— очень
малая величина, на которую по условию возрастает г. Тогда мы
имеем
1(* + Э = ?М + 5ДW+*^+ и т. д.,
где &(z) есть коэффициент при dz, получающийся при нахождении
дифференциала от <р(*)[84], а Г (z) — коэффициент при dz,
получающийся при нахождении дифференциала от А (г). В самом
деле, пусть
<р(*-И)=<р(*)+и;
найдем дифференциал от этой функции, считая z постоянным
(это сделать возможно, так как мы считаем, что в данном
случае изменение z сводится к изменению 5). Тогда мы будем иметь
Полагая
*(* + ?) = *(*)+/•,
ЗАМЕЧАНИЯ ПО ПОВОДУ УСКОРЯЮЩИХ сил 63
Отсюда следует, что, поскольку в случае кривой,
рассматриваемой в качестве ломаной, действие ускоряющей
силы выражается при помощи равномерного движения, при
мы точно так же получим
Полагая, далее,
Г(* + $) = Г(г) + *,
мы получим
<КП (* + $)«</*
Продолжая поступать таким же образом и дальше, мы будем
иметь
*(* + 5) = ?(*) + J d& (z) + J dt J diT (*) +
+ J* j<«J<«II(*)+ и т. д.,
что будет равно
9iz)+^{z)+fT(z) + ±^L+ и т. д.
Установив все это и имея в виду, что
MP=9(t)9
мы будем иметь
BD = 4(t + dt)=i(t) + dtb(t) + 4?^+ ИТ-Д-
CE=4(t+2dt) = <i(t) + 2dtb(t) + 2dt*Y(t)+ и т. д.
Следовательно,
и
RE—ID или — 0£ или — d2e = dt2T (t).
С помощью обычных методов дифференциального исчисления мы
получим
//) = £« Д(*)
и
RE= dtb(t + dt) = ЛД (0 + rf*2 Г (О,
откуда
RE—ID или —0£ или — d*e = dt*T(t).
Следовательно, d2e, получаемое методами дифференциального
исчисления, действительно равно величине ОЕ. (Примечание
Безу.)
64 0БЩ1Ш ЗАКОНЫ ДВИЖЕНИИ II РАВНОВЕСИЯ ТЕЛ
таком предположении отнюдь нельзя считать, что скорость
возрастает постепенно в течение элемента времени ВС, а
нужно полагать, что тело, пройдя путь BD, в начале
элемента времени ВС сразу, скачком, получит все то
увеличение или уменьшение скорости, которое оно в
действительности получает только к концу этого самого элемента
времени.
Для подтверждения этого достаточно указать, что в
случае кривой, рассматриваемой в качестве ломаной, тело
в действительности проходит в течение элементов времени
Вс и ВС расстояния ТЕ' и RE (фиг. 8), пропорциональные
временам. Таким образом, скорость в течение элемента
времени ВС можно считать постоянной, и она относится к
скорости за предыдущий элемент времени ВМ, как RE
относится к ID. Отсюда следует, что в начале элемента
времени ВС скорость меняется скачком в отношении RE
и ID.
Напротив, в случае подлинной кривой действия
ускоряющей или замедляющей силы в течение элементов
времени Вс и ВС выражаются отрезками пе и NE (фиг. 7),
пропорциональными квадратам времен. В этом случае
скорость увеличивается или уменьшается равномерно в
течение всего элемента времени ВС в результате действия
ускоряющей силы, производящей на тело в течение этого
элемента времени ряд равных повторяющихся весьма малых
толчков. Сумма этих малых толчков должна быть равна
тому одному удару, который в случае кривой,
рассматриваемой в качестве ломаной, сообщается телу, как мы
полагаем, в начале элемента времени ВС.
Здесь возможно возражение, которое мы хотим
предупредить. Найденное нами уравнение
d2e=udt2
относится как к случаю подлинной кривой, так и к случаю
кривой, рассматриваемой в качестве ломаной. Поскольку <р
в течение элемента времени ВС можно считать постоянной,
величина d2e или ОЕ должна быть пропорциональной dt2,
т. е. квадрату ВС, и это справедливо даже в случае
кривой, рассматриваемой в качестве ломаной. Нб мы только
ЗАМЕЧАНИЯ ПО ПОВОДУ УСКОРЯЮЩИХ сил 65
что видели, что отрезки Е'О' и ЕО пропорциональны Вс
и ВС. Как же совместить эти два положения? Ответ очень
простой: дело в том, что Е'О' не равно величине d2e,
соответствующей элементу времени Вс; в этом нетрудно
убедиться из простого рассмотрения фиг. 7*).
Замечание V.
26. Геометры не должны забывать об этом различии,
существующем между подлинной кривой и кривой, рассматриваемой
в качестве ломаной, при оценке действия ускоряющих сил
и при сравнении этих действий между собою. Если одно
из действий вычислено исходя из подлинной кривой, то и
другое действие необходимо вычислять также, исходя из
подлинной кривой. В противном случае можно получить
отношение сил,—т. е. отношение действий этих сил,—
вдвое большее против того, которое есть на самом деле **).
*) Необходимо заметить, что отрезок ЕО в качестве второй
разности от линии MP определяется на основании того
допущения, что три точки Р, D и Е лежат на подлинной кривой. Но
рассматривая PD и DE как хорды этой кривой, мы видим, что
Е' не может лежать на кривой, и потому отрезок Е'О' вовсе не
есть d2et соответствующее Вс. Если ЕО есть d2e,
соответствующее ВС, то для того, чтобы найти d2e, соответствующее Вс,
нужно взять Вт, равное Вс, и, проведя тр параллельно BD до
пересечения с кривой в точке р, провести затем прямую pDo до
встречи в точке о с линией сео, параллельной BD. Тогда отрезок
ео и будет d2e, соответствующим Вс. Разница получится та, что
кривая, рассматриваемая .в качестве ломаной, будет иметь теперь
в качестве смежных сторон линии Dp и De вместо DP и DE.
Следовательно, если DN является касательной к подлинной кривой
в точке D и если ое вдвое больше пе, то из пропорции
NE:ne — BC2'Bc2
вытекает пропорция
ОЕ:ое = ВС2:Вс2.
Итак, d2e всегда пропорционально dt2, а отрезки ОЕ и 0'Е\
заключенные между кривой, рассматриваемой в качестве ломаной
и ее касательной, пропорциональны dt. (Примечание Безу.)
**) Действие ускоряющей причины можно определить двумя
способами: или с помощью расстояния, которое она действительно
заставляет тело проходить в течение некоторого элемента времени
или с помощью того расстояния, которое тело прошло бы в те-
б Ж. Даламбер
66 ОБЩИЕ ЗАКОНЫ ДВИЖЕНИЯ II РАВНОВЕСИЯ ТЕЛ
Замечание VI.
27, Если нам задана постоянная ускоряющая сила р, —
скажем, тяжесть,—и под действием этой силы тело
проходит конечный путь z за конечный промежуток времени О,
то мы будем иметь
d2e 2г *)
или
NE z
чение равного элемента времени, двигаясь равномерно со
скоростью, приобретенной в течение первого элемента времени.
В первом случае это действие выражается отрезком NE (фиг. 3 и 4),
причем DIV есть касательная к подлинной кривой. Во втором
случае действие будет выражаться отрезком ОЕ,— вдвое большим,
чем NE,— причем DO будет касательной к кривой,
рассматриваемой в качестве ломаной. От нас зависит, каким именно способом
определять действие ускоряющей причины. Но при сравнении
двух ускоряющих причин нужно помнить, что если одно
действие выражено через NE, отнесенное к кривой, изображающей
пути, пройденные под действием одной причины, то и действие
другой причины должно быть выражено через аналогичный
отрезок, отнесенный к соответствующей кривой, изображающей
пути для второй причины. Это и имеют в виду, когда говорят,
что если одно из действий вычислено, исходя из подлинной
кривой, то и другое действие необходимо вычислять, также исходя
из подлинной кривой, и т. д. (Примечание Безу.)
*) В данном замечании указывается, каким образом любую
ускоряющую силу можно сравнивать с весом. Это сравнение
основывается на следующих соображениях. Уравнение
дает
d2e
Таким же образом мы получим
d2z
d2z
Но вместо отношения -rzr можно взять отношение конечных ве-
d№
личин, имея в виду, что пути, пройденные под действием посто-
ЗАМЕЧАНИЯ ПО ПОВОДУ УСКОРЯЮЩИХ сил 67
Из предыдущего равенства следует
.,а pd2eW
или
2<?zdt2
роз
р¥
Следует остерегаться писать
йЧ-.
pQ2
к чему можно притти, положив d2e, равным NE. В самом
деле, легко видеть, что тогда мы получили бы только
Полиной ускоряющей силы, пропорциональны квадратам времен.
Таким образом, мы получим
d2Z
d2z
(мы взяли в данной пропорции —— вместо d2z ввиду того, что,
как уже было сказано, d2z означает удвоенное расстояние по
сравнению с действительным расстоянием, которое сила
заставляет тело пройти в течение элемента времени Щ. Отсюда следует
d2z _ 2z
d№ -~ 62
и, далее,
_ d2e , 2z
Ч'-Р— dt2 '• Q2 •
Это же можно показать и иначе. Интегрируя уравнение
pd№ = d2zt
мы получим
p№ = 2z.
Сопоставляя последнее равенство с уравнением
d2e = ydt2,
мы получаем то же самое соотношение, {Примечание Везу)
5*
68 ОБЩИЕ ЗАКОНЫ ДВИЖЕНИЯ И РАВНОВЕСИЯ ТЕЛ
ловину величины d2e, равной 2NE, и после
интегрирования мы получили бы лишь половину величины е.
Убедимся в этом на простом примере. Пусть
другими словами, пусть будет сила постоянна и равна
весу. В таком случае, как известно, пути е и z
пропорциональны квадратам времен Ьг и О2. Следовательно,
_ zt*
Это как раз и получается (в результате интегрирования)
из уравнения
ае~- Р№ '
или
тогда как уравнение
привело бы нас к равенству
_ zt*
е— 202 >
т. е. к половине величины е.
Г Л А В А II.
О сложении движений.
Теорема.
28. Если на тело ила на точку А (фиг. 9) действуют
одновременно две какие-либо силы так, что под
действием одной из них тело за известный промежуток
времени прошло бы равномерно путь от А до В, а под
О СЛОЖЕНИИ ДВИЖЕНИЙ
69
К
Ъг
1
/./
и
1
~7С /
W
ч
D\
действием другой оно за тот же промежуток времени
прошло бы равномерно путь от А до С, причем на АВ
и АС можно построить параллелограмм ABDC, то я
утверждаю, что тело А пройдет равномерно диагональ
AD за то же время, за какое
оно прошло бы расстояния АВ
или АС.
Пусть Ag—неизвестная нам
линия, которую будет описывать
тело Л. Не подлежит сомнению,
что эта линия будет прямой (п° '6)
и что тело А будет описывать ее
равномерно. Не менее очевидно и
то, что прямая эта будет
расположена в той же самой плоскости, в L М
которой лежат линии АВ и АС, так фиг> д#
как нет никакого основания для
того, чтобы она вышла из этой плоскости в одну сторону
скорее, чем в другую. Предположим теперь, что когда тело
приходит в некоторую точку g этой прямой, на него
начинают действовать две силы, из которых одна стремится
сообщить телу движение по прямой gc, параллельной АС,
с такой скоростью, какую оно имело в точке А по
направлению АС, но в обратную сторону, а другая стремится
заставить тело пройти путь go, равный и параллельный АВ,
но в противоположную сторону, и за то же время, за
которое тело прошло бы путь АВ. Легко видеть, что при
этих условиях тело будет оставаться в покое в точке g;
ведь скорость данного тела в точке g и его направление
таковы, как будто оно обладает здесь двумя силами,
равными и параллельными силам, направленным по АВ и АС,
и, следовательно, равными и противоположными силам,
направленным по go и gc.
Установив это обстоятельство, представим себе, что
тело Л, описывающее линию Ag, находится на плоскости
KLMH, которая может свободно скользить вдоль двух
направляющих KL и IM, параллельных АСЧ Заставим эту
плоскость двигаться между направляющими таким образом,
чтобы все ее точки g описывали линии gc, равные и
70 ОЫДИЕ ЗАКОНЫ ДВИЖЕНИЯ И РАВНОВЕСИЯ ТЕЛ
параллельные ЛС, за то же время, за какое тело А описало
бы линию ЛС. В то же время пусть обе направляющие
движутся параллельно АВ, но в противоположную сторону,
со скоростью, какой тело А обладало бы по направлению
АВ. При этом своем движении направляющие увлекают
с собой и плоскость. Очевидно, что при этих условиях
все точки g плоскости будут двигаться равномерно и
описывать пути ga, равные и параллельные диагонали AD
параллелограмма ВС, Очевидно также и то, что
движущееся тело или точка А в данном случае будет все время
находиться под действием четырех сил, попарно равных
и противоположных друг другу, вследствие чего тело в
абсолютном пространстве должно будет оставаться в покое.
Отсюда вытекает, что когда движущееся тело, или точка А
приходит в точку g плоскости, эта точка g должна
находиться в том самом месте, которое тело занимало в начале
движения. Но это возможно лишь при том условии, если
линия Ag совпадает с диагональю AD, а точка g — с
точкой D*). Отсюда следует, и т. д. [86].
Замечание.
29, Доказательство, обычно даваемое настоящей теореме,
состоит в следующем. Принимается, что точка А движется
равномерно вдоль линейки АВ с той скоростью, какой она
обладает по направлению АВ, а линейка АВ в то же
время движется по направлению АС с той скоростью, какой
обладает тело А по направлению АС. При такого рода
предположении очень хорошо доказывается, что точка А
описывает диагональ AD.
*) Так как точка А в абсолютном пространстве должна
оставаться в покое, необходимо, чтобы движение плоскости, на
которой по условию находится точка, переносило ее в
противоположную сторону ровно настолько, насколько она продвинулась бы
в том случае, если бы плоскость оставалась неподвижной. Поэтому,
когда точка опишет линию Ag, точка плоскости, находившаяся
в начале движения в g должна описать линию gA и очутиться,
следовательно, в Л. С другой стороны, эта точка должна описать
линию, параллельную диагонали AD. Отсюда следует, что линия
Ag должна совпадать с этой самой диагональю. (Примечание Безу)
О СЛОЖЕНИИ ДВИЖЕНИЙ
71
Вообще большинство обычных доказательств этой
теоремы основывается на том допущении, что обе силы,
действующие одна по направлению АВ, а другая по
направлению АС, действуют на тело А в течение всего времени
движения, а это, строго говоря, не отвечает существу
дела. Ведь по условию тело А в первый момент стремится
одновременно двигаться по направлениям АВ и АС, и
требуется определить направление и скорость, которые
оно должно получить в результате совместного
действия обеих сил. Как только тело приняло некоторое
среднее направление AD, так оба стремления, направленные
но АВ и АС, перестают существовать: существует лишь
стремление, направленное по AD.
Я счел необходимым предупредить такого рода
возражение и показать, что путь тела А не меняется от того,
действуют ли на него данные две силы только в первый
момент, или же они действуют на него непрерывно и
одновременно в течение всего времени движения. И я
полагаю, что в только что приведенном доказательстве я этой
цели достиг.
Следствие I.
30. Пусть тело проходит или стремится пройти отрезок
прямой АС (фиг. 10) с произвольной скоростью. Возьмем
какую-нибудь точку В на пря- _
мой АС или на ее продолже- § "а в £ В
нии. Тогда скорость АС мож- _ 1А
^ Фиг. 10.
но рассматривать как бы
составленной из скорости АВ и скорости ВС. В самом деле,
линию АС можно рассматривать как диагональ
параллелограмма со сторонами АВ и ВС. Отсюда следует, и т. д.
Замечание.
31. Возможно, что кое-кто из читателей будет
удивляться тому, что для доказательства столь простого, пови-
димому, предложения я прибегаю к значительно более
сложному случаю. Мне кажется, однако, что иначе данного
предложения доказать нельзя, если не принять в качестве
?2 ОБЩИЕ ЗАКОНЫ ДВИЖЕНИЯ И РАВНОВЕСИЯ ТЕЛ
бесспорной той аксиомы, что совместное действие двух
причин равно сумме действий этих причин, взятых отдельно;
другими словами, что две причины действуют совместно
так же, как они действуют по отдельности, — принцип, на
мой взгляд, ни достаточно очевидный, ни достаточно
простой. К тому же это положение тесно связано с вопросом
о живых силах и с принципом ускоряющих сил, о котором
мы говорили выше (п° 22). На этом основании я считал
необходимым избегать пользоваться этим положением, не
говоря уже о том, что я в настоящем сочинении задался
целью свести механику к возможно меньшему числу
принципов и все эти принципы получить из одного понятия
движения, т. е. из пройденного пути и из затраченного на
пего времени, совершенно не вводя никаких сил и
движущих причин.
Следствие II.
32. Если тело приводится в движение какими-либо
двумя ускоряющими силами по направлениям АВ и АС
(фиг. 11), то направлением тела
будет диагональ параллелограмма,
построенного на сторонах АВ и
АС, пропорциональных данным
ускоряющим силам. Ускоряющая же
сила данного тела, направленная
по AD, будет так относиться к
любой изданных ускоряющих сил,
направленных по АВ и АС, как
AD относится к АВ и АС, В
самом деле, пусть АЬ и Ас — пути,
которые тело А прошло бы в начале движения под
действием данных сил, взятых по отдельности. Тогда мы будем
иметь
АЬ:Ас — АВ:АС
(п° 22). Отсюда следует, что линии bd и cdy
параллельные линиям АС и АВ, пересекутся в точке d диагонали AD.
Точно так же, если А$ и Ах представляют собой какие-
либо другие пути, которые тело проходит за одинаковые
промежутки времени под действием тех же самых сил, то
О КРИВОЛИНЕЙНОМ ДВИЖЕНИИ
73
отношение ЛЬ к А$ будет равно отношению квадрата
времени, затрачиваемого на АЬ или на Ас, к квадрату времени,
затрачиваемого на А$ или на Ах. Другими словами, это
отношение будет равно отношению Ас к Ах. Отсюда
следует, что точка пересечения 8 линий р§ и хЬ будет также
лежать на диагонали AD. Поэтому, если предположить, что
тело А в первый момент движется по линейке АВ с той
ускоряющей силой, которую оно имеет по направлению АВУ
и что в то же время на линейку действует ускоряющая
сила, направленная по АС и переносящая линейку от А
к С, то точка А будет описывать диагональ Ad за то же
самое время, за которое она описала бы АЬ или Ас; при
этом ее ускоряющая сила, направленная по AD, будет так
относиться к каждой из сил, направленных вдоль сторон,
как диагональ относится к этим самым сторонам.
Отсюда нетрудно видеть, каким образом можно заменить
любую ускоряющую силу другими ускоряющими силами,
взятыми в каком угодно количестве.
Выше (п° 24) мы видели, каким образом мгновенное
действие произвольной силы можно свести к равномерному
движению. Теперь легко понять, что комбинацию действий
любого числа сил и отыскание единого действия,
происходящего от этих сил, можно свести к законам сложения
равномерных движений.
О криволинейном движении и о центральных силах.
33. Так как тело, предоставленное самому себе,
стремится двигаться прямолинейно, то кривую линию оно может
описывать только при действии какой-либо силы,
беспрерывно отклоняющей его от его естественного направления.
Из только что изложенного можно вывести принципы
движения тела по кривой линии.
Доказано, что бесконечно малую дугу произвольной
кривой можно рассматривать как дугу круга с радиусом,
равным радиусу кривизны данной дуги. Поэтому движение
тела по любой кривой сводится к движению того же тела
по некоторому кругу, радиус которого изменяется в
каждый момент.
74 ОБЩИЕ ЗАКОНЫ ДВИЖЕНИЯ И РАВНОВЕСИЯ ТЕЛ
Сила, удерживающая тело на кривой, называется
центральной силой в том случае, когда она направлена в.сегда
к какой-нибудь одной неподвижной точке. Мы, однако,
будем называть эту силу центральной силой независимо от
того, направлена ли она к неподвижной точке, или нет.
По своей природе эта сила есть не что иное, как
ускоряющая или замедляющая сила, направление которой
отлично от направления тела. На основании всего того, что
было сказано выше (п° 24 и 32), мгновенное действие
этой силы можно свести к некоторому равномерному
движению: для этого кривую, описываемую телом в результате
ее действия, нужно рассматривать как ломаную с
бесконечным числом звеньев. При этом действие силы будет в два
раза больше по сравнению с действием центральной силы
в случае подлинной кривой в строгом смысле слова.
Предположим, например, что тело описывает бесконечно
малую дугу RDE окружности (фиг. 6) в результате
действия некоторой силы, отклоняющей тело в точке D от
прямой линии, по данному направлению. Если рассматривать
окружность как многоугольник, то. хорда RD будет
линией, описанной телом в предшествующий элемент
времени, а линия DO, равная RD и являющаяся ее
продолжением, будет той линией, которую тело стремится
описать в последующий элемент времени. Поэтому, если
провести ОЕ параллельно направлению центральной силы в
точке Z), то отрезок ОЕ и будет мгновенным действием
этой силы.
Если теперь мы будем рассматривать окружность в
качестве подлинной окружности, то линией, которую "будет
стремиться описать тело в данном случае, будет служить
касательная DN, действие же силы, удерживающей его
на кривой, будет теперь выражаться линией NE.
Отрезок NE7 деленный на квадрат времени,
затраченного на его прохождение, выражает ускоряющую силу, в
результате действия которой тело описывает кривую
(п° 18, 22 и 26). Но линия NE равна квадрату линии DN,
или дуги DE, или RD, деленному на NQ. Линия же NQ
так относится к диаметру окружности, как синус угла,
образованного центральной силой с кривой, относится к пол-
О КРИВОЛИНЕЙНОМ ДВИЖЕНИЙ
75
ному синусу*). Наконец, так как линия DE} деленная на
время, затраченное на ее прохождение, выражает скорость
тела (п° 15), то отсюда следует, что для произвольной
кривой действие центральной силы пропорционально
квадрату скорости, деленному на радиус кривизны и
умноженному па отношение полного синуса к синусу угла,
образованного силой с данной кривой [88].
Вообще, если считать элемент времени постоянным, то
центральная сила будет выражаться отрезком ОЕ в случае
кривой, рассматриваемой в качестве ломаной, и отрезком
NE в случае подлинной кривой. Поэтому при сравнении
действий двух каких-нибудь центральных сил нужно
помнить об этом различии в выражениях силы: необходимо
или обе кривые рассматривать в качестве ломаных, или же
обе кривые считать подлинными кривыми. В противном
случае одно действие окажется вдвое большим против того,
что должно быть по сравнению с другим действием.
Центральные силы, да и вообще все ускоряющие силы
(под словом «сила» мы будем понимать лишь ее действие),
пропорциональны тем малым расстояниям, которые тело
проходит за одинаковые элементы времени в результате
действия этих сил. Все эти силы обычно сравнивают с
постоянной ускоряющей силой, известной нам лучше всего,—
я говорю о тяжести. Если Е есть расстояние, которое тя-
Edt2
желое тело проходит за конечное время 7, то —~£- будет
тем расстоянием, которое оно пройдет за время dU Если
мы теперь предположим, что за то же время dt тело
описывает дугу DE, то центральная сила будет так относиться
к тяжести, как NE относится к —^- или как OE=^2NE
2Edt*
относится к • Т£- .
Пусть г будет радиус кривизны кривое в точке N\
пусть, далее, S будет синус угла, образованного
направлением центральной силы с кривой, А — полный синус,
*) Это вытекает цз того, что линия NQ или EQ в два раза
больше синуса угла NED [S7J. (Примечание Везу.)
76 ОБЩИЕ ЗАКОНЫ ДВИЖЕНИЯ И РАВНОВЕСИЯ ТЕЛ
е—то расстояние, которое прошло бы тело за время Г,
двигаясь равномерно со скоростью, которой оно обладает
в D. Тогда
DE = ^%
OE=zDE2 •— e4t2A
S ~ T*Sr *
Это значит, что мгновенное действие тяжести так
относится к мгновенному действию центральной силы, как 2Е
е2А е2А
относится к -*- , или как Е относится к ^т. Таким
образом, отношение этих двух действий, которое
большинство геометров принимает за отношение самих причин,
выражено нами в конечном виде *).
ГЛАВА Ш.
Об уничтожении или изменении движения
теми или иными препятствиями.
34, Движущееся тело может встретиться с теми или
иными препятствиями, которые могут изменить или даже
полностью уничтожить его движение. Препятствия эти или
являются непреодолимыми, или же они могут оказывать
сопротивление как раз настолько, чтобы уничтожить лишь
движение, которым обладает тело.
Непреодолимое препятствие может быть такого рода,
что оно не допускает никакого движения тела: примером
может быть случай, когда тело тянет прямолинейный
стержень, закрепленный в неподвижной точке. Далее, непрео-
*) В «Encyclopedie» под словом «Force» читатель найдет ряд
теорем и замечаний, касающихся меры центральной силы. Для
той цели, которую мы для себя ставили здесь, достаточно' того,
что нами только что сказано.
ОБ УНИЧТОЖЕНИИ ИЛИ ИЗМЕНЕНИИ ДВИЖЕНИЯ 77
долимое препятствие может быть и такого рода, что оно
не мешает телу двигаться в каком-то направлении, но
только не в том, какое оно имело: примером может
служить случай, когда тело встречает жесткую неподвижную
плоскость.
35. Если встречаемое телом препятствие, —
непреодолимое или нет, —только -изменяет его движение, не уничтожая
его целиком, так что тело, имея, например, до встречи с
препятствием скорость а, вынуждено в дальнейшем
двигаться со скоростью Ь, отличной от прежней по величине
и по направлению, то очевидно, что скорость а, которой
тело обладало в момент встречи с препятствием, можно
рассматривать как составленную из скорости Ь и некоторой
другой скорости с, утраченной благодаря препятствию.
36. Отсюда следует, что неупругое тело,
ударившееся о неподвижную и непроницаемую плоскость
перпендикулярно к этой последней, должно после удара
остановиться и притти в состояние покоя. В самом деле, пусть
данное тело после столкновения с плоскостью будет иметь
движение. Тогда это может быть только движение назад,
по направлению перпендикуляра к плоскости. Положим,
скорость тела до столкновения была и, а после
столкновения v. Пусть
где т — какое-то неизвестное число. Тогда мы будем иметь
и = — та -]- и -f- та
(п° 30 и 35). Отсюда следует, что скорость, утраченная
телом при столкновении его с плоскостью, равна а-\-та.
Однако, ведь нет никакого основания для того, чтобы т
было каким-нибудь определенным числом предпочтительно
перед другим числом. Единственным условием, из которого
можно найти скорость и-\-та, является то, что эта
скорость уничтожается плоскостью. Но так как плоскость
жесткая и неподвижная (по условию), то нет никакого
основания к тому, чтобы она уничтожила именно скорость а-\-та,
а не, какую-нибудь другую скорость, — скажем, a -f- пи.
Поэтому число т и не может быть каким-либо определен-
78 ОБЩИЕ ЗАКОНЫ ДВИЖЕНИЯ И РАВНОВЕСИЯ ТЕЛ
ным числом предпочтительно перед другим числом. Отсюда
следует, что это число должно равняться нулю.
Действительно, если, как мы предположили, скорость а-\-та
может быть уничтожена благодаря столкновению с
плоскостью, то с гораздо большим основанием при этом
столкновении уничтожится скорость и. Поэтому она и на
самом деле будет уничтожена. Следовательно, та, а
значит и v, будет равно нулю. Отсюда следует, и т. д.
Следствие I.
37. Пусть тело А (фиг. 12) движется по направлению АВ,
встречается с неподвижной и непроницаемой плоскостью BD
и вынуждено дальше дви-
А гаться в этой плоскости.
^S4s-n# D г Тогда скорость тела по на-
Т\~ " I 1 правлению BD будет так
^\^^ / относиться к скорости его
^ч. / по направлению АВ или ВС,
[ _^м/ как СИНУС Уг^а, дополни-
Е с тельного к углу CBD,
относится к полному сину-
фиг* 12- су [39]. В самом деле,
скорость ВС можно
рассматривать как составленную из двух скоростей: одной, BE,
перпендикулярной к плоскости BD, и другой, BD,
лежащей в этой самой плоскости. Но так как скорость BE
уничтожается плоскостью, то тело А будет обладать только
скоростью BD, которая так относится к ВС, как синус
угла BCD, дополнительного к CBD, относится к полному
синусу.
Следствие II.
38. Пусть тело движется по нескольким плоскостям.
АВ, ВС, CD и т. д. (фиг. 13). Тогда продолжим АВ, ВС,...
до какой-то точки F, Е,.., , затем, произвольным
радиусом 01 (фиг. 14) опишем лутуЬМп построим угол LQM,
равный углу CBF. Опустив затем перпендикуляр МК>
опишем радиусом GK дугу NK% так чтобы угол КОМ равнялся
О ДВИЖЕНИИ ТЕЛА ПО КРИВОЙ ПОВЕРХНОСТИ 79
углу DCE. Потом опустим перпендикуляр N1 и так далее.
Я утверждаю, что если скорость по направлению ЛВ
выразить линией GL, то линия GI будет выражать скорость
по направлению CD. Это с очевидностью следует из
предыдущего следствия.
Следствие III.
39. Отсюда следует, что сумма потерянных скоростей
от А до D равна Ы, т. е. равна сумме спнус-верзусов
углов CBF, DCE и т. д., — если полными синусами считать
соответственно линии GL, ОК и т. д. [40].
С л.е д с т в и е IV.
40. Поэтому, если для всех синус-верзусов взять один
и тот же полный синус, а именно GL, то потерянная
скорость будет меньше суммы этих синус-верзусов.
О движении тела по кривой поверхности.
Лемм а.
41. Если к кривой ABCDR (фиг. 15) провести
касательные AY и RY и затем вписать в эту кривую
ломаную ABCDR так, чтобы у этой ломаной внешние
углы BAY, CBFj DCE urn, д> были равны между собой,
80 ОБЩИЕ ЗАКОНЫ ДВИЖЕНИЯ И РАВНОВЕСИЯ ТЕЛ
то я утверждаю, что можно вообразить эту ломаную
со столь большим числом звеньев, что сумма синус-вер-
зусов углов BAY, CBF, ВСЕ, RDS и т. д. будет меньше
любой заданной величины.
Сумма углов BAY, CBF, DCE и т. д. равна углу RYZ,
образованному касательными RY и AY. Поэтому, если
построить угол ryz
% (фиг. 16), равный
,s RYZ, и угол гуп,
равный одному из
углов ЯЛ К или СВ/7,
Фиг. 15.
и если, затем, число этих углов обозначить через п, то
мы будем иметь
arc г/г X я — arc rz
и
(хорда гп)2
rh
Но
Положив
п — сумме синус-верзусов [41].
(хорда гп)2 ^ (атст)2'П (arc rz)2
п <. rh
rh
П'Г/l
(nicrz)2 ,
rh
(где тс будет известным числом, поскольку линии rh и Л
и дуга rz заданы), мы найдем, что
я«/7
сумма синус-верзусов <^—.
Но так как тс и rl суть постоянные числа, то число //
О ДВИЖЕНИИ ТЕЛА ПО КРИВОЙ ПОВЕРХНОСТИ 81
можно взять настолько большим, что -^— будет меньше
любой заданной величины. А в таком случае сумма синус-
верзусов будет и подавно меньше этой заданной величины.
Теорема.
42. Если тело, движущееся по прямой ХА (фиг. 15),
встречается с кривой поверхностью AR} касающейся
линии ХА в точке А, и затем это тело вынуждено
двигаться по этой поверхности, то я утверждаю, что оно
на пути от А до R ничего не потеряет из своей скорости.
В самом деле, в кривую можно вписать ломаную ABCDR
с таким большим числом звеньев, что сумма синус-верзу-
сов ее внешних углов будет меньше заданной величины (п° 41),
и потому утраченная на пути от А до R скорость может
быть сделана и подавно сколь угодно малой (п°40).
Отсюда следует, что если эта ломаная будет совпадать с кри*
вой, то скорость, утраченная телом на пути от А до /?<,
будет равна нулю.
Следствие.
43. Отсюда следует, что когда тело движется по
кривой, скорость его в каждой точке данной кривой, при
прочих равных условиях, меняется точно таким же образом,
как будто это тело движется по касательной к данной
кривой в этой точке.
Замечание.
44. Обычно эта теорема доказывается так, что кривая
рассматривается в качестве ломаной ABCDR с бесконечным
числом звеньев. Тогда внешние углы CBF этой ломаной
будут бесконечно острыми и синус-верзусы этих углов
будут бесколечно малыми второго порядка. Отсюда делается
тот вывод, что в каждый элемент времени тело теряет из
скорости лишь бесконечно малую величину второго порядка,
так что вся потеря от А до R будет лишь бесконечно
малой первого порядка.
6 Ж. Даламоер
85 ОБЩИЕ ЗАКОНЫ ДВИЖЕНИЯ И PABHOBFXHfl ТЕЛ
Хотя мое доказательство, может быть, и длинновато,
но, мне кажется, оно все же яснее, поскольку в нем
скорость, потерянная от А до /?, действительно и точно
оказывается равной нулю, а не бесконечно малой величине.
Если мы хотим доказать свойства кривых со всей
строгостью, то по необходимости приходится мириться с
несколько более длинными доказательствами. Правда, метод
бесконечно малых сильно сокращает эти Доказательства, но
этот метод не так строг. Кроме того, он имеет еще и то
неудобство, что начинающие читатели, у которых понятие
бесконечно малых величин не дошло еще до сознания,
могут усвоить привычку смотреть на эти величины как на
какие-то реальности. Этой ошибки необходимо остерегаться
тем более, что в нее впадал кое-кто из великих людей, и
она послужила поводом для скверных книг, направленных
против достоверности математики *). Метод бесконечно
малых есть не что иное, как метод первых и последних
отношений [43],—другими словами, метод отношений
пределов конечных величин **). Кто понял смысл и принципы
этого метода, тот может с большой пользой применять его
для получения изящных решений.
О равновесии.
45. Если препятствия, встречаемые телом в своем
движении, обладают сопротивлением как раз настолько,
насколько необходимо оно для того, чтобы помешать
движению тела, то говорят, что имеет место равновесие между
телом и данными препятствиями.
*) Сочинение Маклорепа под заглавием «A Treatise on
fluxions» было опубликовано в связи с одной английской книгой
«The Analyst etc.», направленной против достоверности
математики, причем большая часть аргументов в этой книге направлена
против метода бесконечно малых [42].
**) См. «Encyclopedie», слова «Differential» и «Fluxion».
Метафизика дифференциального исчисления изложена в первой из
этих статей, — притом таким образом, что для каких-либо
возражений не остается места [44].
О РАВНОВЕСИИ
83
Т е о р е м а,
46. Если два тела, обладающих скоростями, обратно
пропорциональными их массам, имеют противоположные
направления, так что одно тело не может двигаться,
не сдвигая с места другое тело, то между этими
телами будет иметь место равновесие.
Первый случай.
Если оба тела равны между собой и скорости их также
равны, то совершенно очевидно, что оба тела будут
оставаться в равновесии. В самом деле, нет никакого
основания для того, чтобы одно тело предпочтительно перед
другим двигалось в своем прежнем направлении. Кроме того,
на основании п°36 ясно, что данные тела не могут
двигаться в противоположную сторону. Отсюда следует, и т. д.
Для того чтобы данное доказательство было свободно
от всяких возражений, я здесь предполагаю, что данные
два тела не только равны между собою, но что они и
совершенно подобны друг другу,.— например, это могут быть
два шара, два прямоугольных параллелепипеда и т. д. Для
случая неподобных друг другу тел эта теорема будет
доказана ниже (п°57).
Второй случай.
Если оставить одно из тел без изменений, у другого
же тела массу увеличить в два раза, а скорость уменьшить
в два раза, то также будет иметь место равновесие.
В самом деле, скорость меньшего тела можно
рассматривать как скорость, состоящую из двух скоростей,
каждая из которых равна скорости большего тела (п°30).
С" другой стороны, массу большего тела можно
рассматривать как массу, составленную из двух равных масс,
обладающих той же скоростью. Следовательно, вместо
заданных масс можно представить себе с каждой стороны
по две массы, равные и обладающие одинаковыми
скоростями. Но при таких условиях должно быть равновесие
(случай 1). Отсюда следует, и т. д.
§*
84 ОБЩИЕ ЗАКОНЫ ДВИЖЕНИЯ И РАВНОВЕСИЯ ТЕЛ
Данное предложение можно доказать еще и следующим
образом. Пусть т — масса меньшего тела, 2т— масса
большего тела, и — скорость большего тела и,
следовательно, 2а— скорость меньшего тела. Массу 2т большего
тела я рассматриваю как бы состоящей из двух масс, т и т\
каждая из которых равна массе меньшего тела. Далее,
вместо того, чтобы считать, что каждая из введенных нами
масс, т и т\ обладает скоростью я, я предполагаю, — что
приводит к тому же,—что передняя масса т', — та,
которая приходит в соприкосновение с меньшим
телом,—обладает скоростью 2и вперед и скоростью — и назад, в то
время как задняя масса т сохраняет свою скорость и.
Очевидно, что масса т\ обладающая скоростью — а,
уравновесится равной ей массой'/я, обладающей скоростью и.
Остается, следовательно, масса т', обладающая скоростью 2а,
и масса меньшего тела т> обладающая скоростью 2а. Эти
две массы должны уравновесить друг Apyta (случай 1).
Для того чтобы данное доказательство было свободно
от возражений, я в этом втором случае, как и в двух
следующих, делаю допущение, что тела являются
прямоугольными параллелепипедами с равновеликими и подобными
основаниями, но обладающими различной длиной, и что данные
параллелепипеды сталкиваются друг с другом своими
основаниями. Из такого допущения я исхожу и в следствиях
из данного предложения. Для тел же произвольной формы
настоящая теорема будет доказана ниже (п°57).
Третий случай.
Пусть массы обоих тел относятся друг к другу, как
некоторые два рациональных числа. Положим, М и т
будут эти массы, V и v — их скорости, |х—масса, служащая
общей мерой масс М и т> v — скорость, являющаяся
общей мерой скоростей V и v. Тогда мы будем иметь
т — \хр, М—у.Р,
v = vP, V = vp,
где Р и р — целые числа. Введя эти обозначения, можно,
аналогично предыдущему случаю, доказать, что каждую из
О РАВНОВЕСИИ
85
масс с ее скоростью можно заменить Р-р массами |х,
обладающими скоростью V, так что эти массы будут
уравновешиваться. Отсюда следует, и т. д.
Прежде чем перейти к четвертому случаю, заметим, что
если во всех трех приведенных случаях MV больше или
меньше mv, то равновесия быть не может. Предположим
на один момент, что тела Мит при этих условиях
уравновешивают друг друга. Представим себе, что тела М и м
находятся на некоторой плоскости, и предположим, что
плоскость движется с некоторой скоростью х, увлекая с собой
оба тела. При этом скорость х имеет направление или
одинаковое с К, или ей противоположное; величина же х
такова, что
MV ± Мх = то + /л*.
Легко видеть, что тела Мит, увлекаемые таким образом,
будут сталкиваться друг с другом, обладая в абсолютном
пространстве скоростями Vzbx и w + лг, обратно
пропорциональными массам. На основании уже доказанного тела
должны в этом абсолютном пространстве оставаться в покое.
Однако, в покое они оставаться не могут, поскольку, как
мы предположили, они уравновешивают друг друга, обладая
скоростями V и v. Действительно, скорости К и г> по
условию взаимно уничтожатся при столкновении, и тогда у них
останется лишь общая скорость х, ас этой скоростью
двигаться телам ничто не мешает.
»Отсюда следует, что если две какие-либо соизмеримые
массы уравновешивают друг друга, то с увеличением
или уменьшением скорости одной из этих масс равновесие
будет нарушено. Если же у одного из тел увеличиваются
или уменьшаются сразу и скорость, и масса, то
равновесие нарушится и подавно.
Четвертый случай.
Предположим, наконец, что массы Мит несоизмеримы
между собою, так что
т-=\ьр и Mz=\iP-\-z,
86 ОБЩИЕ ЗАКОНЫ ДВИЖЕНИЯ И РАВНОВЕСИЯ ТЕЛ
где Р и р — целые числа и z<^\x. Я утверждаю, что если
m-v = M-V,
то равновесие также будет иметь место.
Предположим, что равновесия не будет и что для
равновесия необходимо к массе М прибавить или отнять
какую-то добавочную массу t. В таком случае масса
[аР-|-2±^ обладающая скоростью V, будет
уравновешивать массу
m = \ip,
обладающую скоростью v. Величина t должна быть
непременно меньше jji.
В самом деле, если бы t было больше jjl, то мы имели бы
,!/>+*-{-/> цР+,1.
Для того чтобы масса \xP-\-\i могла уравновесить массу /тг,
обладающую скоростью vt она должна обладать сама ско-
ростью —7=5—г— . Но так как
цР + ц
то
<^рЛГ7 или <^
Следовательно, на основании замечания, сделанного в
конце предыдущего случая, масса \iP-\-z-\-t! будучи
mv
больше jiP-J-fx и обладая скоростью V, большей —р-тг~ >
не будет уравновешивать массу т, обладающую скоростью v.
Итак, t должно быть непременно меньше \х. Поскольку,
однако, jx может быть сделано сколь угодно малой
величиной, мы можем сделать заключение, что t должно
равняться нулю. Отсюда следует, и т. д.
Если величину / нужно отнимать, то, предполагая, что
t>p.,
мы будем иметь
О РАВНОВЕСИИ
87
Отсюда следует, и т. д. Что и требовалось доказать.
Произведение массы тела на его скорость называется
количеством движения.
Изложенное приводит нас к аксиоме, что если два тела
имеют равные и прямо противоположные количества
движения, то они уравновешивают друг друга.
Замечание.
47. В конце третьего случая предыдущего п°, когда
массы М и т были соизмеримы, было доказано не только
то, что имеет место равновесие при условии
MV=mv,
но и то, что равновесие невозможно, если MV не равно
mv. Приведенное там доказательство нетрудно применить
и к случаю несоизмеримых масс.
Отсюда следует, что данный за/сон равновесия является
единственным. Это значит, что равновесие возможно только
в том случае, если массы обратно пропорциональны
скоростям и если притом тела стремятся двигаться в
противоположных направлениях.
Следствие I.
48. Положим, три тела, Л, В и С (фиг. 17),
прикреплены к стержню или нити MN произвольной длины и пусть
М
-В-
В
Фиг. 17.
14
этим телам сообщаются по направлениям AM, ВМ и CN
скорости такой величины, что сумма количеств движения
тел А и В равняется количеству движения тела С. В таком
случае будет иметь место равновесие. В самом деле,
скорость тела С можно рассматривать как бы состоящей из
двух скоростей, в сумме равных его полной скорости. Тогда
88 ОБЩИЕ ЗАКОНЫ ДВИЖЕНИЯ И РАВНОВЕСИЯ ТЕЛ
в теле С можно представить себе два количества движения,
одно из которых будет равно и противоположно количеству
движения тела Л, а другое — равно и противоположно
количеству движения тела В. Отсюда следует, и т. д.
Следовательно, вообще, при каком угодно числе тел
равновесие будет иметь место в том случае, если
сумма количеств движения тел, тянущих в одну
сторону, равна сумме количеств движения тел, тянущих
в противоположную сторону [45].
Следствие II.
49. Пусть три тела, В, С и F (фиг. 18),
прикрепленные к нитям или стержням АВ, АС и Л/7, находятся в рав-
/новесии. Найдем отноше-
" ния количеств движения
данных тел.
Заметим прежде всего,
что действие тел В и
С на точку А будет такое
же, как будто бы тела В
. и С находятся в точке А.
Пусть, далее, отношение
отрезков АН и АР
равняется отношению
скоростей тел В и С.
Разложим каждую из
скоростей АН и АР на две
скорости: АО и AN, с
одной стороны, и AQ и
AL, с другой.
Направления этих последних
скоростей мы выбираем таким образом, чтобы скорости АО
и AQ имели взаимно противоположные направления, а
другие две скорости, AN и AL, были направлены по
продолжению FA.
Поскольку имеет место равновесие, можно сделать
заключение, что
B-AO = C-AQ
Фиг. 18.
О РАВНОВЕСИИ
89
и, кроме того, количество движения тела F должно
равняться
B-AN+C-AL.
Через какую-нибудь точку Е на продолжении линии FA
проведем ЕК, параллельно АС, и ED, параллельно АВ.
Тогда я утверждаю, что отрезки АЕ, AD и АК будут
относиться между собою как количества движения тел F, С
и В. Другими словами, должна соблюдаться пропорция [4б]:
\АК\ , (В- АН\
В самом деле,
(АК) , (АК\
АЕ:{ао\-(А0+а^:\ао) =
(АН-КМ\
I АО
PL "Т" АО ' \AP-OD
Ввиду равенства
AL-OD . AN-КМ АО
PL
OD = KM
последнее отношение будет равно
(AL i AN\ J АО
\PL >AG J'
\AP\ '
PL
Заменяя AG и PL пропорциональными им величинами С и
В, мы найдем, что это отношение равно
(AL-C + AN-B)
{АН-В\
:\АР-С)
Что и требовалось доказать.
90 ОБЩИЕ ЗАКОНЫ ДВИЖЕНИЯ И РАВНОВЕСИЯ ТЕЛ
Следствие III.
50. Все то, что было сказано в предыдущих
предложениях по поводу равновесия, останется справедливым и
в том случае, если вместо сообщаемых находящимся в
равновесии телам конечных скоростей мы будем брать
ускоряющие силы, пропорциональные этим конечным скоростям
или, наконец, следуя вышеприведенным определениям (п°22),
движущие силы, пропорциональные соответствующим
количествам движения. Равновесие будет иметь место и здесь:
для доказательства в данном случае нужно лишь
воспользоваться следствием II главы II, вместо следствия I той
же главы.
Замечание.
Об употреблении слова «сила» в статике.
61. Силы, или причины, движущие тела, могут
взаимодействовать друг с другом лишь через посредство тех
самых тел, которые они стремятся приводить в движение.
Отсюда следует, что взаимодействие сил есть не что иное,
как взаимодействие самих тел, обладающих скоростями,
которые сообщаются им этими силами. Таким образом,
под действием сил и под самим словом «сила», которым
обычно пользуются в статике, нужно понимать лишь
произведение тела на скорость или на его ускоряющую силу.
На основании этого определения и предыдущих п°п°
легко притти к заключению, что две равные и прямо
противоположные силы друг друга уравновешивают; что две
силы, действующие в одну сторону, производят то же
самое действие, как и сумма этих сил; что если три силы,
действующие на одну и ту же точку, находятся в
равновесии, то, построив на направлениях двух из этих сил
параллелограмм, мы получим, что диагональ этого
параллелограмма служит продолжением третьей силы, а отношения
данных трех сил равны отношениям диагонали и сторон,
и т. д. Мы получим ряд подобных теорем, обычно
доказываемых в статике. Только в статике это делается, может
быть, с меньшей строгостью, чем это достигнуто нами: со
словом «сила» там обычно не связывается того ясного
понятия, какое даем здесь мы.
О РАВНОВЕСИИ
91
Следствие IV.
52. Пусть две равные силы приложены к концам А и В
прямолинейного жесткого стержня АВ (фиг. 19). Пусть
эти силы действуют в направлении стержня в
противоположные стороны и потому находятся в равновесии.
Представим себе, кроме того, другой стержень АСВ произволь-
Фиг. 19.
ной формы. Очевидно, равновесие от этого не нарушится,
даже если этот второй стержень будет закреплен в какой-
нибудь точке С. Равновесие, очевидно, не нарушится и
тогда, когда силы будут приложены не в точках А и Ву
а в каких-нибудь других точках, лежащих на
продолжении стержня АВ в сторону А или в сторону В. Отсюда
следует, что если предположить, что стержня АВ нет
вовсе, а есть только стержень АСВ, то силы,
приложенные в точках А и В, будучи равными и противоположно
направленными, будут взаимно уравновешиваться.
Следствие V, содержащее правило рычага.
53. Положим, линии АН и BE суть направления двух
сил, находящихся в равновесии на рычаге АСВ, и пусть
отрезки АН и BE относятся друг к другу так же, как
эти силы. Я разлагаю силу АН на две силы, направления
которых АК и АО при своем продолжении проходят
соответственно через точку В и через точку С. Силу BE я
92 ОБЩИЕ ЗАКОНЫ ДВИЖЕНИЯ И РАВНОВЕСИЯ ТЕЛ
также разлагаю на две силы: направление ВР одной из них
должно проходить через точку Л, а направление BF
другой— через точку С. Проведя перпендикуляры CM, CV
и CL к линиям АН, BE и АВ, мы будем иметь
И
RP _ВЕ.СУ*)
D CL #
Но вследствие равновесия
АК=РВ
и поэтому
CM-AH=BE-CV.
Это значит, что силы АН и BE обратно пропорциональны
расстояниям направлений этих сил от неподвижной точки**).
*) Равенство
АН-СМ
АК--
CL
вытекает из того, что стороны АН и АК треугольника Af(H
относятся друг к другу как синусы 'углов АКН и АН К или как
синусы равных им углов CAL и САМ. Если С А принять за
радиус, то
AH\AK=CL\CM.
(Примечание Безу.)
**) Уравнение
или
CM-AH = BE-CV7
СМ.АН — ВЕ-СУ=0,
показывает, что если две силы, приложенные к рычагу, находятся
в равновесии, то должно выполняться следующее условие:
умножив каждую силу на расстояние ее от опоры, мы получим два
произведения, разность которых должна равняться нулю. В
общем случае, для того, чтобы имело место равновесие
произвольного числа сил, расположенных в одной плоскости, необходимо,
чтобы сумма произведений всех сил на расстояния их от опоры
равнялась нулю. При этом силы, действующие в разные стороны,
нужно брать с противоположными знаками. Хотя это предложе-
О РАВНОВЕСИИ
93
Следствие VL
54. Если точка С не закреплена (фиг. 19), то для того,
чтобы узнать, какую силу нужно приложить в точке С,
чтобы уравновесить силы AG и BF> необходимо восполь-
Фиг. 20.
зоваться вышеприведенным следствием II. Силу AG можно
рассматривать как бы составленной из сил АН и Ak,
ние и доказывается в любой книге по статике, тем не менее,
поскольку мы им будем пользоваться в дальнейшем и желая
избавить читателя от труда прибегать к другим источникам, мы дадим
здесь его доказательство. Мы ограничимся при этом случаем трех
сил, но легко видеть, что это доказательство можно
распространить и на случай большего числа сил.
Пусть у нас имеется рычаг APLE (фиг. 20) с опорой в точке
L и пусть в трех точках, Л, Р и Е, приложены силы,
выраженные отрезками AC, PQ и ЕЙ. Силу PQ разложим на две
силы, PV и PR: первая сила проходит через опору, а вторая —
через точку Е. Эту последнюю силу разложим снова на две силы,
EF и Ely одна из которых имеет направление линии АЕ, а другая
направлена к опоре. Силы АС и ЕН также можно разложить
каждую на две силы, из которых одна направлена к опоре, а
другая имеет направление линии АЕ.
Силы, направленные к опоре, будут уничтожены этой опорой.
Отсюда следует, что должны уничтожаться и силы ADf EF и ЕК
94 ОБЩИЕ ЗАКОНЫ ДВИЖЕНИЯ И РАВНОВЕСИЯ ТЕЛ
а силу BF— из сил BE и Вр. Но силы Ak и Вр равны
между собою и должны поэтому взаимно уничтожиться.
Отсюда следует, что силы AG и BF будут
уравновешиваться такой же силой, какую мы найдем, если вместо данных
сил АО и BF мы предположим силы АН и BE,
приложенные в точке С и имеющие прежние направления.
т. е. должно соблюдаться равенство
AD^KE — EF.
Но, во-первых,
PQ:PR (или EG) = LS:LM
и
EG:EF=LT:LS,
откуда
PQ:EF=LT:LM,
или
гг PQ-Ш
EF=-ur.
Во-вторых,
AC:AD = LT:LN
и
EH:EK=LT:LO,
откуда
Ап ЛС-LN D„ EH-LO
AD=-rr и Ек=—пг-'
Следовательно, уравнение
AD = KE—EF •
принимает вид
AC-LN^EH-LO PQ-LM
LT ~~ LT LT '
или
AC-LN + PQ-LM—EH-LO*=b
Что и требовалось доказать.
Следуя тому же методу, который применяется в следствиях
V и VI, можно было бы доказать, что силы, приложенные в
точках Д Р и Е> действуют на опору L точно таким Же образом,
как если бы они были приложены непосредственно в точке опоры.
{Примечание Безу)
О РАВНОВЕСИИ
35
Замечание относительно случая
прямолинейного рычага.
55. Предыдущее доказательство правила рычага
предполагает, что линии АС и СВ образуют между собой
какой-то угол. Может показаться поэтому, что это
доказательство не применимо к тому случаю, когда рычаг
прямолинейный, а направления сил параллельны. Однако
данное предположение справедливо, какой бы тупой угол АСВ
ни был. Поэтому ясно, что оно должно быть справедливо
и в том случае, когда угол АСВ еде- .м
лается равным 180 градусам
Впрочем, можно дать и более строгое
доказательство для указанного случая.
Пусть АР и AR< (фиг. 21) — плечи рычага,
а линии PD и RS суть направления двух I 'ТУ
А
Т
сил, которые, как я предполагаю, уравно- D
вешивают друг друга. Прежде всего
очевидно, что если плечи рычага равны между фиг* 21#
собою, то должны быть равны между собою
и силы Р и R. Положим теперь, что плечи АР и AR не равны
между собой. Проведем тогда произвольным образом
линию AS и представим себе, что эта линия является
жестким стержнем и что к концу S этого стержня приложены
две равные и противоположные силы S и £', направленные
по той же линии, что и сила R. Предположим, наконец,
что одна сила *S', тянущая вниз, уравновешивает силу Р
на рычаге PAS, Очевидно, что противоположная ей сила S
будет уравновешивать силу /?, а это значит, что силы 5
и R равны друг другу (п° 52). Отсюда следует
R = S Р'РЛ
(п° 53), откуда
AR
R:P = AP:AR.
Что и требовалось доказать.
Свойства прямолинейного рычага выводятся из свойств
рычага криволинейного не только мною одним. Ньютон
в своих «Principia», идя, правда, другим путем, поль-
9$ ОБЩИЕ ЗАКОНЫ ДВИЖЕНИЯ И РАВНОВЕСИЯ ТЕЛ
зуется тем же приемом, и можно думать, что этот
великий математик чувствовал те трудности, которые
возникают в том случае, если действовать иначе.
Свойства криволинейного рычага я вывожу из
равновесия двух равных и противоположных сил, а так как эти
две силы в случае прямолинейного рычага исчезают, то
для этого частного случая доказательство можно вывести
из общего случая лишь непрямым путем.
Свойства прямолинейного рычага с параллельными друг
другу силами можно вывести, приводя мысленно эти силы
к одной силе, направление которой проходит через точку
опоры. Этим способом воспользовался Вариньон в своей
«Механике» [47]. Этот метод, наряду с другими преимуще-.
ствами, характеризуется изяществом и единообразием. Но
не обладает ли он, наравне с другими методами, тем
недостатком, что это — непрямой метод и что он выводится
не из истинных принципов равновесия? Здесь приходится
представлять себе, что направления сил при своем
продолжении пересекаются в бесконечности, а затем путем
разложения приводить эти силы к одной силе и, наконец,
показывать,, что направление последней проходит через
точку опоры. Следует ли прибегать к такому способу для
того, чтобы доказывать равновесие двух равных сил,
имеющих параллельные направления и приложенных к равным
плечам рычага? Мне кажется, что понять равновесие в
таком случае столь же легко и просто, как и равновесие
двух прямо противоположных сил или равновесие одной
силы, сдерживаемой закрепленной точкой, и что у нас нет
никакого прямого средства для сведения одного случая
к другому. И если метод доказательства равновесия
рычага, даваемый Вариньоном, является непрямым в одном
случае, то он будет непрямым и в применении к -общему
случаю.
Следствие VII.
56. Если, оставив все условия предыдущего п°, мы
предположим вместо закрепленной точки Л некоторую силу,
уравновешивающую силы Р и /?, то очевидно, что
направление этой силы будет параллельно и противоположно на-
О РАВНОВЕСИИ
97
правлению данных сил, величина же уравновешивающей
силы будет равна сумме данных сил. В самом деле, если
мы принимаем, что некоторая сила уравновешивает две
силы, Р и £', то она должна быть равна P-f-S'*).
Отсюда следует, что она будет равна и P-\-R, так
как
S' = R**).
Замечание I.
57. Когда тело движется или стремится двигаться
в каком-либо направлении, это тело можно представить
себе как бы составленным из бесчисленного множества
малых прямоугольных параллелепипедов одинаковой
плотности, стороны которых параллельны направлению тела.
Эти параллелепипеды будут двигаться или стремиться дви<
гаться в продольном направлении с одинаковыми
скоростями. Тогда на основании правила рычага движение дан-
*) В самом деле, на основании следствия VI силы,
приложенные в точках Р и S', действуют на точку А так, как будто бы
они были приложены в самой точке Л. Но в таком случае точка А
находилась бы под действием одной силы, равной P-{-S\
(Примечание Безу.)
**) Из всей этой теории рычага нетрудно сделать тот вывод,
что для того, чтобы произвольное число сил, действующих на
рычаг по параллельным направлениям и находящихся в одной
плоскости, привести к одной силе, достаточно найти на рычаге
такую дочку, чтобы, прикладывая к ней силу, параллельную
заданным силам и равную их сумме (если они все тянут в одну
сторону), или равную разности между суммой сил, тянущих
в одну сторону, и суммой сил, тянущих в другую сторону, мы
получили бы такое соотношение, что сумма произведений всех
данных сил на их расстояния от любой точки рычага равна
произведению найденной полной силы на ее расстояние от той же
точки.
Вообще, если произвольное число сил, параллельных друг
другу и перпендикулярных некоторой плоскости, находятся в
равновесии, то сумма произведений всех этих сил на расстояния их
до произвольной плоскости, расположенной произвольным
образом, всегда равна нулю.
Оба эти предложения легко доказываются с помощью пра-
рила рычага и их можно найти во многих сочинениях.
(Примечание Безу.)
7 Ж. Даламбер
98 ОБЩИЕ ЗАКОНЫ ДВИЖЕНИЯ И РАВНОВЕСИЯ ТЕЛ
ного тела всегда можно свести к движению одного такого
параллелепипеда, имеющего скорость, равную сумме
скоростей всех параллелепипедов, т. е. равную скорости тела,
умноженной на число параллелепипедов. Отсюда легко
видеть, каким образом равновесие двух тел приводится
к равновесию двух параллелепипедов с равными
основаниями и, следовательно, каким образом теорему n°4G
можно распространить на тела любой формы.
Замечание II.
58. Пусть линии Ее и Zz (фиг. 22) взаимно
перпендикулярны, а линия СЕ' перпендикулярна к их плоскости. •
Фиг. 22.
Вообразим силу О, параллельную линии Се.
Расстояние этой силы до плоскости EZze пусть будет равно £,
а до плоскости Е'Се равно у. Вообразим и вторую
О РАВНОВЕСИЙ
99
силу F, параллельную Сг, и пусть ее расстояние до
плоскости EZze будет равно £, а расстояние до
плоскости E'Cz пусть будет 6. . Наконец, вообразим и
третью силу II, параллельную СЕ\ и ее расстояние до
плоскости Е'Се пусть будет равно |х, а расстояние до
плоскости E'Cz равно v. Действие этих трех сил можно
Фиг. 23.
свести к действию трех других сил. Одна сила будет
равна и параллельна силе G и будет действовать
на точку Z' плоскости E'Cz (фиг. 23), такую, что,
проведя Z'L параллельно СЕ' и Z'U параллельно CZ, мы
будем иметь
* G
Z'U —
G '
7*
100 ОБЩИЕ ЗАКОНЫ ДВИЖЕНИЯ И РАВНОВЕСИЯ ТЕЛ
Вторая сила будет направлена по LZ', параллельно СЕ'
в плоскости E'CZ и будет равна П. Наконец, третья сила
будет направлена параллельно Zz в той же плоскости E'CZ,
будет равна F и будет действовать на таком расстоянии
от Zz, которое нетрудно определить.
Все эти утверждения нетрудно было бы доказать,
опираясь на п°п° 20, 21 и 22 моих «Исследований о
предварении равноденствий» *)»
*) Положим, сила G (фиг. 22) пересекает плоскость E'Cz
в точке Q, а сила F пересекает плоскость Е'Се в точке G.
Проведем QP' параллельно СЕ', QD параллельно Cz, GE'
параллельно Се, GR' параллельно СЕ\ Проведем, наконец, CQ,
которая в точке F пересечется с линией E'F, параллельной Cz.
Вместо силы G, действующей на точку Q, можно взять две
параллельные ей силы, действующие одна в С, а другая в F. Сумма
этих сил должна равняться G и отношение их должно быть равно
отношению FQ и CQ, или, что сводится к тому же самому,
каждая из них должна так относиться к силе G, как FQ, или CQ,
относится к CF,— другими словами, как DE'', или CD, относится
к СЕ'. Таким образом, сила, действующая в С, будет равна
G у , а сила, действующая в F, будет равна -у . Но так как
вторая из этих сил пересекается в некоторой точке К с силой F,
направленной по GIC, то обе эти силы, складываясь вместе, дадут
одну силу, направленную по 1{п. Продолжение этой силы
пересечет в точке N плоскость ErCZ, и можно считать, что она
действует на точку N. Проведя N0' параллельно FK> легко видеть,
что на точку ЛГ действует такая сила, как будто бы к ней были
приложены две силы, направленные по NF и по N0',— а это
суть силы, которые только что действовали по направлениям
GK и FK. Итак, наши две силы приведены к трем: одна из них
G»
равна F и действует по направлению NF, другая равна G у
и действует по Се и, наконец, третья равна -у* и действует по
N0' параллельно Се. Но две последние силы, как мы видели,
могут быть приведены к одной силе, равной их сумме, т. е.
равной (7, и проходящей через В —точку пересечения QD и CN.
В самом деле, CB:CN=CQ:QF=y-:G у, а последнее
отношение равно обратному отношению сил, приложенных в С
и N. Далее, так как две силы, направленные по FK. и GK,
создают вместе силу, направленную по NKn, то очевидно, что если
первую из этих сил выразить отрезком FI(, то вторая сила бу-
О РАВНОВЕСИИ
101
Указанный прием позволяет находить закон равновесия
какого угодно числа сил, действующих в любых
плоскостях и по любым направлениям. Каждую силу нужно раз-
дет выражаться отрезком FN, так что F; у- = FN: FK, или GE'%
или 0. Отсюда
С другой стороны, из треугольников CDQ и CE'F мы имеем
*1
5
E'F=lS
откуда
Следовательно,
**=£-*■
*>-?-*
Таким образом, две данные силы, G к F, приведены к двум
другим силам, также G и F: одна действует в точке В параллельно
FQ
Се на расстоянии рг — х от С£', а другая действует по
направлению NF в плоскости E'Cz на расстоянии С£\
Пусть теперь в точке V (фиг. 23) сила П пересекается с
плоскостью eCz. Проведем через точку В, где теперь
приложена сила О, линию BL параллельно СЕ'. Тогда BL будет
равно 5.
Проведем /,!/. Силу, приложенную в точке В, можно
разложить на две силы: одну действующую по В Г, являющейся
продолжением BD, и другую — по ВК параллельно LV. Последняя
сила при своем продолжении пересечется с направлением VO
силы П. Проведем, далее, VR параллельно Се. Из подобия
треугольников LRV и SB/C мы получим; "что S/C, т. е. сила,
действующая по ВТ, равна ' , а сила, действующая по ВК, равна
■ * . Вторая из этих сил совместно с силой П, направленной
RV
по VO, создает одну силу. Продолженное направление OZ' этой
силы пересекается с BL в некоторой точке Z', и поэтому ее
можно мыслить приложенной к этой точке Z'. Если теперь силу,
направленную по ВК> выразить отрезком ВО, то сила, направ-
102 ОБЩИЕ ЗАКОНЫ ДВИЖЕНИЯ II РАВНОВЕСИЯ ТЦЛ
ложить,— что всегда возможно,— на три силы,
параллельные линиям Се, Cz и СЕ'. Обозначим эти силы через О,
F и II. Для равновесия необходимо:
ленная по VO, будет выражаться отрезком Z'B, так что
BZ^.BO^H:—-.
Отсюда (так как ВО = LV) мы имеем
II. Я V
BZ''>
G '
Но вместо силы, направленной по - Z'O, можно вообразить
в точке Z' силы ВО и Z'B, направленные параллельно ВК и VO,
так что сила Z'B, или II, будет действовать по направлению ZfBt
а сила ВО —по направлению Z'Q параллельно LV. Последнюю
силу можно разложить на две силы: одну, направленную по Z'M
параллельно Се, и другую, направленную по Z'N параллельно Cz,
Из рассмотрения подобных треугольников Z'NQ и LRV мы
найдем, что сила, направленная по Z'M, равна G, а сила, направлеи-
G-LR
пая по Z'N, равна v ■ .
Таким образом, данные три силы приведены нами к пяти
силам: первая равна G и действует в точке Z' перпендикулярно
к плоскости E'CZ на расстоянии
Z'L^BL-BZ'^b-1^
G
п-7 0-LR
от CZ; вторая равна -тку-» и ее можно считать приложенной
в точке Z' и действующей по направлению Z'L'\ третья равна
■ fl.. ■ и ее можно считать приложенной в точке D и действую-
HV
щей по направлению DB\ четвертая равна F и действует по
направлению E'F; наконец, пятая равна П и действует по
направлению Z'B, или LB, на расстоянии
Но силы, приложенные в L', О. и Е', будучи параллельными
О РАВНОВЕСИИ
103
1) если закрепленной точки нет, то должны
соблюдался следующие равенства:
О = 0,*)
О,
\"11 = 0
\>
и, кроме того,
^—11)1 = 0,
Jos—1Ь = 0,
JF6_Ox = 0;
2) если имеется закрепленная точка,— положим, точка С
(это всегда можно предположить), — то для равновесия
необходимо лишь, чтобы соблюдались три последних
равенства, каждое в отдельности.
Для того чтобы доказать последние три уравнения,—
а они только и нуждаются в доказательстве,— заметим,
что, поскольку силы G перпендикулярны к плоскости E'Zz,
тогда как остальные силы лежат в этой самой плоскости,
силы G должны находиться в равновесии сами по .себе,
между собою, приводятся к одной силе, равной
G-LR G-LR . г
RV RV +7<—7*
Ее расстояние СХ до С должно быть таково, что
£~--CL' ——I^.CD + F.CE' =:F*CX.
Отсюда мы получаем
ог-с-^+З -г)
(Примечание Везу),
*) Следуя оригиналу, мы сохранили здесь знак J* вмесю £—
символа, «веденного позже. (Примечание переводчика-)
104 ОБЩИЕ ЗАКОНЫ ДВИЖЕНИЯ И РАВНОВЕСИЯ ТЕЛ
независимо от всех других сил. Отсюда следует, что не
только сумма этих сил должна равняться нулю, но и сумма
их моментов относительно линий CL и CU также должна
равняться нулю. Таким образом,
И?-х)-.
Но отсюда
Jg£ — 1Iv = 0
и
JF0 — Ог = 0.
Поступая точно таким образом с силой Т7,
перпендикулярной к плоскости Е'Се, мы получим
J л;—iijjl=о
и
Наконец, для силы П, перпендикулярной к плоскости Zez,
мы будем иметь
Jllv —GS = 0
и
J/3? —Нц = 0.
Мы получили шесть уравнений, которые приводятся к трем,
приведенным выше.
Следует заметить, что уравнения
Jo=o,
Jo («-■•)-о
О РАВНОВЕСИИ
105
каждое в отдельности необходимы для равновесия. Пусть
мы имеем, например, три силы: Л, В и G (фиг. 24),
перпендикулярные к плоскости LCL*, и пусть эти силы
находятся в равновесии. Для равновесия необходимо:
1) чтобы
л + £+с = о,
2) чтобы точки Л, В и G лежали на одной прямой,
что дает два уравнения
A-AD-\-B-BE-\-G-QF=0
и
A.AK+B.BM-\-G-GO = 0 .
Если точки Л, В и G не лежат на одной прямой, если,
н-пример, точка В будет находиться в Q на продолже-
, О N м к
С
Фиг. 24.
нин BE, то второе уравнение будет справедливо, первое
же нет, и равновесия в таком случае не будет.
Замечание III.
59, Я не буду здесь, в первой части, распространяться
дальше по поводу законов равновесия. Я буду еще иметь
случай говорить о них во второй части настоящего
сочинения. Общий закон равновесия состоит в том, что силы
обратно пропорциональны скоростям, измеряемым по
направлениям этих сил. Иа этот общий закон, о котором
106 ОБЩИЕ ЗАКОНЫ ДВИЖЕНИЯ И РАВНОВЕСИЯ ТЕЛ
весьма кратко упоминает Ньютон в начале своих «Prin-
cipia» [48], опирается доказательство сохранения живых
сил, как это мы увидим во второй части настоящего
сочинения.
Что касается подробностей, относящихся к различным
машинам, о которых обычно упоминается в счатнке, —
таким, как блок, ворот и т. д.,— то я, не имея но этому
поводу сказать чего-либо нового, ограничиваюсь тем, что
отсылаю своих читателей к тем книгам, в которых эти
вопросы разбираются. В частности, я сошлюсь на
вышедшую несколько лет назад «Механику» члена королевской
академии наук Камюса и на сочинение Трабо,
озаглавленное «Принципы, касающиеся равновесия и движения» [49].
В этих книгах данный материал излагается с достаточной
строгостью и ясностью.
^^^
щщ?
<^^®^^0"
ЧАСТЬ II.
ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ ДВИЖЕНИЯ
НЕСКОЛЬКИХ ТЕЛ, ПРОИЗВОЛЬНЫМ ОБРАЗОМ
ДЕЙСТВУЮЩИХ ДРУГ НА ДРУГА, А ТАКЖЕ
НЕКОТОРЫЕ ПРИМЕНЕНИЯ ЭТОГО ПРИНЦИПА*).
ГЛАВА L
Изложение принципа»
Нам известны лишь три различных способа, которыми
те )а действуют друг на друга: эю или непосредственный
толчок/ как при обычном ударе; или действие при
посредстве некоторого промежуточного тела, к которому
данные тела прикреплены; или, наконец, действие в силу
взаимного притяжения, как Солнце и планеты в системе
*) Настоящий принцип, как и большинство последующих
задач, содержался в моем мемуаре, зачитанном в академии в конце
1742 г., хотя первое издание настоящего сочинения вышло в свет
лишь в 1743 г. В тот самый день, когда я начал читать этот
мемуар, Клеро представил свой мемуар, озаглавленный
«Некоторые принципы, облегчающие решение большого числа задач
динамики» [50]. Этот мемуар, напечатанный в томе за 1742 г., был
зачитай после моего мемуара, с которым он к тому же не имеет
ничего общего.
108 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ ДВИЖЕНИЯ
Ньютона. В виду того, что действия последнего рода
исследовались достаточно, я ограничусь здесь рассмотрением
движения тел, во-первых, соударяющихся произвольным
образом, и во-вторых, тех тел, которые тянут друг друга
при помощи нитей или жестких стержней [б1]. Я тем более
охотно останавливаюсь на этом вопросе, что до сих пор
(1742) только небольшое число задач этого рода
разрешено наиболее крупными математиками. И я надеюсь, что
с помощью излагаемого мною общего метода каждый,
владеющий анализом и принципами механики, окажется в
состоянии решать самые трудные задачи указанного рода.
Определение.
Скорость тела с учетом ее направления я буду в
дальнейшем называть движением этого тела. Под
количеством движения я буду понимать, как обычно,
произведение массы на скорость [б2].
Общая задача.
60. Дана система тел, расположенных друг отно«
сительно друга произвольным образом. Каждому из этих
тел передается некоторое движение, которое оно, од-
нако, не может воспринять вследствие действия прочих
тел. Найти движение каждого из данных тел.
Решение.
Пусть система состоит из тел Л, Б, С и т. д., и
предположим, что им передаются движения а, Ь, с и т. д.,
которые, вследствие взаимного действия тел, последние
изменяют в а, б, с и т. д. Ясно, что передаваемое телу А
движение а можно рассматривать как составленное из
воспринятого им движения а и из некоторого другого
движения а. Точно так же и движения Ь, с и т. д. можно
рассматривать как составленные из движений b и р, с и я
и т. д. Следовательно, движение действующих друг на
ИЗЛОЖЕНИЕ ПРИНЦИПА
109
друга тел Л, Б, С и т. д. будет точно такое же, как
если бы вместо импульсов я, Ъ, си т. д. им
передавались сразу по два импульса: а и a, b и [$, с и % и т. д.
Но, по предположению, тела Л, Ву С и т> д. сами по
себе восприняли движения а, Ь, с и т. д. Отсюда следует,
что движения сц f, х и т. д. должны быть таковы, чтобы
нисколько не нарушались движения а, Ь, с и т. д ;
другими словами, если бы тела получили только эти
движения a, ji, я и т. д., 'то эти движения взаимно
уничтожились бы, и тела оставались бы в покое.
Отсюда вытекает следующее правило для нахождения
движения нескольких тел, действующих друг на друга.
Нужно движения а, Ь, с и т. д., передаваемые этим
телам, разложить каждое на два движения: а и а,
b и р, с и х и т. д., причем эти последние движения
должны быть таковы, что если телам будут переданы
лишь движения a, Ь, с и т. д., то тела могут
сохранить эти движения, не мешая друг другу; если же
телам будут переданы лишь движения а, р, я я пг. д.,
то тела будут оставаться в покое.
Ясно, что a, Ь, с и т. д. и будут теми движениями,
которые будут восприняты телами вследствие их
взаимного действия друг на друга. Что и требовалось найти [53].
Следствие.
61. Если какое-нибудь из передаваемых движений равно
нулю, то, очевидно, оно разлагается на такие два
движения, которые равны и противоположны друг другу.
Например, если
а = 0,
то движение а будет равно по величине и
противоположно по направлению движению а. В самом деле, а есть
диагональ параллелограмма, сторонами которого служат а и а.
Но если диагональ равна нулю, то стороны равны друг
другу и друг другу прямо противоположны. Отсюда
следует, и т. д.
ПО ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ ДВИЖЕНИЯ
ГЛАВА II.
Свойства общего центра тяжести нескольких тел,
выведенные на основании предыдущего принципа.
Определение I.
Центром тяжести двух тел я в дальнейшем буду
называть такую точку, которая лежи г па прямой,
соединяющей эти тела, и которая удалена от них на расстояния,
обратно пропорциональные массам тел. И вообще под
центром тяжести нескольких тел я буду всегда понимать
то, что обычно обозначается этими словами в механике,
а именно: такую точку, что если через нее провести
произвольную плоскость, то сумма произведений масс,
расположенных по одну сторону от этой плоскости, на
соответствующие расстояния этих масс до плоскости будет
равна сумме произведений масс, расположенных по другую
сторону, на расстояния их до той же плоскости.
Примечание.
62. В том случае, когда веса тел пропорциональны их
массам, центр тяжести, как мы его только что определили,
будет также той точкой, за которую должна быть
подвешена система для того, чтобы она оставалась в равновесии,—
если бы все тела были соединены друг с другом жесткими
стержнями. Этого нельзя было бы сказать в том случае,
если бы движущие силы или веса тел не были
пропорциональны массам.
То, что мы здесь называем центром тяжести, лучше
было бы поэтому назвать центром масс *). Мы, однако, будем
пользоваться термином центр тяжести для того, чтобы
не расходиться с принятыми обычаями в отношении
терминологии.
*) Термин центр масс употребляет Даниил Бернулли. См. его
«Трактат о приливах и отливах^), глава III, § III [54].
СВОЙСТВА ОБЩЕГО ЦЕНТРА ТЯЖЕСТИ НЕСКОЛЬКИХ ТЕЛ 111
Определение П.
Если несколько сил действуют совместно, то силу,
равную и прямо противоположную той, которая может их
уравновесить, я буду называть равнодействующей
совместного действия данных сил или, короче,
равнодействующей этих сил.
Так, например, если AM (фиг. 21) есть направление
силы, уравновешивающей силы Р и R на рычаге PAR, то
AN будет направлением равнодействующей сил Р и /?,
и эта равнодействующая сила будет равна силе,
направленной по AM,
Следствие.
63. Если каким-либо образом уравновешиваются
несколько сил, то в том случае, если нет закрепленной
точки, равнодействующая должна быть равна нулю. Если
же имеется закрепленная точка, то равнодействующая
проходит через эту точку.
В первом случае, поскольку все силы уравновешивают
друг друга сами собой, постольку должна равняться нулю
та сила, которая способна уравновесить все эти силы.
Поэтому (согласно последнему определению)
равнодействующая данных сил также должна равняться нулю.
Eto втором случае закрепленная точка, очевидно,
заменяет собой ту силу, . которая сдерживает действие всех
других данных сил. Поэтому, если устранить закрепленную
точку и затем отыскивать силу, способную уравновесить
все данные силы, то направление этой силы непременно
будет проходить через эту точку. Отсюда следует, чго
направление равнодействующей также будет проходить
через эту самую точку.
Под «закрепленной точкой» здесь и в нижеследующих
леммах я буду понимать не только математическую
точку (как, например, опора рычага, точка подвеса
стержня или нити), но и вообще любое непреодолимое
препятствие, способное своим сопротивлением
уничтожить действие сил и установить их взаимное равновесие.
112 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ ДВИЖЕНИЯ
Лемма I.
64, Если произвольное число тел движется
равномерно по параллельным направлениям в одной плоскости
или в различных плоскостях, то направление общего
центра тяжести этих тел будет параллельно
направлениям этих самых тел, а скорость центра тяжести
будет равна сумме количеств движения всех тел,
деленной на сумму масс.
Это предложение доказывается во многих сочинениях
и чрезвычайно просто выводится из правила рычага.
Лемма II.
65. Пусть в одной плоскости находятся три тела А,
а и а (фиг. 25) или вообще произвольное число тел.
Пусть точка G
будет общим центром
тяжести этих тел.
Пусть, наконец, GM
будет тем отрезком,
с который проходится
/ этим центром тя-
J жести за то время, за
В какое данные тела
проходят равномерно
какие-то отрезки АС,
ас и ах. В таком
случае я утверждаю, что
если скорости АС, ас и ах разложить каждую на две
скорости, АВ и AD, аЪ и ad, а$ и аЬ, так, чтобы
линии АВ, ab и ар были между собой параллельны, а линии
ВС, be и $х были также параллельны между собой, и если
найти отрезок GN, проходимый центром тяжести G
в том случае, когда тела А, а и а имеют скорости
и направления АВ, аЬ и ар, а также отрезок GO,
проходимый им в том случае, когда тела А, а и а имеют:
скорости и направления AD, ad и аЬ, то диагональ
параллелограмма, построенного на отрезках GN и GO,
В те
и,
С 6 ^—д
d а
Фиг. 25.
СВОЙСТВА ОБЩЕГО ЦЕНТРА ТЯЖЕСТИ НЕСКОЛЬКИХ ТЕЛ 113
даст нам тот отрезок GM, который проходит центр,
когда тела Л, а а а имеют скорости и направления АС,
ас и ах.
В самом деле, предположим, что когда тела А, а и а
достигли В, Ь и [$, а центр G поэтому (согласно условию)
достиг N, им сообщаются по направлениям ВС, be и ря
скорости, равные и параллельные скоростям, направленным
по AD, ad и ab. Ясно, что данные тела достигнут точек
С, сих линий ЛС, яс и ах. Но, по предположению,
когда тела А, а и а будут в С, £ и ж, центр G будет
в Ж. Поэтому, в то время как телами Л, а и а
проходятся отрезки ВС, be и ря, центр тяжести будет проходить
отрезок MW. Этот отрезок NM (согласно лемме I) будет
параллелен линиям ВС, be и $х и будет равен
А-ВС + а-Ъс-\-а.$*
Л + я + а
Отрезок же GO, проходимый центром тяжести О в то
время, когда тела Л, а и а описывают линии /ID, #*/ и
а5, параллельные и равные линиям ВС, be и (&, этот
отрезок GO будет параллелен линиям AD, ad и а§ и равен
i4-i4Z)-f-g,g^-ha ее А-ВС-\-а-Ъс-\-а-$ж .,м
Л-|-я + а А-\-а-\-<х
Отсюда следует, чго отрезок GO равен и параллелен NM.
Следовательно, MG есть диагональ параллелограмма,
построенного на сторонах NG и GO. Что и требовалось
доказать.
Примечание.
66. Легко видеть, что настоящее доказательство можно
распространить и на случай любого числа тел, так что
предложение является общим.
Лемма III.
67. Пусть GM (фиг. 25 и 26) есть отрезок,
проходимый центром тяжести G тел А, а и а., в то время
как эти тела равномерно проходят какие-то отрезки
8 Ж. Даламбер
114 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ ДВИЖЕНИЯ
АС, ас и ак. Перенесем эти тела на другие места F,
f и ср в этой же плоскости, причем они могут быть
теперь расположены одно по отношению к другому
произвольным образом. Пусть при новом расположении тел
их центр тяжести
будет в точке у. Тогда я
утверждаю, что ес.ли
тела будут описывать
отрезки FH, fh и ср7],
и соответственно равные
н и параллельные отрезкам
АС, ас и ах, то отре-
у ш \/ I зок yjx, описанный цент-.
tel Ip р0М тяжеста> будет ра-
J1 вен и параллелен
отрезку GM.
В самом деле, пусть
-^ FL, fl и срХ
соответственно равны и параллель-
фиг- 2б- ны АВ, аЬ и af. Пусть
FP, fp и сртг
соответственно равны и параллельны AD, ad и ai. Пусть, далее,
yv будет путь центра у за то время, когда тела описывают
отрезки FL, fl и <рХ, и, наконец, усо—путь центра тяжести
за то время, когда тела описывают FP, fp и ертт. Ясно, что
отрезок yv будет равен и параллелен ON, а усо равен и
параллелен GO. Отсюда следует, что отрезок у|х будет равен
и параллелен GM. Эти же два отрезка (по предыдущей
лемме) суть как раз те отрезки, которые проходятся
центрами тяжести О и у, когда тела А, а и а и тела F,
/ и ср проходят отрезки АС, ас и ох и отрезки FH, fh
и (j>7). Отсюда следует, и т. д. Что и требовалось
доказать.
Лемма IV.
68. Исходим из тех же предположений, как и в
лемме II, с той только разницей, что отрезки АВ, ab
и а§ и отрезки AD, ad и аЬ (фиг. 27) не параллельны
друг другу. Если GM есть путь центра тяжести за то
СВОЙСТВА ОБЩЕГО ЦЕНТРА ТЯЖЕСТИ НЕСКОЛЬКИХ ТЕЛ 115
время, когда тела А, а а а равномерно проходят
отрезка АС, ас а ах; GN — путь того же центра за то
время, когда тела описывают линии АВ, аЪ и а$; и,
наконец, GO есть путь центра тяжести за то время,
когда тела А, а и а описывают отрезки AD, ad и аЪ,
к
<L N. J* В. О
о
Фиг. 27.
то я утверждаю, что GM будет диагональю
параллелограмма, построенного на сторонах GN и GO.
В самом деле, как и в лемме II, можно доказать, что
NM есть путь центра за то время, когда тела Л, а и а
описывают линии ВС, be и [5*. Но так как AD, ad и аЬ
соответственно равны и параллельны ВС, be и [$#, то
отсюда следует (согласно лемме III), что линия GO равна
и параллельна NM. Отсюда следует, и т. д.
Следствие I.
69. Если каждое из движений АС, ас и ах разложить
на три или вообще на любое число каких-либо движений,
то путь GM центра тяжести будет всегда последней
диагональю параллелограммов, сторонами которых служат отрезки,
которые центр тяжести прошел бы, если бы тела А, а
и а имели отдельно одно за другим каждое из
составляющих движений» Это с ясностью вытекает из предыдущей
леммы.
8*
116 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ ДВИЖЕНИЯ
Следствие II.
70. То же предложение будет справедливым и в том
случае, если число составляющих движений не будет у всех
тел одинаковым,—например, если движение одного тела
будет разложено на три, движение другого — на два
движения и т. д. Действительно, последняя лемма вовсе не
перестает быть справедливой, если предположить, напри*
мер, AD равным нулю, т. е. если движение АС не
разлагается вовсе.
Лемма V»
71. Пусть некоторое произвольное число тел А, В,
С и т. д. связано каким-либо образом^ одно с другим,
причем никакой закрепленной точки в системе не имеется.
Пусть этим телам сообщаются такие движения М, N,
Р и т. д., что в результате тела остаются в равно-
весии. В таком случае я утверждаю, что если бы
данные тела могли свободно получить движения М, N, Р
и т. д., то центр тяжести данных тел оставался бы
в покое.
Разложим каждое из движений М, Л/", Р и т. д. на
два движения, т и jx, п и v, р и тг и т. д., параллельных
двум заданным как угодно расположенным линиям, которые
я назову К и Q. Для того чтобы найти путь центра
тяжести в результате движений М, N, Р и т. д., нужно
найти путь этого самого центра в результате движений /ю>
пу р и т. д., — это будет (согласно лемме I) отрезок,
параллельный К и равный
А-т-\-В-п-\-С-р-\-к т. д.
Л + Я + С + и т. д.
и путь его же в результате движений ji, v, тг и т. д.,—
это будет отрезок, параллельный Q и равный
Л + 5-f С + и т. д.
Диагональ параллелограмма, построенного на этих двух
отрезках, и будет (согласно лемме II) представлять собой
СВОЙСТВА ОБЩЕГО ЦЕНТРА ТЯЖЕСТИ НЕСКОЛЬКИХ ТЕЛ 117
путь центра тяжести. Следовательно, для того чтобы
показать, что путь центра тяжести равен нулю, необходимо
доказать, что каждый из двух указанных отрезков равен
нулю, или, что то же самое, нужно доказать, что
А-т-{-В-п-\-С-р-\-и т. д.=:0
и
А-\1-\-В-у-{-С-у;-\-и т. д. = 0.
Но так как (по условию) тела Л, В, С и т. д.,
получив движения Af, N> Р и т. д., находятся в равновесии
и так как в системе нет закрепленной точки, то
равнодействующая сил А-М, B*N, С'Р и т. д. будет равна
нулю (согласно п° 63). Силы же А-М, B*N, С*Р и т. д.
у нас разложены на силы А*т, и Л-jj., В*п и £-v, С*р
и С«тг и т. д. Следовательно, равнодействующая этих сил
представляет собой ту силу, которая получается из
равнодействующей сил А*т, В*пу С-р и т. д., с одной
стороны, и из равнодействующей сил Л«ц, Z?»v, С*п и т. д.,
с другой. Но эти две равнодействующие силы параллельны
двум различным линиям К и Q. Поэтому для того, чтобы
сила, получающаяся из сложения этих сил, равнялась нулю,
нужно, чтобы каждая из этих сил в отдельности равнялась
нулю. Но одна из этих сил равна
А*т-\-В-п-\- C-/?-j- и т. д.,
а другая равна
Л-ji-j-£-v-f-C-TT-|- и. т. д.
Следовательно, каждая из этих величин равняется нулю.
Что и требовалось доказать.
Лемма VI.
72. Исходим из тех же предположений, как и в
предыдущей лемме, за исключением того, что движения М,
N, Р и т. д. теперь произвольны, т. е. теперь тела
А, В, С и т. д., получив эти движения, могут и не
находиться в равновесии. Кроме того, система может иметь
закрепленную точку. В таком случае я утверждаю,
118 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ ДВИЖЕНИЯ
что если, отвлекаясь от взаимного действия тел друг
на друга, предположить, что тела А, В, Си т. д.
фактически восприняли движения М, N, Р и т. д.,
то путь центра тяжести будет параллелен
направлению равнодействующей сил А*М, B'N, С*Р и т. д.
В самом деле, для того чтобы найти направление этой
равнодействующей, нужно (при тех же построениях, как
и при доказательстве предыдущей леммы) провести
диагональ параллелограмма, стороны которого параллельны К и
Q, а по величине относятся друг к другу, как
А*т-\-В<п-\-С-р-{- и т. д.
относится к
А-\1-\-В'У-\-С>п-\- и т. д.
Для того же, чтобы найти путь центра тяжести в
результате движений Ж, iV, Р и т. д., нужно (согласно лемме II)
провести диагональ параллелограмма, стороны которого
параллельны К и Q, а по величине относятся друг к другу,
как
А-т-\-В*п-\-С*р-\- и т. л
А-\-В + С-\- и т. д.
относится к
Л*{1,-[-В.у-4-С-тс4- и т. д.
А + В + С+ и т. д. #
Следовательно, стороны одного из этих параллелограммов
параллельны сторонам другого параллелограмма, а
отношение сторон одного параллелограмма равно отношению
сторон другого параллелограмма. Отсюда следует, и т. д.
Что и требовалось доказать.
Следствие.
73. Если телам Л, В> С и т. д. сообщить движения
— М> —TV, —Р и т. д., то путь центра тяжести будет
параллелен равнодействующей, но только направление его
будет противоположным.
СВОЙСТВА ОБЩЕГО ЦЕНТРА ТЯЖЕСТИ НБСКОЛЬКИХ ТЕЛ 119
Примечание I.
74. Все только что доказанные нами леммы будут
справедливы и в том случае, когда тела, по предположению,
находятся в разных плоскостях. Действительно, лемма I
справедлива в этом случае так же, как и в других. Что
касается леммы II, то ее доказательство, строго говоря,
не предполагает того, что тела Л, а и а расположены в
одной плоскости; оно предполагает лишь то, что каждое
из движений ЛС, ас и ох может быть разложено на
два движения, параллельных двум заданным линиям.
Отсюда вытекает, что лемма III будет также справедлива
в том случае, если тела находятся в разных плоскостях,
по крайней мере, при том условии, что движения,
сообщаемые каждому телу, могут быть разложены на два
движения, параллельных двум заданным линиям. Но когда
тела расположены в различных плоскостях, каждое
движение, сообщаемое этим телам, может быть разложено на
два движения, из которых одно будет параллельно
некоторой заданной линии, а другое в свою очередь может
быть разложено на два других движения, параллельных
двум другим заданным линиям. Отсюда вытекает, что
лемма III справедлива во всех случаях. Точно так же
справедливы во всех случаях и леммы IV, V и VI, поскольку
они опираются только на первые три леммы и поскольку
они» вовсе не предполагают, что тела находятся в одной
плоскости.
Заметим между прочим, что в приведенных леммах мы
предполагали справедливым предложение, доказанное
Ньютоном, а именно, что центр тяжести нескольких тел,
движущихся равномерно и прямолинейно и не действующих
друг на друга, движется также равномерно и прямолинейно.
Однако нетрудно видеть, что это предложение было бы
также чрезвычайно легко доказать с помощью разложения
данных движений на составляющие движения,
параллельные заданным линиям. Таким образом, наш метод имеет
то преимущество, что он дает возможность доказать, что
центр тяжести нескольких тел движется равномерно и
120 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ ДВИЖЕНИЯ
прямолинейно как в том случае, когда тела действуют
друг на друга, так и- в том случае, когда они друг на
друга не действуют.
Примечание II.
75. Добавим к этому, что если несколько тел,
рассматриваемых как точки, движутся прямолинейно в среде,
сопротивляющейся пропорционально скорости, то и центр
тяжести этих тел будет двигаться прямолинейно с
замедлением движения, пропорциональным скорости. В самом
деле, если сопротивление пропорционально скорости, то
пути, описываемые телами за любой элемент времени,
уменьшаются в отношении этих самых путей. Следовательно,
путь центра тяжести остается и в данном случае
прямолинейным, расстояние же, которое проходится этим
центром, теперь уменьшается за каждый элемент времени на
величину, пропорциональную этому самому расстоянию.
Отсюда следует, и т. д.
Теорема I.
76. Состояние движения или покоя центра тяжести
нескольких тел нисколько не меняется от взаимного
действия этих тел друг на друга, если только система
совершенно свободна, т. е. если она не вынуждена
двигаться вокруг какой-либо неподвижной точки.
Действительно, так как движения а, &, с и т. д.
слагаются из движений а и a, b и {}, с и я и т. д. (и0 60),
то движения a, Ь, с и т. д. можно рассматривать как
составленные из движений а и —а, Ь и —[}, с \\ —х
и т. д. Отсюда следует, что когда тела обладают
движениями а, Ь, с и т. д., путь центра тяжести будет таков,
как будто тела сначала имели движения а, Ъ, с и т. д.,
а затем движения —а, — (5, —к и т. д. (согласно лемме IV).
Но так как, по предположению, в системе нет неподвижной
точки и так как в том случае, если бы телам были
переданы лишь движения а, [5, х и т. д., система находилась
бы в покое, то (согласно лемме V и следствию из леммы VI)
СВОЙСТВА ОБЩЕГО ЦЕНТРА ТЯЖЕСТИ НЕСКОЛЬКИХ ТЕЛ 121
путь центра тяжести благодаря движениям —а, —(5, —я
и т. д. будет равен нулю. Отсюда следует, что когда тела
обладают движениями а, Ь, с и т.д., путь центра тяжести
будет таков же, как если бы тела имели движения а) Ь, с
и т. д., если бы таковые им были сообщены.
Замечание.
77. Если в системе имеется какая-либо закрепленная
точка, то тела, обладающие движениями а, [}, х и т. д.,
могут находиться в равновесии и без того, чтобы
равнодействующая этих движений равнялась нулю: в данном
случае достаточно будет того, чтобы направление
равнодействующей этих движений проходило через закрепленную
точку. В этом случае путь центра тяжести благодаря
движениям— а, —(5, —х и т.д. будет (согласно следствию
из леммы VI) параллелен направлению этой
равнодействующей, но направлен в противоположную сторону. Поэтому
он не будет равен нулю. Отсюда следует, что в данном
случае взаимное действие тел будет нарушать состояние
центра тяжести системы.
Теорема II.
78. При тех же предположениях, что и в теореме I,
если на данные тела действует по параллельным линиям
тяжесть или какая-либо иная ускоряющая сила,
постоянная для каждого тела, но могущая быть различной
для различных тел, общий центр тяжести или, вернее,
центр масс будет описывать такую же кривую, какую
он описывал бы в том случае, если бы тела были
свободными.
Для доказательства возьмем лишь два тела А и В
(фиг. 28) и предположим, что Ла и В$ суть те малые
отрезки, которые эти тела проходят естественным образом
вследствие первоначально сообщенных им скоростей Аа
и ВЪ, с одной стороны, и вследствие ускоряющей силы,
направленной по аа и Ь$, с другой стороны. Пусть С
будет центр масс тел А и В, т. е. такая точка, расстояния
122 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ ДВИЖЕНИЯ
которой до Л и до Б обратно пропорциональны массам А
и В (но не весам А и £, которые могут быть не
пропорциональны массам). Пусть тела А и В, вместо того чтобы
проходить линии Аа и В$, проходят линии Аа и ВЬ. Ясно
(согласно п° 76), что путь центра тяжести Сх в первое
Фиг. 28.
мгновение не будет отличаться от того, какой был бы в
том случае, если бы тела А и В описывали линии Аа и
В$ (п° 76). В следующее мгновение тела будут стремиться
описать
ae = Aa и Ы = ВЪ,
центр же тяжести С будет стремиться пройти прямую линию
хК=Сх
— тот же путь, который был бы им пройден в том
случае, если бы тела продолжали двигаться по направлениям
Аа и В$. Но так как, благодаря ускоряющей силе, тела
А и В описывали бы в этом последнем случае
параллельные друг другу линии е/ и dg, а в первом случае—линии
е<р и §у> соответственно равные и параллельные первым
двум линиям, то путь xk центра масс будет один и тот
же, описывают ли тела линии а/ и [}g, или же линии ау
и by. Однако, какую бы линию вместо аср и by, ни
описывали тела вследствие их взаимодействия, путь центра
тяжести С всегда будет одним и тем же (согласно тео-
СВОЙСТВА ОБЩЕГО ЦЕНТРА ТЯЖЕСТИ НЕСКОЛЬКИХ ТЕЛ 123
реме I). Отсюда следует, и т. д. Легко видеть, что
данное доказательство можно распространить и на случай
большего количества тел. Что и требовалось доказать.
Замечание I.
79. Настоящее доказательство теряет силу в том
случае, если ускоряющие силы не постоянны для того или
иного тела и если направления их действий не параллельны
друг другу. В самом деле, тогда нельзя считать ef равной
и параллельной е<р и dg равной и параллельной 5у> и п0-
тому путь хк центра не будет одним и тем же в обоих
случаях.
Замечание II.
80. Отсюда, однако, следует исключить один случай,
а именно: когда ускоряющая сила направлена к
неподвижной точке и когда эта сила действует пропорционально
расстоянию. В самом деле, в этом случае, как легко
доказать и как это показали многие математики, центр
тяжести совпадает с центром масс, и этот центр притягивается
или отталкивается от неподвижной точки с силой,
пропорциональной расстоянию до этой точки. На этом основании
нетрудно показать, что предыдущая теорема будет
справедлива и в данном случае.
Действительно, так как взаимное действие тел друг на
друга ни в какой мере не нарушает состояния центра масс,
совпадающего в данном случае с центром тяжести,
последний поэтому будет находиться в каждое мгновение на
таком же расстоянии от неподвижной точки, на каком он
находился бы без этого взаимодействия. Следовательно, он
также будет притягиваться с такой же силой. Его
направленная скорость также будет одинаковой в обоих случаях.
Отсюда следует, и т. д.
Итак, в этом последнем случае, согласно известной
теории центральных сил [55], центр масс, или центр тяжести,
будет описывать эллипс, центр которого будет совпадать
124 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ ДВИЖЕНИЯ
с данной неподвижной точкой независимо от того, будут
ли тела действовать друг на друга.
В том же случае, который рассмотрен в теореме, центр
масс будет описывать параболу.
Следствие.
81. Последние две теоремы дают в наши руки очень
простые средства находить движение неизменяемых тел.
В дальнейшем мы покажем некоторые применения этих
теорем.
Примечание.
82. Если тела рассматриваются в качестве точек и если
они движутся в среде, сопротивляющейся пропорционально
скорости, то 1° в случае, если на тела не действует
ускоряющая сила, центр масс будет двигаться прямолинейно и
движение его будет замедляться пропорционально
скорости,— точно так же, как если бы тела были свободны;
2° центр тяжести будет описывать одну и ту же линию и
с одним и тем же законом скоростей независимо от того,
действуют ли тела друг на друга или нет, — лишь бы
тяжесть тел была постоянной или была направлена к
некоторой неподвижной точке и в этом случае была
пропорциональна расстоянию от этой точки. Все это с очевидностью
следует из доказанных выше предложений п°п° 75, 79 и 80.
Теорема III.
83. Если произвольное число тел каким-либо образом
связано друг с другом и если одно или несколько из этих
тел вынуждены двигаться в некоторой плоскости или
в параллельных плоскостях, то я утверждаю, что
движение центра тяжести параллельно этим плоскостям
будет равномерным.
[Так, например, — чтобы конкретно это себе пред-
ставить, — если тело Р (фиг. 38), вынужденное двигать-
ся по прямолинейному жолобу PS, из которого оно
СВОЙСТВА ОБЩЕГО ЦЕНТРА ТЯЖЕСТИ НЕСКОЛЬКИХ ТЕЛ 125
выйти не может, тянет за собой при помощи стержня
РМ другое тело М, то центр тяжести g обоих тел
будет описывать такую кривую, что части прямой KS,
соответствующие дугам, пройденным за одинаковые
промежутки времени центром g, будут равны между со-
бою [66]].
В самом деле, если все потерянные данными телами за
каждый элемент времени движения привести к одной
равнодействующей, то в общем случае очевидно, что
вследствие взаимного уравновешивания этих движений
направление равнодействующей должно быть перпендикулярно к
данным плоскостям. Следовательно, центр тяжести будет
беспрерывно отклоняться от прямой линии силой,
направление которой (согласно лемме VI и п° 77) будет
перпендикулярно к этим плоскостям и действие которой поэтому
будет параллельно данной линии. Отсюда следует, и т. д*
Следствие.
84. Настоящее предложение будет справедливо и в том
случае, если тела обладают какими-либо ускоряющими
силами, постоянными или непостоянными безразлично, лишь
бы эти силы были направлены перпендикулярно к данным
плоскостям. Отсюда следует, что если тела движутся под
действием одних этих сил без всякого первоначального
импульса, то центр масс будет описывать прямую,
перпендикулярную к данным плоскостям. В самом деле, в последнем
случае, если бы тела были свободны, центр тяжести
описывал бы прямую, перпендикулярную к данным плоскостям.
Но его движение будет изменяться только силой,
направление которой перпендикулярно к этим плоскостям.
Следовательно, центр тяжести никогда не отклонится от
перпендикуляра.
Если тела притягиваются к какой-либо неподвижной
точке пропорционально расстоянию и если прямая,
проведенная из центра тяжести к неподвижной точке в первый
момент движения, перпендикулярна к плоскости, то можно
таким же образом доказать, что центр тяжести также
никогда не отклонится от перпендикуляра.
126 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ ДВИЖЕНИЯ
Примечание I.
85. Предыдущие предложения (п°п° 76 и 78) будут
справедливы и в том случае, когда тела действуют друг
на друга силой взаимного притяжения. В самом деле,
пути, которые эти тела проходят, приближаясь друг к
другу вследствие этого притяжения, будут обратно
пропорциональны массам, и потому сумма движений, если брать
их в одну сторону, будет равна нулю. Следовательно, путь
центра тяжести нисколько не изменится благодаря
взаимному действию этих тел друг на друга.
Впрочем, здесь можно применить доказательство,
данное для теоремы I, представляя все эти тела скрепленными
при помощи жестких стержней. Действительно, в этом
случае, если принимать во внимание только их взаимное
притяжение, очевидно, они будут оставаться в равновесии.
Отсюда следует, и т. д.
Примечание П.
86. Мне кажется, с помощью установленных нами
принципов можно доказать или, лучше сказать, объяснить тот
знаменитый закон механики, согласно которому в системе
тяжелых тел, находящихся * в равновесии, центр тяжести
занимает наинизшее положение. В самом деле,
предположим, что система находится в положении В, бесконечно
близком к положению равновесия. Очевидно, в каждом
теле возникнет тогда малое движение, чтобы привести тела
к положению равновесия, и усилие тяжести каждого тела
нужно рассматривать как бы составленным из этого малого
движения и из движения другого, уничтожаемого. Но так как
положение В бесконечно близко к положению равновесия,
уничтожаемые движения будут бесконечно мало отличаться
от полного усилия тяжести; последнее полностью
уничтожается в положении равновесия. Таким образом,
действительные движения любого тела будут представлять собой
бесконечно малую величину по сравнению с теми
движениями, которые имели бы тела, движущиеся свободно
благодаря своей тяжести. Движение центра тяжести будет
СВОЙСТВА ОБЩЕГО ЦЕНТРА ТЯЖЕСТИ НЕСКОЛЬКИХ ТЕЛ 127
нескольких
одинаковых
также бесконечно малым по сравнению с тем движением,
которое имело бы место в том случае, если бы тела
двигались свободно. Это не было бы так, если бы из двух
рассматриваемых здесь бесконечно близких положений одно
не было бы положением равновесия. Отсюда следует, что
можно считать, что от положения В до положения
равновесия центр тяжести .не меняет своего места вовсе;
другими словами, между тем и другими положениями
опускание центра тяжести равняется нулю. А отсюда следует,
что в положении равновесия опускание центра тяжести
представляет собой максимум, в некоторых же случаях —
минимум. Оно представляет собой, например, максимум в
случае цепи и минимум в случае
шариков, образующих свод и
таким образом поддерживающих
друг друга; это будет, как
известно, не что иное, как
перевернутая «цепь».
Может быть, точнее было бы
сказать просто, что в случае
равновесия дифференциал опускания
центра тяжести равен нулю. Как
известно, равенство нулю
дифференциала не всегда указывает
на максимум или минимум.
Этого замечания вполне достаточно, чтобы показать,
что не правильно было бы, как это делают некоторые
авторы, выводить законы равновесия жидкостей из того
мнимого закона, что центр тяжести массы жидкости,
находящейся в равновесии, должен занимать наинизшее
положение. Действительно, если жидкость DOSPE (фиг. 29), все
части которой притягиваются к точке Q пропорционально
расстояниям, находится в равновесии в сосуде MDEN,
то центр тяжести этой жидкости не будет находиться
в наименьшем расстоянии от центра Q. В самом деле,
пусть
MNDE=DOSPE.
Тогда, очевидно, 1° центр тяжести каждой из этих частей
128 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ ДВИЖЕНИЯ
будет совпадать с центром масс этой же части; 2° части
KNP и MOL, взятые вместе, будут равны LSK, и общий
центр масс частей KNP и MOL, более близких к точке Q,
должен быть ниже MN и потому ближе к Q, чем центр
масс LSK, расположенный выше ММ. Отсюда следует, что
так как часть DOLKPE является общей для DOSPE и для
DMNE, то при условии, что
QT= или >QQ,
центр масс жидкости DMNE будет расположен ближе к Q,
чем центр масс жидкости DOSPE. Между тем последняя
находится в равновесии, первая же — нет.
Отсюда следует, и т. д.
Такого рода замечание мною было уже сделано в моем
«Трактате о равновесии и движении жидкостей», п° 13 [б7].
Здесь оно представлено в еще более убедительной форме
с целью предостеречь математиков от такого рода
ошибочных применений принципов механики, которым иногда
придают излишнюю общность.
ГЛАВА III.
Задачи, в которых указывается, как пользоваться
вышеприведенным принципом.
§ 1. О телах, соединенных между собою
при помощи нитей или стержней.
Задача I.
87. Найти скорость стержня CR, закрепленного в
точке С (фиг. 30) и нагруженного произвольным
количеством тел А, В, R, предполагая, что если бы этим
телам не препятствовал укачанный стержень, они в
ЗАДАЧИ
129
равные промежутки времени описывали бы бесконечно
малые линии AOt BQ, RT, перпендикуляр- q
ные к стержню.
Вся трудность сводится к тому, чтобы
найти линию RS, которую какое-либо из тел
R пройдет за тот же промежуток времени,
за который оно в свободном состоянии
прошло бы линию RT; тогда будут известны
скорости Ж/, AM и всех остальных тел.
Будем рассматривать передаваемые
скорости RT, BQ, АО как составленные
(согласно п°п° 30 и 60) из скоростей RS и ST,
BG и — GQ, AM и — МО. В силу нашего
принципа рычаг CAR должен оставаться в
покое, если телам R, В> А передать только движения
ST, — GQ, — МО. Отсюда следует
A.MO.AC-\-B.GQ.BC = R.ST-CR*)}
т. е., вводя обозначения
АО=а, BQ = b, RT = cy
CA = r, CB = v, CR = p и RS=z,
мы получим
откуда
_j_ Aarp 4- Bbrp + Re?2
Следствие I.
88. Пусть F, /, cp будут движущие силы тел Л, 5, R.
Тогда ускоряющую силу тела R мы найдем, подставляя
Р 4 со
вместо a, ft, с их значения т , -^ , i (п° 22). Она будет
*) См. сноску**) на стр. 92. При этом необходимо заметить,
что силами здесь являются величины Л-МО, B-GQ и т. д.
{Примечание Безу.)
9 Ж. Даламбер
130 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ ДВИЖЕНИЯ
равна
Fr+ft + w
Обозначая через ds элемент дуги, описываемой радиусом
С7?, и через а — скорость тела R, мы в общем случае
получим
каковы бы ни были силы Т7, /, ср *). Таким путем нетрудно
решить задачу о центре качания при произвольных
условиях.
Предположим, например, что маятник качается в среде,
сопротивляющейся пропорционально любой степени ип от
скорости. Тогда мы будем иметь <р — kun вместо <р, далее
F—■ вместо г и, наконец, / — вместо /**).
Р Р
Подставим эти значения в последнее уравнение. Обозначая
далее через х длину изохронного, маятника, через М — его
массу и через П — его вес или, вернее, ту часть его веса,
которая действует перпендикулярно к стержню, мы полу-
*) Нужно принять во внимание, что АО, BQ, RT
представляют собой мгновенные импульсы, сообщаемые телам Л, В, R
ускоряющими силами. И так как тело R сохраняет лишь RS или
z, то отсюда следует, что для нахождения движения этого тела
нужно в формулу
yde = udu
(n° 21) подставить z вместо ср и ds вместо de. См. сноску на
стр. 57. {Примечание Безу.)
**) Пусть т будет то сопротивление, которое испытывает со
стороны среды тело /?, движущееся со скоростью р. Если это
тело будет двигаться со скоростью и, то сопротивление станет
тип
равным —— , так что движущая сила тела будет равна всего
тип т
только ср . Очевидно, что величина k, заменяющая —,
зависит от объема, от плотности и от формы тела R. То же
самое можно сказать и о величинах g, h, I. {Примечание Безу.)
ЗАДАЧИ
131
чим уравнение движения этого маятника в виде
llxds Imxn xds Мх2 udu %.
9 9п 9 Р2
откуда
Пр ds iwxn-^ds
~ш—w^—udu--
Сравнивая это уравнение почленно с уравнением движения
сложного маятника, мы найдем значения х и /. Заметим,
что величина / зависит от объема тела Ж, от его формы
*
ganrn
) После подстановки ф— kun и F— и т. д. вместо ф,
' ' рп lt
F и т. д. мы получим уравнение в виде
(P+Qun)ds = uda.
Уравнение же движения простого маятника имеет вид
(П — la'n)ds' = Mu'du'9
где dsr представляет собой малую дугу, описываемую маятником
за какой-либо элемент времени, а и' — его скорость. Но так как
этот маятник, как обычно принимается, описывает дуги, подобные
дугам сложного маятника, мы будем иметь
. , xds , хи
ds'=— и и'=—,
Р Р
Следовательно, проделав все сокращения, мы получим
flip . lanxn-i\
В этом уравнении и к s обозначают те же самые величины a us,
которые мы встречали в уравнении сложного маятника. Поэтому
оба уравнения должны быть совершенно тождественными, и
соответственные члены обоих уравнений должны быть равны друг
другу. Вследствие этого
Et-p
Мх~~~
lxn-1
(Примечание Безу.)
9*
М?*
-г
:<?.
132 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ ДВИЖЕНИЯ
и плотности. Поэтому нельзя считать все эти величины
известными *).
Кроме того, следует заметить, что когда некоторые
авторы говорят, что расстояние х центра качания не
зависит от того, сопротивляющаяся ли среда или нет, — это не
совсем точно. Дело в том, что величины F, <р, /, II и т. д.,
зависящие от веса, сохраняют свое значение только в
пустоте, так как вес тела уменьшается на вес жидкости и
уменьшается в различной степени в зависимости от
плотности, объема и формы того или иного тела. Поэтому
значение х, полученное из сравнения первых членов обоих
уравнений, будет одинаковым только при £, g, h, /,
равных нулю.
Следствие II.
89. Из того, что
A-OM.AC + B-QG-CB = R-ST-CRy
следует, что
А. (AM — АО) • С A -f В • (BG—BQ) -CB = R- (RT—RS). С/?,
откуда
A.AM*CA-\-B'BG.CB-\-R-RS.CR =
= A.AO-CA-{-B-BQCB-\-RRT-CR.
Иначе говоря, силы A-AM, В* EG, R*RS будут
эквивалентны силам А'АОу B*BQ R*RT. Отсюда следует, что
последнюю задачу можно было бы решить также, беря RS
так, чтобы
F>.RS.CR + B-?^ + А.Ц%£
*) Очевидно, что если М известно, то зависящее от него /,
как мы только что видели в сноске**) на стр. 130 , будет также
известным. Поэтому, имея одно неизвестное х и два уравнения
Мх~
и
lX*~l
мра-г — ч*
мы не всегда можем удовлетворить этим >уравнениям. См. «Мё-
moires de I'Academie», 1738. (Примечание Везу)
ЗАДАЧИ
133
равнялось
R-RT.CR-{-B.BQ-CB-\- А-АО-СА.
К этому сводится метод, которым пользуется Бернулли
для нахождения центров качания и который состоит в том,
что в какой-нибудь точке Р стержня нужно поместить тело,
масса которого равна
R-CR2 , В-СВ2 . А-СА2
СР2 ~1~ СР2 ~Т~ СР2 '
а ускоряющая сила такова, что момент этого груза равен
моментам грузов А, В, /?, обладающих их естественными
весами АО, BQ, RT, а скорость равна скорости точки Р
стержня. Отсюда вытекает, что ускоряющая сила тела Р
RS'CP
будет равна г -, так что мы будем иметь
ре CP/R-CR2 , В-СВ2 . А-СА2\ гр_
К°* CR V^CP2"* СР2 ' СР2 )'^ —
= A.AO-CA + B-BQ-CB-{-R-RT.CR.
Очевидно, что первый член этого равенства представляет
собой не что иное, как сумму моментов
A.AM.CA + B'BG-CB + R-RS.CR.
Таким образом, мы показали, что при помощи основного
принципа Бернулли можно решить задачу о центрах
качания гораздо проще, не прибегая к точке Р и не вводя
новых масс.
Только что описанным способом я вначале ,полагал
решать данную задачу, осуществил же это Эйлер в своем
мемуаре, напечатанном в VII томе «Записок Петербургской
академии», где автором используется то положение, что
силы R-RS; B-BG; A-AM должны быть эквивалентны
силам R-RT; B-BQ; А-АО. Однако это положение у Эйлера
никак не доказывается, и доказать его можно, как мне
кажется, только с помощью нашего принципа. Помимо
этого, указанный автор ограничивается применением этого
положения лишь к решению небольшого числа задач,
относящихся к колебаниям изменяемых и неизменяемых тел,
и к тому же, его решение одной из задач этого рода не
134 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ ДВИЖЕНИЯ
совсем верно, как это мы будем иметь случай показать в
дальнейшем.
Уже из этого видно, насколько наш принцип
заслуживает предпочтения и притом не только для решения задач
этого рода, но и вообще всех вопросов динамики.
Лемма VII.
90. Если две бесконечно малые линии Рр и Mm (фиг. 31)
соединить конечными линиями РМ и рт и затем провести
#_ м pix = Pp и т\х==Мт,
то я утверждаю:
1°. Разность РМ — тф.
будет равна удвоенной
разности РМ—рт
минус квадрат угла,
образуемого РМ и рт,
умноженный на РМ.
2°. Угол,
образуемый TTjx и рт, равен
углу, образуемому РМ
и рт, умноженному на
1 i 2(РМ — рт)
*"+" РМ
Проведем линии Ма, не и ja/ параллельно рт, затем
проведем Mb, aPd, сп/ и \ieg перпендикулярно к рт.
Тогда мы получим
Mb = \ig,
Pd—itc.
Отсюда
p.e—v;f=Pa.
Но бесконечно малые углы РМа и етт\х, радиусы которых
РМ и TTjji отличаются друг от друга на бесконечно малую
величину (при равенстве бесконечно малых линий Ра
и е\х), отличаются между собой на бесконечно малую
второго порядка малости, так как разность синусов
Фиг. 31.
ЗАДАЧИ 135
будет равна
jx£ _ Ра Ра (РМ — щ)
яр РМ РМ-щ '
т. е. равна бесконечно малой второго порядка. Умножив
последнее выражение на Ра, мыпол)чим бесконечно малую
третьего порядка. Но
РМ — рт = РМ —Ма -\-Ма—рт = ^~ + Ьт — dp.
Точно так же мы найдем:
pm — lin = —«iLjrmg—cp.
Пренебрегая третьими разностями, мы получим
PM — -w = 2{bm — dp) = 2 (РМ—рт) — ^ =
= 2 (РМ —рт) — (угол аМР)2. РМ.
3°. Угол гтгц, т. е. угол, образуемый рт и тг|1, равен
\ie Ра Ра
%г рт — (bm — dp) Ма —2 (Ьт—dp)
Ра , 2 (bm •— dp) Ра
Ма * Ма ' Ма'
что, если пренебречь третьими разностями, будет равно
углу аМР> умноженному на
Г ( 2(РМ-рт)-\
L ' РМ у
Что и требовалось доказать.
Следствие I.
91. Если линии РМ и рт равны между собою, то
РМ — тт|х = — (угол аМР)2. РМ
и
угол ещ — аМР,
136 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ ДВИЖЕНИЯ
ТО
Следствие II.
92. Если линии Mm и т]Х (фиг. 32) будут равны нулю,
Мтг — РМ=+ 2рО-{
РО*
РМ
угол pMit~PMp = --%!Jft-PMp.
Задача II.
93. Стержень О А (фиг. 33), имеющий неподвижную'
точку G и находящийся в горизонтальной плоскости,
Фиг. 33.
нагружен двумя телами А и D. Тело А наглухо
скреплено со стержнем, а тело D может свободно
скользить вдоль него при помощи кольца. Требуется найти
скорость каждого тела в любое мгновение, а также
найти кривую, описываемую телом D.
Пусть АВ и DE будут бесконечно малые линии,
описываемые телами А и D в течение одного и того же
элемента времени. Если провести дугу ВС) равную АВ, и
ЗАДАЧИ
137
линию El, равную ED и имеющую то же самое
направление, то ясно, что именно эти линии были бы описаны
обоими телами в течение следующего элемента времени, если
бы им не мешал в этом стержень. Правда, тело А по
необходимости опишет дугу ВС, но оно опишет ее не за такой же
элемент времени, как дугу АВ. Пусть BQ — малая линия,
бесконечно мало отличающаяся от ВС, представляет ту
линию, которую описало бы тело А за тот же элемент
времени, за которое оно при своем несвободном движении
проходит линию ВС, если бы оно продолжало после
точки В двигаться далее равномерно с той скоростью, какую
оно имело в В. Пусть за то же время тело D в
равномерном движении описало бы линию Ео. На самом же деле
тело вследствие сопротивления стержня описывает
линию Ер. Будем рассматривать движения BQ и Ео как
сложные движения, состоящие из движений: первое из ВС и
CQ, второе из Ер и El. В таком случае ясно, что если бы
тела А и D обладали лишь движениями CQ и El, то
рычаг оставался бы в равновесии. А так как тело D может
скользить вдоль стержня (по условию), то для равновесия
необходимо, чтобы El было перпендикулярно к рычагу GB.
Кроме того, должно соблюдаться равенство
A-CQ-GA = D.El.GE.
Установив эго, введем следующие обозначения: пусть
GA = a,
AB^dx, GD=y, FD = ~, FE = dy,
CQ = a.
Предположим, что линия BQ описывается с такой же
скоростью, как АВ, а линия Ео — с такой же скоростью, как
DE. В таком случае линии BQ и АВ, и точно так же линии
Ео и DE, относятся друг к другу как времена, затраченные
на их прохождение. А так как линии BQ и Ео
описываются за одно и то же время (по условию), так же как за
одно и то же время описываются линии АВ и DE, то мы
получим
BQiAB (или BCj = Eo:DE (или El).
138 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ ДВИЖЕНИЯ
Отсюда
BC:CQ = DE:io.
Следовательно,
CQ-DE
Далее, из равенства
A-CQ-GA = D-El.GB
мы получаем
r?t Ada
Е1=ро = -щ.
Но угол ЮЕ равен
2dydx
EGD (\— ^)==£G£>-
ay
(п° 92). Если к углу ЮЕ прибавить угол /Go, равный
io DF_CQ.DF_CQ DF_CQ_ а ♦)
Gi' DE~ Gi-BC GD' AB~GA~~~ a '
и угол oGpy равный
то мы получим
угол pGE =
ро Ata
55 —Ду* '
= EGD_2dydXj
ay '
a
• Ada
А так как этот угол pGE равен углу EGD (по построению),
то мы будем иметь
2dydx , a , Ааа
ay * a* Dy2
откуда
2Dydydx
'~Aa2 + Dy*'
= 0,
a =
*) Если из центра G описать дугу is, то мы получим угол
is
iGo = тъ. Вследствие же подобия треугольников DFE и sio мы
будем иметь
(Примечание Безу.)
ЗАДАЧИ 139
Разность Gi— GD равна
(п° 92). С другой стороны, а-~ представляет собой
разность между Gp (или Go) и G/. Следовательно,
откуда
ау~ а* ^Г ах '
или, если подставить вместо а найденное значение, мы
получим уравнение кривой DEp в виде
иУ— а* 'TAa* + Dy**
Для отделения переменных предположим, что
и, вследствие
Тогда
dx:
этого,
мы будем
d2y.
иметь
аЫр
У1* У
~ а »
dpdy
- у
2ydy-aW
f» р2(Аа2 + Dy*) —УаУ-
Умножая это уравнение на , , 2 , 22 и затем интегрируя,
мы получим
= 0- *
2/?2(^2 + ДУ2)2 2£>(Ля2 + Ду2)>
где G—-такая постоянная, что -- в начале кривой
140 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ ДВИЖЕНИЯ
делается равным данному отношению -р \ Таким
образом, мы получим уравнение кривой DEp в следующем виде:
dx=pdy_ adyVD
<* У (Аа2+Dy2) [2GD (Аа2 + Dy2) — 1J •
Что касается скоростей обоих тел, то, обозначая через и
скорость тела Л, мы будем иметь
du CQ
и ВС%
CQ
так как -^ равно отношению второго элемента времени к
первому**). Отсюда следует
du 2Dydy
~~ ~й Aa2-{-Dy2
и
£ Аа2 + РЬ2
g Aa2-\-Dy2>
где g—начальная скорость тела А и где, кроме того,
предположено
у=ь
*) Пусть тело D вначале получает импульс по направлению
РЕ (фиг. 34), и пусть тела А и D вследствие первоначальных
импульсов стремятся за некоторый элемент времени описать линии
АК и Ей Пусть вместо этих линий они на самом деле
описывают линии АВ и Ер. Отношение АВ к Fp следует
приравнять отношению dx к dy в начале координат, а отношение
АВ к Ер — отношению g к /г, где через g и h обозначены
начальные скорости. Следуя в точности тем правилам, которые
приведены в задаче, нетрудно найти все эти величины, — как это
указывает и чертеж. (Примечание Безу.)
**) Мы имеем
AB = udt%
откуда, так как АВ постоянно, мы получим
dudt±ud2t = 0,
или
da __d4 __CQ _CQ
a ~~ dt ~~ AB~ ВС
(Примечание Безу.)
ЗАДАЧИ
141
в начале кривой DEp. Точно так же, если скорость тела D
обозначить через v, мы будем иметь
dv __Ер — Ео _po-FD
Aaa-ydx
со
DE2
Dy*.a(dyz+y**§}
Однако скорость v можно получить и более изящным
способом, на основании принципа сохранения живых сил,
доказательство которого мы даем ниже.
Этот принцип нам дает
Dv2 -f- Ли2 = const.
Отсюда, обозначая через h начальную
скорость тела D, мы получим
D
Замечание I.
94. При решении этой задачи я не
предполагал элемента времени dt
постоянным, так как я хотел получить
уравнение кривой, не зная выражения скорости. Последнее
было бы необходимым, если бы мы считали dt постоянным,
так как
dt = ^
а
и dt можно исключить только в том случае, если известно и.
В подобных случаях я буду поступать таким же образом
и в дальнейшем. Это не значит, что и не может быть
получено тем или иным способом. Я лишь полагал, что
нелишне будет показать, каким образом при решении такого
рода задач можно обойтись без этого,
142 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ ДВИЖЕНИЯ
Замечание II.
95. Предыдущая задача была бы немногим труднее,
если бы тела А и D обладали ускоряющими силами р и /
произвольного направления и произвольной величины. Чтобы
дать пример необходимых в данном случае вычислений, я
буду считать обе ускоряющие силы постоянными и
направленными параллельно вертикали VA. При этом мы должны
представить себе нашу систему движущейся в вертикальной
плоскости. Идя тем же путем, как и в п° 93, мы положим,
сверх того, что тело А вследствие своего веса р проходит
линию QN за такой же элемент времени, за который оно
описывает несвободным движением линию ВС. Так как этот
элемент времени отличается от первого на величину,
бесконечно малую, мы будем иметь
Точно так же
fdx*
и2
A-CN-GA Аа . м
т = D-DG = Qy'[a
, pzdx2\
*) Мы имеем
где ср — ускоряющая сила по направлению QN. Если разложить
тяжесть р на две силы, из которых одна перпендикулярна к QN,
а другая как раз имеет направление QN, то последняя будет
равна ГА . Так как, кроме того,
dx = udt,
то
Q™ GA и*
(Примечание Безу.)
ЗАДАЧИ
143
где через z обозначено GV*). Затем, как в п° 93, мы
получим
2ydxdy
ay*
/ , pzdx2\ Aa t « I fdx2 _£
\ "r au2 J ' Dy2 "I" a "г ц2 ' eJ,
и
•^ a2 * dx * au2
Кроме того,
da a
и dx*
Подставив в первое уравнение на место а его значение,
а именно:
dxdu ududx
или
II2 !
мы (после интегрирования) получим значение и2. Подставив
это значение точно так же, как и найденное уже ранее
значение а, во второе уравнение
мы получим уравнение кривой DEp, В этом уравнении мы
заметим, что
Z ( X \ \™\
— = cos — ) L J
а \а J
и
V a2 — z2 . ( х\
и это даст нам возможность легко исключить z*
*) Здесь предполагается, что к является точкой, куда
приходит D во второй элемент времени. Оно приходит в % вместо z,
где оно очутилось бы вследствие его собственного движения и
тяжести. Разложим (как это показано) вынужденное движение.
Тогда nz должно быть перпендикулярно к GC
и
KZ.D-GK = itz.D-DG = A.CN-AQ.
Отсюда следует, и т. д. {Примечание Безу.)
144 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ ДВИЖЕНИЯ
Замечание III.
96. Пусть сила, приложенная к телу А, заставляет его
двигаться по кривой AN с какой-то скоростью, закон
которой для всех точек нам известен. Требуется найти
траекторию тела D и его скорость. Эта задача приводится
к предыдущей, если мы будем искать ту ускоряющую
силу, которой должно обладать тело А для того, чтобы,
двигаясь в связи с телом Z), оно в каждой точке В
обладало заданной скоростью.
В первом из четырех уравнений предыдущего п° нужно
подставить ср вместо — и, так как и является известной
функцией от х, то можно положить
и = Х,
и тогда
Отсюда
d
а = —х •
Сравнивая это выражение для а. с выражением, полученным
из первого уравнения предыдущего п°, мы найдем
выражение для <р и найдем уравнение кривой DEp.
Пусть, например,
/=0
II
и = постоянной g.
Тогда мы будем иметь
а = 0
и
2dydx ydx2 Аа
~~ау~ "i^ * Dy2'
откуда
2Dg*ydy
• Аа2 dx
и
ydx2
а2 •
da
и '
п _
dX _ а
X dx'
dXdx
d2y=
ЗАДАЧИ
145
Следовательно,
dx — ady
V&fl+y*
При G = 0 мы будем иметь [69]
х
у = са
И 2£
m_2Z)g*cfl
* ~ Ля* '
Тело D в данном случае будет описывать логарифмическую
спираль, так как
dx dy
Если в точке А нет никакого тела, а скорость точки А
в направлении АВ в результате действия некоторой силы,
приложенной к стержню, задана, то задачу можно решить
точно таким же способом. Нужно только представить в
точке А тело произвольной массы и найти, какой ускоряющей
силой должно обладать это тело для того, чтобы, двигаясь в
связи с телом £>, оно имело в любой точке В скорость,
подчиняющуюся данному закону.
Этот метод применим вообще всякий раз, когда тела
как-то связаны друг с другом при помощи нитей или
стержней и когда одна или несколько точек нитей или стержней
движутся с данной скоростью и по данному направлению.
Я допускаю, что эти задачи можно решить и более простым
способом, не определяя, какова должна быть ускоряющая
сила у тела с заданной скоростью в результате действия
других тел. Однако, хотя наше решение и длиннее, тем
не менее оно исходит из истинных принципов, заложенных
в самом предмете, так как совершенно несомненно, что
сила, приводящая тело в движение с заданной скоростью,
отличается от той силы, которая была бы нужна, если бы
были устранены все тела: часть этой силы идет на то, чтобы
10 Ж- Даламбер
146 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ ДВИЖЕНИЯ
преодолеть действие этих самых тел. Наше решение и
определяет разность двух указанных сил и именно в этом и
состоит, как мне кажется, истинная метафизика данной
проблемы.
Замечание IV,
97, В том случае, если стержень нагружен двумя
телами, которые могут свободно скользить вдоль этого
стержня, кривые, описываемые обоими телами, можно найти
следующим образом.
Чтобы сохранить аналогию с предыдущим решением,
мы будем предполагать, что тело Л всегда существует,
однако оно должно быть бесконечно мало по сравнению
с данными двумя телами. Мы будем иметь
2dydx
_i-JL 4-^ = 0,
ау ' а ' у
и если через z обозначить радиус-вектор другого тела,
которое я обозначу буквой Е, мы также получим
2dzdx , а pO'Dy „
Это нам даст
Но
Следовательно,
и
Кроме того, ура;
az ' a Ezz
a 2Dydy + 2Ezdz
dx~ Dyt-i-Ez* '
a _d4
dx dt
dH 2Dydy-\-2Ezdz
dt ~ Dy2 + Ez*
bdt = (Dy2-\-Ez2)dx.
мнения
d*y=ydx*-\-^
*»=***+%
ЗАДАЧИ 147
(если исключить dx2 и подставить ^г вместо -j-\ дают
yd2z — jgrfgy ^
jyate— ^rfj/ dt
Вследствие этого
ydz— zdy=fdt
и потому
Положив
мы получим
fdx(Dy* + Ez>)
ydz— zdy=J— -\^ -.
z=yu,
du fdx
D + EtP'
9 fdt
Мы сможем найти у, если мы найдем еще одно уравнение
с разделяющимися переменными относительно dt и dx. Но
1°. Принцип сохранения живых сил нам дает уравнение
gdt2 = (Dy2 + Яг2) </л;2 + £> dy2 -f £^2,
или уравнение
gdt* = bdtdx + Ddy* + Edz2,
получающееся также и непосредственно из нашего решения.
2°. Уравнение
(Ez2 + Dy2)dx = bdt
после дифференцирования приводит к уравнению
(2Ez dz + 2D у dy) dx = MV
и, затем, после нового дифференцирования
(2 Ez d2z + 2Dyd2y + 2£ ate2 _j_ 2£> dy2) dx = b dH.
Подставим в это уравнение вместо
2Ddy2-\~2Edz2
to*
148 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ ДВИЖЕНИЯ
равную величину
2gdt2 — 2bdtdx,
вместо d2y подставим его значение
вместо d2z — его значение
. о , dHdz
zdx2+ir
и вместо
(Dy2 + Ez2) dx и (2Dydy-{-2Ezdz)dx
также их значения bdt и b d2t. Мы будем тогда иметь
2b dt dx + Ь~ + 2gdt2 — 2b dt dx =- Ь-£ ,
или
bdH bd2t*_n ..
dxdt dxdt~ e U
Интеграл этого уравнения будет иметь вид
bdH п ,, ,
откуда
b dt=zgt2 dx-\~mtdx-\-h dx.
Таким образом, мы получим величину dx как функцию dt.
Отсюда следует, и т. д.
Не нужно опасаться того, что уравнения
f dx da
b —D-\-Eu2
и
. bdt
dx = ~7
-gP + mt + h
смогут оказаться одним и тем же уравнением! для этого
было бы нужно, чтобы da равнялось ndt, где п —
постоянная величина. В таком случае, ввиду того, что
^ da'
ЗАДАЧИ
149
величина у должна была бы быть постоянной, что
невозможно, так как тело D не закреплено (по условию).
В «Memoires de l'Academie» за 1742 г. (стр. 31)
решение не идет дальше того, что находится уравнение,
связывающее dx и dt и тем самым определяющее
положение стержня в каждый момент.
Однако построения кривых, описываемых обоими
телами, там не дается или, если и дается (стр. 35), то оно
производится таким способом, который нельзя признать
геометрическим, поскольку оно не опирается на разделение
переменных. Тем не менее, можно заметить, что уравнения
d2y =у dx2
и
d2z = z dx2}
получающиеся при постоянном dt, приводят к уравнению
(Ру (PZ
У z '
откуда
yd2z — zd2y = 0}
и mi
ydz — zdy=fdt;
отсюда можно получить то же самое построение, которое
нами только что приводилось.
»3ная кривую, описываемую телом D, мы найдем и
кривую, описываемую телом Е, так как
z=yu.
Замечание V.
98. Если мы имеем три тела Z), Е и Я, которые могут
свободно скользить вдоль стержня, то тем же путем, как
и выше, мы найдем уравнение с разделяющимися
переменными относительно dx и dt; далее, таким же способом мы
получим
ydz — zdy =fdt
и
yds — sdy = k dt}
150 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ ДВИЖЕНИЯ
где через s обозначено переменное расстояние от т^ла И
до центра, т. е. до неподвижной точки G, a k
предполагается некоторой постоянной величиной, отличной от /.
Из этих двух уравнений мы получаем
у dz —z dy — -j- (у ds —s dy).
что, после деления на у2 и после интегрирования, дает
Если положить
то мы получим
У ky >
z=yu,
7 = Р«+Г.
где [5 и у — постоянные.
Далее тем же методом, как и раньше, мы получим
bdt = [Dy2 + Е& + Hs2) dxi
откуда
у dz — z dy f dx
или, иначе,
чго дает
Dy2 + Ez* + Яу*~
'(7)
da
~~ b '
fdx
~~ b >
f dx
D+Ett^ + H(^U + ^
Имея эти уравнения, можно построить кривые,
описываемые телами D, Е и Н в этом случае.
Очевидно, задача не будет труднее, каково бы ни было
число тел D, Е} Н и т. д„
ЗАДАЧИ
151
Замечание VI.
99. Если тело А жестко скреплено со стержнем, будучи
удалено от точки G на расстояние а, принимаемое мною
за единицу, а два других тела D и Е могут свободно
скользить вдоль стержня, то мы, идя тем же путем, что
и в п° 97, получим
1°. {Dy*-{-Ez* + A)dx = bdt,
2°. ydz — zdy=fdt>
Положим в последнем уравнении
dx~p dt,
чго дает
d4__dp
dt ~ р *
Тогда из третьего уравнения мы будем иметь
Если положить, далее,
at k '
то вместо этого мы получим
л( bk\_2gdp 2 Ар* dp
\ Р2)~ k к '
или
2gdp 2Apz dp , bdk 2bkdp ~
k k ' p2 ps
Умножая это па —2 и интегрируя, мы получим
2/>* р
где L — постоянная
£-¥-**+*-«>.
152 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ ДВИЖЕНИЯ
Отсюда мы найдем выражение dt и их в виде функции
от р и dp:
dt = Udp
и
dx = XV dp,
где П и lY суть известные функции от р, причем
В таком случае
ЦУ + Е* = %-А=% -Л,
и тогда
у dz — z dу f dt
Dy*-\-Ez* ~Ш ~~A~
Полагая
z
fJldp
Ml .
A
4s
мы получим уравнение с разделенными пере
da fpU dp
D + Eu* b — Ap*
Таким образом, и в этом случае можно также построить
кривые, описываемые обоими телами, и найти положение
стержня для любого момента.
Замечание VII.
100. Если к стержню жестко прикреплены два тела А
и Ву а два других тела могут свободно скользить вдоль
этого стержня, то задача решается все тем же способом.
Вообще задача может быть решена при любом числе
прикрепленных к стержню тел, если предположить, что
кроме того имеются еще два тела, могущих скользить
свободно вдоль данного стержня.
Следовательно, задача может быть решена и в том
случае, если число жестко скрепленных со стержнем тел
станет бесконечным,—другими словами, если принимают
в расчет массу стержня. Легко видеть, что в данном слу-
ЗАДАЧИ
153
чае выкладки будут те же самые, что и в предыдущем п°,
если мы вместо величины А возьмем сумму произведений
всех частиц стержня на квадраты их расстояний от
неподвижной точки G.
Наконец, если вдоль стержня могут скользить тела в
числе, большем двух, то, как можно видеть из п° 97 и
из предыдущего, задача решается теми же самыми способами.
Итак, в общем случае, если произвольный
прямолинейный стержень, находящийся в горизонтальной плоскости,
будет нагружен произвольным числом тел, из которых
одни могут свободно скользить вдоль стержня, другие же
прикреплены к стержню, то всегда можно найти положение
стержня для любого момента, а также можно найти кривые,
описываемые каждым из
свободных тел. При этом
можно, если угодно,
учитывать и массу стержня.
Задача эта до сих пор
решена не была.
Задача III.
101. Тело Р
опускается по кривой СВ
(фиг. 35) и тянет за
собо% тело F при
помощи нити PCF,
.проходящей через блок С.
Найти скорость каж- Фиг. 35.
дого тела.
Пусть тело Р за некоторый элемент времени проходит
элемент пути Рр, а другое тело в течение того же
элемента времени проходит элемент пути
Ff=pV.
В следующий элемент времени, если бы телам ничто
не мешало, они прошли бы элементы пути
рп = Рр
и
154 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ ДВИЖЕНИЯ
Однако вследствие сопротивления нити и вследствие
ее нерастяжимости линия: рте будет пройдена телом Р
в течение элемента времени, отличного от предыдущего
элемента. Тело F за то же время придет в точку со
такую, что
шС+Стт=/С+Ср.
Предположим теперь, что в течение того времени,
за которое тело Р проходит /лт, оно естественным
образом [60] прошло бы путь pi, а тело F естественным
образом прошло бы путь /а). Далее, допустим, что вес тела F
заставил бы его за то же время пройти расстояние cov
но вертикали, часть же веса тела Р, которая действует
по направлению /?/, заставляет его пройти путь //. Если
взять
ро — тг/,
то, согласно нашему принципу, тело F, обладающее одной
только ускоряющей силой, представленной линией oJv,
должно уравновешивать тело Р, обладающее силой ро,
мастью своего веса и своей центробежной силой,
перпендикулярной к кривой Ср, т. е. направленной по pZ.
Проводя из точки о прямую оа до пересечения в точке а
с продолжением Ср и проведя сш, легко видеть, что, так
как остаток силы по направлению pZ уничтожается
вследствие сопротивления кривой поверхности, равновесие будет
иметь место при условии
F'uv — P'pa.
Итак, пусть скорость тела Р будет и, абсолютный вес
его р, абсолютный вес тела F будет g. Далее, пусть будет
Ff—dx, NP=y, Pp^ds,
Тогда мы будем иметь:
.j pdy*ds2
11 ~ u4s *
С другой стороны,
<f>u>;Ff=iTt:Pp}
ЗАДАЧИ
откуда
a dx
4 ds '
и, наконец,
% gds1
00 и2
Обозначив еще
(DV=/Z,
мы найдем
— ., a dx | gds2
4 d$ ' И2
Кроме того, так как
F'W — P.pQi,
мы будем иметь
Р р po'flfo Pflte ^ /pdy-ds2
dx dx * \ a2ds
Отсюда мы получим
Fd*r 1 Fgds*
tuX \ и2
и, следовательно,
/7
Но
Отсюда
, Fa dx Pa ds . Ppds2dy
\ ds flU i и2*/*
Fgtfs2 , Ppds4y
u2 "• н2г/лг , ,
/7 9/7 V*
Fdx2 + Pds2 a"aXm
—Fu4xd2x—Fgds2dx-\-Ppds2dy ,
Fdx2-\-Pds* —uau,
или
о , Fdx2-\-Pds2 , 2Fu2dxd2x 0 , 2^/д;
Полный интеграл этого уравнения (в предположении, ч
а = 0 при у и х, равных нулю) будет иметь вид:
U2.(Pds*-\-Fdx*) _ 2Fgx
156 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ ДВИЖЕНИЯ
Полагая
мы получим
и2 = 2pk,
k= V p '
Pds*-\-Fdx* #
n ndx -
Следует отметить, что -т- есть скорость тела г, так
как при нерастяжимости нити путь тела F за тот или иной
элемент времени так относится к пути тела Я, как dx
относится к ds.
Следствие I.
102. При g=p мы будем иметь
ds*-(Py — Fx)
k = -
Pds2-{-Fdx2 >
что совпадает с формулой, приводимой Бернулли (том II
петербургских «Commentarii») без доказательства[б1]. Эта
формула легко может быть получена на основании
принципа сохранения живых сил.
Следствие II.
103. Если pug равны нулю, т. е. если оба тела
вовсе не имеют веса, то
u*(Pds* + Fdx2) н
—i—rr-r^ ' — постоянной величине.
Pds*
Следствие III.
104. С не меньшей легкостью решалась бы предыдущая
задача и в том случае, если бы оба тела были тяжелыми
и если бы они, к тому же, двигались в среде,
сопротивляющейся пропорционально некоторой функции скорости.
В самом деле, тогда, беря всюду в выкладках
*SHe («>•>•
* Величина* <р(и) обозначает вообще некоторую4 функцию
от up)].
ЗАДАЧИ
157
вместо ~~ и> в уравнениях задачи,
вместо g, мы получим уравнение, в котором переменные
могут быть разделена в некоторых случаях,— например, при
(р(и) = а-\-Ьи2,
где а и Ъ — произвольные постоянные.
Действительно, если известно место тела F, то
известно и место тела Р. Поэтому для любого положения
тел F и Р мы будем иметь отношение dx к ds. Кроме
того, исходя из природы кривой СРр, мы можем знать
отношение dy к ds. Наконец, если положить
dx = qds,
то мы будем иметь
d2x = dqdst
и нам будет известно отношение dq к ds. Поэтому, полагая
dy=zrds
и
dq = zds,
мы в данном случае будем иметь
«=2rfj(pr — a — bu*)—*?pZ.(g+a + bu*q*)<
В этом уравнении переменные могут быть разделены
известными способами, причем мы предполагаем, что
квадратуры кривых возможны.
Следствие IV.
105. В том случае, если оба тела движутся по кривой,
введем обозначения (фиг. 36):
Ff*^dt, Fa=~dx и FN*=dz.
158 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ ДВИЖЕНИЯ
Тогда мы будем иметь
adt
gdz ds2
IT' и2 '
(OV=:
Fndt.
Вместо Fn тогда нужно будет взять —т— *), а вместо
нужно будет написать
Фиг. 36.
С этими незначительными изменениями задача решается,
и мы получим
Pds2 J
\t±
= 2/7^/y -
*) По той причине, что тело Р будет уравновешивать теперь
тело Z7, обладающее не скоростью <*», а скоростью, теряемой
им по направлению нити, в то время как остаток скорости
уничтожается сопротивлением кривой. (Примечание Безу.)
ЗАДАЧИ
159
Это уравнение можно получить также воспользовавшись
принципом сохранения живых сил. Если начальное
значение и равно нулю, то при у = Л и z = 0 мы будем иметь
u*(Pd*+Fdt*) _<>„ (v M_Eii
Следствие V.
106. Если в предыдущем п° положить
и2 = 2рк
л
то
[P(y—A) — Fz\dsi*
k— Pds*~\-Fdt*
Можно, если угодно, положить
в предположении, что тело Р опускается из точки С
и тогда
(Py—Fz)ds*
* =
Pds2-\-Fdt*
Герман (в томе II петербургских «Commentarii»)[63}
дает решение задачи, решаемой нами в п° 105. Формула
Германа (при Л = 0) сводится к следующему:
k--
' CFdx4z\A9
Pds* + Fdx*
а если положить
dt2 = dx2^dq2t
то
k =
»-»+1*&.
ds*
Pds*-\-Fdx*
В нашем же решении (при g=p) мы нашли
, 2/7 [(Ру — Far) ds2 — Fu2 dg2\
2р (Pds2 + Fdx2) *
160 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ ДВИЖЕНИЯ
что к выражению Германа приведено быть не может, так
как отрицательная величина
— Fu2dq2
не может быть равной положительной величине
Поскольку результат нашего решения совпадает с
результатом, полученным с помощью принципа сохранения живых
сил, и поскольку оно опирается лишь на принципы
исключительной ясности, мы можем считать, что в решение
Германа вкрался какой-то недосмотр *).
Примечание,
107. Решение задачи III может показаться несколько
длинным. Но я счел целесообразным показать, как в
данном случае применяется мой принцип. Если же кто желает
*) Решение Германа ошибочно в двух отношениях. Во-первых,
он приравнивает произведение — на мгновенный эффект
движущей силы одного из данных тел сумме количеств движения,
полученных обоими телами за элемент времени, — вместо того, чтобы
приравнивать его, как это показано в п° 107, количеству
движения, получаемому тем телом, движущая сила которого
рассматривается.
Во-вторых, обозначая через и скорость тела Р по
направлению Рр и через v скорость тела F по направлению FC, он
предполагает, что
du:dv — ds:dXi,
Правда,
u:v = ds:dx,
потому что эти малые отрезки, по предположению, описываются
за один и тот же элемент времени с постоянными скоростями.
Но то следствие, которое отсюда Герман получает, справедливо
лишь при условии, что ds и dx постоянны, или, по крайней мере,
если
d2s:d2x~ds:dx.
А принимать это нет никаких оснований. (Примечание Безу.)
ЗАДАЧИ
161
решать эту задачу иным способом, тот может поступить
следующим образом.
Пусть Т будет натяжение нити, одинаковое по
направлению СР и по направлению CF. Тогда в качестве силы,
ускоряющей тело Р по направлению Рр, мы должны взять
Ppdy Tdx
ds ds '
а в качестве силы, ускоряющей тело F по направлению Ff%
мы будем иметь
Tdx Fgdz
dt dt '
Тогда мы получим
(S£-¥)*-**
И
(Tdx Fgdz] ,, F .(a*dt*\
Складывая эти два уравнения и затем интегрируя, мы будем
иметь
u + Pds* —гРУ ^г-
Это решение, несомненно, проще, чем то, которое было
приведено в п° 105. Однако я полагаю, что оно далеко
не такое же ясное и не такое прямое. Дело в том, что,
строго говоря, нить- на тела не действует: она обладает
лишь силой сопротивления, а не силой импульса.
Задача IV.
108*). Тело Р движется по жолобу АРртс (фиг. 37)
и обладает какой-то ускоряющей силой (р. Это тело
тянет за собой два других тела М и М при помощи
*) Хотя эта задача в отношении своего содержания
расположена в надлежащем месте, тем не менее, если кому-нибудь она
покажется чересчур сложной, ее можно разбирать после задачи VII
и после следствий из этой последней.
11 Ж Даламбер
162 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ ДВИЖЕНИЯ
жесткого стержня МРЖ. Найти скорость тела Р и
кривые, описываемые телами М и М.
Пусть тела Р, М и М в течение какого-то элемента
времени описывают линии Р/?, MR и MR. Я провожу
рп = Рр = ра>
и предполагаю, что за тот элемент времени, за который
Фиг. 37.
тело Р в своем несвободном движении проходит линию /ж,
оно естественным образом и равномерно прошло бы о i
резок р/] а под влиянием силы <р, кроме того, отрезок fq.
Провожу, далее,
Ri^MR и Ri^=MR,
ЗАДАЧИ
163
Я также предполагаю, что за то же время, за которое
тело Р проходит /ж, тело М прошло бы отрезок RK,
а тело М — отрезок RK. Согласно нашему принципу нужно
разложить силу, направленную по RK, на две силы, RZ
и Re, а силу, направленную по RK, разложить также на
две силы, RZ и Re; при этом эти силы нужно взять таким
образом, что если бы тела Р, М и М обладали только
силами тг<7, RZ и RZ-, они находились бы в равновесии и
система оставалась бы в покое, а если бы эти тела
обладали лишь движениями /ж, Re и Re, они сохраняли бы
эти движения, нисколько не мешая друг другу. Иначе
говоря, должны соблюдаться равенства:
не = РМ, тге = ЯМ
и
ee = MN[.
Сначала я разлагаю силу, направленную по RZ, на две
силы, из которых одна, RV> должна лежать на
продолжении pR; силу, направленную по RZ, я, далее, разлагаю на
две силы, из которых одна, RV, должна лежать на
продолжении /?R. Кроме того, силы RV и RV я беру такими, что
если бы тела Я, М и М обладали лишь силами щ, RV
и RV, то они находились бы в равновесии: это возможно
в том случае, если, мысленно сложив эти силы в р, мы
получим одну равнодействующую, перпендикулярную к жо-
лобу.»Другими словами, должно иметь место равенство
M.RV.QP , M-RV-gP * ш
*) Силы, направленные по RV и RV, разлагаются здесь на
силы, перпендикулярные к рк, и на силы, направленные по тсрГ.
Первые уничтожаются жолобом. Следовательно, вторые силы
должны уничтожаться силой щ. Но эти силы равны
RV-GP RV-gP
РМ и РМ '
так как, очевидно, pR можно считать параллельной РМ. Отсюда
следует, что
Р.щ = И Т. Д,
(Примечание Везу.)
11*
164 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ ДВИЖЕНИЯ
У тел М и М остаются лишь силы RX и RX. Эти силы
должны уничтожать друг друга, а это возможно лишь в том
случае, когда линии RX и RX лежат на одной прямой RR
И К0ГДа M.RX=M.RX*). (В)
Пусть
РМ=а, GM=yy £М = у, РЖ = Ь
и постоянный перпендикуляр
PQ = c.
Пусть, далее, линия ММ или RR будет обозначена через е>
скорость в точке Р по направлению Рр — через #. Пусть,
наконец,
Pp^zdx, тг/=аа, RX=z и RX —z .
Тогда мы будем иметь
и . <pdx*
Если из центра р описать дугу тгсо и затем провести
линии т и иК и, кроме того, Ro параллельно VK, то ое
будет равна и параллельна RX **). Обозначая через г радиус
кривизны в точке р, мы получим:
*) Можно задать вопрос, нельзя ли сразу предположить, что,
поскольку силы RZ и RZ должны уничтожаться, они совпадают
по направлению с RV и RV и уравновешивают силу,
направленною по nq. Для того, чтобы ответить на этот вопрос, следует
заметить, что подобное предположение повлекло бы за собой
другое предположение , а именно, что тела М и М никак не
действуют друг на друга, — однако сущность дела не позволяет
сделать такое допущение. В самом деле, так как стержень
жесткий и угол МРМ. постоянный (по условию), то тела МиМ ведут
себя так же, как если бы они были соединены друг с другом
жестким стержнем ММ., (Примечание Безу.)
**) В самом деле, проведя линию ZK, мы найдем, что эта
линия будет равна и параллельна Re вследствие разложения,
которое здесь имеет место. Кроме того, линия Ro параллельна VJK
по условию, и их можно считать равными друг другу вследствие
того, что /Со и RV можно считать параллельными друг другу, а
по величине они бесконечно малые второго порядка. Отсюда
следует, что треугольник VZK можно считать подобным и равным
треугольнику Reo и потому линию VZ или RX можно считать
равной и параллельной ое. (Примечание Безу.)
8АДАЧИ
165
1°. Угол, образуемый pR и РМ, будет равен
*У , dx ^
У а2 —у2 "Г" г ''
Но *° """""^ равно квадрату этого угла (п° 91).
Следовательно,
2°. Мы будем иметь, далее,
. -. к<й*М(3 у dx2 ллч
MP га "
где г означает^ радиус кривизны кривой АРр в точке р.
*) Величина ■ . есть дифференциал угла GPM и она
у а2 —у2
должна быть равна TpR — GPM, так как угол GPM мы
рассматриваем не как угол, образуемый линией РМ и линией PQ
в различных ее положениях, а как угол, образуемый линией РМ
со всеми последовательно описываемыми линиями Рр, так что
угол GPM в следующий момент превращается в YpR и потому
TpR—GPM= dy
Va2—y2
dx
Кроме того, угол ТрР равен —, так как угол между двумя
элементами кривой равен углу между соответствующими
радиусами кривизны. Угол же между pR и РМ равен
TpR — GPM+YpP.
Отсюда следует, и т. д. (Примечание Безу.)
**) Мы можем записать
. —, ки • МG
потому что прямоугольный треугольник 1Ш0 с прямым углом в S
подобен треугольнику АГОР, поскольку линию я/ можно считать
параллельной РМ, (примечание Безу.)
166 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ ДВИЖЕНИЯ
3°. Описывая из центра L дуги MN и РТ, а из центра я
дугу iY> мы будем иметь
УК или m — TtK=^jer*).
Ввиду того, что
iK\MR = Kf:Ppy
это нам дает
Yf,_*f-RN_Kf-pT_Kf-PG_*'Va*—y*
А~~ Рр ~ Рр ~ MP — a
4°. Наконец,
тг#— tw = Ko = RV
oe-MQ zVa*—c***)
по— ъе = wy> =—-
MP a
Отсюда следует, что
ue — pR или ve — PM= — z^a2-cZ _/?K —
л
g)/"a2—j/2 , ydx*
4_2**! + *Г ^— +-12.
1 ar ' L У «2 — 3,2 I r J
*) Угол uK бесконечно мало отличается от острого угла PMR,
несмотря на то, что из чертежа этого совсем не видно: чтобы
избежать неясности, на чертеже мы вынуждены были бесконечно
малые, по условию, линии MR и Ri делать довольно большими.
Дуга IY должна упасть дальше //Г, если смотреть из точки тс, и
треугольник iYK будет подобен MRN.
**) Мы можем записать
oe-MQ
ко-
МР
В самом деле, проведя et перпендикулярно к ко, мы можем
разность ко и тс£, равную to, принять за разность ко — кв. Но
. ое • MQ
так как треугольник oet подобен треугольнику MQP вследствие
того, что, как доказано, линия ое параллельна RX или ЛШ, а
линия ot параллельна РМ. {Примечание Безу.)
ЗАДАЧИ
167
Но линия не должна быть равна РМ. Следовательно,
z у а2 — с2
а Ь«Н- а
йУд2 — у2
а
_ydx2 , Г dy , dxV<
Точно так же для другого тела М мы получим
(С)
Ъ t-RVi j =
dy
Yb2 — у2
?]'■
Р)
t/д:
Далее, я замечаю, что величина
MN — РТ
РМ
равна углу, образуемому pR и ЯМ. Но, как мы видели,
этот угол равен
*У , dx
уаъ — уг-Т r •
Следова1ельно,
MN = PT + PM- \—^==Л^^
_ydx . ady adx
Угол4 между (о/ и pR равен углу между pR и ЯЖ (п° 91);
угол между ш и тг/ равен
ЛИ* ;
угол между тг/ и tt# равен
iY _ iK-MN __ Kj-MN .
PAf-Aftf-PAf — Pp-MP '
угол между гс/С, или тго, и пе равен
oe-PQ zc
РМ2 ~~"а2%
168 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ ДВИЖЕНИЯ
Отсюда следует, что угол между не и ш (т. е. вторая
разность от угла между pR и РМ) будет равен сумме
всех этих углов, взятых с соответствующими знаками.
Таким образом, мы будем иметь
ydx
+ —Г'
1 adx у
Точно так же мы получим
dy
dx*- V&—y2
a2r
ady
adx
УЬ2 — у2
чу
+—г
Уф
b2r
I My
-Тг- (E)
Ь » |/~£2__y2
bdx
r
-£• (F)
Если в уравнения (А) и (В) вставить вместо входящих
в них линий соответствующие аналитические выражения,
то мы будем иметь
Ра
jdx?\
и* )
M.RV-YaZ—y*
а
М
м:
и, наконец,
— da
dx
.M.RV.I^I2, (G)
(H)
(L)
Вследствие жесткости стержня угол MP Ж будет
неизменным, так что ■— будет известной функцией от —.
Исключая из последних семи уравнений а, и, RV, RV, z
и z, мы получим в конечном счете одно уравнение,
содержащее лишь dx, у, dy и d2y. Это и будет уравнение
одной из кривых. Уравнение другой кривой после этого
найти будет нетрудно.
Для того, чтобы упростить выкладки, относящиеся
к данной задаче, обозначим угол МРО через (J, а посто-
ЗАДАЧИ
169
янный угол МРЖ через Л. Тогда мы получим
dy
у = д sin I
У а2—у2 = a cos (3,
кроме того,
Yb2 — у2
у = ^ sin (Л — р)
Yb2 — y2 = bcos(A—$)y
или, что то же,
у = Ь sin Л cos [} — 6 sin р cos Л
|/"ft2 — у2 = ^? cos Л cos р + * sin Л sin p.
Установив все это, вставим сначала во все уравнения
вместо а его значение
dudx
Mz
sl вместо z его значение -тт-. Затем, из уравнения (Е)
определим z и, подставив его в уравнения (С) и (D), найдем
RV и RV. Подставив полученные значения RV и RV
в уравнение (G), мы получим уравнение, которое после
интегрирования даст нам значение и. Подставляя это значение
и в уравнение (F), мы придем к окончательному уравнению,
содержащему лишь dх и р с его разностями d$ и d2$.
Если ¥> = 0, то уравнения обеих кривых можно найти
и без уравнения (L). Последнее в таком случае становится
необходимым лишь для нахождения и.
Замечание I.
109. Если MP и РМ представляют собой нити, то силы,
направленные по RX и RX становятся равными нулю, и
мы будем иметь
z = 0 и z = 0.
170 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ ДВИЖЕНИЯ
Но так как нам тогда неизвестна зависимость между у
и у, у нас будет в таком случае шесть уравнений и
четыре неизвестных a, RV, RV и а, подлежащих исключению.
В результате останется два уравнения.
Следствие I.
ПО. Для упрощения задачи предположим, что
г=со, 6 = 0 и <p = Q.
Это значит, что тело Р находится в прямолинейном жолобе
и оно тянет за собой единственное тело М при помощи
стержня или нити, —в данном случае это безразлично.
Тогда мы будем иметь
т/ Раа а У а?—у* , ady2
МУа2 — у2 а ' а2—у2*
Отсюда мы находим
Mady2
и
d
ydx ■
я ""* V а2— у2
a2 dxYaz—У2.
dy 1 _ «
У а2 у2\ а&х
Ma2dy2
~~ У а2—у2 [Ра2 + М {а2 —у2)]
Пусть
а
После подстановок мы будем иметь
— dp | ydy Mydy
р у а2 —у2 "^ {а2 — у2)3/з У а2 —у2 [Ра2 -\~М(а2~ у2)]'
Mcfidy
р {а2 — у2) [Ра2 + М {а2 —у2)]#
Умножая это уравнение на
р(а2-у2)
ЗАДАЧИ
171
п, затем, интегрируя, мы получим
Л~М
May
VPa* + M(a*-y2) " i'VPa*+M(a*-y2)(M+P)>
где Л обозначает некоторую постоянную, взятую при том
условии, что отношение dx к dyy выраженное через — ,
равно данному отнодиенню этих дифференциалов в тот
момент, когда тела начинают свое движение.
Следствие II.
111. Пусть в предыдущем следствии постоянная А
равна нулю. Тогда
р _ _ м . аУ
dx--
М + Р уаг—уъ
Mydy
(M+P)Vd2 — У2'
Последнее уравнение показывает, что в данном случае
искомая кривая есть геометрическая кривая [64]. Для того
чтобы построить эту кривую,
предположим, что СР (фиг. 38)
представляет собой положение
нити в начальный момент.
Описав из центра Р дугу СМК
и опустив из произвольной
точки М перпендикуляр ЛЮ>
отложим
PS-M
NS=GP
РО.
«X G Q N D
Фиг. 38.
Р 0 5
М+Р'
Проведя затем линию ОТ>
равную и параллельную РМУ
мы получим точку Т в качестве одной из точек кривой.
Найдем уравнение относительно координат NQ и QT. Для
этого прежде всего заметим, что
QT=MG=y.
172 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ ДВИЖЕНИЯ
Обозначив, далее, NP через / и NQ через t, мы найдем,
что
Следовательно,
И
Это есть не что иное, как уравнение эллипса, центр
которого D мы найдем, полагая
NP-P
а оси которого суть
DE=a и DX=Cg~- а'Р
'М+Р'
Отсюда следует, что если начальный импульс тел Р
и М будет таков, что начальное dx так относится к
начальному dy, как
— My
(М+Р)Уа*—у2
относится к единице, то тело М будет описывать эллипс, —
такой, как мы только что определили.
Следствие III.
112. Если положить
Рх=*т*М,
то общее выражение для dx примет вид
. У*У _ А УМ dy\ (1 -f-/и) а2 —У2
(1+ «)l/tf —Jf* У^=7а
ЗАДАЧИ
173
Отсюда видно, что если Л не равно нулю, то хотя кривая
и не будет геометрической, но она может быть построена
с помощью спрямления эллипса. В самом деле,
dyV(\ +т) а2 —у* dy У(\-\-т)^а* —ду2
У~а2—у2 Уд. у а2—у2
Но так как общая формула элемента дуги эллипса имеет вид
У а2 — у2
то, положив
(l+m)f = l и —^ = £—1,
откуда
1 р т
мы получим, что
dy V(l-f/я)а2 — .у2
У а2 - у2
есть элемент дуги эллипса, абсцисса которого равна у,
большая ось равна 2а, а отношение параметра к большой
оси равно
т
Притом эта дуга должна быть разделена на }/"#, или же
умножена на ]/ 1 -{- ш. Это значит, что указанное
выражение является элементом дуги эллипса, большая ось
которого равна
2аУТ+т,
абсцисса равна
а отношение параметра к этой оси равно
m
1 + /я'
174 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ „ДВИЖЕНИЯ
Замечание II.
113. То, что мы только что сказали в последних двух
следствиях и что вытекало у нас из общей задачи, можно
получить более просто из двух теорем, приведенных в
начале второй части (п°п° 83 и 84), а именно — что центр
тяжести g тел Р и М (фиг. 39)
S м ** опускается по прямой, перпендн-
[^Ту кулярной к жолобу PQ, или, по
крайней мере, что его движение,
параллельное PQ, является
равномерным. В самом деле, когда
N Г R
V Р Q центр тяжести g опускается по
Фиг. 39. прямой sgV, точка М> как это
известно из учения о
конических сечениях, будет описывать эллипс. И в других
случаях нужно лишь представить себе, что точка g
опускается по прямой, перпендикулярной к жолобу, в то время
как точка Р движется от Р к Q, а точка М описывает
эллипс, и вообразить, что мы заставляем затем всю систему
двигаться параллельно PQ, с той постоянной скоростью,
какую должен иметь центр тяжести параллельно PQ.
Отметим, что все это будет справедливо и в том случае,
когда тела Р и М имеют вес: тогда нужно лишь взять жо-
лоб горизонтальным.
Пусть PQ и MN суть начальные скорости,
сообщенные телам Р и М. Разложим скорость MN на две
скорости, из которых одна, MR, перпендикулярна к жолобу, а
другая, MS, параллельна ему. Отложим на RN такую часть
RT, чтобы соблюдалось равенство
M-RT=P.PQ.
Тогда
TN-M
М+Р
будет скоростью центра тяжести параллельно PQ, и задача
будет полностью решена, если, отвлекаясь от общей
скорости
TN-M
М + Р}
ЗАДАЧИ
175
мы найдем скорость точки М по своему эллипсу и
скорость точки Р. Найти это нетрудно с помощью принципа
сохранения живых сил, который ниже нами будет
доказан. Как видим, метод решения подобных задач довольно
простой.
Замечание III.
114, Если вместо того, чтобы предполагать, что тело
Р обладает ускоряющей силой <р, мы предположим, что
оно вынуждено двигаться по кривой АРр (см. фиг. 37) со
скоростью, изменяющейся по данному закону, то задача
всегда разрешается тем же самым
способом. Весь вопрос будет за- С
ключаться только в том, чтобы
найти силу <р (см. выше, п° 96).
Задача V.
115. Нить СтМ, закреплен-
пая в С (фиг. 40) и нагружен-
ная двумя грузами т и М,
бесконечно мало удалена от
вертикали СО. Найти
продолжительность колебаний этой нити.
Пусть за первый элемент
времени тело т проходит дугу ти>
а тело М за то же самое время —
дугу Mv. Mo^jcho считать, что
тело М имеет одновременно два
движения: движение MV,
равное и параллельное движению ти
тела /л, и движение Vv,
представляющее собой вращение
вокруг центра т или и. Разложим прежде всего
абсолютное усилие веса тела /гс[6Б], направленное по mQ, на два
усилия: одно из них пусть будет способно заставить тело т
пройти за первый элемент времени линию яш, а другое
пусть будет направлено по линии mR, положение которой
неизвестно. Второе" усилие должно уничтожиться, так как
Фиг. 40.
176 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ ДВИЖЕНИЯ
тело т может двигаться только по ти (по условию).
Разложим также абсолютное усилие веса тела М,
направленное по ML, на два усилия: одно из них пусть будет
способно заставить тело М пройти линию MV, а другое, MN,
пусть будет снова разложено на два усилия, из которых
одно способно заставить тело М пройти линию Vv, а
другое должно уничтожиться или, что сводится к тому же
самому, должно уравновешиваться с усилием, которое
направлено по mR и которое также должно уничтожиться.
Для этого необходимо, во-первых, чтобы то усилие тела М,
которое должно уничтожиться, было направлено по МРУ
в сторону продолжения тМ, и во-вторых, чтобы это
усилие так относилось к усилию, направленному по mR,
как бесконечно малый угол SmR (образуемый линией mR
и продолжением Cm) относится к углу MmS*)\ дело в том,
что для равновесия необходимо, чтобы равнодействующая
этих двух усилий была направлена по mS.
Установив всё это, положим
Ст = 1;
вес тела т пусть будет р, вес тела М пусть будет Р,
Mm = L, тК — х, MQ=y
и ускоряющая сила по направлению ти пусть будет ср.
Тогда 1° сила <р будет так относиться к весу р, как угол
RmQ относится к синусу прямого угла Rma. Поэтому,
обозначая полный синус через единицу, мы будем иметь
угол RmQ = ~.
*) Равнодействующая сила и две составляющие силы, как мы
видели, могут быть представлены диагональю и сторонами
параллелограмма, построенного на направлениях последних. Отсюда
нетрудно заключить, что любая из этих трех сил может быть
представлена также синусом угла, образуемого направлениями
двух других. В случае же бесконечно малых углов синусы будут
пропорциональны самим углам. Отсюда следует, и т. д. (Приме*
Нание Везу,)
ЗАДАЧИ
177
2°. Точно так же мы получим, что
угол ЛШ/,=-2-.
Отсюда
угол PMN==j- — ^,
и ускоряющая сила по направлению Vv равна
Усилие тела М по направлению MP бесконечно мало
отличается от усилия этого тела по направлению ML,
поэтому его можно выразить произведением М»Р. Но это
усилие будет так относиться к усилию тела т по
направлению mR (разному /#*р), как угол RmS, равный
относится к углу MmS, равному
у х_
L I •
Следовательно,
..,_вр_*.р(£_*),
откуда
/?лг M-Pf у х\
^~~ / т \L I )'
Таким образом, усилие по направлению Vv будет равно
Ру рх , М-Р/у jr\
L I "г т [ L I ) '
Если обозначить через / время, протекшее с начала
движения, то мы получим (см. п° 20) следующие урав-
1 2 Щ, Даламбер
178 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ ДВИЖЕНИЯ
нения:
-«'*=[f-^(i-i)h' «о
-"-[?-^-т('+¥)]^ <N>
С помощью этих двух уравнений можно определить
движение каждого тела.
Следствие I.
116. Если, по условию, начальные силы по
направлениям та и Vv относятся одна к другой, как тК к MQ,
т. е., другими словами, если
рх | МРх МРу луР М-\-т х (^ ( М-Р\
I ' 1т
МРу уР М-\-т х / , М-Р\ ,~.
Lm L т I у ' т ) -7' v '
то я утверждаю, что тела Мит окажутся на вертикали
СО одновременно. В самом деле, для этого нужно, чтобы
дуги MQ и тК были пройдены за одно и то же время.
Но если указанная пропорция имеет место, то малые части,
на которые за первый и последующие элементы времени
уменьшаются дуги тК и MQ, будут пропорциональны этим
дугам, а ускоряющие силы будут пропорциональны дугам,
которые остается пройти до положения равновесия, Отсюда
следует, и т. д.
Пропорция (О) приводит к уравнению
рху , МРху МРу2 ухР ^ М-\-т х2(п ? М-Р\
I • lm Lm L т
откуда
у М-\-т pLm L ,
х2/ . М-Р\
х 2М 2МР1 21
/pLm , L . /M-\-m pLm /Л 2
MPl I / ' \ 2M 2MPI 2/ J •
*) Выражениям d2x и d2y придан здесь знак минус, хотя
движение и ускоренное. Но нужно заметить, что когда t
увеличивается, хну уменьшаются. (Примечание Везу.)
ЗАДАЧИ
179
или
у-\-х — т-\-М . pLm , L .
х ~~ 2М "+" 2AW/ "Т 27"=tz
-U */pLm 1 ^ 1 (М-{-т pLm L \2
— К Л«Р/ "Г / "Г* V 2М "ШЯ/ 2/ J '
Следствие II.
117. При Р—/?, т. е. если тела Мит имеют
одинаковый удельный вес, мы получим
J>-{-x_Ml — ml-j-ML + mL ,
х ~ 2М1 —
, , /jMmLl + 4APLI +(М1 + ml—ML— ml)*
± К 2ЛЙ *
Выражение, стоящее под знаком корня, может быть
преобразовано, и мы получим другой корень
УШтЬ* + (ml -\-ML-\-Ml — ml)2.
Мы нашли точно такое же отношение у-\-х к х, какое
получено только для данного случая Даниилом Бернулли
(петербургские «Gommentarii», том VI, стр. 111)[66].
Доказательство было дано им же после, в томе VII того же
издания [67]. Решение той же самой задачи дал и Эйлер
в тцме VIII [68]. Я счел необходимым показать, как в
данном случае применяется мой принцип, во-первых, ввиду
того, что это интересно само по себе, и во-вторых, ввиду
того, что он может быть пригоден для решения многих
других задач подобного рода.
Я дальше покажу, что имеются и другие случаи, когда
оба тела достигают вертикальной линии СО одновременно.
Следствие III.
118. Если положение нити СМт в начале движения не
таково, как указано в предыдущем следствии, или если
вообще это положение произвольное, то для того, чтобы
найти движение тел т и М, необходимо в данном случав
12*
180 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ ДВИЖЕНИЯ
прибегнуть к интегрированию уравнений (К) и (N),
приведённых в п° 115. Сначала, для того, чтобы выкладки были
возможно проще, мы предположим, что не только
Р=Р,
но
М=т и 1=1.
Далее, для того чтобы уравнения (К) и (N) сделать
однородными, мы условимся, что время, в течение которого
ускоряющая сила р заставляет тела т и М пройти путь /,
равно 7[69]. Таким образом, уравнения (К) и (N) принимают
вид
и ^(рх = (2х—у)2^ (Р)
-d2ys={2y-2x)?P (Q)
(см. п° 27).
Для интегрирования полученных уравнений я
воспользуюсь методом, указанным мною в «Memoires de l'Acade-
mie des Sciences de Berlin» за 1748 г. и также в другом
месте.
Второе уравнение я умножаю на неопределенный
множитель v и складываю с первым. Я получаю
_d2je_vd2y = 2^.[(2_2v)j: + (2v — l)y]. (R)
Я добиваюсь того, чтобы
(2_2v)*-f(2v — \)у
было кратным—х — vy. Это нам дает
V '
откуда
— V2
ЗАДАЧИ 181
Следовательно, вводя обозначения
х-\-уу=и, т. е. * + --£===«
и
V-2.
мы получим диа уравнения:
— (12ц = (2— V2)-
-^ 2udt»
-r4 2u'dt*
-rfV = (2 + l/2).^l.
Умножая первое уравнение на da, мы получим интеграл
откуда
Va*=u? ТУ
потому что, когда t увеличивается, а уменьшается. Отсюда
следует:
tf = ,4cos r
a' = BcostV*+^.
Это будут полные интегралы, так как, поскольку при /=0
величины dx и 'dy равны нулю, необходимо, чтобы при
* = 0 величины da и duf также обращались в нуль. Из
полученных равенств мы определим х и у, а зная
величины х и у при * = 0, мы найдем постоянные А и В.
182 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ ДВИЖЕНИЯ
Замечание I.
119. Если в только что разобранном случае, т. е. когда
P=zp, М = т и Z, = /,
требуется определить, каково должно быть отношение
линий X и У для того, чтобы тела т и М оказались на
вертикали одновременно, то мы находим (п° 116)
2Х—У_Х
2У—2Х~~ У '
откуда
У2 = 2Х2,
или
Мы получили то же значение, что и для —.Ив самом
деле, стоит лишь немного вдуматься в сущность вопроса,
и мы увидим, что если даны два тела т и Ж, то для
того, чтобы грузы т и М оба оказались на вертикали
одновременно, необходимо, чтобы оба значения — равнялись
Y
значениям -гг. Действительно, поскольку оба тела
приходят на вертикальную линию одновременно, отношение х
к у, отношение dх к dy и отношение d2x к d2y должны
быть неизменными и должны равняться отношению X к У.
Придадим же в таком случае неопределенной величине v
такое значение, чтобы имело место равенство
1 _ У
Тогда очевидно, что в уравнении
-^-v^ = [(2-2v).^ + (2v-l)^]^-
ЗАДАЧИ
183
левая часть обратится в нуль и правая часть поэтому также
равна нулю. Но это возможно лишь в двух случаях: или
когда
2— 2у у_ К J_
2v— 1 х X v »
или когда одновременно
2 — 2v=0
и
2v—1 =0.
Поскольку, однако, последняя возможность содержит
в себе противоречие, отсюда следует, что когда
J^_ Y
v — X'
величина v определяется уравнением
2 —2v 1
2v — 1 v *
Это уравнение ничем не отличается от уравнения,
полученного нами выше в общем случае, когда отношение Y
к X было произвольным. Следовательно, отрицательное
значение — из последнего уравнения должно быть равно
положительному значению отношения У к Х> полученного
из предыдущего уравнения, и, обратно, положительное
значение первого должно быть равно отрицательному значению
второго.
Замечание II.
120. Нетрудно видеть, что рассуждения предыдущего
п° могут быть применены и в том случае, когда ни одно
из равенств
Р=р, М=т и L = /
не имеет места. Действительно, если взять на себя труд
провести нужные выкладки, то можно убедиться в том,
что уравнение относительно— отличается от уравнения от-
Y
носительно -у только знаком во втором члене.
184 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ ДВИЖЕНИЯ
В самом деле, уравнения (К) и (N) п° 115 в общем
случае могут быть представлены в виде
d2x = {ax-\-by)dt*
и
d2y = {cx-\-ey)dt2.
Но для того, чтобы тела приходили на вертикаль
одновременно, необходимо, чтобы соблюдалась пропорция
ах-\-Ьу х
сх-\-еу у
С другой стороны, для определения — необходимо иметь
а -f- £V = ~ .
1 V
Расположив эти уравнения — одно относительно — , а
другое относительно —, мы увидим, что они отличаются
лишь знаком во втором члене.
Легко видеть, что корень в выражении — всегда
будет вещественным числом (см. п° 116). Таким образом,
корни приведенного там уравнения не равны друг другу.
Отсюда следует, что и уравнение относительно v, имею-
у
щее те же самые корни, что и уравнение относительно— ,
но только с обратными знаками, также не может иметь
двух одинаковых корней. Кроме того, совершенно нетрудно
убедиться в том, что радикал будет всегда больше
выражения, стоящего вне радикала. А отсюда следует, что ни
i , ни v не могут обращаться в нуль.
д»
Замечание III.
121. В решении данной задачи я рассматриваю движение
груза М как бы составленным из двух движений, — одного
MV, общего с грузом т, и другого Vv, являющегося
вращением вокруг точки т, как центра, — только для того,
ЗАДАЧИ
185
чтобы подготовить читателя к решению последующих
задач, решение которых при подобном рассмотрении сильно
облегчается. Можно было бы разложить действие тяжести М,
направленное по ML, сначала на два действия: одно
должно создавать движение Mv тела М, а другое, направ-
вленное по MP, должно уничтожаться. Таким путем мы
найдем ускоряющую силу, направленную по Mv и равную
p-slnLMP=Q;
угол SmR будет равен
SmM.P-M^ (у х\ РМ
р-т \L I ) р-т
Отсюда
*««»«-7-[(*-т)-7£].
а следовательно, ускоряющая сила по направлению та
будет равна произведению р на это последнее выражение.
Таким образом, так как х есть то расстояние, которое
эта ускоряющая сила стремится заставить пройти тело т,
а х-\-у есть то расстояние, которое полная ускоряющая
сила стремится заставить пройти тело М, мы будем иметь
и
— d2x — d2y = fxl^2'
Первое из этих уравнений есть не что иное, как
уравнение (К) из п° 115, а второе является не чем иным, как
сочетанием уравнений (К) и (N) из того же п°. Отсюда
следует, что новое решение приводит нас к тому же, что мы
уже имели в п° 115.
Замечание IV.
122. Если расстояния данных двух тел от вертикали,
обозначенные нами в предыдущем п° через х и х-\-у,
обозначить теперь через х и у, то мы получим уравнения
движения обоих тел, подставив у вместо х-\-у и,
следовательно, у — х вместо у.
186 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ ДВИЖЕНИЯ
Положим, что
р=р,
и введем еще следующие обозначения: пусть расстояние,
проходимое свободно падающим тяжелым телом за время Г,
будет равно а; далее, пусть
г 2аМ
1— Lm '
2а
<Р= —v
II = -
Тогда в качестве общих уравнений движения данных тел
мы получим
(см. п° 118).
В точности, следуя методу, указанному в п° 118, мы
найдем два значения v, а именно:
_-Д + П±У(П-Д)» + 4Гу
2?
Обозначив эти значения через v и v', мы будем иметь
и —A cos уКД-f-vcp, и'— В cos уКД-f-v'^,
х
Отсюда, обозначив через а и р значения хну при t — 0,
мы получим
B=a-\-v'$,
(v'a + w'P)cos ^-VA4-v? — (va + vv'P)cos -^A-f V'<P
ДГ = ; >
У V
(a + vg) cos yJ/A + v<o — (a + v'f) cos уУд + v'?
«я- - .
• v — v'
ЗАДАЧИ
187
Отсюда простым построением можно определить х и у,
В самом деле, пусть
х = G cos /?/ -]- rG cos <7^>
j; = Н COS р/ -}" ^ cos ?'•
Опишем дуги окружностей радиусами
С4 = 0, CD = H и СЯ = Л/
(фиг. 41). Построив угол ЛС/,, равный pt, и угол ЛС/7,
равный qt, мы будем иметь
x = CZ + r-CO
CZ-CD , CG-СД
= C4'-fCO.
У~г СА "Т" СЛ
В первом издании настоящего сочинения мною было
'£<^
-" и
/\<^ о
/ /г\
С
к
8
~АГ^^
v^Ni
z ~~/^0\
С
Фиг. 4L
дано другое решение этой задачи. Решение, приводимое
здесь, гораздо проще.
Если
a + vp =0,
или
a + v'p = 0f
т. е. если
р —1 —1
— = , или -—.
что соответствует сл>чаю, рассмотренному в п° 116 и
120, то величины х и у будут состоять только из одного
188 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ ДВИЖЕНИЯ
члена, и отношение х к у будет равно постоянному числу.
Это совпадает с тем, что было замечено в п° 116.
Можно еще заметить, что это единственный случай,
когда величины х и у состоят из одного только члена.
В самом деле, невозможно ни одно из следующих
равенств:
v = 0, v'=0, v = v'
(см. n° 120). Следовательно, один из членов в выражении
х может обратиться в нуль лишь в том случае, если
a-{-vf} = 0 или a-j-v'fi = 0.
То же самое можно сказать и о выражении для у.
Так как v и v' никогда не могут быть равными друг
другу (см. п° 120), отсюда вытекает, что если выражения
для хну состоят из двух членов, т. е. если ни одно
из равенств
a-f-vp = 0, a_|-v'p = 0
не имеет места, то отношение х к у никогда не может
быть постоянным.
Наконец, можно отметить, что ни один из членов в
выражениях для х или у не может быть постоянным числом.
В самом деле, для этого необходимо было бы, чтобы
Д-|~у^=0, или A-J~v'<p=0.
Но это означало бы, что имеет место равенство
1—I
ср —п'
или
L.4- — 4-— = —
/ ' //я ' /я т '
что невозможно.
Замечание V.
123* Читатель может сравнить наше решение с
решением такой же задачи, приведенным Даниилом Бернулли в
«Memoires de PAcademie Royale des Sciences de Berlin»
за 1753 г. [70], и судить о том, какое решение проще и
в особенности какое из них — более прямое.
ЗАДАЧИ
189
Здесь я ограничусь лишь указанием, что в
вышеприведенных выражениях для х и у легко узнать те самые
двойные колебания, которые в рассматриваемом движении
маятника заметил Бернулли. Каждое из колебаний
представлено одним из двух членов, входящих в выражения
х и у.
В самом деле, уравнение движения простого маятника
длиной X имеет вид
или
s = #cos-ij/2?.
Отсюда нетрудно видеть, что движения тел Мит
складываются из двух движений, каждое из которых синхронно
с движением некоторого простого маятника. За
подробностями, если они будут необходимы, можно отослать к статье
Бернулли.
Что, однако, необходимо здесь отметить и что, мне
кажется, должен был отметить Бернулли, это то, что те
два «колебания», о которых здесь идет речь, могут быть
названы колебаниями только не в собственном смысле. Дело
в том, что одно из этих колебаний совершается
относительно движущейся точки,— точки, которая сама
совершает колебания. В силу этого оба колебания будут взаимно
изменять друг друга,— так сказать, искажать друг друга.
Вследствие этого какая-нибудь бесконечно малая часть
колебания, происходящая, например, слева направо
относительно подвижной точки, в действительности в абсолютном
пространстве будет происходить справа налево,— если в
данный момент скорость колебания этой подвижной точки
будет больше и направлена справа налево. Вот почему по
отношению к абсолютному пространству в маятнике,
собственно говоря, вовсе нет двойного колебания, а есть только
одно единственное колебание. Правда, абсолютные
колебания тел не всегда будут происходить одновременно, так
что одно тело может в течение данного времени сделать
190 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ ДВИЖЕНИЯ
больше колебаний, чем другое. Но при этом каждое тело
в отдельности будет совершать в действительности
простые колебания.
Замечание VI.
124. Колебания тела т кончаются тогда, когда dx
становится равным нулю, а колебания тела М — тогда,
когда dy становится равным нулю: скорость тогда'
делается равной нулю.
Таким образом, колебания тела т кончаются, во-первых,
в том случае, когда одновременно будут осуществляться
равенства
sin^]/A-{-v<p = 0
и
sinyj/A + v'cp=0.
Но это будет иметь место в том случае, когда отношение
]/Д-{-У<р к |^Д-[~ч/ср будет равно отношению двух целых
чисел и t будет таково, что --]/ Д-|~^ и ._, ]/д _|-v'tf
будут кратными 180 градусов: тогда синусы обоих углов
будут равны нулю.
Во-вторых, колебания тела т кончаются, когда будет
соблюдаться равенство
sin—l/A + Vcp ]/^ + v<p.v'.(a-fvf*)
sin у-]/Д+ 4'?"_)/Д + у'<р.у.(а + у'Р)
Это последнее равенство будет иметь место только в
том случае, когда отношение V0 не
будет равно отношению двух целых чисел.
Точно так же и колебания тела М кончаются,
во-первых, когда t принимает значения, указанные в первом из
только что приведенных двух случаев; во-вторых, когда
sin-rT/A + v'cp УД-fvcp (о + vf)
ЗАДАЧИ
191
Отсюда следует
1°. Если мы имеем
v'a + vv'j5 = 0
и
что сводится к равенству
то колебания обоих тел кончаются одновременно. Тот же
результат мы будем иметь и в том случае, если
a + v'P = 0.
Легко видеть (см. п° 120), что эти два случая
соответствуют случаю, указанному в п° 116.
2°. Если отношение j/*A~f-v<p к ]/"A-|-v'<p не равно
отношению двух целых чисел, то колебания тел Мит
никогда не будут кончаться одновременно. В самом деле,
значение
sin у УД-f V'^
sin у VA + v<p
для тела т будет относиться к значению того же
выражения для тела Ж, как v' к v. Но v' никогда не может
равняться *v (п° 120). Отсюда следует, что ни при каком
значении t величины dx и dy не могут одновременно
обратиться в нуль.
3°. Если [/"Д-j-vy и [/"Д-j-v'y относятся между собой
как два целых числа, то некоторые колебания обоих тел
будут кончаться одновременно: это будет иметь место тогда,
когда выполняются одновременно два равенства
sin у УД-j-vy — 0
и
sin у\' Д-J-v'y = 0.
192 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ ДВИЖЕНИЯ
Если же оба уравнения, определяющие значение
sin угУ"Д + усР
имеют одно возможное решение, или, по крайней мере,
таковым будет одно из этих уравнений, тогда все
колебания обоих тел не будут кончаться одновременно.
Следует заметить, что решение указанных уравнений
будет невозможно не только в том случае, когда
неизвестное является мнимым, но и в том случае, когда оно
(безразлично, положительное или отрицательное) больше
единицы: ведь синус любого угла не может быть больше
полного синуса.
Если лишь одно из двух уравнений имеет одно
возможное решение, то то тело, к которому это уравнение относится
(скажем, тело т), будет совершать колебаний больше, чем
другое тело. И всякий раз тогда, когда кончается
колебание тела Ж, будет кончаться и одно из колебаний тела т.
4°. Наконец, все колебания обоих тел будут кончаться
одновременно, если отношение ]/"д -[-v<p к "j/д -\-v'cp равно
отношению двух целых чисел и если оба уравнения,
определяющие значения
sin-y-V^ + vcp
вовсе не имеют возможных решений. Пусть, например,
УД + vcp
Тогда
ЗАДАЧИ
193
Отсюда следует, что мы будем иметь одновременно два
равенства
2cosJ-i/T-i _ »'(« + >?)
2cosTKA + ^— 2v(a + v'P)
и
2 cos 4-^1+^==^^^.
Но так как величины a и p совершенно не зависят от
уравнения
Т/Д-f-vcp
поскольку они не входят в это уравнение, то очевидно,
что a-f-v'f} можно предположить столь малым (однако не
равным в точности нулю), что оба выражения
2(a + v'p) 2v(a-f->'W
могут быть больше 2 и, следовательно, больше
2cos^r]/rA-f v<p.
Отсюда с очевидностью вытекает, что первый из указанных
случаев, соответствующий случаю п°116, не единственный
случай, когда колебания обоих тел синхронны, т. е.
начинаются и кончаются в одно и то же время.
Настоящее замечание тем более важно, что до сего
времени, кажется, предполагали обратное.
Замечание VII.
125. Точно таким же образом, приравнивая нулю
выражения для х и у, мы определим, когда оба тела будут
находиться на вертикали, а также и те случаи, когда они
придут туда одновременно. Легко можно убедиться, что
эти случаи не исчерпываются случаями, указанными в п° 116,
когда полуколебания обоих тел (так я называю колебания,
13 Ж. Даламбер
194 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ ДВИЖЕНИЯ
заканчивающиеся на вертикали) всегда будут кончаться
одновременно.
Действительно, если, например,
У д + *р '
то мы имеем
cos у Уд -}- v'cp = cos у УД -f- V'f.
Следовательно, если
C0SyVb-irvy = ti1
то
cos у у д -[- Vy = 4я3 — За;
в этом случае, если
cosy-yX+^^o,
то и
cosy-y Д-j-v'cp^O.
И для того, чтобы все полуколебания кончались
одновременно, нужно, чтобы
4й2 — 3
не было равно ни
v'(« + vE)
v(a + v'P)'
НИ
a-f- vjS
Но это будет иметь место в том случае, если, например,
а и (5 мы возьмем такими, что a-}->'{} будет весьма
малым, но не окончательно равным нулю. И уже этот один
пример показывает, что имеется бесчисленное количество
других подобных случаев, не менее возможных.
ЗАДАЧИ 195
Первый из четырех случаев п°124 точно так же — не
единственный случай, когда и колебания, и полуколебания
синхронны. Пусть, например,
где т — целое нечетное число. Ясно, что если
sinTl/A-|-v<f> =0,
то и
8ln7-yA4-v'v = 0f
так как в таком случае
у У Д + v?
равно некоторому целому числу полуокружностей, и
потому
t . mt _
уУд + v'cp, или T]/A + v?,
будет также равно некоторому целому числу
полуокружностей.
В таком случае легко видеть, что если
cosir]/A^.V(p =о,
то и
с°«7УД + ^=0.
В самом деле,
— У Д + vcp
тогда будет равно 90 градусам, взятым нечетное число
раз, и то же самое можно сказать и о
mt . j
13*
196 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ ДВИЖЕНИЯ
Отсюда следует, что в данном случае как полные
колебания, так и полуколебания всегда будут оканчиваться
одновременно, если соблюдаются другие условия, указанные
выше, в настоящем и предыдущем п°, — если, например,
a-f-v'P очень мало и т. д.
Замечание VIII.
126. Если оба тела обладают некоторой начальной
скоростью, так что
— dx — dy ,
-HT=Z и ~dT=h'
то уравнения интегрируются с неменьшей легкостью. Тогда
нужно принять во внимание, что так как
, v'du — vda' , da — du'
dx=: -, и dy = — ,
V V "' V Y
du du' , Л
то отсюда мы найдем значения — и — при г = 0, и эти
значения будут очень просто выражаться через g и h.
Пусть при t = 0 мы будем иметь
— du — du*
-1Г = П и —=Y-
Из уравнения
— d*u = Kudt*
мы получим
где Л есть заданное нам значение и при / = 0. Отсюда
следует, что
dtVK-- ~~da
y/t + A2_u2
откуда, если обозначить через Ь угол, косинус которого
равен Л, а синус равен ■ !!_■, мы получим
и = cos (/ VK+ 8) = cos S cos / ]/"#— sin д sin / УК,
ЗАДАЧИ
197
что, как легко видеть, дает
и = A cos t УК— —=~ sin t УК.
Vk
Точно таким же образом мы можем найти и значение и\
Следствие IV.
127. В общем случае, когда нить СМт\х (фиг. 42)
нагружена произвольным числом грузов М, т, р. и т. д.,
бесконечно мало
удаленных от вертикали, всегда
можно определить
ускоряющую силу любого из
этих тел,
воспользовавшись одним из двух
способов, указанных вп°115
и в п°121 для случая
двух тел.
Предположим,
например, что мы имеем три
тела М, т и jjl, веса
которых Р, р и тг,
направленные по МА, та и \ха,
разложены каждый на две
составляющие; первыми
из этих двух
составляющих пусть будут "
ускоряющие силы тел М, т
и р., направленные по
MV, та и \хо; вторые
же, направленные по MB, mb и jjlZ, должны
уравновешиваться. Продолжая CM, Mm и т\х, проведем линии MR,
тг и jxZ. Ясно, что силы, направленные по jxZ и тЬ,
следует считать равными весам тел |х и ж, и ясно, что их
можно привести к одной силе, направленной по тг; эту
силу можно рассматривать как сумму данных сил. Таким
же образом силу, направленную по тг, или по Mm, и силу,
направленную по MB, которую можно считать равной весу
Фиг. 42.
198 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ ДВИЖЕНИЯ
тела М, можно привести к одной силе, направленной по
MR. Поэтому ускоряющая сила тела р. будет равна
тт.угол Zjia;
ускоряющая сила тела т будет равна
р • угол гта — угол rm\i -^~- ;
наконец, сила тела М будет равна
Р. [угол RMA — угол RMmp'mp}^ 'Л .
В общем случае очевидно, что если для упрощения
выкладок все веса предположить равными одной и той же
величине g, принятой за единицу, и если буквами /?, д, г, s
и т. д. обозндчить углы МСОу mAIR, \ипг и т. д., а
буквами В, С, Z), Е и т. д. обозначить последовательно все
массы, идя сверху вниз, то ускоряющие силы всех тел,
начиная с самого нижнего, будут равны
P + V + r+s> P + <l + r — s-§,
, E+D E+D + C
Это совпадает с результатами, полученными Д. Бернулли
(см. том VII петербургских- «Commentarib, стр. 170)[71].
Следствие V.
128. Предположим, что нить нагружена только тремя
телами, равными между собой, и пусть их расстояния от
вертикали будут равны (если итти сверху вниз) дг, у и z.
Пусть, кроме того, части нити, заключенные между этими
телами, равны между собою. Тогда для того, чтобы данные
тела одновременно достигали вертикали, необходимо, чтобы
соблюдались пропорции
х:у = (р — Щ:(р-\-Я — г)
и
*'-У = (Р + <1 + г):(Р + <1 — г)>
ЗАДАЧИ 199
или, беря вместо /?, q, г пропорциональные им величины
лг, у— 2х и z — 2у-\-х, мы будем иметь
и
Отсюда
и
х:у = (5х— 2y):(3y — 2x — z)
z:y = (z—у):(3у — 2х — г),
(Зу—2х — z)z = (z—у) у
(Зу — 2х — z) х == (5л: — 2у) у.
Следовательно,
z = — 5^ + ^4-зу— 2* = 1Г — 2у — 2х
Отсюда мы получаем
^-Зу-2х = -% + % + 4у+Ш-Щ-Ш.
Деля все члены полученного уравнения на х и располагая
у
их по степеням — , мы получим
Это уравнение совпадает с уравнением, полученным Д. Бер-
нулли (см. петербургские «Commentarii», т. VI, стр. 112)[72],
который принимает за единицу то, что мы здесь обозначали
через лг, а буквой х обозначает то, что у нас
выражается отношением —.
х
Замечание IX.
129. Вообще, если при произвольном числе тел и при
произвольных расстояниях между ними нужно, чтобы все
тела приходили на вертикаль одновременно, то расстояния
третьего, четвертого и т. д. тела от вертикали будут
200 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ ДВИЖЕНИЯ
всегда выражаться линейно через —. Далее, степень
уравнения, расположенного по степеням — , будет равна числу
тел, и все корни этого уравнения будут вещественными.
Действительно, легко видеть, что если, например, в
случае трех тел допустить, что тело, расположенное выше
всех, отстоит от вертикали на весьма малое расстояние, то
для каждого из остальных двух тел могут быть указаны
три положения, при которых они оба приходят на
вертикаль одновременно с первым: одно положение, когда оба
эти тела находятся по ту же сторону от вертикали, что
и первое тело, и два положения, когда одно тело
находится по одну сторону с первым телом, а другое — по
другую сторону. Вообще, при заданном положении первого
тела второе и остальные тела будут иметь всегда столько
возможных положений, сколько имеется тел. Отсюда
следует, что — имеет столько вещественных значений, сколько
существует тел, а потому у уравнения, расположенного
по степеням —, все корни должны быть вещественными.
Отсюда следует, что при заданном бесконечно малом
расстоянии верхнего тела от вертикали каждое из остальных
тел может иметь столько различных положений, сколько
всего имеется тел.
Следствие VI.
130. Если при тех же предположениях, что и в
следствии V, требуется определить движение каждого тела
в отдельности, не заботясь о том, чтобы все тела
приходили на вертикаль одновременно, то мы получим три
уравнения:
-<Px = (5x-2y).?ff, (S)
-<Py = (3y — 2x — z)-^, (Т)
-cPz = (z-y).%£. (U)
ЗАДАЧИ
201
Для интегрирования этих уравнений я умножаю второе
уравнение на v, третье — на |х и складываю все три
уравнения. Я получаю тогда
— d2x — v d2y — \i d2z =
= [(5_2v)* + (3v-2_^+te-v)*]..^.
Полагаю
5-2у=-2 + 3"-^'1^,
V ц 7
что дает
^ — _ 2 + 3v — 5v -f 2v2 = 2у2 — 2v — 2
и
(5 — 2 v) • (2v2 — 2v — 2) = 2v2 — 3v — 2.
Отсюда мы получаем уравнение
V3 I v2 v ^ —
Располагая последнее уравнение по степеням v, мы найдем,
что оно имеет точно такой же вид, как и уравнение
х* д;2Тд;Т0 v>
полученное нами выше, в п° 128, и что все корни этого
уравнения будут вещественными (п° 129). Впрочем, мы это
докажем иным способом в следующем п°.
Пусть v, v' и v" будут три корня этого уравнения.
Тогда
pL = 2v2 — 2v —2,
p,' = 2v'2 —2v' —2,
jx" = 2v"2 — 2v" — 2.
Полагая
x~\-v'y-\-V-'z =я'|
лг -f- v",y -f- \s!'z — u\
202 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ движения
мы получим три уравнения
— d*u =(5 — 2v). -75-,
7*2 •
— rf»n' = (5 —2v#).
— rfV = (5 —2/)
Отсюда можно, как в п°118, определить значения *и, и9
и и" и, следовательно, х, у п z.
Таким же образом решается задача и при любом числе
тел, каково бы ни было отношение масс этих тел.
Замечание X.
131. В том случае, когда у того уравнения, из
которого определяется v, не все корни вещественны, решение
задачи, как нетрудно убедиться, также возможно. В самом
деле, так как переменные дг, у, z и т. д. должны, очевидно,
иметь вещественные значения, зависящие от /, то мнимые
величины, если они и есть, должны взаимно уничтожиться
в выражениях этих переменных. Действительно, как я
показал в другом месте, любое заданное мнимое выражение
и любой мнимый корень какого-либо уравнения может быть
приведен к виду
где а и р — вещественные величины. Отсюда следует, что
даже в том случае, если у v все корни мнимые, уравнения
относительно и, и' и т. д. можно привести к виду
— Лг ==( + « +РУГ-:^)«<«8.
Это уравнение имеет интеграл
О См. «M&noires de TAcademie do Berlin» за 1748 и
1750 гг. [75].
ЗАДАЧИ
203
Но, как известно,
cz Y~x = cos z ± У— Ь sin z
и
c~z -1 = cos z + ]/"— 1.sinz.
Отсюда следует, что
и = Лс8' (cos at + K^-l • sin s^) -\-
+ £c-s<(cos6/ =f К11"!-sin at).
Такой же вид будут иметь и выражения для и', d' и т. д.
Следовательно, в х, у, z и т. д. могут входить только
выражения вида с5', sin at и cos at с вещественными или
мнимыми коэффициентами. А так как х, уу z и т. д.
должны быть вещественными величинами и так как в силу
того, что данное решение является общим решением и
потому непременно должно дать эти величины, то отсюда
следует, что мнимые величины (если только они будут)
непременно должны уничтожиться.
Однако из самого выражения для и нетрудно показать,
что мнимых величин не будет. В самом деле, уравнения
x-\-vy-\-\i.z = u и т. д.
показывают, что выражения для и, и' и т. д. получаются
из выражений для х> у, z. Но при ^ = 0 должны иметь
место равенства
dx = 0, • dy = 0, dz~0f
так как, по условию, тела выходят из состояния покоя.
Отсюда следует, что при t = 0 мы будем иметь
du = 0, du' — О и т. д.
Следовательно,
ЬА — ЪВ±аУ^-1-АЗ-еУ^Т>В=:0,
откуда или
или
8 = 0 и 8 = 0,
204 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ движения
Можно показать, что 3 должно равняться нулю.
Действительно, величины х, у, z и т. д. должны всегда быть
чрезвычайно малыми по характеру самой задачи: ясно, что
каждое тело может совершать лишь колебания небольшого
протяжения. Поэтому выражения для лг, у, z и т. д. не
могут содержать величин вида сы, так как в таком случае
они возрастали бы до бесконечности. Вследствие этого и и
не должно содержать такого рода величин. Поэтому
§ = 0.
Отсюда следует, что
и = (Л -f В) cos et ± {Л — В) V~—\ • sin st.
И так как и не должно содержать мнимых величин, то
(A — B)V^\-sinet==0,
откуда
А = В.
В результате, так как
и — (Л -f- В) cos et>
мы будем иметь
Поэтому дифференциальное уравнение относительно и
никогда не будет содержать мнимых величин; а так как
коэффициент при и в этом уравнении содержит лишь одну
неопределенную величину v, то отсюда следует, что и v
будет всегда вещественным.
Когда мы имеем больше двух тел, об их движениях
и колебаниях можно было бы, очевидно, сделать несколько
замечаний, аналогичных тем, которые мы сделали по поводу
движения нити, нагруженной двумя телами. Но эти
подробности увели бы нас слишком далеко.
Замечание XI.
132. Если предположить, что тела, прикрепленные
к нити, движутся в среде, сопротивление которой
пропорционально
T-f S
ЗАДАЧИ
205
где у и S — некоторые постоянные, а и — скорость, то и
в этом случае уравнения можно проинтегрировать*
Предположим, например, для простоты выкладок, что
у нас имеется всего только два одинаковых тела. Тогда
мы получим (см. п° 118):
//2*.— (2рх-РУ 7 | *dx\ 21 dt*
а х—\ i MiMdt) рТ* '
,,».. (2ру-2рх Г , b'dy\2ldt*
а У-~\ I M^Mdt) рТ2 #
Эти уравнения можно интегрировать различными
способами,— их я изложил в «Memoires de PAcademie de
Berlin» за 1748 и 1750 гг. Поэтому я больше на этом не
останавливаюсь.
Следствие VII.
133. Пусть кривая нагружена бесконечно малыми
одинаковыми грузами, расположенными на бесконечно малых
расстояниях друг от друга, и пусть все эти грузы
бесконечно мало удалены от вертикали. Пусть х — бесконечно
малые абсциссы этой кривой, у—ординаты, s— дуги,
бесконечно мало отличающиеся от л:, / — длина нити. Из
п° 127 следует, что ускоряющая сила любого из этих
малых грузов будет пропорциональна сумме синусов углов
смежности, начиная сверху, за вычетом произведения угла
смежности на отношение суммы весов всех нижних грузов
к весу рассматриваемого груза. Следовательно, эта сила
для любой точки равна
J ds ds* ''
*) В качестве угла смежности здесь берется величина -—-,
(IS
хотя общее выражение этого угла имеет вид
dx d2y JL_
ds " ds*
•Но так как все точки нити бесконечно мало удалены от верти*
кали, то dx и ds могут заменяться одно другим. (Примечание
Везу.)
206 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ ДВИЖЕНИЯ
Это совпадает с тем, что приводится Даниилом Бер-
нулли (см. т. VII петербургских «Commentarii», стр. 171) [74].
Отсюда Даниил Бернулли вывел уравнение, которое
должна иметь кривая, обладающая тем свойством, что все
ее части одновременно приходят на вертикаль (см. там же,
стр. 171).
Уравнение этой кривой в общем случае имеет вид
dy (l-s)d2y __у т
ds ds2 п '•
Полагая
/ — s — х,
y = Jpdx
и
px=z,
мы получаем уравнение
, , uz2 dx ,
п dzA = — ах.
1 х
Это — не что иное, как уравнение Риккати, которое не
интегрируется известными методами. Это тем более
любопытно, что если положить
x = kum,
где k и т — произвольные постоянные, то мы получим
пи dz -f- nmz2 du -J- kmum du = 0.
Это уравнение немногим сложнее предыдущего уравнения
и тем не менее я не мог отделить в нем переменные,
*) Уравнение кривой имеет вид
dy __ (/ — s) d2y __ у_
ds ds2 ~ n '
потому что ускоряющая сила выражается в виде
dy (I — s) d2y %
ds ds2 '
и так как эта сила, по условию, пропорциональна расстоянию у,
которое остается пройти до вертикали, то все точки кривой
придут иа эту вертикаль в одно и то же время. {Примечание Везу.)
ЗАДАЧИ
207
несмотря на то, что величины k и т могут быть какими
угодно, кроме нуля.
Если кривая не выражается этим уравнением, то ее
уравнение будет меняться от одного момента к другому,
и общее значение ординаты у может быть тогда выражено
лишь в виде функции дуги s, или соответствующей
абсциссы х, и времени t, протекшего с начала движения. Эта
функция при t = 0 даст значение у в функции от s,
заданной уравнением кривой в начале движения *).
Пусть поэтому в общем случае
у = 'ф (t'S) **)
и
dy=pdt-\-qds.
*) Если, по условию, все точки кривой должны приходить
на вертикаль одновременно, то достаточно знать начальную форму
этой кривой, заданную вышеуказанным уравнением, и мы будем
иметь все формы, которые она будет последовательно принимать.
В самом деле, ординаты точек кривой в какой-нибудь из ее форм
находятся всегда в одном и том же отношении к
соответствующим ординатам в начальном положении. Поэтому достаточно
определить величину одной из этих ординат в конце промежутка
времени tt для чего достаточно проинтегрировать уравнение
П
где у' обозначает ординату, соответствующую для данной кривой
той точке нити, которой в первоначальной кривой соответствует у.
Однако, если не вводить условия, что все точки кривой приходят
на вертикаль в одно и то же время, то при заданной начальной
форме кривой нельзя с такой же легкостью найти последующие
формы кривой. Тем не менее, нетрудно видеть, что положение
какой-либо точки нити в конце некоторого промежутка времени t
может зависеть только от следующих трех данных: от длины той
части кривой, на конце которой расположена эта точка, от
времени, которое истекло с начала движения, и от начальной формы
кривой. Отсюда следует, что общее уравнение, из которого можно
определить \у, должно обнимать собою уравнение кривой в
первоначальном виде, и потому оно должно быть таково, что если
положить
y = 9{t*s),
то уравнение начальной кривой должно получиться отсюда, если
положить * = 0. (Примечание Безу.)
**) Выражение y(t*s) обозначает в общем виде некоторую
фуНКЦИЮ ОТ t И 5.
208 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ движения
Пусть, далее, —d2y обозначает вторую разность от у
в предположении, что s остается постоянным (я беру—d2y,
потому что при возрастании t уменьшается у и увеличивается
скорость), a d2y обозначает вторую разность в
предположении, что / остается постоянным.
Тогда
-*Н£-<'-*>-Зг| ■*•*>.
или
Ясно, что dp нужно здесь взять при изменении одного t}
a dq — при изменении одного s. Пусть
dp = adt-\-vds,
dq = bdt-\-m ds.
*) Выше указывалось, что ускоряющая сила любой точки
кривой равна
as (l s> dsz-
Отсюда следует, что для определения движения этой точки нужно
величину
[£-«--•»§]"
приравнять тому малому пути, который сила стремится заставить
пройти точку за время dt, — другими словами, приравнять второй
разности от ординаты у. При этом указанная разность должна
быть взята в предположении, что s постоянно, потому что точка,
движение которой рассматривается, не меняет, по условию, своего
места на нити. Наоборот, в выражении
dy (/ — s) d2y
ds ds2
разности dy и d2y должны быть взяты в предположении
меняющегося s и постоянного £, потому что это выражение обозначает
ускоряющую силу любой точки нити для определенного момента
времени и для определенного положения этой нити. (Примечание
Безу.)
ЗАДАЧИ 209
Так как
pdt-\-qds
представляет собой полный дифференциал, имеет место
равенство
dp dq t
ds ~~Ш'
иначе,
Далее, из уравнения
dt ч ds
вытекает равенство
— а = q — (/ — s) т,
откуда
. q ds4-a.ds
mds — ~ , .
Прибавляя к обеим частям этого равенства bdt или v^W,
мы получим
mds+bdt или </у = у^+**д + у<».
Отсюда
dq-(l — s) — qds = vdt-(l — s)-{-ads
и
q(l—s)= f vdt-(t— $)-\-ads.
Это уравнение должно соблюдаться в том случае, если
все изменяющиеся кривые, о которых идет речь,
обнимаются общим уравнением
y = <p(t-s).
Замечание XII.
134. Можно заметить любопытное сходство между
функцией <p(t*s), выражающей величину у, и дифференциалами
этой функции различного порядка до бесконечности. Пусть
/ — s — u.
14 Ж. Даламбер
210 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ ДВИЖЕНИЯ
Тогда, во-первых, выражение
pdt—qdu
будет полным дифференциалом; во-вторых, мы будем иметь
равенство
— dP — n 1 udct
dt ~CJ~t~ da '
или, иначе,
--dp d(qu)
dt du ;
Из последнего равенства следует, что
qudt—pdu
является полным дифференциалом. Далее, полагая снова
/ — s — uy
мы из последнего следствия получим, что выражения
a dt — v du
и
v и dt — a du,
из которых последнее равно
d[q(l-s)] = d(qu),
являются полными дифференциалами. Отсюда следует, что
если положить
dy=pdt — qda,
dp = adt— vdu,
da = p dt — (oda
и т. д. до бесконечности, то мы будем иметь всякий раз
по паре полных дифференциалов:
pdt — qda и qudt—pdu,
adt — v du и yudt — a du,
pdt — о du и <nudt — p du
и т. д. до бесконечности.
8АДАЧЙ 211
Таким образом, если будет найден какой-либо один
случай интегрируемости, то путем обратного восхождения
можно будет найти и другие, до бесконечности. Пусть,
например,
p = A-\-Bt
и
«> = C-{-Du-1.
Тогда мы найдем, что
р dt — о da
равно полному дифференциалу и что
юи dt — р du
также является полным дифференциалом, если только
С = — В.
Далее, подобно тому, как мы нашли, что
d (qu) — vudt — a du,
мы получим также
d (уи) = ®udt — р da.
Следовательно,
Г* В№
а=\ pdt— ®du = At-\—^ Ви-\-D Aug а-\-Е
и 1 и
Таким же образом, зная а и v, можно найти р и #; и все
остальные величины, которые можно найти попарно путем
восхождения и которые мы обозначим вообще через Р
и Q, будут таковы, что
Pdt—Qda и Qudt — Pda
будут полными дифференциалами.
Вследствие этого данная задача решается
аналитически для бесконечного числа случаев. Я говорю
аналитически, а не в отношении к рассматриваемому вопросу,
так как нужно признать, что ни одно из этих решений не
14*
212 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ ДВИЖЕНИЯ
может дать искомой кривой. Причина этого заключается
в том, что, во-первых, эти решения содержат в себе члены,
в которые входит только одно /, и потому по мере
возрастания / растет до бесконечности и у> чего не должно
быть по условию. Во-вторых, эти решения содержат также
члены вида DAogu, обращающиеся в бесконечность, при и,
равном нулю, т. е. когда s равно всей длине нити.
Замечание XIII.
135. По тем же основаниям нельзя положить
y = S-\-S't2 + S't* и т. д.,
где S, S\ S" и т. д. суть некоторые неопределенные
функции от s. В самом деле, хотя аналитически довольно
легко найти величины S, S\ S" и т. д., тем не менее
величина у, получающаяся отсюда, была бы также
неподходящей в качестве решения рассматриваемой задачи *).
Если положить
y=T-s,
где Т—некоторая неизвестная функция от /, а
5—некоторая также неизвестная функция от s, то уравнение
— dp (/ — s) dq
Ж~ q ds
*) Если в уравнение
подставить вместо у эту величину, соблюдая вышеуказанный
способ дифференцирования, и затем приравнять нулю члены,
содержащие какую-нибудь определенную степень t, то мы найдем,
что уравнение, из которого можно определить S", имеет вид
d*S"__ ds
dS"~ l-s*
Другие допущения, сделанные в тексте относительно у, будут
оправданы несколько ниже. (Примечание Безу)
ЗАДАЧИ
213
примет вид
Hi2 '°="7£Г ds2
Отсюда мы получим
—^L.s—TdS Jl—s)Td2s
— d2T _\_
Tdt2 ~п
и
S^ dS_ /# N d2S
n~ds { 5'~^'
Второе уравнение является уравнением нити, все точки
которой приходят на вертикаль одновременно, первое же
дает
Т— A cos -7г=.,
V п
так как dJ при t = 0 обращается в нуль. Таким образом,
это уравнение еще ничего не дает, так как оно позволяет
найти колебания только в том случае, когда нить имеет
такую форму, что все точки ее приходят на вертикаль
в одно и то же время.
Можно было бы положить также
y=T.S-{-r.S"
и, далее, положить
— d*T _
T'dt2 ~1Пу
где m и m —некоторые неопределенные положительные
постоянные, и, наконец,
<?ш dS" и с\ d2S"
и
ds v ' ds2
Но таким путем мы пришли бы к дифференциальному
уравнению четвертого порядка относительно S". Далее,
214 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ ДВИЖЕНИЯ
величины Т и Т" должны быть таковы, чтобы, во-первых,
у было всегда весьма малым; во-вторых, чтобы при s=0
у обращалось в нуль; в-третьих, чтобы dy при t—0
также обращалось в нуль. Но нетрудно убедиться в том,
что величины Т и Г", найденные из уравнений
//4 v
m"
и
~~ m" dt* '
не могут удовлетворять всем этим условиям одновременно.
Действительно, проинтегрировав первое из этих
уравнений методом, указанным в берлинских «Memoires» за
1748 и 1750 гг. [7б], мы увидим, что Т содержит
выражения вида cbi, где Ь — вещественное число. Отсюда
следует, что все указанные до сих пор методы не позволяют
найти значение у.
Замечание XIV.
136. Однако есть метод, который во многих случаях
ведет к цели. Положим
y = TS-\-T'S'-\-rS" и т. д.,
и пусть
— d4 _ — d4' __ — d*T"
Tdt* —n% Г dt2 m* T" dt* —Г и т< Дм
причем /z, m, г суть какие-то различные величины. Тогда
мы будем иметь
у =* AS cos tVln+BS' cos tVm-\~CS" cost "|/7 и т. д.
Величины Sy S\ S" и т. д. определяются из следующих
уравнений, которые могут быть проинтегрированы с
помощью рядов:
с dS п ,\d2S
С/ dS' II o\d2S'
ЗАДАЧИ
215
Однако в таком случае необходимо, чтобы первоначальное
уравнение кривой при t, равном нулю, имело вид:
y^A-S + B'S' + C'S* и т. д.
Таким образом, этим способом задача может быть решена
лишь в некоторых частных случаях.
Замечание XV.
137. Для того чтобы только что указанные выкладки
провести со всей точностью, необходимо взять уравнение
в виде
2а dt*
■«■•>-[£-"-" SJ
02
где 9 — время, в течение которого тяжелое тело спускается
с высоты а. Тогда мы будем иметь
у = AS cos—~ J- BS cos—-г— и т. д.
Sn dS п оЧ d2S
Ъ-ds-V-^-aW ИТ' Д'
Даниил Вернулли («Memoires de PAcademie de Berlin» за
1753 г., стр. 194 [76]) утверждает, что колеблющаяся
струна Никогда не будет возвращаться в первоначальное
положение за исключением единственного случая, когда
у=зЛ.Scos —-z—i
т. е. того случая, когда (говоря языком этою прославленного
геометра) все колебания простые и одного и того же вида.
Для того чтобы в этом положении можно было не
сомневаться, необходимо доказать, что, во-первых, числа
т, п и т. д., до бесконечности, не соизмеримы между
собой,— чего Бернулли, кажется, не доказал. Правда, он
нашел, что эти числа являются корнями некоторого
сложного уравнения с бесконечным количеством членов, но
216 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ ДВИЖЕНИЯ
этого, мне кажется, недостаточно для того, чтобы
утверждать, что они между собой несоизмеримы. Если же эти
числа не являются несоизмеримыми и если, например,
Ym = qV п у
где q— произвольное,-целое или дробное, число, то легко
видеть, что цепь будет принимать свою первоначальную
форму всякий раз, когда
становятся оба кратными 360 градусов.
Во-вторых, необходимо, кроме того,
уравнение
y = T-S-{-r.S' и т. д.,
или
у=А• 5cos —g \-B-S cos —^—
является единственным уравнением, которое может
выразить колеблющуюся струну. Однако, в этом никак нельзя
быть уверенным.
Замечание XVI.
138. Нами было показано (п° 125), чю случай п° Мб
не является единственным случаем, когда все грузы,
которыми нагружена нить, приходят на вертикаль в одно
и то же время и совершают колебания за одно и то же
время. Вполне возможно, что найденное нами (п° 133)
уравнение — не единственное, делающее колебания цепи
синхронными. Однако об этом трудно высказываться, не
обладая общим методом и полным уравнением
колеблющейся цепи.
доказать, что
и т. д.,
ЗАДАЧИ
217
Лемма VIIL
139. Пусть мы имеем тело CRM (фиг. 43)
произвольной формы с центром тяжести G. Для большей
простоты я буду это тело рассматривать в качестве
плоской фигуры. Пусть все частицы V этого тела
обладают силами VM, направления
которых перпендикулярны к
линии VC, проведенной из
точек V к неподвижной
точке С, взятой произвольно в
теле, и пусть эти силы про-
порцион альны расстояниям VC.
Я утверждаю, что
направлением равнодействующей
будет служить какая-то
линия KL, перпендикулярная к
прямой CG, проведенной через
точку G и через точку С.
Разложим каждую силу VM
на две силы: одну,
направленную по VN,
параллельно CG, и другую,
направленную по VP, перпендикулярно к CG. Легко видеть, что
силы, направленные по V7V, будут пропорциональны
расстояниям CQ этих сил от линии CG и, таким образом,
суммы -этих сил будут равны сумме произведений каждой
частицы на ее расстояние до линии CG. Но так как
линия CG проходит через центр тяжести G, то эта сумма
равна нулю. Отсюда следует, что равнодействующая сил,
направленных но VN, равна нулю. Следовательно,
направлением и величиной той силы, которую мы ищем, будет
направление и величина равнодействующей сил,
направленных по VP, перпендикулярно к СО. Отсюда следует, что
направлением этой силы может быть только какая-то
линия ОАХ, перпендикулярная к CG.
Что касается величины этой силы, направленной по OL,
то эта величина будет равна сумме всех сил,
направленных по VP, умноженных на соответствующие малые массы V.
218 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ ДВИЖЕНИЯ
Так как силы VP пропорциональны VQ, и так как на
основании свойств центра тяжести сумма
равна CG, умноженному на массу MRC, то отсюда
следует, что если ускоряющую силу точки О обозначить
через 'f, то сила, направленная по ОЦ будет равна <f-MRC.
Расстояние СК линии OL от С равно
fy.,.jg.yc [у.УС*
ср. MRC CG-MRC *
Действительно, так как все силы <р приводятся к одной силе,
направленной по OKL, то это значит, что такая же сила,
направленная в противоположную сторону по LKO, будет
эти силы уравновешивать. Если же равновесие имеет
место, то оно не нарушится от того, что точка С будет
взята закрепленной. Но в этом случае момент силы y-MRC,
действующей по направлению LKO, должен быть равен
сумме моментов сил VM (по правилу рычага). Первый
момент будет равен
а второй
Отсюда следует, и т. д.
Следствие I.
140. Из сказанного следует, что положение линии OKL
всегда дано и не зависит от величины (р.
Следствие II.
141. Если совершенно свободное тело CRM обладает
произвольной силой К, направленной по некоторой
линии GBy проходящей через центр тяжести [Q, и если, в
то же время, это тело стремится вращаться с некоторой
ЗАДАЧИ
219
скоростью вокруг своего центра тяжести G, то, как в
предыдущей лемме, можно доказать, что
равнодействующая сила будет равна К и будет направлена по некоторой
линии ОЛХ, параллельной GB. Отсюда следует, что такая же
сила, направленная по LKO, будет уравновешивать силу К,
проходящую через центр G, и те силы, которые
стремятся вращать тело. Следовательно, момент этой силы
относительно точки G должен быть равен моменту силы К
относительно той' же точки О и моменту всех
вращательных сил. Отсюда вытекает, что если через Ч? обозначить
силу, которая стремится вращать вокруг точки G какую-то
произвольную точку, расположенную на расстоянии &, а
через а обозначить сумму произведений частиц на квадрат
их расстояний от точки G, то мы будем иметь
или
Следует заметить, что для того, чтобы сила, направленная
по ОЛХ, действовала в ту сторону, как это мы допустили
на чертеже, вращательная сила должна действовать в ту же
сторону. В противном случае между силой, действующей
по LKO, и вращательной силой равновесия быть не может.
При противоположном условии величина GK будет
отрицательной, и мы будем иметь
K.GK= — *у,
или
Следствие III.
142, Отсюда, заметим мимоходом, нетрудно
заключить, что если свободное и покоящееся тело будет толкать
некоторая произвольная сила К, направленная по OKL> то
центр тяжести G этого тела придет в движение по GB
220 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ движения
параллельно ОЛХ,— как будто сила К проходила через
центр G,— и, кроме того, тело будет вращаться вокруг
этого самого центра О по направлению OKL с такой
скоростью Ч;, что
т. е. с той же скоростью, с какой оно вращалось бы в
том случае, если бы центр G был, по условию,
неподвижен и если бы сила К действовала на точку К по
направлению OKL для того, чтобы заставить тело вращаться.
В самом деле, тело должно получить движение такого
рода, что если бы ему это движение сообщить в обратную
сторону, оно уравновесило бы силу К (п° 61). Отсюда,
на основании предыдущего п°, следует, что тело должно
получить именно такое движение, какое мы только что
указали.
Пусть М есть масса тела. Все части этого тела будут
двигаться параллельно GB со скоростью, равной ~, и,
кроме того, они будут обращаться по направлению OKL
вокруг точки G со скоростью, равной
lVx K-GK-x
Ъ ~ а
где х обозначает расстояние частицы от точки G. Отсюда
нетрудно видеть, что все точки линии CG будут иметь
скорость параллельно GB, равную
К_ K-GK-x
М ~ а
Отсюда следует, что если на линии CG взять такую
точку //, чтобы
0И==М13К'
то скорость эгой точки И будет равна нулю. Это значит,
что эта точка будет находиться в покое и, следовательно,
она будет тем, что Бернулли называет самопроизвольным
центром вращения тела. Этот центр, очевидно, меняется
в каждый момент, потому что в каждый момент меняет
свое положение линия G/C.
ЗАДАЧИ
221
Задача VL
движение, равное и
nail в то же время они
А
143. Тело CRV (фиг. 44) произвольной формы с
центром тяжести в G подвешено на нити АС> причем
линии АС и СО бесконечно мало отклоняются от вертикали.
Найти скорость точек С и О для какого-либо времени t*).
Все части тела CRV имеют
раллельное движению точки С,
обращаются вокруг этой точки
С со скоростями,
пропорциональными расстояниям от
этой точки. Обозначим
через р абсолютный вес какой-
нибудь произвольной частицы 1/,
направленный по вертикали VQ.
Разложим это усилие для
каждой частицы на два
составляющих усилия, из
которых одно, будучи направлено
по Vu, должно быть равно
и параллельно ускоряющей
силе точки С, направленной
по СР, а другое пусть будет
направлено по Vn. Это
усилие Кя, направление которого
нам еще не известно, будет
одинаковым по величине и по направлению для всех
частиц. Вследствие этого все усилия Vn можно
рассматривать как бы соединенными в центре G и действующими
по направлению GA/, параллельному Vn. Разложим, далее,
это усилие Vn для каждой частицы на два составляющих
усилия, из которых одно будет заставлять частицу V
обращаться вокруг точки С, а другое будет уничтожаться.
Это последнее усилие я обозначу через s, и так как все
эти усилия s должны уничтожаться, их равнодействующая
должна быть направлена по АС.
Фиг. 44.
*) Предполагается, что точки А, С, G находятся в одной и
той же вертикальной плоскости. (Примечание Безу>)
222 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ движения
Мы уже нашли, что линия G7V, параллельная линиям Vny
положение которой нам не известно, есть направление
равнодействующей сил Vn. Можно найти положение линии ДХ,
направление равнодействующей всех сил частиц V,
стремящихся заставить их обращаться вокруг точки С, хотя
нам и не известна еще величина этой равнодействующей
(п° 140). Ввиду того, что сила, направленная по GN,
слагается из силы, направленной по /(/,, и из
равнодействующей сил s, эта последняя должна проходить через точку L
пересечения линий GN и KL. Кроме того, она должна
лежать на продолжении АС. Отсюда следует, что точка L
лежит на продолжении АС. Следовательно, линия GM
должна проходить через ту точку, в которой пересекаются
линия KL и продолжение линии АС. Линия CL даст нам
при этом направление равнодействующей сил s.
Пусть тг есть сила точки С по направлению СР: она
будет общей для всех частиц. Пусть ср есть сила точки G,
заставляющая ее обращаться вокруг точки С. Проведем Gi
параллельно СР и GM параллельно АР. Введем
обозначения: пусть
AC = t, CG=r-a, GK=b, СР=х,
пусть т обозначает массу тела т, и — — угол,
образованный линией CG с вертикалью *). Линии GK и GL можно
будет считать равными, и мы будем иметь
угол ом=2£«»_ ({_*)•
Но
сила п=р.1.ам=р [f - (£ -у ) у]
*) Расстояние тбчки G от вертикали, проведенной через
точку С, принято за у. Тогда угол, о котором идет речь, будет
равен —, так как он бесконечно мал. (Примечание Безу.)
ЗАДАЧИ
223
и, с другой стороны, отношение силы, направленной по KL
(равной <р*т), к силе, направленной по GL (равной р «/я),
должно быть равно отношению угла GLM к полному
синусу *). Отсюда следует, что
(у х \ а
откуда
Эти уравнения можно интегрировать методом,
аналогичным тому, которым мы уже пользовались в подобных
случаях в п°п° 118 и 122.
Следствие.
144. Если нам нужно, чтобы точки С и G приходили
на вертикаль в одно и то же время, мы должны положить
„ш%, х y_x_axty ах
откуда
ху ах* ху у2 | аху
Это4 нам даст
у 2* 2а — V а^\ 2а 2} ч
Если / весьма велико по сравнению с а и Ь, то мы будем
иметь
yi
х = ~ и х = —у.
а у
Первое из этих равенств дает
х_ у_
I ~~ а #
*) Угол SLO рассматривается как прямой. В следующем
уравнении Т взято в том же смысле, как ива0 118. (Примечание
Безу.)
224 общий принцип для нахождения движения
Это значит, что если нить достаточно длинна, то для того,
чтобы точки С и G приходили на вертикаль одновременно,
линии CG и АС должны лежать почти точно на одной
прямой. Второе равенство дает нам углы, образуемые
линиями АС и CG с вертикалью: эти углы следует брать в
одну и ту же сторону, и отношение их должно быть
обратным отношению АС к CG. Другими словами, для того
чтобы точки С и G приходили на вертикаль одновременно,
на основании первого равенства нужно, чтобы линии CG и
АС составляли одну прямую, а на основании второго
равенства центр G в первый момент должен быть на
вертикали АР или, по крайней мере, очень близко к этой
вертикали.
Так как настоящая задача совершенно аналогична задаче
о нити с двумя грузами, то по поводу ее можно сделать
такого же рода замечания, какие были сделаны нами выше.
Мы предоставляем их сделать читателю.
§ 2. О телах, качающихся на плоскости.
Задача VII.
145. Произвольная фигура СКО (фиг. 45) расположена
на горизонтальной плоскости MCS таким образом, что
вертикаль GF ее центра
тяжести G не проходит через
точку касания С. Спраши-
\0 вается, что произойдет с
данной фигурой.
Данная фигура может иметь
только два движения: одно —
вращение вокруг точки
касания С, меняющейся в каждый
момент, и другое — движение,
общее для всех частей
фигуры,— скольжение вдоль плоскости по направлению к М
или к S. Поэтому прежде всего нужно определить, в
какую сторону будет направлено это последнее движение, в
сторону М или в сторону S. Во-вторых, нужно определить
ЗАДАЧИ
225
величину силы, производящей это движение, которую я
обозначу через тт. В-третьнх, нужно определить
вращательную силу центра тяжести G, создающую вращение вокруг
точки С, которую я обозначу через <р. Наконец, нужно
определить, в какую сторону эта последняя сила будет
поворачивать точку G, вправо или влево.
Каковы бы ни были силы ср, всегда, как известно, можно
определить направление ZNO равнодействующей этих сил
(п° 140): линия N0 будет перпендикулярна к продолжению
линии CG. Далее, равнодействующая абсолютных усилий
всех частиц вследствие тяжести этих последних будет
направлена no NGF и будет равна р*т) где т— масса тела,
а р — абсолютная тяжесть. Точно так же линия KGR,
параллельная MS, будет направлением равнодействующей всех
сил тг, равной тт-т.
Согласно нашему принципу, силу, направленную по NF,
можно разложить на три силы: одна из них будет
равнодействующей сил <р, другая — равнодействующей сил тг,
третья же должна уничтожаться. Но она может уничтожиться
только в том случае, если она направлена по линии CD,
перпендикулярной к плоскости в точке С. Отсюда, просто
рассматривая чертеж, легко видеть, во-первых, что
равнодействующая сил <р направлена по N0, а не по 7VZ, и
потому фигура будет поворачиваться слева направо; во-вторых,
что сила, направленная по NG, составляется из силы,
направленной по N0, и силы, направление которой NL
проходит через точку N и через точку L пересечения линий
CD и KR\ в-третьих, что фигура будет скользить от G к
К, а не от G к /?; в-четвертых, что если нам дана сила,
направленная по NF, и даны положения линий NL и 7VO,
то тем самым нам дана сила, направленная по N0,—другими
словами, дана сила <р. Точно так же нам дана и сила,
направленная по NL. А так как отношение последней силы к
силе Ti>m равно отношению LQ к QC, то сила тг нам также
дана. Таким образом, задача решена, и нам известно, каково
будет движение фигуры в первый момент.
Выше (п° 84) мы показали, что центр G опускается по
вертикальной прямой. Для того, чтобы определить ту
скорость, с которой он будет опускаться в первый момент,
15 Ж. Даламбер
226 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ ДВИЖЕНИЯ
найдем начальную ускоряющую силу, т. е. ускоряющую
силу в первый момент спуска. Пусть (фиг. 46)
CF=x,
ускоряющая сила точки G, заставляющая ее обращаться
вокруг точки С, равна <р и масса тела равна т. Тогда, во-
первых, сила, направленная по N0, равна <р«/я (см, п° 139),
Фиг. 46.
Далее, поскольку линия GF нам дана, мы можем, зная вид
кривой, найтл GC, которую я обозначаю через X, и ОР,
обозначаемую через z. Сила, направленная по NR,
будет так относиться к силе, направленной по N0, как
синус угла PNG к синусу угла GNR. Отсюда следует, что
сила, направленная по NR, равна
ср./я-С?Р RN
GN ' CF '
а сила, направленная по RL, равна силе, направленной по
RG
NR, умноженной на ~г., т. е. она равна
ср-;?£•(? Р ср. т * GF
GN ~~* CG с
Отсюда следует, что сила точки G, направленная по GL,
так относится к силе 0, поворачивающей вокруг С, как
ЗАДАЧИ
227
GF относится к GC. С другой стороны, сила, направленная
по G/7, так относится к силе у, как CF относится к CG*).
Следовательно, сила, направленная по GF, будет равна
CG '
Далее, сила, направленная по NG (равная р*т), относится
к силе, направленной по N0 (равной ^•/я), как синус угла
RNk к синусу угла RNG, т. е. как Rk к CF. Отсюда
Следовательно, сила, направленная по GF, равна
P-CF*
Rk-CG '
И так как величины С/7, CG и Rk нам даны в виде
функции от дг, то, очевидно, и начальная сила, направленная по
GF, может быть выражена через х.
Аналогичным путем может быть определена скорость и
в последующие моменты. Однако следующий п° даст нам
более простой метод.
Примечание I.
146. Согласно п° 84 ясно, что не только в первый
момент, но и в последующие моменты центр тяжести G
будет опускаться по вертикальной прямой. Но отсюда
совсем нетрудно, без всяких вычислений, определить движение
фигуры.
*) Сила, с которой центр G приближается к плоскости, не
равна весу, потому что, как мы видели, часть веса уничтожается
р точке С. Центр G приближается к плоскости только вследствие
своего вращательного движения вокруг точки С Каково бы ни
Зыло это движение, называемое в тексте буквой ср,
результирующее усилие, с которым центр G приближается к MS, будет равно
yCF
~Ш
(как это нетрудно видеть из операции разложения). Следовательно,
всё дело в том, чтобы определить ср. Величина же этой силы ср
может быть найдена из того условия, что часть веса тела
уничтожается в точке С. {Примечание Безу.)
16*
228 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ движения
В самом деле, в произвольной точке Е (фиг. 45)
проведем касательную BE и опустим на нее перпендикуляр
GB. Когда центр О будет находиться от плоскости на
расстоянии, равном GB, точка Е будет лежать в данной
плоскости.
Если точка С не является точкой касания (фиг. 47),—
например, если данная фигура представляет собой
треугольник и точка С является одной из его вершин,—то в тот
Фиг. 47. Фиг. 48.
момент, когда центр тяжести очутится в точке V, точка С
окажется в Е, так что
VE^GC.
Остается только определить время, в течение которого
фигура достигает того или иного заданного положения.
Довольно простой метод для решения этого вопроса
заключается в следующем. Пусть центр тяжести G (фиг. 48)
за произвольное время t опустился до точки I/, причем
GV = u.
Расстояние х центра тяжести от плоскости в это время
пусть будет равно VF'. Тогда ясно, что
da — — dx
и
~d2a=^d2x.
Отсюда мы получаем
х — А— #,
ЗАДАЧИ
229
где Л представляет сабой значение х при / = 0.
Потерянная сила в вертикальном направлении для всех частей тела
будет равна
md2a
или, более точно,
(п° 27). Кроме того, каждая частица тела, расположенная
на расстоянии b от центра О, опишет за время t
некоторую дугу окружности с центром в точке G. Эта дуга будет
найдена, как функция от А и от #, исходя из формы
фигуры, и потому может быть обозначена через V.
Потерянная сила этой частицы будет равна
— pdtVW
2а dt* #
Поэтому (п° 141), обозначая через Л' сумму произведений
частиц на квадрат их расстояний от точки G, мы можем
написать равенство
РШ \}-2аЖ*)СР - 2abdt* =°'
Величина CF известна, как функция от А и от и, исходя
из формы фигуры.
Пусть теперь
C'F' = u'
и
d*V=rd*u + sdu*f
где г и $ — известные функции а. Тогда мы получим
, pmu'd4W pA'rd2u-№ pA'sdtfi-V* Q
pmU 2a dt* 2abdt* 2abdt* '
Полагая
dt — q du
и подставляя вместо d2u его значение
— dq du
230 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ ДВИЖЕНИЯ
гак как d2t = 0y мы получим следующее дифференциальное
уравнение:
, - , , pmu'dq-V . pA'rWdq pA'sdu-Vq Л
Отсюда известными методами нетрудно найти ^ в функции
и, затем £ в функции и*).
В данном случае можно воспользоваться и принципом
сохранения живых сил. Пусть U будет скорость
вертикального опускания центра О и U его скорость вращения.
Если массу тела обозначить через М, весьма нетрудно
найти отсюда, что сумма живых сил всех частиц будет
равна
U'2A'
MU*-
Ь*
Так как и есть то расстояние по вертикали, на которое
опустился центр тяжести за время t, то на основании
принципа сохранения живых сил мы будем иметь
2puM = MU2+^f-.
Но, во-первых,
U=—
и dt '
во-вторых, путь V, описанный за время t при
вращательном движении, известен в функции и и потому
т „ dV V'da
и илй ж=чг>
где V есть известная функция и. Таким образом, мы
получим
dt* — da2 | А'У2*и*
2/w~r 2pMub* *
Отсюда мы можем найти t в функции и.
*) См. сочинения Бернулли, т. I, Acta eniditorum, 1697 etc.
ЗАДАЧИ
231
Примечание И,
147. Если фигура должна совершать лишь бесконечно
малые колебания, то начальное расстояние GF (фиг. 49)
будет отличаться от линии GC, проведенной к точке
касания С, лишь на бесконечно малую величину второго порядка.
Отсюда нетрудно заключить, что центр G будет опускаться
лишь на бесконечно малую величину второго порядка, тогда
как угол поворота будет
бесконечно малой вели- ^
чиной первого порядка.
Отсюда следует, что и
можно рассматривать как
нуль по сравнению с V.
В таком случае мы
будем иметь
d2a = 0
Фиг. 49.
Но, построив бесконечно близкие радиусы кривизны CR и
С'/?, мы будем иметь угол у или равный ему угол FGF—
= CRC = CGC ~. Отсюда, обозначая CR через г, CG
СА:
через j5, CF через А, мы получим
CF или C'GF-CG = (CGF-\-FGF' ~-CGC)'CG =
— U ^~ь WJ p— + ь ь *
Поэтому вышеприведенное уравнение принимает вид
d*V =
2abdt*
AW
(mA +
m
Щ rmV\
b b у
Таково будет уравнение для того случая, когда
колебания бесконечно малы, или, что в действительности сводится
к тому же самому, когда колебания будут весьма малыми.
232 ОЫЦИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ движения
Если предположить
К'.
так что т§—гт оказывается величиной отрицательной,
и если принять во внимание, что при £ = 0 мы будем
иметь
У=0 и dV=0,
то по соображениям, изложенным в другом месте*), мы
получим
У — 2аЬтЛ Г t 'Уг2а*(тг — т$) Л 2а (тг—т})
v~~~ Л'аз ' [cos rfA' J; ^Р '
Поэтому путь, пройденный в круговом движений частицами,
расположенными на расстоянии b от центра О, будет равен
ЬА
Если
х _ со$ гУ2а(тг — тЩ
Q-fA'
то, согласно известным соотношениям, выражение
cos
t V2a(m$ — mr) —tV2a(mV~mr)
t Y2a(mr — m%) с ьУа> +g ЪУ1'
будет представлять собой вещественную величину, которая
по мере возрастания t будет возрастать до бесконечности.
Это означает, что колебания не будут уже бесконечно
малыми, как это было нами принято, или, точнее говоря,
предыдущее решение уже неприменимо.
Например, если эллипс поставить перпендикулярно к его
малой оси и насколько возможно мало вывести его из этого
положения, то опыт показывает, что он возвращается или
стремится возвратиться в свое первоначальное положение,
совершая весьма малые колебания, как это и следует из
приведенного уравнения. В самом деле, тогда
К л
*) См. «Recherches sur le systeme du monde», часть 1, n° 25,
crp. 30 [77].
ЗАДАЧИ
233
потому что, как всякий знает, радиус кривизны на конце
малой оси эллипса больше этой малой оси. Отсюда
следует, что, поскольку косинус любого угла не может быть
больше единицы, величина bV не может быть больше
Ъ*А
Если, наоборот, эллипс поставить на его большую ось, то
и колебания уже не будут бесконечно малыми. Опытом
это подтверждается, потому что тело «опрокидывается»г
не восстанавливая своего первоначального положения.
Отсюда нетрудно вывести общий метод для решения
вопроса о том, будет ли тело, установленное вначале
в равновесии на плоскости, а затем слегка выведенное из
этого положения, возвращаться в исходное положение или
оно «опрокинется». Весь вопрос сводится к тому, что
больше: радиус кривизны в точке касания или расстояние
центра тяжести от этой точки. Если больше радиус
кривизны, то тело само при помощи бесконечно малых
колебаний восстанавливает свое первоначальное положение;
в противном случае тело «опрокидывается».
Примечание III.
148. Эйлер в VII томе петербургских «Commentarii» [78{
занимается решением задачи VII только для случая, когда
колебания тела на плоскости бесконечно малы. Метод его
состоит в том, что он приравнивает моменты сил,
вызывающих поворот частиц вокруг точки С (фиг. 45),
моментам абсолютной тяжести частиц относительно точки С,
принимаемой за неподвижную. Это сводится к разложению
силы, направленной по NF, на две силы, одна из которых
направлена по Л/О, являясь равнодействующей сил ср,
вызывающих поворот вокруг С, а другая проходит через точки N
и С и уничтожается.
Однако сила, направленная по /VC, может уничтожаться
лишь в том случае, когда NC перпендикулярна к MCS}
234 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ движения
если, по крайней мере, не предполагается, что плоскость
шероховата и шероховатость ее достаточно велика для
того, чтобы уничтожить действие силы NC параллельно
плоскости. Таким образом, для того, чтобы решение Эйлера
имело место, необходимо предположить, что плоскость не
абсолютно гладка. Вероятно, это и хочет сказать автор,
когда он пишет: «In hoc motu vero notandum est planum
super quo fit, aliquantulum asperum esse ponendum, ne
curvae de loco suo inter vacillandum dimoveri queant, quod
eveniret, si planum maxime foret politum» *) [79]. Слова
«ne de loco suo dimoveri queant» («чтобы не могли
сдвигаться со своего места») без сомнения означают: «чтобы
кривые помимо движения вокруг точки касания не могли
скользить параллельно плоскости».
Мне не известно, что помешало Эйлеру остановить свое
внимание на этом последнем движении. Впоследствии
великий геометр оказал мне честь тем, что уведомил меня
в письме от 2 октября 1746 г., чго в то время, когда
он занимался этим вопросом, он не знал, каким образом
учесть в вычислениях поступательное движение.
Наш принцип, как это видно из вышеизложенного,
дает для этой цели весьма простой метод.
Примечание IV.
149. В том случае, если контур фигуры и та плоскость,
но которой эта фигура скользит, не совершенно гладки,
силы р и тг в первый момент могут быть найдены
следующим образом.
Будем рассматривать точку С (фиг. 46) как небольшой
бугорок данной массы и предположим, что нам известно,
какой ускоряющей силой g по направлению CS или СМ
должно обладать это тельце для того, чтобы при
малейшем увеличении этой силы могло быть преодолено
сопротивление, вызываемое неровностями плоскости. Прежде
всего разложим абсолютную силу, направленную по NGy
на две силы, одна из которых будет искомой силой, на-
*) Стр, 108,
ЗАДЛЧТТ
235
правленной по /VO, а другая будет действовать по
неизвестной линии NL, Последнюю силу необходимо в свою
очередь разложить на две силы: одна из них должна быть
направлена по LK и равняться тш, а другая, направленная
по LC и как бы толкающая точку С по направлению СТ,
будет сообщать этой точке С усилие, направленное по CS
и равное заданному усилию g.
Введем обозначения для известных величин. Пусть
GP = a, GN = b,
GO = c, CR = e, RO — f
и пусть неизвестная
GL=y.
Тогда мы можем сказать, что сила, направленная по NLy
будет так относиться к силе, направленной по NG (и рав-
GP
ной рчп), как синус угла GNO, т. е. ^rrv, относится к си-
LZ
нусу угла ZNL, т. е. к ^-.
Но
GP_a_
GN~~ b '
Т7 — ПР OL__a-(c-\-y)
^—Ur'OG~ с
и
NL=Vb*+yK
Следовательно, сила, направленная по NL, будет равна
p-m-NL-OG p-m-C'Vb2-{-y2
GN-OL — b(c+y)
Далее, сила, направленная по LC, будет равна силе,
направленной по NL, умноженной на отношение синуса угла
NLQ, или ^тт, к синусу угла RLCy или к ~. Наконец,
сила, направленная по CS, будет равна силе, направленной
236 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ ДВИЖЕНИЯ
LR
по LC, умноженной на jp • Отсюда следует, что сила,
направленная по CS, будет равна
F ~r ' или p-m-Y . J! »
OL*CR r (с-{'У)*е
Если обозначить через \i массу небольшого бугорка С, то
должно выполняться равенство
c-(y-f)
р-т- ; , ; = g- ц.
Отсюда можно найти у и, следовательно, абсолютные
значения сил, направленных по NL, LK и N0, которые
требовалось найти.
Здесь необходимо сделать одно важное замечание, а
именно: сила точки С, направленная по CS, должна быть
направлена в ту же сторону, в какую части тела CRN
скользят параллельно плоскости. Отсюда вытекает, что
точка L непременно должна быть расположена между
точками /? и Л, где А — точка пересечения прямых NC и RG.
Сила, направленная по СМ, будет тогда равна
р-т.у-у).с
еЛс+У) g *
откуда можно найти у Если найденное значение у больше
С/?, или меньше ОЛ, или если оно отрицательно, то
фигура может только вращаться вокруг точки С, причем эта
точка будет меняться в каждый момент, но в течение
данного момента она может считаться как бы неподвижной.
Значение у равно
pmfc — gy.ec
gpe+pmc
На нашем чертеже это значение, очевидно, не может быть
больше /, потому что
pmfc—gixec < g\ief-\-pmfc.
Но оно будет офицательным, если
ЗАДАЧИ
237
и оно будет меньше GA, или -—Jrr, если
pmfc < g\iec -\- gmcb -f- gmbf.
Если хотят, чтобы была задана не сила, необходимая
для движения точки С, несмотря на сопротивление
плоскости, а только ее отношение к давлению этой точки на
плоскость, то нужно сделать так, чтобы отношение RL
к RC равнялось отношению силы трения к силе давления.
Тогда мы получим точку L. Она всегда будет лежать
между /? и А: в противном случае фигура никакого
движения параллельно плоскости иметь не будет.
Примечание V.
150. Для того, чтобы определить движение фигуры
в последующие моменты, можно воспользоваться методами,
аналогичными указанным выше. Все сводится к тому, чтобы
определить движение центра G параллельно и
перпендикулярно плоскости и, кроме того, вращательное движение
фигуры вокруг этого центра. Обозначим движение
центра G по направлению GK через г\ Тогда потерянная сила
по направлению GK будет равна
— pmd2 v — pmd2 v • О2
г - или —
dt2 ИЛИ 2adt* *
Сохраняя обозначения п° 146, мы должны потребовать,
чтобы равнодействующая потерянной силы
—pmd2V'b2
2adt2
другой потерянной силы
—pmd2u-№
2adt*
и потерянной вращательной силы уничтожалась. А для
этого необходимо, во-первых, чтобы эта равнодействующая
проходила через точку касания С; во-вторых, если эту
равнодействующую разложить на две силы, параллельную
238 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ движения
и перпендикулярную к плоскости, так чтобы эти две силы
имели между собой такое отношение, какого требует
заданный закон трения, то мы получили бы тогда два
уравнения, из которых можно определить неизвестные и и v.
Подробнее объяснять это нет необходимости.
Если фигура движется по негладкой плоскости и если
трение предполагается пропорциональным известной ча£ти
силы давления, то линии CR и CL (фиг. 46) находятся
в постоянном отношении друг к другу. Следовательно,
центр G будет двигаться по кривой так, как будто его
приводит в движение сила, направление которой составляет
всегда один и тот же угол с плоскостью MS.
§ 3. О телах, действующих друг на друга с помощью нитей,
вдоль которых они могут свободно скользить.
Задача VIII.
151. Нить ANPM (фиг. 50) данной длины
прикреплена в точке А к горизонтальной плоскости и
нагружена двумя грузами М и Р,
из которых одиНу а
именно М, укреплен неподвижно
на нити, а другой, Р,
может при помощи колечка
скользить вдоль нити.
Требуется определить
движение каждого из этих тел
в предположении, что
каждое из них получило
некоторый толчок.
Пусть тела Рн М
проходят в течение некоторого
элемента времени линии Рр и Mm, Опишем произвольным
постоянным радиусом AN дугу Nn и /т, равную nN. Вопрос
сводится к тому, чтобы найти величину и положение
отрезка pVy следующего непосредственно за Р/?, а также
положение VT другой части нити.
ЗАДАЧИ
239
Я буду исходить из того, что в течение того элемента
времени, за который тело Р проходит путь pV, оно же
при равномерном движении прошло бы в направлении
прямой Рр отрезок
рр =рп -f ттр = Рр + тгр,
а тело М также при равномерном движении прошло бы
отрезок
то — т\х ~|~1*0 = Mm -|- jxo.
В силу нашего принципа каждое из движений рр и то
нужно разложить на два: рх и pV, с одной стороны, и
mL и тТ, с другой стороны, взяв эти движения таким
образом, что в случае движений pV и тТ тела р и m
нисколько не мешали бы друг другу; т. е. чтобы имело место
равенство
AV+VT = Ap-{-pm,
а, с другой стороны, в случае движений рх и mL данные
тела оставались бы в равновесии. Отсюда следует:
1) что линия mL должна лежать на продолжении рт\
2) что ввиду того, что тело р может скользить вдоль
нити (по условию), равновесие возможно только в том
случае, если направление рх этого тела будет делить угол Арт
пополам;
3) наконец, что сила, направленная по mL> должна так
относиться к силе, направленной по рх, как синус
половины угла Арт относится к синусу целого угла Арт.
Так как положение линий Ар, рт и рх задано, нетрудно
видеть, что если будут известны величины отрезков рх и
тгр, то задача будет решена, и все дело будет только
в выкладках. Но, во-первых, линии рх и тгр должны быть
таковы, чтобы углы VAp и рАР были равны между собой:
во-вторых, если рх и тгр известны, то отрезки AV и VT
> также известны как по величине, так и по направлению,
и сумма этих отрезков должна быть постоянной величиной.
Таким образом, мы имеем два условия, из которых мы
получим два уравнения для нахождения рх и тгр. Проведем
соответствующие выкладки.
240 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ движения
Пусть
AN=\y Nn = dxy АР=у, pQ = dy,
синус половины угла АРМ равен z и длина нити равна d
1°. Разность угла PAp(dx) плюс разность угла АРМ
2dz
V\—z*
в сумме равны углу, образуемому линией РМ с линией рт.
Таким образом, угол, образуемый РМ и рт, равен
2dz
dx-
'V\—z* '
2° Отношения -—— и -р—, т. е. синусы углов pPD
и PpDy даны в виде функции от синуса z и от синуса
угла АрР. Поэтому я их выражу таким образом:
yf*. _Jgf__ ^\ п а(г, . ydx V
V ydy2-hv2rf-W V l^rfya -f-J'^Jf2/
ИЛИ'
Отсюда
РВ=Рр.»(г9 r ydX )
PD = Pp-b[z% , ydX ).
' \ Ydy*-\-y*dx*J
3°. Мы имеем
РМ —р т = dy
т£ — /?D == flfy — u/x -' * -
У~1 — *2
*) Величины -f и А, стоящие перед другой какой-либо
величиной, всегда будут обозначать в дальнейшем некоторую функцию
эгой последней.
ЗАДАЧИ
4°. Полагая
рх=$
и
мы будем иметь (см. п° 92)
. _, 2dy dx
угол nAp — dx~
угол тгЛр =
У
a dx
Ydy*+y4x*
О у
и угол pAV или угол хАр = ±-. Отсюда
2dydx adx , |£ ~
.У Yd^^Wdx2 ' 7_
5°. Мы имеем
Лтг=^у -f- 2dTy -f- j/ ^2i
i4p==^7T+-7=======
I!
AV = Ap — [}]/Т=Гр.
Отсюда
Считая dx постоянным, мы будем иметь
tpy =ydx* + , ady — В VT=P.
6°. Далее, мы имеем
PM-uy. = 2dy-(dx + ^L=ryc-y)
(согласно п° 90);
тго = тг|Л — о/==ттр. — —р--
16 Ж. Даламбер
242 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ движения
(мы предполагаем, что \xt — дуга, описанная из центра тг
радиусом 7TJX, и что MB перпендикулярна Вр). Далее, мы
имеем
• a-pD
ор=тго + -^
и
oV = op — (ЛЛ — z2.
Вследствие равновесия
откуда
оТ=_ Р-$
Следовательно,
Р$
VT = oV.-
2MV\—z*'
В итоге мы будем иметь
VT^c-y-My+^dx + ygL^f (с-у)-
Рр "Г Рр Р^ 2MVT^TJz-
Сложивс полученной величиной VT найденную в п° 5
величину AV, мы должны получить в сумме с. Мы
получим, таким образом, уравнение, из которого совместно с
уравнением (А) можно исключить а и [5.
7°. Мы имеем:
угол A Vp = АрР—dx — рр V
и
угол pVT или угол pVo=ppo-\-ppV-\-poV»
Но
угол pol/ = J~,
at-PD
угол рро =ртю — тгор =zpno «
ррЛс—уУ
ЗАДЛЧ1Г
243
Угол
Но угол /ж|л равен, сумме угла Ррт и угла,
образуемого Tijx с pnty а этот последний угол будет равен
(см. п° 90)
(-+Ffe)-(,+^)-
Таким образом,
AVp-\-pVT=ApP-\-Ppm —dx — ррК+
a'PD ■J-poy-LlL.
Р/> • (с—j/) т HP " "Г c_y •
Но
ApP+Ppm =АРМ+у^.
Следовательно,
Если в это уравнение, а также в уравнение (В)
вставить значения аир, найденные в п° 6, у нас будет всего
два уравнения, содержащих только постоянное dx и
переменные у и z с их разностями. Исключив постоянное dx,
мы получим одно дифференциальное уравнение с двумя
переменными^ и z. Таким образом, задача сводится лишь к тому,
чтобы разделить переменные.
16*
244 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ движения
Уравнения можно еще упростить, обозначив через k
угол, синус которого равен z. Это нам даст
У\— z2 = cosk
и
z = sink.
Замечание I.
152. Если нить ЛВС (фиг. 51) закрепить в точках А
и С и если тело В, весомое или невесомое, может
свободно скользить вдоль
нити, ABC, то очевидно,
что тело В будет
описывать эллипс MBN, в
котором точки А и С
будут фокусами.
Но, кроме того, я
утверждаю, что это тело
будет двигаться по
эллипсу точно таким же
образом и в том
случае, если оно не связано с нитью, а спускается свободно
в полости этого эллипса.. В самом деле, когда тело
движется свободно по эллипсу, то направление движения,
теряемого им в каждое мгновение, будет перпендикулярно
к эллипсу в той точке, где находится сейчас тело. Когда
же оно движется по нити ABC, направление теряемого в
каждый элемент времени движения лежит на линии BF,
делящей угол ABC пополам, и, как известно из учения
о конических сечениях, оно будет перпендикулярно к
эллипсу MBN в точке В. Отсюда следует, и т. д.
Замечание II.
153. Если нить AMBNC (фиг. 52), закрепленная в
точках А и С, проходит сквозь тело KRBQL, которое можег
свободно скользить вдоль этой нити, и если все части
ЗАДАЧИ
245
этого тела KRBGL обладают такими скоростями, что тело
находится в равновесии, то я утверждаю, что
равнодействующая сила будет направлена по линии О/?, делящей
угол AGC пополам, причем угол AGC образован
продолжениями линий АК и CL
В противном случае тело
KRL начало бы скользить Л
или в сторону Л, или в
сторону С, т. е.
равновесия не было бы, что
противоречит условию.
На основании этого
замечания нетрудно будет
найти кривую,
описываемую точками К и Z,, и
скорости этих точек, если
тело получает какой-ли*
бо толчок. В самом
деле, необходимо для каждого момента найти четыре
неизвестных, а именно скорости точек К и Z,, а также их
направления. Но эти скорости и направления должны быть
таковы, чтобы сумма
AK+CL
была постоянной величиной так же, как и длина KL.
Далее, потерянные силы для всех точек тела KRL должны
быть направлены таким образом, чтобы равнодействующая
была направлена по GR. Последнее условие дает два
уравнения/ Действительно, если потерянную силу для
каждой частицы разложить на две силы—одну параллельную
и другую перпендикулярную к GR,—то сумма последних
должна быть равна нулю, а равнодействующая первых
будет направлена по линии GR. Таким образом, мы будем
иметь всего четыре уравнения и четыре неизвестных, и
задача решена.
• Я не привожу здесь соответствующих выкладок,
потому что это было бы, очевидно, весьма долго и весьма
сложно. Достаточно привести смысл этих выкладок#
Фиг. 52.
246 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ ДВИЖЕНИЯ
Замечание III.
154. Я не могу покончить с данным вопросом, не
сделав довольно важного замечания относительно решения
задач, в которых тела соединены друг с другом при
помощи нитей. Нити предполагаются нерастяжимыми, и потому
тела могут быть удалены друг от друга на расстояние,
не большее длины разделяющей их нити. Однако ничто не
мешает- им быть удаленными друг от друга на расстояние,
меньшее этой длины.
Пусть, например, два тела прикреплены к концам нити.
Если этим телам сообщить такие движения, чтобы они
могли фактически иметь эти движения без удлинения нити,
то очевидно, что они будут совершать эти движения
в точности таким же образом, как будто они были совершенно
свободными, и в таком случае никакой задачи, требующей
решения, нет. Поэтому общий принцип, которым мы до
сих пор пользовались, к такого рода случаям применять
нельзя.
В самом деле, если бы мы захотели применить этот
принцип, то оказалось бы, что те движения, при которых
тела должны находиться в равновесии, стремятся не
удлинить нить, а, наоборот, сблизить концы нити. А так как
нить не будет оказывать никакого сопротивления усилию
такого рода, то эти движения и не могут уничтожиться.
Вообще, если тела соединены друг с другом при
помощи нитей, то можно следующим образом удостовериться,
будут ли нити все время оставаться натянутыми:
предположив нити действительно такими, нужно посмотреть,
каково направление сил, которые должны уравновешиваться,
т. е. стремятся ли эти силы удлинить нить или нет. Если
да, то мы вправе полагать, что нити натянуты. Если же
нет, то тела будут двигаться точно таким же образом, как
будто они свободны и друг с другом не связаны.
Во всех этих мерах предосторожности нет
необходимости в том случае, если тела соединены друг с другом
при помощи жестких стержней, на которых они
закреплены неподвижно. Действительно, расстояние между телами
тогда будет непременно равно длине стержня, разделяю-
ЗАДЛЧИ
247
щсго их, и не может быть ни больше, ни меньше. Если
тела соединены между собой при помощи жестких
стержней, которые связаны друг с другом с помощью
шарниров, то только что сделанное нами заметание по поводу
случая с нитями также излишне. Однако в остальном этот
случай совершенно аналогичен со случаем нитей.
В самом деле, если тела, соединенные друг с другом
при помощи нитей, 'движутся таким образом, что нити
вследствие своей нерастяжимости могут изменять эти
движения, то с этими движениями происходят точно такие
же изменения, как будто нити являются жесткими
стержнями, соединенными между собой шарнирами.
Общее примечание.
155. Когда наш общий принцип применяется к решению
какой-нибудь задачи динамики, иногда возможна ошибка,
заключающаяся в том, что мы можем неудачно
предположить, что движения каких-либо тел уменьшаются, тогда
как на самом деле они увеличиваются, или наоборот.
Но здесь дело обстоит так же, как и во многих
других задачах, где вычисления сами исправляют ошибочные
допущения, когда мы вначале принимаем за
отрицательное то, что на самом деле является положительным, или
наоборот.
Нужно только в процессе вычислений внимательно
следить за тем, чтобы не делать никаких отступлений от
сделанных вначале предположений и ни в коем случае не
давать уравнениям такой формы, которая бы противоречила
этим предположениям. Например, представим себе, что а,
($, у и т» Д« СУТЬ силы, потерянные отдельными телами, и
согласно сделанным предположениям и согласно взятому
чертежу эти силы должны быть параллельны друг другу
и направлены в одну сторону. В таком случае, если
условие равновесия требует, чтобы эти силы взаимно
уничтожались (в предположении, что неподвижной точки не
имеется и тело свободно), нужно взять
c*+S+Y=°.
548 СБЩИЙ ПРИНЦИП ДЛЯ^ НАХОЖДЕНИЯ ДВИЖЕНИЯ
а не
и не
<* + Y — ?
и т. д. Если же, по сделанному предположению, сила у,
например, направлена параллельно а и р, но в
противоположную сторону, тогда нужно взять
ИЛИ
e + p_Y=o.
Точно так же, если силы а, [5, у действуют с помощью
плеч х, z9 у и эти плечи взяты все с одной стороны,
силы же все действуют также в одну сторону, мы будем
иметь
ах -j- [te + ЧУ = 0.
Если же, например, j/ взято по другую сторону, чем л; и £.
а все остальное по-старому, то мы получим
алг+р* = у.У»
или
длг + Р*— у„У = 0,
и так в остальных случаях.
Отсюда вытекает, что в указанных случаях уравнения
ИЛИ
a* + p* + Y.y = 0,
полностью и в общем виде представляют условия
равновесия, если только мы не забудем величинам а, р, у и т. д.,
с одной стороны,, и величинам ху у, z и т. д., с другой
стороны, придать знаки согласно сделанным
предположениям и согласно взятому чертежу. То же будет и во всех
остальных случаях.
С такими предосторожностями мы можем совсем не
бояться того, что мы собьемся.
ЗАДАЧИ
249
§ 4. О толкающих друг друга телах, или, иначе,
о телах соударяющихся.
Задача IX.
156, Тело, масса которого т и скорость и, движется
по одной прямой с другим телом, масса которого М, а
скорость О. Найти скорость обоих тел после удара.
Пусть v будет скорость первого тела после удара и V —
скорость второго тела после удара. Запишем (см. п° 61)
так:
u = v-\-u — v
и
u=v+u— V.
Согласно нашему принципу должны соблюдаться равенства
V = v
и
m{u — v)-\-M{U—V) = 0.
Отсюда следует, что
т. та + MU
v или V— г
М-\-т
Следствие.
157. Если тело М произвольной массы, обладающее
данной скоростью £/, испытывает удар со стороны
бесконечно малого тела т, скорость которого равна и, то оно
получит в результате этого удара количество движения,
равное
т (и — U).
Если и будет бесконечно больше, чем U, то это
количество движения будет равно та, т. е. равно количеству
движения ударяющего тела.
Мы видим, таким образом, что когда движение какого-
либо тела ускоряется или замедляется какой-нибудь
понуждающей силой, от которой оно получает, так сказать,
в каждый момент повторяющиеся удары, тогда то коли*
250 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ движения
чество движения, которое тело теряет или приобретает
в каждый момент, можно полагать пропорциональным
понуждающей силе только в том смысле, что сила нами
рассматривается как бесконечно малая масса, обладающая
скоростью бесконечной по сравнению со скоростью толкаемого
тела. В таком случае действие этой силы всегда будет
одно и то же, движется ли данное тело или оно находится
в покое.
Замечание.
158. Здесь будет уместно привести доказательство того,
что мы утверждали выше (см. п° 22), а именно того, что
для определения движений, получающихся в результате
толчка, нельзя пользоваться тем положением, что
ускоряющая сила пропорциональна элементу скорости.
В самом деле, предположим, например, что какое-либо
тело ударилось о другое тело, находящееся в покое.
Количество движения, получаемое ударяемым телом, будет равно
тМа
М + т'
Поэтому и причина, создающая движение, должна была бы
быть пропорциональной
тМа
М+т '
Но, во-первых, как доказать, что движущая причина тела М
пропорциональна
Mm и
М+т'
а не какой-либо другой функции от величин М> /я, и? Не
столь же ли естественно можно было бы считать величину
та пропорциональной движущей причине? А мажду тем
последнее предположение неизбежно приводит к ошибке,,
так как при прочих равных условиях количество движения
тела М вовсе не пропорционально та.
Во-вторых, если бы было известно, что движущая
причина пропорциональна
Mm и
М-\-ту
ЗАДАЧИ
251
то отсюда еще ровно ничего не следует, если не считать
того, что количество движения тела М, рассматриваемое
в качестве действия этой причины, будет пропорционально
Мти
М+т'
При этом вовсе нельзя будет сказать, будет ли эта
величина в точности этим самым количеством движения *).
Таким образом, для того чтобы определить абсолютное
количество движения ударяемого тела, неизбежно
приходится пользоваться иными принципами.
Лемма IX.
159. Пусть по плоскости QR (фиг. 53) может
свободно скользить по направлению от Q к R, или от R
к Q, некоторое тело AKQR
произвольной формы. И пусть на KQ
в произвольном месте положено
какое-либо другое тело М.
Предположим, что тело AKQR
имеет какую-то произвольную
скорость по направлению RQ, а
тело М при этом имеет такую
скорость и такое направление,
что оно уравновешивается с
телом AKQR» Я утверждаю, что это возможно только в том
случае, если, во-первых-, направлением тела М будет
служить линия MG, перпендикулярная к KQ\ во-вторых, если
сила тела М, направленная по МО, и сила тела AKQR,
направленная по RQ, приводятся к одной силе,
направление которой перпендикулярно к плоскости QR.
Следствие.
160. Отсюда следует, что сила тела М должна так
относиться к силе тела AKQRy как OL относится к LS.
• *) См. «Encyclopedic», слово «Cause» (причина) (том II,
стр. 790). См. также слово «Force» (сила) (том VII, стр. 114,
столб. 2) Р].
252 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ движения
Примечание.
161. Направление равнодействующей сил обоих тел
должно быть не только перпендикулярно к плоскости, но
и проходить через основание QR. Отсюда следует, что
если через центр тяжести фигуры AKQR провести прямую,
параллельную QR, то эта' прямая пересечет линию МО в
такой точке, из которой можно опустить перпендикуляр,
падающий на Q/?.
Задача X,
162. Полагая, что тело М обладает какой-то про-
изволъной ускоряющей силой, перпендикулярной к
основанию QRy и сохраняя все остальные условия
предыдущей леммы, найти, каковы будут движение тела М и
движение фигуры.
А а аа
а
Фиг. 54.
Пусть.АВ и ВС (фиг. 54) будут две рядом лежащие
стороны данной фигуры, причем эти стороны таковы, что
AB = BV.
Предположим, что за то время, пока тело М проходит
линию АВ, фигура проходит линию Аа, так что стороны АВ
и ВС будут занимать положения аВ и BD. Пусть, далее,
аа — Аа*
ВЬ = ЛВ
ЗАДАЧИ
253
и пусть линия Ь8 будет тем расстоянием, которое тело М
прошло бы вследствие своей ускоряющей силы; пусть
линии аа и В5 будут теми линиями, которые описали бы наши
два тела в течение следующего элемента времени, не
оказывая никакого действия друг на друга. На самом деле
они вместо этого будут описывать: одно — линию аа, а
другое— линию Ete, оканчивающуюся на стороне bz,
параллельной $d.
Согласно нашему принципу масса тела Ж, обладающая
скоростью г8, должна уравновешивать массу т фигуры,
обладающую скоростью аа. Отсюда вытекает, что bz должно
быть перпендикулярно к bz и должна соблюдаться пропорция
m-aa:M-zb — ib:zbc
Следовательно,
т»аа — М-1Ъ.
Но
ib = kz — bo — аа
и
aa = d(aa).
Поэтому, если ввести обозначения
Aa = du и BK=dy,
мы получим
md2a = Md2y — Md2u,
или
d2u (M-\-m) = Md2y%
Мы получили общее, и притом довольно простое,
уравнение для нахождения движения обоих тел, какова бы ни была
ускоряющая сила, действующая на тело Ж, лишь бы эта
сила была всегда перпендикулярна к QR.
Примечание I.
163. Постоянные, которые нужно прибавить при
интегрировании уравнения
Md*y = (M-\-m)-cPu,
254 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ движения
зависят от dy и du, которые всегда нетрудно найти. Если,
например, направление движения тела М в точке А (фиг. 55)
С
Фиг. 55.
совпадает с касательной к кривой АВ в точке Л, то нужно
провести касательную АР и отложить
PN-M
АО--
М+т
для того, чтобы найти точку О, в которой окажется
фигура в тот момент, когда тело М придет в точку N*).
*) Линия /Ь (фиг. 54) представляет собой ту длину, на
которую убавился путь тела за второй элемент времени по
сравнению с путем за первый элемент, причем путь берется параллельно
плоскости. Но величина замедления за любой элемент времени
есть длина, на которую тело продвигается вперед в силу своего
собственного движения параллельно плоскости, минус движение
фигуры, увлекающее и тело. Поэтому
ib = d2y — d%
где dhi обозначает второе, a d2y — первое движение.
При интегрировании уравнения
Md2y = (M+m)d2u
интегралом от Md2y не всегда нужно брать М*/(В, так как
Sd2y
представляет собой здесь сумму всех малых путей, которые тело
М проходит параллельно плоскости в силу своего собственного
движения. Весь же этот путь определяется первоначальным
движением тела. Если тело в первый момент стремится двигаться по
направлению АК, то $d2y будет равен ВК, так как при
отсутствии кривой поверхности оно пришло бы в точку f(. Если же оно
в первый момент стремится двигаться по направлению АР (фиг. 55),
то $d2y будет равен PN, так как в силу одного этого
стремления оно пришло бы в точку Р. (Примечание Безу.)
ЗАДАЧИ
255
Если тело М будет двигаться только вследствие своей
ускоряющей силы без какого бы то ни было
первоначального толчка, то нужно провести AQ перпендикулярно к BD
и отложить
М-{-т
Впрочем, уже на основании п° 84 явствует, что в
последнем случае общий центр тяжести обоих тел будет
опускаться по вертикальной прямой.
Примечание II.
164. Можно было бы дать и другие решения данной
задачи: все они приводят к уравнению
Md2y = (M-\~m)d2u.
Я предпочитаю всем этим решениям то, которое было
только что указано, из-за того, что оно в высшей степени
простое.
Все задачи, аналогичные этой, какие бы они ни были,
можно решать с помощью нашего принципа. Трудности
будут относиться лишь к вычислениям.
Лемма X.
165. Пусть два шара G и С (фиг. 56) движутся по
GB и CD со скоростями, представленными бес/сонечно
малыми линиями GB и CD.
Ясно, что если
DB = CG,
т. е. если
DE = BF,
то двиэюения обоих шаров
не будут мешать одно дру- фип 5б.
гому.
Отсюда следует вообще, что для того, чтобы данные шары
не мешали друг другу в своих движениях, необходимо,
256 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ ДВИЖЕНИЯ
чтобы скорость точки касания Л но направлению
перпендикуляра С AG к обоим телам была одна и та же как с той,
так и с другой стороны.
Действительно, тогда мы будем им ель
ED = FB,
откуда
DB = CG.
Следствие.
166. Если два тела произвольной формы соприкасаются,
ю, рассматривая точку соприкосновения этих тел как
малую сферическую поверхность, мы увидим, что для того,
чтобы эти тела не мешали друг другу в своих
движениях, скорость точки соприкосновения, измеренная по
направлению перпендикуляра к обеим поверхностям в этой
точке, должна быть одной и той же для обоих тел.
Лемма XI.
167. Если произвольное число тел соударяется таге,
что при условии совершенной твердости и отсутствии
упругости они после удара остаются все в покое, то
я утверждаю, что при условии совершенной упругости
они будут возвращаться обратно с теми же скоростями,
какие были у них до удара.
В самом деле, действие упругости будет состоять в том>
что у каждого тела восстанавливается, только в
противоположную сторону, то движение, которое было утрачено
вследствие действия других тел.
Следствие.
168. Если произвольное число твердых тел [81]
одновременно ударяется друг о друга и если их скорости до удара
были a, b и т. д., а после удара они заменяются
скоростями a, b и т. д., то, рассматривая скорости а, Ъ и т. д.
как составленные из скоростей а и a, b и [J и т. д., мы
найдем, что скорости тех же самых 1ел после удара (в слу-
ЗАДАЧИ
257
чае упругих тел) будут составлены из скоростей а и — а,
b и — (S и т. д.
Поэтому в последующих задачах мы будем говорить
лишь об ударе твердых тел, поскольку отсюда нетрудно
будет вывести и законы движения упругих тел.
Я здесь не рассматриваю вопроса о том, существуют ли
абсолютно твердые тела. Эта проблема относится скорее
к физике, чем к механике, и я здесь принимаю абсолютно
твердые тела лишь в том смысле, в каком обычно в
механике говорят о несгибаемых рычагах, о машинах,
лишенных трения, и т. д. Кроме того, я принимаю как опытный
факт то, что упругость возвращает каждому телу
движение, равное и противоположное тому движению, которое
было потеряно при ударе, не входя в рассмотрение того,
каким образом совершается это восстановление.
Так как довольно хорошо подтверждается то, что
упругие тела при ударе сплющиваются и сжимаются, а затем
снова восстанавливают свою первоначальную форму,
казалось бы, можно думать, что найти законы движения этих
тел так, как мы это делаем здесь,—а именно предполагая,
что тела несжимаемы,—невозможно. И действительно, как
будет показано в дальнейшем, это обстоятельство неизбежно
вносит те или иные изменения в эти законы. Но тем не
менее, мы можем, по крайней мере, принять, что форма
тел меняется весьма незначительно и что как сжатие, так
и восстановление происходят в течение весьма короткого
времени. В таком случае движение после удара не будет
заметно отличаться от.того, какое имело бы место при
условии несжимаемости тел.
Вполне точно эти задачи можно было бы решить в том
случае, если бы нам было известно, по какому закону
меняется при сжатии форма тела. Однако об этом можно
делать лишь предположения.
Задача XI.
169. Предположим, что тело А (фиг. 57) толь/со что
ударилось о другое тело BOQ, находившееся до того в
пд/сое. Удар происходил по направлению АС, не прохо-
17 Ж Дзлал1бг£
258 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ движения
дящему через центр тяжести М ударяемого тела.
Спрашивается, каково будет движение обоих тел после удара.
Какое бы движение ни восприняло тело BOQ,
несомненно то, что его центр М будет двигаться после удара
прямолинейно, а все части этого тела будут вращаться
вокруг этого центра (см. п° 76).
Далее, согласно нашему
принципу, если сообщить этому
телу движение,
противоположное тому, которое оно получн-
ло при ударе, то оно уравнове-
В у/Q Q сится с телом Л, если бы это
yS последнее обладало движением,
' потерянным им при ударе.
Фиг. 57. Выше (п° 141) было
доказано, что если центр тяжести
М какого-нибудь тела движется по некоторому
произвольному направлению и если в то же время это тело
вращается вокруг своего центра, то 'направление
равнодействующей силы будет параллельно направлению центра
тяжести*). Но направлением этой силы может служить лишь
линия СЛ, перпендикулярная в точке касания Л,
вследствие того, что сила эта должна уничтожаться равной ей
силой тела Л, действующей по направлению АС. Отсюда
следует, что движение центра М должно быть
параллельным АС. Далее, скорость вращения должна быть такова,
что если это вращение сложить с движением центра М,
то тела не будут мешать друг другу, т. е. они будут иметь
одинаковую скорость в одну и ту же сторону. Если
опустить на С А перпендикуляр MN% то легко видеть, что
движение точки касания Л по направлению AN будет равно
движению точки N. Таким образом, вся трудность
сводится к нахождению скорости точки М и скорости
вращения точки N.
*) Желающие могут найти более подробное доказательство
этого предложения в наших «Исследованиях о предварении
равноденствий» («Recherches sur la precession des equinoxes»), n° 86
и ел. Однако доказательство, приведенное вп° 141 настоящего
сочинения, мне кажется также достаточным.
Г^\
ЗАДАЧИ
259
Пусть и будет скорость тела А до удара, и — скорость
его после удара, а — скорость центра М, v — скорость
вращения точки N. Тогда мы будем иметь
1* a-ftr = u.
Далее, равнодействующая сила движений частей тела М в
противоположную сторону должна быть равна
А-(и-и).
С другой стороны, эта сила должна быть равна Ж «а иона
должна быть направлена по линии СА. Следовательно, мы
будем иметь
2° ЛЬа = Л-(« —и).
Наконец, если через р обозначить сумму произведений
частей тела М на квадрат их расстояний до центра М> то
мы будем иметь (см. п° 141)
Таковы три уравнения для определения неизвестных
величин а, и и и. Что и требовалось найти.
Задача XII.
170. Два шара А «я (фиг. 58) прикреплены к
стержням рА и са, имеющим неподвижные точки Сие. За-
даны скорости этих шаров. Шары ударяются друг о друга.
Требуется найти скорости тел после удара, предполагая^
что до удара они оба двигались в одну сторону.
Пусть и и v будут скорости центров А и а до удара,
и и v — скорости этих центров после удара. Согласно
нашему принципу необходимо, чтобы скорости и и v были
такими, чтобы тела не мешали друг другу и чтобы, в
случае, если бы центры тел обладали скоростями и — и и v — v,
было бы равновесие. Другими словами, если бы точки А
и а обладали скоростями и — и и v — v, то сила тела Л,
рассматриваемая как бы сосредоточенной в точке А и
действующая по направлению Аа> должна будет равняться силе
17*
260 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ ДВИЖЕНИЯ
тела а, рассматриваемой как бы сосредоточенной в точке а
и действующей по направлению аА.
Если провести к Аа перпендикуляры СО и eg, то
первое условие дает
U'CG v*cg
С А ~7а~т
Далее, если через F обозначить сумму произведений частиц
тела А на квадрат их расстояний до точки С или, вернее,
С
Фиг. 58,
до оси, проходящей через точку С, и через /аналогичную
величину для тела а, то второе условие нам даст
F.{u-u) , /•(»—v)_,
AC-CG ' ас-eg
Из полученных двух уравнений можно определить
значения и и V.
= 0*).
*) В самом деле, если и —и представляет собой скорость
вращения, потерянную центром Л, то скорость, потерянная
всякой другой точкой М, будет равна
tu ^ СМ
а сила, потерянная этой точкой, будет равна
х СМ Ал
ЗАДАЧИ
261
Следствие I.
171. Если тела упруги, то их скорости после удара
(см. п° 168) будут равны
u-j-u— и и v-|-v — V.
Сумма живых сил после удара будет равна
-£2(2u-«)3 + X2_(2v_^ =
Fu2 , fv2 . 4F , , . , 4/ . , .
Но умножая предпоследний член на
а последний член на
что, разумеется, не изменит их величины, мы увидим, что
эти члены взаимно уничтожат друг друга, так как
v-CG и-eg
С А са
и
F-(u — i\) , /•(» —v)_n
СА
СО
са
eg'
CG
' СА>
eg
са'
AC-CG ' ас—eg
Но вместо этой силы можно взять силу, которая действует по
направлению GA или Аа и которая вследствие правила рычага
(если MCG рассматривать как ломаный рычаг) будет равна
(и — и)'СМ*-М
CA-CG
Отсюда следует, что сумма потерянных сил у тела А будет равна
(и -и).СЛЯ.Л! __ и — и f сдр.д! — ^ —иК_
ц —и Г
CA-CG J '
J CA-CG CA-CG J CA-CG
Отсюда следует, и т. д. {Примечание Безу.)
262 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ движения
Отсюда следует, что сумма живых сил после удара будет
равна
Fvfi | fy*
AC*iac2 '
т. е., другими словами, сумма живых сил как до, так
и после удара будет одной и той же.
Следствие II.
172, Если линии С А и са в момент удара параллельны,
то нужно положить
CG=CA и cg^ca,
остальные же рассуждения остаются прежними. Задача
в этом случае была решена в VII томе петербургских
«Comraentarii» И. Бернулли сыном [82], принимавшим тела
упругими. Мое решение резко отличается от его как по
методу, так и по результатам. В то время как в мемуаре
Бернулли скорости после удара выражаются через радикалы,
у нас, как легко убедиться, не будет никаких радикалов.
Величины F и /, единственные величины, которые могут
ввести радикалы в выражение для скоростей, сами
радикалов не содержат. В самом деле, обозначая через J и J
радиусы шаров Л и а и полагая
CN=a и сп = а>
мы получим
F=U*-\-2ab-\- jbA -А
ч
/=(аЧ-2аН-£р).о.
Соответствующие выкладки смотри в указанном мемуаре
Бернулли.
Однако, помимо того, что решение Бернулли — непрямое
решение, так как оно опирается на принцип сохранения
живых сил, оно основывается еще на другом принципе,
который неверен. Принцип этот состоит в том? что тело А
ЗАДАЧИ
263
приводимое в движение при помощи жесткого стержня СА,
рассматривается так, как будто все части его обладают
движением, равным движению центра Л и в то же время
как будто тело А вращается вокруг своего центра,
поворачиваясь на угол, равный углу поворота стержня. В
результате в силу этого принципа получается, что сила
тела А будет такая же, как если бы это тело вовсе не
было прикреплено к стержню и все его части обладали
скоростью, равной скорости его центра без всякого
вращения, что, мне кажется, противоречит законам- механики.
Бернулли в п° XV своего мемуара ограничивается
указанием, что вращается ли тело вокруг точки С или же
все части его движутся со скоростью, равной скорости
центра Л, и в том и в другом случае количество
движения данного тела будет одним и тем же. Против этого
ничего нельзя возразить. Однако в случае, например,
шара, вращающегося вокруг неподвижной точки, количество
движения и сила уже не одни и те же; здесь приходится
учитывать то плечо рычага, при помощи которого
действует та или иная частица. Силой в данном случае будет
служить сумма произведений каждого элемента на его
скорость и на его расстояние от неподвижной точки, а не
просто сумма произведений каждого элемента на его
скорость.
Задача XIII.
173. Два тела А и В (фиг. 59), подвешенные на
нитях СА и GB, укрепленных в точках С и G, толь/со
что ударились друг о друга. Найти их движение после
удара.
Пусть и — скорость обращения точки А вокруг точки С
до удара. Эта скорость будет общая для всех частей тела А.
Пусть, кроме того, v будет скорость обращения центра
тяжести тела А вокруг точки Л, за которую оно
подвешено, до удара. Пусть также U и V будут такие же
скорости, относящиеся к телу В до удара, аналогичные
и и v. Пусть, наконец, все эти скорости после удара
переходят в и и v, U и V. При этом эти последние
скорости таковы, что тела А и В в момент после удара
264 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ ДВИЖЕНИЯ
идут вместе, не мешая др*уг другу» и, кроме того, таковы,
что если бы данные тела обладали только скоростями
и — u, v — v, U—U и V — V, то оба тела взаимно
уравновешивались бы.
Рассматривая все части тела А (фиг. 60) как
обладающие скоростью и — и, можно свести все движения к одной
единственной силе, направление которой ОК будет
проходить через центр тяжести G
тела А и будет
перпендикулярно к линии СД
продолженной к точке L. Далее, если
г с
\ /
Фиг. 59.
центр тяжести тела А будет обладать скоростью v — v
обращения вокруг точки Л, то мы можем найти
направление N0 равнодействующей силы, не зная величины v — v
(см. п° 140). Сила, направленная по ОР, которая, как
я принимаю, является равнодействующей сил, направленных
по ОК и N0, должна уничтожиться. Поэтому она должна
быть такова, чтобы ее можно было разложить на две силы:
одну по направлению PL или СА и другую по
направлению Ра, перпендикулярно к поверхности соприкосновения
двух тел в точке а. Но так как положение точек Р и О
определяется линиями аР и САУ с одной стороны, и
линиями N0 и КО, с другой стороны, — а расположение всех
этих линий известно, — то отсюда следует, что направление
ОР равнодействующей сил, направленных по ОК и 7VO,
ЗАДАЧИ
265
также известно, а следовательно, известно и отношение
сил, направленных по ОК и по N0.
Обозначая через т массу тела Л, мы получим, что
сила, направленная по ОК, будет равна т*{и—и), а сила,
направленная по N0, будет равна т (v — v) (см. п° 139).
Таким образом, отношение и—и к v—v будет известно.
Подобным же рассуждением мы найдем и отношение U—U
к V — V для другого тела. Следовательно, из четырех
неизвестных u, v, U и V можно будет исключить два.
Помимо этого, должны удовлетворяться еще два
условия, а именно: сила, направленная по Ра, должна равняться
силе, действующей в другом теле в противоположную
сторону, и, кроме того, оба тела в момент после удара
должны двигаться вместе: другими словами, скорость точки
касания #, направленная по Ра, должна быть одинаковой
для обоих тел. Эти два условия дают еще два уравнения,
из которых можно найти остальные два неизвестные. И эти
уравнения никогда не будут выше первой степени.
О теле, ударяющем несколько тел одновременно.
Задача XIV.
174. Пусть тело в форме шара А (фиг. 61), движу-
щееся'по направлению данной линии AQ с данной
скоростью, встречается одновременно с двумя телами В и С,
находящимися в покое. Требуется узнать направления
и скорости всех трех тел после удара.
Пусть AN = u— скорость тела А до удара, AR —
искомое направление этого тела после удара, a AV=v —
скорость его после удара. Пусть, кроме того, BZ и СХ—
скорости, которые получают тела В и С. По условию,
все эти линии, AN, AV, BZ и СХ, представляющие
скорости, суть линии бесконечно малой длины.
Скорость BZ тела В и скорость AV тела А должны
быть такими, чтобы соблюдалось равенство
VZ^AB
266 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ ДВИЖЕНИЯ
(см. пб 165). Точно так же скорость СХ тела С и
скорость AV тела А должны быть такими, чтобы соблюдалось
равенство
КАГ== АС.
Далее, если предположить, что тело А в момент удара
обладает движениями AV и VN, или AV \\ Ар, а тела В и С
Фиг. 61.
обладают (п° 61) равными и противоположными движениями
BZ и Bz, с одной стороны, и СХ и Сх, с другой
стороны, то согласно нашему принципу тела А, В и С,
обладающие движениями Л/?, Яг и Сх, должны
уравновешивать друг друга.
Пусть нам даны
AQ = a, QS=T, QT=T;
неизвестные же обозначим следующим образом:
Q/? = /, AV=v.
Тогда, проведя RO перпендикулярно к AS и Ro
перпендикулярно к AT, мы будем иметь
RO_ (T-t).a
AR Ya* + T*-ya*-\-t*'
Ro _ (T + *)-g
AR Уа*-^-Т*-Уа2+Р'
ЗАДАЧИ
267
VZ = AB%
Va2+ T2 (T—t).T \
V a2-\-t2 Ya*-\-T*•Ya*-\-W '
Подобными же рассуждениями мы найдем
\ya* + t* Va2+T2'Va2-{-t2 J '
Но если из точки V провести перпендикуляр VP
к линии AN, то вследствие равновесия мы будем иметь
A.PN=B.B-^Q + C.CX^
И
т D B-BZ-QS | C'CX-QT
А'уи=* AS I Af~'
Вставляя в эти равенства вместо входящих в них линий
соответствующие аналитические выражения, мы сможем
определить v и /.
Если бы мы проделали все выкладки, то мы увидели
бы, что в результате получаются всегда линейные
уравнения. В самом деле, из двух уравнений мы определим
величину
у
У a2+t2
и, сравнивая полученные два выражения, мы исключим
радикал yra2-\-t2 и получим одно уравнение с одним
неизвестным /, входящим в него в первой степени. Таким
образом, мы легко найдем значение t, а подставив его
в одно из выражений
у
Vat+T2'
мы найдем и значение v.
Далее, так как
мы будем иметь
U7 AV-AO
BZ = -AR-'
268 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ ДВИЖЕНИЯ
Замечание 1.
175. Я не вхожу в подробности решения этой задачи
и не стараюсь даже упрощать ее ввиду того, что
прекрасное решение данной задачи можно найти в сочинении Макло-
рена, носящем заглавие «A Treatise on fluxions».
Впрочем, наш принцип позволяет найти законы удара
и в том случае, когда один шар встречается одновременно
с любым количеством шаров. Эта задача была решена
И. Бернулли, но с помощью принципа сохранения живых
сил и только для того случая, когда ударяемые шары
одинаковы и расположены симметрично относительно
направления ударяющего шара [83]. Буге также решил эту
задачу только для такого же случая («Journal des savants»,
апрель 1728 г.) без помощи принципа сохранения живых
сил [84].
Бернулли в «Рассуждении о движении» из своего
решения извлек большое количество изящных следствий,
касающихся движения тел в жидкостях. Там же можно
найти ряд других теорем, им не доказываемых, —
доказательства их приведены мною в моем сочинении «О
равновесии и движении жидкостей», кн. III, гл. 1 [85].
Замечание II.
176. Присмотревшись внимательно к характеру общей
задачи о нескольких одновременно соударяющихся телах,
обладающих заданными скоростями и заданными
направлениями, можно натолкнуться на ряд трудностей, которые
полезно осветить здесь: это даст нам возможность сделать
некоторые новые замечания по поводу законов удара тел.
Предположим, например, что шар А (фиг. 62),
движущийся по направлению AL, встречается одновременно с
шарами С, D, Е и F, симметрично расположенными *
относительно линии AL. Пусть шары F и Е находятся в покое,
а шары С и D движутся параллельно AL со скоростями,
равными скорости тела А. Очевидно, тело А не будет
оказывать на шары С и D никакого действия, и все будет
происходить таким образом, как будто тело А задевает
ЗАДАЧИ
269
только шары Е и F. Если же шары Си D имеют
скорость меньшую, чем скорость тела Л по направлению ALy
то тело А будет оказывать действие на эти шары, и на
первый взгляд кажется, что оно сообщит движение всем
четырем шарам.
Однако трудность здесь вот в чем. Предположим, что
скорость шаров С и D до удара будет весьма немногим
меньше скорости тела Л. Если
эта скорость после удара
увеличится только весьма
незначительно, то, поскольку шары
Л, С и D должны
двигаться вместе, скорость шара А
уменьшится весьма мало.
Далее, так как шары F и Е
также должны двигаться
вместе- с шаром Л, то скорость
этих шаров будет так
относиться к скорости тела А после
удара, как косинус угла BAF к полному синусу, и потому
будет как бы бесконечно больше скорости, потерянной
телом- Л. Но, согласно нашему принципу, тело Л,
обладающее скоростью, которую оно потеряло, должно
уравновешивать тела Е, F, С и D, обладающие скоростями,
противоположными тем, которые они приобрели от удара.
Между тем скорость, потерянная телом Л, весьма мала
(по условию) и потому она не может уравновесить
конечных скоростей тел Е и F. Следовательно, скорость шаров
С и D не может увеличиться на весьма малую величину.
Но, с другой стороны, если скорость их увеличивается на
такую величину, которая не является весьма малой, то они
не будут в состоянии двигаться вместе с телом Л, скорость
которого непременно уменьшится.
При производстве вычислений в настоящей задаче
встречается еще одна трудность. Выражения для скоростей всех
пяти тел после удара найти весьма нетрудно, хотя
согласно только что сделанному нами замечанию может
показаться, что это — дело нелегкое. Вычисления основываются
здесь на тех двух условиях, согласно которым все пять
270 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ ДВИЖЕНИЯ
тел движутся после удара вместе и, далее, на том, чт
если они будут обладать скоростями, противоположными
тем, которые оказались потерянными ими или
приобретенными, то они будут оставаться в равновесии.
Однако, если посмотреть, каким образом вычисления
удовлетворяют этим условиям, то мы увидим, что
последние выражаются аналитически таким образом, что они не
всегда согласуются с физической стороной задачи, вследствие
чего, если ненадлежащим образом применять в данной задаче
вычисления, они могут привести к неправильным выводам.
Для того, например, чтобы тела двигались после удара
вместе, необходимо, чтобы скорости этих тел в направле-.
нии, перпендикулярном к поверхности соприкосновения,
были одинаковыми,—таково условие, которое выражается
аналитически. Но, кроме того, необходимо, чтобы эти
скорости были направлены в одну и ту же сторону или в
противоположные стороны, — смотря по условиям задачи. Это
условие не выражается и не может быть выражено
аналитически.
Точно так же для того, чтобы соблюдалось равновесие
между телами F, С, D, Е и телом Л, недостаточно того,
чтобы сумма движений, взятых в одну сторону, была равна
нулю,— это только и можно выразить аналитически: нужно
еще, чтобы уравновешивающиеся движения были
направлены по АВУ по FA, по СЛ, по DA и по ЕА. Эти
условия не могут быть выражены аналитически, и лишь найдя
величины скоростей и их направления, можно убедиться,
выполняются ли указанные условия или нет.
Если не выполнены все эти условия, как это имеет
место в только что рассмотренном случае, то это служит
признаком того, что некоторые тела системы не
испытывают никакого действия со стороны других тел и
потому в движении их не произойдет никаких изменений.
Так, в данном случае, хотя скорость тел С и D меньше
скорости ударяющего тела А, тем не менее эти тела не
будут претерпевать никаких изменений, и все будет
происходить таким образом, как будто тело А ударит
только два других тела Е и F. Действительно, скорость
тел С и D не может уменьшиться от встречи с телом Л.
ЗАДАЧИ
27\
Они не могут также и получить никакой добавочной
скорости благодаря действию тела Л, поскольку, как мы
видели выше, они не могут после удара двигаться вместе
с телом Л. Но если тела Л, С и D после удара не будут
двигаться вместе, это значит, что между ними нет
никакого взаимодействия. Действительно, в том случае, когда
имеет место взаимодействие между двумя телами, движение
этих тел всегда можно привести к движениям,
направленным в одну сторону — благодаря этим движениям эти трла
нисколько не будут мешать друг другу,—и к движениям
противоположным, которые должны взаимно уничтожиться.
Но противоположно направленные движения могут взаимно
уничтожаться только тогда, когда они, будучи взятыми
в одну сторону, равны между собою. Если первое тело
движется быстрее второго, то между этими телами никакое
взаимодействие невозможно.
Замечание III.
177. Дело будет обстоять иначе в том случае, когда
тела Л, С, D, Е и F являются телами упругими. Скорость
тела Л тогда будет уменьшаться лишь постепенно,
незначительными порциями, и так же постепенно это тело будет
действовать на тела С и D, изменяя их движение, Поэтому
в данном случае для определения скоростей после удара
нужно весьма остерегаться пользоваться правилом,
приведенным лами в п° 168.
Это обстоятельство . навело меня и на другую мысль:
для одновременного соударения нескольких упругих тел
это самое правило может быть совершенно негодным.
Предположим, например, что все пять тел Л, F, £?, С
и D (фиг. 62) являются совершенно упругими. В момент
удара в каждом из этих тел будет происходить сжатие,
причем сжатие это будет таково, что ударяемые тела
в каждый элемент времени будут получать бесконечно
малое количество движения назад по направлениям,
соответственно, FA, С A, DA и ЕАУ равное тому количеству
движения, которое тела Т7, С, D и Е получат вперед.
Таким образом, эти тела будут все более и более
сплющиваться, пока, наконец, они не смогут двигаться все
272 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ движения
вместе со скоростями, равными в одну сторону. Затем
мало-помалу они начнут восстанавливаться и будут снова
терять или приобретать количества движения, равные тем,
которые они перед тем приобрели или потеряли.
Но так как мы совершенно не знаем, по какому закону
упругость создает в телах ускорение, то мы и не знаем,
все ли пять тел одновременно перестают сжиматься, не
начинают ли, например, тела С и D восстанавливаться
в тот момент, когда тела Е и F еще полностью не сжаты.
В таком случае наши пять тел вовсе не могли бы
двигаться после удара вместе даже при том условии, если
допустить, что упругость не восстанавливает их в их
первоначальном состоянии. Но если бы это было так, то для
определения движения после удара не следовало бы
пользоваться методом, указанным в п° 168 и основанным на
том, что тела сначала рассматриваются как твердые, так
как метод этот существенно исходит из того, что наши
тела (отвлекаясь от их упругости) будут после удара
двигаться вместе.
Что во всех телах сжатие заканчивается одновременно,
в этом можно сомневаться хотя бы уже потому, что есть,
бесспорно, случаи, когда это просто невозможно: это будет
в том случае, когда тела С и D, по условию, обладают
скоростью, параллельной AL и чуть-чуть меньшей той,
какой обладает тело А по направлению AL.
Если и бывают случаи, когда сжатие всех тел
заканчивается одновременно, то при изменившихся каким-то
образом условиях, понятно, сжатие может и не кончаться в одно
время для всех тел. Например, если шар А встречает
четыре одинаковых шара С, D, Е и F, находящихся в
покое, и если сжатие в данном случае будет заканчиваться
одновременно для всех шаров (что доказать, однако, было
бы невозможно), то нетрудно себе представить, что при
увеличении массы тел С и D можно достигнуть того, что
эти два шара будут заканчивать свое сжатие или раньше,
или позже, чем шары Е и F. Поэтому абсолютно необходимо
исследовать вопрос, как надлежит поступать в данном
случае для нахождения законов удара. Это будет показано
в следующем п°.
ОБ УДАРЕ УПРУГИХ ТЕЛ
273
Об ударе упругих тел, когда соударяется
несколько тел сразу.
178. Как и многие другие авторы, я буду
рассматривать два соударяющихся упругих шара А и В (фиг. 63 и
64), как будто они сводятся к своим центрам тяжести А
и В и как будто между этими телами помещена пружина,
А а /Г~I
Фиг. 63. Фиг. 64.
способная сокращаться и удлиняться, — что будет
соответствовать сжатию и последующему за ним восстановлению
данных тел. Далее, так как сжатие происходит в течение
весьма короткого времени, то я буду считать, что эта
пружина удлиняется и сокращается незначительно и что,
будучи сжатой весьма мало, она обладает уже весьма
большой силой. Эту силу я буду выражать некоторой функцией
той величины, на которую сократилась или удлинилась
пружина. Другими словами, то малое количество движения,
которое в тот или иной элемент времени одно из наших
тел теряет, а другое приобретает, я буду считать
пропорциональным этой функции. При этом количество движения,
теряемое одним телом,, будет равно количеству движения,
приобретаемому другим телом (см. п° 157), так как
пружина будет стремиться спуститься одинаково в обе
стороны и притом со скоростью, которую нужно считать
бесконечной по сравнению со скоростью тел, поскольку
масса пружины бесконечно мала по сравнению с массой
наших тел.
Исходя из этого, положим, что тела А и В (фиг. 64)
достигли точек а и Ь. Введя обозначения
Аа — ху ВЬ=у,
а также обозначая через / истекшее время, мы будем иметь
— Ai2x = <t{x—y)-dt2,
Btl\\> — y (х-—у)-М2.
@®
10 Ж. Даламбер
274 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ движения
Отсюда мы получим
— Ad2x = Bd2y
и
ndt — A dx = В dy,
где п — некоторое постоянное число, определяющееся из
следующих соображений. Предположим, что при £=0
скорости тел А и В равны а и Ь. Это значит, когда х и у
равны нулю,
~- = а и dy = bdt.
Следовательно,
nz=Aa-\- ВЬ.
Интегрирование уравнения дает
nt — Ах — By
и потому
— Ad2x = <? (x — nt~Ax\dt\
Полагая
nt— Ах
В
-•и,
мы (считая dt постоянным) будем иметь
A-Bd4
В + А
■•<f(u)dt2
A-Bdud2u ,,„ , , ч
Tj^r=dt*.du*{u).
Отсюда мы получаем
A4 dt* - 2(В + А) = dt* f dH ? {U)
dt*
2(B + A)
duVB
Y2-(B + A) ' ^ q-l
duy(u)
179. Впрочем, если я даю здесь это решение, то не
потому, что оно необходимо для определения движения
ОБ УДАРЕ УПРУГИХ ТЕЛ
275
тел А и В. При данных предположениях с этими телами
происходит точь-в-точь такое же изменение, как будто
сжатие и затем восстановление совершаются мгновенно.
А так как мы ищем главным образом движение после
удара и так как нам не известен закон мгновенного
ускорения или мгновенного замедления, то очевидно, что
предыдущее решение нисколько не может пролить свет на
А
Фиг. 65.
этот особенный случай. Поэтому данное решение является
лишь введением к случаям, более сложным.
180. Представим себе, что тела А, С, Д Е и F
(фиг. 65) суть точки, соединенные при помощи пружин
AC, AD и т. д. Нам достаточно найти скорости тел A, F
и С, так как тела Ем D должны претерпевать в точности
те же изменения, как и тела F и С. Пусть тела приходят
в точки а, / и с. Проведем перпендикуляры ау и ах.
Вследствие того, что пружина AF сокращается весьма
незначительно, как мы предположили выше, линии Аа и F/
весьма малы, и мы будем иметь
Обозначая через р косинус угла BAF, а через г—косинус
угла ВАС, и вводя обозначения
Аа = х, Р/=У> Cc = z,
18*
276 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ ДВИЖЕНИЯ
мы получим
— Ad2x =^ [2/?<р (рх —у) + 2лр (rx — z)] dt2 *),
Fd2y = <p(px—y)dt2,
Cd2z — <s>(rx — z)dt2.
В этих уравнениях переменные могут быть разделены в
общем случае при одном условии: если
<Р{РХ—У) = Р-(РХ—У)
и
tp (rx— z) — G-(rx — z),
где G и F — некоторые постоянные. В этом случае можно
найти х, у и z как функции от /, для чего можно
воспользоваться методом, изложенным выше при решении
задачи V, где нами было выяснено, как получить подобные
уравнения.
Сжатие пружины между телами А и F прекратится,
когда pdx сделается равным dy, а между телами Л и С —
когда rdx сделается равным dz.
181. Если тело А ударяет только два тела F и £",
расположенных симметрично, то, поскольку с телом F
будет происходить точь-в-точь то же самое, что и с телом Е,
этот случай представит не больше трудностей, чем
случай, когда тело А ударяет лишь одно тело F и, говоря
приближенно, все будет происходить так, как будто сжа-
*) Если пружина AF сокращается до я/, ее укорочение равно
Af—af^Ay + yF—af.
Но, как уже было отмечено,
Следовательно, укорочение пружины будет равно
4<р—Ff=рх — yt
Сила у{рх—у), направленная по fa, развивает по направлению
Аа действие, выражаемое величиной ру(рх — у). То же самое
можно сказать и о пружине АС. Отсюда
— Ad2x^= и т д.
(Примечание Безу.)
ОБ УДАРЕ УПРУГИХ ТЕЛ
277
тие и восстановление совершаются мгновенно. Поэтому
в данном случае предыдущие вычисления будут необходимы
в весьма малой степени. Однако они позволят точно
определить скорость тела А, а также траекторию тела Z7,
движущегося теперь не по прямой Ffy как мы предполагали и
как можно положить без
ошибки, а по очень малой
кривой.
Предполагая сначала, что
тело F будет двигаться по
линии F/, и принимая af
равным у/, мы получим уравнения
— Ad*x — 2py (рх—у) dt*
и
Fd2y = <р (рх —у) dt29
откуда, как в п° 178, мы и фип 56.
найдем х п у как функции
от t. Но, обозначая /о (фиг. 66) через s, мы найдем, кроме
того, что сила, направленная по /о, будет равна силе,
направленной по ао, умноженной на £у, или, иначе,
умноженной на
а9
хУ~Г-
FA а
(здесь а обозначает FA). Вместо рх~
лее точную величину
-у нужно взять 00-
рх—у-
2а
потому что (пренебрегая третьими разностями)
AF-ao=:Af-Ff-gL*\
*) Мы имеем равенство
AF— aossAy+il—iy — /7 — al~ /о = Л<р — /? — Ff,
так как, как легко видеть,
/о = //
с точностью до бесконечно малых третьего порядка. Далее-, если
278 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ движения
Заметим далее, что в первом из полученных уравнений
вместо 2/7, т е. вместо удвоенного косинуса угла BAF,
нужно взять удвоенный косинус угла Bal, и потому вместо
него мы получим
Установив это и обозначая через а расстояние между
телами, мы будем иметь уравнения
— Ad*x = 2/7(р (и) • dt* — 2д:(1~р2) у (и) dt*
Fd*y = tp{u).dP**).
пренебречь бесконечно малыми величинами третьего порядка, мы
будем иметь
tv-Vl-MF-
(Примечание Безу.)
*) В самом деле,
cos Bal = cos (BAl + Ala) =
= cos BAl • cos Ala — sin BAl • sin Alaf
HO
cos Ala = 1,
так как угол Ala будет бесконечно малым. Далее,
sin BAl = УТ^р*;
с другой стороны,
al AF а
Отсюда следует, и т. д. (Примечание Безу)
**) Здесь мы предполагаем, что сила, направленная по Ff, для
тела F равна силе, направленной по ао% потому что эти силы
отличаются друг от друга лишь на бесконечно малую второго
порядка. Здесь же мы принимаем во внимание лишь бесконечно
малые первого порядка, которыми мы пренебрегали в предыдущих
первоначальных вычислениях. (Примечание Безу.)
ОБ УДАРЕ УПРУГИХ ТЕЛ
279
Далее, мы будем иметь
, , xdx(\ — р2) .
— da = pdx— : £-1—dy>
a
откуда
xdx(l — p2)'
— d2u = pd2x — d2y — d Г
или
-tfgtf —■■ 2^M'^2 ] lpx(\-p*)<t{u).dt*
A ' • aA
cp (u) dt2
F
d\xdx(l—p*)~\ ^
Из первого приближенного решения мы найдем х как
функцию от и и, кроме того, мы будем иметь уравнение
с разделяющимися переменными di и du,—другими
словами, мы будем иметь dt в виде функции от и и du и,
следовательно, du в виде функции от« и dt.
Сделав соответствующие подстановки, т. е. подставляя
в члены
2px(l—p2)<?(u).dt2 d\xdx(\—p*)\
aA а
вместо х его выражение через я, вместо d2x его значение
— 2ру (и) dt2
А
а вместо dx2 его значение, которое, как нетрудно
убедиться, будет равно произведению dt2 на некоторую
функцию от и, мы получим уравнение вида
где V есть некоторая функция от и. Но это уравнение
интегрируемо.
Зная жеи в виде функции от t, или, вернее, зная t
в виде функции от и, мы очень простым способом найдем
и величины х и у. В самом деле, первое решение нам
даст
лг = Д(я),
а второе
dt = duT{u)>
280 ОБЩИЙ ПРИНЦИП, ДЛЯ НАХОЖДЕНИЯ движения
Подставляя к (и) вместо х в выражение
2*(1—/?2)ср(ц)-<Ц2
а '
мы получим
— Ad2x = dt2=.(u)
и
— Ax + Bt-\-C= [dt[dta(u).
Отсюда мы получим х в виде функции от и. Величина у
будет найдена еще более простым путем, так как
Fy-\-Dt-\-Q=^dt\dtif(u).
В конце концов мы получим уравнение
Fd?s=xl*l~pl -dt2'f(px—y).
И так как х и у суть известные функции от /, то здесь,
очевидно, интегрирование никаких затруднений не
представляет.
Замечание.
182. Из предыдущего п° вытекает, что когда тело А
ударяет два упругих тела С и D (фиг. 65), расположенных
симметрично относительно направления АВ ударяющего
тела, скорости этих тел после удара будут если не в
точности такими же, то по крайней мере с большим
приближением такими же, как если бы сжатие и восстановление
пружины совершались мгновенно. Этого не будет в том
случае, если ударяемые шары не расположены симметрично
относительно ударяющего тела.
Действительно, пусть твердый шар А (фиг. 67)
движется по направлению АВ и встречает на своем пути
твердые шары С и D, находящиеся в покое. Скорость тела А
пусть будет представлена линией Аа. Предположим, далее,
что шар А после удара не меняет своего направления и
скоростью его после удара будет линия Аа, Построив парал-
ОБ УДАРЕ УПРУГИХ ТЕЛ
281
лелограммы АпаХ и Apai и проведя линию ах и ad
перпендикулярно к АС и Л£), мы будем иметь
С-А*г = Л./ЛГ
и
D-Ad = A-np*).
Отсюда
/^я/? = С-Ак:£)-Л</.
Другими словами, линия па так относится к линии Ля,
как косинус угла ВАС, умноженный на С, относится к
произведению тела D
на косинус угла BAD.
Отсюда следует, что
произведение тела С
на синус угла ВАС и
на косинус этого же
угла будет равняться
произведению тела D
на синус угла BAD и
па косинус этого же
угла BAD.
Если тела С и D
равны между собою, то
мы получим, что
произведение синуса угла
на косинус этого же
угла будет равняться
произведению синуса
другого угла на
косинус этого последнего угла. Эю возможно только в том
случае, если эти углы будут дополнять друг друга до
*) Все три шара должны после удара двигаться вместе, и
потому тело С должно обладать скоростью Ах (см. п° 165): если
предположить, что тело А будет сохранять скорость Аа, то
в направлении АС оно будет иметь скорость Ах. Но в силу
излагаемого здесь принципа, если бы тело С обладало скоростью Ах,
но направленной в противоположную сторону, то оно бы
уравновесило тело Л, обладающее скоростью iX, которую это тело
потеряло. Отсюда следует, и т. д. Такое же рассуждение можег
быть применено и ко второму уравнению. (Примечание Безу)
282 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ движения
90 градусов, т. е. если угол DAC будет прямым. В таком
случае мы будем иметь
Л1 :Ах = Ар: Ad.
Следовательно, если линию Аа принять за бесконечно
малую линию, то при том условии, что тела А, С и D
упруги и притом действие пружин АС и AD не
пропорционально линиям Ах и Ad, точка А с первого же момента
будет удаляться от прямой Аа и, таким образом, законы
Фиг. 68.
удара этих тел будут сильно отличаться от законов для
того случая, когда сжатие и восстановление совершаются
за одно мгновение.
183. Пусть в общем случае АВ (фиг, 68) будет
направлением ударяющего тела и пусть Аа — кривая, которую
это тело описывает во время сжатия и восстановления
пружины. Пусть, далее,
Ai — x, ai = z, Cc=yt D8 = u
и косинус угла DAC равен г. Тогда мы будем иметь
Ах — С с = х -j- rz — у
и
Ad~ Db — z-\-rx — ищ
ОБ УДАРЕ УПРУГИХ ТЕЛ
283
Мы получим тогда
— Ad2x = <f(x-\-rz—у) • dt2,
— Ad 2z =z<p(z-\-rx — и) • dt2y
Cd2y = tf{x-\-rz —y) dt2,
Dd2u.= <?(z-\-rx — u) dt2,
откуда
и точно так же
— Ad*x = Cd*y
—at— Ax = Cy;
— Ad2z = Dd2a
$t — Az = Da.
Таким образом, подставляя в первые два уравнения вместо
у и и их значения, мы будем иметь два уравнения,
содержащие лишь два неизвестных х ^
и z. С этими уравнениями можно
обращаться при помощи методов,
указанных выше, в том случае,
если
<p(x-\-rz —у) = F- (х-]- rz —у)
и
у (z~\-rx — u) = G-(z-\-rx — и).
184. Пусть два тела Ana
(фиг. 69), соединенные между
собою при помощи пружины Аа,
ударяются друг о друга по
направлению AD и ad так, что если
бы эти тела могли двигаться
по направлению AD и ad> то их
центр тяжести С оставался бы в покое. Во время своего
сжатия оба эти теле будут описывать две подобные кривые
Фиг. 69.
284 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ движения
AG и ag, и сжатие закончится тогда, когда линия Gg будет
перпендикулярна к обеим кривым*). Затем при
восстановлении пружины тела будут описывать кривые GF и gj,
подобные первым двум кривым. Отсюда следует, что
движение тел после удара будет такое же, как будто сжатие
и восстановление происходят мгновенно.
И это будет справедливо в общем случае при любом
ударе двух упругих тел. В самом деле, нетрудно
видеть, что так как движение центра тяжести обоих тел
нисколько не меняется в результате взаимного действия тел
друг на друга, достаточно найти, каковы будут движения
тел после удара для того случая, когда они соударяются
так, что центр тяжести их находится в покое, а потом
сообщить всей системе движение, которое имеет центр
тяжести **).
В том случае, если оба наши тела будут мягкими,
скорости их после удара будут больше, чем в том случае,
когда они являются твердыми. В самом деле, в случае
твердости обоих тел скорости после удара будут
относиться к скоростям до удара, как Cd относится к Са.
В случае же мягких тел, т. е в том случае, когда
пружина сжимается и затем восстанавливается, эти скорости
*) Так как в состоянии центра тяжести в результате
действий самих тел друг на друга не должно происходить никаких
изменений, то центр тяжести при сжатии будет оставаться в
покое, если, как это вытекает из условий, без сжатия он покоился.
Но в таком случае расстояния тел от этой неподвижной точки
будут все время обратно пропорциональны данным телам. Отсюда
следует, что кривые AG и ag будут подобны между собой. То же
самое будет иметь место и после сжатия. Далее, нетрудно видеть,
что сжатие закончится тогда, когда линия Gg, соединяющая оба
тела, будет перпендикулярна к кривым, описываемым ими, так как
тела будут тогда находиться на кратчайшем расстоянии друг от
друга. (Примечание Безу,)
**) В самом деле, так как это движение является общим
для всех частей системы, эти части не будут оказывать друг
на друга никакого действия, кроме того, которое проистекает
из тех движений их, в результате которых центр тяжести
остается в покое. Что касается скорости центра тяжести, то
способ ее определения был указан нами выше (см. п° 72). (Приме-
чание Безу.)
ОБ УДАРЕ УПРУГИХ ТЕЛ
285
будут находиться в отношении Cd к Cg. Но
Cg<Ca.
Отсюда следует, и т. д. *)
Общее примечание.
185. Мы рассмотрели лишь весьма небольшую часть
вопросов, относящихся к соударениям тел. Укажем еще
на некоторые из этих вопросов, заслуживающих внимания
геометров.
I.
В «Encyclopedie5>, в статье «Elastique» (упругий) (т. V,
стр. 447, столб. 2) нами было показано, что пружина,
восстанавливая полностью соударяющимся телам их форму,
утраченную при соударении, может не восстанавливать
их скоростей, и она и в самом деле их не
восстанавливает. Величина утраченной скорости зависит от формы
и от вещества тела, и эту величину можно определить
лишь путем допущений и догадок.
В самом деле, представим себе ряд точек или
абсолютно твердых атомов, расположенных на прямой линии
*) Пусть в случае твердых тел бесконечно малая линия ab
представляет собой скорость до удара. Построим СЬс и проведем
дугу ас% Тогда эта дуга будет представлять собой скорость после
удара, так как, по условию, центр должен оставаться в покое,
а потерянная скорость должна быть направлена по cb. Но
ac:ab = Cd: С а.
В случае мягких тел скорость после удара будет относиться
к скорости до удара, как Cd относится к Cg, вследствие того,
что скорости всякого тела, описывающего некоторую кривую под
действием какой-то силы, направленной к неподвижной точке,
будут обратно пропорциональны перпендикулярам, проведенным из
этой точки на касательные. Но так как
Cg< Са,
то
Cd Cd
Cg> Са
Отсюда следует, и т. д. [Примечание Безу)
286 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ ДВИЖЕНИЯ
и соединяющихся между собой при помощи бесконечно
малых пружин, помещенных между соседними телами.
Такая система абсолютно твердых точек, соединенных друг
с другом указанным образом, довольно точно будет
изображать упругое тело. Положим затем, что эта система
только что ударилась перпендикулярно о некоторую,
жесткую плоскость по направлению линии, проходящей через
все эти малые тельца. Очевидно, первое абсолютно
твердое тельце, ударяющееся непосредственно о плоскость,
утратит мгновенно всю свою скорость. Второе тельце,
непосредственно следующее за первым, сможет при этом
продвинуться дальше вследствие сжимаемости маленькой
пружины, находящейся между первым и вторым тельцем.
Но так как эта пружина бесконечно мала (по условию),
так как, далее, она должна будет прекратить свое сжатие,
как только ее части вступят в абсолютное
соприкосновение друг с другом (а это произойдет весьма быстро)* и так
как, наконец, второму тельцу достаточно пройти
бесконечно малый путь, чтобы настигнуть первое тельце, то не
весьма ли вероятно или даже можно ли сомневаться в том,
что второе тельце не сможет утратить свое движение
полностью, прежде чем оно достигнет крайней точки,
дальше которой ему двигаться уже нельзя? А в таком
случае оставшаяся часть его движения или, вернее, его
стремление к движению будет уничтожено сразу так же,
как это имеет место при ударе абсолютно твердого тела
о жесткую плоскость.
То же самое будет происходить и с рядом следующих
телец. Все эти тельца, утратившие при сжатии пружин
лишь часть своего движения и не имеющие возможности
использовать оставшуюся часть его, потом, при
восстановлении пружины, получат лишь ту часть своего
прежнего движения, которую они утратили в связи со
сжатием пружины, и совсем не смогут вернуть той части его,
которая была уничтожена полностью. Между тем каждая
пружина восстановит свое первоначальное состояние, и
следовательно, вся система примет лишь свою первоначальную
форму, но не первоначальную свою скорость. Найти
скорость каждого тельца после восстановления пружины, а
OB УДАРЕ УПРУГИХ ТЕЛ
287
следовательно, и общую скорость тела, равную сумме
частичных скоростей, разделенной на число телец,
очевидно, очень трудно и даже, может быть, невозможно: ведь
для того, чтобы найти скорость каждого отдельного тельца,
необходимо знать размер и жесткость каждой пружины,
которые будут меняться в каждом отдельном случае.
Что нами было только что сказано об ударе упругого
тела о жесткую плоскость, также будет справедливо и в
случае взаимного удара двух упругих тел: и ими какая-то
часть скорости при ударе будет непременно утрачена.
Обычно принимают, что когда упругое тело ударяет о
жесткую плоскость, только бесконечно малая часть его,
находящаяся около точки соприкосновения, теряет свое
движение сразу, все же остальные части теряют его лишь
постепенно, сохраняя движение и приближаясь к плоскости
до тех пор, пока пружина полностью не сократится.
Предыдущие рассуждения достаточно показывают, насколько
мало соответствует действительности это допущение.
II.
Во всфс предыдущих рассуждениях мы принимали, что
когда два упругих тела соударяются друг с другом,
обладая скоростями, обратно пропорциональными массам,
пружины этих тел сжимаются в каждый момент подобным и
равным образом, так что скорости, теряемые телами за
любой элемент времени, обратно пропорциональны массам,
и точка соприкосновения остается в покое во все время,
пока пружина сжимается и восстанавливается. Если же
пружина данных тел не сохраняется подобной самой себе,
то настоящее допущение уже перестает быть верным, и
это может внести изменение в решения.
Следовательно, предположения, выставляемые рядом
авторов при изложении законов удара упругих тел, являются
слишком ограниченными и мало общими. Они допускают,
что между телами находится пружина и что она одинаково
сжимается как с той, так и с другой стороны, так что оба
тела теряют в каждый элемент времени одинаковые
количества движения, и точка пружины, совпадающая с центром
288 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ движения
тяжести обоих т,ел, остается в покое. Очевидно, это
допущение может соответствовать лишь тому случаю,
когда точка соприкосновения остается в покое как при
сжатии, так и при восстановлении тел.
III.
Если упругое тело только что ударилось
перпендикулярно о некоторую жесткую плоскость и если принять, что
данное тело обладает совершенной упругостью, т. е. если
OI.O- способно вследствие своей упругости восстанавливать
ту скорость, которую оно утрачивает при ударе, то
очевидно, что данное тело после удара отскочит с полной
своей скоростью. Но если в тот момент, когда тело
сплющилось до конца и вследствие сжатия пружины утратило
всю свою скорость, вдруг убрать плоскость, то, очевидно,
ввиду того, что пружина станет совершенно свободной,
она будет стремиться восстановиться в обе стороны, и
потому взаимно противоположные движения, которые она
будет стремиться сообщить, должны взаимно уничтожиться.
Отсюда следует, что теперь тело отскочит со скоростью
гораздо меньшей, чем в первом случае. Может случиться,
что оно даже вовсе не отскочит: это будет в том случае,
когда форма тела в состоянии сжатия будет такова, что
пружина будет восстанавливаться одинаково в
противоположные стороны.
По тем же основаниям можно утверждать, что если
плоскость убрать в то время, когда пружина
восстановилась, но не целиком, то тело отскочит с меньшей
скоростью, чем в случае неподвижной плоскости.
Когда пружины обоих тел совершенно подобны друг
другу, так что они сжимаются и затем восстанавливаются
в одно и то же время, то точка соприкосновения остается
неподвижной в течение всего этого времени, и потому
тела служат друг для друга как бы жесткой опорой.
Поэтому они, очевидно, будут отскакивать друг от друга со
своими первоначальными скоростями. Но если одна из
пружин восстанавливается раньше другой, то не отделяется
ли соответствующее ей тело от другого и не уменьшится
ли та скорость, с которой отскакивает это последнее?
ОБ УДАРЕ УПРУГИХ ТЕЛ
289
IV.
Каковы законы удара жесткого тела об упругое тело?
Вопрос сводится к тому, чтобы выяснить, что произойдет,
если встретятся одно жесткое и другое упругое тело,
причем эти тела обладают взаимно противоположными
скоростями, обратно пропорциональными массам. Очевидно, в
данном случае точка- соприкосновения не останется
неподвижной, как это было в том случае, когда оба тела были
упругими, а пружины их были подобными. Неподвижная
точка (ведь одна такая точка должна существовать!) будет
внутри упругого тела. Но будет ли такой неподвижной
точкой все время одна и та же точка, или в каждый
момент, пока пружина сжимается и восстанавливается, она
будет меняться? Мне кажется, что она должна менять свое
место.
Действительно, во-первых, в первый момент при сжатии
неподвижная точка должна находиться бесконечно близко,
или, говоря точнее, весьма близко к точке
соприкосновения. В самом деле, если бы эта точка не была весьма
близкой к точке соприкосновения, то некоторая конечная
часть упругого тела между этой точкой и точкой
соприкосновения должна была бы внезапно изменить свою
скорость с положительной на отрицательную, а этого в
рассматриваемом упругом теле допустить невозможно, так как
надлежит считать, что любая конечная часть его теряет
свою скорость постепенно. Для того чтобы убедиться в
этом, обозначим через а положительную скорость до удара
и через—Ъ новую отрицательную скорость в той части
тела, о которой идет речь. Отсюда следовало бы, что
эта часть тела теряет скорость а-\-Ь> которая уничтожается
внезапно. Но это в том упругом теле, о котором мы
говорим, невозможно. Поэтому неподвижная точка в первый
момент будет как бы бесконечно близка к точке
соприкосновения.
Во-вторых, поскольку в последующие моменты части
абсолютно твердого тела, двигаясь все вперед, не
смещаются одна относительно другой, постольку они, очевидно,
будут заставлять подаваться неподвижную точку: если бы
19 Ж Ддламбер
290 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ ДВИЖЕНИЯ
эта точка оставалась всегда на одном и том же месте, то
она очутилась бы слишком близко к точке
соприкосновения, а следовательно, и к абсолютно твердому телу.
Поэтому, по мере того как пружина будет сжиматься,
неподвижная точка будет менять свое место.
Далее, когда пружина будет восстанавливаться,
неподвижная точка будет подвергаться всем тем изменениям,
которые она претерпевала при сжатии, но только в
обратном порядке. В каждый момент то и другое тело будет
получать в обратном направлении ту самую скорость,
которой они лишались при соударении. Отсюда следует,
что в последний момент восстановления скорость того и
другого тела будет та же самая (в обратном направлении),
как и в первый момент сжатия.
Таким образом оба тела снова получат всю свою
скорость, и потому законы удара абсолютно твердых тел и
совершенно упругих тел будут такими же, как будто оба
соударяющиеся тела были совершенно упругими.
Из этих отрывочных замечаний, которые можно было
бы продолжить, видно, как много еще остается нерешенных
проблем, относящихся к законам удара тел, и как далеко
еще до того, чтобы весь вопрос можно было считать
исчерпанным теми многочисленными геометрами, которые
занимались им до сего времени.» Эти геометры, в конце
концов, исследовали лишь наиболее простые и наиболее
редко встречающиеся случаи.
ГЛАВА IV.
О принципе сохранения живых сил.
186. Если несколько тел действуют друг па друга
посредством нитей или посредством жестких стержней,
соединяющих их друг с другом, или путем соударений тел
друг с другом,—в последнем случае тела непременно
О ПРИНЦИПЕ СОХРАНЕНИЯ живых сил 291
должны быть совершенно упругими,—то сумма
произведений масс на квадраты скоростей все время остается
постоянной величиной. Если при этом тела обладают некоторыми
силами, то сумма произведений масс на квадраты скоростей
в любой момент равна сумме произведений масс на
квадраты начальных скоростей плюс квадраты тех скоростей,
которые тела приобрели бы в том случае, если бы они,
обладая теми же самыми силами, двигались свободно
каждое по той линии, которую оно описывает. В этих двух
положениях и состоит то, что называют принципом
сохранения живых сил.т
Насколько мне известно, впервые об этих двух
положениях упоминает Гюйгенс. Применение же их для
изящного и простого решения многих задач динамики впервые
показал Бернулли [86].
В настоящей главе я собираюсь дать если не общее
доказательство для всевозможных случаев, то по крайней
мере принципы, достаточные для отыскания доказательства
в том или ином частном случае.
N А В *'
Фиг. 70.
187. Представим себе сначала два тела А и В (фиг. 70)
бесконечно малого объема, прикрепленных к жесткому
стержню АВ. Пусть этим телам сообщаются некоторые
произвольные направления и скорости, изображаемые
бесконечно малыми линиями АК и BD. По нашему принципу
мы должны построить параллелограммы МС и NL такие,
чтобы соблюдались равенства
LC^AB
и
В-ВМ — А-АЫ.
19*
292 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ движения
Тогда линии ВС и AL будут скоростями и направлениями
тел А и В. Но
ВС2 = BD2 — 2СЕ. CD — CD2
и
AD = АК2 + 2PL • KL — KL2.
Отсюда
B.BC2-\-A.AL2 = A-AK2 + B.BD2-\-
-\-A(2PL.KL—KL2) — B(2CE-CD-{-CD*).
Так как
CE = PL
и
A-KL = B-CD,
то последнее выражение равно
A.AK2 + B-BD2 — A-KL2 — B-CD2.
Итак, мы будем иметь
B'BC2-\-A.AL2 = A-AK2-\-B.BD2 — A-KL2 — B-CD2.
Следствие I.
188. В том случае, когда NA и ВМ бесконечно малы,
т. е. если скорости AL и ВС бесконечно мало отличаются
от скоростей АК и BD, имеет место сохранение живых
сил. Действительно, пренебрегая в полученном уравнении
линиями KL и CD, мы получаем
B-BC2-\-A.AL2 = A.AK2 + B-BD2.
Следствие II.
189. В том случае, когда NA и ВМ не бесконечно
малы, проведя в противоположном направлении
CF=CD
и
LO = LK>
О СОХРАНЕНИИ ЖИВЫХ СИЛ
293
нетрудно будет доказать, что
BF2 = BD* — АСЕ-CD
и
A02 = AK2-\-4PL.KL
Отсюда
B.BF*-\~A.AO* = B(BD* — 2ВМ-2СЕ)-\-
+ A(AK2-{-2AN-2PL)=B'BD2'{-A'AK2t
так как
CE=PL
и
A-AN = B-BM.
Следовательно, сохранение живых сил имеет место и
здесь. Но если внимательно рассмотреть этот случай, это
как раз случай удара двух упругих тел (п° 168).
О сохранении живых сил в телах, соединенных
между собою при помощи нитей или жестких стержней.
190. В предыдущем п° мы видели, что если два
тела укреплены на концах жесткого стержня и если им
обоим сообщаются какие-либо скорости, то сохранение
живых сил будет иметь место лишь в том случае, если
воспринятые телами скорости бесконечно мало отличаются
от тех скоростей, которые им были сообщены.
Действительная начальная скорость того или иного тела может
отличаться от скорости, которая ему по тому или иному
направлению сообщается, на конечную величину. Однако,
когда данные тела начали двигаться каждое по своей
кривой, скорость их от одного момента до другого будет
изменяться лишь бесконечно мало*). Таким образом, в
*) Пусть тела А и В, соединенные друг с другом при
помощи жесткой линии АВ (фиг. 71), за какой-нибудь элемент времени
описывают малые линии АС и BD, а в следующий элемент
времени вместо того, чтобы описывать
СЕ=СА
и
DF=DB
(как это было бы в том случае, если бы тела были свободными^
294 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ движения
случае, указанном в п° 188, сумма произведений всех масс
на квадраты их скоростей будет равна сумме произведений
всех масс не на квадрат сообщенных им в первый момент
A G в
Фиг. 71.
скоростей, а на квадрат действительных начальных
скоростей этих масс.
191. Необходимо теперь доказать в общем случае, что
если тела движутся, будучи соединенными между собою
они будут описывать СН и DK- Я утверждаю, что линии ЕН и
FK, представляющие утраченные движения, будут бесконечно
малыми второго порядка.
В самом деле, при всяком положении точек Н и К центр
тяжести g' должен лежать на прямой линии Gg> описываемой им
за первый элемент времени и притом (п° 76) должно быть
g'g = Gg.
Отсюда
g'H=gC=AO.
Но
Е^ — АО,
или (что в данном случае то же самое)
Ef — g'tf
равно
2 (АО —С SH
минус бесконечно малая величина второго порядка (и0 91). А так
как
AQ=€g%
то
Я**-*'//,
а следовательно, и ЕН будет бесконечно малой величиной
второго порядка. Для линии FK доказательство будет такое же.
Отсюда следует, и т. д. (Примечание Безу.)
О СОХРАНЕНИИ ЖИВЫХ СИЛ
295
при помощи нитей или жестких стержней, и если скорость
каждого из них в любой момент изменяется лишь на
бесконечно малую величину, то сумма произведений масс на
квадраты скоростей будет оставаться величиной постоянной,
если данные тела не обладают никакими силами. Если же
тела обладают силами, то эта сумма будет равна сумме
эффектов движущих сил всех тел [87].
Прежде всего,- я замечу, что второй случай
непосредственно вытекает из первого. Другими словами, если
сохранение имеет место в первом случае, то оно необходимо
будет иметь место и во втором случае.
В самом деле, пусть два тела А и а (фиг. 72),
соединенных между собою при помощи стержня Аа, обладают
Фиг. 72.
некоторыми движ)щими силами, направленными по каким-
нибудь линиям EF и е/, расположенным в каждый момент
каким угодно образом; пусть эти тела за какой-нибудь
элемент времени пройдут, соответственно, пути ВА и ab\
эти линии, поэтому, могут изображать скорости тел. Если
бы тела были свободны, они за следующий элемент
времени прошли бы пути АО и ао, равные и лежащие на
296 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ ДВИЖЕНИЯ
одной прямой с АВ и ab. Положим, что прямые AD и ad
изображают эффекты движущих сил за этот элемент
времени. Тогда скорости тел изменятся и будут равны AN
и an. Проведя к линиям АС и ас перпендикуляры ВС и be,
мы будем иметь
AN2 = AB2 + 2.AD-AC
и
an2 — ab2-{-2* ad* ас.
Но так как скорости АВ и аЬ суть действительные
скорости, которыми тела обладают в первый момент, и так
как скорости AN и an от них отличаются бесконечно мало,
то эти самые скорости AN и an лишь бесконечно мало
отличаются от тех скоростей, которыми тела будут
обладать после изменений, вызванных взаимодействием тел.
Обозначив через V и v скорости АВ и ab, через U
и и скорости тел А и а во второй элемент времени, т. е.
скорости, которые они будут иметь вместо AN и ant мы
получим
A.U2-\-a-u2 = A.AN2-\-a.an2 =
= А (АВ2 -|~ 2 AD. С А) + <*> И2 + 2nd. со) =*
= Л- К2-f-tf-f2 + 2Л-AD-CA + 2а-ad-ca.
Отсюда
Л(£/2—У2) + я(я2 — v*) = 2A.AD-CA-\-2a.ad-ca,
или
2Л1/^К+2аг/^ = 2Л.Л£.СЛ + 2а-а^.ш.
Следовательно (принимая в начале движения V—0 и г> = 0),
мы получим
Л1/2 + <w2= [ 2A'AD-CA + ^2a'ad'Ca.
Если бы тела Л и а двигались свободно по кривым
6Л и ga, то, очевидно, величина
[2A-AD-CA
О СОХРАНЕНИИ ЖИВЫХ СИЛ
297
выражала бы собою эффект движущей силы тела А от О
до Л и точно так же величина
\ 2a-ad*ca
выражала бы собою эффект движущей силы тела а от g
до а *). Отсюда следует, и т. д.
Если бы в начале движения мы имели
V = B и v = b,
то, очевидно, мы получили бы
AV*-{-av2 = AB2-{-ab2-{- ^2А.АО-СА + ^2a.ad-ca.
Нетрудно видеть, что настоящее доказательство можно
распространить и на произвольное число тел. В самом
деле, мы исходили здесь лишь из того, что если скорость
от одного момента к другому изменяется лишь бесконечно
мало и если тела не обладают никакими ускоряющими
силами, то сумма произведений масс на квадраты
скоростей остается все время постоянной. Это нам и нужно теперь
доказать в общем виде, для чего необходимо
предварительно доказать нижеследующие леммы.
*) Если ускоряющая сила в точке А выражается линией АО,
то действие ее по направлению кривой будет равно
АР-АС
АВ '
Поэтому если и' есть скорость тела Л, движущегося свободно но
кривой GA, мы будем иметь
AD-АС Аи , , ,
——. АВ = a' du\
Ad
откуда
A.AD-AC = Au'da'f
или
2 f A.AD-AC = Aa'2.
То, что здесь называется эффектом движущей силы, есть
произведение массы на квадрат той скорости, которую эта сила может
сообщить. (Примечание Везу.)
298 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ движения
Лемма XII.
192. Пусть нам дан произвольный параллелограмм
BVbN (фиг. 73). Я утверждаю, что если из одной из
вершин В этого параллелограмма провести линию BD
любого направления и любой величины и если затем из
точки D провести перпендикуляры
Dnt DK и DG на продолжения
линий Bb, BV и BN, то мы будем
иметь равенство
Bb.Bn = BV-BK-\-BN.Ba.
Доказате ль ство.
Проведем из точек N, V и Ь
перпендикуляры NEy VE и ЬН на
продолжение BD. Стороны BV и ВМ
можно рассматривать как силы,
разложенные каждая на две: BF и VF
и, затем, BE и EN. Точно так же
и диагональ ВЬ можно
рассматривать как силу, разложенную на
две силы: ВЫ и ЬН. Так как сила ВЬ эквивалентна силам
BN и BV, то отсюда
BE-{-BF = BH.
Но вследствие подобия треугольников ЬНВ и BDn мы
будем иметь
Bb-Bn = BD.BH=BD'BE-{-BD.BF=^
=:BN-BG-\-BV-BK.
Что а требовалось доказать *).
*) Это предложение можно доказать из чисто
геометрических начал, не прибегая к помощи механики. Приведенное нами
здесь доказательство показывает, насколько различные отделы
математики взаимно разъясняют друг друга.
Фиг. 73.
О СОХРАНЕНИИ ЖИВЫХ СИЛ
299
Замечание.
193, Нетрудно видеть, что смотря по взаимному
расположению точек Е и F и по их положению относительно
точки Н возможно, что вместо суммы произведений BN*BG
и BV'BK придется взять их разность, приравняв ее ВЬ*Вп.
О сохранении живых сил в том случае, когда тела,
рассматриваемые как точки, соединены между собою при
помощи нитей.
194. Представим себе, что три тела А, В и С (фиг. 74)
прикреплены к нити ABC, этим телам сообщаются скорости,
Фиг. 74.
Ла, В§ и Сх и что вследствие взаимодействия друг с
другом тела вынуждены изменить эти скорости: пусть их скорости
теперь будут равны ЛА, BD и СС, причем эти последние
скорости должны быть таковы, чтобы выполнялись равенства
AD = AB
и
DC = BC.
Согласно нашему правилу скорости Аау В$ и Сх мы
должны представить как бы составленными из скоростей ЛА,
BD и СС, с одной стороны, и скоростей А #, ВЬ и Сс,
с другой стороны, причем последние скорости, будучи одни,
оставляют тела в равновесии. Нужно доказать, что
A>AA2 + B>BD2-\-C-CO==A-Aa2JrB-Bp + C'Cx2i
300 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ ДВИЖЕНИЯ
другими словами, что
A*Aa'AQ — B'BN*BO-{-B-BV'BK—C'Cc<CM=0*).
Но
см=вк
и
C.Cc = B-BV
вследствие равновесия. Точно так же
AQ = BG
и
A.Aa = B-BN.
Отсюда следует, и т. д.
Если вместо тела А взять неподвижную точку Л,
вокруг которой могут вращаться тела В и С, то мы будем
иметь
AQ = 0 и BG = 0
и предположение будет также справедливо. Из существа
доказательства с очевидностью вытекает, что оно может
быть обобщено для произвольного числа тел.
Если точка В не закреплена на своем месте, а может
свободно скользить вдоль нити, то линия ВЬ будет делить
угол ABC пополам и мы будем иметь
А.Аа = В-ВМ,
В-ВУ=С-Ссу
B-BN = B-BV
и, наконец,
AQ — BG = BK — СМ
в силу того, что
AD + DC = AB + BC.
*) Это уравнение выводится из предыдущего, если вместо
ЛА2, BD2 и т. д. подставить их значения, полученные на
основании известных свойств квадратов сторон треугольника, и если
при этом принять во внимание сказанное в предыдущем п° 193.
Бесконечно малыми величинами второго порядка нужно при этом
пренебречь. (Примечание Безу.)
О СОХРАНЕНИИ ЖИВЫХ СИЛ
301
Отсюда
A.Aa-AQ — B-BN-BQ-\-B-BV-BK—C-CcCM = 0.
Итак, достаточно ясно видно, что сохранение живых сил
имеет место во всех возможных случаях, когда тела
рассматриваются как точки и когда они соединены между
собой при помощи нитей.
Лемма XIII.
195. Пусть три тела А, В а С обладают
некоторыми силами AQ, BR и Сс (фиг. 75) и находятся в рае-
Q7
Фиг. 75.
новесии на каком-либо рычаге произвольной формы. Пусть
АВ и ВС будут расстояния этих тел друг от друга.
Представим себе рычаг в некотором другом положении,
бесконечно близком к первому, и пусть точки F, G и Е
будут тогда положениями тел А, В и С, так что
FQ=*AB и GE = BC.
Я утверждаю, что если провести перпендикуляры GK,
FX и EZ, мы будем иметь
B.BR.BK=A.AQ.AX-\-C.Cc-CZ.
Доказательство.
Поскольку рычаг ABC не прямолинейный, настоящее
. предложение можно доказывать точно так же, как будто
ABC была нитью, потому что каждая сила может быть
302 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ ДВИЖЕНИЯ
всегда заменена двумя силами, направления которых про*
ходят через точки приложения двух других сил, и таким
образом мы получим шесть сил попарно равных и прямо
противоположных (см. п°п° 192, 193 и 194).
Подобное разложение не может быть произведено
только в одном случае, а именно, когда рычаг ЛВС пря-
Фиг. 76.
молинейный (фиг. 76). Для этого случая необходимо найти
особое доказательство.
Пусть AQ, BR и Сс перпендикулярны к рычагу ABC.
Тогда мы будем иметь
B-BR-BO = C-Cc-CL + A-AQ-AY*).
Но линии ВО и ВК, CL и CZ, AY и АХ отличаются друг
от друга соответственно лишь на величину, бесконечно
малую по сравнению с самими этими величинами.
Следовательно,
B-BR-BK=CCc-CZ-{-A.AQ-AX.
Отсюда следует, и т. д.
Что и требовалось догсазать.
*) Вследствие известного свойства моментов нескольких сил,
находящихся в равновесии. {Примечание Безу)
О СОХРАНЕНИИ ЖИВЫХ СИЛ
303
Замечание.
196. Если рычаг ЛВС (фиг. 77) закреплен в какой-
нибудь точке, например, в точке Г, и если мы предста-
Фиг. 77.
вим себе рычаг в некотором другом положении FYGE, то
предложение будет также справедливо. Доказывается оно
тогда аналогичным образом.
О сохранении живых сил, когда тела соединены между
собой при помощи жестких стержней и когда эти тела
рассматриваются как точки.
197. С помощью предыдущей леммы можно, очевидно,
доказать сохранение живых сил, когда тела соединены
между собой при помощи жестких стержней и когда все
тела закреплены на этих стержнях*).
Если одно из тел, скажем В (фиг. 75), может
скользить вдоль стержня, тогда утраченная им скорость BR
будет перпендикулярна к стержню и в следующий момент
оно окажется не в точке G, — такой, что
FG = AB,
а в бесконечно близкой к ней точке £"**). Вследствие того,
*) Для этого нужно только линии AQ и AF, BR и BG,
Сс и СЕ (фиг. 75) рассматривать в качестве уничтоженных и
остающихся скоростей тел А, В и С и затем в точности следовать
пути, указанному в п° 195. (Примечание Безу.)
**) Здесь мы принимаем, что рычаг ABC, а также и FGE
представляет собой некоторую кривую, a BR—перпендикуляр
к этой кривой в точке В. Нам казалось ненужным давать для
этого случая особый чертеж.
304 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ ДВИЖЕНИЯ
что точки В и G бесконечно близки одна к другой и
вследствие лого, что линии Gg и В А следует считать
параллельными, линию Gg нужно рассматривать как бы
перпендикулярной к линии ВК и, следовательно, линии Bk и ВК
можно заменять одну другой: разность между ними есть
величина бесконечно малая второго порядка.
Итак, сохранение живых сил имеет место и в этом
Случае.
О сохранении живых сил в случае, когда тела
обладают конечными массами и когда они соединены
нитями или жесткими стержнями.
198. В лемме XIII мы видели, что если три тела Л, В
и С, обладающие силами AQ, BR и Сс произвольного на»
правления, находятся в равновесии, то мы будем иметь
C-Cc-CZ-\-A-AQ-AX=B*BR*BK.
Отсюда следует, что если Вг равно и противоположно BR
(фиг. 75), другими словами, если найти
равнодействующую двух сил С'Сс и A'AQ, то выражение
C-CcCZ + A-AQ.AX
всегда можно привести к единственному произведению
В*Вг*ВК. И каково бы ни было число тел,
прикрепленных к жесткому стержню, всегда можно взять точку В,
через которую проходит равнодействующая сила,
представить эту точку перенесенной в G и вместо суммы всех
этих произведений всегда можно взять произведение ВК
на эту равнодействующую силу.
Но для того, чтобы имело место сохранение живых
сил, необходимо, как мы видели, чтобы сумма этих
произведений равнялась нулю. А для этого необходимо: или
чтобы равнодействующая сила равнялась нулю, или чтобы
линия ВК равнялась нулю. Если неподвижной точки нет,
то должна быть равна нулю равнодействующая сила. Если
же неподвижная точка имеется, то скорость точки В должна
О СОХРАНЕНИИ ЖИВЫХ СИЛ
805
быть равна нулю или, по крайней мере, направление точки
В должно быть непременно перпендикулярно к направлению
равнодействующей силы.
В самом деле, если препятствием является математическая
точка,— скажем, точка опоры у рычага,— то либо направление
равнодействующей силы будет проходить через эту точку
опоры и движение точки В будет вращательным
движением вокруг нее, либо сама точка В будет как раз точкой
опоры и движение ее будет равно нулю. Если
препятствием служит неподвижная поверхность, то точка В, через
которую проходит направление равнодействующей силы,
будет непременно лежать на этой поверхности и
направление ее движения в данный момент будет совпадать с
направлением самой этой поверхности, в то время как
направление равнодействующей силы будет перпендикулярно
к поверхности.
Итак, вообще можно сказать, что когда имеется
неподвижная точка, тогда
вк=о.
Таким образом, доказано, что когда тела соединены
друг с другом при помощи жестких рычагов,
закрепленных или незакрепленных, сохранение живых сил имеет
место.
199. Если тела соединены между собой при помощи
нитей, то нужно представить на концах каждой части нити
между двумя телами две равные и противоположные силы,
которые должны тянуть в направлении нити, и тогда
доказательство нетрудно вывести из сказанного выше (п° 194),
когда тела рассматривались как точки.
200. Если нить проходит через одно или несколько
тел, так что эти тела могут свободно скользить вдоль
нее, то ввиду того, что направление равнодействующей
силы, соответствующей потерянным движениям, в каждый
момент проходит через точки О пересечения линий CS и
AR (фиг. 78) и делит соответствующий угол пополам
(п° 153), мы должны вместо этой равнодействующей силы
вообразить две равные силы, которые должны тянуть по
направлению SO и /?G, т. е. по направлению нитей CS
20 Ж. Даламбер
306 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ ДВИЖЕНИЙ
и AR> Далее, если принять, что линии SV и RN являются
путями точек S и /?, и если провести перпендикуляры VD
фиг. 78.
и NP, то в силу того, что сумма
AR-\-SC
является постоянной, мы будем иметь
SD = RP.
Пользуясь двумя последними замечаниями, нетрудно
дать доказательство сохранения живых сил во всех случаях.
О сохранении живых сил в случае удара упругих тел.
201. Сохранение живых сил в случае соударения
упругих тел можно доказать, рассматривая эти упругие тела
как абсолютно твердые тела и принимая вместе с тем,
что как сжатие, так и восстановление пружины совершается
мгновенно. В п° 189 мы уже дали набросок такого
доказательства. Однако нами было замечено (п° 176 и ел.),
что это допущение может привести к ложным выводам
относительно законов соударения упругих тел. Поэтому
здесь мы не будем прибегать к этому допущению и будем
доказывать данное предложение, предполагая, что между
телами помещена пружина, сообщающая обоим телам равные
и противоположные движущие силы.
202. Пусть Л и В (фиг. 79) будут две точки,
соединенные какой-либо пружиной АВ, и пусть эти точки,
получив какие-то произвольные импульсы АО и BF, за время
О СОХРАНЕНИЕ ЖИВЫХ СИЛ
807
сжатия и восстановления пружины опишут кривые Ата и
ВМЬ. Пусть <р будет переменная движущая сила, в любой
момент одинаковая для обоих тел и толкающая их в
противоположные стороны по направлению пружины Mm. Пусть,
наконец, V будет скорость точки М, и — скорость точки
Фиг. 79.
т, G —скорость точки В и g — скорость точки А. Линию
MV обозначим через dz, а линию ти через dx. Тогда мы
будем иметь
B.V2 = BG* — 2^<pdz
и
A-u2 = Ag2-{-2 [ (fdx.
Но 4когда
ab^AB,
тогда
2 \<pdx — 2 [ydz = 0,
так как
dx — dz
есть величина сжатия или расширения пружины за данный
элемент времени и при
ab = AB
пружина приходит в прежнее свое состояние. Отсюда
по окончании сжатия мы будем иметь
A>u*-\~B'V*^A.g*-\-B>G*,
20*
808 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ ДВИЖЕНИЯ
Очевидно, данное доказательство может быть
распространено на случай любого числа точек, соединенных
произвольным образом.
Итак, для точек, соединенных между собой при помощи
пружин, сохранение живых сил, как мы видим, имеет место.
В том случае, когда данные тела имеют конечные размеры,
для доказательства сохранения живых сил достаточно
доказать, что сохранение имеет место t в точке, через которую
проходит направление равнодействующей сил, уравновеши-
q вающихся друг с другом (п° 198). Такой точкой
в том и другом теле будет точка
соприкосновения обоих тел: эта точка, как мы предполагаем,
за время сжатия и восстановления остается
неизменной, а самое сжатие и восстановление, со-
ьУ^\ гласно нашему допущению, заканчиваются в тече-
К-' ние весьма короткого промежутка времени. Мы
должны вообразить, что как раз через эти точки
и проходит пружина, сообщающая им в каждый
момент равные и противоположные движущие силы,
QN распределяющиеся затем на всю массу тела. Таким
" образом, настоящий случай приводится к
предыдущему.
Фиг. 80. 203, Если тела А я В (фиг. 80) соударяются
друг с другом посредством некоторого стержня
С В А, имеющего в С неподвижную точку, то движущие
силы, приложенные в точках А и Ву будут не одинаковы,
будучи обратно пропорциональными плечам СА и СВ.
И так как пути точек В и А за равные промежутки
времени прямо пропорциональны этим плечам рычага, то
произведения движущих сил на пути точек А и В будут
одинаковы в обеих точках.
Таким образом, и здесь сохранение живых сил можно
доказать либо методом п° 189, предполагая тела
несжимаемыми, либо воображая одну бесконечно малую пружину
в точке А и другую в точке В. Для толковых читателей
нет нужды разъясшпь это подробнее.
Итак, сохранение живых сил имеет место и в данном
случае. Комбинируя изложенные принципы, мы всегда
можем доказать его в случае удара упругих тел.
О СОХРАНЕНИИ ЖИВЫХ СИЛ
309
Общее примечание.
204, Из всего сказанного до сих пор следует, что
сохранение живых сил вообще вытекает из того принципа,
согласно которому при равновесии сил скорости их точек
приложения, измеряемые по направлению соответствующих
сил, обратно пропорциональны самим силам. Этот принцип
давно уже признан геометрами в качестве основного
принципа равновесия. Никто, однако, насколько мне известно,
не доказал этого принципа в общем виде и не показал,
что из него в качестве необходимого следствия вытекает
принцип сохранения живых сил.
Только что упомянутый принцип равновесия легко
может быть доказан. В самом деле, могут быть три случая:
или силы равны и противоположны, или они приложены
к различным плечам рычага, или, наконец,
равнодействующая этих сил проходит через какое-нибудь неподвижное
и непреодолимое препятствие, как это мы видели в
задаче X. Уже сказанного выше, мне кажется, достаточно для
того, чтобы доказать наш принцип для первого и второго
случая. Что касается последнего случая, то, очевидно,
составляющие силы в направлении, перпендикулярном к
равнодействующей силе, будут равны между собой,
скорости же, взятые в одну сторону, будут также равны.
Отсюда нетрудно вывести доказательство для того или
иного частного случая. Например, для случая задачи X
доказательство легко получается.
Если ускоряющей силой тел служит сила тяжести g и
если лт, z и т. д. суть вертикальные абсциссы описываемых
телами кривых, то мы будем иметь (п° 191)
AV2-{-av2 и т. д. ==*2Agx-^2agz и т. д.,
если предположить, как и в доказательстве, приведенном
> в п° 191, что тела выходят из состояния покоя. Если же
тела начинают движение с начальными скоростями В и Ь,
то мы будем иметь
AV2^av* и т. д. ***AB2-{-ab*-}-2Agx-\-2agz и т. д.
310 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ ДВИЖЕНИЯ
Следует заметить, что если z отрицательно по отношению
к л;, т. е. если тело а поднимается, в то время как тело
А опускается, мы должны взять — 2agz.
Например, если два равных тела прикреплены к рычагу,
плечи которого суть с и е, и если тело, действующее при
помощи более длинного плеча с рычага, увлекает другое
тело, заставляя его двигаться снизу вверх, то мы будем
иметь
Л1/2 + Лг/2 или AV* + ~^-=*
= 2gAx — 2gAz — 2gAx — ШЕ.
с
Отсюда
т/г — 2gx(c* — ce)
Это же уравнение нетрудно получить и иначе,
пользуясь или нашим принципом, или другими.
Далее, нетрудно видеть, что величина
2Agx -{- 2agz и т. д.
всегда будет равна произведению суммы весов на
удвоенное опускание центра тяжести. В самом деле, опускание
центра тяжести, как это нетрудно доказать методами
статики, равно
Agx-\-agz и т. д.
Ag+ag и т. д.
Таким образом, в том случае, когда тела обладают
весом, сумма живых сил в каждый момент равна сумме
начальных живых сил плюс живая сила груза, равного
сумме всех данных грузов и свободно опустившегося с
высоты, равной той высоте, с которой опустился центр
тяжести.
О сохранении живых сил в жидкостях.
205. Пусть мы имеем какой-нибудь сосуд произвольной
и неопределенной формы POTQ (фиг. 81). Часть этого
сосуда ADCZy ограниченная параллелями AD и CZ,
наполнена жидкостью. Вообразим, что эта жидкость разделена
б СОХРАНЕНИИ ЖИВЫХ СИЛ В ЖИДКОСТЯХ 811
на слои FKQ, параллельные AD, и пусть все точки
каждого слоя обладают некоторой ускоряющей силой,
изображенной соответствующей ординатой kf кривой dfb (при
этом ординаты ad будут представлять положительные
ускоряющие силы, т. е. те силы, которые направлены от L к £,
а ординаты kf—те ускоряющие силы, которые имеют
противоположное направление). Я утверждаю, что если
d
Фиг. 81.
жидкость в данном состоянии находится в равновесии, то
площадь adnmobc будет равна нулю: это значит, что сумма
положительных площадей будет равна сумме отрицательных
площадей.
В самом деле, для равновесия необходимо, чтобы любой
слой FKG испытывал одинаковое давление как снизу
вверх, так и сверху вниз. Но давление на слой FKO по
направлению LB будет такое же, как будто бы этот слой
был нагружен цилиндром EHFG. Если обозначить LK через
х, а ускоряющую силу каждого слоя через ср, то вес этого
цилиндра будет равен
FG • \ <р dx или FG • (adin — nfk).
Точно так же можно доказать, что давление на FQ по на-
812 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ движений
правлению ЯДГбудет равно
FQ (kfm — mog -f- gcb).
Вследствие того, что оба эти давления должны быть равны,
мы будем иметь
adin — nfk = kfm — mog -{- gcb>
или
adin — nfkm -J- mog — gcb = 0.
Отсюда следует, и т. д. Что и требовалось доказать.
Следствие I.
206. Если, считая время постоянным, вместо
ускоряющей силы ф подставить пропорциональную ей малую
скорость duy т. е. малую скорость, с которой данный слой,
взятый изолированно, стал бы опускаться в течение
элемента времени, то мы получим
dudxz=0.
Следовательно, если жидкость движется по направлению
к АВ и если da изображает потерянную или
приобретенную данным слоем скорость, т. е. ту скорость, обладая
которой данный слой уравновешивался бы другими слоями
(п° 60), то мы будем иметь
\ dudx — 0.
Следствие II.
207. Выше нами было показано (п° 191), что сохранение
живых сил в том случае, когда тела обладают весом или
какой-либо иной ускоряющей силой, вытекает из
сохранения живых сил при отсутствии ускоряющих сил. Поэтому
нам достаточно доказать, что сохранение живых сил имеет
место в том случае, когда жидкость ADCZ, приведенная
вначале в движение какой-нибудь причиной (скажем,
поршнем), движется в сосуде POTQ при мысленном отсутствии
тяжести.
О СОХРАНЕНИИ живых сил в жидкостях 313
Для этого мы вообразим жидкость, разделенную на
равные бесконечно малые слои массы т, толщины dx и
ширины у. Тогда мы будем иметь
т =у dx.
Обозначим через и скорость данного слоя, а через
u-\~du скорость его в следующий момент. Тогда, согласно
нашему принципу, если бы слои обладали скоростями du,
они находились бы в' равновесии, т. е., согласно
предыдущему следствию, имело бы место равенство
\ dudx==0.
Но для того, чтобы доказать сохранение живых сил,
необходимо доказать, что
\ mudu — 0 *).
Так как скорость каждого слоя обратно
пропорциональна ширине слоя, мы имеем
С другой стороны,
*) Если
У '
m=ydx.
\ m'idu=:0
и если мы через и! обозначим скорость данного слоя в
следующий элемент времени, то (принимая у dx, или т, постоянным,
на что мы имеем право) мы будем иметь
i
в силу того, что
Следовательно,
(Примечание Везу)
та'2 — ти2 п
ти-
= ти du.
\ ти'2~ \ ти2.
21 Ж. Даламбер
814 ОБЩИЙ ПРИНЦИП ДЛЯ НАХОЖДЕНИЯ ДВИЖЕНИЯ
Следовательно,
\ mudu=\ dudx = 0.
Отсюда следует, и т. д.
Указание.
Даниил Бернулли в своем превосходном сочинении под
названием «Hydrodynamica и т. д.» выводит законы движения
жидкости в сосудах из принципа сохранения живых сил,
не доказывая этого последнего. Так как наш общий
принцип, изложенный в п° 60, привел нас к доказательству
сохранения живых сил, мы могли бы, очевидно,
непосредственно из нашего принципа вывести законы движения
жидкости, причем это был бы способ гораздо более ясный
и прямой. Однако, поскольку в нашу задачу не входит
здесь заниматься жидкостями, мы ограничиваемся тем, что
показали в двух словах применение нашего принципа в этой
области,— области, которая до сих пор казалась столь
трудной.
Слегка наметив здесь эти применения, мы этим и
ограничимся, отсылая интересующихся подробностями к нашему
сочинению «О равновесии и движении жидкостей»* Там мы,
пользуясь нашим общим принципом, получили решение
ряда труднейших задач, какие когда-либо предлагались из
данной области.
Коне ц.
*£&
*2^
ПРИМЕЧАНИЯ К ПЕРЕВОДУ.
[Ц (к стр. 11). Даламбер (Jean Le Rond d'Alembert) родился
в 1717 г. как внебрачный сын генерала Детуш и канониссы Тансен,
и был подброшен матерью около одной из парижских церквей.
Воспитывался в бедной семье ремесленника, с которой и связался
на всю жизнь. Мать всячески избегала потом встречаться с
сыном, боясь скандала, тогда как отец, узнав о его судьбе,
завещал ему ежегодное содержание в 1200 франков. Вскоре отец
умер, поручив заботу о мальчике своим родителям. По их
протекции Даламбер двенадцати лет от роду поступил в
привилегированный коллеж имени Мазарини (так называемый «коллеж
четырех наций»). Коллеж находился в руках янсенистов,
соперничавших с иезуитами в деле уловления душ молодых
людей. В коллеже Даламбер пробыл" пять лет, получив там свою
фамилию.
Математика в коллеже была не в почете, тем не менее тогда
же Даламбер полюбил эту науку. Воспитатели Даламбера
прельщали его то адвокатской, то врачебной деятельностью, которая
была несравненно доходнее, чем научная карьера математика.
Некоторое время по выходе из коллежа Даламбер вынужден был
заниматься t мало приятными для него дисциплинами: в 1738 г.
он получил звание адвоката, и на этом поприще ему, как
превосходному оратору, сулили" блестящую будущность. Даламбера,
однако, интересует другое, и он бросает юридические науки.
Тогда его воспитатели пытаются всячески повлиять на него и
заставить заняться медициной. Они добиваются того, что
Даламбер выбрасывает все свои математические книги и дает
обещание впредь не читать ни одной из них. Но вскоре он нарушает
свое обещание с тем, чтобы окончательно забросить и медицину.
В математике, таким образом, Даламбер был в полном смысле
самоучкой, занимаясь ею, главным образом, в публичной
библиотеке. В своей автобиографии он отмечает, что за эти годы он
испытал немало горечи разочарования от того, что делал много
таких открытий в математике, которые уже давно были сделаны
другими.
Тем не менее занятия математикой идут настолько успешно,
что Даламбер публикует ряд работ по математике и уже в 1742 г»
21*
316
ПРИМЕЧАНИЯ К ПЕРЕВОДУ
в возрасте 25 лет, добивается избрания в Парижскую академию
наук в качестве «адъюнкта» (adjoint)*), перед этим дважды
потерпев неудачу.
В том же 1742 г. Даламбер представил в Академию мемуар,
положенный им в основу своего знаменитого сочинения
«Динамика» («Traite de dynamique»). Это произведение, вышедшее в
свет в 1743 г., послужило поворотным пунктом в развитии
механики: здесь излагался известный «принцип Даламбера» как
универсальный прием решения задач динамики системы со связями.
В трактате Даламбер показывает на ряде трудных примеров
применение своего принципа, и то же самое он делает в своих
позднейших работах по механике.
В 1744 г. Даламбер опубликовал книгу: «О равновесии и
движении жидкостей» («Traite de l'equiiibre et du mouvement des
fluides»), где гидродинамика получила дальнейшее свое развитие
после исторического труда Д. Бериулли «Hydrodynamica» (1738).
Одчако широкую известность Даламбер получил только
благодаря своей книге о причине ветров — «Reflexions sur la
cause generale des vents» (1747). Здесь он показал, как
интегрируются дифференциальные уравнения в частных производных, и
его можно считать основоположником теории этих уравнений.
В 1746—1748 гг. Даламбер обогащает рядом методов
интегральное исчисление (соответствующие мемуары печатались им
в записках Берлинской академии наук).
В 1747 г. в 'записках Берлинской академии наук Даламбер
печатает свой мемуар о колебании струны, вызвавший затем
большую дискуссию **).
В 1749 г. Даламбер опубликовал отдельной книгой свои
исследования о предварении равноденствий, привлекшие к себе
большое внимание научной общественности («Recherches sur la
precession des equinoxes et sur la nutation de Гахе de la terre»).
В 1752 г. выходит книга, посвященная вопросу о
сопротивлении жидкостей («Essai d'une nouvelle theorie sur la resistance
des fluides»).
В 1754 и 1756 гг. выходят его труды по небесной механике
(«Recherches sur les differents points importants du systeme du
monde»), где получает развитие теория возмущения планет и
теория формы Земли как неоднородного тела.
Материальное положение Даламбера, однако, продолжало
оставаться необеспеченным. В 1752 г. прусский король Фридрих II
предложил Даламберу место в своей академии наук. Но Даламбер
не желал покидать родную страну и, не смущаясь неизбежными
*) Полноправные члены академии назывались pensionnaires.
Рангом ниже работники академии назывались associes и еще
ниже adjoints. Денежное вознаграждение получали только
pensionnaires.
**) См. ниже наше примечание.
ПРИМЕЧАНИЯ К ПЕРЕВОДУ
317
гонениями и репрессиями, уже заключил союз с материалистом
Дидро с целью издания знаменитой 33-томной «Энциклопедии»*),
этого тарана, направленного против феодального гнета, давившего
французский народ.
В 1751 г. вышел первый том «Энциклопедии», в котором
напечатано знаменитое предисловие, принадлежащее перу Даламбера.
Это, в сущности, самостоятельное произведение, излагающее
философское кредо Даламбера**). Помимо математических и
физико-математических статей Даламберу принадлежит огромное
количество статей но самым различным вопросам (философия,
история, литература) в первых томах «Энциклопедии». Этим;*
статьями Даламбер приобрел весьма широкую известность, но
они же создали ему и массу врагов из среды реакционеров.
Даламбер приобрел кличку вольнодумца, друга преследуемых
Дидро и Вольтера. В силу этого он, конечно, не мог рассчитывать
на расположение французского правительства.
Все же в 1754 г. Даламбер, опять-таки после трех провалов,
был избран членом Французской академии***).
Первое денежное вознаграждение Даламбер получил лишь в
1754 г., и оно шло от прусского короля под названием pension
в сумме 1200 ливров (около 430 рублей золотом) в год. Лишь
два года спустя расщедрилось и правительство Людовика XV
и назначило Даламберу такую же плату в 1200 ливров в год.
В том же (1756) году Парижская академия наук со своей стороны
назначила ему плату сверх штатов («pension surnumeraire»).
В 1758 г. вышло второе, расширенное, издание «Динамики».
В том же году вышел седьмой том «Энциклопедии», и внимание
сикофантов было привлечено статьей Даламбера «Женева»
(«Geneve»). Реакционеры, и в особенности духовенство, были в высшей
степени раздражены утверждением Даламбера, что
духовенство Женевы принадлежит к деизму и социнианству. Против
Даламбера и против «Энциклопедии» вообще усилились нападки
со стороны реакционных кругов, и Даламбер вышел из редакции,
оставаясь в то же время сотрудником и другом Дидро.
В 1759 г. Даламбер выпустил в свет сочинение
методологического характера «Начала философии» («Elements de philosophie»).
*) Полное название: «Энциклопедия, или толковый словарь
наук, искусств и ремесл» («Encyclopedie, ou dictionnaire raisonne
des sciences, des arts et des metiers»).
**) Это произведение Даламбера переведено на русский язык
,в сборнике «Родоначальники позитивизма» под заглавием «Очерк
происхождения и развития наук» (Издание «Брокгауз-Ефрон», СПБ,
1910, вып. I, стр. 95—169).
***) Не нужно смешивать Французскую академию с Парижской
академией наук: предметом деятельности первой служили
литература и язык, а предметом деятельности второй — математика
и естествознание.
818
ПРИМЕЧАНИЯ К ПЕРЕВОДУ
Живя все еще в условиях материальной необеспеченности и
непрекращающихся нападок и уколов со стороны реакционных
кругов, Даламбер в 1762 г. получил весьма выгодное
предложение от русской царицы Екатерины II занять должность
воспитателя русского наследника. Через год прусский король Фридрих II,
соревнуясь в меценатстве с русской царицей, предложил Даламберу
должность президента Прусской академии наук. Однако
Даламбер неизменно отклонял все эти предложения, не желая уезжать
из пределов своей страны, являя тем самым пример
демократического патриотизма.
Дальнейшие математические исследования свои Даламбер
выпускал в свет в виде сборников «Opuscules mathematiques»
(первый том вышел в 1761 г., последний, восьмой, том — в 1780 г.).
В 1765 г., после смерти Клеро, Парижская академия наук
утвердила, наконец, Даламбера полноправным академиком,
назначив ему pension Клеро. Но и теперь правительство долгое время
не утверждало этого решения Академии, пока, наконец, оно не
было вынуждено уступить давлению научной общественности.
В 1772 г. Даламбер был избран секретарем Французской
академии. Здесь он занялся исторической работой и написал
биографии (eloges) всех академиков, умерших за время с 1700 до 1772 г.
В 1779 г. вышла в свет книга Даламбера «Основы теории и
практики музыки» («Elements de musique theorique et pratique»).
Заслуживает быть отмеченным следующий факт: Даламбер
был настолько известен как философ, что после смерти Вольтера
(1778) он стал первым философом в Академии.
Умер Даламбер в 1783 г., за шесть лет до взрыва
революции во Франции.
Даламбер был первым подлинно французским математиком.
Все свои произведения он писал на французском языке, и он не
переставал думать о благе французской нации.
Первое издание «Динамики» Даламбера вышло в 1743 г.,
второе, значительно дополненное, — в 1758 г. и третье, уже после
смерти Даламбера, в 1796 г. Последнее издание является
перепечаткой со второго. С этого третьего издания и делался
настоящий перевод. (Заметим, кстати, что немецкий перевод из серии
«Ostwald's Klassiker» сделан с гораздо менее полного, первого,
издания.)
При переводе мы больше всего стремились сохранить в
неприкосновенности научный метод Даламбера, те понятия, которыми
он оперирует. Там, где терминология Даламбера может быть
непонятна для современного читателя, мы, сохраняя эгу
терминологию в тексте, поясняли ее в примечаниях.
Как правило, мы стремились сохранить не только
терминологию подлинника, но и его обозначения и символику. Для
примера укажем на следующие особенности символики Даламбера.
Когда у Даламбера производная множится на какой-нибудь
одночлен, то Даламбер записывает символ производной так, как
будто это было отношение дифференциалов. Например, выражение
ПРИМЕЧАНИЯ К ПЕРЕВОДУ
S19
х —■ Даламбер записал бы так: -— Это объясняется тем,
что Даламбер, действительно, смотрел на то, что мы сейчас
называем производной, как на отношение двух дифференциалов.
Мы всюду сохранили обозначения Даламбера.
Даламбер не употребляет совсем слова «отрезок», говоря
всюду вместо него «линия». И здесь мы употребляли терминологию
Даламбера за исключением тех случаев, когда это может привести
к явным недоразумениям.
Даламбер при цитировании журналов весьма неточно
указывает их названия, переводя их, к тому же, на французский язык.
Мы всюду восстанавливали подлинное название журнала, хотя
бы и в сокращенном виде.
Формулы всюду нами выведены в отдельную строку, чего
нет у Даламбера, как и у других авторов его времени.
Другие отступления нами оговариваются в примечаниях.
Опечатки мы исправляли без оговорок.
Все примечания Безу (Bezout, 1730—1783), о которых
упоминает в предисловии автор, нами включены в настоящее издание
и сопровождены соответствующей оговоркой.
[2] (к стр. 11). Различие между необходимыми и случайными
истинами ведет свое начало от Лейбница. Последний под
необходимыми истинами понимал рациональные истины, стоящие выше
опыта, независимые от опыта. Случайные истины, по Лейбницу,
суть истины фактические, зависимые от опыта. Первые истины
априорны, вторые апостериорны. Первые истины содержит
математика, вторые — физика.
[3] (к стр. 12). Сочинение о предварении равноденствий имеет
заглавие: «Исследования о предварении равноденствий и о нутации
земной оси в ньютоновой системе» («Recherches sur la precession
des equinoxes et sur la nutation de Гахе de la terre dans le
systeme newtonien», Paris, 1749). Указываемые здесь добавления
вошли потом в сборник статей Даламбера, посвященных различным
вопросам математики, механики, оптики, астрономии и т. д.
(«Opuscules mathematiques, oil memoires sur differents sujets de geometrie,
de mechanique, d'optique, d'astronomie etc. Paris, 1761—1780),
всего вышло восемь томов. Вопросу о движении тела,
вращающегося вокруг подвижной оси, посвящены следующие статьи:
«О движении тела произвольной формы под действием
произвольных сил» («Du mouvement d'un corps de figure quelconque,
anime par des forces quelconques», t. I, 1761, p. 74—103),
«Исследования по вопросу об осях вращения тела произвольной
формы без ускоряющей силы» («Recherches sur les axes de rotation
d'un corps de figure quelconque, qui n'est anime par aucune force
acceleratrice», t. IV, 1768, p. 1—31), «О движении тела произвольной
формы» ~(«Du mouvement d'un corps de figure qelconque», ibid.,
p. 32—60), «Замечания по поводу одной особенной трудности,
встречающейся при решении задачи о предварении равнодействий
и некоторые другие соображения по поводу этой задачи» («Remar-
320
ПРИМЕЧАНИЯ К ПЕРЕВОДУ
ques sur une difficulte singuliere qui se rencontre dans la
solution du proble-me de la precession des equinoxes avec quelques
autres reflexions sur ce probleme», t. I, 1763, p. 251—293) и «О
вращении тела произвольной формы» («Sur la rotation d'un corps de
figure quelconque», t. VII. 1780, p. 372—377).
[4] (к стр. 12). Речь идет о сочинении Даламбэра «Опыт новой
теории сопротивления жидкостей» («Essai d'une nouvelle theorie
dela resistance des fluides»), вышедшем отдельной книгой. В
основе этого сочинения лежит принцип самого Даламбера,
изложенный им в «Дчнамике». Глава VIII указанного сочинения посвящена
вопросу о движении жидкостей в сосуде, а глава IX — вопросу
о течении рек. "Указываемые здесь добавления вопли потом в
сборник «Opuscules mathematiques», указанный в предыдущем
примечании. Там мы находим следующие статьи: «Замечания по
поводу законов движения жидкостей» («Remarques sur les loix
du mouvemant des fiuides», t. I, 1761, p. 137—163), «О равновесии
жидкостей» («Sur l'equilibre des fluides», t. V, I-re partie 1768,
p. 1—40), «Новые соображения по поводу законов движения
жидкостей» («Nouvelles reflexions sur les loix du mouvement des
fluides», ibid., p. 41—63), «Нэвы'1, строгий и прямой, метод
определения движения жидкостей в сосудах» («Methode nouvelle,
rigoureuse et direct pour determiner le mouvement des fluides
dans les vases», t. VI, 1773, p. 379—390), «Новые соображения
но поводу равновесия жидкостей» («Nouvelle reflexions sur les loix
de l'equilibre des fluides», t. VIII, 1780, p. 1—35) и «Новые
исследования по вопросу о движении жидкостей в сосудах» («Nouvelles ге-
cherches sur le mouvement des fluides dans les vases», ibid.,p.52—230).
Во введении к книге о сопротивлении жидкостей Даламбер
борется с самомнением тех математиков, которые воображают,
что по вопросу о механике жидкостей можно ограничиться одними
математическими выводами. Заканчивается введение такими
словами: «Не нужно думать, чго словечки вроде «Теорема» или
«Короллярий» («Следствие».—3. Е.) об вдают какой-то таинственной
доказательной силой и что, заканчивая какое-либо предложение
словами «Что и требовалось доказать», мы делаем доказанным то,
что таковым не является».
р] (к стр. 12). Указанная статья под заглавием
«Исследования по вопросу о колебаниях произвольного тела, плавающего
в жидкости» («Recherches sur les oscillations d'un corps
quelconque qui flotte sur un fluide») помещена в т. I «Opuscules
mathematiques», p. 104—136. Статья представляет собой развитие книги
о сопротивлении жидкостей.
[6] (к стр. 13). В 1749 г. в журнале Берлинской академии
наук Даламбер напечатал стат ью «Исследования по вопросу о
кривой, которую образует натяну гая струна, приведенная в колебание»
(«Recherches sur la courbe que forme une corde tendue, mise en
vibration») (Histoire de PAcademie Royale des Sciences et belies
lettres, t. Ill, 1747, Berlin, 1749, p. 214—220), и вторую статью, под
заглавием «Продолжение исследований по вопросу о кривой, кото-
ПРИМЕЧАНИЯ К ПЕРЕВОДУ
321
рую образует натянутая струна, приведенная в колебание» («Suite
des recherches stir la courbe que forme une corde tendue, mise en
vibration», ibid., p. 220—249). Через год в том же журнале
появилась статья Эйлера под заглавием «О колебании струн, перевод
с латинского» («Sur la vibration des cordes, traduit du latin»,
«Histoirede Г Academic», t. IV, annee 1743, Berlin, 1750, p. 69—85).
Даламбер выступил с возражениями Эйлеру в статье «Добавление
к мемуару о кривой, которую образует натянутая струна,
приведенная в колебание» («Addition au memoire sur la courbe que
forme une corde tendue, mise en vibration» «Histoire de l'Acade-
mie», t. VI, annee 1750, Berlin, 1752, p. 355—360). Через три года
после этого по тому же вопросу выступил Д. Бернулли со
статьей «Размышления и разъяснения по поводу новых колебаний
струн, указанных в Записках Академии за 1747 и 1748 г.»
(«Reflexions et eclaircissements sur les nouvelles vibrations des
cordes exposees dans les Memoires de l'Academie de 1747 et 1748»,
de l'Academie, t. IX, annee 1753, Berlin, 1755, p. 147—172) и,
кроме того, со статьей «О сочетании нескольких родов простых
изохронных колебаний, сосуществующих в одной и той же
системе тел» («Sur le melange de plusieurs especes de vibrations
simples isochrones, qui peuvent coexister dans un meme systeme
de corps», ibid., p. 173—195). Сейчас же вслед за этим выступил
и Эйлер с «Замечаниями по поводу предыдущих мемуаров г.
Бернулли» («Remarques sur les memoires precedents de M. Bernoulli^,
ibid., p. 196—222). В 1758 г. вышло второе издание «Динамики»
Даламбера, а через год по этому же вопросу выступил молодой
Лагранж со статьей «Исследования по поводу природы и
распространения звука» («Recherches sur la nature et la propagation
du son» в «Miscellanea physico-mathematica societatis privatae
Taurinensis», t. I, 1759, p. 112-f-X). С возражениями Бернулли и
Эйлеру выступил Даламбер в двух своих статьях:
«Исследования по вопросу о колебаниях звучащих струн» («Recherches
sur les vibrations des cordes sonores») и «Дополнение к
предыдущему мемуару о колеблющихся струнах» («Supplement au me-
moire precedent sur les cordes vibrantes») (в «Opuscules mathe-
matiques», t. I, 1761, pp. 1—64 и 65—73).
Одновременно с этим была напечатана статья Лагранжа
«Добавление к первым исследованиям о природе и распространении
звука» («Addition aux premieres recherches sur la nature et la
propagation du son», «Miscellanea physico-mathematica societatis
privatae Taurinensis», t. II, 1760—1761).
[7] (к стр. 13). Вопрос о доказательстве правила
параллелограмма сил привлекал к себе внимание многих математиков и
механиков XVIII столетия. В первом томе петербургских «Commen-
tarii» была напечатана статья Д. Бернулли «Исследование о
принципах механики и геометрические доказательства, относящиеся
к сложению и разложению сил» («Examen principiorum mecha-
nicae et demonstrationes geometricae de compositione et resolu-
tione viriuni/>, t. I ad annum 1726, Petropoli, 1728, p. 126—141).
322
ПРИМЕЧАНИЯ К ПЕРЕВОДУ
Даламбер выступал по этому же вопросу неоднократно. В его
«Opuscules mathematiques», в 1761 г. была напечатана статья
«Доказательство правила сложения сил» («Demonstration du prin-
cipe de la composition des forces», t. I, p. 169—179). В журнале
Парижской академии наук «Histoire de l'Academie Royale des
Sciences. Annee 1769» Даламбер снова выступил по этому вопросу. И,
наконец, в шестом томе «Opuscules mathematiques» (Paris, 1773 г.,
p. 360—370) Даламбер поместил статью «Новое доказательство
параллелограмма сил» («Nouvelle demonstration du parallelogramme
de forces».
Журнал «Ctfmmenlarii» издавался на латинском языке
Петербургской академией наук с 1727 г. Полное его название: «Сот-
mentarii Academiae scientiarum imperialis Petropolitanae». Следует
заметить, что Даламбер всюду при ссылках на этот журнал дает
его название во французском переводе: «Memoires de Petersbourg».
Французское название это издание действительно получило в XIX
столетии («Memoires de l'Academie Imperiale des sciences de
St-Petersbourg»).
[8] (к стр. 15). В подлиннике «Discours preliminaire»
(буквально: «Предварительное рассуждение»).
[9] (к стр. 15). Даламбер, следуя рационалистическим схемам,
не в состоянии надлежащим образом связать математические
науки с физической реальностью. К тому же, Даламбер механику
относит к математическим наукам, а не к физическим.
[Ю] (к стр. 20). «La force d'inertie». Было бы ошибкой этот
термин у Даламбера отождествлять по смыслу с современным
понятием «силы инерции». Выражение «сила инерции» (la force
d'inertie, vis inertiae) в XVII и XVIII столетиях употребляли
в том же смысле, как теперь говорят просто «инерция». С другой
стороны, несомненно и то, что инерция тел в представлении
теоретиков XVII и XVIII столетий связывалась с некоторым
сопротивлением или даже с активным действием инертной массы.
Окончательное формальное уточнение терминов «сила» и «сила
инерции» в механике произошло позже.
[Щ (к стр. 22). Необходимо принять во внимание, что в XVII
и XVIII столетиях понятие скорости не включало в себе
указания на направление, это была чисто алгебраическая (у Декарта
даже чисто арифметическая) величина. Направление движения было
понятием самостоятельным, не зависящим от скорости, и тогда
употреблялось выражение «направление тела», а не «направление
скорости», как сейчас.
[12] (к стр. 24). «Un corps double d'un autre». Это нужно
понимать так, что масса одного тела в два раза больше массы
другого тела. У механиков XVII и XVIII столетий понятие массы
тела настолько сливалось с понятием самого тела, что употреблять
всегда слово «масса» считалось излишним: под массой понималось
количество материи в теле.
[13] (к стр. 24). Сочинение И. Бернулли «Discours sur les
lois de la communication du mouvement» переведено на русский
ПРИМЕЧАНИЯ К ПЕРЕВОДУ
323
язык под заглавием «Рассуждение о законах передачи
движения». См. И. Бернулли. Избранные сочинения по механике.
Перевод под редакцией В. П. Егоршина, ОНТИ, 1937. В
похвальном слове И. Бернулли Даламбер объясняет неполучение
им премии тем, что Академией был поставлен вопрос о законах
соударения абсолютно твердых тел, в то время как И. Бернулли
исследовал законы соударения упругих тел. О сочинении И.
Бернулли Академия высказалась как о сочинении «весьма хорошем
и содержащем блестящие исследованиям.
Iй] (к стр. 25). .Маклорен (Mac-Laurin) — шотландский
математик (1698—1746), занимавшийся также и вопросами
механики. В 1724 г. Парижская академия наук премировала его
работу об ударе (когда «не на тему» представил свое сочинение
и И. Бернулли). В 1742 г. в сочинении «Treatise on Fluxions»
Маклорен указал фигуры равновесия для вращающейся
однородной жидкости (так называемый «эллипсоид Маклорена»)
и ввел неподвижные прямоугольные оси координат. Им же
введено в механику понятие поверхностей уровня. После смерти
Ньютона Маклорен считался крупнейшим английским
математиком.
[151 (к стр. 25). Спор о «силе движущегося тела» начался
не за тридцать, а почти за шестьдесят лет до появления первого
издания «Динамики» Даламбера: в 1686 г. в лейпцигском журнале
«Acta eruditorum» появилась статья Лейбница со следующим
(в переводе на русский язык) заглавием: «Краткое указание ошибки
достопочтенного Декарта и других относительно естественного
закона, согласно которому по божьей воле всегда сохраняется
якобы одно и то же количество движения и которым неправильно
пользуются между прочим в механической практике». Сочинение
Лейбница вызвало сразу же страстную полемику, которую
несправедливо осудил Даламбер, признавший самый вопрос
не подлежащим обсуждению, как совершенно бесполезный для
механики.
'[16] (к стр. 32). Все эти рассуждения Даламбера по поводу
бога-творца,— этого щекотливого для его времени предмета,—
показывают, что он в сущности отвергал бога и его
вмешательство в механические явления. Правда, по форме эти рассуждения
весьма несмелы и расплывчаты, но следует иметь в виду, что до
выхода в свет «Динамики» Даламбера, основные
материалистические и атеистические произведения (Ламетри, Дидро и
Гольбаха) еще не были написаны.
[Щ (к стр. 33). Относительно наименования механической
науки нелишним будет дать следующую историческую справку.
Первоначально (вплоть до конца XVII столетия) словом
«механика» обозначалось лишь учение о равновесии машин, т. е.
статика. Такой смысл вкладывают в это слово Галилей (1638), Ва-
риньон (1687) и отчасти Ньютон (1687). Учение о движении
у Галилея называлось описательно как «наука о пространственном
движении». Лейбниц в противовес механике (т. е. статике) назвал
324
ПРИМЕЧАНИЯ К ПЕРЕВОДУ
эту науку динамикой (1690), понимая под этим прежде всего
учение о живых силах. Лейбницу следовал в этом и его
последователь в XVIII столетии И. Бернулли. Ньютон в предисловии
к своим «Математическим принципам натуральной философии»
(1687) расширяет понятие механики, включая в него и учение
о движении и о силах (причем ньютоновские силы — не то, что
силы у Лейбница). В расширенном смысле понимает механику
также Эйлер (1736). До него Герман озаглавил свое сочинение
о движениях и о силах «Форономия» (1716). Мнение Парижской
академии наук по этому вопросу, очевидно, отражено в
редакционной статье журнала академии «Histoire de. l'Academie Royale des
Sciences» (Annee 1741, Paris, 1744, p. 143—145), в статье,
озаглавленной «По поводу одной задачи динамики» («Sur un probleme
de dynamique»). Тамт говорилось: «Термин динамика с некоторых
пор вошел в употребление среди французских геометров — прежде
всего у Лейбница. Обозначает этот термин спекулятивную (т. е.
теоретическую, В. Е.) и высшую механику, трактующую о
движущих и активных силах тел. По Лейбницу механизм вселенной
и механизм изделий искусства принципиально не отличаются друг
от друга. Вес, говорит би, и упругость,— эти два главных
средства, употребляемых природой при производстве тех или иных
феноменов,—могут быть объяснены механическим образом
подобно нашим обычным машинам: объяснение основывается на
движении эфирной материи. Однако, добавляет этот философ,
первичное движение тел, та сила, которая в них вложена творцом
и которая в них постоянно действует, определяется и изменяется
различным^ образом благодаря взаимным соударениям этих тел.
«Динамикой» он обозначил науку о распознавании (demeler)
и исчислении (evaluer) всех этих различий, а также об
определении эффектов. Механика, статика и то, что обычно называется
наукой о движущих силах (des forces mouvantes), изучают силы
лишь со стороны возможности движения,— т. е. как пассивные
силы. Наоборот, истинным объектом динамики, как мы уже
сказали, является учение о силах, в действительности, приводящих
в движение».
Примыкая к этому мнению, Даламбер дает своему сочинению
название «Динамика», как знак того, что его главная цель
заключается в том, чтобы изложить законы движения тел,
составляющих связанную систему.
Разделение механики как единой науки на статику и
динамику мы находим впервые у Лаграижа в его «Аналитической
механике» (1788).
[18] (к стр. 33). Под «прямыми» методами у Даламбера следует
понимать методы, соответствующие самому существу проблемы.
[19] (к стр. 34). Здесь Даламбер говор it о своем сочинении
«О равновесии и движении жидкостей» («Traite de l'equilibre в
du mouvement des fluides»),
[20] (к стр. 34). Полное заглавие сочинения: «Исследования
о предварении равноденствий и о нутации земной оси в ньюто-
ПРИМЕЧАНИЯ К ПЕРЕВОДУ
325
новой системе» («Recherches sur la precession des equinoxes et
sur la nutation de l'axe de la terre dans le systeme newtonien»).
Указанное сочинение вышло в 1749 г.
[21] (к стр. 35). Полное заглавие «Опыт новой теории
сопротивления жидкостей» («Essai d'une nouvelle theorie sur la
resistance des fluides»). Сочинение вышло в свет в 1752 г.
[22] (к стр. 35). Полное заглавие: «Размышления об общей
причине ветров» («Reflexions sur la cause generate des vents»).
Сочинение вышло в свет в 1747 г. Это сочинение более, чем
какое-либо другое др 1747 г., доставило Даламберу известность.
[23] (к стр. 41). Легко видеть, что логическое доказательство
принципа инерции у Даламбера является мнимым доказательством,
так как в процессе доказательства Даламбер ссылается на то, что
ему нужно доказать.
[24J (к стр. 43). В указанной статье Даламбер подчеркивает,
что сила инерции — это не сила, а свойство материи, так как силу
нужно считать понятием метафизическим. «Тело, говорит Даламбер,
сохраняет свое состояние покоя или движения, причем тело
покоящееся не меньше имеет реальной силы, чтобы сохранять
свое состояние, чем тело движущееся».
В статье «Движение» («Mouvement») в «Энциклопедии»
Даламбер пишет, что тело сопротивляется как движению, так и покою
в равной мере, и это сопротивление пропорционально массе.
«Сопротивление, которое оказывается телом, когда хотят измени!ь
его настоящее состояние, представляет собой основание того
общего закона движения, согласно которому действие всегда
равно противодействию. Установление этого закона было
необходимо для того, чтобы тела могли действовать друг на друга,
и для того, чтобы движение, будучи однажды созданным, могло
передаваться от одного тела к другому с достаточным
основанием. Без этого рода борьбы не могло бы иметь место и
действие: в самом деле, как бы сила могла действовать на то, что
не оказывает ей никакого сопротивления?»
f25) (к стр. 44). У Даламбера, как и у многих других авторов,
процорция записывалась иначе: между отношениями стояло вместо
теперешнего знака равенства два двоеточия. Таким образом,
пропорция имела следующий вид:
BD:CE::AB:AC.
[2б] (к стр. 47). В древности для сравнения промежутков
времени употреблялась так называемая клепсидра,— водяные часы,
представляющие собой в основном сосуд с водой, снабженный
внизу отверстием. Количество вытекшей воды и указывало па
величину истекшего времени.
1*1] (к стр. 49). Приводим соответствующий отрывок из статьи
«Уравнение» («Equation») в «Энциклопедии»: «Когда говорят, что
прямоугольник равен произведению его основания на высоту,
это в более развернутом виде обозначает следующее. Если мы
имеем два прямоугольника и если мы возьмем какую-нибудь ли-
326
ПРИМЕЧАНИЯ К ПЕРЕВОДУ
нейную величину а в качестве общей меры для оснований и высот
этих прямоугольников и если, далее, В будет числом (целым или
дробным, рациональным или иррациональным), выражающим,
сколько раз а содержится в основании первого прямоугольника,
//—числом, выражающим, сколько раз то же а содержится
в высоте первого прямоугольника, далее Ь — числом, выражающим,
сколько раз а содержится в основании второго прямоугольника,
a h — числом, выражающим, сколько раз а содержится в высоте
этого прямоугольника, то площади данных прямоугольников
относятся друг к другу как произведение чисел В и N к
произведению чисел b и h. Точно так же, когда говорят, что скорость
равномерно движущегося тела равна пути, деленному на время,
этим хотят сказать в более развернутом виде следующее. Если
два тела движутся равномерно и одно из них проходит путь
Е за время Г, а другое — путь е за время t, то, взяв отрезок а
за общую меру путей Е и е, а время 0 за общую меру времен
Tut, мы будем иметь, что скорости этих тел будут относиться
Е Т
друг к другу как число — , деленное на число -г-, относится к
е t
числу — , деленному на число у .
[28] (к стр. 52). Вследствие того, что у параболы
J/2 = 2рх,
длина подкасательной равна удвоенной абсциссе точки касания.
р] (к стр. 54). В оригинале стоит «la difference seconde de
Tespace parcouru». Выражением «la difference seconde» обозначали
в XVIII столетии бесконечно малую величину второго порядка
малости, а также дифференциал второго порядка.
[30] (к стр. 59). Статья Д. Бернулли в петербургском
журнале «Commentarii Academiae scientiarum imperialis Petropolita-
nae», t. I, ad annum 1726, называется «Исследование о принципах
механики и геометрические доказательства, относящиеся к
сложению и разложению сил» («Examen principiorum mechanicae et de-
monstrationes geometricae de compositione et resolutione viriuin»).
Начало этой статьи посвящено рассмотрению вопроса о
случайности или необходимости принципов механики. Д. Бернулли
высказывает ту точку зрения, что принцип статики (параллелограмм
сил) можно причислить к необходимым истинам, а принцип науки
о движении, состоящий в том, что «приращения скорости
пропорциональны элементу времени, умноженному на движущие силы
или давления», является только случайной истиной, так как эта
истина была добыта в результате опытов Галилея. Д. Бернулли
говорит, что можно было бы допустить, что приращения скорости
пропорциональны элементу времени, умноженному на некоторую
функцию от силы или давления. Только опыт, а не разум заставляет
нас взять первую степень от силы.
ПРИМЕЧАНИЯ К ПЕРЕВОДУ
327
Даниил Бернулли—швейцарский математик и физик (1700—1782),
сын Ивана Бернулли. В течение сем* лет работал в
Петербургской академии наук. Основное произведение Д. Бернулли,
сделавшее эпоху,-—это «Hydrodynamica», изданное в 1738 г. в
Петербурге.
[31] (к стр. 59). Эйлер (Euler) — швейцарский математик
(1707—1783), надолго связавший свою работу с Россией: с 1727
до 1741 г. и с 1766 г. до своей смерти работал в Петербургской
академии наук. Работы Эйлера являются основоположными для
ряда отделов математики. В 1736 г. вышла его книга «Mechanica
sive motus scientia analytice exposita» или «Механика, т. е. наука
о движении, изложенная аналитическим методом», замечательная
тем, что здесь впервые в механике систематически применяется
анализ бесконечно малых.
В предложении 19 Эйлер «доказывает», что приращение
скорости точки за «промежуточек времени» пропорционально
произведению действующей силы на этот промежуточек времени.
В следствии 2 к этому предложению Эйлер подчеркивает, что
«эта теорема не только правильна, но и по необходимости должна
быть верной, так что если бы мы предположили
dc=p2dt или pHt
или же равным какой-либо другой функции вместо/?, то мы пришли
бы к противоречию». См. русский перевод: Леонард Эйлер. Основы
динамики точки. Перевод с латинского под редакцией В. П. Егор-
шина (ОНТИ, 1938).
[32] (к стр. 59). В соответствии с принятыми тогда
обозначениями (ведущими свое начало от Ньютона) Даламбер различает
движущую силу (la force motrice) и ускоряющую силу (la force
acceleratrice). Первая соответствует теперешнему понятию силы,
вторая же соответствует ускорению, вызываемому силой в данной
точке. У Ньютона это — vis motrix и vis acceleratrix.
'Кроме того, следует заметить, что обе эти величины в
понимании математиков и механиков XVII и первой половины XVIII
столетия отличаются от одноименных величин современной
механики постоянным множителем dt: под движущей силой тогда
часто понимали величину произведения массы на дифференциал
скорости (дифференциал скорости в свою очередь понимался как
приращение скорости за элемент времени dt); под ускоряющей
силой (или ускорением) понимали тогда просто дифференциал
скорости.
[33] (к стр. 59). «Тела, обладающие силами»,—этими словами
мы хотели возможно точнее передать смысл французского
подлинника «les corps animes par des forces» (буквально: «тела,
одушевленные силами») Нельзя этого переводить модернистски:
«тела, находящиеся под действием сил», — так как это исказило
бы мысль Даламбера, считающего, что нет никакой
субстанциальной силы и что сила есть лишь сокращенное обозначение того,
328
ПРИМЕЧАНИЯ К ПЕРЕВОДУ
что тело получает ускорение. В пользу нашего перевода говорит
и то, что у Даламбера встречается выражение «le corps anime
d'une Vitesse», которое можно перевести только как «тело,
обладающее скоростью».
[34] (к стр. 62). Безу таким образом называет производную
<р'(г): он, как и другие авторы долагранжевского периода,
предпочитает иметь дело с дифференциалами, а не с производными.
|35] (к стр. 61). «Courbe polygone» дословно «полигональная
кривая». У Даламбера в дальнейшем различаются courbe polygene
(полигональная кривая) и courbe rigoureuse (подлинная кривая,
т. е. кривая в строгом смысле слова). О различии этих двух
понятий можно прочесть в статье Даламбера в «Энциклопедии»
под словом «Courbe polygone». Там мы находим следующее:
«В отличие от кривой в строгом смысле слова полигональной
кривой называется кривая, рассматриваемая как ломаная с
бесконечным числом звеньев. Такого рода кривые рассматриваются
в геометрии бесконечного. Строго говоря, это означает не что'
иное, как то, что кривая есть предел ломаных, как вписанных,
так и описанных».
[36] (к стр. 70). Данное доказательство правила
параллелограмма является, конечно, доказательством мнимым и оно служит
лишь свидетельством того, как сильно было желание Даламбера
придать всей механике формально логический вид.
[37] (к стр. 75). Тригонометрические величины Даламбер, как
и другие авторы того времени, выражает не отношениями
отрезков, а отрезками. Синус угла выражался длиной перпендикуляра,
опущенного из конца подвижного радиуса на неподвижный.
«Полным синусом» называлась длина самого радиуса в
тригонометрической окружности, т. е. это был синус прямого угла. Для того
чтобы перейти к современным обозначениям, связанным с
отношениями, нужно положить «полный синус» равным единице.
Для того чтобы понять рассуждение Даламбера,
воспроизведем здесь фиг. 6 и проведем на ней диаметр DD\ радиус ОгЕ
и опустим из Ох перпендикуляр ОгК на хорду EQ (фиг. 82).
Тогда, считая дугу DE бесконечно малой, из подобия
треугольников NED и КОхЕ мы будем иметь
EK:0LE= DN:DE,
откуда
EQ\DD' = DN\DE.
Подставляя вместо EQ отрезок NQ, отличающийся от него на
бесконечно малую величину, мы получим
NQ DN . erir>
w — = sin EDOx.
DD' DE
ПРИМЕЧАНИЯ К ПЕРЕВОДУ
329
NE
[38] (к стр. 75). Центральная сила пропорциональна —т-2. Но
NF— 2Ё1 — DE2 — DE2
NQ ~ DD' sin EDOx ~~ 2 p sin EDOx '
Вставляя последнее выражение в выражение силы, мы получим,
DE2
чго центральная сила пропорциональна -—:—+ п , 2, а так как
Фиг. 82.
DE . м
— представляет собой скорость и, то центральная сила
пропорциональна
02 и*
2р sin ^DOx 2? sin (F, 5)'
и2
p sin (F, 5) '
l39] (к стр. 78). Вместо косинуса Даламбер, как и многие
другие авторы его времени, говорил о синусе дополнительного
угла. Обозначения sin и cos в несколько иной, сначала, форме
были введены уже Эйлером, но Даламбер в первой части
трактата пользуется еще словесным наименованием
тригонометрических величии, вводя во второй части почти современную
символику.
[40] (к стр. 79). Синус-верзусом угла ЛОВ (фиг. 83) в
средневековой тригонометрии называли отрезок АС. В современных
обозначениях эта величина соответствует разности 1 — cos ср,
отличаясь от нее множителем, равным радиусу окружности.
|41] (к стр. 80). Для того, чтобы в этом убедиться, заметим,
что хорда
гп = 2R sin %г ,
22 Ж. Даламбер
330
ПРИМЕЧАНИЯ К ПЕРЕВОДУ
где R обозначает радиус круга, а ср — угол пуг. Отрезок rh равен 2/?,
синус-верзус угла ср равен R(\ —cos9). Следовательно, равенство
Даламбера (без умножения на п) принимает следующий вид:
4/?2 sin2-|-
2^> = /? (1 — cos <р).
Производя сокращения, мы получим очевидное тождество:
2 sin2 -7- = 1 — cos ?.
[*2] (к стр. 82). Книга «The Analyst» вышла из-под пера
известного философа-идеалиста, епископа Беркли в 1734 г. В этой книге
Беркли нападает на математику, и в особенности на исчисление беско-
Флг. 83.
нечно малых, с точки зрения правоверия. Беркли упрекал
математику бесконечно малых в недостоверности. Ему отвечал Мак-
лорен.
[Щ (к стр. 82). Термин «первые и последние отношения»
(primae et ultimae rationes) принадлежит Ньютону, который
«методу первых и последних отношений» посвятил первую главу
своих «Начал». Так, одна из теорем указанной главы утверждает,
что «последнее отношение» дуги и стягивающей ее хорды равно
единице. А. Н. Крылов, русский переводчик «Начал», в своем
переводе заменяет термин «первые и последние отношения»
современным термином «предельные отношения».
[44] (к стр. 82). В статье «Дифференциал» (Differentiel) в
«Энциклопедии» Даламбер подчеркивает, что термину «бесконечно
малое» не соответствует реальность: это просто краткий способ
выражения. «В дифференциальном исчислении, собственно говоря,
нет бесконечно малых величин. Там идет речь лишь о таких
величинах, которые называются бесконечно малыми, и об этих вели-
ПРИМЕЧАНИЯ К ПЕРЕВОДУ
331
чинах говорят, что они делятся на другие величины, которые так
же считаются бесконечно малыми. В настоящем своем состоянии
эти величины не есть бесконечно малые величины, точно так же
они не являются такими дробями, у которых числитель и
знаменатель суть бесконечно малые величины: это есть предел
отношения конечных величин... В дифференциальном исчислении
бесконечно малыми величинами пренебрегают, не потому, как это обычно
говорят, что они бесконечно малы по сравнению с теми
величинами, которые оставляются, и не потому, что при этом делается
бесконечно малая или ничтожная ошибка,— этими величинами
пренебрегают потому, что ими необходимо пренебречь для того,
чтобы достичь строгой точности». Другими словами, отбрасывание
бесконечно малых величин есть не приближенная, а точная
операция. «Мы не должны говорить, как это делают многие геометры,
что данная величина является бесконечно малой величиной на том
основании, что она может исчезнуть, или на том основании, что
она исчезнет: мы можем величину назвать бесконечно малой
только в том случае, если она в данный момент исчезает. Ибо
что может дать такого рода псевдо-определение, которое само
в сто раз более непонятно, чем то, что оно должно определить?»
Даламбер далее обвиняет математиков в том, что они сами
подавали повод для всяких возражений. «Сами изобретатели
анализа окутывали свое изобретение таким туманом, какой не
вытекал из его существа. Вообще люди часто питают страсть к
непонятному, если это приводит в результате к чему-то чудесному.
Шарлатанство это и больше ничего! Истина всегда бывает
простои и она может быть понята всяким, кто захочет над ней
потрудиться».
I45] (к стр. 88). Здесь Даламбер формулирует закон,
считавшийся с теми или иными видоизменениями основным законом
статики, начиная с XVI столетия. Этот закон, или правило,
является историческим зародышем современного принципа
виртуальных работ. Современную формулировку принцип виртуальных
работ получил у Лагранжа (за исключением того, что вместо
термина «работа» Лагранж употребляет «момент» — центральное
Понятие' механики Галилея).
Что касается долагранжевской эпохи, то тогда вместо
величины работы в аналитическое выражение принципа входило
«количество движения». Принцип равновесия в том виде, как его мы
находим у Даламбера, является первым приближением к
отображению объективного закона природы: для огромного множества
частных случаев он совпадает с современным принципом
аналитической статики. В самом деле, принцип равновесия у Даламбера
имеет вид
rniVi — m2v2 = 0.
Умножим это равенство на постоянное ускорение силы тяжести £
и на элемент времени S*. Мы будем иметь
migViU — m^gv^t = 0,
22*
332
ПРИМЕЧАНИЯ К ПЕРЕВОДУ
Обозначая mg через Р и vU через 8/, мы получим
Р\Щ — Р2Щ = 0,
или, иначе,
Обратно, можно от последнего равенства притти к равенству
Даламбера.
[4G] (к стр. 89). В приводимых дальше пропорциях нами
сохранен способ обозначения Даламбера целиком. Так как Далам-
беру нужно написать две пропорции, у которых часть членов
одинаковы, то он записывал эти пропорции сокращенно "в виде
одной пропорции, в которой различные члены писались друг над
другом и заключались в фигурную скобку. Так, отношения
АЕ\АК
и
AE\AD
Даламбер записывает в виде одного символа
Нами сохранен способ обозначения, который был у Даламбера.
Заметим, что при обозначении отрезков двумя буквами тогда
большей частью не обращалось внимания на порядок букв.
[47J (к стр. 96). Вариньои (Varignon) —французский
математик и механик (1654—1722). Он впервые точно сформулировал
закон параллелограмма сил и основы теории моментов сил. В 16S7 г,
вышла в свет его книга «План новой механики» («Projet d'tine
nouvelle mecanique»). После смерти Варипьона вышла его более
объемистая книга «Новая механика или статика» («Nouvelle
mecanique ou statique»).
I48] (к стр. 105). В настоящем п° более четко формулирован
принцип виртуальных скоростей, о котором в иной форме
говорилось в п° 46. Заметим, кстати, что автором этого закона
является отнюдь не Ньютон, который говорит о нем только «весьма
кратко». Ньютон, отрицательно относившийся к закону
сохранения движения, не мог уделять достаточно внимания и закону
виртуальных скоростей. Отцом закона виртуальных скоростей
можно считать И. Бернулли (1717), если не говорить о Галилее
и Декарте, которые вплотную подошли к нему.
[49J (к стр. 106). Камюс (Camus) — французский математик,
механик и астроном (1699—1768). Известен определением длины
секундного маятника и участием в знаменитой лапландской
экспедиции Мопертюи и Клеро для градусного измерения. Ему
принадлежат сочинения: «О живых силах движущихся тел» (Traite
sur des forces vives des corps en mouvement») (1728), «Гидрав-
ПРИМЕЧАНИЯ К ПЕРЕВОДУ
333
лика» («Traite d'Hydraulique») (1739), «Основы статической
механики» («Elements de mecanique statique») (1751). В последней книге
второй том посвящен машинам.
Книга Трабо (Trabaud) под заглавием «Принципы, касающиеся
движения и равновесия и могущие служить введением в
механику и физику» («Principes sur le mouvement.et l'equilibre, pour
servir d'introduction aux mecanique et a la physique»), вышла
в Париже в 1741 г.
[&0J (к стр. 107). Клеро (Glairaut) — французский математик
и астроном (1713—1765), в Шлет уже стааший членом Парижской
академии наук. Некоторые его работы были изданы в
Петербурге. Из трудов Клеро по механике должны быть указаны:
«Сборник статей о движении небесных тел» («Recueil de memoi-
res sur les mouvements des corps celestes», 1740), «О форме
Зэмли с рассмотрением вопроса о равновесии жидкостей» («Traite
de la figure de la terre ou il est traite de Tequilibre des fluides»,
1743) «Теория Луны, получающаяся лишь на основании принципа
притяжения» («Theorie de la lune, deduite du seul principe
^attraction», 1752 и 1765) и т. д.
Статья, о которой говорит здесь Даламбер, помещена в
журнале, Парижской академии наук «Histoire de l'Academie Royale
des Sciences» (Annee 1742, Paris, 1745, p. 1—52) и носит
заглавие «Некоторые принципы, дающие решение большого числа
задач динамики» («Sur quelques principes qui doniient la solution
d'un grand nombre de problemes de dynamique»).
[5l| (к стр. 108). Здесь Даламбер справедливо определяет
свою динамику, как динамику системы со связями. До Даламбера
динамика системы разрабатывалась лишь спорадически (Гюйгенс,
Я. Бернулли и др.) и систематической наукой была лишь
динамика точки (Ньютон, Эйлер), достигшая уже к тому времени
относительного формального совершенства. Додаламберовская
механика отличалась и по своему объекту: это была по
преимуществу небесная, а не «земная», не техническая механика.
Даламбера можно считать отцом современной динамики
системы.
[52] (к стр. 108). Остановимся на терминологии Даламбера.
В ней не так трудно разобраться, как это может показаться на
первый взгляд.
В механике XVII и XVIII столетий понятие скорости не
включало в себя направления. Поэтому естественно, что для
обозначения вектора скорости необходимо было изобрести новый
термин. Различные авторы предлагали различные термины. Даламбер
для этой цели употребляет термин «mouvement» (движение).
Заметим, что у Ньютона термином «движение» (motus)
обозначалось понятие «количества движения».
l53J (к стр. 109). В настоящем п° Даламбером формулируется
то правило, которое ныне называется «принципом Даламбера».
Как видно, этот «принцип» выглядит у его автора совсем не
так, как он излагается ныне в учебниках. Форма, близкая к со-
334
ПРИМЕЧАНИЯ К ПЕРЕВОДУ
временной, придана была принципу Даламбера Лагранжем в его
«Аналитической механике».
Даламбер дал изложение своего «принципа» и в
«Энциклопедии», в статье «Dynamique» (Динамика). Приведем здесь это
изложение буквально.
«Положим, что нескольким телам передаются какие-то
движения, которые у них не могут удержаться вследствие их
взаимодействия и которые они вынуждены заменить другими.
Известно, что всякое движение можно рассматривать как сложное
движение, состоящее из двух движений по выбору. Поэтому мы
можем первоначальное движение каждого тела рассматривать как
сложное движение, составленное из двух движений, из которых
одно мы возьмем такое, какое данное тело воспринимает
вследствие действия на него других тел. Но если бы каждое тело
получило это последнее движение вместо своего первоначального,
которое ему было передано, то все тела могли бы сохранить это .
самое движение без всяких изменений: это как раз те движения,
которые тела воспринимают сами по себе. Вследствие этого
другие составляющие движения должны быть таковы, что они
нисколько не будут нарушать первых составляющих движений.
Другими словами, вторые движения должны быть таковы, что
если бы только их сообщить всем телам и ничего больше, то
система оставалась бы в покое.
Отсюда следует, что для того, чтобы найти движение
нескольких тел, действующих друг на друга, нужно разложить
полученные телами движения, т. е. движения, с которыми тела
стремятся двигаться, на два других движения. Эти составляющие
движения должны быть подобраны таким образом, что у каждого
тела одно из этих составляющих движений должно уничтожиться,
а другое должно быть таким и так направленным, чтобы
действие окружающих тел не могло ничего в нем изменить. Отсюда
легко видеть, что все законы движения тел могут быть сведены
к законам равновесия. В самом деле, для решения любой задачи
динамики нужно только разложить движение каждого тела на
два движения. Зная одно из этих составляющих движений, мы
сможем найти другое... Указанные условия всегда дадут все
уравнения. Нет такой задачи динамики, которую нельзя
было бы решить этим приемом или, по крайней мере, привести
- ее к уравнению, — а это есть все, что можно требовать от
динамики.
Мне кажется, что данное правило в самом деле приводит все
задачи, относящиеся к движению тел, к более простой задаче, к
задаче равновесия. Кроме того, этот принцип не опирается ни на какой
вредный или неясный метафизический принцип. Он рассматривает
в движении лишь то, что в нем в действительности имеется, т. е.
пройденный путь и затраченное на это время. Он не пользуется ни
действиями, ни силами,— одним словом, никаким из тех
вторичных начал, которые, может быть, сами по себе и хороши и могут
быть иногда полезными для сокращения и облегчения решения,
ПРИМЕЧАНИЯ К ПЕРЕВОДУ
335
но которые никогда не будут началами первичными, поскольку
метафизика этих начал никогда не станет ясной».
[б4] (к стр. 110). Приводим' соответствующий отрывок из
статьи Д. Бернулли. Говоря об обращении Земли и Луны вокруг
некоторой точки, Д. Бернулли пишет:
«При этом обращении оба тела стремятся удалиться друг от
друга. Однако, это стремление уравновешивается их взаимным
тяготением. А так как Земля проявляет такое же стремление
приблизиться к Луне, какое Луна — приблизиться к Земле, то и
центробежные силы их должны быть равны. Отсюда следует,
что ту точку, вокруг'которой обращаются эти два тела, нужно
расположить таким образом, чтобы центробежные силы были
равны. Поэтому эту точку лучше называть не «центром тяжести»,
а «центром центробежных сил», или, еще лучше, «центром масс»,
поскольку скорости мы предполагаем находящимися в
постоянном отношении. Правда, оба эти названия приводят к тому же
самому и можно говорить о центре тяжести в обычном смысле.
Но спрашивается, какую идею можно связать с этим термином,
когда тяжесть в различных частях тела будет неодинакова?
В этом случае не может быть такой точки, которую можно
было бы назвать центром тяжести, какое бы определение мы ни
давали этому слову. Как бы то ни было, бесспорно то, что
расстояния рассматриваемой нами точки от центров Земли и Луны
будут обратно пропорциональны массам или количествам
материи этих тел». («О морских приливах и отливах»,— трактат,
направленный членам Королевской Академии наук на соискание премии
1740 года», «Traite stir le flux et refjux de U mer, adresse a
Messieurs de l'Academie Royale des Sciences, pour concourir au prix
de 1740». Статья эта напечатана в «Recuell des pieces qui ont
remporte les prix de l'Academie Royale des Sciences», t. IV,
Paris, 1752.)
[бб] (к стр. 123). Речь идет об учении Ньютона, изложенном
в его «Началах». Механика Ньютона это — прежде всего теория
центральных сил.
[56J (к стр. 125). В такой неуклюжей форме Даламбер
говорит о проекции скорости центра тяжести на заданную плоскость.
То же самое в общей форме Даламбер говорит и в самой
теореме III.
[б7] (к стр. 128). В указанном месте трактата о равновесии
и движении жидкостей («Traite de l'equilibre et du mouvement
des fluides») Даламбер анализирует доказательство того
положения, что если жидкость находится в равновесии, то давление
должно быть перпендикулярно к поверхности жидкости.
Доказательство, анализируемое Даламбером, основано на
предположении, что центр тяжести должен быть в наинизшем положении.
Даламбер считает данное доказательство недостаточным, между
прочим, потому, что его нельзя применять к тем случаям,
когда на частицы жидкости действует не тяжесть, а какие-либо
другие силы, неодинаковые для различных частиц. Нельзя
336
ПРИМЕЧАНИЯ К ПЕРЕВОДУ
путать, подчеркивает Дачамбер, центр тяжести и центр
масс.
Положим, все частицы жидкости aj FE (фиг. 84)
притягиваются к точке Q. Тогда в равновесии жидкость будет иметь
уровень оф — дугу круга с центром Q. Центр масс этой жидкости
не будет в наинизшем положении. В наинизшем положении он
будет тогда, когда поверхность жидкости будет горизонтальна,
но тогда не будет равновесиг Возьмем прямоугольный сосуд
F С К '£
Фиг. 84.
Фиг. 85.
ADEB (фиг. 85) и в нем круглое жидкое тело FOSPK, все части
которого притягиваются к центру Q круга. Пусть ширина
сосуда такова, что
D£-2(?C = iu. FOSPK-
Тогда центр тяжести жидкости MDEN, равной FOSPK будет
в точке (?, в то время как центр тяжести жидкости FOSPK
будет выше Q. И гак, масса жидкости FOSPK будет находиться
в равновесии, а центр тяжести ее будет выше Q. С другой
стороны, жидкость MDEN не находится в равновесии (так как
поверхность ее горизонтальная, а не сферическая с центром в Q),
а центр тяжести ее расположен ниже.
Таковы рассуждения Даламбера в указанном трактате.
х
р8] (к стр. 143). Даламбзр обозначает косинус — символом:
х'
cos [ —
а
и поскольку символы sin и cos в те времена быш еще редки в
литературе (впервые они были введены Эйлером), Даламбер в
этом месте делает следующее примечание: «Выражения cos( —
и sin
i)
обозначают косинус и синус от —. И вообще всюду
ПРИМЕЧАНИЯ К ПЕРЕВОДУ
337
в настоящем сочинении я буду обозначать синус и косинус какого-
либо угла р символами sin j* и cos fb>.
[59| (к стр. 145). Буквой с Даламбер обозначает вместе с
прочими авторами своего времени основание натуральных
логарифмов. Буква е для этого числа впервые была взедена Эйлером.
[60| (к стр. 154). Naturellement. Это значит: без всяких
внешних сил, т. е. по закону инерции.
[61| (к стр. 156). Статья И. Бернулли была напечатана в
петербургском журнале «Commentarii Academiae scientiarum impe-
rialis Petropolitanae», t. II ad annum 1727 (Petropoli, 1729) и
носила заглавие «Избранные теоремы о сохранении живых сил,
подлежащие в дальнейшем доказательству и опытной проверке»
(«Theoremataselecta pro conservatione virium vivarum demonstranda
et experimentis confirraanda»). Ср. И. Бернулли «Об истинном
значении живых сил и их применении в динамике» (Избранные
сочинения по механике. Перевод под редакцией В. П. Егоршина.
М. —Л., 1937, стр. 250 — 260). В указанной статье, относящейся
к 1735 г., Бернулли дал доказательство.
[62] (к стр. 156). Функцию ср (и) Даламбер обозначает иначе:
у него она имеет вид ср и. Символ функции был в то время
слишком новым, поэтому Даламбер и сделал здесь подстрочной
примечание.
I63] (к стр. 159). Речь идёт о трактате Германа «Общая
теория движений» («Theoria generalis motuum»), напечатанном в
петербургских «Commentarii», т. II, за 1727 г.
Герман (Hermann) — швейцарский математик (1678—1733),
ученик Я. Бернулли.
[W] (к стр. 171). «Геометрическая кривая», это— такая
кривая, точки которой можно построить при помощи циркуля и
линейки (примечание немецкого переводчика А. Корна).
[65] (к стр. 175). L'effort absolu de la pesanteur.
«Абсолютный». — значит «полный». Под усилием (L'effort)
Даламбер понимает элемент скорости dv.
[66] (к стр. 179). Статья Бернулли в петербургских
«Commentarii» называется «Теоремы о колебаниях тел, соединенных
гибкой нитью, и вертикально подвешенной цепи», «Theoremata
de oscillationibus corporum filo flexili connexorum et catenae
verticaliter suspensae» (t. VI ad annos 1732 et 1733, Petropoli, 1739,
p. 108—122).
[6?] (к стр. 179). Доказательство дано в статье
«Доказательства собственных теорем о колебаниях тел, соединенных гибкой
нитью, и о вертикально подвешенной цепи» (Demonstrationes the-
orematum suorum de oscillationibus corporum filo flexili
connexorum et catenae verticaliter suspensae»), помещенной в
петербургских «Commentarii», t. VII ad annum 1735 (Petropoli, 1740,
p. 162—173).
[68] (к стр. 179). Статья Эйлера называется «О колебаниях
гибкой нити, нагруженной произвольным количеством грузиков»
«De oscillationibus fill flexilis quotcunque pondusculis onusti» и
338 ПРИМЕЧАНИЯ К ПЕРЕВОДУ
помещена в петербургских «Commentarii», t. VIII ad annum 1736
(Petropoli, 1741, p. 30—47).
I69] (к стр. 180). Это значит, что
(где/?—величина, численно равная ускорению), откуда
L — II
р~~ 2'
/ Г3
В уравнениях (К) и (N) Даламбер вместо — подставляет ^ •
Р| (к стр. 188). Речь идет о статье Д. Бернулли «О
сочетании нескольких видов простых изохронных колебаний,
которые могут сосуществовать в одной и той же системе тел» («Sur
le melange de plusieurs especes de vibrations simples isochrones,
qui peuvent coexister dans un meme systeme de corps»),
напечатанной в журнале «Histoire de L'Academie royale des sciences
et belles-lettres»), t. X, annee 1753, Berlin, 1755, p. 173—175.
[71] (к стр. 198). Речь идет о статье Д. Бернулли, указанной
выше (см. примечание 67).
[72| (к стр. 19$). Речь идет о статье Д. Бернулли, указанной
выше (см. примечание 66).
[п\ (к стр. 202). Речь идет о статьях Даламбера
«Продолжение исследований об интегральном исчислении» (Suite des re-
cherches sur le calcul integral») и «Добавления к исследованиям
об интегральном исчислении» («Additions aus recherches sur
caleul integral»), напечатанных в журнале «Histoire de l'Academie
royale des sciences et belles-lettres», t. IV, annee 1748, Berlin,
1750, p. 249—291 и t. VI, annee 1750, Berlin, 1752, p. 361—378.
[74J (к стр. 206). Речь идет о статье Д. Бернулли, указанной
выше (см. примечание 67).
[75] (к стр. 214). Речь идет о статьях Даламбера, указанных
выше (см. примечание 73).
[76] (к стр. 215). Речь идет о статье Д. Бернулли, указанной
выше (см. примечание 70).
[тс} (к стр. 232). Полное заглавие сочинения Даламбера, о
котором идет речь: «Исследования по поводу некоторых
важнейших вопросов о системе мира» («Recherches sur differents
points importants du systeme du monde»). Первая и вторая части
этого сочинения вышли в 1754 г., третья часть — в 1756 г. в
Париже.
р] (к стр. 233). Речь идет о статье Эйлера, имеющей
заглавие «Новый и несложный метод, относящийся к весьма малым
колебаниям как твердых, так и изменяемых тел» («De minimis
oscillationibus corporum tam rigidorum quam flexililium, methodus
nova et facilis»). Статья была напечатана в журнале «Gommenta-
ПРИМЕЧАНИЯ К ПЕРЕВОДУ
839
rii Academlae scientiaruin imperialis Petropolltanae», t. VII ad
annos 1734 et 1735, 1740, p. 99—122.
p9] (к стр. 234). «Надо, однако, заметить, что при данном
движении плоскость, на которой оно происходит, по условию,
должна быть в той или иной степени шероховатой, чтобы
кривые наряду с качанием не могли сдвигаться со своего места, что
может случиться в том случае, если плоскость будет весьма
гладкая».
[80] (к стр. 251). Приводим мысли Даламбера из его статьи
«Причина в механике и в физике» («Cause en mecanique et en
physique»), помещенной в «Энциклопедии».
Пусть тело М движется со скоростью и, а другое тело т
покоится. После удара общая скорость обоих тел будет равна
Ми ~ л
АЛ (—. Эта последняя скорость и будет тем, что называется
«действием». Что же касается «причины», то причиной здесь
служит масса М, обладающая скоростью и. Но какая функция от М
и от и должна быть взята для выражения этой причины? Можно
взять Ми, Ми2, М2и и т. д. Какую бы, однако, функцию здесь мы
ни взяли в качестве выражения «причины», скорость тела т
будет зависеть и от величины т. В таком случае выходит так, что
«причина» не меняется, а «действие» меняется. Впрочем, может
быть, нам скажут, что мы взяли лишь часть «действия» и что
полное «действие» будет равно сумме количеств движения обоих
тел, т. е.
Mhi . Мши
М-\-т "" М-\-т
В таком случае, можно сказать, что это «действие» будет
пропорционально «причине» Ми. Пусть так. Но ведь это полное
«действие» состоит из двух слагаемых, т. е. из двух количеств
движения, каждое из которых необходимо знать в отдельности. Как же
мы их можем узнать с помощью указанного знаменитого
принципа, согласно которому якобы «действие пропорционально
причине»? Здесь нам пришлось бы «причину» разделить на две части,
чтобы каждому из двух действий соответствовала особая часть
причины. Как же нам найти выход из этого затруднения?
Положение о том, что «причина пропорциональна своему действию»,
не только бесполезно, но и прямо вредно. Нужно пожелать, чтобы
механики отчетливо осознали то, что в движении мы ничего не
знаем кроме одного движения, т. е. пройденного пространства
и затраченного времени. Говорить же о какой-то
метафизической, об истинной причине мы не можем, так как мы о ней ничего
не знаем.
. Может быть, спрашивает далее Даламбер, указанный принцип
пропорциональности надлежит понимать таким образом, что одно
действие так относится к другому действию, как причина первого
340
ПРИМЕЧАНИЯ К ПЕРЕВОДУ
действия относится к причине второго действия? Но туг же Да-
ламбер отвечает, что об отношении одной причины к другой
причине говорить нельзя, так как метафизические причины (как
нематериальные действия) сравнивать друг с другом не
представляется возможным.
Данная Даламбером критика принципа о пропорциональности
действия и причины справедлива и направлена против
метафизического толкования «причины» и «действия».
[31] (к стр. 256). «Corps durs». Этим именем Даламбер
обозначает неупругие, абсолютно твердые тела.
I82] (к стр. 262). Речь идет о статье И. Бернулли «О
движении соударяющихся тел». «De raotu corporum se invicem
percutentium», помещенной в журнале «Commentarii Academiae
scientiarum imperialis Petropolitanae, t. VII ad 1735, Petr.opoli,
1740, p. 15—34.
[83j (к стр. 268). Речь идет о сочинении И. Бернулли
«Рассуждение о законах передачи движения» («Discours sur les lois
de la communication du mouvement»), вошедшем в русское издание:
И. Бернулли. Избранные сочинения по механике. Перевод
под редакцией В. П. Егоршииа. ОНТИ, 1937. Указанному вопросу
посвящена у Бернулли глава XII.
[84] (к стр. 268). Речь идет о статье Буге «Решение задачи
Бернулли об ударе тела, встречающегося с несколькими
покоящимися телами, при помощи обычных методов, относящихся
к передаче движений» («Solution, par les settles regies ordinaires
de la communication des mouvements, du probleme de M.
Bernoulli, sur le choc d'un corps qui en rencontre plusieurs autres
qui sont en repos»). Статья была напечатана в журнале,
указанном в тексте.
Буге (Pouguer) — французский математик (1698—1758).
Участвовал в измерениях дуги меридиана на экваторе в Перу (1735—
1742). Ему принадлежат сочинения: «Беседы о причинах
наклонения орбит планет» («Entretiens sur la cause d'inclinaison des or-
bites des planetes», 1734), «Точная форма земли» («La Figure de
la terre determinee», 1749) и др. Главные заслуги Буге — в
области оптики.
Р] (к стр. 268). В указанном сочинении Даламбера законы
движения тел в жидкости выводятся из законов удара одного
тела о многие малые тела. Так же поступает и И. Бернулли.
[86] (к стр. 291). См. на русском языке И. Бернулли,
Избранные сочинения по механике. Перевод под'редакцией В. П. Егор-
шина, М— Л., ОНТИ, 1937. Под именем «принципа сохранения
живых сил» у Бернулли указывается лишь первое из двух положений,
о которых говорит здесь Даламбер. Между этими двумя положени-
яяя существует принципиальная разница, состоящая в том, что в
первом положении говорится о сохранении лишь живых сил, как
таковых, а во втором — о сохранении неизменной суммы живых
сил и потенциальной энергии. Другими словами, хотя Даламбер
и не мог знать о превращениях энергии, тем не менее он, как
ПРИМЕЧАНИЯ К ПЕРЕВОДУ
841
мы видим, подходит весьма близко к этому и в -математической
форме уже отобразил закон сохранения полной механической
энергии.
[87| (к стр. 295). Под эффектом силы (l'effet de la puissance)
Даламбер понимает величину, соответствующую современному
понятию работы. Как видно из дальнейшего, Даламбер этот
эффект выражает величиной
2A-AD-CA
(фиг. 72),—в чем нетрудно узнать интеграл работы. То, что Даламбер
называет «силой», соответствует теперешнему понятию ускорения.
ОГЛАВЛЕНИЕ.
От издательства 5
Предисловие автора ко второму изданию 11
Введение 15
Предварительные определения и понятия 36
ЧАСТЬ I.
Общие законы движения и равновесия тел.
ГЛАВА I.
О силе инерции и о вытекающих из нее свойствах движения. 38
О равномерном движении 43
Замечание по поводу измерения времени 44
Об ускоренном или замедленном движении 49
Замечания по поводу ускоряющих сил и сравнения их между
собою 56
ГЛАВА II.
О сложении движений 68
О криволинейном движении и о центральных силах .... 73
глава ш.
Об уничтожении или изменении движения теми или иными
препятствиями 76
О движении тела по кривой поверхности 79
О равновесии 82
ЧАСТЬ II.
Общий принцип для нахождения движения нескольких тел,
произвольным образом действующих друг на друга, а также
некоторые применения этого принципа.
глава I.
Изложение принципа .107
ОГЛАВЛЕНИЕ
343
ГЛАВА II.
Свойства общего центра тяжести нескольких тел,
выведенные на основании предыдущего принципа ПО
ГЛАВА III.
Задачи, в которых указывается, как пользоваться
вышеприведенным принципом 128
§ 1. О телах, соединенных между собою при помощи
нитей или стержней (128). § 2. О телах, качающихся на
плоскости (224). § 3. О телах, действующих друг на
друга с помощью нитей, вдоль которых они могут
свободно скользить (238). § 4. О толкающих друг друга
телах, или, иначе, о телах соударяющихся (249). О теле,
ударяющем несколько тел одновременно (265)
Об ударе упругих тел, когда соударяется несколько тел
сразу 273
ГЛАВА IV.
О принципе сохранения живых сил 290
О сохранении живых сил в телах, соединенных между собою
при помощи нитей или жестких стержней ....... 293
О сохранении живых сил в том случае, когда тела,
рассматриваемые как точки, соединены между собою при помощи
нитей 299
О сохранении живых сил, когда тела соединены между собой
при помощи жестких стержней и когда эти тела
рассматриваются как точки 303
О сохранении живых сил в случае, когда тела обладают
конечными массами и когда они соединены нитями или
жесткими стержнями 304
О сохранении живых сил в случае удара упругих тел . . . 306
О сохранении живых сил в жидкостях 310
Примечания к переводу 315
Редактор Д. В. Жарков.
Технический редактор Р. А. Негримовская.
Подписано к печати 3/1 1950 г. 21,6 печ.
л. -J-1 вклейка. 18,76 уч,-изд. л. 34 600 тип. зн.
в печ. листе. Т00201. Тираж 4000 экз. Цена
книги 11 р. 25 к. Переплет 2 р. Заказ № 956.
Отпечатано с матриц Первой Образцовой
типографии имени А. А. Жданова в 4-й
типографии им. Евг. Соколовой Главполи-
графиздата при Совете Министров СССР.
Ленинград, Измайловский пр., 29.