ОСНОВЫ
КВАНТОВОЙ
МЕХАНИКИ
Допущено Министерством высшего и среднего,
специального образования СССР в качестве
учебного пособия для университетов
ТРЕТЬЕ ИЗДАНИЕ
Государственное
издательстве
ВЫСШАЯ ШКОЛА
Москва 1961

ОГЛАВЛЕНИЕ
Предисловие '. 11
Введение 13
; Глава 1
* Основы квантовой теории
§ 1. Энергия и импульс световых квантов 15
§ 2. Опытная проверка законов сохранения энергии и импульса для световых
квантов 17
§ 3. Атомизм 21
§ 4. Теория Н. Бора 26 f
§ 5. Элементарная квантовая теория излучения 28
§ 6. Черное излучение 32
§ 7. Волны де Бройля. Групповая скорость 33 **
§ 8. Дифракция микрочастиц 37
Глава 11
Одновы квантовой механик»
§9. Статистическое толкование волн де Бройля 42
§ 10. Вероятность местоположения микрочастицы ' 44
§ 11. Принцип суперпозиции состояний 46
§ 12. Вероятность импульса микрочастицы 48
§ 13. Средние значении функций от координат и функций от импульсов ... 50
§ 14.- Статистические ансамбли квантовой механики 51
§ 15. Соотношение неопределенностей 55
§ 16. Иллюстрации к соотношению неопределенностей 60
§ 17. Роль измерительного прибора 66
Глава 111
Изображение механических величин операторами
§ 18. Линейные самосопряженные операторы 70
§ 19. Общая формула для среднего значения величины и для среднего квадра-
квадратичного отклонения 73
§ 20. Собственные значения и собственные функции операторов и .их физи-
физический смысл. «Квантование» 75
§ 21. Основные свойства собственных функций 78
5

§ 22. Общий метод вычисления вероятностей результатов измерения .... 81
§ 23. Условия возможности одновременного измерения разных механических
' величин 84
§ 24. Операторы координаты и импульса микрочастицы 85
§ 25. Оператор момента импульса микрочастицы 87
§ 26. Оператор энергии и функции Гамильтона 91
§ 27. Гамильтониан 93
Глава IV
Изменение состояния во времени
§ 28. Уравнение Шредингера . . . 96 .
§ 29. Сохранение числа частиц . . „ 100
§ 30. Стационарные состоянии 103
Глава V
Изменение во времени механических величии
§ 31. Производные операторов по времени . » . • « 105
§ /52. Уравнении движений в квантовой механике. Теоремы Эренфеста .... 107
§ 33. Интегралы движении J09
Г л а в а VI
Связь квантовой механики с классической механикой н оптикой
§ 34. Переход от квантовых уравнений к уравненннм Ньютона ....... 112
§ 35. Переход от временного уравнении Шредингера к классическому уравне-
уравнению Гамильтона—Я кобн 116
§ 36. Квантован механика и оптика 119
§ 37. Квазнклассическое приближение .' 121
Г л а в а VII
Основы теории представлений
§ 38. Различные представления состонния квантовых систем 124
§ 39. Различные представлении операторов, изображающих механические
величины. Матрицы 125
§ 40. Матрицы и действии над ними . 127
§ 41. Определение среднего значения и спектра величины, представляемой
; оператором в матричной форме J32
§ 42. Уравнение Шредингера н зависимость операторов от времени в матрич-
матричной форме 134
§ 43. Унитарные преобразования 137
§ 44. Унитарное преобразование от одного момента времени к другому ... 140
§ 45. Матрица плотности , 141
Глава VIII
Теория движении микрочастиц в поле потенциальных сил
§ 46. Вводные замечания 145
§ 47. Гармонический осциллятор 146
§ 48. Осциллятор в энергетическом представлении 151
§ 49. Движение в поле центральной силы 153
§ 50. Движение в кулоновском поле 160
§ 51. Спектр и волновые функции атома водорода 164
6

5 52. Движение электрона в одновалентных атомах 4 - 171
5 53. Токи в атомах. Магнетон 174
$ 54. Квантовые уровни двухатомной молекулы . 176
■§ 55. Движение электрона в периодическом пале 181
Глава IX
Движение заряженной микрочастицы в электромагнитном поле
§ 56. Произвольное электромагнитное поле 189
■$ 57. Движение заряженной свободной частицы в однородном магнитиом поле 193
Глава X
Собственный механический и магнитный моменты электрона (спин)
§ 58. Экспериментальные доказательства существования спина электрона 196
§ 59. Оператор спина электрона 199
§ 60. Спиновые функции . . 202
§ 61. Уравнение Паули 205
§ 62. Расщепление спектральных линий в магнитном поле 207
§ 63. Движение спина в переменном магнитном поле 211
§ 64. Свойства полного момента импульса 214
$ 65. Нумерация термов атома с учетом спина электрона. Мультиплетная
структура спектров . 217
* ^^
Глава XI
Теория возмущений
§ 66. Постановка вопроса 222
§ 67. Возмущение в отсутствии вырождения 224
§ 68. Возмущение прн наличии вырождения 228
§ 69. Расщепление уровней в случае двукратного вырождения 232
$ 70. Замечания о снятии вырождения 234
Г л а в а XII
Простейшие приложения теории возмущений
3 71. Ангармонический осциллятор 237
§ 72. Расщепление спектральных линий в электрическом поле . 239
3 73. Расщепление спектральных линий атома водорода в электрическом поле 242
§ 74. Расщепление спектральных линий в слабом магнитном поле 245
4 75. Наглядное толкование расщепления уровней в слабом магнитном поле
(векторная модель) 250
$ 76. Теория возмущений для непрерывного спектра 251
Глава XIII
Теория столкновений
$ 77. Постановка вопроса в теории столкновений микрочастиц 257
§ 78. Расчет упругого рассеяния приближенным методом .Борна 261
§ 79. Упругое рассеяние атомами быстрых заряженных микрочастиц .... 265
§ 80. Точная теория рассеяния. Фаза рассеянных волн и эффективное сечение 271
§ 81. Общий случай рассеяния 275
§ 82. Рассеяние заряженной частицы в кулоновском поле ' 279
7

х Глава XIV
Теория квантовых переходов
§ 83. Постановка вопроса 281
§ 84. Вероятности переходов под влиянием возмущения, зависящего от временв 284
§ 85. Переходы под влиянием возмущения, не зависящего от времени ..... 287
Глава XV
Излучение, поглощение и рассеяние света атомными системами
§ 86. Вводные замечания 289
§ 87. Поглощение и излучение света 291
§ 88. Коэффициенты излучения и поглощения 294
§ 89. Принцип соответствия 297
§ 90. Правила отбора для дипольного излучения „ . 300
§ 91. Интенсивности в спектре излучения 304
§ 92. Дисперсия , » , 304
§ 93. Комбинационное рассеяние 311
§ 94. Учет изменения фазы'электромагнитного поля волны внутри атома.
Квадрупольное излучение 313
§ 95. Фотоэлектрический эффект 317
-•• Г л а в а XVI
Прохождение микрочастиц через потенциальные барьеры
§ 96. Постановка проблемы и простейшие случаи 324
§ 97. Кажущаяся парадоксальность «туннельного эффекта» . , 32&
§ 98. Холодная эмиссия электронов из металла 330
§ 99. Трехмерный потенциальный барьер. Квазистационарные состояния ... 333
§ 100. Теория радиоактивного а-распада 337
§ 101. Ионизация атомов в сильных электрических полях- 341
Глава XVII
Задача многих тел
§ 102. Общие замечания о задаче многих тел 344
§ 103. Закон сохранения полного импульса системы микрочастиц 347
§ 104. Движение центра тяжести системы микрочастиц ' 349
§ 105. Закон сохранения момента импульса системы микрочастиц „ 352
§ 106. Собственные функции оператора момента импульса системы. Коэффи-
Коэффициенты Клебша—Гордона 357
^§ 107. Связь законов сохранения с симметрией пространства и среды 35&
Глава XVIII
Простейшие применения теории движения многих тел
§ 108. Учет движения ядра в атоме 364
§ 109. Система микрочастиц, совершающих малые колебания 366-
§ ПО. Движение атомов во внешнем поле 370-
§ 111. Определение энергии стационарных состояний атомов методом отклоне-
отклонения во внешнем поле 372
§ 112V Неупругие столкновения электрона с атомом. Определение энергии
стационарных состояний атомов методом столкновений 37&
§ 113. Закон сохранения энергии и особая роль времени в квантовой механике 381
8

Глава XIX
Системы из одинаковых микрочастиц
§ 114. Принцип тождественности микрочастиц 383
§ 115. Симметричные л антисимметричные состояния 387
§ 116. Частицы Бозе и частицы Ферми. Принцип Паули ". . . . 389
§ 117. Волновые функции для системы частиц Ферми и частиц Бозе 395
Г л а в а XX
Вторичное квантование и квантовая статистика
§ 118. Вторичное квантование 399
§ 119. Теория квантовых переходов и метод вторичного квантования ..... 406
§ 120. Гипотеза о столкновениях. Газ Ферми—Дирака и газ Бозе—Эйнштейна 407
Глава XXI
Многоэлектронные атомы
§ 121. Атом гелия 414
§ 122. Приближенная количественнаи теория атома гелия 421
§ 123. Обменная энергия 425
§ 124. Квантовая механика атома и периодическая система элементов Менделеева 428
Глава XXII
Образование молекул
§ 125. Молекула водорода 438
§ 126. Природа химических сил • . 447
§ 127. Межмолекулярные дисперсионные силы 450
§ 128. Роль спина ядер в двухатомных молекулах 453
Глава XXIII
Магнитные явления
§ 129. Парамагнетизм и димагнетизм атомов 455-
§ 130. Ферромагнетизм '. 457
Глава XXIV
Атомное ядро
§ 131. Ядерные силы. Изотопический спин 462'
§ 132. Систематика состояний системы нуклонов 465-
§ 133. Теория дейтона /. . 466
§ 134. Рассеяние нуклонов 468
§ 135. Поляризация при рассеянии частиц со спином 472
§ 136. Применение квантовой механики к систематике элементарных частиц 474
Глава XXV
Заключение
§ 137. Формальная схема квантовой механики 477
§ 138. Границы применимости квантовой механики . 480
§ 139. Некоторые гносеологические вопросы 483
9*

Дополнения
I. Преобразование Фурье 491
II. Собственные функции в случае вырождения '193
III. Ортогональность и нормировка собственных функций непрерывного спектрз.
б-функция 494
IV. Значение коммутативности операторов 497
V. Шаровые функции У(т F, ф) 498
VI. Уравнение Гамильтона 501
VII. Уравнение Шредиигера и уравнения движения в криволинейной Системе
координат . ......... 503
VIII. Требования к волновой функции 506
IX. Решение уравнения для осциллятора . . - . 507
X. Электрон в однородном магнитном поле 511
XI. Координаты Якоби , . . 511

ПРЕДИСЛОВИЕ
ко второму изданию
Второе издание книги «Основы квантовой механики», так же как и пер-
первое (изданное в 1944 г. под названием «Введение в квантовую механику»),
представляет собой, в основном, курс лекций по квантовой механике, читав-
читавшийся автором на протяжении ряда лет на физическом факультете Москов-
Московского государственного университета имени М. В. Ломоносова.
Естественное развитие этого курса лекций побудило меня внести во
второе издание ряд изменений и дополнений.
Существенному изменению подверглась глава, относящаяся к понятию
•состояния в квантовой механике и к дискуссии о соотношении неопределен-
неопределенностей, где внесена большая ясность. В новом издании книги рассмотрены
и подвергнуты критике идеалистические концепции квантовой теории, рас-
распространенные сейчас за рубежом. Кроме того, внесены еще дополнения,
вызванные дальнейшим развитием приложений квантовой механики за
последние годы.
В этой книге, так же как и в первом издании, я стремился дать начи-
начинающему изучать квантовую механику правильное понимание ее физических
■основ, ее математического аппарата, показать на важнейших приложениях
плодотворность этой науки.
Усовершенствованию этой книги в значительной мере способствовали
многочисленные полезные замечания, сделанные моими коллегами, за что
я им много благодарен, особенно С. И. Драбкиной, М. А. Маркову, А. А. Со-
Соколову, С. Г. Суворову и Е. А. Фейнбергу. Разработке последнего параграфа
■книги весьма содействовало обсуждение его на философском семинаре МГУ
« у теоретиков Физического института АН СССР.
Я выражаю также признательность студентам-физикам МГУ, которые
иомогли устранению опечаток и других погрешностей первого издания.
к третьему изданию
Это новое издание «.Основ квантовой механики» существенно перера-
переработано. В него внесен ряд дополнений и изменений.
Дополнения касаются главным образом теории столкновений, прило-
приложений квантовой механики к теории атомного ядра и к теории элемен-
элементарных частиц.
Развитие этих отраслей квантовой механики за последние годы, вы-
вызванное стремительным развитием ядерной физики, было настолько значи-
значительным, что вряд ли эти дополнения нуждаются в оправдании. Сделаны
11

также и некоторые методические дополнения, например, по квазиклас-
квазиклассическому приближению, по теории коэффициентов Клебша—Гордона и
многие другие, в знании которых нуждается современный физик.
Внесенные изменения касаются не только устранения очевидных арха-
архаизмов, но и уточнения различных формулировок и положений. Зтим уто-
уточнениям я обязан многим лицам, которые в разное время сообщили мне
свои критические замечания и пожелания.
Основная идея и дух книги остались теми же, которые были харак-
характерны для первых двух изданий: дать начинающему изучать квантовую
механику правильное понимание ее физических основ, ее математического
аппарата и показать на простейших примерах способы ее применения в
различных областях атомной физики (в теории твердого тела, в атомной
и молекулярной физике, в оптике, в учении о магнетизме, в теории
атомного ядра и др.).
Далее, я все.гда придавал большое значение правильной методологии:
без владения методологией даже самый отличный ум приобретает оттенок
ремесленничества.
Поэтому материалистическая методология, где явно, где менее явно
пронизывает всю книгу. *
За прошедшие годы эта книга была издана во многих странах, и для
меня является большой радостью сознавать, что она способствовала
распространению знания и интереса к современной физике среди многих
народов.
В заключение я выражаю глубокую признательность лицам, которые
помогли мне усовершенствовать эту книгу, моим коллегам и студентам.
Особенно благодарен я М. А. Маркову, который просмотрел новую ру-
рукопись и сделал ряд полезных предложений и замечаний, а также
С. И. Драбкиной, которая самым активным образом участвовала в разра-
разработке изменений и дополнений к новому изданию.
Я признателен также группе сотрудников издательства «Высшая
школа», приложившим немало труда, чтобы хорошо и быстро издать эту
книгу.
Д. И. Блохинцев

ВВЕДЕНИЕ
В последние десятилетия наука об атомных явлениях образовала не
только одну из важнейших глав современной физики, но и получила широ-
широкое применение в современной технике.
Уже самый поверхностный взгляд на замечательную область атомных
явлений обнаруживает новые черты, существенно отличные от тех, которые
свойственны макромиру.
Первое, с чем мы встречаемся в микромире, это — атомизм. Простей-
Простейшие, элементарные частицы характеризуются вполне определенными при-
признаками (зарядом, массой и пр.), тождественными для всех частиц одного
сорта.
Подобной атомистичности не существует в макромире. Макроскопиче-
Макроскопические объекты представляют собой совокупности большого числа элементар-
элементарных частиц. Закономерности макроскопических явлений — это закономер-
закономерности, свойственные совокупности большого числа частиц.
Все это показывает, что было бы методологически неправильно рассмат-
рассматривать микрочастицы по образу и подобию макроскопических тел. Даже
материальная точка классической механики есть абстрактный, идеализиро-
идеализированный образ вовсе не микрочастицы, а макроскопического тела, размеры
которого малы в сравнении с расстояниями, встречающимися в проблеме.
Атомизм микромира не ограничивается определенностью признаков
самих микрочастиц. Он выражается также в существовании некоторой абсо-
абсолютной меры для механического движения. Такой мерой является постоянная
Планка А=1,05- 1СГ27 эрг-сек.Она имеет первостепенное значение в механике
микрочастиц. Физики долгое время игнорировали закон перехода количества
в качество и стремились понять атомные явления, оставаясь в рамках
классических, макроскопических теорий. Открытие постоянной Планка было
первым серьезным предупреждением о несостоятельности механического
переноса закономерностей из области большого в область малого.
В 20-х годах нашего столетия были открыты новые опытные факты,
заставившие окончательно отказаться от этого пути. Было показано, что
электроны обнаруживают волновые свойства: если пропускать поток элек-
электронов через кристалл, то частицы распределяются на экране так же, как
распределяется интенсивность волн подходящей длины волны. Мы получаем
чуждое классической механике явление дифракции микрочастиц. Позднее
было доказано, что это явление свойственно не только электронам, но и вооб-
вообще всем микрочастицам. Таким образом была открыта принципиально новая
и совершенно общая закономерность.
Движение микрочастиц оказалось во многих отношениях более родст-
родственно движению'волн, нежели движению материальной точки по траекто-
траектории. Явление дифракции несовместимо с предположением о движении ча-
частиц по траекториям. Поэтому принципы классической механики, в которой
13

понятие траектории является одним из основных понятий, непригодны для
анализа движения микрочастиц.
Само слово «частица» в применении к индивидуумам микромира вызы-
вызывает в нашем представлении гораздо больше аналогий с материальным»
точками классической механики, нежели это отвечает действительности.
Это замечание следует иметь в виду во всех тех случаях, когда ради
краткости мы будем употреблять в книге слово «частица» вместо «микро-
«микрочастица».
Классическая механика оказывается лишь некоторым приближением,,
пригодным для рассмотрения движения тел большой массы, движущихся
' в достаточно плавно изменяющихся полях (макроскопических полях). При
этих условиях постоянная Планка не имеет значения: ее можно считать пре-
пренебрежимо малой. Становятся также несущественными и явления дифрак-
дифракции. В области малых масштабов, в области микромира, на смену класси-
классической механике приходит механика квантовая. Таким образом предметом
рассмотрения квантовой механики является движение микрочастиц.
Квантовая механика является статистической теорией. Так, с помощью
квантовой механики можно предсказать, как распределяются в среднем на
фотопластинке отраженные от кристалла электроны, но относительно места
попадания каждого отделвного электрона может быть сделано лишь вероят-
вероятностное суждение: «с такой-то вероятностью будет обнаружен там-то».
С подобным же положением дел мы встречаемся и в статистической меха-
механике. Однако между квантовой механикой и классической статистической
механикой есть глубокое различие.
В основе классической статистической механики лежит ньютоновская
механика, допускающая описание истории каждой из частиц, так что в прин-
принципе возможно дать биографию каждого отдельного экземпляра. ,
Современная квантовая механика, в противоположность статистическойг
не построена на основе какой-либо теории индивидуальных микропроцессов.
Она изучает индивидуальные свойства микрочастиц и индивидуальные ми-
микропроцессы, оперируя со статистическими совокупностями — ансамблями.
Эти статистические ансамбли определяются признаками, заимствованными
из классической макроскопической физики (например, импульс, энергия,
координата и т. д.). Поэтому, когда в квантовой механике говорят о воспро-
воспроизведении микроявления, например, о повторении одного и того же опыта,
то имеют в виду воспроизведение макроскопических условий для
микрофизического явления, т. е. осуществление того же ста-
статистического ансамбля.
Таким образом, квантовая механика изучает статистические ансамбли
микрочастиц в их отношении к макроскопическим измерительным аппаратам,
с помощью которых и может быть определено, как говорят, «состояние ча-
частиц», т. е. фиксирован статистический ансамбль.
В круге, ограниченном обрисованной постановкой вопроса, квантовая
механика является крупнейшим шагом в развитии атомной физики XX сто-
столетия, теперь уже выходящей за пределы физики, в область нового инженер-
инженерного искусства.

ГЛАВА I
ОСНОВЫ КВАНТОВОЙ ТЕОРИИ
§1. Энергия и импульс световых квантов
Развитию квантовой механики предшествовало возникновение кванто-
квантовой теории света. В конце прошлого столетия казалось, что в борьбе двух
точек зрения на природу света: корпускулярной и волновой, окончательно-
победила волновая точка зрения в той форме, которую ей придала теория
Максвелла. Опыты Г. Герца с электромагнитными волнами, доказательство-
существования давления света П. Н. Лебедевым и другие факты, добытые
искусством экспериментаторов, видимо, неопровержимым образом доказы-
доказывали справедливость максвелловской точки зрения.
Триумф электромагнитной теории света был, однако, неполным. В тег
время как все проблемы, относящиеся к распространению света, успешно
решались волновой теорией, целый ряд важных явлений, относящихся
к испусканию и поглощению света, упрямым образом не укладывался в рам-
рамки волновых представлений. Так, несмотря на все усилия теоретиков, закон
распределения энергии в спектре черного тела, выведенный на основе вол-
волновой теории, оказывался не только в резком несогласии с опытом,но и содер-
содержал внутренние противоречия.
В 1901 г. М. Планк сформулировал совпадающий" с опытом закон-
распределения энергии в спектре излучения абсолютно черного тела, нахо-
находящегося в тепловом равновесии. Этот закон явился исходным пунктом для
развития квантовой теории. В его основе лежало допущение о прерывном
характере испускания и поглощения света веществом, об испускании и по-
поглощении света конечными порциями — квантами света.
Энергия такого кванта света е пропорциональна частоте, колебаний
света со и выражается равенством:
е = Лсо. A.1>
Здесь Л= 1,05-10~27 эрг-сек есть знаменитая постоянная Планка1.
Это представление о квантах света получило законченную форму
после того, как А. Эйнштейн показал необходимость помимо энергии е
приписать кванту света еще и импульс р = е/с, направление которого-
совпадает с направлением распространения света.
Если ввести волновой вектор k, компоненты которого равны
, 2я , 2я о , 2я
kx = -j- cos a, kv = -г- cos р, kz = т cosj,
1 Под постоянной Планка h в старой литературе подразумевали обычно величину,
в 2я раз большую, т. е. 6,61 -Ю7 эрг-сек, и вместо циклической частоты ш = 2я/Г
(Т—период колебаний) употребляли частоту v=I/7\ Эту же постоянную часто обозна-
обозначают ft. *
15

где К — длина волны, a cos a, cos р и cos у — направляющие косинусы
нормали к световой волне, то формула для импульса кванта света может
быть написана в векторной форме:
p = hk. A.2)
Формулы A.1) и A.2) являются основными уравнениями квантовой
теории света и связывают энергию е и импульс р кванта света с часто-
частотой со, и длиной волны X плоской монохроматической волны, направление
распространения которой определяется вектором* k.
Глубокий смысл квантовой теории света заключается не в том, что
мы представляем себе свет как газ, состоящий из частиц с энергией
Лео и импульсом hk (такое представление полезно ввиду наглядности,
но односторонне), а в том, что обмен' энергией и импульсом между
микросистемами (электрон, атом, молекула и т. п.) и светом происходит
путем порождения одних и уничтожения других квантов света.
Эта мысль получает свое точное выражение- в применении закона
сохранения энергии и импульса к какой-нибудь системе, взаимодействую-
взаимодействующей со светом (точнее, вообще с каким-либо электромагнитным излу-
излучением). Ради наглядности вместо взаимодействия мы будем говорить
более образно: «столкновение».
Обозначим через Е и Р энергию и импульс системы до «столкнове-
«столкновения» с квантом света, а через Е' и Р' — ее энергию и импульс после
«столкновения»; далее, через Лео и hk — энергию и импульс кванта света
до «столкновения», и наконец, через Лео' и hk' — те же величины после
«столкновения».
Точный смысл слова «столкновение» здесь означает, что в резуль-
результате взаимодействия энергия и импульс электромагнитной волны часто-
частоты со и направления k уменьшились соответственно на Лео и hk (квант
света исчез), а энергия и импульс другого электромагнитного колебания
частоты со' и направления k' увеличились на Лео' и hk' (появился квант
света). Образно мы и говорим, что квант света {Лео, hk) «столкнулся»
с системой и изменил свою энергию и импульс (Лео', hk'), т. е. выра-
выражаемся, так, как если бы речь шла о столкновении классических частиц.
В принятых нами обозначениях закон сохранения энергии и импульса
выражается в виде
Лсо + £ = Лсо' + £', A.3)
hk + P^hk' + P'. A.4)
Эги уравнения охватызают все три основных процесса: поглощение,
испускание и рассеяние света.
Если со' = 0 (тогда и #' = 0), то уравнения A.3) и A.4) относятся
к поглощению кванта света Лео; если ео = 0 (fe = 0), то эти же уравнения
определяют излучение кванта Лео.
Если же со и со' отличны от нуля, то эти уравнения относятся
к рассеянию света, когда квант Лео, hk превращается в квант иной
энергии Лео' и иного импульса hk'.
Закон сохранения энергии и импульса в форме.A.3) и A.4) противо-
противоречит как волновому, так и корпускулярному представлению о свете
и вообще не может быть истолкован в рамках понятий классической
физики.
1 Формулы (I.I) и A.2) предполагается справедливыми для любгй частоты со;
они столь жа справздливы для видимого свэта, как и для у-лУчеи- Поэтому вместо
квант свата, квант у-лУчей и т. п. говорят короче—«фотон».
16

Согласно волновой теории энергия волнового поля определяется не ча-
частотой волн со, а амплитудами волн, образующих это поле. С другой стороны,
нет никакой столь общей связи между амплитудой волны и частотой колеба-
колебаний, которая позволила бы связать энергию отдельного кванта с амплитудой
волны. Представим себе, что пучок света встречает на своем пути прозрачную
пластинку. Часть света от нее отразится, часть пройдет через нее. Из волно-
волновой теории следует, что амплитуды падающей, проходящей и отраженной
волн будут различны. Если мы будем теперь каким бы то ни было образом
связывать энергию квантов е с амплитудами волн, то мы придем к заклю-
заключению, что энергия квантов в этих трех пучках различна. Но, согласно
A.1), нельзя изменить энергию кванта, не изменив частоты: часть кванта
всегда «окрашена» иначе, нежели исходный квант.
Поэтому наше предположение о том, что энергия кванта может опреде- .
ляться амплитудой, ведет к тому, что цвет падающего, отраженного и про- '
ходящего пучка должен бы оказаться различным, чего на самом деле при
прохождении через прозрачное тело, конечно, не получается.
Несостоятельно также и допущение, что квант света представляет
собой частицу, находящуюся где-то в пространстве, нечто вроде «поплавка»
на волне.
Квант света по самому определению (уравнения( 1.1) и A.2)) ассоциируется
с монохроматической плоской волной. Такая волна представляет собой чисто
периодический процесс, бесконечный как в пространстве, так и во времени.
Предположение, что квант где-то находится, противоречит совершенной
периодичности волны: синусоидальная волна, будучи как-то деформирован-
деформированной, уже не есть одна синусоидальная волна, а есть совокупность различ-
различных синусоидальных волн.
Таким образом, принимая законы сохранения A.3) и A.4), мы должны
согласиться с недостаточностью классических понятий для выражения явле-
явлений, имеющих место в атомном мире. Свет имеет двойственную природу
и обладает как волновыми, так и корпускулярными свойствами.
Современная квантовая теория электромагнитного поля позволяет
учесть оба эти аспекта, но изложение ее выходит за рамки нашей книги,
посвященной нерелятивистской механике микрочастиц.
§ 2. Опытная проверка законов сохранения энергии
и импульса для световых квантов
Как показал А. Эйнштейн, закон сохранения A.3) позволяет истолковать ■
загадочные с классической точки зрения закономерности фотоэлектрического
эффекта. Суть этого эффекта заключается в испускании металлами электро-
электронов под действием света, падающего на поверхность металла1.
Наблюдающиеся здесь закономерности исключают классическое толко-
толкование. Опыт показывает, что скорость фотоэлектронов зависит исключитель-
исключительно от частоты света со (для данного металла) и совершенно не зависит от ин-
интенсивности падающего света. Последняя определяет только число электро-
электронов, испускаемых металлом в единицу времени.
Как бы хитроумно ни была придумана модель этого явления, прираще-
приращение скорости электрона, согласно уравнению Ньютона, пропорционально
действующей силе. Последняя равна произведению заряда электрона е
на напряженность поля световой волны Е (действием магнитного поля волны
1 Закономерности фотоэффекта исследовались первоначально А. Г. Столе-
Столетовым, В. Хальваксом, А» Риги и др.
2 Д. И. Блохинцев

можно пренебречь). Таким образом, приобретаемая электроном скорость
должна быть пропорциональна Е, а энергия — пропорциональна Е2, т. е.
интенсивности света, чего на самом деле не наблюдается. А. Иоффе и Добро-
Добронравов1 показали, что и при слабых интенсивностях можно наблюдать фото-
фотоэффект, причем оказывается, что электроны излучаются металлом по зако-
законам статистики, так что только среднее число электронов Пропорционально,
интенсивности падающего пучка. Особенно важны были результаты опытов.
Р. Милликэна, строго доказавшего, что энергия испускаемых в фотоэффекте
электронов полностью определяется частотой света, но не его интенсив-
интенсивностью.
Однако этот результат становится очевидным, если применить к фото-
фотоэффекту закон сохранения энергии A.3). Допустим, что на поверхность
металла падает монохроматический свет частоты со. Так как для извлечения
электронов из металла следует затратить некоторую работу, которую-
мы обозначим через % (ее называют работой выхода электронов из металла),,
то первоначальную энергию электрона в металле следует считать равной—%•
Квант света при фотоэффекте поглощается полностью, т. е. йш' = 0. Энер-
Энергия же электрона Е после поглощения кванта света равна m0v2/2,_ где
т0 — масса электрона, а а — его скорость после вылета из металла. Следо-
Следовательно, уравнение A.3) в рассматриваемом случае принимает вид2
he -х-2?. B.1)
Это и есть известное уравнение А. Эйнштейна для фотоэффекта.
Согласно этому уравнению энергия фотоэлектрона mavs/2 линейна
возрастает с частотой света со. Если измерять энергию электрона тормо-
тормозящим потенциалом V так, что eV = mov2/2 (как это делал Милликэн),
то наклон прямой на графике (V, со) должен определяться величиной h/e.
Зная заряд е, определяя из опыта наклон, можно найти h. Милликэн
показал, что значение h получается то же, что и из теории черного-
излучения. Тем самым была доказана справедливость уравнения A.3)
•применительно к фотоэффекту.
В настоящее время уравнение Эйнштейна является одним из основ-
основных уравнений, лежащих в основе теории электронных приборов3.
Совокупность уравнений A.3) и A.4) была экспериментально обосно-
обоснована А. Комптоном, изучившим зависимость частоты рассеянных рентге-
рентгеновских лучей от угла рассеяния. В качестве веществ, рассеивающих
лучи, А. Комптон брал вещества, в которых электроны слабо связаны
с атомом (парафин, графит). Так как энергия кванта рентгеновских лучей
велика, то при расчете можно игнорировать энергию электрона в атоме
(по крайней мере, для электронов в верхних оболочках атома) и рас-
рассматривать электроны как свободные, покоящиеся частицы. Соответствен-
Соответственно этому начальную энергию электрона Е и его импульс Р будем
считать равными нулю.
После столкновения с квантом рентгеновских лучей энергия элект-
электрона может оказаться очень большой, поэтому мы применим формулы
теории относительности, учитывающие зависимость массы частицы от ее
скорости. .Согласно теории относительности кинетическая энергия эле-
1 См. П.. С. Т а р т а к о в с к и й. Кванты света. ГИЗ, 1928.
2 Уравнение A.4) в этом случае не имеет значения, так как оно просто утвер--
ждает, что импульс кванта света передается всему куску металла в целом.
3 Подробности об опытах Р. Милликэна см. Э. Ш польский. Атомная
физика. ГИТТЛ, 1951? см. также книги П. С Тартаковский. Кванты Света. ГИЗ,
1928; Р. Милликэн. Электрон. ГИЗ, 1924.
18

ктрона движущегося со скоростью v, равна
Е'м от°с8 »,/;« B.2)
/l—1,8/0» О V '
где tnt — масса покоя и с — скорость света, а импульс равен
Подставляя эти значения в A.3) и A.4) и имея в виду, что £ = 0, Р = 0,
мы получим:
[] B.4)
hk = hk' + ,щ° , Р = - • B-4')
Здесь со и k — частота и волновой вектор падающего излучения, а со'
и k' — эти же величины для рассеянного излучения.
Из первого уравнения непосредственно следует, что со > со'. Следо-
Следовательно, рассеянное излучение должно обладать большей длиной волны,
нежели падающее. Этот вывод подтверждается опытами Комптона, в то
время как по классической теории частота рассеянного света должна
равняться частоте падающего (рэлеевское рассеяние).
Из уравнений B.4) и B.4') следует один важный вывод: свободный
электрон не может поглощать, а может только рассеивать свет. Действи-
Действительно, полное поглощение означало бы, что со' = 0 (и k' = 0). Тогда
из B.4') следует, что Лиг» одинаково направлены, Поэтому B.4') можно
записать в скалярной форме:
Комбинируя это уравнение с уравнением B.4), получаем, что для погло-
поглощения
, l -I- P
/P» /P2 '
откуда (J = 0, что приводит к k — 0. Этим и доказывается невозможность
поглощения.
Рассмотренный выще фотоэффект, при котором квант поглощается
целиком, возможен лишь по той причине, что электрон связан с метал-
металлом, что выражается в необходимости затратить работу^ % для его выры-
вырывания, и дает возможность передать импульс металлу.
Для того чтобы иметь возможность проверить уравнения B.4),
Комптону предстояла задача определить из них, как зависит частота
рассеянного света со' от угла рассеяния 0. На рис. 1 линия ОА изобра-
изображает направление распространения пучка первичных рентгеновских лучей.
Направление ОС есть направление, по которому наблюдают рассеянные
электронами лучи. Построенный на рис. 1 параллелограмм представляет
импульс падающего кванта hk как сумму импульсов рассеянного кванта
hk' и импульса электрона Р. Угол 9 есть угол рассеяния, а угол а есть
угол между импульсом первичного кванта и импульсом получившего
толчок электрона, так называемого «электрона отдачи». Для нахождения
связи между углом 9 и величиной р?ссеянного кванта Лео' спроектируем
второе из уравнений B.4') на две взаимно-перпендикулярные оси ОА и
2* 19

OB. Замечая, что | k \ ■= со/с, а | k' | = со'/с, получим:
— = — cos 9 -\—- ° cos a,
ее ^ у\— Р2
п Лео' . . /now
О = —- sin 8 - г ° sin а.
с /I—Р2
Исключая из этих уравнений путем несложных алгебраических выкладок р
и угол а, получим:
2Л , . , 9
СО — СО = j- COCO Sin2 -z- *
/«„с2 2
Заменяя здесь со через 2яс/А,, со' — через 2яс/А/, легко находим изме-
изменение длины волны ДА, = sin2-^- •
Эта формула была впервые получена А. Комптоном. Меняя угол, под кото-
которым наблюдалось рассеянное излучение, и измеряя изменение длины волны
при опыте ДА,, Комптон и. By сравнили результаты своих измерений с пред-
предсказаниями теории по формуле B.5) и полу-
получили полное согласие с теорией1.
Поэтому опыты Комптона показывают
полную справедливость предположения о
существовании импульса у кванта света,
величина которого определяется форму-
Л лой A.2). ■
Заметим, что снимки, полученные в ка-
камере Вильсона, позволяют в некоторых слу-
случаях установить направление вылета рас-
рассеянного при комптон-эффекте кванта, а
также путь и энергию электрона отдачи и
тем самым позволяют как бы воочию видеть
сложение импульса электрона и кванта све-
п , г-, v та, приведенное нами2 на рис. 1.
Рис. I. Параллелограмм Комптона встречающаяся в формуле B.5) длина
Л= hlmac = 3,9-10 п см носит название
комптоновской длины. Эта длина имеет фундаментальное значение в ре-
релятивистской теории электрона, являясь одним из масштабов, свойствен-
свойственных микромиру. Зная ДА, B. 5), можно определить h, так что эффект
Комптона дает еще один метод нахождения h.
Явления, в которых постоянная h играет существенную роль, называ-
называются квантовыми. Каждое из них может служить для определения постоян-
постоянной h.
Как и следует ожидать, квантовое явление не может быть истолковано
классически. Согласно классической теории, предполагающей непрерывность
обмена энергией между полем и микросистемами, h = 0, и никакого смеще-
смещения частоты при рассеянии света на свободном электроне не должно полу-
получиться [ДА. пропорционально h, см. B.5)]. Прямой расчет по классической
■ теории приводит именно к такому результату. Под действием переменного
поля частоты со электрон совершает вынужденное колебание той же часто-
частоты. Таким образом возникают колебания заряда е с частотой со. Подобные
1 Подробности об опытах см. в книге П«С, Тартаковский, цит. соч.
8 Там же-
20

колебания порождают переменное поле той же частоты (в силу линейности
уравнений поля); следовательно, рассеянное излучение имеет ту же частоту,
что и падающее.
§ 3. Атомизм
В микромире мы встречаемся с рядом простейших, как принято говорить,
элементарных частиц. В последние годы, благодаря изучению космических
лучей и в результате экспериментов с искусственными быстрыми чзстицами,
получаемыми на ускорителях, список элементарных частиц значительно
расширился. В таблице приведены основные характеристики этих частиц1.
Масса, заряд и другие свойства всех экземпляров элементарных частиц
Таблица элементарных частиц
Название
фотон
нейтрино
электрон
ц-мезон
я-мезоны
К-мезоны
нуклоны
Л — гиперон
2—гиперон
каскадный
гиперон
В этой
тильды (~-).
Символ
Y
v(v)
МЙ
я+
я°
я"
к- (k-)
Р(Р)
п(п)
Ло (Л„)
2*
2»
2" (Z-)
з-
а°
га блице
£- откры
Масса
т
0
0
I
206,7
273,3
264,3
272,8
966
-961
1836,1
1836,6
2181
2327
2340
2340
2585
2585
приведены
т в Дубне
Заряд
е
0
0
— I
— I
+ 1
0
— I
— 1
0
+1
0
0
+1
0
—I
—I
0
тольк
Спин
а
I
1/2
1/2
1/2
0
0
0
0
0
1/2
1/2
1/2
1/2
1/2
1/2
1/2
1/2
э част
Изотопи-
Изотопический спин
Т
—
—
—
—
I
I
I
1/2
1/2
1/2
1/2
0
1
I
Г
1/2
1/2
ицы, а
т3
—
—
—
—
+1
0
— I
1/2
-1/2
1/2
-1/2
0
1
0
—I
-1/2
-1/2
античас
Стран-
Странность
S
—
—
—
—
—
I
I
0
0
— I
— 1
— 1
— I
—2
—2
гицы сбс
Время жизни
оо
оо
оо
2,22- 10"в сек\
2,56-10-в сек
-МО1 сек
'J2,56- Ю-» сек,
— Ю"8 сек
— Ю0 сек
оо
1,04-Ю3 се
2,77-Ю-" се |
0,78-10-" сек
<100 сек
1,58 АЪ-^сек
— Ю0 сек
значены знаком
1 Как видно из таблицы среди характеристик микрочастиц есть специфические
(спнн-ст, изотонический спин — Г, странность — S), не свойственные макрочастицам.
Подробнее об этих характеристиках будет сказано в §§ 58, 59, 131, 136. О новых части-
частицах см. книгу М. А. Маркова «Гипероны и К-мезоны», Физматгиз, 1958.
21

одного рода совершенно тождественны и неизменны. Единственные изме-
изменения элементарных частиц, которые с достоверностью известны в современ-
современной физике, заключаются в превращении одного сорта частиц в другой.
При этом частицы либо уничтожаются, либо возникают, как целое.
Это не означает, что «элементарные» частицы не имеют структуры1.
Это означает лишь то, что в очень широком круге явлений элементарные
частицы можно рассматривать как бесструктурные объекты, имеющие неко-
некоторые глобальные характеристики (массу, заряд, спин и т. д.).
В нашем курсе, посвященном нерелятивистской квантовой механике,
мы будем иметь дело лишь с такими процессами, при которых изменение
энергии частиц много меньше их собственной энергии покоя Ео = тас2.
Процессы, при которых происходят превращения элементарных частиц,
выходят за рамки нерелятивистской механики2.
Существованием элементарных частиц не исчерпывается атомизм,
свойственный микромиру и составляющий его важнейшую отличительную
черту. Сложные частицы, образованные из элементарных частиц (например,
молекулы, атомы, ядра атомов), также обладают атомистическими свой-
свойствами.
Эти атомистические свойства'обусловлены двумя обстоятельствами. Во-
первых, каждый сорт сложных частиц образуется из вполне определенных
элементарных частиц (например, атом водорода образуется из одного про-
протона и одного электрона; ядро урана 238 из 92 протонов и 146 нейтронов
и т. д.). Во-вторых, внутренние состояния сложных частиц прерывны:
для каждой сложной частицы существует своя последовательность вполне
определенных возможных состояний, каждое^из которых отделено от другого
скачкообразными изменениями. Благодаря этому далеко не всякое воздей-
воздействие может перевести сложную систему, например, из состояния с наи-
наименьшей энергией, так называемого нормального состояния, в соседнее —
«возбужденное».
Если энергия внешнего воздействия недостаточна для того, чтобы выз-
вызвать переход системы из нормального состояния в возбужденное, то по пре-
прекращении внешнего воздействия система окажется в том же состоянии, в ка-
-ком она была до применения этого воздействия (в «нормальном» состоянии).
В силу этого атомные системы, подвергаясь какому-либо внешнему воздей-
воздействию, остаются в широких пределах такими же, какими они были до воз-
воздействия, или переходят в новые, вполне определенные состояния. Именно
такая скачкообразность в изменении состояния сложных атомных систем
была той физической (правда, в явном виде неизвестной) причиной, которая
приводила химиков к представлению о неделимости атомов, а физикам позво-
позволяла рассматривать атомы в кинетической теории как неизменные материаль-
материальные точки. Эти неизменность и неделимость соблюдаются лишь до той поры,
пока внешние воздействия не достигнут той степени интенсивности, при кото-
которой' окажутся возможными переходы сложной частицы в соседние состояния.
Благодаря тождественности признаков элементарных частиц и прерыв-
прерывности состояний сложных, частицы микромира не имеют индивидуального
«лица». На характерных признаках электрона или атома водорода не отра-
отражаются происходившие с ними события.
В отличие от этого на макроскопической системе обычно в той или иной
мере запечатлена ее история с тем большей полнотой, чем сложней система.
1 Так, например, сейчас доказано наличие структуры у протона и нейтрона (см.
обзор, Д. Блохинцеа, Б. Барбашоа, В. Барашенкоа, Усп. Физ.
Наук, т. XVIII, стр. 417, 1959).
2 Фотоны н нейтрино имеют массу покоя /no= 0. Поэтому они при асех энергиях
являются релятивистскими частицами и не могут изучаться методами нерелятивистской
квантоаой механики. Подробнее о границах каантоаой механики см. § 128.
22

Прерывность состояний, свойственная микросистемам, доказывается
опытным путем. Франк и Герц пропускали поток электронов, т. е, электри-
электрический ток, через пары ртути. Оказалось, что протекающий ток в зависимо-
зависимости от энергии электронов, имеет максимумы и минимумы, изображенные
на рис. 2.
Первоначально, пока энергия электронов не превосходит 4,9 эв, пучок
электронов проходит через пары ртути, не теряя энергии (на самом деле при
столкновении электрона с атомом ртути, как с целым, происходит некоторый
обмен энергией; однако ввиду того, что масса атома ртути во много раз пре-
превышает массу электрона и удар происходит упруго, этим обменом энергий
можно пренебречь), и поэтому ток растет с ростом напряжения. Но как толь-
только достигается энергия в 4,9 эв, ток падает благодаря тому, что электроны
начинают терять энергию при столкновении с атомами ртути, изменяя их
внутреннее состояние.
Этим и доказывается прерывность возможных значений внутренней
энергии атома ртути: энергия состояния атома ртути, ближайшего к нор-
нормальному, превышает его энергию на
4,9 эв1.
Штерну и. Герлаху удалось по-
показать, что и вращательный импульс
(момент количества движения) атомов
имеет подобно энергии также только
некоторые дискретные значения.
Штерн и Герлах измеряли магнит-
магнитный момент атомов. Этот магнитный
момент обусловлен внутриатомными
токами, и так как последние вызыва-
вызываются движением электронов, то между
магнитным моментом атома и враща-
вращательным импульсом существует связь,
которая будет нами рассмотрена ⧧ 52
и 63. Сущность опытов Штерна и Гер-
лаха заключалась в том, что они про-
пропускали узкий пучок атомов в неодно-
неоднородном магнитном поле. Если атом
имеет магнитный момент $щ, то в магнитном поле напряженности
он получит потенциальную энергию, равную
Рис. 2. Результаты опыта Франка и
Герца
Н
где а — угол между направлением магнитного поля и направлением
магнитного момента атома. Сила, действующая на атом со стороны
неоднородного поля (если оно меняется по направлению оси 0Z), равна
/^-^Sm^cosa.
Градиент поля был направлен перпендикулярно к пучку атомов, и сле-
следовательно, сила F вызывала отклонения атомов от первоначального
направления движения. Если бы были возможны все ориентации магнит-
магнитного момента атома (т. е. любые а), как это следует из классических
•STJ
представлений, то сила F принимала бы все значения от — Щ-s- до
t-ar • Различные атомы отклонялись кбы различно, и при попадании
1 Подробности об опытах Франка и Герца см. Э. В. Ш п о л ь с к и й, цит. соч.
23

пучка на экран мы получили бы размытое изображение щели, ограничи-
ограничивающей пучок. На самом деле получается два резких изображения щели
(рис. 3). Этот результат опыта показывает, что возможны лишь две
дискретные ориентации магнитного момента атома: cos<z=± 1.
Далее, вычисление показывает, что величина отклонения пучков
соответствует значению магнитного момента атома $Щ, равному
8»в = ^- = 9-1(Г21 CGSE,
где е — заряд электрона, |х — его масса, с — скорость света. Это значение
было впервые теоретически найдено Н. Бором из элементарной квантовой
теории и называется магнетоном Бора. Оно является как бы
квантом магнитного момента.
Явление, открытое Штерном и Герлахом, называют пространст-
пространственным квантованием, так как речь идет о дискретности ориен-
ориентации магнитного момента относительно маг-
магнитного поля. На основании упомянутой связи
между вращательным импульсом и магнитным
моментом можно сказать, что опыты Штерна
"и Герлаха доказывают также прерывность воз-
возможных значений вращательного импульса.
Впоследствии мы покажем (гл. X), что наб-
наблюдавшийся Штерном и Герлахом магнитный мо-
момент атома обусловлен не орбитальным движением
электрона (как это первоначально думали), а соб-
собственным магнитным моментом, присущим самому
электрону1.
С интересующей нас сейчас общей точки зре-
зрения мы можем сказать, что опыты Штерна и Гер-
Герлаха показывают, что магнитный момент атома в
целом имеет квантовые, дискретные значения,
и таким образом приносят новое доказательство
прерывности, свойственной возможным состояни-
состояниям атома2.
Мы хотели бы еще обратить внимание читате-
читателя на тот факт, что дискретность атомных состоя-
состояний оказывается также существенной совсем в
другом круге явлений. Согласно очень общим
принципам классической статистической меха-
механики средняя энергия, приходящаяся на одну степень свободы системы,
находящейся в равновесии при температуре Т, равна \ kT, где k —
■ — 1,38- 10~1в эрг/град, есть постоянная Больцмана. На этом
основании, например, одноатомные газы имеют среднюю энергию на один
атом | kT и теплоемкость § k. Этот вывод теории хорошо подтверждается
опытом. Однако он содержит неявное предположение, что атом представляет
собой нечто вроде материальной точки, имеющей три степени свободы
(соответственно трем координатам центра тяжести). Между тем хорошо
известно, что, например, атом Не состоит из трех частиц: ядра и двух элек-
электронов. Мы предполагаем, что эти электроны не способны отдавать или полу-
Рис. 3. .Расщепление пучка
паров натрия в магнитном
поле:
а — в отсутствие поля; 6 — в
присутствии поля
1 Это относится к первым опытам Штерна и Герлаха с Н и Ag в нормальных состо-
состояниях. В общем случае магнитный момент атома обусловлен как орбитальным движе-
движением электронов, так и собственным магнитным моментом этих электронов.
2 Подробности об опытах Штерна и Герлаха см. в книге Э. В. Ш п о л ь с к и й>
ЦИТ. СОЧ.
24

чать энергию и поэтому не участвуют в установлении теплоюго равновесия
в газе. Это предположение не может быть обосновано классической механи-
механикой, так как согласно классической механике, если существует устойчивое
движение с энергией Е, то существует и движение с энергией, мало отличаю-
отличающейся от Е, а это означает, что электроны атомов должны принимать и отда-
отдавать энергию при столкновениях атомов, т. е. должны участвовать в установ-
установлении равновесного распределения энергии. Напротив, с точки зрения кван-
квантовой теории, атом в широких границах действительно может рассматри-
рассматриваться как объект, обладающий только тремя степенями свободы. Согласно
квантовой теории необходима конечная энергия АЕ, чтобы перевести атом
из его нормального состояния в соседнее, возбужденное. Поэтому, если
АЕ^кТ то при столкновениях атомов электроны не будут возбуждаться,
10
А
1
/
\
Л
I
L
К
*****
1,0
1Л
2,2
2,6
Рис. 4. Резонансы во взаимодействии нейтронов с ядром кислорода О8.
По оси ординат отложено сечение взаимодействия в барнах A0~2* см2), по
оси абсцисс — энергия нейтрона в Мэв
и атомы будут вести себя как «твердые» материальные точки. Внутренние
степени свободы будут «заморожены».
Со времени описанных опытов число экспериментальных доказательств
прерывности состояний атомных систем выросло в необозримой степени.
Особенно много новых фактов принесло изучение атомного ядра. Было
показано, что атомные ядра также обладают дискретной системой уровней.
На рис. 4 приведена кривая для сечений взаимодействия нейтронов с ядром
кислорода, в функции энергии нейтронов. Эта кривая имеет острые резонанс-
резонансные пики при определенных энергиях, указывающие на существование
дискретных энергетических уровней в ядре1.
В настоящее время известны резонансные явления и в элементарных
частицах, это резонансы в рассеянии я-мезонов на нуклонах и резонансы
в рассеянии у-лучей на нуклонах2 (см. рис. 5K.
Гипероны распадаются с испусканием я-мезонов или \-квант и превра-
превращаются в результате этих распадов в нуклон. Поэтому гипероны можна
рассматривать как определенные возбужденные, дискретные состояния
нуклонов.
1 См. А. С. Д а в ы д о в. Теория атомного ядра. Физматгиз, 1958.
2 См. обзор, В. П. Джелепов, Б. М. Понтекорво, Успехи Физ~
Наук, т. XIV, стр. 15, 1958.
3 Рис. 5 взят из отчета CERN A958 г.), т. I, стр. 65.
25.

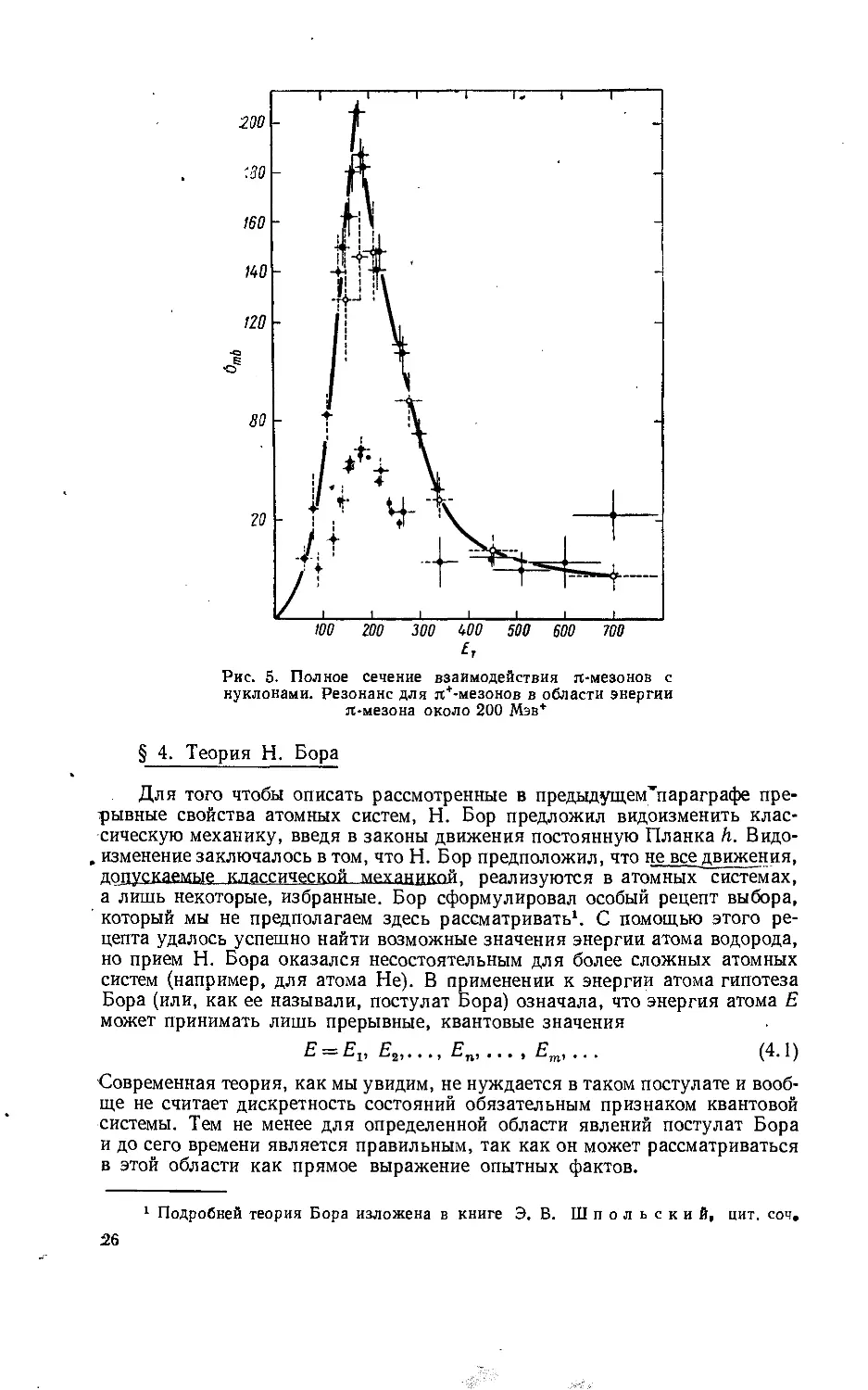
100 ZOO 300 WO 500 600 700
Рис. 5. Полное сечение взаимодействия я-мезонов с
нуклонами. Резонанс для я*-мезонов в области энергии
я-мезона около 200 Мэв*
§ 4. Теория Н. Бора
Для того чтобы описать рассмотренные в предыдущем'параграфе пре-
прерывные свойства атомных систем, Н. Бор предложил видоизменить клас-
классическую механику, введя в законы движения постоянную Планка h. Видо-
. изменение заключалось в том, что Н. Бор предположил, что не все движения,
допускаемые классической ме.хяцикой, реализуются в атомных системах,
а лишь некоторые, избранные. Бор сформулировал особый рецепт выбора,
который мы не предполагаем здесь рассматривать1. С помощью этого ре-
рецепта удалось успешно найти возможные значения энергии атома водорода,
но прием Н. Бора оказался несостоятельным для более сложных атомных
систем (например, для атома Не). В применении к энергии атома гипотеза
Бора (или, как ее называли, постулат Бора) означала, что энергия атома Е
может принимать лишь прерывные, квантовые значения
E = EV Е„...,Еп,...,Ет,... D.1)
Современная теория, как мы увидим, не нуждается в таком постулате и вооб-
вообще не считает дискретность состояний обязательным признаком квантовой
системы. Тем не менее для определенной области явлений постулат Бора
и до сего времени является правильным, так как он может рассматриваться
в этой области как прямое выражение опытных фактов.
1 Подробней теория Бора изложена в книге Э. В. Ш п о л ь с к и й, цит. соч.

Постулат Бора противоречит классической теории излучения, так как
по этой теории возбужденный атом излучает непрерывно, и следова-
следовательно, его энергия может оказаться лежащей между дозволенными
уровнями энергии. Поэтому Бор принял квантовую точку зрения
.(§ 1), согласно которой энергия излучается порциями — квантами света.
Тогда, объединяя закон сохранения энергии с постулатом Бора о дискрет-
дискретности состояний атомов, мы получим написанный впервые Бором закон,
■связывающий частоты ытп, которые может испускать и поглощать атом
{спектр атома), с квантовыми уровнями Еп, свойственными данному
атому, т. е.1
fmmn = Em-En. D.2)
Это уравнение есть не что иное, как закон сохранения энергии при излу-
излучении и поглощении света, и в старой теории Бора представлял один
из постулатов его теории («правило частот» Бора). Разделив урав-
уравнение D.2) на постоянную Планка, мы найдем, что частоты, поглощае-
поглощаемые или излучаемые квантовыми системами, всегда могут быть представ-
представлены в виде разности двух частот:
Ч»„ = О>т-Шп, »т=^. *>п = ^. D.3)
Эти последние называются спектральными термами.
Еще задолго до теории Бора чисто эмпирически было установлено
Ритцем, что наблюдаемые частоты атомов могут быть представлены как
разности термов («комбинационный принцип» Ритца). Поэтому
D.3) можно рассматривать так же, как выражение эмпирического правила
Ритца.
В комбинационном принципе Ритца мы встречаемся с одним фунда-
фундаментальным противоречием между классической теорией и опытом. Если
электрон находится в атоме, то он совершает периодическое или квази-
квазипериодическое движение. В простейшем случае одномерного движения
его координата x(t) может быть разложена в ряд Фурье:
*(')= 2* *n.e*V, D.4)
п=—оо
где ып — пщ, а щ есть частота основного тона, мп есть частота (п— 1)-ого
обертона. Интенсивность /п излучения частоты шп определяется ампли-
тудой (п— 1)-ого обе_ЕШща, т. е. величиной хп (см. § 85). Частоты, сог-
согласно классической теории, могут быть расположены в строку
® = щ, ш2, ..., шп,"... D.5)
Так же могут быть расположены и соответствующие им интенсив-
интенсивности /п или амплитуды х*п. Это очень общее следствие классической
теории противоречит эмпирическому принципу Ритца, так как, согласно
этому принципу, наблюдаемые на опыте частоты всегда определяются
двумя числами пат (номера термовJ, так что в строку располагаются
1 Для поглощения полагаем в A-3): со' = 0, £' = £т, Е = Еп<^ Ет, co = comn, для
излучения: а>'=а>тп, Е' — Еп, Е = Ет, со = 0.
2 Если система обладает f степенями свободы, то она может иметь / основных
тонов <ва (а =1, 2, ...,/), и тогда общее выражение частоты <вп> по классической
теории, будет:
27

не частоты, а термы (шп = £п/Л), частоты же располагаются в квадрат-
квадратную таблицу («матрицу»):
(Л —
О ш12 щ.
О со,, .. . щ„ .. .
........... D-6>
В подобную же таблицу можно расположить соответствующие интенсив-
интенсивности 1тп (или амплитуду колебаний хтп).
Это противоречие можно было бы преодолеть, если предположить,
что каждая из частот штп является одним из основных тонов и соответ-
соответствует своей особой степени свободы. Атом сопоставлялся бы таким
образом роялю, каждая степень свободы — клавише. Но тогда мы должны
были бы допустить существование огромного, в сущности, неограничен-
неограниченного числа степеней свободы и тем самым еще более углубили бы про-
противоречия между предсказаниями классической механики в отношении
теплоемкости атомов и фактами.
В заключение отметим еще то обстоятельство, что теория Бора, хотя
и позволяет, по крайней мере, в простейшем случае атома водорода, опре-
определить частоты comn, т. е. спектр этого атома, но она ничего не говорит об
интенсивностях излучения 1тп этих частот и соответствующих им коэффи-
коэффициентах поглощения. Вычисление этих интенсивностей представляло для тео-
теории Бора непреодолимую и принципиальную трудность. Были возможны
лишь качественные суждения. Расчет по теории Бора атомов более сложных,
чем атом водорода, также привел к принципиальным трудностям. Эти труд-
трудности были преодолены квантовой механикой1.
В 1927 г. В. Гейзенберг предложил все величины, характеризующие
внутриатомные движения, считать матрицами (подобными матрице D.6)).
С этой новой точки зрения координата электрона и его импульс должны
изображаться матрицами хтп и ртп. На этом пути В. Гейзенберг нашел зна-
знаменитое «соотношение неопределенностей» и получил правильные значения
для термов простейших квантовых систем. Его механика называлась «мат-
«матричной» и вскоре слилась с другим, «волновым», направлением, развивав-
развивавшемся де Бройлем и Е. Шредингером.
§ 5. Элементарная квантовая теория излучения
Элементарная теория излучения на основе квантовых представлений
была создана Эйнштейном. Она имеет до некоторой степени феноменологичес-
феноменологический характер2. Тем не менее, она позволяет, опираясь на современную кван-
квантовую механику, решить вопрос об интенсивностях излучения и поглощения
света.
где па—целые числа. Наличие нескольких основных типов не меняет сущности нашего
утверждения о противоречии между классической теорией и принпипсм Ритиа, так как
в этом случае каждый терм- a>n = En/h будет характеризоваться группой чисел
(«1, «г, • • •. "/), а излучаемые частоты опять-таки двумя группами чисел: nlt пг,..., nj)
и (mi, от2, ..., trij).
1 По поводу этих трудностей см. сборник «Основание новой квантовой механики»
пбд ред. А. Ф. Иоффе, Госиздат, 1927.
4 Предположения Эйнштейна получают полное обоснование в современной кван-
квантовой электродинамике. См. В. Г е й т л е р, Квантовая теория излучения, ГИТТЛ,
1940 или А. Ахиезер и В. Берестецкий, Квантовая электродинамика,
Физматгиз, 1959.
28

С квантовой точки зрения интенсивность испускания или поглощения
электромагнитного излучения определяется вероятностью перехода атома
из одного состояния в другое. Решение вопроса об интенсивностях сводится
к вычислению этих вероятностей.
Рассмотрим два состояния какой-нибудь системы, например атома.
Одно обозначим буквой т, а другое буквой п. Энергия первого состояния
пусть будетЕт, а второго Еп. Для определенности предположим, что Ет>Еп,
так что состояние т принадлежит более высокому квантовому уровню
Ет, нежели состояние п, принадлежащее квантовому уровню Еп.
Опыт показывает, что система может сама собой перейти из высшего
состояния т в низшее п, испуская квант света Лш = Ет—Еп с частотой
ш =—т ~ ", имеющий, кроме того, определенную поляризацию и распро-
распространяющийся внутри телесного угла d Q (рис. 6). Любую поляризацию для
определенного направления распространения света мы можем представить
как сложение двух независимых поляризаций /х
и 12, перпендикулярных друг к другу. При перехо-
переходе Ет-^Еп может быть излучен квант света либо
с поляризацией llt либо с поляризацией /2. Поляри-
Поляризацию мы будем отмечать индексом а (а = 1,2). Ве-
Вероятность перехода т —+ п в \ сек, с излучением
£ £
кванта частоты со =—т ч внутри телесного уг-
угла dQ с поляризацией а, мы обозначим через
dW'r-a^dQ. E.1)
Эту вероятность называют вероятностью «спонтан- Рис- 6- Характеристики
J Г \ d излучения
ного» (самопроизвольного) перехода. Возможности н вленне' распростраие.
ТаКОГО Перехода В КЛасСИЧеСКОИ Теории СООТВеТСТВу- иия (угол <W), частота ш, два
ет излучение возбужденного осциллятора. незаполяризХацииаРиВ?2ения
Если имеется излучение, окружающее атом,
то оно оказывает воздействие на атом в двух отно-
отношениях. Во-первых, это излучение может поглощаться, причем атом будет
переходить из низшего состояния п в высшее т. Вероятность такого пере-
перехода в 1 сек обозначим через dWa. Во-вторых, если атом находится в воз-
возбужденном состоянии т, то внешнее излучение может способствовать
переходу атома в низшее состояние п так, что вероятность излучения
увеличится на некоторую величину dW'r. Эту добавочную вероятность мы
будем называть вероятностью индуцированного (или вынуж-
вынужденного) перехода1. Оба типа переходов имеют аналогию в класси-
классической теории: осциллятор, находящийся под влиянием внешнего излуче-
излучения, может как поглощать, так и излучать энергию в зависимости от
соотношения фазы его колебаний и фазы световой волны.
Согласно сказанному полная вероятность излучения равна
Вероятность поглощения d Wa и вероятность вынужденного излучения
■dWr по предположению Эйнштейна, пропорциональны числу квантов света
как раз того сорта, о поглощении и излучении которых идет речь. Опреде-
Определим это число.
Излучение может быть, вообще говоря, не монохроматическим, иметь
различное направление распространения и разную поляризацию. Для опре-
1 На использование индуцированного излучения основаны молекулярные усили-
усилители («Мазоры»).
29

деления характера излучения мы введем величину Qa(^, Q)d(adQ, дающую
плотность энергии излучения, имеющего направление распространения
в пределах телесного угла dQ, поляризацию а и частоту, лежащую
в пределах ш, co + dco. Так как энергия кванта равна /ко, то число квантов
света, частота которого лежит в пределах ш, co + dco, которые распрост-
распространяются в телесном углу dQ и имеют поляризацию а, равно (на 1 см3):
Qa (co0fi) da dQ
ha>
На основании замечания о пропорциональности между числом квантов-
и вероятностями поглощения и вынужденного излучения мы можем
положить:
<Ц, = й"оа(ю, Q)dQ, E.2)
« = Се«(м,^)^ E.3)
Величины а^а, b™a, b^a мы назовем диф^ференц'и'ал ь"н[ыми коэф-
коэффициентами Эйнштейна. Они зависят только от рода систем,
излучающих и поглощающих свет., и могут быть вычислены методами
квантовой механики (см. § 88). Однако можно сделать некоторые общие
заключения о свойствах этих коэффициентов без их вычисления.
Рассмотрим условия, при которых осуществляется равновесие между
излучением и поглощением. Пусть число атомов, находящихся в воз
бужденном состоянии т, есть пт, а число атомов, находящихся в низшем.'
состоянии, пусть равно п„. Тогда число квантов света, излучаемых,
в 1 сек при переходах т—*п, будет равно
а число поглощаемых в 1 сек квантов при переходах п—*т, будег
равно
пп dwa.
В условиях равновесия число актов поглощения должно равняться числу
актов" испускания, т. е.
пп dwa = nm {dw'r + dw").
* Подставляя сюда dw'r из E.1) и dw", dwa из E.2) и E.3), найдем после
сокращения на dQ:
«A™ Qa («>№) = «m tCa C« К Q) + <„] E.4>
(причем co = comn).
Допустим, что мы имеем дело с тепловым равновесием. Тогда числа
атомов в различных состояниях будут функциями температуры Т.
Вместе с тем и плотность излучения q(co, Q) должна быть функцией
температуры. Это будет плотность излучения, находящегося в равновесии'
с веществом при температуре Т, т. е. плотность черного излучения.
Свойства черного излучения, как известно, не зависят от конкретных
свойств вещества, с которым оно находится в равновесии. Поэтому все
выводы, которые будут сделаны на пути исследования черного излуче-
излучения, имеют общее значение. Именно этим обстоятельством и восполь-
воспользовался Эйнштейн, чтобы установить соотношения между коэффициента-
коэффициентами ama- С' С В 0бЩШ ВИДе-
Отношение между числами атомов, находящихся в различных состоя-
состояниях, мы можем определить из статистики. Обычно (см., например, §50).
30

какому-нибудь квантовому уровню Еп отвечает несколько' различны»
состояний квантовой системы. Число таких состояний /„ называют
статистическим весом или степенью вырождения.
Согласно каноническому распределению, справедливому как для клас-
классических, так и для квантовых систем, число атомов Nn, находящихся
в состоянии, принадлежащих энергии Еп, будет равно
-Ел
JVn = const. /ne «\ E.5).
где k — постоянная Больцмана. Если нас интересует число атомов,
находящихся в каком-либо одном из состояний, принадлежащих энер-
энергии Еп, то на основании того же распределения будем иметь:
: hT. E.5'),
in
Подставляя пп и пт из E.5') в E.4) и сокращая на общую постоянную,.
получим:
_ _En_ Em
причем мы ввели в q в качестве аргумента еще и температуру, так как
при тепловом равновесии, как уже указывалось, плотность равновесного
излучения зависит от температуры. При Т—> оо плотность излучения $■
должна неограниченно возрастать, т. е. q—* оо.
Из E.6) при Т —> оо получаем первое важное соотношение:
bm =6" . CS 7\,
па та \°-' )'
На основании этого соотношения, замечая еще, что Em— En — hat,
мы получаем из E.6):
еа(ш, Q, 7) = ^-.-^ E.8),
"та ^у
Чтобы определить отношение —^-, Эйнштейн остроумно воспользовался-
тем обстоятельством, что при высоких температурах, т. е. при' kT > /гш,
полученная квантовая формула E.8) для плотности равновесного излуче-
излучения должна переходить в классическую формулу Рэлея — Джинса. В самом
деле, классическая формула для плотности равновесного излучения
выводится в предположении, что излучение частоты ш может иметь сколь
угодно малую энергию. По квантовой же теории наименьшая энергия'
такого излучения есть Лш. Если kT > Лш, то величиной /гш можно пре-
пренебречь, и тогда основная предпосылка классической теории будет.
, ha
выполнена. Из E.8) при ~г=- < 1, разлагая в ряд еЙТ , получаем:
/,* о т\ "mo kT ,_ п.
Qa{to, ", 1 ) = —п~~'~п— • E-9у
"та
С другой стороны, классическая формула Рэлея—Джинса дает для
плотности равновесного излучения следующее выражение:
(ш п T)r=—^—kT E 10V
Как мы пояснили, для feT >/гш обе формулы E.8) и E.10) должны.
31

совпадать. Поэтому, сравнивая E.9) с E.10), находим:
to3
E.11)
Зта важная формула позволяет вычислить один коэффициент по другому,
так как полученное отношение не зависит от рода вещества (как это
и должно быть), а зависит только от частоты излучения.
Вставляя найденное отношение в E.8), получаем окончательную
формулу для плотности равновесного излучения:
Св(ш,О,
E.12)
§ 6. Черное излучение
Интегрируя ба(со, £2, Т) по полному телесному углу (£2 = 4я) и сум-
суммируя по обеим поляризациям (<х = 1, 2), мы получим плотность излуче-
излучения q(co, T), приходящуюся на интервал час-
ts50" тоты ш, ш-fdu), независимо от направления
распространения и поляризации.
Согласно " E.12) равновесное излучение
изотропно, т. е. не зависит от направления
распространения, и одинаково для обеих по-
поляризаций. Поэтому мы получаем:
но
юо
60
, Т),
F.1)
т. е. плотность равновесного излучения час-
частоты ш при температуре Т равна
Лео3 1
F.2)
' г 3 ц 5 бц
Рис. 7. Распределение энер-
энергии в спектре черного из-
излучения для различных
температур.
ПсГоси абсцисс отложены длины
волн в р.
Эта формула дает спектральное распределение
энергии в спектре черного излучения и впервые
была установлена Планком1. На рис. 7 приве-
приведены графики этого распределения для разных
те ператур Т. В области Лш < kT закон План-
Планка совпадает с классическим законом Рэлея —
Джинса, который для q (ш, Т) гласит:
^ F.3)
kT, имея
В области больших квантов Лш
в виду, что ekT >1,из F.2) получаем:
to3 — -pf
F.4)
Заметим, что в старой литературе формула Планка пишется иначе. Различие
заключается в том, что: 1) вместо нашей постоянной h употребляется (введенная Планком)
в 2я раз большая постоянная; 2) вместо циклической частоты ш употребляется обыч-
обычная v = -h—. Заметим еще, что Q (со, Т) da> = Q (v, Т) dv, т. е. Q (v, Т) = 2яр (со, Т).
32

Формула Рэлея—Джинса выводится из рассмотрения света как непре-
непрерывных волн. Формула F.4) может быть получена, если свет рассматривать
как газ, состоящий из частиц с энергией, равной е = /ко. Первая картина
есть волновая картина света, вторая — корпускулярная картина. Обе кар-
картины являются недостаточными: формула Планка не соответствует ни той,
ни другой.
Легко видеть, что волновая картина применима в той области, где
кванты света малы, а число их велико; напротив, корпускулярная картина
справедлива в той области, где кванты велики, а число их невелико.
Действительно, число квантов в 1 см3 в рэлеевской области (h^ < kT)
в интервале частот от щ до о^ -f- dco есть
а в области Лш > kT (виновская область) оно равно
dN, = -^e-bTdia. F.5')
Отношение dMz к dNt равно
dN1~e kT-щ
при
§ 7. Волны де Бройля. Групповая скорость
Мы не предполагаем здесь следовать историческому развитию кванто-
квантовой механики и, в частности, излагать тот, сам по себе не лишенный
интереса путь аналогий между механикой и оптикой, который привел
де Бройля и позднее Шредингера к установлению исходных пунктов
волновой (или, как теперь чаще называют, квантовой) механики1. Если
не касаться тех сторон первоначальной теории, которые в настоящее время
имеют лишь историческое значение, то основная мысль де Бройля заклю-
заключается в распространении основных законов квантовой теории света A.1)
и A.2) на движение частиц.
Именно, с движением всякой свободно движущейся частицы, имеющей
энергию Е и импульс р, де Бройль связывает плоскую волну
i|)(r, /) = С ё(«*-*г)> G.1)
где г — радиус-вектор продольной точки пространства, / — время.
Частота этой волны ш и ее волновой вектор k связаны с энергией
и импульсом частицы теми же уравнениями, которые справедливы и для
квантов света, т. е.
£ = /№>, G.2)
p = hk. G.3)
Это — основные уравнения де Бройля. Мы имеем здесь дело с историческим
1 Читатель, интересующийся этой стороной дела, иайдет прекрасное изложение
идей де Бройля в книге: Луи де Бройль, Введение в волновую механику, ГНТИ
Украины, 1934.
JJ3

ходом идей, обратным тому, который ведет к квантовой теории света.
Для света мы имели первоначально волновую картину и в квантовой
теории дополнили ее корпускулярной, вводя представления об импульсе
и энергии кванта света. Напротив, для частиц (электронов, атомов и т. п.)
мы имеем в качестве исходного пункта классическое представление
о движении частиц и по идее де Бройля, переходя к квантовой теории,
дополняем эту классическую корпускулярную картину представлениями
волновой теории, вводя частоту ш и длину волны %= -т-^-г, волн, связанных
I» |
с движением частицы.
Подставляя в G.1) ш и k из G.2) и G.3), мы получим новое выражение
для волны G.1), в котором будет в явной форме установлена связь
частоты и длины волны с корпускулярными величинами: энергией частицы Е
и ее импульсом р:
G.Г)
Такую волну мы будем называть волной де Бройля. Вопрос о природе
этих волн и о толковании значения их амплитуды С мы отложим
до следующей главы, тдк как этот вопрос вовсе не является простым.
На первый взгляд может показаться, что движение волны G.1)
не может иметь никакой связи с механическими законами движения частиц.
Однако это не так. Чтобы усмотреть эту связь, обратимся к рассмотре-
рассмотрению основных свойств волны де Бройля. Ради упрощения расчетов выберем
направление оси ОХ, совпадающее с направлением распространения волны;
тогда вместо G.1) мы будем иметь:
г|з (х, t) = Ce{(«"-ft*). G.4)
Величина со/ — kx представляет собой фазу волны. Рассмотрим некоторую
точку х, где фаза имеет определенное значение а. Координата этой точки
определится из уравнения
а = Ы — kx,
откуда видно, что значение фазы а будет с течением времени переме-
I щаться в пространстве со скоростью и, которую мы получим, дифферен-
дифференцируя предыдущее равенство по /:
Эта скорость называется фазовой. Если эта скорость зависит от k,
а следовательно, и от длины волны %■ ( так как % = —г- J , то имеет место
дисперсия волны. В отличие от [электромагнитных волн, для волн
де Бройля существует дисперсия в пустом пространстве. Это обстоятельство
вытекает из уравнений де Бройля G.2) и G.3). Действительно, между
энергией Е и импульсом р существует некоторая связь*
Именно согласно теории относительности при скорости частицы v <rc
(с— скорость света), т. е. в области применимости ньютоновской механики,
энергия свободно движущейся частицы равна:
+ ..., G.6)
где т0 —масса покоя частицы1. Подставляя это значение в G.2) и выражая
р2 через А2, получим:
1 В нерелятивистской теории энергия всегда определяется вплоть до аддитивной
постоянной. Поэтому энергию покоя частицы т0с2, при определении кинетической
энергии, обычно опускают.
34

и, следовательно, ч — ~г есть функция А.
Перейдем теперь к установлению связи движения волны с движением
частицы. Для этого мы рассмотрим не строго монохроматическую
волну G.4), имеющую вполне определенную частоту и длину волны
К = —г-, а почти монохроматическую волну, которую мы будем называть
группой волн. Под группой волн, более обще, мы будем разуметь
суперпозицию волн, мало отличающихся друг от друга по длине волны
и направлению распространения. Для простоты мы рассмотрим группу
из волн G.4), распространяющихся в направлении ОХ. Согласно данному
определению группы, мы можем написать для колебания \|)(я, t) следую-
следующее выражение:
)= \ c(Aj)ei<a>i-ft*)d/2, G.8)
fco-Afc
2я
где k0 = -г— есть волновое число, около которого лежат волновые числа
о
волн, образующих группу (Ak предполагается малым).
Разлагая частоту ш как функцию k (см. формулу G.7)) по сте-
степеням k — kQ, получим:
k=ko+(k-k0).
Взяв k — kj) в качестве новой переменной интегрирования £ и считая
амплитуду с (k) медленно меняющейся функцией k, найдем, что \|) (х, t)
может быть представлено в виде
е LlwV^
С
Выполняя простое интегрирование по |, найдем:
= с(^,0-е1<^'~*«*). G.9)
Ввиду наличия под знаком синуса малой величины Ak, величина с(х, t)
будет медленно меняться*в функции времени t и координаты х, поэтому
с (х, t) можно рассматривать как амплитуду почти монохроматической
волны, а (ш0/ — kox) —■ как ее фазу. Определим координаты х, где ампли-
амплитуда с(х, t) имеет максимум. Эту точку будем называть центром
группы волн. Очевидно искомый максимум будет находиться в точке
.Отсюда следует, что центр группы будет перемещаться со скоростью V,
которую мы найдем, дифференцируя предыдущее равенство по t; именно:
3* 35

Эту скорость мы будем называть групповой скоростью Св отличие
от скорости фазы, равной-^-J. Если бы рассматриваемые волны не обла-
обладали дисперсией, то мы имели бы V — и. В случае волн де Бройля ввиду
наличия дисперсии V фи. Вычислим, пользуясь G.7), групповую
. скорость V:
V— -^ — hk
dk m0
Согласно G.3) hk = p, с другой стороны, p = mQv, где о —скорость
частицы. Поэтому мы приходим к важному выводу:
V = v. G.11)
Итак, групповая скорость волн де Бройля равна механической скорости
частицы v.
Полученные нами соотношения G.10) и G.11) могут быть легко
выведены для распространения волн в любом направлении по отношению
к осям OX, OY, OZ. Предоставляя этот вывод читателю, приведем здесь
лишь окончательный результат:
1/ — дм _ дЕ да дЕ
Vx~ dkx ~~ дРх У
.. да дЕ
; dkz dpz '
или в векторной форме:
V = Vft© = VpE = o. G.10')
Вычислим для двух случаев длину волны А, волн де Бройля. Из G.3)
следует, что
Ь = 15- = -?5*. G.12)
Ограничиваясь случаем малых скоростей v < с и пользуясь равенством
Е =.у— , мы получим:
% = -—= G.12')
Эта формула позволяет вычислять длину волны %, зная массу т0 и энер-
энергию частицы Е.
Применим эту формулу к электрону. В этом случае то = 9-10~28 г.
Выражая энергию электрона в эв, для чего положим Е = eV, где е — за-
заряд электрона, а V — ускоряющая электрон разность потенциалов, изме-
измеренная в вольтах, мы найдем:
%=у^А. G.13)
Для У = 1 эв получаем %= 12,2 А, для V = ЮОООэв получаем А, = 0,122 А,
Вычислим длину волны для молекулы водорода, имеющей энергию 6 ■ 10~14 э,
что равно средней энергии молекулы водорода при температуре 300°.
Масса молекулы равна 2-1,66-10~24 г. Подставляя эти величины в G.12),
найдем К= 1А.
Как видим, длина волны К волн де Бройля очевь мала; она тем
меньше, чем больше энергия частицы и ее масса. Практически, например,
совсем не удается получить длину волны %, равную длине волны види-
видимого света, так как уже с электронами, обладающими энергией в 1 эв,
36

весьма трудно экспериментировать, а при К= 10~8 см мы имели бы дело
с электронами, энергия которых равна всего лишь 1,2-10~4эв.
В современных ускорителях получают частицы очень высоких энергий.
Следовательно, такие ускорители можно рассматривать как источники волн
крайне короткой длины. Если энергия частицы много больше энергии покоя
Е > тоС2, то из G.6) имеем Е <^-.рс и, следовательно, длина волны в этом
случае равна
Ь--^. GЛ4)
Для протонов или мезонов, при энергии Е = 10 -4- 20 Бэв, К = 1,26-104 ч-
~ 6,3-10~16 см. Такие, короткие волны позволяют исследовать внутреннюю
структуру элементарных частиц.
Идея о связи движения частицы с движением волны была столь чужда
установившимся в механике представлениям, что казалась чистой фантазией,
и только опыт мог заставить принять ее как ценный вклад в науку. В каких
же явлениях следовало искать подтверждения или, напротив, опровержения
представления о волновых явлениях при движении частиц? Независимо
от природы волн существует совокупность явлений, присущих только вол-
волнам. Это — явления дифракции и интерференции. Оба явления обусловлены
сложением волн с определенными фазами и амплитудами, и их существова-
существование вытекает из самой природы волнового движения. Поэтому для проверки
идеи де Бройля следовало обратиться к опытам, в которых можно было бы
обнаружить эти явления, оперируя с частицами. Из оптики известно, что
явление дифракции только в том случае заметно, когда расстояние между
штрихами дифракционной решетки сравнимо с длиной волны дифрагирую-
дифрагирующих волн. Если делать опыты с электронами, то согласно приведенному
выше расчету длина волны волн де Бройля по порядку величины равна 1 А,
а для атомов еще меньше. Поэтому условия для наблюдения дифракции
электронов примерно таковы же, как и условия для наблюдения дифракции
рентгеновских лучей, так что подходящей дифракционной решеткой могут
быть лишь кристаллы, где расстояние ^между «штрихами»— атомами кри-
кристалла, по порядку величины, равно 1 А. Опыты, подтвердившие правиль-
правильность точки зрения де Бройля, будут кратко изложены в следующем пара-
параграфе.
§ 8. Дифракция микрочастиц
Переходя теперь к изложению опытов, доказавших правильность идеи
де Бройля, мы начнем с классических опытов Дэвиссона и Джермера. Дэ-
виссон и Джермер изучали рассеяние пучка электронов на поверхности
кристаллов. Наблюдая интенсивность пучков в зависимости от угла рассея-
рассеяния, можно было заметить, 'что распределение электронов по углам весьма
сходно с распределением интенсивности волн при дифракции. На рис. 8
схематически изображен опыт Дэвиссона и Джермера. Электронная пушка
служила источником пучка электронов. Фарадеев цилиндр соединялся
с гальванометром, и по силе тока можно было судить о количестве электро-
электронов, рассеянных поверхностью монокристалла под углом 0 к первоначаль-
первоначальному пучку, который падал нормально к поверхности.
За деталями опыта Дэвиссона и Джермера мы отошлем читателя к спе-
специальным монографиям1. Получающаяся картина рассеяния электронов
весьма сложна.
1 См., например, П. С. Тартаковский. Экспериментальные основания
волновой теории материи. ГТТИ, 1931г.
37

Злектвошя пушка
Электроны небольшой энергии не проникают глубоко внутрь кристалла,
поэтому значительная доля рассеянных электронов рассеивается поверхност-
поверхностным слоем кристалла так, что дифракция происходит в основном от плоской
дифракционной решетки, образованной атомами кристалла, расположенны-
расположенными на его поверхности. Согласно элементарной теории дифракции положение
дифракционных максимумов определяется формулой:
nh — ds'mb, (8.1)
где п — порядок дифракционного максимума, % — длина волны дифраги-
дифрагирующих лучей, d — постоянная плоской поверхностной решетки кристалла,
а в — угол между нормалью к решетке и направлением рассеянного пучка.
Зная энергию первичных электронов, падающих на кристалл (в опытах
Дэвиссона и Джермера энергия электронов могла изменяться примерно от
30 до 400 эв), Дэвиссон и Джермер могли для каждой энергии вычислить
длину волны % по формуле де Бройля G.13) и вы-
вычислить из формулы (8.1) положение максимума
для рассеянных, «дифрагированных», электронов1.
Другой способ проверки формулы де Бройля мог
.заключаться в проверке справедливости (8.1) для
электронов разной энергии. Подставляя в (8.1) X.
из G.13), мы найдем, что в случае правильности фор-
формулы де Бройля должно иметь место равенство
VV sin 0 = const (8.2)
(если угол 0 отвечает положению максимума ин-
интенсивности рассеянных электронов). И тот и дру-
другой путь привел Дэвиссона и Джермера к заклю-
заключению о полной справедливости формулы де Брой-
Бройля G.12), связывающей длину волны % с импуль-
импульсом электронов р.
Дифракцию рентгеновских лучей удается наблю-
наблюдать не только от монокристаллов, но и от поли-
поликристаллических образований, например, от кри-
кристаллических порошков (метод Дебая — Шеррера). П. С. Тартаковский
и Г. П. Томсон впервые применили тот же метод'и к наблюдению дифракции
электронов. В этом методе первичный пучок электронов пропускается через
толщу пленки, имеющей поликристаллическую структуру (во избежание
сильного поглощения электронов пленки берутся очень тонкими, около
10~8 см). В такой пленке отдельные монокристаллики расположены хаоти-
хаотическим образом. В этом методе луч пронизывает кристалл, и мы имеем дело
с пространственной дифракционной решеткой. Условие Брегга—Вульфа
для пространственной решетки гласит:
n'k = 2dsmy, (8.3)
где d — постоянная пространственной дифракционной решетки, ф — угол
между лучом и плоскостью решетки, п, % имеют прежние значения. Если
какой-либо из кристалликов пленки удовлетворяет этому условию (см. рис. 9),
то на фотопластинке Р мы получим пятно Q в точке падения на пластинку
дифрагированного луча KQ. Так как кристаллики расположены хаотически,
то среди них найдутся и такие, что их положение будет отличаться от поло-
Рис. 8. Схема опыта по
дифракции электронов
(Дэвиссон и Джермер)
1 Впоследствии выяснилось, что для электронов малой энергии, в противополож-
противоположность быстрым электронам и рентгеновским лучам, показатель преломления кристалла
отличен от 1. Это обстоятельство нужно учитывать при расчете дифракции медленных
электронов.
38

жения кристаллика К лишь поворотом вокруг оси SO, совпадающей с направ-
направлением падающего пучка. В результате на пластинке вместо пятна Q мы
получим кольцо с радиусом 0Q. Вообще каждому пятну при дифракции от
монокристалла в методе Дебая—Шеррера соответствует дифракционное коль-
кольцо. Легко вычислить диаметр (D)
этих колец. Если расстояние от
пластинки до пленки есть L, то
OK--L
Комбинируя это равенство с (8.3),
получим при малых углах ср:
Рис. 9. Схема опытов по дифракции
электронов (Тартаковский и Томсон)
Подставляя вместо % ее выражение
через энергию электронов, по фор-
формуле де Бройля G.13) мы найдем,
что
DVV = const. (8.4)
Справедливость этого соотношения была полностью подтверждена наблю-
наблюдениями П. С. Тартаковского и Г. П. Томсона1.
В настоящее время достигнуто значительное усовершенствование мето-
методики проведения этих опытов, и дифракция электронов находит столь же
успешное применение для анализа
строения кристаллов (особенно их
поверхностей), как и дифракция рент-
рентгеновских лучей. На рис. 10 мы при-
приводим картину дифракции электронов
от серебряной пленки («электроно-
грамма»). Таким образом реальность
дифракции электронов не вызывает в
настоящее время никаких сомнений.
Вопрос о применимости форму-
формулы де Бройля G.12) к частицам,
более сложным, нежели электрон,
к атомам и молекулам является весь-
весьма принципиальным. Действительно,
возможность применения ее к слож-
сложным системам означает, что волновые
явления не являются результатом осо-
особенностей строения той или иной ча-
частицы, а имеют общую значимость,
выражают общий закон движения
микрочастиц.
Штерн и Эстерман поставили своей
задачей проверить формулу де Бройля для атомов и молекул. Для этой
цели Штерн и Эстерман исследовали отражение Не и Н2 от кристаллов LiF.
Меняя температуру «печи», служившей источником узкого пучка атомных
или молекулярных лучей, экспериментаторы имели возможность менять
энергию исследуемых частиц, а вместе с тем и длину волны де Бройля.
Интенсивность рассеянного кристаллом пучка измерялась с помощью очень
чувствительного манометра.
1 См. ПС. Тартаковский, цит. соч.
39
Рис. 10. Дифракция электронных лучей
от тонкой серебряной пластинки
Скорости электронов C6 kV ускоряющего на-
напряжения) соответствует волиа деБройля
в 0,0645 А. Экспозиция 0,1 сек

Рис. 11. Дифракция нейтронов (лауэграмма)
30
го
w
Ik
Ч
-20'
-10"
10°
20°
Рис. 12." Дифракция атомов Не на
.' кристалле LiF
С05В'„
Рис. 13. Угловое распределение я-ме-
зонов с импульсом 6,8 Бэв/с, упруго
рассеянных на протонах. Рассеяние
сильно направлено вперед и может быть
понято как дифракционное рассеяние
на сильно поглощающем шарике1
1 Рис. 13 взят из работы Ван Ган Чен и др. Объединенный институт ядерных
исследований. ЖЭТФ, 38, 426, 1960.
40

Опыты Штерна и Эстермана вполне подтвердили применимость форму-
формулы де Бройля к указанным сложным частицам. На рис. 12 приведено распре-
распределение интенсивности в рассеянном пучке атомов Не, отражающихся от
кристаллов LiF при Т = 295°. Угол 0° отвечает правильному отражению пуч-
пучка Не от кристалла. Для этого угла имеем резкий максимум. Если учесть та
простое обстоятельство, что размеры атома порядка расстояния между иона-
ионами решетки LiF, то уже наличие правильного отражения невозможно объяс-
объяснить с точки зрения корпускулярной механики.
Помимо максимума, отвечающего правильному отражению, имеется
еще два дифракционных максимума (спектры первого порядка). Положе-
Положение их хорошо согласуется с вычисленным по формуле де Бройля. Подоб-
Подобный же результат получен для молекул Н2.
Дифракционные явления имеют место и для потока нейтронов. Из фор-
формулы G.12), подставляя в нее массу нейтрона т0 = 1,66- 1СГ24 г и выражая
энергию нейтрона в электроновольтах Е = eV, получим длину нейтронных
волн в виде
^i (8.5>
/V
Отсюда видно, что если энергия нейтронов составляет сотые доли электроно-
вольта (так называемые «тепловые» нейтроны), то "К будет сравнима с постоян-
постоянной решетки кристаллов. При этом условии легко получить явление дифрак-
дифракции. Так как нейтроны, в отличие от электронов, но подобно рентгеновским
лучам, мало поглощаются веществом, то с нейтронами можно воспроизвести
дифракцию от объема кристалла (трехмерная дифракция Лауэ). На рис. 11
показана объемная дифракция нейтронов на кристалле хлористого натрия.
Наконец на рис. 13 приведена картина дифракции я-мезонов с энер-
энергией 7 Бэв на протоне. Эта картина соответствует дифракции волн, где
К ~ 10~14 см на сильно поглощающем шарике с радиусом ~10~13 см.
Приведенные в этом параграфе факты с полной очевидностью показы-
показывают, что волновые явления обнаруживают все частицы, независимо от их
природы и строения, а формула де Бройля, связывающая импульс частицы
с длиной волны, имеет всеобщую значимость.

ГЛАВА II
ОСНОВЫ КВАНТОВОЙ МЕХАНИКИ
§ 9. Статистическое толкование волн де Бройля
Физический смысл волн, связанных по идее де Бройля с движением
частиц, был раскрыт не сразу. Вначале были попытки рассматривать сами
• частицы как образования из волн, распределенные в некоторой области
пространства. Интенсивность волны де Бройля рассматривалась в этой кон-
концепции как величина, характеризующая плотность среды, из которой обра-
образована частица. Это понимание волн де Бройля имело совершенно класси-
классический характер. Основанием для него служило то обстоятельство, что в не-
некоторых, весьма частных случаях, оказалось возможным (теоретически)
построить волновые образования, движение которых совпадает с движением
частицы, движущейся по законам классической механики. Примером таких
образований может служить рассмотренная выше группа волн. Как было
показано в § 7, центр группы волн движется как частица. Однако движение
такой группы волн все же не вполне совпадает с движением частицы. Дело
в том, что сама форма группы волн с течением времени изменяется. Именно
как будет показано в § 34, размеры группы возрастают: группа волн расплы-
расплывается. Необходимость такого расплывания можно легко понять из факта
существования дисперсии волн де Бройля в пустоте. Отдельные волны, из
которых образована группа, распространяются с различной скоростью.
Благодаря этому группа волн будет расплываться.
Таким образом, построенная из волн де Бройля частица будет неустой-
неустойчива: даже при движении в пустом пространстве размеры ее будут все время
возрастать неограниченно. Эта неустойчивость будет особенно разительна,
если обратиться к случаю, когда частица движется в неоднородном простран-
пространстве, переходя из одной среды в другую. Примером такого случая являются
классические опыты по дифракции частиц. Когда, например, в опыте Тарта-
ковского—Томсона пучок частиц проходит тонкую фольгу, то он разделяется
на систему конусообразных дифрагированных пучков. Если рассматривать
частицу, в данном случае электрон, как образование из волн, то первоначаль-
первоначально мы должны отождествить с электроном падающую волну, размеры которой
определяются диафрагмами прибора, а после прохождения фольги — всю
систему дифрагированных волн. Каждый дифрагированный пучок должен
был бы представлять некоторую долю электрона. Представим теперь себе,
что мы поставили два прибора, регистрирующих- попадание электронов
(например, фотопластинки), причем в первый прибор направлен только пер-
первый дифрагированный пучок, а во второй прибор — только второй дифраги-
дифрагированный пучок. Тогда, если отождествлять с частицей всю систему дифра-
дифрагированных волн, то мы должны прийти к заключению, что каждый из
приемных аппаратов примет лишь часть частицы. Это и есть'крайнее нару-
42

шение атомизма частицы, приводящее вышеизложенное понимание волн
де Бройля к резкому противоречию с опытом.
В самом деле, частица всегда действует как целое, и обнаруживается
в приборе вся частица, а вовсе не ее доля. В рассмотренном примере электрон
попал бы либо на первый прибор, либо на второй (но не частью на первый
и частью на второй).
В том, что простейшие частицы всегда действуют, как нечто целое,
и заключается атомизм, наблюдаемый в явлениях микромира. Поэтому пред-
представление о частицах как об образованиях из волн де Бройля противоречит
атомизму и должно быть отвергнуто.
Равным образом нельзя допустить, что сами волны являются образо-
образованием частиц или, точнее говоря, возникают в среде, образованной
частицами. Опыт показывает, что дифракционная картина, возникающая
на фотопластинке, не зависит от интенсивности падающего пучка частиц,
а следовательно, и от плотности частиц в единице объема. Чтобы получить
одну и ту же дифракционную картину, можно уменьшить интенсивность,
но увеличивать экспозицию: важно лишь общее число прошедших частиц.
Этот факт определенно показывает, что каждый из электронов дифрагирует
независимо от других1. Поэтому существование волновых явлений нельзя
связывать с наличием одновременно большого числа частиц.
Чтобы еще более подчеркнуть это обстоятельство, заметим, что вол-
волновые явления проявляются при движении электронов в атомах, где
говорить о среде, образованной большим числом частиц, никак не прихо-
приходится. Действительно, такими свойствами обладают электроны, движу-
движущиеся в атомах, где число их совсем невелико (один в водороде, два
в гелии и т. д.).
Правильное толкование волн де Бройля было найдено М. Борном
на совсем другом пути. Чтобы уяснить основную мысль Борна, предста-
представим себе, что мы производим дифракцию электронов и регистрируем
попадание «дифрагированных» электронов на фотопластинке. Пусть перво-
первоначально пропущено небольшое число электронов. Каждый из электронов,
пройдя через дифракционный прибор (например, через фольгу), обнару-
обнаружится в каком-нибудь месте фотопластинки и произведет там фотохими-
фотохимическое действие. Прохождение небольшого числа электронов даст на фото-
фотопластинке картину, похожую на мишень, простреленную плохим стрелком.
Только при большом числе прошедших электронов выявляется регуляр-
регулярность в распределении электронов на фотопластинке и, наконец, обра-
образуется распределение, полностью отвечающее распределению интенсив-
ностей при дифракции волн (например, система дифракционных колец,
изображенная на рис. 10).
Такое поведение частиц привело Борна к статистическому толкованию
волн де Бройля, позволяющему сочетать атомизм частиц с волновыми
явлениями. Согласно статистическому толкованию интенсивность волн
де Бройля в каком-либо месте пространства пропорциональна вероят-
вероятности обнаружить частицу в этом месте. Так, например, если один
дифрагированный пучок направляется на одну фотопластинку,- а второй—
на другую, то при большом числе прошедших через аппарат электронов,
количество попавших на каждую из пластинок, пропорционально интен-
1 При очень больших плотностях в падающем пучке, благодаря нуклоновскому
взаимодействию, может получиться дополнительное рассеяние. Это, однако, имеет вто-
второстепенное значение для рассматриваемого вопроса: важно, что при малых интенсив-
ностях волновые, интерференционные явления не исчезают. Это доказано прямыми опы-
опытами. Г. А. Бибермана, Н. Сушкина и В. Фабриканта (ДАН, XVI, 135 A949)) для
электронов и опытами Л. Яноши для фотонов, см. L. Janossy and Sz. Naray, Hungarian
Acad. of Sciences, Manuscript. Budapest, ХП, Konkoly Thege ut, Hungary, 1957.
43

сивности волн де Бройля, распространяющихся в направлении каждой иа
фотопластинок.
Если фотопластинку поместить так, что направление от дифракцион-
дифракционного аппарата к пластинке совпадает с направлением дифракционного-
минимума (в этом направлении волны гасят друг друга), то частицы
вовсе не будут попадать на такую фотопластинку. Если же речь идет не
о большом числе электронов, а об одном, то интенсивность воли
де Бройля указывает лишь вероятность попадания электрона, но вовсе
не обязывает электрон к тому или иному определенному поведению.
В таком понимании волны де Бройля не имеют ничего общего с вол-
волнами, рассматриваемыми в классической физике. Во всех «классических»
волнах абсолютное значение амплитуды волны определяет физическое
состояние. Если, например, амплитуда колебаний воздуха в одном случае
всюду в два раза больше, чем в другом, то это означает вчетверо большую-
энергию колебаний и вместе с тем другое физическое состояние среды.
В случае волн де Бройля интенсивности определяют вероятности
местонахождения частицы. Поэтому важно лишь отношение интенсив-
ностей в различных частях пространства, а не сама их абсолютна»
величина. Это отношение» показывает, во сколько раз в одном месте про-
пространства вероятнее обнаружить частицы, нежели в другом. Поэтому,
если в одном случае интенсивность волн де Бройля всюду вдвое больше,
чем в другом случае, то физическое состояние частиц все же одно и то же,
так как при таком увеличении амплитуды волн отношения интенсивно-
стей в различных областях пространства остаются неизменными.
Волны де Бройля дают, таким образом, статистическое описание движе-
движения микрочастиц: они определяют вероятность обнаружения {локализации}
частицы в данном месте пространства в данный момент времени1.
§ 10. Вероятность местоположения микрочастицы
Обозначим через х, у, z координаты частицы. Согласно изложенному
в § 9, точный смысл в х, у и z вкладывается следующей измерительной опе-
операцией: величины х, у, z определяются как координаты той точки простран-
пространства, в которой локализуется частица. Так, например, это будут коорди-
координаты пятнышка на фотопластинке, получившегося в результате попадания
на пластинку частицы, или например, координаты, определяющие положе-
положение щели, через которую прошла частица, и т. п.
Координаты пятнышка или щели могут быть определены путем откла-
откладывания твердого масштаба. Такое измерение координаты мы будем назы-
называть «прямы м», так как оно есть как раз то измерение, на котором поко-
покоится само макроскопическое определение понятия координаты частицы.
В тех случаях, когда подобное определение координаты частицы невозмож-
невозможно (например, если частица находится внутри атома), мы будем определять
ее координаты посредством «косвенного» опыта2, т. е. измеряя ука-
указанным выше путем координаты некоторой другой частицы, которая претер-
претерпела столкновение с интересующей нас частицей, и на основании этого изме-
измерения сделаем заключение о координатах частицй, находящейся в атоме,
1 Впоследствии мы увидим, что, зная волну де Бройля, описывающую состояние
частицы, можно найти вероятность не только местоположения частицы, но и вероят-
вероятность любого результата измерения любой механической величины, относящейся
к рассматриваемой частице.
2 Деление опытов на «прямые» и «косвенные» было введено Л. И. Мандель-
Мандельштамом.
44

недоступных прямому измерению. Пример подобного «косвенного» измере-
яия будет приведен в § 16.
Формулируем теперь математически статистическую интерпретацию
волн де Бройля. Заметим, прежде всего, что слово «волны» мы употребляем
сейчас весьма условно. Только в очень специальных случаях состояние ча-
частиц будет описываться простыми плоскими волнами. В общем случае то,
что мы сейчас называем волнами де. Бройля, может представлять собой весь-
весьма сложную функцию координат частицы х, у, z и времени t. Тем не менее,
и для этих сложных случаев мы будем употреблять термин волновая
функция и обозначать последнюю буквой ij;x:
i|> = i|> (х, у, г, t). A0.1)
Как было пояснено в § 9, на основании изложенных фактов мы прини-
принимаем, что вероятность местонахождения частицы определяется интен-
интенсивностью волн, т. е. квадратом амплитуды ty. Имея, однако, в виду,
что i|) может быть комплексной величиной, а вероятность должна быть
всегда действительной и положительной величиной, мы будем брать
за меру интенсивности не г|Д а квадрат модуля г);,' т. е. величину
,где через ij;* обозначена величина, комплексно сопряженная г);2.
Далее следует заметить, что вероятность найти частицу в окрест-
окрестности точки х, у, z зависит, конечно, от размеров выбираемой области.
Рассматривая бесконечно малую область
х, x + dx; у, y + dy; г, z + dz,
■мы можем считатьг); внутри этой области постоянной, а поэтому вероят-
вероятность найти частицу следует считать пропорциональной объему этой
области. Обозначим этот элемент объема через dv = dxdy dz.
Обозначая саму вероятность (бесконечно малую), найти частицу
в элементе объема dv в окрестности точки х, у, z в момент времени t, через
dW (x, у, z, t) мы можем записать статистическую трактовку волн
де Бройля в виде следующего равенства:
dW(x, у, z, *) = |Ф(*. У. 2, t)\*dv. A0.2)
Это равенство позволяет по известной волновой функции ij; (x, у, z, t)
вычислить вероятность местонахождения частицы dW (х, у, z, t). Величину
w(x, у, г, t)^^\^{x,y,z,t)\^ A0.3)
«будем называть плотностью вероятности.
Вероятность найти частицу в момент времени t в объеме V, согласно
теореме сложения вероятностей, равна
W(V, *)=$ dW=\ wdv= \ \У(Х> У> z,t)\2dv. A0.4)
V V V
1 Укажем здесь, что для двух простых случаев мы уже знаем волновую функцию.
Именно, для частиц, движущихся с заданным импульсом р, волновая функция \|>0
^есть монохроматическая плоская волна G.1). Далее, нам известна функция для почти
монохроматической волны, т. е. для группы волн G.8). В ближайшем изложении мы
будем оперировать с произвольными волновыми функциями, оставляя пока в стороне
вопрос о том, как такие функции могут быть определены для заданных физических усло-
условий (ср. § 28). Считая такое определение возможным, мы будем говорить, что ^-функция
описывает (статистически) состояние частицы.
2 В -дальнейшем звездочка всегда будет означать комплексно сопряженную вели-
величину.
45

Если произвести интегрирование по всему объему, то мы получим вероят-
вероятность того, что в момент времени t частица находится где-нибудь. Это —
вероятность достоверного события. В теории вероятностей принято вероят-
вероятность достоверного события считать равной 1. Если принято это согла-
соглашение, то интеграл от | ip |2 по всему объему следует приравнять единице:
y(x,y,z,t)\>dv=\. A0.5)
Это условие называется нормировкой, а функцияijj, удовлетворяющая
этому условию, называется иормироваиной.
Нормировка может оказаться невыполнимой, если интеграл, взятый
по всему объему от | ij;|2, расходится, т. е. функция ty квадратично не инте-
интегрируема. В физически реальных условиях движение частицы всегда про-
происходит в ограниченном пространстве. Это ограничение обусловливается
геометрическими размерами приборов и конечной скоростью движения
частиц. Поэтому вероятность найти частицу отлична от нуля лишь в конечной
области пространства, так что функция ty должна быть интегрируема.
Однако в ряде случаев приходится все же пользоваться некоторыми идеали-
зациями, которые ведут к неинтегрируемым функциям. Простым примером
таких функций является плоская волна G.1). В то время как в действитель-
действительности параллельный пучок всегда ограничен диафрагмами с боков и спереди
своим фронтом, при достаточно больших размерах пучка, когда краевые
эффекты ие играют роли, мы можем рассматривать пучок как плоскую волиу.
Предполагается, что последняя занимает все пространство.
Из G.1) следует, что \ty\2 = |с|2 = const. Это означает, что одинаково
вероятно частицу иайти в любом месте. Нормировать к единице в этом случае
нельзя. В дальнейшем мы дадим, однако, рациональную нормировку и для
этого случая.
Второе замечание относится к зависимости от времени. Нормировка
имеет смысл лишь постольку, поскольку она сохраняется во времени, т. е.
равенство A0.5) должно иметь силу для всех моментов времени (иначе
нельзя сравнивать вероятности, относящиеся к различным моментам вре-
времени). При рассмотрении законов изменения волновой функции во времени
будет показано (§ 28), что нормировка действительно ие меняется, т. е. что
интеграл A0.5) от времени не зависит.
§ 11. Принцип суперпозиции состояний
В данных физических условиях частица может находиться в различ-
различных состояниях в зависимости от способа, каким она в эти условия попа-
попадает. Обращаясь к простейшему случаю свободного движения частицы без
действия внешних сил и без взаимодействия с другими частицами, мы можем
иметь дело с состояниями движения, различающимися как величиной, так
и направлением импульсов. Каждое из этих состояний может быть реали-
реализовано само по себе. Однако существуют и более сложные случаи. Приме-
Примером может служить дифракционный опыт Дэвиссона и Джермера, в котором
падающий на кристалл пучок разбивается на систему дифрагированных
пучков. После взаимодействия с кристаллом движение происходит опять-
таки в пустом пространстве, но представляется уже целой совокупностью
волн де Бройля, отличающихся друг от друга направлением распростра-
распространения.
Бросая на поверхность кристалла пучок определенного направления
и определенной длины волны К, мы не можем получить какую-нибудь из диф-
46

рагированных волн, а получаем сразу всю совокупность этих волн (вместе
с падающей), находящихся к тому же в определенных фазовых отношениях
друг к другу и поэтому способных к интерференции. Вся эта совокупность
волн представляет собой единое волновое поле и изображается одной волно-
волновой функцией г|\ Однако такое волновое поле является совокупностью
простых волн де Бройля typ, каждая из которых сама по себе может описы-
описывать возможное состояние движения частицы в пустом пространстве. В этом
можно убедиться, если выделить с помощью диафрагмы из всего волнового
поля 1|з один из дифрагированных пучков, и затем вторично подвергнуть
его дифракции.
Мы говорим, что состояние, возникающее при дифракции частиц на
поверхности кристалла, является суперпозицией (наложением)
состояний свободного движения, описываемых простыми волнами де Брой-
Бройля. Этот случай суперпозиции является частным выражением общего прин-
принципа суперпозиции состояний, составляющего одну из основ квантовой
механики.
Принцип этот может быть сформулирован следующим образом: если
какая-либо система (частица или их совокупность) способна находиться
в состоянии, изображаемом волновой функцией \|I( и в другом состоянии г|;2,
то она может находиться и в состоянии, изображенном волновой функцией
■ф такой, что
где сх и с2 — произвольные, вообще говоря, комплексные числа, опреде-
определяющие амплитуды и фазы частных состояний ■Ц51 и г|;2. Отсюда следует,'
что если имеется ряд возможных состояний системы, отличающихся друг
от друга значением какой-либо величины (импульса, энергии, момента
импульса и т. п.), которые изображаются волновыми функциями tyu г|;2
то, согласно принципу суперпозиции, существует сложное состояние:
* = c1i|>1+c,i|>,+ ...+cni|>n+...I A1.1)
где с,, с2, . .., сп, ... —произвольные, комплексные амплитуды.
Если состояния, входящие в суперпозицию, отличаются друг от друга
бесконечно мало, то вместо суммы A1.1) мы будем иметь интеграл.
Важным примером суперпозиции последнего рода является представ-
представление произвольного волнового поля ty(x, у, z, t) в виде суперпозиции
волн де Бройля *:
%(х, у, г, *) = —Це * . A1.2)
Именно, волновую функцию любого состояния можно написать в виде
+00
Ф (х, У, г, 0 = J J J с (рх, pv, рг, t) % (х, у, г, t) dPx dpy dpz, A1.3)
где с(рх, ру, pz, ^ — амплитуда волны де Бройля, имеющая импульс
Р(Рх, Ру> Рг)-
Утверждение очевидно, так как A1.3) есть не что иное, как разло-
разложение ty(x, у, z, t) в тройной интеграл Фурье. Чтобы в этом убедиться,
1 Множитель 1/BяЛ3) введен из соображений нормировки, целесообразность кото-
которой вскоре выяснится (см. A2.6)).
47

обозначим
Ф (Рх> Ру Pz> t) = с (рх, ру, pz, t) e " . A1.4)
Тогда на основании A1.2) формула (П.З) может быть записана в виде
. Ух+
(px,py,Pz,t)e n %$/, • (П.5)
Отсюда по известной теореме Фурье об обращении интеграла (П.5) мы
•находим для каждой функции i|) амплитуды ф, а вместе-с тем и с, именно:
+оо Vxx+pyV+pzz
<P(px.Pv,Pz,t)=[\^(x,y,z,t)<T * -^й"- (И-6)
— оо '
Таким образом мы видим, что любое состояние можно рассматривать
лак суперпозицию волн де Бройля, т. е. состояний с заданным импуль-
импульсом частицы р{рх, ру, pz).
§ 12. Вероятность импульса микрочастицы
Мы показали, как на основе статистического толкования волн
де Бройля можно определить вероятность местонахождения частицы.
Сейчас мы увидим, что принцип суперпозиции позволяет расширить ста-
статистическое толкование, так что оказывается возможным определить не
только вероятность тех или иных значений координат частицы, но
и вероятность тех или иных значений ее импульса р.
Формулу де Бройля
мы будем рассматривать как определение величины р, которую в кван-
квантовой механике мы будем называть импульсом частицы 1. Следова-
Следовательно, измерительные операции, которые-определяют р, таковы же, как
и измерительные операции, необходимые для определения направления
распространения волны и ее длины X. Поэтому прибором, измеряющим
импульс частиц, может служить дифракционная решетка. В самом
деле, дифракционная решетка разлагает спектр — разделяет волны с раз-
различными Те, а следовательно, вместе с тем и производит «сортировку»
частиц по различным импульсам р = hie.
Дифракционный опыт, позволяющий определить Тс, мы будем рас-
рассматривать как «прямой» опыт, определяющий и импульс частицы р.
Чтобы рассмотреть теперь вопрос об определении вероятности того
или иного значения импульса частицы, обратимся к опыту по дифракции
частиц (например, электронов), на поверхности кристалла. Суперпозиция
1 В связи с данным нами определением импульса микрочастицы может возник-
возникнуть вопрос: почему вообще величину p=hk следует называть импульсом? Ответ иа
этот вопрос заключается в том, что определенная таким образом величина на самом
деле обладает свойствами, вполне аналогичными свойствам импульса ркл в классиче-
классической механике (ср. §§ 32, 33, 101). В § 34 показано, что классический импульс ркл
{подчиняющийся -уравнению Ньютона) есть среднее квантового импульса
Ркл=р.
В частности, для состояния с определенным значением р имеем ркл=р. Благодаря
этому р может быть также измерено, скажем, по отдаче при ударе, как это делается
в классической механике для определения ркл.
48

волн де Бройля, образующая волновое поле 1|з (х, у, z, t) при дифракции
на поверхности кристалла, схематически изображена на рис. 14, где
показаны падающая (/), отраженная (г) и одна из дифрагированных (d)
волн. В соответствии с реальными .условиями предположено, что пер-
первичная волна представляет собой ограниченный диафрагмой пучок. Такими
же пучками являются и вторичные волны.
Каждый из пучков мы можем представить в виде волны де Бройля
ty(x. у, z, t) с амплитудой с(р), медленно меняющейся в направлении,
перпендикулярном к пучку1. Все
волновое поле ty представим как су-
суперпозицию полей, принадлежащих
отдельным пучкам:
■ф =| 2 с (р) Фр> 02.1)
где сумма взята по всем пучкам.
В целом состояние i|) является
состоянием с неопределенным импуль-
импульсом частиц, так как оно представляет
собой суперпозицию состояний typ
с различными импульсами. Поэтому,
если мы будем производить измере-
измерение импульса частицы, то мы можем
получить в каждом отдельном изме-
измерении одно из значений р, содержа-
содержащихся в суперпозиции A2.1).
Какова вероятность того, что мы
получим значение импульса, равноер?
Дифракционная решетка разложит
нам волновое поле на монохроматиче-
монохроматические (в действительности —'почти мо-
монохроматические) пучки, так же как
она разлагает белый свет на отдельные
спектральные чистые компоненты.
Чтобы подсчитать число частиц, име-
имеющих импульс р, поставим цилиндр
Фарадея и будем определять число
частиц, попадающих в него при раз-
различных его положениях. Вблизи поверхности кристалла мы имеем слож-
сложное волновое поле, представляющее собой результат интерференции всех
пучков. Вдали же от кристалла пучки разделяются. Вероятность того,
что в цилиндре обнаружится частица, согласно статистической 'интер-
'интерпретации волновой функции, будет пропорциональна | 1|з (х, у, z, t) p.
Если мы поставим цилиндр Фарадея достаточно далеко от кристалла,
то отдельные пучки уже разделяются друг от друга и | 1|з (х, у, z, t)\*
сведется к
Цшндр
Фарадея
Рис. 14. При ограниченном^первичном
пучке / отдельные частные волны г, d
и т. д. пространственно разделяются
(х, у, z, t) Р = | с
[х, у, z, t) |2
A2.2)
(для одного из пучков). Используя значение г|з (П.2), получаем:
A2.3)
1 Вне пучка с(р)=0. Таким образом в отличие от A1.3) рассматриваемые сейчас
амплитуды являются функциями координат. Но ввиду медленности изменения они
близки к истинным амплитудам Фурье, встречающимся в A1.3).
Д. И. Блохинцев
49

Следовательно, \с (р) |2 пропорционально вероятности обнаружить электрон
в цилиндре Фарадея, при условии, что он расположен так, чтобы
в него могла быть направлена волна typ. Такой волне принадлежат элек-
электроны, имеющие импульс р. Поэтому величина |сB>)|2 пропорциональна
вероятности обнаружить в состоянии i|) электрон с импульсом р.
Имэл в виду A0.2) и то, что вероятность обнаружить импульс
частицы в интервале
Рх' Px+dPx> Ру Pv + dPy'> Pz> Pz + dpi,
должна быть пропорциональна] dpxdpydpz; мы приходим к выражению
' dW (px, py, pt, t) = \c (px, py, рг, t) |2 dpx dpy dpt A2.4)
и для плотности вероятности:
W (рх, Ри, Pz, t) = \c (px, py, рг, t) |2. A2.5)
Написанные формулы содержат определенный выбор нормировки
вероятностей для импульса.
Пользуясь тем, что ip (рх, ру, рг, t) есть, согласно A1.6), компонента
разложения в ряд Фурье волновой функции г|з (х, у, z, t), нетрудно дока-
доказать, что *
\\ [ I * (Рх> Ру, Рг, t) |2 dPx dPy dPz = ^ ^ I * (X, У, 2, t) |2 dx dy dz. A 2.6)
—oo —oo
Левая часть есть вероятность найти любое значение импульса частицы
(достоверное событие), правая часть есть вероятность найти частицу
в любом месте пространства (также достоверное событие). Поэтому сде-
сделанный выбор нормировки вероятностей целесообразен: вероятности досто-
достоверных событий одинаковы. В частности, если вероятность найти частицу
в любом месте полагается равной единице, то и вероятность найти любой
импульс будет также равна единице. •
§ 13. Средние значения функций от координат
и функций от импульсов
В предыдущих параграфах мы определили вероятность местоположе-
местоположения частицы A0.3) в состоянии ty и вероятность импульса частицы A2.5)
в этом же состоянии. Это позволяет нам тотчас же написать средние
значения любой функции от координат частицы F (х, у, z) и любой функ-
функции от импульса частицы F (рх, р , pz) для состояния, изображаемого
волновой функцией ty. Именно, из A0.3) и A2.5), согласно определению
среднего значения случайной величины, имеем:
F(x,y,z)= ^ F (x, y,z)\q (х, у, z) |2 dx dy dz =
= ^ V (x, У. z) F (x, y, z) if (x, y, z) dx dy dz A3.1)
при условии
5 |1|>(лг, У, z)\*dxdydz=\ A3.2)
и
F (рх, Ру, pz) = 5 F (Px' Py, Pz) I c (Px, Py, Pz) I2 dpx dpy dpz =
= ) c* (Px, Pv, Рг)F (Px, Py, Pz)c (Px, Py, Pz) dpx dpy dpz A3.3)
50

при условии
[PxdpvdPt=l A3.4)
(здесь интегралы взяты по всей области изменения переменных х, у, г
или рх, ру, рг соответственно).
Формулы A3.1) и A3.3) допускают весьма важное преобразование,,
основанное на свойствах интегралов Фурье. Пусть F (х, у, z) есть целая
рациональная функция от х, у, z и F (рх, ру, рг)— целая рациональная
функция от рх, ру, рг.
Тогда формулы A3.1) и A3.3) могут быть переписаны в следующем
виде h
X с (рх ру pz) dpx dpy dpz, A3.5)
(*. У, z)'
Xty(x, y,z)dxdydz. A3.6)
Эти формулы означают, что аргументы функции F следует заменить сим-
символами дифференцирования по указанным аргументам, умноженным на ± ih,
и выполнить операцию дифференцирования над стоящей позади ^-функ-
^-функцией. Так, например, для вычисления среднего значения компоненты
импульса рх поступаем так: F (px, py, pz) = px- Следовательно,
Рх = \ С* (Рх> Pvi Pz) Рх С (Рх, Ру, Pz) dPx dPy dpz, A3.7)
или по формуле A3.6), заменяя рх на —ih^-, получим:
Рх = - [ V (х, У, z) ih^^xy-z) dxdy dz. A3.8)
Подобным же образом среднее значение рх можно вычислить или
по формуле A3.3):
Рх = } с*(рх, ру, рг) рх с (рх, ру, pz) dpx dpy dpz, A3.9)
или по формуле A3.6), заменяя F(px) = px на
Тогда получается:
* (х, у, z) д^ fj' г) dx dy dz. A3.11)
§ 14. Статистические ансамбли квантовой механики
В практической деятельности физика или инженера встречаются два
важных типа задач, на которые должна ответить квантовая механика.
Первая задача такова: по волновой функции предсказать возможные
результаты измерений над микрочастицей («прямая» задача). Второй тип
1 Доказательство эквивалентности A3.1), A3.3) и A3.5), A3.6) срответствеино-
приведено в дополнении I.
4* 54

задачи: по результатам опыта определить волновую функцию частицы
(«обратная» задача).
Предсказания, вытекающие из знания волновой функции, в общем
случае, носят статистический характер. Поэтому если производится какое-то
единичное измерение, то результат этого измерения показывает нам лишь
в какой мере оправдались наши ожидания: произошло ли вероятное или
маловероятное событие. Вполне объективный характер носят лишь рас-
распределения результатов измерения, возникающие при повторении тожде-
тождественных измерений большого числа опытов.
Существенно, что в квантовой области мы не можем повторять опыт
на одной и той же частице, так как измерение, вообще говоря, может изме-
изменить состояние микрочастиц (§ 16).
Поэтому для воспроизведения большого числа (N^>1) тождественных
опытов необходимо представить себе большое число частиц (или систем),
которые, независимо друг от друга, находятся в одном и том же состоянии,
характеризуемом волновой функцией 1|з.
Такой набор частиц (или систем) мы будем называть чистым
ансамблем.
Все вероятности и все средние значения, вычисляемые из волновой
функции, относятся к измерениям в таком ансамбле.
Так, например, утверждение, что вероятность найти координату
частицы х, лежащей около х', равна | i|) (xr) \2dx' означает, что, производя
большое число измерений координаты, в серии одинаковых опытов (одно
и то же ij;!), мы найдем х около х' в N' случаях, причем
^ = \q(x')\*dx'. A4.1)
.Подобным же образом, измеряя в этом же ансамбле импульс частиц рх
и производя всего М измерений (М 2> 1), мы найдем рх вблизи р'х в М'
случаях, причем
^=\с(р'х)\Чр'х, A4.2)
где с{р'х) есть амплитуда в разложении ijj(*) по волнам де Бройля
(ср. § 12).
Зная распределение результатов измерений для х A4.1) и для рх
A4.2), мы можем вычислить средние значения любых функций F (х), Ф(р),
например, среднее значение х, среднее значение рх, средние квадратич-
квадратичные отклонения
_ф-*J_ (Н.З)
и Д~й=(рж1-рж)* A4.4)
и т. п.
Впоследствии мы покажем, что зная волновую функцию 1|з, можно
вычислить вероятности не только для х и рх, но и вообще найти вероят-
вероятности для того или иного результата измерения любой механи-
механической величины, свойственной данной частице или системе.
Совершенно ясно, что из единичного измерения над одной микрочасти-
микрочастицей невозможно определить ее волновую функцию. Зная же распределения
результатов измерения в ансамбле, можно решить и обратную задачу, вос-
восстановить по результатам измерения волновую функцию частицы (конечно,
вплоть до общего нормирующего множителя, который всегда остается
неопределенным) (§ 87).
Таким образом не только предсказания квантовой механики относятся
52

к измерениям в квантовом ансамбле, но и обратно, характер квантового
ансамбля может быть определен из измерений.
Поэтому состояние частицы (или системы), характеризуемое волновой
функцией, следует понимать как принадлежность частицы (или системы)
к определенному чистому квантовому ансамблю. Именно в этом смысле
и будут употребляться в дальнейшем слова: «состояние частицы», «состоя-
«состояние квантовой системы» и т. д.
Приведем теперь конкретный пример чистого ансамбля.
Рассмотрим рассеяния одного электрона на отдельном атоме. Пусть
импульс электрона есть р. Тогда волновая функция электрона ^¥v (х) изо-
бразится в виде суперпозиции волны де Бройля typ (х), изображающей пер-
первичное состояние электрона с импульсом р и волны и(х), представляю-
представляющей собой волну, рассеянную атомом так, что
Vp(x) = %(x) + u(x). A4.5)
Зная рассеянную волну, можно в статистическом смысле предсказать
судьбу рассеянного электрона (ср. теорию столкновений, гл. XIII).
Однако каким же образом воспроизвести этот опыт много раз?
Пусть электроны летят с накаленной нити. С помощью диафрагм выде-
выделим пучок данного направления и сообщим электронам определенную ско-
скорость, прикладывая ускоряющее напряжение. Направим этот пучок в газ
и будем наблюдать интенсивность рассеяния электронов для разных углов.
Если плотность газа невелика и толщина слоя, в котором происходит рас-
рассеяние электронов, не очень большая, то можно пренебречь многократными
рассеяниями электрона.
Если, далее, плотность электронов в первичном пучке настолько мала,
что можно пренебречь их взаимодействиями, то мы имеем дело сразу с вос-
воспроизведением большого числа независимых опытов по рассеянию одного
электрона на одном атоме.
Наконец, если скорость, приобретаемая электронами в ускоряющем
поле, много больше их тепловой скорости и диафрагмы достаточно хорошо
выделяют пучок, то мы можем сказать, что мы имеем дело с электронами
определенного импульса р и, следовательно, приписать им волновую
функцию typ, которая вместе с рассеянной волной и дает У
Таким путем мы на практике осуществляем совокупность тождествен-
тождественных явлений, описываемых одной и той же волновой функцией ^(я),
т. е. - чистый квантовый ансамбль.
С точки зрения квантовой механики задание состояния частицы
с помощью волновой функции является наиболее полным и исчерпывающим.
В действительности, мы часто встречаемся с другими случаями, когда
ансамбль с самого начала содержит частицы в различных состояниях,
описываемых различными волновыми функциями i|3lt г|;2, . .., tyn. При этом
заданы вероятности Рх, Р2, ...,Рп каждого из таких состояний. Такой
ансамбль называется смешанным.
Очевидно, что величины Ръ Р2, ..., Рп указывают вероятность встре-
встретить в смешанном ансамбле соответствующие чистые ансамбли, характе-
характеризуемые волновыми функциями 1|з„ ijj2, ..., г|э„.
Примером смешанного ансамбля будет являться тот случай, когда
к электронам, покидающим накаленную нить, не приложен ускоряющий
потенциал. В этом случае импульс электронов не фиксирован, а фикси-
фиксирована лишь температура накаленной нити Т.
Первичные электроны будут теперь распределены по закону Максвелла.
Вероятность того, что импульс электрона будет лежать между рх, px-\-dpx,
53

Py, Py + dpy, pz, pz + dpz будет
•&_
dPp = Ce to*rdPxdpydp%, A4.6)
где ц — масса электрона, k — постоянная Больцмана, С — нормирующий
множитель ( \ dP = 1 J. Электроны, имеющие импульс р, будут описы-
описываться волновой функцией де Б рой л я typ(x); поэтому dPp A4.6) есть как
раз вероятность того, что электрон будет иметь волновую функцию
%(х), т. е. будет принадлежать к чистому ансамблю typ(x), являю-
являющемуся частью всего рассматриваемого смешанного ансамбля.
Подобный смешанный ансамбль осуществляется в опытах Штерна
и Эстермана по дифракции Не на LiF, где распределение импульсов ато-
атомов Не в первичном пучке задано температурой печи. Напротив в опытах
Дэвиссона и Джермера мы можем полностью игнорировать тепловые ско-
скорости электронов в сравнении со скоростью, приобретаемой ими в уско-
ускоряющем поле. Без большой погрешности можно считать, что все электроны
имеют один и тот же импульс р. Поэтому в этих последних опытах прак-
практически реализуется случай чистого ансамбля, описываемого волновой
функцией rjjp.
Заметим, что часто при определении исходного состояния частиц
вообще не делается никаких измерений, а только предполагается, что
имеется тот или иной чистый или смешанный ансамбль. Справедливость
сделанного предположения проверяется далее по наблюдаемым и измеряе-
измеряемым следствиям, вытекающим из него.
Поэтому волновую функцию или набор волновых функций (в случае
смешанного ансамбля) следует рассматривать как вполне объективную,
не зависящую от наблюдателя, характеристику квантового ансамбля.
В заключение укажем еще на одно существенное различие чистого
и смешанного ансамблей, которое могло остаться незамеченным. Из одних
и тех же волновых функций может быть образован как чистый, так и сме-
смешанный ансамбль. В самом деле, если даны частные состояния т^, г|з2...,
т|з„,..., то из них может быть образована волновая функция Т, предста-
представляющая суперпозицию этих состояний:
п, A4.7)
которая описывает чистый ансамбль. В эту суперпозицию частные состоя-
состояния входят с определенными фазами и амплитудами (Сп = | Сп |eian,
ап-фаза).
С другой стороны, если известно, что система может находиться
в состоянии rj?! с вероятностъю Pv в состоянии \|з2 с вероятностью Р2
и т. д., то мы будем иметь дело со смешанным ансамблем, для харак-
характеристики которого нужно иметь два ряда величин1:
*'■*' *• A4.8,
Вычислим теперь вероятность того, что частица находится в точке х.
В случае чистого ансамбля получим для плотности вероятности:
w (х) = | ф (х) |« = 2 | сп |21 r|jn {xf +22 c*cjf*n{x) rj;m (х). A4.9)
1 В § 44 пояснен другой способ описания смешанного ансамбля с помощью
«матрицы плотности» — величины, аналогичной функции распределения в классической
статистической механике.
54

В смешанном ансамбле эта же вероятность должна быть вычислена так:
вероятность того, что частица будет находиться в точке х, будучи в состоя-
состоянии tyn(x), есть |i|v(*)|2. Вероятность же находиться в состоянии tyn(x)
есть Рп. Поэтому вероятность этого сложного события будет pjtyn(*)|2,
а полная плотность вероятности w(x) будет равна:
оЧ*) = 2рп|фп(*)|«. A4-10)
п
Из сравнения A4.9) и A4.10) мы видим, что в чистом ансамбле имеет место
интерференция между отдельньсми частными состояниями (члены вида
*nCn4J3TO(*); в смешанном ансамбле такая интерференция отсутствует.
Таким образом различие между чистым и смешанным ансамблями
в отношении частных состояний аналогично сложению когерентного и не-
некогерентного света; при вычислении вероятностей в чистом ансамбЬе скла-
складываются амплитуды, а в смешанном ансамбле — интенсивности.
§ 15. Соотношение неопределенностей
Мы перейдем теперь к рассмотрению важнейшего свойства квантовых
ансамблей — к так называемому соотношению неопределенностей.
Напомним, что в классической механике мы интересуемся траекто-
траекториями частиц и их движением по этим траекториям.
Можно было бы думать, что квантовая механика дает некоторое ста-
статистическое описание такого классического движения, подобно тому как
это делается в, классической статистической механике. Простые соображе-
соображения показывают, что это не так. В области микромира механические вели-
величины находятся в иных отношениях, нежели в области макромира, в обла-
области классической механики.
С понятием движения частицы по траектории неизбежно связано пред-
предположение о существовании у частицы в каждый момент времени опре-
определенной координаты х и определенного импульса рх. Первая указывает
положение частицы, а вторая величина указывает, как изменяется это
положение в течение бесконечно малого интервала времени:
x + dx = x + £jj-dt=*x + vxdt, " A5.1)
где т — масса, a vx — скорость частицы.
В статистическом ансамбле частицы могут иметь самые разнообразные
импульсы и координаты, но если это ансамбль классический, то в нем всегда
могут быть выделены подансамбли и с вполне, определенными импульсами
и с вполне определенными координатами. Напротив, такое разложение
квантового ансамбля оказывается невозможным, что указывает на совер-
совершенно отличное от "классического взаимоотношение между локализацией
частицы и ее импульсом. Для того чтобы рассмотреть эту важнейшую осо-
особенность микроявлений, мы будем основываться на опытах по дифракции
микрочастиц. Основной вывод этих опытов заключен в формуле де Бройля,
связывающей импульс и длину волны:
A5-2)
Если под % понимать именно длину волны, то, какова бы ни была при-
природа волн, эта величина не может быть функцией координат х. Выражение
«длина волны в точке х равна Ъ не имеет никакого смысла, ибо по своему
определению длина волны есть характеристика синусоидальной волны,
55

неограниченно простирающейся в пространстве (от х=—со до *= + оо)
% есть «функция» формы волны, а не функция координаты какой-либ<
точки. Поэтому в A5.2) первая часть не может быть функцией координаты х
Следовательно, не может быть функцией координаты х и левая часть равен
ства A5.2), т. е. импульс р.
Подобным же образом нельзя ответить на вопрос: «какова частот;
колебаний маятника в данный момент времени», так как само определени
понятия частоты предполагает, что нужно проследить за многими колеба
ниями маятника1.
Мы приходим к заключению, что коль скоро соотношение де Бройл;
A5.2) признается правильным, то импульс частицы р не может быт
функцией координаты частицы х. В области микромира выражение
«импульс частицы в точке х равен р» не имеет смысла.
Соответственно этому в квантовой области нет таких ансамблей, в кото
рых и импульс и координаты частиц одновременно имели бы вполне опре
деленное значение.
Докажем это важнейшее утверждение сначала для ансамбля, изобра
женного группой волн, рассмотренной в § 7. Как было там показано
группа волн
* йо+Дй
ф (*,*) = ^ c(ft).e-«M'-te>dft A5.3
йо-Дй
может быть представлена в виде [см. G-9)]:
Ik
.e-««/-fco.
A5.4
t—x
Интенсивность | т|з|2 в такой группе волн для некоторого момента времени
изображена на рис. 15. Удвоенное расстояние от точки максимума ||'
/\Л
Рис. 15. Интенсивность | -ф |3 в группе волн в функции х для некоторого
момента времени t
до первого минимума мы можем принять за меру, определяющую раз-
размеры группы. Обозначим его через 2Ах. Из A5.4) следует, что Ах = л/Ыг.
Иными словами,
, Ax-Ak = n. A5.5)
Это чисто волновое соотношение, справедливое для любых волн, показы-
показывает, что произведение линейных размеров группы волн Д* на интервал
1 Эта аналогия принадлежит Л. И. Мандельштаму.
56

волновых чисел Ak тех волн из которых построена группа, есть'величина-
постоянная и равная я.
В частности, если мы желаем послать очень короткий радиосигнал
(малое Ах), то неизбежно в нем будут представлены с заметной интен-
интенсивностью весьма отличающиеся по длине отдельные монохроматические
волны. Поэтому такой сигнал будет принят приемниками, настроенными
на различные волны. Напротив, если мы желаем, чтобы нас принимали
приемники, настроенные лишь определенным образом, то мы должны
посылать монохроматические сигналы, а стало быть, согласно A5-5) —
достаточно длинные.
Возвратимся теперь к квантовой механике. По уравнению де Бройля
px = hk и поэтому, если k меняется в пределах Ak, то импульс р меняется
в пределах
Apx = hAk. A5.6)
Разумея под группой'волн A5.3) группу волн де Бройля, умножим на
постоянную Планка h уравнение A5.5), тогда на основании A5.6) мы
получим:
Apx-Ax^nh. A5.7)
Смысл Арх и А* в формуле A5.7) вытекает из следующего: если мы
будем производить измерение координат частиц, находящихся в состоянии,
описываемом группой волн де Бройля A5.3), то в момент времени t среднее
значение результатов измерения координат будет x==-pnrt. Значения же
результатов отдельных измерений будут разбросаны около х преимуще-
преимущественно в интервале ± Ах. Величина Ах есть неопределенность в коор-
координате х. Если же мы будем в том же состоянии измерять импульс
частиц рх, то среднее значение будет равно рх = ро = hk0, и отдельные
значения будут сосредотачиваться около р0 в интервале Арх = ± h■ Akx.
Величина Арх есть неопределенность в импульсе рх.
Поэтому соотношение A5.7) называется соотношением неопределен-
неопределенностей для импульса рх и сопряженной ему координаты х. Это соотно-
соотношение впервые было установлено Гейзенбергом. Оно является одним из
самых фундаментальных следствий современной квантовой механики
и показывает, что чем уже группа, т. е. чем определеннее значение коор-
координат частиц (малое Ах), тем менее определенно значение импульса
частиц (большое Арх), и наоборот.
Перейдем теперь к доказательству соотношения неопределенностей
для любого состояния частицы, описываемого какой-либо произвольной
волновой функцией ijj. Простоты ради ограничимся одним пространствен-
пространственным измерением; обобщение на большое число измерений совершенно
тривиально. Итак, пусть нам дано какое-либо состояние частицы, изобра-
изображаемое волновой функцией ij; (xI. Волновую функцию мы будем считать
нормированной к единице в области от — оо до +оо.
Для того чтобы установить соотношение неопределенностей в строгой
форме, нам следует прежде всего выбрать меру для отклонения отдель-
отдельных результатов измерений импульса] р и координаты х от их средних
значений ~р и х, иными словами, точнее определить, что мы будем разу-
разуметь под «неопределенностями» Арх и Ах.
1 Время t мы можем не выписывать явно, так как все дальнейшее справедливо
для любого мсЫеита времени. •
57

. В качестве такой меры мы выберем употребляемые в статистике
средние квадратичные отклонения Ар% и Ах21. Эти величины опреде-
определяются следующим образом. Пусть х есть среднее значение величины х.
Если в каком-либо индивидуальном измерении мы получим значение х,
то Ах = х — х будет отклонением результата измерения от среднего зна-
значения х. Среднее значение этого отклонения, очевидно, всегда равно
.нулю:
Ах = х — х = х — х = 0.
Поэтому за меру отклонения индивидуальных измерений от среднего
берут не Ах, а Ах2 — среднее от квадрата индивидуальных отклонений.
Основываясь на этом пояснении, мы можем написать:
Д*« = (*-*)■ = *■-*", A5.8)
Ш = (Рх-Рх)*~Я-р1 .' A5-9)
Не уменьшая общности доказательства, мы можем выбрать для дальней-
дальнейшего подсчета подходящую систему координат. Именно, выберем начало
координат в точке х. Тогда х = 0.' Далее, пусть эта система координат
движется вместе с центром распределения х. Тогда и рх — 0. В этой
-системе координат получим вместо A5.8) и A5.9):
~Ах* = х*, A5.10)
АЙ = Й- A5.10')
Согласно A3.1) и A3.11) имеем:
^ (х) хЦ (х) dx, A5.11)
+00
\d^ A5.11')
Наша задача заключается в установлении связи между Ар% и Ах2. Для
этой цели рассмотрим вспомогательный интеграл:
+ОО
/(£)= ^ |^ + ^|Х "' A5.12)
—00
где £ —вещественная вспомогательная переменная. Раскрывая квадрат
модуля, получаем:
t\^ f) ^d£.^dx. A5.13)
1 Величины У Др|, у Д*2 называк^г «стандартами» или «дисперсией»,
58

Обозначая
+0О
Л= С х211]з|2dx = Дх2, A5.14)
— JO
+0О
—оо
+0О
A5.14')
(здесь произведено интегрирование по частям) \ мы находим
/(Б) = ДБ»-ВБ + С>0. A5.15)
Так как / (£) всюду неотрицательно (при вещественном £), то это
означает, что корни уравнения
/(Е) = 0 A5.16)
комплексны. На основании известной теоремы о корнях квадратного урав-
уравнения, это может быть лишь при условии, что
4ЛС>В2. A5.17)
Подставляя в это неравенство значение Л, В, С из A5.14), A5.14')'
A5.14"), мы приходим к искомому соотношению для Ар% и Д*2:
Apl-Ax2>-j- . A5.18)
Это и есть соотношение неопределенностей в наиболее общем и строгом
виде. Вместе с тем доказано, что нет таких квантовых ансамблей, которые
обладали бы_ тем свойством, что среднее квадратичное отклонение для
импульса Арх и для соответствующей ему координаты Ах2 одновременно
равнялись бы нулю.
Напротив, мы видим, что чем меньше среднее квадратичное отклонение
для одной из этих величин, тем больше оно для другой. Отсюда следует,
что нельзя придумать такой опыт, который позволил бы дать физическое
определение паре х, рх, ибо возможность реализации такого опыта пред-
предполагает существование таких состояний, в которых одновременно Ар%=0
и Дх2=0, что противоречит соотношению неопределенности, основанному,
в конечном счете, на уравнении де Бройля Р=-г~ • Вместе с тем мани-
манипуляции, применяемые в области значимости соотношения де Бройля
(область микромира) для измерения координаты частицы я и ее импульса рх
должны быть взаимно исключающими друг друга: можно рассортировать
частицы либо по их импульсам, либо по их координатам2.
Это выражается в том, что всякая локализация частицы ведет к изме-
изменению ее импульса, которое предсказывается квантовой механикой стати-
статистическим образом.
Нарушение импульса локализацией делает невозможным применение
понятия траектории к движению микрочастиц
1 Мы воспользовались также тем, что в силу интегрируемости гр*гр производные
от 1|з и сама гр исчезают при я^^оо.
2 В работе автора (Journ. of Physics USSR, 2, 71, 1940) показано, что не суще-
существует какой-либо функции распределения, зависящей от (р, х), которая могла бы
изобразить квантовый ансамбль. См. также § 44 этой книги.
89

Стало быть квантовая механика имеет дело с принципиально новыми
объектами, неподчиняющимися классическим законам движения материаль-
материальных точек.
Само название «соотношение неопределенностей» подчеркивает эту
неприменимость: представление «неопределенности» возникает лишь при
неправомерном применении классических величин к новым по своей при-
природе объектам.
В следующем параграфе мы приведем иллюстрации этого положения.
§ 16. Иллюстрации к соотношению неопределенностей
Рассмотрим сначала измерение координаты частицы с помощью щели.
Исходное состояние будем описывать плоской волной де Бройля ijjp.
Пусть волна распространяется по направлению оси ОХ. Это состоя-
состояние обладает той особенностью, что импульс частицы имеет вполне опре-
определенное значение, именно:
„ Px = P>Pv==Pt = °- A6Л)
Таким образом мы имеем дело с ансамблем частиц с заданным импульсом.
Положение частиц (их координаты) в этом ансамбле, напротив, совсем*
неопределено | -фр |2 == const и, стало быть, все положения частиц равно-
равновероятны. Попытаемся фиксировать
хотя бы одну из координат частиц,
например у.
Для этого поставим экран со
щелью, расположив его плоскость пер-
перпендикулярно направлению распрост-
распространения волн так, как это было показа-
показано на рис. 16. Пусть полуширина щели
есть d. Если частица пройдет через
эту щель, то в момент прохождения ее
координата фиксируется положением
щели с точностью до полуширины ще-
щели d. Так как импульс вдоль оси у из-
известен (ру=0), то на первый взгляд ка-
кажется, что мы определили и импульс
ру, и координату у. Однако это совсем
не так. В приведенном рассуждении
пропущено то обстоятельство, что око-
около щели будет иметь место дифракция:
волны будут отклоняться от первоначального направления распростране-
распространения. Вместе с тем импульс частиц при внесении экрана со щелью изменится
и не будет таким, каким он был до внесения экрана.
Среднее значение импульса ру по оси OY останется неизменным: ру=О,
так как дифракция около щели происходит симметричным образом. Оценим
по порядку величины возможное отклонение импульса Ару от среднего
значения. Если мы будем отклонять луч от оси ОХ, то скоро он займет
положение, соответствующее первому дифракционному минимуму (дальше
пойдет первый дифракционный максимум и т. д.). Обозначим угол, образо-
образованный осью ОХ и указанным лучом, через а. Тогда наибольшая интенсив-
интенсивность волн будет приходиться на область от —а до +а. Угол а опре-
определится из того условия, что при этом направлении лучи, исходящие
от двух половин щели, гасят друг друга (разность фаз я). Если длину
60
Рис. 16. Иллюстрация к измерению
Pv и у: дифракция от щели в
экране

волны обозначим через К, то для интересующего нас угла получим из-
известное соотношение
sina = -gy. A6.2)
Полуширина щели d есть не что иное, как неточность Ау, допускаемая
при измерении координаты у.
Далее, psina есть проекция импульса на ось OY. Так как основная
интенсивность волн де Бройля падает в область углов от —а до +а,
то при измерении импульса большинство результатов измерения будет
лежать в интервале от — р sin a до +psina, т. е. разброс измеряемых значе-
значений около среднего значения ру = 0 равен Ар =ps'ma.
Так как по соотношению де Бройля p = 2nh/%, то подставляя в A6.2)
Ару вместо 2nhs'ma/K и Ау, мы получим:
ApyAy^nh. A6.3)
Это соотношение показывает, что чем точнее определяется положение
частиц (чем меньше Ау, т. е. чем уже щель), тем в большей степени
становится неопределенным их импульс (тем больше Ару), и наоборот1.
Благодаря дифракции у щели измерение координаты делает неопре-
неопределенным импульс р, т. е. после прохождения щели частица оказывается
принадлежащей к новому ансамблю, в котором Ару уже не равно нулю.
Другим примером может служить фотопластинка. Мы рассмотрим
идеализированную фотопластинку2. Суть идеализации заключается в том,
что мы будем отождествлять фотопластинку с системой закрепленных ато-
атомов, а ионизацию такого атома — с образованием изображения на фото-
фотопластинке. На самом деле, ионизация одного из активных атомов есть
только начало таких процессов, которые в конце концов приводят к обра-
образованию на фотопластинке проявленного зерна («пятнышка»), которое
и наблюдают на опыте.
Атом можно считать закрепленным или медленно движущимся около
некоторой позиции только в том случае, если он достаточно тяжел 3. Хоро-
Хорошая «идеальная» пластинка должна состоять из бесконечно тяжелых ато-
атомов, имеющих к тому же достаточно малые размеры а, гак как размеры
атома а определяют область, в которой произошла ионизация.
1 Заметим, что в нашем выводе этого соотношения мы воспользовались тем, что
длина волны X, а вместе с тем и полный импульс частицы р не меняются при дифрак-
дифракции. Следовательно, при таком рассмотрении наибольшее значение есть Ару—р, что
соответствует частице, движущейся вдоль экрана. Поэтому может показаться, что
мы можем, ограничившись точностью Дрн=р, добиться сколь угодно большой точно-
точности в определении координаты у, уменьшая ширину щели. Это, конечно, противоре-
противоречит соотношению A5.6). На самом деле это не так. Наше рассмотрение приближенно.
Оно пригодно при условии, что длина волны-X порядка ширины щели. С уменьше-
уменьшением ширины щели характер волнового поля за экраном усложняется. Этому полю
уже нельзя приписать определенной длины волны л. так, как это мы делаем. Разбор
этого случая показывает, что соотношение A5.6) остается верным.
2 Описываемая здесь схема образования изображения осуществляется, напри-
например, в опытах А. П. Жданова (см. Общее собрание Академии иаук СССР 1—4 июля
1946 г.), который фиксирует в толще фоточувствительной эмульсии след частиц косми-
космического излучения. Под эту же схему подпадает образование следов в камере Виль-
Вильсона (см. ниже).
3 Действительно, полагая в соотношении неопределенностей Apx = MAvx, где
М—масса атома, vx— его скорость, мы получим Avx = .. . Отсюда следует, что и
Ах и Avx могут быть малы одновременно только тогда, когда М велико. Бесконечно
тяжелая частица может, стало быть, и занимать вполне определенное положение, и иметь
■определенную скорость (в частности, быть неподвижной).
61

Позднее (§ 51) будет показано, что волновая функция электрона,
находящегося в атоме, отлична от нуля в области порядка а = /г/j/2Ц.У,
где У —энергия ионизации атома, а ц — масса электрона. Величина^, а
равна, по порядку величины, неопределенности в положении электрона
в атоме. Следовательно, этот электрон будет иметь неопределенность
в импульсе Ар ^ /г/а. В этом опыте мы не можем установить, в какой
точке произошла ионизация
атома, а знаем только то, что
область, в которой произошло
столкновение, имеет размеры,
равные примерно а. Поэтому
координата падающего на фо-
фотопластинку электрона х опре-
определяется в лучшем случае с точ-
точностью Ах&iа. С другой сто-
стороны, так какЦ столкновение
происходит с электроном атома,
который имеет неопределен-
неопределенность в импульсе порядка
Ыр ^ /г/а, то после столкнове-
столкновения такую же неопределен-
неопределенность в импульсе Арх будет
иметь и тот электрон, коорди-
координату которого мы определяем.
Умножая Ах^а на^Арж ^ /г/а,
получим
Рнс. 17. Следы я-мезонов с энергией 150 Мэв д„ . Дгг~/г A6 4Л
в камере Вильсона. В центре рисунка упругое х " \ • /
столкновение я-мезона с протоном. Жирный Ичмрпрнир. кпопттинят чягтип
след направо - след протона отдачи. Внизу ИзмеРение' координат частиц
кругообразные следы медленных электронов, всегда связано с существенным
сильно отклоняемых магнитным полем. (Фото воздействием на частицы изме-
выполнено в лаборатории ядерных проблем рительного аппарата. В рас-
в г. Дубне) сматриваемом случае фотогра-
фотографирования положения частицы условием возможности наблюдения коор-
координаты является ионизация атома. Для этой ионизации необходима энер-
энергия J, которая здесь черпается из энергии самой частицы. Если перво-
первоначальный импульс частиц есть р0, то должно быть'
A6.5)
В противоположном случае фотографирование невозможно.
Наблюдение следа частицы в камере Вильсона полностью подходит
под эту схему фотографирования, так как такой след возникает в* ре-
результате последовательных ионизации атомов газа, наполняющего камеру,
т. е. представляет собой ряд последовательных «фотографий», в изложен-
изложенном выше понимании1 (рис. 17).
На основании A6.5) мы можем заключить, что для получения следа
в камере Вильсона необходимо, чтобы_импульс фотографируемой частицы р0
удовлетворял неравенству р0 > У|л/.
1 В камере Вильсона мы наблюдаем след частицы не по ионам} а по капелькам
конденсировавшегося на ионах пара. Пока происходит фотографирование следа, ионы
успевают заметно сместиться из своих первоначальных положений. Поэтому практи-
практическая точность определения положения частицы методом камеры Вильсона несрав-
несравнимо грубее, нежели теоретическая точность, определяемая размерами атома; на самом
деле она определяется размером капелек н их смещением за время фотографирования.
62

Обратимся теперь к косвенному определению координат микрочастиц.
Покажем, что и в этом случае будут возникать ансамбли, удовлетворя-
удовлетворяющие соотношению неопределенностей. В качестве примера косвенного-
опыта можно привести определение положения частиц с помощью микро-
микроскопа (рис. 17). Осветим частицу, находящуюся около *=0, светом
длины волны %. Пучок света паралле-
параллелен оси ОХ. В объектив микроскопа
будет попадать рассеянный свет. Из тео-
теории микроскопа известно, что положе-
положение частицы определяется с точностью
до Ах ^ -h- , где 2е — угол, под которым
sin б
виден объектив из точки положения
объекта1. Таким образом может быть
отобран ансамбль частиц с Ax =
При достаточно малом К величина Ах
в принципе может быть как угодно
мала. Однако при каждом акте рассея-
рассеяния импульс фотона меняется и, как
видно из рисунка, проекция изменения
импульса на ось ОХ будет лежать в пре-
пределах ± ^ sin е ( здесь -v- = -^ есть
■у Рис. 18. Определение;?координат ча~
импульс фотона ) . Этот импульс будет стиц с помощью микроскопа
передаваться частицам так, что они полу-
получат импульсы, разбросанные в пределах Apx^~sine. Отсюда видно, во-
первых что, создавая ансамбль локализованных в малой области (А*)
частиц, мы должны применять очень сильное энергетическое воздействие
(малые % — большие кванты!), во-вторых, что ансамбль с малым Ах будет
иметь большое Арх. Перемножая Арх и Ах, получим Арх- Дх^2яЛ2.
В случае несвободных частиц косвенное измерение является един-
единственно возможным. Например, координата электрона, находящегося
внутри атома, определяется по рассеянию пучка свободных частиц (элек-
(электронов рентгеновских лучей). В этих случаях, однако, всегда получаются
сведения не о положении отдельного электрона в отдельном атоме,
а о распределении этих положений в большой совокупности атомов,
находящихся в одном и том же состоянии, т. е. непосредственно нахо-
находится ItbMl2 (см. теорию столкновений, § 78).
В заключение приведем еще один пример определения координат
частиц. Допустим, что частица заключена внутри ящика с непрозрачными
для частицы стенками. Размер ящика пусть будет I. Будем теперь сдви-
сдвигать стенки ящика (/->0). Тогда положение центра ящика х и опреде-
1 Неточность Ах ■
' sin e
возникает из-за дифракции у объектива микроскопа.
сеяние (после чего она будет принадлежать другому ансамблю), а по одному рассеян-
рассеянному кванту нельзя судить о положении частицы (в фокальной плоскости не будет
изображения). Правильная математическая теория этого опыта, исходящая из статисти-
ческогТтолковаиия ^-функции, была дана Л. Й. Маидельштамом в его лекциях покван-
товой механике.
63

лит положение частицы. По предположению, ящик непрозрачен для час-
частицы. Следовательно, волновая функция частицы отлична от нуля только
внутри ящика. Отсюда следует, что Ах2 э* /2. По мере уменьшения
объема ящика будет'возрастать разброс импульсов
В этом случае р = 0 и, стало^быть, средняя энергия частицы
*г — 2ц ' 8ц/2
Поэтому сжатие ящика требует затраты работы, которая будет неогра-
неограниченно возрастать по мере увеличения степени локализации частицы
'|Ддс = /—>0|. Отсюда следует, что чем в меньшей области пространства
локализованы частицы, тем большей энергией должны они обладать.
'Опыт подтверждает этот своеобразный вывод квантовой теории. Так,
например, электроны в атомах (размеры атомных оболочек 10~9 —10~8 см)
имеют энергию 10 — 100 эв, а нуклоны в^ядрах (размеры ядер 10~13)
■имеют энергию порядка #1 Мэв.
Обратимся теперь к измерению импульса. Рассмотрим прежде всего
дифракционный опыт, положенный нами в основу определения импульса.
На рис. 14 (стр. 49) изображена решетка, первичный пучок (i) и дифра-
дифрагированные пучки (г, d, ...).
Пусть ширина первичного пучка есть /, а постоянная решетки d.
Эффективное для опыта число штрихов решетки будет N = l/d. Из теории
дифракции известно, что ]такая'решетка позволяет различить две волны К
и % + А%, где
^ ?4
Зто есть разрешающая сила дифракционной решетки1. Следовательно,
наша решетка разделит исходный ансамбль на два ансамбля, например,
(г) и (d), характеризуемых двумя различными [импульсами, если эти
импульсы различаются более, чем на
_т. A6.7)
Для того чтобы пучки разделились (условие возможности измерения),
мы должны отойти с цилиндром Фарадея на расстояние Ах (отсчиты-
(отсчитываемое вдоль пучка (г) или (d)), которое больше, нежели l/а, где " -
угол между пучками (г)*и (d). Поэтому Ар- Ах > 2nh у-—. Так как d и %
•одного порядка2, а угол а считается малым, то *
Ар-Ах>2як, A6.8)
т. е. произведение размера пучка Д# (область локализации частицы)
на неопределенность в имйульсе Ар, обусловленную конечной разреша-
разрешающей силой решетки, должно быть больше 2яЛ.
Приведем еще пример определения импульса частиц по частоте рас
сеянного света. Простоты ради ограничимся одним измерением. Пусть рх
есть импульс частиц до столкновения с квантом света, а р'х — то же после
1 См., Г. С. Ландсберг. Оптика. ГТТИ, 1947.
2 При % > d вообще не наблюдается дифракции.
64

столкновения. Частота падающего света пусть будет ш, а рассеянного ш'.
Тогда из закона сохранения энергии имеем:
и из закона сохранения импульса:
= Рх — P-r- (ID. 10)
С С h* rx \ I
Отсюда находим:
Таким образом, зная ш и ш', можно определить импульс частицы рх.
Однако из этого опыта мы не получаем никаких сведений о местополо-
местоположении частицы: место рассеяния совершенно неопределенно. Мы могли бы
определить это место с точностью Ах, если бы вместо монохроматиче-
монохроматической волны послали бы ограниченный сигнал шириною Ах. Но в таком
сигнале, как мы знаем, существует целый набор частот Ak = —&т— •
В силу этого импульса частиц был бы определен с точностью Арх =
= hAK = — , так, что Арх- Ах> як.
В заключение рассмотрим еще один опыт, часто применяемый на практи-
практике. Допустим, что мы намерены определить импульс нейтрона р путем столк-
столкновения его с протоном; импульс протона в исходном состоянии будем
считать равным нулю. После столкновения (предполагая центральный
удар) получим импульс нейтрона равным нулю, а импульс протона будет
равен исходному импульсу нейтрона р (мы считаем массы протона и ней-
нейтрона равными). Этот импульс можно измерить, например, с помощью
измерения искривления следа протона в камере Вильсона, возникающего
под действием магнитного поля. Тем самым будет измерен первоначаль-
первоначальный импульс нейтрона. Однако в этом опыте ничего неизвестно о месте
столкновения. Пользуясь камерой Вильсоиа, мы, конечно, можем просле-
проследить это место —это будет начало трека протона, получившего удар.
Но, как было выяснено ранее, метод камеры Вильсона позволяет опреде-
определить положение частицы, а следовательно, и начало трека с максимальной
точностью Ах^а (а— размеры атома)*. При этом импульс частицы опре-
определяется с точностью Ap^h/a, т. е. мы не будем знать импульс протона
точнее, нежели с этой степенью точности. Тем самым будет внесена
такая же неточность в определении импульса нейтрона. Для произве-
произведения неопределенностей опять получим: Ap-Ax~>h.
Эти примеры служат иллюстрацией отсутствия противоречий между
утверждением о существовании соотношения неопределенностей как след-
следствия общих принципов квантовой механики и возможностями измеритель-
измерительных ацпаратов.
1 Это «идеальная» точность, которая на практике никогда ие достигается; см.
сноску иа стр. F2).
5 Д. И. Влохинцев 65

§ 17. Роль измерительного прибора
При изучении любых явлений статистическими методами измеритель-
измерительные приборы, служащие как для фиксации статистических ансамблей, так
и для анализа распределения в этих ансамблях, должны сами стоять за
пределами этих ансамблей. Иными словами, они должны быть лишены
элементов случайного, свойственного исследуемым с их помощью стати-
статистическим совокупностям 1.
Между тем всякий прибор, как и любое тело, состоит из атомов,
молекул и тому подобных микрообразований, совершающих какие-то движе-
движения, т. е. с точки зрения квантовой механики заведомо принадлежат к не-
некоторому квантовому ансамблю. Поэтому, на первый взгляд создается
некоторое затруднение. Из этого затруднения квантовая механика дает
блестящий по остроумию и эффективности выход: измерительный прибор
должен быть устроен так, что для осуществления его действия в конечном
счете используются только его классические свойства, т. е. такие свойства,
в которых постоянная Планка h не играет роли. Такой прибор мы на-
называем «классическим» или «макроскопическим». Суть его в том, что он
максимально освобожден от квантовой статистичности.
Любой из рассмотренных в § 16 примеров определения рх и х может
служить иллюстрацией «классичности» приборов. В качестве таковых
служили неподвижные экраны со щелями, тяжелый атом идеальной фото-
фотопластинки, ящик с непрозрачными и неподвижными стенками, дифракцион-
дифракционная решетка с жестко фиксированными штрихами или любой спектроскоп
для определения длины волны рассеянного света.
Все эти аппараты мы рассматривали как объекты классической физики,
т. е. рассматривая их действие, мы игнорировали в одном из существен-
существенных пунктов постоянную Планка h. Таким образом приборы измеряют
классические корпускулярные величины.
Набор таких величин, достаточный для определения волновой функ-
функции мы будем называть полным набором, а само измерение пол-
полным измерением.
В классической механике полное измерение состоит в измерении
импульсов и координат частиц. Так как в классической механике все
величины, по крайней мере в принципе, одновременно измеримы, то можно
сказать, что здесь существует лишь одно полное измерение.
Измерив, например, декартовы импульсы и координаты частиц (р, х),
мы можем вычислить все остальные величины, в том числе и обобщенные
импульсы и координаты (Р, Q), которые также образуют полный набор
величин и'так же хорошо определяют движения, как и (р, х). Более того,
ничто не мешает нам, усложнив измерение, измерить и (р, х) и (Р, Q) одно-
одновременно. В силу непротиворечивости классической механики вычислен-
вычисленные значения (PQ) совпадут с измеренными. Поэтому переход от одной
системы полного набора величин к другой системе, в пределах классиче-
классической механики, является несущественным.
В квантовой области полный набор величин, определяющий %р, а вместе
с тем и квантовый ансамбль, так же как и в классической механике, не
является единственным.
Но принципиальное отличие квантовой, механики от классической
заключается в том, что в квантовой механике различные наборы являются,
вообще говоря, взаимоисключающими. Соответственно этому в квантовой
механике существует много различных полных измерений, несовместимых
1 О понятии «случайного» в материалистической диалектике см. Ф. Энгельс,
Диалектика природы.
66

друг с другом. Так, существует квантовый ансамбль, определенный по отно-
отношению к прибору, фиксирующему координаты частиц х, у, z. Это один из
возможных полных наборов.
Такой ансамбль характеризуется волновой функцией tyX'vz'{x, у, z)
(см. § 14), выражающей тот факт, что все частицы ансамбля имеют коорди-
координаты х=х', у=у', z=z'. Другой пример, ансамбль с точно определенным
импульсом рх=рх, Ру—р'у> pz=p'z- Волновая функция такого ансамбля
будет typxpypfa, у, г). Этот ансамбль, опять-таки, с точки зрения кванто-
квантовой механики, определен с предельной полнотой, но он кардинально отли-
отличается от предыдущего.
Следовательно, характер квантового ансамбля совершенно различен
в зависимости от тех признаков, которыми он определен (т. е. в зависимости
от типа полного набора величин) и будет существенно изменяться, если
будут производиться измерения нового полного набора, несовместимого
с исходным. Поэтому состояние квантового ансамбля нельзя понимать без-
безотносительно к тому полному набору величин, которым он определен.
В этой связи измерительные приборы, определяющие различные полные
наборы, следует рассматривать как «системы отсчета», с помощью кото-
рых фиксируется состояние квантового ансамбля1.
Суть столь глубокого различия между определениями состояния в клас-
классической и квантовой области заключается в том, что в классических кон-
концепциях не существовало никакого абсолютного мерила малости. Изучение
микромира открыло существование ряда атомных констант, дающих
такое мерило: элементарный заряд е, элементарная масса электрона и пози-
позитрона ц, массы простейших тяжелых частиц протона тр и нейтрона тп,
постоянную Планка h и другие.
Мы не знаем сейчас в точности тех ограничений классических концеп-
концепций и тех новых понятий и представлений, которые должны вытекать из
существования элементарного заряда и массы, но нам известно, что влечет
за собой существование кванта действия h. Существование кванта действия
ведет к явлению дифракции частиц, которое делает невозможным одновре-
одновременно применение к движению микрочастиц таких, например, величин,
как р и х.
Рассмотрим теперь подробнее, каким образом измерение влияет
на квантовый ансамбль.
Будем считать наш ансамбль заданным волновой функцией ip (х)
(чистый ансамбльJ. Рассмотрим сперва измерения импульса. Для этого
разложим i|) (x) в спектр по волнам де Бройля
A7.1)
Пусть всего сделано /V измерений и в N' случаях получено значе-
значение р, лежащее около р', в М" случаях — около р", в М'" случаях —
около р'" и т. д. {N = N' + M" + N'" + ...)• ТогДа имеем (ср. § 14):
^ ^ ^ , ... A7.2)
1 Это, конечно, не означает того, что если нет измерительного прибора, то нет
и квантового ансамбля: в природе сами по себе осуществляется ситуации, фиксирую-
фиксирующие ансамбль, т. е. соответствующие измерению.
2 Только простоты ради мы рассматриваем чистый случай и ограничиваемся
одним пространственным измерением х, что не существенно для выяснения сущности
дела. О влиянии измерения на смешанный ансамбль см. § 44.
5* 67

В результате произведенных измерений N' частиц выявлен новый
чистый ансамбль с р = р'- характеризуемый новой волновой функцией
typ' (x). Таким образом измерение из первоначального ансамбля с неопре-
неопределенным импульсом выбирает подансямбли с определенными значе-
значениями импульса р', р", р"',..., которые характеризуются новыми
функциями %,'(*), i|v(*), %>"' (*), ... соответственно.
Первоначальное состояние ty(x) переходит в одно из состояний вида
%(х). Это изменение волновой функции называют «редукцией» (све-
(сведением) волнового, пакета. Физически редукция означает, что после изме-
измерения частица оказывается принадлежащей к новому чистому ансамблю.
Весь ансамбль, возникший в результате измерений характеризуется
серией волновых функций tyP'(x), typ»(x), \|v(*). ... с соответствующими
вероятностями | с(р') \2dp', \ c\p")\2dp", \c{p'")\2dp'" т. е. является
ансамблем смешанным.
Подобная же ситуация осуществляется и в других случаях. При-
Приведем еще два примера. Пусть речь идет об измерении координаты х.
Разложим ty(x) в спектр по волновым функциям, характеризующим состоя-
состояние с определенным значением х. Такая функция имеет вид \|v (x) =
= д(х' — х). Поэтому разложение гласит:
= Vc(x')8(x'-x)dx'.
A7.3)
В силу свойств б-функции отсюда сразу же следует с (х') = ^ (х').
Если в N' случаях будет получено х около х', в N" случаях — х около х"
и т. д., то
N
A7.4)
'1 | г (y'"\
-JJ— — \ С(Х )
|2 dx'" — I
| UX — |
""\ I2 dx'
) | UX
При каждом измерении первоначальная функция ty(x) сводится к одной
из функций вида tyX'(x) = 6(x — х')-
Эта редукция показана на рис. 19 \
Мы_ видим, что при измерении координаты опять-таки возникает
смешанный ансамбль, в котором новые чистые подансамбли вида i)v(*),
,,, i|3x»(x), ... представлены с вероят-
вероятностями | г|?(дс') |2, | г)) (хп) |2, т.е. эта
вероятность, как и в случае измере-
измерения импульса, определяется интен-
интенсивностью | с (х') |2, "*с которой чи-
чистое состояние i|v (x) представлено
в исходном чистом состоянии 1|з (х)
Рис. 19. Редукция волнового пакета Щх) ^ этом специальном случае с (х') =
(криваяа)кг()*' (х) (кривая Ь) после измере- ~~ W\x ))
р)ty () (р ) р
иия координаты х, оказавшейся равной л:'
Позднее мы покажем (§ 22), что
б
(§ )
если измеряется любая механичес-
механическая величина L, могущая принимать значения L, L2, L3,..., Ln', то,
чтобы найти вероятность того, что L = £„, нужно разложить г|з (*) в спектр
1 Напомним (см. § 16), что измерение координаты требует энергии, которая
черпается либо из прибора, либо из самой частицы. ' '
68

ГЛАВА III
ИЗОБРАЖЕНИЕ МЕХАНИЧЕСКИХ ВЕЛИЧИН
ОПЕРАТОРАМИ
§ 18. Линейные самосопряженные операторы
Как мы видели, в квантовой области не существует таких состояний,
в которых импульс и координата частиц имели бы одновременно опре-
определенные значения. Это обстоятельство находит свое отображение и в фор-
формальной стороне теории: математический аппарат квантовой механики
резко отличается от математического аппарата классической механики,
в которой задание пары величин р, х имеет полный смысл. Переходя
к изложению этого аппарата, мы в качестве исходного пункта исполь-
используем выражения для среднего значения функций координат или импуль-
импульсов в состоянии ty (х, у, г), приведенные в § 13. Там мы имели для
среднего значения функции координат частицы формулу A3.1):
F (х, у, z) = ^ ф* (х, у, г) F (х, у, г) ф (*, у, z) dx dy dz A8.1)
и для среднего значения функции импульсов формулу A3.6):
F (рх> Ру Рг) =
(x,y,z)dxdydz. A8.2)
Эти формулы получают совершенно одинаковый вид, если проекции
импульса рх, ру, pz изобразить операторами:
Рх= -ihjx, />„--= -ih£, Pz= ~lhjL A8.3)
и соответственно этому обозначению написать A8.2) в виде:
р{Рх< Р'у Рг)= *
= ^* (х, у, z) F (Рх, Ру, Р2) ф (х, у, z) dx dy dz. A8.4)
Таким образом мы приходим к изображению функций от импульса
F(px, Ру, pz) оператором F(PX, Py, Pt).
Этот результат подсказывает, что и другие более сложные механи-
механические величины L(px, py, pz, x, у, z), зависящие как от координат,
так и от импульсов, также должны изображаться операторами. И в са-
самом деле, оказывается, что все взаимоотношения между механическими
величинами в квантовой области могут быть выражены на языке опера-
операторов определенного класса. В этом заключается фундаментальное зна-
значение введения операторов в квантовую механику.
70

Чтобы выделить класс операторов, встречающихся в квантовой меха-
механике, обратимся сперва к общему определению оператора. Независимо
от конкретного вида под оператором L будем разуметь символ, показы-
показывающий, каким способом каждой из рассматриваемого класса функций
и(х) сопоставляется другая функция v(x). Это символически записы-
записывается в виде умножения и на L:
Lu{x) = v(x). A8.5)
В этом равенстве под L можно разуметь, например, умножение на x(L = x),
дифференцирование по x(l = -^ J, извлечение корня {L = Y) и т. п.
Из всего разнообразия мыслимых операторов для изображения меха-
механических величин в квантовой области употребляется только один опре-
определенный класс операторов, так называемые линейные самосопряженные
(иначе — эрмитовские) операторы.
Оператор L называют линейным, если он обладает следующим
свойством:
L{c1u1-\-c2u2) = c1LuJ + c2Lu2, ' A8.6)
где иг и и2 — две произвольные функции, а с1п с2 — произвольные посто-
постоянные. Ясно, что У не является линейным оператором; напротив, -ч—
есть оператор линейный.
Ограничение линейными операторами вытекает из принципа супер-
суперпозиции состояний. Свойство линейности оператора, выраженное в A8.6),
означает, что применение оператора к суперпозиции двух функций и^ и и2
равно суперпозиции результатов применения этого же оператора к каж-
каждой из функций порознь (L (с^^-с2ы2) = clv1 + с2у2, где vx = Lux\ v2 = Lu2),
т. е. мы требуем, чтобы применение операторов не нарушало принципа
суперпозиции.
Линейный оператор!, называют самосопряженным (эрмитов-
ским), если имеет место равенство:
\ u*i (x)-Lu2{x)-dx=\ u2(x)-L*u*(x)-dx, A8.7)
2
где интеграл взят по всей области изменения переменной х, а и* и и,_
суть две произвольные функции весьма широкого класса1. Если пере-
переменных много, то под dx следует разуметь dx dy dz....
Значение условия самосопряженности, как мы увидим позднее, заклю-
заключается в том, что только подчиняющиеся этому условию операторы могут
изображать вещественные (не мнимые) физические величины.
Поясним свойство A8.7^на примере оператора импульса Рх= —ih-^-.
Имеем:
ih \ u2~j dx= J u2-P*u*-dx
1 Они должны быть интегрируемы и иметь производные, равные нулю, на грани-
границах области интегрирования.
71

[так как и*(±со) = и2(±со) = 0]. Таким образом, Рх есть линейный
и самосопряженный оператор. Легко видеть, что оператор -у- линейный,
но не самосопряженный; в самом деле,
Имея в распоряжении некоторые операторы, мы можем построить из них
другие. Способы построения из простых операторов более сложных выте-
вытекают из определения самих операторов и могут быть сформулированы
в виде несложных алгебраических правил. Рассмотрим два линейных
и самосопряженных оператора А и В. Будем называть суммой этих двух
операторов такой оператор С, что
A8.9)
Символически запишем это в виде:
С = А + В. ■ A8.10)
Например, если A = i-^-, а В = х, то из A8.9) следует
Несколько сложнее определится умножение. Под произведением двух
операторов А и В будем разуметь такой оператор С, что
С$ = А(В$), • A8.11)
т. е. сперва следует подействовать на г|з оператором В, а потом на этот
результат подействовать оператором А. Если тот же окончательный
результат может быть достигнут оператором С, то С и будет произведе-
произведением А и В. Символически это запишем так:
= AB. A8.12)
dx
Пример. А = i -д- , В = х, тогда
отсюда следует, что
4-:
Существенно, что произведение операторов зависит от порядка множи-
множителей. В произведенном примере имеем:
= «g, т. е. C = ix±.
Поэтому, если имеются два оператора А и В, то кроме произведения
С можно образовать еще другое произведение:
С' = ВА. A8.12')
Установленные правила позволяют производить с операторами сложе-
сложение, вычитание и умножение так же, как это делается в обычной алгебре,
72

за исключением одного пункта: вообще говоря, нельзя менять порядка
сомножителей. Например
но не А2 — В2.
Такая алгебра, в которой нельзя менять множителей, называется
алгеброй некоммутативных величин, а сами величины некоммутативными
(неперестановочными) или некоммутирующими.
Если оба произведения С и С' равны:
АВ-ВА = 0, A8.13)
то операторы А и В называются коммутирующими (перестановочными).
В противном случае их называют некоммутирующими. Оператор F —
— АВ — ВА называется коммутатором операторов А и В.
При умножении линейных самосопряженных операторов следует иметь
в виду, что произведение их не будет, вообще говоря, также самосопря-
самосопряженным оператором. Именно,
АВ = ^(АВ + ВА) + ^(АВ-ВА). A8.14)
Пользуясь самосопряженностью каждого из операторов А и В, с помощью
A8.7) можно доказать, что оператор
^ • A8.15)
будет самосопряженным, а оператор
^ A8.16)
не будет обладать этим свойством, кроме случая коммутирующих опера-
операторов, когда О = 0. Так как всякий оператор коммутирует сам с собой,
то из сказанного следует, что любая (целая и положительная) степень
линейного самосопряженного оператора А:
Ап = А-А- ... А A8.17)
будет оператором такого же рода.
Пользуясь изложенными правилами, мы можем, исходя из известных
нам операторов проекций импульса Рх, Ру, Рг A8.3) и операторов коор-
координат частицы х, у, z, построить более сложные линейные и самосопря-
самосопряженные операторы L.
§ 19. Общая формула для среднего значения величины
и для среднего квадратичного отклонения
Основная идея применения операторов в квантовой механике заклю-
заключается в том, что каждой механической величине L в квантовой механике
сопоставляется изображающий ее линейный самосопряженный оператор L.
Символически это запишем так:
Вопрос о том, какую именно физическую величину изображает тот

или иной оператор, решается свойствами этой величины и способами ее
наблюдения. В тех случаях, когда изображаемая оператором L квантовая
величина обладает свойствами аналогичными свойствам некоторой класси-
классической величины L, для обеих величин употребляют одно и то же название.
Например, если и имеется классическая величина L —функция импуль-
импульсов и координат L — L(px,py,pz,x,y,z), то линейный и самосопряжен-
самосопряженный оператор L, построенный по правилам предыдущего параграфа из
операторов проекций импульса Рх, Ру, Pz и операторов координат х, у, z,
будет равен:
L = L(PX, Pv, Pz, x, у, z).
Самосопряженный оператор L будет изображать квантовую величину со
свойствами, аналогичными классической величине L(px, ру, pz, x, у, zI.
Разумеется, не все линейные и самосопряженные операторы, образо-
образованные из Рх, Ру, Pz и х, у, z будут изображать величны, имеющие простой
физический смысл и подчиняющиеся простым законам. Так же обстоит
дело и в классической теории. 1ак, величина -£— имеет смысл кинети-
кинетической энергии и подчиняется закону сохранения (в отсутствии внешних
сил), величина же рх3 не имеет какого-либо общего правила поведения
и поэтому не играет никакой роли в механике.
Связь между операторами и измеряемыми величинами устанавливается
с помощью формулы для среднего значения величины L в ансамбле,
описываемом волновой функцией i|). Именно, в квантовой механике при-
принимают, что среднее значение L величины L, изображаемой линейным и са-
самосопряженным оператором L в чистом ансамбле, описываемом функцией
г|з, определяется формулой:
1= ^ V-Lty-dx, A9.1)
где под dx разумеется элемент объема в пространстве независимых перемен-
переменных, и интеграл взят по всей области изменения этих переменных. Ясно,
что наши прежние определения A8.1) и A8.2) являются частным случаем
A9.1). Чтобы получить A8.1) из A9.1), следует положить L = F (х, у, z),
а под dx считать dx, dy, dz. Чтобы получить A8.2), следует положить
На основании свойства самосопряженности оператора L, мы можем написать
A9.1) в эквивалентной форме:
L= \ 1|з • Li];* • dx A9.1')
{для этого полагаем в A8.7) ы* = 1|з*, ы2 = 1|з]. Из сравнения A9.1) и A9. Г)
следует, что
1 = 1*, A9.2)
т. е. среднее значение величины, изображаемой самосопряженным опера-
оператором, вещественно.
1 Поскольку волновая функция рассматривается как функция координат частицы
х, у, г, постольку действие «операторов» х, у, г сводится просто к умножению функ-
функции на х, у или г, действие оператора F (х, у, г)—к умножению на F (х, у, г).
74

Мы получим более детальные сведения о величине L, если вычислим
помимо ее среднего значения L еще и среднее квадратичное отклонение
AL2, указывающее, насколько в среднем отклоняются результаты отдель-
отдельных измерений в ансамбле от их среднего значения. Вычислим AL2. Для
этого следует построить оператор, изображающий величину AL2. Отклоне-
Отклонение от среднего определяется как AL = L — L. Стало быть, оператор,
изображающий его, будет
AL = L-L. A9.3)
Так как квадрат отклонения AL2=(L — LJ, то оператор для AL2 будет:
(ALJ = (L-LJ. A9.4)
Пользуясь общим определением среднего значения A9.1), мы найдем
ДТ2= J y*(ALLp-dx. A9.5)
Таким образом, зная оператор L, мы можем вычислить и AL2.
Величина AL2 должна быть неотрицательной. Это легко доказать,
пользуясь самосопряженностью оператора L. Так как L есть число, то
оператор AL также самосопряженный. Поэтому, пользуясь A8.7) и пола-
полагая в A9.5) ty* = и*, (Д1л|з) = и2, находим:
AT2 = J (ALi|>) (&L*V) dx = ^ | ALi|;21 dx, A9.6)
так как |ALi|J|>0, то из A9.6) следует, что
АТ2>0, A9.7)
(как и должно быть) среднее квадратичное отклонение всегда положи-
положительно или равно нулю.
§ 20. Собственные значения и собственные функции
операторов и их физический смысл. «Квантование»
Формулы предыдущего параграфа дают выражение для среднего зна-
значения L и среднего квадратичного отклонения AL2. Эти формулы ничего
не говорят о том, каковы будут значения величины L в отдельных изме-
измерениях.
Чтобы найти возможные значения величины L, обратимся к таким
состояниям i);L, в которых интересующая нас величина имеет только одно
значение L. В таких состояниях среднее квадратичное отклонение AL2 = 0.
Стало быть, для этих состояний на основании A9.6) имеем:
|ALi|5L |2 dx = 0. B0.1)
Так как под интегралом стоит существенно положительная величина, то
из B0.1) следует:
= 0.
Модуль комплексного числа равен нулю только* тогда, когда само число
равно нулю. Поэтому мы получаем:
75

или, имея в виду значения оператора AL A9.3) и то, что в рассматри-
рассматриваемом состоянии L = L, мы находим окончательно
Lt|}L = b|)L. , B0.2>
Ввиду того, что L есть оператор, найденное нами равенство-
является линейным уравнением для нахождения волновой функции ijjL
того состояния, в котором величина, представляемая оператором L, имеет
единственное значение L. В большинстве случаев, оператор L будет диф-
дифференциальным оператором, и уравнение B0.2) — линейным однородным
дифференциальным уравнением.
Известно, что решение дифференциального уравнения определена
единственным образом только в том случае, когда заданы краевые усло-
условия 1.
С другой стороны, при заданных краевых условиях линейное диф-
дифференциальное уравнение L^ = Lty имеет нетривиальное (т. е. отличное от
нуля) решение, вообще говоря, не при всех значениях параметра L,
а только при некоторых избранных: L — Lv L2, L3, ..., Ln, ... Соответ-
Соответствующие решения %, tjJ, г|;3, ..., tyn, ... называются собственными
функциями, а значения параметра Lv L2, L3, ..., Ln, ..., при которых
существуют решения, называют собственными (иногда говорят харак-
характеристическими) значениями параметра уравнения B0.2).
Наиболее общеизвестный пример такой задачи представляет задача
о колебаниях закрепленной на концах струны. Уравнение движения
в этом случае имеет вид:
S + fe2" = 0' B0-3>
d2
так что L = — ^з > а L = k2. Область, в которой ищется решение, есть
0<л:</, где / — длина струны. Краевые условия будут и = 0 при х = 0
и х = /. Собственные функции для такой задачи равны ип (х) — sin ^- ,
а собственные значения Ln = fe£ = ^-, п— 1, 2, 3,... 2.
В квантовой механике волновая функция всегда определяется во
всей • области изменения тех переменных, которые являются ее аргу-
аргументами (например, ty(x, у, z) определено в области: — оо<х< + °°>
— оо<г/< + °°> — оо < z < -j- °о и т. п.). Поэтому в квантовой механике
мы не можем сформулировать краевые условия для волновой функции
столь непосредственным образом, как они формулируются в классических
задачах о колебании тел.
Однако можно показать3, что из требования сохранения полного
числа частиц вытекают некоторые естественные требования к волновым
функциям, которые оказываются эквивалентными краевым условиям. Тре-
Требования сохранения числа частиц сводится к тому, что вероятность найти
частицу где-либо в пространстве не должна зависеть от времени, т. е. что
)*i|)do = 0. B0.4)
1 Речь идет об уравнениях, не содержащих производных по времени, так что
задание начальных данных отпадает. ~
2 Проблема нахождения собственных значений подробно освещена в книгах:
В. И. Смирнов, Курс высшей математики, тт. III, IV; Р. КурантиД. Г и л_ь-
берт, Методы математической физики, т. I, ГТТИ, 1933.
3 См. дополнение VIII.
76

здесь интеграл распространен по всей области изменения аргументов
^-функции, так что он равен вероятности того, что частица обязательно
где-то находится. Суть дела заключается в том, что условие B0.4) может
быть выполнено только тогда, когда волновые функции имеют достаточно
корректное поведение, а именно: 1) если они конечны во всей области
изменения переменных, за исключением, быть может, некоторых (особых)
точек, где они могут обращаться в бесконечность, не слишком сильно1;
2) если они имеют достаточное число непрерывных производных (также
могущих в отдельных точках не слишком сильно стремиться к бесконеч-
бесконечности); 3) если они однозначны. Более жестко, но достаточно для целей
нерелятивистской квантовой механики эти требования могут быть сфор-
сформулированы в виде трех требований: 1) конечности, 2) непрерывности
и 3) однозначности волновой функции во всей области изменения ее
аргументов.
Эти весьма скромные требования, предъявляемые к решениям урав-
уравнения B0.2), ведут к тому, что во многих случаях решения, обладающие
указанными свойствами A, 2, 3), существуют не при всех значениях L,
а лишь при некоторых, избранных L = Lv L2, L3, ..., Ln, ..., т. е. мы
приходим к задаче о нахождении собственных функций и собственных
значений уравнения B0.2), на основе естественных требований, вытекаю-
вытекающих из условия сохранения числа частиц B0.4).
Вместо «собственные функции уравнения» и «собственные значения
параметра уравнения» мы будем обычно говорить о собственных функ-
функциях и собственных значениях оператора L, которым определяется вид
уравнения B0.2).
Мы будем считать, что никаких значений величины L нельзя наблю-
наблюдать на опыте, кроме тех, которые являются собственными значениями
оператора L. Иными словами, в квантовой механике постулируется:
совокупность собственных значений оператора L: Lt, L2, L3, ..., Ln, ...
тождественна с совокупностью всех возможных результатов измерения
механической величины L, изображаемой оператором L. Это и есть как
раз тот постулат, посредством которого устанавливается связь между-
междуизображением величин операторами и опытом: математика позволяет
предсказать набор собственных значений, а опыт позволяет проверить,
таков ли он, каким его предсказывает теория.
Соответствующие собственным значениям Lv L2. ..., Ln состояния
определяются собственными функциями 1ф1, ty2, ..., tyn, .... В каждом
из этих состояний AL2 = 0 и величина L имеет только одно из значений
Lv Ь2, ..., Ln, ..., соответственно. Совокупность возможных значений
некоторой величины мы будем называть спектром этой величины.
Спектр может быть дискретным, когда возможны только отдельные
значения Lb L2, ..., Ln, ..., либо состоящим из отдельных
тюлос, так что возможные значения L лежат в интервалах: Ьг<сЬ*С
<L2, L3<L<L4, вообще L-< L*cLn+1 либо, наконец, непрерывным,
когда все значения L оказываются возможными. Когда возможные зна-
значения величины являются дискретными, то говорят, что величина имеет
квантованные значения.
В примитивной теории Бора отсутствовали методы, позволяющие
в общем виде решить вопрос о возможных значениях той или иной вели-
величины, в частности, найти квантовые значения ,этой величины. Современ.
1 Если волновая функция не исчезает в бесконечности (например, плоская волна
де Бройля), то вместо ф- для сходимости интеграла в B0.4) следует брать так назы-
называемые «собственные дифференциалы» (см. дополнение III A2) и A2'), где изложено
правило нормировки волновых функций, не исчезающих в бесконечности).
77

ная квантовая механика полностью решает этот вопрос, сводя его к чисто
математической задаче нахождения собственных функций и собственных
значений операторов, изображающих механические величины.
Из самосопряженности оператора L следует, что наблюдаемые зна-
значения L будут вещественны:
Ln = L*n или L = L*. B0.5)
В самом деле, собственное значение Ln (или L) можно рассматривать
как среднее значение величины L в собственном состоянии г|;п (или tyL
соответственно). Но среднее значение величины, изображаемой самосо-
самосопряженным оператором, вещественно (см. A9.2)).
Этим полностью разъясняется значение самосопряженности операто-
операторов: самосопряженные операторы изображают вещественные величины.
§ 21. Основные свойства собственных функций
Обратимся к рассмотрению важнейших свойств собственных функций
самосопряженных операторов. Сперва ограничимся случаем дискретного
спектра. Пусть мы имеем: какие-либо две функции их и ы2. Эти функции
будут называться ортогональными, если
= 0, B1.1)
где интеграл взят по всей области изменения переменных. Для простоты
мы обозначаем все переменные одной буквой х.
Теорема, которую мы докажем, заключается в том, что собственные
функции i|)n и i|)m самосопряженного оператора L, принадлежащие раз-
различным собственным значениям Ln и Lm, ортогональны между собой, т. е.
= 0. B1.2)
В силу предположения о том, что i|)n и tym являются собственными
функциями, мы можем написать:
Ltym = Lmtym', Li];n = Lni];n. B1.3)
Из первого уравнения получим комплексно самосопряженное:
*1|з„ = Lm^, B1.3)
напомним, что согласно B0.5) Lm = L%. Умножив второе из уравнений
B1.3) на i\>m, a B1.3) —на tyn, вычтем второе из первого. Тогда полу-
получится:
Интегрируя это равенство по всей области изменения переменных, будем
иметь
В силу самосопряженности L левая часть равна нулю [следует в равен-
равенстве A8.7), определяющем самосопряженность, положить tym = uv i|;n = u2],
следовательно,
Так как Ln=fcLm, то отсюда следует справедливость B1.2).
78

Функции дискретного спектра всегда интегрируются квадратично,
поэтому мы можем нормировать их к единице:
:*nda:=l. B1.5)
Это последнее равенство можно объединить с равенством B1.2) в одно:
тЦпЛх = дтп, B1.6)
где символ 6тп определяется следующим образом:
б = 1, если п = т,
B1 7 V
бтга = 0, если пфт. \ • г
Системы функций, удовлетворяющие B1.6), мы будем называть ортого-
ортогональными и нормированными системами функций.
В значительном большинстве случаев, встречающихся в квантовой
механике, собственному значению Ln оператора L принадлежит не одна
функция tyn, а несколько собственных функций: 1|з„1, ^„г, • • •» ^«ь • • •, tyni-
Такие случаи называются вырожденными. Если значению L = Ln
принадлежит / собственных функций (/> 1), то говорят о наличии
/-кратного вырождения. Физический смысл «вырождения»
заключается в том, что какое-нибудь определенное значение величины
L = Ln может быть реализовано в разных состояниях.
Доказанная нами теорема об ортогональности собственных функций
относится лишь к функциям, принадлежащим к разным собственным зна-
значениям. В случае вырождения функций 1|з„аF= 1, 2, ..., /) относятся
к одному и тому же собственному значению Ln:
L^nk = Ln^nk, fe=l, 2, ...,/. B1.8)
Поэтому они не будут, вообще говоря, ортогональными. Однако можно
доказать1, что эти функции могут быть всегда выбраны так, что они
будут также ортогональны между собою:
ЦЫхЪи.и. B1.9)
Поэтому условие B1.6) можно считать всегда выполненным, если под т
и п в общем случае разуметь не один индекс, а всю совокупность индек-
индексов, характеризующих собственную функцию (например, вместо т — два
индекса т и k', вместо п также два индекса п и к).
В том случае, когда оператор L имеет непрерывные собственные
значения, доказанные теоремы непосредственно неприменимы. Однако
и в этом случае собственные функции обладают свойствами, аналогичными
свойствам функций дискретного спектра.
Собственные функции непрерывного спектра нельзя перенумеровать
числами. В этом случае функции зависят от собственного значения L
как от параметра, так что мы можем написать:
№) = №' L)> B1Л0>
где через х обозначены переменные, в которых выражен оператор L.
Свойства ортогональности собственных функций непрерывного спектра
проще всего могут быть выражены с помощьюособого символа b(L'—L),
1 См. дополнение II.
79

называемого функцией Дирака или 6-функцией. Эта функция
обладает следующими свойствами:
• 1
\ f(L')8(L'—L)dL' = 0, если точка L' = L лежит вне
£ интервала (a, b): I
j> B1.11)
\ f(L')б(L' — L)dV = /(£), если точка V = L лежит вну-
u три интервала (а, Ь),
где f{L') — любая (достаточно гладкая) функция. Можно доказать1, что
функции непрерывного спектра ^{х, L) могут быть нормированы так, что
= b(L'-L). B1.12)
Зто равенство аналогично B1.6), ибо из B1.11) следует, полагая /(L')= 1,
что 6(L' — L) = 0 всюду, кроме точки L' — L, где б обращается в беско-
бесконечность. Таким образом, символ б (L' — L) играет ту же роль, что
и символ 6Ып в случае дискретного спектра.
В математике доказывается, что система собственных функций опе-
операторов очень широкого класса является не только системой ортогональ-
ортогональных функций, но системой полной.
Это означает, что любую функцию г|з(х), определенную в той же
области переменных и подчиненную тому же классу граничных условий,
что и собственные функции ^п{х), можно представить в виде ряда из
этих собственных функций:
4>(*) = Sc»1>»(*). B1ЛЗ)
П
Пользуясь ортогональностью функций tyn, мы можем определить коэф
фициенты сп и таким образом найти ряд, представляющий ty(xJ.
Для этого умножим B1.13) на i|5*,(x) и проинтегрируем по всему
пространству:
5 (х) dx = 2 сп [ Ч>1 (*) Ч>« (*) dx.
В силу ортогональности и нормировки функций tyn интегралы, стоящие
под знаком суммы, равны бшп (см. B1.6)); таким образом,
Отсюда, меняя обозначение т на п, получаем:
. , B1.14)
1 См. дополнение III.
2 Мы ограничиваемся указанием способа нахождения^ коэффициентов Сп ря-
ряда B1.13). Относительно понятия полноты системы ортогональных функций и схо-
сходимости написанного ряда к функции гр (х) (см. Курант и Гильберт, Методы
математической физики, т. I, ГТТИ, 1933, гл. II, § 1). Сам термин «полнота системы»
функций (иногда говорят «замкнутость» системы) легко может быть уяснен из следую-
следующего соображения. Пусть мы имеем последовательность ортогональных функций, совпа-
совпадающую с последовательностью i|)n, ио ие содержащую, скажем, функции ^iD=l).
Эта система функций (if>2, ^з» •••» Фп, •••). как и система (^ь ф2, ф3. •••» %< •••).
будет ортогональной, но не полной, так как по ней нельзя представить в виде ряда
любую функцию (именно, нельзя представить ifi). Доказательство полноты системы как
раз и заключается в доказательстве отсутствия подобных пропусков.
«О

Таким образом, зная ty и систему ортогональных функций tyn, мы
можем найти все амплитуды сп, встречающиеся в ряде B1.13). Частным
случаем таких разложений по ортогональным функциям являются ряды
Фурье.
В случае непрерывного спектра имеет место разложение в интеграл,
подобный интегралу Фурье. Именно, в этом случае
, L)dL. . B1.15)
Для определения коэффициентов c{L) умножим B1.15) на ty*(x, L')
и проинтегрируем по х:
, L)dx =
= \c{L)dL.b{L'-L)-=c{L').
Меняя здесь обозначение V на L, получим окончательно:
B1.16)
(L)=\
Найденные нами представления любой функции в виде разложений
B1.13) и B1.15) по собственным функциям операторов приводят к очень
важному выводу: любое состояние, изображаемое волновой функцией 1|з (х),
может быть представлено в виде суперпозиции B1.13) или B1.15) состоя-
состояний, относящихся к определенным значениям какой-либо механической
величины. В самом деле, состояния tyn или ty(x, L) по самому своему
определению суть состояния, в которых некоторая механическая вели-
величина L имеет определенное значение Ln (либо соответственно L). А выра-
выражения B1.13) и B1.15) представляют i\>(x) в виде суммы (либо инте-
интеграла) этих частных состояний.
§ 22. Общий метод вычисления вероятностей
результатов измерения
Выше было показано, как находить среднее значение L любой
величины, изображаемой оператором L, и как находить возможные зна-
значения Lv L2, ..., Ln такой величины. Теперь мы перейдем к вычисле-
вычислению вероятности того, что в некотором состоянии г|з(х) в результате
произведенного измерения механической величины L будет обнаружено
значение L=Ln. Основная идея вычисления основывается на принципе
суперпозиции состояний. Пусть собственные функции оператора L будут
tyn(x). На основании свойства полноты и ортогональности этих функций
мы можем представить волновую функцию ty в виде суперпозиции
#(*)=2<V|U*)- B2.1)
п
Для сопряженной функции получим:
i|)*(*) = 2cfti|>5,(*) B2-Г)
m
(где т пробегает те же значения, что и п).
Подставляя эти выражения для г); и г);* в формулу для среднего
значения величины L в состоянии ty, мы найдем:
1= ^ V*-Ly-dx= 2 S c-cn \ ^-L^-dx. B2.2)
n m
6 д. И. Блохинцев 81

Так как tyn есть собственная функция оператора L, то
^п = ^„- B2.3)
Пользуясь B2.3) и ортогональностью функций 1|з£ и tyn, мы получаем
вместо B2.2)
n m
т. е.
^=S|cn|2Ln. B2.4)
п
Далее, умножая B2.1) на B2.Г) и интегрируя по всему пространству,
получаем:
или
У I л 12 = 1 /ОО С\
п
С другой стороны, если через w(Ln) обозначить вероятность того, что
случайная величина L имеет одно из возможных значений Ln, то по
общему определению среднего имеем:
L=J\w(Ln)Ln B2.6)
п
при условии, что
2o>(Ln)=l. B2.7)
Сравнение B2.6) и B2.7), и B2.5) показывает1, что
w(Ln) = [cn\z- B2.8)
Вероятность найти значение механической величины L равной
одному из ее возможных значений Ln равна квадрату модуля ампли-
амплитуды собственного состояния tyn. Иными словами, эта вероятность
определяется интенсивностью |сп|2, с которой собственное состояние tyn
представлено в состоянии г];.
Для вычисления вероятностей того или иного значения величины,
имеющей непрерывный спектр, поступаем совершенно аналогично тому,
как было сделано в случае дискретного спектра. Разложим рассматрива-
рассматриваемое состояние ty по собственным функциям ty(x, L) оператора L:
(L)q(x, L)dL, B2.9)
при этом i\)(x, L) нормировано к б-функцйи, а г|з—к единице.
Вычислим опять среднее значение L в состоянии г|гГ
*(x, L')dL'L ^ c{L)^{x, L)dLdx
и так как ■§ (х, L) есть собственная функция, то
1 Для вполне строгого сравнения B2.6) и B2.4) следует рассмотреть такой опе-
оператор, который есть функция L и равен 1 при L^Ln и 0, если ЬфЬп. Среднее от
такого оператора равно |со|2 по B2.4) и равно Wn по B2.6), откуда и вытекает
82

подставляя это в предыдущее выражение для L и меняя порядок инте-
интегрирования, получим:
,') с (L) dL'dLL \ г|з* (х, L')ty(x, L)dx
и в силу B1.12):
E = ^ с* (L') с (L) dL'dLLb (h' - L).
На основании свойств б-функции отсюда следует, что
1= J \c(L)\zLdL. B2.10)
Подобным же образом получаем
= \\ c*(L')c(L)dL'dL.d(L'-L) =
т. е.
" jc(L)|2dL=l. B2.11)
Если вероятность того, что значение непрерывной, случайной величины
лежит между Ь и L-\- dL есть w (L) dL, то по общему определению сред-
среднего значения
^ B2.12)
при условии
^w(L)dL=l. B2.13)
Сравнивая B2.12) и B2.13) с B2.10) и B2.11), получаем:
w (L) dL = | с (L) \4L. B2.14)
Таким образом и в случае непрерывного спектра мы приходим к ста-
статистической интерпретации интенсивностей собственных состояний
|(L|"
|()|
Приведенные выше формулы справедливы лишь для чистого ансамб-
ансамбля, характеризуемого одной волновой функцией ^{х). Для смешанного
ансамбля предыдущие формулы должны быть несколько обобщены.
Пусть мы имеем смешанный ансамбль, образованный из чистых
ip!, г|з2, ..., г|за, • •., смешанных в пропорции Pv Р2, ..., Ра, Тогда,
если вероятность найти значение Ln некоторой величины в чистом ансамбле
фа есть wa(Ln), то полная вероятность найти L — Ln в смешанном ансамбле
будет равна:
w (Ln) = ^ Pawa\(LJ. B2_ j 5j
1 Заметим, что формула B2.14) содержит как частный елучай формулы A2.4)
для вероятности импульса. Действительно, с (рх, ру, р2) есть амплитуда состояния 1|зр
с определенным импульсом, иными словами, — собственного состояния оператора
импульса. Поэтому с (рх, ру, рг) и с (L) в B2.14) имеют аналогичный смысл. Для пере-
перехода от B2.14) к A2.4) достаточно разуметь под L три компоненты импульеа рх, ру,
pz и соответственно под dL произведение dpxdpydpz.
6* 8а

Подобным же образом для величины, имеющей непрерывный спектр,
будем иметь:
w (L) dL = 2 Pawa (L) dL, B2 j 6)
причем
wd (K) = | can |2; wa (L) = | с„ (L) |2, B2.17)
где can и ca (L) суть амплитуды собственных функций оператора L: г|зп (х)
или соответственно г|з(л:, L) в разложении г|за(*)- В соответствии с фор-
формулами B2.15) и B2.16) среднее значение величины L в смешанном ан-
ансамбле есть
I = 2Pala, B2.18)
a
где La есть среднее значение L в чистом ансамбле tya:
*L%dx. B2.19)
§ 23. Условия возможности одновременного измере-
ния разных механических величин
Мы видели, что в квантовой области не существует таких состояний
частиц, в которых импульс и соответствующая ему координата одновре-
одновременно имели бы определенное значение. В таком же взаимно исключаю-
исключающем друг друга отношении находятся и многие другие величины. В са-
самом деле, чтобы существовали состояния, в которых две величины L и М
одновременно имели бы определенные значения (ALJ = О, (ЛУИJ = О,
нужно, чтобы волновая функция такого состояния была общей собствен-
собственной функцией операторов L и М. Между тем уравнения для собственных
функций операторов L W-M-
B3.1)
имеют, вообще говоря, различные решения tyL Ф tyM.
Поэтому в состояниях i);L, с определенным значением L(AL2 = 0), ве-
величина М не имеет определенного значения (АЛ12 > 0) и, наоборот, в со-
стояни г|зм, с определенным значением УИ(АУИ2 = 0) величина L не имеет
определенного значения (AL2 > 0).
Только в особых случаях две величины L и М имеют одновременно
определенное значение (для этого нужно, чтобы i|>M = i|>iJ. Можно пока-
показать, что условием того, что две величины L и М всевда могли иметь
одновременно определенные значения, является коммутативность
их операторов/, и М. Иначе говоря, должно иметь место оператор-
«ое равенство1:
LM = ML. B3.2)
Напротив, если
LM Ф ML, B3.3)
то величины L и М не имеют одновременно определенных значений
(кроме, может быть, исключительных).
1 См. дополнение IV.
84

Две величины, изображаемые коммутирующими операторами, могут
иметь одновременно определенные значения и поэтому, по крайней мере,
в принципе, могут быть измерены одновременно.
Две величины, изображаемые некоммутирующими операторами,
не могут одновременно иметь определенные значения и поэтому не
могут быть одновременно измерены 1.
Измерение одной из таких величин L приводит к состоянию tyL.
Измеряя в этом состоянии М, мы получим некоторое новое состояние
1|зм, не совпадающее с исходным ^г. Иными словами, измерение одной
из таких величин меняет состояние системы таким образом, что значе-
значение другой величины становится неопределенным.
Мы видим, что и в общем случае мы встречаемся с влиянием изме-
измерительного аппарата на состояние системы подобно тому, которое мы
рассмотрели выше на примере ■ измерения импульса и координаты
(ср. §§ 14, 15). Поэтому всякий аппарат, применяемый в квантовой обла-
области для измерения механических величин, относящихся к микрочастицам,
должен быть тщательно рассмотрен с точки зрения анализа значения
получаемых с его помощью результатов измерения и тех изменений
в состоянии системы, к которым он может приводить. Всякого рода
догматические суждения, не основанные на анализе конкретного устрой-
устройства аппарата, могут привести к ошибочным выводам.
§ 24. Операторы координаты и импульса микрочастицы
Поскольку волновая функция рассматривается нами как функция
координат частицы, постольку оператор координаты частицы х есть само
число х. Действие функции координат частицы F (х, у, г) как оператора
сводится просто к умножению ф(х, у, г) на F (х, у, г).
При этом же выборе переменных2 в волновой функции операторы
проекций импульса частицы, в соответствии с § 13, будут:
P^~ihi' pv--ihi^ p>=-lhi> B4Л>
или в векторной форме:
>=»-iAV, B4. Г)
где V есть оператор градиента (набла).
Операторы проекций импульса и координат подчиняются определен-
определенным правилам перестановки, которые очень облегчают расчеты с ними.
Пусть г|з (х, у, г) есть волновая функция; тогда имеем:
дх '
Рх (хг|;) = _ ih -£- (х\|з) = — ihx ^ — inty.
Вычитая вторую строку из первой, находим:
т. е.
xPx-Pxx = ih, B4.2)
1 См. сноску на стр. 88.
2 Возможность другого выбора независимых переменных в волновой функции
рассмотрена в гл. VII.
85

и аналогичным образом
yPy-Pyy=ih, B4.2')
zPz-Pzz = ih. B4.2")
Эти правила перестановок носят название перестановочных [соотноше-
[соотношений Гейзенберга.
Легко видеть, что
*/>„-/>„* = О, B4.3)
yPt-Pty = 0, B4.3')
zPy-Pf = 0 B4.3")
и т. д.
Подобным же путем можно установить более общие перестановочные
соотношения для любой функции F (х, у, z) и операторов импульса.
Именно:
^
B4.4)
v/ hd-l. B4.4')
Из отношений B4.2) и B4.4) следует, что не существует состояний,
в которых импульс и сопряженная ему координата имеют одновременно
определенные значения. В сущности B4.2) и B4.4) в операторной форме
выражают уже известное нам соотношение неопределенностей.
Определим теперь собственные значения и собственные функции
оператора проекции импульса на какую-нибудь ось (например, ОХ).
Согласно изложенному в § 20, уравнение для собственных функций опе-
оператора импульса имеет вид
РЛ-РхЬ B4-5)
где рх — собственное значение. Имея в виду значение Рх, получаем:
-/Ag-p,* B4.5')
Это уравнение легко интегрируется, и мы получаем:
%х(х) = Ме п , B4.6)
где N — постоянное число. Для того чтобы это решение было всюду
конечным (непрерывность и однозначность этого решения очевидны),
достаточно, чтобы рх было j< любым вещественным числом. Поэтому
спектр собственных значений рх получается непрерывным
-°° </?*< +со. * B4.7)
Множитель N можно выбрать так, чтобы функция typx была нормирована
к б-функции- Для этого нужно положить N = Bпп)-1^1 так, что окон-
окончательно нормированные и ортогональные собственные функции операто-
оператора Рх будут:
^«'¥- B4'8)
] Ч>* х(x) %x(x)dx = 6(p'x-px), B4.9)
1 См. дополнение III, формулу 20.
86

т. е. собственные функции оператора импульса tyPx суть плоские волны
де Бройля. Это не неожиданно. То, что волна де Бройля есть состоя-
состояние с определенным значением импульса частицы, было в сущности
исходным пунктом квантовой механики (§§ 7, 12).
§ 25. Оператор момента импульса микрочастицы
Под моментом импульса частицы (моментом количества движения)
в классической механике понимают векторное произведение радиуса-век-
радиуса-вектора г, проведенного от некоторой избранной точки (например, центра
сил) к частице, на импульс:
М = [гр]. B5.1)
Значение этой величины в механике определяется тем, что она является
интегралом движения в поле центральных сил. В квантовой механике
момент импульса изображается оператором
М = [гР], B5.2)
где Р — векторный оператор импульса B4. Г), а г — радиус-вектор. Осно-
Основанием к такому выбору оператора момента импульса является не только
внешняя аналогия с классическим выражением B5.1), но и то, что изо-
изображаемая оператором М величина является также интегралом движе-
движения в поле центральных сил (ср. § 33) и обладает свойствами, аналогич-
аналогичными свойствам момента импульса в классической механике.
Операторы проекций момента импульса на оси координат, соответ-
соответственно значению векторного произведения B5.2), суть:
B5-3)
и, наконец, оператор квадрата момента импульса есть
Найдем правила перестайовки для компонент момента импульса. Эти
правила понадобятся нам в дальнейшем, а сейчас они могут служить
иллюстрацией приемов алгебры операторов. Вычислим коммутатор б =
= MyMz — MzMy. Подставим сюда вместо Му и Мz их выражение B5.3).
Вычислим MyMz:
MyMt = (Ь* - Pxz) (Pxy - Рух) = PzxPxy - PzyPxy - PzxPyx
= уРухРх - zyPx-x*PzPy + zPyPxx
<так как у и Рг, Рх, г, и Рх, Ру, х, uPz, Py перестановочны). Подобным
же образом:
MzMy = yPzPxx - zyPl - x*PzPy + zPyXPx.
87

Вычитая из первого равенства второе, найдем:
МуМг - МZMу = yPz (хРх - Рхх) + zPv (Рхх - хРх). ■
Пользуясь теперь B4.2), получаем:
Меняя циклически х, у, г, полуним все три перестановки:
М уМ z - MzMy = ihMx, B5.5)
MzMx-MxMz = ihMy, B5.5')
MxMy - M.yM.x = ihMz. B5.5")
Таким образом, операторы компонент момента импульса некоммутивны.
Напротив, каждая из компонент импульса коммутирует с квадратом
полного момента импульса:
М ХМ2 - М *М х = 0, B5.6)
=0, B5.6')
= O. B5.6")
Доказательство предоставляем читателю.
Из этих правил перестановки следует, что проекции момента импульса
Мх, Му, Mz не могут быть одновременно измерены. В состоянии, в кото-
котором одна из проекций имеет определенное значение (ДЛЙ=0), другие
две проекции не имеют определенного значения (AMI > О, AMI > ОI.
Напротив, любая из проекций и квадрат полного момента могут быть
измерены одновременно.
Определим теперь возможные значения проекции момента импульса
на какое-либо произвольное направление и возможные значения абеолют-
(точнее — значения М2). Для решения этой задачи
й б
j^_^[jj ( ) р
удобно перейти к~полярной системе координат, взяв некоторое избранное
направление за ось OZ. В этой системе координат
х = г sin 6 cos ф, у = г sin 6 sin cp, z = r cos 6, B5.7)
где 6 есть угол между осью OZ и радиусом-вектором г, а ср— угол,
отсчитываемый в плоскости ху от оси ОХ.
Несколько громоздкое преобразование формул B5-3) из декартовой
системы координат в полярную приводит к следующему результату:
sq>-!r), B5.8)
mip^), B5.8')
Mz=-ih-^, . - B5.8")
М2 = - A2Ve, Ф , B5.9)
гДе Ve,q> есть, так называемый, оператор Лапласа для сферы:
Так как операторы B5.8) и B5-9) действуют только на углы 6, ср,
то волновую функцию достаточно рассматривать в зависимости лишь
1 Исключением является случай М — 0, из которого следует Мх = Му = Мг = 0.
88

от этих углов, т. е.
1|>=1|>@, ф). B5.11)
Уравнение для определения собственных значений оператора Af2 согла-
согласно B0.2) (полагаем там Z, = Af2, L = MZ) будет
М 2rj3 == М*Ц. B5.12)
Вставляя сюда Af2 из B5-9) и обозначая
b = l£, B5-13)
мы получим уравнение B5.12) в виде:
Это уравнение мы должны решить для всей области переменных
0, ф@<6<я, 0<ф<2я), причем интересующие нас решения должны
быть конечными, непрерывными и однозначными. Уравнение B5.14)
хорошо известно. Это —уравнение для шаровых функций. Подробные
сведения об этих функциях и о решении уравнения B5.14) приведены
в дополнении V. Здесь мы ограничимся лишь кратким резюме.
Оказывается, что решения этого уравнения, удовлетворяющие постав-
поставленным условиям, существуют не ■ при всех значениях "К, а лишь при
* = /(/+1), B5.15)
где / — целое положительное число.
При каждом таком значении / имеется 21-\- 1 решений, которые пред-
представляют собой шаровые функции. Мы обозначим их так:
у и п (е- ф> - /(/7/+й)!24^1) РГ (cos 6)ein*' B5-16>
где т — целое число, ограниченное следующими значениями:
/и = 0. ± 1. ±2, ..., ±1; 1=1, 2, 3, ... B5.17)
(всего 2/+1 значений). Знаком \т\ обозначено абсолютное значение
числа т. Функция Р\т (cos 6) определяется так:
P\m'(l) = (l — V)T-^ЙП^E). i = cos6, B5.18)
причем Pj(|) есть так называемый полином Лежандра:
р (g) = J_^_r(t2_ пи B5.19)
; 2'/! d|l LVi> ; J v
Множитель, стоящий перед Р\т1, выбран так, чтобы ортогональные функ-
функции Ylt m были, кроме того, и нормированными к единице на поверхности
шара, т. е.
я 2я
= fl['[flm'm. B5.20)
(Координаты 6 и ф отмечают Точки поверхности шара. Элемент поверх-
поверхности шара равен sin6d6cfrp.) %
Используем теперь эти результаты для нашей задачи. Как уже было
сказано, уравнение B5-14) имеет однозначные и конечные решения лишь
89

при значениях А, = /(/-}-1). Поэтому собственные значения оператора
квадрата момента импульса будут
M] = h4(l+iy, 1 = 0, 1, 2, ..., B5.21)
а соответствующие собственные функции суть
i|),m(e,» = y,w(e, q>), т = 0, ±1, .... ±/. B5.22)
Собственному значению М\ B5.21) принадлежат всего 21-\-1 собственных
функций, отличающихся значением числа т. Таким образом, мы имеем
дело с случаем вырождения (см. § 21). Сущность этого вырождения
легко уяснить себе, если обратить внимание на то, что собственные функ-
функции оператора квадрата момента импульса Mz являются также собствен-
собственными функциями оператора проекции момента импульса на ось Мг. В самом
деле, уравнение для собственных функций оператора Mz есть
Mxy = Mtyt B5.23)
подставляя сюда Mz из B5.8"), получим:
Если сюда подставить i|)Im, то имея в виду, что tylm пропорционально
•е*т(Р, мы найдем:
- ih- i/
т. е. уравнение B5.23) удовлетворяется функцией г|з[т, причем собствен-
собственные значения оператора Мг равны
Mz = hm, m = 0, ± 1, .... ±1. B5.24)
■Отсюда следует, что состояния tylm при заданном полном моменте М\
(дано /), различающиеся индексом т, суть состояния с различными проек-
проекциями момента на ось 0Z.~
Полученный нами результат показывает, что возможные значения
абсолютной величины момента импульса B5.21) и возможные значения
проекции момента импульса на произвольную ось 0Z B5.24) имеют кванто-
квантовые значения. Никакие другие значения, кроме приведенных, не могут
реализоваться в природе. В состояниях, в которых М2 и Mz имеют опре-
определенные значения, проекции Мх и Му не имеют определенных значений
.(кроме случая 1 = 0, когда М2 = МХ = Му = Mz = 0). Действительно функ-
функции B5.22) не являются собственными функциями операторов Мх и Му
B5.8'), в чем можно убедиться непосредственно. Это же вытекает из
некоммутативности Мх, Му, Mz.
Разумеется, что возможные значения Мх и Му таковы же, как и M
^25.24), ибо направление 0Z ничем не выделено, и чтобы убедиться
в справедливости нашего утверждения, достаточно представить себе, что
•ось ОХ или 0Y принята за полярную, ось. Поэтому, если мы будем
измерять Мх или Му, то мы получим всегда одно из значений htn
(т = 0, ± I, ± 2, ..., ± I), но при этом возникает новое состояние
■с определенным значением, скажем Мх. Это состояние будет состоянием
с неопределенными Му и Mz, т. е. одновременные измерения компонент
момента импульса взаимно исключаются: измерение одной компоненты
делает неопределенным значение другой.
Обратим внимание читателя на некоторые свойства симметрии собст-
собственных функций операторов момента количества движения. Произведем опе-
операцию замены координат х, у, z на — х, —у, —г, соответственно (отражение
от начала координат), которая называется операцией инверсии. В сфери-
•90
z

ческих координатах это означает замену координат г, 0, ср на г, я — 8,'
<р + я, соответственно. При таком преобразовании координат е1тф пере-
переходит в е{(<»+я) = (- 1 )те""ч>, а Р\т{ (cos 8) в Р\т (- cos 0) = (- 1)'+'т I x
ХРГ(cos0) (см. B5.18), B5.19)). Таким образом У1т(8, ф) переходит
в (— l)lVim(e, ф), т. е. умножается на (—1)', независимо от значения т.
Иначе говоря, операция инверсии приводит к умножению волновой функ-
функции на +1 при четном I, и на — 1 при нечетном.
Состояния с (— 1);= -\- 1 (/ — четное) называются четными, или обла-
обладающими положительной четностью, состояниями, с (— 1)'= — 1 (/ — нечет-
flbie) нечетными, или обладающими отрицательной четностью.
Отметим, что понятие четности состояний является более общим,
нежели четность состояния с заданным моментом количества движения
<см. § 105).
§ 26. Оператор энергии и функции Гамильтона
а) Оператор кинетической энергии Т. Опыт показывает, что кине-
кинетическая энергия микрочастиц связана с импульсом таким же образом,
как и для микроскопических тел1, т. е. кинетическая энергия Т частицы,
имеющей массу ц, и импульс р, равна
Т = ^ = ^0& + р1 + Р%- B6.1)
Этот факт заставляет написать оператор кинетической энергии в виде
Вставляя сюда значение операторов PxPyPz из B4*1), находим: .
7=--^V2, B6.2')
' д2 д2 д2 Л
где у2 есть оператор Лапласа f у2 = "gj2"+"g~r + "^a" )• В силу такого
выбора оператора Т его собственные значения Т равны B6.1), если пол
Рх> Pz> РУ разуметь собственные значения операторов импульса Рх,Ру,Рг.
В самом деле, уравнение для собственных функций 1|з (х, у, z) опе-
оператора Т есть
7> = Ту, B6.3)
оно удовлетворяется функцией, представляющей плоскую волну де Бройля
h . B6.4)
Эта же функция является собственной функцией операторов импульса,
так что кинетическая энергия Т измерима одновременно с импульсами
Рх> Ру> Рг (разумеется, операторы Т, Рх, Ру, Рг коммутируют между собой).
Оператор Т может быть легко написан в любой криволинейной системе
координат. Для этого достаточно написать оператор Лапласа V2 в соот-
соответствующей системе координат. В частности, в полярной системе коор-
1 Это обстоятельство в сущности уже использовано в основных соотношениях
де Бройля (см. § 7).
91

динат оператор V2 имеет вид:
где Vbq> следует взять из B5.10).
Подставляя V2 из B6.5) в B6.2') и имея в виду B5.9), мы получим:
Т^-Т + —
где М2 есть оператор квадрата момента импульса, а Тг есть
*V=—£"i-£(/•»£■). B6.7)
Оператор Т может рассматриваться как оператор кинетической энергии,.
Ма
соответствующей движению по радиусу-вектору, а опера тор g-^ —как опе-
оператор кинетической энергии трансверсального движения1.
б) Оператор полной энергии Н. Заметим сперва, что оператор потен-
потенциальной энергии U, поскольку последняя есть функция только коорди-
координат частицы х, у, z, есуь просто. U (х, у, г). В классической механике
полная энергия есть сумма потенциальной и кинетической энергий.
Подобным же образом и в квантовой механике оператор, изображаю-
изображающий полную энергию, есть сумма операторов кинетической и потенци-
потенциальной энергий, т. е.
H = T+U(x, у, г). B6.8)
Вид потенциальной энергии U{x, у, г) так же, как и в классической
механике, заимствуется из опыта и характеризует силовое поле, дейст-
действующее на частицу.
, Заметим, что в кцантовой механике нельзя сказать, что полная энер-
энергия есть сумма кинетической и потенциальной энергий. Кинетическая
энергия есть функция импульсов, а потенциальная — функция координат.
Как мы знаем, не существует таких состояний квантовых ансамблей,
в которых частицы имели бы одновременно определенные импульсы и коор-
координаты .
Поэтому нельзя измерить полную энергию частицы, измеряя порознь
ее кинетическую и потенциальную энергии2.
Полная энергия должна измеряться непосредственно как одно целое.
Возможные значения полной энергии частицы зависят от вида U(x, у, г)>
т. е. от рода частицы и от силового поля, в котором она движется. Нахо-
Нахождение этих значений составляет одну из важнейших задач квантовой
механики и будет рассмотрено позже.
Полную энергию, выраженную через импульсы и координаты, в клас-
классической механике называют функцией Гамильтона. Оператор кинетической
онергии Т у нас выражен через операторы импульса [через B6.2)], поэтому
сператор Н мы будем также называть оператором функции Гамильтона,
или коротко — гамильтонианом.
1 B6.6) вполне отвечает представлению кинетической энергии в классической
механике в виде;
т_Рг А42
2 "
. 2цг« ' ^
где рг—проекция импульса на радиус-вектор.
2 Операторы Т и U, разумеется, не коммутируют, в чем легко убедиться, поль-
пользуясь правилом перестановки B4.4). Отсюда следует, что Т и U ие могут быть Опре-
Определены одновременно для одного и того же состояния 1|з.
92

§ 27. Гамильтониан
Понятие функции Гамильтона может быть распространено также
и на неконсервативные системы. Поэтому оно — несколько общее понятие
механической энергии.
В классической механике существуют простые правила для написания
функции Гамильтона. Ее вид определяется природой механической сис-
системы, т. е. природой частиц и их взаимодействием между собой и с внешним
полем. Зная эту функцию Гамильтона, можно легко найти уравнения дви-
движения в произвольной системе координат.
Подобные же правила для написания оператора функции Гамиль-
Гамильтона — гамильтониана — имеются и в квантовой механике.
Мы ограничимся пока рассмотрением движения одной частицы во внеш-
внешнем поле и только позднее (§ 100) рассмотрим гамильтониан для системы
частиц.
Следует различать два важных случая: когда силы не зависят от ско-
скорости частицы и когда они зависят от нее. В первом случае сила F является
функцией только координат частицы и времени и может быть представлена
как градиент некоторой функции U(x, у, г), которую мы назовем силовой
функциейг:
F=-W'%(x, у, г, t). B7.1)
Если силы не зависят от времени, то U (х, у, z) есть не что иное, как
потенциальная энергия частицы. В этом случае функция Гамильтона
совпадает с полной энергией частицы и равна Т-\-0(х, у, z). Соответ-
Соответствующий гамильтониан есть B6.8) и совпадает с оператором полной
энергии. В более общем случае функция Гамильтона есть сумма кинети-
кинетической энергии Т и силовой функции U:H = T+U(x, у, z, t). Так как
U не является теперь потенциальной энергией, то и Я не есть полная
энергия системы.
В полной аналогии с классическим выражением функции Гамильтона,
гамильтониан напишется в квантовой механике для этого случая в виде:
H = T+U(x, у, z, t), B7.2)
где U — силовая функция.
Остается рассмотреть случай сил, зависящих от скорости частицы.
В микромире единственными известными силами такого рода являются
силы, возникающие в электромагнитном поле (сила Лоренца). Поэтому
достаточно рассмотреть гамильтониан для движения заряженной частицы
(заряд е, масса ц,) в произвольном электромагнитном поле.
Как известно из теории поля, произвольное электромагнитное поле
Е (напряженность электрического поля), Н (напряженность магнитного
поля) могут быть описаны с помощью скалярного потенциала V и вектор-
векторного потенциала А. причем
#=_VV_± **., B7.3)
' Н = rot A. B7.4)
Классическая функция Гамильтона Н, приводящая к правильным урав-
уравнениям движения в электромагнитном поле, имеет вид:
1 Чаще в механике под силовой функцией понимают U. Заметим еще, что, пред-
представляя силу как градиент от U, мы исключаем вихревые поля (случаи, когда
rot F=£0). Однако такого рода силы, не зависящие от скорости, в механике микроча-
микрочастиц неизвестны.
93

где р(рх, ру, рг) есть вектор обобщенного импульса [(так что р — — Л =
= ци, где V— скорость частицы, но р ф ц,Ы 1
Оказывается, что в квантовой механике мы получаем правильный
гамильтониан, если под р будем разуметь оператор импульса Р = —
т. е. оператор гамильтона для этого случая есть
Если помимо электромагнитных сил имеются еще и другие силы, описы-
описываемые силовой функцией U, то общим выражением для гамильтониа-
гамильтониана будет:
B7-7>
Раскроем теперь в явном виде оператор ( Р — — А ~) . Имеем:
По определению, произведения операторов
Далее, на основании B4.4) имеем:
PxAx-AxPx=-ih^,
поэтому
2е . _ ihe дАх , е2 . 3
С С ОХ С
Повторяя вычисления для остальных двух членов в B7.8) и складывая»
результаты, находим
B7.9>
Оператор функции Гамильтона или энергии, как следует из изложен-
изложенного в этом и предыдущем параграфах, определяется двумя обстоятель-
обстоятельствами: 1) природой частицы (в общем случае — системы частиц, ср. § 102I
и 2) природой действующих на нее полей.
Этот оператор является основным для механики, так как, выбира»
его, мы, в сущности, формулируем на математическом языке все особен-
особенности той системы, с которой мы намерены иметь дело.
В частности число независимых переменных, входящих в гамильто-
гамильтониан, по определению, равно числу степеней свободы нашей системы.
Успех решения задачи, в смысле согласия выводов теории с опытом,
уже предопределяется тем, насколько основательно выбран гамильтониан»
(все ли важные взаимодействия учтены!).
Обычно в качестве независимых переменных в гамильтониане берут
декартовы координаты частицы, так как именно при этом выборе перемен-
переменных операторы взаимодействий (например, потенциальная энергия) выра-
1 См. дополнение VI.
94

жаются наиболее просто (числом), а оператор кинетической энергии —
сравнительно простым дифференциальным оператором второго порядка.
Однако возможны и другие выборы независимых переменныхг.
Чтобы получить выражение гамильтониана в произвольной криво-
криволинейной системе координат qxq2q3> достаточно преобразовать полученный
нами для декартовой системы координат гамильтониан в эту систему, сле-
следуя обычным правилам дифференциального исчисления. (Пример такого-
преобразования дает формула B6.5).) Вид гамильтониана в криволиней-
криволинейной системе координат не находится в таком простом отношении к класси-
классической функции Гамильтона, какое имеет место в декартовой системе коор-
координат (замена р на оператор Р). Это обстоятельство не является случайным.
Декартова система в квантовой механике выделена среди всех других коор-
координатных систем тем, что в этой системе кинетическая энергия выражается
суммой квадратов компонент импульса рх, ру, рг так, что, измерив импульс,
мы можем вычислить кинетическую энергию.
В криволинейной системе координат кинетическая энергия выражается
в виде квадратичной функции обобщенных импульсов:
з
Г= 2 aik(qvqi,qs)piph, B7.10)-
t, ft=i
причем коэффициенты aik являются функциями координат. Измерение
Pk№—,\, 2, 3) еще не определяет кинетической энергии, так как нужно еще
знать aih. Последние суть функции координат qh(k — 1, 2, 3) и поэтому не
могут быть определены одновременно с импульсами рк. Таким образом,
только в декартовой системе координат измерение импульсов есть в то же
время и измерение кинетической энергии2.
1 Если частица обладает «спнном» (ср. §§ 58, 59, 60), то наряду с координатами,
в гамильтониан входит спиновая переменная.
2 Об уравнениях квантовой механики в криволинейной системе координат см,
дополнение VII.

ГЛАВА IV
ИЗМЕНЕНИЕ СОСТОЯНИЯ ВО ВРЕМЕНИ
§ 28. Уравнение Шредингера
Пусть в какой-нибудь момент времени ^=0 дана волновая функция
°ty(x, 0), описывающая состояние ансамбля частиц (буквой х мы обозначаем
совокупность всех координат частицы). С помощью этой волновой функции
мы можем вычислять вероятность результатов измерения различных меха-
механических величин для момента времени ^=0 в ансамбле частиц, находя-
находящихся в состоянии ty(x, 0). В этом смысле мы говорим, что волновая функ-
функция ty(x, 0) определяет состояние частицы в момент времени t=0.
Допустим теперь, что мы намерены произвести измерения не в момент
времени ^=0, а позднее, в момент ^>0. За это время состояние частицы
(в общем случае — системы частиц) изменится и будет изображаться неко-
некоторой новой волновой функцией, которую мы обозначим через ty(x, t).
Как мы знаем, волновая функция меняется также в результате измерений
(«редукция волнового пакета», § 17). Сейчас мы предполагаем, что никаких
измерений в интервале от ^=0 до некоторого момента t не производится,
так что речь идет об изменениях состояния, вызванных исключительно
движением частицы (или системы частиц) самой по себе, без вмешатель-
вмешательства измерительного прибора.
Каким образом в этом случае связаны между собой волновые функ-
функции 1|)(ДС, О) И ty(X, t)?
Так как волновая функция полностью характеризует чистый ансамбль,
то она должна также определять и его дальнейшее развитие. Это тре-
требование выражает принцип причинности в применении к квантовой меха-
механике^. Математически это означает, что из волновой функции г|э(х, о)
для ^ = 0 должна однозначно определяться волновая функция ty(x, t)
в более поздние моменты времени.
Рассмотрим функцию г|з в момент времени А^, бесконечно близкий
к ^ = 0. Тогда
Согласно сказанному ( 5'—- j должно определяться из i|) (x, о), т.
1 Мы оставляем открытым вопрос, насколько такая, общепринятая формулировка
принципа причинности является единственной. Возможна и такая постановка вопроса,
когда решение не определяется начальными данными, а выбирается условиями, относя-
относящимися и к прошедшему, и к будущему, так что получается задача на нахождение
собственных решений в пространстве и времени.
S6

где L (х, о) — некоторая операция, которую следует произвести над 1|з (х, о),
чтобы получить (-£-)_•
Так как момент ^ = 0 взят совершенно произвольно, то будем иметь:
, t). B8.1)
Вид оператора L, который можно назвать оператором смещения во
времени, не может быть определен из изложенных выше положений кван-
квантовой механики и должен быть постулирован.
Согласно принципа суперпозиции состояний, этот оператор должен
быть линейным. Далее, оператор L не может содержать ни производных,
ни интегралов по времени. В самом деле, если бы он содержал первую
производную по t, то это означало бы просто, что оператор L есть не тот
оператор, который мы хотим иметь: оператор L выражает первую про-
производную по t через ty(x, t). Если бы он содержал высшие производные
по t, то B8.1) означало бы уравнение для ty более высокого порядка,
чем первый, и следовательно, для определения состояния в последующие
моменты времени нужно было бы знать при г1 = 0 не только ty(x, 0), но
и производные по времени от if ( -Л- ) , ( -~ \ , ... \ т. е. волновая
функция ip не определяла бы состояния системы, что противоречит нашему
основному предположению (ip определяет состояние системы). Наличие
интеграла по t означало бы, что для последующего играет роль значение
\|з на целом отрезке времени, т. е. история процесса. Таким образом L
может содержать t лишь как параметр.
Уравнение B8.1) позволяет по начальной волновой функции гр(х, 0)
найти функцию ty(x, t) и тем самым предсказать вероятность результа-
результатов различных измерений в момент t, в предположении, что в интервале
от ^ = 0 до t система не испытывала никаких дополнительных воздей-
воздействий, в частности, не подвергалась измерению.
Изменение волновой функции, имеющее место при измерениях («редук-
(«редукция»), не описывается каким-либо дифференциальным уравнением, а выте-
вытекает непосредственно из самого результата измерения (§ 17).
Правильный выбор оператора L подсказывается рассмотрением сво-
свободного движения с определенным значением импульса р. Волновая функ-
функция для такого движения есть волна де Бройля:
где
,, дг ~ТГ (Et-Pxx~p у-р z)
у, z, t) = Ne h x v
Pi
Непосредственная подстановка показывает, что эта волна удовлетворяет
уравнению
4J#
Это последнее уравнение можно переписать в виде:
1 Так, например, уравнение для колебаний струны есть уравнение второго поряд-
порядка по времени. Для определения состояния струны в момент £ = 0 нужно знать не толь-
только отклонение струны а (х, t) для а! = 0, но и скорости ее точек -^ при а! = 0.
7 Д. И. Блохиицев
97

если под оператором Н разуметь гамильтониан «для свободного движения
частицы:
Отсюда следует, что для свободного движения оператор смещения во
времени £, = -£- Я.
В квантовой механике делается обобщение этого частного резуль-
результата, именно, принимают, что этот оператор смещения L всегда равен
±
B8.2)
где Я есть гамильтониан (оператор функции Гамильтона), вид которого
для разных случаев рассмотрен в § 27.
В соответствии с этим постулатом уравнение B8.1) для волновой
функции ty может быть теперь записано в виде:
ih^-^Hq. B8.3)
Это уравнение носит название уравнения Шредингера. Оно образует
одну из основ квантовой механики1 и обоснование свое находит не столь-
столько в теоретических и исторических обстоятельствах, приведших к уста-
установлению этого уравнения, сколько в согласии с опытом.
В раскрытом виде уравнение Шредингера B8.3) в отсутствии магнит-
магнитного поля, в соответствии со значением оператора Я (см. 27.2 и 26.2')
имеет вид:
ih Ж = ~ Ж^ + и {х' у> z' ° * {28-4)
[при наличии магнитного поля следует взять Я из B7.9)].
Наиболее важной особенностью уравнения Шредингера является нали-
наличие мнимой единицы перед производной -~. В классической физике урав-
уравнения первого порядка по времени не имеют периодических решений —
они описывают необратимые процессы, например, диффузию, теплопровод-
теплопроводность2. Благодаря мнимости коэффициента при -J- уравнение Шре-
Шредингера, будучи уравнением первого порядка по времени, может иметь и
периодические решения.
По этой же причине волновая функция г|) является, вообще говоря, комплексной
величиной. В классической теории волн также применяют комплексное написание волны
в виде
« = constel( •"-**>,
ио в конечном счете имеют дело лишь с действительной нли мнимой частью и. Напри-
Например, фактическое смещение частиц (например, струны) будет:
и' = const sin (<£>t—kx).
Введение i здесь просто удобный расчетный прием.
1 Во многих курсах стремятся «вывести» уравнение Шредингера. На самом деле,
это уравнение ниоткуда не выводится, а образует основу новой теории. Поэтому мы
предпочитаем постулировать его, ограничившись приведенными выше доводами в пользу
такого постулата.
2 Конечно, характер решения дифференциального уравнения зависит еще н от
краевых условий. Проводя указанное противопоставление, мы имеем в виду случаи,
когда ни U (х, у, г), нн краевые условия не зависят от времени.
98

Иначе обстоит дело в квантовой механике. Если взять вместо волны де Бройля
ее действительную или мнимую часть, например,
то для гр' нельзя найти уравнения первого порядка по времени, которое было бы сов7
местимо с соотношениями де Бройля:
Е и Р
ш=т- к =-г-
Связанная с уравнением Шредингера постановка вопроса «найти ty(x, t),
если дана ty(x, 0)», имеет смысл лишь в том случае, если ty(x, 0) может
быть однозначно сопоставлено с некоторыми определенными физическими
условиями.
Такое сопоставление не является, однако, тривиальным, так как вол-
волновая функция по самой своей природе является величиной неизмеримой
(напомним, что i|) и i|)'==m|), где а —любая постоянная, изображают одно
и то же состояние).
Измеримыми являются значения механических величин L, М, N части-
частицы (или системы частиц) и вероятности, с которыми обнаруживаются эти
значения в ансамбле частиц (или систем).
Поэтому мы могли бы рассчитывать только на то, что по измерениям
вероятностей в ансамбле окажется возможным вычислить волновую
функцию с точностью до несущественного постоянного множителя. Эта
задача вычисления волновой функции по измеренным вероятностям в об-
общем случае совсем не является простой, так как вероятности определяют
только |г);(х)|2 или, вообще, квадраты модулей амплитуд | сп |2 разложения
ty(x) по собственным функциям какого-либо оператора, а фаза ty(x) или
сп остается неопределенной1.
Только в исключительных случаях задача становится простой, или
даже тривиальной.
Например, в § 29 будет показано, что в состояниях, в которых нет
потока частиц, волновая функция действительна. В этих случаях плот-
плотность вероятности w{x) — |г|;(л:)|2 = i|>2(x) и i);(x)^ Yw{x).
Однако вся проблема определения ty(x, о) упрощается тем, что в по-
подавляющем большинстве практически интересных случаев мы имеем дело
с ансамблями частиц, имеющих определенный полный набор механических
переменных L, М, N. Зная их значения из измерений в момент времени
* = 0, можно, пользуясь математическим аппаратом квантовой механики,
вычислить и начальную волновую функцию.
Действительно, если в момент времени ^ = 0 измерены значения L, М, N
этих величин, то мы можем утверждать, что начальная волновая функция
есть общая, собственная функция операторов L, M, N, принадлежащая
собственным значениям2 L, М, N.
На этом пути вся проблема определения волновой функции сводится
■- к выяснению того, какие величины образуют полный набор.
Р. Ниже показано, что эти величины должны обладать следующими
jj свойствами: 1) они одновременно измеримы; 2) число их равно числу сте-
степеней свободы системы; 3) они независимы между собой.
1 См. теорию рассеяния
2 Например,, если начальное состояние характеризуется заданием импульса частицы
р (вэтомслучае L = px, M = py, N=pz), то гр (г, 0) = % (х) есть плоская волна деБрой-
ля, принадлежащая импульсу р.
7* 99

Имея в виду дальнейшие обобщения, будем считать, что волновая функция является
функцией / переменных (система с / степенями свободы).
Интересующая нас функция есть собственная функция и поэтому принадлежит к
полной системе ортогональных функций в пространстве / измерений.
Каждая такая функция характеризуется / параметрами а, р, у («номера функции»).
Если такая функция 1|за р_ v> _ (х, у, г, •••) есть собственная функция опера-
операторов L, M, N, ■•-, то собственные значения L, M, N, ••• будут функциями этих
параметров. Мы будем иметь:
А*о, P,v, ...=L(a> P. Y, •••)%, р, у. м%,», у...=м^ Р- Y. ■■■)%, р, у, ....
B8.5)
Wo,p.v, ...=*("> P. y. •••)*«, в, v, ... • •■■■
Эти уравнения совместны, если
[L, M] = [L, N] = [M, N]= ... =0, B8.6)
т. е. если величины L, М, N одновременно измеримы. Далее, чтобы определить по из-
измеренным L, М, N параметры а, Р, у ..., нужно, решить / таких уравнений:
L = L(a, p, у, -..), М = М(а, р, у, ...), N=N(a, p, у, ...), B8-7)
при этом ни одно из них не должно быть следствием другого, т. е. величины L, М, N
должны быть независимыми1.
§ 29. Сохранение числа частиц
Из уравнения Шредингера можно получить закон сохранения числа
частиц, выражаемый уравнением непрерывности:
-^ + divy-O, B9.1)
где w — средняя плотность числа частиц в точке х, у, z, а j — средняя
плотность потока частиц.
Для того, чтобы получить это уравнение, возьмем уравнение Шредин-
Шредингера сначала для простого случая потенциальных сил B8.4):
Уравнение для комплексно сопряженной функции будет
-'А^=-|г*Ч>* + £Л1>*. B9'2'}
Умножая уравнение B9.2) на г|з*, а B9.2') на ф и вычитая второе урав-
уравнение из первого, получим:
* ■£+♦¥)- -■£■ <♦•*■♦-**■♦•>■
Это равенство может быть переписано в виде:
ж (W0 = ^г div (ГЧ - W); B9.3)
г|)*ф есть плотность вероятности w:
ш = ф*г|з. B9.4)
1 Этн параметры могут быть непрерывными илн дискретными. В простейшем слу-
случае разделяющихся переменных такая функция имеет вид ^ai p, Yi ...(*• У, г) =
— ua(x)vo(y)w (г) ..., см. Р. Курант и Д. Гильберт, Методы математиче-
математической физики, т. I, стр. 49. ГТТИ, 1933.
100

Если через / обозначить вектор:
/ _ ^L (^Vij)* — ij)*Vij)), B9.5)
41JL
то уравнение B9.3) запишется в форме
= 0. B9.6)
Отсюда следует, что вектор j есть вектор плотности тока вероят-
вероятности. Уравнение B9.6) получает более наглядное толкование, если заме-
заметить, что до = ф*ф может рассматриваться так же, ках средняя плотность
частиц. Тогда j следует рассматривать как средний поток частиц через
площадь в 1 см2 в 1 сек. В соответствии с этим уравнение B9.6) нужно
толковать как закон сохранения числа частиц. В частности, интегрируя
B9.6) по некоторому конечному объему V и применяя теорему Гаусса,
получаем:
I^^^ds. B9.7)
где последний интеграл взят по поверхности S, охватывающей объем V.
Распространяя интегрирование по всему пространству (V —> со) и имея
в виду, что волновые функции ф, а вместе с тем и плотность тока j
обращаются на бесконечно удаленной поверхности в нуль1, мы находим:
wdv~Tt $Ф*Ф *» = <>, B9.8)
Tt\
т. е. полная вероятность найти частицу где-либо в пространстве
не зависит от времени. Следовательно, число частиц остается неизмен-
неизменным. Вместе с тем B9.8) утверждает, что нормировка волновых функций
не меняется с течением времени, положение, о котором мы уже упоми-
упоминали в § 10.
Умножим у и до на массу частицы ц:
D»V4>* ф*7ф) B9.9)
Тогда Qp, имеет смысл средней плотности вещества (массы), а /ц—сред-
/ц—средней плотности тока вещества (массы). Из B9.6) следует, что эти вели-
величины подчиняются уравнению непрерывности:
^ + divb = 0, B9.10)
т. е. изменение средней массы в некоторой бесконечно малой области
обусловлено втеканием или вьШеканием этой массы через поверхность,
ограничивающую эту область.
Подобным же образом, умножая до и у на заряд частицы е, получим
среднюю плотность электрического заряда и среднюю плотность элект-
электрического тока:
'| B9Л1>
1 В случае, когда функции \|) не интегрируемы, интеграл \ jnds может и не
обратиться в нуль даже по бесконечно удаленной поверхности. Физически это означает
существование потока частиц из бесконечности или в бесконечность.
101

для которых опять-таки получается уравнение непрерывности
^ 0. B9.12)
Уравнения B9.10) и B9.12) выражают закон сохранения массы и элект-
электричества в квантовой механике.
Если представить волновую функцию ф в виде
1|> = ы<*9, B9.13)
где « — действительная амплитуда, а в — действительная фаза, то под-
подстановка B9.13) в B9.5) дает
У = }ув. B9.5')
Так как ыг есть плотность w, то величина — у© может быть истолкова-
истолкована как средняя скорость в точке х, у, г: ;
y = -V6, B9.14)
h д.
а величина — Ь как потенциал скорости.
Из формулы B9.5') с особой ясностью видно, что плотность тока j
отлична от нуля лишь в том случае, когда состояние описывается ком-
комплексной функцией ф.
При наличии магнитного поля Н, описываемого вектором-потенциалом
А (Н = rot А), формула для плотности тока у должна быть видоизменена1.
Именно, при наличии магнитного поля вместо B9.5) получается выраже-
выражение для плотности тока.
J = |-1W* - Ф*УЧ>] - £ Лф*Ф- B9.5")
Чтобы получить это выражение, следует подставить в уравнение Шре-
дингера B8.3) гамильтониан B7.9) для движения в произвольном
электромагнитном поле. Производя эту подстановку, находим уравнение
Шредингера для этого случая:
ihW= ~|r*N> + ^A^ + ^div4i|> + ^^ + eVi|> + t/i|> B9.15)
и для сопряженной функции
dt 2(г Y \ic Y 2|д,с ^ ' 2(д,са
+ eVty*+Uty*. B9.16)
Умножим опять первое уравнение на г)з*, а второе на ф и вычтем
второй результат из первого. Тогда получается:
Выражение в фигурных скобках может быть преобразовано следующим
образом:
div Л1|5*1|з + Л (i|)*Vi|5 + i|3Vt|J*) = div A^*ty + Av (ф*г|з) = div (Аф*ф).
1 Видоизменение обусловлено тем, что при наличии магнитного поля операторы
Рх, Ру, Pz СУТЬ операторы обобщенного импульса, а не обычного (произведение массы
на скорость). Так же обстоит дело н в классической механике (Ср. дополнение VI,
формула 10).
102

Подставляя этот результат в предыдущее выражение и деля на ih,
получаем:
^Р {^^}0. B9.17)
Это и есть уравнение непрерывности при наличии магнитного поля, опи-
описываемого вектор-потенциалом А. Выражение в фигурных скобках должно
быть плотностью тока у; оно совпадает с B9.5").
Справедливость уравнения непрерывности теснейшим образом связана
с самосопряженностью гамильтониана Н. Это свойство гамильтониана
было неявно использовано нами при. выводе B9.5) и B9.17). В дополне-
дополнении VIII более подробно рассмотрена эта сторона дела и показано,
каким образом из требования самосопряженности оператора Н вытекают
требования к поведению волновой функции в бесконечности в особых
точках (§ 20), обеспечивающие справедливость уравнения непрерывности
во всем пространстве.
§ 30. Стационарные состояния
В отсутствие переменных внешних полей гамильтониан Н не зависит
от времени и совпадает с оператором полной энергии //(*). В этом
случае уравнение Шредингера
ih^^l = H(x)^(x,t) C0.1)
имеет, важные решения, получающиеся, путем разделения переменных
х и t:
y(x,t) = q(x)fV). C0.2)
Подставляя C0.2) в C0.1) и обозначая постоянную разделения перемен-
переменных через Е, мы получаем:
ih%=Ef, . C0.3)
Н(х)Ц(х) = Е$(х). C0.4)
Первое уравнение сразу решается:
= const -e h. C0.5)
Что же касается второго уравнения, то, как видно, оно совпадает с урав-
уравнением для собственных функций оператора энергии1 Н. Если обозна-
обозначить эти функции через tyn(x) (для определенности мы берем случай
дискретного спектра энергии), то окончательное решение C0.2) напи-
напишется в виде:
4>ni(*,.t) = iM*)e h ■ C0.6)
Отсюда следует, что состояния с определенным значением энергии
Еп (Д£2 = 0) гармонически зависят от времени с частотой, равной
con = f. C0.7)
1 Уравнение C0.4) получается из общего уравнения B0.2), если там положить
= H, L=E.
103

Этот результат распространяет соотношение де Бройля Е = шА, приме-
применявшееся первоначально к свободному движению, на любые системы.
Состояние C0.6) с определенным значением энергии по причинам, кото-
которые сейчас выяснятся, называют стационарными. Уравнение же C0.4)
называют уравнением Шредингера для стационарных состояний. В силу
линейности уравнения C0.1) его общее решение ty(x, t) может быть
представлено как суперпозиция стационарных состояний с произволь-
произвольными, но постоянными амплитудами, именно:
г|з (х, t) = 2 софп (х) е~* 'Г. C0.8)
Амплитуды со определяются через начальную функцию ty(x, 0). В самом
деле, в силу ортогональности функций фп имеем:
со=^(*, 0)q*(x)dx. C0.9)
Вычислим теперь вероятность местоположения частицы wn(x, t) и плот-
плотность тока вероятности jn (x, t) в я-ом стационарном состоянии. Согласно
B9.4) и B9.5) имеем:
ял / у т\ —; I ili*** ( v /^ I" — ii*)** ( v ^ ih ( y i\
Подставляя сюда 1|зп(дс, t) из C0.6), находим, что
wn(x,t)=;wn(x,0), C0.10)
/.(*.')=/«(*. 0), C0.11)
т. е. в стационарных состояниях вероятность местоположения части-
частицы и плотность тока вероятности не зависят от времени.
Отсюда же [имея в виду B9.11)] следует, что в этих состояниях
средняя плотность электрических зарядов @е и средняя плотность элект-
электрических токов je не зависят от времени.
Таким образом система, находящаяся в состоянии с определенной
энергией £п(Д£2 = 0), с электрической точки зрения представляет собой
систему статически распределенных зарядов и постоянных токов.
Характеристика стационарных состояний будет более полной, если мы
обратим внимание читателя на то, что в стационарных состояниях
вероятность w (L) нахождения какого-нибудь значения L любой механи-
механической величины (не зависящей явно от времени) не зависит от времени.
Вместе с тем и среднее значение L является постоянным. Для доказа-
доказательства этого положения воспользуемся формулой B2.14):
где с (L) есть амплитуда в разложении ф (х, t) по собственным функциям
^l(x) оператора L, представляющего величину L. Согласно B1.16) имеем
для стационарного состояния tyn(x, t) C0.6):
Ent
h
и, следовательно,
w (L) = | с (L) |2 = | ^ i|>* (x) фп (x) dx 2 = const. C0.12)
104

ГЛАВ-А V
ИЗМЕНЕНИЕ ВО ВРЕМЕНИ МЕХАНИЧЕСКИХ
ВЕЛИЧИН
§ 31. Производные операторов по времени
Уравнение Шредингера позволяет установить простые правила, сле-
следуя которым можно вычислить изменение среднего значения той или
иной механической величины за бесконечно малый промежуток времени,
иными словами, вычислить производную по времени д- L от среднего зна-
значения L некоторой величины L.
Физический смысл этой производной таков. Допустим, что в момент
времени t имеется состояние, описываемое волновой функцией г|)(лг, f).
Произведем измерения величины L в этом состоянии. Мы получим
результаты отдельных измерений L', L", L", .... Среднее из большого
числа измерений будет L(t) и вычисляется по формуле:
C1.1)
Другую серию наблюдений мы проведем в момент времени t' = t + At,
близкий к t. Мы получим новую серию результатов1. Среднее значение
из этих результатов будет другое, так как за время t состояние изме-
изменится и те же результаты L', L", L'", ... будут получаться с иной
степенью вероятности. Кроме того, может случиться, что сама величина
явно зависит от времени так, что и возможные значения L', L", Lm, .. .
будут изменяться с течением времени. Обозначим средний результат
измерений в момент t+At через 1(/+А/),
тогда
Вычислим эту производную. Дифференцируя C1.1) по времени, получаем:
f.L^'dx. C1.3)
1 Измерение значения какой-либо величины точно в данный момент времени
может привести к изменению состояния микрочастицы. Поэтому производство двух
серий измерений в момент t и момент t-\-At подробнее следует представлять себе
следующим образом. Имеется ансамбль из большого числа независимых экземпляров N,
находящихся в состоянии г|) (х, t). Мы разбиваем N на две большие группы Af' и N".
В момент мы производим измерения в первой группе частиц N' и получаем Z (t) [при
этом состояние этих экземпляров, вообще говоря, изменится, и оно уже больше не опи-
описывается функцией ^(х, t)]. Затем в момент t-{-At мы произведем измерения в груп-
пе N" нетронутых первым измерением экземпляров. Из этих измерений и получается
Ut+At).
05

Очевидно, что первый член есть среднее значение -^ и равен нулю,
если L явно не зависит от времени. Два последних члена мы упростим,
пользуясь уравнением Шредингера B8.3). Именно, из B8.3) имеем:
dt ih r
Подставляя эти выражения в C1.3), найдем:
Первый интеграл преобразуем, пользуясь самосопряженностью опера-
оператора /7. Обозначая г|з* = ы*, /,г|> = щ, на основании свойства само-
самосопряженности A8.7) получаем: - '
i-i ■ * dL
Подставляя это в выражение для -тт, находим:
Введем обозначение
[Н, L]=^(LH-HL). C1.5)
Оператор -rr(LH—ffL) будем называть квантовой скобкой Пуассона1.
Введенное обозначение позволяет написать C1.4) в форме
Мы видим, что производная по времени от среднего значения L есть
среднее от некоторой величины, изображаемой оператором
3r+[J5f,L].
Поэтому этот последний оператор следует принять за оператор -л-
производной по времени -г- от величины L, изображаемой оператором L:
§ = §+[//, L]. C1.7)
Это определение оператора, изображающего производную по времени
dL
-^, ведет к тому, что
т. е. производная по времени от среднего равна среднему от производ-
производной по времени.
1 Эта терминология заимствована из классической механики. См. дополнение VI,
формулу D).
106

Если величина L не зависит от времени явно, то формулы C1.6)
и C1.7) упрощаются:
^ = ЩГЦ, C1.9)
^=[Я, L]. C1.10)
В заключение обратим еще внимание читателя, что при вычислении
оператора производной по времени от произведения или от суммы опера-
операторов с квантовой скобкой Пуассона можно обращаться как с обычной
производной (соблюдая, однако, порядок сомножителей). Действительно,
нетрудно видеть, что если L = A+B, то
dt dt dt ^ '
и если L = АВ, то
^=[Я, АВ=[Н. А] В + А[Н, В]^^В + А~. C1.12)
§ 32. Уравнения движения в квантовой механике.
Теоремы Эренфеста
Найдем теперь законы изменения импульсов и координат с течением
времени.
Импульсы и координаты являются величинами, не зависящими явно
от времени. Поэтому согласно C1.10) операторы производных этих
величин по времени выражаются просто через квантовые скобки Пуас-
Пуассона, т. е. в конечном счете через операторы самих этих величин
и гамильтониан Н, характеризующий рассматриваемую механическую
систему.
Обозначим операторы декартовых координат х, у, z и соответствующих
импульсов рх, ру, р2 соответственно через X, У, Z и Рх, Ру, PJ-. Гамиль-
Гамильтониан /У будет функцией этих операторов и, вообще говоря, времени t:
ff = ff(Px,Pv, Pz,X,Y,Z,'t). C2.1)
Обозначим далее через -тг, -тг > ~тг операторы производных коор-
координат по времени, т. е. операторы проекций скорости на оси координат,
w© dPv но,
а через ^-., —~-, ~- — .операторы производных по времени от проекции
импульса.
Подставляя в C1.10) вместо L операторы X, Y, Z, Рх, Ру, Pz,
получим искомые операторные уравнения:
C2-2')
1 Мы ограничиваемся рассмотрением движения в декартовой системе координат.
Об уравнениях в криволинейной системе координат см. дополнение VII.
* 107

Эти операторные уравнения вполне аналогичны классическим уравнениям
Гамильтона и поэтому называются квантовыми уравнениями Гамиль-
Гамильтона 1.
В классической механике первая группа уравнений (производные от
координат) устанавливает связь между скоростью и импульсом, а вторая
группа (производные от импульсов) выражает законы изменения импульса
во времени. Такое же значение имеют и квантовые уравнения Гамильтона.
Для того чтобы в этом убедиться, следует раскрыть явно вид скобок
Пуассона в C2.2) и C2.2'). Ради простоты рассмотрим случай, когда
магнитные силы отсутствуют. В этом случае гамильтониан имеет вид
[см. B7.2)]
Я' (D® _1_ />а _1_ Da\ _l_ 111 Y V 7 /\ /лп о\
= т;— \'х "г 'V "Г 'zl "г и \Л^ ж i ^> Чш IOZ.O)
Ум V /
Рассматривая волновую функцию как функцию координат частицы х, у, z
и времени t, имеем следующие выражения для операторов:
У—v V—a 7—f
Л. Л, Ж у, Ж* С)
Вычислим теперь оператор —^ . Имеем
[Я, X] = ±- (ХН -НХ)=~[ (ХРХ -Р1Х), C2.5)
так как X коммутирует с Ру, Рг, U (х, у, z, t). Правило перестановки
операторов X и Рх B4.2) дает:
Р1Х= Рх (РХХ) = Рх (ХРХ - ih) = (РХХ) Рх - ihPx =
= (ХРХ - ih) Px - ihPx = XPl - 2ihPx. C2.6)
Подставляя это выражение в C2.5), находим:
[Н,Х]=±РХ. C2.7)
Для у, г, очевидно, получим аналогичный результат; поэтому
dX_Px _dY_Pv dZ^_Pz f49R,
af (X af [x af (X v '
т. е. оператор скорости равен оператору импульса, деленному на массу
частицы ц. Иными словами, связь между операторами скорости и импульса
такова же, как и связь между соответствующими величинами в класси-
классической механике.
Найдем теперь оператор—^. Из C2.2') и B4.4) имеем:
[Я, рх] = -L (Pxu- upx) = - 4г - C2-9)
т. е.
dPx dU dpv dU dPz dU
dt — dx ' dt ~ dy ' dt ~ dz '
C2.10)
1 Ср. дополнение VI, уравнение G).
108

—g—, — -5— , —g-суть не что иное, как операторы проекций силы1.
Так что C2.10) можно переписать также в виде
F fF £±F
~SF-t't dt ~tv dt ~*»
т. е. оператор производной по времени от импульса равен оператору силы.
Поэтому C2.10) можно рассматривать как уравнения Ньютона в опера-
операторной форме.
Если мы вычислим среднее значение от величин -^, —Ц*- и т. д.
в каком-нибудь состоянии г|), то из C2.8) и C2.10) на основании C1.8)
получаем:
%=4^)=-1h^ C2ЛЗ>
и т. д. Иначе говоря, производная по времени от средней координаты
х равна среднему импульсу, деленному на массу частицы, и производная
от среднего импульса рх равна средней силе Fx.
В раскрытой форме равенства C2Л2) и C2.13) имеют вид:
C2.12')
C2.13')
Они носят название теорем Эренфеста. Дифференцируя C2.12) по вре-
А.
dt
мени и исключая из C2Л2) и C2.13) -гг(рх), получим квантовое уравне-
уравнение Ньютона:
dt2 дх х' *
§ 33. Интегралы движения
В квантовой механике мы имеем те же интегралы движения, что
и в классической. Величина L будет интегралом движения, если
4г = 4г + [//' Ц =°> C3.1)
Особый интерес представляет случай, когда величина L не зависит явно
от времени; тогда вместо C3.1) имеем:
4г = [//,/,] = 0, ' C3.2)
т. е. для интегралов движения (не зависящих явно от времени) кванто-
квантовая скобка Пуассона равна нулкх
Так как [И, L] определяется коммутатором оператора L и оператора
Гамильтона, то всякая величина L, не зависящая явно от времени, будет
1 Эти операторы являются попросту функциями координат.
109

интегралом движения, если ее оператор коммутирует с оператором
Гамильтона.
Из формул C3.1) и C3.2) следует, что среднее значение интегралов
движения не зависит от времени:
-^-(Г) = 0. C3.3)
Покажем теперь, что и вероятность w(Ln,t) найти в момент времени t
какое-нибудь значение интеграла движения, равное, скажем, Ln, не зависит
от времени1.
Так как операторы L и // коммутируют, то они имеют общие собствен-
собственные функции tyn(x):
Lt|>n = Lnt|>n, C3.4)
Щп = ЕпУ\>п. C3.4')
Разложим произвольное состояние гр (л:, /) по собственным^функциям г|>„.
Эти функции суть функции стационарных состояний, поэтому [ср. C0.8)]
_4Кп1
г|>(£, 0 = 2 спУп (х) е h , . C3.5)
п
ИЛИ
г|з (х, t) = ^ сп @ Ч*п (*)> C3.6)
п
где
_.Ent _.Ent
г ц\ r p h r ICW'o h • (OO.«/
n V / — n — n\/
Разложение C3.6) есть разложение <г|) (х, t) по собственным функциям
оператора L, поэтому
, K>(Ln, *)=К(/)|2 = К@)|* = const. C3.8)
Вид интегралов движения зависит от рода силового поля, в котором дви-
движется частица. Для свободного движения^скловая функция U (х, у, z, t) = 0
и гамильтониан будет равен
Н = Т^-^-(Ря + Р1 + Р1). C3.9)
Как и в классической механике, в этом случае интегралом движения
т. е. сохраняющейся величиной, является импульс, действительно:
[//,/>,] = [#,/>„] = [#,/>,] = 0, C3.10)
т. е.
\^*_п dPy-о АРг -о mm
В поле центральной силы имеет место закон плсщадей — момент
импульса есть интеграл движения. В самом деле, в поле центральной
силы потенциальная энергия U есть функция расстояния от центра силы:
U = U (г). Поэтому для этого случая гамильтониан И может быть написан
в виде [ср. B6.6)]
H=Tr + ^ + U(r). C3.12)
1 Речь идет об интегралах движения, не зависящих явно от времени.
ПО

Операторы квадрата момента импульса Мг и его проекций Мх, Му, Мг
согласно B5.8) зависят только от углов 6, ф, поэтому не действуют
на функции от г. Кроме того, оператор Ж2, входящий в C3.12), комму-
коммутирует с Мх, Му и Мг [см. B5.6)]. Поэтому все четыре названных
оператора коммутируют с Н C3.12) так, что
4J O, C3.13)
l = ^ = ^ = 0. C3.14)
Таким образом, момент импульса в поле центральных сил есть инте-
интеграл движения.
Применим теперь равенство C1.1) к гамильтониану. Полагая L = H,
получаем:
^-f + [ff.ff]-f. C3.15)
Если гамильтониан не зависит явно от времени, то
-^ = 0. ' C3.16)
Однако в этом случае гамильтониан совпадает с оператором полной энергии.
Поэтому C3.16) выражает тот факт, что полная энергия в поле сил,
не зависящих от времени, есть интеграл движения. Иначе говоря, C3.16)
выражает закон сохранения энергии в квантовой механике.
Согласно изложенным выше свойствам интегралов движения уравне-
уравнение C3.16) следует понимать в том смысле, что ни среднее значение
энергии Е, ни вероятности найти отдельные возможные значения энергии
Е = Еп не зависят от времени1.
1 О законе сохранения энергии в квантовой механике см. § 113.

ГЛАВА VI
связь квантовой механики с классической
МЕХАНИКОЙ И ОПТИКОЙ
§ 34. Переход от квантовых уравнений к уравнениям
Ньютона
Доказанные в § 32 теоремы Эренфеста утверждают, что во всяком
состоянии т|з для среднего значения механических величин имеет место
квантовое уравнение Ньютона1:
Представим себе, что г|з отлично от нуля заметным образом лишь
в очень малой пространственной области Л*. Такое состояние мы будем
называть волновым пакетом.
Если бы среднее значение х изменялось согласно классическому
уравнению Ньютона и форма пакета не менялась бы, то движение
пакета | г|з|2 мы могли бы рассматривать как движение материальной точки,
подчиняющейся ньютоновской механике. Вообще говоря, такого движения
по квантовой механике не получается, так как, во-первых, волновой пакет
расплывается, а, во-вторых, чтобы движение центра тяжести пакета х
совпадало с движением материальной точки в поле U (х), нужно, чтобы
осуществлялось равенство
дх
Последнее равенство, вообще говоря, не имеет места. Рассмотрим
все же подробнее те условия, при которых движение пакета приближенно
совпадает с движением материальной точки. Среднее значение х коорди-
*"иаты х, т. е. координата центра тяжести пакета, определяется формулой
х=\ ty*x\pdx. C4.3)
Среднее значение силы есть
\>*-&Vdx C4-4)
1 Мы ограничиваемся одним измерением. Обобщение рассуждений иа пространствен-
пространственный случай не представляет никакого труда.
112

Положим х = х-\-\, тогда
\ dU^l) C4.4')
Допустим, что U (х) достаточно медленно меняющаяся функция перемен-
переменной х в области, где |г|)|2 заметным образом отлично от нуля. Тогда
——_ можно разложить в ряд по степеням |. Производя это разложе-
дх
ние, получим
WW]t-... C4.5)
Но
^ )*|2г|) d£ = | г|>* (л; — 7Jг|) Ах =
Поэтому
Из уравнения C4.1) имеем:
£
Если силовое поле медленно изменяется в пространстве, то, выбрав
достаточно малую ширину пакета А*2, мы можем в этом уравнении пре-
пренебречь всеми членами, кроме первого. _Тогда мы получим уравнение
Ньютона для движения центра тяжести (х) волнового пакета:
которое будет справедливо для того промежутка времени t, для которого
отброшенные в уравнении C4.7) члены малы, т. е. по крайней мере при
условии пока
— '«-Жд*. C4.8)
dU(x)
d~x~
1
2
d*U (х)
. дх*
Величина Л*2, определяющая размеры пакета, есть функция времени и
вообще говоря, растет со^временем (см. ниже)—пакет расплывается. Поэтому,
если даже неравенство C4.8) выполнено в начальный момент времени,
то, начиная с некоторого момента t, оно может нарушиться. Но и выпол-
выполнение неравенства C4.8) еще не означает, что состояние частиц совпадает
с классическим1.
1 Для всех функций U (х) вида: U=a-\-bx-\-cx2, как следует из C4.7), движение
центра тяжести пакета точно совпадает с классическим движением материальной точки
в поле U (х). К числу таких случаев относятся: а) свободное движение, Ь) движение
в однородном поле, с) гармонический осциллятор и некоторые другие -(например, в одно-
однородном магнитном поле получаются те же результаты, что и для осциллятора).
8 Д. И. Блохинцев ""

Действительно, если взять очень узкий пакет (А*2 мало), то средняя
потенциальная энергия частицы по квантовой механике практически равна
потенциальной энергии материальной точки, находящейся в центре волно-
волнового пакета:
XJ = ^ г|)*{/г|) dx^U (*). C4.9)
Но этого нельзя сказать о кинетической энергии Т. Действительно,
f-i^(^+^=W+i' C4J0)
В силу соотношения Гейзенберга
поэтому в C4.10) первый квантовый член может оказаться Гораздо больше
классической энергии частицы, движущейся с импульсом р.
Квантовым членом в C4.10) можно пренебречь, если
ЬЦЬ- <34Л1>
Таким образом, движение частицы можно считать происходящим по законам
классической механики в течение времени t, если в течение этого времени
можно одновременно удовлетворить неравенствам C4.8) и C4.11).
Одновременному удовлетворению обоих этих неравенств благоприятст-
благоприятствуют следующие -обстоятельства: 1) большая кинетическая энергия
частицы Т; 2) поле U (х) представляет собой медленно меняющуюся
функцию координат х.
Таким образом, переход от квантовых уравнений движения к нью-
ньютоновским получается при переходе к большим кинетическим энергиям
частиц и плавно меняющимся полям.
Рассмотрим теперь расплывание пакета для свободного движения частицы. Среднее
квадратичное отклонение Ахг есть среднее от величины
Ах* = х*—х\\
где "х—координата центра пакета. Согласно C4.7) имеем:
dx — —
—=о, x = vt+x0, C4,12)
т. е. центр пакета движется инерциально со скоростью v. Производные величины Ахг
по времени вычисляются по общей формуле C1.7). Полагая там L = Ax2, находим:
> так как для свободного движения оператор //=—— Р*, то
1 1
[Н, *•] =ж [Р\ х<[ =
dAx*
Таким образом оператор . равен
-
-2Ъх. C4.13)
* Во всех дальнейших расчетах пользуемся формулой Рххшш.хРх—:И,
114

Вычислим теперь вторую производную
д Г dAx*
dP
хР+Рх
—~
[я, .£*±*£] =^
OD2 W2y2 2P2 —
C4. H)
Xt=X+\tt
Рис. 20. Движение и расплывание волнового пакета в отсутствии
внешних сил
Ввиду того, что Р2 коммутирует с Н, все высшие производные от Ах2 равны нулю.
Таким образом, разложение Дха в ряд Тейлора по степеням t имеет вид
Переходя от операторов к средним значениям, получим:
C4.15)
C4.16)
Ах2—величина, обязательно положительная, поэтому из C4.16) следует, что A.xt
с ростом t неограниченно растет (может быть, переходя через минимум), т. е. пакет
расплывается. Во многих случаях [в зависимости от вида г|) (х, 0)]
член с t исчезает. Тогда C4.16) получает особенно простой
вид:
C4.17)
где До2—среднее квадратичное отклонение скорости
Расплывание такого пакета совпадает с растеканием роя частиц
в классической механике, если их начальные положения и ско-
скорости распределены около средних значений с квадратичными
отклонениями Ах% и До2. Однако в классической механике мож-
можно взять рой, в котором Ах% и До2 савны нулю. В квантовой
механике этого сделать нельзя в силу соотношения неопреде-
неопределенностей. Рис. 20 иллюстрирует сказанное выше о движе-
движении и расплывании волнового пакета.
В качестве приложения теории движения пакета, изложен-
изложенной в этом параграфе} найдем условия, при выполнении кото-
которых рассеяние частицы в поле атома можно рассматривать
методами классической механики. Пусть радиус сил взаимодей-
взаимодействия между атомом и проходящей около него частицей будет а.
Ясно, что для того, чтобы можно было говорить о траектории
частицы внутри атома, необходимо, чтобы размеры волнового
пакета Д* были много меньше а (рис. 21).
JHIa основании C4.10) и C4.11) заключаем, что кинетическая' энергия'частицы
р 2 А2 А2 V'" '
" ~2 {так как Ах < а). При этом же условии пакет не успевает
Рис. 21. ' Рассеяние
частицы в поле атома:
О — центр атома, а—ра-
а—радиус действия сил, АЛ'—
траектория пакета, рас-
расплывающегося от ширины
Ах до ширины Дх'
2ц
8ца2
8* 115

заметно расплыться за время прохождения частицы через атом, которое по порядку
а а-|х
величины равно г = — ■ = _ _ Действительно, из C4.17) следует, что расширение пакета
составляет Дл:' s= bv-t = ———lp-=—J- а; так как при выполнении C4.11) Др <^ р, то
V- р р
Дх' < а.
Радиус действия сил по порядку величины равен радиусу атома asslO""8 см.
Для a-частицы, с типичной энергией Г = 1 Мэв = 1,6-10 э, p~a=Y2\x^T—4,6-106
(масса a-частицы |ха=6,7-10"г< г). С другой стороны, А/а= 1-10~19. Таким образом, для
a-частицы уравнение C4.11) выполнено. Следовательно, рассеяние a-частицы можно рас-
рассматривать методами классической механики (что и было впервые сделано Резерфордом
в его знаменитой теории рассеяния a-частиц). Однако, если d-частица проходит вблизи
ядра, то необходимо учесть действие ядерных сил, для которых сфера действия a s 10~lsсм,
/i/a=M(Kls и уравнение C4.11) будет выполнено плохо. Поэтому рассеяние а-частиц
ядерными билами («аномальное» рассеяние) нельзя изучать средствами классической
механики. _
Для электронов (це = 9.10~28 г), например, при Т=100эв имеем ре = 5,4-10~19,
так что ре сравнимо с ft/a, и применять классическую механику к этому случаю невоз-
невозможно.
§ 35. Переход от временного уравнения Шредингера
к классическому, уравнению Гамильтона — Якоби
В предыдущем параграфе мы установили связь квантовых уравнений
движения с уравнениями Ньютона и тем самым —связь квантовой механики
с классической. Эта связь может быть обнаружена еще другим способом:
можно показать, что классическое уравнение Гамильтона — Якоби является
предельным случаем временного уравнения Шредингера. Чтобы доказать
это, напомним сперва уравнения Гамильтона — Якоби. Для простоты ограни-
ограничимся рассмотрением движения одной частицы массы ц в потенциальном
поле U {х, у, z, t). Уравнение Гамильтона—Якоби пишется для функции
действия Sn(x, у, z,t), которая обладает тем свойством, что
где рх, ру, рг суть проекции импульса частицы на оси координат. Само
уравнение Гамильтона —Якоби для рассматриваемого случая гласит:
dt 2|.
Так как функция Гамильтона Н (рх, ру, pz, x, у, z, t) равна
Н (рх, ру, рг, х, у, z, t) = -^ (р£ + р\ + pi) + U (х, у, z, t), C5.3)
то из C5.1) и C5.2) следует, что уравнение Гамильтона—Якоби может
быть написано в виде /
о м( » )L У. v и у i \
Э< ч дх ' ду дг *" J
Если функция Гамильтона явно от времени не зависит, то она равна
энергии частицы Е. Тогда из C5.4) следует
dt
116
ds»=E, S0 = Et-s0(x, у, г). C5.5)

Равенства C5.1) показывают, что траектории являются линиями,
ортогональными к поверхностям So = const. Если Я не зависит от времени
явно, то форма этих поверхностей не меняется с течением времени.
На рис. 22 показаны эти поверхности и возможные траектории
частицы.
Частица, находящаяся в момент времени t = О в точке а, будет
двигаться в дальнейшем по траектории а, Ь. Представим себе рой частиц,
имеющих различные начальные координаты х0, у0, z0. Пусть в элементе
объема AV имеется АЛ/ = qAV частиц, где Q— плотность частиц. К моменту
времени t все эти частицы переместятся в некоторую другую область
пространства, но число их, конечно, не изменится. Поэтому, если
следить за движением элемента объема
AV, связанного с этими частицами, то
число частиц в нем остается неизменным.
Обозначая локальную производную че-
D
рез -=гт-, получим:
Но, как известно, локальные производ-
производные от q и AV равны
Рис. 22. Траектория и поверхности
гдеу — скорость движения частиц. Ком- постоянной функции действия
бинируя эти выражения с преды-
предыдущим равенством, мы получаем уравнение непрерывности
divFv)=0.
На основании C5.1)
Поэтому C5.6) можно переписать в виде
L
e о,
-g- = -i- {VqVS0
C5.6)
<35-7)
C5.8)
Таким образом, рой частиц движется, как жидкость. Занимаемый им объем
не «расплывается», а только деформируется.
Уравнения C5.8) можно истолковывать и иначе. Если мы разделим
число частиц AN в объеме АV на общее число частиц N, то -^- можно
рассматривать как вероятность найти частицу в объеме AV, а плотность
q —как плотность вероятности.
Обратимся теперь к квантовой механике. Покажем, что временное
уравнение Шредингера
Н= -~
C5.9)
ведет приближенно к тем же результатам, что и рассмотренное уравне-
уравнение Гамильтона — Якоби. Для этого представим волновую функцию г|> в виде
117

где S —некоторая искомая функция. Замечая, что
*E-_±a-S,h <^_ _±^asY,i, ' d*s .
дх h Ъх ^' Ъхг~ h*\dx) ^~~ hW*1р'
мы получим, подставляя C5.10) в C5.9), уравнение для функции S:
Разложим теперь S по степеням ih:
S = S0 + (ih)S1 + (ih)^S2+... C5.12)
Подставляя C5-12) в C5.11) и сравнивая "коэффициенты при одина-
одинаковых степенях /г, мы получаем уравнения:
9 as0 as, 9 as0 as, „ as0 dst т„ \ _
"a?'- 2^11/ ax ax + ^ a^ dy +z Ж a7 + v ^oj ~~
2|rS1 + V2S0} C5.13')
и т. д. ,
Первое из этих уравнений совпадает с уравнением Гамильтона —Якоби
C5.2), а второе, как легко видеть, совпадает с уравнением непрерывности
C5.8). В самом деле, вероятность найти частицу в окрестности точки
х, у, z есть
е-Ц)|« = вав,+.... C5.Н)
Отсюда
Поэтому, умножая уравнение C5.13') на 2e2S>, мы получаем уравнение
непрерывности C5.8).
Остается выяснить вопрос об области применимости полученного
приближенного решения уравнения Шредингера. При переходе от C5.11)
к уравнению C5.13) мы отбросили член ^-V2S; это возможно сделать,
если
^|f | C5.15)
f V*S0
Пользуясь C5.1), это неравенство можно записать в виде
£»|;|divp|. ^ C5.16)
Это неравенство означает, что кинетическая энергия должна быть
велика, щ изменения импульса |divp| малы. Для одного измерения
получим:
P*»hfx. C5.16')
Вводя длину волны де Бройля Я, = —, находим:
£<2л, C5.17)
т. е. длина волны должна медленно меняться в функции координаты.
ив

§ 36. Квантовая механика и оптика
Исторически одним из истоков квантовой механики послужили па-
параллели, установленные Гамильтоном между геометрической оптикой и
механикой. Эти забытые аналогии были привлечены де Бройлем в совре-
современную физику, и с их помощью были сделаны первые шаги квантовой
(волновой) механики г. Часто говорилось, что Шредингер построил меха-
механику, аналогичную волновой оптике.
Аналогии часто помогают решению той или иной физической про-
проблемы, но все же остаются только аналогиями. Окончательно написан-
написанное Шредингером уравнение не совпадает ни с одним из ранее извест-
известных уравнений для распространения волн. Эти последние—всегда уравне-
уравнения второго порядка по времени, в то время как уравнение Шредингера —
первого порядка по времени; имеются и другие отличия.
Тем не менее все же представляет интерес сравнить уравнение
Шредингера с уравнениями волновой оптики. Допустим, что мы имеем
некоторую однородную среду, в которой распространяются волны со
скоростью v. Тогда уравнение для смещения / при распространении
таких волн будет
*2f-ww = °- C6-D
Для волны, имеющей частоту колебаний to, можно положить
[ = ие-ш, C6.2)
тогда из C6.1) получаем:
0, 62 = J C6,3)
С
= -у—волновое число, Я,—длина волны \ Уравнение C6.3) строго
применимо для однородной среды2. Однако оно описывает явления
дифракции и интерференции и в том случае, если считать скорость v
функцией координат. Поэтому его можно рассматривать как волновое
уравнение и для неоднородной среды. В этом случае кг будет функцией
координат. Условно будем и в этом случае называть k волновым числом,
а Я, = -? — длиной волны,
к
Введем показатель преломления «(л:, у, г):
п (х, у, г) = у = ^ , C6.4)
где К — Длина волны в пустоте. Тогда уравнение C6.4) можно написать
в виде
V2m + &o«2u = O. C6.5)
Если неоднородности среды таковы, что показатель преломления п мало
меняется на протяжении длины волны, то из волнового уравнения C6.5)
можно получить основное уравнение геометрической оптики (в противном
случае мы будем иметь дело с дифракцией волн на этих неоднородно-
стях).
1 См. де Бройль, Введение в волновую механику, ГНТИ Украины, 1934.
2 Уравнение для распространения волн в неоднородной среде (например, электро-
электромагнитных волн в среде с переменной диэлектрической постоянных выглядит иа самом
деле сложнее, чем C6.3).
119

Положим
u = aeihoQ, C6.6)
где а —амплитуда, ko& — фаза волны. Если длина волны мала, то k0
велико. Разложим а и в по обратным степеням k0:
fl = ae+lfl1 + ^a,+ ...f C6.7)
в = в, + 1в1 + 1в,+ .... C6.8)
Подставляя C6.7) и C6.8) в C6.6), а C6.6) в C6.5) и собирая одинако-
одинаковые степени k0, получим уравнение C6.5) в виде
- k\a0 (V60J + %п*ао + О (k0) = 0, C6.9)
где О (k0) означает члены порядка k0 и ниже. Пренебрегая ни зшими сте-
степенями k0, находим отсюда
(V0oJ=n2. C6.10)
Это и есть основное уравнение геометрической оптики, определяющее
поверхности постоянной* фазы
во'(*. у, z)= const C6.11)
через показатель преломления п (х, у, г). Лучи будут линиями, ортого-
ортогональными к этим поверхностям.
Сопоставим с уравнением C6.9) уравнение Гамильтона — Якоби C5.2)
для функции действия So. Производя там подстановку So = £7 — s0, мы
можем написать C5.2) в виде
(Vso)* = 2[i [£-£/(*, у, г)]. C6.12)
Сравнение этого уравнения с C6.10) показывает, что задаче о распрост-
распространении лучей малой длины волны (большое k0) в неоднородной среде
с показателем преломления п (х, у, г) может быть сопоставлена задача
о движении материальной точки в поле сил с потенциальной энергией
U (х, у, г), причем роль показателя преломления играет величина
Jn( — U), а фазы —величина s0. Траектории частиц суть линии, орто-
ортогональные к поверхностям so(x, у, z) = const. Поэтому траектории совпа-
совпадают с лучами света в среде, показатель преломления которой п пропор-
пропорционален ]/2ц {E — U). Таким образом, классическая механика материаль-
материальной точки аналогична геометрической оптике.
Если уравнение C6.3) рассматривать как уравнение волновой оптики,
то можно сказать, что волновая (квантовая) механика аналогична волно-
волновой оптике. В самом деле, уравнение Шредингера
подстановкой
^ = шГ£' - C6-13>
сводится к уравнению
V2u + |^[£-£/]u = 0. C6.14)
Пусть теперь в некоторой области пространства силы отсутствуют:
U = С = const. Обозначим волновое число в этой области через k0. Тогда
kl = $.{E-C) C6.15)
120

(обычно полагают С = 0). Вводя показатель преломления волн по отноше-
отношению к этой области пространства
 = lS = F' <36Л6)
мы можем написать уравнение C6.14) в виде
V2u + k\rPu = 0, C6.17)
что совпадает с C6.5).
Простейшие задачи по расчету преломления и отражения волн при-
приведены в § 94.
При выводе C6.10) из C6.9) мы пренебрегли членами О (k0). Вычислив их, нетрудно
убедиться, что мы пренебрегли членом fc0V260 в сравнении с &§(V60J. Взяв (для про-
простоты) одно измерение, мы можем написать условие справедливости нашего приближе-
приближения в виде , -^
C6.18)
< 2л, C6.19)
Замечая, что к= -г-= к0 ■— , получаем
К ох
дх
что совпадает с ранее полученным условием C5.17) для перехода от уравнения Шре-
дингера к уравнению Гамильтона—Якоби.
Из C6.16) следует, что показатель преломления я, а вместе с ним и длина вол-
волны X=2n/k, заметно меняется лишь в той области пространства, где заметно меняется
потенциальная энергия U, т. е. внутри сферы действия сил а. Если сфера действия
сил а > X, то на протяжении X как U, так и я будут меняться мало (кроме некоторых
исключительных случаев крайне резких изменении потенциальной энергии).1
Поэтому для ориентировочных расчетов условие C6.19) можно заменить более
простым условием:
Я,<о.
Предоставляем читателю применять это условие к примерам, приведенным в § 34.
§ 37. К^вазиклассическое приближение (метод
Вентцеля — Крамерса — Брюльэна)
Изложенная в §§ 35, 36 связь между квантовой механикой и клас-
классической механикой и оптикой позволяет развить приближенный метод
решения уравнения Шредингера, пригодный в тех случаях, когда соблю-
соблюдено условие C6.19), т. е. при слабом изменении длины волны. Говоря
на оптическом языке, в тех случаях, когда показатель преломления
среды п (х) медленно меняется в пространстве.
Тогда, полагая, в соответствии с C6.12) и C6.13)
* = е-Г1'-'-* C7.1)
и s = so + ihs1 + .. . C5.12); получим
■v|) = esie мж-*о>. C7. Г)
1 Может создаться впечатление, что для любых микрочастиц, имеющих достаточ-
достаточно большую энергию и, следовательно, обладающих малой длиной волны X, всегда
будет применима классическая механика. Однако это не так.
При возрастании энергии частицы возникают явления неупрутих ударов (иониза-
(ионизация и возбуждение атомов, тормозное излучение, возбуждение и р|(ЗДеплеиие атомного
ядра и т. п.), которые не могут быть рассчитаны без применения квантовой механики.
121

Рассмотрим в дальнейшем тот случай, когда потенциал U зависит
лишь от одной координаты U = U (л:), тогда s0 и sx также будут функ-
функциями только х.
Теперь Vso = ^-, 0, 0 и из C6.12) следует, что
^(x)dx, C7.2)
где р(х) есть импульс частицы:
г/(*)Н±|р(*)|. C7.2')
Пользуясь C5.13'), вычислим sv причем там следует положить
-А — 0. Получим:
2^-^ + ^ = 0. C7.3)
dx dx ' dx1 v '
Откуда sx = — -^ lg p (x) +"\g с так, что
ib = — fh J . • (oIA)
Yp(x)
В этом приближении вероятность найти частицу в области х, Jc+dJcecTb
'12^ = -Цг7^' C7-5>
т. е. она обратно пропорциональна скорости v (х) = ^-^, стало быть прямо
пропорциональна времени прохождения отрезка dx, как это и должно
быть по классической теории. Учитывая два возможных знака р(х) C6.2'),
полное решение следует написать в виде суперпозиции двух решений:
а . C7.6)
Константы Cj, c2 и а должны быть выбраны из граничных условий
для волновой функции г|> (х) г. Ясно, что из трех констант независимы
только две.
Особого рассмотрения требует случай точек поворота, т. е. таких
точек, где полная энергия Е равна потенциальной V (х). В такой точке
кинетическая энергия и импульс частицы становятся равными нулю:
Г = 0, р = 0.
Согласно классической механики частица в такой точке меняет знак
скорости и начинает двигаться в обратном направлении. .^ Отсюда и наз-
название — точка поворота.
С волновой точки зрения допустимо движение и в области, где
Е < V (х) (об этом подробно будет рассказано в §§ 96, 97). При этом вели-
величина р(х) C7.2') будет чисто мнимой и, конечно, уже не имеет смысла
импульса:
ч Р (*) = ± ' V2p[v(x)-E]= ±i\p(x) |. C7.2" )
При этом одно из- решений в C6.5) будет неограниченно нарастать
с ростом х. Физически имеют смысл только ограниченные волновые
1 См. дополнение VIII.
122

функции, поэтому в области, где Е < U (х), константу с2 следует положить
равной нулю, так что
х
J* Р (х) дх
( J± . C7.6')
Y\p(x)\
Для дальнейшего рассмотрения точек поворота удобно выбрать кон-
константу а равной значению х в точке поворота E — U{a), p(a) = 0.
Как видно из C7.6), C7.6'), найденные приближенные решения обра-
обращаются в бесконечность как раз в точках поворота. Поэтому смыкание
решений по обе стороны от точки поворота требует рассмотрения более
точного решения уравнения Шредингера в окрестности точки поворота.
Это достигается тем, что в окрестности х — а потенциал U (х) пред-
стваляют в виде U(х) = U (а)+ (-,-) (х—а)-\-... и решают для этого
\_иХ /а
линейного потенциала уравнения Шредингера. Мы приведем только
результаты такого расчета.
Будем считать, что для х > а, Е < U {х), а при х < а, Е > U (х),
тогда оказывается, что правильный выбор констант таков, чтох:
х
г|) (х) = у= sin {j- ^ p (x)dx + ±} , x<a, C7.7)
X
[I |p (я) I (fa
, x>a. C7.7')
И для случая, когда E>U{x) в области лг>а:
Предположим теперь, что область движения частицы ограничена и оно
происходит между двумя точками поворота Ь < х < а.
Тогда в 37.7" следует вместо предела а подставить Ь. Очевидно,
что оба решения C7.7) и
{\] <37-8>
в области Ь < х < а должны совпадать. Это возможно лишь при условии:
ь
J = (n+l)*, C7.9)
где л —целое число. **
Распространяя интеграл по всему пути частицы от а до ft и обрат-
обратно, получим
§ ^ ^ C7.10)
Это есть условие квантования по старой, полуклассической теории Бора.
Появление х/2 наряду с целым числом п несущественно, так как, строго
говоря, классическое приближение справедливо лишь тогда, когда п > 1
(условие малости длины волны).
1 См. например, Л. Ландау и Е. Лифшиц, Кваитовая^цмехаиика, ГИТТЛ,
948.
123

ГЛАВА VII
ОСНОВЫ ТЕОРИИ ПРЕДСТАВЛЕНИЙ
§ 38. Различные представления состояния квантовых систем
Как мы видели, для квантовой механики характерно, что одновре-
одновременное употребление ряда классических корпускулярных величин (рх
и х, Т и U, Мх и Му и I1. п.) теряет всякий смысл, так как в природе не
реализуются такие ансамбли, в которых приведенные пары величин суще-
существовали бы одновременно.
Поэтому в отношении каждой квантовой системы все измерительные
аппараты могут быть разбиты на группы. Аппараты одной из таких групп
сортируют частицы (или, общие системы) ансамбля по признакам, исклю-
исключающим сортировку по признакам, характерным для какой-либо другой
группы измерительных аппаратов. Так, например, если мы имеем дело
с частицами, координаты центра тяжести которых суть х, у, г, то мы легко
можем выделить две группы аппаратов; к первой группе можно отнести
аппараты, анализирующие ансамбль таких частиц по координатам х, у, г
и по любым функциям от них F(x, у, г) [например, по потенциальной энер-
энергии U(x, у, г)], а по второй группе — аппараты, анализирующие ансамбль
по импульсам рх, ру, р2 или по любым функциям Ф(рж, ру, pz) от них
[например, по кинетической энергии Т(рх, ру, pz)]. Возможны и другие
группы аппаратов.
До сих пор мы изображали состояние частиц волновой функцией г|)(лг),
беря в качестве переменной координату частицы х (простоты ради, в даль-
дальнейшем мы употребляем лишь одну координату х).
Сортировка частиц по координатам х производится аппаратами, исклю-
исключающими сортировку по рх (далее будем писать просто р вместо рх). Пред-
Представим себе, однако, что мы интересуемся сортировкой частиц не по их
Координатам х, а по их импульсам. Тогда нужно взять аппарат, анализи-
анализирующий ансамбль по р, а не по х. Между тем волновая функция г|), описы-
описывающая ансамбль, взята как функция х. Нельзя ли ойисать состояние
ансамбля так, чтобы волновая функция была функцией импульса р?
В первом случае мы будем говорить, что состояние отнесено к аппа-
аппарату, анализирующему ансамбль по координатам частиц х (первая «система
отсчета»), во втором случае — к аппарату, анализирующему ансамбль по
импульсам рх (вторая «система отсчета»). Коротко говорят: состояние дано
в «^«-представлении или состояние дано в «ps-представлении1.
Найти «р»-представление очень легко. Пусть нам дана волновая функ-
функция г|)(лг, t) («^-представление). Разложим эту функцию по собственным
1 Следует читать: «координатное представление», «импульсное представление».
124

функциям оператора импульса г|)р (х) (т. е. в интеграл Фурье), тогда
г|> (*, t) = ^ с (р, t) % (х) dp, C8.1)
(x,t)^l(x)dx. C8.2)
Если мы знаем амплитуды с(р, t), то мы знаем и г|>(лг, t), задание с{р, t)
вполне определяет г|)(лг, t). Поэтому с{р, t) можно рассматривать как волно-
волновую функцию, данную в функции импульса р и изображающую физически
to же состояние частицы, что и функции г|>(лг, t). Формулу C8.1) следует
рассматривать как преобразование волновой функции от «р»-представле-
ния к «««-представлению, а C8.2) — как преобразование от «««-предста-
«««-представления к «/«-представлению.
Рассмотрим теперь представление состояния, когда за независимую
переменную взята энергия частицы Е. Пусть, для определенности, Е имеет
дискретный спектр значений: Elt E2, £„,.... Соответствующие собствен-
собственные функции обозначим через ty^x), \\>2(x),..., г|)„ (х),.... Волновую функ-
функцию г|)(лг, t) мы можем представить в виде ряда
*). C8.3)
ся @ =$*<*• tWAx)dx. C8.4)
Опять-таки задание всех амплитуд сп @ вполне определяет г|)(лг, t). Обратно,
задание г|)(лг, t) определяет cn{t). Поэтому совокупность всех cn(t) можно
рассматривать как волновую функцию, описывающую то же состояние,
что г|)(лг, t), но в представлении, в котором за независимую переменную
взята энергия1 Е.
С этой точки зрения формула C8.3) есть преобразование волновой функ-
функции от «Еъ-представления к «^-представлению. Формула C8.4) есть фор-
формула обратного преобразования. Из формул C8.1), C8.2), C8.3) и C8.4)
следует, что вероятность найти какое-либо значение независимой переменной
равна квадрату модуля волновой функции в соответствующем представлении.
В самом деле, пусть имеется некоторое состояние г|)(лг, t), тогда вероятность
w(x, t) найти значение координаты, лежащее между х и x+dx, будет
w(x, 0d* = l4>(*. t)\*dx. C8.5)
Вероятность w(p, t)dp найти импульс р между р и p + dp будет
w{p, t)dp = \c{p, 0|2dp. C8.6)
Вероятность найти энергию w(En, t) равной Еп будет
= \c(En,t)\*. . C8.7)
§ 39. Различные представления операторов, изображающих
механические величины. Матрицы.
Для того чтобы изображение состояний г|) в разных независимых
переменных получило полную законченность, нужно еще найти способ
представления операторов в тех же переменных. Между тем до сих пор
мы рассматривали операторы L как «функции» х, считая, что L имеет
1 В полной аналогии с с(р, t) вместо cn(t) (я=1, 2, 3I мы могли бы писать:
с(Е, t) (E=Elt £„..., £„,...).
125

вид L( — *^3i' -О- В этом случае оператор L действует на функции
вида г|>(лг) и производит новую функцию ф(лг) соответственно формуле
>(*). C9.1)
Поэтому можно сказать, что мы брали оператор L в «.хъ-представлении.
Найдем теперь оператор L в энергетическом представлении («£»-пред-
ставление), считая, что энергия имеет дискретный спектр значений Еп.
Соответствующие собственные функции пусть будут г|)п (х). Тогда функции
Ф и г|) можно представить в виде
C9.2)
C9.3)
Совокупность сп есть г|) в «/^-представлении, а совокупность Ьп есть <р
также в «/^-представлении. Оператор L производит из г|) новую функ-
функцию ф, а вместе с тем и^ сп новые амплитуды Ьп. Если мы найдем опе-
оператор, который бы непосредственно выражал Ьп через сп, то тем самым
мы найдем оператор L в «/^-представлении. Для этой цели подставим т|з
и ф из C9.2) и C9.3) в C9.1). Тогда мы получаем:
2 М>п (*) = S Cn'Ltyn{x). [C9-4)
Умножая C9.4) на tym{x) и интегрируя по
получим в силу ортогональности функций
всему пространству х, мы
{)
C9.5)
где
C9.6)
Зна все величины Ьтп, мы можем по формуле C9.5) найти все ампли-
амплитуды (функцию ф в «£»-представленин) по заданным сп (т. е. по
функции г|) в «£»-представлении). Поэтому совокупность всех величин
Lmn следует рассматривать как оператор L в «Е-»-представлении.
Эту совокупность можно расположить в виде квадратной таблицы
Jm3
"тп
C9.7)
имеющей бесконечное число строк и столбцов. Такая таблица называется
матрицей. Сами величины Lmn называются матричными элементами.
Каждый матричный элемент имеет два индекса1. Первый есть номер
1 Часто применяются другие обозначения матричных элементов, введенные-
Дираком, именно, пишут:'
(m\L\n) вместо 1^,
илн еще подробнее:
(Em\L\ En) вместо Lmn.
126

вид L
вида
~-ihj-x,x
jxj. В этом случае оператор L действует на функции
и производит новую функцию ф(х) соответственно формуле
C9.1)
Поэтому можно сказать, что мы брали оператор L в «х»-представлении.
Найдем теперь оператор L в энергетическом представлении («£»-пред-
ставление), считая, что энергия имеет дискретный спектр значений Еп.
Соответствующие собственные функции пусть будут ifn(x). Тогда функции
ф и if можно представить в виде
${х) = '£спЦп(х), C9.2)
ф(*) = 2А %(*)• C9.3)
Совокупность сп есть if в «^«-представлении, а совокупность Ьп есть ф
также в «£»-представлении. Оператор L производит из if новую функ-
функцию ф, а вместе с тем из сп новые амплитуды Ьп. Если мы найдем опе-
оператор, который бы непосредственно выражал Ьп через сп, то тем самым
мы найдем оператор L в «£»-представлении. Для этой цели подставим г|>
и ф из C9.2) и C9.3) в C9.1). Тогда мы получаем:
Ьг$п \х) = 2j cn«Lifo (x). lC9.4)
п п
Умножая C9.4) на ifm(*) и интегрируя по всему пространству х, мы
получим в силу ортогональности функций ifn(x)
C9.5)
Jl»/ri'
где
C9.6)
Зна все величины Ьтп, мы можем по формуле C9.5) найти все ампли-
амплитуды (функцию ф в «/^-представлении) по заданным сп (т. е. по
функции "ф в «£»-представлении). Поэтому совокупность всех величин
Lmn следует рассматривать как оператор L в «Е»-представлении.
Эту совокупность можно расположить в виде квадратной таблицы
L =
■^22 23 • • • -^2
C9.7)
имеющей бесконечное число строк и столбцов. Такая таблица называется
матрицей. Сами величины Lmn называются матричными элементами.
Каждый матричный элемент имеет два индекса1. Первый есть номер
1 Часто применяются другие обозначения матричных элементов, введенные
Дираком, именно, пишут:
(m\L\n) вместо Lmn,
или еще подробнее:
(Em\L\En) вместо Lmn.
126

строки, второй — номер столбца. Безразлично, как мы располагаем в такой
матрице строки и столбцы. Но в каждом расчете необходимо, конечно,
соблюдать одно определенное расположение. Мы условимся нумеровать
строки и столбцы в порядке возрастания собственных значений:
£1<£2<£3< ... <£„< ....
Можно найти представление операторов L и в том случае, когда независимая
переменная имеет непрерывный спектр значений. Обратимся в качестве примера
к «р»-представлению. В полной параллели с C9.2) и C9.3) имеем:
(р)%(х)йр, C9.2')
(p)%(x)dp, C9.3')
с(р) и Ь (р) суть функции i|) и ф в «^«-представлении. Найдем связь между с (р) и Ь(р).
Вставляя C9.2') и C9.3') в C9.1), получаем:
b (p) % (x) dp=\ с (р) ■ L% (x) ■ dp. C9.4')
Умножая это уравнение на г])*, (х) и интегрируя по х, в силу ортогональности функ-
функций ifij, (x),получаем:
\ b (р) б (р' — р) dp = \ с (р) dp
или
b(p')=<\)Lp,pc(p)dp, C9.5')
где
Lp,p = L(p', p)= \ ty*, (x)-Lipp (x)-dx. C9.6')
Величина Lplp есть оператор L в «/«-представлении. Она зависит от двух переменных
р' и р, пробегающих одни и те же значения. Lp,p по-прежнему будем называть
матричным элементом оператора L в «/«-представлении, а всю совокупность значе-
значений Lp,p-—матрицей. Ясно, что в этом случае мы не можем изобразить L , в виде
таблицы. Тем не менее и в этом случае р' будем называть номером строки, а р—
номером столбца.
Мы видим, что в произвольном представлении операторы изобра-
изображаются матрицами1. В <да>-представлении мы имели операторы в виде
дифференциальных операторов. Однако можно показать (см. § 40), что и
в этом представлении операторы можно записать в матричной форме.
§ 40. Матрицы и действия над ними
В матрицах мы отличаем среди всех элементов так называемые
диагональные элементы. Диагональными элементами называются матрич-
В этом последнем обозначении указывается не только оператор (L), которому при-
принадлежит матричный элемент, но и представление, в котором он берется (Е), и, нако-
наконец, номера собственных значений тип, которым принадлежит матричный элемент.
Такое обозначение особенно удобно в случае вырождения (§ 21), когда волновые функ-
функции характеризуются несколькими индексами.
1 В самом деле, под Е или р можно разуметь любую величину L, имеющую
дискретный или соответственно непрерывный спектр значений. Более обще, под Е
или р можно разуметь целую совокупность независимых, одновременно измеримых
величин L, M, N, ... .
Более полное изложение теории представлений и преобразований от одного пред-
представления к другому читатель найдет в книгах: Я. И. Френкель, Волновая меха-
механика, т. II, ГТТИ, 1935; П. М. Дирак, Основы квантовой механики, ГТТИ, 1935.
127

ные элементы, номер строки которых равен номеру колонны, т. е. эле-
элементы вида Lnn. В случае непрерывного спектра диагональными эле-
элементами называют элементы вида L . Если матрица имеет только
диагональные элементы, то ее называют диагональной матрицей. В случае
дискретного спектра такая матрица имеет вид
0 0 ... 0
о
D0.1)
L =
0 L22 0
0 0 0 ... L.
Важным случаем диагональной матрицы является единичная матрица б
с элементами 6mn, равными
т = п.
Эта матрица имеет вид
6 =
1 0 0 0 ...
0 1 0 0 ...
0 0 1 0 ...
о
D0.2)
D0.2')
Из определения матричных элементов единичной матрицы D0.2) следует,
что единичная матрица остается единичной в любом представлении,
ибо равенство D0.2) имеет место для любой системы ортогональных
функций г|)„ (х). Элементы диагональной матрицы L всегда могут быть
записаны в виде:
Lmn = Ln6mn. D0.3)
Часто наряду с какой-либо матрицей L, обладающей элементами Lmn,
приходится рассматривать производные от нее матрицы. Среди таких
отметим сперва комплексно сопряженную матрицу L*. Элементы этой
матрицы комплексно сопряжены соответствующим элементам исходной
матрицы:
(L*)m» = Uw D0.4)
Далее, из данной матрицы можно образовать транспонированную
матрицу L. Эта матрица образуется из исходной путем взаимной замены
строк и столбцов. Элементы этой матрицы определяются формулой
г = ^пт. D0.5)
Если мы возьмем матрицу, комплексно сопряженную транспонированной,
т. е. (L ), то мы получим матрицу, которую называют сопряженной
к исходной и обозначают через L*. Ее элементы определяются формулой
(L+)mn = (L*)mn = L*m. D0.6)
В том случае, когда сопряженная матрица равна исходной:
L*^L (т. е. Lmn = L*nn), D0.7)
то матрица называется эрмшповской или самосопряженной. Это опре-
определение вполне соответствует нашему прежнему определению эрмитов-
128

скоро или самосопряженного оператора A8.7). В самом деле, если опера-
оператор L — эрмитовский, то мы имеем для его матричных элементов:
' *
Рассмотрим теперь алгебраические операции над матрицами. Обра-
Обратимся сначала к сложению матриц. Пусть дан некоторый оператор С,
являющийся суммой операторов А и В. Тогда под суммой матриц А и В
мы будем разуметь матрицу оператора С. Легко найти элементы этой
матрицы. Имеем:
^ ^ m-Bqn-dx, D0.8)
следовательно,
Стп^Лтп+Втп, . D0.9)
т. е. матричный элемент суммы операторов равен сумме соответ-
соответствующих элементов каждого из входящих в сумму операторов. Весьма
важным в смысле приложений является правило умножения матриц.
Для установления этого правила вычислим матричный элемент опера-
оператора С, являющегося произведением двух операторов А и В. Пользуясь
определением матричного элемента, получаем: *
.dx. D0.10)
Величина Btyn сама является некоторой функцией и может быть раз-
разложена в ряд по ортогональным функциям tyk(x):
где
Подставляя это разложение в D0.10), получим:
h ft
Следовательно,
D0.11)
8 D0.11) заключено правило умножения матриц: чтобы получить матрич-
матричный элемент Стп матрицы, представляющей произведение операторов
А и В, нужно элементы т-ой строки матрицы А умножить на эле-
элементы п-го ст.олбца матрицы В и сложить. Правило сложения матриц
D0.9) и правило умножения матриц D0.11) позволят по данным матри-
матрицам операторов А, В, ... находить матрицы, представляющие различные
функции от А, В, ...
Кроме того, правило умножения позволяет в несколько иной форме
представить формулу C9.5), выражающую результат действия опера-
оператора L на волновую функцию. Именно, эту формулу можно рассмат-
рассматривать как матричное произведение. Для этого представим саму волно-
9 Д. И. Блохинцев • 129

вую функцию в «£»-представлении в виде матрицы с одним столбцом:
c2 0 0 ...
D0.12)
Таким же образом представим и функцию
Ь1 0 0 ...
Ь2 0 0 ...
Ф =
D0.13)
Теперь легко видеть, что C9.5) может Цбыть ^написано в виде ма-
матричного произведения
Ф = /4>, D0.14)
где ср есть матрица D0.13), -гр — матрица D0.12), a L — матрица C9.7).
В самом деле, например, Ьт есть элемент m-ой строки и первого столбца
матрицы D0.13). Он должен получиться согласно D0.11) путем пере-
перемножения элементов m-ой строки матрицы C9.7) на элементы первого
столбца матрицы г|з D0.12). Но это как раз и дает уравнения C9.5).
Сопряженную волновую функцию с*, с\, ..., сп, ... можно записать
в виде матрицы, сопряженной-к D0.12), именно в виде матрицы с одной
строкой:
с* с\
0 0
Сп
0
D0.12')
С записью волновых функций в виде матриц D0.12) мы встретимся в тео-
теории магнитного момента электрона.
Заметим еще следующий результат из правила умножения матриц.
Матрица С*, сопряженная к произведению С двух матриц А и В, должна
писаться в виде
= £М+. D0.15)
В самом деле, элементы Стп по определению сопряженной матрицы
равны Спт- Из D0.11) имеем:
р* X1 л* д* V
пп — ^пт — /Ц SinhDhm — Zj
h h
(A*)
hn.
Совершенно аналогичным путем заменяя суммы на интегралы, символ Ьтп на
S (р' — р)] получаем соответствующие формулы для непрерывных матриц.
Именно, вместо D0.2) имеем единичную матрицу
б=б(р'-Р).
Элементы диагональной матрицы запишутся теперь в виде
Lp,p=L(p'N(p'-p).
Свойство самосопряженности выразится формулой
D0.2')
D0.3')
D0.7';
30

Матричный элемент суммы двух матриц А и В будет равен
CP'v=Ap'p+Bp'v> D0-9')
а матричный элемент произведения двух матриц А к В будет равен
Ср'р = ^ Ар'р"Ер"р" dp"' D0-П')
Приведем примеры непрерывных матриц. Рассмотрим сначала оператор координа-
координаты х в «р»-представлении. Согласно определению матричного элемента имеем:
h хе h dx —
П ^-/А^в(р-р'). D0.16)
Далее, по формуле C9.5'), определяющей действие оператора L, данного в матричной
форме, на волновую функцию, имеем:
p)dp= — ih ^ щ^Ь{р' -p)c{p)dp.
Производя здесь интегрирование по частям, находим:
^M,
D0.l7)
т. е. оператор х в «р»-представлении может быть дан либо в виде матрицы D0.16),
либо в виде дифференциального оператора й - D0.17). Последний результат нам уже
знаком (ср. § 13).
Оператор х в своем собственном представлении может быть изображен диагональ-
диагональной матрицей
хх,х=х'6(х — х'), ■ D0.18)
а оператор любой функции V (х)—матрицей
Vx,x=V(x')b(x-x'). D0.18')
В самом деле, по формуле C9.5'), заменяя там обозначения Ь на ср, с на ip, p на х,
получаем:
q>(x) = V(x)i])(x), D0.19)
т. е. действие функции V (х) в «х»-представлении сводится к умножению г]) (х) на V (х).
Результат опять-таки известный.
Подобным же образом оператор Р может быть дан в матричной форме
РХ'Х=+11гГхЬ(х-х')- * D0.20)
Имеем:
<р(*')=^ Px,x^{x)dx = ih[ -^&(x — x')ty(x)dx.
Интегрируя здесь по частям, получаем:
q(x)=-ih^(X), D0.21).
т. е. матричное представление D0.20) оператора Р эквивалентно дифференциальному.
дх
9* 131

умножая слева на г|)т и интегрируя по х, получим:
или
2L
D1.4)
Это —бесконечная система линейных однородных алгебраических уравне-
уравнений для определения амплитуд собственной функции сп и собственных
значений оператора Ln.
Как известно из алгебры, система однородных линейных уравнений
только в том случае имеет решение, отличное от нуля, когда опреде-
определитель, составленный из коэффициентов уравнений, обращается в нуль.
В нашем случае этот определитель имеет бесконечное число строк
и столбцов 1:
Ln-L
J12
L.
13
Lni
-П2
Lnn-L...
= 0.
D1.5)
Это уравнение накладывает ограничения на возможные значения L. Оно
является уравнением бесконечно высокой степени L (трансцендентным)
и будет иметь бесконечно большое число корней: L — Lv L2, . .., La, ...
В алгебре доказывается, что корни такого уравнения обязательно дей-
действительны. Совокупность значений La, при которых разрешима система
уравнений D1.4), и будет совокупностью собственных значений опера-
оператора L. Подставляя в D1.4) один из корней уравнения D1.5), например,
La, мы найдем соответствующее этому корню решение:
L = La, c^c^La), c2 = c2(La) cn = cn(La), ... D1.6)
Совокупность найденных таким образом значений cv с2, . .., сп, ... и
будет собственной функцией оператора L, принадлежащей a-му соб-
собственному значению L — La.
Эта же волновая функция в «.о-представлении будет2
Ы*) = 2>™(^а)^„М- D1.6')
п
В своем собственном представлении всякая величина изображается
диагональной матрицей. В самом деле, если 1|)„(*) есть собственная
функция оператора L, то его матрица имеет элементы:
;'i»i'^ = Mm, D1.7)
где Ln есть n-ое собственное значение оператора L. Поэтому задачу
о нахождении собственных значений оператора L можно рассматривать
1 Такой определитель следует рассматривать как предел определителя, образо-
образованного Для системы конечного числа N неизвестных сп, при N -» оо. Уравнение D1.5)
имеет смысл, если такой предел существует. Пример такого уравнения читатель найдет
в книге: Уиттекер и Ватсон, Современный анализ, ч. 11, стр. 240.
2 функция i])a (x) может быть непосредственно получена путем решения диф-
дифференциального уравнения Z.4p = .Lifi. Решение уравнения D1.4) и D1.5) обычно не проще
решения указанного дифференциального уравнения. Однако при приближенном реше-
решении уравнений (гл. XI) уравнения в матричной форме оказываются весьма полезными.
133

как задачу о приведении матрицы оператора L, данного в произвольном
представлении, к диагональному виду D1.7).
Так как коммутирующие операторы имеют общую систему собствен-
собственных функций, то их матрицы могут быть одновременно приведены
к диагональному виду.
Соответствующие формулы для случая непрерывных матриц получатся из приве-
приведенных выше заменой сумм на интегралы. Вывод их настолько прост, что мы ограни-
ограничимся приведением результатов. Среднее значение величины L будет равно:
L=\ \ dp'dp с* (р') Lptpc (p) D1.2')
(импульсное представление) и
1= \ ^rfx' dx^*(x')Lx,Jf(x) D1.2")
(координатное представление). Вместо уравнения D1.4) будем иметь соответственно
Lp,pc{p)dp = L-c(p'), D1.4')
Lx'x§ (x) dx=L-ty (xf) D1.4")
и, наконец, вместо D0.7):
Pv,v = p'-b(p'-p). D1.7')
хх,х = х'-Ь(х' — х). D1.7")
Уравнения D1.4') и D1.4") будут либо дифференциальными, либо интегральными
уравнениями.
§ 42. Уравнение Шредингера и зависимость операторов
от времени в матричной форме
Уравнение Шредингера B8.3) может быть переписано в матричной
форме, если разложить i|)(jc, t) в ряд по собственным функциям tyn(x)
какого-либо оператора. Подставляя в B8.3) i|)(x, t) в виде ряда
. п>(*,о = 2с«С>Фп(*).
п
умножая слева на ty*m(x) и интегрируя по к, находим:
1кЧГ=ЪНшпСп> Я1=1, 2, 3, .... D2.1)
где
\x)-dx <42.2)
есть матричный элемент гамильтониана Н. Это уравнение по заданным
в начальный момент сп@) [т. е. по г|э(*, 0)] определяет cn{t) [т. е. ty(x, tj\.
Пусть Н есть оператор полной энергии. Возьмем в качестве функ-
функций tyn(x) собственные функции оператора Я. Тогда cn(t) суть ампли-
амплитуды стационарных состояний, а матрица Нтп будет диагональной:
<1х = Епдтп. D2.3)
Подставляя эти замечания Нтп в D3.1), находим уравнения Шредингера
для этого случая:
ih*fc=Encn. _ D2.4)
134

Отсюда
ст(*) = ст@)е~' h , D2.5)
т. е. амплитуды стационарных состояний гармонически зависят
от времени. Это совпадает с выводами § 30.
Применим теперь уравнение Шредингера в матричной форме к вы-
вычислению производной оператора по времени.. Дифференцируя по времени
среднее значение D1.2), находим
d (Г) _ dL_ _ лп >п * дЬтп , vi V ^f™. / г I V V с* L
dt ~~ dt ~ 2л 2л Ст dt п + 2л 2л dt mn»+ Zj Zj m
из D2.1) имеем:
f. / г I V V с L
dt mn»+ Zj Zj m « dt
m n m n m n
- V H*,rl ihdCn-VH с
— 2л nmkCk, ~dT ~~ Zj nhch'
ft "ft
Подставляя эти производные в выражение для -~ , получаем:
„* dLmn «liVVVr*/ И С —
т —ei п ~т~ ~Ж Zj Zj Zj m mn11 nk°k
п ~т~ ~Ж Zj Zj Zj m
m n m n h
~~lh Zj Zj Zj И^^с^ьтпсп-
m n h
Учитывая, что в силу самосопряженности оператора
Н mk = " ftm»
а также то, что индексы т, п и k пробегают одни и те же 'значения,
мы можем (переменив во втором члене обозначение k на п, а в тре-
третьем k на /п) переписать предыдущее уравнение в форме:
~2Г= 2л 2л Ст dt п + "Ж" Zj Zj Ст \ 2л Lmhnhn— 2л
т п т п ft ft
Учитывая, что по правилу умножения матриц
2 LmkHhn = {LH)mn, yj HmkKn
h к
получаем:
где
i (LH - HL)mn = --L 2 (LmhHkn-HmkLkn) = [H, L]mn D2.7)
ь
есть матричный элемент скобки Пуассона. Из сравнения с формулой для
среднего D1.2) следует, что матричный элемент оператора скорости
dL
ж есть
dL_
dt
Формулы D2.6) и D2.8) представляют собой формулы C1.4) и C1.7)
соответственно в матричном представлении.
13

Рассмотрим важный частный случай. Пусть гамильтониан И не за-
зависит от времени, так что Н есть оператор полной энергии. Возьмем
специально энергетическое представление («^-представление). Тогда
матрица Н будет диагональной:
Предполагая еще, что оператор L не зависит явно от времени, мы полу-
получим из D2.7) и D2.8):
dt Jmn ih
ИЛИ
= i(umnLmn> D2.9)
где
ю = Ет—Еп D2.10)
есть боровская частота. В частности, матрица оператора скорости будет
иметь элементы
где хтп— элементы матрицы координаты х. Соотношение между скоро-
скоростью и координатой получается совершенно таким же, как для осцилля-
осциллятора, колеблющегося с частотой и>тп.
Формула D2.9) становится совершенно очевидной, если применить
так называемый гейзенберговский способ представления оператора. Этот
способ заключаетс~Я"~в"™т'ом, что матрица какого-нибудь оператора L стро-
строится с помощью волновых функций стационарных состояний, взятых для
времени t
Ясно, что это можно сделать, так как tyn(x> 0 так же> как и Уп(х)>
образуют полную ортогональную систему функций. Стало быть, в гей-
гейзенберговском представлении матричный элемент оператора L опреде-
определится по формуле
[ 0•£*»(*. t)-dx = Lnmetomni, D2.12)
Отсюда для оператора, не зависящего явно от времени:
Эта формула отличается от D2.9) только тем, что зависимость от времени
перенесена с волновых функций на операторы.
Согласно D2.12) матричные элементы операторов, явно не завися-
зависящих от времени, в гейзенберговском представлении гармонически зави-
зависят от времени, с частотами Бора а>тп-
В случае непрерывных матриц вместо D2.1) будем иметь
или, в координатном представлении:
ihWlp=^Hx.xq(x)dx, D2.1')
136

а вместо D2.8)
Что же касается остальных формул этого параграфа, то они связаны специально с энер.
гетическим представлением.
Введение в рассмотрение непрерывных матриц, как видно из изло-
изложенного в §§ 39 — 42, позволяет сделать матричный способ записи опера-
операторов совершенно единообразным так, что все возможные представления
операторов и волновых функций становятся совершенно равноправными.
Поэтому матричный способ записи операторов особенно удобен при рас-
рассмотрении общих вопросов теории.
При решении же конкретных задач особенно употребительно коор-
координатное представление. Объясняется это тем, что энергия взаимодей-
взаимодействия в нерелятивистской теории зависит только от координат, кинетиче-
/■ р2 \
екая же энергия есть простая функция импульса ( -5— ) ■ В силу этого
в координатном представлении мы получаем уравнение Шредингера
в форме сравнительно простого дифференциального уравнения второго
порядка. Однако при приближенном решении задач другие представления
могут даже иметь преимущества перед координатным.
§ 43. Унитарные преобразования
Рассмотрим преобразование какого-нибудь оператора О от одного
произвольного представления к другому. Пусть в первом представлении
оператор G изображается матрицей G', элементы которой нумеруются
собственными значениями L = LV L2, ..., Ln, ..., Lm, ... оператора L
(«Ls-представление). Во втором представлении пусть тот же оператор G
изображается матрицей G", элементы которой нумеруются собственными
значениями M = MV Mv ..., Ма, ■■■, Мц, ... оператора М («УИ»-пред-
ставление). Для определенности мы предполагаем, что L и М имеют
дискретный спектр. Если оператор О дан первоначально в «.«-представле-
«.«-представлении \ О = G ( — ih-^-, xj\ и собственные функции операторов L и М
суть Tip^x), г|>2(х), ...,г|>п(*). •••- ФтМ- ••• и <b(*)> Ф2 (*)• •••- 4>а(х),...
...фр(л;), .. . соответственно, то матричными элементами оператора G в «L»-
представлении будут
$( ^dx, D3.1)
а в «Л1»-представлении
§(^ )*- D3.2)
Спрашивается, какова связь между матрицей О' с элементами Gmn и матри-
матрицей G" с элементами Ga$ Разложим собственные функции оператора М
по собственным функциям оператора L:
ФЭ (*) =- 2 4>о (*) 5„р, ф2 (х) = 2i|4(*)SiU, D3.3)
n m ч '
137

причем
Snp = \ if* (х) фр (х) Ах, Sma = \ ^m (х) Фа (*) d*. D3.4)
Подстановка D3.3) в D3.2) на основании D3.1) дает
Gap = 2 2 S*«aGmnSnp. D3.5)
Совокупность величин Snp можно рассматривать как матрицу S, строки
которой нумеруются собственными значениями величины L, а столбцы —
собственными значениями величины М. Наряду с матрицей 5 рассмотрим
сопряженную матрицу S+, элементами которой являются
(о )ат = Ьта> D3.0)
так что S+ = S* и, следовательно, строки матрицы нумеруются собствен-
собственными значениями М, а столбцы — собственными значениями L. На осно-
основании D3.6) формула преобразования от Gmn к С?ар D3.5) может быть
написана в виде
Gap = 2 2 (S*)amGmnSnfi, D3.7)
т n ч
или, на основании правила умножения матриц, в матричном виде
G" = S*G'S. D3.8)
Таким образом, матрицу 5 и сопряженную ей матрицу S* можно рассма-
рассматривать как матрицы, с помощью которых совершается преобразование
оператора от одного представления («L») к другому («М»). Матрица 5
обладает важным свойством. Перемножая функции ф£(дг) и фр (х) и инте-
интегрируя результат по х, на основании ортогональности собственных функ-
функций мы получаем:
2 2 S*,aS^6mn = бар, D3.9)
т п ч '
или
* % X"*" ^ — Л /1Q 1Л\
Zj ° an &vR —Оар, Dо. 1U)
п
т. е. в матричной форме
S*S=l. D3.11)
Подобным же образом, разлагая функции т]рп (х) по функциям фр (х), можно
убедиться, что
2Sma S^n=6mn, D3.12)
a
т. е.
SS*=l. D3.1 Г)
Матрица, удовлетворяющая условиям D3.11) и D3.1Г), называется уни-
унитарной. Так как произведение S* на 5 или 5 на S* дает единичную
матрицу, то 5* есть матрица, обратная S, т. е.
S* = S-\ D3.13)
Заметим, что унитарная матрица не является эрмитовской, так как
для эрмитовской матрицы вместо D3.13) мы имели бы S+ = S. На основа-
основании изложенного мы можем сказать, что преобразование оператора от одного
138

представления к другому совершается с помощью унитарной матрицы 5
с элементами D3.4). Само преобразование D3.8) называют унитарным.
Формулу D3.1) можно также рассматривать как унитарное преобразо-
преобразование от координатного представления к «Ls-представлению. Для этого
достаточно написать оператор G ( — ih-=- , х) в матричной форме. Тогда
вместо D3.1) получим
Gmn = \[ 44 (*') Сл г|>п (х) dx dx'. D3.1')
Полагая Smx' = ^m(л:') Ч Sxn = tyn(x), мы приведем преобразование D3. Г)
к виду D3.8). Таким образом, волновые функции tym(x), tyn(x) СУТЬ не чт0
иное, как матричные элементы унитарных матриц S* и S, преобразующих
от координатного представления к «/-«-представлению.
Выше (§ 41) уже было отмечено, что задачу о нахождении собствен-
собственных значений любого оператора можно рассматривать как задачу о при-
приведении матрицы, изображающей оператор, к диагональному виду. В тер-
терминах унитарных преобразований эта задача может быть формулирована
так: найти унитарное преобразование S, которое преобразовывало бы
матрицу оператора G к диагональному виду- Чтобы найти это преобра-
преобразование, умножим уравнение D3.8) слевана 5. Пользуясь D3.11'),
получим:
SG"=G'S, D3.14)
или в раскрытом виде:
S-SmaGe3 = 2GmnSne. D3-15)
Если матрица Gap диагональна, то
SmaGaa = Zj G , S^j.. D3.16)
п
Так как собственные значения Gaa нам неизвестны, то нам следует опу-
опустить индекс а, и мы получим:
m(j = J\ GmaOn, Do. 1 /)
n
что совпадает с уравнением D1.4), если положить G = L, S = C.
Заметим одно важное свойство унитарного преобразования:
унитарное преобразование оставляет неизменным сумму диагональных
элементов матрицы. Эту сумму называют следом (или «шпуром») мат-
матрицы и обозначают так:
Sp. G = 2Gnn. D3.18)
Из D3.7) имеем:
2/-> X"! Х^ Х^ /о+\ /~* с1 Х^ Х^ г> Х^ / о+\ о
Gaa = Zj Zj Zj E )amGmnSna = Zj Zj Gmn 2j E+)am5na =
a a m n m n a
= Zj Zj Gmn6mn= 2 Gnn, D3.19)
m n n
т. е. след матрицы есть инвариант унитарного преоб разевания. Этим
свойством часто пользуются в приложениях.
139

§ 44. Унитарное преобразование от одного момента времени
к другому
Изменение волновых функций с течением времени может быть также рассмотрено
с помощью унитарного преобразования.
Пусть гамильтониан Н не зависит от времени. Обозначим его собственные функции
через фп(дг), собственные значения энергии через Еп. Тогда
Яфи(*) = £АМ- D4.1)
Применим к функции фи (дг) оператор
S(t) = e h D4.2)
значение которого выяснится из дальнейшего.
Из D4.1) следует, что Hstyn (х) = E^i>n (*)> поэтому
оо оо
( £ )' ^ W 2 7Г
sit) *« W=2 ( )
s=0 s=0
= е Л " фа(*)- D4.3)
Пусть теперь дана произвольная, начальная функция ф (лг, 0). Разложим ее по tyn (лг)
^(х,0) = ^сп%(х). D4.4)
Применяя к ф (дг, 0) оператор D4.2), на основании D4.3) найдем:
5 (t) ф (х, 0) = 2 спе h г|зп (лг). D4.5)
Но правая часть есть не что иное, как волновая функция в момент, времени t. Поэтому
(x, 0). D4.6)
Оператор S (t) является унитарным.
Действительно, если оператор 5 (t) взять в энергетическом представлении, то его
матричные элементы, как это непосредственно следует из D4.3), попросту равны
--*-Яп« „ +~Ent
Smn = e -6mn, а матричные элементы сопряженной матрицы (S*)mn=e '^mn-
Поэтому15+=5 !.
Из D4.6) следует, что унитарное преобразование D4.2), выполняемое с помощью
оператора S, вполне заменяет уравнение Шредингера2. Мы можем сказать и иначе:
движение можно рассматривать как последовательность унитарных преобразований3.
1 Этим же путем нетрудло показать, что любой унитарный оператор можно напи-
написать в виде
где ц — эрмитовский оператор фазы.
2 Если гамильтониан Н зависит от времени, то "D4.6) все же остается в силе.
Однако S' (t) в этом случае нельзя написать в виде D4.2). Вместо D4.2) S' (t) = e%
и определяется из соотношения:
at
т. е. для нахождения S' необходимо все же решить уравнение Шредингера. В послед-
последние годы высказывались идеи; что, быть может, оператор фазы i\ (t) является более
фундаментальным, нежели оператор гамильтоновской функции Н, Тогда необходимость
в уравнении Шредингера совершенно отпала бы. Однако не было найдено правил нахож-
нахождения ц для данной физической системы.
3 Подобным же образом в классической механике движение можно рассматривать
как последовательность контактных преобразований.
140

Разложим функции г])(х, 0) и ijj(jc, t) по собственным функциям сра(х) некоторого
оператора L. Тогда D4.6) примет вид:
где Со (t) и са@) суть амплитуды в разложении ty(x, t) и ф (дг, 0) соответственно
Spa {t) — матричный элемент оператора S (t) в «Ls-представлении,
Допустим, что в начальный момент величина L имела определенное значение L=La-
Это означает, что ф(л-, О) = сра(лг), са@) = 1, са, @) = 0, если а'^а. В этом специаль-
специальном, но очень важном случае, вместо D4.6') получим
cP@ = S(ta@. D4.7)
Согласно общей теории (§ 22) вероятность найти L= La в момент t будет равна | с^ (t |2
С другой стороны, было предположено, что при £ = 0 величина L имела единственное
значение, равное La. Поэтому прн этом выборе начальных условий | Са (t) |2 есть вероят-
вероятность найти в момент t: L = La, если при £ = 0 L=La, Иными словами, Р^аA) = \ с^A) [2
есть, как говорят, вероятность квантового перехода1 из состояния L — La в состояние
L=Lg. На основании D4.7) эта вероятность равна
Ppa« = |SpaWI2- D4'8)
Так как матрица 5 есть матрица унитарная, а не эрмитовая, то | Sga |2, вообще говоря
не равно | Sao |2, так что вероятность перехода из состояния а в состояние р, вообще
говоря, не равна вероятности обратного перехода нз состояния р в состояние а.
Отсюда еще не следует делать заключения о необратимости квантовой механики.
Известно из классической механики, что если силы не зависят от скоростей, то измене-
изменение скоростей всех частиц на обратные ведет к тому, что все движение воспроизводится
в обратном порядке.
Можно доказать, что при этих же условиях н в квантовой механике имеет место
совершенно такая же обратимость. Именно, вероятность за время t перейти из состояния,
характеризуемого импульсами частиц р}, р%, ... (состояние а), в состояние с импуль-
импульсами рь р2, ... (состояние Р) равна вероятности за такой же отрезок времени перейти
из состояния, характеризуемого обращенными импульсами —рь —р2, ... (обращенное
состояние Р), в состояние с импульсами — р\, —р§, ... (обращенное состояние аJ.
Из этого краткого очерка унитарных преобразований видно, что весь математиче-
математический аппарат квантовой механики может быть формулирован на языке операторов,
представленных в форме матриц и на языке унитарных преобразований.
§ 45. Матрица плотности
Пусть оператор L дан в координатном представлении в виде матри-
матрицы LX'X. Среднее значение La в состоянии г|за (х) будет (ср. 41,2')
x). D5.1)
Если из чистых ансамблей, характеризуемых волновыми функциями г|за,
образовать смешанный ансамбль, такой, что каждое чистое состояние
будет представлено с вероятностью Ра, то среднее значение L в смешан-
смешанном ансамбле будет (ср. 22.18)
1=2 Ра1а = 2, ра \ \ dx Ах' Га (х1) Lx,xtya (х) D5.2)
1 Ср. §§ 92, 93, где подробно рассматривается проблема квантовых переходов
и даются приближенные методы для вычисления вероятностей перехода.
2 Ср. по этому поводу работу автора, ЖЭТФ 17, 924 A947), где подробно рас-
рассмотрен этот вопрос.
141

(при условии 2^а=0- Равенство D4J2) можно переписать в следующем
виде:
^>Lx-x,' D5.3)
где Qxx' равно
бис' = 2 ЛЛЙ (X') % (X). D5.4)
а
Оператор q, представляемый матрицей с элементами qXX' D5.4), называется
оператором плотности г.
Выражение D5.3) есть не что иное, как сумма диагональных элемен-
элементов оператора qL.
Поэтому мы можем написать D5.3) в виде
I = Sp(eL). D5.5)
В другом представлении, разлагая tya(x) по собственным функциям Ц>п(х)
(некоторого оператора М, имеющего дискретный спектр собственных зна-
значений Mv Мй, ..., Мп, ...), получим из D5.2):
^ = 2 2 1i PaCamLmnCan, D5.6)
а т п
г. е.
Qnm = ^— * aCamCani D5./)
а
где Сап суть амплитуды в разложении tya (x) по ц>п (х). Стало быть, в этом
представлении имеем:
£ = 22QnnAnn = Sp(eL). D5.8>
т п
Диагональный матричный элемент матрицы q имеет смысл вероятности
(или плотности вероятности).
Действительно, полагая в D5.4) х' = х, найдем:
- Qxx = ^Pa\%(x)\2==w(x) D5.9)
а
есть плотность вероятности для координаты х в смешанном ансамбле.
Подобным же образом из D5-7) получаем:
^Рпп=2^а|Сап|а = Ш„, 'D5.10)
а
т. е. вероятности найти в смешанном ансамбле значение М = Мп.
Рассмотрим теперь, как будет меняться оператор q с течением вре-
времени. Матрица D5.4) определяет q для какого-то момента времени, кото-
который мы можем принять за начальный (t ~ 0). Смешанный ансамбль, опи-
описываемый этой матрицей, есть набор независимых систем, каждая
из которых находится (с вероятностью Ра) в одном из чистых состояний
г|за (х) — г|за (х, 0). Система, находившаяся в момент t = 0 в чистом состоянии
tya(x, 0), в момент />0 будет также находиться в чистом состоянии
tya(x, t), которое можно найти из уравнения Шредингера:
ih д-^ф-^ = \ H^fy (x", t) dx" D5-11)
1 Этот оператор был введен Нейманном. См. I. V. Neumann, Gott. Nachr.,
1927.
142

или для сопряженной функции г|>а(*\ t) из сопряженного уравнения:
4*x,x'^Z{x",t)dx". D5.1 Г)
Здесь НХ'Х- есть матричный элемент гамильтониана в «^-представлении.
Вероятности же Ра, будучи вероятностями начальных данных (Ра есть
вероятность того, что при £=0 система находится в состоянии tya(x, 0) =
= i|)a(*))i конечно, не зависят от времени1. Поэтому в момент t > 0
матрица q будет равна:
Qxx' (t) = 2 Л.Ч>а (*', t) $а (х, t). D5-4')
Дифференцируя это уравнение по времени и выражая с помощью D5.11)
и D5.1 Г) производные волновых функций через оператор Гамильтона,
найдем:
Г-^ \ Qxx~Hx.x,dx" D5.12)
(при этом мы воспользовались тем, что Н*>Х' = Нх»х>) или в операторной
форме:
■#=-[Я>в], D5.13)
где [Н, q] есть квантовая скобка Пуассона.
Это операторное уравнение позволяет определить оператор q для любого
момента времени, если он известен при t — 0.
Преимущество описания ансамбля посредством оператора q в сравне-
сравнении с описанием с помощью г|з-функции заключается в том, что опера-
оператор q позволяет единообразно рассматривать как смешанные, так
и чистые ансамбли.
Обратимся теперь к тем изменениям в операторе q, которые возни-
возникают в результате измерения. Пусть производится полное измерение
(измерение величины или набора величин /И). Пусть собственные функ-
функции оператора М будут фп (х). Тогда вероятность найти М = М будет
D5.10). После измерений возникает новый смешанный ансамбль, в кото-
котором новые чистые состояния <$п(х) будут представлены с вероятностями
шп2, т. е. после измерения
Qxx' = 2 ^'™Ф* (*') Фп (*)» <45- И>
и мы получаем совершенно новый смешанный ансамбль-
В квантовой статистике состояния никогда не характеризуются пол-
полным измерением. Поэтому там всегда имеют дело со смешанными ансамб-
ансамблями. В силу этого оператор плотности q приобретает особо большое
значение, именно, в квантовой статистике.
Как известно, в классической статистике ансамбль независимых систем
(который обычно называют ансамблем Гиббса) характеризуется плотностью
вероятности D (р, х) такой, что величина D (p, x)dpdx имеет смысл вероят-
вероятности найти систему с импульсом, лежащим около р, и координатой,
лежащей около хА. Согласно теореме Луивилля эта плотность является
1 Однако Ра могут изменяться в результате измерений. См. ниже.
2 Если, конечно, не произведено выбора подсовокупности, скажем, с М = Мп.
При таком отборе полученный после измерений ансамбль будет чистым (с ty = (fn(x)).
3 Мы пишем в обозначениях, соответствующих ансамблю систем с одной степенью
свободы х. Под р и х можно разуметь совокупность импульсов и координат всех частиц,
входящих в систему.
143

постоянной, так что
ш п, дН дО дН дО] л „ т,
где [п, и\нл — -ау-д з—з-^ есть классическая скобка Пуассона. Из
D5.15) следует, что
^=-[H.DU. D5.15')
Аналогия между D5.15') и D5.13) очевидна.
Классический ансамбль Гиббса и квантовый смешанный ансамбль по
своему существу (набор независимых систем) тождественны. Поэтому опе-
оператор q по аналогии с плотностью вероятности D и называют оператором
плотности. Более полно связь между q и D может быть установлена,
если вместо Qxx> ввести матрицу R (р, х), строки которой нумеруются
импульсом, а колонки координатой:
. р(х-х')
Тогда
^ R (p, *);dp = ^ q^/6 (л: — x') dx' = w{x), D5.17)
ip(x-x')
? (p, x) dx =
где ш (х) и до (р) суть плотности вероятности для координаты х и для
импульсаl p. Эти формулы совершенно аналогичны классическим:
D (р, *) dp = докл (лс), ^ D(p, лг)^лг=до„л(р). D5.18)
Более того, можно показать, что матрица R (р, лг) подчиняется урав-
уравнению, которое при определенных условиях (гладкость полей и гладкость
самой функции R (р, х)) превращается в классическое уравнение D5-15'J-
Поэтому величина R (р, х) вполне аналогична классической вероятности
(плотности вероятности) D(p,x), и ее можно рассматривать как обобще-
обобщение понятия вероятности на случай одновременно неизмеримых величин
(«квазивероятность»). Величина же Qxx аналогична компонентам Фурье
от плотности D (р, х), т. е. величине
. р(х-х')
>(р, х)е h dp. D5.19)
1 Чтобы получить D5.17'), следует иметь в виду, что
~г~лГ
2 Эта матрица' была" введена автором книги. См. Д. Б лох и нц ев, Journ. of
Phys. USSR 2, 71, 1940. Ср. также Я. П. Терлецкий, ЖЭТФ 7, 1937, стр. 1290.

ГЛАВА VIII
ТЕОРИЯ ДВИЖЕНИЯ МИКРОЧАСТИЦ В ПОЛЕ
ПОТЕНЦИАЛЬНЫХ СИЛ
§ 46. Вводные замечания
В этой главе мы рассмотрим простейшие задачи атомной механики,
относящиеся к движению частиц в поле потенциальных сил. Вообще,
если силы не зависят от времени, то основной задачей атомной меха-
механики будет задача о нахождении стационарных состояний системы. Дей-
Действительно, в этом случае согласно C0.8) произвольное состояние ty(x, t)
может быть представлено как суперпозиция стационарных состояний
с постоянными амплитудами сп:
!>(*, 0 = 2 *„!>„(*, 0. D6-1)
п
i(^-0=iW'« h. D6.2)
где tyn(x) суть волновые функции стационарных состояний, а Еп — соот-
соответствующие значения энергии. Волновые функции tyn(x) суть собствен-
собственные функции оператора энергии Н и определяются, согласно C0.4),
из уравнения Шредингера для стационарных состояний
#i]) = £i]x D6.3)
Задача о нахождении стационарных состояний есть вместе с тем задача
о нахождении спектра энергии Е.
Особое значение этой задачи для атомной механики заключается
в том, что в противоположность классической механике квантовая меха-
механика приводит во многих случаях к квантованию энергии, т. е. к дис-
дискретному спектру значений ее Ev Ег, ..., Еп, ... Эти значения часто
называют квантовыми уровнями или уровнями энергии.
Если система (например, электрон в атоме, молекула и т. п.), обла-
обладающая таким спектром энергии, подвергается извне слабому воздействию,
то ее квантовые уровни не меняются (точнее, меняются мало). Однако
благодаря внешнему воздействию система может переходить с одного
уровня на другой так, что ее состояние может измениться значительно.
Вероятности этих переходов мы вычислим значительно позже.
Нахождение же возможных значений энергии позволит нам сразу
сказать, каковы возможные изменения энергии рассматриваемой нами
системы, если между ней и какой-либо другой системой или внешним
полем установлена слабая связь1. Так, если найденные уровни энергии
1 Если связь между системами сильна, то мы имеем одну целую систему. Если
внешнее поле велико, то уровни в системе заметно меняются. Поэтому предположение
о слабости связи является существенным.
10 д. И. Блохинцев 145

будут Ev £2, . .., Еп, ..., Ет, . .., то обмен энергий возможен лишь
порциями:
Ь.Е — Ет — Еп. D6.4)
§ 47. Гармонический осциллятор
В классической механике гамильтонова функция одномерного гармони-
гармонического осциллятора имеет вид
Н = ~+~-х%. D7.1)
Здесь рх — импульс частицы, ц — ее масса, х — отклонение от положения
равновесия, а <в0 — собственная частота (циклическая) осциллятора.
Заметим, что гармонический осциллятор, поскольку речь идет о меха-
механических колебаниях, является идеализацией, так как значение потен-
потенциальной энергии U = ^^x2 означает, что по мере удаления от положе-
положения равновесия сила неограниченно возрастает. Во всех реальных случаях,
начиная с некоторых значений амплитуды, начинаются заметные отступле-
отступления от гармоничности, а при больших значениях х сила взаимодействия
стремится к нулю (а (/-к постоянной величине). Однако для небольших
амплитуд колебаний х вполне можно пользоваться представлением о гар-
гармоническом осцилляторе.
Теория гармонического одномерного осциллятора имеет большое зна-
значение в приложениях, так как подходящим выбором координат («нормаль-
(«нормальные координаты») движение любой системы частиц, совершающих малые
колебания, может быть сведено к движению совокупности независимых
осцилляторов1.
В квантовой механике под одномерным осциллятором мы будем
разуметь систему, описываемую оператором Гамильтона Н, равным,
в полной аналогии с D7.1),
Н = -Щ;+^Х\ D7.2>
где Рх — оператор импульса, гГX — оператор координаты2. Соответствен-
Соответственно этому гамильтониану уравдение Шредингера в «х»-представлении для
стационарных состояний осциллятора имеет вид
-%i£+J!t-***=**• D7-3>
Для решения этого уравнения введем безразмерные величины
цсо0
IE
1 См § 105. Кроме того, теория квантовых гармонических осцилляторов находит
важное применение в квантовой теории света (см. В. Гайтлер, Квантовая теория,
излучения, ГИТТЛ, 1940).
2 Может возникнуть вопрос: почему имеет смысл называть систему с гамильто-
гамильтонианом D7.2) гармоническим, осциллятором? Ответ заключается в тем, что система,
описываемая гамильтонианом D7.2), излучает и поглощает только о,сну частоту со<>
(см. § 88, А) и при h —> 0 переходит в классическую систему с гамильтоновой функ-
функцией'D9.1) (ср. §§ 34, 35).
146

Обозначая дифференцирование по I штрихом и рассматривая ty как
функцию £, после элементарных преобразований мы приведем уравнение
D7.3) к виду
^" + (^-£2И = 0. D7.5)
Нам нужно найти конечные, непрерывные и однозначные решения
этого уравнения в интервале — оо<|< +со. Такие решения уравне-
уравнение D6.5) имеет не при всех значениях параметра X, а лишь при
Я = 2п+1, п = 0, 1,2,3, ..., D7.6)
причем соответствующие функции i])n равны
!>„(&) = е~Яп(!), D7.7)
где //п(|) есть полином Чебышева— Эрмита л-го порядка1, определяе-
определяемый формулой
Щ^; D7.8)
1/2"п!/я ё
при этом множитель перед е^2 выбран так, что функция г|з„(Е) норми-
нормирована по | к 1:
^ [ e-^(S)ds=l. * D7.9)
Таким образом, одного требования непрерывности и конечности if ока-
оказывается достаточно, чтобы параметрах получал лишь дискретные зна-
значения D6.6). Но согласно D6.4) этот параметр определяет энергию.
Сравнивая D6.4) и D6.6), находим, что возможные значения Еп суть
+ |y п = 0, 1,2, 3, ... D7.10)
Эта формула показывает, что энергия осциллятора Е может иметь лишь
дискретные значения. Число п, определяющее номер квантового уровня,
называют главным квантовым числом.
Окончательно мы запишем собственную функцию, принадлежащую
я-му собственному значению и данную в «.«-представлении, в виде
(х\-?—-Н (*) D7.11)
V х0
где £ = -— • *
Эти функции нормированы так, что
+00
Обратим внимание на четность волновых функций осциллятора. Как
легко видеть из формул D7.11) и D7.8), четность состояний осцилля-
осциллятора определяется четностью главного квантового числа п.
1 Подробности, касающиеся решения уравнения D7.5) и в ссобенксст требова-
D7.6), изложены в дополнении IX.
10* 147

Пользуясь формулами D7.7) и D7.8), выпишем несколько собствен-
собственных функций вида D7.11)
D7.12)
D7.12')
п = 2. D7.12")
У х0 > л
1 Л-*2/2*2 Г ^
Первая функция не обращается в нуль нигде (кроме х=±со). Вторая
обращается в нуль при х = 0. Точку, где волновая функция обращается
%(*)
Рис* 23. Волновые функции:
fa —волновые функции осциллятора для п =0, I, 2; Ь — колебания закрепленной струны, t/i —
основной тон, U%, С"з — первые два обертона
i
в нуль, будем называть узлом. Третья функция обращается в нуль при
г и имеет, стало быть, два узла. Мы замечаем, что число узлов
равно номеру функции п. Это свойство справедливо для любого1 п.
Таким образом, квантовое число равно числу узлов собственной функ-
функции. Эти волновые функции изображены на рис. 23, а. Вид функций г|зп (х)
аналогичен виду функции Un(x), изображающей колебание закрепленной
■ на концах струны. Для сравнения на рис. 23, b приведена функция
Uп(х) для основного тона (л = 0), первого обертона (л=1) и второго
обертона (п == 2).
Обнаруживающаяся аналогия между колебаниями струны и волно-
волновой функцией осциллятора не является случайной. Она обусловлена
двумя обстоятельствами. Во-первых, в обоих случаях дело идет об одном
измерении. Во-вторых, колебания струны суть собственные колебания.
Согласно общей теореме об узлах собственных функций (см. примечание
на этой стр.) число узлов функции 1|зп(д:) и функции ип(х) должно быть
одинаково.
Чтобы получить еще более полное представление о квантовых состоя-
состояниях осциллятора, мы приводим на рис. 24 потенциальную функцию
осциллятора
По оси ординат отложена потенциальная энергия, а по оси абсцисс
отклонение х. На этом же рисунке горизонтальными линиями изобра-
изображены уровни энергии Еп D7.10) для разных п. Такие диаграммы, на
1 Всегда номер собственной функции равен числу узлов. Общее доказательство
этой теоремы смотри у Р. Куранта и Д Гильберта. Метолы математической
физики, ГТТИ, 1933, т. I, стр. 429 — 434.
148

которых изображается одновременно энергетический спектр и потенциаль-
потенциальная энергия, употребляются довольно часто. Они позволяют произвести
простое сравнение с классической картиной движения. Рассмотрим,
например, уровень Еу Согласно классической механике частица, имею-
имеющая энергию Е}, могла бы быть обнаружена лишь в области АВ. В самом
деле, А и В суть точки, где потен-
тиальная энергия равна полной. В этих
точках кинетическая энергия Т равна
нулю, так как
E^T + U, T = E~-U. D7.13)
Точки А и В называются точками
поворота. Очевидно, ОА = ОВ есть
амплитуда колебания частицы, имею-
имеющей энергию Ev
Вычислим вероятность w(x)dx
найти частицу в области х, x + dx по Рис 24 Диаграмма ввантовых уров-
классической механике. Эта вероят- ней (£„) и потенциальной энергии
ность пропорциональна времени dt, ,,. . ц ю§ ,
в течение которого частица проходит v^=-~2-x" ^ гармонического ос-
отрезок dx. Если период колеба- циллятора
ний есть Т = —, то мы можем положить:
dx
где и—скорость частицы. Выразим v как функцию х. Имеем:
где а —амплитуда колебаний:
Из D7.15) имеем:
т. е. опять-таки по D7.15):
Следовательно,
х = a sin u>ot,
D7.14)
D7.15)
а-
dx
2яа
1 аг I
-\-a.
D7.16)
D7.17)
D7.18)
Эта вероятность изображена на рис. 25. Наибольшая вероятность падает,
как и следует ожидать, на точки поворота А и В.
Вероятность найти частицу в области х, x + dx по квантовой меха-
механике равна (для /г = 1)
причем
следует взять из D6.12'). Следовательно,
шкв (х) dx = ~±~ e-*V*5i£ AL .
D7.19)
График этой вероятности также изображен на рис. 25. Как видно, кван-
квантовая вероятность также имеет максимумы около классических точек
149

поворота
(
точно, для Et = -к- /н»0, О А = OS = i/
. V
= 1/ ),
но в отличие от классического случая вероятность найти
частицу отлична от нуля и за точками поворота. Это обстоятельство не
представляет в квантовой механике какого-либо противоречия, так как
равенство D7.13) в квантовой механике не имеет силы: кинетическая
энергия Т и потенциальная U не
являются одновременно измери-
измеримыми величинами-
-'* а)
Рис. 25. Сравнение квантовой веро-
вероятности , (№кв) местонахождения
частицы ' (для п=1) с классической
(№кл):
А. В — точки поворота; А', В' — точки
максимума
Рис. 26. Классическая и кван-
квантовая вероятности для состо-
состояния осциллятора с наимень-
наименьшей энергией £0
Особенно сильно подчеркивается различие между квантовым и клас-
классическим случаем, если рассмотреть состояние с наименьшей энергией.
По классической теории наименьшая энергия осциллятора есть £==0
и соответствует покоящейся в положении равновесия частице. Вероят-
Вероятность wun(x) в этом случае имеет вид, приведенный на рис. 26. Она
всюду равна нулю, кроме точки х = 0. По квантовой теории наименьшая
энергия осциллятора есть
р _ /гю0 .
0 2 '
она называется нулевой энергией. Вероятность хюкв (х) в этом случае
равна
Она также приведена на рис. 26.
Выясним подробнее свойства нулевой энергии. Очевидно, что эта
энергия не может быть отнята от осциллятора, ибо по своему существу
она есть минимальная энергия, которую может иметь осциллятор. Ее
можно отнять, лишь изменяя сам осциллятор, именно, уменьшая часто-
частоту соо, т. е. путем изменения коэффициента упругости. Существование
нулевой энергии является типичным для квантовых систем и представ-
представляет собой прямое следствие соотношения неопределенностей
A^-A^>-£. ' D7-2°)
В самом деле, средние значения р и х в состоянии с определенным
значением энергии равны нулю:
х =
\ Упх$п dx= [ ifax dx =
D7.21)
150

(что следует из нечетности подынтегральной функции),
]!l=°- D7-22)
Поэтому для осциллятора соотношения неопределенностей D7.20) можно
переписать в виде
С другой стороны, средняя энергия осциллятора равна
Е = ^ + ^7*. D7.23)
Из сопоставления D7.20') и D7.23) непосредственно видно, что, умень-
уменьшая потенциальную энергию, мы увеличиваем кинетическую, и наоборот-
В частности, состояние с наименьшей потенциальной энергией [7 = 0 есть
состояние с бесконечно большой кинетической энергией Т = со. Объединяя
D7.20') и D7.23), получаем:
+ J^. D7.24)
Отсюда легко найти минимальное значение Е. Именно, из
получаем:
■ >^-, D7.25)
т. е. нулевая энергия есть наименьшая энергия, совместимая с соот-
соотношением неопределенностей.
Примером частиц, совершающих малые колебания, могут служить
атомы в молекуле или в твердом теле. Экспериментально удается дока-
доказать наличие нулевой энергии и нулевых колебаний атомов путем наблю-
наблюдения рассеяния света кристаллами. Рассеяние света обусловлено коле-
колебаниями атомов. По мере уменьшения температуры амплитуда колебаний
согласно классической теории должна неограниченно уменьшаться,
а вместе с тем должно исчезать и рассеяние света. Между тем опыт
показывает1, что интенсивность рассеяния света по мере уменьшения
температуры стремится к некоторому предельному значению, указываю-
указывающему па то, что и при абсолютном нуле колебания атома не прекра-
прекращаются. Этот факт подтверждает существование нулевых колебаний.
§ 48. Осциллятор в энергетическом представлении
Обратимся к представлению, в котором за независимую переменную
взята энергия осциллятора Е. В этом представлении оператор полной
энергии И будет диагональной матрицей с элементами
Ят„=ад„„, D8.1)
1 См. R. W. James, G. W. В rind ley, R. G. Wood, Proc. Roy. Soc,
125, 401 A929).
151

или на основании D7.10):
Н
2
0
0
- 0
з
0
0
о 0
5 ,
у/ш0
0 ...
0 ...
0 ...
D8.2)
Любое состояние осциллятора г|з(.г,/) можно представить как суперпо-
суперпозицию стационарных состояний (ср. § 30):
. Ent
п
где tyn(x) дается формулой D7.11), а Еп — формулой D7.10). Совокуп-
Совокупность всех сп будет волновой функцией в «^-представлении. Вероят-
Вероятность найти в состоянии ty(x, t) значение энергии Еп равна
Эта вероятность не зависит от времени, что соответствует тому, что
энергия есть интеграл движения.
Найдем оператор координаты X в «£»-представлении. По общей
теории он должен изобразиться матрицей с элементами
\}mxr^)ndx. D8.5)
D8.6)
Подставляя сюда г|зт и г|зп из D7.7), получаем:
[ е~*Нт (I) 1Нп (I) dl, х0 =
Этот интеграл может быть вычислен:
для т = п — 1,
D8.7)
0 в остальных случаях.
Пользуясь этим результатом, мы можем написать D8.6) с помощью
символа 6mn в следующем виде:
/ г~г \
D8.8)
Приведем матрицу X Из D8.8) видно, что отличны от нуля лишь
соседние с главной диагональю элементы, именно:
JC — X,
0
о о
VI о
| о
у\ о
/1
D8.9)
152

В- гейзенберговском представлении элементы матрицы оператора X будут
равны (см. D2.12)]
*mn@ = ^n-etom»', D8.10)
где
«m™ = ^i^ = шо(/п-п). D8.11)
Так как хтпф0 лишь для т = п±\, то все матричные элементы коор-
координаты осциллятора колеблются с одной и той же частотой, равной
собственной частоте осциллятора ю0.
Вычислим теперь среднее значение координаты осциллятора х для
произвольного состояния. По общей формуле D/.2) имеем:
W) = ^ctn(t)xmncn(t) = ^c*m(O)xmn(t).cn(O). D8.12)
т п т п
На основании сказанного о матричных элементах xmn{t) среднее значе-
значение х будет гармонической функцией времени с частотой ю0. Иначе
говоря, х зависит от времени так же, как зависит от времени коорди-
координата классического осциллятора1:
q>), D8.13)
где а — амплитуда, ф — фаза.
Матрица оператора импульса в «.Еи-представлении может быть найдена
либо путем вычисления интегралов
Ртп = \ ГшРЛп d* = - »А J 1M, -^?- dx, D8.14)
либо, более просто, на основании квантовых уравнений движения.
Согласно этим уравнениям
Р = ^, D8.15)
т. е.
(^) ■ D8.16)
Пользуясь формулой D2.11), находим:
ртп = 1атпцхтп, D8.17)
или
pmn = i\b(no(m--n)xmn. D8.18)
Разумеется, вычисление интегралов D8.14) ведет к тому же результату.
§ 49. Движение в поле центральной силы •-*
Поле центральной силы характеризуется тем, что потенциальная
энергия частицы в таком поле зависит лишь от ее расстояния г от не-
некоторого центра (силового центра). Законы движения в поле централь-
1 Этот же результат мы можем получить непосредственно из теоремы Эренфеста.
Уравнение C4.1) для осциллятора принимает вид
откуда путем интегрирования находим:
х = а cos (fi>of-[-<p).
153

ной силы образуют фундамент атомной механики: решение общей задачи
о движении электронов в атоме опирается в той или иной мере на
результаты, относящиеся к движению одной частицы в поле центральной
силы.
Обозначая через U (г) потенциальную энергию частицы, мы можем
написать оператор полной энергии И C3.12) в виде:
Н = Тт + ф-в + и(г), D9.1)
где М2 есть оператор квадрата момента импульса, а Тг — оператор кине-
кинетической энергии для радиального движения.
Из общей теории интегралов движения (§ 33) следует, что интегра-
интегралами движения в поле центральной силы будут: полная энергия Е
и момент импульса (т. е. /И2, Мх, Му, Mz). Мы поставим себе задачу
найти стационарные состояния частицы, движущейся в поле U (г).
Уравнение Шредингера для стационарных состояний в нашем случае
гласит:
ТЛ + фгЦ + и(г)Ц = ЕЦ. D9.2)
Волновую функцию "ф естественно искать как функцию полярных коор-
координат г, 0, ф. Мы должны найти однозначные, непрерывные и конечные
решения ty уравнения D9.2) во всей области изменения переменных
г, 0, ф, т. е. в области 0<г<оо, О<0<л, 0<г|з<2л. Так как опера-
операторы И и Ж2 коммутируют, то они должны иметь общие собственные
функции, поэтому мы можем написать второе уравнение для \|>
М2^ = М2^>. D9.3)
Собственные значения Ж2 согласно § 25 равны h4(l-\-\), так что
вместо М2г§ мы можем подставить в D9.2) величину h4(l+ l)ty. Тогда
мы получаем уравнение
!^p1(r)^ = Eip. D9.3')
Это уравнение содержит явно лишь одну переменную г. Полагая теперь
i|>(r, в, Ф) = /?(г)-Уг1тF, ф), D9.4)
где Ylm(b, ср) есть собственная функция оператора М2, мы одновременно
удовлетворяем и уравнению D9.3), и уравнению D9.2'), если функция
R (г) удовлетворяет уравнению
TtR + —'^1R + U(r)R = ER. D9.5)
Это уравнение получается путем деления D9.2') на Ylm. Мы будем
называть его уравнением Шредингера для радиальной функции R(r).
Напомним (см. § 25), что функции Ylm являются также собствен-
собственными функциями одной из проекций момента импульса, именно — при
нашем выборе координат проекции Mz. Поэтому в поле центральной
силы полная энергия, квадрат момента импульса и проекция момента
импульса на некоторое произвольное направление OZ являются величи-
величинами, одновременно измеримыми.
Возможные значения энергии Е определяются из уравнения
D9.5) и зависят от вида U (г). Они могут зависеть от величины
момента импульса М2 (через число /), но они не могут зависеть от
проекции момента импульса Mz (и, следовательно, от числа m): Mz не
входит в уравнение D9.5). Это объясняется тем, что мы имеем дело
154

с полем, обладающим центральной симметрией, так что все направления
в пространстве физически равноправны, и поэтому энергия не может
зависеть от ориентации в пространстве момента импульса. Для дальней-
дальнейших выводов мы должны более подробно определить вид U (г).
Во всех реальных физических системах взаимодействие на беско-
бесконечно больших расстояниях бесконечно мало. Это означает, что асимп-
асимптотически (при г—>оо) потенциальная энергия принимает постоянное
значение:
U (г),-» = const = С, D9.6)
где С-—произвольная постоянная, определяющая уровень потенциальной
энергии в бесконечности.
Мы увидим, что характер решения уравнения D9.5) существенно
зависит от того, больше ли полная энергия Е, чем значение потенциаль-
потенциальной энергии в бесконечности (С), или меньше. Так как С есть произ-
произвольная постоянная, то в тех случаях, когда специально не оговорено,
мы будем полагать ее равной нулю и различать два случая: Е > 0 пЕ < 0.
Определим еще вид U (г) вблизи центра сил (при г—>0). Мы будем
•считать, что U (г) имеет в нуле полюс, порядок которого меньше 2:
U(r)r^=~, «<2. D9.7)
Сделанные нами предположения о виде U (г) охватывают весьма широ-
широкий круг задач атомной механики. Так, например, в проблеме движения
валентного электрона в атоме речь идет о движении электрона в поле
ядра атома, окруженного оболочкой более близких к ядру электронов.
При малых расстояниях действие этих электронов несущественно,
основное поле будет кулоновским полем ядра. Потенциальная энергия
электрона в кулоновском поле имеет вид. — и поэтому входит в класс
D9.7). В случае взаимодействия двух атомов при малых расстояниях
наибольшее взаимодействие есть отталкивание ядер по закону Кулона,
т. е. потенциальная энергия имеет опять-таки вид —. В обоих приме-
примерах U имеет при г = 0 полюс первого порядка.
Для исследования решения уравнения D9.5) представим это реше-
решение в виде
#(г) = ^-. D9.8)
Подставляя это выражение для R в D9.5) и замечая, что согласно B6.7)
мы получаем следующее уравнение для и:
Рассмотрим сначала асимптотические решения этого уравнения при
г —> со. Пренебрегая для больших г членом с — и V (г) [мы считаем С
в D9-6) равной нулю], получаем простое уравнение:
~w^-=Eu- D9J1)
155

Обозначая
&2 = ^ для £>0 и Х2 = -^ для £<0, D9.12)
мы получаем общее решение D9.11) в виде
и = C/hr + С2е~ш, £ > О, D9.13)
м = Q>-M-С2еЛг, £<0, D9.14)
где Cj и С2 суть произвольные постоянные. Согласно D9.8) асимптоти-
асимптотическое решение уравнения D9-5) имеет вид
e Ce—, £>0, D9.15)
# = CX^ + Ca-^, £<0. D9.16)
В первом случае Е > 0 решение ^ конечно и непрерывно при любом
значении постоянных. Как видно, оно представляет собой суперпозицию
сходящихся и расходящихся сферических волн. Вероятность найти
частицу в этом случае не исчезает даже для больших г. Именно, веро-
вероятность найти частицу между г и r-\-dr пропорциональна |^|2 и объему
шарового слоя \nf-dr1:
w{r)dr^\R |2 4лг2 dr = 4л | Сге1кг + С2е~Шг |2 dr.
Такие состояния соответствуют апериодическим орбитам в класси-
классической механике, когда частица движется из бесконечности к центру
сил и уходит опять в бесконечность. Так как рассматриваемое нами
состояние стационарно, то поток приходящих частиц должен равняться
потоку уходящих. Это означает, что амплитуды приходящих и уходящих
волн Cj и С2 должны быть равны по модулю. Если положить С1 = -^- Aeia,
С2 = — -tp Ae~ia, где Л и а действительны, то асимптотическое решение
D9.15) можно представить в виде
R^A^±^, D9.15')
т. е. в виде стоячей, сферической волны.
Иное положение вещей имеет место при Е < 0. В этом случае необхо-
необходимо положить С2 = 0, иначе R становится оо при г—»оо. Поэтому
нужное решение будет
# = СХ-^. ч D9.16')
Для этих состояний
w(r) dr !=a 4л \Сг\2е-2г-г-йг
1 Более детальное исследование (см., например, В. А. Фок, Начала квантовой
механики, КУБУЧ, 1932) показывает, что сделанное нами пренебрежение в уравне-
уравнении D8.10) потенциальной энергией U (г) законно лишь в том случае, если U (г) при
г -I- оо стремится быстрее к нулю, нежели — • В случае кулоновского поля
f7(r)r^=o = —, и асимптотические решения D9.15) и D9.16) несколько видоизменятся,
но не столь существенно, чтобы это видоизменение отразилось на справедливости наших
дальнейших рассуждений.
156

и при больших г величина w (г) —> 0, т. е. частицу можно найти лишь
вблизи центра сил. Такие состояния соответствуют периодическим
орбитам в классической механике, когда частица движется около сило-
силового центра.
Исследуем теперь поведение решений вблизи центра (г—>0). Будем
искать и (г) в виде степенного ряда
w(r) = rV(l + a/ + a2r2+...)- D9.17)
Подставим это выражение для и в уравнение D9.10). Тогда низшей сте-
степенью г будет гу~2 или r"Y~a. Мы видим, что если а < 2, то низшей сте-
степенью будет г*/~2. Член с гу~2 будет наибольшим (при г—>0); поэтому,
игнорируя величины высшего порядка, мы найдем, что результатом под-
подстановки D9.17) в D9.10) будет
[у(у—1) — /(/+1)]^ +члены высшего порядка = 0. D9.18)
Чтобы это равенство было соблюдено тождественно при всех (бесконечно
малых) значениях г, необходимо, чтобы
Y(Y-l) = /(/+l). D9.19)
Отсюда
Y=/+ 1 или Y= ~l- D9.20)
Следовательно, при г—>0 решение R, равное и/г, имеет вид
# = С/ A + агг+ а/2 +•••) + СУ1'1 A + а'гг + а/ +...), D9.21)
где С' и Cj — произвольные постоянные.
Для того чтобы функция оставалась конечной, необходимо положить
С'„ ■= 0. Таким образом, собственная функция R при малых г имеет вид
# = qr'(l + a/+a2r2 +•••)• D9-22)
При г—> со это частное решение перейдет либо в D9.15) (если Е > 0),
либо в D9.16) (если Е < 0). Полагая С'г = 0, мы выбираем частное реше-
решение уравнения D9.10). Поэтому коэффициенты С. и С2 в D9.15) или
в D9.16) будут находиться уже во вполне определенном отношении друг
к другу [абсолютная же величина этих коэффициентов не имеет значе-
значения, так как уравнение D9.10) есть однородное уравнение]. Это отноше-
отношение зависит теперь только от параметров уравнения D9.10), в частности,
от Е. Следовательно, при С^ = 0 имеем: .-$
^ = f(E), D9.23)
где f— некоторая функция Е, зависящая от вида уравнения D9.10),
т. е. от U (г).
Если энергия частицы Е > 0, то оба частных решения в D9.10)
С
конечны, и поэтому при любом отношении ~ решение D9.15) есть допу-
стимое решение, в частности, и при том -~ , которое получается из тре-
1
-бования С2 = 0. Поэтому мы не должны накладывать какого-либо нового
157

ограничения на отношение1 ~. Вместе с тем параметр Е может иметь
любое значение. Отсюда следует, что если энергия Е > О, то энергия
не квантуется, а принимает все значения от 0 до + оо.
Таким образом, при Е>0 мы имеем непрерывный спектр энергии.
Другое положение дел имеет место при Е < 0. Из требования конечности
функции R в нуле {С[ = 0) не следует С2 = 0, так что в общем случае
при R конечном в нуле решение будет возрастать в бесконечности неогра-
неограниченно. Чтобы получить решения конечные и в бесконечности, нужно
дополнительно потребовать С2=0. А это налагает ограничение на воз-
возможные значения энергии Е, так как тогда из D9.23) следует
0. D9.24)
Это будет некоторое трансцендентное уравнение для Е. Корни этого
уравнения
E=EVEV ....£„.... D9-25>
и будут собственными значениями оператора энергии, так как только
при этих значениях Е решение R конечно и при г = 0, и при г-со.
Следовательно, при Е < 0 получается дискретный спектр возможных зна-
значений энергии. Мы получаем в этом случае систему квантовых уровней
D9 25)
Рассмотрим теперь подробней несколько наиболее типичных видов
потенциальной энергии V (г). Во всех случаях мы будем считать, что-
потенциальная энергия имеет (если имеет вообще) при r = U полюс порядка
ниже -1-. Потенциальную энергию в бесконечности условимся считать
равной'нулю. На рис. 27 изображена потенциальная энергия V в функ-
функции расстояния от центра г для случая отталкивания частицы. В этом
случае полная энергия частицы положительна2. При Ь > 0 спектр энер-
1 Из требования С'2 = 0 как раз и вытекает асимптотическое выражение для ff
D9.15'). Полагая Q = 0, мы тем самым выбираем ф без сингулярностей в нуле^ Благо-
Благодаря этому будет справедливо уравнение сохранения для г|)*г|) B9.7) (ср. также допол-
дополнение IX). Для стационарных состояний из B9.7) находим
[ JNdS = O
для любой замкнутой поверхности. Выберем в качестве такой поверхности сферу
с центром в нуле. Тогда JN = Jr- Из B9.5) и D9.4) имеем:
Подставляя в предыдущую формулу и замечая, что
получим
Легко убедиться, что это равенство невозможно, если \С1\ф\Сг\. т
■ В классической механике это следует из того, что кинетическая энергия Г
и если 1/>0, то и £>0. В квантовой механике положение совершенно такое же.
Первый член есть кинетическая энергия и обязательно положителен так как положи-
положительны собственные значения оператора Р2. Если С/> и, то и ь >и.
158

гни непрерывен. Следовательно, в случае отталкивающих сил возможны
все значения энергии от 0 до + со. Это обозначено на рисунке штрихов-
штриховкой. На рис. 28 изображена потенциальная энергия для случая притяже-
притяжения. В этом случае мы должны различать две возможности: Е > 0 и Е < 0.
В первом случае спектр будет непрерывным (штрихованная часть рисунка).
Во втором случае мы получаем дискретный спектр значений Ev Е2, . . .
. .., Еп, ... Эти квантовые уровни изображены на рис. 28 горизонталь-
горизонтальными линиями. Приведенный спектр, состоящий из прерывного и сплош-
сплошного, является как раз тем энергетическим спектром, который свойственен
электрону, взаимодействующему с яд-
ядром или положительным ионом (при-
(притяжение по закону Кулона).
Дискретные уровни отвечают,
как было показано выше, движению
Рис. 27. Потенциальная энергия
для случая отталкивания от
центра:
Энергетический спектр (£ > 0) непре-
непрерывен
Рис. 28. Потенциальная энергия для
случая притяжения к центру:
Энергетический спектр для £ > О непрерывен,
для £ < 0 состоит из отдельных уровней Elt
£2 Еп. J есть энергия ионизации
электрона в атоме (вероятность найти электрон , вдали от атома исчезающе
мала). Напротив, сплошной спектр отвечает ^ионизованному атому, так
как электрон в этом случае может оказаться как угодно далеко от атома.
Энергия, необходимая для иониза-
ионизации, так называемая работа иониза-
ионизации /, легко может быть получена
из приведенной на рисунке диаграм-
диаграммы. Действительно, энергия, кото-
которую имеет электрон в нормальном,
невозбужденном состоянии атома,
есть Ег Для того, чтобы атом был о
ионизован, нужно, чтобы энергия -
его электрона была больше 0, поэ-
поэтому наименьшая работа, которая
будет затрачена на ионизацию атома
в нормальном его состоянии, есть
/ = 0-£х=-£х. D9.26)
Приведем еще другой образец потенциальной кривой, свойственный
двухатомным молекулам АВ. При больших расстояниях атомы А и В
не взаимодействуют, поэтому можно положить U — 0 для г=оо. При
меньших расстояниях атомы притягиваются и, наконец, на малых рас-
расстояниях они отталкиваются из-за отталкивания ядер и электронных
оболочек при проникновении одного атома в другой. Поэтому потенциаль-
потенциальная энергия имеет вид, приведенный на рис. 29. Для Е > 0 мы имеем
опять непрерывный спектр. Вероятность w (г) остается конечной и при
159
Непрерыбный
(пектр
£>0
Дискр
спектр
Рис. 29. Потенциальная энергия V(R)
двух атомов, образующих молекулу,_ в
функции их расстояния R

—>со: атомы А и В могут находиться как угодно далеко друг от друга
(диссоциированная молекула). При Е < 0 получается ряд дискретных
уровней Ev Е2, ..., Еп, ... В этом случае w(r)—>0 при г—>со. Атомы
находятся близко друг к другу и образуют молекулу АВ.
Для диссоциации молекулы, находящейся в нормальном (нижнем)
состоянии, нужно затратить работу диссоциации D:
D=—£г D9.27)
Заметим, что по классической теории эта работа равнялась бы D' — — Dmin,
где t/min означает наименьшую потенциальную энергию. D меньше D'
на величину нулевой энергии -~ .
Из приведенных примеров видно, что, зная потенциальную энергию
U (г), не производя решения уравнения Шредингера, можно сделать
заключение о характере энергетического спектра.
§ 50. Движение в кулоновском поле
Самой простой задачей атомной механики является задача о движе-
движении электрона в кулоновском поле ядра. С такой задачей мы встречаемся
в атоме водорода Н, в ионе гелия Не+, в двукратно ионизованном
литии Li++ и тому подобных ионах, называемых в од ор од on од об ны ми.
Обозначая заряд ядра через -\-eZ, где е—элементарный заряд, a Z—номер
ядра в системе Менделеева, мы получим, что потенциальная энергия
электрона в поле такого ядра будет по закону Кулона равна
U(r)=-^- E0Л)
Чтобы найти квантовые уровни для рассматриваемого движения элек-
электрона, нужно решить уравнение Шредингера для радиальной функции R.
Полагая
R = y, E0.2)
мы получим, как было показано в § 49, для и уравнение D9.10).
Подставляя туда U из E0.1) и разумея под fx массу электрона,
получаем подлежащее решению уравнение
) Ze2 „ ,-п о,
и и —Ей. E0.3)
Рассматриваемый нами случай соответствует притяжению (рис. 28).
Поэтому согласно общей теории движения в поле центральных сил мы
будем иметь непрерывный энергетический спектр для Е > 0 и дискретный
для Е < 0. Мы поставим себе задачу найти этот дискретный спектр
и соответствующие собственные функции R. В целях удобства решения
введем вместо г и £ безразмерные величины
о=^£=!' E0-4)
где
а = — = 0,529-10"8 см, £х = -££ = ■£- = 13,55 эв. E0.5)
Подстановка E0.4) в E0.3) приводит к тому, что в уравнении не будет
160

содержаться атомных постоянных \i, e, h. Именно, вместо D9.3) получаем:
В соответствии с изложенным в предыдущем параграфе об асимптоти-
асимптотическом поведении функции и мы будем искать и в виде
E0.7)
где /(р) — новая искомая функция.
Подставляя « (q) из E0.7) в E0.6), мы найдем уравнение для функ
ции f(Q). Именно, после несложных вычислений получаем:
= 0. E0.8,
Решение этого уравнения будем искать в виде ряда по степеням Q. Из
общей теории мы знаем, что конечное, при г=0, решение уравнения
E0.3) таково, что ряд по степеням г должен начинаться с члена г'*1.
Из E0.7) тогда следует, что конечное в нуле решение E0.8) должно
начинаться с QUl. Поэтому f (q) будем искать в виде
= e!>1 S a%Q\ E0.9)
o
где av —пока неизвестные коэффициенты ряда.
Ряд E0.9) должен быть таков, чтобы функция R (г), которую мы
можем теперь, согласно E0.2) и E0.7), написать в виде
, E0.2')
не нарастала до оо при q—> оо. Для нахождения коэффициентов ряда а,
подставим E0.9) в E0.8) и соберем одинаковые степени Q.
Эта подстановка дает:
o E0.10
Чтобы ряд E0.9) был решением уравнения E0.8), нужно, чтобы E0.10)
было удовлетворено тождественно при всех значениях q от 0 до оо. Это
возможно лишь в том случае, если коэффициенты при каждой степени о
были равны нулю, т. е. когда
+ av[2Z-2a(v + / + l)] = 0 E0.11)
для всех значений v. Эта формула дает рекуррентное соотношение
между av и av+i*
tlt*' v-0, 1,2, 3,.... E0.12)
Первый коэффициент a0, конечно, произволен, так как уравнение одно-
однородно. Дав ему какое-либо значение, найдем из E0.12) а,; по а1 най-
найдем а2 и т. д. Вычисляя все av, мы получим искомое решение в виде
ряда по степеням Q.
Нетрудно видеть, что полученный ряд будет сходиться при всел
g-aQf
значениях q, но при больших q растет столь сильно, что R = при
II Д. И. Блохинцев '61

q—> оо будет стремиться к бесконечности1. Таким образом, как это
и следует из общей теории § 49, конечное при q=0 решение не будет,
вообще говоря, конечным при q=oo. Однако решение будет заведомо
конечно и при q= со, если ряд оборвется на каком-нибудь члене. Тогда
f (q) будет многочленом и R будет стремиться к нулю при q—> оо.
Такое решение будет собственной функцией уравнения, так как оно
конечно во всем интервале от Q — 0 до q= оо и однозначно.
Легко видеть, что обрыв ряда на каком-нибудь члене, например,
номера v = пг, может произойти лишь при особом значении параметра
уравнения а. Действительно, положим, что коэффициент аПг еще не равен
нулю. Чтобы следующий коэффициент cv+i обращался в нуль, необхо-
необходимо, чтобы
2a(nr-H+l) —2Z = 0,
т. е.
- E0.13)
Ясно, что при этом условии не только Оп,.+ 1, но и все последующие
коэффициенты обращаются в нуль, ибо все они пропорциональны anr+i.
Таким образом, E0.13) есть необходимое и достаточное условие, чтобы
решение f (q) обращалось в многочлен, а вместе с тем функция R(q)
оставалась бы всюду конечной. Полагая
п = пг + 1+\ E0.14)
и подставляя в E0.13) значение а из E0.7), получим:
е=-|т- E0-13')
1 Полагая Х = —, s = 2l-\-l, перепишем E0.12) в виде
_ 2a
Отсюда видно, что отношение —— > —-г-у при v —> оо. Далее, мы можем взять
такое v = v', что
V + .+ 1 >?''+"■
где
Начиная с этого значения v, коэффициенты av растут быстрее, нежели коэффициенты
ряда, определяемые рекуррентной формулой
v+i^fT v-
Ряд же с этими коэффициентами дает
Поэтому f (q) растет быстрее /i(q), и, следовательно, функция E0.2') будет стремиться
к оо при q —> оо.
162

Имея в виду выражение Е через е E0.4), мы получаем, что конечны®
и однозначные решения R существуют лишь при следующих значениях
энергии электрона:
Еп--^~, E0.15)
где число п принимает согласно D9.14) значения
я=1,2,3,..., яг = 0, 1, 2, 3 E0.16)
Число п определяет, как мы видим, энергию электрона и называется
главным квантовым числом.
Полученная формула для квантовых уровней Еп электрона, движу-
движущегося в кулоновском поле, найдена впервые Бором на основе полуклас-
полуклассической квантовой теории. В этой теории, где квантование носило харак-
характер искусственного рецепта, приходилось специально оговаривать невоз-
невозможность значения п — 0. В квантовой механике это значение исключено
само собой, так как / принимает значения 0, 1, 2 an, есть номер
члена ряда E0.9) и имеет наименьшее значение 0.
Прежде чем перейти к подробному рассмотрению полученных кван-
квантовых уровней Еп, рассмотрим еще вид собственных решений R(q). Для
собственных решений а = — , поэтому формула E0.12) упрощается:
a /кот
Вычисляя один коэффициент за другим и подставляя их в E0.9), полу.
чим f(Q):
T2l + 2\~J+ 2! BZ + 2) B/ + 3) \ n J +
+ ■■■( 4 nr !B/ + 2)B/ + 3)...B/ + «r) К n J
Отсюда видно, что целесообразно ввести новую переменную:
1 = ^1==21Г. E0.18)
s п па у '
Объединяя все постоянные множители в один фактор Nnl, мы получим
из E0.2'), что функция Япг(о), принадлежащая квантовым числам п и I,
будет равна
RnAD^M^k'L^d), E0.19)
где через L2^^ обозначен многочлен, стоящий в фигурных скобках
в формуле E0.17). Такое обозначение связано с принятым в математике.
Дело в том, что многочлен в E0.17) выражается через производные мно-
многочленов Лагерра, которые определяются формулой
Lh(l) = e^k(e~4k). E0.20)
Тогда под многочленом Д(|) понимают многочлен
Ll(l) = ~Lh{i). E0.21)
Полагая здесь k = n-!rl и s = 2/ —J— 1, легко убедиться, что мы получим
многочлен, заключенный в фигурные скобки в формуле E0.17).
11* 163

Формулы E0.20) и E0.21) легко позволяют вычислять функции /?ы.
Множитель Ып1 в E0.19) мы будем выбирать так, чтобы функция /?„,
была нормирована к единице:
"*,r2dB=l. E0.22>
Полная собственная функция согласно E0.4) будет равна произведе-
произведению Rvl на собственную функцию оператора момента импульса» т. е
9, фН#*(г)У1та(е, ф). E0.23
Энергия Еп, как следует из E0.15), зависит лишь от главного кванте
вого числа п. Если это число задано, то из E0.14) вытекает, что op6t
тальное число / может иметь лишь такие значения:
/ = 0,1,2 п—\ («г=п—1, п —2, ..., 0). E0.2
Далее, как мы знаем, магнитнэе число т при заданном I пробега
значения:
га = 0, ± 1, ±2 . .. ±/. E0.'
Подсчитаем теперь, сколько различных волновых функций принадлея
квантовому уровню Еп. При каждом / мы имеем 2/ -j- 1 функи
отличающихся числом т. Но / пробегает значения от 0 до л— 1, поэт
полное число функций будет
2B/+1) = «2 EС
1=0
Таким образом, каждому квантовому уровню Еп принадлежит л* ра:
ных состояний. Мы имеем дело со случаем «2-кратного вырожде
§ 51. Спектр и волновые функции атома водорода
Подставляя в формулу E0.15) значения универсальных посте»
Е, \i и /г, мы можем вычислить квантовые уровни электрона, дви;
гося в кулоновском поле ядра номера Z. На рис. 30 приведен
уровни для атома водорода (Z—1).
Числа по вертикали слева дают энергию уровней в электронов
(энергия отсчитывается при этом не от 0, а от нижнего уровня Е
видно, по мере роста главного квантового числа п уровни распола
теснее, и при п—со, £^ = 0; далее идет область непрерывного (
Е > 0, соответствующая ионизованному атому. Энергия ионизацш
водорода равна ■>
/= _£1=a^£L= 13.55 эв
Чтобы понять значение чисел, нанесенных на правой ве-
напомним, что частота света ш, излучаемого при переходе из ypoi
в уровень En'i'm't согласно квантовой теории света определяется
яения Бора1-.
1 Это будет доказано. Пока мы опираемся на изложенное в § 2.

Подставляя сюда энергию Еп1т из DР. 15), получим:
п'<п. E1.3)
Эта формула (при Z=l) дает частоту света, излучаемого или поглощао
мого атомом водорода. Ве-
Величина
называется
спектральным термом.
Разности термов дают ча-
частоты. Для атома водорода
терм равен
E1.4)
Величина
Volt
13.53
13
П
Ю,15
10
VCM
= 3,27 X
E1.4')
называется, постоянной
Ридберга — Ритца и впер-
впервые была вычислена теоре-
теоретически Бором. В спектро-
спектроскопии величину термов
чаще указывают не в ча-
Б
стотах -т-, а в волновых
л
числах, показывающих,
сколько длин волн А, укла-
укладывается в 1 см. Если ци-
циклическая частота света
есть а», то обычная частота
v = -=—. Эту-то частоту
и измеряют обычно в v ,
так что спектроскопиче-
спектроскопическая частота (волновое чис-
0
5:
0-
I
I
i ■
2QQDO "
moo-
60000
80000
tooooo
Рис. 30. Схема
квантовых
дорода
ло) равна^обыкновенной частоте v, деленной на скорость света с:
1 V (О
с
уровней атома во
— т- = — = т,— СМ
-1
Постоянная Ридберга — Ритца в волновых числах равна
"d" = 109737,40 см'1.
4л1г3с
Термы водорода в этих же единицах равны
п2
1,09.Ю5
п=1, 2, 3,
E1.4")
E1.4-)
Числа, нанесенные на диаграмме уровней водорода (рис. 30) справа,
дают величину спектральных термов в обратных сантиметрах. Линии,
соединяющие уровни, по своей длине пропорциональны энергии кванта
165

света, излучаемого или поглощаемого цри переходе электрона между
этими уровнями. Указанные на этих линиях числа дают длину волны к
света в А.
Все частоты, относящиеся к переходам, кончающимся одним и тем
же нижним уровнем, образуют так называемую спектральную серию.
Отметим наиболее важные серии водорода. Переходы на уровень п = 1
(нижний) образуют серию Лаймана. Частоты серии Лаймана вычисляются
по формуле:
() п==2' 3 <5Ь5)
Среди этих спектральных линий линия п = 2 имеет наибольшую длину
волны Л, = 1215,68 Л. Она находится в ультрафиолетовой части спектра.
Переходы на уровень п = 2 соответствуют излучению видимого света.
Совокупность этих спектральных линий образует серию Бальмера,
Частоты этой серии суть:
() « = 3, 4, ... E1.6)
Формула D8.6) была найдена Бальмером в 1885 г. на основе анализа
эмпирических данных о спектре водорода. Впоследствии эта формула
сыграла исключительную роль в расшифровке спектров и послужила
пробным камнем для квантовой теории атома. Спектральные линии серии
Бальмера обозначаются буквами
На(п = 3), #в(п = 4), Ну(п = 5) и т. д.
Кроме серии Бальмера и серии Лаймана на диаграмме приведены и дру-
другие серии, соответствующие переходам на уровни п = 3, 4 и 5 (серии
Ритца — Пашена, Брэккета и Пфунда соответственно). Линии этих серий
лежат в инфракрасной области спектра.
Спектры водородоподобных ионов Не+, Li+* и т. п. имеют такой же
вид, как и рассмотренный спектр водорода, но все линии перемещаются
в область более коротких длин волн, так как в этих случаях постоянную
Ридберга следует увеличить в Z2 раз. Именно, согласно E0.3) и E0.4")
частоты для этих ионов будут вычисляться из формулы
^~l), n'<n. E1.7)
Обратимся теперь к более детальному анализу квантовых состояний
и соответствующих собственных функций tynlm{r, 9, ф) E0.23). Любое
определенное состояние, задаваемое тройкой квантовых чисел п, I, т,
представляет собой собственное состояние трех одновременно измеримых
величин: энергии, квадрата момента импульса и проекции момента
импульса на некоторое направление OZ. Все эти три величины имеют
в состоянии tynlm определенные значения, именно:
M! = h4(l + l), / = 0, 1, 2, ..., п-1, E1.9)
Mz = hm, m = 0, ± 1, ±2 ±/. E1.10)
Таким образом, динамическое значение квантовых чисел п, I, m заклю-
заключается в том, что главное число п указывает величину энергии Еп,
орбитальное число I — величину момента импульса М.\ и, наконец, маг-
166

нитное число т —величину проекции момента импульса Мг на некото-
некоторое произвольное направление 0Z *.
Три величины Е, Ml, M2 вполне определяют волновую функцию г|)п!т
и поэтому образуют полный набор величин. Число их, как и должно
быть, равно трем, т. е. числу степеней свободы (ср. § 14).
Квадрат абсолютного значения i|)nim(r, 9, ф) («координатное пред-
представление») дает вероятность того, что при определении положения элек-
электрона в квантовом состоянии п, I, m он будет обнаружен в окрестности
точки г, 9, ф. Точнее эта вероятность определяется так:
w
nim
(r> 9»
гг dr sinQ dQ dy = \
г, 9, ф)|2г2drsin Q
E1.11)
Чтобы нагляднее представить себе характер этой вероятности, мы при-
приводим на рис. 31 полярную систему координат. Полярная ось OZ
выделяется тем, что она есть как раз то направление, на которое про-
проектируется момент импульса Mz = hm. Обозначая через dQ элемент
телесного угла sin 9 dbd ф в обла-
области 9, ф и пользуясь формулой E0.23)
для i|)n[m, мы можем написать ве-
вероятность E1.11) в форме
до.
aim
(г, 9, (p)r2drdQ =
Rh(r)r*dr\Ylm(b,
E1.12)
Рис. 31. Полярные координаты
Если мы проинтегрируем E1.12)
по всем углам dQ, то мы получим
вероятность найти электрон между
двумя сферами радиусов г и г-{-dr.
Обозначим эту вероятность через
wnl{r)dr^-Rh{r)r*dr. E1.13)
На рис. 32 даны эти вероятности
для различных состояний. Числа
на кривых показывают значение чи-
чисел п, 1(пТ = п — 1—\). Например,
31 означаетп = 3, /= 1 (гег = 1). По абсциссе отложено расстояние отцентра
q = ™[cm. E0.4)]. Из графиков легко видеть, что число пт (которое назы-
называют радиальным квантовым числом) равно числу узлов волновой функ-
функции RnV При этом мы1 имеем не узлы в точках, а узловые поверхности,
ибо Rnl обращается в нуль при некотором г —г', а это означает поверх-
поверхность шара радиуса г'. Стало быть, в состоянии, характеризуемом чис-
числами п, I, имеется пг = п— I— 1 узловых поверхностей, имеющих форму
сферы.
Выясним теперь значение введенной ранее длины а. Из вида функ-
функций Rni(Q) E0.19) следует, что при больших r(g—>оо) радиальная функ-
функция Rnl принимает вид
Rni(Q) = Nnle ™» Q^y '■
E1.14)
1 Число / называют орбитальным квантовым числом по той причине, что в старой
боровской теории оно определяло при заданной энергии форму орбиты; m называют
магнитным и по той причине, что оно играет существенную роль в магнитных явле-
явлениях (см. §§ 74, 75, 129, 130).
167

Поэтому при больших значениях г вероятность wnl (r) будет равна
2Zr
па
К па J
E1.15)
Отсюда следует, что длина ^ есть длина, определяющая размеры атома.
так как]"для г > ^ вероятность wnl (r) практически равна нулю.
Приведем более подробный
■ д>5 |A I I I I I 1 расчет для самого нижнего кван-
квантового состояния (п = 1). В этом
случае из E0.19) имеем:
0,1
X
20
30
i<0
01 5 W 15 20
а) 5- состояния A=0)
3D
0,2
0,1
г
к
V
.•*—
01 5 Ю 15 20 25
Ь) р - состояния (I - 1)
30
О 5 Ю 15 20 25
С) d - состояния A-2) и состояние
Рис, 32. Распределение заряда в пер-
вых состояниях водорода:
Абсцисса — г в радиусах водорода, ордииа-
та — вероятность найтн электрон между г а
r+dr
Следовательно,
W
10 ^
и.
Рис. 33. Сравнение Wv.n(r) и
\Укв(г) для состояний п=1
(( = Я1—0)
Zr
Максимальное значение этой вероятности получается при Q — —— !• Отсюда
следует, что в состоянии п = 1 A = т = 0) наиболее вероятно найти элек-
электрон при
А2" 0,529
* О Т ~~~ . . -О^7
10"8 см.
E1.18)
Это есть в точности радиус первой орбиты Бора, величина которого
впервые была получена Бором из старой теории квантования в 1913 г.
Так как нижняя орбита по теории Бора —круговая, то по этой тео-
теории вероятность найти электрон в состоянии п= 1 отлична от нуля лишь
на шаре радиуса /■■= г„. Согласно же новой квантовой механике она отлична
от нуля во всем пространстве. На рис. 33 сопоставлены вероятности
по старой теории (шкл.) и по новой (шкв.) для состояния п= 1 атома
водорода. Приведенное соответствие между шКл. и- шкв. наблюдается и
для других состояний: оно является далеко неполным, что видно уже
из того, что в квантовой механике в нижнем состоянии момент импульса
/И? = 0 (/ = 0), в то время как по старой теории в этом же состоянии
M* = h2. Несмотря на неполноту указанного соответствия, картина
168

распределения вероятности становится более наглядной и указывает на»
связь между квантовой и классической механикой, которая и в самом-
деле существует (ср. гл. VI).
Обратимся теперь к распределению по углам. Если проинтегрировать
E1.11) по г от 0 до со, то мы получим вероятность ш(тF, q>)dQ того,
что электрон окажется лежащим где-то в телесном угле dQ (см. рис. 31)-
около луча (9, ф). В силу нормировки функций Rnl получаем:
Из вида функции Ylm (9, ф) следует, что вероятность не зависит от угла ф
и равна1
wlm (9) dQ = Щт [Р1 Г' (cos 6)]8tdQ. E1.20),
1=0 шжт элеятооны
т=0
Р
электроны
я
электроны
олентронь!
Рис. 34. Угловое распределение электронов Wim(ft) для
s-, р-, d- и /-состояний
Следовательно, распределение по углам обладает симметрией тела вра-
вращения около той оси, на которую фиксирована проекция момента импульса-
(у нас эта ось есть ось OZ).
На рис. 34 мы изобразили графики вероятности wlm для различных
состояний /, т. При этом принята полярная система координат 9, wlm,
так что величина wim откладывается по радиусу-вектору. Для сравнения-
приведены орбиты по Бору, расположенные надлежащим образом. При / = 0,
т = 0 вероятность
не зависит от угла 9, и поэтому мы имеем сферическую симметрию.
Состояние, в котором момент импульса равен нулю (/ = 0), называют
s-состоянием, соответствующий терм называют s-термом; s-состояние
характеризуется, следовательно, шаровой симметрией. Соответствующих
орбит по Бору ' нет. *Это обстоятельство представляло одну из трудно-
— нормировочный множитель, см. дополнение V.
169-

■стей теории Бора, так как приходилось сопоставлять с оптическим s-тер-
мом состояния с /= 1 (т=0, ± 1), в то время как опыт однозначного
показывал, что электрон в s-терме не обладает орбитальным механическим
(и магнитным) моментом.
Состояние с / = 1 (m = 0, ± 1) называется р-состоянием, а соответ-
соответствующий терм — р-термом. Вероятность в этом случае определяется
■функциями P^(cos6) и P°(cos9). Подставляя значения этих функций
из B5.16), имеем:
E1.22)
E1.22')
На рис. 34 изображены вероятности w\y±\, tt>i,o, а также соответ-
соответствующие орбиты по теории Бора. Из рисунков видно, что если по боров-
ской теории в случае, например,
т = ± 1 вероятность найти электров
отлична от нуля лишь в плоскости
орбит ( б = т у » то по квантовой
го- механике она не равна нулю и для
' других значений угла 9 (на конусах
9 = const). Соответствие замечается
в том, что максимум вероятности
лежит при 9 = ^ • Подобное же со-
соответствие имеется и для т = 0 (мак-
(максимум при 9 = 0).
Состояние с / = 2 (т = 0, ± 1, ±2)
называется d-состоянием, а терм —
d-термом- На рис. 34 приведена и
вероятность до21 для 1 = 2. т=\.
Из формул для шаровых функций
B5.16) легко получить
flr=n_J_l сфер, I-,m| конусов, \т\ плос-
й
E1.23)
/ = 2 и т = 1 мы имеем по Бору
совокупность орбит, нормали к ко-
углом раствора, равным 60°. На ко-
конусе с раствором 60° лежит и мак-
максимум вероятности по теории Бора.
По квантовой механике этот максимум приходится на угол 45°.
Вид вероятностей wim(Q) (рис. 34) позволяет нам создать некоторое
представление о форме атома в различных состояниях. Эта форма опре-
определяется значением орбитального числа /, а магнитное число т, как
видно, определяет ориентацию атома в пространстве.
Из приведенных выражений для вероятностей wlm F) видно, что
-функция Р? с / = 0 не имеет узлов, с / = 1 и т = 0 имеет одну узловую
■поверхность Г плоскость е=-|Л, с 1 = 2 и т=1—опять одну узловую
170

поверхность ( плоскость 9 = у j . Вообще уравнение
Р? (cos 6) = О
дает / — \т\ действительных корней 8„ 62, . . ., 6,_)т|. Эти углы и суть
углы раствора конусов F = const), которые образуют узловые поверх-
поверхности. Часть волновой функции i|)n(m, зависящая от угла ф, именно е1™*,
•не имеет узлов, но ее действительная часть cos/Пф или мнимая (i sin ту)
имеют т узлов: ф,, ф2, ...,фт, которые в пространстве дают узловые
плоскости, проходящие через полярную ось.
На рис. 35 изображено семейство узловых поверхностей функции г|зИ[т,
•состоящее из шаров (узлы функции Rnl), конусов (узлы функции РТ)
и плоскостей (узлы функции cos/пф или sin/пф). Число шаров равно пг,
конусов 1 — \т\ и плоскостей \т\. Всего имеется nT-\-l — \m\-\-\m\ =
= nr -\-1 = п — 1 узловых поверхностей. Таким образом, мы опять имеем
иллюстрацию к общей теореме, упомянутой выше.
Приведенные на рис. 35 узловые поверхности характеризуются той же
геометрией, что и узловые поверхности колеблющегося шара. Поэтому
функции 1|з„,т(г, 6, ф) имеют сходство с функциями, изображающими коле-
колебание шара, подобно тому как собственные функции осциллятора г|зп (х)
•имеют сходство с функциями, изображающими колебание струны.
§ 52. Движение электрона в одновалентных атомах
Существует ряд атомов, имеющих один валентный электрон: это
атомы щелочных металлов Li, Na, К, .... Мы будем называть их водородо-
подобными. В этих атомах имеется группа внутренних электронов,
а внешний, валентный электрон движется в поле ядра и этих внутрен-
внутренних электронов.
Строго говоря, мы имеем дело в этом случае с многоэлектронной
проблемой. Однако в перечисленных атомах имеется одна особенность,
позволяющая приближенно свести задачу к задаче о движении одного
электрона в поле центральных сил. Дело в том, что если удалить из та-
такого атома валентный электрон, то оставшиеся электроны образуют элек-
электронную оболочку, характерную для инертных газов. Например, ион Li*
имеет электронную оболочку, аналогичную электронной оболочке атома Не.
И опыт, и теория показывают, что электронная оболочка инертного газа
образует весьма прочную систему, имеющую сферическую симметрию
и мало деформирующуюся внешними воздействиями. Поэтому прибли-
приближенно можно поступить так: считать, что внешний валентный электрон
вообще не влияет на внутренние электроны, и таким образом рассматри-
рассматривать движение внешнего электрона в поле ядра и внутренних электронов.
В силу сферической симметрии распределения последних поле, соз-
создаваемое ими, будет центральным1. Найдем потенциальную энергию
внешнего, валентного электрона (J (г) в поле ядра атома и внутренних
электронов. Обозначим через V (г) потенциал этого поля, тогда
U(r)=-eV(r). E2.1)
Пусть, далее, q(r) есть средняя плотность электрического заряда, созда-
1 Подчеркнем еще раз, что это верно лишь приближенно, так как внешний элек-
электрон на самом деле будет поляризовать внутреннюю электронную оболочку.
171

ваемая внутренними электронами1. Тогда полный электронный заряд.
[ — еМ (r)], заключенный внутри сферы радиуса г, будет равен
г
- eN (г) = 4я \ q (г) г2 dr. E2.2>
о
Учитывая еще заряд ядра + eZ, мы можем представить полный; заряд
в рассматриваемой сфере в виде:
eZ*{r) = e[Z-N(r)], E2.3)-
где через Z* обозначен эффективный номер ядра на расстоянии г. Отсюда
по теореме Гаусса получаем, что поле Щг равно
а потенциал V (г) равен
^^ТГ^- E2'5)
Из E2.3) следует, что действие электронной оболочки сводится к экра-
eZ
нированию поля ядра —, причем это экранирование различно для раз-
различных расстояний от ядра. Вблизи ядра его поле не экранируется.
В самом деле, при г—>0
т1^ г2 dr.
^ о()
r-*0 r r-+0 r
Поэтому в этой области
v _е7.
а потенциал
F(r)=^- + const. E2.6).
Напротив, в областях г > а, где а — радиус электронной оболочки,
N(r)r»a = N,
где N — полное число электронов в оболочке, имеем
* _ e(Z-N)
и потенциал будет равен
V(r) = ^~^-, E2.7).
что соответствует потенциалу ядра, заряд которого уменьшен на заряд
электронов оболочки.
Часто, делая еще более грубое приближение, игнорируют зависимость
эффективного номера Z* (г) от г и берут какое-нибудь наиболее иодхо
1 Вероятность q (г) может быть вычислена методами квантовой механики. Так,
для Li+ речь будет идти о движении двух электронов в поле ядра. Задача здесь
такова же, как и в случае атома Не. Последняя рассмотрена в § J17. Кроме того, Q(r)>
может быть измерена и экспериментально (см. § 79). •
172

постоянное значение для
= Z-N(r0).
E2.8)
•Однако такое приближение очень грубо и не ведет к хорошим результа-
результатам г. Полученная нами потенциальная энергия U (г) = — eV (г) для валент-
валентного электрона водородоподобного атома принадлежит к классу рассмот-
рассмотренных в § 49 С полюс порядка —). Так как N < Z, то мы имеем дело
со случаем притяжения. Отсюда следует, что энергетический спектр
водородоподобного атома будет состоять из непрерывного спектра (Е > 0),
отвечающего ионизованному атому, и
дискретного (Е < 0), образующего сово-
совокупность квантовых уровней атома.
Мы не будем заниматься решением
радиального уравнения D9.5) для этого
вида потенциальной энергии. Оно может
быть решено лишь численным интегри-
интегрированием. Ограничимся лишь изложе-
изложением результатов.
Самым существенным обстоятель-
обстоятельством является то, что энергия Е зави-
зависит в этом случае не только от главного
квантового числа п но и от радиаль-
радиального пт. Это нетрудно понять. В урав-
уравнение D9.5) для функций R, из которого
•определяются и квантовые уровни Еп,
входит орбитальное квантовое число /.
Поэтому Е будет, вообще говоря, за-
зависеть от числа /. Кроме того, значение
Е зависит от номера собственной функ-
функции уравнения D9.5), т. е. от ради-
радиального числа пг Таким образом, в
общем случае собственные значения Е
зависят от двух квантовых чисел, пг
•и /, или так как п = пг -f- / + 1, то можно
сказать, что зависит от п и /. Следо-
Следовательно, полная нумерация уровней и
■свбственных функций будет такая:
ev
4 -
3 -
>■
1 ■
n
Непрерыбный спектр
ls(n'=2,1=0)
Рис. 36. Снятие «/«-вырождения в
одновалентных атомах:
Приведены три первых уровня атома ка-
калия. Уровни 2р, 25, сливающиеся в водо-
водороде, в калии разделены
lm-
1 = 0, 1, 2,...,n-
n=\, 2, 3,...,
E2.9)
а не £„, как в случае кулоновского поля. То, что в кулоиовском поле
энергия зависит лишь от п, есть специальная особенность этого поля,
которая имеет свои основания2. В случае кулоновского поля числа пг
« / входят в выражение энергии в виде суммы n = nr + l+l.
Таким образом, в кулоновском поле, как уже и отмечалось, имеет
место вырождение («/«-вырождение), заключающееся в том, что энергия
при заданном главном числе п не зависит от величины момента импульса (/).
В общем случае центрального поля U (г) это «/«-вырождение снято, и термы
1 Конечно применимость или неприменимость того или иного приближения зави-
зависит еще и от того, какую степень точности желают получить.
2 См. В, А, Фок, Докл. Акад. наук, 1935, № 2, стр. 169.
173

с одним и тем же главным квантовым числом п, но с разными орбиталь-
орбитальными числами / имеют разную величину. На рис. 36 приведены уровни-
для одновалентного атома калия. Как видно, например, главному числу
п=--2 принадлежат два уровня / = 0 (s-терм) и /=1 (р-терм), В случае
водорода эти уровни сливаются вместе.
Что касается магнитного квантового числа т, то оно, как уже объ-
объяснялось, определяет ориентацию атома в пространстве, и поэтому энергия
атома (в отсутствии внешних полей) не может зависеть от этого числа.
§ 53. Токи в атомах. Магнетон
Вычислим плотность электрического тока, текущего в атоме, если-
электрон находится в стационарном состоянии, с определенным значе-
значением проекции момента импульса Mz = hrn. Волновая функция такого
состояния равна
*lW (Л 9, Ф) = Яш (г) Р] Г ' (cos 6) aim*. E3.1).
Согласно B9.11) плотность электрического тока в состоянии i|)alm( будет
выражаться формулой
J = - Щ №nlm Vfc - l&m Vxl>o(m} E3.2)
(мы берем перед е знак — , считая заряд электрона равным — е, е —
= 4,778-10~10 единиц CGSE). Удобно найти вектор J в полярных коор-»
динатах г, 0, ф. Для этого заметим, что в полярной системе проекции
_ did 1 д п
оператора градиента V суть j-, — -^ , —г—»- -^~ . Следовательно, проекции.
вектора J на радиус, меридиан и широту равны соответственно
=0, E3.3)
=0, E3.4>
Uhe f i дх^*1т ,!•* дУп1т) ehm
Первые два результата получаются сразу, если вспомнить, чтоР'Г1 и /?nJ
суть действительные функции переменных 6 и г, а последний следует
из того, что tynlm пропорциональна eim<f. Таким образом, в стационарных
состояниях проекции тока на радиус и меридиан равны нулю (что оче-
очевидно и из геометрических соображений; если, например, Jr Ф О, то заряды,
будут либо растекаться либо накапливаться) и ток течет вдоль широт-
широтных кругов (рис. 37). Это течение вполне соответствует среднему току
по классической механике для совокупности орбит, имеющих один и тот же
полный момент импульса М2 и одну и ту же проекцию этого момента Мг
на ось OZ.
Теперь, основываясь на формуле E3.5) для плотности тока, нетрудно
найти магнитный момент 9JJZ атома. Сила тока dl, протекающего через
площадку da, направленную в меридиональной плоскости,(рис. 37), равна
dI = Jq)da. E3.6)
174

Магнитный момент, создаваемый этим током, равен
E3.7>
где. S — площадь, обтекаемая током dl. Эта площадь равна пг2 sin2 0
(см. рис. 37). Поэтому
яг2 sin2 6
яг2 sin2 6 ehm
с jirsin6
do.
E3.8)
Чтобы получить полный момент $Щг> следует просуммировать по всем
трубкам тока. Тогда мы получим:
J2- E3.9}
Но 2itrsin6dcj есть объем трубки. Так как внутри трубки величина
|i|)n(m|2 постоянна, то интеграл в E3.9) есть просто интеграл от |ipnim|2'
по всему объему. Этот интеграл в силу
нормировки равен 1, следовательно, про-
проекция магнитного момента jia ось имеет
значение
E3.10)
где
£1
Ю-21 единиц CGSM,
E3.11)
т. е. она имеет квантовое'значение, рав-
равное целому числу магнетонов Бора Щв
(см. § 3). Знак минус обусловлен отрица-
отрицательным зарядом электрона.
Произведенный расчет показывает, та-
таким образом, что в состояниях с Mz Ф 0
в атоме течет электрический ток. Этот ток
создает магнитный момент E3.10), так что
атом представляет собой в целом маг-
магнитный диполь. Отношение проекции маг-
магнитного момента Шх к проекции меха-
механического момента Мг равно
е
'2ас
Рис. 37. Токи в атоме при задан-
заданных вращательном моменте М2 и-
его проекции Mz
E3 12}
и в точности совпадает с отношением этих7величин по классической
теории для заряда — е с массой ц, движущегося по замкнутой орбите1.
Заметим, что поскольку ось OZ ничем не выделена, такое же отношение
получится и для проекций £Щ и М на любое направление. Поэтому
E3.12) следует толковать в том смысле, что отношение вектора магнит-
магнитного момента Щ к вектору М механического момента равно — ^— .
1 См., например, И. Е. Тамм, Основы теории электричества, ОГИЗ, Гостех-
издат, 1949, или Р. Б е к к е р, Теория электричества, ч. 11. Электронная теория,
изд. 2. ГИТТЛ, 1941.
175

§ 54. Квантовые уровни двухатомной молекулы
Обратимся к молекуле, образованной из двух атомов Л и Б с мас-
массами гпа и тв- Потенциальная энергия в функции расстояния между
-атомами г пусть будет V (г). Эта энергия имеет вид, приведенный на рис. 38.
Мы ограничимся рассмотрением только относительного движения атомов А
•и В. Из классической механики известно, что относительное движение
двух частиц с энергией взаимодей-
взаимодействия U (г) происходит, как дви-
движение материальной точки с приве-
приведенной массой и:
тв
E4.1)
v
Рис. 38. Потенциальная энергия для ато-
•мов двухатомной молекулы и энергический
спектр:
Для Е>0 спектр непрерывен, для£<0 имеет
место система Уровней Eq, Ei,...
в поле центральной силы U (г), а
общее поступательное движение —
как свободное движение матери-
материальной точки с массой гпа-\-гпв-
Такое же положение вещей имеет
место, как будет доказано в § 104,
и в квантовой механике. Опираясь
на это обстоятельство, мы можем
написать оператор полной энергии
для относительного движения ато-
атомов А и В в виде
где г есть расстояние между атомами, а углы 6 и ф (входящие в М2)
•определяют направление линии, соединяющей А и В.
Уравнение Шредингера для стационарных состояний будет таково же,
■как и D9.2). Волновую функцию можно опять искать в виде
r,e, ф)=Я(г)У,т(в,
причем для и будем иметь уравнение
Член
E4.3)
E4.4)
у
М0Жн0 рассматривать как дополнительную потенциальную
энергию, так что всю потенциальную энергию для движения по радиусу
можно определить в виде
E4.5)
■и переписать уравнение E3.4) в виде
A2 d-
r)'u = Eu. E4.4')
График функции W,(r) для разных I изображен на рис. 39.
В отсутствии вращения (/ = 0) W0(r)=U(r), и мы имеем случай, рас-
рассмотренный в § 49 (рис. 29). Если вращение не сильно (I невелико),
то Wt (г) все еще не сильно отличается от U (г). Последняя кривая лишь
несколько искажается. Если, наконец, I очень велико, то кривая Wt(r)

принимает вид, приведенный на рис. 39 (случай I > 1). Мы знаем, что
для / = 0 молекула имеет дискретный спектр при £<0 и непрерывный
при Е > 0. При сильном вращении Wt (r) всюду положительно. Тогда
из доказанной в § 49 теоремы следует, что Е > 0 и, следовательно, спектр
будет непрерывным. Молекула будет диссоциировать на атомы А и В.
Эта диссоциация является результатом
действия центробежной силы, которая
развивается при вращении молекулы.
Рассмотрим случай, когда враще-
вращение невелико, так что Wl мало отли-
отличается от U (г) —по крайней мере в об-
области минимума U (r) (r = rL). Разло-
Разложим Wt (r) по степеням отклонения
от положения равновесия r — rt. Поло-
Положение равновесия г1 зависит от I и оп-
определится из минимума Wl{r):
dr dr '
dU . h4{l
\ir"
■ = 0.
E4.6)
Отсюда находим r — rt. Далее, имеем:
причем
Введем обозначения:
E4.7)
E4.8)
Рис, 39. Связь колебания и вращения
в двухатомной молекуле
r=r = №?> К-Л» x = r-rt.
E4.9)
Подстановка Wt (r) из E4.7) в E4.4') в обозначениях E4.9) дает
A2 d2u
~2JT rf^~
Обозначая через Е' величину
h4(l+l)
2/7
E4.10)
мы перепишем уравнение E4.5') в виде
ft2 d2u . 1
E4.5")
Это - уравнение для стационарных состояний осциллятора D7.3), обладаю-
обладающего собственной частотой м;. Согласно D7.10) его собственные значе-
значения Е' суть
E4.11)
E4.12)
/z + i.), л = 0, 1, 2
а собственные функции согласно D7.11)
12 Д. И. Блохиицев
177

Находим полную внутреннюю энергию молекулы (пользуясь E4.10)):
, E4.13)
я = 0, 1, 2 / = о, 1, 2 E4.13')
Собственные функции молекулы будут
1W ('. 0. Ф) = ~ «™ (г) У1тF, Ф). E4.14)
Эти волновые функции описывают вращение молекулы и ее колебания.
Энергия молекулы Еп1 оказывается равной сумме энергии колебаний
с частотой с»; и энергии вращения молекулы:
Е^Щ^. E4.15)
Имея в виду, что h4 (/+ 1) есть квадрат момента импульса Ml, мы видим,
что выражение для энергии вращения молекулы в квантовой механике
таково же, как и в классической, так как согласно E4.9) It есть момент
инерции молекулы1. Формула E4.15) показывает, что энергия вращения
квантуется, причем расстояние между соседними уровнями равно
ДЕ, = -£(/ + 1) E4.16)
(если пренебрегать слабой зависимостью момента инерции от /, т. е.
растяжением молекулы под влиянием центробежной силы).
Полученные нами решения, конечно, приближенны. Мы пренебрегли
ангармоничностью колебаний молекулы, отбросив высшие члены в раз-
разложении Wt(r) по степеням r — rl. Это допустимо, если отклонения г — г1
малы в сравнении с расстоянием между атомами г1 (или г0). Из теории
осциллятора следует, что среднее значение х2 — ( я + -?г ) [чтобы в этом
убедиться, достаточно вычислить матричный элемент Хтп, пользуясь матри-
матрий D8.8)]. Поэтому
и условие справедливости нашего приближения может быть написано
в виде
Щ / Y«r<» E4.17)
т. е. приближение тем лучше, чем больше масса атомов молекулы, чем
больше частота колебаний ю0 и чем больше расстояние между атомами г0.
Кроме того, уровень колебаний должен быть не очень высок (п мало).
При больших п и / связь между колебаниями и вращением молекулы
становится сильной, и все наше приближение делается несостоятельным.
Напротив, при малых п и / мы можем вообще пренебречь зависимостью Г;
от / и брать вместо It и юг, /0 и ю0 для / = 0.
Величины /0 и ю0 обычно таковы, что «квант» энергии колебаний ha^
гораздо больше «кванта» энергии вращения -^г • Так, например, для
молекулы водорода
/гюо= 8,75-10'13 эрг. -|^-= 1,15-Ю'1 эрг.
Благодаря этому обстоятельству энергетический спектр молекулы состоит
1 Напомним, что по классической механике энергия вращения равна —у-
178

из системы уровней колебательных (разные значения числа п) и враща-
вращательных (разные I), последние лежат очень близко друг к другу. Схема
энергетического спектра молекулы приведена на рис. 40. Пунктирная
линия на границе с непрерывным спектром есть Е = 0 и соответствует
энергии диссоциирующей молекулы. Это значение энергии может быть
достигнуто при любом п для достаточно больших I.
Энергия диссоциации молекулы D, находящейся в нормальном состоя-
состоянии (/г = / = 0), равна, как было показано в § 49,
D = U0-^. E4.18)
Важнейшая область явлений, в которой обнаруживается квантование
движения молекулы, — это спектры молекул. Пусть возможные уровни
энергии электрона в молекуле суть EN. Тогда полная энергия молекулы
и ее оптического электрона равна
Е =
1) +const.
E4.19)
Написав в таком виде энергию, мы предполагаем, что связь между
движением электронов и движением атомов в молекуле слаба, так что
приближенно можно предста-
Непрерывный спектр
вить энергию в виде суммы
энергии электрона и энергии
атомов. Тем не менее эта связь
все же существует, и даже
при слабой связи изменение
состояния электрона (переход
с уровня EN на другой E'N)
будет сопровождаться измене-
изменением состояния атомов. По-
Поэтому, если молекула погло-
поглощает квант света Аю, то часть
этой энергии пойдет на воз-
возбуждение электрона, а другая
часть на возбуждение движе-
движения атомов молекулы. Обрат-
Обратно, квант частоты ha может
быть излучен не только за
1=1 '-
1=0-
1=2 =
1=0
±е=о
~п--2
Рис. 40. Схема вибрационных (и) и ротационных
уровней (/) двухатомной молекулы
счет энергии электрона, но и за счет энергии движения атомов моле-
молекулы. Поэтому, чтобы получить частоты ю излучаемого и поглощаемого мо-
молекулой света, в правиле частот Бора
следует под Е разуметь энергию всей молекулы в целом. Подставляя
сюда Е из E4.19), получим:
na = tN' — bN-\-ha0(n — п) + -^ [V (/' + 1 ) — 1A + 1I. E4.20)
Обозначая частоту
-пг
vN,N, мы можем переписать E4.20) в виде
д , обусловленную переходами электрона, через.
E4.21),
v,W обычно гораздо больше ш0 и тем более А . Поэтому рядом со спектраль-
спектральной линией, отвечающей чисто электронному переходу (частота v%.N), при
наблюдении в спектроскоп будет наблюдаться ряд линий, очень близких,
12* 179

Почти сливающихся друг с другом1. Такой спектр называют полосатым.
Он характерен для двухатомных молекул (атомы имеют спектр, состоящий
из довольно далеко отстоящих друг от друга линий, иногда, правда, рас-
расщепляющихся на небольшое число соседних). Линии в полосах обусловлены
изменением вращательного движения молекул. Поэтому эти полосы часто
называют ротационными. Кроме ли-
линий, обусловленных изменением враще-
вращения (число I), будут получаться ли-
линии, обусловленные изменением коле-
колебательного движения (число п). Эти ли-
линии часто называют вибрационными.
Таким образом, сложность моле-
молекулярных спектров обусловливается
тем, что в обмене энергией молекулы
со светом участвует, вообще говоря,
О г>о юо 150 200 Т°к вся молекула в целом: не только сос-
Рис. 41. Теплоемкость молекулы Н2, тояния оптического электрона, но
приходящаяся на долю вращательных и состояния колебания и вращения
степеней свободы, молекулы претерпевают изменение.
Теория молекулярных спектров обра-
образует в настоящее время довольно широко разработанную, но все же
далеко не законченную область атомной механики2.
Помимо молекулярных спектров квантовый характер движения моле-
молекулы обнаруживается на теплоемкости двухатомных газов. Согласно клас-
классической теории теплоемкость, приходящаяся на одну степень свободы,
k
равна у, где & —постоянная Больцмана, равная 1,36-10~16 э/град.
Двухатомная молекула имеет всего шесть степеней свободы, поэтому
по классической теории ее теплоемкость должна быть постоянной и рав-
7
нятьсяуй3. Между тем опыт показывает, что при средних темпера-
5 ,
турах теплоемкость действительно постоянна, но равна у к, а при низких
падает до у&. Этот факт находит полное объяснение в квантовой теории.
Если при температуре Т средняя энергия поступательного движения
з
молекулы у kT меньше ha>0, то колебания молекулы не возбуждаются
(точнее, возбуждаются редко). Молекулу можно рассматривать в этом
случае как жесткую и считать число ее степеней свободы равным как бы
не 6, а 5. Говорят, что колебание «замерзает». Температура «замерзания» Tv,
очевидно, определится из неравенства
|ет;<К- , E4.22)
Для Н2 температура «замерзания» Г„ = 4300э. Большой величиной Tv
объясняется, что при обычных температурах теплоемкость двухатомных
газов равна у fe.
1 Конечно, будут эти линии сливаться или нет,—зависит от разрешающей силы
спектроскопа,
2 О молекулах см. подробно в книгах: К. В. Никольский, Квантовая меха-
механика молекулы, ГТТИ, 1934; К р о н и г, Полосатые спектры и строение молекул,
ГНТИ Украины, Харьков, 1935, См. также § 121 настоящей книги.
3 Одна из степеней свободы колебательная и на нее приходится, из-за равенства
кинетической и потенциальной энергии, не у k, a 2yfe.
180

С понижением температуры наступит момент, когда поступательная
энергия окажется меньшей «кванта вращения» у,-, тогда и вращение
не будет возбуждаться и выпадет из теплового баланса. Вращение «замерз-
«замерзнет». Температура «замерзания» вращения Тг определится из неравенства
2 R r - 2/ '
E4.23)
Для Т < Тт теплоемкость вращения равна нулю. Остается только тепло-
3 ,
емкость поступательного движения -wk.
На рис. 41 приведена зависимость теплоемкости вращения сг от тем-
температуры. Как видно, согласие между квантовой теорией и опытом полное.
Пунктиром изображена теплоемкость по классической теории. При низкой
температуре классическая теория противоречит опыту1.
§ 55. Движение"электрона в периодическом поле
К. числу важных случаев движения относится движение электрона
в периодическом потенциальном поле U (х, у, г). Если поле имеет период
а —в направлении ОХ, b — ъ направлении OY и с —в направлении OZ,
то это свойство периодичности может быть выражено равенствами
U{x + a, у, z)=U{x, у, г),
U (х, у + b, z) = U [х, у, г),
U{x, у, z + c) = U{x, у, г).
E5.1)
E5.1')
E5.1")
У(лло)
Такое периодическое поле реализуется внутри идеальных кристаллов,
где ядра атомов, и вместе с тем и средний электрический заряд, распре-
распределены периодически. Потенциал электрического поля будет, конечно,
также периодической функцией коор-
координат х, у, г. Если внутрь такого
кристалла ввести электрон, то он бу-
будет иметь периодическую потенциаль-
потенциальную энергию вида E5.1).
Строго говоря, в этом случае мы
имеем дело с проблемой многих элек-
электронов. Замена такой проблемы более
простой задачей о движении |одного
электрона во внешнем поле является
приближением. Оно, наверно, справед-
справедливо для больших скоростей рассмат-
рассматриваемого электрона (и до той поры,
пока нас не интересуют неупругие
Рис. 42. Кривая потенциальной энер-
энергии электрона в кристалле (в функции
одной координаты х):
Пунктиром изображена волновая функция
(модулированные волны)
столкновения электрона). Что же касается применения такого прибли-
приближения к движению электронов самого кристалла, то до сих пор не дано
обоснования такой возможности, хотя вытекающие и? расчетов следствия
позволяют истолковать множество явлений.
На рис. 42 изображена потенциальная энергия электрона в кристалле
в функции х при условии, что ось ОХ проходит через центры атомов,
1 Подробности о теплоемкости двухатомных газов см. К. Герцфельд, Кинети-
Кинетическая теория материи, ОНТИ, 1935, стр. 403 — 408, а также в книге Fowler, Sta-
Statistical mechanics, 1938.
181

образующих кристалл. В точках ... — 2а, — а, О, + a, -f 2а, ... рас-
расположены центры атомов. В этих точках U имеет полюс первого поряд-
/ 2Z
ка (-
Для выяснения возможных уровней энергии электрона в периодическом
поле и собственных функций энергии нужно решить уравнение Шредингера,
которое мы возьмем сперва в «х»-представлении. Это уравнение гласит:
-~^+Uip = Ey, E5.2)
где fx — масса электрона, a U — потенциальная энергия, подчиняющаяся
условию периодичности E5.1). Ставя себе целью лишь выяснение самых
основных свойств движения в периодическом поле, мы ограничимся одним
измерением. Тогда вместо E5.1) и E5.2) будем иметь:
U(x + a) = U(x), E5.1'")
-|г7§- + г/«1> = £1>. E5-2')
Для исследования этого уравнения перейдем к «р»-представлению.
Положим для этой цели
\^ E5.3)
где рх — импульс по оси ОХ. Соответственно разложим потенциальную
энергию U в ряд Фурье
+оо 2зтгпх
U(x) = l,Une~'^r, Un = UU- E5.4)
— JO
Коэффициенты этого ряда Uп суть не что иное, как U (х) в «^-представле-
«^-представлении. Подставим E5.3) и E5.4) в 'E5.2'):
А2
h— -—\ х +оо
° / с
е—ik'x
е
Умножая это уравнение на — и интегрируя по х от — оо до -f- co>
мы получим б-функции:
+ОО -f-OO +СО
—СО —СО
+
= E\c{k)b(k-k')dk. E5.5')
— со
Выполняя, наконец, интегрирование по k и меняя обозначение fe' на k,
получаем:
+СО
( ^) E5.6)
Это уравнение есть не что иное, как уравнение E5.2') в «^-представлении.
Особенностью его является то, что в него входят лишь те c(k), аргументы
которых отличаются друг от друга величиной 2кп/а (п = 0, ± 1, ± 2, ...).
Величины с (k), с (к + 2лп/а) суть неизвестные, которые нам нужно
вычислить. Все они связаны между собой уравнениями вида E5.6), которые
182

легко получить, если менять в E5.6) к на 2лт/а, где т— целое число.
Перенося в E5.6) член с Е налево, мы без труда можем написать уравне-
уравнения для всех связанных между собою функций c(k-}-2nm/a):
m =
= °- [f*'-£]c(*) +
т=
2я I 2я/г
+
И Т. Д.
E5.7)
Это — система алгебраических линейных однородных уравнений для бес-
бесконечного числа неизвестных c(k-\-— V т = 0, ±1, ±2, ... Для того
чтобы эта система имела отличные от нуля решения, необходимо, чтобы
ее определитель А равнялся нулю. Этот определитель зависит от Е и k
(и всех коэффициентов Un) и является вообще трансцендентной функцией
от Е. Поэтому уравнение
Д(£, £) = 0 E5.8)
имеет бесконечное число корней Е = Ег, Е2, ...,Ej, ..., каждый из кото-
которых является функцией волнового числа к. Отсюда следует, что энергети-
энергетический спектр частицы, движущейся в периодическом поле, будет состоять
из отдельных областей
E = E}(k), /=1, 2, 3 E5.9)
в каждой из которых энергия есть функция волнового числа к. Эти
области называются зонами дозволенной энергии или просто зонами.
Покажем, что в пределах каждой зоны энергия есть периодическая
функция волнового числа к с периодом —. Для доказательства заменим
в системе уравнений E5.7) всюду k на к
2я
Тогда, как непосред-
непосредственно видно из E5.7), такая замена означает просто иной порядок
написания уравнения E5.7), т. е. система уравнений переходит сама в себя.
Поэтому и корни Ej останутся неизменными, так что
Е^к)ч E5.10)
Таким образом, энергия есть в самом деле периодическая функция k и
следовательно, может быть выражена рядом Фурье:
I1 Eim cos (так),
m=0
E5.11)
183

где коэффициенты Ejm зависят лишь от вида потенциальной энергии Щ(х),
т. е. от Uпг. ,
На рис. 43 приведены типичные кривые зависимости Ej (£)"*для двух
первых зон Ег и Е2. В первой зоне энергия меняется от^ минимального
значения Е[ до максимального Е"х, во второй — от Е[ до Е"г. Интервал >£
от Ё[ до Е[ не реализуется и образует запрещенную зону. Таким образом,
£
Рис. 43. Энергетический спектр и энергия в функции волнового
числа k для электрона, движущегося в периодическом поле
спектр состоит из отрезков непрерывного спектра (полос) от Е\ ro~E\,
от £2' до Е"г и т. д. Как правило, запрещенные области суживаются
по мере увеличения номера зоны, вплоть до слияния в непрерывный спектр
в пределе / = со.
Общий вид собственных функций может быть также легко гполучен.
Каждому собственному значению E=Ej(k) принадлежит определенное
решение системы E5.7). Данному значению Ej(k) принадлежит Cj(k)
с вполне определенным значением k, либо отличающимся от него на целое
число —. Если мы хотим записать с;- (k) в виде одной функции, то мы
можем это сделать с помощью б-функций следующим образом:
+00
E5.12)
Это и есть решение, принадлежащее собственному значению Е, (k) и взятое
в «р»-представлении ( так как k' = ~ J. Отсюда получим ар в «^-пред-
«^-представлении:
+00
+ОО +ЛО
—oo n=—=
Производя здесь интегрирование no_fe', получим:
V'Yn '
E5.13)
1 Мы написали ряд по косинусу. Общий ряд Фурье содержит как косинусы, так
и синусы. Однако легко видеть из E5.7), что замена k иа — k не может изменить коэф-
коэффициентов уравнения E5.7). При такой замене они опять переходят сами в себя. По-
Поэтому Е должно быть четной функцией к.
184

Вынося здесь elhx за знак суммирования, получим:
%„ (х) = eihxujh (x), E5.14)
где Ujk (x) есть некоторая периодическая функция х с периодом а:
) = ujk(x). E5.15)
1руь(х) в уравнении E5.14) есть собственная функция оператора энергии
в ««-представлении, относящаяся к собственному значению £,-(&), т. е.
к /-й зоне и волновому числу, равному k. Она представляет собой плоскую
волну (elhx), модулированную в такт периодичности потенциальной энер-
энергии. На рис. 42 изображена действительная часть такой функции (пунктир-
(пунктирная кривая). Точками на оси ОХ отмечены положения ядер атомов [полюса
функции U (х)]. Около этих точек функция %ft(x) близка к тем, которые
свойственны изолированным атомам.
Из решения E5.13) непосредственно следует, что состояния с опре-
определенным значением энергии (Д£'2=0) суть (как и всегда при наличии
поля) состояния с неопределенным значением импульса р. Именно
в состоянии с энергией Ej (k) возможны значения импульса р, равные
( ^y я=0, ±1, ±2, ... E5.16)
с вероятностью
|<^)]2 E5.17)
для рп = /г ( fe-f"—• J • Среднее значение импульса р в состоянии
вообще говоря, не равно нулю.
Докажем теперь теорему о движении группы волн в периодическом
поле, подобную теореме о движении группы волн в отсутствии поля (§7).
Зависимость от времени функции tyjh(x), как представляющих стационар-
стационарные состояния, будет гармоническая с частотой ю = * :
i
. О = %*(*)* " • E5Л8)
Образуем из этих состояний группу, ограничиваясь функциями, принад-
принадлежащими одной определенной зоне (/). Соответственно этому предполо-
предположению индекс /' опустим совсем.
По определению группы имеем:
!>(*, 0= ] с (fe)e1 <**-«"> uh(*)dfe, . E5.19)
Ьо-ЛЬ *
где Ak — малый интервал. Полагая
и считая c(k) и uk(x) медленно меняющимися функциями k (в области
k0 ± Ak), мы получим вместо E5.19)
Aft . г /йй) \ j] д
^ g Г~1"й)о J rffi- E5.19')
-ль
185

Вынесенные за знак интеграла множители являются быстропеременными
функциями х и t. Интеграл по б, напротив, медленно меняется, если Ak
мало. Поэтому этот интеграл можно рассматривать так же, как мы де-
делали в § 7, как амплитуду группы г|з (х, t).
Повторяя в точности все рассуждения § 7, мы найдем, что макси-
максимум амплитуды («центр» группы) перемещается с групповой скоростью,
равной
(%) 1Г^П E5.20)
k yo h V dk /о
■Отсюда следует, что средний импульс такой группы равен
Пользуясь выражением для Е E4.11), мы можем написать выражение
для среднего импульса в группе состояний в /-й зоне около ko = k
в следующем виде:
со
р= --^2 Ejnmsin(mak). E5.22)
Отсюда видно, что на границах зоны ( k = {± — j средний импульс
р = 0. Легко непосредственно убедиться из вида функций ^(я)
E5.13), что в этих случаях мы имеем стоячие медулирсеанные ее/мы
Для значений k Ф — средний импульс вообще не равен нулю. Сле-
Следовательно, состояния с определенной энергией в периодическом поле
суть состояния со средним импульсом, вообще говоря, не равным нулю.
Если ограничиться в ряде E5.11) двумя первыми членами (т = 0
и т=1), то получим:
Е, (k) = £j0 -!- Е}1 cos (ka). E5.11')
В центре зоны (около & = 0, см. рис. 43) можно разложить E5.1 Г)
по степеням k, тогда найдем:
E,(k)=Ei0+ESl(\-k^-+■••'). E5.11")
Для свободного движения энергия равна
Eh = const + ^ E5.11'")
{см. § 7). Поэтому E5.11") можно переписать в виде
Е, (*) = const+ |£, E5.23)
где jj,* есть так называемая эффективная масса:
Соответственно, импульс равен
~P = ^hk, E5.25)
т. е. отличается от импульса свободной частицы коэффициентом ■—
186

Подобным же образом можно представить энергию и на краях зоны
f k — ± — J. Возьмем, например, окрестность точки k = + — . Положим
k = ~ — l. Тогда
cos (ak) = cos (it — |a) = — cos (|a).
В этой области
т. е.
■ E, (k) = const + |il, | = £ _ £, E5.23')
где ц** есть эффективная масса на краю зоны. Из E5.24) следует, что
ц** = — jj,*,
т. е. эффективные массы в середине и на краю зоны имеют противо-
противоположные знаки.
Доказанные в этом отделе теоремы имеют исключительное значение
в современной теории металлов 1. Не имея возможности входить в детали
этой обширной в настоящее время теории, мы ограничимся самыми
краткими замечаниями2. Теорема о движении группы в периодическом
поле показывает, что в периодическом поле электрон движется с неиз-
неизменным средним импульсом, вообще говоря, не равным нулю (это впер-
впервые было показано Ф. Блохом в 1927 г.). Поэтому омическое сопротивле-
сопротивление металла может быть вызвано только тем, что реальный металл не яв-
является средой с идеально периодическим полем. Отступления от строгой
периодичности поля вызывают рассеяние электронных волн [t|)/ft (x)] и при-
приводят к изменению среднего импульса электрона pjh, чем и вызывается
омическое сопротивление. Эти отступления от периодичности обусловлены
двумя причинами: 1) тепловыми колебаниями атомов металла, 2) наличием
посторонних вкраплений в кристалле и случайными микродеформациями.
По мере уменьшения температуры металла уменьшается амплитуда коле-
колебания атомов, а вместе с тем уменьшается рассеяние электронных волн,
и следовательно, падает сопротивление. В хорошо приготовленном кри-
кристалле вторая причина может играть малую роль, поэтому сопротивление
металла будет стремиться к нулю (или очень малой величине) по мере
понижения температуры3. По классической теории оно должно было бы
возрастать («замерзание электронного газа»).
Построенная на основе этой качественной картины количественная
теория омического сопротивления металлов приводит к хорошему согла-
согласию с опытом (см. сноску2).
Отметим еще одно интересное обстоятельство. Несмотря на то, что
•опыты Толмэиа твердо установили, что проводимость металлов обусловлена
движением электронов, оказалось, что в некоторых металлах знак эффекта
1 Мы должны были бы обобщить эти теоремы на три измерения. Однако это
обобщение тривиально сводится просто к увеличению числа переменных (х, у, г вместо х,
kx, ky, k2 вместо k) и все теоремы сохраняют свою силу,
2 Подробно современная теория металлов изложена в книге К. Бете
и А. Зоммерфельд, Электронная теория, ОНТИ, 1938,
3 Это уменьшение сопротивления металлов не следует смешивать с явлением
«сверхпроводимость», которое заключается в резком, скачкообразном исчезновении
сопротивления некоторых металлов при понижении температуры.
187

Холла таков, как если бы проводимость была обусловлена положительно
заряженными частицами. Эта аномалия полностью объясняется с точки
зрения квантовой механики. Можно показать, что если проводимость
металла обусловлена электронами, находящимися на краю зоны, то дело>
будет обстоять так, как если бы это были не электроны, а положительно
заряженные частицы.
Представим себе, что на электрон, находящийся на краю зоны, дей-
~* ~*
ствует электрическое поле Щ. Сила, действующая на электрон, равна её.
Эта сила вызовет изменение среднего импульса, которое по теореме Эрен-
феста равно
£-«*■
Согласно E5.21) получаем:
\i <PE dk
dt dt\hdkj h dk2 dt '
С другой стороны, работа, произведенная полем за 1 сек, равна
d£ _ dE_dk _ _^_. ^ 1 dE
Отсюда
И''
Имея в виду, что согласно E4.23')
мы получаем:
<55-26>
Обычное положение дел таково, что ц* положительно. (Это видно уже
из того, что с уменьшением величины периодического поля U—>0, т. е.
при переходе к свободному движению ц* —>ц.) Но из E4.25) следует,
что ц** = — ц* < 0.
Следовательно, согласно E4.26), электрон, находящийся на крак>
зоны, движется так, как если бы он имел заряд е'\
[X
е = е
[X** '
т. е. заряд, по знаку противоположный заряду в ( так как -^- < 0 \

ГЛАВА IX
ДВИЖЕНИЕ ЗАРЯЖЕННОЙ МИКРОЧАСТИЦЫ
В ЭЛЕКТРОМАГНИТНОМ ПОЛЕ
§ 56. Произвольное электромагнитное поле
Рассмотрим теперь движение частиц с зарядом е и массой и в произ-
произвольном электромагнитном поле. Пусть напряженность электрического
—> —>
поля есть Ш, а напряженность магнитного поля <gffi. Эти напряженности
мы выразим через скалярный потенциал V и векторный потенциал А:
1=-4^-^> E6.1)
d%? = rotA. E6.2)
Гамильтониан для этого случая приведен в § 27 и равен B7.9)
где U — силовая функция и присоединена на тот случай, если помимо
электромагнитных сил имеются еще и другие силы.
Мы не будем сейчас искать стационарные состояния, так как в про-
произвольном электромагнитном поле они не всегда существуют. Ограни-
Ограничимся установлением уравнений движения и из них выведем некоторые
общие заключения-
Для установления уравнений движения мы можем опираться на об-
общую теорию, изложенную в § 32. Согласно C2,2) и C2.2') дело сво-
сводится к вычислению квантовых скобок Пуассона для координат х, у, z
и импульсов Рх, Р , Рг, причем под оператором Н следует разуметь
гамильтониан E6.3)х. | ''
Вычислим сперва оператор скорости -т- (-г-, —г- напишутся тогда
по аналогии J. Имеем:
^^[Н,х]--=±[Р\х]-^[АР,х]. E6.4)
р
Первую скобку мы уже вычисляли C2.5); она равна — . Для второй
[X
1 Дальнейший расчет аналогичен классическому, рассмотренному в дополнении VI.
П9

имеем:
[АЛ х] = [АХРХ, х] = 1 (хАхРх - АхРхх) -
= ~ [хЛхРж - Ах (хРх - Иг)] = АХ. E6.5>
Следовательно,
dX \ / р \ dY I / е ~\ \
ил __ rjj х\ = — ( Р —А )' - — = \Н ц~\ = -—( Р — А I' \
E6.6)
I
Эти операторные уравнения в точности совпадают со второй группой
классических уравнений Гамильтона (см. дополнение VI, формула 10'),.
если под Р разуметь величину, а не оператор.
Первая группа уравнений получается несколько более сложным
путем. Вычислим —г,- :
d-^f=[H, Рх] = - ^[АЛ Ах] + Щ-с [div А, Рх] +
+ ^1А2' P*} + W+U, Px]. E6.7>
Вычислим все эти скобки, начиная с последних:
%%, E6.8)
>-*я.1 ~ 9иг2 Л, II/-2V ^ж л„ Г ^у ^v ~Г^г лу 1>
[\ у дх
i^lrHivA P1 //ге / 02.4ж ^Mv 0Мг \
2[xcL ' xJ~ 2[хс дх ~" 2[хс V. дх* + й(/ дх+ дгдх J '
цсL ' xJ ~ [хс V "й* ж "•" ах и "•" ах
Следовательно,
dt ~~ дх е дх^рс \ дх Vх с Л* J
™^. E6.9>
Чтобы получить производную не от обобщенного импульса, а от обык-
обыкновенного, равного согласно E6.6) >%
PlJ = p*-TA*> E6Л0>
,-„ «ч е dAv т-, е dAу- тт
нужно из E6.9) вычесть -~-. Для этого вычислим -т± . Имеем'
е dAx _ е дАх е ,„ . , .__ . .,
Подставляя сюда Н из E6.3), находим:
{[Н,Ах] = £с [Р\ Ах] - ^ [АЛ Ах]. E6.12)
!90

Далее, вычисляем эти скобки:
[Р'\ AJ = 2[ ~~РГ +-^Р„ +-^ Р* ) — i'/iVa/4T, E6.13)
i > 3cj \ дх х ду У ' дг г J x> v 7
Г А ТУ Л I __ Л X. I У| 3е I У! 5_ f 56 14Л
Отсюда получаем:
Вычитая теперь — —г^Eб. 15) из -rf- E6.9), находим:
— г
дх V с di ^ дх у ^ \ic \ дх ду J \ v с v
_JLfdAJi_dA1^( г_ А\ iMf ^divAN
[ic V dz дх J \ г с J 2[хс \^ х дх J
Но
ду ~ ^ *■< дг дх
Имея еще в виду E6.10), получаем из E6.16):
Операторы скорости -з— и -тт- не перестановочны с полем ^Ж; (если оно
не однородно). Поэтому в E6.17) лучше произвести симметризацию:.
Отсюда следует, что
dY dZ_l ( dY dY dZ dZ \ ih , ~>
J E6.18)
Подставляя E6.18) в E6.17), получаем:
Выражение
£{(^f OC^OI E6-20)
следует рассматривать как оператор силы Лоренца, действующей в поле Ш*
е?в на частицу с зарядом е. В самом деле, классическое выражение
191

для силы Лоренца имеет вид
Остальные два уравнения для осей 0Y и 0Z, очевидно, напишутся путем
циклической подстановки х, у, z.
Переходя от операторного равенства E6.19) к уравнению для сред-
средних значений, для чего умножаем E6.19) слева на чр* (х, -г/, z, t), а справа
на г|з (х, у, z, t) и интегрируем по всему пространству, мы получаем тео-
теорему Эренфеста для движения в электромагнитном поле:
E6.21)
Это уравнение вполне аналогично классическому уравнению Ньютона
<Рх dU , а, , е \ т dy dz\ ,ск О1,>
Рассмотрим теперь специальный случай движения в однородном
электрическом и магнитном поле. В этом случае Ш и ,§№ не зависят
, dX dY dZ
от координат и поэтому коммутируют с операторами^ -тг, -тг и -т-%
В силу этого для однородных полей вместо E6.21) получаем:
{&?£#e); E6.22)
x, у, z суть координаты центра волнового пакета. Сравнение с E6.2Г)
показывает, что в однородном электромагнитном поле центр пакета дви-
движется по законам классической механики как частица с зарядом g
и массой \х.
Если магнитное поле отсутствует, то вместо E6.22) получаем:
(г % = е%х, lc = e-h.t' + vj + x0, E6.23)
т. е. имеет место равномерно ускоренное движение центра волнового
пакета. Заметим, что в однородном электрическом поле не существует
стационарных решений [соответствующие волновые функции обращаются
в бесконечность при х— ±_ со (смотря по направлению поля Шх)]- Дей-
Действительно, согласно E6.23) центр волнового пакета для i = co должен
лежать в бесконечности: поле «сдувает» частицы в сторону падения
потенциальной энергии.
В магнитном поле существуют стационарные решения (см. § 57).
Они существуют также при одновременном наличии электрического и маг-
магнитного полей, если они перпендикулярны друг к другу.
_,. Из E6.1) и E6.2) следует, что если вместо потенциалов А и V [мы введем" новые
А' и V, связанные с прежними формулой:
A' = A+Vf, E6.24)
где f— произвольная функция координат и времени, то потенциалы Л' и V описывают
192

то же поле, что и А и V. Действительно,
1 = rot A' = де-\ rot (V/) =
Таким образом, потенциалы А, V вплоть до преобразования E6.24, 25) произвольны.
Но потенциалы входят в гамильтониан Н. Поэтому может показаться, что физические
выводы могут зависеть от произвола в выборе А и V. .На самом деле это не так.
Физические выводы зависят лишь от поля <§, Ш, а не от потенциалов А, V. В част-
частности, в уравнение движения E6.21) входят лишь напряженности полей, а не потен-
потенциалы. Это пример, иллюстрирующий правильность приведенного утверждения.
Предоставляем самому читателю прямой подстановкой показать что если найдено
решение уравнения Шредингера
ih^ = H% E6.26)
где Н—гамильтониан E5.3), то решение Vp' уравнения Шредингера
Й^- = Я'1|)', E6.26')
где Н' отличается от Н заменой А и V на А' и V по формулам E6.24) и E6.25),
будет получаться из ij> по формуле
так как f—действительная функция, то
|4>'|* = 11>1в. E6-28)
A' = ^-M)'Vi|j'*- г|)'*Ут|/}— -- A'|i|)'|2 = -s^-WVi]J* —i|)*Vi|)} — А | ф |2=Т E6.29)
^[X LIC ^Ll IXC
te -
(так как Уф' = УЧ)е"с ' ■+— Vf-\|/).
То есть вероятность местонахождения частицы и плотность тска остаются неиз-
неизменными при преобразовании потенциалов E6.24) и E6.25), оставляющем неизменным
электромагнитное поле. Подобным же образом и все другие физические величины
остаются теми же.
Это свойство уравнения Шредингера называется электромагнитной или калибро-
калиброванной инвариантностью 1.
§ 57. Движение заряженной свободной частицы
в однородном магнитном поле
Направим ось OZ по направлению магнитного поля. Тогда компоненты
поля будут тх=тч ^ о, тг = т-
Вектор-потенциал А возьмем в виде
Ax=-3W-y, Ay = Az = 0. E7.1)
Тогда из уравнения E7.2) получается как раз нужное поле (чем и оправ-
оправдывается выбор А):
■Жх = 0, ^у = 0, тг^-Ц* = де. E7.2)
1 Этим же свойством обладают классические уравнения Гамильтона (см. допол-
дополнение VI).
13 Д. И. Блохшщеп . *"°

Других полей мы не предполагаем (£/=0, V = 0), поэтому на основании
E6.3) уравнение Шредингера для стационарных состояний напишется
в виде
В этом уравнении мы можем сразу разделить переменные, если положим
i|)(*, у, г) = е*(а*+Э*) ф( у), E7.4)
где а и C—некоторые постоянные.
Подставляя E7.4) в E7.3), находим уравнение для функции ф (у):
eha _ , е2сй?2 , Г и ft2ct2 А2В2П
^+1Е1^}<?- E7-5)
Это последнее уравнение легко приводится к уравнению для осцилля-
осциллятора. Для этого положим:
E7.6')
E7.6»)
Тогда после простых преобразований получаем вместо предыдущего урав-
уравнения новое уравнение
-£$ + ^"ф = «Р- ' E7-7)
Это и есть уравнение для осциллятора массы fx, частоты св0 [см. D7.3)].
Отсюда на основании известных решений для осциллятора мы можем
сразу написать нужные нам решения:
V^') = '~JH.{t), E7-8)
е=/шо( п + у)' п=0, 1, 2 E7.10)
Стало быть, собственные функции частицы в поле будут
%uxp(*, У, z) = е1<««4*г)е 2ЯП(|), E7.11)
а квантовые уровни определятся формулой
!JE. F7.12,
где /г = 0, 1, 2, ... .
Последний член есть не что иное, как кинетическая энергия движе-
движения по оси OZ (вдоль поля), первая же часть
E7.12')
представляет собой энергию движения в плоскости х, у, перпендикуляр-
перпендикулярной к магнитному полю. Эту энергию можно записать в виде потенци-
потенциальной энергии тока, обладающего магнитным моментом Щ, в магнитном
194

поле Ш @, 0, <$?). Именно, положим
е„@) = - фт) = - mzw =
= МвBп + 1)сШ. E7.13)
Из этой формулы мы видим, что проекция магнитного момента $Щг на
направление магнитного поля есть целое кратное от магнетона Бора £ЩВ.
Полученное квантование энергии свободной частицы, движущейся в ма-
магнитном поле, является важным следствием квантовой механики, так как
приводит к наличию диамагнетизма у электронного газа, в то время как
по классической теории диамагнитные свойства у электронного газа
должны отсутствовать1.
Собственные функции {Ы. 11) вполне соответствуют классическому
закону движения в магнитном поле. Именно, по классической теории
мы имеем круговое движение в плоскости х, у с частотой ю0 (как раз
эта часть энергии квантуется) и свободное движение по оси OZ2.
Действительно, волновая функция E7.11) означает, что обобщенный
импульс по оси ОХ равен px = ha и по оси OZ равен р° = Л|3. По оси OY
мы имеем гармоническое движение с частотой ю0 около положения равно-
весия уо~—-ф-• Согласно классической механике импульс по оси ОХ
также постоянен, и это не противоречит тому, что по оси ОХ также
происходит гармоническое колебание около некоторого положения равно-
равновесия х0, так как px = \ivx~\—Ах, а не \ivxl
Обобщенный импульс рх определяет положение равновесия у0, и поэ-
поэтому от него не зависит энергия движения £П(Р).
То обстоятельство, что по квантово-механическому решению как будто
получается гармоническое движение только по оси OY, в то время как
классическое круговое движение означает гармоническое колебание
и по оси Y, и по оси ОХ ( с разностью фаз ~ j, связано с тем,
что волновая функция г|зпар (х, у, z) E7.11) описывает состояние с неопре-
неопределенным положением равновесия х0 колебаний по оси ОХ.
Так как энергия Еп($) не зависит от а, то мы имеем бесконечно
высокое вырождение, соответствующее различным возможным положе-
положениям точки равновесия х0. Поэтому энергии £П(Р) принадлежит не только
найденное нами решение г|?«ар, но и все волновые функции вида
Ц*»(х, у, г)=
где с (а) —произвольная функция а.
В частности, можно подобрать с (а) так, чтобы решение г}зпР соответ-
соответствовало определенному положению точки равновесия по оси ОХ(х0).
1 См., например, К. Бете и А. Зоммерфельд, Электронная теория метал-
металлов, ОНТИ, 1938; Ф. Блох, Молекулярная теория магнетизма, ДНТВУ, 1934, где изло-
изложена теория Л. Д. Ландау.
2 См. дополнение X, где приведен соответствующий расчет по классической
механике.

= ГЛАВЛ Х- -=
СОБСТВЕННЫЙ МЕХАНИЧЕСКИЙ И МАГНИТНЫЙ
МОМЕНТЫ ЭЛЕКТРОНА (СПИН)
§ 58. Экспериментальные доказательства существова-
существования спина электрона
Изложенная в предыдущем теория движения заряженной частицы
в магнитном поле является далеко не полной. Дело в том, что помимо меха-
механического и магнитного моментов, создаваемых движением центра тяжести
электрона, электрону необходимо приписать собственный механический
и магнитный моменты, как если бы он являлся не материальной точкой,
а вращающимся заряженным волчком1. Этот механический и магнитный
моменты называют спиновьши (в отличие от механического и магнитного
моментов, создаваемых движением центра тяжести электрона, которые
мы будем теперь называть орбитальными). Само явление называют спином
электрона2.
Мы изложим кратко те опытные факты, из которых следует существо-
существование спина электрона3. Одно из наиболее простых и прямых указаний
на существование спина электрона получается из опытов Штерна и Герлаха
по пространственному квантованию (§ 3). Штерн и Герлах наблюдали рас-
расщепление надвое пучка атомов водорода, заведомо находящихся в s-состоя-
нии.В этом состоянии механический,а вместе с ним и магнитный орбитальный
моменты равны нулю. Между тем факт отклонения пучка атомов в магнитном
поле показывает,что эти атомы обладают в s-состоянии магнитным моментом.
Расщепление только на два пучка показывает, что проекция этого магнит-
магнитного момента может принимать только два значения. Результаты измере-
измерений показывают, что абсолютная величина этого момента равна магнетону
Бора $ЩВ. Таким образом, в s-состоянии атома, имеющего лишь один элек-
электрон, существует магнитный момент $щ, проекция которого на магнитное
поле принимает лишь два значения ±ЗЛв-
Существование этого магнитного момента в состоянии, где орбиталь-
орбитальный момент заведомо отсутствует, можно объяснить, если предположить,
что этот магнитный момент свойственен самому электрону. Это предположе-
предположение опирается еще и на следующие важные обстоятельства. Спектральные
линии даже тех атомов, которые имеют один оптический электрон, оказы-
1 Теория вращающегося электрона, в рамках классической теории, впервые
была развита Я. И. Френкелем; см. Я- И. Френкель, Электродинамика, т. I,
ОНТИ, 1934.
2 От английского глагола to spin, означающего «вертеть» (веретено).
3 Подробное изложение этих фактов читатель найдет в книге Б. А. Введен-
Введенский и Г. С. Л а и д с б е р г, Введение в современную теорию магнетизма, ГИЗ,
1929.
196

ваются более сложными, нежели это следует из изложенной выше теории
движения электрона в поле центральных сил. Так, например, в атоме Na
вместо одной спектральной линии (а) (рис. 44), отвечающей переходу 2р—>
Is, наблюдаются две очень близкие линии (Ь, с), исходящие из двух близ-
близких уровней. Это — так называемый дублет Na (линии 5895,93А и 5889,95/'.).
Таким образом, р-терм Na следует считать состоящим из двух близких
уровней. Подобная структура спектральных линий наблюдается и в дру-
»{■■
ft.
Рис. 44. Мультиплетная структура
уровня 2 р:
Переходы (Ь) и (с) образуют две близкие
линии (дублет)
гих атомах и носит название мультиплет-
ной структуры спектров. Т-Р
Теория движения электрона в поле
центральных сил показывает, что 2/?-терм
(п=2, / = 1) состоит из трех сливающихся
уровней (т=0, ±1), но вовсе не из двух
близких. Расщепление трех уровней мо-
может получиться лишь во внешнем поле,
а дублет (/>, с) наблюдается в отсутствии /5
поля.
Предположение, что электрон име-
имеет собственный магнитный момент Щ\в,
позволяет сразу объяснить происхож-
происхождение двойного расщепления термов
одновалентных атомов. В атоме, во всех состояниях (р, d,...), кроме
состояния s, в котором орбитальный момент равен нулю, существуют элек-
электрические токи (ср. § 53). Эти токи создают внутреннее магнитное поле.
В зависимости от ориентации спинового магнитного момента электрона
(вдоль этого поля или против него) получается два состояния
с несколько различной энергией, так что каждый из уровней н-\
р, d,... расщепляется на два близких уровня (см. § 62).
Как мы увидим, расщепление спектральных линий атомов
в магнитном поле (эффект Зеемана, § 74) также требует предпо-
предположения о существовании спина электрона и только на его ос-
основе может быть объяснено.
Обратимся теперь к собственному механическому моменту
электрона. Обозначим его через s. Если бы проекция этого
момента sz на любое направление OZ определялась бы целым
числом постоянных Планка mji (как это имеет место для орби-
орбитального момента), то следовало бы ожидать по крайней мере
трех ориентации спина ms = 0, + 1. В самом же деле, упомяну-
упомянутый результат опыта Штерна и Герлаха, а также двойное рас-
расщепление уровней р, d, ... показывают, что возможны только
две ориентации спина электрона. Эти факты привели голланд-
голландских физиков Уленбека и Гаудсмита к предположению, что
проекция собственного механического момента электрона sz на любое
направление измеряется полуцелым числом постоянных Планка и может
принимать лишь два значения
s- = ±y- E8.1)
Это предположение Уленбек и Гаудсмит дополняют, в соответствии
с опытными данными, предположением о наличии у электрона собствен-
собственного магнитного момента Ш, проекция которого Шх на любое направ-
направление может принимать только два значения:
= ±^77" E8-2>
V
Рис. 45.
Схема
опыта
Эйнштей-
Эйнштейна и
де Гааса
197

Из E8.1) и E8.2) следует, что отношение спинового магнитного' момента
к спиновому механическому моменту равно — :
Ш = -±1 E8-3)
в то время как отношение орбитальных моментов равно — к— (см. § 55).
Существование отношения E8.3) между магнитным моментом и меха-
механическим было обнаружено еще в 1915 г. в опыте А. Эйнштейна и де
Гааса. Вкратце сущность этого опыта сводится к следующему. Ферро-
Ферромагнитный стержень / (рис. 45) подвешивается на нитях так, что может
вращаться вокруг своей оси. Если изменить направление продольного
магнитного поля i№, то изменится и направление намагничивания стержня,
т. е. его магнитный момент 2JJ. Так как магнитный момент пропорциона-
пропорционален механическому
Ж=-2-^М, E8.4)
то изменится и механический момент М электронов всего стержня1.
В результате стержень придет во вращение и будет закручивать нить.
Из этого кручения можно определить М, а вместе с тем и проверить
отношение -j-r-. Для электронов это отношение должно быть отрицатель-
отрицательным (заряд электрона равен —в). Это и получилось из опыта, показы-
показывая таким образом, что намагничивание куска ферромагнетика обусловли-
обусловливается движением электронов. Однако отношение получилось равным
не —7Г-, а . Для орбитального движения при самых общих пред-
положениях и классическая, и квантовая теории ведут к значению — —.
Поэтому результат опыта казался загадочным. Если же считать, что намаг-
намагничивание обусловлено не орбитальным движением электрона, а его спи-
ном, то отношение — должно быть равно , что и получается на
/VI [ДгС
опыте. Это предположение позволило не только объяснить результаты опыта
Эйнштейна и де Гааса, но и заложить основы современной теории ферромаг-
ферромагнетизма (см. § 126).
Заметим, что в настоящее время существование спина электрона
может рассматриваться как следствие из релятивистской теории электрона,
развитой Дираком. Однако изложение этой теории выходит за рамки
нашей книги2.
1 Заметим, что формулу E8.4) мы пишем теперь для суммарного момента всех
электронов. Поскольку она справедлива для каждого электрона стержня, то она будет
справедлива и для всей их совокупности. Подробнее об этом см. в книгах:
И. Е. Т а м м, Основы теории электричества, ОГИЗ, Гостехиздат, 1946, Б. А. Вве-
Введенский и Г. С. Ландсберг, цит. соч.
2 См П. Дирак, Основы квантовой механики, ОНТИ ГТТИ, 1937, § 72.
Дирак показал, что из релятивистского уравнения для движения электрона автоматически
вытекает, что электрон должен обладать магнитным моментом E7.2) и механическим
моментом E7.1) и таким образом дал теоретическое обоснование гипотезе Уленбека
и Гаудсмита.
198

§ 59. Оператор спина электрона
Обратимся теперь к математической формулировке гипотезы Улен-
бека и Гаудсмита.
В соответствии с общими принципами квантовой механики собствен-
собственный механический момент электрона (для краткости будем просто гово-
говорить спин электрона) должен изображаться линейным самосопряженным
оператором. Обозначим операторы проекций спина на оси координат
через sx, S , sz. Чтобы определить вид этих операторов, мы потребуем,
чтобы эти операторы подчинялись тем же правилам перестановки, что и
компоненты орбитального момента Мх, Му, Мг. Тогда, заменяя в B5.5)
М на s , получаем1:
1
E9.1)
Проекция спина на любое направление (по исходной гипотезе) может при-
принимать два значения." ± ~ . Поэтому операторы sx, sy, si должны изобра-
изображаться двухрядными матрицами, так как двухрядная матрица, будучи
приведена к диагональному виду, содержит лишь два диагональных
члена и, стало быть, имеет только два собственных значения. Полагая
h
h
E9.2)
мы можем сказать, что операторы ах, оу, oz (спиновые матрицы) должны
быть двухрядными матрицами вида
°У =
Ь,, 6,
ь ь
С-.-, с.
с.Л
E9-3)
имеющими собственные значения
ft2
щая на —г-, получаем:
a*av
1. Подставляя E9.2) в E9.1) и сокра-
E9.4)
E9.4')
E9.4")
ауаг — ozoy = 2iox,
Ввиду того, что собственные значения ах, ау, az равны ± 1, то собствен-
собственные значения операторов ol, а„, а\ суть +1. Стало быть, в своем собст-
собственном представлении эти последние матрицы должны иметь вид
E9.5)
E9.6)
1
0
0
1
g.2
' У
1
0
0
1
_,2
' Z
1
0
0
1
т. е. они являются единичными матрицами б;
1 О
О
6 =
«твенно
1 Опираясь на теорию групп, можно доказать, что правила E9.1) являются един-
:но возможными. См., например, Раи И, Handb. d, Phys., т. XIV, I.
199

Единичная матрица остается единичной во всяком представлении (см. § 40).
Поэтому матрицы ст|, ст§, ol имеют вид E9.5) во всяком возможном пред-
представлении. Рассмотрим теперь комбинацию
2' (о*о-у -Ь оувх) = 2iaxay -\- oy2iox.
На основании E9.4) это можно переписать в виде
но a?j = Ь есть единичная матрица, поэтому
OyOi = •
Следовательно,
E9.7)
т. е. матрицы ах, ау, как говорят, антикоммутируют.
Комбинируя E9.7) с E9.4) и применяя циклическую перестановку ах,
ау, а,, находим:
y v
E9.8)
Найдем теперь явный вид матриц ах, a az. Пусть, скажем, матрица а.
приведена к диагональному виду. Так как ее собственные значения равны
± 1, то диагональный вид а. будет
1 0
E9.9)
Можно показать, что в этом же представлении остальные две матрицы ах,
с,, будут иметь вид
0 И
1 0 '
0у =
0 -i
1 0
E9.9')
Для доказательства образуем произведения ozox и oxoz. По правилу
матричного умножения (§ 40), имеем:
1
0
«п
«21
0
-]
«12
«22
«Л
«2]
1 .
0
«12
«22
0
J
'11
«11 -«12
«21 «22
На основании E9.8) имеем:
— Оо
или
т. е.
200
«11— «]Ц «]2 — «]2' '«21 — ""«21' «22 — «22'
a}J~0,

Поэтому матрица о^. имеет вид
О а
12
Образуем теперь а£:
О ап
ап О
21 О
О а.2
«21 О
E9.10)
0
Сравнивая с E9.5), получаем, что а12а,,= 1. Матрица должна быть само-
самосопряженной, т. е. ап = а*г Стало быть, |а]2|2=1.
Отсюда получаем:
О eia
°~= -ia 0 ' E9-П)
где а — действительное число.
Подобным же образом находим, что
0 е*В
е-*Р 0
E9.11')
Перемножая теперь стс на а , а потом ау на стх и пользуясь E9.8), полу-
получим:
откуда
о
/>-i(a-f
О
0
т. е. а— Р = -у . Таким образом, все соотношения удовлетворены при про-
произвольном значении а. Поэтому без всяких ограничений мы можем взять
а = 0, Р=—о- - Подставляя эти значения в E9.11) и E9.1Г), получаем
E9.9').
Согласно E9.2) из E9.9) и E9.9') получаем матрицы операторов sx, s , sz
в представлении, в котором sz диагоналей (жг-представление):
о 4
о
0 -i
. h
. h
0
А о
о --
E9.12)
Заметим, что значки 1 и 2, нумерующие матричные элементы матриц a
и s, приобретают теперь (поскольку выбрано представление) определенное
значение: значок 1 относится к первому собственному значению s. ( +"о"
а 2 — ко второму ( — ~ j .
Образуем теперь оператор квадрата спина электрона. Из E9.12)
имеем:
1 0
0 1
E9.13)
Вводя квантовые числа ms и /s, определяющие значение проекции
спина на любое направление OZ и его квадрат соответственно, мы можем
написать формулы для квантования спина в полной аналогии с форму-
201

лами E1.9,10) для орбитального момента:
s2 = /i2/s(/s+I), /S = -7T' E9.14)
sz = hms, ms=±Y- E9.15)
§ 60. Спиновые функции
Мы видим, что в квантовой механике состояние спина должно харак-
характеризоваться двумя величинами", абсолютным значением |s| (или s2)
и проекцией спина на какое-либо направление sz. Первая величина (s2)
предполагается для всех электронов одинаковой, поэтому речь может
идти лишь об одной переменной s2. Таким образом, наряду с тремя пере-
переменными, определяющими движение центра тяжести электрона (х, у, г
или рх, р , рг и у. п.), появляется еще одна переменная sz, определяю-
определяющая спин электрона. Поэтому можно сказать, что электрон имеет четыре
степени свободы1.
Соответственно этому волновую функцию if, определяющую состоя-
состояние электрона, следует считать функцией четырех переменных: три отно-
относятся к центру тяжести электрона, а четвертая —к спину (sz). Напри-
Например, в координатном представлении для электрона следует писать;
if = if (х, У, z> sz, t). F0.1)
Так как спиновая переменная имеет только два значения ( ±-о
то можно сказать, что вместо одной функции мы получаем две:
У, 2, + |, f), F0.2)
1>а-!>(*, у, г, -4* ')• F0-2>)
Эти функции мы будем иногда писать в виде матрицы с одним столб-
столбцом
Л о ' (ба3)
я сопряженную функцию —в виде матрицы с одной строкой
F0.3')
Такой способ написания позволит воспользоваться правилами §41 D1.12)-
Ясно, что волновые функции i]^ и т]J будут только в том случае раз-
различны, если существует реальная связь между спином и движением
центра тяжести. Такая связь существует и представляет собой взаимодей-
1 Спиновые переменные sx, sy, sz отличаются от всех известных нам квантовых
величин тем, что они принимают лишь два значения. Это связано с предположением
о строго определенном значении полного момента электрона (s2).
Если бы считали s2 переменными, то мы получили бы не одну, а две степени сво-
свободы, как и должно быть для волчка. Поэтому можно думать, что рассматриваемый
в современной физике спин электрона представляет лишь одно из возможных состояний
вращения электрона (другие значения s2 могут, например, требовать большой энергии
вращения). Этот вопрос следует пока считать открытым. В особенности интересен этот
вопрос по отношению к мезонам, для которых наблюдается целый «спектр» масс.
202

ствие магнитного момента спина с магнитным полем токов, создаваемых
движением центра тяжести заряженного электрона. Это взаимодействие
обусловливает мультиплетную структуру спектров (см. § 58). Поэтому,
если мы игнорируем мультиплетную структуру спектров, то мы можем
вообще пренебречь взаимодействием между спином и орбитальным движе-
движением. В этом приближении
i]^ (x, у, z, £) = т]J(л:, г/, z, t) = i]p(x, у, z, t). F0.4]
Однако, чтобы и в этом случае отметить, что речь идет о частице, обла
дающей спином, пишут функцию F0.1) в виде, соответствующем разделе
ншо переменных:
ty(x, у, z, sz, t) = ty(x, у, z, t)-Sa(sz), F0.5
где через Sa (s2) обозначена спиновая функция. По существу это просто]
значок, указывающий состояние спина частицы.
Значение этого «значка», или иначе, «спиновой функции» таково
индекс а принимает два значения, которые обычно полагают равным.
+ V2 и —1/2 (вместо 1 и 2). Первое значение +1/2 (или 1) означае
что проекция спина на некоторое избранное направление OZ равна + --
Второе значение индекса а означает состояние спина с другим возмож
h
ным значением проекции спина на это же направление, именно — -н-
«Аргумент» sz «функции» Sa рассматривают как независимую переменнун
могущую принимать два значения:^ - -. Тогда
^0, FО.(
так как по смыслу значка в состоянии а= +-н-> sz=+y и в этоМ и
состоянии не может быть sz — —к , поэтому соответствующая функщ
равна нулю. Подобным же образом
= 1. FО.€
Запись же в виде F0.1) и, как частный случай, в отсутствии спи
и орбитального движения, в виде F0.5) позволяет рассматривать спин
как динамическую переменную, подобную любой другой механическ
величине.
Введенные «волновые» функции спина Sa (sz) обладают свойством о pi
тональности и нормировки. Чтобы в этом убедиться, возьмем произ1
дение
где S* означает, как всегда, функцию, сопряженную с S, а а, р = + -
Просуммируем это произведение по всем возможным значениям спиног
переменной sz ( таких значений только два: ± у) • Тогда непосред
венно из F0.6) и F0.6') (имея в виду, что S* — S) следует, что
,) = 6a0. FС

Функция Sa(sz) может быть записана и в матричной форме F0.3). Именно,
F0.8)
F0.8')
Вычислим теперь результат действия любого спинового оператора типа
U.
F0.9)
]
0
]
0
0
0
0
0
S±i/t =
0
0
0
0
0
]
0
на волновую функцию. Значки 1, 2, если оператор L взят в «я2»-пред-
ставлении, означают номера собственных значений sz ( ± у ) • Согласно
формуле C9.5), определяющей действие оператора, данного в матричной
форме, на волновую функцию, мы будем иметь, что оператор L образует
из функции lF(i|3j, ijJ) новую функцию Ф(ф], ф2) по правилу
Ф1 = 1пг|I f LI2\jJ, F0.10)
Ф2 == L21\p1 I-i-22ijJ. F0.10')
Отличие F0.10) от C9.5) заключается лишь в том, что в F0.10) мы имеем
двузарядные матрицы и соответственно функцию из двух компонент,
а в C9.5) мы разумели матрицу с неограниченным числом элементов Lmn
и функцию \!р с бесконечным числом компонент сп(с{,
П ¥ б 603
).
р п( 2 )
Представляя ¥ в виде матрицы (столбца) F0.3), мы можем записать
два уравнения F0.10) и F0.10') в виде одного матричного:
Ф = /Л' F0.11)
[см. D0,14)|. В самом деле, F0.11) в развернутом виде означает
U
U, L,
F0.11')
Ф, 0
ф2 0
что совпадает с F0.10) и F0.10'). В дальнейшем под символом типа Z/F,
если взят оператор, зависящий от спина, мы будем разуметь именно
такого рода произведения, которые в сущности представляют два уравне-
уравнения F0.10, 10') в виде одного матричного.
Среднее значение любого спинового оператора L в состоянии ф,,
г|э2 согласно общей формуле D1.2) есть
L(x, у, z, t) = ty\Llity1Jr\p*L1<ityi-\-ty*L<il\p1-\-ty*LM'\pi. F0.12)
Так как функции ij), и i|J зависят еще и от координат центра тяжести
электрона, то мы написали L(x, у, z, t), имея в виду, что получающееся
по F0.12) среднее есть среднее от L при заданном положении центра
тяжести электрона. Среднее в состоянии г|?3, i|J при любом положении
электрона получится по формуле
L(/)= [1(х, у, г, l)dxdydz.
F0.13)
Формулы F0.12) и F0.13) с помощью представления ¥ в виде матрицы
с одним столбцом могут быть записаны в виде
L(x, у, z, t)^
F0.12')
F0.13')
204

В частности,
ох(х, у, z,
Подобным же образом
аи(х, у, z, t)^
~C!Z(X, у, Z, 0 =
*
0 0
i.1
4-
*A
0
0 1
1 0
1 -
>2*
ipj С
)
гра О
0
F0.14)
F0.14')
F0.14")
§ 61. Уравнение Паули
Рассмотрим движение электрона в электромагнитном поле, учитывая
наличие спина. Согласно основной гипотезе (§ 58) электрон обладает
магнитным моментом
e
(вы;
Благодаря наличию этого момента электрон в магнитном поле (S/в
<М'у, e%?z) приобретает добавочную потенциальную энергию, равную энер-
энергии магнитного диполя в поле
Оператор этой энергии, согласно F.1), есть
F1-2)
F1-3)
где ст— вектор-оператор с компонентами стх, а аг E9.9) и E9.9'). Поэтому
гамильтониан B7.7) для движения заряженной частицы в электромагнит-
электромагнитном поле при учете спина должен быть пополнен добавочным членом F1.3)
так, что он будет равен
Н
2ц
(мы полагаем заряд электрона равным —е).
Уравнение Шредингера для волновой функции XV1
будет иметь вид:
F1.4)
j, гр2) теперь
¥. F1.5)
Это уравнение носит название уравнения Паули. Заметим, что под W
мы разумеем столбец F0.3); поэтому в F1.5) записано в сущности два
уравнения для двух функций ^1 и ^2 в виде одного матричного.
Определим теперь плотность тока. Для этого запишем F1.5) в виде
где через Но обозначены члены, не содержащие операторов ст. Напишем
уравнение для сопряженной функции W*, которую мы будем мыслить

в виде строки F0.3')
Символ ( )+ означает, что в соответствующей матрице столбцы и строки
переставлены и элементы взяты сопряженными.
Умножая теперь F1.6) на W* слева, а F1.6') на Y справа и вычитая
одно уравнение из другого, мы получаем:
цг JL (ifr-гр) = хТ (Ядг) _ {тхр*} W + ~ {¥+ (а^) У - (Cafi) У)* У]. F1.7)
Согласно D0.15) имеем
((ffdi) ЧУ = У* (ff+di) F1.8)
в силу самосопряженности оператора а* = а. Поэтому член в фигурных
скобках равен нулю. Остальные, не содержащие операторов а, после
вычислений, совершенно аналогичных приведенным в § 29 при получении
формулы для плотности тока, дают1
lh ^ A>Г1>1 + 1»Ч) = -1~ div {^Ь - ^г|)Г + ^*V% - i|,2V^} -
_^div[A(^1>1 + ^%)]. F1.9)
Переписывая это уравнение в форме уравнения непрерывности для
плотности вероятности w и плотности потока частиц J, мы находим:
w(x, у, г, 0 = 1>i*1>1 + 1>M>8. F1.10)
J = ^r[(^^-^^1) + (^V^-^V^)] -^А «^ +'ф2Ч2), FЫ1)
или
w(x, у, z, t) = y*y, r=-'-[¥V+«F--Y+V¥] -AV*Y. F1.12)
Эти формулы показывают, что вероятность местонахождения электрона
и плотность токов аддитивно слагаются из двух частей, каждая из кото-
которых относится к электронам с одной определенной ориентацией спина.
Формула для нормировки вероятности имеет вид
\ z=l или ^ W*W dx dy dz = 1. F1.13)
Величины
wx(x, у, z, /) = гр*грг, wz(x, у, г, t) = гр*гр2 F1.14)
суть плотности вероятности найти электрон в точке х, у, г в момент f
cs,= + 2 или sz= —у соответственно. $
Величины
тг = \ -ф*я^х dx dy dz,)
i FЫ5)
Щ = \ ^**2d^ dydz)
1 Пользуясь матричной записью, мы все время оперируем с четырьмя функциями
Ф*, ty%, Фь ^'г сразу. Рекомендуем читателю, впервые знакомящемуся с матричными
методами, иаписать уравнения F1.6) и F1.6') в развернутом виде (четыре уравнения)
и путем умножения первых двух на г|>| и ф*, а двух вторых на ^ и г|J получить
тот же результат.
206

суть вероятности найти электрон со спином sz= -\--~- или со спином
h n
sz = —g" соответственно. Средняя плотность электрических зарядов Qe
и средняя плотность электрического тока Je согласно F1.12) будут равны
е, = - ew*w,
jC = -^i[4r+V¥~-¥V¥+] + — A(Y+Y), F1.16)
Qe и Je не описывают полностью всех источников электромагнитного поля
в случае'электрона. Нужно учесть еще магнитный момент электрона F1.1),
создающий магнитное поле. Из F1.1) и общей формулы E9.12) получаем
выражение для средней плотности магнитного момента (намагничивания I):
T(x,y,z,t)=-^-(WoW). F1.17)
Согласно уравнению Максвелла для магнитного поля имеем уравнения:
rotj# = -^Je, divB = 0, в = ^ + 4я1. F1.18)
Из этих уравнений и определится магнитное поле, создаваемое электро-
—У —V
ном, находящимся в состоянии W, если под Je и I разуметь F1.16)
и F1.17). Вводя в первое уравнение F1.18) вместо <g£ индукцию В,
получим:
{J + tTj F1.18')
rotB {
Таким образом, вместо намагничения I можно рассматривать ток, экви-
эквивалентный этому намагничению, именно:
Js = crotl= _±jLrot(¥W), divJs = 0. F1.19)
Полный электрический ток, соответствующий и орбитальному, и спино-
спиновому движению, есть
j; = -^.'[qr+vY - V¥+¥] +— А (¥+¥) - -J- rot (IW). F1.20)
Для вычисления компонент спинового тока Js следует воспользоваться
формулами F0.14) и F0.14').
§ 62. Расщепление спектральных линий в магнитном поле
Рассмотрим атом с одним валентным электроном, находящийся во
внешнем однородном магнитном поле. Электрон атома будет подвергаться
одновременно действию магнитного поля и электрического поля ядра
и внутренних электронов. Это электрическое поле будем считать централь-
центральным и потенциальную энергию электрона в нем обозначим через U (г).
Магнитное поле направим по оси OZ и возьмем векторный потен-
потенциал А в виде
Ах=-Цу, Ау=+^х, 4 = 0. F2.1)
Магнитное поле по формуле gffi = rot А получается правильное:
<$?« = $?„ = 0, &ег~&е. F2.2)
207

Подставляя это значение А в гамильтониан F1.4), получаем урав-
уравнение Паули:
'^ попр i т 1 / \ 1ТГ trie _
F2.3)
Членом, содержащим (g£% при малых полях, мы можем пренебречь1.
Далее, оператор
\v дх ду J dtp г K '
есть оператор компоненты орбитального момента. Обозначая еще через
tf°=-£v'+tf(r) F2.5)
гамильтониан электрона в отсутствии магнитного поля, мы получаем:
ih -g- = #0VF f -|— {Mz + /ш,) 4х. F2.6)
Из этого уравнения следует, что, поскольку мы пренебрегаем ,J^?2,
постольку член, выражающий действие магнитного поля, может рассма-
рассматриваться как потенциальная энергия AU магнитного диполя с моментом
— 4— (М~\~ ha Л в магнитном поле Ш"-
2[icv ' z/
AU = - {М?Ш) = -^ (Л12 + Act,). F2.7)
Мы будем искать стационарные состояния. Для этого представим
волновую, функцию в виде
pi
F2.8)
. Et
где Е— энергия стационарного состояния. Подставляя ее в F2.6), найдем-.
H°W + ^-(Mz + haz)W^EW. F2.6')
Возьмем представление, в котором матрица ст2 диагональна («s^-представ-
ление); тогда
a.V= J ? *i = +*i F2.9)
и, стало быть, уравнение F2.6') распадается на два уравнения для г]^
и ipg порознь:
Я0^1] "h "о~~^ (^г+ A) ^i = Etyi, F2.10)
= Е%. F2.10')
1 Как будет показано в § 129, пренебрегаемый член определяет слабые диамагнит-
диамагнитные явления.
208

Решение этих уравнений получается тотчас же, если заметить, что
в отсутствии магнитного поля мы имеем два решения:
( ) = ££* для спина sz=-4, F2.1Г)
причем
4W = ^ni(r)-rim@, Ф). F2.12)
Так как Mzt|)nim = hmtynlm, то эти же решения суть решения уравнений
F2.10) и F2.10'), но только принадлежат другим собственным значениям.
Подставляя F2.11) и F2.1Г) в F2.10) и F2.10'), получаем два решения:
n+l), s2=+A, F2.13)
^п-1), sz=-4« F2.13')
т. е. волновые функции (поскольку пренебрегли членом с J£?2) не изме-
изменяются: атом не деформируется магнитным полем. Энергия же начинает
зависеть от ориентации момента относительно поля, т. е. от магнитного
числа т: совпадавшие в отсутствии магнитного поля уровни теперь рас-
расщепляются (снимается «т»-вырождение).
На рис. 46 дано расщепление s- и р-термов. Расщепление р-терма
получается из F2.13) и F2.13'), если перебрать возможные значения т
при Z—1 (т. е. т=±1,0). Расщепление s-терма (/ = 0, т=0) полу-
получается лишь благодаря спину электрона. Это — важный результат теории
спина: как раз это расщепление наблюдали Штерн и Герлах в своих
опытах.
Благодаря расщеплению уровней увеличивается число возможных
переходов, а вместе с тем и число наблюдаемых спектральных линий.
Это явление носит название простого эффекта Зеемана (в отличие от
сложного, см. § 74). Как будет показано в § 90Б, при оптических пере-
переходах число т может изменяться только на ^ 1 или 0. Кроме того,
спиновый магнитный момент очень слабо взаимодействует с полем свето-
световой волны. Поэтому идут в расчет лишь те переходы, при которых спин
не меняется. Эти переходы изображены на рис. 46 линиями (а, Ь, с)
и (а', Ь', с'). Частоты этих переходов вычисляются по формуле
ton'i'm', n"i"m" = 1 = 1 Ь ^- (т - т"). F2.14)
Обозначая частоты в отсутствии поля через ю0, а при наличии поля
через со, мы получаем: »,
сй = ю° + -|^-(т'-т"). F2.15)
Так как т! -~т" — ±_ 1, 0, то имеем три частоты: одну неизмененную
и две —смещенные на ± -=—.
Это расщепление на три линии [нормальный триплет Зеемана) как
раз таково, как оно получается из классической теории эффекта Зеемана.
В классической теории, как известно1, явление Зеемана объясняется
1 См. Г. С Ландсберг, Оптика, Гостехиздат, 1940; Э. В. Ш польский,
Атомная физика, Гостехиздат, 1944; Г. А. Лоренц, Теория электронов, ГТТИ, 1934.
14 Д. И. Блохинцев 209

прецессией орбиты в магнитном поле с частотой, равной частоте Лармора
Ol = -r—• Квантовая формула F2.15) не содержит постоянной Планка/г,
и поэтому результат должен совпадать с классическим (он не может
измениться, если положить h = 0). Это совпадение имеет место.
Покажем, что и в квантовой механике явление Зеемана обусловлено
прецессионным движением момента импульса вокруг направления магнит-
гР.
т-0-
без поля [н-оу
с'
■ 171=0
V г
В none(h*Q)
Рис. 46. Расщепление s- и р-термов в сильном магнитном поле (с учетом
спина)
ного поля. Вычислим для этого производные по времени от орбитального
и спинового моментов. По общей формуле C1.10) имеем:
Я,Ж1, ^ = [H,MZ], F2.16)
dM^[H,Mx],wdp
dt
dsr
dsz
Подставляя сюда^гамильтониан из F2.6)
И = Н° + 4г— (Mz + ha.) = Н° + OjMz + 2OlS,
F2.17)
F2.18)
и замечая.^что"?//0 коммутирует cMhs, а М и s коммутируют между
собою (так как М действует на функции от 6, ф, a s— на функции от
sx, sy, sz), мы находим:
*£ = %
z
dt
Пользуясь B5.5) и E9.1), получаем:
dMx
dt
dsx
= -OLMv, d-§i=->r0LMx,
ЖУ dt
dt
dt
= 0.
F2.19)
F2.20)
Переходя от этих операторных формул к средним значениям и имея
в виду, что OL есть просто число, мы находим:
ds=c
~df
'«' dt
dsv
У dt
dt
dt
F2.21)
F2.22)
210

Из этих уравнений следует, что проекции орбитального и спинового
момента на направление магнитного поля являются, каждая порознь,
интегралом движения. Компонента же орбитального момента, перпенди-
перпендикулярная магнитному полю, вращается с частотой Лармора 0L. Такая же
компонента спинового момента вращается с удвоенной частотой 20ь
[в силу аномального отношения магнитного момента к механическому,
см. F1.1)]. Действительно, из F2.21) имеем:
^* - -О, *EbL- -ОШ М= -^* F2 23)
Отсюда
Mx = A sin @Lt + a), Mv = - A cos @,} f a), Mz = const. F2.23')
Подобным же образом из F1.22) получаем:
~ + $), sy= -BcosB0Li + $), sz = const. F2.24)
5) 63. Движение спина в переменном магнитном поле
В переменном магнитном поле собственный механический момент
частицы не будет интегралом движения, и потому возможны переходы
У///////////Л
р
У/////////////Л\\т Y////////////A
S S
Рис. 47. Схема опыта по измерению магнитных моментов атом-
атомных ядер (Раби):
S — источник пучка частиц (щель), А — первое пространство с неод-
неоднородным постоянным магнитным полем, С — второе, В — простран-
пространство с переменным полем Р — приемник частиц
из одного квантового состояния в другое. Мы рассмотрим в этом пара-
параграфе тот случай движения спина частицы в переменном поле, теория
которого находит важное применение для измерения магнитных моментов
атомных ядер по методу Раби. Схема опыта Раби изображена на рис. 47.
Магниты А и С создают неоднородное постоянное поле, так же как
и в опыте Штерна и Герлаха, однако направления градиентов полей
в магнитах А и С противоположны. Проходя через неоднородное поле
в А, частица отклоняется таким образом, что не может попасть в прием-
приемник Р. Это отклонение выправляется полем в С, которое отклоняет частицу
в противоположном направлении. В результате частица достигает прием-
приемника Р так, как если бы она двигалась попросту по прямой линии (как
в отсутствии полей).
Далее в небольшом пространстве В, расположенном между А и С„
приложено дополнительное переменное поле $£v способное опрокинуть,
магнитный момент частицы. Если магнитный момент частицы при про-
прохождении этого поля опрокинется, то отклонение поля в С уже не будет
компенсировать отклонения, вызванного полем в А, и «опрокинутые»
частицы не будут попадать в приемник Р.
Частоту переменного добавочного поля со и его напряженность J£?,t
подбирают так, чтобы вероятность опрокидывания момента была макси-
14* 21Ь

мальной, и следовательно, поток частиц в приемник Р минимальный. Как
будет показано ниже, зная со и £%?v соответствующие максимуму вероят-
вероятности опрокидывания, можно определить магнитный момент частицы. Этот
метод измерения магнитного момента имеет очень высокую точность. Так
как нас будет интересовать исключительно движение спина (движение
центра тяжести частицы может быть описано методами классической меха-
механики 1), то нам достаточно написать уравнение Шредингера для спиновой
функции S F1.5). Это уравнение имеет вид2:
Простоты ради, мы будэм считать, что частица обладает спином /г/2.
Тогда магнитный момент ЗК изобразится двухрядной матрицей:
!« = №. aJtv = |«V 2Н« = !«Ъ. F3.2)
где ах, ац, а7 — матрицы Паули E9.9,9'), a jj, есть абсолютное значение
проекции магнитного момента на какое-либо направление. Для ядерных
частиц, даже для простейших нуклонов — протона и нейтрона, не суще-
существует столь же простого соотношения между механическим моментом S
и магнитным моментом $Щ> какое известно для электрона E8.3). Поэтому
мы будем считать jj, попросту некоторой константой, характерной для
частицы. Магнитное поле в пространстве В предположим, в соответствии
с постановкой опыта Раби, имеющим вид3
<fflx = Н1 cos at, cWy^H^inat, 3VZ = HO. F3.3)
Подставляя F3.2) и F3.3) в уравнение F3.1), пользуясь видом матриц
Паули E9.9, 9') и правилом действия этих матриц на спиновые функции,
нййдем уравнение для компонент спиновой функции S1 и S2 (первая при-
принадлежит 5Щ2= +ц, а вторая — Щх= — ц):
^ F3.4)-
^ F3.4')
Мы будем считать, что в момент вступления частицы в переменное поле
(t = 0) ее магнитный момент направлен по оси OZ, так что при t = 0
S 1 S 0
(
S1==
2
Положим
1 Это можно сделать для тяжелых частиц (ядра, атомы), но нельзя сделать для
электронов. Н. Бор показал, что методом Штерна—Герлаха вообще невозможно измерить
магнитный момент свободного электрона (см., например, Мотт и Месс и, Теория
атомных столкновений, ОНТИ, 1936, стр. 57).
2 Это уравнение не содержит оператора кинетической энергии, которая в данном
случае должна бы быть кинетической энергией собственного вращэния частицы. Однако,
поскольку 52 остается постоянным, постольку и эту энергию следует считать постоян-
постоянной. Поэтому ее можно не вводить в уравнение.
3 В действительных опытах Раби переменная составляющая магнитного поля
линейно поляризована.
Однако для вычислений удобнее взять вращающееся в плоскости (ху) поле. Резуль
таты ничем существенным не различаются.
212

Тогда уравнения F3.4, 4') можно переписать в виде:
,, F3.6)
S,. F3.6')
Дифференцируя F3.6') по времени, можно, пользуясь ,F3.6), исключить
функцию Sv Заодно выпадет и переменный коэффициент e~iat. После
несложной выкладки получим уравнение для S2:
Это уравнение решаем подстановкой: S2 = aeia(. Характеристическое урав-
уравнение для определения частоты Q будет:
^ ^) 0. F3.8)
Если положить
где 1=~2 есть проекция спина, и ввести tg9 = HjH0, то нетрудно убе-
убедиться, что для Q из F3.8) получается:
Й+ ± (l+
у т | F3.10)
Поэтому общее решение для S2 будет
В соответствии с начальными условиями нужно взять а1= — а2 =
так что
Sa@ = Ле^" sin 6*. F3.1 Г)
Амплитуда Л определится из условия S1@)==l. Подставляя F3.1 Г) в
F3.6') при t = 0, найдем Л = г'уД/б. Поэтому
Cat
'St(t) = ^£-eT sinbt. F3.12)
Вероятность найти в момент t магнитный момент Шг, равный — ц, будет:
sin2 {|-(l + 92 + 29cos6)^}T. F3.13)
Время t в опыте Раби равно времени, в течение которого частица проле-
пролетает через пространство В. Если скорость частицы есть и, а длина про-
пространства В равна /, то t = l/v.
В опыте берут q— 1, а 6^ = я/2 (чтобы получить максимум вероят-
вероятности опрокидывания Р (t)). Отсюда легко оценить, что при v Ss± 105 см/сек,
1=1 см частота переменного поля ю будет равна 10е гц.
Чтобы судить о точности этого замечательного метода, укажем, что
способом Раби были измерены магнитные моменты jj, для протона (р)
и нейтрона (п) и получены значения: цр= 2,7896 ± 0,0002, цп = 1,935 ± 0,02
(за единицу принят ядерный магнетон Бора, равный eh/2Mc, M — масса
протона. Этот магнетон в 1842 раза меньше магнитного момента электрона).
213

§ 64. Свойства полного момента импульса
—> —>
Мы видели, что и орбитальный момент М, и спиновый As представ-
представляют собой величины, принимающие лишь квантовые дискретные значения.
Рассмотрим теперь полный момент импульса, являющийся суммой орби-
орбитального и спинового моментов.
Оператор полного момента определим в виде суммы операторов орби-
орбитального момента М и s:
~ . F4.1)
y vy z = Mz+sz. F4.Г)
Покажем, что операторы компонент полного вращательного момента под-
подчиняются тем же правилам коммутации B5.5), что и компоненты орби-
орбитального момента Мх, Му, Mz. Для этого заметим, что М и s комму-
тируют, так как оператор М действует на координаты, а оператор S на
них не действует. Поэтому
JxJy - JyJx = (Мх + sx) (Му + sy) - (My + sy) (Mx + sx) =
= MxMy - MyMx + sxsy — sysx = ihMz + ihsz F4.2)
[последнее в силу B5.5) и E9.1)]. Таким образом,
F4.3)
F4.3')
F4.3")
(два последних равенства получаются из первого циклической переста-
перестановкой).
Найдем теперь оператор квадрата полного вращательного момента J2.
Имеем
Г- = (М + sJ = Ж2 + s2 + 2Ms =
^M*- + s* + 2(Mxsx + Mysy + Mzsz). ■ F4.4)
Оператор У2 коммутирует с любой проекцией У. Например, рассмо-
рассмотрим проекцию на OZ Jz = Mz-\-sz. Так как Мг коммутирует с /И2, s2
и s. с /И2, б'2, то получим:
J4Z - Л J2 - 2 (Mxsx + Mysy + Mzsz) (Mz + sz) -
Раскрывая здесь скобки, найдем:
J4. - JJ* = 2 {(MXMZ - MZMX) sx + (MyMz - MZMV) sy +
+ Mx (sxsz - szsx) + My (sysz - szsy)},
и, подставляя сюда выражение в круглых скобках из B5.5) и E9.1),
получаем окончательно:
J*JZ - УгУ2 = 2 {- ihMysx + ihMxsy + Мх ( - ihsy) + My ( + ihsx)} = 0.
Подобным же образом доказывается утверждение для остальных двух
компонент. Таким образом,
J4x-JxJ* = 0, F4.5)
У2У,-УуУ2 = 0, F4.5')
У2Уг-У2У2 = 0; F4.5")
214

эти равенства — такого же вида, как и B5.6). Отсюда следует, что опе-
оператор У2 и оператор любой проекции (но одной), например Jz, одновре-
одновременно могут быть приведены к диагональному виду, и, стало быть,
величины у2 и Jz принадлежат к числу одновременно измеримых.
Легко видеть также, что оператор У2 коммутирует с операторами Мг
и s2. Действительно, обращаясь к формуле F4.4), мы непосредственно
видим это свойство оператора у2, так как Ж2 коммутирует с Ж2, Мх,
М , Mz и sx, s ., s, и s2. Равным образом s2, являясь единичной матри-
Г 3
цей умноженной на ~^№, см. E9.13)], коммутирует с sx, sy и sz.
Поэтому
У2Ж2-Ж2У2 = 0, F4.6)
y2s2-s2y2=0. F4.6')
Следовательно, У'2, Ж2 и s2 представляют собой также одновременно изме-
измеримые величины. Из F4.4) имеем:
(Жя)=-^(У2-Ж2-я2). F4.7)
Так как (Ms) образуется из величин одновременно измеримых, то скаляр-
—> —>
ное произведение (Ms) одновременно измеримо с у2, М2 и s2.
Замечая, что
Й«) + «2 = ГЛ), __ F4.8)
мы получаем из F4.7) еще скалярное произведение (Js):
Q~s)=±(J*-M* + s*). F4.9)
Ниже мы покажем, что квадрат полного момента /2 и его проекция
Jг на любое направление квантуются аналогично орбитальному моменту,
но полуцелыми числами. Именно,
/* = А*/(/ + 1), / = |, |, |, ...; F4.10)
Jz = hm.j, /n,= ±y, ±у, .... ±/, F4.11)
причем квантовое число /, определяющее собственные значения полного
момента, может быть выражено через орбитальное число / и спиновое ls
E9.14) по формуле
/ = / + /, или / = |/-/,|. F4.12)
Из формул для собственных значений У2 F4.10), Ж2 B5.21) и s2 E9.14)
получаем важные в спектроскопии выражения для собственных значений
7 /
иг
[/(/+l)-/(/+l)-/,(/8+l)], F4.13)
^-[j(j+\)-l(l+l) + ls(ls+\)]. F4.14)
Эти формулы мы применим позднее к теории сложного эффекта Зеемана.
Обратимся теперь к доказательству формул F4.10) и F4.11). Уравнение для соб-
собственных функций У2 имеет вид
F4.15)
где под *F следует разуметь столбец
Ч>1
^2
F4.16)
215

Пользуясь F4.4), E9.13) и E9.12), находим уравнение F4.15) в раскрытой форме
Ч>*
3
1 0
0 1
ч
Я
h
2
_1_9
——
1 0
0—1
1
г
^2
0 1
1 0
--J*
i
А
0 —г
г 0
Производя здесь умножение и сложение матриц, получаем:
. 3 .„
^ О
и. наконец, сравнивая элементы, получаем два уравнения:
3
4
Эти уравнения легко решаются, если положить
8, ф),
F4.17)
F4.18)
F4.19)
F4.19')
F4.20)
где У;т (9, ф) есть шаровая функция, а а к b — неопределенные коэффициенты. Тогда
имеем:
F4.21)
F4.2Г)
и, далее,
= -h V(l + m)(l-m+l) YU m.lt F4.22)
F4.22')
Эти последние два равенства получаются из свойств шаровых функций1.
Подставляя \|>х и 1>2 из F4.20) в уравнения F4.19) и пользуясь F4.21) и F4.22),
после сокращения первого уравнения на №Y\т, а второго на h2Yi,mti получим:
+ m)(l-m+l) YU m.lt
+ iMv) Ylm= -h V(t-m)(l+m + l)Yi, ma.
где
Л — -
F4.23)
F4.23')
F4.24)
Чтобы эти уравнения имели отличные от нуля решения, необходимо, чтобы их опреде-
определитель равнялся нулю. Это дает нам уравнение для определения X:
= 0.
F4.25)
Отсюда находим два корня
Сравнивая это с F4.24), получаем искомые собственные значения J2:
F4.27)
F4.27')
1 См. дополнение V, формулы C3,34).
216

Первое значение отвечает сложению орбитального [и спинового моментов, а второе —
вычитанию их. Подставляя значение X в уравнения F4.23) и решая их, находим а и 6,
а вместе с тем и собственные функции F4.20). При этом мы еще нормируем их так,
что а2 -|- Ь3 = 1.
Несложные выкладки приводят к следующим функциям: для собственного значе-
значения F4.27):
2/+1
ч>»=-
V1,
F4.28)
и для собственного значения F1.27'):
Г|52 =
2/+1
F4.28')
Решения, как мы видим, вырождены. В самом деле, прн заданном / можно брать раз-
разные числа т==0, +1, i 2, ..., ^ /, а собственное значение /2 от m не зависит. При-
Причина этого вырождения заключается в том, что при заданной абсолютной величине
вращательного момента /2 возможны его различные ориентации в пространстве. Чтобы
в этом убедиться, покажем, что решения F4.28) и F4.28') являются также собственными
функциями оператора Jz проекции полного момента J на OZ.
Действительно, уравнение для собственных функций оператора Jz есть
jz = Jzilp) F4.29)
или, в раскрытом виде,
Ч>1
ч>.
Отсюда, пользуясь F4.21), получаем:
0
т. е. наши решения принадлежат собственному значению
+ —
F4.30)
F4.31)
Обращаясь к решениям F4.28) и F4.28'), мы видим, что в первом решении m может
пробегать значения т=—A-\-\) (при этом ^i = 0), —/, —1-\-\ 0, 1, 2, ..., /,
а во втором решении—значения т= —1, —/-{-'• ••• 0. Ь 2, •.., (/—1) (при т=/
1
1-1-
2
Ч|1 = Ч|2=0). Вводя теперь квантовое число /=/-J- —=/_|_/s или /=|/—ls\ =
мы можем написать F4.27) и F4.27') в виде F4.10). И, наконец, введя обозначение
mj — m-\- ~ на основании сказанного о возможных значениях m при заданном /, полу-
получаем формулу F4.11).
§ 65. Нумерация термов атома с учетом спина
электрона. Мультиплетная структура спектров
Состояние электрона в поле центральных сил мы характеризовали
тремя квантовыми числами п, I, т. Квантовые уровни Еп1 такого элек-
электрона определялись двумя квантовыми числами п, I. При этом мы совсем
игнорировали спин электрона. Если учесть еще и спин, то каждое состоя-
состояние г|)п1та(г, б, ф) окажется в сущности двойным, так как возможны две
ориентации спина
sz = hms, ms=±~, F5.1)
217

Таким образом, к трем квантовым числам, определяющим состояние центра
тяжести электрона, присоединяется четвертое ms, определяющее спин
электрона. Обозначим волновую функцию электрона с учетом спина через
tynimm, {r, 0, ф, s2). Так как взаимодействие спина с орбитальным движе-
движением мы сейчас не учитываем, то согласно F0.5) эта функция может
быть представлена в виде
tynlmms {Г, S, ф, Sz) = 1|>„!т (Г, 6, ф) Sm$ (Sz) F5.2)
(причем значок а функции S мы на этот раз заменяем значком ms).
Соответствующий квантовый уровень есть
Е = Еп1. F5.3)
Четверка квантовых чисел может принимать следующие значения:
«= 1, 2, 3, ..., 0</<я-1,
1, т,= ±у. F5.4)
Для каждого терма Ent мы имеем 21 + 1 состояний, отличающихся
ориентацией орбитального момента, каждое из которых, в свою очередь,
распадается на два состояния, отличающихся спином. Всего 2B1+1)
состояний. Таким образом, налицо 2B/ + 1)-кратное вырождение.
Если учесть теперь слабое взаимодействие спина с магнитным поле!^
орбитальных токов, то энергия состояния будет зависеть еще от ориента-
ориентации спина s относительно орбитального момента М. Мы не будем здесь
излагать расчет этого взаимодействия, так как поправка на взаимодей-
взаимодействие спина и орбитального движения оказывается такого же порядка,
как и поправка, происходящая от зависимости массы электрона от ско-
скорости. Поэтому правильный расчет расщепления уровней требует в этом
случае релятивистского уравнения для движения электрона, рассмотрение
которого выходит за рамки этого курса1. Ограничимся качественным
анализом этого расщепления и оценкой его величины. Магнитный момент
электрона ЭД?В' движется в поле орбитального тока Si?i- Его энергия в этом
поле равна '
ДЕ=-(Ю1вА. F5.5)
Величину магнитного поля <§СХ мы можем оценить как магнитное
поле диполя, эквивалентного орбитальным токам, т. е. диполя с момен-
—¥
том $Щ,. Это поле равно2
Звх =!%>!-%, F5.6)
где г есть радиус-вектор, соединяющий диполи Ш[ и Шв- Поскольку нас
an
an
интересует только порядок величины Д£, то мы можем считать S^i^—г •
где а есть длина порядка внутриатомных расстояний AСГ8 см). Тогда
ДЕ^-^-созШв, т)- F5.7)
Величинымоментов$0};,93£в по порядку равны магнетону Бора (9-10~21 CGSM),
1 См. П. Дирак, Основы квантовой механики, ГТТИ, 1937. Расчет расщепления
приведен в книге Г. Бете, Квантовая механика простейших систем, ОНТИ, 1935.
2 См., например, И. Е. Т а м м, Основы теории электричества, Гостехиздат, 1946,
стр. 269.
218

a cos (Ш, &в), в силу свойств спина может принимать только два зна-
чения ± 1 (смотря по ориентации спина: по полю $@i или против него).
Подставляя в F5.7) численные значения, получаем Д£ «к ± 8- 10~15 эрг.
Эта величина мала в сравнении с разностью энергий между уровнями,
отличающимися числами п, I, и поэтому возникающие новые спектральные
линии близки друг к другу. В частности, одля упоми-
упоминавшегося в § 57 дублета Na (линии 5896 А и 5890 А)
Д£ = 2,8-1(Г15 эрг.
Таким образом, различием в ориентациях спино-
спинового магнитного момента по отношению к внутрен-
внутреннему магнитному полю атома молено объяснить про-
происхождение мультиплетности спектральных линий.
Из изложенного явствует, что для атомов с одним
оптическим электроном возможны только дуплеты (двой-
(двойные линии), соответственно двум ориентациям спина
электрона. Этот вывод теории вполне подтверждается
спектральными данными1.
Обратимся теперь к нумерации уровней атома с уче-
учетом мультиплетной структуры. При учете спиновоорби-
тального взаимодействия ни орбитальный момент М,
„ -»■ Рис. 48. Сложение
ни спиновый s не имеют определенного значения в со- спинового и орби-
стоянии с определенной энергией (они не коммутируют тального момен-
с оператором Гамильтона). По классической механике тов и их прецес-
-* -* сия вокруг направ-
мы имели бы прецессию векторов М и s вокруг вектора ления полного
~t момента /
полного момента J:
/ = M + s", F5.8)
как это показано на рис. 482. Полный момент J остается при этом
постоянным. Соответствующее положение имеет место и в квантовой
механике. При учете спинового взаимодействия только полный момент ./
имеет определенное значение в состоянии с заданной энергией (он комму-
коммутирует с оператором Гамильтона И). Поэтому при учете взаимодействия
спина с орбитой состояния следует классифицировать по значениям пол-
ного момента /.
Как было показано в предыдущем параграфе, полный момент кван-
квантуется по тем же правилам, что и орбитальный момент. Именно, если
ввести квантовое число /, определяющее полный момент J, то
>=й*/(/+1), F5.9)
F5.10)
F5.11)
а проекция J на произвольное направление OZ имеет значения:
Jz^=hmf,
при этом
если спиновой момент параллелен орбитальному, и
/ = |/-/в|, F5.12)
если они антипараллельны. Подобным же образом квантовое число тг
1 Подробности см. в книге С. Э. Фриш, Атомные спектры, ОНТИ—ГТТИ, 1935.
2 Подробности о полуклассической теории см. в книге Л. Бриллуена, Атом
Бора, ДНТВУ, 1935.
219

1
определяющее проекцию J'г, есть
trij = т -f- ^s, ms = ± if •
Так как /, m —целые, a /s и ms —полуцелые, то
. 1 3 5 . _ , i J5_
/ ~' ~' 2 ' ' ' '' J -"- ~2™ ' ^- ~2~
, • ■ • . ± /■
F5-13)
F5.14)
В зависимости от ориентации спина энергия терма будет различной,
именно, она будет разной для j=l-\--^ и /= I — у . Поэтому в этом
случае уровни энергии следует характеризовать значениями главного
числа п, значением орбитального числа I и числом /, определяющим
полный момент, т. е. в этом случае
Е=-Е
nlj-
F5.15)
Волновые функции будут зависеть от спиновой переменной sz и раз-
различны для разных j:
tynljmj — tynljmj (r> 9> ф. sz)- F5-16)
(В этом случае переменные г, 0, ф и sz не разделяются.) Квантовые
уровни при заданном I, различающиеся величиной /, близки друг другу,
так как это есть как раз различие на энергию взаимодействия спина
Р с, а с орбитальным движением для двух
~г~ ' '- ' =2i=oi-J/ рэзных ориентации спина. Четверка
2^ чисел п, I, j, mi может принимать
следующие значения:
л=1, 2, 3, ..., F5.17)
\=-У,У*% 0<Кп-1, F5.17')
ггр,
Р
'Л
2,1эл.б.
11
Рис. 49. Мультиплетная структура
2р — терма атома натрия:
(линии 5890 А и 5896 А образуют известный
дуплет натрия — желтые линии D2 и £>х).
2s - терм далеко отодвинут от 1р - термов,
как это и должно быть в водородоподобных
атомах («Ь — вырождение снято)
1 — l + 's ИЛИ
F5.17")
— j<mf<j. F5.17'")
Величину орбитального момента I
обозначают в спектроскопии буквами
(как мы это уже пояснили)
вают число /. Поэтому,
обозначают так: Зр3/ • Иногда ставят еще один значок:
Главное квантовое число п ставят
впереди буквы. Справа внизу указы-
3
например, уровень (терм) с п = 3, 1=1, 1~т>
32р3/ — двойка
слева вверху указывает, что терм 32р3/ принадлежит к числу дуплетных
(двойных). В случае одного оптического электрона это указание излишне,
т. е. там все уровни дуплетные (j = l + ls и j = \l-— ls\, кроме, конечно,
s-yровней, где / = 0).
При рассмотрении гелия мы встретимся с случаем более сложной
мультиплетной структуры. Так, благодаря наличию двух электронов
имеются одиночные термы (сингулетные) и тройные (триплетные) (см. § 122).
Чтобы различать эти случаи, значок, указывающий мультиплетность
220

уровня, все же сохраняют. Итак, уровень, обозначаемый по обычному
способу F5.15) через Е3> 1(з/2, спектроскопически обозначается через 32р3/»
На рис. 49 приведена схема уровней водородоподобного атома
(т. е. атома с одним оптическим электроном) с учетом мультиплетной
структуры. Там же приведены квантовые числа и спектроскопические
обозначения.
Каждому из рассмотренных уровней EniJ- принадлежит 2/+1 состоя-
ний, различающихся числом т?-, т. е. ориентацией полного момента J
в пространстве. Только при наложении внешнего поля эти сливающиеся
уровни могут разделиться (см. теорию сложного эффекта Зеемана, § 74).
В отсутствии такого поля мы имеем B/+ 1)-кратное вырождение. Так,
2si/2-TepM имеет вырождение 2: два состояния, отличающиеся ориента-
ориентацией спина. 2рз/2-терм имеет 4-кратное вырождение, соответственно
ориентациям J: т, = ± — , ± у •

ГЛАВА IX
ТЕОРИЯ ВОЗМУЩЕНИЙ
§ 66. Постановка вопроса
Лишь в очень немногих случаях задачу о нахождении квантовых уров-
уровней системы (т. е. о нахождении собственных значений и собственных функ-
функций оператора энергии Н) удается разрешить с помощью изученных в мате-
математике функций. В большинстве проблем атомной механики таких простых
решений не существует. Поэтому очень важен весьма обширный класс слу-
случаев, когда рассматриваемая задача может быть приближенно сведена
к задаче, относящейся к более простой системе, для которой собственные
значения Е%, и собственные функции г|)& известны. Такая возможность пред-
представляется в тех случаях, когда оператор энергии Н рассматриваемой
системы мало отличается от оператора Н° более простой системы.
Точное значение слов «операторы мало отличаются» выяснится из
дальнейшего. Сейчас мы укажем те случаи, которые относятся к кругу
задач, могущих быть решенными приближенно. Допустим, что нам изве-
известны волновые функции и квантовые уровни электронов, движущихся
в атоме. Нас интересует, как изменятся квантовые уровни и волновые функ-
функции, если атом поместить во внешнее электрическое или магнитное поле.
Достигаемые на опыте поля обычно малы в сравнении с внутриатомным
кулоновским полем1. Действие внешнего поля можно рассматривать как
малую поправку или, как мы будем говорить, возмущение (этот термин
заимствован из небесной механики и применялся первоначально для обо-
обозначения влияния одной планеты на орбиту другой). Таким же путем могут
быть учтены слабые взаимодействия электронов внутри атомов, например,
магнитные, а в иных случаях даже и кулоновские. Общие методы решения
подобных задач и составляют предмет теории возмущений.
Мы ограничимся пока рассмотрением таких случаев, когда оператор
энергии И обладает дискретным спектром. Пусть данный нам гамиль-
гамильтониан Н равен '»
H = H°+W. F6.1)
Добавок W будем рассматривать как малый и будем называть энергией
возмущения (или иногда кратко—возмущением). Далее, мы предполагаем,
что собственные значения Е°п оператора Н° и его собственные функ-
функции г()п известны, так что
//°г|)п=£М>п- F6.2)
Наша задача заключается в нахождении собственных значений Еп опе-
1 В случае электрического поля можно достигнуть полей, сравнимых с внутри-
внутриатомными. Ср. § 101.
222

ратора Н и его собственных функций. Эта задача, как мы знаем, сво-
сводится к решению уравнения Шредингера
Яг|> = Ег|>. F6.3)
Уравнение F6.3) отличается от уравнения F6.2) одним членом
, который мы считаем малым.
Для приближенного решения задачи методом теории возмущений
пишут прежде всего уравнение F6.3) в таком представлении, в котором
за основную переменную берут собственные значения Е„ оператора Н,
т. е. уравнение F6.2) берут в «£°»-представлении. Если первоначально
оператор Н F6.1) и вместе с тем уравнение F6.3) даны, как это чаще
всего и будет, в координатном представлении, то нужно от этого пред-
представления перейти к «£°»-представлению. Напомним этот переход. Будем
всюду явно писать только одну координату х (в случае надобности
под х можно разуметь любое число переменных так же, как и под знач-
значком п у волновой функции г|)п можно разуметь ряд квантовых чисел).
Пусть в координатном представлении («.«-представление) собственные
функции оператора Н° будут г|)^(х). Разложим искомую функцию г|)(х)
по функциям г|А(х):
Тогда совокупность всех сп есть не что иное, как функция г|) в «Е0»-
представлении.
Подставляя F6.4) в уравнение F6.3), умножая его^на г|)^ (х) и ин-
интегрируя по х, получим:
ЩНтпсп = Ест, F6.5)
п
где Нтп есть матричный элемент оператора Н в «£°»-представлении:
dx. F6.6)
Матрица, образованная из элементов #mn,*IecTb оператор Н в «£°»-пред-
ставлении. Имея в виду F6.1) и F6.2), получаем:
j,°n • ЯЧт" • d* + \ tjj»! • W< • dx = ££ бтоп + Wmn, F6.6')
где Ц7нш есть матричный элемент энергии возмущения в «£°»-представ-
лении:
w,,n= \^m« Wtfk'dx. F6.7)
Матрица, образованная из элементов W п, есть оператор W в этом же
представлении. Подставляя F6.6') в F685), получим:
■ У [Enb*,n+Wmn]cn = Ест. F6.8)
Перенося все члеггы "налево, "находим:
[Eom+Wn.m-E]cm+ %mWmncn = 0, F6.9)
где пит пробегают все значения, которыми нумеруются [функции
невозмущенной системы г|&.
223

где X —малый параметр. При Х = 0 оператор Н переходит в Н". Тогда
уравнение F6.9) запишется в виде
Пока мы никак не использовали предположение о малости W, и
уравнение F6.9) справедливо точно. Задача теории возмущения заклю-
заключается в том, чтобы использовать предположение о малости величин Wmn.
Чтобы явно выразитъ степень малости W, положим:
W-=Xw, F6.10)
. Тогда
[E°m + %wmm-E]cm + KJZ wmncn^0. F6.11)
пфт
Это уравнение мы будем решать по степеням %, считая X малой величи-
величиной. При Х = 0 из F6.11) получается просто уравнение F6.2) в «£0»-
представлении:
(Ет-Е)ст = 0, F6.12)
имеющее решения:
Efm = E°m, ст'=\. F6.13)
При малых значениях X естественно ожидать, что решения уравне-
уравнений F6.11) будут близки к решениям уравнений F6.12), т. е. к F6.13).
Это предположение мы можем выразить явно, если представим собствен-
собственные функции ст уравнения F6.11) и его собственные значения Ет в виде
рядов по степеням малого параметра X:
ст = сЙ? + Ьс&> + №* + . .. F6.14)
и
Ет = Е™ + ХЕт + Л»£'а> + • • • F6.15)
При Х = 0 F6.14) и F6.15) переходят в F6.13), причем Е° должно
равняться Ет- Оказывается, что решение уравнений F6.11) существенно
зависит от того, вырождены ли состояния системы Н° или нет. Если
они вырождены, то каждому собственному значению Еп принадлежит
несколько собственных функций tym, если не вырождены, — то только
одна функция. Эти два случая мы рассмотрим порознь.
§ 67. Возмущение в отсутствии вырождения
Пусть каждому собственному значению El невозмущенного уравне-
уравнения F6.2) принадлежит лишь одна собственная функция tp£, соответ-
соответственно—одна амплитуда с„- Подставим в уравнение F6.11) ряды F6.14)
и F6.15) и соберем члены с одинаковыми степенями. Тогда получается
[Ст — С J Cm ■+- Л \\Wmm — С J Cm + [Em — IZ J Cm +
J_ V 70) r<w\ Л 1%I.\7O) Mi .(I) 17B) „@) i^
пфт
+ [E?n - E«»] c% + 2 wmn c™} + ... = 0. F7.1)
пфт
Это представление уравнения F5.11) позволяет легко решить его методом
последовательных приближений. Мы получим нулевое приближение, если
положим Х = 0; тогда получаем
[Е»т-Ет]с% = 0, т=\*2, 3 k, . .. F7.2)
Это — уравнение для невозмущенной системы Н°. Пусть нас интересует,
224

как меняется уровень El и собственная функция tyl под действием воз-
возмущения W. Тогда из решений F7.2) мы берем ft-oe:
Р<0) ПО „О X /л-у о\
■С — Ek> 6m —°mft> (О/.О)
т. е. все Ст=0, кроме 4°'=1-
Решение F7.3) мы будем называть решением в нулевом приближении.
Это решение мы подставляем в уравнение F7.1) с тем, чтобы найти
'ледующее, первое приближение. Подстановка дает
1ЯА} () = 0, F7.4)
пфт
где через О (к") обозначены члены порядка К2 и выше. Ограничиваясь
первым приближением, мы должны считать эти члены малыми и отбро-
отбросить их. Тогда получаем:
[wmm - &»] bmh + (El - El) С + 2 Wmnbr* = 0-S F7.4')
пфт
Если мы возьмем из этих уравнений уравнение номера m = fe, то получим:
whh-E™ = 0. . F7.4")
Отсюда находим поправку к El первого приближения:
E™ = Wkk. F7.5)
из уравнений с т Ф к находим поправки к амплитудам ст\ именно, если
т Ф к, то F7.4') дает
t = 0. F7.4'")
Отсюда
c™=lf=l^' m^k- F7-6)
Найдем теперь второе приближение; для этого следует учесть члены
с X2. Подставим первое приближение F7.5) и F7.6) в F7.1), тогда
найдем:
F7.7)
n -f - к
где через О (X3) обозначены члены порядка Xs и выше. Пренебрегая
этими членами, получим уравнение для определения Е™ и с™ (второе
приближение). При этом уравнение номера т = k получается в виде
-£<2'+2 §iS|r0- F7-n
Отсюда находим поправку к энергии во втором приближении:
ЕЧ2) _ XT U>bnwnb IP.J С\
£ -- Zi El-El • (О'-°>
Из уравнений с т[Ф[к найдем с'т'.
<2> _ w,<kwmh >п wmnWyh m=hh п Ф k F7 ^
п
15 Д, И. Блохинцев 225

Эту процедуру можно продолжать и дальше, переходя ко все более
и более высоким приближениям. Мы ограничимся вторым приближением
и выпишем результат. Согласно F6.15), F6.16) и F7.3), F7.5), F7.6),
F7.8) и F7.9) имеем:
Ек =Ek + lwkk + К* ^ Щ=Щ + ° (*-'). F7- Ю>
п=И=й
г — 1 п — \ wmh_ ■
Из этих формул видно, что предположение о малости оператора W
в сравнении с Й° означает малость отношения
пфт; F7.12)
po po
при выполнении этого условия поправочные члены в F7.10) :и F7.11)
малы и собственные значения Ек оператора Н и его собственные функ-
функции ст (к) близки к собственным значениям и собственным функциям
оператора Н°. Условие F7.12) —это условие применимости теории возму-
возмущений. На основании F6.10) это условие может быть записано также
в виде
■ iWmll , « 1, пфт, F7.13)
\ьт—tn\ \ '
где Wmn суть матричные элементы оператора возмущения.
Пользуясь F6.4) и F7.6), а также F7.5), мы можем написать наше
решение в <ш>-представлении:
■Ч& (*) + ..., F7.14)
Е,{ = El + Whh + . .., Wkh = ^ С • W^ • cix. F7.15)
Из последней формулы видно, что поправка к уровням в первом прибли-
приближении равна среднему {значению энергии возмущения в невозмущенном
состоянии £)
Из условия пригодности метода теории возмущения F7.13) непосредственно
видно, что успех приближенного расчета зависит от того, какой именно квантовый
уровень мы рассчитываем. Так, например, в кулоновском поле разности энергий
соседних уровней выражаются формулой ,,
я2(«±
"
При малых п эта величина может быть гораздо больше Wn n,±.1 Для больших же «
она стремится к нулю, как 1/я3, и условие F6.13) может оказаться несоблюденным.
Поэтому метод теории возмущений может быть пригодным для расчета поправок ниж-
нижних квантовых уровней и непригодным для расчета поправок для высоких квантовых
уровней. Это обстоятельство нельзя не иметь в виду при приложении теории возмуще-
возмущений к конкретным проблемам.
-> Второе, что следует отметить, — это некоторые особые случаи, когда условие
F6.13) соблюдено и тем не менее квантовые состояния систем Н и Н° радикально
отличаются. Дело в том, что энергия возмущения W может оказаться такого вида, что
существенно изменит асимптотическое поведение потенциальной энергии U {х).
226

Допустим, что к гармоническому осциллятору приложено возмущение
нение Щредингера будет:
=kx3. Урав-
F7 16)
Пои )i-0 мы имеем уравнение для гармонического осциллятора,, имеющего диск-
/ 1 л
ретный спектр энергии En = ha0 ( я+у J • Матричные элементы возмущения
при малом X могут быть как угодно малы в сравнении с Ет — En=ha0(tn — n). Тем
не менее при всяком X уравнение F6.16) имеет непрерывный спектр и только при
Х = 0 оно имеет дискретный спектр собствен-
собственных значений. Действительно, потенциаль-
потенциальная энергия £/(х) = -^-1 \-^х3 ИМеет ВИД-
приведенный на рис. 50. При всяком зна-
значении Е для больших отрицательных х,
U (х) < Е, т. е. асимптотическое значение
потенциальной энергии меньше Е. Поэто-
Поэтому энергетический спектр должен быть
непрерывным.
Спрашивается, какой смысл имеют в
этом случае приближенные функции tyn(x)
и уровни Еп, которые мы можем вычислить
из \]з£ и £« методом теории возмущения,
пользуясь малостью параметра X? Оказыва-
Оказывается, что при малых X найденные методом
теории возмущения функции tyn(x) отли-
отличаются тем, что они велики вблизи потен-
потенциальной ямы U (х) и малы вне ее. На
рис. 51 повторена кривая потенциальной
энергии U (х) (рис. 50) и, кроме того, нанесен квадрат модуля волновой функции
| ty (x) |2. Рис. 51, а соответствует случаю, когда энергия £ = £ns&£?1 Если же энер-
энергия £ не равна Еп, то волновая функция \|)ь> (х) нарастает вдали от потенциальной ямы
U (х) (см. (рис. 51, Ь). В первом случае мы можем сказать, что частицы находятся
около положения равновесия х = 0, так сказать, «в атоме», а во втором случае оии
находятся преимущественно вне его, бесконечно далеко. Стационарность состояний
может получиться лишь в том случае, если существуют волны, как уходящие в беско-
Рис. 50. Кривая потенциальной энергии
v(x) = *—п-^ + Хх3 ( пунктирная кривая
Л2
Uu(x)=
0
Рис. 51. Потенциальная энергия v(x)= ^-я-^ x2JrXx3 и плотность вероят-
вероятности |г|)|2
в — для Е = Е ; Ь — для Е г£ Еп
вечность, так и приходящие нз нее, так что поток частиц через поверхность, окру-
окружающую атом, равен нулю. Такой случай представляется мало интересным. Чаще
приходится иметь дело со случаем, когда имеются лишь уходящие волны (см. § 99).
Тогда стационарных состояний не существует вовсе. Если требовать, чтобы имелись
лишь уходящие волны, то находимые методом теории возмущения функции tyn (x)
описывают поведение частиц лишь в течение не очень большого времени t. Однако
на самом деле это время может быть очень велико, и оно тем больше, чем меньше
значение параметра X. Такого рода состоянии фп (х) и соответствующие им уровни £^
мы будем называть квазистационарными.
15* 227

§ 68. Возмущение при наличии вырождения
В большинстве важных в приложениях задач приходится встречаться
со случаем вырождения, когда в невозмущенной системе (Н°) собствен-
собственному значению Е = Е°п принадлежит не одно состояние гр&, а несколько
ipni, ^n2> -.^ipna 1рй/- Если теперь действует некоторое возмущение
W, то без специального исследования нельзя сказать, какая из функций
tyna будет являться нулевым приближением к собственным функциям
оператора Н = Н°-\- W. В самом деле, вместо ряда функций ip£i, ...
.. ., г|)°ш ■ • •. i|?n/. принадлежащих собственному значению Е„, быть могут
взяты новые функции cp{U, фпг. ■ ■ •» фпа. • • •, фп/> получающиеся из первых
линейным ортогональным преобразованием:
/
2 F8.1)
Р=1
F8.2)
Функции фпа. будучи линейными комбинациями функций г|)пр, будут также
решением уравнения Шредингера
//°Фп = ^Ф„> F8.3)
принадлежащим собственному значению Е°п, и при добавочном условии
F8.2) будут ортогональными, если функции г|#„ ортогональны. Функции
фаа суть поэтому также возможные функции нулевого приближения,
но неизвестно, какие коэффициенты aap следует взять, чтобы получить
правильное нулевое приближение.
Для решения этого вопроса обратимся к уравнению F6.9). Нам,
однако, следует теперь его несколько модифицировать, уточнив обозначе-
обозначения. При наличии вырождения собственные функции оператора имеют
по крайней мере два индекса (п, а). Поэтому в этом случае F6.4) следует
написать подробнее, заменяя индекс п на два: п, а. Тогда мы получим:
1>(*) = 2 cna^°J(x). F8.4)
n, a
Соответственно этому уравнение F6.9) получится (заменяя п на п, а;
т на т, |3) в виде
2 ^mp,r«Cna = 0, F8T5)
где
Wmb na = \ <р • Wy°na • dx F8.6)
есть матричный элемент энергии возмущения и получается из F6.7)
увеличением числа квантовых чисел, нумерующих состояния. Ейт есть
энергия m-го квантового уровня для невозмущенной задачи. Эта энергия
от квантового числа а не зависит (вырождение).
Допустим, что мы теперь желаем найти квантовый уровень возму-
возмущенной системы Ек, близкий к El, и соответствующие собственные функ-
функции tyha(x). Ограничимся решением этой задачи в первом приближении
для уровней и в нулевом приближении для функций.
В отсутствии вырождения мы полагали для функций нулевого при-
приближения, что они просто совпадают с невозмущенными. Соответственно
этому в нулевом приближении с,°от= 1, а остальные равны 0. Этого нельзя
228

сделать при наличии вырождения, ибо, отбрасывая в нулевом приближе-
приближении возмущение W, мы получим из F7.5):
это дает Ck$ Ф 0 для Е = Е%, но при этом не одно Сф а все принадле-
принадлежащие собственному значению Е%, именно с^р для C=1, 2, ...,/. Таким
образом, в нулевом приближении не одна амплитуда, а целая группа
отлична от нуля. Поэтому правильным нулевым приближением для функ-
функций ft-ro уровня будет
), а=1, 2, ...,/
В этом приближении мы возьмем из числа уравнений F8.5) те, которые
содержат не равные нулю сиа- Это будут уравнения:
2 rftp,fea4°a = 0. F8.8)
*£Р
Поскольку мы ограничиваемся нулевым приближением к ft-му уровню,
мы можем опустить индекс ft (держа его просто в уме), положив при этом
= Wkfit ka = $ <р • W|>fca • d*. F8.9)
d$> = c№, a=l, 2, ...,/fc. F8.9')
Тогда уравнения F8.8) запишутся в виде:
0, р = 1. 2, .. ., /г F8.10)
У £ft мы сохранили число ft, чтобы подчеркнуть все же, что речь идет
о группе из /^-состояний, принадлежащих уровню Е%.
Для того чтобы уравнения F8.10) имели отличные от нуля решения,
необходимо, чтобы определитель системы F8.10) обращался в нуль, т. е.
= 0. F8.11)
Это — алгебраическое уравнение степени fk для определения Е. Часто
оно называется вековым1 уравнением. Из него мы получим fk корней".
Ь = -См, -C/j2> ■ • ■, Cka> • • ■, Ekf^ F8.12)
Так как матричные элементы W^a предполагаются малыми, то эти корни
будут близки между собой. Следовательно, мы получаем важный резуль-
результат: при наложении возмущения вырожденный уровень (El) распадается
на ряд близких уровней F8.12). Вырождение снимается. Если некоторые
из корней F8.12) равны, то вырождение снимается лишь частью.
Для каждого из корней Eka F8.12) мы получим свое решение для
амплитуд ср0' из уравнения F8.10). Чтобы отметить, что решение с[°\
с'0', . . ., ср", ..., cffe' принадлежит уровню Eha, мы введем в ср" еще один
индекс а так, что решение уравнений F8.10) для Eka запишется в виде
Е = Eka, c = cZ, cZ, ■ ■ ■, с$, . . ., c$fc, a « 1, 2 fk. FU. 13)
1 Название «вековое уравнение» заимствовано из астрономии.
229

Если бы мы еще удержали индекс k, то полная нумерация для ст была
бы 4ра- Уравнение F8.13) есть приближенная (в нулевом приближении)
волновая функция оператора Н в «£°»-представлении. В ««-представле-
««-представлении решение F8.13) запишется в виде
3=1
F8.13')
Таким образом, каждому уровню Е = Еш принадлежит теперь своя функ-
функция фца» которая и является функцией нулевого приближения для воз-
возмущенной системы (//).
Отличие, функций F8.13') от функций F8.1) заключается в том, что
в F8.1) коэффициенты аар произвольны [вплоть до условия ортогональ-
ортогональности F8.2)], а коэффициенты с«р в F8.13) определены. Следовательно,
функции нулевого приближения cpfta представляют собой частный случай
функций невозмущенной задачи cpft°a. Заметим, что если вычислить следу-
следующие приближения, то нетрудно убедиться, что условием пригодности
метода теории возмущения будет опять-таки F7.12), которое теперь для
вырожденного случая будет иметь вид
В § 41 было показано, что задача нахождения собственных значений и собственн-
ных^функций любого оператора L, заданного в матричной форме, сводится к решению
уравнений D1.4) и D1.5). Разумея в D1.4) под оператором L оператор полной энергии
Н, мы должны в случае вырождения разуметь в D1.4) под индексом я два индекса;
л, а; под т—также два индекса: т., |3. В результате из D1.4) мы получаем уравнения
2 #mp,nacna = £cmP. F8-15>
п, а
которые совпадают с F8.5), так как
a. F8.16)
Уравнение D1.5), соответствующее системе D1.4), в нашем^случае запишется несколько
сложнее (по форме), так как строки и столбцы матрицы оператора Н нумеруются двумя
квантовыми числами п и а. Именно, при каждом я имеется [п разных значений a (/n-
кратное вырождение). Число /„ возрастает с увеличением я. Для первого уровня Д = и
термин «вырождение» не применяется.
Расположить элементы Ятр па в матрицу не представляет труда. Так, можно
нумеровать какой-нибудь столбец 'парой (п, 1), а следующие столбцы номерами: (я, 2I
(я, 3), ..., (я, /п), затем пойдут столбцы с номерами (п+1, 1), (я+1, 2) до
(п+1, /,i+J) и т. д. Подобным же образом нумеруем строки (т, 1), (/я, 2), ..., (т, fm)
и т. д. При такой же нумерации элементов матрицы #тц па уравнение для определения
собственных значений Е может быть написано в следующем виде [это н есть уравнение
D1.5) для нашего случая]:
яи, и— Е
Н
11, 21---
я,
...я
11, ftl-
.Н
и,
Н
21, 11
/2, 21-■■
Я
2/2,
...Н
21, fel-
.я,
2, fel
я,
fel, 11
11
11
1, 21
Р, 21
4.21
.Я
fel,fel"
~E...H
fel, I
.я
ftp, ftl
...H
ft/*, ftl---'
— E
= 0.
F8.17)
230

Обведенные прямоугольниками матричные элементы относятся к одному и тому же кван-
квантовому уровню. Так, например, в первом прямоугольнике (один элемент)—к уровню
&=1, во втором—к уровню fe = 2, в третьем—к /г-му уровню. Если мы пренебрежем
матричными элементами, относящимися к различным уровням, т. е. элементами типа
Ятр па(т^=п) 1ЭТИ элементы согласно F8.16) равны Wma na], то уравнение С67.17)
упростится и примет вид
1-Ё О
О
О
о
о
l, kfk
= 0.
F8.18)
£кую матрицу называют ступенчатой. Ее определитель А" (Е) разбивается на произ-
произведение определителей меньшего ранга, именно1:
2, 21 • ••
Hk\,ki—E---Hk\, kfh
Hkfk,kl---Hhfh,hfh~~E
= 0.
F8.19)
Обозначая входящие сюда определители через Д^ (Е), получим:
А" (Е) = А^ (£)-Д/ (£)... A/fe (E) ... =0.
8.20 )
Уравнение F8.20) будет удовлетворено, если Д, (£)=0 или А, (£)=0 или вообще
'l '2
д (£) = 0. Корни этих уравнений и .дают в первом приближении энергии первого,
второго и вообще /г-го уровин. Уравнение
Af (E) = 0 <t F8.21)
тождественно с уравнением F8.11), установленным другим путем.
В § 41 мы объясняли, что задача нахождения собственных значений оператора
может рассматриваться как задача о приведении к диагональному виду его матрицы.
Из изложенного мы видим, что принимаемое в теории возмущения первое приближение
заключается в том, что мы пренебрегаем матричными элементами, относящимися к раз-
разным уровням, и таким образом задачу о приведении к диагональному виду бесконеч-
бесконечной матрицы сводим к приведению к диагональному виду конечных матриц [отдельных
матриц в ступенчатой матрице F8.18)].
Этот результат получается сразу, если раскрывать определитель F8.18) по
обычному правилу раскрытия: произведение элементов на миноры.
231

§ 69. Расщепление уровней в случае двукратного
вырождения
Рассмотрим частный случай снятия вырождения возмущением, когда
интересующий нас уровень невозмущенной системы двукратно вырожден.
Пусть собственному значению Е^ оператора принадлежат две ^функции
(fft = 2): tjjfei и г|)ь2- Любые две функции q>ki и cpfe2> получающиеся из
tyki и ipfe2 путем ортогонального преобразования, будут также собствен-
собственными функциями оператора Н°, принадлежащими уровню Ей- Это пре-
преобразование мы можем записать в виде [см. F8.1)]:
а1>° + а1>° F8Л)
° 0^ + 0^ F9Л')
Ф°2 = 021^1 + 0
Чтобы удовлетворить условию ортогональности F8.2), положим:
ап= cos6-e*P, a12 = sin
= cos 6 • е~{Р {
ричем 9 и Р здесь два произвольных угла. Таким образом,
фО = cos 6-Ab° + sin 6 • e~iptb9.
„ , F9.3)
, = —sin 6-е*Р-фО± -{-cos6-е-*Ргр°2 '
представляют собой наиболее общие выражения для волновых функций,
принадлежащих двукратно вырожденному уровню Eh-
Ортогональность и нормировку этих функций легко проверить не-
непосредственно и убедиться также, что коэффициенты аар F9.2) удовле-
удовлетворяют условию ортогональности F8.2). При C = 6 = 0 из F9.3) полу-
получаются исходные функции ty°hl и гр^. Пусть теперь наложено некоторое
возмущение W. Нулевое приближение будет выражаться [функциями,
являющимися функциями невозмущенной системы, т. е. функциями F9. l)f
но с вполне определенными коэффициентами; иначе говоря, значения
углов 6 и C будут зависеть от вида возмущений W. Для определения
этих углов будем искать прямо коэффициенты сг и с2 в суперпозиции
F9.4)
Согласно изложенной выше теории эти коэффициенты определяются из
уравнения F8.10), которое в рассмотренном частном случае имеет вид:
где Wu, Wl2, W21, W22 — матричные элементы энергии возмущения:
F9.6)
F9.6')
■ dx. F9.6")
= 0, F9.7)
Вековое уравнение F8.11) имеет тогда вид
7п - е W12
232

где е — поправка к энергии ft-ro уровня:
л = Е-Ен. F9.8>
Раскрывая определитель F9.7) и решая получающееся квадратное
уравнение, мы найдем два корня:
Из уравнений F9.5) находим:
Полагая
F9.9)
F9.10)
F9.11)
и подставляя в F9.10) первый корень (81( знак -f ), получим:
ci _ \W12\e l - _„+„о „я|к F9.12)-
2
а для второго корня (е2, знак —):
с, \W12\e
. F9.12').
Таким образом.Тполучаются следующие решения (в <ш>-представлении):
Фи = cos б-е^гр^ + sin 6- e—^P-
причем
pii2 = — sin 6• e*P• t|)P, -j- cos 6 • e~*P • 1
-tge=- ——
Весьма важным является частный случай, когда
Для этого случая имеем:
F9.13)
F9.13')
F9.14)
F9.15>
F9.16)
F9.17)
F9.17')
Преобразование F9.3) есть поворот. Мы можем получить ^прямую геометрическую
аналогию, если будем считать р = 0 (это требует, чтобы fl7i2=W2i). Тогда коэф-
233-

■фициенты а действительны. Частные значения коэффициентов а—коэффициенты с—
также действительны. Вместо F9.4) мы можем написать, полагая C]=g, с2 = т]:
F9.18)
F9.19)
F9.20)
F9.21)
Это уравнение можно рассматривать как уравнение кривой второго порядка на пло-
.скости (%, г|). Таким образом, среднее значение W есть квадратичная форма от ампли-
t :' туд g, т), представляющих состояние ф.
I ' Введем теперь вместо системы координат £, г\
новые координаты |', г\', отличающиеся от первых
поворотом на угол 6:
|= cos в-1' — sin 6-г)', г) = sin 8 • g'-j-cos в - т)'.
F9.22)
{индекс k мы будем держать в уме). Если потребовать, чтобы
l2 + rf=l.
то средним значением энергии возмущения W в состоянии F9.18) будет
•Согласно F9.6) получим:
Подставляя в F9.18), получим:
F9.23)
Относительно функций (pj и ф§ матрица W должна
быть диагональной. Действительно,
WU =
Щ,=
Рис. 52. Геометрическая иллю-
иллюстрация приведения к диагональ-
диагональному виду матрицы второго ранга
F9.24)
w;2 =
• Поэтому среднее значение W в состоянии ф представится теперь в ином виде:
={ ф
*-
F9.25)
т. е. в новых переменных £', ц' средняя энергия являетси кривой второго порядка,
отнесенной к главным осям (рис. 52).
Таким образом, задача о приведении матрицы W к диагональному виду совпадает
с геометрической задачей о приведении к каноническому виду кривой второго порядка
(отнесение к главным осям). В более общем случае £ и х\ комплексны, поэтому полного
совпадения задач нет, ио аналогия сохраняется, если | и г) и в этом случае рас-
рассматривать как координаты точки.
§ 70. Замечания о снятии вырождения
Мы показали, что при включении возмущения вырождение, свойст-
свойственное невозмущенной системе, снимается: сливающиеся уровни рас-
расщепляются. Чем обусловлено это расщепление? Для ответа на этот вопрос
обратимся прежде всего к причинам вырождения.
Мы видели, что, например, уровни электрона в поле центральных
.сил вырождены 21 + 1 раз (если не считать спинового вырождения). Это
вырождение обусловлено тем, что энергия электрона в поле централь-
центральных сил не зависит от ориентации момента импульса относительно поля.
234

Математически это выражается тем, что гамильтониан в этом случае
■обладает симметрией вращения, именно, гамильтониан
H°=-~^ + U(r) (r = ^a+^ + z2) G0.1)
остается неизменным при повороте системы координат, когда координаты
л, у, г переходят в х', у', г'. В самом деле, при повороте
x^-yz + zz = x'2 + y'2 + z'2, G0.2)
последнее равенство вытекает проще всего из того, что
V* = (V)a,
так как V есть векторный оператор, а квадрат вектора не меняется при
повороте. Таким образом,
Н°(х,у,г) = Н°(х',у',г'). ■ G0.3)
Если наложенное возмущение не обладает сферической симметрией, то
энергия электрона будет зависеть от ориентации момента и произойдет
расщепление уровней. Вместе с тем для оператора И равенство G0.3)
уже не будет иметь места. Этот пример показывает, что наличие вырож-
вырождения связано с той или иной симметрией поля, а снятие вырождения —
■с нарушением этой симметрии.
Приведем еще пример. Пусть мы имеем осциллятор в плоскости х, у,
обладающей одинаковыми частотами со0 для колебаний по ОХ и (по {OY.
Уравнение Шредингера для такого осциллятора имеет вид
<™.4)
Гамильтониан в этом уравнении остается неизменным при поворот-
системы координат вокруг оси OZ. Таким образом, он обладает сим-
симметрией вращения. Согласно сказанному следует ожидать вырождения
Оно действительно имеется. В самом деле, уравнение G0.4) решается
сразу разделением переменных:
W(x, у)=ур1(хIь(у), )
Подставляя G0.5) в G0.4), обычным путем получаем два уравнения:
-|^ + ^^ = £А. . G0-6)
Эти уравнения для осцилляторов имеют известные функции и известные
собственные значения, именно:
= Лй>о(л1 + 4)|. «1 = 0,1,2,..., G0.7)
2 = К)(«2 + 4), «2 = 0, 1, 2, ..,.» G0.7')
Отсюда
235

Введем «главное квантовое число»
я = га1 + я2+1, п2 = п — п1—1. G0.9)
Тогда
Vnn^*, y) = ^n1(x)^n-nl-i(y), En = haon, «=1,2,.... G0.10)
Каждому уровню Еп будет отвечать п функций («1 = 0, ^=1, ...,
п1 = п— 1). Следовательно, вырождение действительно имеется.
Допустим теперь, что возмущение W заключается в изменении коэф-
коэффициента упругости для колебаний вдоль оси OY. Тогда частота колеба-
колебаний по оси OY изменится. Пусть она будет равна сог Гамильтониан
возмущенной системы тогда получит вид:
h2 ( д2 д2 ^ ,
IF здесь—возмущение. JB рассматриваемом примере решение возмущен-
возмущенной системы может быть получено точно. Дело, очевидно, сводится
к замене в G0.7') ю0 на- ю,. В результате решение получит вид:
или
Yn, пг (л;, г/) = г|)„г (л;) ipn-^-i (г/);
п — «j —
G0.10')
Как видим, уровни с различным значением числа пх и одним и тем же
п будут иметь разную энергию. Один уровень Еп невозмущенной системы
расщепился на «уровни £„, 0. £n, v •••> ^n.n-i (числом «). Вырождение
снялось.
Резюмируем вывод из этих примеров. Если гамильтониан H°(x,y,z)
остается инвариантным (неизменным) по отношению к некоторому пре-
преобразованию координат (х, у, z—>х', у', z'), то собственные значения
Е° вырождены. Если возмущение нарушает указанную инвариантность,
то, хотя бы частью, вырождение снимается.

ГЛАВА XII
ПРОСТЕЙШИЕ ПРИЛОЖЕНИЯ ТЕОРИИ
ВОЗМУЩЕНИЙ
§ 71. Ангармонический осциллятор
Гармонический осциллятор является идеализацией реальных механи-
механических систем. Действительная потенциальная энергия частиц никогда
не представляется функцией -^2- х2, а изображается гораздо более слож-
сложной функцией U (х). Первое выражение справедливо лишь для малых х.
Чтобы уточнить выражение потенциальной энергии U (х), мы можем
кроме члена ^-if-х2 учесть еще и более высокие члены разложения U (х)
по степеням отклонения х:
U(x) = -^-x* + lxs + ... G1.1)
Коль скоро добавочные члены остаются малыми, мы имеем дело с гар-
гармоническим осциллятором, несколько возмущенным наличием отступле-
отступлений от кривой, свойственной идеальному гармоническому осциллятору.
Такой осциллятор мы будем называть ангармоническим.
Найдем квантовые уровни ангармонического осциллятора, считая
добавочные члены G1.1) малыми (А, мало). Решим эту задачу методом
теории возмущений, опираясь на уже известные решения для гармониче-
гармонического осциллятора. В качестве возмущения W у нас фигурируют доба-
добавочные члены в выражении для потенциальной энергии1:
Квантовые уровни невозмущенной системы (X = 0) суть уровни гармони-
гармонического осциллятора; его собственные функции обозначим через
) №(х). G1.3)
В данном случае вырождения нет: каждому уровню принадлежит лишь
одно состояние t|£. Матричным элементом энергии возмущения W будет
где через (xs)mn обозначены матричные элементы для х3.
1 Мы можем считать, что спектр возмущенной системы останется все же дискрет-
дискретным, так как %х3 есть поправочный член и он вообще негоден для больших х. Таким
образом, из вида поправки G1,2) не следует делать заключения, что асимптотическое
поведение U (х) радикально изменилось, как это предполагалось в § 66, где добавочный
член Xxs формально рассматривался как пригодный и для больших х.
237

Согласно формуле F7.10) энергия fe-го уровня возмущенной системы
во втором приближении равна
— Fi — ) (Г3\ J- >2 V (X3)"fe (x3)kn
пфк ^h n
Таким образом, .нам достаточно вычислить матрицу (х3)тп. Эту
матрицу мы могли бы непосредственно вычислить из формулы G1.4)
с помощью функций ty°n [см. D7.11)]. Однако мы поступим более просто.
Матрица хтп нам известна [см. D8.8)]. По правилу умножения матриц
мы можем вычислить из матрицы хтп матрицу (ха)тп. Именно,
(х\п = 2 хм {х%п = 2 Чх 2 xlmxmn = 2S xHiXimxma- G1.6>
I I 1
1т
Подставляя сюда значение матричных элементов хк1, х1т, хтп из D8.8),,
получаем:
I m
G1.7>
Ввиду наличия б двойной ряд по / и т просто суммируется, и мы
получаем:
-( h Л3!*! /
8 °h-a,n
6ft+1, И+
Отсюда следует, что {х'3)ш = 0, и поэтому поправка к Ей в первом
приближении равна нулю. Поправка второго приближения, содержащая
сумму по п, также просто вычисляется, так как из суммы остается
согласно G1.8) только четыре члена: n = k±3, « = fe± 1. Кроме того,
(х\п = (х3)п1г. Поэтому, подставляя G1.8) в G1.5) и принимая во внима-
внимание G1.3), находим:
&(^Ж ) k = °> l' 2> -< G1"9>
Это и есть искомое приближенное выражение для энергии квантовых
уровней осциллятора с учетом поправочного ангармонического члена Хх3.
Легко найти условие применимости нашего приближения. Матричный
элемент энергии возмущения X (х3)кп для больших квантовых чисел к
по порядку величины согласно G1.8) равен
w ъ
Разности уровней Е\ — Е„ я» /гю0. Таким образом, условие применимости
теории возмущения F7.13) сводится к
238

Наше приближение применимо, следовательно, для не слишком высокие
уровней, именно
Это условие в переводе на язык классической механики означает, что
амплитуда колебания должна быть не слишком большой.
Формула G1.9) находит свое применение для вычисления колеба-
колебательных уровней молекулы. В § 54, рассматривая двухатомную молекулу,
мы ограничились вторым членом разложения потенциальной энергии 0 (х)
по степеням отклонения (х) от положения равновесия и соответственно
этому получили для молекулы гармонические колебания. Если бы мы
учли и следующий член разложения, что, вообще говоря, приходится
делать, то колебательные уровни молекулы определились бы формулой
G1.9), а не G1.3).
§ 72. Расщепление спектральных линий в электрическом
поле
В электрическом поле спектральные линии атомов, как было обна-
обнаружено на опыте, расщепляются (так называемый эффект Штарка).
Картина расщепления изображена
на рис. 53, где дано расщепле-
расщепление спектральных линий водо-
водорода Яр, Ну, Н6, Не (линии
серии Бальмера). Опыт по-
показывает, что действие электри-
электрического поля на атом водорода
и на другие атомы весьма раз-
различно. В водороде расщепление
спектральных линий пропорцио-
пропорционально первой 'степени электри-
электрического поля %, а во всех осталь- ,,,; . ^ <{t ^g i
ных атомах оно пропорционально
второй степени поля (g2). В силь- Рис. -jg. расщепление спектральных лини»
ных полях (порядка 105 в/см) появ- Бальмеровской серии при больших электри-
ляется дополнительное расщепле- ческих полях!
ние, пропорциональное высшим сте-
степеням if. Кроме того, по мере увеличения поля, как было наблюдено на опыте,,
спектральные линии уширяются и, наконец, вовсе исчезают. Это послед-
последнее явление мы рассмотрим позднее в § 101. Сейчас мы будем рассматри-
рассматривать поля, меньшие Ю5 в/см.
1 Поле возрастает снизу вверх, максимальное значение равно 1,14 миллион*
вольт на см, белые линии — линии постоянного поля. Одновременно сняты невозму-
невозмущенные (без поля) водородные линии; они изображаются средними линиями каждой
картины расщепления, которые на рисунке проходят почти прямолинейно. При срав-
сравнении штарковских линий, соседних с несмещенными линиями, ясно видно, что линия,
лежащая с красной (левой) стороны, всегда удалена от несмещенной линии гораздо
дальше, чем соседняя фиолетовая линия (квадратичный эффект Штарка). Это особенно
хорошо заметно у линии Нр. Далее видно, что все линии перестают существовать при
определенной критической напряженности поля, притом линия Не раньше, чем На,
На раньше, чем Ну и т. д., красные компоненты каждой линии раньше, чем фиолето-
фиолетовые. Явление исчезновения линий сбъяснено в § 101.
239

Из сравнения величины внутриатомного электрического поля
е
0 = -т = 5,13-10» в/см
а
{а —радиус первой орбиты Бора) с внешним полем ф < 105 в/см)
следует, что в широких пределах действие внешнего поля можно рас-
рассматривать как возмущение. Этим мы и воспользуемся для нахождения
квантовых уровней и волновых функций атомного электрона при наличии
внешнего поля %. Обозначим потенциальную энергию оптического элек-
электрона в атоме через U (г). Если теперь еще имеется внешнее однородное
электрическое поле напряженности %, то электрон будет иметь некоторую
добавочную потенциальную энергию W. Эту энергию легко вычислить.
Возьмем ось OZ за направление электрического поля Щ. Тогда по-
потенциальная энергия электрона в поле будет равна
W = e$z= -Dz%, G2.1
где Dz = — ez есть компонента электрического момента на ось1 OZ.
Полная потенциальная энергия электрона будет -равна
U'(r) = U(r) + e$z. G2.2)
Уравнение Шредингера для стационарных состояний будет иметь вид
-|rVsi|>+[£/(r) + egz]i|> = £i|>. ■ G2-3)
Возмущение W относится к случаю, рассмотренному в § 67. Именно,
даже как угодно малое поле % меняет асимптотическое поведение потен-
потенциальной энергии. Если § = 0, то U'—>0 при г—•> ^ со, а если Ш ф 0,
то U' —-> ± оо при z—» ±оо. Поэтому мы можем применить теорию воз-
возмущения (при малых Я) лишь в смысле, разъясненном в § 67. Таким обра-
образом, применяя теорию возмущения, мы будем находить квантовые значения
■ энергии Еп, при которых электрон находится вблизи атома достаточно
большое время («квазистационарные» состояния). Рассматривая в этом
смысле W как возмущение, мы будем считать состояния электрона
в атоме в отсутствии внешнего поля известными.
Рассмотрим сначала водородоподобный атом. Энергию квантовых
уровней атома в отсутствии поля обозначим через:
-1, я=1, 2, 3, ..., G2.4)
а соответствующие волновые функции через
Лт = ^щ('-)^Г(соз6)е{тф, -/<«</. G2.5)
Каждый уровень Eni вырожден 21 -\- 1 раз в силу различных возмож-
возможностей для ориентации орбитального момента Mz. Поскольку мы рас-
рассматриваем определенный уровень п, I, то мы можем опустить индексы п, I,
сохранив лишь т. Тогда для краткости функции, принадлежащие
уровню Eni, обозначим через
Ф-1' Ф-1+i С-.-, !>?. G2.6)
Наиболее общая функция, представляющая состояние с энергией Е°и будет
+i
Ф= 2 СгЖп- G2.7)
т=—1
1 Заряд электрона мы считаем равным —ей начало координат берем в центре
атома.
240

Вычислим, каково будет среднее значение проекции электрического
нта Dz в таком состоянии. Имеем:
Dz = ^ ф*.£>гФ.Л>= 22 с»с»>' \ <-Dzy8n-dv =
3l'(Dz)nn., G2.8)
3i
m m'
где
G2.9)
есть матричный элемент электрического момента Dz. Из G2.1) следует,
что матричные элементы энергии возмущения равны
Wmm, = - (Dz)nn,%. G2.10)
Вычислим (Dz)mm,. Подставляя в G1.10) волновые функции t|£,m из G2.5)
и имея в виду, что z = rcos6, получим:
со я . . 2я
(ГУтт, = - е $ «nir» dr ^ /W cos 6 sin 6 d% { gi(m-»')<P dq>. G2.11)
0 0 0
Если tn Ф т', то этот интеграл равен нулю, так как g*(m-m')<p есть периоди-
периодическая функция ф. Если же т — т, то второй интеграл в G2.11) есть
четная функция cos6 и поэтому равен нулю. Таким образом, (Dz) mm, = 0.
Вместе с тем в любом состоянии, принадлежащем уровню Епь среднее
значение электрического момента DzG2.9) равно нулю. Согласно G2.1)
равна также нулю и энергия возмущения. Отсюда следует, что в водо-
родоподобных атомах не может быть расщепления уровней в электрическом
поле, пропорционального полю, так как средний электрический момент
равен нулю. Расщепление, пропорциональное высшим степеням поля,
конечно, будет иметь место. В самом деле, функции электрона в поле
будут отличны от tynim Wnim — нулевое приближение!). В первом приближе-
приближении мы можем положить:
1W = 1>nim+««jm+-.., G2.12)
где ип1т—некоторый добавочный член, пропорциональный первой степени
поля Щ.
Расчет показывает, что в этом приближении, когда уже учитывается
деформация атома, средний электрический момент Dz не равен нулю,
а пропорционален полю Щ:
Ъг = а%. G2.13)
Этот момент есть результат поляризации атома в поле. Потенциальная
энергия этого момента в поле Щ равна
W=-jP, G2.14)
что соответствует работе поляризации:
ё
W^-\%d (Dz)
о
при увеличении поля от нуля до %.
16 Д. И. Блохиицев 241

Вместе с тем смещение квантовых уровней будет пропорционально
квадрату поля Щ2. В расчет величины а, носящей название поляризуе-
поляризуемости, мы входить не будем1.
Иное положение вещей имеет место в атоме водорода, где помимо
вырождения, связанного с различными ориентациями орбитального момента,
имеется еще «/«-вырождение. Каждому квантовому уровню Еп принадлежит п2
функций вида G2.5), различающихся как числом I A = 0, 1, ..., л—1),
так и числом т. Удерживая в памяти номер уровня п, мы можем выписать
функции, принадлежащие уровню Еп, в виде
i|)?m. / = 0, 1, 2,...,л-1; /n=0, ±[1,...,±/, G2.15)
всего л2 таких функций. Наиболее общим состоянием, принадлежащим
уровню Еп, теперь будет
п-1 +1
2 2
J = 0 т=—I
G2.16)
Средний электрический момент Dz, в состоянии ср, ввиду участия
в суперпозиции G2.16) функций с различными значениями I не равен
нулю (см. расчет в следующем параграфе). Поэтому и средняя добавочная
энергия в поле % в состоянии ср
W=-tDt
G2.17)
будет, вообще говоря, не равна нулю и пропорциональна полю. В резуль-
результате смещение уровней будет пропорционально полю, что и наблюдается
на самом деле. Таким образом сущность различия в поведении в электри-
электрическом поле атома водорода и водородоподобных атомов заключается
в том, что в первом случае в группе состояний, принадлежащих уровню Еп,
имеется электрический момент, а во втором случае в группе состояний
атома, относящихся к уровню Eni, электрический момент отсутствует
и появляется только в результате поляризации (деформации) атома.
§ 73. Расщепление спектральных линий атома водорода
в электрическом поле
Вывод общей формулы для расщепления уровней водорода в элек-
электрическом поле читатель найдет во многих курсах2. Мы ограничимся
разбором примера, на котором легко выяснить всю сущность дела. Именно,
мы рассмотрим расщепление второго квантового уровня атома водорода
(л = 2) (первый уровень не вырожден и потому не расщепляется). Таким
образом, мы берем наиболее простой случай.
Указанному квантовому уровню принадлежат четыре состояния, харак-
характеризуемых следующими волновыми функциями: •»
^2оо= ^20 (г)' ^оо (s-терм),
1
(р-терм).
G3Л)
1 См., например, Г. Бете, Квантовая механика простейших систем, ОНТИ,
1935, стр. 202 — 215, где дан расчет а для Не. Заметим, что формула для поляризуе-
поляризуемости а может быть получена из теории дисперсии (§ 92), если там положить частоту
внешнего поля ш = 0.
2 См., например, Л. Ландау и Е. Лифшиц, Квантовая механика, Гостех-
издат, 1948. ,
242

Согласно B5.18)
1
G3.2)
Далее, из E0.19) получаем радиальные функции Rnl:
г
^20 = У1?е 2А1 — ~2¥
г
Р_. — р~ Ъа. '
G3.3)
~' ]/6а3 ' 2а '
где а —радиус орбиты пора, а , и -у=г — нормирующие множители.
Пользуясь тем, что * = rsin6 cos ср, у — г sin 6 sin cp, z = rcos6, мы можем
написать функции G3.1) в виде:
7 =F(r)z,
х-'у
iii-i — Т4 — |/ зЛ -^21 r " l V)
±zi«
G3.4)
• J
Наиболее общим состоянием, принадлежащим уровню £°, будет
а=1
G3.5)
Чтобы определить приближенно квантовые уровни и волновые функции
при наличии внешнего электрического поля Ш согласно теории возмуще-
возмущения, нужно решить уравнения F8.10), которые в нашем случае гласят:
4
[Е\ -E + Wp'fi] ср + Ц Wf,aca = 0; а, 0 = 1, 2, 3, 4, G3.6)
а=1
pg*e$ztp° dv. G3.7)
Из представления функций в форме G3.4) легко видеть, что все
интегралы G3.7), за исключением двух, именно,
z*dv, G3.8)
в силу нечетности подынтегральной функции относительно z, равны нулю.
Интеграл же G3.8) легко вычисляется в полярных координатах. На осно-
основании G3.3) и G3.4) имеем:
„_ , со я 2я
е$УЪ \ L Г Г
У12
\ \\
обо
Имеем
2а
я 2я
r
2а
2а
о о
z2 sin б d6 d(p = r2 U ^J cos2 6 sin 6 db dq> = ~ r2.
о о
16*

Вводя переменную
получаем окончательно
12
£4 /-/£ —
G3.8')
Напишем теперь систему уравнений G3.6) в явном виде.- На основании
сказанного о матричных элементах Wa$, получаем:
G3.6')
Определитель этой системы Д2 (Е) должен равняться нулю (см. § 68):
Е W
12
*21 C2 C
0
0
О
О
0 £°-£
О
О
О
0 £°2-£
Е.
LU L3 L2
J-П] = 0. G3.9)
Отсюда находим корни £j, £2, £3, £4, которые равны энергии возмущен-
возмущенных уровней:
£ — £» _)_ w £2 = £° — W7 2, Es — Е = Е°. G3.10)
Таким образом вырождение снято только частью: четверной уровень
расщепляется лишь на три разных1. Картина этого расщепления приведена
на рис. 54.
В результате вместо одной спектральной линии, отвечающей пере-
переходу £° —»£" (переход изображен на рисунке стрелкой а), мы получим
Е ——-—— ТРИ линии> отвечающие пере-
' ' ~~ - ' -" ходам:
(а)Е3, £4-»£J,
(b) £,->£•, .
(c) £2 -^ Е\.
Это и есть явление расщеп-
расщепления спектральных линий
Рис. 54. Расщепление уровня я=2 атома водо- в электрическом поле. [Заме-
рода в электрическом поле тим> ЧТо ради Простоты мы
рассчитали расщепление пер-
первой линии ультрафиолетовой серии Лаймана, на самом деле Штарк изучал
расщепление линий серии Бальмера (видимый свет).]
Из G3.10) и G3.8') следует, что разница Д£ в уровнях энергии Е-,
и £2 равна 6efa, т. е. Д£ «к 3- 10~8§ эв, если Ш дано в в/см. Расщепле-
Расщепление маленькое, даже для Ш = 104 в/см, Д£ — 3- 10э<?, а разность
Е\-Е\ «а 10эв.
Вычислим теперь волновые функции ср в нулевом приближении, отно-
относящиеся к уровням £1( £2, £3 и £4. Для этого нужно найти ампли-
амплитуды са из уравнений G3.6'). Подставляя в G3.6')£ = £3 = £4 = £° находим,
5ез поля
В поле
1 Без поля мы имели гамильтониан, обладающий сферической симметрией. При
наличии поля еще остается симметрия вращения вокруг направления поля.
244

что с3 и с4 Ф 0, a Cj = с2 = 0. Следовательно, для несмещенных уровней
наиболее общее состояние описывается функцией:
<P = M>S + c4i|>2, E = E\; G3.11)
с3 и с4 произвольны (вырождение не снято). Подставляя в G2.6')
Е^=Е1 = £° + ^12. получаем cs = c4 = 0, ^ = 03. Поэтому уровню £\ отве-
отвечает волновая функция
V G3.12)
Подобным же путем вычисляем для с3 = с4 = 0 и с, = — с2, и волно-
волновая функция имеет вид
. q>2 = y=-(i|>;-itf) £2 = £°-^12. G3.12')
Г Множитель—— взят из [соображений нормировки ц>х и ф2 к единице. J
Таким образом при наличии поля % волновые функции стационарных
состояний1 будут ф1( ф2 и ф3 = ^з> Ф4 = "ф"- Мы предоставляем читателю
самому убедиться, что, как и должно быть по общей теории, матрица
возмущения W в новом представлении
,dv G3.13)
будет диагональной матрицей,
W' =
ЗеаШ
0
0
0
-ЗеаШ
0
0
0
0
Ь
0
0
0
G3.14)
Отсюда следует, что полученную картину расщепления уровней мы можем
пояснить еще и так: уровни £3 и ^4 не смещаются потому, что в состоя-
состояниях ф3 и ф4 электрический момент равен нулю. Смещения же уровней
Е1 и £2 определяются тем, что в состояниях ц>1 и ф2 момент равен ЪаеЩ
и — ЪаеЩ соответственно, т. е. в первом случае он ориентирован против
поля, а во втором случае — по полю.
§ |74. 'Расщепление спектральных линий в слабом
магнитном поле
Рассмотренная в § 62 теория расщепления спектральных линий
в магнитном поле является далеко не полной, так как не учитывает муль-
типлетной структуры спектральных линий. Введем теперь в рассмотрение
и эту структуру.
Гамильтониан Н атомного электрона, находящегося в магнитном поле,
согласно F2.6) равен
haz) = //« + Ц1 (Мг 4 2sz) G4.
1 Точнее «почти стационарных». Ср. §§ 99, 101.
245

(при этом мы игнорируем члены с сШг как малые). Н° есть гамильтониан
в отсутствии внешнего магнитного поля':
V + t/(r). G4.2)
Учитывая мультиплетную структуру спектра, мы должны дополнить этот
гамильтониан членами энергии взаимодействия спина с орбитальным
движением (они, как объяснялось в § 65, обусловливают структуру
спектров). Далее, напомним замечание в § 65, согласно которому поправка
на зависимость массы электрона от скорости (релятивистский эффект)
такого же порядка, как и взаимодействие спина с орбитой. Все эти допол-
дополнительные члены в энергии электрона, обусловливающие мультиплетную
структуру, обозначим через
W*=W*(*. У> 2, s-ih^, -ih±, -ih±). G4.3)
Мы не будем раскрывать явно вид этого оператора и ограничимся
указанием аргументов, от которых он зависит. Появление в W0 операторов
импульса электрона ясно уже из того, что внутреннее магнитное поле -fflx,
создаваемое орбитальным движением электрона, зависит от скорости
электрона, а следовательно, и от его импульса1. Таким образом, полный
гамильтониан должен быть написан в виде
H = H°+W° + W, W = -^-(M, + 2sz). G4.4)
Мы будем различать два случая: первый, когда магнитное поле настолько
велико, что энергия электрона во внешнем поле W гораздо больше энер-
энергии W0, обусловливающей мультиплетное расщепление, и второй, когда
энергия во внешнем поле W гораздо меньше энергии W0 (малые магнитные
поля).
Уточним понятие «сильного» и «слабого» поля. Заметим, что энергия W0,
которой мы пренебрегаем по порядку величины, равна разности энергий
уровней в дублете (см. рис. 46). Обозначим эту величину через
/±E}r = E°nif-EQnir. G4.5)
Расщепление, создаваемое магнитным полем, равно согласно F2.13) по
порядку величины -^-j Ш. Поэтому рассмотренное в § 62 приближение
соответствует условию
^LM>\bEn,\. G4.6)
Если, например, ДЕ3у = 5,3- 1СГ15 эрг (линии Dx и ZJ в Na, см. рис. 46}
то G4.6) дает $6 > 5- Ю4 эрстед. Напротив, слабое поле Ш
определяется из неравенства W° > W, т. е.
eh
~~ Д Еjj'"
"
G4. У)
eh " %
В первом случае (сильные поля!) мы можем пренебречь величиной W0 по
1 По закону Био и Савара это поле равно:
где v — скорость электрона, а г—радиус-вектор, проведенный от электрона к точке, где
наблюдается поле &в[.
246

сравнению с W- Тогда мы получаем случай, уже рассмотренный в § 62
(простой эффект Зеемана). В случае слабых полей расстояние уровней
eh
в мультиплете АЕ}у гораздо больше -=-— &в\ поэтому в нулевом прибли-
приближении мы можем пренебречь энергией электрона во внешнем поле W по
сравнению с W° и рассматривать в качестве гамильтониана невозмущен-
невозмущенной системы
H = H°+W°, G4.8)
a W— как возмущение. Получающаяся в этом случае картина расщепле-
расщепления уровней и соответственно спектральных линий гораздо сложнее рас-
рассмотренной в § 62. Само явление носит название сложного (иногда гово-
говорят аномального) эффекта Зеемана.
Чтобы рассмотреть это расщепление, заметим, что квантовые уровни
Епц невозмущенной системы [гамильтониан G4.8)], как объяснялось в § 65,
будут вырождены 2/+1 раз, соответственно возможным ориентациям
полного момента J. При наличии внешнего поля такой уровень должен
расщепляться, так как разным ориентациям J будет отвечать разная
энергия магнитного момента во внешнем поле £$. Для того, чтобы найти
это расщепление, мы должны определить собственные значения энергии
возмущения W. Для этого напомним (ср. § 65), что состояния невозму-
невозмущенной системы с учетом мультиплетности характеризуются четырьмя
квантовыми числами п, I, /, m3-. Поэтому матричные элементы энергии
возмущения W будут иметь вид Whijm.., пчч'т'* Если мы ограничимся
первым приближением, то, как излагалось в § 68, нужно пренебречь
матричными элементами энергии возмущения, относящимися к разным
уровням невозмущенной системы. Так как у нас эти уровни нумеруются
числами п, I, /, то в нулевом приближении рассмотрению подлежат
только элементы
Wm.m'. = WnlJm]., nljm,. G4.9)
Пригодность такого приближения обеспечивается малостью магнитного
поля. Так как матричные элементы Wmm> имеют порядок величины -=—-£/в,
то условие G4.7) можно переписать в виде
vnljm,;
«1," G4.10)
что является как раз условием применимости теории возмущения. При
этом мы взяли разность энергий в пределах мультиплета (разные j и /',
но одинаковые п и /). Ясно, что для разных п и / G4.10) выполнено,
если выполнено для одинаковых п и I.
На основании сказанного дело сводится к приведению матрицы Wm.mr
к диагональному виду. Для этого выразим энергию возмущения W через
проекцию Jz наЪсь OZ полного момента J. Имеем:
, G4.11)
где Оь есть частота Лармора. Рассмотрим теперь произведение szj2. Эту
величину можно представить в виде
= Sz (Л + Ji + Jl) = Jt (Sjx + SyJy + SZJZ) +
+ (s,Jx - JMix) -4 + (szJv - Jzsv) Jv,
247

или
sz/2 = /zA7) + Q, G4.12)
Q = (szjx - Jzsx) Jx + (SlJy- Jzsy) Jy. G4.13)
Пользуясь теоремой о сложении вращательных моментов, мы можем
согласно F4.9) переписать G4.12) в виде
sJ2 = Jz^(J2-Mz + s*) + Q. G4.12')
Если мы возьмем теперь такое представление, в котором J2 есть диаго-
диагональная матрица, то тогда G4.12') можно разделить на У2 (ибо диаго-
диагональная матрица ведет себя как обыкновенная величина, а не как опе-
оператор). Поэтому в этом представлении из G4.12') получаем:
sz = ^{JZ-Mz + s*} + -f, G4.13')
и, следовательно, энергию возмущения W можно написать в виде
OL-£ • G4-14)
Матричные элементы оператора Q отличны от нуля лишь в том случае,
когда /¥=/'•
Действительно, оператор Q может быть представлен в виде
Q^yxJy-yyJoc, G4.I5)
где
yx = JvSz—JzSv, yv = JzSx—Jxsz, y- = JxSy—Jysx G4.16)
(индексы получаются циклической перестановкой). Пользуясь правилами перестановки
компонент момента (§ 64), легко доказать, что
Jxyx+Jyyv+Jzyz = O, G4.17)
Jzyx-~yxJz = ihyv, Jzyv — yyJz=—ihyx, Pzyz — yzJz = O G4.18)
(из последних равенств вытекают еще и другие путем циклической перестановки х, у, г).
Если теперь взять три проекции орбитального момента Мх, Му, Mz и три координаты
х, у, z, то нетрудно видеть, что для них имеют [место [совершенно аналогичные алге-
алгебраические равенства, именно:
Mxx+Myy+Mzz = 0, G4.17')
Mzx-xMz-=ihy, M2y—yMz=—ihx, M2z—zMz=0. G4.18')
Сравнение G4.17') и G4.18') с G4.17) и G4.18) показывает, что структура матриц
Jx, Jy, Jz в отношении ух, уц^ yz такова же, как и структура матриц Мх, Му, М:
в отношении матриц х, у, г. В § 90,Б показано, что единственные отличные от нуля
матричные элементы х, у, z имеют вид xL i±1, !/;_ ;±i.zi, ;±i (где / — орбитальное
число). Диагональные элементы хц, уц, z\\ равны нулю. Но / есть как раз номер ссб-
ственного значения /И|. Таким образом, диагональные матричные элементы х, у, г
равны нулю в представлении, в котором М2 диагоналей. Поэтому должны равняться
нулю и диагональные элементы ух, уу, yz в представлении, в котором У2 диагонален,
т. е. матричные элементы
(Yx)im., jm, = 0; {yy)jmU im, = 0; (yz)jm^ jm, = 0. G4.19)
Так как, кроме того, Jx, Jy, Jz коммутируют с J2, то их матричные элементы, не рав-
равные нулю, имеют вид j
V*)jm.tim" Vv)<m.,jm>, (^W, /m'- G4'20> I
> J ' 1 ] I
Из G4.19) и G4.20) следует, что матричные элементы Q вида Qjmjt jm> равны нулю '•■
(в чем легко убеждаемся, образуя Q из у и J по пра_вилу умножения матриц).
248

Таким образом, в интересующую нас матрицу возмущения, элементы
которой относятся к одному и тому же значению полного момента /,
оператор Q не дает никакого добавления. Иными словами, все элементы
матрицы Wm,, m'. образуются за счет части W, не содержащей Q, т. е.
У 3
за счет оператора
w
G4.21)
Так как /z, М2, s2 и У2 коммутируют друг с другом, то их матрицы
могут быть одновременно приведены к диагональному виду. Вместе с тем
приводится к диагональному виду и матрица оператора W (с элемен-
2%.
.tr i
V? l=O,j=1/z;g=Z
тГ-3/г
■">;=-'/г
Рис. 55. Расщепление уровней 2Si/2, 2Pi/2. 3/>з/2в'слабом магнитном поле
тами Wm.mAm Чтобы получить ее диагональные элементы, достаточно под-
1 i
ставить вместо /,, Мг, s2 и J2 собственные значения этих операторов.
Имея в виду, что
мы получаем
W = hOLn4
G4.22)
G4.23)
Эта формула и дает расщепление в слабом магнитном поле кван-
квантового уровня, характеризуемого числами j, l; поскольку речь идет об
одном электроне1, ls — ~. Обозначая теперь поправку W' к энергии
уровня Еп1} через АЕцт., мы можем написать G4.23) в виде
ЬЕ»т. = hOLm.jg, G4.24)
1 Ср. § 105, где дано W для системы электронов.
249

где g означает «множитель Ланде» и равен
b±lL. G4.25)
Так как m3-пробегает все значения от — / до -)-/, то, как видно из G4.24),
каждый уровень ЕпП расщепляется в слабом магнитном Цполе на 2/ -j- 1
уровней.
На рис. 55 приведена схема расщепления уровней:
2С ( J *■ 1 г\\ пт\ I • *
^*/2 I / ~ ~2
1-0
И 2Р:
8/2
I~ 2 ' 1~
При большем поле J£? сложное расщепление упрощается и полу-
получается рассмотренное выше (рис. 46). Это явление упрощения расщепле-
расщепления спектральных линий в магнитном поле при переходе от слабых полей
к сильным наблюдается на опыте1.
\н
с"
§ 75. Наглядное толкование расщепления уровней
в слабом магнитном поле (векторная модель)
Полученная нами формула G4.23) для расщепления квантовых уров-
уровней вГ-слабых магнитных полях может быть наглядно истолкована в тер-
терминах векторной модели. В магнитном по-
\2 ле квадрат полного вращательного момента
/2 и его проекция на магнитное поле /2
являются интегралами движения. Вектор
же полного момента J не является интег-
интегралом движения. Именно, вектор J прецес-
сирует вокруг направления магнитного
поля так, как это показано на рис. 56.
Если связь между орбитальным дви-
движением и спином велика, то относитель-
относительная ориентация вектора спина s и вектора
орбитального момента М( сохраняется, но
оба они прецессируют вокруг полного
момента J. Добавочная энергия W в маг-
магнитном поле равна энергии магнитных ди-
е
и, * s в
{[Д,С
поле Ж':
полей с моментами —
„—^
2[1С
Рис. 56. Прецессия полного мо-
момента J вокруг направления маг-
магнитного поля
[G5.1)
Нам нужно найти среднее значение
величины W. Jz имеет постоянное значение.
Напротив, sz есть переменная величина,
поэтому для вычисления среднего^значения W нужно вычислить сред-
среднее значение sz, имея в виду, что вектор s участвует в двух прецессион-
прецессионных движениях: вокруг вектора J и вместе с J вокруг направления маг-
магнитного поля {ОТ).
'См. Б. А. Введенский и Г. С. Ландсберг, Введение в современную
теорию магнетизма, ГИЗ, 1929.
250

Так как
^?, s), G5.2)
то нам нужно вычислить среднее значение cos {<з№, s). Из рис. 56 видно,
что
cos(J%?, s) = cos(s, J)-cos(J, &£), G5.3)
т. е.
72 = scos(s, J)-cos(J, &e). G5.4)
Но
cos(J, s%) = b-, G5.5)
и из треугольника со сторонами J, M, s получаем:
s/cos(s, J) = (sJ) = y(/2-M2 + s2). G5.6)
Из этих формул получаем
^ ^ G5.7)
Подставляя sz в выражение G6.1) для энергии W, находим
W = 0L (Jz + l) = 0LJz ( 1 + /2~2^+s2 ) . G5.8)
Если в этой формуле разуметь под /2, /2, М2, s2 их квантовые значе-
значения G4.22), то из G5.8) мы получим квантовую формулу G4.23).
§ 76. Теория возмущений для непрерывного спектра
Мы обратимся теперь к тому случаю, когда невозмущенная система
имеет непрерывный энергетический спектр. Обозначим гамильтониан этой
системы через Н°, собственные функции, принадлежащие уровню энергии
Е, — через ipfe. Уравнение Шредингера в этих обозначениях имеет вид
Я°1|>Ъ = Ei|>fc. . G6.1)
Допустим, что на эту систему действует возмущение W. Уравнение
Шредингера для возмущенной системы тогда имеет вид
(//°+W)i|>=Ei|>. > G6.2)
Если возмущение таково, что оно не нарушает непрерывного характера
спектра оператора Н°, т. е. оператор И имеет также непрерывный спектр,
то все действие возмущения сводится к изменению вида собственных
функций, принадлежащих уровню Е. Вместе с тем задача теории возму-
возмущения сводится в этом случае к нахождению функций г|).к, которые при
малом возмущении W могут мало отличаться от функции ipfe. Возможен
однако и другой случай, когда возмущение W приводит к образованию
разрывов в непрерывном спектре. Тогда в задачу теории возмущения
входит не только определение измененных волновых функций, но и опре-
определение положения и величины разрывов в первоначально непрерывном
энергетическом спектре Е.
251

Оба эти случая мы рассмотрим на простом примере частицы, свободно
движущейся вдоль оси ОХ. Уравнение Шредингера в этом случае имеет
вид:
—{ЩП^ = ЕУ° G6-3)
и имеет собственные функции и собственные значения
рх
г Х о2
Возмущенное уравнение напишется в виде
—о—-ту|У(хI|) = £'1|), G6.5)
так что W (х) есть добавочная потенциальная энергия. Значок штрих у Е
присоединен на тот случай, если спектр возмущенной системы изменится.
Без всяких ограничений мы можем положить
G6.6)
!(*). G6.7)
Однако, считая возможным применить теорию возмущений к решению
уравнения G6.5), мы будем считать, что | е | <с Е, | и (х) | < | гр£ (х) |, и будем
пренебрегать произведениями eW, ки, uW как величинами второго порядка
малости. Тогда подстановка G6.6) и G6.7) в G6.5), учитывая G6.3), дает
~^1&-Eu = \*-W (*ШМ. G6.8)
Представим и (х) в виде суперпозиции невозмущенных состояний
и(х)= ^ u(p')typ,(x)dp'. G6.9)
Подставим теперь G6.9) в G6.8), умножим G6.8) на tyP* (х) и проинтегри-
проинтегрируем по х. Имея в виду, что
мы получим:
^u(p')-Eu(p')=,z5(p'-p)-Wv,v G6.10)
[уравнение G6.8) в «/?»-представлении]. Здесь
Wv,v = ^ Цр (х) ■ W (х) i|£ (х) ■ dx = ^ ^ W (х) в * dx G6.
есть матричный элемент в «/^-представлении. Из G6.10) находим:
eb(p—p') — W,
U(P)= £(Р')-£(Р) ' (?6Л2)
В точке р'= р знаменатель G5.12) обращается в нуль. Если мы возьмем
е Ф 0, то мы получим и (р') ^ оо - б (р' — р), и наше решение ни в коем
случае не будет приближением к г|)р. Поэтому следует положить 8 = 0, т. е.
252

Подставляя это значение и (р') в G5.9) и G5.7), мы находим:
Wv,v%, (x) dp'
Е(Р')-Е(Р) ■
G6.14)
Интеграл здесь перечеркнут, что означает, что при интегрировании мы
должны исключить точку р'= р, так как в этой точке формула G6.13)
теряет смысл. К тому же, функция ty°p (х) (р' = р) уже выделена из инте-
интеграла особо1.
Необходимым условием состоятельности нашего метода решения
является малость добавка в G6.14), т. е.
\<\<(х)\. G6.15)
Из G6.13) видно, что и(р') вблизи резонансной точки р = р' будет тем
б б Е. Следова-
Следовачастицы
W(x)
меньше, чем больше р, т. е. чем больше энергия
тельно, наше приближение при-
пригодно при больших энергиях
частицы.
В произведенном расчете мы
считали, что матричный эле-
элемент Wp'p является конечной
величиной. Это будет иметь мес- —**
то в случае, если W (х) доста- ~г= ^ ^
точно быстро исчезает при
\х\ —> со, т. е. для этого воз-
возмущение должно быть сосредо-
сосредоточено в конечной области про-
пространства (рис. 57). В этом слу-
случае, как следует из наших расчетов,
непрерывным2, если добавок и мал.
Если возмущение W (х) распространяется на все пространство так, что Wv>p
бесконечно, то в первоначально непрерывном спектре могут образоваться
разрывы.
В качестве примера приведем возмущение вида
\J
Рис.57. Кривые для энергии возмущения W(x)
энергетический спектр остается
. 2qx
. 2qx
G6.16)
где X и q — некоторые параметры. Вычисляя теперь матричные элементы Wp,v
по формуле G6.11), мы получаем:
G6.17)
1 Точный смысл] знака -V- может быть определен следующим образом:
р~-Д
р
^F{p,p')dP' = UmQ { ^ F(p,p')dP'+ ^ F (p, p') dp'} .
Определенный таким способом предел носит название главного значения интеграла.
2 Если возмущение изображается кривой Ь (рис. 57), то при достаточно глубоком
минимуме могут образоваться дискретные уровни (на рисунке это изображено пункти-
пунктиром). Наш приближенный метод не дает этих уровней, так как он применим лишь для
больших Энергий Е.
253

Подставляя это значение Wpp> в G6.14), мы ввиду наличия 6-функций
сразу выполняем интегрирование и находим:
При малых К это будет пригодное приближение, но оно отказывается
служить в точках
E(p±2q) = E(p), p=Tq, G6.19)
так как в этих точках при любом А, добавок к \|>р обращается в беско-
бесконечность.
Чтобы построить приближенно решение для р — ± q, воспользуемся
тем, что уровню Е (р) принадлежат всегда две функции г|)р и ty°-p. Самое
общее решение, принадлежащее уровню Е (р), будет
i|>lp, G6.19')
где а и Р — неопределенные коэффициенты. Если в G6.7) подставить
теперь ф° вместо typ, то, повторяя все выкладки, мы получим вместо G6.8):
-ж^-~Яи=(8~Г)ф0- G6-8/)
Подставляя сюда и из G6.9), умножая на ^>р' и интегрируя по х, найдем
вместо G6.10):
u(P')(E(p')-E(j>)) = *(a6(p-p') + fi6(p + p'))-(aWp.p + fLWp.,-p) G6.10')
и, наконец, вставляя сюда значение WP'P и Wp>,-P из G6.17), получим:
«(р') (£[(р') - еКр)) =8 [«б (р - р') + Рб (р + р')] -
+ fi{6Bq-p-p')+6(-2q-p-p')}]. . G6.10")
Если р Ф ± q, то мы можем положить е = 0, и взять либо а= 1, Р = 0,
либо а = 0, р = 1. В первом случае получим прежнее решение G6.18),
во втором случае получим решение г|)_р, приближенное к ty-p-
Для р= -\-q имеем из G6.10")
и (р) [Е(р') - Е (q)] = 8 [об (g-p') + fH>{q+ p')]
3<7-Р')]}- G6.10-)
Для р' = q левая часть равна нулю и должна равняться нулю также
и правая. Имея в виду, что при £ ф 0 б (£) = 0, мы получаем:
6@) [sa-^-p] =0 G6.20)
и для р'= -q
6@) [ep-AaJ=o. G6.20')
Сокращая на 6@), получаем систему уравнений:
sa—^Р = 0, ер-А^а = о G6.21)
254

для определения а и р. Легко видеть, что для р — — q из G6.10") полу-
получается опять эта же система G6.21). Система G6.21) однородна. Из ра-
равенства нулю ее определителя получаем:
а соответствующие решения а и Р имеют вид
а = р для е= 4"о
а= —
ДЛЯ 8 =
В результате, для импульса р = ± Ц мы имеем решения:
G6.22)
G6.23)
G6.23')
G6.24)
с* с* / _[ q\ ih_i_ ( у I — гт i ih — ih ^ f 7fi ?4 l
Иными словами, в точке р= ± q энергия претерпевает разрыв. Для
импульсов, лежащих вдали от p = ±q, как было показано, е = 0 и, стало
быть, Е = Е(р). На рис. 58 изображена
кривая энергии Е в функции р: пунк-
пунктиром для невозмущенного движения,
а сплошной линией для возмущенного.
В точках р = ± q получается разрыв
величины X. Другие разрывы р ■=■ ± 2q,
отмеченные на рисунке, получатся при
расчете во втором приближении. (Вообще
разрыв получается в точках р = ± nq,
п= I, 2, 3, . ..). Таким образом получа-
получается спектр-типа, рассмотренного в § 54,
именно, спектр, состоящий из зон доз-
дозволенной энергии от Е ■= 0 до Е =
= £(а)-~ и от £ = £(о) + -о- до
о
следующего разрыва и т. д. v.
запрещенной энергии от £ = Е
до £ = £ (<7) + -у и т. д. Эти
из зон
запре-
Рис. 58. Образование разрывов [(за-
[(запрещенных полос) в непрерывном
спектре при наложении периодиче-
периодического возмущения
щенные участки энергии отмечены на оси ординат штриховкой.
При малой величине возмущенного поля X —> 0 разрывы становятся очень
узкими. Следовательно, спектр частицы, движущейся в периодическом
поле при малой амплитуде поля, является как бы обращением дискрет-
дискретного спектра, характерного, например, для атомов. В дискретном спектре
«дозволены» только некоторые значения энергии Ev E2, ..., а остальные
значения «запрещены». В рассматриваемом случае широкие участки энер-
энергии «дозволены», а некоторые узкие полоски исключены.
На рис. 58 помимо вычисленного нами разрыва в сплошном спектре
Е показано еще плавное изменение Е в функции р вблизи этих точек
разрыва. Это изменение могло бы быть получено и из нашего расчета
если бы мы учли, что решение G6.18) не годится не только в точках
Р = ± <7> где оно просто обращается в бесконечность, но и во всех точ-
точках, где
|Е(р±2<7)-£(/>)!<**,, G6.25)
255

так как в этой области импульсов добавок к Е, хотя и не бесконечен,
но велик. Таким образом, следовало бы исследовать поведение решений
в окрестности точек p— + q- Этот расчет мы опускаем1.
Существенно, что наличие этих разрывов сказывается на виде функ-
функции Е(р) вблизи разрыва и таким образом меняет число состояний грр
(которое мы можем считать пропорциональным dp), приходящихся на
интервал энергии dE. Именно, для невозмущенной задачи —Jw = —, а для
возмущенной -т§- ~ °° в точках разрыва энергии. Этот результат может
быть получен и без специального расчета. В § 54 мы показали в общем
виде, что для частицы, движущейся в периодическом поле, групповая
скорость -
l_ d£ _ d£
V — h dk — dp
на краях зон равна нулю. То, что в нашем примере групповая скорость
на краю зоны равна нулю, следует уже просто из того, что на краях
зон мы имеем не бегущие (е h ) волны, а стоячие G6.24) и G6.24').
1 Этот расчет имеется, например, в книге Л. Бриллуэна Квантовая статисти-
статистика, ОНТИ, 1934, §§ 95 — 97.

гГЛАВА XIII-
ТЕОРИЯ СТОЛКНОВЕНИЙ
§ 77. Постановка вопроса в теории столкновений
микрочастиц
Теория столкновения микрочастиц образует в настоящее время одну
из весьма обширных глав атомной механики1. В нашем курсе мы не
имеем возможности подробно излагать эту теорию и ограничимся лишь
освещением самой постановки вопроса в теории столкновений и изложе-
изложением простейших методов.
Представим себе некоторую частицу А, которую для определенности
будем считать атомом, и падающий на нее поток частиц В, которые для
определенности будем считать электронами. Поток частиц В пусть падает
по направлению 0Z (рис.59). Электроны В, сталкиваясь с атомом, могут
претерпевать изменение своего состояния в двух отношениях. Во-первых,
они изменяют направление своего движения, во-вторых, они могут отдать
некоторую часть е своей энергии Е атому2 А. В этом случае мы гово-
говорим о неупругом столкновении, или неупругом рассеянии. Если 8=0, то
столкновение называют упругим (упругое рассеяние). В опыте интере-
интересуются числом электронов (частиц В), проходящих в 1 сек через площадку
dS (рис. 59), поставленную перпендикулярно к лучу, проведенному
из центра рассеивателя А. Обозначим поток частиц, проходящих через
эту площадку и имеющих энергию Е — к, через dNs. Это число dNs про-
пропорционально размерам площади dS (поскольку она мала) и обратно про-
пропорционально квадрату расстояния до рассеивателя (г). Кроме того, dN&,
очевидно, пропорционально потоку частиц в первичном пучке N. Таким
образом,
dNs = Nq(z, 6, Ф)^, G7.1)
где TV —число частиц, проходящих через площадь в 1 см2 в 1 сек в пер-
первичном потоке, a q(e, б, ср)— некоторый множитель пропорциональности
между dNs и N. Величина —%■ есть телесный угол dQ, под которым вид-
видна площадка dS из центра рассеивателя А. Отношение -~ определяет
вероятность рассеяния в угол dQ с потерей энергии е. Это отношение
1 См., например, монографию Мотт и Месс и, Теория атомных столкновений,
ИЛ, 1951.
2 Если атом А первоначально находился в возбужденном состоянии, то может
быть и такой случай, когда он отдает свою энергию электрону В. В этом случае пер-
первоначальная энергия электрона может увеличиться на некоторую величину е. Такие
удары называют ударами «второго рода».
17 Д. И. Блохинцев 257

равно
^£=<?(8, 6, <p)dQ. G7.2)
Из G7.1) следует, что q имеет размерность площади (так как
±-, W^yjj, то
и называется дифференциальным эффективным сечением (атома А) для
неупругого рассеяния в угол dQ с потерей энергии е.
Величина
л/
б, q>)dQ, G7.3)
где интеграл взят по полному телесному углу 4я, дает так называемое
полное эффективное сечение для неупругого столкновения с потерей
энергии е. /Ve = Q.sN есть число (рассчитанное на 1 сек) частиц, потеряв-
потерявших при столкновении энергию е
при первичном потоке N частиц
через I см2 в 1 сек.
Если потеря энергии е может
, у принимать непрерывные значения,
то для потери энергии, лежащей
между е, е-fete, вместо G7.2)
следует писать:
—-.-A —q (в, б, q>)de,dQ. G7.2')
тш , В этом случае qU, б, q>)de
Падают» tm» \ , будет иметь шысл дифференЦИ-
п ггг. /~ - альиого сечения для неупругого
Рис. 59. Столкновение частиц по квантовой jc\
механике; рассеяния в угол dQ с потерей
А — рассеивающий атом, В-падающий пучок ЭНерГИИ В ИНТерВЭле 8,8 + d&.
частиц- Величина q (e, б, ф) будет в этом
случае также называться диффе-
дифференциальным сечением для неупругого рассеяния, отнесенным к интервалу
телесных углов dQ и интервалу энергии de,. Обычное обозначение: «сече-
«сечение на стерадиан, на единицу энергии».
Заметим, что кроме е, б, ф эффективное сечение может быть функцией
и других параметров, характеризующих столкновение, например, спина
частиц.
Во всех случаях с помощью дифференциального эффективного сечения
можно дать полную статистическую характеристику процессу столкновения.
Поэтому задача в теории столкновений сводится к вычислению сече-
сечения q{&, 6, ф).
Как мы увидим, эта величина, в свою очередь, вполне определяется
амплитудой рассеянных волн.
Оставляя на время вопрос о методах вычисления этой величины в квантовой меха-
механике, рассмотрим, в каких случаях следует для расчета столкновения применять кван-
квантовую механику, а в каких случаях—классическую механику.
Для этого рассмотрим, как протекает столкновение, если применять законы клас-
классической механики. На рнс. 60 изображен атом А с центром в О. Вокруг него прове-
проведена сфера радиуса а, вне которой силы между атомом А и падающей частицей В ма-
малы. Эту сферу мы будем называть сферой действия 1. Частица В, двигавшаяся перво-
1 Эта сфера не всегда может быть определена. Например, для закона Кулона
U— , и ни о какой сфере говорить не приходится. Сферу действия можно опре-
определить лишь в том случае, когда силы достаточно быстро убывают.
258

начально вдоль оси BZ, попадая в эту сферу, будет претерпевать отклонение так, как
показано на рис. 60 (приведен случай отталкивания А и В). Опустим из центра
атома перпендикуляр на первоначальное направление движения частицы BZ. Пусть
длина этого перпендикуляра есть Q. Его называют параметром удара (или прицельным
расстоянием). Частица, имеющая определенный параметр удара, отклонится на вполне
определенный угол 6 так, что q=qF), 6=6(q). Частицы, имеющие параметры удара
между q и Q-j-^Qi отклонятся на углы, лежащие между 0 и b-\-db (угол ер мы сейчас
не рассматриваем, предполагая сферическую симметрию поля атома А). Если предста-
представить себе поток первичных частиц, проходящих через площадку в 1 см2, то из них
в'Ив
2прйр
Рис. 60. Столкновение частицы В с атомом А по классической
(случай отталкивания)
механике
отклонятся на углы G, в-j-de те, которые проходят через кольцо, образованное кругами
радиуса q и Q-f-^Q- Площадь этого кольца есть 2лд dg (рис. 60).
Поэтому на угол 0, 6 —j— cfб отклонятся все те частицы из первичного потока, кото-
которые пойдут через площадку 2яд dq (рис. 60). Стало быть, величина 2я dq и есть эффек-
эффективное сечение для отклонения на угол 0, 6-j-rf6.
Выражая dq через d&, найдем дифференциальное эффективное сечение
! db
G7.4)
Это классическое выражение для q F) не всегда будет применимо к микростолкно-
микростолкновениям. Действительно, ошибка в определении параметра удара Дд должна быть меньше
самого параметра q. С другой стороны, определение q с точностью Дд вносит неопре-
h
деленность в импульс, перпендикулярный первоначальному движению Дрх— -—, а сле-
следовательно, и неопределенность в угле отклонения Дб = ——=- (р— первоначаль-
ный импульс частицы). Отсюда, имея в виду, что 6 > Д6, q > Дд:
6 > 1 . G7.5>
Отсюда видно, что рассмотрение малых отклонений методами классической механик»
бессмысленно. Для рассмотрения же отклонений, удовлетворяющих условию G7.5),
необходимо соблюдение общего условия применимости классической механики, именно,
17* 259

изменения потенциала U (г) на протяжении длины волны % должно быть мало:
1 dU (г) , . . 77 ..
_______ А, «1. G7.6)
Пусть потенциал рассеивающей частицы меняется существенным образом на про-
протяжении а, т. е. а есть по порядку величины область действия потенциала, или
радиус сферы действия. Тогда условие G7.6) может быть заменено более мягким
условием
>.«в G7.7)
^см. § 36). Длина волны ^-электронов с энергией в несколько электроновольт равна,
по порядку величины, 10~8 см, такого же порядка и размеры области а, внутри кото-
которой существенно меняется потенциал в атоме. Поэтому при столкновениях электронов
с атомами G7.7) не соблюдается и необходимо применять квантовую механику. При
•столкновениях а-частиц Ск~10'13 см) с атомом условие G7.7) выполнено и можно
■ограничиться классическим рассмотрением задачи. Однако при столкновениях а-частиц
^нуклонов, вообще тяжелых частиц) с ядром, для которого радиус сферы действия
а—1СГ13 см, опять имеем X—а, т. е. необходимо квантовомеханическое рассмотрение
задачи.
Рассмотрение столкновения лишь с одним атомом, вместо рассмотрения столкнове-
столкновения с совокупностью атомов, образующих газ или жидкое, или, наконец, твердое, тело,
само по себе является абстракцией, пригодной далеко не всегда. Рассматривая лишь
один атом, мы предполагаем, что частица до столкновения с атомом движется свободно.
В этом—самая сущность постановки проблемы о попарном столкновении. Чтобы оценить,
когда такая постановка вопроса возможна, рассмотрим средний путь (свободный пробег),
который частица В пробегает без столкновения в совокупности атомов, образующих
тело.
Для определенности рассмотрим лишь упругие столкновения. Введем критерий
того, что частица В не взаимодействовала с .атомом А (двигалась свободно). В качестве
такого критерия будем считать некоторый угол отклонения 60. Если угол отклонения
6 < 60, то мы будем считать, что частица не отклонилась — двигалась свободно, если
6 > 60, то, напротив, будем считать, что взаимодействие имело место. Эффективное Qo
для отклонения на углы, большие 60, равно
-\
q (е, в, ф) dQ. ■ G7.8)
Знак Qo показывает, что при интеграции мы исключаем малые отклонения (8 < 60). Пред.
ставим теперь себе поток N частиц В, проходящих через площадку в 1 см2. При про-
прохождении длины dx этот поток пронижет объем A см2) dx. Если через п обозначить
число атомов в 1 см3 тела (газообразного, жидкого или твердого), то в указанном
объеме поток частиц В встретит я-A cM2)-dy атомов А. Вероятность столкновения
с одним из атомов А одной из частиц В при прохождении слоя dx равна
cM2).dx=Q0ndx. G7.9)
Обозначим через N (х) величину потока неотклоиенных частиц на глубине х внутри
взщества. Согласно G7.9) убыль этого потока при прохождении слоя х, x-\-dx будет
d-^=-N(x)Qon. G7.10)
Отсюда находим
N(x)=Noe-Qanx . G7.11)
Стало быть, величина
w (x) = e~Ql>nx G7.12)
есть вероятность пройти путь х без столкновения. Следовательно, средний свободный
260

путь / равен
со
[ Q~ . G7.13)
Для того, чтобы мы и в самом деле могли считать частицу, проходящую путь /, сво-
свободно движущейся относительно какого-нибудь из атомов тела, нужно, чтобы свободный
пробег был больше сферы действия а. Иначе частица все время будет находиться в сфе-
сфере действия того атома, с которым ей предстоит столкнуться. Таким образом, условие
применимости теории попарных столкновений как в классической, так и в квантовой
механике есть
Т>а. ' G7.14)
Если сфера действия а не может быть определена, то применение теории попарных
столкновений становится по меньшей мере сомнительным (во всяком случае, для тех
столкновений, для которых / мало).
В квантовой механике условие G7.14) должно быть дополнено еще одним условием
специально квантового характера. Нас интересуют изменения импульса (и энергии) ча-
частицы при столкновениях. Состояние с определенным значением импульса р есть волна
, 2я/г
де Броиля с длиноп волны А,= .
Р
Из условия G7.14) следует, что нам нужно рассматривать движение свободной
частицы на протяжении свободного пробега /, т. е. мы должны иметь дело с группой
волн, размеры которой не превышают /. В такой группе, вообще говоря, Др2 =£0 — это
состояние с неопределенным импульсом. Чтобы можно было пренебречь этой неопреде-
неопределенностью (и оперировать тогда с монохроматической волной), нужно, чтобы
/>А,- G7.15)
В случае невыполнения условий G7.14) и G7.15) необходимо рассматри вать столк-
столкновение сразу со всей совокупностью атомов А или искать особые обходные пути, кото-
которые позволили бы обойти трудности такой прямой постановки задачи.
§ 78. Расчет упругого рассеяния приближенным мето-
методом Борна
Ограничиваясь исследованием упругого рассеяния, мы можем не рас-
рассматривать внутренней структуры атома1 А. Действие атома А на падаю-
падающие частицы В можно в этом случае рассматривать как действие силового
центра. Если атом обладает сферической симметрией, то поле, создаваемое
этим атомом, будет полем центральных сил. Имея в виду именно этот
случай, обозначим потенциальную энергию частицы В в поле атома А че-
через U (г) (г — расстояние от центра А до В). Энергию частицы В обозна-
обозначим через Е. Если считать, что U (г) == 0 при г=оо, то мы должны взять
Е > 0, так как нас интересует такой случай, когда частица В с энергией
Е движется из бесконечности к атому А. Согласно общей теории движе-
движения в поле центральных сил такие состояния частицы В возможны лишь
для Е > 0.
Обозначая волновую функцию частицы В через гр (х, у, г), мы можем
написать для нее уравнение Шредингера в виде
-■^а1|> + £/(гI|> = Е1|> G8.1)
(jj, — масса частицы В). Потенциальную энергию U (г) мы будем считать
достаточно быстро убывающей с возрастанием расстояния г от атома А.
1 Напротив, при расчете неупругих столкновений неизбежно приходится рассмат-
рассматривать структуру атома А. так как при неупругом столкновении изменяется квантовое
состояние этого атома.
261

Введем волновое число
, 2 _ 2цЕ _ р_ ._,„ п\
"• , /г2 /г2 ' ' '
где р — импульс частицы. Обозначим далее
|{7(r) = V(r). G8.3)
Тогда уравнение G8.1) можно переписать в виде
V2^ + ft2^ = V(r)% G8.1')
Решения этого уравнения, принадлежащие энергии Е, очень силь-
сильно вырождены и имеют весьма разнообразную форму.
Мы должны взять такие решения, которые соответствовали бы по-
поставленной физической задаче, т. е. чтобы для больших расстояний от
атома А решение ty были бы совокупностью плоской волны, представляю-
представляющей поток падающих частиц В, и расходящейся волны, представляющей
рассеянные частицы [в общем решении уравнения G8. Г) могли бы, напри-
например, присутствовать еще и сходящиеся волны].
Соответственно этому представим ip в виде суперпозиции:
G8.4)
где ty° представляет поток падающих частиц, а ц —поток рассеянных.
Считая, что падающие частицы движутся вдоль оси 0Z, мы возьмем ч}H
в виде
0 = Je^_ L3=l см3. - G8.5)
Выбранная нормировка функции гр° означает плотность падающих частиц
11|)° |2 = 1 см'3: одну частицу на единицу объема. При этом поток по фор-
формуле B9.5) будет равен
N = Jz = — 1 f p = v \ г|5° |2 = v (сек'1 ■ еж), G8.6)
где V — — = — есть скорость частиц. Функция и, изображающая состоя-
состояние рассеянных частиц, для больших расстояний г от центра атома
должна иметь вид расходящейся волны:
Акт
и (г, 6) = Л F)-^—, G8.7)
Г-УОО
где Л@) есть амплитуда рассеянной волны, а б —угол между г и 0Z,
т. е. угол рассеяния.
Вычислим теперь поток рассеянных частиц на большом расстоянии
от атома. Из формулы для потока частиц B9.5) и из G8.7) следует, что
поток рассеянных частиц будет равен1:
Отсюда поток через площадку dS будет
Q. ' G8.9)
1 См. E2.3). Остальные компоненты /е, /ф в поле центральных сил будут
равны нулю [А F) действительно!]. Заметим еще, что если бы в G8.7) мы взяли
g+ikr вместо e—ikrt то мы получили бы сходящийся поток.
262

И, следовательно, из G8.9) и G7.6) находим:
Ш. G8.10)
Таким образом, для вычисления эффективного сечения q(b) достаточно
знать амплитуду рассеянной волны A(Q). Чтобы найти рассеянную
волну и, мы будем считать V (г) в G8.1') возмущением и применим для
решения уравнения G8. Г) методы теории возмущений1. Подставляя
G8.4) в G8. Г) и пренебрегая членом Vu как членом второго порядка
малости, мы получим:
V2u + k2u = Vty°- G8.11)
Нам нужно теперь найти решение этого уравнения, имеющее асимптоти-
асимптотическую форму G8-7). Вместо разложения и по невозмущенным функциям
мы применим для решения G8.11) более прямой метод. Именно, рас-
рассмотрим функцию
ф(г, Ц = Ф0(г)е~ш, G8.12)
где г—радиус-вектор точки х, у, z, a t будем рассматривать как время,
соответственно этому, со —как некоторую частоту. Будем далее, рас-
рассматривать Ф как скалярный потенциал, создаваемый электрическими
зарядами, распределенными в пространстве, с плотностью
Q(r,t) = Qo(r)e^K G8.13)
Из электродинамики известно, что потенциал удовлетворяет уравнению
Даламбера
где~с — скорость распространения электромагнитных^волн. Решение урав-
уравнения G7-14) известно: именно, если брать волны, излучаемые заря-
зарядом Q(r',t)dv' (мы подразумеваем, что dv' = dx' dy' dz'), расположенным
в точке г', то электрический потенциал в точке^г в момент времени
t равен *
ф(г, 0=^ —-—jV_ri -dv', ' G8.15)
где | г'— г | есть расстояние от точки г', в которой расположен заряд
Qdv', до точки наблюдения г. Подставляя в G8.15) Ф из G8.12) и Q из
G8.13) и сокращая на е~ш, получаем:
Ф0(г)=^-И |Г>_Г| dv'. G8.16)
Если мы подставим в уравнение Даламбера Ф G8.22) и Q G8.13) и сокра-
сократим на e~iat, то получим:
^ G8.17)
Сравнивая это уравнение с G8.11), мы видим, что G8.11) и G8.17)
1 Мы будем, кроме того, предполагать, что V (г) убывает с расстоянием быстрее,
нежели — (см. примечание в § 49). Матричный элемент V (г) будем считать конечным,
так что из изложенного в § 76 следует, что спектр Е останется непрерывным.
263

совпадают, если положить
Отсюда на основании G8.16) заключаем, что
G8.18)
G8.19)
есть [решение уравнения G8.11). При этом у нас уже автоматически
учтено, что и содержит лишь расходящиеся волны, так как решение
G8.15) есть решение для излучаемых, а не «всасываемых» зарядами волн
Рис. 61. Пояснение к выбору векторов, г'—
радиус-вектор от центра атома к элек-
электрону, г — радиус вектор от центра атома
в точку наблюдения R (х, у, ъ), 6 — угол
рассеяния, п0 — единичный вектор по на-
направлению первичного пучка, п — то же
по направлению рассеянного пучка
Найдем теперь вид и (г) вдали от атома А- Для этого^обозначим
единичный вектор в направлении падающего пучка (ось 0Z) через п0,
а единичный вектор в направлении вектора г через п. Преобразуем
сначала | г'— г|. Из треугольника, приведенного на рис. 61, имеем:
где г=|г|, г' = )г'|. Отсюда для г > г' получаем:
G8.20)
(/■' Л г'
— ) означает члены порядка —■ и выше.
Подставляя |г' — г| из G8.20) в G8.19) и пренебрегая в знамена-
знаменателе величиной пг' по сравнению с г, мы получаем выражение для и,
справедливое для больших расстояний г от атома *:
G8.
Подставляя сюда
чаем:
г|)°(г') из G7.5) и имея в виду, что г' = г'п0, мы полу-
u(r)=~-^^^e^-o)y'V(r')dv'. G8.21)
Т. е. для
, где а — радиус сферы действия.
264

Сравнивая G8.21) с G8.7), мы видим, что амплитуда рассеянной волны
равна
А=-^-^eWo-^'V (r')dv'. G8.22)
Введем вектор •
К = £(По-п), /< = £|no-n| = 2/:sin4 = -x-sin4-. G8.23)
Тогда, имея в виду G8.3), получаем:
А (б) = - -ш Цг \ <?ш'и (г') dv'. G8.24)
т. е. амплитуда рассеянной волны пропорциональна компоненте Фурье
в разложении потенциала по плоским волнам eiKt. Подставляя это зна-
значение А F) в G8.10), находим эффективное сечение:
]* G8-25)
Эта формула, как следует из ее вывода, приближенна. В теории столкно-
столкновения это приближение (первое приближение теории возмущений) обычно
называют борновским. Мы не можем входить подробно в рассмотрение
вопроса о точности борновского приближения и пригрдности его в тех
или иных случаяхг. Укажем лишь на то, что интенсивность рассеянной
волны | и (г) |2 вблизи рассеивающего центра должна быть мала в сравне-
сравнении с интенсивностью волны падающей |г|)°(г)|2. Из формулы G8.15)
легко оценить отношение | и |2 к | yf |2, взяв значение этих функций
в центре атома (г = 0). Считая, что силы — центральные, так что V (г') = V (г'),
и полагая в G8.15) г = 0, dv' = r'%dr' sin 6' dO' dtp', kr' = kr' cos б', после
элементарного интегрирования по углам б и ср находим
G8.26)
При k~=> са интеграл справа стремится к 0. Поэтому при достаточно
большой энергии частицы (большое к) метод Борна будет всегда^при-
годен.
§ 79. Упругое рассеяние атомами быстрых заряженных
микрочастиц
Полученная нами формула для дифференциального эффективного
сечения q @) применима для расчета упругого рассеяния достаточно
быстрых частиц. Далее, наш вывод неявно предполагал, что атом и до
удара, и после удара покоится. Если скорость падающих частиц велика,
а скорость атома до удара есть тепловая скорость, то последней можно
пренебречь. Пренебречь же скоростью после удара можно лишь в том
случае, если масса сталкивающейся частицы jj, много меньше массы
атома М. Предполагая, что все эти условия соблюдены, вычислим рас-
рассеяние частиц с массой ц и зарядом <?,. Обозначим через — eg(r")= —eQ (r")
плотность электрического заряда, создаваемого роем электронов атома
в точке г" (предполагаем сферическую симметрию q), а через Z —атомный
1 См. Мотт и М э с с и, ант. соч.
265

"Номер. Тогда электрический потенциал в точке г будет
£Ут' G9Л)
а потенциальная энергия частицы в таком поле будет равна
\g%-. G9.2)
Подставляя это значение U (г) в G8.24), получаем:
А F) = _ Jtiffi С i^!ld0' + i!Li£L С 6гкг' d0- С еЮ^ ,79
л^~ А* 4щ } /■' flU + А* 4щ } 3 I г" — г' [ • \'У-
Входящие сюда интегралы рассмотрим порознь. Для этого заметим, что
интеграл
может рассматриваться как потенциал, создаваемый в точке г" электри-
электрическими зарядами, распределенными в пространстве с плотностью
-Q(r') = eiKr'.
Потенциал ср(г') удовлетворяет уравнению Пуассона:
У2ф (г') = - 4яд (г') = — 4neiKr'. G9.5)
Из этого уравнения сразу находим ср(г'):
<P(r') = 1W"' lK|a = /CI+/CS + /Cl- G9.6)
Из сопоставления G9.4) с первым интегралом в G9.3) следует, что
Для второго, двойного интеграла получаем:
o" о (г") "*'к",' - ||р ^ * е (г) е"". G9.8)
Для выполнения интегрирования в G9.8) возьмем полярную систему
•координат с полярной осью, параллельной К, тогда
dv = r2 dr sin 6 d% dcp, Кг = /(r cos 6.
Получаем:
со 2я Я
(r) eiKt =\я(г) г2 dr^dy'i eiKr cos e sin Б db.
"о о "о
Вводя переменную cos6 = |, легко выполняем интегрирование по £ и ф
и получаем:
со
du q (r) eiKr = 4я ^ ^^ q (г) г2 dr. G9.9)
Подставляя G9.9) в G9.8) и G9.7) в G9.3), мы находим окончательное
выражение для А @):
■266

Имея в виду, что
где о —скорость частицы, и обозначая
= 4я \ ^^ q (г) г2 dr, G9.11)
о
находим окончательно:
А F) = — -^~ {Z — F F)} cosec2-2 . G9.12)
Величину F F) называют атомным фактором. Эта величина, как мы
видим, определяет рассеяние электронов по углам. Заметим, что эта же
величина определяет и рассеяние рентгеновских лучей.
Из G9.12) находим дифференциальное эффективное сечение для
упругого рассеяния электронов с энергией Е в область угла 6:
Чтобы эта формула стала более конкретной, сделаем простое предполо-
предположение о плотности eQ заряда электронного роя. Именно, предположим
{что соответствует выводам квантовой механики), что Q экспоненциально
спадает с увеличением рассеяния от центра атома:
г
Q = Qoe""; G9.14)
где а —«радиус» атома. В целом атом нейтрален, поэтому
{qdv = Z; G9.15)
отсюда находим q0 = -g-^-. Следовательно,
г
Q = -r?-re~4 G9.16)
Вычислим теперь атомный фактор:
о
где £ = /(г. Последний интеграл легко вычисляется:
Е ОО fc
Отсюда
G9.17)
и, следовательно,
|. G9.18)
Для быстрых частиц ka > 1, поэтому в G9.18) для не слишком малых
углов рассеяния можно пренебречь вторым членом выражения в скобках
267

по сравнению с единицей. Тогда получается:
G9Л9>
Эта формула совпадает с формулой для упругого рассеяния частиц
с зарядом е и массой ц в кулоновском поле ядра с зарядом Ze. Впервые
она была получена Резерфордом еще на основе классической механики.
Совсем иной результат получается для малых углов рассеяния. В то
время как из G9.19) при 6 = 0 получаем <7@) = оо, из G9.18) следует,
что при 6 = 0 q @) = const.
То обстоятельство, что для больших углов рассеяние получается
таким, как в кулоновском поле голого ядра, может быть наглядно
истолковано таким образом. Большие отклонения получаются за счет
частиц, пролетающих близко от ядра, благодаря чему на них поле роя
электронов не действует. Малые отклонения получаются, напротив, при
далеких пролетах частиц. В этом случае заряд ядра почти полностью
экранируется отрицательным зарядом электронного роя. Тогда поле очень
сильно отличается от кулоновского.
А. Рассеяние а-частиц
Для а-частиц заряд ег=+2е, масса \i = 4цн = 6,64-10~24 г, где
jj,h — масса атома водорода. Если атомный вес атома А гораздо больше 4,
то мы можем непосредственно применить наши формулы к расчету"рас-
7 сеяния а-частиц атомами, а-части-
$ f цы, излучаемые радиоактивными
\ ,' элементами, имеют скорость v яв
\ ^ у^° яз 109 см/сек. Поэтому из G8.2) по-
<|, \. ^ v'' *& лучаем волновое число k «к 1012 —
v\ '■da / j&- ^ ° — 1013 см'1. Размеры атома а %
^^л- ч\ 'У^ ,^' з. ^ 10^8 еж. Следовательно, ^а «= 104,
\ \ ''/'-V' 3^5^3з(Ра так что вплоть до очень малых уг-
^^т=". лов (sinj^lO^-lO-5) можно
Рис. 62. Рассеяние а-частиц при прохожде- пользоваться формулой G9.19) вме-
нии золотой фольги в 0,001 мм толщиной, сто G9.18). Таким образом, для
Сплошная кривая изображает q(B) в полярной а-ЧЭСТИЦ ИМееМ'
диаграмме. Числа на лучах показывают резуль-
результат наблюдения над числом рассеянных частиц. г4/2 в
Г для s'nY>r~ )■ H'a рис. 62 изображено число рассеянных а-частиц
для разных углов 6 при рассеянии на золоте.
Как уже упоминалось, формула G9.20) была впервые получена
Резерфордом из классической механики путем рассмотрения гиперболи-
гиперболических орбит а-частиц в кулоновском поле атомного ядра. Эта формула
послужила в свое время ключом к открытию ядерной структуры атома1
и носит название формулы Резерфорда. Так как вплоть до самых малых
углов б экранирование заряда ядра роем электронов не играет роли
(F(8)^0), то формула G9.20) есть квантовая формула для рассеяния
а-частиц в чисто кулоновском поле точечного заряда Ze. Таким образом,
1 См. классическую книгу Э. Резерфорд, Строение атома, ГИЗ, 1923.
268

.рассеяние в кулоновском поле оказывается одинаковым по квантовой
и по классической механике1.
Б. Рассеяние электронов
Для электронов jj,~107 г, так что борновское приближение при-
применимо лишь для электронов с энергией в несколько сот электроновольт.
Для 500 eV скорость электронов и=1,3-109 см/сек, £=1,3-109 см1,
т. е. ka ъ 1. Поэтому пренебрегать атомным фактором в G9.18) нельзя.
Эффективное сечение q F) в этом случае равно
i. G9.21)
На рис. 63 изображены кривая рассеяния электронов в Не, вычисленная
теоретически, и результаты измерений Даймонда.
Весьма замечательным обстоятельством является возможность опре-
определить из наблюдений над рассеянием электронов распределение электри-
электрического заряда в атоме. В самом деле,
наблюдая рассеяние электронов для раз-
разных скоростей v и углов б, мы получаем
q F) — дифференциальное эффективное
сечение, а из G9.21) находим тогда
атомный фактор F@), который есть функ-
функция числа /< = ^siny [см. G9:11)].
Соответственно этому будем рассматри-
рассматривать F как функцию К. Из G9.11) имеем:
(г)гйг. G9.22)
Отсюда по теореме Фурье получаем:
со
4яг2О(г)=— [ K-F(K)s\n(Kr)-dK Рис- 63* УпРУгое рассеяние в гелии:
w It J A — теоретическая кривая с учетом экра-
0 В ф
р р у р
нирования, В — резерфордовское рассея-
/7Q 23^ ние> ^ — рассеяние рентгеновского излу-
^ " ' че й К
[Причем МЫ ВОСПОЛЬЗОВаЛИСЬ Тем, ЧТО
> р р у
чения такой же длины волны. Крести-
КИ ~ РезУл"аты измерения Даймонда
Определяя атомный фактор F(К) из опыта, мы находим из G9.23)
Q (г). Величина q (г) есть средняя плотность электрического заряда в атоме,
создаваемого роем электронов. Таким образом, эта величина может быть
получена из опыта. С другой стороны, эту же величину можно вычислить
теоретически, так как вероятность того или иного положения электрона
в атоме определяется через волновую функцию | ^ |2. Как мы уже отме-
отмечали, атомный фактор F (К) может быть также определен из опытов по
рассеянию рентгеновских лучей. Это опять позволяет найти Q.
1 Формула G8.20) получена нами в борновском приближении и для sin -p- > —
гк 2 ka '
Формулу для рассеяния в кулоновском поле можно получить точно (см Мотт
иМэсси, Теория атомных столкновений, ИЛ, 1951, гл. III). Оказывается "что она
точно и для всех углов совпадает с резерфордовской формулой. В случае одинаковых
частиц, например рассеяние а-частиц в Не, квантовая механика дает иной результат.
Опыт подтверждает в этом случае вывод квантовой механики (см. Мотт н Мэсси'
цит. соч. § 4 и § 4,1).
269

Весьма интересно сравнить предсказание квантовой механики с резуль-
результатами опыта в отношении такой деликатной величины, как распределение
среднего заряда внутри атома. Опыт превосходно подтверждает теорию1.
На рис. 64 в качестве иллюстрации мы приводим величину 4ядг2 по
измерениям рассеяния рентгеновских лучей и электронов в Не и теоре-
теоретическую кривую для этой же вели-
величины, которая получается из волновой
функции гр для Не (см § 122).Заме-
122).Замечательно совпадение максимумов и эк-
экспоненциального спадания q при
Зная плотность электронов внутри ато-
атома, мы можем с помощью G9.2) определить,
энергию взаимодействия U (г) между ато-
атомом и рассеиваемым электроном. Таким об-
образом из опытов по упругому рассеянию
частиц может быть определен характер
действующих на эти частицы сил.
Еще более непосредственно этот же
вывод следует из формулы G8.24). Ампли-
Амплитуда рассеянных волн А F) зависит от ft
только через вектор К G8.23), поэтому ее
можно рассматривать как функцию К, т. е.
4 ■
J-
г-
i
/
7
if 3
к- 2
\
О 0,2 0,4 0,6 0,8 г IА0)
Рис. 64. Плотность электрического за-
заряда в Не Dярг2) в функции расстоя-
расстояния г:
I — по рассеянию электронов, 2 — по рассея-
рассеянию рентгеновских лучей, 3 — теоретическая
= А(К). Обращая тогда интеграл Фурье G8.24), найдем:
£/(/-)= —
2jt/z2
Brt)8
e~iKr A{K)dKxdKvdKz.
G9.24),
Поэтому, зная из опыта Л (К), мы найдем U (г), т. е. энергию взаимодействия.
При этом нужно иметь в виду еще следующее. На опыте мы не определяем,
непосредственно Л (К), а определяем эффективное сечение q (Q) — \ А (К)\2. Поэтому,
зная q F), мы можем найти А (К) только в том случае, если амплитуда А (К) действи-
действительна. В противном случае фаза амплитуды А (К) остается неизвестной. Как видно из
G9.24), А (К) будет действительна, если U (r)=U (—г), в частности, для центральных
сил. Далее, обращение интеграла G9.24) требует интегрирования по К.х, Ку, Kz от
— оо до -j-co. Стало быть, для нахождения U (г) мы должны знать рассеяние для
бесконечно больших импульсов рассеиваемых частиц (так как 0^.К ^ 2р/к = 4л/К).
Ограничиваясь импульсом р (энергией £ = p2/2jj,), мы можем вычислить лишь часть
интеграла G9.24):
U(r) =
2яА2
+¥
Bп\ъ I 1 ]
\ / W *J Щ/
2p
-iKr
■A(K)dKxdKv,dKz-
G9.24'),
Если отброшенная часть интеграла мала, то вместо истинной потенциальной энергии
U (г) мы получаем слаженную U (г), т. е. из опыта по рассеянию частиц с импульсом р,
следовательно, с длиной волны ^ = 2itA/p, нельзя сделать вывода об изменениях U (г)
на масштабах порядка %, так как в интеграле G9.24) отсутствуют гармоники е~гКт
с К > 4л/Х = 2р/к. Это есть выражение хорошо известного факта, согласно которому
нельзя получить изображение деталей объекта, размеры которых меньше длины волны,
применяемого для освещения света 2.
1 См. обзор X. Howard Me Millen, Rev. Mod. Phys., т. II, стр.84, 1939.
2 Разумеется, что эти же замечания полностью относятся также к определению-
q (г) через интеграл G9.23).
270

§ 80. Точная теория рассеяния. Фазы рассеянных волн
и эффективное сечение
Обратимся теперь к точному решению уравнения G8.Г):
V2i}) + Щ = V (г) гр. (80.1)'
Это уравнение отличается от уравнения D9.2), подробно рассмотренного
в отделе общей теории движения в поле центральной силы, только мно-
множителем — 2|а//г2 и порядком расположения членов. Поэтому собственное
решение уравнения (80.1), принадлежащее энергии Е = h2k2/2\i, квадрату
момента импульса М2 — к21 (I + 1) и проекции момента Мг = кт, соглас-
согласно D9.4), будет:
причем, если положить Rl = ujr, то из (80.1) получим уравнение для «(:
l = V(r)ul, (80.3)
совпадающее, по существу, с уравнением D9.10). Общее решение уравне-
уравнения (80.1), принадлежащее энергии Е = h2k2/2\i, может быть написано
в виде разложения по ортогональным функциям ipI%m(r, 6, ср):
оо т—-\-1
4>(г, 6,ф) = 2 2 С(т/?((г)У11тF,ф). (80.4)-
1=0 т=-1
Представляя решение в форме (80.4), мы тем самым ищем его в виде
суперпозиции состояний, отличающихся значением момента импульса,
(число /), и его проекции на ось OZ (число т).
Для задачи рассеяния нам нужно, как было объяснено в § 78,,
найти такое частное решение, которое асимптотически имело бы вид:
i|w = eite+4F)^-rf, (80.5).
т. е. представляло бы наложение первичной, плоской волны и волны рас-
рассеянной. Это решение обладает симметрией вращения около оси OZ
и поэтому не зависит от угла ср. Частное решение, не зависящее от ср,
получится из (80.4), если там откинуть все члены суммы с т Ф 0. Так
как Y10 F, ф) только множителем отличается от полинома Лежандра
Pj(coseI, то мы можем представить искомое решение в виде:
1> {г, 6) = ;5 С,/?, (г) Л (cos 6). (80.6).
Дальнейшая задача заключается в определении амплитуд С(. Рассмотрим,
каково будет асимптотическое выражение для функции (80.6). Согласно-
D9.15')Л^[ (г) при г—* оо имеет вид 4-^— г ' ■ Для удобства даль-
дальнейших вычислений целесообразно положить а; = —2^ + Tli и выбрать
такую нормировку для функции Rt(r), что 14=1/ft. Тогда
■ С nl \
smf kr — -^--\-r\i I
RT (rUo, = -^—ьг • (80- 7>
Cm. B5.16).
271-.

При таком выборе нормировки асимптотическое выражение для функ-
функции гр (г, 0) получает вид:
{я! , . , ., , гя! . , }
гкт—г ~г--]-гЛ! -~ihr~\—— —tilt I
е—ш —ш? ■ (80-8)
t=o
Теперь следует выбрать С1 так, чтобы (80.8) совпало с (80.5). Для
этого разложим плоскую волну elkz ■=■ eihr cos 9 по полиномам Лежандра.
Это разложение имеет вид1:
оэ ^
еш = 2 B/ + 1) е*т у~ /,+t/t (kr) PL (cos 6), (80.9)
1=0
где /i-p/2 (kr) есть функция Бесселя порядка / + XU- Физически это раз-
разложение означает представление плоской -волны в виде суперпозиции
стоячих, сферических волн, т. е. разложение по состояниям с различным
моментом импульса относительно начала координат (точка г = 0). Каждый
член суммы (80.9) есть сам по себе решение уравнения (80.1) при V (г) = 0,
т. е. для свободного движения, принадлежащее заданному моменту
импульса (число /). При больших г имеем:
j|(^) (80.10)
Полагая еще
1=0
мы можем представить асимптотическое выражение для гр(г, б) '(80.5)
в виде:
. я1 гкг-г-^- -ikr+t-h-
1=0
• (80.12)
Сравнивая (80.12) почленно с (80.8), находим:
С,е^=B1+\)е1 2, (80.13)
С\е 1 2+гт"=B/+1) + ^1. (80.13')
откуда
Л, = BZ+1) (e2iT1'-l). (80.14)
Стало быть, амплитуда рассеянной волны А F) равна
г=0
Искомое эффективное сечение, согласно G8.10), есть попросту |ЛF)|2:
оэ
= w I ? Bl +!) ^2i11' ~1)р< (cos бJ • (80-1
(=0
1 См., например, В. И. Смирнов, Курс высшей математики, Гостехиздат,
1939, т. III.
272

Полное эффективное сечение для упругого рассеяния будет равно1
(80.17)
1=0
Отсюда мы видим, что как дифференциальное, так и полное сечение
вполне определяются фазами рассеянных волн i\L. Часть полного сечения:
Q, = ^B/+ l)sin2ri, (80.18)
есть эффективное сечение для частиц, обладающих квадратом момента
импульса М2 = НЧ A+ 1) относительно центра сил. Эффективное сечение
<2, часто называют «парциальным». На рассеяние можно распространить
Рис. 65.
а— «s> рассеяние! Qj=O; b—«р» • рассеяние, Qi= — У~2. Заштрихованы области,
где Ri {r) заметно отлично от нуля
систематику термов, принятую для дискретных состояний. Тогда говорят
об «5»-рассеянии (/ = 0), «/«-рассеянии (/=1)и т.д. «ss-рассеяние сфе-
сферически симметрично, «/«-рассеяние обладает симметрией диполя. Проводя
параллель с классической механикой, можно сказать, что рассеяние 1-го
порядка соответствует частицам, проходящим на расстоянии Q, от центра
сил (q, —параметр удара), причем
Q = hVm+i) = х ущ+ту, (8о. 19)
где р — импульс частицы, К — длина волны2.
В квантовой механике состояние с определенным моментом не соот-
соответствует какому-либо определенному параметру удара q. Однако ради-
радиальные волновые функции Rt(r) имеют максимум около r = Qr На рис. 65
заштрихованы области, где R* (г) заметно отлично от нуля.
Как следует из (80.16) и (80.17), для определения рассеяния
достаточно знать фазы рассеянных волн т]. Для нахождения их требуется
найти решение уравнения (80.3) с асимптотическим поведением (80.7).
Задача эта не является простой. В общем случае необходимо численное
интегрирование 3.
Если число существенных фаз невелико, то разумно представить
экспериментально определяемое сечение q(Ь) через эти фазы. Такой спо-
способ анализа опытных данных называется фазовым анализом.
1 Так как \ Pi (cos6)dQ =
4it
Pi (cos 6) Pt, (cos 6) dQ, = 0 Aф1').
г По классической механике /M = pQ, Q—M/p.
3 Только для кулоновского поля ряд (80.15) суммируется в конечном виде и ведет
к формуле Резерфорда.
18 Д. И. Блохинцев
273

Как видно из формулы (80.18) максимальное парциальное сечение
равно j^{2l+ 1) = ~{211-1). Если фаза tj, мала, то Ql = ~Bl + \)ц{-
В том случае, когда все фазы i],«-r, целесообразно применять метод
Борна и вычислять (или определять из опыта) непосредственно А F).
Рассмотрим теперь парциальные волны, принадлежащие орбитальному
моменту I, на больших расстояниях от рассеивающего центра. Из (80.8)
видно, что такую парциальную волну можно представить в виде суперпо-
зиции первичной, сходящейся волны — и рассеянной, расходящейся
волны — :
я/ . / я! ч / та, 1
^!^ ( ) ( )), (80.20)
причем
S, = A (80.21)
Очевидно, что величина St определяет отношение амплитуды расходя-
расходящихся волн к амплитуде сходящихся первичных волн. Эта величина
называется матрицей рассеяния.
В данном случае она дается в диагональном виде
S(E) =eri^(E)blvbmm., (80.22)
Zm, I'm'
где I, m—орбитальное и магнитное квантовые числа.
Если мы будем рассматривать S (Е) для отрицательных значений Е,
т. е. для чисто мнимых значений k: k = — /1/ -^р—' = — т, % > 0, то
гр[ (г, б)г_оэ приобретает вид:
. я( гя! inl „.
; ИГ ^^ "} (80-23)
Мы знаем, что для связанных состояний присутствует только экспо-
е-пг
ненциально убывающая функция . Поэтому для связанных состояний
e2i4j (я) = 0 или J]i(E)=+io3. (80.24)
Таким образом связанные состояния, имеющие дискретные значения
энергии Е = Ev Е2, .. ., Еп, . . . приводят к условию ,,
S(£) = 0 (80.25)
для1 £< 0.
Понятие матрицы рассеяния является весьма широким и в общем
случае она может быть определена как матрица, преобразующая волны,
идущие из бесконечности, в волны, уходящие в бесконечность.
1 В частности, из этого условия можно найти терм Бальмера для водорода, если
исходить из соответствующей матрицы рассеяния (см. Д. Блохинцев, Journ. of Phys.
X. 196, 1946). Позднее С. Т. Ма показал на одном примере, что условие S(Е) = 0
может давать не только правильные уровни, но еще и некоторые лишние корни Е[,
Е'2, .... Вопрос о дополнительных условиях, исключающих эти лишние корни, остается
пока открытым.
274

Значение этой матрицы было особенно подчеркнуто В. Гейзенбергом,
который предлагал положить ее в основу квантовой механики вместо вол-
волновой функции 1.
§ 81. Общий случай рассеяния
С помощью понятия матрицы рассеяния мы можем обобщать получен-
полученные в предыдущем разделе результаты и на случай неупругого рассеяния
частиц. При этом неупругое рассеяние мы будем сейчас рассматривать фено-
феноменологически как поглощение пучка первичных частиц в рассеивающем
центре; именно, каждое неупругое взаимодействие частицы с мишенью вы-
выводит частицу из числа упруго рассеянных. Стало быть, в этом случае
амплитуда волны упруго рассеянного центром, меньше амплитуды SL волны,
падающей на центр. Т. е. |S,|<1, и, следовательно, фазы S, в этом
случае являются комплексными:
6, = 1], + ^, (81.1)
где Y/(£) описывает «поглощение» частиц центром.
Нетрудно видеть, что теперь парциальное сечение упругого рассеяния
напишется, по-прежнему, в форме
Q\ = ^Bt + l)\lSl\s, (81.2)
и совпадаете (80.18) при уг = 0. Вычислим теперь парциальное сечение
неупругих процессов Q]1-
Для этого заметим, что полное число частиц, поглощаемых центром
(или претерпевающих там реакцию), в единицу времени, равно, очевидно,
полному потоку, втекающему в этот центр. Этот поток равен
^""*r^;ds> (8L3)
где интеграл взят по поверхности, окружающей центр (ds = г2 tffi), и под
г|); подразумевается расходящаяся парциальная волна из (80.20). Под-
Подставляя эту волну в (81.3), получим после интегрирования:
/u = gB;+l)A4S(|2). (81.4)
Если в (81.3) вместо грг подставить сходящуюся волну из (80.20), то мы
hk
получим падающий на центр поток /0 = — . Парциальное неупругое сечение
QT будет равно ■— :
'о
£. (81.5)
1 В принципе можно найти S = S(H) или тг) =т| (//)• Однако эти операторные
функции крайне сложны. Тем не менее само их существование указывает на то, что
гамильтониан Н можно было бы заменить оператором 5 или rj. Несколько лет тому
назад Гейзенберг высказал интересное предположение о том, что в релятивистской кван-
квантовой механике волновая функция на малых расстояниях между частицами может быть
вообще лишена физического смысла. Физический смысл сохраняется лишь за волновыми
функциями на бесконечности (см. W. H e i s е п b e г g, Zs. f. Phys. 120,513, 1942). Так
как оператор 5 (или ц) как раз и определяет поведение волновых функций на бесконеч-
бесконечности, то Гейзенберг предложил, что оператор фазы является более фундаментальной
величиной, нежели гамильтониан. Концепция Гейзенберга остается пока общей схемой.
По-видимому, без модификации самой теории относительности для малых пространст-
пространственно-временных масштабов вообще нет никакой необходимости заменять чем-либо тео-
теорию, основанную па гамильтоновском методе (ср. Д. Б л о х и и ц е в. Вестник Моск.
госуд. университета, 1948).
18* 275.

Соответствующие полные сечения получаются суммированием по /:
-St)\\ (81.6)
5,Р) (81.7)
to, наконец, полное сечение всех процессов (упругих и неупругих) равно:
Q* = Qe + Qu = § 2 B1 + 1).A - ReSt). (81.8)
Здесь 7?eS[ означает реальную часть St.
Таким образом, неупругое рассеяние может быть описано с помощью
введения комплексных фаз.
Формально это можно рассматривать как введение комплексного
потенциала W (г) = U (г) + iV (r), так что показатель преломления среды
n(r)= I/ 1+-F становится также комплексным.
Подобное модельное рассмотрение сложной атомной системы, напри-
например атомного ядра, называют «оптической моделью».
Выведем, в заключение, важную оптическую теорему, устанавливаю-
устанавливающую связь между мнимой частью амплитуды рассеяния для угла рассея-
рассеяния 0° = 0 и полным сечением. Из (80.15) и (80.21) видно, что
где 1т Л означает, как обычно, мнимую часть. Сравнивая это с (81.8),
находим:
1тЛ @) = ^Q*. (81.10)
Это и есть так называемая оптическая теорема. Она позволяет опре-
определить мнимую часть амплитуды рассеяния для 6 = 0° из полного сечения
всех процессов.
Рассмотрим теперь два важных случая только что выведенных фор-
формул.
А. Дифракционное рассеяние
Допустим, что при параметрах удара q < R имеет место полное
поглощение. Следовательно, R имеет смысл,радиуса черного, абсолютно
поглощающего шарика.
Далее, будем считать, что 7? > -~-, здесь X— длина волны рассеива-
рассеиваемых частиц.
Только при этом предположении можно получить простые формулы.
В соответствии с формулой G9.19) это означает, что имеет место
полное поглощение для всех / < L, где L(L+ 1) = , —г- ) , L r—=kR.
Но полное поглощение парциальной волны соответствует |S,| = 0
(нет потока от центра системы). Учитывая это, мы можем переписать
формулы(81.6)и (81.7) для полного упругого и неупругого сечений в форме:
L L kR
^E m f \ldl = nR*. (81.11)
0 0 6
•276

Т. е. сечения постоянны и равны поперечной площади черного шарика.
Угловое распределение вычислится с помощью формулы G9.15), кото-
которая теперь гласит:
L
^). (81.12)
Для малых углов б и при больших L (которые здесь и существенныI
Pl(cos0)ss/O@/), где /O(z)—функция Бесселя. Поэтому
Rh
^ (81.13)
и стало быть
^ (81.14)
Это дает кривую с резким максимумом около 0 = 0° и слабыми мини-
минимумами и максимумами вдали от 0°.
Подобные угловые распределения наблюдаются в рассеянии нейтро-
нейтронов на ядрах, при условии % < 2nR или пионов на нуклонах (ср. рис. 13).
В обоих случаях имеет место сильное неупругое взаимодействие.
При %<t 2яг1А^, (го = 1,2-1(Г13 см, Л-атомный вес, a R = г0Л1/8
1^
есть радиус ядра) и при параметре удара q < R нейтрон «запутывается»
в ядре, которое является, таким образом, для него черным телом. В
случае рассеяния пионов на нуклонах, при большой энергии пионов,
где (Е > тс2, т — масса пиона) имеет место сильное неупругое взаимо-
взаимодействие для прицельных параметров q < —=1,4-10'13 см. Почти
каждый пион претерпевает при этом неупругое рассеяние (рождает новые
пионы и теряет свою энергию).
Картина упругого рассеяния при этом близка к картине дифракции
на черном шарике.
Б. Резонансное рассеяние
При взаимодействии сложных систем с частицами могут наблюдаться
резонансные явления, т. е. при определенной энергии частицы Е^ЕТ
наблюдается иногда огромный рост сечения.
Подобное положение является, например, весьма типичным для вза-
взаимодействия нейтронов с ядрами (ср. рис. 4).
Рассмотрим в качестве важного примера резонанс в S-состоянии. В этом
случае волновая функция может быть написана в виде:
p-ihr pikr »
где So — элемент матрицы рассеяния для / = 0. Ясно, что в случае резо-
резонанса So сильно меняется в зависимости от К (от энергии частицы).
Оказывается, что можно выразить So через величины, мало меняющиеся
вблизи резонанса. Для этого выразим So через логарифмическую произ-
производную на поверхности системы (например, ядра), т. е. при r~R. Пред-
Предполагается, что для г > R взаимодействие уже практически отсутствует.
Поэтому производная может быть вычислена с помощью асимптотической
1 См. В. Т. Уиттекер и Г, Н, Ватсон. Курс современного анализа. ГТТИ,
1934, том II, стр. 170.
277

функции i|H(r), с другой стороны, она определяется внутренними свойст-
свойствами системы. Поэтому
(81-16)
где слева написана логарифмическая производная от функции 0(
x — kR, a /(£) значение этой производной как функции энергии, выра-
выраженное через внутренние параметры системы (например, атомного ядра).
Отсюда:
S c (81 17}
^о- е (x+h)+if0 ' [б1Л/)
где положено f(E) — fo(E)—ih(E). Если, при некотором значении
Е = Er, fo(Er) = 0, то наступает резонанс. Действительно, в этой области
значений мы можем положить
J e=e
(81.18)
Вводя обозначения
Ге = -
найдем, что So равно
2k
(81.20)
Подставляя в формулы для упругого сечения ае = -р- ] 1 — So |2 и неупру-
неупругого аи = ~ f 1
)с|2}, получаем:
Е-Е Л- —
sin Jfei?
(81.21)
(81.22)
В этих формулах Г = Ге -]- Гг есть полная полуширина резонанса (при
|Я —Яг| = Г/2 сечение падает в два раза). Величину Г" называют частич-
частичной полушириной упругого рассеяния, Гг — частичной полушириной
реакции (неупругого рассеяния). Амплитуда упругого рассеяния склады-
складывается из двух членов: резонансного рассеяния (член обратно пропорцио-
пропорциональный \Е— Ег -}- y J) и потенциального рассеяния (член, пропорцио-
пропорциональный sinkR). Эта часть рассеяния не зависит от внутренних парамет-
параметров ядра, а только от его размеров R и от энергии частицы.
Формулы (81.21) и (81.22) были выведены впервые Брейтом и Вигне-
ром и описывают рассеяние вблизи резонанса. Они аналогичны известным
из оптики формулам для рассеяния вблизи резонансной спектральной
линии.
На рис. 4 были приведены резонансы в сечении для взаимодействия
нейтронов с ядром кислорода. Каждый из показанных там максимумов,
если вблизи нет соседних, может быть удовлетворенно описан формулами
Брейта — Вигнера.
* 278

Заметим, что резонанс является типично квантовым явлением. Как
видно из формул, при Е = Ег полное сечение
+ k* Г ~ 4л Г
может принимать огромные значения —Я2(Ге~Г), во много раз превос-
превосходящие размеры сферы действия ядерных сил (—я#2).
Например, резонанс в поглощении Хе тепловых нейтронов имеет
сечение, площадь которого в 100 000 раз превосходит площадь геометри-
геометрического сечения ядра Xe'jj5. Этот резонанс имеет большое практическое
значение в эксплуатации ядерных реакторов *.
§ 82. Рассеяние заряженной частицы] в кулоновском поле
В § 50 было изучено движение заряженной частицы в кулоновском
поле. Однако тогда мы интересовались связанными состояниями (Е < 0)
и не рассматривали случая (Е > 0), который осуществляется при рассея-
рассеянии частиц.
Следуя методике § 50, мы могли бы также найти радиальные функ-
функции RL (q) f q = — , / — орбитальное число j и для случая Е > 0.
Однако в случае рассеяния нам пришлось бы искать сложную линей-
линейную комбинацию этих функций, чтобы получить асимптотическое решение
типа (80.5). Поэтому в задаче рассеяния более целесообразно избрать
более прямой и более адекватный задаче метод.
Для этого мы будем исходить из уравнения D9.2) с неразделенными
2ue2Z Z
переменными и положим там G (/•) = ——}—-, здесь eZx и eZ% — заряды
частиц, а г—расстояние между ними.
2u.fi1 2u.£3Z Z
Обозначим теперь № — -р- , ft = — ?2' 2, перепишем уравнение D9.2)
в виде:
Г^Л = 0. (82.1)
Будем теперь искать решение г[) в виде:
$ = eihzF(r~z). (82.2)
Тогда легко убедиться, что для функции / получится уравнение:
^ + Ж{1~т~^р = 0' (82-3)
где £ = г — z. **
Представляя F (£) в виде ряда:
F(Q = ^(l + ^ + a2^+ ...), (82.4)
мы убедимся, обычным путем, что у2 = 0 и, следовательно, F (£,) регулярна
в нуле.
Далее, можно с помощью рекурентных формул вычислить коэффи-
коэффициенты ряда (82.4). Оказывается, что F (£) = 1F1 (— m, I, ikt,) (a = ft/2fe)
1 См. Д. И. Блохинцев, Мирное применение атомной энергии. Доклад на
юбилейной сессии Высшей технической школы в Праге A957).
279

есть функция, связанная с так называемой конфлюэнтной гипергеометри-
гипергеометрической функцией Уиттекера г.
Асимптотическое разложение этой функции известно2 и гласит:
ГA-1а)
Здесь Г (z) есть~гамма-функция. Выбирая теперь гр (г, 6) в виде:
г£(г, 6) = е~~"аГA-Н'а)еш1 Fx (-ia, I, ikQ, (82.6)
где
а = -^~^, ? = r-z = r (l-cos6) (82.7)
и о = р/ц — скорость частицы, получим из (81.6) с помощью (81.5) для гг
£ —> °°:
гр(г, 6)Г( ^со = / + А F) S, (82.8)
где
[— 1 а | | nihz+ialnhfr—z) /ЙО Q\
- L1 ik(r-z) -г ■■• \e ■ \ог-У)
S = i- gJfer-iainfer (82.9')
И
л (о) = 4^4
где e lT1° = n _'■ • Сравнение этих формул с обычными формулами
теории рассеяния показывает, что и падающая волна elhz и рассеянная
волна -— искажены логарифмическими множителями eialnh(-r~z'> и e~ialnkr.
Эта особенность кулоновского поля, которое медленно убывает с расстоя-
расстоянием, и поэтому при как угодно больших расстояниях искажает волны.
Поэтому решений в виде плоских или обыкновенных сферических волн
в кулоновском поле вообще не существует. Эффективное дифференциаль-
дифференциальное сечение q F) в угол б равно | А F) |2:
q F) = e*Z^f cosec4 ~ (82.10)-
совпадает с ранее вычисленным методом Борна (ср. 79.19). Однако ампли-
амплитуды А @) G9-17) и (82.9") отличаются фазой. Отличие будет невелико,,
если а= е '' 2 < 1. Это есть условие применимости метода Борна в рас-
рассматриваемой задаче.
Таким образом, мы доказали, что классическая формула Резерфорда
для рассеяния частиц в кулоновском поле строго следует из квантовой
механики, без каких-либо поправок.
1 См. Е. Т. Уиттекер и Г. Н. Ватсон, Курс современного анализа, ГТТИ,.
1934, т. II, гл. 16.
2 См. Н. Мотт и Г. М е с с и, Теория атомных столкновений, ИЛ, 1951. стр. 69.
280

ГЛАВА XIV
ТЕОРИЯ КВАНТОВЫХ ПЕРЕХОДОВ
§ 83. Постановка вопроса
Одной из важнейших задач квантовой механики является вычисление
вероятностей перехода из одного квантового состояния в другое. Эта
задача может быть обрисована следующим образом. Пусть в момент вре-
времени £ = 0 мы имеем чистый ансамбль систем, характеризуемый тем, что
какая-либо механическая величина L имеет определенное значение L— Ln.
Такой ансамбль будет описываться волновой функцией грп (х), являющейся
собственной функцией оператора L и принадлежащей собственному зна-
значению1 L = Ln. Про системы такого ансамбля говорят, что они находятся
в квантовом состоянии п.
С течением времени, благодаря действию внешних полей или в силу
внутренних причин, состояние систем может измениться.
В результате к моменту времени t наш ансамбль будат описываться
уже некоторой новой волновой функцией, которую мы обозначим через
грп(х, i). Этот новый ансамбль, возникший из прежнего, вообще говоря,
будет ансамблем с неопределенным значением величины2 L.
Если теперь подвергнуть системы, принадлежащие этому ансамблю,
сортировке по величине L, т. е. выполнить спектральное разложение по
признаку L, то получится новый ансамбль (смешанный, ср. § 17). При
этом часть систем будет иметь L — Lm и образовывать чистый ансамбль,
описываемый волновой функцией ^т{х) [Ltym(x) = Lmtym{x)], другая часть
систем будет иметь L ~ Lm- и будет образовывать чистый ансамбль грт' (х)
и т. д. О системах, которые оказались принадлежащими ансамблю
с L~Lm (тфп) говорят, что они совершили квантовый переход из
квантового состояния п в квантовое состояние т.
Сказанное может быть иллюстрировано схемой:
<=о t ^*»(х) L=Lm
L = Ln L неопределенно "—>
На этой схеме сплошной стрелкой показано изменение ансамбля,
1 В общем случае состояние может характеризоваться не одной, а несколькими
механическими величинами L, M, N, .... Соответственно этому число индексов у вол-
волновой функции будет больше \|зп г_ s_ _.
2 Исключение представляет случай, когда L есть интеграл движения. Тогда
_ ■ ^ni
Ln(x, t)=tyn (x)e h и в состоянии \|зп (х, t) опять имеет единственное значение
E=Ln.
281

происходящее само по себе, без вмешательства измерения, т. е. без
осуществления спектрального разложения по признаку L. Это изменение
ансамбля может быть найдено из уравнения Шредингера. На схеме пока-
показано, что это новое состояние ансамбля представляет собой суперпозицию
состояний с различными значениями L (сумма по т). Пунктирными
стрелками показаны изменения ансамбля, возникающие при реализации
спектрального разложения ансамбля в момент t. Как мы знаем (ср. § 17)
такое разложение происходит, в частности, при измерении. Иными сло-
словами, пунктирной стрелкой изображена «редукция пакета» (ср. § 17), при
которой суперпозиция грп (лг, t) превращается в одно из частных состояний
tym(x). Только после этой редукции и можно говорить о квантовом пере-
переходе из состояния L = Ln в состояние, скажем, L — Lm.
Таким образом понятие о квантовом переходе обязательно предпо-
предполагает помимо фиксирования начального состояния (п) также фиксирова-
фиксирование и окончательного состояния (т). Мы подчеркиваем последнее обстоя-
обстоятельство по той причине, что это фиксирование меняет состояние систем
ансамбля. Такое фиксирование будет происходить при всех взаимодей-
взаимодействиях, селективных по отношению к признаку L, т. е. производящих
спектральное разложение ансамбля г|)п(х, t) no i|)m(x), в частности, при
измерениях величины L.
Обращаемся теперь к разъяснению понятия вероятности перехода
из состояния п в состояние т. Согласно общей теории (§ 22) величина
Ртп @ = I cmn {t) I2 есть вероятность найти L = Lm в состоянии грп (х, t)
(см. схему)г. Так как при t = 0 Ртп @) равно нулю, если тФ п (для
т = п, PmJl@)=l), то вероятность Pmn(t) (тфп) называют вероятно-
вероятностью перехода из состояния грп (л:) с L = Ln в состояние i|)m(x) с L — Lm
за время t. Действительно при тфп Pmn(t) дает вероятность найти
в момент t значение L = Lm, которого при t — 0 в нашем ансамбле не
существовало, ибо Pmn@) = 0. Наиболее важными задачами из теории
квантовых переходов являются задачи на вычисление вероятности пере-
перехода из состояния с одной энергией Еп в состояние с другой энергией
Ет или, как говорят, вероятности перехода с одного квантового уровня
на другой. В связи с этим заметим, что если частица (или в общем слу-
случае система) находится под действием зависящего от времени внешнего
поля, то понятие потенциальной энергии, а вместе с тем и полной энер-
энергии лишено смысла (это не относится к кинетической энергии). Поэтому
в общем случае вопрос о переходе частицы с одного квантового уровня
на другой получает смысл лишь тогда, когда причина, вызывающая пере-
переход, действует в течение конечного промежутка времени, скажем, от
^ = 0 до t — Т. Вне этого промежутка полная энергия является интегралом
движения и может быть определена путем надлежащих измерений (см.
§§ 107 и 108). Решение уравнения Шредингера, определяющего гр(х, t)
по г|)(х, 0), представляет большие трудности. Результаты, имеющие общее
значение, могут быть получены лишь в тех случаях, когда переходы
с одного уровня на другой вызываются слабыми воздействиями, так
что эти воздействия можно рассматривать как возмущение.
При этом условии уравнение Шредингера может быть написано
в виде
ih^ = H°(x)-$+ W(x, t)$, (83.1)
где Н° (х) есть оператор полной энергии системы в отсутствии возмуще-
возмущения, a W(x, £) —возмущение. При малом возмущении оператор Я0 (х)
1 Дополнительный значок п у стп указывает на начальное состояние. В § 22
такого указания не давалось.
282

можно рассматривать как оператор полной энергии, и поэтому в этом
специальном случае включение и выключение W(x, t) имеют второсте-
второстепенное значение.
Для нахождения вероятности перехода Pmn(t) с уровня Ет на уро-
уровень Ет удобно написать уравнение (83.1) в «£»-представлении. Разложим
г|)(х, t) по собственным функциям tyk(x) оператора полной энергии //°:
У(х, Ц = ЪскЦ)ук(х)е "ь'; (83.2)
к
подставляя -ф в таком виде в (83.1), умножая на tym(x)e h и интегри-
интегрируя по х, мы получим обычным способом уравнение (83.1) в «^-пред-
«^-представлении:
'^=2^@^*4@ (83-3)
к
(причем принято во внимание, что H°tyh = Ektyh). Здесь Wmk(t) есть
матричный элемент энергии возмущения:
Wmk (t) = ^ t|4 (x) • W (x, t) % (x) ■ dx, (83.4)
a coOTft — б'оровская частота т h h для перехода Em—>Ek. В начальный
момент предполагается, что система находится в состоянии Е = Еп. Сле-
Следовательно, при t = О
сй@) = 1, если k = n, и cfe@) = 0, если k Ф п. (83.5)
Вероятность найти систему в состоянии Е=Ет в момент времени1 t
равна |ст(^)|2. Поэтому вероятность перехода из Еп в Ет к моменту t
равна
Р„ (t) = | ст (t) |2. (83.6)
Таким образом, дело сводится к определению величин ck(t) из уравнений
(83.3) с начальными данными (83.5).
Мы будем рассматривать W (x, t) как малое возмущение. Для реше-
решения уравнения (83.3) заметим, что если совсем игнорировать W, то вели-
величины ск (t) будут постоянными. Поэтому в качестве нулевого приближе-
приближения для cl(t) можно взять их начальное значение (83.5):
г? (f\ — ft /84 7'\
Подставляя эти значения в правую часть (83.3), мы найдем уравнение
для первого приближения с'т (t):
Щ = Wnn (t) еш™\ (83.8)
к
Отсюда
1^ W Ш
mn
Подставляя это первое приближение для Cm (t) в правую часть (83.3),
мы найдем уравнение для второго приближения:
1 = 2 Wnk (t) e^cV (t). (83.10)
к
1 См. § 22.
283

Так как с£' (t) суть опять известные функции времени (83.9), то, инте-
интегрируя (83.10) по времени, мы найдем c'm(t), т. е. второе приближение.
Эту процедуру можно продолжать и дальше, и она ведет к точному
решению для cm(t). Однако, вообще говоря, придется брать много при-
приближений или ограничиваться малыми отрезками времени t. Если же W (x, t)
мало, то достаточно ограничиться первым или вторым приближением.
В дальнейшем мы рассмотрим различные специальные случаи возму-
возмущений и систем.
§ 84. Вероятности переходов под влиянием возмущения,
зависящего от времени
Определим теперь вероятность перехода системы из квантового уровня
Еп в Ет под действием возмущения W (x, t), зависящего от времени.
Допустим, что возмущение равно нулю для t < 0 и для t > Т. Считая,
что Wmn(t) столь малы, что первое приближение пригодно и для t=T,
мы получаем из (83.9) амплитуду dm (t) для (>Г в виде
Т . +ОЭ
Wmn (t) e^n4t = _L ^ Wmn (t) giWdt. тфПщ (84.1)
—оэ
(Заметим, что с'т для t > Т от времени не зависят, так как энергия есть
интеграл движения.)
Полученное выражение для cfm (t) имеет простое значение. В самом
деле, возмущение W (x, t) может быть разложено в интеграл Фурье
W(x, t)= ^ W(x, а)е-шйи>. (84.2)
Отсюда по теореме Фурье получаем:
W(x, <а)=-^ \ W(x, t)eiatdt. (84.3)
Матричный элемент возмущения (83.4) на основании (84.2) может быть
написан в виде
n@ = \rfa(x)-W(x, t) qn(x)• dx =
^ ^ J (со) da, (84.4)
где Wmn(a>) есть матричный элемент компоненты Фурье частоты со. При
меняя к (84.4) теорему Фурье, находим:
+ ОЭ
(84.5)
Сравнивая это с интегралом в (84.1), мы видим, что
Cm=-^Wmn((amn). (84.6)
284

• При этом наше приближение законно, если с1т мало [это —необхо-
—необходимое условие, так как с(т @) = 0'\. Согласно (83.6) и (84.6) вероятность
перехода из состояния Еп в состояние Ет будет равна
^ (84.7)
Эта формула содержит важный результат. Как мы видим, Ртп ф О только
тогда, когда Wmn (tomn) Ф 0, т. е. переход из уровня Еп в уровень Ет
возможен лишь в том случае, когда в спектре возмущения содержится
£ £
частота comn = -^—r—-. Иными словами, переход носит резонансный
характер. Положение выглядит так, как если бы квантовая система
являлась совокупностью осцилляторов с собственными частотами, рав-
равными частотам Бора а>тп. При действии внешнего переменного воздей-
воздействия возбуждаются только те осцилляторы, частоты которых совпадают
с частотами, присутствующими во внешнем воздействии. Ниже мы про-
произведем важные приложения формулы (8ч.7) к оптическим вопросам.
Формула (84.7) выведена для переходов в дискретном спектре. Для
переходов в непрерывном спектре она должна быть несколько видоизме-
видоизменена. Рассмотрим необходимые видоизменения для переходов из дискрет-
дискретного спектра в непрерывный, считая, что система имеет и тот и другой
спектр (таков, например, спектр атомов).
Состояния непрерывного спектра характеризуются непрерывными пара-
параметрами. Мы обозначим их через а, |3, у. (В качестве таковых могут быть,
например, три компоненты импульса частицы рх, ру, pz.) Пока будем явно
писать лишь один из этих параметров и обозначим его через а. Энергия
будет функцией этих параметров £ = £(а). Соответствующей волновой
функцией будет гра(х). Тогда в (83.2) наряду с суммой по состояниям
дискретного спектра появится еще интеграл по состояниям непрерывного
-спектра (интеграл по а):
&г с iE(a)i
*)е h da- (84-8>
Считая, что функции гра(лг) нормированы к б (а—а') и повторяя выкладки,
ведущие от (83.1) к (83.8), мы найдем, что
I tE(a)-Kw
e h dx> (84.9)
если система первоначально находилась в состоянии Еп, причем
Wan (t) = ^ i|>£ (х) ■ W (х, () уп (х) их. (84.10)
Дальнейшие расчеты зависят от предположений о характере зависимости
W (х, () от времени. Мы предположим, что оно монохроматично ^при пере-
переходах в дискретном спектре обязательно нужно учитывать немонохрома-
немонохроматичность реальных возмущений, в случае же переходов в непрерывный
спектр это не обязательно и реальное возмущение можно считать моно-
монохроматическим). Итак, будем считать, что
W (х, t) = W (х) еш + W* (х) е-™(. (84.11)
Тогда
Wan(t) = Wane^ + WZne-™, (84.12)
где Wan и Wan суть матричные элементы компонент Фурье от W(x,t).
285

Подставляя (84.12) в (84.9) и интегрируя по времени, мы находим:
Са ^lhWan 1
--[£(<*)-£„+/но]
1 ih Wan i
-{E(a)-En-fa\
Так как со > О, £ (a) > 0, £n < 0, то первый член мал; второй член велик
для Е(а) = Еп-\--hat. Поэтому мы ограничиваемся вторым членом и полу-
получаем для вероятности перехода из Еп в интервал a, a + da к моменту
времени t:
2
-[E(a)-En-ha]t
— 1
Вероятность же перехода из Еп в а, а + da в 1 сек равна
Panda =
d\ca
sin
dt
[E{a)-En-ha]t
(84.13)
(84.14)
Последний множитель в (84.14) для больших t отличается от б-фукции
только множителем -г. Поэтому вероятность Panda можно написать в виде
2я
Рп (a) da = ^ [ Wan|2 б [Е (а)- Еп- hw] da.
(84.15)
Если состояние непрерывного спектра характеризуется несколькими
параметрами а, |3, у, то подобным же образом получим дли вероятности
перехода из состояния Еп в область a, a + da; fi, P + ^P; Y> Y + ^Y
в 1 сек:
Рп (а, р, Y) da dp dY =
[£ (a, p, Y) - £n - Лео] da dp dY. (84.16)
Нетрудно также получить вероятность переходов в непрерывном
спектре. Именно, беря начальное состояние фа р Y [т. е. capY @) =
= в(а —а0) 6(р—ро) 6(у —Yo)]> аналогичным путем получим для вероят-
вероятности перехода в 1 сек из а0, ро, у0 в интервал a, a + da; p Р ^Р
Y. У + dy:
(«' P. Y) - ^ («о- Ро- Yo)
(84.17)
Эти формулы показывают опять-таки резонансный характер перехода, так
как найденные вероятности отличны от нуля лишь для переходов, для
которых ..,
/гю = £(а, р, у) - £п =/гюарт, п (84. Ш
или
Асо = £ (а, р, у) - Е (а0, р0, у0) = /гюару, адТо> (84.18')
т. е. частота внешнего воздействия равна частоте Бора для возмож-
возможного перехода.
В точке резонанса вычисленные вероятности обращаются в бесконеч-
бесконечность. Однако, по соседству с этой точкой они равны нулю1. Поэтому
1 Это не совсем точно, так как согласно (84.14) мы имеем дело лишь с прибли-
приближением к б-функцпи, а не с самой б-функцией. См. § 112.
286

вероятность перехода в сколь угодно малый интервал энергий, содержащий
точку резонанса, получается конечной. Чтобы в этом убедиться, доста-
достаточно взять вместо параметров а, |3, у, нумерующих состояния непрерыв-
непрерывного спектра, какие-либо новые параметры, в число которых входит энергия.
Пусть это будут параметры Е, а, Ъ. Они суть функции а, |3, у. Имеем:
= Q(E,a, b)dEdadb. (84.19)
q(E,a,b) называют плотностью состояний на интервал энергии, на
интервал а, на интервал Ъ.
Подставляя это значение da, dp, dy в выражение для вероятностей
(84.16) или (84.17) и интегрируя по Е, мы получим нуль, если интервал
интегрирования не содержит точки резонанса, и конечное число, если
содержит эту точку. Именно, из (84.16) и (84.17) получаем:
Рп (Е, a, b) da db = ~\ WEabn |2 Q (Е, а, Ь) da db, (84.20)
PaAYo (Е, a, b) da db = -2^ | WEab> аДТо |2 q (E, a, b) da db, (84.21)
причем здесь разумеется то значение Е, которое следует из условий резо-
резонанса (84.18), или (84.18') соответственно.
В частном случае, когда за параметры а, |3, у взяты три компоненты
импульса частицы рх, р1}, рг, целесообразно рассматривать импульс конеч-
конечного состояния в полярной системе координат р, 0, ср. Тогда имеем:
u, dQ = sinQdQdq>. (84.22)
Энергия частицы есть Е = — , так что p*dp = рг~г dE = \ip dE.
Внося это в (84.22) и сравнивая с (84.19), находим:
q (Е, О, Ф) = q (£) sin 0, q (£) = цр = -1 BцK/2£1/2. (84.23)
Подставляя это в (84.20) и (84.21), находим:
Рп(Е, 0, q,)dQ = ~\WEHn\2Q(E)dQ, . (84.24)
Р„орЛ (Е, 6, ер) dQ = -^ | Wmt9, %РЛ р Q (E) dQ. (84.25)
Эти формулы дают вероятность перехода в 1 сек из состояния п или
ао> Ро> Yo в состояние с энергией Е, причем импульс частицы попадает
в телесный угол dQ.
§ 85. Переходы под влиянием возмущения, не зависящего
от времени
Если возмущение не зависит от времени, то мы можем искать ста-
ционарные решения ty(x)e h уравнения Шредингера и, следовательно,
свести задачу к решению уравнения
методы приближенного решения которого были уже рассмотрены. Однако
можно ставить вопрос и в духе теории квантовых переходов. Обе постановки
вопроса эквивалентно ведут к одним и тем же результатам1.
1 Ср. § 112, где рассмотрено столкновение методом переходов, с § 78, где та же
задача решена методом стационарных состояний.
287

Чтобы получить вероятность перехода под влиянием возмущения,
не зависящего от времени, достаточно в формулах (84.16) и (84.17) поло-
положить со = 0. Тогда условия (84.18) и (84.18') будут иметь вид:
Е(а, Р, у) = Еа или £(а, p,Y) = £(a0, ро, Yo). (85.1)
т. е. переходы возможны лишь без измерения энергии. Это следует из
общей теории, так как энергия в рассматриваемом случае есть интеграл
движения. Следовательно, переходы под влиянием возмущения, не зави-
зависящего от времени, могут быть лишь такого рода, что происходит пере-
перераспределение энергии между частями системы или изменяются какие-
либо другие механические величины (например, направление импульса
частицы).
В непрерывном спектре формула для вероятности перехода в 1 сек
из состояния £(а(>, |30, уп) в состояние Ео, a, a-\~da, b, Ъ-\-&Ъ на основа-
основании сказанного получается прямо из (84.21):
Р*Ауо (Ео, a, b)dadb = ^\ WEoabt %_ ^ ^ |3 q (Eo, a, b) da db% (85.2)
и если взять за а, |3, у импульсы, то
Pvl рЪ р2 (£о> в, Ф) dQ = *%-1 ГЕо, 3> ф, А р.f po ;2 q (£0) dQ. (85.3,
Эти формулы совпадают по виду с (84.21) и (84.25) и отличаются от них
лишь резонансным условием (85-1), выражающим закон сохранения энергии.
Заметим, что в случае не зависящего от времени возмущения не имеет
большого смысла рассматривать переходы только между дискретными
состояниями, так как условие равенства энергий начального и конечного
состояний в этом случае может соблюдаться лишь в исключительных
случаях.

ГЛАВА XV
ИЗЛУЧЕНИЕ, ПОГЛОЩЕНИЕ И РАССЕЯНИЕ СВЕТА
АТОМНЫМИ СИСТЕМАМИ
§ 86. Вводные замечания
Вопросы, связанные с проблемами взаимодействия света и микро-
микрочастиц в их полном объеме выходят за рамки квантовой механики. Они
не могут быть рассмотрены без привлечения дополнительных принципов,
касающихся законов возникновения и исчезновения электромагнитного
поля. Однако мы можем продвинуться довольно далеко, опираясь на полу-
полуфеноменологическую теорию излучения Эйнштейна, существенно базирую-
базирующуюся на законах сохранения энергии и импульса при взаимодействии
между квантовыми системами и полем электромагнитного излучения.
В самом деле, поведение квантовой системы в заданном электромагнитном
поле вполне входит в круг механических задач. Поэтому мы можем, поль-
пользуясь теорией квантовых переходов, вычислить вероятность того, что под
влиянием падающего света атом перейдет в возбужденное состояние или,
напротив, из возбужденного в более низкое. В первом случае энергия атома
увеличится на величину Ет—Еп, если Еп—энергия исходного состояния,
а Ет — энергия возбужденного, во втором — на эту же величину умень-
уменьшится. Рассмотрим сначала первый процесс.
Если мы будем считать, что добавочная энергия атома Еы—Еп заим-
заимствована от электромагнитного поля, то тем самым вероятность перехода
атома из состояния Еп в Ет мы отождествляем с вероятностью поглощения
порции энергии света, равной Ет—Еп, т. е. как раз с той величиной, кото-
которая встречается в теории Эйнштейна (вероятность поглощения кванта
света). Чтобы это отождествление было возможно (не противоречило кван-
квантовой механике), необходимо, чтобы переход атома из Еп в Ет был воз-
возможен лишь в том случае, когда разность энергий Ет—Еп равна энергии
кванта действующего света /ш, т. е. когда соблюдено условие частот Бора:
/ш = £т-£п. (86.1)
Из теории квантовых переходов мы знаем, что это как раз имеет место,
так как переход Еп—>Ет возможен лишь тогда, когда в спектре внешнего
р р
воздействия присутствует частота со = m ——= атп- В нашем случае это
означает, что в спектре падающего света должна содержаться эта частота,
иными словами, должны иметься кванты света с энергией
8 = /ш = £„-£„. (86.2)
Более того, мы знаем, что переход Еп—>Ет целиком осуществляется той
частью возмущения, которая гармонически зависит от времени с частотой
19 Д. И. Блохиицев

а>тп. Таким образом, если мы представим себе, что падающий свет разложен
на совокупность монохроматических волн, то переход Еп—>Ет полностью
реализуется за счет той волны, которая имеет частоту а>тп и соответствую-
соответствующие кванты е = hamn.
Переход атома под влиянием света из возбужденного состояния Ет
в низшее Еп, если опять применять закон сохранения энергии, нужно будет
рассматривать как излучение кванта света к=Ет—Еп. Вероятность этого
перехода мы также можем вычислить. Она будет совпадать с вероятностью
вынужденного излучения в теории Эйнштейна (вероятность излучения под
влиянием излучения).
Мы не можем, однако, в рамках механики рассматривать третий про-
процесс — спонтанное излучение атома, происходящее и в отсутствии внеш-
внешнего действия — в отсутствии, следовательно, падающего света. Если
атом находится в возбужденном состоянии в отсутствии внешнего воздей-
воздействия, то квантовая механика утверждает, что он будет сколь угодно
долго находиться в этом состоянии. Состояния с определенной энергией,
как мы знаем (§ 30), стационарны, а энергия есть интеграл движения. Между
тем опыт показывает, что атом сам собой будет переходить в нормальное
состояние, излучая свет.
Это противоречие не должно вызывать удивления. Мы с самого начала
рассматриваем чисто механическую проблему: движение электрона в задан-
заданном внешнем поле (например, в электростатическом поле ядра), и не учиты-
учитываем того, что движущийся электрон создает электромагнитное поле, кото-
которое действует и на него самого. Короче говоря, мы игнорируем обратное
действие ноля электрона на самый электрон.
С такого же рода положением мы встречаемся и в классической меха-
механике. Если мы рассматриваем движение заряженной частицы, например,
под влиянием квазиупругой силы, то мы получим ответ, что частица, имев-
имевшая в начале энергию Е, будет сохранять это значение энергии и в даль-
дальнейшем. Если же мы учтем, что заряженная движущаяся частица создает
электромагнитное поле, которое действует на нее, то мы обнаружим, что час-
частица на самом деле будет терять свою энергию — излучать свет. Классиче-
Классическая теория дает, как известно1, следующую формулу для энергии -л-,
излучаемой в 1 сек частицей, гармонически колеблющейся с частотой
со0 и обладающей электрическим моментом DKJ1/.
~df = ТЗсз~ (^кл.) » (86.3)
где (DKn J означает среднее по времени от (DKJ1 J. Обратное действие этого
излучения тормозит частицу, так что она постепенно останавливается.
Эта задача об излучении с учетом обратного действия выходит по
существу за рамки квантовой механики; она относится к квантовой электро-
электродинамике. В этой книге мы не предполагаем касаться проблем квантовой
электродинамики, далеких еще от полного решения2. Мы обойдем этот
пункт, постулируя, в соответствии с теорией Эйнштейна, что такое спон-
спонтанное излучение существует.
Имея возможность на основе квантовой механики вычислить вероят-
вероятность поглощения света, мы, опираясь на устанавливаемое в теории Эйн-
Эйнштейна универсальное соотношение E.11) между вероятностью поглощения
1 См., например, И. Е. Т а м м, Основы теории электричества, Гостехиздат,
1949, § 99.
2 Квантовая теория излучения дает возможность обосновать теорию Эйнштейна.
См. по этому поводу книги: П. Дирак, Основы квантовой механики, ОНТИ, 1937
и В. Гайтлер, Квантовая теория излучения, Гостехиздат, 1940.
290

{ сшнтаввого излучения, сможем вычислить и эту послед-
последнюю величину. Реализуем эту программу.
§ 87. Поглощение и излучение света
Для решения задачи о поглощении или излучении света согласно
изложенному в предыдущем параграфе, нам следует подсчитать вероятность
перехода атома с одного квантового уровня на другой под действием пада-
падающего света. Для этого следует прежде всего определить взаимодействие
оптического электрона в атоме со световой волной.
Предположим, что мы имеем дело с поляризованным светом, электри-
электрический вектор которого есть Ш(х, t). Помимо электрического поля имеется
еще и магнитное 3£(x,t); однако действием последнего на электрон
в сравнении с действием электрического поля можно пренебречь1. Дей-
Действие электрического поля существенно различно, смотря по тому, меняется
заметным образом поле Ш (х, i) на протяжении атома или нет. Легко дать
критерий, по которому можно различить эти два случая. Пусть падающий
свет монохроматичен (или почти монохроматичен) и имеем длину волны,
равную к. Тогда
%{х, t) = i0cos^ai0t-^^ (87.1)
( здесь <в0 = —~ ) . Нас, разумеется, интересует поле не во всем простран-
пространстве, а только внутри атома. Пусть размеры атома равны а2. Возьмем
начало координат в центре атома. Тогда в пределах атома фаза волны
2 2
2ях ла
-^— меняется на величину порядка ± —г— и если размеры атома гораздо
меньше длины волны падающего света, то изменением фазы внутри атома
можно пренебречь, так что в каждый момент времени поле внутри атома
может быть описано выражением
|(х, f) = focos(a>0*) (87.1')
и, следовательно, одинаково во всех точках пространства внутри атома.
Условие малости размеров атома в сравнении с длиной волны соблю-
соблюдается в очень широких пределах. Достаточно, чтобы X > 10~8 см
(а^10~8 см). Ультрафиолетовый и видимый свет имеют длины волн,
в тысячи раз больше 10~8 см, так что условие К > а для такого света
вполне соблюдено. Иначе обстоит дело в области рентгеновских лучей,
так как в этой области длина волны далеко не всегда превосходит раз-
Сила, действующая на электрон со стороны магнитного поля, есть сила Лореица
где v—скорость электрона, с—скорость света. Сила действия электрического поля
есть е&. В световой волне % и &в одинаковы, поэтому действие магнитного поля
в — раз меньше. Скорости электрона в атоме в 100 раз меньше с, поэтому магнитное
действие в 100 раз слабее.
2 а есть радиус области, где волновые функции заметно отличаются от 0.
19* 291

меры атома1. Задача о действии таких лучей в этом случае сложнее.
Мы начнем с рассмотрения первого случая, когда длина волны гораздо
больше размеров атома. При этом мы освободимся от частного предполо-
предположения о монохроматичности света, считая все же, что встречающиеся
в спектре длины волн велики в сравнении с размерами атома. Внутри
атома будет тогда действовать электрическое поле света, одинаковое на
всем протяжении атома, но зависящее от времени, обозначим его через
! = !(*). (87.2)
При сделанных нами предположениях легко, не прибегая к общему гамиль-
гамильтониану для электрона во внешнем электромагнитном поле, определить
вид взаимодействия электрона с электрическим полем света (87.2). Поле (87.2)
выводится из скалярного потенциала ср (г, t)= — fr= — (Шхх-\- Шуу-\-Шгг),
так что силовая функция для электрона, находящегося в точке г, в этом
поле будет равна
W{r,t)=-ey=+e (Ir) = - gb, (87.3)
где D= — ex есть электрический момент электрона, если г есть радиус-
вектор, проведенный от ядра к электрону2. Вводя еще единичный вектор 1,
параллельный направлению поля % (t) = \-Ш{£), мы можем написать (87.3)
в виде
W(r, t)= -g(f).(lD). (87.4)
Если через Н° обозначить оператор полной энергии электрона, то урав-
уравнение Шредингера для волновой функции гр (г, t) будет
lh^ = H°^+W(r,t)^. (87.5)
Величину W (г, t) будем рассматривать как возмущение, что оказывается
возможным при всех практически достижимых интенсивностях света3.
Мы поставим теперь задачу вычислить вероятность перехода атома
под влиянием светового поля с квантового уровня Еп (г|? = гр„) на кванто-
квантовый уровень £т(гр = грт). Для того чтобы можно было полностью приме-
применить к этой задаче теорию квантовых переходов, развитую в § 84, мы
сделаем предположение, что поток света начал действовать в момент
времени t = О и был прекращен в момент времени t = Т. Если Т гораздо
больше периода колебаний световых волн, то такое включение и выклю-
выключение не повлияет на спектральный состав падающего света.
Согласно (84.7) вероятность перехода Ртп из состояния Еп в состоя-
состояние Ет к моменту времени t, равному или большему Т, выражается в виде
Pmn = ^\Wmn^mn)\\ " (87.6)
1 Часто интересуются действием рентгеновских лучей на внутренние электроны
(К-оболочка). Размеры К-оболочки для элементов с большим атомным номером гораздо
меньше оболочки, образуемой внешними электронами. Это позволяет расширить область
длин волн, для которых можно пренебречь изменением фазы поля.
2 Направление электрического момента считают от отрицательного заряда к поло-
положительному, а вектор г направлен обратно: от положительного ядра к отрицательному
электрону.
3 Так, поле солнечного света равно —0,1 CGSE, в то время как атомное поле %
равно — яй Ю7 CGSE.
292

где Wmn(a>mn) есть коэффициент Фурье для частоты comn от матричного
элемента энергии возмущения W(r, t). Согласно (87.4) имеем:
(87.7;
(t) (lDnn),
где Dmn есть матричный элемент вектора электрического момента, имеющш
компоненты
= — е
Dmn = - е [
Dmn = — е \
(87.!
Из (87.7) следует, что компонента Фурье от Wmn(t) равна компонег
Фурье от Ш (t), умноженной на—(lDmn) (так как Dmn не зависит от времен
Таким образом, мы получаем, что
^mn («>«„) = - g @)mn) • ( 1 Dmn), (87
где через S (<втп) обозначена компонента Фурье от % (t), принадлежав
частоте comn, т. е. величина
+оо Т
% (comn) = ~ ^ %{t) e-ftWd* = 2^Г ^ ^ @ e-^n(d^. (87
—оо О
Следовательно, вероятность перехода из Еп в Ет согласно (87.6) р
^п = §-2|£К„п)Мштпр. (8'
Квадрат компоненты Фурье электрического поля | Щ (comn) |2 мы м
выразить через количество протекшей за время Т энергии. В самом
плотность электромагнитной энергии равна • (знаменатель 4я, a i
так как имеется еще равная электрической магнитная энергия). 1
энергии равен (где с —скорость света). Отсюда вся протекшая
1 см2 энергия равна
-J-CO
~\~оэ -]-0О
~
dt
~j-co
(а1)
~оо —оо
Интегрируя сначала по t и замечая, что
+
найдем, что
+СС,
~

[так как Щ (со) = %*( — со) ввиду действительности %{t)\. Если через £ (со)
обозначить протекшую энергию на интервал частоты dco, то
Е = ^ £ (со) dco;
о
сравнение с предыдущей формулой показывает, что
Е(<о) = с\ё(а>)\*. (87.13)
Таким образом,
Р —
Е (ffl»)
Количество протекшей энергии £(со) равно, очевидно, плотности лучистой
энергии q(co) на единичный интервал частоты со, умноженной на скорость
света и время протекания энергии Т, т. е.
Е(со) = е(со)с7\ , (87.15)
На основании (87.14) и (87.15) мы можем определить вероятность
ртп перехода из состояния Еп в Ет в единицу времени. Для этого нужно
разделить Ртп на время, в течение которого действует свет, т. е. на Т:
гтп *р
С помощью (87.15) находим, что вероятность перехода в единицу времени
будет равна
Pmn = ^ilDmJ2e(comn). (87.16)
Обозначив еще угол между вектором электрического момента Dmn и направ-
направлением поляризации светового поля 1 через вти, мы получим окончатель-
окончательную' формулу для ртп в таком виде:
ртп = % I Dmn |2 cos* erane (comn). (87.16')
Из этой формулы мы видим, что для вычисления вероятности перехода
достаточно знать матрицу электрического момента Dmn, целиком опре-
определяющуюся свойствами рассматриваемой атомной системы. К этому
важнейшему обстоятельству мы еще вернемся в дальнейшем, а теперь
установим связь вычисленной нами вероятности ртп с коэффициентами
Эйнштейна, рассмотренными в § 5.
§ 88. Коэффициенты излучения и поглощения
Согласно теории Эйнштейна вероятность поглощения кванта света
/гсо= Ет— Еп, имеющего поляризацию а и распространяющегося в телесном
угле dil в 1 сек [см. E.2)], равна
= *naQaKQ)d.Q. (88.1)
Мы же получили вероятностъ ртп в предположении, что волна плоская,
распространяющаяся в некотором вполне определенном направлении. Соот-
Соответственно этому у нас в формулу для вероятности входит лишь спек-
спектральное распределение, а не распределение по углам. Общая связь между
Qa (СО) И Qa (со, Q) еСТЬ
Qa (W) = ^ Qa
294

Так как Qa (со) конечно, a Qa (со, Q) в нашем случае отлично от нуля лишь
для одного вполне определенного направления, то плотность Qa (со, Q)
должна в отношении угла Q носить характер 6-функции:
ga(co, Q) = ea(coN(Q). (88.3)
Интегрируя (88.3) по dQ и пользуясь (88.1), находим вероятность погло-
поглощения в 1 сек для волны, распространяющейся в определенном направ-
направлении (без раствора лучей):
w = @naQ<x (СО)» ^оо.т:^
На основании закона сохранения энергии вероятность поглощения кванта
света ha>,mn должна быть равна вероятности перехода атома из состояния
Еп в Ет, т. е. Wa = рпп. Сравнивая (87.16) „_.
и (88.4), находим, что коэффициент Эйн-
Эйнштейна Ь™а для абсорбции света равен
Ca = ^5-|Dmn|-cos2emn. (88.5)
Нам нужно теперь подробнее разобраться
в значении той или иной поляризации света.
Формула для вероятности перехода ртп
{87.16) получена в предположении, что свет
поляризован в направлении /, образующем
угол 9mn с направлением электрического
момента Dmn. В коэффициентах же Эйн-
Эйнштейна Ь™а индекс a (a = 1,2) указывает на
принадлежность поляризации к одной из
выбранных за независимые Aг или /2). Мы
можем без всяких ограничений выбрать
в качестве первого направления ^(а^^)
направление, перпендикулярное к лучу и
лежащее в плоскости луча и вектора Dmn,
а в качестве второго 12 (а = 2) — направ-
направление, перпендикулярное к этой плоскости (см. рис. 66).
Полагая / = 1г, получаем
„ я
тип 2 тп'
где 6mn есть угол между вектором поляризации Dmn и направлением рас-
распространения поглощаемого излучения. Из (88.5) тогда получаем:
О
Рис. 66. Выбор независимых по-
поляризаций (/j, /2)
>mn|2sin*6mn.
(88.5')
Полагая l —
получаем
п = ~, т. е.
(88.5")
Пользуясь формулой E.11), определяющей отношение коэффициента
■спонтанного излучения а^а к коэффициенту индуцированного излучения
■ftmct = fr,?a tCM- E-7)], мы можем написать вероятность dW'r спонтанного
излучения кванта света /гсо = Ет — Еп поляризации а в телесный угол dQ,
в виде
dQ,
(88.6)
295

где со=:—HLj—- = сотя. На основании (88.5) и (88.5') получаем:
Dmn{*sm4nndQ (88.7)
для света, поляризованного параллельно 1г, и
dW'r2 = 0 (88.7')
для света, поляризованного параллельно 12.
Чтобы получить полную вероятность спонтанного излучения при пере-
переходе из состояния Ет в состояние Еп, нужно проинтегрировать dW'r\ по
всем направлениям распространения. Производя эту интеграцию, получаем:
Если уровня Ет и Еп вырождены, то одна и та же частота comn может
излучаться путем различных переходов из Ет в Еп. Суммируя (88.8) но
всем этим переходам, мы получим полную вероятность излучения частоты
comn в 1 сек. Мы ее обозначим через
дп _ 4@mn Х^ | Г) ~ |2
Величину Л^ называют также коэффициентом Эйнштейна для спонтанного излу-
излучения частоты (оотп. Наряду с Ат вводят соответствующий коэффициент для погло-
поглощения изотропного, неполяризованного излучения частоты comn:
(88.10)
где сумма взята по обеим поляризациям (а=1,2) и по всем переходам из уровня Еп
в уровень Ет. Величина /п означает степень вырождения уровня Еп. Интеграл взят по
всем направлениям распространения света. Подобным же образом можно ввести коэф-
коэффициент В\ для индуцированного излучения:
madQ, (88.10')
где fm—степень вырождения уровня Е^. Пользуясь свойствами bma, bna и ата, легко
доказать, что
t Dn t Dm in —ft^mn r>n /oo 1 i\
tmtim-lntSn, Am-n4sVm. (88.11)
Величина Ат определяет продолжительность жизни атома в возбужденном
состоянии.
Если к моменту времени t мы имеем Nт атомов, находящихся в воз-
возбужденном состоянии Ет, то среднее число атомов, спонтанно переходя-
переходящих в нижнее состояние Еп, будет за время dt равно
откуда
Ыы = Ыте~Ат* — Nme. %mn, (88.12)
где
xmn = -L. (88.I3)
771
Из этих формул следует, что хтп есть средняя продолжительность жизни
атома в возбужденном уровне Ет.
Из (88.9) получаем'.
% = ?£!* . (88.14)
тп 4т3 У ID 1г
*ттп Zj ' mn '
296

Оценим эту величину для видимого света comn да 4-1015; Dmn по порядку
величины равно — еа, где а—размеры атома, так что | Dmn| я» 2-10~18.
Отсюда находим хтп я» 1(Г8 сек, т. е. хтп > Ттп = ~-** Ю'15 сек1.
Вычислим теперь среднюю энергию, излучаемую в 1 сек в элемент
телесного угла du при переходе т—>п. Так как при каждом переходе
излучается энергия Acomn = £т — £„, то средняя энергия, излучаемая в угол
dQ, будет за 1 сек [обозначим ее через d(~j :
d (§ V dW'r- h<*mn = |§£ I Dmn |» sin2GmndQ, (88.15)
(88.16)
а полное излучение за 1 сек получим, интегрируя по всем углам Q:
dE 4o)mn I pv
~dl Зс1"' т
Как распределение излучаемой энергии по углам (88.15), так и пол-
полная энергия, излучаемая в 1 сек, совпадают с соответствующими формулами
для классического осциллятора, обладающего собственной частотой соо= tomn
и средним электрическим моментом:
(D^J2=2|Dmn|2. (88.17)
Кроме того, и поляризация света такая же, как у классического
осциллятора (именно, излучается свет лишь с поляризацией lv см рис. 66).
§ 89. Принцип соответствия
Рассмотрим излучение заряженной частицы (заряд— е), движущейся
согласно законам классической механики. Для простоты ограничимся слу-
случаем одного измерения. Период движения пусть будет то = — . Обозна-
@0
чая координату частицы через x(t), мы разложим ее в ряд Фурье:
-j-co
x(t)= 2 xue^kl, (89.1)
wk=wok, k=±l,±2,..., xk = x*Lk;
co0 будет основной частотой, a cote-—частотами обертонов. Полагая
xte=|xte|ei(Pte(, (89.2>
мы можем записать (89.1) в форме:
оо "
x(t)= E 2|xfe|cos(V + 9te). (89. Г>
fe=i
Электрический момент частицы D пусть равен ex{t), т. е.
~\~со со
D(t)= E Dke^' =* 2 2 | Dk | cos (aht + Фй), (89.3).
где
Dk = exk.
1 Именно это обстоятельство позволяет рассматривать возбужденные состояния
атома как стационарные (по крайней мере, приближенно). Ср. § 113.

Интенсивность излучения частоты wk, его распределение в пространстве
и его поляризация определяются членом
DKn. = 2|Dte|cos(V + cpte). (89.4)
Средняя энергия, излучаемая таким диполем в телесный угол dQ, равна
^ = ^-^(Окл.Jзт29^, (89.5)
а полное излучение равно
dt
где
А С 2@
= "чТгГ ("кл.) i
(Дш.J = 4 | Dh |2 [cos (cohf + ф,)]2 = 2\Dk
Таким образом, мы получаем вместо (87.5) и (87.6)
(89
.6)
(89.7)
(89.
(89.
5')'
6')
dE К
dt Зс3
Из сопоставления этих формул с (88.15) и (88.16) следует, что матричный
элемент электрического момента Dmn является полным аналогом класси-
классических компонент Фурье. Эту аналогию мы можем продолжить, если рас-
рассмотрим изменение по времени электрических моментов Dmn, взяв их
в гейзенберговском представлении. Мы считали Dmn не зависящим от вре-
времени и зависимость от времени переносили на волновые функции. Напро-
Напротив, можно считать волновые функции не зависящими от времени, а зави-
зависимость от времени перенести на операторы (матрицы), как это было в об-
общем виде для любой механической величины пояснено в § 42. Тогда мы
имеем
Dmn @ — Dmn (°) е1атп1 = DmnetfiW. (89.8)
Соответствующее представление в классической теории означает, что
временные множители eftV в (89.3) мы включаем в Dh:
Dk(t) = Dk(O)ei°kt = Dhe^. (89.8')
Таким образом, классически движущаяся частица в отношении излучаемого
ею поля может быть характеризована однорядной последовательностью
гармонически колеблющихся диполей (89.8'):
D/<V, D2ei(V, ..., Dne*V, ... (89.9)
с частотами >t
аI = со0, со2 = 2со0, . . ., соп = «со0, . .., (89.9')
представляющими основной тон и обертоны системы.
Квантовая же система характеризуется в отношении излучения также
совокупностью гармонически колеблющихся диполей, но образующих
гораздо более богатое многообразие. Именно, всю совокупность этих
осцилляторов можно представить матрицей электрического момента
) gfu>21( D
22 "■ *"" ' (89.10)
et(W
298

с частотами
также образующими матрицу
О со12 . .. соап .. .
со2] 0 ... щп ...
(89.10")
со =
Диагональные элементы Dmn(/) матрицы D(/) не зависят от времени,
так как сопп = 0, и представляют собой средний электрический момент
атома в п-и квантовом состоянии. Недиагональные элементы определяют
излучение атома и колеблются с боровскими частотами.
Таким образом, мы приходим к комбинационному принципу Ритца,
выраженному в (89.10), согласно которому частоты атомов выражаются
как разности термов -^, в противоположность выводу классической тео-
теории о кратности всех частот co,t некоторой основной частоте со0.
Еще задолго по квантовой механики Н. Бор высказал предположение, согласно
которому амплитуды классических осцилляторов Dn могут служить для определения
интенсивностей и поляризации излучения квантовых систем. Это предположение носило
название принципа соответствия. Однако до создания квантовой механики применение
этого принципа было весьма неоднозначно и, по меньшей мере, двусмысленно. В самом
деле, в теории Бора квантовые движения представлялись как движения по квантованным
орбитам. Классические амплитуды Dn относятся к движению по какой-либо одной опре-
определенней орбите. Они будут получены, если мы разложим в ряд Фурье радиус-вектор
г (t) частицы, движущейся по я-ой орбите. Излучение же происходит при переходе из
одного квантового состояния в другое, говоря на языке старой боровской теории, при
переходе с одной орбиты (п) на другую (т). Какое из двух движений следует разло-
разложить в ряд Фурье, чтобы получить коэффициенты Фурье О/г, определяющие излучение,—■
на это нельзя было дать ответа.
Однако применение принципа соответствия к переходам между уровнями с боль-
большими квантовыми числами (я > 1), сопровождающимися малыми изменениями квантового
числа (|я — т|=[&|<^я), было вполне рационально. При больших квантовых числах
л квантовые орбиты лежат очень близко друг к другу, образуя практически почти не-
непрерывную последовательность классических неквантованных орбит. Для переходов
между такими орбитами, поскольку изменение числа я мало, можно было однозначно
пользоваться принципом соответствия, считая, что интенсивность излучения определяется
классическими компонентами Фурье D/j, поскольку ввиду малого различия в я-ой и т-ой
орбите безразлично, каксе из этих двух движений подвергнуть разложению на гармони-
гармонические составляющие для определения амплитуд отдельных тонов и обертонов, т. е.
величин Djj.
Существенным затруднением для теории Бора являлась невозможность вычислить
интенсивность излучения для малых квантовых чисел и для больших их изменений.
В этой типично квантовой области переходов принцип соответствия отказывался служить,
и попытки распространить его и на малые значения я вели к двусмысленным результа-
результатам, в лучшем случае позволявшим сделать не количественные, а лишь качественные
высказывания о характере излучения.
В предыдущем мы, исходя из теории Эйнштейна, пришли к заключе-
заключению, что квантовая система поглощает и излучает, как совокупность
классических гармонических осцилляторов с компонентами Фурье электри-
электрического момента, равными Dmneifflmn'- Следовательно, для вычисления погло-
поглощения или излучения света, квантовой системой нужно вычислить погло-
поглощение или излучение классических осцилляторов с моментами Dmneiamnl.
Вычислив энергию, поглощаемую или излучаемую в 1 сек, и разделив ее
на величину поглощаемого или излучаемого кванта света /ico = Ет — Еп,
мы получим вероятность соответствующего квантового перехода в 1 сек.
299

Это утверждение может рассматриваться как современная форма прин-
принципа соответствия между квантовой и классической теорией излучения г,
§ 90. Правила отбора для дипольного излучения
Может оказаться, что некоторые из электрических моментов Dmrtl
равны нулю. Тогда переход т—>п под действием света не реализуется,,
и соответствующая частота comn не поглощается и не излучается, несмотря
на то, что уровни Ет и Еп существуют. В таком случае говорят о пра-
правиле отбора, т. е. о правиле, которое как бы отбирает из числа ecexi
мыслимых переходов Ет ?S En только некоторые, в действительности pea- ]
лизующиеся. Следует иметь в виду, что переход невозможен лишь под!
действием таких возмущений W, матричные элементы которых пропор-
пропорциональны Dmn. Так например, какой-нибудь переход т^п, невозможный
под действием света, вполне может быть реализован в результате столкно-
столкновения с электроном.
Сейчас мы рассмотрим свойства матриц Dmn для важнейших случаев
и выведем правила отбора для поглощения и излучения света.
А. Правила отбора для осциллятора
Пусть мы имеем осциллятор с массой \i, собственной частотой соо
и зарядом е. Квантовые уровни Еп такого осциллятора определяются
формулой
+ у), « = 0,1,2,3 (90.1)
Элементы матрицы электрического момента должны равняться
D = ех р^фтп1 — ру plao (m—n) t /an 9^
где хтп суть элементы матрицы координаты. В § 48 мы вычислили матрицу
координаты и нашли, что элементы ее отличны от нуля лишь для т =
= «±1. Поэтому мы получаем правило отбора:
Dmn ф 0 лишь при т = п± 1, (90.3)
а соответствующие частоты будут равны comn = со0 (т — п) = ± со0, т. е. соб-
собственной частоте осциллятора.
Пользуясь D8.9) и обозначая Do = ехй = е \/ —— , мы можем на-
писать матрицу D (t) в гейзенберговском представлении в виде
0 Doe*<V V41 0 0 ...
e~i(V V41 ° DoeiuV ]/% 0 ...
D{t) =
0 йое-1%*У% 0
(90.4)
1 Более подробную и общую формулировку этого принципа читатель найдет в книге
В. Паули, Общие принципы волновой механики, Гостехиздат, 1947. Можно также
показать (см. там же § 12), что при больших квантовых числах т и п и при )&| =
=--\т—п | < т, п. матричные элементы D^ @==Dm,)m-fe @ приближенно равны клас-
классическим компонентам Фурье: —exk(t)=—ех^ @) elha<)t, так что старая форма прин-
принципа соответствия целиком укладывается в новую. Философский анализ принципа соот-
соответствия читатель найдет в книге: И. В. Кузнецов, Принцип соответствия в совре-
современной физике и его философское значение, Гостехиздат, 1948.
300

Таким образом, осциллятор может поглощать и излучать только соб-
собственную частоту ю0 (так же как и в классической механике).
Установленное правило отбора справедливо не всегда. Мы должны
■вспомнить, что наши расчеты взаимодействия со светом базировались на
предположении, что длина волны света К гораздо больше размеров системы
л. Только при этом условии взаимодействие со светом выражается через
матрицу электрического момента. Размеры осциллятора определяются его
амплитудой. По порядку величины они равны 1/ I/ л + -» ■ Поэтому
правило отбора (90.3) применимо лишь при условии
(90-5)
т. е. для не слишком больших амплитуд колебания.
Следует заметить, что реальные осцилляторы при больших амплиту-
амплитудах колебания (большие п) становятся ангармоническими, и это уже само
яо себе может послужить причиной нарушения простого правила отбора.
Б Правила отбора для о'птического электрона атома
Рассмотрим матрицу электричекого момента для электрона, движу-
движущегося в поле центральных сил. В этом случае волновые функции стацио-
стационарных состояний имеют вид
t|w (г, 8, Ф) = Rnl (r)P? (cos Q) eim<t>. (90.6)
Нам нужно вычислить матрицу электрического момента относительно этой
системы функций. Так как матрицы компонент электрического момента
отличаются от матриц координат электрона только множителем — е, то мы
будем вычислять эти последние. Кроме того, оказывается удобным вычи-
вычислять матрицы не от х, у, z, а от комбинаций
£ — у 4- iu = г sin О-р^'р п — х in = r sin fl ■ р~1ч> £=z (ЯО 71
Пользуясь функциями (90.6), получаем:
оэ я 2я
Ътт, пч'т' = J RmRn>i'rsdr ^ PT-P1?' sin2 9 с
о о
со я 2я
Tbim, «-I'm' = ^ RmRn'1'гЧг ^ Р?Р?' sin2 0 d9 ^ е'(т-"')ч>-1ч>аф,
0 0 0
оо я 2я
Znlm, n'l'm' = ^ RvlRn4-r3dr { PfP™' S\X\ В COS 6 <iO ^ е*(">-"»') Ф ^ф.
0 0 О
0
(90.8)
Интегралы по ф берутся, очевидно, сразу:
.Вводя обозначения
(90.9)
(90.10)
301

я
^ Р? Pf sin2 9 dB = ST', (90.11)
о
я
^ РГР™' sin 9 cos 9 d6 = CmJ"', (90.12)
о
мы можем переписать матричные элементы (90.8) в виде
Snlm. n'l'm' = 2lt/nl, п'Г'5ц' •Omjm/_i, (90.13)
ТЫт, гс'1'т' = 2lt/ni, „■,' • Sa™' • 6т, т< + 1, (90. 1 4)
Znlm, n'l'm' = 2я/„', n'V'Cii' ■ &т, т'- (90Л5)
Эти формулы дают нам сразу правила отбора для изменения магнитного
числа т. Матричные элементы £ отличны от нуля лишь для m' = m-(-l,
элементы т] для т' = т— 1 и элементы 2 для т'~т. Таким образом,
возможны лишь переходы, при которых магнитное число т. изменяется
по правилу
т' —т=±1 или 0. у,
Исследуя интегралы S™?1 и С™т, мы можем установить еще правило
отбора для орбитального квантового числа I. Для этого следует устано-
установить условия, при которых эти интегралы не обращаются в нуль. Рас-
Рассмотрим сперва интеграл С™™'. Нас интересует лишь тот случай, когда
т' = т:
л
СТ™= { Р?Р™cos9sin9dO. (90.16)
о
Вводя переменную x=cos9, получим:
l (x)- Pi'(x)x ах- (90.16)
-1
На основании свойств шаровых функций имеем:
хРТ (х) = ашРГ+1 (х) + blmPT-i (х), (90.17)
где alm и blm — некоторые коэффициенты1.
Имея в виду, что функции РТ ортогональны между собой, и подстав-
подставляя (90.17) в (90.16'), найдем, что С™" имеет вид
Си™=-- alm6r, i+i +blm6l>, i-u (90.18)
и, следовательно, С"г" не равны нулю при I'= I ± 1.
Подобным же образом для интегралов Sir™ (90.11) получаем (при
m =m± 1):
+1
<jm, mil С рт±{ , , -, А] ~Ъ pm/Y\rlv /Qfl I R"V
о£ i' = \ гi' \Х) у 1 — х г\ \х) ах. \jv. 10 }
Пользуясь формулой для шаровых функций2
A - х^!*Р? (х) = almPT-x (x) + PimPl+11 (x), (90.17')
1 См. дополнение V [формула C0)].
2 См. дополнение V [формула C1)].
302

получим, что
S£Vm+1 = a,me,_i, v + Pimei+i, ,/. (90.19)
Применяя предыдущую формулу для (I — х2I1*Р™~* (х), подобным же об-
образом найдем:
, I'+l- (90.19')
Эти формулы показывают, что S™™ фО лишь для Г = I ±- 1.
Таким образом, мы получаем правило отбора для орбитального кван-
квантового числа
Г-г=±1. X (90.20)
Правил отбора для радиального числа «r = « — Z — 1 не существует.!
Последнее найденное нами правило отбора показывает, что оптические!
переходы (для К > а, т. е. для дипольного излучения) возможны лишь]
между состояниями, являющимися соседними в отношении изменения вра-
вращательного момента УИ2= кЧA-\- 1).
Мы объяснили, что в спектроскопии состояние с I = 0 называют s-тер-
мом, состояние с I = 1—р-термом, состояние с I = 2—d-термом и т. д.
Спектроскопистам было давно известно, что оптические переходы совер-
совершаются лишь между s- и р-, р- и d-, d- и f-термами. Как мы видим,
квантовая механика дает объяснение этому факту: только для таких пере-
переходов электрические моменты (диполи) Dmn отличны от нуля.
Рассмотрим подробнее правило отбора для магнитного числа т в применении
к простому эффекту Зеемана. В § 62 нами было установлено, что квантовые уровни
—У
атомов в магнитном поле расщепляются, причем если поле Ш направлено по оси OZ,
то а priori возможные частоты излучения определяются из формулы F2.15):
«njm, п'1'т' = %+°ь(т'-т), (90.21)
где (о0 — частота в отсутствии поля 3$. Соответствующие состояниям Enim функции
равны tynim (88.6) (атом в магнитном поле в первом приближении не деформируется).
Поэтому и матричные элементы Dnlm пЧ,т> останутся такими же, как и в отсутствии
внешнего поля &€. Поэтому мы можем пркменить к оптическим переходам, при нали-
наличии магнитного поля, правила отбора, выведенные нами в предположении отсутствия
какого-либо внешнего поля. На основании этих правил следует, что возможно излуче-
излучение и поглощение не всех частот, предписываемых формулой (90.21), а только трех:
со = ш0 -J- Ol, если т'—/n = ± lf и (л = (л0, если т' = т. (90.22)
Это—как раз то расщепление (нормальный триплет Зеемана), которое мы уже обсуждали
в § 62. Установим теперь поляризацию соответствующих спектральных линий.
Для несмещенной линии (т' = т) отличен от нуля лишь электрический момент по
оси OZ. Следовательно, излучение несмещенной частоты обусловлено диполем, направ-
направленным вдоль магнитного поля &6. Электрический вектор излучения диполя лежит в
одной плоскости с самим диполем. Поэтому излучение частоты будет поляризовано так,
что плоскость поляризации будет проходить через направление магнитного поля. Для
m' = m-(-l матричные элементы z и ц равны нулю [см. (90.13), (90.14) и (90.15)]. На
основании (90.7) тогда получаем:
-i —
2
Уп1т, п'У, m+l—xnLm, n'l', m-fl ' е ■ (90.23)
Подобным же образсм для т' = т—1 получим:
я
Vnlm, n'l', m-l~xnlm, n'l', m-l ' г ■ (90.23')
Эти формулы показывают, что фаза диполя по оси OY смгщена на ^ -^- по сравне-
сравнению с фазой диполя по оси ОХ. Поэтому переход т ■—> т-\- 1 соответствует возбужде-
возбуждению колебаний, поляризованных по правому, а переход т—> т-—1—по левому кругу.
303

Соответственно этому излучение с частотой (о = (о0-)-О£,поляризовано по правому кругу-
а с (о = (о0— Ol — по левому.
Таким образом, и частоты, и поляризации для простого эффекта Зеемана согласно
квантовой теории таковы же, как по классической теории Лоренца. Преимущество
квантовой теории в этом вопросе заключается в том, что она позволяет помимо этих
выводов дать относительную (а если сформулированы условия возбуждения, то и абсо-
абсолютную) величину интенсивностей для всех компонент зеемановского триплета: а = (х>0,
«о ± Ох,.
§ 91. Интенсивности в спектре излучения
Если атом находится в возбужденном состоянии (т),.то возможен
спонтанный переход атома в низкий уровень (л) с излучением кванта света
hamn. В § 88 мы получили выражение для энергии -ф- , излучаемой воз-
возбужденным атомом в единицу времени (88.16). Чтобы получить полную
наблюдаемую интенсивность излучения, следует умножить эту величину
на число атомов Nm, находящихся в возбужденном состоянии (т). Это
число зависит от условий возбуждения. Если, например, возбуждение
тепловое, и светящееся вещество находится в тепловом равновесии при
температуре Т, то
Nm = C(T)e kT, (91.1)
где С — некоторая функция температуры, зависящая от рода излучателей.
Если возбуждение производится ударами электронов и реализовано рав-
равновесие, то число Nm найдется из условий этого равновесия: число пере-
переходов в 1 сек в возбужденные состояния под влиянием ударов электро-
электронов должно равняться числу переходов в 1 сек в низшие состояния,
происходящих благодаря спонтанному излучению и отчасти благодаря
столкновениям с электронами.
В общем случае, не уточняя вида yVm, можно написать для интенсив-
интенсивности Imn излучения частоты comn, вызванного переходом из состояния
{т) в состояние («):
4со4
/ra™ = Afm^f4Dmnp. (91.2)
§ 92. Дисперсия
Задачей теории дисперсии является расчет рассеяния света. При взаи-
взаимодействии со средой свет не только поглощается, но и рассеивается,
меняя направление своего распространения, а в общем случае — и частоту.
Одной из наиболее простых задач теории дисперсии является вычис-
вычисление показателя преломления для газа. Согласно классической теории
поля, по известному соотношению Максвелла, показатель преломления
■среды п равен ]/~е, где е —диэлектрическая постоянная. Диэлектрическая
постоянная в свою очередь связана с поляризуемостью среды а соотно-
соотношением 8=1-1- 4зта так, что
«2-1=4яа. (92.1)
Если N — число атомов в 1 см3, а |3 — коэффициент поляризуемости
отдельного атома, то а = fW и, следовательно,
(92.2)
304

Коэффициент, атомной поляризуемости C определяется из формулы
p = |3g, (92.3)
где р есть электрический момент атома, а I-переменное электрическое
поле световой волны. Задача сводится к вычислению р.
В классической теории оптический электрон рассматривался как части-
частица, движущаяся под влиянием квазиупругой силы. Соответственно этому
предположению для коэффициента поляризуемости C получалось выра-
выражение
iLi (92.4)
r ]1 СО2.—(О2
где е — заряд электрона, jj, — его масса, со0 — собственная частота оптиче-
оптического электрона, а со —частота внешнего поля1. Если в атоме имеются
электроны, обладающие различными собственными частотами со0, coj, ю2, .. .
.. ., (ofe, ... и число электронов с частотой cofe есть fk, то вместо (92.4)
следует иметь в виду более общую формулу
£l Л (92.5)
j3 = _£lv
r u, ZJ и>1—со2
к к
Число fh можно также рассматривать как число осцилляторов в атоме,
обладающих собственной частотой coft. Формула правильно описывает диспер-
дисперсию в смысле зависимости C (а стало быть, и показателя преломления) от
частоты падающего света со. Однако удивительным образом опыт приво-
приводил к тому, что числа fk оказывались меньшими единицы.
Мы перейдем теперь к изложению квантовой теории дисперсии, кото-
которая приводит для когерентного рассеяния к той же формуле (92.5), что
и классическая теория. Но при этом величины fh уже не являются числами
электронов /г-го сорта, а имеют совсем другой смысл. Поэтому мы будем
называть fk иначе, а именно, согласно установившейся терминологии —
силой осциллятора.
Квантовая теория позволяет вычислить силы осцилляторов fh в пол-
полном согласии с опытными данными.
Задача о дисперсии света в квантовой теории может быть поставлена
в полную параллель с квантовой теорией излучения и поглощения света.
Подобно тому, как в этих последних случаях разыскивается вероятность
поглощения или излучения кванта света, так и в случае дисперсии можно
искать вероятность того, что первоначальный квант света (падающий пу-
пучок) изменит в результате взаимодействия с атомом направление своего
импульса, а в общем случае и свою энергию.
Мы, однако, базируясь на принципе соответствия, пойдем более про-
простым и более близким классической теории путем. Именно, мы найдем
электрический момент p(t), который возникает в атоме, находящемся в пере-
переменном поле световой волны. Свет мы будем предполагать монохромати-
монохроматическим, частоты со. Ограничиваясь опять случаем, когда длина волны %
много больше размеров квантовой системы а, мы можем написать электри-
электрическое поле световой волны % (t) внутри системы (атома или молекулы)
в виде
(92.6)
1 См. Р. Бек к ер, Теория электричества, т. II., Электронная теория, § 25,
Гостехиздат, 1941.
20 Д. и. Блохиндев 30J>

Пусть атом до включения светового поля находился в одном из своих
квантовых уровней Еп, собственная функция, соответствующая этому состоя-
состоянию, пусть будет ^n (r, t).
При наличии светового поля состояние атома будет иным (в нем будут
возникать вынужденные колебания). Пусть это состояние описывается
функцией \\>n(r, t). Эта функция должна удовлетворять уравнению Шредин-
гера
'Af = //\+R, (92.7)
где Н° есть оператор полной энергии системы (в отсутствии светового
поля), a W—возмущение, вызываемое световой волной. Согласно (92.6)
W равняется
(92.8)
Для решения уравнения (92.7) представим tyn в виде
где соп = -тг , а ип и vn суть искомые поправки к tj)n. Функция фп есть
функция стационарного состояния невозмущенной системы:
Я°^п ^ЕпЦп. (92.10)
Подставим (92.9) в уравнение (92.7) и в первом приближении пре-
пренебрежем произведениями Wun, Wvn (так как эти члены будут пропорцио-
пропорциональны §2 и уже относятся ко второму приближению). Тогда мы получим:
h (con - со) ипеш +.Л (ю„ + со) ипе~ш = Н°ипеш + Н°опе~ш +
+ е (|„г) е<<" + е Ш ^. (92.11)
Приравнивая здесь коэффициенты при компонентах Фурье, мы получим
уравнения для ип и vn:
—¥
—v
/г(соп + со)»Г1 = Я0Уп + -^|^-^. (92.12')
Для решения этих уравнений разложим и и v в ряды по ортогональ-
ортогональным функциям tj)n:
«n=2-VK- ■ (92.13)
"п = 2ад. " (92.13')
Подставляя эти выражения для ип и vn в (92.12) и (92.12')'и имея в виду,
что функции t]}° удовлетворяют уравнению H°tyl =E1ty1, мы находим:
А2 4|К-«'1-»)*г=«-т^^. (92.14)
Л 2 Вш (ю« -©, + ©) Ц»?=е-^-<. (92.14')
306

Пусть атом до включения светового поля находился в одном из своих
квантовых уровней Еп, собственная функция, соответствующая этому состоя-
состоянию, пусть будет \|)£(r, t).
При наличии светового поля состояние атома будет иным (в нем будут
возникать вынужденные колебания). Пусть это состояние описывается
функцией tyn (r, t). Эта функция должна удовлетворять уравнению Шредин-
гера
'■а| = П.+ %. (92.7)
где Н° есть оператор полной энергии системы (в отсутствии светового
поля), a W—возмущение, вызываемое световой волной. Согласно (92.6)
W равняется
№ = e(§0r)cosfttf. (92.8)
Для решения уравнения (92.7) представим tyn в виде
фп(г, O = *n(r)e-itoni + «n(r)e-i(»n-co)!_|_t,n(r)e-i(con+co)() (92,9)
где соп = -^ , а ип и vn суть искомые поправки к t])n • Функция ^ есть
функция стационарного состояния невозмущенной системы:
Н°^п^Еп^п. (92.10)
Подставим (92.9) в уравнение (92.7) и в первом приближении пре-
пренебрежем произведениями Wun, Wvn (так как эти члены будут пропорцио-
пропорциональны §2 и уже относятся ко второму приближению). Тогда мы получим:
h (con - со) ипеш +. h (ю„ + со) ипе~ш = Н°ипеш + H°vne-iat +
+ e(gor)e Y ф». (92.11)
Приравнивая здесь коэффициенты при компонентах Фурье, мы получим
уравнения для ип и vn:
—¥
/г(соп-сй)«;п = Я°«п + Л^-*п, (92.12)
h((an + «i)vn = Hovn + -^^-^. (92.12')
Для решения этих уравнений разложим и и v в ряды по ортогональ-
ортогональным функциям фп:
«; = 5ХЛ?. ■ (92.13)
»» = 2ад- '* (92-13')
Подставляя эти выражения для «п и vn в (92.12) и (92.12')*и имея в виду,
что функции t])° удовлетворяют уравнению Я0!])? =£°'ф[1, мы находим:
A2^K-ffl,-«>)^=«-^*!l, (92.14)
i
■А2Вп1(Оп-о, + @IЦ=еМ^. (92.14')
i
306

Умножим эти уравнения на i^* и проинтегрируем по всему пространству.
Тогда в силу ортогональности функций t])°, ij)J[ * получим:
*(§ог)>1>п^, (92.15)
|^ *(gor)^du. (92.15')
Отсюда находим Лп); и Bnh:
где
En—Ek
®nh = ®n - «ft = fe
суть собственные частоты атома, a Dhn есть матричный элемент вектора
электрического момента.
Из (92.16) и (92,16') следует, что применимый нами метод решения уравнений.
(92.14) и (92,14') пригоден лишь тогда, когда частота падающего света « не совпадает
ни с одним из собственных частот атома ыпк, т. е. вдали от резонанса. Необходимая
степень удаления от a> = (onh определяется условием;
Только при этом условии Anh и Впъ < 1, Чтобы получить и область резонанса, необ-
необходимо учитывать затухание осцилляторов Ь^пешкп1.
Подставляя найденные значения Anh и Впк в (92.13) и (92.13'), а ип
и ип в (92.9), мы получаем приближенное выражение для ^„(г, t):
2;
p-i (со +со)
2Н
Вычислим теперь в первом приближении электрический момент рпП@> кот°-
—?-
рый индуцируется полем § (t) в состоянии •»])„• Это состояние при нало-
наложении поля переходит в i])n(r, t). Средний электрический момент в этом
состоянии равен•
*п(г, Ог-Ч'п(г- t)dv=-e\ \^n{v, t)\^v-dv. (92.18)
Согласно (90
по Шо, равно
•17) фп(г, 0
2ft 2j a>nk-\-
k
p, с точностью
ш Yn ™к 2ft 2.
ft
ДО
членов
— О) 'Й
eico(
2ft
первого
к
порядка
t
20* 307

Подставляя это в (92.18) и замечая, что
получим:
О (t\— D etCOi ХЛ f (dpDftn) Dfel I (ipPtew) Dfen 
PnnU- nn 2ft ZJ 1 (%n-co + cofen + (o J
e
2ft
f
Мы видим, что электрический момент pnn(t) складывается из двух частей:
из не зависящего от времени момента Dnn и из индуцированного допол-
дополнительного момента, линейно зависящего от поля. Dnn есть не что иное,
как средний-электрический момент атома (или молекулы) в состоянии п.
Так как он не зависит от времени, то в дисперсии света он никакого
участия не принимает. Индуцированный момент меняется периодически во
времени, и притом с частотой, равной частоте падающего света со. Более
того, фаза колебаний этого последнего момента находится в определенной
связи с фазой электрического вектора падающего света. Этот добавочный
момент и ответственен за когерентное рассеяние — дисперсию. Обозначим
его через p'nn(t):
рпп = Рпп Dnn.
Согласно (92.19) этот -индуцированный момент может быть написан (по
компонентам) в виде
(рпп)ж == Ji (ржж©Ожб -]-ржу©Оуб -\-pxzeOze ), \
(о' ) = Ш (Р Ш е*ю' -4- Р Щ е*ю'-4-Р % е*ю') I (92 20)
где через Ж обозначена действительная часть от стоящего за этим знаком
выражения.
Совокупность величин Рху образует тензор атомной поляризуемости
> Р Р f99 2П
I О п
zx "zy rzz
имеющий типичные компоненты вида
Prii== —г /! "{ —; г—~ ~\ i—^~^ г '
i xy fi sLJ I ft)nft —ft) Ыпк-\-Ы )
причем (Dnk)x, (Dkn)y и т. п. суть проекции векторов Dnh, D*n на оси ОХ
и OY. Остальные компоненты тензора р получаются из (92.22) заменой
значков х, у на все возможные пары из х, у, г. Так как Dhn = D*h, то
тензор (92.22) является эрмитовским:
р\сУ = Р£» (92.23)
и, следовательно, диагональные члены Рхж, р , Pzz действительны.
В общем случае, при комплексных Рху, $xz, Руг фаза индуцирован-
индуцированного момента рпп и его направление не совпадают с фазой и направлением
электрического поля световой волны Е(^). Если все компоненты тензора р
действительны, то направление рпп не совпадает с направлением поля, но
фазы их одинаковы.
308

Для сравнения с классической теорией рассмотрим частный, но весьма
важный случай, когда тензор C сводится к одному скаляру, т. е. когда
Рху = Pxz = P,,z = °> Рхх = Руу = Pzz = Р- При ЭТИХ УСЛОВИЯХ И фаза ИНДуЦИ-
рованного момента, и его направление совпадают с фазой и направлением
поля световой волны.
В этом специальном случае проще всего выяснить основное различие
с классической теорией дисперсии. Из (92.22), при сделанном допущении,
имея в виду, что (ohn ■= — conft, получаем:
В = В =6 = В — — V Ыкп ^ (D"ft)* У cqo 24}
nh~
где
и предположено (изотропность системы), что
Полученную формулу (92.24) для поляризуемости В мы можем написать
в виде, совершенно аналогичном классической формуле (92.5), именно:
Р = — S ■/"" т. (92.5')
где
f _ 2р. | хпъ |2(ofew _ 2ix | Dnh I2(ofew ,q9 9t-4
Величину fnk в квантовой теории принято называть силой осциллятора.
Она просто связана с вероятностью спонтанного перехода А%. Именно,
на основании (88.9) имеем:
г -- ^с3 л*
Таким образом сила осциллятора fnk определяет интенсивность спон-
спонтанного излучения.
Величины fnk могут быть вычислены, если известны волновые функ-
функции системы1.
Мы видим, что величины fnk имеют в квантовой теории совсем иное
значение, нежели в классической, где соответствующая величина fk
имела смысл числа электронов /г-го сорта и поэтому была целым чи-
числом. Силы осцилляторов fnk в согласии с опытом не являются целыми
числами. Можно, кроме того, доказать, что их сумма равна Р. Согласно
квантовой теории, как следует из (92.5'), сумма дисперсионных членов
вида —а _ 2- имеется налицо уже для одного электрона, находящегося
в состоянии трЯ- Это находится в прямой связи с тем обстоятельством,
что квантовая система в отношении взаимодействия со светом
ведет себя как совокупность осцилляторов с моментами Dmneia>mnt,
хотя бы даже речь шла лишь об одной частице.
Если атом может находиться не только в состоянии т^, но и в дру-
других (смешанный ансамбль), то, чтобы получить полную поляризуемость В,
нужно поляризуемость, обусловленную атомами, находящимися в состоя-
состоянии \\>п, умножить на вероятность нахождения атома в состоянии \\>п
1 См. Г. Бете, Квантовая механика простейших систем, ОНТИ, 1935.
а См. Г. Бете, цит. соч.
309

и сложить полученные выражения. Обозначая через wn вероятность того,
^ ^n=l, мы получим для
что атом находится в состоянии
причем
поляризуемости а 1 см3 газа выражение:
"ЯП XI
а — ■
(92.26)
где N — число атомов в 1 см3. Показатель преломления в функции частоты
падающего света согласно (92.2) и (92.26) равен
п2 (ю) = 1 + 4"g3iV ^ ^ wn д/^.^ • (92.27)
п h
Часто среди всех членов суммы, входящей в (92.27), один или несколько
преобладают над всеми остальными. Это реализуется в тех случаях,
когда частота со не слишком удалена от резонансной частоты conft.
Сила осциллятора fnk может принимать и отрицательное значение.
Если атом находится в возбужденном состоянии (п), то среди состояний k
L>o
■ и
Рис. 67. Дисперсионные кривые для положительной и отрицательной
дисперсии
будут и такие, для которых coftn < 0 (т. е. Eh<.En). В этом случае дис-
дисперсионная кривая имеет необычный ход —получается, отрицательная
дисперсия. На рис. 67 слева изображен ход дисперсионной кривой в обла-
области "-аномальной дисперсии для классического случая (fnfe>0). Эта дис-
дисперсия была изучена в ряде работ, среди которых особенно обстоятель-
обстоятельны1 работы Д. С. Рождественского1. На том же рисунке справа изобра-
изображена кривая для отрицательной дисперсии (fnh < 0): случай, не преду-
предусмотренный классической теорией. Явление отрицательной дисперсии было
обнаружено Ладенбургом2.
,' Что касается численного значения сил осцилляторбв, то экспери-
экспериментальное их определение не является простой задачей 3.
Для иллюстрации согласия теории с экспериментом приведем данные
Ладенбурга и Карста4 для отношения сил осцилляторов водородных
линий серии Бальмера На и Яр. Эти авторы нашли, что 5,9 : 1 > fa : fp >
> 4,66: 1. Теоретически получается /а : /р = 5,37 : 1.
1 Д. С. Рождественский применил особый метод «крюков». См. Д. С. Рождест-
Рождественский, К исследованию аномальной дисперсии в парах натрия, ДРФХО, часть
физич., 42, 1910.
2 R. Ladenburg, Zs. f. Phys. 65, 167, 1930.
3 R. Ladenburg и A. Carst. Zs. f. Phys. 48, 192, 1928.
4 R. Ladenburg и A. Carst, цит. соч.
310

§ 93. Комбинационное рассеяние
Мы вычислили в предыдущем параграфе электрический момент р'пп,
индуцируемый светом в л-ом состоянии атома. Рассмотрим теперь, какой
добавочный электрический момент pmn индуцируется светом в квантовой
системе при переходе ее из одного состояния т в другое п. Эта задача
легко может быть решена на основе результатов предыдущего параграфа.
Формула (92.17) дает состояние tyn(r, t), возникающее из t])n(i") e~ia>nt под
действием света. Совершенно такую же формулу мы можем написать для
состояния ^m(r, t), возникающего под действием того же света из состоя-
состояния it>m(r)e-f0"nt. Вместо (92.18) мы теперь будем иметь для момента
Pmn @» отвечающего переходу из т в п, следующую формулу:
<(г< 0гФп(г, t)dv. (93.1)
Подставляя сюда значение функций ^n(r, t) из (92.17) и tym (r, t), кото-
которая также получается из (92.17) заменой значка п на т, мы получим:
Vmn \l) Lrmn*' ic "ran I e ишш ^o.z,y
где
Dfcn
Мы видим, таким образом, что помимо уже рассмотренного нами выше
электрического момента Dmn, зависящего от времени периодически
с частотой сот11, появляются еще два дополнительных, индуцированных
светом, электрических момента (93.3) и (93.3'), частоты колебаний кото-
которых суть комбинационные частоты со = comn ± со. Электрический момент
Dnm, как мы знаем, определяет излучение и поглощения для переходов
Ет^-Еп. Полученные нами дополнительные моменты D^ и D^ обуслов-
обусловливают рассеяние падающего света, но с измененной частотой. Эти изме-
измененные частоты представляют собой сумму или разность частоты падаю-
£ £
щего света со и одной из собственных частот системы comn = —г~—— .
Чтобы определить интенсивность этого рассеянного света, мы при-
применим принцип соответствия, согласно которому атом излучает и погло-
поглощает свет как совокупность осцилляторов. Согласно (93.2) мы имеем
теперь три таких осциллятора. Первый из них нами уже рассмотрен
в § 88, а вторые два
О£п&(<отп+а>)' и DSe1'10™-10I (93.4)
согласно формуле (88.16) для средней энергии, излучаемой осциллятором
в 1 сек, дают следующие интенсивности для излучения частоты со' =
= comll-fco и со"-—comn—со соответственно:
dt ~ 3c3 > ""
311
(93-5')

где D^ и Dmn5 определяются выражениями (93.3) и (93.3') и зависят от
интенсивности падающего света. Обращаясь к закону сохранения энергии,
мы можем истолковывать полученное рассеяние с измененной частотой
на основе представления о световых квантах. Пусть атом находится
в состоянии ц, имея энергию Еп. С атомом «сталкивается» квант света
частоты со (энергия e = /zco). В результате столкновения часть энергии
кванта может пойти на возбуждение атома (переход в состояние Ет > Е„).
Тогда рассеянный квант будет иметь энергию, равную
е" = Лео" = /гсо - (Ет - Еп)
(рис. 68, а), и частоту со" = со — отп, со > comn > 0. Если атом находится
в состоянии Ет > Еп, то рассеянный квант может получить энергию от
,£ +ftW атома, который перейдет в низ-
низшее состояние Еп. В этом слу-
случае энергия кванта рассеянного
света е' будет равна (рис. 68, Ь)
е' = /гсо' = /гсо + (Ет - Еп),
а частота будет равна со' = со +
+ comn, где comn > 0. Интенсив-
Интенсивности частоты со' и со" даются
формулами (93.5) и (93.5'). Мы
видим, что применение законов
сохранения энергии между кван-
квантовой системой и излучением
•Е„*Ьы
£
т
3 Э
(а)
(Красная компонента)
n
(Фиолетодая компонента) не допускает рассеяния частот
Рис. 68. Схема переходов при комбинацией- ffl" < °- Этот ВЫВОД не следует
ном рассеянии света автоматически из формулы
(93.5) и является специаль-
специальным требованием, поскольку мы остаемся в рамках принципа соответ-
соответствия 1.
Чтобы определить абсолютные интенсивности рассеяния частот со' и со",
следует умножить (93.5) на число Nm атомов, находящихся в состоянии
т, и (93.5') на число Nn атомов в состоянии п. Частоты со' > со; поэтому
их часто называют «фиолетовыми» компонентами рассеянного комбина-
комбинационного излучения, а со" < со называются «красными» компонентами. Следо-
Следовательно, окончательно для интенсивностей фиолетовых компонент имеем:
Л + > 12
Jrnn >
а для интенсивности красных компонент
г" \Г 4(Ы — (йтп)*
1 — 1\ п у^з
Отношение этих интенсивностей равно
/' = Nm(<i>+<omn)* |РЙ»1
(93.6)
(93.6')
(93.7)
Комбинационное рассеяние было экспериментально установлено
Г. С. Ландсбергом и Л. И. Мандельштамом на твердых телах, а также
Раманом на жидкостях. В обоих случаях частоты comn являлись колеба-
колебательными частотами. В опытах Рамана это были частоты колебаний моле-
1 В квантовой теории радиации этот вывод получается сам собой. См., например,
Г. П л а ч е к, Релеевское рассеяние и рамаи-эффект, ОНТИ УССР, 1935.
312

кул жидкости. В опытах Л. И. Мандельштама и Г. С. Ландсберга
частоты comn являлись частотами молекулярных колебаний кристалла.
В применении к этим опытам особо важный вывод из формулы для отно-
шения-р заключался в том, что интенсивность фиолетовых компонент
должна расти с температурой. В самом деле, число возбужденных колеба-
колебательных состояний кристалла Nт растет с температурой Т по закону
N
m
соответственно этому должна возрастать и интенсивность фиолетовых
компонент в спектре комбинационного рассеяния. Этот вывод теории
вполне подтверждается экспериментально.
Частоты колебаний молекулы определяются ее структурой. Поэтому
исследование молекулярных колебаний является мощным средством изу-
изучения строения молекул. Частоты эти лежат в инфракрасной области,
а многие из колебаний молекул вообще не сопровождаются изменениями элек-
электрического момента (оптически неактивные колебания). Обе эти причины
крайне затрудняют прямое исследование частот колебаний молекулы.
Комбинационное рассеяние в значительной мере облегчает эти трудности.
Изучая комбинационное рассеяние, мы можем иметь дело с видимым све-
светом и по изменению его частоты определить частоты молекулярных коле-
колебаний, независимо от того, являются ли они оптически активными или
нет. Изучение комбинационного рассеяния молекул в настоящее время
образует большую область физической науки.
Подробности, относящиеся к этому явлению, читатель может полу-
получить из цитированной выше книги Г. Плачека.
§ 94. Учет изменения фазы электромагнитного поля волны
внутри атома. Квадрупольное излучение
Все наши расчеты в предыдущем предполагали, что мы имеем дело
со светом, длина волны % которого больше размеров системы а.
Нетрудно модифицировать всю теорию взаимодействия атома со све-
светом таким образом, чтобы освободиться от предположения X > а. Для
этого нужно исходить из гамильтониана B7.9), описывающего поведение
электрона в произвольном электромагнитном поле (при этом мы можем
пренебречь малым взаимодействием спина электрона с полем световой
волны).
Для световой волны вектор-потенциал можно всегда выбрать так,
что divA = 0 и скалярный потенциал V = 0. Таким образом, поле све-
световой волны будет вычисляться по формуле t
1=-^. Ji = rotA. (94.1)
Пренебрегая, кроме того, в B7.9) величиной А2 (как величиной второго
порядка малости), мы можем написать гамильтониан B7.9) в виде
Возмущение (в первом приближении) равно
W(r, *)= — АЯ= —— AV. (94.3)
313

Представим вектор-потенциал в виде интеграла Фурье
А (г, 0=
(94.3')
где к—волновой вектор1. Тогда компонента Фурье от матричного элемента
возмущения, принадлежащая частоте comn, равна:
На основании (94.1)
= - Щ- Ао
0 (О =
(94.4)
где 80(со?гтI есть компонента Фурье от электрического поля. Поэтому
1
(94.5)
Внося это выражение в формулу для вероятности перехода (87.6) и пере-
переjl()|2
р
ходя от jlo(ffl
K плотности излучения так же, как это делалось
1
в § 89, мы получим вероятность перехода в 1 сек в виде:
4я2
Dmn(k)|2Q(comn),
где
(94.6)
(94.7)
Формула (94.6) вполне аналогична (87.16'), и из нее можно получить
коэффициенты Эйнштейна Ъ™а, bma, dma для случая коротких волн.
Различие между (87.16') и (94.6) заключается в том, что в первой
формуле Dmn имеет значение электрического момента, не зависящего от
характера излучения и определяемого свойствами атомной системы,
в то время как вектор Dmn (k) зависит от волнового вектора излучения к.
Поэтому коэффициенты Эйнштейна получатся иными, нежели для диполь-
ного излучения (их общие свойства, установленные в § 5, конечно, оста-
останутся неизменными). Вместе с тем распределение излучения по углам,
его поляризация и зависимость от частоты также изменятся.
Сделанный нами в § 89 вывод о том, что квантовая система взаимо-
взаимодействует с излучением, как совокупность осцилляторов, остается в пол-
полной силе и для излучения любой длины волны. Отличие случая длинных
волн (А, > а) от случая коротких волн (А, С а) заключается лишь в том,
что в первом случае квантовую систему можно рассматривать как совокуп-
совокупность диполей с моментами Dmnei(Omni, в то время как в случае коротких
волн нельзя игнорировать изменение фазы волны внутри системы, и кван-
квантовая система с точки зрения взаимодействия с радиацией уподобляется
системе осцилляторов с частотами comn, размеры которых не меньше размеров
длины волны. В этом случае уместнее говорить о совокупности токов и зарядов,
распределенных в пространстве и зависящих от времени периодически с часто-
частотами comn. Для длинных волн можно пренебречь изменением фазы в пределах
атома и разложить eikr в уравнении (94.7) по степеням кг, а именно:
егкг_ j _j_ j (кг) -+• . ... Так как функции ■фт и i])n отличны от нуля замет-
заметным образом лишь в пределах атома, то это разложение есть разложение
1 Мы будем считать, что направление отдельных частных волн в (94.3') и
поляризации одинаковы.
314

7 2na ,
по степеням ка-—г отношения размеров атома а к длине волны Л.
Из (94.7) тогда получаем:
Dmn (k) = \ 'ф^'У'фп dv -\- ■ \ tym (кг) Xtyn dv -\- ... =
= Umn -р Umn + • • ■ (У4.О)
Первый член D^n есть
ho Г ^ р ->
ran— w \ ^m'Vl^n'UC — ^ *mn> \Vt.J)
где Pmn—матричный элемент оператора импульса. На основании кванто-
квантовых уравнений движения имеем:
Ртп=щатпгтп, (94.10)
где гтп есть матричный элемент радиуса-вектора. Следовательно,
DSS, = Dmn, (94.11)
т. е. при длинных волнах в первом приближении мы получаем из (94.6)
формулу (87.16') для дипольного излучения. Если Dmn Ф 0, то следую-
следующим членом Итп можно пренебречь. В тех же случаях, когда в силу правил
отбора Dmn = 0, второй член в (94.8) может и не равняться нулю. При
Dmn = 0 излучение будет определяться вторым членом D™. Мы сейчас
покажем, что излучение, связанное с этим дополнительным членом, состоит
из квадрупольного электрического и дипольного магнитного излучения.
Согласно (94.8) D^'n может быть написано в виде:
~\ • (94.12)
т. е. выражается через матричный элемент оператора1
Этот оператор, с помощью правила, установленного в §31, может быть
тождественно переписан в такой форме:
(94.13)
Переходя от операторов к матричным элементам и пользуясь тем, что
где М —оператор момента импульса, получим:
£ ((кг) Р}тп = ^Р ((кг) г}mn +1 {[кМ]}„„. (94.14)
к п
Подставляя этот результат в (94.12) и замечая, что ■ = —, где
/
п —единичный вектор по направлению распространения излучения f сле-
1 Чтобы избежать путаницы в значении различных скобок, в этих выкладках мы
обозначаем (ab) — скалярное произведение, [ab] — векторное произведение, {Lmn} или
Lmn — матричный элемент оператора L.
315

k 1
дует вспомнить, что—■ = —, co = comn J , и имея в виду равенство
— ое-М = 5Ш (ЗК-магнитный момент атома), найдем:
DS= -* у{(кг) г}„,+ [nimn]. 2(94.15)
Здесь первый член может быть представлен в виде произведения
вектора—{'к на матричный элемент тензора второго ранга:
е , е е
уа Y1I Yy
о о У 2
е е 9 е
е е е 2
9~ ZX тг ZIJ -к- Z
(94.16)
Этот тензор называют квадрупольным моментом атома. С его помощью
(94.15) запишется в виде:
D£« = - / (kQmn) + [nilmn]. (94.17)
Первый член обусловливает электрическое квадрупольное излучение,
а второй — дипольное магнитное.
Пользуясь правилом отбора для дипольного излучения Г = / ± 1
(Ср. § 90) и правилом умножения матриц, нетрудно получить правила
отбора для квадрупольного излучения. Имеем:
и так как I" = 1 ± 1, V = Г ± 1, то l' = l, l± 2.
Такой же результат получится и для остальных компонент тензора.
Таким образом, правило отбора для квадрупольного излучения гласит
V = I или t ± 2. Что касается магнитного излучения, то матрица оператора
—>
3JJ диагональна относительно / и магнитное излучение получается при
переходах с изменением магнитного числа т, т. е. правило отбора будет
гласить:
V — I, m' — m ± 1.
Интенсивность квадрупольного излучения много меньше интенсив-
интенсивности дипольного (если последнее существует). В самом деле, Dmn при-
2яа гт
мерно в-г— раз меньше неисчезающего дипольного момента. Поэтому
вероятность перехода с квадрупольным излучением по порядку величины
/ 2яаЛ2
в ( "~х~ ) Раз меньше вероятности перехода с дипольным излучением.
CooTBeTcfBeHHO этому время жизни атома в возбужденном состоянии, коль
(Я Л2'
-S— ) раз больше времени
жизни для незапрещенного дипольного перехода, которое мы оценили в § 88
примерно в 10~8 сек. Отсюда для видимого света Я~5-103А и а~1 А
время жизни х в возбужденном состоянии, из которого возможен переход
в нижнее состояние только путем квадрупольного излучения, равно при-
примерно 10~2 сек. Такие состояния атомов называют метастабильными
состояниями.
Так как магнитный момент атома значительно меньше электрического,
то и магнитное излучение приводит к очень малой вероятности перехода,
т. е. также к метастабильным уровням.
316

Таким образом, в атомах квадрупольное излучение и магнитное излу-
излучение существенны лишь в том случае, когда дипольное излучение запре-
запрещено правилами отбора.
В атомных ядрах, испускающих у-лучи, запрещение дипольного излу-
излучения является обычным делом. Поэтому излучение у"лУчей зачастую
обусловливается квадрупольным или магнитным моментом ядра1.
§ 95. Фотоэлектрический эффект
В этом параграфе мы рассмотрим теорию фотоэлектрического эффекта
на атомах. Задача, стоящая перед нами, заключается в вычислении веро-
вероятности ионизации атома действием световой волны и в определении
углового распределения вылетающих электронов. Таким образом, речь
идет о переходе электрона из нормального уровня (нижний уровень дис-
дискретного спектра) в уровни непрерывного спектра.
Энергию нормального уровня обозначим через Ео (Ео < 0), а соот-
соответствующую волновую функцию — через i]H(r)- Волновые функции непре-
непрерывного спектра, принадлежащие энергии Е, ввиду большого выро-
вырождения можно брать весьма различным образом, лишь бы они образовы-
образовывали полную систему ортогональных функций. Мы возьмем такие функ-
функции, которые встречались нам в теории упругих столкновений, т. е. супер-
суперпозицию плоской волны, с определенным импульсом электрона р (рх, ру, pz),
и волны, рассеянной атомом. Для больших расстояний от атома такие
волновые функции будут иметь вид (ср. § 79):
= const* \е
где /г — волновое число. Такого типа функции являются одной из воз-
возможных форм волновых функций стационарных состояний непрерывного
спектра. Энергия Е состояния (95.1) будет равна
Функции (95.1) будем считать нормированными к Ь(рх — р'х), &(ру—р'у)>
b(pz — p'z). Возмущение, вызывающее переходы, согласно (94.3) возьмем
в виде
t)=-fcAV, (95.3)
где А — вектор-потенциал световой волны. Волну мы предположим моно-
монохроматической и возьмем А в виде
А = \ А> <»г-кг> + -1 Аое~* («*~kr\ (95.4)
где к есть волновой вектор волны. Так как волна поперечная, то
div~A = 0, т. е.
А0к = 0. (95.5)
Для вычисления интересующей нас вероятности* перехода мы можем
прямо применить формулу (84.24), так как последняя как раз выведена
для переходов из дискретного спектра в непрерывный под влиянием воз-
возмущения, гармонически зависящего от времени.
1 Подробности об этом см. в книге: А. Ахиезер и И. Помераичук, Некоторые
вопросы теории ядра, Гостехиздат, 1948.
317

Разумея в (84.24) под Еп энергию нормального состояния атома Ео>
под импульсом рх, ру, pz(p, 8, ф) — импульс фотоэлектрона, мы должны
согласно (95.3), (95.4) и (84.12) взять в качестве матричного элемента
возмущения величину
ф.
(95.6)
Тогда вероятность перехода электрона в 1 сек из состояния Ео в состоя-
состояние Е = E0-\-ha с импульсом, лежащим внутри телесного угла di~i, будет
равна
Ро (Е, 8, Ф) йп = -£ Щ^- (Ео + hafl* | WVxVyVz, о |2 • dQ, (95.7)
причем сюда входят лишь такие значения импульса рх, ру, рг, которые
удовлетворяют резонансному условию
^ ±(pl + pl + pl) = E0 + ha. (95.8)
Переходы в другие уровни Е невозможны. Замечая, что Ео= — I, где
/ — работа ионизации, мы можем переписать (95.8) в виде
P~ = hu-l. (95.9)
Это есть уравнение Эйнштейна для фотоэффекта на атоме.
Для того чтобы получить окончательное выражение для Р0(Е, 8, ф),
необходимо вычислить матричный элемент (95.6). Для этой цели необхо-
необходимо знать волновую функцию исходного состояния г|H и функции непре-
непрерывного спектра typ р р. Допустим, что мы интересуемся фотоэффектом
с /^-оболочки (тогда — Ео = 1 есть ионизационный потенциал /(-оболочки).
Эта оболочка расположена близко к ядру атома, и поэтому (игнорируя
взаимодействие двух /(-электронов) можно взять для ^0 функцию нижнего
уровня Ео для движения в кулоновском поле. Это будет (п = 1, 1 = т = 0)
I/2<^, (95.10)
где Z — номер элемента, а а — радиус первой боровской орбиты.
Такая функция будет весьма близко аппроксимировать истинную.
Мы ограничимся весьма грубым приближением для функций непрерывного
спектра. Именно, мы будем попросту игнорировать изменение плоской
волны вблизи атома благодаря действию его поля и соответственно этому
вместо точной функции возьмем невозмущенную действием атомного поля
плоскую волну
. (Pxx+PyV+Pzz)
(нормирована по р к б-функции). Такое приближение мало годится для
точного расчета, однако все же в нем еще сохраняются существенные
черты явления. Оно будет тем лучше, чем больше энергия фотоэлектрона,
т. е. оно пригодно для Е > — Ео = /. При таком предположении о функ-
функциях непрерывного спектра матричный элемент (95.6) может быть вычислен
без большого труда. Подставляя (95.10) и (95.11) в (95.6), мы получим:
Wррр.0=- р. —L_ ( ilУ* х { е (kr~^) Ao (Ve~ % dx dy dz. (95.12)
318

Пусть волна распространяется по направлению оси ОХ, а электрический
вектор (поляризация) направлен по оси 0Z. Тогда ОХ есть направление
вектора k, a OZ —вектора Ао. Тогда А0 = 0, О, Ао, и, следовательно,
^ ^Xk^^)^ (95.12')
Расположение векторов к, р, Ао дано на рис 69. Для выполнения инте-
интегрирования в (95.12') возьмем вектор
/гк—р за полярную ось сферической
системы координат G, Ф.
Если ось OZ в этой системе имеет
углы в', Ф', то
г = (г), = г cos (OZ, r).
Косинус угла между OZ и г, если век-
вектор г имеет полярные координаты в, Ф,
будет равен:
cos (OZ, г) = cos в • cos в' +
+ sin в sin В' cos (Ф' — Ф).
Угол между Ak-р И Г есть в. Поэ- Рис- 69' Расположение векторов А,
,пг 1 п,ч k и р при?,фотоэффекте
тому (95.12) можно записать в виде: F v "л ч
 Y/a A Z J f95 \2"\
где
\ sir
COS 0-—-
a fcosGcosB'-
0 0 0
+ sin 6sin в' cos (Ф' — Ф)}.
Интеграл по Ф от соб(Ф — Ф') дает, очевидно, нуль, поэтому
■k_$|rcoee--^
J = 2я cos 6' ^ г2 dr ^ sin В
о 6
Вводя переменную £ = cos G и обозначая.
(95.13)
(95.13')
со -f 1
= 2ясозВ' \r2dr-\ Idle
г через q, мы получим:
Zr
о -l
и, выполняя здесь простые интегрирования, найдем окончательно
J = cos в'
8го'
к —
к—Р-
(95.13")
Остается выразить cos В' через углы в той системе координат, где за по-
полярную ось принято направление распространения света (ось ОХ, вектор к).
Пусть угол между плоскостью, образованной векторами р и к — —- и плос-
плоскостью ZX, будет qp (см. рис. 69). Угол между /гк и /гк—р, пусть будет 8'.
319

Обозначая еще угол между ОХ и р через 8, мы получим из сферического
треугольника со сторонами в', 8' и у:
cos в' = sin в'совф
и из треугольника со сторонами Лк, р, /гк—р:
sin 8' = sin 8 ,hkp__ . .
Поэтому
/ = sine cos(p-p^ 8шр„ ,., ■ (95.14)
к—-
На основании (95.12")
— 8яе I Y_£f_
Z2
г-гг- sin 8 cos ф. (95.15)
Далее,
к —
= * +&—7Tcos9-
Из закона сохранения энергии (93.9), считая, что |~ > / (это — условие
применимости нашего приближения), мы найдем:
Аи
с
Обозначая через v скорость электрона — , получаем lik--^- p, и, стало
быть,
к-Т
а2
4с2
Мы оперируем с нерелятивистской теорией, поэтому пригодность наших
формул ограничена не только со стороны малых скоростей (^г^О>
но и со стороны больших. Необходимо, чтобы скорость фотоэлектрона
была значительно меньше скорости света с. Поэтому членами порядка -^-
следует пренебречь (учет их находится за пределами применимости нере-
нерелятивистской теории). Поэтому •
к—£
/г2
= Ef i-4-cos
(95.16)
Z2
Заметим, что мы еще можем отбросить член —^ по сравнению с
к- р
В самом деле,
2 д2 /j2
"» р» а а = —5. Следовательно,
Z2
а2
__ 2р.
/г*
Тг2" 2/г2 "
Но согласно формуле Бальмера
2А2
■=-£„ = /,
320

т. е. условие — <С ~ эквивалентно / < -|~ . Таким образом, имея в виду
Z2
быстрые фотоэлектроны, мы должны опустить в (95.15) член —% в зна-
знаменателе.
Подставляя (95.16) в (95-15), мы найдем окончательное выражение
для искомого матричного элемента:
w 4яе 1 / Z3 У/з 1 у, /i" sin 6 cos ф /rie , 7Ч
Подставляя, наконец, это значение матричного элемента в выражение
для^вероятности (95.7), мы получим1:
Р (Е 8 ш) dd dd 2e* B^)8/2/l4 Л*(гЛЬ (to)/2-sin2 e cos2 Ф (95.18),
Вместо Л^ можно ввести поток световой энергии. Из (95.4) получаем
—>
электрическое поле %
Величина магнитного поля gffl такова же, и так как оно перпендикулярно
то вектор Пойнтинга S равен по величине
с с со2 . ■
4я 4я с2 ° *
Среднее значение его равно
Подставляя это значение А\ в (95.18), найдем:
r
f , v
1-
V с
„ Л4
cosB
У
Объединяя все постоянные в одну 6 и замечая, что р6 = Bji£K = Bji/zcoK,
мы получим:
Р0(Е, 8, 9)rfQ^feco-9/2-iin29cosa(p SrfQ, . (95.21)
( 1—-cos8 )
V с J
J
где
(95-22)
Из полученной нами формулы, следуют самые основные черты фотоэлек-
фотоэлектрической эмиссии. Во-первых, число фотоэлектронов пропорционально
интенсивности падающего света S, скорость же фотоэлектронов зависит
согласно (95.9) лишь от частоты падающего света со, т. е. мы получаем
как раз те особенности фотоэффекта, которые представляют принципиаль-
принципиальные трудности для понимания с точки зрения классических концепций.
1 При переходе от (95.7) мы пренебрегли начальной энергией электрона Ео по срав-
сравнению с Аи.
21 Д. И. Блохинцев 321

Далее, формула (95.21) дает угловое распределение фотоэлектронов. Так
как угол 8 отсчитывается от направления распространения света, а ф —
от электрического вектора, и максимум фотоэмиссии лежит при 8 = ±"о"'
Ф = 0, то это означает, что наибольшее число фотоэлектронов летит в на-
направлении 0Z, т. е. в направлении электрического вектора световой волны.
При увеличении частоты падающего света скорость фотоэлектронов
возрастает так, что начинает играть роль множитель ( 1 cos 8
в (95.21), в силу чего максимум фотоэмиссии сдвигается в направлении
меньших 8, т. е. в направлении распростране-
распространения света. Этот вывод находится в согласии
с опытом. На рис. 70 изображены резуль-
результаты опыта. По оси ординат отложен ко-
косинус угла 8 между направлением распро-
распространения света и направлением максималь-
максимальной эмиссии, по оси абсцисс отложена ско-
скорость фотоэлектронов, причем за единицу
скорости взята скорость света. cos8m=0
отвечает направлению вдоль электрического
вектора волны, a cos 8m = 1 — направлению
вдоль луча света. Как видно, результаты
расчета хорошо совпадают с данными опыта
(кружки). С помощью формулы (95.22) мы
можем получить и абсолютную величину
фотоэффекта. Обычно в таких случаях вы-
вычисляют коэффициент поглощения для подаю-
подающего света т. Для нахождения его поступаем
следующим образом.
Представим себе, что на слой вещества толщиною Ах падает поток
света S. Тогда, если в 1 см3 вещества содержится п атомов, то в объеме
1 см2 X Ах в I сек произойдет в среднем
Рис. 70. Сдвиг вперед макси-
максимума фотоэффекта:
мак (Уг°л между направленном
распространения света и направле-
направлением максимума фотоэмиссии) в
функции р=—
1
, 8, <p)dQ
ионизации атомов. Поглощенная при этом энергия будет равна этой вели-
величине, умноженной на /гсо (так как при каждой ионизации поглощается
квант света Лео). С другой стороны, в этот же слой в 1 сек входит энер-
энергия S х 1 см2. Таким образом, убыль потока энергии S при прохождении
тонкого слоя Ах равна
AS = - hum Ах \ Ро (Е, 8, ф) dQ.
Подставляя сюда Р0(Е, 8, ф) из (95.21), мы получим:
д5= _ л.... a ..t..-9/..F С sin28cos2<
Полагая
мы получим:
322
7i С
sin2 8 cos2 ф
[ cos
с
(95.23)
AS = - tSAx;

отсюда следует, что х есть коэффициент абсорбции. Число атомов в еди-
единице объема пропорционально плотности вещества Q, именно:
где Л —атомный вес вещества. Подставляя это значение в (95.23) и обоз-
обозначая
мы получим величину так называемого массового коэффициента абсорб-
х
ции — в виде
-=-4т-- (95-24)
Q со7/* v ;
Эта зависимость от частоты также подтверждается опытами над поглоще-
поглощением рентгеновских лучей. Следует впрочем иметь в виду, что (95.24)
выведено для поглощения в /(-оболочке. На самом деле поглощение про-
происходит сразу несколькими оболочками. Мы не будем рассматривать
относящиеся сюда усложнения и отсылаем интересующегося читателя
к специальной литературе1.
1 М. Stobbe, Ann. d. Phys. 7, 661 A930); A. Sommerfeld undC. Schur
Ann. d. Phys., 4, 409 A930).

ГЛАВА XVI
ПРОХОЖДЕНИЕ МИКРОЧАСТИЦ
ЧЕРЕЗ ПОТЕНЦИАЛЬНЫЕ БАРЬЕРЫ
§ 96. Постановка проблемы и простейшие случаи
Если мы имеем две области пространства, в которых потенциальная
энергия частицы меньше, нежели на поверхности, разделяющей эти
области, то мы говорим, что области разделены потенциальным барьером.
Простейшим примером потенциального барьера может служить барьер
в одном измерении, изображенный на рис. 71. По оси ординат отложена
потенциальная энергия 11 (х) в функции координаты частицы х. В точке х0
потенциальная энергия имеет максимум Um. Все пространство — оо < х <
< + оо делится в этой точке на две области; х < х0 и х > х0, в которых
U < Um. Значение термина «потенциальный барьер» сейчас же выяснится,
если мы рассмотрим движение части-
частицы в поле U (х) на основе классиче-
классической механики. Полная энергия час-
частицы Е равна
Е = -K— + U (х), (96.1)
где р — импульс частицы, a |i — ее
масса. Решая (96.1) относительно
импульса, получим:
р(х)=±
Рис 71. Потенциальный барьер в од-
одном измерении
(96.2}
Знаки J- следует выбрать в зави-
зависимости от направления движения
частицы. Если энергия частицы Е
больше «высоты» барьера Um, то
частица беспрепятственно пройдет барьер слева направо, если начальный
импульс р > 0, или в противоположном '^направлении, если начальный
импульс р< 0.
Допустим, что частица движется ^слева, имея полную энергию Е,
меньшую Um. Тогда в некоторой точке хг потенциальная энергия U (хх) = Е.
p(xl) = 0, частица остановится. Вся ее энергия обратится в потенциаль-
потенциальную, и движение начнется в обратном порядке: хх есть точка поворота.
Поэтому при Е < Um частица, движущаяся слева, не пройдет через
область максимума потенциала (х = х0) и не проникнет во вторую область
х > х0. Подобным же образом, если частица движется справа налево,
имея Е <Um, то она не проникнет в область за второй точкой поворота хг,
324

в которой U(Xz) = E (см. рис. 71). Таким образом потенциальный барьер
является «непрозрачной» перегородкой для всех частиц, энергия которых
меньше Um (напротив, он «прозрачен» для частиц, обладающих энергией
Е > Um). Этим и разъясняется название «потенциальный барьер».
Совсем иначе протекают явления вблизи потенциальных барьеров,
если речь идет о движениях микроскопических частиц в микроскопиче-
микроскопических полях, т. е. о движениях, при рассмотрении которых нельзя игно-
игнорировать квантовые эффекты. В этом случае, как мы сейчас увидим,
в противоположность выводам классической механики, частицы с энер-
энергией Е, большей высоты барьера Um, частично отражаются от барьера,
а частицы с энергией, меньшей Uт, Частично проникают через барьер.
Для того чтобы в этом убедиться, мы рассмотрим совсем простой
случай барьера, изображенный на рис. 72. Именно, мы будем считать,
что потенциальная энергия частицы U (х) всю- , ^ i
ду равна нулю, кроме области 0<х</, где j
она имеет постоянное значение, равное Um. Такой
барьер представляет собой, конечно, идеализа-
идеализацию, но на нем особенно просто можно просле-
проследить интересующие нас стороны проблемы. Мы
можем себе представить, что такой прямоугольный '
барьер возникает путем непрерывной деформации
плавного барьера, изображенного на рис. 72. Рис. 72. Самый простой
Будем искать стационарные состояния части- потенциальный барьер
цы, движущейся в поле такого барьера. Обозна-
Обозначая потенциальную энергию через U (х), мы получим уравнение Шредин-
гера в виде
It2 d-ty , , , , . , r^ . /OR Q\
+ U (x) * = .с'ф. (96.3)
ujp
Обозначая в дальнейшем дифференцирование по х штрихом и вводя
оптические обозначения
*.' = ¥' ^[E-U(x)] = ky~(xy, (96.4)
где п (х) — показатель преломления (см. § 36), мы перепишем уравнение
(96.3) в виде
ty" + kZn2(x)H? = 0. (96.5)
Уравнение (94.5) распадается на три уравнения для трех областей про-
пространства:
' М> = 0, x<0, U(x) = Q, (96.5')
b(x)y = O, 0<x</, U(x) = Um, (96.5")
ф' + ед> = 0, х>1, U(x) = O. (96.5"')
Решения в этих областях могут быть написаны сразу:
■ф (Х) = % (х) = Aeih»x + Be-ih°x, (96.6)
■ф (х) = фп (х) = aeift°nmx + pe-«onmx) (96.6')
■ф (х) = %п (х) = а^х + be-ih<*, (96.6")
где А, В, a, J3, аи b — произвольные постоянные. Однако это—общие
решения трех независимых уравнений (96.5), (96.5'), (96.5") и они, вообще
говоря, не образуют какой-либо одной волновой функции, описывающей
состояние частицы, движущейся в силовом поле О (х). Для того чтобы
они давали действительно одну функцию ф>(л'), мы должны соблюсти
краевые условия, которые мы сейчас установим.
325

Для этого будем рассматривать U (х) и, следовательно, п (х) как
плавную функцию х. Интегрируя тогда уравнение (96.5) около точки
х = 0, получим:
+д +д
^ ф" dx + kl^ л2 (х) ф dx = 0.
-Д -Л
Отсюда
+д
ф' (+ А) - ф' (- А) = - К \ п2(х)Ц (х) dx. (96.7)
-Д
Переходя к пределу А—>0, получаем краевое условие1;
Ф'( + 0) = Ф'(-0). (96.7')
Далее, согласно общему требованию о непрерывности волновых функций
имеем второе краевое условие:
Ф( + 0) = ф(-0). (96.7")
Точка х = 0 ничем не выделена, поэтому условия (96.7') и (96.7") должны
быть соблюдены в любой точке, в частности, и при х = 1.
Чтобы решение (96.6) трех уравнений (96.5) можно было рассматри-
рассматривать как предел решения одного уравнения при переходе от плавного
изменения U (х) к скачкообразному, нужно, чтобы эти решения в точках
х = 0 и х = 1 удовлетворяли краевым условиям (96.7') и (96.7"), т. е.
Подставляя сюда значение функций из (96.6), получаем:
(96.9)
aeikonml _|_ ^e-ikonml —. aeikol
ikonm (aeihor>ml— pe-ifto"mi) = ik0 (aeih°l —
Мы имеем четыре уравнения для шести постоянных. Произвол в выборе
постоянных объясняется тем, что могут быть волны, падающие на барьер
слева, а могут быть — падающие на него справа.
Если мы, например, возьмем А, В Ф 0, 6 = 0, то Aeihr>x может рас-
рассматриваться как падающая волна, Be~ihr^ — как отраженная, a aeiftox —
как проходящая. Если бы мы взяли I Ф 0, то это означало бы, что есть
еще падающая волна с другой стороны барьера. Эти возможности соот-
соответствуют в классической механике случаям движения частиц к барьеру
слева, либо справа.
Мы рассмотрим для определенности случай падения частиц слева.
Тогда мы должны взять 6 = 0. Кроме того, без всяких ограничений мы
можем принять амплитуду падающей волны за единицу: Л=1. Уравне-
Уравнения (96.9) принимают тогда вид:
aeihonml
n
(96.10)
1 Ср. дополнение VIII.
326

Из этих алгебраических уравнений находим а, C, В и а:
а== _ и+"ш) (96 11)
e-iftonmlA_j_nmJ__eiftonmlA_nmJ ' <■ I
e (i«) C96 12)
_nmJ ' V • /
"> , (96.13)
aeViol — 1^™ (96 14)
-ik0nml A +J1копт1 A ПJ
e
-ik0nml
Если энергия частицы £ больше высоты барьера Um, то показатель пре-
преломления пт действителен. В этом случае интенсивность отраженной
волны | В |2 равна
4 i^0
d 12 4С — "mJsina(^o»m0 /ПС 1 с\
1 A + »L + A-«тL-2A-п^ cos Bйопга/) ' ^и' -1
а интенсивность проходящей волны
1 с*~2
(96.15')
A +nmL + (l — nmL — 2A — njyzcos
Вычислим по формуле для плотности тока поток частиц в падающей
волне (Jo), отраженной (Jr) и проходящей (Jd). Из B9.5) имеем:
1 = !l^ I А 2_^п / _ ^о | п |2 / ___ j^o ] ]2 /ng Jg\
0 (Л1 |.i ' г (Л11' d [i ' ' ■ V'-'
Отношение потока отраженных частиц к потоку падающих:
1<4|2
(96.17)
называют коэффициентом отражения. Отношение потока проходящих
частиц к потоку падающих:
Jd - |a|2-|a|2 = D (96.18)
называют коэффициентом прозрачности барьера.
Из закона сохранения числа частиц (уравнение непрерывности для
тока) следует, что
R + D=\ (96.19)
(приведенные выше выражения для i? и D позволяют непосредственно
убедиться в справедливости этого равенства).
По классической механике, если E>Um должно иметь место R = 0,
D—l: барьер совершенно прозрачен. Из (96.15) следует, что | В |2 Ф О,
поэтому в квантовой механике R > О, D<1. Частицы частью отра-
отражаются так же, как отражаются световые волны на границе двух
сред.
Если энергия частицы Е меньше высоты барьера Um, то по класси-
классической механике имеет место полное отражение D = 0, R=l. При этом
частицы совсем не проникают внутрь барьера. В оптике такой случай
•отвечает полному внутреннему отражению. Согласно геометрической оптике
лучи света не проникают во вторую среду.
Более тонкое рассмотрение на основе волновой оптики показывает,
•что в действительности световое поле при полном отражении все же про-
проникает в среду, от которой происходит отражение, и если эта среда
представляет собой очень тонкую пластинку, то свет частично проходит
327

через нее. Квантовая механика в случае Е <Um (случай отражения) при-
приводит к выводу, аналогичному выводу волновой оптики (см. аналогии
в § 36). Действительно, если Е < Um, то показатель преломления пт
является чисто мнимой величиной [см. (96.4)]. Поэтому мы положим
^ . (96.20)
Внося это выражение для пт в (96.14), вычислим теперь |а|2. Тогда
считая e''oli»m|i ^ 1, получаем:
lm'iVeftolnm"- (96-21>
Обозначая первый дробный множитель через Do (он не очень отличается
от 1) и имея в виду значение k0, получаем:
Г (9б22>
Таким образом, при Е < Um, в противоположность выводам классической
механики, частицы проходят через барьер.
Явление прохождения через потенциальный барьер получило образное-
название туннельного эффектах.
Очевидно, что туннельный эффект будет иметь заметное значение
лишь в тех случаях, когда D не слишком мал, т. е. когда
-E)l^l. (96.'23>
Нетрудно видеть, что с туннельным эффектом мы можем встретиться
лишь в области микроскопических явлений. Так, например, для Um —
— Е— Ю1 эв. (около десяти электрон-вольт), jj,— КГ27 г (масса электрона)
и /^ 10~8 см, из (96.22) получим D я» е~г. Но если мы возьмем, напри-
например, / = 1 см, то из той же формулы получим D — е"х°8. Увеличение-
массы частицы и превышение Um над Е еще более уменьшат D. Подоб-
Подобным же образом можно показать, что рассмотренное выше отражение
исчезает с ростом энергии частицы —квантовая механика переходит
в классическую.
Формулу (96.22) для коэффициента прозрачности D, выведенную-
нами для прямоугольного барьера, мы можем обобщить и на случай
барьера произвольной формы. Мы произведем сейчас это обобщение про-
простым, хотя и не вполне строгим путем.
Пусть мы имеем потенциальный барьер U (х), изображенный на>
рис. 71. Представим его приближенно в виде совокупности прямоугольных
барьеров с шириной dx и высотой U (х). Эти барьеры на рисунке заштри-
заштрихованы. Частица, имеющая энергию Е, вступает в барьер в точке х = хг
и покидает его в точке х = х2. Согласно (96.22) коэффициент прозрачности
для одного из этих элементарных барьеров равен
D' — D'e- y Уац1Щх)-Е] dx
потенциальная энергия U (х) должна быть достаточно плавной, чтобы dx-
можно было взять достаточно большим]. Коэффициент прозрачности для
всего барьера должен равняться произведению коэффициентов прозрач-
1 Впервые это явление было рассмотрено Л. И. Мандельштамом и М. А. Леонто-
вичем в связи с квантовой теорией ангармонического осциллятора (ср. конец § 67).
328

ности для всех элементарных барьеров. Тогда показатели в формуле для
D' сложатся и мы получим1
- -Д 1 V2\x{U{x)~E] dx
D = Doe *i . (96.24)
§ 97. Кажущаяся парадоксальность «туннельного эффекта»
Прохождение частиц через потенциальные барьеры представляется на
первый взгляд парадоксальным. Эту парадоксальность усматривают в том,,
что частица, находящаяся внутри потенциального барьера при полной
энергии Е, меньшей высоты барьера Um, должна иметь отрицательную
кинетическую энергию 7 = -—, ибо полная энергия, как это имеет место
в классической механике, является суммой энергий кинетической и потен-
потенциальной:
В области, где U (х) > Е, 4- < 0, это бессмысленно, так как им-
пульс р есть действительная величина. Как раз эти области, как мы
знаем из классической механики, недоступны для частицы. Между тем
согласно квантовой механике частица может быть обнаружена и в этой
«запретной» области. Таким образом, получается, будто квантовая меха-
механика приводит к заключению, что кинетическая энергия частицы может
быть отрицательной, а импульс частицы мнимым. Это заключение и на-
называют парадоксом «туннельного эффекта».
На самом деле здесь нет никакого парадокса, а само заключение
неверно. Дело в том, что, поскольку туннельный эффект есть явление
квантовое [при /г—*0 коэффициент прозрачности D (96.24) стремится
к нулю], постольку он может обсуждаться лишь в рамках квантовой
механики. Полную же энергию частицы можно рассматривать как сумму
кинетической и потенциальной энергий только на основе классической
механики. Формула Е = -£- -\- U (х) предполагает, что мы одновременно
знаем величину как кинетической энергии Т, так и потенциальной U (х).
Иными словами, мы приписываем одновременно определенное значение
координате частицы х и ее импульсу /?, что противоречит квантовой
механике. Деление полной энергии на потенциальную и кинетическую
в квантовой механике лишено смысла, а вместе с тем несостоятелен
и парадокс, основанный на возможности представить полную энергию Е
как сумму кинетической энергии (функция импульса) и потенциальной
энергии (функция координат).
Нам остается лишь посмотреть, не может ли все же оказаться так,
что путем измерения положения частицы мы обнаружим ее внутри потен-
потенциального барьера, в то время как ее полная энергия меньше высоты,
барьера.
Обнаружить частицу внутри барьера действительно можно, даже если
E<cUm; однако, коль скоро фиксируется координата частицы х, при этом
создается согласно соотношению неопределенности дополнительная диспер-
1 Эта формула может быть получена более строго методом квазиклассического
приближения (§ 37). См. также В. Паули, Общие принципы волновой механики, § 12,
Гостехиздат A947).
329.

сия в импульсе (Ар2), так что уже нельзя утверждать, что энергия частицы,
после того как определили ее положение, равна Е. (Ср. §§ 14, 15.)
Из формулы для коэффициента прозрачности следует, что частицы
проникают заметным образом лишь на глубину /, определяемую равен-
равенством (96.23). Чтобы обнаружить частицу внутри барьера, мы должны
фиксировать ее координату с точностью Ах < /. Но тогда неизбежно воз-
/г2 /г2
никает дисперсия импульса Ар2 > = -^. Подставляя сюда /2 из
4Дх2 4'
(96.23), находим:
4^>Um-E, (97.1)
т. е. изменение кинетической энергии частицы, вносимое вмешательством
измерения, должно быть больше той энергии, которой ей недостает до
высоты барьера Um.
Приведем пример, иллюстрирующий это утверждение. Пусть мы желаем определить
координату частицы, находящейся внутри потенциального барьера, таким путем, что
будем посылать узкий пучок света в направлении, перпендикулярном к направлению
движения частицы. Если пучок рассеется, то, значит, на его пути попалась частица.
Как объяснялось выше, точность нашего измерения должна быть такова, чтобы
Ах<^1; с другой стороны, нельзя создать пучок света, ширина которого была бы
меньше длины световой волны Я. Таким образом Дх]>Я, а следовательно, длина волны
света должна быть меньше /, т. е.
(97.2)
/2цA/т-Е)
так какЯ= — , где v—частота световых колебаний, а с—скорость света, то отсюда сле-
следует, что
/г2т2>2(лс2 (Um—E).
Встречающиеся в нерелятивистской механике энергии должны быть меньше собствен-
собственной энергии частицы (лс2, поэтому
h\>Um — E, (97.3)
т. е. энергия применяемых в световом пучке квантов света должна быть больше, нежели
разность между высотой потенциального барьера и энергией частицы.
Таким образом, этот пример иллюстрирует положение о необходимости применить
для измерения координаты аппараты, обладающие достаточно большой энергией, чтобы
можно было локализовать частицу.
§ 98. Холодная эмиссия электронов из металла
Если к металлу приложить большое электрическое поле (порядка
106 в/см) так, чтобы он являлся катодом, то такое поле вырывает элек-
электроны: получается электрический ток. Это, явление получило название
«холодной эмиссии». Оно может быть легко истолковано на основе кван-
квантовой теории прохождения частиц через потенциальный барьер и притом,
в общих чертах, в согласии с опытом.
В этом параграфе мы рассмотрим теорию этого эффекта, представля-
представляющую одно из наиболее простых приложений теории прохождения через
потенциальный барьер. Обратимся сначала к картине движения электро-
электронов в металле в отсутствии внешнего электрического поля.
Чтобы удалить электрон из металла, необходимо затратить некоторую
работу. Следовательно, потенциальная энергия электрона в металле
меньше, нежели вне металла. Наиболее простым образом этот факт может
быть выражен, если мы примем потенциальную энергию электрона U (х)
внутри металла равной 0, а вне металла равной С > 0, так что потен-
330

Металл
им
Вакуум
<?. *
г-
г
диальная энергия имеет вид, изображенный на рис. 70. Схематизируя
таким образом истинный ход потенциальной энергии, мы в сущности
оперируем со средним полем в металле. На самом деле, потенциал внутри
металла меняется от точки к точке с периодом, равным постоянной кри-
кристаллической решетки. Наше приближение соответствует гипотезе свобод-
свободных электронов, так как, поскольку U (х) = 0, то внутри металла нет
никаких сил, действующих на электрон.
Здесь мы не можем обсуждать вопрос о степени правильности такого
приближения1. Ограничимся лишь указанием на то, что рассмотрение
электронов в металле как свободно движущихся частиц («электронный
газ») позволяет уяснить многие
явления в металлах и поэтому,
в определенных рамках, является
законным. Распределение по энер-
энергиям электронов этого газа тако-
таково, что подавляющее большинство
электронов имеет энергию £<С
{при абсолютном нуле температу-
температуры электроны заполняют все уров-
уровни энергии от Е = 0 до Е = е0 < С,
где е0 есть так называемая нуле- ' с
вая энергия; см. § 120). Поток Рис- 73- Поле на Палице металла:
^ттр^тплнпп мртяттгтя пяпяи-,тттин Сплошная линия — в отсутствии внешнего поля,
j,jic.r\ ijjunuD mcidji^id, исздсзгищпп пунктирная линия—при наличии внешнего поля
ИЗНуТрИ Металла На еГО ПОВерХ- s- ПРИ наличии поля образуется барьер ОВС1
ность, обозначим через Jo. Так
как электроны имеют энергию Е < С, то этот поток полностью отра-
отражается от скачка потенциала С, имеющего место на границе металл —
вакуум.
Представим теперь себе, что наложено электрическое поле Щ, направ-
направленное к поверхности металла. Тогда к потенциальной энергии элек-
электрона U (х) (рис. 73) добавится потенциальная энергия электрона в постоян-
постоянном поле I, равная —еЩх ( —е — заряд электрона). Полная потен-
потенциальная энергия электрона будет теперь равна
1]> (у\ J1(y\ pf Y Г р¥ Y ( Y ^. 0\ \
]]>1у\ п lv ^ Л\ I \&о- i.)
U (X) = U (X <^ U). I
Кривая потенциальной энергии примет теперь иной вид. Она изображена
на рис. 73 пунктиром. Заметим, что внутри металла нельзя создать боль-
большого поля, поэтому изменение U (х) произойдет лишь вне металла.
Мы видим, что образуется потенциальный барьер. По классической
механике электрон мог бы пройти через барьер лишь в том случае, если
его энергия Е > С. Таких электронов у нас очень мало (они обусловли-
обусловливают малую термоионную эмиссию). Поэтому никакого электронного тока
по классической механике при наложении поля получиться не должно2.
Однако, если поле Щ достаточно велико, то барьер будет узок, мы будем
иметь дело с резким изменением потенциальной энергии и классическая
механика будет неприменима: электроны будут проходить через потен-
потенциальный барьер.
1 См., например, Г. Бете и А. Зоммерфельд, Электронная теория метал-
металлов, ОНТИ, 1938.
2 Если поле понижает высоту барьера, tos если высота последнего С станет
меньше ~ё0, то же самое будет иметь место и по классической механике. Но это будет
колоссальный ток: электроны хлынут лавиной через барьер. На самом деле имеет место
постепенное нарастание тока с ростом поля.
331

Вычислим коэффициент прозрачности этого барьера для электронов,
имеющих энергию движения по оси ОХ, [равную Ех. Согласно (96.24)
дело сводится к вычислению интеграла
S = J V2]i[U'(x)-E] dx,
где xt и х2 — координаты точек поворота. Первая точка поворота есть
(см. рис. 73), очевидно, хх = 0, так как для всякой энергии Ех < С гори-
горизонтальная прямая Ех, изображающая значение энергии движения по ОХ,
пересекает кривую потенциальной энергии в точке х = 0. Вторая точка
поворота х2 получится, как видно из чертежа, при
отсюда
следовательно,
С-Ех
S= С l/2jT[C-egx-£x]dx. (98-2)
Введем переменную интегрирования g = „■■_ - х. Тогда мы получим
Ц§^. (98.3>
Таким образом, коэффициент прозрачности D для электронов, обладающих
энергией движения по оси ОХ, равной Ех, равен
D(Ex)=Doe~3 h °<S ' (98.4)
Коэффициент этот несколько различен для разных £ж, но так как С > Ех,
то средний (по энергиям электронов) коэффициент прозрачности будет
иметь вид
где Do и Що — константы, зависящие от рода металлов. Ток холодной
эмиссии будет равен »
_ _i?
J(%) = J0D = Ae S. (98.6)
Эта зависимость тока от поля вполне подтверждается экспериментами1.
1 Они были выполнены П. И. Лукирским.
332

§ 99. Трехмерный потенциальный барьер. Квазистационарные
состояния.
Рассмотрение в §§ 97 и 98 задачи о прохождении через потенциаль-
потенциальный барьер отличалось той особенностью, что в них речь шла о потоке
частиц, приходящих из бесконечности и встречающих на своем пути
потенциальный барьер. В дальнейшем (теория радиоактивного распада,
.автоионизация атомов) нам встретятся такие случаи, когда речь будет
идти о потоке частиц, выходящих из некоторой ограниченной области
пространства (ядро атома, атом), окру-
окруженной потенциальным барьером.
Пусть шар с центром в О и радиу-
радиусом г0 (рис. 74, а) есть та поверхность,
.на которой потенциальная энергия U (г)
принимает максимальное значение, так
что для г <r0U <Um и для г >ro(J <
< Uт. Соответствующий пример графика
U (г) дан на рис. 74, Ъ. Допустим, что
нас интересует прохождение через барь-
барьер частиц, первоначально находившихся
Рис. 74. Потенциальный барьер, ог-
ограничивающий замкнутую область
(г<г0)
внутри него. Соответственно предположению, что частицы, падающие извне,
отсутствуют (нет «бомбардировки»), мы должны взять вне барьера лишь
уходящие волны
i[> = С ~ , k > 0. (99.1)
Это условие мы будем называть условием излучения. Ясно, что урав-
уравнение Шредингера
..3ib Л« ,
в этом случае может иметь лишь нестационарные решения. Действи-
Действительно, применим закон сохранения числа частиц к сфере радиуса г:
~
Из (99.1) имеем:
и, стало быть,
>=-Wrds=-\ Jrr2dQ.
s
, ih С . дг|>* Л|>
Г 2(Л V.Y дг дг
А ['
At
dv = - - [ | С |2 dQ < 0,
(99.3)
(99.4)
, (99.5)
т. е. среднее число в объеме сферы V убывает так, что if не может
гармонически зависеть от времени.
Задачу об истечении частиц из барьера можно1* решать, исходя из
уравнения (99.2) с начальным условием таким, что функция Ир (г, 0)
отлична от нуля лишь внутри барьера (чтобы выразить тот факт, что при
t — Q частица находилась внутри барьера). Можно, однако, исходить из
другого условия, до некоторой степени противоположного, именно считать,
что истечение частиц происходит уже давно и значительная часть их уже
находится вне барьера. Такой подход к решению мы рассмотрим под-
подробнее. Он удобен тем, что допускает разделение переменных г и t
33 3

в уравнении (99.2). Положим сразу:
■ S1
При этом величина Е будет комплексной, и ее нельзя рассматривать как
энергию частиц (см. об этом ниже). Мы положим1
F—F lhX
(99.7)
Тогда среднее число частиц в объме Уо, заключенном внутри барьера,
согласно (99.6) и (99.7) будет
U{rj
N(t) =
[ ф* (г) ц (г) dv,
-С
т. е.
■£.'
N(t) = e~M-N(O). (99.8)
Величину X будем называть константой рас-
распада. Подстановка (99.6) в (99.2) дает
и г' г? —— V2\b 4- U (г) * == (Е — — ^1 * С99 9>
Рис. 75. Потенциальный г ч у
барьер, ограничивающий ,г ,
замкнутую область (г<гх) и Чтобы выяснить принципиальную сторону дела,
имеющий простую прямо- мы рассмотрим схематичный пример, взяв фор-
угольную форму2 му барьера U (г), изображенную на рис. 75.
Рассмотрим далее, для простоты, состояния
с орбитальным моментом, равным нулю: / = 0. Тогда, полагая
y(r)=!L£L, (99.10)
мы получим из (99.9)
(99.11)
/г2 d2u
Согласно нашему предположению о виде U (г) уравнение (99.11)
разобьется на три:
u" + k2u = 0 @ <r ОО, (99.12)
u"-q4i = 0 (rj<r<r2), (99.12')
«" + /г2« = 0 (r.2<r), (99.12")
где
m-£0 + ^Y (99.13)
(99.14)
(99.14')
(99.14")
(99.15)
~A« V"° 2
Решения этих уравнений имеют вид
ui = A'e-ihr + Beihi @ < г < гг),
qr (rt<r< ra),
Из условия конечности i]> в нуле следует, что
А' = —В, «1 = Л sin/гг.
1 Из (99.6) и (99.7) видно, что если взять Х = 0, то мы получили бы стационар-
стационарные состояния, что противоречит, согласно (99.5), условию излучения.
2 потенциальная кривая О, гь Um соответствует потенциальной яме, получаю-
получающейся из барьера отодвиганием гг в бесконечность. Е\, Е\ — уровни энергии в такой
яме.
334

Кроме того, условие излучения дает 6 = 0 (только уходящие волны).
Краевые условия на границах r — rt и г = г2, как мы установили в § 96,
сводятся к равенству функций и их первых производных:
^e-qr\ (99.16)
kA cos кгг = 9 (ae9ri- 0е"9^) для л = гх, (99.16')
аевг« + ре-вг« = аеш*, (99.17)
iftra для г = г2. (99.17')
На этот раз мы имеем четыре однородных уравнения для четырех коэф-
коэффициентов Л, a, P, а. Поэтому необходимо, чтобы определитель А системы
уравнений (99.16) и (99.17) обращался в нуль. Несложные вычисления
дают:
()|± () O, (99.18)
где / означает ширину барьера г2 —гг (99.18) есть трансцендентное урав-
уравнение для k. Определим его корни приближенно, считая д/ > 1. Тогда
в нулевом приближении можно отбросить член с e~ql, и мы получаем
-f-tgAr1+l=O. (99.19)
Это —точное уравнение для нахождения собственных значений для потен-
потенциальной ямы @, rv Um), изображенной на рис. 75 и получаемой из потен-
потенциального барьера рис. 75 при г2 = оо. В такой потенциальной яме
имеются дискретные уровни энергии (для E<Um). Если корни уравне-
уравнения (99.19) обозначить через km, km, .... kon, .... то энергия этих уров-
уровней будет [согласно (99.13)] равна
Корни действительны1, если ^ = 0, и по порядку величины равны
—. В этом случае мы имеем стационарные состояния. При конечной
ширине барьера асимптотическое поведение потенциальной энергии таково,
что U (г),.^ < Е, и вместо дискретного спектра (99.20) мы получаем
непрерывный. Однако условие излучения выбирает из непрерывного спектра
уровни, близкие к Еоп, но они не будут теперь стационарными (кп Ф 0).
При малых Хп они будут почти стационарными. Это — квазистационарные
уровни, упоминавшиеся в § 67. Определим величину Хп, считая ее малой.
Для этого разложим член с eql в (99.18) по степеням Ak = k — k0, где
/г0 — один из корней уравнения (99.19) для стационарных состояний потен-
потенциальной ямы, а в член с e'ql подставим /г = /г0; замечая, что '
получим:
Отсюда находим А/г.
1 Для достаточно глубокой ямы (Um -* оо) qm -» оо, вместо (99.19) имеем tgfo-1 = O,
= ял, л= 1, 2, 3, ....
335

При этом малую поправку к действительной части /г0 мы также можем
опустить, как не представляющую интереса. Мнимая же часть будет
равна
Пренебрегая также малой поправкой к действительной части k в (99.13),
мы можем положить -р-2 = &ц. Из (99.13) получаем:
* = *o-SS- (99.22)
Сравнивая это с предыдущим выражением для А/г, мы находим:
Имея в виду, что —- есть скорость частицы v0 внутри барьера и что
И1
k0 % — = — (г—радиус ямы), мы получаем из (99.23) и (99.13):
^^Wl. (99.24)
Эта формула имеет простое наглядное толкование. =— есть число ударов
частицы о внутреннюю стенку барьера в 1 сек, а экспоненциальный мно-
множитель есть коэффициент прозрачности.
Отметим еще некоторые особенности рассмотренной задачи. Мнимое значение
волнового вектора к приводит к тому, что интенсивность излучаемой волны — eihr
неограниченно растет по мере удаления от потенциального барьера:
Рост г|)п1 вытекает из требования, чтобы имелось только излучение, и отвечает
тому факту, что на больших расстояниях находятся частицы, вылетевшие раньше, еще
тогда, когда интенсивность | фх |2 внутри самого барьера была больше. Однако в нашем
методе решения мы не учли того обстоятельства, что излучение на самом деле когда-то
началось (а не длилось все время от t=—оо) и что к моменту начала излучения | г|зх |2
было конечно. Поэтому наш вывод о том, что "ф1П ->■ оо при г -»• оо, вывод, относящийся
к частицам, вылетевшим очень давно, неверен, и само найденное решение справедливо
„ 2koh
лишь для небольших г, именно для г /Ц .■ - ■
Далее отметим, что в связи с формулой (99.7) в литературе часто говорят о мни-
мнимой энергии. Следует иметь в виду, что такое выражение имеет лишь чисто формаль-
формальный смысл. Найденное нами состояние
•ф (г, t) = %(T)e h 2 (99.25)
не есть стационарное состояние с определенным значением энергии (стационарные
состояния гармонически зависят от времени).
Чтобы определить вероятность, найти то или иное значение энергии Е
в этом состоянии, нужно разложить if (г, t) по собственным функциям
1|)Е (г) оператора Н. Так как U (г) > 0, то собственные значения этого
оператора образуют непрерывный спектр 0<i:<-f-oo (ср. § 49). Если
положить
ср _,Et
ф (г, t) = ^ С (Е) е l h % (T)dE, (99.26)
о
336 .

■о w (E) dE=\C (E) |2 dE дает искомую вероятность. Однако мы не можем
юспользоваться для вычисления С (Е) функцией Ир {г, t) (99.25), так как
)на правильна лишь для не очень больших г. Поэтому мы изберем
)бходыый путь, именно, будем считать, что Ир (г, t) имеет корректное
юведение в бесконечности, а начальная функция Ир (г, 0) отлична от нуля
сметным образом лишь внутри барьера, так что вид функции Ир (г, 0)
■.оответствует тому факту, что при t = 0 частица находится во внутренней
области барьера. Определим амплитуду a (t), с которой представлено
состояние Ир (г, 0) в состоянии Ир (г, t). Имеем:
t), Ир* (г, 0)dv. (99.27)
Подставляя сюда Ир (г, t) и Ир* (г, 0) из (99.26) и пользуясь ортогональ-
ортогональностью функций ^(г), найдем:
. К/ °° . Ei
(E)dE= \ e^ w(E)dE. (99.28)
Величина Р {t) — \a (t) j2 дает, очевидно, закон распада состояния
vjj (г, 0). Как видно, форма этого закона определяется распределением
энергии w (E) dE в начальном состоянии1.
Вернемся теперь к нашей задаче. Выберем Ир(г, 0) так, чтобы
*ф(г, O) = t])o(r) внутри барьера и Ир (г, 0) = 0 вне его. Подставляя теперь
Ир (г, t) из (99.25) в (99.27), мы можем игнорировать возрастание Иро{г)
вне барьера, так как там Ир (г, 0) = 0. В силу совпадения Ир (г, 0) и Нр0 (г)
внутри барьера и считая, что Ир (г, 0) нормировано к 1, получим:
На основании (99.28), теперь нетрудно убедиться, что w (E) dE должно
быть- равно2:
w (E) dE = -g ^-^, (99.30)
т. е. мы получаем дисперсионную формулу для распределения энергии.
Величину АЕ — -^- называют шириной квазистационарного уравнения Ео.
Если через т= 1Д обозначить среднюю продолжительность жизни части-
частицы в состоянии t])(r, O)=t])o(r), то мы получаем
Д£-т = 4 . (99.31)
—соотношение между шириной квазистационарного уровня и длитель-
длительностью жизни частицы в этом уровне.
§ 100. Теория радиоактивного а-распада
Известно, что многие радиоактивные элементы распадаются, испуская
a-частицы. По вылете из атомного ядра a-частица, имея двукратный поло-
положительный заряд (+2е), ускоряется в кулоновском поле атомного ядра,
1 Эта теорема принадлежит Н. С. Крылову и В. А. Фоку (ЖЭТФ, 17,
93, 1947).
2 Интеграл в (97.28) в этом случае легко вычисляется посредством вычетов
в комплексной плоскости.
■" Д. И. Блохинцеп

[=13 Ю'6эрг
заряд которого обозначим через Ze (под Z будем подразумевать номер эле-
элемента после вылета а-частицы, Z=Z'-2, если Z' есть номер элемента да
радиоактивного распада).
Большая прочность а-частицы позволяет предполагать, что она суще-
существует в ядре в виде самостоятельного объекта, являясь одним из простых
образований, из которых строится атомное ядро1. Ясно, что а-частица может
длительно находиться в атомном ядре лишь в том случае, если область
вблизи атомного ядра является минимумом потенциальной энергии а-час-
тицы. Кулоновская потенциальная энергия а-частицы, равная —, где
г — расстояние от ядра до частицы, по мере приближения к ядру, как это
изображено на рис. 76 пунктирной кривой, все время возрастает моно-
тонно. Поэтому минимум энергии вблизи
ядра может получиться лишь в том случае,
если на близких расстояниях на а-частицу
действуют какие-то иные силы, помимо элект-
электрических. Такими силами являются ядерные
силы, действующие между нуклонами. Эти
силы весьма велики и действуют лишь на очень
малых расстояниях. Именно этими силами w
обусловливается смена кулоновского оттал-
отталкивания на резкое притяжение вблизи ядра,,
изображенное на рис. 76 сплошной кривой.
Такое поведение потенциала называют обра-
образованием потенциальной ямы или кратера.
При наличии таких сил а-частица, находя-
находящаяся в области г<г0, т. е. в поле притяга-
притягательных сил, будет длительно удерживаться
внутри ядра.
Как же происходит а-распад? Долгое'
время это оставалось загадкой. Еще Кельвин предполагал, что частицы,
испускаемые радиоактивным элементом, как бы кипят внутри потенциаль-
потенциального кратера Время от времени одна из частиц получает избыток энергии
над средней, преодолевает барьер и, вылетев за него, ускоряется отталки-
вательным полем, приобретая большую энергию.
Однако эта наглядная картина, как было показано Резерфордом, про-
противоречит опыту. К изложению этого опыта мы сейчас и перейдем.
Резерфорд бомбардировал атомы радиоактивного урана а-частицами
тория С Энергия а-частиц тория С равна 13- 1(Г6 эрг. Такие частицы,
преодолевая кулоновское отталкивание, могут весьма близко подойти
к ядру. Оценим расстояния наибольшего сближения гг. Очевидно, что гд
есть то расстояние, при котором потенциальная энергия частицы -j— будет
равна исходной кинетической, т. е. ^ = 13X Ю эрг, Z' есть номер ура-
урана и равен 92. Поэтому мы находим, что г1=3-10~12 см.
Наблюдение показывает, что рассеяние таких частиц строго такое,
каким оно должно быть при действии на а-частицу кулоновского поля.
Это означает что ядерные силы начинают действовать на а-частицу на рас-
расстояниях, меньших, нежели 3-Ю2 см. Поэтому а-частицы, заключенные
в ядре, находятся внутри области, радиус которой меньше 3-Ш см.
Or' r0 ЗЮ'асм г^6-Ю''2см г
Рис. 76. Кривая потенциальной
энергии а = частицы в функции
расстояния от ядра (г, Um, r').
Та же кривая схематизирована
(г, Um, г0) (резкое падение пос-
после г0)
Это предположение не является обязательным. Возможно, что перед выле-
вылетом из ядра а-частица образуется из более простых частиц: нейтронов и протонов, мы,
будем считать в дальнейшем, что она существует в ядре постоянно.
338

С другой стороны, уран, сам является радиоактивным элементом и испу-
.кает а-частицы. Измерение энергии этих частиц показывает, что она равна
1,6- Ю эрг.
Эти а-частицы вылетают из ядра, т. е. с расстояний, меньших 3-10~12 см.
Гогда, ускоряясь в кулоновском поле, они должны были бы приобрести
1нергию, равную высоте потенциального барьера (см. рис. 76) и во всяком
-.лучае большую, нежели 13-10~6 эрг. Получается же так, как если бы они
шлетали с расстояния г— 6-10~12 см. Таким образом опыт приводил с точки
(рения классической физики к парадоксальному положению: нужно было
предположить, что кулоновское электрическое поле ядра действует
ia падающие извне а-частицы, но не действует на вылетающие из. ядра,
шбо считать, что закон сохранения энергии не выполняется при радио-
радиоактивном распаде.
Решение этого парадокса вытекает из квантовой механики, приводящей
к возможности туннельного эффекта через потенциальный барьер, разде-
разделяющий область притяжения (/"</■„) от области отталкивания г>/■„).
В самом деле, тогда парадокс полностью решается: частица, находя-
находящаяся внутри ядра, может иметь энергию, меньшую, нежели высота барье-
барьера, и все же пройти через него. Частица же, пролетающая извне, ввиду
малой прозрачности барьера лишь в очень редких случаях будет за-
захватываться ядром (так как время пребывания ее около ядра очень
мало). Поэтому рассеяние а-частиц, падающих извне, будет обусловли-
обусловливаться кулоновскими силами, действующими за пределами барьера. Предпо-
Предположенная малая прозрачность барьера согласуется с. тем фактом, что
периоды радиоактивного а-распада весьма велики.
Применяя теорию прохождения через потенциальные барьеры, легко
облечь изложенную идею в математическую форму и найти выражение
для константы радиоактивного распада X. Напомним, что эта константа
определяется следующим образом. Если имеющееся к моменту времени t
число нераспавшихся атомов dN будет равно
djV= -X-N-dt, N(t) = N@)e-u. A00.1)
Для вычисления константы распада X мы можем применить кванто-
квантовую теорию просачивания частиц через потенциальные барьеры, изложен-
изложенную в предшествующем параграфе. Согласно этой теории а-частицу вну-
внутри ядра следует рассматривать как находящуюся в «квазистационарном»
состоянии. Обозначая скорость частицы в этом состоянии через v{, радиус
барьера через г0 и, наконец, его коэффициент прозрачности через D, мы
получим:
^ = §-oD. A00.2)
Остается вычислить D. Ввиду более сложной формы барьера вместо
(99.24) мы получим [см. (96.24)]:
Из рис. 76 следует, что первая точка поворота гг есть г0 (радиус
ядра), вторая (г2) определится из условия
A00.4)
22* 339

С другой стороны, уран сам является радиоактивным элементом и испу-
испускает а-частицы. Измерение энергии этих частиц показывает, что она равна
* 6,6-10 эрг.
Эти а-частицы вылетают из ядра, т. е. с расстояний, меньших 3-10~12 см.
Тогда, ускоряясь в кулоновском поле, они должны были бы приобрести
энергию, равную высоте потенциального барьера (см. рис. 76) и во всяком
случае ббльшую, нежели 13-10 эрг. Получается же так, как если бы они
вылетали с расстояния г~6-10~12 см. Таким образом опыт приводил с точки
зрения классической физики к парадоксальному положению: нужно было
предположить, что кулоновское электрическое поле ядра, действует
на падающие извне а-частицы, но не действует на вылетающие из. ядра,
либо считать, что закон сохранения энергии не выполняется при радио-
радиоактивном распаде.
Решение этого парадокса вытекает из квантовой механики, приводящей
к возможности туннельного эффекта через потенциальный барьер, разде-
разделяющий область притяжения (/"<г0) от области отталкивания г>л0).
В самом деле, тогда парадокс полностью решается: частица, находя-
находящаяся внутри ядра, может иметь энергию, меньшую, нежели высота барье-
барьера, и все же пройти через него. Частица же, пролетающая извне, ввиду
малой прозрачности барьера лишь в очень редких случаях будет за-
захватываться ядром (так как время пребывания ее около ядра очень
мало). Поэтому рассеяние а-частиц, падающих извне, будет обусловли-
обусловливаться кулоновскими силами, действующими за пределами барьера. Предпо-
Предположенная малая прозрачность барьера согласуется с тем фактом, что
периоды радиоактивного а-распада весьма велики.
Применяя теорию прохождения через потенциальные барьеры, легко
облечь изложенную идею в математическую форму и найти выражение
для константы радиоактивного распада К. Напомним, что эта константа
определяется следующим образом. Если имеющееся к моменту времени t
число нераспавшихся атомов dN будет равно
dN~—%-N-dt, N (t) = N @) g-«. A00.1)
Для вычисления константы распада X мы можем применить кванто-
квантовую теорию просачивания частиц через потенциальные барьеры, изложен-
изложенную в предшествующем параграфе. Согласно этой теории а-частицу вну-
внутри ядра следует рассматривать как находящуюся в «квазистационарном»
состоянии. Обозначая скорость частицы в этом состоянии через vit радиус
барьера через г0 и, наконец, его коэффициент прозрачности через D, мы
получим:
X = ^D. A00.2)
Остается вычислить D. Ввиду более сложной формы барьера вместо
(99.24) мы получим [см. (96.24)]:
« • A00.3)
Из рис. 76 следует, что первая точка поворота гг есть г0 (радиус
ядра), вторая (л2) определится из условия
27'р2 97'<>2
22* 339,

Таким образом,
г2
S = Jj Vfy [U (г) -Е] dr = J/2JI ^ j/~-£dr. A00.5)
ro
Вводя сюда новую переменную | = —, мы получаем
1
го.
1- ld£, A00.5')
и, полагая, наконец, еще g = cos2«, мы без труда вычислим вышена-
писанный интеграл:
A00.6)
COS «0-7;-2Z^-
Воспользуемся тем, что отношение — меньше единицы, и разложим
ы0 и sin 2«0 в ряд по степеням — (достаточно ограничиться двумя первы-
первыми членами). Тогда мы получим:
S = ^^-2e |/j!]AZr7, A00.7)
где » —скорость вдали от ядра, равная у —. Итак, выражение для кон-
станты распада A00.3) раскрывается следующим образом:
_4jtc2Z' | 4еУЛ |Г^7—
^ = 2~|е Ло h , A00.8)
или
, , 4jtc2Z'
Наиболее замечательным выводом из этой формулы является зависимость
между X и скоростью а-частицы v. Подобная зависимость еще задолго
до квантовой теории этого явления была установлена на опыте Гайгером
и Нэттолом.
Далее мы видим, что In К зависит от номера элемента Z (Z = Z' — 2)
и радиуса ядра.
Из опыта известно, что константы распада варьируют в очень широких
пределах: от 106 се/с до 10~18 сек'1. Если бы в таких же пределах
приходилось варьировать параметры, определяющие X, то теория была бы
наверно неправильной. Замечательным следствием формулы (98.9) является
то, что если по эмпирическим данным для X определять радиусы ядер,
то окажется, что они все лежат в тесных границах, примерно от
5-Ю2 см до 9-102 см. Значительное различие в величине К для разных
элементов определяется не различием в радиусах ядер, а различием в энер-
энергии вылетающих частиц. Слабую зависимость X от г0 и резкую от v
следует рассматривать как подтверждение теориих
1 Подробности теории радиоактивного распада см. А. С. Давыдов, Теория
атомного ядра, Фнзматгиз, 1958.
340

§ 101. Ионизация атомов в сильных электрических полях
Подобно тому, как сильное электрическое поле вырывает электроны
из металлов (холодная эмиссия, § 96), оно вырывает их также и из отдель-
отдельных атомов газа. Явление это называют иногда «автоионизацией» атомов
и его причину легко понять, если рассмотреть вид потенциальной энергии
электрона в атоме при наличии внешнего электрического поля. Пусть
потенциальная энергия электрона в отсутствии внешнего поля есть 0(г).
Внешнее электрическое поле % пусть направлено по оси OZ. Тогда вся
потенциальная энергия электрона равна
U'(r)=U(r)+eEz. A01.1)
Рассмотрим вид потенциальной кривой на оси OZ (х=у=0, r=\z\). В отсут-
отсутствии внешнего поля (%=0)U' = U(r) и имеет вид, изображенный на рис. 77
пунктиром. Дополнительная потенциальная энергия во внешнем поле еЩг
изобразится прямой аа . Кривая полной потенциальной энергии U', полу-
получающаяся сложением, проведена на рис. 77 сплошной линией а'Ь' и аЬ.
Мы видим, что около точки 20 образуется потенциальный барьер, разде-
разделяющий пространство на две области: внутреннюю z>z0 и внешнюю z<.z0,
в каждой из которых потенциальная энергия U' меньше U'(zo) = Um. На чер-
чертеже приведены также два уровня
энергии Е' и Е". Если энергия Е—Е"~>
>0т, то электрон не будет удержи-
удерживаться вблизи атома, а будет удалять-
удаляться в область отрицательных z. Если
же энергия электрона E=E'<cUm, то
согласно законам классической меха-
механики электрон останется во внутренней
области. По квантовой механике в этом
случае просачивание через барьер все
же будет иметь место. Таким обра-
образом, здесь создается положение ве-
вещей, вполне аналогичное тому, ко-
которое имеет место при радиоактивном
распаде.
- Теперь уже совсем легко видеть
причину ионизации атомов полем.
При включении поля получается барьер, через который электроны прони-
проникают во внешнее пространство. Если высота барьера Um меньше энергии
электрона, то частицы будут проходить («над барьером») и по классиче-
классической механике. Поэтому и классическая механика приводит к возможности
ионизации атома внешним электрическим полем. Различие заключается
лишь в том, что по законам квантовой механики эта ионизация должна
наступать при меньших полях, нежели это предписывается механикой
классической, так как согласно квантовой механике для возможности иони-
ионизации не нужно, чтобы барьер оказался ниже энергии электрона. Ясно,
однако, что при малых полях барьер будет очень широким и прозрачность
его будет очень мала.
Явление автоионизации можно наблюдать таким образом: допустим,
что мы наблюдаем какую-либо спектральную линию, обусловленную элек-
электронным переходом из состояния Е' в Ео (см. рис. 77). По мере увеличения
электрического поля эта линия будет смещаться (штаркэффект), и если
поле достигнет столь большой величины, что прозрачность барьера будет
велика, то электрон в состоянии Е' будет чаще вылетать из атома, проходя
341
Рис. 77. Сложение атомного поля

через барьер (ионизация), нежели падать в нижнее состояние (Ео), излучая
свет. Благодаря этому спектральная линия будет слабеть, пока, наконец,
совсем не исчезнет. Это явление можно наблюдать на бальмеровской серии
атомного водорода1.
Для того чтобы иметь возможность проследить действие электрического
поля различной напряженности, устраивают так, что различные части
спектральной линии обусловливаются светом, исходящим от атомов, нахо-
находящихся в полях различной силы. Именно в объеме светящегося газа элек-
электрическое поле возрастает в направлении, параллельном щели спектро-
спектроскопа (до некоторого предела, достигнув которого оно вновь падает).
На фотографии (см. рис. 53) приведены результаты подобного опыта.
Буквами р, y, б, е обозначены линии серии Бальмера (Яр— переход п~-
=-4—>п=2, Ну— переход «=5—>п=2, Н&— переход «= 6—>«=2 и Не—
переход «=7—>п=2). Приложенное электрическое поле растет снизу вверх.
Белые линии на фотографии суть линии одинаковой напряженности поля.
Из фотографии видно, что линии сначала расщепляются. Это расщепление
увеличивается по мере роста поля (из расщепления линии Нр легко видеть
положение линии максимальной напряженности поля). При некоторой
напряженности поля спектральная линия исчезает.
Сравнение линий J3, у, б, е показывает, что они исчезают в последова-
последовательности е, б, у (при достигнутых полях р полностью не исчезает). Это есть
последовательность возрастания энергии возбужденного состояния.
Из рис. 77 явствует, что чем выше энергия электрона, тем меньше при
заданном поле ширина и высота барьера, т. е. тем больше его прозрачность.
Таким образом, наблюдающаяся последовательность в исчезновении спект-
спектральных линий вполне соответствует нашему толкованию этого явления
как результата туннельного эффекта. То обстоятельство, что красные
компоненты расщепленных линий исчезают раньше фиолетовых, также полу-
получает полное разъяснение при более детальном рассмотрении волновых функ-
функций электрона. Именно, состояния, отвечающие линиям, смещенным в крас-
красную сторону, обладают тем свойством, что в них интенсивность электрон-
электронного облака больше в области барьера, нежели в состояниях для фиоле-
фиолетовых компонент. Благодаря этому ионизация протекает более благопри-
благоприятным образом.
Сформулируем несколько детальнее те условия, при которых следует
ожидать исчезновения спектральной линии в электрическом поле. Пусть
вероятность оптического перехода электрона в нижнее состояние будет
— '(т—время жизни в возбужденном состоянии). Время жизни электрона
в возбужденном состоянии есть х я» 10"8 сек. Вероятность перехода элект-
электрона в нижнее состояние в 1 сек будет —. Вероятность туннельного
эффекта (ионизации) будет равна (так же, как и при расчете радиоактив-
радиоактивного распада) числу ударов электрона о внутреннюю стенку потенциаль-
потенциального барьера в 1 сек, умноженному на коэффициент прозрачности D.
Число ударов о барьер по порядку величины равно к—, где о —скорость
электрона, а гп—радиус барьера, примерно равный радиусу орбиты а.
Скорость равна, опять-таки по порядку величины, £> = }/ —■—-, где |£| —
энергия электрона, a jj, — его масса.
1 Заметим, что наблюдение числа электронов, вырываемых полем, в данном
случае затруднено, так как в условиях газового разряда трудно установить, за счет
каких именно причин возрастает электронный ток.
342

Следовательно,
/ е2 Л2 Л
i так как Е = — ^-, а = —^ ) • Следовательно, вероятность автоионизации
равна 1016 D сек'1. Чтобы преобладала автоионизация (условие исчезно-
исчезновения спектральной линии), нужно, чтобы — <D-1016, т. е. D > 10~8.
Количественная теория автоионизации находится в хорошем согласии
с опытом1.
1 См. Г. Бете, Квантовая! механика простейших систем, ОНТИ, 1935,
стр. 193—197.

ТЛАВА XVII
ЗАДАЧА МНОГИХ ТЕЛ
§ 102. Общие замечания о задаче многих тел
Квантовая механика одной частицы во внешнем поле может быть обоб-
обобщена на случай движения многих частиц. Для этого так же, как и в класси-
классической механике, достаточно рассматривать систему из N частиц как одну
частицу с 3iV степенями свободы (если не считать спина частиц; с учетом спи-
спина будем иметь AN степеней свободы). Все общие положения квантовой меха-
механики, имеющие силу для системы с несколькими степенями свободы, могут
быть сразу же перенесены на систему, состоящую из ЛГ частиц. Тем не менее
существуют некоторые специфические моменты, свойственные' системам из
многих частиц и заслуживающие специального рассмотрения.
Среди этих специфических моментов особо важные выясняются для
систем, состоящих из одинаковых частиц. В дальнейшем нам придется
подробно остановиться на них. Свойства систем из одинаковых частиц
образуют одну из наиболее замечательных глав квантовой механики. Однако
пока мы оставим в стороне эти особенности систем с одинаковыми частицами
и обратимся к некоторым вопросам, общим для систем любых частиц.
Всегда ли можно рассматривать совокупность частиц как механическую
систему с соответственно большим числом степеней свободы? Ответ должен
быть отрицательный. Рассмотрение системы частиц с координатами x1ylz1,
x2y.2z2, ..., xNyNzN как механической системы с 31V степенями свободы воз-
возможно лишь при условии, что между частицами не действуют запаздываю-
запаздывающие силы (или при приближенном рассмотрении таких сил). Иначе говоря,,
все силы взаимодействия должны зависеть лишь от мгновенных значений
механических величин, относящихся к нашим частицам (например, от их
координат и скоростей в данный момент времени), а не от их значений
в прошлом, как это бывает при действии запаздывающих сил. Это условие
не является особенностью квантовой механики. Оно таково же и в класси-
классической механике.
Поясним это условие на примере электромагнитных сил. Пусть рас-
расстояние между частицей номера / и частицей номера k есть rJfe. Тогда время,
в течение которого распространится электромагнитное возмущение
rih
от одной частицы [к другой, равно т = —, где с —скорость света.
Для того чтобы можно было считать силы мгновенными, необходимо,
чтобы за время х расстояние между частицами мало изменилось. Если
относительная скорость частиц вдоль rjh есть vih, то изменение rjh
за время т есть Дг3'к = »3уг = • Следовательно, наше условие гласит:.
Vj^-_<rik' т. е. vjk<£ с.
3 44

Следовательно, относительные скорости частиц должны быть гораздо
меньше скорости света с. Короче говоря, это всегда можно сделать, если
мы ограничиваемся нерелятивистской областью скоростей.
Если и~с, то сверх того, что мы должны будем учитывать и реля-
релятивистские, и квантовые эффекты, мы должны будем вместе с механи-
механическими уравнениями для частиц рассматривать еще и уравнения электро-
электромагнитного поля, которые управляют распространением взаимодействия
от одной частицы к другой.
Относящиеся сюда вопросы выходят за рамки этой книги и вообще
они еще не разрешены полностью современной теориейх.
Поскольку же v < с, мы можем рассматривать квантовую механику
системы частиц как механику одной частицы с многими степенями свободы.
Если у нас имеется N частиц с координатами xhykzk (k=\, 2, 3, . .., N)
и с массами mh, то волновая функция Ир в этом случае будет, как всегда,
функцией координат всех степеней свободы нашей системы и времени t,
т. е. функция 3N-\- 1 аргументов2:
Ир = 1|з(х„ yv zv ..., xh, yh, zh, ..., xN, yN, zN, t). A02.1)
Она определяется таким образом в пространстве 3N измерений, в так
называемом пространстве конфигурации системы. Название этого фик-
фиктивного пространства проистекает от того, что задание координат точки
в этом пространстве есть задание трехмерных координат (хк, yk, zh) для
всех частиц (k=l, 2, 3, ..., N) нашей системы и, следовательно, опре-
определяет расположение (конфигурацию) всех частиц системы в трехмерном
пространстве. Поэтому точку пространства конфигураций с 3N коорди-
координатами (хх, yv zv ..., xN,yN, z?f) называют изображающей (систему) точкой.
Обозначим бесконечно малый элемент объема в пространстве кон-
конфигураций через dQ:
dQ = dx1dyxdz1 ... dxkdykdzk ... dxNdy^, dzjy A02.2)
Тогда величина
* w (xv yv г,, >.., xk, yh, zk, . .., xN, yN, z'N, t) dQ. = Hp*HpdQ A02.3)
есть вероятность того, что изображающая точка лежит в элементе
объема dQ пространства конфигураций в момент времени t, т. е. вероят-
вероятность конфигурации системы, при которой в момент t координаты первой
частицы лежат между xlr x1~\-dxi, уЛ, y1~\-dy1, zv z1~\-dz1, ..., /г-ой
частицы - между xh, xh +dxh, yk, yh + dyh, zk, zk + dzh и т. д.
Наряду с элементом объема A02.2) рассмотрим элементы объема
в подпространствах ^типа dQft, dQft3-, ... |_и т. д., определенные по фор-
формулам:
dQ = dxkdyhfdzHdQH, A02.4)
dQ = dxH dyk dzn dxj dyj dzj dQhj" iih. n. A02.4')
Интегрируя A02.3) по координатам всех частиц кроме' k-ой, т. е. по dQk,
мы найдем вероятность того, что координаты /г-ой частицы лежат между
xk> xhJr dxk, yh, yh+dyh, zk, zk+ dzh при любом положении других, иными
словами, мы найдем вероятность того, что /г-ая частица находится в данном
1 См. В. Гайтлер, Квантовая теория излучения, ГИТТЛ, 1940; П. Дирак,
Основы квартовой механики, гл. XIV; Г. Вентцель, Введение в квантовую теорию
волновых полей, Гостехиздат, 1947. Особенно: А, И. АхиезериВ. Б. Бересте ц-
к и й, Квантовая электродинамика. Физматгиз 1959.
2 Чтобы не усложнять вопроса, мы не рассматриваем сейчас спина частиц
345

месте пространства. Обозначая эту вероятность через w(xh, yh, zk, t), мы
получаем:
w(xh, yk, zh, t)dxhdyhdzu — dxkdykdz \ ij>*ij) dQfe. A02.5)
Подобным же образом величина
®(xk> Ун> zk> xi> Уз, Zi< t)dxhdyhdzhdXjdyjdzj =
= dxk dyk dzh dxj dy, dz,- [ ty*tydQkj A02.5')
есть вероятность того, что /г-ая частица находится около точки xhybzk,
j-ая частица одновременно около точки х^у^. Таким образом, зная волно-
волновую функцию ty, заданную в пространстве конфигураций, можно опреде-
определить вероятность данной конфигурации системы A02.3), вероятность
положения любой из частиц A02.5) и, наконец, вероятность того или
иного положения пары частиц A02.5') и т. п. Равным образом по общим
формулам квантовой механики, разлагая \р по собственным функциям
какого-либо из интересующих нас операторов, можно вычислить и вероят-
вероятности того или иного значения любой механической величины.
Мы будем считать, что волновая функция Hp(xv ...,zn, t) так же,
как и волновая функция одной частицы, подчиняется уравнению Шре-
дингера
ИгдЛ = Ну, A02.6)
причем Н означает здесь гамильтониан для системы частиц. Последний,
в полной аналогии с классической гамильтоновой функцией для системы
N частиц с массами тъ ..., тк, ..., mN
N , N
где Uk(xk, yk, zk, t) — силовая функция /г-ой частицы во внешнем поле,
a Ukj(xk, ..., Zj)~ энергия взаимодействия /г-ой и /-ой частиц, напишется
в виде
JV N
И = ^ { - ^ VI + Un (xk, ук, гк, О} + 2 иы (xk> Ук> гк, хи yh z3),
A02.6')
где
Очевидно, что этот гамильтониан представляет собой простое обобщение
гамильтониана для одной частицы х.
Из уравнения A02.6) следует уравнение непрерывности для вероят-
вероятности w в пространстве конфигураций. Чтобы получить его, умножим
A02.6) на ф* и вычтем сопряженную величину. Имея в виду значение
гамильтониана A02.6'), мы получим:
N
* i (***) = - £ S i
k—i
1 Можно было бы выписать гамильтониан при наличии магнитного поля и с учетом
спина. Он равен сумме гамильтонианов отдельных частиц плюс члены, определяющие
взаимодействие частиц между собой.
346

Полагая
— ih
-. д д д
где \h — оператор с проекциями -=— , ^— , -^—, мы можем написать полу-
полученную формулу в виде
^2 = 0. m A02.8)
ft=i
Это уравнение показывает, что изменение вероятности конфигурации w
обусловливается потоком этой вероятности. Так Jft есть функция коор-
координат всех частиц (и времени) и имеет смысл плотности тока, обуслов-
обусловленного движением /г-ой частицы при заданных координатах всех осталь-
остальных (N — 1) частиц. Чтобы получить плотность тока /г-ой частицы )k при
любом положении остальных, следует интегрировать A02.7) по всем коор-
координатам, кроме координат /г-ой частицы:
h (xh> Ун> zh> 0 = \ Jft (xv ■■■, Ч> У к' zk> ••■■> z"x> *) dQu- A02.9)
Этот ток также удовлетворяет уравнению непрерывности, но уже в трех*
мерном пространстве. Именно, интегрируя A02.8) до dQft, мы получаем:
w (Л* Z *) dQ
Далее,
Так как dQft [см. A02.4)] как раз содержит координаты всех частиц
кроме /г-ой, то интегралы вида \ div&Jfc' dQ!t можно преобразовать в по-
поверхностные и если о|з исчезает в бесконечности, то они равны нулю.
Так как, напротив в интеграле \ d\vkJkdQk дифференцирование и интег-
интегрирование идут по различным переменным, то
ivhJft dQk = d\v,t ^ Jk dQk = div,jr
= ~dt [ w (■*!• • • •' Zjv' /) dQft = Ж w
Таким образом, мы получаем закон сохранения для каждой из частиц
0 = 0, • (Ю2.10)
-сформулированный уже в трехмерном пространстве (xh, yh, zh).
§ 103. Закон сохранения полного импульса системы микрочастиц
В классической механике, как известно, полный импульс системы
частиц, находящихся под , действием лишь внутренних сил, остается
постоянным. При этом центр тяжести системы движется по инерции
прямолинейно и равномерно. Если же имеются внешние силы, то измене-
изменение полного импульса в единицу времени равно результирующей всех
347

внешних сил, действующих на частицы системы. Мы покажем, что эти
положения классической механики сохраняют свою силу и в квантовой
области. Определим для этой цели оператор полного импульса всех микро-
частиц системы Р- Под оператором полного импульса всей системы частиц
мы будем подразумевать сумму операторов импульса Рк всех частиц
k=l, 2, ...,'N:
я=2 ?ft=-«viSvft. (юз.1)
—>
Вычислим оператор производной импульса Р по времени. Согласно общим
формулам квантовой механики
^ 4 A03.2)
Подставляя сюда Н из A00.6') и замечая, что Р коммутируем с опера-
тором кинетической энергии частиц / = —о~ 2j — "^» мы ПОЛУЧИМ> что
JV JV N
h=l k=£j=i k=i
Далее, замечаем, что
tf*(Svft)-(Svfc)£/ft=-W. A03-3>
ft=l ft=l
JV
Наконец, вычислим перестановку оператора 2 Vft и взаимной энергии
частиц 2 Ukj. При этом мы сделаем предположение, что силы между
ft=3
частицами зависят лишь от взаимных расстояний между частицами гы-
так, что Uk] = UM-(rkj). Тогда на Uk]- действуют только те операторы V&'
из суммы 2 Vh, Для которых k' = k или fe' = /, т. е. на Uhj действует
ft=i
пара: Vft + V,-- Имеем:
^w (Vfc + V3-) - (Vft + Vy) 1/ы- = - VkU,l3- - Vy^, (Ю3.4)
HO
Следовательно,
Wj + W>, = 0. (Ю3.5)
Это есть выражение закона о действии и противодействии. Из него,
следует, что перестановка операторов A03.4) равна нулю.
348

Таким образом, получается:
di с?.
k, yk,zh,t),
A03.6)
т. е. оператор производной полного импульса по времени равен оператору
результирующей силы, действующей со стороны внешних полей на нашу
систему.
Эта теорема является полным аналогом классической теоремы о дви-
движении центра тяжести системы. Различие заключается лишь в том, что
в квантовой механике она формулируется не для самих механических
величин, а для изображающих эти величины операторов и, следовательно,
для средних значений величин.
Если внешние силы отсутствуют (Uk = 0), то из A03.6) следует, что
dP -0
A03.7)
т. е. полный импульс системы частиц, взаимодействующих между собой,
в отсутствии внешних сил сохраняется.
Напомним, что операторное равенство A03.7) означает, что: 1) сред-
среднее значение полного импульса не меняется с течением времени, 2) ве-
вероятности w(р) того или иного значения р также остаются неиз-
неизменными.
§ 104. Движение центра тяжести системы микрочастиц
Докажем важную для приложений теорему о независимости движе-
движения центра тяжести системы от относительных движений частиц, обра-
образующих эту систему. Для этого преобразуем гамильтониан системы
Частиц Н, подверженных действию лишь внутренних сил:
Я =
■W,
N
=2^vi и w= 2
A04.1)
A04.2)
к новым координатам: координатам центра тяжести системы X, Y, Z
и 3N — 3 относительным координатам. Удобно взять так называемые
координаты Якоби, которые определяются следующим образом:
ВД
Х3,
tt = -
i*v
A04.3)
349

Совершенно такие же формулы имеют место для осей 0Y и 0Z:
mlyl+...+mjyf )
m++m I A04.3'}
Эти формулы представляют собой обобщение обычных формул для коор-
координат центра тяжести и относительных координат двух частиц. Коор-
Координаты Якоби являются ортогональными. С помощью обычных правил
перехода от дифференцирования по одним переменным к дифференциро-
дифференцированию по другим переменным можно доказать, что1
ЛГ-1
где
Д2 Л2 Я2
V2< = — 4-— 4-— , П04.6У
д|^ <?т]'^ о^2. v '
М есть масса всей системы, а ^ — приведенная масса центра тяжести /
первых частиц и (/+1)-ой:
М = ь|т„ A04.7)
±=—L- + ^- A04.8)
ft=i
Из этих формул следует, что гамильтониан A04.1) может быть написан
в виде
W-1
+ W(llt ...,In-i, i\v ..-.Tiw-i, Si. ...,Sw-i), A04.10)
причем оператор
'--и»1—иСич-да+Bi) <104Л1>
есть оператор кинетической энергии центра тяжести всей системы,.
а оператор
3=1
есть оператор кинетической энергии относительного движения частиц.
1 См. дополнение XI.
350

Существенно, что в энергию взаимодействия W координаты центра тяже-
тяжести не входят. Преобразуя %v ..., &у_ь цг, ..., тцу-i, Z,v ..., S/v-i
к любым новым относительным координатам, qx, q2, ..., 931V-3. мы не
изменим оператора Т. Поэтому вообще вместо A03.6') можно написать
иг
Hr + H^^ 3), (Ю4.13)
где Hi есть гамильтониан для относительного движения и не содержит
координат центра тяжести. Далее, на основании A04.9) и A03.1) полу-
получаем новое выражение для оператора полного импульса:
p*=-ihM' ру=-шж> p^-ihi- A04Л4)
Волновую функцию ¥ будем рассматривать как функцию координат цен-
центра тяжести X, Y, Z и относительных координат qv q2, ..., дзя-з-
Уравнение Шредингера с гамильтонианом A04.13) допускает разделение
переменных, если положить
¥(Х, Y, Z, qv q2, ...,q3N_3, t) =
= Q>(X,Y,Z,tL(qvq» • •., qsN-s, t). A04.15)
Подставляя A04.15) в уравнение Шредингера, получим:
^4 ^ . A04.16)
Разделив это 'на <Dij) и приравнивая порознь члены, зависящие от X, Y, Z
и qv 92, ..., 93JV-3, мы найдем два уравнения:
4!=4^ A04Л7)
ih^- = H&. A04.18)
Первое из уравнений относится к движению центра тяжести, второе —
к относительному движению. Как мы видим, первое есть уравнение
движения свободной частицы с массой М: центр тяжести в отсутствии
внешних сил движется как свободная материальная точка. Простейшее,,
частное, решение уравнения A04.17) есть волна де Бройля
Ф (X, Y, Z, t) = -^r Д {Et-px^-pvr-p^z\ (Ю4.19)
Она же, как следует из A04.9), есть собственная функция оператора пол-
полного импульса Рх, Ру, Pz, принадлежащая собственным значениям
Рх, Ру, Pv E есть собственное значение кинетической энергии движения
центра тяжести системы:
Длина волны К этих волн, как это следует из A04.19), так же, как
и для элементарной частицы, равна
+^' A04-2°)
где V — групповая скорость движения центра тяжести.
Вывод этот важен, так как особенно подчеркивает, что волны де Бройля
не являются какими-то колебаниями, связанными с природой (например,
351

структурой частиц), а выражают в квантовой области общий закон дви-
'жения свободных частиц или закон движения центра тяжести системы,
не подверженной действию внешних сил.
§ 105. Закон сохранения момента импульса системы
микрочастиц
Пусть мы имеем систему из N частиц. Обозначим операторы проек-
проекций момента импульса /г-ой частицы на оси координат через Мх, My, М}
A05Л)
A05.1")
где xk, yh, zh — координаты /г-ой частицы.
Соответственно этому операторы проекций полного момента импульса
всей системы частиц Мх, Му, Мг определим по формулам:
N
Мх= 2 Мх, (Ю5.2)
N
Му= S Ml, A05.2')
A05.2")
Покажем, что оператор производной по времени от момента импульса
равен моменту сил, действующих на систему (точнее, оператору момента
1 сил). Согласно общему определению производной оператора мы имеем:
^ ^-МХН). A05.3)
Гамильтониан Н согласно A05.6') равен:
JV JV
{£2} 2 ии- A05-4)
Для вычисления перестановки операторов в A05.3) мы должны иметь
в виду, что каждое слагаемое Мх в операторе Мх действует лишь на те
члены в Н, которые содержат координаты k-ак частицы.
Операторы Vft коммутируют с оператором Мх- Действительно, как мы
знаем, оператор кинетической энергии можно представить в виде
где ГГA —оператор той части кинетической энергии частицы, которая
отвечает движению частицы по радиусу-вектору rH, a (MftJ — квадрат
момента импульса /г-ой частицы. Мх коммутирует и с Тг , и с (Ж*J,
поэтому МКх коммутирует с — -^— V^.
352

Вычислим теперь перестаножу М* и Uk» Имеем:
Наконец, найдем еще перестановку:
rhj * rkj J v >*' >yh> drh. rh.
A05.7)
Подставляя A05.6) и A05.7) в A05.3), мы найдем:
JV JV
dzh Z" dyk J 2j ^ftS'i уьг»*дгк. rh. ■
Последняя сумма равна нулю, в чем убеждаемся сразу, переменив местами
индексы k и /. Поэтому получаем:
dMx __ -sn f dUn dUk
-Г-Ъ\У-5Г—гЖ
Стоящее справа выражение есть не что иное, как оператор проекции
на ось ОХ суммы моментов внешних сил, действующих на систему.
Совершенно таким же образом получаем:
dt ^-l
N
dMz VA / uu/ft ииц \ И ПК Я"\
dt ZJ V. " дуй oxk J v '
k=i
Таким образом, мы получаем теорему, известную из классической меха-
механики: изменение момента импульса в единицу времени равно моменту
внешних сил, действующих на систему. Эта теорема в квантовой меха-
механике, подобно теореме о полном импульсе, формулируется для операторов.
Если момент внешних сил равен нулю, то полный момент импульса
системы сохраняется:
^г- = т—^ = °- - A05-9)
Следовательно, при отсутствии внешних сил среднее значение момента
импульса Мх, Му, Мги вероятности w(M'x), w(My), w (M'z) нахождения
определенного значения какой-либо из проекций момента не изменяются
с течением времени.
23 д. и- Блохинцев 353

, Если учесть спин частиц, то оператор полного момента импульса
должен быть определен по формулам
N
Mx=^)(Mx + skx), A05.10)
My=^](Mk + shv), A05.10')
ft=l
N
Mz= ^{Mk + skz), A05.10")
ft=i
где s£, sk, sh — операторы (двухрядные матрицы) проекций собственного
механического момента /е-ой частицы. Теорема о сохранении полного
момента импульса остается в силе и в этом случае. Если нет сил, дей-
действующих на спины, то доказательство этой теоремы ничем не отличается
от приведенного выше, так как при таком предположении гамильтониан
системы коммутирует со всеми операторами sh.
Так как операторы Ж\, Мк, Mkz, sk, s*, s£, принадлежащие разным
частицам (разные /г), коммутируют между собой, то из известных правил
перестановки для компонент орбитального момента B5.5) и спинового
момента E9.1) одной частицы легко получить правила перестановки для
полного момента импульса системы частиц:
A05.11)
MyMz-MzMv=-ihMx, A05.11')
A05.11")
A05.12)
M2My - MyM2 = 0, A05.12')
M2MZ — MZM2 = Q, A05.12")
где M2 есть оператор квадрата полного момента импульса:
М2 = Мх + Му + Mz. A05.13)
Ниже на основании этих правил перестановки доказывается, что
полный момент импульса для системы частиц квантуется по формулам:
M2 = h4(J + 1), A05.14)
Mz — hm, |m|</, A05.15)
причем J есть либо целое число 0, 1, 2, 3, ..., либо полуцелое -^ , 3/2,
5/2, .. ., в зависимости от числа частиц и их спина. Неравенство | т I < /
означает, что m = J, У —1, / — 2, .. . — J'. Иначе говоря, мы имеем всего
2J + 1 квантовых ориентации полного момента относительно любого напра-
направления (OZ).
Заметим, что так как у электрона спин полуцелый ( -=- J, то для чет-
четного числа электронов J всегда целое, а для нечетного—полуцелое.
Проекции A05.2, 2', 2") полного орбитального момента
-> N ~*
ML= S Мк A05.16)
354

полного спинового момента
N ^
Ж,= 2 sk A05.17)
дчиняются тем же правилам перестановки, что и проекции полного
мента. Поэтому они квантуются по аналогичным формулам:
L = 0, 1, 2, 3, ..., A05.18)
MzL = hmL, \mL\<L, A05.19)
ll = h"S(S+l), S = 0, 1, 2, 3, ..., или S' = l, 4'. I- •••> A05.20)
Mzs = hms, |ms|<S. A05-21)
[ри заданном значении полного орбитального момента L и заданном зна-
ении полного спинового момента S возможны различные значения /
—>■ —у
зависимости от взаимной ориентации векторов М1 и Ms. Рис. 48 (стр. 219)
гожет служить иллюстрацией сложения этих моментов.
Очевидно, что J может принимать все значения от L+S, соответс-
соответствующего параллельной ориентации М, и Ms, до \L — S\, соответствую-
цего антипараллельной ориентации этих векторов, т. е.
S-1|, \L + S-2\, .... \L-S\. A05.22)
Всего BS+1) значений. Все состояния с одними и теми же L и S
образуют один мультиплет — группу уровней, находящихся, ввиду слабости
взаимодействия между спином и орбитальным движением (ср. § 65),
в соседстве друг с другом. Кратность (число уровней) в мультиплете
равна, как мы видим, 2S+ 1.
Полный момент системы ■/, ее орбитальный момент L и спиновый
момент S служат для обозначения терма атома в целом. Так же как
и для одного электрона (ср. § 65), термы с L = 0, 1, 2, 3,... обозна-
обозначают S, P, D, F, ... (на этот раз большими буквами) соответственно.
Справа внизу приписывают значок, указывающий значение полного
момента J, а слева вверху значок кратности мультиплета, к которому
принадлежит терм, а тем самым указывают и полный спин. Например,
*Рз/2 означает терм, для которого L=3, / —Ь1%, 6' = 3/2; Ь8ь^ означает
терм, для которого L = 0, / = 5/2, S = 5/а.
Формула A05.15) доказывается сразу, если заметить, что отдельные члены в сумме
A05.10") коммутируют между собой и, следовательно, могут быть одновременно приве-
приведены к диагональному виду так, что собственное значение Mz равно сумме собствен-
собственных значений M^~\-s^. Но собственные значения последних суть hm^, где т& — целое
или полуцелое число, смотря по значению спииа частиц. Таким образом,
N N
AJZ= ^ hmk=hm, m= ^ mh. A05.23)
ft=l fc=i
Для определения собственных значений М2 введем операторы
Пользуясь A05.12) получаем:
AMZ— MZA = — hA, BMz — MzB=hB. A05.24)
Напишем эти равенства в виде произведений матриц, беря представление, а кото-
котором Mz диагонально. Тогда получаем:
Am,m.hm"-htn'Am,n.= -hAm,m.,
23* 355

или
m"-m'-l) = O. A05.26)
Отсюда следует, что единственные неисчезающие элементы А и В суть Ат, т_1
и flm.mti- Оператор квадрата полного момента М* можно выразить через операторы А
я В двояким образом, именно:
* — hMz, A05.27)
A05.27')
Беря диагональный элемент (яг, яг) от этих равенств, получим:
= Am,m^Bm^,m = M2+~-
Отсюда
A05.28)
A05.28')
A05.29)
-. h* ( m+~ ) . A05.29')
Будем теперь считать величину М2 заданной. Тогда возможные значения j m | неизбежно
ограничены. В самом деле,
собственное значение М^.~\-Му не может быть отрицательным. Обозначим нижнее зна-
значение m через яг', а верхнее—через т". гДа из A05.29) и A05.29') следует (так как
Отсюда
1 т /"Ж2 Г
У+Т' A05-30)
Г+J- A05.30')
Разность т" — т'~\-1 есть число целое, равное числу различных возможных Mz при
данном М2. Обозначим т" — яг'-f-l == 2У —[— 1. Тогда из A05.30) и A03.30') получаем:
A05.31)
В силу полной равноправности положительных и отрицательных значений Mz мы
должны положить яг"=—т'. Вместе с A05.15) это нам дает
!т{</, где яг=0, ±1, ±2 ±J или т=±~, ± -| , .... ±7.
При доказательстве мы пользовались только правилами перестановки операторов
проекций импульса A05.11). Так как таким же правилам перестановки подчиняются
порознь проекции оператора полнэго орбитального момента A05.16) и полного спинового
момента A05.17), то тем самым доказаны и формулы A05.18), A05.19) и A05.20),
A05.21).
Из этих формул и из A05.14) следует, цто оператор скалярного произведения
2MMS = А12 — \ \
имеет собственные значения
A05.32)
такЗчто формула F4.13) для одной частицы является частиым случаем A05,32),
356

Повторяя рассуждения § 74, можно легко вывести формулу для энергии в MaF-
иитном поле для системы частиц:
-\" ТТ1—i—Г\ f • A05.33)
J \J —\-1) j
так что G4.23) будет частным случаем A05.33) для одной частицы. Формула A05.33)
дает расщепление уровней в магнитном поле для системы электронов (сложный атом).
§ 106. Собственные функции оператора-момента импульса системы.
Коэффициенты Клебша — Гордона *
Собственные функции оператора полного момента системы являются
сложными функциями угловых и спиновых координат частей системы и их
квантовых чисел. Однако в большем числе часто встречающихся случаев
их можно выразить через функции моментов импульса отдельных частей.
Рассмотрим наиболее простой случай системы, состоящей из двух под-
подсистем. Пусть Мг и М2 суть операторы моментов импульса этих подсистем,
коммутирующие друг с другом. Мг и М2 могут быть орбитальными спи-
спиновыми моментами двух частиц, орбитальным и спиновым моментом одной
частицы и т. д.
Полный момент импульса будем считать интегралом движения. Состоя-
Состояние системы может быть охарактеризовано как квантовыми числами jlt jv
tnv m2 (/j, /2 — собственные значения моментов импульса подсистем,
щ, т2 — их проекций), так и четверкой чисел J, m, jlt j3 (J, m —соб-
—собственные значения полного момента системы и его проекции, причем
m = /71,4-/71, A05.23)).
Поставим задачу определить волновые функции системы через вол-
волновые функции подсистем.
Пусть Y] т общие собственные волновые функции операторов М\
и Mlz, Y] т то же для Ж\ и M2z. Тогда произведение Y, mjYf m будет
собственной функцией оператора проекции полного момента
С собственным значением m = /n1 + m2.
Обозначим через У^у у общую собственную функцию операторов Ж2
Ее можно представить как линейную комбинацию произведений YjymYj m%
y\i%= S S UJ2fn1m2\Jm)Y]ny,tmt. A06.1)
Коэффициенты (j1j2mltn21 Jm) являются действительными числами
и называются коэффициентами Клебша—Гордона (ЖорданаI. Они равны
нулю при т Ф т1 + т2, так что двойная сумма в A06.1) фактически сводится
к однократной. Функции У£ у зависят от тех же переменных, от которых
зависят функции У j^nx, У'} т • В частности, если одна из них есть функ-
функция угловых координат, другая спиновых, то соответствующая У™- у назы-
называется сферической функцией со спином. Именно этот случай был нами
рассмотрен в § 63, где находились собственные функции полного момента —
спинового и орбитального для одной частицы. Коэффициенты при Ylt m
и ^i, m*i в формулах F4.28) и F4.28') и суть ничто иное, как коэффи-
1 Подробно см. Кои дон К.., Шорт ли Г., Теория атомных спектров, ИЛ, 1949,
По поводу обозначений см. А. С. Давыдов, Теория атомного ядра, Физматгиз, 1958.
357

циенты Клебша — Гордона для случая1 /2 = х/2. Спиновые волновые функ-
функции в этих формулах заменены их значениями @.1).
Выражение A00.1) допускает обратное преобразование:
Г3-1т1ГЗЛ= S2 2 Uil2rn1m,\Im)y?ilil A06.2)
. J=\ Jj-Zj | m=~J
(сумма по т содержит фактически один член т = т1~\-т2).
Из условий ортогональности систем функций Yjm и У7^у2 следуют
условия ортогональности для коэффициентов Клебша — Гордона, а именно:
Zj . Zj . \}\12т1Г'
!\+Н J
/=l Ji—J"B I m=-J * 2
i21 Itn) Ц^щт'^
A06.3)
A06.4)
Коэффициенты Клебша — Гордона удовлетворяют также некоторым
условиям симметрии, а именно:
(j1jim1m2\Jm) = (-iyi+^-J(j1i2, —rnv -mi\J1, — m), A06.6)
• (/i/V«im21 /m) = (— 1 )n+i2-i (/2/1m2m11 /m), A06.7)
\j%mxm% \Jm) = {- 1)^т* V2J+1 (Jj2, -m, m%\ \v - m,),
A06.8)
1 (),Ц, - от | /а, - mt), A06.9)
/, + 1 • (hktn.tn, \Jm) = (-
у21 + 1 (/2/m2, - m \ jv - щ).
A06.10)
Приведем таблицу коэффициентов Клебша—Гордона для / = |- и 1
Таблица 1
Коэффициентов Клебша—Гордона
/
h+ 2
1
h 2
1
I 1 \ 2
/ /i + m+ у J
V 2/i+i ;
1
/ 1 \ 2
V 2h+l У
_ 1
m2— 2
1
( ■ ! ' V
V 2h+i ;
i
/ /i + m+-s- 1
V 2h+l У
1 га в F3.28') соответствует яг. в A06.1) , t -* h, т±-д--» т.
358

Таблица 2
Коэффициенты Клебша—-Гордона (jxj \ тхт^ \ 1т)
/n»= — 1
Г (h-w)(h-/w+l)-]2
L B/i+l)Bj1 + 2) J
(h—m)(ii+m+\)
J
/г-1
l-m)(j1+m) 2
2;1B/1+1)
Благодаря свойствам симметрии коэффициентов Клебша — Гордона
эти таблицы могут использоваться во всех случаях, когда любое из кван-
квантовых чисел /1( j2j равно 1/2, 1. Обратим внимание читателя на значение
некоторых коэффициентов Клебша — Гордона. Если / = j1 + /2, то
(hh> /ib
A06.11)
для любых значений j1 и /2. Для случая сложения двух антипараллель-
антипараллельных спинов имеем
_L i_JL
^'2 2
00
Л
2 ' 2 ' 2 ' 2
00 ) =
^-,A06.12)
т. е. волновая функция системы двух антипараллельных спинов будет
i(szl)S i(sia)-S
+2
(sz2)] A06.13)
<CM. 117.13)
Общая формула для коэффициентов Клебша — Гордона приведена
в работе Вигнера 1.
§ 107. Связь законов сохранения с симметрией пространства и времени
Физическое пространство обладает свойством однородности и изотроп-
изотропности. Время—свойством однородности. Кроме того, в отношении обрати-
обратимых процессов имеется равноправие по отношению знака времени.
Эти свойства пространства и времени отображаются в основных
законах сохранения квантовой механики для замкнутой системы.
А. Закон сохранения энергии
Рассмотрим следствия однородности времени. Произведем бесконечно
малый сдвиг ко времени At. Тогда волновая функция системы г|з перейдет
в г|)' = t|)(x,, x2, ...,xK, t-\-At). Это изменение функции мы можем рас-
рассматривать как действие бесконечно малого унитарного преобразования
1 Wigner E. P., Gruppentheorie, Braunschweig, 1931.
359

St (см. § 28):
\J3'=S;aJ3, A07.1)
где St = 1 + iLAt и"L — эрмитов оператор.
С другой стороны, г|з' —г|з = -^Л^ и, сравнивая с A07.1), получим
dt т*
Это уравнение совпадает с уравнением Шредингера и
Но в силу однородности времени L, а следовательно, и If не должны
зависеть от времени, т. е. ^- = 0, а следовательно, и
d|=[/f, Я] = 0, A07.2)
что и выражает закон сохранения энергии в замкнутой системе.
Б. Закон сохранения импульса
Рассмотрим замкнутую систему частиц и произведем смещение
—>
всех координат (радиусов-векторов) xh на бесконечно малую величину
Ах. Тогда
У =ty{xl+Ax,...,xs + Ax, t) = ty(xlt...txN,t) + Ax ^ Vh^. A07.3)
где Vft — градиент по координатам /г-ой частицы.
Рассматривая это смещение как бесконечно малое унитарное преоб-
преобразование
Sx = 1 + CgAx,
где g эрмитов оператор, найдем
i=-»Svft. A07-4>
Оператор g" только множителем h отличается от оператора полного
импульса системы Р A03.1).
Так как операции смещения в пространстве Sx и во времени St могут
выполняться в любом порядке (в отсутствие внешних сил), то Sx и St
коммутируют, т. е. [Lg] = 0, а следовательно, [РН] = 0. Это означает
A07)
т. е. сохранение полного импульса замкнутой системы.
В. Закон сохранения момента импульса
Рассмотрим бесконечно малое вращение системы"в изотропном прост-
пространстве вокруг оси OZ на угол Асрг. Это вращение приведет к изменению
координат /с-ой частицы на
Л% = {УкЛфг- -**Аф;. 0}- A07.6)
360

Новая функция г|з' = ty(x1 + Axv ...,xN-\- Лхл-> t) может быть полу-
получена из первоначальной с помощью бесконечно малого^ унитарного пре-
преобразования
S^ = 1 + мп,Дф,; ^' = 5ф2-ф. (Ю7.7):
С другой стороны, учитывая A07.6), получим
N
^xN,t) = ^{х1..., xN,t) - 2 Щк Q^J
fe=l
A07.8>
Сравнивая A07.7) и A07.8), получим
«.=-«'£ 0^-*»-О- A07-9)
т. е. mz только множителем отличается от оператора 'Мг проекции пол-
полного момента на OZ. Аналогичные соотношения получим для вращения
вокруг двух других осей и таким образом
где М оператор момента импульса системы.
В силу изотропности пространства и однородности времени операторы
S<p и S,, а следовательно Ж и Я—коммутируют между собой, т. е.
[МН] = 0. Поэтому
^? = 0, A07.11)
т. е. момент импульса системы есть интеграл движения.
Г. Закон обратимости процессов
в квантовой механике
Рассмотрим преобразование Т обращения времени: t—>—t. Уравне-
Уравнения движения инвариантны по отношению к этому преобразованию для
случая обратимых процессов. В квантовой механике все процессы обра-
обратимы1. Поэтому операции Т должно соответствовать некоторое унитарное
преобразование волновой функции и операторов, отображающее свойство
обратимости.
Рассмотрим уравнение Шредингера сперва в отсутствии электромаг-
электромагнитных полей: *
^ ff = -£-(-Ihyy + U. A07.12)
При замене t на — t мы получим:
-Ш^- = Щ', A07.12')
где г|)' = г|)(х1 xN, —t) = STty.
1 Это утверждение не относится к процессу измерения, который может быть и не-
необратимым.
361.

Сравнивая A07.12') с уравнением Шредингера для комплексно-сопря-
комплексно-сопряженной функции
^ A07.12")
мы видим, что
^' = ST^ = ^*, A07.13)
т. е. функция, описывающая обращенное во времени движение, совпадает
• с комплексно-сопряженной.
В случае заряженных частиц, движущихся во внешнем электромаг-
электромагнитном поле, при обращении времени нужно одновременно переменить
.знак магнитного поля и знак спинов:
STA = - AST, [A07.14)
ST~o=—~oST. A07.15)
Действительно, при таком преобразовании уравнение Паули F1.5):
-при замене t—> — t, А—>—А, а—> — о Я = rot Л—> — Н перейдет в урав-
ление для комплексно-сопряженной функции ■»])*, т. е. сохранит силу ра-
равенство1 A07.13).
Д. Закон сохранения ч е"т ности]
Рассмотрим теперь преобразование инверсии Р: х—> — х, у—>—у,
■Z—> — z. Это преобразование соответствует переходу от правой системы
координат к левой.
В нашем пространстве нет различия между правыми и левыми вин-
винтами. Поэтому теория должна быть инвариантна по отношению к преоб-
преобразованию инверсии Р. Это требование налагает условие на возможные
гамильтонианы, именно:
РИ=ИР. A07.17)
Соответствующее унитарное преобразование волновой функции будет:
у, z, t). A07.18)
Равенство A07.17) означает, что оператор инверсии есть интеграл
движения:
■^ = 0. A07.19)
Далее, очевидно, что Я2г|) = +1|). Отсюда следует, что собственные зна-
значения оператора инверсии равны ± 1. Волновые функции (или состояния),
принадлежащие р= + 1, называют четными(+),а принадлежащие р= — 1,
— нечетными (—).
Если состояние в какой-то момент времени обладает определенной
■четностью, то в силу A07-19) эта четность не может измениться. Поэто-
Поэтому четность является одним из признаков, которым характеризуется кван-
квантовая система.
В частности, для частицы в состоянии с орбитальным моментом /
четность равна (—1)г (§ 25). Для системы частиц, обладающих момента-
1 Ср. по этому поводу § 44 и сноску на стр. 111.
:362

ми lv ...,In, четность состояния будет определяться четностью произве-
произведения Yhmv . .., YiNmN, что дает (— 1)'i+;2+--+'-n.
В заключение заметим, что если квантовая система находится не
в пустом пространстве, а в какой-то среде, во внешнем поле или внутри
кристалла, то свойства симметрии среды будут также отображаться в су-
существовании некоторых интегралов движения.
Например, если атом вкраплен в кристалл такой, что он обладает
2я -
■осью симметрии «-ого порядка, то при повороте на угол -- среда будет
переходить в самою себя. Операция поворота на угол ф = —■ будет инте-
интегралом движения, а волновая функция атома if будет подвергаться при
этом,определенному унитарному преобразованию.

ГЛАВА XVIII
ПРОСТЕЙШИЕ ПРИМЕНЕНИЯ ТЕОРИИ
ДВИЖЕНИЯ МНОГИХ ТЕЛ
§ 108. Учет движения ядра в атоме
При рассмотрении движения оптического электрона в атоме мы пред-
предполагали ядро атома неподвижным, рассматривая его как источник
центральных сил. Такое приближение тем лучше, чем больше масса
ядра т. Пользуясь доказанной выше теоремой о центре тяжести, легко
учесть поправки, обусловленные конечностью массы ядра. Уравнение для
определения энергии Е и собственных функций ¥в будет, с учетом
движения ядра, писаться в виде
ft2 / а2 , д* , д* л
оФ-yt \ /)v*2 i Л /» a i Л *^> 2 / О #>? \ н v* ' s^ft^ ' Ят'^
+ U(r)Y-EW, A08.1)
где /nx —масса ядра, х1( j/j, гх —его координаты, т2 —масса электрона,
л:2, у2, z2 — его координаты, г есть расстояние между ядром и электроном:
r2 = (^ — a:2J + (j/1 — у2J + B1 — z2J. A08.2)
Вводя координаты Якоби, согласно A04.3) получим:
^" t Ut^X\_ I i-1%Xq \r /i r\Q Q\
tot t 2 i b2 fflj-|-ffl2 ' V -1
так что et, Tin Ci в этом случае суть просто относительные координаты
ядра и электрона, X, Y, Z —координаты центра тяжести электрона
и ядра. В этих координатах гамильтониан уравнения A08.1) перепишется
согласно A04.10) в виде:
/ , , . I I \ ., I
On \ Л^2 l^ Л,,2 " Я, 2 i Л
2iM V дХ2 "^ ЭК2 "^ EZ2 У 2|i V. f?xa ~ ду*
+ U(rL = E4, A08. Г)
где
M = ml + m2, L = ± + -L. A08.4)
Разделим переменные X, Y, Z и х, у, z так же, как это делалось
в § 104 [см. A04.15)]:
V(X, Y, Z, х, у, z) = e~T;(P*X+P"Y+P*Z) у(х, у, г). A08.5)
364

Это решение означает свободное движение центра тяжести атома с им-
лульсом рх, ру, рг. Для функции ty(x, у, г), описывающей относительное
движение, получим:
\-^-J + U(r)^ = e\lp, A08.6)
'где
V P С \ P
Уравнение A08-6) совершенно одинаково с уравнением для движения
частицы с массой \а в заданном силовом поле U (г), е имеет смысл внут-
внутренней энергии атома (энергии относительного движения), а полная энер-
энергия Е складывается из энергии относительного движения е и энергии
движения центра тяжести атома -—-. Когда мы решали задачу о движе-
движении электрона в атоме, то мы имели дело с таким же уравнением, как и
{108.6), но вместо приведенной массы |i стояла масса электрона. Поэтому
нам нет надобности заново решать задачу о движении электрона в атоме
с учетом движения ядра. Чтобы теперь найти ей ty(x, у, z), достаточно
заменить во всех прежних формулах массу электрона на приведенную
массу ji. Так как масса ядра т, во много раз больше массы электрона /п2,
то из A08.4) следует, что jj, да т2, так что вызываемые движением ядра
лоправки к с и f будут малы. Если считать массу ядра бесконечно боль-
большой, то \л = т2 (масса электрона). При этом условии в § 51 нами было
найдено значение постоянной Ридберга R. (мы обозначим ее теперь через
Ri, и массу электрона через /п2), равное
S <108-8>
Мы видим, что для то "О, чтобы получить истинное значение постоянной
Ридберга, определяющей оптические частоты электрона, движущегося
в кулоновском поле, нужно заменить тг на приведенную массу jj,. Так
как jj, для различных атомов различно, то это обстоятельство позволяет
определить из спектральных наблюдений массу электрона. Это было
•сделано Хаустоном с помощью точных измерений линий На и Hg водорода
и сравнения их с соответствующими линиями иона Не*. Так, например,
для На частоты vH для водорода равна
— постоянная Ридберга для водорода. Ддя иона гелия и для
того же квантового перехода имеем:
где ^не — постоянная Ридберга для Не+. Множитель 4 появляется по той
причине, что величина термов атома (см. § 51) пропорциональна квадрату
заряда ядра Z2. Заряд же ядра Не вдвое больше заряда ядра Н.
Из предыдущих формул следует, что
VHe—VH Пне —!lH
= A08.9)
где jj-не и цн суть приведенные массы иона гелия и водорода. Согласно
365

A08.4) имеем:
_ I I *-—*!* Л 08 ГОН
где /Пц — масса ядра водорода, а тне — масса ядра гелия. Подставляя,
это j предыдущую формулу, мы получим:
_Не Н_._2. A08.9')
Отсюда видно, что, определив спектроскопически у и зная атомные
веса Н v Не, мы можем вычислить отношение —-, т. е. «атомный вес»
Электрона. Указанным путем Хаустон нашел
— = 0,000548, — =1838,2 ± 1,8. A08.1 IV
Этот же эффект является средством для определения масс изотопов.
В самом деле, линии, соответствующие одинаковым квантовым переходам,
у .разных изотопов несколько различны из-за различия в приведенных.
массах. Таким путем была установлена масса тяжелого водорода (дей-
тона): то = 2/пц.
§ 109. Система микрочастиц, совершающих малые
колебания
Рассмотрим сначала систему из двух одинаковых частиц, совершаю-
совершающих малые колебания. Обозначим отклонение первой частицы от положе-
положения равновесия через хх, а второй —через х2. Потенциальная энергия
U (xv x2) для малых отклонений может быть разложена в ряд
\ 1* 2/ О11О 2' 121*""* \ '
Здесь jj, — масса частиц (одинаковая для обоих), со0—частота колебаний
частиц в отсутствии взаимодействия между ними, 'кх1хг — энергия взаимо-
взаимодействия частиц (для малых хх и х2).
Оператор полной энергии частиц, имеющих потенциальную энергию
A09.1), имеет вид
Из классической механики известно, что для системы частиц, совер-
совершающих малые колебания, можно ввести так называемые «нормальные
координаты» qv q2, в которых потенциальная энергия U выразится в виде
суммы квадратов qv q2, а кинетическая энергия — в виде суммы квадра-
квадратов соответствующих импульсов, так что мы будем иметь дело с двумя
независимыми нормальными колебаниями. В рассматриваемом частном
случае эти нормальные координаты связаны с хх и хг формулами
Xb = y={qx-qd. A09.3).
Эта особенность нормальных координат сохраняется и в квантовой меха-
механике. Введем в A09.1) вместо хх и х2 нормальные координаты qx и q2
366

Для этого заметим, что
д$ _ <Эгр дх1
dqx ~ dxi dqx
' дх2 dqx ~ у<Г \дх~[ '
2 V, *tf "Г" дх\ + дхг дх2
подобным же образом
Следовательно,
дх\ ~ дх\ ' dq{ "•" dq\ ш
На основании этого равенства получаем:
где
ца>2 = ца>; + Ь, iicoaa = iiffloa - к A09.5)■
Из A09.4) следует, что гамильтониан двух связанных осцилляторов
в нормальных координатах представляется в виде суммы гамильтонианов
для двух независимых осцилляторов, одного с частотой сох и другого
с частотой соа (тот же результат, что и в классической механике).
Найдем квантовые уровни и соответствующие им собственные функции
системы связанных осцилляторов. Оператор содержит координаты qx и 9г
и, следовательно, волновая функция i]) должна рассматриваться как функ-
функция д, и q2. Уравнение Шредингера для стационарных состояний нашей
системы имеет вид
Это уравнение легко решается разделением переменных. Для этого
положим:
A09.7).
A09.8)
Подставляя A09.7) и A09.8) в A09.6), деля результат на if, (93) ty2 (92)
и приравнивая порознь постоянным Et и Е2 члены в левой части, завися-
зависящие от qx и 92 соответственно, получим:
— "о Д2"+ г^^'Фа^-^г'Фг' (Ю9.9 )•
Первое из этих уравнений есть уравнение для осциллятора с частотой со1г
а второе —для осциллятора с частотой со2. Поэтому собственными функ-
функциями уравнений A09.9) будут
A09.10)
а собственными значениями
: = 0, 1, 2, .... A09.11)

Подобным же образом для уравнения A09.9') имеем:
4
/ 11@,
= V —
A09.10')
TJ, я2 = 0, 1, 2, 3, .... A09.11')
Отсюда следует, что собственные функции исходного уравнения A09.6)
имеют вид
х\>пп (9i> 9г) = '*1}п (9i)'*l}n (9г)> A09.12)
а соответствующие собственные значения оператора энергии равны
t + Y^ + ^Tna + y) • A09.13)
Нулевая энергия системы равна
£оо = -1г- + -^г-- A09.14)
Вероятность найти нормальные координаты, лежащими в интервалах
qv 9x + ^9] и q^J]<i,-\-dq^ равна
w(qv q2)dq1dq2 = ^ n (qv q^dq^dq^. A09.15)
Если мы желаем определить вероятность того, что координаты частиц
лежат в интервалах xv Xy + dxx и х2, x2~\-dx2, то для этого достаточно
заметить, что
dq1dq2 = dx1dx2,
и выразить в A09.15) ql и q2 через xL и х2. Тогда получим:
w (Xy, xz) dxx dx2 =
I^2. A09.16)
Сходные результаты^получаются для системы с любым числом сте-
степеней свободы. Пусть мы 1имеем N частиц, совершающих малые колеба-
колебания около положения равновесия. Обозначим отклонения /е-ой частицы
от положения равновесия через xh, yk, zk. Тогда потенциальная энергия
равна
N
+ EibXlzu + Fihyizh) + hm. ;A09.17)
причем величины А.к, Blk, Cik, Dlh, EVl, Fih суть вторые производные
потенциальной энергии по смещениям. Так, например,
lh dxi dxh '
Из классической механики известно1, что в этом случае можно ввести
нормальные координаты qs, s = 1, 2, . .., ЗА/ такие, что гамильтонова
функция распадается на сумму гамильтоновых функций гармонических
осцилляторов.
1 См., например, М. Б о р н, Теория твердого тела.
368

Нормальные координаты qs и декартовы хк, yk, zk связаны ортого-
ортогональным преобразованием:
93 = 2KA + iWft + Ys)A). s=l, 2, .... 3N, A09.18) ■
h
гдета8Й, f5sfe, Ysk СУТЬ коэффициенты преобразования. В нормальных коор-
координатах qs — гамильтониан нашей системы
N N
2 (VA++^^ A09.19)
преобразуется к виду
8=1 8
где jj, — некоторая эффективная масса, a ojs —частоты k нормальных коле-
колебаний. Уравнение Шредингера для стационарных состояний имеет вид
злг
= £¥(9l, 92, ...,Ы- A09.21)
Очевидно, что это уравнение распадается на ЗЛГ уравнений для ЗЛ'
независимых осцилляторов, если представить W в виде произведения
функций от qv q2, ..., qsN. Уравнение для осциллятора, представляю-
представляющего s-oe нормальное колебание, будет
^^Г ^ (Ю9.22)
Отсюда
^1/% (/^7.), (Ю9.23)
2 A09.24)
Собственные же функции и собственные значения всей системы осцил-
осцилляторов определяются выражениями
■фп^...na...n3iV(9v 9г> • • • > 9s' • • • > 7sJv) =
n2 (9a) • • • Ф». (9s) • • • \n (Q3N)> A09.25)
»зДГ = А ( ) ^ )
( i) A09.26)
где nr n2, .. ., ns, ..., «3,Y — целые положительные числа, включая нуль.
Нулевая же энергия системы равна
Ео = 4 K + ffl2+ ...+©.+ ... +co3iv). A09.27)
Перебирая всевозможные значения чисел п3 в A09.26), мы"^гполу-
чим все квантовые уровни системы колеблющихся частиц. Из A09.26)
следует, что для определения этих уровней достаточно знать частоты
нормальных колебаний cos.
24 Д. И. Блохинцев 369

Примером систем, имеющих квантовые уровни вида A09.26), могут
служить молекулы и твердые тела. И в тех, и в других атомы совер-
совершают малые колебания около положений равновесия*.
Заметим, что при больших амплитудах колебаний следует учесть
высшие члены в разложении потенциальной энергии, именно, члены вида
Wdx~d—dz~ xiVhzi + • • • и т> п> Колебания тогда будут нелинейными,
и наши результаты будут иметь лишь приближенное значение. В частно-
частности, формула A09.26) будет справедлива лишь для малых квантовых
чисел п..
§ ПО. Движение атомов во внешнем поле
Рассмотрим движение системы частиц (атома, молекулы) во внешнем
поле сил. В целях большей конкретности мы ограничимся системой из
двух частиц с массами т1 и т2 и координатами xv yv zx и хг, у2, z2.
Обобщение на случай большего числа совершенно тривиально.
Обозначим энергию взаимодействия частиц через W(x1 — x2, ух — у2,
zi — гг)> энергию первой частицы во внешнем поле через ll-y (xv у„ Zj),
а энергию второй —через U2 (x2, у2, z2). Уравнение Шредингера для вол-
волновой функции системы XY (xv yv zv x2, y2, z2, /) будет иметь вид
|^ ^ A10.1)
Введем в это уравнение вместо координат частиц xv yv zx и х2, у2, z2
координаты центра тяжести X, Y, Z и относительные координаты х, у, г
[см. A08.3)]. Переходя в A10.1) к этим новым координатам и замечая,
что по A08.3)
A10.2)
z1=Z+y1z,
мы получим:
Y +
+ U2(X-y2x, Y-y2y, Z-y2zL' + W(x,y,z)W, A10.1')
где
2--^ i
x dx2 r
dKa ~1~ dZ~ ' x dx2 r dya "•" dz2 •
Переменные X, У, Z и х, у, г в этом уравнении ввиду наличия поля
(Ul и f/2) не разделяются. Поэтому в общем случае исследование этого
уравнения весьма затруднительно.
Предположим, однако, что размеры системы малы. Это означает, что
мы ограничиваемся рассмотрением таких систем и таких состояний, когда
1 Квантование энергии колебаний атомов в твердом теле находит свое выражение
в квантовом характере теплоемкости твердого тела, которая при достаточно низких
температурах меньше той, которая полагалась бы по классической теории Cfe, где
й—постоянная Больцмагш), именно, теплоемкость твердого тела убывает с уменьшением
температуры пропорционально Т3, Расчет теплоемкости твердого тела на основе кван>
товой теории изложен почти во всех курсах по статической физике.
370

элновая функция У достаточно быстро убывает с увеличением относи-
ельно расстояния г = Yx% + У2 + z2 ДВУХ частиц. Пусть это убывание
аково, что вероятность найти частицы на расстоянии г > а друг от друга
рактически равна нулю. Тогда а можно рассматривать как размер нашей
истемы (например, «радиус» атома, «длина» молекулы и т. п.).
В этом случае в уравнении (ПО. Г) играют роль лишь такие области
:, у, г, для которых г < а- При таком предположении мы можем разло-
кить Ьх и U2 по степеням х, у, г (если f/t и U2 достаточно гладкие
рункции). Это разложение мы напишем в виде
U1(X + ylx, У + YiJ/. Z + Y]Z)+£/2(X-y2x, У-УъУ' 2~Ъ^) =
= t/1(X, Y, Z) + Ut(X, Y, Z) + ^-x+ . . . +^-*+ • •. =
= V(X, Y, Z) + w(X,Y,Z, x, y, z)+..., A10.4)
где V (X, Y, Z) есть потенциальная энергия центра тяжести системы,
а через w обозначены члены, содержащие х, у, г. Этот член связывает
движение центра тяжести с относительным движением. Уравнение Шре-
дингера (ПО.Г) теперь можно записать в виде
+ w(X,Y,Z,x,y,z)W. A10.5)
Пусть в отсутствии внешнего поля собственные функции для внут*
реннего движения будут tyn (x, у, г), а собственные значения энергии fen-
Очевидно, что ajjn есть решение уравнения
1,2
—ЩГ V^« + ^(х,у,г)Гп^ &№■ (И0.6)
Если мы учтем влияние внешнего поля, то к этому уравнению добавится
член w (X, У, Z, х, у, z), и мы получим уравнение
' —!^nq + W(x,y,z)\p + w(X,Y,Z,x,y,z)ip = E'ty. A10.7)
В это уравнение координаты центра тяжести X, Y, Z входят как пара-
параметры, и от них будут зависеть как волновые функции, так и собствен-
собственные значения этого уравнения.
Во многих случаях w(X, Y, Z, х, у, г) можно рассматривать как
возмущение. Это обстоятельство позволяет решить уравнение, если
известны решения уравнения A10.6). Обозначим собственные функции
уравнения A10.7) и его собственные значения через
Ъп = $п(х. У, г, X,Y,Z), En = En(X,Y,Z). A10.8)
Разложим теперь Чр (х, у, г, X, Y, Z, t) по собственным функциям \ра.
Тогда получается:
У (х, у, г, X, Y, Z, t) = 2 Ф„ (X, Y, Z, /) \рп (х, у, г, X, Y, Z). A06.9)
п
Подставляя это разложение в уравнение A10.5), умножая на т|)т(*, у, г,
X, Y, Z) и интегрируя по х, у, z, получим (в силу ортогональности
функции tyn) уравнения для функций Фп:
A10.9')
24* 37i

где
ата = ] i& • ЧхЪп ■dx dy dz> A10.10)
A10.10')
Эти два последних члена отличны от нули лишь в том случае, если
функции aj}n зависят от координат центра тяжести X, Y, Z и приводят
к возможности переходов системы из одного состояния в другое. Действи-
Действительно, если при / = 0 все ФA = 0, кроме Фп, Ф 0, то при t Ф 0 -^~ Ф 0,
и с течением времени из состояния <£„- будет возникать суперпози-
суперпозиция A10.9).
Если 1|эп не зависят от X, Y, Z, то атп и Ьтп равны 0. Если эта
независимость имеет мг>_то, хотя бы приближенно, то мы можем пре-
пренебречь величинами а,иа и Ьтп в A10.9') и тогда получим:
4 ^ф + [^(^ Y Z) + E(X, Y, Z)]On. A10.11)
Это есть ура р. я-ние для движения центра тяжести системы в потен-
потенциальном поле с потенциальной энергией, равной
Un*=V(X,Y,Z) + En(X,Y,Z), A10.12)
при условии, что внутреннее состояние системы есть n-ое квантовое
состояние. Уравнение A10.11) таково же, как уравнение, для движения
материальной точки.
§ 111. Определение энергии стационарных состояний атомов
методом отклонения во внешнем поле
В этом параграфе мы рассмотрим теорию опытов, в которых опре-
определяют энергию стационарных состояний атома, подвергая пучок атомов
отклонению внешним полем; важнейший из них — опыт Штерна-Герлаха.
Обычно его рассматривают как опыт по определению магнитного момента
атома. Будучи рассматриваем более непосредственно, он является опытом
по определению энергии атома во внешнем магнитном поле.
Из теории движения атомного электрона при наличии магнитного
поля (§ 62) следует, что, поскольку пренебрегают высшими степенями
магнитного поля, постольку действие магнитного поля можно выразить
через добавочную потенциальную энергию F2.7), равную энергии магнит-
магнитного диполя (орбитального и спинового) в магнитном поле. Поэтому мы
можем применить к интересующему нас случаю теорию предыдущего
параграфа. Из расчетов § 62 следует, что в указанном приближении вол-
волновые функции электрона tynlm не зависят от магнитного поля, а собствен-
собственные значения энергии равны F2.13):
Еп1,т = Е°П1 + е-щ~(т±1). A11.1)
При этом мы считали поле J£? однородным. Если оно достаточно плавно
(для микроскопических полей нужная плавность всегда обеспечена), то
372

его можно рассматривать, как функцию координат центра атома X, Y, Z
без того, чтобы нарушалась справедливость1 A11.1).
Таким образом, мы можем написать
■■E°ni + -£;(m±l)&?(X, У, Z). A11.2)
nlm (X, Y, Z)
-ZL
Волновые функции tynlm от X, Y, Z зависеть не будут, так как они
не зависят от поля е%?. Стало быть, мы имеем дело со случаем, когда
вместо общих уравнений A10.9) для волновых функций Ф, описывающих
движение центра тяжести, можно написать уравнения A10.11). Эти урав-
уравнения в нашем случае будут:
rXD i Л2
ih п^т __ V2 Ф -1- F
V 7\&Г
A11.3)
Так как масса атома М велика, а внешнее поле g/в всегда плавно меняется
от точки к точке, то мы имеем налицо как раз те условия, при которых
применимо приближение классической механики. Положив
Фп1т(Х, Y,Z, t)=
, Y, Z,
(UL4)
где Snlm — функция действия, a Qnlm — плотность атомов в пространстве,
мы получим для Snim и gnim в первом приближении классические урав-
уравнения [см. §§ 35 C5.8) и C5.13)]
FF^ = ~1M
dt
М
A11.5)
A11.6)
Первое уравнение есть уравнение Гамильтона-Якоби; оно утверждает, 'что
частица будет двигаться по классическим траекториям. Второе уравнение
есть уравнение непрерывности; оно утверждает, что рой частиц будет
двигаться так, чтобы поток частиц,
проходящий через любое сечение трубки,
образованной траекториями, был постоя-
постоянен.
Обратимся теперь к чертежу (рис.
78). Пусть на протяжении от D до Р
действует магнитное поле, направленное
по оси OZ. В D сделана диафрагма, через
которую поступают атомы. Ширина
щели в диафрагме равна AZ0. Пучок
атомов, входящий в D, будет расщеп-
расщепляться. Те из атомов, которые окажут-
окажутся в состоянии с магнитным моментом
дат=0, будут двигаться без действия
сил. Из уравнений A11.5) и A11.6) мы
получим проходящий без отклонения
пучок. Атомы, находящиеся в каком-
либо другом состоянии с 5Шт Ф 0, образуют отклоненные пучки (на рис. 78
приведены два таких пучка).
Рис. 78. К теории опытов Штер-
Штерна—Герлаха
1 Для этого достаточно, чтобы поле <SS? мало менялось в пределах размеров
атома а, т. е. должно соблюдаться условие
дХ
dY
dm
dZ
373

Существенно, что магнитный момент $Щт меняется от состояния
к состоянию скачкообразно. Благодаря этому пучки, вообще говоря, раз-
разделяются так, что по месту падения атомов на экран (или фотопластинку)
Р мы можем решить, в каком из возможных состояний 1|эет находятся
атомы, т. е. определить их стационарные состояния. Траектории, при-
принадлежащие пучкам, легко вычислить из уравнений A11.5), A11.6), учи-
учитывая расположение диафрагмы D, ее форму и начальное распределе-
распределение скоростей атомов.
Можно и прямо воспользоваться уравнениями Ньютона:
м d*X _ дЕп1т \
М- ^ \ AП.7)
dt2 dY
M-^§- = -dEnlr
dt2 dZ ' J
Будем считать, что магнитное поле <§№ зависит лишь от г (по крайней
мере на большей части отрезка DP). Тогда из A11.7) получаем:
X = vt + X0, , A11.8)
Y = Y0, A11.8')
где у —скорость атомов (мы предполагаем, что они первоначально дви-
„,, d&e
жутся параллельно ОХ, и, кроме того, градиент поля -^- в пределах
области движения атомов считаем почти постоянным). Обозначая длину
DP через / и пользуясь A11.2), мы получим отклонение
-т- -т- 1 eh . , ,. йЗв /3 /111 п\
Произведенный нами расчет лишь приближенный. В действительности
атомы, проходящие диафрагму, не будут двигаться по классическим
траекториям: пучок будет расползаться.
Чтобы учесть это явление, следует сделать еще один шаг в прибли-
приближенном решении уравнения A11.3), учтя члены в Snlm и Qntm,
содержащие первые степени h (см. § 35). Мы не будем этого делать,
а ограничимся лишь оценками.
Пусть ширина пучка в направлении OZ есть AZ0. Тогда скорости ато-
атомов в направлении OZ в силу соотношения неопределенности
AZ0-Apz>h A11.10)
не могут равняться нулю (как это допускалось в классическом расчете).
Если среднее значение pz = 0, то из A11.10) следует, что AZ0-yWyI> h, т. е.
°*>-тщ- <шло'>
При прохождении через поле в течение времени t, благодаря наличию
разброса в скоростях vz, ширина пучка AZ возрастает и будет равна
Для того, чтобы мы были еще в состоянии решить, к какому из состоя-
состояний ЕП1т или E»im' относится атом, падающий на экран Р, необходимо,
374

чтобы | Zm> — Zm | > AZt, т. е. на основании A11.8")
дЕ„
2М dZ" dZ
ИЛИ
dEnlm' л у дЕп1т
U
dZ " dZ
Но так как в силу слабой зависимости Enim> и Enim от Z
nlm' д у ОД та; m д у
Л7 "^0 лт ^^О
t>h. A11.13)
I J~'nlm' — l~"iilm I ^*
то последнее неравенство можно записать также в виде
\Enlm,-Enlm\t>h, A11.14)
т. е. для того, чтобы различать стационарные состояния атома (Enim' или
Enim), измерение должно производиться в течение достаточно большого
времени t:
t > Гр р—г- A11.15)
■ ^nlm' ^nlm I
К этому обстоятельству мы еще вернемся в § 112.
В заключение теории опытов по определению стационарных состояний
атомов методом отклонения пучка атомов во внешнем поле рассмотрим
более сложный случай, когда первоначальная волновая функция представ-
представляет состояние с неопределенным значением энергии.
По общей теории вероятность получить при измерении в таком состоя-
состоянии значение энергии Еп равна |с„|2, где сп — амплитуда в разложении
ф по собственным функциям оператора энергии1. Покажем, как относится
это общее утверждение к определению энергии методом отклонения пучков.
Если система находится во внутреннем состоянии tyn(x, у, z), то полная
волновая функция, с учетом движения центра тяжести, будет равна
W (X, Y, Z, х, у, z) = Фп (X, Y, Z) фп (х, у, г), A11.16)
причем Ф„ определяется из уравнения A11.3) [или вообще A10.11)].
Если состояние т|з есть суперпозиция о|зп, то в силу линейности уравнений
квантовой механики общая функция имеет вид
Ч(Х, Y, Z, х, у, г) = ^с„Фп(Х, Y. Z)-tyn(x, у, z). A11.17)
п
Непосредственно на опыте мы измеряем не внутреннюю энергию атома,
которая нас интересует, а положение атома X, Y, Z. Определим вероят-
вероятность того, что атом находится в области
X, X + dX, Y, Y + dY, Z, Z + dZ.
Эта вероятность равна
w (X, Y, Z) dX dY dZ = dX dY dZ \ \ Y |2 dx dy dz = "^ I cn I2' I ®nl2 dX dY dZ.
A11.18)
Измерение энергии атома Еп заключается в том, что мы решаем,
к какому из пучков (см. рис. 78) относится атом. Каждый пучок описы-
описывается своей функцией Фп (X, Y, Z). Для того, чтобы наш опыт был дей-
1 Для простоты мы обозначаем все квантовые числа (п, /, т) одной буквой п.
375

ствительно опытом по измерению энергии атома, нужно, чтобы различные
пучки были разделены друг от друга, иными словами, функции Фп (X, Y, Z)
должны быть отличны от нуля в различных областях пространства [для
этого должно быть обязательно выполнено условие A11.15)].
Найдем теперь, какова вероятность wn того, что атом принадлежит
пучку т. Для этого нужно проинтегрировать A11.18) по объему этого
пучка. Мы обозначим этот объем через Vm:
wm= ^ w(X, Y, Z)dXdYdZ=^\cn\*- ^ \On\*dXdYdZ. A11.19)
Vm n Vm
Если пучки разделены, то все интегралы равны нулю, кроме интеграла
®n\*dXdYdZ,
Vm
равного единице в силу того, что Фт нормирована. Таким образом,
wm=\cm\\ A11.20)
Но wm есть как раз вероятность того, что энергия атома равна Ет (так
как атомы с различной энергией принадлежат различным пучкам). Поэтому
рассмотренное нами определение энергии атома находится в полном согла-
согласии с интерпретацией величин \сп\2 как вероятностей найти значение энер-
энергии атома Еп. При этом измерительным аппаратом служил сам атом: внут-
внутренняя энергия Еп определялась по положению центра тяжести атома.
Обратим внимание еще на одно важное обстоятельство. В § 16 мы
утверждали, что измерение всегда превращает чистый ансамбль в смешан-
смешанный. Легко убедиться, что в рассматриваемом случае это превращение на
самом деле имеет место. Определим вероятность найти электрон в окрест-
окрестности точки х, у, z при заданном положении центра тяжести атома X, Y, Z.
Имеем:
w(x, у, z, X, Y, Z) = |¥|2=2 ^спс*тх^п{х, у, г)i&(х, у, z) x
ХФЯ(Х, Y, Z)Om(X, Y, Z). A11.21)
В области, где Фя и Ф,п перекрываются, мы имеем интерференцию состоя-
состояний %, t])m и для определения w важны фазы сп, с?п. В области, где Ф„
и Фт не перекрываются (измерение!), мы получаем:
w(x, у, г, X, Y, Z) = |Y|»=2 |сп|2-|фп(*. у* г)\2-\ф»(Х' Y Z)l2.
A11.21')
т. е. фазы сп выпали. Вероятность w образуется теперь некогерентно иэ
•»])„, как это характерно для смешанного ансамбля (ср. § 16).
§ 112. Неупругие столкновения электрона с атомом. Определение
энергии стационарных состояний атомов методом столкновений
Одним из простых приложений теории движения многих тел является
расчет неупругих столкновений с атомами. С такого рода столкновениями
мы встречаемся в опытах Франка и Герца (§ 3). Однако наш расчет нельзя
будет непосредственно применить к этим опытам, так как мы будем пред-
предполагать, что сталкивающийся электрон имеет энергию, значительно пре-
376

вышающую знергию электрона в атоме (при этом условии можно будет
применить теорию возмущений). Оператор полной энергии двух электро-
электронов1 имеет вид
Я(г„ r2) = #(r1) + #(r2)+ W(rlf г2) = Я°(Гх, ra)+W(rlf r2), A12.1)
Я(г1)=--|-^+[;(г1), A12.2).
" (Г2)= ~и"
A12.3).
W(rlt r2) = [/(r2)H
1 — Г2|
Здесь U (г^ означает потенциальную энергию атомного электрона в поле
е2
остова (ядра и остальных электронов атома). -, г есть кулоновская
энергия взаимодействия атомного электрона с электроном, летящим извне.
U (г2) есть энергия этого последнего электрона в поле остова атома. Осталь-
Остальные члены имеют само собою понятное значение.
Кинетическую энергию летящего извне электрона мы считаем столь
большой, что все его взаимодействие с атомом W будем рассматривать
как возмущение. Тогда уравнение Шредингера для невозмущенного дви-
движения будет иметь вид
но ir т \ .ко ir r \ р.|,о (гг\ /] 10 4Y
\'т» 2/т \1* 2/ — т\1'2/* ^l li.iy
Оно имеет решение
•2). A12.5)
где фп — волновая функция стационарного состояния электрона в атоме,
принадлежащая энергии Е"п, a t])Po — волна де Бройля, описывающая сво-
свободное движение летящего извне электрона с импульсом р0.
Нас интересует вероятность перехода нашей системы из двух элек-
электронов в какое-нибудь другое состояние:
Для вычисления этой вероятности применим теорию' квантовых пере-
переходов под влиянием возмущения, не зависящего от времени (§ 85). Таким-
возмущением является у нас энергия W A12.3). Вычислим сначала мат-
матричный элемент этого возмущения для перехода п, р0—>т, р. Имеем:
1. г2) A12.8>
(здесь dvv dv2 означает интегрирование по координатам первого и соот-
соответственно второго электрона). Вычислим сначала интеграл по dvv Введем:
Qmn(«-i)=-e<(r1)^(r1). (П2.9)
Эту величину будем называть матричным элементом плотности заряда для
перехода п—>т (очевидно, что Qnn есть среднее значение плотности
в состоянии t])n). Учитывая ортогональность функций фп» мы полу-
1 Движение атома в целом мы можем игнорировать ввиду большой величины,
массы ядра по сравнению с массой электрона.
377

чаем:
= Vmn(r2). A12.10)
Последняя величина может рассматриваться как матричный элемент потен-
потенциальной энергии сталкивающегося электрона B) в поле ядра и атомного
электрона A).
Если т-=п, то столкновение будет упругим. Vnn совпадает с той
энергией возмущения, которая встречалась в § 79 в теории упругого рас-
рассеяния электронов. Подставляя V'mn(r2) в A12.8) и имея в виду, что
i РоГ2 . РГ2
р h P к
£*Р (r2) = -1—эГ > A12.11)
мы получим:
1 <• i (р°-р) Г2 1
"'mp, ripo — ^я/г)*" J 2 ' ли >Г8' е ~ Bл/гK mn *• '' (''2.12)
где через К обозначен вектор
K = !V=JL = k0-k, A12.13)
где к0 и к—волновые векторы электрона до и после столкновения.
Для вычисления вероятности перехода в 1 сек из начального состоя-
состояния Еп, р%, ру, p°z в конечное Ет, р, dQ (dQ — элемент телесного угла,
в котором лежит направление импульса электрона р после столкновения)
применяем формулу (85.3). Плотность состояний на интервал полной энер-
энергии системы, обозначенная в (85.3) через q(E), будет у нас такая же,
как и для одной частицы [см. (84.23)], так как
Следовательно, Q(E) = \ip. Поэтому согласно (85.3) и A12.12) имеем:
Рпро(т, p)dQ = ^^y|Fmn(K)|2^pdQ. A12.14)
Чтобы вместо вероятности перехода в 1 сек получить эффективное
сечение q (р0, р, 0, ф) для перехода р0—> р, dQ, нужно иначе нормировать
функции падающего электрона. Именно, их нужно нормировать так, чтобы
поток через 1 см2 в 1 сек равнялся единице. Для этого вместо A12.11)
нужно взять
t, ' A12.1 Г)
где v0 — скорость падающего электрона:
v -12°1 = Ь- ш ■ A12.15)
•Функции A12.11) и A12.11') отличаются множителем
Так как в вероятность A12.14) начальная функция входит в квадрате,
то, переходя от нормировки A12.11) к нормировке A12.1 Г) (для падаю-
378

щих частиц), мы получим в A12.14) множитель Bя/гK — . Вместе с тем
Ро
вероятность Рпра (pi, р) примет размерность площади. Так как принятая
нами нормировка для падающей волны есть как раз та, которая прини-
принимается для расчета эффективного сечения (поток: одна частица в 1 сек
через 1 см2), то полученная вероятность совпадает с эффективным сече-
сечением. На основании сделанных замечаний получаем эффективное сечение
в виде
()V^- (П2.16)
При этом условие резонанса, совпадающее с законом сохранения энергии,
в случае возмущения, не зависящего от времени, имеет вид:
A
2ц
-2-
2ц
A12.17)
Для упругого рассеяния т = п, р = р0, и формула A12.16) в точности
совпадает с выведенной в § 78 методом стационарных состояний. Для
неупругого рассеяния вид атомного фактора Fmn несколько иной [см. A12.12)].
'Кроме того, в q входит множитель р/р0, смысл которого легко уяснить.
q dQ есть отношение потоков падающего и рассеянного в угол dQ. В это
отношение потоков входит отношение скоростей, которое как раз равно
р/р0 и выпадает для упругого рассеяния. Обозначая р через ртп, К через
Ктп-= Ро~Ртп-, часто пишут A12.16) в форме
qmn(Q,
Fmn(Kmn)\*dQ.
A12.16')
Отсюда, интегрируя по всем возможным углам рассеяния dQ, мы получим
эффективное сечение для любого столкновения, при котором энергия элект-
электрона меняется на величину Ет — Еп, а атом переходит из состояния Еп
в Ет\
Qmn = \ Чтп (9, Ф) dQ. A12.18)
4л
Если Еп— нижнее нормальное состояние атома,"*то соударяющий электрон
может только возбуждать атом (Ет > Еп). В этом случае Qmn называют
эффективным сечением для возбуждения
атома. На рис. 79 приведена типичная
зависимость этого сечения от энергии элек-
электронов. На основании закона сохранения
A12.17) мы можем, измеряя изменение
Р2 Ра
энергии падающих электронов -^ ■—- ,
определить разности Ет — Еп и тем са-
самым установить энергетический спектр ато-
атома. Это и было впервые проделано в опы-
опытах Франка и Герца.
Если, как это обычно делают,
принять границу (т = со) между ди-
дискретным и непрерывным спектрами
атома за нуль при отсчете энергии атом-
атомного электрона, то, определяя ту потерю энергии первичных
0
Рис. 79. Зависимость эффектив-
эффективного сечения (Qmn) для возбуж-
возбуждения ударами электронов от
энергии электронов Е
нов
ЦХ,
электро-
тр-, при которой начинается ионизация атома (появляются вто-
втоРо2
ричные электроны), мы можем также измерить энергию состояния атома,
37»

в котором он находился до столкновения. В самом деле, в этом случае-
из A12.17) имеем:
Таким образом, следовательно, мы можем определить стационарное
состояние атома. Отличие этого измерения от измерений отклонением
атомов внешним полем заключается в том, что состояние атома после
измерения меняется (например, происходит ионизация атома), в то время
как в опытах по отклонению оно остается неизменным.
Обратим внимание на то обстоятельство, что при измерении энергии
атома методом столкновений требуется, как и в методе отклонения, неко-
некоторое минимальное время. Действительно, измерение основывается на законе
сохранения энергии A12.17). Этот закон выражается наличием 6-функцш
в вероятности перехода [ср. § 84 формулы A5), A6) и A7), при этои
в них следует положить ha — Q].
На самом деле мы имеем дело не с б-функцией, а с приближенны!
ее выражением (84.14):
(.1'
которое лишь при t—> со переходит в 6 (£—£„). Функция 6'(Е—Е
отлична от нуля заметным образом только для интервала разности А (Е — Е
для которого
Д (Е - £0) ■ t ъ h,
и становится малой для
Д(Е-Е0).*»А, A12.
т. е. имеется неопределенность в разности начальной энергии Ео и not
ной Е, связанная с длительностью промежутка времени t между нача,
измерения (начало взаимодействия падающего электрона с атомом) и кон
измерения (определение энергии падающего электрона после столкновен
Предположим теперь, что энергию падающего извне электрона \
и после столкновения мы знаем точно. Тогда из A12.20) следует соо
шение для длительности измерения t и неопределенности А(Еп —
в разности начальной и конечной энергии измеряемой системы (ат<
&(EU-En.).t>h. A1
Чтобы определить уровни нашей системы (опыт Франка и Ге
фиксируем еще и конечную энергию. Для этого будем отмечать те ел
когда в результате столкновения атом ионизуется (Еп- > 0), и изм<
энергию вылетающего из атома электрона. Тогда вся неопределен
перенесется на начальное состояние, и из A12.21) мы получим:
A(EJ-t>h. A1
Чтобы можно было знать, какую из энергий Еп или Ет имел ат
столкновения, нужно, очевидно, чтобы А (Еп) < | £„— Ет |, т. е.
\En-Em\.t>h, (]
т. е. для того, чтобы отличить, в каком из состояний находилс
до опыта, нужна достаточная длительность измерения (при этом s
после опыта предполагается известной). Если же ограничиться оп
иием энергии только до опыта (в исходном состоянии) или тольк<
опыта, то соотношение A12.21') не имеет места.

§ 113. Закон сохранения энергии и особая роль вре-
времени в квантовой механике
В классической теории закон сохранения энергии утверждает, что
энергия замкнутой системы остается неизменной, так что, если обозначить
энергию такой системы в момент t=0 через Ео, а в момент t через Еи то
В квантовой механике закон сохранения энергии формулируется аналогич-
«ым образом. Именно, согласно § 33 энергия является интегралом движения,
я вероятность w(E, t) найти в момент t значение энергии, равное Е, не зави-
зависит от времени:
^£ = 0. A13.2)
Закон сохранения энергии в только что высказанной форме предполагает
■возможность определения энергии в данный момент времени без того, чтобы
■подвергнуть ее неконтролируемому изменению. В классической механике
возможность такого измерения не вызывает сомнений. В квантовой механике,
•напротив, такого рода возможность ввиду того, что вмешательство прибора
вообще говоря, меняет состояние системы, не является самоочевидной.
Рассмотренные в §§ 111, 112 измерительные устройства для определения
энергии показывают, что энергия без нарушения ее величины может быть
измерена лишь с точностью
ДЕ>4» A13.3)
•где т— длительность измерения. Однако это не представляет трудности
для закона сохранения энергии, так как энергия является интегралом дви-
движения, и мы располагаем как угодно большим временем, чтобы произвести
длительное измерение. Так, например, если мы проведем измерение в течение
времени т, а затем предоставим систему самой себе на время Т, а затем вновь
определим энергию, то закон сохранения энергии A13.2) утверждает, что
результат этого второго измерения с точностьюАЕ^и —совпадаете резуль-
результатом первого измерения. Если же не требовать неизменяемости энергии
при ее измерении, то никаких ограничений на точность кратковременного
{мгновенного) измерения энергии не наложено, так как соотношение A13.3)
содержит лишь неопределенность АЕ разности энергий до опыта и после
опыта [ср. A13.21)]. Поэтому можно получить сколь угодно точное зна-
значение о величине энергии в данный момент времени, если ограничиться зна-
знанием ее величины либо до опыта, либо после опыта. Так, например, мож-
можно определить значение энергии в момент г"=0 после опыта и в момент
t = T до опыта. Тогда закон сохранения энергии утверждает, что оба
значения энергии будут равны друг другу.
В заключение вопроса об энергии укажем на то, что соотношения
между неопределенностью АЕ значения энергии Е в данный момент вре-
времени t и точностью фиксации этого момента At:
AE-At>~, A13.4)
подобного соотношению для импульса и сопряженной координаты
Арх-Ах>\, A13.5)
381

в квантовой механике не существует так же, как не существует и соотно-
соотношения t -Н — Ht = ih в отличие от соотношения xPx — Pxx = ih.
Мы могли бы рассчитывать на подобное соотношение лишь в том случае,
если бы энергии Е можно было бы сопоставить оператор ih -^- подобно
д
тому, как величине рх сопоставляется оператор — ш-^— . На самом же деле,
в квантовой механике оператор энергии Н есть «функция» операторов
импульса и координат: Н == Н (Рх, Ру, Pz, x, у, z). Поэтому с точки зрения
общих принципов квантовой механики энергия есть величина, которая
в данный момент времени может иметь вполне определенное значение,
а время t, в отличие от координат х, у, z, не является оператором.
Однако все же можно получить соотношение A13.4), если вложить
надлежащий смысл в понимание величин АЕ и At. Приведем примеры.
Пусть мы имеем группу волн (см. §§ 7 и 14), движущуюся с групповой
скоростью v и имеющую размеры (неопределенность в координате) Ах.
Введем время At — Ax/v, в течение которого группа проходит через какую-
нибудь фиксированную точку пространства х. Имея в виду, что
Р%
АЕ = А -— = v ■ Арх, A13.6)
мы получим из A13.5):
А .- U
(П3.7)
Здесь АЕ есть неопределенность в энергии, a At — время прохождения
группы через фиксированную точку пространства х. Можно сказать и иначе:
это есть время, в течение которого среднее значение х меняется на вели-
величину неопределенности в координате Ах.
Другим примером соотношения вида A13.4) может служить рас-
рассмотренное в § 101 явление распада, исчезновения некоторого заданного
первоначального состояния ty(x, 0). Именно там было показано, что если
неопределенность энергии АЕ отождествлять с шириной квазистационар-
квазистационарного уровня АЕ = hk/2, а под At разуметь длительность жизни состояния
x=l/K = At, то АЕ и At связаны соотношением A13.4) [ср. формулу (99.31)].
Л. И. Мандельштамом и И. Е. Таммом было показано1, что рас-
рассмотренные здесь примеры являются частным случаем весьма общего
толкования соотношения A13.4), заключающегося в следующем: пусть L
есть любая механическая величина, не являющаяся интегралом движения.
Тогда, если состояние нестационарно, то среднее значение L будет
меняться с течением j'времени. Пусть At есть тот промежуток времени,
в течение которого среднее значение L меняется на величину неопределен-
неопределенности AL (AL есть корень квадратный из среднего квадратичного откло-
отклонения AZ>): \L (t + At) —T(t) | = AL. Тогда At связано с неопределенностью
в энергии АЕ (причем АЕ = V АЕ2) соотношением A13.4).
Изв. Акад. наук СССР (сер. физ.). 9, 122, 1945.

SEssEEEEs ГЛАВА XIX =
СИСТЕМЫ ИЗ ОДИНАКОВЫХ МИКРОЧАСТИЦ
§ 114. Принцип тождественности микрочастиц
Мы перейдем теперь к рассмотрению свойств систем, состоящих из оди-
одинаковых частиц. Одинаковыми частицами мы будем называть частицы, имею-
имеющие одинаковые массу (т), заряд (е), спин (s) и т. д., так что в равных
условиях (внешнее поле, присутствие других частиц) такие частицы ведут
себя одинаковым образом.
С точки зрения атомизма естественно, но не необходимо считать, что все
экземпляры частиц одного рода (электроны, протоны, нейтроны и т. д.)
между собой тождественны. В самом деле, измерение величин, характери-
характеризующих частицы (m, e, s), производится, конечно, лишь с некоторой точ-
точностью (Am, Де, As), и всегда законно предполагать, что, по крайней мере
в пределах точности измерения, разные экземпляры могут отличаться друг
от друга.
Одинаковы или неодинаковы все экземпляры одного рода, это можно
было бы решить лишь в том случае, если бы поведение совокупности оди-
одинаковых частиц качественно отличалось от поведения совокупности различ-
различных, хотя бы и сколь угодно мало различных частиц. Именно к такому
качественному отличию свойств совокупности одинаковых частиц от свойств
совокупности различных частиц приводит квантовая механика. Поэтому,
опираясь на квантовую механику и опыт, можно решить на первый взгляд
нерешимый вопрос о том, тождественны ли друг другу все представители
частиц одного рода или нет.
Чтобы уяснить себе, каким путем решается этот вопрос, мы должны
обратиться сначала к изучению наиболее простых особенностей совокупно-
совокупностей, состоящих из одинаковых частиц. Пусть мы имеем N одинаковых
частиц. Координаты, принадлежащие /г-ой частице, обозначим буквой qk,
так что под qk следует разуметь три координаты, определяющие положения
центра тяжести частицы (хк, yh, zk) и, может быть, еще четвертую, опре-
определяющую спин частицы (sj, если она таковым обладает.
Обозначим массу частиц через т, энергию во внешнем поле через U(qk, t),
а энергию взаимодействия /г-й и /-й частиц через W(qk, д3), тогда гамиль-
гамильтониан системы таких частиц будет равен
И (9i- 92 Qk 9i 9jv- t) =
N N
= 2 [ —шЪ+и<Я» ')+ 2 W(qk,q,). A14.1)
Предположение об одинаковости частиц выразилось здесь в том, что массы
частиц, энергия во внешнем поле U и энергия взаимодействия W для всех
38а

частиц взяты одинаковыми. Эта особенность гамильтониана сохраняется
•в любом внешнем поле: на одинаковые частицы любое внешнее поле
действует одинаковым образом.
Для проведения общих выводов не очень удобно опираться на спе-
специальный вид гамильтониана1 A14.1). Поэтому мы должны выразить тот
факт, что гамильтониан описывает систему одинаковых частиц, не прибегая
•к явному его виду.
Исходя из A14.1), легко уяснить себе, в чем заключается обязатель-
обязательная и наиболее общая особенность гамильтониана системы одинаковых
частиц. Если в гамильтониане A14.1) мы переставим местами координаты
•&-й частицы (qh) и /-й частицы (д;), то гамильтониан не изменится. В самом
деле, такая перестановка обозначает просто перестановку слагаемых в сум-
суммах, входящих в гамильтониан:
Н (qv 92 9ft- • • • > Qi' • ■ ■ > 9.v. 0 =
= #(9i> 92, •■■> 9j, •••, 9fe- •••, 9л-> 0 A14.2)
для всех пар (/, k) N частиц, образующих систему. Если бы среди N
частиц была бы хоть одна отличная, то это равенство не имело бы места
•как раз для перестановки этой отличной частицы с любой другой. Таким
образом, равенство A14.2) и выражает самое общее свойство гамильтониана,
относящегося к совокупности одинаковых частиц.
Коротко это свойство может быть сформулировано так: гамильтониан
системы одинаковых частиц инвариантен (симметричен) относительно
перестановки координат любой пары частиц.
Ввиду того, что нам в дальнейшем придется часто встречаться с пере-
перестановками, нам удобно ввести новый оператор — оператор перестановки
частиц Рм. Под этим оператором мы будем подразумевать символ, указы-
указывающий на то, что координаты /г-й и /-й частиц должны быть перестанов-
перестановлены. Например, если мы имеем функцию f(...,qk, ..., qp ...), то
Pkif(.,., qh, ..., q}, ...) = /(..., 9У, ...,9ft» >••)• (П4.3)
Этот оператор, очевидно, принадлежит к числу линейных операторов,
так как для того, чтобы переставить координаты в сумме двух функций,
«ужно переставить их в каждой из функций.
С помощью оператора Рк,; равенство A14.2) можно написать в виде
Рк,Н (9ъ •••> 9;, 9,, •••> 9jv-O =
- Я (,?1 qH q,,..., (In. 0 Ph} A М.4)
для всех пар к, /. Таким образом, оператор Phj коммутирует с гамиль-
гамильтонианом системы одинаковых частиц. Действительно, если мы применим
к некоторой функции \|> оператор РН, то в силу A14.2) это все равно,
что применить к \|> оператор HP, ибо оператор Р оставляет неизменным
•согласно A14.2) гамильтониан Н.
Опираясь на это свойство гамильтониана, докажем важную вспомо-
вспомогательную теорему относительно волновых функций, описывающих состоя-
состояние систем из одинаковых частиц. Пусть волновая функция системы
/V частиц есть W (q± qh qi 9лг> 0; она должна удовлетворять
1 Написав гамильтониан Н в форме A14.1), мы исключили непотеициальные пода
■(например, магнитное поле), также исключили взаимодействие, могущее зависеть от ско-
скоростей частиц (магнитные силы). Все это могло бы быть учтено и нисколько не изме-
изменило бы хода дальнейших рассуждении.
384

уравнению Шредингера
, дЧ(д„ ...,д,,, ..., qu ...,qN,t) __ „ , ,ч
in- ^ — п (qv ..., </fc, .. ., qjt .. ., qiX, i) x .
x¥(9l, ..., qh, ..., qjt ..., qN,t). A14.5)
Переставим в этом уравнении координаты k-й и /-Й частиц. Для этого
подействуем на обе его части оператором Phi:
ih~(P^Y) = Phi(HW). A14.5')
В силу того, что гамильтониан Н для одинаковых частиц симметричен
относительно перестановки частиц, мы можем на основании A14.4) пере-
переставить в A14.5') операторы Phf и Н. Тогда мы получим:
ih^-(PkjY) ^ H (PhjY). A14.6)
Из сопоставления A14.6) с исходным уравнением A14.5) следует, что если
¥ (qv .. ., qh <7У, . . ., qN, t) есть решение уравнения Шредингера A09.5),
то и
¥' = Pk)W = ¥ (qv ...,qjt...,qh qN, t) A14.7)
есть также решение этого уравнения, и, следовательно, ¥' наряду с ¥
представляет одно из возможных состояний системы. Оно отличается от
прежнего ¥ тем, что k-я частица находится теперь в состоянии, ранее
занимавшемся /-Й частицей, и /-я занимает теперь состояние k-я. Продол-
Продолжая перестановки, мы можем получить новые возможные состояния
системы ¥", ¥'", .. ., отличающиеся друг от друга распределением частиц
по состояниям.
Утверждая, что первая частица находится в состоянии а (первое место
в волновой функции), вторая частица — в состоянии Ь (второе место )и т. д.,
мы встречаемся с одной характерной трудностью. Дело в том, что, стано-
становясь на атомистическую точку зрения, считая разные экземпляры частиц
одного рода одинаковыми, мы можем различать частицы только по их состоя-
состоянию — например, по их положению в пространстве, по величине их импуль-
импульса, энергии и т. д. Разумеется, что с течением времени состояние частиц
может измениться, и они могут обменяться своими состояниями. Поскольку
в классической механике принципиально возможно проследить за траекто-
траекторией частиц, постольку, отметив частицы, например, по их положению
в момент времени t=Q, мы можем в любой момент сказать, находится ли
в данном месте та частица, которую мы назвали первой, или та, которую
назвали второй. Между тем, в квантовой области этого сделать нельзя.
Если бы мы отметили частицы по их положению в момент t=0, то волновые
пакеты, относящиеся к различным частицам, быстро бы растеклись и пере-
перекрылись, так что, обнаружив в момент г">0 где-либо какую-нибудь из частиц,
мы уже никак не могли бы сказать, какая же это из частиц — первая или
вторая.
Эти рассуждения иллюстрируются рис. 80. На рис. 80, а изображены
положения частиц х1 и х2 в момент ^=0 и дальнейшие движения их по клас-
классическим траекториям. На рис. 80, Ь изображены волновые пакеты частиц
в момент г1—0 около хг и х2 (заштрихованные области) и их дальнейшее
рассеяние. Следует отметить, что заштрихованы только те области, где
} -ф |2 имеет большую величину, так что в незаштрихованных областях пакеты
также перекрываются, только значение |\|)J2 там мало. Найдя частицу
в области пространства, где волновые пакеты перекрываются, мы уже не
можем решить, с какой из двух частиц мы имеем дело.
385

Приведем еще другой пример. Пусть частицы находятся в ящике, раз-
разделенном перегородкой (рис. 81). Непрозрачные стенки ящика означают,
что по мере приближения к стенкам потенциальная энергия частиц возраста-
возрастает. В частности, перегородка есть не что иное, как потенциальный барьер.
Этот барьер изображен на рис. 81 снизу, под ящиком. Если энергия частиц
меньше высоты барьера, то согласно классической механике частицы неспо-
неспособны проникнуть через него — перегородка для них непрозрачна. Поэтому
мы можем различать частицы по их положению в левой или правой полови-
половине ящика.
t-t
Рис. 80. Нумерация частиц по их положениям в пространстве:
о — в классической механике; Ь — квантовой. В области, заштрихованной
дважды, нумерация спуталась
. Согласно же квантовой механике для всякого барьера конечной высоты
есть вероятность, что частица проникает через него благодаря туннельному
эффекту. Если первоначально волновые функции частиц суть ¥а и ¥ь
(рис. 81), то по истечении некоторого
времени они превратятся в ¥« и Чгь
(пунктирные кривые), так что частица а
может быть найдена справа, а частица
Ь — слева. При t—> со волновые функ-
функции ¥а и "Рь станут одинаковыми
и будут иметь симметрично располо-
расположенные максимумы в обеих половинах
ящика. Вероятность найти частицу а
в одном из отделений ящика будет
равна той же вероятности для части-
частицы Ь, так что всякий след исходной
несимметрии будет утерян.
Аналогичные рассуждения можно
провести и в тех случаях, когда
частицы отмечаются не по их положе-
положению в пространстве, как в приведенных
примерах, а по каким-либо другим приз-
признакам, характеризующим их состоя-
состояние. Пусть, например, в момент времени /"==0 частица а имеет импульс ра,
а частица Ь — импульс рь. Так как состояния с заданным импульсом зани-
занимают все пространство, то всегда существует некоторая вероятность столкно-
столкновения частиц, в результате которого частицы обменяются импульсами так,
что частица а будет иметь импульс рь, а частица Ъ — импульс ра.
386
1
ш
ж
_л
y-N.
-
(f) V/
" V
Ш
т
1
(-^
■~—
%
%
1
'/У/
%,
1
1.
ШШШжШШШжШ
Рис. 81. Две частицы в ящике, раз-
разделенном перегородкой. Внизу изо-
изображен ход потенциала вблизи сте-
стенок и волновые функции частиц

Таким образом, в квантовой области единственный способ, по которо-
которому можно различать одинаковые частицы — различие по состояниям, отка-
отказывается служить. В этой связи мыслимо предположение, что встречающиеся
в природе системы устроены так, что вообще проблема различения одина-
одинаковых частиц является надуманной, т. е., что состояния совокупности
одинаковых частиц всегда таковы, что можно говорить лишь о состоя-
состоянии всей совокупности в целом, а не о распределении частиц по со-
состояниям. Это предположение оправдывается на самом деле. Его мы
формулируем в форме принципа тождественности частиц: в совокупно-
совокупности одинаковых частиц реализуются лишь такие состояния, которые
не меняются при обмене одинаковых частиц. Это означает, что веро-
вероятность найти при измерении какой-либо механической величины Ь,
относящейся к системе одинаковых частиц или к ее части, значение, рав-
равное Ь', не меняется при обмене частиц их состояниями.
Высказанный принцип не вытекает из изложенных ранее положений
квантовой механики, но, как мы увидим, он вполне подходит к ней
и обязателен, если мы хотим получить из квантовой механики выводы,
согласующиеся с опытом.
§ 115. Симметричные и антисимметричные состояния
Пусть Y (<7j, .. ., qh, . . ., q3, . . ., <?#, t) есть волновая функция, описы-
описывающая состояние системы из N одинаковых частиц. Тогда, если мы
обменяем состояниями, скажем, k-ю и /-ю частицы, то получим новое,
как следует из теоремы A14.7), возможное состояние системы, описывае-
описываемое волновой функцией ¥' (qv .. ., q-v . .., qh, .. ., qN, t). Принцип тож-
тождественности частиц утверждает, что это новое состояние неотличимо от
прежнего, т. е. 1Р' и ¥ описывают фактически очно и то же состояние
системы.
Волновые функции, описывающие одно и то же физическое состояние,
могут отличаться друг от друга только постоянным множителем. Следо-
Следовательно, из принципа тождественности вытекает, что
V (<Ь ■■■, 4f qh, ..., qs, t) = XY (qv ...,qh, ...,qu ...,qN, I),
где X — некоторый постоянный множитель. Это равенство с помощью
оператора перестановки может быть написано в виде
PkjV = XY. A15.1)
В уравнении слева A15.1) на функцию действует оператор Pki, а справа
стоит эта же функция, умноженная на число X. Следовательно, уравне-
уравнение A15.1) есть уравнение для собственных функций ¥ и собственных
значений % операторов перестановки Pkl-. Мы можем поэтому сказать, что
условие A15.1), накладываемое принципом тождественности на возможные
состояния системы, заключается в том, что волновые функции Y, описы-
описывающие состояние системы, должны быть собственными функциями опе-
операторов Pkj (для любых k, /). Нетрудно определить, каковы эти соб-
собственные функции и собственные значения X. Для этого применим к A15.1)
еще раз оператор перестановки Pkj. Имеем:
XPhjY. A15.2)
Два раза применяемый оператор перестановки Pki не меняет функции ¥.
Поэтому в A15.2) слева стоит просто ¥(..., qh, ..., qf, ...), а справа
в силу A15.1) X2Y(. .., qk, ...,q,,...), так что A15.2) переписывается
25* 387

в виде
т. е.
^2=1. A15.3)
Отсюда получаем собственные значения оператора перестановки Puj:
К= ± 1, A15.4)
а соответствующие собственные функции обладают в силу A15.1) следую-
следующими свойствами:
PkiW= +W, Я= -г 1, A15.5)
или
Ph,V=-W, X=-l, A15.6)
т. е. собственными функциями оператора перестановки Phi являются
функции, которые при перестановке координат /г-ой частицы (qh) и /-ой ча-
частицы (<7у) либо не меняются A15.5), либо меняют свой знак на противопо-
противоположный A15.6). Первые функции A15.5) мы будем называть симметрич-
симметричными, а вторые A15.6) антисимметричными относительно перестановки
частиц номера k и /.
Таким образом, возможные состояния системы из N одинаковых частиц
должны описываться волновыми функциями ¥ (qv . .., qh, .. .,<?,■,..., qN, t),
которые либо меняют свой знак при перестановке любой пары частиц (к, /),
либо остаются неизменными. Из соображений равноправности всех частиц
нетрудно предвидеть, что возможные функции ¥ таковы, что они либо
симметричны во всех парах одинаковых частиц, либо антисимметричны
во всех парах частиц, так что не может быть функций, которые в части
частиц симметричны, а в другой —антисимметричны^. Окончательно
из принципа тождественности частиц следует, что возможны только два
класса состояний для одинаковых частиц:
ph AFS = ¥s (/г, / - любые) A15.7)
— симметричные во всех частицах и
PkjWa = - ¥а (k,j- любые) A15.8)
— антисимметричные во всех частицах.
Мы сейчас покажем, что переходов между этими состояниями быть
не может: если в какой-то момент времени система находится в симмет-
симметричном (lFs) или антисимметричном (¥а) состоянии, то она всегда находится
в симметричном или соответственно антисимметричном состоянии. Для
доказательства этого важного положения достаточно воспользоваться
уравнением Шредингера и тем обстоятельством, что гамильтониан обяза-
1 Если встречаются перестановки и того и другого рода, тоЧг = 0. Действительно,
пусть ¥ симметрична при перестановке k и /, / и i, но антисимметрична при перестановке
i и k. Тогда имеем:
= -¥(..., <7Ь ...,<7у qu ...)=- ^(...,9у, ■••,% qi, •■•) =
= —-Чг(...,<7г qh, •••,9J. •••)•
Отсюда
¥(...,G,- qk,...,qj,...) = O, т. е. Ч> (..., qt qk qh ...) = 0.
Подобным же образом проводится доказательство в предположении, что две перестановки
антисимметричны, а третья симметрична.
388

телЬно симметричен относительно одинаковых частиц. Уравнение Шре-
дннгера
ih-^-^HW A15.9)
нам удобно переписать в форме:
d,Y = -~/M dt, A15.10)
где dt будет означать приращение волновой функции за время dt. Допустим,
что в момент времени t = 0W есть симметричная функция координат частиц
(W = Ys). Тогда в силу симметрии Н величина ff¥s будет также сим-
симметричной функцией координат частиц, а следовательно, и приращение
функции dtY будет симметричной функцией от координат частиц.
С помощью оператора перестановки эти рассуждения могут быть
записаны так:
отсюда с помощью A15.10) следует:
Pu(dtWs) = dtWt A15.11)
для всех пар к, /. Наше доказательство, таким образом, утверждает, что
функция, симметричная в какой-то момент времени (^ = 0), остается сим-
симметричной и в соседние моменты времени как в прошлые, так и будущие,
ибо доказательство одинаково применимо и к dt > 0 и dt < 0. Следова-
Следовательно, симметрия функции остается неизменной для всех моментов времени
от t = — оо до t=-\-co. Совершенно аналогичным образом проводится
соответствующее доказательство для антисимметричных функций. Пусть
в момент ^ = 0 функции Ч*4, описывающая состояние системы, антисим-
антисимметрична (lF = lF(l). Тогда
р w — _ иг
hj а а*
Далее,
из A15.10) тогда следует:
/>И(ед=-ЙДи, A15.12)
т. е. приращение антисимметричной функции Wa само антисимметрично.
Поэтому, если система находится в состоянии, описываемом антисим-
антисимметричной функцией Wa, то она всегда остается в таком состоянии.
Доказанная теорема показывает, что деление состояний на два класса
носит «абсолютный» характер: если какая-либо система в какой-либо момент
времени обнаружена в состоянии того или иного класса AF5 или ¥а), то
она никогда не перейдет из одного класса в другой. Такой переход невоз-
невозможен, как бы мы ни меняли внешнее поле, так как всякое внешнее поле
одинаково действует на одинаковые частицы, и, следовательно, при любом
изменении внешнего поля гамильтониан остается симметричным.
Нам надлежит теперь решить вопрос о том, в каких случаях какую
из двух возможностей (*Р = XVS или lF = lFa) следует применять для описа-
описания состояния системы из одинаковых частиц.
§ 116. Частицы Бозе и частицы Ферми. Принцип Паули
Как мы видели, квантовая механика на основе принципа тождествен-
тождественности одинаковых частиц ведет к двум классам состояний, абсолютно не
смешивающимся между собой. Поэтому выбор того или иного класса
' " ' 389

состояний для какой-либо системы частиц может быть продиктован
только природой частиц, образующих систему, а не характером внешнего
поля или каким-либо подобным обстоятельством.
Опытным путем установлено, что в природе существуют частицы, при-
принадлежащие обоим классам. При этом наблюдается следующее правило:
частицы, обладающие спином, равным целому числу постоянных Планка:
s=hm, m = 0, I, 2, A16.1)
описываются симметричными функциями (Ys). Мы будем называть такие
частицы частицами Бозе, а совокупности таких частиц — ансамблями Бозе —
Эйнштейна, по имени физиков, разработавших статистику для таких частиц.
Напротив, частицы, имеющие спин, равный полуцелому числу постоян-
постоянных Планка:
s = hm, m = Y> Y' Т' (П6.2)
описываются антисимметричными функциями (Ya). Мы будем называть
такие частицы частицами Ферми, а совокупность таких частиц ансамблями
Ферми — Дирака, по имени физиков, построивших статистику для частиц
такого рода Ч
Все простейшие «элементарные» частицы обладают спином О, V2 или 1
(см. таблицу на стр. 475).
Спином гА обладают электроны, протоны, нейтроны, гипероны, ц-мезон,
нейтрино и их античастицы. Поэтому они все являются частицами Ферми
(«фермионами»).
Спин 0 имеют я-мезоны и fe-мезоны — они являются частицами Бозе
(«бозонами»).
Единственная элементарная частица со спином 1 есть фотон. Он также
подчиняется статистике Бозе.
Принадлежность сложной системы, например атома и ядра, к тому или
иному классу частиц будет определяться числом и классом более простых
частиц, из которых образована сложная система. Рассмотрим для примера
атом водорода. Атом водорода представляет собой систему из двух частиц
Ферми: протона и электрона. Суммарный механический момент атома водо-
водорода в нормальном состоянии складывается из механического момента
(спина) протона и из спина электрона. Так как каждый из них имеет момент,
равный J- ^, то суммарный момент атома водорода в нормальном состоянии
может быть равен 0 или ±h, т. е. измеряется целым числом постоянных
Планка.
Рассмотрим теперь ансамбль из атомов водорода. Координаты протона
fe-ro атома обозначим через Qk, а координаты электрона fe-ro атома через |й.
Тогда волновая функция, описывающая ансамбль, состоящий из N атомов
водорода, будет иметь вид:
V - W(QV £„ . . ., Qk, g,t, ..., Q,, ey, . .., QN, lN, t). A16.3)
Будем рассматривать каждый из атомов водорода как одну частицу
(это можно сделать во всем том круге явлений, где можно игнорировать
возможность возбуждения электрона атома водорода). Тогда обмен состоя-
1 Пользуясь теорией относительности, Паули показал, что это правило может быть
обосновано теоретически. Однако мы не имеем возможности обсуждать здесь его аргу-
аргументацию и отсылаем читателя к оригиналу: В. Паули, Релятивистская теория эле-
элементарных частиц.
390

ниями двух атомов водорода — fe-ro и /-го — означает одновременную пере-
перестановку в ¥ и координат ядер Qk, Qj, и координат электронов £h, S,j,
принадлежащих /г-му и /-му атомам. Но так как мы считаем протоны
и электроны частицами Ферми, то волновая функция ¥ должна быть анти-
антисимметрична относительно перестановки любой пары ядер (Qk и Qj). Рав-
Равным образом она должна быть антисимметрична и при перестановке любой
пары электронов (gft и £;-). Таким образом, при перестановке /г-ro и /-го
протона ¥ меняет знак, при перестановке /г-го и /-го электрона она также
меняет знак. Следовательно, при перестановке атомов водорода, когда сразу
переставляется и пара протонов, и пара электронов, ¥ не изменится вовсе,
т. е. относительно перестановки атомов водорода ¥ симметрична, и атомы
водорода, поскольку они рассматриваются как простые частицы, принадле-
принадлежат к числу частиц Бозе.
Подобным же образом можно провести рассуждения и для а-частицы,
которая состоит из двух протонов и двух нейтронов. Исходя из того, что
волновая функция для системы а-частиц должна быть антисимметрична
относительно перестановки протонов и относительно перестановки нейтро-
нейтронов, легко прийти к заключению, что относительно перестановки а-частиц
волновая функция должна быть симметрична, т. е. а-частицы должны отно-
относиться к числу частиц Бозе. Этот вывод соответствует тому, что суммарный
механический момент а-частицы должен быть целым числом h, так как он
должен составляться из четырех спинов, каждый из которых равен у .
В самом деле механический момент а-частицы равен 0.
Обратимся теперь к рассмотрению основной особенности частиц типа
Ферми. Эта фундаментального значения особенность заключается в том, что
частицы этого рода подчиняются так называемому принципу Паули, который
еще задолго до разработки квантовой механики был сформулирован В. Паули
на основании анализа эмпирических данных о спектрах сложных атомов.
Принцип этот (в элементарной форме) утверждает, что в данной систе-
системе в одном и том же квантовом состоянии не может находиться более
одного электрона.
Поясним этот принцип примером. Квантовое состояние электрона, дви-
движущегося в поле центральных сил, характеризуется тремя квантовыми
числами п, I, т, определяющими энергию электрона («), его орбитальный
момент (/) и одну проекцию орбитального момента на какое-либо направле-
направление (т),а также четвертым квантовым числом (ms=± -~-\ определяющим
проекции спина электрона sz на то же направление. Таким образом полностью
квантовое состояние задается четырьмя числами п, I, m, ms. Принцип Паули
утверждает, что в таком состоянии либо вообще нет электрона, либо есть
только один. Более же одного электрона там быть не может. В состоянии
с одними и теми же квантовыми числами, относящимися к движению центра
тяжести электрона (п, I, т), можно поместить два электрона с противополож-
противоположными направлениями спина тя= + у .
Приведенная формулировка принципа Паули проста, но страдает
тем недостатком, что она приближенна. В самом деле, когда мы помещаем
второй электрон в состояние с заданными числами п, I, т, то все это состоя-
состояние в результате взаимодействия первого электрона со вторым изменяется.
Поэтому в элементарной формулировке не вполне ясно, в какое именно
состояние нельзя поместить более одного электрона. Тем не менее, ввиду
того, что состояние электронов из-за их взаимодействия во многих случаях
меняется незначительно, уже элементарная формулировка принципа Паули
оказывается весьма плодотворной.
391

Сформулируем принцип Паули так, чтобы освободиться от только что
указанного затруднения. Для этого заметим, что электрон С илидругаячасти-
ца со спином -к ) есть частица, обладающая четырьмя степенями свободы:
три относятся к движению его центра тяжести, четвертая есть спин. Поэто-
Поэтому для указания состояния отдельного электрона, принадлежащего систе-
системе или одинокого, достаточно измерить четыре величины Lv L2, L3, s, кото-
которые должны обладать следующими свойствами: а) все они должны быть
одновременно измеримы; Ь) первые три должны характеризовать движение
центра тяжести и быть независимыми; с) четвертая должна определять состоя-
состояние спина электрона.
Совокупность четырех величин такого рода образует полный набор
механических величин для электрона. Одновременное измерение их являет-
является полным измерением, в результате которого возникает состояние ^ыь21^(Я)Х
в котором заданы четыре величины Llt L2, L3, s. Ради краткости мы обозна-
обозначим определенное значение четверки таких величин одной букой п, так что
4>n foft) = tLA-Las Ы- (П6.4)
Приведем примеры таких четверок. Можно взять за три величины компо-
компоненты импульса рх, р,;, pz, а в качестве четвертой величины, определяющей
спин электрона,— например, проекцию спина на направление импульса
электрона sp. Тогда L1=px, L2=py, L3=pz, s=sz. Подчеркнутая нами неза-
независимость трех величин Lv L2, L3 исключает, например, такой выбор
■^1=Рх' L%~PV, L3—px, так как в этом случае L3 есть функция Lv Другой
выбор величин может быть, например, таким: в качестве Lt возьмем энергию
движения электронов в поле ядра Еп1т (^1=^„гт), за Ln_ возьмем момент
импульса электрона (L2=M), за Lg—проекцию момента импульса на какое-
либо направление (L3=MZ) и, наконец, для определения спинового состоя-
состояния возьмем проекцию sz спина на ось OZ. При первом выборе величин
L1, L2, Ls, s после измерения получается состояние
$n(qk) = %xPvPzsz(qk)> A16.5)
при втором выборе
^г.Ы = ^п!тзгЫ. A16.5')
Эти состояния, возникающие в результате измерения, не будут вообще
стационарными состояниями, что явствует уже просто из того, что в системе
электронов ни импульс отдельного электрона, ни энергия отдельного электро-
электрона не являются интегралами движения. Для нас сейчас существенна другая
сторона дела. Введя в рассмотрение состояния отдельного электрона tyn(qk),
возникающие в результате измерения, произведенного на электроне системы,
мы освободились от употребления неясного термина «состояние электрона
в системе», так как состояние системы характеризуется одной волновой функ-
функцией 1|э(^1, •••, qu, •••> qN> 0> и выделить там состояние одного электрона без
изменения системы вообще невозможно. Если мы производим измерение
величин, относящихся к отдельному электрону (Llt L2, L3, s), то по крайней
мере в момент времени ^=0, в который было произведено измерение, состоя-
состояние электрона будет
Таким образом вместо «состояния отдельного электрона в системе» мы опери-
оперируем с состоянием отдельного электрона, возникающим в результате
произведенного над ним полного измерения. Эти замечания позволяют
нам формулировать принцип Паули в самой общей форме, не прибегая
к неточным словам «квантовые состояния отдельного электрона».
392

В этой общей форме принцип Паули гласит: в системе электронов
в каждый момент времени при измерении любых четырех величин Lx, Ь„, L3,
s, характеризующих состояние отдельного электрона, каждое значение
четверки величин Llt L2, L3, s может быть получено только для одного
электрона системы.
Теперь мы докажем, что эмпирически установленный принцип Паули
есть следствие принципа тождественности частиц в квантовой механике.
Именно, частицы, описываемые антисимметричными волновыми функциями
(частицы Ферми), подчиняются принципу Паули.
Сначала мы проведем доказательство, простоты ради, для ансамбля,
состоящего только из двух частиц. Обобщение на любое число частиц будет
уже совершенно просто.
Допустим, что состояние частиц характеризуется антисимметричной
функцией W(qlt 9г> f) (<?]> Ц% означают, как и раньше, совокупность всех
координат, включая спин первой и соответственно второй частицы). Допу-
Допустим, что мы измеряем для первого электрона совокупность четырех вели-
величин, характеризующих полностью его состояние. Их значения обозначим
одной буквой «j. Значения тех же величин для второго электрона обозна-
обозначим через п2.
Состояние первого электрона, когда измеряемые величины имеют зна-
значение н,, пусть описывается волновой функцией 1|>п (qj, соответственное
состояние второго электрона г|зп (q2). Так как речь идет об измерении меха-
механических величин, то функция г|з„ (qj является собственной функцией
операторов этих величин, и следовательно, функции для разных значений
п: образуют ортогональную систему функций:
>*{ М Ч\ Ы dql = bn^i. A16.6)
То же самое, конечно, относится и к функции г|)„2(д2). При этом, так как
под п2 разумеются те же механические величины, что и под пг> то я|зПз—
такие же функции, как и г|зП1, с той лишь разницей, что они относятся ко
второму электрону, так что у них в качестве аргумента вместо q1 стоит q2.
Разложим функцию W (qlt q2, t), описывающую состояние системы,
по собственным функциям измеряемых на электронах величин, т. е. по
%AQi) и УпЛяд- Получим:
¥ (qlr q2, t) = 2j2j c {nn n2> О Ч>™ {Qi)-4>^2(Qz)^ A16.7)
где
с {nv n2, t) — \ ¥ (qt, q2, t) г|)*х (дх) г|)*2 (g2) ^g, ^92-> 0 16.8)
при этом, написав в A16.7) сумму по их и и„, мы предположили, что изме-
измеряемые величины принимают лишь дискретные значения. Если бы они
принимали непрерывные значения, то следовало бы вместо суммы писать
интегралы. Это не изменило бы дальнейшего хода рассуждений. Поэтому
ради определенности мы сохраним обозначение через сумму. Сумма по пг
и п2 распространена по всем значениям пх и п2; кроме того, пх и п2 пробегают
одинаковые значения (так как речь идет об одних и тех же механических
величинах как для первого, так и для второго электрона).
Согласно общей теории величина
w (nv щ, t) - | с (nlt ла, t) ]2 A16.9)
есть вероятность того, что в момент времени t на первом электроне будет
получено значение измеряемых величин, равное пъ а на втором — значение
тех же величин, равное п.,. Переставим в ¥ (qlt q%, t) первый и второй элек-
39S

троны. По предположению мы имеем дело с частицами Ферми, так что функ-
функция ¥ изменит^при этой перестановке свой знак. Следовательно,
¥ (q2, glt t) = 2 2 с (гц, щ, t) Ц (д2) гр (?1) = - ¥ (дъ дг, t), A16.10)
2 2c(rti, "г. О ^.(tfa)^ Ы =
т. е.
Y1
Если мы теперь изменим обозначения, заменив лх на п%, а л2 на nv
все останется по-прежнему, так как суммы распространены по всем зна-
значениям пх и п2, и они пробегают одни и те же значения. На основании
этого замечания мы можем переписать A16.11) в виде
= - S 2 с К, л2, 0 гр (9l) г|)П2 Ы. A16.12)
Эти ряды по ортогональным функциям могут равняться друг другу только
при условии, что коэффициенты при одинаковых функциях равны между
собой, т. е.
0= -с(я2, «]. ^)- A16.13)
Для пг=-п2, мы получаем, что:
С(П], tlv t)= —C(tlv tlv t), A16.13')
но функция, равная самой себе с обратным знаком, равна нулю. Следо-
Следовательно,
с(п, п, 0 = 0. A16.14)
Подставляя это в A16.9), находим, что если значения и; и л2 одина-
одинаковы, то вероятность w (n^, n2, t) равна нулю:
w (п, п, 0 = 0. A16.15)
Тем самым наше предположение доказано: вероятность того, что одновре-
одновременно в системе двух электронов будут измерены на обоих электронах
одни и те же значения одной и той же совокупности механических величин,
характеризующих состояние электрона, равна нулю. Следовательно, такой
результат измерения невозможен, что и составляет содержание принципа
Паули.
Обобщение на N частиц проводится без труда путем таких же рас-
рассуждений как те, что были нами только что проведены для двух частиц.
Волновая функция системы ¥ (qv .. ., qk, ..., qit . . ., q^, t) разлагается
в этом случае следующим образом:
t ¥ (qlt . .., qh, . . ., qf, ...,qN,t) =
= 2 • • • 2 • • • 2 • • • 2 c (n,, . ... nk, .... ny, .... nN, t) X
nl "ft nj nN
x ФП1 {ч,) ■ ■ ■ Ч4 Ы ■ ■ • % Ш • • • 4>njv M, A16.7')
394

c(nv ..., nh, ..., rif, ..., nN, t) =
= С . . . С dqx . . . dqNW (qx qN, t)Mp* (qj . . . tf (qN). A16.8')
гроятность найти значения измеряемых величин равными пх на первом
тектроне, nk — на 6-ом, п,- — на /-ом, nw — на iV-ом, равна
W («j Пк, . . . , П}, . . . , nN, t) =
= j c(n1( ..., nh, .. ., rij, ..., nN, t)\2. A16.9')
[роизводя в A16.7') перестановку fe-ой и /-ой частиц и меняя суммиро-
ание по пк на суммирование по п: и наоборот, мы в полной аналогии
A15.11) и A15.12) получим:
c(nlt .. ., щ, ..., пк, .... nN, 0 =
= -c(nx nft л,, ..., n№0, A16.13")
откуда следует, что
с(пх щ, . . ., nh, . .., nN, t) = 0 для nh = nj. A16.14')
Следовательно,
о>(Я], . . ., пк пи • •-. nN, 0 = 0 для nh = nr A16.15')
Гак как это доказательство применимо к любым парам частиц (k, j) из
числа N частиц, то все nk должны быть различны, иначе w = 0. Таким
образом, вероятность найти в системе частиц Ферми хотя бы пару
частиц, для которых результаты измерений всех величин, характери-
характеризующих состояние частицы (nk), одинаковы, равна нулю.
Например, два электрона не могут иметь одинаковый импульс и оди-
одинаково направленный спин (в этом случае пк = п}, причем под п следует
разуметь рх, ру, pz, s). Подобным же образом нельзя обнаружить в одной
и той же точке пространства два электрона с одной и той же ориентацией
спинов (тогда qH = q-, причем под q разумеются х, у, z, s; при qh = qt
функции A16.7,7') имеют узел так, что j Ч? |2 обращается в нуль).
Эти же утверждения справедливы также и для всех других частиц
Ферми, для позитронов, протонов и нейтронов.
В заключение отметим, что так как электроны являются составной
частью атомов, а протоны и нейтроны — составной частью атомного ядра,
то принцип Паули имеет первостепенное значение как в теории электрон-
электронной оболочки атомов, так и в теории атомного ядра.
§"17. Волновые функции для системы частиц Ферми
и частиц Бозе '
Рассмотрим несколько подробнее волновые функции, обладающие свой-
свойством симметрии или антисимметрии в частицах. Начнем с антисимметрич-
антисимметричных функций, принадлежащих частицам Ферми. Сначала обратимся к слу-
случаю двух частиц. Антисимметричная функция двух частиц W(qvq2,t)
может быть разложена по собственным функциям ^ni(<?i) и tyn2 (9г)> ПРИ'
надлежащим отдельным частицам:
Выражение A17.1) мы можем представить в ином виде, разбив сумму
395

на две части, в одной пусть nl>n2, а в другой n1<n2[n1 = n2 выпадает,
так как с (nv nv /) = 0]:
n2
Меняя во второй сумме индексы суммирования пу на и2 и и2 на
получим:
j, мы
< ГЦ
и, наконец, переставляя п1 и и2 в с(и2, п1( £), мы получим на основании
A16.13):
выражение в скобках мы можем представить в виде определителя и записать
*Р в виде
= 2
«2 П2
A17.3)
Таким образом, антисимметричная волновая функция представляется в виде
суммы (или интеграла) определителей вида
»№ (qv qa) -
П2 (qj
A17.4)
Если мы имеем дело с N частицами, то подобным же образом легко полу-
получить, опираясь на A16.13), в общем случае
W(qlt . . ., qh, . . ., qj, .. ., qN, t)= У!"-2 c(nv . . ., nk, . ..
qh,
A17.5)
где
nh,
{qk) ■ ■ ■ 44 (qj) •••
(9h) ■ ■ ■ 4>ni (qj) . . .
• . . г|5„л (qu) ■ . ■ 44
A17.6)
\>nN (qd ■■■ %N (qk) ■ ■■ %N (qj) ■ ■ ■ 4>nN (qs)
Раскрывая определитель, мы можем написать Ф также в виде
Фгц nh nj nlV (qx, • • •, qk, ■ ■ ■, qj qN) =
Ргц (q%) • ■ ■ tynh (q,) ■ ■ ■ ipny (qj) ■ • • ^njV (qN)- A17.6')
Здесь сумма взята по всем N\ перестановкам частиц qlt ...,q?t, причем
знак + или — берется перед слагаемым в A17.6'), смотря по тому полу-
396

■чается ли некоторое расположение величин q из расположения в порядке
возрастающих номеров qv q2 qk, qli+:s, ..., qN путем четного числа
парных перестановок или путем нечетного числа парных перестановок.
Приведенное представление антисимметричных волновых функций
в виде суммы определителей очень важно в практических приложениях
теории при приближенном решении задачи о движении многих тел. Допу-
Допустим, что нас интересуют волновые функции стационарных состояний двух
электронов в атоме. Такие функции найти, вообще говоря, довольно трудно.
Напротив, функции одного электрона найти значительно проще. Допустим,
что эти функции мы знаем — пусть это будут функции %рщ (qj и 1|)„2 (q2).
Если взаимодействие электронов не сильно, то волновая функция системы
двух электронов будет такова, что состояние каждого из электронов будет
мало отличаться от состояния одного электрона в атоме в отсутствии
другого электрона. Если же один электрон мы помещаем в квантовое
состояние, характеризуемое величинами (квантовыми числами) пх, то веро-
вероятность найти какое-нибудь иное значение п[ в этом состоянии равна нулю.
Подобным же образом, помещая второй электрон в состояние щ, мы
должны будем утверждать, что вероятность найти п'2 равна нулю. Если
мы теперь имеем дело сразу с двумя электронами в атоме, то в случае
слабого взаимодействия между электронами состояние при помещении
второго электрона должно мало измениться. Это означает, что если теперь
вероятность найти пл — п'х и л2 = п'2 и будет отлична от нуля, то она
все же будет мала, а стало быть, все c(n'v n'2, t) в A17.3) малы, кроме
c(nv n2, t). Пренебрегая всеми с, кроме с (пх п2, t), мы получим из A17.3)
волновую функцию гГ° для двух электронов атома в нулевом приближении:
и так как общий множитель с (nv n2, t) не играет роли, то
U*> ' <Ш-7)
ЧГО = Ф„1П.(?1, ?а). (П7.8)
Аналогично и в случае многих частиц, при условии слабого взаимодей-
взаимодействия между ними, функцией нулевого приближения для системы частиц
¥° является Ф„х> ...,„/!; ...,„у, ...,nN(qv ..., qh, ..., qh ..., qN) A17.6),
если i|;ni(9i), г|)„2(д2) %n(qn) суть функции электронов без учета
взаимодействия.
Таким образом, представление антисимметричной волновой функции
в виде определителя A17.4) или A17.6) дает приближенный способ для
представления волновых функций системы слабо взаимодействующих частиц
через функции отдельных частиц в отсутствии взаимодействия между ними.
Для частиц Бозе мы имеем другое разложение волновой функции
системы частиц W по произведениям функций отдельных частиц:
^п! Ы tyns (q2) ■ ■ ■ tynh(qh) ■ ■ ■ ^.foj) • • • ^nN{qN)- Переставляя в разложе-
разложении волновой функции системы
У (Чг ■ • ■ > Чч Qh ■ ■ ■' Qn, 0 = 2 • • • 2 с ("i> • ' '' "Л"' *) х
X г|5П1 (?]) ... %k (qk) . .. г|)„. (q,) . . . %N (qN) A17.9)
координаты &-ой и /'-ой частиц и замечая, что функция Чг для частиц
Бозе при этом не должна измениться, мы, сравнивая коэффициенты при
одинаковых произведениях, найдем, что
С (rt,, . .., Пк, ..., Щ, . . ., nN, t)= +C(/t,, .. ., Ilj, . . ., П„, . . ., nN, t).
A17.10)
397

Для двух частиц будем поэтому иметь:
7а) = S C("J' ^{^гц^О^ЫЧ- ifftlfct?!)}' A17.11)
Если взаимодействие между частицами слабо, то приближенное выраже-
выражение для волновой функции состояния двух частиц, близкого к состоянию
невзаимодействующих частиц, в котором одна из частиц находится
в состоянии Я], а другая в п2 имеет вид
4го = *н Ы ЧЧ Ы + ЧЧ (Яг) ЫЧ*)- A П-12>
В случае N частиц на основании сходной аргументации получим1.
4го = 2 *п (Яг) ■ ■ - ЧЧ (9*) • • • *.у (W) • • ■ ^«д, Ы, (И7.13)
р
где V означает сумму по всем .V! перестановкам координат частиц
р

= ГЛАВА :
ВТОРИЧНОЕ КВАНТОВАНИЕ И КВАНТОВАЯ
СТАТИСТИКА
§ 118. Вторичное квантование
Ансамбли одинаковых частиц могут быть рассмотрены особым мето-
методом, носящим название вторичного квантования. Сущность этого метода
заключается в том, что в качестве независимых переменных для описания
ансамбля вместо полного набора механических величин, характеризующих
индивидуальные состояния отдельных частиц, берут число частиц в этих
состояниях. Каждое из этих состояний будем характеризовать тремя
переменными: Lv L2, L3, относящимися к движению центра тяжести частицы
и спиновой переменной s, если частицы имеют спин. Ради упрощения
математического аппарата будем считать, что эти переменные имеют
дискретный спектр, так что все состояния можно перенумеровать числом п
так же, как это делалось в § 116 (под п разумеется совокупность значе-
значений четырех величин: Lv L2, L3, s).
Обычно гамильтониан дается в координатном представлении, поэтому
мы выполним сперва преобразование от координатного представления
к «/.«-представлению, которое будем считать дискретным1.
Если в координатном представлении волновая функция системы N
одинаковых частиц будет ^>(qvq2 qN, t), то уравнение Шредингера
для этой системы гласит:
,)\
где Н (qh) = - -^- Vl + U (qh) есть оператор энергии k-й частицы, U (qk) -
потенциальная энергия к-я частицы во внешнем поле, a W (qk, qj) — энер-
энергия взаимодействия fe-й и /-й частиц. Разложим теперь волновую функцию т|>
по собственным функциям tynh(qk) операторов Lit L2, Ls, s точно таким же
1 В теории вторичного [квантования часто берут импульсное представление
(L1 = pXt L2 = py, Ls = pz)- Однако импульсное представление непрерывно. Поэтому при-
прибегают к искусственному приему, полагая px = 2nhnx/l, py = 2nhny/l, pz = 2nhn2/l, где
пх, пу, nz—целые числа, а /—некоторая большая длина (ср. § 120). Тогда импульсное
представление становится дискретным. В окончательном результате переходят к /—>оо
и тем самым освобождаются от этого искусственного допущения. Исчерпывающая теория
вторичного квантования, применимая также и к случаю непрерывной последовательности
состояний, была разработана В. А. Фоком (V. A. Foe k, Phys. Zs. d. Sov. Union,
6 425, 1934).
3S9

путем, как это делалось в § 116. Тогда получим:
У (<7i, <?2 дп, 0 = 2 2 • • • 2с (">• "г- • • •. nN, t) x
X г|)П1 (9l) г|)„2 (<?2) • . • ^>nN Ы- (П8.2)
с (пх, п2, . ,.,«jv, t) есть, очевидно, волновая функция нашей системы
в «/^-представлении. [ c(nv п2, .. ., «n, f) |2 есть вероятность того, что пер-
первая частица находится в состоянии пг (имеет четверку Lu L2, La, s, обо-
обозначенную одной буквой «j), вторая частица в состоянии «2 (имеет четверку
L[, L'2, Lg, s', обозначенную через п2) и т. д. Подставляя A18.2) в A18.1),
умножая уравнения слева на tymi (qj tymi (q2) .. . ipmN (<?n) и интегрируя
по qv q2, ..., qN, получим:
., d
in-т. с (mv m2, . . ., mk, . . ., rrij, .. ., tnN, t) —
= 2 S Hmk; nk С (tni} m2 nh, ..., rtlj, . . ., W.N, t) +
N
+ 222 Wm m nn c(m1} m2 nk, .. ., nh . .., mN, t). A18.3)
Здесь Wm ■„ и Wmfem-,nftn- суть матричные элементы:
\(qn)H(^^h(%)dqk, (П8.4)
m. (<73-) W (<7ft, <7,) ij)n (qlt) г|)„. (<73-) dqkdqj. A18.5)
Уравнение A18.3) есть уравнение A18.1) в «^-представлении. В силу
одинаковости частиц матричные элементы A18.4,5) зависят лишь от значе-
значения квантовых чисел тк, пг}; пк, tij, а не от номера частиц k, j. Обозна-
Обозначая какое-нибудь значение тк через т, пк через п, подобным образом m.j
через т', щ через п', координаты k-й частицы через q, а /—через q', мы
можем написать A18.4) и A18.5) в виде:
|г W ^ ^ (q) U (q)
t.2
m G) f/ (<?) t|>« (<?) d<? = ^-»», (П8.6)
G) <V (9') W (9, 7' )ф„ G) г|)„- • (<?') d<7 dG' = Wmm', nn'- A 18.7)
Амплитуды с (inv m2, . . ., m^, t) (волновые функции в «^-представле-
«^-представлении) суть симметричные функции квантовых чисел mv m2, . . ., т^ для
частиц Бозе и антисимметричные функции для частиц Ферми (см. § 116).
Поэтому значения этих амплитуд зависят лишь от того, сколько аргу-
аргументов из их полного числа N (ть т2, .. ., tnN) равно т, сколько равно
tn', in", ... и т. д., а не от того, какие именно из этих аргументов равны
т, т, т", ..., т. е. эти амплитуды являются функциями числа частиц
в каждом из состояний. Обозначим эти числа через Nu Л/2, . . ., Nm, ...
. . ., Nm', . . ., Nm", ■ • •, и т. д. Следовательно, например, Nm равно числу
чисел тн среди аргументов с {mv m2, . .., mN, t), значение которых равно
in, Nm' равно числу чисел тк, значение которых равно т' и т. д.
В случае частиц Бозе числа Nm могут быть любыми. Напротив, в слу-
случае частиц Ферми, в силу принципа Паули, функция c(mv m2 mN, t)
обращается в нуль, если хотя два числа mh, щ равны между собою, так
что Nm принимает только два значения 0 или 1: состояние может быть
занято только одной частицей или вообще не занято.
400

Дальнейшие преобразования мы произведем для частиц Бозе. Наша
задача заключается теперь в том, чтобы написать уравнение Шрсдингера
A18.3), взяв в качестве переменных вместо квантовых чисел тг, т%, ...
...,iriN числа частиц в этих состояниях Nv N2, ...,Nm, .... Для этого
нам нужно прежде всего изменить нормировку амплитуд с. В самом деле,
если рассматривать с как функцию чисел Nv N2, ..., Nm, то
I c {Nv ^2> • • • > Nm, ..., t) |2 есть вероятность нахождения Nl частиц в состоя-
состоянии 1, N2 частиц в состоянии 2, .. ., Nm частиц в состоянии тит. д. Эта
.же вероятность выразится через c(m.i,m2, ...,tn^,t) в виде
\c{N1, Nv ..., Nm, ...,t)\2=2\c(mvrn» "^mN,t)\\ A18.8)
где сумма взята по всем c(mrm2, ...,tnN,t), имеющим Nl чисел tnk,
равных 1, N2 чисел тк, равных 2, и т. д. В силу симметрии все эти с
равны между собою. Поэтому
|c(/Vr N2, ..., Nm, ..., 012 = -лПлП 1~7П
A18.8')
откуда
c_(m1, m2, . *., m^ 0-
A18.9)
Подставляя теперь в A18.3) вместо с (mv tn2, ...,triN,t) амплитуды
c(Nv N2, .. ., /Vm, ...,/), мы можем выполнить суммирование по номерам
частиц k и /. Для этого воспользуемся A18.6) и A18.7) и заметим, что
c(mv т2, ..., т1{, ..., тг .. ., tnN, t) отличается от c(mv пг2, .. ., пк, ...
..., т}, . ,., nix, t) тем, что число частиц в состоянии mh —m уменьши-
уменьшилось на 1, а число частиц в состоянии пк = п увеличилось на 1.
Подобным же образом с (т,, т2, ..., пк, ..., п,, ..., т«, /) отличается
от с(ти т2, ..., тк, . . ., mh .. ., din, t) тем, что число частиц в состоя-
состояниях mh = tn, mj — tn' уменьшилось на 1, а в состаяниях пк = п, щ = п'
увеличилось на 1.
На основании этих замечаний находим:
.. d I ( Nil ... Nm] ... Nm,\ ... Nn\ ... Nn,\ ...
in ,, \\ щ
Xc(Nl,
H
... Nn,\ ...V/i
J
T 2 E # JVm WW. nn, X
V
J
X
m, m' n, n'
v
AM J X
Xc(Nv ...,Nm-\, ..., iVe.- 1, ...,Nn +1, ..., iVn.+ l, ...,/).
A18.10)
26 Д. И. Блохинцев 401

Деля на ( -дПдП ^ - получим:
ili-~c(Ni: ..., Nm, ...,Nm., ...,Nn, ...,Nn., ...,/) =
= 2 NVz(Nn-\-l)V*Hmnx
n, m
Xc(Nv ..., /Vm-1, ..., Nm,, ...,Nn-\-l, ..., Nn,, ...,t) +
XciN,, ..., Nm-\, ...,Nm>-\, ..., Nn+l, ...,Nn--l, ..., 0-
A18.11)
Это и есть искомое уравнение, в котором за независимые переменные
взяты числа частиц в отдельных состояниях. Это уравнение может быть
записано в очень удобной форме, если ввести операторы ап и а„, которые
действуют на функции от чисел Nn, следующим образом:
anf{Nlt /V2, . .., Nn, ...,Nm, . ..) =
= (Nn+lY'*f(Nlt Nt, ...,Nn+l, ...,Nm, ...), A18.12)
atf{Nv N2, ...,Nn,...,Nm,...) =
l, .-.,Nm, ...), A18.12')
Nm, ...) = 0. A18.12")
Эти операторы, очевидно, обладают следующими свойствами:
a*nan = Nn, anat = Nn+l, A18.13)
amaZ-aiam = 6mn. A18.14)
Теперь нетрудно видеть, что с помощью этих операторов уравнение A18.11)
может быть написано в виде
') fj|^i|i|f)i A18.15)
где
Я=^«;ЯгаА+|2 2 c&<&Wmm:nn'anan: A18.16)
т, п in, таг п, пг
Оператор Н есть гамильтониан системы, выраженный через операторы
ап и а'п- Его обычно называют вторично квантованным, Это уравнение
вполне эквивалентно исходному уравнению A18.1) для N частиц в кон-
конфигурационном пространстве. В сущности, уравнение A18.15) есть ура-
уравнение A18.1) в «^-представлении, т. е. в представлении, в котором
в качестве переменных взяты числа частиц Nv N2, . .., /Vm, ... в различ-
различных квантовых состояниях 1, 2,...,т, .. . .
Однако уравнение A18.15) в одном отношении—общее уравнения A18.1);
последнее написано для системы N частиц, в уравнении же A18.15)
полное число частиц явным образом не входит. Оно является постоянной
интегрирования. Действительно, оператор Н A18.16) в каждом члене
содержит одинаковое число операторов а и операторов а*. Так как опе-
операторы а увеличивают число частиц в каком-либо из состояний на 1,
а операторы а* уменьшают число частиц в каком-то из состояний на 1,
то полное число частиц N = 2^'т П°Д действием оператора Н не меняется,
так что
^ = [Я,Л/] = 0. A18.17)
402

Таким образом N = const. Поэтому уравнение A18.15) справедливо для
любого числа N одинаковых частиц Бозе.
Гамильтониан A18.16) теории вторичного квантования можно напи-
написать в другой форме, которая соответствует энергии некоторого волнового
поля.
Пусть волновая функция одной частицы есть я|) (q). Разложим эту
функцию по собственным функциям tyn(q) операторов Lv L2, L3, s:
1>G) = ^МЛ?)- A18.18)
n
Будем теперь рассматривать амплитуды ап не как числа, а как операторы,
со свойствами A18.14). Тогда сама функция я|) будет оператором
T(<?)=S«»t(<?). A18.19)
п
действующим на числа Nlt N2, . . ., Nm, . .. . Переход от A18.18) к A18.19)
означает, что мы перешли от чисел к операторам, т. е. мы как бы перешли
от классической теории к квантовой. Но так как описание движения одной
частицы с помощью волнового поля я|)(<7) уже само по себе является
квантовым, то замену амплитуд ап на операторы ап называют вторичным
квантованием, а волновую функцию W называют квантованной волновой
функцией1.
Заметим, что переход от неквантованной волновой функции A18.18)
к квантованной A18.19) может быть сформулирован непосредственно
без обращения к операторам ап. Действительно, из A18.14) и A18.19)
следует: •■ " ■
V (q) ¥* (q) - Ч* (q') V (q) = 2 (апа*т - «* ап) я|)й (q) ^ (q') = '
т, п
= 2^*™(?li(?)=E«(?')t,(?).
т, п п
где сумма распространена по всем собственным функциям. Такая сумма,
как можно доказать, равна б (q' — q). Поэтому квантование волновой
функции можно записать в виде:
W (q) W* (q') - Ч>* (q') 4{q) = 6 (q' - q). A18.20)
С помощью квантованной волновой функции ~*¥ (q) A18.19) гамильтониан
A18.16) может быть написан в виде:
[ V* (q) U (q) V (q) dq + ,
[A18.21)
Эквивалентность A18.21) и A18.16) очевидна, если учесть A18.19) и вы-
выражения для матричных элементов A18.6) и A18.7).
В этой форме гамильтониан // A18.21) можно рассматривать как
энергию некоторого волнового поля, которое «квантовано» в том смысле,
что классическое поле я|) [q) заменено на оператор 4f (q). Действительно,
1 Следует не упускать »з виду, что волновой функцией в обычном понимании
чтой величины в теории вторичного квантования является функция с (Л/1; Л/2 Nm, ..., t),
а не Ч\
26* 403

будем понимать под я|) (д) волновое поле де Бройля-Шредингера и пред-
предположим, что отдельные элементы этого поля взаимодействуют между
собой так, что энергия взаимодействия двух элементов пропорциональна
произведению плотностей |я|) (q) |2 |я|)(<7') i2- «Классическое» уравнение для
такого поля будет1:
ih^t = ~~T V2y>(q) + u(q)ty(q) + ty(q) )W(qq')\q(q')\2dq'. A18.22)
Полная энергия такого поля будет равна2
+ т $ Ж?) Iе К to') I2 w to- я') &я W- С118-23)
Если теперь расположить здесь -ф и яр* надлежащим образом и заменить
их на операторы У и W*, подчиняющиеся правилу перестановки A18.20),
то мы получим в точности гамильтониан A18.21) теории вторичного кван-
квантования. Отсюда видно, что теория вторичного квантования допускает
следующий замечательный подход к теории систем одинаковых частиц:
рассматривается некоторое классическое поле яр. Для него нахо-
находится выражение энергии //. В этом выражении классическое поле яр
заменяется на оператор W. Тогда мы приходим к гамильтониану Н
теории вторичного квантования и получаем право говорить о частицах,
свойственных данному полю яр: после квантования поле обнаруживает
дискретную, корпускулярную природу. Эта процедура носит название
«квантования поля». Сила ее заключается в том, что она применима
к любому, классическому полю3.
В приведенном выше примере речь шла о квантовании поля де Бройля-
Шредингера для случаи частиц Бозе.
Совершенно таким же путем можно выполнить квантование для слу-
случая частиц Ферми. Различие заключается лишь в свойствах операторов а,
а*. Чтобы найти эти операторы, нужно выполнить заново преобразование
уравнения A18.3) от переменных щ]( т2, ...,т^ к переменным Л/,, /V2,...
...,Л/т, ..., которое для частиц Ферми несколько более кропотливо
ввиду того, что при перестановке частиц функции с(тЛ, т2, .. ., nix, t)
меняют свой знак. Далее, как уже отмечалось, числа Nm могут иметь
лишь два значения: 1 и 0. Выполняя сходные преобразования4, мы
получим из A18.3) опять уравнение A18.15) с гамильтонианом A18.16),
но операторы ап, а*п будут определены в этом случае иначе, именно:
aj(Hv /V2, ...,0n,...,/Vm, ...) =
Л/2, ..., ln, ..., Nm, ...), A18.24)
Jv Л/2, ..., 1., ..., /Vm, ...) = 0, A18.24')
...,0„, ..., Nn, ...) = 0, ' A18.24")
1 Это уравнение отличается от правильного уравнения Шредингера для одной
частицы последним членом, который выражает допущенное нами самовоздействие гр-воли.
2 Пользуясь уравнением A18.22), можно убэдиться, что ~/7- = 0, т. е. Н есть инте-
интеграл движения. Так как второй член в A18.22)) завэдомо есть потенциальная энергия
во внешнем поле, то все выражение, поскольку //=const., следует рассматривать как
полную энергию поля.
3 Общая теория этого квантования изложена в книге: Г. Вентцель, Введе-
Введение в квантовую теорию волновых полей, Гостехиздат, 1947.
4 См., например, Дирак, Основы квантовой механики, § 80, или оригинальную
работу В. А. Фока, Zs. f. Phys, 75, 622, 1932.
404

aZf{NxtN2,...,ln,...,Nn,...) =
N,,...,On,...,Nm,...), A18.24'")
причем знак -\- или — берется, смотря по тому, четное или нечетное
число занятых (Nm=l) состояний предшествует состоянию п, если состоя-
состояния расположить в порядке возрастания1 п.
Из этих правил следует:
а£ап=Ып@ или 1), ana*=l-Nn, A18.25)
апс& + е&ап = 6тп. A18.26)
Как видно, правило перестановки для операторов а в случае частиц Ферми
отличается знаком от правил перестановки для частиц Бозе.
Пользуясь A18.18) и повторяя выкладки, ведущие к A18.20), получим:
W (д) W* (д1) + У* (д1) W (д) = б (д1 - д). A18.27)
Все остальные формулы, в частности, выражение для И A18.21), остаются
без изменения. Таким образом гамильтониан И совместно с правилом
квантования A18.27) можно рассматривать как вторично квантованный
гамильтониан для электронных волн, «классическое» уравнение для кото-
которых есть A18.23). Правило квантования для обоих случаев может быть
записано в одной формуле:
= b(q'-q\ (И8.28)
причем знак -f берется для частиц Ферми, а знак — для частиц Бозе.
В современной физике приходится иметь дело с явлениями рождения
и уничтожения частиц. Эти явления, строго говоря, выходят за рамки
квантовой механики. Однако метод вторичного квантования ввиду того,
что в него не входит явным образом полное число частиц, допускает
простое обобщение на случай переменного числа частиц и тем самым
оказывается пригодным для описания явлений рождения и уничтожения
частиц. Действительно, если к гамильтониану Н A18.16) добавить член
вида
Q=lQnan+ 2 Qtat, A18.29)
п п
где Оп, (?п суть некоторые операторы, характеризующие взаимодействие
частиц с какими-либо другими частицами, способными поглощать или
излучать первые, то полное число частиц N уже не будет интегралом
движения, так как [Q, N] =£ 0. При этом члены, содержащие «, описы-
описывают рождение частиц, а члены, содержащие а*, — их уничтожение [см.
A18.12') и A18.12")].
Если кванты света (общее — фотоны) рассматривать как частицы, то
можно процессы испускания и поглощения света рассматривать как про-
процессы рождения и уничтожения фотонов. Основанная на этой мысли
квантовая теория излучения была развита Дираком 2. Подобным же путем
можно изучить явления возникновения и уничтожения электронов и пози-
1 Можно ввести вигнеровскую функцию \п, определяемую формулой:
Vn= П A-2Л/т),
вместо знака Ht; в формулах A14.24) писать vn(vn — ±; 1).
2 См. П. Дирак, Основы квантсвс й механики, ОНТИ, 1937, §§ 62 — 67; Гейтлер,
Квантовая теория излучения, ГИТТЛ, 1940.
405

тронов при р±-распаде, при рождении и уничтожении пар, явления обра-
образования и распада мезонов и др. Все эти явления рассматриваются кван-
квантовой теорией полей 1
Помимо квантовой теории поля, теория вторичного квантования нахо-
находит также обширные приложения в области квантовой статистики.
§ 119. Теория квантовых переходов и метод вторичного
квантования
Вычислим теперь вероятности перехода под влиянием возмущения
из' одного квантового состояния в другое в ансамбле одинаковых частиц.
Для расчета воспользуемся методом вторичного квантования. Чтобы кон-
конкретизировать задачу, рассмотрим переходы под влиянием слабого взаимо-
взаимодействия между частицами.
В этом случае целесообразно выбрать переменные Lv L.2, L3, s, опи-
описывающие состояние частиц таким образом, чтобы одна из них (скажем Lj)
равнялась энергии частицы L, (<7,L) = E (qh). Тогда матрица Н-тп будет
диагональной. Если через гт обозначить собственные значения энергии
частиц, то Нтп = е,т-Ьтп. При таком выборе переменных уравнение A18.15)
имеет вид:
ih 1 с {Nv ЛГ8, ...,*) = S e™^™c (/Vi> N*> • • •' 0 +
т
+ ~ 2 c&aZl>Wmm'nn'anan.c(NvNs, ...,t). A19.1)
Сумма ^>jEmN,m — E есть полная энергия всех частиц без учета их взаи-
т
модействия. Вводя вместо функций с (Nv Ыг, . . ., t) медленно меняю-
меняющиеся амплитуды b(NvN2,...,t) = c(Nl,Ni,...,t)eh m т, получим
вместо A19.1) уравнение для b(Mu Nv . . ., t):
ih~b(N\,N,,...,t)=,
= у Zi e atndm', Wmm*nn> anan' b (N1, N2, ..., t).
m,m',n,rV (liy.Zj
Допустим, что в начальный момент времени населенность различных
состояний характеризуется числами №v N°, ■ . ■, так что все амплитуды b
при / = 0 равны нулю, кроме
Пользуясь обычным приемом теории возмущений, подставим в пра-
правую часть уравнения A19.2) начальное замечание 6°. Тогда, имея в виду
свойства операторов а%,, ««-. о,п, аП' [см. A18.12') и A18.12"]), получим
уравнение для определения 6A) в первом приближении:
ih jt b^(N\, N1,.... №т+ 1, ..., №т> + 1,..., №п- 1, .... №- 1, ..., t) =
=£Т^п^-*п-*п') ' {N0m+ 1I/я {Nm> + 1I/2 Mony.2 NOXJ2 Wmm/i nn,_ A19.3)
1 II. Н. Боголюбов и Д. В. Ширков, Введение в теорию квантовых полей,
ГИТТЛ, 1957; А. И. Ахиезер и В. Б. Берестецкий, Квантовая элек-
электродинамика, Физматгиз, 1959.
406

Интегрируя это уравнение по времени и вычисляя вероятность перехода
в единицу времени Ртт>,пП' = ^\ &A) |2 (ср. вычисления § 84), найдем:
Ртт; пп> = (№т+\) № + 1) №п№п,~ J Wmm., nw|26(em + em,—en-«v), (П9.4)
причем наличие «б»-функции обеспечивает закон сохранения энергии.
Подобным же образом, разумея в A19.2) под «£,, ат', ап и «„< опе-
операторы Ферми—Дирака A18.26), получим для случая частиц Ферми:
Pmm>,nn> = (\~N^)(l~Nl,)N^'^\Wmm',nn'\2b(en-yzm'~-zn~en')- (П9.5)
Эти формулы показывают, что в системе одинаковых частиц вероят-
вероятность перехода из начального состояния (п, п') в конечное (т, т) зави-
зависит не только от числа частиц в начальном состоянии (п, п'), но от на-
населенности конечного состояния (т, т'). Это совершенно новый результат
квантовой теории, не имеющий места в классической механике. Для час-
частиц Бозе вероятность перехода тем больше, чем больше частиц уже нахо-
находится в конечном состоянии. Частицы Бозе имеют, таким образом, тен-
тенденцию накапливаться в одном состоянии. Напротив, для частиц Ферми
вероятность перехода равна нулю, если состояние, в которое происходит
переход, занято (№т=\ или Nm'=l). Это есть новое выражение для
принципа Паули.
§ 120. Гипотеза о столкновениях. Газ Ферми—Дирака и газ
Бозе—Эйнштейна
В классической кинетической теории предполагается, что вероятность
перехода частиц в результате столкновения из некоторого состояния п
и п' (энергии частиц еп и еП') в другое состояние т и т (энергии час-
частиц е„ и е„/) пропорциональна числам частиц в начальных состояниях N п
и Nnr-
А . hi М /1 9П 1 \
mm , пи — ^^тпт , nn' ** п п \ ■ /
Если Nn и Nn' — среднее число частиц в состояниях п и п', то предпо-
предполагается в соответствии с A20.1), что среднее число переходов из п, п'
в гп, т' равно
jt mm', nn' = "mw', nn' NnNn'i A20.1 )
при этом Ammr, nn' = Ann-, mm' (так называемый «принцип детального баланса»1).
На основании квантовой механики мы должны для газа, состоящего
из одинаковых частиц, сделать другое предположение о среднем числе
переходов под влиянием столкновений. Как было показано в предыдущем
параграфе, вероятность перехода зависит не только от числа частиц в ис-
исходных состояниях, но и от степени населенности конечных состояний,
1 Этот принцип справедлив не всегда. Он во всяком случае справедлив в первом
приближении теории квантовых переходов (см. §§ 83, 84), и строго справедлив, если
силы взаимодействия между частицами — центральные (ср. § 44 и цитированную там
работу Д. И. Блохннцева).
407

именно, вместо A20.1)' в согласии с A19.4) и A19.5) имеем для вероят-
вероятности столкновения в случае частиц Ферми:
Ртт>.««' = Amm,t nn,{\~ NJ A - Nm.) NnNn, A20.2)
(Nm, Nm', Nn, Nn> = 1 или О). В этой формуле явно выражен принцип
Паули: если оно из конечных состояний занято Nm=\ или Цт, = \, то
перехода быть не может. Подобным же образом для частиц Бозе имеем:
Ртт',пп> = Атт,,пп(Ыт+\)(Ыт> + \)ЫжЫп,. A20.3)
Здесь множители (N_m+ 1) и (Nm,-\-\) не имеют столь наглядного значе-
значения, какое имеют множители A — Nm), A—/Vm') в случае частиц Ферми.
Однако необходимость наличия таких множителей была нами доказана
(§ 119). Как уже отмечалось, частицы Бозе имеют тенденцию к ассо-
ассоциации: они переходят в наиболее населенные состояния 1.
Равенство величин Атт^п„ и Апп>,тт' (обратный переход) вытекает
в квантовой механике из того факта, что Атт<,пп, пропорционально квад-
квадрату модуля матричного элемента энергии взаимодействия Wmm>tnn',
a Wmm>,nn-=W*n',mm> (см. сноску к стр. 407).
В соответствии с A20.2) и A20.3) для газа из одинаковых частиц
в квантовой механике для среднего числа переходов под влиянием столкно-
столкновений берут вместо A20. Г) выражение
Ртт'. пп' = Атт „„' A ± NJ A' ± Nm') ^гДп' ( 1 20.4)
причем знак— берут для частиц Ферми, а знак + для частиц Бозе.
Формулу A20.4) мы будем рассматривать как новое предположение о сред-
среднем числе столкновений частиц, основанное на квантовой механике2.
Очевидно, что A20.4) превращается в классическое выражение A20.1),
если среднее число частиц в каждом из состояний мало в сравнении с еди-
единицей.
Найдем теперь распределение по энергиям при тепловом равно-
равновесии в газе частиц Бозе или Ферми. При тепловом равновесии число
переходов в состояния п и п' в результате столкновения частиц, нахо-
находившихся в состоянии т и т', должно равняться числу обратных пере-
переходов. Из A20.4) тогда получаем (в силу равенства Amm>t fcn/ = Ann>, mm')'-
A ± NJ A ± Nm,)NnNn, = (\ ±Nn)(\± Nn>)NmNm>. A20.5)
Далее, при равновесии среднее число частиц в каждом из состояний Nт
будем считать только функцией энергии это.-о состояния e,,v[iVlft= iV(e,J].
На основании закона сохранения энергии при столкновениях [ср. A19.4)
и A19.5)] имеем:
= ев+е„». A20.6)
1 Это приводит к замечательному свойству газа из частиц Бозе: при низкой тем-
температуре наступает своеобразная конденсация этого газа, даже если предположить,
что газ — совершенно идеальный, так что силы взаимодействия бэсконечно малы. См.
A. Einstein, Berichle der Preuss. Akad., 3, 1925. Теория идеального газа Бозе
была развита Н. Н. Боголюбовым (Journ. Phys. USSR, XI, 23, 1947). Эта теория поз-
позволяет дать толкование интересному явлению сверхтекучести гелия.
2 Мы назовем A20.4) «предположением», так как в выражзнии для вероятности
перехода A20.2) разумеются истинные значения населенности уровней Nn, Nn,, Nт, Nт.
а в A20.4) стоят средние значения Nn, Nn,, Nm, Nm,. Равенство (lztNm) A±#т,) {NnNn,=
= A rb Nm) (l±JVm/) NnNn, не является очевидным и выполняется не при всех условиях.
408

Из A20.5) получаем, что
-^— = C, A20.5')
1 ± Nm \±Nm> l±Nn l±Nw
где С — некоторая постоянная, которая может зависеть [на основании
сделанного предположения об Л/ и закона сохранения A20.6)] лишь
от суммы вт4-ет< (или en +en'= em+em')- Таким образом
:(ет+вт')- A20.5")
1 ± Л/т I ± Л/т'
Обозначая 2?=г—- = ф(вт), мы перепишем A20.5") в виде
A20.7)
Дифференцируя это равенство один раз по ет и другой раз по ет< и деля
один результат на другой, найдем:
Ф' (ет) = Ф'
Ф (е-т) Ф (8т')
A20.8)
где в — некоторая постоянная, не зависящая от е. Интегрируя теперь
A20.8) по ет, находим:
Ф(вт) = в-^+\ A20.9)
где а — постоянная интегрирования. Отсюда находим" для среднего числа
частиц в состоянии с энергией е,„:
. Й» = ЛМО = —_i A20.10)
—а
е ° ±1
(знак — для частиц Бозе, знак -\- для частиц Ферми). При большой
энергии частицы (е —-» со) закон распределения по_энергиям должен сов-
совпадать с классическим законом Больцмана
yV(eJ = const.. е~"\ A20.11)
где k — постоянная Больцмана, а Т — абсолютная температура. Переходя
в A20.10) к пределу ет—> со и сравнивая с A20.11), находим, что 6 =
= kT. Таким образом, окончательно
Nm = - 1- . A20.12)
Постоянная интегрирования а определится из условия равенства числа
частиц во всех состояниях полному числу частиц в рассматриваемом
экземпляре газа:
2Йт = Л/. A20.13)
m
Совокупность частиц, подчиняющихся закону распределения A20.12)
со знаком ( Ь), носит название газа Ферми — Дирака, а со знаком ( — ) —
газа Бозе — Эйнштейна. Закон A20.12) явно написан для дискретных
состояний.
40»

Введем число состояний на интервал энергии de. Обозначим его
через Vq(e)de, где V — объем всего газа. Тогда, суммируя A20.12)
по всем квантовым состояниям, энергия которых попадает в интервал е, е-(-
■fcfe, мы получаем среднее число частиц газа, имеющих энергию
между е, e-\-de (закон распределения по энергиям):
«
и деля на V, получаем то же число для единицы объема газа:
jf(e)fife = —J(e)de , A20.14)
Вместо A20.13) теперь следует написать:
со со
-р^— = п, A20.15)
о
где п — -у—плотность числа частиц1.
Распределение A20.14) со знаком ( + ) носит название распределения
Ферми — Дирака, а со знаком ( —,) — распределения Бозе — Эйнштейна.
Наиболее существенной особенностью распределения Ферми —Дирака
является существование нулевой энергии газа. Чтобы в этом убедиться,
положим а = -77"; тогда имеем:
j(s) de, = ^ / (е) -= Е^Е(в)—. A20.16)
0 е w 4-1 е~®~+1
При в—>0 (низкие температуры) е0 должно быть больше нуля (если энер-
энергию е отсчитывать от нуля так, что е > 0), иначе при в —> 0 / (е) —> 0
и нельзя удовлетворить первому равенству A20.16). Далее, мы видим,-
что при в—» 0 / (е) = q (е) для е < е0 и / (е) = 0 для е > е0, т. е. при абсолют-
абсолютном нуле все состояния в 'газе Ферми — Дирака заняты вплоть до состоя-
состояний с е = е0, остальные же состояния свободны. Энергия частиц, занимающих
состояния от е = 0 до е = е0, и есть нулевая энергия газа. Более подробное
рассмотрение показывает, что такое распределение очень мало меняется с тем-
температурой, если только температура остается такой, что ® — kT<€ eo.eo, оче-
очевидно, есть максимальная энергия частицы в газе Ферми — Дирака
при абсолютном нуле температуры.
Мы вывели распределения Ферми —Дирака и Бозе — Эйнштейна,
исходя из гипотезы о столкновениях A20.4). Эти же распределения могут
быть найдены из общих положений термодинамической статистики
(ансамбль Гиббса) без каких-либо предположений о кинетике процессов2.
Отличие расчетов, базирующихся на квантовой механике, от расчетов,
базирующихся на классической механике, заключается в разном способе
подсчета числа возможных состояний. В квантовой механике состояние
1 Очевидно, что q (в) не может зависеть от объема газа, так как иначе функция
распределения также зависела бы от него. Такая независимость q (e) от V всегда имеет
место, если объем газа V значительно больше X3, где %—длина волны в преобладаю-
преобладающем числе занятых состояний.
3 См. М. А. Лео пто вич, Статистическая физика, Гостехиздат, 1944.
410

характеризуется заданием симметричной или антисимметричной волновой
функции х¥, и различные перестановки частиц по отдельным состояниям
не дают нового состояния (¥ переходит сама в себя или меняет знак).
С точки зрения классической механики каждая такая перестановка озна-
означает новое состояние частиц. Классическая статистика, базирующаяся
на таком подсчете состояний, представляет собой предельный случай
квантовой статистики, в которой число состояний исчисляется по числу
различных волновых функций (можно показать, что классическая стати-
статистика получается из квантовой, если число частиц в объеме средней
длины волны К3 много меньше единицы). В квантовойобласти различают две ста-
статистики— статистику Ферми — Дирака (для частиц, подчиняющихся
принципу Паули, — антисимметричные W) и статистику Бозе —Эйн-
—Эйнштейна (симметричные W, частицы Бозе). В своих принципиальных осно-
основах эти две статистики, конечно, не различаются.
Применим статистику Ферми — Дирака к электронам проводимости
в металле. Последние приближенно можно рассматривать как свободные
частицы *. Подсчитаем число состояний на интервал энергии q (e).
В объеме металла L3 = F состояния свободных частиц будут стоячими
волнами. Удобнее рассматривать бегущие волны, считая металл бесконечно
большим, но мы будем предполагать, что в каждом объеме L3-=V состоя-
состояние полностью повторяется («условие периодичности»). Такое рассмотре-
рассмотрение вполне законно, если L > К, где X есть длина волны преобладающего
числа занятых состояний. Волновые функции будут плоскими бегущими
волнами вида
i(hxx~\~kyy-\-k~ z)
Ч~ A20Л7>
.(нормированы к 1 в L3), причем kx, ky, kz имеют значения
kx = jH*_t kv = ^-f kz=*^-. A20.18)
Благодаря такому выбору kx, ky, kz состояние в объемах L3 повторяется.
•Состояния у нас нумеруются числами пх, пу, пг. Эту тройку чисел и сле-
следует теперь разуметь под одним индексом т, фигурировавшим в A20.12).
Образуем сумму ^AnxAnyAnz '(Ап=±1) по состояниям, которые
попадают в интервал энергии е, e-f-fife. На основании A20.18) имеем:
AnxAnyAnz
следовательно,
в, e+ds е, в-fde
= v_ re kiMd dQ=wk2M A2019
s, E-fd8
Замечая, что для свободных частиц г — -к—кг и что каждому значению к
соответствуют два состояния с различной ориентацией спина электрона,
мы получаем:
B13/2el^rfe- ■A20-2°)
1 Строгое доказательство возможности такого приближения, и установление гра-
границ его применимости до сих пор еще не произведены.
411

Подставляя это значение Q (е) в A20.14), находим закон распределения
свободных электронов:
f /,л л,, _ 8я BИ-K/г еу2 йг Л9П9П
Вычислим максимальную энергию е0 для 6 = 0. Так как при в = О
f(e) = O для е>е0, то из A20.16) и A20.21) имеем:
r°f,. , 8я BA)'/г ? ,, , 8я B|хK/г 2 3, /1ОГ1 оо.
п = ^ / (е) da = -^5-*^- ^ е /» de = ^^ ^- у е*'к A20.22)
'е 6
Отсюда
Величина максимальной энергии электрона е0 для металлов (п—
■— 1022 см 3) получается равной нескольким электроновольтам. Такого же
порядка величины средняя нулевая энергия электронов е @) [точ-
[точно е @) = я/6е0]. По классической теории средняя энергия электронов должна
быть гораздо меньше C/2kT). Более детальное исследование показывает,
что е0 очень мало зависит от температуры, если только последняя много
меньше То=~. Эта температура для электронного газа составляет ~ 10 000°.
Для температур Т^>Т0 можно доказать, что распределение Ферми —Ди-
—Дирака переходит в максвелловское распределение
/ (е) cfe = ccnst.e~~eV2 de. A20.24)
Температуру То назывяют температурой вырождения газа. Применение
статистики Ферми — Дирака к электронному газу позволило преодолеть
многочисленные принципиальные затруднения классической электронной
теории металлов и в настоящее время является исходным пунктом совре-
современной теории1.
В качестве примера распределения Бозе — Эйнштейна рассмотрим чер-
черное излучение. Будем считать кванты света (фотоны) частицами. Соотно-
Соотношение между энергией е и волновым числом k для этих частиц есть е =
= кш ■= hck, т. е тг = he. Так как состояния фотона представляются
плоской волной, то число состояний на интервал энергии будет A20.19).
При этом еще нужно умножить A20.19) на 2, так как для каждого зна-
значения к возможны две независимые поляризации. Следовательно, из A20.19)
получаем:
(iJirfe- ' A20-25)
Таким образом, закон распределения фотонов по энергии получается
в виде
-f^--- A20-26>
1 Литература по квантовой теории металлов весьма обширна. Укажем книги:
Я- И. Френкель, Введение в теорию металлов, Гостехиздат, 1948; Г. Бете и А. 3 ом-
мерфельд, Электронная теория металлов, ОНТИ, 1938; Р. Пейерльс, Электрон-
Электронная теория металлов, ИЛ, 1948.
412

Полное число фотонов неопределенно ( = оо), поэтому условие A20.15)
для определения а не может быть использовано. Энергия в единице объ-
объема в интервале de будет равна еу (е) de. Имея в виду, что е = /гсо, перей-
перейдем к плотности излучения и(ш) на интервал частот d<a: и(ш)Ло =
= eg(e) h dw. На основании этого получаем:
При ha < 6 закон распределения должен переходить в классический закон
Рэлея-—Джинса (§ 6). Чтобы получить этот закон, следует взять а = 0.
Таким образом, получаем:
«H = w-sr— A20-26">
т. е. формулу Планка1.
1 Применяя метод Гиббса, можно непосредственно вывести формулу A20.26"),
яе прибегая к классическому закону Рэлея—Джинса. (См. М. А. Леонтович,
цит. соч.)

ГЛАВА XXI
МНОГОЭЛЕКТРОННЫЕ АТОМЫ
§ 121. Атом гелия
Атом гелия, второй атом периодической системы, является наиболее
простым из многоэлектронных атомов. Однако уже на нем классическая
механика потерпела полный крах. Попытки рассчитать его методами
классической механики (с учетом квантовых условий Бора) привели
к выводу о невозможности применения классической механики к атомным
системам с двумя и большим числом электронов. Было сделано предпо-
предположение о существовании некоторого рода «немеханических действий».
Современная квантовая механика в проблеме многоэлектронных систем не
встречает никаких принципиальных трудностей (вычислительные трудности
довольно значительны).
Начнем с качественного анализа возможных состояний атома гелия,
опираясь при этом на общую теорию систем, состоящих из одинаковых
частиц, изложенную в §§ 114—117. Определим прежде всего вид опера-
оператора Гамильтона Н для электронов атома гелия. Взаимодействия в атоме
гелия можно разбить на две группы. В первую входят значительные куло-
новские взаимодействия между ядром и электронами, во вторую — слабые
магнитные взаимодействия, обусловленные взаимодействием спинов элек-
электронов между собой и с орбитальным движением1.
Обозначим координаты электронов через xv yv z, (г,) и х2, у2, z2 (r2),
а их спины через s3 и s2. Оператор кулоновских взаимодействий будет
равен
и=-^--~~ + ~, ■ A21.1)
Г1 гъ Г12
где первые два члена представляют энергии взаимодействия первого
и соответственно второго электрона с ядром атома, имеющим заряд -f 2е,
а третий член определяет энергию кулоновского взаимодействия электро-
электронов (рис. 82).
Оператор магнитных взаимодействий обозначим через W. Он будет
зависеть от спинов, положения и скоростей электронов:
W=W(sv s2, r,, r2, -ihVlt -ihV2). A21.2)
Учитывая еще кинетическую энергию обоих электронов, мы можем напи-
написать полный гамильтониан электронов атома гелия в виде
Л (г,, r2, Sj, s0=_|_v;-|rv;-^—^-4-^-+V. A21.3)
1 В эту же группу следует отнести поправки, обусловленные зависимостью массы
электрона от скорости (ср. § 65).
114

Последний член, как мы знаем (ср. § 74), очень мал и обусловливает
мультиплетную структуру спектров. Ограничиваясь в дальнейшем каче-
качественным анализом мультиплетного строения уровней гелия, мы вовсе
отбросим этот член и будем исходить из гамильтониана
И (г г ) — V2 — V2 — ^е" — -1 — A21 4)
В этом приближении, когда игнорируются малые спиновые взаимодействия,
переменные, относящиеся к движению центров тяжестей электронов и к их
спину, разделяются. Выбирая в качестве спиновых переменных проекции
:пинов на некоторое направление (например, OZ): szl и si2, мы можем
ср. § 60) написать полную волновую функцию
цзух электронов атома гелия в виде
¥(г„ r2, s2j, 8.а) = Ф(г„ r2)-S(s2J, sz2), A21.5)
а,е через S (szl, s.2) обозначена часть волновой
ункции W, зависящая от спинов.
Оператор Гамильтона Н A21.4) [а также и
)чный A21.3)] симметричен относительно обоих
тектронов ввиду их тождественности.
Поэтому к рассматриваемому случаю приме-
[мо утверждение общей теории (§ 115), согласно
торому волновая функция W A21.5) должна быть
тисимметричной или симметричной относительно Рнс- 82- Взаимодействия
к г в атоме Не
:тиц, в зависимости от того, подчиняются ли
i принципу Паули или нет.
Опыт показывает, что электроны подчиняются принципу Паули (впер-
: именно для электронов он и был установлен). Следовательно, волно-
функция A21.5) должна быть антисимметричной относительно пере-
човки электронов, т. е.
оатор перестановки мы можем представить в виде произведения двух
аторов перестановки Р'12 и Р^, из которых первый переставляет коор-
ты центра тяжести электронов гг и г2, а второй — спины электронов
s,2. Тогда A21.6) с помощью A21.5) можно написать в виде1
/>цФ(г„ r2)-P;'2S(s21, sz2)= -Ф(гх, r2)-S(szl, sI2). A21.7)
да мы получаем две возможности: либо
P'ltO(rv г2)=+Ф(г3, г.г), A21.8)
да
P"nS(szv sz2)= -S(szv sza), A21.9)
ке
Р;2Ф(гх, г2)= -Ф(гр г2), A21.8')
а
^Mszl, Sza)= +S(ss], s;2). A21.9')
возможность означает, что координатная функция симметрична,
>вая антисимметрична, вторая возможность означает, что коорди-
функция антисимметрична, а спиновая — симметрична. Поэтому мы
вержденне A21.6) справедливо и в тех условиях, когда спиновым взаимодей-
: пренебрегают. Дальнейшее, напротив, базируется на приближении A21.5).

получаем два класса волновых функций для возможных состояний атома
Не, именно:
Ч^ФЛг,, r2)Sa(sZJ> sr2), A21.10)
Ъг = Фа(Гг, r2)Ss(sn> sz2), A21.10')
где значками s и а обозначены симметричные и соответственно антисим-
антисимметричные функции.
Рассмотрим теперь подробнее спиновые функции Sa и Ss. Поскольку
мы игнорируем взаимодействие спинов, каждую функцию можно было бы
написать в виде произведения спиновых функций, рассмотренных в § 60
F0,6), F0,6'), относящихся к каждому электрону в отдельности, т. е.
в виде
S(szV sl2) = Sai(szi)Sa2(sz2), A21.11)
где значки аг и а2 и указывают, как направлен спин электрона—по
оси 01 или против нее. Но функция A21.11) не является ни симмет-
симметричной, ни антисимметричной функцией спинов электронов. Легко, однако,
построить из функций A21.11) антисимметричные функции Sa и симмет-
симметричные Ss.
Рассмотрим сначала случай, когда спины электронов противоположны
друг другу. Тогда волновая функция A21.11) имеет вид
S'(szl, srt) = S+1/l(sI1)S_v,(s«), A21.12)
но возможно и другое состояние, когда спин первого электрона проти-
противоположен оси 01, а спин второго—направлен по оси 01:
S"(szv sz2) = S_1/2(szl)S+1/2(sz2). A21.12')
Оба состояния отвечают суммарному спину по оси OZ, равному нулю,
и оба принадлежат одной и той же энергии Е. Поэтому этой же энергии
может принадлежать и любая суперпозиция этих состояний. Среди них
единственная, описываемая антисимметричной функцией Sa, имеет видх
у 2 2 s 2 2 г%
Таким образом мы определили вид антисимметричной спиновой функции.
Если спины электронов параллельны, то антисимметричные состояния,
очевидно, невозможны. В этом случае мы можем иметь следующие состоя-
состояния спина электронов:
^sWzl» ^22) == ^-bV2 (^*l) 04-V2 \^х2/> A^1.14)
S" (с с \ Q /Ч\*ч /с\ (\0\ ) А'\
8 \ Z I' z2/ — От— 3 /о W* 1/ О — 1/о \ 22/ * !*^.1«1
Эти состояния с самого начала симметричны по спину электронов. Кроме
того, из функций A21.12), A21.12') можно образовать еще одну симме-
симметричную в спинах электронов функцию, именно:
s" (szi, szz) = -~ {S+1/2 (szl) S_1/2 (sz2) + S_1/2 (szl) S-h/i (sz2)}. A21.14")
1 Множитель —jz^ присоединен из соображений нормировки Sa к 1. В самом
У 2
деле, функции S±l/2 (s2) нормированы к 1 согласно F0.7). Если мы образуем произве-
произведение
« S* (szl, s22) Sa (szu s22)
и просуммируем no обоим спинам szi = ^:~^-, .S22 = ±-?r' To мы> как легко убедиться,
пользуясь F0.7), получим 1 (см. также § 106).
416

Таким образом мы имеем всего три симметричные по спину функции
S's, S's и S's". Первые две относятся к суммарному спину 1, но в состоя-
состоянии S's спин направлен по оси OZ, а в состоянии S's —против оси OZ.
Несколько менее ясно то обстоятельство, что состояние Ss" также отно-
относится к суммарному спину 1, но только он ориентирован перпендику-
перпендикулярно оси OZ. В этом можно убедиться проще всего следующим образом.
Мы берем в качестве спиновых переменных проекции спина на ось OZ.
Если речь идет о состоянии, в котором спин ориентирован перпендику-
перпендикулярно оси OZ, то эти переменные szl
и sz2 должны иметь неопределенное
, h
значение ±-?г, т- е- состояние со
..
Пара - гелий
Орто - Шип
спином перпендикулярно оси OZ,
должно записываться в szl и sz2 пере-
переменных так, чтобы фигурировали все
возможные значения szl и sz2. Кроме
того, мы ищем состояние, симмет-
симметричное в спинах. Тогда A21.14")
есть единственный способ написать
волновую функцию этого состояния 1.
На рис. 83 приведено схематически
расположение спинов для найденных
нами состояний.
Таким образом, состояния симмет-
симметричные в координатах центров тяже-
тяжести электронов Ф8, суть состояния с
суммарным спином электронов, рав-
равным нулю. Состояния, антисимметричные в координатах центров тяжести
электронов Фа, суть состояния с параллельными спинами электронов
(суммарный спин равен 1). Таких состояний имеется три соответственно
трем квантовым ориентациям суммарного спина. Уровни атома гелия рас-
распадаются поэтому на два класса: на уровни с антипараллельными спи-
спинами и на уровни с параллельными спинами.
Если мы учтем, что от ориентации спина по отношению к орбиталь-
орбитальному движению хотя очень мало, но все же зависит энергия квантового
уровня, то мы должны будем прийти к заключению, что уровни с анти-
антипараллельными спинами будут одиночные (сингулентные), а уровни с па-
параллельными спинами будут распадаться на три близких, соответственно
Полный спин-0 Полный спин-/
Рис. 83. Схема сложения спинов двух
электронов:
На схеме отмечены принятые в тексте обоз-
обозначения волновых функций соответствующих
состояний
1 Утверждение о принадлежности состояний S's, S" и S's" к спину 1 (сложение
спинов электронов) может быть проверено прямым вычислением. Если обозначить
операторы спинов электронов, определяемые матрицами F8.12), через Sj и s%, то опе-
оператор полного спина представится матрицей
Собственная функция S оператора s2 должна удовлетворять уравнению
где 's — число, определяющее полный спин. Из этого уравнения можно убедиться, что
/3 имеет всего два значения: /s=0 (антипараллельные спины) или /s=l (параллель-
(параллельные спины). Далее непосредственной подстановкой в это же уравнение Sg, Sg и S^"
можно убедиться, что эти функции суть функции, принадлежащие /s=l.
Простые выкладки, нужные для доказательства этих предложений, предоставляем
сделать самому читателю.
27 Д. И. Блохинцев
417

трем возможным ориентациям суммарного спина относительно магнитного»
поля, создаваемого орбитальным движением. Таким образом эти уровни
будут тройные (триплетные)г.
Самым замечательным свойством этих двух классов состояний гели»
является то, что между ними невозможны (почти невозможны) квантовые
переходы. В самом деле, спиновые взаимодействия очень малы, и если их
совсем игнорировать, то гамильтониан электронов атома гелия, даже при
действии внешних полей, например, светового поля, будет симметричным
относительно координат электронов, так как внешнее поле одинаково дейст-
действует на оба электрона. Таким образом,
#(<-!, г2) = #(г2, Г1). A21.15)
Изменение волновой функции W (гь r2, szl, sz2, t) за время dt дается урав-
уравнением Шредингера, которое мы напишем в виде.
dt4 (Г!, r2, szl, sZ2, t)=^frff(rvr2)W(r1, r2, s21, sat)dt A21.16)
подобно тому, как мы это делали в § 115. Если xV(ru r2, s2l, sz2, t) есть
в какой-то момент симметричная функция координат электронов г1( г2,
то приращение этой функции dtxV, согласно A21.16) и ввиду A21.15), будет
также симметричным. Подобным же образом, если ¥ (г,, r2, szi, sz2, t) анти-
антисимметрично, то и приращения будут антисимметричными. Следовательно,
симметричное в координатах состояние остается симметричным при всех
возможных изменениях. Равным образом, антисимметричное состояние
также остается антисимметричным. Следовательно, невозможны переходы
из состояний vFi A21.10) в состояния ¥ц A21.10') и обратно.
Заметим, что следует иметь в виду отличие доказанной сейчас теоремы
от общей теоремы § 115. Функции Ч^ и х¥ц являются антисимметричными
функциями в частицах, поэтому между состояниями VF| и Уц сточки зрения
общей теоремы § 115 возможны переходы. Мы доказываем сейчас невозмож-
невозможность перехода между Wi и Чгц при условии, что игнорируются взаимодей-
взаимодействия со спином. Поскольку эти взаимодействия все же существуют, то
переходы между Wi и lVn на самом деле возможны, но ввиду малости
взаимодействия со спином они будут очень мало вероятны.
В качестве иллюстрации приведем оценки для действия световой волны.
Энергия взаимодействия световой волны с зарядом электрона, по порядку
величины, будет равна
где а—размеры атома, е — заряд электрона, а % — электрическое поле
световой волны (еа есть электрический момент атома). Взаимодействие же
световой волны с магнитным моментом электрона, по порядку величины,
eh
равно произведению магнитного момента электрона -у— на магнитное поле
волны $в:
так как % и <§}в в световой волне равны, то
W"_ h_
W ^
1 Расчет величины этого расщепления см. в книге Г. Бете, Квантовая
механика простейших систем, § 22, ОНТИ, 1935.
418

h h
— есть, по порядку величины, импульс электрона в атоме, а его ско-
рость v. Итак,
W" v
Это отношение составляет менее 1/j00. Поэтому весьма мало вероятно, что
свет вызовет переход, при котором изменится направление спина электро-
электрона1. Иными словами, будут преобладать переходы без изменения спина,
т. е. переходы между состояниями с одинаковой симметрией в координатах
электронов. Это и утверждает только что доказанная теорема.
Следовательно, если гелий находится в состоянии с параллельными
спинами (антисимметричное в координатах состояние), то весьма мало
вероятно, чтобы его состояние изменилось на состояние с антипараллельны-
антипараллельными спинами (симметричное в координатах), и наоборот. Положение вещей
/laps - ге/шц Орто - гелии
Рис. 84. Расположение спинов в орто-и пара-гелии
таково, как если бы существовало два сорта гелия — с параллельными
и с антипараллельными спинами. Первый сорт гелия называют орто-гелием,
а второй — пара-гелием (см. схему на рис. 84). Для того чтобы перевести
один сорт гелия в другой, нужно изменить направление спина одного из
электронов. Ввиду малости магнитного момента спина это изменение про-
произвести весьма трудно. Легко видеть, что энергетически нижнее состояние
гелия должно быть состоянием пара-гелия. В самом деле, мы неоднократно
указывали на то, что нижнее состояние характеризуется волновой функцией
без узлов. Но антисимметричная функция Фа (г1( г2) имеет узел (узловую
поверхность при гг=г2). В самом деле,
ФаОч. Г2)=-Ф„(г2, rj;
при Гу=гг—г получаем:
Ф„(г, г)=-Фо(г, г),
т. е. Фа (г,г)=0. Поэтому функцией нижнего состояния должна быть сим-
симметричная функция Ф3 \rlt г2). Следовательно, это будет состояние, анти-
антисимметричное в спинах, т. е. состояние пара-гелия. Таким образом, гелий
в нормальном состоянии есть пара-гелий.
В связи с этим возникает вопрос: как получить орто-гелий? Если осве-
освещать светом, то практически будут получаться возбужденные состояния
опять-таки с антипараллельными спинами, т. е. пара-гелий. Таким путем
мы не добьемся никакого результата. Иначе обстоит дело, если бомбардиро-
бомбардировать гелий электронами. В этом случае мы имеем дело с тремя одинаковыми
частицами: два электрона атома гелия и один падающий извне. Поэтому
данный нами анализ состояний для двух одинаковых частиц будет в этом
1 Следует еще учесть, что вероятность перехода пропорциональна квадрату
энергии возмущения, поэтому отношение вероятностей будет 10~4.
27* 419

случае непригоден. Физически дело сводится к тому, что падающий элек-
электрон может стать на место атомного, а атомный вылететь из атома. Так как
в пучке падающих электронов есть электроны со всяким направлением спи-
Вольт
го, 55 J
Рис. 85, Схема спектральных термов гелия
на, то в результате такого обмена в атоме могут оказаться электроны с оди-
одинаково направляемым спином: пара-гелий превратится в орто-гелий.
Доказательство существования двух гелиев (точнее двух классов состоя-
состояний гелия) позволило полностью истолковать всю совокупность спектроско-
спектроскопических данных, относящихся к спектру гелия и к его поведению в раз-
различных условиях. На рис. 85 мы приводим схему уровней атома гелия.
В пара-гелии суммарный спин равен нулю. Мультиплетная структура
отсутствует. Линии являются одиночными (сингулентными). Соответствую-
Соответствующие термы обозначаются буквами, с присоединением слева вверху значка 1
420

(например: ^-S, 1P). Напротив, термы орто-гелия распадаются на три, близ-
близких между собою. Спектральные линии ортогелия соответственно этому
расщеплению уровней состоят из трех близких линий (триплеты). Термы
орто-гелия обозначаются присоединением слева вверху значка 3 (триплет),
например, 3S, 3Р. На рис. 85 отмечено состояние орто-гелия 23S как мета-
стабильное. Дело в том, что это состояние есть низшее состояние орто-
ортогелия. Переход в нижнее состояние есть переход в состояние 1XS пара-гелия
и связан с изменением направления спина. Он мало вероятен, и атом гелия,
оказавшийся в таком состоянии, будет находиться в нем весьма долго,
несмотря на наличие запаса энергии в 19,77 эв.
На этом мы закончим качественный анализ состояний атома Не
и перейдем к приближенной количественной теории.
§ 122. Приближенная количественная теория атома гелия
Для расчета квантовых уровней атома гелия мы применим метод,
который хотя и не является лучшим с точки зрения достигаемой точности
расчетов, но зато отличается простотой и наглядностью. Уравнение Шре-
дингера для определения квантовых уровней атома Не и волновых функ-
функций стационарных состояний имеет вид
H(rlt r2;szl, s^Wir,, r2, szl, sz2) = EW(rv r2, szl, sz2). A22.1)
Так как мы пренебрегаем спиновыми взаимодействиями, то это урав-
уравнение, пользуясь A21.5), можно сократить на S(szv sz2). Тогда мы получим:
H(rlt г2)Ф(г1; г2) = £Ф(Г1, г2), A22.2)
причем оператор полной энергии дается формулой A21.4). Этот оператор
можно написать в виде
ff(rv г2) = #0(г„ r2)+W(rl2), A22.3)
где
О I 1' 2/ Oil 1 Oit 2 f f О V 1 / ^ 0 I 2/' V * /
W(s~n)=y-- A22.5)
Оператор ffo(rlt r2) есть оператор полной энергии двух электронов в поле
ядра без взаимодействия их между собой. W(r12) есть энергия взаимодей-
взаимодействия электронов. Наше приближение будет заключаться в том, что эту
энергию взаимодействия мы будем рассматривать как малую поправку
и в качестве нулевого приближения будем брать движение невзаимодей-
невзаимодействующих электронов в поле ядра '.
Волновые функции и квантовые уровни для такого движения известны,
так как это есть движение в кулоновском поле. Пусть первый электрон
находится в состоянии ^„(г^, энергия Еп, а второй электрон —в состоя-
состоянии я|)ш(г2), энергия Ет. Тогда в качестве функции нулевого приближе-
приближения, принадлежащей энергии Еп-\-Ет, можно взять
■фх(г,, г2) = я|)„(г1)я|)т(г2). A22.6)
1 В конце концов оказывается, что энергия взаимодействия не очеиь мала (поэтому
приближение не является особенно хорошим), но все же она меньше разности энергии
низших уровней примерно в три раза.
421

В самом деле,
#o(i"i, r2)\Mri, г2) = Яо (гх) фп (гх) я|)га (г2) + Яо (г2) фп (гх) фт (г2) =
= £пг|)п (гг) грт (r2) + £тг|)п (Г]) грт (г2),
т. е.
Я0(г1> г2) ^ (г1( г2) = (Еп+ Ет) ^ (г1; г2). A22.7)
Однако, энергия Еп + Ет принадлежит, очевидно, и другое состояние,
когда первый электрон находится в состоянии Еп, а второй в состоянии Ет.
Волновая функция этого состояния есть
Ф«(Г1, г2) = чрт (Г1) Ч>» (гя). A22.6')
Подобно тому как мы нашли A22.7), мы найдем, что
#0(г1; г2)гМг1; h) = (En + Em)^(ri, r2). A22.7')
Таким образом, уровню Еп-\-Ет невозмущенной системы принадлежат
два состояния г^ и \]з2, отличающихся обменом состояний электронов A)
и B). Мы имеем дело с вырождением. Это вырождение называют обмен-
обменным. Согласно общей теории возмущений (§ 69) правильная волновая
функция нулевого приближения должна быть суперпозицией вырожденных
состояний1'.
Ф(гх, rs) = c1q1(r1, г2) + с2я|J (tv r2). A22.8)
Амплитуды с1 и с2 и квантовые уровни Е возмущенной системы опреде-
определятся из основных уравнений теории возмущения. Так как мы ограничи-
ограничиваемся рассмотрением двукратного обменного вырождения (функции ^ и \]з2),
то мы можем прямо применить теорию для двукратного вырождения,
изложенную в § 69. Для определения амплитуд сг и с2 тогда получаются
уравнения F9.5), которые в нашем случае имеют вид:
1,20, |
)ci = 0, I ( У)
где Епт есть энергия невозмущенного движения:
Е°пт = Еп + Ет A22.10)
(в обозначениях § 69 индексы п, т обозначены одной буквой k), а вели-
величины Wu, Wlit WM, W2X суть матричные элементы энергии возмущения W
[см. F9.6)]. Так как в F9.6) имеется в виду интегрирование по всем пере-
переменным, от которых зависят волновые функции, то в нашем случае фор-
формулы F8.6) получают вид:
^dvidv2, A22.11)
dvidv* ' A22.12')
1 Строго говоря, мы должны были бы снабдить волновые функции фп тремя
индексами (п, I, т), ибо, как мы знаем, уровню Е71 принадлежит всего п2 различных
состояний (вырождение в кулоновском поле!). Соответственно этому для правильного
расчета уровней Не в качестве функции нулевого приближения следует брать супер-
суперпозицию состояний, отличающихся не только обменом электронов, как мы это сделали,
но и всех состояний, принадлежащих уровням Еп и Ет и отличающихся вращатель-
вращательными моментами и их ориентациями. Мы, однако, будем вести расчет так, как если бы
уровни Еп не были вырождены. Это делается только для того, чтобы выявить особенности
задачи, вытекающие исключительно из того факта, что мы имеем дело с двумя одина-
одинаковыми частицами.
422

где dvx = dxl dy1 dzv dv2 = dx2 dy^ dz2, a W есть энергия возмущения A22.5).
Уровни энергии возмущенной системы Е определяются из векового
уравнения F9.7), которое полностью сохраняет свой вид:
Wn-s Wl2 A22.12)
W2l W22-&
где в теперешних обозначениях поправка к энергии равна
г = Е-Е*пт = Е-(Ел + Ет). A22.13)
Прежде чем решать это уравнение, установим некоторые специальные
особенности матричных элементов A22.11). Подставляя в A22.11), A22.11'),
вместо \|)t и \|з2 их значения из A22.6) и W из A22.5), мы получаем:
Далее, легко видеть, что W х2 равно W21. В самом деле,
Wl2 = г* \ JM^(ri) *«{г^ Г™ ^ dvl dv2, A22.15)
с другой стороны, 168
W2l = U:• W^-dv, dvt = e* { Гт (ri) ^tLiD) *" <r«) ^^ (rA rfOl dvt. A22.16)
Так как переменные интеграции rl(xl, yv zr) и r2(x2, y2, z2) пробегают
одни"и те же значения, то мы можем заменить xv ух, zl на х2, у2, z2,
а%2, у2, z2 на хл, yv z1 (это просто новое обозначение), и так как rl2 = r2V
то при такой замене Wl2 просто совпадает с W21. Следовательно,
т. е. величины Wi2 действительны. Мы положим
Wu = Wn = K, Wl2 = W2l = A, A22.18)
К. и А суть действительные величины. В этих обозначениях вековое урав-
уравнение A22.12) принимает вид
Д'-е А
А К-е.
•откуда получаем
(Д-_еJ==Л2, в = К±А. A22.20)
Уравнения A22.9) с помощью новых обозначений запишутся в виде
(К- е)с1 + Лс2 = 0, (К-г)с2 + Ас1 = 0. A22.9')
Подставляя сюда первый корень (е) из A22.20), находим ct = c2. Подставляя
второй корень е, находим ct = — с2. Следовательно, решение A22.8) будет
^ , A22.21)
A22.22)
= 0, A22.19)
; множитель —=- введен дл я нормировки J .
Таким образом, благодаря обменному вырождению получается два рода
состояний: симметричные Ф3 и антисимметричные Фа [напомним, что
согласно A22.6) и A22.6') при перестановке координат электронов tyl
423

переходит в \]з2]. Существование этих двух родов состояний находится
в полном согласии с общей теорией § 115. Мы знаем, что первые состояния
суть состояния пара-гелия, а вторые —состояния орто-гелия. Формулы
A22.21) и A22.22) суть, следовательно, приближенные выражения для
функций пара- и орто-гелия.
Излагая качественную теорию атома гелия, мы указали на то, что
нормальное состояние должно описываться симметричной функцией (пара-
(парагелий). Этот результат также содержится в решениях A22.21) и A22.22).
В самом деле, нижнему уровню Ех принадлежит лишь одна волновая
функция "ф100 (rL). Поэтому, чтобы образовать нижнее состояние атома гелия,
имеется лишь одна возможность — поместить второй электрон в это же
состояние (отсюда, уже из элементарного понимания принципа Паули,
следует, что второй электрон должен иметь спин, противоположный спину
первого). Следовательно, в ниж-
<-К+А
Е,*Ег
--t-
1
I
I
ZE,
I
I
_j
i
I
Рис.
Схема обменного расщепления уров-
уровней гелия
нем состоянии чрг = \|J и Фа = 0.
Таким образом, для нижнего сос-
состояния имеем единственное ре-
решение
A22.23)
E = 2Et + K + A. A22.23')
Разность энергии пара- и
орто-состояний согласно A22.21)
и A22.22) равна 2Л. Следова-
Следовательно, система уровней гелия,
распадается на две энергетически
различные системы уровней пара-
и орто-гелия. Каждому уровню
атома гелия Еп-\-Ет, которые
получаются без учета взаимо-
взаимодействия электронов, соответст-
соответствуют при учете взаимодействия,
два уровня — уровень пара-гелия
Еп-\-Ет-\-К + А и уровень орго-
гелия Еп -f- Em -\- К — А. Так, например, если один электрон находится в-
нижнем соотоянии Ev а второй в следующем верхнем Е2 (энергия Е1-^-Е2),
то, учитывая обмен электронов и их взаимодействие, мы получим два уровня:
El -f- £2 -\- К + А и Е1 + Е2 + К — А. Это расщепление, а также уровень
2Е1-\-К + А, изображены на диаграмме рис. 86. Эта диаграмма дает менее-
многообразное расщепление, чем приведенное в полной спектроскопической
схеме рис. 85. Это объясняется тем, что мы. игнорировали (для простоты)
то обстоятельство, что уровни невозмущенной проблемы (например, Е2)
вырождены (кроме первого). Более полный расчет показал бы, что расщепление
уровней получается не только благодаря обменному вырождению, но и благо-
благодаря снятию «/«-вырождения. Последнее ясно уже из того, что «Ь-вырождение
существует только в кулоновском поле ядра. Присутствие второго электрона
неминуемо должно его снять. Учет этого снятия «/«-вырождения дает
более богатую картину расщепления уровней, совпадающую со схемой
рис. 86.
Отсылая читателя, интересующегося вычислительными вопросами,,
к специальной литературе1, ограничимся здесь указанием на положение
дел с теоретическим расчетом уровней Не. Расчеты гелия по методу,.
1 См. Бете, Квантовая механика простейших систем, §§ 11—24, ОНТИ, 193£н
424

изложенному выше, приводят к далеко не идеальному согласию с опытом.
Именно, поправка е отличается на 10 — 20% от той, которая следует
из экспериментальных измерений. В настоящее время существуют гораздо
более совершенные методы расчета. Хиллераас получил (в восьмом при-
приближении) значение для основного уровня гелия (ионизационный потенциал)
величину 7 = 198 308 см'1 (мы приводим величину энергии в обратных
сантиметрах, как это принято в спектроскопии), в то время как эксперимен-
экспериментальное значение ионизационного потенциала Не равно / = 198 298 ± 6 см'1.
Совпадение теории и эксперимента поразительное, особенно если иметь
в виду, что в расчет не входят никакие произвольные постоянные, которые
можно было бы «подгонять» к опытным данным.
Вычисление возбужденных термов благодаря «Ь>-вырождению гораздо
сложнее, и достигнутая там точность значительно меньше приведенной
для основного терма.
§ 123. Обменная энергия
Рассмотрим теперь подробнее значение поправки е = /(-)-Л, обусловлен-
обусловленной кулоновским взаимодействием электронов. Для этого вместо волновых
функций я|)„ и я|)т введем новые величины
Qnn(r1)=-e|41n(ri)|2, Qmm(r2)= -е|яЫг2)|2, A23.1)
Qmn(ri)=-^(r1)il)n(r1), Qmn(r2)=-^m(r2)i))*(r2). A23.2)
Первые две имеют простой физический смысл. Именно, Qnn(r1), очевидно,
означает среднюю плотность электрического заряда в точке rJ; создаваемую-
электроном, находящимся в состоянии i|>n(rj). Подобным же образом Qmm(r2)
означает среднюю плотность электрического заряда в точке г2, создаваемого
электроном, находящимся в состоянии я|)т (г2).
Две последние величины qmn (rs) и Qmn(r2) не имеют такого простого
смысла. Это —плотности зарядов, обусловленные тем, что каждый из элек-
электронов может находиться частью в состоянии я|)„(г,), частью в состоянии
я|)ет(г2). Мы будем называть их обменными плотностями. Эти величины
могут быть комплексными, поэтому название «плотность заряда» употреб-
употребляется здесь весьма формально. С помощью введенных плотностей вели-
величина К на основании A22.18) и A22.14) может быть написана в виде:
Qnn I
A23.3)
а величина Л на основании A22.8) и A22.15) в виде:
( Qmn VV Qmn (r2) j,, -J-, /104 A \
Величина К. имеет простое и наглядное значение. В самом деле, интеграл
в A23.3) есть не что иное, как взаимная кулоновская энергия двух зарядов,,
один из которых распределен в пространстве с плотностью Qnn, а второй —
с плотностью Qmm. Образно мы могли бы истолковать эту энергию как
энергию кулоновского взаимодействия двух электронов, заряды которых
размазаны в пространстве. Поэтому эту часть энергии взаимодействия
электронов называют кулоновской (в узком смысле слова). Другая часть (Л)
не может быть наглядно истолкована. Формально величину А можно рас-
рассматривать как электростатическую энергию двух зарядов, распределенных
425*

с плотностями Qmn и Qmn- Эту часть энергии взаимодействия электронов
называют обменной энергией- В этом смысле говорят, что энергия взаимо-
взаимодействия Двух электронов состоит из двух частей — кулоновской К и обмен-
обменной А.
На самом деле следует иметь в виду, что как К, так и А обусловлены
кулоновским взаимодействием (при е — 0 иД" = 0, и Л = 0). Различие между
кулоновской энергией (в узком смысле слова) и обменной А основано
на приближенном представлении функций системы Фо и <DS в виде
-^=~(Я131 ± 'Фг)* Тем не менее, это разделение энергии взаимодействия на куло-
новскую и обменную части оказывается очень плодотворным и поэтому
получило право на существование.
Согласно теории возмущений поправка к энергии е должна просто
равняться средней энергии возмущения в соответствующем состоянии. Это
утверждение легко проверить для рассматриваемого нами случая. Энергией
возмущения является кулоновская энергия взаимодействия электронов
с2 тт ,
— . Чтобы вычислить среднее значение этой энергии в некотором состоя-
'12 2
нии Ф(гх, г2), нужно умножить — на вероятность положения первого
электрона в области dvt и второго в области dv2, т. е- на | Ф j2 dvv dv2, и про-
проинтегрировать по всем возможным положениям электронов, т. е. вычислить
интеграл
Г-|Ф|2^1^2- A23.5)
12
Подставляя Фа или Ф3 из A22.21) и A22.22) вместо Ф, мы находим:
\Ъг I2 ± l>il>2 ± ^я|>2}сЦ dv2, A23.6)
что в силу A22.6) и A22.6') равно
JL = K±A, A23.6')
'12
т. е. поправка е есть просто средняя энергия кулоновского взаимодействия
электронов в состоянии Ф3 или Фа.
Этот расчет позволяет нам глубже взглянуть на происхождение обменной
энергии. Величина | яр, |2 dvldv.2 есть вероятность того, что первый электрон
находится в области dvl и в состоянии п, а второй — в области dv2
и в состоянии т. Аналогично величина [ я|J12 dvY dv2 есть вероятность того,
что первый электрон находится в области dvl и в состоянии т, а вто-
второй — в области dv2 и в состоянии п. Если бы состояния i]^ и я|J были
независимы, то мы получили бы, что вероятность первому электрону
находиться в области dv^, а второму — в области dv%, независимо оттого,
в каких состояниях эти электроны находятся, равна (считая ^ и \|J
равновероятными):
^12 = 4{Ы2 + 1^12}^1^2- A23.7)
На самом деле состояния tyt и я|J оказываются не независимыми, и факти-
фактически реализующееся состояние есть
Ф = у1(^1±^2)- A23.8)
Волновые функции ярг и я|J находятся при этом в определенных фазовых
соотношениях, и мы получаем в выражении для вероятности нахождения
426

частиц в областях dv1 и dv2 интерференционный член
dP[, = | Ф |2 dVl dv2 = dP12 ± (^ + ярмд dvx dv2, A23.9)
■который и приводит к существованию обменной энергии.
Легко видеть, что обменная энергия вовсе не связана специально
<с кулоновским взаимодействием электронов. Предположив любое другое
взаимодействие наших частиц W(rt2), мы все равно получили бы среднюю
энергию W{rl2) в виде двух частей: W — энергии в узком смысле слова,
■которая получилась бы, если бы в A23.3) вместо — ввести W(г12),
.и обменной энергии А, которая получилась бы из A23.4), если опять-таки
вместо — ввести туда W(rl2). Таким образом, всякое классическое
■взаимодействие IF(r12) двух одинаковых частиц ведет к обменной энергии.
Обменная энергия не имеет никаких аналогов в классической меха-
механике. Открытие ее существования является одним из фундаментальных
и новых результатов квантовой теории.
Название «обменная энергия» выяснится гораздо полнее, если мы
рассмотрим состояния Ф, в которых распределение частиц по состояниям п
и т фиксировано. Для этого обратимся к временной зависимости состоя-
состояний Фа и Ф3. Так как это—стационарные состояния, то
- 4" (Eo+K+A) t
h
1 - -i- (E° + K-A) f
Обозначим
A23.10)
^о = -^-, A23.11)
и рассмотрим вместо Ф3 и Фа состояние, являющееся их суперпозицией
(это будет уже не стационарное состояние):
Ф = -~ {Ф8 + Ф„) = 1 г~ы^ {яр! (е~ш + еш) + ^2 (е~ш - еш), A23.12)
я л и
<D = M*Hi + cs@1>s. A23.13)
-где
cl(t) = e~i*'>tcas6t, c2(t) = ie'^' sin6t. A23.14)
Согласно статистическому значению амплитуд с, и с2, величина [сх|2 есть
вероятность нахождения системы в состоянии я|I (т. е. первый электрон
в п, а второй в т), а [ с212 — вероятность того, что система находится
в состоянии я|J (т. е. первый электрон в т, а второй в п). Имеем:
I ^'.@11" = coss M. |c2@l2 = sin26^ A23 15)
отсюда взятое нами состояние Ф A23.12) таково, что при £ = 0 первый
электрон находится в состоянии я|)п, второй в состоянии я|),„. Спустя время
т = -5т- получим [Cj|2 = 0, |c2|2= 1, т. е. первый электрон перейдет в состоя-
состояние я|)ш, а второй в я|)п — произойдет обмен состояниями. На основании
427

A23.11) мы видим, что это время обмена можно выразить через обменную
энергию. Именно, мы' получаем, что
t = -g-. A23.16)
Отсюда следует важный вывод: время обмена состояниями обратно про-
пропорционально обменной энергии-
Интересно посмотреть те условия, при которых обменная энергия
столь мала, а время обмена столь велико, что обменом можно совсем
пренебречь. Обменная энергия зависит от плотности Qmn(r) = я|)т(г)я|)п (г),,
следовательно, она зависит от того, насколько перекрываются функции
состояний я|)т и я|)п. Если т|)т = 0 там, где я|)п ф О, или i|)m^=0 там, где
я|)п = 0, то Qmn = 0 и обменная энергия вовсе отсутствует. Этот крайний
случай является, однако, идеализацией. Тем не менее мы можем вывести
из него важное заключение: если состояния я|)т и я|)п таковы, что | я|)т |2'
и | я|)п ]2 сосредоточены в разных частях пространства, то обменная энергия
мала (стремится к нулю).
Допустим теперь, что состояния \\>п суть состояния электрона
в атоме, но энергии Еп и Ет предположим сильно отличающимися:
Ет > Еп- Тогда функция я|)п сосредоточена в области, очень близкой
к ядру, а я|)т довольно широко распространяется от ядра. Так как обе
функции нормированы к 1, то это означает, что я|)т мало там, где я|)п
заметно велико. Следовательно, плотность Qmn опять-таки мала. Таким'
образом, обменная энергия мала и обменом можно пренебречь, если идет
речь либо об обмене состояниями, сосредоточенными в разных частях
пространства, либо об обмене состояниями, сильно отличающимися по-
энергии.
Последнее обстоятельство оправдывает, например, то, что во многих
случаях можно пренебречь обменом оптического электрона с электронами*;
внутренних оболочек. !
§ 124. Квантовая механика атома и периодическая
система элементов Менделеева
Открытый Менделеевым периодический закон является важнейшим
законом природы. Он составляет основу не только химии, но и вообще всей
современной атомной и ядерной физики.
Теория этого закона далеко еще не завершена. Проблема структуры
атомных ядер находится еще в зачаточном состоянии, а между тем именно-
ядро атома определяет полностью структуру его электронной оболочки,
а вместе с тем — химические и физические свойства атома в целом. Однако,
если рассматривать характеристики атомных ядер как данные из опыта,
то квантовая механика позволяет понять периодичность в структуре элек-
электронных оболочек атомов, исходя из теории движения системы электронов
в электрическом поле ядра. Таким образом для выяснения природы перио-
периодичности можно ограничиться расчетом движения электронов в атомах
исходя из заданной массы ядра и его заряда. Поставленная таким образой
задача представляется все же еще чрезвычайно трудной математически из-з<
большого числа электронов в атомах. Напомним, что в классической механи
ке даже проблема движения трех тел не получила до сих пор общего и norf
ного решения. К счастью, в атомной механике положение лучше и мног»
практически важные результаты могут быть получены с помощью прибли
женных методов. Причиной такого упрощения является дискретность состоя
ний электронов в атомах. Благодаря этому, на основе принципа Паул
428

и теории движения электрона в поле центральной силы, удается достигнуть
существенных результатов в понимании распределения электронов в атомах
и, вместе с тем, периодичности в химических свойствах элементов.
При этом первостепенное значение имеет понятие порядкового номе-
номера (Z) элемента в таблице Менделеева. Это понятие было введено еще самим
Менделеевым, поскольку в ряде мест своей таблицы он отступил от исход-
исходного принципа — расположения элементов по возрастающему атомному
весу и придал большее значение периодичности химических свойств. Позднее
классические исследования Резерфорда и Мозли показали, что атомный номер
имеет глубокий физический смысл, именно номер элемента Z равен заря-
заряду ядра, измеренному в единицах элементарного заряда (+е). Вместе
с тем этот же номер для нейтрального атома равен числу электронов в его
электронной оболочке. Поэтому, зная номер элемента Z, мы знаем важней-
важнейшие для атомной механики данные — заряд ядра и число электронов в ато-
атоме. Как теперь хорошо известно, ядра атомов образуются из незаряженных
частиц — нейтронов (заряд 0, масса 1,00845, если массу кислорода принять
за 16) и протонов (заряд -\-е, масса, 1,00807). Число протонов в ядре, соглас-
согласно сказанному выше, должно быть равно Z. Атомы с одинаковым числом
протонов, но отличающиеся друг от друга числом нейтронов, имеют один
и тот же номер Z, но разный атомный вес А. Такие атомы называются изо-
изотопами. Химические свойства зависят от числа электронов в нейтральном
атоме, т. е. от Z, поэтому изотопы химически равноценны *, и совокупность
изотопов, принадлежащих одному и тому же Z, представляет собой один
и тот же химический элемент. Оказывается, что атомный вес A %2Z, так что
число протонов и нейтронов в ядрах приблизительно равно друг другу.
Благодаря этому расположение элементов в порядке возрастания атомного
веса ведет (за немногими исключениями) к тому же расположению, что
и расположение по заряду ядра -\-eZ.
Чтобы разобраться в распределении электронов в элементах, мы будем
■представлять себе каждый последующий элемент образованным из преды-
предыдущего путем прибавления к ядру одного протона (и надлежащего числа
нейтронов) и, соответственно, прибавления одного электрона в электронной
■оболочке атома. Далее, мы будем игнорировать взаимодействие электронов
и внесем, где будет нужно, поправки на это взаимодействие2.
Нейтрон можно рассматривать как нулевой элемент периодической
системы (Z=0), образующий нулевой период. Первым элементом будет
водород (Z=l). Ядро водорода образовано из одного протона3.
Нормальное состояние единственного электрона атома водорода харак-
характеризуется квантовыми числами п=\, 1=0, m=0, ms=± у.Соответствую-
у.Соответствующая волновая функция будет tynimms (q), где через q обозначены координа-
координаты центра тяжести электрона и спиновая координата.
Увеличивая заряд ядра на -j-e, мы получим ядро гелия. В состояние
п = 1, I = 0, т = 0 можно поместить второй электрон, если спин его про-
1 Речь идет о свойствах валентности. В кинетике реакций имеет значение не
только число электронов, но и масса атома. Поэтому нельзя сказать, что изотопы
с химической точки зрения вполне тождественны. Однако различия, возникающие
из-за изотопии, все же крайне малы, если не считать, например, изотопов водорода,
для которых массы сильно различны, именно, равны 1, 2 и 3.
2 Этот путь толкования периодической системы иа основании атомной меха-
механики был впервые указан Н. Бором. См. Н. Бор, Три статьи о спектрах и о строе-
строении атома, ГИЗ, 1923.
3 Кроме того, имеются изотопы водорода, встречающиеся в естественных усло-
условиях в незначительных количествах; именно: 2=1, А = 2 (дейтерий) и Z=l, Л = 3.
Первый из них удается получать в довольно больших количествах («тяжелая'вода»).
429

тивоположен спину первого электрона ( для одного ms= + ~rf > Для другого
ma=—-wj. Точнее говоря, мы должны из функций я^, о, о, +i/2(<7i)'
и ipi, о, о,-i/2(<7a) образовать антисимметричную волновую функцию так,
как это делалось в § 117. Два электрона гелия занимают все возможные
состояния, принадлежащие п=\. Эта группа состояний ( п =■ 1, 1 = 0,-
т = 0, т3= ± тг ) называется К-оболочкой (рентгеноскопическое обозначе-
обозначение термов). Таким образом /(-оболочка заполнена, вместе с тем закончен-
первый период периодической системы, состоящий всего из двух элемен-
элементов Н и Не.
Увеличивая заряд ядра еще на + е и добавляя один электрон, мы
перейдем к Li. При этом приближенной волновой функцией должна быть,
антисимметрическая комбинация из
принадлежащая наименьшей энергии (нормальное состояние Li). Следуя?
таким образом далее, мы можем сказать, что в нашем приближении волно-
волновая функция многоэлектронного атома, номера Z, будет являться анти-
антисимметричной комбинацией из функций tyrikikmkm,(qk), каждая из которых
описывает движение одного электрона в кулоновком.поле ядра, с зарядом-
-\-eZ. На основании A17.6') мы можем написать эту функцию в виде:
Эта функция равна нулю, если для двух электронов числа п, I, т, тв
совпадают (принцип Паули!). Так как нас интересует нормальное состояние-
атома, то числа nlf /j, ..., nz, lz должны быть выбраны так, чтобы,
энергия всей системы электронов
£= S Enhih A24.2)-
была наименьшей. Если под функциями tynhLm,m^, разуметь волновые
функции для движения в кулоновском поле ядра (полное игнорирование-
взаимодействия электронов), то энергия отдельных состояний Еп1 зависит
лишь от п. На самом деле существует зависимость Еп1 от I, так как
электроны движутся не только в поле ядра, но и в поле других электронов.
Эта зависимость более слабая, но все же для достаточно больших п может
оказаться, что состояния с большим п и малым I могут иметь меньшую
энергию, нежели состояния с малым п, но с большим I. Такой случай,
как мы увидим, впервые встречается для калия.
Итак, для Li приближенная волновая функция имеет вид A24.1)
при Z = 3. Так как /{-оболочка уже заполнена, то третий электрон дол-
должен быть помещен в состояние п = 2, / = 0, m = 0, ms— ±1/г. Группа
состояний с п = 2 называется L-оболочкой. Таким образом, в Li начинает
заполняться L-оболочка. Всего в L-оболочке имеется 2«2 = 2-22 = 8 состоя-
состояний. Два из них принадлежат s-терму ( I = 0, т = 0, ms==±Yj'
и шесть — р-терму ( I = 1, т = 0, ± 1, ms = ± -х- J .
Увеличивая далее заряд ядра и прибавляя электрон, мы перейдем
от Li к Be, от Be к В и т. д. через С, N, О, F до Ne. В неоне все
8 мест L-оболочки заняты. Мы получаем опять инертный газ и вместе
430

с тем заканчиваем второй период периодической системы. Дальнейшие
электроны могут быть помещены лишь в состояния с « = 3. Это — так
называемая УИ-оболочка. В УИ-оболочке имеется всего 2-32= 18 состояний
(/ = 0, 1=1, 1 = 2). Группа состояний с 1 = 0 и /=1 вполне аналогична
L-оболочке и заполнится на протяжении от Na до Аг. Мы получим третий
период периодической системы. Увеличивая заряд Аг на -\- е и добавляя
электрон, мы получим калий. Если бы мы поместили электрон калия
в УИ-оболочку, то состояние этого электрона характеризовалось бы 1 = 2
(rf-терм). Однако и в оптическом, и в химическом отношениях атом К
вполне схож с атомами Li и Na, которые имеют внешний валентный
электрон в s-терме. Поэтому мы должны поместить электрон калия.
в состояние п = 4, / = 0, начав новую оболочку (Л/-оболочка), не закон-
закончив заполнение УИ-оболочки. Это означает, что состояние п = 4, I — 0 имеет
меньшую энергию Е4о, нежели состояние п — 3, 1 = 2 (Е32), что вполне
может быть, если учесть взаимодействие электронов. Таким образом мы
получаем в калии распределение электронов, вполне аналогичное их рас-
распределению в Na (см. таблицу).
Следующий за калием элемент есть кальций (Са, 2=20). Опять-таки
спектроскопические данные указывают на необходимость поместить элек-
электрон Са в s-терм (N-оболочка). В дальнейших элементах происходит
заполнение /И-оболочки [от Sc(Z = 21) до Zn(Z = 30)]. Далее заполняется
Л/-оболочка до криптона (Кг, Z = 26), и этим заканчивается следующий
период (мы получаем инертный газ). Таким образом, для инертных газов
(кроме Не) характерна конфигурация из 8 электронов; два в s-состоянии
и шесть в р-состояиии.
Следующий за криптоном элемент—рубидий (Rb, Z = 37). Он анало-
аналогичен Na и К. Следовательно, внешний электрон Rb помещается не
в Л/-оболочке, а начинает новую оболочку (« = 5; О-оболочка). Электрон Sr
(щелочно-земельный) находится опять в О-оболочке, так что Sr аналоги-
аналогичен Са. В следующих за Sr элементах заполняются О-оболочка и свобод-
свободные места в А/-оболочке (см. таблицу). С цезия начинает заполняться
Р'-оболочка (п = 6).
Элементы группы редких земель (от La, Z = 57, до Hf, Z = 72, вклю-
включительно) обладают сходными химическими свойствами, так как они все
имеют сходное распределение электронов в О- и Р-оболочках. Они отли-
отличаются друг от друга степенью заполнения УУ-оболочки и в отдель-
отдельных случаях — заполнением оболочки О (см. таблицу). Это заполнение
начинается от Се и заканчивается у Lu. Группу редких элементов часто
называют «лантанидами». 72-й элемент (Hf) долго считали также редкой
землей. Однако, как мы видели, в Lu вся оболочка Hf уже заполнена и сле-
следующий 72-й электрон должен быть помещен в оболочку bd. Это обстоятель-
обстоятельство привело Бора к заключению, что Hf должен быть аналогом Zr. И дей-
действительно, этот элемент вскоре был найден в циркониевых рудах.
В последнее время система Менделеева была пополнена вновь откры-
открытыми заурановыми элементами: нептунием (Np), плутонием (Ри), америци-
ем (Am), кюрием (Cm) и др. Эти элементы образуют группу, весьма анало-
аналогичную группе редких земель. Роль лантана в этой группе играет актиний-
(Ас). Поэтому элементы этой группы объединяют под названием «актинидов».
Элементы группы имеют сходные внешние оболочки и, в основном, отли-
отличаются заполнением оболочки 5/1.
Приведенная здесь таблица могла бы быть заменена символической
1 Подробности об электронных оболочках и термах лантанидов и актинидов см^
Н. Хайд и Г. С и б о р г, Трансурановые элементы, ИЛ, 1959; Химия изотопов,
ИЛ. 1948.
431

Таблица 3
Распределение электронов в атомах
Элемент
Н 1
Не 2
Li 3
Be 4
В 5
С 6
N 7
О 8
F 9
Ne 10
Na 11
Mg 12
Л1 13
Si 14
Р 15
S 16
Cl 17
Аг 18
К 19
С а 20
Sc 21
Ti 22
V 23
Cr 24
Mn 25
Fe 26
Co 27
Ni 28
Cu 29
Zn 30
Ga 31
Go 32
As 33
Se 34
Br 35
Kr 36
К
1,0
Is
1
2
2
2
2
2
2
2
2
2
L
2,0
2s
—
1
2
2
2
2
2
2
2
2,1
2p
—
1
2
3
4
5
6
Конфигурация
неона
M
3,0
—
—
1
2
2
2
2
2
2
2
3,1
3p
—
—
1
2
3
4
5
6
Конфигурация
аргона
3,2
3d
—
—
—
1
2
3
5
5
6
7
8
10
10
10
10
10
10
10
10
N
4,0
4s
—
—
—
1
2
2
2
2
1
2
2
2
2
1
2
2
2
2
2
2
2
4,1
4p
—
—
—
—
1
2
3
4
5
6
Основ-
Основной
терм
^1/2
XSO
^/2
4S3/2
3P2
2^/3
ts./,
2 p
^1/2
зл>
4S*/2
3P2
xs0
2<?
^1/2
xs0
2£)з/2
3F2
4f3/2
4f°/2
2<?
51/2
XSO
2D
*1'2
3^o
3P2
2Рз/з
XS0
Ионизаци-
Ионизационный по-
потенциал (в
электроно-
вольтах)
13,539
24,45
5,37
9,48
8,4
11,217
14,47
13,56
18,6
21,5
5,12
7,61
5,96
7,39
10,3
10,31
12,96
15,69
4,32
6,09
6,57
6,80
6,76
6,74
7,40
7,83
7,81
7,606
7,69
9,35
5,97
7,85
9,4
11,80
13,940
432

Продолжение табл. 3
Элемент
Rb 37
Sr 38
Y 39
Zr 40
Nb 41
Mo 42
Tc 43
Ru 44
Rh 45
Pd 46
Ag 47
Cd 48
In 49
Sn 50
Sb 51
Те 52
J 53
Xe 54
Cs 55
Ba 56
La 57
Ce 58
Pr 59
Nd 60
Pm 61
Sm 62
Eu 63
Gd 64
Tb 65
Dy 66
Ho 67
Er 68
Tu 69
Yo 70
Lu 71
Конфигу-
Конфигурация
внутренних
СЛОсв
Конфигура-
Конфигурация крип-
криптона
Л
4,2
и
—
—
1
2
4
5
6
7
8
10
Конфигурация
палладия
•
Слои от Is до 4d
содержат
46 электронов
7
4,3
4/
—
—
—
—
—
—
—
—
—
—
—
—
—
—
—
—
_
—
—
2
3
4
5
6
7
7
9
10
11
12
13
14
14
О
5,0
5s
1
2
2
2
1
1
1
1
1
—
1
2
2
2
2
2
2
2
5,1
5р
—
—
—
—
—
—
—
—
—
—
—
1
2
3
4
5
6
Слои
5s
и Ър
содержат
8 электронов
5,2
—
—
—
—
—
—
—
—
—
—
—
—
—
—
—
_
—
1
—
—
—
—
—
1
—
—
—
—
—
1
Р
6,0
6s
—
—
—
—
—
—
—
—
—
—
—
—
—
—
—
—
—
1
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
Основ-
Основной
терм
2 С
XS0
^/2
^2
6D1/9
7S3
2sv2
Vx/S
4S»/B
2%
2sv2
2ZK/2
"H
4
4
■ 7P
w
"Я
»H
is
3A./2
Ионизаци-
Ионизационный
потенциал
в электроно-
вольтах)
4,16
5,67
6,5
7,35
7,7
7,7
8,5
7,54
8,95
5,76
7,37
8,5
10,44
12,078
3,88
5,19
28 Д. и. Блохиицев
433

Продолжение табл. 3
Элемент
Nf 72
Та 73
W 74
Re 75
Os 76
Ir 77
Pt 78
Au 79
Hg 80
Tl 81
Pb 82
Bi 83
Po 84
At 85
Rn 80
Fr 87
Ra 88
Ac 89
Th 90
Pa 91
U 92
Np 93
Pu 94
Am 95
Cm 96
Bk 97
Cf 98
Es 99
Fm 100
Md 101
102
103
Конфигура-
Конфигурация
внутренних
слоев
Слои от Is
добр содер-
содержат 68
электронов
О
5,2
2
3
4
5
6
7
8
Слои от Is до 5d
содержат 78
электронов
Слои от Is до 5d
содержат 78
электронов
5,3
5/
—
—
—
—
—
—
—
—
—
—
—
—
2
3
4
6
7
7
8
10
И
12
13
14
14
Р
6,0
6s
2
2
2
2
2
2
2
1
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
6,1
6р
—
—
—
1 '
2
3
4
5
6
6
6
6
—
6
6
6
6
6
6
6
6
6
6
6
6
6
6,2
6d
—
—
—
—
—
_
1
2
1
1
—
1
1
—
—
—
—
—
1
Q
7,0
7s
—
—
—
—
—
—
1
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
Основ-
Основной
терм
4F3/2
6S5/2
4fV2
2Sl/2
чр
3Р2
2Р3/а
'So
,SI/1
'S,,
зр .
4К
*
Ионизаци-
Ионизационный
потенциал
(в электро-
новольтах)
9,20
10,39
6,08
7,39
8,0
10,689
1
134

формулой, указывающей распределение электронов в атоме по различным
оболочкам. Например, для Li такая формула гласит (IsJ 2s, что означает
что в атоме лития два электрона находятся в состоянии Is и один в состоянии
2s. В предпоследней колонке таблицы указан основной терм атома. Напом-
Напомним, что основной терм атома в целом обозначается большими буквами
S, Р, D, F соответственно значению квантового числа L=Q, 1, 2, 3, ...,
определяющего суммарный орбитальный момент (ср. § 101). Справа, внизу
символа указано число J, определяющее полный момент. Слева, вверху
индексом указана мультиплетность терма 2S+1, где 5 — число, определяю-
определяющее полный спин. Для лития орбитальный момент электронов равен нулю,
а спины двух внутренних электронов компенсированы. Поэтому основной
уровень атома Li будет дуплетным 2Si/2.
Подобная же формула, например для неона, гласит (IsJ BsJ BрN.
Все спины и все орбитальные моменты компенсированы, поэтому основной
терм неона, так же как и всех других инертных газов, будет lS0. В алюминии
мы имеем дело с одним р-электроном (Зр), орбитальный и спиновой момент
которого нескомпенсированы. Поэтому его основной терм будет 2Pi/2 (фор-
(формула строения оболочек (IsJ BsJ Bp)eCsJ Зр). Не трудно разобраться
и в обозначениях для других элементов.
Как мы видим, открытая Менделеевым периодичность в химических
свойствах элементов, с точки зрения атомной механики, означает повтори-
мость в структуре внешних электронных оболочек. Так, инертные газы Ne,
Ar, Kr, X и Em имеют одинаковые внешние оболочки из 8 электронов. Все
щелочные металлы имеют один электрон в s-терме, сверх оболочки инертно-
инертного газа (терм 2Si/2). Щелочно-земельные металлы имеют два электрона сверх
оболочки инертного газа (терм 1S0). Галоиды F, Cl, Br, J имеют оболочки,
в которых недостает одного электрона до оболочки инертного газа (терм
2Рз/2). Длина же периодов, в существенном, определяется числом квантовых
состояний в каждой из оболочек. Это число, согласно E0.26), если еще учесть,
что в каждом из состояний могут находиться два электрона с различно
направленными спинами, будет 2«2 (п — главное квантовое число, харак-
характеризующее оболочку). Поэтому длина периодов определяется числами 2,
8, 18, 32, ....
Таким образом современная атомная механика внесла существенный
вклад в понимание одного из самых замечательных законов природы —
закона периодичности химических свойств элементов, открытого нашим
великим соотечественником.
На рис. 87 приведена таблица Менделеева в схематической форме, при-
приданной ей Бором.
Как уже отмечалось, представление волновой функции системы электронов в виде
антисимметричной комбинации индивидуальных функций,электронов tynlmm (<?) A24.1)
является приближенным. Это приближение будет совсем грубым, если в качестве этих
функций взять функции для движения электрона в кулоновском поле ядра, совсем не
учитывая взаимодействие электронов.
Можно, однако, поставить вопрос: как иайти такие функции tynlmm (q), чтобы
истинная функция системы электронов Ф (gb q2, ••-, qw) наилучшим образом представ-
представлялась в виде определителя A24.1)? На этот вопрос отвечает метод Фока1. Сущность
этого метода заключается в отыскании таких ^n(mm (q), которые обращают в минимум
полную энергию системы:
E=\<!)*-ff<$dq1dqi...dqN, A24.3)
1 См. Я. И. Френкель, Волновая механика, ч. II, ОНТИ, 1935, или Бете,
Квантовая механика простейших систем, ГНТИ УССР, 1938.
28* 43,5-

и
2
Не
3
Li
'it-
Be
11
Na
5
В
12
Мд
6
С
13
Al
7
N
/4
Si
8
0
15
P
9
F
16
s
10
m
17
Cl
18
An
19
К
?0
Ca
37
Rb
.--
■
71
Sc
38
Sr
,-—
7?
n
39
Y
,—-
23
V
l>0
Ir
Cr
и
Nb
25
Mn
Mo
26
Fe
из
ТС
27
Co
44
Ru
'-^
■^^
-^.
28
Ni
U5
Rh
\
■^-^
29
Си
U6
Pd
31)
In
31
&a
4<?
Cd
32
&e
U9
In
33
As
50
Sn
34
Se
51
Sb
35
Br
52
Tt
36
Kr
53
J
Редкие земли
55
Cs
56
Ba
87
Fr
57
La
88
Ra
89
Ac
58
Ce
1
1
90
Tb
59
Pr
1
1
1
91
Pa
60
Nd
i
i
i
i—
92
U
61
Pm
i
i
i
93
Np
62
Sm
j
i
i
9k
Pu
63
Eu
i
i
i
95
Am
6k
Qd
i
i
i_
96
Cm
65
Tb
i
i
i—i—i
97
Bk
66
Dy
i
i
i
98
cf
67
Ho
1
1
1
99
ES
68
Er
i
i
i
100
Fm
69
Tu
i
i
i
101
Md
70
Yb
71
Lu
72
Hf
73
Та
74
W
75
Re
76
Os
77
Ir
78
Pt
79
Аи
80
Hg
81
Tl
82
Pb
83
Bi
84-
Po
85
At
86
Rn
i
i
i
Рис. 87. Периодическая система элементов

при добавочном условии (условие нормировки):
{ O*(Ddqidqa... dqN=l. A24.4)
Здесь под Н разумеется гамильтониан всей системы электронов. Эта вариационная за-
задача приводит к системе нелинейных уравнений для определения индивидуальных функ-
функций ^n(mm (q). Получаемое при этом значение энергии для нижнего терма Ед является
наиболее точным из совместимых с видом функции A24.1).
Эта же вариационная задача может быть решена прямыми методами вариационного
исчисления (метод Ритца). В этом методе в качестве нулевого приближения рассматри-
рассматривается некоторый класс функций Ф, зависящий от параметров а, 6,... (например, а, Ь,...
могут быть и радиусами электронных оболочек). Выполняя интегрирование, найдем Е
как функцию а, Ь,...
Из условия минимума
• |£-0, ^ = 0, A24.5)
da db K
и условия A24.4) найдутся те значения параметров, которые дают наилучшее прибли-
приближение для Е и Ф, совместимое с избранным классом функций. Точность приближения
в значительной мере зависит от того, насколько хорошо удается угадать тип функций Ф„
допущенных к конкуренции в качестве первого приближения. Этот метод, практически,
оказывается весьма эффективным (см., например К. Бете, цит. соч., §§ 11 —14).

ГЛАВА XXII
ОБРАЗОВАНИЕ МОЛЕКУЛ
§ 125. Молекула водорода
Теперь мы рассмотрим на основе квантовой механики молекулу водо-
водорода Н2.
Молекула Н2 обладает типичной гомополярной связью. Поэтому,
рассмотрев этот простейший случай гомополярной молекулы, мы можем
рассчитывать на выяснение природы сил, обусловливающих гомополярные
валентные'связи. Для того, чтобы вычислить силу взаимодействия между
двумя атомами водорода, нужно определить их потенциальную энергию
О (R) как функцию расстояния между центрами атомов (между ядра-
ядрами) R. U (R) складывается из двух частей: из энергии кулоновского
взаимодействия ядер -f ^- и из энергии электронов Е, которая зависит
от расстояния между ядрами и поэтому входит в потенциальную энергию
взаимодействия двух атомов. Итак, мы можем написать, что искомая
энергия U (R) равна
U(R)=^ + E(R). A25.1)
Таким образом, задача сводится к определению энергии электронов E(R).
Для больших расстояний R между атомами, очевидно, можно пренебречь
влиянием одного атома на движение электрона в другом атоме, поэтому
для R-^oo энергия электронов просто равна сумме энергий электронов
в каждом из атомов водорода.
В дальнейшем нас будет интересовать молекула водорода в нижнем
энергетическом состоянии. Соответственно этому при удалении атомов на
бесконечное расстояние друг от друга, мы получим атомы водорода в нор-
нормальном состоянии. Обозначим энергию атома водорода в нормальном
состоянии через Ео (Ео равна 13,55 eV). Тогда для интересующих нас
состояний молекулы энергия для больших R равна 2Е0. Мы положим:
E(R) = 2E0 + b(R), ' A25.2)
Очевидно e,(R) будет означать изменение энергии электронов при сближе-
сближении атомов водорода. Эту величину нам следует определить.
Вся энергия электронов Е (R) определится из уравнения Шредингера
как собственное значение оператора Гамильтона для нашей системы электро-
электронов. Этот оператор Гамильтона легко написать:
tf=-^V2-^V2---™----+-. A25.3)
" 2jxvi 2jxVs ral rb2 гы ra2^ r12 K '
Здесь кроме очевидных операторов кинетической энергии обоих электро-
электронов входят: а) потенциальная энергия первого электрона A) и первого
438

ядра ( — —- ), b) потенциальная энергия второго электрона B) и второго
-—), с) потенциальная энергия первого электрона A) и второго
ь
Схема решения Ф,
ft)
~^*4Ъ
ядра ( — — J , d) потенциальная энергия второго электрона B) и первого
(е2 Д
] и, наконец, е) энергия взаимодействия обоих электронов
Рис. 88 поясняет приме-
примененные здесь обозначения для рас-
расстояний rav rbl, гш, га2, гп.
Если волновую функцию для
системы наших электронов мы обо-
обозначим через
Ф(г1; г2),
то уравнение Шредингера для оп-
определения Фи £ будет иметь вид
Я(г1; г2) = £Ф, A25.4)
где Н дается выражением A25.3).
Решить уравнение A25.4) мож-
можно лишь приближенно. Мы будем
здесь следовать методу, который
хотя и не является самым лучшим
в смысле достигаемой точности, но
зато он отличается большой просто-
простотой и наглядностью и весьма бли-
близок к методу, применяемому при
решении задачи об атоме Не, рас-
рассмотренной в § 122.
В качестве исходного прибли-
приближения для волновой функции в этом методе принимаются волновые функ-
функции невзаимодействующих атомов водорода. Иными словами, нулевое приб-
приближение есть решение для далеко раздвинутых друг от друга атомов
H(R-^ со). Соответствующее значение энергии системы есть 2£0. Мы мо-
можем считать расстояния R большими до тех пор, пока изменение энер-
энергии электронов при сближении атомов мало в сравнении с разностью
между нижним уровнем 2Е0 и ближайшим высшим ЕО-\ГЕ1:
Рис.
Схема решения <j>
Схема взаимодействия в
ле Н2:
молеку-
Сплошные линии соединяют частицы, между кото-
Йыми взаимодействие учтено в решении \|>i или т|>2.
[унктирные линии соединяют частицы, взаимодей-
взаимодействие между которыми в нулевом приближении
игнорируется.
\s(R)\<£\(El-E0)
A25.5)
Последняя величина составляет 10, 15 eV. Для таких расстояний вели-
сину e(R) можно рассматривать как поправку к энергии невзаимодей-
чтвующих атомов 2Е0, а саму волновую функцию системы электронов
Ф—как функцию, близкую к волновой функции невзаимодействующих
атомов водорода.
Для того чтобы произвести подсчет таким путем, т. е. исходя из
удаленных друг от друга атомов водорода, мы должны подробнее рас-
рассмотреть гамильтониан нашей системы A25.3). Обозначим через На(\)
часть гамильтониана Н A25.3), равную
Н l\\=—^~V2 —
A25.6)
439

а через Нь B) —другую его часть, равную
"bB)=-£vj-£. A25.7)
Очевидно, что гамильтониан Иа(\) есть гамильтониан, соответствующий
движению первого электрона A) вокруг ядра (а), а Мь{2) есть гамиль-
гамильтониан для движения второго электрона около ядра F). Полный гамиль-
гамильтониан Н может быть написан в виде
H = Ha(l) + HbB) + W(l, 2), A25.3')
где
W(l,2)=-£—£- + ■£-. A25.8)
га2 'Ы '12
Обратимся к случаю больших расстояний R. Пусть первый электрон
находится в атоме (а) (около ядра а), а второй — в атоме F) (около
ядра Ь). Тогда величиной W(\, 2) можно пренебречь, так как эта величина
есть энергия взаимодействия второго электрона с ядром (а) плюс энергия
взаимодействия первого электрона с ядром (Ь) и, наконец, плюс энергия
взаимодействия обоих электронов. Если атомы далеки друг от друга, то
все эти три величины малы. Поэтому приближенно в уравнении A25.4)
величину W(l, 2) можно отбросить, и мы получим уравнение:
[ЯОA) + ЯЬB)]Ф = ЕФ. A25.9)
Это уравнение описывает два невзаимодействующих атома водорода при
условии, что первый электрон находится в атоме (а), а второй в атоме F).
Решение этого уравнения тотчас же может быть написано. Это — не что
иное, как произведение волновых функций для нормального состояния
атома водорода. Действительно, пусть ^а(га1) есть волновая функция
нормального состояния атома водорода (а) для первого электрона,
а %(гЬ2)— волновая функция нормального состояния атома F) для вто-
второго электрона; тогда в силу A25.6) и A25.7)
ЯоA)фо(го1) = ад«('-о1). A25.10)
HbB)%(rb2) = E<$b(rb2). A25.10')
В качестве решения уравнения A21.9) мы можем взять
$i(rv Г2) = 1>„(го1I>ь(ги). A25.11)
Соответствующее ему значение энергии Е будет 2Е0.
Если бы не было вырождения, то решение A25.11) и было бы нуле-
нулевым приближением. Однако на самом деле в рассматриваемой задаче
имеется обменное вырождение. Очевидно, что кроме решения 1|зг A25.11)
возможно и такое решение, когда на первом атоме (а) находится второй
электрон B), а на втором атоме (Ь) находится первый электрон A).
Чтобы усмотреть это решение, разобьем гамильтониан A25-3) на отдель-
отдельные слагаемые следующим образом:
H = HaB) + Hb(l) + WB, 1), A25.3")
где
ЯаB)=-|^-£, A25.6')
ЯьA)=-|[^-£ A25'Г)
440

суть гамильтонианы для атомов водорода, когда второй электрон B)
находится в атоме (а) и соответственно когда первый электрон находится
в атоме (Ь). Далее,
WB,l) =-■£—£•+£• A25.8')
fal rb2 ru
есть взаимодействие электронов и электронов и ядер, принадлежащих
разным атомам. При достаточно большом расстоянии межну атомами (а)
и (Ь) этой величиной можно пренебречь, и уравнение A25.4) превратится
в упрощенное:
A25.9')
Это опять, подобно A25.9), есть уравнение для двух невзаимодействук>
щих атомов водорода, и его решение будет
*, (Г1, г8) = фв (гаВ) фь (гЬ1), A25.11')
т. е. отличается от A25.11) перестановкой (обменом) электронов. Разу-
Разумеется, соответствующее значение энергии Е есть опять-таки 2Е0. Таким
образом, для больших R уравнение A25-4) имеет два решения A25.11)
и A25.1 Г), принадлежащих энергии 2Я0- Эти два решения иллюстри-
иллюстрируются схемой, изображенной на рис. 85. При учете взаимодействия
между атомами W(\, 2) и W B, 1) решение Ф не будет, конечно, совпа-
совпадать ни с \|)j, ни с г|J, но нулевое приближение к Ф будет линейной
комбинацией из i^i и \]з2, как всегда, при наличии вырождения. Поэтому
мы можем положить:
. A25.12)
где с1 и с2 — подлежащие определению коэффициенты, а ф —малый (по-
(поскольку расстояния R не очень малы) добавок к нулевому приближению.
Рассматривая ф как малый добавок, мы будем пренебрегать произ-
произведениями W(\, 2) ф, И7 B, 1)ф, еф, так как W и 8 сами рассматриваются
как малые величины. Вставляя A25.12) в A25-4) и пользуясь обозначе-
обозначением A25.2), мы получим:
+ е)Ф. A25.13)
Здесь мы произведем разбиение на части согласно A25.3') и A25.3"):
= 2Е0(с1Ч>1 + с2г|>2) + 8 (с^+с^г) + B£0-е) <р. A25.14)
Пользуясь тем, что \|)t и \]з2 суть решения уравнений A25.9) и A25.9')
с Е~2Е0, и пренебрегая произведениями Wq>, еф, мы найдем:
[ЯаA) + ЯьB)]ф-2£оФ=[в-И7A,2)]с1г|I+[в-^B, \)]с^2. A25.15)
Это — неоднородное уравнение для определения поправок к волновой
функции ф и к собственному значению е. Однако у нас еще не определе-
определены коэффициенты с1 и с2, входящие в правую часть уравнения A25.15).
Для определения их заметим, что если бы справа в A25.15) стоял
нуль, то мы имели бы для ф однородное уравнение, совпадающее с A25.9),
которое имеет решение \]зг Согласно известной математической теореме
неоднородное уравнение имеет решение лишь в том случае, если его пра-
441

вая часть ортогональна к решению однородного уравнения. Иными сло-
словами, должно иметь место равенство
{[8-117A, 2)]с1ЦI + [в-И7B, l^c^^dv.dv^O, A25.16)
где dvl = dxldyldz1, dv2~dx2dy2dz2. Это дает нам одно уравнение для
двух коэффициентов ct и с2. Легко получить и второе. Для этого в A25.13)
член //ф представим в другом виде, именно:
пренебрегая опять Й7ф как величиной второго порядка малости, мы полу-
получим вместо A25.15):
[HaB) + Hb(l)]<p-2Eo<p = [B-W(l,2)]c11?l + [B-WB, 1)]с2г|>2. A25.15')
Левая часть совпадает с уравнением A25.9'), которое имеет решение \]J.
Опять-таки правая часть неоднородного уравнения для ср должна быть
ортогональна к решению однородного уравнения гр2. Это и дает нам второе
уравнение:
[e-B7(l, 2)] с^-г-[е-IF B, 1)] c^J ^ dot do8 = 0. A25.16')
Для дальнейшего введем сокращенные обозначения:
2, A25.17)
^2- A25.18)
Приведенные здесь равенства интегралов вытекают из того, что IF A,2) =
= Pi2lFB, 1) и 1|з2 = -Pi2^i, так что интегралы отличаются лишь обозна-
обозначением подынтегральных переменных и поэтому равны. Функции \|)t и \]з2
неортогональны между собой, поэтому мы введем еще третий интеграл1:
lv2. A25.19)
С помощью этих обозначений A25.16) и A25.16') записываются в виде
(e-K)c1+(eS2-A)c2 = 0, A25.20)
(eS2 - А) сг + (8 - К) с2 = 0. A25.20')
Отсюда находим сначала уравнение для е:
(e-KJ-(eS2-AJ = 0. A25.21)
Это уравнение дает два корня:
ei=fe£, A25.22)
A25.22')
Подставляя эти значения в A25.20), найдем две системы решений для cv c2.
Именно, для 8 = et
с1= -са A25.23)
И ДЛЯ 8 = 82
6! = ^. A25.23')
1 фх и ф2 ортогональны лишь для i? = oo. Для R=Q S=l. Поэтому излагаемая
теория не является вполне строгой теорией возмущения, в которой всегда предпола-
предполагается ортогональность исходных, иевозмущенных решений.
442

Следовательно, наши решения могут быть написаны в таком виде:
£о = 2Е0 + £^-, Фв = Ч»1 — 4>в A25.24)
(антисимметричное решение) и
Es = 2E0 + ~±4, 0>s = 4|3j_ -f- -ф2 A25.24')
(симметричное решение).
Рассмотрим теперь подробнее значение полученных поправок к энер-
энергии. Для этого выпишем подробное значение интегралов A25.17) и A25.18).
Подставляя в A25.17) W(\, 2) из A25.8) и ■ф1 из A25.11), мы получим1:
= \ 1 ~7
е2 в2
так как член — не содержит координат второго электрона, а коор-
координат первого, и так как в силу нормировки
то, обозначая через qb B) — — etyf, (rb2) среднюю плотность электрического
заряда, создаваемую электроном B) в атоме F), через Qa(l)= — e^l (ral) —
среднюю плотность электрического заряда, создаваемую электроном A)
в атоме (а), мы сможем выразить /( в новой форме:
К= \ ~-Qb{2)dvs + \^.Qa(l)dvl+ \ ^{l)Qb{2)dVldv2. A25.25)
Первый интеграл есть средняя потенциальная энергия электрона B)
атома F) в поле ядра (а), второй интеграл — та же величина для первого
электрона A) атома (а) в поле ядра F) и, наконец, третий интеграл есть
средняя потенциальная энергия электронов A) и B), находящихся в раз-
разных атомах. Таким образом, К есть не что иное, как средняя энергия
электростатического взаимодействия атомов, кроме взаимодействия
ядер, которое мы считаем отдельно [см. A25.1)].
Интеграл A25.18) представляет собой обменную энергию. Подставляя
в A25.18) значение W(\, 2) и \|)t и \]з2, мы получим:
А = [ { - J~2 - ^ + ^ } ^а (Гад ^Ь Ы ^а (Г,а) % (hi) ^l dv2-
Обозначая обменную плотность так, как мы это делали при рассмотрении
атома Не, через
6аьA)= — е^а (га1) ^ъ (гы),
Qab B) = — бЧ'а (Га2> $Ь (Гы)'
мы можем написать А в виде
Л Л / 1 \ Л /О\
ytdy2; A25.26)
последний член есть обменная энергия электронов совершенно такого же
вида, как та, что была нами получена при рассмотрении атома Не. Раз-
Различие заключается в том, что там речь шла об обмене электронов, состоя-
состояния которых различались энергией электронов, а здесь состояния \]за и \]зь
1 Если подставить W B, 1) из A25.8) и ф2 из A25.11), то читатель сможет непо-
непосредственно убедиться в справедливости равенства двух интегралов в A25.17).
443

различаются положением электронов у атома (а) или у атома F). Обмен
электронами происходит между (а) и F).
Первые два члена представляют собой поправки к обменной энергии,
происходящие из-за неортогональности волновых функций, именно:
)^^ ^ Уа Са2) Уъ Ы dvt. A25.19')
При R—>co волновые функции \]за и \]зь в силу экспоненциального убы-
убывания с увеличением расстояния от ядер (а) и F) столь мало перекры-
перекрываются [\])а отлично от нуля вблизи ядра (а), а -фь — вблизи ядра F)], что
S очень мало и стремится к 0. Напротив, при R = 0 ядра (а) и F) сов-
совпадают. Тогда \|за и \|зь суть волновые функции одного и того же атома
водорода. В силу нормировки \]за и \\>ь при R = 0 S равно 1. Поэтому
0<S<l. A25.27)
Равным образом и S2 A25.19) также заключено в этих пределах. Таким
образом полученные нами формулы A25.24) и A25.24') для энергии двух
атомов водорода совпадают по своему физическому смыслу с формулами
A22.21), A22.22) для энергии атома Не, именно, и там, и здесь поправки
складываются из энергии кулоновского взаимодействия К и обменной
энергии А. Некоторое различие обусловлено лишь неортогональностью
волновых функций (члены с S и S2). Мы можем теперь написать энергию
U (R) двух атомов водорода для антисимметричного состояния Фа и сим-
симметричного Ф3.
На основании A25.1), A25.2) и A25.24), A25.24') имеем:
Ua ~ ■"i о ~Ь ~д~ ~Ь j £2 '
Эти формулы можно переписать в виде:
-A-S*^, A25.28)
A25.28')
Члены -D- + A" представляют собой среднюю кулоновскую энергию двух
атомов водорода, находящихся на расстоянии R между собой, Л —обмен-
—обменная энергия. Последний член, пропорциональный S2, включает поправки
на неортогональность волновых функций, послуживших нам в качестве
нулевого приближения.
С помощью формул A25.25) A25.26) может быть вычислена и куло-
новская, и обменная энергия. Для этого достаточно подставить в эти
интегралы выражение для волновой функции нормального состояния
водорода. Эта функция известна и есть просто экспоненциальная функция:
L~^l A25.29)
где г —расстояние электрона от ядра, а а —радиус первой орбиты Бора.
Чтобы получить функции 1|зо(го1), \]5ь(гЬ2) и т. д., нужно вместо г в пре-
предыдущую формулу подставить га1 или гЬ2 и т. д., так как эти величины
суть как раз расстояния какого-либо из электронов до одного из ядер
(см. рис. 88).
444

и, и,
Мы не будем производить здесь вычисления |этих интегралов. Заме-
Заметим лишь то, что как интеграл К, так и А содержат волновые функции,
относящиеся к различным атомам [например, \]за (га1) и tyb (гЬ2): каждая из
этих функций экспоненциально убывает с увеличением га1 и гЬ2]. Поэтому
оба интеграла К и А отличны от нуля лишь постольку, поскольку вол-
волновые функции, а, стало быть, и электронные оболочки атомов взаимно
перекрываются.
В результате оба интеграла убывают с увеличением расстояния между
_ ?к.
атомами R, как е а . На рис. 89 изображена взаимная энергия атомов
Ua(R) и US(R) как функция расстояния между атомами R, получающаяся
в результате вычисления кулоновской К,
и обменной А энергий1. Величина 2Е0
принята за 0 отсчета энергии. Расстоя-
Расстояние R измерено в единицах воровского
радиуса, так что по оси абсцисс ОТЛО-
жено не R, а —■. Как видно из рисунка,
для антисимметричного состояния (Фа)
энергия Ua(R) отвечает отталкиванию
двух атомов водорода, так что молекула Н2
образоваться не может. Напротив, для
симметричного состояния Ф3 энергия
US(R) имеет минимум при ^0=1,4-а =
= 0,74•10~8 см, так что атомы водорода
будут в этом случае иметь тенденцию
находиться на расстоянии Ro друг от
друга. В симметричном состоянии, сле-
слеб
Рис.
Энергия взаимодействия
g_ - „ двух атомов водорода для триплет-
довательно, образуется устойчивая моле- ного з2 сингулетного *2 состояний,
кула водорода Н2. Мы сейчас свяжем в последнем состоянии образуется
эти два рода состояния с направлениями устойчивая молекула Н2
спинов электронов. Это совсем нетрудно
сделать, если вспомнить результаты, полученные нами для атома Не
(§ 122). Полученные нами волновые функции для молекулы Н2 зависят
лишь от координат центров тяжестей электронов хг и г2. Полная волно-
волновая функция W должна еще зависеть и от спинов электронов szl и sz2.
Так как взаимодействием спинов с орбитальным движением и взаимодей-
взаимодействием спинов между собой мы пренебрегали, то волновая функция W
представляется как произведение функции Ф от координат центров
тяжести, электронов на функцию S от спинов szl и sz2. Так как элект-
электроны подчиняются принципу Паули, то волновая функция W должна
быть антисимметрична при перестановке электронов. Так же как и в случае
атома Не, мы имеем две координатные функции Ф: симметричную Ф3
и антисимметричную Фо.
Чтобы в обоих случаях вся функция W была антисимметрична, нужно,
чтобы для Ф —Ф3 спиновая функция S(szl, s,2) была антисимметрична по
спину (S = Sa). Напротив, для антисимметричной функции Ф = Фа спино-
спиновая функция должна быть симметрична (S = Ss). Очевидно, что спиновые
функции Sa и Ss будут совершенно такими же, как и полученные нами
в § 122. Именно, Sa описывает состояние с антипараллельными спинами
(см. § 122). Таким образом, состояние Фв с энергией Us (R) есть сингу-
летное состояние (противоположно направленные спины). Такое состояние
в молекулах обычно обозначают знаком 1S. Состояние Фа с энергией Ua(£>),
1 По поводу вычисления интегралов К и А см. Г. Бете, Квантовая механика
простейших систем, ОНТИ, 1935, стр. 360—361.
445

напротив, есть триплетное состояние (параллельные спины). Это состояние
обозначают знаком 32.
Обращаясь к кривым для Ua и Us рис. 86, мы можем выразить при-
приведенный там результат так: два атома водорода, имеющих электроны
с противоположно направленными спинами (^-состояние), притягиваются
и образуют молекулу. Два атома водорода, имеющих электроны с парал-
параллельными спинами C2-состояние), отталкиваются.
Притяжение или отталкивание атомов водорода зависит от знака
обменной энергии А (так как энергии Uа и Us отличаются лишь знаком Л).
Таким образом, образование гомополярной молекулы На определяется
обменными силами, и этим объясняется то, что ни в классических теориях,
ни в примитивной квантовой теории Бора нельзя было построить теорию
гомополярной связи. Мы обратимся теперь к некоторым подробностям,
касающимся потенциальной энергии US(R) молекулы водорода На. На
рис. 89 кривая US(R) изображена отдельно от кривой триплетного состоя-
состояния Ua(R)- Зная аналитическое выражение для US(R), мы можем найти
положение равновесия (точку R = Ro) из уравнения
^МВ1 = 0. A25.30)
Разлагая далее U^iR) по степеням отклонения от положения равно-
равновесия (R= Ro), мы получим:
A25.31)
Это разложение справедливо для малых отклонений (R — Ro). Если было
бы достаточно, в смысле точности, ограничиться только членом разложе-
разложения с (R — RoJ' т0 мы имели бы дело с гармоническим осциллятором.
Частота этого осциллятора может быть получена следующим образом.
Потенциальная энергия осциллятора, обладающего массой |л и частотой ш0
и совершающего колебания около положения равновесия Ro, равна
U(R) = const. + £p (R - £0J.
Сравнивая это с предыдущей формулой для US(R), мы находим:
A@8 = ^^^ . A25.32)
Отсюда
(О =1/ — ( —~г^ 1
Заметим, что так как речь идет об относительном движении ядер, то под
[Л следует разуметь приведенную массу двух атомов водорода, т. е.^если
через т# обозначить массу атома водорода, то
— == —. A25.33)
С помощью формулы A25.32) мы можем найти частоту молекулярных
колебаний ш0 по кривизне -гщ- потенциальной кривой US(R) в точке рав-
равновесия Ro. Третий член в A25.31) дает поправку на отклонение от гар-
гармоничности.
Для больших энергий колебания эта поправка будет играть все воз-
возрастающую роль. Если энергия колебания Е будет больше значения
446

потенциальной энергии US(R) на бесконечности [на рис 89 Us(oo) поло-
положено равным нулю, так что речь идет о Е > 0], то молекула вообще не
будет колебаться, а диссоциирует. Энергия D, необходимая для диссо-
диссоциации, по классической механике была бы равна — US(RO)-
Чтобы получить правильное значение энергии диссоциации молекулы,
нужно еще учесть, что в самом нижнем состоянии молекула имеет положи-
положительную нулевую энергию колебаний -^ (см. рис. 88). Эту энергию нужно
вычесть.
Таким образом D равно
Теоретическое
значение
0,735-10"8 см
4280 см'1
4,37 eV
Экспериментальное
значение
0,753-10-8 см
4390 см~1
4,38 eV
таким путем мы можем найти и энергию диссоциации.
Итак, произведенный расчет позволяет найти: 1) положение равнове-
равновесия Ro, 2) частоту молекулярных колебаний ш0 и 3) энергию диссоциации D
молекулы Н2. Все эти вели-
величины известны из опыта. Be- Таблица 4
личина Ro входит в момент
инерции молекулы /, который
равен I—\iRl; он может быть
определен по спектральным
данным из формулы Деландра
[(см. 54.20)]. Частота колеба-
колебаний ш0 опять-таки определяет-
определяется по спектральным данным.
Величина работы диссоциа-
диссоциации может быть определена и оптически, и химически. Здесь мы при-
приводим таблицу, в которой даны результаты вычислений Хиллерааса1
для Н2 и опытные данные. Эти данные показывают прекрасное согласие,
особенно если учесть то, что первые две величины (Ro и ш0) очень чувстви-
чувствительно зависят от формы кривой US(R). Кроме того, отметим, что достигну-
достигнутая Хиллераасом точность не является предельной и могла бы быть еще
повышена. Достигнутый квантовой механикой успех в расчете молекулы Н2,
основанном лишь на том факте, что эта молекула состоит из двух протонов
и двух электронов (без привлечения каких-либо произвольных констант),
является одним из крупнейших успехов квантовой механики.
§ 126. Природа химических сил
В химии различают два рода связей, приводящих к образованию моле-
молекул: ионные (гетерополярные) и гомополярные. Ионная связь реализуется
в тех случаях, когда молекулу можно представить себе как образование
из положительных и отрицательных ионов (пример NaCl). Гомополярная
связь реализуется в тех случаях, когда деление на ионы провести невозмож-
невозможно. Типичным случаем гомополярной связи являются молекулы из одина-
одинаковых атомов (пример Н2).
Теорию ионных связей разрабатывали еще и до квантовой механики
и не без успеха. Простейшая идея о природе ионной связи (валентности)
заключается в следующем: гетерополярная валентность элемента попросту
определяется числом электронов, которое нужно отнять (у электроположи-
электроположительного элемента) или прибавить (к электроотрицательному элементу),
1 Сводные данные о молекуле Н2 см. у Г. Б е т е, Квантовая механика про-
простейших систем, ОНТИ, 1935, стр." 370.
447

чтобы получить ион, имеющий электронную оболочку ближайшего инертного
газа. Так, от Na нужно отнять один электрон, чтобы получить оболочку Ne.
К С1 нужно прибавить один электрон, чтобы получить оболочку Аг. Таким
образом Na+ и СГ являются как бы заряженными атомами инертных газов.
При этих условиях основную роль в ионной связи должно играть куло-
новское притяжение разноименно заряженных ионов, поскольку электрон-
электронные оболочки инертных газов химически неактивны. Однако известно, что
одни электростатические силы не могут обеспечить устойчивого равновесия.
Поэтому помимо кулоновского притяжения зарядов ионов —^ необходимо
ввести еще некоторое отталкивание на близких расстояниях. Эти отталки-
вательные силы в классической теории не могли быть рассчитаны, но введе-
введение их казалось эмпирически обоснованным, поскольку атомы инертных
газов отталкиваются друг от друга на малых расстояниях. Отталкиватель-
ные силы брались в виде
а
где а и т — эмпирически определяемые константы. Полная потенциальная
энергия двух ионов имеет поэтому вид *
U(r)= -— +-w- A26.1)
Если на указанном пути удавалось подойти к проблеме гетерополярной
связи, то проблема гомополярной связи оставалась совершенно темной.
Попытки рассчитать молекулу Н2 никогда не приводили к удовлетворитель-
удовлетворительному результату. Из изложенной выше квантовой теории молекулы Н2
ясна и причина этих неудач. Главную роль в образовании молекулы Н2
играют обменные силы, существование которых является особенностью
самой квантовой механики. Сами по себе эти силы не требуют привлечения
какого-либо нового взаимодействия частиц. Они возникают из того же куло-
кулоновского взаимодействия электронов в молекуле Н2. Кроме того, как мы
видели, для построения правильной теории молекулы Н2 необходим учет
принципа Паули, т. е. принципа неразличимости частиц. Незнание этих
сторон дела и являлось причиной невозможности решить проблему строе-
строения даже простейшей молекулы до открытия квантовой механики.
Напротив, успешное решение проблемы молекулы Н2 средствами кван-
квантовой механики послужило исходным пунктом для квантовой теории гомо-
гомополярной валентности. Не имея здесь возможности входить в подробное
освещение этого вопроса, ограничимся немногими замечаниями. Для Н2
мы получили два состояния: с параллельными и антипараллельными спина-
спинами. На рис. 90 изображено распределение плотности электрического заряда
электронов q для этих двух состояний. Плотность электрического заряда
в точке г вычисляется из волновой функции O(rt, r2) по формуле
е(г)= -2е^ |Ф(г, r')\2dv'. A26.2)
Если спины атомов параллельны, то Ф=Фа. В точке г=г' функция Фа=0
(узловая плоскость). Благодаря этому плотность q в области между атомами
имеет минимум (рис. 90, а). Напротив, в состоянии с антипараллельными
спинами Ф=Ф5 узловой плоскости не имеется и плотности зарядов обоих
атомов как бы сливаются (рис. 90, Ь). Слияние плотностей (образование гомо-
1 Заметим, что квантовая механика дает иной вид отталкивательного члена,
лучше согласующийся с опытом.
448

олярной связи) мы сопоставляем валентному штриху Н — Н. Образование
инимума плотности — отсутствию такой связи.
Можно показать, что силы гомополярной связи обладают свойствами
асыщения — признаком, характерным для валентных сил. Нетрудно
идеть, что присоединение третьего атома Н к молекуле Н2 не приводит
созданию обменных сил между электронами молекулы и третьим атомом.
> самом деле, обозначим волновую функцию электронов молекулы (атомов
и Ь) через Osd^, r2) Sa(sv s2). Волновую функцию электрона третьего
тома (с) обозначим через я|)с (r3)Si/2(s3). Спин третьего электрона мы
зяли направленным по оси OZ. Можно было бы взять и противополож-
ое направление. Важно лишь то, что спин третьего электрона противопо-
ожен_спину одного~из электронов молекулы. Чтобы получить функцию
Рис. 90. Распределение плотности зарядов в двух отталкивающих атомах
/У(а2)—(а) и распределение плотности зарядов в молекуле Н2 (Х2)—(в)
зсей системы, нужно из ФК5Я и я|)с51/2 образовать антисимметричную в ча-
:тицах функцию (учет принципа Паули). Единственная антисимметричная
функция, которую можно построить из Ф35а и i|)cS, есть:
Ф (rlf г2, г3, sv s2, s8) = у= {Ф8 (rlf г2) я|)с (г3) Sa (sp s2) Si/2 (s8) +
Г1, г8) я|>с (r2) Sa (s3,
2, r3)
5a (s2,
A26.3)
Функции Su(s1, s2) согласно A17.13) имеют вид:
• yj [S1/t (S|) 5_1/2 (s2) - 51/2 (*s) 5_1/3
Исходя из свойств ортогональности и нормировки спиновых функций
Sa(s) fa — ± ^ ) [см- F0.7)], легко убедиться, что все три спиновые
функции, фигурирующие в суперпозиции A26.3), ортогональны между
собой. Поэтому, если мы возьмем | Ф |2 и просуммируем по всем значе-
значениям ( ±-о-) всех тРех спинов, чтобы получить вероятность w(rv г2, г3)
положения электронов в окрестности точек rt
w(rv r2, rs)= 2 4
r2, г3, то мы получим:
с(г1)|2|. A26.4)
Обозначая, как мы это делали в предыдущем параграфе, плотность заряда
электрона, находящегося на атоме (а), через qa, на атоме F) — через Qb,
наконец на атоме (с) — через qc, а обменную плотность через qab, мы
29 д. и. Блохинцев 449

можем, пользуясь значением Ф3 A25.24'), A25.11), A25.11'), написат
полученную вероятность конфигурации электронов в виде
W (Гц Г2, Г3) = т {[Qa (rt) Qb (Г„) + 2Qab (Г0 Qab (rs)] Qc (r8) +
+ [Qo (rl) 6b (гз) + 26аЬ (rt) Qab (Г3)] Qc (Г2) +
+ [Qa (rs) Qb (r8) + 2Qab (r2) Qab (r8)] qc (rj}, A26. J
где
Qub ('l) = ~ «M'la) 1>Ь ('ib)- A26.6
Из этого выражения мы видим, что для третьего атома (с) не возникае
обменной плотности (типа Qac, Qbc), а следовательно, обменных сил с атоме
ми (а) и F), образующими молекулу. Кулоновское же взаимодействие остает
ся. Поэтому третий атом будет отталкиваться. Этим и доказывается способ
ность обменных сил к насыщению и правомочность сопоставления валет
ного штриха слиянию плотности электрических зарядов двух атомов.
Заметим, что никакого строгого разграничения между гомополярно
и ионной связью на самом деле провести нельзя. Это — просто два крайни:
случая. В типичном случае гомополярной связи заряд распределен сим
метрично между обоими атомами. Если атомы неодинаковы, то такая сим
метрия нарушается. Если, наконец, симметрия нарушается резко, так 4Ti
заряд электронов сосредоточивается преимущественно около одного и,-
атомов, то мы получим случай ионной связи.
§ 127. Межмолекулярные дисперсионные силы
Выше были рассмотрены валентные силы. Эти силы, будучи связань
с ориентацией спинов электронов, обладают свойством насыщения. Кроме
того, эти силы действуют на коротких расстояниях. Они определяютс?
степенью перекрытия электронных плотностей, принадлежащих взаимодей
ствующим атомам. Так как по мере удаления от атома электрическая плот>
ность убывает экспоненциально с увеличением расстояния от центра атома
то и валентные силы убывают экспоненциально с увеличением расстояни?
между атомами.
Помимо этих валентных сил, между атомами и молекулами действую!
еще особые силы, имеющие всегда характер сил притяжения. Это — меж-
межмолекулярные дисперсионные силы, или силы Ван-дер-Ваальса. Замечатель-
Замечательным свойством этих сил является то, что они действуют между электрически
нейтральными системами и системами, не обладающими электрическим
моментом. Так, например, они действуют между атомами Не, распределение
заряда в которых обладает шаровой симметрией, так что эти атомы не обла-
обладают ни дипольным, ни квадрупольным, ни каким-либо высшим электриче-
электрическим моментом. Второе важное свойство этих сил заключается в том, что эти
силы не зависят от температуры. Природа этих сил оказывается также
квантовой.
Силы Ван-дер-Ваальса можно вычислить, если рассмотреть взаимодей-
взаимодействие достаточно удаленных друг от друга атомов. На большом расстоянии
между атомами валентные силы, вычисляемые из первого приближения теории
возмущения, очень малы. Напротив, на этих расстояниях оказывается уже
невозможным игнорировать второе приближение, в котором учитывается
деформация электронных оболочек атомов. Объясняется это тем, что допол-
дополнительные поправки к энергии ваимодействия атомов, вычисляемые во
450

втором приближении, убывают с увеличением расстояния R между атомами
пропорционально ™ , в то время как энергия валентных связей.убывает
пропорциональное ".При больших R второе приближение оказывается
больше первого.
Производя для больших расстояний подсчет энергии во втором прибли-
приближении, можно вычислить силы Ван-дер-Ваальса. Не входя в эти расчеты,
мы поясним основную идею квантовой теории сил Ван-дер-Ваальса на простом
примере, допускающем точное решение задачи. Вместо реальных атомов
рассмотрим два одномерных осциллятора с собственной частотой со0 (такая
модель атома фигурирует в классической теории дисперсии). Обозначим
координату электрона в первом атоме черех хи а его импульс через plt коор-
координату электрона во втором атоме через х2, импульс через р2. Расстояние
между «атомами» пусть будет R. Электрический момент первого атома есть
ехи а второго] ех2. Если расстояние R между этими атомами достаточно
велико, то энергия взаимодействия этих атомов может быть представлена
как потенциальная энергия взаимодействия двух диполей с моментами ехг
и ех2. Эта энергия равна
Если осцилляторы покоятся, то хг=х2=0 и их дипольные моменты равны
нулю. Так как, кроме того, оба «атома» электрически нейтральны, то ника-
никакого взаимодействия между ними не получается.
Согласно классической теории, взаимодействие возникает лишь между
колеблющимися осцилляторами. Не вдаваясь в расчет этого взаимодействия,
мы можем предсказать, что его величина будет зависеть от температуры Т.
Это ясно уже из того, что при Т=0° абс. колебаний нет и л:1=х2=0. Иное
дело получается по квантовой механике. Даже при абсолютном нуле имеют-
имеются нулевые колебания, которые приводят к тому, что средняя энергия взаи-
взаимодействия рассматриваемых нами осцилляторов не равна нулю.
Для вычисления этой энергии обратимся к расчетам § 109, где как раз
рассмотрен интересующий нас случай взаимодействия двух одномерных
осцилляторов, обладающих чистотой со0 и массой ц. Энергия взаимодействия
осцилляторов, была предположена в виде Xxtx2 [см. A09.1)]. В нашем слу-
случае энергия взаимодействия осцилляторов выражается формулой A27.1).
Стало быть, полагая в формулах § 109
Л = -^, ' A27.2)
мы можем воспользоваться всеми результатами этого параграфа. Сейчас
нас интересует наименьшая нулевая энергия наших осцилляторов. Эта
энергия равна
Eo = ~y~ + ~2А = -2-К + «2). A27.3)
где о)! и со2 определяются из формулы A09.5)
< = <+~, <о22 = ^--^.
Я,
Отсюда, считая ш^ > — , находим:
29* 451

и, следовательно,
ш1 + (Оо = 2ш0-4-^Ч- A27.4)
Имея в виду значение К для нашего случая A27.2), находим из A27.3)
и A27.4) нулевую энергию двух дипольно взаимодействующих осцилля-
осцилляторов:
Яо(*)-к-тл£п?+-"- A27-5)
Мы видим, что нулевая энергчя оказывается функцией расстояния к
между осцилляторами—«атомами» и, стало быть, играет роль потенци
альной энергии взаимодействия этих «атомов».
Отбрасывая несущественную аддитивную постоянную /гш0, получаа
для этой энергии выражение
Мы видим, что эта энергия обусловлена притягательными силами (знак — !
Эти силы можно рассматривать как силы Ван-дер-Ваальса для нашу
идеализированных атомов. Квантовая природа этих сил ясна уже из тог
что при /i = 0 G = 0, так что в предельном случае классической механш
эти силы равны нулю.
Таким образом, ван-дер-ваальсовское притяжение есть результс
уменьшения нулевой энергии при сближении осцилляторов. Форму
A27.6) мы можем преобразовать, введя в нее коэффициент атомной noj
ризуемости р для постоянного поля. Из теории дисперсии мы знаем, i
коэффициент атомной поляризуемости для осциллятора массы [г и часто
ш0 равен1 (§ 92)
полагая здесь ш=0, получаем коэффициент поляризуемости для посте
ного поля
Р = -А-. A2
Внося его в формулы для потенциальной энергии ван-дер-ваальсовс
силы A27.6), получаем:
где
е = /ш0, A:
т. е. в разности между квантовыми уровнями осциллятора. Так как в
мулу для ван-дер-ваальсовых сил входит коэффициент поляризуем
получаемый из теории дисперсии, то эти силы в последнее время и назь
дисперсионными.
Расчет, проведенный во втором приближении для реальных ат
приводит в основном к тому же результату, что и полученный нами (
для модели атома в виде линейного осциллятора. Именно, квантовая ф
ла для потенциальной энергии сил Ван-дер-Ваальса для реальных а
1 Эта формула—классическая. Квантовая формула (90.5') для осциллятор;
к тому же результату, в чем предлагаем убедиться читателю самостоятельно, в
зовавшись матрицей х,& для координаты осциллятора и формулой (92.25).
452

Таким образом спин ядер благодаря принципу Паули оказывает значи-
значительное, косвенное влияние на орбитальное движение ядер в молекуле.
Это влияние выражается замечательным образом в чередовании интенсивно-
стей во вращательных спектрах молекул и в их теплоемкости1. Остановимся
на этом последнем влиянии. Допустим, что установилось тепловое равнове-
равновесие при столь низкой температуре, что вращение вымерзло (ср. § 54). Тогда
водород будет находиться в состоянии параводорода (/=0). Если теперь
такой водород нагревать, то вероятность изменения направления спина ядер
при столкновениях молекул будет очень мала (из-за малости взаимодействия
с малым магнитным моментом ядер). Поэтому, несмотря на столкновения,
водород будет оставаться в парасостоянии, и теплоемкость за счет вра-
вращения будет определяться переходами / = 0—>/ = 2—^/ = 4, ....
Если же дать водороду постоять при этой повышенной температуре
(для этого требуется много дней), то спины ядер успеют перераспреде-
перераспределиться. Наряду с параводородом возникнет также и ортоводород. Тогда
окажутся возможными также и переходы типа / = 1 —з>-/ = 3 —>/ = 5, ... .
Так как'изменения вращательной энергии Д£ = -57 тО + у) ~ОЧ~Тг) Г
различны для четных и нечетных I, то теплоемкости параводорода и орто-
водорода различны. В силу этого медленный процесс установления равно-
равновесия между пара- и ортоводородом будет сопровождаться изменением
теплоемкости водорода.
При равновесии число молекул ортоводорода в три раза больше
молекул параводорода (так как для параллельных спинов имеется три
симметричных функции Ss, а для антипараллельных —только одна, анти-
антисимметричная Sa; ср. § 125). Поэтому нормально водород представляет
собою смесь орто- и параводородов в отношении 3:1.
Это поразительное явление изменения теплоемкости водорода находит
в квантовой механике не только описанное качественное объяснение, но
и может быть рассчитано количественно в полном согласии с опытом2.
1 Относительно чередования интенсивностей в спектрах молекул см.
К. В. Никольский, Квантовая механика молекулы, ГТТИ, 1934; К р о н и г,
Полосатые спектры и строение молекул, ГНТИ Украины, 1935; В. Н. Кондрат ь-
е в, Структура атомов и молекул, изд-во АН СССР, 1946.
2 См. Крониг, цит. соч.; Fowler, Statistical mechanics, Cambridge, 1929.

zz ГЛАВА XXIII ^ee
МАГНИТНЫЕ ЯВЛЕНИЯ
§ 129. Парамагнетизм и диамагнетизм атомов
Основной и простейшей задачей атомной механики из области магнит-
магнитных явлений является вычисление магнитных моментов атомов, помещен-
помещенных во внешнее магнитное поле. Мы уже вычисляли элементарным спо-
способом магнитный момент орбитальных токов в атоме (§ 53). Обратимся
теперь к общим методам.
Наиболее общим образом операторы" проекций магнитного момента
могут быть определены как производные (с обратным знаком) от опера-
оператора полной энергии (точнее гамильтониана) по проекциям магнитного
поля:
аия» ы
В частности, для одного электрона гамильтониан Н, описывающий дви-
движение электрона в магнитном поле, имеет вид:
(знак + перед вектором-потенциалом А взят потому, что мы считаем
заряд электрона равным — ё). Направим ось 01 по направлению магнит-
магнитного поля и возьмем вектор-потенциал в форме
А*=-™У, Ау' = 1Гх> А* = °- A29-3)
Дифференцируя И по ^€г, мы найдем:
>]-1пг8*- A29-4)
Оператор, стоящий в прямых скобках, есть оператор проекции на 01
момента истинного импульса1. Далее, Рух — рху есть оператор проекции
на 01 момента обобщенного импульса Mz- Пользуясь A29.3), представим
A29.4) в виде
а»,- -щ-с(мж+2sz)-^g(*■ + & =~^c(jz+sz)-
A29.5)
1 Напомним, что в магнитном поле оператором скорости является не —Р,
455

Как мы видим, оператор состоит из двух частей: не зависящей от магнит-
магнитного поля и зависящей от него. Рассмотрим их порознь. Первая часть
3^=-2Jrc ('* + **) [A29.6)
имеет собственные значения, которые мы уже находили в теории эффекта
Зеемана. Действительно, энергия возмущения в магнитном иоле W =
= — (e^'lz)- Собственные значения оператора W различны, смотря по
тому, имеем мы дело с сильными магнитными полями (простой эффект
Зеемана) или со слабыми (сложный эффект Зеемана). В последнем случае
собственные значения W Даются формулой G4.23). Эти собственные зна-
значения отличаются от собственных значений 3J?2 множителем—^'. По-
Поэтому из G4.23) находим:
те' he
\
2,'
n
J '
где rrtj есть магнитное число, / — число, определяющее полный механиче-
механический момент, / — орбитальный, /s — спиновый. Потенциальная энергия
этого момента во внешнем магнитном поле есть как раз W. Она может
принимать как положительные, так и отрицательные значения, смотря по
значению т,- = ± у , ± у , . . ., ±j.
При термодинамическом равновесии будут предпочитаться отрицатель-
отрицательные значения W и, следовательно, положительные значения yj}'z. В резуль-
результате получится средний момент, направленный по полю, т. е. случай.
парамагнетизма. Существенно, что gj^ не может равняться нулю. Сле-
Следовательно, одноэлектронные атомы всегда парамагнитны. Второй член
в A29.5)
ж"=-^5(-*2+^) A29-8>
представляет собой магнитный момент, который всегда направлен (как
непосредственно видно) против поля. Таким образом, этот момент обуслов-
обусловливает диамагнетизм. Он никогда не может быть равен нулю, так как
л:2+г/2>0, и поэтому диамагнитный эффект имеет место во всех атомах.
Однако легко видеть, что момент W1" значительно меньше ?j им можно
пренебречь в сравнении с последним. Действительно, 5Шг по порядку
eh гШ1
eh a еШ1
величины равняется магнетону у-, а да! ^ y-^"^3, где а—размеры атома.
Ш'г > Ж" для всех полей СШ, Для которых
^«£-£=137^. A29.9),
Все практически достижимые поля удовлетворяют этому условию.
Если число электронов в атоме четное, полный момент импульса
может оказаться равным нулю. Вместе с тем, будет равен нулю и маг-
магнитный момент ад2, обусловливающий парамагнетизм. Такой атом будет
диамагнитным. Так, например, в атоме гелия, в основном состоянии,
как мы знаем, орбитальный момент равен нулю, а спиновый компенсиро-
компенсирован благодаря противоположному направлению спинов. Поэтому 9),г = 0.
Гелий должен быть диамагнитным, что и наблюдается в действительности.
Диамагнитную восприимчивость гелия можно вычислить, имея в виду,,
что для двух электронов ж" будет равно
2WT^ + ^+^)- A29.10)
456

Средние значения х\, у\, х\, у\ в силу сферической симметрии основного-
состояния гелия и симметрии электронов в нем равны между собой.
и равны -^-, где г2 —средний квадрат радиуса-вектора. Таким образом,.
4-а
Диамагнитная восприимчивость, рассчитанная на один атом, будет равна
С помощью волновых функций для электронов атома гелия A22.23) можно
вычислить среднее значение г2 и получить численное значение магнитной
восприимчивости.
Вычисление % с помощью волновых функций дает %— — 1,87* 10"'.
Экспериментальное значение % — — 1,88-10 6. Заметим, что выражение
A29.8) для диамагнитного момента совпадает с тем, которое получается
из классической электронной теории 1. Однако только квантовая механика
позволяет вычислить х2-\-у2, исходя из констант, характеризующих атом.
Если мы имеем дело с многоэлектронным атомом, то вместо A29.7) мы пслучим
на основании изложенного в § 105 [см. формулу A03.33)]:
s|S+"b
где J есть число, определяющее полный момент импульса всех электронов, L—число,
определяющее полный орбитальный момент, a S—число, определяющее полный спиновый
момент, | rrij | < J и определяет проекцию полного момента на магнитное поле.
Если J = 0, что может быть лишь для атомов с четным числом электронов, то ЭО?' = 0
и атом будет диамагнитным, причем J.
JV
47^2). ('29.13)
fe=i
где N—число'электронов. Если J Ф 0, то величиной SO?" можно пренебречь в сравнении-
с SO?j. Атомы с J Ф0 будут парамагнитными.
§ 130. Ферромагнетизм
Происхождение постоянного магнетизма ферромагнитных веществ пред-
представлялось в течение длительного времени совершенно загадочным. Сущ-
Сущность явления заключается, как известно, в том, что ферромагнитные
тела могут оставаться намагниченными и в отсутствии внешнего магнит-
магнитного поля £%?. Для объяснения свойств ферромагнетиков Вейсс предложил
теорию, объясняющую постоянный магнетизм наличием внутреннего магнит-
магнитного поля e%?v которое и заставляет ориентироваться элементарные магниты,,
даже если внешнее поле равно нулю. Теория Вейсса позволяла объяснить
многие свойства ферромагнетиков, однако, происхождение внутреннего
поля £%?{ оставалось неразъясненным.
Для приведения теории Вейсса в согласие с опытом приходится1
допускать, что поле 36\ имеет колоссальную величину: 106- э. Прямые
1 Ср. Р. Беккер, Теория электричества, т. II, ГИТТЛ, 1941, Электронная тео-
теория, § 29.
457

опытых показывают, что такого магнитного поля внутри ферромагнетика
на самом деле не существует. Гейзенбергу удалось показать, что силы,
ориентирующие элементарные магниты, — обменные силы. Этим была
объяснена природа загадочного вейссового поля. Гейзенберг, в согласии
с данными опыта Эйнштейна и де Гааса (см. § 57), предполагает, что
намагничивание ферромагнитных тел обусловлено не орбитальным движе-
движением электронов, а магнитным моментом спина. Далее, ферромагнетизм,
по-видимому, следует отнести не за счет валентных электронов («электроны
проводимости»), а за счет электронов внутренних, незаконченных оболочек
атомов ферромагнетиков (см. распределение электронов в Fe, Ni и Со
в таблице на стр. 432).
Для простоты допустим, что в каждом из атомов, образующих кри-
кристалл, имеется лишь один такой электрон. Взаимодействие такого элек-
электрона с соседними атомами можно считать малым и поэтому можно рас-
рассматривать волновую функцию всех электронов, обусловливающих ферро-
ферромагнетизм (числом N), как соответствующую системе невзаимодействующих
электронов.
Для нумерации состояний заметим, что положение центров атомов
в кристалле (узлы решетки) определяется вектором
A30.1)
где я,, п2, п3 — целые числа, а а,, а2 и а3 — основные векторы решетки.
Таким образом, положение каждого атома определяется тройкой чисел
л,, п2, п3. Ради краткости эту тройку будем обозначать одной буквой п
и называть номером атома. Пусть волновая функция &-го электрона, нахо-
находящегося на п-м атоме, есть
где Sa— спиновая функция.
Поскольку мы пренебрегаем взаимодействием с соседними атомами,
постольку волновая функция всего кристалла в целом будет антисимме-
антисимметричной комбинацией вида A17.6') из произведений функций Ф„, относя-
относящихся к отдельным электронам. Выбор значков а ( +1/2 или — 1/2) у каждой
из функций Sa будет означать выбор определенного распределения спинов
(направленных по оси 01 или против нее) среди атомов кристалла. Если
спины всех электронов ориентированы в одном направлении, например,
по 01, то мы будем иметь дело с полным насыщением (максимальное
намагничивание). Рассмотрим такое состояние, когда все спины направлены
по 01, за исключением одного, направленного против 01. Пусть такой
•спин находится на атоме номера I. Тогда согласно сказанному выше вол-
волновая функция W всех N электронов имеет вид
2 (± 1) РЬ (Гг) S+1/a (sh) г[>2 (га) S+i/, (sg — Ч»* (г,) S-
2
A30-2)
Учтем теперь взаимодействие электронов с соседними атомами. Для этого
применим теорию возмущений. Мы имеем дело со случаем вырождения,
так как, очевидно, электрон со спином, направленным против оси 01,
может находиться на любом из атомов. Поэтому правильная функция
1 Я. Г. Дорфман пропускал пучок быстрых электронов через намагниченную
ферромагнитную фольгу. Поле в 106 э должно было бы отклонять электроны, чего на
самом деле не наблюдалось.
45 8

нулевого приближения будет линейной суперпозицией из Ч^
¥=2 ai'Yf, A30.3)
причем амплитуды a,i> надлежит еще определить. Для этого заметим, что
оператор полной энергии Н электронов равен:
JV JV
Н = Н°+ У, — + 2 ип(гт), A30.4)
пут= 1 п~>т= 1
JV
п=1
где //„—оператор полной энергии п-го электрона, находящегося на
п-ом атоме, ■ энергия взаимодействия п-го и m-го электронов,
a Un (гт) — энергия взаимодействия m-го электрона с и-ым ионом (пфт).
Все члены в Н, кроме Н°, будем рассматривать как возмущение. Под-
Подставляя в уравнение Шредингера HW = EW вместо W приближенную функ-
функцию A30.3) и имея "в виду, что
//п (г„)г|з„(г„) = £01|5„(гп), A30.6)
где Ео—энергия электрона в атоме, мы получим:
JV
y,ai,Yi. = E-y,ai,Wi,. A30.7)
[ (£ )]
V n>m=l " I' V
Умножим теперь это уравнение на W*% проинтегрируем результат по коор-
координатам всех электронов и просуммируем по двум значениям спина
sz — ± -к каждого из электронов. При этом мы будем считать функции
^„(г) и tym(r), относящиеся к различным атомам, ортогональными1. Далее
при суммировании по спину следует иметь в виду ортогональность функ-
функций Sa(sz) (ср. § 60). В результате мы получим вместо A30.7)
N-E0.ai+2 Iw [ai> - а4] = fia., A30.8)
с
где Iw есть обменный интеграл (матричный элемент энергии возмущения):
hi' =T\Vl (fl) 4*' (Г2) У* (Г2) **' (ri) {~Г + Ul (Г1) + Ul' (Г2) +
}v1dvi. A30.9)
Волновые функции г|зг (г) быстро убывают с увеличением расстояния г
от центра атома. Поэтому обменный интеграл 1ц, быстро убывает с уве-
увеличением расстояния между атомами I и I'. Благодаря этому при решении
уравнений A30.8) можно ограничиться матричными элементами 1ц>, отно-
относящимися к ближайшим соседям. Так как в кристалле все ближайшие
соседние атомы равноправны, то обменный интеграл имеет для них одно
и то же значение /. Таким образом, уравнения A30.8) можно написать
в виде
ai,] = 0, A30.9')
1 На самом деле они ортогональны только приближенно.
459

где сумма распространена по атомам Г, соседним атому I. Число ближай-
ближайших соседей и их расположение зависят от типа кристаллической решетки.
Для простой кубической решетки соседние с атомом I (lv /2, /3) атомы
имеют числа /', равные 1г±\, /2, 1Ъ\ lv /2 ± 1, /3; lv /2, 1%± 1-
Легко видеть, что уравнения A30.9') имеют решения
а, = 01^,3= const.•е|(9»11+в*'»+в«'з) , A30.10)
где qv q9, qs— некоторые безразмерные величины. В самом деле, подста-
подстановка A30.10) в A30.9') дает
Е —iVE0 =2/[3—cos<7j.-cos <7г—cos <78], A30.11)
откуда
+ 2/[3—cos<7i-cos<72—cos<78]. A30.12)
Замечая, что 1га, \%а, 13а, где а—постоянная решетки, суть координаты
узла решетки, мы видим, что A30.10) может рассматриваться как плоская
волна с волновым вектором к= —Г —, —, —J. Вероятность найти
спин, направленный против OZ, есть | а, |2 = const., т. е. все положения
спина равновероятны. Таким образом амплитуды at, определяющие состояние
спина, весьма аналогичны волновой функции свободно движущейся частицы,
имеющей заданный импульс. Зта аналогия еще усугубляется тем, что, ПО'
крайней мере, для малых к энергия A30.12) может быть написана в виде
£ = const. + —№-{ , A30.13)
Л2 г ^
где -н-^г = /а , т. е. в виде, совпадающем с выражением энергии для сво-
свободной частицы. Величину ц* можно рассматривать как эффективную
массу. Ввиду наличия такой аналогии между распространением в кристалле
спина определенной ориентации и движением свободной частицы состоя-
состояние A30.10) называют спиновой волной.'
Если в кристалле имеется не один, а несколько (г) спинов, ориенти-
ориентированных против оси OZ, то расчет протекает аналогичным образом, но
усложняется тем, что при наличии многих спинов, ориентированных против
оси OZ, могут встретиться пары соседних атомов со спинами, направлен-
направленными против OZ. Для этих пар обменные интегралы не равны нулю.
Однако при небольшом числе г такие случаи будут встречаться редко,
и полное решение может рассматриваться как совокупность невзаимодей-
невзаимодействующих спиновых волн вида A30.10) (или, с корпускулярной точки
зрения как «спиновый газ»). Энергия будет суммой энергий для каждой
из спиновых волн. Если мы обозначим вектор q для k-ой спиновой волны
через q,4, то вся энергия спинового газа будет jj
г
Из этой формулы следует, что при отрицательном / ферромагнетизма
быть не может, так как при / < 0 энергия имеет минимум при наиболь-
наибольшем г. Поэтому при тепловом равновесии первоначальная ориентация всех
спинов по оси будет стремиться расстроиться. Напротив, при положи-
положительном обменном интеграле минимум энергии будет достигаться при
наименьшем г, так что если некоторая часть спинов ориентирована против,
оси OZ, то эти спины будут иметь тенденцию ориентироваться по оси OZ
(число г будет уменьшаться). Поэтому положительное значение обменного
интеграла является необходимым условием ферромагнетизма (только в этом
случае состояние с наименьшей энергией может быть состоянием, в котором
460

все спины электронов направлены одинаково). Причиной, приводящей
к ориентации спинов в одну сторону, являются, таким образом, не фиктив-
фиктивное магнитное поле Вейсса, а обменные силы. Ферромагнетизм есть явле-
явление квантовое. Наконец, мы видим, что ферромагнетизм не является
свойством отдельных атомов, а представляет собой свойство кристалла,
что находится в согласии с тем фактом, что ферромагнитных газов не
существует.
Для вычисления намагничения ферромагнетика при какой-либо тем-
температуре Г следует найти, методами статистики, среднее значение г. Тогда
магнитный момент куска ферромагнетика, содержащего N электронов,
будет, очевидно, равен
-2г), A30.15)
где 2Kb есть магнитный момент одного электрона (магнетон Бора). За соот-
соответствующими вычислениями и другими подробностями мы отсылаем чита-
читателя к специальной литературе1.
1 См. С. Н. Вонсовский, Современное учение о магнетизме, УФН, 35, 556,
1948; 36, 30, 1949; 37, 1, 1949; 37, 237, 1949.

ГЛАВА XXIV
АТОМНОЕ ЯДРО
§ 131. Ядерные силы. Изотопический спин
Взаимодействие нуклонов в ядре представляет собою еще далеко не
решенную проблему. Однако принципы квантовой механики оказываются
применимыми как к движению нуклонов в ядре, так и к взаимодействию
нуклонов с ядром. На этом пути за последние годы достигнуты значи-
значительные успехи и квантовая механика оказывается настоящим путеводите-
путеводителем физика в сложной картине ядерных взаимодействий.
Отсылая читателя к специальным курсам1, мы остановимся здесь лишь
на наиболее простых и важных обстоятельствах.
До сих пор никому еще не удалось написать выражения для потенциа-
потенциала протонов и нейтронов (как принято говорить, нуклонов) в атомном ядре.
По-видимому, это очень сложная функция положений, скоростей и спинов
нуклонов. Весьма вероятно, что она вообще непредставима в виде суммы
попарных взаимодействий отдельных нуклонов.
Но не установлен «потенциал» и для пары нуклонов. Вообще простое
представление о силах применимо здесь лишь на больших расстояниях
нуклонов друг от друга. Тем не менее, могут быть даны довольно далеко
идущие заключения о характере ядерных взаимодействий, которые позволя-
позволяют разобраться в сложном комплексе опытных фактов.
Взаимодействие двух нуклоно.в зависит от расстояния между ними г12,
от их относительной скорости vn и от их спинов sx и s2, а также, как пока-
показывает опыт, существенно зависит от типа взаимодействующей пары, т. е.
являются ли нуклоны этой пары протонами, нейтронами или один из них
есть протон, а другой нейтрон. Далее, в процессе взаимодействия может
происходить, как говорят, «перезарядка», и протон может превратиться
в нейтрон и обратно2.
Оказывается, что если мы будем рассматривать протон и нейтрон как
два состояния одной и той же частицы — нуклона, то основные особен-
особенности взаимодействия нуклонов могут быть выражены в виде очень простых
закономерностей на языке так называемого зарядового или, как чаще, гово-
говорят, изотопического спина.
Так как у нас имеется только два зарядовых состояния нуклонов, то
естественно ввести новую динамическую переменную ts, которая принимает
только два значения так, что волновую функцию нуклона (опуская пока
зависимость от обычного спина s) можно записать в виде матрицы с одной
1 См, А, С. Давыдов, Теория атомного ядра, Физматгиз, 1958.
2 См. например, Д. И. Б л о х и н ц е в, ЖЭТФ, т. 29, стр. 33, 1955,
462

колонкой:
W(x, t) =
состояние «протонное»,
состояние «нейтронное»,
A31.1)
также, как мы это делали в теории обычного спина (ср. § 60, 60.3
и 60.3'). В соответствии с оптической терминологией, по которой состоя-
состояния, отличающиеся только проекцией спина, называются мультиплетом,
протонное и нейтронное состояния называют изотопическим (зарядовым)
триплетом.
Все операторы, изменяющие зарядовые состояния нуклонов, так же
как и в случае обычного спина, можно выразить с помощью двухрядных
матриц Паули, таких как ах, ау, az (ср. § 59). Мы обозначим эти матрицы,
действующие теперь на зарядовый индекс 1,2, через
Любой оператор, действующий на пару функций (<ф1, г|з2), может быть
выражен через линейную комбинацию матриц (г1у т2, т3). Введем вектор.
изотопического спина t, аналогичный вектору обычного спина s:
7=4-*. о31-3)
где х есть вектор с тремя компонентами: т1( т2, т3. Ясно, что этот «вектор»
ничего общего не имеет с обычным пространством: он определен в абстракт-
абстрактном, зарядовом пространстве, или, иначе, в пространстве изотопического
спина.
«Повороты» в этом пространстве означают линейные преобразования
над tyi и ty2 такие, что в качестве базисных функций выбираются различ-
различные линейные комбинации протонного и нейтронного состояний нуклонов.
Например, вместо ^ и ty2 можно взять новые базисные функции:
Ф1 = ■—— (% + 1|з2) и ф2 =-—^ (г|з1—г|з2) —симметричную и антисимметрич-
антисимметричную. Переход от (г|з1; г|з2) к ф15 ф2) есть поворот в изотопическом про-
пространстве.
—*■
Введение оператора изотопического спина нуклона t позволяет нам
применить теорию обычного спина к теории спина изотопического.
В частности, ясно, что операторы t% и ts одновременно приводятся
к диагональному виду и имеют собственные значения:
(ср. 59.14 и 59.15).
Отметим, что t2 является инвариантом при вращениях в изотопическом
пространстве. Очевидно также, что правила сложения векторов изотопи-
изотопического спина в системе нуклонов будут те же, что и для обычного спина.
В частности, для вектора полного изотопического спина системы из jV
нуклонов /:
. 7= 2 7h A31.5)
(k— номер нуклона), будут справедливы формулы A05.20) и A05.21):
/2 = 7G+1), 7 = 0, 1, 2, 3,..., A31.6)
или 7' = у, 3/2, 6/2.-->
/з = П |73|<7. A31.7)
463

"Ясно также, что скалярные произведения изотопических спинов вида:
—*■
(здесь t's, s= 1, 2, 3 — суть компоненты вектора Г, а ^ — то же для вектора
второго нуклона t") будут так же, как и t2 = (t, t) инвариантами в изото-
изотопическом пространстве.
Приведем еще формулу, выражающую заряд Q системы N нуклонов
через изотопический спин:
^] A31.9)
В частности, для одного нуклона:
Q = |-(l + t3). A31.9')
Существенным физическим фактом, является то обстоятельство, что взаи-
взаимодействие двух нуклонов оказывается изотонически инвариантным (т. е.
не зависящим от возможных вращений в изотопическом пространстве) и что
при взаимодействии полный изотопический спин сохраняется 1.
Эти два фундаментальных факта и оправдывают введение новой дина-
динамической переменной — изотопического спина нуклона.
Далее взаимодействие нуклонов, конечно, должно быть инвариантно
относительно вращений, отражений и инверсий координат в обычном про-
пространстве. Если ограничиться малыми скоростями нуклонов и учитывать
—Э» —> —Э»
только зависимость от их относительного расстояния г, их обычных sv s3
и изотопических спинов tv tv то можно образовать следующие инварианты:
г, (sv s2), (tv t%), (sv r) (s2, г), которые, в свою очередь, могут быть выра-
жены через полный спин S = st-|-s2 и полный изотопический спин I = tl-\-t2
так, что вместо названных инвариантов ввести новые:
(ХЛ2)->8\ A31.10)
(V)(ssr^-^Sls=6^p-2-2S*. A31.10")
Последний инвариант построен так, что его среднее значение по углам
будет равно нулю. Это обычно принятый выбор. Очевидно, что взаимо-
взаимодействие, определяемое этим членом, будет нецентральным. Его называют
тензорным взаимодействием. Если учитывать зависимость от скоростей,
то можно образовать много и других инвариантов. Однако опыт показы-
показывает, что пока скорости малы по сравнению со скоростью света, среди
возможных инвариантов важен лишь инвариант спинорбитального взаимо-
действия (LS); здесь L означает вектор суммарного орбитального момента
нуклонов. Вместо него можно ввести вектор полного момента количества
движения нуклонов J = L-\-S и соответственно инвариант (/S).
1 Этот факт особенно точно и полно обоснован в экспериментальных работах объе-
объединенного института ядерных исследований. См. В. П. Джелепов и Б. М. Пон-
Понтекорво, Усп. Физ. наук, VXIV, стр. 15, 1958.
464

Учитывая все эти инварианты, мы можем записать энергию взаимо-
взаимодействия двух нуклонов в виде:
U (l,2) = A (r, S2, /2) + В (г, S2, P)-S12 (гТS) + С (г, S2, /2) (JS). A31.11)
Относительно функций А, В и С известно очень мало. С точки зре-
зрения мезонной теории ядерных сил эти функции должны иметь характер-
характерную зависимость от расстояния вида ~- е~г/а/г для г > а, где а = — =
trie
= 1,4 - Ю~13 еж —есть комптоновская длина я-мезона.
Поэтому приведенный выше вид возможного взаимодействия нукло-
нуклонов A31.11) более полезен для систематики возможных состояний нукло-
нуклонов, нежели для количественных вычислений уровней или матрицы рас-
рассеяния.
§ 132. Систематика состояний системы нуклонов
Гамильтониан системы нуклонов инвариантен не только относительно
преобразований вращения, отражения и инверсии, но и относительно пере-
перестановки нуклонов.
Отсюда, совершенно таким же образом, как было описано в §§ 115, 116,
следует, что волновая функция должна быть либо симметричной, либо
антисимметричной при перестановке любой пары нуклонов. Но так как
нуклоны имеют спин Уг, то для них должна быть выбрана вторая возмож-
возможность — антисимметричные функции, приводящие к принципу Паули
и к статистике Ферми.
Рассмотрим теперь состояния двух нуклонов. Обратимся сперва
к изотопическому спину. Очевидно, что возможны всего четыре состояния:
Г=0 и Г=1, Г3=0,±1. В первом случае состояние антисимметрично
в изотопических переменных, во втором — симметрично (точно так, как
для обычного спина, см. теорию атома гелия, § 121). В состоянии с Т=\,
поскольку гамильтониан не зависит от Г3, энергия трех состояний с Г3=
=0>=bl будет одинакова.
Однако эта одинаковость имеет место лишь до той поры, пока не
учитываются относительно слабые электромагнитные взаимодействия.
Ввиду различия зарядов и магнитных моментов у протона и нейтрона
совпадающие уровни 7'8=0,±1, вообще говоря, расщепятся. Поэтому эти
три состояния называют зарядовым триплетом, а само состояние Т—\ —
триплепгным. Состояние Г=0 будет зарядовым синглетом.
Дальнейшее различие состояний определяется суммарным спином S.
Именно, возможны опять-таки четыре состояния: S-—1, ог=0,±1 — три-
плетное состояние и S=0 — синглетное. Симметрия функции в простран-
пространственных координатах определяется симметрией по зарядовым и спиновым
переменным. В таблице 5 приведены все возможные симметрии функции
для двух нуклонов.
Таблица 5
Симметрия функций системы двух нуклонов
7 = 0
а
S = 0
а
L нечетн.
а
S=l
s
L четн.
s
s
S = 0
а
L четн.
s
S=l
s
L нечетн.
а
30 Д. И. Блохинцеа
465

В этой таблице знак а означает антисимметричную, а знак s — симметрич-
симметричную функцию. Напомним (ср. § 124), что в случае двух частиц переста-
перестановка Рп эквивалентна операции /^—инверсии, т. е. замене относитель-
-> ->
ных координат х на — х. Четность состояния в этом случае совпадает
с четностью орбитального числа L.
Если для систематики нуклонных состояний сохранить обозначения
S, P, D, F для L = 0, 1, 2, 3 ... соответственно, а также принятое обоз-
обозначение полного момента J и мультиплетности, то полное обозначение
состояния будет иметь вид:
Здесь первый индекс означает зарядовую мультиплетность BГ+ 1), вто-
второй B5+1) —спиновую, индекс (±) четность терма, индекс / — его пол-
полный момент, L = S, P, D, F, ... — означает орбитальный момент. Для
системы из двух нуклонов знак ± опускают, так как он определяется
четностью L; кроме того часто опускают.и индекс изотопического спина Т.
Для двух нуклонов получаем теперь следующую систему возможных
состояний для У = 0, 1,2, ...
Таблица 6
Состояния двух нуклонов
J
0
1
2
7 = 0
S=0
xPi
S=l
3Sb 3Оц
7=1
S=0
XSO
S=l
*Po
sPi
3P2- 3^2
§ 133. Теория дейтона
Как известно, дейтон является изотопом водорода и его ядро состоит
из протона и нейтрона. Известно далее, что его спин равен S= 1. Далее,
зарядовое состояние только одно; следовательно, Г = 0. Из таблицы 6
видно, что возможное основное состояние дейтонов должно быть Т = 0,
sSj. или может быть 3DV Однако мы знаем, что в основном состоянии
волновая функция должна иметь наименьшее возможное число узлов.
Поэтому мы должны приписать дейтону основной терм 3S1. Из-за нали-
наличия тензорных сил орбитальный момент в дейтоне не сохраняется, поэто-
поэтому возможна и примесь состояния SD,, которая на самом деле и имеется
и приводит к существованию квадрупольного электрического момента
у дейтона. Из величины этого момента можно судить о том, что примесь
состояния SD] невелика (около 5%).
Таким образом опыт показывает, что состояние Г = 0, S=l является
нижним. Других связанных состояний в системе из двух нуклонов неиз-
неизвестно.
Ввиду того, что функции А (г), В (г) и С (г) в энергии взаимодействия
нуклонов A31.11) нам неизвестны, мы определим волновую функцию дей-
дейтона в основном состоянии окольным путем, воспользовавшись тем опыт-
опытным фактом, что энергия связи нуклонов в дейтоне £0= — 2,1 • 106 эв ма-
мала в сравнении с собственной энергией я-мезонов тяс2=140-10в эв.
466

Действительно, при заданных Г, S и / (или L) энергия взаимодей-
взаимодействия нуклонов U (г) A31. 11) становится попросту некоторой функцией
их относительного расстояния г (тензорным и спин-орбитальным взаимо-
взаимодействиями мы пренебрежем. Кстати, в дейтоне они дают лишь малые
поправки—примесь 3Di состояния). Тогда уравнение для радиальной функ-
функции, дейтона \]з (г) = —" будет гласить:
A33.1)
где
- = — + -
и Г|Л— приведенная масса протона и нейтрона (сравни
104.4); тр — масса протона, тп — нейтрона. Так как они мало отличаются, то
V-
Уравнение A33.1) переписывается в виде:
A33.2)
Здесь х2= — гг Ео, — = 4,ЗЬ10~13 см. Эта длина определяет асимптота-
ческое поведение функции дейтона \]з (г). Действи-
Действительно, при г—^со(у-^>0) из A33.2) получим
е-иг
\|з (г) = С •- . С другой стороны,
Щп
т. е.
где а — —g= 1,4-10"
—g
СМ,
U (г) убывает как -
т. е. гораздо быстрее %р (г). Поэтому мы можем
считать, что ядерные силы действуют лишь на
очень малом расстоянии и вообще пренебречь ими
для г~>а. Это иллюстрируется рисунком 91, на
котором изображена кривая потенциальной энергии
V (г) для системы протон-нейтрон.
Нормируя теперь -ф (г) на единицу
со
Ал \ %J32(r)r2dr = 1, A33.3)
что
A33.4)
Рис. 91. Потенциаль-
Потенциальная кривая для сил
протон-нейтрон в дей-
дейтоне:
Уровень Eq лежит на глу-
глубине 2 Mev. Глубина ямы
составляет около 25 Mev;
радиус а— 1,4 • 10~13 см
найдем константу С. Легко убедиться,
С = у -~ . Таким образом мы получаем:
YoC")— у ~2лТ
Эта функция может быть использована для расчета фоторасщепления
дейтона, для расчета некоторых ядерных реакций с дейтоном, в которых
важны большие прицельные параметры и т. п.
Заметим, что по самому смыслу вывода этой функции она не приме-
применима для расстояний1 г меньших а= 1,4-10~13 см.
1 В опытах М. Г. Мещерякова было показано, что при столкновениях быст-
быстрых нуклонов с ядрами в большем числе из ядер вылетают дейтоны. Это указывает на
существование в дейтоне очень большой связи на малых расстояниях. См. по этому по-
поводу также Д. И. Блохинцев, ЖЭТФ, 33, 1295, 1957.
30* 467

§ 134. Рассеяние нуклонов
Проблема рассеяния нуклонов очень обширна и включает в себя столь
различные явления, как например рассеяние медленных тепловых нейтро-
нейтронов в водороде и столкновение быстрых нуклонов, вплоть до самых высо-
высоких энергий, когда наряду с упругим рассеянием возникают мощные не-
неупругие процессы, в которых рождаются я-мезоны или другие новые
частицы. Мы рассмотрим здесь два важных примера:
А. Рассеяние медленных нейтронов на протонах
В этом случае имеет значение только S-состояние, поскольку длина
волны у- считается гораздо большей, нежели радиус действия ядерных
сил а. Напомним, что высшие состояния ''удут пространственно удалены
на расстояния, большие А,/2л (сравни рис. 61). Из таблицы возможных
состояний двух нуклонов видно, что в рассеянии (р, п) участвуют оба
изотопических состояния Т = О и Г=1, причем возможные S-состояния
отличаются суммарным спином: 3SX и 1S) соответственно (триплетное
и синглетное состояния). Таким образом нам необходимо вычислить две
фазы Зт}1 и 1ц0.
Рассмотрим сперва триплетное состояние. В этом случае уравнение
для волновой функции U (г) будет совпадать с уравнением A33.2). Одна
ко теперь мы будем считать Е > 0 и положим ^ Е = к2.
Асимптотический вид и (г) при г У а будет:
Предполагая, что энергия нейтрона Е мала в сравнении с энергне
взаимодействия нуклонов 0 (г), мы можем, решая уравнение A33.2), bi
обще пренебречь членом Е в сравнении с (У, а это означает, что лог;
рифмическая'; производная —- при г < а почти не зависит от Е (при м
лом Е). Обозначим ее а.
Так как; на границе г = а логарифмические производные должны бы
равны, то используя решение A34.1), получим:
Ъ)=-а. A34
A34
Пренебрегая малой величиной кг, найдем:
Откуда, согласно обще л фэрмуле (80.18.), дифференциальное сече!
равно
dq (9) = ± sin2 (Ч) dQ= k.^a2 sin б de. A3<
Теперь мы установим связь между а и х. Напомним, что согла
§ 80 для связанного состояния фаза г\ равна -\-ioo. Приравнива
A34.3) Зт1,= +/со, находим, что k=+ia, а следовательно, волне
функция и (г) будет вести себя для связанного состояния как е~аг. С
нивая это с A33.4), мы видим, что сс = и.
Таким образом, формулу A34.4) можно переписать в виде:
^% (lc
468

причем, теперь величина % известна из энергии связи дейтона. Полное
сечение в триплетном состоянии (S = 1) будет равно:
3<? = ^- A34-6)
Подобным же образом получим для синглетного состояния (S = 0):
где — уже некоторая новая длина, определяемая потенциалом взаимо-
взаимодействия в синглетном состоянии. Так как она входит в формулу для
сечения совершенно аналогично х3.= х, то соответствующую ей энергию
Ех = -— > 0 называют энергией «виртуального» уровня дейтона.
.£[1
Б. Упругое^1 рассеяние нуклонов]
В этом разделе мы рассмотрим упругое рассеяние нуклонов на нук-
нуклонах. Следует заметить, что при энергии нуклона Еа > 292 Мэв могут
образоваться мезоны, однако, вклад этого неупругого процесса еще не
велик и при энергиях Еа — 400 Мэв.
Рассмотрим сперва первичную волну Ц>°, изображающую движение
двух нуклонов до их рассеяния. Мы будем рассматривать только относи-
относительное движение так, что Ч'° зависит лишь от разности координат нук-
нуклонов г^г^ — г2.^Очевидно, что
Y0 = V(r)S°(S2],Sz2O°(^, tS2), A34.8)
где S° —спиновая функция '(см. § 121), а Т° —функция изотопического
спина; szl, sz2—проекции спинов нуклонов на ось OZ, C1, C2— третьи
компоненты изотопического спина нуклонов. Причем, согласно A31.4) для
протона ts=-\-112, для нейтрона t3—— 1/г, Структура функции T(t3vtS2)
совершенно такова, как и структура функции S (s2l, s22). Оба нуклона мы
рассматриваем теперь как две тождественные частицы, подчиняющиеся прин-
принципу Паули; поэтому функция Ч>° должна быть антисиммеп.рична отно-
относительно перестановки нуклонов. При этом г переходит в—г, так что сим-
симметрия г|)°(г) совпадает с ее четностью. Симметрия функций -ф0 (г), 5° и
Т° должна быть выСрана так, чтобы вся функция 4го была антисиммет-
антисимметрична. Если координатная функция г|)° (г) изображает первичную плоскую
волну с импульсом p = hk, то вместо eik r (ср. 80.5) следует брать сим-
метризованную функцию
Эта симметризация выражает тот факт, что мы теперь" не различаем,
какой из нуклонов 1 или 2 являются мкиенью и какой рассеивается.
Если мы теперь обозначим амплитуду волны, рассеянной в угол 9 от
первичной волны eih r через А (Ь), то очевидно, что волна, рассеянная от
e-ik т будет А (я — 6). Действител1гно, замена г на — г означает замену 6
на я — Ь. Поэтому для одинаковых чгстац, в отличие от (80.5), вся
волна, падающая вместе с рассеянной, для больших г представляется
в виде: ^.^
Фа, s Й = ^ ± e-S7 + ylkr [Л(Ь)±А(я-Щ A34.10)
469

Соответствующее дифференциальное сечение q F) будет равно:
Л(я~6)р. A34.11)
В A34.10) мы не выписали спиновой зависимости функции tyayS
и амплитуд А. Запись, учитывающая эти зависимости, гласила бы:
¥(г с с f t \ ,1,0 jr\ CO (a Q \Т° If t \ 4-
V' zV uz2> LSv '32/— та. s УI ^ X^zV zit 1 l'3lf '32/1
+ y Г[А(Ь, szl, sz2, t31, t32)±A{a-b, szl, sz2, t3l, t32)\. A34.12)
Рассмотрим теперь некоторые частные случаи. Сперва обратимся
к рассеянию протона на протоне («рр»-столкновение). В этом случае
T=l, T3=-fl, S = 0 или 1. Спиновая функция S° (szV sz2) совпадает
с одной из функций S(szl, sz2) A21, 13, 14, 14', 14"), в зависимости от значе-
значения спина S и его проекции на ось oz. Функция для 7|=1и713= + 1 равна
Т° (t f \ 9' A t \ П 44 1 V\
где S's есть функция A21.14), в которой szl заменено на t3l и sz2— на t3r
Полное сечение рассеяния протонов дается теперь квадратом модуля
амплитуды при расходящейся волне — в A34.13). Обозначим это сече-
сечение для триплетного состояния S = 1 через:
sq (9) = р А F) + SA {л — 6) |2. A34.14)
Причем мы не выписываем здесь спиновых переменных. Сечения для всех
трех ориентации спина Sz = 0, ± 1, очевидно, равны. Сечение в синглет-
ном состоянии будет
-6)[3. A34.15)
Если в исходном пучке все ориентации спинов равновероятно {пучок
неполяризован), то каждое из состояний спина имеет вероятность 1/4.
Поэтому дифференциальное сечение рассеяния неполяризованных протонов
будет:
7(9)^F)+1^6)
При пренебрежении электромагнитными взаимодействиями (взаимодей-
(взаимодействие зарядов и магнитных моментов) оператор Т3 не входит в гамиль-
гамильтониан. Поэтому взаимодействие нуклонов, в этом приближении, должно
быть изотонически инвариантно. Иными словами, оно может зависеть
только от значения полного изотопического спина, но не от его проекций.
Для столкновения двух нейтронов (««««-столкновение) имеем Т=1,
Т3 = — 1. Отсюда следует, что сечение рассеяния двух нейтронов равно
сечению для рассеяния протонов:
?пп(в) = <7рРF). A34.17)
Несколько сложнее обстоит дело при столкновении протонов с ней-
нейтронами («р«»-столкновение). В этом случае мы имеем дело с суперпози-
суперпозицией двух состояний: Г=1, Г3 = 0 и Г = 0, Г3 = 0.
Действительно, если мы рассмотрим первичную волну в A34.8),
то видно, что Т° (t31, t3i) может быть равно либо S's" (tsv t32) для T=l,
Г3 = 0 (ср. 121.14"), либо Sa(t3l,t32) (ср. 121.13), для Г = 0, Г3 = 0:
T°(t3l, tS2) = ~{S ,i(*8l)S ,(/8a)±S , (gSj(a, A34.18)
У г -t- 2 2 +2 2
470

причем, индекс + 1/2 означает протон, а индекс — 1/2 —нейтрон. Оба
возможных состояния являются суперпозициями состояний протона и ней-
нейтрона.
Чтобы получить состояние протона и нейтрона, следует взять супер-
суперпозицию состояний с 7=1 и Т = 0. Например, для синглетного состоя-
состояния S — 0, необходимая первичная волна напишется в виде:
~
+ 2
^(г)S
Sa (sxvs2,)
A34.19)
Действительно, эта суперпозиция представляет собой такую волну,
что частица, имеющая импульс + k, имеет изотопический спин t3 = + 1/2
(т. е. является протоном), а частица, имеющая импульс — k, имеет изо-
изотопический спин ts= — V2 (т е. является нейтроном). Это есть правиль-
правильный выбор первичной волны, представляющей протон с импульсом + k
и нейтрон с импульсом —k. Нумерация же частиц 1 и 2 не имеет ника-
никакого значения.
В силу линейности уравнений, амплитуда рассеянной (р, п) — волны
Fpnity будет также суперпозицией амплитуд /^F) = А1(Ь) + Л1(л — 9)
и ^о (в) = А> (9) + А, (л - 9) для со- 4П .„_
стояний Т — \ и Т — 0, соответствен- 24 -
но, и притом с теми же коэффициен-
коэффициентами, что и суперпозиция первичных ™
волн ( + 1/У2), т. е.
смг страд
+pom-
A34.20)
Поэтому дифференциальное сечение
для «р«»-рассеяния будет равно
= Ugl (9) +
+ Re [Fo F)^F)].
A34.21)
Рассмотрим теперь сумму qpn F)+
+ 7pn(n — 6). Очевидно, что эта сумма
дает сечение для наблюдения любой
рассеянной частицы р или п. Действи-
ТеЛЬНО, еСЛИ ПрОТОН рассеян В уГОЛ 6,
то нейтрон рассеян в угол л —9.
Но при замене 6 на л-6 имеем F;(n -6) = ^1(б
координатная функция симметрична, а_^0(л-6) =
I — U она антисимметрична. Поэтому:
n(б) 4-7Рп(я- 6) = 7i(9) + <7о(в).
U5"
Рис, 92. Угловая зависимость упругого
рассеяния нуклонов в различных изо-
изотопических состояниях:
^=Od7oF)) и 7"=l(i7i(8)) для энергии нукло-
нуклонов 400 Мэв; для Т= 1 рассеяние изотропно!.
Но
так как при Г=1
Falb), так как при
A34.22)
()
Следовательно, измеряя qpn(%) и qpp{%), мы
CERN, Symposium A956), доклад В. П. Джелепова.
471

можем вычислить сечение рассеяния qo(Q) в изотопическом состоянии
7 = 0.
На рис. 92 показана угловая зависимость <7ОF) и <7,*F) при энергии
380 — 400 Мэв. Как видно, взаимодействие в состояниях Т — 0 и Г=1
совершенно различно. Полные сечения «/о и Я\ также совершенно раз-
различны: сечение q^ в области высоких энергий практически постоянно,
а сечение q0 уменьшается с энергией.
§ 135. Поляризация при рассеянии частиц со спином
Как мы видели, ядерные взаимодействия зависят от спинов частиц.
Это приводит к тому, что при столкновении нуклонов друг с другом или
с ядрами амплитуда рассеянной волны оказывается различной для различ-
различных ориентации спина рассеянных частиц: возникает спиновая поляриза-
поляризация. Первоначальные частицы обычно неполяризованы. Поэтому исходное
состояние является обычно не чистым, а смешанным; оно представляет
собою набор состояний с различными ориентациями спинов, причем каждая
ориентация имеет свою вероятность Ра. Такой пучок более целесообразно
описывать матрицей плотности q (см. § 45), нежели волновой функцией.
Рассмотрим поляризацию частицы со спином 1/2. Выберем в каче-
качестве базисных спиновых функций функции ф, и ф2.
Пусть в первоначальном пучке смешаны с вероятностями Pt и Р2
два спиновых состояния я|), и я|J. Эти состояния можно представить как
линейную комбинацию базисных состояний фг и ф2:
2
я|>г= Y cihc?k, t=l, 2. ' ' A35.1)
k=\
Согласно D5.4), элементы матрицы рассеяния q определятся фор-
формулой
2
Qik = Y РпСщСпъ. A35.2)
71=1
Среднее значение любого спинового оператора О, согласно общей фор-
формулы D5.10), запишется теперь в виде:
0 = Sp(q0). A35.3)
Так как q есть двухрядная матрица, то она может быть представлена
в виде линейной комбинации матриц Паули:
q = A+(§■&). A35.4)
Выразим теперь коэффициенты А, В через среднее значение спина частицы
S = -н- а, или, что удобнее, через среднее значение а. Для этого заметим,.
что
Spa=0, Spe%=2. A35.5)
Поэтому
°х = SP (Qax) = ASpax + Spax (Ba) = Bx,
т. е. а=В. Далее, условие нормировки требует, чтобы Spg = 2A = I,.
т. е. Л = 1/2. Таким образом, матрица:
(,= 1-)-а.а A35.6)
472

характеризует состояние поляризации в исходном пучке. Как видно, она
непосредственно выражается через вектор спина а и его среднее значе-
значение а. Для неполяризованного пучка q = 1/2. После рассеяния спиновые
состояния изменятся и вместо смеси состояний \]з1 и \]з2 мы получим смесь
некоторых новых состояний ty[ и ty'2. Эти новые состояния могут быть
выражены через старые с помощью матрицы рассеяния Sik F)
A35.7)
Элементы этой матрицы зависят от угла 9 и импульса частиц к. При
6 Ф 0 матрица рассеяния S (9) пропорциональна амплитуде рассеяния А(Ь).
Согласно правил преобразования матриц новая матрица плотности q' будет
равна:
q' = S*qS, A35.8)
где S+ матрица, сопряженная к S (см. стр. 470). Если исходный"*пучок был
не поляризован, то q = х/2 и
q' = 1s+S. A35.9)
Эта величина не нормирована к 1, так как S, кроме спиновых переменных,,
содержит и другие F, k, ...). Поэтому среднее значение после рассеяния
следует вычислять по формуле
—у
Эту величину и называют поляризацией Р:
Р = а'. . A35.11)
Конкретное значение Р зависит от матрицы рассеяния S или, что тоже,
от амплитуды рассеяния А. Однако можно показать, что вектор поляриза-
поляризации Р перпендикулярен плоскости рассеяния, образованной двумя век-
торами: волновым вектором k до рассеяния и волновым вектором к' после
рассеяния.
Действительно, Р есть среднее от а, поэтому Р есть псевдовектор
и, следовательно, правая часть в A35.10) есть также псевдовектор. Но
единственный псевдовектор, который мы можем построить из величин,
характеризующих амплитуду рассеяния, есть векторное произведение
k х k'. Поэтому мы можем утверждать, что
P = a(kxk'), A35.12)
где а есть некоторый множитель пропорциональности, зависящий от углов
и энергии. Отсюда видно, что поляризация для малых углов равна 0.
Если направить k по оси oz, то при перемене азимута рассеяния с ф
на л — ф (в частности, рассеяние направо или рассеяние налево) поляриза-
поляризация меняет свой знак.
Опыт подтверждает существование поляризации *. При рассеянии про-
протонов на протонах при энергии 600 Мэв поляризация достигает 40%.
1 См. В. П. Джелепови Б. М. Понтекорво, Усп. Физ. наук, XXIV,
стр. 15, 1958.
473

§ 136. Применение квантовой механики к систематике
элементарных частиц
В § 3 сведена в таблице довольно большая совокупность известных
к настоящему времени элементарных частиц.
Существенной особенностью большинства элементарных частиц являет-
является их неустойчивость — они распадаются в течение короткого времени
(см. время жизни в последнем столбце таблицы), превращаясь в другие,
тоже элементарные, частицы.
Среди других превращений этих частиц особую роль играет процесс
взаимодействия частиц с античастицами (электрон-позитрон, протон-анти-
протон-антипротон и т. д.), так называемый процесс аннигиляции. В процессе аннигиля-
аннигиляции частица и античастица исчезают как таковые, превращаясь в мезоны,
■у-кванты, электроны и нейтрино. Эти процессы взаимодействия не могут
быть рассмотрены в рамках нерелятивистской квантовой механики,
в которой как и в классической механике имеет место закон сохранения
числа частиц. Поэтому теория элементарных частиц не может быть дана
без привлечения квантовой теории полей и релятивистской квантовой
механики. Тем не менее, основные принципы квантовой механики доста-
достаточны для пояснения систематики элементарных частиц.
Совокупность элементарных частиц можно прежде всего разбить по
массам на тяжелые частицы — барионы, средние — мезоны и легкие —
лептоны. К барионам относятся нуклоны (протон, нейтрон) и гипероны
(сверхтяжелые). В настоящее время известны гипероны: Ло (лямбда-
частица), 2 (сигма-частица) и каскадный гиперон S (кси-частица). Все
гипероны имеют спин, равный Уг, и следовательно, являются фермионами
(§ П6). При распаде гиперонов в конечном счете получаются нуклоны.
Поэтому гипероны могут рассматриваться как возбужденные состояния
нуклона, причем мерой возбуждения служит масса. В соответствии с этим
на диаграмме (рис. 93) гипероны показаны в виде горизонтальных черточек-
уровней, указывающих массу (в единицах электронной массы). Штрихо-
Штрихованные линии показывают квантовые переходы, сопровождающиеся испу-
испусканием л-мезонов или -у-квантов и переходом на нижний уровень возбу-
возбуждения (превращением в более легкий гиперон). Как видно из таблицы,
уровни нуклона состоят из групп линий, представляющих близкие по массе
частицы с различным зарядом. Каждой группе частиц можно приписать
общее значение изотопического спина с различными значениями его проек-
проекций, т. е. такая группа является изотопическим мультиплетом (§ 131).
Протон и нейтрон (нижнее состояние) представляют дублет: Т= Уъ, Г3= ± Уъ.
Л0-гиперон, нейтральная частица, не имеющая близких соседей, обладает
изотопическим спином: Г=0, Г3=0. 2-гиперон имеет три зарядовых состо-
состояния @, ±е). В соответствии с этим его изотопический спин Т=\, Г3=
=0, ±1. Наконец, Н-гиперон является дублетом (заряд 0, —ё), что соот-
соответствует изотопическому спину: Т = 1/2, Т3= ±-к •
Приведенная единая картина гиперонов наталкивается, однако, на труд-
трудность. Именно, связь заряда частиц с их изотопическим спином, выражен-
выраженная формулой A31.9), не выполняется для возбужденных состояний. Для
разрешения этой проблемы Гелль-Манн и Нишижима предложили обоб-
обобщить формулу A31.9), введя новую характеристику элементарных частиц —
«странность», выражаемую новым квантовым числом S. С учетом этого
числа вместо A31.9) следует писать
Q = e(~N + Tb + ±s\ A36.1)
где N — число бариснов.
474

Для нуклонов S = 0, для Ло- и 2 -гиперонов S = — 1 для Н-гиперонов
S = —2. Таким образом, полный индекс частицы содержит значения
спина а, изотопического спина и его проекции G, Т3) и странности (S).
Например, 2~-гиперон имеет: о — -^, Г=1, Т3= — 1, S= —1. Эти чет-
четверки чисел указаны на диаграмме (рис. 93) и в таблице элементарных
Масса в
3000-
Масса в
электронных массах -
2100
W00-
1900
1838,6
1836.1
1800
Рис. 93. Схема элементарных частиц и их распадов:
а) бариоиы (уровни нуклона), б) мезоны и лептоиы
частиц на стр. 27 для всех частиц. Для античастиц Т3 и S имеют обрат-
обратные знаки. Античастицы обозначены знаком «тильда» (—), напимер, Ло.
Состояния античастиц изображены на диаграмме отдельно. Мезоны и леп-
тоны изображены в правой части диаграммы1. Наиболее тяжелыми мезо-
мезонами являются Д"-мезоны. По всей совокупности данных спин Д"-мезона
1 Указанные в диаграмме справа К\ и К^-частицы явлются суперпозициями
■состояний К0 и К0.
475

а = 0, изотопический спин Т = -^, T3=±-x- (изотопический дублет с заря-
зарядами 0 и е). Странность Д"-мезонов S= 1. Как видно из схемы Д"-мезоны
распадаются либо на л-мезоны, либо на лептоны.
Три л-мезона (л° и л±-мезоны) имеют спин а=0. Они являются бозо-
бозонами (§ 116) и образуют изотопический триплет сТ= 1, Г3 = 0, f 1. Стран-
Странность л-мезонов, как легко проверить на формуле для заряда, S — 0.
При сильных взаимодействиях мезонов и барионов имеет место закон
сохранения странности, т. е. изменение s при таких взаимодействиях равно
нулю. Это обстоятельство находит выражение в экспериментально уста-
установленном законе парного рождения «странных» частиц (частиц с S Ф 0).
Например, реакция образования Л0-гиперона: п~-\-р—>Л0-|-л0 невозможна,,
так как в результате реакции имеется лишь одна странная частица Ло.
Напротив, реакция п~-{-р—>Л0 + /@ является обычной реакцией получе-
получения Л0-гиперонов и Д"-мезонов. При распадах странных частиц (так назы-
называемое слабое взаимодействие) странность не сохраняется. Например, при
распаде Ло—>р-|-л~, AS Ф 0.
Обратимся к последней группе частиц — лептонам. К ним относят
электрон е (и его античастицу— позитрон е), нейтрино v (и антинейтрино v),
а также (л-мезон (и цГ).
В настоящее время не существует определенной систематики лептонов-
и применение к ним понятий изотопического спина и странности не оче-
очевидно.
Особое место в систематике занимает также фотон у, имеющий спи»
<т= 1.
Возможно, что лептоны и фотоны имеют особо фундаментальное зна-
значение в мире элементарных частиц, так как все неустойчивые частицы*
в конце концов распадаются либо на электроны и нейтрино, либо на фотоны.

ГЛАВА XXV
ЗАКЛЮЧЕНИЕ
§ 137. Формальная схема квантовой механики
Излагая основные положения квантовой механики, мы не стремились
к строгой дедуктивной последовательности. Логическая стройность дедук-
дедуктивного изложения неизбежно влечет за собой абстрактность, которая
скрадывает опытные основания того или иного обобщающего положения.
Напротив, в заключение книги целесообразно коротко резюмировать основ-
основные положения и задачи квантовой механики.
Квантовая механика изучает статистические ансамбли микрочастиц
и решает три главные задачи:
1) Определение возможных значений физических величин (определение
спектра величин).
2) Вычисление вероятности того или иного значения этих величин
в ансамбле микрочастиц.
3) Изменение ансамбля во времени (движение микрочастиц).
Принадлежность микрочастицы к определенному ансамблю характери-
характеризуется в квантовой механике волновой функцией г|з.
Эта функция есть функция полного набора величин, который мы обозна-
обозначим через1 х. Число величин, входящих в полный набор, определяется
природой системы и равно" числу ее степеней свободы.. В зависимости от
выбора набора величин, являющихся аргументами волновой функции,
говорят о том или ином представлении1 состояния.
Волновая функция имеет еще (часто опускаемый) индекс («), напри-
например, tyn(x), указывающий на другой набор, которым определена сама волно-
волновая функция.
Статистический ансамбль, описываемый определенной волновой функци-
функцией, называют чистым. Ансамбль, не имеющий определенной волновой функ-
функции, называют смешанным. Он характеризуется матрицей плотности.
Основное свойство чистых квантовых ансамблей выражается в прин-
принципе суперпозиции: если два возможных состояния изображаются
волновыми функциями ■vjI и iJj2, то существует и третье состояние,
изображаемое волновой функцией:
■^ = c^L + c2Mp2, (I)
где сг и с2 — произвольные амплитуды.
Далее, все соотношения между физическими величинами выражаются
в квантовой механике на языке линейных, самосопряженных операторов
1 Здесь под х не следует понимать обязательно координату или координаты.
.Этой буквой мы обозначаем любую совокупность переменных, дискретных или непре-
непрерывных, образующих какой-либо полный набор.
77

таким путем, что каждой действительной физической величине L сопо-
сопоставляется изображающий ее линейный, самосопряженный оператор L.
Изображение величин с помощью операторов связывается с изме-
измеримыми величинами с помощью формулы, определяющей среднее значение
величины L в состоянии if. Эта формула гласит:
(II)
при условии нормировки1:
Это определение среднего позволяет найти спектр величины L, т. е.
возможные ее значения. Для этого разыскиваются состояния, в которых
величина L имеет только одно определенное значение, т. е. такие состоя-
состояния, в которых AL2 = 0. Это требование ведет к уравнению для собствен-
собственных функций оператора L (ср. § 20):
Отсюда находится спектр L (непрерывный или дискретный) и соответ-
соответствующие собственные состояния ifL(x). Принимается, что собственные
значения оператора L и суть те значения величины L, которые наблю-
наблюдаются на опыте.
Так как собственные функции образуют ортогональную систему
функций, то любая волновая функция if (х) может быть разложена в спектр-
по собственным функциям г|з^ (х):
где
c(L) = (ifL) if), A37.2)
а знак суммы ^ Должен пониматься как знак интеграла \ dL . s,, если
спектр L непрерывный.
Это спектральное разложение фактически осуществляется в устрой-
устройстве, которое разлагает ансамбль if (х) по подансамблям ^l(x), в частно-
частности, в измерительном аппарате, измеряющем величину L.
Вероятность найти значение величины равным L в ансамбле,
характеризуемом волновой функцией if (x), равна | с (L) |2 (в случае непре-
непрерывного спектра |c(L)j2 есть плотность вероятности).
С другой стороны, с (L) есть волновая функция того же ансамбля,
но взятая в «/^-представлении. Иначе говоря, с (L) и if (л:) изображают
один и тот же ансамбль.
Четвертый существенный пункт квантовой механики относится
к изменению ансамблей во времени; именно изменение во времени волно-
волновой функции, описывающей ансамбль, находится из уравнения Шредингера:
|f (IV)
где оператор Н есть гамильтониан системы, зависящий только от при-
природы системы и от рода действующих на нее внешних полей. Оператор Н
1 Символом («, Lv) мы обозначаем «скаллрноз произвгдэние» и и Lv, которое
в случаэ непрерывных паремгнных ишегт вид интеграла: [(к, Lv) — \ u*-Lvdx, а в
случае дискретных переменных вид суммы: (и, Lv) = ^ 2 KJJLnmom.
478

будет оператором полной энергии системы, если внешние поля не зависят
от времени. Обычно
H = T+U, A37.3)
где Т есть оператор кинетической энергии, а (У —оператор, представляю-
представляющий потенциальную энергию или силовую функцию.
Оператор Т есть функция оператора импульса Р. Опыт показывает,
что в отсутствии магнитных сил:
^ A37.4)
где Pk — импульс fe-й частицы, a mh — ее масса. В случае наличия магнит-
магнитного поля Ph следует заменить на
Ш = ^--Г^> A37.5)
где Ак — вектор-потенциал в точке нахождения fe-й частицы.
Из уравнения Шредингера (IV) и из определения среднего значе-
значения A1) следует, что
^4f ) (ф, [Я, L]4>). A37.6)
Поэтому оператор —п-, изображающий производную величины L по
времени, имеет вид:
-§- = 4г+[Я' Ц, A37.7)
где [И, \L\ — -г- (HL — LH) есть квантовая скобка Пуассона.
Интегралы движения характеризуются тем, что
•^ = 0. A37.8)
В отсутствии внешних сил важнейшими интегралами движения будут:
энергия, полный импульс системы:
^ = |]Pfc=-iA|]yfc A37.9)
и момент импульса:
M = 2[rvPfe] + 2Sfe, A37.10)
к k
где Sk—спиновый момент fe-й частицы.
Вид оператора Р как раз и может быть определен из того факта,
что он изображает величину, являющуюся интегралом движения, т. е.
коммутирует с оператором Н в отсутствии внешних сил. Из операторов
Рк и rfe можно строить и другие, более сложные операторы, физическое
значение которых может быть весьма специальным. Таким образом вид
важнейших операторов определяется сам собою, если постулировать вид
оператора Гамильтона (т. е. уравнение Шредингера).
Последнее из основных предположений квантовой механики относится
к системам одинаковых частиц. Это —принцип тождественности.
Согласно этому принципу, обмен любой пары одинаковых частиц (k, /')
не ведет к физически новому состоянию. Математически это выражается
479

в форме условия, накладываемого на волновые функции:
Pk}4 = W, (V)
где Я,= ± 1 есть собственное значение оператора перестановки pk}-. Это
условие ведет к делению состояний на два класса:
W = WS (симметричные), A37.11)
W — Wa (антисимметричные). A37.1 Г)
Далее, из уравнения Шредингера следует, что симметрия не может
измениться с течением времени. Поэтому принадлежность частиц к сорту
«s» или сорту «а» может определяться только природой частиц. Частицы,
состояния которых описываются антисимметричными волновыми функ-
функциями Wa суть частицы Ферми. Они подчиняются принципу Паули, который
вытекает как следствие из свойств ансамбля, описываемого антисимметрич-
антисимметричными волновыми функциями.
Частицы, состояния которых описываются симметричными функция-
функциями W., называются частицами Бозе.
Таким образом мы видим, что в основе квантовой механики лежат пять
фундаментальных положений: (I) — принцип суперпозиции состояний,
(II) — определение среднего значения, (III) — толкование собственных
значений как единственно возможных, (IV) — уравнение Шредингера
и (V) — принцип тождественности частиц одного сорта. Физические основа-
основания этих положений были подробно обсуждены в соответствующих главах
курса.
§ 138. Границы применимости квантовой- механики
Вполне строго и точно границы применимости физической теории могут
■быть указаны лишь на основе более общей теории, включающей рассматри-
рассматриваемую как частный или предельный случай. В настоящее время не суще-
существует теории микроявлений, более обширной и глубокой, нежели кванто-
квантовая механика. Поэтому границы квантовой механики могут быть проведены
лишь очень ориентировочно. Можно наверное сказать лишь то, что кванто-
квантовая механика неприложима к системам, состоящим из частиц, движущихся
со скоростями, сравнимыми со скоростью света с, т. е. в релятивистской
•области.
Квантовая механика является механикой систем с ограниченным,
конечным числом степеней свободы. В этом отношении она является анало-
аналогом классической механики систем материальных точек. Если скорости
движения частиц становятся сравнимыми со скоростью света, то вообще
не приходится говорить о системе с конечным числом степеней свободы.
В самом деле, в этом случае нельзя не учитывать конечной величины скоро-
•сти распространения электромагнитных полей. Если за время At расстоя-
расстояние между частицами rik изменится на Ar3-fe,To при условии, что относитель-
относительная скорость частиц -^ близка к скорости света, примерно такое же время
нужно для распространения электромагнитного поля на расстояние Дг3-,<.
Поэтому наряду с частицами нужно рассматривать электромагнитное поле,
которое само и создается этими частицами и на них действует. Иными сло-
словами, в систему должны быть включены не только все частицы (что дает
3iV степеней свободы для N бесспиновых частиц и 4/V для N частиц со
•спином), но и электромагнитное поле, состояние которого определяется
•бесконечным числом степеней свободы.
•480

Это электромагнитное поле в последовательной теории должно также
рассматриваться квантовым образом, так как известно, что импульс и энер-
энергия поля передаются фотонами.
Когда энергия фотонов или частиц превышает собственную энергию
частиц т0с2, то частицы могут возникать и исчезать. Так, фотон у с энер-
энергией /гш>2тос2 может исчезнуть и превратиться в пару частиц: эле-
электрон (е~, т0) и позитрон (е+, т0). Наоборот, позитрон и электрон могут
превратиться в фотон *.
Эти процессы превращения можно выразить в виде схемы.
у ^± е++е". A38.1)
В приведенном примере частицы возникают и уничтожаются благодаря
электромагнитному взаимодействию.
Другого рода процессы, при которых возникают частицы, это про-
процессы так называемого сильного взаимодействия. Примером такого взаимо-
взаимодействия может служить реакция
. A38.2)
В этом процессе я"-мезон сталкивается с протоном и рождает пару
/(-мезонов.
Элементарные частицы превращаются также друг в друга при сла-
слабых взаимодействиях, ведущих к радиоактивному распаду частиц. Напри-
Например, нейтрон спонтанно превращается в протон, излучая электрон е~
и нейтрино v:
n-±p + e- + v. A38.3)
В радиоактивном, позитронном распаде ядер возможна и обратная
реакция:
p->n + e* + v. A38.31)
Распадаются и мезоны, в частности
n+-^n+-fv, A38.4)
\i+-*[e* + hv+'v. A38.4')
Сопоставление приведенных схем показывает, что нейтрон нельзя
рассматривать как сложную частицу, состоящую из протона и электрона.
Равным образом нельзя и протон рассматривать как состоящий из нейтрона
и позитрона. Мы имеем дело не с выбрасыванием готовых частиц, а с рожде-
рождением новых частиц (е+, е", hv) при превращении n~Zp (подобно тому, как
излучаемый атомом квант света не скрывается в готовом виде внутри атома,
а возникает заново, в результате превращения энергии возбужденного
электрона в энергию излучения).
В реакциях A38.4) и A38.4')мы опять имеем дело нес распадом мезонов
на готовые частицы, из которых они состоят, а с превращением их, с воз-
возникновением новых частиц.
Во всех этих явлениях нет уже ничего общего с механикой системы
частиц: само число частиц и их природа подвергаются изменениям. В этих
явлениях мы имеем дело с системами, которые обладают неопределенным,
неограниченно большим числом степеней свободы. Такого рода системы
скорее родственны полям, нежели механическим системам материальных
частиц. В частности, в области больших энергий исчезает та грань, кото-
которая позволяла нам различать «истинные» частицы: электроны, протоны,
нейтроны, атомные ядра, атомы и т. п. от «эфемерных» фотонов. Закономер-
Закономерности, управляющие частицами первого рода, и составляли, в сущности
31 И. Д. Блохинцев 481

предмет квантовой механики, напротив, фотоны мы рассматривали как
объекты изучения теории электромагнитного поля1. Эта грань основывалась
на том факте, что перечисленные частицы имеют массу покоя ти, так что
они остаются неизменными и не могут возникать заново при нерелятивист-
нерелятивистских энергиях E<tm0c2.
Напротив, масса покоя фотона равна нулю, так что он при всех
обстоятельствах является релятивистской частицей, способной рождаться
и исчезать при как угодно малых энергиях.
Если энергии становятся сравнимыми с энергией покоя частиц, то
все частицы уподобляются фотонам: рождаются, исчезают и превращаются '
друг в друга. Поэтому при этих больших энергиях более целесообразно
говорить об электронно-позитронном поле, о мезонном поле, о поле протон-
протонном или нейтронном («нуклонные» поля), нежели о системе данных частиц2.
За последние годы теоретическая мысль сделала существенные успехи
в развитии квантовой теории полей. Однако нигде и никому еще не удалось
достигнуть окончательного успеха.
Уже в квантовой теории электромагнитного поля выяснилось, что
распространение теории поля за рамки простейших процессов поглощения,
излучения и рассеяния фотонов на любые электромагнитные процессы,
включая взаимодействие частиц, ведет к принципиальным трудностям.
В этих случаях приходится иметь дело с бесконечно большим числом фото-
фотонов. Вместе с тем оказывается, что так же, как и в классической электрон-
электронной теории, электромагнитная масса заряженных частиц равна бесконеч-
бесконечности.
Этот результат получается и в теории других полей. Проблема массы
частицы видимо есть проблема структуры частицы и представляет собою
труднейшую и до сих пор нерешенную задачу теории.
Особо важное место занимает в современной теории релятивистская
теория электрона, развитая П. Дираком. Она является обобщением нереля-
нерелятивистской квантовой механики электрона на случай больших скоростей.
Эта теория, в сочетании с квантовой теорией поля, позволяет рассчи-
рассчитать многие релятивистские явления такие, как превращение кванта света
в электроны и позитроны, и обратно, рассеяние света на электронах и дру-
другие. Она дает полную теорию движения быстрого электрона во внешнем
поле например, в кулоновском поле ядра атома. Особенно интересны поп-
поправки, вносимые в это движение нулевыми колебаниями электромагнитного
поля и поляризацией вакуума. В настоящее время эти эффекты получили
экспериментальное подтверждение и являются доказательством изумитель-
изумительного факта: в вакууме существуют постоянные нулевые колебания, подобно
тому, как они существуют в твердом теле, более того, из-за образования
пар позитронов и электронов и последующей их аннигиляции происходит
поляризация этого вакуума. Все эти эффекты удается вычислить применением
теории возмущения, основанной на малости электрического заряда элек-
электрона.
При этом для устранения бесконечностей из расчетов применяются
специальные методы «перенормировки», позволяющие последовательно
устранять бесконечность в каждом приближении3.
Применение этих же методов к сильным взаимодействиям таким, как
взаимодействие мезонного поля с нуклонами, пока не удается. Причина
1 Ср. § П8.
2 Подобно тому, как говоря о фотонах, мы имеем в виду квантовую теорию
электромагнитного поля.
3 См. А. И. Ахиезер, В. Б. Берестецкий, Квантовая электродина-
электродинамика, Физматгиз, 1959, Н. Н. Боголюбов и Д. В. Ширков. Введение в тео-
теорию квантованных полей, 1957. . ;
482

лежит в том, что сами методы «перенормировки» не решают проблемы
собственной массы частицы и их структуры, а представляют собой лишь
искусственный прием, позволяющий обойти явное рассмотрение физичес-
физических процессов в области особо малых масштабов.
§ 139. Некоторые гносеологические вопросы
С развитием квантовой механики теоретическая мысль в области физи-
физики вступила в период новой ломки основных физических представлений,
казавшихся очевидными и ненарушимыми. Эта радикальная перестройка
основных физических представлений касается, главным образом, понятия
частицы и принципов ее движения и сейчас вступает в новую еще более
углубленную фазу.
Философы-идеалисты стремятся представить эту ломку как кризис
материализма.
Известно, что в период выхода книги В. И. Ленина «Материализм
и эмпириокритицизм» философствующие реакционеры также пытались
опровергнуть материализм с помощью «самоновейших» данных тогдашней
физики. В своем глубоком и остром анализе Ленин показал Несостоятель-
Несостоятельность этих попыток и разъяснил, что научные положения диалектического
материализма не могут быть поколеблены открытием «электромагнитной»
или какой-либо другой природы вещества. Что же касается ломки физиче-
физических понятий, то с точки зрения материалистической гносеологии она являет-
является необходимым моментом в процессе развития познания. Ленин объяснил,,
в какие дебри философской путаницы может забраться исследователь, не
различающий ломки конкретных физических представлений о материи от
проповедуемого реакционерами кризиса материализма.
Современная ситуация в методологии теоретической физики, характер-
характерная для науки капиталистических стран, в принципе, не отличается от
рассмотренной Лениным в «Материализме и эмпириокритицизме». Буржуаз-
Буржуазная философская мысль, в соответствии с самой ее социальной природой,
по-прежнему опирается на идеалистическую философию, пытается и теперь
использовать развитие естествознания в реакционных целях.
Идеалистическая философия оказывает свое влияние на толкование
сущности и значения квантовой механики во многих зарубежных научных
школах. Копенгагенская физическая школа еще при самом своем возник-
возникновении связывала себя с позитивизмом и в дальнейшем весьма способ-
способствовала развитию субъективистских взглядов на сущность квантовой
механики.
Н. Бор в своем толковании квантовой механики1 исходит из прин-
принципа дополнительности. Согласно этому принципу возможны два класса
экспериментальных установок: первый класс допускает определение
импульсно-энергетических соотношений, второй — пространственно-времен-
пространственно-временных. Одновременное применение обеих установок принципиально исклю-
исключается. Таким образом «квантовое описание» явлений распадается на два
взаимоисключающих класса, которые являются дополнительными друг
к другу в том смысле, что их совокупность в классической физике дает
полное описание.
Из изложенного содержания принципа дополнительности видно, что
в нем подчеркивается не факт существования новых по своей природе-
1 См. Н. Бор, Можно ли сказать, что квантовомёханическое описание физи-
физической реальности является полным? УФН, XVI, 446, 1936.
31* 483-

объектов, а возможности макроскопических измерительных приборов.
Иными словами, на первый план выдвигаются не объективные особенности
микромира, следствием которых и является невозможность изучать их
методами классической физики, а возможности наблюдателя, оперирующего
с макроскопическими величинами и понятиями.
Такая направленность воровского принципа дополнительности ведет
к двоякого рода последствиям.
Во-первых, Бор и в еще большей степени его последователи разви-
развивают этот принцип в особую философскую концепцию дополнительности,
которая ведет к отрицанию причинности и объективности микроявле-
микроявлений1. Исходя из этой концепции, Н. Бор говорит «о непригодности обыч-
обычной точки зрения натуральной философии для описания физических
явлений того типа, с которыми мы имеем дело в квантовой механике2.
П. Иордан же прямо заявляет о «ликвидации материализма»3.
Во-вторых, применение рассматриваемого принципа в физике ведет
к субъективному толкованию волновой функции и понятия состояния
в квантовой механике. Волновая функция рассматривается не как объектив-
объективная характеристика квантового ансамбля, а как выражение сведений наблю-
наблюдателя, полученных в результате измерений. Реальность того или иного
состояния микросистем становится в таком понимании тождественной со
сведениями наблюдателя о микросистеме, т. е. превращается из объектив-
объективной категории в субъективную.
При анализе этих воззрений следует иметь в виду, что копенгагенская
школа исходит из позитивистских позиций, т. е. с самого начала отрицает
объективное существование материи, «ограничиваясь» упорядочением
«результатов наблюдения». В позитивистском понимании как классическая,
так и квантовая физика не являются отображением объективного мира,
а представляют собой математические конструкции. Для первой из этих
«конструкций» характерна возможность разделения понятий субъекта
и объекта, а для второй это разделение невозможно, так как субъект измере-
измерением «приготовляет физическую реальность». Таким образом, речь идет
не об анализе отношений познающего субъекта и объекта как частей объек-
объективного мира, а об анализе этих конструкций, т. е. об анализе в сфере
понятий.
С этих позиций позитивисты пытаются опровергнуть материализм таким
путем, что сначала его связывают с определенными, ограниченными физи-
физическими и философскими представлениями, а затем объявляют несостоя-
несостоятельными.
С точки зрения материализма сама возможность познания обусловлена
наличием материальных связей между познающим субъектом и объектом
исследования. В физике эта связь осуществляется с помощью различных
приборов. Такие приборы всегда влияют на объект, и обратно, объект влияет
на прибор. В классической физике предполагалось, что это взаимовлияние
может быть сделано как угодно малым; в квантовой области обнаружилось,
что это влияние не может быть как угодно малым. Мы видели, что измери-
измерительные приборы на самом деле меняют состояние систем и тем самым пре-
превращают один ансамбль в другой.
Было бы, однако, абсурдом, связывать материализм с принципиальной
малостью взаимодействий. Открытая в квантовой области конечность взаи-
взаимодействий не подрывает материализма и не ставит каких-либо границ
познанию.
1 См. N. Bohr, Atorntheorie und Naturbeschreibung, J. Springer, Berlin, I£31.
2 См. Н. Бор, цит. соч. УФН, XVI, 446, 1936.
3 P. J о г d a n, Physics of 20th century, Phil, library, New Jork, 1944.
484

Так, изучая космические лучи, применяют счетчики или другие при-
приборы. Эти приборы изменяют состояние обнаруживающихся в них отдель-
отдельных частиц, переводят их в новый ансамбль, но они не меняют в целом того
квантового ансамбля, который можно назвать ансамблем космических
лучей. Вносимое этими приборами нарушение в ход явления космических
лучей в целом, конечно, ничтожно, и поэтому ничто не мешает выяс-
выяснению объективных закономерностей, свойственных космическим лучам.
Таким образом, квантовая механика на самом деле изучает объектив-
объективную, существующую независимо от наблюдателя природу квантового
ансамбля.
При этом свойства .единичного микроявления квантовая механика
исследует посредством изучения статистических закономерностей. Эти
статистические закономерности имеют совершенно объективный характер.
Так, например, распад радиоактивных атомов, протекающий статистически
закономерно, происходит в природе сам по себе, без какого-либо вмеша-
вмешательства измерения.
Поэтому неправильно утверждать, что статистика вносится в явление
измерением: статистическая' закономерность существует независимо от
измерений, как объективная закономерность природы.
В классической физике закономерность может быть сформулирована
в другой форме, нестатистической. Именно состояние изолированной
системы в любой момент времени однозначно определяется ее состоянием
в некоторый начальный момент времени. Такое выражение закономерных
связей, господствующих в мире физических явлений, на самом деле прибли-
приближенно. Изоляция системы может осуществляться в природе лишь с некото-
некоторой степенью точности, но никогда полностью, и на самом деле, даже
и в классической области, возможна лишь для выражения простейших
закономерностей.
Будучи распространена на все явления, такая причинность ведет
к кальвинизму, предопределенности, когда по выражению Энгельса сама
«необходимость низводится до ранга случайности»1. Между тем, позитиви-
позитивисты навязывают материализму эту ограниченную точку зрения на причин-
причинность, и когда оказывается, что она не является универсальной, то объявля-
объявляют несостоятельным материализм2.
В квантовой области возможна изоляция только ансамбля в целом.
Волновая функция, выражающая состояние ансамбля, однозначно опреде-
определяется по уравнению Шредингера:
ih^ = H$ A39.1)
для любого момента времени, если она известна в начальный момент. Таким
образом, простейшая форма причинной связи сохраняется для ансамбля.
Единичные же события управляются статистической закономерностью.
Эта последняя закономерность не есть результат отсутствия закономерных
связей внутри мира единичных явлений, как это утверждают позитивисты;
напротив, статистическая закономерность как раз и есть выражение обще-
общего, закономерного в единичных явлениях.
Было бы неправильно полагать, что можно применять (или что впослед-
впоследствии станет возможным применить) к отдельным микроявлениям понятие
классической причинности, пригодное для изолированных систем. Скорее
всего, что такой изолированности в мире атомных явлений вообще не
существует.
1 Ф. Энгельс. Диалектика природы.
2 См. П. Иордан, цит. соч.
485

Если это так, то и последующее развитие атомной физики пойдет по
пути развития и углубления статистического метода, сквозь призму кото-
которого будут выясняться дальнейшие закономерности в строении атомов,
атомных ядер и самих элементарных частиц1. Открытие квантовых уровней
атомов, затем их тонкой, и, наконец, сверхтонкой структуры (разности
энергий порядка 10~12, КГ15 и 108 эрг, соответственно), достигнутое разви-
развитием техники статистического эксперимента, может служить прекрасной
иллюстрацией мощи этого метода и замечательным подтверждением ленин-
ленинского тезиса о познаваемости материи и о неисчерпаемости ее свойств.
Обратимся теперь к рассмотрению позиции копенгагенской школы
в понимании волновой функции. С наибольшей ясностью эта позиция может
быть разобрана в связи с дискуссией А. Эйнштейна и Н. Бора2. В этой
дискуссии был рассмотрен такой пример. Имеются две частицы 1 и 2,
претерпевающие столкновение. Пусть их состояние до столкновения,
в начальный момент времени, характеризуется волновой функцией
у¥°{х1,хг) = Мр0{х1)ч>°{хг). A39.2)
Волновую функцию этих частиц после столкновения, по истечении доста-
достаточно большого времени, обозначим через ^(л^, х2). Эта функция уже не
будет произведением функций, зависящих от xt и х2 порознь.
Измерим теперь какую-либо величину, относящуюся только к первой
частице для определенности, скажем, импульс чтой частицы pv После этого
измерения волновая функция первой частицы будет \]зР1 (л^). Разложим
¥ {xv x2) по функциям 1|зр {xt):
¥ {хи х2) = ^ Фр (х2) фр (xt) dp, A39.3)
где фр (х2) суть амплитуды в разложении Wp{x-l, х2) по \]зр(л:1). Если изме-
измерение импульса, произведенное над первой частицей, даст импульс pv
то волновая функция редуцируется к одному члену суперпозиции A39.3):
4(xvxi)-+<pPl{xi)Tl?Pi{xl). A39.4)
Таким образом, меняется и состояние второй частицы, хотя над ней
не производилось никаких измерений и она уже давно перестала взаимо-
взаимодействовать с первой. Следовательно, говорят, изменились «сведения»
об этой частице, а стало быть, и ее состояние, т. е. понятие состояния
в такой трактовке оказывается равносильным понятию «сведения о состоя-
состоянии».
Это и есть субъективная трактовка волновой функции. Эта трак-
трактовка связана с тем, что копенгагенская школа вообще отодвигает
на задний план статистический характер квантовой механики.
В квантовой механике состояние частицы характеризуется действи-
действительно не «само по себе», а принадлежностью частицы к тому или иному
ансамблю (чистому или смешанному). Эта принадлежность имеет совершен-
совершенно объективный характер и не зависит от сведений наблюдателя. Если эти
1 Впоследствии могут обнаружиться такие новые физические явления, о кото-
которых мы сейчас и не в состоянии подозревать и которые быть может позволят построить
иестатистическую теорию микроявлений. Сочетания утверждений, представляющихся
сейчас противоречивыми, могут гармонически согласоваться в будущем. Так, во вре-
времена расцвета классической термодинамики всякое утверждение о том, что тепло может
само собой перейти от холодного тела к более теплому, было бы воспринято как, оче-
очевидно, не научное, противоречащее «второму началу» термодинамики. Но мы зиаем,
что позднейшее развитие примирило подобную возможность с классической формули-
формулировкой второго начала в новых рамках кинетической теории материи.
2 См. УФН, т. XVI, вып. 4, 1936.
486

сведения не соответствуют природе ансамбля, то из них никаких новых
сведений, кроме разве нелепых, получиться не может.
Измерительные приборы, как мы пояснили в курсе, являются спектраль-
спектральными анализаторами: они разлагают исходный ансамбль по подансамблям,
характер которых зависит не только от природы ансамбля, но и существен-
существенным образом от рода самого прибора — анализатора.
В рассмотренном выше примере производится анализ по признаку,
относящемуся к первой частице. Но так как в исходном ансамбле х¥ (xv х2)
существовала корреляция между обеими частицами, обусловленная их
взаимодействием, то разложение по признаку pt одновременно выделяет
подансамбль для второй частицы, т. е. после измерения она оказывается
принадлежащей другому подансамблю, характеризующемуся волновой
функцией ц>щ{х2).
Поэтому изменение состояния второй частицы вызвано не изменением
«сведений» о ней, а взаимодействием первой и второй частиц до измерения.
Если бы такого рода взаимодействия не было, то и изменения состояния
первой частицы не оказывали бы влияния на состояние второй (волновая
функция ¥ (хт; хг) оставалась бы произведением функций от хх их2). В нашем
примере особенно ясна сущность корреляции, вызванной взаимодействием.
Действительно, пусть до столкновения импульс первой частицы был pj, вто-
второй — pi. Тогда, если после столкновения импульс первой частицы оказы-
оказывается равным рл, то импульс второй частицы, в силу закона сохранения
импульса, обязан быть равным p2=p\Jrpl—Р\ (стало быть ц>р (х2) есть волна
де Бройля с импульсом p2=Pi+p"—Pi)- Поэтому сортировка частиц 1 по
их импульсу является в то же время сортировкой по импульсу частиц 2.
Мы видим таким образом, что субъективная трактовка волновой функции
покоится на забвении ее статистической сущности.
Волновая функция, или, общее, матрица плотности на самом деле дает
совершенно объективную характеристику квантового ансамбля1. Задание Ч;
(или матрицы плотности) определяет все возможные разложения данного
ансамбля по отношению к любым анализаторам-измерителям.
Процесс разложения исходных ансамблей по какому-либо признаку
на подансамбли осуществляется не только в лаборатории, но и непосред-
непосредственно в природе. Во всех случаях, когда возникает такая ситуация, что
фазовые соотношения между различными состояниями tyn{x), входящими
в суперпозицию
^{x) = J]cn^n(x), A39.5)
становятся несущественными, мы можем говорить об «измерении» вели-
величины п, так как в этих случаях чистое состояние \]з (х) может быть
заменено смесью состояний tyn(x) с вероятностями2 —\сп\2.
После этого анализа мы можем обратиться к рассмотрению самой
сути дискуссии А. Эйнштейна и Н. Бора. В своей статье А. Эйнштейн
1 Значение волновой функции как характеристики квантового ансамбля весьма
основательно подчеркнуто в изложении К. В. Никольского. См. К- В. Николь-
Никольский, Квантовые процессы, ГИТТЛ, 1940.
2 Так, например, получается, если пучки, принадлежащие различным tyn(x),
пространственно расходятся. Заметим еще, что если бы указанное разложение ансамбля
не происходило в природе объективно, то не имело бы никакого смысла использовать
вычисляемые из квантовой механики вероятности в кинетических уравнениях. Между
тем, это приложение квантовой механики практически оказывается, пожалуй, одним
из самых важных.
487

и его соавторы1 высказали утверждение о неполноте квантовой механики2.
Именно они указали, что невозможно одновременно измерить р и х
у частицы, несмотря на то, что каждую из этих величин порознь можно
измерить, не влияя непосредственно на саму частицу. В приведенном
ими примере берется специальный вид функции:
*-^Pdp = 2n-b(xl-x2-x0), A39.6)
где х — некоторая постоянная. Пусть мы измеряем сначала импульс пер-
первой частицы и получаем значение р, тогда из .разложения A39.6) непосред-
непосредственно видно, что импульс второй частицы будет — р. Координата же ее
х2 будет совершенно неопределенной. Вместо импульса мы могли бы также
измерять координату первой частицы хх = х. Тогда из A39.6) следует, что вол-
волновая функция второй частицы будет ~ б(л:—х2—х0), что соответствует
х2=х—х0, т. е. мы определили координату второй частицы хг. Импульс же
второй частицы р2 в этом состоянии оказывается полностью неопределенным.
А. Эйнштейн и его соавторы сделали отсюда заключение, что квантовая
механика неполна, так как она не дает возможности определить одновремен-
одновременно р2 и хг, хотя при измерениях на вторую частицу прибором не воздей-
воздействовали.
Н. Бор в своем ответе А. Эйнштейну и его соавторам опровергает эту
точку зрения, исходя из принципа дополнительности. Именно, Бор утвер-
утверждает, что измерительные приборы в принципе всегда устроены так, что
возможно определение или только р, или только х. Поэтому квантовая
механика полна, так как полностью соответствует возможностям макроско-
макроскопических приборов. Ответ Бора был только полуправдой. Беря в основу
своего ответа принцип дополнительности, Бор выдвигает на первое место
возможности измерительных приборов, между тем как суть дела заключается
в новой природе объектов измерения — микрочастиц, к которым непримени-
неприменимо классическое понятие движения по траектории. Далее, Н. Бор оставляет
встороне статистическое толкование волновой функции. Изэтого толкования,
как это впервые с полной ясностью было показано Л. И. Мандельштамом3,
следует, что в приведенном А. Эйнштейном примере речь идет о разложении
исходного ансамбля ^(л:,, х2) на различные, исключающие друг друга
ансамбли (один раз по признаку рл, другой раз по признаку л:,). Изменение
же «состояния» второй частицы, как мы это поясняли выше, связано не
с воздействием прибора, а с корреляцией состояний первой и второй частиц,
обусловленной взаимодействием этих частиц, имевшим место до измерения.
Таким образом А. Эйнштейн и его соавторы, критикуя квантовую меха-
механику в связи с невозможностью измерить рих одновременно, даже в слу-
случае отсутствия прямого вмешательства прибора, упускают из виду прин-
принципиально иную природу микрочастиц: они неявно допускают, что микро-
микрочастицы не отличаются от классических частиц и только воздействие при-
прибора является причиной соотношения неопределенностей. Однако измери-
измерительные приборы являются классическими как в макроскопической, так
и в квантовой физике. Стало быть, дело не в приборах, и невозможность
1 См. А. Эй'н штейн, Б. Подольский и Н. Розен, Можно ли считать,
что кваитовомехапическое описание физической реальности является полным?
УФН, XVI, 440, 1936.
2 Речь идет о полноте квантовой механики внутри области ее применения.
То, что развитие физической теории микромира не закончилось на квантовой механике,
не оспаривается никем.
3 Неопубликованные лекции по квантовой механике, читанные Л. И. Мандель-
Мандельштамом в МГУ в 1939 году. ,

одновременно измерить р и х вытекает не из дефектов современных измери-
измерительных аппаратов, а обусловлена иной сущностью микрочастиц, отличной
от сущности частиц классических.
Вообще, неверно думать, .что современный физический эксперимент
недостаточен по точности для измерения «истинных» одновременных зна-
значений импульса и координаты микрочастиц. Напротив, он достаточно точен
для доказательства того, что для микрочастиц одновременно эта пара вели-
величин не существует в природе. Приведем пример, иллюстрирующий это утвер-
утверждение*. Из рассеяния рентгеновских лучей или электронов на атомах мож-
можно найти распределение электронов внутри атомов (т. е. |я|з(г)|2 ср. § 79).
Этот эксперимент означает определение координат электронов внутри атома.
На рис. 64 был приведен результат такого опыта для атомов гелия. Из него
следует, что значительная часть электронов обнаруживается столь да-
далеко от центра атома, что полная энергия Ео исходного состояния оказы-
оказывается меньше потенциальной и (г). Если мы допустим, что электрон
в атоме имеет и некоторый импульс р и некоторую координату г, то полная
р2
энергия будет равна Ео — £—|- г (г) и для всех электронов, обнаруживаю-
/ATI
щихся на расстоянии большем, нежели 0,6 А, окажется, что— < 0, т. е.
импульс будет мнимым. Это — очевидный абсурд, с любой точки зрения.
Другая возможность заключалась бы в предположении, что истинная
р2 р2
энергия электрона в атоме все же равна Е — х—Ь U (г)! £~ > 0 ). а Рас"
сматриваемая в квантовой теории энергия Еоесть лишь некоторое среднее из
этих «истинных» энергий: Е0=Е.Такое предположение означает, что энергия
ионизации различных экземпляров атомов одного и того же вещества, нахо-
находящихся, с точки зрения квантовой механики, в одном и том же состоянии
Ео, на самом деле различна. Разброс этой энергии АЕ=Е—Ео по порядку
величины равен Ео, что составит для атома Не около 20 эв; число элек-
электронов, заведомо участвующих в этом разбросе (т. е. электроны с U (г)>Е)
будет равно 20%. Этот вывод полностью противоречит любому опыту по
определению энергии ионизации, например, опыту Франка — Герца или
опытам по определению границы фотоэффекта. Ничего подобного такому
разбросу в значении энергии ионизации в действительности не наблюдается1.
Таким образом, предположение о том, что электрон в атоме, в состоянии
с заданной энергией, имеет какие-то скрытые значения пары величин (р, л:)
противоречит опыту.
Из того факта, что классическая пара величин (р, х) не является харак-
характеристикой движения микрочастиц, позитивисты делают вывод о существо-
существовании частиц вне времени и пространства. При этом они рассматривают
частицы не как объективную реальность, а лишь как понятие, служащее для
приведения в стройную математическую схему результатов наблюдения1.
Между тем, в квантовой механике имеется простое выражение того
факта, что частица существует независимо от наблюдателя, в пространстве
и времени, именно условие нормировки:
*)|ad*=l. [A39.7)
Это условие означает, что в любой момент времени (t) частица может
быть локализована в одной из точек пространства (х). Иначе говоря, частица
всегда может быть приведена в такое взаимодействие, что она обнаружит
свою корпускулярную природу. При этом она перейдет в такое состояние,
в котором импульс как физическая характеристика состояния частиц поте-
1 В сущности любой квантовый опыт мог бы служить такой иллюстрацией.
489

ряет свой смысл. Если же мы имеем дело с состоянием, в котором импульс
частиц имеет определенное значение (очень широкая группа волн де Бройля),
то в этом состоянии частицы могут быть локализованы в любой точке боль-
большой (по сравнению с длиной волны) области пространства, в любой момент
времени.
Поэтому нет такого случая, когда квантовая механика оперировала бы
с объектами вне времени и пространства; реальный квантовый ансамбль
всегда осуществляется в конечной области пространства и как таковой
существует конечное время. Квантовая механика показывает, однако, что
движение микрочастиц в пространстве и времени нельзя отождествлять
с движением материальных точек по траекториям. Движение по траектории,
согласно квантовой механике, является частным случаем движения, реали-
реализующимся лишь приближенно при определенных условиях (ср. § 34).
Кажущаяся парадоксальность квантовой механики возникает только
в тех случаях, когда новые, устанавливаемые ею закономерности стремятся
понять с точки зрения классической механики. Между тем, квантовая меха-
механика обобщает классическую, расширяет и углубляет понятие движения за
узкие пределы представлений классического атомизма. В силу этого было
бы неверно рассматривать представление о движении частиц по траектории
как «истину в последней инстанции». В. И. Ленин в книге «Материализм
и эмпириокритицизм», подчеркивая, что основное для материалистической
гносеологии есть признание объективности природы и объективности свойст-
свойственных ей закономерностей, говорит: «Но диалектический материализм
настаивает на приблизительном, относительном характере всякого научного
положения о строении материи и свойствах ее, на отсутствии абсолютных
граней в природе, на превращении движущейся материи из одного состоя-
состояния в другое, по-видимому, с нашей точки зрения, непримиримое с ним
и т. д. Как ни диковинно с точки зрения «здравого смысла» превращение
невесомого эфира в весомую материю и обратно, как ни «странно» отсутствие
у электрона всякой иной массы, кроме электромагнитной, как ни необычно
ограничение механических законов движения одной только областью
явлений природы и подчинение их более глубоким законам электромагнит-
электромагнитных явлений и т. д.— все это только лишнее подтверждение диалектиче-
диалектического материализма»1.
Квантовая механика показала ограниченность классического атомизма
и вскрыла качественно новые особенности микромира, нашедшие полное
подтверждение в технике и в практике физического эксперимента.
Поэтому с точки зрения диалектического материализма квантовую меха-
механику следует рассматривать как важнейший этап в развитии атомистики
20-го столетия. Этот этап свидетельствует об исключительной силе челове-
человеческого разума, сумевшего обнаружить в кажущемся хаосе микроявлений
поразительные по своей общности и точности закономерности.
1 См. В. И. Л е и и и, Материализм и эмпириокритицизм, Соч., IV изд. т. 14
стр. 248.

ДОПОЛНЕНИЯ
I. Преобразование Фурье
Напомним сначала интеграл Дирихле, фигурирующий в теории
интегралов Фурье:
\
с? (z)s-^dz, A)
z
а
где ф(г) —произвольная функция. Этот интеграл обладает следующими
свойствами: 1) если а, Ъ > 0 или а, Ь < 0, то этот интеграл равен 0;
2) если а < 0, Ь > 0, то он равен ф @) (для непрерывных функцийI.
Наличие функции — под знаком интеграла и взятие предела (т—>оо)
мы можем обозначить одним символом б (z), так что предыдущий инте-
интеграл напишем в виде
, \ * / \ ( — 0, если а' b > 0 или а, Ь < 0,1
(z) б (z) B)
JW ul = ?@), если а<0, Ь > 0. j (>
Символ б (z) часто называют б-функцией (дельта-функция). Общее опре-
определение символа б дано в дополнении III. Переходя к доказательству
эквивалентности формул A3.1), A3.3) и A3.5), A3.6), соответственно,
мы рассмотрим ради сокращения выкладок случай одного измерения
и докажем справедливость равенства
Pi = \ Ф* (Рх) PS<P (Px) dPx = \ Г (x) (-ihgz)* W dx> <3)
—ОЭ —ОЭ
где ф(рж) есть компонента Фурье от
dx, D)
а « — целая положительная степень. Для доказательства подставим
в C) вместо ф(рж) и ф*(рж) их выражения из D). Тогда имеем:
Рхх'
1 См., например, В. И. Смирнов, Курс высшей математики ОНТИ
1937, т. II, стр. 369. '
491

Вместо произведения рхе. h можно написать (ih-~r ) е * h . Тогда
получаем:
+оо -{-со р^' -f-эо рхх
Ш ~ [ ^§-хУе-г~с1х. F)
Проинтегрируем в последнем интеграле п раз по частям, причем
будем предполагать, что \]з (х) и ее производные обращаются в нуль
на границах интегрирования х=^со. Выполняя интегрирование, найдем:
+со _ х 1 х
\ 1— J -i~^(£fdx; G)
переменим теперь порядок интегрирования и будем интегрировать
сначала по рх.
+со +со -(-со _ рх(х' — х)
— со —со —оо
Введем теперь переменные t, = ~, z = x' — x. Выполняя в последнем
интеграле в (8) интеграцию по £ в конечных пределах от — т до + от,
а затем переходя к пределу от—>оо, мы можем написать (8) в виде
. , sin тг
—со —со
+_°° . +=°
iE*(A:+zN(z)rfz. (8')
На основании B) (а = — со, Ь=-(-оо), ф(г) = >ф* (л: + г) имеем:
х. (9)
Тем самым доказано C). Целая рациональная функция от рх имеет
вид F{px) = 1. а„-р"- Имеем:
{x)dx. (Ю)
Таким образом, эквивалентность A3.3) и A3.6) для случая одного
измерения доказана. Обобщение на три измерения сводится просто
к увеличению числа интегрирований и поэтому совершенно тривиально
[достаточно доказать эквивалентность A3.3), A3.6) для среднего от
Px-p™-plz, где т, п, / — целые и положительные степени].
Справедливость равенства
\ \ {P)Q^y( A1)
— ОО —СО
492

следует из справедливости C), если заметить, что по теореме Фурье
+со i—г—
Заменяя в C) \]з на ф, рх на х и меняя одновременно знак у мни-
мнимой единицы в показателе формулы D), мы получаем из C) и D) фор-
формулы A1) и D'). Из A1) далее следует
dpx. A2)
Это —частный случай A3.5) для одного измерения. Обобщение на три
измерения опять-таки тривиально.
II. Собственные функции в случае вырождения
Собственные функции \|зпй(&=1, 2, ...,/), принадлежащие соб-
собственному значению Ln, линейно независимы, т. е. между ними не суще-
существует соотношений вида
/
JNA* = o, A)
где ah— некоторые постоянные. Если бы такие соотношения существовали,
то они означали бы,' что одна или несколько функций выражаются через
другие, т. е. фактическое число различных собственных функций, при-
принадлежащих Ln, было бы не /, а меньше. Если функции tynh не ортого-
ортогональны между собой, то мы можем ввести новые функции, получающиеся
из "рпк линейным преобразованием
/
фпа = 2 «ай^пй, а = 1, 2, ...,/. B)
k=i
В силу линейности уравнения для собственных функции функции фп„
будут опять-таки собственными функциями оператора L и принадлежа-
принадлежащими собственному значению Ln.
Из уСЛОВИЯ ОрТОГОНалЬНОСТИ фуНКЦИЙ фтмх'-
*аф«Р dx = ба0 C)
следуют условия для определения .коэффициентов аак:
t 1
S S aakapn'Shk' = 6ag, D)
ft=i ft'=i
где s^' есть
= \ tyfjitynk'dx. E)
Возможность найти коэффициенты аа^, удовлетворяющие условиям
D), следует из геометрической аналогии. Будем рассматривать функ-
функции \|зп/1 как единичные векторы jh в пространстве / измерений, а shh' —
как скалярные произведения (jh, }к,). Тогда B) можно рассматривать
как преобразование в пространстве / измерений от косоугольной системы
493

координат к прямоугольной1. Отсюда ясно, что преобразование B) —
не единственное: получив ортогональную систему координат, мы можем
ее еще вращать любым образом.
Так, например, если функции i|)nfe уже ортогональны, то Skk' = &kk',
и из D) тогда следует
/
2 Къа^к = бар. F)
Это и есть условия для коэффициентов ортогонального преобразова-
преобразования системы ортогональных функций tynk в новую систему опять-таки
ортогональных функций фпа. Таким образом, собственные функции,
принадлежащие одному собственному значению Ln, определяются лишь
с «точностью» до ортогонального преобразования вида B) с коэффициен-
коэффициентами, подчиняющимися условию F).
III. Ортогональность и нормировка собственных функций
непрерывного спектра, 6-функция
Проинтегрируем уравнение для собственных функций
{х, L) = Lty (х, L) A)
по Ь в малом интервале AL. Мы получим:
L+AL
£Д\|) (х, L) = \ £д|з (x, L) dL, B)
где
L+AL
■ф (л:, L) dL. C)
Эту величину называют собственным дифференциалом (оператора L).
Примером такого собственного дифференциала является рассмотренная
в § 7 группа волн. Мы докажем, что не сами функции, а собственные
дифференциалы являются ортогональными и могут быть нормированы.
Для этого проинтегрируем подобным же образом сопряженное уравнение
по Ь'; мы найдем
L'+AL'
L* Л-ф* (х, L') = ^ L>* (^, L') dL'. , E)
Умножим B) на Д\]з* (л:, L'), а E) на Д\]з (л:, L), вычтем один результат
из другого и проинтегрируем по х. Тогда получим:
dx {А-ф* (л:, L') ■ L Д\|з (л:, L) — А-ф (х, L) ■ L* Д^^лг/'Ь')} =
L+AL L'+AL'
\ dL \ dL'(L — L')\|j* (л:, Ь') ip (л:, L). F)
L L'
1 Подробности об ортогонализации функций см. в книге Р. Курант и
Д. Гильберт, Методы математической физики, т. I, Гостехиздат, 1945, гл. II, § !.
494

Левая часть равна нулю в силу самосопряженности оператора L, а справа
при малых AL и AL' мы можем вынести L — L' за знак интеграла.
Тогда получим:
{L—L'){dx- Дг|з* {х, L') А-ф (х, L) = 0. G)
Если интервалы AL и AL' не перекрываются, то L Ф L'. Отсюда следует
\ dx ■ Аф* (х, L') А-ф (х, L) = 0, (8)
т. е. ортогональность собственных дифференциалов. Если AL и AL' совпа-
совпадают, то интеграл (8) не равен нулю. Нетрудно показать, что он будет
первого порядка малости относительно AL. В самом деле, интеграл
, L) (9)
можно заменить интегралом
I'=\ dx- Аф* (х, L) ^ ф {х, L) dL, A0)
причем £it и L2 выбраны так, что участок (L,L-\-AL) лежит внутри
участка (Lls L2)- В силу ортогональности собственных дифференциалов
интеграл по участкам (L,, L) и {L-\-AL, L2) ничего не добавит к инте-
интегралу (9). Поэтому (9) и A0) равны. Но при AL—>0 A0) стремится к 0
как AL. Поэтому, выбирая подходящий нормировочный множитель, можно
всегда сделать так, чтобы
lim -тТ-= 1,
т. е.
\dx-A^*{x,L)A${x,L) = M A1)
при АЬ—>0.
Формулы (8) и A1) можно объединить в одну, выражающую норми-
нормировку и ортогональность собственных дифференциалов:
dx Аф* {х, L') Аф (х, L) = AL или 0 A2)
в зависимости от того, совпадают интервалы L, L-j- AL и I/, L' + AL,
или нет. Освобождаясь от одного интегрирования (по dL) в A2), мы можем
написать A2) в виде
dx.Mp*{x,L')$(x,L) = l или 0, A2')
смотря по тому, попадает ли точка L' — L в интервал L' L' + AL, или
нет. Условие ортогональности и нормировки A2) или A2') может быть
с помощью особого символа сформулировано для самих функций. Для
этого поменяем в A2') порядок интегрирования по х и dL':
L'+AL
^ dL' ^ (х, L) ф* {х, U) dx = 1 или 0. A3)
Введем обозначение
^ L'-L). A4)
495

Тогда из A3) следует
L'+AL
^ dL'.6(L' —L)=l или 0, A5)
смотря по тому, попадает ли точка L'=L в интервал L', L'-}-AL, или
нет. Это последнее равенство мы будем рассматривать как определение
символа б (Z/ — L), называемого Ь-функцией или функцией Дирака (на
самом деле это не функция, а просто обозначение).
Из A5) следует [B1.11)], что
ь
\f(L')b(L'-L)dL = f(L) или 0, A6)
а
смотря по тому, попадает ли точка L'' = L в интервал (а, Ь), или нет.
Для доказательства A6) достаточно разбить интервал (а, Ь) на столь
малые участки, чтобы в каждом из них можно было вынести функцию
f [L') за знак интеграла (для этого она должна быть гладкой). Во всех
участках результат интеграции в силу A5) будет равен нулю, кроме,
однако, как угодно малого, содержащего точку L' — L. В этом участке
интервал от б согласно A5) будет равен 1.
Вместо того, чтобы говорить о нормировке и ортогональности
собственных дифференциалов A2), мы будем говорить, что собственные
функции нормированы к б-функции A4).
В качестве примера приведем нормировку собственных функций
оператора импульса рх. Эти функции суть
*pxix) = NPxe \ A7)
где Np — искомый нормирующий множитель, могущий a priori зависеть
от рх. Образуем интеграл A4):
dx =
\ e
3
h px
-h-lim — \ --A8)
~ _, ,. 1 sin mz .
Сравнивая это с множителем Дирихле lim —•- , обладающим
m-м» л z
свойством б-функции от z [см. дополнение I, формулу A)], мы находим,
что
{p'x-Px). A9)
Отсюда определяем нормирующий множитель
\NPx\22nh=\, NPx = {2nh)~lh B0)
(разумеется, еще можно было бы включить фазовый множитель егч"-Рх >
где ф —действительная функция, однако в этом нет накакой надобности).
496

IV. Значение коммутативности операторов
Докажем теорему: если два оператора L и М имеют общую полную
систему собственных функций, то они коммутируют. Обозначим общие
собственные функции через ifn (x)- Тогда имеем:
Ь|>п=М>,и ЛИ>„ = МПЧ>П. A)
Действуя на первое уравнение оператором М, а на второе оператором L
и вычитая один результат из другого, получим:
ML^n=LnMn^n, LM^n = LnMj?n, (ML-LM)^n=0. B)
Так как любую функцию можно разложить по функциям 1|зп, то мы имеем:
H=0, C)
т. е., применяя оператор ML — LM к любой функции, мы получаем
нуль. На языке ^операторов это означает коммутативность операторов:
ML-LM = 0. D)
Покажем теперь, что если операторы L и М коммутируют, то они
имеют общие собственные функции. Уравнение для собственных функций
оператора L будет
L-ty = Li|j. E)
Действуя на это уравнение оператором М и меняя порядок ML и LM,
мы получаем:
F)
Отсюда следует, что г|/ = Mty есть также собственная функция опера-
оператора L, принадлежащая собственному значению L. Если вырождение
отсутствует, то значению L принадлежит лишь одна функция, а, стало
быть, \|/ может отличаться от \]з ?лишь [постоянным множителем, т. е.
i|/ = мф. Таким образом
М^ = М^, G)
откуда следует, что \]з есть также собственная [функция оператора М-
В случае наличия вырождения \|/ может быть i! линейной комбинацией
функций i|3h(fe=l, 2, ..., /), принадлежащих собственному значению L:
f
^' = yW^h= Y} Musty', fe=l, 2, ..., f, (8)
ft'—l
Однако, вместо функций \]зй можно взять их линейные комбинации
(см. дополнение II):
Ф= S «А. (9)
ft'=i
причем ак могут быть выбраны так, что новые функции ср будут собствен-
собственными функциями 'оператора М-
Мф = Мр. A0)
Подставляя сюда ф из (9) и пользуясь (8), найдем путем сравнения
коэффициентов при \|)ft:
i
2 Mkk.ak. = Mak, k=\,2,..,,f. A1)
h' =^ i
32 Д. И. Блохннцев • 497

Это —система однородных алгебраических уравнений для определения
коэффициентов ак. Она имеет решение лишь в том случае, когда ее
определитель равен нулю: ■
Ми-М М12 ... Му
М21 М22 — М ... M2f
Mfl ... Mff - М
= 0. A2)
Из этого уравнения найдем корни Mv Mz, ..., Mf. Для каждого из
этих корней {Ма) получим свое решение уравнений A1) аа1, aaz, ...,aaf
и, следовательно, согласно (9) свою функцию ср: 17
фа = S'flMV A3)
fe=l
Новые функции сра(а=1, 2, ..., /), будучи линейными комбина-
комбинациями 1|зЛ, будут собственными функциями оператора L, принадлежащими
значению L, а вместе с тем и собственными функциями оператора Mr
принадлежащими значениям M — Mv М2, ..., Ма, . .., Mf соответственно.'
V. Шаровые функции Y,m(Q,q>)
В проблеме нахождения собственных значений оператора момента
импульса М2 мы встречаемся с уравнением для шаровых функций B5.14):
sm6 38 v 36 у ' sin2 в дер2 ' т ^ /
Нам нужно найти собственные функции этого уравнения (т. е. непре-
непрерывные, однозначные и конечные решения во всей области изменения
переменных 0<6<л, 0<ф<2я).
Разделим прежде всего переменные б и ср. Для этого положим:
B)
Подстановка B) в A) приводит к разделению переменных, если положить
Отсюда
Фт(ф) = в*т". D)
Чтобы Фт было однозначной функцией ф, необходимо, чтобы т было
целым числом
« = 0, ±1, ±2, .... E)
Подставляя D) в A) и деля на Фт, получим уравнение для в:
sin6 ,36 V db J sin26
Введем вместо б новую переменную
£ = cos8, — 1<|< + 1, d|=—sin8d8 G)
и будем рассматривать в как функцию %. Тогда из F) получается:
498

Рассмотрим поведение решения в вблизи особых точек уравнения
1= ± 1- Обратимся сначала к точке |=-)-1. Введем переменную.
z — %— 1- Тогда из (8) получаем:
Будем искать в в виде ряда по степеням г:
6 = zvu, v = ao + alz + a2z2 + ... + avzv + A0)
Нам нужно сперва определить степень -у, с которой начинается ряд.
При z->0
Подставляя это решение в (9) и пренебрегая бесконечно малыми мень-
меньшего порядка, нежели zv~2, мы получим из (9):
откуда
у=±т- *
То же значение у получается для разложения вблизи особой точки
|= — 1. Чтобы решение оставалось конечным при £= ± 1, нужно в A0)
взять
т. е. для т > 0 "Y = -у ' для m < ^ Y — ~ "f" • Второе решение A1) обра-
обращается в бесконечность. Таким образом, мы можем взять в в виде
1 ОТ 1
е = A-|2) 2 v, A3)
где у—ряд по степеням z. Нам теперь удобнее взять v в виде ряда по |:
со
о = ?■ &viv- A4)
v=0 v л
Подставляя A3) и (8), получим:
Внося сюда ряд A4) и сравнивая коэффициенты при одинаковых степе-
степенях |, мы получаем рекуррентную формулу для определения коэффициен-
коэффициентов bv:
(v + 2)(v + lNv+2 = [v(v-l) + 2(|/n| + l)v-X, + |/7i +m2]bv. A6)
Если ряд A4) оборвется на каком-то члене номера v = fe, то и будет
многочленом fe-ой степени, и, следовательно, A3) будет конечным, непре-
непрерывным и однозначным решением, т. е. собственной функцией уравне-
уравнения A). Из A6) следует, что ряд может оборваться лишь в том случае,,
если
т. е.
X = (k + \m\)(k + \m\ + l). . . A7)
Полагая
k + \\ = l, A8)
32* 49»

мы получаем:
Я. = /(/ + 1), / = 0, 1, 2, 3, ..., A9)
|т| = 0, 1,2, ...,/. B0)
Можно доказать, что никаких других собственных функций уравнения A)
не существует1.
Решение в, принадлежащее характеристическим числам I и т, мы
обозначим через
в(£)=Р[т|(£), | = cos8. B1)
Если уравнение A5) дифференцировать по |, то получается уравнение,
в котором \т\ заменяется на |т|+1. Поэтому если решение для т = 0
обозначать через Р1 (|), то
Pim|(i) = (l-^J J-^P^i). B2)
Р( (I) есть многочлен степени I и называется многочленом (или полино-
полиномом) Лежандра. Коэффициент при нем обычно нормируется так, что
Р(A) = 1. ' B3)
Из A6) при |т| = 0 получаем:
Отсюда мы видим, что если взять Ьоф0, Ьг = 0, то многочлен РХ будет
содержать лишь четные степени |, если же Ьо = 0, Ьгф 0, то только
нечетные. Выбирая Ьо (при четном /) или Ьл (при нечетном /)'так, чтобы
соблюдалось B3), мы можем вычислить все коэффициенты в многочлене Р(.
Можно проверить, что получающийся многочлен может быть представлен
формулой
Р?(|) = Р((|)=2Г7Г^г(^-1)'. B5)
Имея в виду B), D) и B1), мы получаем собственную функцию уравне-
уравнения A) в виде
Ylm F, Ф) = Ы1тР1Г] (cos 6) <*™р, B6)
где Nlm — нормировочный множитель. Вычисление этого нормировочного
множителя, которое мы опускаем2, приводит к значению
Функции B6) образуют полную систему ортогональных функций на
поверхности шара 6, ср. Поэтому любая интегрируемая квадратично
и однозначная функция \]з F, ср) может быть представлена в виде ряда
со -|_;
Ч>F,Ф)=2 2 clmFImF,q>), B8)
i=0 m=~l
где
Я 2Я
Clm = \ \$ (в, Ф) Y*m (S, ф) Sin 6 db dy. B9)
о о
1 См. Bechert, Ann. d. Phys., 83, 906A927).
2 См., например, В. А. Фок, Начала квантовой механики, КУБУЧ, 1932i
стр. 124—125.
500

В заключение приведем результаты применения некоторых операто-
операторов к шаровым функциям, встречающихся в приложениях:
а) умножение на cos 6 = | или sin 6 = ]/l — l2;
PY - i/e+m+tHf-M+Oy , /
S im V B/+1)B/ + 3) l + Ь m "Г у
B/+1)B/ + 3) l + Ь m Г у B^-j-l) B/— 1)
+ K B/4-1) B/—1) r'-L m-i
б) действие операторов проекций вращательного момента УЦХ, Му, Мх-
, C2)
x + iMy)Yln=-hV(l-m){l+m+l)Yltm+v C3)
)У1>т.1. C4)
Доказательство этих формул приведено в специальных курсах шаровых
функций. См. также Бете, Квантовая механика простейших систем, § 65.
VI. Уравнение Гамильтона.
Пусть <7i> <7г> • • • > <7s» • • ■• > Qf СУТЬ обобщенные координаты, опреде-
определяющие конфигурацию системы, а ри р2, ..., рв, ..., /^ — соответствую-
соответствующие обобщенные сопряженные импульсы. Функция Гамильтона Н есть
функция этих координат и импульсов и, вообще говоря, времени t.
Уравнения Гамильтона, как известно, гласят:
d£l=^J^L dqs___dH_ ■ ,,,
dt ~ dqs ' dt ~ dps ■ *• '
Производная по времени от любой функции F обобщенных коорди-
координат, импульсов и времени будет
*L— 1L ! V Л1*5± *s>J£dPs /9v
dt "+"
dt dt ~i~ ^-1 dqs dt ^ ^ dps dt ' K '
a=l a=l
Пользуясь уравнениями Гамильтона A), мы можем переписать B) в виде
где [Я, F] равно
/
8=1
и называется скобкой Пуассона.
Очевидно, что сами уравнения Гамильтона A) [могут быть также
записаны с помощью скобок Пуассона
H,pt], ^r = [H,qa], s=l, 2, ...,/ E)
[для этого полагаем в C) F=ps и F = qs]. Как мы увидим (§ 31),
в совершенно аналогичном виде пишутся уравнения движения в кванто-
квантовой механике. В частном случае декартовой системы координат и одной
501

частицы, движущейся в поле сил, выводимых из силовой функции
U (х, у, z, t), имеем:
+f+pl +U{x,y,z, t) ■ F)
(<7i = *>' <72 = «/. <7s = z, P! = px, ft = /V Ps = Pz)- Ha основании E) полу-
получаем отсюда:
-rfr-Ltf.AJ- аг~ - ах ' rf^ ~l ' J~ дРх - [1 ^'
и аналогичные уравнения для остальных двух координат и импульсов.
Из G) находим:
d4 dU /£Л
т. е. уравнение Ньютона.
В случае движения заряженной частицы с зарядом е и массой ц
в электромагнитном поле, описываемом скалярным потенциалом V и век-
векторным А, так что
^ = rotA, A0)
-+■ -—>
где ^ —напряженность электрического поля, а J^ — магнитного, функция
Гамильтона пишется в виде
Докажем, что вытекающие из этой функции уравнения Гамильтона
dpx __ дН dpy дН dpz _ дН .„,.
~1Г~ ~~~W ' ~dT~~ ду ' Л — <Эг ' ^ '
dx^__dH_ dy____dH_ dz _ дН ?„.
Л -^" ' ~dT дру ч dt ~ dpz \ '
эквивалентны уравнениям Ньютона для той же частицы, движущейся
под действием силы Лоренца:
Подставляя в G') и G") Я из F') и производя дифференцирование,
получим:
Из G') получаем:
dy - — ( п - Л
502

Из A0) следует, что
dPx _.. d2x e dAa
ЧГ-Р d(* + с dt •
Так как значение вектора-потенциала Ах берется в точке, где находится
заряд е, то полная производная по времени от Ах будет
dAx_dAx . дЛх dx дАх dy дАх dz
dt " dt ^ dx dt "^ dy dt "^ dz dt/
Подставляя в (9') значения ( px —-Ax j , Г py —— Лу j , Г pz —- Az J из
A0') и значение -^- из A1) и пользуясь A2), найдем:
d2x e dAx dV e \ dy f dAy dAx \ dz f dAz dA
dt2 с dt dx ~ с L dt V dx dy
dAx\l
~ ~dz~ J j ■
Отсюда на основании формул (9) и A0), связывающих поле и потен-
потенциалы, находим:
т. е. первое из уравнений (8'). Подобным же образом получаются
и остальные два уравнения (8") и (8'").
Таким образом уравнения Гамильтона G') и G"), вытекающие из
функции Гамильтона F), эквивалентны уравнениям Ньютона (8).
Потенциалы А и V могут быть выбираемы произвольно, лишь бы по
(9') и A0') получалось нужное электромагнитное поле. Если мы вместо
А и V возьмем
A' = A + V/, V'-V-^, (И)
где /—произвольная функция координат и времени, то %' = %, 3$' = 3$.
Подставляя в функцию Гамильтона F) А' и V вместо А и V, мы,
очевидно, придем к уравнению движения A3), если там под А и V
разуметь А' и ]/'■ Пользуясь A4), убеждаемся, что новый выбор потен-
потенциалов не меняет уравнения (8). Это свойство уравнений Гамильтона
называют электромагнитной инвариантностью.
Заметим, что в отличие от уравнения движения (8) функция Гамиль-
Гамильтона Н меняется при преобразовании A4). Например, движение в одно-
однородном постоянном электрическом поле %, направленном по оси ОХ,
может быть описано потенциалами А = 0, V=— %x. Вместо этих потен-
потенциалов можно взять по A4) другие потенциалы, например, Ах= — сШ,
А'у = Лг = 0, 1/' = 0. Предоставляем читателю самому убедиться в том,
что в обоих случаях мы получаем уравнение Ньютона для равноускорен-
равноускоренного движения, но при первом выборе потенциалов функция Гамильтона
имеет смысл полной энергии частицы, а при втором она равна кинети-
кинетической энергии частицы.
VII. Уравнение Шредингера и' уравнения движения в
криволинейной системе координат
В § 27 мы объясняли причину, по которой декартова система коор-
координат в квантовой механике занимает особое положение среди всех дру-
других возможных систем: в декартовой системе координат измерение
проекций импульса рх, ру, pz дает нам также значение кинетической
503

энергии. Поэтому исходные уравнения квантовой механики пишут обычно
в декартовой системе координат. Уравнение Шредингера легко может
быть написано и в любой криволинейной системе координат qlt q2, qSr
поскольку оно дано в декартовой системе. В этой последней оно гласит:
ih *Иу г'° = _ |L V^ (х, у, z,t) + U (х, у, г, t) 4, (*, у, z, t) A)
[простоты ради, мы пишем уравнение для одной частицы и в отсутствии
магнитного поля1]. При переходе от декартовых координат к криволи-
криволинейным ij) и U будут функциями от qlt q2, q3. Все дело сводится к пре-
преобразованию оператора Лапласа V2. Пусть квадрат линейного элемента
ds2 в криволинейной системе координат q есть
з
ds« = d*s + dj,« + dz2= 2 gskdqsdqk, B)
s, fe=l
где g-^ — компоненты метрического тензора. Далее, пусть ■D2 = ||gt.fe|| есть
определитель матрицы gsll. Введем еще элементы обратной матрицы gsk,
так что
gsagak = b*, 6J=1 (k = s), 6^=0 (кфз). C)
[В C) по а суммируют от 1 до 3.}
Тогда оператор V2 в этих обозначениях запишется в виде 2
D V dqs \ « dqh у
(где суммировано по s и k), и соответственно этому уравнение Шредингера
получает вид
+ U (qu q2, q3, t) \!p (qv q2, q3, t). E)
Оператор Гамильтона будет
Беря скобку Пуассона
^=[H,qt], G)
мы получим контравариантную компоненту скорости ^1— . Умножая на
массу \1, мы получим такую же компоненту импульса P(s). Чтобы получить
ковариантную компоненту импульса Ps, преобразуем P(s) по формуле пере-
перехода от контравариантных к ковариантным компонентам:
Ps = gsuP(k)- (8)
В качестве примера рассмотрим полярную систему координат г, б, ср.
В этом случае
f f ^2 2i2da gu=l, g2a = r-, g33 = rasin2 9; (9)
33==7?J_^r D = r2sin6; (9')
Общий случай см. W. Paul i, Handb. d. Phys., XXIV, ч. I.
См., например, А. Эйхенвальд, Теоретическая физика, ч. 1, ГИЗ, §§ 157—166.
504

Гамильтониан будет равен
2 . 2 д . 1 1 д / . „ д
++E1П9
Найдем первую группу уравнений (операторы скорости). Согласно G)
имеем:
■ЗИЛ.']. ■§ = [!*, в], ^ = [Я,Ф]. ' (И)
Вычислим сначала первую скобку Пуассона. Для этого заметим, что
* 2 д \ / д» 2 д \ „ 1 / д
+ J + ) 2{г
В силу этого первая скобка Пуассона A1) дает
<>4Н-«7О ■■)=""'
Для второй скобки Пуассона из перестановки
д \ 1 д / . п д
;С51п9
получаем:
d6 I ih д i, г . - \ _^(в)
^^^ ~^уй^ж^51п6- • •) = /) 03)
и, наконец, для третьей скобки совсем просто получается :
r dt r2sin26 дф r '
Переходя по формуле (8) к ковариантным компонентам рг, Pj, Рф> мы
получаем на основании (9), A2.13) и A2.14):
д-(УЛпВ...),
/sine - A5)
г* - "* дер *
Вычислим теперь вторую группу квантовых уравнений Гамильтона:
Для этого целесообразно представить A0) в виде
где 7W2 —оператор квадрата момента импульса, а Рг— первый из операто-
операторов A5). Несложное вычисление скобок Пуассона A6) с помощью A7)
дает:,
dPr __ _ М2 __ dU_ dPb ^ ctg6 Г 2 _ h?_ \ __ дЦ_
dt ~ 2(аг3 дг ' dt ~~ p,r2sin6 \ "ф 4~ j W '
dt dcp *■ '
Из этих трех уравнений два (для рг и Рф) совпадают по форме с соот-
соответствующими классическими уравнениями Гамильтона. Уравнение для ре
505

вместо р% содержит р% -т- . Появление ^-связано с существованием
в квантовой механике устойчивых состояний с М2 = 0, в конечном счете
с нулевой энергией квантовых систем.
VIII. Требования к волновой функции
При формулировке требований к г|)-функции естественней всего исхо-
исходить из свойств гамильтониана Н, поскольку именно этим оператором
определяется физическая природа системы. Из уравнения Шредингера для
г|5 и г|)* нетрудно получить следующее равенство:
1 Г 1 Г Г
-тт- \ ib*//ib dv гг- \ я|)//гЬ* dv= — \ div J dv, A)
где выражение для плотности тока у совпадает с полученным в § 29.
С другой стороны, условие самосопряженности для оператора Н гласит:
\>-H*ty* dv, B)
и стало быть, для того класса волновых функций, для которого оно выпол-
выполнено, мы должны иметь:
dv = — \ div J dv — — \ JNdS = 0. C)
dt
Обратимся сперва к случаю одного измерения — оо < х < t со..
Имеем: [dv = dx, div./ = —p-. Если в некоторой точке х = х1 нарушается
непрерывность потенциальной энергии U (х) (скажем, она претерпевает
скачок), то при интегрировании в C) мы должны исключить эту точку.
Выполняя интегрирование, получим:
«U*i-0)-4(-«>) = 0. D)
Плотность тока Jх (± оо) должна равняться нулю (противоположный
случай означал бы, что волновые функции в бесконечности не исчезают
и все интегралы были бы расходящимися; заметим, что при рассмотрении
самосопряженности собственные функции г|)ь операторов с непрерывным
спектром L, не исчезающие в бесконечности, должны быть заменены
исчезающими в бесконечности собственными'дифференциалами, ср. дополне-
дополнение III).
Таким образом из D) следует непрерывность плотности тока
Jx(Xl + 0) = JX (*,-()). E)
Подставяя сюда значение Jx из B9.5), получим:
Л (
т. е. непрерывность волновой функции и ее первой производной.
Предположим теперь задачу трехмерной и положим, что в точке г = О
оператор Гамильтона имеет особую точку. В этой точке теорема Гаусса C)
опять-таки не будет применима, и мы должны исключить ее из объема
интегрирования, окружив ее сферой малого радиуса R. Тогда интеграл
по поверхности в формуле C) разобьется на два: по бесконечно удален-
506

ной поверхности, в пределе охватывающей весь объем, и по поверхности
шара радиуса R—» 0:
lim R2\JRdQ-\- \/ivds = 0, G)
oo
причем в первом интеграле мы выразили элемент поверхности шара в виде
ds = ft2 dQ, где dQ — элемент телесного угла. Ввиду исчезновения в бес-
бесконечности волновых функций (или их собственных дифференциалов) второй
интеграл равен нулю. Подставляя в первый интеграл JR= ^-f г|)-^— 'Ф*л^ )
и полагая г|з=: —, где и регулярно при г—» 0, получим:
что возможно лишь в том случае, если а<1. Отсюда мы видим, что
волновые функции во всяком случае не могут обращаться в бесконечность
быстрее, нежели 1/га, а< 1.
Неоднозначность в волновой функции может возникнуть в том случае,
когда мы имеем дело с циклическими координатами, например, с углом ср,
отсчитываемым вокруг некоторой оси. Тогда угол ср и угол ср + 2л озна-
означают одно и то же положение в пространстве, поэтому вероятность г|)*г|),
как величина наблюдаемая, обязана быть однозначной функцией угла ср.
A priori этого нельзя сказать про саму гр-функцию. Однако на основании
свойств шаровых функций и уравнения непрерывности A) путями, сходными
с изложенными в этом дополнении, можно показать, что г|>функция должна
быть однозначна (иначе самосопряженность оператора Н не может быть
обеспеченаI. Таким образом естественные условия, предъявляемые к волно-
волновой функции на основе требования сохранения числа частиц C), в конечном
счете сводятся к требованию выполнения условия самосопряженности опе-
оператора B).
Будут ли при этом выполнены условия самосопряженности для других
операторов L —это будет зависеть от их природы, поскольку класс допу-
допущенных волновых функций уже определен оператором Н и допущенными
в нем нарушениями непрерывности.
IX. Решение уравнения для осциллятора
Задачи о нахождении квантовых уровней осциллятора приводит к урав-
уравнению
Нам нужно найти конечные и непрерывные решения этого уравнения.
Исследуем асимптотическое поведение решения A), т. е. для g = ± оо.
Эти точки одновременно являются особыми точками уравнения. Для этого
положим
^ С?^ = е/E)у^).1 B)
Подставляя B) в A), находим:
1 Ср. В. Паули, Общие принципы волновой механики, Гостехиздат, 1947, § 6.
507

Чтобы функция е;E) явилась фактором, определяющим асимптотическое
поведение г|з(£), нужно выбрать / так, чтобы коэффициент f' + /'2— £2
в особых точках £=±оо был регулярным, т. е. чтобы член £2 уничто-
уничтожался. Это дает
/(S)=±-g"S2. D)
Стало быть, решение уравнения A) можно представить в виде
^{1)^с,е-11&\{1)А-с^хк1\{1). E)
Мы интересуемся конечными решениями г|), поэтому берем частное
решение с2 — 0, т. е. берем г|з в виде
V® = e-1'*tv(l)i F)
Для функции v будем теперь иметь уравнение
w'-2£w' + (a,-l)w = 0. G)
Точка £ = О есть регулярная. Поэтому о можно искать в виде ряда
Тейлора
Подставляя (8) в G) и собирая одинаковые степени £, получим рекуррент-
рекуррентную формулу для определения коэффициентов afe:
(Н2)(Н1)аы-2Ч+(^-1)йь = 0. (9)
откуда
2fe—(А.—1)
a a
Если ряд (8) оборвется на члене номера п, то и будет многочленом п-ой
степени. Тогда решение F) будет конечным и непрерывным и однозначным
во всей области — сх> < | < + сх>. Такие решения и будут собственными
функциями уравнения A). Из A0) следует, что ряд может оборваться
лишь при тех значениях Я., которые определяются формулой
, я = 0, 1, 2, ... A1)
Это и есть формула C7.7), приведенная в тексте.
Многочлен и(£) с коэффициентами, определяемыми формулой A0) для
Я. = 2п+1, носит название многочлена Чебышева — Эрмита.
Его обозначают обычно через Нп (£), и он удовлетворяет уравнению G)
при Я. = 2п+1, т. е. уравнению
= 0. A2)
Легко проверить, что этому уравнению удовлетворяет многочлен
Поэтому Нп только множителем отличается от этого последнего много-
многочлена. Следуя обычному определению, мы положим:
ЯпA)=(-1Г^^(е-52). A3)
[Нетрудно убедиться, что многочлен A3) имеет коэффициенты, удовле-
удовлетворяющие рекуррентной формуле A0) при Я. = 2п+1.]
508

1риведенный в тексте C7.9) многочлен Нп отличается от A3) мно-
1ем ]/2"п! У~я, который выбран так, что функция i|>n (g) нормиро-
к 1. Именно, в тексте мы даем нормированный полином Чебышева—
та
твенное решение уравнения A), принадлежащее собственному значе-
А, = 2и + 1, может быть теперь записано в виде
^п{1)^е-1!^Нп{1), A5)
под Ип (|) будем разуметь нормированный полином Чебышева—
шта A4).
Функции г|)п(£) ввиду самосопряженности оператора, определяющего
!внение A), должны быть ортогональными. В этом легко убеждаемся
юсредственно. В самом деле, для двух функций i|)n и tyn,, имеем:
Jg?- + Bn+l-&»№„ = О,
+ Bл' + 1 — Sa) 4>n. = 0.
множая первое уравнение на г|)п,, а второе на г|зга, вычитая и интегрируя
) |, получаем:
— ОО — ОЗ
1евая часть есть
+00
м
d£ =
= 0,
— ОО
т. е.
= o.
С помощью интегрирования по частям можно также убедиться, что
следовательно,
+оо
№n>dl = bnn,, A6)
т. е. функции г|)„ образуют систему ортогональных и нормированных функ-
функций. Любая функция г|)(£) (с несущественными для нас ограничениями'
может быть представлена в виде ряда
ОО
*Н£)= 2 <vi>«(£)> A7
где
+ОО
1EA) I|)n(g) fi(g. A(

Обратимся теперь к свойствам ненормированных многочленов Чебы-
шева —Эрмита A3). По формуле Коши производная -р^е-& может быть
представлена в виде интеграла по замкнутому контуру
din e - 2ni ) B-|)«+i ' V 7
причем контур обходит точку g. Поэтому из A3) имеем:
е-62Я (Р\ = (— 1)п— { — dz.
Полагая z — 1 — t, получим:
(контур обходит вокруг t = 0). Из последней формулы следует, что
оо
е-/2+2/6= 2-^Hn(l)tn, B1)
т. е. е~/2+2/5 есть производящая функция для #„(£).
Производящая функция B1) позволяет установить важное рекуррент-
рекуррентное соотношение между полиномами Чебышева — Эрмита. Для этого диф-
дифференцируем B1) по t:
п=1
т. е.
оо
2 § яп (|) *» - 2 4- я« (S) ^n+1 = 2 -(^гугя»(g) 'я'1- B2)
п=0 п=0 п=1
Собирая коэффициенты при одинаковых степенях t, получаем:
2|Яп(|) = Яя+1(|) + 2пЯя.1(|). B3)
Умножая эту формулу на | и применяя B3), еще раз получим:
Ч2НпA) = Bп+ 1) Hn{l) + ^Hn^{l)+2n{n-\) Hn.t{\). B4)
Умножим эти равенства на е~^ и заменим в них ненормированные поли-
полиномы Эрмита на нормированные [для чего в B3) и в B4) каждый поли-
полином Нт умножаем и делим на У2пт\у"л]. После сокращения на общие
множители получим рекуррентные соотношения для волновых функций A5).
Именно:
Ып (I) = |/^ 4W (S) + |/у *n-i (S)- B5)
Отсюда получаем интеграл, встречающийся в §§ 48, 47. Умножая B5)
на \!рт (|), интегрируя по g и принимая во внимание ортогональность
и нормировку функции г|)„ A6), получим:
/
у в«, n-i, B6)
что дает интеграл D8.7).
Подобным же путем, исходя из B5) и ортогональности, можно
вычислить интегралы от любой целой и положительной степени g.
510

X. Электрон в однородном магнитном поле
Функция Гамильтона [см. дополнение VI, формулу F)] при сделанном
нами выборе вектора-потенциала А E7.1) имеет вид
Отсюда
dpx
dt
dx дН
dt дрх
Следовательно,
0
дх
Л'-
ар у
dt
dp.
dt
С J
дН e&t
ду \х,с
дН Q
dz '
' dt дру
' ( л. е чр ~\
°v dz дН pz
ц ' dt dpz ц
B)
px = const. =p°, Pz = const. = pi,
- = — a>lY, Y — asm a>ot + 6cos
cp°
у = a sin су + 6 cos oy — -r^ •
Полагая
получим:
и стало быть,
Далее,
т. е.
х = — a cos (o0t -f b sin a>ot -f- jc0,
т. е. движение происходит по кругу
/ cp° n2
(x — xoJ + (y + -^ \ -=а? + b2t
cp°
с центром в х = x0, у = —-~ф и с радиусом /? = j/a2 -f 627Энергия движе-
движения не зависит от р\ — эта величина определяет положение центра круга.
Полная параллельность этого классического расчета с приведенным
в § 57 квантовым очевидна.
XI. Координаты Якоби
Согласно формулам преобразования A04.3) имеем:
D)
F)
G)
(8)
(9)
A0)
причем
B)
511

есть масса первых / частиц. С помощью A) и B) находим:
Лт N N N N
2л "а****" ~~ 2л Zj *э|7"Ж5"~~ ~~ 2л |7 2л ~дх^~~
N
VI Й f
т. е. мы получаем формулу A02.9), приведенную в основном тексте.
Сходиым же образом вычисляется оператор кинетической энергии. Доста-
Достаточно вычислить оператор
N N N
v J v V
"^ ~~ ZJ mk дх\ - ^ mk ^J ZJ dlj d|f. d^ 3^ "
С помощью A) и B) находим:
N N N 2 ЛГ
«■ф — Zj "йг)Г 1 ^-1 ZJ MjM{, dlj д%}. 2j^ ~Щ dljdl^ ^ ~Щ~ J ~~
N N N , ЛГ
,-уи., a|,a| z Zj уи,- ^/а^1
Первая сумма по k в E), как легко видеть (путем изменения порядка
суммирования по k, j и /'), равна нулю. Вторая сумма преобразуется
следующим образом:
' . N N N j JV-1
Zj тД Zj л« а|* + а|* j Zj Zj щ щ + Zj mft+1 a|»
- Zj m, di* + Zj mUx щ ~ м d?N + Zj ^ ж,- + mui
' 1 ) 1 У= 1
i'= 1 ) = 1
т. e.
V
N )=i ' '
где [х, есть приведенная масса центра тяжести первых / частиц и (/ 4- 1)-ой:
— = — + -±— (8)
Имея в виду, что
из*G) получаем A02.4):
JV-1
Huvc. (.1 ?
i Ин-- |
t БИБЛИОТЕК ^ !i

ЗАМЕЧЕННЫЕ ОПЕЧАТКИ
Стр.
23
72
78
79
91
94
94
98
!07
1!4
122
274
Строка
!8 снизу
!4 сверху
1! снизу
3 сверху
17 сверху
2 ссерху
14 сверху
12 снизу
12 сверху
7 сверху
7 снизу
3 снизу
19 снизу
10 сверху
Напечатано
§§ 52 и 63
я /
А~ дх
а B1.3)
^ *Mndx=l
для микроскопических
р Ф \xv]
{рх-~Ах *+(рх-±.Ах )
и = const еш~кхУ
%-1Н.АВ-
т-^-^{р-р+ру^
Ар2 . Р
2^ + 2^,
уравнения C6.4)
в C6.5)
X
h | 1 Р (х) 1 dx
/P(^,8)r_= +
B/+!)Р, cos 6* Д Г
2ik V
Должно быть
§§ 53 к 64
A-i ~
дх
а B1.3')
для макроскопических
р =£ [га1
(^Px-jAxy(^Px^~Ax^
; u=constei(<0/-fex)
rfi [Я ЛВ]
it
Ар2 р2
2ц + 2ц
уравнения C6.3)
в C7.6)
X
|/р(х)
B/+ !) Р; cos 8 i Цг {
2ik \
Блохинцев. Основы квянторой механики