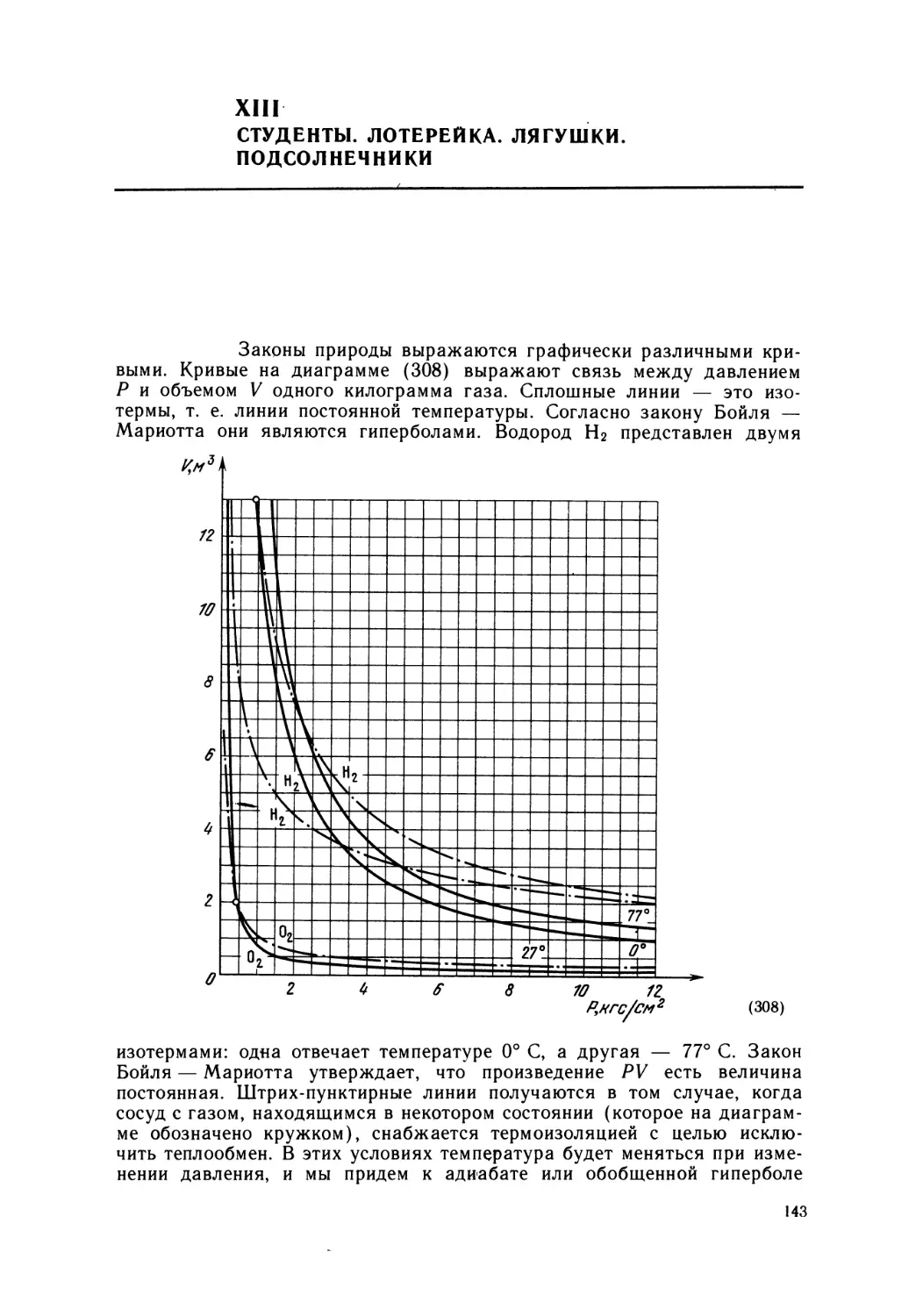
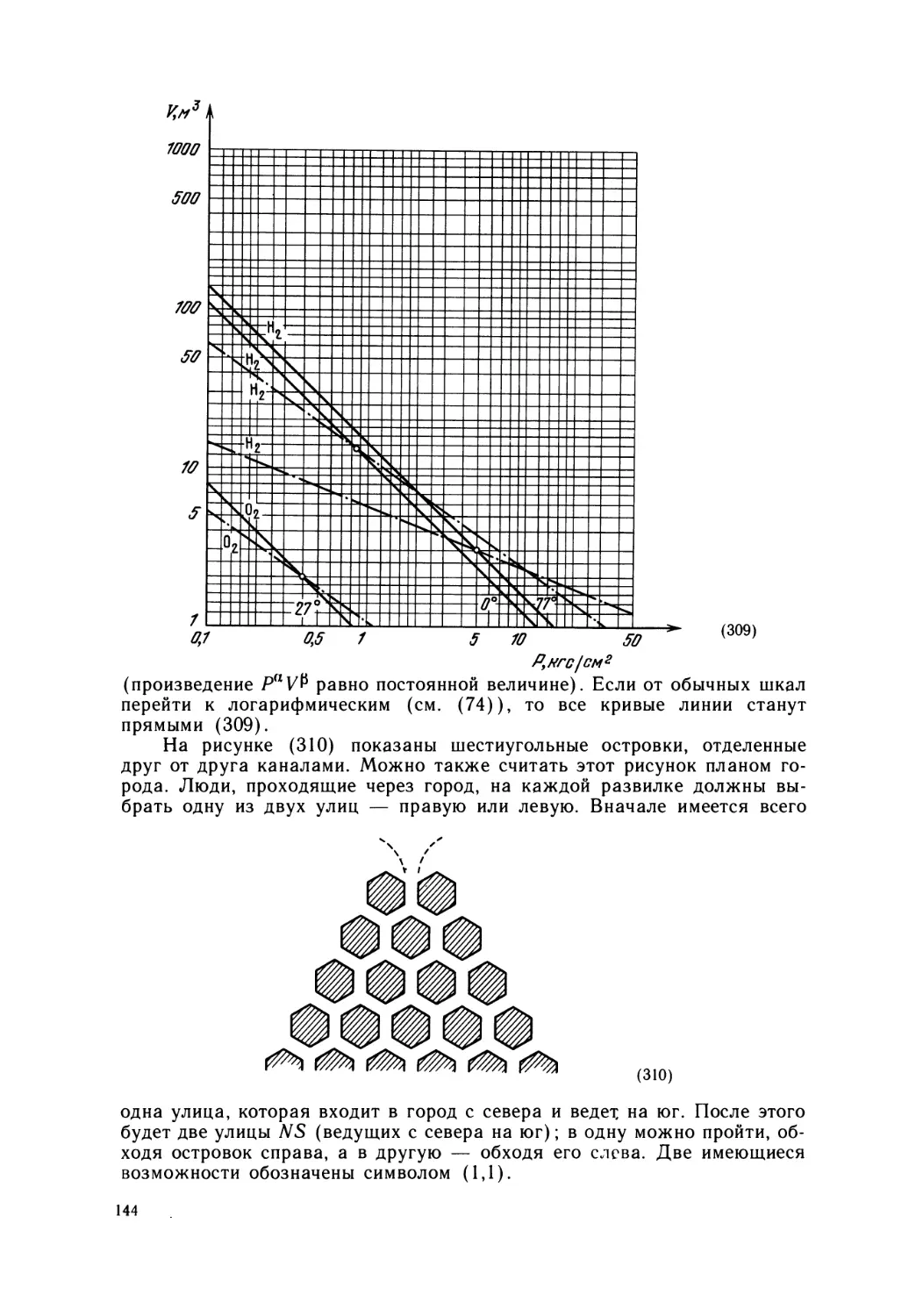
Text
БИБЛИОТЕЧКА-КВАНТ-
ВЫПУСК 8
Г. ШТЕЙНГАУЗ
МАТЕМАТИЧЕСКИЙ
КАЛЕЙДОСКОП
БИБЛИОТЕЧКА «КВАНТ*
выпуск 8
Г. ШТЕЙНГАУЗ
МАТЕМАТИЧЕСКИЙ
КАЛЕЙДОСКОП
Перевод с польского ф. Л. Варпаховского
МОСКВА <НАУКА>
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
I 9 « 1
Scan ДАW
22.10
Ш 88
УДК 51
РЕДАКЦИОННАЯ КОЛЛЕГИЯ:
Академик И. К. Кикоин (председатель), академик А. Н. Колмогоров (заместитель
председателя), кандидат физ.-матем. наук И. Ш. Слободецкий (ученый секретарь), член-кор-
респондент АН СССР А. А. Абрикосов, академик Б. К. Вайнштейн, заслуженный учитель
РСФСР Б. П. Воздвиженский, академик В. М. Глушков, академик П. Л. Капица, профес-
сор С. П. Капица, член-корреспондент АН СССР Ю. А. Осипян, член-корреспондент
АПН СССР В. Г. Разумовский, академик Р. 3. Сагдеев, кандидат хим. наук М. Л. Смолян*
ский, профессор Я. А. Смородинский, академик С. Л. Соболев, член-корреспондент АН СССР
Д. К. Фаддеев, член-корреспондент АН СССР И. С. Шкловский.
Редактор выпуска Ф. А. Кабаков.
Штейнгауз Г.
III 88 Математический калейдоскоп: Пер. с польского.— М.: Наука.
Главная редакция физико-математической литературы, 1981.
Популярные книги замечательного польского математика Г. Штейнгауза хорошо знакомы советскому чи-
тателю. В них автор пытается показать, что математика пронизывает всю окружающую нас реальную жизнь.
Для понимания книги достаточно тех знаний математики, которые дает средняя школа. Отдельные трудные
места читатель без особого ущерба может опустить. Имеются вопросы, на которые автор не знает ответа,
а есть и такие, на которые ответа не знает никто.
ш WW <”-80 .702000000
ББК 51
22.10
Гуго Штейнгауз
МАТЕМАТИЧЕСКИЙ КАЛЕЙДОСКОП
(Серия: Библиотечка «Квант»)
М., 1981 г., 160 с. с илл.
Редактор И. А. Райская
Технический редактор С. Я. Шкляр Корректор А. Л. Ипатова
ИБ № 11630
Сдано в набор 22.04.80. Подписано к печати 07.01.81. Бумага 70Х lOO'/ie. тип. № 2
Гарнитура литературная. Печать офсетная. Условн. печ. л. 13 Уч -изд. л. 12,98.
Тираж 150 000 экз. Цена книги 75 коп.
Заказ № 1073
Издательство «Наука»
Главная редакция физико-математической литературы
117071, Москва, В-71, Ленинский проспект, 15
Чеховский полиграфический комбинат
Союзполиграфпрома Государственного комитета СССР
по делам издательств, полиграфии и книжной торговли
г. Чехов Московской области
Ш 91-80 1702000000
иэо(02)-о 1
©Перевод на русский язык.
Издательство «Наука»,
Главная редакция физико-мате-
матической литературы, 1981
ПРЕДИСЛОВИЕ АКАДЕМИКА А. Н. КОЛМОГОРОВА
Доказательства математических гео-
рем следуют строгим законам логики. Подобно это-
му школьник, решив задачу, обязан отчетливо из-
ложить решение и обосновать законность каждого
шага решения. Но в случае сколько-нибудь слож-
ной задачи сначала надо придумать решение и лишь
потом его обосновать. Подобно этому интересные
новые теоремы математики сначала придумывают
«по догадке», или, как говорят более учено, по ин-
туиции.
Математическая интуиция часто руководству-
ется представлениями о красоте. Решение хорошо
поставленной, естественной задачи обычно оказы-
вается красивым. Конечно, не каждая красиво вы-
глядящая гипотеза оправдывается. Но искать под-
линное решение проблемы часто бывает разумным
среди предположений, выделяющихся своей кра-
сотой.
Известный польский математик Гуго Штейн-
гауз в своей книге «Математический калейдоскоп»
стремится увлечь читателя математикой именно с
этой стороны: красотой математических фактов и
возможностью их усмотреть интуитивно еще до ло-
гического обоснования. Доказательства тоже быва-
ют красивы своей неожиданной простотой. Они
конечно, тоже имеются в книге Штейнгауза, но мно-
гие факты сообщаются и без доказательств, чтобы
увлечь читателя своей красотой, в то время как
само доказательство может оказаться и недоступ-
ным читателям из-за недостатка у них знаний.
«Математический калейдоскоп» можно читать
разными способами. Нет ничего зазорного и в том,
чтобы перелистывать его, останавливаясь подроб-
нее на картинках, поражающих своей красотой, ли-
бо обращая внимание на простоту формулировок
ответов в тех случаях, когда, казалось бы, задан-
ные вопросы простых ответов не обещают. Но, ко-
нечно, читатель получит больше пользы и больше
удовольствия, если разберется в доказательствах
там, где они приведены, и попытается их найти
там, где они не даны автором.
Книга Штейнгауза переведена на много языков.
В 1949 г. был издан и ее русский перевод, сделанный
с первого, менее полного, польского издания. Всюду
книга пользовалась большим успехом. Я надеюсь,
что новое ее издание тоже завоюет ей много друзей
среди читателей «Библиотечки «Кванта».
А. Колмогоров
ПРЕДИСЛОВИЕ
Предлагая польскому читателю второе (а в общем счете —
седьмое) издание моего «Калейдоскопа», должен сразу же оговорить,
как и в предисловии к первому изданию, что эта книга не претендует
ни на систематическое построение какого-либо раздела математики, ни
на популярное изложение тех или иных математических задач. Это про-
сто книжка с картинками. Основная ее цель — представить математику
в зримой форме — сохраняется в качестве главной и в новом издании,
хотя я и допускал более длинные словесные комментарии там, где без
них было не обойтись.
Ошибался бы тот, кто считал «Калейдоскоп» собранием шарад и
курьезов, поскольку серьезные вопросы подменяются в нем детскими
игрушками. Это верно, что «Калейдоскоп» обращен к любознательности
ребенка, которому он показывает неведомые и захватывающие вообра-
жение предметы. Но не так ли поступает с нами сама природа? И разве
из-за этого мир превращается в магазин с игрушками? Думаю, что нет.
А если и так, то можно ли это вменять в вину «Калейдоскопу»?
Немало найдется таких рисунков, в которых читатель не увидит
математики. Эти рисунки просто красивы. Когда они пришли мне в голо-
ву, хотелось увидеть модель, а когда модель была готова, хотелось
посмотреть, как она выйдет на фотографии — взрослые люди и даже
взрослые математики тоже должны иногда поиграть. Все это было бы
невозможно без помощи рисовальщиков, модельщиков и фотографов.
В первом издании было 180 иллюстраций, во втором число их перевалило
за 300. Для первого издания рисунки делали Энгельштейн, Грюнберг и
Халицка, а фотографии — Ванда Диамандувна; к этим именам, которые
я вспоминаю с благодарностью, должен присоединить теперь имена
Бронислава Купца с кафедры фототехники Вроцлавского политехническо-
го института и рисовальщиков В. ВдовЯка, А. Трояновского и А. Ты-
чыньского. Модели для нового издания изготовил Рышард Новаков-
ский; эти модели принадлежат математическому кабинету Вроцлавского
университета им. Болеслава Берута.
Для понимания книги не требуется знания высшей математики.
Есть в ней, правда, и трудные места, но их можно опустить, так как
«Калейдоскоп» не является каким-либо систематическим руководством.
5
Кто пожелает, может поразмыслить над предлагаемыми вопросами;
некоторые из них легкие, ответы на некоторые другие автору неизвестны,
но встречаются и такие, которые в настоящее время никто не умеет
решать.
Примечания в конце книги указывают на источники, в которых
автор почерпнул большую часть своих замыслов.
Несколько лиц критически прочли рукопись: М. Кац (первое изда-
ние), Г. С. М. Коксетер и Г. Роббинс (американское издание); при
подготовке настоящего издания я пользовался помощью Я. Мыцель-
ского. Название книги придумано моей женой.
Какова основная идея книги? Их две: 1) предметом математики
является действительность, 2) математика универсальна — нет вещи,
которая была бы ей чужда. Этих идей читатель не откроет ни в одном
рисунке в отдельности, но обозрев их все, почувствует, что таков именно
их совокупный смысл.
Вроцлав, 16 сентября 1954 г.
Г. Шт.
I
ТРЕУГОЛЬНИКИ. КВАДРАТЫ. ИГРЫ.
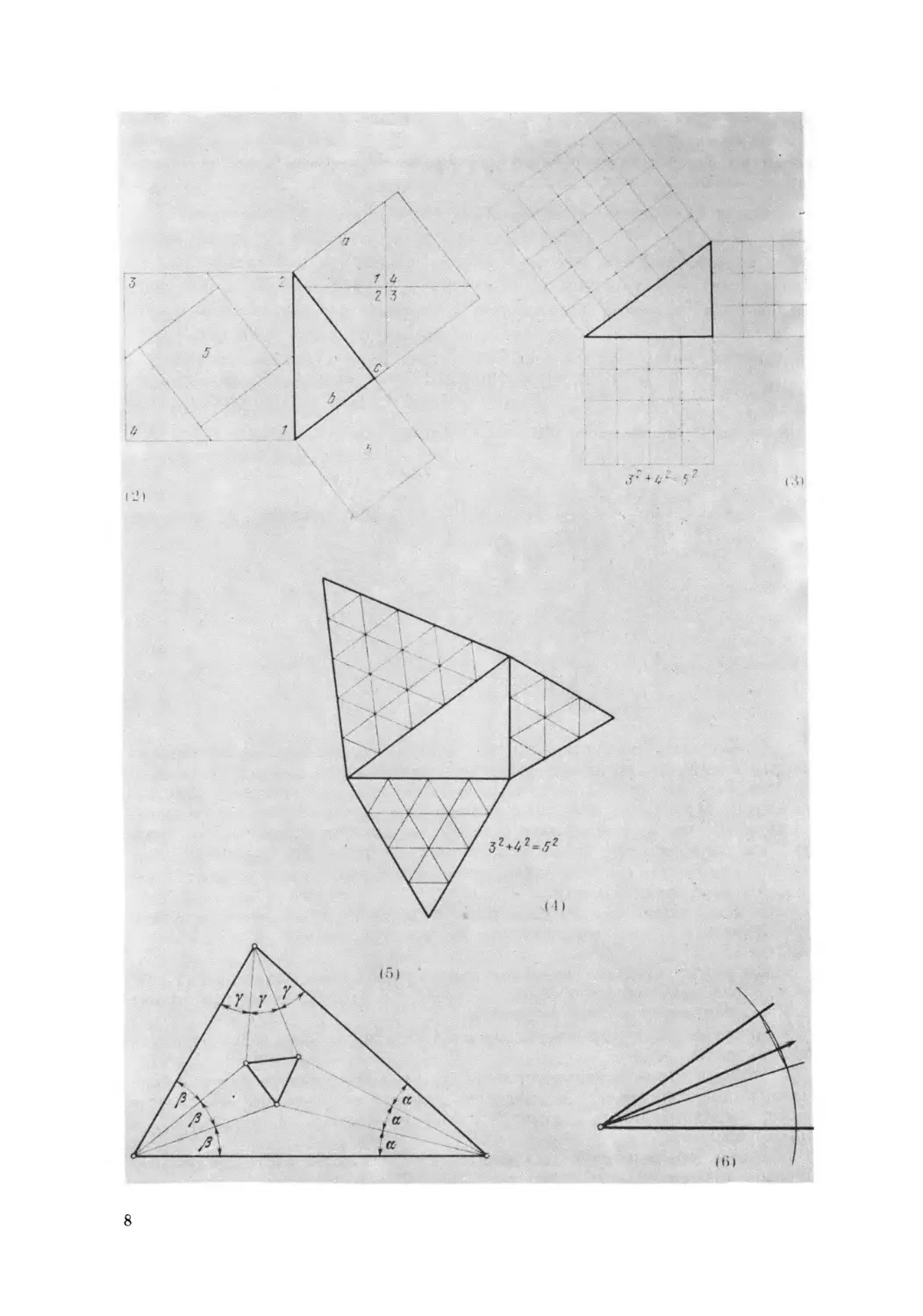
Из этих четырех дощечек (1) составится квадрат или рав-
носторонний треугольник, в зависимости от того, в какую сторону повер-
С помощью прямоугольного треугольника можно разложить квадрат
на два квадрата (2); чтобы убедиться, что больший квадрат складыва-
ется из двух меньших, проведем через центр среднего квадрата горизон-
тальную и вертикальную прямые и сместим, не поворачивая, получившие-
ся четыре части в углы большего квадрата; сместив теперь малый квад-
рат, мы покроем оставшуюся незанятой среднюю часть большего квад-
рата. Из равенства а= Ь+с видно, что малый квадрат точно соответствует
размеру этой средней части.
Смысл только что доказанного утверждения становится особенно
прозрачным в случае треугольника (3) со сторонами 3, 4 и 5. Имеем:
9+16 = 25.
Мы можем, следовательно, построить прямой угол с помощью 12-сан-
тиметровой нитки со связанными концами и с отметками на расстоянии
3, 4 и 5 сантиметров одна от другой.
То же свойство прямоугольного треугольника можно проверить и
без квадратов (4).
Чтобы построить равносторонний треугольник, можно взять произ-
вольный треугольник (5) и разделить каждый его угол на три равные
части; тогда внутри его получится малый треугольник, который и будет
равносторонним.
Угол с большой точностью делится на три равные части следующим
образом (6): сначала угол делится пополам, а затем хорда половинного
7
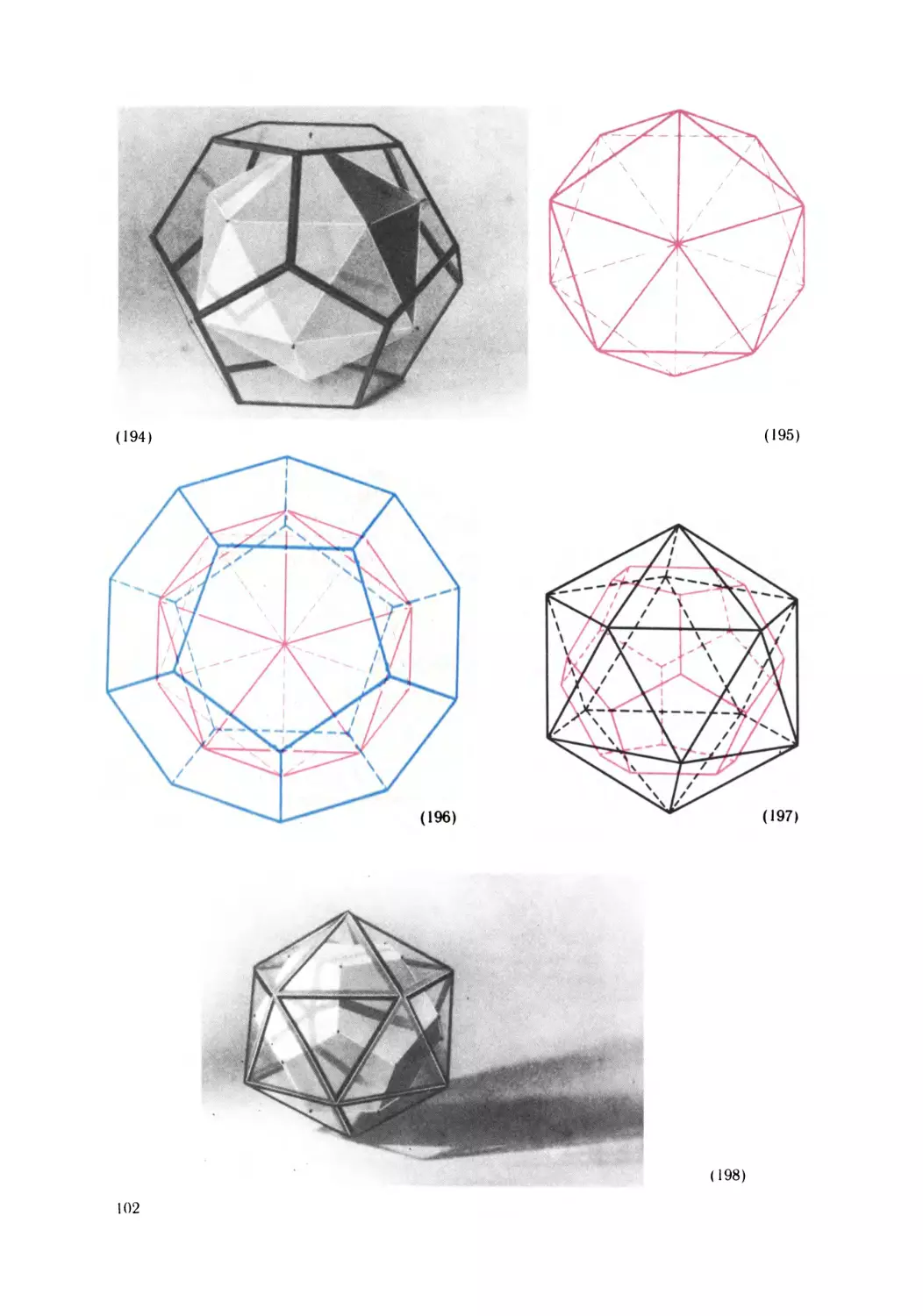
8
угла делится на три; луч, отсекающий 2/3 этой хорды, отделяет одну треть
всего угла.
Данный способ не является абсолютно точным.
Всю плоскость можно покрыть квадратными плитками нескольких
разных размеров (7).
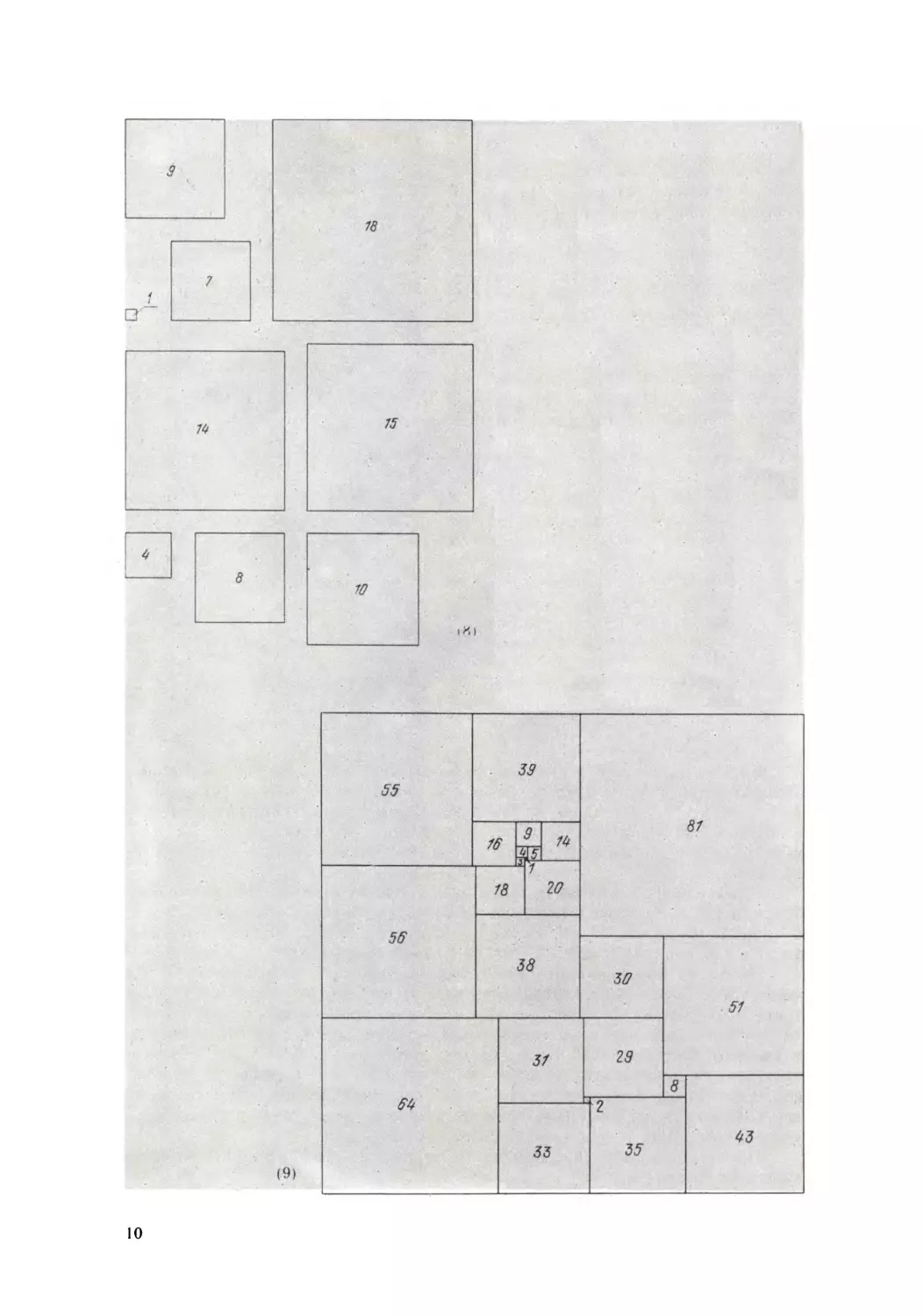
Весьма интересно разбиение прямоугольника на одни только разные
квадраты. На стр. 10 представлены (8) девять квадратов со сторонами
1, 4, 7, 8, 9, 10, 14, 15, 18. Задача: составить из этих квадратов прямо-
угольник. Это простейший пример разбиения прямоугольника на раз-
ные квадраты. Ни в каком разбиении не может быть меньше девяти ква-
дратов.
Даже квадрат можно разбить на разные квадраты. Мы здесь изо-
бразили (9) одно такое разбиение на 24 квадрата со сторонами 1, 2, 3, 4,
5, 8, 9, 14, 16, 18, 20, 29, 30, 31, 33, 35, 38, 39, 43, 51, 55, 56, 64, 81. Можно
ли разбить квадрат менее чем на 24 разных квадрата?
Чтобы из произвольного треугольника вырезать треугольник с пло-
щадью в семь раз меньше, отделяем (10 Д) от каждой стороны по одной
трети и соединяем полученные точки с противоположными вершинами;
то, что площадь красного треугольника равна одной седьмой площади
исходного треугольника, видно из соседнего рисунка (10 В): красный
треугольник равновелик каждому из шести серо-крричневых треугольни-
ков; выступающими коричневыми треугольниками можно покрыть синие
треугольники; следовательно, общая площадь семи равновеликих тре-
угольников равна площади исходного треугольника.
Простейшее разбиение плоскости на равные квадраты (11) исполь-
зуется во многих играх.
9
18
55 35 87
16 - 9 /4
56 75 1 20
35 30 51
37 29
8 1/3
33 u 2 35
Ю
(io A)
(Ю В)
На доске (12) размером 3x3 можно играть в крестики-нулики сле-
пующим образом. Игроки поочередно ставят по одному крестику (пер-
вый игрок) или нулику (второй игрок). После того, как выставлено по
три крестика и нулика, каждый игрок при очередном ходе имеет право
переставить один свой крестик или нулик на одну из соседних свободных
клеток (но не наискосок). Выигрывает тот, кто первый займет три клет-
ки по вертикали, горизонтали или диагонали. Начинающий обеспечит
себе выигрыш, если он своим первым ходом займет центральную клетку,
а затем будет должным образом отвечать на ходы противника. Действи-
тельно, если первый игрок поставит сначала крестик в клетку е, то вто-
рой игрок может поставить нулик либо в одну из прилегающих, либо в
угловую клетку. Пусть нулик поставлен в угловую клетку, например,
клетку а. Тогда первый игрок должен поставить крестик в клетку А, вы-
нуждая противника занять клетку/?; на это первый игрок отвечает заня-
тием клетки с, и второй игрок должен будет поставить нулик в клеткуg.
Теперь первый игрок за два следующих хода переставляет крестики из
клетки е в клетку / ь из клетки h в клетку i и выигрывает. Если второй
игрок займет сначала одну из прилегающих к е клеток, например, клет-
ку /?, то первый займетg , второй должен будет занять с\ тогда первый
займет а, вынуждая второго занять d — и второй игрок не успеет поме-
шать первому переставить крестик с g сначала на й, а затем на i. Можно
условиться, что начинающий не имеет права занимать первым ходом
центральную клетку, тогда при правильной игре обоих партнеров игра
никогда не закончится.
(12)
11
Некоторые шахматные позиции можно точно проанализировать. На-
пример, в эндшпиле д-ра Бергера (13) у белых имеется только один ход,
ФЫ — Ь8, обеспечивающий им победу. При этом ходе и дальнейшей
правильной игре белых их выигрыш уже после восьми ходов становится
очевидным. При всяком же другом ходе белых и правильной игре черных
победу одерживают черные.
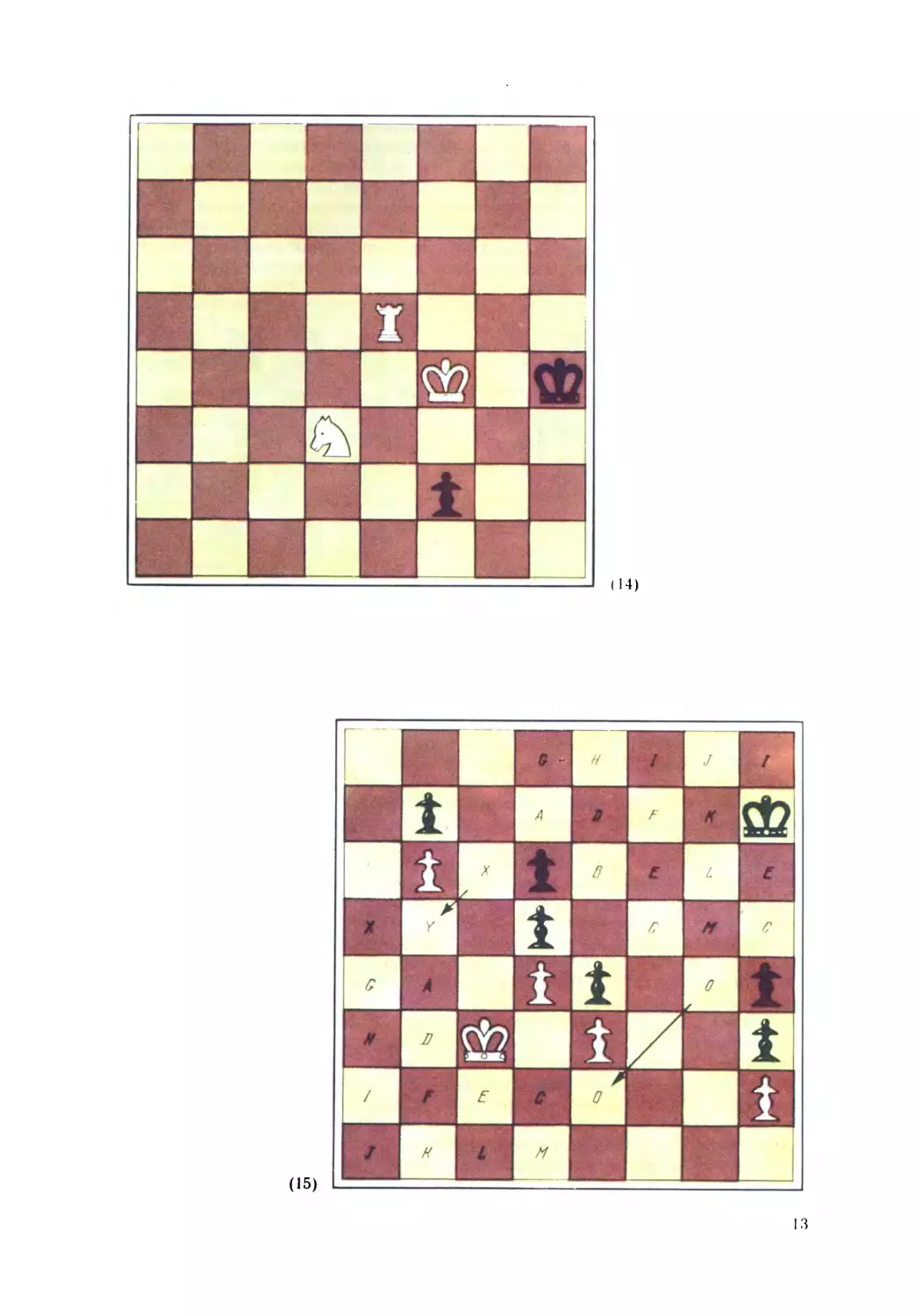
Некоторые эндшпили замечательны богатством вариантов и нео-
жиданностью внешне скрытого решения. Так, например, начинающему
игроку нелегко будет догадаться, каким образом в этой позиции (14) бе-
лые дают мат самое большее в четыре хода.
Эндшпиль д-ра Эберса (15) носит чисто математический характер.
Можно точно доказать, что белые не позволят черному королю взять
какую-либо из своих пешек, если только всегда будут ходить своим ко-
ролем на поле, обозначенное той же буквой, что и поле, на котором стоит
черный король. В соответствии с этим правилом первый ход белых есть
ход В — F. Если белые ни разу не отступят от этого правила, то резуль-
тат будет ничейным. Если они нарушат его хотя бы однажды, то черные
смогут при желании не позволить белым вернуться к указанной тактике,
их король проникнет в лагерь белых по одной из диагоналей X — Y или
О — О и черные добьются победы.
Читателю не нужно быть блестящим игроком, чтобы добиться ре-
зультата 1:1 в одновременной игре на двух досках против двух мастеров.
Достаточно потребовать, чтобы один из мастеров (А) играл белыми,
а другой (В) — черными и чтобы матч начинался ходом мастера А. Тем
же самым ходом читатель должен начать свою партию с В, а когда тот
ответит — повторить его ответ в партии с А и т. д. В итоге на обеих досках
будет разыграна одна и та же партия. Читатель либо выиграет на одной
доске и проиграет на другой, либо сделает ничью на обеих досках, по-
этому в любом случае он и оба его партнера вместе наберут по одному
очку.
Мы не располагаем математической теорией игры в шахматы, однако
для некоторых более простых игр такая теория построена. Рассмотрим,
12
(14)
13
например, следующую игру (16). В квадратной коробочке имеется 16 яче-
ек; одна из них свободна, а остальные заполнены фишками, занумерован-
ными числами от 1 до 15. На рисунках (16) и (17) показаны два располо-
жения фишек, в ячейках коробочки, первое из которых считается началь-
ным, а второе выбрано произвольно. Можно ли, передвигая фишки внутри
коробочки, перевести произвольно выбранное расположение в начальное?
Ознакомимся с теорией этой игры. Припишем свободной ячейке номер 16;
каждому расположению фишек, отвечает некоторая расстановка чисел 1,
2, 3,...15, 16. От расстановки этих чисел, в их естественном порядке можно
перейти к любой другой расстановке за несколько шагов, каждый из кото-
рых состоит в перестановке двух соседних чисел. Например, расстановку
2, 1,3, 4,..., 16 можно получить за один шаг — переставив единицу с
двойкой.
Одни расстановки требуют четного числа шагов, другие — нечетного,
но никакая расстановка не может быть получена из начальной как за
четное, так и за нечетное число шагов. Если бы к некоторой расстановке
вело два пути — с четным и нечетным числом шагов, то можно было бы
пойти первым путем и затем вернуться вторым путем, выполняя соответст-
вующие шаги в обратном порядке. В результате получился бы путь, веду-
щий от начальной расстановки к ней же, в котором число шагов, будучи
суммой чисел разной четности, было бы нечетным. Это, однако, невоз-
можно — никакую расстановку нельзя перевести в себя за нечетное число
шагов. Ведь на каждом шагу переставляются какие-нибудь два числа:
если имеется шаг, преобразующий пару соседних чисел (3, 7) в пару
(7, 3), то должен существовать обратный шаг, преобразующий пару
(7, 3) в пару (3, 7). Действительно, пусть, например, в исходной расста-
новке, к которой мы хотим вернуться, тройка стояла слева от семерки;
тогда мы должны скомпенсировать перескок тройки направо от семерки —
при любых дальнейших перемещениях тройка не сможет вернуться на
.свое место иначе, как перескочив снова налево от семерки. Это относит-
ся ко всем парам —- число шагов, в которых участвуют любые два задан-
ных числа, четно. Следовательно, четно и общее число шагов. Мы убе-
дились, таким образом, что существуют расстановки четные и нечетные —
первые получаются из начальной расстановки за четное, а вторые —
за нечетное число шагов. Если какая-нибудь расстановка четна, то она
не может быть нечетной.
14
Все сказанное относится к расстановке фишек в один ряд. При пе-
ремещениях внутри коробочки нельзя выполнять произвольные шаги.
Можно, правда, принимать за расстановку любое расположение фишек,
если читать номера от левого верхнего угла до правого нижнего, однако,
теперь всякий шаг заключается в перестановке пустой ячейки 16 с со-
седней фишкой, номер которой может быть каким угодно. Если соседняя
фишка расположена справа или слева, то при этом получится шаг в преж-
нем смысле, как если бы числа были расставлены в один ряд. Однако
если она находится сверху или снизу, то при расположении в один ряд
этому соответствует перестановка двух чисел, между которыми стоят
три числа. Такая перестановка требует семи шагов.
Если мы хотим перейти от расстановки (16) к расстановке (17), то
нам во всяком случае придется вернуть пустую ячейку 16 в ее исходное
положение в правом нижнем углу; следовательно, влево ее нужно будет
переместить столько же раз, сколько и вправо, и вниз столько же раз,
сколько и вверх. Таким образом, получится четное число 21г горизонталь-
ных и четное число 2v' вертикальных перемещений. Этому соответству-
ет 21г + 2и-7 шагов, т. е. четное число шагов. Но за четное число шагов
четная расстановка переходит всегда в четную, а нечетная — в нечетную
(почему?). Между тем расстановка (17) нечетна, так как она получается
из начальной за один шаг — перестановкой единицы и двойки, а расста-
новка (16) четна, так как она получается из начальной за нуль шагов;
в силу этого переход от (16) к (17) неосуществим. В то же время всегда
можно перейти от любой четной расстановки к любой другой четной рас-
становке, а от любой нечетной — к любой другой нечетной; предлагаем
читателю доказать это самостоятельно.
Игра «в пятнадцать» была какое-то время популярной, но после
опубликования в 1879 г. ее теории вышла из моды.
Все упоминавшиеся здесь игры имеют нечто общее, роднящее
их также со многими другими играми. Не только для шахматных эндшпи-
лей, но и для таких игр, как «крестики — нулики» или «волки и овцы»,
теория позволяет установить, какая из сторон выиграет при условии
правильной игры. Одновременно теория указывает, как играть пра-
вильно. Этому как, будто противоречит возможность ничьей в шахматах,
однакр, такую возможность можно исключить, если условиться,
что проигравшим считается партнер, который в случае повторе-
ния позиции сыграет так же, как он сыграл раньше.
Общее утверждение об играх подобного рода гласит, что вся-
кая игра либо несправедлива, либо нейтральна. При этом нейтральной
считается игра, которая при правильной тактике обоих партнеров
всегда заканчивается вничью. В некоторых играх ничьи отсутствуют;
такие игры называют категоричными. В ряде случаев ничейный исход
можно исключить с помощью дополнительных соглашений (как в
только что приведенном примере). Согласно сделанному утвержде-
нию, всякая категоричная игра является несправедливой.
Условимся, что в игре белых и черных начинают всегда белые;
тогда, например, в игре в «волки и овцы» белые всегда могут добить-
ся победы; сделанное выше утверждение означает, что и в любой,
другой категоричной игре одна из сторон всегда может добиться
победы, так что исход борьбы предрешен еще до ее начала. При этом
победа достигается независимо от того, как играет другая сторона.
Ясно, что только одна сторона располагает такой выигрышной тактикой.
Иногда эту тактику найти легко, как в случае «волков и овец», иногда
15
трудно, как в некоторых шахматных эндшпилях, иногда неясно даже,
удастся ли это сделать в пределах обозримого будущего, как в слу-
чае обычной игры в шахматы, однако, всегда для одной из сторон
такая тактика существует. (В случае шахмат необходимо принять
указанное выше дополнительное соглашение, а также считать, что
пат означает проигрыш для стороны, не имеющей хода.)
Для доказательства рассмотрим эндшпиль, в котором белые дают
мат самое большее в 4 хода. Обозначим эту позицию через EG4. Белые,
очевидно, располагают таким первым ходом, что при любом ответе на
него черных получится позиция EG$. Они, таким образом, распола-
гают хорошим ходом, если хорошим считать ход, приводящий к пози-
ции EG3. Точно так же и в позиции EG3 у белых имеется хороший ход,
который приводит к позиции EG2, а в этой позиции — хороший ход,
дающий позицию EG\. Наконец, в этой последней позиции у белых также
имеется хороший ход — шах и мат! Разумеется, плохая защита черных
может облегчить белым задачу: белые смогут поставить мат за три,
а не за четыре хода; в любом случае белые располагают последователь-
ностью хороших ходов, позволяющей им поставить мат самое большее
в четыре хода. Теперь понятно, что означает позиция EGn. Все по-
зиции EGn (п=1, 2, 3, ...) будем называть выигрышными позициями
для белых.
Пусть теперь на шахматной доске все 32 фигуры стоят в своей
исходной позиции. Логика учит, что существуют лишь две возможности,
каждая из которых исключает другую: (I) — позиция является выигрыш-
ной для белых, (II) — позиция не является выигрышной для белых.
В первом случае исход любой шахматной партии заранее предопре-
делен в пользу белых, поскольку начальная позиция есть EGn. Во
втором случае начальная позиция не есть EGn. Это означает, что на
каждый ход белых черные могут ответить ходом, который приводит к
позиции, также не являющейся EGn. Ведь если бы у белых был та-
кой ход М, что при любом ответе черных получалась бы выигрышная
для белых позиция, то и исходная позиция была бы для них выигрышной,
а это противоречит принятому нами допущению (II). То же рассуж-
дение применимо и к позиции, возникающей после первого ответа
черных: снова на каждый ход R белых черные могут ответить так,
чтобы получилась позиция «не-ЕСл». Белые, следовательно, не могут
выиграть — им для этого нужно добиться позиции EGi, чего черные
не допустят, если будут играть правильно; но в таком случае ввиду
категоричности игры черные должны выиграть.
Мы не знаем, какая из возможностей, (I) или (II), осуществля-
ется в шахматах на самом деле при дополнительном соглашении, исклю-
чающем ничьи, но нам известно, что осуществляется одна и только
одна из этих возможностей, и поэтому шахматы являются игрой неспра-
ведливой.
Такое же рассуждение применимо к шашкам и многим другим
играм. Любая из этих игр, если она не категорична, может быть
справедливой, но тогда она нейтральна. Неизвестно, является ли игра
в шахматы (без дополнительных правил) нейтральной или нет. В послед-
нем случае шахматы — игра несправедливая, но можно еще не знать,
какая из сторон обеспечивает себе выигрыш. Если это известно, то
неизвестной еще может оставаться тактика выигрывающей стороны,
а в случае, когда шахматы являются нейтральной игрой, — тактики
обеих сторон, гарантирующие каждой из них ничью.
16
Существуют игры иного рода, к которым
изложенная выше теория неприменима.
Доску для игры в «крестики — нулики» мож-
но использовать и для такой игры: в каждую
клетку доски (18) заранее и на всю игру впи-
сывается какая-нибудь цифра — либо белая, либо
черная; первый партнер (белые) ставит в свою
карточку одну, две или три белые палочки, а
второй партнер (черные) — одну, две или три
черные палочки в свою карточку, но ни один
из них не видит, что поставил другой; затем
карточки открываются и тем самым опреде-
ляются вертикаль и горизонталь доски; цифра, стоящая в клетке их пере-
сечения, определяет размер выигрыша для белых, если эта цифра белая,
и для черных, если она черная. Особенность этой игры состоит в том,
что она не является замкнутой. Поясним это.
Допустим, белые решили все время ставить в своей карточке две
палочки и черные поняли это, играя с белыми достаточно долго. Тогда
они примут наиболее выгодную для них тактику, проставляя постоянно
в своей карточке две палочки, обеспечивая себе тем самым выигрыш
размера 3 при каждом розыгрыше. Через некоторое время белые раз-
гадают их систему игры и изменят свою тактику: будут ставить все
время одну палочку. Это будет давать им выигрыш размера 2, пока
черные не решатся на смену своей тактики. Ясно, что такое взаимное
приспосабливание не дает ни одному из партнеров какого-либо опре-
деленного плана игры.
В шахматах дело обстоит иначе. В задаче д-ра Бергера можно
точно указать, как должны играть оба партнера, если каждый из
них действует наилучшим для себя образом (см. примечание (13)
в конце книги). Если белые знают, что черные действуют* безошибоч-
но, то они должны начать с ходаФЫ—Ь8, иначе им не удастся поста-
вить мат на тринадцатом ходу. Если черным известно, что они играют
с идеальным противником, то они ответят ходом Cgl—сб; при всяком
другом ответе им будет поставлен мат еще до тринадцатого хо-
да. Так разворачивается борьба в соответствии с «главной игрой»,
указанной в тексте. Здесь каждый из партнеров действует наилуч-
шим для себя образом. Наличие «главной игры» делает игру замкнутой.
Шахматы, шашки, «волки и ов-
цы» и почти все игры с поочеред-
ными явными ходами противников
относятся к замкнутым играм — не-
зависимо от того, нейтральны они
или несправедливы: в то же время
игра на девяти клетках, проиллюст-
рированная на рисунке (18), не
является ни замкнутой, ни неспра-
ведливой, ни нейтральной — это
игра открытая, справедливая и ка-
тегоричная. И причиной, как- не-
трудно видеть, служит то, что ходы
делаются одновременно.'
По известной легенде мудрец,
который изобрел шахматы, потре-
17
бовал в награду от персидского шаха такое количество пшеницы,
чтобы им можно было покрыть шахматную доску (19), положив на
первую клетку одно зерно, на вторую — два, на третью — четыре и
вообще на каждую следующую клетку, вплоть до последней, — в два
раза больше, чем на предыдущую. Оказалось, что такого количества
зерна не наберется не только в хранилищах шаха, но и всего мира.
Мудрец скромно потребовал, чтобы ему дали 1 + 2 + 22 + ... + 263 =
= 264—1 зерен. Это двадцатизначное число. Оно имеет делители (какие?).
Если тем же способом покрыть зернами две шахматные доски,
а потом с последней клетки второй доски одно зерно убрать, то на
этой клетке оказалось бы р = 2127 — 1 зерен, т. е.
170141183460469231731687303715884105727
зерен. Это число р не имеет делителей; оно является простым и
состоит из 39 цифр. Можно доказать, что существует большее прос-
тое число из 39 цифр, не указывая самого этого числа. Недавно
установлено, что число 180 р2+ 1 также является простым. Вот это число:
5210644015679228794060694325391135853335898
483908056458352201854618372555735221.
7 октября 1952 г. на электронно-вычислительной машине SWAC
был получен рекордный результат — доказана простота числа
22281—1 Этот великан представляет собой 687-значное число. Какие
у него первая и последняя цифры? [Примечание при переводе.
К настоящему времени, используя более совершенные ЭВМ, удалось
доказать простоту некоторых больших чисел вида 2" — 1, например,
чисел 24423— 1 и 211213—1.]
Евклид доказал, что простых чисел бесконечно много. Установ-
лено, что число 2257—1 не является простым, однако пока не удалось
найти ни одного его делителя.
Можно проделать следующий эксперимент с шахматной доской:
смазать поверхность доски клеем, а затем, подражая жесту сеяте-
ля, бросать с высоты на доску по нескольку зерен, пока на ней не
окажется 64 зерна. Ясно, что зерна распределятся на доске неравно-
мерно: некоторые клетки останутся пустыми, на других будет по
одному зерну, на третьих — по два и т. д. Согласно теории вероят-
ностей можно ожидать примерно такого результата: 24 клетки оста-
нутся пустыми, на 24 клетках будет по одному зерну, на 12 — по
два, на 3 клетках — по три, на одной четыре. При точном подсчете
для чисел клеток получаются дробные значения, однако, сумма этих
чисел, умноженных на числа содержащихся в них зерен, по-прежнему
равна 64.
А вот еще более интересный вариант этого эксперимента: на
карту центральной Европы наносится рисунок шахматной доски (с
64 клетками) и в границах этого рисунка отмечаются 64 самых круп-
ных города. Если окажется, что города распределяются по клеткам в
соответствии с предсказаниями теории, то это будет свидетельство-
вать о том, что на размещение городов влияли многие различные не-
зависимые обстоятельства.
Можно указать простую запись для очень больших чисел. Напри-
мер, многие гигантские числа удается представить в весьма обо-
18
зримой форме, если принять следующие обозначения (20): пусть
означает аа, [а] ~^а в а треугольниках, — а в а квадратах.
Тогда число МЕГА =(5) окажется слишком большим, чтобы ему можно
было приписать какой-либо физический смысл. Это число читается
как «256 в 256 треугольниках» и становится понятно, почему нам
(20)
пришлось отказаться от обычного способа записи чисел. Предлагаем
читателю самому охарактеризовать число МЕДЗОН = (з).
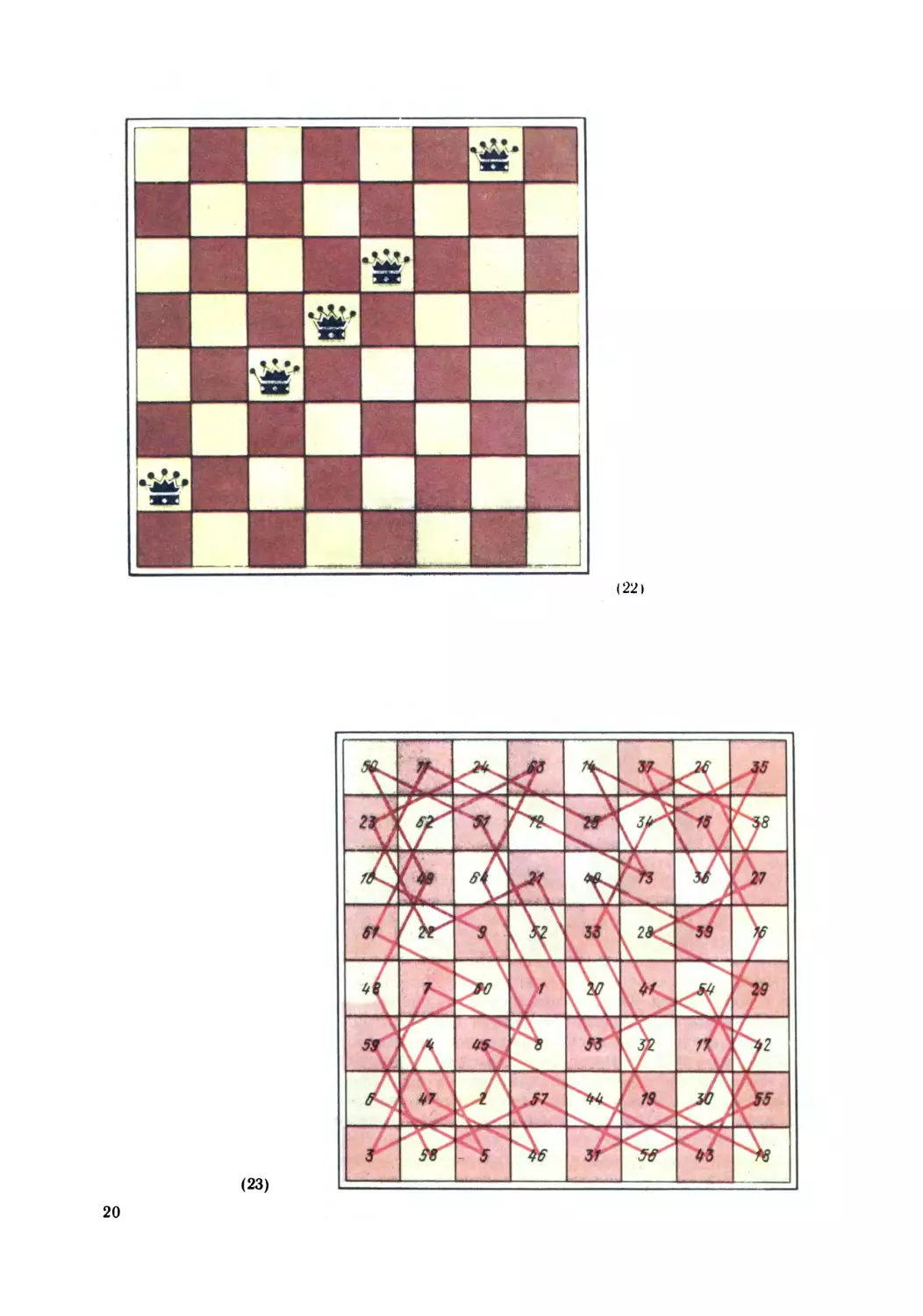
Шахматная доска явилась источником многих задач и игр.
Укажем, например, такую задачу: сколькими способами можно рас-
ставить на доске 8 ферзей (21) так, чтобы ни один из них не бил
другого? Оказывается, имеется всего 92 таких расстановок и все
(21)
они получаются из 12 существенно различных расстановок с помощью
поворотов и зеркальных отражений доски.
На шахматной доске можно расставить 5 ферзей таким образом
(22), что любое поле доски окажется под боем. Всего существует
4 860 решений и все они получаются из 638 существенно различных
расстановок. Задача имеет решение и в том случае, если потре-
бовать дополнительно, чтобы никакие два ферзя не били друг друга.
Предоставляем читателю найти такое решение.
Представим себе, что заминировано такое множество полей
доски, что ни с какого поля левого края доски король не может
19
(22)
(23)
20
добраться до правого края, минуя заминированные поля. Тогда ладье
удастся пройти от верхнего края доски до нижнего, двигаясь по
одним только заминированным полям. То же верно для любой
прямоугольной доски размером тхп. Это утверждение кажется
достаточно очевидным, однако, его доказательство требует опре-
деленных усилий.
Можно обойти всю шахматную доску ходом коня и на шесть-
десят четвертом ходу вернуться в исходное положение. Можно даже
сделать это так, что в результате обхода получится многоугольник
с центром в центре доски, а номера ходов, проставленные в соот-
ветствующих клетках доски, дадут так называемый «магический
квадрат» (23), т. е. суммы номеров в каждой горизонтали и в каж-
дой вертикали окажутся одинаковыми и будут равны 260, поскольку
иное значение для суммы невозможно (почему?).
Великого математика Эйлера привлекали задачи с конем и неко-
торые другие подобные задачи, например, задача о 36 офицерах,
которая заключается в следующем: как построить офицеров шести пол-
ков по одному полковнику, подполковнику, майору, капитану, поручику
и подпоручику от каждого полка — так, чтобы ни в одной шеренге и
ни в одном ряду не повторялись ни звания, ни полки? Это задача
не имеет решения, но в случае 25 офицеров пяти разных полков и пяти
званий задача легко решается (на рис. (24) разные цвета отвечают
полкам, а разные буквы — званиям).
«Игра в офицеров» Эйлера получила впоследствии практическое
применение — так называемые греко-латинские квадраты используются
в настоящее времЪ в агрономических опытах. Для изучения влияния
различных условий на различные сорта какой-либо культуры участок
делится на 25 малых участков: пусть буквы А, В, С, D, Е означают
пять разных сортов культуры, а буквы g, h, i, j, I — пять видов
удобрений; на плане, приведенном на рисунке (25) указаны всевоз-
можные комбинации сортов культуры и видов удобрений — каждому
малому участку отвечает своя комбинация.
Если горизонтальным рядам соответствуют различные степени
влажности, то, как видно из плана, каждый сорт выступает в со-
четании с каждой степенью влажности. Скажем, влажность гх со-
четается с А, В, С, D и Е, но- то же самое распространяется и на
влажности г2, гз, г4 и г5. В то же время все степени влажности
21
сочетаются со всеми видами удобрений. Вертикальные ряды соответст-
вуют различным способам обработки земли; видно, что в каждом
таком ряду встречаются все сорта, все виды удобрений и все степени
влажности.
Имеются еще две диагональные системы участков: т, п, р, q, t и
и, v, ш,х, у. Первая из них отвечает различным датам сева, а вторая —
различным датам сбора. Возьмем, например, диагональ т; она пересека-
ет все горизонтальные ряды, все вертикальные ряды, все линии системы
и—у, все участки А—Е и все участки g—l- Поэтому если подсчитать
средний урожай т с пяти участков, обозначенных этой буквой, то мож-
но будет сказать, что на величину этого урожая влияет дата сева — одна
и та же для всех пяти участкрв (скажем, 1 марта), тогда как, влияние
различий в сортах культуры и видах удобрений устранено. Подсчитав
средний урожай А с пяти участков, обозначенных этой буквой, мы устра-
няем влияние всех факторов за исключением сорта культуры.
Эти замечания, вытекающие из непосредственно очевидных свойств
греко-латинского квадрата, приводят к следующему методу. Подсчитаем
средний урожай М с малого участка, поделив общий урожай со всего
участка на 25. Пусть теперь какие-либо пять участков обозначены какой-
нибудь одной буквой; обозначим той же буквой средний урожай с одного
такого участка, полученный делением общего урожая со всех пяти участ-
ков на пять. Затем вычислим такие суммы:
(М—Л)2Ч- (Л1—В)2'+ (Л4 —С)2Ч- (M — D)2*+ (М—Е)2;
(M—g)2'+ (M-h)24- (M—i)2'+ (M — j)2'+ (M — l)2;
и т. д. Следующий шаг заключается в сравнении этих сумм. Если, напри-
мер, первая из них больше второй, то мы вправе считать, что сорт куль-
туры влияет на урожай больше, чем вид удобрения.
22
Однако точный «дисперсионный анализ» (так принято называть этот
метод) на самом деле оказывается более сложным, поскольку исследу-
ется еще и вопрос о том, нельзя ли объяснить слишком большие расхож-
дения между суммами случайными отклонениями.
Весьма интересны такие игры как, тотализатор, где важно уметь
разбираться не только в лошадях, но и в людях. Ведь на очень хорошую
лошадь, достоинства которой всем известны, ставят почти все играю-
щие, поэтому даже если эта лошадь и придет первой, тот, кто поставил
на нее, выигрывает мало, либо совсем ничего не выигрывает. Следова-
тельно, выгодно ставить на лошадь, достоинства которой хотя и замет-
ны, однако, большинству играющих неизвестны.
Можно устроить тотализатор без лошадей и вообще без каких-
либо приспособлений. Пусть каждый из собравшихся в комнате внесет
в банк, по одному злотому и напишет на отдельном листочке, так, чтобы
не видели остальные,— число, которым он оценивает в сантиметрах
высоту комнаты. Листочки собираются, для написанных чисел подсчи-
тывается среднее, и тот, кто написал самое близкое |<, этому среднему
число, забирает содержимое банка ... высота же комнаты вообще не из-
меряется! Хозяин комнаты, знающий ее настоящую высоту, не имеет,
однако, никаких преимуществ перед своими гостями. В этой игре пони-
мание людей, их образа мышления и манеры восприятия, не менее важ-
но, чем в тотализаторе.
II
ПРЯМОУГОЛЬНИКИ. ЧИСЛА и тоны
Будем говорить, что лист бумаги нормальный, если при
сложении его вдвое получится подобный ему лист (26). Если а и & оз-
начают длинную и короткую стороны нормального листа, то имеет место
пропорция a:b = b:a/2.
Возьмем два одинаковых нормальных листа и приклеим основание
b одного из них к длинной стороне а другого (27). Получится большой
прямоугольник со сторонами а + b и b (заштрихованный на рисунке)
и малый прямоугольник со сторонами Ь, а — b (незаштрихованная чадть
рисунка). Из пропорции a:b = b:a/2 следует равенство а2 = 2д2, откуда
вытекает пропорция (а + b) :Ь = Ь: (а—Ь). Следовательно, заштрихован-
ный прямоугольник подобен незаштрихованному. Но этот последний ра-
вен дважды заштрихованному прямоугольнику. Таким образом, заштри-
хованный прямоугольник подобен дважды заштрихованной своей части.
Назовем лист, подобный заштрихованному на рисунке, гипернор-
мальным. Мы только что показали, что если отрезать от гипернормаль-
ного листа два квадрата, то получится новый гипернормальный лист.
Допустим, что длины сторон нормального листа выражаются целы-
ми числами сантиметров — а см и b см. Из двух таких листов можно ука-
занным выше способом получить гипернормальный лист, длина каждой
стороны которого также выражается целым числом сантиметров. Пусть
длинная сторона имеер р см, а короткая — q см. Отрезав от этого листа два
квадрата, получаем новый гипернормальный лист со сторонами q см и
24
р—2q см. Ясно, что эти числа тоже целые и
что новая длинная сторона меньше половины
прежней. Продолжая этот процесс, мы будем
получать все меньшие гипернормальные ли-
сты с целочисленными сторонами. Но так
как длины сторон — целые числа, то на каж-
дом шагу длинная сторона уменьшается, по
крайней мере на сантиметр; поэтому самое боль-
шее через р шагов длинная сторона исчезнет.
Это противоречие доказывает, что не может
существовать нормального листа с целочис-
ленными сторонами независимо от единицы из-
мерения — будь то сантиметры, дюймы, мил-
лиметры или микрометры.
Отношение сторон нормального листа рав-
но V2~. Это число, которое, будучи помножено
на себя, дает 2. Мы показали сейчас, что л/2~
не является числом рациональным, т. е. что его нельзя представить
в виде отношения а /Ь двух целых чисел а и Ь.
Этот результат наглядно демонстрируется на «решетке целых чисел*
(28). Такую решетку можно представить себе как результат расстановки
точек в шеренги и колонны на равных расстояниях друг от друга напо-
добие того, как расставляют в поле шесты с хмелем. Проводя прямые ли-
нии вдоль шеренг и колонн, получим шахматную доску, покрывающую
всю плоскость.
Приложив нормальный лист к левому нижнему углу рисунка, про-
ведем на нем прямую по диагонали этого листа (наклонная прямая
на рисунке). Взгляд наблюдателя, направленный по этой прямой, не
встретит на своем пути ни одного шеста (почему?).
Число 1/2~ .можно записать в таком виде:
Действительно, если обозначить всю эту дробь через х, то дробь под
первой чертой будет 1 + х. Таким образом,
х2—1 = 1, х2 = 2, х = л/2“.
Мы будем получать приближенные значения 1, 3/2, 7/5, 17/12,... чис-
ла V2? обрывая дробь перед первым, вторым, третьим, четвертым и т. д.
знаком плюс. Угловой коэффициент наклонной на рисунке есть V2~.
Числа 1, 3/2, 7/5, 17/12, ... определяют некоторые точки решетки; напри-
мер, 3/2 означает точку, расположенную на две единицы правее и на три
единицы выше точки в левом нижнем углу. Мы видим, что эти точки
(крупные колечки на рисунке) все ближе подходят к наклонной прямой.
Нам уже известно, что V2~ не является отношением никаких целых
чисел а и Ь. Следовательно, не существует целых чисел а и bt таких, что
25
а2 = 262. Другими словами, два одинаковых военных подразделения,
построенные в квадраты, нельзя перестроить в один квадрат. Это, однако,
всегда можно сделать, если брать одним солдатом больше или меньше.
Такие построения можно осуществить как,раз с помощью найденных выше
дробей:
22 + 22 = 32 —1, 52 + 52 = 72 + 1, 122 + 122 = 172— 1.
Все эти дроби получаются из дроби 1/1: сумма 14-1=2 дает зна-
менатель следующей дроби, а сумма 2+1 — ее числитель; сумма
3 + 2 = 5 есть третий знаменатель, а 2 + 5 = 7 — третий числитель
и так далее:
tUWtL ™
Арифметические формулы, связывающие любую дробь p/q этого ряда
со следующей за ней дробью Р/Q, таковы:
Q = р + р, P = p + Q= p + 2p.
Допустим, что дробь p/q определяет перестройку двух* квадратов
в один с ошибкой ±1:
р2_2^2= ±L
Тогда легко убедиться, что то же самое верно и для следующей дро-
би P/Q:
Р2_2Q2= (р + 2р)2^2(р + р)2^
= р2 + 4рр + 4р2 — bpq—2p2 — 2q2 = 2q2 — р2 = ± 1.
Но дробь 1/1 годится для требуемой перестройки: I2 — 2 • 12 = — 1.
Отсюда следует, что следующая дробь нашего ряда тоже годится, и так
далее; все дроби ряда дают требуемые квадраты. Об этом уже было ска-
зано выше, но теперь мы имеем доказательство.
Наше рассуждение напоминает детский фокус с домино (29); кости
домино устанавливаются в ряд и первая из них опрокидывается; тогда
опрокидываются и все остальные кости (30). Чтобы это предвидеть,
не нужно знать ничего, кроме следующего: первая кость повалена и кости
установлены так, что любая поваленная кость повалит следующую.
Утверждая, что при этих условиях фокус с домино должен получиться,
мы пользуемся правилом, называемым математической индукцией.
26
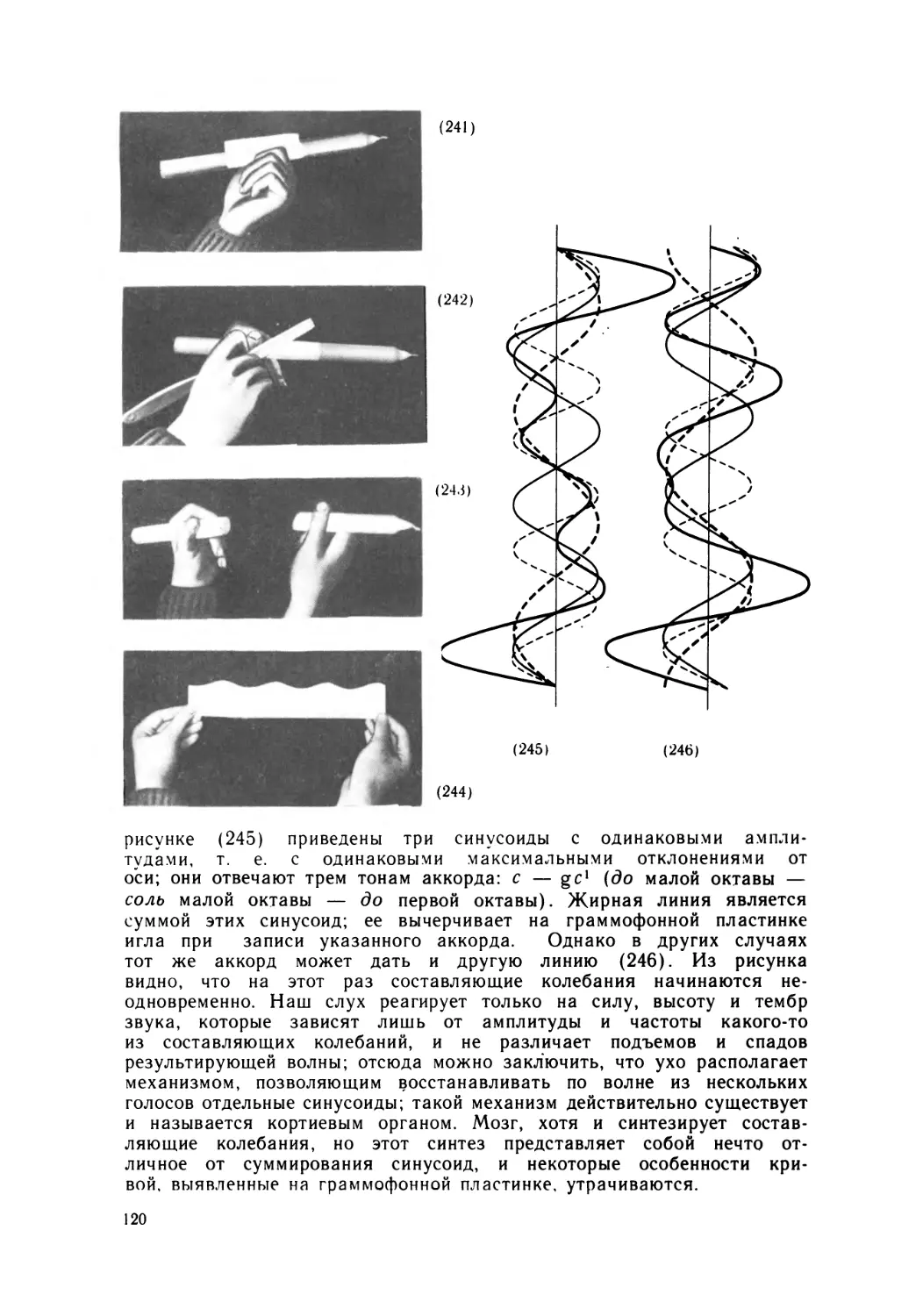
Числа рациональные и иррациональные связаны с проблемой музы-
кальной гаммы (31). Иррациональными называют такие числа, которые
подобно числу V2” не могут быть представлены в виде отношения а/6
двух целых чисел а и Ь. В гамме c-dur интервалы с—d, d—е, f—g, g—a,
a—h, (32) должны быть одинаковы (один тон), а интервалы е — f
и h — с — в два раза меньше (полтона). Давно уже опробованы на моно-
хорде простейшие аккорды. Выяснилось, что совместное звучание тем при-
ятнее для слуха, чем меньше целые числа, выражающие отношение чисел
(32>
колебаний в секунду. Высокому с отвечает в два раза большее число коле-
баний в секунду, чем низкому с, поэтому октава выражается отношением
2:1. Отношение 3:2 дает квинту (g:c)y 4:3 — кварту (f:c), 5:4 — большую
терцию (е:с), 6:5 малую терцию (f:d). Интервал с — с содержит 12 полу-
тонов, или 4 малые терции, следовательно, должно быть (6/5)4 = 2. Однако
дробь слева составляет 2,0736, т. е. больше 2. С этим ничего нельзя поде-
лать: невозможно так, установить высоту тонов, чтобы все аккорды выра-
жались бы отношениями целых чисел и не менялись бы с изменением то-
нальности.
Между f и g лежит fis (черная клавиша в самой середине октавы);
интервал от низкого с до fis таков же, что и интервал от fis до высокого
с — увеличенная кварта. Если отношение чисел колебаний в секунду
fis:с обозначить через х, то должно получиться х • х = 2, т. е., х = '\/2 >
а это — число иррациональное.
Фортепиано — темперированный инструмент: все полутоновые интер-
валы у него одинаковы и, значит, теоретически отвечают отношению чисел
колебаний V2; зато аккорды на фортепиано не являются чистыми.
Поэтому скрипач, следуя своему слуху, отступает от фортепиано, хотя
и настраивает по нему перед концертом скрипку: у него увеличенная квар-
та выражается отношением 7:5, так что его кварта так же близка к тем-
перированной увеличенной кварте, как точка 7/5 на решетке целых чисел
(28) — к наклонной прямой.
27
Бесконечная дробь, выражающая не является простейшей.
Простейшей, очевидно, будет дробь
Обозначим величину этой дроби через х. Под первым числителем стоит
та же самая дробь, следовательно,
х=14-1, х2—х=1, х = 1(л/5"4-1) = 1,618...
Прямоугольник назовем «золотым» (33), если при отсечении от него
квадрата остается прямоугольник, подобный первоначальному. Пусть дли-
ны его сторон будут а и Ь. Тогда
a:b = b : (а—Ь), * а2—ab = b2, (a/b)2 — (alb) =*= 1.
Дробь alb удовлетворяет тому же уравнению, что и х, и поэтому рав-
на (и5 + 1) /2. Это число иррациональное (почему?), так, что никакие
а
£3 (33)
целые а и b не дают золотого прямоугольника. Можно, однако, поступить
также, как и в случае V2? обрывая нашу дробь на первом, втором, третье-
ем и т. д. знаке плюс. При этом получатся дроби
1/1, 2/1, 3/2, 5/3, 8/5, 13/8,
которые дают все более точные приближения золотого числа 1,618... Зна-
менатели этих дробей 1,1,2,3,5,8,13,21,... образуют последовательность
чисел, называемых числами Фибоначчи. Каждое из чисел в этой последо-
вательности, начиная с числа 2, получается сложением двух предыдущих
чисел:
1 + 1=2, 1+2 = 3, 2 + 3 = 5, 3 + 5 = 8,
Пользуясь методом математической индукции, можно показать, что
п-й по порядку член последовательности чисел Фибоначчи равен
Золотой прямоугольник, раскладывается на бесконечное число квад-
ратов: сначала от него отделяется квадрат, затем от оставшегося прямо-
28
угольника снова отделяется квадрат
и т. д. Из рисунка видно, что верши-
ны этих квадратов, оказавшихся
внутри большого прямоугольника,
лежат на двух прямых: диагонали
большого прямоугольника и диаго-
нали прямоугольника, получивше-
гося после удаления первого квад-
рата (почему?). Это разложение
на квадраты служит геометриче-
ским образом бесконечной дроби,
составленной из одних только
единиц.
Если ствол (34) пускает новую
ветвь, то на следующий год он «отды-
хает» и только через год пускает еще одну ветвь — точно так,же ведет себя
каждая ветвь. Поэтому сначала имеется только главный ствол, на следую-
щий год — две ветви, еще год спустя — 3, потом 5, 8, 13, ...— как, в после-
довательности Фибоначчи.
Внутренние дворы дворца (35), обрамленные колоннадами, имеют
форму, близкую к форме золотого прямоугольника. Золотым сечением
называется такое деление отрезка на два отрезка, при котором отношение
всего отрезка к,большему равно отношению большего к, меньшему. В этом
случае оба отношения выражаются золотым числом (почему?).
Представим себе, что трем пастухам поручили стеречь скот на квад-
ратном пастбище. Пастухи, скорее всего, поделят пастбище на три прямо-
угольных участка (36), каждый расположится в центре своего участка
и будет стеречь скот только на этом участке.
29
Если пастух С окажется смекалистей своих товарищей, то он предло-
жит им другое деление на участки, при котором все три пастуха будут на-
ходиться на одинаковом расстоянии от наиболее удаленных точек, своих
участков (37). Это расстояние, равное половине диагонали каждого из но-
вых участков, будет меньше, чем для прежних участков.
Через некоторое время А и В заметят, что их участки больше, чем
у С, и предложат .новый раздел на участки, при котором все трое останутся
на своих местах, расстояния до наиболее удаленных точек, не изменится,
но будет соблюдено естественное условие, что каждая точка квадрата конт-
ролируется тем пастухом, который расположен к, ней ближе других (38).
Однако у С по-прежнему останется самый маленький участок, и В
предложит еще одно изменение, при котором за счет увеличения участка,
отведенного С, участки станут равными, пастухи останутся на прежних
местах и расстояния до наиболее удаленных точек, тоже останутся преж-
ними (39).
Но когда предложение В будет принято, А заметит, что вне его участка
имеются точки, до которых ему ближе, чем двум другим пастухам. Тогда
С укажет, как должны изменить свои позиции А и В, чтобы выполнялось
условие ближайшего пастуха без изменения границ участков (40). Послу-
шавшись С, пастухи А и В вскоре обнаружат, что у них расстояния до
наиболее удаленных точек,больше, чем у С. В конце концов пастухи согла-
сятся вернуться к, первоначальному разделу на три одинаковых прямо-
угольных участка.
Ill
ВЗВЕШИВАНИЕ. ИЗМЕРЕНИЕ.
СП РА В ЕД Л И ВЫ Й РАЗДЕЛ
Посмотрим еще раз на рисунок (19) — на первой клетке
шахматной доски лежит 1 зерно, на второй 2, на третьей 4, на восьмой
128. На первой и второй клетках вместе лежат 3 зерна, на первой и третьей
5 зерен, на второй и третьей 6 зерен и т. д. Легко убедиться, что путем
сложения некоторых из восьми указанных чисел можно получить любое
число — от 1 до 255.
Любую массу от 1 до 40 г можно взвесить, пользуясь 4 гирями, если
гири разрешается ставить на обе чашки весов (41). Это основывается
Й Й Й А
на представлении чисел с помощью степеней тройки. Все целые числа от
—40 до 40 (исключая нуль) получаются из выражения ±27±9±3± 1, в
котором каждое слагаемое берется с определенным знаком или просто
отбрасывается.
Этим пользуются в фокусе с угадыванием имен. Составляется
список из 80 женских имен, занумерованных числами от —40 до 40. Берут-
ся четыре карты; на обеих сторонах первой карты изображается блондин-
ка, на второй — брюнетка, на третьей — шатенка, на четвертой — русая.
Изображения на двух сторонах каждой карты отличаются цветом глаз,
на одной стороне глаза голубые, на другой черные. Если в списке имен
имя Тереза стоит под номеррм —25, то, учитывая, что —25 = —27 + 3—1,
записываем это имя трижды, а именно, на тех сторонах трех карт, где
изображены голубоглазая блондинка, черноглазая шатенка и голубогла-
зая русая. Правило состоит в следующем: 27, 9, 3 и 1 означают соответ-
ственно блондинку, брюнетку, шатенку и русую, знак плюс — черные
глаза, а знак минус — голубые. Непосвященный получает карты, на кото-
рых записано 80 имен, задумывает имя и отыскивает его на картах, а
список остается у фокусника. Он сообщает фокуснику, что это либо го-
лубоглазая блондинка, либо черноглазая шатенка, либо голубоглазая
31
русая; тогда тот, сложив в уме числа —27, +3 и —1, получает число —25
и находит под этим номером в своем списке имя Тереза.
Если сравнивать два предмета по массе на весах без гирь, то можно
только определить, который из них тяжелее. Как узнать, какой из предме-
тов самый тяжелый, если имеется больше двух предметов, а сравнивать
их можно только парами? Сделать это нетрудно: надо найти более тяже-
лый из каких-нибудь двух, сравнить его с каким-нибудь третьим, потом
более тяжелый из них сравнить с четвертым и т. д. В случае п предметов
для определения таким способом самого тяжелого из них потребуется
п—1 взвешиваний.
Точно так же обстоит дело с теннисными соревнованиями: чтобы
выявить сильнейшего из п игроков, достаточно провести п—1 матчей.
Но меньшего числа матчей недостаточно. Ясно, что чемпион должен до-
казать свое превосходство над каждым игроком либо непосредственно
(по итогу матча с ним), либо косвенно (по итогам цепочки матчей).
Пусть точки на плоскости означают игроков, а соединяющие их отрез-
ки — матчи между ними. Чемпион должен быть соединен с каждым игро-
ком либо отрезком, либо ломаной, вследствие чего все п точек должны
быть соединены друг с другом либо непосредственно, либо через другие
точки.
Отсюда легко вывести, что для соединения п точек потребуется
не менее п—1 отрезков (42). Строгое доказательство можно дать по
индукции (ср. (29), (30)). Для соединения двух точек один отрезок, без-
условно, необходим. Пусть для соединения п точек необходимо не менее
п—1 отрезков. Пусть, однако, для некоторого /г<тг существует система
из /г+1 точек, соединенных k отрезками. В этой системе обязательно
найдется точка, из которой исходит только один отрезок (почему?). Если
эту точку и этот отрезок удалить из данной системы, то остается система
из п точек, соединенных k—1 отрезками, где k—1 <л—1, а это противо-
речит нашему условию о том, что для соединения любых точек требуется
не менее п—1 отрезков. Значит, для соединения любых /г+1 точек необ-
ходимо не менее п отрезков.
Спортивные соревнования проводятся обычно по кубковой системе:
участники разбиваются на пары и проводится первый тур; победители
снова разбиваются на пары, после чего проводится второй тур и так да-
лее, пока не определятся два участника последнего, финального матча,
который выявит победителя соревнования. Так, в случае восьми участни-
ков (43) проводится 4 матча первого тура, 2 матча второго тура и один
матч третьего — всего 7 матчей. Меньшим числом матчей, как было пока-
зано, обойтись невозможно.
Обычно второе место присуждают игроку, проигравшему в финаль-
ном туре. Такое правило нельзя, разумеется, признать справедливым,
поскольку второй финалист (Е) не встречался ни прямо, ни косвенно с иг-
роками В и С, проигравшими победителю и поэтому выбывшими из
соревнований. В соревнованиях с 8 участниками число игроков, проиг-
равших победителю, равно 3. Необходимо еще два матча, чтобы выявить
сильнейшего из них (44). В любом случае достаточно провести
32
(44)
О
U 4
п—l + [log2(n—1)] матчей, чтобы определить двух сильнейших игроков
среди п участников (через [а] обозначается наибольшее целое число
не превосходящее а). Меньшее число матчей, вообще говоря, недоста-
точно.
Выражение «вообще говоря» означает, что не существует никакого
метода, который в любом случае позволял бы выявить двух лучших игро-
ков за меньшее число матчей, чем это указано в приведенной выше фор-
муле. Однако случайно может оказаться, что в списке участников игроки
расставлены в порядке, соответствующем их силе; при наличии только
одного корта сначала проводится матч между А и В, а после того как В
выиграет,— матч между В и С и т. д. После п—1 матчей мы имеем не
только победителя, но и полную классификацию N, М, L, ..., С, В, А.
Но это обстоятельство нельзя считать доводом в пользу такой последо-
вательной системы розыгрыша и против кубковой системы (с дополни-
тельными матчами для определения второго по силе игрока). Ведь только
случай позволил уменьшить число матчей: при иных исходах матчей
соревнования растянулись бы. В то же время кубковая система (с допол-
нительными матчами) всегда укладывается в число матчей, указанное
в формуле.
Чтобы упорядочить предметы взвешиванием на весах без гирь (или
расклассифицировать игроков с помощью матчей по двое), можно по-
ступить следующим образом (45). Пусть мы упорядочили некоторое
число предметов и хотим определить место между ними для нового пред-
мета. Найдем сначала серединный предмет S, а именно предмет, который
уступает по массе такому же числу предметов, какое он превосходит;
если число предметов четно, то серединное место пусто, и тогда середин-
ными будем считать два предмета, разделенные этим местом. Сравним
теперь новый предмет А с серединным предметом S (или с любым из двух
серединных предметов). Если А окажется тяжелее S, то сравним его
с серединным предметом группы более тяжелых предметов, если легче —
то с серединным более легких. Так поступаем до тех пор, пока предмет
А не займет место А"' между двумя соседними предметами в. исходном
ряде предметов.
2. Г. Штейнгауз 33
Начнем с двух „предметов — чтобы узнать, какой из них легче, а какой
тяжелее, требуется одно взвешивание; чтобы теперь найти место для
третьего предмета, потребуется самое большее два взвешивания; чтобы
найти место для четвертого предмета, сравним его с серединным, а затем,
смотря по тому, будет он тяжелее или легче, с самым тяжелым или
с самым легким. В любом'случае хватит двух взвешиваний. Получаем сле-
дующую зависимость:
Число взвешиваний, которое достаточно, чтобы найти место для но-
вого предмета среди
2, 3, 4, 5, 6, 7, 8, ...
ранее упорядоченных предметов, равно
1, 2, 2, 3, 3, 3, 3, ...
Поэтому число взвешиваний, достаточное для упорядочения
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, И, 12, ...
предметов, равно
0, 1, 3, 5, 8, 11, 14, 17, 21, 25, 29, 33, ...
Можно получить такую общую формулу для п предметов:
число взвешиваний = 1+Лп—2*, где Л=1+ [log2n].
Не так давно Слупецкий доказал, что этот метод является кратчай-
шим. Метод этот применим не только для классификации игроков или
спортивных команд, но и для упорядочения любых предметов (например,
карточек в алфавитной картотеке).
Указанное выше решение напоминает решение одной артиллерий-
ской задачи (46). Наблюдатель сообщает, на каком участке шоссе нахо-
дится танк, Артиллерист может попасть в любую точку шоссе, но о резуль-
татах выстрела он может судить лишь по сигналам наблюдателя «недолет»
и «перелет». Как действовать артиллеристу?
(46)
Наилучшая тактика состоит в следующем: сначала произвести вы-
стрел в середину участка, затем при сигнале «перелет» в середину бли-
жайшей половины участка и вообще каждый раз целить в середину участ-
ка, на котором в соответствии с сигналами наблюдателя находится танк.
Если L — длина исходного участка, то какой-нибудь из первых п снаря-
дов ляжет не дальше, чем на расстоянии L/2" от цели, т. е. в наихудшем
случае отклонение от цели будет равно L/2". Этот наихудший случай про-
изойдет лишь тогда, когда танк стоит на одном из концов отрезка.
34
Задачу в целом можно представить в виде игры. Если неприятелю
известен метод, которому следует артиллерист, то он постарается распо-
ложить танк как можно дальше от мест попаданий первых п снарядов.
В случае метода, основанного на делении участков пополам, наилучший
выход заключается в том, чтобы поместить танк в одно из двух крайних
положений — это гарантирует расстояние Л/2Л до ближайшей точки попа-
дания.
Что произойдет, если артиллерист изберет иной метод, а разведка
противника этот метод раскроет? Всякий метод приводит к серии выстре-
лов, основанной исключительно на серии сигналов «недолет» и «перелет»,
поскольку этими сигналами исчерпывается вся получаемая артиллери-
стом информация.
Рассмотрим случай, когда производится только один выстрел, п=1.
Невозможно произвести один выстрел так, чтобы была гарантирована
ошибка, меньшая L/2. Существует единственная возможность обеспечить
ошибку, не большую L/2 — выстрелить в середину участка. Пусть такой
выстрел сделан; тогда при втором выстреле максимальная возможная
ошибка окажется наименьшей лишь в том случае, если артиллерист будет
целить в середину ближней или дальней половины участка — в соответст-
вии с сигналами «перелет» или «недолет»; при этом наибольшая возмож-
ная ошибка будет равна L/4. С другой стороны, если первый снаряд не
был бы направлен в середину участка, то танкист, знавший о месте попа-
дания снаряда перед сражением, имел бы в своем распоряжении безопас-
ный участок длиною более, чем L/2. Мы знаем, что артиллерист, действуя
наилучшим образом, может уменьшить этот участок вдвое своим следую-
щим выстрелом, но все равно наибольшая возможная ошибка превзойдет
L/4. Это доказывает, что пользующийся популярностью метод половинок
оказывается наилучшим при п = 2. Пользуясь индукцией, можно убедить-
ся, что то же верно и при любом другом п. Таким образом, с точки зрения
теории игр данный классический метод оказывается наилучшим. Мы, од-
нако, не исследовали, как оценивается этот метод с точки зрения теории
вероятностей, где требуется, чтобы ожидаемое отклонение от цели было
наименьшим. Если считать все местоположения танка на участке равно-
вероятными, то получится в точности такое же решение, какое было толь-
ко что найдено.
Сравнение предметов по массе приводит к задачам совершенно иного
характера, чем ранее рассмотренные, если на чаши весов разрешается
класть по нескольку предметов. Если имеется восемь монет, не отличаю-
щихся по внешнему виду, и известно, что одна из них фальшивая, легче
остальных, то эту монету можно найти за два взвешивания.
Положим по три монеты на каждую чашу и если одна из них перетя-
нет, то сравним следующим взвешиванием любые две монеты с более
легкой чаши: в случае равновесия фальшивой будет оставшаяся третья
монета, в противном случае — более легкая из двух. Если первое взвеши-
вание дает равновесие троек, то второе взвешивание используется для
сравнения двух оставшихся монет — одна из них должна быть более
легкой.
Задача усложняется, если дано тринадцать монет, в том числе одна
фальшивая, отличающаяся по массе от двенадцати настоящих, но неизве-
стно, тяжелее фальшивая монета, чем настоящая, или легче. В этом слу-
чае фальшивую монету можно найти за три взвешивания (47). На рисун-
ке монеты обозначены буквами, образующими надпись ПРАВИЛЬНЫЙ
КОД. Монету с обозначением «И» откладываем, а с остальными произво-
35
®®®®®®©®®®®@©
©@@® ®@©@
Z
@©@©---®@@@
iZU |Х7 4 IА | | | И 4 4ZU | £ 4
|ЛЧ 1д/1 И |ЛЧ IZ7 4
(47)
дим три взвешивания, помещая всякий раз на каждую чашу весов по че-
тыре монеты. Сочетания НАРЫ — КИЛЬ, ЛАПЫ — ВИНО, РОЛЬ —
ДИВА, приведенные на рисунке, указывают, какие монеты помещаются
на каких чашах в очередных взвешиваниях. Результат каждого взвеши-
вания можно выразить с помощью черточек: / (левая чаша тяжелее),\
(правая чаша тяжелее), — (чаши весят поровну). На рисунке изоб-
ражены 13 таких симметричных иероглифов, а над ними обозначения
всех 13 монет. Если, скажем, взять левую половину одиннадцатого иерог-
лифа, то читая ее сверху вниз, получим следующий набор 3 знаков:
V — > —•
Такой набор встречается только в левой половине одиннадцато-
го иероглифа и означает, что в первом взвешивании перетянула правая
чаша, а во втором и третьем чаши весили поровну. Это означает, что
фальшивой является монета К и что она весит больше остальных. Если
результаты трех взвешиваний дают правую половину какого-либо иерогли-
фа, то это будет указывать на то, что фальшивая монета весит меньше
остальных.
Заметим, что в случае иероглифа, указывающего на монету Й, соот-
ношение между весом фальшивой и весом настоящей монеты остается
неизвестным (почему?).
Чтобы процедура выделения фальшивой монеты стала понятной,
рассмотрим несколько возможностей. Пусть в двух взвешиваниях, скажем,
первом и втором, имело место равновесие (—). Тогда монеты Н, А, Р,
Ы, К, И, Л, Ь, П, В, О — настоящие* поэтому в третьем взвешивании не-
равновесие может быть обусловлено только монетой Д. Еще пример:
допустим в первом взвешивании перетянула левая чаша (/), а во втором —
36
правая (\). Следовательно, фальшивая монета перешла с одной чаши
весов на другую и, значит, это либо монета Л, либо монета Н. Если третье
взвешивание дает равновесие (—), то фальшивой была монета Н\ если
же и в третьем взвешивании перетянет правая чаша, то монета Л весит
меньше остальных. (Заметим, что случай /, \, /, а также случай \, /, \ неосу-
ществимы — почему?) Наконец, третий пример: пусть в каждом из трех
взвешиваний перетягивает левая чаша. Это означает, что фальшивая
монета остается все время на одной и той же чаше весов, т. е. это монета
И, В нашем случае она легче остальных.
Доказано (сравнительно недавно), что для выделения фальшивой
монеты среди (Зл—1) /2 монет достаточно п взвешиваний и что меньшее
число взвешиваний недостаточно. Смысл подобного утверждения был вы-
яснен в задаче о соревнованиях: хотя не существует способа, позволяю-
щего всегда обойтись меньшим чем п числом взвешиваний, в отдельных
случаях удается найти фальшивую монету быстрее; если м^З, то
(3 —1)/2= 13, однако могут быть случаи, когда фальшивая монета обна-
ружится уже после двух взвешиваний.
Для измерения количества жидкости пользуются сосудами извест-
ной емкости. Имеются три сосуда емкостью 12, 7 и 5 литров, самый боль-
шой из них наполнен вином. Можно разлить это вино на две равные пор-
ции с помощью бильярда (48), имеющего форму параллелограмма с
острым углом 60°. Представим себе, что сосуды лежат на плоскости биль-
ярдного стола и что перпендикулярные к сосудам прямые, проведенные из
точки стола, в которой находится шар, определяют в каждый момент
уровни вина в сосудах. На рисунке представлен полный путь шара в виде
ломаной, каждый отрезок которой соответствует одному переливанию из
сосуда в сосуд. Всего имеется 11 отрезков, т. е. можно обойтись 11 перели-
37
ванйями и это дает самое короткое решение. Если Л
первым ударом направить шар от левого нижнего угла Г
вдоль короткой стороны параллелограмма, то полу- i
чится другое решение (сколько в этом случае будет I
переливаний?).
с
(49В)
(49А)
. В прямоугольном бильярде, отношение сторон которого выражается
отношением целых чисел (скажем, 5:3), шар, пущенный из угловой точки
стола в направлении биссектрисы угла (49 А), после нескольких рико-
шетов (здесь после шести) снова попадет в какой-нибудь угол стола.
На рисунке (49 В) ломаный путь шара представлен в виде прямой, а все
прямоугольники получены из ис-
ходного путем последовательных
зеркальных отражений, отвечаю-
щих рикошетам шара от сторон
стола. Если отношение сторон стола
равно отношению двух целых чисел
р и q и дробь pjq несократима,
то попаданию шара в угол стола
будет предшествовать p+q—2 ри-
кошетов (почему?).
Желая попасть шаром А в шар
В (50) так, чтобы шар ударился
перед этим' в правый, нижний,
левый и верхний борты, найдем
зеркальное отражение Вх точки
В относительно верхнего борта,
отражение В2 точки В} отно-
сительно левого борта, отраже-
ние В3 точки В2 относительно
нижнего борта и отражение В4
точки В3 относительно правого
борта, а затем будем целить ша-
ром А в точку В4. Все возмож-
ные способы попадания в шар В
можно получить с помощью ре-
шетки прямоугольников, подобной
Вц той, которая изображена на рисунке
38
(49 В), отмечая образы Вь В2, Вз, • точки В в последовательных прямо-
угольниках. Одна из этих точек соединяется отрезком прямой с точкой А.
Чтобы найти истинную ломаную траекторию, нужно по очереди сложить
прямоугольники вдоль их общих сторон, начиная с последнего; в ре-
зультате все прямоугольники наложатся на исходный и если бумага будет
прозрачной, то мы увидим всю ломаную траекторию. Этот прием можно
испробовать и в случае, когда требуется попасть в угловую точку.
Желая поделить такую вещь, как торт, на две равные части, мы можем
прибегнуть к давнему способу, когда одно заинтересованное лицо разре-
зает торт, а другому предоставляется выбор. Достоинства такого способа
очевидны. Ни один из партнеров не может считать себя обойденным:
первый партнер обеспечивает причитающуюся ему долю тем, что разре-
зает торт на две части, которые представляются ему равноценными;
второй по меньшей мере не обделяет себя, выбирая лучшую, на его взгляд,
из двух частей или же, если он не видит оснований для предпочтения, —
любую из них. При этом предполагается, что вещь в целом не теряет в
ценности при разрезании, т. е. ценность двух частей вместе та же, что и
всей вещи в целом, и что' партнеры с этим согласны, хотя соотношение
целого и части может оцениваться ими по-разному. Такие «делимые»
объекты встречаются; примером может служить куча угля.
Возникает вопрос: как произвести справедливый раздел между тремя
или более партнерами? Мы укажем решение на примере пяти партнеров —
оно легко переносится на случай любого числа партнеров.
Обозначим пять участников буквами А, В, С, D н Е. Участнику А
предоставляется право отрезать от торта любую порцию; В, если пожелает,
может эту порцию уменьшить; после этого уменьшенная или первоначаль-
ная порция переходит к С, который также может ее уменьшить либо не
менять и т. д. Когда, наконец, Е воспользуется своим правом уменьшить
порцию или оставить ее без изменений, порцию получает тот из партне-
ров, который отрезал от нее последним (скажем, D), а оставшаяся часть
торта, вместе со всеми отрезанными кусочками,— делится между
остальными участниками (т. е. между А, В, С, Е). На этом втором этапе
еще один участник получает свою долю торта, на следующем этапе —
еще один, после чего останутся двое; эти двое делят оставшуюся часть
торта по принципу: «один делит, другой выбирает».
Теперь убедимся, что каждый из партнеров получит долю, которая
его устраивает независимо от образа действий его товарищей. Если А
отрезал порцию, которая, по его мнению, составляет у5 всего торта, а все
остальные участники пропустят эту порцию без изменений, то порция до-
станется Л, и Л не будет обделен. Если же кто-нибудь отрежет от этой
порции, то Л ее не получит, поскольку она достанется последнему из тех,
кто от нее отрезал. Раз Л полагал, что отрезал У5 часть торта, то после
уменьшения этой части он должен считать, что она станет меньше у5, а то,
что останется — больше 4/5 всего торта; в дележе этого остатка Л примет
участие с правом на */4 часть (ведь одного партнера уже не будет). На вто:
ром этапе ему следует действовать, как и прежде, и если ему придется
резать торт первым, то он должен постараться отрезать часть, стои-
мость которой оценивается им как У4 стоимости всего торта.
Но это предписание недостаточно — нужно еще указать, как должны
действовать другие участники, отличные от начинающих. Допустим, В
сочтет : >рцию, отрезанную Л, слишком большой, т. е. превышающей
7s часть всего торта. Тогда ему следует уменьшить эту порцию до разме-
ра, отвечающего, по его представлению, такой именно части; если никто в
39
дальнейшем этой порции не уменьшит, то В и получит ее — такой, какой
сам отмерил. Если же кто-нибудь от нее отрежет, то она уже В не доста-
нется, а поскольку В сам довел эту порцию до Vs» то при последующем
отрезании получится, на взгляд В, порция, меньшая Vs» и такой она пой-
дет одному из партнеров, так что в дележе на втором этапе В будет пре-
тендовать на V4 часть остатка, который по его оценке составляет более
всего торта, причем В будет одним из четырех участников (так как один
участник отпадет).
Теперь понятно, каково общее правило: на каждом этапе начинаю-
щий должен отрезать порцию, которая, по его мнению, составляет \/п
часть торта, подлежащего дележу на этом этапе между п участниками.
Если же участник, не является начинающим на данном этапе и считает
порцию, отрезанную партнерами, большей 1/п, то он должен постараться
уменьшить ее до 1/п; если же порция — по его оценке — составляет 1/п
торта или меньше, ему следует оставить ее без изменений. Это правило
позволяет каждому участнику получить как минимум такую долю, какая
ему причитается по его собственной оценке.
Способ справедливого раздела приводит к такой игре (51). Участ-
ники игры складываются в равных долях, получившаяся кучка монет раз-
ного достоинства помещается внутри круга, а затем происходит дележ
этой кучки. Вместо ножа, которым резали торт, для извлечения монет из
кучки или их возвращения в кучку пользуются грабельками — эти дейст-
вия соответствуют отрезанию от торта или возвращению кусочков, от-
резанных от чужой порции. Монеты разрешается перемещать только од-
ним движением грабелек, так что на результат игры влияет не только
верный глаз, но и ловкость рук.
Иное правило используется для дележа неделимых предметов. Объяс-
ним это правило на примере четырех братьев, которым нужно поделить на-
следство, состоящее из радиоприемника, мотоцикла и часов. Каждый из
братьев сам оценивает стоимость всех трех вещей. Скажем, один из них
(4) пишет: приемник,— 3000, мотоцикл — 5000, часы — 1500 злотых.
Остальные братья тоже оценивают стоимость каждой вещи. Затем кар-
точки с оценками всех четверых собираются и составляется таблица:
А В С D
Приемник 3000 .1 5000 1 2500 3000
Мотоцикл 5000 4000 4000 I 6000 |
Часы 1 1500 I 1000 1000 500
Итого 9500 10000 7500 9500
1/4 часть 2375 2500 1875 2375
Из таблицы видно, что А оценивает причитающуюся ему долю наследства
в 2375 злотых, В свою — в 2500 злотых и т. д. В первых трех строчках
таблицы рамками отмечены максимальные оценки; каждый из братьев
получает ту вещь, которую он оценил дороже других братьев; поэтому
40
А получит часы, В — приемник, D — мотоцикл, а С ничего не получит.
В результате сложится такая ситуация:
Получили вещей на сумму (злотых
Причиталось
А В С D
1500 5000 — 6000
2375 2500 1875 2375
Недоплачено
Переплачено
875 1875
2500 3625
Поэтому В и D должны внести наличными 2500 + 3625 злотых, всего
6125 злотых; из них А получит 875, а С — 1875 злотых, всего 2750 злотых.
Оставшаяся сумма 6125—2750 = 3375 злотых распределяется поровну
между всеми братьями, так что каждый получит по 843 злотых 75 грошей.
В итоге А и С получат доплату наличными:
А С
875 .1875
+ 843,75 + 843,75
1718,75 2718,75
При этом В и D внесут наличными:
В D
_2500 _3625
843,75 843,75
1656,25 2781,25
Теперь сумма, внесенная В и D, распределена между А и С. Легко убе-
диться, что после распределения вещей и расчетов наличными каждому
из братьев достается на 843 злотых 75 грошей больше, чем доля, которая
причиталась ему по его собственной оценке. Например, D причиталось
2375 злотых, а он получил мотоцикл, который сам оценил в 6000 злотых,
и заплатил наличными 2781 злотых 25 грошей, т. е. получил в чистом виде
3218 злотых 75 грошей, что ровно на 843 злотых 75 грошей больше, чем
сумма в 2375 злотых, которую он сам считал одной четвертой наследства.
То же самое выходит и у остальных братьев.
Участки удобнее всего делить с помощью их планов. Если три лица,
совместно владеющие участком земли, желают поделить его между собой,
то им следует начертить на кальке три одинаковых плана участка (52),
после чего каждый из партнеров должен провести на своем экземпляре
плана две перпендикулярные к улице прямые, которые, по его мнению,
делят участок на три равноценные части (эти части необязательно будут
равными по площади ввиду неравномерной плодородности земли; к тому
же один квадратный метр земли ценится выше, если он расположен бли-
же к дому владельца; речь, таким образом, идет о субъективной оценке
участков). Теперь, после наложения калек, на совмещенном плане полу-
чится шесть линий — по две линии от каждого из трех участников
41
А, В и С. Если линии идут так, как показано на рисунке, то посредник
признает за А участок /, за В — участок //, за С — участок ///. Мы видим,
что каждый из владельцев получает больше одной из трех частей, которые
он сам считал равноценными. Линии могут располагаться по-разному,
всего имеется восемь существенно различных возможностей и в каждом
случае осуществимо такое распределение, при котором надел всякого
участника будет не меньше одной из трех частей, являющихся в его пред-
ставлении равноценными.
Иногда арбитр может установить новые границы посередине погра-
ничных полос, но может обойтись и без этого.
Достоинством дележа с помощью планов является одновремен-
ность предложений партнеров, когда никто из них не знает заранее, что
предлагают другие. Посреднику остается лишь проследить за исполне-
нием договоренности, основное положение которой состоит в том, что
каждый из партнеров должен получить надел, содержащий одну из трех
указанных им частей.
Этот способ можно применить и для дележа торта. Однако проще
всего торт делится между тремя партнерами следующим образом.
Партнер А делит торт на три части. Партнеры В и С, каждый в от-
дельности, указывают, какие части годятся, а какие малы, при этом, одна-
ко, каждый из них должен признать хотя бы одну из частей достаточной.
Если оба они сочтут таковой только одну часть и притом оба одну и ту же,
то А выбирает любую из двух других частей, а В и С делят между собой
две оставшиеся: В может добавить к одной из них кусочек, отрезанный
от другой, после чего С предоставляется выбор. Если же В признает одну
часть достаточной, а С — другую, то они берут себе эти части, а третья
достается А. Этот способ имеет то преимущество, что при разрезании тор-
та получается самое большее 4 куска.
В ряде стран парламентские выборы проводятся по системе пропор-
ционального представительства. Пусть, например, в некотором округе
должны быть избраны пять членов парламента и в выборах участвуют
три партии А, В и С. Эти партии делят между собой мандаты пропорцио-
нально числу голосов, поданных за списки их кандидатов. Возникают
затруднения с дробями: скажем, если из общего числа 150 000 подан-
ных голосов партия А получила 43 500, партия В — 69 000, и партия С —
37 500 голосов, то число мандатов для партии А будет 1,45, для партии
В — 2,3, для партии С — 1,25. Дроби могут учитываться по-разному.
Простейший способ заключается в следующем. Числа разбиваются на
целые части и правильные дроби и сначала распределяются места соот-.
ветственно целым частям, т. е. Л и С получают по одному мандату, а В —
два. Затем сравниваются дробные остатки 0,45, 0,3 и 0,25; наибольший из
них 0,45, поэтому оставшийся свободный мандат получает Л. В результате
Л достанется два мандата, В — 2, С — 1.
На рисунке (53) изображен равносторонний треугольник высотой
10 см; следовательно, такой же будет сумма расстояний от любой внутрен-
ней точки до сторон А, В, С треугольника. Можно считать, что каждая
точка отвечает одному из возможных исходов голосования, условившись,
что 1 мм соответствует 1500 голосам. Например, отмеченная на рисунке
точка представляет результат Л — 43 500, В — 69 000, С — 37 500, по-
скольку такие цифры получаются при умножении расстояний до сторон
треугольника (в миллиметрах) на 1500.
Однако и многие другие результаты голосования, не слишком сильно
отличающиеся от приведенного, дают по правилу остатков такое же рас-
42
пределение мандатов (2, 2, /). Имеется, следовательно, много точек, кото-
рым отвечает распределение (2, 2, /).
Множество точек, отвечающих распределению (2, 2, /), образует
правильный шестиугольник, обозначенный на рисунке этой тройкой
чисел. Это объясняет разбиение треугольника на шестиугольные участки.
Стрелка на рисунке заканчивается в точке, принадлежащей участку
(/, 2, 2). Отсюда видно, что в случае признания первого голосования не-
действительным, может случиться, что по итогам второго голосования,
в котором примет участие такое же число избирателей, партия А потеряет
мандат, хотя и соберет большее число голосов — на это указывает подъем
стрелки; этот утраченный мандат не может, однако, перейти к партии,
потерявшей часть голосов. (Но как тогда читатель объяснит перераспре-
деление мандатов, отвечающее измененному направлению стрелки?)
Описанная выше система называется системой наибольших остатков.
Существуют и другие системы пропорционального распределения, но ни од-
на из них не свободна от парадокса: партия, отбирая голоса у другой пар-
тии и тем самым увеличивая число своих сторонников, тем не менее теряет
мандат. В самом деле, каждой системе отвечает разбиение равносторон-
него треугольника на участки. Три участка, соответствующие тройкам
(2, 2, /), (2,1, 2), (1, 2, 2), будут граничить друг с другом (54). Желая из-
бежать парадокса, мы должны будем в качестве двух границ участка
(/, 2, 2) взять две линии, удаляющиеся от основания А треугольника,
т. е. линии, соответствующиё'углу больше 180°. Но то же относится и
к, двум другим участкам, а все три угла не могут быть больше 180°, так
как в сумме они дают 360°.
IV
ПАРКЕТЫ. ПЧЕЛИНЫЕ СОТЫ. БОТИНКИ.
ПЛОЩАДИ И ДЛИНЫ
Разбиение треугольника на предпоследнем рисунке напоми-
нает пчелиные соты. На фотографии (55) запечатлены шестиугольные
отверстия, заполняющие плоскость. В каждой точке сходится не более
тоех шестиугольников: только разбиение плоскости на шестиугольники
(56) обладает этим свойством — при любом другом разбиении будут су-
ществовать точки, в которых сходится более трех областей.
Нам уже известно разбиение плоскости на квадраты (шахматная
доска). Деформации этого разбиения дают всевозможные паркеты из
четырехугольников (57).
Последний паркет этого класса — треугольный (58); не может
быть никакого паркета из одинаковых правильных многоугольных пли-
ток, кроме указанных трех.
Существуют еще однородные паркеты: однородный паркет составлен
из нескольких видов правильных плиток, причем в каждом стыке сходится
равное число плиток одного и того же вида. Поскольку угол правильного
n-угольника составляет 2—4/и прямых или 1/2—1/h часть полного угла,
то всякому однородному паркету отвечает некоторый набор натуральных
чисел п, р, q, г, ..., удовлетворяющих уравнению
l__L + _L_l+_L__L + ±__L+ ...
2 п 2 р 2 q 2 г
Это уравнение имеет 17 решений, но только 11 из них можно реализовать
в виде паркетов, плитки которых заполняют всю плоскость и не находят
одна на другую. Три из них уже известны, некоторые другие показаны на
рисунках (59—64). Быть может, еще более красивы неоднородные парке-
ты (65—68). Неоднородных паркетов бесконечно много (почему?).
44
-z <М:
(56)
45
46
(62)
(63)
47
'▼▼▼▼▼▼▼▼TV
z
F
'▼▼▼▼▼▼▼▼▼▼
AAAAAAAAAA
F
1111 A 1 1 Д 1 1 1
(64)
(65)
48
(66)
(67)
(68)
Какому из паркетов следует отдать предпочтение? В известном смыс-
ле можно выделить первый, составленный из шестиугольников, который
мы видим на фотографии пчелиных сот. А именно, если мы пожелаем
разбить бесконечное поле на участке размером в 1 гектар так, чтобы на
ограждения пошло как, можно меньше материала, то участкам нужно
будет придать форму правильных шестиугольников. (Каково точное со-
держание этого утверждения?)
Связанные с этим расчеты находят применение в обувной промыш-
ленности. И ширина, и длина ступни у всех людей разные; если к углу
дощечки приложить прямоугольник, такой ширины и длины, как у ступни,
то противоположная вершина прямоугольника даст нам некоторую точку
дощечки; разным ступням будут отвечать разные точки. Фабрика, же-
лающая производить мужскую обувь, должна получить через обувные
магазины замеры стоп большого числа покупателей; в результате на изме-
рительной дощечке появится целый ряд точек, Если наберется несколько
сотен* или тысяч точек, то окажется, что точки довольно плотно запол-
няют некоторую область и только несколько точек лежит за ее пределами.
Для этих немногих аномальных стоп фабрика производить обуви не бу-
дет. Для нормальных мужских стоп можно будет ограничиться, скажем,
27 типами обуви разной ширины и длины, Фабрика должна изготовить
27 различных колодок, и возникает вопрос: как выбрать размеры этих
колодок? Понятно, что на дощечке нужно нанести 27 точек с таким рас-
четом, чтобы каждая точка выделенной области оказалась как можно
ближе к, одной из них.
Обычно точки расставляются так, как, на рисунке (28); каждую точку
можно считать центром квадрата, что отвечает квадратному паркету.
Можно, однакр, пользоваться паркетом из шестиугольников; тогда каж-
дая точка будет центром правильного шестиугольника (69).
50
Оказывается, второй способ выгоднее: при одном и том же числе
27 колодок применение шестиугольной сетки позволяет уменьшить макси-
мальное расстояние точек области до ближайших центров, что дает воз-
можность точнее подобрать нужный размер обуви. Можно изготовить
дощечку, выложенную шестиугольниками с указанными на них номерами
обуви (70); приставив ступню к бортам дощечки и примкнув к ней по-
движный угольник, мы по его вершине найдем шестиугольник с нужным
нам размером обуви.
Трещины в подсушенном на солнце иле на берегу реки или в эмали
на кафельных плитках (71) кажутся совершенно беспорядочными. Но
если присмотреться к ним внимательнее, то становится заметно, что углы
между трещинами близки к прямым. Это явление можно объяснить,
допустив, что трещины образуются в результате сокращения поверхно-
стного слоя ила. По законам механики трещина должна пойти таким обра-
зом, чтобы работа, затраченная на ее образование, была наименьшей.
Эта работа пропорциональна площади сечения вдоль линии разрыва.
Поэтому разрыв должен происходить по линии, отвечающей наименьшему
возможному сечению. В случае однородного поверхностного слоя из
этого вытекает, что трещины образуют прямые углы. Меняющаяся тол-
шина слоя обусловливает искривления трещин (почему?).
Каждая точка ветвления является точкой гладкой линии, в которой
берет свое начало некоторая боковая линия; гладкая трещина — более
старая. Это замечание позволяет проследить всю генеалогию трещин и в
конце концов найти предков всего семейства.
Представим себе, что вначале на рисунке (72) были изображены две
области, А и В. При добавлении новой линии, соединяющей две точки
первоначальных линий, получается новая область С; поскольку каждая
из прежних дуг делится новой на две части, то общее число дуг увеличи-
вается на три. Через п шагов получаем карту с новыми п странами, при-
чем число границ увеличится на Зп. Вначале было две страны и три гра-
ницы, поэтому теперь получится п + 2 стран и Зп + З границ. Если внеш-
нюю область также считать страной (океан), то придем к п + 3 странам
с Зп + З границами. Каждая граница разделяет две соседние страны,
т. е. на любую границу приходится два соседства: ХсУиУсХ. В резуль-
тате имеем 2(3п + 3)=6п + 6 соседств и п + 3 страны; значит, среднее
51
число соседей на страну будет
(6п + 6)/(п + 3) = 6—12/(п + 3).
Это число меньше шести, но приближается к шести с ростом числа стран;
напомним, что океан считается за страну, а число k материковых стран
есть п4-2, так что среднее число соседей на страну составляет
6-12/(fe+l).
Исключим теперь океан и морские границы. На этом мы потеряем
одну страну и по крайней мере шесть соседств, если не менее трех стран
имеют морские границы. Тогда среднее число соседей на одну страну
снизится и будет меньше 6—12/(6 +1), а значит, заведомо останется
меньше шести.
Мы предположили, что число стран с морскими границами (при
6>3) не меньше трех. Но легко нарисовать карту с несколькими страна-
ми (например, с 10), из которых только одна или две имеют выход к мо-
рю; это можно будет сделать, если допустить существование стран,
имеющих форму кольца, или же стран, которые граничат с какой-нибудь
другой страной по двум отдельным границам. Не учитывалось также и
то, что в одной точке могут граничить более трех стран.
Мы хотели бы знать, для всякой ли карты среднее число соседей
у одной страны меньше шести? С этой целью рассмотрим произволь-
ную карту — только каждую страну будем предполагать связной
(Германия накануне 1870 г. не отвечала бы этому требованию).
Нашу карту можно получить, начав с одной страны и пририсовывая
затем поочередно новые границы: каждый раз будем соединять две
граничные точки (которые, в частности могут, совпадать) или ри-
совать замкнутую линию внутри одной страны. Это необязательно
даст новую страну (почему?), но в таком случае не возникнет и
новых соседств. Если получится новая страна, то только одна, а
число границ может увеличиться на 1, 2 или 3. Следовательно, при-
бавится самое большее шесть соседств, и мы, рассуждая как, прежде,
убеждаемся, что среднее число соседей на страну не превзойдет шес-
ти. На этот раз, однако, океан не исключался и считался за страну.
Если учитывать только материковые .страны и сухопутные границы,
то, как, показывают многие примеры, полученная оценка для среднего
числа соседей остается в силе. Доказать, что это так, по-видимому,
нелегко, и автор не гарантирует, что это вообще возможно.
52
Представим себе, что, начиная с года, мы регулярно измеряем
рост ребенка, нанося метки на рейке и проставляя рядом возраст
ребенка: 1 год, 1,1 года, 2 года и т. д.
Пусть скорость роста обратно пропорциональна времени: двух-
годовалый ребенок, растет в два раза медленнее, чем годовалый,
трехлетний — в три раза медленнее годовалого и т. д. Тогда числа на
рейке дадут шкалу, которая называется логарифмической. Такие имен-
но шкалы видим мы на логарифмической линейке (73). Их на ней
53
четыре: две верхние и две ниж-
ние; две средние нанесены на
подвижной планке. Обе верхние
шкалы одинаковы, обе нижние
тоже одинаковы, но увеличены
в два раза по сравнению с верх-
ними. При любом положении
подвижной планки числа верх-
ней неподвижной шкалы будут
пропорциональны стоящим не-
посредственно под ними числам
верхней подвижной шкалы.
Например, в положении, пока-
занном на рисунке (74), числа
самой верхней шкалы в 2,45 ра-
за больше чисел примыкающей
к ней подвижной шкалы, по-
этому чтобы умножить 3,45 на
2,45, достаточно установить
риску окошечка на делении 3,45
подвижной шкалы — она ука-
жет тогда на верхней неподвиж-
ной шкале искомое произведе-
ние 8,45. Ошибка будет не
более 3%. Числа самой верх-
ней шкалы являются квадра-
тами стоящих под ними чисел
самой нижней шкалы. Риска
на снимке показывает, что
2,912 = 8,45. Следовательно, линейка позволяет находить квадрат-
ные корни (как?). Логарифмическая линейка особенно удобна для вы-
числений по тройному правилу.
Если смешиваются две жидкости разной плотности, например,
два сорта бензина или бензин и нефть, то для определения плотности
смеси можно воспользоваться номограммой (75). Широкая наклон-
ная шкала — подвижная. Плотность более легкой жидкости дается
показанием подвижной шкалы в точке пересечения с левой вертикалью,
плотность, более тяжелой — показанием той же шкалы в пересечении
с правой вертикалью; в точке пересечения наклонных шкал показа-
ние неподвижной шкалы означает процент объема смеси, приходя-
щейся на более тяжелую жидкость, а показание подвижной — плот-
ность смеси. Чтобы .определить плотность смеси, составленной на 55% из
нефти с плотностью 0,830 и на 45% из бензина с плотностью 0,543,
совмещаем деления 0,830’ и 0,543 подвижной шкалы с правой и
левой вертикалями и, передвигая шкалу вдоль этих вертикалей, до-
биваемся, чтобы точка пересечения наклонных шкал пришлась на
деление 55 неподвижной шкалы. В той же точке подвижной шкалы
снимаем показание 0,701 — это и будет искомая плотность смеси. До-
казательство основывается на подобии треугольников, получающихся в
пересечении шкал и вертикалей. Если жидкости отличаются по плот-
ностям меньше, чем на 20%, то вместо вертикалей следует восполь-
зоваться двумя параллельными наклонными прямыми. Зная любые три
из четырех величин, можно определить четвертую; например, по плот-
54
ностям смешиваемых жидкостей и самой смеси с помощью номограм-
мы легко найти процентное содержание жидкостей в смеси (как,?).
Некоторые номограммы более просты, например, номограмма фо-
тографов. Расстояния f, g, h от линзы до предмета, изображения и
фокуса (76) удовлетворяют на основании законов оптики соотноше-
нию 1 /f 4- 1 / g = 1 /h. Если на номограмме (77) провести прямую
Фохуе
Изо&ражем/е
через деления, отвечающие двум из этих величин, то мы найдем третью.
Например, в нашем случае предмет расположен на расстоянии 7,5
дюйма от линзы, фокусное расстояние которой равно трем дюймам,
поэтому изображение по другую сторону линзы будет находиться от
нее на расстоянии пяти дюймов.
По этой номограмме можно определить, сколько времени (Л)
потребуется двум людям на совместное выполнение некоторой работы,
если один из них может выполнить ее сам за / часов, а другой за
g часов. (Если один рабочий нагружает машину за 5 часов, а другой
за 7,5 часа, то работая вместе, они закончат погрузку за 3 часа.)
Можно строить номограммы, не градуируя шкалы числами.
Формула Мерсенна
выражает число п колебаний струны в секунду через длину струны
L в метрах, радиус сечения струны г в миллиметрах, силу натяжения
струны Р в килограммах силы и плотность материала струны d в
граммах на кубический сантиметр; в формулу входит также число
л = 3,14159... Если заранее считать, что длина струны составляет
1 м, а сила натяжения — 100 кгс, то можно будет построить номограм-
55
(78)
му (78), которая позволит определять радиус сечения струны по
высоте звука и материалу, из которого она изготовлена. Например,
на нашем рисунке пунктирная прямая в пересечении с остроконеч-
ной кривой дает радиус сечения железной струны (Fe), издающей
звук, ля. Номограмма строится сначала в числах: берутся логариф-
мы обеих частей формулы и строятся соответствующие логарифми-
ческие шкалы (как, на логарифмической линейке); потом числа на
шкале частот колебаний заменяют нотным станом со скрипичным
ключом, т. е. вместо частот колебаний указывают отвечающие им
тоны; вместо плотности металла проставляют название металла данной
плотности, а за величину радиуса принимают величину отрезка,
высекаемого подходящей кривой. Если известны материал струны и ее
радиус, то по номограмме можно определить высоту тона. Некоторые
из промежутков между нотными делениями больше других (почему?)
Изображенный на целочисленной решетке многоугольник (79) ил-
люстрирует следующее утверждение: если внутри многоугольника с
вершинами в точках решетки лежит /, а на его границе — b точек
решетки, то плошадь многоугольника
равна произведению площади
единичного квадрата решетки
на сумму
i + ь/2 — 1.
Например, в данном случае
площадь равна
6+11/2—1 = 10,5.
Это утверждение легко
проверяется для прямоуголь-
ника. Если на его основании
лежит т + 1 точек, а на вы-.-
соте п + 1 точек, то площадь
прямоугольника будет равна
тп квадратных единиц. На
границе лежат четыре точки
в вершинах и еще по т — 1
56
точек на горизонтальных сторонах и по п—1 на вертикальных,
поэтому для числа b граничных точек имеем
&=4 + 2(т—1) +2(п—1) = 2m + 2n.
Точки решетки внутри прямоугольника образуют т—1 колонн и
п—1 рядов, поэтому произведение этих чисел дает число внутрен-
них точек;
/= (т—1) (и—1).
Подсчитаем далее сумму Z+&/2—1:
(т— 1) (и—1) +-i- (2m + 2n) —1 = тп.
Эта сумма, как мы видим, численно равна площади прямоугольника.
Заметим теперь, что .из двух многоугольников, имеющих одну
общую сторону, можно сделать один, если эту сторону удалить; при
этом число i + b/2—1 для полученного многоугольника будет суммой
соответствующих чисел для исходных многоугольников (почему?). Тем
самым число i + b/2—1 для треугольника, полученного в результате
деления прямоугольника диагональю, будет равно половине соответ-
ствующей суммы для прямоугольника и, следовательно, — ввиду справед-
ливости утверждения для прямоугольников, — будет выражать площадь
треугольника. Но любой многоугольник, с вершинами в точках решет:
ки можно получить, объединив, а затем удалив несколько таких тре-
угольников. Поэтому наше утверждение верно для любого многоуголь-
ника с вершинами в точках решетки.
Решетки целых чисел можно использовать и для измерения пло-
щадей произвольных областей, а не только многоугольников. Любую
область можно расположить на решетке таким образом, что число
точек, попавших внутрь области, будет больше или равно площади
области, выраженной в квадратных единицах решетки.
Площадь заштрихованной области (80) равна 11 квадратным еди-
ницам. Расположим эту область на решетке произвольным образом
и произведем разрезы вдоль линий решетки. Вся фигура разобьется
на отдельные квадратики. Сложив их в одну стопку (81), мы сможем
проткнуть эту стопку булавкой в таком месте, что по меньшей мере
57
*
•
• • •
(82)
резания (82). Во всей области
11 заштрихованных частей бу-
дут проколоты. Иначе булавка
протыка/ia бы всегда не более
10 таких частей и оказалось бы,
что проекции этих частей По-
крывают нижний квадрат не бо-
лее 10 раз, т. е. площадь
всей области не превосходит
10 квадратных единиц решет-
ки,— а нам дано, что она
равна 11 квадратным едини-
цам. Отыскав нужную точку
и сделав прокол, расставим
снова квадраты по своим ме-
стам, так, как было до раз-
останется не менее 11 следов
прокола; передвигая область по вертикали и горизонтали, совмещаем
один из следов с точкой решетки; тогда и все другие следы окажутся
в точках решетки и область будет содержать не менее 11 таких точек.
Если большой точности не требуется, то решетку целых чисел
можно использовать для измерения площадей. Например, можно изме-
рить площадь листка, наложив на него кальку (или целлулоидную
пластинку)^ на которую нанесены точки по образцу (79). Если на
листок, придется п точек, и расстояние между соседними точками бу-
дет. 3,16 мм, то площади листка будет около 10м мм2. Можно улуч-
шить этот метод, если расставить точки так, как показано на рисунке (83).
(Какими должны быть расстояния между соседними точками?)
Пусть выпуклая фигура площади 4 имеет центр, т. е. точку, в
которой любая проходящая через нее хорда делится пополам. Наложим
эту фигуру на решетку целых чисел так, чтобы центр совпал с
точкой решетки, а в остальном произвольно (84); тогда внутри фигу-
ры (или на ее границе) окажется по меньшей мере еще 2 точки решет-
ки. Эта теорема принадлежит Минковскому; доказать ее не просто.
Мы воспользуемся теоремой Минковского, чтобы оценить, как, да-
леко можно видеть сквозь чащу шестов для хмеля (85). Удалим один
шест и расположим в этом месте наблюдателя. Маленькие кружки
изображают проекции шестов; пусть их радиус будет г. Всякий луч
просматривается до тех пор, пока точки решетки отстоят от него бо-
(83)
(84)
58
лее чем на г. Построим ка-
кую-нибудь прямоугольную по-
лоску с центром в наблю-
дательном пункте шириной 2г
и длиной 2/г. Площадь этой
полоски равна 4, а центр
находится в точке решетки;
следовательно, по теореме Мин-
ковского внутри полоски или
на ее границе окажутся по
меньшей мере еще две точки
решетки. Кружки с центрами
в этих точках пересекут сред-
нюю линию полоски (отстоя-
щую от краев полоски на рас-
стояние г) или будут касаться
этой линии и закроют обзор.
Следовательно, дальность об-
зора не превышает 1/г.
С другой стороны, иногда
удается видеть почти на такое
расстояние. А именно, будем
смотреть по касательной к бли-
жайшему кружку в той же ко-
лонке; продолжим эту пря-
о о о о о о
о о о о о
о \° о А о о
о о' ° 1 о о
о о о/ о о
о о О\ ф о о
о о о \*\- -ф о о
о о о о о
о о о о о о
о о о о О о
о о о о о\ о
о о о о о о
о о о о о о о
О
О
О
О
О
О
О
О
О
.О
О
О
О
(85)
мую до пересечения с пунк-
тирной линией центров ближайшей колонки и подсчитаем, на ка-
ком расстоянии находится точка пересечения. Большой прямоуголь-
ный треугольник подобен малому, а требуется вычислить гипоте-
нузу большого. Подобие треугольников дает пропорцию h : 1 = 1 : г,
откуда h = 1/г. Однако дальность обзора будет меньше /г, так
как на пути встретятся кружки ближайшей колонки. Сдви-
нем такой кружок вдоль линии центров так, чтобы он касался
выбранной прямой. Получится еще один малый треугольник, равный
прежнему. Его сторона на выбранной прямой равна V1—г2, поэтому
в наихудшем случае дальность обзора составит 1/г—V1—г2. Правда,
на пути еще раньше стоит точка касания с ближайшим к наблюда-
телю кружком, но это препятствие будет устранено, если мы чуть-
чуть изменим угол зрения, что почти не уменьшит дальности. Таким
образом, мы увидим некоторые точки на' расстоянии, чуть меньшем
1/г—V1 —г2, но точки, отстоящие на расстояние 1/г, уже не будут
видны. Если, например, расстояние между шестами равно 50 см, а
их диаметр — 5 см, то приняв за единицу решетки 50 см, получим:
г = 0,05 единицы, 1/г = 20 единиц=10 м, 1/г—V1—г2 = 19,0013 единиц»
»9,5 м; следовательно, расстояние до наиболее удаленной точки бу-
дет лежать в пределах от 9,5 до 10 метров. Измерение площадей' проще
измерения длин. Если контур области задан с некоторой точностью,
то площадь области, можно оценить с ошибкой, которая уменьшается
по мере уточнения контура; если контур можно указать с какой угод-
ной точностью, то и ошибку можно сделать как угодно малой-
. Иначе обстоит дело с длинами. Две весьма близко расположен-
ные кривые могут значительно отличаться по длине: например, зиг-
загообразная ломаная (86) почти на 40% длиннее прямой.
59
Существуют также линии бесконечной длины — если мы допуска-
ем существование объектов, имеющих корректные математические оп-
ределения, и не интересуемся вещественными моделями. Математикам
нужны такого рода линии в их теоретических исследованиях. Так, в
одном из исследований решается задача об описании кривой, про-
ходящей через все точки квадрата — и внутренние, и граничные. Строя
.свое решение, Серпинский начинает с многоугольника (87), потом из
Четырех подобных многоугольников составляет крест (88), потом из
четырех подобных крестов составляет новый крест (89) и продолжает
так, далее (90, 91), раз за разом повторяя один и тот же прием. В
пределе эти приближения дают кривую, заполняющую квадрат: мо-
жем считать ее траекторией движущейся точки и для каждой точки квад-
рата указать, в какой имейно момент через нее пройдет движущаяся
60
точка. Эта кривая имеет бесконечную длину. Она не может быть нари-
сована в своей последней, идеальной стадии (почему?).
Всматриваясь в рисунок, (91), мы замечаем, что он покрыт как.
бы сеткой диагональных прямых (почему?).
Вокруг области, ограниченной замкнутой кривой, например, облас-
ти, имеющей форму озера Снярдвы (92), можно описать квадрат.
В этом легко убедиться, если провести сначала пару горизонталь-
ных касательных к, контуру области, затем пару перпендикулярных
к, ним касательных, и после этого повернуть рамку касательных вокруг
контура на 90°. В результате горизонтальные касательные станут
вертикальными и обратно. Поэтому если расстояние между касатель-
ными у одной пары было больше, чем у другой, то после поворота
оно сделается меньше; следовательно, в какой-то момент эти расстоя-
ния должны сравняться, а как раз тогда в пересечении касатель-
ных получится квадрат. Гораздо труднее доказать, что во всякий контур
можно вписать квадрат; однако на самом деле это так (93).
Для измерения длин можно пользоваться клетчатой сеткой —
по образцу шахматной доски. На прозрачную кальку наносится
сетка, каждое очко которой представляет собой клетку со стороной
3,82 мм. Прямые одного из двух направлений сетки проводятся под
углом 30° к. ее краю. Чтобы измерить, например, длину Вислы, нужно
положить кальку на карту, совместив их края (94), и пройти Вислу
от истока до устья, двигаясь по клеткам сетки ходом шахматной ладьи
и считая число переходов (95); затем калька переворачивается на
другую сторону и проделывается то же самое; наконец, совместив одну
из прямых сетки с краем карть}, повторяют эту операцию третий раз.
Суммарное число переходов дает искомую длину в миллиметрах.
Масштаб нашей карты равен 1:5 000 000, поэтому чтобы найти длину
Вислы в километрах, нужно умножить полученное число на 5.
Объясним принцип действия такого лонгиметра на примере
измерения отрезка прямой длиною L миллиметров. Число ходов шах-
матной ладьи вдоль отрезка равно сумме проекций отрезка на оба
направления сетки, если принять сторону клетки за единицу измере-
ния. После трехкратного наложения • лонгиметра получим сумму проект
61
ций на шесть направлений. Из сказанного ранее видно, что эти направ-
ления образуют звезду, между лучами которой заключен угол 30°.
Если с одним из направлений отрезок составляет угол а, то со всеми
шестью направлениями он образует углы
а -I- 0°, а + 30°, а -I- 60°,
а+ 90°, а 4-120°, а+150°.
62
Поэтому сумма проекций равна
L [sin (а -I- 0°) -I- sin (а + 30°) + sin (а + 60°) +
+ sin (а + 90°) +sin (а+ 120°) + sin (а-I- 150°)]
Выкладки показывают, что эта сумма имеет наименьшее значение при
а = 0° и наибольшее значение при а=15°. Таким образом, при любом
а сумма проекций будет не меньше
L(0+ 1/2 +VT/2+ 1 + VT/2+ 1/2) = 3.732L.
и не больше
+ + + + _3,864L.
В качестве единицы измерения мы взяли отрезок длиной 3,82 мм;
поэтому чтобы выразить сумму проекций в миллиметрах, нужно разде-
лить полученные результаты на 3,82. Тогда вместо точного значения
L мы получим величины 0,977L и 1,011L. Следовательно, лонгиметр
измеряет длину отрезка с ошибкой от —2,3% до 1,1%. Но любую кри-
вую можно считать составленной из небольших отрезков прямой,
поэтому относительная ошибка при определении длины всей кривой
также будет лежать в этих пределах; как, правило, она будет даже
меньше (почему?).
На некоторых картах приводятся горизонтали (изогипсы), кото-
рые дают представление о перепадах высоты на местности. Изме-
ряя общую длину этих горизонталей, можно оценить среднюю кру-
тизну местности.
При использовании для этой цели лонгиметра подсчитывается
число пересечений его прямых с горизонталями.
Для определения направления и величины максимального уклона
плоской покатой местности (что может иметь практическое значе-
ние, например, при дренаже местности) не требуется ни сложных
измерений, ни сложных выкладок, Измеряется уклон в произвольном
направлении ОХ и на карте в этом направлении откладывается от-
резок, длина которого в сантиметрах равна величине уклона в про-
центах; затем то же самое повторяется
для направления ОУ, перпендикулярного
к ОХ, после чего фигура достраивается
до прямоугольника; его диагональ дает
направление и величину максимального
уклона; в примере на рисунке (96) наи-
больший уклон составляет 5%. Рулетка,
шест с делениями и уровень с визиром —
вот все, что нужно для измерений.
Все еще остается открытым вопрос
о длине линий, которые дает нам при-
рода, а не математическое определение.
Когда измеряется длина реки, возника-
ет трудность, связанная с мелкими изви-
линами в ее течении. Такие реки или
горные хребты служат иногда граница-
ми между странами. Переходя ко все более
подробным картам и соответственно
63
увеличивая точность измерений,
мы можем оказаться в ситуа-
ции, когда длина возрастает
неограниченно.
Лонгиметр позволяет обой-
ти эту трудность, но имеет тот
недостаток, что его точность
ограничена величиной квадра-
та земной поверхности, пред-
ставляемого на карте клеткой
лонгиметра. Эта величина ме-
няется с изменением масш-
таба карты, и в разных
случаях следовало бы рекомендовать разные масштабы и надле-
жащие лонгиметры. Такие рекомендации составить было бы нелегко.
Можно, однакр, измерять длины, подсчитывая число пересечений
параллельных линий на кальке с кривой на карте (мы уже упоминали
этот метод в связи с измерением горизонталей). Пусть п—число пе-
ресечений, d—расстояние между параллельными линиями, a k—число
различных положений кальки: тогда число
j _ nnd
2k
дает приближенное значение длины. Все k положений кальки полу-
чаются последовательными поворотами на угол 180° /k.
Этим мы еще не освобождаемся от парадокса бесконечной дли-
ны. Чтобы избежать парадокса, условимся, что на каждой прямой
все точки пересечения, начиная с одиннадцатой, считаться не будут.
Указанное ограничение приведет нас к, определенной величине, кото-
рую мы обозначим Аю и назовем длиной десятого ранга. Это понятие
свободно от парадокса длины; если переходить к более подробным
картам и увеличивать точность измерений путем увеличения k и умень-
шения d, то, ограничивая число учитываемых точек пересечения десятью,
мы будем получать по формуле для L числа, все более близкие к не-
которому пределу — идеальной длине Аю- Точно так же определяются
длины любых рангов Lb L2, •••, L™, ...
Это правило позволяет указать процедуру измерения, которая сво-
бодна от таких единиц длины, как километры, мили или версты: для
сравнения длин границ различных стран можно было бы, например,
во всех случаях пользоваться длиной двенадцатого ранга.
Пусть Um и L'm означают длины левого и правого берегов Вислы
одного и того же ранга tn. Парадокс длин может проявиться теперь
в новой форме:
limZ4=oo, limL" = oo.
m—>оо m—>оо
Можно, однако, ожидать, что отношение имеет конечный
предел. Чтобы найти этот предел с любой желаемой точностью, нуж-
но только выбрать т достаточно большим и пользоваться разлинован-
ной калькой, как, было указано. Такой метод позволяет определить
отношение длин двух берегов Вислы, хотя сами эти длины остаются
при этом неизвестными.
V
ВЫБОР ПУТИ. ПОИСКИ БЛИЗКИХ СОСЕДЕЙ.
ПРЕСЛЕДОВАНИЕ КОРАБЛЕЙ
Кратчайший путь ведет по прямой. Бедуин возвращается
к, шатру (97), но хочет по дороге сводить крня на пастбище и к реч-
ке. Что ему сделать раньше?
Зеркальное отражение шатра от берега реки дает точку аь а
эта точка при зеркальном отражении от границы пастбища перехо-
дит в точку а?. Производя отражения в обратном порядке, получаем
точки Ai и А2. Выделенная на рисунке ломаная линия является крат-
чайшей дорогой к, шатру: длина ее равна расстоянию между бедуином
и точкой а2. Пожелай бедуин сперва напоить крня, он должен был
бы преодолеть по меньшей мере такое же расстояние, как, между ним
и точкой А2, а оно было бы больше.
Бедуин не чертил плана; он просто прицелился ружьем в точку,
где сходятся река и пастбище и, увидев, что шатер оказался справа,
поехал налево. Чтобы объяснить его поведение, заметим, что точки
а2 и Л2 строятся независимо от того, где находится всадник. Он может
оказаться либо ближе к а2, либо ближе к Л2, либо на одинаковом расстоя-
нии от а? и А2. Точки, равноудаленные от 02 и Л2, образуют прямую;
это нейтральные точки. Одной из них будет точка, лежащая на берегу
реки и на границе пастбища, однако, и шатер находится в нейтраль-
ной точке. Ведь если бедуину, проследовавшему от шатра к, реке, за-
тем к, пастбищу и снова к, шатру, покажется, что всякая дорога к, шатру
3. Г. Штейнгауз
65
через пастбище и реку длиннее этой, то, проделав тот же путь в об-
ратном порядке, он должен будет убедиться в своем заблуждении.
Итак, мы имеем две нейтральные точки — шатер и точку, где сходятся
река и пастбище. Разделяющая прямая должна пройти через обе
эти точки. Увидев, что вторая из точек расположена левее шатра,
бедуин поймет, что и сам он находится по левую сторону разделяю-
щей прямой, т. е. ближе к, точке а^, чем к, Л2. Поскольку длины двух
кратчайших путей равны расстояниям до точек, а* и Л2, то бедуин
выберет путь, отвечающий меньшему расстоянию, т. е. расстоянию
до а^, как, на рисунке. Метод зеркальных отображений, использван-
ный здесь, — тот же, что и в задачах с бильярдом.
Три деревни должны построить общую школу. Чтобы суммарное
время, затрачиваемое на хождение в школу, было . наименьшим, ее
следует расположить в подходящем месте. Детей в деревнях — 50,
70 и 90. Разложим на столе карту района и там, где на карте обозна-
чены деревни, просверлим в столе отверстия (98); пропустим через
эти отверстия веревочки, свяжем их верхние концы в узел, а к ниж-
ним привяжем гири массой 50, 70 и 90 г.; тогда узел, установив-
шись, укажет нам место, где должна строиться школа.
Можно, однако, и не портить стола. Построим сначала треуголь-
ник (99) со сторонами 50, 70 и 90. Нас будут интересовать внешние
углы )С, )£, )$С этого вспомогательного треугольника. Теперь на
карте нужно отыскать такую точку, из которой деревни видны
под этими углами. Например, деревни 50 и 90 должны быть видны
из нее под углом, равным внешнему углу между сторонами 50 и 90 вспо-
могательного треугольника (100). Множество точек, удовлетворяющих
этому условию, представляет собой окружность, проходящую через
точки 50 и 90; чтобы найти ее центр, достаточно заметить, что точки 5и и
90 видны из центра под вдвое большим углом, чем соответствующий
внутренний угол вспомогательного треугольника. Построив эту окруж-
ность, повторяем построение для точек 50 и 70 — получаем еще
одну окружность; пересечение двух окружностей дает нам место под
школу.
Первый способ с гирями основан на законах статики: система на-
ходится в равновесии, когда ее центр тяжести занимает самое низкое
возможное положение. Передвигая узел, мы удлиняем или укорачиваем
свисающие части веревочек, вследствие чего центр тяжести перемещается
в вертикальном направлении; смещение центра тяжести вниз пропор-
66
ционально сумме приращений этих частей, умноженных на массы при-
крепленных к ним гирь. В силу этого центр тяжести займет самое низкое
положение в том случае, когда сумма длин горизонтальных частей ве-
ревочек, умноженных на массы соответствующих гирь, будет наименьшей.
Но в этом случае сумма расстояний, пройденных всеми детьми до шко-
лы, также будет наименьшей, поскольку она тоже равна сумме произве-
дений горизонтальных частей веревочек на массы гирь. (Если каждый
сантиметр на карте означает километр на поверхности земли, а каждый
грамм — одного ребенка, то сумма в сантиметро-граммах дает сумму в
километро-детях.)
Задача о расположении телефонной станции, к которой должны
быть проложены кабели от подстанций, ничем, по существу, не отличается
от задачи о выборе места для школы.
Способ с гирями имеет то преимущество, что всегда дает требуемое
решение — даже когда масса одной из гирь настолько велика, что две
другие не могут ее уравновесить. Ведь в этом случае узел (если только
он достаточно толст) застрянет в одном из отверстий и, таким образом,
укажет искомое место. В то же время вспомогательный треугольник во-
обще нельзя будет построить, если в одной из деревень детей окажется
больше, чем в двух других, взятых вместе. Но и тогда, когда треугольник
существует, дальнейшие построения могут не привести к правильному
ответу (в каких случаях?).
Мы только что воспользовались следующим законом статики: если
три силы находятся в равновесии, то можно построить треугольник, сторо-
ны которого выражают эти силы по величине и направлению. Если по-
вернуть треугольник (99) на подходящий угол, то его стороны станут
параллельны жирным линиям на рисунке (100); это как раз объясняется
действием упомянутого закона — нужно только применить его в обратном
порядке, исходя из треугольника сил.
Последнее замечание приводит нас к так называемым взаимным
фигурам Кремоны. Пусть для примера имеется десять стержней, соеди-
ненных шарнирами в точках А, В, С, D, Е, О (101); мы получаем шесть
3*
67
областей: 1, 2, 3, 4, 5, 6. Построим теперь взаимную фигуру — многоуголь-
ник сил (102); на этой фигуре области будем обозначать буквами, а вер-
шины цифрами. На рисунке (101) вершина С принадлежит областям
2, 3 и 6 и в ней соединяются стержни ВС, ОС и DC; на рисунке (102)
вершины 2, 3 и 6 принадлежат области С, а границы областей В и С,
О и С, D и С соответственно параллельны ВС, ОС, DC на рисунке (101).
Эта закономерность распространяется на весь многоугольник сил.
Шарнир С конструкции находится в равновесии, если приложенные
к нему силы направлены так, как указано стрелками, и по величине
равны сторонам теугольника С. Подобное же условие должно выпол-
няться и для других шарниров. Например, силы, приложенные к шарниру
D, определяются сторонами треугольника D, однако стрелка вдоль
стержня CD должна теперь указывать в сторону D, так как согласно
закону равенства действия и противодействия стержень, оказывающий
давление на шарнир С, должен оказывать точно такое же давление
и на шарнир D. Следовательно, расставив стрелки в треугольнике С мно-
гоугольника сил, мы должны, рисуя стрелку вдоль стороны 6—3 внутри
D, обратить стрелку, идущую вдоль этой же стороны внутри С. Но
стрелки внутри каждой области задают обход ее контура в некотором
направлении, так что мы получаем направления всех стрелок в области D,
потом в области Е и так далее. Это дает возможность построить весь
многоугольник сил, если известна одна его сторона и направление со-
ответствующей стрелки. Следовательно, зная усилие в одном из стержней
конструкции, мы можем найти и все остальные. Изменение величины
этого усилия приведет лишь к пропорциональному изменению размеров
многоугольника, но форма его останется прежней. Например, усилие
в стержне ОЕ всегда будет в 7/4 раза больше, чем в стержне ВС
(поскольку на рисунке 102 отрезок 5—4 равен 35 мм, а отрезок 6—2 —
20 мм); при этом,если стержень ВС растягивается, то стержень ОЕ сжи-
мается (почему?).
Решая задачу о выборе места для постройки школы, мы исходили
из треугольника сил, а затем определяли по нему расположение стерж-
ней в условиях равновесия (веревочки играли роль стержней).
Поиск кратчайшего пути может оказаться иногда весьма трудной
задачей. Если после того, как разбиты палатки лагеря, комендант поже-
лает выбрать для себя такую из них, чтобы обход всех палаток занял
у него как можно меньше времени, то ему достаточно перепробовать по
очереди все возможные варианты. Если, однако, палаток больше десяти,
то проверка вариантов растянется на многие годы.
68
Поставим перед собой более легкую задачу: как соединить палатки
тропинками, чтобы из каждой можно было попасть в каждую и чтобы
общая длина всех тропинок была как можно меньше. Тропинки
могут разветвляться, но только у палаток.
Проще всего сделать это так. Начнем с любой палатки и соединим
ее тропинкой с ближайшей. Для каждой из этих двух палаток найдем
ближайшую к ней среди остальных палаток; ту, которая расположена
ближе к своей палатке, соединяем с ней тропинкой. Это будет третья
палатка, и мы имеем уже три палатки, соединенные двумя тро-
пинками, для каждой из этих трех палаток снова ищем ближай-
шую к ней и снова из ближайших выбираем ближайшую в качестве
четвертой палатки. Продолжаем действовать так до тех пор, пока тро-
пинки не соединят всех палаток. Тропинок получится на одну меньше,
чем палаток, а все они вместе составят некоторое дерево. Так мы будем
называть систему тропинок, соединяющих все палатки, в которой из
каждой палатки в каждую ведет только один путь. Существует несколько
(103)
- - дядявх I ммгевщши
- - - Пореви т ха/пево/ши
таких деревьев, но то, которое мы нашли, будет самым коротким. На ри-
сунке (103) изображено кратчайшее, или минимальное, дерево дорог, со-
единяющих польские воеводские центры. Каждый из этих центров соеди-
няем с ближайшим к нему — получим дороги первой категории, образую-
щие одно или несколько деревьев первой категории. Теперь представим се-
бе, что из каждого центра одного дерева проведены дороги во все центры
другого дерева и из всех этих дорог выбрана кратчайшая; длину этой доро-
ги принимаем за расстояние между деревьями. Соединив каждое дерево
первой категории с ближайшим к нему деревом, получаем дороги второй
категории, образующие вместе с дорогами первой категории одно или не-
69
сколько деревьев второй категории. Соединяя деревья второй категории
с ближайшими к ним деревьями, получаем деревья третьей категории
и так далее, пока все центры не будут охвачены одним деревом.
Построенное здесь дерево дает мало что нового, так как обычные
карты позволяют судить о расстояниях не только между городами дере-
ва, но и между любыми другими. Иначе обстоит дело в ситуациях, кото-
рые мы сейчас рассмотрим, поскольку речь будет идти не о точках
плоскости, как в случае городов, но об элементах пространств очень боль-
шого числа измерений (читай — об элементах, обладающих большим
числом свойств); мы же, строя дерево, будем поступать‘подобно бота-
нику, засушивающему объемный цветок в плоском гербарии и тем са-
мым сохраняющим лишь наиболее существенные расстояния между от-
дельными частями цветка.
Можно, однако, и из дерева городов извлечь полезные сведения.
Если, скажем, кто-нибудь пожелал бы охватить все воеводские центры еди-
ной кратчайшей железнодорожной сетью без развилок в промежутках
между городами, то ему пришлось бы запроектировать эту сеть как раз
в виде дерева, указанного на рисунке (103).
О деревьях можно говорить всегда, когда даны, какие-то элементы
и указаны расстояния между ними; при этом элементы вовсе не обяза-
ны быть точками на плоскости. Выберем, например, 28 контрольных пунк-
тов в лесах Силезского Бескида и будем регистрировать в этих пунктах
наличие определенных мхов, скажем, печеночников (Hepaticae). В Бески-
де встречается несколько различных видов печеночников, а именно 31.
Ботаники оценивают распространенность растений (частоту их появления)
по шкале: 0, 1,2, 3, 4. Так на западном склоне Смерековца вид Alicyjaria
scalaris выступает с частотой 1/ Cephalozia biscyjndata — с частотой 2,
a Cephalozia connivens — с частотой 0. Смерековцу соответствуют числа
1, 2, 0,... — всего 31 число, ибо таково общее число видов печеночников.
В другой местности — Стожек Вельки — имеем числа 0, 1, 0,... Сравнение
Смерековца со Стожком дает следующие разности: 1, 1, 0,... (всюду из
большего числа вычитается меньшее) — всего 31 разность. Сумма раз-
ностей равна 13. Число 13 можно принять за расстояние между Смереков-
цем и Стожком. Это не расстояние в обычном смысле, а лишь в смысле
различий в распространенности видов печеночников: чем больше разнят-
ся леса в отношении видов мхов, тем больше это расстояние. Теперь мож-
но составить таблицу расстояний между отдельными лесными пунктами:
имеется 28 пунктов, следовательно, расстояний будет 364. Пользуясь
этой таблицей, можно составить минимальное дерево для 28 бескидских
лесов. Но если построить его на обычной карте, то картина получится
искаженная, ибо карта дает буквальные расстояния, тогда как в случае
дерева расстояния берутся «по печеночникам». Поэтому следует пере-
рисовать дерево, не считаясь с обычными расстояниями и размещая леса
в соответствии с ботаническими расстояниями между теми точками дере-
ва, которые соединяют в процессе его построения. Таких расстояний по-
лучится 27; длины отрезков на рисунке (104) выбраны в соответствии с
этими расстояниями.
Кружки на рисунке обозначают различные лесные пункты: темными
кружками представлены буковые леса, заштрихованными — еловые, а
наполовину темными, наполовину заштрихованными — смешанные. Ле-
са различных типов вышли на дереве отдельно стоящими группами: почти
отсутствуют темные кружки, попавшие в окружение иных кружков. Из
этого становится ясно, что виды печеночников связаны с типом леса, так
70
Я юзу от Ч.диселни
баранья Гура О--------О---------О Чень
хМагура
См ер ено Seif О--О Сто^ дёмнц
Магрра
U ^г-^дХааоры
б о то я ЯоорнинХ
Хблатня Хаменны Чантория больна
Старь/ Гронь ф----Ф-------ф---ф-—ф---------ф
I Гура бу нови Шыдзелы/а
Хребет между ф блатней а Клинтоном
о—
Кубалонна
Козины/
4|________ф Потом Гаура
Потом барбара
ф----------ф Рубийца
о—
Хребет между
Сонрастнои а
дрловои
I Сальмололь
^К югу от д. диселни
•0 Чпнтория дельна
0 баранья
О -Еловые леса
ф -бунобь/е леса
ф-Смеи/иннь/е леса
(4 Кобыла (южн.)
(104)
что по ним можно судить о типе леса. Любопытно отметить, что по типу
леса нельзя судить о видах печеночников.
Рассмотренный здесь метод пригоден для классификации челове-
ческих черепов (105), языков, авиационных двигателей и многих других
вещей.
Задачу о кратчайшем пути приходится решать в процессе преследо-
вания. Ясно, что если преследование ведется в неограниченном простран-
стве (океане), то наилучший метод — это постоянно держать курс на
преследуемую цель. Однако далеко не всем ясно, что именно мы называем
«наилучшим методом». Если, например, на преследуемом корабле не зна-
ют, что за ним ведется погоня, и поэтому он сохраняет свой курс незави-
симо от наших действий, то у нас имеется лучший метод, чем просто дер-
жать курс на цель. Зная отношение скоростей V:vy мы можем указать
курс, позволяющий догнать преследуемый корабль в кратчайшее воз-
можное время. Для этого нужно найти все те точки, до которых корабли
71
могли бы дойти от своих исходных позиций за одно и то же время (т. е. точ-
ки, отстоящие от них на расстояния, пропорциональные скоростям V и и);
эти точки составляют окружность, так называемую окружность Аполло-
ния (106). Если курс преследуемого корабля пересекает эту окружность,
то следует держать курс на точку пересечения, если он ее не пересекает,
то догнать корабль вообще невозможно.
В последнем случае можно постараться подойти к нему как можно
ближе. Его скорость v больше скорости V преследователя. Допустим,
когда его заметили, он шел перпендикулярно к направлению, в котором
был виден (107). На рисунке указано построение, позволяющее найти
требуемый курс. В момент наибольшего сближения удаляющийся корабль
будет виден прямо по курсу (почему?). Этой позиции на рисунке отвеча-
ют черные корабли, начальной — белые.
Может,, однако, случиться, что капитан корабля увидит преследова-
телей и изменит свой курс; тогда методы, основанные на его неосведомлен-
ности, потеряют свою силу. В отыскании наилучшего метода мы должны,
следовательно, исходить не из наиболее благоприятных, а из наименее
благоприятных условий, как это было с шахматами и другими играми.
Будем именовать преследуемый корабль Черным, а корабль-пресле-
дователь Белым. Допустим, что скорость Белого V больше скорости Чер-
ного v. Эффективность метода преследования можно оценивать временем,
которое потребуется Белому, чтобы догнать Черного: метод будет тем луч-
ше, чем меньше это время.
В открытом море Черный может неизменно следовать разумному
правилу: что бы ни делал Белый, уходить от него по его курсу. Тогда ско-
рость, с которой Белый будет догонять Черного (относительная скорость),
72
будет не больше, чем I/—v, а время, за которое Белый догонит Черного —
не меньше, чем dl (V—v), где d означает исходную дистанцию между
кораблями. Но раз Черный располагает простым способом, позволяю-
щим ему продержаться по меньшей мере в течение этого времени, то и
Белый не может гарантировать, что закончит погоню за меньшее время.
Если он хоть раз изменит правилу — держать курс на преследуемого,
то Черный продержится еще дольше. Однако Белый может гарантировать,
что догонит Черного за время dl (V—v) — для этого нужно только посто-
янно держать курс на Черного и идти с максимальной скоростью I/.
Если Черный попробует иногда уклоняться от своего разумного правила —
уходить от Белого по его курсу — или если он снизит свою скорость, то
Белый сможет догнать его быстрее, чем за гарантированное им время.
Теперь нетрудно указать наилучшую тактику для каждого: «прямо
на преследуемого» для Белого и «прямо от преследователя» для Черного.
При такой тактике Белый гарантирует время d/(V—v), Черный — то
же самое время. Из одного этого уже следует, что Белый не может гаран-
тировать меньшее время, чем d/(V—v), а Черный — большее. Наилуч-
шее время оказывается одним и тем же для обеих сторон, и поэтому по-
гоня представляет собой замкнутую игру.
Чтобы подчеркнуть сходство между погоней и обычными играми,
обозначим время от начала до конца погони через Т и, выражая Т в часах,
d — в километрах, a v и V — в километрах в час, будем по окончании
погони присуждать либо d/(V—v) — Т очков Белому, либо Т—d/ (V—v)
очков Черному, смотря по тому, какая из этих величин положительна.
Это приводит нас к игре, которая будет справедливой и, как мы уже ви-
дели, замкнутой.
Погоня усложняется, когда корабли находятся вблизи берега (108).
Если линия берега прямая (или незначительно искривлена), то наилуч-
ший метод для каждого из кораблей состоит в следующем. На карте
строится уже рассмотренная выше окружность Аполлония; она меняется
с изменением позиций кораблей. Наиболее удаленную от преследуемого
корабля морскую точку этой окружности назовем точкой Аполлония. Са-
мое лучшее для обоих кораблей — держать курс на эту точку. В откры-
том море такая тактика не отличается от прежней, но в случае, когда по-
гоня начинается вблизи берега, новое правило может предписывать иной
образ действий, поскольку точка
Аполлония не обязана лежать на
прямой, соединяющей корабли, тог- х.
да как прежнее правило требует, -----
чтобы оба корабля следовали вдоль
этой прямой. Если оба корабля будут MRgXXV х7
придерживаться нового, общего для 4 11
них правила, то точка Аполлония / \ \
будет оставаться неподвижной, а I \
курсы кораблей — постоянными; | iKxXx
если же один из кораблей станет от ' \ /
него уклоняться, то точка Аполло- I \ \
ния может начать смещаться вдоль \
линии берега, и второй корабль, еле- гр
дуя новому правилу, должен будет ]|LJ X ’щхХ
менять свой курс. Близость берега ' Гр------
приводит к уменьшению времени I
погони и поэтому благоприятна для (Н)«) I | |
73
преследователя. Интересно отметить, что понятие «близость» получает
здесь точный смысл: корабли находятся вблизи берега, если точка Аполло-
ния лежит на береговой линии.
Если два корабля преследуют третий, нужно построить, две окруж-
ности Аполлония — по одной для каждого корабля-преследователя.
Позиции этих кораблей и точка пересечения окружностей, наиболее уда-
ленная от преследуемого корабля, дадут три вершины треугольника.
Если преследуемый корабль окажется внутри этого треугольника (109),
то наилучший образ действий для каждого из трех кораблей — держать
курс на указанную точку пересечения. Если преследуемый корабль нахо-
дится вне треугольника (НО), то двум другим лучше всего держать курс
прямо на него, т. е. следовать прежнему правилу. Что же касается пре-
следуемого корабля, то он должен уходить по курсу наиболее опасного из
преследователей — именно того, для которого время преследования,
вычисленное по формуле Т = d/ (V —v ), окажется наименьшим.
Следует помнить, что треугольник подвижный и преследуемый ко-
рабль может попасть на одну из его сторон. Этого, однако, не случится,
если вначале он был внутри треугольника и все три корабля строго
придерживались общей для них рекомендации; в этом случае^ все они
будут сохранять постоянный курс (почему?).
Решение задачи о двух преследователях оставлено нами без до-
казательства. Читателю предоставляется самому проверить, верно ли
это решение. Особенно интересно выяснить, обоснован ли наш метод
в том случае, когда преследуемый корабль «берется в клещи».
Пусть один корабль, преследуя другой, не меняет своего курса
относительно прямой, соединяющей корабли, и пусть второй корабль
также идет под некоторым неизменным углом к этой прямой. Тогда
оба корабля будут двигаться по кривым, закручивающимся вокруг
общего полюса (111). Чтобы найти этот полюс, являющийся, очевидно,
местом перехвата, построим две1 окружности: окружность Аполлония и
окружность, проходящую через три точки — начальные позиции корабля
и точку пересечения их начальных курсов. Эти окружности пересекутся
в двух точках, наиболее удаленная из которых будет искомым полюсом.
Угол между курсами кораблей равен углу между направлениями от
кораблей к полюсу; это вытекает из того, что полюс лежит на второй
окружности.
Рассмотрим теперь треугольник: корабль — корабль — полюс.
Угол, под которым основание этого треугольника видно из полюса, равен,
как показывает рисунок (111), разности углов между курсами кораблей
и основанием; отношение же боковых сторон равно отношению ско-
ростей V:v, поскольку полюс лежит на окружности Аполлония. Так
74
СССе
(ШУ (112)
как углы между курсами кораблей и соединяющей их прямой, а также
величины скоростей V и v не меняются, то треугольник корабль — ко-
рабль — полюс, построенный для любого другого момента времени,
будет подобен исходному. Пусть теперь новый треугольник строится
по истечении малого промежутка времени /. Тогда концы основания
сместятся вдоль курсов на отрезки Vt и vt и полюс для нового треуголь-
ника совпадет с прежним (почему?). Итак, полюс остается на месте,
корабли видны из него под неизменным углом и углы между курсами
кораблей и направлениями от них к полюсу также не меняются.
Каждый корабль, следовательно, движется по кривой, которая составляет
один и тот же угол с любой прямой, проходящей через некоторую опре-
деленную точку; такая кривая (112) имеет название — логарифмическая
спираль. Если вращать эту спираль вокруг неподвижного полюса,
то кажется, что она расширяется или сжимается. Две спирали, со-
ставляющие с лучами из полюса одинаковые углы, конгруэнтны.
Такими именно являются траектории кораблей на рисунке (111).
А теперь пусть корабль-преследователь действует наилучшим обра-
зом, т. е. держит курс непосредственно на преследуемый корабль, ко-
торый по традиции пиратов предпочитает, чтобы его курс шел всегда
под прямым углом к курсу преследователя. Как мы уже выяснили,
траектории кораблей будут конгруэнтными логарифмическими спира-
лями. Если в начальный момент расстояние между кораблями было d,
а скорость преследователя V, то время, за которое преследуемый ко-
рабль будет настигнут, составит величину dIV, независимо от скорости v
последнего, так как эта скорость никак не- влияет на расстояние
между кораблями. В силу этого расстояние по спирали от исходной
позиции преследователя до самого полюса будет равно d. Но поскольку
любой момент может считаться начальным, то длина спирали от ко-
рабля-преследователя до полюса всегда равна расстоянию между ко-
раблями. Угол между лучами из полюса к кораблям всегда прямой,
ибо он равен углу между курсами кораблей, как было отмечено при описа-
нии рисунка (111), а этот угол прямой.
Возможно ли, чтобы траектории двух кораблей совпадали? Это
зависит от отношения скоростей v:V. Когда оно равно 3,644, путь
будет один и тот же и, — что кажется удивительным, — преследуемый
корабль, идущий с большей скоростью, будет повторять путь преследо-
вателя, пока не столкнется с ним у полюса (ИЗ).
75
Так полученная спираль обладает особым свойством — она будет
своей собственной эволютой; ее можно описать концом нитки, на-
крученной на дугу спирали и подходящим образом продолженной.
На рисунке (113) этой дугой является участок спирали между ко-
раблями, а продолжением нитки — соединяющий их прямолинейный
отрезок; большой корабль накручивает нить на спираль и одновременно
описывает эту спираль концом нити. Полюс всегда виден справа по бор-
ту под углом 74°40' к его курсу — это относится к каждому из кораблей.
Три собаки А, В и С, расположенные на одинаковых расстояниях
друг от друга, срываются в погоню: А гонится за В, В за С и С за А —
все с одинаковой скоростью v. Сближение собак А и В происходит не
только за счет собственной скорости и первой из них, но и за счет со-
ставляющей скорости второй, бегущей за С; эта составляющая равна
ц/2, так как cos 60° = 1/2. Следовательно, скорость, с которой сближаются
А и В, равна Зи/2. Если начальное расстояние между ними было s, то
продолжительность погони будет s: (3v/ 2) = 2s/ Зу. Собаки будут все
время находиться на равных расстояниях одна от другой и подобно
кораблям опишут логарифмические спирали. Длина каждой спирали
равна произведению времени погони на скорость, (2s/3v)v = 2s/3, а точка
встречи лежит в центре первоначального треугольника.
При сматывании нитки с круглой катушки получается другая спи-
раль (114). Ее эволюта — окружность. Вообразим, что какой-нибудь пред-
мет перестал испытывать силу тяготения (и сопротивление воздуха);
тогда он унесется с поверхности Земли как раз по такой спирали (почему?).
Муха, ползущая по радиусу равномерно вращающейся граммофон-
ной пластинки, опишет другую спираль, так называемую спираль Ар-
химеда(115). Расстояние мухи от центра диска будет в этом случае
пропорционально углу, на который повернется радиус. Кулачок, составлен-
ный из двух дуг такой спирали и прикрепленный к диску (116), преобра-
зует равномерное вращение диска в равномерное движение поршня по-
переменно в одну и другую сторону (почему?).
76
VI
ПРЯМЫЕ ЛИНИИ. ОКРУЖНОСТИ. СИММЕТРИЯ.
ОПТИЧЕСКИЕ ИЛЛЮЗИИ. ПРЕВРАЩЕНИЕ НЕВИДИ-
МОГО В ВИДИМОЕ
Стержневой многоугольник позволяет проводить прямые
линии без помощи линейки. Инверсор (117) состоит из шести стержней:
четыре одинаковых коротких стержня образуют подвижный ромб,
а два одинаковых длинных стержня соединяют две вершины этого ромба
с неподвижной точкой F^. Если соединить теперь третью вершину ромба
с другой неподвижной точкой F2 еще одним стержнем, равным по длине
расстоянию FiF2, и если все соединения шарнирные, то при деформации
ромба его свободная вершина будет описывать прямую.
Чтобы определить центр тяжести палки, будем, поддерживая палку
в горизонтальном положении ребрами ладоней, постепенно сдвигать
руки (118). Если центр тяжести находится первоначально между руками,
то палка будет оставаться в равновесии: при смещении центра тяжести
в сторону одной из рук, давление на нее будет становиться во много раз
больше, чем на другую; в конце концов произведение давления на коэф-
фициент трения окажется больше для ближайшей к центру тяжести ла-
дони и тогда движение палки относительно нее прекратится и палка
начнет перемещаться относительно другой ладони. В этой игре палки
с ладонями руки будут чередоваться до тех пор, пока не сойдутся.
А так как центр тяжести остается все время между ладонями, то он
окажется в месте их соприкосновения (119).
Если палка гладкая, то этот фокус проделывается чисто механи-
чески, без всякого сознательного усилия и даже — с завязанными гла-
зами.
Все построения, которые выполняются циркулем и линейкой, можно
произвести и без линейки. Если, например, заданы только концы от-
резка 1—2 и нужно найти его середину, то проводим сначала две окруж-
77
ности радиуса 1—2 с центрами в точках 1 и 2 (120) и находим точку
3 их пересечения; из этой точки проводим окружность того же радиуса и
получаем точку 4\ из точки 4 проводим окружность того же радиуса
(через точки 3 и 2), пересекающую окружность с центром 2 в точке 5;
из точки 5 радиусом 5—3 и из точки / радиусом 1—5 проводим еще две
окружности и находим точки их пересечения 6 и 7; наконец, из этих
точек проводим две окружности через точку 5; в их пересечении полу-
чаем точку М, которая и будет искомой серединой отрезка. В построении
участвует восемь окружностей. (Может ли их быть меньше?)
Если даны две пересекающиеся окружности (121), то их центры
можно найти, пользуясь только линейкой. Выбираем точку а на
78
одной из окружностей и проводим
из нее прямую через точку пересече-
ния окружностей — получаем точ-
ку Ь\ по прямой из b через вторую
точку пересечения попадаем в точку с\
выбрав вместо а другую точку А,
получаем таким же образом точки В
и С. Пунктирные прямые соединяют а
с с и А с С, а также А с а и С с с\
получаем две точки, которые соедине-
ны на рисунке штрих-пунктирной
прямой. Эта прямая проходит че-
рез центр окружности аАсС. По-
вторяя то же построение с другими исходными точками, находим еще
одну такую прямую и центр. (Сколько раз мы пользовались ли-
нейкой?)
Нельзя указать правило, которое позволяло бы по заданной
окружности только циркулем и линейкой построить отрезок той же
длины, что и окружность. Отношение длины окружности к диаметру
равно 3,141592653... Ксендз А. А. Коханьский, состоявший библиоте-
карем при короле Яне III, изобрел приближенное построение (122).
Из точки А на окружности проводится окружность того же радиуса —
получается точка /. Окружность того же радиуса, проведенная из
точки 1, дает точку 2. Прямая 2—0 в пересечении с касательной к окруж-
ности в точке А дает точку 3. Откладывая по касательной от точки 3 от-
резок, равный тройному радиусу, находим точку 6; отрезок В — 6 при-
ближенно выражает длину полуокружности (с какой точностью?).
Если построить всевозможные окружности, проходящие через две
заданные точки (123), то можно будет найти другое семейство окруж-
ностей, пересекающих все окружности первого семейства под .прямыми
углами. Все окружности второго семейства являются окружностями Апол-
лония (см. (106) ).
Если на плоскости даны три области произвольной формы, то
можно провести такую окружность, которая делит каждую из них на
79
(125)
две равновеликие части (124). Чтобы разделить область пополам,
достаточно одной прямой. Соответствующее свойство пространства
выражается «теоремой о бутербродах»: любой ломтик хлеба с маслом
и ветчиной можно одним плоским разрезом поделить так, что хлеб,
масло и ветчина поделятся пополам.
Когда одна монета катится по другой такой же монете, точка
касания монет обегает полностью обе монеты — подвижную и не-
подвижную (125). Обводы монет равны, поэтому когда точка касания
пройдет половину обвода неподвижной монеты, она пройдет поло-
вину обвода подвижной. Однако, после этого, как показывает опыт,
подвижная монета снова ляжет «головой вверх» (почему?).
Коперник установил, что окружность, которая катится по окруж-
ности вдвое большего радиуса, находясь внутри ее, каждой своей точкой
описывает прямую (126). Представим себе хорду меньшей окружности
в виде спички, прикрепленной к ней своими концами, и проследим движе-
ние спички от момента, когда она коснется своей головкой большей
окружности, до момента, когда другой ее конец достигнет центра этой
окружности. За этот промежуток спичка заметет область, заключенную
80
(128)
внутри прямоугольного треугольника, каждая точка которой пройдет
под спичкой ровно один раз. В этом смысле каждый треугольник
можно замести спичкой, перемещая ее подходящим образом (127).
Движение спички, скользящей своими концами вдоль двух пере-
секающихся прямых, совпадает с ее движением в качестве хорды малой
окружности в коперниковой системе двух окружностей. Нужно только
принять точку пересечения прямых за центр большей окружности,
а малую окружность провести через этот центр и оба конца спички.
В каждый момент своего движения малая окружность (с прикреплен-
ной к ней спичкой) будет проходить через эти три точки. Если длина
спички равна диаметру малой окружности, то спичка заметет внутрен-
ность звезды, называемой астроидой (128).
Когда круг катится по прямой (129), точка на его обводе (гвоздь)
описывает циклоиду. В каждый момент точка обвода либо приближа-
ется к наивысшей точке, либо удаляется от нее, а скорость подвижной
точки пропорциональна ее расстоянию от самой низкой точки круга.
(Какова скорость самой низкой точки?).
Пусть по прямой катятся одновременно два круга с одной и той
же скоростью и один из них в два раза больше другого; если в начальный
момент провести в большем круге вертикальный диаметр, то в про-
цессе всего движения этот диаметр будет касаться циклоиды, описыва-
емой точкой меньшего круга (130).
Отметим какую-нибудь точку ближе к центру круга (131), тогда
ее траекторией будет гладкая кривая, а если взять точку на продолжении
радиуса, то получим кривую с петлями (132).
Длина циклоиды равна периметру квадрата, описанного вокруг
катящегося круга.
Повернем рисунок (129) на 180°. Будем теперь считать, что тяжелый
маленький шарик Р скатывается по желобу, имеющему форму циклоиды;
движение шарика под действием силы тяжести будет таким же, как
если бы он был закреплен на обводе равномерно катящегося круга.
Шарик, скатывающийся по такому желобу, опередит другой шарик,
скатывающийся по наклонной плоскости, даже если первому шарику
81
часть пути придется пройти в гору (133). На нашем эскизе указано
положение шарика, скатывающегося по наклонной плоскости (кото-
рая обозначена пунктирной линией), в момент, когда шарик, скатываю-
щийся по циклоиде, пересечет эту плоскость.
Расчеты в подобных задачах значительно упрощаются, если опи-
раться на следующий факт, обнаруженный Кантом: шарики, которые
начинают одновременно скатываться из одной й той же точки по разным
наклонным плоскостям, будут в каждый момент времени располагаться
на некоторой окружности (134). Из всех шариков, скатывающихся по
разным желобкам в определенную точку, быстрее всех у цели окажется
шарик, скатывающийся по циклоиде.
Круг имеет наибольшую площадь по сравнению со всеми другими
фигурами с тем же периметром. Отсюда следует, что площадь, ограни-
ченная замкнутой кривой длины L, никогда не превышает величины
Л2/(4л), (почему?).
Если фигура ограничена кривой, отличной от окружности, то ее
площадь можно увеличить за счет деформации фигуры, не меняющей
длины ограничивающей кривой. Это легко проверяется в случае фигуры
с двумя перпендикулярными осями симметрии (135): фигура разрезается
вдоль осей симметрии на четвертушки, две из них переворачиваются на
другую сторону, после чего все они снова складываются вместе (136).
Длина периметра не изменилась, но в центре новой фигуры образовался
квадрат, который как, раз и дает приращение площади.
Круг имеет постоянную ширину: можно катить его рукой по столу,
не опуская и не поднимая руки. Но тем же свойством обладают и раз-
личные другие фигуры. Если из каждой вершины равностороннего
треугольника провести окружность через две другие вершины, то по-
лучится фигура постоянной ширины (137).
Чтобы получить фигуру постоянной ширины с гладким контуром,
нужно продолжить стороны правильного треугольника, отложить на
продолжениях один и тот же отрезок, а затем провести из каждой его
вершины по две окружности: одну радиусом, равным отложенному
82
отрезку, а другую — радиусом, равным стороне треугольника, увели-
ченной на этот отрезок (138). Если катить такой контур по прямой, то вы-
сота его самой верхней точки будет оставаться неизменной.
Длина контура постоянной ширины равна длине любого другого кон-
тура той же постоянной ширины. Очевидно, что измерение длины
лонгиметром дает в обоих случаях одинаковый результат — это и есть
доказательство. Отношение длины контура к его ширине равно
3,14159 ... (почему?).
Круг можно вращать внутри треугольника, сохраняя его касание
со сторонами треугольника. В случае равностороннего треугольника
фигурой наименьшей площади с таким же свойством является линза
(139), ограниченная двумя дугами окружности, радиус которой равен
высоте треугольника.
Одно из свойств круга состоит в том, что шест кругового сечения,
изготовленный из однородного материала с меньшей, чем у воды плот-
ностью, остается неподвижным на поверхности воды, как, бы ни повора-
чивать его вокруг собственной оси. Нарисованные здесь контуры (140),
(141) обладают таким же свойством при условии, что материал, из
которого изготовлен шест, в два раза легче воды; эти контуры так, по-
добраны, что любая хорда, делящая их пополам, делит пополам и
заключенную внутрь них площадь. Таким образом, свойство одновремен-
ного деления пополам контура и площади не является исключительной
привилегией круга. Контур, представленный на рисунке (141), имеет
три оси симметрии и содержит три прямоугольных отрезка.
Солдаты разошлись из. пункта Р в разных направлениях и останови-
лись через 30 шагов после того как миновали ров, расположенный
на расстоянии 60 шагов от Р (142). В результате возникла кривая.
83
называемая конхоидой Никомеда. Потом все они пошли назад прежней до-
рогой, сделав три остановки — через 60, еще через 30 и снова через 30 ша-
гов. Так появились две новые линии: сплошная линия на рисунке и линия
с петлей. Пунктирная линия соединяет точки, в которых были сделаны
первая и последняя остановки.
Если бы ров шел не по прямой, а по окружности диаметром
в 60 шагов (143), то линии, отвечающие первой и второй остановкам,
соединились бы в одну гладкую кривую, называемую улиткой Паскаля.
Круг — самая симметричная из фигур — у него бесконечно много
осей симметрии. Чтобы получить симметричный образ какого-либо пред-
мета, можно воспользоваться зеркалом. В этом случае зеркало
будет плоскостью симметрии. Пусть таким предметом служит диск,
наклоненный к, плоскости зеркала (144); нарисуем на диске два
диаметра — один параллельный плоско-
сти зеркала, и второй, перпендикулярный
к первому. По другую сторону зеркала
увидим отражение диска и его диаметров.
Соединяя накрест концы диаметров с их
образами, получим точку на зеркале. Дан-
ную точку можно считать вершиной кону-
са, в основании которого лежит реальный
диск. Отражением этого конуса будет дру-
гой, воображаемый, конус, который мы
видим за зеркалом. Но оба конуса, настоя-
щий и воображаемый, можно считать за
один, так как образующие воображаемого
конуса служат продолжениями образую-
84
щих настоящего конуса. Так
получается модель, представ-
ленная на фотографии; зеркало
из нее изъято.
Однако прямая, соединяю-
щая центр диска с вершиной ко-
нуса, не проходит через центр
другого диска, как об этом
наглядно свидетельствует чер-
ный стержень модели. В этом
можно убедиться, если провести
секущую плоскость через чер-
ные диаметры, наклоненные к
зеркалу. На плоскости получат-
ся два симметрично располо-
женных диаметра, два белых
стержня, соединяющих накрест
их концы, и черный стержень,
проходящий через середину од-
ного из диаметров; то, что сере-
дина второго диаметра не по-
падет на черный стержень, есть
очевидный факт планиметрии.
Отсюда вытекает невоз-
можность построения центра
круга с помощью одной только
линейки. Ведь такое построение
заключалось бы в проведении
(144)
системы прямых, две из которых
пересекались бы в центре круга. Проектируя эту систему на второй диск
из вершины конуса как из центра, мы получили, бы новую систему прямых,
отвечающих в отношении второго диска тому же предписанию, что и
исходная система в отношении первого диска, поскольку граничная ок-
ружность первого диска перейдет в граничную окружность второго,
прямые — в прямые, точки пересечения прямых — в точки пересечения
соответствующих прямых. Следовательно, центр первого диска, который
является одной из этих точек, должен перейти в центр второго диска,
но, как мы видели, не перейдет. Это доказательство невозможности весьма
показательно как пример применения математического метода.
Чтобы получить плоское изображение трехмерного предмета, мы при-
бегаем к геометрической перспективе. Фотографическая камера дает ее
автоматически, но мастера живописи также пользовались ею, желая
создать впечатление глубины пространства (145).
Горизонтальные параллельные прямые всегда пересекаются в одной
точке на линии горизонта картины. Если эти прямые перпендикулярны
к фону, то точка их пересечения является главной точкой картины
(точка пересечения красных линий на репродукции). Чтобы получить
правильное зрительное ощущение реального трехмерного пространства,
нужно, чтобы глаз располагался на прямой, проходящей через главную
точку перпендикулярно к плоскости картины. Если глаз отклонится
от этой линии, то получится иной, искаженный образ модели
(почему?)
85
Оптическая иллюзия зрителя, ощущающего на себе провожающий
взгляд с портрета, мимо которого он проходит, легко объясняется.
Если бы вместо портрета у стены неподвижно стоял живой человек,
то по мере того, как мы его минуем, он представал бы перед нами в ме-
няющемся виде (146): сначала голова скрыла бы одно ухо, потом за
переносицей стал бы скрываться один глаз и т. д. Но если бы этот че-
ловек, когда мы идем мимо, поворачивал голову вслед за нами, оста-
ваясь лицом к нам, то мы бы видели все время оба уха, оба глаза
(146)
и т. д. Минуя же портрет, мы из любого положения видим оба уха и
оба глаза, так что у нас возникает ощущение, что человек с портрета по-
ворачивается к нам лицом.
Однажды в летний день автору довелось наблюдать рой мушек,
которые танцевали подобно комарам на одном месте, затем неожиданно
перекидывались все на несколько метров дальше, чтобы и там потанце-
вать парами и через какую-нибудь минуту вернуться на прежнее место —
эта их общая игра повторялась снова и снова. Так продолжалось доволь-
но долго, благодаря чему автор смог грубо оценить скорость, с которой
совершались перелеты; она составляла примерно 60 км в час.
При внимательном наблюдении во время перелетов видны были
светлые точки (147). Они прочерчивали в воздухе пунктирные прямые
с расстоянием между точками приблизительно в один сантиметр.
Это был, конечно, эффект наклонного солнечного освещения: насекомые
86
(147)
становились видимыми в момент, когда взмахивали крылышками.
Каждая вереница блесток принадлежала одной мушке, а блестки видны
были во множестве на траектории мушки благодаря свойству сетчатки
глаза удерживать изображение в течение некоторой доли секунды.
Но 60 км в час — это 6 000 000 сантиметров за 3600 секунд или
1667 сантиметров в секунду, а значит, 1667 взмахов крылышками в
секунду. Даже если допустить, что из-за ошибки, связанной с грубой
оценкой скорости полета и расстояния между блестками, найденное
число следует уменьшить на 40%, то и тогда итогом наблюдения будет
по меньшей мере тысяча взмахов в секунду. Любопытно, что этот ре-
зультат удалось получить, не прибегая к инструментам.
Один взмах крылышками для мушки — это то же самое, что для
человека шаг. Человек делает два шага в секунду, мушка — 1600 взма-
хов; значит, жизнь мушки протекает в 800 раз быстрее: две минуты для
нее означают то же, что для нас сутки, так что игры мушек в течение
одного описанного выше цикла можно сравнить с утренними и вечерними.
Законы симметрии используются в такой игрушке. На деревянной
подставке помещается стальной шарик (148). Короткая трубочка, вде-
ланная в подставку, служит опорой шарику, так что шарик находится
на высоте примерно 2 см над подставкой. На подставке смонтирован дер-
жатель, заканчивающийся таким же блестящим шариком, который на-
ходится на высоте около 30 см над подставкой. Держатель несет также
горизонтальную стеклянную пластинку, которая располагается на та-
ком расстоянии от подставки, чтобы служить плоскостью симметрии
для шариков. Глядя сверху, мы видим нижний шарик, так как пластинка
прозрачна, а также верхний, поскольку пластинка играет роль зеркала.
Однако виден будет только один шарик под пластинкой, ибо зрительные
образы шариков сливаются благодаря их симметричному расположению.
87
Уложим теперь глиняную куклу
на подставку таким образом, чтобы
нижний шарик оказался внутри кук-
лы (149); глядя, как и раньше,
(150)
сверху, мы увидим шарик на преж-
нем месте, поскольку по-прежнему
будет видно отражение верхнего ша-
рика. Но зрительно это отражение
будет восприниматься так же, как ес-
ли бы был виден нижний шарик.
Мы сможем убедиться в этом на
ощупь, если, добираясь до шарика
сквозь глину пальцами или щипцами,
безошибочно достигнем его, словно
бы глина была прозрачной.
Для этой идеи можно найти
практическое применение, использо-
вав ее для локализации чужеродных
предметов в теле человека. Здесь, од-
нако, нужен будет рентгеновский ап-
парат (150). Сначала нам неизвест-
но местонахождение предмета в теле
пациента (скажем, кусочка иголки) и просвечивание лучами рентгенов-
ской лампы, находящейся под операционным столом, даст на экране,
расположенным над пациентом, только проекцию иголки (151). Лампа
подвешена на маятнике, отклонение которого приводит к смещению этой
проекции. Но и при новом положении лампы можно вернуть проекцию
на прежнее место, поднимая или опуская всю установку (с помощью
зубчатого колесика с рукояткой). Стеклянная пластинка и ма-
ленькая лампочка, находящиеся над пациентом, связаны с осью
маятника таким образом, что в момент возвращения проекции на
88
прежнюю отметку лампочка займет симметричное с отыскиваемой
иголкой положение относительно пластинки. В этот момент экран
убирается, в операционной включается обычный свет, и хирург видит
перед собой изображение, подобное изображению на фотографии (149):
глядя сквозь пластинку, он видит пациента (152), а в нем лампочку как
раз в том месте, где находится игла. Теперь можно оперировать, не под-
вергаясь действию рентгеновских лучей, так как рентгеновский аппарат
выключен. Точность локализации не зависит от угла зрения хирурга,
как и в описанной выше игрушке.
Некоторые оптические иллюзии весьма поразительны. Будем раз-
глядывать проволочную сетку такого вида, как на рисунке (11),
но сконцентрируем наш взгляд на точке, находящейся перед сеткой,
а потом постепенно, не отводя взгляда от этой точки, станем присматри-
ваться к сетке. Квадраты сетки покажутся/Ииеньше обыкновенного,
а когда мы попробуем дотронуться до сетки, то протянем руку не-
достаточно далеко и промахнемся. Иллюзия объясняется тем, что
квадраты сетки одинаковы и, глядя в точку перед сеткой, мы правым
глазом видим квадрат, находящийся слева, а левым — другой квадрат,
лежащий правее первого. Оба квадрата дают такие же образы, как один
меньший квадрат, находящийся на уровне выбранной точки. Эта точка
расположена ближе к нам, чем настоящая сетка, и эффект получается
такой, как если бы вся сетка переместилась на уровень выбранной
точки, а размеры сетки соответствующим образом уменьшились. Можно
и отдалить от себя сетку, но сделать это труднее (почему?).
Различие в образах у правого и левого глаза лежит в основе
стереоскопического видения. Такого видения (когда рисунок на бумаге
воспринимается как пространственная модель) можно достигнуть с по-
мощью анаглифов. Нужно построить два перспективных изображения:
проекцию предмета на бумагу из правого глаза как из центра и такую же
проекцию для левого глаза. Первое изображение выполняется синим
цветом, второе — красным, и рисунок разглядывается сквозь двухцветные
очки, у которых правое стеклышко красное, а левое — синее. Тогда
изображение получается рельефным (почему?). I
Когда стержень находится перед нами в горизонтальном положении,
но поддерживающих его опор не видно, то трудно оценить расстояние
до него. Причина заключается в однородности стержня. Стоит нанести
на стержень пятнышко лака, и иллюзия исчезнет — сосредотачивая
взгляд на пятнышке, мы создаем у себя ощущение вполне определенного
расстояния. В случае отсутствия пятнышка достаточно слегка склонить
голову к плечу (почему?).
89
Vll
СОЛЬ. ПАУКИ И МУХИ. ДВОРЦЫ И КИРПИЧИ
Природа реализовала куб в виде кристалла соли NaCl (153).
Кубами можно заполнить все пространство.
Можно раскрасить грани куба в различные цвета и притом 30 различ-
ными способами. Любой из этих 30 раскрашенных кубов можно склеить
с некоторыми 8 другими так, чтобы получился большой куб той же
раскраски, а каждые две склеиваемые грани были одного цвета.
Из этих шести фигурок (154) можно составить . куб (155), но
сделать это вовсе не легко. Существуют два способа. Если сторона куба
равна 9 см, то можно считать, что три фигурки склеены из 5 кубиков со
стороной 3 см, а три — из 4 таких кубиков. Две фигурки симметричны
друг другу (можно ли этого избежать?).
Составляя фигурки так, как показано на фотографии (156А), мы
построим изящный архитектурный макет (156В). Таких макетов сущест-
вует больше, чем мог бы собрать один человек, беспрестанно занимаясь
этим в течение всей своей жизни.
Если куб поделить пополам плоскостью, проходящей через его
центр перпендикулярно к диагонали, то в сечении получится правильный
шестиугольник (157).
Глядя на куб сверху в направлении большой диагонали, пер-
пендикулярной к горизонтальной плоскости проекций, мы также увидим
правильный шестиугольник (158).
Нарисовав любые три отрезка, выходящие из одной точки, и дополнив
рисунок параллельными им пунктирными прямыми, мы всегда можем
считать получившуюся фигуру (159), (160) некоторой косой проекцией
куба (теорема Польке).
Изготовим модель куба из белой проволоки (161) и сфотографируем
ее несколько раз на одной пластинке после каждого поворота на один
и тот же угол вокруг большой диагонали; мы получим изображение фигу-
ры (162), составленной из двух конусов и гиперболоида вращения. На
снимке отчетливо видна гипербола, являющаяся меридианом этого гипер-
90
(157)
91
92
болоида. Видно также, что на
поверхности гиперболоида ле-
жат два семейства прямых ли-
ний.
Кратчайший путь ведет
по прямой. Если паук и муха
сидят на противоположных гра-
нях куба (163), то, желая
добраться до мухи кратчайшим
путем, паук проложит свой
маршрут по прямой на разверт-
ке куба (164).
Если муха хочет обойти все
грани куба, чтобы удостове-
(167)
риться в отсутствии паука и как можно скорее вернуться на прежнее
место, то ее путь на развертке куба также изобразится в виде пря-
мой (165). Как видно из рисунка, длина кругового пути мухи будет одной и
той же, откуда бы она ни вышла (166).
У мухи, однако, всегда имеются две дороги на выбор. Эти крат-
чайшие круговые дороги представляют собой шестиугольники одного
и того же периметра, и через каждую точку на поверхности куба прохо-
дят две такие линии, пересекаясь в этой точке под прямым углом. Но ри-
сунок (165) показывает, что всякое семейство параллельных дорог покры-
вает лишь половину поверхности куба; стало быть, всего насчитывается
четыре семейства (почему?). Если каждое из них выложить нитками
своего цвета, то возникнет столько оттенков, сколько будет пар цветов,
т. е. 6 (ибо через каждую точку пройдут две нитки). На каждой грани
появится четыре оттенка, и каждый оттенок охватит треугольную
четвертушку грани. (Будут ли расцветки всех граней различны?)
Желая найти кратчайшую дорогу, можно нередко с успехом поль-
зоваться способом паука и мухи: разложить поверхность на плоскости,
начертить прямую, а потом свернуть поверхность, восстановив ее
прежнюю форму. Конус, например, представляет собой поверхность,
составленную из прямых линий. Муха, которой нужно обойти конус и как
можно скорее вернуться на прежнее место, опишет петлю (167), имею-
щую излом в исходной точке. Конус, разрезанный вдоль одной из обра-
зующих и распластанный на плоскости, перейдет в сектор круга (168),
а путь мухи составится из двух прямолинейных отрезков, перпендику-
93
лярных к граничным радиусам сектора. Однако если угол развертки
конуса равен 180° и уже подавно, когда он больше, решение будет
иным: муха взбирается по образующей прямо на вершину и, оглядев-
шись по сторонам, тем же путем возвращается назад.
Существуют, однако, поверхности, которые нельзя распластать
наподобие конуса; например, нельзя сделать этого со сферой. Кратчай-
ший путь на сфере ведет по окружности большого круга; такие окруж-
ности называют ортодромами. Каждый меридиан является ортодромой.
Допустим, что нам удалось разложить сферу на плоскости без растяже-
ний. Тогда ортодромы, сохранив свою длину, перейдут в кратчайшие
линии на плоскости, т. е. в прямые. Но ортодромы — замкнутые линии,
а прямые — нет. Уже из одного этого вытекает, что сферу нельзя разло-
жить на плоскости. Но даже если ограничиться частью сферы, скажем,
ее полярной зоной, то и тогда мы приходим к противоречию. Меридианы,
сходящиеся в северном полюсе, (169), при распластывании сферы перей-
дут в прямолинейные отрезки равной длины (170), а вся сфера превра-
тится в диск, границей которого будет окружность. Эта окружность
представляющая собой окружность полярного круга, также сохраняет
свою длину, поэтому ее радиус равен радиусу полярного круга, который
изображен в виде жирного горизон-
тального отрезка на рисунке (169).
Но радиус окружности на рисун-
ке (170) получился из отрезка мери-
диана, изображенного на рисун-
ке (169) в виде жирного криволиней-
ного отрезка; он, следовательно, ра-
вен длине этого отрезка, которая, од-
нако, больше длины горизонтального
отрезка. Итак, полярная зона, распо-
ложенная на плоскости, должна быть
кругом, и длина его радиуса должна
совпадать с длиной каждого из этих
двух отрезков, один из которых ко-
роче другого, что невозможно.
Мы уже упоминали о заполне-
нии кубами всего пространства. Из
него можно следующим образом по-
лучить новое заполнение. Кубы бе-
рутся поочередно белыми и черными
и располагаются как бы в про-
94
странственно-шахматном порядке,
после чего черные кубы убираются.
В каждую из образовавшихся пу-
стот вставляем шесть пирамид с об-
щей вершиной в центре выброшен-
ного куба. Если представить себе, что
к белому кубу присоединены все при-
легающие пирамиды, то получим
двенадцатигранник с одинаковыми
ромбическими гранями и вписанным
в него кубом (171). Теперь видно
(172), что все пространство запол-
няется этими ромбическими двена-
дцатигранниками. Нетрудно под-
считать объем каждого двенадца-
тигранника: один двенадцатигранник
строится из двух кубов и по- (171)
этому его объем равен удвоен-
ному объему куба, т. е. 2а3, где а означает ребро куба. Меньшая диагональ
грани равна а, большая — а^Г, следовательно, сторона ромба 6 =
= яУЗ/2 , а объем составляет 1663/ (Зл/3~).
Вершины получаются двух видов: в одних сходятся четыре две-
надцатигранника, в других — шесть.
Если взять два слоя полых двенадцатигранников и снять по три
свободные грани с каждого из них, то образовавшиеся шестиугольные
отверстия,дадут нам систему пчелиных сот (173). Отсюда следует, что
в пчелиных сотах имеются точки, в которых сходятся четыре ячейки,
и точки, в которых сходятся шесть ячеек.
Интересно выяснить, можно ли заполнить все пространство одина-
ковыми многогранниками таким образом, чтобы в каждой вершине
сходилось по четыре из них (по три многогранника сходиться в вершинах
не могут). С этой целью рассмотрим кирпичную кладку, наращиваемую
(172)
(173)
95
96
во всех направлениях. Укладывая первый слой, будем действовать по
примеру каменщика, который следит за тем, чтобы стыки шли в пол-
кирпича (174). Отметим, что такой слой (жирные линии на рисунке)
не дает нам существенно нового паркета на плоскости. Если считать
каждую точку, в которой сходятся три кирпича, за вершину, то верхние
грани кирпичей окажутся шестиугольниками, а часть рисунка (174).
выполненная жирными линиями, будет лишь деформацией картины
пчелиных сот (55).
Укладывая второй слой (пунктирные линии на рисунке), накрываем
кирпичами все вершины первого слоя. Теперь уже в каждой вершине,
замурованной между слоями, сходится по 4 кирпича. Третий слой
укладываем так же, как первый — вершина против вершины. Таким же
образом надстраиваются дальнейшие слои. Подсчитаем теперь, сколько
соседей получилось у каждого кирпича (175). Их будет 6 в том же
самом слое и по 4 в соседних слоях — всего 14.
Выкрасим ребра всех кирпичей в черный цвет. Постепенно разбирая
кладку (176), (177), мы увидим на белых кирпичах не только их собствен-
ные черные ребра, но и черные следы, оставленные ребрами прилегавших
кирпичей. Каждый кирпич, следовательно, окажется четырнадцатигран-
ником, сплющенным в форму обыкновенного кирпича. Желая предста-
вить его себе в несплющенном виде, заметим, что на его поверхности
имеется 6 «квадратов» и 8 «шестиугольников». Это позволит нам вос-
становить искомый четырнадцатигранник (178), который, скажем попут-
но, можно было бы получить, срезав вершины восьмигранника. Такими
раздутыми кирпичами, как и обычными кирпичами, можно выложить все
(179/
пространство (179), причем в каждой вершине, по-прежнему, будет схо-
диться по четыре кирпича. Найденные четырнадцатигранники семире-
гулярны (полуправильны) — все их грани являются правильными мно-
гоугольниками. Других тел с такими же свойствами не существует, так
,что мы пришли к простейшему заполнению пространства одинаковыми
фигурами.
4. Г. Штейнгауз
VIII
ПЛАТОНОВЫ ТЕЛА. КРИСТАЛЛЫ. ДРОЖЖИ. МЫЛО
Уже Платону было известно, что существует только пять ви,-
дов правильных многогранников.
Как составить четыре треугольника из шести спичек? Для этого нужно
из трех спичек составить треугольник, лежащий в основании пирамиды,
а три другие сделать ее боковыми ребрами. В результате получится пра-
вильный четырехгранник — первое из платоновых тел (180). Его прямо-
угольная проекция на плоскость основания выглядит так, как показано на
рисунке (181). Одна из проекций представляет собой квадрате диагоналя-
ми (182), а модель фигуры можно изготовить, исходя из развертки, пока-
занной на рисунке (183).
наковых кубов можно составить один больший куб. Выкрасив грани боль-
шего куба в черный цвет и разложив его.снова на маленькие кубы, получим,
что некоторые из них будут иметь по три черные грани, другие по две,
98
третьи— по одной, наконец, среди кубов окажутся и такие, на которые
краска вообще не попала. По сколько кубов будет в каждой из этих групп?
Из восьми равносторонних треугольников удается составить еще одно
платоново тело — правильный восьмигранник (184). Если установить его
на одной из граней как на основании и спроектировать на плоскость этого
(186)
(187)
основания, то мы получим рисунок (185), из которого видно, что центры
граней правильного восьмиугольника являются вершинами куба (186).
Обратно, центры граней куба служат вершинами правильного восьмигран-
ника (187).
Следующее платоново тело — правильный двенадцатигранник —
имеет пятиугольные грани (188). Модель двенадцатигранника легко полу-
4
99
(188)
чается из его развертки (189). Нужно перочинным ножиком сделать на
ребрах надрезы (с внешней стороны будущей модели) и, поделив развертку
на две звезды, наложить одну на другую так, чтобы вышла одна десяти-
угольная звезда (190); затем эту звезду следует обвязать резинкой, обходя
ею углы поочередно сверху и снизу и прижимая модель свободной рукою
юо
(191)
(192)
к столу. Отпустив теперь руку, мы увидим, что, раскрывшись (191),
звезда превратится в пространственную модель двенадцатигранника
(192).
Для раскраски двенадцатигранника с условием, чтобы соседние грани
были разного цвета, потребуется не менее четырех красок. Если выбраны
четыре цвета (например, красный, синий, зеленый и желтый), то раскраску
можно произвести только двумя различными способами; при этом предпо-
лагается, что раскраски, переходящие друг в друга в результате поворотов
и зеркальных отражений, не считаются различными.
Последнее правильное тело — двадцатигранник (193). Его развертка
состоит из двадцати равносторонних треугольников (194).
Горизонтальную проекцию двадцатигранника (195) можно получить
одновременно с проекцией двенадцатигранника (196); действительно,
как видно из модели (193), центры граней двенадцатигранника служат
вершинами двадцатигранника. Обратно, центры граней двадцатигранника
дают вершины двенадцатигранника (197), (198). Что же касается четы-
рехгранника, то он отвечает сам себе: центры его граней являются вер-
шинами меньшего четырехгранника (199). В двенадцатигранник можно
также вписать и куб, выбрав в качестве его вершин подходящие вершины
двенадцатигранника (200); пусть читатель вообразит себе тело, образо-
ванное всевозможными кубами, вписанными в двенадцатигранник.
101
102
Одинаковыми шарами нельзя заполнить всего пространства. То же
относится и к кругам на плоскости (201): уложив их с максимальной
возможной плотностью, мы получим нечто вроде пчелиных сот и легко
представим себе, как при деформации круги перейдут в шестиугольники.
103
Чтобы наиболее плотно заполнить пространство шарами, следует разбить
его на кубические ячейки (кубы берутся без граней, лишь в виде проволоч-
ных каркасов), и, считая ячейки попеременно белыми и черными, ставить
в каждую белую ячейку такой шар, который касался бы тех ее ребер.
При этом половина ячеек будет занята шарами и нетрудно подсчитать,
какая часть пространства окажется заполненной шарами. Если через а
обозначить ребро ячейки, то радиус шара как половина диагонали
квадрата аХа будет a/V5~. Поэтому объем шара составит 3/а (а/^2~)3,
а учитывая, что объем двух ячеек есть 2а3, получим, что искомое отно-
шение равно л V2/6^ 0,7405.
Итак, при максимально плотном заполнении шары занимают при-
мерно 74% всего пространства. Поэтому если в бензиновой эмульсии
мыла содержится более 75% мыла, то можно быть уверенным, что не
мыльные шарики взвешены в бензине, а шарики бензина в мыле. Такая
смесь не воспламеняется (почему?) и мыло, содержащее менее 25% бен-
зина, безопасно в домашнем обиходе.
Наиболее плотное заполнение пространства шарами может быть
достигнуто и другим способом. Располагаем сначала шары в один слой
так, чтобы вид сверху совпадал с рисунком (201). На этот слой наклады-
ваем следующий, точно такой же слой, так, чтобы каждый шар верхнего
слоя оказался в ямке, образованной тремя шарами первого слоя. Заме-
тим, что не все ямки окажутся заполненными: если шар ляжет в
какую-нибудь ямку, то соседние с ней ямки останутся свободными.
В связи с этим третий слой можно будет разместить двумя способами: ша-
ры этого слоя располагают либо над свободными ямками первого слоя
(202), либо как, раз над шарами первого слоя (203); так, укладывается
(202)
(203)
слой за слоем. В любом случае каждый шар среднего слоя будет касаться
двенадцати соседних шаров. В первом случае точки касания дадут вер-
шины «кубооктаэдра» или кристалла аргентита Ag2S (204) — эта фигура
вырезается из правильного восьмигранника кубом, проходящим через
середины его ребер. Во втором случае точки касания дадут вершины дру-
гого четырнадцатигранника (205), который также составлен из 6 квадра-
тов и 8 равносторонних треугольников. Если рассечь такой четырнадца-
тигранник,плоскостью, проходящей через шесть его ребер, повернуть одну
104
(204)
(205)
половину на 60° относительно другой и затем склеить обе половины, то мы
снова получим кубооктаэдр.
Теперь представим себе, что шары сделаны из дрожжей и разрастают-
ся одинаково. Пустоты между ними заполнятся и место каждого шара
займет многогранник, описанный около породившего его шара. Первому
способу размещения шаров будет отвечать ромбический двенадцатигран-
ник, изображенный на рисунках (171) и (172), а второму — тело, пред-
ставленное на рисунке (206), ограниченное 6 ромбами и 6 трапециями.
Ромбический двенадцатигранник можно получить из тела (206),
разрезав его по экватору (черная линия на рисунке) и повернув верхнюю
половину вокруг вертикальной оси на 60°. Из этого следует, что оба
тела имеют одинаковые объемы и поверхности, одно и то же число много-
гранных углов каждого типа, а их соответствующие грани — одинаковые
площади, периметры и углы. Двугранные углы тел также одинаковы.
Первый способ размещения ша-
ров показывает, что кубооктаэдр
можно вписать в ромбический двена-
дцатигранник; второй способ приво-
дит к сходному выводу (какому?).
Мы видим, что пространство
можно заполнить ромбическими две-
надцатигранниками; тела, изобра-
женные на рисунке (206), как пока-
зывает опыт с дрожжами, также по-
зволяют осуществить такое за-
полнение.
Ячейки пчелиных сот можно по-
лучить, сжимая между двумя доска-
ми два слоя шариков, уложенных
наиболее плотным образом. В резуль-
(206)
105
тате образуются два слоя шестигранных призм, заканчивающихся сводча-
тыми колпачками, которые составлены из трех ромбов каждый; колпачки
одного слоя служат также колпачками другого. Это позволяет предполо-
жить, что форма пчелиных сот обязана своим происхождением действию
эластичных шариков; в данном случае шариками являются головки пчел,
предельно густо усеивающие каждую из двух поверхностей тонкой воско-
вой пластинки.
Возникает вопрос, какому способу заполнения пространства следует
отдать предпочтение — двенадцатигранникам (171), (172) или полупра-
вильным четырнадцатигранникам (178), (179). Речь идет о том, который
из двух способов более экономичен, т. е. в каком случае на изготовление
граней уйдет меньше материала. Оказывается, расходы на материал при
втором способе заполнения (названном нами простейшим) будут примерно
на 6 промиллей меньше. Иными словами, поверхность четырнадцатигран-
ника приблизительно на шесть тысячных меньше поверхности равновели-
кого ему двенадцатигранника. Весьма интересно, что такая незначитель-
ная разница заметна на глаз: а именно, видно, что четырнадцатигранник.
по своей форме стоит ближе к, шару, который является наиболее экономич-
ным из тел, о чем будет сказано ниже.
Кристалл флюорита CaF2 (207) напоминает полуправильный че-
тырнадцатигранник, тот самый раздутый кирпич, который изображен на
рисунке (178). Кристалл пирита FeS2 (208) близок к правильному двенад-
цатиграннику. Кристаллы же других минералов принимают любопытные
неправильные формы: кристалл сфалерита ZnS (209) имеет 12 граней,
являющихся одинаковыми дельтоидами, а у куприта Си2О (210) 24 грани,
каждая из которых представляет собой неправильный пятиугольник,
Если через каждое ребро правильного двенадцатигранника провести
плоскость, перпендикулярную к, плоскости симметрии, в которой лежит
это ребро, то получится ромбический тридцатигранник, (211). Диагонали
его граней являются ребрами правильных многогранников: большие
диагонали служат ребрами двадцатигранника, а меньшие — ребрами
двенадцатигранника. Повторяя эту процедуру в отношении тридцатигран-
ника, придем к, шестидесятиграннику (какими будут его грани?).
Результаты выборов по системе пропорционального представи-
тельства определялись в случае трех партий с помощью треугольника
(53); при наличии четырех партий треугольник заменяется правильным
четырехгранником, который делится на части, равноотстоящими плоско-
стями, параллельными граням (212). Если провести параллельно каждой
грани бесконечно много равноотстоящих плоскостей, то мы придем к за-
106
(212)
107
(215)
(216)
полнению всего пространства правильными восьмигранниками и четырех-
гранниками.
Кроме обычных правильных многоугольников (213), существуют
еще и звездчатые (214 А,В,С). Звездчатый пятиугольник, pentagramma
mysticum был излюбленной фигурой астрологов и чародеев. Имеются трй
правильных семиугольника — один обычный и два звездчатых.
Фотография (215) дает представление о том, как, выглядит много-
гранник, ограниченный 12 звездчатыми пятиугольниками.
Можно выбрать такие четыре вершины куба, которые служат верши-
нами правильного четырехгранника. Это можно сделать двумя способами
(216), а в сплетении соответствующих двух четырехгранников получится
звездчатый восьмигранник,
IX
МЫЛЬНЫЕ ПУЗЫРИ. ЗЕМЛЯ И ЛУНА. КАРТЫ
И ДАТЫ
Проще всего получить шар, выдувая мыльные пузыри (217).
Силы поверхностного натяжения вызывают сокращение поверхности
мыльной пленки. Внутри мыльного пузыря содержится некоторая пор-
ция воздуха. Поэтому пленка принимает такую форму, которой при задан-
ном объеме соответствует наименьшая поверхность. Единственное тело,
удовлетворяющее этому условию, есть шар.
Луна была когда-то жидким телом. Поскольку любая капля жидкой
массы притягивала любую другую такую каплю, частицы жидкости
располагались так, что любое изменение формы требовало затраты
(218В)
энергии. Можно доказать математически, что сферическая (т. е. шаро-
вая) форма обладает таким свойством. Фотография (218 А) является
109
снимком шара, освещенного сбоку, а фотография (218 В) — снимком
Луны
Если выдувать мыльные пузыри через трубку с двумя отверстиями
(219), то на них появятся две выпуклости из мыльной пленки Qi), которые
будут расти одинаково вплоть до момента, пока они не превратятся в полу-
сферы (6). Затем произойдет нечто удивительное: один пузырек, будет
продолжать расти, а другой начнет уменьшаться (с). Причина этого
кроется в том свойстве шара, о котором мы говорили выше: при заданном
объеме шар имеет наименьшую возможную поверхность. Когда мы вдуем
в трубку некоторую порцию воздуха, природа должна будет распорядиться
о размещении данной избыточной порции внутри как, можно более малой
поверхности, при условии, что эта поверхность состоит из двух пленок,
краями которых служат границы круглых отверстий. Это равнозначно
тому, чтобы заключить избыток, воздуха внутри пленки, одна часть ко-
торой расположена над отверстием, а другая под ним, ибо (с) две
пленки всегда можно соединить в одну, не меняя ни их объема, ни их по-
верхности. Пока избыток, воздуха недостаточен, чтобы заполнить сферу
радиуса, равного радиусу отверстия, пленка будет иметь симметричную
чечевицеобразную форму (а). Как,только эта форма станет сферической
(£), начнет расти сфера, опирающаяся на границу отверстия и заключаю-
щая в себе весь избыток,воздуха. Такая сфера показана на рисунке (с),
ее нижняя часть обозначена пунктиром; стоит только перенести эту
нижнюю часть на второе отверстие, чтобы стало понятно, почему вторая
пленка оседает (почему?).
Земля имеет форму шара (220). Одна из двух черных линий, соеди-
няющих Лиссабон с мысом Фарвель (на фотографи она получилась
почти прямой), дает кратчайший путь между данными пунктами. Это ду-
га большого круга шара, так, называемая ортодрома. Меридианы тоже
являются ортодромами, а из параллелей — только экватор. Вторая ли-
ния — это локсодрома, или линия постоянного курса; она пересекает все
меридианы под одним и тем же углом. Мореплаватель, который выбрал
свой курс по компасу и сохраняет его неизменным, движется по локсодро-
ме. Это упрощает управление кораблем, но удлиняет путь. Мы видим,
что в дальнейшем своем течении локсодрома закручивается спирально
вокруг полюса и становится совершенно непригодной для прокладыва-
ния курса в полярных широтах.
но
(220)
Проекция Меркатора (221) представляет собой карту, которая вер-
но передает углы на земной поверхности; меридианы и параллели обра-
зуют на ней прямоугольную сетку. Локсодромы изображаются на этой
карте прямыми. Действительно, любая локсодрома пересекает все мери-
дианы на поверхности Земли под одним и тем же углом, а, значит, и на
карте Меркатора тоже, поскольку углы на ней сохраняются. Но мериди-
аны на этой карте изображаются параллельными прямыми, поэтому лок-
содрома, пересекающая все эти прямые под одним и тем же углом, сама
будет прямой. Ортодрома, напротив, изгибается наподобие синусоиды.
Если спроектировать поверхность земного шара из южного полюса
на плоскость, касающуюся шара в северном полюсе (стереографическая
проекция), то получится карта (222), которая окружности на поверхности
Земли переводит снова в окружности и сохраняет углы. На такой карте
ортодрома будет представлена окружностью (большей, чем сама орто-
дрома), а локсодрома — логарифмической спиралью. Последнее
вытекает из того, что меридианы на карте изображаются прямы-
ми, пересекающимися в полюсе, а локсодрома пересекает их под одина-
ковыми углами.
Если спроектировать земную поверхность из центра Земли на
плоскость, касающуюся земной поверхности в северном полюсе (гномо-
ническая проекция), то ортодрома перейдет в прямую (223). Поэтому
такая карта будет удобна для полетов в арктических районах.
111
(221)
Поместив глобус внутрь цилиндра, касающегося его по экватору
(224 А) и продолжив плоскости параллелей и меридианов до пересече-
ния с цилиндром, получим карту Земли на поверхности цилиндра (224 В).
Если разрезать эту поверхность и разложить ее на плоскости, то мы при-
дем к карте с прямолинейными взаимно перпендикулярными меридиана-
ми и параллелями. Эта карта обладает тем специфическим свойством
(известным еще Архимеду), что она сохраняет площади. Если покрыть
глобус равномерным слоем краски или глины и если каждую частицу
этого покрытия перенести в соответствующее место карты на цилиндре,
т. е. в горизонтальном направлении (225 А), то получится равномерное
покрытие цилиндрической поверхности; если перенести всю массу покры-
тия в обратном направлении на общую ось цилиндра и шара, то эта
ось также покроется равномерно. Последнее покрытие можно было бы
получить сразу, без вспомогательного цилиндра. Но к тому же покрытию
можно прийти и по-другому, в два приема: сначала вся масса проектиру-
ется на плоскость экватора (225 В) — каждая частица массы как бы спа-
дает на эту плоскость или возносится к ней, а затем это плоское распреде-
ление массы прямоугольно проектируется на какой-нибудь диаметр эк-
ваториального сечения, что, очевидно, снова приведет к равномерному
распределению (225 С). Мы получили попутно такое распределение мас-
сы на круглом диске, прямоугольная проекция которого на любой диаметр
диска дает равномерное распределение вдоль этого диаметра. Существу-
ет лишь одно такое распределение массы на диске.
из
(224А)
(225A)
IIIIIIIIIIIIIIIIIIIIIIIIIHIIIIIIIIIIIIIIIIIIIIIII
114
Чтобы объяснить парадокс даты на нашей планете, представим се-
бе, что карта (224 В) нарисована на прозрачной кальке и снова наклеена
на цилиндр, на который она проектировалась. Пусть поверхность цилинд-
ра изготовлена из стекла и неподвижна. Один из меридианов, отделяю-
щий Азию от Америки и пересекающий Тихий океан, считаем линией да-
ты (226). Календарь будет представлять собой бумажную ленту, втяги-
ваемую под стекло через щель вдоль линии даты и накручиваемую на
невидимый деревянный барабан, который вращается в указанном стрел-
кой направлении; неподвижная же стеклянная поверхность будет ими-
тировать Землю. Ненакрученная часть ленты означает будущее, накру-
ченные ее витки, закрытые другими витками, означают прошлое, а на-
крученная часть ленты, видимая через стекло,— это настоящее. На ленте
указаны дни, месяцы и годы. Дни разделены поперечными линиями на
часы. Даты меняются в полночь, поэтому поперечные линии, означающие
О часов (жирные линии на ленте) служат также границами дат. В связи
с этим на Земле получаются две границы дат: неподвижная граница дат и
подвижная граница полуночи. На нашем рисунке ВТОРНИК простирает-
ся от неподвижной до подвижной границы, которая находится западнее
неподвижной (в момент, представленный на рисунке, подвижная
граница проходит через северную Японию). На запад от нее еще
продолжается ПОНЕДЕЛЬНИК, который охватывает все пространство
западнее подвижной границы вплоть до самой неподвижной границы.
По мере того как подвижная граница в результате вращения деревян-
ного барабана смещается на запад, ВТОРНИК увеличивает свою тер-
риторию за счет сокращающейся территории ПОНЕДЕЛЬНИКА. Нако-
нец, наступает момент, когда ВТОРНИК владеет всем земным шаром.
Но это только один момент, так как начинается СРЕДА — линия
полуночи сходит с неподвижной линии даты, и, двигаясь на запад, остав-
ляет между собой и неподвижной границей узкую полоску на новый день.
ВТОРНИК начинает клониться к упадку, и вся игра возобновляется
снова.
Если бы Земля была цилиндрической формы, то можно было бы про-
вести на ней круговые параллели и перпендикулярные к ним прямоли-
нейные меридианы. Представим себе, что на такой цилиндрической пла-
нете все эти линии видимы — как на суше, так и на море. Тогда навига-
ция упростилась бы, ибо, как мы уже знаем, кратчайшими линиями на
цилиндре являются винтовые, а они пересекают параллели и меридианы
под одними и теми же углами. На Земле, имеющей форму шара, невоз-
можно построить координатную сетку меридианов и параллелей, которые
пересекали бы все ортодромы (т. е. большие круги) под одинаковыми
углами. Однако помимо цилиндра существуют и другие тела, допускающие
такую удобную сетку. Как известно, конус можно разрезать и развернуть
на плоскости; кратчайшими линиями будут тогда прямые. Но на плоскости
обычная квадратная сетка, такая как на рисунке (11), обладает тем
свойством, что любая прямая пересекает все параллели под одинаковыми
углами, и все меридианы под одинаковыми углами. Если теперь нам
удастся свернуть эту плоскую сетку в конус, то наша цель будет достиг-
нута. Но здесь возникает одна трудность: желая, чтобы линии сетки были
гладкими, мы должны разрезать ее подходящим образом, а именно, вдоль
самих этих линий. Угол при вершине А на рисунке (227) может иметь ве-
личину 90°, 180° или 270°. Получатся три разных конуса. У первого из
них (228) будет лишь одно семейство «меридйано-параллелей», причем
каждая из этих линий пересекает каждую другую, а также и саму себя,
115
(228)
(229)
116
(232)
в единственной точке. Второй конус (229) будет иметь сетку меридианов
и параллелей и каждый меридиан пересекает каждую параллель ровно
один раз. На третьем конусе (230) получится три семейства линий; их
можно назвать меридианами, параллелями и связующими. Каждое се-
мейство пересекает два других и через каждую точку конуса проходят
линии двух семейств. На фотографиях конусов, обращенных вершинами
к объективу (231, 232, 233), видно, как пересекаются линии их сеток.
X
БЕЛКИ. ВИНТЫ. СВЕЧИ. ТЕНИ. АККОРДЫ
Забавно выглядят белки, когда они гонятся друг за другом
по дереву. Белки бегут по винтовым линиям. Действительно, чтобы найти
кратчайший путь на цилиндре, можно разрезать его вдоль прямой и раз-
ложить на плоскости (234) как карту (224 В). Кратчайший путь между
(234)
любыми двумя точками будет идти тогда по прямой, а эта прямая при
свертывании всей поверхности в цилиндр перейдет в винтовую линию
(235). Проекция винтовой линии дает в некоторых точках острия (236).
Это особенность каждой спиральной линии — любая точка такой линии
при подходящем проектировании может перейти в конец острия (237).
(235)
118
Обычный винт имеет своим кра-
ем винтовую линию. Так назы-
ваемый бесконечный винт пре-
образует равномерное враща-
тельное движение в равномер-
ное поступательное (238).
Когда отрезок постоянной
длины одним своим концом
скользит по винтовой линии, а
другим по ее оси, он описывает
винтовую поверхность (239).
Эту поверхность описывает так-
же и «плечо», укрепленное на
стержне под прямым углом, ког-
да оно равномерно вращается
вокруг стержня, а стержень в
свою очередь равномерно сме-
щается вдоль самого себя. Если
не считать некоторых поверхно-
стей вращения, то винтовая по-
верхность — единственная, ко-
торая может скользить по са-
мой себе. Сфера, цилиндр и пло-
скость являются поверхностями
вращения; они не только могут
скользить по себе, но могут при
этом перевести любую свою точ-
ку в любое положение и к тому
же по любой траектории. По
этой именно причине четыре
перечисленные поверхности
всегда будут играть наиболее
важную роль в машинострое-
нии.
В сечении цилиндра пло-
скостью получается эллипс
(240). Ошибочно было бы счи-
тать, что эллипс, будучи пло-
ской кривой, представляет со-
бой кратчайшую линию на по-
верхности цилиндра.
Если обернуть свечку бу-
магой (241), а потом разрезать
свечу наискосок острым ножом
(242, 243) и развернуть бумагу,
то получится синусоида (244).
Каждую кривую можно
получить, складывая синусои-
ды. Бороздка, оставляемая на
граммофонной пластинке иглой
при записи одного чистого тона,
будучи развернута на плоскости,
превращается в синусоиду. На
119
(241)
рисунке (245) приведены три синусоиды с одинаковыми ампли-
тудами, т. е. с одинаковыми максимальными отклонениями от
оси; они отвечают трем тонам аккорда: с — gc1 (до малой октавы —
соль малой октавы — до первой октавы). Жирная линия является
суммой этих синусоид; ее вычерчивает на граммофонной пластинке
игла при записи указанного аккорда. Однако в других случаях
тот же аккорд может дать и другую линию (246). Из рисунка
видно, что на этот раз составляющие колебания начинаются не-
одновременно. Наш слух реагирует только на силу, высоту и тембр
звука, которые зависят лишь от амплитуды и частоты какого-то
из составляющих колебаний, и не различает подъемов и спадов
результирующей волны; отсюда можно заключить, что ухо располагает
механизмом, позволяющим восстанавливать по волне из нескольких
голосов отдельные синусоиды; такой механизм действительно существует
и называется кортиевым органом. Мозг, хотя и синтезирует состав-
ляющие колебания, но этот синтез представляет собой нечто от-
личное от суммирования синусоид, и некоторые особенности кри-
вой, выявленные на граммофонной пластинке, утрачиваются.
120
(247)
Электрокардиограмма регистрирует (247) колебания электри-
ческого потенциала, вызванные периодическими сокращениями сер-
дечной мышцы. Расшифровка ее зубцов — дело трудное.
Три кривые стали известны раньше других: эллипс, парабола
и гипербола. Их можно получить, выполняя подходящие сечения ко.-
нуса плоскостью. Вследствие этого они могут быть реализованы в
виде теней, отбрасываемых круглым кольцом. Поместив кольцо так,
чтобы все его точки проектировались на стену, получим эллипс
(248); если часть кольца не проектируется на стену, то тень при-
нимает форму гиперболы (249); когда же на стену проектируются
все точки кольца, кроме одной, тень дает параболу (250). Шар,
лежащий на столе и освещенный сверху, дает тень в виде эллипса,
а точка, в которой он касается стола, является одним из фоку-
сов этого эллипса.
Планеты движутся по эллипсам. Солнце находится в одном из
фокусов. Радиус Солнце — планета заметает ежедневно одну и ту
(248)
121
122
же площадь (251), равно как и за каждый месяц, но из рисунка вид-
но, что пройденный Землей путь меняется от месяца к месяцу.
Если м пустить шар от борта эллиптического бильярда так,
чтобы он прошел не между фокусами, то шар будет двигаться по
ломаной, звенья которой служат касательными к меньшему эллипсу
с теми же фокусами (252). Если, однако, пустить его так, чтобы он
прошел между фокусами, то отразившись, он снова пройдет между
фокусами, и, стало быть, всегда будет так двигаться. Траектория
шара составится из отрезков, касательных к некоторой гиперболе
с теми же фокусами, что и у бильярда (253). Если шар пущен из
фокуса, то, отразившись, он пройдет через другой фокус, после сле-
дующего отражения — через первый фокус и так далее (254);
после нескольких отражений прямолинейные звенья траектории будут
мало отличаться от большой оси бильярда.
XI
ПОВЕРХНОСТИ ИЗ НИТОК. ЦЕПОЧКА. КОЛЯСКА.
МИНИМАЛЬНАЯ ПОВЕРХНОСТЬ.
Все линии на поверхности шара кривые, но есть и кривые
поверхности, которые сотканы из прямых линий. Такими, например, яв-
ляются поверхности конуса и цилиндра.
Мы уже видели (162), что куб, вращаясь, может скользить своими
ребрами по двум конусам и гиперболоиду вращения. Вообще же каждый
однополостный гиперболоид (255) соткан из двух семейств прямых и,
глядя на него сверху, мы видим эллипс с касающимися его прямыми (256).
Параболоид вращения .образуется при вращении параболы вокруг
ее оси симметрии. Автомобильные фары нередко бывают параболоидаль-
ной формы. В сечениях параболоида плоскостями, параллельными оси,
получаются параболы и притом одинаковые. Таким образом, на поверх-
ности параболоида через любую ее точку можно провести бесконечно
много одинаковых плоских кривых. Тем же свойством обладают шар и
плоскость (существуют ли другие примеры?).
Центр тяжести пространственного четырехугольника (257), в вер-
шинах которого помещены одинаковые грузы, можно найти, .если опре-
делить сначала центр тяжести одной пары грузов и, поместив в нем оба
этих груза, сделать то же самое с двумя другими грузами, а затем опре-
делить центр тяжести двух найденных центров с двойными грузами. В ито-
ге получится, что центр тяжести всей системы попадет в середину отрез-
ка, соединяющего середины двух противоположных сторон. Но можно
124
было бы начать с другой пары противоположных сторон и прийти, оче-
видно, к аналогичному результату. Отсюда видно, что отрезки, соединяю-
щие середины сторон произвольного пространственного, в частности,
плоского четырехугольника, пересекаются и делятся в точке пересече-
ния пополам. Когда грузы a, b, с, d не равны, но пропорциональны
(a:b = c:d) мы получаем отрезки, которые делят одну пару противополож-
ных сторон в отношении а:Ь, а другую — в отношении b:d. Эти отрезки
тоже пересекаются, как показывают рассуждения, аналогичные приве-
денным. Если менять массы грузов, сохраняя их пропорциональность,
то получатся два семейства прямых, образующие кривую поверхность
(258), как бы ткань натянутую на четырехугольной раме (металлический
контур, который виден на снимке, является вспомогательным; чтобы вы-
делить четырехугольник, достаточно выбрать по две нитки из каждого
семейства). Сбоку полученная поверхность выглядит как седло (259);
эту поверхность называют гиперболическим параболоидом.
(258)
125
260)
Существует простой способ образования поверхности, содержащей
семейство прямых: берется плоская кривая с касательными — в виде
проволоки с приделанными к ней полосками — и проволока изгибается
произвольным образом в пространственную кривую. В результате возни-
кает двусторонняя поверхность (260), сотканная из одного семейства
прямых; проволока будет ее ребром, общим для обеих сторон и ограни-
чивающим каждую из них.
Если два соосных проволочных кольца (расположенных как нижнее
и верхнее основания усеченного конуса) погрузить в мыльную воду, то
образовавшаяся между кольцами пленка даст наименьшую из всех по-
верхностей вращения, какие могут быть между ними натянуты (261),
ибо пленка стремится сократиться максимально возможным образом. На
снимке рядом с поверхностью видна ее проекция на экран. Параллелями
поверхности являются окружности, а форма меридианов отчетливо пере-
дается верхним контуром проекции поверхности. Нитка, подвешенная
на экране, сфотографирована вместе с проекцией, чтобы показать, что
меридиан имеет форму цепной линии, т. е. повторяет линию цепочки,
подвешенной на двух гвоздях (262). Уравнение этой линии может быть
представлено в виде у = 10' -Ь10;х, при подходящем выборе единиц изме-
рения для х и у.
Минимальная поверхность, образованная мыльной пленкой, может
быть получена вращением цепной линии вокруг оси х. Как найти эту ось
по имеющейся цепочке? Нужно разрезать цепочку в самой нижней точке
и дать ей распрямиться. Для этого следует зафиксировать цепочку гвоз-
дями, вбитыми с внутренней ее стороны, на стене, где она висит, а затем
предоставить разрезанную цепочку действию силы тяжести. Конец це-
почки опишет тогда ту же самую кривую, что и коляска, которую ребенок,
идущий по краю тротуара, тянет за собой (263). Коляска, катящаяся
126
(263)
по мостовой, будет приближаться к краю тротуара, но никогда его не
достигнет. Край тротуара будет искомой осью. Следовательно, осью мож-
но считать наивысшую из горизонтальных прямых, которой еще не коснут-
ся свободно падающие концы разрезанной цепочки.
Вращая трактрису, описанную коляской (или концом цепочки), во-
круг прямой, которая является границей тротуара (т. е. осью цепной ли-
нии), мы получим новую поверхность вращения. Эта поверхность облада-
ет особым свойством: любой листок (например, листок позолоты или ста-
ниоля), покрывающий некоторую ее часть, можно передвигать по всей
поверхности так, чтобы листок не растягивался, не разрывался и не мор-
щился и вместе с тем плотно прилегал к поверхности. Тем же свойством
обладают шар, цилиндр, конус и плоскость, а также любая поверхность,
полученная сворачиванием или изгибанием плоскости и, стало быть, лю-
бая драпировка из нерастягивающейся ткани.
Но трактрисоида вращения отличается еще и тем, что ее кривизна
всюду отрицательна, т. е. все ее точки — седловые. Эта кривизна остается
одной и той же во всех точках — как у шара, что вытекает из опыта с пе-
ремещением листочка. Поэтому трактрисоида является псевдосферой,
а еще правильнее — антисферой.
127
XII
ПРОГУЛКА ПО МОСТАМ. ТРОПИНКИ. ЗАВЯЗЫВАНИЕ
УЗЛОВ. ПРИЧЕСЫВАНИЕ ВОЛОС.
Уже говорилось, что существует только пять видов пра-
вильных многогранников, или платоновых тел, но не говорилось, почему
это так.
Нарисуем на поверхности шара фигуру из L линий, V вершин
и S граней. Иными словами, поделим территорию земного шара между S
странами, считая, что вся эта территория сухопутная. Какими бы между-
народными отношениями не диктовался подобный раздел, всегда будет
выполняться условие V + S = L + 2. Убедиться в справедливости этого
условия, найденного великим математиком Эйлером, нетрудно. Начнем
с одной вершины (264). Понимая условие Эйлера буквально, видим,
что оно выполняется, ибо имеется одна вершина (V=l), одна страна
(S=l) и границы отсутствуют (L = 0), так что 14-1=0 + 2. Если про-
вести из вершины одну линию, то получим новый раздел территории
Земли (265), но и для него наше правило сохраняет силу, так как V = 2,
S=l, L=\ и 2+1 = 1+2. Пусть теперь имеется произвольная фигура,
удовлетворяющая правилу Эйлера (266); проведем новую линию, сое-
диняющую две ее вершины (267), (268). От этого число вершин не
изменится, а число граней и число линий увеличится на 1; следовательно,
после проведения новой линии и левая, и правая части формулы Эйлера
увеличатся на 1. Поэтому, если эта формула была верна для прежней
фигуры, то она останется верной и для новой. Формула Эйлера сохранит
силу и в том случае, когда новая линия соединит одну из вершин преж-
ней фигуры с новой вершиной (269), так как в этом случае число
128
граней не изменится, а число линий и число вершин увеличится на 1.
Но поделить поверхность Земли между странами всегда можно, начав
с одной вершины и пририсовывая затем одну за другой все необходимые
границы; следовательно, формула Эйлера справедлива для любой
фигуры. (Как в этом рассуждении используется принцип домино?)
Правильные разделы сферы отличаются от всех других тем, что
в них все грани ограничены одним и тем же числом s линий и в каждой
вершине сходится одинаковое число v линий. Если имеется S граней
(стран), то произведение Ss дает удвоенное число линий, так как каж-
дая линия принадлежит двум граням и поэтому считается дважды.
Таким образом, 2L = Ss. Можно также пересчитать линии, перебирая
одну за другой все вершины; это даст формулу 2L = Vv. (Здесь под-
разумевалось, что в первом случае S>1, а во втором V>1. Если усло-
виться, что v = 2L при V = 1 и s = 2L при£=1, то обе формулы будут
верны и тогда, когда есть только одна грань или только одна вершина.)
Подставляя выражения
S=2L V- 2L
S ’ V
в формулу Эйлера, находим
—+ —= L + 2.
V S
Это можно переписать так:
Проще всего удовлетворить уравнению (Е), положив
s = 2, v = L или v = 2, s =L.
Первый способ дает S = L, V = 2. Имеется только две вершины
и столько граней, сколько линий. Поскольку v = L, каждая линия про-
ходит через каждую вершину, а поскольку s = 2, каждая грань ограничена
двумя линиями. Мы, следовательно, имеем два полюса, соединенных
Л меридианами (270); меридианов может быть любое число (L = 1,2,3,...).
Второй способ дает V = L, S = 2. На этот раз получается только две
грани и столько вершин, сколько линий. Поскольку s = L, каждая линия
принадлежит каждой грани; иными словами, каждая граница граней
состоит из L линий и L вершин. Следовательно, шар разделится на две
полусферы, ограниченные L-угольником (271); число L может быть
любым.
Эти два случая будем считать особыми. Отметим, что особый случай
s = 2, v = 2 (272) получается как по первому, так, и по второму способу.
5. Г. Штейнгауз
129
Вернемся теперь к, уравнению (Е) и попробуем решить его при
L = 1. Легко убедиться, что в этом случае получатся только два решения:
v = 1, s = 2 и и = 2, s = 1. Оба они будут особыми. Одно из них пред-
ставлено на рисунке (265). Как, изобразить второе?
Положив L = 2, получим v = 2, s = 2, т. е. особое решение, отве-
чающее рисунку (272).
Желая найти другие решения, мы должны подставлять вместо L
числа 3,4,5,... Тогда правая часть уравнения (Е) будет меньше единицы,
а поскольку она всегда больше 72, то
Значение s = 1 не удовлетворяет правому неравенству, а значение
s = 2 дает особые решения, представленные на рисунке (270), которые
мы уже учли.
Итак, мы должны начать со случая s = 3. Тогда в качестве v нужно
испробовать лишь одно из трех значений — 3, 4 или 5, так как, v = 1
не удовлетворяет правому неравенству, v = 2 приводит к, уже учтенному
особому случаю, который представлен на рисунке (271), а при и>6
величина '/s + x/v будет меньше или равна х /2 — вопреки левому нера-
венству. Рассуждая таким же образом и учитывая левое неравенство,
мы убеждаемся, что величина v не может принимать других значений
и в случае s>3. Но все, что здесь сказано, остается в силе, если s и
v поменять ролями. Таким образом, отбрасывая невозможные и особые
случаи, мы можем ограничиться 9 случаями, которые получаются при
s = 3, 4, 5 и v = 3, 4, 5. Из них четыре случая:
5 = 4, v = 4,
5 = 5, v = 4,
5 = 4, v = 5,
5 = 5, v = 5
невозможны из-за левого неравенства: уже сумма 74 + 74= 7г оказы-
вается меньше требуемой. Остается пять случаев:
5 = 3, v = 3; (а)
подстановка в (Е) дает 1/3+1/3—1/2= 1/L, (b)
£ = 6, 5 = 4, У = 4; s = 3, v = 4;
подстановка в (Е) дает 1/3+1/4—1/2= 1/£, £=12, 5 = 8, V = 6; s = 3, v = 5; (с)
подстановка в (Е) дает 1/3 + 1/5—1/2 = 1/£, £=30, 5=20, V = 12; s = 4, v = 3; (d)
подстановка в (Е) дает £=12, 5 = 6, V = 8; 5 = 5, v = 3; (е)
подстановка в (Е) дает £=30, 5 = 12, V = 20.
130
В случаях (d) и (е,) «мы не производили выкладок, так как эти
случаи можно получить из (Ь) и (с), если поменять ролями s и v,
а также S и V. В итоге мы нашли пять правильных, или платоновых, разде-
лов сферы. Особые решения не дают многогранников, так как не су-
ществует ни плоских двухугольников с прямолинейными сторонами, ни
пространственных двугранников с плоскими гранями. Пять платоновых
тел, отвечающих правильным разделам сферы (a), (b), (с), (d) и (е), —
это четырехгранник, восьмигранник, двадцатигранник, куб и двенадцати-
гранник; теперь уже доказано, что других правильных многогранников
не существует.
Следует отметить, что на самом деле доказано значительно больше,
чем было обещано. А именно, мы нашли все правильные разделы сферы
независимо от того, какими являются границы областей — дугами
окружностей, зигзагообразными или какими-либо иными кривыми линия-
ми. Больше того, сказанное относится не только к сфере: наши рассужде-
ния оставались бы в силе, если бы, например, речь шла о планетах
кубической или чечевицеобразной формы.
Известна старая головоломка — обвести контур фигуры, не отрывая
карандаша от бумаги и не обводя ни одной линии контура дважды.
На рисунке (273) изображена фигура, которую удается обвести по-
добным образом.
Эйлер стал интересоваться такими фигурами, когда ему предложили
задачу о мостах города Кенигсберга (нынешнего Калининграда): можно
ли обойти город так, чтобы пройти по семи его мостам (274) ровно по
одному разу?
Если обозначить остров через А, левый берег реки через В, пра-
вый — через С, а область между рукавами реки в ее верхнем течении —
через D, то задача сведется к обводу контура (275) одним непрерывным
движением. Но это невозможно, так как выбрав одну из точек А, В, С, D
за начало пути, а другую (или ту же самую) за его конец, мы должны
будем пройти по ходу движения через остальные две (или три) точки,
не являющиеся ни начальными, ни конечными; при этом одна дорога
должна вести к точке, а другая — от нее, но в каждой точке сходятся
три или пять дорог, вследствие чего некоторые дороги останутся не-
пройденными.
С другой стороны, если все точки контура — четные (т. е. такие,
в которых сходится четное число дорог) или если только одна или две
из них нечетные, то фигуру можно обвести одним непрерывным движе-
5*
131
нием лишь бы она была связной. Проверим это для фигур с одними
только четными точками. Выберем какую-нибудь точку контура в качестве
стартовой. Как бы ни идти из этой точки, мы рано или поздно снова
в нее вернемся, так как никогда не попадем в тупик; из любой другой
точки, в которой мы окажемся по ходу движения, всегда будет вести
хотя бы одна нехоженная дорога. Можно поэтому считать, что мы пройдем
по замкнутому маршруту. Если это не весь контур, то наш маршрут пе-
ресекает непройденную часть контура в некоторой точке А (276).
Из общего числа дорог, ведущих в эту точку, было использовано лишь
четное число дорог и, значит, осталось их тоже четное число. Изменим
теперь первоначальный план движения и пройдем прежний путь от А до
А (жирная линия на рисунке). Но точка А принадлежит непройденной
части контура, поэтому, вернувшись в эту точку, мы можем начать
из нее путешествие по оставшейся части; новое путешествие, очевидно,
снова закончится в точке А (пунктирная кривая на рисунке). Однако
две замкнутые кривые, пересекающиеся в какой-нибудь точке, состав-
ляют вместе одну-единственную замкнутую кривую (примером может
служить цифра 8). Если эта последняя кривая не исчерпывает всего
контура, то она пересекается с оставшейся его частью в некоторой точке
В, и мы можем действовать далее прежним способом; в конце концов
будет найден маршрут, охватывающий весь контур.
Подобным же образом решается задача и в том случае, когда только
две точки нечетные. Ввиду связности фигуры можно указать маршрут,
ведущий из одной нечетной точки (точки О) в другую (точку О').
Если при этом мы не обойдем всей фигуры, то оставшаяся ее часть,
поскольку она не содержит нечетных точек, будет замкнутым контуром
(277); этот контур пересечет путь О — О' в некоторой точке А. Двигаясь
из О в О', мы дойдем до точки Д, обойдем замкнутый контур (пунктирная
линия на рисунке), вернемся в точку А и завершим обход по участку А — О'
маршрута О — О'.
Посмотрим на скрещенную цепочку (278). Расправляя ее на столе
с целью освободиться от скрещения, мы должны будем пройти через
такое положение (279), когда цепочка «переламывается», т. е. когда
в некоторой ее точке получается острие. Это можно доказать, исследуя
поведение касательной (280). По мере передвижения вдоль цепочки
угол между касательной и некоторым постоянным направлением меняется,
но при обходе всей скрещенной цепочки приращения этого угла компен-
132
сируются его уменьшениями, так что в итоге полное приращение ока-
зывается нулевым. В случае несмещенной цепочки полное приращение
составляет 360°. Следовательно, должна существовать переходная форма
цепочки, когда она из скрещенной с приращением 0°, превращается в
нескрещенную с приращением 360°; это как, раз и будет форма с острием,
в котором скачкообразно сбрасывается приращение угла касательной,
получившееся в результате обхода всего контура.
Рисунок (281) служит иллюстрацией к задаче, родственной задаче
о мостах. Имеются три дома, голубятня, колодец и навес для сена;
требуется проложить от каждого дома тропинки к голубятне, колодцу
и навесу таким образом, чтобы тропинки между собой не пересекались.
133
(282)
Эта задача неразрешима. Действительно, если идти от первого дома
по тропинкам, ведущим к голубятне, колодцу и навесу, а затем двигаться
от них дальше по тропинкам, соединяющим их со вторым домом, то
окажется, что три непересекающиеся линии идут от первого дома ко
второму (282). Такие линии делят всю плоскость на три области:
Сь С2 и С3. Следовательно, третий дом должен находиться в одной из
этих областей. Если он попадет в Сь то навес будет отделен от него
замкнутым контуром; если он попадет в С2, то другой замкнутый кон-
тур отделит от него голубятню; если же этот дом попадет в С3, то он
окажется внутри контура, отделяющего его от колодца. В первом случае
третий дом нельзя будет соединить тропинкой с навесом, во втором —
с голубятней, в третьем — с колодцем, поскольку такая тропинка будет
пересекать другие тропинки.
Представим себе четыре страны, каждые две из которых имеют
общую границу. Столицы любых двух стран можно будет в таком случае
соединить железнодорожной линией, проходящей только по их террито-
риям. Начнем с трех столиц А, В и С. Соединяющие их линии образуют
как бы треугольник. Четвертая столица D будет находиться либо внутри,
либо вне этого треугольника. Соединяя эту столицу с остальными, мы
в любом случае получим большой треугольник, составленный из трех
граничащих друг с другом малых треугольников. Пусть теперь Е будет
столицей пятой страны (283); она либо окажется вне большого треуголь-
ника, либо попадет в один из малых. В обоих случаях среди столиц
А, В, С, D найдется такая столица X, которая будет отделена от Е тре-
угольником железнодорожных линий. (На рисунке представлены оба
случая: одному отвечают буквы Е и X, а другому — буквы Е' и X'.)
Но эти линии не проходят по территории стран со столицами Е и X
и поэтому эти страны не могут граничить друг с другом. Итак, мы прихо-
дим к выводу, что не может быть пяти стран, каждая из которых грани-
чила бы с каждой другой.
Все эти задачи относятся к специальному разделу геометрии, называ-
емому топологией; в топологию входит также учение об узлах.
На шнуре, концы которого соединены (284), никогда не получится
узла, если его не было перед скреплением концов; если же узел был (285),
то он не исчезнет (286), пока шнур не будет разрезан. Простейший узел
имеет две формы (287); каждая из них является зеркальным отраже-
нием другой.
Узел можно смещать вдоль шнура как угодно далеко. Но завязать
на концах шнура такие два узла, чтобы при встречном движении они
взаимно уничтожились, невозможно. Только в самое последнее время
этот факт, известный из опыта, удалось доказать математически.
134
(284)
(285)
(286)
(287)
Нетрудно так сплести три шнура, чтобы никакие два из них не были
сплетены друг с другом (288) ; из рисунка видно, что достаточно разре-
зать какой-нибудь один шнур, чтобы расплелись все три. Можно построить
модель, обладающую аналогичным свойством с любым числом замкнутых
линий (289 А, В).
Бумажная лента, перекрученная на 180° и затем склеенная (лента
Мёбиуса), представляет собой одностороннюю поверхность (290). Муха
может перебраться из любой ее точки в любую другую, не переползая
через край поверхности. Этот край является замкнутой, свободной от
узлов кривой.
Если бы лента Мёбиуса была сделана из очень эластичной резины,
то ее край можно было бы деформировать в окружность; а тогда сама
лента превратилась бы в торбу (291), которая пригодна для ношения
вещей, хотя у нее нет ни внутренней, ни внешней стороны.
Если разрезать ленту Мёбиуса вдоль черной серединной линии, па-
раллельной ее краю, то лента не распадется, а перейдет в двустороннюю
поверхность (292). Краями полученного таким способом пояса будут две
замкнутые линии без узлов, сплетенные, однако, друг с другом. Теми
же свойствами (двусторонностью, наличием двух сплетенных между
собой краев без узлов) обладает лента, перекрученная перед склеива-
нием на 360° (293); лента, полученная разрезанием мёбиусовой, пе-
рекручена на 720°. Имеется еще одна поверхность с точно такими же
свойствами, что и поверхность, модель которой представлена на снимке
(293) — а именно, зеркальное отражение этой модели: ни одна из двух
указанных поверхностей не переводится в другую никаким изгибанием
или растяжением.
135
(288)
136
(294)
(295)
(297)
Разрезав ленту (293) вдоль серединной линии, мы получим две спле-
тенные между собой ленты (294); обе они копируют первоначальную
ленту.
Если на ленте Мёбиуса провести линию на расстоянии одной трети
ширины ленты от края (295) и затем разрезать ленту вдоль этой линии,
то получатся две сплетенные между собой ленты (296); меньшая из них
будет подобна первоначальной ленте, а большая примет ту же форму,
что и лента, которую мы уже видели на снимке (293).
Если перед склеиванием перекрутить ленту на 540°, т. е. на три
полоборота, то снова получится односторонняя поверхность (297), край
которой имеет узел «клеверного» типа, т. е. такой, как на снимке (287).
Каким именно из двух узлов снимка будет этот узел — правым или
левым?
Обычный кусок поверхности, например, листок, имеет две стороны,
а его край представляет собой линию без узлов. В связи с этим возникает
вопрос: существует ли двусторонняя поверхность, край которой содержит
137
(298)
узлы? Положительный ответ на него
дает модель (298). В этой модели
край поверхности имеет форму кле-
верного узла левого типа (287),
а для различения сторон поверхности
одна из них на фотографии заштри-
хована, а на другой штриховка от-
сутствует.
Существует гипотеза, что любую
карту можно раскрасить четырьмя
красками так, чтобы всякие две стра-
ны, имеющие общий участок гра-
ницы, были закрашены в разные
цвета. Это до сих пор не доказано,
но все примеры подтверждают такую
гипотезу. В случае тора (299), т. е.
тела в форме камеры автомобильной
шины, требуется целых семь красок,
так, как поверхность тора можно раз-
бить на семь областей, каждые две
из которых граничат друг с другом
вдоль некоторой линии. Такое раз-
биение поверхности тора (кольца)
показано на рисунке (300), на ко-
тором тор приводится в двух видах —
сверху и снизу. {Хотя поверхность
тора значительно менее обычна, чем
плоская или сферическая, удалось доказать, что семи красок, на торе
всегда хватает. Правда, доказано, что в случае плоскости или сферы всегда
можно обойтись пятью красками, но не найдено примера, в котором четы-
рех красок, было бы недостаточно. [Примечание при переводе. Уже после
смерти автора книги проблема четырех красок была решена: американские
математики Аппель и Хакен показали, что достаточно проверить лишь
конечное — хотя и очень большое число типов карт; им удалось осущест-
вить эту проверку с помощью ЭВМ, и машина подтвердила, что четырех
красок всегда достаточно. См. Appel Kenneth, Н a ken W о 1 4 -
gang, Every planar map is four colorable, Bull. Amer. Math. Soc. 1976,
82, № 5, 711—712.]
На поверхности тора можно начертить замкнутую линию, представ-
ляющую собой левый клеверный узел и вместе с тем не имеющую само-
138
пересечений (301 А). Если разрезать тор вдоль черной линии, т. е.
линии узла на торе, то получится двусторонняя поверхность (301 В)
с двумя сплетенными между собой краями, каждый из которых повто-
ряет исходный узел. Чтобы получить эту поверхность непосредственно,
нужно перекрутить бумажную ленту на три полных оборота (1080°),
завязать полученную ленту узлом, а затем склеить.
Двустороннюю поверхность с двумя не сплетенными между собой
краями, имеющими форму узлов (302), можно получить, соединив труб-
кой две одинаковые поверхности того же типа, что и поверхность, ко-
торую мы уже видели на снимке (298).
На торе можно расположить сколько угодно узлов левого клеверного
типа (287), которые не пересекают ни себя, ни друг друга (303). Од-
139
(303)
(304)
нако, если поместить на торе по одному клеверному узлу каждого типа —
правого и левого, то эти узлы пересекутся в 12 точках (304).
Растянем плоский кусок резины, ограниченный каким угодно конту-
ром, а затем отпустим его, позволив резине принять первоначальную
форму (305 А, В); если вся резина* окажется внутри той области,
которую она покрывала в растянутом состоянии, то некоторая ее точка
140
Р займет то же положение, какое она занимала, когда резина была
растянута.
Приведем здесь доказательство, основанное на одном свойстве
шахматной доски (21—23), следуя идее, принадлежащей В. Стожку.
Пусть резина растянута до размеров шахматной доски и пусть через
Q обозначена точка, в которую переходит точка Р растянутой резины
(305А)
(305В)
после того как ее отпустят. Поле доски назовем красным, если для каж-
дой его точки Р точка Q лежит ближе, чем Р, к правому краю доски;
в случае, когда всякая точка Р поля переходит в точку Q, которая ближе,
чем Р, к левому краю доски, будем называть поле зеленым; желтым
назовем поле, если оно не является ни красным, ни зеленым. Легко убе-
диться, что все поля крайней левой вертикали — не зеленые, а поля
крайней правой — не красные. Очевидно, кроме того, что красные и зеле-
ные поля не могут быть соседними, так как соседние поля имеют (по край-
ней мере одну) общую точку. Поэтому, если запретить королю ходить по
желтым полям, то он не сможет пройти от левого края доски до правого, а
тогда ладья может пройти от верхнего до нижнего края доски, двигаясь по
одним только желтым полям (это свойство шахматной доски было отме-
чено на стр. 19). Таким образом, можно провести от верхнего до ниж-
него края доски такую линию, которая проходит только по желтым полям.
Из каждой точки этой линии проведем стрелку PQ. Не может быть, чтобы
все эти стрелки вели выше (иначе говоря, точки Q не могут быть всегда
выше точек Р), так, как, начальная точка линии не может перейти в точку
за пределами доски. Точно так, же не может быть, чтобы все они ве-
ли ниже.
Направление стрелки по ходу движения меняется непрерывно, следо-
вательно, на линии найдется такая точка Р', в которой стрелка P'Q' на-
правлена горизонтально. Но из определения желтого поля вытекает, что
в поле, содержащем точку Р', найдется такая точка Р", где стрелка P"Q"
направлена вертикально. Если поле мало, то подобный скачок в перемене
направления стрелки возможен лишь при условии, что сами стрелки малы
для всех точек Р в этом поле. Деля область на п2 полей и увеличивая и,
мы получаем в пределе точку Ро, в которой стрелка PoQo исчезает
(т. е. Ро= Qo), а это означает, что после того, как резину отпустили, точка
Ро остается на месте.
Если сплющивать произвольным образом шарик, сделанный из
эластичного материала (не разрывая его), то всегда найдутся антиподы
(диаметрально противоположные точки) L и М такие, которые после сплю-
щивания сольются в одну точку (306 А, В). Из этого можно вывести та-
кое интересное следствие: на поверхности Земли в каждый момент време-
141
ни найдутся два антипода с одной и той же температурой и одним и тем
же атмосферным давлением.
Шар, покрытый волосами, никогда не удастся гладко расчесать;
всегда найдется, по крайней мере одна точка, в которой волосы создадут
полюс без определенного направления (307 А, В).
XIII
СТУДЕНТЫ. ЛОТЕРЕЙКА. ЛЯГУШКИ.
ПОДСОЛНЕЧНИКИ
Законы природы выражаются графически различными кри-
выми. Кривые на диаграмме (308) выражают связь между давлением
Р и объемом V одного килограмма газа. Сплошные линии — это изо-
термы, т. е. линии постоянной температуры. Согласно закону Бойля —
Мариотта они являются гиперболами. Водород Н2 представлен двумя
изотермами: одна отвечает температуре 0° С, а другая — 77° С. Закон
Бойля — Мариотта утверждает, что произведение PV есть величина
постоянная. Штрих-пунктирные линии получаются в том случае, когда
сосуд с газом, находящимся в некотором состоянии (которое на диаграм-
ме обозначено кружком), снабжается термоизоляцией с целью исклю-
чить теплообмен. В этих условиях температура будет меняться при изме-
нении давления, и мы придем к адиабате или обобщенной гиперболе
143
Р’ХГС/СМ2
(произведение P(lV$ равно постоянной величине). Если от обычных шкал
перейти к логарифмическим (см. (74)), то все кривые линии станут
прямыми (309).
На рисунке (310) показаны шестиугольные островки, отделенные
друг от друга каналами. Можно также считать этот рисунок планом го-
рода. Люди, проходящие через город, на каждой развилке должны вы-
брать одну из двух улиц — правую или левую. Вначале имеется всего
одна улица, которая входит в город с севера и ведет на юг. После этого
будет две улицы NS (ведущих с севера на юг); в одну можно пройти, об-
ходя островок справа, а в другую — обходя его слева. Две имеющиеся
возможности обозначены символом (1,1).
144
Теперь имеется на выбор три улицы NS. В восточную улицу может
войти только тот, кто на предыдущей развилке пошел налево. К средней
улице ведут два пути — кто раньше пошел налево, может пойти теперь
направо, а кто раньше пошел направо, может свернуть теперь налево.
К западной улице ведет только один путь. Все указанные возможности
выражаются символом (1, 2, 1). Складывая соседние числа 1,2 и 2,1, по-
лучаем набор (1, 3, 3, /), который указывает, сколькими способами мож-
но войти в каждую из следующих четырех улиц NS. Так шаг за шагом
строится треугольник Паскаля:
/
/ 1
1 2 1
13 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 > 36 84 126 126 84 36 9 1
В последней строке этого треугольника указано, сколькими способа-
ми можно пройти к первой, второй, ...десятой улице в десятом ряду остров-
ков. В общей сложности получается следующее число способов:
1+9 + 36 + 84+126+126 + 84 + 36 + 9+1 =512 = 29.
Можно считать, что на рост человека влияет множество различных
факторов, действующих в период его развития, а также в период разви-
тия его предков; одни их них ведут к увеличению роста, другие — к умень-
шению. Представим себе, что каждый человек подбрасывает монету и
жребий решает, должна ли природа увеличить его рост на дюйм (орел)
или на столько же уменьшить (решка). Допустим, что сначала все были
одного роста. Если каждый из 512 человек проходит такую жеребьевку
девять раз (или, что то же самое, подбрасывает сразу 9 монет), то резуль-
тат, скорее всего, будет такой, какого можно ожидать по опыту выбора
улиц в городе. Ведь приобретение дополнительного дюйма можно рассмат-
ривать как решение пойти направо, а потерю дюйма — как решение свер-
нуть налево. Поскольку имеется 512 человек, то можно исчерпать все
возможности, указанные в последней строке треугольника Паскаля. Если
все они осуществятся, то рост одного человека будет на 5 дюймов ниже
среднего, девяти человек — на 4 дюйма, ..., 126 человек — на 1 дюйм;
затем 126 человек будут на 1 дюйм выше среднего, 84 человека — на
2 дюйма, ..., 1 человек — на 5 дюймов.
Если расставить всех этих людей так, чтобы в первой шеренге были
самые высокие, во второй те, рост которых на один дюйм меньше и так
далее, то получится 10 шеренг; если же затем выравнять эти шеренги по
левому флангу, то правый фланг даст кривую, определяемую числами
Паскаля. Таким образом, чтобы наметить эту кривую — кривую Гаусса, —
достаточно просто построить ординаты по числам Паскаля.
145
(311)
Можно также собрать всех студентов, зачисленных в университет
в каком-нибудь году, и расставить их по росту тем же способом, каким
были расставлены люди нашего воображаемого контингента (311).
Наконец, можно изготовить деревянную лотерейку (312) с шести-
угольными островками и каналиками между ними. Будем сыпать дробь
через верхнее отверстие наклонной лотерейки; она тогда распределится
между перегородками, установленными непосредственно под лотерейкой,
(312)
146
(313)
(314)
и мы сможем убедиться в справедливости случайного закона Гаусса, про-
верив, что высоты столбиков дроби между перегородками пропорцио-
нальны числам Паскаля.
Этот эксперимент можно упростить (313), (314), заменив лотерейку
обычной доской (лучше обтянуть ее сукном): дробь, высыпаемая из од-
ной точки, скапливается между перегородками. Это соответствует беско-
нечно большому числу бесконечно малых островков. Строго говоря, закон
Гаусса, который приближенно описывается треугольником Паскаля, до-
казан математически в предположении, что имеется бесконечно много
бесконечно малых независимых воздействий — обычная доска как раз
точнее отвечает таким условиям. (Перегородки обязательны, потому что
иначе очередные скатывающиеся дробинки могли бы разбросать уже
скатившиеся.)
Диаграмма (315) получена из опытов Тревана на лягушках, которые
подвергались действию наперстянки (digitalis); цифры на нижней (лога-
(315)
/ \
—I » 1 1 1 г 1 1 1 1 I 1 1 1 1 | 1 1 1 1 I 1 ' 11 | 11 1 П 1 1 1 I I1 I Ii|iiii|ini|iin|iiii|iiiq-- ф
0,1* 0,5 0,5 0,7 0,8 0,9 7,0 см3
147
рифмической) шкале означают дозы инъекций наперстянки в расчете на
100 г массы лягушки; левее каждой вертикали, отвечающей какой-либо
дозе, нарисовано столько лягушек, сколько их погибает из ста при инъек-
ции этой дозы. Например, введение дозы 0,4 см3 убивает 6 лягушек из
100, а доза 0,6 см3 оказывается смертельной в 50 случаях из 100. (Какая
доза необходима, чтобы погибли 99 лягушек из 100?) Разумеется, все
эти данные получены как средние из большого числа опытов.
«Лягушечья кривая» также является кривой Гаусса; ее уравнение
следующее:
у = А • Юс(х-6)2 (коэффициент с отрицателен).
В явлениях, связанных с размножением организмов в ограниченном
пространстве, мы встречаемся с кривыми иного рода. Торнтон обнаружил,
что объем, который занимают бактерии, находящиеся в замкнутом сосуде,
увеличивается со временем по тому же закону (316), что и закон (317),
148
(319)
которому подчиняется рост подсолнечников (опыты Рида и Холланда),
или же закон (318), определяющий рост протяженности железнодорожных
линий в США. Причина заключается в том, что рост числа организмов
пропорционален количеству уже живущих организмов и имеющемуся
свободному пространству (которое уменьшается). На рисунках видны так-
же небольшие отклонения истинных величин от значений теоретической
кривой. Рост населения США подчиняется такому же закону (319); этот
закон выражается формулой
у__ 190830,35 1 ллл
1 ~ + 101,542035 - 0ДО62К5[/- ЮТ] * 1иии
(/ — означает год, Y— численность населения).
Кривая имеет в некоторой точке перегиб; можно доказать, что верх-
няя граница, к которой приближается кривая, лежит в два раза выше
точки перегиба. Исходя из этого, статистики предсказывали, что числен-
ность населения США не превысит 160 миллионов. Из формулы получает-
ся, что число жителей может дойти до 191 миллиона. Расхождение вызва-
но тем, что трудно точно определить положение точки перегиба, так как
149
OS I
-
ООО О
0003
для истинной кривой известны лишь отдельные точки, через которые не
удается провести гладкой линии с единственной точкой перегиба.
Что бы ни говорить о таких предсказаниях, фактом остается то, что
законы об ограничении иммиграции появились вскоре после достижения
точки перегиба; тогда же обнаружились и дали о себе знать и другие
признаки ограниченности пространства.
В области естественных наук встречается множество различных кри-
вых, хотя теоретическое обоснование выражаемых ими законов зачастую
неизвестно; одним из примеров служит кривая (320), дающая распреде-
ление суши и водного пространства на разных высотах (по нижней шкале
видно, что на глубине 8000 м суша занимает все 100%, на глубине
4000 м — только 60%, на уровне моря — около 30%, а на высоте 8000 м
все пространство занимает атмосфера); еще один пример — это кривая
(321) смертности среди мужского населения США.
ПРИМЕЧАНИЯ
Число (и) в начале каждого примечания означает, что оно относится к рисун-
ку с этим номером или к, тексту, который его сопровождает.
(1) Дудни (Dydney Н. Е., Amusements in Mathematics — London:, 1917, p. 27).
(2)Пифагор Самосский (582—507 до н. э.), автор теоремы о квадратах сторон пря-
моугольного треугольника, занимался паркетами и теорией гармонии. Разбиение на ри-
сунке — индусского происхождения. На оригинальном рисунке стоит надпись «Гляди!»,
которая более красноречива, чем любое словесное доказательство.
(4) Идея принадлежит профессору Яну Минусинскому.
(5) Морли (Morley F. On Reflexive Geometry — Trans. Amer. Math. Soc., 1907, v. 8,
p. 14—24); Чайлд (Child L. J. M., Proof of Morley’s Theorem — Math. Gazette, 1923, v. 11,
p. 171).
(6) Важевский указывает на некоего адвоката по фамилии Раппапорт как на автора
этой трисекции (Wazewski Т.— Rocznik Pol. Tow. Mat. 1945. t. 18, s. 164). Ошибка не пре-
восходит 22'23"; для углов, меньших 30°, ошибка меньше Г.
(7) Можно рассматривать задачу о покрытии, в котором все квадратные плитки раз-
ные. Если потребовать дополнительно, чтобы сторона каждой плитки не превосходила опре-
деленной величины, скажем, 1 м, то задача становится значительно сложнее.
(8) На это разбиение прямоугольника указал Моронь (Moron Z — Przeglad Mat.-Fiz.
1925, t. 3, s. 152—153).
(9) На это разбиение указал Уилкокс (Willcocks Th.— Fairly Chess Rev. 1948, v. 7).
Первым, кто разложил квадрат на различные квадраты, был Шпраг (Sprague R.— Math. Z.
1939, В. 45, S. 607—608); в его разложении содержится 55 квадратов. Невозможность раз-
ложения прямоугольника менее чем на 9 разных квадратов доказали Рейхардт и Топкен
(Reichardt Н., Toepken Н.— Jahresber. Deutsch Math. Vereinigung, Aufgaben u. Losungen,
1940, B. 50, S. 13—14).
(10) Книга (1), c. 27. Минусинский приводит графическое доказательство (Miky.-
sinski J.— Ann. Univ. Marii Curie-Sklodowskiej, Lublin, 1946, t. 1, s. 45—50; рисунок поме-
щен на с. 49).
(12) Теории различных игр рассматриваются в книге Аренса (Arens W. Mathematische
Unterhaltungen und Spiele — Leipzig: Teubner, 1910, B. 1, S. 172—176).
Моргенстерн и Нейман подвергли в своей книге теорию игр обстоятельному матема-
тическому и логическому анализу (Morgenstern О., Neumann J. V. The theory of Games and
Economic Behaviour.— 2-nd ed.— Princetone:, 1947). В более доступной форме теория игр
излагается в книге МакКинси (McKinsey J. С. С. Introduction to the Theory of Games —
New York:, McGraw-Hill, 1952).
(13) Бергер (Berger J.— Columbia Chess Chronicle, 1888).
Согласно анализу В. Хетпера самая длинная оборона черных такова:
Белые Черные
1. ФЬ8 6. <t>g4 10. Фа1 Сс4 Саб Ch5
2. Феб 7. <t>dl 11. ФЬ8 + Саб СЬ7 Cg4
3. Фе1 8. Kpg3 12. Ф:СЬЗ + СЬ5 Се4 Ch3
4. Фс1 9. Фс1 13. Ф:СЬ2-Х СП Cf3 Ch2
5. <Df4
152
Кр — король, Ф — ферзь, С — слон, : — бьет, 4--шах, -X — мат, abcdefgh — вертикали
слева направо, 12345678 — горизонтали снизу вверх.
(14) Массман (Massman W.— Neue Leipziger Zeitung, 1936). Эту задачу можно найти
в книге: Прокоп (Prokop F. J. 1000 auserlesene Schachaufgaben, Prague, 1944, № 423).
На польском языке имеется книжка Врубеля (Wrobel М. Tajemnice dwuchodowki,
Warszawa:, 1950). Это исчерпывающая оригинальная монография о двухходовках.
(15) Эбере (Ebersz К. Magyar Sakkvilag, 1940). Анализ приводят Дюшан и Халбер-
стадт (Duchamp, Halberstadt. L’Opposition et les Cases Conjuguees — Paris—Bruxelles;
Lancel et Legrand, 1930, p. Ill, № 244).
Торрес-и-Кеведо сконструировал автомат, который ладьей и королем матует одино-
кого короля играющего против него человека, начиная с любой позиции в наименьшее воз-
можное число ходов. (Torres у Quevedo — Sci. Amer. Suppl. 1915, v. 6., p. 296). Современная
электронная техника предоставляет значительно большие возможности. Винер (Winer N.
Cybernetics — New York; Wiley 1948). Русский перевод: Винер Н. Кибернетика,— М.: Со-
ветское радио, 1958.
(16) Книга (12), В. 2, S. 226—260. Игру изобрел, по-видимому, известный шахматист
Лойд (Loyd S.). Теорию разработали Джонсон и Стори (Johnson W., Story W. Е.— Amer. J.
Math. 1879, v. 2, p, 397—404).
(17, 18) Категоричность шахмат и аналогичных игр первым доказал Ласло Кальмар
(Kalmar L. Zur Theory der abstrakten Spiele — Acta Litterarum ac Scientiarum R. Univ.
Hungaricae; Sec. Sc. Math., 1928, v. 4, p. 65—85).
(19) Евклид, один из величайших математиков всех времен, жил в Александрии око-
ло 300 г. до н. э. Автор первого систематического изложения геометрии.
Простоту числа 2127—1 доказал Фокенберг в 1917 г.
Лемер (Lehmer D. Н.) сконструировал машину фотоэлектрического действия, про-
веряющую делимость чисел-великанов; она демонстрировалась в 1933 г. на выставке
«А Century of Progress» в Чикаго. С того времени вычислительная техника значительно
усовершенствовалась, особенно в связи с выяснением возможности применения электрон-
ных ламп. См. Литтлвуд (Littlewood J. Е.— Math. Gazette, 1948, v. 32, р. 163—171); Сер-
пйнский (Sierpihski W.— Matematyka, 1950, № 3 (10), s. 12—20); Миллер и Уиллер
(Miller J. С. Р., Wheeler D. J — Nature, 1951, v. 168, р. 838); У лер (Uhler Н. S — Scripta
Math, 1952, v. 18, р. 122—131); Серпйнскйй (Sierpihski W.— Matematyka, 1954, № 1, s. 3).
(21) Роуз Болл (Rouse Ball W. W. Mathematical Recreations and Essays — London:,
Macmillan, 1939, p. 165, 171). См. также книгу (12), с. 225, 293.
(22, 23) Студент Вроцлавского университета Хуляницкий (Hulaniski А.) нашел простое
доказательство теоремы о заминированных полях шахматной доски и опубликовал его в
журнале Wiadomosci Matematiczny.
(23) Книга (1), с. 102—103; книга (12), с. 381. Это решение задачи об обходе доски
конем нашел русский офицер Янич (Jaenisch — Chess Montly, 1865).
(24) Леонард Эйлер (1707—1783). Написал несколько сотен работ, охватывающих
почти все разделы высшей и элементарной математики.
Невозможность расстановки 36 офицеров доказали Фишер и Ятс (Fisher, Yates —
Proc. Cambridge Phil. Soc., 1944, v. 30, p. 492—507); см. также Брук и Райзер (Bruck, Ryser —
Canad. J. Math., 1949, v. 1, p. 88—93).
(25) Фишер (Fisher R. A. The Design of Experiments — Edinburg: 1947).
(26) Платон (429—348 до н. э.), ученик Сократа, говорит об иррациональности V2 и
других чисел.
(29) Блез Паскаль (1623—1662), геометр и философ, изобретатель барометра и вы-
числительной машины, основоположник теории вероятностей, применил математическую ин-
дукцию в своей книге Traite du triangle arithmetique. Мауролико (Maurolico F.) (1494—1575)
опередил его на целое столетие, но работа его была забыта.
(30) Имеется стопка запечатанных конвертов. В каждый конверт вложено письмо
следующего содержания: «Открой следующий конверт, прочитай письмо и сделай то, чего
153
оно от тебя требует». На первом конверте написано: «Открой этот конверт, прочитай письмо
и сделай то, чего оно от тебя требует». Принцип математической индукции утверждает,
что всякий, кто согласится выполнить предписание, имеющееся на первом конверте, должен
будет открыть все конверты.
(31) Рисе (Reiss /. W., Elementarz muzyezny — Warszawa: 1949).
Эйлер придал проблеме музыкальной гаммы точный смысл (1739 г.) и обратил внима-
ние на то, аккорд звучит тем лучше, чем меньше числа, выражающие отношение чисел ко-
лебаний. Клавдий Птолемей из Александрии (140 г. н. э.) взял, кроме октавы, принты
и крарты, также большую терцию 5:4 за основу диатонической гаммы с интервалами 9 /8,
10 /9, 16 /15, 9 /8, 10 /9, 9 /8, 16 /15. Здесь все аккорды, включая малую терцию, выражаются
числами, меньшими десяти, но секунды разные: то 9Д то 10/9. Если настроить так,фортепья-
но, то произведение в тональности D-dur звучало бы иначе, чем в тональности C-dur.
Темперированную шкалу ввел органист Андреас Веркмейстер в 1691 г.
Что касается теории, то см.: Релей (Lord Rayleigh, The Theory of Sound — London:
1894 — 6). Русский перевод: Стрэтт Дж. В. (Лорд Релей. Теория звука.— 2-е изд.— М.:
Гостехиздат, 1955.) Минусинский исследовал возможные способы усовершенствования му-
зыкальной шкалы (Mikysihski J. Problemy, 1954).
(33) Цейзинг преувеличивает значение золотого сечения в своей книге (Zeizing А.
Neue Lehre von der Proportionen des menschlichen Korpers, 1854).
(34) Л. Фибоначчи жил в Пизе около 1200 г.
Идея дерева возникла в связи с другой идеей, высказанной Жилинским на математи-
ческом конгрессе в Болоньи (Zylihski Е.— Atti del Congr. Bol., 1928, v. 4, p. 153—\56).Шим-
кевич обсуждает роль чисел Фибоначчи в ботанике в связи с так, называемым законом
Людвига (Szymkiewicz D.— Acta Soc. Botan. Poloniae 1928, t. 5, s. 380—391).
(35) План дворца в Риме, называемого Палаццо Канчеляриа.
(37) На рисунке (37) участок, который достался С, составляет 1 /8 всего пастбища,
на (38) — 1 /4. Точка, в которой сходятся все три участка, имеет на (38) координаты
(1 /2, 5 /8), если считать, что противоположные вершины квадратного пастбища имеют коор-
динаты (0, 0) и (1, 1). На рисунке (39) общей является точка 1 /2, 13 /24. На (40) самая
длинная дорога для А составляет 505 /48, для С — 601/48, а общая точка та же, что и на (39).
Банкофф из Лос-Анжелеса предлагает другое
решение (Bankoff L.— Amer. Math. Monthly,
1952, v. 59, p. 634). Приводим здесь его чертеж:
треугольник, АВС равносторонний, а его высоты,
проведенные из центра, делят квадрат на три равно-
великих участка, поручаемых пастухам А, В и С.
(Сначала проводится вспомогательная прямая pq,
которая делит квадрат на два прямоугольника в
отношении 2:1, а затем отрезок, pq делится на че-
тыре части и через крайние точки деления прово-
дятся две наклонные прямые под углом 30° к,
прямой pq\ вершина С треугольника получается в
пересечении пунктирных прямых.) При таком
разделе имеем: I — участки равновелики, II — расстояния до наиболее удаленных то-
чек участков равны, III — каждая точка пастбища контролируется ближайшим пастухом,
однако, одним достоинством этот раздел не обладает, а именно, не выполнено условие IV, тре-
бующее, чтобы позиции пастухов были выбраны так, что их расстояния до наиболее уда-
ленных точек, участков минимальны. Из наших пяти решений только первое, т. е. решение
(36) обладает всеми преимуществами I—IV; для (37) выполняются II и IV, для (38) —
II, III и IV, для (39) — I, II и IV, для (40) — I и III. Банкофф считает, что его раз-
дел предпочтительнее раздела (36) на том основании, что у него расстояния до наиболее
удаленных точек, меньше. Однако ведь не исключено, что среди разделов, удовлетворяющих
свойствам I—IV, раздел (36) дает наименьшие расстояния до наиболее удаленных точек!
Понимает ли читатель, в чем здесь заключается вопрос?
154
(42) Шрейер (Schreier J.— Mathesis Polska, 1932, t. 7, s. 154—160).
(45) Слупецкий (Stypecki J.— Colloq. Math., 1951, v. 2, p. 286—290).
(47) Смит (Smith С. A. B.— Math. Gazette, 1947, v. 31, p. 31—39).
Более простой способ предложила Декарт (Descartes Blanche — Eureka, 1950, № 13).
Наш рисунок, является графическим воплощением ее идеи.
Русецкий предложил еще один способ выявления фальшивой монеты с помощью трех
взвешиваний в предположении, что среди четырнадцати монет 0, 1, 2,..., 13 имеется одна
фальшивая более легкая или более тяжелая, чем остальные и что она отлична от монеты 0.
Произведем три взвешивания, помещая каждый раз по 5 монет на каждую чашу весов:
а= (0, 6, 8, 10, 12) —(5, 7, 9, 11, 13), Ь= (2, 4, 5, 7, 12) —(0, 3, 6, 11, 13),
с = (0, 4, 5, 10, И) —(1, 2, 7, 8, 13).
Пусть а равно 4-1, если в первом взвешивании перетягивает левая чаша, —1 — если пра-
вая, и 0 в случае равновесия. Аналогично определяются числа b и с для второго и третьего
взвешиваний. Если
п = (9а + ЗЬ+с)(—\)а+ь+с,
то при /г > 0 число п дает номер фальшивой монеты, которая тяжелее остальных, а при n<jO
число — п дает номер фальшивой монеты, которая легче остальных.
(48) Твиди привел графическое решение задачи о разливе вина; наш рисунок,следует
его идее. (Tweedie М. С. К.— Math. Gazette, 1939, v. 23, р. 278—282)
(49) На это указали Ауэрбах и Мазур.
(50) Кнастер и Штейнгауз (Knaster Br., Steinhays Н.— Rocznik Pol. Tow. Mat. 1946,
t. 19, s. 228—231).
Штейнгауз (Steinhaujs H. The Problem of Fair Division — Econometrica, 1948, v. 16,
p. 101 — 104).
(53) Пойа (Polya G.— L’Enseignement Mathematique, 1919, v. 4, p. 355—379).
Постоянство суммы расстояний от точки до сторон равностороннего треугольника до-
казал Вивиани.
Изменение направления стрелки означало бы, что сначала происходили выборы, ко-
торым отвечает более высокая точка и результат (1, 2, 2), а затем те, которые дали более
низкую точку и результат (2, 2, 1). Здесь партия А теряет голоса и приобретает манда^
что как, будто противоречит сказанному в тексте. Объяснение таково: утверждалось, что
партия, потерявшая голоса, не может получить мандата за счет партии, которая собрала
дополнительное число голосов, но не утверждалось, что она вообще не может получить
мандата: при измененном направлении стрелки партия А получает дополнительный мандат
за счет партии, которая также потеряла голоса — партии С. Стало быть, здесь нет проти-
воречия: партия, потерявшая голоса, может приобрести новый мандат, но только за счет
партии, которая также потеряла голоса.
(72) Та же ситуация, что и в (264). Автор предложил эту задачу своим студентам
и получил решение от К. Флорка и других.
(73, 74) Принцип действия логарифмической линейки указал Гюнтер в 1623 г. В 1771 г.
Партридж изобрел устройство, близкое к, современной логарифмической линейке.
Если произведение не получается в пределах шкалы, то нужно против множителя
установить не 1, а 10.
(75) Штейнгауз (Steinhcu^s Н. О roznych skalach funkcyinych i ich zastosowaniu —
Parametr, 1935, t. 2, s. 1 —12).
Создателем номографии является Докань (1884).
(76, 77) Закон линзы открыл в 1693 г. знаменитый астроном Эдмунд Холли
(1656—1724).
(78) Мерсенн (1588—1648) нашел формулу для частоты колебаний натянутой струна
опытным путем. Формула верна в системе СГС. Если сила измеряется в граммах силы,
то при подстановке в формулу ее нужно взять с коэффициентом 981.
155
(79) Пик, (Pick G. Geometrisches zur Zahlenlehre — Z. d. Vereines Lotos, Praga, 1899).
Штейнгауз (Steinhaus H. О polu figur plaskich — Przeglgd Mat.-Fiz 1924).
Каким было бы правило в пространственном случае?
(80, 81, 82) Блйчфельдт (Blichfeldt Н. F.— Trans. American Math. Soc., 1914, v. 15,
p. 227—235).
(83, 84) Вармус (Warmus M.— Golloq. Math. 1947, v. 1, p. 45—46).
(84) Минковский (Minkowski H. Geometric der Zahlen — Leipzig:, Teubner, 1912.
Упрощенное доказательство дано Гильбертом и Кон-Фоссеном (Hilbert, Cohn-Vossen,
Anschauliche Geometric — Berlin:, Springer, 1932. В этой книге отличные рисунки и фото-
графии. Русский перевод: Гильберт и Кон-Фоссен, Наглядная геометрия,— М.— Л.:,
ОНТИ, 1936).
(85) Задачу поставил и решил Пойа. Мы выбрали иной путь решения.
(86) Серпинский (Sierpihski W.— Bull. Acad. Sci. de Cracovie: A, 1912, p. 463—478).
Первым построил такую кривую итальянский математик. Пеано.
(93) Шнирельман — УМН, 1944, т. 10, с. 120—130. Это перепечатка значительно более
ранней работы.
(94—96) Штейнгауз (Steinhays Н.— Mitt. Sachsischen Acad. 1930, В. 82, S. 120—130).
В работе того же автора (Steinhays Н.— Przeglad Geografiszny, 1947, t. 21) приводит-
ж *
ся следующая формула для подсчета среднего уклона в области g~——, где В — площадь
В
области, h — расстояние между соседними горизонталями по вертикали, Ц — длина i-и го-
ризонтали, g — уклон. Величина Ц определяется по числу точек пересечения /-й горизонтали
с параллельными прямыми сетки.
См. также Штейнгауз (Steinhays Н.— Sprawozdania Wroclawskiego Towarzystwa
Naukowego, 1949, t. 4, приложение 5); определяется понятие длины порядка п и указывается
на возможность применения этого понятия в географии.
(101, 102) Итальянский геометр Кремона- и английский физик, Максвелл изобрели
около 1875 г. графостатику, основанную на свойст^ах взаимных фигур. Благодаря этому упро-
стились расчеты металлических конструкций, таких, например, как, Эйфелева башня.
(104, 105) Гроховска (Grochowska I. Chynniki ecologiczne i rozmieszczenie geograficzne
w^trobowcow Beskidu Sigskiego — Polska Acad. Umiejgtnosci, Wydawnictwa &l$skie, Prace
Biologiczne, 1950, t. 2, s. 1—72).
Стенсьлицка-Мыдлярска (Stpslikra-Mydlarska W.) Stanowisko systematyzne czfowieka
z Ngan-Dong — Ann. Uniw. Marii Curie-Sclodowskiey: Sec. C, 1947, t. 2, s. 37—109+1—VIII.
Этот метод разработан отделом приложений Государственного математического
института и получил название вроцлавской таксономии.
(106) Аполлоний Пергский (270—200 до н. э.) изучал свойства конических сечений.
(108) Вармус приводит это решение без доказательства (Warmys М.— Rocznik Pol.
Tow. Mat., 1946, t. 19, s. 233—234).
(109) Зиеба-высказал это решение без доказательства (не опубликовано).
(112) Рене Декарт, создатель аналитической геометрии, упоминает об этой спирали в
письме к Мерсенну^ 1638 г.
В природе логарифмическая спираль связана с явлением роста организмов, форма
которых на каждой очередной стадии подобна той, какую они имели на предшествующей
стадии.
(См.: Томсон (Thompson D'Arcy W. Science and the Classics, Oxford Univ. Press, 1940,
p. 114—147).
(ИЗ) Эта спираль описывается уравнением r = aecq (е = 2,71828..., с = 0,274411...,
а — любое). Здесь г означает расстояние до полюса, а ср — угол относительно фиксиро-
ванного направления.
Курс корабля составляет с направлением корабль — полюс 74°39'12".
(115) Архимед (287—212 г. до н. э.), один из знаменитейших математиков старого и но-
вого времени, подсчитал отношение длины окружности к диаметру с точностью до третьего
156
десятичного знака, открыл закон о силе, действующей на погруженное в жидкость тело, за-
ложил основы высшей математики.
(См. Роуз Болл (Rouse Ball W. W.) Short Account of the History of Mathematics — Lon-
don: Macmillan, 1935.)
(116) Браун (Brown H. T. 507 Mouvements mecaniques — Liege: Deseer., p. 28,
№ 96, № 97).
(117) Поселье, французский морской офицер, открыл этот механизм в 1864 г. Его опере-
дил Саррю, применивший иной подход к. проблеме (см. Comptes Rendus de 1’Academie,
1853, v. 36, p. 1036).
(120) Маскерони (Mascheroni L Geometria del Compasso — Pawia: 1797). Наполеон I
читал эту книгу.
Mop (Mohr G. Euclides Danicus — Amsterdam:, 1672) опередил Маскерони в построе-
ниях одним только циркулем, но был забыт.
См. также: Курант и Роббинс (Courant R., Robbins Н. What is Mathematics? Oxford
Univ. Press, 1941, p. 5. Русский перевод: Курант и Роббинс, Что такое математика? — 2-е
изд. — М.: Просвещение, 1967).
(121) Радемахер и Топлиц (Rademacher Н., Toeplitz О. Zahlen und Figuren — Berlin:
Springer, 1930, S. 164).
(122) Ксендз Адам Адаманды Кохачьский привел эту конструкцию в Acta Eruditorum
в 1685 г. Он первым применил стальную пружину для подвески часового маятника.
(124) Об этом см.: Стоун и Тьюки (Stone А. И., Тцкеу L. 1F.— Duke Math. J. 1942,
v. 9, р. 356—359) и Штейнгауз (Steinhaus Н.— Fundamenta Math., 1945, v. 33, р. 245—263).
(128) Николай Коперник (1473—1543), великий астроном. Доказал, что планеты кру-
жатся вокруг Солнца и что Земля также подчиняется этому закону. Его работа De revolutio-
nibus orbium coelestium увидела свет в 1543 г.
(129) Иоганн Бернулли, один из создателей математического анализа, родившийся
в 1667 г., в 1696 г. поставил задачу о брахистохроне, или линии кратчайшего спуска, и на
следующий год решил ее.
Угловая скорость со круга, его радиус г и ускорение g силы тяжести связаны формулой
g = rco2.
(134) Иммануил Кант, немецкий философ (1724—1804).
(135) См. книгу 120, VII, § 8.
(137) См. книгу 121.
(139) В СССР эта задача предлагалась ученикам средних школ. См.: УМН, 1948, т. 2,
№ 2, с. 239.
(140) Циндлер обнаружил контуры, отличные от окружности, у которых любые хорды,
делящие контур пополам, делят также и фигуру, ограниченную этим контуром, на две равно-
великие части. (Zindler К. Uber konvexe Gebilde, II — Monatshefte f. Math. u. Phys., 1921,
B. 31, S. 25—29).
См. также Ауэрбах (Auerbach H. Sur un probleme de M. Ulam concernant I’equilibre des
corps flottants — Studia Math. 1938, v. 7, p. 121, 122).
(141) Cm. (29). Никомед жил около 200 г. до н. э.
(144) См. книгу (120).
(145) Репродукция картины «Возвращение Одиссея» Бернардино Пинтуриккио
(1454—1513). Оригинал хранится в лондонской Национальной галерее.
(150) Штейнгауз (Steinhaus Н. Sur la localisation au moyen des rayons X.— C. R. Acad.
Sci. 1938, p. 206).
Об оптической локализации предметов и одном ее применении см. Archiwum Lw. Tow.
Naukowego, III, 1938, t. 9, s. 335—343; Urz^d Patentowy Rzeczypospolity Polskiej, patent
№ 34108 zgtoszony 8.3.1938, udsielono 29.4.1950.
(154, 155) Идея принадлежит Яну Минусинскому.
(159) Польке сформулировал эту теорему в 1858 г. и опубликовал ее без доказательства
в 1860 г. Ее элементарное доказательство было найдено Шварцем (Schwarz И. А.— J. reine
u. angewandte Mathematik, 1864, В. 63, S. 309—314).
157
(161) При быстром вращении модели появятся неожиданного вида темные линии. Они
составлены из точек мнимых пересечений ребер.
(171) Брюкнер (Bruckner М. Vielecke und Vielflache,— Leipzig: 1900, S. 130). Косинус
острого угла ромба равен
(181) Ломницкий (tomnickiA. О. wieloscianach umiarowych, Bibl. Matematyczna, nr. 9).
Коксетер (Coxeter H. S. M. Regular Polytopes — New York: 1949, p. 22).
Объемы пяти планотовых тел с ребром а таковы:
<Д/2~/12, а3, аУ2"/3, а3(15 + 7л/5") 14,
5а3(3 + л/5")/12.
(201) О наиболее плотном заполнении пространства одинаковыми шарами см. Куль-
чицкий (Kyjczyski St.— Mlody Matematyk, dodatek do czasopisma Parametr, 1931, № 4—5,
s. 61—69).
(208) Грани этого двенадцатигранника не могут быть правильными пятиугольниками,
так, как это несовместимо с законами кристаллографии.
См. вторую из книг (181), с. 63.
(218) Здесь помещен снимок. Луны, перевернутый телескопом, сделанный в Парижской
обсерватории 26 апреля 1898 г. в 19 ч. 09 мин.
(219) Это явление обнаружил Вармус.
(221) Герард Меркатор (1512—1594). Не существует проекций, сохраняющих длины.
(227—230) Третий конус нашел Р. Новаковский.
Зенобия Мазурувна нашла еще ряд конусов, в том числе такие, которые получаются
из треугольного паркета (58) или наложения двух квадратных паркетов (Mazurowna Z.—
Matematyka, 1954, № 1).
(244) Уравнение этой кривой у = а sin bx.
Функцию синус ввел во втором веке н. э. великий александрийский астроном
Птолемей.
(248) Ср. (106).
(251) Законы движения планет открыл в 1609 г. Иоганн Кеплер (1571 —1630).
(247) Эту электрокардиограмму снял д-р Коважика, профессор вроцлавской Медицин-
ской академии.
(258) Если отношение (а : Ь) : (с : d) постоянно, но не равно 1, то получится иной па-
раболический гиперболоид, отличный от описанного в тексте.
(261) Эта минимальная поверхность называется катеноидом.
Мыльная пленка, натянутая на какой-либо контур, дает наименьшую из всех поверх-
ностей с таким контуром.
Бойс (Boys С. V. Soop Bubbles — London: Romance a. Sci. Ser., 1924, A.5. Там же име-
ется рецепт приготовления мыльной воды).
(263) Ф. Миндинг (1806—1885) открыл эту «антисферу», а Э. Бельтрами заметил, что
для ее обитателей естественной была бы геометрия Лобачевского, в которой сумма углов
треугольника меньше 180°.
Н. Лобачевский (1793—1856) и Я. Бойаи мл. (1802—1860) открыли существование
непротиворечивых геометрий, отличных от евклидовой. См. книгу (120), IV, § 9.
(264) См. вторую из кни1 (181), с. 5—12.
Если бы один конец новой линии находился в старой вершине, а другой давал новую
вершину на одной из старых линий, то V и S увеличились бы на 1, a L — на 2 и формула
V+S = L + 2 оставалась бы в силе. Если бы оба конца новой линии были новыми вершинами
на одной из старых линий, то S возросло бы на 1, V — на 2, a L — на 3, и формула Эйлера опять
оказалась бы справедливой. Наконец, может случиться, что новая линия одним своим концом
связана с сетью прежних границ, а другой ее конец «свободный». Тогда новая страна не воз-
никнет, S не изменится, а и V, и L увеличатся на 1 — если новая линия начинается в старой
вершине, кдк.на рисунке (269), или на 2 — если новая линия начинается в новой вершине на
старой линии. И в том, и в другом случае формула Эйлера сохраняет силу.
158
(268) Франкль и Понтрягин (Frankl F., Pontriagin L.— Math. Annalen, 1930, В. 102,
S. 785—789).
(274) См. (24).
(282) Листинг (1808—1882) опубликовал в 1847 г. первую книгу по топологии.
См. книгу (120), гл. V.
(286) Задачу о развязывании узлов сообщил автору К. Борсук. Решил эту задачу Мы-
цельский: (Mycielski J.— Fundamenta Math. 1954, v. 42).
(299) Проблему четырех красок сформулировал Мёбиус в 1840 г. Франклин привел до-
казательство для любой карты, содержащей не более 37 стран (Franklin Ph.— J. Math.
Phys. 1937, v. 16, p. 172—184). Простое доказательство теоремы Хивуда о достаточности
пяти красок.содержится в третьей из книг (180), в приложении к гл. V. О проблеме 7 красок
см. книгу (21), с. 235.
(305) Лебег (Lebesgue Н.—Math. Annalen, 1911, В. 70, S. 166 и далее); доказательство
неполное. Полное доказательство дал Брауэр (Brouwer L. Е.— J. reine u. angewandte Math.,
1913, В. 142, S. 150 и далее).
(306) Задача поставлена Уламом и решена Борсуком (Borsuk К.— Fundamenta Math.
1933, В. 20, S. 177—190).
(307) Теорема Брауэра.
Закон адиабат открыл Пуассон (1781 —1840). Закон Бойля открыт в 1662 г.
(308) Смит и Дункан (Smith J. G., Duncan A. J. Sampling Statistics and Applica-
tions — New York: McGraw Hill, 1945, p. 137—152). Данные взяты из реального опыта.
(315) Треван (Trevan J. В. — Proc. Roy. Soc., 1927, v. 101, p. 483).
(316) Лотка (Lotka A. J. Elements of Physical Biology — Baltimore: Williams a. Wil-
kins, 1925). Там же ссылки: с. 70: Торнтон (Thornton Н. G. — Annual of Applied Biology, 1922,
c. 265); c. 74: Риди Холанд (Peed H. S., Holland R. H.— Proc. Nat. Acad. Sci. 1919, v. 5, c. 140),
c. 360: American Reference Book, 1914, p. 235; World Almanac, 1921, p. 277; Statistical
Abstracts, 1920, p. 814; c. 103: Таблицы Главера.
Пользуясь этими данными, Лотка подобрал функцию. Наш рисунок основан на его
данных.
(319) Крокстон и Кауден (Croxton F. Е., Cowden D. I. Applied General Statistics —
New York, Prentice Hall, 1946, v. 16, p. 452—458) ; график 171, c. 457. Логистическую кривую
нашел бельгийский математик Верхульст.
Ср. Пирл (Pearl R. The Biology of Population Growth — New York: A. A. Knopf, 1925,
v. 18).
СОДЕРЖАНИЕ
ПРЕДИСЛОВИЕ 5
I. ТРЕУГОЛЬНИКИ. КВАДРАТЫ. ИГРЫ 7
II. ПРЯМОУГОЛЬНИКИ. ЧИСЛА И ТОНЫ 24
III. ВЗВЕШИВАНИЕ. ИЗМЕРЕНИЕ. СПРАВЕДЛИВЫЙ РАЗДЕЛ 31
IV. ПАРКЕТЫ. ПЧЕЛИНЫЕ СОТЫ. БОТИНКИ. ПЛОЩАДИ И ДЛИНЫ 44
V ВЫБОР ПУТИ. ПОИСКИ БЛИЗКИХ СОСЕДЕЙ. ПРЕСЛЕДОВАНИЕ
КОРАБЛЕЙ 65
VI. ПРЯМЫЕ ЛИНИИ. ОКРУЖНОСТИ. СИММЕТРИЯ. ОПТИЧЕСКИЕ
ИЛЛЮЗИИ. ПРЕВРАЩЕНИЕ НЕВИДИМОГО В ВИДИМОЕ 77
VII. СОЛЬ. ПАУКИ И МУХИ. ДВОРЦЫ И КИРПИЧИ 90
VIII. ПЛАТОНОВЫ ТЕЛА. КРИСТАЛЛЫ. ДРОЖЖИ. МЫЛО 98
IX. МЫЛЬНЫЕ ПУЗЫРИ. ЗЕМЛЯ И ЛУНА. КАРТЫ И ДАТЫ 109
X. БЕЛКИ. ВИНТЫ. СВЕЧИ. ТЕНИ. АККОРДЫ 118
XI. ПОВЕРХНОСТИ ИЗ НИТОК. ЦЕПОЧКА. КОЛЯСКА. МИНИМАЛЬНАЯ
ПОВЕРХНОСТЬ 124
XII. ПРОГУЛКА ПО МОСТАМ. ТРОПИНКИ. ЗАВЯЗЫВАНИЕ УЗЛОВ.
ПРИЧЕСЫВАНИЕ ВОЛОС 128
XIII. СТУДЕНТЫ. ЛОТЕРЕЙКА. ЛЯГУШКИ. ПОДСОЛНЕЧНИКИ 143
ПРИМЕЧАНИЯ 152
Цена 75 коп.
БИБЛИОТЕЧКА «КВАНТ»
ВЫШЛИ ИЗ ПЕЧАТИ
Вып. 1. М. П. Бронштейн. Атомы и электроны.
Выл. 2. М. Фарадей. История свечи.
Вып. 3. О. О р е. Приглашение в теорию чисел.
Вып. 4. Опыты в домашней лаборатории.
Вып. 5. И. Ш. С л об о д ецк и й, Л. Г. Асламазов. Зада-
чи по физике.
Вып. 6. Л. П. Молчанов. Головоломки.
Вып. 7. П. С. Александров. Введение в теорию групп.
Вып. 8. Г. Штейнгауз. Математический калейдоскоп.
ГОТОВЯТСЯ К ПЕЧАТИ:
Вып. 9. Замечательные ученые.
Вып. 10. В. М. Глушков, В. Я. Валах. Что такое ОГАС!