Вычислительные методы для инженеров - Копченова Н.В., Амосов А.А., Дубинский Ю.А.

Author: Копченова Н.В. Амосов А.А. Дубинский Ю.А.
Tags: железные скобяные изделия слесарное дело розлив напитков лампы с горючими веществами и горелки печи вычислительная техника микропроцессоры математика инженерная математика
ISBN: 5-06-000625-5
Year: 1994
Similar
Основы слесарного дела
Слесарное дело
Нестандартная оснастка для слесарных работ
Text
                    A.A. АМОСОВ
DA. АУБИНСКИЙ
КВ. КОПЧЕНОВА
ВЫЧИСЛИТЕЛЬНЫЕ
МЕТОДЫ
ДЛЯ ИНЖЕНЕРОВ
Рекомендовано Государственным комитетом Российской Федерации
по высшему образованию в качестве учебного пособия
для студентов высших технических учебных заведений
Москва «Высшая школа» 1994

ББК 32.97
А 62
УДК 683.1
Федеральная целевая программа книгоиздания России
Рецензенты: кафедра прикладной математики МГТУ им. Баумана (зав.
кафедрой д-р техн. наук, проф. В.С.Зарубин); чл.-кор. РАН, д-р физ.-мат.
наук, проф. Н.Н.Калиткин
Амосов А.А, Дубянский Ю.А., Копченою Н.В.
А62 Вычислительные методы для инженеров: Учеб. пособие. —
М.: Высш. шк., 1994. — 544 с: ил.
ISBN 5-O6-000625-5
В книге рассматриваются вычислительные методы, наиболее часто ис-
используемые в практике инженерных и научно-технических расчетов: методы
решения задач линейной алгебры и нелинейных уравнений, проблема собствен-
собственных значений, методы теории приближения функций, численное дифференци-
дифференцирование и интегрирование, поиск экстремумов функций, решение обыкновенных
дифференциальных уравнений. Значительное внимание уделяется особенностям
реализации вычислительных алгоритмов на ЭВМ и оценке достоверности
полученных результатов. Имеется большое количество примеров и геометриче-
геометрических иллюстраций.
Для студентов и аспирантов технических вузов, а также для инженеров и
научных работников, применяющих вычислительные методы.
1602120000 - 002
001@1) - 94
ISBN 5-06-000625-5
Без обьявл.
ББК 32.97
6Ф7.3
© А.А.Амосов, Ю.А.Дубинский, Н.В.Копченова, 1994
Цель расчетов — не числа, а пони-
понимание.
Р.В.Хемминг
Из нашего девиза "Цель расчетов — не
числа, а понимание" следует, что чело-
человек, который должен этого понимания
достигнуть, обязан знать, как происхо-
происходит вычисление. Если он не понимает,
что делается, то очень маловероятно,
чтобы он извлек из вычислений что-
нибудь ценное. Он видит голые цифры,
но их истинное значение может оказать-
оказаться скрытым в вычислениях.
Р.В.Хеммит
ПРЕДИСЛОВИЕ
В настоящее время имеется значительное число учебников и монографий,
посвященных методам вычислений (часть из них отражена в списке литерату-
литературы к данному пособию). Однако, на наш взгляд, большинство этих книг ори-
ориентировано на студентов-математиков или на специалистов по вычислительной
математике. В то же время практически отсутствует отечественная учебная
литература, в которой доступным для студента технического вуза или инжене-
инженера образом были бы изложены основы вычислительных методов, применяемых
сегодня для решения инженерных задач. Особенно острой, по мнению авторов,
является потребность в книге, которая содержала бы не только изложение
начал численных методов, но и давала бы представление о реально использу-
используемых в вычислительной практике алгоритмах. Данное учебное пособие призва-
призвано в определенной степени восполнить этот пробел.
Настоящее пособие адресовано в первую очередь студентам и аспирантам
высших технических учебных заведений, изучающим основы математического
моделирования и численные методы. Авторы надеются на то, что эта книга
будет полезна широкому кругу инженерных и научно-технических работников,
которые намерены применять ЭВМ для решения прикладных задач.
При написании книги авторы использовали многолетний опыт преподава-
преподавания курса вычислительных методов студентам и аспирантам различных спе-
специальностей Московского энергетического института, а также опыт работы на
вычислительном центре МЭИ. Значительное влияние на выбор материала и
характер изложения оказали также многочисленные дискуссии со слушателями
существующего при МЭИ факультета повышения квалификации преподавате-
преподавателей вузов страны.
3

Авторы стремились, изложить материал по возможности наиболее простым
и доступным образом. Объем знаний высшей математики, необходимый для
понимания содержания книги, не выходит за рамки программы младших
курсов втуза. Пособие содержит довольно много примеров, иллюстрирующих те
или иные положения теории, а также демонстрирующих особенности вычисли-
вычислительных методов или работу конкретных алгоритмов. Тем не менее многие из
рассматриваемых вопросов трудны для восприятия и требуют внимательного
изучения. К сожалению, в учебной литературе они нередко опускаются. К
таким центральным вопросам относятся, например, понятия корректности,
устойчивости и обусловленности вычислительных задач и вычислительных
алгоритмов, особенности поведения вычислительной погрешности. Важность их
понимания для эффективного применения ЭВМ сегодня велика и не акценти-
акцентировать на них внимание авторы посчитали невозможным.
Дадим краткое изложение основного содержания книги. Важную идейную
нагрузку несут на себе первые три главы. Рассматриваемые в них вопросы
закладывают фундамент, необходимый для правильного понимания рассматри-
рассматриваемых в остальных главах вычислительных методов.
В гл. 1 дается общее представление о методе математического моделирова-
моделирования, в том числе о процессе создания математических моделей, о последова-
последовательности этапов решения инженерной задачи с применением ЭВМ, о вычи-
вычислительном эксперименте.
В гл. 2 наряду с введением в элементарную теорию погрешностей содер-
содержится изложение основных особенностей машинной арифметики. Понимание
этих особенностей необходимо тем, кто заинтересован в эффективном примене-
применении ЭВМ для решения прикладных задач.
В гл. 3 обсуждаются важнейшие свойства вычислительных задач, методов
и алгоритмов. Дается общее представление о корректности, устойчивости и
обусловленности вычислительной задачи. Приводится описание основных
классов вычислительных методов. Значительное внимание уделяется устойчи-
устойчивости вычислительных алгоритмов, их чувствительности к ошибкам. Дается
представление о различных подходах" к анализу ошибок, в том числе и об
обратном анализе ошибок. Обсуждаются требования, предъявляемые к вычис-
вычислительным алгоритмам.
Конкретные вычислительные задачи и методы их решения рассматривают-
рассматриваются начиная с гл. 4. Здесь авторы стремились к тому, чтобы не только изло-
изложить простейшие подходы, но и дать представление об алгоритмах, которые
реально используются для решения соответствующих задач.
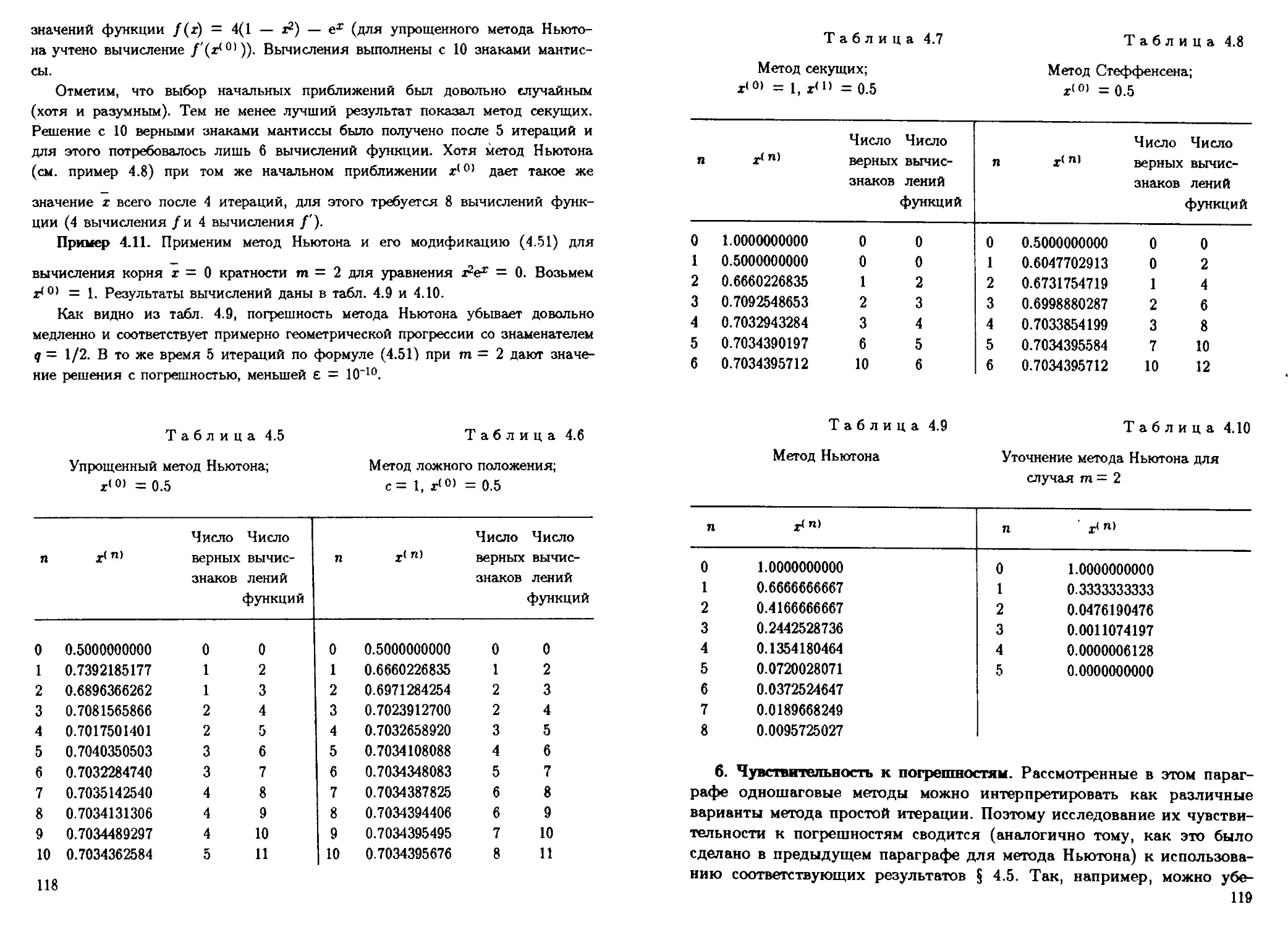
В гл. 4 рассматриваются методы отыскания решений нелинейных уравне-
уравнений. Значительное внимание уделено постановке задачи и ее свойствам, в
частности — чувствительности корней нелинейных уравнений к погрешностям.
Среди различных методов отыскания корней более подробно излагаются метод
простой итерации, метод Ньютона и различные их модификации.
4
В гл. 5 рассмотрены прямые (точные) методы решения систем линейных
алгебраических уравнений. Основное внимание уделяется методу Гаусса и его
различным модификациям. Рассматривается использование LLf-разложения
матриц для решения систем линейных уравнений, метод квадратных корней,
метод прогонки, методы вращений и отражений. Обсуждается алгоритм итера-
итерационного уточнения.
В гл. 6 рассматриваются итерационные методы решения систем линейных
алгебраических уравнений: метод простой итерации,' метод' Зейделя, метод
релаксации и другие методы.
В гл. 2 рассматривается задача отыскания решений систем нелинейных
уравнений, ибсуждаются не только соответствующие итерационные методы, но
и различные подходы к решению сложной задачи локализации.
В гл. 8 дается представление о проблеме собственных значений и о различ-
различных подходах к вычислению собственных значений и собственных векторов.
Излагаются степенной метод и обратный степенной метод, обсуждается QR-
алгоритм.
В гл. 9 излагаются наиболее известные численные методы решения задачи
одномерной минимизации, в том числе метод деления отрезка пополам, метод
Фибоначчи, метод золотого сечения и метод Ньютона.
В гл. 10 рассматриваются различные методы решения задачи безусловной
минимизации. Наиболее полно изложены градиентный метод, метод Ньютона и
метод сопряженных градиентов.
В гл. 11 рассмотрены наиболее важные и часто встречающиеся в приложе-
приложениях методы приближения функций. Значительное внимание уделено интерпо-
интерполяции, причем рассматривается интерполяция не только алгебраическими
многочленами, но и тригонометрическими многочленами, а также интерполя-
интерполяция сплайнами. Достаточно подробно обсуждается метод наименьших квадра-
квадратов. Дается понятие о наилучшем равномерном приближении и дробно-раци-
дробно-рациональных аппроксимациях.
В эту главу включены также некоторые вопросы, имеющие непосредствен-
непосредственное отношение к методам приближения функций. Это конечные и разделенные
разности, многочлены Чебышева, быстрое дискретное преобразование Фурье.
В гл. 12 рассматриваются различные подходы к выводу формул численного
дифференцирования, обсуждается чувствительность этих формул к ошибкам в
вычислении значений функции.
В гл. 13 излагаются методы вычисления определенных интегралов. Выво-
Выводятся квадратурные формулы интерполяционного типа и квадратурные форму-
формулы Гаусса. Дается представление о принципах построения адаптивных проце-
процедур численного интегрирования и, в частности, об используемых в них спосо-
способах апостериорной оценки погрешности. Рассматриваются различные подходы
к вычислению интегралов от функций, имеющих те или иные особенности. В

частности, затрагивается проблема интегрирования быстро осциллирующих
функций.
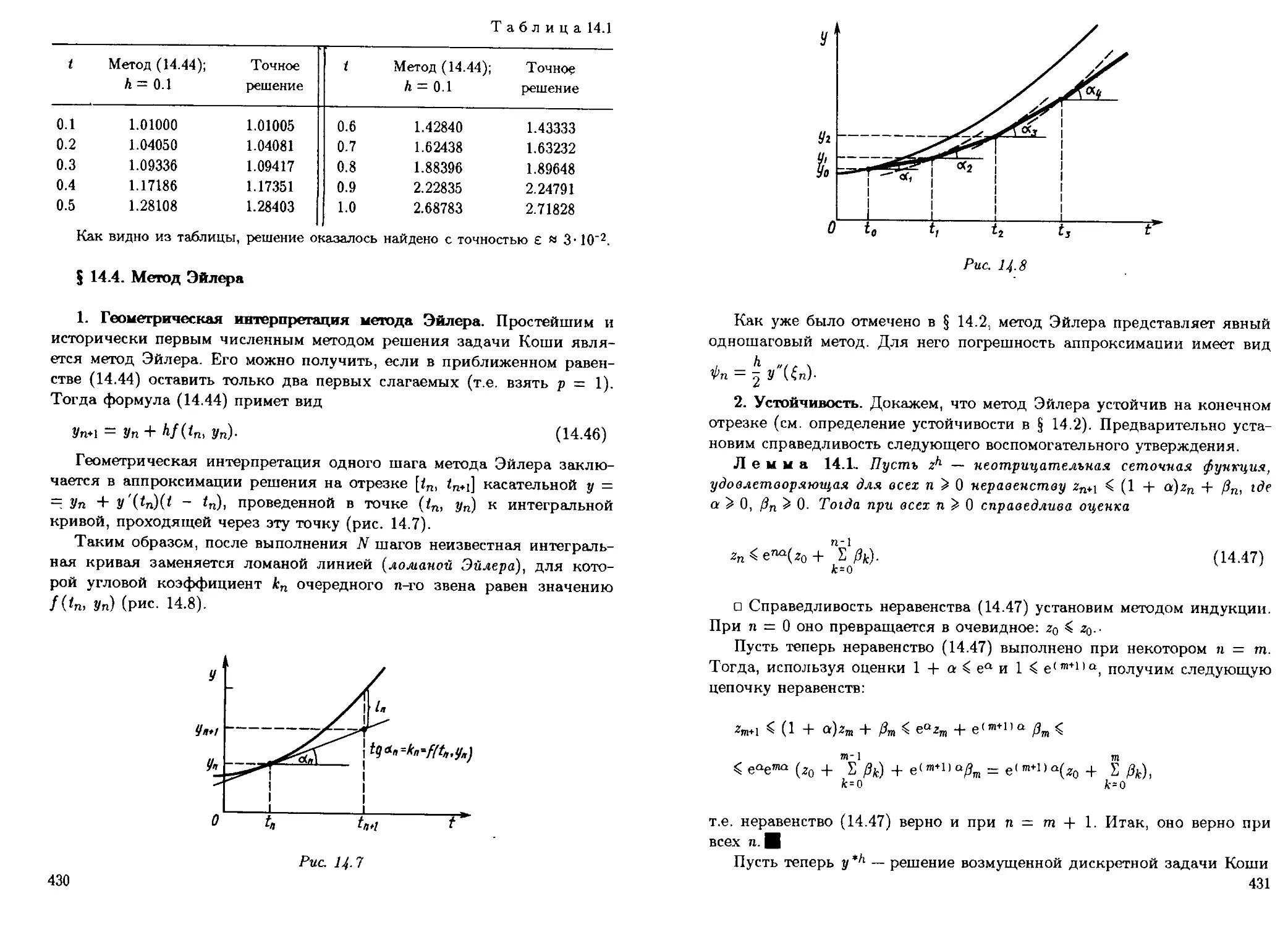
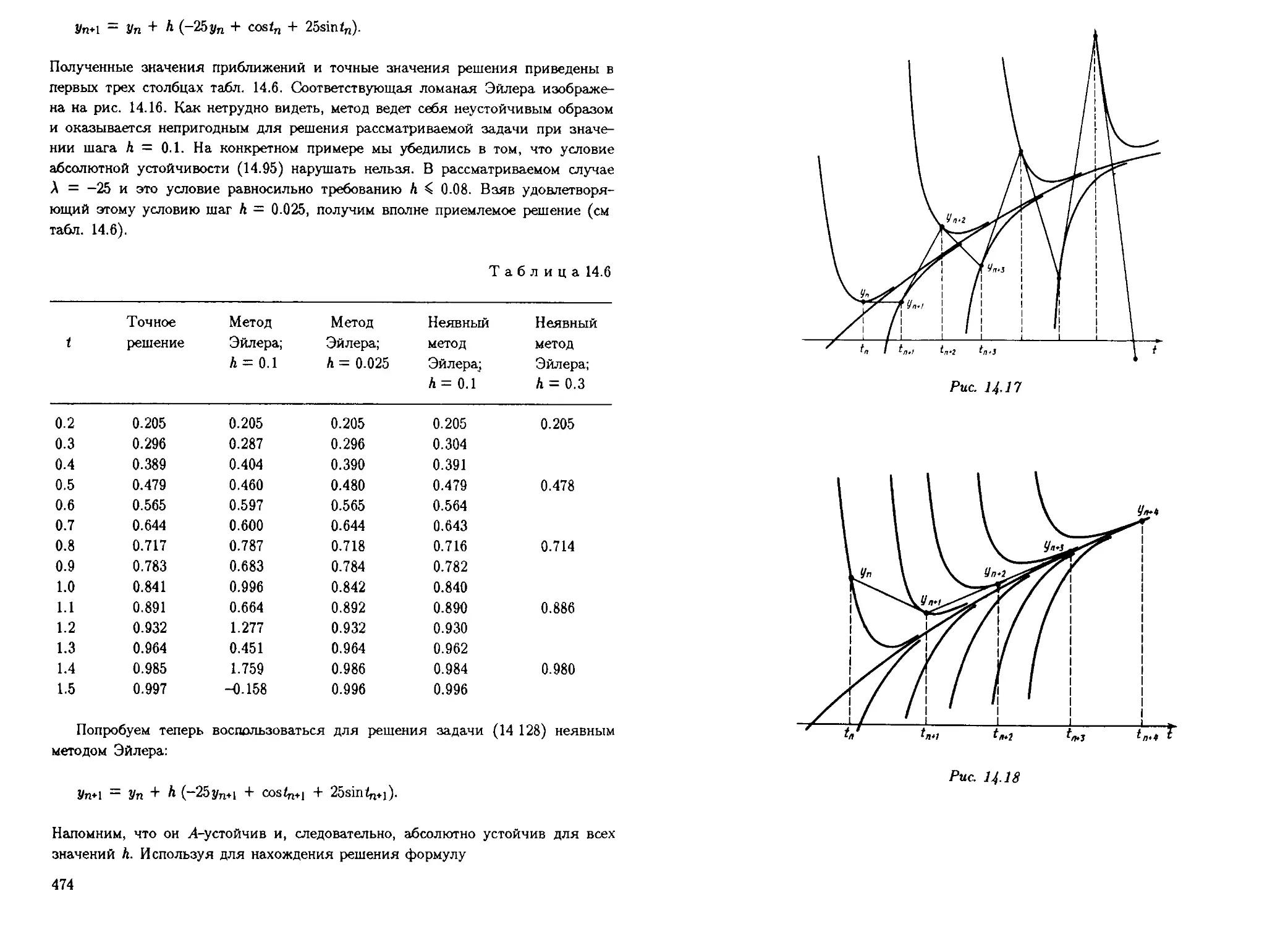
Гл. 14 посвящена численным методам решения задачи Коши для обыкно-
обыкновенных дифференциальных уравнений Подробно рассматриваются метод
Эйлера и его различные модификации. Значительное внимание уделено рас-
рассмотрению классических методов Рунге—Кутты и Адамса. Обсуждаются раз-
различные свойства устойчивости численных методов решения задачи Коши, в
том числе нуль-устойчивость, абсолютная устойчивость, Л-устойчивость, А(а)-
устойчивость. Специально рассматриваются жесткие задачи и методы их
решения.
В гл. 15 изучаются методы численного решения двухточечных краевых
задач. Подробно излагается применение метода конечных разностей к решению
краевых задач для обыкновенного дифференциального уравнения второго
порядка. Дается представление о проекционных методах Ритца и Галеркина;
обсуждается один из их современных вариантов — метод конечных элементов.
Завершает главу рассмотрение метода пристрелки.
.» Можно предположить, что к изучению отдельных параграфов или даже
глав этой книги читатель приступит, только столкнувшись с необходимостью
решить на ЭВМ важную для него задачу. Вероятно, в этом случае польза от
изучения соответствующего раздела будет наибольшей. Многие вопросы рас-
рассмотрены очень кратко или не рассмотрены вообще. Авторы надеются на то,
что соответствующие пробелы можно восполнить, используя сделанные в тексте
ссылки на известные учебники и монографии.
В ряде случаев авторы позволяют себе интерпретировать те или иные
результаты, делать определенные выводы и даже давать рекомендации в
надежде на то, что для новичка соответствующие рассуждения дадут полезный
начальный ориентир. В целом же ко всяким рекомендациям в такой сложной
и многообразной области, как применение вычислительных методов для реше-
решения прикладных задач на ЭВМ, следует отнестись с осторожностью. Они не
могут претендовать на бесспорность и их следует рассматривать скорее как
отражение точки зрения авторов.
Иногда то или иное положение обосновывается ссылкой на вычислительную
практику. Хотя критерий практики и играет при отборе методов вычислений
существенную роль, все же оценки методов, основанные на результатах их
применения для решения конкретных задач, нередко бывают весьма субъек-
субъективны и противоречивы.
В заключение отметим, что никакие теоретические положения и советы не
могут заменить собственного опыта вычислительной работы Как надеются
авторы, параллельно с изучением данной книги такой опыт может приобрести
читатель переходя от решения задач учебного характера к серьезным практи-
практическим задачам
Авторы
ГлавУП
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
И РЕШЕНИЕ ИНЖЕНЕРНЫХ ЗАДАЧ
С ПРИМЕНЕНИЕМ ЭВМ
В этой главе дается общее представление о методе математического
моделирования, в том числе о процессе создания математических
моделей, о последовательности этапов решения инженерной задачи с
применением ЭВМ, о вычислительном эксперименте.
Разделение решаемых с применением ЭВМ прикладных задач на
инженерные, научные, экономические и т.п. является до известной
степени условным. Тем не менее при написании данного пособия авто-
авторы ориентировались на читателя, интересующегося решением именно
инженерных задач. Попытаемся охарактеризовать этот класс задач,
выделив его некоторые характерные особенности.
1.Инженерные задачи имеют ярко выраженную практическую на-
направленность. Целью их решения является создание новой конструк-
конструкции, разработка нового технологического процесса, минимизация
затрат на производство некоторого изделия и т.д. Поэтому для таких
задач характерна необходимость доведения результатов до конкретных
чисел, графиков, таблиц, на основании которых можно принимать
решения.
2. Эти задачи характеризуются значительным объемом выполня-
выполняемой вычислительной работы.
3. Для этих задач характерно использование достаточно сложных
математических моделей и серьезного математического аппарата.
4. Как правило, инженерные задачи решают специалисты, имеющие
техническое образование, но не являющиеся профессионалами в облас-
области разработки математических методов и программного обеспечения
ЭВМ. Поэтому естественно желание этих специалистов использовать
готовые вычислительные методы и стандартное математическое про-
программное обеспечение.
Наконец, условимся считать, что в рассматриваемый класс задач
входят задачи только умеренной сложности. Для их решения не тре-
требуются сверхбольшие скорости вычислений и сверхбольшие объемы
7

памяти для хранения данных. Таким образом, эти задачи могут быть
решены с помощью ЭВМ, доступных массовому пользователю. Те же
задачи, которые требуют для решения сверхмощной вычислительной
техники и принципиально новых алгоритмов, будем относить к катего-
категории научных задач.
$ 1.1. Математическое моделирование
и процесс создания
математической модели
Математическое моделирование представляет собой метод исследо-
исследования объектов и процессов реального мира с помощью их приближен-
приближенных описаний на языке математики — математических моделей. Этот
метод чрезвычайно плодотворен и известен уже несколько тысячеле-
тысячелетий. Насущные задачи земледелия и строительства еще в древние
времена приводили к необходимости определения площадей и объ-
объемов, а следовательно, и к рассмотрению элементарных геометрических
фигур, дающих пример простейших математических моделей. Возмож-
Возможности математического моделирования и его влияния на научно-техни-
научно-технический прогресс неизмеримо возросли в последние десятилетия в
связи с созданием и широким внедрением ЭВМ.
Процесс создания математической модели условно можно разбить
на ряд основных этапов: 1) построение математической модели; 2)
постановка, исследование и решение соответствующих вычислительных
задач; 3) проверка качества модели на практике и модификация моде-
модели. Рассмотрим основное содержание этих этапов.
1. Построение математической модели. Предполагается, что с по-
помощью наблюдений и экспериментов, практики (понимаемой в самом
широком смысле) получена достаточно подробная информация об
изучаемом явлении. Для рассматриваемого этапа характерно глубокое
проникновение в полученные факты с целью выяснения главных зако-
закономерностей. Выявляются основные "характеристики" явления, кото-
которым сопоставляются некоторые величины. Как правило, эти величины
принимают числовые значения, т.е. являются переменными, вектора-
векторами, матрицами, функциями и т.д.
Установленным внутренним связям между "характеристиками"
явления придается форма равенств, неравенств, уравнений и логиче-
логических структур, связывающих величины, включенные в математическую
модель. Таким образом, математическая модель становится записью на
языке математики законов природы, управляющих протеканием иссле-
исследуемого процесса или описывающих функционирование изучаемого
8
объекта. Она включает в себя набор некоторых величин и описание
характера связи между ними.
Построение математических моделей — существенная и очень важ-
важная чнЬть естественных и технических наук. Эта задача, требующая от
исследователя глубокого знания предметной области, высокой матема-
математической культуры, опыта построения моделей, развитой интуиции и
многого другого. Создание удачной новой модели — всегда крупное
достижение соответствующей науки, а иногда и целый этап в ее разви-
развитии.
Подчеркнем, что математическая модель неизбежно представляет
собой компромисс между бесконечной сложностью изучаемого явления
и желаемой простотой его описания. Модель должна быть достаточно
полной, для того чтобы оказаться полезной для изучения свойств
исследуемого явления. В то же время она обязана быть достаточно
простой, для того чтобы допускать возможность ее анализа существу-
существующими в математике средствами и ее реализации на ЭВМ. Из огром-
огромного числа характеристик явления и действующих на него факторов
требуется выделить основные, определяющие, отбросив при этом вто-
второстепенные, несущественные.
Нередко в математическую модель закладываются некоторые гипо-
гипотезы, еще не подтвержденные на практике. Такую математическую
модель часто называют гипотетической.
Приведем пример простейшей математической модели.
Пример 1.1. Пусть исследуется движение тела, брошенного со скоростью ц
под углом а к поверхности Земли.
Будем считать, что в рассматри- у\
ваемом случае можно пренебречь
сопротивлением воздуха, считать
Землю плоской, а ускорение свобод-
свободного падения д — постоянной.
Введем систему координат, ее
начало поместим в точку бросания,
ось Ох направим горизонтально в
направлении бросания, а ось Оу —
вертикально вверх (рис. 1.1). Пусть
и (<) и w (t) — горизонтальная и
вертикальная составляющие скорости v(t) в момент времени t (в начальный
момент t = О, v = vq).
Согласно законам механики, при сделанных предположениях движение тела
в горизонтальном направлении является равномерным, а в вертикальном —
9
У
Рис. 1.1

равноускоренным с ускорением, равным — д. Поэтому справедливы следующие
равенства:
и = Ц) cos а, х = (vo cos a)t,
w = vq sin a - gt, у = (ц> sin a)t - ^— .
A.1)
A.2)
Формулы A.1), A.2) и дают простейшую математическую модель рассматрива-
рассматриваемого явления, созданную в XVII в. Г.Галилеем1. Заметим, что при 0 < а <
< ir/2 траектория движения представляет собой параболу
У=-;
cos-2 a
х2 + (tg а) х.
Математические модели часто разделяют на статические и динами-
динамические. Статическая модель описывает явление или ситуацию в пред-
предположении их завершенности, неизменности (т.е. в статике). Динами-
Динамическая модель описывает, как протекает явление или изменяется ситу-
ситуация от одного состояния к другому (т.е. в динамике). При использо-
использовании динамических моделей, как правило, задают начальное состоя-
состояние системы, а затем исследуют изменение этого состояния во времени.
2. Постановка, исследование и решение вычислительных задач. Для
того чтобы найти интересующие исследователя значения величин или
выяснить характер из зависимости от других входящих в математиче-
математическую модель величин, ставят, а затем решают математические задачи.
Выявим основные типы решаемых задач. Для этого все величины,
включенные в математическую модель, условно разобьем на три груп-
группы: 1) исходные (входные) данные х; 2) параметры модели а; 3) иско-
искомое решение (выходные данные) у. В динамических моделях искомое
решение часто является функцией времени у = у (<); переменная t в
таких моделях, как правило, бывает выделенной и играет особую роль.
Наиболее часто решают так называемые прямые задачи, постановка
которых выглядит следующим образом: по данному значению входно-
входного данного х при фиксированных значениях параметров а требуется
найти решение у. Процесс решения прямой задачи можно рассматри-
рассматривать как математическое моделирование причинно-следственной связи,
присущей явлению. Тогда входное данное х характеризует "причины"
явления, которые задаются и варьируются в процессе исследования, а
искомое решение у — "следствие".
1 Галилео Галилей A564 — 1642) — итальянский физик, механик, астро-
астроном, один из основателей точного естествознания.
10
Для того чтобы математическое описание было применимо не к
единичному явлению, а к широкому кругу близких по природе явле-
явлений, в действительности строят не единичную математическую модель,
а некоторое параметрическое семейство моделей. Будем считать, что
выбор конкретной модели из этого семейства осуществляется фиксаци-
фиксацией значений параметров модели а. Например, в роли таких параметров
могут выступать некоторые из коэффициентов, входящих в уравнения.
С помощью выбора параметров может производиться указание типа
функциональной зависимости между некоторыми из величин. Наконец,
если используемые математические модели разбиты на классы, то
параметром может служить и класс используемой модели.
Пример 1.2. Для модели A.1), A.2) прямую задачу естественно формулиро-
формулировать как задачу вычисления величин и (<), w (t), x (t), у (t) по задаваемым
входным данным щ, а. Параметром модели здесь является величина ускоре-
ускорения свободного падения д. Ее значение зависит от того, производится ли
бросание тела с поверхности Земли на уровне Мирового океана, в глубокой
шахте или же на большой высоте. Заметим, что та же модель пригодна для
описания движения тела, брошенного на любой другой планете, если значение
параметра д для этой планеты известно.
Большую роль играет решение так называемых обратных задач,
состоящих в определении входного данного х по данному значению у
(параметры модели а, как и в прямой задаче, фиксированы). Решение
обратной задачи — это в определенном смысле попытка выяснить,
какие "причины" х привели к известному "следствию" у. Как правило,
обратные задачи оказываются сложнее для решения, чем прямые.
Пример 1.3. Для модели A.1), A.2) обратную задачу можно сформулиро-
сформулировать так: по заданным и (<), w (t), x (<), у (t) требуется найти значения % а.
Заметим, что для однозначного определения % а достаточно задать в любой
фиксированный момент <о > 0 одну из пар величин ( и (fe), w Aq)) или (х (to),
У (А)))-
Помимо двух рассмотренных типов задач следует упомянуть еще
один тип — задачи идентификации. В широком смысле задача иденти-
идентификации модели — это задача выбора среди множества всевозможных
моделей той, которая наилучшим образом описывает изучаемое явле-
явление. В такой постановке эта задача выглядит как практически нераз-
неразрешимая проблема. Чаще задачу идентификации понимают в узком
смысле, как задачу выбора из заданного параметрического семейства
моделей конкретной математической модели (с помощью выбора ее
параметров а), с тем чтобы оптимальным в смысле некоторого крите-
11

рия образом согласовать следствия из модели с результатами наблюде-
наблюдений.
Пример 1.4. Применительно к модели A.1), A.2) задача идентификации
может состоять в определении величины ускорения свободного падения плане-
планеты д по результатам наблюдений за параметрами траектории.
Указанные три типа задач (прямые, обратные и задачи идентифи-
идентификации) будем называть вычислительными задачами. Для удобства
изложения в дальнейшем независимо от типа решаемой задачи будем
называть набор подлежащих определению величин искомым решением
и обозначать через у, а набор величин — входным данным и обозна-
обозначать через х.
Пример 1.5. При описании многих явлений используют модель полино-
полиномиальной зависимости между величинами х и у :
у - Рп(х) = oq + <цх + ... + апзР- .
A.3)
Здесь во, ai, ..., On — коэффициенты многочлена, являющиеся параметра-
параметрами модели (в число параметров модели можно включить и степень многочле-
многочлена). При фиксированных значениях параметров прямая задача состоит в
вычислении значения многочлена у = Рп(х) по заданному х. В таком случае
целью решения обратной задачи является определение по заданному значению
у соответствующего ему значения х. Нетрудно видеть, что это есть задача
отыскания корней многочлена, отличающегося от Рп{х) заменой коэффициента
oq на ао — до ~ У- Если же из практики известна некоторая информация о
зависимости у от х, то определение параметров ао. "ь ¦••. ап> ПРИ которых
модель A.3) наилучшим в некотором смысле образом описывает эту зависи-
зависимость, представляет собой задачу идентификации. Например, если задана
таблица значений xt, yt, то такую задачу в зависимости от ситуации можно
решать, используя известные методы итерполяции и наименьших квадратов
(см. гл. 11).
Пример 1.6. Нередко входящие в модель функции х (<) и у (t) бывают
связаны равенством
t
у A) = \ х (г) Ат + С.
о
Например, так связаны между собой скорость х (<) и путь у (t) при прямоли-
прямолинейном движении. Тогда при фиксированном значении постоянной С прямая
12
задача (задача интегрирования) состоит в вычислении первообразной у (<) по
заданной функции х (<). Обратная задача (задача дифференцирования) зак-
заключается в вычислении х (<) = у' (t) по заданной функции у (t).
Как правило, решение вычислительной задачи не удается выразить
через входные данные в виде конечной формулы. Однако это совсем
не означает, что решение такой задачи не может быть найдено. Су-
Существуют специальные методы, которые называют численными (или
вычислительными). Они позволяют свести получение численного
значения решения к последовательности арифметических операций
над численными значениями входных данных. Эти методы были изве-
известны давно: в качестве примера, уже ставшего классическим, можно
привести открытие Леверье1 в 1846 г. новой планеты Нептун. Однако
для решения задач численные методы применялись довольно редко,
так как их использование предполагает выполнение гигантского объ-
объема вычислений2. Поэтому в большинстве случаев до появления ЭВМ
приходилось избегать использования сложных математических моде-
моделей и исследовать явления в простейших ситуациях, когда возможно
найти аналитическое решение. Несовершенство вычислительного аппа-
аппарата становилось фактором, сдерживающим широкое использование
математических моделей в науке и технике.
Появление ЭВМ кардинально изменило ситуацию. Класс математи-
математических моделей, допускающих подробное исследование, резко расши-
расширился. Решение многих, еще недавно недоступных, вычислительных
задач стало обыденной реальностью.
3. Проверка качества модели на практике и модификация модели.
На этом этапе выясняют пригодность математической модели для
описания исследуемого явления. Теоретические выводы и конкретные
результаты, вытекающие из гипотетической математической модели,
сопоставляют с экспериментальными данными. Если они противоречат
друг другу, то выбранная модель непригодна и ее следует пересмот-
пересмотреть, вернувшись к первому этапу. Если же результаты совпадают с
допустимой для описания данного явления точностью, то модель
1 Урбен Жан Жозеф Леверье A811 — 1877) — французский астроном. На
основании законов небесной механики, используя данные об аномалиях в
движении планеты Уран, Леверье рассчитал траекторию движения гипотетиче-
гипотетической неизвестной планеты. В том же году немецкий астроном Галле обнаружил
Нептун в указанном Леверье месте.
2 Расчет траектории планеты Нептун потребовал от Леверье нескольких
месяцев кропотливой вычислительной работы.
13

можно признать пригодной. Конечно, необходимо дополнительное
исследование с целью установления степени достоверности модели и
границ ее применимости.
На определенном этапе развития науки и техники постепенное
накопление знаний приводит к моменту, когда результаты, получаемые
с помощью математической модели, вступают в противоречие с данны-
данными практики или перестают удовлетворять ее требованиям в смысле
точности. Тогда возникает необходимость модификации модели или
же создания принципиально новой, более сложной модели. Таким
образом, цикл создания математической модели повторяется много-
многократно.
Пример 1.7. Рассмотрим задачу внешней баллистики, т.е. задачу о движе-
движении артиллерийского снаряда. Простейшая модель A.1), A.2) дает параболиче-
параболическую траекторию движения снаряда, что, как было замечено еще 9 XVII в.,
противоречит данным практики. Существенным неучтенным фактором здесь
является сопротивление воздуха.
Приведенная ниже модификация модели Галилея принадлежит И.Ньюто-
И.Ньютону1. Известно, что величина F силы лобового сопротивления воздуха пропор-
пропорциональна квадрату скорости, т.е. F = —fii?. При этом /? = Q.bCSp, где р —
плотность воздуха, S — площадь поперечного
п,(г сечения, С— коэффициент лобового сопротивления
(для многих задач баллистики С» 0.15).
Обозначим через Fx и Fy горизонтальную и верти-
вертикальную проекции вектора лобового сопротивления.
Заметим, что Fx/F = u/v, Fy/F = w/ц v =
Следовательно Fx —
Рис 1.2
= \u2 + v? (рис. 1.2).
= -/? и \ч? + «P, Fy = -/? w \t? + v?.
Пусть т — масса снаряда. Тогда в силу второго закона Ньютона справед-
справедливы уравнения
dw
mdt~~
+
г
V?,
dr
dl
= %
dy
dt
A.4)
A.5)
1 Исаак Ньютон A643 — 1727) — английский физик, механик, астроном и
математик, заложивший основы современного естествознания.
14
которые необходимо дополнить начальными условиями
и @) = чэ cos о, w @) = vo sin а, х @) = 0, у @) = 0.
A.6)
Полученная модель является более сложной, чем рассмотренная ранее
модель A.1), A.2), однако она содержит ее как частный случай. Действитель-
Действительно, в случае /? = 0 (сопротивление воздуха отсутствует) уравнения A.4) —
A.6) и A.1), A.2) эквивалентны.
Естественно, что модель A.4) — A.6) непригодна для решения задач совре-
современной баллистики и реально используемые модели значительно сложнее.
Заметим, что работа по созданию математической модели, как
правило, проводится объединенными усилиями специалистов, хорошо
знающих предметную область, и математиков, владеющих соответству-
соответствующими разделами прикладной математики и способных оценить воз-
возможность решения возникающих вычислительных задач.
§ 1.2. Основные этапы решения
инженерной задачи
с применением ЭВМ
Решение серьезной инженерной задачи с использованием ЭВМ —
довольно длительный и сложный процесс. С определенной степенью
условности его можно разбить на ряд последовательных этапов. Вы-
Выделим следующие этапы: 1) постановка проблемы; 2) выбор или по-
построение математической модели; 3) постановка вычислительной зада-
задачи; 4) предварительный (предмашинный) анализ свойств вычислитель-
вычислительной задачи; 5) выбор или построение численного метода; 6) алгорит-
алгоритмизация и программирование; 7) отладка программы; 8) счет по про-
программе; 9) обработка и интерпретация результатов; 10) использование
результатов и коррекция математической модели.
1. Постановка проблемы. Первоначально прикладная задача бывает
сформулирована в самом общем виде: исследовать некоторое явление,
спроектировать устройство, обладающее заданными свойствами, дать
прогноз поведения некоторого объекта в определенных условиях и т.д.
На данной стадии происходит конкретизация постановки задачи, и
первостепенное внимание при этом уделяется выяснению цели иссле-
исследования. От исследователя требуется глубокое понимание существа
задачи и умение сформулировать ее так, чтобы найденное решение
было полезным и в то же время могло быть получено с помощью суще-
существующих методов и в реальные сроки. Неудачная постановка пробле-
проблемы может привести к тому, что длительный и дорогостоящий процесс
15

решения задачи завершится получением бесполезных или тривиаль-
тривиальных результатов (в этом случае возможно и отсутствие каких-либо
результатов).
Этот очень важный и ответственный этап завершается конкретной
формулировкой проблемы на языке, принятом в данной предметной
области. Знание возможностей, которые дает применение ЭВМ, может
оказать существенное влияние на окончательную формулировку
проблемы.
2. Выбор или построение математической модели. Для последующе-
последующего анализа исследуемого явления или объекта необходимо дать его
формализованное описание на языке математики, т.е. построить мате-
математическую модель (см. § 1.1). Часто имеется возможность выбора
модели среди известных и принятых для описания соответствующих
процессов, но нередко требуется и существенная модификация
известной модели, а иногда возникает необходимость в построении
принципиально новой модели.
Рассматриваемый этап — едва ли не самый важный и трудный.
Часто удачный выбор математической модели является решающим
шагом к достижению цели. Одна из существенных трудностей такого
выбора состоит в объективном противоречии между желанием сделать
описание явления как можно более полным (что приводит к усложне-
усложнению модели) и необходимостью иметь достаточно простую модель
(чтобы была возможность реализовать ее на ЭВМ). Важно, чтобы
сложность математической модели соответствовала сложности
поставленной проблемы. Если поставленных целей можно достичь,
используя более простую математическую модель, то ей и следует
отдать предпочтение. Как правило, полезно иметь несколько
упрощенных вариантов принимаемой модели. Заметим, что грамотное
упрощение модели — непростая задача, однако анализ упрощенных
моделей весьма полезен в течение всего процесса решения задачи.
Такие упрощенные модели часто позволяют ответить на многие
принципиальные вопросы и понять основные закономерности
поведения более сложной модели.
3. Постановка вычислительной задачи. На основе принятой матема-
математической модели формулируют вычислительную задачу (или ряд
таких задач). Анализируя результаты ее решения, исследователь пред-
предполагает получить ответы на интересующие его вопросы.
4. Предварительный анализ свойств вычислительной задачи. На
этом этапе проводят предварительное (предмашинное) исследование
свойств вычислительной задачи. Большое внимание уделяют анализу
корректности ее постановки, т.е. выяснению вопросов существования и
единственности решения, а также исследованию устойчивости решения
16
задачи к погрешностям входных данных (эти вопросы более подробно
рассматриваются в гл. 3). Такое исследование, как правило, относится
к компетенции профессиональных математиков. Тем не менее инжене-
инженеру полезно быть в курсе современного состояния названных проблем,
уметь самостоятельно проводить простейшие исследования.
К сожалению, для многих имеющих практическую ценность задач
их строгое исследование в полной постановке провести не удается и к
решению приступают без детального анализа математических свойств
этих задач. Это нежелательная, но вынужденная мера, так как в прик-
прикладных исследованиях существенное значение имеют конкретные
(часто — весьма сжатые) сроки получения результата. На этом этапе
полезным оказывается изучение упрощенных постановок задачи. Иног-
Иногда для них удается провести исследование, позволяющее понять ос-
основные особенности исходной вычислительной задачи. Особую цен-
ценность имеют различные аналитические решения; они оказываются
полезными не только для анализа явления, но и как основа для тесто-
тестовых испытаний на этапе отладки программы.
5. Выбор или построение численного метода. Для решения вычис-
вычислительной задачи на ЭВМ требуется использование численных ме-
методов.
Часто решение инженерной задачи сводится к последовательному
решению стандартных вычислительных задач, для которых разработа-
разработаны эффективные численные методы. В этой ситуации происходит либо
выбор среди известных методов, либо их адаптация к особенностям
решаемой задачи. Однако если возникающая вычислительная задача
является новой, то не исключено, что для ее решения не существует
готовых методов. Построение численного метода для такой задачи
может оказаться очень трудной проблемой и потребовать привлечения
специалиста по вычислительной математике. Умение различать отме-
отмеченные две ситуации необходимо, и наличие его уже говорит об опре-
определенной квалификации в области вычислительных методов.
Для решения одной и той же вычислительной задачи обычно мо-
может быть использовано несколько методов. Необходимо знать особен-
особенности этих методов, критерии, по которым оценивается их качество,
чтобы выбрать метод, позволяющий решить проблему наиболее эф-
эффективным образом. Здесь выбор далеко не однозначен. Он сущест-
существенно зависит от требований, предъявляемых к решению, от имеющих-
имеющихся в наличии ресурсов, от доступной для использования вычислитель-
вычислительной техники и т.д.
Возникающим на этом этапе вопросам и посвящена большая часть
данной книги.
6. Алгоритмизация и программирование. Как правило, выбранный
17

на предыдущем этапе численный метод содержит только принципиаль-
принципиальную схему решения задачи, не включающую многие детали, без кото-
которых невозможна реализация метода на ЭВМ. Необходима подробная
детализация всех этапов вычислений, для того чтобы получить реали-
реализуемый на ЭВМ алгоритм. Составление программы сводится к перево-
переводу этого алгоритма на выбранный язык программирования. Заметим,
что в настоящее время для вычислительных задач наиболее широко
используется алгоритмический язык ФОРТРАН.
В книге значительное место уделяется алгоритмам (в гл. 3 обсужда-
обсуждаются их общие свойства и критерии оценки качества) и практически
не рассматриваются вопросы собственно программирования. Конечно,
алгоритмизация и программирование очень тесно связаны. Более того,
практика показывает, что небольшие, на первый взгляд, различия в
программах могут привести к значительным различиям в их эффек-
эффективности. Тем не менее вопрос разработки качественного программного
продукта мы не затрагиваем (этому предмету посвящено большое
число пособий). Подчеркнем лишь, что большинство пользователей
справедливо предпочитает строить свои программы из готовых моду-
модулей и использовать стандартные программы, реализующие те или
иные алгоритмы. Разумеется, отсутствие в библиотеке стандартных
программ той или иной программы не должно быть непреодолимым
препятствием.
7. Отладка программы. На этом этапе с помощью ЭВМ выявляют и
исправляют ошибки в программе.
Как правило, начинающий пользователь ЭВМ убежден, что ошибок
в составленной им программе нет или же они могут быть легко обнару-
обнаружены и исправлены. Однако совершенно неожиданно для него отладка
программы и доведение ее до рабочего состояния нередко оказывается
длительным и весьма трудоемким процессом. Приобретая определен-
определенный опыт в составлении и отладке сравнительно сложных программ,
пользователь убеждается в справедливости популярного афоризма: "В
любой программе есть по крайней мере одна ошибка".
Таким образом, наличие в программах ошибок — вполне нормаль-
нормальное и закономерное явление. Поэтому подготовку к отладке следует
начинать уже на этапе алгоритмизации и программирования. Заметим,
что эффективность отладки самым существенным образом зависит от
общей методики разработки программ.
После устранения ошибок программирования необходимо провести
тщательное тестирование программы — проверку правильности ее
работы на специально отобранных тестовых задачах, имеющих извест-
известные решения.
18
Основные вопросы методики отладки программ можно найти, на-
например, в [10].
8. Счет по программе. На этом этапе происходит решение задачи на
ЭВМ по составленной программе в автоматическом режиме. Этот про-
процесс, в ходе которого входные данные с помощью ЭВМ преобразуются
в результат, называют вычислительным процессом. Как правило, счет
повторяется многократно с различными входными данными для по-
получения достаточно полной картины зависимости от них решения
задачи.
Первые полученные результаты тщательно анализируются, для того
чтобы убедиться в правильности работы программы и пригодности
выбранного метода решения. Счет по программе продолжается не-
несколько секунд, минут или часов. Именно быстротечность этого этапа
порождает распространенную иллюзию о возможности решать важные
прикладные задачи на ЭВМ в очень короткое время. В действительно-
действительности же, конечно, необходимо принимать во внимание весь цикл от
постановки проблемы до использования результатов. Для серьезных
задач часто полезные результаты получаются только в результате
многолетней работы.
9. Обработка и интерпретация результатов. Полученные в результа-
результате расчетов на ЭВМ выходные данные, как правило, представляют
собой большие массивы чисел. Начинающий пользователь часто пыта-
пытается вывести эти массивы на печать с тем, чтобы "потом провести их
анализ". Обычно первый же опыт анализа распечатки, содержащий
сотни тысяч чисел, приводит к пониманию того, что эта работа непо-
непосильна для человека и следует постараться возложить ее на ЭВМ.
Зачастую первоочередной интерес представляет лишь небольшая
часть полученной информации (например, значения одной из функций
в выделенных точках) или даже некоторая грубая интегральная харак-
характеристика (максимальное или минимальное значение, оценка энергии
системы и т.д.).
Для того чтобы исследователь мог воспользоваться результатами
расчетов, их необходимо представить в виде компактных таблиц, гра-
графиков или в иной удобной для восприятия форме. При этом следует
максимально использовать возможности ЭВМ для подготовки такой
информации и ее представления с помощью печатающих и графиче-
графических выходных устройств.
Для правильной интерпретации результатов расчетов и оценки их
достоверности от исследователя требуется глубокое знание существа
решаемой инженерной задачи, ясное представление об используемой
математической модели и понимание (хотя бы в общих чертах) особен-
особенностей применяемого вычислительного метода.
19

Вопросы обработки и интерпретации результатов вычислений будут
затронуты при рассмотрении конкретных вычислительных методов и
алгоритмов.
10. Использование результатов и коррекция математической моде-
модели. Завершающий этап состоит в использовании результатов расчетов
в практической деятельности, иначе говоря, во внедрении результатов.
Не стоит огорчаться, если большинство полученных сначала результа-
результатов окажется бесполезным. Действительно полезные для практики
результаты являются плодом серьезной целенаправленной работы, в
процессе которой цикл решения задачи повторяется неоднократно.
Очень часто анализ результатов, проведенный на этапе их обработ-
обработки и интерпретации, указывает на несовершенство используемой мате-
математической модели и необходимость ее коррекции. В таком случае
математическую модель модифицируют (при этом она, как правило,
усложняется) и начинают новый цикл решения задачи.
$1.3. Вычислительный эксперимент
Создание математических моделей и решение инженерных задач с
применением ЭВМ требует выполнения большого объема работ (см.
§ 1.1, 1.2). Нетрудно заметить аналогию с соответствующими работами,
проводимыми при организации натурных экспериментов: составление
программы экспериментов, создание экспериментальной установки,
выполнение контрольных экспериментов, проведение серийных опытов,
обработка экспериментальных данных и их интерпретация и т.д. Од-
Однако вычислительный эксперимент проводится не над реальным объ-
объектом, а над его математической моделью, и роль экспериментальной
установки играет оснащенная специально разработанной программой
ЭВМ. В связи с этим естественно рассматривать проведение больших
комплексных расчетов при решении инженерных и научно-техниче-
научно-технических задач как вычислительный эксперимент, а описанную в предыду-
предыдущем параграфе последовательность этапов решения как один его цикл.
Широкое применение ЭВМ в математическом моделировании, раз-
разработанная теория и значительные практические результаты позволя-
позволяют говорить о вычислительном эксперименте как о новой технологии и
методологии научных и прикладных исследований. Серьезное внедре-
внедрение вычислительного эксперимента в инженерную деятельность лишь
начинается, но там где оно происходит реально (в авиационной и
космической промышленности) его плоды весьма весомы.
Отметим некоторые достоинства вычислительного эксперимента по
сравнению с натурным. Вычислительный эксперимент, как правило,
20
дешевле физического. В этот эксперимент можно легко и безопасно
вмешиваться. Его можно повторить еще раз (если в этом есть необхо-
необходимость) и прервать в любой момент. В ходе этого эксперимента мож-
можно смоделировать условия, которые нельзя создать в лаборатории.
Заметим, что в ряде случаев проведение натурного эксперимента
затруднено (а иногда и невозможно), так как изучаются быстропроте-
кающие процессы, исследуются труднодоступные или вообще пока
недоступные объекты. Часто проведение полномасштабного натурного
эксперимента сопряжено с губительными или непредсказуемыми по-
последствиями (ядерная война, поворот сибирских рек) или с опас-
опасностью для жизни или здоровья людей. Нередко требуется исследова-
исследование и прогнозирование результатов катастрофических явлений (авария
ядерного реактора АЭС, глобальное потепление климата, землетрясе-
землетрясение). В этих случаях вычислительный эксперимент может стать основ-
основным средством исследования. Заметим, что с его помощью оказывается
возможным прогнозировать свойства новых, еще не созданных конст-
конструкций и материалов на стадии их проектирования.
Существенным недостатком вычислительного эксперимента являет-
является то, что применимость его результатов ограничена рамками приня-
принятой математической модели.
Конечно, вычислительный эксперимент никогда не сможет пол-
полностью заменить натурный, и будущее за их разумным сочетанием.
Действительно, построение математической модели основано на ре-
результатах наблюдений, опыта, а достоверность ее выводов проверяется
с помощью критерия практики.
Для инженерных задач характерно наличие значительного числа
параметров (конструктивных, технологических и др.). Создание нового
изделия или технологического процесса предполагает выбор среди
большого числа альтернативных вариантов, а также оптимизацию по
ряду параметров. Поэтому в ходе вычислительного эксперимента рас-
расчеты проводятся многократно с разными значениями входных пара-
параметров. Для получения нужных результатов с требуемой точностью и в
приемлемые сроки необходимо, чтобы на расчет каждого варианта
тратилось минимальное время. Именно поэтому при создании програм-
программного обеспечения так важно использовать эффективные численные
методы.
Разработка программного обеспечения вычислительного экспери-
эксперимента в конкретной области инженерной деятельности приводит к
созданию крупного программного комплекса. Он состоит из связанных
между собой прикладных программ и системных средств, включающих
средства, предоставляемые пользователю для управления ходом вы-
вычислительного эксперимента, обработки и представления его результа-
21

тов. Такой комплекс программ иногда называют проблемно-ориентиро-
проблемно-ориентированным пакетом прикладных программ.
§ 1.4. Дополнительные замечания
1. Математическое моделирование является основой современной методо-
методологии решения инженерных задач, и его роль объективно возрастает в связи с
необходимостью решения все более сложных прикладных проблем.
2. Эффективность применения ЭВМ в той или иной области науки и
техники тем выше, чем совершеннее ее математические модели. В то же время
использование ЭВМ для исследования каких-либо процессов часто служит
серьезным стимулом для создания новых математических моделей и детально-
детального изучения этих процессов другими методами.
3. Само по себе применение ЭВМ не позволяет решить инженерную задачу,
а лишь дает в руки исследователя мощный инструмент познания. Использова-
Использование ЭВМ не только не освобождает от необходимости глубоко осмыслить
решаемую проблему, но и заставляет уделять постановке задачи гораздо боль-
больше внимания.
4. Вычислительный эксперимент не противоречит натурному эксперименту
и классическому математическому анализу инженерной задачи, а, напротив,
находится с ними в органическом единстве.
5. Для успешного применения метода математического моделирования с
использованием ЭВМ необходимо гармоническое владение всеми его составля-
составляющими. В настоящем пособии основное внимание уделено вычислительным
методам и алгоритмам, анализу свойств вычислительных задач, интерпретации
получаемых результатов.
6. Дополнительную информацию о методологии современного математиче-
математического моделирования и концепции вычислительного эксперимента можно полу-
получить из следующих источников: [65], [78], [81], [47], [58].
7. Популярное изложение принципов организации и функционирования
проблемно-ориентированных пакетов прикладных программ содержится, напри-
например в [45].
Глава 2
ВВЕДЕНИЕ
В ЭЛЕМЕНТАРНУЮ ТЕОРИЮ
ПОГРЕШНОСТЕЙ
§ 2.1. Источники и классификация
погрешностей результата
численного решения задачи
Для правильного понимания подходов и критериев, используемых
при решении прикладной задачи с применением ЭВМ, очень важно с
самого начала признать, что получить точное значение решения прак-
практически невозможно и не в этом цель вычислений. Получаемое на
ЭВМ решение у* почти всегда (за исключением некоторых весьма
специальных случаев) содержит погрешность, т.е. является прибли-
приближенным. Невозможность получения точного решения следует уже из
ограниченной разрядности вычислительной машины.
Наличие погрешности решения обусловлено рядом весьма глубоких
причин. Перечислим их.
1°. Математическая модель является лишь приближенным описани-
описанием реального процесса. Характеристики процесса, вычисленные в
рамках принятой модели, заведомо отличаются от истинных характе-
характеристик, причем их погрешность зависит от степени адекватности моде-
модели реальному процессу.
2°. Исходные данные, как правило, содержат погрешности, по-
поскольку они либо получаются в результате экспериментов (измере-
(измерений), либо являются результатом решения некоторых вспомогательных
задач.
3°. Применяемые для решения задачи методы в большинстве случа-
случаев являются приближенными. Найти решение возникающей на прак-
практике задачи в виде конечной формулы возможно только в отдельных,
очень упрощенных ситуациях.
4°. При вводе исходных данных в ЭВМ, выполнении арифметичес-
арифметических операций и выводе результатов на печать производятся округ-
округления.
Пусть у — точное значение величины, вычисление которой является
23

целью поставленной задачи. Соответствующая первым двум из указан-
указанных причин погрешность 8ну называется неустранимой погрешностью.
Такое название вызвано тем, что принятие математической модели и
задание исходных данных вносит в решение ошибку, которая не может
быть устранена далее. Единственный способ уменьшить эту погреш-
погрешность — перейти к более точной математической модели и задать более
точные исходные данные.
Погрешность 8му, источником которой является метод решения
задачи, называется погрешностью метода, а погрешность 6ъу, возника-
возникающая из-за округлений при вводе, выводе и вычислениях, — вычисли-
вычислительной погрешностью. Таким образом, полная погрешность результа-
результата решения задачи на ЭВМ 8у = у - у* складывается из трех состав-
составляющих: неустранимой погрешности, погрешности метода и вычисли-
вычислительной погрешности, т.е. Ьу = 6Иу + 6му + 6ву.
Будем далее исходить из предположения, что математическая мо-
модель фиксирована и входные данные задаются извне, так что повли-
повлиять на значение величины Ьну в процессе решения задачи действитель-
действительно нельзя. Однако это совсем не означает, что предварительные оцен-
оценки величины неустранимой погрешности не нужны. Достоверная ин-
информация о порядке величины 6ну позволяет осознанно выбрать метод
решения задачи и разумно задать его точность. Желательно, чтобы
величина погрешности метода была в 2—10 раз меньше неустранимой
погрешности. Большее значение 6иу ощутимо снижает точность резуль-
результата, меньшее — обычно требует увеличения затрат, практически уже
не влияя на значение полной погрешности. Иногда характер использо-
использования результата таков, что вполне допустимо, чтобы величина 6иу
была сравнима с 8ну или даже несколько превышала ее.
Величина вычислительной погрешности (при фиксированных моде-
модели, входных данных и методе решения) в основном определяется
характеристиками используемой ЭВМ. Желательно, чтобы величина
6ву была хотя бы на порядок меньше величины погрешности метода и
совсем не желательна ситуация, когда она существенно ее превышает.
Умение анализировать погрешности при решении прикладной
задачи и соблюдать между ними разумный компромисс позволяет
существенно экономить используемые ресурсы и является признаком
высокой квалификации.
§ 2.2. Приближенные числа.
Абсолютная и относительная погрешности
В предыдущем параграфе было отмечено, что числа, получаемые
при решении на ЭВМ прикладных задач, как правило, являются
24
приближенными. Следовательно, вопрос о точности результатов, т.е. о
мере их уклонения от истинных значений, в теории и практике мето-
методов вычислений приобретает особое значение. Начнем его рассмотре-
рассмотрение с введения основных понятий элементарной теории погрешностей.
Условимся относительно обозначений, которые в дальнейшем будут
использоваться при сравнении величин. Кроме привычных знаков,
" = ", " t ", " < ", " < ", будем использовать знаки приближенного
равенства " й " и приближенного неравенства " < ". В случае, когда
положительные величины а и 6 являются величинами одного порядка
(т.е. 10 < а/Ь < 10), будем использовать обозначение а - Ь. Если же а
много меньше 6, то будем писать а < Ь, что эквивалентно соотношению
а/Ь € 1.
1. Абсолютная и относительная погрешности. Пусть а — точное
(вообще говоря, неизвестное) значение некоторой величины, а* —
известное приближенное значение той же величины (приближенное
число). Ошибкой (или погрешностью) приближенного числа а* называ-
называют разность а- а* между точным и приближенным значениями.
Простейшей количественной мерой ошибки является абсолютная
погрешность
= |а- а
B.1)
Однако по величине абсолютной погрешности далеко не всегда можно
сделать правильное заключение о качестве приближения. Действитель-
Действительно, если Д(о*) = 0.1, то следует ли считать погрешность большой или
нужно признать ее малой? Ответ существенным образом зависит от
принятых единиц измерения и масштабов величин. Если а я 0.3, то
скорее всего точность приближения невелика; если же а«3-108, то
следует признать точность очень высокой. Таким образом, естестверно
соотнести погрешность величины и ее значение, для чего вводится
понятие относительной погрешности (при a t 0)
«(а*) =
B.2)
Использование относительных погрешностей удобно, в частности,
тем, что они не зависят от масштабов величин и единиц измерения.
Заметим, что для приведенного выше примера 8(а*) и 0.33 = 33% в
первом случае и 6(а*) и 0.33-Ю"9 = 0.33-10% во втором.
Так как значение а неизвестно, то непосредственное вычисление
величин А(а*) и 6(а*) по формулам B.1), B.2) невозможно. Более
25

реальная и часто поддающаяся решению задача состоит в получении
оценок погрешности вида
2. Правила записи приближенных чисел. Пусть приближенное
число а* задано в виде конечной десятичной дроби:
\a-a*\
\a - o*|
B.3)
B.-4)
где Д(л*) и S{a*) — известные величины, которые мы будем называть
верхними границами (или просто границами) абсолютной и относи-
относительной погрешностей.
Если величина Д(а*) известна, то неравенство B.4) будет выполне-
выполнено, если положить
в(О = _Д(О ¦ B.5)
Точно так же если величина Ь{а*) известна, то следует положить
Д(а») = |а|«(а*)- B-6)
Поскольку значение а неизвестно, при практическом применении
формулы B.5), B.6) заменяют приближенными равенствами
Д(а 1 й \а \о(а ). \^'')
Замечание. В литературе по методам вычислений широко
используется термин "точность". Принято говорить о точности
входных данных и решения, о повышении и снижении точности
вычислений и т.д. Мы также будем использовать эту терминоло-
терминологию, за которой скрывается довольно простой смысл. Точность в
качественных рассуждениях обычно выступает как противополож-
противоположность погрешности, хотя для количественного их измерения ис-
используются одни и те же характеристики (например, абсолютная и
относительная погрешности). Точное значение величины — это
значение, не содержащее погрешности. Повышение точности вос-
воспринимается как уменьшение погрешности, а снижение точности —
как увеличение погрешности. Часто используемая фраза "требуется
найти решение с заданной точностью е" означает, что ставится
задача о нахождении приближенного решения, принятая мера
погрешности которого не превышает заданной величины е. Вообще
говоря, следовало бы говорить об абсолютной точности и относи-
относительной точности, но часто этого не делают, считая, что из кон^-
текста ясно, как измеряется величина погрешности.
26
а* = ап
Значащими цифрами числа а* называют все цифры в его записи,
начиная с первой ненулевой слева.
Пример 2.1. У чисел а* = О.ОШ и а* = 0.0103000 значащие цифры под-
подчеркнуты. Первое число имеет 3, а второе — б значащих цифр.
Значащую цифру числа а* называют верной, если абсолютная
погрешность числа не превосходит единицы разряда, соответствующе-
соответствующего этой цифре.
Пример 2.2. Если Д(а*) = 2-Ю, то число а* = 0.0103000 имеет 4 верные
значащие цифры (они подчеркнуты).
Следует отметить, что широко распространенной ошибкой при
записи приближенных чисел является отбрасывание последних знача-
значащих нулей (даже если они представляют собой верные цифры).
Замечание. Верная цифра приближенного числа, вообще
говоря, не обязана совпадать с соответствующей цифрой в записи
точного числа. Таким образом, термин "верная цифра" не следует
понимать буквально (см. пример 2.3).
Пример 2.3. Пусть а = 1.00000, а* = 0.99999. Тогда Д(о*) = 0.00001 и у
числа а* все подчеркнутые цифры — верные, хотя они и не совпадают с
соотвествующими цифрами числа а.
Количество верных значащих цифр числа тесно связано с величи-
величиной его относительной погрешности. Приведенные ниже утверждения
позволяют в дальнейшем связывать точность числа с количеством его
верных значащих цифр и трактовать потерю точности как потерю
верных цифр.
Предложение 2.1. 1°. Если число а * содержит N верных
значащих цифр, то справедливо неравенство 6(а*) < A0№l - I)'1 и
и Ю-ЛМ.
2°. Для того чтобы число а* содержало N верных значащих цифр,
достаточно, чтобы было выполнено неравенство 6(а*) < (lO^-fl)'1 и
и 10"*.
27

3°. Если число а* имеет ровно N верных значащих цифр, то
Ю-т < 6(а*) < 10"№1 и таким образом 6(а*) ~ 10"^.
Пример 2.4. Что можно сказать об относительной погрешности числа а*,
если оно содержит 3 верные цифры?
В силу утверждения 1° имеем 6(а*) < 10~2 = 1%.
Пример 2.5. С какой относительной точностью следует найти число а*,
чтобы верными оказались 6 значащих цифр?
Из утверждения 2° следует, что достаточно найти а* с относительной
точностью е и Ю~6.
Заметим, что границы абсолютной и относительной погрешностей
принято записывать с одной или двумя значащими цифрами. Большая
точность в записи этих величин, как правило, не имеет смысла, так
как обычно они являются довольно грубыми оценками истинных
значений погрешностей, и кроме того, для практического использова-
использования часто бывает достаточно знать только их порядок.
Пример 2.6. Информация о погрешности вида 6(а*) в 0.288754-10~5
практически равноценна информации 8(а*) и 3-Ю, причем последняя вызы-
вызывает больше доверия. Скорее всего, вполне удовлетворительной в данном
случае является и запись 6(а*) ~ 10~6.
Неравенство B.3) эквивалентно двойному неравенству
а* - Д(а*) <а<а* + Д(я')
и поэтому тот факт, что число а * является приближенным значением
числа а с верхней границей абсолютной погрешности Д(а*) (с абсо-
абсолютной точностью е = Д(а*)), принято записывать в виде
а= а* ± Д(в*).
Как правило, числа а* и Д(а*) указывают с одинаковым числом цифр
после десятичной точки.
Пример 2.7. Пусть для числа а известны приближенное значение а* =
= 1.648 и граница абсолютной погрешности Д(а*) = 0.002832. Тогда можно
записать а = 1.648 ± 0.003. Записи вида а = 1.648 ± 0.002832 или а =
= 1.648 ± 0.1 являются неестественными.
28
Из неравенства B.4) следует, что значение а заключено примерно
между а*A - 1(а*)) и а*A + *(а*)). Поэтому тот факт, что число а*
является приближенным значением числа а с границей относительной'
погрешности 6(а*) (с относительной точностью в = 6(а*)), принято
записывать в виде а = а*A ± 6(а*)).
Пример 2.8. Оценим точность часто используемого в простейших расчетах
приближения ir* = 3.14 к числу зг. Известно, что ж = 3.14159..., поэтому -к -
— it* = 0.00159... Следовательно, можно принять Д(т*) = 0.0016 и 6(it*) и
и 0.0016/3.14 и 0.00051 = 0.051%. Итак, ir = 3.14 ( 1 ± 0.051%).
Замечание. Если число а * приводится в качестве результата
без указания величины погрешности, то принято считать, что все
его значащие цифры являются верными. Начинающий пользова-
пользователь часто слишком доверяет выводимым из ЭВМ цифрам, предпо-
предполагая, что вычислительная машина придерживается того же согла-
соглашения. Однако это совсем не так: число может быть выведено с
таким количеством значащих цифр, сколько потребует программист
заданием соответствующего формата. Как правило, среди этих
цифр только небольшое число первых окажутся верными, а, воз-
возможно, .верных цифр нет совсем. Анализировать результаты вычис-
вычислений и определять степень их достоверности совсем непросто.
Одна из целей изучения вычислительных методов и состоит в дос-
достижении понимания того, что можно и чего нельзя ожидать от
результатов, полученных на ЭВМ.
3. Округление. Часто возникает необходимость в округлении числа
а, т.е. в замене его другим числом а * с меньшим числом значащих
цифр. Возникающая при такой замене погрешность называется по-
погрешностью округления.
Существует несколько способов округления числа до п значащих
цифр. Наиболее простой из них — усечение состоит в отбрасывании
всех цифр, расположенных справа от п-й значащей цифры. Более
предпочтительным является округление по дополнению. В простейшем
варианте это правило округления состоит в следующем. Если первая
слева из отбрасываемых цифр меньше 5, то сохраняемые цифры оста-
остаются без изменения. Если же она больше либо равна 5, то в младший
сохраняемый разряд добавляется единица.
Абсолютная величина погрешности округления при округлении по
дополнению не превышает половины единицы разряда, соответству-
соответствующего последней оставляемой цифре, а при округлении усечением —
единицы того же разряда.
29

Пример 2.9. При округлении числа а = 1.72631 усечением до трех знача-
значащих цифр получится число а* = 1.72, а при округлении по дополнению —
число а* = 1.73.
Границы абсолютной и относительной погрешностей принято всег-
всегда округлять в сторону увеличения.
Пример 2.10. Округление величин Д(а*) = 0.003721 и 7(а*) = 0.0005427 до
двух значащих цифр дает значения Д(я*) = 0.0038 и S(a*) = 0.00055.
§ 2.3. Погрешности арифметических операций
над приближенными числами
Исследуем влияние погрешностей исходных данных на погрешность
результатов арифметических операций. Пусть а* и Ь* —
приближенные значения чисел а и Ь. Какова соответствующая им
величина неустранимой погрешности результата?
Предложение 2.2. Абсолютная погрешность алгебраиче-
алгебраической суммы (суммы или разности) не превосходит суммы абсолютных
погрешностей слагаемых, т.е.
Д(а* ± Ь*) < Д(а*) + ДF*).
а Имеем
B.8)
Д(а* ± 6*) = \(а ± Ъ)-(а* ± Ь*)\ = |(а- а*) ± (Ь - Ь*)\ <
< Д(а*) + ДF*). ¦
Следствие. Б силу неравенства B.8) естественно положить
Д(а* ± Ъ*) = Д(а*) + ДF*). B.9)
Оценим относительную погрешность алгебраической суммы.
Предложение 2.3. Пусть а и Ь — ненулевые числа одною
знака. Тогда справедливы неравенства
8(а*+ 6'HW, *(a*-O<^max,
ide «„.ax = max {6(a*), S(b*)}, v = \a + b\/\a- b\.
B.10)
d Используя формулу B.2) и неравенство B.8), имеем
\а± Ь\ 6(а* ± 6*) = А(а* ± Ь*) < Д(а*) + ДF*) =
= \а\6(а*)+ \Ь\6(Ь*)$(\а\ + \Ь\) W= |a+6|W.
Из полученного неравенства сразу следуют оценки B.10). Ш
Следствие. В силу неравенств B.10) естественно положить
6(а*+Ь*)= W, *(«*-Л*) = "«««.
ufc «„„„ = max fS(a*),l(b*)}, v= \a+ 6|/|a-6|.
B.11)
30
Первое из равенств B.11) означает, что при суммировании чисел одно-
одного знака не происходит потери точности, если оценивать точность в
относительных единицах. Совсем иначе обстоит дело при вычитании
чисел одного знака. Здесь граница относительной ошибки возрастает в
v > 1 раз и возможна существенная потеря точности. Если числа а и Ь
близки настолько, что \а + Ь\ > | a — 6|, то i/ > 1 и не исключена
полная или почти полная потеря точности. Когда это происходит,
говорят о том, что произошла катастрофическая потеря точности.
Пример 2.11. Пусть решается инженерная задача, в которой окончательный
результат у вычисляется по формуле у = 1 - х с помощью предварительно
определяемого значения х. Предположим, что найденное приближение х* =
= 0.999997 к значению х содержит 6 верных значащих цифр. Тогда у* = 1 -
- 0.999997 = 0.000003 и в процессе вычисления оказались потерянными 5 вер-
верных цифр. Если же учесть, что 6(х*) ~ 0.0001%, а 6(у*) ~ 33%, то следует
признать, что произошла катастрофическая потеря точности.
Подчеркнем, что здесь виновником "катастрофы" является не операция
вычитания, а предложенный метод решения задачи, где окончательный ре-
результат получается с помощью вычитания двух близких чисел. Выполнение
этой операции лишь делает очевидным то, что действительно полезная инфор-
информация о значении у уже оказалась потерянной до вычитания. Если нет друго-
другого варианта расчета, то для получения приемлемого результата следовало бы
предварительно вычислить х с существенно большим числом верных знаков,
учитывая, что 5 старших значащих цифр при вычитании будут потеряны.
Итак, получаем следующий важный вывод. При построении чис-
численного метода решения задачи следует избегать вычитания близких
чисел одного знака. Если же такое вычитание неизбежно, то следует
вычислять аргументы с повышенной точностью, учитывая ее потерю
примерно bi/= | a + 61 /1 о — 61 раз.
Предложение 2.4. Для относительных погрешностей произ-
произведения и частного приближенных чисел верны оценки
31

6(а*Ь*) < S(a*) + 6(b*) + S(a*N(b*),
B.12)
§ 2.4. Погрешность функции
6(a /& } < 1 - 6(b*) ' B13)
в последней из которых считается, что i(b*) < 1.
D Выполним следующие преобразования:
\аЬ\6(а*Ь*) = А(а*Ь*) = \аЪ - а*Ь*\ = \(а - а*)Ъ +
+ (Ь- Ъ*)а-(а- а*)(Ъ-Ь*)\ < |6|Д(а*) + |а|ДF*) +
+ Д(а*)Д(&*) = \аЪ\F(а*) + 6(Ь*) + 6(а*N(Ь*)),
т.е.
\ab\6(a*b*) < \аЬ\F(а*) + Ь(Ъ*) + 8{а*N(Ь*)).
Разделив обе части этого неравенства на \ab\, получаем оценку B.12).
Для вывода второй оценки предварительно заметим, что |&*| =
= \Ь+ (Ь*-Ь)\ > \Ь\ -А(Ь*) = \Ь\A- 8(Ь*)). Тогда
1. Погрешность функции многих переменных. Пусть / (х) = f(x\, X2,
¦¦¦I хт\ — дифференцируемая в области G функция т переменных,
вычисление которой производится при приближенно заданных значе-
значениях аргументов г*, х*, ..., х^. Такая ситуация возникает, например,
всякий раз, когда на ЭВМ производится расчет по формуле. Важно
знать, какова величина неустранимой ошибки, вызванной тем, что
вместо значения у = / (х) в действительности вычисляется значение
Введем обозначения: пусть [х, х*] — отрезок1, соединяющий точки
х и х*, и /' = df/dij.
Xj
j
Предложение 2.5. Для абсолютной погрешности значения
у*= f(x*) справедлива следующая оценка:
B.15)
D Оценка B.15) вытекает из формулы конечных приращений
Лагранжа2:
_ \а(Ъ*-Ь)+Ь(а-а*)\ , | д
~~ [«PI ¦
а*)
_ 6(b*)+6(a*) я
~ 1-6(Ь*) ¦"
Следствие. Если 6(а*) < I и 6(Ь*) К 1, то для оценки границ
относительных погрешностей можно использовать следующие прибли-
приближенные равенства:
6(а*Ь*) я 6(а*) + 6(Ь*), 6(а*/Ь*) и 6(а*) + 6(Ь*).
B.14)
Именно равенства B.14) чаще всего и используют для практиче-
практической оценки погрешности.
Итак, выполнение арифметических операций над приближенными
числами, как правило, сопровождается потерей точности. Единствен-
Единственная операция, при которой потеря не происходит, — это сложение
чисел одного знака. Наибольшая потеря точности может произойти
при вычитании близких чисел одного знака.
32
f(x)-f(x*)=
/
Гх х}
х,-О, ie[x, х*}.\
Следствие. Если х* я х, то в силу оценки B.15) можно
положить
\
т
}-\ х)
т
J
B.16)
B.17).
Равенство B.16) удобно для практических оценок, а равенством
B.17) мы воспользуемся в дальнейшем для теоретических построений.
1 Отрезком, соединяющим точки г и г* в m-мерном пространстве, называет
ся множество точек вида ах + A - а)х*, 0 ^ а ^ 1.
2 Жозеф Луи Лагранж A736 — 1813) — французский математик, механик и
астроном. Один из создателей математического анализа, вариационного исчис-
исчисления, классической аналитической механики.
2-28 33

Из формул B.16), B.17) вытекают приближенные равенства для
оценки границ относительных imi \>< Гппостой:
B.18)
Здесь
!/(*•)!
B.19)
Пример 2.12. Пусть корни квадратного уравнения г2 .+ frz + с = 0 вычис-
вычисляются при значениях коэффициентов Ь и 103, с и 1! Каково влияние погреш-
погрешностей задания коэффициентов на точность вычисляемых значений?
Воспользуемся явными формулами для корней: х\ = f (b, с) = (-b -
— [d)/2, х2 = д (b, с) = (-ft + 4~rf)/2, где <f = б2 - 4с Заметим, что х\-х2 — с
Тогда при заданных значениях коэффициентов получим \d я \ 106 — 4 я 103,
Ч « (-103 - 103)/2 = -103, х2 = с/з\ и 1/(-Ю3) = -10. Далее, имеем /^ =
= (-1 - 6/.Й/2 « (-1 " Ю3/Ю3)/2 = -1, /; = 1/р и Ю-з, д'ь = (-1 +
+ b/[d)/2 = F - jd)/Bf5) = -ъ/fd и 10, ?^ = -1/jrf и -10. Применяя
первую из формул B.19), для корня i\ находим и* , = | Ь*\ \^\/\ х*\ и 1,
{/т. = | с*| |/' |/| г.*| й 10. Аналогично для корпя х2 имеем V2\ =
,2
= l**
Ujl/lx2*l й *' 2 = lc*ll»cl/lr2l й L Таким образом,
6(х*) « 6F*) + 10-«6(с*), «(г*) и 6F*) + в(с').
B.20)
Следовательно, точность первого корня практически определяется только
точностью задания коэффициента Ь, в то время как коэффициент с может
быть задан очень грубо. Для второго корня влияние погрешностей в задании
коэффициентов бис практически одинаково.
2. Погрешность функции одной переменной. Формулы для границ
погрешностей функции / (х) одной переменной являются частным
случаем формул B.16) — B.18) при m = 1:
»), Д(з,*) я
B-21)
B.22)
гдеИ=
3. Погрешность неявной функции. Нередко приходится сталкивать-
сталкиваться с ситуацией, когда функция у = f (х\, х2, ..., хт) задается не явной
формулой, а как решение нелинейного уравнения F (у, хь х2, ..., хт) =
= 0, т.е. неявно. Если для такой неявной функции воспользоваться из-
известными формулами вычисления производных
B.23)
то исследование неустранимой погрешности неявной функции сразу же
сводится к рассмотренному выше случаю.
Пример 2.13. Для проведенного в примере 2.12 исследования совсем не
обязательно было выписывать явные формулы для корней. В этом случае
величины ij = / F, с) и х2 = д (Ь, с) можно рассматривать как неявные
функции, заданные уравнением F (х, Ь, с) = 0, где F = з? + Ъх + с.
Здесь F'x = 2х + b, F'b = х, F'c = 1. Следовательно,
34
= ,., b= 10з, с = !
Вычисления при i = 1, х* » -103 и i = 2, х* я -10 дают те же значения
коэффициентов v* v v* 2, v* v v* 2, что и в примере 2.12, а, следовательно,
те же формулы B.20).
$ 2.5. Особенности
машинной арифметики
Знание основных особенностей машинной арифметики необходимо
для грамотного использования ЭВМ при решении научно-технических
задач. Пользователь, не учитывающий эти особенности, вряд ли может
рассчитывать на высокую точность и эффективность вычислений.
Невнимание к ним часто приводит к неверным результатам. Подчерк-
Подчеркнем, что в основе причин появления вычислительной погрешности
лежит сам способ представления чисел на ЭВМ.
35

1. Системы счисления. Принятый способ записи чисел состоит в
представлении их упорядоченным набором цифр. В привычной нам
десятичной позиционной системе счисления вещественное число х
представляют последовательностью символов, которая начинается со
знака (+ или -) и продолжается цепочкой десятичных цифр а, и /3},
разделенных десятичной точкой:
х = ±ап
¦¦¦ Рт
B.24)
Здесь каждой позиции (разряду), которую занимает цифра
относительно десятичной точки, отвечает определенная степень числа
10. По существу, равенство B.24) представляет собой принятое
сокращение полной записи числа г, имеющей вид
х = ±(а„-10п + ... + Qi-101 + ао-Ю° + А-10 +
Пример 2.14. Запись х =. 20.5 означает, что х - 2-101 + 0-10° + 5- КГ1.
Для представления чисел в вычислительных машинах также ис-
используют позиционные системы счисления, однако основаниями сис-
систем служат, как правило, степени числа 2. Это вызвано способом хра-
хранения чисел в устройствах памяти ЭВМ, каждое из которых можно
рассматривать как набор однотипных элементов, способных находиться
только в одном из двух возможных устойчивых состояний — "вклю-
"включен" или "выключен". Эти состояния интерпретируются соответствен-
соответственно как 0 или 1 — значения двоичного числа. Наиболее распространены
системы счисления с основанием 2 (базисная двоичная система счисле-
счисления), 8 и 16.
Игнорируя некоторые малосущественные детали, будем считать,
что все вычислительные машины работают в двоичной системе счисле-
счисления. В ней вещественное число х по-прежнему записывается в виде
B.24), однако а, и fy — уже двоичные цифры @ или 1). В этом случае
полная запись выглядит так:
±(ап-2" + ... + «1-21 + ао-2° +
V22 92 )
Пример 2.15. Запишем число х = 20.5 в двоичной системе счисления. Для
этого разложим его в сумму по степеням двойки: х — 1-24 + 0-23 + Ь22 +
+ 0-21 + 0-2° + 1-2. Опуская степени двойки, получаем х = A0100.1J.
Здесь нижний индекс 2 указывает на основание системы счисления.
36 '
Для хранения числа в памяти ЭВМ отводится поле стандартной
длины {машинное слово), в котором число записывают в виде последо-
последовательности двоичных цифр. По форме представления, способу хране-
хранения и реализации арифметических операций существенно различаются
два типа используемых на вычислительных машинах чисел: целые
числа и вещественные числа.
2. Представление целых чисел. Целое число п представляют в виде
и = ±(aL2L
а,2' + ао2°),
B.25)
где L — некоторое стандартное для ЭВМ целоо число, а, — двоичные
цифры. Всего для хранения числа п отводят L %- 2 разрядов (один из
них для хранения знака).
Из представления B.25) видно, что максимальное по модулю целое
число, представимое в ЭВМ, есть п,паХ = 2^ + ... + 21 + 2° = 2^+1 - 1.
Обычно это значение не очень велико. Например, при стандартном
формате записи целых чисел на компьютерах типа IBM PC щ^х =
= 231 - 1 я 2-Ю9.
Операции сложения, вычитания и умножения над целыми числами
реализованы так, что если результат не превышает по модулю число
nmax> т° он получается точным. Отметим, однако, следующую неприят-
неприятную особенность. Если модуль результата превышает птлх, то на боль-
большинстве вычислительных машин эта ситуация не доводится до сведе-
сведения пользователя, происходит присвоение результату некоторого зна-
значения (меньшего nmax по модулю) и вычисления продолжаются далее.
3. Представление вещественных чисел. В большинстве современных
ЭВМ для вещественных чисел принята форма представления с плава-
плавающей точкой, когда каждое число представляют в виде
г =
72.2-2
B.26)
Здесь 7ь 72i ¦•¦, It — двоичные цифры. Число г нормализуется так,
чтобы 71 = 1> и поэтому в памяти ЭВМ хранятся только значащие
цифры. Число fi = ±Gi*2'1 + 72'2 + ••• + 7t'2 называется мантис-
мантиссой числа х. Количество t цифр, которое отводится для записи мантис-
мантиссы, называемое разрядностью мантиссы, зависит от конструктивных
особенностей конкретной вычислительной машины, но всегда является
конечным. В представлении B.26) р — целое цисло, называемое двоич-
двоичным порядком. Порядок также записывают как двоичное целое число
р = ±(<7;<77-i ... <ТоJ, для хранения которого в машинном слове отводит-
отводится / + 2 двоичных разрядов. На рис. 2.1 схематически представлена
структура машинного слова для хранения вещественного числа.
37

+
Г,
+
Мантисса
ДШчный порядок
Рис. 2.1
Поскольку нуль — ненормализуемое число (его нельзя представить
в виде B.26) при 7i * 0)> Для его хранения предусматривают особый
способ записи.
Пример 2.16. Представим число х — 20.5 в двоичной системе счисления в
нормализованной форме с плавающей точкой. Так как х = A0100.1J (см.
пример 2.15), то, перемещая двоичную точку на 5 позиций влево, получаем
х= @.101001J-25.
На основании имеющихся сведений о представлении чисел в ЭВМ
можно сделать ряд важных выводов.
1°. На ЭВМ представимы не все числа, а лишь конечный набор
рациональных чисел специального вида. Эти числа образуют предста-
вимое множество вычислительной машины. Для всех остальных чисел
х возможно лишь их приближенное представление с ошибкой, которую
принято называть ошибкой представления (или ошибкой округления).
Обычно приближенное представление числа х в ЭВМ обозначают1
как t* = п(х). Если округление производят по дополнению, то
граница относительной погрешности представления равна единице
первого отброшенного разряда мантиссы, т.е. 6(х*) = ем = 2~* (поря-
(порядок числа не влияет на относительную погрешность представления).
Если же округление производят усечением, то 6{х*) = ем= 21"'.
Величина ем играет в вычислениях на ЭВМ фундаментальную роль; ее
называют относительной точностью ЭВМ, а также машинной точ-
точностью (или машинным эпсилон). Всюду в дальнейшем ем — это отно-
относительная точность ЭВМ. Заметим, что значение этой величины опре-
определяется разрядностью мантиссы и способом округления.
Важно с самого начала иметь четкое представление о том, что поч-
почти наверняка в представимом множестве ЭВМ нет числа у, являющего-
являющегося решением поставленной задачи. Лучшее, что можно попытаться
сделать, — это найти его представление у* — п(у) с относительной
точностью порядка ем.
Полезно отметить, что среди представимых на ЭВМ чисел нет не
только ни одного иррационального (в том числе и таких важных по-
постоянных, как it, e, \2), но и даже такого широко используемого в
вычислениях числа, как 0.1. Дело в том, что двоичная запись числа
0.1 является бесконечной периодической дробью: 0.1 =
= @.0001100110011...J- Поэтому это число всегда представляется на
ЭВМ приближенно, с погрешностью, вызванной необходимостью ок-
округления.
2°. Диапазон изменения чисел в ЭВМ ограничен. В самом деле, так
как 7i = 1> т0 Для мантиссы ц справедливы оценки 0.5 ^ |/х| < 1.В то
же время для представления в. ЭВМ порядка р используется конечное
число (/ + 1) двоичных цифр и поэтому |р| < Ртах = 2м - 1. Таким
образом, для всех представимых на ЭВМ чисел г (за исключением
нуля) имеем 0 < Хо < |i| < ХЛ, где *0 = 2~*Р«МХ+Ч Х^ = 2?тах.3аме-
тим, что диапазон представления чисел на ЭВМ всецело определяется
разрядностью порядка.
3°. Все числа х, по модулю большие Х^, не представимы на ЭВМ и
могут рассматриваться как машинная бесконечность. Попытка полу-
получить такое число приводит к аварийному останову ЭВМ по переполне-
переполнению. Все числа х, по модулю меньшие Хо, для вычислительной маши-
машины не различимы и представляются как нуль (машинный нуль). Полу-
Получение числа х такого, что \х\ < Хо, называют исчезновением порядка
(или антипереполнением). Обычно при исчезновении порядка автома-
автоматически полагается fl(z) = 0 и вычисления продолжаются.
Замечание. Не следует смешивать машинную точность ем с
минимальным положительным представимым на ЭВМ числом Xq.
Это совершенно разные числа, причем Xq < ем-
Машинная
бесконечность
Машинный
нут
Рис. 2.2
Машинная
бесконечность
1 fl — начальные буквы англ. floating — "плавающий".
38
4°. На машинной числовой оси (рис. 2.2) числа расположены нерав-
неравномерно. Плотность их возрастает по мере приближения к нулю и
падает с удалением от нуля. Чтобы убедиться в этом, заметим, что
39

расстояние от одного представимого на ЭВМ числа х до другого бли-
ближайшего представимого равно единице последнего разряда мантиссы,
умноженной на 2Р, т.е. равно IP'*-. Так как t фиксировано, то рассто-
расстояние уменьшается с уменьшением порядка р и возрастает с увеличени-
увеличением р.
Для компьютеров типа IBM PC (при вычислениях на ФОРТРАНЕ)
представимые числа расположены в диапазоне 10~38 < |г| < 3-Ю38,
вполне достаточном для большинства приложений. Однако разряд-
разрядность мантиссы невелика (t — 23) и ем и 10~7; в десятичной арифмети-
арифметике это эквивалентно тому, что мантисса содержит 7 десятичных цифр.
Заметим, что для большинства ЭВМ, используемых для научно-техни-
научно-технических расчетов, мантисса имеет разрядность, эквивалентную 7—14
десятичным разрядам.
4. Арифметические операции над числами с плавающей точкой.
Правила выполнения арифметических операций в двоичной системе
счисления чрезвычайно просты и легко реализуются на ЭВМ.
Однако в силу ограниченной разрядности мантиссы операции сло-
сложения, вычитания, умножения и деления над представимыми в ЭВМ
вещественными числами не могут быть реализованы точно. Дело в том,
что арифметические операции над числами, мантиссы которых содер-
содержат t разрядов, приводят, как правило, к результатам, содержащим
более I разрядов. Округление результата до t разрядов и служит глав-
главным источником погрешности. Для того чтобы отличать машинные
арифметические операции от идеальных' математических операций +,
-, х, :, будем обозначать их через ©, 6, ®, ©. Игнорируя несуществен-
несущественные детали, можно считать, что результат машинной арифметической
операции совпадает с результатом точного выполнения той же опера-
операции с погрешностью, приближенно равной погрешности округления.
Таким образом,
Д(а® Ь) я \а + Ь\ем, Д(а в 4) я | а - 6|ем,
Д(а ® Ь) я | а х 6|еМ) Д(а © Ь) « | а : Ь\ем.
Конечно, в некоторых ситуациях округление может отсутствовать.
Например, полезно знать, что умножение и деление числа на целую
степень двойки выполняется на ЭВМ точно, так как в этом случае
мантисса не меняется.
Пример 2.17. Рассмотрим гипотетическую ЭВМ, в которой числа представ-
представляются всего лишь с 6 двоичными разрядами мантиссы, а округление произ-
производится по дополнению. Пусть на такой ЭВМ вычисляются сумма и произве-
40
дение двух представимых на ней чисел а = 20.5 = A0100.1J и Ь = 1.75 =
= A.11J- Производим вычисления в двоичной арифметике:
а+ Ь- A0100.1J
а х Ь = A0100.1J
A.11J = A00011.111J.
После округления до 6 значащих цифр получим а ® Ь — A0110.1J = 22.5,
а® Ь = A00100.)г = 36. Очевидно, что эти результаты отличаются от точных
значений а + Ь- 22.25, ах Ь= 35.875.
Заметим, что машинные арифметические операции обладают иными
свойствами, нежели обычные математические операции. Например, не
выполняется известное правило арифметики "от перемены мест слага-
слагаемых сумма не меняется". Покажем это на примере.
Пример 2.18. Пусть вычисления производятся на ЭВМ из примера 2.17,
причем а = (l.J, b = с - @.000001J. Тогда а + b = A.000001J и после
округления имеем а® Ь = A.00001J- Далее, (а ® Ь) + с = A.000011J и после
округления получим (а ® b) ® с — A.00010J- Сложение в ином порядке дает
с® Ь = @.000010J, (с® Ь) ® а = A.00001J. Таким образом, (а в 6) в с +
Ф (с® Ь)® а.
5. Удвоенная точность. На многих вычислительных машинах воз-
возможна реализация арифметических действий над числами, разряд-
разрядность мантисс которых примерно вдвое превосходит стандартную
разрядность i. Это приводит к существенному повышению машинной
точности. Например, на компьютерах типа IBM PC (при вычислениях
на ФОРТРАНЕ) в режиме удвоенной точности ем ~ 10~16. Для сравне-
сравнения напомним, что обычная точность этих ЭВМ есть ем ~ 10~7, так что
следует говорить не об удвоении точности, а о повышении точности на
много порядков.
На тех ЭВМ, где арифметика удвоенной точности реализована
аппаратурно, время исполнения программ возрастает не более чем
вдвое (часто этот коэффициент ближе к единице). Если же реализация
вычислений с удвоенной мантиссой осуществляется программным
образом, то время счета увеличивается в несколько раз. Поскольку
для хранения числа с удвоенной мантиссой отводится два машинных
слова, в этом случае вдвое возрастает используемая память.
Отметим, что удвоенная точность не ликвидирует ошибки округле-
округления, а только уменьшает их величину.
6. Вычисление машинного эпсилон. Для приближенного вычисле-
вычисления величины ем удобно пользоваться следующим определением.
Машинное эпсилон — это минимальное из представимых на ЭВМ
чисел е, для которых 1 © е > 1.
41

Величину ем можно оценить непосредственно в ходе вычислитель-
вычислительного процесса. Для этого достаточно включить в программу фрагмент,
реализующий следующий метод. Полагая е<0) = 1, следует вычислять
последовательно е'1» = 0.5е@), еB> = 0.5еA>, ..., е<п> = О.бе'"-", ...,
проверяя каждый раз выполнение неравенства 1 © е(п) > 1. Как толь-
только при некотором п окажется, что 1 © е(п) = 1, следует положить ?м =
= ?<n'i> и перейти к следующему этапу вычислений. Хотя полученное
таким способом значение может отличаться от ?м в 2 раза, обычно оно
используется так, что эта погрешность не имеет значения.
Пример 2.19. Покажем, что ем = 2~6 = @.000001J — машинное эпсилон
для ЭВМ из примера 2.17. В самом деле, 1 + ем = A.000001J и после округ-
округления имеем 1 © ем = A.00001)г. Если же к единице добавить любое положи-
положительное е < ?м, то в седьмом разряде результата будет стоять нуль и после
округления получим 1 © е = 1.
Всюду в дальнейшем, приводя конкретные числовые примеры, мы
откажемся от использования двоичной арифметики. Десятичная ариф-
арифметика привычнее, а основные закономерности поведения ошибок
округления не зависят от основания используемой системы. В боль-
большинстве расчетов, которые будут приведены для иллюстрации поведе-
поведения ошибок округления, имитируется выполнение вычислений на
гипотетической вычислительной машине, имеющей б десятичных
разрядов мантиссы и производящей округление по дополнению. Будем
называть эту машину 6-разрядной десятичной ЭВМ. Для нее ем =
= 5-Ю, так что по точности она сравнима с компьютером типа IBM
PC (при вычислениях на ФОРТРАНЕ с обычной точностью).
§ 2.6. Дополнительные замечания
1. Более подробно приближенные числа и погрешности арифметических
операций над ними изложены в известном учебном пособии [28]. Здесь же
приведены правила подсчета оставляемых значащих цифр, которые рекоменду-
рекомендуется применять при массовых "ручных" вычислениях без точного учета по-
погрешностей.
2. Дополнительную информацию об особенностях арифметических опера-
операций над числами с плавающей точкой можно найти, например, в [19], [83].
3. В последнее время в практике вычислений в качестве меры ошибки
приближенного числа а* часто используют величину
а-а
1+
Глава 3
ВЫЧИСЛИТЕЛЬНЫЕ ЗАДАЧИ,
МЕТОДЫ И АЛГОРИТМЫ.
ОСНОВНЫЕ ПОНЯТИЯ
§ 3.1. Корректность вычислительной задачи
1. Постановка вычислительной задачи. Под вычислительной зада-
задачей будем понимать одну из трех задач, которые возникают при ана-
анализе математических моделей: прямую задачу, обратную задачу или
задачу идентификации (см. § 1.2). Слово "вычислительная" подчер-
подчеркивает, что основные усилия будут направлены на то, чтобы найти
(вычислить) ее решение.
Будем считать, что постановка задачи включает в себя задание
множества допустимых входных данных X и множества возможных
решений Y. Цель вычислительной задачи состоит в нахождении реше-
решения у€ У по заданному входному данному хвХ. Для простоты понима-
понимания достаточно ограничиться рассмотрением задач, в которых входные
данные и решение могут быть только числами, наборами чисел (векто-
(векторами, матрицами, последовательностями) и функциями. Предположим,
что для оценки величин погрешностей приближенных входных данных
х* и приближенного решения у* введены абсолютные и относительные
погрешности А(х*), Д(з/*), 6(х*), 6(у*), а также их границы Д(я*),
Д(У*)> Жх*)' Жу*)- Определения этих величин в случае, когда х и у —
числа, были даны в § 2.2. В тех случаях, когда входные данные или
решение не являются числами, эти характеристики погрешностей
также можно ввести естественным образом; мы будем это делать по
мере необходимости.
2. Определение корректности задачи. Анализ важнейших тре-
требований, предъявляемых к различным прикладным задачам, приводит
к понятию корректности математической задачи, которое было
впервые сформулировано Ж.Адамаром1 и развито затем И.Г.Петров-
объединяющую в себе черты абсолютной и относительной погрешности. Она
близка к Д | а*\ при \а\ < 1 и практически совпадает с 6(а*) при \ а\ > 1.
42
Жак Адамар A865 — 1963) — французский математик.
43

ским1. Вычислительная задача называется корректной (по Адамару —
Петровскому), если выполнены следующие три требования: 1) ее реше-
решение у& Y существует при любых входных данных х€Х; 2) это решение
единственно; 3) решение устойчиво по отношению к малым возмуще-
возмущениям входных данных. В том случае, когда хотя бы одно из этих
требований не выполнено, задача называется некорректной.
Существование решения вычислительной задачи — естественное
требование к ней. Отсутствие решения может свидетельствовать, на-
например, о непригодности принятой математической модели либо о
неправильной постановке задачи. Иногда отсутствие решения является
следствием неправильного выбора множества допустимых входных
данных X или множества возможных решений У.
Пример 3.1. Рассмотрим задачу о решении квадратного уравнения
+ Ьх + с = 0.
C.1)
Старший коэффициент а считается равным единице; этого всегда можно
добиться делением уравнения на о. Если считать входным данным пару коэф-
коэффициентов 6, с и искать решение в множестве вещественных чисел, то сущест-
существование решений
XI = (-6 - \Р - 4с )/2, *2 = (-Ь +
- 4с )/2
C.2)
будет гарантировано только в том случае, если ограничить множество входных
данных коэффициентами, удовлетворяющими условию ft2 - 4с > 0. Если же
расширить множество возможных решений и считать, что корни C.2) могут
принимать комплексные значения, то задача будет иметь решение при любых
Ь, с.
Так как математическая модель не является абсолютно точным
отражением реальной ситуации, то даже в случае, когда исходная
проблема заведомо имеет решение, соответствующая вычислительная
задача может и не оказаться разрешимой. Конечно, такая ситуация
говорит о серьезном дефекте в постановке задачи. В некоторых случа-
случаях отсутствие решения математической задачи приводит к пониманию
1 Иван Георгиевич Петровский A901 — 1973) — российский математик.
того, что первоначально сформулированная проблема неразрешима и
нуждается в серьезной корректировке.
3. Единственность. Для некоторых вычислительных задач единст-
единственность является естественным свойством; для других же .решение
может и не быть единственным. Например, квадратное уравнение C.1)
имеет два корня C.2). Как правило, если задача имеет реальное содер-
содержание, то неединственность может быть ликвидирована введением
' дополнительных ограничений на решение (т.е. сужением множества У).
В некоторых случаях проблема снимается тем, что признается целесо-
целесообразным найти набор всех решений, отвечающих входным данным х,
и тогда за решение у принимается этот набор. Например, для уравне-
уравнения C.1) решением можно назвать пару (ib x2).
Неединственность решения вычислительной задачи — весьма непри-
неприятное свойство. Оно может быть проявлением неправильной постанов-
постановки исходной прикладной проблемы, неоднозначности ее решения или
сигналом о неудачном выборе математической модели.
4. Устойчивость решения. Решение у вычислительной задачи назы-
называется устойчивым по входным данным х, если оно зависит от входных
данных непрерывным образом. Это означает, что для любого е > О
существует 8 — 6(г) > 0 такое, что всякому исходному данному х*,
удовлетворяющему условию Д(я*) < 6, отвечает приближенное
решение у*, для которого А(у*) < е. Таким образом, для устойчивой
вычислительной задачи ее решение теоретически можно найти со
сколь угодно высокой точностью ?, если обеспечена достаточно
высокая точность 6 входных данных. Схематически ситуация
изображена на рис. 3.1. Множества тех х* и у*, для которых Д(х*) <
6 и Д(?/*) < е, изображены как окрестности точек г и у, имеющие
радиусы 6 и ?. Требование увеличить точность решения приводит
автоматически к повышению требований к точности данных;
соответствующие окрестности на рис. 3.1 отмечены пунктиром.
Рис 3.1
44
45

Неустойчивость решения у означает, что существует такое во > О,
что какое бы малое 8 > 0 ни было задано, найдутся такие исходные
данные г*, что А(х*) < 8, но А(у*) > ?о-
Приведем простейшие примеры устойчивых и неустойчивых задач.
Пример 3.2. Задача вычисления корней квадратного уравнения C.1) устой-
устойчива, так как корни C.2) являются непрерывными функциями коэффициентов
бис.
Пример 3.3. Задача о вычислении ранга матрицы в общем случае неустой-
неустойчива. В самом деле, для матрицы А = \ ранг равен 1, поскольку detA — О
и существует ненулевой элемент ац — 1. Однако сколь угодно малое возмуще-
возмущение коэффициента аъг на величину ? + О приводит к матрице А = ,
для которой detA = ? ф 0 и, следовательно, ранг равен 2.
Пример 3.4. Покажем, что задача вычисления определенного интеграла / =
dx устойчива.
Пусть f*(x) — приближенно заданная интегрируемая функция и I* —
dx- Определим абсолютную погрешность функции /* с помощью равен-
а
ства Д(/*) = sup|j(a:) — /*(х)|, в котором знак sup можно заменить на max,
если /и /* непрерывны. Так как
Д(Г) = \1- 1*\ = |/(/(*) -Г(*))<1х| < F- а)Д(/*),
C.3)
то для любого ? > 0 неравенство Д(/*) < ? будет выполнено, если
потребовать выполнение условия Д(/*) < 8 = ?/F - а).
Пример 3.5. Покажем, что задача вычисления производной и (х) = f'(x)
приближенно заданной функции является неустойчивой.
Пусть /*(а) — приближенно заданная на отрезке [а, 6] непрерывно
дифференцируемая функция и и*(х) = (f*)'(x). Определим абсолютные
погрешности с помощью равенств Д(/*) = rmax.|/ (х) - f*(x)\, Д(«*) =
- maxЛи{х) - и\х)\.
[а ,Ь\
Возьмем, например f*(x) = / (х) + a sin(ar/a2), где 0 < а < 1. Тогда
и*(х) — и (х) + acos(ar/a2) и Д(и*) = а, в то время как Д(/*) = а. Таким
образом, сколь угодно малой погрешности задания функции / может отвечать
сколь угодно большая погрешность производной /'.
46
Различие в ситуациях, возникающих при приближенном задании
функции /в задачах интегрирования и дифференцирования, отражено
на рис. 3.2. Видно, что уменьшение величины 6 = Д(/*) влечет за
собой уменьшение Д(/*) (эта величина не превышает заштрихованной
площади), в то время как производные /' и (/*)' могут отличаться
сколь угодно сильно.
Рис. 3.2
Одна и та же задача может оказаться как устойчивой, так и неус-
неустойчивой в зависимости от выбора способа вычисления абсолютных
погрешностей Д(г*) и Д(у*). В реальных задачах этот выбор
определяется тем, в каком смысле должно быть близко приближенное
решение к точному и малость какой из мер погрешности входных
данных можно гарантировать.
Пример 3.6. Рассмотрим задачу о вычислении суммы сходящегося ряда
S — S at с приближенно заданными слагаемыми а ? и at. Если a t определяет-
Jfc=o * *
ся таким образом, что гарантируется малость Д(в?) для всех к, то для после-
оо
довательности a* = {a*}jt=o естественно положить Д(а*) — sup|a^ - a?|. В
такой постановке задача неустойчива. Чтобы убедиться в этом, достаточно
положить а? = at + 8 (где 8 > 0) для к < N и а? = ajt для к 2 N. Тогда для
оо
суммы ряда 5* = Е а? имеем ДE*) = N8. Следовательно, как бы ни была
fc=o
мала величина Д(а*) — 8, абсолютную погрешность суммы ряда S* с по-
помощью выбора N можно сделать сколь угодно большой. Если же положить
47

ak ~ ak "*" ^ для всех Ь то сумма ряда S* вообще станет бесконечной, т.е. ряд
станет расходящимся.
В то же время, если можно задавать а? так, чтобы оказалась малой вели-
величина Д(а*) = Е \ак - а?|, то ДE*) = | Е (а* - а?)| < Д(а') и в такой
постановке задача устойчива.
5. Относительная устойчивость решения. Часто требование малости
абсолютной погрешности является неоправданным или трудно прове-
проверяемым. В таких случаях полезно рассмотреть относительную устой-
устойчивость решения, определение которой отличается от данного выше
определения устойчивости (абсолютной устойчивости) только тем,
что А(х*) и Д(у*) заменяются на 6(х*) и 6(у*) соответственно.
оо
Пример 3.7. Вернемся к задаче вычисления суммы ряда S — S ajt из
Jt=o
примера 3.6. Предположим, что a* t 0 для всех к. Часто можно гарантировать
малость величины 6(а*) = sup{ | ajt - a?|/|ajt|}. Тогда Д(а?) < |ajt| • 6(а*) и
&0
поэтому ДE*) < Е | afc| • 6(а*). Таким образом,
6(s*) < f_S | ofcl/l.? «*|
'*)¦ C.4)
Следовательно, задача вычисления суммы сходящегося ряда S относитель-
оо
но устойчива, если он сходится абсолютно (т.е. сходится ряд S | а^|).Если же
ряд сходится только условно, т.е. S | ед| = оо, то задача не является относи-
к-о
тельно устойчивой.
Замечание. Так как для решения вычислительных задач
используют ЭВМ, точность которых определяется разрядностью
мантиссы или эквивалентной величиной границы относительной
погрешности округления ем, то представляется более естественным
исследование относительной устойчивости.
6. О некорректных задачах. Длительное время считалось, что не-
некорректные задачи, решения которых неустойчивы, не имеют физи-
физического смысла и не представляют ценности для приложений. Однако
это мнение оказалось ошибочным. Как выяснилось, многие важные
прикладные задачи некорректны. Не вызывает, например, сомнения
48
практическая важность решения некорректных задач дифференциро-
дифференцирования и суммирования ряда (см. примеры 3.5, 3.6). К некорректным
задачам относятся также обратные задачи геофизики, астрофизики,
спектрографии, многие задачи распознавания образов, задачи синтеза
и ряд других прикладных задач.
К настоящему времени разработана теория решения многих классов
некорректных задач. Важная роль в создании методов решения таких
задач принадлежит российским математикам, в первую очередь
А.Н.Тихонову1. Эти методы (методы регуляризации) довольно сложны
и выходят за рамки данной книги. Для первого знакомства с ними
можно рекомендовать учебное пособие [79].
§ 3.2. Обусловленность вычислительной задачи
1. Определения. Пусть вычислительная задача корректна (ее реше-
решение существует, единственно и устойчиво по входным данным). Теоре-
Теоретически наличие у задачи устойчивости означает, что ее решение
может быть найдено со сколь угодно малой погрешностью, если только
гарантировать, что погрешности входных данных достаточно малы.
Однако на практике погрешности входных данных не могут быть
сделаны сколь угодно малыми, точность их ограничена. Даже то, что
исходные данные нужно будет ввести в ЭВМ, означает, что их относи-
относительная точность будет заведомо ограничена величиной порядка ?м
(см. § 2.5). В реальности, конечно, уровень ошибок в исходной инфор-
информации будет существенно выше. Как же повлияют малые, но конечные
погрешности входных данных на решение, как сильно способны они
исказить желаемый результат? Для ответа на этот вопрос введем новые
понятия.
Под обусловленностью вычислительной задачи понимают чувстви-
чувствительность ее решения к малым погрешностям входных данных. Задачу
называют хорошо обусловленной, если малым погрешностям входных
данных отвечают малые погрешности решения, и плохо обусловленной,
если возможны сильные изменения решения.
Часто оказывается возможным ввести количественную меру степени
обусловленности вычислительной задачи — число обусловленности.
Эту величину можно интерпретировать как коэффициент возможного
возрастания погрешностей в решении по отношению к вызвавшим их
погрешностям входных данных.
Андрей Николаевич Тихонов A906—1993) — российский математик.
49

Пусть между абсолютными погрешностями входных данных х и
решения у установлено неравенство
Д(у») < "дД(О- C.5)
Тогда величина 1/д называется абсолютным числом обусловленности.
Если же установлено неравенство
6(у<) < vs5{t*) C.6)
между относительными ошибками данных и решения, то величину vg
называют относительным числом обусловленности. В неравенствах
C.5), C.6) вместо погрешностей Д и 8 могут фигурировать их границы
Д и 8. Обычно под числом обусловленности v задачи понимают одну
из величин i/д или i/g, причем выбор бывает ясен из смысла задачи.
Чаще все же под числом обусловленности понимают относительное
число обусловленности. Для плохо обусловленной задачи v > 1. В
некотором смысле неустойчивость задачи — это крайнее проявление
плохой обусловленности, отвечающее значению v = <». Конечно, v —
это максимальный коэффициент возможного возрастания уровня оши-
ошибок, и для конкретных исходных данных действительный коэффици-
коэффициент возрастания может оказаться существенно меньше. Однако при
выводе оценок C.5) и C.6) стремятся к тому, чтобы не завышать зна-
значений i/д и Ug и поэтому соотношение v > 1 все же свидетельствует о
реальной возможности существенного роста ошибок. Грубо говоря,
если v ~ 10^, где v — относительное число обусловленности, то поря-
порядок N показывает число верных цифр, которое может быть утеряно в
результате по сравнению с числом верных цифр входных данных.
Каково то значение и, при котором следует признать задачу плохо
обусловленной? Ответ на этот вопрос существенно зависит, с одной
стороны, от предъявляемых требований к точности решения и, с дру-
другой — от уровня обеспечиваемой точности исходных данных. Напри-
Например, если требуется найти решение с точностью 0.1%, а входная ин-
информация задается с точностью 0.02%, то уже значение v = 10 сигна-
сигнализирует о плохой обусловленности. Однако (при тех же требованиях
к точности результата) гарантия, что исходные данные задаются с
точностью не ниже 0.0001%, означает, что и при v = 103 задача хоро-
хорошо обусловлена.
С простым, но очень важным примером плохо обусловленной зада-
задачи мы уже познакомились в § 2.3. Это задача вычитания приближен-
приближенных чисел одного знака. Оценка B.10) дает для нее значение относи-
50
тельного числа обусловленности v — |а+6|/|а— 6|. Так как в приме-
примере 2.11 имеем i/ » |1 + х*|/|1 — г*| я 7-Ю5, то потеря пяти верных
значащих цифр здесь не представляется удивительной.
2. Примеры плохо обусловленных задач. Первым рассмотрим клас-
классический пример, принадлежащий Дж.Уилкинсону [83].
Пример 3.8. Пусть требуется найти корни многочлена
Р(х) = (х- 1)(аг-2) ... (х- 20) = х20 - 210 х19 + ...
по заданным значениям его коэффициентов. Из теории известно, что эта
задача устойчива. Возьмем коэффициент а = -210 при г19 и изменим его
значение на а * = -210 + 23. Как повлияет эта, казалось бы, незначительная
ошибка на значения корней? Заметим, что ху = 1, х^ = 2, ..., x^q = 20 —
точные значения корней.
Вычисленные с высокой точностью корни возмущенного многочлена таковы:
х* я 1.00000; х* я 2.00000; х* я 3.00000; х* а 4.00000; х* и 5.00000;
х* и 6.00001; х* я 6.99970; х* и 8.00727; х* и 8.91725;
2г*011 и 10.0953 ± 0.64350b; х*2<13 и 11.7936 ± 1.65233»;
х4 ,
13.9924 ± 2.518832; х*6
16.7307 ± 2.81262г;
х* 10 и 19.5024 ± 1.94033»; х* » 20.8469.
1 3,1У ? U
х
Как нетрудно видеть, корни х\, ..., х& оказались практически нечувствительны
к погрешностям в коэффициенте а. В то же время некоторые корни преврати-
превратились в комплексные и имеют относительные погрешности от 6 до 18%, несмот-
несмотря на то, что 8(а*) я 6-10"8%.
В данном случае нетрудно провести анализ чувствительности корней. Пусть
F[x, а) = х20 + ai19 + ... .Будем рассматривать корни Хк как функции
параметра а, т.е. г^ = хк(а). Равенство F (х^а), а) = 0, выполненное в
окрестности а = -210, задает ifc как неявную функцию от а. Пользуясь
второй из формул B.22) для границы относительной погрешности и применяя
формулу B.23) для производной неявной функции, имеем
\a\-\FjFL\
?) я Vk8(a*), где
. Учитывая, что
-хк
а=-210
20
= . П ( х - i), получаем v^ —
dF
—
да
dF
—-
дх
= Р\х) =
Q=-210
210/с18
51

Вычисление чисел z/jt дает следующие значения:
j/j я 2-Ю5, J/2 й 9-Ю"8, и3 я 10, J/4 я 10м, J/5 й 3-Ю1,
i/6 я 2-Ю3, 1/7 я 8-104, i/8 я 2-Ю6, i/9 я 2-Ю7, »/10 « 2-Ю8,
J/ц я 9-Ю9, 1/12 й 4-109, //и я Ю10, 1/м й 2-Ю10, fis я 3-Ю10,
1/16 Я 3-Ю10, 1/17 й 3-Ю10, fig и Ю10, 1Л9 й 3-Ю9, 1/20 й 5-Ю8,
свидетельствующие о чрезвычайно плохой обусловленности старших корней.
Следует обратить серьезное внимание на то, что задача вычисления
корней многочленов высокой степени часто оказывается плохо обусло-
обусловленной. Поэтому имеет смысл с определенной осторожностью отно-
относиться к алгоритмам, составной частью которых является вычисление
корней многочленов высокой степени.
К сожалению, эта задача может быть плохо обусловленной и для
многочленов невысокой степени, в особенности, если вычисляются
кратные корни.
Пример 3.9. Пусть ищется решение уравнения (г - IL = 0 с кратным
корнем. Ошибка в младшем коэффициенте, равная 10"8, приводит к уравне-
уравнению (х - IL = 10"8, имеющему следующие корни: ц^ = 1 ± 10~2, 1&,4 =
= 1 ± 10-«. В этом случае ошибка в 10% в одном из коэффициентов приве-
привела к погрешности решения в 1%, что явно говорит о плохой обусловленности
задачи.
3. Обусловленность задачи вычисления значения функции одной
переменной. Пусть задача состоит в вычислении по заданному х значе-
значения у = / (х) дифференцируемой функции /. В силу формул B.21),
B.22) для этой задачи имеем
« I/'(*)!,
¦!/'(*)
C.7)
C-8)
Воспользуемся этими формулами для оценки обусловленности
задачи вычисления значений некоторых простейших функций.
Пример 3.10. Для задачи вычисления значения функции у = ех в силу
формулы C.8) относитечьное число обусловленности Vc приближенно равно | х\
и при реальных вычислениях эта величина не может быть очень большой.
Например, при вычислении экспоненты на компьютере типа IBM PC всегда
|г| < 88, так как в противном случае возможно переполнение или
антипереполнение. Следовательно, задача вычисления этой функции хорошо
обусловлена, однако в случае 10 < \х\ < 102 следует ожидать потери 1—2
верных значащих цифр по сравнению с числом верных цифр аргумента х.
Подчеркнем, что эта потеря точности объективно обусловлена погрешностью
задания аргумента и не связана с используемым алгоритмом.
Пример 3.11. Для задачи
вычисления значения функции У
у = sinх в силу формулы C.7)
имеем i/д = |cosx| < 1, что гово-
говорит о хорошей абсолютной обус-
обусловленности этой задачи при всех
х. Однако если важен результат с
определенным числом верных
знаков, то нужно исследовать
относительную обусловленность.
Согласно формуле C.8) имеем -
1Л- = | х ctg х\. На рис. 3.3 приве-
г
in.
ден график этой функции при х
г? 0 (она четная).
Рис. 3.3
Так как
оо при X
¦кк
(для к = ± 1, ± 2, ...), то при х я жк задача обладает плохой относительной
обусловленностью, и можно лишь утешаться тем, что мала абсолютная
погрешность значения у* — sini*. Если же значение |х| очень велико, то i/j >
> 1 и вычислять значение синуса просто бессмысленно. Например, если вы-
вычисления ведутся на компьютере типа IBM PC, где ?м ~ 10, то уже для
|r| ~ 107 одна только абсолютная ошибка представления числа х есть
величина порядка единицы, так как А(х*) я |г|-ем. Нетрудно понять, что
при Д(я*) - 1 вычисленное любым способом значение sinr* не представляет
никакой .ценности. Вывод, который можно сделать, довольно прост: при ис-
использовании функции у = sinx желательно проводить вычисления так, чтобы
аргумент находился в диапазоне |г| < 2, поскольку здесь Vc ^ 1.
Ь
4. Обусловленность задачи вычисления интеграла / = [/ (x)dz. Как
а
следует из оценки C.3), в этом случае абсолютное число обусловленно-
обусловленности имеет вид 1/д = (Ь - а). Если же перейтрТк рассмотрению относи-
относительных погрешностей и положить 6(f*) = sup |/*(i) - /
для тех, х, где f(x) t 0, то используя неравенство
¦ A(r)<nr(x)-/(i)|dx<f|/(i)|d*.*(n,
x)\
52
53

получим оценку
ь ь
в которой vs= [ |/ (г) | dr/1 \ f (x)dx\.
C.9)
Если подынтегральная функция знакопостоянна, то Vg = 1 и задача
хорошо обусловлена. Если же функцТия / на [а, Ь] принимает значения
разных знаков, то vs > 1. Для некоторых сильно колеблющихся (ос-
(осциллирующих) около нуля функций может оказаться, что Vg > 1 и
тогда задача вычисления интеграла является плохо обусловленной. '
Иногда причиной появления плохо обусловленных задач становит-
становится отсутствие у пользователя ЭВМ элементарного представления об их
существовании. В связи с этим заметим, что в последнее время получа-
получает развитие опасная тенденция пренебрежительного отношения к
математическим знаниям вообще и к знанию вычислительной матема-
математики, в частности. Вера в могущество ЭВМ и надежность стандартных
программ бывает так велика, что считается совсем ненужным знать о
вычисляемой математической величине что-либо кроме ее определения
и, возможно, геометрического или физического смысла. Приведем
простой пример, иллюстрирующий оценку C.9) и заодно показыва-
показывающий, что иногда аналитическая выкладка бывает эффективнее, чем
применение самого современного компьютера.
Пример 3.12. Пусть в распоряжении пользователя имеется высокопроизво-
высокопроизводительная ЭВМ и стандартная программа для вычисления интегралов вида
Ь
I— \ f(x) dx. Предположим, что нужно вычислить коэффициенты Фурье
а
1 2
9п — 1 9 (х) sinffnr dx для функции д (х) = х + Aecos х при п > 1 и А > 1.
-1
Использование для вычисления дп указанной стандартной программы при
/(г) = д (х) simrnx автоматически означает, что ставится вычислительная
задача, рассмотренная выше. При этом величина относительной погрешности
8 (/*) вычисляемой на ЭВМ функции /* и / заведомо не может быть меньше1
2
Оценим величину Vg. Заметим, что функция Ае008 х sirnrnx нечетная и,
1 Если учитывать погрешность вычисления функции siinrnr, то следует
ожидать, что эта величина будет значительно больше ?м.
54
следовательно, интеграл от нее равен нулю. Поэтому возможно аналитическое
вычисление интеграла:
дп - \ х sinxrur dx cosxnj
-1 я-п
-1
кп -
2
|ylecos х\ — \х\ ) Л- 1 и поэтому
xS» (A - 1) f |sin?rnx|dx = A - I.
-l
Кроме того, |^(х)
I |/(г)| dx= i\g(x)\ •
-l -l
Таким образом, us > (A - l)jrn/2 я 1.5 An. Если ^ вычисляется, например,
при A = 1(И и n = 102, то Vg > 1.5* 106. Следовательно, для этих значений
параметров принятое решение о вычислении интеграла по простейшей стан-
стандартной программе может- обойтись в потерю примерно 6 значащих цифр
результата. Если вычисления ведутся на ЭВМ, имеющей лишь порядка 7
десятичных значащих цифр, то возможна катастрофическая потеря точности.
Заметим, что в этих рассуждениях никак не учтены погрешность реализован-
реализованного в программе метода и вычислительная погрешность, наличие которых
усугубляет ситуацию.
5. Обусловленность задачи вычисления суммы ряда. Рассмотрим
задачу вычисления суммы абсолютно сходящегося ряда с ненулевыми
слагаемыми. В силу оценки C.4) эта задача устойчива, а за относи-
относительное число обусловленности следует принять величину
ие= Е \ак\/\ Е ак\.
к-0 к=0
C.10)
Заметим, что для ряда с положительными слагаемыми имеем vs = 1,
т.е. задача хорошо обусловлена. Если же ряд не знакопостоянный, то
vs > 1 и при Vg > 1 задача оказывается плохо об>словленной.
§ 3.3. Вычислительные методы
Обсудив некоторые важные особенности вычислительных задач,
обратим внимание на те методы, которые используются в вычислитель-
вычислительной математике для преобразования задач к виду, удобному для реа-
реализации на ЭВМ, и позволяют конструировать вычислительные алго-
алгоритмы. Мы будем называть эти методы вычислительными. С некото-
некоторой степенью условности можно разбить вычислительные методы на
следующие классы: 1) методы эквивалентных преобразований; 2) мето-
55

ды аппроксимации; 3) прямые (точные) методы; 4) итерационные
методы; 5) методы статистических испытаний (методы Монте-Карло).
Метод, осуществляющий вычисление решения конкретной задачи,
может иметь довольно сложную структуру, но его элементарными
шагами, являются, как правило, реализации указанных методов. Да-
Дадим о них общее представление.
1. Методы эквивалентных преобразований. Эти методы позволяют
заменить исходную задачу другой, имеющей то же решение. Выполне-
Выполнение эквивалентных преобразований оказывается полезным, если новая
задача проще исходной "или обладает лучшими свойствами, или для
нее существует известный метод решения, а, может быть, и готовая
программа.
Пример 3.13. Эквивалентное преобразование квадратного уравнения х2 +
Г j]2 J2 - 4с
+ Ьх +с = 0 к виду \х + - = — (выделение полного квадрата) сводит
[ 2J 4
задачу к проблеме вычисления квадратного корня и приводит к известным
для ее корней формулам C.2).
Эквивалентные преобразования иногда позволяют свести решение
исходной вычислительной задачи к решению вычислительной задачи
совершенно иного типа.
Пример 3.14. Задача отыскания корня нелинейного уравнения f (х) — О
может быть сведена к эквивалентной задаче поиска точки глобального мини-
минимума функции Ф (г) = (/(г)J. В самом деле, функция Ф (г) неотрицательна
и достигает минимального значения, равного нулю, при тех и только тех х,
для которых /(г) = 0.
2. Методы аппроксимации. Эти методы позволяют приблизить
(аппроксимировать) исходную задачу другой, решение которой в
определенном смысле близко к решению исходной задачи. Погреш-
Погрешность, возникающая при такой замене, называется погрешностью
аппроксимации. Как правило, аппроксимирующая задача содержит
некоторые параметры, позволяющие регулировать величину погреш-
погрешности аппроксимации или воздействовать на другие свойства задачи.
Принято говорить, что метод аппроксимации сходится, если погреш-
погрешность аппроксимации стремится к нулю при стремлении параметров
метода к некоторому предельному значению.
Пример 3.15. Один из простейших способов вычисления интеграла I —
Ь
= ] f(x)Ax состоит в аппроксимации интеграла на основании формулы прямо-
а
угольников величиной
56
Ih=hl /(« + (•- \)h).
Шаг h = (b — а)/п является здесь параметром метода. Так как Р1 представляет
собой специальным образом построенную интегральную сумму, то из определе-
определения определенного интеграла следует, что при k -» 0 метод прямоугольников
сходится, т.е Z'1 -» /.
Пример 3.16. Учитывая определение производной функции f'(x) —
f(x + Л) - f(x)
—i i-i , для ее приближенного вычисления можно исполь-
= 1 im
Л-о
зовать формулу f\x)
. Погрешность аппроксимации этой
0.
формулы численного дифференцирования стремится к нулю при k
Одним из распространенных методов аппроксимации является
дискретизация — приближенная замена исходной задачи конечномер-
конечномерной задачей, т.е. задачей, входные данные и искомое решение которой
могут быть однозначно заданы конечным набором чисел. Для задач,
которые не являются конечномерными, этот шаг необходим для после-
последующей реализации на ЭВМ, так как вычислительная машина в
состоянии оперировать лишь с конечным количеством чисел. В приве-
приведенных выше примерах 3.15 и 3.16 была использована дискретизация.
Хотя точное вычисление интеграла и предполагает использование
бесконечного числа значений f(x) (для всех z€ [a, b]), его приближен-
приближенное значение можно вычислить, используя конечное число п значений
в точках а + (i - ^/-ijh. Аналогично, задача вычисления производной,
точное решение которой предполагает выполнение операции предель-
предельного перехода при h -» 0 (а следовательно, использование бесконечного
числа значений функции f), сводится к приближенному вычислению
производной по двум значениям функции.
При решении нелинейных задач широко исполь-
используют различные методы линеаризации, состоящие
в приближенной замене исходной задачи более
простыми линейными задачами.
Пример 3.17. Пусть требуется приближенно вычислить
значение х — ?~а для а > 0 на ЭВМ, способной выпол-
выполнять простейшие арифметические операции. Заметим,
что по определению х является положительным корнем
нелинейного уравнения гг — а — 0. Пусть xi0) — неко-
некоторое известное приближение к \а. Заменим параболу
у= х2 - а прямой у = (г<°>J - а + 2z@> (х- г<°»),
являющейся касательной, проведенной к ней в Рис. S.4
57

точке с абциссой х — х@) (рис. 3.4). Точка пересечения этой касательной с
осью Ох дает лучшее, чем г@1 , приближение и находится из линейного
уравнения (г@)J — а + 2г@)(.г — г@)) = 0. Решая его, получаем
приближенную формулу
fa» х* =
r@) _
J-
C.11)
Например, если для х — \2 взять г'0) = 2, то получится уточненное
значение
J2 и *• = i B + ! = 1-5.
При решении разных классов вычислительных задач могут исполь-
использоваться различные методы аппроксимации; к ним можно отнести и
методы регуляризации решения некорректных задач. Заметим, что
методы регуляризации широко используют и для решения плохо обус-
обусловленных задач.
3. Прямые методы. Метод решения задачи называют прямым, если
он позволяет получить решение после выполнения конечного числа
элементарных операций.
Пример 3.18. Метод вычисления корней квадратного уравнения
х2 + Ъх +
+ с = 0 по формулам г\2 — (—Ь ± \ б2 - 4с)/2 является прямым методом.
Элементарными здесь считаются четыре арифметические операции и операция
извлечения квадратного корня.
Заметим, что элементарная операция прямого метода может ока-
оказаться довольно сложной (вычисление значений элементарной или
специальной функции, решение системы линейных алгебраических
уравнений, вычисление определенного интеграла и т.д.). То, что она
принимается за элементарную, предполагает во всяком случае, что ее
выполнение существенно проще вычисления решения всей задачи.
При построении прямых методов существенное внимание уделяется
минимизации числа элементарных операций.
Пример 3.19 (схема Горнер а1). Пусть задача состоит в вычисле-
вычислении значения многочлена
Рп(х) =
C.12)
Вильяме Джордж Горнер A786 — 1837) — английский математик.
по заданным коэффициентам ао, Дь ..., ап и значению аргумента х. Если
вычислять многочлен непосредственно по формуле C.12), причем х2, z3, ..., х"-
находить последовательным умножением на х, то потребуется выполнить 2п - 1
операций умножения и п операций сложения.
Значительно более экономичным является метод вычисления, называемый
схемой Горнера. Он основан на записи многочлена в следующем эквивалентном
виде:
= ((¦¦¦
Расстановка скобок диктует такой порядок вычислений: So = an, S\ =
= Sox + an-i, 52 = Six + an-2, ..., 5, = St-\x + а„-„ ..., Sn - Sn-\x + oq- Здесь
вычисление значения Рп{х) — Sn потребовало выполнения только п операций
умножения и п операций сложения.
Схема Горнера интересна тем, что дает пример оптимального по числу
элементарных операций метода. В общем случае значение Рп(х) нельзя полу-
получить никаким методом в результате выполнения меньшего числа операций
умножения и сложения.
Иногда прямые методы называют точными, подразумевая под
этим, что при отсутствии ошибок во входных данных и при точном
выполнении элементарных операций полученный результат также
будет точным. Однако при реализации метода на ЭВМ неизбежно
появление вычислительной погрешности, величина которой зависит от
чувствительности метода к ошибкам округления. Многие прямые
(точные) методы, разработанные в домашинный период, оказались
непригодными для машинных вычислений именно из-за чрезмерной
чувствительности к ошибкам округления. Не все точные методы тако-
таковы, однако стоит заметить, что не совсем удачный термин "точный"
характеризует свойства идеальной реализации метода, но отнюдь не
качество полученного при реальных вычислениях результата.
4. Итерационные методы. Это — специальные методы построения
последовательных приближений к решению задачи. Применение мето-
метода начинают с выбора одного или нескольких начальных приближе-
приближений. Для получения каждого из последующих приближений выполня-
выполняют однотипный набор действий с использованием найденных ранее
приближений — итерацию1. Неограниченное продолжение этого
итерационного процесса теоретически позволяет построить
бесконечную последовательность приближений к решению —
1 От лат. iteratio — "повторение".
58
59

итерационную последовательность. Если эта последовательность
сходится к решению задачи, то говорят, что итерационный метод
сходится. Множество начальных приближений, для которых метод
сходится, называется областью сходимости метода.
Заметим, что итерационные методы широко используются при
решении самых разнообразных задач с применением ЭВМ.
Пример 3.20. Рассмотрим известный итерационный метод, предназначенный
для вычисления [а (где а > 0), — метод Ньютона. Зададим произвольное
начальное приближение г@) > 0. Следующее приближение вычислим по
формуле г(
= I|,<0> +
2Г х@>
выведенной с помощью метода линеаризации
в примере 3.17 (см. формулу C.11)). Продолжая этот процесс далее, получим
итерационную последовательность г@), гA), гB), ..., г( п), ..., в которой
очередное (Jfc + 1)-е приближение вычисляется через k-e по рекуррентной1
формуле
r( Jt+l) = I г( к) +
Х 2
C.13)
Известно, что этот метод сходится при любом начальном приближении
г@) > Qt так что его область сходимости — множество всех положительных
чисел.
Вычислим с его помощью значение %2 на 8-разрядной десятичной ЭВМ.
Зададим г@) =2 (как в примере 3.17). Тогда хA) = 1.5, iB) = 1.4166667,
гC) - 1.4142166, гD) = 1.4142136, тE) = 1.4142136. Дальнейшие вычисления
бессмысленны, так как из-за ограниченности разрядной сетки все следующие
уточнения будут давать тот же результат. Однако сравнение с точным значе-
значением |2 = 1.41421356... показывает, что уже на третьей итерации были полу-
получены 6 верных значащих цифр.
Обсудим на примере метода Ньютона некоторые типичные для
итерационных методов (и не только для них) проблемы. Итерационные
методы по своей сути являются приближенными; ни одно из получа-
получаемых приближений не является точным значением решения. Однако
сходящийся итерационный метод дает принципиальную возможность
найти решение с любой заданной точностью е > 0. Поэтому, применяя
итерационный метод, всегда задают требуемую точность е и
итерационный процесс прерывают, как только она достигается.
1 От лат. recurrens — "возвращающийся".
Хотя сам факт сходимости метода безусловно важен, он недостато-
недостаточен для того, чтобы рекомендовать метод для использования на прак-
практике. Если метод сходится очень медленно (например, для получения
решения с точностью в 1% нужно сделать 106 итераций), то он непри-
непригоден для вычислений на ЭВМ. Практическую ценность представляют
быстро сходящиеся методы, к которым относится и метод Ньютона
(напомним, что точность ? = Ю~5 в вычислении [2 была достигнута
всего за три итерации). Для теоретического исследования скорости
сходимости и условий применимости итерационных методов выводят
так называемые априорные1 оценки погрешности, позволяющие еще до
вычислений дать некоторое заключение о качестве метода.
Приведем две такие априорные оценки для метода Ньютона. Пусть
г( 0) > [а. Известно, что тогда х< "> > [а для всех п > 0 и погрешности
двух последовательных приближений связаны следующим неравен-
неравенством:
Здесь
(t
( п) -
"'
C.14)
— величина, характеризу-
ющая относительную погрешность n-го приближения. Это неравенство
говорит об очень высокой квадратичной скорости сходимости метода:
на каждой итерации "ошибка" 6( "> возводится в квадрат. Если
выразить Sin) через погрешность начального приближения, то
получим неравенство
6(п) < (^@)JП_ (з.15)
из которого вида роль хорошего выбора начального приближения. Чем
меньше величина 6'°' = 6(х@>)/2, тем быстрее будет сходиться метод.
Практическая реализация итерационных методов всегда связана с
необходимостью выбора критерия окончания итерационною процесса.
Вычисления не могут продолжаться бесконечно долго и должны быть
прерваны в соответствии с некоторым критерием, связанным, напри-
например, с достижением заданной точности. Использование для этой цели
априорных оценок чаще всего оказывается невозможным или неэффек-
неэффективным. Качественно верно описывая поведение метода, такие оценки
являются завышенными и дают весьма недостоверную количественную
информацию. Нередко априорные оценки содержат неизвестные вели-
1 От лат. a'priori — "до опыта".
60
61

чины (например, в оценках C.14), C.15) содержится величина j~a),
либо предполагают наличие и серьезное использование некоторой
дополнительной информации о решении. Чаще всего такой информа-
информации нет, а ее получение связано с необходимостью решения дополни-
дополнительных задач, нередко более сложных, чем исходная.
Для формирования критерия окончания по достижении заданной
точности, как правило, используют так называемые апостериорные1
оценки погрешности — неравенства, в которых величина погрешности
оценивается через известные или получаемые в ходе вычислительного
процесса величины. Хотя такими оценками нельзя воспользоваться до
начала вычислений, в ходе вычислительного процесса они позволяют
давать конкретную количественную оценку погрешности.
Например, для метода Ньютона C.13) справедлива следующая
апостериорная оценка:
|х'"> - [а\ < |z<"> - z<"-4 |, п> 1,
позволяющая оценивать абсолютную погрешность приближения через
модуль разности двух последовательных приближений. Она дает воз-
возможность сформулировать при заданной точности ? > 0 очень простой
критерий окончания. Как только окажется выполненным неравенство
(п) _
C.16)
вычисления следует прекратить и принять х( n) за приближение к [а с
точностью ?.
Пример 3.21. Если значение %2 требуется найти с точностью ? = 10~5, то
неравенство C.16), как видно из приведенных в примере 3.20 вычислений,
будет выполнено при п = 4. Так как |хD) - rt3) | = 3-Ю, то с учетом
погрешности округления можно записать результат:- %2 = 1.41421 ± 0.00001.
5. Методы статистических испытаний (методы Монте-Карло). Это —
численные методы, основанные на моделировании случайных величин
и построении статистических оценок решений задач. Этот класс мето-
методов, как принято считать, возник в 1949 г., когда Дж. фон Нейман2 и
1 От лат. a'posteriori — "после опыта".
2 Джон фон Нейман A903 — 1957) — американский математик, физик,
инженер-изобретатель. Оказал значительное влияние на развитие современной
математики. Один из создателей первых ЭВМ.
62
С.Улам1 использовали случайные числа для моделирования с
помощью ЭВМ поведения нейтронов в ядерном реакторе. Эти методы
могут оказаться незаменимыми при моделировании больших систем,
но подробное их изложение предполагает существенное использование
аппарата теории вероятностей и математической статистики и выходит
за рамки данной книги.
§ 3.4. Корректность вычислительных
алгоритмов
1. Вычислительный алгоритм. Вычислительный метод, доведенный
до степени детализации, позволяющий реализовать его на ЭВМ, при-
принимает форму вычислительного алгоритма.
Определим вычислительный алгоритм как точное предписание
действий над входными данными, задающее вычислительный процесс,
направленный на преобразование произвольных входных данных х (из
множества допустимых для данного алгоритма входных данных X) в
полностью определяемый этими входными данными результат.
Реальный вычислительный алгоритм складывается из двух частей:
абстрактною вычислительного алгоритма, формулируемого в обще-
общепринятых математических терминах, и программы, записанной на
одном из алгоритмических языков и предназначенной для реализации
алгоритма на ЭВМ. Как правило, в руководствах по методам вычисле-
вычислений излагаются именно абстрактные алгоритмы, но их обсуждение
проводится так, чтобы выявить особенности алгоритмов, которые
оказывают существенное влияние на качество программной реали-
реализации.
2. Определение корректности алгоритма. К вычислительным алго-
алгоритмам, предназначенным для широкого использования, предъявляет-
предъявляется ряд весьма жестких требований. Первое из них — корректность
алгоритма. Будем называть вычислительный алгоритм корректным,
если выполнены три условия: 1) он позволяет после выполнения ко-
конечного числа элементарных для вычислительной машины операций
преобразовать любое входное данное х?Х в результат у; 2) результат у
устойчив по отношению к малым возмущениям входных данных; 3)
результат у обладает вычислительной устойчивостью. Если хотя бы
одно из перечисленных условий не выполнено, то будем называть
алгоритм некорректным. Уточним и более подробно обсудим эти ус-
условия.
1 Станислав Улам A909 — 1984) — американский математик.
63

Необходимость выполнения первого условия понятна. Если для
получения результата нужно выполнить бесконечное число операций
либо требуются операции, не реализованные на ЭВМ, то алгоритм
следует признать некорректным.
Пример 3.22. Известный алгоритм деления чисел "углом" некорректен, так
как он может продолжаться бесконечно, если не определен критерий оконча-
окончания вычислений.
Пример 3.23. Отсутствие критерия окончания делает "некорректным и
алгоритм Ньютона вычисления \а (см. пример 3.20).
Пример 3.24. Алгоритм вычисления корней квадратного уравнения C.1) по
формулам C.2) некорректен, если он предназначен для использования на
вычислительной машине, на которой не реализована операция извлечения
квадратного корня.
3. Устойчивость по входным данным. Устойчивость результата у к
малым возмущениям входных данных {устойчивость по входным
данным) означает, что результат непрерывным образом зависит от
входных данных при условии, что отсутствует вычислительная пог-
погрешность. Это требование устойчивости аналогично требованию устой-
устойчивости вычислительной задачи. Отсутствие такой устойчивости де-
лаег алгоритм непригодным для использования на практике.
Отметим, что в формулировку устойчивости алгоритма по входным
данным неявно входит одно весьма важное предположение, а именно,
что вместе с входным данным х в множество допустимых входных
данных X входят и все близкие к х приближенные входные данные х*.
Пример 3.25. Пусть алгоритм предназначен для вычисления корней квад-
квадратного уравнения C.1) с коэффициентом, удовлетворяющими условию d —
= б2 - Ас ^ 0. Если в нем используются формулы C.2), то этот алгоритм
некорректен. В самом деле, значение d*, отвечающее приближенно заданным
коэффициентам Ь* и с*, может оказаться отрицательным, если d и 0. Тогда
вычисления завершатся аварийным остановом при попытке извлечь
квадратный корень из отрицательного числа. Если же в формуле C.2)
заменить d на max {d, 0}, то алгоритм становится корректным.
4. Вычислительная устойчивость. Из-за наличия ошибок округле-
округления при вводе входных данных в ЭВМ и при выполнении арифмети-
арифметических операций неизбежно появление вычислительной погрешности.
Ее величина на разных ЭВМ различна из-за различий в разрядности
и способах округления, но для фиксированного алгоритма в основном
величина погрешности определяется машинной точностью ем.
64
Назовем алгоритм вычислительно устойчивым, если вычислитель-
вычислительная погрешность результата стремится к нулю при ?м -» 0. Обычно
вычислительный алгоритм называют устойчивым, если он устойчив по
входным данным и вычислительно устойчив, и неустойчивым, если
хотя бы одно из этих условий не выполнено.
Пример 3.261. Пусть требуется составить таблицу значений интегралов
1п = \ х'^'Мх для п = 1, 2, ... на 6-разрядной десятичной ЭВМ
о
Интегрируя по частям, имеем
„ ( () | j
О 0 0 &
Следовательно, справедлива формула
In ~ nIn-\ ~ 1, п > 1. C.17)
1
Кроме того, /0 = ( е\-Чх = е - 1 а /* = 1.71828.
Воспользуемся формулой C.17) для последовательного вычисления приб-
приближенных значений интегралов 1п:
h й /* = 17* - 1 = 0.71828;
h й 7* = 31* - 1 = 0.30968;
h « /' = 57* - 1 = 0.19360;
h « 7* = 77*- 1 = 0.13120;
h K 7* = 97*- 1 =-0.55360;
h й /' = 27* - 1 = 0.43656;
Ц я /4* = 41* - 1 = 0.23872;
/6 » /* = 6/* - 1 = 0.16160;
h й /8* = 8/7* - 1 = 0.00496;
1ю « /*0 = 10/* - 1 =-6.5360 .
Здесь вычисления следует прекратить. Искомые значения интегралов очевид-
очевидно, положительны, а найденные значения при п = 9 и и = 10 отрицательны. В
чем причина появления такой большой ошибки?
В данном примере все вычисления проводились точно, а единственная и,
на первый взгляд, незначительная ошибка была сделана при округлении
значения /0 до 6 значащих цифр (заметим, что До = |/0 - /*| и 2-Ю'6).
Однако при вычислении 1\ эта ошибка сохранилась, при вычислении 1^ умно-
умножилась на 2!, при вычислении 73 — на 3!, .... при вычислении /9 — на 9! и т.д.
1 Идея примера заимствована из [5], [86].
3-28
65

Таким образом, Д„ = \1п~ Щ = п! До. Уже при п = 9 имеем 9! = 36880 и
поэтому Д9 = 9! До й 0.73.
Если вычисления производятся без ограничений на число я, то рассматри-
рассматриваемый алгоритм следует признать вычислительно неустойчивым. Ошибки
растут пропорционально п! настолько быстро, что уже при довольно скромных
значениях п попытки добиться приемлемого результата даже за счет увеличе-
увеличения разрядности мантиссы заранее обречены на неудачу.
Как изменить алгоритм, чтобы сделать его устойчивым? Перепишем фор-
формулу C.17) в виде
-к+1
-—
C.18)
и будем вести вычисления значений /п в обратном порядке, начиная, напри-
например, с п = 54. Положим /54 я /,4 = 0. Так как /м < е|г?4с1г = е/55, то Д54 <
< е/55 и 5-Ю. Однако при вычислении /5з эта ошибка уменьшится в 54
раза, при вычислении /52 — еще в 53 раза и т.д.
В результате значения /„ при п = 50, ..., 1 будут вычислены с шестью
верными значащими цифрами. Здесь погрешности не растут, а затухают. Ясно,
что модифицированный алгоритм вычислительно устойчив.
Вычислительная неустойчивость алгоритма часто может быть выяв-
выявлена благодаря анализу устойчивости по входным данным, так как
неустойчивость к малым ошибкам округления входных данных автома-
автоматически свидетельствует о вычислительной неустойчивости алгоритма.
Пример 3.27. Предположим, что величины уп для п = 1, 2, ... вычисляются
по рекуррентной формуле
Уп = «„ИгМ + fin, (ЗЛ9>
а величина jfo задана. Пусть у* — заданное приближенное значение величины
Уо. Тогда (если вычисления ведутся абсолютно точно) определяемые по фор-
формуле C.19) приближенные значения содержат ошибки, связанные равенством
Уп~Уп~ ап(Уп-\. ~ Уп-\)- Следовательно, Д(з/*) = | а„| Д(у*м) и при выпол-
выполнении условия |ап| < 1 алгоритм устойчив по входным данным, поскольку
Д(у*) < Д(у*) для всех п. Если же \ап\ > q > 1, то Д(у*) > рЬ(у%) и
абсолютная погрешность неограниченно возрастает при в -» оо. В этом случае
алгоритм неустойчив по входным данным, а потому и вычислительно неус-
неустойчив.
66
Справедливости ради следует заметить, что алгоритм C.19) был
признан нами неустойчивым в случае \ап\ > q > 1 при выполнении
двух условий, на которых не было достаточно акцентировано внима-
внимание. Первое из них состоит в предположении о неограниченной про-
продолжительности вычислительного процесса (п -» оо), что невозможно на
практике. В действительности такой характер неустойчивости говорит
о тенденции к неограниченному росту погрешности при неограничен-
неограниченном продолжении вычислений. Правда, если ошибки растут очень
быстро, то вычисления могут довольно скоро завершиться аварийным
остановом по переполнению. Второе условие касается выбранной меры
погрешности. Совсем не обязательно, чтобы рост абсолютной погреш-
погрешности всегда был неприемлем в конкретных вычислениях. Если он
сопровождается сильным ростом точного решения и при этом относи-
относительная погрешность остается малой, то алгоритм можно признать
относительно устойчивым. По-видимому, при анализе вычислительной
устойчивости более естественным является рассмотрение относитель-
относительных погрешностей.
Пример 3.28. Пусть в формуле C.19) все /?„ = 0 и ап Ф 0. Тогда 6(у*) =
= Д(О/1*>1 = l°nl A(d)/l«n*>-i| = *(»n-i)- Следовательно, 6(у*) =
= 6[Vq) и при любых значениях ап t 0 алгоритм относительно устойчив по
входным данным.
§ 3.5. Чувствительность вычислительных алгоритмов
к ошибкам округления
Выполнение вычислений на ЭВМ сопровождается появлением
вычислительной погрешности, связанной в первую очередь с необходи-
необходимостью округления результата каждой арифметической операции.
Даже если разрядность ЭВМ велика, существует реальная опасность,
что выполнение большого числа операций приведет к накоплению
погрешности, способной значительно или даже полностью исказить
вычисляемый результат. Однако и при небольшом числе действий
результат вычислений может оказаться совершенно неправильным,
если алгоритм слишком чувствителен к ошибкам округления.
Начинающий вычислитель часто склонен игнорировать ошибки
округления. На первых порах при решении простых задач, в особен-
особенности если новичок не задумывается о точности найденных решений,
его позицию нетрудно понять. Однако решение серьезных задач (ког-
(когда число арифметических операций превышает миллиарды, в вычис-
67

ления вкладываются значительные средства, а результат следует полу-
получить с гарантированной точностью и за принятые на основании расче-
расчетов решения приходится нести ответственность) предполагает совсем
иное отношение к вычислительной погрешности.
1. Порядок выполнения операций. Решение математической задачи
на ЭВМ сводится в конечном итоге к выполнению последовательности
простейших арифметических и логических операций. Однако часто
одно и то же математическое выражение допускает различные способы
вычисления, отличающиеся только порядком выполнения операций.
Если вычисления производить точно, то они (при любом способе
вычисления) будут приводить к одному результату. Однако результа-
результаты вычислений на ЭВМ уже зависят от порядка выполнения операций
и различие в вычислительной погрешности может быть весьма значи-
значительным.
Рассмотрим простой, но полезный пример вычисления на ЭВМ
N
суммы 5дг = S а,. Пусть а* — положительные представимые на вычис-
i=i
лительной машине числа. В каком порядке следует их суммировать
для того, чтобы сделать вычислительную погрешность по возможности
минимальной?
к
Пусть Sk = ? flf — частичная сумма, a St — ее приближенное зна-
чение, вычисляемое по формуле S? = S?_, © а*. Погрешность значения
ST складывается из погрешности значения S^.l и погрешности выпол-
выполнения операции S^ © ajt- Следовательно,
+ ак)еи и A(SjJ_i) + S*?M. Поэтому
= ((N- l)a, + {N- l)a2 + (tf
дцЕм + - +
aN )eM.
Так как множитель, с которым входит а, в формулу для оценки
погрешности, убывает с ростом «, в общем случае ошибка окажется
наименьшей, если суммировать числа в порядке возрастания их значе-
значений, начиная с наименьшего.
Иногда неудачно выбранный порядок операций либо приводит к
полной потере точности, либо вообще не дает возможности получить
результат из-за переполнения.
Пример 3.29. Пусть на ЭВМ типа IBM PC требуется вычислить
произведение v = oq * сц * oq х ••• х «49 х «50. где а, « 1025Ч Если
производить вычисления в естественном порядке, то уже oq * а\ и 1044 дает
аварийный останов по переполнению. Вычисление произведения в обратном
порядке сразу же приводит к исчезновению порядка, так как a$Q * a4g и
и 10'49 < Xq. В результате aso ® 049 = 0 и после выполнения всех умножений
будет получено нулевое значение и В данном случае вполне приемлем
следующий порядок операций: v = oq * a5o * ai х <Чэ х ••• х «24 х *2б * «25.
исключающий возможность переполнения или антипереполнения.
2. Катастрофическая потеря точности. Иногда короткая последова-
последовательность вычислений приводит от исходных данных, известных с
высокой точностью, к результату, содержащему недопустимо мало
верных цифр или вообще не имеющему ни одной верной цифры. В
этом случае, как было отмечено в § 3.2, принято говорить о катастро-
катастрофической потере точности. В примере 3.29 мы сталкивались с ситуаци-
ситуацией, когда неудачный порядок вычисления произведения привел к
неверному нулевому значению результата. Рассмотрим другие при-
примеры.
Пример 3.301. Известно, что функция е1 может быть представлена в виде
сходящегося степенного ряда:
2! 3!
п<
C.20)
Возможность вычисления значения экспоненты прямым суммированием ряда
C.20) кажется привлекательной. Пусть для вычислений используется 6-раз-
6-разрядная десятичная ЭВМ. Возьмем х - -8.1 и будем вычислять значения
частичных сумм до тех пор, пока добавление очередного слагаемого еще меня-
меняет значение суммы:
e'8'i и 1.00000 в 8.10000 © 32.8050 6 88.5737 ® 179.362 в 290.566 ©
© ... © 16.4111 в 7.81941 Ф ... = 0.000649915.
В сумму вошло 36 слагаемых и значение очередного C7-го) слагаемого оказа-
оказалось уже не в состоянии изменить результат. Можно ли считать результат
удовлетворительным? Сравнение с истинным значением е"8- 1 и 0.000303539
показывает, что найденное значение не содержит ни одной верной цифры.
В чем причина катастрофической потери точности? Дело в том, что вычис-
вычисленные слагаемые ряда неизбежно содержат погрешности, причем для некото-
некоторых (для слагаемых с 5-го по 13-е) величина погрешности превосходит значе-
значение самого искомого результата. Налицо явный дефект алгоритма, к обсужде-
обсуждению которого мы еще вернемся в конце этого параграфа.
В данном случае переход к вычислениям с удвоенной длиной мантисс л
позволит получить значение е"8*' с шестью верными значащими цифрами.
Идея примера заимствована из [86].
69

Однако всего лишь удвоенное значение аргумента х — —16.2 снова возвращает
нас к той же проблеме. Поступим иначе. Используя разложение C.20), вычис-
вычислим е8-1 я 1.00000 в 8.1000 © 32.8050 © ... = 3294.47 и тогда е"8-1 = 1/е8-1 «
и 0.000303539. Предложенное изменение алгоритма позволило получить искомое
значение на той же 6-разрядной десятичной ЭВМ, но уже с шестью верными
значащими цифрами.
Заметим тем не менее, что реальные машинные алгоритмы вычисления ех
устроены совсем иначе.
Приведем теперь пример, когда к катастрофической потере точно-
точности приводит еще более короткая последовательность вычислений.
Пример 3.31. Пусть при х = 1/490 на 6-разрядной десятичной ЭВМ вычис-
вычисляется значение функции
у = cos* - cos2x.
C.21)
Заметим, что при х и 0 величины с\ — cost и 1 - — и сг = cos2z и 1 - 2х*
близки. Так как вычисленные их приближенные значения с* и с? будут
содержать ошибку, то возможна серьезная потеря точности. Действительно,
с* = 0.999998, с* = 0.999992 и у* = с* - с* = 0.000006. При вычитании
старшие разряды оказались потерянными и в результате осталась только одна
значащая цифра.
х Зх
Вычисление по эквивалентной формуле у = 2sin - sin —, позволяет избе-
избежать вычитания близких чисел и дает значение у* — 0.624741-10 с шестью
верными цифрами.
Интересно отметить, что у и 1.5*2, причем использование этой приближен-
приближенной формулы в данном случае дает 6 верных значащих цифр, в то время как
вычисления по формуле C.21) — только одну верную цифру.
Замечание. Не всегда катастрофическая потеря точности в
промежуточных вычислениях действительно является катастрофой.
Все зависит от того, как в дальнейшем используется результат.
3. Обусловленность вычислительного алгоритма. По аналогии с
понятием обусловленности математической задачи можно ввести поня-
понятие обусловленности вычислительного алгоритма, отражающее чувст-
чувствительность результата работы алгоритма к малым, но неизбежным
ошибкам округления. Вычислительно устойчивый алгоритм называют
хорошо обусловленным, если малые относительные погрешности округ-
округления (характеризуемые числом ем) приводят к малой относительной
70
вычислительной погрешности 6(у*) результата у*, и плохо обусловлен-
обусловленным, если вычислительная погрешность может быть недопустимо боль-
большой.
Если 6(у*) и ем связаны неравенством М,(у*) ^ «М^м, то число v&
следует называть числом обусловленности вычислительною алгоритма.
Для плохо обусловленного алгоритма i/yi > 1.
При очень большом значении числа обусловленности алгоритм
можно считать практически неустойчивым1.
Применим, например, алгоритм, первоначально предложенный в
примере 3.26, для вычисления конечной серии из N интегралов 1\, 12,
..., 1ц. Тогда коэффициент роста ошибки v& окажется конечным.
Иными словами, при вычислении конечной серии интегралов алгоритм
формально оказывается устойчивым. Тем не менее уже при не очень
больших значениях N он настолько плохо обусловлен, что в практиче-
практическом плане может считайъся неустойчивым.
Для решения хорошо обусловленной задачи нет смысла применять
плохо обусловленный алгоритм. Именно такими являются алгоритмы,
первоначально предложенные в примерах 3.26 и 3.30.
Вернемся к примеру 3.30. Задача вычисления функции ех хорошо
обусловлена (см. пример 3.10). Можно ли было предвидеть катастро-
катастрофическую потерю точности при вычислении значения е"8*1 прямым
суммированием ряда C.20)?
оо
Рассмотрим задачу суммирования ряда Е at со слагаемыми ajt =
= -ц . Каждое из этих слагаемых вычисляется с относительной ошиб-
ошибкой 6(а?) > ем. При х < 0 формула C.10) с учетом разложения C.20)
2*
00 I x\ °° x^ I I
дает значение v& = S -M- / I E —p— = e2'*!. Рост модуля г (для г
< 0) приводит к резкому ухудшению обусловленности вычислений.
Для г = -8.1, как в примере 3.30, имеем vs — е16-2 и 107. Поэтому
неудивительна полная потеря точности при вычислениях на 6-разряд-
6-разрядной десятичной ЭВМ.
Рассмотрим теперь обусловленность алгоритма прямого вычисления
по формуле C.21). Еели величина х не слишком мала Bт2 > ем), то
значения с* я 1 - — и с* й 1 - 2х2 будут содержать ошибки порядка
1 Иногда такие плохо обусловленные алгоритмы называют численно неус-
неустойчивыми.
71

ем Поэтому А(у*) ~ 2ем Учитывая, что у я 1.5х2, найдем оценку гра-
границы относительной погрешности ~6(у*) ~ x'2zu. Число обусловленности
v ~ х'2 растет с уменьшением |х|. В случае, когда 2х2 < ?м, в результа-
результате вычислений будут получены значения с* = 1, с* = 1 и у* — с* -
- Cj = 0. Здесь 6(у*) = \у ~ у*\/\у\ = 1 и происходит полная потеря
точности.
Если алгоритм, предназначенный для решения хорошо обусловлен-
обусловленной задачи, оказался плохо обусловленным, то его следует признать
неудовлетворительным и попытаться построить более качественный
алгоритм. В примерах 3.30 и 3.31 это удалось сделать сравнительно
легко.
Однако для плохо обусловленных задач дело обстоит иначе. Ключ
к пониманию дает следующее высказывание [67]: "Если задача плохо
обусловлена, то никакие усилия, потраченные на организацию изощ-
изощренных вычислений, не могут дать правильных ответов, исключая
случайности" Здесь требуется серьезное переосмысление постановки
вычислительной задачи.
§ 3.6. Различные подходы к анализу ошибок
1. Прямой анализ ошибок. Общий эффект влияния ошибок обычно
учитывают следующим образом. Изучают воздействие ошибок вход-
входных данных, метода и округлений на получаемый результат у* и пыта-
пытаются оценить некоторую меру близости у* к истинному решению у.
Такой метод исследования называяют прямым анализом ошибок В
большинстве случаев в данной книге мы будем следовать этому тради-
традиционному пути. Во многих (но далеко не во всех) случаях оценки
погрешности удается получить; однако довольно часто они оказывают-
оказываются сильно завышенными и приводят к неоправданному пессимизму в
оценке качества приближенного решения. Реальная величина погреш-
погрешности у - у* часто значительно меньше, чем ее оценка, рассчитанная
на самый неблагоприятный случай и выведенная с помощью прямого
анализа. Особенно трудным является прямой анализ вычислительной
погрешности.
2. Обратный анализ ошибок. В последнее время получил широкое
распространение другой подход к оценке влияния ошибок. Оказывает-
Оказывается, что довольно часто приближенное решение у* можно трактовать
как точное решение той же задачи, но отвечающее возмущенным ис-
72
ходным данным х*. Оценка величины такого эквивалентного возмуще-
возмущения и является целью обратного анализа ошибок.
В прикладных задачах входные данные, как правило, содержат
погрешности. Обратный анализ показывает, что ошибки, внесенные в
решение в процессе его вычисления, оказываются равносильными
некоторым дополнительным ошибкам, внесенным во входные данные.
Сопоставление величины эквивалентного возмущения и уровня ошибок
входных данных позволяет судить о качестве найденного решения. На
рис. 3.5 представлена графическая иллюстрация обратного анализа
ошибок. Здесь данное х* таково, что решением задачи,
соответствующим х *, является у * — результат приближенного решения
задачи с входным данным х. На рисунке заштрихована область
неопределенности входного данного; в пределах этой области входные
данные для решающего задачу неразличимы. В представленном
случае х* оказалось внутри этой области, поэтому результат у* следует
признать вполне приемлемым.
Область неопределенности
входною данного
Область неопределенности
решения
Рис. 3.5
Каждый из указанных двух подходов к оценке погрешности имеет
свои достоинства и полезным является разумное их сочетание.
Пример 3.32. Пусть на 6-разрядной десятичной ЭВМ вычисляется корень
уравнения
г> - 12.5^ + 62.513 - 156.25*? + 195.3125* - 97.65625 = 0.
При вводе в ЭВМ последние два коэффициента будут округлены до шести
значащих цифр и уравнение примет вид
Р*(х) = г>
+ 62.5I3 - 156.25I2 + 195.313* - 97.6563 = 0. C.22)
Допустим, что некоторый алгоритм, примененный к этому уравнению, дал
значение приближенного решения х* - 2.6. Следуя логике прямого анализа
73

ошибок, чтобы оценить качество полученного приближения нужно было бы
задаться вопросом: насколько отличается г* от истинного решения х уравне-
уравнения C.22)? Мы поступим иначе. Подставляя г* в левую часть уравнения
C.22), получим значение Р*(х*) = 0.00126. Заметим теперь, что х* = 2.6
является точным решением уравнений
** - 12.5*4 + 62.5*3 - 156.25л2 + 195.3125* - 97.65626 = 0,
I5 - 12.5*4 + 62.5*3 - 156.25*? + 195.31252* - 97.656312 = 0,
которые после округления коэффициентов совпадают с уравнением C.22) и
становятся неотличимы от исходного уравнения. Найденное решение следует
признать превосходным с точки зрения "философии" обратного анализа оши-
ошибок, так как оно является точным решением задачи, лежащей в пределах
области неопределенности задачи C.22). Рассчитывать на то, что после записи
уравнения в виде C.22) удастся получить лучший ответ, просто бессмысленно.
Конечно, это немного обидно, особенно если учесть, что исходное уравнение в
действительности есть развернутая запись уравнения (х — 2.5M = 0 и истин-
истинным значением корня является х = 2.5.
Представляется, что значение обратного анализа ошибок недоста-
недостаточно осознанно, в особенности среди непрофессиональных вычислите-
вычислителей. Этот подход показывает на возможность иного взгляда на оценку
качества приближенного решения, а, значит, и на качество многих
вычислительных алгоритмов. Сложившийся стереотип заставляет
искать приближенное решение у* математической задачи, мало отли-
отличающееся от ее истинного решения у. Однако для большинства прак-
практических задач в силу неопределенности в постановке и входных дан-
данных в действительности существует и область неопределенности реше-
решения (см. рис. 3.5). Поскольку эта область неизвестна, оценить степень
близости вычисленного решения у* к ней очень трудно. Гораздо про-
проще, быть может, получить ответ на аналогичный вопрос для входного
данного г*, соответствующего решению у*. Поэтому можно сформули-
сформулировать цель вычислений и так: "найти точное решение задачи, кото-
которая мало отличается от поставленной задачи" или же так: "найти
решение задачи с входным данным х*, находящимся в пределах облас-
области неопределенности заданного входного данного х".
Пример 3.33. Пусть для задачи Коши
у - Гу = а(х)х, у A) = 2,
где а(х) = 2.6 + O.Ole, найдено приближенное решение у =
его качество?
74
C.23)
Как оценить
Условие у A) = 2, очевидно, выполнено. Подставляя у (х) в левую часть
уравнения, убеждаемся, что у (х) удовлетворяет уравнению C.23) с коэффици-
коэффициентом а* = 4 - B и 2.586 вместо а. Обратим внимание на то, что "истинное"
значение <*о коэффициента а нам в действительности неизвестно и а (г) —
лишь некоторое его приближение. Числовой параметр 2.6 в лучшем случае
получен округлением "истинного" значения, и, следовательно, а может отли-
отличаться от ад и на 0.05. Так как |а* — а\ ^ 0.03, то в силу естественной
неопределенности в постановке задачи функция у = 2& с позиции обратного
анализа ошибок может считаться таким же равноправным решением поставлен-
поставленной задачи, как и найденное сколь угодно точно решение задачи C.23). Во
всяком случае теперь для того, чтобы отказаться от найденного приближенного
решения, нужны довольно веские аргументы.
Подчеркнем, что в основе методов решения некорректных и плохо
обусловленных задач также лежит существенное переосмысление пос-
постановок вычислительных задач.
3. Статистический анализ ошибок. Даже для простых алгоритмов
строгий анализ влияния ошибок округления очень сложен. При боль-
большом числе выполняемых операций гарантированные оценки погрешно-
погрешности, рассчитанные на самый неблагоприятный случай, как правило,
бывают сильно завышенными.
Можно надеяться на то, что появляющиеся в реальном вычисли-
вычислительном процессе ошибки округления случайны и их взаимное влия-
влияние приводит к определенной компенсации результирующей ошибки.
Статистический анализ ошибок, исходящий из предположения об их
случайности, направлен на исследование не максимально возможных, а
наиболее вероятных ошибок.
Для сравнения покажем отличие в результатах на примере задачи
N
вычисления суммы 5дг = Е ajt большого числа положительных слага-
Jfc=i
емых. Гарантированная оценка погрешности дает значение относитель-
относительной погрешности S(S^), растущее пропорционально N. В то же время
статистический анализ показывает, что если ошибки округления явля-
являются случайными с нулевым средним значением, то S(S^) растет про-
пропорционально fN, т.е. гораздо медленнее. К сожалению, на тех ЭВМ,
где округление производится усечением, последнее предположение не
выполнено, так как ошибки округления смещены в одну сторону и
поэтому имеют ненулевое среднее значение. Здесь 6(S^) растет опять
пропорционально N.
4. Некоторые нестрогие способы анализа. Распространенным мето-
75

дом оценки влияния вычислительной погрешности является расчет с
обычной и удвоенной точностью. Если результаты двух вычислений
получаются существенно различными, это является свидетельством
плохой обусловленности алгоритма. В то же время есть надежда на то,
что совпадающие в ответах цифры верны.
Примерно такие же суждения о чувствительности решения к ошиб-
ошибкам округления можно сделать, если провести вычисления на двух
различных вычислительных машинах или использовать различные
компиляторы. Разумеется, такое исследование имеет смысл провести
на одном-двух типичных примерах до начала массовых однотипных
расчетов.
Влияние ошибок во входных данных на результат вычислений
можно увидеть, если решить задачу несколько раз, изменяя случай-
случайным образом входные данные в пределах ошибки их задания. Проде-
Проделав такой эксперимент несколько раз, можно грубо оценить погреш-
погрешность решения, вызванную погрешностями входных данных.
§ 3.7. Требования, предъявляемые
к вычислительным алгоритмам
В § 3.4 и 3.5 были сформулированы два важнейших требования —
корректность и хорошая обусловленность. Помимо них к алгоритмам
предъявляется еще целый ряд существенных требований.
1. Требования к абстрактным алгоритмам. К числу этих требований
относятся: 1) экономичность; 2) надлежащая точность; 3) экономия
памяти; 4) простота.
Экономичность алгоритма измеряется числом элементарных опера-
операций, необходимых для его реализации, и в конечном итоге сводится к
затратам машинного времени. Это требование формулируют иногда
как требование максимальной быстроты исполнения алгоритма. Эко-
Экономичность особенно важна при массовых расчетах. Естественно, что
при создании алгоритмов большое внимание уделяют минимизации
числа операций. Для некоторых задач разработаны алгоритмы, требу-
требующие минимально возможного числа операций. Пример такого алго-
алгоритма — схема Горнера (см. пример 3.19). Отметим, что ряд математи-
математических алгоритмов, созданных в домашинный период, оказался удиви-
удивительно неэкономичным. Приведем классический пример такого алго-
алгоритма.
Пример 3.34 (правило Крамер а1). Для решения системы линей-
1 Габриэль Крамер A704 — 1752) — швейцарский математик.
76
ных алгебраических уравнений Ах = 6 порядка m по правилу Крамера предла-
предлагается вычислять компоненты вектора х как отношения специальным образом
построенных определителей: xt — At/A, t = 1, 2 т. Если вычислять опре-
определитель непосредственно по его определению, то нужно выполнить (т — 1)т !
умножений и т! сложений. Пусть для вычислений используется ЭВМ с
производительностью 106 умножений в секунду и решается система с числом
неизвестных т = 15, весьма скромным для приложений. Тогда вычисление
только одного определителя потребует 14*15! и 1.8* 1013 умножений, в резуль-
результате чего на вычисление решения уйдет около 10 лет непрерывной работы
ЭВМ. Вместе с тем для решения той же системы на той же ЭВМ методом
Гаусса (см. гл. 5) потребуется примерно 0.002 с. Естественно, что как вычисли-
вычислительный алгоритм правило Крамера следует забраковать.
Даже для самых простых задач выбор экономичного алгоритма
может дать существенное уменьшение числа операций.
Пример 3.35. Пусть требуется вычислить х"-, где п — натуральное число.
Вычисление этой величины последовательным умножением на х предполагает
выполнение п - 1 операций умножения. Нетрудно убедиться в том, что этот
способ не самый экономичный. Например, х*4 можно найти, выполнив не 63, а
всего 6 операций умножения, если последовательным возведением в квадрат
вычислить г2, х*, Xs, х16, г?2, г?4.
В общем случае представим п в виде разложения B.25) по степеням двой-
двойки (именно так число п хранится в памяти ЭВМ). Тогда
х°°
C.24)
Заметим, что в произведении C.24) следует учитывать при вычислении только
те сомножители, для которых at t 0 (т.е. а, = 1). Алгоритм, основанный на
разложении C.24), называется бинарным алгоритмом. Он позволяет найти х"-
не более чем за 21og2n операций умножения.
Требование точности означает, что вычислительный алгоритм
должен давать решение задачи с заданной или приемлемой для зада-
задачи точностью е.
Важным является требование экономии памяти. Хотя в последнее
время доступная память ЭВМ существенно расширилась, для "боль-
"больших" задач требование экономии памяти может в ряде случаев стать
основным. Интерес к экономному размещению информации в памяти
возрастает в связи с более широким использованием персональных
ЭВМ для решения научно-технических и инженерных задач.
Учитывая необходимость дальнейшей программной реализации
алгоритма, подчеркнем, что простота алгоритма также является
весьма желательным его свойством.
77

2. Требования к программным реализациям алгоритмов. К насто-
настоящему времени выработан ряд требований к программам, реализу-
реализующим вычислительные алгоритмы и предназначенным для длительно-
длительного и широкого использования. Перечислим некоторые из них: 1) на-
надежность; 2) работоспособность (робастность); 3) переносимость (порта-
бельность); 4) поддерживаемость; 5) простота в использовании и др
Рассмотрим эти требования более подробно.
Надежность программы означает, что она не содержит ошибок и
вычисляет именно тот результат, для которого она предназначена.
Работоспособность (робастность) включает в себя надежность и
предполагает, что программа способна выявлять недопустимые исход-
исходные данные, обнаруживать различные критические для задачи или
алгоритма ситуации. Робастная программа реагирует на такие ситу-
ситуации приемлемым для пользователя образом. Она составлена так,
чтобы исключить какие-либо аварийные остановы, в том числе по
переполнению, из-за деления на нуль, неудачной попытки применить
операцию извлечения квадратного корня или взятия логарифма от
отрицательного числа.
Алгоритм может "потерпеть неудачу" при решении задачи, если
заданное входное данное не является для него допустимым. Конечно,
в простых ситуациях пользователь должен сам различать допустимые
для алгоритма входные данные от недопустимых. Однако чаще всего
сделать это до вычислений очень трудно или невозможно, и в про-
программе должен быть предусмотрен анализ данных и сообщение пользо-
пользователю о недопустимых или сомнительных данных. Необходимо иск-
исключить ситуацию, характерную для некачественных программ, когда
реакцией на задание данных, при которых алгоритм не может по
объективным причинам найти решение задачи, является аварийный
останов или же выдача внешне вполне правдоподобного, но совершен-
совершенно бессмысленного результата.
Переносимость (портабельностъ) означает, что программа может
работать на различных ЭВМ без изменения или с незначительными
изменениями. Всякая характеристика ЭВМ, используемая в программе
(например, значение машинного эпсилон ем), должна или вычисляться
самой программой, или задаваться пользователем.
Поддерживаемость означает прежде всего требование легкости
модификации. Для того чтобы была возможность внесения в програм-
программу изменений с минимальной вероятностью появления ошибок, она
должна быть составлена максимально ясно и логично. Полезно вносить
в текст программы содержательные комментарии. Разобраться в плохо
составленной программе может оказаться труднее, чем создать новую.
Поддерживаемая программа должна быть хорошо документирована.
78
Плохое описание программы в лучшем случае способно вызвать к ней
недоверие, а в худшем — может не позволить пользователю правильно
ее эксплуатировать. К сожалению, нередка ситуация, когда предназна-
предназначенная для широкого использования программа настолько плохо доку-
документирована, что пользователь предпочитает потратить время на напи-
написание аналогичной программы (возможно, гораздо худшего качества)
либо вообще отказаться от решения задачи.
Простота о использовании программы — весьма желательное, но
трудно достижимое свойство. Зачастую добиться простоты в использо-
использовании можно только жертвуя надежностью или экономичностью. Су-
Существует ряд широко используемых программ, которые, в первую
очередь, популярны, благодаря простоте в использовании.
3. Противоречивость требований. Можно продолжить перечисление
требований к вычислительным алгоритмам, добавив, например, требо-
требования универсальности и гибкости. Однако нетрудно понять, что
сформулированные требования противоречивы. Большинство из них
вступает в противоречие с экономичностью, выраженной через затраты
машинного времени. В разных ситуациях на первый план может высту-
выступать то или иное требование и, удовлетворяя в большей степени одним
требованиям, программа с неизбежностью в меньшей степени удовлет-
удовлетворяет другим. Это частично объясняет наличие большого числа про-
программ, предназначенных для решения одной и той же задачи.
Естественно, что хорошая программа, которую можно предъявить
для широкого использования, не может быть простой. Следует приз-
признать, что составление таких программ — это работа, требующая высо-
высокой квалификации и специальных знаний. Бе выполняют специалисты
по созданию математического обеспечения ЭВМ. Рядовой пользова-
пользователь должен по возможности стремиться максимально использовать
стандартные программы, а не создавать новые.
§ 3.8. Дополнительные замечания
1. Учебное пособие [79] можно рассматривать как введение в теорию мето-
методов решения некорректных задач. Ее удачно дополняют следующие книги: [7],
[59], [80]. Отметим, что [80] содержит не только теорию и алгоритмы, но и
тексты соответствующих программ.
2. Весьма содержательное изложение проблемы обусловленности вычисли-
вычислительных задач и обратного анализа ошибок содержится в [67]. Здесь же под-
подробно обсуждаются проблема создания высококачественного математического
обеспечения и требования, предъявляемые к вычислительным алгоритмам.
79

Глава 4
МЕТОДЫ ОТЫСКАНИЯ РЕШЕНИЙ
НЕЛИНЕЙНЫХ УРАВНЕНИЙ
В этой главе рассматривается задача отыскания корней нелинейных
уравнений и излагаются методы ее решения. Это делается несколько
подробнее, чем обычно принято в учебниках по численным методам.
Дело в том, что нелинейное уравнение представляет собой редкий
пример задачи, которая может быть сравнительно полно исследована
элементарными средствами и допускает наглядные геометрические
иллюстрации. В то же время многие проблемы, возникающие при
отыскании корней нелинейных уравнений, типичны, а некоторые мето-
методы их решения (в особенности метод простой итерации и метод Нью-
Ньютона) допускают широкие обобщения и играют в вычислительной
математике фундаментальную роль.
§ 4.1. Постановка задачи.
Основные этапы решения
1. Постановка задачи. Задача отыскания корней нелинейного урав-
уравнения с одним неизвестным вида
/(*)=0
D.1)
имеет многовековую историю, но не потеряла свою актуальность и в
наши дни. Она часто возникает как элементарный шаг при решении
различных научных и технических проблем. Напомним, что корнем
(или решением) уравнения D.1) называется значение х, при котором
/(*) = 0.
Для справедливости большинства рассуждений данной главы доста-
достаточно предположить, что в окрестности каждого из искомых корней
функция }{х) дважды непрерывно дифференцируема.
80
Корень х уравнения D.1) называется простым, если f'(x) Ф 0. В
противном случае (т. е. в случае f'(x) = 0) корень х называется крат-
кратным. Целое число m назовем кратностью корня х, если /к) (х) = 0
для к — 1, 2, . ., m — 1 и fm)(x) ф 0. Геометрически корень х соответ-
соответствует точке пересечения графика функции у = / (х) с осью Ох. Ко-
Корень х является простым, если график пересекает ось Ох под ненуле-
ненулевым углом, и кратным, если пересечение происходит под нулевым
углом. Функция / (х), график который изображен на рис. 4.1, имеет
четыре корня. Корни хх и х3 —
_ У
простые, i2 и Х4 — кратные.
Задача отыскания простых
корней является существенно
более простой (и чаще встре-
встречающейся), чем задача отыс-
отыскания кратных корней. В
действительности большинство
методов решения уравнения
D.1) ориентировано именно на
вычисление простых корней.
2. Уточнение постановки задачи. В конкретной задаче часто инте-
интерес представляют не все корни уравнения, а лишь некоторые из них.
Тогда постановку задачи уточняют, указывая на то, какие из корней
подлежат определению (положительные корни, корни из заданного
интервала, максимальный из корней и т.д.).
В подавляющем большинстве случаев представить решение уравне-
уравнения D.1) в виде конечной формулы оказывается невозможным. Даже
для простейшего алгебраического уравнения n-й степени
D.2)
Рис. 4-1
хп +
+ ... + ахх + ао = 0
явные формулы, выражающие его корни через коэффициенты с помо-
помощью конечного числа арифметических операций и извлечения корней
степени не выше п, найдены1 лишь при п = 2, 3, 4. Однако уже для
1 Алгебраические уравнения третьей и четвертой степени не поддавались
усилиям математиков около 2000 лет. Эту задачу решили итальянские мате-
математики эпохи Ренессанса: Сципион дель Ферро A456—1526), Никколо Тарта-
лья A500—1557), Джироламо Кардано A501—1576), Людовико Феррари A522—
1565).
81

уравнений пятой и более высоких степеней таких формул не существу-
существует. Этот замечательный факт, известный как теорема Абеля, был уста-
установлен в 30-е годы XIX в. Н. Абелем1 и Э.Галуа2.
Невозможность найти точное решение нелинейного уравнения ка-
кажется огорчительной. Однако нужно признать, что желание найти
точное числовое значение решения вряд ли следует считать разумным.
Во-первых, в реальных исследованиях зависимость у = f(x) является
лишь приближенным описанием, моделирующим истинную связь меж-
между параметрами у и х. Поэтому точное решение х уравнения D.1) все
равно является лишь приближенным значением того параметра х,
который в действительности соответствует значению у = 0. Во-вторых,
даже если уравнение D.1) допускает возможность нахождения решения
в виде конечной формулы, то результат вычислений по этой формуле
почти с неизбежностью содержит вычислительную погрешность и
поэтому является приближенным.
Пример 4.1. Предположим, что исследование некоторого явления привело к
необходимости решить уравнение
2.7 = 0.
D.3)
Воспользовавшись формулами C.2) для корней квадратного уравнения, полу-
получим значения х\ = 1.5, ij = 1-8- Найдены ли нами точные значения параметра
*? Очевидно, нет. Скорее всего коэффициенты уравнения D.3) известны
приближенно и в лучшем случае они представляют округленные значения
"истинных" коэффициентов. В действительности можно лишь утверждать, что
«1 я 1.5, 12 и 1.8.
Предположим теперь, что "истинный" вид уравнения D.3) таков: л? —
— 3.3287г + 2.6631 = 0. Тогда точные значения параметра можно вычислить
по формуле 11,2 = C.3287 ± V3-32872 — 4-2.бб31)/2. Однако она лишь
указывает на то, какие операции и в каком порядке следует выполнить. В
данном случае точное вычисление по формуле невозможно, так как она
содержит операцию извлечения квадратного корня. Вычисленные по ней
значения *j, хз неизбежно окажутся приближенными.
1 Нильс Хенрик Абель. A802—1829) — норвежский математик. Теорема, о
которой идет речь, была доказана им в возрасте около 22 лет.
2 Эварист Галуа A811—1832) — французский математик, один из создате-
создателей теории групп.
82
В дальнейшем мы откажемся от попыток найти точные значения
корней уравнения D.1) и сосредоточим внимание на методах решения
более реалистичной задачи приближенного вычисления корней с
заданной точностью е.
В данной главе под задачей отыскания решений уравнения D.1)
будем понимать задачу вычисления с заданной точностью е конечного
числа подлежащих определению корней этого уравнения.
3. Основные этапы решения. Решение задачи отыскания корней
нелинейного уравнения осуществляют в два этапа. Первый этап назы-
называется этапом локализации (или отделения) корней, второй — этапом
итерационною уточнения корней.
Локализация корней. Отрезок [а. 6], содержащий толь-
только один корень х уравнения D.1), называют отрезком локализации
корня х. Цель этапа локализации считают достигнутой, если для
каждого из подлежащих определению корней удалось указать отрезок
локализации (его длину стараются по возможности сделать минималь-
минимальной).
Прежде чем переходить непосредственно к отысканию отрезков
локализации, имеет смысл провести предварительное исследование
задачи для выяснения того, существуют ли вообще корни уравнения
D.1), сколько их и как они расположены на числовой оси.
Способы локализации корней многообразны, и указать универсаль-
универсальный метод не представляется возможным. Иногда отрезок локализа-
локализации известен либо он определяется из физических соображений. В
простых ситуациях хороший результат может давать графический
метод (см. пример 4.2). Широко применяют построение таблиц значе-
значений функций /вида yt = f(xt), t = 1, 2, ..., п. При этом способе лока-
локализации о наличии на отрезке [x,-i, z,] корня судят по перемене знака
функции на концах отрезка (см. пример 4.3). Основанием для приме-
применения указанного способа служит следующая хорошо известная теоре-
теорема математического анализа.
Т е о р е и а 4.1. Пусть функция f непрерывна на отрезке [а, Ь] и
принимает на его концах значения разных знаков, т. е. /(а)*/F) < 0.
Тогда отрезок [а, Ь] содержит по крайней мере один корень уравнения
f(x) = 0.
К сожалению, корень четной кратности не удается локализовать на
основании перемены знака с помощью даже очень подробной таблицы.
Дело в том, что в малой окрестности такого корня (например, корня x%
на рис. 4.1) функция /имеет постоянный знак.
Важно подчеркнуть, что далеко не всегда для успешного отыскания
83

корня х уравнения D.1) необходимо полное решение задачи локализа-
локализации. Часто вместо отрезка локализации достаточно найти хорошее
начальное приближение г@) к корню х.
Пример 4.2. Локализуем корни уравнения
4(l-z2)-e* = 0. D.4)
Для этого преобразуем уравнение к виду 1 — х2 — 0.25е1 и построим графики
функций у = 1 — г2 и у = 0.25ех
(рис. 4.2). Абсциссы точек пересече-
пересечения этих графиков являются корня-
корнями данного уравнения. Из рис. 4.2
видно, что уравнение имеет два
корня Х[ и xi, расположенные на
отрезках [-1, 0] и [0, 1]. Убедимся,
что функция f(x) = 4A — г2) — е1
принимает на концах указанных
отрезков значения разных знаков.
Действительно, /(-1) = -е < 0,
/@) = 3 > 0, /A) = -е < 0.
Следовательно, в силу теоремы 4.1 на каждом из отрезков [-1, 0] и [0, 1]
находится по крайней мере один корень.
Пример 4.3. Локализуем корни уравнения
г3 - 1.1г2-2.2г+ 1.8 = 0.
Для этого составим таблицу значений функции f{x) — i? — l.lz2 — 2.2а1 + 1.8
на отрезке [-2, 2] с шагом 0.4.
Таблица 4.1
Рис 4-2
-2.0
-1.6
-1.2
-0.8
-0.4
0.0
/(г) -6.200 -1.592 1.128 2.344 2.440 1.800
Продолжение табл. 4-1
0.4
0.8
1.2
1.6
2.0
0.808
-0.152 -0.696
-0.440
1.000
Из табл. 4.1 видно, что функция / меняет знак на концах отрезков [-1.6,
-1.2], [0.4, 0.8], [1.6, 2.0]. Теорема 4.1 дает основание утверждать, что каждый
из этих отрезков содержит по крайней мере один корень. Учитывая, что в
силу основной теоремы алгебры многочлен третьей степени не может иметь
более трех корней, заключаем, что полученные три отрезка содержат ровно по
одному корню. Таким образом, корни локализованы.
Итерационное уточнение корней. На этом этапе
для вычисления каждого из корней с точностью е > 0 используют тот
или иной итерационный метод, позволяющий построить последова-
последовательность г@), тA), ..., г(п), ... приближений к корню х.
Общее представление об итерационных методах и основные опреде-
определения были даны в § 3.3. Введем дополнительно некоторые определе-
определения.
Итерационный метод называют одношаювым, если для вычисления
очередного приближения х{п*Х) используется только одно предыдущее
приближение г(п) и к-шаювим, если для вычисления z(n+1) использу-
используются Jb предыдущих приближений я< "¦*¦'>, х<п~к*2), ^ х<п> _ Заметим,
что для построения итерационной последовательности одношаговым
методом требуется задание только одного начального приближения
z<0), в то время как при использовании Jb-шагового метода — к началь-
начальных приближений г@), гA), ..., г1*1.
Скорость сходимости — одна из важнейших характеристик итера-
итерационных методов. Говорят, что метод сходится со скоростью геомет-
геометрической прогрессии, знаменатель которой q < 1, если для всех п спра-
справедлива следующая оценка:
|z<n> -~х\ < со?". D-5)
Как нетрудно видеть, из оценки D.5) действительно вытекает сходи-
сходимость метода.
Пусть одношаговый итерационный метод обладает следующим
свойством: существует <г-окрестность корня х такая, что если прибли-
приближение г( п) принадлежит этой окрестности, то справедлива оценка
-х\Р,
D.6)
84
где С > 0 и р П - постоянные. В этом случае число р называют
порядком сходимости метода. Если р=1иС<1,то говорят, что
метод обладает линейной скоростью сходимости в указанной «т-окрест-
ности корня. Если р > 1, то принято говорить о сверхлинейной ско-
скорости сходимости. При р = 2 скорость сходимости называют квадра-
85

тичной, а при р = 3 — кубической. При наличии оценки D.6) у ib-шаго-
вого метода (при к > 1) число р также будем называть порядком схо-
сходимости метода.
Лемма 4.1. Пусть одношаювый итерационный метод обладает
линейной скоростью сходимости в некоторой о-охрестности корня х.
Тогда при любом выборе начального приближения х@) из а-
окрестности корня х итерационная последовательность х(п) не
выходит за пределы этой окрестности, метод сходится со скоростью
геометрической прогрессии со знаменателем q — С и имеет место
следующая оценка погрешности:
0.
D.7)
а Заметим, что принадлежность х(П) окрестности (х — а, х + о)
является следствием неравенства D.7). В самом деле, так как q < 1, то
|r<n) — х\ ^ |гю) _ г| < а Сходимость х<п) кг также вытекает из
D.7).
Справедливость неравенства D.7) установим методом индукции.
При п = 0 оно переходит в очевидное: |х@) — т\ < |z@> — х|.
Пусть неравенство D.7) выполнено при п = m — 1. Тогда
— х| <
т. е. неравенство выполнено и при п = т. Ш
Лемма 4.2. Пусть k-шаговый итерационный метод в некоторой
а-окрестности корня х имеет р-й порядок сходимости. Выберем 6 > 0,
так, чтобы выполнялись неравенства 6 К а и С6Р~1 < 1, где С — пос-
постоянная из неравенства D.6). Тогда при любом выборе начального
приближения х@) из S-окрестности корня х итерационная последова-
последовательность х{ п) не выходит за пределы этой окрестности, метод
сходится и справедлива оценка
где q = С\
, п>0,
-i|, С, =
D.8)
а Заметим, что принадлежность z(n) окрестности (х — S, х + 6)
является следствием неравенства D.8). В самом деле, так как q < 1 и
рп, то из D.8) вытекает, что
— х|
= |г@) — х\ < 6.
Сходимость г("' к i также следует из D.8).
86
Справедливость неравенства D.8) установим методом индукции.
При п = 0 оно переходит в очевидное: |г<0) — х\ < |г@) — х|. Пусть
неравенство D.8) выполнено при п = т — 1. Докажем, что оно верно и
при п = т. Используя условие D.6), получаем
- х|
- x|P
С помощью доказанных лемм исследование сходимости итерацион-
итерационных методов сводится только к получению оценки D.6).
J 4.2. Обусловленность задачи
вычисления корня
Пусть х — корень уравнения D.1), подлежащий определению. Бу-
Будем считать, что входными данными для задачи вычисления корня г
являются значения / (х) функции / в малой окрестности корня. Так
как значения / (х) будут вычисляться на ЭВМ по некоторой програм-
программе, то в действительности задаваемые значения являются приближен-
приближенными и их следует обозначать через /*(х). Ошибки в f*(x) могут быть
связаны не только с неизбежными ошибками округления, но и с ис-
использованием для вычисления значений функции / приближенных
методов. К сожалению, нельзя ожидать, что в окрестности корня отно-
относительная погрешность 8{{*) окажется малой. Достаточно обратиться к
примерам 2.11 и 3.11, чтобы установить, что для чрезвычайно простых
функций у =. \ — х и у = sin х в окрестности корней х — 1 и х = л
значения этих функций не могут быть найдены с малой относительной
погрешностью. Реально рассчитывать можно лишь на то, что малой
окажется абсолютная погрешность вычисления значений функции.
Будем предполагать, что в достаточно малой окрестности корня
выполняется неравенство \f(x) — /*(х)| < Д, где Д = Д(/*) — граница
абсолютной погрешности. Сама погрешность корня ведет себя крайне
нерегулярно и в первом приближении может восприниматься пользова-
пользователем как некоторая случайная величина. На рис. 4.3, а представлена
идеальная ситуация, отвечающая исходной математической постановке
задачи, а на рис. 4.3, б — реальная ситуация, соответствующая вычис-
вычислениям значений функции /на ЭВМ.
87

Рис. 4-3
Если функция / непрерывна, то найдется такая малая окрестность
(х — е, х + е) корня х, имеющая радиус е > 0, в которой выполняется
неравенство
I/O0I < Д- D.9)
Для х € (х — е, х + е) знак вычисленного значения /*(г), вообще
говоря, не обязан совпадать со знаком f (х) и, следовательно, становит-
становится невозможным определить, какое именно значение х из интервала
(х — е, х + е) обращает функцию /в нуль (рис. 4.3, 5).
Будем называть этот интервал интервалом неопределенности корня
х. Найдем оценку величины е. Пусть корень х — простой. Для близких
к х значений х справедливо приближенное равенство
Поэтому неравенство D.9) примет вид \f'(x)(x— x)\ < Д, откуда полу-
получаем
х —
Д Д
< X < X +
\Г(*)\
Следовательно,
D.10)
Здесь vK =
1Я*)
Рас.
— число, которое в рассматриваемой задаче играет
роль абсолютного числа обусловленности. Действительно, если г* —
корень уравнения }*{х) = 0, то |/(х*)| < Д и тогда выполнено нера-
неравенство
|г-х*| <Д(О<ёи*дД(/*). D.U)
Заметим, что радиус интервала неопределенности прямо пропор-
пропорционален погрешности Д вычисления значения /. Кроме того, е воз-
возрастает (обусловленность задачи ухудшается) с уменьшением |/'(ж)|,
т. е. с уменьшением модуля тангенса угла наклона, под которым гра-
график функции пересекает ось Ох (рис. 4.4, а, б).
Если же f'(x) — 0 (т. е. корень х — кратный), то формула D.10) уже
не верна. Пусть кратность корня равна т. Тогда в силу формулы
Тейлора1 справедливо приближенное равенство
*/(*)
- X)
(X -
(х-
1 Брук Тейлор A685—1731) — английский математик и философ. Широко
известная формула разложения функции в степенной ряд была получена им в
1712 г.
89

в правой части которого все слагаемые, кроме последнего, равны нулю.
Следовательно, неравенство D.9) имеет вид
/""(*)
(г -
< Д .
Решая его, получаем аналогично D.10) оценку радиуса интервала
неопределенности:
ml Vm_ly
()
Эта оценка означает, что для корня кратности m радиус интервала
неопределенности пропорционален Д , что свидетельствует о плохой
обусловленности задачи вычисления кратных корней. С этой неприят-
неприятностью мы уже сталкивались при рассмотрении примера 3.9.
Отметим, что ? не может быть меньше величины |х|ем — погреш-
погрешности представления корня х в ЭВМ.
В реальной ситуации оценить величину и даже порядок радиуса
интервала неопределенности довольно сложно. Однако знать о его
существовании нужно по крайней мере по двум причинам. Во-первых,
не имеет смысла ставить задачу о вычислении корня х с точностью
е < е. В условиях неопределенности, вызванных приближенным зада-
заданием функции, любое значение г* ? (г — е, х + е) может быть с одной
и той же степенью достоверности принято за решение уравнения. Во-
вторых, нельзя требовать от алгоритмов отыскания корня получения
достоверных результатов после того, как очередное приближение
попало в интервал неопределенности или оказалось очень близко от
него; в этой ситуации вычисления следует прекратить и считать, что
получен максимум действительно возможного.
Для большинства итерационных методов определить этот момент
можно, поскольку начиная с него поведение приближений i(n) стано-
становится крайне нерегулярным. Если вдали от интервала неопределеннос-
неопределенности величина
qin) - |х(п) _
_ х(п-2)
D.12)
обычно бывает меньше единицы (|г(п) — х1"'11 | < |r(n"u — r<n> |),
то появление при некотором п значения qln) > 1 свидетельствует,
скорее всего, о начале "разболтки" — хаотического поведения итераци-
итерационной последовательности. В этой ситуации вычисления имеет смысл
прервать, чтобы выяснить причину явления и принять правильное
90
решение. Лучшим из полученных приближений к решению следует
считать, конечно, х<п'п. Использование для контроля вычислений
величины D.12) называют часто правилом Гарвика.
§ 4.3. Метод бисекдии
1. Описание метода. Пусть требуется с заданной точностью е > 0
найти корень г уравнения D.1). Отрезок локализации [а, Ь] (т. е. отре-
отрезок, содержащий только один корень х) будем считать заданным.
Предположим, что функция / непрерывна на отрезке [о, Ь] и на его
концах принимает значения разных знаков, т. е.
/(а) /F) < 0.
На рис. 4.5 изображен случай, когда f (а) < 0 и /F) > 0.
Для дальнейшего будет удобно обозначить
отрезок [а, Ь] через [а@), Ь@)]. Примем за приб-
приближенное значение корня середину отрезка —
точку х@) = (а@> + 6<О))/2. Так как положение
корня х на отрезке [а<0), 6@>] неизвестно, то
можно лишь утверждать, что погрешность этого
приближения не превышает половины длины
отрезка (рис. 4.5):
D.13)
_ х|
Рис. 4.5
Уменьшить погрешность приближения можно,
уточняя отрезок локализации, т. е. заменяя начальный отрезок [а@),
6<0)] отрезком [аA), 6A)] меньшей длины. Согласно методу бисекции
(половинного деления) в качестве [аA),6A)] берут тот из отрезков
[а<0), х@)] и [х@), 6@)], на концах которого выполняется условие
/(аA))/FA))<0. Этот отрезок содержит искомый корень. Действи-
Действительно, если /(аA)) f(bll)) < 0, то наличие корня следует из теоремы
4.1; если же /(аA)) /FA)) = 0, то корнем является один из концов
отрезка. Середина полученного отрезка гA) = (аA) + 6A))/2 дает
теперь приближение к корню, оценка погрешности которого составля-
составляет
|Х(П _
= (Ь- а)/22.
За очередное уточнение отрезка локализации [аB), 6B)] снова берут
тот из отрезков [аA), хA)], [хA>, 6A)], на концах которого выполняет-
выполняется условие /(аB>) /(&B)) < 0.
91

Опишем очередную (п + 1)-ю итерацию метода. Пусть отрезок
[<!<">, 6'п>] уже найден и вычислены значения z(n>, /(a(n)), f(btn)).
Тогда производят следующие действия:
1°. Вычисляется f(xin)).
2°. Если /(a') /(z(">) < 0, то в качестве отрезка локализации
[e(n+D] j<n+i>] принимается отрезок [а<">, х'">]. В противном случае
/(*<">) /F(п>) < 0 и за [а<«+1>, &сп*п] принимается отрезок
[X(n)) J(n)].
3°. Вычисляется z<"+1> = (а<"+1> + 6<"+D)/2.
Неограниченное продолжение итерационного процесса дает после-
последовательность отрезков [а@>, 6@>], [а'1', ftA>], ..., [а(п>, 6<">],
содержащих искомый корень. Каждый из них (за исключением на-
начального) получен делением пополам предыдущего отрезка.
2. Скорость сходимости. Середина n-го отрезка — точка х1п) —
= (а(п) + 6(п))/2 дает приближение к корню х, имеющее оценку пог-
погрешности
| г< "> - г | <(&<"> - а' п> )/2 = F - а)/2"+1.
D.14)
Из этой оценки видно, что метод бисекции сходится со скоростью
геометрической прогрессии, знаменатель которой q = '/2- По сравне-
сравнению с другими методами метод бисекции сходится довольно медленно.
Однако он очень прост и весьма непритязателен; для его применения
достаточно, чтобы выполнялось неравенство D.13), функция / была
непрерывна и верно определялся ее знак. В тех ситуациях, где не
нужна сверхвысокая скорость сходимости (а это часто имеет место при
простых инженерных расчетах), этот метод весьма привлекателен.
Заметим, что число итераций, которое требуется при применении
метода бисекции для достижения разумной точности е, не может быть
очень большим. Например, для уменьшения первоначального отрезка
локализации в 106 раз нужно 19 итераций.
3. Критерий окончания. Итерации следует вести до тех пор, пока
не будет выполнено неравенство 6(n) — а(п) < 2е. При его выполне-
выполнении в силу оценки D.14) можно принять х1п) за приближение к корню
с точностью е.
I итерация. Вычисляем /(х@)) а 1.3512. Так как
/(а<°))/(г<°)) > 0, то за очередной отрезок локализации принимаем
[а<», ft'1'] = [0.5, 1]. Вычисляем *"> =@"» + ft'1' )/2 = 0.75.
II итерация. Вычисляем /(хA)) я -0.3670. Так как /(вA))
/(я'1») < 0, то [а<2>, б'2'] = [0.5, 0.75] и *<2' = (а<2> + ft<2>)/2 = 0.625.
Результаты следующих итераций (с четырьмя цифрами после десятичной
точки) приведены в табл. 4.2.
Таблица 4.2
Знак Знак
Номер
итера-
итерации к
0
1
2
3
4
5
6
а(п)
0.0000
0.5000
0.5000
0.6250
0.6875
0.6875
0.7031
1.0000
1.0000
0.7500
0.7500
0.7500
0.7187
0.7187
0.5000
0.7500
0.6250
0.6875
0.7187
0.7031
0.7109
1.3513
-0.3670
0.5693
0.1206
-0.1182
0.0222
&(п> _ а(п)
1.0000
0.5000
0.2500
0.1250
0.0625
0.0312
0.0156
При п = 6 имеем ЬF) — аF) и 0.0156 < 2-10. Следовательно, заданная
точность достигнута и можно принять х и агF). Окончательно получим х =
= 0.71 ± 0.01.
4. Влияние вычислительной погрешности. При использовании
метода бисекции принципиально важным является правильное опреде-
определение знака функции / В случае, когда г(п) попадает в интервал
неопределенности корня (см. § 4.2), знак вычисленного значения
/*(я(п)) не обязан быть верным, и последующие итерации не имеют
смысла. Однако этот метод следует признать очень надежным; он
гарантирует точность приближения, примерно равную радиусу интер-
интервала неопределенности е. Как было отмечено в предыдущем парагра-
параграфе, большего требовать нельзя.
Пример 4.4. Найдем методом бисекции с точностью е = 10 положитель-
положительный корень уравнения 4A — х2) — е* = 0.
В примере 4.2 этот корень был локализован на отрезке [0, 1], причем
/@) > 0, /A) < 0. Положим а<°> = 0, 6@» = 1, z<°> = (а<°> + 6<°>)/2 =
= 0.5.
92
§ 4.4. Метод простой итерации
1. Описание метода. Чтобы применить метод простой итерации для
решения нелинейного уравнения D.1), необходимо преобразовать это
уравнение к следующему виду.
93

x=
D.15)
Это преобразование (приведение уравнения к виду, удобному для итера-
итерации) можно выполнить различными способами; некоторые из них
будут указаны ниже. Функцию <р далее будем называть итерационной
функцией.
Выберем каким-либо образом приближенное значение корня х@) и
подставим его в правую часть уравнения D.15). Получим значение
rA) = ip(xl0)). Подставляя теперь xli) в правую часть уравнения
D.15), имеем xl2) = <p(xil)). Продолжая этот процесс неограниченно,
получим последовательность приближений к корню, вычисляемых по
формуле
D.16)
Очевидно, что метод простой итерации — одношаговый (см. § 4.1).
Если существует предел построенной последовательности х =
lim xln), то, переходя к пределу в равен
№+00
функцию ip непрерывной, получим равенство
= lim xln), то, переходя к пределу в равенстве D.16) и предполагая
№+00
х=
D.17)
Это значит, что х — корень уравнения D.15).
2. Геометрическая иллюстрация. Из рис. 4.6 видно, что корень х
уравнения D.15) является абсциссой точки пересечения графиков двух
функций: у = х и у = tp(x). Возьмем некоторое начальное приближение
г@), которому отвечает расположенная на кривой у — <р(х) точка А/@)
с координатами (г@), хП)) (напомним, что хA) = ^(х@))). Соединим
точку М@) отрезком прямой у = х{1> с лежащей на прямой у = х
точкой Nil) с координатами (гA), хA)). Проведем теперь через точку
Nil) прямую х — х{1] до пересечения с кривой у = tp(x) в точке МA) с
координатами (х11), гB)). Продолжая этот процесс далее, получаем
ломаную линию A/t0) Лг<1) МA) ЛгB) Л/B)..., для которой абсциссы
точек М( п) представляют собой последовательные приближения г1 п)
к решению х.
3. Сходимость метода. На рис. 4.7, а—г представлена геометричес-
геометрическая иллюстрация поведения итерационного процесса в четырех прос-
простейших случаях взаимного расположения прямой у = х и кривой
У - f{x).
94
yvM
Рис 4-6
/ N
Рис П
В случаях (в) и (<5) метод простой итерации сходится, причем, как
нетрудно заметить,- при произвольном начальном приближении.
Напротив, в случаях (в) и («) метод расходится при любом выборе
начального приближения. Заметим, что в случаях (а) и @) \<р (х)\ < 1

(как видно из рисунка, модуль тангенса угла наклона кривой у = tp(x)
к оси абсцисс меньше единицы), а в случаях (в) и (t), наоборот,
|у/(гI > 1- Таким образом, можно предположить, что сходимость
метода простой итерации связана с выполнением условия I^X1)! < А.
Действительно, имеет место следующий результат.
Теорема 4.2. Пусть в некоторой а-окрестности корня х функ-
функция <р дифференцируема и удовлетворяет неравенству
\ч>'(х)\ < q, D.18)
где 0 < q < 1 — постоянная.
Тогда независимо от выбора начального^ приближения х@) из ука-
указанной а-окрестности корня итерационная последовательность не
выходит из этой окрестности, метод сходится со скоростью геомет-
геометрической прогрессии и справедлива следующая оценка погрешности:
|х
(в) _
D.19)
о Вычитая из равенства D.16) равенство D.17) и используя форму-
формулу конечных приращений Лагранжа, получим
-х =
< п>) -
Здесь а(п+1) =
)> где
-х). D.20)
— некоторая точка, расположенная
между х( п) и х. Если х(п) € (х — <т, х + а), то |ain+1> | < q в силу
условия D.18). Тогда на основании равенства D.20) получаем
-х\
Это означает, что метод простой итерации обладает линейной скорос-
скоростью сходимости и поэтому доказательство теоремы завершается приме-
применением леммы 4.1. И
Оценка погрешности D.19) является априорной. Она показывает,
что метод простой итерации сходится со скоростью геометрической
прогрессии, знаменатель которой равен q. Чем меньше q, тем выше
сокрость сходимости. Видна и роль правильного выбора начального
приближения: чем меньше погрешность начального приближения, тем
меньше итераций потребуется сделать для достижения заданной точ-
точности е.
Неравенство D.19), как правило, не используется для практической
оценки погрешности. Одна из причин этого состоит в том, что значе-
значение х, входящее в правую часть оценки, неизвестно. Кроме того,
96
использование неравенства D.19) приводит к существенно завышенной
оценке погрешности.
4. Критерий окончания. Выведем апостериорную оценку погреш-
погрешности, пригодную для практического применения.
Теорема 4.3. Пусть выполнены условия теоремы 4.2 и х@)-е
? (х — G, х + &). Тогда верна следующая апостериорная оценка погреш-
погрешности:
D В силу равенства D.20) имеем
Отсюда
— «' п>
Х( п) - X = f т( П-1) _ х( П) )
пМ.
— х<п>)
D.21)
— х).
D.22)
Взяв модуль от левой и правой частей этого равенства и воспользовав-
воспользовавшись неравенством
а< п)
1 - а'"»
1 -
получим требуемое соотно-
шение D.21). В
Если величина q известна, то неравенство D.21) дает эффективный
метод контроля погрешности и можно сформулировать следующий
критерий окончания итерационного процесса. Вычисления следует
Я
вести до выполнения неравенства
равносильного ему неравенства
1 - q
|x(n) _
D.23)
Если это условие выполнено, то можно считать, что х( п) является
приближением к х с точностью е.
Пример 4.5. Используем метод простой итерации для вычисления положи-
положительного корня х уравнения 4A — х2) — ех = 0 с точностью е = 10. Резуль-
Результат примера 4.4 дает для корня отрезок локализации [а, Ц = [0.70, 0.72].
Преобразуем уравнение к виду D.15), где ip(x) = i/l — ех/4. Заметим, что
. Так как
- е*/4), <р"(х)
ip" < 0 на [а, Ь], то производная ip' монотонно убывает и q =.max,.| y?'(x)| =
= ip'(b) я 0.37. Следовательно, условие сходимости D.18) выполнено. Возьмем
х10) = 0.7 и будем вести итерации до выполнения критерия D.23). В табл. 4.3
соответствующие приближения приведены с 10 знаками мантиссы.
4-28 97

n
0
1
2
3
4
5
0.7000000000
0.7046714292
0.7029968319
0.7035984939
0.7033824994
0.7034600632
Табл
9 | x( n\
1 - g1
и ц а 4.3
(
X
3-Ю
1-10
4-10
2-10
5-Ю
Критерий окончания выполняется при п = 5. После округления значе-
значения г15) до четырех значащих цифр получим х = 0.7035 ± 0.0001.
Замечание. Часто в практике вычислений вместо критерия
D.23) используется привлекательный своей простотой критерий
|х«п)-1«"-1)|<е. D.24)
В случае 0 < q < 1/2 использование критерия D.24) оправдано.
Действительно, здесь A — q)/q > 1 и поэтому выполнение неравен-
неравенства D.24) влечет за собой выполнение неравенства D.23).
В то же время в случае 1/2<д<1
использование критерия D.24)
может привести к преждевремен-
преждевременному прекращению итераций.
Дело в том, что когда величина q
близка к единице, итерационный
процесс сходится медленно и
расстояние между двумя последо-
¦" вательными приближениями г( п)
и z<n-n не-характеризует рассто-
Ох
Рис. 18
яния от х
4.8).
1 п)
до решения х (рис.
Пример 4.6. Пусть метод простой итерации используется для решения
10~4
уравнения х- 0.9999г + 10/Д Здесь <р(х) = 0.9999* + , ?'(() - 0.9999
и, следовательно, условие D.18) сходимости метода выполнено. Для вычисле-
вычислений по формуле D.16) используем 6-разрядную десятичную ЭВМ. Возьмем
г@) = 0.715010. Тогда хA) = 0.715009 и, если доверять критерию D.24), то
следовало бы считать, что решение получено с точностью ? = 10'6. Продолжая
вычисления, получим гB> = 0.715008, хC> = 0.715007, гD> = 0.715006,
гE) = 0.715005, хF) = 0.715005. Дальнейшие итерации теряют смысл. Сколь-
Сколько же верных знаков найдено? Сравнение с точным значением решения
х — = 0.707106... показывает, что верными в приближении хF) являются
V2
только две значащие цифры. Использование критерия D.24) в данном случае
категорически недопустимо. В дальнейшем мы еще вернемся к обсуждению
этого примера.
Использование критерия D.23) предполагает знание величины q,
входящей в условие D.18). Однако далеко не всегда эта величина
известна, либо может быть легко вычислена. В тех же случаях, когда
удается оценить q, эта оценка оказывается довольно грубой.
Исключим из критерия окончания итераций величину q. Заметим,
что в малой окрестности корня величина производной <р' практически
постоянна: <р'(х) я f'{x). Поэтому в равенстве D.22) величину а(п) =
— <P'((in~l)) можно приближенно заменить на ip'(x). Далее в силу
равенства
где ?(гг) — промежуточная между г'"1 и г'"'2' точка, имеем а(тг) =
= (г(гг) _ х(п-1))/(х(п-п _ г(п-2)) = р'(?<">) й <p'(i). Таким образом,
в равенстве D.22) можно положить а(тг) и а(тг) и поэтому при опреде-
определенных условиях можно использовать следующий практический крите-
критерий окончания итерационного процесса:
\xin) _ X(n-U I <
1 ' IV
а(п)
5. Дополщгтельные сведения о характере сходимости. В случае,
когда производная (р' знакопостоянна на отрезке локализации, итера-
итерационная последовательность обладает некоторыми полезными допол-
дополнительными свойствами. Заметим, что при <р'(х) Ф 0 в достаточно
малой окрестности корня знак производной ip'(x) действительно пос-
постоянен.
Теорема 4.4. Пусть [а, Ь] — отрезок локализации корня уравне-
уравнения D.15). Предположим, что на этом отрезке функция <р непрерывно
дифференцируема, а ее производная <р'(х) знакопостоянна и удовлетво-
удовлетворяет неравенству D.18) при 0 < q < 1. Пусть х@) € [а, Ь] — произ-
99

вольное начальное приближение и в случае ip' < 0 выполнено дополни-
дополнительное условие гA) = y>(zl0)) € [а, Ь] (первое приближение не выходит
за пределы отрезка локализации).
Тогда итерационная последовательность не выходит за пределы
отрезка [а, Ь], метод простой итерации сходится и верны оценки
погрешности D.19), D.21).
Кроме того, справедливы следующие свойства:
1°. Если <р' > О на [а, Ь], то г( п| сходится к х, монотонно возрас-
возрастая в случае а ^ il0) < х, и монотонно убывая в случае х < х{0) Kb.
2°. Если <р' < О на [а, 6], то сходимость i(n) ki носит колебатель-
колебательный харакитер, т. е. при всех п > О значения г< п) и z'"*1' расположены
по разные стороны от х, причем последовательности приближений с
четными и нечетными номерами сходятся к х монотонно. В этом
случае верна апостериорная оценка погрешности
rln) -
D.25)
и справедлив критерий D.24) окончания итерационного процесса.
Мы не будем приводить здесь полное доказательство теоремы. Оно
основано на использовании равенства D.20), установленного при дока-
доказательстве теоремы 4.2. Докажем только справедливость свойств 1° и
2°.
d Если 0 < <р' ^ q, то знаки величин г1 п) — х и х1""'' — х совпада-
совпадают, в то время как |х1п) — х\ < q\xln'1] — x\. Следовательно, последо-
последовательность монотонно приближается к х с той стороны, где лежит
х@). Если же -q < <р' < 0, то из равенства D.20) следует, что знаки
величин z( п) — х и х1™'11 — г различны. Это подтверждает колеба-
колебательный характер сходимости. ¦
Замечание. Монотонный и колебательный характер сходимос-
сходимости итерационной последовательности, указанные в теореме 4.4,
иллюстрируют соответственно рис. 4.7, а и 4.7, б.
6. Приведение уравнения к виду, удобному для итераций. Ключе-
Ключевой момент в применении метода простой итерации — эквивалентное
преобразование уравнения D.1) к виду D.15). Конечно, такое преобра-
преобразование имеет смысл только тогда, когда оказывается выполненным
условие D.18) при 0 < q < 1. Укажем один из простых способов такого
преобразован ия.
100
Предположим, что производная /' на отрезке [а, Ь] непрерывна и
положительна. Тогда существуют положительные постоянные т и М
такие, что 0 < m < f'(x) < М, х G [а, Ь]. Приведем уравнение D.1) к
виду
х- х- а/(х),
D.26)
где а > 0. В этом случае итерационная функция ip имеет вид <р(х) =
= х— а/(х). Как выбрать а, чтобы выполнялось условие D.18), при-
причем q было бы по возможности минимальным?
Заметим, что 1 — аМ < <р'(х) = 1 — af'(x) < 1 — am и поэтому
\<р'(х)\ < q (а) - max {|1 — аМ\, |1 — ат\]. Для того чтобы было
выполнено неравенство q(a) < 1, достаточно взять любое а ? @, 2/М).
Конкретный выбор параметра а зависит от наличия информации о
числах т и М. Если известны обе эти величины, то лучшим является
выбор а = а0 = 2/(М + т). В этом случае q(a0) = (М — т)/(М + т).
Если же известно только М, то можно положить а = щ — —. В этом
м
случае q (а{) = 1 — — Кроме того, при а = щ производная <р'{х) неот-
неотрицательна, и в силу теоремы 4.3 сходимость является монотонной.
Замечание. Случай, когда производная /' отрицательна,
сводится к рассмотренному выше умножением уравнения / (г) = 0
на -1.
Пример 4.7. Для решения задачи, поставленной в примере 4.5, можно
воспользоваться преобразованием уравнения D.4) к виду D.26). Будем считать
известным, что х € [0.70, 0.72]. Так как на отрезке локализации выполнено
условие DA — i2) — ех)' = -8г — в? < 0, то перепишем уравнение в виде
Л(х) = 0, i • Hi) = е* - 4A - г2). Тогда /,'(*) = е* + 8г и для
х G [0.70, 0.74 ¦ ,.ны оценки 0 < т - /,'@.70) ^ /,'(*) < /,'@.72) = М. Выберем
2
в уравнении D-26) ft =
т + М
, возьмем х<0) = 0.7 и будем вести итерации
г(п)
по формуле il"+4 = г(п) — «[е — 4A — аг1п)J]. Выбранному ft соответ-
соответствует q = а 0.013 и поэтому сходимость должна быть более быстрой,
чем в примере 4.6. Действительно, уже первая итерация дает гA) =
= 0.7034025118, и так как
прекратить и считать х = 0.7034 ± 0.0001.
|г<4- г<°> | и 5-Ю, то итерации следует
101

$ 4.5. Обусловленность метода простой итерации
В § 4.4 метод простой итерации был рассмотрен при идеальном
предположении о возможности точного вычисления значений функции
<р(х). В действительности же вычисления на ЭВМ дают приближенные
значения <р*(х). Поэтому вместо последовательности г1п), удовлетво-
удовлетворяющей равенству х(пП) = <р(х1п)), получается последовательность
z<п), для которой
-,„¦1, =(р »(~<п)). D.27)
Известно, что метод простой итерации и многие другие итерацион-
итерационные методы устойчивы к ошибке, допущенной на одной из итераций.
Такая ошибка эквивалентна некоторому ухудшению очередного приб-
приближения; если она не вывела приближение за пределы области сходи-
сходимости, то итерационная последовательность по-прежнему будет схо-
сходиться к решению х, а внесенная ошибка — затухать. Поэтому о таких
итерационных методах говорят, что они обладают свойством самоисп-
равляемости.
Однако погрешности допускаются не на одной, а на всех итерациях
и совокупное их влияние несколько иное.
1. Обусловленность задачи. Прежде чем сформулировать результат
о поведении метода простой итерации при наличии погрешности в
вычислении функции ip, отметим, что преобразование уравнения
f(x)= 0 к виду х — <р(х) изменяет обусловленность задачи. Запишем
это уравнение в виде / (г) = 0, где / (г) = х — <р(х), и воспользуемся
результатами § 4.2. Заметим, что Д(/*) = Д(у>"), поскольку в действи-
действительности приближенно вычисляется только. функция <р. Поэтому
оценка D.11) в данном случае выглядит так:
А(х') <
D.28)
Здесь v = 1/| 1 — <р'(х)\ — абсолютное число обусловленности корня х.
Грубо оценивая при выполнении условия | <р' \ < q < 1 величину v
1
числом v = , приходим к оценке
D.29)
102
В случае, когда <р' < 0 или <р' « 0, ее можно уточнить. Действительно,
как нетрудно установить, v < 1, если <р' < 0; следовательно,
А(х*) <А(<р*). D.30)
Заметим, что в оценках D.28)—D.30) величины Д (х*) и Д (^*)
можно заменить на 8(х*) и 8(<р*). Чтобы убедиться в этом, достаточно
разделить левую и правую части оценок на величины \х\ и |^(г)|,
которые равны между собой. Например, оценка D.28) преобразуется к
виду
~б(х*) < vl(<p*) D.31)
и, следовательно, абсолютное и относительное числа обусловленности
здесь совпадают.
Сделаем некоторые выводы. Задача вычисления корня х уравнения
х = <р(х) плохо обусловлена, если <р'(х) и 1. В этом случае сле-
следует ожидать, что количество верных цифр корня х по сравнению с
количеством верных цифр в вычисляемых значения <р *(х) должно быть
меньше примерно на N = lg v цифр. Для радиуса интервала неопреде-
неопределенности е и i/A(<p*) корня х в случае \<р'\ ^ q < 1 справедлива оцен-
оценка ? < ?* = -——. В случае, когда -1 < <р' < 0, уточненная оценка
такова: ? < ? * = А(р*); здесь потери верных цифр быть не должно.
Пример 4.9. Для уравнения х — *р(х) при ip(x) = 0.9999* + 10/^/2 имеем
<р'(х) = 0.9999 и, следовательно, v — 104. Поэтому при решении этого уравне-
уравнения методом простой итерации на ЭВМ будет потеряно примерно четыре
значащих цифры. Вычисления на 6-разрядной десятичной ЭВМ (или на
близкой ей по точности ЭВМ типа IBM PC) могут дать в таком случае всего
лишь две верные значащие цифры. Это вполне согласуется с результатом,
полученным в примере 4.6.
2. Чувствительность метода простых итераций к погрешности вы-
вычислений. Сформулируем основной результат данного параграфа.
Теорема 4.5. Пусть выполнены условия теоремы 4.2 и для всех
х € (х — а, х + а) имеет место неравенство \<р(х) — <р(х*)\ < Д(^*).
103

Предположим также, что е* = ^ ^ ' < а (т. е. величина Д(у*)
достаточно мала).
Если вычисления по формулам D.16) и D.27) начинаются с одною
начальною приближения xi0) = х@) € (х — «tj, x + <ti) (icte <7i =
= min {G, }, то последовательность x(n) не выходит за преде-
пределы <т-окрестности корня х и для всех п > 1 справедливы следующие
оценки погрешности:
ё*.
D.32)
D.33)
D.34)
Здесь С -
1 - q
Замечание 1. В случае ip' < 0 в неравенствах D.32)—D.34)
можно положить е* й Д(у>*), Си 1.
Замечание 2. При достаточно больших п в оценках D.32)—
D.34) величину е * можно считать приближенно равной радиусу
интервала неопределенности е = Уг_)—
1 -?'(*)
D Докажем по индукции, что для всех п > 0 справедливы неравенст-
неравенства D.32), D.33) и х<"> € (х — а, х + <г). Очевидно, что при п = 0 это
верно.
Предположим, что доказываемое утверждение справедливо при
некотором п > 0. Вычитая из равенства D.27) равенство D.16), получа-
ем
(г — <т, г + (т),
где Д("» = <р*(х1п)) — 1р(х(Ы), |Д(") | < Д(р*). Как следствие полу-
полученного равенства и сделанных предположений, имеем
_х(п»
= е*.
104
Объединяя эту оценку с оценкой D.19), получаем
|х(п+1) _ х| < 9п+1|х@) _ х| + ё*.
Поэтому
Нужное утверждение доказано для номера, равного п + 1, а следова-
следовательно, и для всех п > 0.
Вычитая из равенства D.27) равенство D.17), получаем
х<п+1>_ г = а(Щ(х(п>_ х) _|_ Д(п)( а(п) = ^'(^(Ш),
^(п) е (l— <Т, X + (Т).
Таким образом,
п)
)_ т —
аШ) ^г г ^ + 1 _ а(п) '
Из полученного равенства вытекает оценка D.34).Ш
Итак, итерационный процесс не ухудшает обусловленность корня х.
Как оказывается, гарантированная точность метода простой итерации
ограничена снизу величиной, примерно совпадающей с радиусом е
интервала неопределенности. Критерий D.23) окончания итераций
применим, если е * < е.
Входящую в соотношения D.29), D.30) величину Д(у*) в общем
случае оценить сверху достаточно сложно. Оценка снизу очевидна:
*) > Ы^м- В благоприятной ситуации, когда вычисления ведутся
окажется
по простым формулам, можно надеяться на то, что
величиной порядка |г|ем.
§ 4.6. Метод Ньютона
Знаменитый м"етод Ньютона является одним из наиболее эффектив-
эффективных методов решения самых разных нелинейных задач. Расчетную
формулу метода можно получить, используя различные подходы.
Рассмотрим два из них.
105

1. Метод касательных. Выведем расчетную формулу метода для
решения нелинейного уравнения
D.1) из простых геометрических
соображений. Соответствующая
иллюстрация приведена на рис.
4.9.
Пусть х@) — заданное начальное
приближение к корню х. В точке
М@) с координатами (г@),
д /(z'0))) проведем касательную к
х графику функции j = /(г) и за
новое приближение г111 примем
абсциссу точки пересечения этой
касательной с осью Ох. Аналогич-
Xя х<*
Рис. 19
но, за приближение zB) примем абсциссу точки пересечения с осью
Ох касательной, проведенной к графику в точке МA) с координатами
(гA), /(хA))). Продолжая этот процесс далее, получим последователь-
последовательность r@), xA), zB), ..., z(n), ... приближений к корню х.
Напомним, что уравнение касательной, проведенной к графику
функции у = /(г) в точке (г', f(x(n))), имеет вид
у =
D.35)
Полагая в равенстве D.35) у = 0, замечаем, что при выполнении усло-
условия f'(xin)) + 0 абсцисса х(п+1) точки пересечения касательной с осью
Ох удовлетворяет равенству
О =
D.36)
Выражая из него х(п+1>, получаем расчетную формулу метода Ньюто-
Ньютона:
— х( П) _
/(*'"')
, п>0.
D.37)
Благодаря такой геометрической интерпретации этот метод часто
называют методом касательных.
2. Метод линеаризации. С более общих позиций метод Ньютона
можно рассматривать как итерационный метод, использующий специ-
специальную линеаризацию задачи и позволяющий свести решение исход-
исходного нелинейного уравнения к решению последовательности линейных
уравнений.
106
Пусть приближение i( n) уже получено. Представим функцию в
окрестности точки z( n) по формуле Тейлора:
/(г) = /(х< «>) + /'(*' "I )(г - х<»!) + Ц& (х - х<"»У. D.38)
Здесь ^ — некоторая точка, расположенная между г и г( п). Заменяя в
уравнении /(г) = 0 функцию /(г) главной линейной частью разложе-
разложений D.38), получим линейное уравнение
= 0-
D.39)
Принимая решение уравнения D.39) за новое приближение г(п+1),
приходим к формуле D.37).
3. Основная теорема о сходимости метода Ньютона.
Теорема 4.6. Пусть х — простой корень уравнения f (х) — 0, о
некоторой окрестности которою функция f дважды непрерывно диф-
дифференцируема. Тогда найдется такая малая а-окрестность корня х,
что при произвольном выборе начальною приближения х@) из этой
окрестности итерационная последовательность метода Ньютона не
выходит за пределы окрестности и справедлива оценка
-х|2
х|2, п>0,
D.40)
где С = (Г1, означающая, что метод сходится с квадратичной скорос-
скоростью.
Следствием оценки D.40) является априорная оценка
, п>0,
D.41)
в которой q = а'1 |х@) — х|.
D Так как /'(х) + 0 (по определению простого корня), то в силу
непрерывности функций /' и f найдется 6о~°кРестность корня, в кото-
которой при некоторых постоянных а и /? выполнены неравенства 0 < а <
Пусть х(п) 6 (х — а, х + а), где а = min {60, -*-}. Подставляя х = х
в D.38), получим равенство
О = /(х< п>) + /'(*'п) )(х - х< п>) 4-
в котором ^ 6 (г — и, х + с). Вычитая из него равенство D.36), имеем
107

-
-x)=
Тогда, приравняв модули обеих частей этого равенства и используя
условия ограниченности \f'(x)\ и \f'(x)\, приходим к неравенству
а|г(п+п _ г| ^ с |г(п) _ J.|2) откуда следует справедливость оценки
D.40). Доказательство теоремы завершается применением леммы 4.2. И
Таким образом, при выборе начального приближения из достаточ-
достаточно малой окрестности корня метод Ньютона сходится квадратично.
Это означает, грубо говоря, что на каждой итерации число верных
цифр приближения примерно удваивается.
Приведенные в теореме 4.6 оценки погрешности являются априор-
априорными (см. § 3.3) и их использование в практике вычислений для коли-
количественной оценки погрешности неэффективно или чаще всего невоз-
невозможно.
4. Критерий окончания. На практике предпочтительнее использова-
использование простой апостериорной оценки
\х(п) _ jl ^ I xtn) _ х( n-i) | ] D-42)
справедливость которой обосновывается следующим утверждением.
Теорема 4.7. Пусть выполнены условия теоремы 4.6 и х{0) €
6 (х — -, х + -). Тогда для всех п > 1 верна оценка D.42).
id di
о Из оценки D.41) следует, что Ix'"' — х| ^ оаг
п-\
aq = |х@> -
— х\ < —. Поэтому, применяя неравенство D.40), получим цепочку
неравенств 2|х<"> - ~х\ < 2cr-i|x<n-» - х|2 < |г<"-1> - х| < \х^п'" —
— х< 1) | _|_ | г( п) — х|, из которой вытекает оценка D.42). И
Наличие оценки D.42) позволяет сформулировать следующий прак-
практический критерий окончания итераций метода Ньютона. При задан-
заданной точности е > 0 вычисления нужно вести до тех пор, пока не ока-
окажется выполненным неравенство
[п) _ Х[п-П
Пример 4.8. Используя метод Ньютона, найдем с точностью е — 10 поло-
положительный корень уравнения 4A — г2) — е* = 0.
В примере 4.2 корень был локализован на отрезке [0, 1]. Для /(г) =
108
= 4A — г2) — еГ имеем f'(x) = -8г — еГ. Очевидно, что f'(x) Ф 0, т. е. х —
простой корень. Возьмем начальное приближение г@) = 0.5 и будем
выполнять итерации метода Ньютона по формуле
4С1 _ (х^п)J) - exin)
gx(n) + eidi
Результаты первых итераций с 10 знаками мантиссы приведены в табл. 4.4.
Таблица 4.4
г(П)
\xtn) _ х( п-1) I
0
1
2
3
4
0.5000000000
0.7392185177
0.7042444088
0.7034399951
0.7034395712
2.4-10-1
3.5-10
8.0-10
4.3-10
При п = 4 вычисления следует прекратить и после округления получим
х = 0.703440 ± 0.000001.
Сравнение результатов итераций со значением х показывает, что прибли-
приближения гA), хB), гC) содержат 1, 3, 6 верных значащих цифр соответственно.
Можно показать, что приближение гD) содержит 10 верных цифр. Это подт-
подтверждает отмеченный ранее общий факт: при каждой итерации метода Ньюто-
Ньютона число верных значащих цифр примерно удваивается.
Пример 4.9. Используя метод Ньютона, укажем итерационный процесс
вычисления <Ja, где а > 0, р — натуральное число.
Р-
По определению, х = уа — это неотрицательная.величина, удовлетворяю-
удовлетворяющая равенству хР = а. Таким образом, задача сводится к вычислению положи-
положительного корня уравнения f(x) = 0, где f (х) — хР — а. Итерационная форму-
формула метода Ньютона примет вид
= г< то _:
У-а_р-1
[га)\р-1 р
D.44)
*• ' При р — 2 эта формула уже была получена в примере 3.17.
5. Связь с методом простой итерации. Метод Ньютона можно рас-
рассматривать как один из вариантов метода простой итерации, связан-
связанный со специальным преобразованием уравнения /(i) = 0k виду
109

х-
D.45)
где ip (x) = х — f(x)/f'(x). В самом деле, итерационная формула мето-
метода простой итерации x(n*l) = ip (x(n)) совпадает с формулой D.37).
N
Исходя из этого с учетом оценки D.19), можно было бы сделать
вывод о том, что метод Ньютона сходится только линейно. Однако
заметим, что <р'(х) — f (х) , v ' Так как f (х) = 0, то tp'(x) = 0 и
величина а<п+1> = |^>'(?(п)I> определяющая в силу равенства D.20)
коэффициент сжатия ошибки, стремится к нулю при п -* <». Скорость
сходимости возрастает по мере приближения к корню, отсюда и ее
сверхлинейный характер.
В качестве аналога теоремы 4.4 для метода Ньютона приведем
следующий результат.
Теорема 4.8. Пусть [а, Ь] — отрезок локализации простою
корня х уравнения D.1). Предположим, что на этом отрезке функция f
дважды непрерывно дифференцируема, а ее производные f'(x) и f'(x)
знакопостоянны. Пусть х<0) 6 [а, 6] — произвольное начальное прибли-
приближение, и в случае /(х@)) f(x@)) < 0 выполнено дополнительное усло-
условие гA) € [а, Ь] (первое приближение не выходит за пределы отрезка
локализации).
Тогда начиная с п = 1 итерационная последовательность метода
Ньютона х(п) сходится к х монотонно с той стороны отрезка [а, Ь],
tdef(x)f(x)>0.
Иллюстрацией монотонного характера сходимости может служить
рис. 4.9.
Следствие. Пусть уравнение f(х) имеет корень х, функция
f(x) дважды непрерывно дифференцируема на всей числовой оси, а ее
производные /' и /' знакопостоянны. Тогда метод Ньютона сходится
при любом начальном приближении г@) (т. е. является глобально
сходящимся), причем начиная с п = 1 последовательность сходится
монотонно с той стороны от корня, где f (x) f'(x) > 0.
б. Трудности использования. Простота, логическая стройность и
высокая скорость сходимости делают метод Ньютона чрезвычайно
привлекательным. Однако для его практического применения нужно
преодолеть две существенные трудности. Одна из них состоит в необ-
необходимости вычисления производной f'(x). Часто бывает невозможно
найти аналитическое выражение для f'(x), а определить приближенное
значение с высокой точностью очень трудно. Иногда вычисление
ПО
/'(я) — вполне реальная, но весьма дорогостоящая операция. В этих
случаях приходится модифицировать метод, избегая непосредственно-
непосредственного вычисления производной. Некоторые из таких модификаций приве-
приведены в § 4.7.
Более существенно то, что метод Ньютона обладает, вообще говоря,
только локальной сходимостью. Это означает, что областью его сходи-
сходимости является некоторая малая <т-окрестность корня х и для гаран-
гарантии сходимости необходимо выбирать хорошее начальное приближе-
приближение, попадающее в эту ег-окрестность. Неудачный выбор начального
приближения может дать расходящуюся последовательность (рис.
4.10) и даже привести к аварийному останову (если на очередной
итерации f'(x( п)) а 0). Для преодоления этой трудности часто исполь-
используют метод Ньютона в сочетании с каким-либо медленно, но гаранти-
гарантированно сходящимся методом типа бисекции. Такие гибридные алго-
алгоритмы находят в последнее время широкое практическое применение.
Рис 4-Ю
7. Влияние погрешности вычислений. Пусть х — простой корень.
Если метод Ньютона рассматривать как вариант метода простой итера-
итерации, связанный с преобразованием уравнения f (х) = 0 к виду D.45),
то можно воспользоваться результатами § 4.4 и § 4.5.
Поскольку ip'(x) = 0, справедливо неравенство D.30) и радиус
интервала неопределенности корня х равен примерно Д(у>*). В
оценках D.32)—D.34) можно считать е* и Д(^*) и С и 1. Для того
111
чтобы сделать окончательные выводы, остается оценить

Пусть /* и (/')* — приближенные значения функций /и /', вычис-
вычисляемые в малой окрестности корня х. Будем считать, что производная
/' вычисляется хотя бы с точностью до 1—2 верных значащих цифр. В
противном случае (особенно, если неверно определяется знак /') из
геометрического смысла метода легко понять, что его применять не
следует. В силу предложения 2.5 в малой окрестности корня имеем
Так как ip* (х) = х в f\*( у т0> учитывая погрешность и |х|ем,
вносимую в <р* вследствие выполнения операции вычитания, получим
Д(?р и i + |г|ем.
Таким образом, преобразование уравнения Xх) = 0 к виду D.45)
практически не меняет обусловленность и радиус е интервала неопре-
неопределенности корня х. Итерационный процесс Ньютона дает возмож-
возможность вычислить решение с точностью е > е. Отметим, тем не менее,
что эти достоинства метода Ньютона реализуются, вообще говоря,
только в малой окрестности корня.
5 4.7. Модификации метода Ньютона
В предыдущем параграфе в качестве недостатка метода Ньютона
была отмечена необходимость вычисления значения производной /'(г)
на каждой итерации. Рассмотрим некоторые модификации метода
Ньютона, свободные от этого недостатка. Заметим, что, по существу,
излагаемые в этом разделе итерационные методы решения нелинейно-
нелинейного уравнения на каждой итерации используют некоторую процедуру
его линеаризации, т. е. исходное нелинейное уравнение заменяется
приближенно более простым линейным уравнением.
1. Упрощенный метод Ньютона. Если производная f'(x) непрерыв-
непрерывна, то ее значение вблизи простого корня х почти постоянно. Поэтому
можно попытаться вычислить /' лишь однажды в точке г@), а затем
заменить в формуле D.37) значение /'(*(п)) постоянной /'(х@)). В
результате получим расчетную формулу упрощенною метода Нью-
Ньютона:
112
D.46)
Геометрическая иллюстрация метода приведена на рис. 4.11. В
точке (я@), /(г@))) к графику
функции у = f(x) проводится
касательная /0 и за приближе-
приближение гA) принимается абсцисса
точки пересечения этой каса-
касательной с осью Ох (как в методе
Ньютона). Каждое следующее
приближение х<п+1> получается
здесь как абсцисса точки пере-
пересечения с осью Ох прямой,
проходящей через точку А/< п) с
координатами (r(n), f(x{n))) и
параллельной касательной /о-
Упрощение вычислений по сравнению с методом Ньютона достига-
достигается здесь ценой резкого падения скорости сходимости. Сходимость
этого метода является уже не квадратичной, а линейной.
Метод D.46) можно рассматривать как метод простой итерации с
итерационной функцией tp(x) = х — /vg(o>y Так как ? ^ = 1 ~~
"(*)
то для знаменателя q соответствующей геометрической
прогрессии имеем q и
. Следовательно, скорость сходи-
сходимости тем выше, чем ближе начальное приближение х@) к решению х.
2. Метод ложного положения. В основе этой и следующих двух
модификаций метода Ньютона лежит приближенное равенство
J K
.,...
2( п) \ _ f ( xi п) \
i I Li±—I
zm) _ xtn)
D.47)
Оно верно при условии zln) я r<«> и следует из определения произ-
водной: f'{x) = lim /(?__~/(j* •
Пусть с — фиксированная точка, расположенная в окрестности
простого корня х. Заменим в расчетной формуле метода Ньютона
D.37) производную f'{xln)) правой частью приближенного равенства
D.47), полагая z(n) = с. В результате придем к расчетной формуле
метода ложного положения:
113

— т(п) _.
/(с)-/ (*<">)
/(*<•»>), ">0.
D.48)
Геометрическая иллюстрация метода приведена на рис. 4.12. Оче-
Очередное приближение x(n*i] получается здесь как абсцисса точки пере-
пересечения с осью Ох прямой, проведенной через расположенные на
графике функции у — f(x) точки Ми М(п) с координатами (с, /(с)) и
У
0
i
х<" /" х'
у
М"/
1\
1 1
1 J
Рис. 4-12
Рас. 113
Метод D.48) обладает только линейной сходимостью. Его можно
рассматривать как метод простой итерации с итерационной функцией
<р(х) — х — ~гг\ ттт /(г)- Так как скорость сходимости определя-
т (с) — г (х\
ется вблизи корня величиной q» \tp'{x)\ =
1 —
(с -г) f\x)
/(с)- f{~r)
, то она
тем выше, чем ближе окажется выбранная точка с к х.
3. Метод секущих. Замена в формуле метода Ньютона производной
f /xi n-l) \ _ f /х( n) )
—-—(п_1) ^ - приводит к расчетной
f'(x( n)) приближением
формуле метода секумщг.
х( п+1) _
г( п-1) _
:/(*<"»), п>1.
D.49)
Заметим, что этот метод двухшаговый, так как для нахождения
очередного приближения х<п+1> требуется знание двух предыдущих
приближений х(п) и г'"1. В частности, для того чтобы начать вы-
вычисления, необходимо задать два начальных приближения х@) и хA).
Все рассмотренные ранее методы требовали для вычисления х[ n+1'
только знание z(n), т. е. были одношаговыми.
114
На рис. 4.13 приведена геометрическая иллюстрация метода. Оче-
Очередное приближение xtn*l) получается здесь как абсцисса точек пере-
пересечения с осью Ох секущей, соединяющей точки Л/'"1 и Min) графи-
графика функции f(x) с координатами (r(n"n, f(xln'l])) и (xin], f(x(n))).
Примечательно то, что эта модификация метода Ньютона сохраняет
свойство сверхлинейной сходимости, если вычисляется простой корень
х. Точнее, верно следующее утверждение.
Теорема 4.9. Пусть х — простой корень уравнения f (х) = 0, в
некоторой окрестности которого функция f дважды непрерывно диф-
дифференцируема, причем f'(x) i- 0. Тогда существует а-окрестность
корня х такая, что при произвольном выборе приближений х@) и гA)
из этой а-окрестности метод секущих сходится с порядком р —
— — я 1.618, т. е. для п > 1 справедлива оценка
— Х\
-х\Р, р =
Так как одна итерация метода секущих требует только одного
нового вычисления значения функции /, а метод Ньютона — двух
вычислений значений функций (/ и /'), то трудоемкость двух итера-
итераций метода секущих приблизительно эквивалентна трудоемкости од-
одной итерации по Ньютону. Две итерации метода секущих дают поря-
порядок р2 « 2.618 > 2, поэтому его можно расценивать как более быстрый
по сравнению с методом Ньютона.
К сожалению, метод обладает, вообще говоря, только локальной
сходимостью. Он требует выбора двух близких к г (в общем случае —
очень близких) начальных приближений г@) и хA). Если эти прибли-
приближения выбраны неудачно, то метод расходится (рис. 4.14).
х""
1
«'"
У
0
xw у
М1"
==—- х"> х
Рис. Щ
115

4. Метод Стеффевсена. Итерационная формула метода Стеффенсе-
Стеффенсеимеет вид
_ Г(П) _
/(*'"')
), n>0. D.50)
Можно считать, что она получена в результате замены производной
/'(г<">), входящей в расчетную формулу метода Ньютона, приближе-
приближением D.47), где г<"> = г'"' + /(*<">).
Метод Стеффенсена интересен тем, что он является одношаговым,
не требует вычисления производной /' и в то же время, как и метод
Ньютона, сходится квадратично, если корень г — простой, функция /
дважды непрерывно дифференцируема в окрестности корня, а началь-
начальное приближение z( 0) выбрано близко к х.
Геометрическая иллюстрация метода Стеффенсена приведена на
рис. 4.15. Приближение xin*1) получается как абсцисса точки пересе-
пересечения с осью Ох секущей,
проходящей через точки
Af( n) и ЛГ( п) с координатами
(г<»>, /(*<•»>)) и (*<»»,
f(zin))). Значение г(п>
отвечает абсциссе , точки
пересечения с осью Ох пря-
прямой у = /(г"") — (х —
— х1п)), проходящей через
точку М1 п) и параллельной
прямой у = -х.
Несмотря на свойство квад-
ратичной сходимости, метод
Стеффенсена уступает методу
секущих, поскольку требует большей вычислительной работы для
достижения toft же точности е. Это связано с тем, что на каждой
итерации рассматриваемого метода вычисление функции производится
дважды, а в методе секущих лишь один раз.
5. Уточнение метода Ньютона для случая кратного корня. В прин-
принципе для вычисления корня уравнения /(г) = 0 кратности m > 1
можно использовать и стандартный метод Ньютона. Однако в этом
случае скорость его сходимости является только линейной. Можно
показать, что знаменатель q соответствующей геометрической прогрес-
прогрессии приближенно равен 1 .
116
Рис. 4-15
Для того чтобы сохранить квадратичную скорость сходимости,
метод Ньютона нужно модифицировать следующим образом:
r(n+n - g(n) -mJtl) ,„,{, n>0.
D.51)
Можно показать (это достигается раскрытием неопределенностей с
помощью формулы Тейлора), что при таком выборе итерационной
функции f{x) = х — m -777-7 получим ip'(x) = 0, и сходимость снова
окажется квадратичной.
На рис. 4.16, а, б проиллюстрировано поведение последовательных
приближений стандартного метода Ньютона и его модификации D.51)
для случая отыскания корня кратности m = 2.
Рис. 4-16
Для метода D.51) значение г'п+1> получается следующим образом.
В точке М( п) с координатами (x(n), f(x(n))) к графику функции
проводится касательная. Пересечение ее с осью Ох дает вспомогатель-
ную точку xln*l). Для получения точки х(п+1) нужно воспользоваться
равенством z(n+1
— xin) =
= m(xln+1) —
Пример 4.10. Применим методы, рассмотренные в данной главе, для вычис-
вычисления положительного корня уравнения 4A — z2) — ех = 0, считая известным,
что х € [0, 1] (см. пример 4.2).
Результаты вычислений приведены в табл. 4.5—4.8. В них для каждого
приближения дается число верных знаков и требуемое число вычислений
117

значений функции f(x) = 4A — г2) — ех (для упрощенного метода Ньюто-
Ньютона учтено вычисление /'(г<0))). Вычисления выполнены с 10 знаками мантис-
мантиссы.
Отметим, что выбор начальных приближений был довольно случайным
(хотя и разумным). Тем не менее лучший результат показал метод секущих.
Решение с 10 верными знаками мантиссы было получено после 5 итераций и
для этого потребовалось лишь 6 вычислений функции. Хотя метод Ньютона
(см. пример 4.8) при том же начальном приближении г@) дает такое же
значение х всего после 4 итераций, для этого требуется 8 вычислений функ-
функции D вычисления /и 4 вычисления /').
Пример 4.11. Применим метод Ньютона и его модификацию D.51) для
вычисления корня х = 0 кратности т = 2 для уравнения jPe? = 0. Возьмем
fio) = i Результаты вычислений даны в табл. 4.9 и 4.10.
Как видно из табл. 4.9, погрешность метода Ньютона убывает довольно
медленно и соответствует примерно геометрической прогрессии со знаменателем
q - 1/2. В то же время 5 итераций по формуле D.51) при m = 2 дают значе-
значение решения с погрешностью, меньшей ? = 1О~10.
Таблица 4.5
Упрощенный метод Ньютона;
г'°> =0.5
Таблица 4.6
Метод ложного положения;
с= 1, лг«°> = 0.5
п
0
1
2
3
4
5
6
7
8
9
10
Х(П)
0.5000000000
0.7392185177
0.6896366262
0.7081565866
0.7017501401
0.7040350503
0.7032284740
0.7035142540
0.7034131306
0.7034489297
0.7034362584
Число
верных
знаков
0
1
1
2
2
3
3
4
4
4
5
Число
вычис-
вычислений
функций
0
2
3
4
5
6
7
8
9
10
11
п
0
1
2
3
4
5
6
7
8
9
10
х[п)
0.5000000000
0.6660226835
0.6971284254
0.7023912700
0.7032658920
0.7034108088
0.7034348083
0.7034387825
0.7034394406
0.7034395495
0.7034395676
Число
верных
знаков
0
1
2
2
3
4
5
6
6
7
8
Число
вычис-
вычислений
функций
0
2
3
4
5
6
7
8
9
10
11
118
Таблица 4.7
Таблица 4.8
Метод секущих;
х@) = 1(
Метод Стеффенсена;
г<°> =0.5
п
0
1
2
3
4
5
6
х<п>
1.0000000000
0.5000000000
0.6660226835
0.7092548653
0.7032943284
0.7034390197
0.7034395712
Число
верных
знаков
0
0
1
2
3
6
10
Число
вычис-
вычислений
функций
0
0
2
3
4
5
6
п
0
1
2
3
4
5
6
х(п)
0.5000000000
0.6047702913
0.6731754719
0.6998880287
0.7033854199
0.7034395584
0.7034395712
Число
верных
знаков
0
0
1
2
3
7
10
Число
вычис-
вычислений
функций
0
2
4
6
8
10
12
Таблица 4.9
Метод Ньютона
Таблица 4.10
Уточнение метода Ньютона для
случая т— 2
п
0
1
2
3
4
5
6
7
8
1.0000000000
0.6666666667
0.4166666667
0.2442528736
0.1354180464
0.0720028071
0.0372524647
0.0189668249
0.0095725027
71
0
1
2
3
4
5
' х(п)
1.0000000000
0.3333333333
0.0476190476
0.0011074197
0.0000006128
0.0000000000
б. Чувствительность к погрешностям. Рассмотренные в этом параг-
параграфе одношаговые методы можно интерпретировать как различные
варианты метода простой итерации. Поэтому исследование их чувстви-
чувствительности к погрешностям сводится (аналогично тому, как это было
сделано в предыдущем параграфе для метода Ньютона) к использова-
использованию соответствующих результатов § 4.5. Так, например, можно убе-
119

диться в хорошей обусловленности модифицированного метода Ньюто-
Ньютона и метода ложного положения.
Высокая скорость сходимости метода секущих делает его привлека-
привлекательным для применения. Однако вызывает беспокойство тот факт,
ftx{n-\) \ _ f (r(nn
что в формулу D.49) входит величина —-—(п-п _ (nl 1 аппрок-
аппроксимирующая производную. Вблизи корня, когда z(n) я г(пМ) и
/(х'п>)я /(г') я 0, погрешность вычисления функции начинает
существенно сказываться на точности этой величины, и метод секущих
теряет устойчивость. Этим он существенно отличается от методов
простой итерации и Ньютона, для которых приближения х( п) равно-
равномерно устойчивы к погрешности независимо от числа итераций п.
Тем не менее при грамотном использовании метод секущих дает
возможность получить почти столько же верных значащих цифр корня
х, сколько вообще позволяет обусловленность задачи (см. § 4.2). Воз-
Возможная (но не обязательная) ¦ потеря точности составляет 1—2 верные
цифры. Необходимо лишь прервать итерационный процесс в тот мо-
момент, когда приближения окажутся в опасной близости к интервалу
неопределенности. Один из способов заметить этот момент состоит в
использовании правила Гарвика (см. § 4.2).
Отметим, что при попадании очередного приближения в малую
окрестность решения теряет устойчивость и метод Стеффенсена.
§ 4.8. Дополнительные замечания
1. Метод обратной квадратичной интерполяции. Пусть приближения
r(n-2)| r( n-Dj r(n) уЖе найдены, а соответствующие значения функции /
различны (последнее предположение заведомо будет выполнено, если функция
/ строго монотонна). Тогда строят такой квадратичный многочлен Р2(у) от
переменной у, что г( " = Рг(/(*(" )) Для г = п — 2] п — 1, п. За очередное
приближение к решению принимается г( п*1 > = Рг@).
Этот трехшаговый метод обладает локальной сходимостью с порядком р в
и 1.839; для начала его работы требуется задание трех хороших начальных
приближений.
2. Методы с порядком сходимости выше второго. Приведем пример одноша-
гового метода, обладающего кубической сходимостью:
/'(*<»>) 2(/'(*(п))J
Существуют и другие методы с порядком сходимости выше второго, теорети-
теоретически очень быстро сходящиеся вблизи корня. Однако они редко используют-
120
ся на практике, так как их преимущество в скорости сходимости начинает
проявляться лишь тогда, когда итерации уже почти сошлись и в действитель-
действительности осталось сделать 1—2 итерации либо вообще пора прекратить вычисле-
вычисления. Чтобы ощутить преимущество таких методов над методами Ньютона и
секущих, нужна ЭВМ с очень высокой разрядностью и желание получить
решение с чрезвычайно высокой точностью.
3. Вычисление корней многочленов. Вычисление корней многочленов Рп(х)
степени п — специальная задача, для решения которой разработано большое
число эффективных алгоритмов. Укажем на один из них — метод Мюллера. В
нем по трем ранее найденным приближениям xin'2),
Х1 п)
СТроЯТ
интерполяционный многочлен второй степени Q>(:r), т. е. такой многочлен для
которого (Эз(г(") = /(г(" ) при i = п — 2, п — 1, п. За очередное приближе-
приближение г(п+1) принимают тот из двух корней многочлена Qi(x) (в общем случае
являющихся комплексными), который расположен ближе к xin).
Вплоть до начала 60-х годов задача вычисления корней многочленов была
весьма распространенной. Одна из основных причин состояла в том, что к
отысканию корней характеристического многочлена сводилась одна из важней-
важнейших задач алгебры — задача вычисления собственных чисел матриц. В нас-
настоящее время существуют другие, гораздо более эффективные численные
методы вычисления собственных значений (см. гл. 8), и, по-видимому, задача
вычисления корней многочлена во многом потеряла свою актуальность.
Как было отмечено ранее, к задаче отыскания корней многочлена высокой
степени с приближенно заданными коэффициентами следует отнестись очень
внимательно: она может оказаться плохо обусловленной (см. в гл. 3 пример
Уилкинсона). Вообще, можно посоветовать избегать применения методов реше-
решения вычислительных задач, в которых используются многочлены высокой
степени.
4. Гибридные алгоритмы. В последние годы получили признание алгорит-
алгоритмы, которые называют гибридными (или регуляризированными). Они представ-
представляют собой комбинации надежных, но медленно сходящихся методов типа
бисекции с недостаточно надежными, но быстро сходящимися методами типа
секущих и Ньютона. Результирующие алгоритмы обладают высокой надежнос-
надежностью и гарантированной сходимостью. В тех же случаях, когда в окрестности
простого корня функции /— гладкая, сходимость становится сверхлинейной.
Алгоритм ZEROIN, изложенный в [86], является примером эффективного
гибридного алгоритма, на каждом шаге которого принимается решение о том,
какой из трех методов: бисекции, секущих или обратной квадратичной интер-
интерполяции — следует использовать для вычисления очередного приближения.
5. Критерии окончания. Проблема выбора правильного критерия окончания
итерационного процесса часто оказывается достаточно сложной. Следует иметь
в виду, что наряду с обсуждавшимся в предыдущих параграфах условием
|я(п)_г( n-i) |< ?j нередко используется следующее условие: |/(я(п')|< ?г-
121

Глава 5
ПРЯМЫЕ МЕТОДЫ РЕШЕНИЯ
СИСТЕМ ЛИНЕЙНЫХ
АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
§ 5.1. Постановка задачи
В вычислительной линейной алгебре выделяют четыре основные
задачи: 1) решение систем линейных алгебраических уравнений; 2)
вычисление определителей; 3) нахождение обратных матриц; 4) опре-
определение собственных значений и собственных векторов. Задачи 2 и 3
обсуждаются в § 5.6, последней по порядку (но не по значению) зада-
задаче 4 посвящена гл. 8.
В основном же данная глава посвящена задаче 1, а более точно —
прямым методам решения систем линейных алгебраических уравнений
с вещественными коэффициентами:
E.1)
а2тхт ~
= ьт.
В матричной форме записи эта система принимает вид
Ах=Ь,
где
E.2)
А =
он
«21
1
°12
0-12
2
«13 ••¦
«23 ¦•¦
lira
«2 m
аз*
«m3
"mm .
6 —
ь2
122
Итерационные методы решения системы E.1) будут рассмотрены в
гл. 6.
Уделим основное внимание задаче вычисления вектора х, являюще-
являющегося решением системы E.2), по входному данному — вектору Ь. Будем
предполагать, что матрица А задана и является невырожденной. Из-
Известно, что в этом случае решение системы существует, единственно и
устойчиво по входным данным. Это означает, что рассматриваемая
задача корректна.
Хотя задача решения системы E.1) сравнительно редко представ-
представляет самостоятельный интерес для приложений, от умения эффектив-
эффективно решать такие системы часто зависит сама возможность математичес-
математического моделирования самых разнообразных процессов с применением
ЭВМ. Как будет видно из дальнейшего изложения, значительная
часть численных методов решения различных (в особенности — нели-
нелинейных) задач включает в себя решение систем E.1) как элементар-
элементарный шаг соответствующего алгоритма.
Пусть I* = (х*, х*, ..., х^)т — приближенное решение системы E.1).
В этой и следующих главах мы будем стремиться к получению реше-
решения, для которого погрешность е = х — х* мала (количественные ха-
характеристики "величины" погрешности будут введены в следующем
параграфе). Тем не менее заметим, что качество полученного решения
далеко не всегда характеризуется тем, насколько мала погрешность
х — г*. Иногда вполне удовлетворительным является критерий малос-
малости невязки г = Ь — Ах*. Вектор г показывает, насколько отличается
правая часть системы от левой, если подставить в нее приближенное
решение. Заметим, что г — Ах — Ах* = А(х — х*) и поэтому погреш-
погрешность и невязка связаны равенством
е= х-х* =
E.3)
§ 5.2. Нормы вектора и матрицы
1. Норма вектора. Решением системы линейных алгебраических
уравнений является вектор х = (хь х2, ..., хт)Т, который будем рассмат-
рассматривать как элемент векторного пространства Rm. Приближенное реше-
решение х* = (х*, х*, ..., х*)т и погрешность е = х— х* = (xj — х*, ..., х„ —
— х^)т также являются элементами пространства Я™. Для того чтобы
анализировать методы решения систем, необходимо уметь количествен-
количественно оценивать "величины" векторов х* и х — х*, а также векторов Ь и
123

4—6*, где b* — (b*, b*, ..., b?)r — вектор приближенно заданных
правых частей. Удобной для этой цели количественной характеристи-
характеристикой является широко, используемое понятие нормы вектора.
Говорят, что в R задана норма, если каждому вектору х из Rm
сопоставлено вещественное число ЦхЦ, называемое нормой вектора хи
обладающее следующими свойствами:
1°) ||х| > 0, причем ||z| = 0 тогда и только тогда, когда х = 0;
2°) |ах| = \а\ |х| для любого вектора хи любого числа а;
3°) | х + у\ ^ I х| + У у| для любых ьекторов х и у;
последнее неравенство принято называть неравенством треугольника.
Заметим, что такими же свойствами обладает обычная геометричес-
геометрическая длина вектора в трехмерном пространстве. Свойство 3° в этом
случае следует из правила сложения векторов и из того известного
факта, что сумма длин двух сторон треугольника всегда больше длины
третьей стороны.
Существует множество различных способов введения норм. В вы-
вычислительных методах наиболее употребительными являются следую-
следующие три нормы:
m
|x|i=S \Xi\,
1=1
l/
)
= max
E.4)
Первые две из них являются частными случаями более общей нормы:
1=1
E.5)
(при р = 1 и р =2), а последняя, как можно показать, получается из
нормы E.5) предельным переходом при р -»<».
Замечание 1. Норма |х|2 является естественным обобщением
на случай m-мерного пространства понятия длины вектора в двух-
и трехмерных геометрических пространствах. Поэтому ее называют
евклидовой нормой.
Замечание 2. Справедливы неравенства
IxL<||x||2<
E.6)
указывающие на то, что в определенном смысле все три введенные
нормы эквивалентны: каждая из них оценивается любой из двух
других норм с точностью до множителя, зависящего от т.
Пример 5.1. Найдем |x|i, Н2. Но. для вектора х = @.12, -0.15, 0.1б)т.
124
По формулам E.4) определяем Hi = 0.12 + 0.15 + 0.16 = 0.43, |х|2 -
= @.122 + 0.152 + 0.162)'/2 = 0.25, И» = тах {012, 0.15, 0.16} = 0.16.
2. Скалярное произведение. Напомним, что скалярным произведе-
произведением векторов х = (хи х2, ..., хт)Т и у = (уи у2, ..., ут)Т называется
величина
т
(х, у) = ххух + х2у2 + ... + хтут - ? rtyt. E.7)
!=]
Нетрудно установить, что |х|2 = (х, хI/2.
В случае, когда векторы х, у имеют комплексные компоненты,
скалярное произведение понимают так:
(х, у) =
х2у2 + ... + хтут.
3. Абсолютная и относительная погрешности вектора. Далее будем
всюду считать, что в пространстве m-мерных векторов Rm введена и
фиксирована некоторая норма |х|| (например, одна из норм |х[р, 1 ^
< р < оо. В этом случае в качестве меры степени близости векторов х и
х* естественно использовать величину |х— г*|, являющуюся аналогом
расстояния между точками х и х*. Введем абсолютную и относитель-
относительную погрешности вектора х* с помощью формул
Выбор той или иной конкретной нормы в практических задачах
диктуется тем, какие требования предъявляются к точности решения.
Выбор нормы flxfli фактически отвечает случаю, когда малой должна
быть суммарная абсолютная ошибка в компонентах решения; выбор
\х\2 соответствует критерию малости среднеквадратичной ошибки, а
принятие в качестве нормы ЦхЦ^ означает, что малой должна быть
максимальная из абсолютных ошибок в компонентах решения.
4. Сходимость по норме. Пусть {x(nl}n=i — последовательность
векторов х(п) = (х[п), x2n)i •¦•> •С7пП1)т- Говорят, что последователь-
последовательность векторов х{ п) сходится к вектору г при п -> <ю (х( п) -» х при
п -»оо), если А(х1п)) = |г(п| — х|| -» 0 при п -»со.
Замечание. Сам факт наличия или отсутствия сходимости
х( п| к х при п -» № в конечномерных пространствах не зависит от
выбора нормы. Известно, что из сходимости последовательности по
125

одной из норм следует сходимость этой последовательности в Д по
любой другой норме. Например, для норм |z|i, i*|hi В1!», это выте-
вытекает из неравенств E.6). Более того, х(п) -» х при п -» <» тогда и
только тогда, когда для всех х = 1, 2, ..., т имеем х[п) -> xt при
п -> оо, т. е. сходимость по норме в R эквивалентна покомпонентной
(покоординатной) сходимости.
5. Норма матрицы. Величина
E.9)
называется нормой матрицы А, подчиненной норме векторов, введен-
введенной в Л™.
Заметим, что множество всех квадратных матриц размера т х т
является векторным пространством. Можно показать, что введенная в
этом пространстве формулой E.9) норма обладает следующими свойст-
свойствами, аналогичными свойствам нормы вектора:
1°) ||j4|| > О, причем ||.4f = 0 тогда и только тогда, когда А = 0.
2°) || а>4|| = | а| • Ц.А|| для любой матрицы А и любого числа а.
3°) \А + В\ < \А\ + \В\ для любых матриц А и В.
Дополнительно к этому верны следующие свойства:
4°) |i4-B| < ЦАЦ- |В| для любых матриц А и В,
5°) для любой матрицы А и любого вектора х справедливо неравен-
неравенство
E.10)
Докажем, например, свойство 5°. Если |х|| ± О, то неравенство E.10)
эквивалентно неравенству ЦЛхЦ/ЦхЦ ^ \А\, справедливость которого
следует из определения E.9). Если же Цх|| - 0, то неравенство E.10)
превращается в верное числовое неравенство 0^0.
Как следует из определения E.9), каждой из векторных норм |х||
соответствует своя подчиненная норма матрицы А. Известно, в част-
частности, что нормам ||x|i, |х|2 и flxf^ подчинены нормы |j4|i, \А\2 и
вычисляемые по формулам
1 = шах
m
Е
E.11)
E.12)
где Xj(ATA) — собственные числа1 матрицы АГА;
= max E |ау|. E.13)
Нормы |A|i и Й-АЦ^ вычисляются просто (см. ниже пример 5.2).
Для получения значения первой из них нужно найти сумму модулей
элементов каждого из столбцов матрицы А, а затем выбрать макси-
максимальную из этих сумм. Для получения значения Ц-АЦ^ нужно анало-
аналогичным образом поступить со строками матрицы А.
Как правило, вычислить значение нормы Ц-АЦг бывает трудно, так
как для этого следует искать собственные числа А;. Для оценки вели-
величины |Л|2 можно, например, использовать неравенство
E.14)
величина, называемая евклидовой нормой
Здесь || Л Ц
= \ s
|2 _
матрицы А.
Норма E.9) имеет простую геометрическую интерпретацию. Для
того чтобы ее привести, заметим, что операцию умножения матрицы А
на вектор х можно рассматривать как преобразование, которое перево-
переводит вектор х в новый вектор у — Ах. Если значение Jx|| интерпретиру-
интерпретируется как длина вектора х, то величина [Лх||/||х| есть коэффициент
растяжения вектора х под действием матрицы А. Таким образом,
величина
\АЛ
= \А\ =тах
E.15)
представляет собой максимальный коэффициент растяжения векторов
под действием матрицы А. Полезно отметить, что для невырожденной
матрицы А минимальный коэффициент растяжения к^п отвечает нор-
норме обратной матрицы и вычисляется по формуле
*min =
- min
E.16)
1 Напомним, что число А называется собственным числом матрицы А, если
det (.4 — \Е) — 0. Каждая матрица порядка m имеет ровно тп собственных
чисел (вообще говоря, комплексных) с учетом их кратности.
127

Заметим, что в случае \А\ < 1 происходит сжатие векторов под
действием матрицы А.
Пример 5.2. Для матрицы
0.1
0.2
0
-0.4
0
0.1
0
-0.3
0.3
.А ~~
найдем [А\[, \А\^ и оценим \А\2
В соответствии с формулами E.11), E.13) и неравенством E.14) имеем
|il|i = max {0.1 + 0.2 + 0, 0.4 + 0 + 0.1, 0 + 0.3 + 0.3} = 0.6,
\a\j= max {0.1 + 0.4 + 0, 0.2 + 0 + 0.3, 0 + 0.1 + 0.3} = 0.5,
1а\2<№е=[1\1оЦ
* 0.63.
$ 5.3. Типы используемых патриц
Эффективность вычислений в линейной алгебре существенно зави-
зависит от умения использовать специальную структуру и свойства исполь-
используемых в расчетах матриц. Напомним некоторые важные типы матриц.
Квадратная матрица А называется диагональной, если ее элементы
удовлетворяют условию ау = 0 для i t j (все отличные от нуля эле-
элементы расположены на главной диагонали):
А =
ап 0 0 ... 0
0 022 0 •¦• 0
0 0 а33 •¦¦ 0
0
<hm
Диагональную матрицу, у которой все элементы ац главной диаго-
диагонали равны единице, называют единичной и обозначают буквой Е:
1
0
0
0
1
0
0
0
1
... 0
... 0
... 0
Е =
О 0 0 ... 1
Пример 5.3. Вычислим норму единичной матрицы К
По определению, \Е\ — max ¦!—Д = max -й =1. Следовательно, \Е\ =1.
хФО
128
Важную роль в численном анализе играют треугольные матрицы.
Квадратная матрица А называется нижней треугольной, если все ее
элементы, расположенные выше главной диагонали, равны нулю (Ду =
= 0 для i < j). Если же равны нулю все элементы матрицы, располо-
расположенные ниже главной диагонали (ау = 0 для i > ]), то она называется
верхней треугольной.
Нижняя и верхняя треугольная матрицы имеют соответственно
следующий вид:
ап 0 0
«21 <»22 0
... 0
... 0
¦•¦ 0
°т2
022 023
0 а33
a2m
а3т
О О
О
Отт J
Треугольные матрицы обладают рядом замечательных свойств.
Например, для таких матриц определитель легко вычисляется по
формуле
det A = au
¦¦¦ атт-
E.17)
Квадратная матрица А называется симметричной, если она совпа-
совпадает со своей транспонированной матрицей Ат(или, что то же, Оу = пц
для всех i, j).
Будем называть симметричную матрицу А положительно определен-
определенной и писать А > 0, если для всех векторов х Ф 0 квадратичная форма
т
(Ах, х) = Е uifiXj
принимает положительные значения.
Обозначим через А,щП и А^х минимальное и максимальное собствен-
собственные значения матрицы А. Известно, что для симметричной матрицы
Amin Ы2<(Ах, *)<Атах И2
и матрица А положительно определена тогда и только тогда, когда все
ее собственные значения положительны.
Одна из трудностей практического решения систем большой раз-
размерности связана с ограниченностью оперативной памяти ЭВМ. Хотя
объем оперативной памяти вновь создаваемых вычислительных машин
растет очень быстро, тем не менее еще быстрее возрастают потребности
практики в решении задач все большей размерности (напомним, что
5-28 ¦ 129

для хранения в оперативной памяти ЭВМ матрицы порядка т требу-
требуется т2 машинных слов). В значительной степени ограничения на
размерность решаемых систем можно снять, если использовать для
хранения матрицы внешние запоминающие устройства. Однако в этом
случае многократно возрастают как затраты машинного времени, так и
сложность соответствующих алгоритмов.
Поэтому при создании вычислительных алгоритмов линейной ал-
алгебры большое внимание уделяют способам компактного размещения
элементов матриц в памяти ЭВМ. Заметим, что для хранения диаго-
диагональной матрицы достаточно отвести массив длины m и расположить в
нем элементы ац, а22, ..., amm. Для хранения треугольной матрицы
достаточно m (тп + 1)/2 ячеек памяти, что примерно вдвое меньше
места, отводимого для хранения матрицы общего вида. Столько же
ячеек используется для хранения симметричной матрицы, поскольку
такая матрица полностью определяется, например, заданием своей
нижней треугольной части.
К счастью, приложения очень часто приводят к матрицам, в кото-
которых число ненулевых элементов много меньше общего числа элементов
матрицы. Такие матрицы принято называть разреженными. Напротив,
матрицы общего вида называют плотными (или заполненными).
Разреженность матрицы является очень ценным свойством, поскольку
объем информации, который следует обрабатывать и хранить в памяти
ЭВМ, для таких матриц даже очень большого размера может оказать-
оказаться не слишком большим. Для хранения всех ненулевых элементов и
информации об их расположении оказывается достаточным использо-
использовать только оперативную память ЭВМ. Иногда элементы матрицы
известны либо вычисляются по простым формулам и необходимость в
их хранении отпадает.
Одним из основных источников разреженных матриц являются
математические модели технических устройств, состоящих из большо-
большого числа элементов, связи между которыми локальны. Простейшие
примеры таких устройств — сложные строительные конструкции и
большие электрические цепи. Другой важный источник разреженности
— метод конечных разностей и метод конечных элементов, используе-
используемые для решения уравнений математической физики.
Известны примеры решенных в последние годы задач, где число
неизвестных достигало сотен тысяч. Естественно, это было бы невоз-
невозможно, если бы соответствующие матрицы не являлись разреженными
(число элементов матрицы при т — 105 равно m * m — 1010).
Простой пример разреженной матрицы дает трехдиаюналъная мат-
матрица
130
all
1
0
0
0
a12
2
<*32
0
0
0
<»23
«33
0
0
0
0
4
0
0
... 0
...0
...0
... a
... 0
11-1,111-2 <hn-\,m-l am-l, т
'hn.m-l Omm
все ненулевые элементы которой расположены на главной и двух со-
соседних с ней диагоналях. Число этих элементов равно Зт — 2, что при
большом m много меньше общего числа т2 эле-
элементов матрицы.
Многие приложения приводят к системам
уравнений с так называемыми ленточными мат-
матрицами. Матрица А называется ленточной с
полушириной ленты, равной /, если ai} = 0 для
I * — ]\ > I- Все ненулевые элементы такой матри-
матрицы расположены на s = 2/ + 1 ближайших к
главной диагоналях матрицы; число s принято
называть шириной ленты. Схематически ленточ- ^ис- **¦!
ная матрица представлена на рис. 5.1. Частным
случаем ленточной матрицы при & = 3 является трехдиагональная
матрица. Ясно, что в случае s < m ленточная матрица является разре-
разреженной.
§ 5.4. Обусловленность
задачи решения системы линейных
алгебраических уравнений
Оказывается, что решения различных систем линейных алгебраи-
алгебраических уравнений обладают разной чувствительностью к погрешнос-
погрешностям входных данных. Так же как и другие задачи (см. § 3.2), задача
вычисления решения х системы уравнений
Ах=Ь
E.18)
может быть как хорошо, так и плохо обусловленной.
Исследование обусловленности задачи начнем со случая, когда
элементы матрицы А считаются заданными точно, а вектор-столбец
правой части — приближенно.
Лемма 5.1. Для погрешности приближенного решения системы
E.18) справедлива оценка
131

Д(х*)<|Л-1|-|г|, E.19)
tde r= Ь — Ax* — невязка, отвечающая х*.
Для доказательства достаточно взять норму левой и правой частей
равенства E.3) и воспользоваться свойством E.10).
Теорема 5.1. Пусть х* — точное решение системы Ах* = Ь*, в
которой правая часть Ь* является приближением к 6. Тогда верны сле-
следующие оценки абсолютной и относительной погрешностей:
А(х*) < j/д Д(П, E.20)
6(х*)<^6(Ь*), E-21)
где^=[А%и6=[А^{ [Ь[Дх[
D В рассматриваемом случае г = 6 — Ах* = 6 — Ь* и неравенство
E.19) принимает вид E.20). Разделив теперь обе части неравенства
E.20) на \х\ и записав его в виде
приходим к оценке E.21). Щ
Замечание 1. Величина уд = [А~1\ для задачи E.18) играет
роль абсолютного числа обусловленности (см. § 3.2).
Замечание 2. Величина vs = v^x) = \А~*\-16||/||*| называет-
называется естественным числом обусловленности. Она зависит от конкрет-
конкретного решения х и характеризует коэффициент возможного возрас-
возрастания относительной погрешности этого решения, вызванного пог-
погрешностью задания правой части. Это означает, что i/Дх) для зада-
задачи вычисления решения х системы E.18) играет роль относительно-
относительного числа обусловленности (см. § 3.2).
Замечание 3. Полученные в теореме 5.1 оценки точны в том
смысле, что для системы Ах = Ь с произвольной невырожденной
матрицей А и любой заданной правой частью 4*0 найдется сколь
угодно близкий к 6 приближенно заданный вектор Ь* ф Ъ, для
которого неравенства E.20) и E.21) превращаются в равенства.
Вычислим максимальное значение естественного числа обусловлен-
обусловленности, используя определение E.4) нормы матрицы:
E.22)
Полученную величину принято называть стандартным числом обус-
обусловленности (или просто числом обусловленности) матрицы А и обоз-
обозначать через v(A) или cond(j4). Таким образом,
E.23)
Сформулируем важное следствие из теоремы 5.1.
Следствие. В условиях теоремы 5.1 справедлива оценка
6(х*) <cond(А)-6(Ь*). E.24)
Для ее доказательства достаточно воспользоваться оценкой E.21) и
заметить, что в силу определения E.22) верно неравенство vg<cond(A).
Замечание. Оценка E.24) точна в том смысле, что для систе-
системы E.18) с произвольной невырожденной матрицей А найдутся
правая часть Ь t 0 (и отвечающее этой правой части решение х) и
сколь угодно близкий к 6 приближенно заданный вектор Ь* Ф b
такие, что неравенство E.24) превращается в равенство.
Величина cond(-A) является широко используемой количественной
мерой обусловленности системы Ах — Ь. В частности, систему и матри-
матрицу А принято называть плохо обусловленными, если cond(v4) > 1. В
силу оценки E.24) и последнего замечания для такой системы сущест-
существуют решения, обладающие чрезвычайно высокой чувствительностью
к малым погрешностям задания входного данного Ь. Тем не менее
заметим, что не для всякого решения х коэффициент v^x) роста отно-
относительной ошибки достигает значений, близких к максимально воз-
возможному значению cond(.A).
Отметим следующие свойства числа обусловленности.
1°. Для единичной матрицы cond(?) = 1.
а Пользуясь тем, что Е~1 = Е и \Е\ = 1 (см. пример 5.3), получим
cond(J5)= JJB-M'I^I = l.B
2°. Справедливо неравенство cond(vi) > 1.
а Из равенства Е = А-А'1, свойства 4° норм матриц и равенства
| = 1 следует, что 1 = \Е\ < М Ч |Л[ = cond(vi).B
3°. Число обусловленности матрицы А не меняется при умножении
матрицы на произвольное число а Ф 0.
D Заметим, что (аА)'1^ о'М'1. Поэтому cond(<b4) = [aA\ • [(аА)'1\=
= \а\-\А[ |а|-1|Л-Ч B
х*0
132
Замечание. Пользуясь приведенной в § 5.2 геометрической
интерпретацией норм матриц А и Ал (см. формулы E.15) и E.16)),
число обусловленности можно интерпретировать как отношение
133

максимального коэффициента растяжения векторов под действием
матрицы А к минимальному коэффициенту: cond(A) = Amax/*min-
Величина cond(A) зависит, вообще говоря, от выбора нормы век-
векторов в пространстве Л1*. Фактически это есть зависимость макси-
максимального коэффициента роста ошибки от способа измерения вели-
величины входных данных и решения. В частности, выбору нормы [г|р
A < р < <ю) отвечает condp(v4) = М"Чр-1 А[р.
Пример 5.4. Вычислим condJ^A) для матрицы
« A.981, 0.4735)т и получим v?x) =
« 187.2-2.51/1.981 « 237.
_ Г 1.03 0.991 1
[ 0.991 0.943 J"
Сначала найдем обратную матрицу
E.25)
. Г -87.4 91.8 1
й[ 91.8 -95.4 J'
Тогда condao(j4)=
\А~1\
2.021-187.2 я 378. Если входные данные для
системы уравнений с матрицей E.25) содержат относительную погрешность
порядка 0.1—1%, то систему можно расценить как плохо обусловленную.
Пример 5.5. Рассмотрим систему уравнений
1.03x1 + 0.991*2 = 2.51,
0.991x1 + 0.943x2 = 2.41
E.26)
с матрицей E.25). Ее решением является xi я 1.981, х2 я 0.4735. Правая часть
системы известна в лучшем случае с точностью до 0.005, если считать, что
числа 2.51 и 2.41 получены округлением "истинных" значений при вводе в
память трехзначной десятичной ЭВМ. Как влияет погрешность во входных
данных такого уровня на погрешность решения? Возмутим каждую из компо-
компонент вектора правой части Ь - B.51, 2.41)т на величину 0.005, взяв Ь* =
= B.505, 2.415)т. Решением системы, отвечающим Ь*, является теперь х* я
и 2.877, х* я -0.4629. Таким образом, решение оказалось полностью искажен-
искаженным. Относительная погрешность задания правой части 6(Ь*) —
= \Ь— Ь*|оо/1М«> = 0.005/2.51 я 0.2% привела к относительной погрешности
решения 6(х*) = [х — **|оо/М<» й 0.9364/1.981 я 47.3%. Следовательно,
погрешность возросла примерно в 237 раз.
Можно ли ввести в правую часть системы E.26) такую погрешность, чтобы
получить существенно большее, чем 237, значение коэффициента роста ошиб-
ошибки? Вычислим естественное число обусловленности, являющееся максималь-
максимальным значением рассматриваемого коэффициента, отвечающим решению г и
134
Таким образом, на поставленный вопрос следует ответить отрицательно.
Можно дать следующую геометрическую интерпретацию рассмотренного
примера. Каждому уравнению системы E.26)
соответствует прямая на плоскости Oxixj. По
коэффициентам при i) и ^ в этих уравне-
уравнениях видно, что прямые почти параллельны.
Так как вблизи точки пересечения прямые
почти сливаются, то даже незначительная
погрешность в задании положения этих
прямых существенно меняет положение
точки пересечения (рис. 5.2).
Пример 5.6. Традиционным примером
очень плохо обусловленной матрицы являет-
является матрица Гильберта1 — матрица И с риа jf
элементами Лу = l/(i + j— 1).
Из табл. 5.1, заимствованной из [87], видно, что для матрицы И даже
сравнительно невысокого порядка число обусловленности оказывается
чрезвычайно большим.
Таблица 5.1
Порядок
матрицы
Гильберта
10
Приближенное
значение числа 2-Ю1 5-Ю2 2-Ю4 5-Ю5 2-Ю7 5-Ю8 2-Ю10 5-1011 2-1013
обусловленности
До сих пор мы- предполагали, что матрица А задана точно. Однако
на практике это часто не так. Как выясняется, введенная выше вели-
величина cond(A) характеризует также и чувствительность решений систе-
системы к малым погрешностям задания элементов матрицы А. В подтверж-
подтверждение сказанного приведем следующий результат.
Теорема 5.2. Пусть х* — точное решение системы Atx* = Ь с
приближенно заданной матрицей А+. Тогда верна следующая оценка
относительной погрешности:
1 Давид Гильберт A862—1943) — немецкий математик, исследования кото-
которого оказали большое влияние на развитие современной математики.
135

6*(x*)<cond(A)-6(At), E.27)
где 6*(x*) = \x- x*\/\x% S(At) = |A - it,|/|A|.
а В данном случае невязка г имеет вид г = Ь — Ах* — Л,г*— Ах*=
= (At — А)х*. Применяя неравенство E.19), получим цепочку
неравенств
5\х*) = \х-х*\ДхЦ < |Л-Ч-|0*.- А)хЦ/\\хЦ <
<|А-1|-М,-^|-|'*|/1>*1 =cond(A)-6(At). Ш
Следствие. В условиях теоремы 5.2 справедливо приближенное
неравенство
S(x*)<cond(A)-6(At). E.28)
Замечание 1. В случае, когда с погрешностью заданы как
правая часть системы, так и матрица (т. е. х* является решением
системы Atx* = Ь*), причем cond(A) • 6(А t) < 1, можно доказать
справедливость неравенства
6(x*)<cond(A)(8(b') + 6(А.)).
Замечание 2. Распространенным является представление о
том, что по величине определителя матрицы А можно судить о
степени близости системы уравнений к вырожденной или об обус-
обусловленности системы. Для того чтобы убедиться в ошибочности
этого мнения, умножим каждое из уравнений системы E.1) на пос-
постоянную а ± 0. Ясно, что такое преобразование никак не меняет
решение системы и его чувствительность к малым относительным
ошибкам в данных. Однако определитель умножается на число от,
и поэтому с помощью выбора а может быть сделан как угодно
большим или малым. Подчеркнем, что число обусловленности
cond(A) при таком преобразовании системы не меняется в силу
свойства 3°.
Замечание 3. Вычисление чисел обусловленности vg —
= \A'l\'\b[/\x\ и cond(yl) = | A J • J Л fl непосредственно по указан-
указанным формулам предполагает предварительное вычисление обратной
матрицы А'1. Вследствие большой трудоемкости этой операции (как
показано в § 5.6, для ее выполнения в общем случае требуется
примерно 2т3 арифметических операций) на практике избегают
такого способа вычисления. При этом важно отметить, что в боль-
большинстве случаев достаточно лишь грубой оценки числа обусловлен-
136
ности с точностью до порядка. С эффективными методами, дающи-
дающими оценки величин vg и сопс!(Л), можно познакомиться в [67], [86].
Проверить чувствительность решения системы Ах = 6 к погрешнос-
погрешностям можно и экспериментально. Для этого достаточно решить задачу
несколько раз с несколькими близкими к Ь правыми частями 6A),
4B), ..., Уп). Можно ожидать, что величина ug — max e)ui)( Даст
оценку значения vg. Во всяком случае эта величина дает оценку снизу,
так как
cond(X).
§ 5.5 Метод Гаусса
Рассмотрим один из самых распространенных методов решения
систем линейных алгебраических уравнений — метод Гаусса1. Этот
метод (который называют также методом последовательною исключе-
исключения неизвестных) известен в различных вариантах уже более 2000 лет.
Вычисления с помощью метода Гаусса состоят из двух основных
этапов, называемых прямым ходом и обратным ходом (обратной под-
подстановкой). Прямой ход метода Гаусса заключается в последователь-
последовательном исключении неизвестных из системы E.1) для преобразования ее
к эквивалентной системе с верхней треугольной матрицей. Вычисления
значений неизвестных производят на этапе обратного хода.
1. Схеыа единственного деления. Рассмотрим сначала простейший
вариант метода Гаусса, называемый схемой единственного деления.
Прямой ход состоит из т — 1 шагов исключения.
1-й ш а г. Целью этого шага является исключение неизвестного ц
из уравнений с номерами t = 2, 3, ..., m. Предположим, что коэффици-
коэффициент а\\ ± 0. Будем называть его главным (или ведущим) элементом 1-го
шага.
Найдем величины
рй =
(« = 2, 3, ..., т),
E.29)
называемые множителями 1-ю шага. Вычтем последовательно из вто-
второго, третьего, ..., m-го уравнений системы E.1) первое уравнение,
умноженное соответственно на /<2i, /<зь ¦••> Iha- Это позволит обратить в
1 Карл Фридрих Гаусс A777—1855) — немецкий математик и физик, рабо-
работы которого оказали большое влияние на дальнейшее развитие высшей алгеб-
алгебры, геометрии, теории чисел, теории электричества и магнетизма.
137

нуль коэффициенты при х\ во всех уравнениях, кроме первого. В ре-
результате получим эквивалентную систему
E.30)
«с *.=
и вычтем последовательно из (Jfc + 1)-го, ..., m-го уравнений получен-
полученной на предыдущем шаге системы Jfc-e уравнение, умноженное соответс-
соответственно на ЦЫ,Ь Рк*2,к, -, Ртк-
После (т — 1)-го шага исключения получим систему уравнений
xm=
E.33)
в которой ajy и 60* (i, j = 2, 3, ..., m) вычисляются по формулам
-(\\ _ . - Lf 1) L .. И /с oi\
д v *.' ~ и** ~ tlfi ui ч. О - Oi ~~ tit\ 0\. @.011
2-й шаг. Целью этого шага является исключение неизвестного х2
из уравнений с номерами i = 3, 4, ..., т. Пусть ai,^ t 0, где а2^' —
коэффициент, называемый главным (или ведущим) элементом 2-ю
шага. Вычислим множители 2-го шага
Й2= eJJ'/eJJ' (« = 3, 4, ...,m)
и вычтем последовательно из третьего, четвертого, ..., m-го уравнений
системы E.30) второе уравнение, умноженное соответственно на /*32i
/*42> --I A*m2- В результате получим систему
012*2
E.32)
Здесь коэффициенты at?' и 6(^2) («, j = 3, 4, ..., m) вычисляются по
формулам
Аналогично проводятся остальные шаги. Опишем очередной Jb-й
шаг.
Jb-й ш а г. В предположении, что главный (ведущий) элемент к-го
шага uj-jf11 отличен от нуля, вычислим множители k-to шага
матрица Л'1 которой является верхней треугольной. На этом вычис-
вычисления прямого хода заканчиваются.
Обратный ход. Из последнего уравнения системы E.33)
находим хт. Подставляя найденное значение хт в предпоследнее урав-
уравнение, получим z,n-i. Осуществляя обратную подстановку, далее после-
последовательно находим хт-2, хт-з, ..., х\. Вычисления неизвестных здесь
проводятся по формулам
хт—
хк =
(к = т - 1, ..
E.34)
Трудоемкость метода. Оценим число арифметических
операций, необходимых для реализации схемы единственного деления.
Вычисления 1-го шага исключения по формулам E.29), E.31)
требуют выполнения m — 1 деления, (т — 1)т умножений и (т — \)т
вычитаний, т. е. общее число арифметических операций составляет
Qi = 2(m — IJ + 3(m — 1). Аналогично, на 2-м шаге требуется Qi =
= 2(m - 2J + 3(m - 2) операций, а на к-ы шаге — Qk = 2(m - JfcJ +
+ 3(m — Jfc) операций.
Подсчитаем теперь приближенно общее число Q арифметических
операций прямого хода, считая размерность системы m достаточно
большой:
m-l m-1 m-\ т-1
Q= ? Qk=2 Y, (m-JfcJ + 3E (m-Jfc) = 2S
Jt = i fc=i fc=i t=i
_ 2(m - 1) m Bm - 1) 3(m - l)m 2
~ 6 + 2 Й3Ш-
т-\
Jfc =
138
139

Как нетрудно видеть, для реализации обратного хода по формулам
E.34) нужно всего т2 операций, что при больших то пренебрежимо
мало по сравнению с числом операций прямого хода.
Таким образом, для реализации метода Гаусса требуется примерно
B/3)т3 арифметических операций, причем подавляющее число этих
действий совершается на этапе прямого хода.
E.35)
Пример 5.7. Методом Гаусса решим систему
10*1 + 6*2 + 2*з = 25,
5*i + . *2 — 2*з + 4*4 = 14,
3*1 + 5*2 + *3 — *4 = Ю,
6*2 — 2*з + 2*4 = 8.
Прямой ход. 1-й шаг. Вычислим множители /^l =
= 5/10 = 0.5, /*3i = a3i/an = 3/10 = 0.3, /i4i = 041/111 = 0/10 = 0. Вычитая
из второго, третьего и четвертого уравнений системы E.35) первое уравнение,
умноженное на fch Л31 и ^41 соответственно получим
+ 6*2 + 2*з = 25,
— 2*2— 3*3 + 4*4 = 1.5,
3.2*2 + 0.4*з— *4 = 2.5,
6*2— 2*з + 2*4 = 8.
E.36)
2-й шаг. Вычислим множители /*зг = аз2>/а22> = 3-2/(-2) = -1.6, /*42 —
= 6/(-2) = -3. Вычитая из третьего и четвертого уравнений системы E.36)
второе уравнение, умноженное на A^2 и /*42 соответственно, приходим к системе-
10*1 + 6*2 + 2*з = 25,
— 2*2— 3*з+ 4*4 = 1.5,
— 4.4*з + 5.4*4 = 4.9,
- 11*з + 14*4 = 12.5.
E.37)
3-й шаг. Вычисляя множитель /143 = (-И)/(-4.4) = 2.5 и вычитая из
четвертого уравнения системы E.37) третье уравнение, умноженное на /<4з.
приводим систему к треугольному виду:
10*1 + 6*2+2*3 = 25,
— 2*2— 3*з + 4*4 = 1.5,
-4.4*3 + 5.4*4 =4.9,
0.5*4 = 0.25.
E.38)
Обратный ход. Из последнего уравнения системы находим
*4 = 0.5. Подставляя значение *4 в третье уравнение, находим *з =
140
= D.9 — 5.4*4)/(-4-4) = -0.5. Продолжая далее обратную подстановку, получа-
получаем ^ = A.5 + Зла - 4*4)/(-2) = 1, *, = B5 - 6*2 - 2xs)/10 = 2. Итак, i\ =
= 2, *2 = 1, *з = -0.5, *4 = 0.5.
Результаты вычислений можно свести в следующую таблицу.
Таблица 5.2
Исходная система
1-й шаг прямого хода
2-й шаг прямого хода
3-й шаг прямого хода и обрат-
обратный ход
Oil
10
5
3
0
10
0
0
0 ,
10
0
0
0
10
0
0
0
«й
6
1
5
б
6
-2
3.2
б
6
-2
0
0
б
-2
0
0
*
2
-2
1
-2
2
-3
0.4
-2
2
-3
-1.4
-11
2
-3
-4.4
0
«44
0
4
-1
2
0
4
-1
2
0
4
5.4
14
0
4
5.4
0.5
к
25
14
10
8
25
1.5
2.5
8
25
1.5
4.9
7.5
25
1.5
4.9
0.25
0.5
0.3
0
-1.6
-3
2
1
-0.5
0.5
Необходимость выбора главных элемен-
элементов. Заметим, что вычисление множителей, а также обратная подста-
подстановка требуют деления на главные элементы ajjj >. Поэтому если один
из главных элементов сказывается равным нулю, то схема единствен-
единственного деления не может быть реализована. Здравый смысл подсказыва-
подсказывает, что и в ситуации, когда все главные элементы отличны от нуля, но
среди них есть близкие к нулю, возможен неконтролируемый рост
погрешности.
Пример 5.8. Используя метод Гаусса, решим систему уравнений
2*i - 9i2 + 5*з = -4,
1.2*1-5.3999^+ б*з = 0.6001,
XI- j^ — 7.5гз =-8.5
на 6-разрядной десятичной ЭВМ.
E.39)
141

Прямой ход. 1-й шаг. Вычисляем множители /«21 = 0.6 и
= 0.5 и преобразуем систему к виду
2*i - 9*2 + 5*з = -4,
0.0001*2 + 3*з = 3.0001,
3.5*2-
E.40)
Все вычисления на этом шаге выполняются без округлений.
2-й шаг. После вычисления множителя ц^ — 3.5/0.0001 = 35 000 пос-
последнее уравнение системы должно быть преобразовано к виду «j2'*3 = Ц2)'
где a[f = -10 - З-/432 = -105010, 6321 = ~^ъ — 3.0001-/х32 = -105010. Одна-
Однако на используемой ЭВМ будет получено уравнение
-105010*з = -105011. E.41)
Действительно, коэффициент а(^] определяется точно, так как при его вычис-
вычислении не возникает чисел, мантиссы которых имеют более 6 разрядов. В то же
время при вычислении Ь{г2) умножение коэффициента 3.0001 на /132 Дает 7-
разрядное число 105003.5, после округления которого до 6 разрядов получится
105004. Вычисление 6^2> завершается выполнением операции вычитания:
5<2) к _g 5 — 105004 = -105010.5. После округления последнего числа до 6
разрядов мантиссы приходим к уравнению E.41).
Обратный ход. Из уравнения E.41) находим *з и 1-00001. Сравне-
Сравнение с истинным значением *з = 1 показывает, что эта величина получена с
очень высокой для используемой ЭВМ точностью.
Дальнейшие вычисления дают
*2 = C.0001 - 3*3)/0.0001 = C.0001 - 3.00003)/0.0001 = 0.7,
Ш = (-4 + 9*2 - 5г3)/2 = (-4 + 6.3 - 5.00005)/2 = -1.350025.
После округления имеем *i = -1.35003.
Как нетрудно видеть, найденные значения неизвестных имеют мало общего
с истинными значениями решения *1 = 0,*2 = 1,гз = 1-
В чем же причина появления такой значительной погрешности? Говорить о
накоплении ошибок округления не приходится, так как всего было выполнено
28 арифметических операций и лишь в 4 случаях потребовалось округление.
Предположение о плохой обусловленности системы не подтверждается; вычис-
вычисление сопс^Л) дает значение и 100.
В действительности причина состоит в использовании на 2-м шаге малого
ведущего элемента aSQ — 0.0001. Следствием этого стало появление большого
142
множителя /<32 и существенное возрастание коэффициента в последнем уравне-
уравнении системы.
Таким образом, изложенный выше вариант метода Гаусса (схема
единственного деления) оказался некорректным и, следовательно,
непригодным для вычислений на ЭВМ. Этот метод может привести к
аварийному останову (если a^JT" = 0 при некотором Jfc), и вычисления
по нему могут оказаться неустойчивыми.
2. Метод Гаусса с выбором главного элемента по столбцу (схема
частичного выбора). Описание метода. На Jb-м шаге прямого
хода коэффициенты уравнений системы с номерами i = Jt + 1, ..., m
преобразуются по формулам
», i= Jt + 1, ..., т. E.42)
Интуитивно ясно, что во избежание сильного роста коэффициентов
системы и связанных с этим ошибок нельзя допускать появления
больших множителей /4,*.
В методе Гаусса с выбором главного элемента по столбцу гаранти-
гарантируется, что \ftik\ < 1 для всех к - 1, 2, ..., m — 1 и t = Jt + 1, ..., т.
Отличие этого варианта метода Гаусса от схемы единственного деле-
деления заключается в том, что на /Ь-м шаге исключения в качестве глав-
главного элемента выбирают максимальный по модулю коэффициент а .
1к
при неизвестной х* в уравнениях с номерами i = Jt, к + 1, ..., т. Затем
соответствующее выбранному коэффициенту уравнение с номером i*
меняют местами с t-м уравнением системы для того, чтобы главный
элемент занял место коэффициента iJ^jT1' •
После этой перестановки исключение неизвестного г* производят,
как в схеме единственного деления.
Пример 5.9. Решим систему уравнений E.39) методом Гаусса с выбором
главного элемента по столбцу на 6-разрядной десятичной ЭВМ.
Прямой ход. 1-й шаг. Максимальный в первом столбце элемент
матрицы находится в первой строке, поэтому перестановка уравнений не нуж-
нужна. Здесь 1-й шаг проводится точно так же, как и в примере 5.8.
2-й шаг. Среди элементов а22' = 0.0001 и aj'1 = 3.5 матрицы системы
E.40) максимальный принадлежит третьему уравнению. Меняя местами второе
и третье уравнения, получим систему
2х[ — 9*2 + .5*3 = -4.
3.5*2 — 10*з = -*-5,
0.0001*2 + Зг3 = 3.0001.
143

После вычисления /*32 = 0.0001/3.5 » 2.85714-10 последнее уравнение
системы преобразуется к виду 3.00029*з = 3.00029.
Обратный ход. Из последнего уравнения находим г3 = 1. Далее,
имеем х2 = И-5 + Ю*з)/3.5 = 1, ц = (-4 + 9х2 - 5г3)/2 = (-4 + 9 - 5)/2 =
= 0. В данном случае ответ получился точным.
Заметим, что дополнительная работа по выбору главных элементов
в схеме частичного выбора требует порядка т2 действий, что практи-
практически не влияет на общую трудоемкость метода.
Вычислительная устойчивость схемы час-
частичного выбора. Детальное исследование метода Гаусса пока-
показывает, что действительной причиной неустойчивости схемы единст-
единственного деления является возможность неограниченного роста элемен-
элементов промежуточных матриц ЛA), А{2), ..., А(т'1] в процессе прямого
хода. Так как на Jfc-м шаге схемы частичного выбора |од| '^ 1, то для
вычисленных по формулам E.42) элементов а(^> справедлива оценка
|a(*;> | < I <*;?"" I + lai^r" I- Следовательно, максимальное по модулю
значение элементов матрицы возрастает на одном шаге не более чем в
2 раза и в самом неблагоприятном случае т — 1 шаг прямого хода
даст коэффициент роста <р(т) = 2.
Гарантия ограниченности роста элементов матрицы делает схему
частичного выбора вычислительно устойчивой. Более того, для нее
оказывается справедливой следующая оценка погрешности:
6(x*)<f(m)condir(A)-EH. E.43)
Здесь г* — вычисленное на ЭВМ решение системы; й(г*) =
= J х — х * || г/1| х[ 2 — его относительная погрешность; cond^-A) =
= И^ИяМ'Ия ~~ число обусловленности матрицы А; ?ц — машинное
эпсилон; наконец, f (m) = С (т) <р(т), причем С (т) — некоторая
медленно растущая функция, зависящая от порядка m системы (типа
степенной функции с небольшим показателем), <р{т) — коэффициент
роста.
Наличие в оценке E.43) множителя <р(т) = 2mrl указывает на то,
что при большом m схема частичного выбора может оказаться плохо
обусловленной и возможна существенная потеря точности. Однако
практика матричных вычислений показывает, что существенный рост
элементов матрицы происходит крайне редко. В подавляющем боль-
большинстве случаев действительное значение коэффициента роста не
превышает 8—10. Если система хорошо обусловлена, то погрешность
вычисленного решения оказывается, как правило, малой.
Иногда для проверки качества приближенного решения х* вычис-
144
ляют невязку г= b — Ах* и о степени близости приближенного реше-
решения к точному пытаются судить по тому, насколько мала невязка.
Этот метод ненадежен по отношению к схеме частичного выбора, так
как известно, что она гарантированно дает малые невя,э*ш. Более
точно это утверждение можно сформулировать так: справедлива оцен-
оценка
*Ьем, E.44)
где / (т) то же, что и в оценке E.43). Заметим, что в неравенство
E.44) не входит число обусловленности.
3. Метод Гаусса с выборок главного элемента по всей матрице
(схема полного выбора). В этой схеме допускается нарушение естест-
естественного порядка исключения неизвестных.
На 1-м шаге метода среди элементов ay определяют максимальный
по модулю элемент а, . Первое уравнение системы и уравнение с
Vi
номером i] меняют местами. Далее стандартным образом производят
исключение неизвестного х из всех уравнений, кроме первого.
h
На ib-м шаге метода среди коэффициентов a\fu при неизвестных в
уравнениях системы с номерами i — k, ..., ?п выбирают максимальный
по модулю коэффициент a\jl)- Затем k-е уравнение и уравнение,
содержащее найденный коэффициент, меняют местами и исключают
неизвестное z- из уравнений с номерами i = jfc + 1, ..., т.
На этапе обратного хода неизвестные вычисляют в следующем
порядке: х. , х- , ..-, х..
]п 3m-i h
Пример 5.10. Решим систему E.39), используя схему полного выбора на 6-
разрядной десятичной ЭВМ.
Прямой ход. 1-й шаг. Максимальный по модулю элемент а^.— -9
содержится в первом уравнении, поэтому перестановка уравнений не нужна.
Исключаем неизвестное *2 из второго и третьего уравнений, и используя
множители ^21 = -5.3999Д-9) и 0.599989 и /?3i = -1/(-9) и 0.111111. В резуль-
результате получим систему
2*1 — 9*2 + 5*з = -4,
2.2-10-5*1 + З.ООООбгз = 3.00006,
0.777778*1 - 8.05556*з = -8.05556.
2-й шаг. Среди коэффициентов при неизвестных во втором и третьем
уравнениях максимальным является коэффициент а^' = -8.05556. Перестав-
145

ляя местами второе и третье уравнения и исключая неизвестное а$ (соответст-
(соответствующий множитель /*32 = 3.00006/(-8.05556) « -0.372421), приходим к системе
2*1 — 9*2 + 5г3 = -4,
0.77777811 - 8.05556^. = -8.05556,
0.289683ч = 2.89240 -10.
Обратный ход. Из последнего уравнения находим i\ =
= 2.89240• 10-7/0.289683 я 9.98470-10. Далее, имеем *3 = (-8.05556 -
- 0.777778*i)/(-8.05556) а 1.00000, ъ = (-4 - 2*i - 5*3)/(-9) = 1.00000.
Округляя найденные значения до пяти цифр после десятичной точки,
получим ответ: ц = 0.00000, ^ = 1.00000, т3 = 1.00000. Заметим, что в данном
случае получено решение, совпадающее с точным.
Схема полного выбора по сравнению со схемой частичного выбора
дает существенное замедление роста элементов матрицы. Доказано, что
для нее коэффициент роста уэ(т), входящий в оценку E.43), не превы-
превышает величины т'2 {У-Ъ^-А^ ... m^<m"n)^2 < 1.8m°-25ln m (что
значительно меньше соответствующего значения <fi(m) = 2*и для схе-
схемы частичного выбора). Подчеркнем, что до сих пор еще не найдено
матрицы, для которой полный выбор дал бы значение у(т) > т.
Таким образом, для хорошо обусловленных систем этот вариант мето-
метода Гаусса является хорошо обусловленным.
Однако гарантия хорошей обусловленности достигается здесь ценой
значительных затрат на выбор главных элементов. Для этого дополни-
дополнительно к B/з)т3 арифметических действий требуется произвести при-
примерно т3/3 операций сравнения, что может ощутимо замедлить про-
процесс решения задачи на ЭВМ. Поэтому в большинстве случаев на
практике предпочтение отдается все же схеме частичного выбора. Как
уже отмечено, ситуации, когда при использовании этого варианта
метода Гаусса происходит существенный рост элементов, встречаются
чрезвычайно редко. Более того, эти ситуации могут быть легко выяв-
выявлены с помощью заложенных в современных программах эффективных
методов слежения за ростом элементов матриц.
4. Случаи, когда выбор главных элементов не нужен. 'Известно, что
для некоторых классов матриц при использовании схемы единственно-
единственного деления главные элементы гарантированно располагаются на глав-
главной диагонали и потому применять частичный выбор нет необходимос-
необходимости. Так, например, обстоит дело для систем с положительно опреде-
определенными матрицами, а также с матрицами, обладающими следующим
свойством диагонального преобладания:
146
3=1
<4j\ < l«nl> * = 1. 2, ..., т.
E.45)
Матрицы, удовлетворяющие условию E.45), таковы, что в каждой из
строк модуль элемента ац, расположенного на главной диагонали,
больше суммы модулей всех остальных элементов строки.
5. Масштабирование. Перед началом решения целесообразно мас-
масштабировать систему так, чтобы ее коэффициенты были величинами
порядка единицы.
Существуют два естественных способа масштабирования системы
Ах = Ь. Первый заключается в умножении каждого из уравнений на
некоторый масштабирующий множитель /<t. Второй состоит в умноже-
умножении на масштабирующий множитель otj каждого j-ro столбца матрицы,
что соответствует замене переменных г- = ot~lZj (фактически — это
замена единиц измерения). В реальных ситуациях чаще всего масшта-
масштабирование может быть выполнено без существенных трудностей. Одна-
Однако подчеркнем, что в общем случае удовлетворительного способа мас-
масштабирования пока не найдено.
На практике масштабирование обычно производят с помощью
деления каждого уравнения на его наибольший по модулю коэффици-
коэффициент. Это вполне удовлетворительный способ для большинства реально
встречающихся задач.
$ 5.6. Метод Гаусса и решение систем уравнений
с несколькими правыми частями, обращение матриц,
вычисление определителей
Рассмотрим применение метода Гаусса к решению следующих
задач линейной алгебры: 1) вычисление решений системы уравнений с
несколькими правыми частями; 2) вычисление обратной матрицы; 3)
вычисление определителя.
1. Вычисление решений системы уравнений с несколькими правыми
частями. Довольно часто на практике встречается ситуация, когда
нужно решить несколько систем уравнений
Ах- id,, Ax- dB), ..., Ах= d(p) E.46)
с одной матрицей А и различными правыми частями du], rfB), ...,
Конечно, применяя метод Гаусса к каждой из систем E.46) незави-
независимо от других, можно найти соответствующие решения *<d, *B>> •••>
147

r(p), затратив примерно B/з)рп»3 арифметических операций. Однако
при одновременном решении систем E.46) число операций можно
существенно сократить. Как было отмечено в § 5.5, основные вычисли-
вычислительные затраты в методе Гаусса связаны с преобразованием матрицы
к треугольному виду. Преобразование же правой части производится
параллельно и требует примерно т2 арифметических операций. Если
параллельно с приведением матрицы А к треугольному виду преобра-
преобразовать по однотипным формулам все р правых частей, то на прямой
ход метода будет затрачено только примерно B/3)т3 + рт2 операций.
С учетом обратного хода общие вычислительные затраты составят
примерно B/з)т3 + 2рт2 арифметических операций.
Преобразование правых частей не обязательно производить парал-
параллельно. Каждую из правых частей rf(i), <fB), ..., dip) можно обрабо-
обработать последовательно, если после приведения матрицы А к треугольно-
треугольному виду Л1' сохранить в памяти ЭВМ множители /*у и матрицу
2. Вычисление обратной матрицы. Прежде чем переходить к изло-
изложению метода вычисления обратной матрицы А'1 для квадратной
невырожденной матрицы А, отметим, что в действительности проблема
вычисления обратной матрицы возникает не так часто, как это можно
предполагать.
К сожалению, зачастую обращение матрицы А производится с
единственной целью вычислить по известному вектору Ь вектор х вида
х = A'lb. Умножение матрицы Л на вектор требует примерно 2т2
арифметических операций. Однако вычисление А'1 обходится (как
будет показано ниже) примерно в 2т3 операций. Это означает, что на
вычисление решения системы Ах = 6 по формуле г = А'1Ь будет затра-
затрачено примерно 2т3 операций. В данном случае х можно найти в 3 раза
быстрее методом Гаусса и вычисление А'1 не нужно. Более того, можно
ожидать, что вычисленное методом Гаусса решение окажется точнее,
так как потребуется выполнение меньшего числа операций.
Может показаться особенно выгодным предварительное вычисление
матрицы А'1, если далее потребуется найти большое число векторов по
формулам
= A'ld
B),
E.47)
Однако суммарные затраты при таком подходе составят примерно
2т3 + 2рт2 операций, в то время как при одновременном решении
методом Гаусса эквивалентной системы E.46) получаем значения хA),
ХB), .-., Х(Р) примерно за B/з)п*3 -f 2pm2 операций. Следовательно, и
в этом случае вычисление А'1 нецелесообразно.
148
Иногда в пользу необходимости вычисления А'1 приводится сле-
следующий довод. Если известно, что в течение длительного времени
потребуется неоднократно решать системы уравнений вида E.46) с
фиксированной матрицей А и различными правыми частями d( д.), то
имеет смысл предварительно вычислить А'1. Записав А'1 в память
ЭВМ, можно затем по мере необходимости быстро вычислять х{к) по
формуле Z( /t) = A^dik)- Однако использование L {/-разложения матри-
матрицы А (см. § 5.7) позволяет вычислять г< к) столь же быстро, а предва-
предварительная работа на этапе разложения дает трехкратную экономию.
Таким образом, и этот довод в пользу необходимости вычисления
обратной матрицы неубедителен.
Довольно часто при решении различных задач средствами линей-
линейной алгебры возникают выражения типа
v = В СЛ WD~l w. E.48)
Если у исследователя нет достаточного опыта решения задач линей-
линейной алгебры на ЭВМ, то он может принять решение о необходимости
вычислять матрицы В, A'1, Л, с тем чтобы действовать далее по
формуле E.48). Однако и в этом случае можно поступить иначе и
найти v с меньшими затратами. Решая систему Dx = to, найдем
х = D~xv>. Затем вычислим у = Wx и, решая систему Az = f, найдем
г— А'1у. Наконец, вычислим и = Сг и, решая систему Bv = «, найдем
tr= B-i«.
Сказанное выше вовсе не означает, что нет ситуаций, когда вычис-
вычисление матрицы А'1 необходимо и оправдано. В ряде технических при-
приложений и статистических задач непосредственный интерес представ-
представляет анализ свойств именно обратной матрицы. Тем не менее, как мы
видим, в матричных вычислениях можно и следует обходиться без
вычисления обратных матриц. Авторы настоятельно рекомендуют не
вычислять обратные матрицы, если только в дальнейшем не предпола-
предполагается анализ элементов этих матриц.
Покажем, как вычисление обратной матрицы' можно свести к рас-
рассмотренной выше задаче решения системы уравнений с несколькими
правыми частями. Обозначим матрицу А'1 через V, ее столбцы — через
V[, «г, ..., Ощ и столбцы единичной матрицы Е— через е\, ег, ..., е*,.
Согласно определению обратной матрицы верно равенство AV = Е,
эквивалентное совокупности равенств
= e2,
= em
E.49)
Таким образом, столбцы матрицы V = А'1 (а следовательно, и саму
матрицу), можно найти, решая m систем уравнений с общей матрицей
149

А. Согласно изложенному выше, для этого потребовалось бы примерно
(8/з)т3 арифметических операций, однако учет специального вида
правых частей системы E.49) позволяет вычислять матрицу А'1 при-
примерно за 2т3 операций.
3. Вычисление определителя. Воспользуемся алгоритмом метода
Гаусса с выбором главного элемента по столбцу и заметим, что иско-
искомый определитель и определитель полученной треугольной матрицы
Aim'l) связаны равенством
det A = (-l)*det A""'1',
где s — число потребовавшихся перестановок строк. Остается восполь-
воспользоваться формулой E.17) и тогда получим
det А = (-1)* a}?» en' ... в»-"» , E.50)
где <z{J> = лц- Отметим, что вычисление по формуле E.50) требует
особой аккуратности, в особенности если число m велико. Как мы
убедились в примере 3.29, при вычислении произведений следует
специальным образом упорядочивать сомножители. Неудачный поря-
порядок их расположения может привести к аварийному останову по пере-
переполнению либо к исчезновению порядка.
Можно избежать переполнения и исчезновения порядка, если для
вычисления det А воспользоваться формулой
In|det A| =2 ln|a«;-»|-
t=i '
Однако следует иметь в виду, что ее использование может привести к
некоторой потере точности.
Замечание. Действительная необходимость в вычислении
определителей возникает довольно редко. Во всяком случае осно-
основанные на их использовании алгоритмы оказываются весьма неэф-
неэффективными (как в примере 3.34, где обсуждалось правило Краме-
Крамера), и поэтому вычисление определителей давно уже не является
элементом современных алгоритмов линейной алгебры. Кроме того,
из результатов в § 5.4 следует, что использование величины det A
для определения степени близости системы уравнений к вырожден-
вырожденной дает весьма ненадежный и сомнительный критерий.
Пример 5.11. Используя метод Гаусса с выбором главного элемента по
столбцу вычислим определитель матрицы
150
2
1.
1
2
-9
-5.
-1
3999
5
6
-7.5
А =
на 6-разрядной десятичной ЭВМ.
Повторяя преобразования из примера 5.9, получим матрицу
2-9 5
0 3.5 -10
0 0 3.00029
Так как была сделана одна перестановка строк, то формула E.50) дает
и (-1)-2-3.5-3.00029 и -21.0020.
Можно с достаточной степенью уверенности предположить, что во
многих технических науках, где традиционно используются определи-
определители, в ближайшее время неизбежен переход к использованию других
более содержательных характеристик линейных моделей. Такими
естественными характеристиками могут служить, например, собствен-
собственные числа и собственные векторы матриц (см. гл. 8).
§ 5.7. Метод Гаусса
и разложение матрицы на множители.
L ^-разложение
Вернемся еще раз к методу Гаусса с тем, чтобы рассмотреть его с
более общих позиций. Излагаемый ниже подход оказался чрезвычайно
плодотворным и привел не только к более глубокому пониманию мето-
метода, но и позволил создать высокоэффективные машинные алгоритмы
его реализации, а также рассматривать другие точные методы с еди-
единой точки зрения.
Рассмотрим сначала простейший вариант метода Гаусса для реше-
решения системы линейных алгебраических уравнений
Ах=Ь. E.51)
1. Схема единственного деления и L {^-разложение. При выполнении
вычислений 1-го шага исключения по схеме единственного деления
система уравнений приводится к виду
где
E.52)
151

«11 в12
0 дп.
0 a<i>
0 aA)
а коэффициенты aW
13
«2^
¦ii'
<з'
, 6U>
Д
«ii'
•ii'
ТОГО
i =
621>
(i, j = 2, 3, ..., m) вычисляются по форму-
формулам E.29), E.31).
Введем матрицу
l
-/*21
-/*31
0
1
0
0 .
0 .
1 .
.. 0
.. 0
.. 0
0 0 ... 1
Как нетрудно проверить, справедливы равенства
Л"» = AM, »"> = А/,6,
т. е. преобразование системы E.51) к виду E.52) эквивалентно умноже-
умножению левой и правой частей системы на матрицу М\.
Аналогично можно показать, что вычисления 2-го шага исключе-
исключения приводят систему E.52) к виду
Л<2>Х =
где
Л<2> =
= A/26">,
Л<2) =
«11
0
0
0
«12
A)
°22
0
0
fl13
A)
°23
атз'
- «im
( 1)
••• a2m
- -i?'
... a*2»
TOTR
,M2
' 1
0
0
. 0
0
1
-Лз
-Mm
0
0
г 1
2 0
... 0 '
... 0
... 0
... 1
,6»2) =
»i
All)
62
6<2)
M 2)
ГО
После (т — 1)-го шага, завершающего прямой ход, система оказы-
оказывается приведенной к виду
E.53)
с верхней треугольной матрицей .Л1'. Здесь
152
u
яA)
Я22
О О
23
„B)
3
о о
б'2»
i -™m-l —
1 0 0 ... О О
О 1 0 ... О О
0 0 0 ... 1 0
0 0 0 ... -//„,,„,-! 1
Заметим, что матрица Л1' получена из матрицы А последова-
последовательным умножением на Mlt M2, ..., Мп-\:
A«"-») = AV! ... JT2J<iA.
Аналогично,
Из равенства E.54) вытекает следующее представление:
А= Mil*T2l... Jfti
Как легко проверить,
E.54)
E.55)
E.56)
«яй =
1
/i21
Л31
.Л.1
1
0
0
0
0
1
0
0
0
1
0
0
0
0
1
0
0
0
0
0
... 0
... 0
... 0
... 1
... 0
... 0
... 1
0 '
0
0
. 1
1
0
0
0
0
1
Д32
Ыг
0
0
1
0
... 0
... 0
... 0
... 1
,....,
Для этого достаточно перемножить матрицы Щ1 и Afjt (к = 1, ...,
т — 1), в результате чего получится единичная матрица.
153

Введем обозначения U = Aim~li, L = M{lM^ ... AfmM- Вычисляя
матрицу L, убеждаемся в том, что она имеет следующий вид:
о о
1 О
032 1
...О
...О
...о
... 1
E.57)
Тогда равенство E.56) в новых обозначениях примет вид
А = LU. E.58)
Это и есть1 L U-разложение матрицы А — представление матрицы А в
виде произведения нижней треугольной матрицы L и верхней тре-
треугольной матрицы U.
Таким образом, прямой ход метода Гаусса без перестановок можно
рассматривать как процесс вычисления I {/-разложения матрицы
системы, на Jfc-м шаге которого определяются элементы i-го столбца
матрицы L и к-Л строки матрицы U.
Возможность L [/-разложения обосновывается следующей теоремой.
Теорема 5.3. Если все главные миноры матрицы А отличны
от нуля, то существуют единственные нижняя треугольная матрица
L вида E.57) и верхняя треугольная матрица U такие, что А = LU.
Структура матриц L и U позволяет организовывать компактное
размещение элементов этих матриц в памяти ЭВМ по мере их вычис-
вычисления. На fc-M шаге исключения в области памяти, где первоначально
располагалась матрица А, размещается матрица
"п
2
„A)
а22
aim
И2,Ь1
4*1,
fl
I*m2
¦Nik
п<*>
1 Обозначения треугольных матриц буквами L и U вызваны тем, что эти
буквы являются начальными в английских словах lower — "нижний" и up-
upper — "верхний".
154
При этом вся необходимая для дальнейших вычислений информация
сохраняется.
Пример 5.12. Проиллюстрируем LtZ-разложение на примере решения
системы E.35). На основании данных табл. 5.2 можно записать
L =
10 0 0
0.5 1 0 0
0.3 -1.6 1 0
0 -3 2.5 1
и=
10 6 2
0 -2 -3
0 0 -4.4
0 0 0
0
4
5.4
0.5
Следовательно, LU-разложение матрицы системы имеет вид
10 6 2 0
5 1-24
3 5 1-1
0 6-22
10 0 0
0.5 1 0 0
0.3 -1.6 1 0
0 -3 2.5 1
10 6 2
0 -2 -3
0 0 -4.4
0
4
5.4
0.5
2. Использование Z {/-разложения. В современных программах,
реализующих метод Гаусса на ЭВМ, вычисления разбивают на два
основных этапа. Первый этап — это вычисление L {/-разложения матри-
матрицы системы. Второй этап — обработка правых частей и вычисление
решения.
Смысл выделения первого этапа состоит в том, что он может быть
выполнен независимо, для его проведения не нужна информация о
правой части системы. Это как бы этап предварительной подготовки к
быстрому вычислению решения. Именно для получения L {/-разложе-
{/-разложения производится основная масса вычислений (примерно B/3)ш3
арифметических операций).
На втором этапе выполняют следующие действия:
1°. Преобразуют правую часть Ь по формулам прямого хода; необ-
необходимые для вычисления коэффициенты иц берут из матрицы L. В
результате получают вектор 6( яг1', связанный с вектором 6 формулой
E.55).
2°. С помощью обратной подстановки решают систему Ux = 6( т'.
Для непосредственного вычисления решения х на втором этапе
требуется примерно 2т2 арифметических операций.
В случае, если необходимо решить р систем уравнений с фиксиро-
фиксированной матрицей А и различными правыми частями ^пь ^B>> ¦¦-<
dip), первый этап проводят лишь один раз. Затем последовательно р
раз проводят вычисления второго этапа для получения решений г< i >,
ХB), ..., Х(р). Для этого, как и в § 5.6, требуется примерно B/з)пг3 +
+ 2pm2 арифметических операций.
155

Пример 5.13. Решим систему
lOxi +6*2 + 2^ =8,
Ъх\ + »2 — 2гз + 4*4 = 7,
3xi + 5хг + гз — х4 = 2,
6я2 — 2гз + 2х4 = 2.
Воспользуемся LCJ-разложением матрицы системы, указанным в примере
5.12. Сначала преобразуем вектор правой части 6 = (8, 7, 2, 2)т по формулам
прямого хода.
1-й шаг. fr2n = Ьг - /<2i*i = 7 - 0.5-8 = 3, ft'1' = *з - 03i*i = 2 —
— 0.3-8 = -0.4, fr4n = 64 — 041*1 = 2 — 0-8 = 2. После 1-го шага получим
*A) = (8, 3,-0.4, 2)т.
2-й шаг. 6<2> = &'1» - 0з2*2п = -0-4 - (-1.6)-3 = 4.4, fr<2> = &4" -
- 042b2U = 2 - (-З)-З = 11. После 2-го шага найдем 6«2> = (8, 3, 4.4, 11)т.
3-й шаг. 643> = fr42) — 114зЦ2) = И — 2.5-4.4 = 0. В результате пря-
прямого хода получен вектор 4<3> = (8, 3, 4.4, 0)т и система приведена к виду
10«i + 6i2 + 2*з = 8,
— 2x2 — 3*з + 4х4 = 3,
— 4.4х3 + 5.4х4 = 4.4,
0.5х4 = 0.
Обратный ход дает значения неизвестных Х4 = 0, хз = -1, i% — 0, zj = 1.
3. Метод Гаусса с выбором главного элемента и разложение матри-
матрицы на множители. В отличие от схемы единственного деления схема
частичного выбора предполагает на it-м шаге прямого хода перестанов-
перестановку уравнений системы с номерами «* и к (при выборе в качестве глав-
главного элемента Jt-ro шага элемента а: ^). Это преобразование эквивален-
эквивалентно умножению системы на матрицу Pjt, которая получается из еди-
единичной матрицы перестановкой «jt-й и ifc-й строк (см. пример 5.14).
Исключение неизвестного на к-м шаге по-прежнему эквивалентно
умножению системы на матрицу Afjt.
Таким образом, после 1-го шага система Ах = Ь преобразуется к
виду А">х = i*1», где А»1' = Aft Pi А, Ь11» = AftPjb. После 2-го шага
система преобразуется к виду AB)i = ЬB), где АB) = Af^A111,
*<2> = Af2P2*<l>.
После завершающего (т — 1)-го шага прямого хода система оказы-
оказывается приведенной к виду А{т'1]х = bim'i], где А(яН) =
Как нетрудно видеть,
М2Р2М1Р1Ь.
E.59)
E.60)
Равенство E.59) равносильно следующему разложению матрицы А на
множители:
А =
E.61)
где U= A1' —верхняя треугольная матрица.
Разложение E.61) не является L [/-разложением матрицы А. Однако
прямой ход по-прежнему равносилен L (/-разложению, но уже не самой
матрицы А, а матрицы А, полученной из нее в результате соответству-
соответствующей перестановки строк. Это разложение имеет вид
А= LU,
E.62)
где А = Pm-iP-m-2 ¦¦¦ Р2Р1А, L — нижняя треугольная матрица, отлича-
отличающаяся от матрицы E.57) перестановкой множителей в столбцах.
Пример 5.14. Найдем разложение вида E.62) для матрицы системы E.39),
используя результаты вычислений примера 5.9. Так как 1-й шаг прямого хода
не потребовал перестановки, а на 2-м шаге были переставлены второе и третье
уравнения, то
1
0
0
0
1
0
0
0
1
, Р2 =
1
0
0
0
0
1
0
1
0
, А =
2
1
1.2
-9
-1
-5.3999
5
-7.5
6
1
0.5
0.6
0
1
2.9-10
0
0
1
, u=
2
0
0
-9
3.5
0
5
-10
3.00029
156
Для матрицы А прямой ход уже проводится по схеме единственного деления.
Отличие от вычислений примера 5.9 состоит в том, что на 2-м шаге множители
/*2i и 031, а также второе и третье уравнения системы E.40) меняются места-
местами. В результате получим разложение вида E.62), где
L-
После получения разложения вида E.62) для решения системы
Ах = Ь выполняют следующие действия.
1°. Правую часть перестановкой элементов приводят к виду
* = Pm-iPm-2 ... РгРхЪ.
2°. Преобразуют вектор 6 по формулам прямого хода; необходимые
Для вычислений множители 0у берут из матрицы L. В результате
Получают вектор 6( т'1'.
3°. Обратной подстановкой решают систему Ux = bim'i).
157

Заметим, что матрица перестановки Рк полностью определяется
заданием номера »* уравнения, которое переставляется с Jfc-м уравнени-
уравнением. Поэтому для хранения всей информации о перестановках достаточ-
достаточно целочисленного массива длины m — 1.
Пример 5.15. Решим систему E.39), используя полученное в примере 5.14
разложение матрицы А
Здесь вектор Ь = (-4, 0.6001, -8.5)т преобразуется в вектор Ь — (—4, -8.5,
0.6001)т перестановкой второго и третьего элементов.
Прямой х о д. 1-й шаг.
= 62 —
= -8-5 — 0.5(-4) = -6.5,
= Ь3 — /*31*1 = 0.6001 — 0.6-(-4) = 3.0001. В результате 1-го шага имеем
*ч» = (-4, -6.5, 3.0001)т.
2-й шаг.
= б'1' -
= 3.0001 - 2.9-10- (-6.5) и 3.00029. В
результате прямого хода правая часть оказалась приведенной к виду ЬB) =
= (-4, -6.5, 3.00029)т.
Обратный ход проводится точно так же, как в примере 5.9, и дает
значения хз = 1, x-i — 1, ц = 0.
§ 5.8. Метод Холецкого (метод квадратных корней)
1. Описание метода. Пусть требуется решить систему линейных
алгебраических уравнений
Ах = Ь
E.63)
с симметричной положительно определенной матрицей А. Линейные
системы такого типа часто встречаются в приложениях (например, в
задачах оптимизации, при решении уравнений математической физики
и др.). Для их решения весьма часто применяется метод Холецкою
(другое название — метод квадратных корней).
В основе метода лежит алгоритм построения специального LU-
разложения матрицы А, в результате чего она приводится к виду
А = Ш.
В разложении E.64) нижняя треугольная матрица
L-
/,, 0 ...0
hi '22 •¦• 0
Art 'm2 ••• 'л
E.64)
E.65)
уже не обязательно должна иметь на главной диагонали единицы, как
это было в методе Гаусса, а требуется только, чтобы диагональные
элементы 1ц были положительными.
Если разложение E.64) получено, то решение системы E.63) сво-
сводится к последовательному решению двух систем с треугольными
матрицами:
Ly=b,
E.66)
Для решения систем E.66) требуется выполнение примерно 2т2 ариф-
арифметических операций.
Найдем элементы матрицы L. Для этого вычислим элементы матри-
матрицы LL1 и приравняем их соответствующим элементам матрицы А. В
результате получим систему уравнений
п
h 1 = «it.
'ti'i l = ai l. »' = 2, 3 т,
hi + '2 2 = а22>
+ /12*22 = <»i2. • = 3, 4 т,
¦¦¦+
+ '.2'fe2+ • • • + liklkk= <4k, i = k+ 1, ..., m,
'J2 + - +
Решая систему E.67), последовательно находим
E.67)
'«1 = anlhu » = 2, 3, ... , m,
h2 = a/«22 - Щу
'i2 = (Ч12 - 'ti'21 )/'22. « - 3, 4 m,
E.68)
- (<4k~ 'ii'
— ¦¦¦ -'i.Jfc-1 lk,k-l)/lkk< «= *+ 1, •-, Щ
158
W = ч/вши-fii- lla---ll,m-l-
Заметим, что для вычисления диагональных элементов использует-
используется операция извлечения квадратного корня. Поэтому метод Холецкого
159

называют еще и методом квадратных корней. Доказано, что положи-
положительность соответствующих подкоренных выражений является следст-
следствием положительной определенности матрицы А.
2. Достоинства ыетода. Метод Холецкого обладает рядом ценных
качеств, которые позволяют предпочесть его методу Гаусса, если тре-
требуется решить систему линейных алгебраических уравнений с симмет-
симметричной и положительно определенной матрицей.
Как нетрудно подсчитать, число операций, выполняемых в ходе
вычисления разложения E.64) по формулам E.68), равно примерно
т3/3. Учитывая, что для решения систем E.66) требуется примерно
2т2 арифметических операций, убеждаемся, что при больших m метод
Холецкого требует вдвое меньше вычислительных затрат по сравнению
с методом Гаусса.
Учет симметричности матрицы А позволяет экономно использовать
память ЭВМ при записи исходных данных задачи и результатов вы-
вычислений. Действительно, для задания матрицы А достаточно ввести в
память ЭВМ только элементы ау (i > j), расположенные на главной
диагонали и под ней. В формулах E.68) каждый такой элемент а1}
используется лишь однажды для получения /у и далее в вычислениях
не участвует. Поэтому в процессе вычислений найденные элементы /у
могут последовательно замещать элементы ау.
В результате нижняя треугольная матрица L может быть располо-
расположена в той области памяти, где первоначально хранилась нижняя
треугольная часть матрицы А. Применение для решения системы
E.63) метода Гаусса потребовало бы использования примерно вдвое
большего объема памяти.
Безусловным достоинством метода Холецкого является также его
гарантированная устойчивость.
Пример 5.16. Используя метод Холецкого, найдем решение системы уравне-
уравнений с симметричной положительно определенной матрицей:
6.25*i — *2 + 0.5*з = 7.5,
-*! + 5*2 + 2.12*з = -8.68,
0.5*i + 2.12*2 + 3.6*з = -0.24.
По формулам E.68) последовательно находим
/ц = увц = ^6.25 — 2.5, B1 = a2iMi = —1/2.5 = -0.4,
fei = W11 = 0.5/2.5 = 0.2,
'32 = (а32 —
'зЗ = Va22 "
160
Следовательно, матрица L такова:
= V<*22 — & = V5 — 0.16 = 2.2,
= B.12 - 0.2(-0.4))/2.2 = 1,
- 2 = /3.6 - 0.22 - I2 = 1.6.
2.5 0 0
-0.4 2.2 0
0.2 1 1.6
Система Ly=b имеет вид
2-5jn
-0.4й
= 7.5,
. =-8.68,
1.6 & = -0.24.
Решая ее, получаем j/i = 3, & = -3.4, y3 - 1.6.
Далее из системы Ux = у, которая имеет вид
2.5*1 - 0.4*2 + 0.2*3 = 3,
2.2*2 + *з = -3.4,
1.6*3 = 1.6,
находим решение *i = 0.8, *2 = -2, *3 = 1.
§ 5.9. Метод прогонки
Рассмотрим метод прогонки^ — простой и эффективный алгоритм
решения систем линейных алгебраических уравнений с трехдиагональ-
ными матрицами:
q*2
02*1
*3
= <*!¦
= d2,
at*i-i
c,*,«
E.69)
атхт-1 + Ьтхт =
Системы такого вида часто возникают при решении различных задач
математической физики, а также при решении других вычислитель-
вычислительных задач (например, приближения функций сплайнами).
1 Метод прогонки был предложен в начале 50-х годов независимо несколь-
несколькими авторами, в том числе российскими учеными И.М. Гельфандом,
О-В. Локуциевским, B.C. Владимировым, А.С. Кронродом.
•-28 161

1. Вывод расчетных формул. Преобразуем первое уравнение систе-
системы E.69) к виду
Х\ = <*\Х2 + 01,
E.70)
где ац = -С)/6Ь Д = V*i-
Подставим полученное для х\ выражение во второе уравнение систе-
системы:
a2(aii2 + А) + hx2 + С2*з = d2.
Преобразуем это уравнение к виду
Х2 = «2*3 + 02, E-71)
где <*2 = -C2/(h ¦+ a2«i), А> = (<^2 — a20\)l(h + a2«i)- Выражение E.71)
подставляем в третье уравнение системы и т. д.
На j-m шаге этого процесса A < i < m) i-e уравнение системы пре-
преобразуется к виду
= atxiH + 0t,
E.72)
где а, = -с,/F, + a,a,-i), /3, = (i, - a,0i-i)/(bt + atat.i).
На m-м шаге подстановка в последнее уравнение выражения rm.j =
= атЛхт + 0m-i дает
«jn(am-lZm + An-l) + &iA = <*т-
Отсюда можно определить значение хт:
Хт = An = (dm - ат0пЛI(Ьт + amOtm-i).
Значения остальных неизвестных г, для t = гг. — 1, m — 2, ..., 1
теперь легко вычисляются по формуле E.72).
2. Алгоритм прогонки. Сделанные преобразования позволяют орга-
организовать вычисления метода прогонки в два этапа'.
Прямой ход метода прогонки (прямая прогонка) состоит в вычисле-
вычислении прогоночных коэффициентов а, A < > < т) и 0Х A < % < т). При
j = 1 коэффициенты вычисляют по формулам
«1 = -ci/7ii 0\ =¦ */7ь 71 = *1, E-73)
а при » = 2, 3, ..., m — 1 — по рекуррентным формулам
at = -C1/711 0i=(dt- ai0i-i)/fu 7. = 6. + etai-i- E-74)
При t = m прямая прогонка завершается вычислением
Pm=(dn- Oj9«-i)/7m, 7m = 6m +
E.75)
Обратный ход метода прогонки (обратная проюнка) дает значения
неизвестных. Сначала полагают хт = 0т. Затем значения остальных
неизвестных вычисляют по формуле
xt = a,Xf, + A, i = m - 1, m - 2, .:., 1. E.76)
Вычисления ведут в порядке убывания значений « от m — 1 до 1.
Пример 5.17. Используя метод прогонки, решим систему
5*1 — гь
= 2.0,
— Ч = 3.3,
+ 3.6г3 — 0.8*4 = 2.6,
Зг3 + 4.4*4 = 7-2-
Прямой ход. Согласно формулам E.73)—E.75) получаем
162
7! = 6, = 5, <ч = -С!/7i = 1/5 = 0.2, А = rf,/7i = 2.0/5 = 0.4,
72 = *2 + Л2«1 = 4.6 + 2-0.2 = 5, а2 = -сц/ъ - 1/5 = 0.2,
02 = (d2 - а2А)/72 = C.3 - 2-0.4)/5 = 0.5,
73 = &з + а3а2 = 3.6 + 2-0.2 = 4, а3 = -<&/7з = 0.8/4 = 0.2,
03 = (<*з - а3/?2)/Тз = B.6 - 2-0.5)/4 = 0.4,
74 = Ь4 + О4а3 = 4.4 + 3-0.2 = 5,
04 = (d4- <H0z)/lA = G.2 - 3-0.4)/5 = 1.2.
Обратный ход. Полагаем х4 — 04 — 1.2. Далее находим хз =
= а3*4 + 0з = 0.2-1.2 + 0.4 = 0.64, *2 = «2*3 + 02 = 0.2-0.64 + 0.5 = 0.628,
II = ai*2 + 0\ — 0.2-0.628 + 0.4 = 0.5256. Итак, получаем решение: х\ =
= 0.5256, г2 = 0.628, *3 = 0.64, г4 = 1-2.
3. Свойства метода прогонки. Непосредственный подсчет показыва-
показывает, что для реализации вычислений по формулам E.73)—E.76) требу-
требуется примерно 8т арифметических операций, тогда как в методе Гаус-
Гаусса это число составляет примерно B/з)т3. Важно и то, что трехдиаго-
нальная структура матрицы системы позволяет- использовать для ее
хранения лишь Зт — 2 машинных слова.
Таким образом, при одной и той же производительности и опера-
оперативной памяти ЭВМ метод прогонки позволяет решать системы гораз-
гораздо большей размерности, чем стандартный метод Гаусса для систем
уравнений с заполненной матрицей.
Приведем простые достаточные условия на коэффициенты системы
E.69), при выполнении которых вычисления по формулам прямой
прогонки могут быть доведены до конца (ни один из знаменателей 7i
не обратится в нуль). В частности, это гарантирует существование
решения системы E.69) и его единственность. При выполнении тех
же условий коэффициенты а, при всех г удовлетворяют неравенству
163

I a, I < 1, а следовательно, обратная прогонка по формуле E.76) устой-
устойчива по входным данным (см. пример 3.27). Положим а{ = О, Ья = 0.
Теорема 5.4. Пусть коэффициенты системы E.69) удовлетво-
удовлетворяют следующим условиям диагонального преобладания:
|, |6*|
(KJKrn).
E.77)
Totda 7i t 0 и \ati\ ^ 1 для всех i = 1, 2,..., m.
а Воспользуемся принципом математической индукции. Из условий
теоремы имеем 71 = &i * 0 и | <*i | = | q j /1 Ь\ | < 1.
Пусть теперь 7fc-i * 0 и | ajt-! | < 1 для некоторого к > 1. Тогда
|7*1 = \h + ajtaifc-i I > I 6*1 - |afc||a*-il > |6fc| — |а*|.
Из полученной оценки в силу условий E.77) вытекает справедливость
неравенств 17fc| > 0 и | 7fcl ^ \ск\- Следовательно, 7* * 0 и | ajt| =
||/Ы
4. Метод прогонки и разложение матрицы иа множители. Описан-
Описанный вариант метода прогонки можно рассматривать как одну из схем
метода Гаусса (без выбора главного элемента), в результате прямого
хода которого исходная трехд и атональная матрица
А =
«2
0
0
0
Cl
62
«3
0
0
0
0
0
0
0
cz
0
0
... 0
... 0
... 0
••• Om-1
... 0
0
0
0
Ьщ-Х
a,
0
0
0
cm-i
представляется в виде произведения двух двухдиагональных матриц:
Л = LU. E.78)
Здесь
L-
7i 0 0 ... 0 О
а2 72 0 ... О 0
0 аэ 7з ••• О О
0 0 0
7т
а! 0 ... 0 0
1 -а2 ... 0 0
О 0
0 0
0 - 1 -am-i
0 ... 0 1
Так как для определения L и U нет необходимости вычислять
коэффициенты /3„ то общее число операций на получение разложения
E.78) составляет примерно Зт.
164
Подобно тому как это описано в § 5.7, разложение E.78) можно
использовать для решения систем с многими правыми частями. Если
нужно решить р систем с матрицей Л, то общее число операций соста-
составит примерно Зт + Ътр.
К сожалению, при обращении матрицы А теряется ее трехд и ато-
атональная структура. Обратная матрица является заполненной, однако
для ее вычисления с помощью разложения E.78) требуется примерно
2.5т2 арифметических операций.
Так как det A = det Z-det U, а det U = 1, то определитель
трехдиатональной матрицы, после того как получено разложение
E.78), вычисляется по элементарной формуле
det А = 7172 ••• 7я-
б. Некоторые варианты метода прогонки. Наряду с изложенным
выше "стандартным" вариантом метода прогонки (правой прогонкой)
существует большое число других вариантов этого метода. Это методы
левой прогонки, встречных прогонок, немонотонной прогонки, потоко-
потоковый вариант метода прогонки. В ряде случаев эти модификации могут
существенно улучшить обусловленность прогонки.
Для систем уравнений, обладающих близкой к E.69) структурой,
разработаны методы циклической прогонки, матричной прогонки и
ДР-
С указанными вариантами метода прогонки можно подробно озна-
ознакомиться в [42], [72].
§ 5.10. ДО-разложение матрицы.
Методы вращений и отражений
Метод Гаусса не является единственным методом исключения,
используемым для решения систем линейных уравнений и приведения
матриц к треугольному виду. Рассмотрим два метода исключения,
обладающих в отличие от метода Гаусса гарантированной хорошей
обусловленностью — метод вращений и метод отражений. Оба этих
метода позволяют получить представление исходной матрицы А в виде
произведения ортогональной1 матрицы Q на верхнюю треугольную
матрицу R:
1 Напомним, что матрица Q называется ортогональной, если для нее вы-
выполнено условие (J = Q1, что эквивалентно равенству Qff = R
165

A = QR. E.79)
Представление E.79) — это QR-разложение матрицы на множители.
1. Метод вращений. Опишем прямой ход метода. На 1-м шаге неиз-
неизвестное х\ исключают из всех уравнений, кроме первого. Для исключе-
исключения х\ из второго уравнения вычисляют числа
«12 =
1
обладающие следующими свойствами:
С12 + «12 = *> ~S12all + Ci2a2l = 0.
E.80)
E.81)
Затем первое уравнение системы заменяют линейной комбинацией
первого и второго уравнений с коэффициентами с\2 И $12, а второе
уравнение — аналогичной линейной комбинацией с коэффициентами
-«12 и Cj2- В результате получают систему
E.82)
в которой
, (KjKtn), E.83)
Ъ\ = С12&1 + S\2b2, Ь2 =-«1261+ С12&2-
Заметим, что o2l' = -в^пц + 012021 = 0 в силу специального выбора
чисел Ci2 и 5i2 (см- равенства E.81)).
Естественно, что в случае a2i = 0 исходная система уже имеет вид
E.82) и в исключении неизвестного хх из второго уравнения нет необ-
необходимости. В этом случае полагают с^ = 1 и вх2 = 0.
Как нетрудно видеть, преобразование исходной системы E.1) к
виду E.82) эквивалентно умножению слева матрицы А и правой части
6 на матрицу Т\2, имеющую вид
си «12 0 0 ... 0
"«12 Ci2 0 0 ... 0
0 0 1 0 ... 0
0 0 0 1 ... 0
0 0 ... 1
Для исключения неизвестного х\ из третьего уравнения вычисляют
числа
„A)
С13 =
1
E.84)
такие, что с23 + «1з = 1, -«1зои' + С13Л31 = 0- Затем первое уравнение
системы E.82) заменяют линейной комбинацией первого и третьего
уравнений с коэффициентами Ci3 и «13, а третье уравнение — аналогич-
аналогичной комбинацией с коэффициентами — s13 и с^. Это преобразование
системы эквивалентно умножению слева на матрицу
Т,з =
С13
0
«13
0
0
1
0
0
«13
0
ci3
0
0
0
0
1
... 0
... 0
... 0
... 0
О
1
и приводит к тому, что коэффициент при х\ в преобразованном треть-
третьем уравнении обращается в нуль.
Таким же образом xi исключают из уравнений с номерами i = 4, ...,
m. В результате 1-го шага (состоящего, как мы видели, из m — 1
"малых" шагов) система приводится к виду
О22
 3
2
= Ь2
=63",
E.85)
В матричной записи получаем
166
где ЛП) = Ты ... Т,зГ,2Л, б»» = Т1ш ... Т13Т12Ь.
Здесь и далее через Ты обозначена матрица элементарного преоб-
преобразования, отличающаяся от единичной матрицы Е только четырьмя
элементами. В ней элементы с индексами (к, к) и (/, Q равны од, эле-
167

мент с индексами (Jt, /) равен зд, а элемент с индексами (/, к) равен
-ski, причем выполнено условие
ch+sh=l. E.86)
Действие матрицы Tki на вектор х эквивалентно его повороту вокруг
оси, перпендикулярной плоскости Ox^xi на угол (ры такой, что од =
= cos ipki, ski = sin fkl (существование такого угла гарантируется ра-
равенством E.86)). Эта геометрическая интерпретация и дала название
методу вращений. Операцию умножения на матрицу Tki часто называ-
называют плоским вращением (или преобразованием Гивенса). Заметим, что
т "I
Tki = Tki и, следовательно, матрица Ты ортогональная.
На 2-м шаге метода вращений, состоящем из т — 2 "малых" шагов,
из уравнений системы E.85) с номерами « = 3, 4, ..., m исключают
неизвестное Х2- Для этого каждое к>е уравнение комбинируют со вто-
вторым уравнением. В результате приходим к системе
(m-1) , „(m-1)
j22 x2 + a2a
J 2' „
a3 3 X3
a2m % = &2 .
*3
*3
.12).
J 2)
- 1B)
В матричной форме записи получаем
= Т2п... Т2ЛТ23А">, 6<2> = T2m... TuT
После завершения (т — 1)-го шага система принимает вид
„(m-1) _ i(m-l)
"mm *т ~ °т i
или в матричной форме записи
168
где , ^!,,,
Введем обозначение Д для полученной верхней треугольной матри-
матрицы Л1™'. Она связана с исходной матрицей А равенством
Д= ТА,
где Г= Тт-1(Я, ... T2m...T23Tim' ... Ti3T12 — матрица результирующего
вращения. Заметим, что матрица Т ортогональна как произведение
ортогональных матриц. Обозначая Q = Г = Гт, получаем QR-
разложение матрицы А.
Обратный ход метода вращений проводится точно так же, как и
для метода Гаусса.
Метод вращений обладает замечательной численной устойчивостью.
Для него оценка E.43) справедлива с коэффициентом /(т) = 6т.
Однако этот метод существенно более трудоемок по сравнению с
методом Гаусса. Получение Qit-разложения для квадратной матрицы
А общего вида требует примерно 2тп3 арифметических операций.
Пример 5.18. Используя метод вращений, решим на &-разрядной
десятичной ЭВМ систему уравнений
2xi — 9»2 + 5х3 = -4,
1.2x1 - 5.3999*2 + 6г3 = 0.6001,
xi — г>2 — 7.5г3 = -8-5.
Прямой ход. 1-й шаг. Исключим х\ из второго уравнения. Для
этого вычислим С[2 и «12 по формулам E.80):
V22 + 1.22
и 0.857493,
1.2
и 0.514495.
V22 + 1.22
Преобразуя коэффициенты первого и второго уравнений по формулам
E.83), приходим к системе
2.33238x1 - 10.4957x2 + 7.37444хз = -3.12122,
7.85493-10-5г2 + 2.57248гз = 2.57256,
xi - *2 — 7.5*3 = -8-5.
Далее вычислим коэффициенты ci3 и si3 по формулам E.84):
2.33238 „_ 1
и 0.919087,
я 0.394055.
V^.332382 + I2
V2.332382 + I2
169

Заменяя первое и третье уравнения их линейными комбинациями с коэффи-
коэффициентами Ci3i Чз и -sl3i C13 соответственно, получим систему
2.53772Г1 - 10.0405i5 + 3.82234x5 = -в. 21814,
7.85493-10" ъхг + 2.57248хз = 2.57256,
3.21680г2 - 9.79909*3 = -6.58231.
2-й ш а г. В полученной системе имеем
3.21680. Поэтому
= 7.85493-10,
азг =
A)
С23 =
¦и 2.44185-10, «23 и 1.00000.
Заменяя второе и третье уравнения системы их линейными комбинациями с
коэффициентами С23, «гз и ~*23. сгз соответственно, приходим к системе
2.53772x1 - 10.0405x2 + 3.82234х3 = -6.21814,
3.21680x2 - 9.79903хз = -6.58225,
- 2.57272хз = -2.57272.
Обратный ход дает последовательно значения х$ — 1, х% =
= 0.999994, щ =-1.58579-10.
2. Метод отражений. Матрицами Хаусхолдера (или отражений)
называются квадратные матрицы вида
V= E
Здесь w — вектор-столбец в Л™, имеющий единичную длину. Матрица
V является ортогональной и симметричной. Умножение на нее называ-
называют преобразованием Хаусхолдера (или отражением). Действие матрицы
V на вектор х можно интерпретировать как ортогональное отражение
вектора в Я™ относительно гиперплоскости, проходящей через начало
координат и имеющей нормальный вектор, равный to.
Как и вращения, отражения используются для обращения в нуль
элементов преобразуемой матрицы. Однако здесь с помощью одного
отражения можно обратить в нуль не один элемент матрицы, а целую
группу элементов некоторого столбца или строки. Поэтому, являясь
почти столь же устойчивым, как и метод вращений, метод отражений
позволяет получить фЯ-разложение квадратной матрицы общего вида
примерно за D/3)т3 арифметических операций, т.е. в полтора раза
быстрее.Изложение самого метода можно найти, например, в [9].
170
\ 5.11. Итерационное уточнение
В большинстве случаев метод Гаусса с выбором главного элемента
позволяет найти приближенное решение с довольно высокой точнос-
точностью. Однако иногда возникает необходимость найти решение с боль-
большей точностью. Полезно знать, что существует метод, позволяющий
найти приближенное решение с относительной точностью, сравнимой с
ем, если только число обусловленности не слишком велико. Этот ме-
метод, называемый итерационным уточнением, требует небольшого
(примерно на 25%) увеличения машинного времени по сравнению с
затратами на получение решения методом Гаусса.
Пусть т@) — найденное на ЭВМ приближенное решение системы
Ах = Ь. Напомним (см. § 5.1), что невязка г@) = b — Лг@) и погреш-
погрешность е@) = х — i@) связаны равенством
Ле<°' = г'°>. E.87)
Если бы удалось найти е@) как точное решение системы E.87), то
вектор гA) = г10' + е@) дал бы точное решение системы Ах = Ь.
Однако в действительности вычисленное на ЭВМ значение хA> неиз-
неизбежно будет содержать ошибку. Тем не менее можно ожидать, что гA)
окажется лучшим приближением, чем г@). Используя приближение
хA), аналогичным образом можно найти приближение хB).
Опишем более подробно очередной (Jt + 1)-й шаг метода.
1°. Вычисляют r(fc) а Ь — Ах{к). Исключительно важно, чтобы
вычисление И*' производилось с повышенной точностью. Дело в том,
что Ь и Ах1 *' и поэтому при вычислении невязки неизбежно вычита-
вычитание близких чисел, а следовательно, потеря большого числа значащих
цифр. Одна из возможностей состоит в использовании для вычисления
Лх<*> и 6— Axik) арифметики удвоенной точности.
2°. Вычисляют решение системы >4с( *' = г( *'. Так как матрица А
не меняется, то получение очередного приближения с использованием
однажды вычисленного I [/-разложения матрицы А (с учетом необхо-
необходимых перестановок строк) требует сравнительно небольшого числа
(примерно т2) арифметических действий.
3°. Вычисляют г'^11 и r(fc» + e(*>.
Если число обусловленности не очень велико (например,
cond (A) < e^Oi TO метод довольно быстро сходится. Сходимость
характеризуется постепенным установлением значащих цифр в
приближениях x(fc). Если же процесс расходится, то в приближениях
не устанавливаются даже старшие значащие цифры.
Необходимо отметить одну интересную особенность. В процессе
171

итерационного уточнения невязки г<*> обычно не уменьшаются, а
даже несколько возрастают по величине.
Кроме того, как оказывается, приближения х( k) могут быть исполь-
использованы для грубого по порядку оценивания естественного числа обус-
обусловленности v?x). Для этого достаточно воспользоваться приближен-
приближенной формулой
E.88)
Пример 5.19. Используя алгоритм итерационного уточнения, найдем реше-
решение системы
1.03x1 + 0.991x5 = 2.51,
0.991x1 + 0.943*2 = 2.41
E.89)
на 3-разрядной десятичной ЭВМ, считая, что режим вычислений с удвоенной
точностью на ней эквивалентен использованию 6-разрядной десятичной ЭВМ.
Вычислим множитель первого (и в данном случае последнего) шага прямо-
прямого хода метода Гаусса: ц = 0.991/1.03 и 0.962. Так как при вычислении на 3-
разрядной ЭВМ имеем 0.943 — 0.991-0.962 и -0.01 и 2.41 — 2.51-0.962 и 0, то
второе уравнение системы E.89) приводится к виду -0.01*2 = 0.
Обратная подстановка дает, приближенное решение г{0) = 2.44, i^0) = 0.
Итерационное уточнение. 1-й шаг. Вычислим (с удвоен-
удвоенной точностью) компоненты невязки:
г<0) =2.51- 1.03г«°> -0.99Ц0' =-0.00320,
г<20) = 2.41 _ 0.99Ц0' - 0.9434°' = -000840
Вычисляя методом Гаусса решение системы
1.03е<°> + 0.99Ц°> = -0.00320,
0.991е<°> + 0.943е2°> = -0.00840,
получим ej0) = -0.481, е?0) = 0.496. Завершается 1-й шаг вычислением
II = г[0) + eJ0), xi — 4°' + «2°'' пРивоДЯЩим на 3-разрядной ЭВМ к
значениям г'1' = 1.96, г2п = 0.496.
2-й шаг дает значения г}1» = -4.000336, т\1) = -0.000088, е<" =
= 0.0223, е2и = -0.0235 и г<2> = 1.98, *<2> = 0.473.
3-й ш а г дает значения г[2> = 0.00186, г?2> = 0.00178, е<2> = 0.00084,
е?2> = 0.001 и *«3> = 1.98, *<3> = 0.474.
Сравнивая *B( и *C), замечаем, что последние значащие цифры практи-
172
чески установились и, следовательно, процесс следует завершить, приняв xj и
и 1.98, *2 « 0.474.
Использование формулы E.88) с ем = 5-Ю дает следующую оценку
естественного числа обусловленности:
"/*) * ?м' |е@) loo/I**0) L * 2-103-0.496/1.96 и 407.
Приведем для сравнения действительные значения решения и естественно-
естественного числа обусловленности: Х[ и 1.9812, а^ и 0.4735, J^*) и 273 (см. пример 5.5).
§ 5.12. Дополнительные замечания
1. Более подробное и в то же время доступное изложение рассмотренных в
этой главе вопросов можно найти, например, в [38], [39], [67], [87].
2. Предположим, что требуется решить систему я линейных алгебраических
уравнений с m неизвестными, где m < п. Так как число уравнений превышает
число неизвестных, то вполне вероятно, что рассматриваемая система не имеет
решения. Хотя уравнения системы нельзя удовлетворить точно, можно попы-
попытаться удовлетворить их как можно точнее, минимизируя величину вектора
невязки г = Ь — Ах . Выбор в качестве минимизируемой величины
евклидовой нормы невязки
| г, |2 приводит к методу наименьших
квадратов решения переопределенных систем линейных уравнений [50].
Отметим, что в гл. 11 метод наименьших квадратов рассматривается в
связи с задачей приближения таблично заданной функции.
3. Интересной модификацией метода Гаусса является алгоритм Краута,
основанный на изменении порядка выполнения арифметических операций.
Существуют два случая, когда эта модификация может иметь преимущества.
Во-первых, алгоритм Краута выгоден тогда, когда для вычислений использует-
используется микрокалькулятор, так как алгоритм позволяет избегать выписывания
промежуточных результатов. Во-вторых, он приводит к меньшей вычислитель-
вычислительной погрешности при условии, что вычисления ведутся на ЭВМ, обладающей
сравнительно быстрой арифметикой с расширенной точностью или особенно
быстрой операцией вычисления скалярных произведений (х, у) = S г,у,.
i=i
Обсуждение модификации Краута можно найти, например, в [67], [87].
4. Следует отметить, что в данной главе оказались практически не отра-
отраженными прямые методы решения систем уравнений с разреженными матрица-
матрицами (исключение составляет § 5.9, посвященный методу прогонки). Желающим
найти доступное изложение современных прямых методов, предназначенных
для решения очень больших линейных систем с разреженными матрицами,
можно посоветовать обратиться к [40]. Укажем также на книги [30], [63], [94],
специально посвященные технологии разреженных матриц.
173

$ 6.1. Метод простой итерации
Глава 6
ИТЕРАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ СИСТЕМ
ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
Системы линейных алгебраических уравнений можно решать как с
помощью прямых, так и итерационных методов. Для систем уравнений
средней размерности чаще используют прямые методы.
Итерационные методы применяют главным образом для решения
задач большой размерности, когда использование прямых методов
невозможно из-за ограничений в доступной оперативной памяти ЭВМ
или из-за необходимости выполнения чрезмерно большого числа
арифметических операций. Большие системы уравнений, возникающие
в приложениях, как правило, являются разреженными. Методы
исключения для решения систем с разреженными матрицами не-
неудобны, например, тем, что при их использовании большое число
нулевых элементов превращается в ненулевые и матрица теряет свой-
свойство разреженности. В противоположность им при использовании
итерационных методов в ходе итерационного процесса матрица не
меняется, и она, естественно, остается разреженной. Ббльшая эффек-
эффективность итерационных методов по сравнению с прямыми методами
тесно связана с возможностью существенного использования разрежен-
разреженности матриц.
Применение итерационных методов для качественного решения
большой системы уравнений требует серьезного использования ее
структуры, специальных знаний и определенного опыта. Именно по-
поэтому разработано большое число различных итерационных методов,
каждый из которых ориентирован на решение сравнительно узкого
класса задач, и существует довольно мало стандартных программ,
реализующих эти методы.
В этой главе будут рассмотрены наиболее простые и известные
итерационные методы, позволяющие решать достаточно широкий
класс систем.
174
1. Приведение системы к виду, удобному для итераций. Для того
чтобы применить метод простой итерации к решению системы
линейных алгебраических уравнений
Ах = Ь
F.1)
с квадратной невырожденной матрицей А, необходимо предварительно
преобразовать эту систему к виду
х = Вх + с.
F.2)
Здесь В — квадратная матрица с элементами btJ (i, j = 1, 2, ..., m), с —
вектор-столбец с элементами С{ (i = 1, 2, ..., m).
В развернутой форме записи система F.2) имеет следующий вид:
Х\ - b\\X\
Х2 = Ь2\Х\
613*3
+ СЬ
Ь2пХт + С2,
F.3)
bn2x2
Вообще говоря, операция приведения системы к виду, удобному для
итераций (т.е. к виду F.2)), не является простой и требует
специальных знаний, а также существенного использования специфики
системы. В некоторых случаях в таком преобразовании нет необходи-
необходимости, так как сама исходная система уже имеет вид F.2).
Самый простой способ приведения системы к виду, удобному для
итераций, состоит в следующем. Из первого уравнения системы F.1)
выразим неизвестное х^.
= ап
- 012*2 ~
из второго уравнения — неизвестное х2:
х2 = 022 (h - а-г\х\ ~ «^з^з - •••
и т.д. В результате получим систему
Х2 - Ь2\Х\
F.4)
в которой на главной диагонали матрицы В находятся нулевые эле-
элементы. Остальные элементы выражаются по формулам
175

«, j = 1,2, ..., m, j * j).
F-5)
Конечно, для возможности выполнения указанного преобразования
необходимо, чтобы диагональные элементы матрицы А были ненуле-
ненулевыми.
Часто систему F.1) преобразуют к виду х = х - т(Ах — 4), где т —
специально выбираемый числовой параметр (см. п. 5).
2. Описание метода. Выберем начальное приближение х@) =
= (х\0), г<0), ..., х^у. Подставляя его в правую часть системы F.2) и
вычисляя полученное выражение, находим первое приближение
Подставляя приближение хA) в правую часть системы F.2), получим
Х<2> = Вх<1> + С
Продолжая этот процесс далее, получим последовательность х@), хA),
..., х(п), ... приближений, вычисляемых по формуле
+ с, к = 0, 1, 2, ... . F.6)
В развернутой форме записи формула F.6) выглядит так:
С2,
F.7)
В случае, когда для итераций используется система F.4) с коэффи-
коэффициентами, вычисленными по формулам F.5), метод простой итерации
принято называть методом Якоби^.
3. Сходимость метода простой итерации.
Теорема 6.1. Пусть выполнено условие
\В\
F.8)
Тогда: 1°) решение х системы F.2) существует и единственно; 2°) при
произвольном начальном приближении х@> метод простой итерации
сходится и справедлива оценка погрешности
1 Карл Густав Якоб Якоби A804 — 1851) — немецкий математик.
|*<°>-х|. F.9)
D 1°. Из курса линейной алгебры известно, что система линейных
алгебраических уравнений имеет единственное решение при любой
правой части тогда и только тогда, когда соответствующая однородная
система имеет только нулевое решение. Пусть х — решение однородной
системы х = Вх. Тогда |х| = \Вх\ < |Б||х|. Так как по условию
\В\ < 1, это неравенство возможно только при |х| =0. Следователь-
Следовательно, х = 0 и тем самым первое утверждение теоремы доказано.
2°. Вычитая из равенства F.6) равенство х = Вх + с, получим
х= В(хЧс) _i). (б10)
Вычисляя норму левой и правой частей этого равенства и используя
неравенство |В(х<*> - х)| < |В||х<*> - х|, имеем [х'^1' - х| <
< \В\ Jx'k' - х|. Так как это неравенство верно для всех it > 0, то
- х|
' - х|
- х|
«|х<1> - х|
Справедливость неравенства F.9) установлена. Учитывая, что
|г@) _ z| не зависит от п, а |В|" -» 0 при п -» оо, получаем из него,
что | т' п) - х| ¦* 0 при п -» оо. И
Замечание 1. Теорема 6.1 дает простое достаточное условие
F.8) сходимости метода простой итерации. Грубо это условие мож-
можно интерпретировать как условие достаточной малости элементов Ь1}
матрицы В в системе, приведенной к виду F.2).
Замечание 2. Если \В\ = \В\Ж, то условие F.8) принимает
вид
\В\ - max ? |6„| < 1.
Для метода Якоби это условие в силу равенств Ьи = 0, btJ = -atJ/au
эквивалентно условию диагонального преобладания E.45). Если же
воспользоваться условием F.8) при \В\ = \B\i, то для метода
Якоби получим другое условие диагонального преобладания:
? \at}\ < \an\, j= 1,2, ..., m.
F.11)
i*J
176
177

Таким образом, для сходимости метода Якоби достаточно, чтобы
матрица А была близка к диагональной.
Замечание 3. Из оценки F.9) следует, что при выполнении
условия F.8) метод простой итерации сходится со скоростью гео-
геометрической прогрессии, знаменатель которой q = |B|. Скорость
сходимости тем выше, чем меньше величина \В\. Хотя метод схо-
сходится при любом начальном приближении х@>, из оценки F.9)
можно сделать полезный вывод: начальное приближение желатель-
желательно выбирать близким к решению.
Замечание 4. Оценка погрешности F.9) является априорной.
Ее использование для формулировки критерия окончания итера-
итераций затруднительно, так как значение |х@> - x\ неизвестно, а его
грубое оценивание заведомо приведет к завышению необходимого
числа итераций.
4. Апостериорная оценка погрешности.
Предложение 6.1. Если выполнено условие F.8), то спра-
справедлива апостериорная оценка погрешности
~xln'u
а Запишем равенство F.10) при Jfc = n - 1 в виде
х<"> - х =
Тогда
-г).
Для завершения доказательства достаточно заметить, что полученное
неравенство эквивалентно неравенству F.12). И
~ -3 амечание. Величину, стоящую в правой части неравенства
F.12), можно легко вычислить после нахождения очередного при-
приближения х( п).
Если требуется найти решение с точностью е, то в силу F.12) сле-
следует вести итерации до выполнения неравенства
Таким образом, в качестве критерия окончания итерационного
процесса может быть использовано неравенство
|г(п) _ж(п-11| < ?ь F.13)
где ?1 =
В практике вычислений иногда используют привлекательный
своей простотой критерий окончания
|х(п> - х11 < е. F.14)
Отметим, что для метода простой итерации его применение обосно-
обосновано только тогда, когда \В\ <1/2 (в этом случае A - |Б|)/|Б| > 1
и выполнение неравенства F.14) влечет за собой выполнение нера-
неравенства F.13)). Однако в большинстве реальных случаев величина
JBJ оказывается близкой к единице и поэтому A - |В|)/|Б| < 1. В
этих случаях ?i < e и использование критерия F.14) приводит к
существенно преждевременному окончанию итераций. Величина
|х(п) - х') здесь оказывается малой не потому, что
приближения х' и х(п) близки к решению, а потому, что метод
сходится медленно (ср. с замечанием на с. 98).
Пример 6.1. Используя метод простой итерации в форме Якоби, найдем
решение системы
6.25x1 - х2 + 0.5*з = 7.5,
-X) + 5x2 + 2.12i3 = -8-68, F.15)
0.5x1 + 2.12*2 + 3.6*з = -0-24.
с точностью е = 10 в норме | • Ц^.
Вычисляя коэффициенты по формулам F.5), приведем систему к виду
F.4)
XI = 0.16*2- 0.08г3 + 12,
*5 = 0.24 -0.424г3 - 1-736,
г3 = -0.138911 - 0.5889г2 - 0.0667.
F.16)
178
В последнем уравнении коэффициенты даны с точностью до погрешности
округления. Здесь
179

0
0.2
-0.1389
0.16
0
-0.5889
-0.08
-0.424
0
c =
1.2
-1.736
-0.0667
в =
Достаточное условие сходимости метода простой итерации выполнено, так
как |BL = max {0.24, 0.624, 0.7278} = 0.7278 < 1.
Примем за начальное приближение к решению вектор х<0) = @, 0, 0)т и
будем вести итерации по формуле F.6) до выполнения критерия окончания
F.13), где в данном случае ?i = A - 0.7278)/0.7278-10'3 « 0.37-10~3. Значения
приближений в табл. 6.1 приводятся с четырьмя цифрами после десятичной
точки.
Таблица 6.1
xin)
0.0000
0.0000
0.0000
_
1.2000
-1.7360
-0.0667
1.7360
0.9276
-1.4677
0.7890
0.8557
0.9020
-1.8850
0.6688
0.4173
0.8449
-1.8392
0.9181
0.2493
12
13
14
15
0.8006
-1.9985
0.9987
0.0018
0.8003
-1.9993
0.9990
0.0008
0.8002
-1.9995
0.9995
0.0005
0.8001
-1.9998
0.9997
0.0003
При п — 15 условие F.13) выполняется и можно положить г\ = -0.800 ±
± 0.001, *2 = -2.000 ± 0.001, хз = 1.000 ± 0.001. В данном случае точные
значения решения ij = -0.8, а& = -2, а& = 1 нам известны (см. пример 5.16).
Заметим, что в действительности решение с точностью до ? = 10'3 было полу-
получено уже при п = 13.
5. Система с положительно определенной матрицей. В случае, когда
А — симметричная положительно определенная матрица, систему
Ах = Ь часто приводят к виду
180
х= х-т(Ах-Ь),
которому отвечает метод простой итерации:
- Ь),
F.17)
F.18)
Здесь В = Е - г А и параметр т > 0 выбирают так, чтобы по возмож-
возможности сделать минимальной величину \В\%.
Пусть Amin и Атах — минимальное и максимальное собственные
значения матрицы А. Известно, что условие |Д|2 < 1 будет выполне-
выполнено, если взять т 6 @, 2/Ащах). Оптимальным является выбор т =
= 2/(А,шп + Ащах). В этом случае JjBj2 принимает минимальное значе-
значение, равное (Апах - Amin)/(Amax + А^п)-
Чаще известны не значенияА,иП и Ащах, а их оценки вида 0 < ft <
^ ^min ^ -^max ^ М либо вида А^х < М. В первом случае полагают
г — 2/(/х + М), а во втором г < 2/М (например, т = \/М).
Заметим, что в случае, когда А^п < -^тах (а так бывает очень часто)
при любом выборе т е @, 2/Атах), имеем \В\2 « 1. Поэтому в этом
случае метод F.18) сходится очень медленно.
6. Влияние ошибок округления. Из-за наличия ошибок округления
реально вычисляемые на ЭВМ приближения г("' отличаются от иде-
идеальных приближений х( п). Поэтому нельзя утверждать, что для
любого ? > 0 найдется номер щ(&), начиная с которого все приближе-
приближения будут находиться в е — окрестности решения.
В действительности же существует некоторая ? — окрестность реше-
решения, после попадания в которую приближения г(п) дальнейшего
уточнения при выполнении итераций не происходит. В подтверждение
сказанного приведем следующий результат.
Теорема 6.2. Пусть \В\ < 1. Предположим, что вычисляемая
на ЭВМ с помощью метода простых итераций последовательность
х( п) удовлетворяет равенствам
с+ ?<п\ п>0,
F.19)
где ?<"> € Д™, |?(п> | < 6. Если вычисления по формулам F.6) и F.19)
начинаются с одного начального приближения х@) = х@>, то для всех
п ^ 1 справедливы следующие оценки погрешности:
|i<n> - х<п>| <?, F.20)
F.21)
181

r( л) _
r( П) _ Ti П-1
e.
F.22)
*<*¦" =
e =
-—-та ¦
1 - \B\
Таким образом, метод простых итераций устойчив, но гарантиро-
гарантированная точность метода ограничена величиной е. Критерий окончания
F.13) применим, если е < е.
§ 6.2. Метод Зейделя
1. Описание метода. Пусть система F.1) приведена к виду F.4) с
коэффициентами, вычисленными по формулам F.5).
Метод Зейделя1 можно рассматривать как модификацию метода
Якоби. Основная идея модификации состоит в том, что при вычисле-
вычислении очередного (Jfc + 1)-го приближения к неизвестному ц при t > 1
используют уже найденные (к + 1)-е приближения к неизвестным х\,
..., ц-\, а не к-е приближения, как методе Якоби.
На (к ¦+• 1)-й итерации компоненты приближения г***1' вычисляют-
вычисляются по формулам
х\Ы) =
Ьих2к) +b13xCk)
+ CU
+ c2l
+ c3, F.23)
l
Введем нижнюю и верхнюю треугольные матрицы
0
621
6ml
0
0
632
&m2
0 ..
0 ..
0 ..
ЬтЗ ¦
. 0
. 0
. 0
. 0
О b\
О 0
О 0
623 ...
0 ...
Тогда расчетные формулы метода примут компактный вид:
1 Людвиг Зейдель A821 — 1896) — немецкий астроном и математик.
182
F.24)
Заметим, что В = Вх + Дг и поэтому решение х исходной системы
удовлетворяет равенству
х = Дх + Вг* + с F.25)
Метод Зейделя иногда называют также методом Гаусса—Зейделя,
процессом Либмана, методом последовательных замещений.
2. Достаточные условия сходимости.
Теорема 6.3. Пусть [В\ < 1, где \В\ — одна из норм \В\ ,
\B\i- Тогда при любом выборе начального приближения х<0) метод
Зейделя сходится со скоростью геометрической прогрессии, знаме-
знаменатель которой q < \В\.
Доказательство этой теоремы опускаем. Оно довольно громоздкое,
хотя и не сложное. Приведем более компактное доказательство следу-
следующей теоремы, близкое к доказательству теоремы 6.1.
Теорема 6.4. Пусть выполнено условие
\Bi\ + |Bi| < 1. F.26)
Тогда при любом выборе начального приближения метод Зейделя схо-
сходится и верна оценка погрешности
tdtq=\Bt\/(l-\Bl\)<l.
О Вычитая из равенства F.24) равенство F.25), имеем
- i=
- х) + Я2(х<*> - х).
F.27)
F.28)
Вычисляя нормы левой и правой частей этого равенства и используя
свойства норм, получим
- х| =
- х)
Следовательно,
x|<?Ix<*> -x\,q=
Так как это неравенство верно для всех ifc ^ 0, то из него следует оцен-
183

ка F.27). В силу условия F.26) имеем 0 < q < 1. Поэтому х(п) -» х при
П -> оо. Ц
Особо выделим часто встречающийся на практике случай систем с
симметричными положительно определенными матрицами.
Теорема 6.5. Пусть А — симметричная положительно опреде-
определенная матрица. Тогда при любом выборе начального приближения х@>
метод Зейделя сходится со скоростью геометрической прогрессии.
Отметим, что никаких дополнительных априорных условий типа
малости нормы некоторой матрицы здесь не накладывается.
3. Апостериорная оценка погрешности.
Предложение 6.2. Если выполнено условие \В\ < 1, то для
метода Зейделя справедлива апостериорная оценка погрешности
- х| < ,
1 ~
"-i)|, n> 1.
F.29)
а Положим it = п — 1 и запишем равенство F.28) в следующем виде:
- х =
- х)
Тогда
- х| < |ВЦ|х<"> - х|
откуда и следует неравенство F.29). И
Полученное неравенство позволяет сформулировать простой крите-
критерий окончания итерационного процесса. Если требуется найти реше-
решение с точностью е > 0, то итерации метода Зейделя следует вести до
выполнения неравенства |х(п) - х' ||В2||/A - fBf) < е.или эквива-
эквивалентного ему неравенства
I*
(n) _ -( n-1)
e2l
F.30)
где е2 =
е.
4. Геометрическая интерпретация метода. Приведем геометрическую
интерпретацию метода Зейделя в случае m = 2, т.е. в случае решения
системы
184
+ 2*2 =
Первое уравнение задает на плоскости хх0х2 прямую /Ь второе — пря-
прямую /2 (рис. 6.1). Расчетные формулы метода принимают вид
где 612 = -ai2/an, q = Ьх/аи, Ь2\ = -a2i/a22, c2 =
прямой xi = х\ до пересечения с прямой 12. Координата
Рис. 6.1
Пусть приближение г( *> уже найдено. Тогда при определении
х[к+1) координата х2 = х2 ' фиксируется и точка х перемещается па-
параллельно оси Ох\ до пересечения с прямой \\. Координата х\ точки
пересечения принимается за х\ ". Затем точка х перемещается вдоль
р 2 р г точки
пересечения принимается за 4 1' ¦
На рис. 6.1, а, б приведены геометрические иллюстрации, отвеча-
отвечающие сходящемуся и расходящемуся итерационному процессу Зейде-
Зейделя. Видно, что характер сходимости может измениться при переста-
перестановке уравнений.
Пример 6.2. Используя метод Зейделя, найдем решение системы F.15) с
точностью ? = 10~3.
После приведения системы к виду F.16) убеждаемся, что ИВЦ^ < 1 и
поэтому в силу теоремы 6.2 метод Зейделя сходится
Положим х@) = @, 0, 0)т и будем вычислять последовательные приближе-
приближения по формулам
185

= -0.1389г<*+1> -О.
+ 1.2,
-1.736,
-0.0667.
Здесь
0
0
0
0.16
0
0
-0
-0
0
.08
.424
и 1^21» = 0.424. Будем вести итерации до выполнения критерия окончания
F.30), где е2 = 10-A - 0.7278)/0.424 и 0.64-10. Значения приближений с
четырьмя цифрами после десятичной точки приведены в табл. 6.2.
Т а б л и ц а 6.2
_ fl П-1)
0.0000
0.0000
0.0000
1.2000
-1.4960
0.6476
1.4960
0.9088
-1.8288
0.8841
0.3328
0.8367
-1.9435
0.9616
0.1147
0.8121
-1.9813
0.9873
0.0378
*<">
0.8040
-1.9938
0.9958
0.0125
0.8013
-1.9980
0.9986
0.0041
0.8004
-1.9993
0.9995
0.0014
0.8001
-1.9998
0.9998
0.0005
!*<«>-
При п = 8 критерий окончания выполняется и можно положить Х\ =
= 0.800 ± 0.001, х2 - -2.000 ± 0.001, х3 = 1.000 ± 0.001. Заметим, что в
действительности решение с точностью ? = 10'3 было получено уже при п = 7.
186
Замечание. Существует устойчивое заблуждение, связанное с
представлением о том, что метод Зейделя сходится быстрее, чем
метод Якоби. Это действительно так, если матрица А симметрична
и положительно определена (мы убедились в преимуществе метода
Зейделя для системы уравнений с такой матрицей, решая примеры
6.1 и 6.2). Однако в общем случае возможны ситуации, когда метод
Якоби сходится, а метод Зейделя сходится медленнее или вообще
расходится. Возможны и противоположные ситуации. Дело в том,
что эти методы ориентированы на решение разных классов систем:
метод Якоби — на системы с матрицами, близкими к диагональным,
а метод Зейделя — на системы с матрицами, близкими к нижним
треугольным.
§ 6.3. Метод релаксации
Метод последовательной верхней релаксации является одним из
наиболее эффективных и широко используемых итерационных методов
для решения систем линейных алгебраических уравнений с симмет-
симметричными положительно определенными матрицами А. Этот метод
часто называют 50Л-методом1. Частично популярность SOR-члетода
можно объяснить его простотой и тем, что он хорошо известен
широкому кругу прикладников.
Суть метода релаксации состоит в следующем. После вычисления
очередной i-й компоненты (Jfc + 1)-го приближения по формуле метода
Зейделя
(k)
+ ...+ bimx(m
производят дополнительно смещение этой компоненты на величину
(и- l)(x\k*u - x[k)), где ш — параметр релаксации. Таким образом,
t-я компонента (it + 1)-го приближения вычисляется по формуле
На рис. 6.2 показано несколько первых итераций метода при значе-
значении параметра релаксации и = 1.25.
1 От англ. successive over relaxation.
187

/
Put tf.i
В обозначениях предыдущего параграфа компактная формула для
вычисления х<*+1> записывается следующим образом:
ис.
Как нетрудно видеть, при и = 1 метод релаксации совпадает с
методом Зейделя. При и > 1 его было принято называть методом
последовательной верхней релаксации, а при и < 1 — методом после-
последовательной нижней релаксации. В последнее время метод релаксации
называют методом последовательной верхней релаксации для любых
значений и.
Если А — симметричная положительно определенная матрица, то
при любом значении параметра ш @ < ш < 2) метод релаксации схо-
сходится. Часто оказывается возможным выбрать 'Параметр и > 1 так,
чтобы SOR-метод сходился существенно быстрее, чем методы Якоби и
Зейделя. Однако выбор параметра релаксации — довольно трудная
задача. Во многих случаях она решается экспериментальным путем.
Существуют различные модификации метода релаксации. Распро-
Распространенный вариант метода связан с использованием различных пара-
параметров w, для вычисления различных компонент х, очередного (к + 1)-
го приближения к решению.
Пример 6.3. Используя метод последовательной верхней релаксации с
параметром ш = 1.12, найдем решение системы F.15) с точностью ? = 10'3.
188
Приведем систему к виду F.16), положим **<•>= @. 0, 0)т и будем вычис-
вычислять последовательные приближения по формулам:
и
^^1» = и (-0.1389x<fc+1> -0.
+ 1.2),
- 1.736),
)*<fc) - w-0.6667.
Значения приближений с четырьмя цифрами после десятичной точки
приведены в табл. 6.3.
Т а б л и ц а 6.3
Х(П)
0.0000
0.0000
0.0000
1.3440
-1.6433
0.8001
0.8166
-1.9442
0.9846
0.8094
-1.9973
0.9986
0.7995
-1.9998
1.0001
0.8001
-2.0000
1.0000
Сравнение с точным решением щ = 0.8, *j = -2, 15 = 1 показывает, что для
получения приближения к решению с точностью ? = 10 потребовалось всего
4 итерации. Напомним, что для достижения той же точности при том же
начальном приближении методами Якоби и Зейделя потребовалось соответст-
соответственно 13 и 7 итераций.
§ 6.4. Дополнительные замечания
1. При изложении итерационных методов решения систем линейных алгеб-
алгебраических уравнений нам пришлось ограничиться простейшими методами. В
данной главе оказались не рассмотреннымси такие известные и популярные
методы, как метод наискорейшею спуска, метод сопряженных градиентов
(называемый еще методом Ланцоша1), метод минимальных невязок, линей-
линейный многошаговый метод с чебышевским набором параметров и др. Эти
методы изложены, например, в учебниках [9], [71] и в специальной литературе
[20], [72], [89]. Отметим, что методы наискорейшего спуска и сопряженных
градиентов будут рассмотрены в гл. 10 в связи с задачей минимизации квад-
квадратичной функции F.31).
1 Корнелий Ланцош A893 — 1974) — физик-теоретик и математик. Родился
в Венгрии. Работал в Германии, США, Ирландии.
189

2. Многие итерационные методы решения систем с симметричными поло-
положительно определенными матрицами основаны на замене задачи отыскания
решения системы Ах = Ь эквивалентной задачей отыскания минимума квадра-
квадратичной функции
F.31)
В частности, метод Зейделя дает ту же последовательность приближений,
что и метод покоординатного спуска, примененный к функции F.31). Подроб-
Подробнее об этом будет сказано в § 10.2; см. также [9].
3. В настоящее время наиболее глубоко развиты методы решения систем
уравнений с симметричными положительно определенными матрицами. Иногда
этого достаточно, так как в принципе существует возможность симметризовать
любую систему Ах = Ъ с невырожденной квадратной матрицей, т.е. свести ее к
эквивалентной системе с симметричной положительно определенной матрицей.
Для этого можно умножить обе части системы на матрицу А7. В полученной
таким образом системе
А^Ах- АГЬ
F.32)
матрица А — AFA обладает всеми нужными свойствами.
Однако указанным образом поступают сравнительно редко. Дело в том, что
при переходе от А к А может быть потеряно свойство разреженности. Кроме
того, вообще говоря, существенно ухудшается обусловленность системы. На-
Например, для матриц, близких к симметричным, cond(yl) и (cond(j4)J. Следова-
Следовательно, имеется реальная опасность, что система F.32) окажется очень плохо
обусловленной.
4. Как уже было отмечено, одно из важнейших достоинств итерационных
методов заключается в возможности эффективного использования разреженно-
разреженности матрицы А. Поясним сказанное на примере метода простой итерации.
В случае когда матрица В — заполненная, для вычисления по формуле
F.6) требуется выполнить примерно 2т? арифметических операций. Однако
для разреженной матрицы с М (М < т2) ненулевыми элементами требуется
лишь примерно 2М арифметических операций (одно умножение и одно сложе-
сложение на каждый ненулевой элемент). Таким образом, общее число операций
составляет примерно 2Мп (е), где п (е) — число итераций, необходимое для
достижения заданной точности ?.
Глава 7
МЕТОДЫ ОТЫСКАНИЯ РЕШЕНИЙ
СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
В этой главе рассматривается задача отыскания решений систем
нелинейных уравнений, существенно более сложная, нежели задачи
отыскания решения одного нелинейного уравнения или системы ли-
линейных алгебраических уравнений. Тем не менее достаточно подробное
знакомство с содержанием глав 4 и 6, а также § 5.1 — 5.3 позволяет
увидеть соответствующие аналогии в постановках проблем и методах
их решения для нелинейных систем.
Будем считать, что в множестве m-мерных векторов введена некото-
некоторая норма, порождающая соответствующую норму для квадратных
матриц порядка m (см. § 5.2).
§ 7.1. Постановка задачи.
Основные этапы решения
1. Постановка задачи. Задача отыскания решения системы нели-
нелинейных уравнений с m неизвестными вида
/2D,
= 0,
- 0,
G.1)
= 0,
является существенно более сложной, чем рассмотренная в гл. 4 задача
отыскания решения уравнения с одним неизвестным. Однако на прак-
практике она встречается значительно чаще, так как в реальных исследова-
исследованиях интерес представляет, как правило, определение не одного, а
нескольких параметров (нередкр их число доходит до сотен и тысяч).
Найти точное решение системы, т.е. вектор х — (xlt г2, ¦••, я»п)т, удов-
191

летворяющий уравнениям G.1), практически невозможно. В отличие
от случая решения систем линейных алгебраических уравнений ис-
использование прямых методов здесь исключается. Единственно реаль-
реальный путь решения системы G.1) состоит в использовании итерацион-
итерационных методов для получения приближенного решения х* = (х*, х*, ...,
хп)Т' Удовлетворяющего при заданном е > 0 неравенству \х* - х\ < е.
Прежде чем перейти к изучению методов решения системы GJ),
подчеркнем важность понимания того факта, что эта задача может
вообще не иметь решения, а в случае, когда решения существуют, их
число может быть произвольным. В общем случае весьма сложно
выяснить, имеет ли система решения и сколько их.
Пример 7.1. Рассмотрим систему уравнений
4*2 + % = 4,
*2-*2+ 1=0.
Здесь 1\, х2 — неизвестные, t — параметр. Первое уравнение задает на плоско-
плоскости г\Ох2 эллипс, второе уравнение — параболу. Координаты точек пересече-
пересечедх\ дх2 дхт
дх\
Рис 7.1
192
ния этих кривых дают решения системы. Если значения параметра t изменя-
изменяются от -2 до 2, то возможны следующие ситуации (рис. 7.1): а) 1 = -2 —
решений нет; б) t = -1 — одно решение; в) t = 0 — два решения; г) t = 1 —
три решения; д) t = 2 — четыре решения.
Для дальнейшего удобно использовать сокращенную векторную
форму записи систем. Наряду с вектором неизвестных х = (х\, х2, ...,
х„)т рассмотрим вектор-функцию /= (Л, ?, ..., /т)т. В этих
обозначениях система G.1) примет вид
/(*) = О- G.2)
Будем считать функции ft{x) непрерывно дифференцируемыми в неко-
некоторой окрестности решения х. Введем для системы функций J5, /2, ...,
/га матрицу Якоби
G.3)
которая будет использована в дальнейшем.
2. Основные этапы решения. Как и в случае уравнения с одним
неизвестным (см. гл. 4), отыскание решений начинают с этапа локали-
локализации. Для каждого из искомых решений г указывают множество,
которое содержит только одно это решение и расположено в достаточ-
достаточно малой его окрестности. Часто в качестве такого множества выступа-
выступает параллелепипед или шар в m-мерном пространстве.
Иногда этап локализации не вызывает затруднений; соответству-
соответствующие множества могут быть заданными, определяться из физических
соображений, из смысла параметров х, либо быть известными из опыта
решений подобных задач. Однако чаще всего задача локализации (в
особенности при больших т) представляет собой сложную проблему,
от успешного решения которой в основном и зависит возможность
вычисления решений системы G.1). На этапе локализации особое
значение приобретают квалификация исследователя, понимание им
существа решаемой научной или инженерной проблемы, опыт решения
этой или близких задач на ЭВМ. Во многих случаях полное решение
задачи локализации невозможно и ее можно считать решенной удов-
удовлетворительно, если для х удается найти хорошее начальное прибли-
7-28 193

жение х@). В простейших случаях (например, для системы двух урав-
уравнений с двумя неизвестными) могут быть использованы графические
методы (см. пример 7.1).
На втором этапе для вычисления решения с заданной точностью ?
используют один из итерационных методов решения нелинейных
систем.
Будем считать, что определения § 4.1, связанные с характеризацией
сходимости итерационных методов, остаются в силе, причем в нера-
неравенствах D.5) и D.6) знак модуля заменен на знак нормы, а 6-окрест-
ность решения х понимается как множество точек х, удовлетворяющих
условию | х - х| < 6.
Пример 7.1. Произведем локализацию решений системы
=8*1*,,
G.4)
На плоскости цОз^ построим графики уравнений системы. График первого
уравнения — это лист Декарта1 (рис. 7.2, а). График второго уравнения
состоит из луча — биссектрисы первого координатного угла и кривой, пересе-
пересекающей эту биссектрису в точке (et e)T (рис. 7.2, б).
Из рис. 7.3 видно, что эти кривые пересекаются в трех точках А, В, С, т.е.
система имеет три решения. Так как оба графика симметричны относительно
прямой XI = x>i, то координаты точки В равны и их легко вычислить: *i = 4,
zj = 4. В силу этой же симметрии достаточно определить только координаты
Х[, Xi точки С, так как точка А имеет координаты х\ = zj и xj = *1- Из рис.
7.3 замечаем, что точка С содержится в прямоугольнике П = {(аг, у) : 3.5 <
< xi < 4, 1.5 < щ < 2.5} и ~х\ я 3.8, г2 я 2.
Подчеркнем, что только по виду уравнений системы G.4) без ис-
использования графического метода установить число решений и найти
приближения к ним было бы весьма трудно. К сожалению, при числе
уравнений m > 3 геометрические иллюстрации теряют свою эффектив-
эффективность.
Замечание. Иногда удается понизить порядок m системы,
выразив одно или несколько неизвестных из одних уравнений
системы и подставив соответствующие выражения в другие уравне-
уравнения.
1 Рене Декарт A596 — 1650) — французский философ, математик, физик
физиолог. Впервые ввел понятие переменной величины и функции. В анали-
аналитической геометрии создал метод прямоугольных координат.
194
Рис. 7.2
Пример 7.2. Система уравнений
Рис. 7.5
x3 + у3 = 8*у,
*lny = 1пг
сводится к одному нелинейному уравнению *> + & = 8 х+* после того, как
из второго уравнения выражается у = х*
3. Корректность н обусловленность задачи. Будем считать, что
система G.1) имеет решение ~х, причем в некоторой окрестности этого
195

решения матрица Якоби /'(х) невырождена. Выполнение последнего
условия гарантирует, что в указанной окрестности нет других решений
системы G.1). Случай, когда в точке х матрица /'(х) вырождена, явля-
является существенно более трудным и нами рассматриваться не будет. В
одномерном случае первая ситуация отвечает наличию простого корня
уравнения f(x) = 0, а вторая — кратного корня.
В § 4.2 было установлено, что погрешность вычисления функции /
приводит к образованию вокруг корня уравнения /(х) = 0 интервала
неопределенности , внутри которого невозможно определить, какая из
точек является решением уравнения.
Аналогично, погрешности в вычислении век-
вектор-функции /приводят к появлению области
неопределенности D, содержащей решение х
системы G.1) такой, что для всех х € D вектор-
векторное уравнение /(х) = 0 удовлетворяется с точ-
точностью до погрешности. Область D может
иметь довольно сложную геометрическую
структуру (рис. 7.4). Мы удовлетворимся толь-
Рис 7.4
ко лишь оценкой радиуса е этой области.
Предположим, что для близких к х значений х вычисляемые
значения /*(х) удовлетворяют неравенству |/(х) - /*(х)| < Д(/*).
Тогда ? можно приближенно оценить с помощью неравенства ? <
< 1(/Ч*))м|Д(/*)- Таким образом, в рассматриваемой задаче роль
абсолютного числа обусловленности играет норма матрицы, обратной
матрице Якоби /(х).
§ 7.2. Метод простой итерации
1. Описание метода. Предположим, что требуется найти решение
х = (xi, х2, ..., хж)т системы G.1) с заданной точностью ? > 0. Преобра-
Преобразуем систему G.1) к следующему эквивалентному виду (к виду, удоб-
удобному для итераций):
.  **•).
Если ввести вектор-функцию <р = (ipu tfr, ..., tpn)i, то система G.5)
запишется так:
* = *<*)• G.6)
Пусть начальное приближение х@) = (х<°>, х120], ..., *^°>)т задано.
Подставляя его в правую часть системы G.6), получим хA) = р(х@>).
Подставляя хA> в правую часть G.6), найдем хB) = у>(хA') и т.д.
Продолжая вычисления по формулам
Г(Ы) _ <p(xik))i *>о, G.7)
получим последовательность х@), х'1', ..., х(п), ... приближений к
решению х.
Запись G.7) означает, что очередное приближение x(fc+1> вычисля-
вычисляется через предыдущее приближение х( ki следующим образом:
= ы*\к),
*<*'
)•
Отметим существенную аналогию с методами простой итерации для
решения одного нелинейного уравнения (см. гл. 4) и системы линей-
линейных алгебраических уравнений (см. гл. 6).
2. Сходимость метода. Пусть ip'(x) — матрица Якоби, отвечающая
вектор-функции у(х) (см. § 7.1). Сформулируем теорему о сходимости
метода простых итераций, являющуюся аналогом теорем 4.2 и 6.1.
Теорема 7.1. Пусть в некоторой о-окрестности решения х
функции ipt(x) (г = 1, 2, ..., т) дифференцируемы и выполнено неравен-
неравенство
< Я,
G.8)
196
где 0 < q < 1, q — постоянная.
Тогда независимо от выбора начального приближения х@> из ука-
указанной ff-окрестности корня итерационная последовательность не
выходит из этой окрестности, метод сходится со скоростью геомет-
геометрической прогрессии и справедлива следующая оценка погрешности:
G.9)
197

Замечание 1. Условие G.8), грубо говоря, означает, что в
окрестности решения производные -j— для всех t и ) должны быть
ах,
"достаточно малы по модулю". Иными словами, систему G.1) сле-
следует преобразовать к такому виду G.5), чтобы функции <р, слабо
менялись при изменении аргументов, т.е. были "почти постоянны-
постоянными". Каких-либо общих рецептов, как это следует делать, в общем
случае нет.
Замечание 2. В условиях теоремы 7.1 верна апостериорная
оценка погрешности
- г|
1 - q
G.10)
которая удобна для формулирования критерия окончания итера-
итераций, если известна величина q. Однако найти значение q, удовлет-
удовлетворяющее неравенству G.8) для всех х из некоторой <г-окрестности
корня, далеко не просто. В ряде случаев при наличии достаточно
хорошего начального приближения i@) можно, считая, что q и q0 =
= |р'(х<0>I> использовать следующий практический критерий
окончания итерационного процесса:
_ 1 ~ *>
е.
Пример 7.3. Используя метод простой итерации, найдем с точностью ? =
10~3 решение х\, х2 системы G.4).
Приведем систему к виду, удобному для итераций:
" 'г3
Здесь >p\ {x\, X2) = J82jx2 — x23 , ^2D. fy) —  + ; i— • Проверим
выполнение условия сходимости вблизи точки С. Вычислим матрицу Якоби
8г2
дхх
Так как *i и 3.8 и *2 и % то Для * и * имеем
<p'(xi, X2) и ^'C.8, 2) и
3.379
3.188
0.4361
.0.361 "
Тогда |»»'(Ч. »г)|„ и |у>'C-8, 2I. и 0.379 + 0.436 = 0.815. Следовательно,
метод простой итерации
G.11)
будет сходиться со скоростью геометрической прогрессии, знаменатель которой
примерно равен 0.815, если начальные приближения брать в достаточно малой
окрестности решения.
Возьмем х[0) = 3.8, г20) = 2 и будем вести итерации по формулам G.11),
используя критерий окончания G.10), в котором ? = 10~3, q = 0.815. Резуль-
Результаты вычислений с шестью знаками мантиссы приведены в табл. 7.1.
к
к
0
3.80000
2.00000
5
3.77198
2.07920
1
3.75155
2.03895
6
3.77399
2.07850
2
3.74960
2.06347
7
3.77450
2.07778
Та
3
3.75892
2.07498
8
3.77440
2.07732
б л и ц а 7.1
4
3.76720
2.07883
9
3.77418
2.07712
198
При к = 9 критерий окончания выполняется и.можно положить *i = 3.774 ±
± 0.001, *2 = 2.077 ± 0.001.
199

3. Влияние погрешности вычислений. В силу наличия погрешнос-
погрешностей при вычислении на ЭВМ получается не последовательность z( k>,
удовлетворяющая равенству G.7), а последовательность х1к), удовлет-
удовлетворяющая равенству
G.12)
Будем считать, что абсолютная погрешность вычисляемых значе-
значений <р*(х) вектор-функции <р мала и что \(р(х) - <р*(х)\ < Д(у>*)-
Наличие погрешности вычисления ip приводит к появлению области
неопределенности решения х, радиус е которой можно приближенно
оценить, пользуясь неравенством е < ?* = Д(у>*)/A - q) в том случае,
если |р'(*I < q.
Сформулируем следующий результат, являющийся аналогом теорем
4.5 и 6.2.
Теорема 7.2. Пусть выполнены условия теоремы 7.1 « для всех
х из с-окрестности решения х выполнено неравенство 1<р(х) - ф*(х)\ <
< Д(у»*). Предположим, также что е* = ¦ _ ' < а (т.е. величина
*) достаточно мала). Тогда если вычисления по формулам G.7)
«G.12) начинаются с одною начальною приближения х@) = i@),
принадлежащею <г\-окрестности решения х (где <Т\ —
— min {о~, (a — е *)/?}), то последовательность х(п) не выходит за
пределы а-окрестности решения х и для всех п ^ 1 справедливы оценки
r(fc) ¦(¦<*) Xlk) Г<*
т(Ы) r(Jt) zik) х1к
Ji i J2 > гЗ
' •¦¦> xm I '
Более общий вариант метода Зейделй состоит в следующем: t-я
компонента решения на (к + 1)-й итерации метода определяется как
решение нелинейного уравнения
где *¦(*.) = /,(х<^), ...,
Преимущества этого подхода состоят в возможности использования
методов решения уравнений с одним известным и в отсутствии необхо-
необходимости приведения системы уравнений к виду, удобному для итера-
итераций. Указанный метод сходится, если для матрицы Якоби /'(г) выпол-
выполнены условия диагонального преобладания.
Иногда существенный выигрыш дает использование метода, явля-
являющегося аналогом метода релаксации (см. § 6.3). В нем после вычисле-
вычисления очередной i-й компоненты (к + 1)-го приближения по формуле
метода Зейделя
приближение
+ (и- lX
вычисляют по формуле
-x\
- rj
1 - q
|г
(п) _
е*.
4. Модификации метода простой итерации. В некоторых случаях
для ускорения сходимости полезно использовать следующий аналог
метода Зейделя (см. § 6.2):
200
§ 7.3. Метод Ньютона
для решения систем
нелинейных уравнений
1. Описание метода. Обобщим метод Ньютона, изложенный в § 4.6
•для решения одного нелинейного уравнения, на решение систем не-
нелинейных уравнений G.1). При этом будем исходить из трактовки
метода Ньютона как метода линеаризации.
- 201

Предположим, что исходя из начального приближения х@) к реше-
решению х построены приближения хA>, хB), ..., х<">. Заменим в системе
G.1) каждую из функций /,(« = 1, 2, ..., т) линейной частью ее разло-
разложения по формуле Тейлора в точке х( п):
/,(*) « /,(*< "> ) + ? Щ^ (г, - *< »> ).
В результате придем к системе линейных алгебраических уравнений
«(п)
*<«>) = О,
() У (
имеющей в матричной форме записи следующий вид:
G.13)
Здесь /* — матрица Якоби G.3).
Предположим, что матрица /'(х(п)) невырожденная, т.е. существует
обратная матрица (/'(х(п))). Тогда система G.13) имеет единственное
решение, которое и принимается за очередное приближение х<п+1> к
решению х. Таким образом, приближение х(п+1> удовлетворяет равен-
равенству
/(*<"') + /'(х(п>)(*(п+1) - г"»») = 0,
G.14)
выражая из которого х(п+1), выводим итерационную формулу метода
Ньютона:
= г(п) _
G.15)
Замечание. Формула G.15) предполагает использование тру-
трудоемкой операции обращения матрицы (см. гл. 5), поэтому непо-
непосредственное ее использование для вычисления xl n+1' в большинст-
большинстве случаев нецелесообразно. Обычно вместо этого решают эквива-
эквивалентную системе G.14) систему линейных алгебраических уравне-
уравнений
/'(х<п))Дх<"+1> = -/(х<">) G.16)
относительно поправки Дх(п+1) = х<п+1> - х(п). Затем полагают
x(n*U = х(п) + Дх<п+1). G 1?)
2. Сходимость метода. Сформулируем основную теорему о сходимо-
сходимости метода Ньютона.
Теорема 7.3. Пусть в некоторой окрестности решения х систе-
системы G.1) функции /,(i = 1, 2, ..., m) дважды непрерывно дифференциру-
дифференцируемы и матрица f'(x) невырождена. Тогда найдется такая малая 6-
окрестность решения х, что при произвольном выборе начального
приближения х<0) из этой окрестности итерационная последователь-
последовательность метода Ньютона не выходит за пределы окрестности и спра-
справедлива оценка:
|х<"+ч - хЦ < й-1|х<") - х|2, п>0.
Эта оценка означает, что метод сходится с квадратичной ско-
скоростью.
Квадратичная скорость сходимости метода Ньютона позволяет
использовать простой практический критерий окончания:
(п) _
G.18)
Пример 7.3. Используя метод Ньютона, найдем с точностью ? = 10~4 реше-
решение Xi, X2 системы G.4).
Возьмем х{ = 3.8, ^2 = 2 и будем вести вычисления по формулам
G.16), G.17), в которых
Г г? + xl - 8412 1
3*1 - 8*2 Ъх\ - Ьх
*1 Т1
Результаты вычислений с шестью знаками мантиссы приведены в табл. 7.2.
Т а б л и ц а 7.2
0
1
3.80000 3.77258 3.77388 3.77389
2.00000 2.07189 2.07708 2.07710
202
203

При к — 3 критерий окончания \^к) — jt* *~1 'loo < е = Ю~4 выполняется и
можно положить щ - 3.7739 ± 0.0001, г2 = 2.0771 ± 0.0001.
3. Трудности использования. Изложенные в § 4.6 трудности исполь-
использования метода Ньютона не только сохраняются при применении его к
решению систем нелинейных уравнений, но и усугубляются. Во-пер-
Во-первых, возникает проблема вычисления на каждой итерации матрицы
/Xх) из т2 частных производных, что само по себе может оказаться
весьма сложным делом. Во-вторых, обостряется проблема нахождения
хорошего начального приближения. Ее решить в многомерном случае
гораздо труднее, чем в одномерном.
4. Влияние погрешности вычислений. Пусть /* и (/')* — вычисля-
вычисляемые на ЭВМ приближенные значения вектор-функции / и матрицы
Якоби /'. Пусть для решения системы линейных алгебраических урав-
уравнений используется схема частичного выбора (см. § 5.5). Будем счи-
считать, что матрица /' достаточно хорошо обусловлена (cond(/') е^, < 1)
и вычисляется не слишком грубо (|/* - (/')*| < \f\). Тогда при'выбо-
ре начального приближения из малой окрестности решения метод
Ньютона является устойчивым и дает возможность найти решение с
гарантированной точностью е > е* = |(/'(х))"ЧД(/*).
§ 7.4. Модификации метода Ньютона
Если оценивать качество метода Ньютона только по числу необхо-
необходимых итераций, то следовало бы сделать вывод о том, что этот метод
стоит применять всегда, когда он сходится. На практике для достиже-
достижения разумной точности е при выборе достаточно хорошего начального
приближения х@) требуется, как правило, 3—5 итераций.
Однако при оценке общей трудоемкости метода следует учитывать,
что на каждой итерации требуется выполнение следующей дополни-
дополнительной работы:
1) вычисление m компонент вектора /(х(п));
2) вычисление т2 компонент матрицы Якоби f'(xln));
3) решение системы линейных алгебраических уравнений G.16).
Существует большое число модификаций метода Ньютона, позволя-
позволяющих в тех или иных ситуациях снизить его трудоемкость либо избе-
избежать необходимости вычисления производных. Рассмотрим кратко
некоторые из таких модификаций, учитывая, что их одномерные нало-
налоги были изучены более подробно в § 4.7.
204
1. Упрощенный метод Ньютона. Заменим в расчетных формулах
метода Ньютона G.16), G.17) матрицу /'(х(п)), зависящую от п, пос-
постоянной матрицей А = /'(х@)). В результате получим расчетные фор-
формулы упрощенного метода Ньютона:
ЛДх<"+1> = -/(*<"'),
= г(п)
G.19)
G.20)
Можно показать, что этот метод сходится со скоростью геометри-
геометрической прогрессии, если начальное приближение х@) выбрано доста-
достаточно близким к решению х, причем знаменатель прогрессии q тем
меньше, чем ближе г@) кг.
По сравнению с методом Ньютона число итераций, необходимое
для достижения заданной точности е, существенно возрастает. Тем не
менее общие вычислительные затраты могут оказаться меньше. Причи-
Причины этого состоят в следующем. Во-первых, вычисление матрицы Якоби
производится здесь только один раз; во-вторых, как нетрудно видеть,
при использовании упрощенного метода Ньютона G.19), G.20) много-
многократно решается система линейных уравнений с фиксированной мат-
матрицей А и различными правыми частями. Это означает, что при реше-
решении систем G.19) методом Гаусса возможно применение Ш-разложе-
ния матрицы А, которое резко уменьшает число операций, необходи-
необходимых для вычисления Дх(п+1) (см. гл. 5).
2. Использование формул численного дифференцирования. Доволь-
но часто вычисление производных —, являющихся элементами
дх}
матрицы /', затруднено или вообще невозможно. В такой ситуации
для приближенного вычисления производных можно попытаться ис-
использовать формулы численного дифференцирования (см. гл. 12).
Например, можно использовать следующую конечно-разностную ап-
аппроксимацию производной:
«Vi
г(п) х(п) л. kin) xl n) x(n)) -
шаги.
Параметры hln) t 0 (j = 1, 2, ..., m) — это конечно-разностные
205

Если в расчетных формулах метода Ньютона G.16), G.17) заменить
матрицу /'(х( п)) аппроксимирущей ее матрицей J( "> с элементами
7((п), то получим следующий итерационный метод:
G.22)
G.23)
В простейшем варианте этого метода шаги h} ( j = 1, 2, ..., m) не
зависят от п. Отметим, что выбор величины шагов представляет собой
не очень простую задачу. С одной стороны, они должны быть доста-
достаточно малыми, чтобы матрица J(nl хорошо приближала матрицу
/'(х(п)), с другой, они не могут быть очень малы, так как в этом
случае влияние погрешностей вычисления функций fj на погрешность
формулы G.21) численного дифференцирования становится ка-
катастрофическим (выполняется вычитание близких приближенных
чисел).
Следующие три метода можно рассматривать как варианты метода
G.22), G.23), в которых реализованы специальные подходы к вычисле-
вычислению вектора Л<"> = (Л{п), Л^п>, ..., h{mn))T. Для того чтобы приведен-
приведенные ниже рассуждения были формально корректными, в формуле
G.21) положим J[™ = -^ (х<">), если оказалось, что Л^"' = 0.
3. Метод ложного положения. Пусть с — фиксированный вектор.
Положим А(п) = с - х(п). Тогда формулы G.21) — G.23) определяют
метод ложного положения, обладающий линейной скоростью сходимо-
сходимости в случае, если вектор с и начальное приближение г<0) выбраны
достаточно близко к решению.
4. Метод секущих. В одном из наиболее популярных своих вариан-
вариантов метод секущих можно рассматривать как метод G.21) — G.23), где
д(п) = г(п-п _ х(п). Метод секущих является двухшаговым: для
вычисления очередного приближения ж1п*1) используют два предыду-
предыдущих приближения х(п) и х'. Для того чтобы начать вычисления,
необходимо задать два начальных приближения х@) и хA).
При удачном выборе начальных приближений х@) и хA) метод
секущих сходится со сверхлинейной скоростью с порядком сходимости
р = 05 + 1)/2.
5. Метод Стеффенсена. Вычисления по методу Стеффенсена про-
производят по формулам G.21) - G.23), где Л<"> = /(х<">).
Замечательно то, что хотя этот метод не требует вычисления произ-
206
водных и в отличие от метода секущих является одношаговым, он, как
и метод Ньютона, обладает свойством квадратичной сходимости. Прав-
Правда, как и в методе Ньютона, его применение затруднено необходи-
необходимостью выбора хорошего начального приближения.
По-видимому, для решения нелинейных систем вида G.1) метод
Стеффенсена чаще окажется лучшим выбором, чем метод секущих или
метод ложного положения.
Как и в одномерном случае (см. § 4.7), следует отметить, что мето-
методы секущих и Стеффенсена теряют устойчивость вблизи решения
(фактически это происходит при попадании приближения х( п> в об-
область неопределенности решения х). Поэтому при использовании этих
методов важно вовремя прекратить выполнение итераций.
§ 7.5. О некоторых подходах к решению задач
локализации и отыскания решений
систем нелинейных уравнений
Подчеркнем еще раз, что одной из наиболее трудных проблем,
возникающих при решении систем нелинейных уравнений, является
задача локализации решения. Изложим некоторые подходы к ее реше-
решению, широко применяемые в практике вычислений. Указанные методы
можно применять и для вычисления решения с заданной точностью е.
1. Использование методов минимизации. Иногда бывает полезно
свести задачу отыскания решения системы нелинейных уравнений к
задаче отыскания минимума функции многих переменных. В простей-
простейшем варианте это сведение выглядит следующим образом. Введем
га
функцию Ф (х) = ? (/,(х)J. Она неотрицательна и достигает своего
минимума (равного нулю) тогда и только тогда, когда /,(х) = 0 для
всех 1=1,2, ..., т, т.е. х является решением системы G.1).
Применяя для отыскания минимума функции Ф один из итераци-
итерационных методов минимизации — методов спуска (см. гл. 10), можно
найти вполне удовлетворительное приближение к решению х, которое
затем имеет смысл использовать как начальное приближение х<0) в
одном из итерационных методов решения нелинейных систем.
Выгода от указанного сведения исходной задачи к задаче миними-
минимизации состоит в том, что, как правило, методы спуска имеют более
широкую область сходимости. Использование методов спуска можно
рассматривать и как один из способов локализации решений системы
G.1). Применение на заключительном этапе методов, специально ори-
207

ентированных на решение нелинейных систем, вызвано тем, что вблизи
искомого решения методы спуска сходятся медленее.
Следует отметить, что функция Ф (г) может иметь и ненулевые
локальные минимумы, и в зависимости от выбора начального прибли-
приближения методы спуска могут приводить к точкам локального минимума,
не являющимися решениями системы G.1).
Пример 7.4. Решения системы G.4) являются точками глобального мини-
минимума функции
= (г?
х\ -
+ (i,ln x2 - х2\п xtf.
2. Метод продолжения по параметру. Сначала заметим, что доволь-
довольно часто на практике встречаются ситуации, когда система нелиней-
нелинейных уравнений естественным образом зависит от некоторого параметра
t, т.е. имеет вид
/(*. О = 0,
G.24)
а решение ее следует найти при некотором фиксированном значении
параметра, например при I = 1. В частности, этим свойством обладает
система из примера 7.1. Предположим, что при каждом <€[0, 1] система
G.24) имеет решение х = х (<), непрерывно зависящее от параметра t,
причем при t = 0 решение системы /(х, <) = 0 известно либо легко
вычисляется.
Таким образом, семейство решений х (I) описывает в пространстве
Д™ траекторию, начальная точка х@) которой известна, а конечная
хA) подлежит определению (рис. 7.5).
x(i)-x(tN
x(O)'*(t,)
Рис. 7.5
И в тех случаях, когда система не зависит от параметра, можно
ввести параметр t так, чтобы были выполнены указанные выше усло-
условия. Например, если х* — известное приближение к решению системы
/(х) = 0, то можно рассмотреть систему вида G.24), полагая /(х, <) =
= /(*) ~ A " *)/(«*)¦
Введем на отрезке [0, 1] набор точек 0 — to < t\ < ... < tf/ = 1.
Используя тот или иной итерационный метод, решим последовательно
для Jfc = 0, 1, 2, ..., N системы /(г, <*) = 0. При этом за начальное
приближение к х (<*) будем принимать решение х (<jt-i) Если разность
ik ~ h-i достаточно мала, то можно ожидать, что х (ijt-О будет доста-
достаточно хорошим начальным приближением к х {ik), обеспечивающим
сходимость используемого итерационного метода.
Замечание. Довольно часто на практике проводится
исследование зависимости определенных характеристик объекта от
некоторого параметра t. Для таких задач метод продолжения есте-
естествен. Более того, точки <0, <ь ¦¦¦, 'лг можно выбрать, используя
дополнительные соображения, причем решение х (<jt) представляет
интерес не только для ifc = N, но и для всех к — 0, 1, ..., N.
3. Метод дифференцирования по параметру. Предположим, что
решение г (<) системы G.24) является гладкой функцией параметра t.
Дифференцируя тождество /(г (<), t) = 0 по t, получим
fx (г @, t)x'(t) + f't
dfx
208
Здесь Г (г, t) — матрица с элементами —- (г, t) (t, j — 1, 2, ..., m), a
ft (г, i) — вектор-столбец с элементами -^ (х, t) (i = 1, 2, ..., m). Таким
образом, если матрица f'x невырождена (det f'x t 0), то х (t) является
решением задачи Коши для системы обыкновенных дифференци-
дифференциальных уравнений
«'@ = -(/х (« @, i))'4't (* (t), 0, х @) = х @). G.25)
Интересующее нас значение решения х A) можно теперь найти приб-
приближенно, применяя численные методы решения задачи Коши.
209

Например, метод Эйлера приводит к процессу
(,
(*1
-i/j (,(*), tk), к = о, 1,..., лг-1,
где х<°> = х @), x(fc) — приближение к х (<*) (рис. 7.6). Конечно,
метод Эйлера приведен здесь только для удобства иллюстрации, а в
реальной ситуации используется один из методов более высокого
порядка точности.
Полученное указанным способом_зяачение z(N) можно использовать
и как хорошее начальное приближение к
итерационных методов решения системы G.24).
хA) в одном
из
Замечание 1. Иногда метод дифференцирования по парамет-
параметру называют методом Давиденко.
Замечание 2. Методы продолжения и дифференцирования по
параметру нередко позволяют успешно преодолевать непростую
проблему локализации. Однако следует отметить, что эти методы
далеко не всегда оказываются эффективными и их практическое
применение требует определенной осторожности.
§ 7.6. Дополнительные замечания
1. Существенно более подробная и богатая информация о системах нели-
нелинейных уравнений и методах их решения содержится в книгах [61], [32]. Реко-
Рекомендуем также обратиться к учебнику [9].
2. В последнее время значительный интерес проявляется к так называемым
квазиньютоновским методам, которые получаются при специальных аппрокси-
аппроксимациях матрицы Якоби. Часто такая аппроксимация сочетается с использова-
использованием гибридных алгоритмов подобно тому, как это делается для решения
одного нелинейного уравнения (см. § 4.8). Полезные обсуждения таких методов
можно найти в [32].
3. Иногда подходящим для решения задачи методом оказывается метод
установления (см. [9]). Чаще это бывает тогда, когда решение системы G.1)
описывает устойчивое стационарное состояние некоторой физической системы
4. Рекомендовать тот ичи иной метод как наиболее подходящий для реше-
решения системы нелинейных уравнений невозможно без тщательного изучения
конкретной задачи.
Глава 8
МЕТОДЫ РЕШЕНИЯ ПРОБЛЕМЫ
СОБСТВЕННЫХ ЗНАЧЕНИЙ
Вычисление собственных значений и собственных векторов — одна
из тех сложных вычислительных задач, с которой часто приходится
сталкиваться инженеру или научному работнику, занимающемуся
конструированием или анализом больших технических систем. В
электрических и механических системах собственные числа отвечают
собственным частотам колебаний, а собственные векторы характеризу-
характеризуют соответствующие формы (моды) колебаний. Знание собственных
чисел позволяет анализировать многие процессы, исследовать и управ-
управлять ими. Оценка величин критических нагрузок при расчете строи-
строительных конструкций также основана на информации о собственных
значениях и собственных векторах матриц.
Собственные числа и собственные векторы являются важнейшими
характеристиками, отражающими существенные стороны линейных
моделей. Поэтому, конечно, дальнейшее расширение процесса матема-
математического моделирования приведет к тому, что владение методами
решения проблемы собственных значений станет неотъемлемым эле-
элементом инженерного образования.
§ 8.1. Постановка задачи.
Некоторые вспомогательные
сведения
1. Постановка задачи. В данной главе мы ограничимся рассмотре-
рассмотрением методов решения проблемы собственных значений только для
квадратных матриц А порядка m с вещественными элементами atJ
(г, j - 1, 2, ..., m). Будем всюду под |г| понимать норму |х|2 и под
(г, f) — скалярное произведение векторов х, у (см. § 5.2).
Напомним, что число А называется собственным значением (собст-
211

венным числом) матрицы А, если существует ненулевой вектор х, удов-
удовлетворяющий уравнению
Ах = Ах
(8.1)
и называемый собственным вектором матрицы А, отвечающим собст-
собственному значению А.
Запишем систему (8.1) в виде
(А-ХЕ)х=0.
Эта однородная система имеет ненулевое решение х тогда и только
тогда, когда определитель матрицы системы равен нулю, т.е.
det(A - ХЕ) = 0.
(8.2)
Раскрытие этого уравнения приводит к так называемому характери-
характеристическому (или вековому) уравнению
\т
рт = 0,
(8.3)
представляющему собой алгебраическое уравнение степени т.
Известно, что характеристическое уравнение имеет в области комп-
комплексных чисел ровно т корней Аь А2, ..., Ат (с учетом их кратности).
Таким образом, каждая квадратная матрица А порядка m обладает
набором из т собственных значений Ai, A2, ..., Ат.
Если матрица А симметричная, то все ее собственные значения
являются вещественными числами. Для несимметричных матриц воз-
возможно наличие комплексных собственных значений вида А = а + ф с
ненулевой мнимой частью. В этом случае собственным значением мат-
матрицы обязательно является и комплексно-сопряженное число А = а -
-,13.
В ряде задач механики, физики, химии, техники, биологии требу-
требуется получение всех собственных значений некоторых матриц, а иног-
иногда и всех собственных векторов. В такой постановке задачу называют
полной проблемой собственных значений.
Довольно часто определению подлежат не все собственные значения
и собственные векторы, а лишь небольшая их часть. Например, суще-
существенный интерес во многих приложениях представляют максимальное
или минимальное по модулю собственное значение или же собственное
значение, наиболее близко расположенное к заданному значению.
Такие задачи являются примерами частичных проблем собственных
значений.
Может показаться, что достаточно ограничиться только рассмотре-
рассмотрением методов решения полной проблемы собственных значений, так
212
как все остальные проблемы являются ее частными случаями. Однако
такой подход неоправдан, поскольку ориентирует на работу по получе-
получению значительного объема заведомо ненужной информации и требует
существенно большего объема вычислений, чем это необходимо в дей-
действительности. Поэтому для решения различных частичных проблем
собственных значений разработан ряд специальных методов.
Пример 8.1. Найдем собственные числа матрицы
2
1.2
1
-9 5
-5.3999 6
-1 -7.5
(8.4)
Запишем характеристический многочлен
Г2-А -9
Р3(А) = det(A - ХЕ) = det
1.2
1
-5.3999-А
-1
5
6
-7.5-А
= -А3 - 10.8999А2 - 26.49945А - 21.002.
Используя один из итерационных методов решения нелинейных уравнений
(например, метод Ньютона), нетрудно определить один из корней уравнения
Р3(Х) = 0, а именно А! я -7.87279. Разделив Р3(Х) на А - Аь имеем
787070 й Р^ = *2 + 3.02711 А + 2.66765. Решая квадратное уравнение
Р2(Х) = 0, находим корни А2K я -1.51356 ± 0.613841 t
Таким образом, матрица А имеет одно вещественное собственное значение
Ai и -7.87279 и два комплексно-сопряженных собственных значения А2)з й
я -1.51356 ± 0.613841 1.
Численные методы решения проблемы собственных значений, ис-
использовавшиеся до конца 40-х годов, сводились в конечном счете к
решению характеристического уравнения (8.3). Этой классической
схеме следовали и мы в примере 8.1. При реализации такого подхода
основные усилия были направлены на разработку эффективных мето-
методов быстрого вычисления коэффициентов характеристического уравне-
уравнения. Методы такого класса получили названия прямых; к ним отно-
относятся пользовавшиеся популярностью методы Крылова1, Данилевско-
Данилевского, Леверье и др.
1 Алексей Николаевич Крылов A863 — 1945) — русский математик, меха-
механик и кораблестроитель, является автором первого в мировой научной литера-
литературе курса по численным методам — изданных в 1911 г. "Лекций о прибли-
приближенных вычислениях".
213

Однако указанный подход становится неудовлетворительным, если
речь идет о вычислении собственных значений матриц, имеющих
порядок т в несколько десятков (и тем более сотен), т.е. матриц
довольно скромных по современным понятиям размеров.
Одна из причин состоит в том, что хотя задачи (8.1) и (8.3) фор-
формально эквивалентны, они имеют разную обусловленность. Так как
корни многочлена Рт(х) высокой степени чрезвычайно чувствительны
к погрешностям в коэффициентах, то на этапе вычисления коэффици-
коэффициентов характеристического уравнения может быть в значительной
степени потеряна информация о собственных значениях матрицы.
С появлением ЭВМ широкое распространение получили итерацион-
итерационные методы решения проблемы собственных значений, не использу-
использующие вычисление характеристического многочлена. К началу 60-х
годов эти методы практически полностью вытеснили прямые методы
из практики вычислений.
2. Преобразование подобия. Говорят, что матрицы А и В подобны,
если существует невырожденная матрица Р (матрица подобия) такая,
что В = Р~1АР. Само преобразование матрицы А к виду В = Р~1АР
называется преобразованием подобия. Преобразование подобия матри-
матрицы возникает естественным образом как результат замены переменных
(или перехода к новому базису) в пространстве m-мерных векторов.
Действительно, пусть у — результат применения матрицы А к вектору
х, т.е. у = Ах. Произведем замену переменных х — Рх', у = Ру'. Тогда
равенство у = Ах примет вид у' = Р~1АРх'. Это означает, что в новых
переменных то же самое преобразование осуществляется уже не матри-
матрицей А, а матрицей Р~1АР, подобной А.
Важно то, что и полученная в результате преобразования подобия
матрица имеет тот же набор собственных чисел. В самом деле, рассмот-
рассмотрим характеристический многочлен для матрицы Р~1АР и воспользу-
воспользуемся тем, что определитель произведения квадратных матриц равен
произведению соответствующих определителей:
- XE) - det(P-'(>4 - \Е)Р) =
= detP-ldet(A - XE)detP = det(A - XE).
Таким образом, характеристические многочлены, а следовательно, и
собственные числа матриц А и Р~1АР совпадают. Соответствующие
собственные векторы х и х' не совпадают, но, как нетрудно устано-
установить, они связаны равенством t = Рх'.
Если бы матрицу А с помощью преобразования подобия или после-
последовательности таких преобразований удалось привести к верхнему
треугольному виду, то проблему вычисления собственных значений
214
можно было бы считать решенной. Дело в том, что у верхней треуголь-
треугольной матрицы
В =
... b
!¦
(8.5)
собственными числами являются элементы главной диагонали 6„. В
этом нетрудно убедиться, если записать характеристический много-
многочлен: det(B- XE) = (Ьп - А)F22 - А) ... Fmm - A).
Оказывается, что преобразованием подобия матрицу А можно при-
привести к еще более простому виду, чем (8.5). Справедлива (см. [23])
следующая теорема.
Т е о р е и а 8.1. Любую квадратную матрицу А с помощью преоб-
преобразования подобия можно привести к следующему виду:
Г* АР = А =
Ai <Ti 0 О
О А2 <т2 О
О О А3 ffS
ОООО
0 0 0 0
0
(8.6)
Здесь Ai, A2, ..., Ат — собственные числа матрицы А. Числа <г, прини-
принимают одно из двух значений 0 или 1, причем если <т, = 1, то обяза-
обязательно А, = А^ц.
Матрица (8.6) называется жордановой формой матрицы А.
3. Матрицы простой структуры. В этой главе особое внимание
будет уделено матрицам простой структуры, т.е. матрицам, которые
с помощью преобразования подобия можно привести к диагональному
виду:
R1AP - D =
Aj 0 ... О
О А2 ... О
О 0 ... А.
(8.7)
Запишем равенство (8.7) в виде АР — DP и заметим, что оно верно
тогда и только тогда, когда каждый j-й столбец матрицы Р является
собственным вектором матрицы А, отвечающим собственному значению
Xj. Таким образом, верна следующая теорема.
215

Теорема 8.2. Матрица А является матрицей простой струк-
структуры тогда и только тогда, когда она имеет т линейно независимых
собственных векторов ех, е2, ..., ещ, отвечающих собственным значе-
значениям Ai, A2, ..., Am соответственно.
Указанные в теореме собственные векторы ei, е2, ..., ет образуют
базис в пространстве m-мерных векторов. Поэтому каждый т-мерный
вектор х может быть однозначно представлен в виде линейной комби-
комбинации этих векторов:
х =
с2е2
(8.8)
Какие же матрицы заведомо могут быть приведены к диагональ-
диагональному виду? Следующие два предложения частично отвечают на этот
вопрос.
Теорема 8.3. Если все собственные значения матрицы А раз-
различны, то она является матрицей простой структуры.
Теорема 8.4. Если А — вещественная симметричная матрица,
то она подобна диагональной матрице, причем матрица подобия Р
может быть выбрана ортогональной (т.е. удовлетворяющей условию
Р"» = Р*).
4.Локализация собственных значений. С помощью так называемых
теорем локализации иногда удается получить грубые оценки располо-
расположения собственных чисел. Изложим самый известный из этих резуль-
результатов — теорему Гершгорина1.
т
Пусть г, = Г |ау| — сумма модулей внедиагональных элементов j-й
j
строки матрицы А. Обозначим через 5t круг радиуса rt на комплек-
комплексной плоскости с центром в точке а„, т.е. S, = {г ?С : \z - аи\ < г,}.
Будем называть круги 5, кругами Гершгорина. Имеет место следующее
утверждение.
Теорема 8.5 (теорема Гершгорина). Все собственные значения
матрицы А лежат в объединении кругов 5j, S2, ¦••, Sm.
? Возьмем произвольное собственное значение А матрицы А и соот-
соответствующий собственный вектор х. Пусть х, — максимальная по мо-
модулю координата вектора х. Запишем г-е уравнение системы (8.1) в
следующем виде:
(а„- А) х, = -S a,;xj.
1 Семен Аронович Гершгорин A901 — 1933) — российский математик. Ре-
Результат, о котором идет речь, был опубликован им в 1931 г.
216
Из этого равенства с учетом оценки \х1/х1\ < 1 следует неравенство
\ап - А|
\at]\
<rf.
Таким образом, А€5,. Ш
Пример 8.2. Для матрицы
А =
-2
0.5
-0.5 -3.5
0.5
1.5
0.5
0.8 -0.5
круги Гершгорина изображены на рис. 8.1. Здесь т\ = 1,
= 2и гз = 1.3.
Рис. 8.1
Следующий результат является полезным дополнением к теореме
Гершгорина.
Теорема 8.6. Если к кругов Гершгорина образуют замкнутую
область G, изолированную от других кругов, то в G находится ровно к
собственных значений матрицы А (с учетом их кратности).
Следствие. Если какой-либо круг Гершюрина изолирован, то
он содержит ровно одно собственное значение матрицы А.
Пример 8.3. Для матрицы А из примера 8.2 в объединении кругов Si и 5г
находится ровно два собственных значения \\ и А2) а круг 5з содержит ровно
одно собственное значение A3.
5. Отношение Рэлея. При вычислении собственных чисел и собст-
собственных векторов симметричных матриц важную роль играет функция
217

(8.9)
называемая отношением РэлеяК Следующее предложение частично
объясняет значение этой величины.
Теорема 8.7. Пусть А — симметричная матрица. Тогда спра-
справедливы следующие утверждения:
1°) минимальное и максимальное собственные значения матрицы А
вычисляются по формулам
= min p (х),
т Ф О
= max p (х);
х Ф О
2°) вектор х является стационарной точкой функции р (х) (т.е.
удовлетворяет условию grad p (х) = 0) тогда и только тогда, когда
х — собственный вектор матрицы А.
При построении методов решения проблемы собственных значений
существенно используется то обстоятельство, что если х — хорошее
приближение к собственному вектору е]у то р (х) — хорошее приближе-
приближение к собственному числу А^.
6. Обусловленность задачи вычисления собственных значений и
собственных векторов. Пусть А » — матрица с приближенно заданными
элементами а* я а . Обозначим через A* (j = 1,2, ..., т) собственные
числа матрицы А„. Рассмотрение вопроса о том, как влияет погреш-
погрешность задания матрицы на погрешность искомых собственных значе-
значений, начнем с формулировки следующего известного результата.
Теорема 8.8. Пусть А и А„ — симметричные матрицы, a Aj и
А * — их собственные числа, упорядоченные по возрастанию. Тогда
справедливы оценки погрешности
\j-\* | <||Л-Л,||2,
max
(8.10)
(8.11)
Теорема 8.8 означает, что задача вычисления собственных значений
симметричных матриц очень хорошо обусловлена. Следовательно, в
20
0
0
0
0
20
19
0
0
0
0
20
18
0
0
0 ...
0 ...
20 ...
0 ...
0 ...
0
0
0
2
0
0
0
0
20
1
1 Джон Уильям Рэлей A842 — 1919) — английский физик и математик.
218
этом случае собственные числа надежно определяются заданием эле-
элементов матрицы. К сожалению, для несимметричных матриц дело
обстоит совсем иначе. Хотя задача вычисления собственных значений
и в этом случае является устойчивой, для многих несимметричных*
матриц собственные значения чрезвычайно чувствительны к погрешно-
погрешностям задания коэффициентов.
Пример 8.4. Приведем принадлежащий Дж.Х.Уилкинсону [83] пример мат-
матрицы, очень плохо обуословленной по отношению к проблеме собственных
значений.
Собственными числами верхней треугольной матрицы 20-го порядка
А =
являются числа А] — 1, Аг — 2, ..., А20 = 20. Заметим, что для этой матрицы
характеристический многочлен Рго(А) = B0 - А)AЭ — А)...A - А) только лишь
знаком отличается от многочлена, рассмотренного в примере 3.8 в связи с
плохой обусловленностью его корней. Добавим малое е к элементу 020,1 = 0. В
результате характеристическое уравнение примет вид
B0 - А)A9 - А) ... A - А) = 2019е.
При ? = 10~10 собственные значения возмущенной матрицы таковы: А* я
я 0.996, А* я 2.11, А* я 2.57, А*_5 я 3.97 ± 1.09 i, А*7 я 5.89 ± 1.95 i, A*9 я
я 8.12 ± 2.53 I, А*оп я Ю.5 ± 2.73 г, А*213 я 12.9 ± 2.53 i, A*415 я 15.1 ±
± 1.95 г, А*6Д7 я 17.0 ± 1.09 г, А*8 я 18.4, А*9 я 18.9, А*о и 20.0 Как
нетрудно видеть, большинство значений оказались полностью искаженными.
Отметим, что число обусловленности cond (А) матрицы А не харак-
характеризует обусловленность матрицы по отношению к проблеме собствен-
собственных значений. Оказывается, что такой характеристикой чувствитель-
чувствительности собственных значений относительно погрешности задания мат-
матрицы для матрицы простой структуры служит число обусловленности
матрицы Р, столбцы которой являются собственными векторами мат-
матрицы А. В подтверждение сказанного приведем следующий результат.
Теорема й.Я.Пустъ P~lAP = D, где D — диагональная матрица
219

из собственных значений матрицы А, и пусть d — cond2(.P)|./l - Ал\.
Тогда каждое собственное значение матрицы А, удалено от некоторо-
некоторого собственного значения матрицы А не более чем на d.
Пусть х — собственный вектор матрицы А, отвечающий собствен-
собственному значению А, а х* — собственный вектор приближенно заданной
матрицы A t, отвечающий собственному значению Л *. Прежде чем
обсуждать обусловленность задачи вычисления собственного вектора х,
заметим, что здесь вопрос о выборе меры близости векторов х* и х не
является тривиальным. Выбор в качестве такой меры величины
|х-х*| неудачен. Дело в том, что собственные векторы х* и г не
определяются однозначно. Во всяком случае после умножения
каждого из них на любые числа а\ Ф 0 и «2 * О полученные векторы
а\х* и <*2Х снова являются собственными. Поэтому имеет смысл
стремиться не к тому, чтобы векторы х* и х были близки по норме, а
к тому, чтобы они были близки по направлению. Исходя из этого,
примем в качестве меры близости х* к х величину |sin tp\, где <р —
угол между векторами х* и х, вычисляемый по формуле
<р = arccos
(**. *)
WU4
Задача вычисления собственных векторов симметричной матрицы
хорошо обусловлена, если собственные значения хорошо отделены
друг от друга. В подтверждение сказанного приведем следующий
результат.
Теорема 8.10. Пусть А и А„ — симметричные, матрицы. Тогда
верна оценка
|sin <p\
\Л - At\
7
Здесь if — угол между векторами х* и х, а ^ — расстояние от А* до
ближайшего из несовпадающих с А собственных значений матрицы А.
В случае, когда матрица А несимметрична, собственные векторы
могут оказаться очень плохо обусловленными.
Замечание. Подавляющее большинство встречающихся на
практике матриц являются матрицами простой структуры. Это
обстоятельство, а также большая простота анализа методов вычис-
вычислений и формулировок соответствующих результатов позволяют
220
нам в основном остановиться на проблеме собственных значений
для матриц простой структуры.
§ 8.2. Степенной метод
Пусть требуется вычислить максимальное по модулю собственное
значение А! матрицы А, причем известно, что
|А2| > |Аа| >...>\\т\.
(8.12)
Замечание. Собственное значение Ai в данном случае должно
быть вещественным, поскольку в противном случае собственным
значением было бы также равное ему по модулю число Аь
1. Степенной метод без сдвигов. Опишем простейший вариант
степенного метода, применяемого для вычисления Ар Возьмем произ-
произвольный начальный вектор х@) и построим последовательности векто-
векторов {x(fc)}^=0 и приближений {A}fc)}^=0 к Аь используя формулы
(8.13)
Замечание. Правая часть формулы (8.14) — это просто отно-
отношение Рэлея, вычисленное при х = х1^'. В самом деле, А<*> =
Справедлива следующая теорема.
Теорема 8.11. Пусть А — матрица простой структуры, для
которой выполнено условие (8.12). Предположим, что в разложении
,х@) _
+ ... +
(8.15)
по базису из собственных векторов коэффициент с\ не равен нулю.
Тогда Ар' -» Ai при к -»оо и верна оценка относительной погрешности
(8.16)
221

D Как легко установить, вектор х( *> удовлетворяет равенству х( к) =
— Дкх( 0) > т е получается из х( 0> умножением на к-ю степень матрицы
А (отсюда и название метода). Так как Аег = А,е„ то Акег — А,е, и,
следовательно,
х(к] -
(8.17)
r( к)
X* ' i.
Положим z(fc) = и заметим, что z(fc) -> с\е\ при к -»оо, причем
it
Л _
+ -
Так как
<*>
1"
:Z<
Al
-
<
А2
Ai
А2
AT
fc
t\ =
ДЛЯ
A2
A,
BC(
(8.18)
Теперь нетрудно установить, что
при А -»oo. Более того,
. (8.19)
Используя неравенство Коши—Буняковского |(х, у)\ < Ы*М>
имеем
w
lk) -
(8.20)
Из равенства (8.19) и оценок (8.18), (8 20) следует, что
fc-1)
-1)
Замечание 1. В действительности теорема 8 11 справедлива
для произвольных матриц, удовлетворяющих условию (8.12). Пред-
Предположение о том, что матрица А — простой структуры, потребова-
потребовалось лишь для упрощения доказательства.
Замечание 2. Если | Aj | > 1, то |*<*> | -> оо при it -» oo (см.
формулу (8.17)) и при вычислении на ЭВМ возможно
переполнение. Если же |Ai| < 1, то |x(fc)| -» 0 и возможно
исчезновение порядка. Для предупреждения этих ситуаций обычно
вектор x(fc) нормируют, например, так, чтобы Jx(fc)J = 1 для всех
к > 1. Одна из используемых модификаций такова:
xik) =
(8.21)
Предполагается, что |х@) Ц = 1.
Теорема 8.11 для метода (8.21) остается справедливой. Более того,
последовательность х( *' сходится к собственному вектору по на-
направлению, т.е. sin <pik) ¦* 0 при к
рами х<fc) и е\.
оо, где <pik) — угол между векто-
вектоЗамечание 3. Крайне маловероятно, чтобы в разложении
(8.15) вектора х@) по собственным векторам коэффициент q при ei
оказался равным нулю. Теоретически в этой исключительной ситу-
ситуации метод не должен давать сходящуюся к Ai последовательность.
Однако при вычислении на ЭВМ по формулам (8.12) через не-
несколько итераций вследствие погрешностей округления почти на-
наверняка появится ненулевой коэффициент при ег в разложении
вектора х( *'. Итерационный процесс снова окажется сходящимся
(правда, потребуется выполнить большее число итераций).
2. Апостериорная оценка погрешности. В общем случае для реше-
решения проблемы собственных значений не существует эффективных
апостериорных оценок погрешности, в особенности для собственных
векторов Более простой эта проблема выглядит для симметричных
матриц
Для оценки погрешности приближения А * к собственному значе-
значению А симметричной матрицы полезно использовать следующую тео-
теорему.
Теорема 8.12. Пусть А * — произвольное число, ах* — произ-
произвольный ненулевой вектор. Тогда для любой симметричной матрицы А
существует собственное значение этой матрицы А такое, что спра-
справедлива оценка
222

IA — Л *|
\A**-
PI
(8.22)
Если x* — приближенно вычисленный собственный вектор, то нера-
венствр (8.22) позволяет дать простую апостериорную оценку погреш-
погрешности вычисленного собственного значения А *. В частности, для сте-
степенного метода (8.13), (8.14) из (8.22) следует такая апостериорная
оценка:
x<*>-
(напомним, что здесь предполагается симметричность матрицы А).
Пусть х* — ненулевой вектор, рассматриваемый как приближение к
собственному вектору х, который отвечает собственному значению А.
Далее, пусть р* = р (х*) — отношение Рэлея, г = Ах* - р*х* — вектор
невязки, <т = ]Дтг . Если собственное значение А хорошо отделено от
остальных собственных значений матрицы А, то для оценки погрешно-
погрешности может быть использован следующий результат.
Теорема 8.13. Пусть А — ближайшее к р * собственное значение
симметричной матрицы А, х — соответствующий собственный век-
вектор и /р — угол между векторами х* и х. Тогда справедливы оценки
|sin <p\ <~ , |А -р*\ <~- ¦
Здесь 7 = min |A, - р*\ — расстояние от р* до ближайшего из отлич-
отличных от А собственных значений матрицы А.
Приведем еще одно важное свойство симметричных матриц.
Теорема 8.14. Пусть А — симметричная матрица, х* — произ-
произвольный ненулевой вектор, р* = р (х*). Тогда р* и х* являются точ-
точными собственным числом и собственным вектором некоторой мат-
матрицы А „ для которой
\A-A,U=a. (8-23)
Оценка (8.23) может оказаться очень полезной для обратного ана-
анализа ошибок (о существе такого подхода к анализу ошибок мы говори-
говорили в § 3.6). Например, очень часто матрица А, для которой на ЭВМ
производится вычисление собственных значений, является лишь приб-
224
лиженным представлением "истинной" матрицы А, собственными
значениями и векторами которой в действительности и интересуется
исследователь Пусть известен порядок погрешности а — \А - А\-А
приближенно заданной матрицы и для найденной пары х*, р* =
*х \Ах* - р*х'\
— р (х ) величина а = *—][~*1Г оказывается сравнимой с вели-
величиной е или даже существенно меньше ее. В такой ситуации р* и х*
оказываются собственными значением и вектором матрицы А», кото-
которая отличается от "истинной" матрицы почти так же, как отличается
от нее матрица А. Вряд ли тогда следует стремиться к получению
"более точных" решений.
Пример 8.5. Используя степенной метод, найдем для матрицы (8.5) макси-
максимальное по модулю собственное значение Ai, а также отвечающий ему собст-
собственный вектор.
Возьмем х*01 = A, 0, 0)т и будем вести вычисления по формулам (8.21).
I итерация. Вычисляем yj11 = 2г{0) - Эг^01 + 5г^01 = 2, у!,1' =
^ +
- 5.39994°'
Тогда А;11 = (у'1',
+ 1.2-0 + 1-0 = 2.
= у[1> х\°> +
= 2-1 +
Далее, fir1'! = {22 + 1.22 + I2 я 2.53772 и
_ У
I П
« п)« * @.788110,
0.472866, 0.394055)т.
Результаты десяти первых итераций с шестью знаками мантиссы приведе-
приведены в табл 8.1.
Номер
итера-
итерации it
0
1
2
3
4
5
6
А|*>
_
2.00000
-1.24159
-6.08121
-9.50971
-8 23499
-7.94591
1.000000
0.788110
-0 250056
-0.611733
0.700557
-0.716752
0.720030
Х2Ь
0.000000
0.472866
0.266743
-0.593143
0.583736
-0.579514
0.578443
Т а б л и ц а 8.1
xik)
о
0.000000
0.394055
-0.930763
0.523415
-0.410455
0.387853
-0.383353
8-28
225

Продолжение табл. 8.1
Номер
итера-
итерации к
7
8
9
10
А|*>
-7.88567
-7.87462
-7.87294
-7.87277
-0.720635
0.720729
-0.720739
-0.720739
ХШ
-0.578216
0.578174
-0.578167
0.578167
Т( к)
0.382446
-0.382446
0.382437
-0.382437
Хотя мы не имеем в данном случае обоснованного критерия окончания, по-
видимому, при Jt = 10 следует прекратить вычисления и, округляя результаты,
положить Xi и -7.873, «i и (-О.7207, 0.5782, -0.3824)т.
Важными достоинствами степенного метода являются его простота,
возможность эффективного использования разреженности матрицы и
отсутствие необходимости преобразования матрицы А.
Недостаток метода в применении к многим прикладным задачам —
довольно медленная сходимость. Часто в приложениях значение |А2|
оказывается близким к | Aj |. Так как скорость сходимости степенного
метода определяется величиной |-г^| и 1, то в этом случае сходимость
«I
будем очень медленной.
3. Степенной метод со сдвигами. Существует несколько способов
преодоления указанной трудности. Один из них заключается в приме-
применении степенного метода не к матрицеЛ, а к матрице А = А - оЕ, где
<т — некоторое число. Собственными значениями матрицы А являются
числа А, - G, получаемые сдвигом собственных значений А, на число а.
Если число \\ — с по-прежнему остается максимальным по модулю, то
следует попытаться подобрать а так, чтобы сделать величину
[A, - <т\
|A! - c\
минимальной. Если, например, все собственные зна-
max
2< i<n
чения положительны, то такой минимум достигается при а = (А2 +
+ Ат)/2.
После того как приближение А* к собственному значению вычисле-
вычислено, степенной метод можно использовать для вычисления очередного
собственного значения. Один из приемов такого использования состо-
состоит в сдвиге собственных значений на а = А*. В этом случае число
226
Ai — А * станет минимальным по модулю, а максимальным по модулю
окажется сдвиг другого собственного значения.
Существует несколько способов избавления от уже вычисленных
собственных чисел и соответствующих собственных векторов с целью
избежать их повторного вычисления. Эти способы принято называть
исчерпыванием. Более подробную информацию о них можно найти,
например, в [19], [62].
§ 8.3. Метод обратных итераций
1. Вычисление собственных векторов методом обратных итераций.
Многие из методов решения проблем собственных значений лучше
приспособлены для вычисления собственных значений, чем собствен-
собственных векторов. Поэтому целесообразно рассмотреть задачу вычисления
собственного вектора е; при условии, что уже найдено достаточно
точное приближение А * к собственному значению А^.
Если исходить непосредственно из определения собственного векто-
вектора, то е; следует искать как нетривиальное решение однородной систе-
системы уравнений
(Л - \jE)z = 0
(8.24)
с вырожденной матрицей А - XjE. Однако Xj известно лишь прибли-
приближенно и в действительности при таком подходе вместо системы (8.24)-
придется решать систему
(А-Х*Е)х=0. (8.25)
Так как матрица А - Х*Е заведомо невырождена, то решением систе-
системы (8.25) является только х = 0. Следовательно, непосредственное
численное решение системы (8.25) не дает возможность вычислить
собственный вектор.
Одним из эффективных методов вычисления собственных векторов
является метод обратных итераций. В этом методе приближения к
собственному вектору определяют последовательным решением систем
уравнений
(а- а;
с последующей нормировкой решения:
(8.26)
227

.(fc+l)
(8.27)
В качестве начального приближения берут ненулевой вектор х<0) с
произвольно выбираемыми или даже случайными компонентами. Часто
удовлетворительным является выбор х@) = A, 1, ..., 1)т.
Чтобы понять механизм действия метода, рассмотрим случай, когда
А — матрица простой структуры, a Xj — простое собственное значение.
Представим векторы х@) и fA> в виде линейных комбинаций собст-
собственных векторов в], «2, ..., «я,:
m m
Так как (А - A??)fA) = Е а*(А* - А*)е^, то систему уравнений (8.26)
при it = 0 можно записать в виде
m m
?а,<А<- Х*)е{= S c«ei.
Приравнивая коэффициенты при t{, получим а, = . 1_ . » . Следова-
Следовательно,
t i
(8.28)
Если | Aj; - А *| < | А| - А *| для всех i ^ j, то второе слагаемое в правой
части формулы (8.28) мало по сравнению с первым. Поэтому fA) »
с,-
-г—1
Л,-
j и вектор
оказывается близким по направлению к
вектору ej.
Можно показать, что вектор х'*1, вычисляемый на к-й итерации,
имеет вид
«ГА- - А*
с,е, ,
где 10( *' | -» | с j | при к -»оо. Вектор х( *' сходится к еу по направлению
со скоростью геометрической прогрессии, знаменатель которой g =
IA. - АЛ
max
[a, -
228
Если абсолютная погрешность значения А* много меньше рассто-
расстояния от Xj до ближайшего из остальных собственных чисел (что экви-
эквивалентно выполнению условия |Aj - А*| < |А; - А*| для всех i t j), то
метод обратных итераций сходится очень быстро. Чаще всего доста-
достаточно сделать 1—3 итерации.
Пример 8.6. Используя метод обратных итераций, найдем на 6-разрядной
десятичной ЭВМ собственный вектор матрицы (8.4), отвечающий собственному
значению Ai » А * = -7.8728.
Возьмем х<0) = A, 1, 1)т. Тогда система (8.26) при к = 0 примет вид
9.8728Й - %У2 + Ьуз = 1,
1.2М + 2.4729з/2 + 6з/3 = 1,
й - 3/2 + 0.3728уз = 1-
Вычисляя ее решение методом Гаусса, получим з/'11 = -123909, у^ —
= 99398.3, з/^1' = 65749. После нормировки имеем х\и = -0.720736, г2" =
= -0.578166, я",1' = 0.382440.
Подставляя в правую часть системы (8.26) вместо вектора г101 вектор гA)
и вычисляя решение, находим j/|2> = -59671.5, з/221 = -47867.7, у132) =
= 31663.1. Полученные после нормировки значения г'2> — -0.720737, г?2) =
= —0.578166, х^2> = 0.382440 с машинной точностью совпадают со значениями,
полученными на первой итерации. Итерации следует прервать и считать ре-
результатом вектор q « (-0.720737, -0.578166, 0.382440)т.
Замечание 1. Так как А * почти совпадает со значением А^,
при котором det(>l - X Е) = 0, то матрица А - Х*Е очень плохо
обусловлена. Возникает естественное опасение, что большие по-
погрешности, неизбежные при реализации вычислительного процесса
(8.26), (8.27) на ЭВМ, могут существенно повлиять на свойства
приближений. К счастью, это не так; ошибка, возникающая при
229

численном решении системы (8.26) (которая может быть по величи-
величине сравнима с yik)), оказывается почти пропорциональной вектору
ty В данном случае плохая обусловленность системы не ухудшает, а
улучшает ситуацию.
В справедливости сказанного легко убедиться, если повторить
вычисления из примера 8.5, используя микрокалькулятор. Полу-
Полученные значения уA) и уB) наверняка будут иметь мало общего с
указанными в примере. Тем не менее приближения гA) и гB)
практически совпадут с вычисленными выше, отличаясь, возможно,
только знаком.
Замечание 2. Записав равенство (8.26) в виде у<**п =
= (А - Х*Е)'1х(к), замечаем, что метод обратных итераций — это
просто степенной метод, примененный к матрице (А - А *?)''.
2. Метод обратных итераций с использованием отношения Рэлея.
Одной из проблем применения метода обратных итераций является
необходимость получения хорошего приближения к собственному
значению. В случае, когда А — симметричная матрица, можно попы-
попытаться использовать для оценки А^ отношение Рэлея Этот подход
приводит к следующему комбинированному методу.
(8.29)
(8.30)
(8.31)
Предполагается, что начальный вектор х@) нормирован, т.е. |х@)| =
= 1.
Если начальное приближение хорошо аппроксимирует по направле-
направлению вектор tp то метод (8.29) — (8.31) сходится очень быстро. Напри-
Например, если \j — простое собственное значение, то сходимость оказывает-
оказывается кубической. Одним из способов получения удовлетворительного
начального приближения х@) является выполнение нескольких ите-
итераций степенного метода.
Замечание. В случае, когда метод (8.29) — (8.31) сходится, он
позволяет одновременно эффективно вычислять и собственное
значение \} и соответствующий собственный вектор е;.
230
(A- A<fc>
y( fr+
§ 8.4. дД-алгоритм
В настоящее время лучшим методом вычисления всех собственных
значений квадратных заполненных матриц общего вида (умеренного
порядка) является фД-алгоритм1.
1. Основной QA-алгоритм. Опишем итерационную процедуру, явля-
являющуюся основой алгоритма. Она существенно использует возможность
разложения произвольной матрицы в произведение ортогональной и
верхней треугольной матриц, т.е. так называемое фД-разложение (см.
§ 5.10).
На 1-й итерации с помощью метода отражений или метода враще-
вращений вычисляют фД-разложение матрицы j4@) = А, имеющее вид
(8.32)
Затем строят матрицу ЛA)= R\Qi. Заметим, что из равенства (8.32)
следует, что Ri = ф^Л101 и поэтому А{1) = Q^A@) Qv Таким обра-
образом, матрицы А{1) и j4@) подобны (см. § 8.1) и поэтому имеют общий
набор собственных значений Ai, A2, ..., Am.
На 2-й итерации находят фД-разложение матрицы Ап\ имеющее
вид Ail) = ОгЯг! и вычисляют матрицу ЛB) = R2Q2, подобную мат-
матрице АA >.
На (ib + 1)-й итерации вычисляют разложение А(к) = Qk+\Rk+\ и
строят матрицу Aik*l) = Rk*iQk*i- Неограниченное продолжение этого
процесса дает последовательность матриц j4A), AB), ..., >4(п), . .,
подобных матрице А.
К сожалению, в общем случае, когда собственные значения матри-
матрицы могут быть кратными или комплексными, строгое изложение пре-
предельных свойств последовательности Л'*' потребовало бы введения
ряда довольно сложных математических понятий. Поэтому ограничим-
ограничимся указанием на то, что при определенных условиях в случае, когда
собственные значения матрицы А вещественны и различны по модулю,
причем lA^ > |А2| > ... > |Ат|, последовательность Л(п) сходится к
верхней треугольной матрице А вида
Л =
A2 x
О А3
ООО
(8.33)
1 Этот метод независимо был предложен в 1960 г. в России математиком
В.Н.Кублановской и в 1961 г. в Англии системным программистом Дж.Фрэнси-
сом.
231

Здесь крестиками помечены элементы, в общем случае не равные
нулю.
Известно, что в рассматриваемом случае элементы а[к) матриц
А{ к), стоящие ниже главной диагонали, сходятся к нулю со скоростью
геометрической прогрессии, причем
7( к)
(8.34)
т.е. скорость сходимости а'*' к нулю определяется величиной отноше-
отношения А, к Aj (заметим, что
*
< 1 при г > j).
Следует подчеркнуть, что фЯ-алгоритм не обеспечивает обычной
поэлементной сходимости и речь идет о сходимости к треугольной
матрице (8.33) по форме. Она характеризуется сходимостью к нулю
поддиагональных элементов, тогда как наддиагональные элементы от
итерации к итерации могут существенно изменяться.
2. Ускорение фД-алгоритма. Приведенный выше вариант QR-алго-
ритма очень неэффективен по двум основным причинам. Первая из
них состоит в том, что для реализации только лишь одной итерации
этого метода требуется выполнить порядка т3 арифметических опера-
операций, если А — матрица общего вида. Вторая причина заключается в
том, что при наличии двух близких собственных значений А, и A,_i
метод сходится очень медленно, так как, например, элемент а**' j
сходится к нулю со скоростью геометрической прогрессии, знамена-
и 1.
тель которой q = U——
I A,-i
Для того чтобы уменьшить число арифметических операций, мат-
матрицу А предварительно с помощью подобных преобразований отраже-
отражения или вращения приводят к так называемой форме Хессенберга^:
(8.35)
Ли
0
hu ...
h22 ...
Л32 ...
*l
h2
Лз
,m-\
,m-\
,m-\
him
h2m
h3m
0 0
''mm .
Матрица Н, в которой равны нулю все элементы Л,;, такие, что г > j'
Герхард Хессенберг A874 — 1925) — немецкий математик.
232
+ 1 (т.е. все элементы, расположенные ниже диагонали, непосредствен-
непосредственно примыкающей к главной диагонали), называется матрицей Хессен-
Хессенберга. Существуют эффективные стандартные процедуры преобразова-
преобразования матрицы А к виду (8.35), поэтому мы не будем останавливаться
подробно на этом преобразовании. Для дальнейшего важно то, что
матрицы А и И подобны и обладают общим набором собственных
значений, а матрица подобия Р, для которой выполняется равенство
И=
(8.36)
ортогональна.
После преобразования матрицы А к виду (8.35) к матрице Н приме-
применяют фД-алгоритм. Эффективность такого подхода обусловлена на-
наличием следующих двух замечательных свойств матриц Хессенберга.
1°. Матрицы Я( к), порождаемые QR-алгоритмом из матрицы
Я<0) = Н, сами являются матрицами Хессенберга, т.е. для них
h[f = 0 при г > j¦+ 1.
2°. Для выполнения одной итерации QR-алюритма для матрицы
Хессенберга требуется число арифметических операций, пропорци-
пропорциональное т2.
Однако, как уже было отмечено, даже достигнутая благодаря пред-
предварительному преобразованию матрицы А к виду (8.35) существенная
экономия числа арифметических операций недостаточна для практи-
практического использования (ЗД-алгоритма. Дело в том, что при наличии
близких соседних собственных значений А, к A,.j элемент А^*t-i
А,
ет очень медленно пропорционально qK, где q =
А,-,
я 1. Для реше-
решения этой проблемы используют различные варианты QR-алюритма со
сдвигами.
Поясним суть этого подхода. Допустим, что для А, известно
хорошее приближение А *. Тогда собственными значениями матрицы
Iflk) = jj(k) _ д *е являются Д; = А7 - A*, j - 1, 2, ..., т. В этом слу-
случае вместо отношения -г—- « 1 скорость убывания поддиагонального
А,-]
х А'А
=
элемента Ji{k) определяет величина
т
-j— я 0. После
нескольких итераций фЯ-алгоритма, которые практически сделают
элемент ft< fc)t -1 равным нулю, следует выполнить обратный сдвиг, пола-
233

гая #' к) = В(к) + А *Е. После выполнения этой операции матрицы А
и #'*> снова имеют общий набор собственных значений.
Последовательное осуществление сдвигов для t = m, m — 1, ..., 1,
сопровождаемых итерациями по фД-алгоритму, дает возможность
быстро привести матрицу А к виду (8.33). Остающийся, невыясненным
вопрос о том, как получить приближенные значения А* « А„ снимает-
снимается, если учесть, что в ходе фД-алгоритма диагональные элементы /»<*>
сходятся к А, при к -> оо. Следовательно, в качестве А* можно, напри-
например, брать элементы1 Л<*>.
Итак, прежде чем применять <?Д-алгоритм, следует преобразовать
исходную матрицу А к форме Хессенберга. Без такого преобразования
#Д-алгоритм практически не применяется. Затем целесообразно ис-
использовать один из вариантов фД-алгоритма со сдвигами.
Пусть теперь собственные значения найдены и требуется найти
один собственный вектор е; матрицы А, отвечающий собственному
значению Хр или несколько собственных векторов. Тогда целесообраз-
целесообразно сначала найти соответствующий собственный вектор е; матрицы Н<
(например, методом обратных итераций), а затем вычислить е; по
формуле С] = P-Vj, где Р — матрица подобия из (8.36).
Замечание1. Вычисление собственного вектора е} непосредст-
непосредственным применением метода обратных итераций к матрице А воз-
возможно, но потребует большего числа арифметических операций по
сравнению с указанным выше подходом.
Замечание 2. Проведенное в этом параграфе обсуждение
алгоритма носило в значительной степени ознакомительный харак-
характер. Практически не был затронут случай, когда матрица имеет
кратные или комплексные собственные значения. Не рассматрива-
рассматривались и особенности применения фД-алгоритма для комплексных
матриц.
Замечание 3. фД-алгоритм обладает хорошей обусловлен-
обусловленностью. Например, как показано в [19], в одном из его вариантов
после числа итераций, не превосходящего 5, для каждого собствен-
собственного значения получаются приближения А*, А*, ..., А^, являющи-
1 Чаще всего в библиотечных программах используется либо указанная
стратегия сдвигов (сдвигов по Рэлею), либо стратегия сдвигов по Уилкинсону
[84].
234
еся точными собственными значениями некоторой матрицы А,
такой, что
\А-А.\Е<ттЧи\\А\Е
(это утверждение сформулировано в терминах обратного анализа
ошибок).
$ 8.5. Дополнительные замечания
1. В данной книге не рассмотрены некоторые весьма популярные методы
решения проблемы собственных значений. Изложение метода бисекций,
метода вращений Якоби, QL-алюритма (являющегося вариантом QR-
алгоритма), LR-алюритма и других методов можно найти, например в [19],
[20], [62], [83], [84].
Авторы советуют обратить внимание на книгу [41], содержащую изложение
современных численных методов решения проблемы собственных значений,
вполне доступное для студента или выпускника технического вуза.
2. Если А — заполненная матрица общего вида умеренного порядка, то
лучшим выбором для вычисления всех собственных значений служит один из
вариантов (ЗЯ-алгоритма со сдвигами. Необходимо только предварительно
преобразовать матрицу к форме Хессенберга.
3. В случае, когда А — симметричная матрица умеренного порядка, ее
обычно приводят сначала с помощью последовательных преобразований Хаус-
холдера к трехдиагональному виду. Для вычисления собственных значений
полученной трехдиагональной матрицы можно использовать <2Д-алгоритм, но
по-видимому, чаще более предпочтительным является метод бисекций. Одно
из достоинств этого алгоритма состоит в том, что он позволяет находить не все
собственные значения, а одно или группу нужных собственных значений.
4. Если приближенное значение собственного числа найдено, то подходя-
подходящим методом вычисления соответствующего собственного вектора является
метод обратных итераций.
5. Методы, которые используются в настоящее время для решения пробле-
проблемы собственных значений в случае, когда А — разреженная матрица большой
размерности, можно разделить на две основные группы: методы одновремен-
одновременных итераций (или итерирования подпространства) и методы типа Ланцо-
ша... Их обсуждение можно найти, например, в [41]. Один из простейших
возможных подходов — степенной метод — был рассмотрен в § 8.2.

х, выполняется неравенство f(x) < /(г), то г называется точкой стро-
юю локальною минимума.
Глава 9
МЕТОДЫ ОДНОМЕРНОЙ МИНИМИЗАЦИИ
Одно из важнейших направлений в конструировании изделий, а
также проектировании и эксплуатации технологических процессов
состоит в оптимизации (минимизации или максимизации) некоторой
характеристики f(x). Функцию /(х) часто называют целевой функцией.
Заметим, что основное внимание может быть уделено минимизации
целевой функции, так как максимизация сводится к минимизации с
помощью введения новой целевой функции J (х) = -f(x). В случае,
когда варьируется один скалярный параметр х, возникает задача одно-
одномерной минимизации.
Необходимость изучения методов решения задачи одномерной
минимизации определяется не только тем, что задача может иметь
самостоятельное значение, но и в значительной мере тем, что алгорит-
алгоритмы минимизации являются существенной составной частью алгоритмов
решения задач многомерной минимизации (см. гл. 10), а также других
вычислительных задач.
$ 9.1. Задача одномерной минимизации
1. Постановка задача. Определения. Пусть /(х) — действительная
функция одной переменной, определенная на множестве X С ( -оо, со).
Напомним, что точка х € X называется точкой глобальною минимума
функции /на множестве X, если для всех х € X выполняется неравенс-
неравенство /(х) < /(х). В этом случае значение /(х) называется минимальным
значением функции /на X.
Точка х € X называется точкой локальною минимума функции /,
если существует такая 6-окрестность этой точки, что для всех х из
меножества X, содержащихся в указанной ^-окрестности, выполняется
неравенство /(х) < /(х). Если же для всех таких х, не совпадающих с
236
Пример 9.1. Для функции, график которой изображен на рис. 9.1, точки
л?з и *4 являются точками строго локального минимума, а в точках х, удовлет-
удовлетворяющих неравенству х^ < х < *2. реализуется нестрогий локальный мини-
минимум.
Рис. 9.1
Известно, что необходимым условием того, чтобы внутренняя для
множества X точка х была точкой локального минимума дифференци-
дифференцируемой функции /, является выполнение равенства
/'(*) = 0. (9.1)
Число х, удовлетворяющее этому равенству, называется стационарной
точкой функции /. Конечно, не всякая стационарная точка х обязана
быть точкой локального минимума. Для дважды непрерывно диффе-
дифференцируемой функции достаточным условием того, чтобы стационар-
стационарная точка х была точкой строгого локального минимума, является
выполнение неравенства f(x) > 0.
Существуют различные постановки задачи минимизации. В самой
широкой постановке требуется найти все точки локального минимума
и отвечающие им значения функции / В приложениях чаще всего
возникает задача вычисления конкретной точки локального минимума
или точки глобального минимума. Иногда представляет интерес толь-
только лишь минимальное значение целевой функции, независимо от того,
в какой именно точке оно достигается.
2. Отрезок локализации. Подобно тому, как алгоритмы решения
нелинейных уравнений настроены на отыскание одного изолированно-
237

го корня (см. гл. 4), большинство алгоритмов минимизации осуществ-
осуществляет лишь поиск точки локального минимума функции /. Для того
чтобы применить один из таких алгоритмов минимизации, следует
предварительно найти содержащий точку х отрезок [а, Ь], на котором
она является единственной точкой локального минимума. Этот отрезок
в дальнейшем будем называть отрезком локализации1 точки х. К
сожалению, не существует каких-либо общих рецептов относительно
того, как найти отрезок локализации. В одномерном случае полезным
может оказаться табулирование функции с достаточно мелким шагом и
(или) построение графика. Отрезок [а, Ь] может быть известен из фи-
физических соображений, из опыта решения аналогичных задач и т. д
Для некоторых алгоритмов (например, для метода Ньютона) достаточ-
достаточно иметь не отрезок локализации, а хорошее начальное приближение
г@)
К X.
Пример 9.2. Для функции / (г) = х3 —
— х + е'х произведем локализацию то-
точек локального минимума.
Из графика функции, изображенного
на рис. 9.2, видно, что функция /(г)
имеет две точки локального минимума xi
и Г2, первая из которых является и точ-
точкой глобального минмума. Для точки х\
за отрезок локализации можно принять
отрезок [-4, -3], а для точки Гг — отре-
отрезок [0, 1].
Докажем теперь, что на отрезке [0, 1]
действительно содержится точка локаль-
локального минимума. Для этого заметим, что
/'(г) = З*2 - 1 - ех и /'@) = -2 < 0,
= 2 — е > 0. Так как значения
Рис 9.2
f@) и /'A) имеют разные знаки, то на отрезке [0, 1] содержится точка г, для
которой f'(x) = 0. Но f(x) = бх + е'х > 0 для всех х € [0, 1]. Следовательно,
/"(г) > 0 и точка х на отрезке [0, 1] есть единственная точка локального ми-
1 В теории оптимизации отрезок [а, 6] чаще называют интервалом неопре-
неопределенности. Мы понимаем интервал неопределенности иначе (см. § 9.2).
238
кимума. Аналогично доказывается, что отрезок [—4, —3] также является отрез-
отрезкам локализации.
3. Унимодальные функции. Пусть / — функция, определенная на
отрезке [а, 6]. Предположим, что на этом отрезке содержится единст-
единственная точка х локального минимума функции /, причем функция
строго убывает при х < х и строго возрастает при х > г. Такая функ-
функция называется унимодальной1. Возможны три случая расположения
точки х на отрезке [а, Ь]: точка х является внутренней для отрезка, х
совпадает с левым концом отрезка и х совпадает с правым концом
отрезка. Соответственно и график унимодальной функции может иметь
одну из форм, схематично изображенных на рис. 9.3.
б)
I I
I I I
OX, X2 *3 Ь X. PUC. 9.4
Замечание. Унимодальная функция, вообще говоря, не обяза-
обязана быть непрерывной. Например, функция, изображенная на рис.
9.4, унимодальна и имеет три точки разрыва.
Приведем достаточное условие унимодельности функций на отрезке
[а, Ь].
Предложение 9.1. Если для всех х € [а, Ь] выполнено условие
f(x) > 0, то функция унимодальна на отрезке [а, Ь].
Пример в.З. Функция /(г)=х3 — г + е'х унимодальна на каждом из
отрезков [-4, —3] и [0, 1]. Чтобы убедиться в этом, достаточно заметить, что
1 Иногда такую функцию называют строго унимодальной, а унимодальной
называют функцию, которая строго убывает при х < xj, равна постоянной при
х\ < х ^ *2 и строго возрастает при х 2 х^ [Щ-
239

f'(x) - 6г + e1 > 0 для всех х € [-4, -3], х € [О, 1], и воспользоваться пред-
предложением 9.1.
Для сужения отрезка локализации точки минимума унимодальной
функции полезно использовать следующее утверждение.
Предложение 9.2. Пусть / — унимодальная на отрезке [а, Ь]
функция и а < а < -у < 0 < Ъ. Тогда:
1°) е<м« /(а) </(/?), тох€[л,0[;
2«) ecAuf(a))f(p), mo~x?[a, 6];
30) если f(a)> f(t), и /G) < /(/?), то i 6 [а, Д.
о 1°. Предположим противное: х > /?. Тогда вследствие унимодаль-
унимодальности /получим /(а) > f(ff), что противоречит условию.
2°. Предположим противное: х < а. Тогда вследствие унимодаль-
унимодальности /получим /(а) < /(/?), что противоречит условию.
3°. В силу п. 1° имеем г ? [а, ft, a в силу п. 2° имеем г 6 [а, 6]
Следовательно, г € [а, Д.
Геометрическая иллюстрация пп. 1° и 2° приведена на рис. 9 5. II
иобып отрезок
о)
новый отрезок
б)
Рис. 9.5
Рис. 9.6
240
Многие алгоритмы одномерной минимизации построены в расчете
на то, что на отрезке локализации целевая функция унимодальна. В
частности, такими являются алгоритмы, рассматриваемые в § 9.3.
4. Об одном подходе к локализации точки минимум». На практике
часто бывает неизвестно, является ли данная функция унимодальной.
Однако во многих случаях из дополнительных соображений следует,
что при г ^ го функция /сначала убывает, а затем, начиная с некото-
некоторого значения х = х, становится возрастающей (правда, не исключено,
что далее она снова может стать убывающей). Для того чтобы в таком
случае локализовать точку г, используют различные нестрогие
методы. Один из распространенных подходов состоит в следующем.
Выбирают начальный шаг Л > 0, в несколько раз меньший предпола-
предполагаемого расстояния от точки xq до точки х. Затем вычисляют и срав-
сравнивают значения /(г0) и /(ii), где тл = rc + A
Если оказывается, что f(xo) > f(x\), то последовательно вычисляют
значения функции /в точках хк = яо + 2^'Л для к Ъ 2. После обнару-
обнаружения первой же точки, для которой /(ц) ^ /(гы), за отрезок лока-
локализации принимают отрезок [rjt-j, хы]. В случае, изображенном на
рис. 9.6, а, за отрезок локализации принят отрезок [т2, г4]
Если же / (хо) < /(zi)> то последовательно вычисляют значения в
точках хк = io + Л/2'с"!, к ^ 2. После обнаружения первой же точки ц,
для которой /(ц) < / (zo)> за отрезок локализации принимают отре-
отрезок [г0, ?fc-i]. В случае, изображенном на рис 9 б, б, за отрезок локали-
локализации принят отрезок [х0, х2].
Описанный метод не является строгим и не гарантирует, что отре-
отрезок локализации всегда будет найден. Например, для функции, гра-
график которой изображен пунктиром на рис. 9.6, а, при выбранном шаге
h справедливы неравенства /(г0) > /(rj) > 1(хг) > f (x3) > f (x^) и
поэтому отрезок локализации точки г обнаружен уже не будет Тем не
менее этот или близкий к нему методы часто используются на практи-
практике.
Пример 9.4 Локализуем указанным выше образом точку локального мини-
минимума функции /(х) = хг — х+ е'х.
Возьмем хъ = -5, А = 0.2 и положим г\ = ц + Л = -4.8. Так как /(*ь) «
я 28.4 > /(ч) й 15.7, то будем последовательно вычислять значения функции
/в точках j-fc = г§ + 2^'Л. Из табл. 9.1 видно, что при к = i впервые выпол-
выполняется неравенство /(zfc) < f {гк+\)- Поэтому за отрескж локализации следует
принять отрезок [хз, i$] — [-4.2, -1.8].
241

Таблица 9.1
it
*к
f(*k)
0
-б
28.4
1
-4.8
15.7
2
-4.6
6.74
3
-4.2
-3.30
4
-3.4
-6.94
5
-1.8
2.02
{ 9.2. Обусловленность задачи минимизации
Пусть х — точка строгого локального минимума функции / вычис-
вычисляемой с погрешностью. Будем считать, что в некоторой окрестности
точки х вычисляемые приближенные значения /*(х) удовлетворяют
неравенству |/(х) — /*(х)| < Д = Д (/*), т. е. имеют границу абсолют-
абсолютной погрешности, равную Д. Как нетрудно понять, существует такая
малая окрестность (х — е, х + е) точки минимума х, для которой,
, , основываясь на сравнении вычисля-
емых значений / (х), нельзя досто-
достоверно определить ту точку, в кото-
которой действительно достигается ми-
wf*(x) У нимум функции / Эта ситуация
1 схематично изображена на рис. 9.7.
Интервал (х — е, х + е) будем назы-
/-ё х х+ё х* вать интервалом неопределенности
Рис. 9.7 точки х локального минимума.
Оценим величину е радиуса интервала неопределенности в
предположении, что функция /дважды непрерывно дифференцируема
и выполнено условие /*(х) > 0. В этом случае с учетом того, что
/'(х) = 0, для значений функции /в точках х, близких к х, справедли-
справедливо приближенное равенство
Оценим минимальное расстояние между точками х и х, начиная с
которого заведомо будет выполнено неравенство /*(х) > /*(х), т. е.
точка х перестанет попадать в интервал неопределенности. Имеем
242
/*(х) - /*(х) = /(х) - /(г) + (Г(х) - /(*)) - (Г(г) - f{x)) >
> /U) - /(«) - 2Д « ?& (х - хJ - 2Д.
Следовательно, /*(х) — /*(х) > i (х — хJ — 2Д и неравенство
/*(х) > /*(х) выполнено, если (х — хJ > 4Д//"(х). Таким образом,
(9.2)
Заметим, что любое приближение х* к х, попавшее в интервал неопре-
неопределенности, нельзя отличить от точного значения х точки минимума,
используя только вычисляемые значения /* функции /. Поэтому
Итак, рассматриваемую задачу минимизации нельзя назвать хоро-
хорошо обусловленной. Если задача хорошо масштабирована, т. е. х ~ 1,
1/(гI ~ 1| Г(х) ~ 1| то соотношение (9.3) можно записать в терминах
относительных погрешностей так:
_ -Я1/.
Отсюда следует, что если ?(/*) ~ 10"™, то 8{х*) ~ 10 . Иными слова-
словами, если значения функции вычисляются с m верными значащими
цифрами, то приближенное значение точки минимума можно найти
примерно лишь с т/2 верными значащими цифрами.
Таким образом, точность определения положения точки минимума
гладкой функции существенным образом зависит от точности вычисле-
вычисления функции /. При этом если для поиска х используются только
приближенные значения /*(х), вычисляемые для различных х, то
неизбежна потеря примерно половины верных значащих цифр.
Предположим теперь, что для отыскания точки локального мини-
минимума можно использовать вычисляемые каким-либо образом прибли-
приближенные значения (/') *(х) производной функции /. Как уже отмечалось
в § 9.1, в рассматриваемом случае задача минимизации эквивалентна
задаче отыскания корня х нелинейного уравнения f'(x) = 0. Из ре-
результатов § 4.2 вытекает, что последняя задача обладает значительно
243

меньшей чувствительностью к ошибкам. В частности, справедлива
следующая оценка границы абсолютной погрешности:
Д
А*)
(9.4)
Сравнение (9.4) с оценкой (9.3) показывает, что алгоритмы, исполь-
использующие для отыскания решения г уравнения (9.1) вычисление значе-
значений производной, могут достигать более высокой точности, чем алго-
алгоритмы, использующие для минимизации функции /только вычисление
ее значений.
Пример 0.5.Оценим радиус интервала неопределенности для каждой из
точек «! и -3,7, х2 я 0.7 локального минимума функции /(х) = х3 — * + е'х в
случае, когда вычисление функции производится на 6-разрядной десятичной
ЭВМ1.
Заметим, что f(x{) я /(-3.7) я -6.5, /(х2) я /@.7) и 0.14. Так как для
используемой ЭВМ2 ?м = 5-Ю, то в малой окрестности точки "х\ верхняя
граница Ai абсолютной погрешности вычисления / приближенно равна
?м |/п)| и 5-10-7-6.5 = 325-Ю6. Аналогично, Д2 я ем |/(х2)| я
« 5-10-0 14 = 7-Ю"8.
Вычисляя значения второй производной f'(x) - 6* + е'х при х = xj, x =
- xi, получаем /"(xj) я 18, f(z2) я 4.7. В силу формулы (9.2) радиусы
интервалов неопределенности оцениваются следующим образом:
El и 2\Ai/f(xi) я 2 V3-25-10-6/18 я 8-Ю,
Е2 « 2.J А2/Г(х2) й 2 V7-Ю-8/4.7 и 2-10.
Следовательно, точку х2 можно найти с большей точностью, чем точку х), если
использовать сравнение вычисляемых на 6-разрядной десятичной ЭВМ значе-
1 Напомним, что 6-разрядной десятичной ЭВМ мы условились называть
гипотетическую ЭВМ, имеющую 6 десятичных разрядов мантиссы и произ-
водяющую округленир по дополнению.
2 Напомним, что через Ем обозначено машинное эпсилон — величина, ха-
характеризующая относительную точность представления чисел в ЭВМ.
244
ний функции / При этом каждую из точек можно найти с точностью е = 10,
но вряд ли удастся найти с точностью е = 10.
Пример 9.6. Пусть теперь точки xi и х2 локального минимума функции
/(х) = х3 — х + е ищутся как решения нелинейного уравнения
/'(х) = Зх2-1-е-*=0. (9.5)
Оценим в этом случае радиус интервала неопределенности для каждой из
точек X], х2, если вычисления ведутся на той же ЭВМ, что и в предыдущем
примере.
Оценим сначала границу абсолютной погрешности вычисления производной
исходя из приближенного равенства
Д =
Тогда
е-*).
Ai я eMC"ri + е**) « 4-10'5, Д2 я емCг1 + е'2) я Ю.
На основании формулы (9.4) имеем
Ё, я Д,//*(^) я 2-10, ё2 я Ai/fC'i) й 2- Ю-7. (9.6)
Заметим, что погрешности представления чисел *t, r2 на 6-разрядной
десятичной ЭВМ таковы: ?M|^| я 2-Ю, Ем|х2| я 4-Ю. Поэтому получен-
полученные оценки (9.6) означают, что, решая уравнение (9.5), можно найти точки Т[
и х2 с максимальной для используемой ЭВМ точностью, равной соответственно
2-Ю и 4-10 (ср. с результатом предыдущего примера).
§ 9.3. Методы прямого поиска.
Оптимальный пассивный поиск.
Метод деления отрезка пополам.
Методы Фибоначчи и золотого сечения
Ряд методов минимизации основан на сравнении значений функции
/, вычисляемых в точках х\, г%, •¦-, Ш Эти методы часто называют
методами прямою поиска, а точки х, — пробными точками.
Прежде чем перейти к изложению некоторых из наиболее извест-
известных методов прямого поиска, уточним постановку задачи. Будем счи-
245

тать, что требуется найти приближение х* к точке минимума х унимо-
унимодальной на отрезке [а, Ь] функции /. Предположим также, что число
пробных точек N заранее фиксируется и за приближение х* к точке
минимума принимается одна из этих точек.
1. Оптимальный пассивный поиск. Метод решения поставленной
задачи, в котором задается правило вычисления сразу всех пробных
точек xi, r2, ..., хц и за х* принимается та точка xjt, для которой
/(rjt) = min /(*i)> называется методом пассивною поиска. Соот-
ветствующая геометрическая иллюстрация приведена на рис. 9.8.
Оценим погрешность этого
метода. Для удобства положим
= а,
= Ь. В силу выбо-
выбора точки х* —
справедливы
неравенства /(zjh) ^ f(xk) и
/(**) < /(*ы)- Поэтому из
п. 3° предложения 9.2 следует,
0 Xt ti X/,-1 A* Xtw KH ft X
Рис. 9.8 - -
что х € [xic-i, Xkn\. оначит, | х —
— xjt| ^ max {xjt — xjt-i, x^+i — x^}. Так как положение точки минимума
х на отрезке [а, 6] заранее неизвестно, то для х* = xjt справедлива
лишь следующая гарантированная оценка погрешности:
\х- х*\
max
(9.7)
Можно показать, что величина, стоящая в правой части неравенст-
неравенства (9.7), станет минимальной, если точки х\, Х2, ..., xn расположить на
отрезке [а, Ь] равномерно в соответствии с формулой х, = а + ih, где
А = Д/(# + 1), Д = Ь — а. Метод с таким выбором пробных точек
называется оптимальным пассивным поиском. Гарантированная оцен-
оценка погрешности для него выглядит так:
Пример 9.7. Используем оптимальный пассивный поиск для того, чтобы
найти с точностью е = 0.1 точку г локального минимума функции /(г) = г3 —
— х + е"х, локализованную на отрезке [0, 1].
Из формулы (9.8) следует, что для решения задачи потребуется вычислить
значения функции в девяти пробных точках вида ц = 0.Ц где t = 1, 2 9.
Приведем таблицу этих значений:
246
х 0.1 0.2 0.3 0.4 0.5
Таблица 9.2
0.6 0.7 0.8 0.9
у 0.81 0.63 0.47 0.33 0.23 0.17 0.14 0.16 0.24 '
Так как минимальное значение достигается в точке ху= 0.7, то х = 0.7±0.1.
Если бы мы попытались найти х с точностью ? = 10, то оптимальный
пассивный поиск потребовал бы вычисления значений функции уже в 99
точках.
2. Метод деления отрезка пополам. Пусть для решения поставлен-
поставленной задачи последовательно вычисляются значения функции / в N
пробных точках х\, х2, ..., хц, причем для определения каждой из
точек Хк можно использовать информацию о значениях функции во
всех предыдущих точках х\, х2, ..., zjt-i- Соответствующие методы назы-
называют методами последовательною поиска. Рассмотрим простейший из
методов этого семейства — метод деления отрезка пополам. В нем, как
и в двух других рассматриваемых в этом параграфе методах (методах
Фибоначчи и золотого сечения), используется принцип последователь-
последовательного сокращения отрезка локализации, основанный на предложении
9.2 и на следующем простом утверждении.
Предложение 9.3. Если функция унимодальна на отрезке
[а, &], то она унимодальна и на любом отрезке [с, J\ С [а, 6].
Для удобства изложения обозначим отрезок [а. Ь] через [а@), 6@)].
Поиск минимума начинают с выбора на отрезке [а<0), 6@)] двух сим-
— 6, /?@) =
метрично расположенных точек а<01 =
„(О +
а@)
Ь - а
(- S. Здесь 0 < 6 < —-—, 6 — параметр метода. Далее
вычисляют значения /(а@)) и /(/?@))- Сравнение этих значений в
силу предложения 9.2 позволяет сократить отрезок локализации сле-
следующим образом:
если /(«<»>) < /(/?10)), то r€ [a<D, 6<П] = [в<°>,
если/(о<°») > /(/3@)), то г€[а<»
Если описанную процедуру принять за одну итерацию метода и
продолжить аналогичные операции для образования последователь-
последовательности сокращающихся отрезков локализации, то получим итерацион-
итерационный метод. Опишем очередную его итерацию исходя из того, что
отрезок локализации [a(fc), b{k)] уже найден. Выполняют следующие
действия:
247

1°. Вычисляют а(к) =
6, р{ к> =
e(fc)
2 ». л- - 2
2°. Находят значения /(<*<*>) и f(P(k))-
3°. Новый отрезок локализации определяют по правилу:
если /(<*<*>) < /(/?<*>), то
J1
fk.il
если /(<*<*>) > /(/?<*>)> то
1
'{*")])№ */М В первом случае за очередное
приближение к точке минимума
Первый
смчаи
а(к.п
а во
ь
Второй
случаи
Рис. 9.9
Как нетрудно заметить, справедливо равенство
принимают
втором случае x(**n = /?(fc) (рис.
9.9).
Обозначим через Д<п> = bin) —
— а{п) длину отрезка [а(п), 6(п)].
(9.9)
Поэтому, если параметр S достаточно мал F < Д(п)). то длина вновь
полученного отрезка почти вдвое меньше длины предыдущего отрезка.
Отсюда — и название метода.
Используя равенство (9.9), с помощью метода математической ин-
индукции легко показать, что
Заметим, что Д<п) убывает и при п -» <х> стремится к величине 28,
оставаясь при каждом п больше этой величины. Поэтому сделать при
некотором п длину Д<п> отрезка локализации [а(п), 4<п)] меньше
заданного е > 0 можно лишь, выбрав 6 < е/2. В этом случае из оче-
очевидной оценки погрешности \xin) — х\ < Д(п) следует, что значение
х действительно можно найти с точностью е и справедлив следующий
критерий окончания итерационного процесса. Вычисления следует
прекратить, как только окажется выполненным неравенство
до) <е. (9.10)
Тогда за приближение к х с точностью е можно принять х* = х(п).
248
Замечание. При реализации метода на ЭВМ необходимо
учитывать, что вычисления значений функции / будут произво-
производиться с погрешностью. Для того чтобы знак разности /*(а(п)) —
— /*(?<п)) совпадал со знаком разности /(а(п)) — /(/?<п))> необхо-
необходимо, чтобы выполнялось условие В > е (см. равенство (9.2)). По-
Поэтому 6 нельзя задавать слишком малым.
Пример 9.8. Применяя метод деления отрезка пополам, найдем с точностью
? = 10 точку х локального минимума функции /(*) = г3 — х + е'х, локали-
локализованную на отрезке [0, 1]. Вычисления будем вести на 6-разрядной десятич-
десятичной ЭВМ.
Зададим 6 = 10, о@> = 0, 6«°» = 1.
а@) 4-
I итерация. 1. Вычислим а@) =
— 6 — 0.499,
„@)
+ 6 = 0.501.
2. Определим значения /(а<°>) и 0.232389, /(/?<0)) « 0.230676.
3. Так как /(«<<») > /(/?<°»), то следует положить [ аA), *<>>] =
.= [0.499, 1].
Результаты следующих итераций приведены в табл. 9.3.
Таблица 9.3
п
0
1
2
3
4
5
6
7
0<п)
0.000000
0.499000
0.499000
0.623750
0.686125
0.686125
0.701607
0.710141
bin)
1.000000
1.000000
0.750500
0.750500
0.750500
0.719088
0.719088
0.719813
а(П)
0.499000
0.232389
0.748500
0.143924
0.623750
0.154860
0.686125
0.140403
0.717088
0.139821
0.701607
0.139549
0.708348
0.139543
0.501000
0.230676
0.750500
0.144350
0.625750
0.154131
0.688125
0.140230
0.719088
0.139940
0.703607
0.139520
0.711348
0.139587
Д(П)
1.000
0.501
0.252
0.125
0.063
0.033
0.017
0.010
249

Так как АG> < е, то при п = 7 итерации прекратим и положим х
= 0.711348. Таким образом, 1с = 0.71 ± 0.01. Заметим, что для
достижения точности ? = 10~2 потребовалось 14 вычислений функции.
3. Метод Фибоначчи. Заметим, что метод деления отрезка пополам
требует на каждой итерации вычисления двух новых значений функ-
функции, так как найденные на предыдущей итерации в точках а(п> и
/?< п) значения далее не используются. Обратим теперь внимание на то,
что одна из этих точек (обозначенная в предыдущем параграфе через
х(п)) является внутренней для отрезка [o(n), bin)] и поэтому дальней-
дальнейшее сокращение отрезка можно произвести, вычислив дополнительно
значение функции лишь в одной новой точке. Это наблюдение приво-
приводит к методам, требующим на каждой итерации (кроме первой) расче-
расчета лишь одного нового значения функции / Два наиболее известных
среди них — методы Фибоначчи и золотого сечения.
Метод Фибоначчи1 является оптимальным последовательным мето-
методом, т. е. методом, обеспечивающим максимальное гарантированное
сокращение отрезка локализации при заданном числе N вычислений
функции. Этот метод основан на использовании чисел Фибоначчи Fn,
задаваемых рекуррентной формулой
Fn = Fn-x + Fn.2 (n > 2)
и начальными значениями Fo = 1, Fi = 1. Укажем несколько первых
чисел: FQ = 1, Fx = 1, F2 = 2, F3 = 3, F4 = 5, F5 = 8, F6 = 13, F7 = 21,
F6 = 34, F9 = 55, Flo = 89, Fn = 144.
Метод Фибоначчи состоит из N — 1 шагов. Очередной (к + 1)-й
шаг выполняют здесь аналогично (it + 1)-й итерациии метода деления
отрезка пополам. В отличие от него точки о(к), /?(fc) здесь находят по
формулам
( к) = а( it)
l д ( к) о( k) — а( к)
Д ( к) _
Новый отрезок локализации определяют по тому же правилу:
если /(«<*») </(/?<*>). то [
если /(«<*>) > /(/?<*>), то
1 Фибоначчи (Леонардо Пизанский) A180—1240) — итальянский математик.
250
В первом случае за очередное приб-
приближение к точке минимума прини-
принимают г1**1' = а( *>, а во втором слу-
случае г'**1' = /?<*> (рис. 9.10).
Важно то, что в любом случае точка
z(fc+n совпадает с одной из точек
<м
а("
i
а"""
' 1
b!M)
Первы?
случаи
второй
c/igvau
FN-k-l
Рис. 9.10
Поэтому на очередном шаге достаточно вычислить значение функции
лишь в одной недостающей точке.
В результате выполнения iV — 1 шагов отрезок локализации умень-
уменьшается в Fn*\/2 раз, а точка xiN'l) оказывается центральной для пос-
последнего отрезка локализации [aiN'1), б'^11]. Поэтому для x(N'l)
справедлива следующая оценка погрешности:
1
(9.11)
Пример 9.9. Применяя метод Фибоначчи, найдем с точностью ? = 10~2
точку х локального минимума функции f(z) = i3 — г + е'х, локализованную
на отрезке [0, 1]. Вычисления будем вести на 6-разрядной десятичной ЭВМ.
Первым среди чисел Фибоначчи, для которого выполняется условие
&/Ffft\ < ? (где Д = 1), является число Fn — 144, отвечающее ЛГ = 10.
Зададим а<°> = 0, Ь<°> = 1.
Первый шаг. 1. Вычислим а'0» = а<°> + (Ь<°> - а§ ^
F\ 1 144
и 0.381944, /?<о> = в<0) + (ft@) _
= ?Lw 0.618056.
144
2. Определим значения /(а<°>) и 0.356308, /(/?@)) и 0.157028.
3. Так как/(а'0') >/(/?@)), то положим [а<1>, 6")] = [а<°>, Ь<°>].
Второй шаг. 1. Учитывая, что аA) = /?10) и 0.618056, вычислим
= а<1> + F"> - a<i>)fyFl0 и 0.763889.
2. Вычислим значение /(/?A)) « 0.147712.
3. Так как/(а'1») >/(/?">), то положим [а<2', б'2'] = [о'1),
Результаты остальных шагов приведены в табл. 9.4.
251

Таблица 9.4
n
0
1
2
3
4
5
6
7
8
9
а(П)
0.000000
0.381944
0.618056
0.618056
0.618056
0.673611
0.673611
0.694445
0.694445
0.701389
fclnl
1.000000
1.000000
1.000000
0.854167
0.763889
0.763889
0.729167
0.729167
0.715278
0.715278
a(n)
/(«<"»)
0.381944
0.356308
0.618056
0.157028
0.763Й89
0.147712
0.708334
0.139527
0.673611
0.141905
0.708334
0.139527
0.694445
0.139805
0.708334
0.139527
0.701389
0.139553
0.708334
/(/?<">)
0.618056
0.157028
0.763889
0.147712
0.854167
0.194672
0.763889
0.147712
0.708334
0.139527
0.729167
0.140830
0.708334
0.139527
0.715278
0.139731
0.708334
0.139527
0.708334
Д(«)
1.000
0.618
i).382
0.236
0.119
0.090
0.056
0.035
0.021
0.014
После 9 шагов вычисления прекращаем и полагаем г « /9(8) = 0.708334. Та-
Таким образом, х = 0.71 ± 0.01. Заметим, что для достижения точности ? = 10~2
потребовалось 10 вычислений значения функции, в то время как при исполь-
использовании метода деления отрезка пополам необходимо 14 вычислений.
Хотя метод Фибоначчи и оптимален в указанном выше смысле,
зачастую он неудобен для использования. В частности, это касается
возможного применения поиска Фибоначчи для решения одномерных
подзадач в алгоритмах многомерной минимизации. Здесь нередко
эффективность алгоритма одномерной минимизации оценивается не по
тому, какая точность в значении х получена, а совсем по другим кри-
критериям, к которым метод плохо приспособлен. Например, бывает важ-
важно достичь минимального значения функции /с некоторой относитель-
относительной точностью 6 либо уменьшить значение / на определенную величи-
величину.
4. Метод золотого сеченая. Из-за указанных недостатков вместо
252
метода Фибоначчи чаще используется теоретически почти столь же
эффективный метод золотою сечения.
Напомним, что золотым сечением1 отрезка называется такое раз-
разбиение отрезка на две неравные части, что отношение длины всего
отрезка к длине его большей части равно отношению длины большей
части к длине меньшей части отрезка.
Золотое сечение отрезка [а, А] осуществляется каждой из двух сим-
симметрично расположенных относительно центра отрезка точек
(Ь -а)
(рис. 9.11). Действительно, как нетрудно проверить,
Замечательно то, что точка а осуществляет золотое сечение не
только отрезка [о, Ь], но и отрезка [а, Р].
— а
Действительно, ——- - ^ _ а - 2
Точно так же точка Р осуществляет золотое
сечение не только отрезка [а, Ь], но и отрезка [в, Ь]. Этот факт далее
существенно используется.
Очередная (Jfc + 1)-я итерация метода золотого сечения произво-
производится аналогично (к + 1)-й итерации метода деления отрезка пополам.
В отличие от него точки о( *>, Р{ к) находятся по формулам
= alk)
Важно то, что какой бы из отрезков [al*>, 6(fc)] или [a<*>, &'*>] не
был бы выбран за очередной отрезок локализации, точка z(fc+1) (в
первом случае r(fc+1> = a<*>, а во втором случае *<ы> = Р1к)) совпа-
совпадает с одной из точек a(fc+1), /?(Ы). Поэтому на очередном шаге дос-
• Термин "золотое сечение" ввел Леонардо да Винчи. Принципы золотого
сечения широко использовались при композиционном построении многих
произведений мирового искусства (в особенности, архитектурных сооружений
античности и эпохи Возрождения).
253

таточно вычислить значение функции лишь в одной недостающей
точке.
Заметим, что точка г(п) отстоит от концов отрезка [ain), bin)] на
2
величину, не превышающую Д <п). Поэтому верна оценка
Таблица 9.5
1 +
-х\
Д(П) _
(9-12)
которую можно использовать для апостериорной оценки погрешности.
Заметим, что каждая итерация сокращает длину отрезка локализации
в (V5 + 1)/2 раз. Поэтому б' - а<п> = Д<»»> = B/(^5 + 1))п Д и
справедлива следующая априорная оценка погрешности:
-х\
1 +
п+1
д.
(9.13)
Таким образом, метод золотого сечения сходится со скоростью геомет-
геометрической прогрессии, знаменатель которой q = 2/(^5 + 1) « 0.62.
Пример 9.10. Найдем методом золотого сечения с точностью ? = 10 точку
г локального минимума функции f(x) = х3 — х + е'х, локализованную на
отрезке [0, 1].
Положим а<°> = 0, 6@> = 1.
I итерация. 1. Вычислим а@) = а<°> +
(i<0) _ в<<») я
я 0.381966, /?@> = а<°> +
F@) _ „@)) a 0.618034.
2. Вычислим /(о<°>) й 0.356280, /(/?@)) й 0.157037.
3. Таккак/(а@») > /(/?<0>), то положим [а(»), ftd)] = [а@)' ft@)].
II и т е р а ц и я. 1. Учтем, что аA) = /И0) и 0.618034, и вычислим
= в(П
_ а(П
а(П) й 0.763936.
2. Вычислим /С^*1») и 0.147725.
3. Так как /(«*<») = /(^@)) > /(/9">), то положим [а<2>,
- [а'1', *(»)].
Результаты остальных итераций приведены в табл. 9.5.
254
п
0
1
2
3
4
5
6
7
8
9
а(п)
0.000000
0.381966
0.618034
0.618034
0.618034
0.673764
0.673764
0.695051
0.695051
0.695051
6<п>
1.000000
1.000000
1.000000
0.854102
0.763936
0.763936
0.729493
0.729493
0.716337
0.708204
а(п)
/(а"»)
0.381966
0.356280
0.618034
0.157037
0.763936
0.147725
0.708204
0.139526
0.673764
0.141883
0.708204
0.139526
0.695051
0.139774
0.708204
0.139526
0.703182
0.139525
/(/?<«>)
0.618034
0.157037
0.763936
0.147725
0.854102
0.194622
0.763936
0.147725
0.708204
0.139526
0.729493
0.140868
0.708204
0.139526
0.716337
0.139782
0.708204
0.139526
Д(П*1)
0.618
0.382
0.236
0.146
0.090
0.056
0.034
0.021
0.013
0.008
Так как ДA01 < е, то итерации следует прекратить и положить х я а<8) w
я 0.703182. Таким образом, х — 0.70 ± 0.01. Отметим, что для достижения точ-
точности е = 10~2 потребовалось 10 вычислений значений функции, как и в
методе Фибоначчи.
5. Эффектшгаость методов прямого поиска. Эффективность указан-
указанных методов можно оценивать, например, тем, во сколько раз умень-
уменьшается после использования N вычислений значений функции перво-
первоначальная длина Д отрезка локализации. Другой критерий — величи-
величина гарантированной оценки погрешности. Табл. 9.6 позволяет сравнить
по этим критериям рассмотренные выше методы. Как видно, очень
неэффективен пассивный поиск. Метод деления отрезка пополам
уступает почти эквивалентным по эффективности методам Фибоначчи
и золотого сечения.
255

Таблица 9.6
Метод прямого поиска
Длина отрезка
локализации
Величина гарантирован-
гарантированной оценки погрешности
Оптимальный пассивный 2 .
поиск N+ 1
Метод деления отрезка попо-
лам (N - четное, величиной 6 1 д и ^ д
пренебрегаем) "/2
2
Метод Фибоначчи —— Д « 1.7• @.62)^-Д
1
N+ 1
и 0.5-@.71)*- Д
«0.85- @.62)*- Д
Метод золотого сечения
Д «16-@.62)*- Д
и @.62)*
- Д
Приведем еще одну таблицу (табл. 9.7), из которой видно, сколько
вычислений функции /нужно сделать для того, чтобы достичь точнос-
точности ?. Предполагается, что начальный отрезок локализации имеет
единичную длину.
Таблица 9.7
Метод прямого поиска
Оптимальный пассивный
поиск
Метод деления отрезка
пополам F < ?)
Метод Фибоначчи
Метод золотого сечения
? = 10
9
6
5
5
Число
? = 10 ?
99
12
10
10
N при заданном ?
¦ = 10
999
18
15
15
? = 10
9999
26
19
20
? = Ю-5
99999
32
24
24
6. Влияние погрешности вычислений. Одна из самых распростра-
распространенных ошибок при обращении к стандартным программам, реализую-
реализующим тот или иной метод на ЭВМ, состоит в завышении требуемой
точности Необходимо понимать, что при наличии погрешностей в
вычислении значений функции /достижимая точность е методов пря-
256
мого поиска ограничена снизу величиной е « 2\ Д(/*)//'(х), где е —
радиус интервала неопределенности (см. § 9.2). Это означает, напри-
например, что прямые методы не позволяют найти на 6-разрядной десятич-
десятичной ЭВМ точку х2 локального экстремума функции /(х) = х3 — х + е~х
с точностью ? < ?2 и 2 • 10. Задание е < ?г приведет лишь к бесполез-
бесполезной трате машинного времени.
§ 9.4. Метод Ньютона и другие методы
i гладких функций
Отметим, что применение рассмотренных выше методов деления
отрезка пополам, Фибоначчи и золотого сечения не позволяет извлечь
никакой выгоды из возможной гладкости функции. Существуют мето-
методы, которые могут оказаться более эффективными, если минимизируе-
минимизируемая функция достаточно гладкая. Часть из них является просто моди-
модификациями известных методов решения нелинейных уравнений (см.
гл. 4) применительно к уравнению
/'(*) = 0.
(9.14)
1. Метод бисекции. Пусть /— унимодальная непрерывно дифферен-
дифференцируемая на отрезке [а<0), 4@)] = [а, Ь] функция и на отрезке [а, 4]
точка х является единственной стационарной точкой. Применительно
к решению уравнения (9.14) одна итерация метода бисекции выглядит
следующим образом.
Пусть отрезок локализации [а(п), 6(п)] известен и найдено значе-
значение x(n) = (o(nl + 4(п))/2. Тогда производят следующие действия.
1°. Вычисляют значение /'(х(п)).
2°. Если /'(х<">) < 0, то полагают [a<n+1\ 6<n+1>] = [x<n>, ft<">]. В
противном случае полагают [a(n+1), b(n*l)] = [о(п), х(п)].
3°. Вычисляют х'"*11 = (а'п+1> + 6<"+1>)/2.
В рассматриваемом случае метод сходится с оценкой погрешности
(П) _
(9.15)
И обладает всеми присущими методу бисекции решения нелинейных
уравнений достоинствами и недостатками (см. § 4.3). Возникает лишь
дополнительная проблема, связанная с необходимостью вычисления
Производной /'.
257

2. Метод Ньютона. Для решения уравнения (9.14) можно попытать-
попытаться воспользоваться методом Ньютона (см. § 4.6), расчетная формула
которого в данном случае принимает вид
=r xln) -'¦
п>0.
Следствием теоремы 4.6 является следующее утверждение.
(9.16)
Теорема 9.1. Пусть в некоторой окрестности точки х функ-
функция f трижды непрерывно дифференцируема и выполняется условие
f(x) > 0. Тогда найдется такая малая а-окрестность корня х, что
при произвольном выборе начальною приближения г'01 из этой а-ок-
рестности метод Ньютона (9.16) сходится квадратично.
В силу сверхлинейной сходимости для метода Ньютона можно
использовать следующий критерий окончания итераций:
|Х(П) _г(Я-1)| <?. (917)
. . Пример 9.11. Используя метод бисекции, найдем с точностью ? = 10~2
точку локального минимума функции /(х) = х3 — х + е'х, локализованную на
отрезке [0, 1].
Положим а<°> = О, 6(О> = 1, х<°> = (а<°> + 6<°>)/2 = 0.5. Заметим, что
У(х) = 3x2 - 1 _ е-*
I итерация. 1. Вычислим /(х@>) и -0.856531.
2. Так как/'(х<0») < 0, то [а"», 6A>] = [х<°>, 6<°>].
3. Вычислим *"> = (о'1» + 6<1>)/2 = 0.75.
Результаты остальных итераций приведены в табл. 9.8.
Таблица 9.8
п
0
1
2
3
4
5
6
а<")
0.000000
0.500000
0.500000
0.625000
0.687500
0.687500
0.703125
Ьш
1.000000
1.000000
0.750000
0.750000
0.750000
0.718750
0.718750
х<">
0.500000
0.750000
0.625000
0.687500
0.718750
0.703125
0.710938
-0.856531
0.215133
-0.363386
-0.084863
0.062444
-0.011882
(*->-.««.)/2
0.500
0.250
0.125
0.063
0.031
0.016
0.008
После выполнения шести итераций вычисления можно прекратить и поло-
положить х и хF). Таким образом, х = 0.71 ± 0.01. Отметим, что для достижения
точности е = 10~2 потребовалось шесть вычислений значения производной
258
Пример 9.12. Используя метод Ньютона, найдем с точностью ? = 10~6
точку локального минимума функции / (х) = х3 — х + е'х, локализованную на
отрезке [0, 1].
Положим х@) = 0.5. Результаты вычислений по формуле (9.16), имеющей
в данном случае вид
2 (П)
) - 1- е"*
(п)
приведены в табл. 9.9.
Таблица 9.9
г<п)
I х{ п) _
0
1
2
3
4
0.5000000
0.7374944
0.7062126
0.7056421
0.7056419
2-Ю
3-Ю
6-Ю
2-Ю
При п = 4 итерации прерываются. Можно считать, что х = 0.705642 ± 10"в.
Заметим, что точность е = 10~2 была достигнута уже после выполнения двух
итераций.
3. Метод последовательной параболической интерполяции. Этот
метод предназначен для минимизации гладких функций, но в отличие
от методов бисекции и Ньютона не требует вычисления производных.
Опишем одну итерацию простейшего варианта этого метода. Пред-
Предположим, что уже известны три предыдущих приближения r(fc),
X(t-D) x(fc) к точке 1с. Пусть у = Р2{х) = т<*> + п<*>(х - х<*>) +
+ p(fc)(r — x(fc)J — уравнение параболы, проходящей через три точки
плоскости с координатами (х<*-2\ /^ (*1 Я*1'))
(*«*>,/(!<*>)). Здесь
*(*)*' Л ;
x(Jt)_
k-1) _
р( К) —
( fc-2)'
x(ifc)_
259

За очередное приближение г'**11 кг принимается та точка, в кото-
которой функция /^(z) достигает минимума. Из уравнения
получается формула
г'**» = *<*> ~^ш- (9.18)
Естественно, что для начала работы этого метода требуется выбор трех
начальных приближений х@), хA), х<2).
Пусть функция / трижды непрерывно дифференцируема в некото-
некоторой окрестности точки х и удовлетворяет в ней условию f(x) > 0.
Можно показать, что в этом случае выбор начальных приближений
х<0), хA), г<2) из достаточно малой окрестности точки х гарантирует,
что ptkl ф 0 для всех к и метод последовательной параболической
интерполяции сходится сверхлинейно, с порядком, приближенно рав-
равным 1.324. Поэтому в качестве критерия окончания итерационного
процесса можно принять неравенство (9.17).
Отметим, что в описанном методе используются только значения
функции / вычисляемые в точках х( *'. Поэтому (как и для методов
прямого поиска) при его реализации на ЭВМ достижимая точность
метода ограничена снизу величиной, равной радиусу е интервала
неопределенности. После того как очередное приближение х(п) попа-
попадет в интервал (х — е, х + е), дальнейшие вычисления теряют смысл
(см. § 9.2).
Существуют различные модификации метода последовательной
параболической интерполяции. Одна из них, например, обеспечивает
принадлежность очередного приближения предыдущему отрезку лока-
локализации и дает последовательность стягивающихся к точке х отрезков.
4. Гибридные алгоритмы. Лучшими среди универсальных методов
одномерной минимизации считаются так называемые гибридные (или
регуллризованные) алгоритмы. Они представляют собой комбинации
надежных, но медленно сходящихся алгоритмов типа бисекции (если
возможно вычисление /'(х)) или золотого сечения с быстро сходящи-
сходящимися методами типа последовательной параболической интерполяции
или Ньютона. Эти алгоритмы обладают высокой надежностью и гаран-
гарантированной сходимостью, причем сходимость становится сверхлиней-
сверхлинейной, если в окрестности точки строгого минимума функция /(х) доста-
достаточно гладкая.
260
Примером эффективного гибридного алгоритма является алгоритм
FMIN, изложенный в [86]. Алгоритм FMIN осуществляет поиск мини-
минимума методом золотого сечения, переключаясь по возможности на
параболическую интерполяцию.
5 9.5. Дополнительные замечания
1. Дополнительную информацию о методах одномерной минимизации
можно найти, например, в пособии [18].
2. Описанные выше методы приспособлены, как правило, для минимизации
унимодальных функций. Если эти методы применить для минимизации непре-
непрерывной функции, не являющейся унимодальной на рассматриваемом отрезке,
то мы получим, вообще говоря, лишь точку локального экстремума. Поэтому
такие методы часто называют локальными методами минимизации. К настоя-
настоящему времени разработан ряд методов, которые предназначены для поиска
глобального минимума. С некоторыми из них можно ознакомиться в [18].
3. Решение задачи минимизации существенно усложняется, если на значе-
значения функции накладываются случайные ошибки (помехи). Так бывает, на-
например, тогда, когда значения функции получают в результате измерений
какой-либо физической величины. В том случае, когда ошибки являются
случайными величинами и обладают определенными вероятностными характе-
характеристиками, для поиска минимума можно использовать метод стохастической
аппроксимации. Понятие об этом методе можно получить из [18]; там же содер-
содержатся ссылки на соответствующую литературу.

= X П Цх выполняется неравенство /(х) < /(х). Если же для
Глава 10
МЕТОДЫ МНОГОМЕРНОЙ МИНИМИЗАЦИИ
Одной из наиболее часто встречающихся в инженерных расчетах и
научных исследованиях вычислительных задач является задача мини-
минимизации1 функции m действительных переменных /(хь х2, ..., хт).
Функция /(целевая функция) минимизируется на некотором множестве
X С Я. В случае, когда X = Л™ (т. е. ограничения на переменные xit
Г2, ..., хп отсутствуют) принято говорить о задаче безусловной миними-
минимизации. В противном случае (т. е. тогда, когда X t №") говорят о задаче
условной минимизации.
В данной главе рассматриваются методы решения задачи безуслов-
безусловной минимизации. Многие из них являются основой для перехода к
более сложным методам решения задач условной минимизации.
§ 10.1. Задача безусловной минимизации
функции многих переменных
1. Постановка задачи. Определения. Пусть /(х) = }{х\, х2, ..., хт) —
действительная функция многих переменных, определенная на мно-
множестве X С Д™. Точка х € X называется точкой глобальною минимума
функции /на множестве X, если для всех х € X выполняется неравенс-
неравенство /(х) < /(х). В этом случае значение /(х) называется минимальным
значением функции /на X.
Точка х & X называется точкой локальною минимума функции /
если существует такая 6-окрестность Ug этой точки, что для всех
1 Как и в случае одной переменной, задача максимизации сводится к за-
задаче минимизации заменой функции /на -/
262
всех х 6 Х$ (х Ф х) выполняется строгое неравенство /(х) < /(х), то х
называется точкой строгою локального минимума.
Подавляющее большинство методов решения задачи безусловной
минимизации в действительности являются методами поиска точки
локального минимума. За исключением весьма редких случаев для
нахождения точки глобального минимума, вообще говоря, не остается
ничего иного, как найти все точки локального минимума и, сравнивая
вычисленные в этих точках значения функции /, выделить среди них
точку глобального минимума. Однако такой подход связан с чрезмер-
чрезмерно большими вычислительными затратами и вряд ли перспективен. На
практике чаще используется другой подход к нахождению точки
глобального минимума, который состоит в том, чтобы определить ее
местоположение из анализа самой решаемой задачи, а затем применить
для вычисления один из методов поиска точки локального минимума.
2. Поверхность уровня, градиент и матрица Гессе. Необходимые и
достаточные условия локального минимума. Напомним некоторые
определения и факты, известные из стандартного курса теории функ-
функций многих переменных.
Множество точек, для которых
целевая функция принимает постоян-
постоянное значение /(х) = с, называется
поверхностью уровня. В случае т =
= 2 это множество называют линией
уровня. На рис. 10.1 показано, как
получаются линии уровня для функ-
функции двух переменных. Функция
fixii X2) задает в трехмерном прост-
пространстве некоторую поверхность и =
= /(гь хз), низшая точка которой и
дает решение задачи минимизации.
Для того чтобы изобразить рельеф рис jq j
этой поверхности, проведем несколько
равноотстоящих плоскостей и =
= const. Проекции на плоскость Ох[Х2 линий пересечения этих плос-
плоскостей с поверхностью и дают линии уровня.
Для дифференцируемой функции определен вектор из первых
частных производных
263

Анти
который называется градиентом.
Если в точке х градиент не равен
нулю, то он, как известно, пер-
перпендикулярен проходящей через
эту точку поверхности уровня и
указывает в точке х направление
наискорейшего возрастания фун-
функции. Вектор — g (x) называется
антшрадиентом и указывает направление наискорейшего убывания
функции (рис. 10.2).
Известно также, что равенство нулю градиента в точке х является
необходимым условием того, чтобы внутренняя для множества X точка
х была точкой локального минимума дифференцируемой функции /
Точка х, для которой выполняется равенство
Рис. 10.2
/'(*) = 0,
A0.1)
называется стационарной точкой функции /. Равенство A0.1) предс-
представляет собой систему т нелинейных уравнений относительно компо-
компонент г\, ?2| ¦•¦) ** вектора х, имеющую вид
•щ К *2. -., *я) = 0,
-г- (хи х2, ..., х-) = 0.
A0.2)
Однако не всякая стационарная точка является точкой локального
минимума. Пусть функция / дважды непрерывно дифференцируема.
Тогда достаточным условием того, чтобы стационарная точка х бы-
была точкой локального минимума, является положительная определен-
определенность1 матрицы
<7 («) = /(«) =
дх\дх
(*)
A0.3)
1 Определение положительно определенной симметричной матрицы см. в
§5.3.
264
составленной из вторых частных производных функции /. Матрицу
A0.3) принято называть матрицей Гессе1.
3. Выпуклые функции. Понятие выпуклости
играет значительную роль в теории методов
минимизации. Функция / называется строго
выпуклой, если для любых х Ф у, 0 < А < 1
выполняется неравенство
/(А х + A - А)») < А /(«) + A - А) /(у).
Это определение имеет наглядный геометри-
геометрический смысл — график функции / на ин-
интервале, соединяющем точки г и у, лежит Рис. 10.3
строго ниже хорды, проходящей через точки
(*, /(х)) и (у, /(у)) (рис. 10.3). Для дважды
непрерывно дифференцируемой функции положительная определен-
определенность матрицы Гессе f(x) является достаточным условием строгой вы-
выпуклости.
Функция / называется сильно выпуклой с постоянной ее > 0, если
для любых х, у, 0 < А < 1 выполнено неравенство
/(Ах+ A - А)у) < А/(«) + A - А) /(у) -f АA - А)|х- „|2.
A0.4)
Дважды непрерывно дифференцируемая функция / является сильно
выпуклой тогда и только тогда, когда для всех х матрица Гессе удов-
удовлетворяет условию
(Г(хК, fl>« \(\2, ?€ Я*,
где ее > 0 — постоянная, входящая в неравенство A0.4).
4. Задача минимизации квадратичной функции. Часто первона-
первоначальное исследование свойств методов безусловной минимизации про-
проводится применительно к задаче минимизации квадратичной функции
F(xu г2, ..., хт) = ^ Д ^ а,]Х,Х]-
A0.5)
коэффициенты ау которой являются элементами симметричной поло-
положительно определенной матрицы А. Используя матричные обозначе-
обозначения, запишем функцию F так:
1 Людвиг Отто Гессе A811—1874) — немецкий математик.
265

F{*) = \ {Ax, x) - (I, x).
A0.6)
Вычислим градиент и матрицу Гессе для функции A0.5). Диффе-
Дифференцирование F по хк дает
6F
1 Я
1
1!
2 j = i
A0.7)
A0.8)
= <Чк-
Пользуясь симметрией матрицы А, получим формулу
dF Я .
— = Д W-»b
Таким образом,
*"(*) = 4х-Ь
Дифференцируя обе части равенства A0.7) по ц, получим
Это означает, что для квадратичной функции A0.5) матрица Гессе не
зависит от х и равна А.
Задача минимизации квадратичной функции представляет интерес
по многим причинам. Отметим две основные из них. Во-первых, в
малой окрестности точки минимума гладкая целевая функция хорошо
аппроксимируется суммой первых трех слагаемых ее разложения по
формуле Тейлора:
/(*) « F,(x) = /(*•) + (, («•), х- х*)+ i(G(»•)(*- »*), х- х*) A0.9)
с центром в точке х* и х. Функция F» с точностью до постоянного
слагаемого может быть записана в виде A0.6) с матрицей А = G (х*) и
» G (х). Поэтому можно ожидать, что вблизи точки минимума качест-
качественный характер поведения последовательности х( п), генерируемой
методом минимизации, для функции /окажется почти таким же, как и
для квадратичной функции F.
Во-вторых, хорошо известно, что в случае, когда А — симметричная
положительно определенная матрица, задача минимизации квадратич-
квадратичной функции A0.6) эквивалентна задаче решения системы линейных
алгебраических уравнений
Ах=Ь.
A0.10)
Более того, решение х° системы A0.10) дает точку минимума функции
266
A0.6). Действительно, F'(iP) = Ах° — Ь = 0, т. е. х° является стацио-
стационарной точкой функции F. Так как матрица Гессе F"(x°) = А поло-
положительно определена, то в точке г° выполнены достаточные условия
минимума и, значит, х° = х.
Таким образом, всякий метод безусловной минимизации, будучи
примененным к поиску минимума функции A0.6), порождает некото-
некоторый метод решения системы A0.10).
Отметим, что поверхностями уровня квадратичной функции A0.6)
служат m-мерные эллипсоиды (при т = 1 — эллипсы) с центром в
точке х. Отношение большей оси каждого из этих эллипсоидов (эл-
(эллипсов) к меньшей оси равно cond2(j4) = Ащах/А^п — числу обуслов-
обусловленности матрицы А. Здесь Хпах и Л,щП — максимальное и минимальное
собственные значения матрицы А. Чем больше отношение Лщах/Лпйт
тем сильнее вытянуты поверхности (линии) уровня.
5. Обусловленность задачи минимизации. В § 9.2 достаточно под-
подробно обсуждалась обусловленность задачи поиска строгого локально-
локального минимума функции одной переменной. Так как ситуация в много-
многомерном случае аналогична, то здесь изложим соответствующие положе-
положения более кратко.
Пусть х — точка строго локального минимума дважды непрерывно
дифференцируемой функции / матрица Гессе которой в точке х поло-
положительно определена. Предположим, что в некоторой окрестности
точки минимума вычисляемые приближенные значения /*(х) удовлет-
удовлетворяют неравенству |/(х) — /*(х)| < Д = Д(/*). Тогда для радиуса
соответствующей области неопределенности справедлива грубая оценка
? и 2 \ Д/Amin, где А„пп > 0 — минимальное собственное значение
матрицы Гессе f{x).
Отсюда следует, что методы приближенного решения задачи мини-
мизациии, в которых используются только значения /*, не могут,
вообще говоря, гарантировать получение приближенного решения х* с
погрешностью меньшей чем Д(х*) и 2 \ Д/А„йп- Это означает, на-
например, что даже для хорошо масштабированных задач (т. е. при
|х| ~ 1, |/(х)| ~ 1, Amin ~ 1) неизбежна потеря примерно половины из
того числа верных значащих цифр, которые содержались в прибли-
приближенных значениях /*(х).
Пусть теперь для решения задачи минимизации доступны приб-
267

лиженные значения градиента (/') *. Тогда сведение задачи поиска
точки минимума х к эквивалентной задаче решения системы уравне-
уравнений /'(*) = 0 существенно улучшает обусловленность задачи. В част-
частности, справедлива такая оценка границы абсолютной погрешности:
Здесь А ((/') *) — граница абсолютной погрешности значений (/') *,
считающаяся достаточно малой величиной. Поэтому если для вычис-
вычисления х можно использовать значения градиента, то такой возможнос-
возможностью не следует пренебрегать.
§ 10.2. Понятие о методах спуска.
Покоординатный спуск
1. Методы спуска. Большинство итерационных методов, применя-
применяемых для решения задачи безусловной минимизации функций многих
переменных, относятся к классу методов спуска, т. е. таких методов,
для которых каждая итерация (шаг) приводит к уменьшению значе-
значения целевой функции: /(х(п+1)) < /(х(п)) для всех п > 0.
Опишем структуру типичной (п + 1)-й итерации метода спуска в
предположении, что приближение х( п) к точке минимума уже найдено
и х<п) Ф х.
1°. Находят ненулевой вектор р< п), называемый направлением спус-
спуска. Этот вектор должен быть таким, чтобы при всех достаточно малых
а > 0 выполнялось неравенство
/(х< п) + ау( ">) < /(х< ">). A0.11)
Если ввести функцию одной переменной а, имеющую вид
?„(<*) =/(х<"> + aj><">), A0.12)
то неравенство A0.11) можно записать так: <рп(<х) < уп@)-
2°. Вычисляют положительное число ап (шаг спуска), для которого
выполняется неравенство
/(х<
">
</(*(п)),
или, что то же самое, -неравенство <рп((*п) <
268
A0.13)
3°. За очередное приближение к точке минимума принимают
г<n+1 > = х( п) + апр{ п) ¦
4°. Проверяют выполнение критерия окончания итераций. Если
критерий выполняется, то итерации прекращают и полагают г и
ft х<п+1). В противном случае итерации продолжают далее.
Последовательность точек г<0>, г'11, ..., х(п), ..., генерируемую
йетодом спуска, иногда называют траекторией спуска.
2. Направление спуска. Заметим, что вектор у(п) не может быть
задан произвольно. В силу требования A0.11) функция <рп{а), опреде-
определяемая формулой A0.12), должна убывать в точке о = 0. Для того
чтобы это условие выполнялось, достаточно потребовать выполнения
неравенства ^@) < 0. Так как <р^(а) = (/'(x(n> + ap(n))> Pin)), то
вектор р( п) является направлением спуска, т. е. удовлетворяет
условию A0.11), если
A0.14)
Можно показать, что для строго выпуклой функции / это неравенство
выполняется тогда и только тогда, когда вектор р<п) задает направле-
направление спуска.
Обычно именно способ выбора направления спуска р( п) определяет
конкретный численный метод, а различные варианты метода опреде-
определяются далее алгоритмом вычисления шага спуска ап. Например,
выбор в качестве j>(n) антиградиента р'п) = -/'(х(п)) задает градиент-
градиентный метод (см. § 10.3). В этом случае (/'(*'п)). р<п>) = -|/'(*(п)I2 <
< 0, т. е. условие A0.14) выполняется.
3. Выбор шага спуска. Следует иметь в виду, что шаг an спуска
определяет "истинную" величину шага А„ = |х(п+1) — х<п)| =
= <*„ | р( п) |, но совпадает с ней только тогда, когда вектор р1 п) имеет
единичную длину.
В качестве ап можно выбирать значение параметра о, которое
обеспечивает достижение наименьшего значения функции /вдоль луча
ж = x(n) + apin), а > 0. В этом случае для вычисления ап требуется
решение одномерной задачи минимизации функции <рп(а). Этот путь
достаточно надежен, однако может быть связан с большими вычисли-
вычислительными затратами.
Существуют и активно применяются другие подходы к выбору ап,
гарантирующие выполнение условия A0.13). Один из простейших
подходов, называемый дроблением шага, состоит в следующем. Фикси-
Фиксируют начальное значение шага а и выбирают параметр -у, 0 < 7 < 1
269

(часто 7 = '/г)- За шаг спуска принимают ап = а- -у'п, где in — первый
из номеров i = 0, 1, 2, .. , для которого выполнено условие
/(*< "> + а- 7'J»( п)) - /(г<"') < 0- а- 7'(/'(*( n)), J»( ">). A0.15)
Здесь 0 < 0 < I, 0 — некоторый дополнительный параметр.
4. Критерии окончания итераций. На практике часто используют
следующие критерии окончания итераций:
|x(n*i) _х(п) | < ?Ь A0.16)
П+П)./(х(п.)| <?2) A017)
п)I<?з, A0.18)
где ?i, е2, бз — заданные положительные числа. Нередко используют
различные их сочетания, например требуют, чтобы одновременно
выполнялись условия A0.16) и A0.17) или даже все три условия
A0.16)—A0.18).
Нередко вместо критериев A0.16), A0.17) применяют их аналоги,
основанные на сочетании понятий относительной и абсолютной пог-
погрешностей:
На втором шаге производят спуск по координате х2. Значения х\ =
\ | ^(
!/(«"•¦»)-/(*(я)I
|),
!/(*< «¦»)!),
A0.19)
A0.20)
а также другие критерии.
К сожалению, надежные критерии окончания счета, которые были
бы применимы к широкому классу задач и гарантировали бы достиже-
достижение нужной точности, пока не известны.
5. Покоординатный спуск. В методе покоординатного спуска в
качестве очередного направления спуска выбирают направление одной
из координатных осей. Наиболее известным является метод цикличес-
циклическою покоординатною спуска. Опишем очередной (п + 1)-й цикл одно-
одного из вариантов этого метода, считая приближение х( п) уже найден-
найденным.
Цикл с номером, п + 1 состоит из m шагов. На первом шаге произ-
производят спуск по координате х\. Значения х2 — х?п), ..., хт = х^п) ос-
остальных координат фиксируют, а х|п+1) выбирают из условия
= mm /(л
Фактически решается задача минимизации функции одной перемен-
переменной
270
= г}"*1'
= г
х3 = х^п), ..., хт = х^п) остальных координат фиксируют и
i) выбирают как решение задачи одномерной минимизации
x2,
Аналогично осуществляют остальные шаги. На последнем m-м шаге
координату х^п*1) определяют из условия
= min
В результате получается очередное приближение х<"+1> к точке
минимума. Далее цикл метода снова повторяют.
На рис. 10.4 изображена геометрическая иллюстрация цикличес-
циклического покоординатного спуска.
Рис 10.4
Применим метод циклического покоординатного спуска для мини-
минимизации квадратичной функции A0.5). Так как на Jfc-м шаге очередно-
очередного цикла значение координаты xj.n+1) определяется из условия мини-
минимизации функции F по направлению xjt, то необходимо, чтобы в точке
/
(х{п+1>, ...,
х^п')т производная dF/dxk обраща-
обращалась в нуль. Учитывая формулу A0.7), получаем уравнение
-bk = 0,
271

откуда находим
Ё1
A0.21)
Последовательные вычисления по формуле A0.21) для ? = 1, 2, ...,
m и составляют один цикл метода покоординатного спуска. Заметим,
что этот метод применительно к решению системы линейных алгебраи-
алгебраических уравнений Ах — Ь с симметричной положительно определенной
матрицей дает известный итерационный метод Зейделя (см. гл. б),
сходящийся со скоростью геометрической прогрессии
§ 10.3. Градиентный метод
Рассмотрим задачу безусловной минимизации дифференцируемой
функции многих переменных /(х). Пусть х(п) — приближение к точке
минимума х, & gin) — д (х( п)) — значение градиента в точке х("'.
Выше уже отмечалось, что в малой окрестности точки х( п) направле-
направление наискорейшего убывания функции / задается антиградиентом
-0( п>. Это свойство существенно используется в ряде методов миними-
минимизации. В рассматриваемом Ниже градиентном методе за направление
спуска из точки х< п> непосредственно выбирается р("> = -д( п). Таким
образом, согласно градиентному методу
Х(П*\) -
(п)
A0.22)
Существуют различные способы выбора шага ап, каждый из кото-
которых задает определенный вариант градиентного метода.
1. Метод наискорейшего спуска. Рассмотрим функцию <рп(а) =
— f (х<п) — ау<п)) одной скалярной переменной а > 0 и выберем в
качестве ап то значение, для которого выполняется равенство
= min
0<о
A0.23)
Этот метод, предложенный в 1845 г. О. Коши1, принято теперь назы-
называть методом наискорейшею спуска.
1 Огюстен Луи Коши A789—1857) — французский математик, один из
создателей современного математического анализа, теории дифференциальных
уравнений и др.
272
рис
На рис. 10.5 изображена геомет-
геометрическая иллюстрация этого метода
для минимизации функции двух
переменных. Из начальной точки
х<°» перпендикулярно линии уровня
/(х) = /(х@)) в направлении р@) =
= -$@) спуск продолжают до тех
пор, пока не будет достигнуто мини-
минимальное вдоль луча х@> + ар[0)
(а > 0) значение функции / В най-
найденной точке хA> этот луч касается
линии уровня /(х) = /(хA)). Затем из точки хA) проводят спуск в
перпендикулярном линии уровня направлении рA) = -$d) до тех пор,
пока соответствующий луч не коснется в точке х<2) проходящей через
эту точку линии уровня, и т. д.
Отметим, что на каждой итерации выбор шага ап предполагает
решение задачи одномерной минимизации A0.23). Иногда эту
операцию удается выполнить аналитически, например для
квадратичной функции.
Применим метод наискорейшего спуска для минимизации квадра-
квадратичной функции
F(x) = l-(Ax,x)-(b,x)
с симметричной положительно определенной матрицей А.
Согласно формуле A0.8), в этом случае д{п) = Ах1п)
формула A0.22) выглядит здесь так:
xin*n = х<п> -
Заметим, что
= I (А
2
-*)¦
A0.24)
Ь. Поэтому
A0.25)
х< "> -
- (*, х< "> -
Эта функция является квадратичной функцией параметра а и дости-
достигает минимума при таком значении а = ап, для которого
= 0.
Таким образом, применительно к минимизации квадратичной функ-
273

ции A0.24) метод наискорейшего спуска эквивалентен расчету по фор-
формуле A0.25), где
_
A0.26)
Замечание 1. Поскольку точка минимума функции A0.24)
совпадает с решением системы Ах = Ь, метод наискорейшего спуска
A0.25), A0.26) может применяться и как итерационный метод
решения систем линейных алгебраических уравнений с симметрич-
симметричными положительно определенными матрицами.
Замечание 2. Отметим, что а'п1 = Р (я(п)), где р (х) =
= (Ах, х)/{х, х) — отношение Рэлея (см. § 8.1).
Пример 10.1. Применим метод наискорейшего спуска для минимизации
квадратичной функции } (х\, ъ) = ^ + 2^ — 4*1 — 4^.
Заметим, что /(Ч, ъ) = (Ч - 2J + 2{я2 — 1J _ б. Поэтому точное
значение х = B, 1)т точки минимума нам заранее известно. Запишем данную
функцию в виде A0.24), где матрица А - и вектор Ь = D, 4)т. Как
нетрудно видеть, А = AF > 0.
Возьмем начальное приближение х<0) = @, 0)т и будем вести вычисления
по формулам A0.25), A0.26).
]
4-42 3'
=D/3,4/3)'.
II итерация. ,">= ^ж<"- » = (-4/3, 4/3)^, ^ = j^')'1 ^ " j =
= A6/9, 8/9)Т.
Можно показать, что для всех п > 1 на n-й итерации будут получены
значения
= =| A, (-1)п)т,
= z _ J B, (_1)п)г.
Заметим, что | х<п) — х| = — -¦ 0 при п -> <ю. Таким образом, последова-
274
тельность х*п), полученная методом наискорейшего спуска, сходится со ско-
скоростью геометрической прогрессии, знаменатель которой q — 1/3.
На рис. 10.5 изображена именно та траектория спуска, которая была полу-
получена в данном примере.
Для случая минимизации квадратичной функции справедлив сле-
следующий общий результат [ 18].
Теорема 10.1. Пусть А — симметричная положительно опре-
определенная матрица и минимизируется квадратичная функция A0.24).
Тогда при любом выборе начального приближения метод наискорейшего
спуска A0.25), A0.26) сходится и верна следующая оценка погрешнос-
погрешности:
tin)
^шах — -"ппп
@) _ .
A0.27)
Здесь Апйп и Ащах — минимальное и максимальное собственные значения
матрицы А.
Отметим, что этот метод сходится со скоростью геометрической
прогрессии, знаменатель которой q = (Хтих — -*min)/(Amax + Amin), при-
причем если А,п1П и Ащах близки, то q мало и метод сходится достаточно
быстро. Например, в примере 10.1 имеем А^п = 2, А^х = 4 и поэтому
q = D — 2)D + 2) = 7з- Если же Amn < Amax, то q и 1 и следует ожи-
ожидать медленной сходимости метода наискорейшего спуска.
Пример 10.2. Применение метода наискорейшего спуска для минимизации
квадратичной функции /(ц, 1%) = г? + 10д^ — 44—4^ при начальном
приближении х<0) = @, 0)т дает последовательность приближений *<п) = х —
Г 9ln
— 2 — -A, (-1)п)т, где х = B, 0.2)т. Траектория спуска изображена на
рис. 10.6.
Рис. 10.6
Последовательность х*п) сходится здесь со скоростью геометрической
прогрессии, знаменатель которой равен q = 9/11, т. е. существенно медленнее,
275

чем в предыдущем примере. Так как здесь А =
О 20
, то Amin = 2,
= 20, (Лщах — ^min)/(Amax + A,njn) = 9/11, и полученный результат вполне
согласуется с оценкой A0.27).
Замечание 1. Мы сформулировали теорему о сходимости
метода наискорейшего спуска в случае, когда целевая функция
является квадратичной. В общем случае, если минимизируемая
функция строго выпуклая и имеет точку минимума х, то также
независимо от выбора начального приближения полученная указан-
указанным методом последовательность х<п) сходится к * при п •* «>. При
этом после попадания х( п| в достаточно малую окрестность точки
минимума сходимость становится линейной и знаменатель соответс-
соответствующей геометрической прогрессии оценивается сверху величиной
q и (Ащах — Amin)/(Amax + Лиц,,), где Amin и Хшх — минимальное и
максимальное собственные числа матрицы Гессе G (х).
Замечание 2. Для квадратичной целевой функции A0.24)
решение задачи одномерной минимизации A0.23) удается найти в
виде простой явной формулы A0.26). Однако для большинства
других нелинейных функций этого сделать нельзя и для вычисле-
вычисления оп методом наискорейшего спуска приходится применять чис-
численные методы одномерной минимизации типа тех, которые были
рассмотрены в предыдущей главе.
2. Проблема "оврагов". Из проведенного выше обсуждения следует,
что градиентный метод сходится достаточно быстро, если для мини-
минимизируемой функции поверхности уровня близки к сферам (при m =
= *2 линии уровня близки к окружностям). Для таких функций ае =
= ^max/^min и 1- Теорема 10.1, замечание 1, а также результат примера
10.2 указывают на то, что скорость сходимости резко падает при
увеличении величины ае. Действительно, известно, что градиентный
метод сходится очень медленно, если поверхности уровня мини-
минимизируемой функции сильно вытянуты в некоторых направлениях. В
двумерном случае рельеф соответствующей поверхности u = f {х\, хг)
напоминает рельеф местности с оврагом (рис. 10.7). Поэтому такие
функции принято называть овражными. Вдоль направлений, характе-
характеризующих "дно оврага", овражная функция меняется незначительно, а
в других направлениях, характеризующих "склон оврага", происходит
резкое изменение функции.
276
Рис. 10.7
Если начальная точка х@) попадает на "склон оврага", то направ-
направление градиентного спуска оказывается почти перпендикулярным "дну
оврага" и очередное приближение хA) попадает на противоположный
"склон оврага". Следующий шаг в направлении ко "дну оврага" возв-
возвращает приближение хB) на первоначальный "склон оврага". В ре-
результате вместо того чтобы двигаться вдоль "дна оврага" в направле-
направлении к точке минимума, траектория спуска совершает зигзагообразные
скачки поперек "оврага", почти не приближаясь к цели (рис. 10.7).
Для ускорения сходимости градиентного метода при минимизации
овражных функций разработан ряд специальных "овражных" методов.
Дадим представление об одном из простейших приемов. Из двух близ-
близких начальных точек z@) и zA) совершают градиентный спуск на
"дно оврага". Через найденные точки х@) и хA) проводят прямую,
вдоль которой совершают большой "овражный" шаг (рис. 10.8). Из
найденной таким образом точки zB) снова делают один шаг градиент-
градиентного спуска в точку х( 2). Затем совершают второй "овражный" шаг
вдоль прямой, проходящей через точки хA) и х<2), и т. д. В результа-
результате движение вдоль "дна оврага" к точке минимума существенно уско-
ускоряется.
Рис. 10.8
Более подробную информацию о проблеме "оврагов" и "овражных"
Методах можно найти, например, в [9], [18].
277

3. Другие подходы к определению шага спуска. Как нетрудно
понять, на каждой итерации было бы желательно выбирать направле-
направление спуска р( п), близкое к тому направлению, перемещение вдоль
которого приводит из точки х(п) в точку х. К сожалению, антигради-
антиградиент f(n) = -$<"• является, как правило, неудачным направлением
спуска. Особенно ярко это проявляется для овражных функций. По-
Поэтому возникает сомнение в целесообразности тщательного поиска
решения задачи одномерной минимизации A0.23) и появляется жела-
желание сделать в направлении р{ п> лишь такой шаг, который бы обеспе-
обеспечил "существенное убывание" функции /. Более того, на практике
иногда довольствуются определением значения а„ > 0, которое просто
обеспечивает уменьшение значения целевой функции.
В одном из простейших алгоритмов (типа дробления шага) такого
выбора шага ап фиксируют начальное значение а > 0 и значение
параметра -у, 0 < -у < 1. За а„ принимают а„ = а-71", где in — первый
из номеров i = 0, 1, 2, ..., для которого выполнено условие убывания
/(х< п> - a-f§<п)) - /(х< ) < 0. A0.28)
Однако при таком выборе а„ нет гарантии, что последовательность
х<п> будет сходиться к точке минимума даже для простой квадратич-
квадратичной функции A0.24). Условие A0.28) является слишком слабым: пос-
последовательность х( п), незначительно уменьшая значения функции /
может "останавливаться", не доходя до точки х. Такое поведение
последовательности х(п) можно предотвратить, если заменить условие
A0.28) условием "существенного убывания" функции / на каждой
итерации:
A0.29)
Здесь /? @ < /3 < 1) — дополнительный параметр. Заметим, что для
рассматриваемого метода y(n> = -y'n» = -/'(х(п)) и поэтому неравенс-
неравенство A0.29) в точности совпадает с неравенством A0.15), используемым
в методах спуска при дроблении шага.
Пример 10.3. Продемонстрируем применение градиентного метода с дробле-
дроблением шага к задаче минимизации квадратичной функции f(i\, ъ) = ^ +
+ 2л2» — 4xi — 4*2 из пример» 10.1. Для выбора значения шага будем исполь-
использовать условие A0.29). Воспользуемся следующими краткими обозначениями:
о, = а-f1, х<п'1) = г<п)— а,*п>. Заметим, что *"> = Bг|п)— 4, 4*<п> — 4)т.
278
Выберем начальное приближение *<<» = @, 0)т, начальное значение шага
о = «о = 1, значения параметров 7 = 1/2, 0 = 3/4. Вычислим значения
/(*•<») = 0, /о. =(-4,-4)т
I и т е р а ц и я. Вычисляем *<о.о> = *<0) _ а^О) = D, 4)т, /(ж<0.0)) =
= 16. Так как значение функции не уменьшилось, то следует уменьшить шап
ei = ао/2 = 0.5.
Вычисляем х">,1) = *<0) _ ^0) = B| 2)т, /(*о,1>) = ^ Поскольку
/(*<о,1>) _/(««») = ^ > -/for,|*<0) |2 = _12, условие A0.29) не выполняет-
выполняется и следует снова уменьшить шаг: а2 = aj/2 = 0.25.
Вычисляем х*°.2> = г<0> - а2*0' = A, 1)т /(г<о.2)) = -Ъ. Имеем
/С**0'21) - /(*<0)) = -5 > ~Ы*0) I2 = -6, т. е. условие A0.29) не выпол-
няется. Уменьшаем шаг: аз = а2/2 = 0.125.
Вычисляем х">.31 = *<0) _ аз*°> = @.5, 0.5)т, /(**<М>) = -3.25. Так
как /(*»>.»») - /(*««») = -3.25 < -раз\^)\2 = _3> то условие A0щ
выполнено.
Положим *<!> = @.5, 0.5)т; напомним, что /(«"») = -3.25. Вычислим
/>' = (-3, -2)т и положим «о = 1.
Далее вычисления следует продолжить до выполнения какого-либо приня-
принятого критерия окончания итераций.
4. Влияние погрешности вычислений. Один из существенных недос-
недостатков градиентного метода связан с его чувствительностью к погреш-
погрешностям вычислений. Особенно сильно этот недостаток сказывается в
малой окрестности точки минимума, где антиградиент, задающий
направление поиска, мал по модулю. Поэтому эффективность градиен-
градиентного метода на завершающей стадии поиска существенно ниже, чем
на начальной стадии.
$ 10.4. Метод Ньютона
1. Простейший вариант метода Ньютона и метод Ньютона с дробле-
шага. Пусть в некоторой окрестности точки минимума х функция
/ является сильно выпуклой и дважды непрерывно дифференцируе-
дифференцируемой. Далее, пусть х(п| — хорошее приближение к х. Тогда в малой
окрестности точки х(п) функция /достаточно точно аппроксимируется
квадратичной функцией Fn(x) = /(х<п>) + (з(п), * — х(п>) +
+ -(G<")(x — х(п>), х — х(п|), являющейся суммой первых трех
членов ее разложения по формуле Тейлора (ср. с формулой A0.9)).
Здесь $<п> = /'(*(п|). <?<"> = Г(х(п))-
279

Можно ожидать, что точка *< ">, в которой достигается минимум
функции Fn, будет значительно лучшим приближением к х, чем х<п|.
Учитывая, что F^(x) = д(п) + Gin](x — *<n)), замечаем, что точка
х("' может быть определена из необходимого условия экстремума:
j< П) _|_ Д< П) ( j< П) _ г( П) ) = 0.
Таким образом, чтобы попасть из точки г( п) в точку х( п), нужно
переместиться вдоль вектора р(п> = х(п) — х(п), который определяет-
определяется из системы линейных алгебраических уравнений
QI п) р( n) = _
( n)
A0.30)
Вектор р1п) принято называть ньютоновским направлением, а метод
спуска
A0.31)
с таким выбором р1 п) — методом Ньютона.
Отметим, что ньютоновское направление является направлением
спуска. В самом деле, в силу равенства A0.30) для р1п) верна формула
pin) — _[?<n)]-ij<n) Матрица [С'] положительно определена (это
следует из положительной определенности матрицы G1 п)). Поэтому
(/'(*<"')> j><«>) = -([<?< "Ч!1"'. *<">) < 0.
Таким образом, условие A0.14) выполняется и р(п) действительно
задает направление спуска.
Различные варианты метода A0.31), A0.30) связаны с различными
способами выбора шагов ап. Заметим, что при выборе ап = 1 рассмат-
рассматриваемый метод в точности совпадает с методом Ньютона решения
систем нелинейных уравнений, примененным к решению системы
f(x) — 0. Отсюда — и название метода.
Простым следствием теоремы 7.3 о сходимости метода Ньютона
решения систем нелинейных уравнений является следующая теорема.
Теорема 10.2. Пусть в некоторой окрестности U точки мини-
минимума х функция f является сильно выпуклой и трижды непрерывно
дифференцируемой. Тогда найдется такая малая 6-окрестность точки
х, что при произвольном выборе начальною приближения z@) из этой
окрестности последовательность х("', вычисляемая с помощью мето-
280
да A0.30), A0.31) при ап = 1, не выходит за пределы 6-окрестности
точки х и сходится к ней квадратично.
Замечание. Квадратичная скорость сходимости метода позво-
позволяет использовать простой практический критерий окончания:
(xin+n -х(п) | < е. A0.32)
Теорема 10.2 указывает на то, что метод Ньютона сходится очень
быстро, и практика вычислений это подтверждает. Однако существен-
существенным недостатком рассмотренного варианта метода является необходи-
необходимость выбора достаточно хорошего начального приближения, которое
на начальной стадии поиска точки минимума, как правило, отсутству-
отсутствует. Поэтому метод Ньютона с выбором ап — 1 чаще применяют на
завершающем этапе поиска г, когда с помощью других методов уже
найдено достаточно точное приближение к точке минимума.
Указанного недостатка в значительной степени лишен вариант
метода Ньютона, в котором в качестве" шага спуска выбирается ап =
= 7lni где in — первый среди номеров i > 0, для которых выполняется
неравенство /(х(п) + 7'Р<П)) - /(*<п)) < /М?(Г1). »"")• Здесь
0<7<1|0</?< 1/2 — параметры метода. Метод Ньютона с таким
выбором ап для широкого класса функций сходится при любом выбо-
выборе начального приближения х@> ? U и этим выгодно отличается от
метода с выбором ап= 1.
Теорема 10.3. Пусть трижды непрерывно дифференцируемая в
Rn функция /имеет точку минимума х и ее матрица Гессе f'^поло-
f'^положительно определена. Totda при любом начальном приближении х@)
последовательность х( п|, вычисляемая методом Ньютона с выбором
ап = i%n сходится к х с квадратичной скоростью. Более тою, найдет-
найдется номер по такой, что для всех п ^ щ выполняется равенство ап — 1.
Замечание. Используют и другие способы выбора ап. Напри-
Например, иногда ап выбирают из условия <рп(ап) = niin <pn(a), где
0<а<1
M*) = f(*n) +«Р(П))-
Квадратичная скорость сходимости метода Ньютона, а также воз-
возможность использования матрицы Гессе для контроля за соблюдением
достаточных условий экстремума делают этот метод чрезвычайно
привлекательным при решении задачи безусловной минимизации.
281 •

Пример 10.4. Применим метод Ньютона A0.30), A0.31) с ап = 1 для
поиска точки минимума функции f(z\, #2) = t( + Ю(»2 — sin *iJ с точностью
е = 10. Будем использовать критерий окончания итераций A0.32) и вести
вычисления на 6-разрядной десятичной ЭВМ. Отметим, что минимальное и
равное нулю значение функция /достигает в точке г = @, 0)т.
Имеем
#<»• = /(х< *>,*<">) =
= Br<"> + 20(sin r<"> - r<«>)-cos г<">,
G<n, = /-(*»>) f2
-sin
-20cos x\n)
20
Возьмем за начальное приближение Xй' = A, 1)т.
I итерация. Вычислим
[0.2869281
[3.17058 J'
Л10-
[-10.
,5065 -10.8060
.8060 20
Таким образом, при п = 0 система A0.30) принимает следующий вид:
10.5065р|0) -10.8060р?°> = -0.286928,
-10.8060р<0) + 20р?°> = -3.17058.
Решая ее, получаем р<°> = -0.428445, р?0) = -0.390018. Далее в соответствии
с формулой A0.31) полагаем г<1> = г<°> + р<°> = 0.571555, 4" = 4°' +
+ р^0) = 0.609982. Так как It*!' — х<0) | и 0.6 > Е, то вычисления следует
продолжить далее.
Результаты следующих итераций приведены в табл. 10.1.
Таблица 10.1
(П)
0
1
2
3
4
5
1.00000000
0.57155400
0.15541900
0.00824200
0.00000082
0.00000000
1.00000000
0.60997200
0.19094400
0.00939200
0.00000101
0.00000922
6-Ю
6-Ю
2-10-1
1-Ю
2-Ю
При п = 5 критерий окончания выполняется и вычисления следует прекра-
прекратить. Итак, ~х я @.00000, 0.00000)т.
2. Понятие о квазиньютововских методах. Высокая скорость схо-
сходимости метода Ньютона связана с тем, что в нем используется матри-
матрица Гессе, содержащая информацию о кривизнах функции / В резуль-
результате минимизируемую функцию удается достаточно точно аппрокси-
аппроксимировать последовательностью квадратичных функций Fn. В методах,
которые называют квазиньютоновскими1, также фактически исполь-
используется квадратичная аппроксимация функции / но в отличие от ме-
метода Ньютона в них не применяется вычисление вторых производных.
Информация о кривизнах функции / здесь накапливается посте-
постепенно и является результатом наблюдений за изменением градиента
#<п).
Направление спуска в квазиньютоновских методах определяется
как решение системы уравнений
в которой В( п) — текущее приближение к матрице Гессе. Начальное
приближение Б@) обычно полагают равным единичной матрице. В
таком случае р@) = —^<0) и первая итерация совпадает с одним шагом
градиентного метода.
После того, как найдено приближение xln*l), вычисляют матрицу
g(n*i) = д(п) + ABin), где АВ1п) — некоторая поправочная матрица.
Во всех правилах пересчета неизменным является выполнение квази-
квазиньютоновскою условия
Известно, что при определенных условиях квазиньютоновские
методы сходятся сверхлинейно. Для квадратичных же функций они
дают точное значение точки минимума после конечного числа итера-
итераций, которое не превышает2 т.
Первый из квазиньютоновских методов был предложен в 1959 г.
Дэвидоном. С тех пор эти методы непрерывно совершенствовались и к
аастоящему времени стали одними из наиболее популярных и широко
282
1 Первоначально эти методы называли методами переменной метрики.
2 Естественно, что это верно только при отсутствии вычислительной пог-
<вешности.
283

применяемых на практике. Весьма интересное и содержательное обсуж-
обсуждение квазиньютоновских методов содержится в книгах [24], [32], [91].
Замечание. В некоторых вариантах квазиньютоновских мето-
методов направление спуска вычисляется по формуле р( п) = -Я( п) д1 п),
где Я( п) — матрица, аппроксимирующая матрицу, обратную матри-
матрице Гессе.
3. Метод Ньютона и квазиньютоновские методы при наличии по-
помех. Вычислительные ошибки (помехи) оказывают существенное вли-
влияние на поведение метода Ньютона. Природа этих ошибок может быть
различной (вычисление $<п), решение системы уравнений G1 п) р1 п) =
= -д1п) и др.). В результате вместо ньютоновского направления р<п)
получается направление р'«п). Пусть |р(п) — р(«п) | < ?. Как известно,
метод Ньютона сходится, вообще говоря, лишь в некоторой окрест-
окрестности U точки минимума. В случае, когда радиус этой окрестности
меньше ?, очередное приближение xin*l) = x(n) + QnP(*n) скорее всего
окажется вне окрестности U и метод не будет сходиться. Таким обра-
образом, метод Ньютона сохраняет свои преимущества лишь при высокой
точности вычислений.
Квазиньютоновские методы оказываются весьма чувствительны к
ошибкам в вычислении градиента. Причина здесь состоит в том, что в
основе этих методов лежит идея восстановления матрицы Гессе по
результатам вычисления градиента f(x) в точках х(п). Как и в методе
Ньютона, здесь необходимо очень аккуратное вычисление градиента.
$ 10.5. Метод сопряженных градиентов
Метод Ньютона и квазиньютоновские методы, обсуждавшиеся в
предыдущем параграфе, весьма эффективны как средство решения
задач безусловной минимизации. Однако они предъявляют довольно
высокие требования к объему используемой памяти ЭВМ. Это связано
с тем, что выбор направления поиска pfn) требует решения систем
линейных уравнений, а также с возникающей необходимостью хране-
хранения матриц типа В( п), Я( п). Поэтому при больших т использование
этих методов может оказаться невозможным. В существенной степени
от этого недостатка избавлены методы сопряженных направлений.
1. Понятие о методах сопряженных направлений. Рассмотрим зада-
задачу минимизации квадратичной функции
F (г) = -2(Ах,х) -(*,*)
A0.33)
с симметричной положительно определенной матрицей А Напомним,
что для ее решения требуется один шаг метода Ньютона и не более
чем m шагов квазиньютоновского метода Методы сопряженных на-
направлений также позволяют найти точку минимума функции A0.33) не
более чем за m шагов. Добиться этого удается благодаря специально-
специальному выбору направлений поиска.
Будем говорить, что ненулевые векторы у'01, рA), ..., р"»' явля-
являются взаимно сопряженными (относительно матрицы А), если
(Ар1 п}, р(") = 0 для всех п t I.
Под методом сопряженных направлений для минимизации квадра-
квадратичной функции A0.33) будем понимать метод
- xtn)
(п = о, 1, 2, ..., m - 1),
в котором направления р@), pil), ¦¦¦, plm'l) взаимно сопряжены, а
шаги
,(п)
D(n)
)
-"- (V, р(п))
получаются как решение задач одномерной минимизации:
<Рп(<*п) = min <pn(a), ipn(a) = F (г«п) + ар'"').
Теорема 10.4. Метод сопряженных направлений позволяет
найти точку минимума квадратичной функции A0 33) не более чем за
т шаюв.
Методы сопряженных направлений отличаются один от другого
способом построения сопряженных направлений. Наиболее известным
среди них является метод сопряженных градиентов
2. Метод сопряженных градиентов. В этом методе направления р1 п|
строят по правилу
=-,@»,
где
A0.34)
A0.35)
284
Так как j»<°'= -gl0), то первый шаг этого метода совпадает с шагом
метода наискорейшего спуска. Можно показать (мы этого делать не
^Удем), что направления A0.34) действительно являются сопряжен-
285

ными относительно матрицы А. Более того, градиенты д1п) (п = 0, 1,
..., m — 1) оказываются взаимно ортогональными.
Пример 10.5. Применим метод сопряженных градиентов для минимизации
квадратичной функции / (щ, 15) = *? + 2х^ — 4щ — 4*2 из примера 10.1.
Запишем /в виде - (Ах, х) — (h, x), где
*-[::]¦-О-
Возьмем начальное приближение *<°> — @, 0)т.
1-й шаг метода совпадает с первым шагом метода наискорейшего спус-
спуска. Поэтому (см. пример 10.1) *<°> = (-4, -
= D/3, 4/3)*.
2-й шаг. Вычислим *"> = Л^1' -Ь = (-4/3, 4/3)т,
р@> = -дш,
= D/3,
A/9X4, 4)т = A6/9, -8/9)*,
, р)_ Н/)(/)(/)(/) _
, j.4)) C2/9)¦ A6/9)+(-32/9)• (-в/9) 81
aip4) = D/3, 4/3)т + C/8)A6/9, -8/9)т = B,
Так как j<2> = Л*12' — Ь = 0, то г = х<2) = B, 1)т и решение оказалось
найденным за два шага.
3. Метод сопряженных градиентов для минимизации неквадратич-
неквадратичных функций. Для того чтобы указанный метод можно было приме-
применить для минимизации произвольной гладкой функции /, формулу
A0.35) для вычисления коэффициента Рп.\ преобразуют к виду
'~MJ A0.36)
^n"J ~ I д{ П- 1 ) 12
или к виду
_ |,'"Ч2
|2 ¦
A0.37)
Преимущество формул A0 36), A0.37) в том, что они не содержат
явным образом матрицу А.
286
Минимизацию функции / методом сопряженных градиентов произ-
производят в соответствии с формулами
п>0,
a>0
A0.38)
A0.39)
A0.40)
Коэффициенты $п.\ вычисляют по одной из формул A0.36), A0.37).
Итерационный процесс здесь уже не оканчивается после конечного
числа шагов, а направления р1 п) не являются, вообще говоря, сопря-
сопряженными относительно некоторой матрицы.
Решение задач одномерной минимизации A0.40) приходится осу-
осуществлять численно. Отметим также то, что часто в методе сопряжен-
сопряженных градиентов при п = т, 2т, Зт, ... коэффициент fin-x не вычисля-
вычисляют по формулам A0.36), A0.37), а полагают равным нулю. При этом
очередной шаг производят фактически методом наискорейшего спус-
спуска. Такое "обновление" метода позволяет уменьшить влияние вычис-
вычислительной погрешности.
Для сильно выпуклой гладкой функции /при некоторых дополни-
дополнительных условиях метод сопряженных градиентов обладает высокой
сверхлинейной скоростью сходимости. В то же время его трудоемкость
невысока и сравнима с трудоемкостью метода наискорейшего спуска.
Как показывает вычислительная практика, он незначительно уступает
по эффективности квазиньютоновским методам, но предъявляет значи-
значительно меньшие требования к используемой памяти ЭВМ. В случае,
когда решается задача минимизации функции с очень большим чис-
числом переменных, метод сопряженных градиентов, по-видимому, явля-
является единственным подходящим универсальным методом.
§ 10.6. Методы минимизации
без вычисления производных
1. Методы прямого поиска. Метод деформируемого многогранника.
Существует большой класс методов минимизации, каждый из которых
основан на сравнении значений целевой функции в последовательно
вычисляемых пробных точках. Это так называемые методы прямою
поиска. Обычно они применяются тогда, когда в любой окрестности
точки локального минимума целевая функция не является гладкой, а
множество точек, в которых она недифференцируема, имеет слишком
сложную структуру. К сожалению, методы прямого поиска в большин-
большинстве случаев очень неэффективны. Обращаться к ним, по-видимому,
287

имеет смысл только тогда, когда есть уверенность, что никакие другие
подходы к решению задачи минимизации невозможны.
Рассмотрим кратко один из наиболее известных методов прямого
поиска — метод деформируемою многогранника. Сначала необходимо
задать т + 1 точку х<0), х^0), ..., х^$> так, чтобы векторы х?°> -=¦ х<°>,
х?°> — х<0), ..., х^°» — х<0) были линейно независимы. Тогда эти точ-
точки можно интерпретировать как вершины m-мерного многогранника.
Обычно начальный многогранник выбирают правильным.
Опишем очередную (п + 1)-ю итерацию простейшего варианта
метода. Будем предполагать, что точки х<п), х?">, ..., x^J> являются
вершинами многогранника, полученного на предыдущей итерации, и
занумерованы так, что /(*<">) = min f(*\n)), /(rm?i) =
Ki<mfl
= max /(x<n)). Отбрасывают точку *$\ как самую неудачную.
<<
1 т
я<п) = _ ? х(п) и СТроят пробную точку
Затем вычисляют "центр тяжести" оставшихся точек по формуле
' = м|п) + («<"> —
ra+{)' отРазив симметрично вершину х^\ относительно точки м(п).
Геометрическая иллюстрация этой операции в случае m = 2 приведена
на рис.' 10.9, а. Заметим, что в плоском случае роль многогранника
играет треугольник.
Рис. 10.9
Далее возможны три случая.
Случай 1: /(х'п)) < /(х^">) < f(xmn))> т- е- пробная точка не
привела к уменьшению значения целевой функции, но и не стала
"худшей" в наборе х[п), х^">, ..., х^п), х^"'. В этом случае точку
признают удовлетворительной и х^?> заменяют на
288
Случай 2: /(х^">) < /(х'">), т. е. выбор пробной точки привел
к уменьшению значения целевой функции. Тогда направление отраже-
отражения считают удачным и делают попытку "растянуть" многогранник в
этом направлении с коэффициентом растяжения /? > 1 (обычно 2 К /3 К
<3). Находят точку х^"> =1»"») + /?(«<"> — xj">). Есля /(х?п>) <
)> то растяжение прошло удачно и точку
заменяют на
х'"'. В противном случае растяжение было неудачным и производят
замену *^,"\ на х^™1. На рис. 10.9, б показано "растяжение" с коэффи-
коэффициентом /9 = 2.
Случай 3: /('„p1 )-*/(*&"')• ^ этом случае считают, что много-
многогранник следует сжать. Если /(х^™1) > f(*lm?\)t то вершину x^yj заме-
заменяют точкой х<.п> = ¦<"' - 7(«(п) - x^y'j). Если же /(х?">) < /(*<,?}),
то х^> заменяют на х<.п'= в(п'+ 7(«(п)— *??{)• Здесь 0 < f < 1, 7 —
коэффициент сжатия (обычно 7 = 1/2)- На рис. 10.9, в показано "сжа-
"сжатие" с коэффициентом f — 1/2.
Помимо операций отражения, сжатия и растяжения периодически
(после выполнения определенного числа итераций) производят опера-
операцию замены текущего многогранника правильным многогранником —
так называемое восстановление. При восстановлении сохраняются
лишь две лучшие точки последнего многогранника. Расстояние между
этими точками принимают за длину ребра вновь генерируемого пра-
правильного многогранника. Эта операция позволяет ликвидировать
излишние деформации, возникающие в ходе итераций.
Известно большое число различных модификаций этого метода.
Подробно они описаны в книгах [24], [91]. Там же указаны различные
критерии окончания.
2. Методы минимизации гладких функций, использующие конечно-
разностные аппроксимации производных. Довольно часто в приложе-
приложениях возникает необходимость в минимизации функций, обладающих
достаточным числом производных, которые тем не менее недоступны
для прямого вычисления. Например, такая ситуация имеет место
тогда, когда значение функции является результатом решения слож-
сложной математической задачи. В этом случае приходится применять
алгоритмы, использующие лишь вычисляемые в различных точках
значения функции / Здесь обращение к методам прямого поиска
(типа метода деформируемого многогранника), специально разработан-
разработанным для минимизации негладких функций, вряд ли целесообразно,
10-28 289

так как эти методы не позволяют извлекать никакой выгоды из воз-
возможной гладкости функции. Часто существенно лучший результат
можно получить, заменив в одном из алгоритмов спуска используемые
в нем производные их аппроксимациями в соответствии с формулами
численного дифференцирования (см. гл. 12). Например, для производ-
производной f'x простейшая аппроксимация такова:
уЬ ..., хт) — /(zb х2, ..., хт)).
Подобная модификация алгоритмов не является тривиальной и
требует достаточной осторожности в реализации. Это связано с высо-
высокой чувствительностью формул численного дифференцирования к
ошибкам в вычислении функции (см. § 12.3). Более подробное обсуж-
обсуждение методов минимизации, использующих конечно-разностное ап-
аппроксимации производных, можно найти в [24] и [32]. В заключение
все же отметим, что конечно-разностные аппроксимации производных
используются в алгоритмах минимизации тогда, когда аналитическое
вычисление производных невозможно. Бели же производные можно
вычислить аналитически, то усилия, потраченные на такое вычисле-
вычисление, как правило, окупаются.
§ 10.7. Дополнительные замечания
1. Задача о наименьших квадратах. Среди задач безусловной минимизации
особое место занимает задача минимизации функций вида
Ф (*) =
A0.41)
где Ji(r), ..., fs(x) — некоторые функции т переменных.
Необходимость в минимизации таких функций возникает, например, при
использовании метода наименьших квадратов для решения задачи аппрокси-
аппроксимации функции (см. гл. 11) либо для решения проблемы идентификации
математической модели по данным эксперимента. К поиску точки минимума
функции вида A0.41) сводится и задача решения системы нелинейных уравне-
уравнений
= 0 0=1,2 N) A0.42)
(см. гл. 7). Действительно, если решение х системы (Ш.42) существует, то оно
совпадает с точкой глобального минимума функции Ф, причем Ф (х) = 0.
290
- Для минимизации функции A0.41) в принципе можно применить любой из
универсальных методов минимизации. Однако, как правило, этого не делают, а
используют алгоритмы, специально разработанные для решения задачи о
наименьших квадратах. Достаточно подробное их обсуждение можно найти,
например, в [32].
2. Естественно, что в данной книге содержится лишь краткое введение в
методы решения задач безусловной минимизации, Более подробное изложение
можно найти, например, в [6], [18], [24], [32], [64], [66], [76], [91] и др.
3. Задачи условной минимизации. Множество , X, на котором
минимизируется функция / часто задается с помощью системы неравенств
вида
2, .... *т) > 0, i= 1, 2, .... к.
Если целевая функция /и задающие множество X функции $ линейны, то
задачу минимизации называют задачей линейного программирования. Если же
хотя бы одна из этих функций нелинейна, то говорят о задаче нелинейною
программирования.
Обсуждение методов решения задач условной минимизации при всей их
важности выходит за рамки данной книги. Укажем, например, на книги [18],
[24], [76], [91], содержащие достаточно подробное и доступное введение в соот-
соответствующие методы.
4. Особый класс задач составляют так называемые задачи дискретной
минимизации. В этих задачах множество X, на котором минимизируется функ-
функция / является конечным или счетным. Часто X — множество точек с цело-
целочисленными координатами, удовлетворяющими некоторым ограничениям.
Методы решения таких задач описаны, например, в [76].
5. Авторы рекомендуют обратить внимание на книгу [24], в особенности на
ее последние главы ("Моделирование", "Практические вопросы" и "Вопросы и
ответы"). В них содержится большое число весьма интересных замечаний,
полезных рекомендаций и советов для широкого круга специалистов, заинтере-
заинтересованных в решении практических задач минимизации.

Глава И
ПРИБЛИЖЕНИЕ ФУНКЦИЙ
И СМЕЖНЫЕ ВОПРОСЫ
В этой главе рассматриваются наиболее важные и часто встречаю-
встречающиеся в приложениях методы приближения функций одной перемен-
переменной. Значительное внимание уделено интерполяции, причем рассмат-
рассматривается интерполяция не только алгебраическими многочленами, но
и тригонометрическими многочленами, а также интерполяция сплайна-
сплайнами. Довольно подробно обсуждается метод наименьших квадратов,
широко используемый в практике инженерных расчетов. Дается поня-
понятие о наилучшем равномерном приближении и дробно-рациональных
аппроксимациях.
В главу включены также некоторые вопросы вычислительной мате-
математики, имеющие непосредственное отношение к методам аппроксима-
аппроксимации (приближения) функций. Это конечные и разделенные разности,
многочлены Чебышева, быстрое дискретное преобразование Фурье.
$ 11.1. Постановка задачи
приближения функций
Вычисление значения функции у = /(х) — одна из тех задач, с
которой постоянно на практике приходится сталкиваться. Естественно,
что при решении на ЭВМ серьезных задач желательно иметь быстрые
и надежные алгоритмы вычисления значений используемых функций.
Для элементарных, а также для основных специальных функций такие
алгоритмы разработаны, реализованы в виде стандартных программ и
включены в математическое обеспечение ЭВМ. Однако в расчетах
нередко используются и другие функции, непосредственное вычисле-
вычисление которых затруднено либо приводит к слишком большим затратам
машинного времени. Укажем на некоторые типичные ситуации.
1. Функция /задана таблицей своих значений:
а вычисления производятся в точках х, не совпадающих с табличны-
табличными.
2. Непосредственное вычисление значения у — /(х) связано с прове-
проведением сложных расчетов и приводит к значительным затратам ма-
машинного времени, которые могут оказаться неприемлемыми, если
функция /вычисляется многократно.
3. При заданном значении х значение f(x) может быть найдено из
эксперимента. Ясно, что такой способ "вычисления" в большинстве
случаев нельзя использовать в вычислительных алгоритмах, так как он
связан с необходимостью прерывания вычислительного процесса для
проведения эксперимента1. В этой ситуации экспериментальные дан-
вые получают до начала вычислений на ЭВМ. Нередко они представ-
представляют собой таблицу типа A1.1) с тем отличием, что табличные значе-
' вия у * отличаются от "истинных" значений у,, так как заведомо
содержат ошибки эксперимента.
Возникающие проблемы нередко удается решить следующим обра-
образом. Функцию f(x) приближенно заменяют другой функцией д (х),
вычисляемые значения которюй и принимают за приближенные значе-
значения функции /. Конечно, такая замена оправдана лишь тогда, когда
значения д (х) вычисляются быстро и надежно, а погрешность прибли-
приближения / (х) — д (х) достаточно мала. Обсудим кратко некоторые вопро-
вопросы, с которыми в каждом конкретном случае приходится сталкиваться
при выборе постановки задачи приближения и метода ее решения.
1°. Необходимо решить, какую информацию о функции / можно
использовать как входные данные для вычисления приближения д.
Например, часто известна или может быть получена таблица значений
функции вида A1.1), а иногда — и таблица ее производных. В некото-
некоторых случаях можно использовать информацию о значениях функции
на всем отрезке [а, Ь].
2°. Полезно иметь некоторую дополнительную априорную информа-
информацию об аппроксимируемой функции. Часто она бывает качественного
характера, например известно, что функция / "достаточно гладкая"
("плавно меняющаяся"), периодическая, монотонная, четная и т. п.
Иногда удается получить некоторые количественные характеристики
функции /, например, бывают известны верхние оценки для максимума
= 0, 1,2, ..., п),
292
A1.1)
1 Правда, в некоторых алгоритмах такое прерывание естественно, например
если ЭВМ используется для управления технологическим процессом, сложной
технической системой или включена в систему обработки и планирования
физического эксперимента.
293

модуля некоторых ее производных, величина периода, оценка уровня
погрешности в заданных значениях.
3°. Знание свойств функции /позволяет осознанно выбирать класс
G аппроксимирующих функций. Часто такой класс представляет собой
параметрическое семейство функций вида у = д (х, а) = д (х, oq, au ...,
Ош) и выбор конкретной аппроксимирующей функции д осуществляет-
осуществляется с помощью выбора параметров во, <»i, —i <Чл- Широко используются
классы функций вида
ат<ря(х),
A1.2)
являющихся линейными комбинациями фиксированного набора неко-
некоторых базисных функций <ро(х), <pi(x), ..., yjm(x). Функцию Фт(х) часто
называют обобщенным многочленом по системе функций у>о. Уь •••, <Рт,
а число m — его степенью.
Если в качестве базисных функций берутся степенные функции
<Р)^х) = I*, то возникает задача приближения алгебраическими много-
многочленами
Рт(х) = во + <Ч* + ... + <Jm*m- A1.3)
Отметим, что методы приближения функций алгебраическими много-
многочленами играют важную роль в численном анализе и наиболее глубоко
разработаны. Одна из причин этого состоит в том, что многочлены
A1.3) легко вычисляются, без труда дифференцируются и интегриру-
интегрируются.
Тригонометрические многочлены
Sm(x) = а0 +
(
KKm/2
cos 2хкх + fits sin 2irJbx),
A1.4)
часто используемые для аппроксимации периодических на отрезке
[О, 1] функций, также могут быть записаны в виде A1.2), если в качес-
качестве базисных функций выбрать функции <ро(х) = 1, ^(х) = cos 2тх,
<f>2(x) = sin 2тг, <р3(х) = сое 4тг, (р4(х) = sin 4тг, ... . Используя форму-
формулу Эйлера ехр {«у} = cos у + > sin у, можно записать тригонометричес-
тригонометрический многочлен A1.4) в виде
Sm(x)=
-т/ККт/2
A1.5)
что соответствует выбору базисных функций <pk(x) — ехр {2xikx},
-т/2 < * < т/2.
Используются также и некоторые нелинейные комбинации функ-
функций, отличные от A1.2). Например, в ряде случаев эффективным
является использование класса дробно-рациональных функций
294
1 + bjr + ... +
Выбор класса G аппроксимирующих функций осуществляется с
учетом того, насколько хорошо может быть приближена функция /
функциями из этого класса.
4°. Необходим критерий выбора в классе G конкретной аппрокси-
аппроксимирующей функции д, являющейся в смысле этого критерия наилуч-
наилучшим приближением к / Например, требование совпадения функции д
с функцией / в некоторых фиксированных точках приводит к задаче
интерполяции. Другой распространенный критерий — требование
минимизации среднеквадратичного уклонения — лежит в основе мето-
метода наименьших квадратов. Существует большое число других критери-
критериев, естественных в конкретных прикладных проблемах.
5°. Важно понимать, что решение указанных выше вопросов тесно
связано с тем, как мы собираемся использовать приближение д и ка-
какая точность нам нужна.
Замечание. Задачу выбора в классе G конкретной приближа-
приближающей функции можно рассматривать как задачу идентификации
(см. § 1.1), если интерпретировать функцию у = д (х, а) как матема-
математическую модель реальной функциональной зависимости у = /(х).
J 11.2. Интерполяция обобщенными многочленами
1. Постановка задачи интерполяции. Пусть в точках хо, х\, ••-, хп,
расположенных на отрезке [а, 4] и попарно различных, задана таблица
A1.1) значений некоторой функции /. Задача интерполяции состоит в
построении функции д, удовлетворяющей условию
Я (*,) = К (» = 0, 1, .-, п). (П.6)
Другими словами, ставится задача о построении функции д, график
которой проходит через заданные
точки (ij, yt) (рис. 11.1). Указанный
способ приближения функций приня-
принято называть интерполяцией (или
интерполированием), а точки ц —
узлами интерполяции.
Нетрудно видеть, что выбор функ-
функции д неоднозначен, так как по задан-
заданной таблице можно построить беско-
бесконечно много интерполирующих функ-
295
Хц X,
Рис. 11.1

ций. На практике, как правило, функцию д выбирают иа достаточно
узкого класса G функций, в котором единственность выбора гаранти-
гарантируется.
2. Экстраполяция. Пусть Zjnin и Япвх ~ минимальный и максималь-
максимальный из узлов интерполяции. В случае, когда интерполяция использу-
используется для вычисления приближенного значения функции /в точке х, не
принадлежащей отрезку fanlm Зпах] {отрезку наблюдения), принято
говорить о том, что осуществляется экстраполяция. Этот метод приб-
приближения часто используют с целью прогнозирования характера проте-
протекания тех или иных процессов при значениях параметров х, выходя-
выходящих за пределы отрезка наблюдения. Заметим, что надежность такого
прогноза при значениях х, удаленных на значительное расстояние от
отрезка [zmin> Zmxh как правило, невелика.
3. Задача интерполяции обобщенными многочленами. Рассмотрим
более подробно задачу интерполяции обобщенными многочленами
Фя(х) вида A12). Назовем обобщенный многочлен Фт(х) интерполяци-
интерполяционным, если он удовлетворяет условию
¦«(*«) = ». 0 = 0,1 я), A1.6)
или, что то же самое, системе линейных алгебраических уравнений
A1.7)
= Уп,
относительно коэффициентов во, аи ..., ат.
Заметим, что систему уравнений A1.7) можно записать в следую-
следующем виде:
где
Voi'n)
во
<Ч
УО
У\
. Уп.
A1.8)
A1.9)
Введем векторы <р, = (р/х0), <pfa)> ¦••> <Pj(xn))T, J = 0, 1, . ., m. Бу-
Будем говорить, что система функций <fio, <Pi, ¦¦¦, fm линейно зависима а
точках xq, xu ..., хп, если один из векторов <р} системы <f>o, <f\, ..., <Рт
296
может быть представлен в виде линейной комбинации остальных век-
векторов этой системы:
<р}
Jfc=0
A1.10)
В противном случае систему функций щ, <р\, ..., <рп будем называть
линейно независимой в точках xq, x\, ..., хп.
Пример 11.1. Покажем, что при m < п система функций 1, х, а?, ..., i
линейно независима в точках хо, i\, ..., tn, если они попарно различны.
Допустим противное. Тогда справедливо равенство A1.10), которое в дан-
данном случае (при од = (*8i 4i ¦••) *п)т) принимает вид
*{ = 2 а
Jt=O
к*)
= 0, 1, .... п).
A1.11)
m
Полагая а, = -1, получаем, что многочлен Рщ(х) = ? а*я* степени1 m обрг-
Jt=o
щается в ноль в точках xq, x\, ..., хп, число которых равно п+ 1 и, следова-
следовательно, больше т. Однако в силу основной теоремы алгебры многочлен степе-
степени т, тождественно не равный нулю, не может иметь более т корней. Полу-
Полученное противоречие доказывает линейную независимость рассматриваемой
системы функций
Рассмотрим матрицу Грама2 системы функций <ро, <р\, ..., <рп, име-
имеющую вид
(<Р0, Ч>0) (<Р1, <Ро) - (<Рт, *>о) '
Г = Р*Р =
A1.12)
. .90. Vm) (<(H, <Рт) ••• (<Рт, фт)
Здесь в случае, когда функции <р} могут принимать комплексные зна-
значения, под Р* понимается сопряженная к Р матрица, а элементы Tjfc
матрицы Грама вычисляются по формуле
1 В данной главе для упрощения формулировок будем говорить, что мно-
многочлен Рт имеет степень m даже в случае, когда а* = 0, т. е. фактическая его
степень меньше т.
2 Иорген Педерсен Грам A850—1916) — датский математик.
297

Ijk = Ы, <Pj) = S <Pk (Xi) <Pj(xi),
i=0
A1.13)
Если же функции ipj принимают только вещественные значения, то
Р* = Р1 и элементы матрицы Грама вычисляются по формуле
tjk =
,) = I <fk (r«)
«=o
A1.14)
Определитель матрицы Грама det Г принято называть определите-
определителем Грама.
Как следует из курса линейной алгебры, справедлив следующий
результат.
Теорема 11.1. Система функций <ро, ip\, ..., <рп является линей-
линейно независимой в точках х0, хи ..., хп тогда и только тогда, когда
т < п и определитель Грама det Г отличен от нуля.
Известно, что при т > п система функций <р0, <р\, ..., <рт линейно
зависима в точках х0, xi, ..., хп. Отсюда вытекает неединственность
решения а системы (П.8) (если оно существует). Действительно, в этом
случае справедливо представление A1.10) и вместе с вектором а реше-
решением системы A1.8) является вектор а' = я + <Д«, где Да = (а0, аи
..., atj-i, -I, atjn, ..., аж)т, a t — любое число. Бели же га< и, то реше-
решение системы A1.8) существует не для всякой правой части у.
В силу указанных причин при интерполяции обобщенными много-
многочленами число параметров т + 1 обычно берут равным числу п + 1
заданных точек. В этом случае Р — квадратная матрица и для того,
чтобы система A1-8) была однозначно разрешима при любой правой
части у, необходимо и достаточно, чтобы определитель матрицы Р был
отличен от нуля. В свою очередь при m = п это условие в силу равен-
равенства det Г = det P* det Р = |det P\2 и теоремы 11.1 дает следующий
результат.
Теорема 11.2. Если т = п, то решение задачи интерполяции
обобщенным многочленом A1.2) существует и единственно при любом
наборе данных у0, У\, ..., уп тогда и только тогда, когда система функ-
функций <ро, <pi, ..., <Рп линейно независима в точках х$, гь ..., хп.
Назовем систему функций <ро, <р\, ..., <рп ортогональной на множест-
множестве точек хо, щ, ..., хп, если (^, <pj) = 0 при к Ф j и (<рк, <р3) * 0 при к =
= j для всех it = 0, 1, ..., m; j = 0, 1, ..., т. Очевидно, что для ортого-
ортогональной на множестве z0, ri, ..., хп системы функций матрица Грама
диагональна, а определитель Грама отличен от нуля. Поэтому всякая
ортогональная на множестве точек xq, x\, ..., хп система функций
заведомо является линейно независимой в этих точках.
298
Пример 11.2. Покажем, что система функций у?0, <Pi, —, fN-\, где <Рк(х) =
— exp {2xijfcr}, ортогональна на множестве точек щ = '/№ ' = 0, 1, ..., N — 1.
Здесь I — мнимая единица.
Для доказательства ортогональности рассматриваемой системы функций
достаточно установить, что справедливо равенство
A1.15)
(ИЬ fj) = Щ (*= 0, 1 N- 1; j= 0, 1, .... N- 1),
где Skj = 0 при к Ф j w Skj = I при к = j. Введем обозначение и =
= exp {2xi/JV}. Тогда y>Jt(x;) = exp {2icikl/N} = ш*' и согласно формуле A1.13)
имеем
l*o
A1.16)
При к = j правая часть равенства A1.16), очевидно, равна N. При к Ф j, ис-
используя формулу суммы членов геометрической прогрессии и равенство
u,< k-j) N = exp {21Г<* - ])} = 1, имеем
j) = A -
= 0.
Таким образом, равенство A1.15), а вместе с ним и ортогональность системы
функций <fik(x) = exp {2xikx} доказаны.
В случае, когда система функций р0, ipi, ..., <рп ортогональна на
множестве точек хо, х\, ..., хп, решение задачи интерполяции не пред-
представляет затруднений. Действительно, система уравнений A1.8) после
умножения на матрицу Р* преобразуется к виду
Га=*, Ь=Р*Г
A1.17)
Заметим, что элементы вектора * = F0, 6ь —¦ *т)т вычисляются по
формуле
= (f, <Pj) =
A1.18)
Так как матрица Г диагональна, то решение системы A1.17) находит-
находится в явном виде:
:0, 1, ..., т. A1.19)
299

$ 11.3. Полиномиальная интерполяция.
Многочлен Лагранжа
1. Интерполяционный многочлен. Начнем с рассмотрения задачи
интерполяции в наиболее простом и полно исследованном случае ин-
интерполирования алгебраическими многочленами. Для заданной табли-
таблицы A1.1) многочлен Рп(х) = Е ад.х* степени л называется интерполя-
интерполяционным многочленом, если он удовлетворяет условиям
Лт(*«) = У, (i = 0, 1, ..., п). A1.20)
Равенство A1.20) можно записать аналогично A1.7) в виде системы
уравнений
во +
Оо +
+ «2*0 + - + «П*0 = УО.
+ 02*? + ... +
A1.21)
= Уп
относительно коэффициентов многочлена. Эта система однозначно
разрешима, так как система функций 1, х, х2 хп линейно независи-
независима в точках го, xi, ..., х„ (см. пример 11.1 и теорему 11.2). Однозначная
разрешимость системы A1.21) следует и из того хорошо известного
факта, что определитель этой системы (определитель Вандермонда1)
*? ... af
= П (х,-х;)
1 *h «n ••• *п
отличен от нуля, если узлы интерполяции попарно различны. Таким
образом, верна следующая теорема.
Теорема 11.3. Существует единственный интерполяционный
многочлен степени п, удовлетворяющий условиям A1.20).
Замечание. На практике система A1.21) никогда не использу-
используется для вычисления коэффициентов интерполяционного многочле-
300
1 Александр Теофил Вандермонд A735-1796) — французский математик.
на. Дело в том, что часто она является плохо обусловленной. Кроме
того, существуют различные удобные явные формы записи интерпо-
интерполяционного многочлена, которые и применяются при интерполя-
интерполяции. Наконец, в большинстве приложений интерполяционного
многочлена явное вычисление коэффициентов од не нужно.
2. Многочлен Лагранжа. Приведем одну из форм записи интерпо-
интерполяционного многочлена — многочлен Лагранжа
Ln(x) = EQ j,;/n;<x).
Здесь
М*) = "
A1.22)
к=1
- *к
Как нетрудно видеть, 1п](х) представляет собой многочлен степени п,
удовлетворяющий условию
0 при i Ф j.
Таким образом, степень многочлена Ln равна п и при х = х, в сумме
A1.22) обращаются в ноль все слагаемые, кроме слагаемого с номером
)= г, равного yt. Поэтому многочлен Лагранжа A1.22) действительно
является интерполяционным.
Замечание 1. Запись интерполяционного многочлена в фор-
форме Лагранжа A1.22) можно рассматривать как его запись в виде
обобщенного многочлена A1.2) по системе функций <р?х) ¦=¦ lni?x),
к= 0, 1, ..., п.
Замечание 2. Как правило, интерполяционный многочлен
Лагранжа используется так, что нет необходимости его преобразо-
преобразования к каноническому виду Ln(x) = Е а^х*. Более того, часто
Jt« о
такое преобразование нежелательно.
В инженерной практике наиболее часто используется интерполяция
многочленами первой, второй и третьей степени (линейная, квадратич-
квадратичная и кубическая интерполяции). Приведем соответствующие формулы
для записи многочленов Лагранжа первой и второй степени:
301

"*\
+ yj
(
A1.23)
Ъ <11Л4>
Пример 11.3. Пусть задана таблица значений функции у = In x:
Таблица 11.1
1.0
1.1
1.2
1.3
1.4
у 0.000000 0.095310 0.182322 0.262364 0.336472
Для приближенного вычисления значения In A.23) воспользуемся линей-
линейной и квадратичной интерполяцией.
Возьмем цэ = 1.2, ц = 1.3. Вычисление по формуле A1.23) дает значение
In A.23) « IiA.23) « 0.206335.
Для применения квадратичной интерполяции возьмем xq = 1.1, х\ = 1.2,
Х2 = 1.3 — три ближайших к точке х = 1.23 узла. Вычисляя по формуле
A1.24), имеем In A.23) и ?гA.23) и 0.207066.
Заметим, что пока нам не известна погрешность полученных приближенных
значений.
§ 11.4. Погрешность интерполяция
Приведем без доказательства наиболее известную теорему о пог-
погрешности интерполяции.
Теорема 11.4. Пусть функция f дифференцируема п + 1 раз на
отрезке [а, Ь], содержащем узлы интерполяции xt, i = 0, 1, ..., п. Тогда
для погрешности интерполяции в точке х € [а, Ь] справедливо равенс-
равенство
A1.25)
в котором wn+i(r) = (г — Хо)(х — Х!)...(г — хп), а ? — некоторая точка,
принадлежащая интервалу (а, Ь).
Основное неудобство в использовании этой теоремы состоит в том,
что входящая в формулу A1.25) для погрешности точка ( неизвестна.
Поэтому чаще используется не сама теорема, а ее следствие.
302
Следствие. В условиях теоремы 11.4 справедлива оценка
погрешности интерполяции в точке х € [а, 6], имеющая вид
A1.26)
а также оценка максимума модуля погрешности интерполяции на
отрезке [а, Ь], имеющая вид
max |/(г)-Р„(х)|
г и
[о, Ь]
(H-27)
Здесь
= max
[а.*]
Пример 11.4. Оценим погрешность приближений к In A.23), полученных в
примере 11.3 с помощью интерполяции многочленами первой и второй степени.
В этих случаях неравенство A1.26) примет вид
-«01.
A1.28)
A1.29)
1 2
Заметим, что для f(x) - In (х) имеем / 2) (х) = - -$ и /3) (х) = -j. Поэто-
Поэтому здесь М2 = max |/2)(х)| = у-^ и 0.69 и А/3 = max \P3)(x)\ =
[1.2,1.3] [1.1,1.3]
2
= —j-j и 1.5. Тогда в силу неравенств A1.28) и A1.29) получаем следующие
оценки погрешности:
е!=|1пA.23) - IiA.23)| < !у!|A.23—1.2X1.23-1.3I « 7.3-Ю,
е2=|1пA.23)-?2A.23)| < ^р|A.23-1.1)A.23-1.2)A.23-1.3)| W6.9-10.
Если на отрезке [а, 6] производная /"¦!> меняется слабо, то вели-
величина абсолютной погрешности \f(x) — Рп(х)| почти полностью опре-
определяется значением функции Шпц(х). Представление о типичном ха-
характере поведения этой функции можно получить из рис. 11.2.
303

Рис 11.2
Обратим внимание на то, что при
выходе аргумента х за пределы
отрезка наблюдения [%;„, a^J зна-
значение |u/n+i(i)| быстро становится
очень большим. Это объясняет нена-
ненадежность экстраполяции функции
для значений аргумента, удаленных
от отрезка наблюдения.
Пусть теперь г0 < *i < ••¦ < хп и
пусть Л, = х, — xt-i — t-й шаг табли-
таблицы, а Ащах = max А,. Несколько
К t<n
огрубляя оценку A1.27), можно получить следующее неравенство:
max \f(x)-Pn(x)\<
Mn*i
4(п
A1.30)
Оно позволяет утверждать, что для достаточно гладкой функции /
при фиксированной степени интерполяционного многочлена погреш-
погрешность интерполяции на отрезке [хо, я„] при АтаХ -+ 0 стремится к нулю
не медленнее, чем некоторая величина, пропорциональная Ь^. Этот
факт принято формулировать так: интерполяция многочленом степени
п имеет (п + 1)—й порядок точности относительно Атах. В частности,
линейная и квадратичная интерполяции имеют второй и третий по-
порядки точности соответственно.
§ 11.5. Интерполяция с кратными узлами
1. Интерполяционный многочлен с кратными узлами. Иногда в
узлах г, (i = 0, 1, ..., т) бывают заданы не только значения у, = /(я,)
функции / но и значения ее производных у'г = f'(x,), y"t = Г(хг), ...,
у**») = /<*г1'(г,) до некоторого порядка it, — 1. В этом случае узел х,
называют кратным, а число kt, равное количеству заданных значений,
— кратностью узла. Пусть п = k0 + k\ + ... + кт — 1. Можно доказать,
что существует единственный многочлен Рп(х) степени п, удовлетворя-
удовлетворяющий условиям
= У„
= У[,
для всех i = 0, 1, ..., т. Этот многочлен называют интерполяционным
многочленом с кратными узлами. Можно указать и явную формулу его
записи, аналогичную форме Лагранжа A1.22). Мы этого делать не
будем и отметим лишь два важных частных случая.
1°. Пусть на концах отрезка [хо, X]] заданы значения уо, уи у^, у[.
Тогда m=l,ifco = 2, Jbi=2, п = 3и интерполяционный многочлен
Р3(х), удовлетворяющий условиям Р3(х0) = Jfo, Р^Ы) = у'о, Pz{*\) = У\,
Р'3(х\) = у[, может быть представлен (что проверяется непосредствен-
непосредственно) в следующем виде:
A1.31)
"Г П дз -г »1 Л2
где А = Х\ — х0. Многочлен A1.31) принято называть кубическим ин-
интерполяционным многочленом Эрмита1.
2°. Пусть в точке х0 заданы значения у0, у'о, ¦¦¦, у10п) ¦ Тогда много-
многочлен Рп(х), удовлетворяющий условиям Pn(io) = Уо, ^(^о) = ?о> ¦¦-,
= у^оп) представляется в виде
(*) . A1.J2)
Рп(х) =
Как нетрудно видеть, многочлен Рп(х) представляет собой отрезок
ряда Тейлора. Таким образом, формула Тейлора дает решение задачи
интерполяции2 с одним узлом кратности п + 1.
2. Погрешность интерполяции с кратными узлами.
Теорема 11.5. Пусть функция f дифференцируема п + 1 раз на
отрезке [а, 6], содержащем узлы интерполяции rt (t = 0, 1, ..., т).
Тогда для погрешности интерполяции с кратными узлами в точке
х€ [а, Ь] справедливы равенство A1.25) и неравенства A1.26), A1.27),
в которых un+i(x) = (х - хо)I (г - ziP ... (г - rm) , а ? — некоторая
точка, принадлежащая интервалу (а, Ь).
Для формулы Тейлора (т = 0, *0 = п + 1) теорема 11.5 дает извес-
известную формулу остаточного члена в форме Лагранжа. Для кубического
304
1 Шарль Эрмит A822—1901) — французский математик.
2 Заметим, что в действительности с ее помощью осуществляется экстра-
экстраполяция.
305

многочлена Эрмита (т = 1, Jfco = 2, к{ = 2) неравенство A1.27) приво-
приводит к следующей оценке погрешности:
max
A1.33)
Здесь учтено то, что максимум функции 014A) = (х — гоJ(х — х\J на
отрезке [го, *\] достигается в точке х = (х0 + хх)/2 и равен Л4/16.
§ 11.6. Минимизация оценки погрешности интерполяции.
Многочлены Чебышева
1. Постановка задачи минимизации оценки погрешности. Предполо-
Предположим, что значение заданной на отрезке [а, ft] функции /можно вычис-
вычислить в произвольной точке х. Однако по некоторым причинам1 целе-
целесообразнее заменить прямое вычисление функции / вычислением зна-
значений ее интерполяционного многочлена Рп. Для такой замены необ-
необходимо один раз получить таблицу значений функции / в выбранных
на отрезке [а, 6] точках х$, x\, ..., хп. При этом естественно стремиться
к такому выбору узлов интерполяции, который позволит сделать ми-
минимальной величину Д(Р„) = max \f(x) — Рп{х)\ — погрешность
интерполяции на отрезке [a, ft].
Пусть о функции / известно лишь то, что она непрерывно диффе-
дифференцируема п + 1 раз на отрезке [a, ft]. Тогда неравенство A1.27) дает
верхнюю границу погрешности интерполяции:
, Ь]
A1.34)
Поставим теперь задачу: определить набор узлов интерполяции х0, хи
..., хп, при котором величина А(Рп) минимальна. Для решения этой
задачи нам потребуются некоторые сведения о многочленах Чебыше-
Чебышева2.
1 Например, вычисление значений / (х) — трудоемкая операция.
2 Пафнутий Львович Чебышев A821—1894) — русский математик, один из
создателей современных теории чисел, теории вероятностей, теории прибли-
приближений функций.
306
Замечание. Формула A1.34) остается справедливой и в слу-
случае, когда некоторые из узлов хо, х\, ..., хп совпадают, т. е. имеет
место интерполяция с кратными узлами.
2. Многочлены Чебышева. Введенные П.Л. Чебышевым многочлены
Тп(х) широко используются в вычислительной математике. При п = 0
и п = 1 они определяются явными формулами
ВД = 1, Т,(х) = х, A1.35)
а при п > 2 рекуррентной формулой
Тп(х) = 2хТп.1(х) - Тп.2{х). A1.36)
Запишем явные формулы для многочленов Чебышева Тп{х) при
п = 2, 3, 4, 5:
ВД = 2гВД - ВД = 2*2-1,
ВД = 2*Г2(г) - ВД = 4x3 - з*.
Т4(х) = 2хГ3(г) - Т2(х) = 8** - в*2 + 1,
Т5(х) = 2хТ4(х) - Т3(х) = 16г5 - 20гЗ + 5г.
Аналогично можно записать явные формулы и при n ^ 6.
Приведем некоторые свойства многочленов Чебышева.
1°. При четном п многочлен Тп(х) содержит только четные степе-
степени х и является четной функцией, а при нечетном п многочлен Тп(х)
содержит только нечетные степени х и является нечетной функцией.
2°. При п > 1 старший коэффициент многочлена Тп(х) равен 2",
т. е. Г„(г) = 2п'1хп + ... .
Справедливость свойств 1° и 2° следует непосредственно из опреде-
определения A1.35), A1.36).
3°. Для х € [-1, 1] справедлива формула
Тп(х) = cos (n arccos x). A1.37)
D При п = 0 и п = 1 формула A1.37) верна, так как
cos @-arccos x) = 1, cos (I-arccos x) = х. Для того чтобы доказать
справедливость формулы для всех п > 0, достаточно показать, что
функции Сп(х) = cos (n arccos х) удовлетворяют такому же, как и
многочлены Чебышева, рекуррентному соотношению
Сп(х) = 2х Спл{х) - Сп.2(х) A1.38)
(ср. с A1.36)). Соотношение A1.38) получится, если в легко проверяе-
проверяемом тригонометрическом тождестве
307

cos [(m + 1) <fi] + cos [(m — 1) tp] = 2cos tp cos mip
положить m = n — l и tp = arccos x. Ш
4°. Яри n > 1 многочлен Тп(х) имеет ровно п действительных кор-
корней, расположенных на отрезке [-1, 1] и вычисляемых по формуле
B*
хк = cos v 2
к - О, 1, ..., п - 1.
A1.39)
5°. При п > 0 справедливо равенство max | Тп(х)| = 1. Если в > 1,
[-1.1]
то этот лаксилул (Jocmwtoemcji роемо в п + 1 точках, которые нахо-
находятся по формуле
Гтт] _ ,
= сов — , т = 0, 1, ..., п.
A1.40)
При этом Тп(хт) — (-1I", т. е. максимумы и минимумы многочлена
Чебышева чередуются.
Доказательство свойств 4° и 5° основано на применении формулы
A1.37). Например, в силу этой формулы корни многочлена Тп{х),
расположенные на отрезке [-1, 1], совпадают с корнями уравнения
cos (n arccos x) = 0. Эквивалентное преобразование этого уравнения
дает n arccos х = т/2 + хк, к - О, ±1, ±2, ... . Так как 0 < arccos x < т,
то заключаем, что имеется ровно п корней ц, отвечающих значениям
к = 0, 1, ..., п — 1 и удовлетворяющих равенствам arccos зд =
= i— —, эквивалентным формуле A1.39).
2п
Назовем величину max | Pn(x) \ уклонением многочлена Рп(х) от
[-1.1]
нудя. Эта величина характеризует максимальное отклонение (уклоне-
(уклонение) графика многочлена Рп от графика функции у = 0 на отрезке
Н, 1].
6°. Среди всех многочленов фиксированной степени п > 1 со стар-
старшим коэффициентом ап, равным 1, наименьшее уклонение от нуля
(равное 21'") имеет многочлен Г„(х) = 21"" Гп(х).
Благодаря этому свойству, Имеющему особую ценность для прило-
приложений, многочлены Чебышева иногда называют наименее уклоняющи-
уклоняющимися от муля. Свойство 6° иначе можно сформулировать так: для
любого многочлена вида Рп(х) = хп + an-ixn~l + ... + ао, отличного от
Тп(х), справедливо неравенство
21"п = max | fn(z) | < max | Pn(x) \.
[-1.1] [-1.1]
308
Приведем графики многочленов Тп(х) для п = 1, 2, 3, 4, 5 (рис.
11.3).
T,fx)
Замечание. Из свойства 6° следует, что среди всех многочле-
многочленов Рп(х) фиксированной степени п > 1 со старшим коэффициентом
ап Ф 0 наименьшее уклонение от нуля (равное |ап|2''") имеет мно-
многочлен ап Тп(х).
Формулы A1.39) и A1.40) позволя-
позволяют дать следующую геометрическую
интерпретацию построения корней и
точек экстремума многочлена Т^х).
Разделим полуокружность, опираю-
опирающуюся на отрезок [-1, 1] как на
диаметр, на In равных частей и
спроецируем полученные точки на
отрезок [-1, 1]. На рис. 11.4 изображен Рис. 11.4
случай п = 5.
Нумеруя проекции справа налево, получим, что все проекции с
нечетными номерами являются корнями многочлена Тп (на рис. 11.4
309

они помечены кружочками), а все проекции с четными номерами —
точками экстремума (они помечены крестиками). Заметим, что корни и
точки экстремума сгущаются к концам отрезка [-1; 1].
3. Решение задачи минимизации оценки погрешности. Найдем
сначала решение задачи в предположении, что отрезок интерпо-
интерполяции [а, Ь] совпадает с отрезком [-1, 1]. В этом случае величина
A1.34) будет минимальной при таком выборе узлов xq, х\, ..., хп, при
котором минимальна величина max |wn+1(x)|, т. е. минимально укло-
[-1:1]
нение многочлена u>n*i{x) = (х — xQ)(x — xi)...(x — хп) от нуля. В силу
свойств 4° и 6° многочленов Чебышева решение задачи дает набор
узлов
2* + 1
являющихся нулями многочлена Тп+и так как в этом случае ы„+1 =
Заметим, что при таком выборе
(n + 1)! 2" '
A1.41)
причем в силу свойства 6° любой другой выбор узлов дает большее
значение верхней границы погрешности. Для сравнения укажем, что
при использовании для приближения функции / отрезка ряда
п А к) (ft)
Тейлора Рп(х) = S , ' хк верхняя граница оценки погрешности
такова:
Следовательно, она в 2П раз хуже, чем при интерполяции с оптималь-
оптимальным выбором узлов.
Пусть теперь отрезок интерполяции [а, Ь] произволен. Приведем его
к стандартному отрезку [-1, 1] заменой
а+ b b- a
х = —о" + "о-
A1.42)
где t € [-1, 1]. Как нетрудно видеть, в этом случае и>пц(х) =
310
= (t - to)(t - «,)...(/ _
_ b a
- 2 *" —2— tk ДЛЯ k = °' l> -' n- Следовательно,
„ Zk _
6 - a
n+l
max I
[-1.1]
и минимум этой величины достигается при значениях to, t\, ..., <„,сов-
падающих с нулями многочлена Т^. Значит, решение поставленной
задачи дает выбор узлов
4 =
а+ b . b-a
¦ cos
2*+
' *=0'1 п-
A1.43)
которому отвечает минимальное значение верхней границы погрешнос-
погрешности интерполяции, равное
(я + 1)! 2"
§ 11.7. Конечные разности
1. Таблица конечных разностей. Пусть функция у = f(x) задана
таблицей A1.1) своих значений, причем г0 < х\ < ... < хп и расстояние
h = Xi — Zj-i между соседними узлами таблицы значений аргумента
постоянно. В этом случае величину h называют шагом таблицы, а
узлы — равноотстоящими.
Величину Ду, = j/ffi — yx принято называть конечной разностью
первою порядка функции у = /(г) в точке Х{ (с шагом А). Конечная
разность второю порядка определяется формулой A2yt = Ay^i — Дзд.
Аналогично определяются конечные разности третьего и более высо-
высоких порядков. Общее определение конечной разности порядка к тако-
таково:
Здесь к > 1 и Д°у, = yt.
Таблицу конечных разностей (которые называют еще конечными
разностями вперед) обычно располагают следующим образом:
311

Таблица 11.2
Д3»
ft
«2
Д2»ь
ДУп-2
Д3Уп-3
Vn-1
Vn
2. Свойства конечных разностей. Можно показать, что конечные
разности порядка к выражаются через значения функции в it + 1
точке по формуле
(
1*0
A144)
где Cl = ' — биномиальные коэффициенты. В частности,
"¦ I '\к —1I
— »„
Приведем без доказательства важное утверждение, указывающее на
тесную связь между производными гладких функций и их конечными
разностями.
Теорема 11.6. Пусть функция / дифференцируема к раз на
отрезке [г,, r^fc]- Тогда справедливо равенство
Д*Л =**/*» @, A1-45)
в котором ? — некоторая точка из интервала (х„ znfc)-
312
Замечание. При к = 1 формула A1.45) совпадает с форму лий
конечных приращений Лагранжа.
Следствие. Для многочлена у = Рп{х) — S о^т конечная
разность порядка п является постоянной величиной, равной hnn'.an.
Разности порядка k > n тождественно равны нулю.
Конечные разности имеют разнообразные практические примене-
применения. Например, если производная Jb-ro порядка / к) слабо меняется на
отрезке [х„ х^^, то в силу равенства A1.45) для х € [г„ х^к] справедли-
справедлива следующая формула численного дифференцирования:
/ *1
A1.46)
В § 11.9 конечные разности будут использованы для построения
интерполяционного многочлена Ньютона. Рассмотрим еще два прило-
приложения конечных разностей, связанных с анализом погрешностей таб-
таблиц, а именно задачу об оценке уровня "шума" таблицы и задачу
обнаружения единичных ошибок.
Заметим, что в реальных вычислениях таблица конечных разностей
Д*у, строится по значениям у* каждое из которых содержит погреш-
погрешность е; = у} — у* Тогда в силу формулы A1.44) найденные значения
Д*у* содержат неустранимые ошибки
1
Г = S (-1)*"' qt e,»|.
A1.47)
Как нетрудно видеть, имеется тенденция к росту погрешностей ?<*> с
ростом к. Если известно, что |е,| < е для всех i, то можно гарантиро-
гарантировать справедливость лишь следующей оценки:
A1.48)
3. Оценка уровня "шума" в таблице. На практике часто возникает
следующая задача. Для набора г0, х\, ..., хп равноотстоящих узлов
каким-либо образом построена таблица приближенных значений глад-
гладкой функции у = f(x). Требуется оценить уровень погрешности (уро-
(уровень "шума") таблицы.
Полученная выше гарантированная оценка погрешности A1.48) не
Дает удовлетворительного ответа на поставленный вопрос. Она лишь
313

указывает на то, что в самом неблагоприятном случае рост ошибки
произойдет с коэффициентом, равным 2к. Проведем статистический
анализ погрешности. Будем предполагать, что ошибки ед (j = 0, 1, ...,
п) являются независимыми случайными величинами с математическим
ожиданием A/ [ej = 0 (это эквивалентно отсутствию систематической
составляющей погрешности) и дисперсией М [е^] = а2.
В силу формулы A1.47) М [&\к)\ = 0 и тогда для дисперсии
погрешности k-й разности имеем:
= М
(ff<*>J = Л/[(Е(-1)Ы
>o
S (-l
Mr
( ? (-I)*"' CTkew)]
г-О
СГк
Заметим, что E (ClJ = Сгк и A/ [e,*/ e^r] = 0 при / Ф г, так как
величины e^i и е^г независимы. Следовательно, (<г(*>J =
Принимая за уровень "шума" таблицы величину а квадратного
корня из дисперсии (среднеквадратичную ошибку), получим равенство
A1.49)
которое дает более оптимистичное по сравнению с оценкой A1.47)
значение коэффициента роста ошибки, так как \ С^к < %к-
Бели конечные разности Аку* строятся для гладкой функции, то
они часто имеют тенденцию с ростом к уменьшаться по абсолютной
величине, а затем, начиная с некоторого к = р, возрастать, испытывая
сильные колебания в пределах одного столбца. При этом для к > р
основной вклад в значение Д*у* вносит величина е',*'. Это обстоя-
обстоятельство позволяет считать, что в оценке дисперсии (<г(Р>J »
1 П^Р
« 7 ^ (?(.р)J величины е'Р' можно приближенно заменить
п — р + 1 ,«о 1 '
на ДРу*. Вычислив <г(Р', затем достаточно воспользоваться формулой
A1.49) для оценки уровня "шума" таблицы.
Пример 11.5. Оценим уровень "шума" в таблице значений функции у =
— In х, заданной с шагом А = 0.1 (первый и второй столбцы табл. 11.3). Сос-
314
тавив таблицу конечных разностей1, замечаем, что, начиная с Jfc = 5, абсолют-
абсолютные значения разностей Аку} начинают возрастать. Оценим <тE) следующим
образом:
<т<5>
у 1*0
(Д5У,)
«3.5-10-1
Учитывая, что Cj0 = 252, имеем а = <гE)Д/252 « 2-10. Таким образом,
погрешность таблицы составляет примерно две единицы 5-го разряда, а 6-4 и
7-й разряды уже не содержат полезной информации. Если бы таблицу предпо-
предполагалось использовать на практике, то, по-видимому, имело бы смысл округ-
округлить значения у, до 5 значащих цифр после десятичной тоаки.
Таблица 11.3
г
1.0
1.1
1.2
1.3
1.4
1.5
1.6
1.7
1.8
1.9
2.0
У
0.0000000
0.0953274
0.1823232
0.2623748
0.3364634
0.4054856
0.4700009
0.5306478
0.5877802
0.6418666
0.6931428
Ду
953274
869958
800516
740886
690222
645153
606469
571324
540864
512752
Д2у
-«3316
-69442
' -59630
-50664
-45069
-38684
-35145
-30460
-28102
ДЗу
13874
9812
8966
5595
6385
3539
4685
2358
Д<2,
-4062
-846
-3371
790
-2846
1146
-2327
Д5у
3216
-2525
4161
-3636
3992
-3473
1 Следуя общепринятым обозначениям, мы записываем конечные разности
так, как если бы десятичная точка следовала за последними разрядами, от-
отведенными для значения функции.
315

4. Обнаружение единичных ошибок. Анализ таблиц конечных
разностей позволяет в некоторых случаях обнаруживать грубые еди-
единичные ошибки в таблицах гладких функций и даже частично их
устранять. Прежде чем продемонстрировать сказанное на примере,
рассмотрим, как распространяется в таблице конечных разностей
ошибка е, допущенная только в одном значении щ. Пользуясь форму-
формулой A1.47) или равенством e'fc) = ejjfj1' — е'*' (где е^°> = е при j =
= t и е'0) = 0 при j Ф i), получим следующую таблицу распростране-
распространения единичной ошибки, т. е. ошибки, допущенной в одной точке.
Таблица 11.4
?<0) ?<1) ?B) ?C) ?D)
?<*>
«1-1
О е
е
е -4с
-Зе
-2е бе
Зе
е -4е
-е
О е
Пример П.в. Пусть на отрезке [1.5, 2.8] задана таблица значений функции
у = In r (первый и второй столбцы табл. 11.5). Составим для нее таблицу
конечных разностей. Аномальное поведение разностей третьего и четвертого
порядка указывает на наличие в таблице значений функции ошибки. Сравне-
Сравнение с табл. 11.4 распространения единичной ошибки приводит к заключению о
том, что погрешность допущена в значении у, отвечающем х = 2.2. Тогда
погрешностям е, -4е,. бе, -4е, ? табл. 11.4 приближенно отвечают значения
316
262-10-6, -1231-10-6, 1774-10, -1222-10-6, 282- Ю'б табл. 11.5. Это соответст-
соответствие имеет место при е « 298-10'6. Следовательно, табличное значение 0.788757
нужно заменить на 0.788459.
Таблица 11.5
X
1.5
1.6
1.7
1.8
1.9
2.0
2.1
2.2
2.3
2.4
2.5
2.6
2.7
2.8
У
0.405465
0.470004
0.530628
0.587787
0.641854
0.693147
0.741937
0.788757
0.832909
0.875469
0.916291
0.955511
0.993252
1.029619
д»
64539
60624
57159
54067
51293
48790
4682Q
44152
42560
40822
39220
37741
36367
My
-3915
-3465
-3092
-2774
-2503
-1970
-2668
-1592
-1738
-1602
-1479
-1374
Дз,
450
373
318
271
533
-698
1076
-146
136
123
105
*у
-77
-55
-Л1
262
-1231
1774
-1222
282
-13
-18
Замечание. Часто вместо конечных разностей вперед
Аку{ используют разности назад, определяемые рекуррентной фор-
формулой
317

Здесь it > 1, V°yt = yv Заметим, что разности вперед и назад связа-
связаны равенством
§ 11.8. Разделенные разности
1. Таблица разделенных разностей. Пусть функция / задана на
таблице Xq, х\, .,., хп значений аргумента с произвольным (не обяза-
обязательно постоянным) шагом, причем точки таблицы занумерованы в
произвольном (не обязательно возрастающем) порядке. Величины
~/(Ti)
принято называть разделенными разностями первого порядка функции
/. Разделенные разности второго порядка определяются формулой
J \-H -»»,, -,т4/
Xt*2 — ХХ
Аналогично определяются разделенные разности третьего и более
высоких порядков. Общее определение разделенной разности порядка
к> 2 таково:
-/О* ¦¦¦;
Таблицу разделенных разностей обычно располагают следующим
образом:
Таблица 11.6
ч)
' /(ад ч; •••;
h /(n)
2. Свойства разделенных разностей. Разделенные разности облада-
обладают рядом замечательных свойств. Перечислим без доказательства
некоторые из них.
318
1°. Разделенная разность f (х{, хм\ ...; **¦*) является симметричной
функцией своих аргументов г,, гпЬ ..., x^jt (m. e. ее значение не меняет-
меняется при любой их перестановке).
2°. Пусть функция /имеет на отрезке [а, Ь], содержащем точки г,,
X производную порядка к. Тогда справедливо равенство
=
A1.50)
где ? — некоторая точка, расположенная на интервале (а, ft).
3°. В случае, когда таблица значений аргумента имеет постоянный
шаг h, разделенная и конечная разности связаны равенством
/(х,; **,;...;х**)=р§- A1.51)
Пример 11.7. Приведем таблицу (табл. 11.7) разделенных разностей для
функции, заданной табл. 11.1. Вычисления произведены на 6-разрядной
десятичной ЭВМ.
Таблица 11.7
1.0
1.1
1.2
1.3
0.000000
0.095310
0.182322
0.262364
0.953100
0.870120
0.800420
0.741080
-0.414900
-0.348500
-О.296700
0.221333
-0.121665
0.172667
1.4 0.336472
Перенумеруем теперь узлы, положив щ — 1.2, 1\ = 1.3, ъ = 1.1, хд = 1.4,
<4 = 1-0. Тогда таблица разделенных разностей примет следующий вид:
Таблица 11.8
1.2
1.3
1.1
1-4
i
1.0
0.182322
0.262364
0.095310
0.336472
0.000000
0.800420
0.835270
0.803873
0.841180
-0.348500
-0.313970
-0.373070
" 0Л 72650
-0.121750
0.197000
319

В табл. 11.8 подчеркнуты разделенные разности, которые совпадают (как и
должно быть в силу свойства 1°) с точностью до вычислительной погрешности
с соответствующими разделенными разностями из табл. 11.7 (они также под-
подчеркнуты).
§ 11.9. Интерполяционный многочлен Ньютона.
Схема Эйтнена
1. Интерполяционный многочлен Ньютона с разделенными разнос-
разностями. Используя разделенные разности, интерполяционный многочлен
можно записать в следующем виде:
/(ад ч)
/(ад *i; х2)(х-х0)(х - хх)
п
+ /(х0; хп ..., xn)(x-x0)(x-xl)...(x-xn.l) = Е /(ад xi; ...,
Jt=o
). A1.52)
Здесь wo(z) = 1, wjt(*) = (x — zo)(r — zi)...(x — zfc-О- Записанный в та-
таком виде интерполяционный многочлен называют интерполяционным
многочленом Ньютона с разделенными разностями.
Замечание 1. Отметим очевидную (с учетом равенства
A1.50)) аналогию между формулой Ньютона A1.52) и формулой
Тейлора A1.32).
Замечание 2. Формулу A1.25) для погрешности интерполя-
интерполяции в точке х, не являющейся узловой, можно уточнить следующим
образом:
/(х) - Р„(х) = /(х0; ...; х„; х)шп<г1(х).
A1.53)
Мы не приводим доказательства этой замечательной формулы.
Отметим лишь, что если воспользоваться свойством 2° разделенных
разностей, то из нее немедленно получается формула A1.25).
В практическом плане формула A1.52) обладает рядом преиму-
преимуществ перед формулой Лагранжа. Пусть, например, по каким-либо
причинам необходимо увеличить степень интерполяционного много-
многочлена на единицу, добавив в таблицу еще один узел xn+i. При исполь-
использовании формулы Лагранжа A1.22) это приводит не только к увеличе-
увеличению числа слагаемых, но и к необходимости вычислять каждое из них
заново. В то же время для вычисления Pn*i(x) п0 формуле Ньютона
320
A1 52) достаточно добавить к Рп(х) лишь одно очередное слагаемое,
так как
Заметим, что в случае, когда величина \хп*у — х\ мала, а функция /
достаточно гладкая, справедливо приближенное равенство
/(х0; ...; хп, I) * f(x0; .. ; хп; хп+1),
из которого с учетом равенств A1.53) и A1.54) следует, что
fix)- Рп(х) * РпН(х) - Рп(х).
Таким образом, величину
?n= \Pn*i(x)- PrXx)\ A1.55)
можно использовать для практической оценки погрешности интерпо-
ляцнп.
Пример 11.8. По табл 11.1 значений функции у -= In x из примера 11.3
найдем приближенное значение In т при х = 1.23, используя интерполяцион-
интерполяционные многочлены Ньютона с разделенными разностями Pk(x) для к = 0, 1, ..., 4.
Оценим при к — 0, 1, 2, 3 погрешность интерполяции по формуле A1.55).
Занумеруем узлы таблицы в следующем порядке: х0 = 1.2, i\ = 1.3, ^ =
= 1.1, г> = 1.4, ?4 = 1 -0, т. е. в порядке возрастания расстояния до точки г =
~ 1 23. Соответствующие этой нумерации разделенные рачности приведены в
табл 11.8 (мы используем только подчернутые разности).
Вычисления на б-разрядной десятичной ЭВМ дают следующие значения:
Р*(г) = О 1Я2322. Р,(х) - Р0(х) + f(x0, jj) o.'i(г) й 0 182322 +
+ 0 80042-A.23 - 1 2) » 0 206335. е( = | Р^х) - Р0(х)| «2 4-10.
Р,{х) - Р{{х) г f(x0. j\. х2) и,(х) « 0.206335 — 0.3485A.23 — 1.2)A.23 —
- 1 3) й 0 207СЙ7, Z; -- \Р2(х) - Р,(х)\ й 7.3-10"'1.
Аналогично получаются значения Р-Л(х) ~ 0.207020, Е-> и 4.7-10, Рц{х) ~
« 0.207014, ?о -s 6-10"'5
EciH бы задача состояла в определении значения In f i.23) с точностью с =
= 10'А, то вин имения следовало бы окончить поте получения ?¦> < ?.
Результат был бы таким: !и A.23) « Р>(х) й 0 2071
11-28 * 321

2. Интерполяция с использовавшем схшы Эйткена. Рассмотрим
один из алгоритмов решения задачи интерполяции. Предполагается,
что задана таблица значений функции / Требуется при заданном х
вычислить с помощью интерполяции значение /(х) с заданной точнос-
точностью е либо с максимально возможной при имеющейся информации
точностью. Считается, что функция /достаточно гладкая.
Обозначим через P(k,k*i, •••,*)(г) интерполяционный многочлен
степени m — Jb с узлами интерполяции ц, rjt*i, ..., хп. В частности,
положим Р( к) (х) = Ук- В этих обозначениях справедливо равенство
р
Р(к,Ы, ...,
A1.56)
В самом деле, правая часть представляет собой многочлен степени
т + I — к. Непосредственная проверка показывает, что этот многочлен
совпадает с у, в точках х — sc, для i = Jfc, к + 1, ..., m+ 1 и, значит, по
определению равен Р(к, •••,я*пA)-
Удобный и экономичный способ вычисления значения многочлена
Рп(х) = Л од, ,п)(х), лежащий в основе рассматриваемого алгоритма,
дает схема Эйткена1. Она заключается в последовательном вычисле-
вычислении с помощью формулы A1.56) элементов следующей таблицы:
Таблица 11.9
Л 0,1,2) W .
Р{п-г,п-1,п){*)
Л п) (*) = Уп
Для решения поставленной задачи интерполяции при заданном
значении z узлы нумеруют в порядке возрастания их расстояния
|г — хк\ до точки г. Затем последовательно вычисляют значения Р\(х),
во. Рг(х), ?i, •••) ^i»h(*)i ?m Если при некотором m оказывается,
Александр Крог Эйткен A895—1967) — английский математик.
что ет < е, то полагают f(x) и рт(х). Если же ет > е для всех т, то
полагают f(x) и Рк(х), где к — степень, при которой достигается мини-
минимум оценки погрешности: 6fc = min em.
Пример 11.9. Для решения задачи из примера 11.8 воспользуемся схемой
Эйткена. В этом случае (как и в примере 11.8} ч> = 1-2, г\ = 1.3, ъ = 1.1,
*5 = 1.4, х4 = 1.0. После завершения вычислений табл. 11.9 принимает
следующий вид:
Таблица 11.10
0.182322
0.262364
0.095310
0.336472
0.206335
0.203895
0.199814
0.20706^
0.206752
0.207020
Подчеркнутые числа дают те же, что и в примере 11.8, значения Рк(х), к = 0,
1, 2, 3. Естественно, что теми же окажутся и значения е*.
3. Интерполяционный многочлен Ньютона с конечными разностя-
разностями. Пусть интерполируемая функция задана на таблице с постоянным
шагом А (т. е. х, = х0 + «A, i = 0, 1, ..., п). В этом случае, используя
формулу A1.51) связи между разделенными и конечными разностями
и вводя безразмерную переменную i - (х — хь)/Л, многочлен Ньютона
A1.52) можно записать в следующем виде:
A1.57)
322
Многочлен A1.57) называется интерполяционным многочленом Нью-
Ньютона с конечными разностями для интерполяции вперед.
Заметим, что в формуле A1.57) используются только конечные
разности, расположенные в верхней косой строке табл. 11.2. Можно
использовать конечные разности, расположенные и в нижней косой
строке табл. 11.2, записав многочлен в виде интерполяционною много-
многочлена Ньютона с конечными разностями для интерполяции назад:
323

Pn(x) = Pn(xn+hq) =
A1.58)
Я (« + 1)(« + 2) + - + ^-f f (« + 1)...(« + •» - 1).
Здесь q = (х - х„)/Л.
| 11.10. Обсуждение глобальной
полиномиальной интерполяции.
Понятие о кусочно-полиномиальной
интерполяции
Пусть функция интерполируется на отрезке [а, Ь]. Метод решения
этой задачи с помощью интерполяции единым для всего отрезка мно-
многочленом Рп(х) называют глобальной полиномиальной интерполяцией.
При первом знакомстве с интерполяцией этот подход кажется привле-
привлекательным. В самом деле, неплохо иметь один многочлен, пригодный
для приближения функции /во всех точках х € [о, Ь]. В то же время
известные результаты теории аппроксимации позволяют надеяться на
то, что удасться приблизить функцию с любой требуемой точностью е
с помощью соответствующего выбора степени многочлена и узлов
интерполяции на отрезке [а, 6]. Приведем один такой классический
результат.
Теорема 11.6 (аппроксимационная теорема Вейерштраееа1).
Пусть функция /непрерывна на отрезке [а, Ь]. Тогда для любою е > 0
существует полином Рп(х) степени п = п (е) такой, что
max|/(x)-Pn(r)| <e.
Заметим, что теорема Вейерштраееа не дает конструктивного спосо-
способа построения соответствующего многочлена.
Несмотря на приведенные выше аргументы, существуют весьма
веские причины, по которым глобальная интерполяция многочленами
высокой степени в вычислительной практике, как правило, не ис-
используется. Обсудим некоторые из этих причин.
1 Карл Теодор Вильгельм Вейерштрасс A815—1897) — немецкий математик,
один из основоположников современного математического анализа и теории
аналитических функций.
324
1. Сходимость при увеличении числа узлов. Всегда ли можно до-
добиться повышения точности интерполяции благодаря увеличению
числа узлов (и соответственно степени п интерполяционного многочле-
многочлена)? Хотя положительный ответ на этот вопрос напрашивается сам
собой, не будем торопиться с выводами.
Уточним постановку задачи. Для того чтобы реализовать процесс
интерполяции функции / многочленами возрастающей степени п,
необходимо указать стратегию выбора при каждом п набора узлов
интерполяции х10п), х[п), ..., х^"'. Такая стратегия задается указанием
интерполяционною массива — треугольной таблицы
хо
Х0 Х1
Х0 ' Г12' Х22)
,(П)
•" ХП '
в каждой строке которой все х[п) различны и г', € [а, Ь]. Будем
говорить, что при заданной стратегии выбора узлов метод интерполя-
интерполяции сходится, если max |/(r) — Рп(*)| "* 0 ПРИ »"¦<*>•
Рассмотрим сначала простейшую стратегию, состоящую в равно-
равномерном распределении на отрезке [а, Ь] узлов интерполяции, т. е. в
выборе х<п> = а + ih (i = 0, 1, ..., п), где h = (Ь — а)/п. Следующий
пример показывает, что такая стратегия не может обеспечить сходи-
сходимость интерполяции даже для очень гладких функций.
Пример 11.10 (пример Рунг е1). Используем глобальную полино-
полиномиальную интерполяцию с равномерным распределением узлов для приближе-
приближения на отрезке [-1, 1] следующей функции:
1
/(г) +25*2
A1.59)
Вычисления показывают, что при больших п интерполяция дает превосходные
результаты в центральной части отрезка. В то же время вопреки ожиданиям
Последовательность Рп(х) расходится при п -»оо для 0.73 < |г| < 1. Соответст-
Соответствующая иллюстрация приведена на рис. 11.5.
1 Карл Давид Тояьме Рунге A856—1927) — немецкий физик и математик.
325

л 6-я cmen
I \
I \
\1.0х
Рис 11.5
Равномерное распределение узлов интерполяции для функции
Рунге A1.59) оказалось неудачным. Однако проблема сходимости для
этой функции исчезает, если в качестве узлов интерполяции брать
корни многочлена Чебышева Т„ц(х). Существует ли единая для всех
непрерывных на отрезке [а, Ь] функций / стратегия выбора узлов ин-
326
терполяции, гарантирующая ее сходимость? Отрицательный ответ на
этот вопрос дает следующая теорема.
Теорема 11.7 (теорема Фабера1). Какова бы ни была страте-
стратегия выбора узлов интерполяции, найдется непрерывная на отрезке
[а, Ь] функция /, для которой max \f(x) — Рп(х)\ -» « при п ¦* со.
[а,Ь]
Теорема Фабера отрицает существование единой для всех непре-
непрерывных функций стратегии выбора узлов интерполяции. Однако для
гладких функций (а именно такие функции чаще всего и интерполи-
интерполируются) такая стратегия существует, о чем говорит следующая теоре-
теорема.
Теорема 11.8. Пусть в качестве узлов интерполяции на отрез-
отрезке [а, Ь] выбираются чебышевские узлы A1.43). Тогда для любой непре-
непрерывно дифференцируемой на отрезке [а, Ь] функции f метод интерпо-
интерполяции сходится.
Замечание. Практическая реализация стратегии выбора узлов
интерполяции A1.43) возможна и оправдана в довольно редких
случаях и просто невозможна тогда, когда приходится иметь дело с
заданной таблицей значений функции.
2. Чувствительность интерполяционного многочлена к погрешнос-
погрешностям входных данных. Помимо погрешности, которая возникает от
приближенной замены функции / интерполяционным многочленом,
возникает еще дополнительная погрешность, связанная с тем, что
значения интерполируемой функции также задаются с погрешностью.
Пусть заданные в узлах х, значения у* содержат погрешности ?,.
Тогда вычисляемый по этим значениям многочлен Р^(х) = ? У,*'„Xх)
содержит погрешность
ад - p*(t) = ?о ьм*у (и-60)
Например, при линейной интерполяции по приближенно заданным
значениям справедливо равенство
Рх{х) - Р*(х) = ео/1О(г)
где
1 Жорж Фабер A877—1966) — швейцарский математик.
327

X —
> '"Vх) =
Воспользуемся тем, что
тельно,
max
(*)| + |'п(*)| = 1 Для х € [xq, х{\. Следова-
Следова-P;(r)| <тах{|ео|, |е,|}.
показать это, приведем отрезок [а, Ь] к стандартному отрезку [-1, 1] с
помощью линейного преобразования х = — \- —-— t. Тогда х, =
а + b , Ъ - а . _ ,
= —¦?— + —т.— «I и константа Лебега приводится к виду
An = max E |7n
[-1,1] J'-°
Таким образом, при линейной интерполяции погрешность, возникаю-
возникающая вследствие погрешности значений функции, не превосходит верх-
верхней границы погрешности этих значений.
Рассмотрим теперь общий случай. Пусть известно, что верхняя
граница погрешности значений у* равна Д(»*), т. е. |е,| < Д(у*) для
всех i = 0, 1, ..., п. Тогда для верхней границы соответствующей пог-
погрешности многочлена Д(Р^) = max \Pn(x) — Р^(*)| в силу равенства
[а,Ь]
A1.60) справедлива оценка
Д(Р*)<Л„Д(у«).
Здесь Л„ = max ? К,
A1.61)
— величина, которую называют констан-
той Лебею,1.
Замечание. В случае, когда |е,| = Д(у*) для всех t, выбором
знаков погрешностей е, можно добиться выполнения равенства
Д(Р*) = Л„Д(у*). Это означает, что в самом неблагоприятном
случае погрешность входных данных при интерполяции может
возрасти в Лп раз. Таким образом, в задаче интерполирования
константа Лебега играет роль абсолютного числа обусловленности.
Величина Л„ не зависит от длины отрезка [а, Ь], а определяется
лишь относительным расположением узлов на нем. Для того чтобы
1 Анри Леон Лебег A875—1941) — французский математик, один из созда-
создателей современной теории функций вещественной переменной и теории ин-
интегрирования.
328
= П
Естественно поставить задачу о таком оптимальном выборе узлов
интерполяции, чтобы величина Ля оказалась минимально возможной.
Для малых значений п эту задачу решить нетрудно. При п = 1 выбор
(q = -1, <i = 1 дает Л) = 1. При п = 2 оптимальное значение Л2 = 5/4
достигается, например, при <о = -1> 'i = 0, <2 = 1. В общем случае
оптимальный выбор узлов неизвестен. Установлено, однако, что почти
оптимальным является выбор в качестве узлов интерполяции нулей
многочлена Чебышева
2
. При таком выборе Лв» — 1п(п+1)
1.
С рассматриваемой точки зрения крайне неудачным при больших п
является выбор равноотстоящих узлов интерполяции. При таком выбо-
для п > 4 и обусловленность задачи резко ухудша-
реЛ„>
Bn - l)Vn
ется с ростом п. Сказанное позволяет сделать важный вывод: в вычис-
вычислениях не следует использовать интерполяционные многочлены высо-
высокой степени с равноотстоящими узлами.
3. Обусловленность задачи вычисления многочлена с приближенно
заданными коэффициентами. Обратим внимание на еще один потен-
потенциальный источник потери точности при использовании многочленов
Р„(х) высокой степени. Для определенности будем считать, что много-
многочлен вычисляется на отрезке [а, 6], где \а\ < Ь, причем предваритель-
предварительно он представлен в виде
Jt'O
Здесь
A1.62)
— некоторый набор базисных многочленов у>*(х), обла-
обладающий тем свойством, что всякий многочлен Рп(*) степени п может
быть однозначно представлен в виде A1.62). Например, можно ис-
329

пользовать степенной базис {z*}?*0> нормированный стеленной базис
Таблица 11.11
{
базис
локальный степенной базис
г -
b -
, лагранжев базис
чебышевский
. (см. § 11.3) и
т. д.
При вычислении коэффициентов а* неизбежны погрешности, при-
приводящие к приближенным значениям а?. Поэтому в действительности
будет вычисляться многочлен
Примем за относительную погрешность вектора «* = (о*, в* а*)т
величину
6(а*) - (max |а,-a*|)/max |а,|,
(К i<n 0<i<n
а за относительную погрешность многочлена Р*(т) — величину
6(Р*) =( max | Рп(х) - Р*(
[в, Ь]
max | Рп(х) |.
[а,Ь]
Числом обусловленности задачи вычисления многочлена с приближенно
заданными коэффициентами назовем величину condn, равную мини-
минимальной из постоянных Кп, для которых выполняется неравенство
Величина condn, характеризующая чувствительность вычисляемых
значений многочлена к погрешностям в коэффициентах ед, существен-
существенно зависит от выбора базиса {pt(iO}J5«0- Неудачный выбор базиса мо-
может сделать эту, казалось бы, элементарную задачу очень плохо обус-
ловенной. Доказано, например, что даже для вполне "разумного"
локального степенного базиса
г — а
U
число обусловленнос-
обусловленносЬ - а]
ти оценивается снизу величиной ТпC). Как видно из табл. 11.11,
использование указанного базиса для представления многочленов
высокой степени сопряжено с опасностью значительной потери точнос-
точности.
330
я 12 3 4 5 б
Г„C) 3 17 99 577 3363 19601 114243 665857 3880899
Отметим, что для чебышевского базиса condn < fe (n + 1). Для
лагранжева базиса число обусловленности совпадает с константой
Лебега Ап. Напомним, что при почти оптимальном выборе узлов ин-
2
терполяции Лп и — In (п + 1) + 1.
Итак, глобальная полиномиальная интерполяция многочленом
высокой степени может привести к неудаче или оказаться неэффектив-
неэффективной. Альтернативный подход состоит в локальной интерполяции, когда
функция / аппроксимируется интерполяционным многочленом Рт(х)
невысокой степени т на содержащемся в [а, Ь] отрезке [а, 0\ малой
длины. Естественно, что при этом используется лишь часть табличных
значений. Рассмотрим два подхода к приближению функции, основан-
основанные на локальной интерполяции.
4. Интерполирование с помощью "движущегося" полинома. Строят
набор полиномов P@,i, •••,«,), Ли, •••,*¦!), •••, Лп-т,п-т*1, —.и) фикси-
фиксированной степени т, каждый из которых совпадает с табличными
значениями в m + 1 последовательных точках. Каждый такой полином
используют для приближения функции в тех точках х из отрезка
[а, Ь], для которых выбранные узлы таблицы являются ближайшими.
Пример 11.11. Пусть функция задана следующей таблицей:
Таблица 11.12
1
Ух
1.0 1.8 2.2 1.4
1.0
Для интерполяции этой функции воспользуемся "движущимся" полиномом
второй степени. Заметим, что при х ? [0.0, 1.5] для приближения используется
многочлен Р( о,1,2) (*)> ПРИ х ? [1-5, 2.5] — многочлен Р< 1,2,31(^I Щ>и х 6
€ [2.5, 4.0] — многочлен РB,а,4)(*)- Соответствующая геометрическая иллюст-
иллюстрация приведена на рис. 11.6. Заметим, что полученная таким способом ап-
аппроксимирующая функция имеет разрывы в точках г = 1.5 и х— 2.5.
331

J_
1
2 J
Рис. 11.6
и х
У
2
у
0
\
1
V
2
Г ft
4 х
Рис 11. 7
5. Кусочно-полиномиальная интерполяция. Исходный отрезок [а, Ь]
разбивают на несколько отрезков меньшей длинь% на каждом из кото-
которых функция интерполируется своим многочленом.
Пример 11.12. Для интерполяции функции из примера 11.11 используем
кусочно-полиномиальную интерполяцию. На отрезке [0, 2] аппроксимируем
функцию многочленом Р<о,1,2)(*)> а на отрезке [2, 4] — многочленом
РB,3,4)(*)• Соответствующая геометрическая иллюстрация приведена на рис.
11.7. Заметим, что результирующая аппроксимирующая функция непрерывна,
но в точке х = 2 график ее имеет излом, соответствующий разрыву первой
производной.
Заметим, что интерполяцию "движущимся" полиномом можно
рассматривать как частный случай кусочно-полиномиальной интерпо-
интерполяции.
Как следует из оценки A1.30), метод кусочно-полиномиальной
интерполяции при использовании многочленов фиксированной степени
m имеет (т + 1)-й порядок точности относительно А
332
5 11.11. Интерполяция сплайнами
1. Определение сплайна. Проведенное выше обсуждение интерполя-
интерполяции показывает, что повышение точности приближения гладкой фун-
функции благодаря увеличению степени интерполяционного многочлена
возможно (см. теорему 11.8), но связано с существенным повышением
сложности вычислений. К тому же использование многочленов высокой
степени требует специальных мер предосторожности уже при выборе
формы их записи, и вычисления сопровождаются накоплением ошибок
округления.
Поэтому на практике предпочитают кусочно-полиномиальную ин-
интерполяцию с использованием многочленов невысокой степени. Однако
этот способ приближения имеет недостаток: в точках "стыка" двух
соседних многочленов производная, как правило, имеет разрыв (см.
пример 11.12). Часто это обстоятельство не играет существенной роли.
Вместе с тем нередко требуется, чтобы аппроксимирующая функция
была гладкой и тогда простейшая кусочно-полиномиальная
интерполяция становится неприемлемой.
Естественная потребность в наличии аппроксимирующих функций,
которые сочетали бы в себе локальную простоту многочлена невысокой
степени и глобальную на всем отрезке [а, Ь] гладкость, привела к
появлению в 1946 г. так называемых сплайн-функций или сплайнов —
специальным образом построенных гладких кусочно-многочленных
функций. Получив в 60-х годах распространение как средство интер-
интерполяции сложных кривых, сплайны к настоящему времени стали важ-
важной составной частью самых различных вычислительных методов и
нашли широчайшее применение в решении разнообразных научно-
технических и инженерных задач.
Дадим строгое определение сплайна. Пусть отрезок [а, Ь] разбит
точками а = хо < х\ < ... < хп = b нь п частичных отрезков [xt-i, rj.
Сплайном степени т называется функция Sm(x), обладающая следую-
следующими свойствами:
1) функция Sm(x) непрерывна на отрезке [а, Ь] вместе со всеми
своими производными S^^x), 5jj,2)(x), ..., 5jJ,P'(x) до некоторого поряд-
порядка р;
2) на каждом частичном отрезке [zt-i, xj функция Sm(x) совпадает с
некоторым алгебраическим многочленом Ря,Кх) степени т.
Разность m — р между степенью сплайна и наивысшим порядком
непрерывной на отрезке [а, Ь] производной называется дефектом
сплайна.
Простейший пример сплайна дает непрерывная кусочно-линейная
333

функция (рис. 11.8), являющаяся сплайном первой степени (линейным
сплайном) с дефектом, равным единице. Действительно, на отрезке
[а, Ь] сама функция Si(x) (нулевая производная) непрерывна. В то же
время на каждом частичном отрезке Si(z) совпадает с некоторым мно-
многочленом первой степени.
У
х, х2
Рис. 11.8
х„ х
Х„ X
Рис. 11.9
Наиболее широкое распространение на црактике получили сплайны
5з(х) третьей степени (кубические сплайны) с дефектом, равным 1 или
2. Такие сплайны на каждом из частичных отрезков [r,-i, xj совпадают
с кубическим многочленом:
и имеют на отрезке [а, Ь] по крайней мере одну непрерывную произ-
производную Sj'(z).
Термин "сплайн" происходит от английского слова "spline" (гибкая
линейка, стержень) — названия приспособления, использовавшегося
чертежниками для проведения гладких кривых через заданные точки.
Бели гибкую стальную линейку поставить на ребро и, изогнув, зафик-
зафиксировать ее положение в узловых точках (рис. 11.9), то получится
механический аналог кубического сплайна. В самом деле, из курса
сопротивления материалов известно, что уравнение свободного равно-
равновесия профиля S (х) линейки таково: 5М)(г) = 0. Следовательно, в
промежутке между двумя соседними узлами 5 (х) представляет собой
многочлен третьей степени. В то же время отсутствие у линейки изло-
изломов свидетельствует о непрерывности касательной к графику функции
5 (г) и кривизны, т. е. производных 5'(х) и 5"(х).
2. Интерполяционный сплайн. Пусть функция у = /(х) задана
таблицей своих значений у, = f(xt), i = 0, 1, ..., п. Сплайн Sm(x) назы-
называется интерполяционным, если 5m(zt) = Ш ДЛЯ всех ' = 0| 1, ..., п.
Значение Sj = S^(xt) называется наклоном сплайна в точке х%.
Заметим, что на отрезке [xj-i, х<] интерполяционный кубический
сплайн однозначно определяется заданием значений y,-i, щ, я,-ь ^,. В
самом деле, из равенства A1.31) вытекает следующая формула:
334
I
+¦
Si.
A1.64)
Здесь hi = Xi — Xi-i.
Различные методы интерполяции кубическими сплайнами отлича-
отличаются один от другого способом выбора наклонов s*. Обсудим некото-
некоторые из них.
3. Локальный сплайн. Если в точках zt известны значения произ-
производной у'{ — f'(xi), то естественно положить а, = y't для всех i = 0, 1,
..., п. Тогда на каждом частичном отрезке [ц.и х<\ в соответствии с
формулой A1.64) сплайн однозначно определяется значениями ун, yi,
y'i-i' У| (поэт°му его и называют локальным сплайном). Заметим, что
он совпадает с кубическим интерполяционным многочленом Эрмита
A1.31) для отрезка [x,-i, x<].
Из неравенства A1.33) получается следующая оценка погрешности
интерполяции локальным кубическим сплайном:
A1.65)
где Ащах = max hi — максимальная из длин частичных отрезков.
1 < i<n
Заметим, что для построенного указанным образом сплайна можно
гарантировать непрерывность на отрезке [а, Ь] только функции S$ и ее
первой производной 5}', т.е. его дефект равен 2.
Существуют и другие способы выбора коэффициентов а^ приводя-
приводящие к локальным сплайнам (кубический многочлен Бесселя1, метод
Акимы и др. [16]).
4. Глобальные способы построения кубических сплайнов. Для того
чтобы сплайн Ss(x) имел непрерывную на отрезке [а, Ь] вторую произ-
производную Sj(r), необходимо выбирать наклоны s, так, чтобы в точках х,
"стыка" многочленов P3)t и Рз,«+1 совпадали значения их вторых про-
производных:
, «=i.2 n-i.
(и.66)
Фридрих Вильгельы Бессель A784—?184б) — немецкий астроном.
335

Пользуясь формулой A1.64), найдем значение
Из подобной формулы, записанной для многочлена Рз,1+ь имеем
Р"зы(Хг) = - -р- - ^~ + 6 V*p~ * ¦ A168)
Таким образом, равенства A1.66) приводят к следующей системе урав-
уравнений относительно коэффициентов я,:
30. Полагая в уравнениях A1.71), A172) f(a) - 0, f(b) = 0
(независимо от того, выполнены ли эти условия для интерполируемой
функции), придем к системе уравнений, определяющих так
называемый естественный кубический сплайн.
4°. Часто нет, никакой дополгительной информации о значениях
производных на концах отрезка. Один из применяемых в этой ситуа-
или подходов состоит в использовании условия "отсутствия узла".
Выбор наклонов s, производят таким образом, чтобы для получаемого
сплайна выполнялись условия Р2,\(х) = Р^ЛХ)> Pa.n-i(x) = -Рз,п(*) Для
этого достаточно потребовать совпадения в точках Т\ и хп-х соответст-
соответствующих третьих производных:
- у,)].
«= 1,2, ..., n-1.
A1.69)
Заметим, что эта система уравнений недоопределена, так как число
уравнений системы (равное п — 1) меньше числа неизвестных (равного
п + 1). Выбор двух оставшихся уравений обычно связывают с некото-
некоторыми дополнительными условиями, накладываемыми на сплайн в
граничных точках о и 6 (граничными условиями). Укажем на некото-
некоторые из наиболее известных граничных условий.
1°. Если в граничных точках известны значения первой производ-
производной /'(а) и f'(b), то естественно положить
«о = /'(<,), in = f'(b). A1.70)
Дополняя систему A1.69) уравнениями A1.70), приходим к системе
уравнений с трехдиагональной матрицей, которая легко решается
методом прогонки (см. гл. 5). Полученный таким образом сплайн
называется фундаментальным кубическим сплайном.
2°. Если в граничных точках известны значения второй производ-
производной f(a) и f(b), то можно наложить на сплайн граничные условия
S(a) = P<i(xo) = Г(а)> S(b) = Р;пЫ = f(b), что приводит к сле-
следующим уравнениям:
4*0 2ц
"л7~аГ
- уо
(достаточно в равенстве A1.68) взять i
. = п).
336
A1.71)
A1.72)
0, а в равенстве A1.67)
Эквивалентные алгебраические уравнения выглядят так:
2A(jo- й) + A;2(s0 + Sl) = 2Л-з(у, - у2) + h^(Sl + ъ),
Sn).
A1.73)
AL74)
Та же аппроксимирующая функция может быть получена несколь-
несколько иначе. Уменьшим число частичных отрезков, объединив попарно
отрезки [io, *i], fa, хг] и [хп-2, хп.\], [хп-], аг„]. Это отвечает разбиению
отрезка [а, 6] точками а = г0 < *i < ¦•• <*п-2 - ^ гДе xi — r«i Для
i = 1, 2, ..., п — 3. и построению соответствующего интерполяционного
сплайна ^з(^)- Условия "отс>тч-твия узла" эквидаленты требованию
совпадения значений сплайна 53(г) в точках хх и хп-\ со значениями yi
И Уп-1-
5°. Если /— периодиг,еская функция с периодом, равным о -- а, то
систему A1.69) следует дополнить условиями
«с = «п.
Существуют и другие подходы к заданию граничных условий
(подробнее об этом см. [16]).
Пример 11.13. Для функции, заданной табл. 11.12, построив (естественный)
кубический сплайн. В этом случае система уравнений для наклонов «о, s\, ...,
s4 в точках хо, ц, ..., х4 записывается следующим образом:
337

Рис 11.10
sq = -0.5s, + 1.2, A1.75)
Ж, + 4*i + «г = 3.6, A1.76)
* + 4*2 + *з = -1.2, A1.77)
*2 + 4*з + «4 =-3.6, A1.78)
«4 = -0.5*3 - 0.6. A1.79)
Решая ее, получаем значения sq — 57/70,
si = 54/70, *г = -ЗУЮ, *з = -54/70, гц =
= -3/14. Теперь на каждом частичном
отрезке значения сплайна можно вычис-
вычислить по формуле A1.64). Соответствующий
график приведен на рис 11.10 (ср. с рис.
11.6 и 11.7).
¦* Пример 11.14. Интерполируем функ-
функцию, заданную табл. 11.12, кубическим
сплайном, используя условие "отсутствия
узла". В этом случае уравнения A1.76)—
A1.78) останутся прежними, а уравнения A1 75) и A1.79) заменяются следую-
следующими:
«э-*2 = 0.8, *2-«4=-0.8. A1.80)
Решая систему A1.76)—A1.78), A1.80), получаем значения sq = 8/15, «i = 5/6,
*2 = -4/15, *з = -29/30, 54 = 8/15. График соответствующего сплайна мало
отличается от графика, изображенного на рис. 11.10.
5. Погрешность приближения кубическими сплайнами.
Теорема 11.9. Пусть функция f имеет на отрезке [а, Ь] непре-
непрерывную производную четвертою порядка и М+ = max |У4)(Г)|- Тогда
для интерполяционного кубическою сплайна 5з(г), удовлетворяющего
граничным условиям типов 1°, 2°, 4° или 5° (последнее — для случая
периодической функции), справедлива следующая оценка погрешности:
max \f(x)-Sa(x)\ < СА/4Сх- A1.81)
Заметим, что сплайн S3(x) не только сам аппроксимирует функцию
/(г), но его производные 53'(r), 5j(r), 5^3)(г) приближают соответству-
соответствующие производные функции / Сформулируем соответствующую теоре-
теорему в наиболее простом случае, когда таблица задана с постоянным
шагом А.
Теорема 11.10. При выполнении условий теоремы 11.9 для ука-
указанных в ней сплайнов справедливы неравенства
338
max
[а,Ь]
(г) - S^ (х) \
к = 1, 2, 3.
A1.82)
Замечание. Благодаря большей простоте записи и благозвуч-
благозвучному названию естественные сплайны получили значительное расп-
распространение. Однако искусственное наложение условий f(a) — 0,
f(b) = 0 при интерполяции функций, которые этим условиям не
удовлетворяют, приводит к значительной потере точности. Вместо
четвертого порядка точности (как локальный кубический сплайн
или кубические сплайны с граничными условиями типов 1°, 2°, 4°,
5°) естественный сплайн обладает лишь вторым порядком точности.
Если использование естественного сплайна не вызвано какими-либо
специальными причинами, то следует, по-видимому, отказаться от
него в пользу кубического сплайна с граничным условием типа 4°.
$ 11.12. Понятие о дискретном преобразовании Фурье
и тригонометрической интерполяции
1. Дискретное преобразование Фурье. В прикладных исследованиях
широко используются различные варианты преобразования Фурье1
функций непрерывного аргумента, а также представление функций в
виде сходящихся тригонометрических рядов (рядов Фурье). Известно,
например, что всякая непрерывно дифференцируемая периодическая с
периодом 1 функция / может быть разложена в ряд Фурье:
f(x) = Е акехр{2хгкх}.
A1.83)
Здесь i — мнимая единица. Коэффициенты разложения вычисляются
по формулам
= / /(г) ехр{-2хгкх} dx.
о
A1.84)
Однако во многих случаях функция /бывает задана лишь в конеч-
конечном числе точек х} = j/N, j = 0, 1, ..., N — 1. В этом случае аналогом
формулы A1.83) является разложение вида
J:
/(«,) =NJ: в*ехр{2яЦ}, 0 < j < N.
Jt=o
A1.85)
1 Жан Батист Жозеф Фурье A768—1830) — французский математик, один
из основоположников математической физики.
339

Заметим, что это разложение имеет место тогда и только тогда, когда
тригонометрический многочлен
Е
A1.86)
интерполирует функцию / по ее значениям в точках х}, 0 < j < N.
Выше (см. пример 11.2) было доказано, что система функций <pk(z) =
= exp{2tikx}, О < к < N ортогональна на множестве точек х; = j/N,
О < j < N, причем (wt, ft) = N. Следовательно, разложение A1.85)
действительно имеет место, причем в силу равенства A1.19) коэффици-
коэффициенты йк определяются по формуле
ак = Ъ
/(xj) exp{-2rikxi), 0<k<N.
A1.87)
Операцию преобразования набора значений /(хо), /(xi), ..., f(xf/-\)
в набор коэффициентов во, <Ji, ..., a#-i принято называть прямим диск-
дискретным преобразованием Фурье, а обратную операцию — обратным
дискретным преобразованием Фурье. Осуществление этих операций
является важной составной частью многих алгоритмов.
Для удобства изложения введем обозначение и = exp{2xi/JV} и
перепишем формулы A1.85), A1.87) в следующем виде:
fc«o
4 JV» 1
± E
0<>< ЛГ,
0
ЛГ.
A1.88)
A1.89)
2. Быстрое дискретное преобразование Фурм. Если вычисления
проводить непосредственно по формулам A1.88) и A1.89), то на вы-
выполнение каждого из преобразований потребуется примерно № ариф-
арифметических операций. (Здесь под арифметической операцией понима-
понимается умножение двух комплексных чисел с последующим сложением.
Величины и№ считаются вычисленными заранее.)
Однако в случае, когда число N не является простым, количество
арифметических операций, требуемых для вычисления по формулам
A1.88) и A1.89), можно существенно уменьшить. Поясним сказанное на
примере вычислений по формулам A1.88). (Вычисления по формулам
A1.89) производятся аналогично с заменой и на и>~1.)
Пусть N = N\N2, где 2 < N\, 2 < ЛГ2 — целые числа. Представим
индекс j в виде j — j\N\ + jb, где 0 < л < N2, 0 < jo < N\. Положим к =
340
+ ко, где 0 < kt < Nu 0 < ко < N2. Пользуясь тем, что kj =
+ ЫоЪ + koj и ukJlN = 1, имеем w*J = a.*1**2^ Заменяя в
формуле A1.88) суммирование по индексу к операцией повторного
суммирования по индексам ко и к\, получим
= Е
где
2-1 ЛГГ1
Е
Jti«O
12 "О
У
fco«
A1.90)
A1.91)
Массив а содержит N чисел и для его вычисления требуется NN\
арифметических операций. После того как найдены значения а (ко, jo),
на вычисления по формуле A1.90) требуется NN2 операций. Таким
образом, общее число арифметических операций равно N (N\ + N2).
Заметим, что достигнута экономия в числе операций, поскольку Л^ +
+ N2 < N\N2 = ЛГ, как только N > 4. Выигрыша удалось достичь
благодаря тому, что оказалось возможным выделить группы слагаемых
A1.91), которые используются для вычисления значений /(х;) при
различных j, но сами вычисляются лишь однажды.
Указанная выше идея развита в алгоритмах быстрою дискретною
преобразования Фурье. В случае, когда N = N\-N2 ... Nm, (где 2 < Ns), с
помощью быстрого дискретного преобразования Фурье можно выпол-
выполнить дискретное преобразование Фурье за N (М + N2 + ... + ЛГт)
арифметических операций. Особенно эффективным является этот
алгоритм, когда число ЛГ является степенью числа 2 (т. е. N = 2"). В
этом случае вместо № операций требуется выполнить лишь 2N log2N
операций. Например, для N = 1024 = 210 этот алгоритм позволяет
ускорить вычисления в —. -. = 1024/20 и 50 раз.
2lOg2n
Широкое внедрение алгоритма быстрого дискретного преобразова-
преобразования Фурье в практические вычисления привело к подлинной револю-
революции во многих областях, связанных с обработкой числовой информа-
информации. Программы, реализующие различные варианты этого алгоритма,
входят в стандартное математическое обеспечение ЭВМ и доступны
массовому пользователю.
Замечание 1. Часто разложение A1.85) записывают в эквива-
эквивалентном виде:
341

-ЛГ/2<КЛ/2
что соответствует интерполяции тригонометрическим многочленом
-N/2<KN/2
A1.92)
Здесь коэффициенты а& по-прежнему задаются формулой A1.87).
Замечание 2. Хотя интерполяционные тригометрические
многочлены A1.86), A1.92) и совпадают в точках х}, они принима-
принимают существенно разные значения в точках z, отличных от узловых.
3. Тригонометрическая интерполяция. Рассмотрим кратко задачу
интерполяции функции /, заданной в точках 0 < х0 < х\ < ... < ж/^i < 1
тригонометрическим многочленом A1.92). К ней приводит, например,
типичная радиотехническая задача о тригонометрической интерполя-
интерполяции периодического сигнала.
Не вдаваясь в довольно сложную проблему оценки погрешности
тригонометрической интерполяции, отметим тем не менее, что для
гладкой периодической с периодом 1 функции / есть основание рас-
рассчитывать на выполнение приближенного равенства /(х) и Sy(x) для
всех х € [0, 1].
Рассмотрим важный вопрос о чувствительности многочлена S\ к
погрешностям в исходных данных. Пусть значения у* и f(xt) интерпо-
интерполируемой функции задаются с погрешностями е, и известно, что |ef| <
< Д(у*) для t = 0, 1, ..., N — 1. Тогда вычисляемый по значениям у*
тригонометрический интерполяционный многочлен 5* содержит пог-
погрешность. Для нее справедлива оценка
= max
[0,1]
аналогичная оценке A1.61) для алгебраических многочленов. Здесь \у
— постоянная, являющаяся аналогом константы Лебега \ff.
Примечательно то, что в отличие от задачи интерполяции алгебра-
алгебраическими многочленами (см. § 11.10) оптимальным (т. е. дающим
минимальное значение Ад) является равномерное распределение узлов,
~ 2
которому отвечает значение А.\ и - In [(N + 1)/2].
342
Таким образом, при тригонометрической интерполяции выбор
узлов ij = j/N @ < j < N) является наиболее естественным с точки
зрения как простоты вычисления коэффициентов многочлена (быстрое
дискретное преобразование Фурье), так и минимизации влияния оши-
ошибок исходных данных.
| 11.13. Метод наименьших квадратов
Задача наименьших квадратов возникает в самых различных облас-
областях науки и техники. Например, к ней приходят при статистической
обработке экспериментальных данных с помощью регрессионного
анализа. В инженерной деятельности задача наименьших квадратов
используется в таких областях, как оценивание параметров и филь-
фильтрация.
1. Линейная задача наименьших квадратов. Пусть функция у =
= / (х) задана таблицей приближенных значений
»."/(*•), 1 = 0,1,..., я, A1-83)
полученных с ошибками ?, = у0, — ух, где у\ — f(xt). Если значения у,
получены из эксперимента, то ошибки носят случайный характер и
зачастую уровень погрешности ("шума" таблицы) бывает значитель-
значительным (рис. 11.11, а).
Предположим, что для аппроксимации функции / используется
линейная модель:
у = Фт(х) н аоро(х) + о,^(х) + ... + ап<р„Лх). A1.94)
Здесь ро(х), ipi(x), ..., <рм(х) - заданные базисные функции1, во, <Ч> •¦•,
1 В данном параграфе рассматриваются функции, принимающие только
вещественные значения.
343

Ощ — параметры модели, являющиеся коэффициентами обобщенного
многочлена Фя(х). Как уже отмечалось выше, одной из наиболее прос-
простых и часто используемых линейных моделей вида A1.94) (при <pi?x) —
= х*) является полиномиальная модель
у = Рт(х) = во +
+ ... +
A1.95)
В случае, когда уровень неопределенности исходных данных высок,
неестественно требовать от модели A1.94) выполнения условий A1-7)
совпадения значений обобщенного многочлена Фт(х) в точках xt с
заданными значениями у,, т. е. использовать интерполяцию. Как не-
нетрудно видеть (см. рис. 11.11, б), при интерполировании происходит
повторение ошибок наблюдений, в то время как при обработке экспе-
экспериментальных данных желательно, напротив, их сглаживание.
Отказываясь от требования выполнения в точках х, точных ра-
равенств A1.7), следует все же стремиться к тому, чтобы в этих точках
выполнялись соответствующие приближенные равенства
У\,
A1.96)
Уп-
Используя обозначения A1.9), запишем систему приближенных ра-
равенств A1.96) в матричном виде:
Реи f.
A1.97)
Из различных критериев, позволяющих выбрать параметры ас, а1}
..., ат модели A1.94) так, чтобы приближенные равенства A1.96) удов-
удовлетворялись наилучшим в некотором смысле образом, наиболее часто
используется критерий наименьших квадратов. Согласно этому крите-
критерию параметры выбираются так, чтобы минимизировать среднеквадра-
среднеквадратичное уклонение
обобщенного многочлена Фя(х) = Е л^р^х) от заданных табличных
значений у, @ < > < п). Заметим, что минимум среднеквадратичного
уклонения достигается при тех же значениях а$, аь ..., ат, что и мини-
минимум функции
344
1
(«, »)•
п + 1
Итак, линейная задача метода наименьших квадратов состоит в
следующем. Требуется найти (при фиксированном наборе функций <р0,
<Р\, ..., <рт) обобщенный многочлен Ф?(х), для которого среднеквад-
среднеквадратичное уклонение принимает минимальное значение:
* (*1, У) = min 6 (Фт, у).
Ф.
Искомый обобщенный многочлен Ф? будем далее называть многочле-
многочленом наилучшего среднеквадратичного приближения.
2. Нормальная система. Существуют различные подходы к реше-
решению поставленной задачи. Простейший из них состоит в использова-
использовании необходимого условия экстремума функции s:
^ = 0, *= 0, !,...,«
A1.98)
Вычисляя частные производные функции s и изменяя порядок сум-
суммирования, от равенства A1.98) переходим к системе линейных алгеб-
алгебраических уравнений
Е (Е
j=o t-o
(* = 0,1,..., т),
(Ц.99)
которая называется нормальной системой метода наименьших квадра-
квадратов.
Как нетрудно видеть, нормальную систему можно записать в виде
1*Рш=1Ху, A1.100)
или, используя матрицу Грама Г = i*P (см. § 11.2) и вводя вектор b =
= P*i, в виде
Г-=*. A1.101)
Лемма 11.1. Пусть л — решение системы A1.101). Тогда для
любого ¦' = ¦ + Д« имеет место равенство
(¦',») =
|РД«|2
345

? Имеем
f) =
= 5 (а,
- И2 = |
+ 2(/*Pe-
, Да) + |РД«|2
Остается заметить, что второе слагаемое в правой части полученного
равенства в силу A1.100) равно нулю. ¦
Теорема 11.11. Пусть система функций <ро, <р\, ..., <рп линейно
независима в точках xq, х,, ..., хп. Тогда многочлен наилучшею средне-
квадратичною приближения Ф{ существует и единствен.
d В силу теоремы 11.1 det Г * 0. Поэтому решение с системы
A1.101) существует и единственно. Таким образом, если многочлен Ф{
существует, то его коэффициенты aoi дь •••) *я определяются единст-
единственным образом.
Заметим теперь, что согласно лемме 11.1 для любого «' Ф ш имеем
а («', f) > s (в, у), т. е. на решении • нормальной системы действитель-
действительно достигается минимум функции «.'
Замечание 1. Если т = п и система функций <ро, <р\, ..., <рп
линейно независима в точках хо, х,, ..., хП) то многочлен Ф^, найден-
найденный методом наименьших квадратов, совпадает с интерполяцион-
интерполяционным многочленом Ф„. В самом деле, ФП(Х|) = У» для всех i = 0, 1,
..., п и поэтому 8 (Ф„, f) = 0. Так как среднеквадратичное уклоне-
уклонение не может быть отрицательным, то Фп — многочлен наилучшего
среднеквадратичного приближения. В силу его единственности
Фп = Н-
Замечание 2. Как правило, при использовании метода наи-
наименьших квадратов предполагается, что т < п. В этом случае метод
обладает некоторыми сглаживающими свойствами.
Очень часто для приближения по методу наименьших квадратов
используются алгебраические многочлены степени m < п. Поскольку
система функций 1, х, ..., х" линейно независима в точках хо, «i, ..., х„
при т < п (см. пример 11.1), в силу теоремы 11.11 алгебраический
многочлен наилучшего среднеквадратичного приближения существует
и единствен.
Так как в случае приближения алгебраическими многочленами
<pi?z) - х*, то нормальная система A1.99) принимает следующий вид:
7= 1ухх\, к =0,1,...,
т.
A1.102)
Запишем систему A1.102) в развернутом виде в двух наиболее
простых случаях га = 1 и m = 2. В случае, когда приближение осу-
осуществляется многочленом первой степени Р\{х) = Oq + a\x, нормальная
система имеет вид
(п+ 1)во+ ? х,\<ц = ? у*,
?x,]oo+ [?xfL= 1ухх{.
=o J Lt-o J i=o
A1.103)
Бели же используется многочлен второй степени Рг(х) = flo+ a\x +
+ a2x2, то нормальная система имеет вид
[n "I Г «  n
? x, a( + E t\ o2 = E yu
i'O J U'O J i=O
\ L X{\Oq + L x" a, + L x 02 = iy yiXi, Ц1.1Ц4)
Li=o J Lt=o J Li=o J i=o
[?^1л x Г v тз]„ , Г Я д1 л 8,j
\ L х во + I Zj х, в, + ii х • a2 = i/ У|Х.'.
Lt=o J Li=o J li»o J t=o
П{жмер 11.15. Пусть функция у = /(г) задана следующей таблицей:
Таблица 11.13
0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8
0.9
у 0.21 0.23 0.31 0.29 0.42 0.35 0.58 0.61 0.59 0.66
Используя метод наименьших квадратов, аппроксимируем ее многочленами
первой и второй степени и найдем соответствующие среднеквадратичные укло-
уклонения 8\ И ^2-
Вычислим коэффициенты и правые части нормальных систем A1.103),
A1.104): Е х, = 4.5, Е г2 = 2.85, Е х\ = 2.025, Е х\ = 1.5333, Е и = 4.25,
1=0
1=0
t'O
t=0
9 9
Е yin = 2.356, Е у,*2 = 1.6154.
t-o t=o
Для многочлена первой степени нормальная система имеет вид
+ 4.5о, =4.25,
4.5во + 2.85а, = 2.356.
346
347

Решив ее, получим значения оо * 0.183, <ц « 0.538 коэффициентов многочлена
Р{(х) = оо + <tix наилучшего среднеквадратичного приближения. Его график
изображен на рис. 11.11, в.
Запишем теперь нормальную систему для многочлена второй степени:
4.5а! + 2.8502 = 4.25,
4.5ао + 2.85ai + 2.025O2 = 2.356,
2.85ао + 2.025О! + 1.533302 = 1.6154,
Решив ее, получим значения oq * 0.194, oi * 0.452, ог * 0.0947 коэффициентов
многочлена Р2(*) = "о + <ч* + "г*2 наилучшего среднеквадратичного прибли-
приближения.
Вычисления по формуле
б, = У
для т = 1 и га = 2 дают значения 6\ « 0.0486, <2 й 0.0481.
Так как средняя погрешность е исходных данных заведомо превышает
0.01, нетрудно заключить, что приближения многочленами первой и второй
степени дают в данной ситуации практически эквивалентный результат.
Учитывая большую простоту использования линейных функций, достаточно,
по-видимому, остановиться на приближении }{х) я 0.183 + 0.538*
3. Некоторые вычислительные аспекты задачи наименьших квадра-
квадратов. Метод вычисления параметров оо, а\, ..., а* с помощью решения
нормальной системы A1.101) кажется весьма привлекательным. Дейст-
Действительно, задача сводится к стандартной проблеме линейной алгеб-
алгебры — решению системы линейных алгебраических уравнений с квад-
квадратной матрицей. Более того, можно показать, что в случае, когда
функции <ро, <Pi, .., fm линейно независимы в точках хц, х\, ..., х„,
матрица системы Г является симметричной и положительно определен-
определенной. В частности, это означает, что при решении нормальной системы
методом Гаусса не нужен выбор главных элементов; возможно также
использование метода Холецкого (см. гл. 5).
Следует тем не менее обратить серьезное внимание на то обстоя-
обстоятельство, что при отсутствии специального выбора базисных функций
Vo. <Pi, •¦•< <Рт уже при т > 5 нормальная система обычно оказывается
очень плохо обусловленной. Казалось бы, из теоремы 11.11 следует,
что единственное ограничение на систему базисных функций состоит в
том, что она должна быть линейно независима в заданных точках.
Однако, будучи формально линейно независимой, система функций ipo,
348
ifii, ..., <Рш может оказаться очень близкой к линейно зависимой. Ис-
Использование такой "почти линейно зависимой" системы базисных
функций делает задачу метода наименьших квадратов плохо обуслов-
обусловленной. При переходе от задачи наименьших квадратов к задаче ре-
решения нормальной системы Р*Рш = РТ% происходит как бы симметри-
симметризация системы Рш « f (см. § 6.3). При этом еще более ухудшается
обусловленность задачи. В этом случае вычисленные на ЭВМ как
решение системы A1.101) параметры модели могут оказаться полнос-
полностью искаженными ошибками округления.
Простейший пример такой "почти линейно зависимой" системы
базисных функций при больших т дает система 1, г, ..., х*, широко
применяемая при аппроксимации алгебраическими многочленами. При
m > 5 соответствующая нормальная система, как правило, здесь на-
настолько плохо обусловлена, что ее использование практически беспо-
бесполезно.
В определенном смысле "наиболее линейно независимой" является
система функций <ро, ipi, ..., <рп, ортогональных на множестве точек zq,
xi, ..., х„. Матрица Грама такой системы длатональна, а потому реше-
решение нормальной системы A1.101) вычисляется легко:
bk/m, ьк = 2
Ikk
= 2
к = О, 1, .... m.
Хотя выбор ортогональной на множестве точек xq, гь ..., хп системы
функций и желателен, он далеко не всегда возможен и удобен. Поэто-
Поэтому часто используются системы базисных функций, для которых мат-
матрица Грама лишь близка к диагональной. При аппроксимации на
отрезке [-1, 1] алгебраическими многочленами степени т пример такой
системы дает система многочленов Чебышева 7o(z), Ti(z), ..., TJ^z).
Заметим, кстати, что найденный методом наименьших квадратов мно-
многочлен Рп(х) = воГо(г) + oi Г^*) + ... + «жГ^аг) дает лишь иное, от-
отличное от стандартного A1.95) представление многочлена наилучшего
среднеквадратичного приближения. Однако задача определения пара-
is» ы 'л»
метров оо, О], ..., аш обладает существенно лучшей обусловленностью и
поэтому предпочтительнее с вычислительной точки зрения.
Существуют методы решения задачи наименьших квадратов, пред-
предваряющие решение нормальной системы численной ортогонализацией
системы базисных функций (см., например, [50], [60]). Однако в
настоящее время в серьезной вычислительной практике нормальная
система, как правило, не используется. Применяются другие, более
надежные методы (учитывающие, например, информацию об уровне
349

погрешности данных и относительной точности используемой ЭВМ). С
одним из таких методов, основанном на сингулярном разложении
матрицы Р, можно познакомиться в [86].
4. Понятие о статистических свойствах метода наименьших квадра-
квадратов. Пусть значения yt функции / в точках х( определяются в результа-
результате эксперимента. Предположим, что ошибки наблюдения et = y°t — yt
являются независимыми случайными величинами с нулевым средним
значением и дисперсией, павной а2, т. е.
Af [e,ej = 0
= е* A=0,1, ...,«),
j, i = 0, 1, .... n, j= 0, 1, ..., n).
A1.105)
A1.106)
Рассмотрим сначала простейший случай, когда измеряемая величи-
величина постоянна, т. е. /(г) = а. В этом случае естественно искать прибли-
приближение в виде постоянной oq. В изложенной выше схеме это соответст-
соответствует выбору m = 0, <ро{х) = 1 и Фо(х) = <»о, а нормальная система прев-
п
ращается в одно линейное уравнение (п + 1)oq = Е yt. Таким образом,
1=0
оценкой постоянной величины а по методу наименьших квадратов
является среднее арифметическое значение
ao =
1
A1.107)
т. е. измеренные значения осредняются так, как это принято в статис-
статистике.
Пусть Дао = а — во — ошибка оценки A1.107). Заметим, что Дао =
п + 1 t=
Е|, а потому
o
= —L- 2 M [ej = 0,
п + 1 t=o
Итак, математическое ожидание ошибки Дао равно нулю, причем,
как видно из равенства A1.108), ее дисперсия стремится к нулю при
п -» оо. Аналогично усредняются случайные ошибки с ростом числа
наблюдений и в общем случае.
О 1Я
Пусть Ф| (г) = S аЪ
fc=o
шего среднеквадратичного приближения, первый из которых отвечает
350
), Ф]К(г) = S
к-о
— многочлены наилуч-
вектору у0 = (yo, y°, ..., уп)т данных, не содержащих ошибок, а второй
вектору у = (у0, за, ..., уп)т данных, содержащих случайные ошибки.
Положим «° = (ао, аи ..., а?)т, Да = (Дао, &ah ..., Даш)т (где Aajt =
= а? — at, к = 0, 1, ..., ш)ис = (e<j, ?1, ..., ?п)т- Рассмотрим многочлен
ГД«=
Отсюда вытекает равенство
Лг»О
Так как векторы а и «° удовлетворяют системам уравнений Те =
= Р^, Г*° =-Рг|°, то вектор Дв является решением системы
A1.109)
A1.110)
Заметим, что ДФт(х) и Даь — это случайные ошибки значения
многочлена Ф|(х) и его коэффициентов а&, вызванные наличием слу-
случайных ошибок е, в исходных данных. Покажем, что эти ошибки
имеют нулевое математическое ожидание.
Действительно, из формулы A1.110) следует, что
А/[Да] = rii*A/[E] =0,
откуда в свою очередь имеем
U [ДФт(х)] = 1м [Да*Ых) = 0.
Введем величину
равную среднеквадратичному значению ошибки ДФт(х).
Теорема 11.12. Справедливо равенство
МГ 21 - т+ 1
а Заметим, что
1
а1.
A1111)
= -~-{ (РАа, РД«) = ^j-L-j- (Д.,
351

n + 1
, Fe) =
n + 1
, e).
Из определения операции умножения матриц следует, что элемент ау
матрицы А — РТ'1РТ имеет вид ау = Е S Pt/Tifc" Pfc,i гДе Tjjt" ~
элементы матрицы Г, pL — элементы матрицы Р1. Поэтому
,?0 Д,
m+1
Л
Здесь 7t/ = ? pI.Pt/ ~" элементы матрицы Г. I
1=0 *
Замечание 1. Величина М [р2] представляет собой среднее по
точкам х, значение дисперсии случайной ошибки ДФт(г,) Из тео-
теоремы 11.12 следует, что М [р2] -> 0 при п ¦* оо, т. е. при неограничен-
неограниченном росте числа наблюдений среднее значение дисперсии ошибки
стремится к нулю.
Замечание 2 Равенство A1.111) подтверждает представление
о том, что статистические свойства метода наименьших квадратов
проявляются при п > т, т. е. тогда, когда число наблюдений много
больше числа параметров модели
Введем обозначения 6т = 6 (Ф& »), б? = S (Ф? , j°), dm= 6 (Ф& |°)
Заметим, что величина dm представляет собой среднеквадратично*'
уклонение многочлена наилучшего среднеквадратичного приближения
Ф% (построенного по вектору f исходных данных, содержащих случай-
случайные ошибки) от вектора jP точных значений функции /, которую мы и
пытаемся оценить. Именно эту величину следует считать "истинной"
мерой погрешности. Вычислим математические ожидания величин 6„ и
Теорема 11.13. Справедливы равенства
A1.112)
A1.113;
а В силу леммы 11.1 имеет место равенство
a («, *>) = 8 (*>, f)
которое в принятых выше обозначениях примет вид di = (б*J + р2.
Вычислив математическое ожидание и использовав теорему 11.12,
получим равенство A1.112).
Заметим теперь, что в силу леммы 11.1 а (ё>, у) = а (а, у) + |РДв|2.
Преобразуем левую часть этого равенства:
s (*, f) =
Таким образом,
rl 1
~\
2(P«° - »о, е)
-^ е).
З = (п + 1) а2, М [р2] =
Учитывая, что
М[\е\2] = |о
А/ [(Р«° - s°, е)] = (РвР - jo, А/ [е]) = 0,
получим равенство A1.113). И
5. О выборе степени обобщенного многочлена. Пусть функцию /
можно аппроксимировать с достаточно высокой точностью е обобщен-
обобщенным многочленом Фт(х) = Е акръ{х) некоторой степени т. Если эта
степень заранее не известна, то возникает проблема выбора оптималь-
оптимальной степени аппроксимирующего многочлена Ф| в условиях, когда
исходные данные у, содержат случайные ошибки е,.
Пусть ipo, ipi, ..., <рт — фиксированный набор базисных функций,
линейно независимых в точках х0, ij, ..., хп. Предположим, что n > m,
а ошибки е, удовлетворяют условиям A1.105), A1.106). Будем решать
задачу наименьших квадратов для m = 0, 1, 2, ..., постепенно увеличи-
увеличивая число параметров модели. Отметим, что значения среднеквадра-
среднеквадратичных уклонений 6т и 6$, должны с ростом m убывать. Действитель-
Действительно, множество всех многочленов Ф^ степени т+1 включает в себя
множество всех многочленов степени Фт и поэтому
6ml = min S
min 6 (Фт, j) = Sm, m > 0,
= min 6 (Фти »°) < min 6 (Фт, f°) = С т > 0.
352
353

Заметим также, что в силу теоремы 11.13 и закона больших чисел
(при п > 1) справедливы следующие приближенные равенства:
п— тп
n+ 1 '
ТИП
о*.
A1.114)
A1.115)
Как нетрудно видеть, с ростом m первое слагаемое в правой части
равенства A1.115) убывает, а второе возрастает. Поэтому следует ожи-
ожидать, что величина dm (именно она и характеризует уклонение вычис-
вычисляемого многочлена Ф| от функции f) с ростом т должна сначала
убывать, а затем, достигнув своего минимума при некотором m = mo,
начать возрастать.
Итак, существует оптимальная (в смысле критерия dm) степень
аппроксимации то. Однако несмотря на то, что увеличивая т, можно
получать все лучшее соответствие многочлена Ф| с экспериментальны-
экспериментальными данными, следует иметь в виду, что начиная с m = m0, многочлен
будет все хуже соответствовать приближаемой функции.
Выбор оптимальной степени то не представлял бы труда, если бы
значения dn можно было вычислять. Однако в действительности пря-
прямому вычислению поддаются только значения среднеквадратичного
уклонения 6т, анализируя которые мы и должны выбрать степень
многочлена.
Предположим, что дисперсия с2 (или ее оценка) случайных ошибок
?, известна. Пусть также известно, что для некоторого значения m < п
возможно приближение, для которого 6„ < <т. Тогда, начиная с этого
значения тп, согласно формуле A1.114) с у
будет иметь место приближенное равенство
значения тп, согласно формуле A1.114) с учетом того, что » 1,
п + 1
а.
A1.116)
Таким образом, за оптимальное значение степени многочлена следует
принять то значение т, при котором впервые будет выполнено приб-
приближенное равенство A1.116). При имеющейся информации лучший
выбор вряд ли возможен.
Пусть теперь значение а2 дисперсии ошибок е, нам не известно.
Зато известно, что функция / либо представляет собой обобщенный
многочлен Фт некоторой степени тщ (и тогда 6„ = с0 = 0 для всех
354
m > mo), либо же, начиная с некоторого m = mo, увеличение степени
многочлена в широком диапозоне значений п»о < m < mi практически
не влияет на качество приближения (т. е. 6* я с0 = const для всех
то < т < mi). Согласно формуле A1.114) справедливо приближенное
равенство
п +
п— тп
п— тп
' + <*
A1.117)
При m > то величина, стоящая в правой части этого равенства, приб-
п + 1 2
лиженно равна
со + а1 и не убывает по т. Это наблюдение
п — тп
позволяет использовать в рассматриваемой ситуации следующее прак-
практическое правило выбора: за оптимальное значение степени многочле-
многочлена следует принять то значение тп, начиная с которого величина <т\
стабилизируется или начинает возрастать.
Пример 11.16. Найдем оптимальную степень алгебраического многочлена
для аппроксимации функции, заданной табл. 11.13.
Заметим, что фактически оптимальная степень m = 1 уже была найдена
при решении примера 11.15. Основанием для такого вывода послужило сравне-
сравнение среднеквадратичных уклонений Ь\ и 0.0486 и 6г и 0.0481 с оценкой уровня
"шума" таблицы — грубый аналог критерия A1.116).
Попробуем получить тот же вывод, используя значения величин A1.117).
Найдем дополнительно P0(z) = 0.425 и 60 и 0.162. Тогда <& = — 6% и 0.292,
, тоза
о{ = Щ ft и 0.00295, <72 = Щ $ и 0.00381. ^
о 7
оптимальное значение степени следует принять m = 1.
6. Нелинейная задача наименьших квадратов. Часто из физических
или каких-либо других соображений следует, что зависимость у = / (х)
между величинами у и х должна хорошо описываться моделью вида
у = д (х, в), где функция д (х, в) = д (х, во, аи ..., а„) нелинейно зави-
зависит от параметров uq, аь ..., а„.
Пусть функция у = /(г) задана таблицей значений yt = f(xt),
t = 0, 1, ..., п, где п > тп. Тогда применение критерия наименьших
квадратов приводит к задаче определения искомых параметров во, а\,
..., ат из условия минимума функции
(а, у)=1(д (х„ а) - у,J-
355

Нелинейная задача наименьших квадратов (особенно при большом
числе параметров) весьма трудна для решения. Обычно для вычисле-
вычисления параметров ш применяются специальные методы минимизации [32].
В некоторых весьма специальных случаях решение нелинейной
задачи наименьших квадратов можно свести к решению линейной
задачи. Пусть, например, зависимость у от х ищется в виде у = аеЬх,
где а > 0. Логарифмируя это равенство, приходим к линейной зависи-
зависимости In у = ш а + Ьх величины Y = In у от г. Теперь по таблице
значений У, = In у, (i = 0, 1, ..., п) можно легко определить значения
In а и 6. Подчеркнем вре же, что найденные таким образом значения
параметров а и 6 отличаются от тех значений, которые могут быть
найдены непосредственной минимизацией функции Е (ое • — у,J.
0
J 11.14. Равномерное приближение функций
1. Задача о наилучшем равномерном приближении. Пусть /(х) —
заданная на отрезке [а, И\ непрерывная функция. Будем говорить, что
многочлен Рп(х) приближает функцию / равномерно на отрезке [а, 4] с
точностью е, если Д(Л0 = max |/(х) — Рп(х)\ ^ ?• Таким образом,
величина А(РП) играет здесь роль погрешности приближения.
Естественно поставить следующую задачу: среди всех многочленов
фиксированной степени п найти многочлен Qn(x), для которого вели-
величина погрешности равномерного приближения минимальна, т. е.
A(Qn) < Д(РП) для любого многочлена Рп(х) степени п. Поставленная
задача называется задачей о наилучшем равномерном приближении, а
искомый многочлен Qn(x) — многочленом наилучшего равномерного
приближения. Справедливо следующее утверждение.
Теорема 11.14. Для любой непрерывной на отрезке [а, Ь] функ-
функции f многочлен наилучшего равномерного приближения Qn степени п
существует и единствен.
Пример 11.17. Покажем, что многочленом наилучшего равномерного приб-
приближения нулевой степени для функции у = Jx на отрезке [0, 1] является
Qb(x) = 1/2. Заметим, что A(Q,) = max \J~x- 1/21 *= 1/2 (рис. 11.12, а) и
[0,1]
этот максимум достигается в точках xt) = 0 и х\ = 1. Для любого другого
многочлена Р(?х) = а, где a t 1/2, значение Д(Ро) > 1/2. В самом деле, если
а > 1/2, то Д(Р0) > Цъ - а\ = а > 1/2. Если же а < 1/2, то Д(Р0) >
^-а\ = 1 _а> 1/2.
Рис 11.12
Приведем без доказательства один из наиболее известных результа-
результатов о многочленах наилучшего равномерного приближения.
Теорема 11.15 (теорема Чебышева). Для того чтобы многочлен
Qn(x) был многочленом наилучшего равномерного приближения
непрерывной на отрезке [а, Ь] функции /(*), необходимо и достаточно,
чтобы на отрезке [а, Ь] нашлись по крайней мере п + 2 точки xq <
< xi < x2 < ... < xmi такие, что
f(xt)-Qn(xt) = а(-1)« max |/(х)-<?„(*)|, t = 0, 1, .... п + 1. A1.118)
Здесь а — постоянная, равная 1 или -1 для всех i одновременно.
Точки хо, х\, ..., Хпц, удовлетворяющие условиям теоремы, принято
называть точками чебышевского альтернанса1. Равенство A1.118)
накладывает на точки чебышевского альтернанса два требования:
1) в точках xt модуль погрешности приближения функции /много-
/многочленом Qn достигает максимума: |/(х,) — Qnix,)\ = max |/(x) —
[-.Ч
-Qn(x)\;
2) для всех i = 0, 1, ..., п погрешность /(х,) — Qn(xt) меняет знак
при переходе от точки х, к следующей точке xni.
1 От лат. alternate — "чередоваться".
357

Пример 11.18. В примере 11.17 точками чебышевского альтернанса являют-
являются точки яо = 0 и х\ — 1 (число точек равно двум, так как п = 0). В самом
деле, в этих точках достигается максимум модуля погрешности, а сама пог-
погрешность меняет знак при переходе от щ к Х[.
Пример 11.19. Найдем многочлен наилучшего равномерного приближения
первой степени для функции у = Jx на отрезке [0, 1].
В рассматриваемом случае п = 1 и должны быть по крайней мере три
точки чебышевского альтернанса. В частности, это означает, что графики
функций у — V* и у = Qi(x) = ах + Ь должны пересекаться хотя бы дважды
(рис. 11.12, <5). Функция <р(х) = Ji — Q(*) вогнута и потому может иметь на
отрезке [0, 1] лишь одну внутреннюю точку экстремума Х[. Следовательно, две
из точек чебышевского альтернанса совпадают с концами отрезка: х$ = 0, *5 =
= 1. В т^чке г\ функция <f(x) удовлетворяет необходимому условию экстрему-
экстремума <р'(х\) — 0, что эквивалентно уравнению
— -о=0. A1.119)
С учетом равенств (р(гь) = -Ь, <р(х{) = ¦& — ац — Ь, p(jfe) = 1 — а — b
условие перемены знака ip{i^) = -<р(х\) = (р(х$ эквивалентно двум уравнениям
A1.120)
A1.121)
-Ъ = -/ч + <Щ + Ь,
-6=1 -а- Ь.
Из уравнения A1.121) сразу находим, что в = 1. Затем из уравнения A1.119)
определяем, что ц = 0.25. Наконец, из A1.120) получаем 6 = 1/8.
Таким образом, Qi(x) = * + 1/8 — многочлен наилучшего равномерного
приближения первой степени, аппроксимирующий функцию Jx с погрешностью
A(Q) = 1/8.
2. Задача о понижении степени многочлена. Пусть Р^х) = ащЖ* +
+ ат-1гт + ... + ао — многочлен степени m > 1, значения которого
вычисляются на стандартном отрезке [-1, 1] (напомним, что к стан-
стандартному отрезку можно перейти от произвольного отрезка [в, Ь] ли-
линейной заменой переменных). Поставим следующую задачу о пониже-
понижении степени многочлена: аппроксимировать Рт(х) на отрезке [-1, 1]
многочленом Qn-i(x) наилучшего равномерного приближения на еди-
единицу меньшей степени.
Заметим, что RJix) = Ря(х) — Qn-i(*) — многочлен степени m со
старшим коэффициентом, равным старшему коэффициенту ап много-
многочлена PB(z). Поставленную задачу можно иначе сформулировать так:
среди всех многочленов степени т с фиксированным старшим коэф-
358
фициентом Ощ найти многочлен Rm для которого величина
max \Rm(x}\ минимальна. Как известно (см. § 11.6), решение этой
[-1.1]
задачи дает многочлен Дп(г) = ^Ч Т»(г) и для нег0 max IRm^ I =
V [-1,1]
_ I Дли таким образом, решением поставленной задачи является мно-
= ад-#гвд- A1Л22)
2
гочлен
Соответствующая погрешность приближения равна ?х-
Замечание. Тривиальный способ понижения степени много-
многочлена Рт{х) — отбрасывание старшего слагаемого атхт дает погреш-
погрешность, равную \а„\, т.е. в 2я раз большую, чем приближение
многочленом A1.122).
3. Нахождение многочленов, близких к наилучшим. В большинстве
реальных случаев задача о наилучшем равномерном приближении
непрерывной функции / является очень трудной Для ее решения
развиты специальные численные методы, реализованные в виде стан-
стандартных программ. Заметим, однако, что во многих ситуациях доста-
достаточно ограничиться нахождением многочлена, близкого к наилучшему,
либо просто найти многочлен, равномерно приближающий функцию /
с заданной точностью е. Укажем на два случая, когда возможно на-
нахождение многочленов, близких к наилучшим.
1°. Пусть производная /ntl>(z) функции /слабо меняется на отрез-
отрезке [а, Ь]. Тогда интерполяционный многочлен Рп(г) с чебышевскими
узлами A1.43) близок^к многочлену наилучшего равномерного прибли-
приближения.
2°. Пусть функция f(x) задана на отрезке [-1, 1] равномерно сходя-
сходящимся степенным рядом (рядом Тейлора):
f(x) = 2 в***.
к-0
A1.123)
Требуется найти многочлен минимальной степени, равномерно прибли-
приближающий функцию /на отрезке [-1, 1] с заданной точностью е.
Излагаемый ниже метод решения этой задачи часто называют
жономиэацией степенных рядов. Сначала берут отрезок ряда Тейлора
т
Рш{х) = Е а*!*, аппроксимирующий функцию / с точностью Е0 < ?•
Jt= 0
Далее степень многочлена последовательно понижают. Если погреш-
359

ность
UJ
J
^- понижения степени такова, что е0 + ?i < e, то много-
многочлен Рт заменяют многочленом /V, = Рп - -ЦЬ- Tm = "Ё о("г* Если
2^ Jt=o *
погрешность е2 =
такова, что ?0 + б! + е2 < е, то снова пони-
жают степень многочлена P^i по формуле Рщ-2 =
.A)
, - m;' rm.i и
т. д. Процесс прерывают тогда, когда вычисление очередного ejt дает
ео + ?i + ••• + ?fc > е. В этом случае полагают f(x) и
Пример 11.20. Найдем многочлен минимальной степени, аппроксимирующий
функцию у = sin г на отрезке [-1, 1] с точностью е = КГ3.
Ряд sin х = Е (-1)к ^ — знакопеременный, а его слагаемые убыва-
убывают по модулю. Поэтому погрешность приближения функции sin х отрезком
ряда Тейлора P2n*i(*) = Е (-1)* оценивается величиной е0 =
1
Bп + 3)!'
максимуму модуля первого отброшенного слагаемого.
Выбор п = 2 дает значение е0 = ^щ и 2-Ю < ?. Следовательно, многочлен
Рь\ч — х — jj- + j2« аппроксимирует функцию у = sin я с точностью е<> и
« 2-104
Понижение степени многочлена Рь будет сопровождаться дополнительной
погрешностью е, 1
ь у
= -Ц|1 = щй 5.2-КГ»
-Ц|
5.2-КГ». Следовательно, е0 + ?i < e и
после понижения степени по формуле
w ~ ш Ts(r) =х - т+ ш - ш
получим многочлен
р, ч 383 5 ,
A1-124)
дающий приближение к sin х на отрезке [-1, 1] с точностью 7.2-10'4.
Так как е3 = — • ^ > Ю'3, то дальнейшее понижение степени невозмож-
невозможно и решением задачи является многочлен A1.124).
360
§ 11.15. Дробво-рациональные аппрокс
и вычисление элементарных функций
ации
При создании стандартных программ вычисления элементарных и
специальных функций специалистами по математическому обеспече-
обеспечению ЭВМ применяются разнообразные приемы, требующие глубоких
профессиональных знаний. Используемые вычислительные методы не
являются здесь машинно-независимыми, а, наоборот, существенно
учитывают разрядность мантиссы, скорость выполнения арифметичес-
арифметических операций и другие особенности конкретной ЭВМ. Отметим, что к
указанным стандартным программам обычно предъявляется требова-
требование обеспечения относительной точности результата порядка машин-
машинного эпсилон ем.
Использование богатой дополнительной информации об аналити-
аналитических свойствах элементарных и специальных функций позволяет
значительно уменьшить объем вычислений. Существенно используется
возможность представления вычисляемых функций сходящимися
степенными рядами вида
A1.125)
Здесь 2 = х — xq\ х0 — точка, в которой осуществляется разложение
функции в ряд. Отметим, однако, что вопреки распространенному
мнению такие ряды непосредственно практически никогда не исполь-
используются для вычисления функций.
Широко применяемым в настоящее время способом представления
функций является приближение их рациональными дробями вида
oo +
A1.126)
К дробно-рациональным аппроксимациям приходят различными путя-
путями. В ряде случаев используется рациональная интерполяция — интер-
интерполяция функции рациональной дробью A1.126). Тогда коэффициен-
коэффициенты a, (j = 0, 1, ..., п), Ьк (к = 0, 1, ..., т) находятся из совокупности
соотношений R (zt) = щ @ < ii < N, N = n + m + 1), которые можно
записать в следующем виде:
2 4-zj = Vi E
Эти соотношения образуют систему N линейных алгебраических урав-
уравнений относительно # + 1 неизвестных. Такие системы всегда имеют
361

нетривиальные решения. Можно записать Я (г) и в явном виде, если
использовать аппарат обратных разделенных разностей [9].
Один из возможных путей состоит в использовании теории цепных
(или непрерывных) дробей. Например, функция tg x представляется
цепной дробью
1 —
3 *
Обрывая такую бесконечную дробь, получают некоторую конечную
дробь, аппроксимирующую функцию.
Все более популярным в последние годы способом приближения
аналитических функций становится аппроксимация Ладе — такая
дробно-рациональная аппроксимация A1.126), для которой
2 C
о
A1.127)
Равенство A1.127) означает, что коэффициенты oq, аи ..., ап, 60, hu
•••, bm дроби A1.126) подбираются так, чтобы в разложении ее в ряд
Тейлора первые п + т + I слагаемых в точности совпадали с соответ-
соответствующими слагаемыми ряда A1.125).
В качестве примера приведем две аппроксимации Паде функции ех
в случаях п = 2, m = 2 и п = 3, m = 3:
е1 и
12 + 6х +
12
- бг +
10) +
л? '
60)
10) -
A1.128)
Отметим, что при \х\ < 0.5 In 2 аппроксимация A1.128) обеспечивает
точность 9-Ю"9.
В заключение параграфа рассмотрим, как вычисляется в одной из
стандартных программ функция у = In x. Аргумент х представляют в
виде х = [i-2P, где р — двоичный порядок, ц — мантисса, 0.5 < /i < 1.
Затем используют разложение
In х = (р - 0.5Iп 2 + 2« S
*0
Заметим, что | v\ < а = (^ -
L
где » =
— «2*
+ 1) < 0.172. Ряд Е
it
1
fc-o 2/t + 1 r
заменяют затем на отрезке [-а, а] многочленом, близким к многочлену
362
четвертой степени наилучшего равномерного приближения. В
результате получается формула
In х и (р - 0.5Iп 2 + v B.000000815 + 0.666445069»2 +
+ 0.415054254V4),
погрешность которой для всех х не превышает 3 ¦ 10~8.
$ 11.16. Дополнительные замечания
1. Хотя в данном пособии интерполирование рассматривается довольно
подробно, все же за пределами обсуждения оказывается ряд полезных приемов
интерполирования и соответствующих приложений (таких, как, например,
интерполяционный многочлен Бесселя и обратная интерполяция). Подробности
можно найти в [9].
2. Тем, кто интересуется практическим применением сплайнов, рекомендуем
книгу [16]. В ней можно найти не только изложение теории и алгоритмов
решения задач, но и полезные практические советы и тексты соответствующих
фортранных программ.
3. Изложение современных вычислительных методов решения линейных
задач метода наименьших квадратов содержится в общепризнанном учебнике-
справочнике [50]. Заметим, что в оригинальное издание этой книги включены
и тексты соответствующих фортранных подпрограмм, которые были, к сожале-
сожалению, опущены при переводе.
4. Исключительно богатый материал по специальным и элементарным
функциям содержит справочник [1]. Эта книга пользуется заслуженной попу-
популярностью у специалистов, и тот, кто занимается вычислением специальных
функций лишь эпизодически, может найти в ней ответы на большинство
интересующих его вопросов. Правда, большая часть приведенных в справочни-
справочнике результатов была получена до 1960 г. Как дополнение к [1] можно рассмат-
рассматривать книгу [51].
5. Желающим более глубоко ознакомиться с аппроксимациями Паде и
непрерывными (цепными) дробями рекомендуем обратиться к специальной
литературе [11], [31].
6. Подчеркнем, что в данной главе рассматривались методы приближения
функций только одной вещественной переменной. В случае аппроксимации
функций многих переменных можно использовать аналогичные подходы (см.,
например, [9], [54]).

Глава 12
ЧИСЛЕННОЕ
ДИФФЕРЕНЦИРОВАНИЕ
Численное дифференцирование применяется тогда, когда функцию
трудно или невозможно продифференцироать аналитически. Напри-
Например, необходимость в численном дифференцировании возникает в том
случае, когда функция задана таблицей. Кроме того, формулы числен-
численного дифференцирования широко используются при разработке вы-
вычислительных методов решения многих задач (решение дифференци-
дифференциальных уравнений, поиск решений нелинейных уравнений, поиск
точек экстремума функций и др.).
$ 12.1. Простейшие формулы
численного дифференцирования
1. Вычисление первой производной. Предположим, что в окрестно-
окрестности точки х функция / дифференцируема достаточное число раз. Ис-
Исходя из определения производной
Ax
естественно попытаться использовать для ее вычисления две простей-
простейшие приближенные формулы:
Пх) и П* + *) - / (*)
А . '
A2.1)
A2.2)
соответствующие выбору фиксированных значений Ах — А и Дх = -А
Здесь А > 0 — малый параметр (шаг). Разностные отношения в правых
364
частях формул A2.1) и A2.2) часто называют правой и левой разност-
разностными производными [70].
Для оценки погрешностей
п(х, А) = }'(х) -
г.(х, Л) = f'(x) -
А) - f(x)
f{x) - /(г - А)
введенных формул численного дифференцирования (погрешностей
аппроксимации) воспользуемся формулами Тейлора:
/'«¦)
f(x±h) = f(x)±f'(x)h
А2.
A2.3)
Здесь и ниже ?+ и ?- — некоторые точки, расположенные на интерва-
интервалах (х, х + А) и (х - А, х) соответственно. Подставляя разложения
A2.3) в выражения для г+, получаем rv(z, А) = - - /' (?+) А, г.(х, А) =
= - /' (?.) А. Следовательно,
\r.(x,h)\<l-M2h,
= max
[х, х + А]
= max
[, - А,
A2.4)
A2.5)
Таким образом, формулы A2.1), A2.2) имеют первый порядок
точности по Л. Иначе говоря, правая и левая разностные производные
аппроксимируют производную }'(х) с первым порядком точности.
х-»
к+Ь
0 x-h
x+h
S)
Рис. 12.1
365

Приведенные формулы численного дифференцирования имеют
простую геометрическую интерпретацию (рис. 12.1, а). Пусть ^Vo, N. и
N+ — расположенные на графике функции у = f (r) точки с координа-
координатами (х, f(x)), (х - Л, /(г - Л)) и (х + A, f (х + Л)). Напомним, что
производная f'(x) равна тангенсу угла а наклона к оси Ох касатель-
касательной, проведенной к графику функции в точке No. Формула A2.1)
соответствует приближенной замене производной f'(x) = tga правой
разностной производной — { — , равной тангенсу угла «¦
наклона к графику функции секущей, проведенной через точки No и
N+. Формула A2.2) соответствует аналогичной замене левой разностной
^ т-^
производной
равной тангенсу угла а. секущей,
проведенной через точки No и N..
Естественно предположить (рис. 12.1, а и 12.1, б), что лучшим по
сравнению с tga* и tga. приближением к f'(x) = tga является тангенс
угла наклона а0 секущей к графику, проведенной через точки N. и N+.
Соответствующая приближенная формула имеет вид
Пх) т
A2.6)
Величину в правой части этой формулы часто называют центральной
разностной производной.
Подставляя в выражение для погрешности
Для вычисления f'(x) можно получить формулы любого порядка
точности (см. § 12.2). Однако в таких формулах с ростом порядка
точности возрастает и число используемых значений функции. В каче-
качестве примера приведем формулу
/'(*) «
f{*-2h) - Sf(x-h)
12А
A2.8)
имеющую четвертый порядок точности.
Пример 12.1. Пусть функция /(г) = е1 задана на отрезке [0, 1] таблицей
значений с шагом Л = 0.2:
Таблица 12.1
0.0
02
0.4
0.6
0.8
1.0
/(*) 1.000000 1.22140 1.49182 1.82212 2.22554 2.71828
Используя формулы численного дифференцирования, найдем значения произ-
производной f'(x) в узлах таблицы.
В точках х = 0.0 и х = 1.0 из приведенных в этом параграфе формул
можно воспользоваться лишь формулами A2.1) и A2.2). В остальных точках
применим формулу A2.6), имеющую более высокий порядок точности. Вы-
Вычисления дают следующую таблицу производных:
Таблица 12.2
соответствующие разложения по формуле Тейлора
A3,
получим, го(г, А) = -
Д2 Следовательно, справедли-
справедлива оценка погрешности
I ro(x, Л) | <!?- A2, M3= max
[x - h , z + A]
A2.7)
Таким образом, центральная разностная производная аппроксимирует
производную f'(x) со вторым порядком точности относительно А.
366
0.0
0.2
0.4
0.6
0.8
1.0
/(г) 1.10700 1.22955 1.50180 1.83430 2.24040 2.46370
г (г) -0.10700 -0.00815 -0.00998 -0.01218 -0.01486 0.25458
Здесь же приведены значения погрешностей г (г), которые в данном случае
легко вычисляются (ведь f'(x) = t? = /(*)). Как и следовало ожидать, значе-
значения погрешности в крайних точках (здесь использовались формулы первого
порядка точности) существенно больше, чем во внутренних точках.
Заметим, что значения погрешностей можно было оценить и заранее, ис-
используя априорные оценки A2.4), A2.5), A2.7). Например, неравенство A2 4)
дает в точке х = 0 оценку
, | г 1 ,. , 1
I г| ч - М2п = - max
[0,0.2]
•A = i-1.22140-0.2« 0.13.
367

В точке х — 0.2 из неравенства A2.7) следует, что
| г| < \ Л/3Л2 = \ max | J" | A2 = 1-1.49182-0.04 и 0.01, и т.д.
6 б [0,0.4] 6
Для вычисления / (х) при х = 0.4 и * = 0.6 можно также применить
формулу A2.8) и получить значения /@.4) и 1.49176 и /'@.6) и 1.82203 с
погрешностями, приближенно равными 6-10 и 9-Ю соответственно.
2. Вычисление второй производной. Наиболее простой и широко
применяемой для приближенного вычисления второй производной
является следующая формула:
/•(«) м
Я* ~ ») ~ 2/(х) + /(х + А)
A2.9)
Величину в правой части этого приближенного равенства часто назы-
называют второй разностной производной [70].
Подставляя в выражение для погрешности
*>
соответствующие разложения по формуле Тейлора
fix ± h) = fix) ± f'ix)h + Ц^- h2 ± /11W дз
24
А4,
f **(?*) + f4)(?)
получим г (x, A) = - -—" ' —^-^ А2. Следовательно,
|г(х,А)| <^Л2, Л/< = max
[*-h, x+h]
A2.10)
Таким образом, формула A2.9) имеет второй порядок точности.
Для вычисления /*(х) можно получить формулы любого порядка
точности. Например, формула
Г/Гч п ~/(*-2А) + 1б/(х-А) - 30/(х) + 1б/(г+А) - /(r+2/Q
имеет четвертый порядок точности.
368
Пример 12.2. Используя табл. 12.1 значений функции fix) = е*. найдем с
помощью формул численного дифференцирования значения /"(х) во внутрен-
внутренних узлах таблицы.
Вычисление по формуле A2.9) дает значения, приведенные в табл. 12.3:
Таблица 12.3
X
f(')
r(x)
0.2
1.22550
-0.00410
0.4
1.49700
-0.00518
0.6
1.82800
-0.00588
0.8
2.23300
-0.00746
Применение формулы A2.11) позволяет получить значения /@.4) и
и 1.49204, /"@.6) и 1.82183 с погрешностями, приближенно равными
-2-10-1, -3-НГ».
§ 12.2. О выводе формул численного
дифференцирования
Хотя простейшие формулы численного дифференцирования можно
получить сравнительно элементарно, для вывода и анализа таких
формул в более сложных случаях необходимо использовать значитель-
значительно более серьезный математический аппарат. Заметим, что основой для
построения различных приближенных формул вычисления производ-
производных являются методы теории приближения функций, элементы кото-
которой были изложены в предыдущей главе.
Предположим, что в окрестности точки х функция / аппроксимиру-
аппроксимируется некоторой другой функцией д, причем производная j( k) в точке х
легко вычисляется. Естественно в такой ситуации попытаться восполь-
воспользоваться приближенной формулой
^|A)«|}(*>(г). A2.12)
Наиболее просто этот подход реализуется в случае, когда приближе-
приближение осуществляется с помощью интерполяции.
1. Формулы численного дифференцирования, основанные на интер-
интерполяции алгебраическими многочленами. Пусть Рп(х) — интерполяци-
интерполяционный многочлен степени п с узлами интерполяции хо < х\ < Хг < ...
... < х„ и х€[хо, х„]. В этом случае формула A2.12) принимает вид
0<*<n.
A2.13)
369

При этом справедлива следующая оценка погрешности формулы
A2.13):
|/it)(l) _ рШ(х)\ < CntkMnnh%?l<, 0 < * < п. A2.14)
Здесь CHik — положительные числа, а Мп+1 = max |/*+1(z)|.
[х о , Ы
Замечание 1. Порядок точности формулы A2.13) относитель-
относительно Лтах равен разности между числом узлов интерполяции и по-
порядком вычисляемой производной.
Замечание 2. Если формула A2.13) применяется для вычис-
вычисления производной в точке, относительно которой узлы таблицы
расположены симметрично, и число п - к четно, то порядок точно-
точности формулы повышается на единицу по сравнению с порядком п +
+ 1 - к, гарантируемым оценкой A2.14). Таковы, например,
формулы A2.6), A2.8), A2.9), A2.11).
Заметим, что Р1пп] (х) = n! f(x0; х\\ •••, хп) (это следует, в частности,
из формулы A1.52)). Таким образом, справедлива приближенная
формула (она вытекает и из A1.50))
п!/(х0; ч; .... хп),
A2.15)
имеющая по крайней мере первый порядок точности. Ее частными
случаями являются следующие формулы:
A2.16)
<Ш7>
При выборе в качестве узлов интерполяции значений х0 = х, х\ =
= х + h формула A2.16) превращается в формулу A2.1). При выборе
т0 = х - h, X] = х из A2.16) получается формула A2.2), а при х0 —
= х - h, xi = х + h — формула A2.6). Аналогично из формулы A2.17)
получается формула A2.9).
2. Использование таблиц с постоянным шагом. Наиболее простой
вид принимают формулы численного дифференцирования при исполь-
370
зовании таблиц у, — f(xt) с постоянным шагом. Например, формула
A2.15) в этом случае выглядит так: fn)(x) и —rjp
В тех случаях, когда значение производной необходимо вычислять
в крайних для таблицы точках хо и хп, используются односторонние
формулы численною дифференцирования Рк)(хо) w P^k) (xq) и fk)(xn) и
s P^1 (in). Приведем односторонние формулы (их легко получить
дифференцированием многочленов Ньютона A1.57) и A1.58)) для
вычисления первой производной /':
f'(x0) н i S Ц
т S
имеющие ге-й порядок точности.
При п = 2 из A2.18), A2.19) получаются формулы
/'(in) й ai
имеющие второй порядок точности.
A2.18)
A2.19)
A2.20)
A2.21)
Пример 12.3. Вычисление значений производной функции /(г) = еР,
заданной табл. 12.1, по формулам A2.20), A2.21) дает значения /'@.0) «
и 0.98445, /'A.0) и 2.68700 с погрешностями, равными 0.001555 и 0.03128.
Для сравнения напомним, что погрешности значений, найденных в примере
12.1 по простейшим формулам С12.1), A2.2) соответственно равны — 0.10700 и
0.25458.
3. Другие подходы. Применение формулы A2.13) для вычисления
производной fk) фактически основано на кусочно-полиномиальной
интерполяции. Полученная таким образом производная в точке "сты-
"стыка" двух соседних многочленов может иметь разрыв. Поэтому, если
требуется глобально на отрезке [а, Ь] аппроксимировать производную
гладкой функцией, то целесообразно использовать сплайны. Производ-
371

ная S^k) (х) сплайна Sm(x) при к < т - г (где г — дефект сплайна) дает
гладкую глобальную аппроксимацию для fk)(x).
В случае, когда значения функции сильно "зашумлены" случайны-
случайными ошибками, полезным может оказаться использование метода на-
наименьших квадратов.
§ 12.3. Обусловленность формул
численного дифференцирования
Несмотря на внешнюю простоту формул численного дифференци-
дифференцирования, их применение требует особой осторожности. Отметим, что
используемые при численном дифференцировании значения f*(x)
функции f(x) непременно содержат ошибки. Поэтому к погрешности
аппроксимации формул численного дифференцирования добавляется
неустранимая погрешность, вызванная погрешностями вычисления
функции / Для того чтобы погрешность аппроксимации была доста-
достаточно малой, требуется использование таблиц с малыми шагами А.
Однако, к сожалению, при малых шагах формулы численного диффе-
дифференцирования становятся плохо обусловленными и результат их при-
применения может быть полностью искажен неустранимой ошибкой. Важ-
Важно понимать, что действительная причина этого явления лежит не в
несовершенстве предложенных методов вычисления производных, а в
некорректности самой операции дифференцирования приближенно
заданной функции (см. гл. 3, пример 3.5)
Поясним сказанное на примере использования формулы A2.1).
f(x + А) - /*(*)
А
вычисляемого значения правой разностной производной представляет
собой сумму погрешности аппроксимации г*(х, А) =
f{x + А) - /(г)
А
Полная погрешность г*(х, А) = /'(
реально
= / (х) —
и неустранимой погрешности гн{х, А) =
= I ((/(* + Л) - Пх + А)) - (/(*) - /•(*)))•
Пусть Д — верхняя граница абсолютной погрешности Д(/*(г)) =
= \f(x) — f*(x) | используемых значений функции. Тогда погрешность
гн оценивается следующим образом:
i i ^2Л
A2.22)
Оценка A2.22) означает, что чувствительность формулы A2.1) к пог-
погрешностям входных данных характеризуется абсолютным числом
372
обусловленности j/д = -. Так как j/д -» <» при А -> 0, то формула A2.1)
при малых Л становится очень плохо обусловленной. Поэтому несмотря
на то, что погрешность аппроксима-
аппроксимации стремится к нулю при А -> 0 (см.
оценку A2.4)), следует ожидать, что
полная погрешность будет неограни-
неограниченно возрастать при А -¦ 0. Во всяком
случае так ведет себя верхняя граница
полной погрешности г (Л) = - M2h +
2Д -
+ т— (график функции г (Л) для слу-
случая, рассмотренного в примере 12.4,
приведен на рис. 12.2).
Выберем оптимальное значение шага
А, при котором величина г (А) достигает минимального значения.
Приравнивая производную г'(Л) = - М2 - -гг- к нулю, получаем
значение АоПТ = 2\А/М2, которому отвечает величина г,,цП = г (АоПТ) =
= 2J ДМ2.
Таким образом, при использовании формулы A2.1) для вычисле-
вычисления производной функции /, заданной с погрешностью, следует обра-
обратить особое внимание на выбор шага А. Однако даже при оптимальном
выборе шага полная погрешность окажется величиной, пропорци-
Рис 12.2
ональной лишь \ Д.
Формулы для вычисления производных порядка к > 1 обладают
еще большей чувствительностью к ошибкам задания функций. Поэто-
Поэтому значения производных высокого порядка, найденные с помощью
таких формул, могут быть очень неточными.
Пример 12.4. Рассмотрим результаты применения формулы A2.1) с разны-
разными значениями шага А для вычисления производной функции f(x) = ё° в
точке х = 1.
В табл. 12.4 приведены значения приближений (/')* к /'A) = ей 2.71828,
полученные на 6-разрядной десятичной ЭВМ и отвечающие значениям А =
= 10, 10, ..., 10'6. Для удобства анализа указаны также значения
погрешностей г*.
373

Таблица 12.4
10"
10-2
10
-з
10
-5
10
(/')* 2.85890 2.73200 2.72000 2.70000 3.00000 0.00000
г* 14-10 14-Ю 17-Ю -18-Ю 28-10 -27 • 10
Из таблицы видно, что погрешность г* с уменьшением А сначала убывает по
модулю, а затем начинает резко возрастать. При Л = 10:6 значения функции в
точках х = 1 + h к х = 1, найденные с шестью знаками мантиссы, совпадают,
и поэтому вычисление по формуле A2.1) дает приближение к /'A). равное
нулю. Ясно, что при Л < 10 будет получаться тот же результат.
На рис. 12.2 точками помечены значения модуля погрешности г*, отвеча-
отвечающие различным А из диапазона 10 < А ^ 10. Сплошной линией изображен
- 10
график функции г (А) = 1.4А + —;-, являющейся верхней оценкой для
л
|г*(Л)| (в данном случае Мг = max \еР°\ < 2.8 и Д = 5-10). Отметим,
[1, 1.01]
что хотя реальное значение погрешности г* и оказывается меньше получаемо-
получаемого с помощью оценки г, все же функция г (А) правильно отражает основные
особенности поведения погрешности.
$ 12.4. Дополнительные замечания
1. Формулы численного дифференцирования применяются и для
приближенного вычисления частных производных функций многих
переменных. Для их построения используются различные приемы. Среди них
последовательное применение одномерных формул численного
дифференцирования и дифференцирование интерполяционных формул.
Распространенным является и метод неопределенных коэффициентов [9]
(иногда он используется и в одномерном случае).
2. При наличии в значениях функции случайных ошибок нередко
применяют некоторые процедуры предварительного сглаживания. В последнее
время получила распространение группа методов численного
дифференцирования, в которых используются идеи регуляризации (см. [79,
гл. 4, § 6].
3. Дополнительную информацию о методах численного дифференцирования
можно найти, например, в [43].
Глава J3
ЧИСЛЕННОЕ
ИНТЕГРИРОВАНИЕ';
§ 13.1. Простейшие квадратурные формулы
1. Постановка задачи. В прикладных исследованиях часто возника-
возникает необходимость вычисления значения определенного интеграла
/= ffyxjdx
A3.1)
Этот интеграл может выражать площадь, объем, работу переменной
силы и т.д
Если функция f{x) непрерывна на отрезке [а, Ь] и ее первообраз-
первообразную F (х) удается выразить через известные функции, то для вычисле-
вычисления интеграла A3.1) можно воспользоваться формулой Нъютона-Лейб-
ница1:
lf(x)dx= F(b)- F(a)
A3.2)
К сожалению, в подавляющем большинстве случаев получить значение
определенного интеграла с помощью формулы A3.2) или других ана-
аналитических методов не удается.
X 2
Пример 13.1. Интеграл )е"' At широко используется при исследовании
о
процессов теплообмена и диффузии, в статистической физике и теории веро-
вероятностей. Однако его значение ке может быть выражено в виде конечной
комбинации элементарных функций.
1 Готфрид Вильгельм Лейбниц A646 — 1716) — немецкий математик, фи-
физик и философ. Один из создателей дифференциального и интегрального
исчислений.
375

Заметим, что даже в тех случаях, когда удается получить первооб-
первообразную функцию F (х) в аналитической форме, значительные усилия,
затраченные на это, часто оказываются чрезмерно высокой платой за
окончательный результат. Добавим еще, что вычисления интеграла в
этих случаях по формуле A3.2), как правило, приводят к громоздким
(а часто — и приближенным) вычислениям. Следует отметить также,
что зачастую найти точное значение интеграла A3.1) просто невозмож-
невозможно. Например, это имеет место, когда функция / (х) задается таблицей
своих значений.
Обычно для вычисления значения определенного интеграла приме-
применяют специальные численные методы. Наиболее широко используют
на практике квадратурные формулы — приближенные равенства вида
f/(x)dx
1=0
A3.3)
Здесь х, — некоторые точки из отрезка [а, Ь] — узлы квадратурной
формулы; At — числовые коэффициенты, называемые весами квадра-
N
турной формулы; N ^ О — целое число. Сумма ? AJ(xt), которая
1=0
принимается за приближенное значение интеграла, называется
- ?
турной суммой Величина R = f/(x)dx - ? AJ(xt) называется по-
а 1=0
грешностью (или остаточным членом) квадратурной формулы.
Будем говорить, что квадратурная формула A3.3) точна для много-
многочленов степени т, если для любого многочлена степени не выше m эта
формула дает точное значение интеграла, т.е.
fP«(x)dx =
a t=0
При оценке эффективности квадратурных формул часто исходят из
того, что наиболее трудоемкой операцией при вычислении по формуле
A3.3) является нахождение значения функции / Поэтому среди двух
формул, позволяющих вычислить интеграл с заданной точностью е,
более эффективной считается та, в которой используется меньшее
число узлов.
Выведем простейшие квадратурные формулы, исходя из наглядных
геометрических соображений. Будем интерпретировать интеграл A3.1)
как площадь криволинейной трапеции, ограниченной графиком функ-
функции у = /(х) (при f(x) } 0), осью абсцисс и прямыми х = а, х = b
(рис. 13.1, а).
376
Рис. 13.1
0 а*х0 х,
Рис. 13.2
Разобьем отрезок [а, 6] на элементарные отрезки [х,-Ь х,] точками
а = х0 < хх < ... <х„ = Ь. Интеграл / разобьется при этом на сумму
элементарных интегралов:
i
A3.4)
где 7, =J f(x)dx, что соответствует разбиению площади исходной
криволинейной трапеции на сумму площадей элементарных криволи-
криволинейных трапеций (рис. 13.1, б).
Введем обозначения: /, = /(*,), /, . 1/2 = /(г, . 1/2), где xt . 1/2 =
- (r,-i + z,)/2 — середина элементарного отрезка. Для простоты шаг
Л = х, - r,-i будем считать постоянным.
2. Формула прямоугольников. Заменим приближенно площадь
элементарной криволинейной трапеции площадью прямоугольника,
основанием которого является отрезок [х,.и rj, а высота равна значе-
значению /, - 1/2 (на рис. 13.2, а через N,. 1/2 обозначена точка с коорди-
координатами (г,. i /2, /,. j /г)). Так мы приходим к элементарной квадра-
квадратурной формуле прямоугольников:
377

Л
- 1/2-
A3.5)
Производя такую замену для всех элементарных криволинейных тра-
трапеций, получаем составную квадратурную формулу прямоугольников-
- + /п- 1/2) = Л S
n
= h У.
1=1
[13.6)
Эта формула соответствует приближенной замене площади исходной
криволинейной трапеции площадью ступенчатой фшуры, изображен-
изображенной на рис. 13 2. б.
Замечание. Иногда используют формулы
п-\
/и h Е /„
1-0
i
A3 7)
A3.8)
называемые соответственно составными квадратурными формулами
левых и правых прямоугольников. Геометрические иллюстрации
приведены на рис. 13.3, о и б. В соответствии с этим формулу A3.6)
иногда называют составной квадратурной формулой центральных
прямоугольников.
3. Формула трапеций. Соединив отрезком точки JV,-i(r,-i, /t-i) и
Щх„ ft) на графике функции у = /(г), получим трапецию (рис 13.4,
а). Заменим теперь приближенно площадь элементарной криволиней-
криволинейной трапеции площадью построенной фигуры. Тогда получим элемен-
элементарную квадратурную формулу трапеций:
I, « \ (/,-1 + /.)¦
A3.9)
Пользуясь этой формулой при % - 1, ..., п. выводим составную квадра-
квадратурную формулу трапеций:
= h [^
/«-1 + ff\ =
4
A3.10*
Эта формула соответствует приближенной замене площади исходной
378
Рис. 13.4
Рис. 13.5

криволинейной трапеции площадью фигуры, ограниченной ломаной
линией, проходящей через точки Nq, Ni, ..., Nn (рис. 13.4, б).
4. Формула Симпсона1. Если площадь элементарной криволиней-
криволинейной трапеции заменить площадью фигуры, расположенной под парабо-
параболой, проходящей через точки Ni-\, #t - 1/2 и N{ (рис. 13.5, а), то полу-
*t
чим приближенное равенство U и } P2(x)dx. Здесь Р2(х) — интерполя-
*ы
ционный многочлен второй степени с узлами x,-i, х*- i/2> xt- Как не-
нетрудно убедиться2, верна формула
= U -
- ъ -1/2)
Ее интегрирование приводит к равенству
J P2(x)dx=hfi.l/2 + Ji h Л'х J (x,-rl-i/2)dx +
i h ~. 2/t -1/2 + /t-1 f /„ _ _ . ЛОЛ* —
= A/i - 1/2
? (/< " Vi - 1/2 + A-l) = J (/И
/0-
Таким образом, выведена элементарная квадратурная формула Симп-
Симпсона:
/< м ? (Д-1 + 4JJ - 1/2 + Л)- A311)
Применяя эту формулу на каждом элементарном отрезке, выводим
составную квадратурную формулу Симпсона:
1 Томас Сиштсон A710—1761) — английский математик.
2 Проверку того, что PjD-i) = /:-ь РЖ* - i/г) = /t- 1/2.
= /.,
рекомендуем провести самостоятельно.
380
П / I J / lQ.fl iQ.f i
- Ад + 4/3Л + Ih + ¦¦¦ + 2/n-i +
+ 4/n - 1/2 + fn) = ^ (A + /„ + 4 g fi. 1/2 + 2 "Ё1 /,). A3.12)
Замечание 1. Учитывая геометрическую интерпретацию
формулы Симпсона, ее иногда называют формулой парабол.
Замечание 2. В случае, когда число элементарных отрезков
разбиения четно (я = 2т), в формуле Симпсона можно использо-
использовать лишь узлы с целыми индексами:
При выводе этой формулы роль элементарного отрезка играет
отрезок [x2i-2, r2j] длины 2А.
5. Оценка погрешности. Оценим погрешность выведенных квадра-
квадратурных формул в предложении, что подынтегральная функция /дос-
/достаточно гладкая. Как и в предыдущих главах, будем использовать
обозначение Мк = max \fk)(x)\.
[«, Ч
Теорема 13.1. Пусть функция f дважды непрерывно дифферен-
дифференцируема на отрезке [а, Ь]. Тогда для составных квадратурных формул
прямоугольников и трапеций справедливы следующие оценки погреш-
погрешности:
A3.13)
A3.14)
12
D Выведем сначала оценку A3.13). Представим погрешность R —
— I ~ ^пр формулы прямоугольников в виде
Л= f f(x)dx-h g /,.ly2= § / (f(x)-f(xt.1/2))dx.
О 1=1 t=l *,-j
Используя формулу Тейлора
/(*) =/(*i - 1/2) + /'(*• - 1Л)(*- *• - 1/2)
где х € [х,-ь xj, ^ = ({х)е [xi-u xt], имеем
(Х-
381

Д, = J (/ (x) - / (x, - ! /2))dr = I J Г(«х))(х - x, - , ^dx,
J
Vi
2 x
t-1
o r-r,.1/2K
24
Так как R = ? Д„
1
то
1=1
< S ^ A3 = ^ Лзп. Замечая, что пА =
i=l ^4 ^4
= Ь - а, приходим к оценке A3.13).
Для вывода оценки A3.14) воспользуемся тем, что отрезок, соеди-
соединяющий точки N,-\ и Ni представляет собой график интерполяцион-
интерполяционного многочлена первой степени у — Р\(х) = ft-\ -Ц- + Л —г——.
п п
Поэтому для элементарной формулы трапеций верно равенство
Д, = / f(x)dx - | (Л-, + /,) = \ (f(x) - P,(x))dx.
r ^ r
Используя оценку A1.28) погрешности линейной интерполяции, имеем
-t-1 *
Следовательно, для R = I - I^p справедлива оценка
Приведем теперь без доказательства теорему об оценке погрешности
формулы Симпсона.
Теорема 13.2. Пусть функция f имеет на отрезке [а, Ь] непре-
непрерывную производную четвертого порядка /4). Тогда для формулы
Симпсона A3.12) справедлива оценка погрешности
jh. М4(Ь - а)
С1 2880
A3.15)
Замечание 1. Оценки A3.13), A3.14) и A3.15) означают, что
формулы прямоугольников и трапеций имеют второй порядок
точности относительно А, а формула Симпсона — четвертый поря-
порядок точности. Из тех же оценок следует, что формулы прямоуголь-
382
ников и трапеций точны для многочленов первой степени, а форму-
формула Симпсона — для многочленов третьей степени
Замечание 2. Формулы A3.7) и A3.8) имеют лишь первый
порядок точности (абсолютная погрешность каждой из формул не
превышает 0.5 М\{Ь - а)А) и поэтому для вычисления интегралов на
практике они используются крайне редко.
1 ,
Пример 13.2. Вычислим значение интеграла / е'х dx, используя квадратур-
о
ные формулы прямоугольников, трапеций и Симпсона с шагом h = 0.1.
Сначала составим таблицу значений функции у = е'*2:
Таблица 13.1
X
0.00
0.05
0.10
0.15
0.20
0.25
0.30
0.35
0.40
0 45
0.50
е-*2
1 0000000
0 9975031
0.9900498
0.9777512
0.9607894
0.9394131
0 9139312
0.8847059
0.8521438
0 8166865
0.7788008
X
0.55
0 60
0.65
0.70
0 75
0.80
0.85
0.90
0.95
1.00
е-*2
0.7389685
0.6976763
0.6554063
0.6126264
0.5697828
0.5272924
0.4855369
0.4448581
0.405554К
0.3678794
Производя вычисления по формулам A3 6), A3 10), A3 12), получим Т^р =
= 0.74713088, 4р = 0.74621079, / = 0.74682418.
Оценим погрешность каждого из полученных значений, используя неравен-
неравенства A3.13) — A3.15). Вычислим f2)(x) = (Ах2 - 2)е'х2. Как нетрудно видеть
|/2) | < Л/г = 2. Следовательно,
/ - 4Р < ^ @-1J й о.84 • Ю-з, | / - 4Р | ^ ~ @.1J я 1.7 • Ю-з.
Далее, Р4)(х) = (Ш* - 48г* + \2)ех2, |/4> | < 12. Поэтому
@.1L и 0.42-10
383

Таким образом, из вычислений по формуле прямоугольников с учетом
погрешности следует, что I — 0.747 ± 0.001; по формуле трапеций — что / =
= 0.746 ± 0.002; по формуле Симпсона — что / = 0.7468242 ± 0.0000005.
6. Случай переменного шага. Приведем составные квадратурные
формулы прямоугольников, трапеций и Симпсона в случае переменно-
переменного шага hi = Xi - Xj-i.
/«4= ? fi-xnK
? /i-i + Л
A,,
-й jfc = g /,-1 + ifi-in + /¦ h._
i-i
Вывод этих формул и их геометрический смысл остаются теми же, что
и для случая постоянного шага. Теоремы об оценках погрешности
также останутся справедливыми, если в неравенствах A3.13) - A3.15)
заменить Л на Лщах = max h{.
1 < ii < n
$ 13.2. Квадратурные формулы интерполяционного типа
Для приближенного вычисления определенных интегралов часто
используется следующий естественный для методов приближения
функций прием. Подынтегральную функцию / аппроксимируют на
отрезке [а, Ь] некоторой функцией д, интеграл от которой легко вычис-
вычисляется, а затем полагают
\ f{x)dx» \ g (x)dx. A3.16)
а а
Точность формулы A3.16) можно повышать за счет усложнения
метода глобальной аппроксимации. Однако чаще используется другой
подход. Интеграл / представляют в виде суммы A3.4) интегралов по
элементарным отрезкам [ц-х, хг]. На каждом таком i-м отрезке функ-
функцию f(x) аппроксимируют некоторой легко интегрируемой функцией
gi(x). В результате получается составная формула
ь п xi
\ f(x)dx*> ? ( g,{x)dx.
t=l *
t=l
384
1. Вывод квадратурных формул интерполяционного типа. Рассмот-
Рассмотрим более подробно этот подход в случае, когда аппроксимация осу-
осуществляется с помощью интерполяционного многочлена. Зафиксируем
некоторые значения to, ti, ..., im€[-l, 1]. Аппроксимируем функцию
f(x) на i-м элементарном отрезке [x,--i, x<\ интерполяционным многочле-
многочленом Рт<г(х) с узлами интерполяции г'1' = г» - i /г + HjA,/2, j = 0, 1, 2,
..., т. В случае, когда все значения tj различны, можно воспользо-
воспользоваться записью интерполяционного многочлена в форме Лагранжа:
A3.17)
Используя замену переменной х = ц . i п + —-, вычислим интеграл
от Pmi на отрезке [xj-l rj:
J Pm,,<z)dx= S/(zJ«)) f /i«.
rt-l r° xi-i ''
{
dt.
= hi E ajfixi .1/2+ tjhi/2), aj={- 1 П |f-
j=0 2 -! fc=0 (<; -
Hi
n i
Приближенная замена интеграла / суммой Р1 — S \ Pmti(x)dx
•=l xi-\
приводит к следующей составной квадратурной формуле интерполя-
интерполяционною типа:
4
;=0
A3.18)
Замечание. Квадратурные формулы интерполяционного типа,
построенные на основе равноотстоящих значений <о> *ь •••) 'пи назы-
называют формулами Ньютона— Котеса1.
Рассмотренные в предыдущем параграфе простейшие квадратурные
формулы являются формулами интерполяционного типа; более того,
1 Роджер Котес A682 — 1716) — английский математик, друг и ученик
И.Ньютона.
13—28 385

они относятся к классу формул Ньютона—Котеса. Формулы прямо-
прямоугольников A3.6), трапеций A3.10) и Симпсона A3.12) отвечают ис-
использованию интерполяционных многочленов соответственно нулевой,
первой и второй степени.
2. Оценка погрешности. Приведем теорему об оценке погрешности
формулы A3.18).
Т е о р е ы а 13.3. Пусть функция f имеет на отрезке [а, Ь] непре-
непрерывную производную порядка т + 1. Тогда для погрешности квадра-
квадратурной формулы A3.18) справедлива оценка
A3.19)
ide
Ст =
1)!
? Представим погрешность R = / - Ih формулы A3.18) в виде
Ь п *i n *•'
R = \ f(x)dx- E J PmXx)dx = Е J (f(x) - Pm,t{x))dx.
Пользуясь оценкой A1.26) погрешности интерполяции, в данном слу-
случае принимающей вид
и производя замену переменной х =
неравенств
ц - \п + thi/2, получаем цепочку
х.
Учитывая, что Е
t=i
A3.19). ¦
386
Е А, = A^Ii F - о), приходим к оценке
=i
Замечание 1.Теорема остается справедливой и в случае, когда
для построения квадратурной формулы используется интерполяция
с кратными узлами (т.е. когда некоторые из значений <о, tlt ..., tm
совпадают).
Замечание 2. Как следует из оценки A3.19), квадратурные
формулы интерполяционного типа A3.18) точны для многочленов
степени т.
Отметим, что для некоторых симметричных квадратурных формул
оценка погрешности A3.19) является грубой и не отражает истинный
порядок их точности. Например, согласно этой оценке формулы пря-
прямоугольников и Симпсона должны иметь лишь первый и третий поря-
порядок точности соответственно, а в действительности они имеют на еди-
единицу больший порядок точности (см. теоремы 13.1, 13.2 и замечание 1
на с. 382). Поясним причину этого явления на примере формулы
прямоугольников.
Аппроксимируем функцию /на отрезке [ян, *t] интерполяционным
многочленом Piit(x) = /(zi-1/2) + f'(xi -1/2X1 - Zi-1/2) с кратным
узлом Xj-i/2. Интегрирование многочлена Pit^x) дает значение Д и
i
и [ Piti(x)dx =
совпадающее со значением, получаемым по
элементарной формуле прямоугольников A3.5). Геометрическая иллю-
иллюстрация, приведенная на рис. 13.6, пока-
показывает, что формулу (центральных) пря-
прямоугольников с равным основанием мож-
можно было бы назвать и формулой трапе-
трапеций. Действительно, площадь fi-\n'^i
элементарного прямоугольника ABCD
совпадает с площадью трапеции AEFD,
одна из сторон EF которой является
касательной к кривой у = f(x), прове-
проведенной в точке Ni. 1 /2 (ведь площади
треугольников EBNi - \п и Ni . 1 p,FC
равны).
Таким образом, можно считать, что
формула прямоугольников построена на основе интерполяции функции
/ многочленом первой степени с кратным узлом. Теперь из теоремы
13.3 с учетом замечания 1 следует, что эта формула действительно
имеет второй порядок точности.
Формула Симпсона может быть получена (аналогично) на основе
интерполяции многочленом третьей степени с узлами X(-i, Zt-1/2,
387

xt, центральный из которых является кратным. Следовательно, эту
формулу с достаточным основанием можно было бы называть и форму-
формулой кубических парабол. Закономерно, что формула Симпсона имеет
четвертый порядок точности.
3. Обусловленность квадратурных формул интерполяционного типа.
При вычислении интегралов, как правило, приходится использовать
не точные значения f(x) подынтегральной функции, а приближенные
значения /*(х). Напомним (см. § 3 1), что задача вычисления опреде-
определенного интеграла от приближенно заданной функции является устой-
устойчивой. В предположении, что \f(x)j- f*(x)\ < Д(/*) для всех хб[а, 4],
справедлива оценка
= \1-Г\ =
- ?/*(x)dx| < D-
указывающая на то, что абсолютное число обусловленности этой зада-
задачи равно b - а, т.е. длине отрезка интегрирования.
Какова же чувствительность квадратурной формулы A3.3) к по-
погрешностям задания функции /? Заметим, что
\ZAJ(x,)- l
«=о «=о
[2 |Л,|]д(Л.
Li=o J
Таким образом, квадратурная формула устойчива к ошибкам задания
функции и ее чмгпо обусловленности //д равно ? \At\.
1 = 0
Заметим, что все квадратурные формулы интерполяционного типа
6
точны для многочленов нулевой степени и поэтому 4 - а = Jl-dz =
j/д « 560 D - а) при m = 30. В силу плохой обусловленности эти
формулы уже при m > 10 используются весьма редко.
$ 13.3. Квадратурные формулы Гаусса
1. Построение квадратурных формул Гаусса. Из результатов пре-
предыдущего параграфа следует, что квадратурная формула \f(x)dx »
а
N
» ? AJ(xt), построенная интегрированием интерполяционного много-
многого
члена степени N с фиксированными узлами xq, х\, ..., ад, точна для
всех многочленов степени N. Однако, если имеется свобода в выборе
узлов, то можно распорядиться ею так, чтобы получить формулу,
точную для всех многочленов некоторой степени, превышающей N.
Поставим следующую задачу: при заданном числе N + 1 узлов
построить квадратурную формулу, точную для многочленов наиболее
высокой степени. Формулы, удовлетворяющие этому условию, принято
называть квадратурными формулами Гаусса. Как правило, сначала
строят формулы Гаусса
« ?
1=0
A3.20)
для стандартного отрезка [—1, 1]. Затем с помощью замены переменной
а + b 4 - а
х = — 1 ¦?— t осуществляют переход к формулам интегрирова-
интегрирования на произвольном отрезке:
N " Ь4-а#,Га+6 Ь-а 1
= Е А,. Следовательно, если все веса А, квадратурной формулы ин- \f(x)dx и —-— h aj —-p. 1 5— '« •
1=0 a l «=o I *• *¦ J
A3.21)
терполяционного типа положительны, то ее число обусловленности //д
совпадает с 4 — а. Чувствительность такой формулы к ошибкам аде-
адекватна чувствительности вычисляемого интеграла. Если же среди весов
N N
At имеются отрицательные, то i/. = S \At\ > S At = b - a.
1=0 1=0
Известно, что при больших значениях m среди весов квадратурной
формулы A3.18) появляются отрицательные и значение числа обуслов-
обусловленности j/д становится большим. Например, для формул Ньюто-
Ньютона—Котеса «/д и 3.1 D - а) при m =10, v^ « 8.3 D - а) при m = 20,
388
Заметим, что формула A3.20) точна для многочленов степени т
тогда и только тогда, когда она точна для функций /(<) = 1, t, t2, ...
..., tm. Это эквивалентно тому, что узлы <, и веса а, формулы A3.20)
должны удовлетворять системе нелинейных уравнений
S a/t = )tkdt = * , I |)Ы, k = 0, 1, ..., m.
«=0 -1 к т 1
A3.22)
Можно показать, что система A3.22) имеет единственное решение по,
389

au ..., aN, t0, tu ..., tN (причем it € [-1, 1]) тогда и только тогда, когда
число уравнений системы совпадает с числом неизвестных т е в слу-
случае m = IN + 1.
Пример 13.3. Построим квадратурную формулу Гаусса A3.20) с двумя
узлами.
В этом случае, т.е. при N - 1, т - 3, система A3.22) примет вид
=2,
. 2
3'
0!<! = \iAt - 0,
-l
axi = ]fdt = 0.
-1
Решая ее, находим значения а0 = а, = 1, t0 = - L ц = L . Таким
получаем квадратурную формулу Гаусса
Д
Ы
точную для многочленов третьей степени.
Для квадратурной формулы Гаусса справедлива следующая оценка
погрешности:
Входящий в нее коэффициент aN = B> + з^А^ЭДЗ °ЧеНЬ
ро убывает с ростом N. Приведем, например, несколько первых его
значений: а0 й 4-Ю, сц я 2-Ю, а2 й 5-Ю, а3 й 6-100 а4 й
й4-103.
Можно было бы разбить отрезок интегрирования на частичные
отрезки и исходя из формулы Гаусса построить составную формулу,
имеющую порядок точности, равный 2N + 2. Однако при интегриро-
интегрировании достаточно гладких функций в этом нет необходимости, так как
уже при небольшом числе узлов D < N < 10) формула Гаусса обеспе-
обеспечивает очень высокую точность. На практике используются и формулы
с десятками и сотнями узлов.
2. Узлы и веса квадратурной формулы Гаусса. Приведем значения
узлов и весов квадратурной формулы Гаусса с числом узлов от 1 до б
(табл. 13.2):
390
Таблица 13.2
Число
Узлы и\узлов
веса
к
h
0.00000000000
2.00000000000
-0.5773502692
1.0000000000
0.5773502692
1.0000000000
-0.7745966692
0.5555555556
0.0000000000
0.8888888888
0.7745966692
0.5555555556
Число
Узлы и\узлов
веса
<0
к
щ
к
02
h

и
о4
-0.8611363115
0.3478548451
-0.3399810436
0.6521451549
0.3399810436
0.6521451549
0.8611363115
0.3478548451
-0.9061798459
0.2369268851
-0.5384693101
0.4786286705
0.0000000000
0.5688888888
0.5384693101
0.4786286705
0.9061798459
0.2369268851
-0.9324695142
0.1713244924
-0.6612093864
0.3607615730
-0.2386191861
0.4679139346
0.2386191861
0.4679139346
0.6612093864
0.3607615730
0.9324695142
0.1713244924
Пример 13.4. Найдем значение интеграла \e~x2dx,. используя квадратурную
о
формулу Гаусса с двумя, тремя и четырьмя узлами.
В данном случае а — 0, 6 = 1, /(г) = е'г2 и формула A3.21) принимает
вид
= fe-^dx я/jy = 1 Е?-|С'Ш(«'
Взяв из табл. 13.2 значения узлов it и весов аг при N — 1, 2, 3, получим
следующие приближения:
2
т _ 1 / -@.211324865J , -@.
'1 ~ о Vе т е
788675135
I ) и 0.7465946885;
391

I» h = \ @.555555555б-е'(ОЛ127О11665>2 + 0.8888888888-e'25 +
+ 0.5555555556-e0'887298335» ) и 0.7468145842;
/« h = \ @.3478548451-e-(o-069431844'2 + 0.6521451549.e-(o-33OOO9478>2 +
+ 0.6521451549-e-@-669990522J + 0.3478548451-e"'°'930568156i *) w
и 0.7468244681.
Эти значения содержат такие абсолютные погрешности: A(/i) й 2-Ю,
Д(/г) *> 10'5, Д(/з) й 3-Ю. Для сравнения укажем, что значение того же
интеграла, полученное в примере 13.2 по формуле прямоугольников с 10 узла-
узлами, имеет абсолютную погрешность примерно 3-Ю, а по формуле Симпсона с
21 узлом — абсолютную погрешность примерно 5-Ю'8.
3. Обусловленность квадратурных формул Гаусса. Квадратурные
формулы Гаусса обладают еще одним замечательным свойством: их
весовые коэффициенты всегда положительны. Это свойство (как следу-
следует из рассуждений предыдущего параграфа) гарантирует хорошую
обусловленность квадратурной формулы. Более того, число обуслов-
обусловленности равно 4 - а и не зависит от числа узлов. Это позволяет при-
применять на практике квадратурные формулы Гаусса с числом узлов,
достигающим сотен.
§ 13.4. Апостериорные оценки погрешности.
Понятие об адаптивных процедурах численного интегрирования
Применение неравенств типа A3.13), A3.14), A3.15), A3.19) для
априорной оценки погрешности квадратурных формул в большинстве
случаев оказывается неэффективным или вообще невозможным. Это
связано как с трудностями оценивания производных подынтегральной
функции / так и с тем, что получаемые оценки, как правило, бывают
сильно завышенными. На практике обычно используются иные подхо-
подходы к оценке погрешности, позволяющие строить процедуры численно-
численного интегрирования с автоматическим выбором шага.
1. Главный член погрешности. Пусть Ih — приближенное значение
6
интеграла /= f/(r)dr, вычисленное по некоторой квадратурной фор-
а
муле и использующее разбиение отрезка [о, Ь] на элементарные отрез-
отрезки длины Л. Предположим, что для погрешности этой формулы спра-
справедливо представление1
1 Напомним, что запись <р (h) = о (Л*) (читается "<р (Л) есть о малое от
А*") означает, что <р (Л)/Л* -» 0 при h -» 0.
392
I- Ih = Chk + о (hk), A3.23)
где СФ0ик>0 — величины, не зависящие от h Тогда величина Chk
называется главным членом погрешности квадратурной формулы.
Заметим, что из неравенства A3.23) следует справедливость оценки
|/ - Ih\ < Chk с некоторой постоянной С > \С\. Поэтому число к пред-
представляет собой не что иное как порядок точности соответствующей
квадратурной формулы.
Если подынтегральная функция /достаточно гладкая, то для каж-
каждой из составных квадратурных формул
/и Ih= §ЛЕ aj
1=1 J = 0
A3.24)
существует главный член погрешности. Приведем без доказательства
соответствующий результат.
m
Теорема 13.4. Пусть Е о, = 1 и к — минимальное среди нату-
З'О
ральных чисел, для которых величина
jl m ,
fffc = - (ЛИ - Е afi
2 -1 j=o
отлична от нуля. Если функция f непрерывно дифференцируема к раз
на отрезке [а, Ь], то для погрешности квадратурной формулы A3.24)
справедливо представление A3.23), в котором
Следствие 1. Если функция f дважды непрерывно дифференци-
дифференцируема на отрезке [a, ft], то для погрешностей составных квадратурных
формул прямоугольников и трапеций справедливы следующие представ-
представления:
/ - 7ЙР = СпрЛ2 + о (Л»), Спр = ^ jff(x)dz,
Стр = - l- |
A3.25)
A3.26)
Следствие 2. Если функция f четырежды непрерывно диффе-
дифференцируема на отрезке [а, Ь], то для погрешности составной квадра-
квадратурной формулы Симпсона справедливо представление
A3.27)
393

В силу предположения A3.23) для погрешности квадратурной
формулы при достаточно малом h справедливо приближенное равен-
равенство
- /Л я Chk.
A3.28)
Несмотря на элементарный характер формулы A3.28), она позволяет
сделать ряд важных выводов. Первый из них состоит в том, что умень-
уменьшение шага h в М раз приводит к уменьшению погрешности квадра-
квадратурной формулы примерно в Мк раз. Действительно, при h\ = h/M
имеем
имеем
В частности, уменьшение шага h в два раза приводит к уменьше-
уменьшению погрешности примерно в 2* раз:
фA-П A3.29)
2. Правило Рунге практической оценки погрешности. Как следует
из теоремы 13.4, главный член погрешности квадратурной формулы
интерполяционного типа имеет вид
Непосредственное использование этой формулы для оценки погрешно-
погрешности / - Ih неудобно, так как требует вычисления производных функ-
функций / В более сложных ситуациях выражение для главного члена
погрешности может оказаться существенно более громоздким. Поэтому
в вычислительной практике часто применяются методы оценки
погрешности, не использующие явное выражение для главного члена.
Вычитая из равенства A3.28) равенство A3.29), получим
Учитывая приближенное равенство A3.29), приходим к следующей
приближенной формуле:
2* - 1
A3.30)
Использование этой формулы для апостериорной оценки погрешности
значения Р1'2 принято называть правилом Рунге (или правилом двой-
двойною пересчета).
Замечание 1. Так как / - Ih и 2*(/ - Ih'2), то из A3.30) следу-
2k(fi/2 - рЛ
ет формула / - Р1 и —Ц-^ —?, которую можно было бы использо-
использовать для приближенной оценки погрешности значения Ih. Как
правило, этого не делают, поскольку среди двух вычисляемых
значений интеграла Ih и Ih'2 второе является более точным и имеет
смысл оценивать именно его погрешность.
Замечание 2. Заменой h на 2А формула A3.30) приводится к
следующему виду:
A3.31)
Для формул прямоугольников и трапеций Jfc = 2 (см. A3.25) й~
A3.26)), а для формулы Симпсона Jfc = 4 (см. A3.27)). Поэтому для
этих квадратурных формул равенство A3.31) принимает следующий
вид:
*пр й о
394
A3.32)
A3.33)
/-^4(^"/c/l)i A3-34>
Пример 13.5. Применяя правило Рунге, оценим погрешность приближенных
значений /?р = 0.74713088, т?р = 0.74621079, 1^ = 0.74628418, полученных в
примере 13.2 при вычислении интеграла / = fe~l2dr и использующих формулы
о
прямоугольников, трапеций и Симпсона с шагом Л = 0.1.
Вычислим приближенные значения интеграла по указанным квадратурным
формулам с удвоенным значением шага. В результате получим /Пр =
= 0.74805326, lip = 0.74436832, /?Л = 0.74682495.
Применяя теперь формулы A3.32) — A3.34), находим
395

/- A> « \ @.74713088 - 0.74805326) я -3-Ю'4, 7- Д> я | @.74621079 -
О О
- 0.74436832) я 6-Ю'4, I- 1% я L @.74682418 - 0.74682495) я -5-Ю"8.
Естественно, что кроме правила Рунге существуют и другие спосо-
способы апостериорной оценки погрешности. Например, можно использо-
использовать значения А> и Г}р, вычисленные по формулам прямоугольников и
трапеций с одним и тем же шагом, для практической оценки погреш-
погрешности каждого из этих значений. Действительно, в равенствах A3.25),
A3.26) Сгр = -2 Спр. Поэтому
А, - Д. = (^пр-
Отсюда следует, что
/-iftp«|(A,-jftp), A3.35)
/-A>*-f(A»-A»)- <13-36)
Пример 13.6. Применяя формулы A3.35), A3.36), оценим погрешности
значений А> = 0.74713088, /?р = 0.74621079, являющихся приближениями к
значению интеграла / = je'^dt (см. пример 13.2).
о
Имеем / - А> я \ @.74621079 - 0.74713088) я -3-Ю"», / - $р я
я-2 (-3* 10~4) = 6-10. Отметим, что полученные оценки совпадают с
соответствующими оценками из примера 13.5.
Наличие некоторого правила получения апостериорной оценки
погрешности позволяет строить процедуры вычисления интеграла / с
заданной точностью е, достигаемой последовательным дроблением
шага интегрирования. Простейшая процедура такого типа состоит в
последовательном вычислении значений Г1 и соответствующих апосте-
апостериорных оценок погрешности е, (например, по правилу Рунге) для
Л, = Ао/21, где Aq — начальное значение шага, t = 1, 2, ... . Вычисления
прекращаются тогда, когда при некотором t оказывается |е,| < е
(требуемая точность достигнута) либо тогда, когда величина |et|
начинает возрастать (точность не может быть достигнута из-за вли-
влияния вычислительной погрешности).
396
Пример 13.7. Найдем значение интеграла I = fe"l2dr с точностью е = 10"*,
о
используя формулу трапеций и применяя процедуру последовательного дроб-
дробления шага интегрирования, описанную выше.
Возьмем Ло = 0.2. Значения fa = 0.74436832, fa = 0.74621079 (где А, =
= Ао/2 = 0.1) и ?i = 6-Ю были уже получены (см. пример 13.5). Так как
|ei| > е, то уменьшаем шаг вдвое: Аг = Aj/2 = 0.05 и вычисляем fa =
= 0.74667084, Z2 = \ (fa - fa) - \ @.74667084 - 0.74621079) я 1.5-10. Так
О О
как |е2| > е, то снова дробим шаг: А3 = кг/2 = 0.025, вычисляем fa -
= 0.74678581, е3 = I (fa - fa) = i @.74678581 - 0.74667084) я 4-Ю,
о о
Поскольку |бз| < ?, требуемая точность достигнута и с учетом округления
получаем / = 0.7468 ± 0.0001.
3. Экстраполяция Ричардсона. Наличие приближенного равенства
1 . Chk jh/2 - ]h
/_ jkn a GA* и формулы yj- я . ^ — позволяют получить уточ-
уточненное значение интеграла
A3.37)
Таким образом, квадратурная формула Р1 порождает новую квадратур-
квадратурную формулу A3.37), имеющую более высокий порядок точности.
Если этот порядок известен, то процесс уточнения можно продолжить.
Предположим, например, что для погрешности квадратурной фор-
формулы справедливо представление
N+ о (А *
A3.38)
при всех N = 1, 2, ..., причем 0 < Jti < к2 < ... < Jfcjv < ••• • В этом слу-
случае формула A3.37) приводит к следующему методу уточнения, кото-
который называют также методом экстраполяции Ричардсона1. Пусть шаг
h измельчается по правилу А^ = A^-i/2, j = 1, 2, ..., N. Сначала полага-
полагают /g1 = Ih. Для вычисления всех последующих приближений исполь-
используют рекуррентное соотношение
1 Арчибалд Рид Ричардсон A881 — 1954) — английский математик.
397

/ft _ jhfl
JN ~ lN-1
=1,2,..
- 1
Пример 13.8. Так как для формулы трапеций равенство A3.38) имеет
место, причем Aj = 2, J>2 = 4, ..., Jb/v = 2N, то к ней можно применить экстра-
экстраполяцию Ричардсона. В результате получается так называемый метод Ром-
берш. Существуют стандартные программы вычисления интегралов методом
Ромберга. Правда, следует отметить, что эффективность этого метода не
велика. Как правило, лучший результат дает применение квадратурных фор-
формул Гаусса или рассматриваемых ниже адаптивных процедур численного
интегрирования.
Замечание. Первый же шаг метода Ромберга приводит к
уточнению квадратурной формулы трапеций, совпадающему с
формулой Симпсона. Действительно,
ift/2 , I
jtp "•" з
ifl _ jh ч _ 4
р Чр> з
тр
_1 Л _
з 'тр
4. Адаптивные процедуры численного интегрирования. До сих пор
нам было удобнее рассматривать методы численного интегрирования с
постоянным шагом. Однако они обладают значительно меньшей эф-
эффективностью и используются в вычислительной практике существен-
существенно реже, чем методы с переменным шагом. Объясняется это тем, что,
равномерно распределяя узлы по отрезку интегрирования, мы пол-
полностью игнорируем особенности поведения подынтегральной функции.
В то же время интуитивно ясно, что на участках плавного изменения
функции достаточно поместить сравнительно небольшое число узлов,
разместив значительно большее их число на участках резкого измене-
изменения функции. Распределение узлов интегрирования в соответствии с
характером поведения подынтегральной функции часто позволяет при
том же общем числе узлов получить значительно более высокую точ-
точность. Тем не менее выбор соответствующего неравномерного распреде-
распределения узлов интегрирования является очень сложной задачей и вряд
ли мог быть широко использован на практике, если бы для решения
этой задачи не удалось привлечь ЭВМ.
Современные процедуры численного интегрирования (адаптивные
квадратурные программы) используют некоторый алгоритм автомати-
398
ческого распределения узлов интегрирования. Пользователь такой
программы задает отрезок [а, 6], правило вычисления функции / и
требуемую точность ? > 0. Программа стремится, используя по воз-
возможности минимальное число узлов интегрирования, распределить их
так, чтобы найденное значение Р1 = Е 7|' удовлетворяло неравенству
A3.39)
Здесь Ту1 — приближенное значение интеграла /, = \ /(х)Aх,вычисля-
емое по некоторой формуле.
Типичная программа разбивает исходный отрезок [а, Ь] на элемен-
элементарные отрезки [x,-i, х,] так, чтобы для погрешностей R, = /, - Ту вы-
выполнялось неравенство
< е.
A3.40)
При этом каждый из элементарных отрезков получается, как правило,
делением пополам одного из отрезков, найденных на более раннем
шаге алгоритма. Заметим, что неравенство A3.40) выполняется, если
каждая из погрешностей R, удовлетворяет условию \Rt\ < hfi/(b - a).
Действительно, тогда \I - Ih\ = | S (/, - 7^)| < Е | Д,| < -r^- E А, =
Ь-а ,>!
1=1
= е.
Рассмотрим, например, одну из простейших адаптивных процедур,
основанную на формуле трапеций
'•"¦ft,, = ?(/•-! + /•) A341)
и использующую для контроля точности составную формулу трапеций
с шагом А,/2:
Ч- 1/2 + ft)-
A3.42)
Заметим, что если значение 7^' t уже найдено, то для нахождения
значения TV* требуется лишь одно дополнительное вычисление функ-
функции /в точке х,. 1 /2-
399

Можно показать, что для оценки погрешностей квадратурных
формул интерполяционного типа на элементарных отрезках правило
Рунге сохраняет силу. Поэтому погрешность приближенного значения
ц можно оценить по формуле
3 тр,!'- A3.43)
В рассматриваемой адаптивной процедуре последовательно выбира-
выбирают точки ц и вычисляют значения
St=
последнее из которых Sn совпадает с Ih и принимается за приближен-
приближенное значение интеграла /. Перед началом работы полагают So — О,
хо = а и задают некоторое начальное значение шага h\.
Опишем f-й шаг процедуры в предположении, что значение SH уже
найдено и очередное значение шага Л< определено.
1°. По формулам A3.41) - A3.43) вычисляют значения т?« {, 7*«, е{.
2°. Если \ei\ > h?/(b - а), то шаг А, уменьшают в 2 раза и повторя-
повторяются вычисления п. 1°.
3°. После того как очередное дробление шага приводит к выполне-
выполнению условия |ej| < h?/(b - а), вычисляют значения xt = zH + A,, Si =
4°. Если Xi + hi > Ь, то полагают A^i = 6 - г*. В противном случае
полагают A^i = Aj. На этом »-й шаг завершается.
Замечание 1. В некоторых адаптивных процедурах при вы-
выполнении условия типа |е,| < hfi/(b - о) очередное значение шага
удваивается: Л*ц = 2 Aj. Таким образом, шаг интегрирования в
зависимости от характера поведения подынтегральной функции
может не только измельчаться, но и укрупняться.
Замечание 2. Известно [9], что при оптимальном распределе-
распределении узлов интегрирования модули погрешностей, приходящихся на
элементарные отрезки интегрирования, должны быть примерно
одинаковыми. Распределение узлов, полученное с помощью адап-
адаптивных процедур, как правило, не является таковым. Однако для
большинства функций оно является вполне удовлетворительным.
400
§ 13.5. Вычисление интегралов
в нерегулярных случаях
Нередко приходится вычислять интегралы
)F(x)dx
A3.44)
от функций, имеющих те или иные особенности. Например, сама
функция F (или ее производная некоторого порядка) имеет участки
резкого изменения, точки разрыва или является неограниченной.
Такие функции плохо аппроксимируются многочленами и поэтому для
вычисления соответствующих интегралов может оказаться неэффек-
неэффективным непосредственное применение стандартных квадратурных
формул, рассчитанных на возможность кусочно-многочленной аппрок-
аппроксимации функции F. Случай, когда в интеграле A3.44) промежуток
интегрирования бесконечен, также требует специального рассмотрения.
! _ 2
Пример 13.9. Функция — е'х имеет особенность в точке х — 0. Попробуем
Г-
применить для вычисления интеграла
1 •*
1- \— ех dx* 1.689677
формулу прямоугольников с постоянным шагом:
A3.45)
A3.46)
1*1 -1/2
Результаты вычислений для нескольких значений шага А приведены в
табл. 13.3. Заметим, что значения ТНр сходятся к / очень медленно. Теоретиче-
Теоретический анализ погрешности показывает, что она убывает пропорционально лишь
А1 /2, а не А2, как в регулярном случае.
Таблица 13.3
'пр
0.200
0.100
0.050
0.025
1.420
1.499
1..555
1.594
2.7-10'1
1.9-10
1.4-КГ1
9.6-Ю
401

Укажем на некоторые подходы к вычислению интегралов в нерегу-
нерегулярных случаях, позволяющие учесть особенности поведения функции
F и благодаря этому значительно сократить затраты машинного време-
времени или достичь большей точности.
1. Разбиение промежутка интегрирования на части. Пусть подын-
подынтегральная функция F является кусочно-гладкой и су < с2 < ... < ср —
известные точки разрыва функции F либо ее производных. В этом
случае имеет смысл представить интеграл A3.44) в виде суммы:
f
1 2 Ь
F(x)dx= \ F(x)dx+ \ F(x)dx+...+ \ F(x)dx.
а с
A3.47)
Вычисление каждого из входящих в сумму A3.47) интегралов пред-
представляет собой стандартную задачу, так как на каждом из частичных
отрезков [о, с\], [с\, с2], ..., [ср, Ь] подынтегральная функция является
гладкой.
Разбиение промежутка интегрирования на части может оказаться
полезным приемом и в других случаях, например тогда, когда имеет
смысл на разных частях применять различные квадратурные форму-
формулы. Другой пример дает стандартный прием вычисления несобствен-
ных интегралов вида lF(x)dx. Если требуется вычислить такой интег-
а
рал с точностью е > 0, то его представляют в виде суммы:
Ъ
\F.(x)dx = \F(x)dx + (F (x)dx. Затем благодаря выбору достаточно
а а о
оо
большого Ь добиваются выполнения неравенства | (F (x)dx\ < е/2 и
вычисляют интеграл \ F {x)dx с точностью е/2.
а
2. Выделение веса. В некоторых случаях подынтегральная функция
допускает разложение на два сомножителя: F (х) = p(x)-f(x), где
функция р (х) является достаточно простой и имеет те же особенности,
что и F (x), a f (х) — гладкая функция. Тогда имеет смысл рассматри-
рассматривать интеграл A3.44) в виде
г =}/>(*)/(
x)dx.
A3.48)
Здесь функция р (х) называется весовой функцией (или весом). При
построении численных методов вычисления интеграла A3.48) весовая
402
функция считается фиксированной. В то же время f(x) может быть
произвольной достаточно гладкой функцией.
Примерами весовых функций могут служить постоянный вес р (х) =
= 1, весовые функции Якоби р (х) = (х - а)а(Ь - а)Р (а < х < Ь),
Лагерра1 р (х) = i^e'^O < г < оо) и Эрмита р (х) = е'х2 (-оо< х < оо),
6 6
соответствующие интегралам вида \f{x)dx, \{х — а)а(х — b)Pf(x)dx,
а а
]x**-xf {x)dx, le-*?f(x)dx.
о -*>
Методы приближенного вычисления интегралов, рассмотренные в
предыдущих параграфах, применимы и к задаче вычисления интегра-
интегралов с весом.
Пусть Рт<1 — интерполяционные многочлены A3.17). Приближенная
замена-интеграла A3.48) суммой:
= 2 ( p{x)Pn<i (x)dx
1=1 *t\i
приводит к следующей квадратурной формуле интерполяционного
типа:
/*/*= Е hiZ
1=1 j=0
Здесь коэффициенты ву вычисляются по формуле
A3.49)
Hi
Если функция / имеет на отрезке [о, Ь] непрерывную производную
порядка m + 1, то для погрешности формулы A3.49) верна оценка
\I-Ih\ <CmMml
Пример 13.10. Выведем аналог формулы прямоугольников с постоянным
шагом для вычисления интеграла
Эдмунд Никола Лагерр A834 — 1886) — французский математик.
403

1= I— J
A3.50)
Заменяя функцию /на элементарном отрезке [zt-i, г,] постоянной U- \п и
учитывая, что
*' 1
*«-i г:
2Л
получим следующую квадратурную формулу:
- 1/2.
A3.51)
Пример 13.11. Применим квадратурную формулу A3.51) для вычисления
интеграла A3.45) при тех же значениях шага, что и в примере 13.9.
В рассматриваемом случае формула A3.51) принимает вид
-т*
*И +
A3.52)
Полученные с ее помощью результаты приведены в табл. 13.4. Сравнение с
результатами примера 13.9 показывает, что для вычисления интеграла A3.45)
формула A3.52) имеет безусловное преимущество перед формулой прямоуголь-
прямоугольников A3.46).
Таблица 13.4
I-P*
0.200
0.100
0.050
0.025
1.686276
1.688958
1.689521
1.689642
3.4-Ю
7.2-Ю
1.6-10"<
3.5-10
Для вычисления интегралов A3.48) применяют и квадратурные
формулы Гаусса \р (x)f(x)dx и Е AJ(xt), точные для многочленов
а 1=1
наиболее высокой степени. Они строятся аналогично тому, как было
сделано в случае постоянного веса р (х) = 1 (см. § 13.4).
Пример 13.12. Для вычисления интеграла A3.50) построим квадратурную
формулу Гаусса с одним узлом:
404
— /(r)dr«
A3.53)
Потребуем, чтобы формула A3.53) была точна для многочленов первой степе-
степени. Это эквивалентно выполнению равенств 2 = | — dx = q, s = | — ^г =
or- -1 о г^
= d*i. Таким образом q = 2, ^ = 1/3 и формула A3.53) принимает вид
A3.54)
Хотя формула A3.54) и кажется примитивной, применяя ее для вычисле-
вычисления интеграла A3.45), получаем значение / и 1.789679, абсолютная погреш-
погрешность которого равна 0.1 и практически совпадает с погрешностью значения,
найденного в примере 13.9 по формуле прямоугольников с шагом h = 0.025.
Замечательно то, что формула Гаусса A3.54) достигает точности е = 0.1 при
использовании только одного вычисления значения функции /(г) = е'х . В то
же время формула A3.46) для достижения той же точности требует вычисле-
вычисления 40 значений функции.
3. Формула Эрыита. Для вычисления интегралов вида
т.е. в случае р (х) = 1/J 1-х2, а = -1, Ь = 1, используют квадратур-
квадратурную формулу Гаусса
)M±dx«*l f(xt),
называемую формулой Эрмита. Узлами этой формулы являются нули
многочлена Чебышева Тп(х), т.е. числа х, = сое
—
, 1 < i < п.
4. Интегрирование быстро осциллирующих функций. В задачах
радиотехники часто встречается проблема вычисления интегралов
вида
I f(x)e dx = )
а а
I coaux dx + jjj(r)sinuir dr.
а
A3.55)
1 Например, F (x) = f(x)etwx отвечает несущему высокочастотному колеба-
колебанию еюх с модулированной амплитудой f(x).
405

Здесь ш (b - а) У I, f(x) — некоторая достаточно гладкая функция,
a t — мнимая единица. Функции f(x)cosu x и /(i)sinw x являются
быстро меняющимися и имеют на отрезке [а, Ь] порядка (Ь — а)ш/т
нулей. чЕсли попытаться вычислить интеграл A3.55) с помощью стан-
стандартных квадратурных формул, то для обеспечения приемлемой точ-
точности на каждый "полупериод" колебаний подынтегральной функции
потребуется поместить хотя бы несколько (например, порядка десяти)
точек. Так как на отрезок [а, Ь] приходится примерно F - а)ш/т таких
"полупериодов", то необходимо по меньшей мере порядка и (Ь — а) > 1
узлов интегрирования. Следовательно, стандартный подход к вычисле-
вычислению интегралов вида A3.55) потребует слишком больших затрат ма-
машинного времени.
Для существенного уменьшения объема вычислений в равенстве
A3.55) полезно рассматривать функцию р (х) = ешх как весовую. Тог-
Тогда кусочно-полиномиальная интерполяция функции f(x) приводит к
квадратурным формулам интерполяционного типа, которые принято
называть формулами Филона.
Выведем одну из таких формул, основанную на интерполяции
функции f(x) на каждом из элементарных отрезков [xk-\, Хк] линейной
функцией Л,*(г) = Л-1 + (fie ~ fk-\)(x ~ Zit-i)/Ajfc и являющуюся анало-
аналогом составной квадратурной формулы трапеций. Положим
Л Хк
/*=[ f(x)etu"dx*I* = f Plifc(x)e""dr.
rfc-l к хк-1
Вычислив интеграл I , получаем формулу
Здесь
. _ sinpfc Рксоирк - sinpt sinpt Pifccospfe -
Лк — — h I -~ , -Djfc = I 1—2
Рк П Рк П
Pk =
J
2 '
В результате приходим к составной формуле вида
f/(r)e""d*«S^
a «=1 ^
5. Аддитивное выделение особенности. Иногда подынтегральную
функцию удается представить в виде суммы F (г) = ip (x) + ф (г), где
функция <р (х) содержит особенность, но интегрируется аналитически,
а функция ф (х) является достаточно гладкой. Тогда интеграл от
функции F представляют в виде суммы двух интегралов:
6 6 Ъ
] F(x)dx= I <p(x)dx+ } ф(х^х= /<l» + /<2).
а а а
Первый из них вычисляется аналитически, а значение второго можно
найти с помощью той или иной квадратурной формулы.
Пример 13.13. Указанный прием можно использовать для вычисления
интеграла A3.45). Представим интеграл в виде
е-*2 - 1 +
Г*
dx =
Интеграл /A) вычисляется аналитически: /A) = 1.6. В то же время функция
e-I
( - 1 + я2)/^ трижды непрерывно дифференцируема на отрезке [0, 1].
Поэтому интеграл /B) можно вычислить по формуле прямоугольников. В
результате приходим к формуле
/и 7й = 1.6 + А Е
(А-1/2
Найденные по ней приближенные значения интеграла приведены в табл. 13.5:
Таблица 13.5
0.200
0.100
0.050
0.025
1 687874
1.Ш227
1.689565
1.689649
1.8-lO'3
4.5-10-4
1.1-10-4
2.8-10
406
Конечно, отмеченные приемы представляют лишь небольшую часть
тех средств, которые применяются при вычислении интегралов в нере-
нерегулярных случаях. Иногда, например, оказывается полезной замена
407

= ip (<), приводящая интеграл к виду \ F (x)dx =
переменных т
$
= \ F{v{t))<p
а
§ 13.6. Дополнительные замечания
1 Мы не рассматриваем проблему вычисления кратного интеграла
»(*) = i f(Qi{, а<х<Ь.
G
A3.56)
поскольку это потребовало бы привлечения достаточно сложного математи-
математического аппарата. Ограничимся указанием на то, что в принципе вычисление
интегралов A3.56) можно проводить методами, аналогичными рассмотренным в
этой главе. Соответствующие ку^птурные формулы1 для вычисления кратных
интегралов имеют вид
?
A3.57)
Среди формул A3.57) есть кубатурные формулы интерполяционного типа и
кубатурные формулы Гаусса. Иногда для вычисления кратного интеграла
оказывается целесообразным сведение его к повторному вычислению
однократных интегралов. Для первоначального знакомства с методами
вычисления кратных интегралов можно рекомендовать книги [9], [43].
2. Вычисление кратных интегралов уже при не очень больших значениях
т > 6 является очень сложной задачей. Применение для вычисления таких
интегралов кубатурных формул типа A3.57) требует (даже при очень скромных
запросах к точности) такого большого числа N вычислений значений функции
/ что решение задачи даже при использовании самых современных ЭВМ
становится нереальным. Привлекательной альтернативой в такой ситуации
становится использование метода Монте-Карло. Простейшее представление
об этом методе (на примере вычисления однократного интеграла) можно
получить из учебника [21]. Мы все же рекомендуем обратиться и к весьма
содержательному обсуждению метода Монте-Карло, проведенному в книге [9].
3. Иногда возникает необходимость по известной функции f(x), заданной
на отрезке [a, ij, восстановить ее первообразную
A3.58)
При каждом фиксированном х функцию A3.58) можно рассматривать как
определенный интеграл вида A3.1) и вычислять с помощью одного из извест-
известных методов. Однако если требуется находить значения у (х) в большом числе
различных точек, то такой подход становится нецелесобразным. Оказывается
более выгодным разбить отрезок [а, § на элементарные отрезки точками а =
= xq < х\ < Х2 < ... <хп — 6, а затем составить таблицу значений у, и у (х,),
0^1^ п. Значения j/, можно найти, например, по формуле yt = yt.\ + /, ,
1 ^ i ^ п. Здесь уо — 0, а /,' — приближение к интегралу ? f(x)dx,
T,-i
полученное с помощью одной из квадратурных формул. Значение у (х) в
любой из промежуточных точек можно затем приближенно восстановить, ис-
используя интерполяцию. Так как значения y'(xt) — f(x^) фактически также
известны, то весьма подходящим для интерполяции на каждом элементарном
отрезке [r,-i, rj является кубический многочлен Эрмита (см. § 11.5).
Использование этого способа интерполяции позволяет находить значения у (х)
с довольно высокой точностью по сравнительно редкой таблице значений.
4. В данной главе в основном обсуждались не вычислительные алгоритмы,
а методы дискретизации, т.е. методы замены определенных интегралов соот-
соответствующими квадратурными суммами. Как бы ни был организован алгоритм,
он все же предполагает вычисление квадратурной суммы. С увеличением числа
слагаемых возрастает влияние вычислительной погрешности на результат
суммирования. При очень больших значениях N даже для хорошо обусловлен-
обусловленных квадратурных формул соответствующий вычислительный алгоритм может
стать плохо обусловленным. Тем не менее при умеренном значении числа
узлов влияние ошибок округления невелико и им часто можно пренебречь.
Впрочем, формулы A3.57) называют также и квадратурными.
408

езных затруднений (по крайней мере формального характера). Некото-
Некоторые особенности решения задачи Коши для систем уравнений изложе-
изложены в § 14.10 и 14.11. При этом значительное внимание уделяется проб-
проблеме устойчивости численных методов и так называемым жестким
задачам.
Глава Ц
ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ
ЗАДАЧИ КОШИ ДЛЯ ОБЫКНОВЕННЫХ
ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Инженеру часто приходится иметь дело с техническими системами
и технологическими процессами, характеристики которых непрерыв-
непрерывным образом меняются со временем1 t. Соответствующие явления, как
правило, подчиняются физическим законам, которые формулируются
в виде дифференциальных уравнений. Одной из основных математиче-
математических задач, которые приходится решать для таких уравнений, являет-
является задача Коши (или начальная задача). Чаще всего к ней приходят
тогда, когда начальное состояние некоторой физической системы в
момент времени <0 считается известным, и требуется предсказать ее
поведение при t > t0. Понимание того, что задача Коши описывает
развитие тех или иных процессов во времени, значительно упрощает
восприятие как подходов к ее решению, так и критериев оценки каче-
качества получаемых приближений.
Подавляющее большинство возникающих на практике начальных
задач невозможно решить без использования вычислительной техники.
Поэтому в инженерных и научно-технических расчетах численные
методы решения задачи Коши играют особую роль.
Моделирование самых разнообразных процессов приводит к
необходимости решать системы дифференциальных уравнений (иногда
довольно высокого порядка). Тем не менее большая часть этой главы
(§ 14.1 — 14.9) посвящена рассмотрению методов решения задачи
Коши для одного дифференциального уравнения первого порядка.
Это традиционный подход, упрощающий как изложение методов, так
и понимание их существа. Переход от случая одного уравнения к
случаю систем дифференциальных уравнений не вызывает затем серь-
1 В роли t может выступать и другая (например, пространственная) пере-
переменная. Тем не менее в этой главе переменную t будем называть временем.
410
§ 14.1. Задача Коши для дифференциального уравнения
первого порядка
1. Постановка задачи. Напомним, что решением обыкновенного
дифференциальною уравнения первою порядка
»'(<) =/(',*(<)) A4.1)
называется дифференцируемая функция у (<), которая при подстанов-
подстановке в уравнение A4.1) обращает его в тождество. График решения
дифференциального уравнения называют интегральной кривой. Про-
Процесс нахождения решений дифференциального уравнения принято на-
называть интегрированием этого уравнения.
Исходя из геометрического смысла про-
производной у' заметим, что уравнение A4.1)
задает в каждой точке (<, у) плоскости пе-
переменных i, у значение /(*, у) тангенса
угла а наклона (к оси Ot) касательной к
графику решения, проходящего через эту
точку. Величину k = tga = f(t, у) далее
будем называть угловым коэффициентом
(рис. 14.1). Если теперь в каждой точке
Рис. Ц.1
(t, у) задать с помощью некоторого вектора направление касательной,
определяемое значением /(<, у), то получится так называемое поле
Рис. Ц.2
411

направлений (рис. 14.2, а). Таким образом, геометрически задача ин-
интегрирования дифференциальных уравнений состоит в нахождении
интегральных кривых, которые в каждой своей точке имеют заданное
направление касательной (рис. 14.2, б). Для того, чтобы выделить из
семейства решений дифференциального уравнения A4.1) одно кон-
конкретное решение, задают начальное условие
\Щу)\
A4.4)
У (<о) = Уо-
A4.2)
Здесь t0 — некоторое фиксированное значение аргумента I, а у0 —
величина, называемая начальным значением. Геометрическая интерпре-
интерпретация использования начального условия состоит в выборе из
семейства интегральных кривых той кривой, которая проходит через
фиксированную точку (t0, уо)-
Задачу нахождения при t > t0 решения у (t) дифференциального
уравнения A4.1), удовлетворяющего начальному условию A4.2), будем
называть задачей Коши. В некоторых случаях представляет интерес
поведение решения при всех t > t0- Однако чаще ограничиваются
определением решения на конечном отрезке [<0, Т\-
2. Разрешимость задачи Коши. Пусть П — множество точек (I, у),
удовлетворяющих условию <0 < t < Т, - <» < у < со; это множество бу-
будем называть полосой.
Приведем одну из теорем о разрешимости задачи Коши.
Т е о р е ы а 14.1. Пусть функция /(<, у) определена и непрерывна в
полосе п Предположим также, что она удовлетворяет условию Лип-
Липшица
A4.3)
для всех <о ^ i ^ Т и произвольных у\, у%, tde L — некоторая постоян-
постоянная (постоянная Липшица).
Toida для каждою начальною значения уо существует единственное
решение у (t) задачи Коши A4.1), A4.2), определенное на отрезке
Замечание 1-. Для дифференцируемых по у функций / усло-
условие A4.3) выполняется тогда и только тогда, когда для всех
(t, у)€Пт справедливо неравенство
Рудольф Липшиц A832 — 1903) — немецкий математик.
412
Поэтому условие A4.4) можно также называть условием Липшица.
Замечание 2. Теорема 14.1 остается справедливой, если в ее
формулировке условие Липшица A4.3) заменить менее ограничи-
ограничительным односторонним условием Липшица
(fit, й) -fit, у2))(У1 -У2)<<? (У1 - Ы2- A4-5)
Подчеркнем, что входящая в это условие постоянная <т может иметь
произвольный знак.
Для дифференцируемых по у функций /условие A4.5) выполняется
тогда и только тогда, когда для всех (I, 3/)бП справедливо
неравенство
fyit, У) < °- A4.6)
Ясно, что для функций, удовлетворяющих условию Липшица с
постоянной L, одностороннее условие заведомо выполнено с постоян-
постоянной а < L.
Пример 14.1. Функция /(<) = cos (i + у) удовлетворяет условию Липшица
с постоянной L = 1, так как f = -sin (t + у) и |/'| < 1. Отсюда следует, что
решение задачи Коши у' = cos (t + у), у Aq) — уо существует и единственно
на любом отрезке [t$, Т\.
Пример 14.2. Функция / (t, у) — t - у3 не удовлетворяет условию Липши-
Липшица, поскольку /' = -Зу2 и модуль этой величины не ограничен. В то же время
одностороннее условие A4.6) выполняется с постоянной о~ — 0. Следовательно,
можно утверждать, что решение задачи Коши у' = t - $, у A$) — уо сущест-
существует и единственно на любом отрезке [($, 7].
Пример 14.3. Функция f(t, у) — t + j/3 не удовлетворяет одностороннему
условию A4.6), так как частная производная /' = Зу2 не ограничена сверху.
Поэтому вопрос о разрешимости задачи. Коши у' = / + $, у (to) — уо требует
дополнительного исследования.
Отметим следующий полезный результат, указывающий на зависи-
зависимость степени гладкости решения задачи Коши от степени гладкости
правой части дифференциального уравнения.
Теорема 14.2. Пусть функция / непрерывно дифференцируема т
раз в полосе П^ Тогда если функция у является на отрезке [<о, 3]
решением задачи Коши A4.1), A4.2), то она непрерывно
дифференцируема т + 1 раз на этом отрезке.
413

Это утверждение непосредственно вытекает из возможности диффе-
дифференцирования тождества y'(t) = f (t, у (<)) не менее чем т раз.
В дальнейшем функции f и у будем предполагать дифференциру-
дифференцируемыми столько раз, сколько потребуется при рассмотрении соответст-
соответствующих численных методов.
3. Устойчивость решения задачи Коши на конечном отрезке. Этот
вопрос весьма важен для понимания особенностей методов численного
интегрирования дифференциальных уравнений. Рассмотрим сначала
процесс распространения погрешностей, внесенных в начальные значе-
значения. Пусть у* — возмущенное начальное значение, ?0 = Уо - У^ — его
погрешность, а у *(t) — решение соответствующей задачи Коши
(«*)'(/) = /(/, «*(<)). A4-7)
Вычтем из уравнения A4.1) уравнение A4.7) и воспользуемся фор-
формулой конечных приращений Лагранжа:
/(*, у @) - /О. vV)) = а @B/ @ - »*@). а @ = /у (*, у @).
где у (<) — некоторое промежуточное между у (<) и y*(t) значение. В
результате получим, что погрешность ? (t) = у (t) - y*(t) удовлетворя-
удовлетворяет дифференциальному уравнению
и начальному условию
? (to) = Go-
Решение задачи A4.8), A4.9) выражается формулой
? @ = еоехр I j A(r)drj.
о
Таким образом, величина
С @ = exp J j A(r)drj = exp J J /у(г, у (r))d
о о
играет в задаче Коши роль коэффициента роста ошибки.
414
A4.8)
A4.9)
Заметим, что знак производной /' оказывает существенное влияние
на поведение погрешности ? (t). Если fy > 0, то величина С (t), a
вместе с ней и модуль погрешности монотонно возрастают. При этом
соответствующие интегральные кривые расходятся. Иллюстрацией
такого поведения погрешности может служить рис. 14.3, а. Иначе
ведет себя погрешность в случае fy < 0. Здесь С (t) и |е @1 с ростом
t монотонно убывают, а соответствующие интегральные кривые сбли-
сближаются. Ошибка, внесенная в начальное значение, имеет тенденцию к
затуханию (рис. 14.3, 6). В случае, когда производная /' незнакопосто-
незнакопостоянна, поведение погрешности может быть более сложным.
/' ?0
Но
Рис. Ц.З
Важно отметить, что в любом случае выполнение одностороннего
условия Липшица A4.5) гарантирует, что коэффициент С (i) роста
ошибки окажется ограниченным, если задача решается на конечном
отрезке [t0, T\. В самом деле, в этом случае
I f'(r, у (r))dr < \ adr = a (t - t0)
и поэтому С (t) < К (Г) для всех <0 < t < Г, где
К(Т) = Г1
при ff > 0,
A4.10)
Таким образом, при выполнении условия /' < а справедлива оценка
max \y(t)-y*(t)\
A4.11)
415

выражающая устойчивость на конечном отрезке [t0, Т\ решения задачи
Коши по начальным значениям.
4. Модельное уравпеьие. Наиболее простым образом ведет себя
погрешность в случае, когда решается линейное уравнение
y'(t) = \y (t) + f(t)
с постоянным коэффициентом А. В этом случае погрешность ? удов-
удовлетворяет уравнению ? '(<) = А? (t) и выражается формулой
?(<) = ?OeA((~V. A4-12)
Поскольку функция /(<) не влияет на характер распространения
погрешности, при изучении устойчивости по начальным значениям
естественно ограничиться случаем / (<) е 0 и рассматривать уравнение
y'(t) = \y(t). (H.13)
Уравнение A4.13) часто называют модельным уравнением. Оно играет
важную роль при исследовании свойств численных методов решения
задачи Коши.
Как следует из формулы (.14.12), модуль погрешности решения
уравнения A4.13) изменяется в е раз за интервал времени т = 1/|А|.
Поэтому величину т = 1/|А| иногда называют временной постоянной
или постоянной времени модельного уравнения A4.13). Если же пара-
параметр А является комплексным числом, то временной постоянной назы-
1
вают величину г — -i-fj гг.
| Ке л I
В случае, когда рассматривается распространение малого возмуще-
возмущения, внесенного в решение у (<) уравнения у' = /(*, у) в малой окрест-
окрестности точки 1, значение коэффициента А (<) в уравнении A4.8) оказы-
оказывается близко к постоянной А" = f'y(i, у (<)). Поэтому при i » t спра-
справедливо приближенное равенство e'(t) » Xz (t). Это означает, что
поведение погрешности для уравнения у' = Ху моделирует локальное
распространение погрешности для общего уравнения A4.1). Роль
временной постоянной играет здесь величина т (i) = —^- -
|А|
может принимать комплексные значения, то формула для т имеет вид
. Так как ее значение меняется с изменением точки t
\fy(l у 0I
то ее называют локальной временной постоянной. Если же функция /
416
5. Устойчивость по правой части. Будет ли решение задачи Коши
устойчивым не только по отношению к погрешности ?0 задания на-
начального значения, но и К погрешностям ф (<) задания правой части
уравнения? Положительный ответ на этот вопрос дает следующая
теорема.
Теорема 14.3. Пусть выполнены условия теоремы 14.1. Далее,
пусть у (<) — решение задачи A4.1), A4.2), а у*A) — решение задачи
Тогда справедлива оценка
max \y(t)-yV)\'<K(T)(\yo-y*\
\r(,(t)\dt),
A4-14)
A4.16)
выражающая устойчивость на конечном отрезке [tu, Т] решения задачи
Коши по начальным значениям и правой части. Здесь К (Т) =
И T-t )
= е о .
Замечание. Величина К (Т) играет в задаче Коши роль оцен-
оценки числа обусловленности1. Если в теореме 14.1 условие Липшица
A4.3) заменить односторонним условием A4.5), то оценка A4.16)
будет выполнена с постоянной К (Т), определенной формулой
A4.10).
6. Устойчивость решения на неограниченном промежутке. При
решении самых разнообразных прикладных задач особый интерес
представляет изучение описываемых дифференциальными уравнени-
уравнениями процессов на больших временных отрезках. В такой ситуации
недостаточно наличия у задачи Коши свойства устойчивости на конеч-
конечном отрезке. Если входящая в неравенство A4.16) величина К (Т)
может неограниченно расти с ростом Т, то это означает, что допускает-
допускается неограниченный при Г -> оо рост погрешностей. Как следствие, при
достаточно больших Г такая задача является плохо обусловленной и
найти ее решение на отрезке [<0, Т] с приемлемой точностью оказыва-
оказывается невозможно.
1 Напомним, что общее понятие о числе обусловленности вычислительной
задачи содержится в гл. 3.
14-28 417

Пример 14.4. Рассмотрим задачу Коши у '(<) - У (<) ~ sin t + cos t,
y@) = 0. Ее решением, как нетрудно
проверить, является функция у (t) =
= sin t.
Внесем в начальное значение погреш-
погрешность, заменив условие у @) = 0
условием у @) = е. Решением соответ-
соответствующей задачи служит уже функция
у (<) = sin < + ее*. Погрешность ее* с
ростом t быстро увеличивается и, как
видно из рис. 14.4, уже при не очень
больших t ее значение становится
Рис. U-4 неприемлемо большим.
Для того чтобы обусловленность
задачи Коши не ухудшалась с ростом Г, в силу замечания 1 к теореме
14.3 достаточно потребовать, чтобы правая часть уравнения удовлетво-
удовлетворяла неравенству fy (t, у) < 0 для всех t > t0 и произвольных у. Более
того, можно доказать, что при выполнении условия f'y (t, у) < а < 0
справедлива следующая оценка:
'@-у*(
>-»«*! +
max
A4.17)
Предположим, что на каждом отрезке [to, 1] (t0 < T — произволь-
произвольное) неравенство A4.6) выполнено с некоторой постоянной <т = <т(Т).
Тогда решение у (t) определено для всех <о < t < оо. Пусть у* (t) —
решение уравнения A4.7), отвечающее произвольному начальному
значению у*. Назовем решение задачи Коши A4.1), A4.2) устойчивыми
по Ляпунову1, если справедлива оценка max \y (t) - У*@1 *
<о< «Г
< К\Уо ~ у о |, где постоянная К не зависит от Т. Если дополнительно
известно, что у* (t) - у (t) -* 0 при t -» «, то решение у (t) называется
асимптотически устойчивым.
Замечание 1. Решения модельного уравнения A4.13) с
вещественным параметром А устойчивы по Ляпунову тогда и только
1 Александр Михайлович Ляпунов A857—1918) — русский математик и
механик. Приведенное здесь определение устойчивости по Ляпунову является
более грубым, чем классическое определение [93].
418
тогда, когда А < 0, и асимптотически устойчивы тогда и только
тогда, когда А < 0. Этот вывод легко следует из формулы A4.12).
Если же параметр А — комплексное число, то из той же формулы
, ,.ч. . . ReA(T-<o) „
следует, что |е (i)| = |ео| е . Поэтому решения модельного
уравнения устойчивы по Ляпунову тогда и только тогда, когда
Re A ^ 0, и асимптотически устойчивы тогда и только тогда, когда
ReA < 0.
Замечание 2. Для решения задачи Коши A4.1), A4.2) (как
вытекает из неравенства A4.11) и формулы A4.10)) грубым доста-
достаточным условием устойчивости по Ляпунову служит выполнение
неравенства /' ^ 0. Следствием выполнения условия /' < а с посто-
постоянной а < 0 является асимптотическая устойчивость решения.
§ 14.2. Численные методы решения задачи Коши.
Основные понятия и определения
1. Сетки и сеточные функции. Первый этап на пути построения
численного метода решения задачи Коши состоит в замене отрезка
[<о, Т\ - области непрерывного изменения аргумента t - множеством иА,
которое состоит из конечного числа то-
точек t0 < ti < ... <tN - Т и называется Ut, tn., tn tH*T
сеткой. Сами точки /, называются узла- * *
ми сетки, а величина hn = tn — tn-i —
шагом сетки (рис. 14.5). Для того что-
Рис. Ц.5
бы упростить изложение, будем рассматривать, как правило, равномер-
равномерные сетки, т.е. такие сетки, для которых шаг hn постоянен. В этом
случае kn = h = —— и tn = t0 + nh, n = 1, 2, ..., N.
Наряду с функциями непрерывного аргумента будем рассматривать
и сеточные функции, т.е. такие функции, которые определены лишь в
узлах сетки оА Для того чтобы отличать сеточные функции от
функций непрерывного аргумента, будем помечать их индексом h. Так,
например uh — сеточная функция. Для краткости записи значения
иН^п) сеточной функции а'1 в узлах tn сетки цЛ будем обозначать через
ип.
2. Дискретная задача Коши. Следующий этап в построении числен-
численного метода состоит в замене задачи Коши ее дискретным аналогом -
системой уравнений, решая которую можно последовательно найти
значения уь у2, ..., ум сеточной функции yh, играющие роль приближе-
приближений к значениям решения задачи Коши в узлах сетки uA
419

В основе построения конкретного численного метода лежит тот или
иной способ замены дифференциального уравнения у' = f(t, у) его
дискретным аналогом - уравнением вида
- E atji/n^.j = Ф (in, Уп+1-к, ¦¦-, Уп, Уп+и Л),
A4.18)
в которое входят значения сеточной фунции yh в к f 1 последователь-
последовательных точках tn*i-k, ¦•¦! <m 'n+i- Предполагается, что а0 t 0.
Во всех рассматриваемых в этой главе методах сумму
<*кУп*1-к),
A4.19)
стоящую в левой части уравнения A4.18), можно рассматривать как
разностную аппроксимацию производной у' в соответствии с одной из
формул численного дифференцирования (см. гл. 12). Правую часть Ф
уравнения A4.18) можно рассматривать как специальным образом
построенную аппроксимацию функции /.
Значение yn+i приближенного решения в очередной точке находит-
находится из уравнения A4.18). При этом используются найденные ранее
значения сеточной функции у11 ъ к предыдущих точках tn*i-k, ¦¦¦, <п-
Поэтому такие методы получили название к-шаговых. Как нетрудно
видеть, для того чтобы найти значения сеточной функции yh во всех
узлах сетки пА, используя ifc-шаговый метод, необходимо задать к
начальных значений:
»4«o) = ft. yh(h) = Уи .... yh(tk-i) = Ук-v A4-20)
Задачу вычисления сеточной функции yh, удовлетворяющей урав-
уравнению A4.18) для всех n > it - 1 и принимающей заданные начальные
значения A4.20), будем называть дискретной задачей Коши.
Замечание. Принято считать, что уравнением A4.18) задается
численный метод решения задачи Коши. Далее мы будем отождест-
отождествлять свойства численного метода, дискретного уравнения A4.18) и
соответствующей дискретной задачи Коши.
При к = I уравнение A4.18) упрощается и принимает вид
A4.21)
Соответствующий метод принято называть одношаювым. Вычисление
значения уп*\ осуществляется здесь с использованием только одного
предыдущего значения уп. Поэтому одношаговые методы часто назы-
называют самостартующими.
420
Пример 14.5. Простейший дискретный аналог дифференциального уравне-
уравнения A4.1) представляет собой уравнение
A4.22)
приводящее к известному методу Эйлера}.
Пример 14.6. Метод Эйлера является примером одношагового метода.
Вычисление очередного значения ynt\ осуществляется здесь по формуле
Уп+1 - Уп+ hf(tn, yn).
A4.23)
При к > 1 численный метод называют многошаговым. Примеры
таких методов можно найти в § 14.7 и 14.10.
Замечание. Использование многошагового метода предполага-
предполагает преодоление одной специфической трудности, не возникающей
при применении одношаговых методов. Как уже отмечалось выше,
^-шаговый метод требует задания к начальных значений A4.20), в
то время как в постановке задачи Коши содержится только одно
начальное значение у0. Поэтому при к > 1 метод не является само-
самостартующим и для вычисления дополнительных значений у\, у2, ...
..., yk-i необходимы специальные подходы.
3. Явные и неявные методы. Реализация численного метода на
ЭВМ предполагает построение алгоритма, позволяющего вычислить
решение поставленной дискретной задачи Коши. В случае, когда вхо-
входящая в уравнение A4.18) функция Ф не зависит от yn*i, вычисление
значения упы не вызывает затруднений и осуществляется по явной
формуле
г it
Уп+1 = «о* Г ^азУп*1-3
+
<> Уп+\-к, ••¦, Уп, А) .
Поэтому соответствующие методы называют явными. В противополож-
противоположность им, методы, в которых функция Ф зависит от j/n+1, называют
неявными. При реализации неявного метода при каждом п (или, как
говорят, на каждом шаге) возникает необходимость решения относи-
относительно уп+1 нелинейного уравнения A4.18).
Пример 14.7. Метод Эйлера, для которого вычисления уп*\ производятся
по явной формуле A4.23), представляет собой явный метод.
1 Леонард Эйлер A707 — 1783) — математик, физик, механик, астроном.
Родился в Швейцарии, с 1726 по 1741 г. и с 1776 по 1783 г. работал в России.
421

Пример 14.8. Простейшим примером неявного метода является неявный
метод Эйлера, соответствующий аппроксимации дифференциального уравне-
уравнения A4.1) дискретным уравнением
Уп+1 ~ Уп _ tt4
д f(Utn.
A4.24)
Другим примером неявного метода может служить правило трапеций
•а
г—- = о (/(*»>¦ У") + /(*п*ь Уп+i))- A4.25)
Как в том, так и в другом методе значение Уп*\ определяется уравнением
неявно, и для его вычисления приходится использовать один из итерационных
методов решения нелинейных уравнений.
4. Устойчивость. Если решение дискретной задачи Коши не обла-
обладает устойчивостью по отношению к малым возмущениям начальных
значений и правой части уравнения, то соответствующий численный
метод нельзя использовать в практических вычислениях. Приведем
определение устойчивости, достаточное для понимания основного
содержания этого и следующих четырех параграфов. Более подробно
обсуждение этой проблемы будет проведено в § 14.8.
Внесем в правую часть уравнения A4.18) и в начальные условия
A4.20) произвольные малые возмущения фп и е0, ?i, t2, ..., ?jt-i соответ-
соответственно. Положим Уо = Уо ~ ?о, У* = У1 - ?ь •••, у?м = Ук-1 - ?fc-i- Пусть
у *Л — решение соответствующей возмущенной задачи
(<о) = Уо*> У*Л(<1) = У,*. -, У*М<
= 9k-v
A4.26)
A4.27)
Будем называть дискретную задачу Коши A4.18), A4.20) и соответст-
соответствующий численный метод устойчивыми на конечном отрезке (или
просто устойчивыми), если при всех А < Ао (где До достаточно мало)
справедливо неравенство
max \yn-y*n\
N-1
max |е„| + Е
A4.28)
где величина К не зависит от А, е„ @ < п < Jfc-1) и фп (Jfc-1 < п < JV-1).
422
Замечание. Неравенство A4.28) является дискретным анало-
аналогом неравенства A4.16), выражающего устойчивость задачи Коши.
Для одношаговых методов (т.е. при к = 1) неравенство A4.28)
принимает вид
"ъ\
max \уп-.у*\ <А-(ГК|ео| +"ъ\Фп\- А),
и аналогия с A4.16) становится еще более очевидной. Действитель-
Действительно, сумму Е |У>п|* А можно рассматривать как дискретный аналог
П'О
интеграла J | ф (t)\dt, построенный по формуле левых прямоугольни-
прямоугольников (см. § 13.1).
5. Аппроксимация. Пусть у (<) — произвольная гладкая функция.
Зафиксируем значение t = tn и устремим А к нулю (а п соответственно
— к бесконечности). Будем предполагать, что замена в формуле A4.19)
значений yn*i-j сеточной функции уЛ соответствующими значениями
У (<—^^—1)А функции у дает величину
+ А) + on у @ + ... + аку (<-(*- 1)А)),
стремящуюся к y'(t) при А -» 0.
Аналогично предположим, что
A4.29)
Ф (t, y(t-(k- 1)A, ..., у (<), у (t + к),к)) -/(*,» @) при А - 0.
Замечание. Из сделанных предположений следует, что коэф-
коэффициенты а0, аь ..., ajt должны удовлетворять условию
«о + «1 + •¦• + ак = 0.
A4.30)
В самом деле, для у (t) = 1 величина A4.29) превращается в —г,
А
где а = Ё а}.
лишь при а = 0, что эквивалентно равенству A4.30).
По условию, -г- -» y'(t) = 0 при А -» 0. Но это возможно
Пусть у (i) — решение задачи Коши A4.1), A4.2). Назовем сеточ-
сеточную функцию ф*1, определяемую формулой
423

k
?
"- У
), ¦¦-, 3/ (<n*i), A),
погрешностью аппроксимации дискретного уравнения A4.18) на реше-
решении у. Эта же формула, записанная в виде
1 *
^ ? а^ (<n+i-;) = Ф (tn, у (<n+i-Jfc). •-, У (<n+i). A))
A4.31)
позволяет заметить, что функция у (t) удовлетворяет* уравнению
A4.18) с точностью до погрешности аппроксимации фп.
Сеточную функцию фЬ используют для предварительной оценки
того, насколько точно аппроксимируется дифференциальное уравнение
его дискретным аналогом. Говорят, что дискретное .уравнение A4.18)
аппроксимирует дифференциальное уравнение A4.1), если
max \Фп\ "• 0 при Л -» 0, и аппроксимирует его с р-м порядком,
если справедлива оценка max \фп\ < ChP, р > 0.
Часто для оценки качества одношаговых методов A4.21) использу-
используют не погрешность аппроксимации, а другую величину — локальную
погрешность. Пусть yn+i — значение, найденное из уравнения
Vn*\-y(tn) _ ф ^ у Dд уп+]) д^ A4.32)
т.е. из уравнения A4.21), в которое вместо уп подставлено точное
значение решения дифференциального уравнения в точке t — tn.
Тогда разность 1п = у (<п+1) - уп+\ называется локальной погрешностью
метода (или его погрешностью на шаге). Другими словами, /п — это
погрешность, которую допускает за один шаг метод, стартовавший с
точного решения.
В случае, когда Ф не зависит от уп+\ (т.е. метод A4.21) является
явным), локальная погрешность и погрешность аппроксимации оказы-
оказываются связаны простым равенством /п = фпЬ, что непосредственно
вытекает из данных определений.
Пример 14.9. Покажем, что метод Эйлера имеет первый порядок аппрокси-
аппроксимации.
Известно, что
У (in + h) - y(tn) _ h
д У \гп) т 2
где tn < ?п < <n+i (см. § 12.1). Учитывая равенство y'(tn) = f (tn, у (<n)),
для погрешности аппроксимации получаем следующее выражение:
Vn
f(. {t^- v"
/ I'm У {in}) - 2 У
Поэтому
max \фп\
0<n<N
Mo • ,,
-г-=- Л, Л?2 = max
[to.
A4.33)
A4.34)
т.е. метод действительно имеет первый порядок аппроксимации.
Пример 14.10. Для погрешности аппроксимации неявного метода Эйлера
A4.24) также справедлива оценка A4.34) и поэтому он также имеет первый
порядок аппроксимации. Простое доказательство этого факта рекомендуем
провести в качестве упражнения.
Пример 14.11. Найдем выражение для локальной погрешности метода
Эйлера.
По определению, /„ = у (tn^) - уп+\, где yntl = у (tn) + hf (tn, у (<„)). Но
в силу равенства A4.33) у (<n*i) = у (<n) + A/(tn, у (tn)) + Л^„ = уп*\ + Л^п-
Л2
Поэтому 1п — Ифп = — у (?п)- Таким образом, локальная погрешность метода
Эйлера имеет второй порядок малости относительно шага Л.
6. Сходимость. Пусть у (t) — решение задачи Коши. Назовем гло-
глобальной погрешностью (или просто погрешностью) численного метода
сеточную функцию е'1 со значениями еп = у (tn) - yn в узлах tn. В
качестве меры абсолютной погрешности метода примем величину
Е (Л) = max \y (in) ~ Уп\-
0<n<iV
Численный метод решения задачи Коши называют сходящимся,
если для него Е (Л) -» 0 при А -» 0. Принято говорить, что метод схо-
сходится с р-м порядком точности (или имеет р—й порядок точности),
если для погрешности справедлива оценка Е (Л) < ChP, p > 0.
Покажем теперь, что для устойчивого численного метода из на-
наличия аппроксимации с порядком р следует сходимость с тем же
порядком. Будем предполагать, что начальные значения у\, у2, ..., yk-i
заданы с р-м порядком точности1, т.е. верна оценка
max \y (in) — уп\ < CohP.
Справедлива следующая основная теорема.
424
Для одношаговых методов это предположение излишне.
425

Теорема 14.4. Пусть численный метод устойчив на конечном
отрезке и имеет порядок аппроксимации, равный р. Тогда если началь-
начальные значения у\, ..., уь-i заданы с р-м порядком точности, то и метод
сходится с р-м порядком точности.
D Пусть Vn — погрешность аппроксимации. Положим у? = у (<„).
Равенство A4.31) позволяет утверждать, что сеточная функция y*h
является решением дискретной задачи Коши A4.26), A4.27). Устойчи-
Устойчивость метода означает выполнение неравенства A4.28), которое в силу
равенств у*= у (tn) и у (to) = у0 можно переписать так:
Неявный метод Эйлера
прямоугольников:
A4.38)
= Уп + hf(tmi) Дает формулу правых
y(in)«yn=h
1=1
а правило трапеций A4.25) приводит к известной формуле трапеций
max \y(tn)-
0<n<N
Учитывая, что
<К(Т) Г max \y(tn)-yn\ +
[Кя<Ы
Ё'
.A4.35)
"Ё1 К|-А<(Т-<о) max Ц,п\ < (Г- t0) Ctf,
п'Ы 0<n<N
правую часть неравенства A4.35) можно оценить величиной
К(Т)(С0 + (Т- tQ)C)hP = Ch?. Итак, max \y (tn) - уп\ < Ы. Ш
в. Связь с задачей вычисления интеграла. Существует тесная связь
между проблемой решения задачи Коши и задачей вычисления интег-
интеграла с переменным верхним пределом
(<) = |/(r)dr, <0 < t < Т.
A4.36)
Действительно, вычисление интеграла A4.36) эквивалентно решению
задачи Коши
A4.37)
являющейся частным случаем более общей задачи A4.1), A4.2).
Таким образом, всякий численный метод решения задачи Коши
порождает соответствующий метод численного интегрирования. На-
Например, метод Эйлера j/n+i = Уп + ЛХ<п) приводит к формуле левых
прямоугольников:
426
»(п)? (
На примере формулы A4.38) легко увидеть различие между ло-
локальной и глобальной погрешностями. Локальная погрешность — это
погрешность, допускаемая на одном элементарном отрезке, т.е.
/п= \ f(i)dt-hf(tn),
tn
а глобальная погрешность — это результирующая погрешность, т.е.
?„= ( f(t)dt-h Е /(<,).
. 1=0
У\
№j
о и
t, Ь
а)
Г
Рис. Ц.б
В данном случае в силу линейности задачи A4.36) глобальная
n-i
Е /
ni
погрешность есть просто сумма локальных погрешностей: е„ = Е /,.
1 = 0
Для нелинейного уравнения у' — /(<, у) это уже не так. В зависимости
от характера поведения интегральных кривых глобальная ошибка
427

может оказаться больше (рис. 14.6, а) или меньше (рис. 14.6, б) суммы
соответствующих локальных погрешностей.
§ 14.3. Использование формулы Тейлора
Один из наиболее простых для понимания подходов к решению
задачи Коши основан на использовании формулы Тейлора
y'{t)h + ^
«2 + ... + "—fL АР + Rpn(t, A).A4.39)
„( p* i ) ( c\
Здесь Rpn(i, A) — —:— . j Лр* — остаточный член формулы Тейлора,
f — некоторая точка, принадлежащая отрезку [t, t + A].
Отбрасывая остаточный член, получаем приближенное равенство
у A + Л) я у (t) + у '(t)k + ЦЙ Л2 + ... + *if|^ hP. A4.40)
Если значение решения у в точке < известно, то в силу равенства
У '(<)=/(<, У @) A4.41)
значение производной ^'(<) также можно считать известным. Для того
чтобы вычислить производные у", у"', ... более высокого порядка,
входящие в формулу A4.40), продифференцируем равенство A4.41) по
t, используя правило дифференцирования сложной функции. Тогда
получим
У" = f't + ГУУ' = /; + fyf, A4.42)
У" = ftV +Ъ1]У' + (Л?' + hV У')/+ /„(/; + f'y') =
= ftV + 2f\l]f+ fyf't + (Q2f+ fyy'P A4-43)
и т.д. Как нетрудно заметить, выражения для производных у{ к) ус-
усложняются по мере роста порядка к.
Использование приближенной формулы A4.40) приводит к следу-
следующему явному одношаговому методу.
Уп+i =
АР.
A4.44)
Здесь у'п = f(tn, yn); значения у'^ и у"^ получаются в результате под-
428
становки в формулы A4 42) и A4.43) значений / = tn и у — уп\ анало-
аналогично вычисляются значения у^ при Jb > 3.
Локальная погрешность этого метода 1п совпадает с величиной
Rp+iAru h) остаточного члена формулы Тейлора, пропорциональной
}J'*X Пользуясь этим, можно доказать, что метод A4.44) сходится и
имеет порядок точности, равный р.
Несмотря на то, что рассматриваемый метод теоретически дает
возможность найти решение с любым порядком точности, на практике
он применяется довольно редко. Дело в том, что использование фор-
формулы A4.14) приводит к необходимости вычисления большого числа
частных производных ^ , что чаще всего является весьма трудоем-
трудоемкой и нередко аналитически невыполнимой операцией.
Более существенный аргумент против использования метода A4.44)
состоит в том, что к настоящему времени разработаны эффективные
численные методы решения задачи Коши (например, методы Рун-
ге—Кутты и Адамса), предполагающие необходимость вычисления
значений только функции / и не использующие ее частные производ-
производные. Именно этим методам, реализованным в виде стандартных прог-
программ и пакетов прикладных программ, мы и уделим основное внима-
внимание в дальнейшем.
Тем не менее для решения некоторых специальных классов задач
приведенный выше метод может быть полезен. В частности, он исполь-
используется при решении некоторых задач небесной механики, в которых
вычисление производных j^1 не требует существенных дополнитель-
дополнительных затрат в силу специальной структуры правых частей.
Пример 14.12. Найдем численное решение задачи Коши
у' = 21у, 3/@) = 1 A4.45)
на отрезке [0, 1], используя метод A4.44) при р — 2, обладающий вторым
порядком точности. Как нетрудно проверить, точным решением этой задачи
2
является функция у (t) — et .
Дифференцируя уравнение по <, получим следующее выражение для вто-
второй производной, у" — 2у + 2ty' =2A + 2fi)y. Поэтому расчетная формула
A4.44) в данном случае примет вид
- уп
h2tnyn + j 2
2)y =
2t2n)yn =
2tnh
уп.
Найденное по этой формуле для h = 0.1 приближенное решение приведено в
табл. 14 1. Для сравнения в ней же приведены значения точного решения.
429

Таблица 14.1
t
0.1
0.2
0.3
0.4
0.5
Метод A4.44);
h =0.1
1.01000
1.04050
1.09336
1.17186
1.28108
Точное
решение
1.01005
1.04081
1.09417
1.17351
1.28403
t
0.6
0.7
0.8
0.9
1.0
Метод A4.44);
h = 0.1
1.42840
1.62438
1.88396
2.22835
2.68783
Точное
решение
1.43333
1.63232
1.89648
2.24791
2.71828
Как видно из таблицы, решение оказалось найдено с точностью ? и 3-10~2.
§ 14.4. Метод Эйлера
1. Геометрическая интерпретация метода Эйлера. Простейшим и
исторически первым численным методом решения задачи Коши явля-
является метод Эйлера. Его можно получить, если в приближенном равен-
равенстве A4.44) оставить только два первых слагаемых (т.е. взять р = 1).
Тогда формула A4.44) примет вид
Уп+1 = Уп+ hf(tn> yn).
A4.46)
Геометрическая интерпретация одного шага метода Эйлера заклю-
заключается в аппроксимации решения на отрезке [/„, tn*{\ касательной у =
= Уп + y'(tn)(t ~ tn)t проведенной в точке (in, yn) к интегральной
кривой, проходящей через эту точку (рис. 14.7).
Таким образом, после выполнения N шагов неизвестная интеграль-
интегральная кривая заменяется ломаной линией (ломаной Эйлера), для кото-
которой угловой коэффициент кп очередного n-го звена равен значению
/(/„, уп) (рис. 14.8).
430
Рис. Ц.8
Как уже было отмечено в § 14.2, метод Эйлера представляет явный
одношаговый метод. Для него погрешность аппроксимации имеет вид
Фп = \ y"Un)-
2. Устойчивость. Докажем, что метод Эйлера устойчив на конечном
отрезке (см. определение устойчивости в § 14.2). Предварительно уста-
установим справедливость следующего воспомогательного утверждения.
Лемма 14.1.. Пусть zh — неотрицательная сеточная функция,
удовлетворяющая для всех п ^ 0 неравенству zn*\ < A + a)zn + /?п, где
а > 0, fin ^ 0. Тогда при всех п ^ 0 справедлива оценка
zn<ena(z0+ V/?fc). A4.47)
п Справедливость неравенства A4.47) установим методом индукции.
При п = 0 оно превращается в очевидное: zq ^ zq.-
Пусть теперь неравенство A4.47) выполнено при некотором п — т.
Тогда, используя оценки 1 + а < eQ и 1 < е(т+1)а, получим следующую
цепочку неравенств:
zm+l
<*)zm
е"»"' * /Jm
(го
т-1
S /
т.е. неравенство A4.47) верно и при п = т + 1. Итак, оно верно при
всех п.Ш
Пусть теперь y*h — решение возмущенной дискретной задачи Коши
431

A4.48)
A4-49)
Теорема 14.5. Пусть функция f удовлетворяет условию
|/'| К L. Тогда справедливо неравенство
LiT-t.)
°
max|j,*-j,n|
А ?
A4.50)
означающее, что метод Эйлера устойчив на конечном отрезке.
о Вычитая из уравнения A4.48) уравнение A4.46) и пользуясь
формулой конечных приращений Лагранжа
/(*„> У„) "/(*„> Уп) = fy(tn> Уп)(Уп ~ »„)-
получаем равенство
У*пн - Упн = A +
откуда следует
A4.51)
Заметим теперь, что для zn = | г/* - yj, а = hL и /?п = Л|^п| в
силу A4.51) справедливо неравенство 2п+1 < A + а)гп + /9П. Согласно
п-1
лемме 14.1, имеем \у* - yj < en/lL(|j/' - у \ + S |^„|А)- Учитывая,
к = 0
что nh К Nh = Т - <oi приходим к неравенству A4.50). Я
3. Оценка погрешности. Так как метод Эйлера устойчив на конеч-
конечном отрезке и имеет первый порядок аппроксимации (см. пример
14.9), то из теоремы 14.4 следует, что он сходится с первым порядком
точности. Точнее, верна следующая теорема.
Теорема 14.6. Пусть функция f удовлетворяет условию
|/'| ^ L. Тогда для метода Эйлера справедлива такая оценка
глобальной погрешности:
max \y{tn)-yn\<C(T)h,
A4.52)
ideC(T)-e
432
(T- to)M2/2, M2 = max \y"(t)\.
Приведем доказательство теоремы, не использующее теорему 14.4.
а Пусть фп — погрешность аппроксимации. Перепишем ее определе-
определение A4.33) в виде
У (*n*i) = У (tn) + А (/(*„, У (*„)) + Фп)-
Полагая у? = у (/„), замечаем, что сеточная функция y*h является
решением дискретной задачи Коши A4.48), A4.49), где у* = yQ. Тогда
в силу теоремы 14.5 справедлива оценка
max \y (tn) -jn|
S |
n=o
S |
Учитывая, что S |^гг|А < max
n=0
- 'o)i и используя оценку
A4.34) для погрешности аппроксимации, получим неравенство
A4.52).i
Пример 14.13. Найдем численное решение задачи Коши у' = 2ty,
у @) = 1, на отрезке [0, 1], используя метод Эйлера. Заметим, что та же
задача другим методом была решена в примере 14.12.
В данном случае расчетная формула A4.46) принимает вид
З/mi = Уп + ЮгпУп = A + 2А<„)г/п.
A4.53)
Полученные с помощью этой формулы для значений шагов А = 0.1, А = 0.01 и
h — 0.001 приближенные решения приведены в табл. 14.2. Для сравнения в
последнем столбце даны значения точного решения у (t) = е' . Нижняя строка
таблицы содержит значения абсолютной погрешности Е (А). Как и следовало
ожидать, при уменьшении шага в 10 раз погрешность уменьшается также
примерно в 10 раз.
Таблица 14.2
t
0.1
0.2
0.3
0.4
0.5
Метод Эйлера;
А= 0.1
1.00000
1.02000
1.06080
1.12445
1.21440
Метод Эйлера;
А =0.01
1.00903
1.03868
1.09071
1.16835
1.27659
Метод Эйлера;
А =0.001
1.00995
1.04060
1.09383
1.17299
1.28328
Точное
решение
1.01005
1.04081
1.09417
1.17351
1.28403
433

Продолжение табл.
t
0.6
0.7
0.8
0.9
1.0
E(h)
Метод Эйлера;
Л = 0.1
1.33584
1.49615
1.70561
1.97850
2.33463
3.9 -Ю
Метод Эйлера;
А =0.01
1.42277
1.61733
1.87513
2.21724
2.67379
4.5-10-2
Метод Эйлера;
Л= 0.001
1.43226
1.63080
1.89432
2.24480
2.71376
4.6-Ю-з
Точное
решение
1.43333
1.63232
1.89648
2.24791
2.71828
-
4. Влияние вычислительной погрешности. Оценивая метод Эйлера
необходимо учитывать, что при его реализации на ЭВМ неизбежно
возникнут ошибки округления. В результате фактически вычисляемые
значения у? будут удовлетворять соотношению
Величины Ьп учитывают вклад погрешностей округления. Это соотно-
соотношение можно рассматривать как возмущенное уравнение вида A4.48),
в котором фп — 8n/h. Тогда неравенство A4.50) дает следующую оцен-
оценку влияния погрешностей округления:
max |
0<п<Лг
п=0
A4.54)
Здесь Ь — некоторое среднее значение величины 8п, а N = (Т - <о)/Л.
Таким образом, с учетом неравенств A4.52) и A4.54) получается
следующая оценка погрешности фактически вычисляемых значений
max \y(tn) - у*\ <
(f-4
Схематически график функции Е? (Л) приведен на рис. 14.9.
Оказывается, что полная погрешность убывает только лишь при
уменьшении шага h до некоторого значения ЛоПТ. Достижимая точность
метода ограничена снизу величиной Е^п и попытка увеличить точ-
точность за счет уменьшения шага h при h < ЛоПТ приводит лишь к рез-
резкому росту погрешности.
434
Е'
Emln
О
I
(tn*l,y(tn.,))
(tn.y(tn))
"опт
Рис. Ц.9
Рис. Ц.10
Значение ЛоПТ, как правило, бывает очень трудно определить зара-
заранее. Однако если очень высокая точность не нужна, то необходимый
для ее достижения шаг h обычно бывает много больше Л0Пт-
Если же требуется высокая точность решения, то достичь ее с
помощью метода Эйлера нельзя, даже если пойти на значительные
затраты машинного времени (неизбежные при расчете с малым значе-
значением шага Л). Необходимо иметь в своем распоряжении методы, име-
имеющие более высокий порядок точности и позволяющие вести расчет со
сравнительно крупным шагом h.
§ 14.5. Модификации метода Эйлера
второго порядка точности
Медленная сходимость метода Эйлера (его погрешность убывает
пропорционально лишь первой степени А) является серьезным препят-
препятствием для использования его на практике. Из рис. 14.7 видно, что
уже один шаг по касательной к интегральной кривой приводит к
значительной величине локальной погрешности /„. Можно ли так
подправить расчетную формулу метода, чтобы существенно уменьшить
величину /„?
Пусть у (t) — решение дифференциального уравнения
A4.55)
y'(t) = f(t,y(t)),
удовлетворяющее условию у (tn) = уп- Далее, пусть
кп = У (W ~ У ('"> = tgTn A4-56)
— угловой коэффициент секущей, проходящей через точки (tn, у {tn})
и (*п+ь У (tn+i)) графика функции у (<) (рис. 14.10).
435

Ясно, что "метод", состоящий в вычислении но формуле
Vn*\ ~ Vn -f hkn, A4 57)
имеет нулевую локальную погрешность Дтя того чтобы воспользовать-
воспользоваться этой формулой, нужно лишь "научиться вычислять значение кп"
Интегрируя обе части уравнения A4 55) по i от /,, до <,,¦] и исполь-
зуя формулу Ньютона—Лейбница [ y'(t)dt = у (<n+i) - У (tn), прихо-
приходим к равенству
У (tn*\) ~ У (tn) = \ fU,y(t))di A4 58)
Из равенств A4 56) и A4 5Я) следует, что
, tm\
Построим на основе правила трапеций явный метод. Для этого
A4 59)
Заметим теперь, что применение для приближенного вычисления
интеграла, стоящего в правой части выражения A4 59). формулы
левых прямоугольников | /(/, ц (t))dt и hf (tn, y (tn)) немедленно
приводит от A4 57) к методу Эйлера A4 46)
Известно (см гл 13), что больший порядок точности имеет форму-
формула трапеций
/ f(i, У @) di « | (/(<„, у (/„)) + /(«„¦,, у (Vi)))
Непосредственное ее применение к вычислению кп приводит к
правилу трапеций
подставим в правую часть формулы A4.60) значение уп+
ваемое" методом Эйлера. В результате получается метод
Уп+i = Уп+2
+ /(<п*ь Уп + А/(<„, у„))),
"предсказы-
"предсказыA4.61)
который называют методом Эйлера—Коши (или методом Хьюна).
Геометрическая иллюстрация этого метода представлена на рис.
14.11. Вычисления разбивают на два этапа. На первом этапе (этапе
прогноза) в соответствии с методом Эйлера у\?\ = уп + hk(nl), ?„" =
= /('m Уп) вычисляют грубое приближение к значению у (tn*i)- В
точке (<mi, yml) определяют угловой коэффициент kn2) = f{tn*\, Уп+\)-
На втором этапе (этапе коррекции) вычисляют усредненное значение
углового коэффициента кп = (Jfc^11 + k^2))/2. Уточненное значение уп+\
находят по формуле утх = уп + hkn, что соответствует шагу по
прямой, проходящей через точку (tn, • уп) и имеющей угловой
коэффициент, равный кп.
Vn+I = Vn + j (/('"' Уп) + /(Vl- Уп*]))
A4.60)
Рис. Ц.11
Замечание. Метод Эйлера—Коши относится к классу мето-
методов прогноза и коррекции (иначе говоря, методов типа предик-
предиктор—корректор1).
(ср с A4 Q4)) Этот метод имеет второй порядок точности, но является
неявным Поэтому его реализация связана с необходимостью решения
относительно у„+1 нелинейною уравнения A ) 60)
1 От англ. to predict — "предсказывать", "прогнозировать"; to correct —
"исправлять", "корректировать".
437

Метод A4.61), который можно рассматривать как модификацию
метода Эйлера, имеет второй порядок точности. Еще одну модифика-
модификацию второго порядка точности можно получить с помощью формулы
(центральных) прямоугольников
п1
\ f{t,y (t))dt и hf(tn.l/2, у
, <n*i/2 = <n + Л/2,
если для приближенного вычисления значения у (tn+i /2) применить
метод Эйлера. В результате получим расчетные формулы усовершенст-
усовершенствованною метода Эйлера
Упн/г= Уп+~к1пи , кпи = /(<„, уп)>
A4.62)
Уп*\ = Уп + hkn, kn = /(<п+1/2. Уп*\ /г)-
Геометрическая иллюстрация этого метода приведена на рис. 14.12.
Иы.Упч)
I
Пример 14.14. Применим рас-
рассмотренные в этом параграфе
методы для численного решения
задачи A4.45) с шагом Л = 0.1.
Расчетная формула метода
Эйлера—Коши принимает вид
Л
Уп*\ = Уп + j B*лУп +
+ 2<п+1(з/„ + h2tnyn)) = A4.63)
,*4 tn.i t
Рис. 1112 + 2ktntn+1)].
Вычисления усовершенствованного метода Эйлера производим по формуле
Лч Л
Правило трапеций A4.60) приводит к уравнению
А
З/n+l = Уп + о
438
которое в данном случае линейно и легко разрешается относительно уп*\:
Уп+i = »пA + Л<п)A - Л<„+0- A4.65)
Результаты вычислений по формулам A4.63), A4.64) и A4.65) приведены в
2
табл. 14.3. Там же для сравнения представлены значения решения у (<) = е .
Нижняя строка таблицы содержит величину абсолютной погрешности Е (Л).
Таблица 14.3
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0
Метод Эйлера-
Коши; Л = 0.1
1.01000
1.04070
1.09399
1.17319
1.28347
1.43236
1.63059
1.89345
2.24260
2.70906
Усовершенство-
Усовершенствованный метод
Эйлера; h = 0.1
1.01000
1.04060
1.09367
1.17253
1.28228
1.43038
1.62749
1.88870
2.23546
2.69843
Правило
трапеций;
А =0.1
1.01010
1.04102
1.09468
1.17450
1.28577
1.43624
1.63700
1.90390
2.25958
2.73660
Точное
решение
1.01005
1.04081
1.09417
1.17351
1.28403
1.43333
1.63232
1.89648 '
2.24791
2.71828
E(h) 0.93-10
2.0-10'2
1.9-10
Как видно из сравнения табл. 14.3 с табл. 14.2, проведенные в этом параграфе
модификации метода Эйлера действительно привели к повышению точности.
§ 14.6. Методы Рунге—Кутты
Наиболее популярными среди классических явных одношаговых
методов являются методы Рунге — Кутты1. Методы Эйлера, Эйлера —
Коши и усовершенствованный метод Эйлера можно рассматривать как
простейших представителей этого класса методов.
1. Вывод расчетных формул. Поясним вывод расчетных формул
метода Рунге—Кутты. Пусть (как и в § 14.5) у (<) — решение диффе-
1 В.М.Кутта A867—1944) — немецкий математик.
439

ренциального уравнения у' = /(<, у), удовлетворяющее условию
у (<„) = уп. Запишем равенство A4.58) в следующем виде:
У (W = У («я) + f /((,У(<Р. A4.66)
Если бы входящий в это равенство интеграл можно было вычислить
точно, то получилась бы простая формула, позволяющая последова-
последовательно вычислить значения решения в узлах сетки. Поскольку в дей-
действительности это невозможно, попробуем получить приближенную
формулу, заменив интеграл квадратурной суммой (см. гл. 13).
Введем на отрезке [tn, <n+i]"» вспомогательных узлов tn1] = tn + ajA,
f*,21 = tn + a2h, ..., tnm) = tn + amh, где 0 = <ц < а2 < ... < ап < 1.3аме-
тим, что
а2 <
= tn, tnm) < inn- Заменяя входящий в равенство A4.66)
интеграл квадратурной суммой с узлами tn1], ..., tnm), получаем приб-
приближенное равенство
У (W « У (in) + Л Е cj(inl), у (tnl))). A4.67)
t=i
Однако воспользоваться равенством A4.67) для вычисления у (<n*i)
нельзя, так как значения функции у в точках tnl) для t = 2, 3, ..., m
,
неизвестны. Чтобы найти эти значения, запишем равенства
У (#') = У (in) + С /(<, У (O)d' (« = 2, 3, ..., m),
A4.68)
аналогичные равенству A4.66). Заменяя для каждого t входящий в
формулу A4.68) интеграл соответствующей ему квадратурной форму-
формулой с узлами tnn, <n2), •¦¦, <п'1], придем к приближенным равенствам
у (^3))« у (tn)
, у
tnl)) « У (in)
y(tnm))*y(in)
m-l
У , у
позволяющим последовательно вычислять приближения к значениям
У (гп ), ¦¦¦, У \tn )¦
Обозначим теперь через уп1) вспомогательные величины, имеющие
смысл приближений к значениям у (tnt]); пусть klni] — f (t(nl), у{пг)) -
приближение к значению углового коэффициента к в точке tnt]. Тогда
расчетные формулы примут вид
Уп*1 - Уп+
kn= Y, ctkln
1=1
Ук1) =Уп,
ll)
(m) _
— J/n + " Ь Pn]Kn ¦
Часто из этих формул исключают вспомогательные величины уп1) и
записывают формулы так:
т
Уп+i = Уп + hkn, kn = E ctkn'',
t=i
№ =
m-l
440
Заметим, что выведенные формулы задают явный одношаговый
метод вида уп*х = уп + НФ (tn, yn, h), где для вычисления значений
функции Ф (<„, уп, h) = E ct/kn" используются значения правой части
t=i
/ в т вспомогательных точках. Поэтому этот метод называют явным
т-этапным методом Рунге—Кутты.
Выбор конкретных значений параметров с,, а,, /?у осуществляется
исходя из различных соображений. Естественно, что одним из основ-
основных является желание сделать порядок аппроксимации р максимально
возможным.
441

2. Устойчивость и сходимость. Следующая теорема позволяет в
дальнейшем называть методы Рунге—Кутты, имеющие р-й порядок
аппроксимации, методами р-го порядка точности.
Теорема 14.7. Пусть правая часть дифференциального уравне-
уравнения удовлетворяет условию |/'| < L. Тогда всякий явный т-этапный
метод Рунге—Кутты устойчив на конечном отрезке
Следствие. Пусть выполнено условие |/'| < L. Тогда если
явный т-этапный метод Рунге—Кутты имеет р-й порядок аппрокси-
аппроксимации, то он сходится с р-м порядком точности.
Справедливость следствия вытекает из теоремы 14 4.
3. Семейство явных двухэтапных методов. Выведем расчетные фор-
формулы семейства явных двухэтапных методов Рунге—Кутты второго
порядка точности. Запишем формулы явного двухэтапного метода
Уп*\ = Уп+ h(ClklnX) + c2k{n2)),
kkl) = f(in, Уп), kn2) = /On + ah, yn + hj3knu)
в виде
^'A~ Уп = с,/A„, уп) + c2/0n + ah, yn + ДО/On, Уп)).
Параметрами этого метода являются величины с\, с2, а, /?.
Представим погрешность аппроксимации
ф =
~ cj(t, у) - c2f(t + ah,y
, у)),
(где t = tn, у = у (tn), у (t) — решение дифференциального уравнения
у' = f [t, у)) в виде разложения по степеням h
Формула Тейлора
О
у 0 + Л) = у 0) + У'О)А + l
с учетом равенств у' - /, у" - f't + fyf {см A4.42)) дает формулу
y{t
\ (/;
о
(аргументы t, у у функции / и ее частных производных /(', f'y
опускаем).
442
Представим значение функции /в точке (< + аЛ, j/ + hftf), исполь-
используя формулу Тейлора для функции двух переменных с центром в
точке It, у):
f(t+ah,y+ h/Jf) = f(t, у) + f'tah + /y
Таким образом,
ф = A - с, - с2)/+ [A/2 - c2a)f't + A/2 - с2/?)/у/] А + О (А2).
Если потребовать, чтобы выполнялись условия с\ + с2 = 1, c2a = 1/2,
с2/? =1/2 (что эквивалентно выбору С] = 1 - —, с2 = —, /? = а), то
первые два слагаемых в формуле для ф обратятся в нуль, и поэтому
метод будет иметь второй порядок аппроксимации.
Итак (с учетом следствия из теоремы 14.7), можно утверждать, что
при любом а€@, 1) метод
A4.69)
^ /On + ah, yn + aft/On, Уп))}
имеет второй порядок точности.
Заметим, что при а — 1 формула A4.69) дает метод Эйлера—Коши,
а при а = 1/2 — усовершенствованный метод Эйлера (см. § 14.5).
4. Метод Рунге—Кутты четвертого порядка точности. Наиболее
известным из методов Рунге—Кутты является классический 4-этапный
метод четвертого порядка точности:
Уп+i = Уп+ hkn, kn=1- (knl) + 2kln2)
nU = /0„, Уп), ^2> = /0n + !
A4.70)
^3) = I (in + | Уп + \ kn2)), С = f(tn +h,yn+ hknS)).
Этот метод весьма прост и, как показывает практика, довольно
эффективен в обычных расчетах, когда отрезок [l0, T] не очень велик
и нужна сравнительно невысокая точность.
Замечание. Применение метода A4.70) к решению задачи о
вычислении интеграла A4.36) порождает формулу Симпсона
Уп*\ = Уп + g (/On) + 4/0„+1/2) + /On+i)).
443

Таким образом, классический метод Рунге-Кутты четвертого поряд-
порядка точности A4.70) можно рассматривать как аналог формулы
Симпсона, отвечающий решению задачи Коши.
Пример 14.15. Продемонстрируем работу метода Рунге-^Кутты четвертого
порядка точности применительно к решению «задачи Коши A4.45).
В этом случае расчетные формулы принимают вид
= У»
h)(yn
Найденные с шагом Л = 0.1 приближенные значения решения уп и их
погрешности ?п приведены в табл. 14.4.
Таблица 14.4
0.1
0.2
0.3
0.4
0.5
Уп
1.010050167
1.040810770
1.094174265
1.173510814
1.284025256
?п
10"9
4-Ю"9
2-Ю"8
6-Ю"8
2Ч0
0.6
0.7
0.8
0.9
1.0
Уп
1.433328994
1.632315187
1.896478467
2.247902590
2.718270175
еп
5-Ю
2-Ю
3-10'6
6-Ю
2-Ю
5. Обсуждение методов Рунге—Кутты. Методы Рунге—Кутты имеют
несколько достоинств, определивших их популярность среди значи-
значительного числа исследователей. Эти методы легко программируются1.
Они обладают достаточными для широкого круга задач свойствами
точности и устойчивости. Эти методы (как и все одношаговые методы)
являются самостартующими и позволяют на любом этапе вычислений
легко изменять шаг интегрирования.
Увеличивая число m вспомогательных точек, можно построить
методы Рунге—Кутты любого порядка точности р. Однако уже при
1 Это очень важно, если отсутствуют или по каким-либо причинам недо-
недоступны соответствующие стандартные программы. Если же используются
развитые пакеты прикладных программ, то сложность программирования
метода не интересует пользователя, поскольку он обращает внимание на другие
свойства метода.
144
р > о эти методы используются довольно редко. Это объясняется как
чрезмерной громоздкостью получающихся вычислительных формул,
так и тем, что преимущества методов высокого порядка точности р над
методами, в которых р — 4 и р = 5, проявляются либо н тех задачах,
где нужна оч^нь высокая точность и используются ЭВМ высокой
разрядности, либо в тех задачах, где решение очень гладкое. Кроме
того, методы Р^нге—Кутты высокого порядка точности р часто оказы-
оказываются менее эффективными по сравнению с методами Адамса того же
порядка точности (см. § 14 7).
Замечай и е. Кроме описанных выше классических явных
методов Рунге—Кутты используются и более сложные в реализации
неявные тп-этапные методы Рунге—Кутты:
Уп*\ = У г) +
"¦:ii кп — и сгкп
m
aA Уп + hYj ft
= I, 2,
т.
Эти методы имеют ряд преимуществ перед явными методами, одна-
однако это достигается за счет существенного усложнения вычислитель-
вычислительного алгоритма, так как на каждом шаге необходимо решать систе-
систему т нелинейных уравнений. В настоящее время неявные методы
Рунге—Кутты применяются в основном для решения так называ-
называемых жестких задач (см. § 14 11).
6. Автоматический выбор шага. Отметим, что в современных прог-
программах, реализующих методы Рунге—Кутты, обязательно используется
некоторый алгоритм автоматического изменения шага интегрирования
Лп+1 = tn+\ - 'л
Интуитиыю ясно, чго на участках плавного изменения решения
счет можно вести с достаточно крупным шагом. В то же время па тех
участках, где происходят резкие изменения поведения решения, необ-
необходимо выбирать мелкий шаг интегрирования. Обычно начальное
значение шла hi jdAdei гкиьзоьсаел!,. Долее шаг интегрирования
меняется в соответствии с величиной получаемой в ходе вычислений
оценки локальной погрешности. Само по себе изменение шага hn для
методов Рунге—Кутты (впрочем, как и для всех других одношаговыч
методов) не представляет сложности. Действительная проблема состоит
в том, как оценить локальную погрешность и выбрать очередной шаг
интегрирования.
Один из распространенных подходов состоит в использовании
правила Руте {правила двойною пересчета) Пусть значение в точке 1п
4-15

уже найдено и у (t) — решение уравнения у'{1) = /(<, у), удовлетворя-
удовлетворяющее условию у (tn) = уп- Обозначим через у n+1 приближение ymi к
значению у (tn+\), найденное с помощью одношагового метода
A4.71)
У ml = Уп + hn+l$An, Уп, Уп+i, hn*l),
который имеет порядок точности, равный р. Можно показать, что для
методов Рунге—Кутты локальная погрешность /„ = у (<n+i) - У п+'
допускает представление
к = г (<„, уп) Л&! + о (Agtl),
где г (<, у) — непрерывная функция. Следовательно, при достаточно
малых Лп+1 справедливо приближенное равенство
tn, УпН:\-
A4.72)
Уменьшим теперь шаг интегрирования вдвое, положив hn+x п —
= hn+x/2, и вычислим приближение к значению решения в точке <п+1 с
помощью того же одношагового метода. Для этого потребуется выпол-
выполнить уже два элементарных шага по формулам
Уп+1 /2 = Уп + hn+l /2$ (in, Уп, Уп*\ /2, hn+l /2),
Уп+i = Уп*\ /г + hn*i /2$ (in+i/2, Уп+\/г, Уп+i, hn+xn)-
Полученное таким образом значение у +1/2 = j/n+i будет, конечно,
отличаться от значения, найденного по формуле A4.71). Достаточно
ясно, что два шага величины Л„+1 /2 приведут здесь к локальной пог-
погрешности
У (<„*0 - /ml п « 2г (/„, уп) h%\ n. A4.73)
Вычитая из равенства A4.72) равенство A4.73), получим формулу
Сравнение ее с A4.73) приводит к приближенному равенству
/2
2P_\
A4.74)
Использование этой формулы для апостериорной оценки локальной
погрешности значения у п*х п (которое в дальнейшем принимается за
приближенное значение решения задачи Коши в точке <п+1) и называ-
называют правилом Рунге*. Заметим, что этот способ контроля точности
приводит к увеличению времени счета примерно на 50%.
Существуют более экономичные методы оценки локальной погреш-
погрешности, основанные на использовании для контроля точности двух
различных методов Рунге — Кутты. В настоящее время одним из са-
самых эффективных методов такого типа является метод Рунге—Кут-
Рунге—Кутты—Фельберга. В этом методе для оценки погрешности метода пятого
порядка точности используются формулы метода четвертого порядка
точности, причем на одном шаге требуется всего лишь шесть вычисле-
вычислений значений правой части2 /
После того как тем или иным способом оценена локальная ошибка,
программа принимает решение о том, оставить ли шаг интегрирования
прежним, уменьшить ли его вдвое или увеличить в два раза. Это про-
происходит примерно по той же схеме, что и в адаптивных программах,
предназначенных для вычисления определенных интегралов (см. §
13.5). Известно, что при оптимальном выборе шагов интегрирования
абсолютные погрешности, приходящиеся на каждый из шагов, должны
быть примерно равны (см. [9]). Этот результат учитывается при созда-
создании стандартных программ с автоматическим выбором шага.
7. Влияние вычислительной погрешности. Влияние погрешностей
на результат вычислений с помощью явных методов Рунге — Кутты
примерно таково же, как и для метода Эйлера (см. § 14.4). Однако
для них Ё1 (h) = С {Т)(М^\ЬР + т). Кроме того, высокая точность
Т г п
методов позволяет вести интегрирование со сравнительно большим
шагом h > ЛоПТ и поэтому влияние вычислительной погрешности
обычно бывает несущественным.
44 fi
1 Отметим, что использование правила Рунге требует определенной осто-
осторожности, так как равенство A4.72) имеет место, вообще говоря, лишь при
достаточно малом значении шага /ц,+1.
. 2 Более подробное описание этого метода можно найти в [86]. К сожалению,
'в приведенном в этой книге тексте соответствующей ФОРТРАН-программы
Лмеются досадные опечатки.
447

§ 14.7. Линейные многошаговые методы.
Методы Адамса
1. Методы Адамса. В одношаговых методах после того как найдено
очередное значение уп в точке tn, значение уп.\ отбрасывают и уже не
используют в последующих вычислениях. Естественно все же попы-
попытаться извлечь определенную пользу из информации о значениях
решения уп-ы, •••> Уп-и Уп не в одной, а в к предыдущих точках <п-Ь-ь
•••> 'п-ь <п> т.е. применить многошаговый метод.
Среди многошаговых методов наибольшее распространение в прак-
практике вычислений получили методы Адамса1
Уп*\ ~ Уп
1 =
A4.75)
г с
Здесь /?0, А, ¦••, h — числовые коэффициенты, fn+\-} = f (in*\-p Уп+i-j)-
Уравнение A4.75) позволяет найти новое значение ynti, используя
найденные ранее значения уп, yn-i, ¦¦¦, Уп-Ы- Поэтому предварительно
требуется задание к начальных значений уо, у\, ..., yk-i-
В случае /?0 = 0 метод Адамса является явным, так как значение
jfo+i выражается через найденные ранее значения по явной формуле
Уп+1 = Уп + Л S /?/„¦]-_,.
A4.76)
Если же /?0 ± 0, то для нахождения yn+1 приходится решать нелинейное
уравнение
Уп*\ =
n+\, Уп+\) + 9т
A4.77)
где дп = Уп + ЛЁ/?,/п+1-, — известное значение. Поэтому при /?0 t О
метод Адамса A4.75) является неявным.
Существуют различные способы вывода формул A4.75). Приведем
два из них. Воспользуемся, как и в предыдущем параграфе, равен-
равенством
»(W = »(«n)+ ( f(t,y(t))dt A4.78)
1 Джон Кауч Адаме A819 — 1892) — английский астроном и математик
Метод типа A4.75) был разработан им в 1855 г. по просьбе известного англий-
английского специалиста по внешней баллистике Башфорта.
448
Заменим приближенно функцию F (<) е /(<, у (<)) интерполяционным
многочленом (к - 1)-й степени Ph-i(t), принимающим значения fn, fn-\,
¦ ¦¦, /n-Ы в тех узлах tn, <п.ь .., tn-k+], где значения сеточной функции
yh уже найдены. Интегрирование этого многочлена дает приближенное
равенство
f(t, у
= h E
A4.79)
В результате от A4.78) приходим к формуле A4.76), соответствующей
явному t-шаговому методу Адамса—Башфорта.
Замечание Так как многочлен Р^-\ используется для приб-
приближения функции F вне отрезка, на котором известны ее значения,
то в действительности равенство A4.79) основано на экстраполяции.
Поэтому соответствующий метод называют еще жстраполяционным
методом Адамса.
Если же в интеграле, входящем в равенство A4.78), заменить
подынтегральную функцию интерполяционным многочленом к-й степе-
степени Qk(t), совпадающим со значениями fm\-k, •••, fn, fn+\ в узлах <n+i-A;,
..., tn, tmit T0 получится формула
Уп+i = уп+ Л S /yn+i-,,
J = 0
A4.80)
соответствующая /t-шаговому методу Адамса — Моултона. Заметим,
что этот метод — неявный.
Замечание. Метод A4.80) принято называть также интерпо-
интерполяционным методом Адамса.
Выведем формулы двухшагового метода Адамса—Башфорта и одно-
шагового метода Адамса—Моултона.
Интерполяционные многочлены P\(t) и Q\{t) таковы:
- /„(<„¦! - О/Л + fn+l(t - fn)/*.
Их интегрирование по t дает следующие значения:
449

Таким образом, двухшаговая формула Адамса—Баш форта имеет вид
Уп*\ = Уп + j ("*/" ~ /n-l)i
а одношаговая формула Адамса—Моултона — вид
Уп*1 = Уп + 2 ^п+1 + ^
Предложение 14.1. Пусть решение задачи Коши у (<)
непрерывно дифференцируемо к раз на отрезке [t0, T]. Тогда к-шаговый
метод Адамса—Башфорта и (к - 1)-шаювый метод Адамса—Моултона
имеют порядок аппроксимации, равный к.
Следующая теорема дает основание называть методы Адамса, име-
имеющие р-й порядок аппроксимации, методами р-го порядка точности.
Теорема 14.8. Пусть выполнено условие |/'| < L. Тогда явные
методы Адамса устойчивы на конечном отрезке. Кроме тою, при
выполнении условия h < /io = о| а \ Т устойчивыми на конечном отрез-
Уп+i = Уп + j (/n+i + /n), P = 2;
Ут1 - 3/п + уз E/n+i + 8/п - /n-i), Р = 3;
ке являются и неявные методы Адамса.
Замечание. Если выполнено условие /' < 0, то неявные мето-
методы Адамса устойчивы при любых h.
Следствие. Пусть выполнено условие |/'| < L. Тогда если k-
шаговый метод Адамса имеет р-й порядок аппроксимации, а началь-
начальные значения у\, у2: ..., уы определяются с р-м порядком точности,
то метод сходится также с р-м порядком точности.
Следствие верно в силу теоремы 14.4.
Приведем расчетные формулы методов Адамса—Башфорта р-го
порядка точности при р = 2, 3, 4:
Уп*\ = Уп + 2 ^fn ~ fn-l), V = 2;
Упн - Уп+уг B3/п - 16/n-i + 5/„-2), Р = 3;
= Уп + 2i
Приведем также расчетные формулы методов Адамса—Моултона р-
го порядка точности при р = 2, 3, 4.
450
Упн = Уп + 24
/n_2), p = 4.
2. Методы прогноза и коррекции. Может показаться, что при нали-
наличии явных формул Адамса высокого порядка точности нет необходи-
необходимости в использовании неявных формул. Однако в вычислительной
практике явные методы Адамса используются очень редко. Одна из
основных причин этого состоит в том, что в представляющих наиболь-
наибольший интерес для приложений задачах неявные методы обладают
лучшими свойствами устойчивости и позволяют вести расчет с
существенно большими шагами, нежели явные методы.
Сложность использования неявных методов Адамса заключается в
необходимости решать уравнение A4.77) относительно уп+1. Значение
yn+i можно найти, используя, например, метод простой итерации
2/n+i" = Ф (ут\ ),в>О,ф (у) = hfafitnn, у) + дп. A4.81)
Так как ф'(у) = hflof'(in*u у), то при достаточно малых h условие
сходимости \ф'\ < д < 1 выполнено (см. § 4.4) и метод A4.81) сходит-
сходится.
Часто за начальное приближение yln+\ принимают значение, получа-
получаемое по явной формуле Адамса, и выполняют только одну итерацию
метода A4.81). В результате приходят к методу прогноза и коррекции.
Один из широко используемых методов прогноза и коррекции получа-
получается при совместном использовании методов Адамса—Башфорта и
Адамса—Моултона четвертого порядка точности:
Прогноз: у<°{ = Уп + Л E5/„ - 59/n-i + 37/„-2 - 9/„-а),
f@) _ i i у @) \
in* 1 — / \ t n* 11 Уп*1)-
Коррекция: уп+1 = уп + — (9/п?1 + 19/„ - 5/n-i + fn.2).
Следует подчеркнуть, что результирующий метод оказался явным.
Пример 14.16. Применим описанный выше метод Адамса—Башфорта—Мо-
Адамса—Башфорта—Моултона четвертого порядка точности для решения задачи Коши A4.45) с
шагом Л = 0.1.
451

В качестве начальных значений у\, У2, Уз, необходимых для начала вычис-
вычислений, примем значения, полученные методом Рунге—Кутты четвертого поряд-
порядка точности и приведенные в табл. 14.4. Затем воспользуемся формулами
Уп°\ = Уп + у2 (ЪЪ1пУп ~ 59<„-1У„-1 + 37tn-2yn-2 ~ Ып-зУп-з),
УпН = Уп + jTj (9*п+1Уп+\ + 19<n!/n - btn-Wn-l + <п-2Рп-2).
Найденные значения и соответствуюащие погрешности приведены в табл. 14.5.
Таблица \А.Ъ
in
0.4
0.5
0.6
0.7
0.8
0.9
1.0
Прогноз
«@)
Уп
1.173420048
1.283880725
1.433111448
1.631994012
1.896003688
2.247194327
2.717200091
Погрешность
прогноза е^01
9.1-10
1.5-10
2.2-Ю-1
3.3-10
4.8-10
7.2-10
1.1 -Ю
Коррекция
Уп
1.173518429
1.284044297
1.433364614
1.632374743
1.896572568
2.248046603
2.718486351
Погрешность
метода ?п
-7.6-10~6
-1.9-10
-3.5- Ю-5
-5.9-10
-9.2-10
-1.4-10
-2.1-Ю
3. Общие линейные многошаговые методы. Эти методы, включа-
включающие в себя методы Адамса, задаются формулами вида
1 *
т 2
/
}-0
A4.82)
Предлагается, что а0 t 0, |а^| + |/7jt| t 0. Они называются
линейными, так как значения yt и /, ( г — п + 1 - к, ..., n, n + 1)
входят в формулу A4.82) линейно.
Замечание. Методы A4.82) принято также называть конечно-
разностными методами, а дискретную задачу Коши для уравнения
A4.82) — конечно-разностной схемой (или просто — разностной
схемой).
4. Методы с переменным шагом и переменным порядком. На основе
методов Адамса создан ряд весьма сложных, но и эффективных прог-
программ. В них предусматривается не только автоматический выбор шага
(подобно тому, как это делается для методов Рунге—Кутты), но и
452
автоматический выбор порядка метода. И шаг метода, и его порядок
(в некоторых программах порядок точности может достичь 13) меня-
меняются в ходе вычислительного процесса, приспосабливаясь к характеру
поведения искомого решения.
Методы Адамса требуют меньшего числа вычислений правой части
дифференциального уравнения по сравнению с методами Рунге—Кутты
того же порядка точности. Для них существуют эффективные методы
апостериорной оценки локальной погрешности. Недостатком методов
Адамса является нестандартное начало вычислений. Для определения
значений уи у2, ..., уы, необходимых для работы it-шагового метода,
используются методы Рунге—Кутты либо другие многошаговые мето-
методы. В разработанных к настоящему времени стандартных программах
эта проблема решена.
§ 14.8. Устойчивость численных методов
решения задачи Коши
Как в теории численных методов решения задачи Коши, так и в
практическом плане вопросы об устойчивости методов к малым ошиб-
ошибкам задания начальных данных и правой части уравнения, а также об
устойчивости к погрешностям вычислений являются одними из цент-
центральных. Рассмотрим некоторые естественные требования устойчиво-
устойчивости, которые накладываются на дискретные методы
1
\-] = Ф (<гг, Уп*к-и ¦•-, Уп, Уп+l,
A4.83)
Уделим сначала основное внимание исследованию устойчивости
дискретной задачи Коши для уравнения A4.83) к малым
погрешностям в начальных данных. Пусть yh — решение дискретной
задачи, соответствующее начальным значениям
у\,
ук-\, а y
tfl —
решение той же задачи, соответствующее начальным значениям у*, у*,
..., з/?_] Если отрезок [<о, Т], на котором ищется решение, и шаг Л
фиксированы, то для всякого приемлемого метода решения задачи
Коши его решение непрерывным образом зависит от начальных
значений. Более того, если погрешности et= yt - у* (i = 0, 1, ..., k-l)
задания начальных данных достаточно малы, то ошибку значений у*
можно оценить следующим образом:
max \y*-yn\<XhA) max |e,|. A4.84)
-1
453

Величина к\т), входящая в правую часть неравенства A4.84), играет
роль числа обусловленности метода. Подчеркнем, что в общем случае
она зависит как от Т, так и от Л.
1. Нуль—устойчивость. Будем стремиться к тому, чтобы при доста-
достаточно малых значениях шага А дискретная задача Коши не только
имела близкое к у (t) решение yh, но и обладала другими важными
свойствами, аналогичными свойствам исходной задачи. В силу нера-
неравенства A4.11) ошибка, внесенная в начальное значение задачи Коши,
на отрезке [to, Т] возрастает не более, чем в К (Т) раз (где К (Т),
вообще говоря, растет с ростом Т). Поэтому в общем случае рост вели-
величин 1&{Т) с ростом Т также допустим. Однако если коэффициент
может неограниченно возрастать при h -» 0, то уменьшение шага
Л приведет не к уточнению решения, а, наоборот, к неограниченному
росту погрешности. Таким образом, следует потребовать, чтобы для
дискретной задачи Коши при всех достаточно малых h было выполне-
выполнено неравенство
max \y*-yn\ < K(T) max |е,|,
0<n<N 0<
A4.85)
где К (Т) не зависит от h.
Методы, для которых неравенство A4.85) выполнено в случае,
когда решается задача Коши для однородного уравнения у' — О,
будем называть нуль-устойчивыми.
Чтобы отбросить те из методов A4.83), которые заведомо не обла-
обладают свойством нуль—устойчивости, применим метод A4.83) к реше-
решению задачи Коши для уравнения у' = 0. В этом случае / н 0, Ф = 0 и
уравнение A4.83) принимает вид
+ <*1Уп + ¦¦¦ +
= 0.
A4.86)
Такие уравнения называют линейными однородными разностными
уравнениями k-го порядка с постоянными коэффициентами.
Пусть y*h — решение того же уравнения, .соответствующее возму-
возмущенным начальным значениям у*, у*, ..., у?_{. Тогда в силу линейно-
линейности уравнения погрешность tn = уп - у* также является его решением:
+ - + <х)?п-Ы = 0.
A4.87)
Будем искать частное решение уравнения A4.87) в виде е„ — qn.
Подставляя ?n+i-j = ?п+1'-? 0 = 0, 1, ..., к) в A4.87), и сокращая на об-
454
щий множитель
уравнению
видим, что величина q должна удовлетворять
A4.88)
которое называют характеристическим уравнением, соответствующим
методу A4.83). Многочлен Р (q) = aoqk + а^ + ... + afc называется
характеристическим многочленом.
Приведем некоторые факты, известные из теории линейных разно-
разностных уравнений. Пусть q — корень уравнения A4.88) (вообще говоря,
комплексный). Тогда сеточная функция ега = qn является решением
разностного уравнения A4.87). Если же q — кратный корень кратности
m > 2, то ему отвечают частные решения qn, nqn, n2qn, ..., nm'1qn. Опи-
Опишем теперь структуру общего решения разностного уравнения. Пусть
9ь 92i •••) <?г — корни характеристического уравнения, а Ш], т2, ..., тТ —
их кратности (mi + m2 + ... + mr ~ k). Тогда всякое решение урав-
уравнения A4.87) может быть представлено в виде1
?„=
I =0
ТП2-1
Е с
тг-1
Е с
(=о
A4.89)
В частности, если все корни qu q2, .., qr — простые, то для всякого
решения уравнения A4.87) справедливо представление
?n= cl9"+ с2?«+ ... + crqnr.
Оказывается, что наличие или отсутствие у метода A4.83) нуль-
устойчивости определяется исключительно расположением корней
характеристического уравнения.
Будем говорить, что выполнено корневое условие, если все корни q\,
q2, ..., qT характеристического уравнения лежат внутри или на границе
единичного круга комплексной плоскости (т.е удовлетворяют условию
|gt| < 1, г = 1, 2, ..., г), причем на границе единичного круга нет крат-
кратных корней. Заметим, что в силу равенства A4.30) число q = 1 всегда
является корнем характеристического уравнения.
Теорема 14.9. Для того чтобы метод A4.83) обладал нуль-
устойчивостью, необходимо и достаточно, чтобы выполнялось корне-
корневое условие.
о Ограничимся доказательством необходимости выполнения корне-
корневого условия. Предположим, что метод обладает свойством нуль-устой-
1 Если среди корней характеристического уравнения имеется корень q — 0
кратности s, то представление A4 89) верно при п ^ s.
455

чивости, а корневое условие не выполнено. Тогда характеристическое
уравнение имеет либо корень q такой, что |д| > 1, либо корень q
кратности т > 2 такой, что \q\ = 1. В первом случае сеточная функ-
функция е'1 со значениями en = eqn есть решение разностного уравнения
A4.87), соответствующее заданию начальных значений е, = eql (i = 0,
1, ..., Jfc-1). Во втором случае решением, соответствующим заданию
начальных значений е, = ?igl (i = 0, 1, ..., it - 1), является функция е'1
со значениями en = enqn. И в том, и в другом случаях благодаря
выбору ? начальные погрешности могут быть сделаны сколь угодно
малыми, но в то же время |еп| -> <*> при п -»оо.
Т - to
Учитывая, что N =
оо при Л -> 0, получим | у^ - yN\ =
— |е#| -» а> при h -> 0, т.е. неравенство A4.85) не может выполняться
для всех k. Итак, необходимость корневого условия доказана. |Р
Теорема 14.10. Методы Руте—Кутты и Адамса обладают
свойством нуль-устойчивости.
а Методам Рунге—Кутты соответствует однородное разностное
уравнение ут1 - уп = 0, а ему, в свою очередь — характеристическое
уравнение q - 1 =0. Последнее имеет один простой корень q = 1, т.е.
корневое условие выполнено.
Аналогично, ^-шаговому методу Адамса соответствует разностное
уравнение упц - уп + Q-yn-i + ... + O-j/n-Ы = 0, а ему — характеристи-
характеристическое уравнение qk - q^1 = 0. Последнее имеет один простой корень
}i = 1 и корень q2 = 0 кратности Jb - 1, т.е. корневое условие здесь
также выполняется.ИГ
Пример 14.17. Рассмотрим метод
Уп*\ + Уп~ 2уп-1 _ 5/п + /п-1
ЗЛ
б
A4.90)
имеющий второй порядок аппроксимации1. Попытаемся применить его для
численного решения задачи Коши y'(t) = cos t, у @) = 0. Заметим, что функ-
функция у (<) = sin< является ее решением.
Возьмем шаг h = 0.1. Положим jfo = 0 и в качестве второго начального
значения, необходимого для расчета по методу A4.90), примем эд = 0.1. Так
как у @.1) = 0.099833..., то абсолютная погрешность значения у\ не превышает
2-Ю.
1 В наличии второго порядка аппроксимации можно убедиться самосто-
самостоятельно.
456
График полученного приближения изображен на рис. 14.13. При t > 0.7
погрешность уже становится заметной. Далее она быстро развивается и при
t и 1.4 потеря точности становится катастрофической. Попытка увеличить
точность решения за счет уменьшения шага вдвое приводит лишь к еще более
быстрому нарастанию погрешности. Полная потеря точности происходит здесь
уже при t и 0.9. Проверим теперь, выполняется ли для метода A4.90) корне-
корневое условие. Характеристическое уравнение имеет вид q2 + q — 2 = 0. Корня-
1.0
0.3
0.6
ом\
о.г
ЛриВмлкенное
решение, шаг
h-0.1
aoV-л—i—i—i—i—i—i—i—У—i—i—,—,—,—,—,
0.0 0.1 0.1 0.3 ОМ 0.S US ОЛ 0.8 0.91.0 U 1.2 13 /A I.S t
Рис. Ц.13
ми уравнения являются числа fl = 1, ф = -2. Так как |ф| = 2 > 1, то
корневое условие нарушено. Отсутствие у метода A4.90) нуль-устойчивости и
служит причиной наблюдаемого неконтролируемого роста погрешности. Такого
рода колебания приближенного решения, вызванные ростом погрешности,
иногда называют четно—нечетной болтанкой1.
Таким образом, для того чтобы численный метод можно было
использовать на практике, необходимо, чтобы он был нуль—устойчи-
нуль—устойчивым. Игнорирование этого требования даже для методов, обладающих
высоким порядком аппроксимации, приводит к катастрофической
потере точности.
1 Конечно это не математический термин, а жаргон.
457

Оказывается, что для линейных многошаговых методов выполнение
корневого условия гарантирует не только нуль-устойчивость метода, но
и устойчивость метода на конечном отрезке по начальным значениям и
правой части в смысле определения устойчивости A4.28), введенного в
§ 14.2.
*? L. Предполо-
Теорема 14.11. Пусть выполнено условие |/'|
Тогда метод A4.82)
жим, что линейный многошаговый метод A4.82) удовлетворяет
корневому условию и при /30 Ф 0 (т.е. для неявного метода) выполнено
дополнительное условие на шаг: h < h = 11 J
2\
устойчив на конечном отрезке.
Доказательство этой теоремы можно найти в [71]
2. Абсолютная устойчивость. Как уже отмечалось в § 14.1, необхо-
необходимость решения задачи Коши на больших временных отрезках [to, T\
возникает в самых различных областях науки и техники. Наибольший
интерес в этих случаях представляет изучение устойчивых решений.
Отметим, что нуль—устойчивость гарантирует устойчивое развитие
погрешностей при h -> 0 только в том случае, когда отрезок интегриро-
интегрирования [to, 7] фиксирован Однако наличие нуль—устойчивости вовсе не
исключает того, что сколь угодно малая погрешность в начальных
значениях при неограниченном росте tn (при Г->оо) может приводить
к сколь угодно большой погрешности решения. Значительную часть
таких заведомо непригодных для решения задачи Коши на больших
временных отрезках методов можно отбросить, если исследовать
результат их применения к решению модельной задачи
у' - Ху, у (tQ) = Уо.
A4.91)
Напомним (см. § 14.1), что решение этой задачи устойчиво по Ляпуно-
Ляпунову, если комплексный параметр А удовлетворяет условию ReA ^ 0, и
асимптотически устойчиво, если ReA < 0.
Большинство используемых дискретных методов (в том числе и
методы Рунге—Кутты и Адамса) в применении к задаче A4.91) стано-
становятся линейными и приобретают вид
1 k
-hE
+\-} = A
A4.92)
Здесь fij(h\) — некоторые зависящие от величины z = Xh функции.
В силу линейности уравнения A4.92) ошибка еп = уп - у*, возни-
458
кающая из-за погрешностей в начальных значениях, удовлетворяет
тому же уравнению:
i к
it
= XT,
Перепишем это уравнение в виде
А:
? Ъ(г)гп*\-] - О,
A4.93)
где yj(z) = а} - zfij(z), z — hX. Заметим, что A4.93) — это линейное
однородное разностное уравнение. Поэтому для того чтобы при
фиксированном z погрешность еп оставалась ограниченной при п -» оо,
необходимо и достаточно выполнение корневого условия для отвеча-
отвечающего уравнению A4.93) полинома.
Назовем метод A4.83) абсолютно устойчивым для данного z = hX,
если при этом z все корни полинома устойчивости
P(q,z)=
A4.94)
лежат в комплексной плоскости внутри единичного круга и на границе
этого круга нет кратных корней. Множество D точек комплексной
плоскости, состоящее из тех z, для которых метод абсолютно устойчив,
называют областью абсолютной устойчивости метода.
Пример 14.18. Найдем область абсолютной устойчивости метода Эйлера.
Применительно к модельному уравнению у = Ху расчетная формула
метода Эйлера принимает вид j/n+i = уп + hXyn. Запишем соответствующее
разностное уравнение для погрешности
е„ч - A + hX)en = 0 A4.95)
и заметим, что полином устойчивости Р (q, z) — q— A + z) имеет один прос-
простой корень 9=1 + z. Область абсолютной устойчивости состоит здесь из тех
z = hX, для которых 11 + z\ < 1, и представляет собой в комплексной плоско-
плоскости круг единичного радиуса с центром в точке zq = -1 (рис. 14.14, а).
Тот же результат нетрудно установить, не используя полином устойчивости
и корневое условие. Действительно, из уравнения A4.95) следует, что ?п —
= A + hX)n?,Q. Поэтому |еп| = |1 + ЛА|п?о и ?п -» оо при п •* оо, если |l +
+ ЛА | > 1. В этом случае метод не является устойчивым. Наоборот, если
|1 + АА| < 1, то |еп| < |ео| и метод устойчив.
459

1ml
Рис. Ц.Ц
Пример 14.19. Найдем области абсолютной устойчивости для неявного
метода Эйлера A4.24), правила трапеций A4.25), метода Эйлера—Коши A4.61)
и усовершенствованного метода Эйлера A4.62).
Применительно к модельному уравнению неявный метод Эйлера принимает
вид j/n+1 = уп + ftAj/n*). Соответствующий полином устойчивости A - z)q - 1
имеет единственный корень q = A - г)'1. Условие | ?| < 1 эквивалентно здесь
условию 11 - г| > 1. Таким образом, область устойчивости представляет собой
внешнюю часть единичного круга с центром в точке 2^=1 (рис. 14.14, б).
Для правила трапеций уп+\ = уп + — (уп + yn+i) полином устойчивости
2 Z
Р (q, г) = A - -) q - A + -) имеет корень q = B + z)/B - z). Условие | q\ <
4 1 эквивалентно здесь неравенству Rez < 0. Поэтому область устойчивости
представляет собой левую полуплоскость (рис. 14.14, в).
Применительно к уравнению у' = Ху расчетные формулы методов A4.61) и
A4.62) совпадают: j/n+1 = уп + — B + h\)yn. Корнем полинома устойчивости
Z2 Z1
Я - 0- + г+2~) является q — 1 + z + —. Область абсолютной устойчивости
изображена на рис. 14.14, «. Для сравнения на рис. 14.14, д схематично
изображена область абсолютной устойчивости метода Рунге— Кутты четвертого
порядка точности.
460
Предположим, что параметр Л, входящий в модельное уравнение
A4 91), отрицателен. Тогда условие абсолютной устойчивости метода
Эйлера 11 + h\ \ < 1 оказывается экзивалентным неравенству
A4.96)
Такое же ограничение на шаг возникает при использовании метода
Эйлера—Коши и усовершенствованного метода Эйлера. В то же время
метод Рунге—Кутты четвертого порядка точности оказывается абсо-
абсолютно устойчивым при выполнении чуть менее ограничительного
условия
h < h0 и
2.8
A4.97)
Отметим, что при А < 0 неявный метод Эйлера и правило трапеций
оказываются абсолютно устойчивыми при любых h.
3. yl-устойчивость. Для того чтобы исключить ограничение на шаг
h при решении устойчивой по Ляпунову модельной задачи A4.91),
необходимо потребовать, чтобы область абсолютной устойчивости
метода включала в себя полуплоскость Rez < 0. Численный метод,
обладающий таким свойством, называют А-устпойчивым.
Примерами Л-устойчивых методов служат неявный метод Эйлера и
правило трапеций. В то же время метод Эйлера и метод Рунге—Кутты
четвертого порядка точности не являются Л-устойчивыми.
§ 14.9. Неявный метод Эйлера
Как следует из результатов предыдущего параграфа, простейшим
представителем семейства ^устойчивых методов является неявный
метод Эйлера
Уп*\ - Уп+
A4.98)
Как нетрудно понять, геометрическая интерпретация одного шага
метода A4.98) заключается в том, что решение на отрезке [tn, tn+{\
аппроксимируется касательной у = ym\ + y'(tn*i)(t - tn*i), проведен-
проведенной в точке (<п+ь Уп*\) к интегральной кривой, проходящей через эту
точку (рис. 14.15).
Достоинства неявного метода Эйлера проявляются при решении
461

»»
Рис. Ц.15
задачи
дифференциальных уравнений, имеющих
устойчивые по Ляпунову решения. Как
уже отмечалось в § 14.2, достаточным
условием такой устойчивости является
выполнение одностороннего условия
Липшица /' < 0.
Пусть yh — решение дискретной задачи
Коши для уравнения A4.98)
соответствующее начальному условию
a y
*h —
решение возмущенной
A4.99)
где (т/i = -» а при h -» 0.
1 - ah
Из того, что неявный метод Эйлера устойчив и имеет первый поря-
порядок аппроксимации, вытекает (в силу теоремы 14.4) его сходимость с
первым порядком. Приведем соответствующий результат.
Теорема 14.14. Пусть функция f удовлетворяет условию f < 0.
Тогда для неявного метода Эйлера справедлива следующая оценка
погрешности:
max \уп-у*\ < ( \y"(t)\dl-h.
t0
A4.102)
Если же функция f удовлетворяет условию /' < а < 0, то верна
оценка
Аналогично теореме 14.5 можно доказать следующий результат.
Теорема 14.12. Пусть д
Тогда справедливо неравенство
max \yn-y*\<\uo-y^\+h'X\i>n\, A4.100)
Теорема 14.12. Пусть функция f удовлетворяет условию /' < 0.
ЛГ-1
А Ъ\фп\,
k
означающее, что неявный метод Эйлера устойчив на конечном отрез-
отрезке.
Заметим, что неравенство A4.100) является дискретным аналогом
оценки A4.16), справедливой для погрешности решения задачи Коши
(при этом К (Т) = 1). Следует отметить, что оно верно для метода
A4.98) при любых А, в то время как для явного метода Эйлера это
неравенство имеет место только если -i ^ /' < 0 и А ^ /to = 2/L.
Для неявного метода Эйлера справедлив и дискретный аналог
оценки A4.17).
Теорема 14.13. Пусть функция f удовлетворяет условию
/' < а < 0. Тогда справедливо неравенство
max \фк\,
A4.101)
max \Уп-уп\ < у-
0< '"
А А,
A4.103)
где М2 = max |y"(<)|.
Последняя оценка замечательна тем, что ее правая часть не растет
с ростом Т, если вторая производная решения ограничена.
§ 14.10- Решение задачи Коши для систем
обыкновенных дифференциальных уравнений
и дифференциальных уравнений m-го порядка
1. Задача Коши для систем дифференциальных уравнений первого
порядка. Как правило, возникающие в приложениях проблемы приво-
приводят к необходимости решать задачу Коши не для одного дифферен-
дифференциального уравнения, а для систем дифференциальных уравнений
вида
= Ж*.
»2'@ = Ш, й@. »г@. ¦¦- Ы0)
462
A4.104)
463

Здесь yi(t), УгС)) •¦•> Jm(') — искомые функции, значения которых
подлежат определению при <б[<о, Т]- В момент времени i = <o задаются
A4.105)
yi(<o) = Ую, Уг(<о) = Уго, -, Ут(<о) = Уто,
определяющие начальное состояние физической системы, развитие
которой описывается уравнениями A4.104).
Введем вектор-функции у (t) = (yi(t), y2(t), ..., ym(t))r, f(t, y) =
= Ш<> У), h (*, У), ¦¦-, fm(t, У))т и вектор ft = (y10, y2o, ¦¦-, Уто)т- Тогда
задачу Коши A4.104), A4.105) можно записать в компактной форме:
!'(*)=/(«, f@),
»(*о) = *>•
A4.106)
A4.107)
Для того чтобы охватить ряд важных для технических приложений
задач (электротехника, радиотехника и др.), будем считать, что функ-
функции ух и /, (i = 1, 2, ..., т) могут принимать комплексные значения.
2. Разрешимость задачи Коши. Пусть Пт — множество таких точек
(i, у), для которых t€[t0, Т], а уь у2, ...., ут — произвольные
комплексные числа. Это множество будем называть слоем. Будем, как
m _ m 1/2
и ранее, использовать обозначения (у, г) — S ytzt и |у| = (Е |у,|2)
«-1 t=i
для скалярного произведения и нормы m-мерных комплексных
векторов.
Сформулируем аналог теоремы 14.1 о разрешимости задачи Коши.
Теорема 14.15. Пусть вектор-функция /(/, у) определена и
непрерывна в слое Пг- Предположим также, что она удовлетворяет
условию Липшица
l/(*,fl)-/(<,f2)l<i|fl-fcl, A4.108)
для всех <о ^ t < Т и произвольных yj, уг, где L > 0 — некоторая посто-
постоянная (постоянная Липшица).
Тогда для каждого начальною значения ft существует единственное
решение у (<) задачи Коши A4.106), A4.107), определенное на отрезке
[к,Ц.
Замечание 1. Можно показать, что если функции /i, /2, ..., fm
непрерывно дифференцируемы по ylt yi, ..., ут, то условие Липшица
A4.108) выполняется с постоянной L тогда и только тогда, когда
матрица Якоби
464
/;с») =
, У) f[yii, У) ... fxy(t, у)
- Г2у (*, у)
УЯ1
удовлетворяет неравенству |/'(<, уI < X.
Замечание 2. Теорема 14.16 остается справедливой, если в ее
формулировке условие Липшица A4.108) заменить менее ограничи-
ограничительным односторонним условием Липшица
Jft -
«г|у, -
A4.109)
Назовем систему дифференциальных уравнений диссипативной,
если вектор-функция /удовлетворяет неравенству
Re(f(t,m)-f(t, fc), л - fc) < 0
(т.е. если /удовлетворяет одностороннему условию Липшица с посто-
постоянной <т = 0).
3. Устойчивость решения задачи Коши. Приведем аналог теоремы
14.3.
Теорема 14.16. Пусть выполнены условия теоремы 14.15.
Далее, пусть у (<) — решение задачи A4.106), A4.107), a y*(t) —
решение задачи
A4.110)
A4.111)
Тогда справедлива оценка
max
Т
\
A4.112)
выражающая устойчивость на конечном отрезке [t0, T\ решения задачи
UT-t )
Коши по начальным значениям и правой части. Здесь К (Т) — е
Если в теореме 14.15 условие Липшица A4.108) заменить односто-
465

ронним условием A4.109), то оценка A4.112) будет выполнена с посто-
янной К (Т) = е при а > 0 и с постоянной К (Т) = 1 при а < 0.
Следствие. Если система A4.106) диссипативна, то справед-
справедлива оценка
max
A4.113)
Замечание. Можно показать, что если условие A4.109) вы-
выполнено с постоянной <т < 0, то для всех t?[to, T] справедлива оцен-
оценка
If 0)" 1*0I
llb-fo*l
max
A4.114)
По аналогии со случаем одного дифференциального уравнения (см.
§ 14.1) рассмотрим вопрос об устойчивости решения задачи Коши к
возмущениям начальных данных при Т -* <х>. Будем считать, что на
каждом отрезке [to, 1\{to < T — произвольно) неравенство A4.109)
выполнено с некоторой постоянной а = о\Т). Тогда решение у (<)
определено для всех <о ^ < < °°- Пусть у*(<) — решение задачи A4.110),
A4.111), отвечающее произвольному начальному значению у* и
ф (f) = 0. Будем называть решение задачи Коши A4.106), A4.107)
устойчивым по Ляпунову, если справедлива оценка max |у(<) -
1o<t'<T
~ У*0I ^ -^Ifo ~ foli гДе постоянная К не зависит от N. Если
дополнительно известно, что |у (<) - !*(<)! ¦* 0 при i -» оо, то решение
называется асимптотически устойчивым.
Замечание 1. При ф (t) = 0 из неравенства A4.113) получаем
оценку max |jO) - у*0I < lib - Jq|. Поэтому всякое решение
диссипативной системы является устойчивым по Ляпунову.
Замечание 2. Предположим, что одностороннее условие Лип-
Липшица A4.109) для всех <о < < < <» выполняется с одной и той же
постоянной а < 0. Тогда при ф (<) = 0 из неравенства A4.114)
получаем оценку
If 0)" 1*0I
||Ь-»0*|,
откуда следует, что \у (<) - y*(t)\ -* 0 при / -» оо, те. решение у (/)
асимптотически устойчиво.
4. Система линейных уравнений с постоянными коэффициентами.
Рассмотрим систему
'(t) = Ay(t),
A4.115)
являющуюся простейшим примером системы дифференциальных
уравнений первого порядка; здесь А — квадратная матрица порядка
т. В теории численных методов решения систем дифференциальных
уравнений система A4.115) играет роль, аналогичную той, которую
при исследовании методов численного интегрирования одного уравне-
уравнения у' — /(<, у) выполняет модельное уравнение y'(t) = \y (t) (см. §
14.1).
Напомним структуру решения системы линейных уравнений с по-
постоянными коэффициентами в наиболее простом и важном случае,
когда матрица А имеет простую структуру. В этом случае существует
набор в], в2, ..., ет собственных векторов матрицы А, соответствующих
собственным значениям Aj, A2, ..., Am, который образует базис в прост-
пространстве m-мерных векторов. Матрица Р, столбцами которой служат
векторы ei, e2, ..., ет, не вырождена и такова, что
= A =
А; О
О А2
0 0 ... А„
A4.116)
Обозначим через z\(t), Z2(i), ..., zm(t) координаты вектора у (t) в базисе
ei, ..., еп. Так как
у @ = *,(l)ei + z2(t)e2 + ... +
A4 117)
то вектор у (<) связан с вектором г (<) = (z\(t), z2(t), ..., zm(t))T равенст-
равенством у (t) = Pz(t). Умножив обе части системы A4.115) слева на Р~1,
получим для вектор—функции z (<) систему уравнений
z'(t) = Az(t).
466
467

В силу диагональной структуры матрицы А эта система распадается на
т независимых дифференциальных уравнений
't(t) =
= 1,2, . ., т.
A4.118)
Заметим, что уравнение A4.118) для i-й компоненты вектора есть
модельное уравнение с параметром Л = Л,.
Таким образом, в рассматривармом случае интегрирование системы
линейных дифференциальных уравнений эквивалентно интегрирова-
интегрированию т модачьных уравнений A4 118). Решая каждое из них, получим
z,(<) =
, с, = гг(*о) и в силу равенства A4.117) находим
Здесь с = (с,, с2, ..., cm)T =
Пусть е (<) = у (t) - y*(i) — погрешность решения, вызванная пог-
погрешностью начальных значений ?о = 9Ь - у*- В силу линейности сис-
системы A4.117) погрешность является решением той же системы: е'@ —
= Ае (I). Следовательно,
е @ = ?
t=i
A4.119)
стоянных г, =
i = 1, 2,
m Наличие в решении задачи
где а = (а,, а2, ..., ат)т = Р'е0 '
Формула A4.119) позволяет сделать ряд важных выводов В частно-
частности, и:1 нее следует, что решение системы A4 115) с постоянной матри-
матрицей А простой структуры устойчиво по Ляпунову тогда и только
тогда, когда ReAt < 0 для всех i — 1,2, . ., тп и асимптотически
устойчиво тогда и только тогда, когда ReAt < 0 для всех i = 1, 2,
..., тп. Отметим также, что в отличие от случая одного дифференци-
дифференциального уравнения для систем характерно наличие тп временных по-
1
|ReA,|
физических компонент с существенно различными временными посто-
постоянными может привести к серьезным затруднениям при численном
решении соответствующих задач Более подробно этот вопрос рассмат-
рассматривается в следующем параграфе.
Пусть теперь y*(t) — решение нелинейной системы
(»Т@ = /(<.»•(<))> 04.120)
отвечающее возмущенному начальному условию у*(<о) = Vq Вычитая
из уравнения A4.120) уравнение y'(i) = f(i, у {t)) и используя приб-
приближенное равенство
468
<, »*(*)) " f(t, У @)
@ " »'@).
получаем, что погрешность е @ = У @ ~ »*@ удовлетворяет прибли-
приближенному равенству
Таким образом, можно предположить, что в малой окрестности точки
Gi У (')} эволюция погрешности е @ происходит примерно так, как и
для системы A4.117), т.е.
е @
t=i
Здесь А, и е, (« = 1, ..., тп) — собственные значения и собственные
векторы матрицы А = f'(t, у A)).
5. Понятие о численных методах решения задачи Коши для систем
уравнений первого порядка. Описанные выше применительно к реше-
решению задачи Коши для одного уравнения методы можно использовать
и для систем уравнений первого порядка, причем форма их записи
претерпевает минимальные изменения. Следует лишь заменить в рас-
расчетных формулах числа уп на векторы уп = (у1п, у2п, ..., Уяп)т,
функцию / — на вектор—функцию / и т.д. Ё результате дискретное
уравнение A4.18) преобразуется в систему дискретных уравнений
9п*1-к, ¦¦-, 9п,
Например, расчетная формула метода Эйлера уп+] = уп + Л/(<„, уп)
применительно к решению системы A4.106) принимает вид
9п*1 = 9п+
Покоординатная запись этого соотношения выглядит так:
У1,п*\ = У\п + Л/(<п, ton, У2п, •¦•, Утпп),
У2,п*\ = V2n + V2(<n, ton, УЪп, ¦¦¦, Утп),
Ут,п*1 — Утр. + ЛЦ<п> ton, Угп, ¦¦¦, Утп),
Аналогично, метод Рунге—Кутты четвертого порядка точности
A4.70) порождает для систем дифференциальных уравнений первого
порядка следующий метод:
= Уп
469

? ,„
*,
* *(, 2)
Теория численных методов решения задачи Коши для систем
дифференциальных уравнений имеет много общего с соответствующей
теорией решения задачи Коши для одного дифференциального урав-
уравнения. В частности, справедливы аналоги всех изложенных выше
результатов, касающихся устойчивости и сходимости дискретных
методов на конечном отрезке. Однако имеют место и существенно
новые явления. Один из таких эффектов-жесткость — будет рассмот-
рассмотрен в следующем параграфе. Прежде чем переходить к его изложению,
выясним, какие изменения появляются в случае применения дискрет-
дискретных методов к решению задачи Коши для системы уравнений с посто-
постоянными коэффициентами A4.115).
Рассмотрим линейный многошаговый метод
\ S
Предположим для простоты, что матрица А имеет простую структуру.
Положим Zn = P^jfn, где Р — матрица, удовлетворяющая равенству
A4.116). Умножив обе части уравнения A4.121) на матрицу Р слева и
учитывая, что
получим соотношение
к
к
i-j = Е /?;Ayn+i-;.
}0
Так как матрица Л — диагональная, то оно эквивалентно следующей
системе уравнений для компонент вектора Zn = (zin, z2n, •••,
it
1 к к
1 S q,z, „¦]-, = Ь /J,Ai2,,nti-j, * = 1, 2, ..., m.
A4.122)
Заметим, что A4.122) есть не что иное, как результат применения
линейного многошагового метода к решению уравнений A4.18).
Таким образом, если решения системы A4.115) устойчивы по Ляпу-
Ляпунову, то для того чтобы погрешности еп оставались ограниченными
при п -» оо, необходимо потребовать, чтобы для всех г — 1, ..., m вели-
величина h\t принадлежала области D абсолютной устойчивости применя-
применяемого метода. Можно показать, что такой же вывод справедлив и для
методов Рунге—Кутты. Требование, чтобы h\t 6 D при всех г = 1, 2, ...,
470
m, для методов, не обладающих свойством ^-устойчивости, может
приводить к существенным ограничениям на величину шага h.
Предположим, например, что все собственные значения матрицы А
отрицательны. Тогда условие A4.96) абсолютной устойчивости метода
Эйлера приводит к следующему ограничению на длину шага интегри-
интегрирования:
2
Такое же ограничение на шаг возникает при использовании метода
Эйлера—Коши и усовершенствованного метода Эйлера. Метод Рун-
Рунге—Кутты четвертого порядка точности, как следует из неравенства
A4.97), оказывается абсолютно устойчивым при таком ограничении на
длину шага:
h < hn a
2.8
ma х | А, I
Следовательно, для явных методов шаг интегрирования должен не
превышать значения k0, пропорционального наименьшей из временных
постоянных системы.
6. Сведение задачи Коши для уравнения m-го порядка к задаче
Коши для системы уравнений первого порядка. Задача Коши для
дифференциального уравнения m-го порядка состоит в нахождении
функции у (<), удовлетворяющей при t > t0 дифференциальному
уравнению
ylm)(t) = f(t, y(t), y'(t), -, у(я
а при t = t0 - начальным условиям
У (<о) = Ую, У'(t0) = г/го, •••,
Рассмотрим функции z/,(<) = у (t), y2(t) - y'(t), ..., ym(t) = у*-11 (<)•
Заметим, что yi^t) = (ук-{) '(<). Поэтому введенные функции удовлетво-
удовлетворяют системе дифференциальных уравнений первого порядка
A4.124)
A4.125)
y2V) =
A4.126)
471

Начальные условия A4.125) в новых обозначениях принимают вид
УтЫ = УтО- A4.127)
= »Ю,
= У20,
Пример 14 21 Задача Коши для дифференциального уравнения второго
порядка у" = -25у + sin*, у@) = 0, »'@) = 1 введением новых искомых
функций й(*) = y(t), й@ = У '@ годится к эквивалентной задаче Коши
для системы дифференциальных уравнений первого порядка ух - щ, У2
- 25?/, х sirf. ^@) - 0. WO" = 1.
Для решения задачи Коши A4.124), A4.125), приведенной к виду
A4126) A4 127) можно воспользоваться известными методами или
даже готовыми программами. Часто именно так и поступают. Следует
все же иметь в виду, что вычисления можно организовать и так, что
сведение уравнения A4.124) к системе A4.126) не потребуется. Напри-
Например, для решения дифференциального уравнения второго порядка
у" = f(i у) используется ряд специальных методов [88]. Одним из
наиболее'популярных среди них является метод Нумерооа четвертого
порядка точности:
Уп-l _
Л2
L
12
Ю /0„, Уп)
§ 14.11. Жесткие задачи
1 Понятие о жестких задачах. В последние годы при решении
задачи Коши явными методами Рунге-Кутты и Адамса значительное
число „следователей сталкивается с весьма неожиданным и неприят-
„„„ явчгнпем. Несмотря на медленное изменение искомых функции
ргкчет приходится вести, казалось бы, с неоправданно мелким шагом
h Ben попытки увеличить шаг и тем самым уменьшить время решения
задачи приводят лишь к катастрофически большому росту погрешно-
погрешности Обладающие таким свойством задачи получили название жест-
Кш. Сразу же подчеркнем, что жесткость является свойством задачи
Коши (а но используемых численных методов).
Жесткие задачи встречаются в самых различных областях науки и
техники Традиционными источниками появления таких задач явля-
являются химическая кинетика, теория ядерных реакторов, теория^автома-
теория^автоматического управления, электротехника, электроника и т.д. Жесткие
затчи «ошикают также при аппроксимации начально-краевых задач
для уравнений в частных производных с помощью полудискретных
методов (методов прямых).
Трудности, возникающие при численном решении жестких задач,
продемонстрируем на таком примере.
Пример 14.22. Вычислим значения приближенного решения задачи Коши
y'(t) = -25у (<) + cos* + 25sin<, у @) = 1, A4.128)
используя метод Эйлера. Решением этой задачи является функция у (<) =
= sint + еЧ Как нетрудно видеть (рис. 14.16), на начальном переходном
участке 0 < t < 0.2 решение быстро меняется. Однако уже через небольшой
интервал времени переходная часть решения e5t практически исчезает и
решение становится медленно меняющимся.
0.5
Рис. Ц.16
Естественно, что приближенное решение на переходном участке приходится
вычислять, используя достаточно мелкий шаг. Однако при t > 0.2, когда
переходная часть решения, казалось бы, уже практически отсутствует, возни-
возникает желание перейти к вычислению со сравнительно крупным шагом.
Предположим, что при t - 0.2 найдено значение решения у @.2) и 0.205 с
точностью ? = 10~3. Возьмем шаг h = 0.1 и будем вычислять решение при
t > 0.2, используя метод Эйлера:
473
472

Уп*1 = Уп
cos<n + 25sin<n).
Полученные значения приближений и точные значения решения приведены в
первых трех столбцах табл. 14.6. Соответствующая ломаная Эйлера изображе-
изображена на рис. 14.16. Как нетрудно видеть, метод ведет себя неустойчивым образом
и оказывается непригодным для решения рассматриваемой задачи при значе-
значении шага Л = 0.1. На конкретном примере мы убедились в том, что условие
абсолютной устойчивости A4.95) нарушать нельзя. В рассматриваемом случае
А = -25 и это условие равносильно требованию А < 0.08. Взяв удовлетворя-
удовлетворяющий этому условию шаг Л = 0.025, получим вполне приемлемое решение (см
табл. 14.6).
Таблица 14.6
t
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0
1.1
1.2
1.3
1.4
1.5
Точное
решение
0.205
0.296
0.389
0.479
0.565
0.644
0.717
0.783
0.841
0.891
0.932
0.964
0.985
0.997
Метод
Эйлера;
Л = 0.1
0.205
0.287
0.404
0.460
0.597
0.600
0.787
0.683
0.996
0.664
1.277
0.451
1.759
-0.158
Метод
Эйлера;
Л = 0.025
0.205
0.296
0.390
0.480
0.565
0.644
0.718
0.784
0.842
0.892
0.932
0.964
0.986
0.996
Неявный
метод
Эйлера;
Л = 0.1
0.205
0.304
0.391
0.479
0.564
0.643
0.716
0.782
0.840
0.890
0.930
0.962
0.984
0.996
Неявный
метод
Эйлера;
Л = 0.3
0.205
0.478
0.714
0.886
0.980
Попробуем теперь воспользоваться для решения задачи A4 128) неявным
методом Эйлера:
Уп*\ = Уп
Напомним, что он Л-устойчив и, следовательно, абсолютно устойчив для всех
значений Л. Используя для нахождения решения формулу
'I
Рис. Ц.П
tn;
t~*t
Рис. Ц.18
474

_ Уп
при Л = 0.1 получим значения, совпадающие с соответствующими значениями
решения с точностью 2-Ю (см. табл. 14.6). Если же нас устраивает точность
? = 6-Ю, то шаг Л можно утроить. Вычисленные с шагом h = 0.3 значения
также указаны в табл. 14.6.
Приведенная в примере ситуация типична для жестких задач. При
использовании классических явных методов наличие в решении быст-
быстро меняющийся жесткой компоненты даже на том участке, где ее
значение пренебрежимо мало, заставляет выбирать шаг Л из условия
абсолютной устойчивости. Для жестких задач это ограничение приво-
приводит к неприемлемо малому значению шага Л. Поэтому численное реше-
решение таких задач требует применения специальных неявных методов.
Простейшим из них является неявный метод Эйлера. На рис. 14.17 и
14.18 проиллюстрировано принципиальное отличие результатов вычис-
вычислений, осуществляемых с помощью явного и неявного методов Эйлера.
2. Жесткие задачи для систем дифференциальных уравнений.
Рассмотрим задачу Коши для системы линейных дифференциальных
уравнений с постоянными коэффициентами
y'(t) = Ay(t).
A4.129)
Предположим, что А — матрица простой структуры и все собственные
числа этой матрицы имеют отрицательные вещественные части (ReAm <
^ ReAm-i< ... ^ ReAj < 0). Как отмечалось в предыдущем параграфе, в
этом случае решение задачи асимптотически устойчиво и представля-
представляется в виде
, (i) = с
Если среди собственных чисел At имеются числа с сильно различа-
различающимися значениями вещественных частей, то возникает проблема,
связанная с наличием в решении у компонент, имеющих существенно
1 „
различные временные постоянные г, = . . i. Через довольно корот-
|НеА,|
кий интервал времени поведение решения будет определяться наибо-
наиболее слабо меняющейся (медленной) компонентой решения. Так, если
ReAm < ... < ReA2 < ReA! < 0, то при < - <0 > г2 = . „ . . справедливо
| КеЛ2|
приближенное равенство у (<) и qe «i- В то же время применя-
476
емый для решения задачи Коши метод должен обладать свойствами
устойчивости, позволяющими подавлять наиболее быстро меняющуюся
(жесткую) компоненту сте
погрешности
е @ =
Отметим, что для медленной компоненты решения временной постоян-
постоянной является величина ( min iReAjtl), а для жесткой компоненты
погрешности — величина ( max iReAjtl) Их отношение и определяет
степень жесткости задачи.
Приведем применительно к системе A4.129) одно из определений
жесткости. Пусть ReAjt < 0 для всех it = 1, ..., т. Определим число
жесткости системы A4.129) с помощью формулы
max
s =
min
|ReAjt|
A4.130)
Систему уравнений A4.129) назовем жесткой, если для нее s > 1.
Пример 14.23. Рассмотрим систему
у' = -7501»- 24992,
z' = -7497»- 2503г,
у @) = 0, г @) = 4.
Собственные значения матрицы коэффициентов
Г-7501 -2499]
А =
-7497 -2503J
таковы; Aj — —4, Ат = -10000. Здесь число жесткости s = | = 2500 много
I Ai |
больше единицы и поэтому систему можно квалифицировать как жесткую.
Общее решение системы имеет вид
с2е00001, 2 (*) =
У @ = с,е-
Начальным значениям у @) — 0, z @) = 4 отвечает решение
,, (А — —f,-4t J- р-10000( -г / f\ — 4P-4t + p-10000(
477

Жесткая компонента решения здесь быстро затухает и через очень небольшой
интервал времени решение будет практически совпадать с у (<) = —e'4t, г (<) =
--= Зе"Ч
Решение этой задачи с помощью явных методов очень неэффективно.
Например, для метода Рунге—Кутты четвертого порядка точности условие
2.8
устойчивости л < г^—;—г в данном случае приводит к необходимости
~ max|ReAjt|
использования очень мелкого шага Л < 2.8-10~4.
Замечание. В приведенном выше наиболее простом определе-
определении жесткости требовалось, чтобы ReA^ < 0 для всех к. Более об-
общие современные определения жесткости [9], [26] не исключают
наличия собственных чисел At с положительными вещественными
частями при условии, что для них ReAt < max |ReAfc|.
К Km
В случае, когда матрица А зависит от t (т.е. решается система
линейных уравнений с переменными коэффициентами), число жестко-
жесткости также зависит от t и определяется по формуле A4.130), в которой
уже Хк = Л-кA)- Так как s = s (<), то система у' — A (t)y может
оказаться жесткой на одном интервале времени t и нежесткой — на
другом.
В настоящее время нет общепринятого математически корректного
определения жесткости задачи Коши для системы нелинейных уравне-
уравнений
»'=/(*,»)¦ A4-131)
Чаще всего эту задачу называют жесткой в окрестности точки
(Л У (J))> если жесткой является соответствующая линеаризованная
система
= Ay(t),
= fy(lyG))-
A4.132)
Ь подтверждение правомерности такого определения жесткости можно
сослаться на то, что (см. предыдущий параграф) погрешность Е (t)
решения нелинейной системы удовлетворяет приближенному равенству
?.'(<) й As (t) и поэтому в малой окрестности точки A, у (^погрешно-
(^погрешности решений линеаризованной системы A4.132) и системы A4.131)
должны вести себя примерно одинаковым образом.
К счастью, для того чтобы распознать жесткую задачу на практике,
iacxo совсем не обязательно проводить математически строгое ее ис-
исследование. Если система уравнений A4.131) правильно моделирует
473
реальное физическое явление, включающее процессы с существенно
различными временными постоянными, то соответствующая задача
Коши должна быть жесткой. Как правило, исследователь проявляет
интерес к изучению поведения медленно меняющихся характеристик
процесса в течение длительного времени. Наличие же быстро меня-
меняющихся физических компонент при использовании классических
явных методов решения задачи Коши заставляет его выбирать шаг А
порядка наименьшей из временных постоянных, что делает процесс
численного решения чрезвычайно дорогостоящим и неэффективным.
Существующие в настоящее время методы решения жестких задач
позволяют использовать шаг А порядка наибольшей из временных
постоянных, подчиняя его выбор только требованию точности.
Замечание 1. В последнее время задачу не принято квалифи-
квалифицировать как жесткую на переходном участке. Если исследователь
проявляет интерес к изучению переходного режима, то для нахож-
нахождения решения на переходном участке могут оказаться вполне
приемлемыми и явные методы Рунге—Кутты и Адамса.
Замечание 2. Обычно при определении жесткости делается
явное или неявное предположение о том, что среди собственных
чисел матрицы А отсутствуют такие, для которых |ImA,| > 1. Это
означает, что предполагается отсутствие быстрых осцилляции в
компонентах погрешности. Если же такие осцилляции возможны, то
необходимо использовать специальные методы подавления соответ-
соответствующих компонент погрешности.
3. Понятие о методах решения жестких задач. Для решения
жестких задач было бы желательно использовать Л-устойчивые ме-
методы, так как они не накладывают никаких ограничений на шаг А.
Однако оказывается, что класс таких методов весьма узок. Например,
среди явных линейных многошаговых методов нет А-устойчивых.
Доказано также, что среди неявных линейных многошаговых методов
нет А-устойчивых методов, имеющих порядок точности выше второго.
Многие из возникающих на практике жестких задач таковы, что
для них собственные значения матрицы Якоби удовлетворяют нера-
неравенству |arg (-А,)| < а (г = 1, 2, ..., т), где а > 0 — некоторое число.
В частности, если все собственные значения вещественны и
отрицательны, то указанное неравенство выполняется для любого
сколь угодно малого а > 0.
Для таких задач требование ^-устойчивости методов является
чрезмерным и его можно заменить менее ограничительным требовани-
требованием наличия у метода А ((^-устойчивости. Численный метод решения
479

задачи Коши называют А (а)-устойчиаым, если область его абсолют-
абсолютной устойчивости включает угол | arg(—г) | < а (рис. 14.19). В частно-
частности, при а — KJ1 определение А (о)-устойчивости совпадает с опреде-
определением Л-устойчивости.
Рис. 14-19
Рис. Ц.20
Известно, что среди явных линейных многошаговых методов нет
А (а)-устойчивых ни при каком а > 0. Однако среди неявных линей-
линейных многошаговых методов имеются А (а)-устойчивые методы высоко-
высокого порядка точности. Важный класс таких методов (формул диффе-
дифференцирования назад) относится к так называемым чисто неявным
методам:
1
Чисто неявные методы получаются в результате замены в системе
дифференциальных уравнений A4.131) при t - in*\ производной у'@
ее разностной аппроксимацией, использующей значения функции в
точках I^n, in, —¦> *п*1-к- Если Для этого используется односторонняя
разностная производная (см. § 12.2), то получается формула дифферен-
дифференцирования назад.
Приведем формулы дифференцирования назад при к = 1, 2, 3, 4,
имеющие /fc-й порядок точности
г — ./(,'n+li Уп+1,11 K —
n
(это неявный метод Эйлера);
In
— 1\Чг*1, tln+l), К —
A4.133)
A4.134)
6Л
— /('п+ь Уп+0) ^— 3;
- 48уга + Збуп-i - 16уп-2
12А
¦ = /(<п+1, Уп+i), fc= 4.
A4.135)
A4.136)
Напомним, что метод A4.133) является Л-устойчивым. Как видно из
рис. 14.20, а и 14.20, б, для формул A4.134) и A4.135) области их
абсолютной устойчивости почти целиком содержат левую полуплос-
полуплоскость Re.z < 0. Поэтому свойства устойчивости1 этих методов вполне
достаточны для решения большинства жестких задач.
Весьма популярный и широко используемый при решении жестких
задач алгоритм Гира основан на использовании формул дифференци-
дифференцирования назад порядка точности к = 1, 2, ..., 6 и представляет собой
метод с автоматическим выбором шага интегрирования и порядка
метода. Один из первых вариантов алгоритма реализован в форт-
ранной программе DIFSUB.
§ 14.12. Дополнительные замечания
1. К настоящему времени разработано большое число различных численных
методов решения задачи Коши и работа в этом направлении ведется очень
активно. Тем не менее наиболее популярными остаются классические методы
Рунге^—Кутты и Адамса, а также их современные модификации. Каждый из
этих двух классов методов имеет определенные достоинства и недостатки,
некоторые из них уже обсуждались выше. Не имея перед собой конкретной
задачи, вряд ли можно дать рекомендации в пользу того или иного метода,
тем более что до сих пор в этом вопросе нет достаточной ясности. Однако
ориентируясь на серьезное обсуждение оценки качества методов, приведенное в
книге [74], можно попытаться грубо описать ситуации, в которых они обладают
большей эффективностью. При этом следует иметь в виду, что одним из
основных показателей эффективности метода является количество вычислений
правых частей дифференциальных уравнений, которое требуется для достиже-
достижения заданной точности решения.
Предположим, что решаемая задача Коши не является жесткой. Предполо-
Предположим также, что вычисление правых частей дифференциальных уравнений не
является слишком трудоемкой операцией. Тогда целесообразно применение
методов Рунге—Кутты с автоматическим выбором шага, наиболее эффектив-
эффективным среди которых для широкого класса задач является метод Рунге^—Кут-
1 При 1 < к < 6 формулы дифференцирования назад обладают так называ-
называемой жесткой устойчивостью [68], [74].
480
16-28
481

ты—Фельберга пятого порядка точности. Если же к точности решения не
предъявляются слишком высокие требования, то хороший результат следует
ожидать и от применения классического метода Рунге—Кутты четвертого
порядка точности.
В том случае, когда вычисления правых частей трудоемки (на каждую из
них приходится в среднем более 25 арифметических операций) имеет смысл
предпочесть использование качественной программы, реализующей метод
Адамса с автоматическим выбором шага и порядка метода. По-видимому,
именно эти методы в будущем станут наиболее употребительными.
2. После того как приближенные значения уп решения задачи Коши в
узлах in (n = 0, 1, ..., N) определены, для вычисления значений решения у (t)
в промежуточных точках можно использовать интерполяцию. В связи с этим
полезно отметить, что наряду со значениями вектор-функции уп фактически
оказываются вычисленными значения производной у^ = /(<п, уп)- Поэтому в
данном случае для интерполяции естественно использование кубического
интерполяционного многочлена Эрмита или локального кубического сплайна
(см. гл. 11). Для методов первого или второго порядка точности вполне удов-
удовлетворительный результат дает использование линейной интерполяции.
3. Поиск эффективных методов решения жестких задач еще находится в
начальной стадии. Тем не менее разработан ряд популярных алгоритмов
(среди которых наиболее известен алгоритм Гира) и создано значительное
число качественных программ. Вопрос о наиболее эффективном методе реше-
решения жестких задач остается открытым и какие-либо рекомендации здесь
преждевременны. В последнее время выявилась достаточная перспективность
применения для решения таких задач специальных неявных методов Рун-
Рунге—Кутты [26]. Подчеркнем еще раз, что явные методы Рунге—Кутты для этой
цели совершенно непригодны.
4. Дополнительную информацию о методах решения задачи Коши (и
полезное обсуждение жестких задач) можно найти, например, в учебниках [9],
[14], [43], [60], [69], [71], [86]. Настоятельно советуем обратить внимание на две
весьма содержательные книги [74] и [88]. Вторая из них содержит систематиче-
систематическое и доступное широкому кругу читателей изложение численных методов
решения нежестких задач. Методам решения жестких задач специально посвя-
посвящены монографии [68], [26], последняя из которых содержит современный
взгляд на эту проблему.
Глава 15
РЕШЕНИЕ ДВУХТОЧЕЧНЫХ
КРАЕВЫХ ЗАДАЧ
Двухточечная краевая задача — это задача отыскания решения
обыкновенного дифференциального уравнения или системы обыкно-
обыкновенных дифференциальных уравнений на отрезке а < х < Ь при усло-
условии, что дополнительные условия на решение налагаются в двух точ-
точках аи Ь — "краях" отрезка [а, Ь] (отсюда — и название задачи).
Решить краевую задачу, вообще говоря, значительно труднее, чем
задачу Коши и для этого используются разнообразные подходы. Наи-
Наиболее распространены различные методы дискретизации, позволяющие
заменить исходную задачу некоторым ее дискретным аналогом. Полу-
Получающаяся дискретная краевая задача представляет собой систему
уравнений (возможно, нелинейных) с конечным числом неизвестных и
может быть решена на ЭВМ с помощью специальных прямых или
итерационных методов. Одним из простейших и весьма популярных
подходов к дискретизации является использование метода конечных
разностей. В §§ 15.2 и 15.3 рассматриваются некоторые из основных
моментов применения этого метода.
В § 15.4 дается представление о другом подходе к дискретизации
краевых задач. В нем описываются проекционные методы Ритца и
Галеркина и обсуждается один из их современных вариантов, имею-
имеющий большое практическое значение, — метод конечных элементов.
В заключение главы рассматривается метод пристрелки.
§ 15.1. Краевые задачи
для одномерного стационарного
уравнения теплопроводности
1. Дифференциальное уравнение и краевые условия. Рассмотрим
дифференциальное уравнение второго порядка
jz) + q(x) u = f(x), а<х<Ь. A5.1)
483

Оно называется одномерным стационарным уравнением теплопровод-
теплопроводности и возникает при математическом моделировании многих важных
процессов. Например, это уравнение описывает установившееся распре-
распределение температуры и (г) в теплопроводящем стержне длины / = b —
— а. В этом случае к (г) — коэффициент теплопроводности; w (х) =
= -it (г) - плотность потока тепла; { (х) — коэффициент теплоотда-
теплоотдачи (qu — мощность стоков тепла, пропорциональная температуре м);
/(г) — плотность источников тепла (при / < 0 — плотность стоков
тепла).
Уравнение A5.1) описывает также установившееся распределение
плотности нейтронов в реакторе, характеристики которого зависят от
одной пространственной переменной х. В такой трактовке1 и (х) — это
полный поток нейтронов, Jfc (х) — коэффициент диффузии, q (г) —
сечение поглощения, /(г) — плотность источников нейтронов. То же
уравнение описывает и стационарные процессы диффузии газов (раст-
(растворов) в пористых средах; и (х) рассматривается тогда как концентра-
концентрация диффундирующего вещества. Поэтому уравнение A5.1) часто
называют одномерным уравнением диффузии. Рассматриваемое уравне-
уравнение имеет приложения и в других областях техники и естествознания
(деформации струн и стержней, распространение электромагнитных
волн и т. д.)
Далее будем считать функции Jfc (x), q (x), /(х) заданными и пред-
предполагать, что выполнены неравенства
*(x)>Jfco>0, q(x)>Q.
A5.2)
Так как уравнение A5.1) является дифференциальным уравнением
второго порядка, то для того чтобы однозначно найти функцию
и (х) — распределение температуры в стержне, необходимо задать два
дополнительных условия. Простейшая постановка краевых условий
такова:
и (а) = иа, и F) = щ.
Краевые условия такого типа принято называть краевыми условиями
первою рода. Физическая интерпретация этих краевых условий состо-
состоит в том, что в рассматриваемой задаче на торцах стержня поддержи-
поддерживаются фиксированные значения температуры иа и щ.
Возможны и другие постановки краевых условий. Так, если извест-
известна плотность потока тепла через левый торец стержня, то условие
и (о) = иа можно заменить краевым условием второю рода:
Аналогичное условие для правого торца имеет вид
-Jfc F) «'F) = wb.
Основное внимание в этой главе будет уделено краевой задаче
?[«](*)=/(г), <.<х<6,
и (а) = «а, и (Ь) = щ.
A5.3)
A5.4)
-к (а) и'(а) = wa.
484
Здесь L — дифференциальный оператор, определяемый следующим
образом:
L[u](x)=-(k(x)u'(x))- + q(x)u(x).
2. Разрешимость' краевой задача. Будем считать, что коэффициен-
коэффициенты q и / непрерывны на отрезке [а, Ь], коэффициент Jfc непрерывно
дифференцируем на [а, Ь\ и выполнены условия A5.2).
Назовем дважды непрерывно дифференцируемую на отрезке [а, Ь]
функцию и (х) решением (классическим решением) краевой задачи
A5.3), A5.4), если и (х) является решением дифференциального урав-
уравнения A5.3) и удовлетворяет краевым условиям A5.4).
Приведем без доказательства известные из теории дифференциаль-
дифференциальных уравнений результаты о разрешимости рассматриваемой краевой
задачи и о гладкости ее решения.
Т е о р е м а 15.1. Решение краевой задачи A5.3), A5.4) существу-
существует и единственно.
Теорема 15.2. Пусть коэффициенты q и f являются т раз, а
коэффициент Jfc — т + 1 раз непрерывно дифференцируемыми на отрез-
отрезке [а, Ь] функциями. Toida решение и (х) краевой задачи A5.3), A5.4)
есть непрерывно дифференцируемая m + 2 раза на отрезке [а, Ь] функ-
функция.
3. Принцип максимума. Важным свойством уравнения A5.3) являет-
является наличие так называемого принципа максимума. Приведем один из
вариантов его формулировки.
Теорема 15.3. Пусть и (х) — решение задачи A5.3), A5.4).
Тогда если f {х) < 0, иа < 0, щ < 0, то и (х) < 0.
Теорема 15.3 имеет простой физический смысл. Если отсутствуют
источники тепла и температура торцов стержня неположительна, то ни
в одной из внутренних точек стержня температура не может стать
положительной.
Заметим, что произвольную дважды непрерывно дифференцируе-
дифференцируемую функцию и (х) можно рассматривать как решение краевой задачи
A5.3), A5.4), если специальным образом выбрать правую часть / и
краевые значения иа, щ, а именно положить f(x) = L [u](x), ua = « (а),
щ = и (Ь). Учитывая это замечание, сформулируем теорему 15.3 иным
образом.
485

Теорема 15.4. Пусть и (х) — дважды непрерывно дифференци-
дифференцируемая на отрезке [а, Ь] функция, удовлетворяющая неравенствам
L [и] < 0, и (а) < О, и (Ь) < 0. Тогда и (х) < 0.
Из теоремы 15.4 вытекает следующее утверждение.
Теорема 15.5 (теорема сравнения). Пусть и (x), v (x) — дважды
непрерывно дифференцируемые на отрезке [а, Ь] функции, удовлетворя-
удовлетворяющие неравенствам L [и] < L [v], и (а) < v (а), и (Ь) < v (b). Totda
u(x)<v (х).
4. Априорная оценка и устойчивость решения. Используя теорему
сравнения, можно вывести оценку максимума модуля решения и (х)
через данные краевой задачи.
Теорема 15.6. Справедлива следующая оценка решения краевой
задачи A5.3), A5.4):
max |и(х)| <тах{|иа|, Ы} + A'-max |/(х)|. A5.5)
[а, Ь) [а,Ь]
Здесь K=^,R = f ?-., 1= Ь-а.
4 а к (х)
Замечание 1. Неравенства типа A5.5) принято называть
априорными оценками решения.
Замечание 2. Если коэффициент Jfc (х) рассматривать как
коэффициент теплопроводности, то т-/~\ ~~ это коэффициент тепло-
* \х)
сопротивления, а К = ] т-7"\ ~ это полное теплосопротивление
а * (х)
стержня.
Замечание 3. При к (х) = 1 уравнение A5.3) принимает вид
-«'(г) + q (х) и (х) = f{x).
A5.6)
В этом случае R = / и оценку A5.5) можно уточнить следующим
образом:
max |и(*)| <тах{|ив|,
j- max |/(x)|.
[а,Ь]
A5.7)
Рассмотрим теперь вопрос о влиянии погрешностей задания крае-
краевых значений иа, щ и правой части / на решение краевой задачи.
Пусть и (х) — решение краевой задачи A5.3), A5.4), а и*(х) — решение
краевой задачи
L {и*](х) = Г(х), а<х<Ь,
486
Здесь f*(x) — непрерывная функция, рассматриваемая как приближен-
приближенно заданная (с погрешностью 6f*(x) = / (х) — /*(х)) правая часть урав-
уравнения; и*, «j — приближенно заданные (с погрешностями еа = иа —
— и*,?.ь=щ — «?) краевые значения.
Теорема 15.7. Справедлива оценка
max |и(г)-«*(г)| <max{|ee|, |е*|} + К- max \Sf(x)\, A5.8)
[a,b] [a,b]
tde К — та же постоянная, что и в неравенстве A5.5).
? Для доказательства достаточно заметить, что функция е (х) =
= и (х) — и*(х) является решением краевой задачи
L[e](x) = 6f(x),a<x<b,
е (а) = еа, е F) = еь,
и воспользоваться для оценки величины max |e (х)| теоремой 15.6. И
[а,Ь]
Из оценки A5.8) видно, что в случае, когда величина К не очень
велика, краевая задача A5.3), A5.4) хорошо обусловлена. Если же
#> 1, то задача является плохо обусловленной. В этом случае погреш-
погрешности порядка 6 задания правой части уравнений может отвечать
погрешность порядка Кб решения задачи. Ниже при рассмотрении
численных методов решения краевой задачи будем предполагать, что
она хорошо обусловлена.
Замечание. Если рассматривается устойчивость решения
краевой задачи для уравнения A5.6), то в оценке A5.8) следует
заменить К на Р/8.
§ 15.2. Метод конечных разностей:
основные понятия
Метод конечных разностей (или метод сеток) является одним из
универсальных и широко используемых методов решения краевых
задач. Его популярность во многом объясняется относительной просто-
простотой подхода к дискретизации дифференциальных уравнений. Суть
метода состоит в следующем. Область непрерывного изменения аргу-
аргумента заменяют конечным (дискретным) множеством точек (узлов),
называемым сеткой. Вместо функций непрерывного аргумента рассмат-
рассматривают функции, определенные только в узлах сетки, — сеточные
487

функции. Производные, которые входят в дифференциальное уравне-
уравнение и краевые условия, заменяют их разностными аналогами — линей-
линейными комбинациями значений сеточных функций в некоторых узлах
сетки. В результате краевую задачу заменяют дискретной краевой
задачей (разностной схемой), представляющей собой систему конечно-
конечного числа линейных или нелинейных алгебраических уравнений. Реше-
Решение разностной схемы (предполагается, что оно существует) принима-
принимают за приближенное решение краевой задачи.
Несмотря на кажущуюся простоту метода, при его использовании
приходится решать ряд проблем. Например, следует иметь в виду, что
для одной краевой задачи можно построить большое число различных
разностных схем, среди которых далеко не все пригодны для исполь-
использования на практике.
В этом параграфе мы покажем, как применяется разностный метод
для решения краевой задачи A5.3), A5.4), ограничиваясь для просто-
простоты изложения случаем уравнения с постоянным коэффициентом
it (х) — 1. В этом случае краевая задача принимает вид
-«"(*) + q(x)u(x) = f
и (а) = иа, и (Ь) = щ.
а<х<Ь,
A5.9)
A5.10)
1. Построение сетки и введение сеточных функций. Произведем
дискретизацию области непрерывного изменения аргумента х, заменив
отрезок [а, 6] сеткой иЛ — конечным
набором точек а = хо< xi< ... < xn =
— b (рис. 15.1). Точки X, называются
О'ка х, х2
кы--Ь
Рис. 15.1
узлами сетки оЛ
Для простоты изложения в этом параграфе будем считать сетку
равномерной с шагом А = F — a)/N. Тогда г, — Х{.\ = А для всех i = 1,
2, ..., N. Заметим, что при N -»оо шаг А -» 0 (сетка измельчается).
Сетка (J* естественным образом разбивается здесь на два подмно-
подмножества: иА = иА U ih. Множество внутренних узлов iJ1 состоит из тех
узлов xj, A < I < N — 1), которые лежат внутри интервала (а, 6). Мно-
Множество граничных узлов 7^ состоит из двух узлов xq = а и xn = Ь,
лежащих на границе отрезка [а, 6].
Далее будем вычислять решение краевой задачи не в произвольных
точках отрезка [а, Ь], а только в узлах сетки аЛ Таким образом, иско-
искомой окажется не функция и, а сеточная функция1 «А Значения и^(х,)
1 Сеточные функции использовались нами и в предыдущей главе.
этой функции в узлах Х( будем обозначать через щ и рассматривать
как приближения к значениям и (xt) решения задачи A5.9), A5.10).
Введем также сеточные функции ^ и /¦, принимающие в узлах сетки
иА значения g, = q (х,) и J, = /(ц).
2. Построение разностной схемы. Напомним (см. гл. 12), что произ-
производную и"(я) можно аппроксимировать второй разностной производ-
производной:
U (X) N
h)
A5.11)
с погрешностью r/,(z) =
)—, где ? € [х — Л, х + А]. Используя
формулу A5.11), заменим теперь в каждом из внутренних узлов ц
A < I < N — 1) дифференциальное уравнение A5.9) приближенным
равенством
_и(г{.0-2и(гд+иЫ)+^(х^к nujf.^ A5.12)
связывающим неизвестные значения решения в трех последовательных
узлах сетки.
Потребуем теперь, чтобы значения искомой сеточной функции иЛ
удовлетворяли во всех внутренних узлах сетки уравнениям A5.12), в
которых знак приближенного равенства заменен на знак равенства:
+ ^ 1<|<„_1 A513)
В результате дифференциальное уравнение A5.9) оказалось аппрокси-
аппроксимированным его дискретным аналогом — разностным уравнением
A5.13).
Естественно потребовать, чтобы в граничных узлах сеточная функ-
функция и'1 удовлетворяла равенствам
ИЛAо) = ,„, „A(XJV) = щ. A5.14)
Таким образом, мы пришли к системе линейных алгебраических
уравнений A5.13), A5.14), в которой число уравнений совпадает с
числом неизвестных щ = иЛ(х,) (i = 0, 1, ..., N) и равно N + 1. Решая
эту систему (которую мы будем называть системой сеточных уравне-
уравнений), можно найти сеточную функцию uh.
Введем линейный разностный оператор Lh с помощью равенства
488

и запишем систему сеточных уравнений A5.13), A5.14) в следующем
виде:
щ =
иЛ(г0) = «а,
= иь
A5.15)
A5.16)
Дискретную задачу A5.15), A5.16), зависящую от параметра А, приня-
принято называть разностной схемой для краевой задачи A5.9), A5.10).
3. Вычисление решения разностной схемы с помощью метода про-
прогонки. Приведем систему сеточных уравнений к виду
- «и + B
«о = иа, uN =
= h>fu К i < N- 1,
A5.17)
A5.18)
Как нетрудно видеть, эта система есть частный случай системы
линейных алгебраических уравнений вида
6о«о
CiUj+! = diy
N — 1,
A5.19)
матрица которой трехдиагональна. Здесь
а, = -1, bt = 2 + A29j, a = -1, dt = A2/i, 1 < i < N,
b0 = 1, c0 = 0, do = ua, ajv= 0, 6#= 1, ^лг = 4-
Напомним, что эффективным методом решения таких систем явля-
является метод прогонки (см. § 5.9), вычисления которого состоят из двух
этапов: прямого и обратного хода.
Прямой ход метода прогонки заключается в вычислении прогоноч-
ных коэффициентов а* и fa @ < i < JV). При i = 0 коэффициенты вы-
вычисляют по формулам
«о = -со/7о, А) = «fc/То. 7о = *0i
а при I = 1, 2, ..., N — 1 — по рекуррентным формулам
оч = -Ci/ъ, Pi={di— аД-0/7.. Ъ = bi + «чаи-
При i = N прямой ход завершают вычислением значения
Обратный ход метода прогонки дает значения неизвестных. Снача-
Сначала полагают и# = fa, а затем значения остальных неизвестных находят
по формуле
490
Вычисления ведут в порядке убывания значений индекса t от N — 1
до 0.
Применительно к решению системы A5.17), A5.18) расчетные фор-
формулы метода прогонки упрощаются. \
Прогоночные коэффициенты вычисляют по формулам
-0/7«, 7. ='2 + A29l - аи, A5.20)
«о = 0, /90 = иа,
оч = 1/7., ft = (A2/i
гдв! = 1,2, ..., N-l.
Обратный ход дает значения неизвестных щ, и2, ..., «/v-i (напомним,
что значения «о = иа, «дг = щ известны). Для этого производят вычис-
вычисления по формулам
= Ч,
A5.21)
A5.22)
Замечание. Очевидно, что коэффициенты A5.19) удовлетво-
удовлетворяют неравенствам
< 0, bi > 0, с* < 0, а( + Ь{ + с, > 0, К « < N
A5.23)
Отсюда следует, что для системы A5.17), A5.18) выполнены усло-
условия диагонального преобладания: |60| ^ |со|, l^il ^ |at-| + \ci\ >
> | a^l A < i < N), \bf/\ > \(in\- Поэтому в силу теоремы 5.4 вычис-
вычисления по формулам A5.20) могут быть доведены до конца (ни один
из знаменателей 7« не обратится в нуль). Кроме того, обратная
прогонка устойчива по входным данным.
4. Существование и единственность решения. Согласно последнему
замечанию, систему сеточных уравнений A5.17), A5.18) с помощью
эквивалентных преобразований можно привести к системе вида A5.21),
A5.22), из которой однозначно находятся неизвестные. Таким обра-
образом, справедлива следующая теорема.
Теорема 15.8. Решение разностной схемы A5.15), A5.16) су-
существует и единственно.
Как будет показано ниже, разностная схема A5.15), A5.16) облада-
обладает рядом свойств, аналогичных соответствующим свойствам краевой
задачи A5.9), A5.10).
5. Принцип максимума. Как уже отмечалось ранее, важным свойст-
свойством задачи A5.9), A5.10) является принцип максимума. Естественно
491

потребовать, чтобы и для разностной схемы был справедлив дискрет-
дискретный аналог этого свойства. Более того, невыполнение для разностной
схемы принципа максимума можно рассматривать как серьезный де-
дефект, ставящий под сомнение возможность ее использования на прак-
практике.
Л е к м а 15.1 (принцип максимума для системы сеточных уравне-
уравнений). Пусть сеточная функция uh является решением системы сеточ-
сеточных уравнений
OiUi-i + М* + Win = 4 1 < i < N, A5.24)
«о = иа, «ЛГ = «6
коэффициенты которой удовлетворяют условиям A5.23). Тогда если
иа < 0, щ < 0 и di < 0 для всех i = 1, 2, ..., N — 1, то а* < 0.
D Предположим, что неравенство иЛ < С не выполнено. Так как по
условию значения uh в граничных узлах неотрицательны («о = «a ^ 0,
up/ = щ < 0), то максимальное значение функции «Л положительно и
достигается во внутреннем узле сетки: щ^х — max щ > 0.
Пусть j — максимальный среди индексов «', для которых щ = «max-
В силу такого выбора j справедливы неравенства ttj-i ^ Uj = Un»x> uj*\ <
< Uj = «max. Так как a; < 0, Cj < 0, то ajUj < ujVj-i, CjUj < cju^\. Учиты-
Учитывая, что aj + bj + Cj > 0, dj < 0, из равенства A5.24), взятого при i = j,
получим следующую цепочку неравенств:
0 < (aj + bj + c})uj < ajUj-i + bjUj + cju^i = <f; < 0
Полученное противоречие @ < 0) доказывает, что vf1 < 0.Н
Теорема 15.9 (принцип максимума). Пусть сеточная функция
uh является решением разностной схемы A5.15), A5.16). Тогда если
/> < 0, иа < 0, щ $ 0, то мЛ < 0.
а Для доказательства достаточно заметить, что коэффициенты
соответствующей системы сеточных уравнений A5.17), A5.18) удовлет-
удовлетворяют условиям A5.23), di = Л2 /i < 0, и воспользоваться леммой
15.1. ¦
Заметим, что произвольную сеточную функцию uh можно считать
решением разностной схемы A5.15), A5.16), если выбрать правую
часть и граничные значения специальным образом, а именно положить
/> = 1Л[и'1], иа = «Л(а:о), щ = uH.xn)- Учитывая это замечание, сформу-
сформулируем теорему 15.9 иным образом:
Теорема 15.10. Пусть сеточная функция к'1 удовлетворяет
неравенствам Lh[uk] < 0, uh(x0) < 0, иЛ(хл/) ^ 0- Тогда ил < 0.
Из этой теоремы вытекает следующий важный результат.
492
Теорема 15.11 (теорема сравнения). Пусть сеточные функции
uh и iA удовлетворяют неравенствам |1Л[ыЛ]| < Lh[vh], lu^xo)! <
< *Ч*о), |иЛЫ| < vh(xN). Тогда \ и*| < »*.
Согласно условию, сеточная функция уЛ = иЛ — vh удовлетворяет
неравенствам ?Л[|Л] = Lh[uh] — Lh[vh] < 0, y^i0) = «h(xo) - ^(xo) < 0,
y^xs) = иЛ(ялг) ~ "*(w) ^ 0- Поэтому в силу теоремы 15.10 уЛ < 0, что
эквивалентно неравенству и'1 < iA.
Аналогично, sf1 — —ift — и'1 удовлетворяет неравенствам I^f^A] =
= -Щи*} - Щч*\ < 0, z^xo) = -tfi(to) - «ft(xo) < 0, zfixN) = -v^xn) -
— мЛ(хл) < 0. Следовательно, 2^ < 0, что эквивалентно неравенству
-в* < гЛ
Итак, -iA < иЛ < 1)Л. ¦
6. Априорная оценка решения. Оценим максимум модуля решения
«Л разностной схемы через данные дискретной задачи (правую часть
уравнения и краевые значения). Предварительно установим справедли-
справедливость двух вспомогательных утверждений.
Лемма 15.2. Для решения разностной схемы
A5.25)
A5.26)
A5.27)
а Введем сеточную функцию tA = М = const, М = max {| иа\, | щ\}.
Заметим, что \L[yh]\ = 0 < L[rA] = q^M, \у\хо)\ = \иа\ < М = ь^ю),
\yH.xtd\ = luil ^ М = v^(xff). Поэтому в силу теоремы сравнения
Л М, что эквивалентно оценке A5.27). И
Лемма 15.3. Для решения разностной схемы
= 0, х € <Л
ул(г0) = иа, yh(xN) = щ
справедлива оценка
max \у,\ <тах{|иа|,
Lh[zh] = Д х 6 оЛ,
оцекка
0<
A5.28)
A5.29)
A5.30)
а Введем сеточную функцию v^zj) = — (r^ — a)(b — Xi), где
^4 = max |/5|. Заметим, что t/1 ^ 0. Непосредственной проверкой не-
0< i<N
трудно убедиться в том, что Ih[tA] = А + j^A Таким образом,
493

|И1 1 ЩЛ 1 = 0
и поэтому в силу теоремы сравнения \zh\
iA. Так как максимум
_. -4 , w, . а + b
квадратичной функции — (х — а)(Ь — х) достигается при х — —-— и
it 2i
равен — Р, то
8
< - Р и из неравенства
8
< г* следует оценка
Сформулируем теперь основной результат этого пункта.
Теорема 15.12. Для решения разностной схемы A5.15), A5.16)
справедлива априорная оценка
max
<max
т-max
0<
A5.31)
а Заметим, что сеточную функцию иЛ можно представить в виде
суммы: и'1 = у* + 2h, где г/1 — решение разностной схемы A5.25),
A5.26), a zh — решение разностной схемы A5.28), A5.29). Пользуясь
неравенством max |«,| < max |j/,| + max |z,| и оценками A5.27),
A5.30), приходим к неравенству A5.31).Н
7. Устойчивость. Рассмотрим вопрос о чувствительности решения
разностной схемы к погрешностям задания правых частей разностных
уравнений. Пусть иЛ — решение разностной схемы A5.15), A5.16), а
и *h — решение разностной схемы
r€
где
A5.32)
A5.33)
= /> — б/1, и * = иа — еа, иь* = иь — ej.
Назовем разностную схему A5.15), A5.16) устойчивой, если при
любых еа, ?ь, б/1 справедлива оценка
ЛГтах \6ft\, A5.34)
Q<t<N
max |«,-ш*| <тах{|ев|,
где постоянная К не зависит от Л. Отметим, что эта оценка является
аналогом оценки A5.8), справедливой для краевой задачи.
Теорема 15.13 (об устойчивости разностной схемы). Для раз-
разностной схемы A5.15), A5.16) справедлива оценка A5.34) с постолмиой
I2
К=Г
а Заметим, что сеточная функция е'1 = иЛ — и *^ является решением
разностной схемы
494
= «А х €
Применяя для оценивания eh теорему 15.12, приходим к неравенству
A5.34). ¦
Замечание. Значение Р/8 постоянной К в неравенстве A5.34)
для разностной схемы A5.15), A5.16) совпадает в силу замечания
на с. 487 со значением соответствующей постоянной в неравенстве
A5.8). Этот факт говорит о том, что разностная схема обладает
такой же чувствительностью к ошибкам задания исходных данных,
что и краевая задача.
8. Аппроксимация. Пусть « (г) — решение дифференциального
уравнения L[u] = f. Назовем сеточную функцию ijft = Lh[u] — f1 пог-
погрешностью аппроксимации разностного уравнения
?Л[ИЛ] = Д x
Из определения
Щь] = р + il
следует, что справедливо равенство
xtuA,
A5.35)
A5.36)
означающее, что функция и удовлетворяет разностному уравнению
A5.35) с точностью до погрешности аппроксимации.
Сеточную функцию i/A используют для предварительной оценки
того, насколько точно аппроксимируется дифференциальное уравнение
его разностным аналогом. Говорят, что разностное уравнение A5.35)
аппроксимирует дифференциальное уравнение L[ii\ = / если
max \фх\ -» 0 при А -» 0, и аппроксимирует ею с т-м порядком (при
0<КЛГ
m > 0), если справедлива оценка max | ^i| < Chm.
0<t<N
Лемма 15.4. Пусть коэффициенты q и f дважды непрерывно
дифференцируемы на отрезке [а, Ь]. Тогда разностное уравнение A5.15)
аппроксимирует дифференциальное уравнение L[u] — f со вторым по-
порядком, причем справедлива оценка
max
М±р, М<= тах|«н.(г)|.
[а,Ь]
A5.37)
d Прежде всего заметим, что в силу теоремы 15.2 функция « (г)
имеет на отрезке [а, Ь] непрерывную производную mD)(z).
495

В силу определения погрешности аппроксимации имеем
где rh(xt) = иD)(?,)Л2/12 — погрешность аппроксимации производной
и"(х) ее разностным аналогом по формуле A5.11). Таким образом,
max |У>,| = max 10 ^ ^ Т? ^2' т" е' справедливость оценки
0< i<N 0< i<N
A5.37) установлена. В
В общем случае дополнительно возникает проблема изучения пог-
погрешности аппроксимации краевых условий. Однако для краевых усло-
условий A5.10) эта проблема отсутствует, так как сеточная функция удов-
удовлетворяет им точно.
9. Сходимость. Пусть и (г) — решение краевой задачи, а и'1 — реше-
решение соответствующей разностной схемы. Назовем погрешностью раз-
разностной схемы сеточную функцию ел, принимающую значения ?* =
= e^Zj) — и (xj) — u\xi) в узлах сетки сА
Будем говорить, что разностная схема сходится при А -» 0, если
max |е,| -» 0 при А -» 0, и сходится с т-м порядком точности (при
0< KN
т > 0), если для погрешности справедлива оценка max |е,| < Chm,
(К i<N
где С некоторая постоянная, не зависящая от А.
Покажем, что разностная схема A5.15), A5.16) сходится со вторым
порядком точности.
Теорема 15.14. Пусть функции q (х), }{х) дважды непрерывно
дифференцируемы на отрезке [а, Ь]. Тогда для погрешности разностной
схемы A5.15), A5.16) справедлива оценка
max |и(хО-и*| < СА2,
0<i<JV
tde с = ш max
[Ч
A5.38)
[Ч
d Введем сеточную функцию а*Л, значения которой в узлах сетки
совпадают с точными значениями решения краевой задачи, т. е.
u*4xi) = и (*0- Равенство A5.36) означает, что u*h можно рассматри-
рассматривать как решение разностной схемы A5.32), A5.33), где /*А = f1 + ijft,
и* = иа, и? = щ. В силу теоремы 15.13 для еЛ = uh — u*h справедлива
оценка
496
max |?j| < т- max
0<i<JV
т
A5.39)
0<«<ЛГ
Учитывая теперь неравенство A5.37), из A5.39) получаем оценку
A5.38). ¦
Замечание. Сходимость разностной схемы A5.15), A5.16) со
вторым порядком точности вытекает из того, что схема устойчива и
обладает аппроксимацией со вторым порядком относительно А.
10. Оценка погрешности по правилу Рунге. Полученная в теореме
15.14 априорная оценка A5.38), как правило, оказывается непригодной
для практической оценки погрешности разностной схемы. На практике
чаще применяются апостериорные оценки погрешности, использующие
расчеты на сгущающихся сетках. Пусть, например, иЛ и u2h — решения
разностной схемы A5.15), A5.16), соответствующие шагам Aj = А и
Aj = 2А. Тогда в соответствии с правилом Рунге при определенных
условиях справедлива приближенная формула
ел(г) = и (х) - и^х) и ——
A5.40)
Отметим, что она применима только в узлах сетки w2'1, т. е. там, где
определены обе сеточные функции uh и u2h.
Пример 15.1. Используя разностную схему A5.15), A5.16) с шагом А = 1/8,
найдем приближенное решение краевой задачи
-и"(х) + ?и (х) = (¦? + ^)cos ^1, 0 < х < 1,
м@)=-1, иA) = 0
A5.41)
и оценим его погрешность по правилу Рунге. Вычисления будем вести с шес-
шестью значащими цифрами.
¦к2 т
В данном случае q (х) = г2, /(г) = (— + л^соз - х и система сеточных
уравнений A5.17), A5.18) примет вид
«0=1.
-КИ + B + к2$щ - nj»! = (j- + ^)cos | »ь 1 < i < N- 1,
«N=0.
A5.42)
497

При Aj = 1/8 приходим к следующей системе уравнений относительно
неизвестных и, « u (i'A) (i = 0, 1, ..., 8):
«0= 1,
-«о + 2.00024ц - «г = 0.0380518,
-а, + 2.00098»2 - «3 = 0.0365207,
-иг + 2.00220«з - «4 = 0.0338827,
-чз + 2.00391 ц, - us = 0.0300233,
-щ + 2.00610% - U6 = 0.0248099,
-щ + 2.00897«в - «7 = 0.0181171,
-«6 + 2.01196^ - щ = 0.0098552,
щ = 0.
Решая ее с помощью метода прогонки, находим значения, представленные в
3-м столбце табл. 15.1. Заметим, что в данном случае точное решение задачи
известно: и (х) = cos — х. Значения точного решения и вычисленные с их
it
использованием погрешности приведены во 2-м и 4-м столбцах той же табли-
таблицы.
Таблица 15.1
0.000
0.125
0.250
0.375
0.500
0.625
0.750
0.875
1.000
X
1.000000
0.980785
0.923880
0.831470
0.707107
0.555570
0.382683
0.195090
0.000000
Л
h= 1/8
1.000000
0.981114
0.924413
0.832097
0.707733
0.556116
0.383082
0.195300
0.000000
Л
А,= 1/8
0
-3-Ю
-5-Ю-4
-6-ю-4
-6-Ю'4
--5-10-4
-л- ю-4
-2-10
0
Л
h= 1/4
1.000000
-
0.926080
-
0.709703
-
0.384324
-
0.000000
Оценка погреш-
погрешности по прави-
правилу Рунге
0
-
-6-Ю
-
-7-Ю'4
-
-МО
-
0
Оценим теперь погрешность, используя правило Рунге. Возьмем шаг
= 2Aj = 1/4. Решая соответствующую систему сеточных уравнений:
«0=1,
-ко + 2.00391ц - «г = 0.146083,
-ц + 2.01563мг - «з = 0.120093,
-«2 + 2.03516«з - и, = 0.0724683,
«4 = 0,
498
получаем .значения, представленные в 5-м столбце табл. 15.1. В последнем
столбце этой таблицы даны приближенные значения погрешности, полученные
по формуле A5.40). Заметим, что в данном примере правило Рунге дает весьма
хорошие результаты.
11. Влияние вычислительной погрешности. При расчетах с доста-
достаточно крупными шагами А влиянием вычислительной погрешности на
решение часто можно пренебречь. Однако все же следует иметь в виду,
что при решении системы A5.17), A5.18) методом прогонки происхо-
происходит накопление вычислительной погрешности. Известно1, что при
А -> 0 вычислительная погрешность может возрастать здесь пропорцио-
пропорционально ем/А2, где ем — относительная точность представления чисел в
ЭВМ. Таким образом, при достаточно малых значениях шага А
возможна катастрофическая потеря точности.
Сделанное выше утверждение перестанет казаться неправдоподоб-
неправдоподобным, если мы убедимся в том, что при малых А вычислительная пог-
погрешность может привести к существенному искажению решения уже на
этапе составления системы сеточных уравнений. Пусть, например, для
решения краевой задачи A5.9), A5.10) используется разностная схема
с шагом А = 10, а вычисления ведутся на 6-разрядной десятичной
ЭВМ. Заметим, что для такой ЭВМ ем = 5-Ю'7. Так как здесь Л2*2, <
< 10'6 = 2ем, то результатом вычисления коэффициента bt = 2 + A2z,
после округления до 6 значащих цифр мантиссы является число Ь* =
= 2. Следовательно, даже если остальные вычисления будут произво-
производиться точно, то фактически окажется найденным не решение системы
A5.42), а решение системы
«о = 1.
uN= 0,
соответствующей
г2
-и"(х) = (— 4
« @) = 1, и(
краевой задаче
¦ г2) сое - х,
1) = 0.
сое ! *„
JV—
1 Бахвалов Н.С. О накоплении вычислительной погрешности при
численном решении дифференциальных уравнений. В сб.: Вычислительные
методы и программирование. М.: Изд-во МГУ, 1962, с. 47—€8.
499

Поскольку в результате оказалась решенной "не та задача", найденные
значения и* будут существенно отличаться от искомых и,. В данном
конкретном случае погрешность будет достигать и 5%. В общем случае
погрешность может оказаться значительно больше.
§ 15.3. Метод конечных разностей:
аппроксимации специального вида
1. Случай переменного коэффициента к (х). Вернемся к проблеме
численного решения краевой задачи
-(к (х) «'(*)) ' + «(*)« (х) = /(г), а < х < 4;
и (а) = иа, и F) = щ.
A5.43)
A5.44)
По сравнению со случаем А: = 1, рассмотренным в предыдущем параг-
параграфе, единственное видимое отличие состоит в необходимости выбора
подходящей аппроксимации для выражения1 — (it (г) и'(х))' = w'(x).
Рассмотрим некоторые из возможных подходов к выбору аппроксима-
аппроксимации.
Введем обозначения х^ д = (х, + х^{)/2, jfc^i р. = к (х„\ #), 0 < i <
^ N. Аппроксимируем производную w'(x) при г = х, следующим обра-
образом:
W '(X,) И - (W
- W (*,-! /г)).
Используя далее приближенные формулы
/г) =
/2
м (*и /г) = *и /г« '(*м /г) й *t-i /г * "д" ,
получаем аппроксимацию
A5.45)
A5.46)
A5.47)
k
1/2 А *'/2А
В результате приходим к разностной схеме вида A5.15), A5.16), где
1 Напомним, что величина w (х) = -к (х) и'(х) имеет физический смысл
потока тепла, если уравнение интерпретируется как уравнение теплопровод-
теплопроводности.
500
A5.48)
Отметим, что коэффициенты а, = -i,.j /2, bt = kt-i ^ + кп1 # + h2qt,
с, = -ktn /2 соответствующей системы сетояных уравнений удовлетворя-
удовлетворяют условиям A5.23). Следовательно, при любом А решение разностной
схемы существует и единственно. Кроме того, в силу леммы 15.1 для
разностной схемы справедлив принцип максимума. Можно показать
также, что разностная схема устойчива и сходится со вторым поряд-
порядком точности, если коэффициенты к, q, /являются дважды непрерыв-
непрерывно дифференцируемыми на отрезке [а, Ь] функциями.
Формальный подход к выбору аппроксимации дифференциального
уравнения может давать разностные схемы, обладающие теми или
иными дефектами. Например, кажется удобным предварительно преоб-
преобразовать первое слагаемое уравнение A5.43) следующим образом:
(itu')' = ки" + it'и'. После такого преобразования для этого слагаемо-
слагаемого естествен выбор аппроксимации
v ' \х=х, v " А2
приводящей к разностной схеме с оператором
2А
2А
+
Заметим, что коэффициенты соответствующей системы сеточных урав-
уравнений
а, = -it
)- К = 2* (г,)
<ь, с, = -* (г,) - ? *'(*,)
удовлетворяют условиям A5.23), гарантирующим наличие принципа
максимума, только если
Л max
<2.
A5.49)
Таким образом, в случае, когда коэффициент it может резко ме-
меняться на отрезке [а, Ь], ограничение A5.49) приводит к необходимос-
необходимости выбора очень мелкого шага А для получения приемлемых результа-
результатов.
2. Случай неравномерной сетки. Часто возникает необходимость
использования неравномерной сетки аЛ, т. е. сетки, у которой шаг Л, =
501

= X{ — X(-i зависит от i. Положим Aj+i p. = x^i /2 — *н /г- Заменяя в
формулах A5.45), A5.46), A5.47) А на At+i /2j At+i, h соответственно,
придем к разностной схеме A5.15), A5.16), в которой
14*1/2
Aj+j
Bi-1 /2
Щ -Щ-1
Нетрудно убедиться в том, что при такой аппроксимации справедлив
принцип максимума и разностная схема устойчива. Можно показать,
что при некоторых дополнительных предположениях она сходится со
вторым порядком точности относительно Лщах.
3. Разности "против потока". Как отмечалось выше, уравнение
A5.43) описывает установившееся распределение температуры в непод-
неподвижной среде. В том случае, когда исследуются тепловые процессы в
движущейся среде (например, рассматривается поток жидкости), урав-
уравнение модифицируется следующим образом:
-(* (х)и'(*))' + v (х)и'(х) + q (x)u (х) = /(*).
Здесь v (х) — величина, пропорциональная скорости потока жидкости.
При дискретизации этого уравнения возникает новый момент,
связанный с необходимостью аппроксимации слагаемого v (х)и'(х). Ка-
Кажется естественным воспользоваться для аппроксимации производной
и' центральной разностной производной. В результате к разностному
оператору A5.48) добавится слагаемое и,
2Л
Выясним, удовлетворяют ли коэффициенты
/2
« = *«-i /2
*t*i /2
где щ = .
/2
соответствующей системы сеточных уравнений условиям A5.23), гаран-
гарантирующим выполнение принципа максимума. Как нетрудно видеть,
неравенства A5.23) выполняются, если h\vt\ < 2 min {Jti-i/2. ^1/2}-
В том случае, когда скорость потока велика, это неравенство приво-
приводит к весьма жесткому ограничению на шаг Л. Его можно избежать,
если использовать односторонние разностные производные. В задачах
динамики жидкостей и газов широко используются аппроксимации
вида
¦ « (Xj) - U
+ v,
. U
- И
A5.50)
где v'{ = min {v (х$, 0}, и* = max {v (х{), 0}. Они называются аппрок-
502
симациями "против потока" (или "против ветра"). Такой выбор
аппроксимации слагаемого м' приводит к системе сеточных уравне-
уравнений с коэффициентами
с, =
<Ч = -(*«ч /2+ Ц), *i = *i-i /2+ *t*i /2 + A«i + ;
Легко убедиться в том, что условия A5.23) здесь всегда выполняются.
Таким образом, принцип максимума выполняется при любых шагах А.
Правда, при использовании приближения A5.50) порядок аппроксима-
аппроксимации снижается со второго до первого.
4. Случай разрывных коэффициентов. Одна из специфических
особенностей, присущих многим техническим задачам, заключается в
том, что среда, в которой изучаются те или иные процессы, как прави-
правило, существенно неоднородна и состоит из материалов с разными
физическими свойствами. При математической формулировке таких
задач эта особенность проявляется в том, что коэффициенты диффе-
дифференциальных уравнений становятся разрывными. Это существенно
усложняет построение эффективных численных методов.
Предположим, например, что коэффициенты к, q, / входящие в
уравнение A5.43), могут иметь на отрезке [а, Ь] конечное число М
точек разрыва ?, (а < ft < ?2 < ••• < ?м < *) первого рода. Будем
предполагать, что всюду за исключением этих точек коэффициенты А,
q, /непрерывны и удовлетворяют условиям Jt (х) > Jto > 0, q (x) > 0.
В этом случае решение краевой задачи A5.43), A5.44) уже нельзя
понимать в классическом смысле. Уточним постановку задачи для
уравнения с разрывными коэффициентами. Назовем функцию и (х)
решением задачи A5.43), A5.44), если:
1) функция и (х) непрерывна на отрезке [а, Ь] и удовлетворяет
краевым условиям и (а) = иа, и F) = щ;
2) поток w (х) = -к (х)м'(х) непрерывен на отрезке [а, 6];
3) всюду за исключением точек ft, ft>, ..., ?м функция w (x) непре-
непрерывно дифференцируема и удовлетворяет уравнению
q(x)u(x) =
A5.51)
Для вывода разностных уравнений воспользуемся методом балан-
баланса1. Запишем уравнение теплового баланса для отрезка [х*-1/2> ^i+i/Ji
где 1 < i < N — 1. Для этого проинтегрируем уравнение A5.51) по х от
xi-i /2 Д° ^i+i /2- В результате получим равенство
1 Иногда метод баланса называют интегро-интерполяционнъии. методом
[70].
503

^«¦1/2 xi*\/2
- w (xi-i n) + I qudx= J /dr.
zi-\f2 xi-l /2
Воспользовавшись приближенной формулой
A5.52)
zi*\ /2
J qu dx и
4-1/2
*i*\ p.
и « (ii) f q dx и разделив обе части равенства A5.52) на Л*ц #,
xi-\ /2
получим
A5.53)
/2
4*1/2 j 4+1/2
/ q (x)dx, /* = -r / / (x)dx — средние зна-
чения функций q и /на отрезке [ii-i/2, a?i+i /2]-
Далее заметим, что
« (х^) - и (xt)
Таким образом,
t + 1
) J.
w
A5.54)
[1 *'*' А -1
т— | , — эффективное значение коэффициента
Л,+1 1 « (-f)J
теплопроводности на отрезке [г*, ij+i]. Заметим (это важно!), что усред-
усредняется фактически не коэффициент теплопроводности к (х), а обрат-
обратный к нему коэффициент теплового сопротивления (Jt (x))'1.
Перейдем теперь от приближенных равенств A5.53), A5.54) к
разностному уравнению
Добавляя к A5.55) уравнения
«о= иа, илг= «6, A5.56)
приходим к разностной схеме A5.55), A5.56).
Замечание. Разностные уравнения A5.55) записываются
единообразно во всех внутренних узлах сетки независимо от того,
504
где расположены точки разрыва коэффициентов дифференциально-
дифференциального уравнения. Это означает, что рассматриваемая разностная схема
относится к классу однородных разностных схем [70].
5. Аппроксимация краевых условий. Выше при аппроксимации
краевой задачи краевые условия первого рода и (а) = «а, и (Ь) = щ не
вызывали каких-либо затруднений и потому основное внимание уделя-
уделялось аппроксимации дифференциального оператора. Однако краевые
условия могут иметь более сложный вид и тогда возникает проблема
их аппроксимации.'
Рассмотрим, например, краевое условие второго рода
-* (а)и '(в) = wa.
A5.57)
Простейший подход к его аппроксимации состоит в замене производ-
ной и (а) разностным отношением —^ т )s-L. В результате
л
получается разностное краевое условие
-к (а) *р>
A5.58)
Так как
то разностное уравнение A5.58) аппроксимирует краевое условие
A5.57) лишь с первым порядком относительно А, что приводит к пони-
понижению порядка точности разностной схемы. Порядок аппроксимации
краевого условия можно повысить разными способами. Например,
можно заметить, что в силу дифференциального уравнения A5.43) при
х = а для решения и справедливо равенство
к (а)и"(а) = -к'(а)и'(а) + q (a)« (a) - /(a).
Таким образом,
-' W
и мы приходим к разностному краевому условию
505

- «о
А
2
Л
2
аппроксимирующему краевое условие A5.57) со вторым порядком.
Другая аппроксимация второго порядка относительно А получится,
если использовать метод баланса. Проинтегрируем уравнение A5.51)
по х от г0 до х\ /2 = х0 + А/2. В результате, учитывая, что w (х0) = wa,
*i /2 х\ п
получим равенство w (xin) — wa + J qudx — J f dx. Отсюда, исполь-
зуя приближенное равенство A5.54), приходим к разностному уравне-
уравнению
,h Щ - "о
-*1 п д
где
_
~ а
/2
А А
2 ¦'0'
$ 15.4. Понятие о проекционных
и проекционно-разностных методах.
Методы Ритца и Галеркина.
Метод конечных элементов
Наряду с методом конечных разностей значительной популярнос-
популярностью пользуются проекционные методы Ритца и Галеркина, а точнее —
их современные варианты, объединяемые названием "метод конечных
элементов" или "проекционно-сеточные методы".
1. Вариационная постановка краевой задачи. Вариационные мето-
методы, представляющие собой частный случай проекционных методов,
используются для решения самых разнообразных задач на протяже-
протяжении многих Десятков лет. Эти методы применяются для решения тех
задач физики и техники, которые могут быть описаны с помощью так
называемых вариационных принципов. В соответствии с одним из прос-
простейших вариационных принципов функция и (х), являющаяся решени-
решением задачи, должна быть стационарной точкой вариационною функци-
функционала
J (и) = J F (х, и, и') dx.
а
A5.59)
Вариационный функционал, как правило, имеет определенный физи-
физический смысл. Нередко он выражает потенциальную энергию физичес-
физической системы.
Обозначим через U множество функций, на котором определен
функционал J («). Будем считать, что входящие в U функции удовлет-
удовлетворяют условиям
«(в) = «в, и(Ь) = щ, A5.60)
где значения «„ и щ фиксированы. Предположим также, что в множес-
множество U входят все непрерывные кусочно-гладкие функции, принимаю-
принимающие на концах отрезка [а, Ь] значения A5.60).
Предположим, что дважды непрерывно дифференцируемая функ-
функция и (х) является стационарной точкой функционала A5.59). Тогда,
как известно из курса вариационного исчисления [93], эта функция
должна удовлетворять дифференциальному уравнению
~\\К'(*' «>"') + К(х' «¦«') = 0- A5-61)
которое принято называть уравнением Эйлера (или уравнением Эйле-
Эйлера — Лагранжа). Таким образом, решение вариационной задачи оказы-
оказывается решением краевой задачи A5.61), A5.60). Более того, при неко-
некоторых условиях эти задачи оказываются эквивалентными и возникает
возможность решать определенный класс краевых задач, используя
методы вариационного исчисления.
Рассмотрим теперь функционал
Ь Ъ
х, A5.62)
,
506
где k (x), q (x), f(x) — кусочно-непрерывные функции, удовлетворяю-
удовлетворяющие условиям к (х) > ко > 0, q (x) > 0. Поставим вариационную задачу
о поиске точки минимума функционала A5.62) на множестве U. Как
нетрудно видеть, в рассматриваемом случае
F(x, «,«') = \ (* (*)(«'J + « (*)«')-/(*)«
и уравнение Эйлера принимает следующий вид:
-iku')'+ qu = f. A5.63)
Можно доказать, что функция и является точкой минимума функцио-
функционала A5.62), т. е. удовлетворяет условию
507

J(«) = min J(v),
A5.64)
тогда и только тогда, когда она является решением краевой задачи
A5.63), A5.60).
Отметим одно достоинство вариационной постановки задачи
A5.63), A5.60). Она исключает необходимость требования наличия у
рассматриваемых функций второй производной и даже непрерывности
первой производной. Это обстоятельство оказывается весьма ценным
для многих приближенных методов.
2. Метод Рнтца. Рассмотрим приближенный метод решения вариа-
вариационной задачи о поиске точки минимума функционала J (и) на мно-
множестве U. Будем искать приближенное решение uN в виде следующей
линейной комбинации:
Ъ
A5.65)
Здесь ipo(x)y <ft(x), ¦i <Ptl(x) — некоторые фиксированные функции,
которые далее мы будем называть базисными. Предполагается, что
система базисных функций линейно независима и линейными комби-
комбинациями A5.65) при соответствующем выборе коэффициентов с*о, а\,
..., а# можно аппроксимировать решение и с желаемой степенью точ-
точности.
Обозначим через UN множество всех функций вида A5.65) (при
фиксированных <р0, <рх, ..., <рн), удовлетворяющих условиям uN(a) = иа,
uN(b) = u\y Предположим далее, что базисные функции удовлетворяют
следующим условиям: tpo(a) = 1, <Pj(a) = 0 для всех j > 1; wvF) = li
tp0) = 0 для всех j < N — 1. Тогда, как нетрудно видеть, условия
A5.60) для и = uN выполняются тогда и только тогда, когда справед-
справедливы равенства
ао=иа, ан=иь. A5.66)
Согласно методу Ритца1, приближенное решение uN определяется
как функция, минимизирующая функционал J на множестве UN. Та-
Таким образом, по определению
J (v).
A5.67)
Заметим, что задача A5.67) представляет собой задачу минимиза-
Вальтер Ритц A878—1909) — швейцарский физик и математик.
ции функции многих переменных. В самом деле, величина J (v) =
= /(? aj<pj) является функцией N — I переменных «ь а2, ..., a^-i
(значения а0 = иа, ац = щ фиксированы). Согласно необходимому
условию экстремума, минимум этой функции достигается при тех
значениях параметров ац, а2, ..., адм, для которых выполняются
равенства
A5.68)
Добавляя к этим равенствам условия A5.66), приходим к системе
уравнений A5.68), A5.66), из которых можно определить значения
коэффициентов о; (j = 0, 1, ..., TV) и тем самым — приближение «*.
Применим метод Ритца к решению краевой задачи для уравнения
A5.63) с краевыми условиями первого рода. Для функционала A5.62)
имеем
I /
-?. J (la/pj) = / [к (Д
Я
/ / Ъ
- / f <р( dx =;
\
= .? (/
j-0 a
Я <Pi<Pj) dx)aj - Iffi dr.
a
Система A5.68), A5.66) в данном случае превращается в систему ли-
линейных алгебраических уравнений
S ujjOtj = bi, i = 1, 2, ..., If- 1,
°0 = «a. <*v = 4,
A5.69)
A5.70)
508
6 6
где aij = / (к <р\<р' + q щ<р>) dx, bt = J f ipf dx.
a ' a
Исключая переменные а0 и адг, систему A5.69), A5.70) можно свес-
свести к эквивалентной системе уравнений
Здесь а = (оь о2, ..., алц)т, А — матрица порядка N — 1 с элементами
509

«у («> J = 1. 2, ..., N - 1), i= (du d2, ..., dN-iy, где <f, = 6, — аюиа —
, « = 1> 2, ..., ЛГ- 1.
Отметим, что матрица А — симметричная и положительно опреде-
определенная.
3. Проекционная постановка краевой задачи. Краевая задача
L[u] = f, х€ [«,»], A5.71)
и (а) = иа, и (Ь) = щ A5.72)
допускает вариационную постановку тогда и только тогда, когда диф-
дифференциальное уравнение A5.71) является уравнением Эйлера для
некоторого функционала J. Таким образом, этим свойством обладают
далеко не все задачи. Например, краевая задача для уравнения
vu'
A5.73)
при v (х) f 0 не допускает классической вариационной постановки.
Приведем проекционную постановку краевой задачи, которая имеет
место и в том случае, когда задача не может быть сформулирована как
вариационная.
Будем называть пробной функцией всякую непрерывную на отрезке
[а, Ь] кусочно-дифференцируемую функцию <р (г), обращающуюся в
нуль при х = а, х = 6. Множество всех пробных функций обозначим
через Ф. Умножив уравнение A5.71) на произвольную функцию <р € Ф
и проинтегрировав полученное равенство по х от а до Ь, получим ин-
интегральное тождество1
Ь Ь
JL [и] <pdx = f fipdx.
A5.74)
Итак, если функция и является решением дифференциального уравне-
уравнения A5.71), то она должна удовлетворять интегральному тождеству
A5.74). В то же время, как следует из основной леммы вариационного
исчисления [93], если интегральное тождество A5.74) выполняется для
любой пробной функции if, то L[u] = /
Таким образом, краевую задачу A5.71), A5.72) можно сформулиро-
сформулировать в следующей проекционной постановке. Требуется найти такую
функцию и, которая удовлетворяет интегральному тождеству A5.74)
1 Равенство A5.74) называют интегральным тождеством, подчеркивая тем
самым, что оно выполняется для любой пробной функции <р.
510
для произвольной пробной функции ip € Ф и для которой выполнены
краевые условия A5.72).
Приведем в качестве примера интегральное тождество
* ь
/(-(*«')' + »«' + <?«) <fi dx = / / <р dx,
A5.75)
соответствующее дифференциальному уравнению A5.73). Придадим
тождеству A5.75) несколько иную форму. Для этого преобразуем сла-
ь
гаемое — / (ku')' <p dx. Используя формулу интегрирования по частям,
а
с учетом равенств ip (а) = 0, <р F) = 0 получим
ъ
-f(ku')'
ь ь
J ku'<p' dx = J ku'f' dx.
В результате интегральное тождество примет вид
ь ь
J (ku'tp' + vu'tp + quip) dx = J f(p dx.
A5.76)
Отметим, что при замене уравнения A5.73) интегральным тождест-
тождеством A5.76) отпадает необходимость рассматривать только лишь функ-
функции и (х), обладающие вторыми производными. Это обстоятельство
играет важную роль при построении и исследовании методов решения
рассматриваемой задачи, а также ряда других задач. Кроме того,
проекционная постановка оказывается удобной при рассмотрении
уравнений с разрывными коэффициентами.
5. Метод Галеркина. Как и в методе Ритца, в методе Галеркина1
приближенное решение ищется в виде
«"(*)=
Однако в отличие от метода Ритца основой для построения метода
является не вариационная, а более общая проекционная постановка
задачи. За приближенное решение в методе Галеркина принимается
функция uN € UN, которая удовлетворяет интегральному тождеству
1 Борис Григорьевич Галеркин A871—1945) русский инженер, ученый,
специалист в области строительной механики и теории упругости.
511

b b
J L[u"\ <p dx = f f <p dx
для любой пробной функции <р = <pi, x = 1, 2, ..., TV— 1.
Для задачи A5.71), A5.72) метод Галеркина с использованием
интегрального тождества A5.76) приводит к следующей системе урав-
уравнений:
/ [к ( Е а#'Л р' + 1)(Е аур'Л <р{ + q ( ? a^) y>J dx =
( #
a >=0 y
= ff<Pidx
a
«0 = «a, O
(
>=0
i=l, 2, ..., /V-l),
Заметим, что эта система при v (х) = 0 в точности совпадает с систе-
системой A5.69), A5.70), полученной методом Ритца. Таким образом, при-
применительно к решению краевой задачи A5.63), A5.60) методы Ритца и
Галеркина оказываются эквивалентными.
Замечание. Приближенное решение uh, определяемое методом
конечных разностей, задается только в узлах сетки иА. Поэтому для
получения значения решения в произвольной точке приходится
производить интерполяцию. В то же время проекционные методы
дают в качестве приближенного решения функцию A5.65), вычис-
вычисляемую в произвольной точке х.
Как мы отмечали в предыдущих параграфах, системы сеточных
уравнений, получаемые методом конечных разностей, обладают тем
важным свойством, что матрицы коэффициентов, этих систем являются
разреженными (более того, в рассмотренных примерах матрицы были
трехдиагональными). Для решения таких систем разработаны эффек-
эффективные методы.
В общем случае применение методов Ритца и Галеркина к решению
краевых задач приводит к необходимости вычислять решения систем
уравнений вида Аа = i с заполненными (и зачастую плохо обуслов-
обусловленными) матрицами А. Современные варианты проекционных мето-
методов, объединяемые термином "метод конечных элементов", свободны
от указанного недостатка. Перейдем к их рассмотрению.
6. Метод конечных элементов. Метод конечных элементов предс-
представляет собой разновидность проекционных методов, основанную на
специальном выборе базисных функций.
512
История метода весьма поучительна. Метод конечных элементов
впервые был предложен Р. Курантом1 в 1943 г., но тогда его важная
работа опередила потребности практики и фактически осталась неза-
незамеченной. Затем в начале 50-х годов инженерами — специалистами по
строительной механике был разработан новый подход к решению
задач теории упругости. В тех случаях, когда расчетная область имела
сложную геометрию, она разбивалась на подобласти простой геомет-
геометрии, в каждой из которых решение могло быть найдено аналитически.
Эти подобласти были названы конечными элементами, а сам подход —
методом конечных элементов. Только в начале 60-х годов математи-
математиками были осознаны практическое значение и математическая природа
метода. В 60 и 70-х годах шло бурное развитие теории метода, он
завоевывал все более широкие области применения. К настоящему
времени метод конечных элементов получил самое широкое распрост-
распространение в вычислительной практике. На его основе разработано боль-
большое число пакетов прикладных программ для решения разнообразных
инженерных и научных задач.
Отметим характерные черты метода конечных элементов, выделяю-
выделяющие его среди других проекционных методов.
1) Расчетная область (множество изменения независимой перемен-
переменной) разбивается на конечное число элементарных подмножеств стан-
стандартной формы (которые и называют конечными элементами).
2) Используемые базисные функции ipj таковы, что они:
на каждом элементе имеют простой вид (чаще всего — многочлены);
отличны от нуля лишь на нескольких соседних элементах.
Покажем, как применяется метод конечных элементов к решению
краевой задачи A5.63), A5.60). Разобьем отрезок [a, b] точками
п — xq < х\ < ... < XN = Ь на N элементарных отрезков [zt-ь *J Длины
Aj. Таким образом, в роли конечного элемента выступает элементарный
отрезок [X(_i, rj.
Введем базисные функции <р3(х) для j — 1, 2, ..., N — 1 следующим
образом
(х-
при х€ [x
- x)/hrl при xe [x
0 При Z$ [Xj-i,
A5.77)
График такой базисной функции ("шапочки") изображен на рис. 15.2.
Подчеркнем, что функция <pj отлична от нуля только лишь на двух
1 Рихард Курант A888—1972) — немецкий математик.
17-28
513

соседних конечных элементах (отрезках [xj.\, х}] и [ij, х^{\) и является
кусочно-л инейной.
«i*i =
0 х„ х,
х О
а)
Б)
Рис. 15.2
Хц-1 X* X
0)
- *)/*1 при х 6 fo, ч],
о
0
при
При
Введем также функции <р}{х) для j = 0 и j'• = N (рис. 15.2, а, б):
A5.78)
A5.79)
Будем искать приближенное решение задачи в виде
и^(х) = Е <*j<Pj(z)- A5.80)
Заметим, что базисные функции обладают тем свойством, что ipfa) =
= 1 и ipjiii) = 0 при i t j. В силу этого aj = un(xj), т. е. коэффициенты
линейной комбинации A5.80) представляют собой значения функции
uN в узлах xj. После введения обозначения «J = и^(х;) функцию A5.80)
можно записать так:
Величины и; = a, (j = 0, 1, ..., N) удовлетворяют системе уравне-
уравнений A5.69), A5.70), которую в данном случае можно получить как
методом Ритца, так и методом Галеркина. Заметим, что базисные
функции <р,(х) и <pj(x) одновременно могут быть отличны от нуля толь-
Ь
ко, если | j — j\ < 1. Поэтому при | i — j| > 1 элементы <iy = /(it^,V,' +
a J
+ 4<Pi<Pj) dx равны нулю. Таким образом, для определения неизвестных
и^ получаем следующую систему уравнений с трехдиагональной матри-
матрицей:
514
«О = «а.
Так как
г= Ч-
A5.81)
A5.82)
\/kj при г 6 (г^-
-1/А^! при X е (Xj,
0 При Х$. [Xj-i,
то
/2
где
i/2
A5.84)
A5.85)
A5.86)
Систему уравнений A5.81), A5.82) принято называть сис-
системой метода конечных элементов или проекционно-разностной схе-
схемой1.
Можно показать, что проекционно-разностная схема имеет единст-
единственное решение uN(x) и при выполнении некоторых условий на сетку
иА и коэффициенты Jfc, q, /она имеет второй порядок точности.
Существует весьма тесная связь между теорией разностных схем и
теорией проекционно-разностных схем. В подтверждение сказанного
ограничимся тем, что преобразуем систему A5.81), A5.82) так, чтобы
она обрела внешнее сходство с соответствующей разностной схемой.
Разделив каждое уравнение A5.81) на Aj+i p. и воспользовавшись равен-
равенствами A5.83)—A5.87), получим систему уравнений
1 Используется также термин проекционно-сеточний метод. Та же система
уравнений может называться вариационно-разностной схемой, если она по-
получена с помощью метода Ритца.
515

A5.87)
>•«-! + rf-* + A
i/ a«
«0 =
г= Ч-
A5.88)
В такой форме записи она действительно оказывается похожа на раз-
разностную схему A5.55), A5.56).
Замечание. При построении системы уравнений метода конеч-
конечных элементов, как правило, возникает необходимость вычисления
некоторых интегралов1. Для проекционно-разностной схемы
A5.87), A5.88) в случае, когда коэффициенты к, q, f— гладкие, эта
проблема легко решается применением квадратурных формул.
Например, можно положить
J к (х) dx и hik (х,ч п), J q
t ~1 " ~1
dx и
J f(x)Vi dx я /(хи п) J ?_?i dx + f(xM n)J
При этом второй порядок точности сохраняется.
7. Специальная проекционно-разностная схема. Предположим, что
коэффициенты к, q, /, входящие в одномерное уравнение диффузии
A5.63), могут быть разрывными. В этом случае можно, как и ранее,
использовать кусочно-линейные базисные функции A5.77), A5.78),
1 Аналогичная проблема возникает и при реализации некоторых разност-
разностных схем, например, однородной разностной схемы A5.55), A5.56).
516
A5.79). Полученная таким образом проекционно-разностная схема
сходится, однако по скорости сходимости она существенно уступает
однородной разностной схеме A555), A5.56).
Чтобы получить качественную проекционно-разностную схему для
уравнения диффузии с разрывными коэффициентами, воспользуемся
специальными базисными функциями <р}{х). Эти функции для j = 1,2,
..., N - 1 имеют следующий вид:
Ф) =
Здесь Д, =
пр»
1 Ч*
Xi
A5.89)
при
Jt ТВ
. Кроме того,
при х $ [хо, х\]\
при xi [xf/.h
при х€ [rjv-i,
A5.90)
A5.91)
Выбранные базисные функции <pj интересны тем, что всюду за
исключением узлов сетки они удовлетворяют дифференциальному
уравнению {к<р',)' = 0.
Применение этих базисных функций приводит к проекционно-
разностной схеме вида A5.87), A5.88), где все коэффициенты находят-
находятся по формулам A5.85), A5.86) за исключением коэффициентов J^-i/2,
^гм /2, которые вычисляются по формулам
dx
т. е. так же, как и в разностной схеме A5.55), A5.56).
Эта проекционно-разностная схема имеет второй порядок точности
517,

и решается методом прогонки. Отметим одно замечательное свойство
указанной схемы. В случае q (х) = 0 полученные с ее помощью значе-
значения «, совпадают с истинными значениями краевой задачи а (г,) в
узлах сетки (схема точна в узлах сетки). Отметим, что базисные функ-
функции A5.89), A5.90), A5.91) и в случае, когда коэффициенты уравнения
диффузии являются гладкими, но сильно меняющимися, дают боль-
большую точность по сравнению с простейшими кусочно-линейными базис-
базисными функциями.
§ 15.5. Метод пристрелки
Метод пристрелки (он называется также методом стрельбы или
баллистическим методом) позволяет свести решение краевой задачи к
решению системы нелинейных уравнений относительно так называе-
называемых пристрелочных параметров, а также к решению (вообще говоря,
многократному) задачи Коши.
Сначала рассмотрим этот метод на примере решения следующей
краевой задачи для системы двух дифференциальных уравнений пер-
первого порядка:
y'(x) = f(x,y(x),z(x)),
z'(x) = g(x,y(x),z(x)),
у (a) = ya, z(b) = zb.
Наряду с этой задачей рассмотрим задачу Коши
у'(х, а) = f(x, у (х, a), z (x, а)),
z'(x, а) = д (х, у (х, а), г (х, а)),
A5.92)
A5.93)
A5.94)
A5.95)
A5.96)
у(а) = уа, *(а) = а. A5.97)
Решение задачи A5.95)—A5.97), т. е. пара функций у (х, a), z (x, а),
зависит не только от переменной х, но и от пристрелочном параметра
а. Подобрав значение параметра а, при котором z F, а) = гь, получим
решение задачи Коши, совпадающее с решением краевой задачи
A5.92)-A5.94).
Таким образом, для того чтобы найти решение краевой задачи
нужно решить нелинейное уравнение
ф (а) = 0, A5.98)
где ф (а) — z (Ь, а) — гь. Отметим, что функция ф (а) не задана какой-
либо явной формулой и вычисление каждого ее значения предполагает
518
вычисление решения задачи Коши A5.95)—A5.97). Как правило, для
решения задачи Коши приходится использовать тот или иной числен-
численный метод.
Уравнение A5.98) можно решать, используя один из известных
методов решения нелинейных уравнений. Довольно часто успешным
оказывается применение метода бисекции, метода секущих или метода
Ньютона (см. гл. 4).
Замечание. Применение метода Ньютона
<*ы = «к-ф (ак)/ф'(ак) A5.99)
сопряжено с необходимостью вычисления значений не только фун-
функции ф (а), но и ее производной ф'(а). Покажем, как можно вы-
вычислить ф'(а) = — г D, а) в рассматриваемом случае.
Дифференцируя по параметру а уравнения A5.95), A5.96) и
начальные условия A5.97), замечаем, что функции и (х, а) =
= —- у (х, a), v (х, а) = — z (х, а) удовлетворяют следующим урав-
уравнениям и начальным условиям:
«' = #*, У (*, a), z (х, а))« + f'z(x, у (х, а), г (х, a))v, A5.100)
«' = 0у(*. У (х> °). 2 (*. <*))* + 9'z(x, у (х, a), z (x, a))v, A5.101)
«(а,а) = 0|«(а,а)=1. A5.102)
Решая теперь относительно функций у, z, u, v задачу Коши для
системы уравнений A5.95), A5.96), A5.100), A5.101) с начальными
условиями A5.97), A5.102), можно определить ф (а) = z (Ь, а) — гь
и ф'(а) = «D, а).
Пример 15.2. Применим метод пристрелки к решению краевой задачи
A5.103)
A5.104)
Положим ф (а) = гA, а) — 1, где у (х, a), z(x, a) — решение задачи
Коши
х ,, *
Wy
у @, а) = 1, г @, о) = о.
A5.105)
A5.106)
519

Для решения уравнения ф (а) = 0 воспользуемся методом секущих:
= (*к-Ф («*
Ф (<**) - ф (art-,)-
A5.107)
Возьмем щ = 0.5, ai = 1 и будем вести итерации по формуле A5.107) до тех
пор, пока не выполнится условие |У>(од)| < Ю'6. Результаты вычислений
приведены в табл. 15.2.
Таблица 15.2
Ф(<*1д
0
1
2
3
4
0.500000
1.000000
0.873956
0.881517
0.881612
-0.632121
0.213061
-0.013596
-0.167833-10
0.151260-10
Заметим, что в общем случае вычисление значения ф (а) производится с
помощью численного решения задачи Коши. Однако в рассматриваемом случае
задача A5.105), A5.106) допускает аналитическое решение
у (х, а) = e2Q, z(x, a) = 2ае 2а. A5.108)
Поэтому можно воспользоваться явной формулой
_ 1_
ф (а) = 2ое га _ !.
В результате применения метода пристрелки для задачи A5.103), A5.104)
получаем решение A5.108), где а и 0.881612.
Замечание. Своим названием метод пристрелки обязан оче-
очевидной аналогии между процессом его реализации при решении
краевой задачи и процессом пристрелки при артиллерийской
стрельбе по цели. После выбора очередного значения од пристре-
пристрелочного параметра (выбора угла стрельбы) решается задача Коши
(производится "выстрел"). Если 2 F, од) совпадает с z\> с заданной
точностью, то "цель считается пораженной", а краевая задача —
решенной. В противном случае производится корректировка значе-
значения пристрелочного параметра и процесс продолжается дальше.
520
Использование для решения уравнения A5.98) метода бисекции
еще более усиливает эту аналогию. Здесь результат того "выстре-
"выстрела", при котором ф (од) > 0, может восприниматься как "перелет
снаряда", а того, при котором ф (од) < 0, — как "недолет".
Покажем теперь схематично, как применяется метод пристрелки
для решения общей двухточечной краевой задачи для системы диф-
дифференциальных уравнений первого порядка
у[{?) = Л(*> Sft(*)> •••> Уп(х)),
Уп(х) = fn(x, У\(х), .-, Уп(х)),
), .... Уп(Ь)) = 0,
<Рп(У\(а), ¦-, Уп(а), yi(b), ..., уп(Ь)) = 0.
Запишем эту задачу в векторной форме:
Рассмотрим также задачу Коши
у'(х, а) = f(x, j(z, a)),
У (а, а) = о.
A5.109)
A5.110)
A5.111)
A5.112)
Здесь a — («i, aj, ..., an)T — вектор пристрелочных параметров. Решив
задачу Коши A5.111), A5.112) при фиксированном значении вектора
а, получим решение у (z, а). Далее взяв у (а) = а и у F) = у F, а) и
подставив эти значения в систему A5.110), приходим к системе урав-
уравнений
*(в) = 0, A5.113)
где ф (а) = <р (а, у F, о)). Наконец, решив систему A5.113), получаем
набор a = (а\, а2 an)T значений пристрелочных параметров, при
которых решение задачи Коши A5.111), A5.112) совпадает с решением
краевой задачи A5.109), A5.110).
Практическая реализация метода пристрелки при большом числе
уравнений (часто уже при п > 3) оказывается довольно сложным де-
делом. Действительно, даже сама по себе проблема решения системы
521

нелинейных уравнений A5.113) является весьма трудной. Серьезные
затруднения могут возникнуть здесь уже на этапе выбора хорошего
начального приближения <ц>. Необходимо также учесть, что каждое
вычисление вектор-функции ф (о) является здесь весьма трудоемкой
операцией: оно предполагает (численное) решение задачи Коши
A5.111), A5.112).
Метод пристрелки достаточно эффективен в том случае, когда
задача Коши A5.111), A5.112) является хорошо обусловленной. Одна-
Однако если задача Коши плохо обусловлена, то метод оказывается прак-
практически непригодным. Дело в том, что при решении системы A5.113)
значения пристрелочных параметров а обязательно будут найдены с
некоторой погрешностью, (относительная величина которой не может
иметь порядок, меньший чем машинное эпсилон ем). Соответствующее
решение задачи Коши (в случае плохой обусловленности) в результате
этой погрешности окажется полностью искаженным. Однако даже в
том идеализированном случае, когда вектор а найден абсолютно точ-
точно, при численном решении задачи A5.111), A5.112) на ЭВМ в приб-
приближенное решение будут внесены ошибки, которые сделают его не-
непригодным. Для некоторых систем эти ошибки могут приводить даже
к аварийному останову вычислительного процесса.
Пример 15.3. Рассмотрим краевую задачу
у\х) = z (г), z\x) = 100у (а) + е* 0 < х< 2,
у@) = 0, *B) = 0.
Как нетрудно проверить, ее решением является пара функций
у (х) = qe10* +
z(x) =
A5.114)
A5.115)
|f
—
99'
где
_ 1 Юе-Ю +е->8
Q=990 1 + еч"о w 153838-10-",
1 10 -
990 1 +
« 0.0101010.
Попробуем решить задачу A5.114), A5.115) методом пристрелки, используя
6-разрядную десятичную ЭВМ. Соответствующая задача Коши имеет вид
у'(х, а) = х {х, a), z'(x, а) = 100» (х, а) + е*
у @, а) = 0, z @, а) = а.
522
Ее решением являются функции
г^-ае-'й-
99
.±|^.a|e-iox.l_ex.
A5.116)
A5.117)
Уравнение ф (а) — 0 (где ф (а) = z B, а)) для определения пристрелочного
параметра а является линейным. Поэтому для определения а достаточно
сделать одну итерацию метода секущих:
1
- «о)
A5.118)
Возьмем ao = 0, «i = -1. Тогда вычисления по формуле A5.117) на
6-разрядной десятичной ЭВМ дают значения, ф (ao) = zB, 0) « 2.69536-107,
ф (ai) = z{2, -1) я -2.15629-108. В соответствии с формулой A5.118) получа-
получается следующее значение пристрелочного параметра:
a = -1 —
-2.15629-108(-1 - 0)
-2.15629-10« -2.69536-107
и а* = -1 + 0J
= -0.111112.
Подстановка в формулы A5.116), A5.117) значения о = о* приводит к приб-
приближенному решению
. .,«„ 1 .
у\х)=
- -^ e*.
Здесь
20
20
7 = ^ Itt - a*l и \к @.
0909091 + 0.111112) я 0.0101011.
Тогда q — с* « 5-10'8, сг — с* и -10'7. Это означает, что
у (г) _ у*(г) к 5-10'8e101 - 10-V1O:c,
z (г) - z*(x) и 5- lO'V01 + lO'V10*.
Наличие в погрешности компоненты, пропорциональной е1Ог, приводит к тому,
что при х = 2 погрешности решения достигают следующих величин: у B) —
- у*B) я 24.3, z B) - г*B) я 243.
523

§ 15.6. Дополнительные замечания
1. В этой главе метод конечных разностей и метод конечных элементов
рассматривались только лишь применительно к решению двухточечных крае-
краевых задач для обыкновенных дифференциальных уравнений второго порядка.
Значительно более широкую область применения этих методов представляют
собой различные задачи для дифференциальных уравнений в частных произ-
производных. Ограниченный объем книги не позволяет отразить здесь богатство
существующих подходов и разнообразие используемых приемов. Тем, кто
интересуется решением уравнений в частных производных с помощью метода
конечных разностей, рекомендуем первоначально обратиться к учебникам [43],
[60], [71], а затем — к книгам [ 54], [70].
Как доступное введение в метод конечных элементов, можно рекомендовать
книги [3], [27], [57], [75]. В дальнейшем следует обратиться к [35], [36], [55],
[73], [85].
2. Так как мы рассматривали краевые задачи только для обыкновенных
дифференциальных уравнений, то тем самым фактически лишили себя воз-
возможности обсуждать достоинства и недостатки метода конечных разностей и
метода конечных элементов в их сравнении между собой. Ограничимся лишь
констатацией того, что для решения дифференциальных уравнений существу-
существуют два мощных метода, каждый из которых не обладает, вообще говоря,
безусловным преимуществом над другим. Тем не менее отметим, что нередко
наиболее эффективньши оказываются именно те приближенные методы, кото-
которые сочетают в себе достоинства обоих методов.
3. При математическом моделировании различных физических явлений
часто приходится решать краевые задачи, в которых дифференциальные
уравнения или краевые условия являются нелинейными. Примером может
служить дифференциальное уравнение -(к (г, «)«')' = /(*, «), описывающее
установившееся распределение тепла в стержне, теплофизические характерис-
характеристики которого зависят от температуры и. Для решения таких задач широко
используются метод конечных разностей и метод конечных элементов. Возни-
Возникающие здесь дискретные краевые задачи нелинейны и требуют для вычисле-
вычисления решений использования специальных итерационных методов.
4. В последние десятилетия было осознано, что решение проблемы числен-
численного решения дифференциальных уравнений основано на использовании
специальных методов теории приближения функций. Однако глубокая связь
между проблемой аппроксимации функций и проблемой решения дифферен-
дифференциальных уравнений осталась за рамками данной книги. Отметим лишь, что
приближенное решение »A(r), полученное с помощью проекционно-разностной
схемы A5.81), A5.82), представляет собой линейный сплайн.
524
ЛИТЕРАТУРА
1. Абрамовиц М., С т и г а н И. (ред.). Справочник по специальным
функциям с формулами, графиками и математическими таблицами. — М.:
Наука, 1979.
2. А л б е р г Дж., Нилсон Э., Уолш Дж. Теория сплайнов и ее
приложения. — М.: Мир, 1972.
3. Андреев В.Б., Руховец Л.А. Проекционные методы. — М.:
Знание, 1986.
4. Бабенко К.И. Основы численного анализа. — М.: Наука, 1986.
5. Бабушка И:, ВитасекЭ., ПрагерМ. Численные процессы
решения дифференциальных уравнений. — М.: Мир, 1969.
в. Базара М., Шетти К. Нелинейное программирование. Теория и
алгоритмы. — М.: Мир, 1982.
7. Бакушинский А.Б., Гончарский А.В. Некорректные
задачи. Численные методы и приложения. — М.: Изд-^о МГУ, 1989.
8. Б а х в а л о в Н.С. Численные методы. — М.: Наука, 1973.
9. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Числен-
Численные методы. — М.: Наука, 1987.
10. Безбородое Ю.М. Индивидуальная отладка программ. — М.:
Наука, 1982.
11. Б е й к е р Дж., Грейвс — Моррис П. Аппроксимации Паде. —
М.: Мир, 1986.
12. Беклемишев Д.В. Дополнительные главы линейной алгебры. —
М.: Наука, 1983.
13. Блехман Н.Н., М ы ш к и с А.Д., П а н о в к о Я.Г. Механика и
прикладная математика. Логика и особенности приложений математики. — М.:
Наука, 1983.
14. БоглаевЮ.П. Вычислительная математика и программирование. —
М.: Высшая школа, 1990.
15. Боголюбов А.Н. Математики. Механики. Биографический спра-
справочник. — Киев: Наукова думка, 1983.
16. Д е Б о р К. Практическое руководство по сплайнам. — М.: Радио и
связь, 1985.
17. Бородин А.Н., Бугай АС. Выдающиеся математики. — Киев:
Радянська школа, 1987.
525

18. Васильев Ф.П. Численные методы решения экстремальных задач.
— М.: Наука, 1980.
19. Воеводин В.В. Вычислительные основы линейной алгебры. — М.:
Наука, 1977.
20. Воеводин В.В., Кузнецов Ю.А. Матрицы и вычисления. —
М.: Наука, 1984.
21. В о л к о в Е.А. Численные методы. — М.: Наука, 1987.
22. Галлагер Р. Метод конечных элементов. Основы. — М.: Мир,
1984.
23. Гантмахер Ф.Р. Теория матриц. — М.: Наука, 1988.
24. Г и л л Ф., М ю р р е й У., РайтМ. Практическая оптимизация. —
М.: Мир, 1985.
25. Горинштейн А.М. Практика решения инженерных задач на
ЭВМ. — М.: Радио и связь, 1984.
26. ДеккерК., ВерверЯ. Устойчивость методов Рунге—Кутты для
жестких нелинейных дифференциальных уравнений. — М.: Мир, 1988.
27. Д е к л у Ж. Метод конечных элементов. — М.: Мир, 1976.
28. Демидович Б.П., Марон И.А. Основы вычислительной мате-
математики. — М.: Наука, 1966.
29. Демидович Б.П., Марон И.А., Шувалова Э.З. Числен-
Численные методы анализа. — М.: Наука, 1967.
30. Джордж А., Л ю Дж. Численное решение больших разреженных
систем уравнений. — М.: Мир, 1984.
31. Д ж о у н с У., Т р о н В. Непрерывные дроби. — М.: Мир, 1985.
32. Д э н н и с Дж., Шнабель Р. Численные методы безусловной
оптимизации и решения нелинейных уравнений. — М.: Мир, 1988.
33. Жаблон К., Симон Ж.—К. Применение ЭВМ для численного
моделирования в физике. — М.: Наука, 1983.
34. Завьялов Ю.С., Квасов Б.И., Мирошниченко В.Л.
Методы сплайн-функций. — М.: Наука, 1980.
35. Зенкевич О. Метод конечных элементов в технике. — М.: Мир,
1975.
36. Зенкевич О., Морган К. Конечные элементы и аппроксима-
аппроксимация. — М.: Мир, 1986.
37. Иванов В.В. Методы вычислений на ЭВМ. Справочное пособие. —
Киев: Наукова думка, 1986.
38. Икрамов Х.Д. Численные методы линейной алгебры. (Решение
линейных уравнений.) — М.: Знание, 1987.
39. Икрамов Х.Д. Численные методы для симметричных линейных
систем. — М.: Наука, 1988.
40. Икрамов Х.Д. Вычислительные методы линейной алгебры. (Реше-
(Решение больших разреженных систем уравнений прямыми методами.) — М.: Зна-
Знание, 1989.
41. И к р а м о в Х.Д. Несимметричная проблема собственных значений. —
М.: Наука, 1991.
42. И л ь и н В.П., Кузнецов Ю.И. Трехдиагональные матрицы и их
приложения. — М.: Наука, 1985. '»
43. Калиткин Н.Н. Численные методы. — М.: Наука, 1978.
44. Канторович А.В., А к и л о в Г.П. Функциональный анализ. —
М.: Наука, 1977.
45. Карпов В.Я., К о р я г и н Д.А. Пакеты прикладных программ. —
М.: Знание, 1983.
46. Копченова Н.В., Марон И.А. Вычислительная математика в
примерах и задачах. — М.: Наука, 1972.
47. Краснощекое П.С, Петров А.А. Принципы построения
моделей. — М.: Изд-во МГУ, 1983.
48. Кронрод А.С. Узлы и веса квадратурных формул. — М.: Наука,
1964.
49. Крылов В.И., Бобков В.В., Монастырный П.Н.
Вычислительные методы, том 1. — М.: Наука, 1976.
50. ЛоусонУ., ХенсонР. Численное решение задач метода наи-
наименьших квадратов. — М.: Наука, 1986.
51. Люк Ю. Специальные математические функции и их аппроксима-
аппроксимации. — М.: Мир, 1980.
52. Люстерник Л.А., Червоненкис О.А., Янпольс-
к и й А.Р. Математический анализ. Вычисление элементарных функций. М.:
Физматгиз, 1963.
53. М а к-К р а к е н Д., Д о р н У. Численные методы и программирова-
программирование на ФОРТРАНЕ. - М.: Мир, 1977.
54. М а р ч у к Г.И. Методы вычислительной математики. — М.: Наука,
1989.
55. М а р ч у к Г.И., А г о ш к о в В.И. Введение в- проекционно-сеточные
методы. — М.: Наука, 1981.
56. М а р ч у к Г.И., Шайдуров В.В. Повышение точности решений
разностных схем. — М.: Наука, 1979.
57. М и т ч е л л Э., У а й т Р. Метод конечных элементов для уравнений
с частными производными. — М.: Мир, 1981.
58. Моисеев Н.Н. Математика ставит эксперимент. — М.: Наука, 1979.
59. МорозовВ.А. Регулярные методы решения некорректно поставлен-
поставленных задач. — М.: Наука, 1987.
60. О р т е г а Дж., П у л У. Введение в численные методы решения
дифференциальных уравнений. — М.: Наука, 1986.
526
527

61. ОртегаД., Рейнболдт В. Итерационные методы решения
нелинейных систем уравнений со многими неизвестными. — М.: Мир, 1975.
62.ПарлеттБ. Симметричная проблема собственных значений. — М.:
Мир, 1983.
63. Писсанецки С. Технология разреженных матриц. — М.: Мир,
1988.
64. Пол як Б.Т. Введение в оптимизацию. — М.: Наука, 1983.
65. Попов Ю.П., Самарский А.А. Вычислительный экспери-
эксперимент. — М.: Знание, 1983.
66. Пшеничный Б.Н., Данилин Ю.М. Численные методы в
экстремальных задачах. — М.: Наука, 1975.
67. Райе Дж. Матричные вычисления и математическое обеспечение. —
М.: Мир, 1984.
68. Ракитский Ю.В., Устинов С.М., Черноруцкий М.Г.
Численные методы решения жестких систем. — М.: Наука, 1979.
69. Самарский А.А. Введение в численные методы. — М.: Наука,
1982.
Ж Самарский А. А. Теория разностных схем. — М.: Наука, 1977.
71. Самарский А.А., Г у л и н А.В. Численные методы. — М.:
Наука, 1989.
72.Самарский А. А., Николаев Б.С. Методы решения сеточных
уравнений. — М.: Наука, 1978.
73. С е г е р л и н д Л. Применение метода конечных элементов. — М.:
Мир, 1979.
74. Современные численные методы решения обыкновенных дифференци-
дифференциальных уравнений (под ред. Дж. Холла и Дж. Уатта). — М.: Мир, 1979.
75. Стренг Г., Фикс Дж. Теория метода конечных элементов. — М.:
Мир, 1977.
76. Сухарев А.Г., Т и м о х о в А.В., Федоров В.В. Курс мето-
методов оптимизации. — М.: Наука, 1986.
77. С ь я р л е Ф. Метод конечных элементов для эллиптических задач. —
М.: Мир, 1980.
78. Тихонов А.Н. Математическая модель. Математическая энцикло-
энциклопедия, т. 3. — Сов. энциклоп., 1982.
78. Тихонов А.Н., А р с е н и н В.Я. Методы решения некорректных
задач. — М.: Наука, 1986.
80. Тихонов А.Н., Гончарский А.В., Степанов В.В.,
Я г о л а А.Г. Численные методы решения некорректных задач. — М.: Наука,
1990.
81. Т и х о н о в А.Н., Костомаров Д.П. Вводные лекции по прик-
прикладной математике. — М.: Наука, 1984.
82-ТьюарсонР. Разреженные матрицы. — М.: Мир, 1977.
528
83. Уилкинсон Дж. X. Алгебраическая проблема собственных значе-
значений. — М.: Наука, 1970.
84. Уилкинсон Дж. X., Р а й н ш К. Справочник алгоритмов на
языке Алгол. Линейная алгебра. — М.: Машиностроение, 1976.
85. ФлетчерК. Численные методы на основе метода Галеркина. — М.:
Мир, 1988.
86. Форсайт Дж., Мальком М., М о у л е р К. Машинные мето-
методы математических вычислений. — М.: Мир, 1980.
87. Форсайт Дж., М олерК. Численное решение систем линейных
алгебраических уравнений. — М.: Мир, 1969.
88. ХайрерЭ., НерсеттС, ВаннерГ. Решение обыкновенных
дифференциальных уравнений. Нежесткие задачи. — М.: Мир, 1990.
89. Хейгман Л., Я н г Д. Прикладные итерационные методы. — М.:
Мир, 1986.
90. Хемминг Р.В. Численные методы для научных работников и
инженеров. — М.: Наука, 1972.
91. ХиммельблауД. Прикладное нелинейное программирование. —
М.: Мир, 1975.
92. Ш у п Т. Решение инженерных задач на ЭВМ. — М.: Мир, 1982.
93. Эльсгольц Л.Э. Дифференциальные уравнения и вариационное
исчисление. — М.: Наука, 1969.
94. Эстербю О., 3 л а т е в 3. Прямые методы для разреженных
матриц. — М.: Мир, 1987.

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Абсолютная погрешность 25
-- вектора 125
- точность 28
- устойчивость 459
Абстрактный вычислительный алго-
алгоритм 63
Автоматический выбор шага 445
Адаптивные квадратурные програм-
программы 398
- процедуры численного интегриро-
интегрирования 398
Алгоритм бинарный 77
- вычислительно устойчивый 65
- вычислительный 63
- - абстрактный 63
- Гира 481, 482
- Краута 173
- неустойчивый 65
- плохо обусловленный 71
- устойчивый 65
- хорошо обусловленный 70
-1Д235
-QL235
- QR 231
- - основной 231
- - со сдвигами 233
Алгоритмы гибридные 111, 121, 260
- регуляриэованные 121, 260
Анализ ошибок обратный 73
- - прямой 72
- - статистический 75
Антиградиент 264
Антипереполнение 39
Апостериорные оценки погрешнос-
погрешности 62
Аппроксимационная теорема Вейер-
штрасса 324
Аппроксимация дифференциального
уравнения 424, 495
530
с р-м порядком 424
- краевых условий 505
- Паде 362
Априорные оценки погрешности 61
- - решения краевой задачи 486
разностной схемы 494
Базис лагранжев 330
- локальный степенной 330
- нормированный степенной 330
- степенной 330
- чебышевский 330
Базисные многочлены 329
- функции 508
- - кусочжьлинейные 514
- - специальные 517
Баллистический метод 518
Быстрое дискретное преобразование
Фурье 341
Вариационная постановка краевой
задачи 506
Вариационно-разностная схема 515
Вариационные принципы 506
Вариационный функционал 506
Вековое уравнение 212
Векторы взаимно сопряженные 285
Верная цифра 27
Верхняя граница абсолютной пог-
погрешности 26
- - относительной погрешности 26
Вес 402
Весовая функция 402
Веса квадратурной формулы 376
Гаусса 390
Временная постоянная 416
--локальная 417
Входное данное 10, 12
Вычислительная задача 12, 43
- - корректная 43
- - некорректная 44
- - плохо обусловленная 49
- - хорошо обусловленная 49
- погрешность 24
Вычислительный алгоритм 63
- - абстрактный 63
- - корректный 63
- - некорректный 63
- - неустойчивый 65
- - устойчивый 65
- процесс 19
- эксперимент 20
Вычислительные методы 13, 55
Гибридные алгоритмы 111, 121, 260
Главный член погрешности квадра-
квадратурной формулы 393
Глобальная погрешность 425
полиномиальная интерполя-
интерполяция 324
Градиент 264
Градиентный метод 272
Граница абсолютной погрешности 26
- относительной погрешности 26
Граничные условия 336
Данные входные 10
- выходные 10
- исходные 10
Двоичный порядок 37
Двухточечная краевая задача 483
Дефект сплайна 333
Дискретизация 57
Дискретная задача Коши 420
- краевая задача 488
Дискретное преобразование Фу-
Фурье 340
быстрое 341
обратное 340
прямое 340
- уравнение 419
Диссипативная система дифферен-
дифференциальных уравнений 465
Дробление шага 269
Дробь непрерывная 362, 363
- цепная 362, 363
Евклидова норма вектора 124
- - матрицы 127
Естественный кубический сплайн 337
Жесткая задача Коши 472, 478
- система дифференциальных урав-
уравнений 477
Жорданова форма матрицы 215
Задача безусловной минимиза-
минимизации 262
- вычислительная 12, 43
- - корректная 44
- - некорректная 44
- - плохо обусловленная 49
- - хорошо обусловленная 49
- дискретной минимизации 291
- жесткая 472
- идентификации 11
- интерполяции 295
- - обобщенными многочленами 296
- конечномерная 57
- линейного программирования 291
- Коши 410, 412
- - дискретная 420
- - для обыкновенного дифферен-
дифференциального уравнения первого поряд-
порядка 412
m-го порядка 471
системы обыкновенных диффе-
дифференциальных уравнений первого по-
порядка 463
- - жесткая 472, 476
для системы дифференциаль-
дифференциальных уравнений 476
- краевая двухточечная 483
- минимизации оценки погрешнос-
погрешности интерполяции 306
- начальная 410
- наименьших квадратов линей-
линейная 343, 345, 363
нелинейная 355
531

нелинейного программирова-
программирования 291
- о наилучшем равномерном приб-
приближении 356
- о наименьших квадратах 290
- о понижении степени многочле-
многочлена 358
- обратная 11
- одномерной минимизации 236
- прямая 10
- условной минимизации 262, 291
Золотое сечение 253
Значащая цифра 27
Инженерная задача 7
Интегральная кривая 411
Интегральное тождество 510
Интегрирование дифференциального
уравнения 411
Интегро-интерполяционный ме-
метод 503
Интервал неопределенности корня
нелинейного уравнения 88
- - точки локального минимума 242
Интерполирование 295
Интерполяционный массив 325
- многочлен 300
- - кубический Эрмита 305
--Лагранжа 301
- - Ньютона с конечными разностя-
разностями для интерполяции вперед 323
------ для интерполяции на-
назад 323
- - - с разделенными разностя-
разностями 320
- - обобщенный 296
- - с кратными узлами 305
Интерполяция 295
- глобальная полиномиальная 324
- квадратичная 301
- кубическая 301
- кусочно-полиномиальная 332
- линейная 301
532
- локальная 331
- рациональная 361
- тригонометрическая 342
Искомое решение 10, 12
Исчезновение порядка 39
Исчерпывание 227
Итерационная последовательность 60
- функция 94
Итерационное уточнение 171
- - корней нелинейного уравне-
уравнения 83, 85
Итерационные методы 59
Итерационный метод одношаго-
вый 85
- - ib-шаговый 85
- процесс 59
Итерация 59
Катастрофическая потеря точнос-
точности 31, 69
Квазиньютоновские методы 283
Квазиньютоновское условие 283
Квадратурная сумма 376
- формула 376
- - Гаусса 389, 405
- - интерполяционого типа 385, 403
- - левых прямоугольников 378
- - Ньютона - Котеса 385
- - правых прямоугольников 378
- - прямоугольников элементар-
элементарная 377
составная 378
- - Симпсона элементарная 380
составная 380
- - точная для многочленов степе-
степени т376
- - трапеций элементарная 378
составная 378
- - центральных прямоугольни-
прямоугольников 378
Конечномерная задача 57
Конечно-разностная схема 452
Конечно-разностные методы 452
- шаги 205
Конечные разности 311
- - вперед 311
- - назад 317
- - порядка Jfc 311
Конечные элементы 513
Константа Лебега 328
Корень нелинейного уравнения 80
простой 81
кратный 81
Корневое условие 455
Корректность вычислительного алго-
алгоритма 63
- вычислительной задачи 44
Коэффициент роста 144
Краевая задача двухточечная 483
- - дискретная 488
Краевые условия первого рода 484
- - второго рода 484
Кратность корня нелинейного урав-
уравнения 81
- узла интерполяции 304
Критерий окончания итерационного
процесса 61, 270
Круги Гершгорина 216
Кубатурные формулы 408
Кусочно-полиномиальная интерполя-
интерполяция 332
Линейная задача наименьших квад-
квадратов 343, 345, 363
Линия уровня 203
Локализация корней нелинейного
уравнения 83
- собственных значений 216
- точки минимума 241
Локальная интерполяция 331
- погрешность 424, 427
- сходимость 111
Локальный сплайн 335
Ломаная Эйлера 430
Мантисса 37
Масштабирование 147
Математическая модель 8
- - гипотетическая 9
- - динамическая 10
- - статическая 10
Математическое моделирование 8
Матрица
- верхняя треугольная 129
-Гессе 265
- Гильберта 135
- Грама297
- диагональная 128
- единичная 128
- заполненная 130
- ленточная 131
- нижняя треугольная 129
- ортогональная 165
- отражения 170
- плотная 130
- плохо обусловленная 133
- подобия 214
- положительно определенная 129
- простой структуры 215
- разреженная 130
- симметричная 129
- трехдиагональная 130
- треугольная 129
- Хаусхолдера 170
- Хессенберга 233
- Якоби 193
Матрицы подобные 214
Машинная бесконечность 39
-точность 38
Машинное слово 37
- эпсилон 38, 42
Машинный нуль 39
Метод Адамса 448
- - интерполяционный 449
- - экстраполяционный 449
- Адамса - Башфорта 449
- Адамса - Моултона 449
- баланса 503
- баллистический 518
533

- бисекции 91, 257
- бисекции 235
- вращений 166
- - Якоби 235
- Галеркина 511
- Гаусса 137
- - с выбором главного элемента по
всей матрице 145
столбцу 143
- Гаусса - Зейделя 183
- градиентный 272
- Давиденко 210
- Данилевского 213
- деления отрезка пополам 247
- деформируемого многогранни-
многогранника 288
- дифференцирования по парамет-
параметру 209
- Зейделя 182, 201
- золотого сечения 253
- итегро-интерполяционный 503
- касательных 106
- квадратных корней 158
- конечных разностей 487
- - элементов 512
- Крылова 213
- Ланцоша 189
- Леверье 213
- линейный многошаговый с чебы-
шевским набором параметров 189
- ложного положения 113, 206
- минимальных невязок 189
- Монте - Карло 408
- Мюллера 121
- наименьших квадратов 173, 343
- наискорейшего спуска 189, 272
- Нумерова 472
- Ньютона вычисления \а 60
- - минимизации 258, 280
- - решения нелинейных уравне-
уравнений 106
534
- - - систем нелинейных уравне-
уравнений 201
- - упрощенный 112, 205
- обратной квадратичной интерпо-
интерполяции 120
- обратных итераций 227
- - - с использованием отноше-
отношения Рэлея 230
- отражений 170
- пассивного поиска 246
- покоординатного спуска 270
- половинного деления 91
- последовательного исключения
неизвестных 137
- последовательной верхней релак-
релаксации 188
- - параболической интерполя-
интерполяции 259
- - нижней релаксации 188
- последовательных замещений 183
- пристрелки 518
- прогонки 161, 490
- продолжения по параметру 208
- простой итерации решения систем
линейных алгебраических уравне-
уравнений 175
систем нелинейных уравне-
уравнений 196
нелинейных уравнений 93
- релаксации 187
- Ритца 508
- Ромберга 398
- Рунге - Кутты 439
неявный лнэтапный 445
- - - четвертого порядка точнос-
точности 443, 469
явный т-отапный 441
- Рунге - Кутты - Фельберга 447,
482
-секущих 114, 206
- сеток 487
- сопряженных градиентов 189, 285
- - направлений 285
- Стеффенсена 116, 206
- степенной 221
стохастической аппроксима-
аппроксимации 261
- стрельбы 518
- установления 210
- Фибоначчи 250
- Холецкого 158
- Хьюна 437
- Эйлера 421, 430, 469
- - неявный 422, 461
- - усовершенствованный 438
- Эйлера - Коши 437
- экстраполяции Ричардсона 397
- Якоби 176
- SOR 187
Метода Гаусса ведущий элемент k-ro
шага 138
- - главный элемент fc-ro шага 138
- - множители it-го шага 138
- - обратный ход 139
- - прямой ход 137
Методы Адамса 448
- аппроксимации 56
- вычислительные 13, 55
- итерационные 59
итерирования подпространст-
подпространства 235
- квазиньютоновские 210, 283
- конечно-разностные 452
- линеаризации 57, 106
- линейные многошаговые 452
- Монте - Карло 62
- "овражные" 277
- одновременных итераций 235
- переменной метрики 283
- последовательного поиска 247
- прогноза и коррекции 437, 451
- прямого поиска 245, 287
- прямые 58, 213
- регуляризации 49, 58
- Рунге - Кутты 439, 444, 481, 482
- спуска 268
- статистических испытаний 62
- типа Ланцоша 235
- - предиктор - корректор 437
- точные 59
- численные 13
- эквивалентных Преобразований 56
Минимальное значение функ-
функции 236, 262
Многочлен интерполяционный 300
- - кубический Эрмита 305
- - Ньютона 320, 323
- - обобщенный 296
- - с кратными узлами 305
- Лагранжа 301
- наилучшего равномерного прибли-
приближения 356
- - среднеквадратичного приближе-
приближения 345
- обобщенный 294
- характеристический 455
Многочлены наименее уклоняющие-
уклоняющиеся от нуля 308
- Чебышева 307
Модельное уравнение 416
Множество граничных узлов сет-
сетки 488
- внутренних узлов сетки 488
- возможных решений 43
- допустимых входных данных 43
Надежность программы 78
Наименьших квадратов задача ли-
линейная 343, 345, 363
нелинейная 355
Наклон сплайна 334
Направление ньютоновское 280
- спуска 268, 269
Начальная задача 410
Начальное значение 412
-условие 412
Начальные значения 420
535

- условия i64, 471
Невязка 123, 132
Некорректная задача 44, 48
Непрерывная дробь 362
Неравенство треугольника 124
Неустранимая погрешность 24
Неявный метод Эйлера 422, 4о1
Норма вектора 124
- - евклидова 124
- матрицы подчиненная 126
- - евклидова 127
Нормальная система метода нлимень-
ших квадратов 345
Нуль-устойчивость 454
Область абсолютной устойчивос-
устойчивости 459
- неопределенности 73. 196
- сходимости метода 60
Обобщенный многочлен 294
Обратная задача 1!
- прогонка 163
Обратный анализ ошибок 73
- ход метода Гаусса 139
прогонки 163
Обусловленность вычислительного
алгори-ма 70
- вычислительной задачи 49
Односторонние формулы численного
дифференцирования 371
Округление 29
- по дополнена - -;./
- усечением 2°
Определитель Вандермондь. ^00
- Грама 298
Оптимальный пассивный пс ick 246
Остаточный член кчащ>агурной фор-
формулы 376
Относительная погрешность 25
- - вектора 125
- точность 29
- - ЭВМ 38
Отношение Радел 218
536
Отражение 170
Отрезок локализации корня нели-
нелинейного уравнения 83
- - точки локального минимума 238
- наблюдения 296
Оценки погрешности априорные 61
- - апостериорные 62
Ошибка 25
- округления 38
- представления 38
Пакет прикладных программ проб-
проблемно-ориентированный 22
Параметр пристрелочный 518
- релаксации 187
Параметры модели 10
Переносимость 78
Переполнение 39
Плоское вращение 168
Плохо обусловленная вычислитель-
вычислительная задача 49
-- матрица 133
- - система линейных алгебраичес-
алгебраических уравнений 133
Плохо обусловленный вычислитель-
вычислительный алгоритм 71
Погрешность 23, 25
-абсолютная 25
- аппроксимации 56
- - дискретного уравнения 424
- - разностного уравнения 495
- - формулы численного дифферен-
дифференцирования 365
- вычислительная 24
- квадратурной формулы 376
- локальная 424
- метода 24
- на шаге 424
- неустранимая 24
- округления 29
- относительная 25
- разностной схемы 496
- численного метода решения зада-
задачи Кош и 425
глобальная 425, 427
локальная 424, 427
Подобные матрицы 214
Поверхность уровня 263
Поддерживаемость 78
Поле направлений 411
Полином "движущийся" 331
- устойчивости 459
Портабельность 78
Порядок сходимости итерационного
метода 85
Постановка краевой задачи вариа-
вариационная 506
проекционная 510
Постоянная временная 416
-Липшица 412, 464
Правило Гарвика 91
- двойного пересчета 395, 445
- Крамера 76
- Рунге практической оценки пог-
погрешности 394, 445, 447, 497
- трапеций 422, 436
Представимое множество ЭВМ 38
Преобразование Гивенса 168
- подобия 214
- Фурье дискретное 340
быстрое 341
обратное 340
прямое 340
- Хаусхолдера 170
Приближенное число 25
Приведение к виду, удобному для
итераций, системы линейных алгеб-
алгебраических уравнений 175
нелинейного уравнения 94,
100
Пример Рунге 325
- Уилкинсона 51, 219
Принцип максимума 485, 492
- для системы сето'эдых уравне-
уравнений 492
Пристрелочные параметры ">!«, 521
Проблема "оврагов" 276
- собственных значений полная 212
частичная 212
Пробная функция 510
Пробные точки 245
Прогонка обратная 163
- прямая 162
Прогоночные коэффициенты 162
Проекционная постановка краевой
задачи 510
Проекциокнс-разностная схема 515
специальная 516
Проекционно-разностный метод 515
Порядок двоичный 37
- сходимости итерационного мето-
метода 85
- точности численного метода реше-
решения задачи Коши 425
Процесс вычислительш-'й 19
- Либыана 183
Прямая задача 10
- прогонка 162
Прямой анализ ошибок 72
- ход метода Гаусса 137
прогонки 162
Прямые методы 58
- - решения проблемы собственных
значений 213
Работоспособность 78
Разделенные разности 318
Разложение матрицы на множите-
множители 154, 156, 166
-11/154
- QR 166
Разности конечные 311
--вперед 311
- - назад 317
- "против ветра" 503
- "против потока" 503
537

- разделенные 318
Разностная производная вторая 368
- - левая 365
-- правая 365
- - центральная 366
- схема 452, 488, 490
- - однородная 505
Разностное уравнение 489
- - Jb-ro порядка линейное однород-
однородное с постоянными коэффициентами
454
Разрядность мантиссы 37
Регуляриэованные алгоритмы 121
Рекуррентная формула 60
Решение краевой задачи для одно-
одномерного стационарного уравнения
теплопроводности 485
с разрывными коэффи-
коэффициентами 503
- нелинейного уравнения 80
- обыкновенного дифференциально-
дифференциального уравнения первого порядка 411
Робастноегь 78
Сетка 419, 487, 488
- равномерная 419
- неравномерная 501
Сеточные функции 419, 487
Сдвиги по Рэлею 234
- - Уилкинсону 234
Система линейных алгебраических
уравнений плохо обусловленная 133
- функций линейно зависимая в
точках 296
независимая в точках 297
- - ортогональная на множестве то-
точек 298
Скалярное произведение векто-
векторов 125
Скорость сходимости итерационного
метода квадратичная 85
кубическая 86
линейная 85
538
сверхлинейная 85
Собственное значение матрицы 211
- число матрицы 127, 212
Собственный вектор матрицы 212
Сплайн 333
- интерполяционный 334
- кубический 334
- - естественный 337
- - фундаментальный 336
- линейный 334
- локальный 335
- степени m 333
Сплайна дефект 333
- наклон 334
Среднеквадратичное уклонение 344
Статистический анализ ошибок 75
Стационарная точка функции 237,
264
Степенной метод 221
- - без сдвигов 221
- - со сдвигами 226
Схема Горнера 58
- единственного деления 137
- конечно-разностная 452
- разностная 452, 490
- полного выбора 145
- частичного выбора 143
- Эйткена 322
Сходимость итерационного метода 60
со скоростью геометрической
прогрессии 85
- локальная 111
- метода аппроксимации 56
- - интерполяции 325
- к треугольной матрице по фор-
форме 232
- последовательности векторов по
направлению 223
норме 125
покоординатная 126
- разностной схемы 496
с m-м порядком точности 496
- численного метода решения зада-
задачи Коши 425
Таблица конечных разностей 311
- разделенных разностей 318
Теорема Вейерштрасса аппроксима-
ционная 324
- Гершгорина 216
- локализации 216
- сравнения 486, 493
- Фабера 327
- Чебышева 357
Точка минимума глобального 236,
262
- - локального 236, 262
- - строгого локального 237, 263
- стационарная 237, 264
Точки пробные 245
- чебьгшевского альтернанса 357
Точность 26
-абсолютная 28
- машинная 38
- относительная 29
- удвоенная 41
- ЭВМ относительная 38
Точные методы 59
Траектория спуска 269
Угловой коэффициент 411
Удвоенная точность 41
Узлы интерполяции 295
- - кратные 304
- квадратурной формулы 376
Гаусса 390
- равноотстоящие 311
- сетки 419, 487, 488
- - внутренние 488
- - граничные 488
Уклонение многочлена от нуля 308
- среднеквадратичное 344
Унимодальная функция 239
Упрощенный метод Ньютона 112, 205
Уравнение диффузии одномер-
одномерное 484
- линейное однородное разностное с
постоянными коэффициентами 454
- модельное 416
- теплопроводности одномерное ста-
стационарное 484
- характеристическое 212, 455
- Эйлера 507
Усечение 29
Условие диагонального преоблада-
преобладания 147, 177
- корневое 455
-Липшица 412, 413, 464
- - одностороннее 413, 465
- "отсутствия узла" 337
Условия граничные 336
- краевые второго рода 484
- - первого рода 484
Усовершенствованный метод Эйле-
Эйлера 438
Устойчивость алгоритма 65
- - вычислительная 65
- - по входным данным 64
- разностной схемы 494
- решения вычислительной задачи
абсолютная 48
относительная 48
по входным данным 45
- решения задачи Коши асимптоти-
асимптотическая 418, 466
на конечном отрезке по на-
начальным значениям 416
и правой части 417,
465
по Ляпунову 418, 466
- численного метода решения зада-
задачи Коши 422
Форма матрицы жорданова 215
- - Хессенберга 232
Формула Ньютона - Лейбница 375
- парабол 381
- рекуррентная 60
- Эрмита 405
539

Формулы дифференцирования на-
назад 480
- квадратурные 376
- кубатурные 408
численного дифференцирова-
дифференцирования 364
односторонние 371
- Филона 406
Фундаментальный кубический
сплайн 336
Функция весовая 402
- - Лагерра 403
- - Эрмита 403
- - Якоби 403
- выпуклая 265
- овражная 276
- пробная 510
- сеточная 419, 488
- сильно выпуклая 265
- строго выпуклая 265
- унимодальная 239
- целевая 236, 262
Характеристический многочлен 455
Характеристическое уравнение 212,
455
Хорошо обусловленная вычислитель-
вычислительная задача 49
Хорошо обусловленный вычисли-
вычислительный алгоритм 70
Целевая функция 236, 262
Цепная дробь 362
Цифра значащая 27
- - верная 27
Числа Фибоначчи 250
Численные методы 13
Численный метод решения задачи
Коши абсолютно устойчивый 459
А-устойчивый 461
Л(а)-устойчивый 480
для систем дифференциаль-
дифференциальных уравнений первого порядка 469
fc-шаговый 420
----- линейный многошаго-
многошаговый 452
многошаговый 421
неявный 421
нуль-устойчивый 454
одношаговый 420
самостартующий 420
сходящийся 425
устойчивый 422
на конечном отрезке 422
явный 421
Число жесткости 477
- обусловленности вычислительной
задачи 49
абсолютное 50
относительное 50
- - вычислительного алгоритма 71
- - задачи вычисления многочлена
с приближенно заданными коэффи-
коэффициентами 330
- - естественное 132
- - матрицы 133
стандартное 133
- приближенное 25
Шаг конечно-разностный 205
- сетки 419
- спуска 268, 269
-таблицы 311
- формулы численного дифферен-
дифференцирования 364
Ширина ленты 131
ЭВМ б-разрядная десятичная 42
Экономичность алгоритма 76
Экономизация степенных рядов 359
Экстраполяция 296
- Ричардсона 397
ОГЛАВЛЕНИЕ
Предисловие 3
Глава 1. Математическое моделирование и решение инженерных задач с
применением ЭВМ 7
§ 1.1. Математическое моделирование и процесс создания математичес-
математической модели 8
§ 1.2. Основные этапы решения инженерной задачи с применением ЭВМ 15
§ 1.3. Вычислительный эксперимент 20
§ 1.4. Дополнительные замечания 22
Глава 2. Введение в элементарную теорию погрешностей 23
§ 2.1. Источники и классификация погрешностей результата численного
решения задачи 23
§ 2.2. Приближенные числа. Абсолютная и относительная погрешности . 24
§ 2.3. Погрешность арифметических операций над приближенными чис-
числами 30
§2 4. Погрешность функции 33
§ 2.5. Особенности машинной арифметики 35
§ 2.6. Дополнительные замечания 42
Глава 3. Вычислительные задачи, методы и алгоритмы. Основные поня-
понятия 43
§ 3.1. Корректность вычислительной задачи 43
§ 3.2. Обусловленность вычислительной задачи 49
§ 3.3. Вычислительные методы 55
§ 3.4. Корректность вычислительных алгоритмов 63
§ 3.5. Чувствительность вычислительных алгоритмов к ошибкам округ-
округления 67
§ 3.6. Различные подходы к анализу ошибок 72
§ 3.7. Требования, предъявляемые к вычислительным алгоритмам 76
§ 3.8. Дополнительные замечания 79
Глава 4. Методы отыскания решений нелинейных уравнений 80
§ 4.1. Постановка задачи. Основные этапы решения 80
§ 4.2. Обусловленность задачи вычисления корня 87
§ 4.3. Метод бисекции 91
§ 4.4. Метод простой итерации 93
§ 4.5. Обусловленность метода простой итерации 102
§ 4.6. Метод Ньютона 105
§ 4.7. Модификации метода Ньютона 112
§ 4.8. Дополнительные замечания 120
Глава 5. Прямые методы решения систем линейных алгебраических
уравнений 122
§ 5.1. Постановка задачи 122
§ 5.2. Нормы вектора и матрицы 123
§ 5.3. Типы используемых матриц 128
§ 5.4. Обусловленность задачи решения системы линейных алгебраичес-
алгебраических уравнений 131
§ 5.5. Метод Гаусса 137
541

§ 5.6. Метод Гаусса и решение систем уравнений с несколькими правыми
частями, обращение матриц, вычисление определителей 147
§ 5.7. Метод Гаусса и разложение матрицы на множители. Ь^Аразложе-
ние 151
§ 5.8. Метод Холецкого (метод квадратных корней) 158
§ 5.9. Метод прогонки 161
§ 5.10. Qii-рэзложение матрицы. Методы вращений и отражений 165
§ 5.11. Итерационное уточнение 171
§ 5.12. Дополнительные замечания 173
Глава 6. Итерационные методы решения систем линейных алгебраичес-
алгебраических уравнений 174
§ 6.1. Метод простой итерации 175
§ 6.2. Метод Зейделя 182
§ 6.3. Метод релаксации 187
§ 6.4. Дополнительные замечания 189
Глава 7. Методы отыскания решений систем нелинейных уравнений . . . 191
§ 7.1. Постановка задачи. Основные этапы решения 191
§ 7.2. Метод простой итерации 196
§ 7.3. Метод Ньютона для решения систем нелинейных уравнений 201
§ 7.4. Модификации метода Ньютона 204
§ 7.5. О некоторых подходах к решению задач локализации и отыскания
решений систем нелинейных уравнений 207
§ 7.6. Дополнительные замечания 210
Глава 8. Методы решения проблемы собственных значений 211
§ 8.1. Постановка задачи. Некоторые вспомогательные сведения 211
§ 8.2. Степенной метод 221
§ 8.3. Метод обратных итераций 227
§ 8.4. фй-алгоритм 231
§ 8.5. Дополнительные замечания 235
Глава 9. Методы одномерной минимизации 236
§ 9.1. Задача одномерной минимизации 236
§ 9.2. Обусловленность задачи минимизации 242
§ 9.3. Методы прямого поиска. Оптимальный пассивный поиск. Метод де-
деления отрезка пополам. Методы Фибоначчи и золотого сечения . . 245
§ 9.4. Метод Ньютона и другие методы минимизации гладких функций . 257
§ 9.5. Дополнительные замечания 261
Глава 10. Методы многомерной минимизации 262
§ 10.1. Задача безусловной минимизации функции многих переменных . 262
§ 10.2. Понятие о методах спуска. Покоординатный спуск 268
§ 10.3. Градиентный метод 272
§ 10.4. Метод Ньютона 279
§ 10.5. Метод сопряженных градиентов 284
§ 10.6. Методы минимизации без вычисления производных 287
§ 10.7. Дополнительные замечания 290
Глава 11. Приближение функций и смежные вопросы 292
§ 11.1. Постановка задачи приближения функций 292
542
§ 11.2. Интерполяция обобщенными многочленами , . . . . 295
§ 11.3. Полиномиальная интерполяция. Многочлен Лагранжа 300
§ 11.4. Погрешность интерполяции 302
§ 11.5. Интерполяция с кратными узлами 304
§ 11.6. Минимизация оценки погрешности интерполяции. Многочлены
Чебышева 306
§ 11.7. Конечные разности 311
§ 11.8. Разделенные разности 318
§ 11.9. Интерполяционный многочлен Ньютона. Схема Эйткена 320
§ 11.10. Обсуждение глобальной полиномиальной интерполяции. Поня-
Понятие о кусочно-полиномиальной интерполяции 324
§ 11.11. Интерполяция сплайнами 333
§ 11.12. Понятие о дискретном преобразовании Фурье и тригонометри-
тригонометрической интерполяции 339
§ 11.13. Метод наименьших квадратов 343
§ 11.14. Равномерное приближение функций 356
§ 11.15. Дробно-рациональные аппроксимации и вычисление элементар-
элементарных функций 361
§ 11.16. Дополнительные замечания 363
Глава 12. Численное дифференцирование 364
§ 12.1. Простейшие формулы численного дифференцирования ....... .364
§ 12.2. О выводе формул численного дифференцирования 369
§ 12.3. Обусловленность формул численного дифференцирования 372
$ 12.4. Дополнительные замечания 374
Глава 13. Численное тгтегрирование 375
§ 13.1. Простейшие квадратурные формулы 375
§ 13.2. Квадратурные формулы интерполяционного типа 384
§ 13.3. Квадратурные формулы Гаусса 389
§ 13.4. Апостериорные оценки погрешности. Понятие об адаптивных
процедурах численного интегрирования 392
$ 13.5. Вычисление интегралов в нерегулярных случаях 401
§ 13.6. Дополнительные замечания 408
Глава 14. Численные методы решения задачи Коши для обыкновенных
дифференциальных уравнений 410
§ 14.1. Задача Коши для дифференциального уравнения первого по-
порядка 411
§ 14.2. Численные методы решения задачи Коши. Основные понятия и
определения 419
§ 14.3. Использование формулы Тейлора 428
§ 14.4. Метод Эйлера 430
§ 14.5. Модификации метода Эйлера второго порядка точности 435
§ 14.6. Методы Рунге-Кутты 439
§ 14.7. Линейные многошаговые методы. Методы Адамса 448
5 14.8. Устойчивость численных методов решения задачи Коши 453
§ 14.9. Неявный метод Эйлера 461
§ 14.10. Решение задачи Коши для систем обыкновенных дифференци-
дифференциальных уравнений и дифференциальных уравнений т-го порядка 463
§ 14.11. Жесткие задачи 472
§ 14.12. Дополнительные замечания 481
543

Глава 15. Решение двухточечных краевых задач 48;
§ 15.1. Краевые задачи для одномерного стационарного уравнения тепло-
теплопроводности 48
§ 15.2. Метод конечных разностей: основные понятия 48
§ 15.3. Метод конечных разностей: аппроксимации специального вида . . 50
§ 15.4. Понятие о проекционных и проекционно-разностных методах. Ме-
Методы Ритца и Галеркина. Метод конечных разностей 50
§ 15.5. Метод пристрелки 51
§ 15.6. Дополнительные замечания 52
Литература 52
Предметный указатель 53<
Учебное издание
Амосов Андрей Авенирович, Дубинекий Юлий Андреевич,
Копченова Наталья Васильевна
ВЫЧИСЛИТЕЛЬНЫЕ МЕТОДЫ ДЛЯ ИНЖЕНЕРОВ
Редактор А.М.Суходский. Художественный редактор Т.А.Коленкова. Технически
редакторы С.В.Светикова, И.А.Балелина. Корректор В.В.Кожуткина. Операторы
Т.М.Дородных, В.Н.Думбар.
ИБ № 8157
ЛР № 010146 от 25.12.91. Изд. № ФМ-55. Сдано в набор 02.02.9
Подп. в печать 18.10.93. Формат 60x88/16. Бум. офс. № 2. Гарнитура "Тайм^
Печать офсетная. Объем 33,32 усл.печ.л. 33,32 усл.кр.-отт. 28,15 уч.изд.)
Тираж 10000 экз. Заказ № 28.
Издательство "Высшая школа", 101430, Москва, ГСГМ, Неглинная ул., д. 29/14
Набрано на персональных компьютерах издательства
Отпечатано в Московской тип. № 8 Министерства печати и массовой
информации РФ. 101898, Москва, Хохловский пер., 7.