Процессы и аппараты химической технологии. Общий курс - Айнштейн В.Г.

Предисловие к пятому øэлектронномуù
издани
1.1 3. Перенос субстанции в химической технологи
1.1.4. Размерности. Системы единиц. Единицы измерени
1.2.3. Основные характеристики øсвойстваù рабочих те
1.3. Общие подходы к анализу процессов перенос
1.3.3. Подходы к анализу и установлению общих закономерностей процессов перенос
1.5. Уравнения переноса импульса, теплоты и веществ
1.5.2. Дифференциальное уравнение переноса теплоты в движущейся жидкост
1.5.3. Дифференциальное уравнение переноса вещества в движущейся жидкост
1.6.2. Различные конфигурации потоков субстанци
1.8.2. Геометрическое и физическое подобие. Масштабные преобразования. Критерии подоби
1.8 3. Обобщенные переменные на базе основных уравнений перенос
Подобие в переносе различных субстанци
1.8.4. Обобщенные переменные на базе других уравнений и представлени
1.8.6. Обобщенные переменные и пропускные способност
2.1.2. Давления и поверхности уровня в покоящемся сосуд
2.1.3. Давления и поверхности уровня в случае относительного поко
Вертикальный цилиндрический сосуд, вращающийся вокруг своей ос
Горизонтальный сосуд, вращающийся вокруг своей ос
2.1.4. Силы давления на дно и боковые стенки сосуд
2.2.4. Законы ламинарного течения ньютоновских жидкосте
Распределение скоростей в турбулентном поток
Коэффициент гидравлического сопротивлени
2.2.7. Характер изменения напора по длине трубопровод
2.3.2. Наивыгоднейший диаметр трубопровода. Диапазоны рекомендуемых скоросте
2.3.4. Трубопровод с путевым и транзитным расходам
2.4. Гравитационное течение тонких плено
2.5.2. Пластичное течение бингамовских жидкосте
2.5.3. Пластичное течение псевдопластичных и дилатантных жидкосте
Истечение через отверстие в боковой стенк
2.6.2. Истечение жидкости при переменном напор
2.7. Элементы гидравлики дисперсных систе
Гидравлическое сопротивление псевдоожиженного сло
Стесненное витание и расширение псевдоожиженного сло
2.7.5. Образование и движение жидких капель и газовых пузыре
О скорости движения капель и пузырей в сплошной сред
2.8.2. Транспортные системы с твердой фазо
2.8.3. О двухфазных течениях типа жидкость-жидкость и жидкость- га
2.9. Об особенностях молекулярного течени
3.1.2. Основные характеристики насосной установк
3.1.3. Предельная геометрическая высота всасывания насосо
3.2.3. Закон движения поршня. Диаграмма подач
3.2.4. Работа и расчет воздушных колпако
3.2.7. Расчет мощности, потребляемой поршневым насосо
3.2 8. Регулирование производительности поршневых насосо
3.3.3. Характеристики центробежных насосо
Универсальная характеристика центробежного насос
3.3.4. Параллельная и последовательная работа насосо
3.5. Достоинства и недостатки насосов различных типов. Области их применени
4.2. О термодинамических основах работы компрессоро
4.3.2. Удельные затраты энергии в поршневом компрессор
4.3.3. Производительность поршневого компрессор
4.3.4. Степень сжатия в поршневом компрессор
4.3.5. Сжатие газа в многоступенчатых компрессора
Оптимизация распределения степени сжатия по ступеням компрессор
Оптимизация распределения степени сжатия при промежуточном отборе части газ
4.3.6. Об охлаждении поршневых компрессоро
4.3.8. Регулирование производительности поршневых компрессоро
4.4. Некоторые специальные объемные компрессор
4.5.2. Производительность турбокомпрессоро
4.5.3. Напор, развиваемый турбокомпрессорам
4.5.5. Регулирование производительности турбокомпрессоро
4.7. Области применения компрессоро
4.8. Вакуумировани
4.8.2. О вакуум-насосах глубокого вакуум
5.1.3. Центробежное осаждение в неоднородных жидкостных система
5.1.4. Центробежное осаждение в неоднородных газовых система
5.1.5. Некоторые другие процессы осаждени
5.2.3. Основные характеристики фильтрационного процесс
5.2.5. Отдельные режимы периодического фильтровани
Фильтрование при постоянной скорости фильтраци
5.2.6. Непрерывный процесс фильтрования на барабанном вакуум-фильтр
5.2.7. Определение параметров процесса фильтровани
5.2.8. Фильтрование в поле центробежных си
Основные проблемы процессов перемешивани
Способы перемешивани
5.3.2. Пневматическое перемешивани
5.3.4. Перемешивание лопастными мешалкам
Затраты энергии на перемешивание лопастными мешалкам
5.3.5. О перемешивании паст и сыпучих материало
5.4.2. Диспергирование при истечении из отверстий и сопе
6.2. Виды теплопереноса. Общее математическое описани
6.2.3. Об уравнении Фурье—Кирхгоф
6.3. Стационарный кондуктивный перенос теплоты через стенк
6.4.2. Аналогия в процессах конвективного переноса количества движения и теплоты, а также веществ
6.4.3. Теплоперенос в условиях вынужденной конвекци
6.4.4. Теплоперенос в условиях естественной конвекци
6.7. Теплоотдача от поверхности в псевдоожиженном сло
6.9.2. Лучистый теплоперенос между двумя телам
Приложение 6.2. К расчету относительного коэффициента теплоотдачи при кипени
7.3.2. Расчет коэффициентов теплопередач
7.3.3. Коэффициент теплопередачи при параллельном теплоперенос
7.4.2. Перенос теплоты через стержень бесконечной длин
7.4.3. Критическая и целесообразная толщина тепловой изоляци
7.5. Теплообмен øосновные проблемы и положения
7.5.2. Потоки энтальпий и тепловые баланс
7.7.2. Тепловой поток при прямоточном и противоточном движении теплоносителе
7.8. Изменение температур вдоль теплообменной поверхност
7.9. Лимитирующие стадии в процессах теплоперенос
7.9 2. Пропускные способности и лимитирующие стадии при стационарном теплоперенос
7.9 3. О пропускных способностях в нестационарных процесса
7.10. Нестационарный теплообмен с твердыми телам
7.10.2 Нестационарный безградиентный теплообмен с твердым тело
7.10.3. Нестационарный теплообмен с шаром в граничных условиях III и I род
7.11. Межфазный теплообмен в псевдоожиженном сло
7.11.2. Вырождение смешанной задачи в потоковую øбалансовую
7.12. Регулярный режим теплообмена тела со сплошной средо
7.15.2. Нагрев псевдоожиженного слоя потоком горячего газа в условиях балансовой задач
7.15.3. Нестационарный теплообмен между двумя интенсивно перемешиваемыми жидкостям
7.15.4. Безградиентное остывание тела за счет лучистого теплообмен
8.2. Влияние продольного перемешивания на эффективность ХТ
8.3. Структура потоков в случае простейших идеальных моделе
Кривые отклик
Результирующий эффект процесса Uре
8.3.2. Идеальное перемешивани
8.3.3. Параметры кривых отклика и простейших моделей продольного перемешивани
8.4. Структура потоков в реальных система
8.4.2. Диффузионная модель потока с продольным перемешивание
8.5 Общая оценка моделей структуры потоко
8.5.2. Общая оценка моделей продольного перемешивани
8.6. Об экспериментальном изучении продольного перемешивани
8.6.3. К выбору модели и определению ее параметро
8.6.4. Определение параметров моделей методом моменто
8.7. Структура потоков в технологических расчета
8.7.2. Распределение элементов потока по времени пребывания при гравитационном течении тонких плено
8.7.3. Конвективный теплообмен при ограниченном продольном перемешивании одного из теплоносителе
9.3. Физико-химические основы процесса выпаривани
9.4. Схема работы выпарных аппаратов. Количество удаляемого растворител
9.4.2. Определение количества øпотока ù удаляемого растворител
9.5. Выпарные аппараты периодического действи
9.5.1. Периодическое выпаривание с однократной загрузкой исходного раствора в аппара
9.5.2. Периодическое выпаривание с постоянным уровнем раствора в аппарат
9.6. Выпарные аппараты непрерывного действи
9.6.3. Схема и расчет вакуумной выпарной установк
Расчет прямоточной многокорпусной установк
9.6.6. Выпарной аппарат с полным тепловым насосо
9.6.7. Выпарной аппарат с частичным тепловым насосо
9.6.8. Повышение эффективности выпарных установок за счет утилизации теплот
9.8. Выбор размеров сепарационного пространства выпарных аппарато
Приложения к главе
Приложение 9.2. Значения поправочного множителя φ* øКкг растворителя/кДжù в зависимости от рабочих температур кипения растворителя tp ø°Сù и давлений р øкПа
10.1.2. Составляющие описания массоперенос
10.2.2. Расчет некоторых свойств смесей с использованием концентраци
10.2.3. О концентрациях в технологических расчета
10.3 2. Равновесие в системах класса 3ø2-2ù
10.4.2. Виды массопереноса. Об уравнении Фик
10.5. Элементы материального баланса для фаз
10.6. Массопередача и баланс для процессов класса 3ø2-2ù
10.6.3. Пропускные способности массообменного процесс
10.7 Рабочие линии в аппарате для непрерывного процесса класса 3ø2-2ù
10.7.3. Рабочие линии в некоторых специфических случая
10.8. Средняя движущая сила для процессов класса 3ø2-2ù
10.8.2. Прямоточное движение фаз в режиме И
10.8.3. Противоточное движение фаз в режиме И
10.8.4. Основные размеры массообменных аппарато
10.9. Поток вещества в процессах класса 3ø2-2ù
10.9.2. Прямоточное движение фаз в режиме И
10.9.3. Противоточное движение фаз в режиме И
10.10. Пропускные способности и лимитирующие стадии для процессов класса 3ø2-2ù
10.10.3. О подмене задачи в массоперенос
10.11. Сети аппаратов øобщая характеристика
10.12. Ступенчатый противоток для процессов класса 3ø2-2ù
10.12.2. Аналитический расчет идеального процесс
10.12.3. Аналитический расчет реального процесс
Ступенчатый противоток для цепочки из n одинаковых аппарато
10.12.4. Оценка эффективности функционирования ступенчато-противоточной цепочки реальных массообменных аппарато
10.12.5. О расчете противоточных аппаратов и их цепочек по «методу ВЭТС
10.13. Перекрестное соединение аппаратов в сети для процессов класса 3ø2-2ù
10.13.2. Оптимизация ступенчато-перекрестных процессов при идеальном контакте фа
10.13.3. Массоперенос в реальных ступенях контакта в случае прямой линии равновеси
10.14. Периодические и полунепрерывные процессы класса 3ø2-2ù
10.15. О расчете массообменных процессов иных классов, нежели 3ø2-2ù
Массообмен в псевдоожиженном слое в условиях внешней задач
10.16.5. О смешанных задачах массоперенос
11.2. Конструкции абсорбционных аппарато
11.3. Фазовое равновесие в системе газ-жидкост
11.3.2. Фазовое равновесие при абсорбции, сопровождаемой химической реакцие
11.3.3. Фазовое равновесие в некоторых специальных случая
11.4.2. Высота абсорберов с непрерывным контактом фа
11.4.3. Высота абсорберов со ступенчатым контактом фа
11.4.4. О целесообразности рециркуляции рабочих потоко
11.5. Особенности расчета некоторых специальных случаев абсорбци
11.5.2. Абсорбция нескольких компонентов из газовой смес
11.5.3. Абсорбция при химическом взаимодействии поглощаемого компонента с абсорбенто
Нагревание абсорбент
Понижение давления над абсорбенто
11.7. Гидравлическое сопротивление абсорберо
12.2. Физико-химические основы процессов перегонк
12.2.2. Правило фаз и равновесие в системах жидкость-па
12.2.4. Равновесие для реальных бинарных смесе
12.2.5. Равновесие для многокомпонентных систе
12.3.3. О дистилляции в токе инертного газ
12.3.5. О некоторых других дистилляционных процесса
12.3.6. Общая оценка процессов дистилляци
12.4.2. Типовая схема, потоки, терминологи
12.5. Об аппаратурном оформлении и работе ректификационных установо
12.6. Материальные и тепловые потоки в ректификационной колонн
12.7. Непрерывная ректификация бинарных смесе
Последовательность расчета ректификационной колонн
12.7.2. Основные размеры ректификационных колон
12.7.4. Воздействие на эффективность работы колонн
12.7.5. Влияние агрегатного состояния исходной смеси на работу ректификационной колонн
12.7.6. Некоторые особенности работы ректификационных колон
12.8. Расчет ректификации бинарных смесей с помощью энтальпийной диаграмм
Общая последовательность расчета ректификационной колонн
12.9. Ректификация бинарных смесей с применением разделяющего агент
12.10. Периодическая ректификация бинарных смесе
12.10.2. Ректификация при постоянном составе дистиллят
12.10.3. Ректификация при постоянном флегмовом числ
12.11. О расчете ректификации многокомпонентных смесе
12.11.2. Разделение многокомпонентных смесе
13.2. Основные конструкции экстракционных аппарато
13.2.2. Экстракторы со ступенчатым контактом фа
Ступенчатые смесительно-отстойные экстрактор
13.4. Выбор экстрагента и подходы к анализу экстракционных процессо
13.5.2. Экстракция при частичной взаимной растворимости экстрагента и разбавител
Некоторые особенности треугольной диаграммы для процессов экстракци
14.2. Физико-химические основы адсорбционных процессо
14.3.2. Адсорберы непрерывного действия с движущимся слоем сорбент
14.3.3. Адсорберы полунепрерывного действия с неподвижным слоем сорбент
14.4. О технологическом расчете адсорбционных процессо
14.5. Расчет непрерывных процессов адсорбции в псевдоожиженном слое сорбент
14.5.2. Ступенчато-противоточный адсорбер с псевдоожиженным слое
Об адсорбции в условиях внутренней задач
14.6. Расчет непрерывного процесса противоточной адсорбции в движущемся слое сорбент
14.7. Расчет полунепрерывного процесса адсорбции в неподвижном слое сорбент
Статическая и динамическая емкости сорбент
Задачи технологического расчет
14.7.2. Расчет процесса идеальной адсорбци
14.7.3. Уравнение связи хпр и L для процесса реальной адсорбци
14.7.4. Об экспериментальном определении параметров уравнения Ӹилов
14.7.5. Расчетное определение параметров формулы Ӹилов
14.7.6. Определение динамической емкости сорбент
14.7.7. Расчет количества десорбируемого поглощенного компонент
15.2. Физико-химические основы процесса конвективной сушк
15.2.3. Свойства влажного твердого материал
15.3.4. О распределении в простой сушилке подводимой теплоты между калорифером и сушильной камеро
15.5. Сушилка с частичным возвратом отработанного воздух
15.5.2. Идеальная сушилка с частичной рециркуляцие
15.5.3. Реальная сушилка с частичной рециркуляцие
15.6. О некоторых других вариантах сушильного процесс
15.7.2. Приближенный аналитический расче
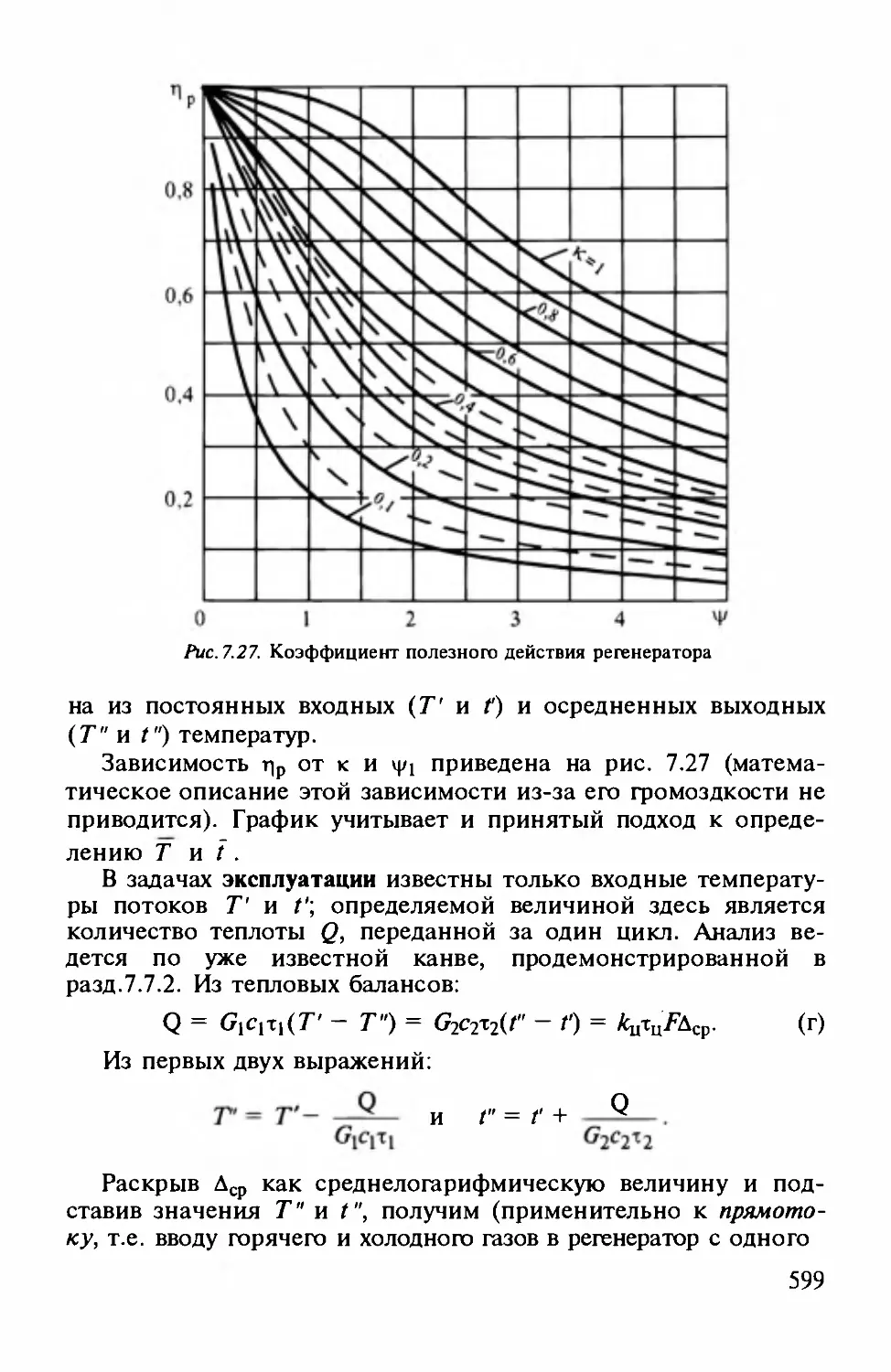
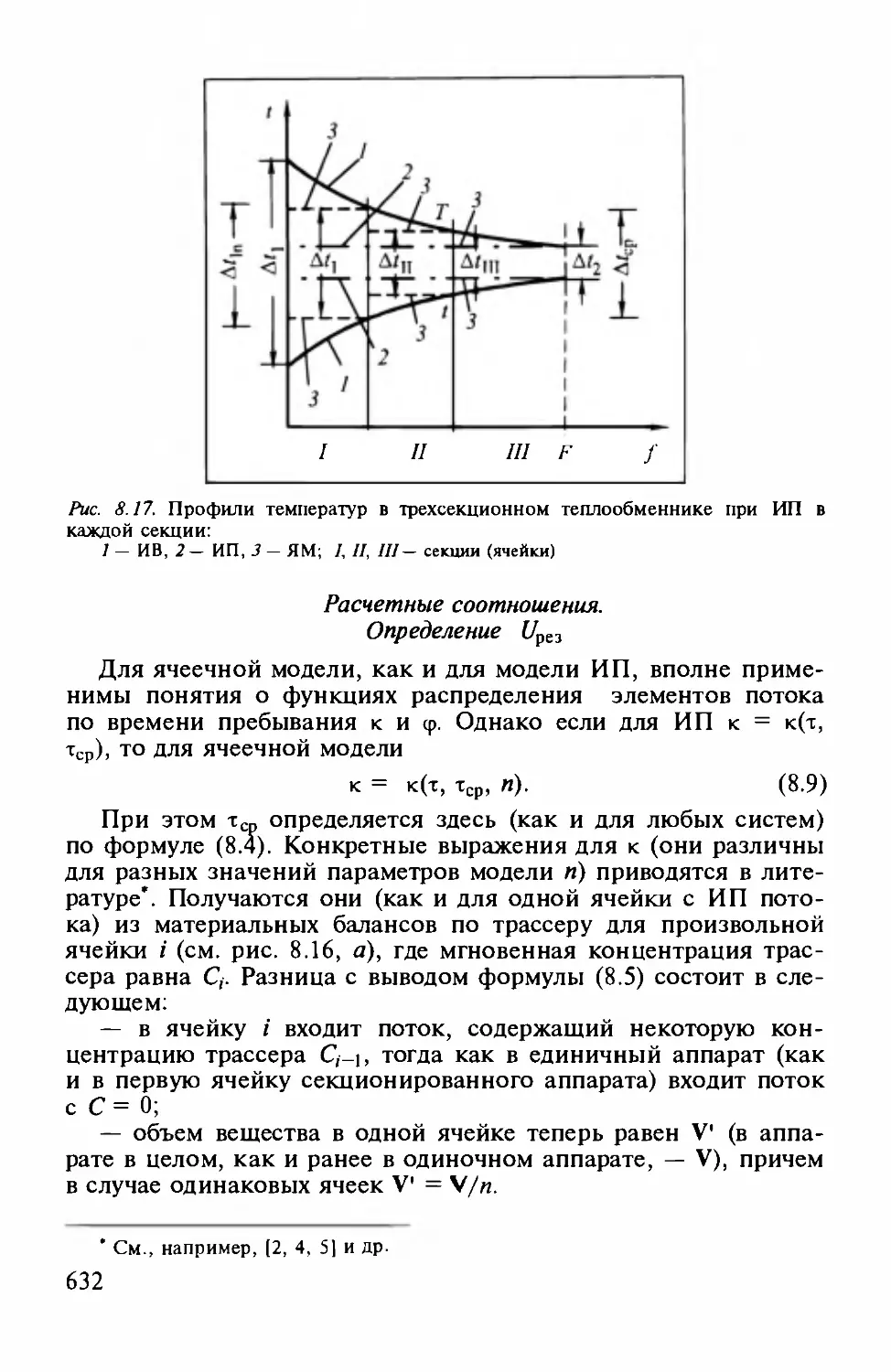
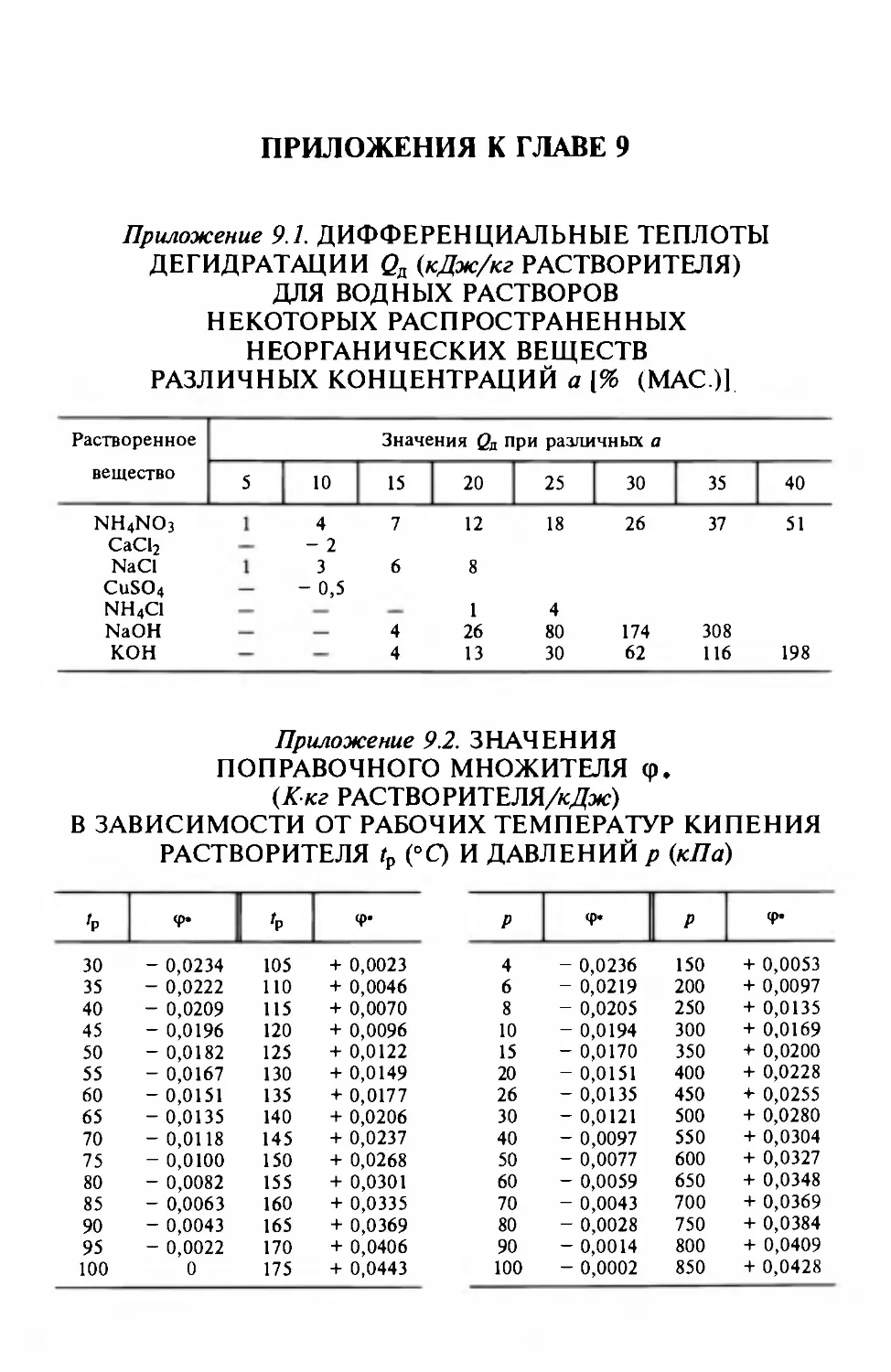
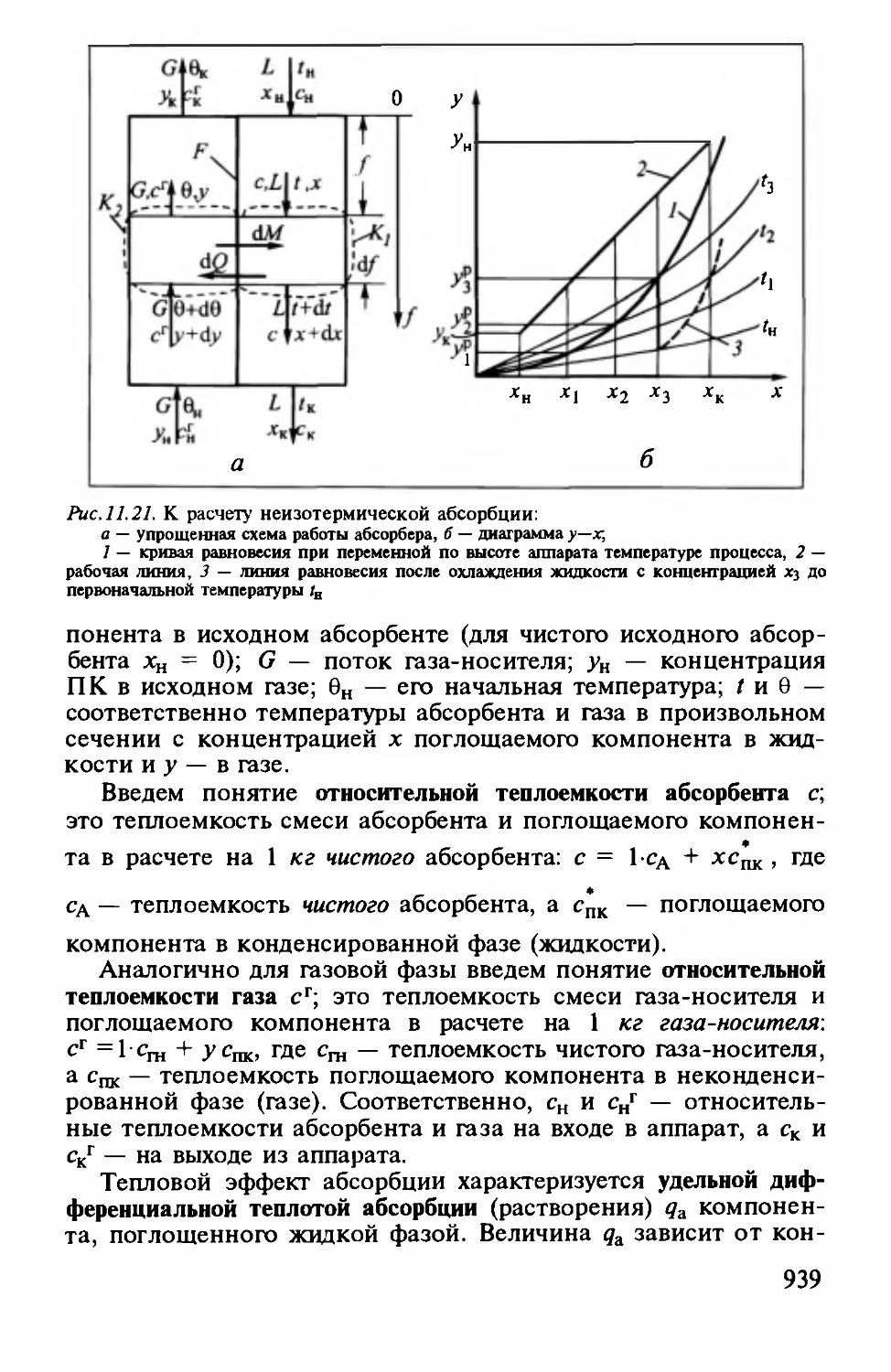
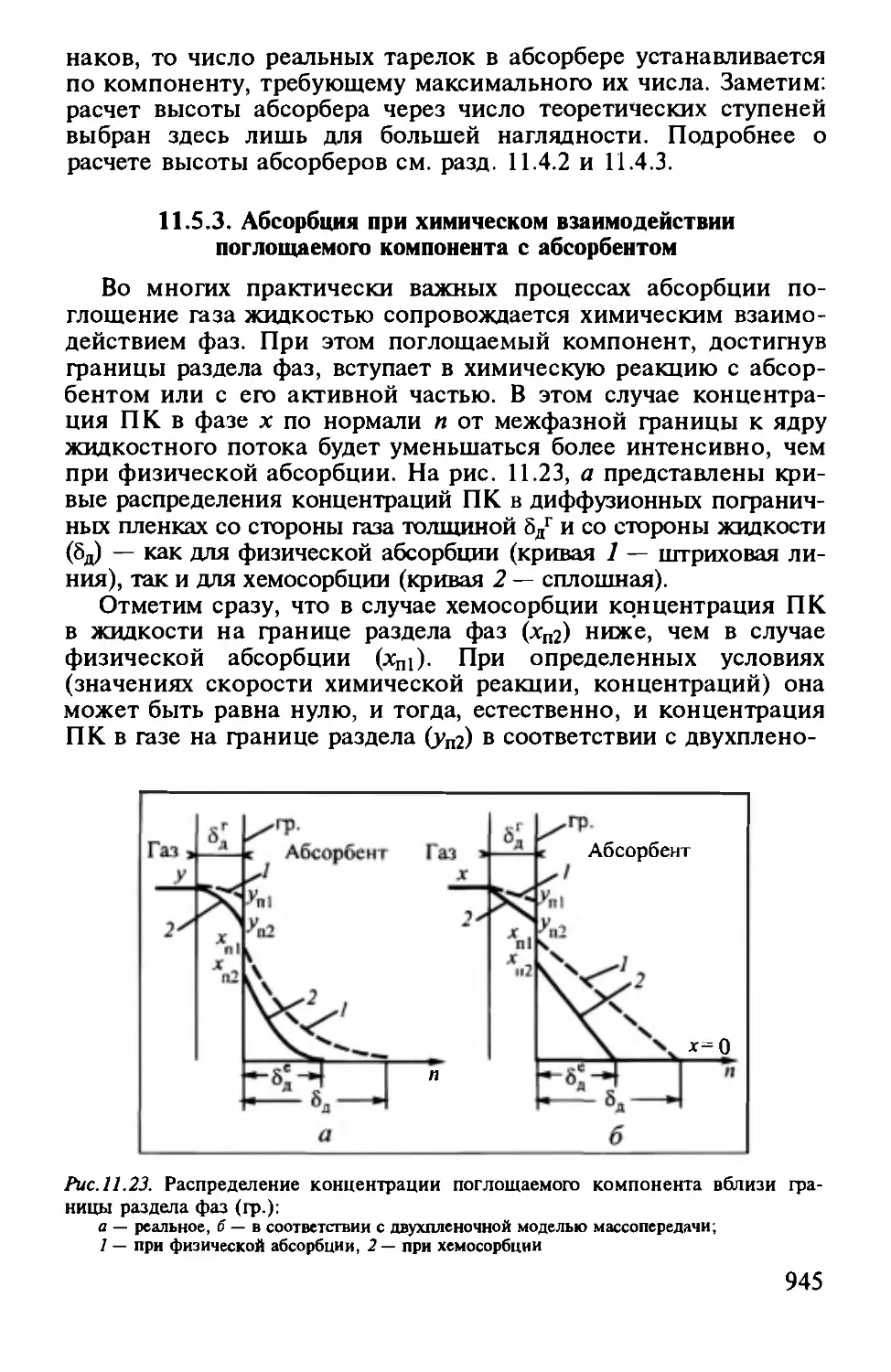
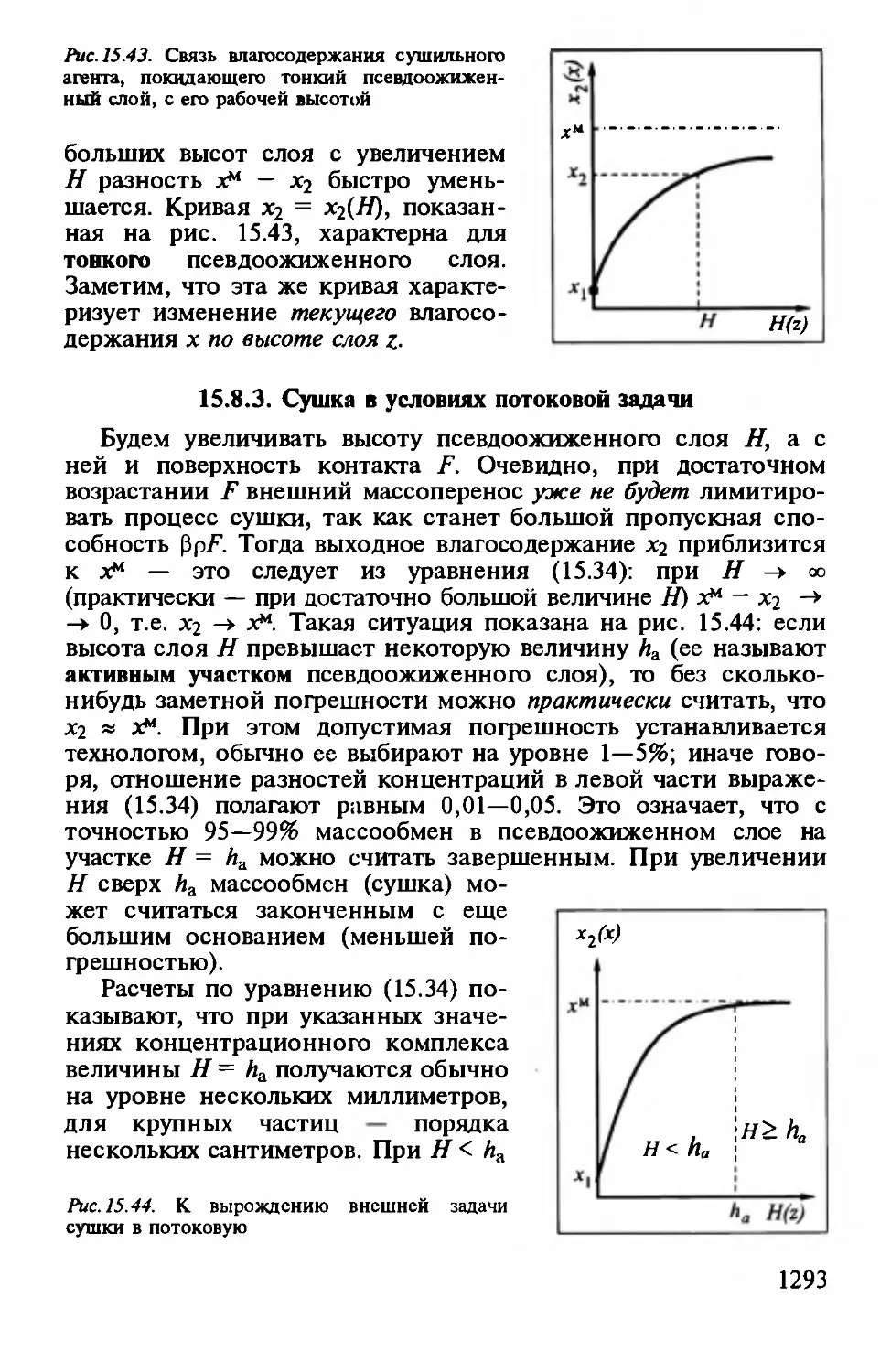
15.8.3. Сушка в условиях потоковой задач
15.8.4. Сушка в условиях внутренней задач
16.3.4. Переход расплава индивидуальных веществ в твердое состояни
16.3.5. Кристаллизация бинарных и многокомпонентных смесе
16.5.2. Массовая кристаллизация с отводом теплоты через охлаждаемые поверхност
16.5.3. Массовая кристаллизация при непосредственном контакте с хладоагенто
16.5.4. Кристаллизация с частичной отгонкой растворител
16.5.5. Кристаллизация на охлаждаемых поверхностя
16.6.2. Перекристаллизация с использованием растворителе
17.2. Аппаратурное оформление процессов растворени
17.3. Физико-химические основы растворения твердых вещест
17.5. Способы и схемы процессов растворени
17.6.2. Частичное растворение веществ с инертным компоненто
17.7. Отдельные задачи растворения и выщелачивани
17.7.2. Выщелачивание в потоке растворителя в условиях балансовой задач
17.7.3. Протяженность рабочей зоны для процесса противоточного выщелачивания с непрерывным контактом фа
18.2. Основные особенности процессов сублимации и десублимаци
18.3. Возможные варианты организации процессов сублимации и десублимаци
18.4. Аппаратурное оформление сублимационных процессо
18.6. Технологический расчет процессов сублимации и десублимаци
19.1.2. Основные механизмы взаимодействия частиц в гранул
19.1.3. Классификация процессов гранулировани
19.1.4. Элементы типовой технологической схемы гранулировани
19.2. Аппаратурное оформление процессов гранулировани
19.2.2. Гранулирование прессованием и формование
19.2.3. Гранулирование кристаллизацией капель расплав
19.3. Гранулирование мелкодисперсных материало
19.3.2. Материальные и тепловые балансы гранулятор
19.3.3. Кинетика и расчет гранулирования окатыванием и агломерацие
19.3.4. Расчет гранулирования прессование
19.3.5. Расчет гранулирования формование
19.4.2. Кинетика кристаллизации капель расплав
19.4.3. Кристаллизация расплава на поверхности растущих грану
19.5. Гранулирование кристаллизацией из растворов и паровой фаз
19.6. О капсулировании гранулированных продукто
20.2. Основные механизмы переноса вещества через мембран
20.2.2. Механизм переноса вещества через пористые мембран
20.3. Мембранные процессы разделения и способы их организаци
20.3.2. Процессы разделения с химическим взаимодействием проникающих компонентов и материала мембран
20.4. Основные конструкции мембранных ячее
20.5. Основы расчета процессов разделения в мембранных ячейка
20.5.2. Идеальное вытеснение потока в надмембранном пространстве с отводом пермеата от поверхности мембраны в подмембранном пространств
20.5.3. Идеальное вытеснение потока в надмембранном и идеальное перемешивание потока в подмембранном пространства
20.5.4. Перепад давления в потоках, движущихся в подмембранном и надмембранном пространства
20.6. Простейшие каскадные схемы разделени
20.6.2. Замкнутый каскад с возвратом проходящего потока на предыдущую ступен
21.2.2. Реальная паровая компрессионная холодильная машин
21.2.3. О воздушной компрессионной холодильной машин
21.2.4. Двухступенчатая паровая компрессионная холодильная машин
21.2.6. О некоторых других холодильных машинах умеренного охлаждени
21.2.7. Рабочие тела, охлаждающие и охлаждаемые среды, промежуточные хладоагент
21.2.8. Об аппаратурном оформлении процессов умеренного охлаждени
Адиабатическое расширение с отдачей внешней работ
Сопоставление αh и α
21.3.3. Усовершенствованные циклы с дросселирование
21.3.6. Об аппаратурном оформлении процессов глубокого охлаждени
21.3.7. Двухколонный ректификационный агрегат для разделения воздух
22.1.2. О затратах энергии на измельчени
22.1.3. Основные требования к размольным машинам. Типовые схемы размольных установо
Производительность щековой дробилки и еб регулировани
О расчете затрат энергии на измельчение в щековой дробилк
Производительность валковой дробилки и ее регулировани
О расчете затрат энергии на измельчение в валковых дробилка
22.4. Барабанные мельниц
22.4.2. Основные режимы движения насадки в барабанной мельнице øкачественный анализ
Некоторые эксплуатационные характеристики барабанных мельни
О затратах энергии на измельчение в барабанных мельница
Глава 23 КЛАССИФИКАЦИЯ ЗЕРНИСТЫХ МАТЕРИАЛО
23.2.3. Элементы технологического расчет
23.3.2. Элементы технологического расчет
23.4. Гидравлическая и пневматическая классификаци
К инженерному расчету классификаторов, работающих в поле сил тяжест
23.4.3. Классификация с использованием инерционных си
23.4.4. Классификация псевдоожижаемых твердых части
Сепарация на основе сегрегации в псевдоожиженном сло
23.5. О некоторых других возможностях классификации твердых материало
Глава 24 СОПРЯЖЕННЫЕ И СОВМЕӹЕННЫЕ ПРОЦЕСС
24.2.2. Ректификация азеотропообразующих смесей в двух колоннах, работающих пол разными давлениям
24.2.7. Некоторые другие сопряженные процесс
24.3.2. Массообменно-массообменные процесс
24.3.3. Процессы, включающие механические или гидромеханические операци
Перечень учебников по общему курсу ПАХТ на русском язык
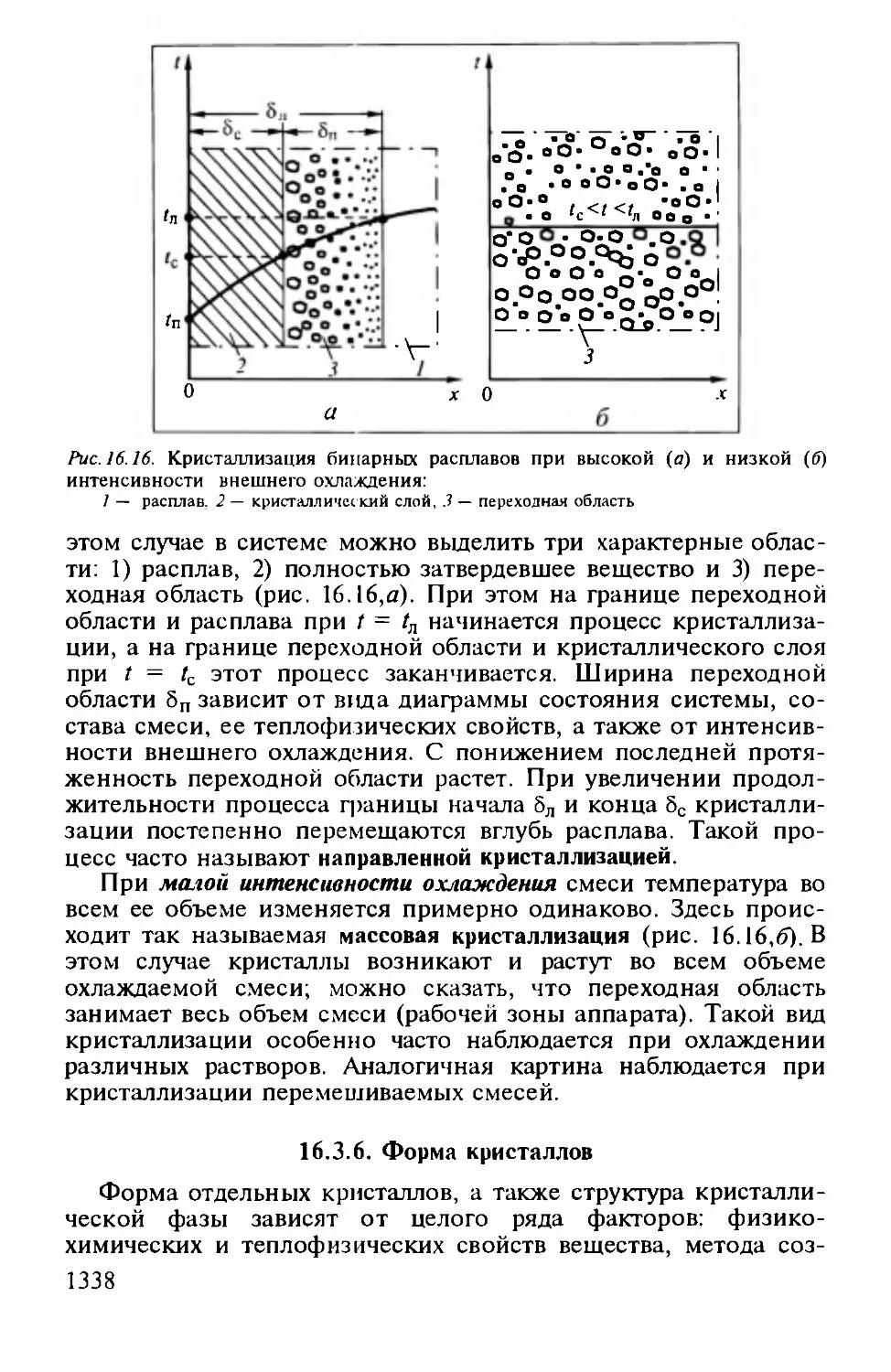
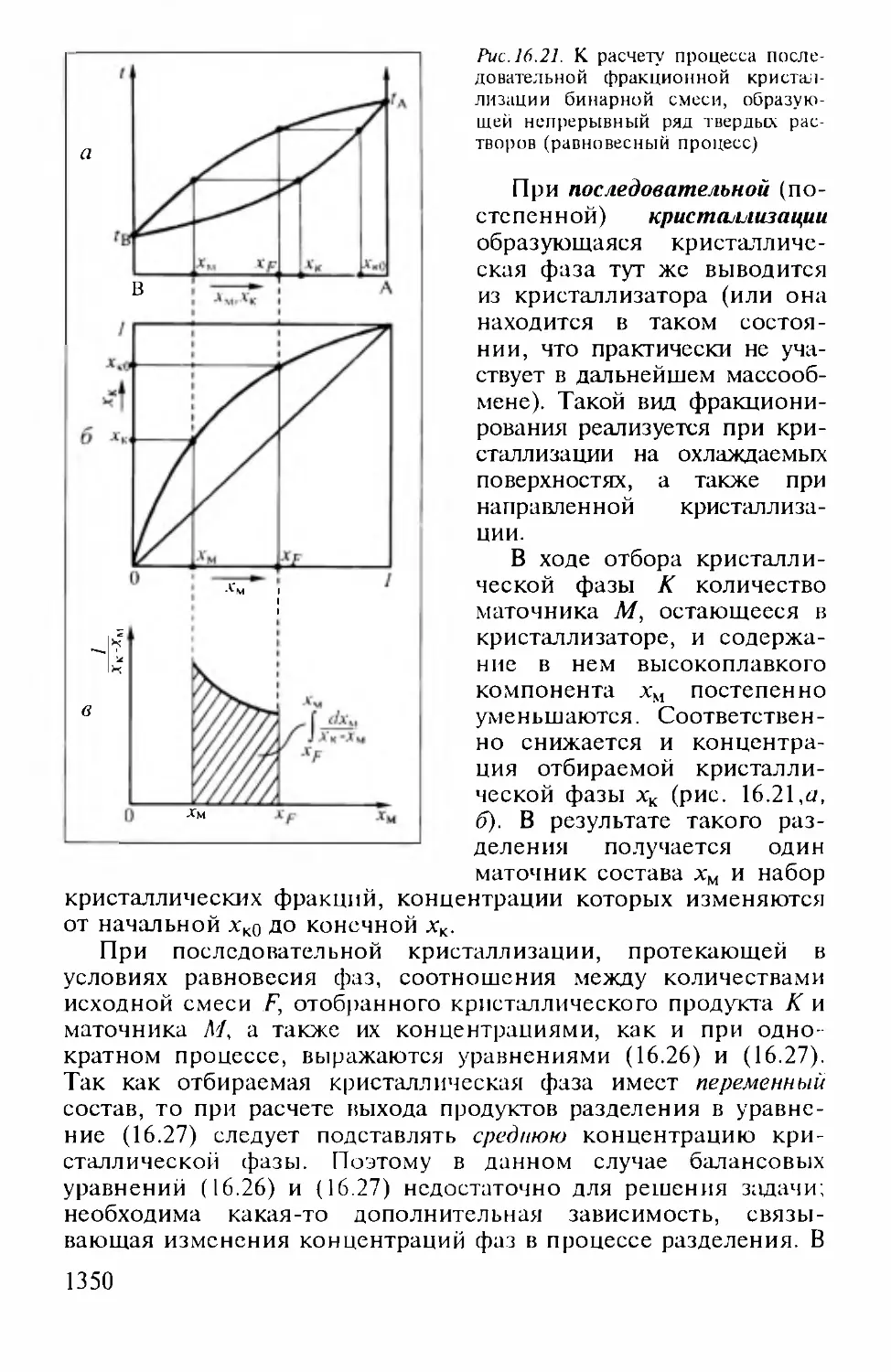
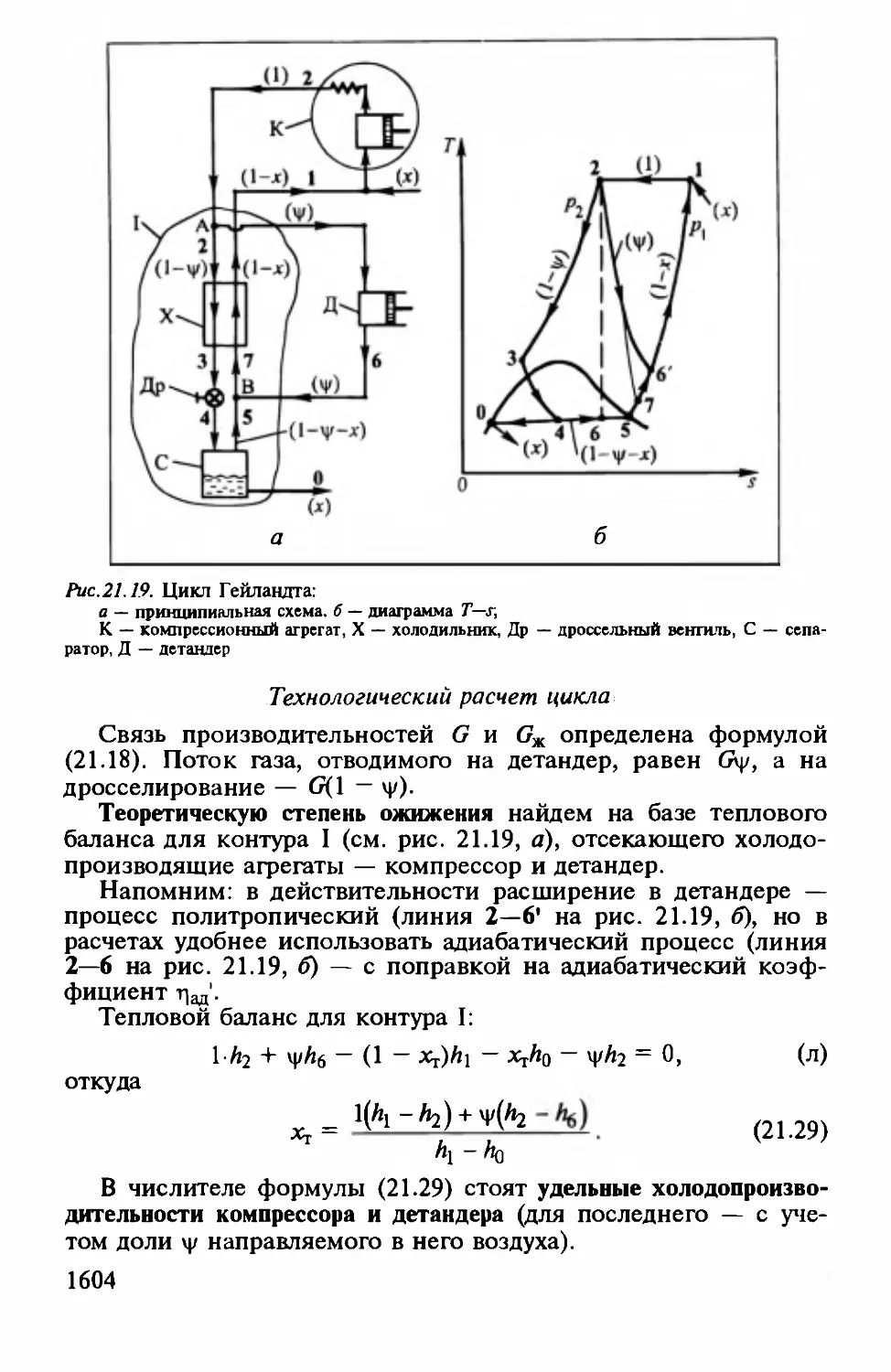
Author: Айнштейн В.Г.
Tags: химическая технология химическая промышленность основные процессы и аппараты химической технологии химические технологии
ISBN: 978-5-9963-2214-5
Year: 2014
Similar
Процессы и аппараты химической технологии. Часть 1. Теоретические основы процессов химической технологии. Гидромеханические и тепловые процессы и аппараты
Процессы и аппараты химической технологии. Часть 2. Массообменные процессы и аппараты
Проектирование и расчет аппаратов основного органического и нефте-химического синтеза
Основные процессы и аппараты химической технологии
Text
                    Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ПРОЦЕССЫ И АППАРАТЫ
ХИМИЧЕСКОЙ
ТЕХНОЛОГИИ.
ОБЩИЙ КУРС
Под редакцией В. Г. АЙНШТЕЙНА

В двух книгах

Рекомендовано
Министерством образования Российской Федерации
в качестве учебника
для студентов высших учебных заведений, обучающихся
по химико-технологическим направлениям и специальностям

5-е издание (электронное)

Москва
БИНОМ. Лаборатория знаний
2014

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

УДК 66-93 (075.8)
ББК 35.11
П84
Авторы
В. Г. Айнштейн, М. К. Захаров, Г. А. Носов, В. В. Захаренко,
Т. В. Зиновкина, А. Л. Таран, А. Е. Костанян
Рецензенты:
Кафедра процессов и аппаратов химической технологии РХТУ
им. Д.И. Менделеева;
доктор технических наук, профессор Б.С. Сажин
(МГТА им. А.Н. Косыгина)

П84

Процессы и аппараты химической технологии. Общий курс : [Электронный
ресурс] : в 2 кн. / В. Г. Айнштейн, М. К. Захаров, Г. А. Носов [и др.] ; Под ред. В. Г. Айнштейна. — 5-е изд. (эл.). — М.: БИНОМ. Лаборатория знаний, 2014. — 1758 с. : ил.
ISBN 978-5-9963-2214-5

В учебнике, написанном опытными преподавателями Московского государственного университета тонких химических технологий имени М.В. Ломоносова (МИТХТ им.
М. В. Ломоносова), рассмотрены теоретические основы построения, математического
описания и инженерного расчета основных химико-технологических процессов, а также
принципы устройства и функционирования технологической аппаратуры. В книге 1 раскрываются основные понятия и соотношения, основы тепло- и массопереноса, основные
закономерности переноса импульса, теплоты, вещества. Особое внимание уделяется вопросам гидравлики, перемещения жидкостей, сжатия газов, гидромеханическим процессам,
теплопередаче и теплообмену, структуре потоков, а также выпариванию.
Книга 2 — логическое продолжение книги 1, здесь наряду с традиционными для учебника главами, посвященными абсорбции, дистилляции и ректификации, жидкостной экстракции, адсорбции, сушке твердых материалов, кристаллизации, охлаждению, измельчению и классификации твердых материалов, приводится ряд новых глав: «Гранулирование»,
«Сублимация и десублимация», «Сопряженные и совмещенные процессы».
Авторы учебника удостоены премии Правительства Российской Федерации в области
образования за 2005 г.
Для студентов и аспирантов высших учебных заведений, обучающихся по химикотехнологическим направлениям и специальностям, а также для специалистов химической
промышленности.

УДК 66-93 (075.8)
ББК 35.11
По вопросам приобретения обращаться:
«БИНОМ. Лаборатория знаний»
Телефон: (499) 157-5272
e-mail: binom@Lbz.ru, http://www.Lbz.ru

ISBN 978-5-9963-2214-5

© БИНОМ. Лаборатория
знаний, 2014

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ОГЛАВЛЕНИЕ
Книrа

1

Предисловие ко пятому изданию . . . . . . ... .................... ...............................
Предисловие к первому изданию .. ............................".." .. "" ... "."..........
Основные условные обозначения . . .
.. .. . ... ... ......... ......... ........

13
14

26

Глава 1
ОСНОВНЫЕ ПОНЯТИЯ И СООТНОШЕНИЯ .. """"""""""."."..

31

1.1. Введение ."".. "."".."......"..."......""."."""...."".." ..""."..".""""""" ... ".
1.1.1. Предмет и место курса """"""""""""""""""""""""""".. """"

31
31
35
38
41

1.1.2.

Краткие исторические сведения"""". .. "".. """""""""""""""".

1.1.3.
1.1.4.
1.1.5.

Перенос субстанции в химической технологии"""""""""""""
Размерности. Системы единиц. F,диницы измерения":"".. ".""
О точности инженерных расчетов""""""."... """" .. """"""".""

1.2. Основные понятия.""."... """..""""".."""."""...""""""".""."""" ....".
1.2.1. Обобщение и конкретизация"""."....".."""".. """"""."""."."".
1.2.2. Некоторые физические понятия "".""".""""."""".""""""""".
1.2.3. Основные харакrеристики (свойства) рабочих тел """""".. ""...
1.3. Общие подходы к анализу процессов переноса".. """""""""""""""".
1.3.1. Уравнения баланса"""".".""""".. """...."."."""""."""""""."...
1.3.2. Интенсивность процессов переноса""""".""""".""""""".. "....
Потенциалы и потоки субстанций """""""." .."""."."""""""".."".
О перекрестиых эффекrах Онзаrера". "" """"".".""".. """".""."".
"

Пропускные способности"""""""""... ".."."""..""....... ""..."........"
1.3.3. Подходы к анализу и установлению общих закономерностей
процессов переноса""... "."..".."...."""......"..""""... """".""......
1.3.4. Общая канва анализа" ... ".".. ".""""""" ... """""""""""""..""".
1.4. Уравнения неразрывности и расхода ""..... ".. "."""."""""".. """""" .. "
1.4.1.

Уравнение неразрывности ".. "."...... "...... "" ... "...".""...""""... ".

1.4.2.

Уравнения расхода".... "" .. """."..." ... "..... "...... ""........""".........

1.5. Уравнения переноса импульса, теплоты и вещества """"""".. """.......
1.5.1.
1.5.2.
1.5.3.

.жидкости " ..""""."""..""..""."" ..."""". """"""""" .. """."".. "".

83

Дифференциальное уравнение переноса вещества в движущейся жидкости...........................................................................

86

1.8. Физическое подобие"."""."."".. """""..""".... ".".""." ..... """""."""".

1.8.З.

69
73
74
74
77
79
79

1.6.2. Различные конфиrурации потоков субстанции"""""""""""""
1.6.3. Анизотропные среды "."""... "."""."""""""".. """."""""""."...
1.7. Условия однозначности""."".""""..""""".. """ .... ""..""""""."""""".
1.8.1.

45
45
47
50
55
55
60
60
66
67

Дифференциальное уравнение движения несжимаемой жидкости (перенос импульса).""""... """""" .. ".. """."."".""".........
Дифференциальное уравнение переноса теплоты в движущейся

1.6. Модификации уравнений переноса""""."".. "."."."""""""""""...."...
1.6.1. Ус.ловия протекания процесса переноса".""""""" .. ".."""".. ""

1.8.2.

44

Обобщенные переменные""""" .. "".... "." .. """"."..""""."."."".
Геометрическое и физическое подобие. Масипабные преобразования. Критерии подобия".. "".. ""..... """"""."..."""." .. "."".
Обобщенные переменные на базе основных уравнений переноса ..............................................................................................

89
89
91
95
97
99
99
101
106

3

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Гидродинамическое подобие.............................................................
Теruювое подобие..............................................................................
Диффузионное подобие .. ..................................................................
Подобие в переносе различных субстанций .... ... ........
.. .... ....
· · · ·.· · · · . . .

.

106
110
111
112

1.8.4.

Обобщенные переменные на базе других уравнений и предстаалений . "..................................................................................

1.8.5.

Критериальные уравнения...........................................................

1.8.6.

Обобщенные переменные и пропускные способности...............

112
114
115

Литература к главе 1.....................................................................................

118

Глава 2
ГИДРАВJIИКА .. .... ...... ...... .... "...................................................................

119

2.1. Гидростатика. .... .. ... .... ".""."".....""...." .............. ".........."......................

119
120
122
124

2.1.1.
2.1.2.

Основные уравнения rnдростатики и поверхностей уровня . .....
Дааления и поверхности уровня в покоящемся сосуде..............

2.1.3. Дааления и поверхности уровня в случае относительного покоя
Цистерна, движущаяся с постоянным ускорением по горизонтальной плоскости ..... ."........"...........................................................
Вертикальный цилиндрический сосуд, вращающийся вокруг своей
оси ..... "................................"............................................................
Горизонтальный сосуд, вращающийся вокруг своей оси.................
2.1.4. Силы дааления на дно и боковые стенки сосуда........................
2.2. Гидродинамика (общие проблемы)........................................................
2.2.1.
Уравнение БернуJUIИ . ... "........................................."...................
Уравнение Бернулли для идеальной жидкости.".. ... ... "..................
Уравнение Бернулли для реальной жидкости""."""."."""... """"".
2.2.2. Уравнение Дарси-Вейсбаха . "."""."" ....""""..".""."""."""""".
2.2.3. Режимы течения жидкости... ""...."""""""...."......""""...."."""
2.2.4. Законы ламинарного течения ньютоновских жидкостей " .. """.
2.2.5. Законы турбулентного течения... .. "".....""....""......""""..".."""
Общая картина течения.". ..... """""...."""..""......"".. " .."""......... ".
Распределение скоростей в турбулентном потоке ".".. .".""....... ".".
Коэффициент rnдраалического сопротиаления"."""""""".".. "...".
2.2.6. Mecrnыe сопротиаления" ." ..."""""""""".""""".""""""...... ....
2.2.7. Характер изменения напора по длине трубопровода"".".".... ".
2.3. Трубопроводы ... .. "............."......."....."...................................................
2.3.1.
Простой трубопровод .. .... " ................. ".......................................
2.3.2. Наивыгоднейший диаметр трубопровода. Диапазоны рекомендуемых скоростей. ..... "...................."...........................................
2.3.3. Разветвленный трубопровод ... .. ...... ........ ..... .......".........."...........
2.3.4. Трубопровод с путевым и транзитным расходами......... "......... "
2.3.5. Газопровод...................................................................................
2.3.6. Гидраалический удар .. ".............................."......"............".........
.

.

2.4. Гравитационное течение тонких пленок........ "......................................
2.5. Течение неньютоновских жидкостей .. .......... "................"........... "........
2.5.1.
2.5.2.
2.5.3.

Классификация и общие свойства неньютоновских жидкостей
Пластичное течение бингамовских жидкостей ...........................
Пластичное течение псевдопластичных и дилатантных жидкостей."........................................................................................

125
126
128
130
132
133
134
137
139
142
146
151
151
155
159
163
166
167
168
172
173
176
179
182
185
190
190
195
199

2.6. Истечение жидкостей и газов..... "................................"....."..".""".... "

202

Истечение жидкости при постоянном напоре................... .. ".."

202
203
205

2.6.1.

.

Истечение через отверстие в дне сосуда .. "......""""......"............."..
Истечение через отверстие в боковой стенке... "".....".......".... ".......

4

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

2.6.2. Истечение :жидкости при переменном напоре .............. .............
2.6.3. Об истечении rазов......................................................................
2.7. Элементы гидравлики дисперсных систем.............................................
2.7.1. Общая характеристика дисперсных систем с твердой фазой.....
2:7.2. Неподвижный слой......................................................................
2.7.3. Движущийся слой ........................................................................
2.7.4. Псевдоожиженный слой ..............................................................
Кривые псевдоожижения .................................................. ................
Гидравлическое сопротивление псевдоожиженного слоя.................
С корость начала псевдоожюкения ............................................... ... ..
Скорость уноса .. ................................ .......... . . ... . ........... .. ............. . . . ...
Стесненное витание и расширение псевдоожиженноrо слоя...........
2.7.5. Образование и движение жидких капель и rазовых пузырей....
Оценка размеров элементов дисперсной фазы.................................
О скорости движения капель и пузырей в сплошной среде ............

2.8. Двухфазные течения ..... ......................................... ................... ..............
2.8.1. Общие положения .......................................................................
2.8.2. Транспортные системы с твердой фазой.....................................
Общие характеристики пневмотранспортных систем.......................
Гидравлическое сопротивление.........................................................
2.8.3. О двухфазных течениях типа жидкость-жидкость и жидкостьrаз............................ .....................................................................
2.9. Об особенностях молекулярного течения..............................................
Литература

к

главе 2.....................................................................................

207
209
213
214
217
222
224
227
228
230
232
236
241
241
244
246
246
250
250
253
255
257
260

Глава 3
ПЕРЕМЕЩЕНИЕ ЖИДКОСТЕЙ........................................................
3.1. Классификация насосов. Типовая схема и основные характеристики
насосной установки ............................................................... ...............
3.1.1. Классификация насосов ..............................................................
3.1.2. Основные характеристики насосной установки..........................
3.1.3. Предельная геометрическая высота всасьmания насосов............
3.1.4. О мощности и КПД насосов.......................................................
3.2. Поршневые насосы.................................................................................
3.2.1. Принцип действия и классификация насосов............................
3.2.2. Производительность....................................................................
3.2.3. Закон движения поршня. Диаrрамма подачи.............................
Закон движения поршня .................................. ........................ .........
Диаrрамма подачи ........ . ....................................................................
3.2.4. Работа и расчет воздушных колпаков ................................... """
3.2.5. Характеристика поршневых насосов .........".".............................
3.2.6. Предельная высота всасывания...................................................
3.2.7. Расчет мощности, потребляемой поршневым насосом ..............
3.2.8. Регулирование производительности пор шневых насосов... "......
3.3. Центробежные насосы............................................................................
3.3.1. Основное уравнение. Напор .................".... "...............................
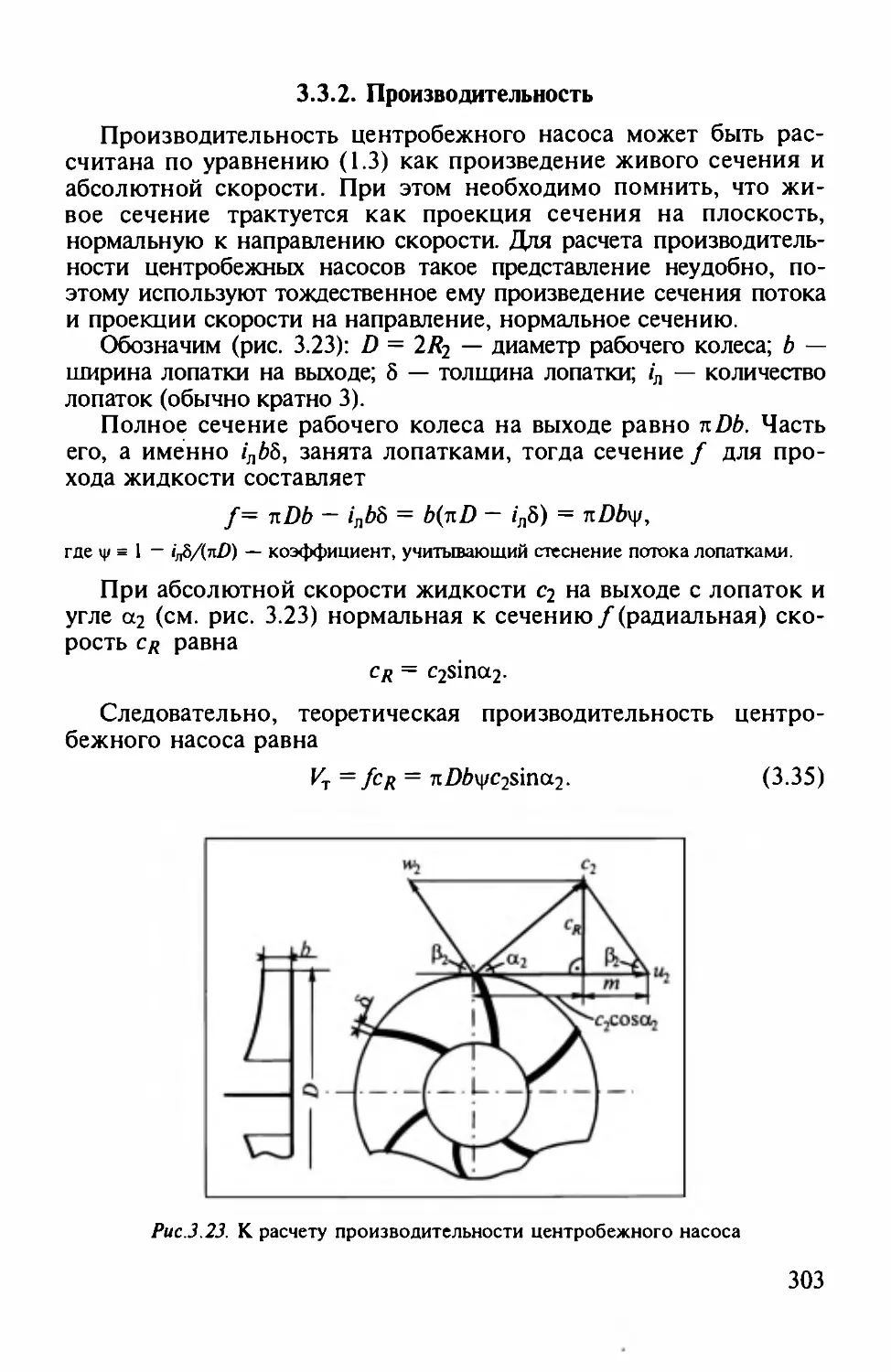
3.3.2. Производительность....................................................................
3.3.З. Характеристики центробежных насосов.........................."..... "...
Частная характеристика центробежного насоса..................... .. ".......
Рабочая точка центробежного насоса .........................................."....
З аконы пропорциональности............................................................
Универсальная характеристика центробежного насоса. .............."....

261
262
262
267
270
273
274
274
279
281
281
283
285
289
290
293
294
295
298
303
304
304
306
308
309

5

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

3.3.4.
3.3.5.

Параллельная и последовательная работа насосов......................

311

Предельная высота всасывания ..""......".."."""..."""......."".."..

313

3.4. Немеханические насосы ........... "".""."."."".....".....""........"."....".".".
3.4.1. Га.злифrы......................................................................................
3.4.2. Струйные насосы """"..""""""........"....."."..."""..""".......""...
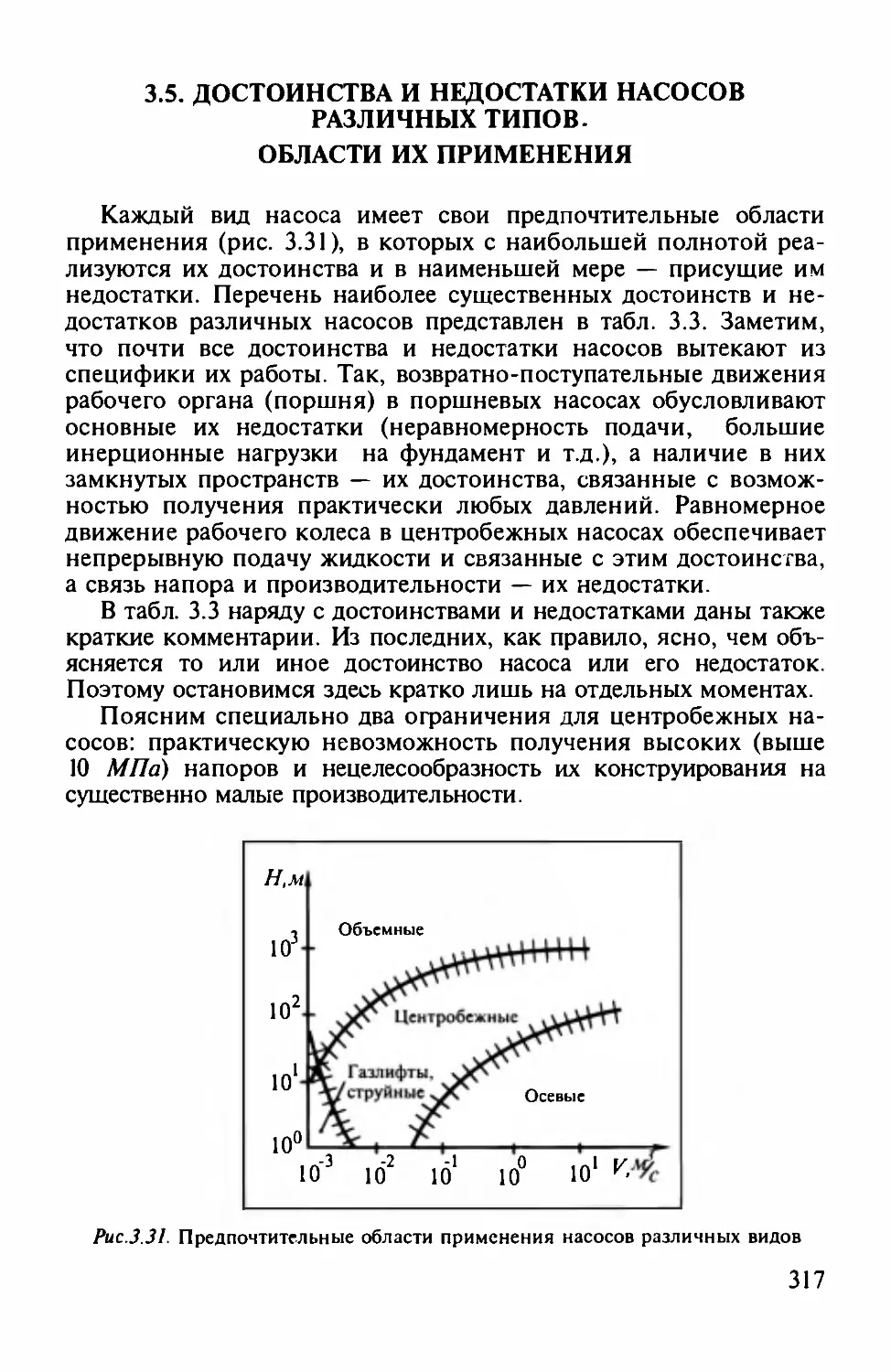
3.5. Достоинства и недостатки насосов различных типов. Области их
применения...........................................................................................

Литература

к

главе].....................................................................................

314
314
316
317
322

Глава 4
СЖАТИЕ ГАЗОВ................................................................................

323

4.1. Классификация компрессоров ".. .................... "........"....."""......""".."
4.2. О термодинамических основах работы компрессоров......... "".........."..
4.3. Поршневые компрессоры.......................................................................
4.3.1. Устройство и работа поршневых компрессоров .."""....."".....".
4.3.2. Удельные затраты энергии в поршневом компрессоре .... ".."""
4.3.3. Производительность поршневого компрессора .. """"".".""" .."
4.3.4. Степень сжатия в поршневом компрессоре... ""........."........."".
4.3.5. Сжатие rаза в многоступенчатых компрессорах ...""".."""""""

324
325

Схема многоступенчатой компрессионной установки ."......... "....."
ОIТТИмизация распределения степени сжатия

330
330
332
337
342
343
343

по ступеням ком-

прессора .............................................................................................

345

ОIТТИмизация распределения степени сжатия при промежуточном
oroope части газа..... "....."".........".....""....."""..""....".........""........

4.3.6.
4.3.7.
4.3.8.

Об охлаждении поршневых компрессоров .. ".."."""""..""""....
Расход энергии. Мощность """""......""".. """.."..""""..""""...
Реrулирование производительности поршневых компрессоров.

350
351
352
354
356
356

4.4. Некоторые специальные объемные компрессоры "".". ".."""..""""...
4.4.1. Пластинчатые ротационные компрессоры""""."........... """""..
4.4.2. Водокольцевые компрессоры ....... "...."..................""......"".."...
4.5. Центробежные компрессоры ..................................................................
4.5.1. Устройство и принцип действия турбокомпрессоров"...".."...".
4.5.2. Производительность турбокомпрессоров."""".... ".".........."."...
4.5.3. Напор, развиваемый турбокомпрессорами"""""... """"."""."..
4.5.4. Характеристики турбокомпрессоров ."".".""."""""""..."""."".
4.5.5. Реrулирование производительности турбокомпрессоров """"...
4.5.6. Центробежные вентиляторы ".... "......."""..""...........""...""".""
4.6. Другие динамические компрессоры""""""..... """""".......""..".. """".
4.7. Области применения компрессоров"..""."..."".""""."."..""".".."""...
4.8. Вакуумирование .. ........................ .... .................. " ................... "............
4.8.1. Поршневые вакуум-насосы """.. "."..."..."".".............""""""""
4.8.2. О вакуум-насосах глубокого вакуума ""."".... ""..."".""""""..".
4.8.3. Время вакуумирования сосудов.... "."...."."...............""...""""".

358
359
359
360
361
364
365
366
367
368
368
369
372
374

Литература

375

"

.

к

.

.

главе 4" ....".."..."...""""....."..."........."....."".............""..".".

Глава 5
ГИДРОМЕХАНИЧЕСКИЕ ПРОЦЕССЫ" ........".."""..............."""".

377

5.1. Осаждение...............................................................................................
5.1.1. Общие положения ""."."..""."."""""""..""".....""""""""""""
5.1.2. Естественное осаждение ."............".....""""."".""".".".".."""."

378
378
383

6

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

5.1.3.

Центробежное . осаждение в неоднородных ЖJЩКОСПIЫХ сисrемах
Связь свойств су.спензии с геометрическими размерами це.�приq�уги и ее производительностью............................................................

Затраты энергии на работу центрифуги............................................
5.1.4. Центробежное осаждение в неоднородных rазовых системах"..
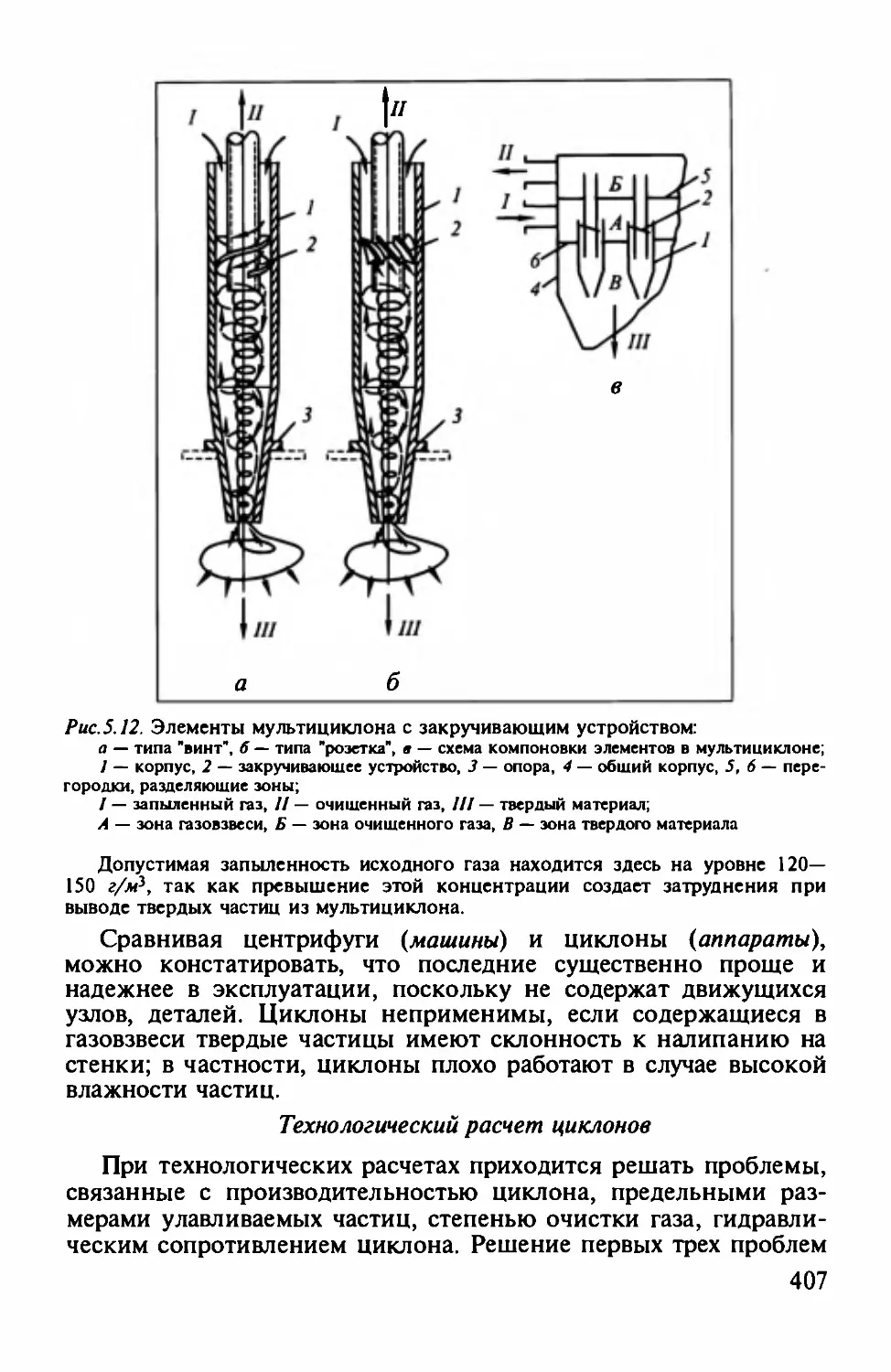
Устройство и принцип работы циклонов "..""....."."....."".....".""..
Технологический расчет циклонов....................................................

5.1.5. Некоторые другие процессы осаждения " .... ""....."""...""".......
5.2. Фильтрование ........ .. ... ........ ..... ... ........ ".................................................
5.2.1. Общие положения ...... .. ""....""............................."....................
5.2.2. Устройство и работа фильтров ... ... ....... "..........................".........
5.2.3. Основные характеристики фильтрационного процесса..............
5.2.4. Основное уравнение фильтрования .. "".".."..................."....."...
5.2.5. Отдельные режимы периодическоrо фильтрования ...................
.

Фильтрование при постоянной движущей силе...............................
Фильтрование при постоянной скорости фильтрации....... .. ..... .. "".
О других режимах и моделях фильтрования ..... ............ ."................

5.2.6.

392
395
399
404
404
407
412
413
413
415
418
419
422
422
424
425

Непрерывный процесс фильтрования на барабанном вакуумфильтре .. ......................................................................................

5.3.5. О перемешивании паст и сыпучих материалов . .... ."""..............
5.4. Диспергирование жидкостей и rазов " ...................................".........."..
5.4.1. Механическое диспергирование ...... . .. ...... ......... .... .".........."."..
5.4.2. Диспергирование при истечении из отверстий и сопел .... ... . "..

426
428
430
435
436
436
436
437
441
441
443
445
446
452
453
460
461
462
465

Литература к главе 5.....................................................................................

467

5.2.7.
5.2.8.
5.2.9.

Определение параметров процесса фильтрования......................
Фильтрование в поле центробежных сил..... ............... "..............

Промывка осадка ..... . . ... ...... .... ... .. ............ ... .. ... .."....................".
5.3. Перемешивание .". .... "......."......."......."................................................
5.3.1. Общие положения ..... ...... .. ." .................................... ".................
Цели процесса перемешивания"...... ...... ........... ....... . ... "..................
.

.

.

Основные проблемы процессов перемешивания..............................
Способы перемешивания ... .. ........ ..... .. ... ... "....."...............................

5.3.2.
5.3.3.
5.3.4.

Пневматическое перемешивание."..............................................
Циркуляционное перемешивание .. ..... ................... ...... .."...........
Перемешивание лопастными мешалками .. ...... ... ....... .. "......".....

Движение жидкости в окрестности вращающейся лопасти . ............
Центральная воронка...... ..... . .. .... ".............................."....................
.

Затраты энергии на перемешивание лопастными мешалками.........

.

.

.

Глава 6
ОСНОВЫ ТЕШIОПЕРЕНОСА " ......"............................".....................

469

6.1. Основные понятия."......... .. "......"......."..........."...........................".......
Теплофизические свойства рабочих тел ...... "..............."...................
Характер процессов переноса теплоты......... .. ... .. .. .. ""................."...
6.2. Виды теплопереноса. Общее математическое описание.. ".....".............
6.2.1. Виды теплопереноса ... ..... ...... ... ......... .......... ... .... .".................."..
6.2.2. Удельные тепловые потоки ... "".................."......"."...................
6.2.3. Об уравнении Фурье-Кирхrофа......... ........ ......... ... .... .. .. . ".......
6.3. Стационарный кондуктивный перенос теплоты через стенки..............
6.3.1. Плоская однослойная стенка.. .."........................................."......
6.3.2. Плоская многослойная стенка.....................................................
6.3.З. Цилиндрические стенки"................................... "" ..... ... ......... ....

471
472
474
475
475
477
478
478
479
481
482

.

.

7

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

6.3.4. Сферические стенки....................................................................
6.4. Конвективный теплоперенос..................................................................
6.4.1. Коэффициент теплоотдачи и число Нуссельта ... ....... .................
6.4.2. Аналогия в процессах конвективного переноса количества
6.4.3.
6.4.4.
6.4.5.
6.5.
6.6.
6.7.
6.8.
6.9.

движения и теплоты, а также вещества.......................................
Теплоперенос в условиях вынужденной конвекции...................
Теплоперенос в условиях естественной конвекции....................
Конвективная теплоотдача к шару..............................................

Теплоперенос при конденсации пара ....................................................
Теплоперенос при кипении жидкости...................................................

Теплоотдача от поверхности в псевдоожиженном слое..... . ".................
Порядок коэффициентов теплоотдачи...................................................
Теплоперенос излучением......................................................................

6.9.1.
6.9.2.
6.9.3.
6.9.4.

Общие понятия............................................................................
Лучистый теплоперенос между двумя телами.............................
Экранирование ............................................................................
Об излучении газов......................................................................

Литература

484
485
485
487
490
491
495
496
502
506
508
509
510
512
515
516

главе 6.....................................................................................

518

Приложении к главе 6 .......................................................... . .........................

519

к

Приложение 6.1. К

определению

среднего

коэффициента

рядности

д1lЯ пучков горизонтальных труб...............................

519

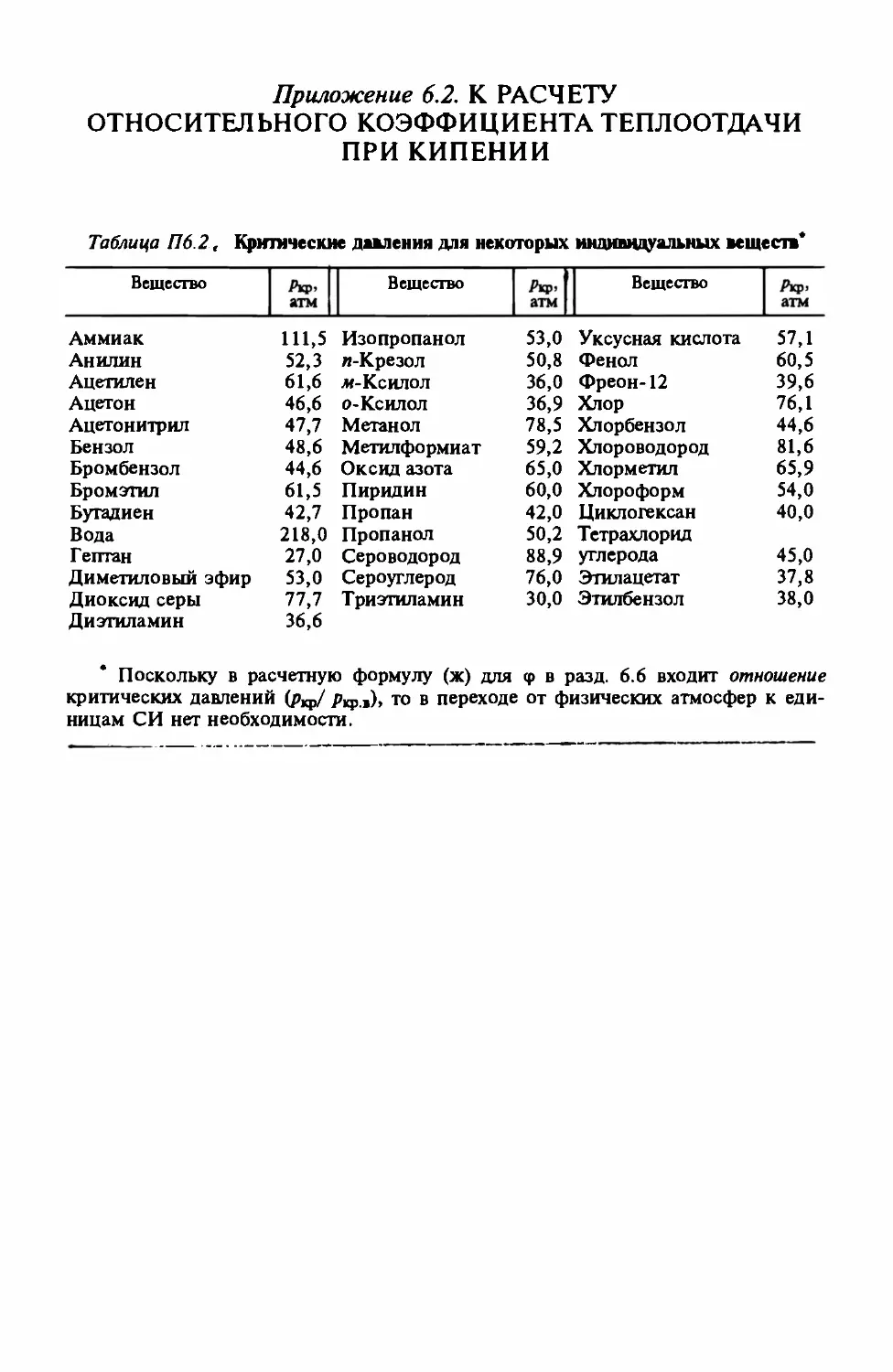
при кипении .. .......................................................

522

Приложение 6.2. К расчету относительного коэффициента теплоотдачи

Глава 7
ТЕПЛОПЕРЕДАЧА И ТЕПЛООБМЕН...............................................

523

7.1. Классификация теплообменников .. .......................................................
7.2. Теплопередача (основные понятия).......................................................
7.3. Коэффициент теплопередачи.................................................................
7.3.1. Общая концепция коэффициента теплопередачи при последовательном теплопереносе................................ .............................
7 .3.2. Расчет коэффициентов теплопередачи........................................
7.3.3. Коэффициент теплопередачи при параллельном теплопереносе
7.4. Отдельные задачи теплопередачи...........................................................
7.4.1. Распределение температур в катализаторной зоне в круглой

523
527
529

7.4.2.
7.4.3.

трубе.............................................................................................
Перенос теплоты через стержень бесконечной длины ...............
Критическая и целесообразная толщина тепловой изоляции....

7.5. Теплообмен (основные проблемы и положения)..................................
7.5.1. Круг задач ....................................................................................
7.5.2. Потоки энтальпий и тепловые балансы......................................
7.6. Средний температурный напор. ..... ........... ..... . ......... ".... ""..................
7 .6.1. Характерные температурные профили........................................
7.6.2. Средние температурные напоры .................................................
7.6.3. Проектный выбор теплообменника ............................................
7.7. Тепловой поток.......................................................................................
7.7.1. Тепловой поток при движении теплоносителей в режиме идеального перемешивания .. ................. . ........ ..................................
7.7.2. Тепловой поток при прямоточном и противоточном движении
теплоносителей . ...........................................................................
7.8. Изменение температур вдоль теплообменной поверхности..................
.

8

.

529
531
534
535
535
539
541
544
544
546
550
550
551
558
559
559
561
565

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

7.9.

Л имити рующие стадии
7.9.1.
7.9.2.

в процессах теплопереноса ..............................
Общие понятия............................................................................
Пропускные способности и лимитирующие стадии при стационарном теплопереносе. ..... ...... .. .. .. ... ..... ................. . . ......... ...
О пропускных способностя х в нестационарных процессах........
.

7.9.3.

.

7.10. Нестационарный теплообмен с твердыми телами ...............................
7.10.1. Основные понятия... ....... .... ......... ... .... ... ........... .... ....... ................
7.10.2. Нестационарный безградиентный теплообмен с твердым телом
7.10.3. Нестационарный теплообмен с шаром в граничных

567
567
568
574
574
574
576

услови-

111 и 1 рода ... ... ... ... ............ ..... .... ........... .. .. ... ... ... .......... ...........

7.11.1. Межфазный тешюобмен в тонком псевдоожиженном слое.......

577
583
584

7.11.2. Вырождение смешанной задачи в потоковую

586

ях

7.11. Межфазный теплообмен в псевдоожиженном слое.............................

( балансовую) ..... .

7.12. Реrуля рный режим теплообмена тела со сплошной средой.. ...... .. ..... .

588
589
590
592
594
601

7.12.1. Реrулярный режим 1- го рода........ .. ...... ................ ........... ...........

7.12.2. Реrулярный режим 2- го рода............. ... ........ ........... ... .... .. .. ........
7 .13. О термосифонах и тепловых трубах.....................................................
7.14. Приближенный расчет реrенсраторов.... ..... ..... ....... ..... ... ...... ........ ...... .
7.15. Отдельные задачи теплообмена ....... . ...... ......... .. .... .. ................ ... ..... .... .
7.15.l. Нагрев

конденсирующимся
паром интенсивно перемеши
ваемой жидкости..........................................................................

-

7.15.2. Нагрев псевдоожиженного слоя потоком горя чего

rаза

в условиях балансовой задачи ...................................................................
7.15.3. Нестационарный теплообмен между двумя интенсивно перемешиваемыми жидкостя ми ................. .............. ............ ... ... ...... ..
7.15.4. Безградиентное остывание тела за счет лучистого теплообмена.

Литература

к

Z11аве 7.....................................................................................

601
602
603
605
606

Глава 8
СТРУКТУРА ПОТОКОВ.........................................................................

607

8.1. Общие понятия......... .. ... ..... .. .... ..... .......... ............... .... ........ ...... ..............

608
612
618
618
618
618
621
621
621
623

8.2. Влия ние продольного перемешивания на эффективность ХТП. .. .... . . .
.

8.3. Структура потоков в случае простейших идеальных моделей"". ..........

Идеальное вытеснение................................ .................................
Время пребывания ............................................................."".".........
Кривые отклика .... ... ..."".""...."."."."..."..................".."... ".............
Результирующий эффект проце сса Uрез ..
8.3.2. Идеальное перемешивание."......"....."............. ""........ ".......... ".
Время пребывания ... .....""....."............. "... "."... "......... "...................
Кривые отклика ...... . ........... ."...""......................".................."...... "
Результирующий эффект процесса Uрез.". ."".....""........"""..""......
Параметры кривых отклика и простейших моделей продольно8.3.3.
го перемешивания ". ""........"................" .......... "."......"...........

8.3.1.

"" .. " .. . . . " .. """"."."". .. . . . . .•

.

"

8.4. Структура потоков в реальных системах." .. """..."............ ".. ""..........
"

8.4.1.

Ячеечная (каскадная , ступенчатая" ..) модель потока с продольным перемешиванием...... "....."...................................................

Сущность модели...... .... .. ... ................... ........ ....... ... .............. .............
Расчетные сооrnошения. Определение Uроз .......... .."."... "............".
8.4.2. Диффузионная модель потока с продольным перемешиванием
Сущность модели..... ... .. ...... ... ... ""...".......................................... ......

624
627

628
629
629
632
634
634

Расчетные сооrnошения. Определение Uрез ..... "".".................... .. ...

637

8.5. Общая оценка моделей структуры потоков ".. .. "......""""".."........ .......

638

9

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

8.7.1.

Химическая реакция в потоке"""""""""""""""""""""""""".

638
640
644
644
647
648
650
655
656

8.7.2.

Распределение элементов потока по времени пребывания при
гравитационном течении тонких пленок """"""""""""""""""

658

8.7.3.

Конвективный теплообмен при ограниченном продольном перемешивании одноrо из теплоносителей""""""""""""""""""

8.5.1.
8.5.2.

Сопоставление моделей продолъноrо перемешивания""""""".
Общая оценка моделей продолъноrо перемешивания""""""""

8.6. Об эксперимекrальном изучении продольноrо перемешивания """""
8.6.1. Общие положения """"""""""""""""""""""""""""""""""".
8.6.2. О среднем времени пребывания"""""""""""""""""""""""""
8.6.3. К выбору модели и определению ее параметров""""""""""""
8.6.4. Определение параметров моделей методом моментов "" """".
8.7. Структура потоков в технологических расчетах"""""""""""""""""".
"

Литература

к

главе 8.....................................................................................

661
666

Глава 9
ВЫПАРИВАНИЕ......................................................................................

667

9.1. Сущность процесса. Цели и области применения"""""""""""""""".
9.2. Основные типы выпарных аппаратов """""".""""""""""""""""""".
9.2.1. Классификация вьmарных аппаратов""""""""""""""".."""""
9.2.2. Конструкции вьmарных аппаратов """""""""""""""".""""""

667
669
669
671
675
683

9.3. Физико-химические основы процесса вьmаривания"""""""""""""".
9.4. Схема работы вьmарных аппаратов. Количество удаляемого растворителя
9.4.1. Типовая схема выпарноrо аппарата. Обозначение параметров
процесса ..".......""....."."....."....."""...."......"..."".......""............
9.4.2. Определение количества (потока ) удаляемого растворителя"".
9.5. Выпарные аппараты периодическоrо действия"""""""""""".. ..""""
9.5.1. Периодическое выпаривание с однократной загрузкой исходного раствора в аппарат""""""""""""""""""""""""""".. """.
9.5.2. Периодическое выпаривание с постоянным уровнем раствора
в аппарате"...""".....""..."".."""...""......"......"......""."...........".
9.6. Выпарные аппараты непрерывноrо действия """ """"""""" """ " ""
9.6.1. Однокорпусный выпарной аппарат """."""""""""""""."""""
9.6.2. Выбор рабочеrо давления процесса""""""""""""""".. ".. """".
9.6.3. Схема и расчет вакуумной выпарной установки """"""""""""
9.6.4. Пути экономии греющеrо пара """"""""""""""""""""".""""
9.6.5. Многокорпусные вьmарные установки.."""""""""""""".""""
Схема и работа мноrокорпусных установок """""""""""""""".""
Расчет прямоточной многокорпусной установки""""""""."."""".
9.6.6. Выпарной аппарат с полным тепловым насосом """""""" " "".
9.6.7. Выпарной аппарат с частичным тепловым насосом"""".. """".
Расход пара ....""....""......".....".....".............."..................................
Расчет коэффициента инжекции.......................................................
9.6.8. Повышение эффективности выпарных установок за счет утилизации теплоты .................................................. . .......................
.

"

"

683
684
685
686
690
693
693
695
696
702
704
704
708
716
719
719
720

9.7. Пленочные выпарные аппараты"""""""""""""".""""""""""""""""
9.8. Выбор размеров сепарационноrо пространства выпарных аппаратов "
Литература к главе 9" .."".".."."....""....."....."".............."".."."".......".......

725
727
730
733

Приложения к главе 9 """""""." """""""""""""""" """"""""""""""."".

734

Приложение 9.1.

Дифференциальные теплоты дегидратации
Qд
(к.Дж/кг растворителя) для водных растворов неко
торых распространенных неорrанических веществ
различных концентраций а(% (мае.)]""""""""""".

10

734

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Приложение 9.2. Значения поправочного множителя <f>• (Ккг раство
рителя/кДж) в зависимости от рабочих температур
кипения растворителя fp (0С) и давлений р (кПа) .. . .

734

Глава 10
ОСНОВЫ МАССОПЕРЕНОСА ............. .............

.

............................ . ..
.

10.1. Общая характеристика массопереноса ....................."".......................
10.1.1. Классификация массообменных процессов ................................
10.1.2. Составляющие описания массопереноса ............................ "......
10.1.3. Массообменные устройства .........................................................
10.1.4. Порядок последующего изложения.............................................
10.2. Концентрации........................ ..............................................................
10.2.1. Способы выражения и пересчета концентраций ........................
10.2.2. Расчет некоторых свойств смесей с использованием концентраций.............................................................................................
10.2.3. О концентрациях в технологических расчетах ............................
10.2.4. Правило рычаrа.. ........."...............................................................
10.3. Равновесие ...............................""......"................................................
10.3.1. Общие положения ...................................... ...... " ........... "............
10.3.2. Равновесие в системах класса 3(2-2)1 ..............".........................
10.4. Кинетика массопереноса в фазе.................................................. ... .....
10.4.1. Общие положения . ...."....."........................................................
10.4.2. В иды массопереноса. Об уравнении Фика ......".........................
10.4.3. Диффузионный массоперенос.....................................................
10.4.4. Конвективный массоперенос "............ .. ....................................
10.5. Элеме1пы материального баланса для фазы .......................................
10.6. Массопередача и баланс для процессов класса 3(2-2)1 ................ . ..
10.6.1. Массопередача ........"..."......"...........................................".........
Составление уравнения массопередачи........................"...................
Двухпленочная модель массопередачи ....................."".....................
Расчет коэффициентов массопередачи............. .................................
10.6.2. Материальный баланс аппарата...................................................
10.6.3. Пропускные способности массообменного процесса.................
10.7. Рабочие линии в аппарате для непрерывного процесса класса 3(2-2)1
10.7.1. Уравнения и положение рабочих линий........................... ..........
10.7.2. Построение рабочих линий...."...................................................
10.7.3. Рабочие линии в некоторых специфических случаях.................
10.8. Средняя движущая сила для процессов класса 3(2-2)1 .................. . ..
10.8.1. Идеальное перемешивание обеих фаз ..."....................................
10.8.2. Прямоточное движение фаз в режиме ИВ............"" .... "............
10.8.3. Противоточное движение фаз в режиме ИВ ..."..........................
10.8.4. Основные размеры массообменных аппаратов ............ ".............
10.9. Поток вещества в процессах класса 3(2-2)1 ........................................
10.9.1. Идеальное перемешивание обеих фаз.........................................
10.9.2. Прямоточное движение фаз в режиме ИВ..................................
10.9.3. Противоточное движение фаз в режиме ИВ...............................
10.10. Пропускные способности и лимитирующие стадии для процессов
класса 3(2-2)1 .................................................... ........"........""...........
10.10.1. Пропускная способность массообменного аппарата .................
10.10.2. Лимитирующие стадии процесса ............. ................. .................
10.10.3. О подмене задачи в массопереносе .... ......................................
10.11. Сети аппаратов (общая характеристика) ............ . ............ ..."..........
10.12. Ступенчатый противоток для процессов класса 3(2-2)1 ....................
10.12.1. Общие положения. Графоаналитический расчет.......................
.

.

.

.

.

.

.

.

.

.

.

.

735
736
736
742
744
748
750
751
755
758
759
762
762
766
768
768
770
772
773
778
780
780
781
781
785
788
791
792
793
797
801
805
806
808
811
814
817
818
821
823
825
825
828
829
830
833
834

11

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

10.12.2. Аналитический расчет идеальноrо процесса..............................

83S

10.12.3. Аналиrический расчет реальноrо процесса................... .............
Сrупенчатый противоток для цепочки из двух аппаратов .... . ..........

841

Ступенчатый противоток для цепочки из п одинаковых аппаратов

843

10.12.4. Оценка эффективности функционирования

841

ступенчато-про-

тивоточной цепочки реальных массообменных аппаратов .......
10.12.5. О расчете противоточных аппаратов и их цепочек по

848

"методу ВЭТС" .. ..... .. . .... ... .... .. ...... ..... .. ..... .......... ...... ... .. .. . ..... .... ..
10.13. Перекрестное соединение аппаратов в сети для процессов класса

851

3(2-2) 1

········· · · · · · ············ ·························· · · · · · · · · · · · · · · · · · ··· ········· · · · · · · · · · · · · · · ·

10.13.1. Массоперенос при идеальном контакте фаз в ступенях...........
10.13.2. Оптимизация ступенчато-перекрестных процессов при идеальном контакте фаз.................................................................
Оптимизация потоков распределяемой фазы ...................................
Оптимизация числа ступеней............................................................
Выбор распределяемой фазы.............................................................
10.13.3. Массоперенос в реальных ступенях контакта в случае прямой
линии равновесия .... . ........... ........ .........:..................................
10.14. Периодические и полунепрерывные процессы класса 3(2-2)1..........
10.14.1. Периодические процессы...........................................................
10.14.2. Полунепрерывные процессы...... ........................ ... ..... "..............
10.15. О расчете массообменных процессов иных классов, нежели 3(2-2) 1
10.16. Массообмен с твердыми телами.........................................................
10.16.1. Общие положения .... ........... ... .......... ...... ................ ............ "......
10.16.2. Внешняя задача массопереноса...... ...... " ...................... "............
Соста811Яющие внешнего массопереноса . . ........... ........... .......... .... ....

851
853
857
857
859
860

Нбl
R6l

X6.\
X65
ХЫ!
R7 I
R7 I

10.16.4. Потоковая задача массопереноса ..... .......................... ...... ..... .....

R73
873
875
877
880

10.17. К оценке качества ра:шеления .. .......... .......... ......................................

882
884

Литература к главе 10...................................................................................

8SS

Массообмен в псевдоожиженном слое в условиях внешней задачи
10.16.3. Внутренняя задача массопереноса ........ ................ ...... .. ........ . . .. .
10.16.5. О смешанных задачах массопереноса ..................... ..... ... .. ...... .. .

Книrа 2
Оглавление

891

Глава 11.

907

Глава 12.
Глава 13.
Глава 14.
Глава 15.
Глава 16.
Глава 17.

Глава 18.
Глава 19.
Глава 20.
Глава 21.
Глава 22.
Глава 23.
Глава 24.

АБСОРБЦИЯ
дисrилляция и РЕКТИФИКАЦИЯ
ЖИДКОСfНАЯ ЭКСfРАКЦИЯ
АДСОРБЦИЯ
СУШКА ТВЕРДЫХ МАТЕрИАЛОВ
КРИСfАJVIИЗАЦИЯ
РАСfВОРЕНИЕ И ВЫЩЕЛАЧИВАНИЕ
СУБЛИМАЦИЯ И ДЕСУБЛИМАЦИЯ
ГРАНУЛИРОВАНИЕ
МЕМБРАННЫЕ ПРОЦЕССЫ РАЗДЕЛЕНИЯ
УМЕРЕННОЕ И ГЛУБОКОЕ ОХЛАЖдЕНИЕ
ИЗМЕЛЬЧЕНИЕ ТВЕРДЫХ МАТЕРИАЛОВ
КЛАССИФИКАЦИЯ ТВЕРДЫХ МАТЕРИАЛОВ
СОПРЯЖЕННЫЕ И. СОВМЕЩЕННЫЕ ПРОЦЕССЫ

Перече" уче61н(ов nо общему курсу Процессw н апnара11.1 ХН1МЧесхой тeXJЮJIOIIOI
Пред.w-...�й ухаза�nе.

969
1103
1157
1213
1307
1393
1435
1469
1519
1551
1619
1655
1697
1733
1735

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ПРЕДИСЛОВИЕ К ПЯТОМУ (ЭЛЕКТРОННОМУ) ИЗДАНИЮ
Первое издание учебника увидело свет в конце 1999 г. (кн. 1) – начале 2000 г. (кн. 2) в издательстве «Химия» (Москва) при поддержке центра
«Интеграция». Тираж первого издания был ограничен (1000 экз.) и целиком распределён по вузам и НИИ РАН, в свободную продажу учебник не
поступал. Между тем, издательство и авторы получили многочисленные
заявки на учебник от научных организаций, предприятий, вузов и частных
лиц – научных работников, инженеров, аспирантов, преподавателей и студентов вузов.
В 2002 и 2003 гг. учебник вышел в свет в издательствах «Логос», «Высшая школа», в 2006 г. – в издательствах «Университетская книга», «Логос»,
«Физматкнига» (совместное издание). Настоящее (пятое) издание учебника выходит в электронном виде.
Авторы учебника внимательно изучили замечания, полученные от
читателей и рецензентов, большинство замечаний нами учтено (в полной
мере или частично). Лишь немногие из поступивших замечаний мы отклонили, и на то было две причины. Во-первых, при анализе некоторых
объектов мы придерживаемся других взглядов и считаем нашу методику
изложения учебного материала более рациональной. Во-вторых, будучи
даже согласны с некоторыми замечаниями по сути, мы не хотели нарушать
целостность нашей авторской концепции (см. предисловие к первому изданию учебника и главу 1). Здесь мы осмелимся напомнить, что учебная
дисциплина почти всегда преподносит теоретические положения и закономерности науки в обобщённом и в какой-то степени упрощённом виде. Мы
старались следовать строгому научному изложению (конечно же, хорошо
понимая различие между наукой и её «учебной долей») и найти разумное
соотношение научного и учебного начал. Мы полагаем, что более строгому
анализу того или иного объекта место в научной литературе, но не в учебнике, тем более по общей учебной дисциплине.
В настоящем издании исправлены ранее допущенные и замеченные
опечатки и неточности. В остальном пятое издание является стереотипным.
Все замечания и предложения читателей авторы по-прежнему примут
с благодарностью.
13

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Светл ой памяти Уч ителя выдающегося педагога,
ученого и инженера
Нисона Ильи'lа Гел ьперина
посвящаем

ПРЕДИ СЛОВИ Е К ПЕРВОМУ ИЗДАНИЮ
Развитие научной мысли, расширение масштабов научного
знания и прони кн овение в его глубины сопровождается диффе
ренциа цией науки , возни кн овением и вьщелением новых ее об
ластей, более дробной рубрикацией , усилением разобщенности
между раз.л ичными научными дисциплинами и разделами внут
ри дисциплин, ослаблением и даже утерей связей (по крайней
мере - ясно видимых) между ними. Это приводит к потерям в
осознании единства природных явлений, общности в закономер
ностях дисциплин и отдельных их разделов, в подходах к их
изучению - движение мысли происходит по обособл енн ым тра
екториям. В результате появляются затруднения в изучении
(усвоении) научных дисципл и н, в использовании успехов одной
науки (одного раздела науки ) при теоретическом и эксперимен
тал ьном изучении проблем и практической ре али зации решений
- в другой области знаний (нередко - достаточно бл и зкой) .
Растущее принципи ал ьное противоречие (развитие науки и
потеря общности между разными областями знания) особенно
так
негативно влияет на про це сс
обуч е н ия студентов,
как именно в этот пери од закладывается научное мировоззрен и е
будущих специ ал истов. Поэтому одна из важнейших задач пр и
написании вузовского учебника состоит в том, чтобы вскрыть
перед студентами при чинно -следственные связи изучаемой дисц и 
плины с другими (предьщущими, с м ежными , последующими) и
между разделами (а также внутри разделов) изучаемой дисци
плины. Применительно к курсу " Про цессы и аппараты хими
ч еской технологии " ( ПАХТ) необходимо подчеркнуть в первую
очередь тесную связь с Высшей м ате м атикой (это для ПАХТ не
только инструментарий, но во многом еще и наука, определяю
щая пути и методы анализа явлений и про цессов, в ряде случаев
- просто способ мышления), Ф изико.й (прежде всего речь здесь
ид ет о п оюп ий но м аппарате и феноме н ологическо м подходе
к анализу явлений) , Физической хи мией (в наибольшей мере с раздело м " Термодинамика" , отчасти - с кинетикой химиче·

14

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ских реакций), а также с рядом других дисциплин. В то же вре

мя при изучении курса ПАХТ необходимо прокладывать мости

ки (далее они будут расширены и конкретизированы) к курсам
"Общая химическая технология", "Реакторные устройства и
моделирование", "Системы управления", "Оборудование заво
дов", а также к курсам специальных технологий.
МЕТОДОЛОГИЧЕСКИЕ И МЕТОДИЧЕСКИЕ АСПЕКТЫ
КУРСА ПАХТ. Вряд ли следует жестко противопоставлять со
держательную и методическую стороны учебного материала.
Важны обе проблемы:
Чему учить и Как учить, - но вторая
представляется сегодня более острой, что и обусловило повы
шенное внимание в учебнике к методологии и методическим
вопросам.
ПАХТ - курс синтетический. Он формировался на протяже
нии десятков лет из отдельных (нередко - обособленных) об
ластей знания и дисциплин, зачастую подходящих к анализу и
описанию явлений и процессов с совершенно разных позиций.
Разумеется, одновременно происходил и обратный процесс:
некоторые разделы ПАХТ выделялись в самостоятельные учеб
но-научные дисциплины. Но при создании учеб ника интеграция
занимает нас больше, нежели дифференциация, поскольку
именно при интеграции возникает проблема осмысления и пояс
нения общности в подходах (при дифференциации - лишь во
прос о сохранении или несохранении этой общности).
Современные учебные курсы ПАХТ содержат анализ тради
ционного набора технологических приемов; вариации - весьма
невелики (наличие или отсутствие некоторых глав: "Измельчение
и классификация твердых материалов", "Холодильные процессы"
и т.п.). Формируя содержательное наполнение учебника, мы
сочли
целесообразным дополнительно
включить в него ряд
технологических приемов, приобретающих значимость в наши
дни и имеющих достоверную перспективу на будущее: "Сублима
ция и д е сублимация ", "Гранулирование", "Сопряженные и
совмещенные процессы". Кроме того, нетрадиционно расстав
лены акценты в главе "Мембранные процессы разделения".
Объединить методологически и методически
отдельные
(часто разрозненные, имеющие разные базы) подХоды к анализу
процессов, явлений - весьма непросто. Но если этого не сде
лать, то перед студентом курс не будет выступать в виде едино
го, логически увязанного целого; скорее, он предстанет как со
брание отдельных рецептов, применяемых к решению тех или
иных задач. Иными словами, будет набор проблем, подпроблем,
вопросов и задач, каждую из которых надо решать своим специфи
ческим способом. Излишне rоворить, что такой курс окажется гро
моздким, лоскутным, не обьединенным общей идеей.
15

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Со:щанию методологически выдержанного курса преmпствуют:
- тр адиции, громадный накопленный опыт, выраженный
прежде всего в многочисленных практических рекомендациях,
эмпирических формулах, прагматических рецептах решения
отдельных задач;
- различия в подходах к решению разных проблем - как до
статочно общих, так и сугубо частных.
Видимо, поэтому в ряде учебников по курсу ПАХТ ощущает
ся четко выраженное стремление к обобщению излагаемого мате
риала, иначе говоря - к интеграции знания. В учебники вклю
чаются главы общего характера, на основе которых далее трак
туются технологические приемы и описания конкретных про
цессов (конкретных в смысле ПАХТ, но не отдельных техноло
гий) . Цель - выявить и проследить перед студентами эту общ
ность, показать связи дисциплин по вертикали и горизонтали,
базируя новый материал на уже известном. Подчеркнем, что
интеграции знаний способствует акцент в учебнике прежде
всего на фундаментальные положен ия курса. Это позволяет от
эвристических правил перейти к структурированию учебно
научного материала на уровне принципов, что в конечном итоге
приводит к репрографии (более сжатому и емкому представле
нию) информации и ускоряет познание.
Существенной помехой в последовательной реализации идеи
обобщен ия является желание авторов многих учебников охва
тить в ходе анализа и описания крайне широкий круг процессов
и задач. Эта многоохватность в условиях любой разумной огра
ниченности объема учебника возможна только за счет глубины
проработки основ; многочисленные частности (под эгидой
" практической важности " или " освоен ия последних достижений
науки и техники " ) можно включить в учебник только в ущерб
выявлению общности и анализу физического смысла явлений,
процессов. Кстати, ограниченность времени на изучение в вузе
курса ПАХТ делает освоение такого учебника практически не
возможным. Разумеется, учебник по охвату проблем должен
быть шире курса ПАХТ в любом химико-технологическом вузе,
дабы в ходе обучения можно было выбрать разделы, коим жела
тельно (соответственно направленности и традициям вуза, фа
культета, а может быть - и пристрастиям кафедры, преподавате
лей) уделить более пристальное внимание (сократив или опустив
изучение других). Однако существующие учебники, на наш
взгляд, отличаются тенденцией к рассмотрению чрезмерного
множества отдельных объектов, в том числе таких, место которым
(при всей их практической значимости) - в научных публикаци
ях, справочной литературе. Не в подробном описании многочис
ленных объектов видятся нам цели вузовского учебника.
16

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Соответственно указанным выше положениям при создании
учебника мы исходили не из тезиса "Что можно добавить", а из
тезиса "Без чеrо нельзя обойтись", имея в виду прежде всего об
щие подходы к рассматриваемым явлениям и типовым процес
сам (конечно, насколько это возможно на существующем уров
не науки о ПАХТ) . Мы считали целесообразным ограничить
изложение курса основн ым и проблемам и (вопрос в том, насколь
ко правильно мы смогли установить и отобрать основное), ти
повым и пр им ерам и , привлекая наиболее интересные (пол езные!)
частности лишь для иллюстрации - в целях лучшего усвоения
основ.
При отборе материала мы отдавали предпочтение методически
сущес111е1D1ЫМ моментам перед прикладными (пусть даже практи
чески важн ыми), полагая главной целью - раскрыть перед сту
дентом подходы к анализу процесса и методы проведения анализа.
Надо исходить из того, что, восприняв общие подходы и приемы,
студент (а впоследствии научный работник, инженер) с анализом
множества конкретных процессов и ситуаций справится само 
стоятельно .

ПРИНЦИПЫ ИЗЛОЖЕН ИЯ КУРСА. Существующая ныне
градация усвоения знания насчитывает четыре уровня:
"Распознавание" (узнавание ранее изученного объекта при его
предъявлении); "Воспроизведение " (умение воспроизвести объ
ект, его описание, математический вывод) ; "Понимание "
(овладение связями различных факторов, умение установить и
объяснить их, предсказать поведение объекта при изменении
условий,
т. е. активное применение знаний) ; "Творчество"
(создание новых подходов к описанию объекта, выявление но
вых факторов, новых объе ктов, новых областей знания). Мы
полагаем , что инженер или научный работник, владея уровнями
Распознавания и Воспроизведения, должен в основном функ
ционировать на уровнях Понимания и Творчества (доля послед
него особенно высока у научного работника). По этой причине
мы старались построить учебник на уровне Понимания - это
предпосылка Творческого уровня, когда вопросы становятся
важнее ответов. В конце концов, сверхзадача - не в том, чтобы
студент знал описание того или иного процесса, а в том, чтобы
он усвоил общие подходы (к рассмотрению явлений и процес
сов, к постановке технологических задач) и приемы (анализа
этих явлений, процессов, задач) , чтобы смог подойти к описа
нию любого (даже незнакомого) процесса, провести его анализ
синтез на уровне ПАХТ.
В соответствии с этим в учебнике особенно тщательно и де
тально проработаны общие главы, где изложены основные по
ложения, важные для ряда конкретных (последующих) глав.
Общность в физико-химических закономерностях, технолоrиче-

17

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ских аспектах, методических вопросах, в подходах к анализу
подчеркивается нередкими перекрестными ссьтками в тексте на
материалы других глав (чаще - предыдущих, в основном общих). Специально заметим, что в согласии с концепцией
учебника оправдано . место главы "Основы массопереноса": тра
диционно ее включают в тот том, где изучаются конкретные
массообменные процессы; в данном учебнике она помещена в
томе (книге), содержащем все общие главы. Это позволяет про
следить общность различных процессов переноса.
Заметно расширена и углублена глава "Кристаллизация",
ставшая фундаментом для глав "Растворение и выщелачивание",
"Сублимация и д есублимация", "Гранулирование". Значительно
шире (в виде отдельной главы) представлена общая проблема
структуры потоков. Для главы 10 "Основы массопереноса" сущест
венно вьщеление систем класса 3(2-2) 1 - анализ разнообразных
массообменных процессов этого класса (скажем, многих про 
цессов абсорб ции и экстракции) ведется по единой канве.
Общность подчеркивается и внутри глав. Так, с единых по
зиций анализируется кристаллизация из растворов и расплавов.
При изложении некоторых разделов нам пришлось в ряде
случаев использовать базу (подходы, приемы, методы), традици
онно выпадающую из общих (устоявшихся) подходов к курсу (это
относится, например, к главе "Выпаривание", в еще большей мере
- к главе "Сушха", отчасти - к главе "Адсорбция"). Мы постара
лись и :щесь показать связи этой базы с общими подходами - в
балансовых соотношениях, в кинетических закономерностях и т.п.
М ногие фундаментальные (концептуальные, методологиче
ские) положения научный работник, преподаватель, инженер (и
не каждый!) начинают чувствовать и понимать через 15-20 лет
профессиональной деятельности, т.е. далеко за предел ами вуза.
Для студента они остаются не только непознанными, но чаще
всего - да:же не обозначенными. Авторы учебника постарались
сделать акцент на некоторых таких моментах (примеры приве
дены ниже), наиболее концентрированно - в первой главе. Их
осмысление способствует становлению методо.11оги11еского харак
тера мышления студентов, поиску ими причинно-следственных
связей. При этом появляются вопросы и сомнения, а это пред
посьтка успешной творческой учебы и работы.
В ходе изложения материала в учебнике авторы постарались
показать и подчеркнуть общность рассматриваемых проблем:
- на содержательном уровне (вывод и вид дифференциаль
ных уравнений переноса различных субстанций; представление
равновесия и кинетики переноса, и т.п.);
- на методолоrическом уровне (линейность-нелинейность
модельных описаний; уровень абстрагирования модели от объ
екта; концепция пропускных способностей и лимитирующих
18

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

стадий; место обобщенных переменных; правомерность исполь
зования коэффициентов незнания и т.д. );
- на методическом уровне (сходное построение большинства
глав, техника составления балансов; выбор подходящего типа
концентраций компонентов для обеспечения постоянства рас
четных потоков; определение числа теоретических ступеней ;
равноточность инженерных расчетов и др.).
В настоящем учебнике отдельных технологических задач
рассмотрено меньше, чем в других учебни ках. Скажем, в разделе
"Дистилля ц ия " опущены некоторые способы осуществления
этого процесса, не содержащие оригинальных методических
решений; по той же причине в главе " Экстракция " не рассмат
ривается экстрагирование с флегмой (в таких случаях читатель
обычно отсьшается к соответствующей литературе) . Мы поста
рались использовать предоставленные нам страницы для углуб
ленной (в плане ПАХТ) проработки физического смысла, под
ходов и приемов, детального рассмотрения тех процессов и си
туаций, которые характерны для возможно более широкого
круга " процессных" задач . В ряде случаев приводится несколько
возможных путей анализа объектов; в качестве примеров можно
привести распределение скоростей при течении тонких пленок
(глава " ГИдравлика " ) или формирование напора центробежного
насоса (глава " Перемещение жидкостей " ).
Все это предопределило ряд особенностей учебника .
1 . Главное внимание уделено вопросам, разделам, главам,
дающим наиболее общие представ.ления о процессах и группах
сходных процессов, о постановке задач, приемах анализа, алго
ритмах расчетов, о физическом смысле явлений и процессов.
2. Основные вопросы в учебнике - не "как ?" и "что ?", а
''за чем ?" (постановка проблемы) и ''п о чему ?" (обоснование хода и
результатов анализа) . Поэтому, где возможно, мы стремились
дать образы, модельные представ.ления о явлении, процессе, соче
тая феноменологический и аналитический подходы. При этом в
ходе получения ответов на вопросы "зачем?" и "почему?" разре
шаются многочисленные вопросы типа " что? " , " как? " : в есте
ственно-научном и техническом образовании важны не столько
факты и эмпирические связи, сколько постижение их физи
ческой сущности и доказательность анализа . А эмпирику и ак
сиоматику мы постарались свести к минимуму.
3. В учебник включено рассмотрение отдельных вопросов, не
очень существенных с прагматической точки зрения, но важных
в методическом отношении (в смысле нетривиальности подхода,
не потерять метод, вооружить
приема анализа) . Здесь цель
студента достаточно широким и действенным инструментарием
в
для разрешения технологических ситуаций (пусть даже
-

19

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ущерб перебору более широкого круга конкретных практиче
ских задач ) .
4. М ы особо старались обратить внимание студентов на те
моменты курса ПАХТ , которые (мы знаем это из опыта препо
давания) вызывают у них затруднения при постижении физи
ческой сущности процесса и осмыслении полученного результа
та либо вообще ускользают от их внимания.
5. В качестве основного мы старались вьщержать дедуктивный
метод построения курса и изложения материала , не отказываясь
в отдельных случаях и от других способов его подачи.
При написании уч ебника мы стремились:
- найти разумное соотношение научного и учебного начал, сохра
нить приемле м ый научный уровень (но без глубоких научных
изысков - их рассмотрение в учебнике может затруднить усвое
ние материала студентом; место им - в научной литературе, т.е.
на более высокой ступени овладения научной дисци пл иной) ;
- выдержать методич еский уровень, позволяющий студенту
уяснить суrь и двигаться дальше.
Мы старались соблюсти известную меру научной строгости
(не опускаясь до вульгаризации), понимая в то же время разли
чие между наукой и ее учебной долей, преподносимой в учеб
нике. Поэтому мы считали возможным в ряде случаев посту
питься строгостью научного изложения , если это помогало соз 
данию образа (облика) , модели явления, процесса и способство
вало лучшему осмыслению проблемы. Полагаем, что строгость
научного восприятия и анализа придет к студенту , инженеру,
научному работнику (или они придуr к ней) при более глубокой
проработке проблемы, если им доведется столкнуrься с ней в
будущей учебе и деятельности.
Достаточно строгое изложение материала в уч ебнике для ес
тественных и технических вузов не отрицает целесообразности
(если удается) эмоциональной пода чи материала, повышающей
интерес к предмету, способствующей усвоению и запоминанию.
Речь идет об интересных технологических ситуациях, запоми
нающихся эпизодах, элегантных пуrях решения задач, ярком
языке - образности, эпитетах, метафорах. Одним словом, во
втузовском учебнике есть место для восклицательного знака (и
не только в изображении факториалов) и для многоточия (и не
только при указании на прерывание записи бесконечных после
довательностей) .
Авторы в основном придерживались терминологии, устано
вившейся в науке о ПАХТ, не отказываясь вм есте с тем от ее
изменения и уrочнения там, где это представлял ось целесооб
разным. Так, в главах "Основы тепл опереноса" , "Теплопередача и
теплообмен" разведены (им придан конкретный смысл) понятия
"теплоперенос" , "теплоотдача" , "теплопередача" , "теплообмен " .

20

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

В учебник включались только те вопросы, которые авторы “пропустили через себя”, т.е. по которым у них была достаточная ясность. По этой причине из рассмотрения исключен, например, такой
вопрос (интересный методически и важный для химической технологии), как истечение на водосливах: в существующих учебниках он
дан с недопустимыми ошибками, а более строгое решение отличается неприемлемой громоздкостью. Пока же компактного, строгого,
но доступного студентам решения этого вопроса, к сожалению, нет.
Изложенные выше подходы представляются нам важными вообще, в том числе и при написании учебника по курсу ПАХТ, в особенности – в связи с намечающимся в перспективе возникновением
более общей научной (впоследствии и учебной) дисциплины “Технологические процессы и аппараты” (ТПА), в которую дисциплина ПАХТ войдет как составная часть со своим характерным (для
химической технологии) содержанием. Но методология и методика
у ТПА и ПАХТ будут общими (вероятно, обогащенными новыми
подходами). Подчеркнутое внимание в учебнике к общим моментам
и выявлению связей — существенно еще и в этом аспекте.
ПРЕДСТАВЛЕНИЕ МАТЕРИАЛА ЧИТАТЕЛЮ (СТУДЕНТУ).
Учебник разделен на две примерно равные по объему книги. Отдельные книги не являются тематически обособленными: вторая
книга представляет собой продолжение первой; нумерация страниц
у книг — общая. Представление материала в учебнике учитывает
развитие науки “Процессы и аппараты химической технологии” —
сложный нелинейный переход от эвристических правил (в период
становления технологии) к основополагающим принципам (глобальным, общим, отраслевым, частным) на основе фундаментальных
представлений в исследуемой и смежных областях Знания.
Причинно-логические связи анализируются, а математические
преобразования приводятся в учебнике достаточно подробно, чтобы студенту были вполне ясны постановка задачи, канва вывода,
анализ полученного результата. Мы считаем неприемлемой нередко реализуемую в учебниках практику, когда результат приводится
сразу, а ход решения изымается. Ведь в самом ходе решения часто
встречаются поучительные приемы, а порой и неожиданные повороты.
21

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Сведения из других курсов (предьщущих и смежных) , на кото
рых базируется понимание и описание отдельных вопросов кур
са ПАХТ, представлены только в необходи м ых объемах, без их
детализации и подробного повторения.
Конструкции аппаратов, в которых протекают изучаемые
процессы, приводятся схематично, стилизованно, без несуще
ственных (в аспе кте курса ПАХТ) узлов, описание их работы
дается лаконично. Основная цель здесь - дать студенту пони
мание принципа работы аппарата, в котором происходит анали
зируе м ый процесс; частные практические рекомендации сведе
ны к миниму му. Предполагается, что в идеале теоретическому
учебнику по курсу ПАХТ должно сопутствовать отдельное учеб
ное пособие с детальным описанием конструкций аппаратов и
изложением принци п ов и особенностей их работы.
При необходимости более подробного расс мотрения каких
либо вопросов, касающихся теоретического анализа, инженер
но-технологических расчетов, сведений из других курсов, кон
струкций аппаратов и т.п. , следует воспользоваться помещен
ными в учебнике ссылками на учебную и научную литературу.
Список рекомендуемой литературы в алфавитном порядке раз
мещается после каждой главы. Кроме того, во второй книге
перед " Предметным указателем" дан перечень известных нам
учебников по обще му курсу "Процессы и аппараты химической
технологии " , изданных на русском языке.
Нумерация рисунков, таблиц, основных формул дана по гла
вам арабскими цифрами , например (2. 1 ) , (5.2); в ряде сл учаев
(составные рисунки, модификация формул) при меняется запись
вида ( 10.7б) . Нумерация вспомогател ьных соотношений обозна
чается русскими буквами (а) , (б) и т.д. и ведется заново с каж
дого подраздела уровня (7.3).
В редких случаях отдельные главы учебника заканчиваются
приложениями, включающими необходимые для расчетов мате
риалы, не содержащиеся в распространенной учебной и спра
вочной литературе.
В тексте учебника принято испол ьзован ие разл ичн ых шрифт ов
( полужирного, курсива, петита) с целью акцентирования и об
особления отдельных моментов - ключевых, углубляющих ана
лиз, методически важных (или , наоборот, необязательных) для
понимания учебного материала, изучаемого в данном и последую
щих ра:щелах. О назначении каждой формы шрифrовых вьщелений
см. соответствующий подраздел в "Основных условных обозначе
ниях " .

Список основных условных обозначений помещен в каждую из
к н и г , Предметны й указатель дан во второй к н и г е . В Оглавлении

22

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

первой книги приведен также перечень глав второй книги, а во вто
рой книге - глав первой книги. Мы вообще старал ись излагать и
размещать материал т-ак, чтобы это было удобно читател ю, студенту.
Учебник включает целый ряд идей (как содержательного, так
и методического характера) заслуженного деятеля науки и тех
ники, лауреата Государственной премии, доктора технических
наук профессора Нисона Ильича Гельперина, в том числе разра
батываемых им в последние годы жизни, - он не успел их реа
лизовать. Существенную роль в вьщвижении и осмысл ении во
шедших в учебник хи м ико-технологических проблем сыграли
некоторые преподаватели кафедры ПАХТ М ИТХТ, не приняв
шие участия в написании учебника; среди них - один из пер
вых учеников И . И . Гельперина в М ИТХТ, опытнейший препо
даватель профессор В.Л. Пебалк. Авторам хотелось бы рассмат
ривать предлагаемый учебник как определенный шаг в развитии
научно -учебной школы Уч ителя .

Изучение весьм а нел егкого для студентов курса ПАХТ (а по
тому - и материала в учебнике) требует грамотной постановки
задач, логически вьщержанного хода решений, анализа найден
ных результатов, т.е. постоянной работы на понимание. Поэтому
сам им способо м п одачи учебного материала авторы стремились
убедить студента, что ход решения задачи важнее полученного
результата (факта, рецепта действий), а метод решения - еще
важнее, поскольку относится не к единичной задаче - он охва
тывает группу задач. Иными сл овами , основой науки и учебной
дисциплины "Процессы и аппараты химической технологии "
является никак не Know how (" Знаю как" ) , а Кпоw why ( " Знаю
почему" ) и не менее важное, а зачастую и более сложное Know
what for ( " Знаю зачем " ) . И еще: необходимо, чтобы учебник был
проникнут духом движения научн ой мысли - это относится не
только к быстро изменяющемуся прикладному материалу, част
ностя м , накопленны м фактам, рецептам, но и к более стабиль
ным фундаментальны м знаниям. Студент должен вынести из
учебника понимание незавер ш енности дисциплины как в науч
ном, так и в методическом аспекте.
В этом плане, как ни парадоксально, одна из главных задач
курса (а значит, и учебника по курсу) состоит в том, чтобы при
изучении материала студент чего-то не понял (или не до конца
понял ). Осознанное непонимание рождает вопросы - это первый
шаг к уиубленному пониманию

.

23

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

И если работать над курсом ПАХТ в таком ключе, если постичь связи
между разделами дисциплины (и внутри разделов), а также с другими науками, то пытливый студент может вынести из учебника больше, чем
заложено в него авторами.
Авторами конкретных глав (их номера указаны в скобках) являются:
– проф. В.Г. Айнштейн: Основные понятия и соотношения (1), Гидравлика (2), Сжатие газов (4), Гидромеханические процессы (5), Основы теплопереноса (6), Адсорбция (14), Сушка (15), Измельчение твердых материалов (22), а также (с участием доц. В.В. Захаренко) – Структура потоков
(8);
– проф. В.Г. Айнштейн и доц. В.В. Захаренко: Теплопередача и теплообмен (7), Основы массопереноса (10);
– проф. В.Г. Айнштейн, проф. М.К. Захаров, проф. А.Е. Костанян: Дистилляция и ректификация (12);
– проф. В.Г. Айнштейн и доц. Т.В. Зиновкина: Классификация твердых
материалов (23);
– проф. М.К. Захаров: Перемещение жидкостей (3), Выпаривание (9), Абсорбция (11);
– доц. Т.В. Зиновкина: Умеренное и глубокое охлаждение (21);
– проф. А.Е. Костанян: Жидкостная экстракция (13);
– проф. Г.А. Носов: Кристаллизация (16), Растворение и выщелачивание (17), Сублимация и десублимация (18), Сопряженные и совмещенные
процессы (24);
– доц. А.Л. Таран: Гранулирование (19), Мембранные процессы разделения (20).
Авторы благодарны рецензентам – заведующему кафедрой “Процессы
и аппараты химической технологии и безопасности жизнедеятельности”
Московской государственной текстильной академии доктору технических
наук профессору Б.С. Сажину и кафедре “Процессы и аппараты химической технологии” РХТУ им. Д.И. Менделеева (заведующий кафедрой – доктор технических наук профессор А.А. Титов), а также эксперту – заведующему лабораторией Теоретических основ химической технологии ИОНХ
им. Н.С. Курнакова РАН доктору технических наук профессору Н.Н. Кулову
– за внимание к рукописи учебника, доброжелательную критику и ценные
замечания.
Все вопросы читателей, замечания и предложения – как общего характера, так и по конкретным разделам и главам – авторы воспримут с благодарностью.
24

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

И в заключение – особенности подхода авторов учебника, выраженные
титульным редактором книги В.Г. Айнштейном в предельно компактной
форме:
Эти строки оды хвалебной
Посвящаю группе фанатов,
Написавших смелый учебник
По процессам и аппаратам.
Он останется ярким следом
В смутных дебрях сложной науки.
Вклад его нам еще неведом –
Оценить его смогут внуки.
В нем – явления переноса,
Но готовых рецептов нету;
В нем важнее ответов – метод,
А еще важнее – вопросы.
Мы процессы свели в модели,
Их исток – в бесконечно малом.
Чтоб пробиться к расчетным целям,
Подружились мы с интегралом.
За стеною из заблуждений –
Безобразно серой, безликой,
Мы увидели суть явлений,
Протыкая привычность мнений
Пропускных способностей пикой.
Проработать учебник – значит:
Видеть смысл Приходов и Стоков,
Распознать подмену задачи,
Взвесить вклад структуры потоков,
Общность в разных найти явленьях,
Вникнуть в свежих идей побеги,
Вскрыть потоковых стадий значенье –
Их порой не приемлют коллеги.
Что ж, нам тоже было непросто
Мир порадовать новым словом.
Но без трудностей – нету роста,
Не окажется слово новым.
В гневе тот – наши книги топчет,
Этот – славит их гимном звучным.
Но учебник наш, знаю точно,
Никому не кажется скучным.
Мы благое сделали дело –
Каждый автор может быть гордым.
Я хочу, чтоб оно звенело
Не последним для нас аккордом.

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ОСН ОВН Ы Е УСЛ ОВН Ы Е ОБО ЗНАЧ Е Н И Я
Настоятельно рекомендуем студентам (вообще - читателям учебни
ка) оmестись к этому разделу с большим вниманием: ознакомление с
ним поможет лучшему усвоению изложенного в учебнике материала.
Выбор символики (условных обозначений) в учебнике основан на
следующих положениях и подходах:
- число используемых в учебн ике понятий больше количества
имеющихся символов ; при совпадающей символике смысл разных
величин различается с помощью индексов;
- потоки , силы, геометрические размеры и прочие величины обо
значаются латинскими символами (исключения - единичны) ; при
выборе символов исходили из латинского, английского или немецкого
корня соответствующего понятия либо из установившихся традиций ;
- расходы , потоки (теплоты , вещества) и другие величи н ы , обозна
ченные латинскими символами, изображены курс и в н ы м шрифтом ,
количества (в редких случаях - другие характеристики) - прямы м ;
- индексы при величинах обозначены чаще всего русскими буква
ми ; они обычно соответствуют начальным буквам поясняющего поня
тия .
В не которых случаях возможны вынужденные отступления от сфор
мулированных выше подходов.
Для облегчения работы с материалом учебника (иногда - и для
уточнения) смысл обозначений , содержащихся в приводимом ниже
перечне (и, естественно, дополнительно вводимых) , поясняется также в
каждой главе.
С целью сокращения записей и акцентирования внимания читателя
в ряде глав прописными буквами выделены ключевые слова, их смысл
специально пояснен в тексте.
В заголовках разделов и подразделов учебника выдержана иерархия
шрифтов. В тексте учебника тоже используются различные шрифrовые
аwделения, что способствует смысловой рубрикации материала и рас
становке акцентов.
Ниже последовательно приведены (где возможно - в алфавитном
порядке) основные условные обозначения , используемые в учебнике:
понятийная символика, аббревиатура ключ е вых слов (тех, что приме
няются в учебнике широко) и другие сокращения , некоторые матема
тические символы, виды шрифтовых выделений в тексте.

26

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

с и м в о л ы
а

Ь
С
с

D

DиD
d
Е
F

f

GиG

g

Н
h
/

-

-

-

-

-

-

i
k

L

L
LиL

-

М
М иМ
т

-

-

тем пературопроводность;
удел ьная поверхность; кон
цеп ция (преимущественно
массовая )
линейный размер, ш ирина
константа излучения; концентрация ком понента (вещества)
в потоке, в одной из фаз
абсолютная скорость; теплоем кость
диаметр; коэффициент диффузии
количество и поток пара
диаметр
плотность луч истого потока;
эффекти вность; коэффициент
эффективной диффузии ( про
дольного перемешивания)
сила; поверх ность теплооб
мена или контакта фаз
площадь попереч ного сечения; частота
м ассовые количество и рас
ход вещества, твердой фазы
ускорение свободного падения
высота
высота; энтальпия (удел ьная)
условное
теплосодержание
воздуха; момент инерции
энтальпия (удельная)
коэффициенты теплопередачи
или массопередачи ; показа
тель адиабаты ; константа ско
рости химической реакции
расход воздуха ( в расчете на
абсолютно сухой); удельный
(на 1 к г топлива) расход воз
духа; удельная работа
работа
количество и расход жидко
сти
линей н ы й размер, дл ина;
удел ь н ы й (на 1 к г удаляемой
влаги) расход воздуха
молярная м асса
межфазные кол ичество и по
ток передан ного вещества
м асса; показатель политроп ы ; ко:�ффи циент распределени я

N

-

п

р

р

-

Qи Q q
R
-

r

s
SиS
т.
и

s

1

-

V
V
v
W и W -

и. v

-

Х
w

-

-

х

У

у

х.
а

р

Г

у,

z

-

мощность; ч исло я чеек пол
ного перемешивания; число
ступеней
число оборотов; кратность
циркуляци и ; число ступеней
сила
давление, п арциальное дав
ление
количество и поток теплоты
удельные потоки - теплоты
( напряжение теплового потока) или вещества (массы,
компонента)
радиус; газовая постоя нная
(индивидуальная,
универ
сальная)
радиус, радиальная коорди
ната; теплота парообразова
ния ( конденсации)
поперечное сечение
количество и поток раствора
энтропия (удельная)
тем пература
влажность
относител ьная
твердого материала
скорость
объем
объемный расход
удел ьный объем
межфазные количество и поток удаленной влаги
скорость
относительная концентрация
вещества в фазе х; степень
сухости влажного пара
воздуха;
влагосодержание
мольная (или какая-либо иная)
концентрация вещества в фазе
х; степень ожижения воздуха
относительная концентрация
в фазе у
какая -л ибо
(или
мольная
иная) концентрация вещества
в фазе у
координаты
коэффициент теплоотдачи; относительная летучесть; угол
коэффициент объемного расширения; коэффициент маесоотдачи
плотность орошения
27

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

у
л

-

линейный размер,
стенки или пленки

'1

А.

толщина

порозность; степень черноты;
холодильный коэффициент

Е

к

движущая сила процесса (Лt,

ЛС, ЛХ, ... )

8

е

угол

коэффициент

пластической
вязкости (пластичности) ; коэффициент полезного действия, эффективность

температура,
-

безразмерная температура; безразмерное время
коэффициент расхода

коэффициент гидравлического сопротивления ; теплопроводность; теплота плавления
(затвердевания )

µ

�

v

п

7t

р

(1
t

<р
ro

-

-

динамическая

вязкость; номинальная (расходная) концентрация твердой фазы
кинематическая вязкость
коэффициент

местного

со-

противления
-

периметр
осмотическое давление
плотность; абсолютная маесовая концентрация

-

-

поверхностное натяжение
время; напряжение трения
плотность
распределения;
относительная
влажность;
доля; угол
угловая скорость; абсолютная влажность твердого матер и ала

И Н Д Е КС Ы
Верхние
кр
р

-

критический

л

ламинарный

т

турбулентный

-

конец, на выходе
•

равновесное значение

-

знак безразмерной величины
средний,

усредненный

(над

символом)

начало, на входе
Нижние

а
вл
вх

-

-

о

аппарат

-

начальный, исходный; нуле-

-

пар
плавление

влажный

вой

на входе
на выходе

п
пл

газ, газообразный

пп

продольное перемешивание

гр

граничный; греющий

р

реальный

д

диффузионный,

с

сплошная среда; сухой; стес-

вых
г

-

дисперсная

фаза
е

-

ненный
свободный

эквивалентный

св

ж

жидкость, жидкий

и

истинный

см
ер

ид

идеальны й

ст

стенка

инерт, инертный

т

твердый; тяжелый; трения

конечный

у

условный

кипение
конденсация

уд
ч

легкий, локальный

э

ин

к
кип
конд
л
м
н

28

-

местный; материал
началы�ый

F
v

-

-

смеси
средний

удельный
частица
эффективный
поверхностный
объемн ы й

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

А Б Б Р Е В И АТУРА КЛ Ю Ч Е В Ы Х СЛОВ И ТИ П О В Ы Е СОКРАЩЕ Н ИЯ
ГУ

ив
ип

-

гра11 и ч ное у сл о 11 и е

-

идеал ь н о е в ы тес н с 1 1 11 ::

-

КПД
нс
НУ

ОБС

ПАХТ -

п р о це с с ы и а п п араты х и м и 
ч е с к о й технологии

коэ фф и ц и е н т п о л е з н о г о де й -

Ис

-

тверды й м атериа.11

СТВ11Я

ПС
ТМ

непо дв и ж н ы й слой

Нак

-

н а коп ле н 11 е

идеал ьное п е ре м е ш и в а н и е

-

н а ч ал ь ное у с л о в и е

-

основное

балансовое

соот-

ношение

псе вдоо жиже н н ы й слой

-

источ н и к

llp

-

п р и ход

Рез

резул ьтат

Ст

-

Ух

-

у х од

сток

О БО Б ЩЕ Н Н Ы Е П Е Р Е М Е Н Н Ы Е
к р и т е р и и п од о б и я и д р у г и е к о м п л е к с ы

Аг =

gd

v2

a, Sx =

_

3

Рт р

-

kx F

L

aR
Bi = � .
Ат

ь , sУ

с' =
Eu

-

-

-

Ат

k F

D

= -у-

L
--

с=

р

mD ,
mD
-L

= Лр
pw

2

D т Dт
.
F1 =
· R1
_

7

ат �

- 12

Fo =
Fr -

=

д!_2
w

•

R2

-

критери й
А р х и м еда

3

d
Gr = g
P Лt
;
ad
= а/ '

ЧИСЛО

единиц переноса

Nu

кр итер и й
Био

Ре д

число единиu переноса

Ре т

фактор ы
м ассопереноса

Ре з

А

А

wl
=-

D

wl
=-

а

wl
=Е

-

критери й
Грасгофа

-

ч исло Нуссельта

-

кр итери й
Пекле диффузи о н н ы й

-

критерий
Пекле теnловой

-·

кр итери й
Пекле для
п родольного
перем ешиван ия (эффекти в н ы й )

ч исло Эйлера
критер и й
Ф и ка

а

Pr = �
wl p

-

кр итери й
Фурье

Re

=

-

критери й
Фруда

Sc

=�

µ

D

,

wdp
µ

,

wd
v

критери й
Прандтля
-

критери й
Рейнольдса

-

критерий
Ш м идта
29

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

S h = 13 1
D

'

St = �

Pd

-

D

St д

кр 1пер11й
Шерпу да

-

CP\V

Ч И СЛО

Стан-

то11а тепло-

=!

We =

-

w

pw2 d

--

вое

(J

ч исло Стантона диффузио н ное
критерий
Вебера

МЛ ТЕМАТИ Ч ЕСКАЯ И ЗНАКОВАЯ С И МВОЛИКА

const

-

idem
lim
m ax
min
opt

l l OCTO Я l l l Н I Я n e J l ll Ч lt l l a

-

экспо1 1е1rrа: ехр у оз11ачает е1

-

r 1 редел

-

макс и м у м

-

м и 11имум

-

о пт и м у м

-

ехр

од и 1 1ако о ы й (-ая, -ое, -ые)

v

z

п

I:

-

1 1

л

-

разность, п р и раще н и е

произведен ие
сумма
абсолютная вел и ч и н а

0- е

о перация сопоставлен и я

=

з н ак тождества; обозначе11ие
пропорционалыюсть

"

прибл иженное равенство

перем е 1 1 1 1 ая вел и ч и 11 а

var

лапласиа11

ШРИФТО В Ы Е ВЫДЕЛЕНИЯ
В т е к с т е

1 . Полуж и р 11 ы й п р я м о й - ру бр11кацио1шые в ьщелен и я ( в начале строки), н овые,
п р и н ц и п и ал ы 1 ы е для дан11ого текста по11ятия, терм и н ы ; для некоторых обоб
щающих 1ю1 1ят11 й 11спол ьзуется полу ж и р н ы й ку рсив.

2.

С ветл ы й 11ря м о й в разрядку - рубри кацион 1 1 ы е в ыделе 1 1 и я ( в 11ач але стро к и ;

подч и 11е11ы 11олуж11 р 1 ю м у п р я м о м у ) .

3. С оетл ы й курс и в - с м ысловые акцент ы ; определения, форму лировки законов
правил.

4 . П р опи сные бу к в ы - аббревиатура ключевых слов и н аи более распростра11ен
ных понятий.

5.

С 11роп11сной бу квы - составля ющие балансо вых соотношений ( в обобщен н ом

виде, безот1юсителыю к перенос и м о й субстан ц и и ) .

6.

Мел к и й ш рифт - констру к ц и и аппарато в; фрагменты, и ногда - элементы текста

(у rлублсш1е а1 1ализа), без проработки которы х 11е нару ш аются связность изложе1 1 11 я и 1 ю 1 1 и м а1 1 11е rюследу юще1·0 материала, а также подп и с и к рису н кам и с1юски .

Н а р и с у н к а х

/, //,

(/), (/),

30

-

...
...

поток и веществ, рабочих тел (си м волы е11абже н ы 11 а рисунках

стрел кам и )
- т е же вещества, рабочие тела, за1 1 и м ающие пространства (области,
зо1 1 ы а1111арата)

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Глава 1

ОСНОВНЫЕ ПОНЯТИЯ И СООТНОШЕНИЯ

" Процессы и аппараты химической технологии " (ПАХТ) наука о принципах организации и расчета химико
технологических процессов и принципах (не деталях) конструи
рования технологической аппаратуры. ПАХТ - один из разде
лов более широкой области знаний - теоретических основ хи
мической технологии. (ТОХТ) ; но они выходят за пределы
ТОХТ, включая некоторые прикладные аспекты.
1 . 1 . ВВЕДЕНИЕ
1 . 1 . 1 . Предмет и место курса

Номенклатура веществ (продуктов) , получаемых химической
и смежными отраслями промышленности, исчисляется ныне
десятками тысяч наименований. Разумеется, ни одной науке в
рамках химической технологии не под силу изучить даже не
большую часть процессов получения этих соединений. Поэтому
каждая наука классифицирует упомянуrые соединения и про
цессы по каким-то сушественным признакам, например: по
типу веществ (органические, неорганические, полимерные;
иногда с более дробной рубрикацией); по фазовому состоянию
(гетерогенные процессы или гомогенные; в жидкой, газовой или
твердой фазе); по условиям проведения процесса (высоко- и
низкотемпературные, под высоким или низким давлением и
т. д.). ПАХТ классифицируют процессы по элементарным техно
лоПtЧеским приемам (например, фильтрование, экстракция, суш
ка, гранулирование) ; таких приемов - около двух десятков. При
этом рассмотрение технологических приемов в рамках ПАХТ
ведется в общем
безотносительно к участвующим в процессе
веществам, численным значениям их конкретных свойств и па
раметров процесса. Эта конкретика проявляется уже в ходе
применения методов ПАХТ к инженерному расчету того или
иного технологического процесса и реальному его воплоще
нию - при совместных действиях специалистов в области
ПАХТ и технологии производства интересующего нас продукта.
-

31

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

И м енно в см ысле использования того или иного технологиче
ского прие м а трактуется в курсе ПАХТ сам терм ин процесс .
Р азличие отдельных хи мико-технологических процессов с точки
зрения ПАХТ состоит в выборе (использовании) тех или иных
прие мов, в их числе и последовательности . Замети м , что м ногие
из расс матривае мых в курсе ПАХТ прие мов находят широкое
при м енение также в пищевой, фармацевтической , м еталлурги
ческой и других областях про м ы шленности.
Основная цель науки о ПАХТ состоит в ан ал изе эле м ентар
ных технологических прие мов и функционирования типичных
аппаратов - в отдельности и в различных сочетаниях. В ка
честве главных вьщели м здесь две задачи:
а) изучение законо мерностей и мате матическое о п исание
технологических прие м ов и их совокупностей, разработка рас
четных методов перехода от процесса в лабораторной установке
к крупны м про м ы шл енны м аппаратам (часто говорят: " от стекла
к металлу" ) ;
б) усовершенствование существующих и разработка новых
технологических прие мов, создание методи ки их расчета.
Ан ал из явлений и процессов предполагает установление свя
зей (качественных и количественных - их не надо противопо
ставлять) между объектам и , потокам и рабочих тел, их свойства
м и , парам етрам и. При это м ка чественные связи направлены
прежде всего на установление характера влияния тех или иных
парам етров на ход технологического процесса, количествен
н ые - на доведение анализа "до числа" , т. е. на расчет требуе
м ых характеристик процесса. В конечно м итоге реализация ка
чественных и количественных связей в аспекте ПАХТ должна
привести к созданию и нженерной методики расчета технологи
ческого аппарата и проводи мого в не м процесса.
Специально подчеркне м , что стадия доведения конкретного
процесса до промы шл енных масштабов зачастую зани м ает су
щественно больше вре мени, нежел и его л абораторная проработ
ка. Оказывается, мало создать химико-технологический процесс
в пробирке или лабораторной трубке, мало изучить его м еха
низ м и кинетику, отработать оптим ал ьные условия его осущест
вления; надо еще обеспечить такие условия в пром ы шл енно м
агрегате, чтобы механизм и кинетика были достаточно хорошо
воспроизведены. Эти м и зани м ается наука ПАХТ - ан ал изо м и
расчетом гидродинам ической, тепловой , диффузион ной обста
новки, наЙденной в лабораторных условиях и необходи м ой для
успешного проведения про мы шл е н ного процесса.
Проимюстрируем роль ПАХТ ярким примером из истории отечественной
химической промышленности. В начале 30-х годов американцы продали нашей
стране и смонтировали в Бобриках (ныне Новомосковск) колонны синтеза

32

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

аммиака по новейшей (тогда) технологии ; однако в обусловленные сроки за
пустить их с гарантированной производительностью они не сумели. Выяснить
причину было поручено молодому профессору И.И.Гельперину. Он вскрыл
колонны, проанализировал работу их теплообменных зон и выявил недопусти 
мые температурные перекосы. На основе его расчетов была изменена кон
струкция теплообменного устройства в колоннах, и они бьии запУШены (на
том же катализаторе, с тем же синтез-газом, при тех же параметрах работы) с
производительностью, заметно выше проектной. (Между прочим, американцы
купили у нас лицензию - за немалые деньги - на свою колонну, но с нашей
теплообменной начинкой!) Таким образом, в ОСУШествлении каталитического
процесса решающей явилась тепловая обстановка, обеспеченная грамотным
анализом и созданной на его основе рациональной конструкцией теплообмен
ной зоны реактора.

Приведенный при мер не дол жен создавать впечатл ения , что
наука ПАХТ сегодня способна давать однозначные и исчерпы
вающие ответы на все технологические вопросы. До сих пор в
хи м ической технол огии до трети капитальных затрат уходит на
переделки и модернизацию оборудования - в значител ьной
степени пото му, что его не сумел и достаточно хорошо рассчи
тать и сконструировать сразу. Это обусл овлено, во-первых,
сложностью самих технологических процессов, недостаточной
изученностью м еханиз мо в их протекания ; отсюда приближен
ность анализа и расчета, введение "коэффициентов незнания "
(обоснованных и не очень) - разл ичного рода коэффициентов
полезного действия (КПД) , степени прибл ижения к опти мал ь
ному процессу и т.п. Это обусл овл ено, во-вторых, прин ципи
альной вариативностью разумных технол огических решений, да
и не всегда заранее можно сказать, какое решение лучше в дан
ной конкретной ситуации. Повышение эффективности хи м ико
технол огических процессов возможно путе м кол ичественных и
качественных изменений. При количественных из менениях
(вел ичин и соотношений потоков, технол огической аппаратуры
и т.п.) за повышение эффективности, как правило, приходится
" пл атить" усл ожнением и удорожание м (процесса, аппаратов,
систем управления) . Повышения эффективности при одновре
менно м упрощении и удешевл ении технол огического процесса
удается добиться при качественных из менениях посл еднего:
принципиал ьно новых подходах к его осуществлению, возм ож
но - на основе новых технологических прием ов.

ПАХТ являются в значительной мере "синтетической " наукой; здесь широко
используются инструментарий Математики и знания из ряда областей Физики,
Прикладной механики, Технической термодинамики, Физической химии
(прежде всего термодинамики и кинетики) и других дисциплин. Так, некото
рые задачи ПАХТ прямо решаются с испол ьзованием понятийного аппарата
Прикладной механики (например, задача о гидравлическом ударе) , Электротех
ники (расчет электрофильтров), Физичес кой химии (задачи макрокинетики) и
т. п.

33

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

В свою очередь курс ПАХТ слу ж ит базой для ряда других наук, использую
щих его методы и результаты при решени и своих научных и и нженерных задач .
В то же время ПАХТ нередко вторгаются в область некоторых друг их наук, в
чем-то пересекаJ1сь с ними, исследуя проблемы, предстамяющие совместный
и нтерес.
Материалы учебного курса ПАХТ прл мо используются при изучении дис
циплины "Реакторные устройства и модел и рование" - эта дисциплина в науч 
ном плане вообще состамяет единое целое с ПАХТ. Некоторые идеи и методы
ПАХТ применяются и получают дальнейшее развитие:
- при изучении закономерностей поведения достаточно сложных химико
технолоrических систем (ХТС) в курсах "Общая химическая технология ",
"Системные характеристики ХТС" и т. п . ;
- при изучении проблем управления эти ми системами в курсе
"Автоматические системы уп равления хи м и ко-техн ологическими процессам и"
(контроль и регулирование процесса, поддержание стабильного технологиче
ского режима) и в курсе "Химическая кибернетика", призванном обеспечить
уп равление процессами в глобальном смысле - на уровне анализа-синтеза
ХТС.
Положения и методы науки ПАХТ испол ьзуются та кже в курсах конкрет
ных техн ологий и оборудования заводов, и зучающих специальные технологиче
ские схемы и аппаратуру для производства определенной химической продук
ции .

Научная дисципл ина ПАХТ непрерывно развивается , углуб
ляя и расширяя исследования и сферы своих интересов. Учеб
ная дисципл ина ПАХТ наряду с не к оторыми другими завершает
общеинженерное образование; далее инженерное образование
продолжается в рам к ах отдельных технологий .
Жи знь постоянно предъявляет все более высо ки е требования
к качеству химичес к ой продукци и , а оно сегодня в значитель
ной мере зависит от совершенства используемых технол огиче
ских методов. Стремление к повышению к ачества продукц ии
привело к технологичес к ой револ юции , и , вероятно, этот уже
наступ ивший этап развития технологии будет достаточно про
должи тельным; по к райней мере, возможности совершенствова
ния технологии еще далеко не ис ч ерпаны. Значительное место в
развитии технологических методов прин адл ежит науке о ПАХТ:
тут и проникновение в механиз м процессов, и углубление и
расширение знани й об их оптимальном проведении ( маршруты
процессов, предпочтительные усл овия, режимы, технологиче
ские запреты, рациональные констру к ции) , и разработка новых
эффе ктивных приемов. Успех здесь - в сочетании фундамен
тальных построений наук и о П АХТ и специфи к и к он к ретных
технологий. И как бы ни шло развитие химичес к ой технологии,
к а к бы ни изменялись ее потребности и направленность, ПАХТ
всегда будут занимать серьезное место в подготовке инженера
химика-технолога. При этом фу ндамент науки П АХТ будет
оставаться относительно стабильн ы м (постепенно расширяясь и
углубл яясь) , а вот ориентиров к а и к он к ретное наполнение учеб 34

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ных курсов могут, конечно, нескол ько смещаться в соответствии
с потребностя м и отдельных наук и технологий.
Курс ПАХТ призван дать студенту химико-технологического
вуза достаточно широкие сведения, позволяющие е му в даль
нейшем самостоятельно ориентироваться в конкретных техноло
гических процессах - в их анализе, мате м атическо м описании и
инженерном расчете, в подходах к конструированию аппаратуры.
1 . 1 .2. Краткие исторические сведения

Почти каждая наука, в особенности связанная с последую
щим
практическим
использованием
ее
теоретических
изысканий, проходит "собирательную" стадию, когда она опери
рует разрозненными объектами и фактами . По-настояще му нау
кой она становится на стадии обобщений, когда появляется
возможность интерпретировать эти факты с общих позиций,
обосновывать некие общие законо мерности, п рогнозировать
ситуацию. Так, общая химия стала наукой с появлением Перио
дического закона.
Вплоть до конца XIX века технол оги в построении промыш
ленных процессов ориентировались на знание отдельных фактов
и правил - ПАХТ находились на описательном (собира
тельно м ) этапе, преобладающую роль играло инженерное искус
ство. Успех в производстве того или иного конкретного продук
та определяли всесторонние знания деталей данного производ
ства ( п о существу - эвристические правила) - общие законо
мерности и связи в раз.личных химико-технологических процес
сах не прослеживались. В месте с тем передовые деятели науки и
промышленности в России и за рубежом уже в конце XIX начале ХХ века ясно видели необходимость таких обобщений
(формирования технологических принципов) , установления
достаточно общих законо мерностей явлений и процессов. Одна
ко попытки такого подхода к описанию п роцессов с единых
научных позиций до начала 20-х годов ХХ века нельзя считать
успешными. Видимо, неудачи были предопределены неразрабо
танностью необходи мого понятийного аппарата и подспудным
стремлением (в соответствии с тогдашними традициями) уде
лять большое вни мание частностям , рецепта м (в то м числе для конкретных производств) . В результате не оставалось (или
почти не оставалось) места для общего анализа. Только по от
дельным технологическим приемам удавалось выйти на уровень
обобщений, отвечающий (не по содержанию, конечно, а по
направленности подхода) современным представлениям (при
меро м может служить брошюра И .А.Тищенко "Теория расчета
многокорпусных выпарных аппаратов " , изд. М ВТУ, 1 9 1 1 г. ).
35

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Вряд ли можно назвать дату создания науки и курса ПАХТ в
современном их понимании, становление происходило посте
пенно. В начале 20-х годов появились одна за другой две книги
Л .Ф.Фокина "Методы и орудия химической техники" ( Госиздат,
М . - П . , 1 923 и 1 925 гг.) , где в отдельные главы были вьщелены
некоторые технологические приемы в их современной класси
фикации , например: компрессоры, разделение газов, центрифу
гирование, фильтрация, выпаривание, дистилля ц ия и ректифи
кация и др. Однако все же это бьш преимущественно подход на
описат ельном уровне, а расчетные формулы приводились без их
вывода и анализа.
Структурно и методически ближе к современным курсам
ПАХТ стоит книга американских ученых W. H.Walker,
W. К. Lewis, W. H .McAdams "Principles of Chemical Engineering"
( McGraw Hill Со. ; N.Y.
London, 1 923 г. ) . Она содержит обыч
ные для теперешних курсов главы: гидравлика, теплообмен ,
фильтрация, выпаривание, сушка, ректификация и др. ; этим
главам предпосланы методические и физико-химические осно
вы (промышленная стехиометрия, включающая балансовые со
отношения ; пограничные пленки ; основы испарения и сушки и
т. п . ) . Правда, авторам не удалось полностью отойти от рас
смотрения конкретных производств, составляющих предмет
теплотехники и еще более - общей химической технологии
(главы: топливо и энергия, сгорание, печи для обжига и сушки,
газогенераторы) .
Важным этапом становления науки о ПАХТ стала книга
W. L. Badger, W.L. McCabe "Elements of Chemical Engineering"
( McGraw Hill Со . ; N .Y.-London, 1 93 1 г. ) , оперативно переведен
ная на немецкий ( 1 932 г.) и русский ( 1 933 г.) языки . Здесь рас
ширен круг рассматриваемых проблем (например, добавлены
процессы выщелачивания, кристаллизации и др. ) и , по
видимому, впервые введен термин " главные операции" - сино
ним применяемого ныне "технологические приемы" .
Однако и в двух последних книгах обстоятельный анализ ря
да процессов чередуется с рецептурными рекомендациями рас
чета по готовым формулам и с описательным материалом.
Можно также констатировать (не в упрек авторам, конечно),
что с современных позиций в этих монографиях еще не про
изошло дифференциации дисциплин "Процессы и аппараты
химической технологии" и "Машины и аппараты химических
производств".
В последующие десятилетия наука и учебный курс ПАХТ
претерпевают существенные количественные и качественные
изменения. В курс вливаются новые элементарные технологиче -

36

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ские приемы, обогащающие химическую технологию; с другой
стороны, отдельные раздел ы курса выделяются в самостоятель
ные научные и учебные дисциплины. Появляются общие учеб
ники по ПАХТ и учебники (моногр афии) по отдел ьным техно
логическим приемам и группам п р иемов. Постепенно усилиями
отечественных и зарубежных учен ых наука и учебные курсы
ПАХТ приобретают современ ные очертания - как по структуре,
так и по содержанию. В нашей стране развити е этой науки свя
зано с именами И . И . Гельпер и на, А . Г. Касаткина, А. Н . Плановс
кого и ряда других ученых и педагогов.
Первонач ал ьно отдельные технологические приемы ан ал изи
ровались исследователями, группами исследователей со специ
фи ческих (" удобн ых" ) позици й - вне связи с другими приема
ми, так что вопрос об общности механизма протекания и зако
номерностей при емов просто не возн икал . В ходе развития нау
ки о ПАХТ происходит постепенная " притирка" различных тех
нологических приемов, их математических описаний. В резуль
тате укрепляются связи между технологическими приемами,
выявляются возможности общего подхода к их рассмотрению,
хотя и в настоящее время в оп исании некоторых технологиче
ских приемов достаточно большое место зан и мают, к сожале
нию, обособленные подходы. Тем не менее основная тенденция
развития ПАХТ бесспорна: повышение общности подходов к
анализу и оп исанию различных технологических приемов, к
объединению их в более крупные группы приемов и к поиску
базы для дальней ших обобщений .
Н а современной стадии развития науки и учебной дисциплины ПАХТ сно
но на совершенно ином, более
ва возрастает значимость описательного,
высоком уровне. Речь идет о выявлении связей и обосновании математического
анализа - от построения моделей до осмысления результатов.Так реализуется
диалектическая спираль познания : описательное - теоретический анализ описательное.

Другая тенденция развития теории ПАХТ состоит в увеличе
нии крена в сторону изучения (анализа, математического опи
сания) собственно процесса, происходящего в том или ином
аппарате. Детал ьное рассмотрение конструкции самого аппарата
на стадию практического
выносится за пределы курса ПАХТ
внедрения, отчасти отдается смежной дис ци плине "Маш ины и
аппараты хи мических производств" .
Содержан ие отдельных глав, подходы к анализу и сам пере
чень тем, рассматриваемых в различных курсах и учебниках по
ПАХТ, не совпадают, они подвижны . Нередко из рассмотрения
исключают, например, некото р ые механические процессы
( измельч ение, классификация), иногда - холодильны е. Почти
всегда из курса ПАХТ в отдельную дисциплину вьщеляют реак-

37

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

торные устройства и их моделирование. Круг вопросов, вклю
ченных в настоящи й учебник, соответствует традициям Москов
ской государственной академии тонкой химической технологии ;
о н ясен из "Содержания" .
1 . 1 .3. Перенос субстанции в химической технологии

Химическая технология имеет дело с крайне широким разно
образием аппаратов. Среди них, разумеется, реакторы , в кото
р ых происходят химические превращения и получаются целевые
продукты. Однако перечень химико-технологической аппарату
ры далеко не исчерпывается химическими реакторами по ряду
причин. Во-первых, реагенты надо подготовить к проведению
процесса в реакторе: подать их туда при определенных давлении
и температуре, в определенном (часто - отличающемся от ис
ходного) агрегатном состоянии, с заданным соотношением ком 
понентов и т.д. Во-вторых, в ходе химической реакции из-за
нестрогой селективности (наряду с основными протекают и по
бочные реакции) и неполноты превращения почти всегда полу
чаются смеси различных продуктов реакции и исходных реаген
тов, так что целевые продукты надо отделить от побочных (с
целью их особого использования) и непрореагировавших ком
понентов (чтобы вернуть их в реактор) . В-третьих, химическая
технология использует ряд операций , вообще не включающих
собственно химические превращения. Наконец, в-четвертых,
сами м химически м превращениям сопутствуют физические
(физико-химические) явления, прямо не относящиеся к хими
существенное (иногда ческой реакции, но оказывающие
определяющее) влияние на результат химико-технологического
процесса.
Таким образом , наряду с химическими превращениями хи
мическая технология использует многочисленные явления и
процессы нехимического характера, требующие определенных
способов организации и осуществляемые в соответствующих
аппаратах и процессуально-технологических схемах. Протекание
таких процессов (собственно химических - тоже, конечно) в
той или иной мере связано с пер еносом какой-либо субстан
ции
количества движения (импульса) , теплоты , вещества
(массы) , иногда нескольких субстанций одновременно. Этот
перенос характеризуется (вызывается или сопровождается) из
менением технологической ситуации (параметров процесса), в
общем случае - во времени в рассматриваемой точке аппарата,
а в самом аппарате - от одной точки к другой, в более простых
случаях - только во времени или только от точки к точке .
-

38

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Изучение переноса импульса связано с анализом сил
(внешн их, вн уrренних), действующих на объект, рабочее тело;
переноса теПJJоты - с перемещением и подводом (отводом) теп
ловой энергии (иногда с изменением агрегатного состояния, с
тепловыделением) ; переноса вещества - с его перемещением в
пределах какой-нибудь одной фазы и (или) между различными
фазами. Все эти явления переноса могут быть использованы
направленно - для осуществления про цесса (скажем, тепло
ты - для нагрева объекта), а могут и сопровождать какой-либо,
в том числе химический, про цесс (скажем, отвод теплоты реак
ции или вывод одного из продуктов реакции).
Отдельные явлен ия переноса затрагивались (в определенных
аспектах) в ряде предшествующих дисципл и н - в физике, тех
нической механике, физической химии и др. ; ины е будут затро
нуты в последующи х дис циплинах. Курс ПАХТ анализирует эти
явления в плане построен ия и описания отдельных приемов
(про цессов) или их совокупностей; при этом в ряде случаев ис
следуется перенос сразу нескольких субстанций .
В зависимости от преобладания переноса той или иной суб
станции в курсе ПАХТ вьщеляют и изучают следующие группы
процесс08:
- nщромеханические, где основные явления связаны с пере

носом импульса (количества движения) в жидкостных и газовых
потоках, реже - в системах с твердыми телами. К этой группе
примыкают механические про цессы, базирующиеся в основном
на законах механ и ки твердого тела;
- теПJJовые, где наблюдаются явления, связанные с различ
ными формами переноса теплоты в области умеренных, низких
или высоких температур. Пр и этом обычно приходится учиты
вать и закономерности переноса импульса, поскольку он сопут
ствует переносу теплоты;
- массообменные (прежде всего - диффузионные) , куда отно
сят многочисленные про цессы, связанные с переносом вещест
ва. При этом обычно приходится учитывать и закономерности
переноса импульса, а довольно часто - и теплоты;
- химические процессы в научном плане, конечно, тоже от
носятся к дис циплине ПАХТ. В учебном аспекте в нашей стране
их принято вьщелять в самостоятельные курсы, прежде всего в курс " Реакторные устройства и моделирование " , с определен
ных позиций - в " Общую химическую технологию" , в некото
рые разделы "Химической кибернетики " и т. д. Еще раз под
черкнем, что любой химический процесс сопровождается пере
носом импульса, теплоты, вещества; в ряде случаев именно яв
ления переноса, а не собственно химическое превращение,
определяют течение химического процесса и успех в его осу-

39

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ществлении (приведенный в разд. 1 . 1 . 1 пример с синтезом ам
миака - убедительная тому иллюстрация). Это означает, что в
такого рода ситуациях анализ химико-технологического процес
са должен обязательно учитывать закономерности переноса со
ответствующей субстанции.
Приведенная выше классификация П АХТ по переносимой
субстанции не является единственно возможной. Не менее важ
ны и полезны также другие классификационные срезы.
При неизменны.х во времени характеристиках процесса в каж
дой точке технологического аппарата говорят о стационарном
(установившемся) процессе; при этом упомянутые характеристи
ки могут изменяться от одной точки аппарата к друтой . Такая
ситуация характерна для непрерывных процессов. При изменяю
щихся во времени характеристиках в аппарате в целом или в
каких-либо его точках говорят о нестационарном (неустановив
шемся) процессе - такая ситуация характерна для периодических
процессов либо для полунепрерывных (так нередко именуют про
цессы, когда некоторые - прежде всего входные - потоки ра
бочих тел и их параметры поддерживаются постоянными , но
тем не менее характеристики процесса изменяются во времени ) .
Заметим : если в стационарном процессе отслеживать характери
стики какого-либо элемента потока при его перемещении в ап
парате, то они претерпевают из м енения - в пространстве (в
аспекте мгновенного положения этого элемента), во времени (в
аспекте самого элемента) . В этих случаях, не отказываясь от
термина "стационарность" относительно процесса в целом, не
редко вводят еще термин "квазистационарность" - относительно
исследуемого элемента.
Стационарные процессы отли ч аются стабильностью как си
туации в технологическом аппарате , так и характеристик полу
чаемого продукта; они легко контролируются и управляются ;
для них обычно характерна высокая производительность. По
этим причинам чаще всего стремятся к осуществлению техноло
гических процессов в непрерывном режиме. Однако в ряде слу
чаев технологические особенности процесса приводят к необходи
мости его проведения в периодическом режиме. Это нередко ха
рактерно для малотоннажных производств и при использовании
одной и той же аппаратуры для попеременного получения партий
разных продуктов; возможны и иные причины. С некоторыми из
таких процессов нам предстоит встретиться в курсе ПАХТ.
Для организации технологического процесса существенно аг
регатное состояние рабочих тел , отсюда - возможность класси
фикации на основе фазового состояния. В зависимости от коли
чества участвующих в процессе фаз различают rомо- и гетеро
фазные процессы. В зависимости от чиеда компонентов, входя40

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

щих в состав рабочего тела, различают процессы с одно- и мно
гокомпонентными потоками (иногда удобно среди последних
выделить еще и процессы с двух- и трехкомпонентными потока

ми). Процессы переноса приводят к разным результатам в зави
симости от взаимного направления потоков, участвующих в тех
нологической операции, от некоторых внутренних характери
стик каждого из потоков. Все эти классификационные срезы
будут рассмотрены позднее.
С точки зрения постановки организационно-расчетных про
блем различают задачи:
- эксщатационные : здесь речь идет о готовом аппарате с из 
вестными конструкционными характеристиками, направлением
потоков, заданными начальными (входными) потоками и их
параметрами; требуется определить результаты процесса - на
выходе из аппарата или в конечный момент времени. Пример:
надо определить конечные температуры теплоносителей в теп
лообменнике с известной поверхностью F при заданных началь
ных температурах и режимных характеристиках работы;
- проектные: здесь также известны (заданы) начальные
(входные) поток.и и их параметры, но кроме того задаются неко
торые конечные (выходные) параметры целевого потока; тре
буется определить конечные (выходные) параметры остальных
потоков и основные конструктивные характеристики (объемы,
поверхности, форму, габариты и т. п.) проектируемого аппарата,
иногда - разработать процессуально-технологическую схему.
Пример: определение теплообменной поверхности F, необходи
мой для нагрева одного из теплоносителей до заданной темпе
ратуры, если потоки и начальные температуры обоих теплоно
сителей известны.
Как правило, для данного аппарата (технологической схемы)
возможны одна эксплуатационная и несколько проектных по
становок задач расчета.
Следует подчеркнуть известную условность (незавершен
ность, открытость) приведенных классификаций. В зависимости
от постановки проблем (здесь играют роль и соображения
удобства анализа и систематизации) , а также от уровня наших
знаний - эти классификации могут быть изменены, дополнены,
а иногда и изъяты из обращения.
1 . 1 .4. Размерности. Системы единиц .
Единицы измерения

Ч исленные значения величин , входящих в математическое
описание технологического процесса, зависят от единиц измере
ния этих величин. Совокупность согласованных единиц измере41

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ния составляет систему единиц. Разумеется , в расчетах возможно
использование различных систем единиц; важно только выбрать
определенную систему и последовательно ее придерживаться.
Смешение разных систем единиц и использование внесистем
ных единиц - одна из наиболее часто встречающихся причин
ошибок в технологических расчетах.
В качестве предпочтительной в настоящее время принята
Международная система единиц - СИ (System Intemational SI) , базирующаяся на единицах длины / (м - метр),
массы т
(кг - килограмм) и времени t (с - секунды) ; к ним примыкает
единица температуры Т, t (К - градус Кельвина: " Кельвин " ).
Отсюда получаются производные размерности и единицы измере
ния (в принятой системе единиц) , например для скорости w =
= //t (м/с), силы Р = mlf'r 2 (кг·м/с2> = Н - ньютон), давления
р = Р// � (Н/м2 = Па - паскаль) , работы L = р. / ( Нм = Дж джоуль) и др. Для указания на то, что речь идет о размерности ,
обычно используют квадратные скобки; например, [т] = кг.
Размерности и единицы измерения играют важнейшую роль
в расчетах для любой научной дисциплины; курс ПАХТ в этом
отношении - не исключение: инженерно-технологические рас
четы без указания единиц измерения теряют содержательность.
Размерность отражает физический смысл используемой величи
ны, а единицы измерения позволяют оценить и представить ее
порядок (вне единиц измерения такая оценка невозможна) . Со
поставление размерностей величин в ходе теоретического опи
сания процесса может служить способом проверки правиль
ности математических преобразований: если размерности левой
и правой частей равенства и отдельных их слагаемых не совпа
дают, то в анализе есть ошибка (правда, совпадение размерно
стей еще не гарантирует правильности анализа, а говорит лишь
о тщательности преобразований, - ведь ошибка может содер
жаться и в постановке задачи) .
Ранее в курс "Процессов и аппаратов" (и не только химической технологии)
достаточно обширным разделом входила ''Теория размерностей" с отдельным
понятийным аппаратом, теоремами и методами исследования. Эта теория не
редко использовалась для перехода к обобщенным переменным: искомую вели 
чину выражали как функцию (предпочтительно - степенную) набора других
величин, выбираемых исходя из имеющегося научно-производственного опыта
и здравого смысла (т.е. феноменологически); сопоставление размерностей по
зволяло сформировать безразмерные критерии (см . разд. 1 .8), контролирующие
технологический процесс. С течением времени и развитием аналитических
методов область применения этих подходов существенно сузилась, уступив
место иным приемам. Дело в том , что надежда на "здравый смысл" не всегда
оправдывалась - были вскрыты ошибочные решения задач, обусловленные
недостаточностью феноменологических представлений, возможной субъектив
ностью в выборе переменных и т. д. (в истори и науки известна "ошибка Рэлея" ,
упустившего влияние одного и з факторов и получившего деформированные

42

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

критерии подобия) . Однако наметившийся отход от некоторых методов
''Теории размерностей", конечно, не затрагивает сущности понятий "раз
мерность", "единицы измерения" и необходимости грамотного их применения.

Рекомендуется первоначально выразить единицы измерения
всех величин в единой системе единиц (например, в С И ) , только
после этого приступать к расчетам. Попытка вести пересчет
единиц в ходе самого расчета - источник ошибок.

Перевод единиц из одной системы в друI)'Ю ведется на основе известного
соотношения эталонов основных единиц измерения . Пусть, например, в спра
вочнике приведены значения динамической вязкости в сантипуазах: 1 сп =
= 0,01 дн·с/см2 ; надо выразить ее в СИ. Зная , что 1 дн " 1 г· см/с , 1 г = 1 0-з кг,
1 см = 1 0-2 м, запишем:

д
г СМ · С = -2 _
г _ 1 0 -2 1 0- 3 кг =
1 йl = 0,0 1 ....!!.:.!_ = 1 0 -2 ·
10
см · с
см 2
с 2 - см 2
1 0-2 м - 1с
м
м
Н
= 1 0 - 3 � - . � = 1 0- 3 кг - , ..!.___ 1 0 -3
с = 1 0- 3 Па · с.
М ·С м с
2
м
м2
с2
Для установления размерности и единицы измерения какой
=

=

либо величины используются два основных способа:
1 ) на основе физического смысла (определения) самой вели
чины; если, например, скоростью называется путь, пройденный
в единицу времени, то, очевидно, единица измерения скорости
будет м/с; если давление или напряжение трения определяется
как сила, приходящаяся на единицу поверхности, то единица
измерен ия для этих величин выразится как Н/м2, и т. д.;
2) исходя из какого-либо теоретического соотношения, содер
жащего искомую величину, при условии, что единицы измере
ния остальных входящих в это соотношение величин известны.
Пусть, скажем, имеется формула для теплоотдачи Q = a · f'.Лt,
причем поток теплоты Q выражен в Дж/с = Вт, поверхность
теплообмена F - в м2, температурный напор Лt - в К; тогда
единица измерения коэффициента теплоотдачи на основе соот
ветствующей размерности выразится так:

[а] -

(Q]
[ F] · ( Л t)

Дж

С · м2 · К

=

Вт
м2 · К .

Выше указывалось на связь физического смысла величины с ее размерно
стью и единицей измерения. Однако эта связь может оказаться завуалирован
ной при стремлении к сокращению записи единицы измерения . Так, единицу
измерения коэффициента теплопроводности Л. в СИ записывают упрощенно:
Дж/(с·м·К) - здесь физический смысл остается неясным. Это произошло из-за
сокращения (м] ; полная запись имеет вид Дж/( с·м2 · К/м) , и тогда физический
смысл становится ясным; коэффициент теплопроводности есть поток теплоты в
единицу времени между двумя плоскими поверхностями площадью в 1 м2, если
при расстоянии между этими плоскостя ми в 1 м температурный напор равен

43

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

1 К. Пользоваться упрощенной записью размерности и единицы измерения Л,
конечно, можно; надо только понимать, что скрывается за упрощением.
В ряде случаев полная запись единицы измерения является обязательной.
Так, при выражении концентрации [ q = кг/кг совершенно необходимо указы
вать, о каки х "кг" идет речь (особенно в знаменателе): о кг вещества, приходя
щихся на 1 кг смеси или на 1 кг какого-либо отдет.ноrо к:омпонеита.

В ходе технологических расчетов нередко приходится исполь
зовать величины, не имеющие размерности. Некоторые из них
безразмерны изначально (числа 7t , е) , другие - по определению
(различные коэффициенты поле з ного действия) , третьи - по
происхождению (ком пл ексы, у которых размерности в числите
ле и знаменателе одинаковы и потому сократились) .
1 . 1.S. О точности инженерных расчетов

Технологические расчеты должны проводиться с определен
ной точностью. Уровень этой точности (допустимая погреш
ность) обусловливается ответственностью расчета (скажем,
учебный расчет нередко проводится с меньшей точностью, не
жели проектный в конструкторском бюро) и точностью исход
ных величин, которыми мы располагаем. В равной мере непри 
емлемы как недостаточная , так и избыточная точность расчета
(последняя чаще всего - следствие недостаточной грамотности
лица, ведущего расчеты).
Обычно точность получаемого результата не п ревышает точ
ности исходных (заложенных в расчет) величин.

Покажем это на примере произведения двух величин z = ху. Пусть абсо
лютные поrрешности х и у составляют лх и Лу; тогда относительная ошибка
будет Бх = ЛХ/х (в долях от х) ; соответственно для у: Бу = Лу/у. Примем (это
наиболее частый практический случай) , что абсолютные погрешности много
меньше сами х величин: лх << х, Лу << у; тогда значения лх и лу в математи
ческом плане можно трактовать как дифференциалы dx и dy и использовать
аппарат дифференциального исчисления. Максимальная абсолютная ошибка
исследуемого произведения лz = Л(х·у) = d(x·y) = y·dx + x·dy. Оrносительная
ошибка произведения Бz = Л(ху)/(ху) = (ydx + x·dy)/(x-y) = dx/x + dy/y = Бх +
+ Бу. Таким образом, максимальная относительная ошибка произведения равна
сумме относительных ошибок сомножителей . Иначе говоря, она больше, чем
относительная ошибка любого из сомножителей. И если один из сомножителей
взят с поrрешностью 1 %, то произведение не может получиться точнее, сколь
ко бы цифр ни высвечивалось на дисплее калькулятора или компьютера. И
записывать результат нужно с тем числом значащих цифр, которое отвечает
поrрешносm рассчитанной величины. При этом последняя из записанных
цифр указывает абсолютную погрешность: если, например, записано 1 ,25, это
означает, что найденная величина равна 1 ,25 ± 0,0 1 ; а если записано 1 ,250, то,
значит (должно означать!), что расчет произведен с большей точностью, и най
денная величина равна 1 ,250 ± 0,00 1 .

Ч аще всего допускаемая погрешность в инженерных расчетах
составляет доли процента. Ч тобы вьщержать эту точность, реко-

44

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

мендуется брать величины с тремя значащими цифрами
(например: 65,2, или 6,52 , или 0,652, или 0,0652 и т. п . ) . Исклю
чением являются числа, начинающиеся с 1 ; во избежание сни
жения точности их целесообразно брать с четырьмя значащими
цифрами ( 1 5 , 3 7 или 1 , 537 и т. д.). И менно с таким числом зна
чащих цифр следует представлять результаты расчета (выходные
сведения ) . Поскольку в ходе расчетов (а они бывают весьма
громоздкими и многоступенчатыми) ошибка может накапл и 
ваться, то промежуточные величины целесообразно брать с од
ной дополнительной значащей цифрой. Представление резуль
татов с излишней точностью (нередкая ситуация!), т. е . с числом
значащих цифр, не отвечающих реальной погрешности и разум
ной точности расчета, - неграмотно и неправомерно.
1 .2. ОСНОВНЫЕ ПОНЯТИЯ
1 .2. 1 . Обобщение

и

конкретизация

Объекты и процессы, изучением которых занимаются ПАХТ
и другие науки , характеризуются многочисленными конкретны 
ми особенностями и связями ; досконально и точно учесть их
трудно, чаще всего - просто невозможно. Поэтому в ходе науч 
ного анализа вьщеляют основные (общие) моменты, давая
упрощенное, идемизированное (пусть приближенное) представ
ление о характеристиках изучае мых объектов, о закономерно
стях явлений и процессов - это придает общность устанавли 
ваемым закономерностям. Такие закономерности часто именуют
законами природы. Не исключено, что в отдельных случаях и
ситуациях принятый уровень идеализации (абстрагирования)
может оказаться чрезмерным; при переходе к рассмотрению
конкретного объекта, явления, процесса в целях уточнения ана
лиза потребуется снижение уровня идеализации. Тогда учиты
вают проигнорированные ранее более тонкие эффекты, вьще
ляющие данный объект из группы сходных с ним.
Характерным примером абстрагирования может служить понятие идеально
подчиняющегося закону Клапейрона - Менделеева и справед11 и вого
(пусть не вполне точно) д11Я всех газов в весьма широком диапазоне температур
и давлений. Однако в определенных условиях (высокие давления , низкие тем
пературы , близость к состоянию насыщения и т.п . ) использование этого закона
приводит к большим ошибкам , причем разным д11Я отдельных газов. Поэтому
уравнение Клапейрона - Менделеева приходится модифицировать, переходЯ к
уравнению Ван-дер- Ваальса или вводЯ коэффициенты сжимаемости .

rо rаза,

Вообще , физические представления и созданные на их осно
ве математичес ки е построения (иначе: физические и математи
ческие модел и) должны приводить к достаточной (разумной)

45

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

точности описания объекта, процесса, адекватно отражая его
основные (обусловленные постановкой задачи) закономерности .
Говорят: "Любая модель - всегда карикатура на действитель
ность". Это, конечно, так, но ведь карикатура должна быть по
хожей, реальный объект должен быть в ней узнаваем . Строя
физические и математические модели , необходимо представлять
уровень абстрагирования (т. е. роль и вклад принятых допуще
ний), чтобы можно было ограни ч ить (оконтурить) область при
менения получаемых закономерностей и в случае необходимос
ти наметить пути уточнения анал иза.
Идеализация объектов и явлений нередко упрощает их мате
матическое описание, хотя и делает результаты анализа и расче
та приближенными . Отказ от упрощений уточняет результат, но
обычно заметно усложняет выражение связей и получаемые
закономерности . Поэтому всегда следует оценивать целесооб
разность отказа от упрощений ; иногда уточнение столь несуще
ственно, что отказ от упрощений совершенно не оправдан , ска
жем , в аспекте повышения точности и нженерного анализа.
Среди общих путей упрощения изучаемых закономерностей
особо вьщеляют линеаризацию связей между рассматриваемыми
объектами , явлениями, процесса м и . М ногообразие и сложность
этих связей обусловливают (за крайне редким исключением) их
заведомо нелинейную природу, а это создает серьезные затруд
нения при анализе и математическом описании процесса. Пере
ход к линейным связям (линеаризация) существенно упрощает
анализ; однако при этом снижается точность анализа - он ста
новится приближенным. Важно, ч тобы погрешности анализа
при таком прибл ижении не нарушил и необходимую точность
расчета.
Математически сформулированные выше положения наглядно иллюстри
руются с позици й разложения функций в ряд Тейлора. Пусть мы хотим устано
вить некую закономерность, выражающую зависимость определенного эффекта
j(x) от перемен ной х в относительной близости к значению х = а. Тогда

/" (а)
/{х) = /{а) + f'(a) (х - а ) +
(х - а) 2 +
--

\!

+

/"' (а)

--

--

2!

(х - а)3 + . . . .

3!
При достаточно малых отклонениях (рассогласованиях) х от а все сла
гаемые, кроме первых двух, будут существенно малы из-за высоких степеней
малой разности (х - а ) . Поэтому без сколько-нибудь заметной погрешности
можно считать, что зависимость j(x) я вляется линейной относительно (х - а) , а
значит и относительно х. Таким образом , дпя окрестности точки х = а предпо
ложение (упрощение!) о линейном характере закономерности j{x) является
достаточно точным. Здесь крайне важно понимать, что при увеличении рассо
гласования (х - а) возрастает роль отброшенных членов бесконечного ряда

46

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Тейлора. Так что при достаточно больши х значен иях разности (х - а) погреш
ности анализа на основе линейного соотношения выходят за допустимые пре
делы, и тогда игнорирование нелинейных членов ряда (третье и последующие
слагаемые) становится неправомерным.
Строго говоря, использование линейных соотношений оправданно лишь
после предварительной оцен ки вклада отброшенных нелинейных членов и
установлен ия диапазона значений (х - а) , в котором функцию ./(х) можно счи
тать линейной (или же, в более общем случае, - в котором допустимо брать
ограниченное число членов разложения). Попьггка "принудительного" сохране
ния линейного характера соотношений за пределами этого диапазона приводит
либо к значительным ошибкам, либо к тому, что во избежание таких ошибок
постоянные коэффициенты (множители) перед аргументом х или (х - а) в
формуле Тейлора приходится принимать переменными ; таким способом отра
жают объе ктивно сушествующую нелинейность, проявляющуюся при достаточ
но больших отклонениях х от некоего важ ного для процесса значения а.

М ногообразие связей и недостаточная познанность явлений,
лежащая в основе анализируемых процессов, не дают оснований
считать, что результат математического исследования проблемы
и конструктивное решение должны быть единственными, жест
ко обусловленными: постановкой задачи; системой ограниче
ний; сведениями, имеющимися в распоряжении научного ра
ботника или конструктора; ресурсами. В технике вообще, тем
более на данном (еще не всегда высоком с позиций технологи
ческих задач) уровне развития науки и технических возможно
стей, совсем не исключены различные пути и результат ы реше 
ния проблемы. При этом среди вариантов решений (научных,
конструкторских) далеко не всегда можно с полной определен
ностью установить оптимум во всех отношениях ; приходится
сопоставлять достоинства и недостатки предложенных вариан
тов. Окончательный выбор (на стадии формулирования целей
осуществления процесса либо при получении конечных реше
ний) часто реализуется на основе технологическою компромисса.
Сегодня уже ясно, что неоднозначность технологических ре
шений - следствие объективного развития технологии. Дело в
том, что с течением времени неизбежно происходят более или
менее существенные изменения во взглядах на цели, возмож
ности, пути реализации (а также ограничения) химико
технологических процессов, в таком случае говорят о вариатив
ности критериев оптимальности . Это закономерно приводит к
изменениям в конечных результатах (включая и конструктивное
оформление процессов) , в таком случае говорят о поливариант
ности решений.
1 .2.2. Некоторые физические понятия

Введем некоторые физические понятия, необходимые для
анализа и математического описания в ближайших разделах
курса ПАХТ (другие понятия будут вводиться в последующих
разделах по мере необходимости).
47

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Сплошная среда. Жидкие, твердые, газообразные тела состоят
из атомов, молекул, ионов и других элементарных образований ;
число и х в единице объема в условиях, интересующих хими
ческую технологию, очень велико. Например, в 1 смЗ воздуха
при нормальных условиях содержится ,,, 2 ,1. 1 0 1 9 молекул; даже в
крайне разреженной атмосфере Луны их ,,, 1 0 1 0 в 1 смз . В рас
сматриваемых курсом ПАХТ объектах (рабочих телах) атомы,
молекулы, ионы и расстояния между ними, как правило, значи
тельно меньше масштабов (размеров) объекта. Поэтому в подав
ляющем большинстве случаев можно считать, что рабочее тело
целиком заполняет рассматриваемую в ходе анализа часть про
странства, т. е. является сплошной средой. Дискретность про
странства (т. е. различия в свойствах атомов, молекул и проме
жутков между ними) здесь в расчет не принимается.

В некотор ых (весьма редких) случаях дискретность пространства приходится
учитывать: например, в разреженных газах, когда расстояния между молекула
ми и путь их свободного пробега сопоставимы с характерным размером аппара
та. В этих случаях делаются специальные оговорки и анализ ведется вне посту
лата о сплошности среды (см. разд. 2.9).

Представление о сплошной среде физически оправдано тем,
что рассматриваемые химической технологией фрагменты про
странства, в том числе трактуемые как бесконечно малые , прак
тически всегда содержат достаточно большое число элементар
ных частиц (атомов, молекул и т. д.) ; поэтому можно считать,
что они сохраняют общие свойства рабочего тела и закономер
ности изменения его состояния в ходе проведения с ним техно
логических операций. Идеализация систем путем введения по
нятия о сплошных средах позволяет в ходе анализа объектов,
явлений, процессов пользоваться математическим аппаратом
непрерывных функций, прежде всего - дифференциальным и
интегральным исчислением.
Идеальная жидкость. Идеальной называется жидкость, абсо 
лютно не сопротивляющаяся сдвигу и разрыву (т.е. обладающая
абсолютной текучестью и полным отсутствием сил сцепления
между частицами, значит, - вязкости и липкости) и абсолютно
сопротивляющ аяся сжатию (т.е. абсолютно несжимаемая). Трак
товка жидкости в качестве идеальной приводит к значительному
упрощению рЯда закономерностей, используемых в " Техничес
кой гидравлике " (раздел ПАХТ, изучающий закономерности
покоя и движения жидкости) . Реальные жидкости, как правило,
близки к идеальным в смысле несжимаемости : нужны очень
высокие давления (в сотни и тысячи атмосфер) , чтобы сжимае
мость реальной жидкости стала заметной. Однако реальные
жидкости могут весьма значительно сопротивляться сдвигу
(свойство вязкости) и растяжению (свойство липкости) . Заме 48

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

тим, что газы существенно сжимаемы (скажем, идеальные соответственно закону Клапейрона- Менделеева); реальные
газы сопротивляются сдвигу (т. е. обладают вязкостью) , хотя и
не столь сильно, как реальные жидкости .
И зотропные и анизотропные среды . Е сл и интересующее нас
свойство рабочего тела не изменяется в занимаемом им про
странстве, то это пространство и среда в нем называются изо
троlПIЫМИ относительно данною свойства. Е сли же наблюдается
изменение свойства от точки к точке (иногда считают : и во вре
мени) , то пространство трактуется как неизотропное, и.л и анизо
тропное. Такое широко е понимание термина " изотропность "
обычно используется в термодинамике и ряде других научных
дисциплин .
В более узком смысле анизотропными считаются про
странства (среды), в пределах которых изменяются некоторые
удельные свойства (теплоемкость, вязкость, плотность, прозрач
ность и т . п . ) ; но здесь термин " изотропность " не распростра
няется на изменение интенсивных величин - температуры,
давления, концентрации и др. В другом (тоже узком) смысле
признаком анизотропности считают неодинаковость какого
либо свойства по разным направлениям пространства (скажем,
вдоль координатных осей); примером может служить теплопро
водность вдоль разных направлений в кристалле или прочность
древесины (например , на сдвиг) вдоль и поперек древесных
волокон. Именно такая - узкая - трактовка чаще всего ис
пользуется в задачах науки ПАХТ.
Иде альное вытеснение и идеальное перемешивание. При изуче
нии движения потоков в рабочих зонах технологических аппа
ратов удобны два упрощенных модельных представления.
Согласно первому из них все элементарные частицы потока
движутся в рабочей зоне с одинаковыми скоростями и минуют
эту зону за одинаковые промежутки времени. Такой характер
движения называют идеальным вытеснением (ИВ). Здесь для всех
элементов потока одинаково время пребывания • ив в рабочей зоне
< т ив - сосредоточенная величина) , а интересующий нас признак
( температура, концентрация, какое-нибудь свойство) изменяется
по ходу потока. При этом на вы х оде из рабочей зоны все эле
менты потока в силу равенства для них значений • ив имеют
одинаковое значение температуры, концентрации , свойства.
Заметим, что эту модель используют при анализе технологиче
ских процессов наиболее часто и , к сожалению, без необходи
мых оговорок .
Согласно второй модели - о н а носит название иде ального
перемешивания (ИП) - элементы потока полностью перемеша
ны в рабочей зоне. Поэтому всякая интересующая нас характе 49

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ристика потока (температура, концентрация, любое свойство

рабочего тела) во всех точках в пределах рабочей зоны и на вы
ходе из нее имеет одинаковые значения. Однако время пребыва
ния элементов потока в рабочей зоне - распределенная величи
на: некоторые элементы мoryr быстро " проскочить" через рабо
чую зону, почти не задерживаясь в ней (выходные характери
стики таких элементов будут мало отличаться от входных); дру
гие будут весьма долго (часто - бесполезно долго) находиться в
ней (здесь характеристики элементов на выходе из рабочей зоны
будут существенно отличаться от входных). Использованию этой
модели в расчетах обычно предшествуют специальные оговорки.
Математические описания процессов с использованием мо
делей И П, и особенно И В, часто привлекают простотой полу
чаемых решений. Реальную ситуацию в рабочей зоне чаще всего
(не обязательно!) следует трактовать как промежуточную. Спо
собы анализа и математические описания простейших идеали
зированных моделей и более сложных, ближе отвечающих ре
альным ситуациям, рассмотрены в гл.8.
1 .2.3. Основные характеристики (свойства) рабочих тел

Свойства,

характеристики

рабочих

тел,

свойства делят на экстенсивные и интенсивные.

субстанций.

Эти

Экстенсивным называется свойство, имеющее меру в самом се
бе; количество этого свойства измеряется на основе одноимен
ного эталона (скажем, длина - в м, масса - в кг и т. д. ; здесь м
и кг
эталоны той же природы, что и измеряемая величина:
длина, масса) . Интенсивные вели11ины не имеют меры в себе, они
-

измеряются косвенно, на основе экстенсивных (или производ
н ых от них) величин: например, температура измеряется по вы
соте столбика термометра, по объему газа в баллончике, по
электрическим характеристикам термометра сопротивления или
термопары.
Экстенсивные величины пропорциональн ы количеству суб
станции (скажем, массе) , при суммировании их количество уве
личивается; именно эти величины имеются в виду, когда гово
рят, что часть меньше целого. Возможность суммирования экс
тенсивных величин лежит в основе расчета некоторых свойств
субстанции (интенсивных, удельных - см. ниже) по адди тив
ности.
Интенсивная величина не зависит от количества субстанции;
при увеличении ее количества простого суммирования интен
сивной величины не происходит (скажем, при сложении двух
масс одинаковой или разной температуры результирующая тем
пература не равна сумме исходных). Интенсивная величина при
50

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

наращивании

няется.

количества субстанции некоторым образом усред

Перенос субстанции (теплоты , вещества и других экстенсив
ных величин) возможен, если в разных точках технологической
системы (аппарата, потока) различны значения интенсивных
свойств (температуры, давления и др.). Разница в значении ин
тенсивных свойств ( потенциалов) является причиной и движущей
силой переноса экстенсивных величин.
В ряде случаев удобно вьщелять еще одну группу свойств удельные свойства. Это какое-либо экстенсивное свойство, отне
сенное к единице субстанции (например, к 1 кг) и потому не
зависящее (подобно интенсивной величине) от количества суб
станции. Примерами могут служить плотность вещества или его
теплоемкость. Удельные свойства вещества, как и интенсивные,
при сложении субстанции тоже усредняются.
Схема усреднения удельного или интенсивного свойства С на
примере смешения двух порций (массовые количества - а и Ь,
значения свойства - СА и Св соответственно) показана на
рис. 1 . 1 .
В простейших случаях усреднение интенсивных и удельных
величин при изменении количества субстанции (например, при
смешении нескольких порций вещества) нередко производят по
аддитивности. Такая процедура усреднения подразумевает: ма
тематически - линейность рассматриваемого свойства, физиче
ски - справедливость закона сохранения для экстенсивной вели
чины, используемой для расчета этого свойства.
Абсцисса точки смеси (т) зависит от количеств а и Ь взятых
порций (или, что то же, - от концентраций) , она определяется
по правилу рычага - см.разд. 1 0.2.4. В случае аддитивного расче
та рассматриваемого свойства для смеси
С = (а СА + Ь Св) / (а + Ь)

линия смешения - прямая (на рисунке - сплошная линия J).
Однако при наращивании количества субстанции (при сме
шении) нередко наблюдаются и нелинейные эффекты: например,
выделение или поглощение теплоты смешения в случае расчета
теплоемкости смеси. Тогда усредненное значение свойства сле
дует рассчитывать с учетом таких нелинейных эффектов. В этом
случае
требуется
написание
баланса
по
субстанции
(см. разд. 1 .3 . 1 ) с учетом ее Источников ( Ис) и Стоков (Ст), что
приведет к отклонению от адди тивности - вверх или вниз от
прямой на рис. 1 . 1 (в зависимости от знака нелинейного эффек
та) . Если искомое усредненное значение свойства, отвечающее
точкам М, больше рассчитанного по адди тивности , то говорят о
синерrизме данного свойства (штриховая линия на рисунке),
51

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 1. 1. К усреднению интенсивных
удельных свойств :

с

ссн +-----.....L

с

сАн +---�--«

�
1

или

1 - аддити в ность свойства, 2 - синергизм ,
J - антагонизм; С - свойство, К - количе
ство, М, МСн и М"" - точки, характеризующие
свойства смеси для случаев /, 2 и J

если меньше, - то об антаrониз
ме (штрих-пунктирная линия).

Напомним сущность некото
рых экстенсивных и удельных
т
а
к
ь
свойств рабочего тела (либо свя
занн ых с ними характеристик) ,
используемых в ближайших раз
делах курса; во многом эти характеристики хорошо известны из
предшествующих учебных дисциплин. Размерности приводимых
величин даны в СИ.
Масса т - важнейшая физическая характеристика рабочего
тела, определяющая его инерционные свойства. В механике
масса является коэффициентом пропорциональности между
действующей на тело силой и его ускорением. В СИ масса из
меряется в кг.
ПлО'Пlость р и удельный объем v. Масса, содержащаяся в еди
нице объема V, называется плотностью тела: р = m/V, кг/мз .
Величина, обратная плотности и представляющая собой объем,
занимаемый единицей массы, называется удельным объемом: v =
= V/m, мЗ/кг. Совершенно очевИдно (из физического смысла, из
сопоставления размерностей) , что в любой системе единиц
pv = 1 , соответственно р = l/v и v = l/p.
Скоростью w (в курсе ПАХТ будут использованы и иные сим
волы) называется путь /, отнесенный к единице времени t ; еди
ница измерения скорости - м/с. Если скорость во времени не
изменяется, то она рассчитывается по формуле
w = l/t ;

(1.1)

если же скорость переменна во времени, то мгновенная скорость
(в момент t) выразится как
( l . l a)
w = d //dt ,
а формула ( 1 . 1 ) в этом случае определяет осредненную во времени
скорость w.
Скорость потока ЖИдкости (газа, твердого материала) в неко
торой точке аппарата называется локальной. На ее основе опреде
ляется (из физических соображений, из сопоставления размерно
стей) поток ЖИдкости (газа и т.д. ) d V через элементарное живое
сечение <if (площадку, нормальную к направлению скорости):
( 1 .2)
d V = wdf или w = d V/df .
52

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Выражение ( l .2) именуется уравнением расхода в дифференци
альной форме. Для определения средней по всему поперечному
сечению / скорости потока Wcp предварительно определяют пол
ный расход:

V=

f w d/

!

( 1 .2а)

и, исходя из ( 1 .2), записывают уравнение расхода в интегральной

форме:

Wcp =

V/f ИЛИ

V = Wcp f ·

( 1 .3)

Заметим: в ряде технологических задач полный расход V за
дан, так что нет необходимости в использовании формулы
( l .2a) ; кроме того, индекс "ер " нередко опускают.
Силы. В механике, гидравлике, ряде других разделов и дис
циплин анализ взаимодействия сил равнозначен (в аспекте по
лучаемых результатов) анализу потоков импульса (количества
движения), поскольку поток импульса, отнесенный к единице
времени, представляет собой силу. Единица измерения силы в
СИ - ньютон Н = кг·м/ с2.
Обычно используют следующую классификацию сил: массо
вые (объемные), поверхностные, линейные.
Массовыми называют силы, действующие на каждую частицу
внутри данной массы (объема) рабочего тела. Примером массо
вых сил могут служить силы всемирного тяготения (в част
ности - вес) , центробежные силы, инерционные силы. Если
источник массовых сил лежит вне тела, то говорят о внешних
силах (источник веса тела - притяжение Земли); если силы
проявляются независимо от внешних воздействий, то это внут
ренние массовые силы (силы инерции). Массовые силы пропор
циональны массе рабочего тела; они могут быть представлены
как произведение массы на ускорение:
Р = та.

( 1 .4)

В этом смысле ускорение выступает как единичная (удельная)
массовая сила, т. е. отнесенная к единице массы: а = Р/т = Р'.
В ходе анализа будет удобно использовать проекции единичных
внешних массовых сил на оси координат: Рх, Ру, Р�.Поверхностными называют силы, действующие на поверх
ность и пропорциональные ей . Различают нормальные и танrен
циа.rо.ные поверхн0С1Н ые силы. Первые действуют нормально к
поверхности - это силы давления (сжатия и т.п.). Их пропорцио
нальность величине поверхности выражается соотношениями
( 1 . 5)
dРн = pdf ИЛИ Рн = р/
в дифференциальной (для локальной силы давления dРн )
или в интегральной (для полной силы давления Рн ) форме соот53

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ветственно. Связь между выражениями ( 1 .5) очевидна: Рн =

=

fp df Удельная (приходящаяся на единицу поверхности) нор

/

мальная сила называется давJiением:
- локальным (в точке поверхности) р = d Pнfdf,
- средним (по всей поверхности j) р = Pнff
Вдоль поверхности (тангенциально) действуют силы сдвига (в
гидравлике - силы трения) . Их удельная характеристика, отне
сенная к единице поверхности, называется напряжением сдвиrа
(трения). Пропорциональность силы и поверхности здесь выра
жается соотношениями
( 1 . 6)
в дифференциальной и интегральной формах, причем в первом
случае tт = dPт/d/ - локальное напряжение сдвига (в точке по
верхности) , во втором tт = Рт// - среднее его значение по по
верхности /
Удельные характеристики поверхностных сил р и tт измеря
ются в Н/м2 = Па (паскаль) .
Примером линейных CИJI является сила поверхностного натя
жения, действующая по периметру П и пропорциональная ему.
Для полной силы поверхностного натяжения пропорциональ
ность периметру выразится как
( 1 .7 )
Рп = сr П ,
где а - средний (по периметру П) коэффицне�rr поаерхноС'JИоrо натяж:еНИJ1;
[а) = Н/м .
ТеПJiоемк:остью называется количество теплоты, необходимое
для нагревания рабочего тела на 1 градус. Удобно оперировать
удельной теПJiоемкостью с, отнесенной к единице массы тела. В

курсе ПАХТ чаще всего используют теплоемкость при постоян
ном давлении ( с == ср) . Единица измерения теплоемкости:

Дж/(кг·К).

Другие необходимые характеристики будут вводиться по ходу
изложения курса.

В заключение раздела заметим: при изложении курса нам придется неодно
кратно КJ1ассифицировать явления, процессы, ситуации - подобно тому, как
это сделано выше в отношении сил. Надо ясно понимать, что природа - еди
на, у нее нет классификаций; это мw вводим классификации в целях удобства
восприятия и систематизации тех или иных фактов, явлений, закономерностей.
В этом смысле любая классификация - условна, даже субъективна (хотя она
вполне может бытъ удачной); нередко общепринятая классификация - просто
дань традиции.
Покажем условностъ классификации на примере выталкивающей силы,
действующей на тело объемом V и поверхностью F, погруженное в жидкость
плотностъю р (рис. 1 .2.). На произвольную элементарную площадку dF, распо-

54

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

-f
�

-

Рис. 1. 2. К
а

-

тело

-:.---=--

1

Среда

� �·�

_-

IL

-

v

-

р -

'lf �_ -�
-

а

р

d

<2. _

dF

z

б

формированию архимедовой силы:
в жидкости:

схема сил, 6 - увеличенный фрагмент элементарной поверхности

ложенную на глубине z (там дааление р = pgz) действует по нормали к площад
ке элементарная 0011epxнoC11UU1 сила dP = pdF. Если угол силы dP с вертикаль
ной осью z равен 1р (в месте расположения площадки), то составляющая силы
dP вдоль вертикальной оси будет (dP)cos1p = p(dF)co51p = pdxdy (поскольку
проекция dF на плоскость ух, равная (dF)cosip, записывается как d.x·dy) . Чтобы
получить полную силу вдоль вертикальной оси, надо просуммировать dP по
всей поверхности F:
р=

fJ р dxdy .
(F)

Но по формуле Остроградского-Гаусса между интегралами по поверхности
и по объему существует связь:
d
fJ Р Фdу = fff p dV .
(V) dz
(F)

В рассматриваемом случае dp/dz = pg, так что

d
fff p dV = fJJ р gdV = pgV .
(V) dz
(V)

(а)

Эrо и есть зuон Архимеда: на погруженное в жидкость тело действует вы
талкивающая сила, равная весу жидкости в объеме тела. Таким образом, закон,
представленный первоначально как результат действия поверхностных сил,
получил конечное выражение (а) в форме массовых сил - в такой форме трак
товать и использовать этот закон удобнее.
Проведенный анализ показывает условность введенной ранее классифика
ции сил: архимедову силу можно относить как к поверхностным, так и к мас
совым - все зависит от стадии и целей анализа.

1.3. ОБЩИЕ ПОДХОДЫ
К АНАЛИЗУ ПРОЦЕССОВ ПЕРЕНОСА
1 .3. 1 . Уравнения баланса

Среди разнообразных типов соотношений , встречающихся в
химической технологии (во многих других учебно - научных дис
циплинах - тоже), часто используются уравнения баланса. Эти
55

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

уравнения нередко выступают как математическое выражение
законов сохранения какой-нибудь субстанции (массы, коли
чества движения, теплоты, какого-либо вещества) . Однако ба
лансовые соотношения можно записать и для таких ситуаций,
когда законы сохранения не действуют. Так, баланс может быть
записан для одного из веществ, участвующих в химической реак
ции: здесь сохранения (скажем, массы или числа молей) именно
этого вещества - нет, так как оно может исчезать или возни
кать в ходе химической реакции. К этой же категории относятся
балансы объемов рабочих тел, энтропии (здесь отсутствие зако
нов сохранения - фундаментальный факт) . Таким образом,
понятие баланса шире, нежели закона сохранения (по крайней
мере, в рамках конкретной учебно -научной дисциплины) .
Сущность метода балансов и последовательность составления
балансовых соотношений заключается в следующем:
а) определяют, для какой именно субстанции необходимо за
писать баланс;
б) вьщеляют пространственный контур , для которого состав
ляется баланс;
в) устанавливают временной интервал, для которого будет со
ставлен баланс.
Затем обозначают и выражают: потоки субстанции, входящие
в контур (Приход = Пр) и выходящие из него (Уход = Ух) ; Ис
точники (Ис) субстанции и ее Стоки (Ст) внутри контура; На
комение ( Нак) субстанции (или Результат процесса, сокращен
но - Рез) в контуре за исследуемый временной интервал. Далее
записывают Основное Балансовое Соопtоmение (ОБС):
( l .8)
+ Пр - Ух + Ис - Ст = Нак(Рез) .
ОБС может быть записано для л юбой характеристики объек
та, относящейся к экстенсивным величинам.
Основные цели составления баланса:
- проверка сходимости баланса , т.е. выявление невязки ба
ланса и ее причин, принятие решения об уточнении модели
процесса или о повышении точности определения величин,
ВХОДЯЩ И Х в ОБС;
- нахождение неизвестного эл емента баланса; здесь должны
быть известны все элементы баланса, кроме определяемого;
- отыскание функциональной связи между элементами ба
лансового соотношения (непосредственно или в результате ма
тематических преобразований).
В качестве субстанции , для которой записывается балансовое
соотношение, может выступать масса (или поток массы) . В этом
случае чаще всего предполагается справедливость закона сохра
нения массы (дефект массы в ходе ядерных реакций в хими56

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ческой технологии обычно не рассматривается). Баланс импуль
са (количества движения) часто используется при изучении ме

ханических и гидромеханических процессов. Следует иметь в
виду, что эти балансовые выражения, отнесенные к единице вре
мени, приобретают форму балансов взаимодействующих сил. Су
щественно, что при переносе импульса в поле внешних массовых
сил причины их появления лежат за пределами вьщеленного
контура; поэтому внешние массовые силы трактуются как Ис
точники или Стоки импульса внутри контура. Кроме того, в
этом случае обычно говорят не о Накоплении, что физически
оправданно для количества движения, а о Результате (Рез) - из
менении ситуации под влиянием равнодействующей сил.
При составлении энерrетическоrо баланса в качестве субстан
ции целесообразно (если это допустимо) вьщелить какой-либо
определенный вид энергии, например - тепловой ; тогда энер
гетический баланс превращается в тепловой; в других ситуациях
приходится использовать полный энергетический баланс.
Баланс по веществу может б ыть записан для какого-нибудь
одного или для нескольких участвующих в процессе компонен
тов либо для всех компонентов смеси.
Пространственный контур (рис. 1 .3) выделяет из технологи
ческой системы один аппарат, несколько аппаратов или часть
аппарата (возможно, бесконечно малую его часть). После вьще
ления контура все потоки , пересекающие его границы (жирные
линии), трактуются как Пр и ход ы субстанции в контур или ее
Уходы из него. Есл и между потоками происходит обмен суб
станцией, нередко при выборе контура потоки целесообразно
формально обособить ( сегрегировать)
примеры этому будут в
курсе.
В качестве временно'rо интервала можно выбрать время проте
кания всего процесса от на
-

чала до конца либо от нача

ла до некоторого промежу
точного состояния (так по

ступают при необходимости
установления закономерно
стей изменения исследуе
мой характеристики во вре
мени) . Для периодических
процессов нередко прихо
дится начинать с составле
ния баланса в д и ффе рен
-

Рис. 1.З. К составлению баланса:

Пр - приход, Ух - уход, Ис источник, Ст - сток, К - кон1)'р

57

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

циальной форме
для бесконечно малого (элементарного) про
межутка времени d't'. Для стационарных процессов за временной
интервал чаще всего удобно выбирать единицу времени ( 1 с).
-

Без выбора субстанции, определения пространственного конту
'
ра и установления временного интервала составление баланса лишено смысла.
При написании балансовых соотношений в дифференциальной форме
(вообще - при состаалении любых дифференциальных уравнений) необходимо
С11ЮГО следовать математическому правилу: если какая-либо независимая пере
менная х (пространственная или временная координата, другой аргумент) по
лучила приращение dx, то исследуемая функция у тоже получает приращение dy,
которое всегда считается положительным. Математике безразлична физическая
сущность описываемого процесса; поэтому не нужно пьrrаться "догадываться",
каким должен быть знак этого приращения dy в свете физических предстаале
ний о процессе. Присущий физическому смыслу знак dy проявится сам - при
подстановке пределов интегрирования или граничных условий; вот их форму
лирование - дело исследователя (физика, химика, технолога), но не математи
ка. Попытка учесть знах приращения на стадии состааления дифференциально
го уравнения - источник ошибок. Их потом приходится мучительно устранять,
приче м "нечестными путями": делать где-то еше одну ошибку в знаке
(например, произвольно меняя пределы интегрирования); объяснять, что знак
"минус" означает расход (вещества, энергии и т. п.), а не их получение; а то и
просто "забывать" про неестественно появившийся в формуле знак.
Итак: при положительном приращении аргумента будем всегда полагать при

ращение функции по.сожшnиьнwм.

И еще. В качестве пределов интегрирования должны подставляться только
начальные или конечные (либо текущие) значения величин, являющихся пара
метрами интегрирования, т. е. стоящих в подынтегральном выражении под
знаком дифференциала (в рассматриваемом случае - величин х и величин у) . И,
разумеется, при подстановке нижнего ("н") и верхнего ("в") пределов в правой и
левой частях равенства необходимо выдерживать горизонтальное соответствие:
величине Хн отвечает Ун. величине Ха отвечает Уа·
В качестве Прихода и Ухода мoryr выступать потоки субстан

ции в единицу времени (в непрерывных стационарных процес
сах) либо ее количества (в периодических нестационарных про
цессах) - конечные (за весь процесс или часть его) или беско
нечно малые (за элементарный промежуток времени d't') .
Источники и Стоки вводятся в балансовые уравнения, когда в
изучаемой ситуации для субстанции отсутствует закон сохране
ния. Это тоже могут быть потоки субстанции (в единицу вре
мени) либо ее количества (за конечный или бесконечно малый
промежуток времени). На рис. 1.3 Источники и Стоки изобра
жены крестиками или жирными точками в кружках малого раз
мера.
В результате алгебраического сложен ия Приходов, Уходов,
Источников и Стоков количество рассматриваемой субстанции
в пределах контура может изменяться или не изменяться : про
исходит или не происходит Накопление субстанции. В стацио 
нарном состоянии (непрерывные процессы) таких изменений не
58

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

наблюдается, так что здесь Накопление субстанции Нак = О .
Для нестационарных процессов типично изменение количества
балансируемой субстанции внутри контура. При этом Накопле
ние всегда есть разность между конечным и начальным коли
чествами субстанции; эта разность получится положительной,
когда количество субстанции нарастает, и отрицательной, когда
оно убывает.
Пусть, например, речь идет о балансе массы М . В стацио
нарном процессе ее количество в контуре не изменяется во вре
мени, так что Нак = Мк - Мн = О. В периодическом процессе
конечное количество массы Мк может быть не равно начально
му Мн; тогда Нак = Мк - Мн "* О. При рассмотрении бесконеч
но малого промежутка времени dt Накопление субстанции
(здесь - массы) тоже бесконечно м ало. Пусть в начале элемен
тарного промежутка ( момент t) количество массы равно М, а в
конце его ( момент t + dt) - равно М + dM. Тогда Нак = ( М +
+ dM) - М = dM. Если изменение массы зависит от ряда фак
торов (и время t
лишь один из них) , то количество массы в
дМ
момент t + dt составит М +
dt, так что Нак = д М d t .
-

дt

--

дt

--

Заметим, что Накопление субстанции может быть равно О и в
случае нестационарного процесса, когда пространственный кон
тур стягивается, например, в поверхность (граница раздела фаз
и т. п . ) : накопление субстанции в таком контуре нулевого объема
означало бы бесконечно большое повышение потенциала
(температуры, концентрации) , чего физически происходить не
может. Такая ситуация встретится , например, при записи гра
ничных условий к дифференциальным уравнениям переноса.
В практических ситуациях ОБС ( 1 . 8 ) нередко может быть
упрощено и записано в урезанном виде. Так, для стационарных
процессов ( Нак = О) оно принимает вид
( l . 8a)
+ Пр - Ух + Ис - Ст = О .
В условиях действия законов сохранения из ОБС вьmадают Источ
ники и Стоки:
( 1 . 8б)
+ Пр - Ух = Нак,
а если речь идет еще и о стационарных процессах, то
( 1 .8в)
+ Пр - Ух = О .
Последнее соотношение нередко представляют в форме
( 1 . 8г)
Пр = Ух.
В ряде случаев здесь применяют иную запись; например, при
переносе теплоты между двумя теплоносителями в отсутствие
59

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

теплопотерь в окружающую среду: сколько теплоты отдал один
поток, столько получил друтой.
Для изолированных систем (нет Приходов и Уходов субстан
ции) :
+ Ис - Ст = Нак.
( 1 .8д)
Разумеется, возможны и иные случаи и соответствующие им
формы записи. В простейших случаях можно, конечно, сразу
записать баланс в какой-либо усеченной форме. Надо только
ясно представлять себе , что эта форма записи всегда является
модификацией ОБС ( 1 .8). Подчеркнем, что в ряде сложных си
туаций попытка упрощенной записи баланса может привести к
ошибкам, чаще всего - в знаке какого-нибудь элемента баланса
(такие ошибки известны в истории науки о ПАХТ) .
1 .3.2. Интенсивность процессов переноса
Потенциалы и потоки субстанций

Потенциалы и их поля. В разных точках рабочего объема тех
нологического аппарата в общем случае значения интенсивных
величин (потенциалов) и некоторых друтих параметров - раз
личны. Точки с одинаковыми значениями параметров образуют
(рис. 1 .4) изоповерхности (например, одинаковой температуры) .
На рисунке эти поверхности представлены в виде изолиний сечений изоповерхностей плоскостями, паралл ельными плос
кости отсчета интенсивной величины (подобно тому, как это
делается на географических картах при обозначении линий рав
ной высоты над уровнем моря). Поскольку на изоповерхности
значения свойства (потенциала, например температуры) не из
меняются, то движущая сила, вызывающая перемещение суб
станции (в рассматриваемом примере - теплоты) вдоль изоли
нии, изоповерхности, отсутствует, так что направленного пере
мещения субстанции вдоль этой линии, поверхности - не про
исходит. Однако значения потенциалов на разных изо
поверхностях различны; существующая (и, как правило, под
держиваемая внешними факторами) разность потенциалов яв
ляется основой движущей силы переноса субстанции между изо
поверхностями : так, температурный напор - причина возник
новения переноса теплоты. При этом по 1 1 закону термодина
мики субстанция самопроизвольно переносится от большего ее
потенциала к меньшему (для рассматриваемого примера: поток
теплоты - от горячих зон к холодным) .
Интенсивность переноса (поток субстанции) возрастает с
увеличением движущей силы, приходящейся на единицу рас
стояния между изоповерхностями потенциала. Поскольку эти
60

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 1.4. Изолинии потенциального поля с верши
ной А (жирной стрелкой показано направление
потока субстанции в точке В, тонкой - направле
ние градиента)

расстояния зависят от принятого направ
ления их отсчета, то возникает неопреде
ленность в оценке интенсивности пере
носа субстанции. Поэтому целесообразно
выбрать определенное направление, кон
кретизирующее оценку интенсивности
переноса. В качестве такого направления берут самое короткое
- нормаль к изоповерхности; в этом случае разность потенциа
лов, приходящаяся на единицу длины, будет наибольшей (в
сравнении с другими направлениями расстояний между изопо
верхностями), так что рассчитываемый поток субстанции будет
выражен наибольшей величиной.
Изменение потенциала на единицу длины по нормали назы
вается его градиентом. Согласно общепринятой гипотезе, интен
сивность удельных (отнесенных к единице времени и единице
поверхности, нормальных к изоповерхностям) потоков субстан
ции, выражающих скорость ее переноса, пропорциональна гра
диенту соответствующего потенциала. При этом градиент, со
гласно установлениям математики , принимается направленным
в сторону повышения потенциала; между тем субстанция перено
сится от большего потенциала к меньшему. Поэтому в соотноше
ниях:, связывающих удельные потоки субстанции и градиенты,
перед последними ставится знак "минус". Очевидно, что полный
поток субстанции в единицу времени получается как произведе
ние удельного потока на величину поверхности, через которую
переносится субстанция.
Удельные потоки субстанции. Рассмотрим удельные потоки
(иногда используют термин "плотность потока") применительно
к переносу различных субстанций.
Пусть вдоль неподвижной поверхности (рис. 1 . 5, а) движется
жидкость, причем непосредственно у поверхности (стенки ) ско
рость ее относительно стенки равна О - так называемая
"концепция прилипания" (жидкости к поверхности). По мере
удаления от стенки по нормали п скорость возрастает по неко
торому закону: на расстоянии п от стенки она равна w, на рас
стоянии п + лп равна w + Лw. Таким образом, на участке норма
ли лп наблюдается приращение скорости Лw, так что среднее
равно
(на участке Лп ) значение градиента скорости
Лw/Лп, а локальное (в точке п) составляет lim (Лw / Лп) = дw/дп .
Поскольку слои жидкости на расстояниях п и п + Лп движутся
дn-+0

61

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Удельные поrоки и
градиенты:
а - к переносу импульса, б
- к переносу теплоты (или
вещества)

Рис. 1.5.

п
w +Лw
п+лп�-----,.....,�

с разными скоростями,
то между этими слоями
возникают силы трения:
импульс от слоев с
большей скоростью пе
w
редается
к слоям
с
о
а
6
меньшей. Удельный по
ток импульса (если его
отнести к единице вре
мени , то речь пойдет о напряжении трения tт
см. разд. 1 .2.3),
согласно упомянутой выше общей гипотезе, на участке Лп про
порционален величине Лw/Лп . Локальное значение потока им
пульса или напряжения tт на расстоянии п от стенки получается
в результате предельного перехода Лп --+ О : tт 1 дw/дnl , причем
символ абсолютного значения градиента призван учесть проти
воположность направлений потока импульса и градиента. Связь
tт и градиента, записанная в форме равенства (т.е. с коэффици
ентом пропорциональности) , называется формулой Ньютона:
-

-

tт

=

-

µ

дw
дп

=

1 l

д
µ w.
дп

( 1 .9)

Важно, что обоснованный выше знак "минус" относится не к
коэффициенту пропорциональности µ, а к градиенту дw/дп. Ина
че говоря, более строго надо бы записывать не tт = -µ(дw/дп), а
tт = µ(- дw/дп) ; это замечание относится также к удельным ха
рактеристикам переноса и других субстанций.
Множитель µ называется коэффициентом динамической вяз
кости (иногда кратко - динамической вязкостью) . Согласно
формуле ( 1 .9) он представляет собой силу, действующую между
1 м2 )
двумя вьщеленными в жидкости единичными (в СИ
паралл ельными площадками , находящимися на расстоянии 1 м,
при разности скоростей между площадками в
м/ с. Единица
измерения в СИ:
-

[ µ) =

м 2

1

н

----

м/с '
м

после формальных сокращений: ( Н/м2 )-с = Па·с.
В ходе анализа нередко оперируют кинематической вязкостью
v = µ/р ; ее формальная размерность / 2/t , а единица измерения в

62

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

СИ - м2/с; физически это следует понимать как перенос им
пульса в единицу времени с объемным потоком между двумя па
ралл ельными площадками в 1 м2 , находящимися друг от друга на
расстоянии 1 м, при движущей силе переноса, равной единице:
мз
[v ] =
2 1

С М
·

·

М

· 

Аналогичные рассуждения можно провести для переноса теп
лоты (рис. 1 .5, б) между изотермическими поверхностями. Ее
удельный поток q (в СИ: Вт/м2 ) согласно той же гипотезе будет
пропорционален градиенту дt/дп. В форме равенства получаем
закон Фурье:
q=

-л}!__
дп

=

л.1�дп11 .

0 . 10)

Множитель Л. называется коэффициентом теплопроводности
(или просто теплопроводностью) . Он представляет собой поток
теплоты, проходящий в единицу времени между двумя парал
лельными единичными площадками ( 1 м2 ), находящимися на
расстоянии 1 м, при разности температур между ними 1 градус;
Вт
в СИ [Л] =
, сокращенно обычно записывают [Л] =
2
К/м
м
·

·

= Вт/(м · /().
В ходе анализа нередко оперируют температуропроводностью
а = Л./ср, имеющей формально размерность м"'l/с. Физически же,
как и в случае переноса импульса, а следует понимать как ха
рактеристику переноса субстанции (здесь - теплоты) с объем
ным потоком между единичными плоскими поверхностями в
условиях, сформулированных при рассмотрении кинемати
ческой вязкости v:
Дж кг К · м 3
= / 2/r: = м2/с .
[ а] =
2

С М
·

·

·

·

К дж кг
·

·

Наконец, перенос вещества по рассматриваемой гипотезе вы
ражается законом Фика, согласно которому удельный поток ве
щества q8 пропорционален градиенту концентраций д С/дп:
qв =

D

-

D ac
дп

=

D

l дп l
ac

·

(1.1 1)

Здесь
коэффициент диффузии ; аналогично v и а он измеря
ется в м3/(м2 ·с· l/м) , формально - в м2/с и характеризует пере-

63

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

нос вещества в единицу времени между двумя единичными
плоскостями , находящимися на расстоянии 1 м, при единичной
разности потенциалов между ними . Заметим: q8 здесь выражен в
мЗ/(м 2 ·с) ; при необходимости выражения массового потока в
формулу ( 1 . 1 1 ) следует (ер. размерности) ввести плотность р :
ас
а
pD
( 1 . 1 l a)
.
qв м с =
дп
В ходе анализа и расчета процессов переноса субстанции не
обходимо располагать закономерностями изменения градиентов
по объему технологического пространства (аппарата) . Реально
эти закономерности удается установить и использовать лишь в
достаточно простых ситуациях: чаще - при переносе субстан
ции в твердых телах или через них, реже - в случае жидкост
ных и газовых потоков. Нередко эти подходы не удается реали
зовать в силу недостаточного уровня знаний о механизме про
цесса. Кроме того, такой путь иногда затруднен из-за сложно
стей теоретического анализа, а также громоздкости получаемых
соотношений. В этих случаях прибегают к упрощенным пред
ставлениям о механизме переноса, что позволяет получить до
статочно простые расчетные выражения . Чаще всего к упомяну
тым упрощениям обращаются в случае переноса теплоты и ве
щества.
Пусть имеется (рис. 1 .6) холодная теплообменная поверх
ность, омываемая горячим потоком жидкости или газа (перпен
дикулярно плоскости рисунка). Около этой поверхности темпе
ратура изменяется от 0 на самой поверхности до t на некотором
удалении от нее (далее - изменением t можно пренебречь) .
Область (по нормали к поверхности) , в которой наблюдается
значимое изменение потенциала (при анализе теплоты - тем
пературы), называется пограничным слоем (ПJiенкой) , в данном
случае - тепловым. Это близкое к реальному представление
удобно заменить упрощенным - модельным, согласно которому
все изменение температуры от 0 до t сосредоточено в достаточно
тонком модельном тепловом поrраничном слое толщиной От, так
что за его пределами температура потока t по нормали к по
верхности не изменяется. Согласно такому модельному пред
ставлению (дt / дп) п=о = Лt/&т , где Лt =: t 0. Тогда удельный теп
ловой поток к стенке, соответственно выражению ( 1 . 10), равен q
-

-

= Л(Лt/0т) = (Л/0т) Лt.

Важно, что речь идет не о реальной толщине пограничного
слоя (вследствие асимптотического характера температурной
кривой точно зафиксировать границу изменения t невозможно) ,
64

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 1. 6. К модели пограничной пленки (/ поток жидкости или газа по нормали к
плоскости рисунка)

а о модельной, т. е. расчетной тол
щине Б,.. В подавляющем боль
шинстве случаев значение Б,. неиз
вестно. Поэтому комIUiекс Л/Б,.
трактуется в целом как особая
удельная характеристика интенсив
ности конвективного теIUiоперено
са. Она носит название коэффици

�-t
е

ента теплоотдачи:

( 1 . 1 2)
который представляет собой поток теIUiоты в единицу времени
через единичную поверхность при температурном напоре в 1 К;
в СИ [а] = Вт/(м2 ·К) .
Аналогичная характеристика
коэффициент массоотдачи
вводится при описании переноса вещества:
( 1 . 13)
13 = D/f:Jд ,
причем f:Jд
толщина (то.же модельная, расчетная
гипотетическая) диффузионного пограничного слоя, получаемая при
спрямлении концентрационной кривой около поверхности мас
сообмена. В СИ [ 13) = м3/(м2 ·с· l ), формально [ 13 ) = м/с.
Значения Б,. и Бд часто бывают достаточно близкими между
собой (особенно для газов, когда налицо сходство в механизмах
переноса теIUiоты и вещества) , но они не обязательно совпада
ют по величине.
Аналогичные подходы могут быть реализованы и при пере
носе других субстанций. При необходимости расчета полных
потоков субстанций в единицу времени значения а и 13 следует
умно.жить на величину поверхности F и соответствующую дви
жущую силу ( Лt, ЛС).
а = Л/Б,. ,

-

-

-

Несмотря на крайне широкое использование коэффициентов отдачи (типа
и �) в технологических расчетах, надо понимать, что их применение обуслов
лено недостаточными знаниями о механизме процессов, а также иногда чисто
счетными осложнениями. Поэтому расчетная концепция, основанная на коэф
фициентах тепло- и массоотдачи , является ограниченной; она сушественно
уступает прямым методам расчета, базирующимся на соотношениях типа ( 1 .9)
- ( 1 . 1 1 ) . Недостатки использования коэффициентов отдачи проявляются осо
бенно ярко, когда эти коэффициенты получаются зависящими от движущих
сил Лt, ЛС или уровней температур, концентраций. Можно предвидеть отказ в
будушем от использования коэффициентов отдачи ; в основу расчетов будут
положены закономерности, связанные с характером потенциальных полей температурных, концентрационных и других.
а

65

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

О перекрестных эффектах Онзагера
С позиций неравновесной термодинамики приведенные выше
подходы к выражению удельного потока q; произвольной суб
станции мoryr быть представлены в обобщенном виде.

Движущая сила, отличная от нуля, приводит к возникнове
нию потока некой конкретной (i-й) субстанции. При этом из
феноменологических соображений ограничиваются линейной
связью типа ( 1 .9) - ( 1 . 1 3) между удельным потоком q; и соот
ветствующей движущей силой (ра�ностью потенциало в) Л;_· Да
лее принимают, что результирующии поток переносимоиu суостан
ции ЯRЛЯется линейной комбинацией потоков, вызываемых характер
ными для рассматриваемых процессов движущими силами.
Пусть: i
вид субстанции; j
тип движущей силы, вызы
вающей ее поток; q;
вектор удельных потоков субстанций,
содержащий i элементов; Лj - вектор движущих сил переноса,
содержащий j элементов; Ау - матрица коэффициентов про
порциональности, содержащая ij элементов. Тогда
-

-

-

q; =

L Аилj .
(j)

(а)

Выражение (а) представляет собой общую запись законов пе
реноса субстанций в линеаризованной форме. Применительно к
конкретным субстанциям ·
q,

q,

=
=

lл �1
дп

адt

!!!!

'!::Б Лt = Ап Л t

А,,Л,
=

перенос
кондукти вны й
теплоты ( закон Фурье) ;
перенос
конвективный
теплоты ( закон
Н ьютона) ;
диффузионн ы й перенос
вещества ( закон Фика) ;
конвекти вны й перенос
вещества
( уравнение
массоотдачи) ;
перенос
электричества
(закон О ма) ;

и т. Д.

ламинарное
течение
жидкости ( закон П уазей 
ля , закон Дар ен )

• Для сокращения записи удельный поток теплоты
индекса t.
66

q

в ( 1 . 1 0) записан без

(6)

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Не введенные ранее обозначения : о
удельное электрическое сопротивление; U
радиус трубопровода.

-

пуrь переноса субстанции ;
электрический потенциал;

R

Р/

-

Согласно второму принципу неравновесной термодинамики
входящие в (а) и (б) коэффициенты пропорциональности удо
влетворяют перекрестным эффектам Онзаrера (иначе
эквива
лентным соотношениям взаимности) для паралл ельного переноса
какой-либо субстанции :
AiJ = Aji .
(в)
О нзагера
(Заметим: правомерность перекрестных эффектов
ограничена "однородными" явлениями · . )
Поясним смысл выражения (в) н а примере тепло- и массопе
реноса. Пусть в процессе переноса этих субстанций участвуют
две движущие сил ы - перепад температур Л1 и перепад кон 
центраци й Л т . Тогда возможно возни кновение двух паралл ель
ных потоков переноса - теплоты q1 и вещества qm, базирую
щихся на перепадах температур и перепадах концентраций со
ответственно. Для рассматриваемых случаев эти потоки можно
описать соотношениями типа (а) , (б).
Перенос теплоты:
(г)
Перенос вещества:
(д)
qm = АттЛ т + AmtЛt
-

·

Здесь основная составляющая переноса теплоты A ttЛ1 (она ба
зируется на движущей силе Л1) дополнена составляющей теплово
го потока А 1тЛ т за счет переноса вещества (движущая сила Л т). Эту дополнительную составляющую переноса теплоты на
зывают эффектом Дюфо. Аналогично: основная составляющая
переноса вещества АттЛт (она базируется на движущей силе Лт )
дополнена составляющей переноса вещества A m tЛ r за счет разно
сти температур Л1. Дополнительная составляющая переноса ве
щества носит название эффекта Соре.
Из соотношений Онзагера (в) следует, что, например, в слу
чае малого вклада теплопереноса в массоперенос (мал коэффи
циент Ат 1, поэтому мала и величина Ат tЛ1) коэффициент A rm, а с
ним и вклад А 1тЛ т массопереноса в теплоперенос,
тоже мал.
-

Пропускные способности

В отечественной литературе достаточно широко используют
ся понятия о сопротивлении пере н осу - удельном и (реже) пол
ном; чаще всего это понятие используют при переносе теплоты

• Подробнее об упомя нуrых ограничени я х см.

[ 1 , 2).

67

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

и вещества. Под сопротивлением переносу понимают отношение
движущей силы, т.е. разности потенциалов (в более общем смыс
ле: характерного перепада потенциалов) , к потоку субстанции удельному или полному. Обознач им: Лt и Л С - температурный
и концентрационный напоры (разности потенциалов, здесь движущие силы рассматриваемых процессов переноса); о толщина прослойки, через которую происходит перенос суб
станции (пусть прослойка будет плоской; это может быть твер
дая стенка или гипотетическая пограничная пленка). Тогда
удельное сопротивление теплопереносу выразится как Лt/q =
= о/Л, полное: Лt/ Q = &/(ЛF), где Q = qF - поток теплоты через
теплообменную поверхность F При использовании коэффици
ента теплоотдачи: Лt/q = 1 /а и Л t/ Q = l/aF В случае переноса
вещества - аналогично: Л С/q8 = О/ D и Л С/М = o/(DF) ; Л С/q8 =
= 1 /13 и Л С/ М = l/j3F, причем М = q8F - поток переносимого
вещества в единицу времени через поверхность контакта F
В аспекте сопротивления переносу могут рассматриваться не
только потоки субстанции , нормальные к поверхности контакта F
(часто - одновременно и к направлению движения рабочего
тела) , и соответствующие движущие силы, но и продольные по
токи и перепады потенциалов. Так, во многих задачах гидравли
ки поток G движется под действием перепада давлений Р 1 (на
входе в объект) и р2 (на выходе); при переносе потока теплот ы
наблюдается характерное изменение температур теплоносителя
от входа в аппарат t' до выхода из него t" и т.п.
В последние годы выявилась большая плодотворность ис
пользования для анализа процессов переноса величин, обратных
сопротивлениям. Они получили название пропускных способно
стей и представляют собой отношение полного потока субстан
ции к соответствующей движущей силе (в более общем плане к характерному перепаду соответствующего потенциала) . Так,
для переноса потока теплоты Q нормально к теплопередающей
поверхности F характерным перепадом температур будет дви
жущая сила (температурный напор) Лt. Тогда пропус кная спо
собность Q/Лt для переноса теплоты путем теплопроводности
выразится как (Л/&)F, а путем конвекции - как aF; аналогич
но - для массопереноса: (D/&)F и j3F. Применительно к про
дольному переносу теплоты ( например, при нагреве потока G
жидкости с теплоемкостью с от температуры t' до t") поток теп
лоты, как будет показано в разд . 7 .5 и следующих, выразится:
Q = Gc( t" - t'). Следовательно, пропускная способность Q/(t" - t') в этом случае составит Gc.
Понятийный аппарат пропускных способностей для различ
ных процессов и их отдельных стадий будет достаточно широко
представлен в этой и последующих главах курса.
68

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Заметим, что в случае линейных соотношений (для постоян
ных µ , А., D, а также а , 13 и т.п.) понятия "сопротивление пере
носу" и " пропускная способность " имеют четкий физический
смысл и определенное математическое выражение. Для нели
нейных процессов и соотношений такой ясности пока нет, но
общие качественные представления сохраняются.
1 .3.3. Подходы к анализу и установлению общих закономерностей
процессов переноса

Основу инженерного анализа составляет выявление количе
ственных связей между различными факторами технологическо
го процесса. Наиболее достоверные результаты дает строгий
анализ, основанный на фундаментальных физических законах и
учитывающий конкретную технологическую обстановку. В идеа
ле такой анализ не должен привлекать каких-либо опытных
данных, он должен исходить из физических основ явлений и
процессов (англичане говорят: "from first principles " ). Однако из
за многообразия и сложности причинно-следственных связей
реализовать такой подход удается весьма редко - лишь для са
мых простых процессов. Между тем инженерная практика зача
стую не может ждать строгих теоретических решений и потому
ищет дополнительные возможности .
На ранних стадиях создания и развития технологического
приема, процесса нередко приходится ограничиваться практиче
скими рекомендациями, базирующимися на положительном и
отрицательном инженерном опыте осуществления этого или
аналогичного процесса. Такие рекомемдации частично сохраня
ют силу и на последующих стадиях модернизации данного и
сходных процессов. Явная недостаточность этих рекомемдаций
приводит к необходимости математических описаний
первона
чально на уровне эмпирических соотношений, связывающих
основные характеристики процесса и вытекающих поначалу из
самых примитивных, а затем и более достоверных представле
ний о физической сущности явлений и процессов (фено
менологический подход). Такого рода расчетные соотношения
носят, как правило, частный характер, и х прогнозные возмож
ности - невелики ; применение их даже для сходных процессов
и ситуаций, но с другими веществами , температурами и тому
подобными условиями, конфигурациями рабочих зон аппаратов
- чревато ошибками. Для расширения сферы использования
таких соотношений и повышения их прогнозных возможносте й
приходится расширять диапазоны исследований (условий, рабо
чих тел, объектов) , охватывая значительное число факторов
-

69

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

(хотя набор их по-прежнему определяется общими представле
ниями о закономерностях процесса) . Тогда устанавливаемые
при обработке опытных данных соотношения получаются более
надежными; за это приходится платить более обширным экспе
риментом, а иногда и усложнением найденных расчетных соот
ношений. В рамках рассматриваемого подхода нередко проводят
чисто формш�ьную обработку опытных данных, строя соотноше
ния (типа регрессионных моделей и др. ) вне физических пред
ставлений о механизме протекания процесса и тем самым заве
домо ограничивая возможности использования расчетного урав
нения узкими рамками проведенного эксперимента. Во всех
рассмотренных случаях нет гарантии приемлемой надежности (в
том числе - прогнозности) получаемых расчетных уравнений ,
поскольку в своей основе они в значительной мере базируются
на чисто инженерной интуиции исследователя - такая база не
всегда надежна.
На более поздних этапах развития науки, технологии обра
щаются к аналитическим исследованиям, строя математические
модели , глубже учитывающие взаимосвязи между отдельными
факторами процесса. Этот путь обычно получает развитие после
накопления солидного объема эмпирических сведений и соот
ношений - без этого не проверить правильность результатов
анализа.
Немалую роль в развитии аналитических методов играет осо
знание недостаточности упомянутых ранее эмпирических и по
луэмпирических подходов. Здесь также остается место феноме
нологическим моментам; однако это происходит на уровне эле
ментарных актов процесса (например, переноса), где прини
маемые феноменологические представления уже достаточно
полно и убедительно апробированы. Далее вьщвигают предпо
ложения о роли и месте упомянутых элементарных актов, о
связях различных факторов, вьщеляя характерные особенности
процесса, обозначают условия его проведения , в том числе ситуацию в начале процесса и в ходе его на границах рабочей
зоны. Последующий анализ должен в идеале привести к матема
тическим выражениям, позволяющим осуществить инженерный
расчет процесса. Нередко в этих случаях математические описа
ния содержат некие численные коэффициенты (множители ,
слагаемые и т . п . ) , значения которых заранее н е известны; и х в
дальнейшем находят из специального опыта, поставленного в
соответствии с полученным математическим описанием, - так
теоретический анш�из и эксперимент дополняют друг друга.

Такой путь должен привести к получению надежных расчет
ных соотношений, применимых в широких рабочих диапазонах,
70

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

но при условии, что удалось достаточно полно выявить элемен
тарные акты и выразить их связи, а потом разрешить возникшие
математические проблемы. В противном случае решения полу
чаются чрезмерно приближенными, описывающими процесс
лишь в общих чертах, так что приходится проводить оценку:
отвечает ли точность решения требованиям инженерного расче
та, т. е. адекватны ли построенная модель процесса и получен
ное решение реальному процессу. Заметим, что особая труд
ность во многих случаях состоит в формулировании начальных
и граничных условий (см. разд. 1 .7): от правильности их записи
в значительной мере зависит адекватность получаемого реше
ния.
В ходе разработки математической модели, базирующейся на
физических представлениях о механизме процесса, иногда полу
чаются весьма сложные (например, трансцендентные) соотно
шения , не разрешимые в явном виде относительно искомой
величины. Здесь приходится обращаться к численным методам
решения (в том числе с использованием ЭВМ); однако при этом
в известной мере теряется общий взгляд на протекание процес
са, зачастую возникают затруднения в определении характера
wrияния отдельных факторов на процесс в целом.
Обилие переменных, громоздкость эмпирических соотноше
ний и приближенность многих аналитических решений способ
ствовали появлению (и крайне широкому распространению в
предшествующие полвека) метода обобщенных переменных. Суть
его заключается в том, что отдельные переменные объединяются в
комплексы - не произвольно, конечно, а по определенным пра
вилам, отвечающим физическому смыслу рассматриваемых яв
лений, процессов. Ч исло таких комплексов, разумеется, меньше
числа отдельных (исходных, натуральных) переменных . Это
позволяет ставить эксперимент, варьируя меньшее число факто
ров (теперь это комплексы вместо натуральных величин) и по
лучать более компактные (иногда и достаточно прогнозные)
расчетные соотношения.
Обобщающий характер комплекса, состаwrенного из
нескольких натуральных (и потому - размерных) величин, су
щественно возрастает, если этот комплекс является безразмер
ным. В качестве таких комплексов выступают критерии подо
бия, числа переноса и некоторые другие величины - о них речь
поЙдет ниже. Каждый такой комплекс имеет определенный фи
зический смысл; поэтому недостаточно представить набор нату
ральных величин в безразмерной форме, чтобы получить обоб
щенную переменную. Это важно подчеркнуть, поскольку в пе
риод уwrечения обобщенными переменными было предложено
71

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

немало безразмерных комIUiексов, лишенных физического
смысла; их использование приводило к формальным расчетным
уравнениям, не обладающим прогнозностью, а зачастую имею
щим мало общего с физическим смыслом процесса.
Аналитический метод и метод обобщенных переменных не
противостоят один другому; их нередко используют совместно.
Так, аналитические выражения часто представлены в диффе
ренциальной форме или весьма громоздки для практического
использования. Можно, не решая этих уравнений, на их основе
сформировать обобщенные переменные и грамотно поставить
эксперимент: ведь теперь уже ясно, какие именно обобщенные
переменные надо варьировать в ходе опыта, чтобы установить
достаточно надежные количественные связи между ними.
При анализе явлений, процессов нередко удается получить
уравнения, качественно правильно отражающие взаимосвязи
между различными факторами; однако количественно результа
ты могут при этом заметно отличаться от наблюдаемых на прак
тике. В этих случаях вводят поправочные коэффициенты; фак
тически это коэффициенты незнания
в их роли часто высту
пают различного рода КПД, коэффициенты эффективности ,
поправочные множители и т. д. Если они лишь несколько
(скажем, на 1 0% или немногим более) корректируют получен
ное ранее решение, то это допустимо: значит, основные эффек
ты учтены, а отклонения обусловлены менее значимыми факто
рами. Конечно, желательно в дальнейшем учесть эти дополни 
тельные эффекты, но и с поправочными коэффициентами фор
мула работоспособна. Однако бывает, что эти коэффициенты
призваны скорректировать аналитическое решение в несколько
раз (скажем, предложена расчетная формула для некоего про
цесса с КПД на уровне 0, 1 -0,2). Это означает, что выявить
основные эффекты и влияющие на них факторы не удалось, и
модель процесса построена на базе второстепенных эффектов.
Успеха на таком пути создания расчетных соотношений не бу
дет; полученные расчетные формулы ненадежны, в изменив
шихся условиях их использование может привести к ошибоч
ным результатам.
В практике анализа явлений и процессов нередко производят
подмену задачи, описывая одно явление в терминах и символах
другого. В ряде случаев эту подмену проводят намеренно, тогда
мы осознаем последствия подмены и можем оценить границы ее
правомерности. В частности , мы осуществляем такую подмену,
когда от выражения IUiотности потока через градиенты темпера
тур и концентраций пере ходим к выражениям через коэффици
енты тeIUio- и массоотдачи; или сложные эффекты в переносе
-

72

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

импульса в некоторых течениях тра ктуем как проявление некой
эффективной вязкости µ 3 , отличающейся от вязкости рабочего
тела µ . Нам придется неоднократно использовать такую подмену
в курсе ПАХТ.
Но в ряде случаев исследователь проделывает такую подмену
неосознанно в порядке "добросовестного заблуждения"; таких
примеров в науке предостаточно. Результат - недостоверный и
неубедительный (а то и просто ошибочный) ход рассужден и й ,
нен ад ежное (иногда неверное) решение. Примером может слу
жить упомянутый выше анализ процесса без предварительного
выявления основных факторов, построение модели на базе ма
лозначащих для процесса эффе ктов. Неосознанная подмена
з адачи неоднократно в истории ПАХТ приводила к казусам , к
совершенно неверным выводам и рекомендациям .
-

1 .3.4. Общая канва анализа

В последующих разделах представлены выводы общих диф
ференциальных уравнений переноса субстанций. Существуют
различные пути анализа, приводящие к конечному результату.
Выберем наиболее наглядный путь, использующий балансовые
соотношения типа ( 1 . 8 ) ; он основан на рассмотрении непо
движного бесконечно малого постоянного объема в движущейся
жидкости (при необходимости - газа, твердого тела) . Удобнее
всего вести анализ в декартовой системе координат (рис. 1 . 7 ) ,
выделяя в качестве пространственного контура элементарный
прямоугольный паралл елепипед с ребрами d.x, dy, dz и рассматри
вая (для единицы времени или бесконечно малого промежутка
dt) потоки соответствующей субстанции через пары граней dxdy,
dxdz и dydz, а также изменения, происходящие внутри выделен
ного элементарного объема dV = dxdydz. В зависимости от рас
сматриваемой субстанции получают дифференциальные уравне
ния неразрывности и переноса субстан ции . И нтегрирование
этих дифференциальных уравнен и й
с установленными условиями одно
z
значности должно привести к урав
нениям, которые можно использо
вать в инженерных расчетах. Фор
мулирование упомянутых услови й и
процедуры интегрирования (или
Рис. 1. 7. К выводу дифференциальных урав
нений переноса: эл ементарный контур в
декартовой системе координат

у

� d'
d�
d.x

х

73

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

способы замены этих математических операций при возникно
вении определенных трудностей ) рассматриваются в соответ
ствующих главах курса.
В подходах к выводу уравнений неразрывности и переноса
различных субстанций (а для последних - и в конечных выра
жен иях) и меется много общего. Последующий анализ ведется с
подчеркиванием этих общих моментов и вместе с тем с указани
ем (для каждой субстанции) на особенности выводов и полу
ченных закономерностей.
1 .4. УРАВНЕНИЯ НЕРАЗРЫВНОСТИ И РАСХОДА
1 .4. 1 . Уравнение неразрывности

Запишем закон сохранения массы для неподвижного прямо
угольного элементарного паралл елепипеда (контур) в движу
щейся жидкости (рис. 1 . 8 ; координатные оси в целях упрощен ия
рисунка не показаны) для бесконечно малого промежутка вре
мени d<. Закон сохранения предполагает отсутствие Источников
и Стоков массы внутри контура. Предварительно укажем , что
элементарные объемный и массовый потоки жидкости , прохо
дящей в единицу времени через элементарное сечение d/ нор
мально к нему, составляют
( 1 . 1 4)
d G = p wd/,
d V = wdf,
может изменяться во вре
причем в общем случае плотность
р
мени и по координатам.
Вдоль оси х через левую грань dydz со скоростью wx в контур
за время d• входит элементарное количество жидкости Прх
уходит Ухх =
= p w ydzd• , через правую
PWx +
( х
) dx: dyd zd • . Для оси х разность + Прх - Ухх составляет
+д
х
(после раскрытия скобок и очевидных сокращений)

�
�

r

J

(а)
- д(рwх ) dxdydzd•, или - д(рwх ) dVd<.
х
х
д
д
Аналогичные разности + Прj - Yxj (j = у, z) для осей у и z

запишутся:

- д(рw у ) dVd't и - д(рw, ) dVd't.
у
z
д
д

(б)

Соответственно основному балансовому соотношению ( 1 . 8)
необходимо выразить накопление м ассы в контуре за время d<.
74

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

---� P w х

dz

Рис. 1 . 8. К

+ д( р их
дх

) dх

выводу уравнения неразрывности

Количество массы в объеме dV в момент ' равно p dV. Посколь
ку р может изменяться по координатам (х, у, z) и+ во времени
(•) , то Накопление массы к моменту времени '
d• записы
вается в частных производных:
д( рd V)
др
(в)
Нак =
dт = - dVdт.

д't

т

Собирая теперь найденные выше элементы баланса (а) , (б) и
(в) в ОБС ( 1 .8 ) , получаем после сокращен ия на dV и d• уравне
ние неразрывности (сплошности) :

- др
т

=

+

д(рw х )
дх

д(рw у )
ду

или в несколько иной форме :

др
т

+

д(р w х )
дх

+

д(рw у )
ду

+

+

д(pw z )
дz

( l . 1 5)

д( pw z ) = О
.
дz

( l . 1 5')

И нтегрирование полученного уравнения с конкретными
условиями однозначности приводит к закону сохранения массы
в интегральной форме.
Применительно к ряду частн ых случаев общее уравнение
( 1 . 1 5) существенно упрощается.
Для стационарных процессов др/m = О, и тогда

д(рw х )
дх

+

д( рw у )
ду

+

д( pw z )
дz

=

О

.

В случае однонаправленных течен ий, скажем вдоль оси
дет wy = wz = О, так что

- др
т

=

д(рw х )
дх

( l . l 5a)
х,

бу

( l . 1 5б)

а если такое движение является еще и стационарным, то
d(p wx )
( l . 1 5в)
= О'
dx
причем частные производные заменены здесь на обыкновенные,
поскольку осталась только одна независимая переменная х.

75

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

В случае несжимаемой жидкости (практически - при не
сли шком больших изменениях давления, когда можно считать р
"" const) справедливо дp/dt = О; кроме того, р может быть выне
сено из - под знака производной в оставшихся слагаемых уравне
ния ( 1 . 1 5) и сокращено. Тогда

дw у
дw х
+ дх
ду

+ - = О'

дw z
дz

( 1 . 1 5г)

а для однонаправленного движения несжимаемой жидкости - еще
проще:
дwх = d w ., О
( 1 . 1 5д)

дх

dx

=

.

Если поток представляет собой смесь N компонентов, то
уравнение неразрывности может быть записано не только для
всей смеси в форме ( 1 . 1 5) , но и для отдельного i-го компонента
(i = 1 , 2, " " N) . Для этого вводится понятие о парциальной плот
ности (по суmеству - о массообъемной концентрации , кг/м3 )
данного компонента: р; = dm;/dV, где т; - масса i-го компо
нента в контуре dV. В принятых обозначениях уравнение нераз
рывности в отсутствие Источников и Стоков компонента i при
нимает вид

др ; = д(р;wх) + д(р ; wу ) + д(р;w,) .
дt
дz
дх
ду

- -

( l . 1 5e)

Для различных частных случаев уравнение (l . 1 5e) также мо
жет быть представлено в упрощенных формах записи.
При налич и и химических реакций закон сохранения массы i
го компонента может быть нарушен из-за появления Источн и 
ков и ( или ) Стоков этого компонента. Пусть интенсивность его
появления ( исчезновения) в результате реакции характеризуется
приращением количества его молей кv; - в единице объема и в
единицу времени ; значит, при
ращение массы составит к v;М;,
где М; - молярная масса ком
z
понента i (размерности : [ кv;] =
кмоль/(мЗ·с) ;
[ М;] = кг/кмоль;
[кмоль/(м3 ·с) ] х
[ кv;М;]
кг/(м 3 ·с). Тогда
х(кг/кмоль)
входящая
в ОБС ( 1 .8) раз
ность Ис - Ст для элементар
ного объема dV за бесконечно
=

Рис. 1. 9. Связь декартовых и цилин
дрических координат

76

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

малое время d-r запишется как к v; M,<lVd-r. С учетом Источников
и Стоков уравнение неразрывности после сокращения на dVd-r
(см. вывод уравнения) примет вид

др; + д(р;W х ) + д(р;W у )
д't
ду
дХ

+

д(р;w,; ) =
дz

к V/·М·1 .

( 1 . 1 6)

Разумеется, при сложении уравнений ( 1 . 1 6) для всех N компонентов смеси мы придем к выражению ( 1 . 1 5), поскольку
N

:L

i=1

кv;М; = О

, так что для смеси в целом закон сохранения мас

с ы остается справедливым.

В технологической практике рабочее тело (rаз, жидкость и т.п.) часто дви
жется в пространстве цилиндрической конфигурации - трубе, колонне, ци
линдрическом аппарате. В этом случае бывает удобной запись уравнения не 
разрывности в 14ш11Ндри•ескмх координатах (рис. 1 .9): декартовы координаты х и
у заменяются на радиальную г и угловую q>, а координата z
сохраняется.
Связь координат - очевидна: х = r cosqi, у = r sinq>, z = z.
В результате преобразования координат (ввиду громоздкости оно здесь не
приводится) общее уравнение неразрывности типа ( 1 . 1 5') в отсутствие Источ
ников и Стоков массы приобретает вид

-

-

др + !. д(р . г . w, ) + !. д(pw 'I' ) + д(p wt ) = О
дt
г
дг
г дq>
дz

( 1 . 1 5ж)
'

где w, и wqi
радиальная и угловая составляющие скорости.
В случае несжимаемой жидкости (р = const) первое слагаемое обращается в
нуль, а в остальных слагаемых р сокраща ются. Тогда
!. д( г . w, ) + !. дw'I' + д wt
г
дг
г дq>
дz

=

(

)

дг + !. дw ср + дwt = О.
!. r дw , +
w,
дz
г
дr
дг
г дq>

После раскрытия скобок и сокращений
дw , w , + !. дw'I' + дw t
+
дr
г
г дq>
дz

= О.

(г)

( ! . ! Sз)

Из ( 1 . 1 5е) и ( l . 1 5ж) нетрудно получить выражения для частных случаев
движения жидкости, например для осесимметричного течения, т. е. при
дwqi/дq> = О .

1 .4.2. Уравнения расхода

На основе введенных ранее понятий элементарных потоков
d V и d G получают уравнения расхода для конечных живых сече
ний и участков аппаратов, трубопроводов. Для нахождения пол
ного массового потока в единицу времени через живое сечение f
проинтегрируем второе из выражений ( 1 . 14) по сечению f и ис
пользуем теорему о среднем:
(д)
G = f р wd/ = (pw)cp/ .
1

77

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Будем в дальнейшем пренебрегать возможными, но весьма
малыми изменениями плотности потока в сечении f, тогда
(pw) cp = p wcp · В результате из (д) получ ают уравнение массовоrо
расхода для лiобой жидкости (в том числе сжимаемой, т.е. для газа):
G = P Wcrf = pw/ ,
( 1 . 1 7)
причем в правом фрагменте формулы под w понимают среднюю
скорость (индекс " ер" здесь просто опушен).
Если между двумя сечениями, помеченными индексами " l " и
" 2 " , нет Прихода и Ухода жидкости (газа, твердого) , то в отсут
ствие Накоплений (для стационарных процессов)
( 1 . 1 7а)
G = P 1 W i/i = P 2 w'J.h ;

в случае несжимаемых жидкостей это соотношение записывает
ся в форме
( 1 . l 7б)
G = pwifi = pw'J.h
и может быть использовано также для нестационарных течений.
Заметим, что выражения ( l . 1 7)
( l . 1 7б) могут быть получе
ны из уравнения неразрывности для однонаправленного движе
ния типа ( l . 1 5в) - до сокращения на d V = dxdydz = dxd/
Для несжимаемых жидкостей (практически для реальн ых
жидкостей, а также приближенно для газов, если перепад дав
ления между сечениями '' ! '' и "2" мал в сравнении с абсолютны
ми давлениями) из выражений (1 . 1 7) и (l . 1 7б) получаются урав
нения объемного расхода V = G/ p :
( l . 1 8)
V = wf
При отсутствии Приходов и Уходов жидкости между рас
сматриваемыми сечениями
V = wifi = w'Jh,
( l . 1 8a)
причем в силу несжимаемости жидкостей (здесь Нак = О ) фор
мула ( l . 1 8a) справедлива также для нестационарных течений.
Из ( l . 1 8) и ( 1 . 1 8а) следует, что при постоянном расходе V
увеличение живого сечения потока f сопровождается понижени
ем его скорости w.
Выражения типа ( l . 1 7) , ( 1 . 1 7а) , ( l . 1 7б), ( 1 . 1 8) и ( l . 1 8a) широ
ко используются в инженерных расчетах.
Специально подчеркнем, что в технологической практике
нередки ситуации с неравномерным во времени движением по
тока, значит и с изменяющейся во времени скоростью (эта не
равномерность может быть специально организована либо обус
ловлена природой явления). В таких случаях тоже приходится
усреднять скорость , но уже во времени : говорят об осредненных
скоростях. Надо обязательно видеть разницу в усреднении локаль
ной скорости по живому сечению и в осреднении мгновенной ско
-

рости по времени.

78

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

1 .5. УРАВНЕНИЯ ПЕРЕНОСА ИМПУЛЪСА,

ТЕПЛОТЫ И ВЕЩЕСТВА

1 .5. 1 . Ди фференциал ьное уравнение движен и я
несжи маемой жидкост и (перенос и мпульса)

Перенос и мпул ьса ( коли чества движения) детал ьно изучается в
главе " Гидравл и ка" . Кардинальн ая п роблема при анал изе переноса
и м пул ьса состоит в определении давления и скорости в и нтере
сующей нас точке технологичес кого пространства в произвол ь н ы й
момент времен и :

р

=

p(x, y, z, 1 ) ; w w(x, y, z, 1 ) .
=

(а)

В кон кретных задачах гидравл ики уравнение переноса и м пул ь
са испол ьзуется совместно с уравнениями неразрывности и (или)
расхода.
Будем рассматри вать контур - элементарн ы й прямоугол ь н ы й
параллелепи пед, выделен н ы й в движущейся несжимаемой ж идко
сти (рис. 1 . 1 О). Как и при вы воде уравнения неразрывности, огра
н и ч и мся вначале изучен ием ситуации применител ьно к одной из
осей координат ( например, оси х); полученные закономерности
распространи м в дальнейшем на течение вдоль осталь ны х осей.
А нал и з можно вести для переноса импульса и кол ичества д ви
же ния л ибо относя все потоки этой субстанции к еди н и це времени,
т.е. для действующих c wi , - результат будет одинаковы м. Выберем
второй путь: будем выражать соответствующие с и л ы и зап исывать
балансы сил согласно ОБС ( 1 . 8), отслежи вая одновременно (в це
лях уяснения физического смысла) и составляющие переноса и м 
пул ьса (кол и чества движения) з а един и цу времени .
Но р м ал ь н ы е п ове р х н остн ые с ил ы ( с ил ы давл е н и я ) , дейст
вующие вдол ь оси х н а л е вую гра н ь dy dz равн ы pdy dz (с поз и ц и й
переноса и м пул ьса - это е г о П р и ход в ко нту р dV через л е ву ю

---- р +

i}- dx

' dz
' '
' V.

0с" ...

Рис. 1. 10. К выводу основного уравнения гидродинам и ки

79

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

грань) . Справа, где давление на элементарную грань равно
др dx, нормальная сила против оси х запишется:
р+
(р +

дх
др
+
dx)dydz (с позиций переноса импульса - это его Уход из
дх
контура dV через правую грань) . Разность этих нормальных сил
(в символике ОБС:
+ П р н - Ух н ) составляет
р
д
dx)dydz, или - др dxdydz = - др dV. (б)
pdydz - (р +
дх
дх
дх

Танrенциальные поверхностные силы (сдвига, внуrреннего
трения) рассмотрим сначала для какой-нибудь пары граней ,
например верхней и нижней (см. рис. 1 .8). Вдоль нижней грани
dxdy действует сила tнdxdy, где tн - напряжение трения на
н ижн ей грани. Эта сила выражает перенос импульса из объема
жидкости снизу через грань dxdy в элементарный контур dV,
получающий импульс (это Приход: ПРт) . Через верхнюю грань
dxdy контур dV теряет импульс (это Уход: Ухт) в жидкостное
пространство; в силовом выражении эта потеря импульса запи
сывается как t8dxdy, где t8 - напряжение трения на верхней
грани . Обозначим составляющие скорости
по оси х на

н ижнеи и верхней гранях соответственно
�

Wx и Wx

+

дw х d
z. Для
дz

--

рассматриваемой пары граней речь идет об изменении скорости
Wx при переходе от нижней грани к верхней, т. е. вдоль оси z;
ось z здесь - нормаль к элементарной площадке dxdy. Выразив
теперь tн и t8 по формуле ( 1 .9), получим силы, действующие на
н ижн юю и верхнюю грани (соответственно Приход и Уход им
пульса через упомянутые грани) -

дw х dxdy ,
µ __
дz
дw
д
µ - (Wx + х dz)dxdy .
дz
дz

tнdxdy =
t8dxdy =

-

-

__

Разность этих тангенциальных сил или потоков импульса (по
символике ОБС: + Пр' - Ух') составляет - после раскрытия
скобок и очевидных сокращений -

д2w
д 2w
(tн - t8)dxdy = µ ---f dxdydz = µ ---f dV.
дz
дz
Тангенциальные силы вдоль оси х действуют не

(в)

только на
рассмотренную пару граней. В той же манере могут быть про -

80

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

анализированы силы, действующие, например, на ближнюю и
дальнюю грани dxdz; разница в том, что нормаль к этим пло
щадкам направлена по оси у. Поэтому в результате преобразо
ваний, аналогичных тем, что привели к выражению (в) , полу-

2
µ д �х dV. Соответствующий анализ для левой и правой
ду
д2 w
граней дает µ ---f- dV. В целом баланс всех тангенциальных сил
дх
вдоль оси х (в символах ОБС: + Пр - Ух) выражается суммой:
2 х
a 2 w_
a2w
х + д w_
х dV = µV2 wx<IV,
_
µ
+
(г)
дz 2
дх 2
ду 2

ч ится

(

__

__

J

__

причем оператор Лапласа (лапласиан) v 2 означает сумму вторых
производных по осям координат от величины, стоящей под зна
ксм этого оператора (в рассматриваемом случае - от Wx) .
На массу жидкости плотностью р в объеме dV могут действовать
внешние массовые силы; в терминах ОБС ( 1 .8 ) - это Источники
и Стоки . Обозначим Рх проекци ю равнодействующей единич
ной массовой силы вдоль оси х. Тогда сила, приложенная по
оси х к массе жидкости в объеме dV (с позиций переноса внешний импульс; в символах ОБС: + Ис - Ст) , составит
(д)
Рх pdV .
Равнодействующая всех рассмотренных выше сил обусловит
Результат ( Рез - в терминах и символах ОБС) . П о 11 закону
Ньютона он равен произведению массы жидкости в контуре
(объеме) dV на ускорение вдоль оси х:

р dV

.

dwx
dt '

(е)

связывая систему координат с неподвижным элементарным па
ралл елепипедом , эту величину тра ктуют в смысле силы инерции .
С позиций переноса рассматриваемой субстанции Результат
надо понимать как Накопление количества движения ( Нак) объемом dV, массой p dV.
Собирая теперь найденные величины по (б), (г) , (д) , (е) и
следуя ОБС ( 1 . 8 ) , приходим после сокращения на dV к балансо
вому соотношению для оси х:

д
дх

р + µУ' 2 w + Р р = р
-х
х

-

dwx
.
dt

(ж )

Обычно каждое из слагаемых делят на р и, подставляя
81

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

µ/р =

v, записывают (ж) в виде

d wx = p _ ..!_ дp + vV 2
wх
х р дх
d't
р

или

..!_ др
р дх = х

- d w,
+ vV 2 w
х
d 't

( 1 . 1 9)

( 1 . 1 9а)

Скорость wx, согласно (а) , является функцией координат и
времени. Поэтому ее полный дифференциал равен

дw
дw
дw
дw
х dz
х d't + --х dх + -х dу + -dwх = -дх
д't
.
дz
ду
Отсюда, имея в виду, что dx/dт = Wx, dy/dт = Wy, d </dт = wz,
легко найти полную производную d wxfdт (ее еще называют суб
станциональной производной* и обозначают Dwxfdт), поделив
каждое слагаемое на dт:
dwx -дwх +
дwх
дw х + w --(з)
w дwх
х дх + w у -z дz
d't = дт
ду
С этим значением производной dwxfdт выражение ( 1 . 1 9)
принимает вид

дw
дw
д
д
х = р _ ..!_ р + vV 2w . ( 1 . 1 9б)
х + w wх + w
х
х
х
z
дх
д
у ду
дх
р
д't
Существенно, что при стационарном течении дwхfдт = О, но
dwxfdт совсем не обязательно равно нулю, поскольку силы
дw

х +w

z

инерции возникают не только при изменении с течением вре
мени скорости в точке - первое слагаемое в правой части вы
ражен ия (з), но и при ее изменении от точки к точке вдоль оси
координат - остальные слагаемые в правой части (з) .
Специально напомним, что при выводе уравнений ( 1 . 1 9) на
стадии получения соотношений (6) , (в), (д) и (е) нас не должны
заботить знаки разностей типа (Пр - Ух) или величин Рх и
dwxfdт. Согласно правилам математики все эти приращения
принимаются положительными, а знак скажется (проявится) при
подстановке пределов интегрирования или условий однознач
ности (скажем, граничных условий) либо при конкретизации
технологической проблемы (где знак, например Рх, будет просто

• Субстанциональная производная - особый вид полной производной. Суб
станциональная производная подразумевает, что определяется полная произ 
водная при движении субстанции ; при этом входящие в математические выра
жения производные от координат по времени имеют смысл скоростей по соот
ветствующим осям координат.
82

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

задан условиями задачи). Это положение полностью относится
также к анализу переноса теплоты и вещества, изложенному в
последующих разделах.
Выражения, аналогичные ( 1 . 1 9 - 1 . 1 9б), могут быть получе
ны и для других осей координат. Чаще всего их записывают
решенными относительно слагаемых типа др/дх, т.е. в форме
( 1 . 1 9а):

..!. др Р d wx + v'V2 w
dt
р дх =
dwY
1 др
+ v 'V 2 wY
Р
�
=
у
р ду
..!. др р d w, + v'V 2 w
р дz =
dt
-

х

х

-

-

z

( 1 . 20)

z

Эта система уравнений и представляет собой основное урав
нение rидродинамики (уравнение Навье-Стокса) для несжимаемой

жидкости.
Зафиксируем: в терминах баланса сил (и потоков импульса
соответственно) член в левой части выражает силы давления
(разность Приходов потоков импульса в контур и Уходов из
него за счет нормальных сил); первое слагаемое в правой час
ти - массовые силы (внутренний Источник импульса в контуре
или его Сток - за счет внешних причин); второе - силы инер
ции ( Накопление контуром dV количества движения); третье силы внуrреннеrо трения, вязкости (разность Приходов потоков
импульса в контур и Уходов из него - под действием тангенци
альных сил). Смысл обыкновенных производных dwy/d't и dwJd't
раскрывается аналогично тому, как это было сделано для суб
станциональной производной вдоль оси х: dwxfd't.
Для сжимаемых жидкостей (газов) основное уравнение гид
родинамики записывается более сложно; в нем появляются до
полнительные слагаемые, учитывающие сжимаемость (с исполь
зованием отдельных моментов, связанных с уравнением нераз
рывности).
1.5.2. Дифференциальное уравнение переноса теплоты
в движущейся жидкости

Перенос теплоты детально изучается в главах " Основы тепло
переноса " и "Теплопередача и теплообмен " . Кардинальной про
блемой при анализе теплопереноса является определение темпе
ратуры в интересующей нас точке технологического про
странства в произвольный момент времени:
(и)
t = t(x, у, z, 't ) .
83

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

выводу основного урав
нен ия теплопереноса
Рис. 1. 11. К

Поскольку в общем случае
распределение температур свя
зано с закономерностями течеОсь х
ния, то в конкретных технологических задачах уравнение
теплопереноса используется
совместно с уравнениями неразрывности , расхода и гидродина
мики .
Будем рассматривать перенос те пл оты за бесконечно малый
промежуток времени dt применительно к контуру - элементар
ному прямоугольному параллелепипеду (рис. 1 . 1 1 ) , первона
чально - вдоль оси х.
Приход теплоты в контур за счет теплопроводности (кондук
ции) через левую грань dydz, где температура равна t, согласно

дt dydzdt.
dt составляет Прх = -Л. дх
дt dx, теп
Ч ерез правую грань dydz, где температура равна t + дх
лота уходит из контура - за время dt в количестве Ухх =
д
дt
= -Л. - (t + - dx)dydzdt.
дх
дх
закону Фурье ( 1 . 1 0) за время

Разность этих Прихода и Ухода (потоки теплоты на рисунке
показаны стрелками) после раскрытия скобок и очевидных со
кращений выразится так:
+

Прх - Ухх =

д 2 t dVdt.
д 2 t dxdydzdt = Л. Л. дх 2
дх 2

(к)

Аналогичные разности кондуктивных потоков теплоты вдоль
осей у и z запишутся как
+ Пру -

2
д2t
Л. �2 dVdt и + Пр, - Ух, = Л. -2 dVdt. (л)
дz
ду
Общее количество теплоты, воспринятое объемом dV за вре
мя dt путем теплопроводности, будет равно:
Уху =

=
84

(

+ Пр - Ух = I ( + Прj - Yxj) =
j

)

2
2
2
Л. �2 + �2 + � dVdt = Л.V2tdVdt,
дх
ду
дz 2

(м)

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

причем j = х, у, z - направление по осям координат (индекс сум
мирования); символ v 2 обозначен и использован в разд. 1 .5. 1 .
В общем случае в контуре dV мoryr существовать Источники
и(или) Стоки теплоты - за счет экзо- или эндотермической
реакции, индукционного нагрева, ряда других причин. Обозна
чим Источник (Сток) теплоты, отнесенный к единице объема и
единице времени, через Qv (в 1 СИ: Дж/м3· е) . Тогда для элемен
тарного объема dV и временного промежутка dt можно записать
алгебраическую сумму:
+ Ис - Ст = QvdVdt.
(н)
В результате кондуктивных потоков по (м) и тепловыделения
(теплопоглощения) по (н) произойдет Накопление теплоты, т.е.
нагрев или охлаждение жидкости в элементарном контуре dV температура изменится на величину dt:
Нак = epdVdt,
(о)
rде с

-

теплоемкость рабочего тела в объеме dV.

Собирая теперь найденные в (м) , (н) и (о) элементы баланса
в общее соотношение ( 1 .8.), приходим после сокращения на dV
и dt к следующему выражению:

dt
dt

ер - .

(п)

= aV 2 t + � .

( 1 .2 1 )

ЛV 2 t +

Qv

=

Обычно каждое слагаемое делят на ер и предстаwхяют резуль
тат решенным относительно d t/dt . Тогда после замены Л/ер = а
получ ается

�
dt

ер

Поскольку температура по (и) есть функция координат и
дt

дt

дt

-

времени, то d t = - dt +

дх

дt
dx + dy +
ду

дt

-

дz

dz. Отсюда, поде-

лив все слагаемые на dt и выражая производные пути по време
ни вдоль осей координат в виде соответствующих скоростей (см.
раздел 1 . 5. 1 . ) , имеем

dt =

�

дt

дt

+

+ wу � + wz �
х�
�
�
�

w

(р)

С этим значением полной (субстанциональной) производной
выражение ( 1 .2 1 ), предстаwхяющее собой дифференциальное

уравнение переноса теплоты в движущейся жидкости (уравнение
Фурье - Кирхrофа) , принимает вид:
дt

дt

+ wх � +
дх

w
У

�
ду

+

� aV2 t + Qv
z дz =
ер

w

( I .2 l a)
85

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Существенно, что при стационарных течениях дt/дт = О, но
dt/d.x и другие производные от температуры по осям координат

совсем не обязательно равны нулю, поскольку температура мо
жет изменяться не только во времени, но и от точки к точке.
Первое слагаемое в левой части уравнения ( l .2 1 ) характери
зует локальное НакоПJJение теПJJоты объемом dV за счет измене
ния температуры во времени в рассматриваемой точке. Сла
гаемые типа wхдt/дх выражают Накопление теплоты при переме
щении элемента dV от точки к точке - это перенос субстанции
(здесь - те пл оты) путем ВЬIН)']IЩенной конвекции (т.е. потоком,
движущимся со скоростью Wx и т.п.). Первое слагаемое в правой
части отвечает за перенос теплоты теПJJопроводностью; второе за теПJJовыделение (теплопоглощение) внутри контура dV.
1 .S.3. Дифференциальное уравнение переноса вещества
в движущейся жидкости

Общие закономерности переноса вещества детально изучают
ся в главе " Основы массопереноса" , а применительно к отдель
ным случаям, вариантам, условиям - в конкретных главах, опи
сывающих различные массообменные процессы. Кардинальная
задача при анализе переноса вещества состоит в определении
концентрации компонента (выбранного нами i-го или каждого)
в какой-либо точке технологического пространства в произ
вольный момент времени:
С; = С,{х, у, z, t).
(а)

Поскольку распределение концентраций в общем случае свя
зано с закономерностями течения, а зачастую и теплопереноса,
то в конкретных технологических задачах уравнение массопере
носа используется совместно с уравнениями неразрывности,
расхода, переноса импульса, а при необходимости - и переноса
теплоты.
Анализ переноса вещества будем вести по той же канве, что
и импульса, и теплоты; в качестве потенциала здесь выступает
концентрация интересующего нас компонента смеси С;. В целях
согласования с уравнением
неразрывности ( 1 . 1 6) будем
оперировать (это необяза
д С; dx
тельно) мольно-объемными
�----°"' С +
; --ох
СИ:
концентрациями
[в
( кмоль
компонента i)/мЗ ] ;
' dz
Ось х

86

Рис. 1. 12. К выводу основного урав
нения переноса вещества

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

-

связь такой концентрации с массообъемной Cfl/0 (в кг i/м3 )
молярная масса [в СИ [ М;] =
очевидна: Cf11° = С;М;, где М;
= (кг компонента i)/(кмоль компонента i) ] , это ясно из сопостав
ления размерностей:
кг i
кг i
к.моль i
= з .
з
к.моль
i
м
м

-

Рассмотрим мольный поток вещества (компонента i) вдоль
оси х за счет диффузии
за бесконечно малый интервал време
ни dt применительно к бесконечно малому объему - контуру
dV (рис. 1 . 1 2). Пусть концентраци я компонента i на левой грани
dydz равна

С;,

на правой С; +

д С1·
-дх

dx. Тогда согласно закону

Фика ( 1 . 1 1 ) Приход вещества в объем dV через левую грань
выразится: Прх =

dx)

--

-D д Сх1· dydzdt,
д

а Уход Ухх =

(

д
- Dдх С;

+

д С; dуdzd1. Разность этих мольных потоков вещества пос
дх
ле раскрытия скобок и сокращений составит
а 2 с1. dxdydzdt = D-а 2 с1. dVdt.
+ Прх - Ухх = D-(т)
дх 2
дх 2
+

Аналогичные разности потоков того же компонента вдоль
осей у и z запишуrся как
+ Пру - Уху =

-

D а 2С·-1dVdt
ду 2

и + Прz - Yxz =

-

.
D а2 с'2 dVdt .
дz

(у)

Тогда общее количество компонента i, воспринятого за счет
диффузии элементарным объемом dV за время dt, будет равно
+ Пр - Ух = L ( + Прj - YXj) =

(

)

(ф)
D д 2х�i + д 2�; д 2�; dVdt lJV2 C,dVdt ,
ду дz
д
причем j = х, у, z
направления осей координат (индекс сум
=

j

-

=

мирования); оператор v 2 обозначен и использован в разделах
1 .5. 1 и 1 .5.2.
В общем случае в элементарном объеме dV мoryr существо
вать Источники и (или) Стоки компонента i за счет химических
превращений. Эти Источники (Стоки) в молях компонента i,
отнесенные к единице объема и единице времени, были в разд.
87

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

1 .4 обозначены к vi· Тогда для объема dV и временн ого интервала

dt можно записать:

K v;

(х)
В результате диффузии компонента по (ф) и его возникнове
ния (исчезновения) по (х) в элементарном объеме dV может
происходить Накопление компонента, т.е. изменение его кон
центрации - за время dt на величину d С;:
(ц)
Нак = dVd C;.
Собирая теперь найденные в (ф) , (х) и (ц) элементы баланса
в общее соотношение ( 1 .8), после сокращения на dV и dt при
ходим к следующему выражению:
+ Ис - Ст

=

IJV 2 C1 + к VI

·

dVdt.

dC·
= -dt
'

(ч)

Это выражение обычно записывают решенным относительно

d C;/dt, причем индекс "i " часто опускают, подразумевая, что
речь идет об определенном компоненте, концентрация которого

С = С;:

dC
dt

- = DV 2 C + к v ·

( 1 .22)

Поскольку С изменяется по координатам и во времени, то
точно так же, как при переносе и м пульса или теплоты (разд. 1 .5 1
и 1 .52),
ас
ас
ас .
d c ас
(ш)
=-+ w +w +w z az
х ах
у ау
дt
dt
С этим значением полной (субстанциональной) производной
выражение ( l .22) , представляющее собой дифференциальное

уравнение переноса вещества в движущейся жидкости (уравнение
Фика), принимает вид

ас
+w
at

х

ас
ах

-

+w
у

ас
ау

-

+w

ас

z

az

-

- IJV 2 С + K v,

_

( 1 .22а)

причем в случае стационарных течений д С/дt = О , но совсем не
обязательно равны нулю слагаемые типа wх(дС/дх) - в полном
соответствии с замечаниями, сделанными в разд. 1 .5 1 и 1 .52.
Первое слагаемое в левой части уравнения (l .22) характери
зует изменение локмьной концентрации (Накопление) компо
нента во времени в объеме dV . Слагаемые типа wх(дС/дх) также
характеризуют Накопление компонента, но в связи с перемеще
нием объема dV в технологическом пространстве - говорят о
переносе вещества путем вынужденной конвекции. Первое ела88

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

гаемое в правой части отвечает за перенос компонента пуrем

диффузии; второе слагаемое - за пояВJiение (исчезновение) этого

компонента внуrри объема dV в результате химической реакции .
Выражение типа ( 1 .22а) может быть записано и для массо
объемной концентрации компонента; для этого следует каждое
слагаемое умножить на молярную массу М = М; рассматри
ваемого компонента:

а с мо
а с мо
ас мо
а с мо
+ w -- + w
+ w -- = Dv 2 c м o + к v М' ( l .22б)
х
z
дt
дх
у
ду
дz
причем,
как указывалось в разд. 1 .4, массообъемная концентрация смо представляет собой парциальную плотность i-го ком
понента.
--

--

Сходство полученных выше математических описаний про
цессов переноса импульса, теплоты, вещества указывает на
сходство в глобальных закономерностях и механизме самих про
цессов. Проблемы аналогии в переносе различных субстанций
затронуrы в последующих разделах этой главы, а более подроб
но - в главах 6 и 1 0.
1.6. МОДИФИКАЦИИ УРАВНЕНИ Й ПЕРЕНОСА

Уравнения переноса ( 1 . 1 9) , ( 1 .20) , ( 1 .2 1 ) , ( 1 .22) в разд. 1 . 5
представлены в достаточно общем виде (иногда с ограничения
ми; скажем, уравнение Навье-Стокса - для несжимаемой жид
кости) . Применительно к ряду конкретных случаев и условий эти уравнения могуr быть модифицированы; при этом зачастую
они упрощаются (иногда - весьма существенно) или становятся
удобнее для аналитических решений. Примеры таких упроще
ний уравнения неразрывности были приведены в разд. 1 .4. Про
демонстрируем некоторые возможности модификаций уравне
ний переноса (в основном на примере уравнения Фурье
Кирхгофа).
1 .6. 1 . Условия протекания процесса переноса

В случае стационарных процессов из приведенных выше
уравнений переноса выпадает член, содержащий частную произ
водную по времени: �/дt, дt/дt, дС/дt. Тогда принятое в качестве
итпострирующего примера уравнение ( 1 .21а) запишется так:

w

дl

-

х

дх

+w

У

дl
+w
ду

qv
дl
2
- = a"V t +
дz
ер

-

=

·

( 1 .2 1 б)
89

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

В отсутствие Источников и Стоков субставнции (внешних мас
совых сил и импульса; теплоты; вещества) выпадает слагаемое,
содержащее соответственно Рх (либо Ру, Рт) , qv, кv. Тогда урав
нение ( l .2 l a) примет вид

дt

дt

дt

дt

- + wx - + wy - + w. - = aV 2 1 ,
ду - дz
дх
д-t

а в случае стационарного процесса - еще проще:

дt
дх

дt
у ду

дt
; дz

( 1 .2 1 в)

w - + w - + w - = aV 2 / .

( 1 .2 1 г)

д 2 t qv
дt
дt
- + w - = а- + - ·

( 1 .2 1д)

х

Заметим, что при переносе импульса (баланс сил) в уравне
нии Навье - Стокса ( 1 .20) нередко выпадают слагаемые � лишь
по отдельным осям координат j = х, у либо z. Так, при рассмот
рении течения в поле сил тяжести (пусть она направлена вдоль
вертикальной оси z обраща тся в нуль величины Рх и
а
!
�
Р�,
проекция единичнои массовои силы на вертикальную ось Pz =
= -g, где g - ускорение свободного падения, знак " минус " от
ражает противоположное направление оси z и этой массовой
силы.
В процессах с однонаправленным перемещением субстанции
(скажем, вдоль оси х) в уравнениях остаются лишь члены, со
держащие скорости и производные вдоль данного направления,
поскольку вдоль других осей эти величины обращаются в нуль.
Например, для теплопереноса

дх

х

дх

дх 2

ер

В рассматриваемой ситуации в системе уравнений ( l .20) нас
будет интересовать лишь первое из них - для оси х. Выражение
( 1 .2 lд) в свою очередь упрощается для стационарных процессов
(дt/m = О), при отсутствии Источников и Стоков теплоты (qv =
О) и т. п. Заметим также, что практически вполне возможно
однонаправленное движение потока рабочего тела (пусть вдоль
оси х, так что wy = wz = 0) , но кондуктивный перенос теплоты
происходит по разным направлениям; тогда

дt
дt
qv
- + w - = aV 2 t + - ,
д-t

х

дх

ер

( 1 . 2 1 е)

причем лапласиан здесь, в отличие от ( l .2 1д) , сохраняет произ
водные по всем осям координат, не только по х. Вообще, анали
зируемое направление движения жидкости (газа и т.п.) не обя
зательно совпадает с направлением переноса другой субстанции;
поэтому в уравнения переноса вполне могут входить слагаемые
90

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

(отвечающие, с одной стороны, за конвективный перенос суб
станции, а с другой, - за перенос путем трения , теплопровод
ности, диффузии), содержащие производные по разным осям
координат.
В случае переноса в твердых телах выпадают конвективные
состаWIЯющие, так как скорости wj равны нулю. Тогда

дt = V 2 t + qv .
a
д-t
р

( 1 .2 1 ж)

aV 2 t + !Ь_ = О ;

( 1 .2 1 ж1 )

е

Разумеется, это уравнение для ряда ситуаций будет выглядеть
еще проще:
- стационарный перенос теплоты (дt/m = О):

ер

- отсутствие Источников (Стоков) теплоты

� = aV 2 t ;

(qv = О):

д-t

( 1 .2 1ж 11 )

стационарный теплоперенос в отсутствие Источников и
Стоков теплоты (дt/m = О , fJv = О, возможность сокращен ия а) :
v2 1

( 1 .2 I ж1 II )

= о,

а если при этом анализируется еще и однонаправленный перенос
теплоты (например, вдоль оси х) , то совсем просто:

fi t d 2 t
-2 = дх d x 2

- О.
-

( 1 .2 1ж 1У)

Рассмотренные примеры, разумеется, не охватывают всего
многообразия конкретных случаев, но приведенных иллюстра
ций вполне достаточно для модификации уравнений перено
са - применительно к другим субстанциям и некоторым воз
можным ситуациям.
1 .6.2. Различные конфиrурации потоков субстанции

Существует иной срез модификации уравнений переноса,
связанный с конфиrурацией потоков субстанции, объекта
(технологического аппарата, его рабочей зоны), в которых пере
мещается субстанция. В расчетно-аналитическом плане пробле
мы здесь прежде всего связаны с выражением лапласиана, запи
санного ранее в декартовых координатах:

2
2
2
V2 = 8 2 + 0 + 0 ·
дх ду 2 дz 2
-

-

-

(а)
91

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Использование этих координат удобно в случае плоских те
чений : движение жидкости в узкой щели, в виде тонких пленок
и т. д. Однако при движении жидкости, например, в цилиндри
ческих трубах или кольцевых каналах уравнения переноса при
выражении лапласиана по (а) становятся крайне неудобными
для решения , но ситуация обычно значительно упрощается при
переходе к цилиндрич еским координатам.
При решении технологичес ких задач чаще всего наряду с де
картовыми приходится использовать цилиндрические и сфериче
ские координаты . В первом случае - это в равной мере отно
сится к течениям в цилиндриче ских аппаратах и трубах и к пе
реносу субстанции в твердых телах цилиндриче ской формы, во
втором случае - это чаще всего перенос субстанции в сфериче
ских телах. Переход от декартовых координат к цилиндриче 
ским и сферическим производится по известным из математики
правилам преобразован ия коорди нат. Н иже эти весьма громоз
дкие преобразован ия опущены , приводятся результирующие
выражения для лапласианов (и других слагаемых уравнений пе
реноса, если в этом есть необходимость).
Связь цилиндрических координат - радиальной r, полярной q>
и продольной (направим ее вдоль оси z) с декартовыми дана в
разд. 1 .4: х = rcosq>, у = rsinq>, z = z (см. рис. 1 .9).
Лапласиан
величин,
имеющих
скалярную
природу
(температуры, концентрации) , записывается в виде
1 а + 1 а2 + а2
v 2 = а2 + -- -·
( 1 .23)
-

дr2

, дr , 2 дq> 2

В частности , для переноса теплоты:
2 д 2 t + 1 дt + 1 д 2 t

-

дz 2

+ д2 t ·
-- V t=
2
дr r дr ,2 дq> 2 дz 2
-

--

--

( 1 .23а)

Практиче ский интерес зачастую представляют следующие ва
рианты процессов переноса:
- симм етричный перенос субстанции; в рассматриваемом
примере - симметричный теплообмен, когда iflt/дq> 2 = О, т.е.
нет изменения потенциала (здесь - температуры) по полярному
углу: на одинаковых радиусах - одинаковые температуры;
- перенос субстанции в рабочих зонах большой протяжен
ности по оси z; тогда интенсивность переноса субстанции
(здесь - теплоты путем теплопроводности) вдоль этой оси мо
жет оказаться существенно ниже, чем в радиальном направле
нии - можно принять a2t/дz2 � О.
Трансформация выражения ( 1 .23а) для каждого из этих слу
чаев затруднений не вызывает. Если, например, реализуются
92

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

сразу оба условия (а) и (б) , то
'\l t =

2

а2 t
дr 2

+ -- .

ас
r дr

( 1 .23б)

1

При переходе к цилиндрическим координатам изменения за
трагивают не только лапласиан, но и конвективные составляю
щие переноса. Например, в часто встречающемся и достаточно
общем случае осесимметричного потока (жидкости, газа) и не
симметричного переноса теплоты (скажем, вследствие неравно
мерного обогрева стенок канала) уравнение теплопереноса
имеет вид
2
qv
ar
ar
а1
a r
1 ar
1 а21 + а21
, ( 1 .23в)
- + wг - + w z
+
+
+
--= а
2
2
2
2
ер
r
,
r
r
дt
z
д
д
д
az
дr
д<р

- (- - -

) -

причем индексы при скоростях отвечают координатным осям.
Для величин, имеющих векторную природу (в курсе ПАХТ
речь идет о скорости и ее составляющих по осям координат) ,
выражение для лапласиана получается сложнее * ; одновременно
изменяются и выражения для конвективных составляющих пе
реноса. Обозначим скорости вдоль осей цилиндрических коор
динат r, q> и z соответственно Wr, wч>, wz; другие слагаемые с эти
ми индексами также относятся к соответствующим осям коор
динат. Наиболее актуально в практическом аспекте течение
вдоль продольной оси z. Для несжимаемой жидкости уравнение
Навье-Стокса в цилиндрических координатах имеет вид

! др = Pzр дz

+

v

{

[ дt

дwz

+w

r

дwz + wcp дwz
д wz
+ wz
r дq>
дz
дr

}

д 2 w, + .!. дw, + -1 д 2 w, + д 2 wz ·
дr 2 r дr , 2 дq> 2 дz 2

]

+

( 1 .24)

Здесь
в
квадратных
скобках
стоит
полная
(субстанциональная) производная dwJdt, а в фигурных лапласиан скорости wz. При симметричном относительно оси z
течении становятся равными нулю слагаемые, содержащие про
изводные от скорости wz по координатному углу <р , и выражение
( 1 .24) упрощается.
Можно виде'JЪ, 'П'О выражения лапласиана д11Я продольной оси (заме-mм, конвек
тивной составляющей - также) в случае величин скалярной и векторной природы
совпадают. Иначе обстоит дело с уравнениями относительно осей r и ер. Приведем в
качес111е примера запись уравнения Навье-Стокса для движения в направлении
• См ., например, ( 1 , 3) .

93

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

[

w" дw" w"w, .
r д<р

угла <р (это акtуально для закрученных потоков):
1 др
pr д<р

_

- - - Р<р

+

v

{

+w - - + w - + - - + -r
дw"
дt

дw"
' дr

t

дw"
дz

]

}

+

2
д2 w
д2
'4> + ! дw'Р + _!_ w'4> + 2. дw, + a w'4> w'P .
д1р
,
дlр
2
,2
2
2
r
r
гz 2 - ,2
дr
д

( 1 .25)

Как и ранее, в квадратных скобках здесь субстанциональная производная,
но уже от скорости w<p , а в фиrурных - ее лапласиан. При отсуrствии движе
ния жидкости (газа) вдоль радиальной координаты (это справедливо в боль
шинстве практических случаев, если нет Источников и Стоков жидкости, а
стенки канала непроницаемы для нее) и при осесимметричном течении, когда
дw<р/д<р и w, равны нулю, уравнение ( 1 .25) сушественно упрощается:
дw'Р
дw<Р
1 др _ р
д 'w. J дw. д ' w. w. .
( 1 .25а)
pr д1р -

[

<р - � + w z

] {

ЭZ- + v 7 + -; г;- + --гт - 7

}

Здесь, в отличие от записи для скалярных величин, в лапласиан входит слагае
мое w<p/r2.

При переносе субстанции в шарообразных телах или техно
логических пространствах используют сферические координа
ты - радиальную r и характерные угловые координаты, широко
используемые в географии, - долготу <р и широту IJI. Переход от
декартовых координат к сферическим производится на основе
соотношений х = rsin<psinljl, у = r cos<psinljl, z = rcoSIJI.
Технологические задачи чаще всего требуют установления
температурных или концентрационных полей (при переносе
теплоты или вещества соответственно) в сферическом про
странстве - здесь потенциалы (температуры, концентрации)
имеют скалярную природу. Для этого случая преобразование
координат дает
пv 2 =- -д2 + 2 д2
д + 1
д
д
1
. 2 1j1
( 1 .26)
SJO
+
дr2

r дr

r 2 д(cos lJI)

[

д(соs <р )

]

·

r2 sin 2 IJI д<р 2

·

Это громоздкое выражение существенно упрощается для
симметричного (относительно центра сферы) переноса, когда

производные потенциала по координатным углам <р и 1J1 обра
щаются в нуль:

v2

=

- + --;

( 1 .26а)

д2 t + � дt .

( 1 .2 6б)

д2

дr 2

2

r

д

дr

например, для симметричного переноса те плоты в сфере

v2 1

=

дr2

r

дr

Для величин векторной природы выражения лапласиана получаются весьма
громоздкими и здесь не приводятся. Эти случаи могут представлять практиче-

94

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ски й интерес, например, при изучении движения жидкости в сферической
капле или пузыре.

Особо подчеркнем, что при выражении уравнений в цилин
дрических и сферических координатах нередко (симметричный
перенос, несущественное изменение потенциала вдоль продоль
ной оси) удается свести задачу к одномерной (однонаправленный
перенос). Тогда актуальным является установление закономер
ности изменения потенциала (температуры, концентрации)
только вдоль радиальной координаты - см. уравнения ( 1 .23б) ,
( 1 .26б). Это существенно упрощает математическую формули
ровку задачи и само решение.
1 .6.3. Анизотропные среды

До сих пор анализировались процессы переноса в средах

изотропных в смысле постоянства коэффициентов пропорциональ
ности µ(v) , Л(а) , D - в законах ( 1 .9), ( 1 . 1 0) и ( 1 . 1 1 ) , связы

вающих удельные потоки субстанции с градиентами потенциа
лов, в самих уравнениях переноса типа ( 1 .20) - ( 1 .22). В этих
случаях рассматриваемые соотношения являются линейными, что
облегчает (иногда жестче: делает возможным) их аналитическое
решение. В случае анизотроm1ых сред возникают существенные
осложнения как в формулировании задач и записи уравнений
переноса, так и (особенно) в их решении.
Наиболее простыми являются случаи, когда упомянутые ко
эффициенты различаются только по направлениям осей коорди
нат, но не изменяются от точки к точке вдоль осей
(физически - не зависят от уровня потенциала субстанции,
например температуры или концентрации). Здесь нужно· опери
ровать (скажем, при переносе теплоты) не единым коэффици
ентом теплопроводности, а коэффициентами , специфичными в
направлении осей - декартовых Лх, Л.у, Л.z или цилиндрических

Л.r, Л."' , Л.z и т.п. Тогда, очевидно, вместо а

уравнение ( 1 .2 1 ) должен входить фрагмент
ах

--

--

(

д2t
д2 t
д2 t
.
+
ау -- + az
дх 2
дz 2
ду 2

д2t
дх 2

+

д2 t
ду 2

+

д2 t

дz 2

)

в

(б)

Здесь усложнение уравнения не сопровождается нарушением
его линейности. Однако на практике нередко встречаются тех
нологические ситуации, когда упомянутые выше коэффициенты
изменяются от точки к точке и во времени, поскольку физиче
ски зависят от изменяющегося потенциала субстанции . Так, Л. и
95

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

а моrут зависеть от температуры t; при небольших ее изменени
ях этой зависимостью пренебрегают и оперируют " постоян
ными " (средними) значениями Л. и а
так зачастую и делают
при анализе процессов теплопереноса; для больших изменений
(диапазонов) температур игнорирование изменения Л. и а с тем
пературой приводит к ошибочным результатам.
При наличии существенной зависимости Л. от t надо в ходе
анализа теплопереноса (разд. 1 .5.2; рис. 1 .9) учитывать прира
щение Вдоль оси х не только температуры, но и всего произве
дt
дения Л. , так как изменяются одновременно t и Л.. Иначе го
дх
воря, кондуктивный поток теплоты через правую грань dydz за
дt dx dydzdt;
д t время dt неправомерно выражать в виде л. +
дх
дх
дt
к потоку теплоты через левую грань -Л. - dydzdt надо добавить
дх
д -Л. дt
приращение - dх dydzdt. Тогда разность кондуктивных
дх
дх
тепловых потоков вдоль оси х составит
-

(

[

]

)

[

(
) ] dydzdt =
= � ( л. �) dydzdt = � ( л. �) dVdt.
(в)
дх
дх
дх
дх

дt dх
д -Л. дt дt
+ Прх - Ухх = -Л. dydzdt - -Л. +
дх
дх
дх дх

После деления на dV и dt вместо первого слагаемого в
2t
лапласиане Л. д 2 будет стоять более сложное
нелинейное дх
выражение:
� л. � ;
(г)
дх
дх
аналогичные выражения будут записаны и для других осей ко
ординат. Решения таких уравнений будут существенно затруд
нены, так как надо зн·ать связь Л. с t и суметь аналитически раз
решить уравнение, содержащее такую связь.
Совершенно очевидно, что при Л. = const нелинейный фраг2
мент (г) переходит в линейный Л. д , характерный для записи V2t.
--

-

( )

дх

96

�

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Практически при решении задач теплопереноса весьма часто Л. и а можно
считать не зависящими от температуры. Но вот при переносе импульса в дви
жущейся среде встречаются ситуации, когда пренебрегать нелинейностью нель
зя: значения µ и v могут существенно зависеть от градиентов скоростей. Это
происходит, когда нарушается связь tт и дw/дп, заданная формулой Ньютона:
либо µ не является постоянной величиной из-за происходящих в жидкости
структурных деформаций, так что µ зависит от градиента скоростей, либо осу
ществляется намеренная подмена задачи, когда нелинейные эффекты вихреоб
разования в жидкости выражают в терми нах и символах нормального переноса
импульса, т.е. в манере формулы ( 1 .9). Такие случаи будут освещены в главе
''Гидравлика". При переносе вещества коэффициенты диффузии D также не
редко зависят от уровня концентраций С. С этим встречаются , например, при
массопереносе в твердых телах (процессы адсорбции, сушки), когда с измене
нием концентрации вещества в твердом теле изменяются скоростные характе
ристики диффузии, а иногда и сам механизм массопереноса (по крайней мере,
изменяется вклад различных механизмов в перенос вещества). Тогда вместо

2с

-( )

а
фрагмента D а 2 в уравнение будет входить слагаемое
D; аналогича
с
&
&
&
ные замены надо будет сделать и для осей у и z. В целом уравнение переноса
получится более сложным и возникнут уже упомянутые затруднения: надо бу
дет знать (установить) зависимость D от С; надо суметь разрешить усложненное
дифференциальное уравнение. Чаше всего в таких ситуациях (в равной мере
при переносе импульса, теплоты, отдельного компонента) приходится привле
кать численные методы.

1.7. УСЛОВИЯ ОДНОЗНАЧНОСТИ

При решении основных уравнений переноса - типа ( 1 .20) ( 1 .22), а также ряда других, менее общих дифференциальных
уравнений, встречающихся в курсе ПАХТ, необходимо отыскать
постоянные интегрирования (или установить пределы интегри
рования) , дабы полученное в общем виде решение конкретизи
ровать применительно к определенному интересующему нас
технологическому процессу. С этой целью должны быть зафик
сированы условия однозначности, вьщеляющие конкретное ре
шение из более общего, записанного для группы сходных про
цессов. В широком смысле к условиям однозначности относят
физические свойства рабочих тел (среды и др. ), конфигурацию
и размеры рабочей зоны аппарата. Без этого не удастся сформу
лировать начальное и граничные условия .
В случае нестационарных (периодических) процессов в ка
честве одного из условий однозначности используют начальное
условие (НУ) , фиксирующее ситуацию в начальный момент
времени ('t = О) - до начала процесса. Так, могут быть заданы
начальная температура или же начальное распределение темпе97

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ратур в теле, в технологическом пространстве (если исходные
температуры в разных точках различны) , начальная концентра
ция , начальный уровень жидкости и т.п.
В случае стационарных (непрерывных) процессов начальное
условие, естественно, не задается, поскольку ситуация во вре
мени не изменяется. Уменьшение числа условий однозначности
на единицу (по сравнению с периодическим процессом) не ве
дет к потерям в математических решениях, поскольку отвечает
уменьшению на единицу числа переменных: отсутствуют част
ные (в ряде задач - обыкновенные) производные по времени.
Наличие в уравнениях переноса и других дифференциальных
уравнениях пространственных изменений (они отражены произ
водными различных порядков по пространственным координа
там) приводит к необходимости установления rраничных условий
(ГУ) , т.е. ситуации на границе рабочей зоны, технологического
аппарата.
Так, при движении сплошной среды в канале общепринятой является
согласно которой скорость среды относительно поверх
н ости в точках контакта с ней равна нул ю. Другой пример: при записи уравне
ний движения нормальная составляющая скорости среды на границе с любой
непроницаемой для нее поверхностью тож е равна нулю. В случае теплообмена
в качестве грани ч ного условия может, например, быть задана температура (или
распределение температур), поддерживаемая на границе тела, рабочей зоны . В
случ ае массообмена при течении среды в канале поток вещества на границе со
стен ками канала по нормали к ним также равен нулю (если, конечно, стен ки
непрон ицаемы для вещества и не вступ ают с ним в химическую реакцию), а
вот в случае теплопереноса тепловой поток вполне возможен и , как правило,
существует (кстати, его интенсивность тоже может быть задана в качестве гра
нич ного условия, если эту интенсивность возмож но зафиксировать - напри
мер, в случае регулируемого электрообогре ва).
В самом общем плане используется следующая классификация
"концепция прил пания ",
и

граничных условий (в качестве примера ниже приводится тер
минология и символика переноса теплоты как наиболее на
глядная) .
ГУ 1 рода
задано распределение потенциалов субстанции на
границе тела, рабочей зоны - постоянное или изменяющееся во
времени (например, распределение температур на границе тела).
В простейшем случае распределение потенциала на границе не
изменяется во времени и однородно (например, температура
одинакова на поверхности тела, на границах рабочей зоны) тогда задача решается наиболее просто.
ГУ 11 рода
задано распределение удельных потоков субстан
ции (либо постоянный удельный поток) через границу тела, ра
бочей зоны [ например , величина q по ( 1 . 1 0) на границе тела] .
ГУ 111 рода - заданы распределение потенциала субстанции
(либо постоянное его значение) в среде, окружающей тело, ра
бочую зону (скажем, температура среды вокруг тела) и коэффи
циент обмена (коэффициент теплоотдачи а) тела со средой .
-

-

98

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ГУ IV рода - задано распределение удельных потоков субстан
ции (либо постоянный ее поток) на границе двух соприка
сающихся тел - твердых, жидких, твердого и жидкого или газо
образного и т.д. [например, величина q по ( 1 . 1 0) с разными зна

чениями Л. по разные стороны границы раздела - соответствен
но различиям в свойствах этих тел] .
Наконец, возможны условия (таковы свойства тела или спе
цифика рабочей зоны аппарата) , при которых не существует
градиента потенциала субстанции в теле, рабочей зоне: в этом
случае говорят о безrрадиентном переносе субстанции. Напри
мер, при отсутствии температурного градиента температура тела
будет одинакова во всех его точках в каждый момент времени,
хотя, разумеется, она может в периодическом процессе изме
няться во времени, а в непрерывном процессе возможен подвод
или отвод теплоты.
Заметим, что формулирование начальных и граничных усло
вий необходимо не только для решения дифференциальных
уравнений, но в ряде случаев и при описании технологических
процессов, когда составляющие уравнений конечны.
Формулирование условий однозначности - весьма ответ
ственная процедура при математическом описании технологиче
ских процессов. Зачастую именно от правильности представле
ний об условиях однозначности - в особенности о граничных
условиях - зависит адекватность модели реальному объекту.
Особые трудности нередко возникают при оценке технологи
ческой ситуации как раз на границах объекта - с ограничи
вающей его поверхностью, с окружающей средой и т.п.
Более детально НУ и ГУ различных видов будут рассмотрены
и использованы в общих главах ''Гидравлика" , " Основы теплопе
реноса", "Теплопередача и теплообмен", " Основы массоперено
са" , а также в ряде других глав - для решения конкретных на
учных и технологических задач .
1.8. ФИЗИЧЕСКОЕ ПОДОБИЕ
1 .8. 1 . Обобщенные переменные

Теоретические построения могут быть широко и последова
тельно использованы в технологической практике чаще всего
лишь при условии представлени я их в форме количественных
соотношений. Различные возможности установления таких со
отношений показаны в разд. 1 .3.3. При этом многообразие свя
зей между свойствами объектов и параметрами процессов,
осложненное часто недостаточным проникновением в механизм
99

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

происходящих явлений, приводит к существенным затруднени 
ям в установлении количественн ы х закономерностей , иногда к получению весьма громоздких расчетных соотношений .
Здесь сл едует указать на разрыв в уровне ряда техноло гических задач и в
возможн остях аналитических ре шений уравнений (п ервоначально зачастую
достаточно точных) . Возникающие трудности вынуждают идти на уп рощен ия
(самих уравнений и условий однозначности ) , а это нередко приводит к потере
точности решений. Численные методы могут быть свободны от этого недостат
ка, но они привязаны к кон кретным условия м процесса, ограничены пр и н ятым
диапазоном изменения пере м енных; кроме того, они н е обнажают внутренних
связей явления, процесса - такова цена, уп лачиваемая нами за их испол ьзова
н ие . Существуют попытки снизить отмеченные недостатк и , п ол учая сн ач ала
численные решения теоретичес ких уравнений в достаточно ши роких диапазо 
нах изменения пере менных ( условий), а затем - подбирая приближенные
уравнения связи ; это по существу полуэм пир ический метод разработки расчет
ных соотношений. Разумеется, при большом числе переменных реализация
это го метода отличается высокой трудое м костью, причем п ро гнозность п олу
чаемых расчетных соотношений не всегда может быть гарантирова н а .

К успеху в создавшейся проблемной ситуа ц ии может привес
ти переход к обобщенны м переменным , когда натуральные пе
ременные (их число зачастую достаточно велико) объединяют в
существенно меньшее число безраз мерных ком nл ексов, имеющих
определенный физический смысл . В результате устанавливаются
связи не ме жду натуральными п еременным и , а ме жду обоб
щающими комплекса ми . Расчетные соотношения в обобщенных
переменных обладают следующи ми особенностями :
- выглядят менее громоздко (более к омпактно) , нежели со
отношения , использующие натур ал ьные ( ра зм ерные) перемен
ные;
- оказываются полезными на тех стадиях исследования яв
ления, процесса, пока задачу не удается решить строгими ана
литическими методами ;
- позволяют представить в ла к оничной форме строгие ана
литические решения;
- позволя ют вести расчеты и интерпретировать их результа
ты в любой систе ме единиц, пос к ольку численные значения
безразмерных комплексов не зависят от выбранно й систем ы
единиц.
Возможность перехода к обобщенны м переменным обуслов
лена тем , что влияние отдельных пере м енных (факторов) в те х 
нологическом процессе проявляется не порозн ь , а совместно,
поэтому и рассматривать их влияние на процесс надо не раздел ь 
но, а в совокупности . Использован ие обобщенных переменных,
каждая из которых включает несколько натуральных, повышает
общность описания процесса, пос к ольку одно значение обоб
щенной переменной может быть ре ал и з овано при м ноги х соче
тания х численных значений входя щ их в него натуральны х пере 1 00

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

менных. Отсюда следует, что полученные безразмерные ком
плексы могуr характеризовать не единичное явление или процесс,
а группу сходных явлений и процессов, для которых такие ком
плексы имеют одинаковые численные значения
это положение
лежит в основе понятия о физическом подобии.
Существуют различные пути формирования безразмерных
обобщенных комплексов. Наиболее обоснованный - на базе
аналитических выражений, описывающих процесс (в том чис
ле - в дифференциальной форме ) . Другой путь имеет феноме
нологическое происхождение - здесь исходят из общих пред
ставлений о факторах, влияющих на протекание процесса, и о
его закономерностях. При этом действуют на чисто интуи
тивной основе либо используют теорию размерностей (см. разд.
1 . 1 .4) , формируя перечень перемен н ых также интуитивно. Есте
ственно, в обоих последних случаях обоснованность получаемых
безразмерных комплексов существенно ниже, чем установлен
ных на основе моделей, представлений о механизме процесса,
его теоретического описания . В ряде случаев новая обобщенная
переменная может быть получена путем комбинации уже из
вестных.
П осле формирования обобщен н ых переменных необходимо
установить между ними количественные связи , позволяющие
вести и нженерные расчеты с целью определения искомых нату
ральных переменных, входящих в безразмерные комплексы.
-

1 .8.2. Геометрическое и физическое подобие.
Масштабные преобразования.
Критерии подобия

Как указано выше , математические описания, представлен
ные в обобщенных переменных, охватывают группы сходных
объектов, явлений , процессов - их называют подобными. Поня
тие геометрического подобия (фигур, тел) введено в средней
школе. Но термин " подобие " в термодинамике , физике, химии,
технологии и меет более широкое толкование. В курсе ПАХТ
рассматривается и используется физическое подобие примени
тельно к переносу различных субстанций для очень широкого
круга задач - от общетеоретических описаний до прикладных
расчетных формул .
Приведем определение физически подобных явлений и про
иллюстрируем его на примере течения жидкостей.
Два физических явления подобны, ее.ли в сходственных точках
геометрически подобных систем одноименные характеристики разли
чаются только постоянными коэффициентами (множителями подо
бия). Математические описания подобных систем идентичны.

101

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

1. 13. Подобные течения :
( № 1 ) и образец (№ 2)

Рис.

№

модель

Пусть имеются два геометрически подобных канала (рис.
В,
1 . 1 3) - малого (его обычно на
зывают " модель" ) и большого
( " образец" ) размеров; в этих
каналах текут жидкости с раз№2
В1
ными свойствами (плотность,
вязкость, теплоемкость и т. п . ) .
Выберем в малом (система J ) и
большом (система 2) каналах
две пары сходственных точек А 1
и А2, В1 и В2, причем для каждой пары характерно свое геомет
рическое соответствие типа r1 /l1 = '2/ /2 . Оrношение r1/'2 = 11 //2 =
. . . = mr представляет собой множитель геометрического подо
бия, постоянный для любой пары сходственных точек в рас
сматриваемых канал ах . По определению физического подобия
для
как для пары точек А1 и А2, так и для В1 и /h (вообще
любой пары сходственных точек в модели и образце) характер
ны равенства
1

Az1• ъ._"

Е
.

t

-

� = тР '· ..!:!.. = тµ•· .:L = тС•· ..!!l.. = тР•· � = тw и т. д . ' (а)
Р2

µ2

С2

w2

Р2

причем m; - множители подобия, разные для разных характери
стик, но одинаковые в предел ах одной характеристики для каж
дой пары сходственных точек. Иначе говоря, значения, скажем,
вязкостей µ 1 и µ 2 или скоростей w 1 и w2 мoryr быть разными в
сходственных точках модели и образца, но численные значения
отношений µ 1 /µ 2 или w1/w2 для всех пар сходственных точек (А 1
и А2, В1 и В2 и др.) в модели и образце - одни и те же: mµ , m w и
т.д. (разумеется, в общем случае mµ * mw * . . ) . При переходе от
одной пары сходственных точек к другой значения mµ , mw, . . не
изменяются. В этом смысле каждый множитель подобия высту
пает в качестве масштабной характеристики соответствующей
физической величины.
Понятие о множителях подобия служит основой получения об
общенных переменных. Путь их формирования с помощью таких
множителей именуется масштабными преобразоt1аниями. Проде
монстрируем поначалу получение одной из обобщенных перемен
ных на весьма простом примере уравнений неразрьmности ( 1 . 1 5).
Запишем эти уравнения для двух подобных течений, отмечая
их принадлежность к модели либо образцу индексами 1 и 2:
.

.

др.

1 02

сп .

+

д(р . w. )
ах .

+ . . . = О,

1)

др 2
Ut z

+

д(р 2 w2 )
дх 2

+ ... = О ;

(2)

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

остальные слагаемые в левой части здесь опущены, поскольку
по своей структуре они совпадают со вторыми слагаемыми.
Применим к ( 1 ) и (2) масштабные преобразования :
(б)
P t = трр2 ; • i = т.- 2; w1 = mww2; х 1 = т1х2,
причем множитель подобия для координат обозначен т1 - он
общий для всех координат (в том числе у1 и У2, z1 и z2 ) и линей
ных размеро в /1 2·
Подставим rеперь в уравнение ( 1 ) значение Р1 = трр2, а также
всех других параметров процесса в модели, выражая их через соот
ветствующие множиrели подобия и параметры процесса в образце.
Тогда, имея в виду, что постоянные множители мoryr быть вьrnе
сены за знаки производных, получим новую запись для модели:
mP др 2 + m p m w д(р 2 w2 )
1 ')
+ .
О.
т,

0. 2

. .

т1

дх 2

=

(

Обращаем внимание на то, что (1 ' ) описывает систему 1
(модель), но с множителями подобия и в символах системы 2
(образца).
Согласно определению физического подобия, уравнения ( 1 )
и (2) для систем 1 и 2 должны быть идентичны. Это возможно,
'

если комплексы, содержащие множители подобия, mpm w

---

т1

тР

и

тт

- сокращаются, а возможность сокращения этих ком

плексов означает их равенство:
тр
тт

=

mp mw
т1

(в)

Разумеется, в данном примере множитель тР можно сократить:
_1_
тт

=

тw
т1

(г)

W 1 /2
W 2 /1

(д)

Теперь значения множителей подобия по (а) , (б) - т.
mw = w1/wъ т 1 = /1//2 - подставим в выражени е (г):
�

= • 1/•2,

Ч

=

=

Собирая величины с одинаковыми индексами (т.е. относя
щиеся к каждой из систем) в разные части равенства, находим

(е)

причем последний комплекс не снабжен индексом, что означает
справедливость рассматриваемого равенства (одинаковые чис1 03

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ленные значения полученного комплекса wt/ l) для всех подобных
течений. Этот комплекс, как и другие обобщенные переменные,
безразмерен.

Совпадение численного значения безразмерного комплекса
(в рассмотренном примере - wt/l} , или в других ситуациях нескольких комплексов, является необходимым и достаточным
условием подобия группы систем, объектов, течений, процессов.
Ком пл екс wt // называют критерием rомохронности и обозначают
символом Но. Чаще обобщенным безразмерным комплексам
присваивают фамилии крупных ученых, обозначая комплексы
первыми двумя буквами фамилий этих ученых.
Физический смысл комплекса Но = wt// ясен из предпосылок
анализа: сравнивались (см. вывод уравнения неразрывности) два
конкурирующих эффекта - вынужденный перенос массы жид
кости (под действием перепада давления , разности уровней и
т. п . ) и ее накопление в вьщеленном объеме. Специально под
черкнем, что численное значение безразмерного комплекса
(здесь Но; однако замечание относится к любой обобщенной
переменной) не есть прямое отношение конкурирующих эффек
тов, факторов. Это их соотношение (т. е. отношение в каком-то
масштабе; говорят: " масштаб отношений " ) , поскольку все по 
стоянные коэффициенты, выражающие связи количественно, в
комплексах, как правило, опускаются. Можно лишь утверждать,
что при увеличении комплекса возрастает влияние фактора,
стоящего в числителе (для Но - переноса массы за счет вынуж
денной конвекции) , а при уменьшении комплекса - фактора,
стоящего в знаменателе (для Но - накопления массы во време
ни). В частности , для стационарных процессов, где отсутствует
накопление массы в рабочей зоне, критерий Но вырождается ,
его численное значение стремится к бесконечности.
Конкретизация значения обобщенной переменной, при ко
торой тот или иной эффект (фактор) становится доминирую 
щим, обусловлена постановкой конкретной задачи ; иногда это
значение устанавливается экспериментально.
Метод масштабных преобразований может быть реализован в
упрощенной форме, что, конечно, приводит к тем же результа 
там. Будем вести сопоставление (его принято обозначать симво 
лом о • ) конкурирующих эффектов, не принимая во внима
ние операцию дифференцирования, поскольку масштабные
множители безразличны к этой операции. Тогда сопоставление
эффектов накопления массы и ее продольного конвективного
переноса изобразится в форме
-

Е.
t

-

pw
.
/

(ж)

Сокращая на р и собирая все величины в одной части ра
венства, сразу получим критерий гомохронности; для всех по1 04

о

•

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

добных течений он в сходственных точках имеет одинаковое
значение:
W 't =
-

/

(з)

Н о = i'dem.

В целях экономии места и времени при последующем изло
жении курса, как правило, используется упрощенный метод
масштабных преобразований.
В тех случаях, когда безразмерные комплексы, определяющие
протекание процесса, заданы по условию технологической зада
чи, их обычно называют критериями подобия. Комплексы, со
искомые зна
держащие текущие значения переменной (часто
что
Заметим,
числами.
безразмерными
называть
принято
чения),
в зависимости от постановки технологической задачи одна и та
же обобщенная переменная может выступать в роли критерия
или числа.
Нередко приходится иметь дело с безразмерными перемен
ными, записанными в виде отноше ния одноименных величин,
координата, а / основной (характерный,
например х//, где х
определяющий ) линейный размер, или С/ С0 , где С текущая, а
начальная концентрация. Такие параметриче ские безраз
Ч>
мерные переменные в силу их простоты в сравнении с комплек
сами называют симплексами. Заметим, что с помощью масштаб
ных преобразова ний не всегда удается в полной мере выявить
симплексы, влияющие на процесс.
При установлени и понятия физического подобия говорилось
о соблюдении геометрического подобия. Для многих технологи
ческих задач полное геометрическое подобие не является необ
ходимым - достаточно приближенного. Здесь две главные при
чины. Первая обусловлен а разумной точностью инженерных
решений: в ряде задач отказ от строгого геометричес кого подо
бия не приводит к существенн ым погрешностям, точность оста
ется практически приемлемо й. В основе второй причины лежит
достаточн о очевидный (и экспериме нтально подтвержденный)
факт разного влияния отдельных геометрич еских характери стик
системы (рабочей зоны) на ход технологи ческого процесса. Яс
но, например , что толщина стенки трубопровода бет в подав
ляющем большинстве случаев не сказывается на характере тече
ния в нем жидкости или газа, поэтому не требуется геометри че
ского подобия типа 6 1//1 = 62//2 • Менее очевиден пример, ка
сающийся формиро вания поля скоросте й потока, поступив шего
в канал. Это формиро вание происходит на начальны х участках
канала; на некотором расстоян ии от входа в канал оно практи
чески завершается, после чего поле скоросте й сколько- нибудь
заметно не изменяется. При этом на входном участке поле ско-

-

-

-

-

1 05

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ростей зависит как от продольной координаты в направлении
потока (т. е. расстояния до входного сечения), так и от нор
мальной к этому направлению (диаметра, ширины или глубины
канала и т. п.). Но за пределами входного участка влияние про
дольной координаты вырождается, влияет лишь поперечный
размер канала (диаметр и т. п.). Поэтому для каналов достаточ
но большой протяженности во многих задачах обобщенные пе
ременные (безразмерные комплексы и симплексы) формируют
ся на основе только характерного нормального (к направлению
течения) размера: диаметра канала, толщины зазора и т. д.
Установление определяющего размера - задача исследователя,
инженера.
1 .8.3. Обобщенные переменные

на базе основных уравнений переноса
Н иже рассмотрено формирование обобщенных переменных
на основе дифференциальн ых уравнений переноса импульса,
теплоты и вещества, а также некоторых соотношений иного
происхождения и вида. По ходу изложения курса в дальнейшем
будут вводиться и использоваться и другие обобщенные переменные.
Гидродинамическое подобие

Для иллюстрации достаточно сложного случая (в сравнении с
уравнением неразрывности) проведем по уже известной канве
подробные масштабные преобразования уравнения Навье
Стокса для стационарного течения. Выберем одну из осей коор
динат, например ось z (во избежание громоздкости записи ин
декс "z" опустим) ; тогда имеем для подобных течений в модели и
образце (индексы 1 и 2)
1 др 1
_
Р 1 дz 1

_1_ др 2
Р 2 oz 2

=

=

(
(

дw 1
Р1 - w 1
дz 1

дw 2
Р2 - w 2
oz 2

+

+

)
)

...

...

+

+

v1

(� ]
( � ·]

v2

02 1
oz 1

д2 2
oz 2

+

+

... '
..

(1)

'

(2)

причем выражения в скобках записаны в усеченном виде, по
скольку структура опущенных слагаемых та же, что и оставлен
ных (поэтому в аспекте множителей подобия и операций с ни
ми потери информации здесь не будет) .
Выразим характеристики системы 1 через множители подо
бия и характеристики системы 2: Р 1 = mp p 2; Р1 = mJPl; Z 1 = m ,z2 ;
Р1 = тм Р2 (индекс "м" означает, что множитель mм одинаков для
всех массовых сил); w1 = mww2 ; v 1 = mvv2.
1 06

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

др2 =
;. ( дw 2
Р"-; дz 2 тмР2 --;;; w 2 дz 2

2
...) + � v 2 [ ддzw2i + . . .)

Подставим полученные произведен ия в уравнение ( 1 ) :

тр

тр т1

1

т

+

m v mw

( 1 ')

Заметим : вторая производная по смыслу математической операции есть
частное от повторенного дважды деления дифференцируемой величины на
аргумент (именно поэтому в знаменателе записывается "квадрат" аргумента) ;
вот почему в последнем слагаемом выражения ( 1 ') т" получается в первой
степени, а т1 - в квадрате.

Математические описания ( 1 ') для системы 1 и (2) для си
стемы 2 по условию подобия должны быть идентичны. Этому
условию отвечает равенство комплексов, составленных из мно
жителей подобия (тогда эти комплексы можно сократить) :

mpml
тр

силы дав
ления

тм

т;

массовые силы

силы
и нерции

т1

m v mw
--

j

т
силы
вязкости

(а)

Здесь под каждым из комплексов записаны силы (могут быть
записаны потоки импульсов), за которые по смыслу слагаемых
уравнения Навье-Стокса "отвечают" соответствующие комплексы.
Сравнивая попарно рассматриваемые эффекты (в принятой
трактовке - силы), можно получить 6 равенств, из коих три
являются независимыми и дают три "основные" обобщенные пе
ременные (остальные 3 равенства приводят к производным об
общенным переменным, которые могут быть также получены
комбинацией трех основных) . Выбор равенств в качестве основ
н ых обусловлен более всего историческими причинами
(традицией) ; в настоящее время в качестве базы приняты силы
и нерции , выражаемые комплексом mw2/m1•
Сопостав.ление сил дав.ления и инерции. Здесь тр/ (тр т1) о •
о
• т � / т 1 . После сокращения на т1 и подстановки значения мно
жителей тр = р1/р2, тР = р 1/р2 и mw = w 1/w2 имеем

-

-

2
w1

�·
2

откуда, разводя величины с оди н ако в ы ми индексами в разные
части равенства, получаем для всех подобных течений в сход
ственных точках

-

Р2
P2wi

=

р

pw 2

=

Eu

= idem

- критерий (число) Эйлера.

(б)
1 07

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Смысл

Eu

ясен из названия про цедуры сопоставления: это

соотношение сил даВJiения и инерции.

В технологических процессах нас чаще всего интересует не дав
ление р в какой-либо точке или сечении аппарата (канала, трубы),
а перепад давлений Лр межцу определенными точками или сечения
ми (при рассмотрении подобных течений - межцу сходственными
сечениями ). Поэтому используют несколько иное выражение Eu:
Лр .
Eu (в)
=
pw

2

-

тм

СопостаВJiение массовых сил с силами инерции. В этом случае
2
о - • mw /m1. После подстановки значений mм = Р1 / Р2 (при

этом вдоль оси z, если она направлена вертикально, речь может
идти о единичной массовой силе тяжести, численно равной ее
ускорению g), mw и т1 имеем

g. w� /2
g 2 = w; z, '

откуда, повторяя проведенную выше операцию, получаем для
всех подобных течений в сходственных точках
g 1 l2
g 1 /1
gl
= Fr = idem - критерий (число) Фруда. (r)
w 12

=

=

w2
w 22
Смысл Fr ясен из названия про цедуры сопостамения: это
соотношение массовых сил и инерции. Заметим, что в разных
учебниках и монографиях дается разное написание Fr: gl/w2;
w2/gl; w/ Jii и др. ; поэто му каждый раз надо оговаривать, о ка

ком написании Fr идет речь.

Разумеется, если рассматривается течение не в поле сил тя
жести, а в каком-либо ином внешнем силовом поле, то во Fr вмес
то ускорения свободного падения g войдет характерное ускорение
соответствующего поля (например, центробежного или др.).
Сопостав.ление сил инерции и вязкости. Сооmосятся коМТUiексы
mw2/m1 о • m.;nw/m(. После сокращения на mw/m1 и подстановки
значений всех множителей подобия (включая mv = = v 1 /v2) имеем
-

w1
v J2
� = у 2 /1 '

откуда, разводя величины с оди н ако в ы ми индексами в разные
части равенства, получаем для всех подобных течений в сход
ственных точках

w 1 l1
v1

1 08

w 2 /2
v2

w/
v

-

=

Re

=

idem

-

критерий (число) Рейнольдса. (д)

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Смысл числа Re, крайне широко используемого при описа
нии процессов переноса, ясен из названия процедуры сопостав
ления: это соопtошение сил инерции и сил вязкости. Заранее
нельзя с определенностью сказать, при каких именно числен
ных значениях Re будут доминировать сил ы инерции л ибо силы
вязкости. Это зависит от типа рассматриваемой системы и осо
бенностей течения. Конкретные численные значения Re, отве
чающие преобладанию тех или иных сил , зачастую можно уста
новить только экспериментально. Априори можно лишь
утверждать, что увеличение Re означает относительное возрас
тание сил инерции, уменьшение Re
возрастание сил вязкости
(внутреннего трения) .
Технологический процесс может протекать в условиях, когда
численное значение Re очень велико (можно считать, стремится
к бесконечности) или очень мало (стремится к нулю) . Это озна
чает, что оди н из конкурирующих факторов (в гидравлике одна из сил , для Re - сила и нерции или сила вязкости) стано
вится исчезающе мал в сравнении с другим. Тогда критерий
перестает контролировать процесс; говорят, что он сам (здесь Re) и его влияние вырождаются.
Продемонстрируем, как можно получить Re, используя упро
щенные масштабные преобразования. С этой целью примени
тельно к стационарному течению сопоставим второе и третье
слагаемые в правой части уравнения ( l . 20) , например для оси z,
опуская символы дифференцирования:
-

w
w-

w

(е)
о -· v - .
1
12
Произведя очевидные сокращения и собрав все величины в
одну часть равенства, приходим к числу Рейнольдса:
wl
- = Re = idem.
v

(ж)

Равенство численных значений каждой из обобщенных пере
менных - Eu, Fr, Re -является необходимым и достаточным
признаком подобия для широкой группы стационарных течений.
Аналогичные равенства численных значений соответствующих
обобщенных переменных служат признаками подобия в процес
сах переноса других субстанций. В качестве линейного размера
в Re, Fr был введен некий конечный характерный размер / (его
конкретный смысл устанавливается при анализе конкретного
процесса) . В ряде задач технологическая ситуация зависит от
координаты точки, и тогда число Рейнольдса может быть пред
ставлено, например, в виде Rex = wx/v. Такое написание крите
рия не всегда удобно, так как обобщенная переменная содержит
сразу две натуральные переменные, контролирующие процесс: х
и w. В этом случае иногда удобна замена Rex на две обобщенные

1 09

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

переменные:

wx

wl х
= -- ,
v
v /
т.е. на Re = wVv и симплекс х// - относительную координату.
Выше бьuю указано, что сравнение других пар эффектов мо
жет привести к другим обобщенным переменным. Так, сопо
ставление сил тяжести и вязкости (ил и соответствующих им
потоков импульса) дает
2
силы тяжести
( з)
силы тяжести
силы инерции
Fr Re - g/
wv '
Rex =

{

силы вязкости

}{
=

-

силы инерции

}{
.

силы

вязкости

}

=

.

=

.

здесь фигурные скобки означают, что речь идет не об отноше
н иях с ил , а об их соотношениях (в некоем масштабе) .
Можно получить и другие комбинации критериев (без
размерных чисел), также имеющие четкий физический смысл .
Тепловое подобие
Применим к уравнению Фурье- Кирхгофа ( l .2 l a) упрощен
ные масштабные преобразования .
Сопоставление локальной накопленной теплоты с теплотой, пе
ренесенной путем теплопроводности. Сопоставим первые сла
гаемые в левой и правой частях уравнения :
t
t
- о- • а
(и)
t
х2 .
Сокращая на t и перенося все величины в одну часть ра
венства, переходим к безразмерно м у комплексу at/x2, содержа
щему две переменные t и х, а потому - не всегда удобному при
анализе и решении технологических задач . Простые преобразо
вания, аналогичные показанным выше для Rex, приводят к двум
обобщенным переменным, содержащим каждая по одному нату
ральному параметру (t или х) :
-

2

2

1 .
at 1
-;r
/2 [2 -;r
=

01:

Первый из полученных комплексов at/ 12 = Fo носит название
критерия (числа) Фурье, второй х// является параметрическим
критерием (относительной координатой) . Число Фурье широко
используется в задачах, где основными в переносе теплоты яв
ляются принятые для сопоставления локальное накопление и
кондуктивный поток теплоты (в их соотношении и заключается
физический смысл Fo), в частности - в периодических процес
сах нагревания (охлаждения) твердых тел .
Сопоставление конвективного (перенос с движущейся средой) и
КОН,!JУКтивноrо потоков теплоты. Сравниваются второе и т.п. сла
гаемые в левой части уравнения Фурье и первое слагаемое в

1 10

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

правой его части:

t
t
w- o - • a- .
(к)
х
х2
После преобразований, аналогичных выполненным ранее,
приходим к не всегда удобному безразмерному комплексу w.x/a;
умножая его на Vl, получаем уже известный симплекс х/1 и об
общенный комплекс, называемый числом (критерием) Пекле:
wl/a = Ре. Этот комплекс широко используется в задачах, где
основу процесса составляют конвективный и кондуктивный тепло
вые потоки (в их соотношении и заключается физический смысл
Ре), в чаС'Пiости - во многих задачах непрерьmноrо и периодиче
ского теплообмена с участием жидкостных и газовых потоков.
Сопоставление первого и второго слагаемых в левой части
( 1 .2 1 а) приведет к уже знакомому нам критерию гомохронности.
Можно, конечно, проследить результаты сопоставления и дру
гих пар слагаемых в уравнении переноса теплоты, получив кри
терии , характеризующие соотношения соответствующих тепло
вых потоков. Численные значения полученных критериев в
сходственных точках систем для всех подобных процессов теп
лопереноса - одинаковы.
Диффузионное подобие

Сопоставление потоков вещества, накопленною и перенесенною

дн

фф

С
t

u

узиеи. Здесь - о - •

DC2

приводит к параметрическому
х
критерию х/1 и диффузионному критерию Фурье, иначе - кри
терию Фика Fi = Dt//2. Физический смысл этого комплекса - в
соотношении потоков вещества, указанных в заголовке проце
дуры сопоставления. Как и в случае теплообмена, эта обобщенная
переменная широко используется в задачах, связанных с описани
ем периодической диффузии в твердых телах. Заметим: аналогич
ный критерий используется и при описании нестационарных гид
родинамических процессов: Zh = vt/J2 число Жуковскою.
--

Сопоставление потоков вещества, переносимых конвекцией (с
движущейся средой) и диффузией. Здесь операция сопоставления
-

С

w-

DC

о - • -- приводит, наряду с симплексом х/1, к диффузих
х2
онному критерию Пекле Ред = wl/D. Его физический смысл - в
соотношении потоков вещества, указанных в заголовке проце
дуры сопоставления. Как и в случае теплообмена, эта обобщен 
ная переменная используется в задачах непрерывного и перио
дического массопереноса с участием потоков сплошной среды.
Разумеется, сопоставление других пар потоков вещества
(слагаемых уравнения Фика) приведет к формированию соответ111

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ствующих комШiексов, характеризующих сооrnошение рассматри
ваемых эффектов. Все эти обобщенные переменные имеют одина
ковые численные значения в подобных процессах массопереноса.
В заключение заметим, что обобщенным переменным нередко
присваивают название на1)'ра.11Ьных, но выражеЮIЪIХ в безразмерной
форме. Так, Re трактуют как безразмерную скорость, Fo
как без
размерное время, Eu - как безразмерный перепад давлений и т. п.
-

Подобие в переносе различных субстанций
До сих пор подобие явлений анализировалось в пределах пе
реноса отдельной субстанции - импульса, теплоты или вещест
ва. Однако сходство уравнений переноса (а в его основе, конеч
но, - сходство в физических явлениях, в механизмах переноса
разных субстанций) позволяет сопоставлять сходные эффекты
для различных субстанций - независимо от их природы. Осо
бенно ШIОдотворным оказалось сопоставление потоков субстан
ций , выражаемых слагаемыми с лаШJасианом. Эти слагаемые,
изначально сформулированные на основе удельных потоков
импульса, теШiоты, вещества и градиентов соответствующих
потенциалов, характеризуют в конечном итоге поля скоростей,
температур, концентраций.
Если отвлечься от природы субстанции, то сопоставление
указанных потоков импульса и теплоты дает безразмерный ком
плекс Pr = v/a
число (критерий) Прандтля, характеризующий
связь скоростного и температурного полей. Заметим, что Pr мо
жет быть получен также как отношение чисел Ре и Re, сформу
лированных при сопоставлении сходных пар слагаемых в урав
нениях Навье-Стокса и Фурье- Кирхгофа:
-

;

Ре = wl wz = � =

(л)
Pr.
Re
а
а
v
Проведенное в этой манере сопоставление для таких же по
токов импульса и вещества приводит к безразмерному числу
(критерию) Шмидта, характеризующему связь скоростного и
концентрационного полей: Sc = v/D. Этот критерий также мо
жет быть получен как отношение Ред и Re. Заметим, что в оте
чественной литературе число Шмидта нередко называют диффу
зионным критерием Прандтля и обозначают Рrд.
Значительно реже используют критерий Льюиса Le = a/D, по
лучаемый при сопоставлении кондуктивного потока теплоты и
диффузионного потока вещества и характеризующий связь тем
пературного и концентрационного полей.
1 .8.4. Обобщенные переменные
на базе друrих уравнений и представлений
Обобщенные переменные могут быть сформированы на
основе различных модельных представлений и теоретических

1 12

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

соотношений; обоснованность таких переменных определяется
достоверностью предпосылок, на которые опираются эти пред
ставления и соотношения. Продемонстрируем упомянутые воз
можности на некоторых примерах,
В ра:щ. 1 .3.2 на основе понятия о поrранwnюм слое бьmо получе
но выражение ( 1 . 12), согласно которому а = Л/&г. Эrо выражение, за
очень редким исключением, не является расчетным ввиду неопреде
ленности толщины тепловой поrраничной пленки &г. Однако мас
штабные преобразования позволяют и :щесь путем замены &r на
определяющий .линейный размер / сформировать безразмерный ком
плекс, имеющий впoJllie определенный физический смысл:
Л
а/
(м)
а о - • - � - = Nu - число Нуссельта '

бт

Л

представляющее собой соотношение интенсивностей теплового
потока по одну сторону поверхности теплообмена, выраженных в
форме конвективного (а) и кондуктивного (Л и [) эффектов.
В той же манере получается и выражается аналогичная об
общенная переменная для массоопереноса:
131
D
(н)
= Sh - число Шервуда,
13 о - • & �
D
д

имеющее тот же физический смысл , только не для тепло-, а для
массоотдачи . В отечественной литературе Sh иногда именуют
диффузионным критерием Нуссельта и обозначают Nuд .
Обобщенная переменная может быть сформирована на базе
граничных условий. Покажем это на примере ГУ 1 1 1 рода. Де
тально это условие будет рассмотрено в разд. 7. 1 0 . 3 ; здесь мы
воспользуемся самыми общими представлениями . Рассмотрим
некий участок поверхности лF на границе твердого тела (пусть
горячего) и омывающей
жидкости
его холодной
(рис. 1 . 14). Удельный по
ток теплоты из внутренних
зон твердого тела к его
Среда
границе согласно ( 1 . 1 О)
01
составляет
а
ЛF
Среда
, где х - нормаль
1
о
&l rp
Твердое
0гр
01
тело
а
Рис. 1. 14. К формированию кри
__ ,
терия Био:
•
Г аница
х
а - нестационарный режим
а
б
(выпуклое тело), б - стационар
ный режим (плоская стенка)

л.тl�I

0,Лт�q
1

1 13

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

к ruющадке лF. Поскольку на границе теплота накапливаться не
может, то она целиком отводится конвекцией, причем удельный
конвективный поток равен Q. Лt, где Лt = е - t - разность темпера
тур поверхности тела и среды (движущая сила конвективной теп
лоотдачи). Для поверхности ЛF полные потоки теплоты (изнутри
тела на его границе и снаружи) запишутся в виде равенства

�1�1

=
дх гр М ��
�
После сокращения на ЛF, путем упрощенных масштабных
преобразований �

J

a.t получаем безразмерный комплекс

а.1/� = Bi - критерий Био. Важно: поскольку речь идет о потоке
теплоты на границе [индекс "гр" в выражении (о)], то в Bi входит не
переменная координата х, а определяющий линейный размер /.
Несмотря на внешнее сходство, критерий Bi не является ана
логом числа Nu. (Внимание: в знаменателе Nu стоит теплопро
водность среды, омывающей твердое тело, в знаменателе Bi теплопроводность этого тела.) Число Нуссельта возникло как
результат разной формы записи потока теплоты от тела к
сплошной среде (в терминах и символах конвекции и теплопро
водности) . Но это один и тот же поток снаружи тела; в этом
смысле Nu - формален . Критерий Био сформирован на основе
анализа тепловых потоков по разные стороны от границы тела и
омывающей его среды. Поэтому Bi - физически обоснованный
критерий, выражающий соотношение тепловых потоков снару
жи и внутри тела.
о- •

По ходу изложения курса будут вводиться и использоваться
также другие обобщенные переменные.
1 .8.S. Критериальные уравнения

Количественные связи обобщенных переменных устанавли
вают путем теоретического анализа (это удается далеко не всег
да) или с помощью специально поставленного эксперимента.
Эти связи носят название критериальных уравнений , например
типа Eu = /(Re, Fr, . . . ) или Nu = j{Re, Pr, . . . ). Полученные урав
нения справедливы ("работают") для подобных процессов (в
гидравлике - течений , в теплообмене - процессов теплопере
носа определенного типа и т.д.) в найденных теоретически или
проверенных экспериментально диапазонах изменения обобщен
ных переменных. Поскольку здесь устанавливаются диапазоны в
обобщенных переменных, то составляющие их натуральные пе
ременные могут варьироваться более широко (кстати , и более

1 14

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

узко), лишь бы обобщенные переменные в своем изменении не
выходили за обусловленные границы. Важно понимать, что кри
териальные уравнения за пределами установленных диапазонов
теряют надежность, точность, прогнозность в количественном
смысле, а в ряде случаев - и в качественном.
Вид критериальных уравнений при теоретическом отыскании
количественных связей вытекает из математического анализа.
При эмпирическом подходе эти связи чаще всего представляют
в виде степенных функций , например Nu = aRenPrm, причем
параметры уравнения а, п, т определяются обработкой экспе
риментальных данных. Степенной вид критериальных формул в
общем случае, конечно, не отражает какого-либо физического
закона (природа совсем не отдает предпочтения степенным за
висимостям) . Просто степенные зависимости удобны, поскольку
в логарифмических координатах они изображаются прямыми
линиями (это, кстати, облегчает определение параметров урав
нения); кроме того, такая манера представления опытных дан
ных в какой-то мере еще и дань традициям.
Надежность полученных критериальных уравнений опреде
ляется правильностью физических представлений и построен
ных на их основе моделей (если речь идет о теоретических зави
симостях), обоснованностью выбора переменных и достаточной
широтой эксперимента (если зависимости - эмпирические). Во
всех случаях должны быть указаны границы применимости кри
териальных зависимостей.
Различные критериальные зависимости будут качественно
обоснованы и представлены в количественной форме (с указа
нием диапазонов их правомерного использования) при изложе
нии соответствующих разделов курса.
1 .8.6. Обобщенные переменные и пропускные способности
Обобщенные переменные (безразмерные числа, критерии по
добия - комплексы и симплексы) представляют собой соотно
шения конкурирующих факторов, эффектов. В качестве таких
факторов могут выступать потоки субстанции (или их коренные
фрагменты), определяющие сущность технологических процес
сов. В этом аспекте обобщенные переменные (по крайней мере
многие из них) вполне могут трактоваться как соотношения про
пускных способностей тех или иных стадий процесса.
При таком подходе яснее очерчиваются диапазоны условий,
в которых та или иная стадия процесса становится доминирую
щей или, наоборот, ее влияние будет исчезающе малым (так что
ее можно игнорировать при описании процесса) - выше такие
ситуации мы связывали с вырождением критериев подобия.
Продемонстрируем высказанные положения некоторыми
примерами.
1 15

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рассмотрим сначала перенос теплоты от горячей плоской
стенки (см. рис. 1 . 14, б) к потоку омывающей ее (пусть справа)
холодной среды. Будем рассматривать две последовательные
стадии теплопереноса: через стенку (ее теплопроводность Лт,
толщина 8) и от стенки к среде (интенсивность теплообмена
определяется коэффициентом теплоотдачи а ) . Кондуктивный
поток теплоты внутри тела через поверхность F составляет
Лт

1�
&

F; очевидно, что для плоскои стен ки
u

е
л
l�
&

=-,
8

где Л0 =

= 0 1 - 0 2 - разность температур на левой и правой сторонах
стенки (детально описание кондуктивного теплопереноса будет
рассмотрено в главе 6). Пропускная способность кондуктивной
стадии теплопередачи (согласно определению пропускных способностей) составляет

ле

_О_ = � F . Тот же поток
8

теплоты, отва·

димый к среде путем конвективной теплоотдачи , согласно вы
ражению (о) в разд. 1 .8 .4, равен Q = aЛtF, причем здесь Лt =
= 0 2 - t. Тогда пропускная способность конвективной стадии
теплопередачи составляет Q/Лt = aF. Отношение пропускных
способностей конвективной (снаружи стенки) и кондуктивной
(внутри нее) стадий теплопередачи приводит к уже полученному
ранее критерию Био:
aF

= а8 = Bi.
(Л. , / 8)F Л. 1

При таком подходе к формированию критерия четко видны
как его физический смысл, так и условия вырождения. Действи
тельно, если теплопроводность стенки высока, да еще мала
толщина ее 8, а теплообмен со средой затруднен (низкие а ) , то
пропускная способность кондуктивного потока много больше,
нежели конвективного. В этих условиях интенсивность теплопе
редачи всецело определяется стадией конвекции: сколько на этой
стадии будет пропущено теплоты (от стенки к среде) , столько
вообще будет передано теплоты в ходе теплопередачи (т.е. на
обеих стадиях вместе). А кондуктивный перенос теплоты в этом
случае может протекать очень интенсивно, поэтому он совсем
не сдерживает (не лимитирует) интенсивность теплопередачи .
Можно считать, что здесь кондуктивная пропускная способ
ность (Л-r,/O)F ..._. оо (характерный температурный напор Л0 ..._. О);
критерий Био Bi....,.O , т.е. его влияние на процесс теплопереноса
вырождается. В обратной ситуации крайне интенсивен конвек
тивный теплоперенос, т.е. aF ..._. оо (при этом Лt ..._. О), а вот теп
лоперенос в стенке будет малоинтенсивным - в силу низкой
теплопроводности стенки Лт и (или) большой ее толщины 8.
1 16

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Тогда теплопередача контролируется (еще говорят: определяется,
лимитируется) кондуктивной стадией, Bi --+ ао и его влияние на
процесс также вырождается.
Вырождение критериев Био означает, что в обоих рассматри
ваемых случаях Bi не войдет в уравнения, описывающие эти край
ние случаи теплопередачи. Однако при сопоставимости пропускнЬIХ
способностей конвективной и кондуктивной стадий пренебрегать
интенсивностью какой-либо одной из них относительно другой
нельзя - тогда критерий Био будет (прямо или в завуалированной
форме) входить в расчетные соотношения теплопередачи.
Аналогичным образом, применительно, например, к трубе
диаметром d и длиной /, могут быть сформированы критерии
Пекле Ре и Ред - как соотношения пропускных способностей
продольного переноса теплоты (соответственно, вещества) путем
7td 2
вынужденной конвекции _Q
__ = Gc = pwfc = pw-- с (либо
t" - t'
4
G = pwf - в случае массопереноса) и нормального к направлению движения среды кондуктивного теплового потока

=

Л.

-

7tdl (либо диффузионного

В

-

d

d
янных множителей
Gc
= wd !!._ = Ре !!._ и

'!:_ р

а 1

1

F= р

л.

d

F =

D
7td/) . С точностью до посто d
.

-

�
F = D 1 = Ред
wd d

G

p-

d

d
d
Специально подчеркнем, что сопоставление пропускных спо
собностей продольного конвективного потока (теплоты или ве
щества) и нормального кондуктивного (соответствующей суб
станции) приводит к произведению Ре или Ред на симплекс d/l.
Заметим : при строгом геометрическом подобии множитель d/I
принял бы для подобных явлений постоянное значение; в кри
терии он просто не был бы включен. При сопоставлении про
пускных способностей продольных конвективного и кондук
тивного потоков множители d/l отсутствовали бы.
В той же манере формируется, например, число Нусселъта
Nu - как соотношение пропускн ых способностей aF и

� F,

а

также ряд других обобщенных переменных. В частности, при сопо
ставл ении пропускных способностей конвективных тепловых пото
ков - нормального к поверхности теплообмена aF = = a7tdl и пpo7td 2
дольного вынужденного Gc = pw
с
получается дЛЯ теплооб4
--

-

1 17

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

менной трубы диаметром d и длиной / безразмерное число
aF
aтtdl
а
1
- = ---.,,..Gc
wpc d" '
тtd 2
c
pw
4
причем безразмерный комплекс a/wpc используется при описа
нии теплообменных процессов.
Аналогичная обобщенная переменная получается при анали
зе массопереноса:
13F
13тtdl
13
- = -- = - - ,
v
тtd2 w (/
--

w

4

--

причем безразмерный комплекс 13/w используется при описании
массообменных процессов.
Из приведенных выше примеров видно, что сопоставление
пропускных способностей стадий позволяет (помогает) выявить
определяющий линейный размер, входящий в критерии подо
бия для конкретного анализируемого явления , процесса.
Сопоставление пропускных способностей нередко приводит
к обобщенным переменным, не используемым (обычно или
пока еще) в качестве безразмерных чисел и критериев подобия.
И ногда выражение отношений пропускных способностей стадий
указывает на необходимость корректировки общепринятого на
писания критериев подобия или объясняет появление поправок
в критериальных и других соотношениях. В целом метод про
пускных способностей расширяет возможности использования
обобщенных переменных для решения технологических задач. При
этом в ряде случаев существенно яснее становятся физический
смысл явлений и процессов, а также границы (диапазоны) целесо
образности использования того или иного расчетного метода.
Л ИТЕРАТУРА

к главе

1

Е. Явления переноса: Пер. с анrл./ Под
ред. Н . М . Жаворонкова, В.А. Малюсова. М.: Химия, 1 974. 688 с.
2. Де Граот С., Мазур П. Неравновесная термодинамика: Пер. с анrл./ Под
ред. Д.Н. Зубарева. М . : Мир, 1 964. 456 с.
3. Патрашев А.Н. Гидродинамика. М . : Военно-морское изд-во, 1 953. 720 с.

1.

Берд Р" Стюарт В., Лайтфут

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Глава 2

ГИДРАВЛ И КА

Гидравлика - часть механики, изучающая равновесие и
движение жидкостей , в более широком смысле - также газов и
твердых тел. Учебник ПАХТ включает элементы технической
гидравлики:
- проблемы теоретического характера, составляющие базу
для подходов к некоторым задачам этой главы и разнообразным
проблемам ряда других глав;
- некоторые прикладные вопросы, имеющие существенное
значение для освоения общего подхода к анализу процессов, для
решения групп задач гидравлики , для практических расчетов в
других разделах курса.
Как указано в гл. 1 , гидравлика изучает проблемы, связанные
с переносом импульса (количества движения). В основе многих
построений настоящей главы лежат уже введенные ранее поня
тия о сплошной среде, идеальной Жидкости, ряд других поня
тий , а также полученные выше уравнения неразрывности, рас
хода, Навье-Стокса.
Гидравлика включает несколько разделов, из коих здесь рас
сматриваются два основных: весьма кратко - rидростатика
(равновесие жидкостей и других рабочих тел) и более подробно
- rидродинамика (движение жидкости, газа и т.п . ) . Ряд вопро
сов, имеющих меньшее значение для химической технологии,
оставлен за пределами учебника• (например, истечение на водо
сливах, струи, течение при высоких скоростях, потенциальное
течение или же такой специфический раздел, как плавание
тел).
2 . 1 . ГИДРОСТАТИКА

Гидростатика изучает жидкость в абсолютном и относитель
ном покое. Кардинальная проблема этого раздела, лежащая в
основе ряда конкретных задач, - определение давления в про
извольной точке технологического пространства:
(а)
р = р(х, у , z)
.

•

Эm вопросы см. ( 1 , 18,

22, 25 и др. ] .

1 19

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

В задачах гидростатики давление в точке не зависит от про
странственной ориентации ruющадки, на которую оно действует.
Признаком, позволяющим отнести решаемую задачу к гидро
статике , является неподвижность отдельных слоев (частиц) жид
кости относительно друг друга и относительно границ технологи
ческого пространства (стенок аппарата) . При этом сам аппарат,
сосуд >
совсем не обязательно должен быть неподвижным важно лишь отсутствие относительного перемещения жидкости
внутри сосуда. Иногда говорят: если удается выбрать систему
координат (жестко связанную с аппаратом, сосудом), относи
тельно которой не происходит движения жидкости, то задача
относится к гидростатике. А сам рассматриваемый сосуд может
находиться в покое или перемещаться по отношению к непо
движному наблюдателю (при этом возникают поля внешних
массовых сил ) .
2. 1 . 1 . Основные уравнения rидростатики и поверхностей уровня

К закону распределения давления (а) можно прийти, сопо
ставляя силы, отвечающие постановке задач гидростатики: нор
мальные поверхностные (давления) и внешние массовые. Одна
ко нам проще воспользоваться уже выведенным уравнением
Навье-Стокса ( 1 .20) , отбросив в нем слагаемые, связанные с
перемещением жидкости относительно зафиксированной на
сосуде системы координат. При этом все скорости жидкости (их
производные - тоже, конечно) относительно этой системы ко
ординат обращаются в нуль. Это означает, что в ( l .20):
= О - ведь ситуация в принципе стационарная
= 0), и значения � и �/дj равны нулю (j = х, у, z - коор
динатные оси, относительно которых жидкость неподвижна);
= О, так как под знаком v 2 каждое слагаемое д2 w/дj2 =
= О; при этом совсем . не обязательно рассматривать идеальную
жидкость с µ,
= О - все последующие рассуждения справед
ливы и для реальной жидкости (напомним, что она практически
несжимаема, так что ее плотность постоянна) : сила вязкости не
проявляется
= О ) и не влияет на ситуацию не вследствие µ =
= О, а из-за отсутствия градиента скоростей .
Таким образом, в ( l .2U) остаются лишь слагаемые, отве
чающие силам давления и внешним массовым силам - эти силы
взаимно уравновешены. В этом случае уравнения ( l .20) суще
ственно упрощаются; например, для оси х:
.!. др = р
(б)
х.
р дх
Аналогичные соотношения, называемые уравнениями Эйлера
для гидростатики , записываются и для других осей. И ногда их
преобразуют, перенося р в правую часть равенства и домножая

dw/dt
(дwj/'lf.r
vV2wj

1 20

v
(tт

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

обе части равенства на приращение координаты вдоль соответ
ствующей оси:

дхдр

dx = pPxdx

(в)

.

Такая форма записи позволяет путем суммирования выраже
ний типа (в) для всех осей координат получить полный диффе-

дрх дур dy дрz dz:
д д д
dp = p(Pxdx + PyJy + P{Jz) .

ренциал давления dp =

dx +

+

(2. 1 )

Эго выражение называют основным уравнением пщростатики в
дифференциальной форме. Его физический смысл обозначен вы
ше: равенство си.л давления и внешних массовых си.л. С позиций
переноса импульса: импульс нормальных поверхностных сил
равен импульсу внешних массовых сил .
Интегрирование выражения (2 1 ) должно привести к закону
распределеИИJ1 давлеИИJI (а) а интеrральной форме. Для несжи
маемых жидкостей (теоретически - для идеальных , практиче
ски - для реальных в диапазонах давлений, используемых хи
мической технологией):
у
р
z
(2.2)
f dp = - Р о = р f Px dx + f Py dY + f Pz dZ .
.

�

р

[х

�

h

�

)

Для нахождения интегралов в правой части (2.2) надо знать
законы изменения единичных массовых сил Рх, Ру, Pz по соот
ветствующим осям координат х,
а также значение коорди
нат какой-либо точки .хо,
ZQ, давление в которой
известно.
В результате выполнения операций интегрирования выраже
ния (2.2)
получаются значения давления в разных точках.
Точки пространсrва с одинаковым даалением образуют поверх
ности равного дааления, называемые поверхностями УJЮВИЯ. Вдоль
каждой такой поверхности дааление не изменяется (р = const), так
что dp = О. Тогда из (2. 1 ) , после сокращения на р � О, получается
уравнение поверхнОС111 уровня в диффереtЩИальной форме:
(2.3)
Pxdx + Py;Iy + P{Jz = О .
Зная законы изменения 1'j по соответствующим координатам
j = х, у, z, после операции интегрирования
(2.4)
fPxdx + f Py;Iy + f P{J = С
получаем уравнение поверхностей уровня в интеrральной форме (с
постоянной интегрирования С):
(r)
ft.x, у, = С, или /{х, у, z, С) = О .

у0,

у, z,

р0

z

z)

121

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Пусть среди бесконечного множества поверхностей уровня
(соответственно бесконечному числу значений С) есть поверх
ность, на которой известно давление (вьщелим параметры, отве
чающие этой поверхности , и ндексом "О"):
(2.5)
f{xo, Уо , Zo) = Со ;

тогда можно подставить в выражение (2.2) сопряженные значе
н ия Ро и хо, Уо , ZQ, и задача отыскания давления р в точке с ко
ординатами х, у, z - решена.
Обычно в качестве известной выступает свободная поверх
ность - поверхность раздела фаз (чаще всего - между жид
костью и газом); именно она далее отмечена индексом О Кон
кретное значение С0 определяется объемом жидкости У в техно
логическом аппарате (иначе: материальным балансом по объему
жидкости) и , разумеется, его конфигурацией.
Последовательность (алгоритм) расчета давления в точке за
пишем в следующем виде:
"

(2.5)

У � Со

�

хо, Уо ,

Zo

(2 2)

Рх , Ру, Р, ;

Ро

Р

".

·

(д)

Некоторые примеры реализации этого алгоритма представле
ны ниже .
2. 1 .2. ДаВJiения и поверхности уровня в покоящемся сосуде

Пусть жидкость находится в неподвижном сосуде (рис. 2 . 1 ) .
Координатные оси удобно зафиксировать, совместив плоскость
ху с дном сосуда; ось z направим вертикально вверх. В качестве
внешних массовых сил здесь выступает только сила тяжести (ее
ускорение - ускорение свободного падения - равно g) , направ
ленная против оси z. Для произвольной точки А (ее вертикаль
ная координата z) , очевидно, Рх = О, Ру = О , Р._ = -g; и если
известно ZQ, то из (2.2)
Р - Ро = p (-g) (z Zo ) = pgh
или
(2.6)
Р = Ро + pgh ,
-

где

h

=

( ZO - <:)

глуб и н а погружен ия т очЮI А ( под свободной поверхностью )

Координа1·а свободной поверхности Zo принята постоянной;
это отвечает повседневному опыту (поверхность покоящейся
жидкости - горизонтальна) и логике анализа (как и любая по
верхность уровня, она нормальна к единственной внешней мас
совой силе - силе тяжести) .
Величина р называется полным давлением, р0 - внешним,
гидростатическим. Если сосуд соединен с атмосферой , то
pgh
-

1 22

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 2. 1. Дааление в точке и свободная поверх
ность в неподвижном сосуде

z

Ро равно атмосферному давлению р3, а
Ро
величина pgh будет тра ктоваться ка к
избыточное давление (сверх атмосфер
А
ного).
у
g
В практических задачах координата
х
z точки, где нужно отыскать дамение
р, задана; однако
(а с ней и h) надо
найти - до этого фор мула (2. 6 ) дает
лишь ал горитм (способ, путь) решения . Чтобы довести ее до
"расчетного состояния", необходимо воспользоваться уравнени
ем поверхности уровня (2.4) :
f (-g) dz = С; иначе z = ( - C/g) const.
(2.7)
Последнее выражение отвечает горизонтальной плоскости ,
что теоретически подкрепляет принятый ранее постулат о
const. Заметим, что этот факт, как и отсутствие в формулах
(2.6) и (2. 7) координат х и у, обусловлен действием мщ:совых
с ил только по оси z.
Величина
либо задана изначально как уровень жидкости в
сосуде, либо ее находят по объему жидкости У . Например, для
сосуда постоянного поперечного сече ния f при отсчете z от дна
сосуда
У//
Формула (2.6) ямяется математическим выражением закона
Паскаля, устанамивающего связь полного дамения с внешним.
Эта же формула демонстрирует возможность измерения давле
ния в метрах жидкостного столба:
Р - Ро
(е)
h =

Zo

=

Zo =

=

Zo

Zo =

pg '
что находит свое отражение в названии правой части (е) или ее
состамяющих p/pg, pafpg-. пьезометрическая высота. Это выра
жение лежит в основе измерения давления пьезометрами, мано
метрами и вакуумметрами (см. рис. 2.2, а): правая трубка пьезометр , измеряющий избыточное давление (р - Pa )/pg в м
столба рабочей жидкости плотностью р; левая - И-образная
трубка - манометр, измеряющий избыточное давление (в дан
ном примере - в пространстве над жидкостью) hм = <Ро p3)/p,..g в м столба манометрической жидкости плотностью Р м·
Заметим , что расположение жидкости в к оленах манометра на
рисунке отвечает неравенству Ро > Ра · При Ро < Ра уровень жид
кости в левом колене будет ниже , че м в правом ; такая U
образная трубка, показывающая разрежение в аппарате по срав
нению с атмосферным давлением, называется вакуумметром.
1 23

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ОР.

..!

о

Р"

а

А

А

б

Рис. 2.2. П рактические приложения (а, б) уравнения '(2.6)

р = pgh и h = p/pg '
а также получаемые на их основе широко используются в по
следующих разделах.
Исходя из уравнения (2.6) можно записать закон сооб
щающихся сосудов в общем виде . Пусть в двух сообщающихся
сосудах находятся несмешивающиеся жидкости (их плотности р 1
и Р 2 ) , над свободными поверхностями которых давления равны
Р 1 и Р2 (см . рис. 2.2, б) . Жидкости в сосудах относительно гра
ницы их раздела А-А (жирная линия в левом сосуде) устана
вливаются на уровнях h 1 и h 2 · Если рассматривать равновесие
жидкостей для сечения А-А (ниже этого сечения столбы тяже
лой жидкости плотностью р 2 уравновешены) , то, согласно (2. 6 ),
легко выразить давление р в этом сечении и установить связи
между свойствами и параметрами жидкости в сосудах:
(ж)
Р = Р1 + P 1 gh 1 = Р2 + p �h 2 .

Соотношения типа

Отсюда нетрудно получить выражения для различных част
ных случаев (р1 = р2 ; р 1 = р 2 и др. ) , в том числе найти условия,
при которых жидкости в сообщающихся сосудах устанавливают
ся на одинаковом уровне.
2. 1 .3. Давления и поверхности уровня

в случае относительною покоя

Основная характерная особенность здесь в том , что сосуд
может перемещаться относительно неподвижного наблюдателя;
но относительно системы координат, зафиксированной на движу
щемся сосуде, жидкость остается неподвижной, поскольку в каж
дой ее точке внешние массовые силы уравновешены силами
давления . Основная проблема - в выражении единичных мас
совых сил Рх, Ру, Р,.
Рассмотрим отдельные примеры - соответственно различ
ным вариантам формирования внешних массовых сил.
1 24

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Цистерна, движущаяся с постоянным ускорением
по горизонтальной плоскости
Здесь (рис. 2.3, а) единичные массовые силы не изменяются

вдоль осей координат. Наряду с силой тяжести (ее ускорение по
оси z, как и в случае абсолютного покоя , равно -g) действует
еще и массовая сила вдоль оси х: единичная сила, численно
равная ускорению, составляет -а (знак "минус" показывает, что
в системе координат, закрепленной на сосуде, массовая сила
направлена против ускорения а) . Массовые силы вдоль оси у
отсутствуют, поэтому в решение координата у не войдет.
Ограничим задачу нахождением положения свободной по
верхности жидкости в цистерне. Подставим в (2.4) значения Рх =
= - а и Р, = - g и проинтегрируем:
f( - a) d.x + f ( - g)dz = С; - ах - gz = С.
Обозначив
C/g = С' = const , придем к уравнению плоской
поверхности:
(з)
z = - (a/g)x + с· '
наклоненной к горизонту под углом а , тангенс которого tga =
= -a/g. Значен ия постоянных С, С' для свободной поверхности
зависят от количества жидкости , первоначально залитой в
цистерну (они определяются из материального баланса по жид
кости) . Зная С' = Со и tga, найдем координату любой точки на
свободной поверхности ; определение далее по (2.2) давления р в
произвольной точке с координатами х, z затруднений не вызывает.
z

t
!

::i::

z
х

z

м
х
а

б

в

Рис. 2.3. Давление в точке и свободная поверхность - относительный покой:

а - цистерн а с ускорен и ем н а гор и зон тал ьной пл оскости , б - вертикальн ый сосуд,
вра щающийся вокр уг своей оси, " - гор и зонтальны й сосуд, враща ющийся вокруг свое й ос и

1 25

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Вертикальный цилиндрический сосуд,
вращающийся вокруг своей оси
Здесь (и в следующем примере) единичные массовые силы
изменяют свои значения вдоль некоторых осей координат (рис.
2.3, б) . Определим положение свободной поверхности и давле
ние в произвольной точке В
в сосуде радиусом R, вра
щающемся вокруг своей оси с постоянной угловой скоростью ro
(напомним: ro = 2 ттп, где п число оборотов сосуда в секунду;
[ro] = с- 1 ) . Первоначальный уровень жидкости в сосуде h0.
Поместим начало координат в центре дна сосуда, ось z (ось
вращения) направим вверх. Решение задачи начнем с выраже
ния единичных массовых сил , обозначив координаты точки В
х, у, z или, переходя к цилиндрическим координатам, r, <р и z.
Радиальная (центробежная) единичная массовая сила на коор
динате r составляет ro2r. Тогда (см. рисунок) :
Рх = ro2r cos<p = ro2x; Ру = ro2r sin<p = ro2y; как и ранее , Pz = -g.
-

p[f

]

Подставим эти значения в (2.2) и проинтегрируем:

Р - Ро
=

{

=

2
"'2 {х 2

Хо

-

ro 2 xdx +

-

Ро

Zo

=

х5 ) + "'22 {У 2 - У5 ) - g(z - < о )

Поскольку х2 + у2 =
сать компактнее:

Р

J ro 2 ydy - J gdz

Уо

=

r2 и XQ2

+

у02

=

}

(и)

r02, то (и) можно запи-

Р[ "' 2 {r 2 - r,' } - g(z - z o )] .
2

(2. 8 )

где г, z координаты точки, где оп ределяется дамение р; fЬ , � - координаты любой
точки на свободной поверхности
там постоянно (и известно) дамение Ро·
-

-

До тех пор, пока координаты r0, � какой-либо точки на сво
бодной поверхности не найдены, задача не может считаться
решенной, так как уравнение ( 2 . 8 ) для конкретной ситуации
использовать еще нельзя . Для определения пары сопряженных
значений r0 , � необходимо найти уравнение свободной поверх
ности . На основании (2.4) имеем

fro2xdx + fro2ydy - fgdz = С;
0) 2
(1) 2
0) 2
2 x 2 + 2 y 2 - gz = C ; 2 r 2 - gz = C .

(к)

Последнее из соотношений (к) позволяет найти уравнение
1 26

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

поверхности уровня в общем в ид е (здесь обозначено:
=

-C/g = const) :

2

(!)
z = С' + r2 .

2g

С '=·

(л)

Таким образом, поверхности уровня представляют собой па
раболоиды вращения с координатами вершины С'. Вьщелим
среди них свободную поверхность:
(!) 2

(.о = Со + - ro2 .

(м)

(.о = z. + - ro2 .

(н)

У = 1t R2h0 = 1t R2 z. + 2. 1t R2(H - Z• ) ,

(о)

2g

На рис. 2.3, б координата вершины параболической свободной поверхности обозначена z. ; при r0 = О имеем (.о =
Z• ,
тогда по (м) получается тождественная замена С0 = Z• , так что
(!)

2

Без знания z. нельзя найти по (н) искомую пару сопря 
женных значений (.(), r0. Для определения z. запишем матери
альный баланс по жидкости: сколько ее было залито в сосуд (У
- до уровня h0) , столько и находится во вращающемся сосуде:
2g

1

причем первое слагаемое в правой части - объем цил индри
ческой части жидкости высотой z . , второе - ее объем выше
уровня z. (известно, что объем параболоида вращения равен
половине объема цилиндра той же высоты). Из (о) после со
кращения на 7tR2 имеем
Н + Z• = 2h0, Н = 2h0 - Z• и т. п .
(п)
Величину Н можно найти не только из материального балан
са (о) , но и из соотношения сил по (н) : Zo = Н при ro = R
(стенка сосуда) :
2

Н = Z• + !!:_ R2

2g
Приравнивая величины Н по (п) и (р), получим
ro 2 R 2
z · = h0 - -4g

(р )
(с)

Подставив это значение z. в (н) , приходим к расчетному вы
ражению для свободной поверхности �
7�
'VJ

00 2 R 2 00 2 ГО2 .
- h0 - -+ 4
g

2g

(2.9)
1 27

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Теперь, задаваясь произвольно значением r0, находим по (2.9)
отвечающее ему значение z.o. Для отыскания давления р в точке
с координатами r, z необходимо в (2.8) подставить эти сопря
женные значения r0 , z.o.
Из полученных соотношений следует:
- по выражен иям (с) и (п) либо (р) можно найти выражение
для высоты подъема жидкости у стенки вращающегося сосуда:

Н = ho

+

(J) 2 R 2
4g

--

(т)

- высота Н растет, а Z• понижается с увеличением скорости
вращения сосуда ffi . При этом сопоставление (с) и (т) показы
вает, что подъем жидкости у стено к и опускание вершины пара
болоида (относительно первоначального уровня ho ) выражаются
одинаковыми высотами : ffi 2 R2/(4g) .
Важно, что соотношение сил (центробежных и тяжести) , вне
зависимости от параметров вращения и геометрических характе
ристик (R, h0), всегда выражается соотношением (н) ; кстати ,
именно по этой причине величин ы Z• и Н не зависят от плот
ности жидкости р. А вот материальный баланс по жидкости (о)
ранее записан лишь для случая , когда вершина параболоида
остается выше дна сосуда (или его касается) . Значение ffi , при
котором происходит касание дна, легко определяется из (с) при
Z• = О: ffi = (2/R) �gho . При бол ьш их ffi ( z. < О, Н > 2ho) матери
альный баланс по (о) неправомерен , его надо составлять заново.
При расчете давления по (2.8) может получиться р < р0, ина
че: р - Ро < О. Эго означает, что точка В оказалась над свободной
поверхностью, и в действительности давление в ней равно JJo.
Замети м ,
что при ffi = О задача сводится к покоящейся
жидкости, и выражения (2.8), (2.9) закономерно обращаются в
(2.6) и (2.7). Но (2.8) также обращается в (2.6) , если точку на
свободной поверхности взять над точкой В: ro = r. Надо, однако,
понимать, что в этом случае в отличие от (2.6) локальная глу
бина h погружения точки В для вращающегося сосуда будет за
висящей от параметров вращения, так как координата <.о по (2.9)
связана с ffi .
Горизонтальный сосуд, вращающийся вокруг своей оси

Ограничимся получением уравнения свободной поверхности .
Совместим (рис.2 . 3 , в) ось у с горизонтальной осью вращения
сосуда (вдоль этой оси массовые с илы не действуют) . Выразим
единичные массовые силы, действующие в точке М:
Рх = ffi2r cosq> = ffi 2x; Ру = О; Pz = g + ffi 2r sinq> = - g + ffi 2Z.
-

1 28

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Подставим эти значения в (2.4), выполним операцию инте
грирования и перейдем к записи уравнения свободно й поверх
ности . В ходе вывода заменим постоянную интегрирования С,
с
обозначив
через С', а для свободной поверхности
(1) 2 / 2
через Со . Тогда
(1) 2
(1) 2
fro2xdx + f(-g + ro 2 z)dz = С;
z 2 - gz = с;
+

2х 2 2

х

2�

2g z
2 + z2 <.() = Со .
= С' и Хо2 + (.()2 ro 2
ro
Добавив к обеим частям последнего равенства постоянную
величину (g/ro 2)2 , получим
'
2
С
<о +
о+
,
• СО ,
-

или

хБ +Б

, (:,J}

:

( - :2) 2

xJ + z o

(: )

(у)

= Со

- уравнение окружности (в пространстве
цилиндра) радиу
сом ro = ../Со , не соосно й с цuл индром, конкретно - с ц ентром ,
поднятым над осью вращения сосуда (точка О) на высоту е = g/ro 2
Для сосуда радиусом R и длиной / при объеме первоначально
залитой жидкости V значение r0 определяется из материального
баланса по жидкости V = rt ( R2 - r02) /, причем, очевидно, r0 2 =
= .хо 2 + <.()2 . Итак, поверхности уровня (в их числе - свободная
поверхность) представляют собой цилиндры, оси которых сме
щены вверх относительно оси вращения сосуда на величину
эксцентриситета е. Из выражения (у) видно, что с увеличением
скорости вращения сосуда ro эксцентриситет е уменьшается; при
высоких значениях ro (теоретически - при ro � оо) получается
е � О, и свободная поверхность становится практически соос
ной с цилиндрическим сосудом.

.

-

Задачи на абсолютный покой или относительный
для ц истерны, верти
кального вращающегося сосуда и ряд других - принадлежат к гидростатике с
полным основанием - теоретически и практически . Задачу для горизонтал ьно
го вращающегося сосуда к гидростатике можно отнести лишь умозрительно: в
действительности же для поддержания найденной выше ц илиндрической фор
мы свободной поверхности необходимо постоянное (мгновенное) перетекание
жидкости из верхних зон в нижние. Реально это протекание не успевает за
вращением сосуда, и практически эксцентриситет е получается менее рассчи
танного, р <i11ного g/ro2.

1 29

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

2. 1 .4. Силы давления на

дно

и боковые стенки сосуда

Будем решать задачу определения сил давления для покояще
гося сосуда, жидкость в котором находится под действием силы
тяжести.
Сила даВJ1ения на дно сосуда. Пусть в сосуде, площадь днища
которого Fдю находится жидкость плотностью р; уровень жид
кости в сосуде h, давление над свободной поверхностью р0. Тог
да во всех точках днища давление одинаково и, согласно (2.6) ,
равно р = Ро + pgh. Сила полного давления на дно сосуда по
второму из выражений ( 1 .5) составляет:
(2. 1 0)
Рдн = рFдн = (Ро + pgh)Fдн = РоFдн + pghFдн .

Первое из слагаемых в правой части представляет собой силу
внешнего давления, второе - гидростатического. Подчеркнем,
что сила давления на дно сосуда не зависит от его конфигура
ции - важны лишь площадь днища Fдн и уровень жидкости в
сосуде h (разумеется, также плотность жидкости р и внешнее
давление Ро).
Сила даВJlения на боковые стенки сосуда. Ограничимся реше
нием задачи применительно к плоской вертикальной стенке • она показана в изометрической проекции на рис.2.4. Необходи
мо найти силу давления, действующую на интересующий нас
фрагмент поверхности F, и точку приложения ее равнодей 
ствующей . Поскольку глубина погружения различных точек
площадки F относительно свободной поверхности (ее уровень
обозначен х - х)
различна (h = var), то найдем сначала эле
ментарную силу давления dP, действующую на бесконечно ма
лую поверхность d/, находящуюся на некоторой текущей глуби
не h. Для этого воспользуемся выражением (2.6) и первой из
формул( 1 .5):

dP = (Ро + pgh)d/
Проинтегрируем это уравнение по всей поверхности F:
Р = Po F + p g I h df .

(ф)

( F)

Второе слагаемое в правой части содержит статический мо
мент площади J h d}; по теореме о среднем он равен произведе
(F)

нию некой "средней" глубины погружения hц площадки F на
величину этой площадки F:
I h dF = hц F .
( F)

• Для плоской наклонной и криволинейной стенок задача рассмотрена в (6) .

1 30

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис.2.4. К определению силы давления на боковую стенку и центра
давления:
ЦТ - центр тяжести (массы), lJД
центр давл ения

-

При этом координата hц
представляет собой rлубииу

F. Тогда сила полного
давления на боковую стенку
Р = PoF + pghцF . (2. 1 1 )
-Боковая
Первое слагаемое в правой
стенка
части есть сила внешнего дав
"""--.--днище
ления, второе - гидростати
ческого. Заметим, что во
многих практических задачах (прежде всего для открытых аппа
ратов) сила внешнего давления уравновешивается аналогичной
силой снаружи аппарата, так что в расчетном плане иногда ин
терес может представлять только сила избыточного давления.
В отличие от днища, для боковой поверхности сила давления
(гидростатического, полного) изменяется с глубиной. Поэтому
возникает проблема отыскания точки приложения ее равнодей
ствующей; эту точку называют центром дав.ления. Найдем коор
динату центра гидростатического давления hд , для чего приме
ним теорему механики, гласящую, что относительно некоторой
оси момент равнодействующей СШIЫ равен сумме моментов со
ставляющих. Моменты будем брать первоначально относительно
оси х - х, совпадающей с положением свободной поверхности в
плоскости боковой стенки :
(х)
Pr;chд = f h d Pr/c .
(F)
Раскроем смысл полной силы гидростатического давления
Pr/c по (2. 1 1 ) и элементарной dPr/c по ( 1 .5): Pr/c = pghцF; dPr/c =
= pghdf, подставим эти значения в (х) . После сокращения на pg
получим
(ц)
hцhд F = f h 2 d/ = lx:x ,
(F)
где lxx называется момеиrом инерции плоЩIДJ[И F произвольной формы отно-

поrруж:евия центра масс wо

щади

сительно оси х - х.

Если подставить в (ц) значение hц через статический момент
площадки F, то получится, что hд есть отношение моментов
этой площадки 2-ro (инерции) и 1 -то (статического) порядков
относительно оси х - х. Обычно удобнее оперировать моментом
131

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

инерции /о относительно горизонтальной оси О - О, проходя
щей через центр масс площадки F (его легче рассчитать; он
приводится в справочниках) . Формула определения моментов
для параллельного пе еноса осей известна из теоретической
механики: lxx = Io + hu F. Подставим это значение lxx в (ц) :

�

huh4F = Io + hu2 F ,

откуда

Из

h4

(2. 1 2)

=

hu

.

+

Io

Fhu

(2. 1 2)

--

следует, что точка приложения равнодействующей

для вертикальной (наклонной - тоже) поверхности находится

ниже

центра тяжести площади - это следствие нарастания дав
ления по мере увеличения глубины .
Определение /0 п р и известной конфигурации площадки F
принципиальных затруднений не вызывает.
Приведем пример расчета /0 для прямоугольной площадки основанием а и
высоrой Ь. ОчевИдНо, что rориэонтальная ось О - О проходит через середину
площадки и делит ее пополам, так что для каждой половины высоn.� h изме
няются от О до Ь/2. Элементарная площадка равна od h . Тоrда момент /0 для
обеих мощадок вместе равен

Ь/2

lo ""' 2 f h2 od h
о

•

�Ь/2

2а h

3

=

3

!!!.__ .

Дпя случая , коrда а = a(h) = var, e ro нельзя выносить иэ-под знака инте
грала, но общий подход к определению /0 сохраняется.
о

12

2.2. Г ИДРОДИНАМИКА (ОБЩИЕ ПРОБЛЕМЫ)
Кардинал ьная задача гидродинамики, как указывалось в разд.
состоит в определении взаимосвязанных давления и скорос
ти в какой-либо точке технологического пространства в произ
вольный момент времени. При этом в отличие от гидростатики
давление в точке (его называют rидродннамическим) эдесь по
разным направлениям
Решение кардинальной зада
чи позволяет проследить траектории и характеристики движе
н ия жидкости в зависимости от конфигурации канала и условий
течения - это зачастую отправная точка для решения конкрет
l:fЫХ технологических задач.
Общий характер течения жидкости наглядно представляется
в виде линий тока, в каждой точке которых вектор скорости
движен ия совпадает с касательной к этой линии (рис. 2.5). При
установившемся движении линии тока сохраняются неизменны-

1 . 5,

-

1 32

различно.

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис.2.5. Линия тока и трубка тока

ми, при неустановившемся - это мгно
венная характеристика, изменяющаяся
во времени. В непосредственной бли
зости к рассматриваемой проходят дру
гие линии тока, создавая совместно
трубку тока. Совокупность трубок тока в
канале образует поток рабочего тела
(жидкости, газа и т. п.). Ряд гидродина
мических соотношений, справедЛивых для трубки тока (ее жи
вое сечение можно трактовать как бесконечно малое) , в практи
ческих целях нередко распространяют на поток в целом - это
загрубляет анализ, делая полученные соотношения в известной
мере приближенными, но зато позволяет использовать выявлен
ные закономерности для решения некоторых инженерных задач .
Различают внуrренние и внешние задачи гидродинамики . Пер
вая группа задач относится к течениям внутри каналов, труб,
аппаратов - поток ограничен наружной стенкой , закон о мерно
сти течения определяются взаимодействием потока с этими
стенками. Вторая группа задач изучает течение снаружи тел, его
закономерности зависят от взаимодействия обтекаемых тел с
невозмущенной (в идеале - неограниченной) средой. Более
сложными я вля ются смешанные задачи, когда движущаяся среда
(жидкости , газы, твердые тела, их смеси) гидродинамически
взаимодействует со стенками канала и обтекаемыми телами посторонними (при движении однофазных сред) либо состав 
ляющими поток (при движении многофазных систем). Здесь
нередко вводятся термины " стесненное движение " , " стесненное
обтекание" и т.п.
Заметим: в основе закономерностей движения потоков в
условиях внутренних и внешних задач лежат общие предпосьш 
ки , в частности устанавливаемые законом ( 1 .9). Поэтому при
решении упомянутых задач возможны общие подходы; в ряде
случаев к успеху приводит подмена одной задачи другою.
В химической технологии достаточно часто встречаются все
три вида задач. Ниже последовательно анализируются сначала
внутренние задачи гидродинамики (разд. 2 . 2 . l - 2.6), а затем
внешние (разд. 2.7) и кратко - смешанные (разд. 2.8).
2.2. 1 . Уравнение Бернулли

Уравнение Навье-Стокса ( l .20) чаще всего весьма сложно
для аналитического решения инженерных задач (даже в случае
стационарных течений)
из-за многочисленности связей
(часто - нелинейных) между входящими в уравнение величи1 33

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

нами, трудностей в достаточно точном формулировании гра
ничных условий и возникающих чисто математических ослож
нений. За довольно редким исключением решить эти уравнения
аналитически не удается, причем наибольшие трудности пред
ставляет операция двойного интегрирования фрагментов урав
нения, включающих лапласиан. Чтобы создать основу для ин
женерных решений, уравнение Навье-Стокса значительно
упрощают, проводя анализ первоначально для идеальной жид
кости, т. е . отбрасывая слагаемые, содержащие v, µ = О. Это,
однако, может привести к существенным погрешностям при
описании и расчете течения реальных жидкостей . Поэтому в
дальнейшем в полученные решения вводят поправки, призван
ные учесть сделанные ранее допущения, т. е. скомпенсировать
слагаемые, отброшенные в уравнении Навье-Стокса.

Уравнение Бернулли для идеальной жидкости
Будем рассматривать частный, но наиболее часто встречаю
щийся случай течения в поле сил тяжести.
Уравнение Навье-Стокса ( 1 .20) может быть записано для
любого направления. Выберем (рис. 2.6) бесконечно малый
участок трубки тока d/, наклоненный к горизонту под углом а , и
запишем применительно к этому участку уравнение Навье
Стокса для идеальной жидкости
в направлении /:
dw
1 др
(2. 1 3)
- - = -g sш a - - .
-=-

р д/

.

dt

Здесь gsina - единичная массовая сила вдоль оси / (ось z
по-прежнему направлена вертикально вверх, единичная массо
вая сила вдоль нее равна -g) , w - скорость потока вдоль оси /.
Пусть течение является стационарным: дw/дt = О; поскольку
движение - однонаправленное• , то dw/dt = w(дw/дl). В резуль
тате в уравнении остается одна независимая переменная /, так
что частные производные можно заменить обыкновенными:
dw
.
1 dp
-

- - = -g SIП а
р

d/

-

W

d/

-

•

Домножим каждое слагаемое на d/, произведем замены
( d/)sina = dz, wdw = dw2/2 и соберем все слагаемые в одну часть
равенства:
dw 2
1
(а)
=о
gdz + - dp +
р

2

-

* Это утверждение я вляется прибл и же н н ы м , поскол ьку в общем случае не
обязател ьно /1
f;, так что составляющие этих скоростей вдол ь других
направле н и й не строго равны нулю. Замети м , что точ н ы й анализ, требующий
вес ьма громоздких п реобразова н и й , при водит к тем же конеч ным резул ьтатам .
=

1 34

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис.2.6. К

или

выводу уравнения Бернулли

--

dp + dw 2 = о .
dz + -

z

(2. 1 4)

2g
pg
выражения

Эrи
представляют
собой уравнения Бернулли в диффе

ренциальной форме.

Поскольку сумма дифференциа
лов равна дифференциалу суммы, то для несжимаемой жид
кости ( р = const)

(

2
d z + _!!_ + w

2g

pg

)=

О ,

откуда получается уравнение Бернулли в интегральной форме:

z+

-р + -w 2
2g

pg

=

(2. 1 5)

const.

Уравнение пока что записано для трубки тока. Чтобы это
уравнение можно бьvю применять для инженерных расчетов,
его распространяют на течение в канш�е в целом (потери в точ
ности при таком заrрублении невелики}, относя характеристики
течения к полному живому сечению потока /; тогда скорость w
принимает смысл средней скорости в сечении потока.
Нередко удобно анализировать изменение характеристик те
чения между двумя сечениями fi и f2. Пусть между этими сече
ниями нет дополнительных Приходов и Уходов жидкости
(помимо Прихода поступающей жидкости через сечение fi и
Ухода через h жидкости, покидающей рассматриваемый учас
ток) . В этом случае выражение (2. 1 5) можно записать для сече
ний fi и h прямого канала:
Z1

_

w
+ f!l_ + l

2

pg

2g

= Z2

w 22
+ .!!1_ + pg

2g

·

(2. 1 5а)

В выражениях (2. 1 5) и (2. 1 5а) все слагаемые имеют размер
ность длины (в СИ измеряются в м) и представляют собой в
геометрической интерпретации некие высоты. При этом z1 и
z2
расстояния центров сечений канала от некоторой произ
вольно выбранной горизонтальной ПJJоскости отсчета. Под
черкнем, что ее расположение - безразлично (обусловлено
лишь соображениями удобства) , поскольку для течений суще
ственна разность уровней z 1 - z2 . Каждое из этих слагаемых на-

-

1 35

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

а

б

в

Рис.2. 7. Илл юстрация эффекта Бернулли:
да,

а

-

легкий шар ик в п ото ке воздуха, 6 - чел о ве к н а платформе вбл изи мча щегося поез 
параллельн о движущихся корабля

в - два

зывается rеометрической, или нивелирной высотой. Слагаемые
вида p/(pg) называются пьезометрическими высотами (см. разд.
2. 1 .2); на такую высоту поднимается жидкость плотностью р под
давлением р. Подчеркнем, что и здесь уровень отсчета давлений
безразличен (можно вести отсчет от нуля, от атмосферного или
какого-либо иного давления ) , так как для течения существенна
разность давлений P t - Р2 · Наконец, слагаемые вида w2/(2g) назы
ваются скоростными (реже - кинетическими) высотами.
Наряду с термином "высота" в гидравлике для этих слагаемых
используют термин напор. Высоты, напоры измеряются в м
столба движущейся (рабочей) жидкости. Сумма трех рассматри
ваемых слагаемых называется полным, или динамическим напо
ром (высотой).
Из выражений (2. 1 5) и (2. 1 5а) следует, что при течении иде
альной жидкости геометрическая, пьезометрическая и скорост
ная высоты могут изменять свои значения от сечения к сече
нию, но сумма их (при отсутствии дополнительных Приходов и
Уходов жидкости между сечениями) есть величина постоянная .
Это означает, что при уменьшении (увеличении) какого-либо
одного из слагаемых обязательно увеличится (уменьшится) ка
кое-нибудь из остальных (или они оба). Так, при увеличении
скорости (особенно - при сильном) уменьшается давление (на
этом принципе работают инжекционные устройства).
Наглядная иллюстрация эффектов Бернулли представлена на
рис. 2.7: легкий шарик не выпадает из наклонной газовой струи
(внутри нее - область высоких скоростей и пониженных давле
ний); нельзя находиться на платформе близко к быстро идуще
му поезду (человека может притянуть к мчащемуся составу) ; не
допускается быстрое параллельное движение двух рядом идущих
кораблей (скорость воды между ними больше, чем снаружи , так
что возникающая разница в давлениях может привести к их
бортовому столкновению) . На использовании уравнения Бер
нулли основано применение напорных трубок для измерения
1 36

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

скоростей: очевидно, что пьезометр, присоединенный к трубке ,
отверстие которой выставлено против потока, покажет суммарный напор

р

+

w2

, откуда нетрудно, зная давление, найти скорg 2 g
рость w. Примерами практических приложений уравнения Бер
нулли могут также служить инжекторы и эжекторы (см. разд.
3 .4.2, 4.6 и 9.6.7).
Для энергетической интерпретации уравнения Бернулли надо
представить слагаемые в форме , аналогичной (а) , и домножить
их на кг/кг. Тогда слагаемые приобретают смысл , ясный из coм - м кг кг · м м
пос-rавления размерностеи ; например: [ z·g) --- -= -- - =
с 2 кг
с 2 кг
-м
Н
Дж
= -- =
- это удельная энергия (т.е. отнесенная к 1 кг
-

-

v

--

кг
кг
жидкости) . При этом z·g - удельная потенциальная энергия
жидкости, поднятой на высоту z; р/р - удельная потенциальная
энергия даВ.11ения; w2/2 - удельная кинетическая энергия . Сумма
этих энергий представляет собой полную энергию потока. В
этом аспекте уравнение Бернулли означает , что потенциальные
энергии и кинетическая энергия могут изменяться от сечения к
сечению, но суммарно их энергия (при отсутствии дополнитель
ных Приходов и Уходов энергии между рассматриваемыми сече
ниями) остается неизменной. Таким образом, уравнение Бернул 
ли является одним и з выражений Закона сохранения энерПIН .
Заметим , что слагаемые уравнения Бернулли в его энергети
ческой и нтерпретации , будучи умножены на плотность р , при
обретают смысл соответствующих удельных энерги й , отнесен 
ных к единице объема.
Уравнение Бернуми для реальной жидкости

Анализ течения идеальной жидкости проведен при игнори
ровании сил трения, что позволило отбросить слагаемые vV 2 w в
уравнении Навье - Стокса. При течении реальных жидкостей
необходимо внести поправки , отражающие действие сил трения ,
т . е . уч итывающие затраты энергии на преодоление этих сил, и
тем самым компенсировать отброшенные члены уравнения,
выражающие силы вязкости (вязкостные члены) .
Пусть реальная жидкость в сечении 1 характеризуется теми
же составляющими напора и полн ы м напором (или энергией) ,
w 12
· к сечению 2 этот напор (энерчто и идеальная: z1 + f!l_ +
рg 2 g '
-

1 37

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

w2

гия) z2 + !2.. + 2 будет для реальной жидкости меньше, неже2g
рg
ли для идеальной, поскольку часть энергии по пуrи от сечения
1 к сечению 2 затрачена на преодоление сил трения - происхо
дит рассеяние (диссипация) энергии, часть ее переходит в теп-

2

w
лоту. В результате для реальной жидкости z2 + Р 2 + _l_ <
2g
pg

z1

+

w2

1 . Ч тобы верн ься к записи в форме
+ lL + уr

равенства, необрg 2 g
ходимо для сечения 2 ввести дополнительное слагаемое, выра
жающее упомян уrые потери энергии. В терминах геометри
ческой интерпретации говорят о потерянном напоре (потерянной
высоте) , обозначаемом символом hп и измеряемом (как и другие
слагаемые) в м жидкостного столба. Таким образом, для реаль
ной жидкости
w2

1
Z 1 + 12_ + - =

w2
z2 + 12._ + 2 + h n·
2

(2. 1 6)
pg 2 g
pg
g
Итак, при течении идеальной жидкости полный напор в се
чении 2 бьш равен зафиксированному в сечении J, а при тече
нии реальной жидкости - он в сечении 2 стал меньше. Важно
установить, за счет какой составляющей произошло уменьшение
напора в сечении 2 при переходе от идеальной жидкости к реаль
ной. Величина z2 (как и z1) - характеристика канала, она от
свойств протекающих по нему жидкостей не зависит и потому на
переход к реальной жидкости повлиять не может. Величина w2
при заданном объемном расходе V так.же не изменяется при пере
ходе от идеальной жидкости к реальной, поскольку жидкость
несжимаема (идеальная - теоретически, реальная - практиче
ски); это следует из уравнения расхода w2 = V/h (площадь живо
го сечения h от свойств жидкости, естественно, не зависит). Зна
чит, при переходе от идеальной жидкости к реальной изменение
претерпевает давление Р2 · Если сопоставить правые части уравне
ний (2. 1 6) и (2. 1 5а) , обозначив давление для идеальной жидкости
Р2 " , то при одинаковых левых частях уравнений имеем
и
Z2 + Р 2

pg

-

+

-

w2

2 = Z2 + Р 2
2g
pg

-

+

w 22

2g

-

+

Отсюда видно, что l!1... = Р2 + hn , так что
pg
pg

1 38

и

hn

.

(б)

потери давления

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

(напора) при течени и реальной жидкости от сечения 1 к сече
нию 2 состамяют:

hп

и

=

Р2 - Р 2

pg

=

Лр п

--

pg

(в)

Таким образом, введение hп позволяет обойти сложности ре
шения уравнения Навье-Стокса, связанные с учетом
(интегрировани ем) вязкостных членов. Теперь все трудности
расчета перенесены на определение hп. Расчет этой величины
является одной из важнейших проблем гидродинамики: знание
hп необходимо при расчете напорных устройств (насосов и т.п.),
определении основных параметров течен ия в трубопроводах
(задачи эксплуатации и проектирован ия), выборе режи мных
характеристик при осущестмении ряда процессов и т.д. Значи
тельная часть последующих разделов этой главы (включая и
внешние задачи гидродинамики) связана с определением поте
рянного напора .
2.2.2. Уравнение Дарси-Вейсбаха
Для определения потерь напора hп при течении жидкости

рассмотрим прямолинейный участок трубопровода длиной / с
произвольной (но постоянной) формой поперечного сечения f,
пусть периметр этого сечения равен П, причем канал заполнен
движущейся жидкостью, так что речь идет о смоче1П1ом периметре.
Воспользуемся общим при емом, нередко применяемым в
курсе ПАХТ для определения неизвестной величины: приравня
ем два выражения, первое из которых содержит искомую величи
ну и формально описывает некое ямение, процесс, а второе дает
физически обоснованное описание того же ямения, процесса.
Потеря дамения Лрп обусломена силой трения . Выразим эту
силу формально - по ( l .5) и (в) через потерянный напор hп:
Лрr/ = hпpgf. Эта же сила может быть запи сана, согласно ( l .6),
как произведен и е напряжения трения на стенках канала tт = ts и
поверхности трения - боковой поверхности канала П /:
t.fП /.
Таким образом,
(г)
hпркf = tsПI ,
откуда
Пlt s
(д)
=

hп

/pg

Это выражение демонстрирует характер мияния отдельных
параметров потока на hп . Преобразуем (д) к виду, более удоб
ному для инженерных расчетов.
Отношение живоrо сечения потока f к смоченному периметру
П характеризует форму канала и называется rидраалическим ра1 39

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис . 2. 8. К расчету эквивалентного диаметра жи 
вого сечения (П - смоченный периметр; тонкая
линия А в смоченный периметр не включается)

диусом живого сечения :
Rr = //11 .

идет о се
а
б
чении и периметре не канала, а живого сечения
потока - эти понятия совпадают только для
каналов, в которых все сечение занято жид
костью (рис . 2 .8, а). Если же живое сс;чение потока составляет некоторую долю
сечения канала (рис. 2.8, б), то часть периметра потока, соприкасающегося не
со стенкой, а с газом, не включается в смоченный периметр. (Молчаливо пред
полагается, что трением потока на грани це с газом можно пренебречь.) Смо
ченный периметр потока на рис. 2 .8, б обозначен более жирно.
Существен н о .

'ТТО

р е ч ь здесь

(е)

Для наиболее часто встречающихся заполненных потоком
круглых сечений радиусом R имеем по (е) : Rr = (nd 2 /4)/(nd) =
= d/4, т.е. гидравлический радиус не совпадает с геометриче
ским : Rr = R/2. Это создает неудобства при расчетах; поэтому
вводят эквиваленmый диаметр de , равный учетверенному гидрав
лическому радиусу:
(ж)
de = 4Rr = 4//11 .
Для круглых сечений de = d.
Введение Rr и d, обусловлено предположением, что в случае канала с про
извольной формой сечения можно воспользоваться расчетными соотношения
ми, установленными для крутлого сечения, если вместо диаметра подставить в
эти соотношен ия величину d" Это предположение не является строгим, но для
ряда задач (прежде всего для окрутлых сечений без внутренних выступов и
острых утлов) оно существенно упрощает расчеты, не снижая сколько-нибудь
заметно их точности .

П одставив в (д) 4//11

= de ,
hп

пол уч им

= _1_ 4t s .
d e pg

(з)

Трудноопределимым в этом выражении является напряжение
трения на стенках канала ts. Or него избавляются, подставляя
вместо 4тs /(pg) пропорциональную ей иную величину той же
размерности: м. В качестве такой величины не следует выбирать
z или p/pg-. из-�а неопр еделенности начала отсчета; из-за изме
нения значении z и p/pg по длине канала; из-за того, что харак
теристики течения вообще зависят не от значений z и p/pg, а от
их разностей Лz = Z 1
z2 и Лр = Р1 Р2 · Комплекс 4тs /(pg) при
нимается пропорциональным скоростному напору:
-

-

4t s
pg

=

Л.

г

�
2
g

(и)

Это удобно, поскольку в каналах постоянного сечения ско
рость w не изменяется по их длине; а при изменении сечения -

140

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

w легко пересчитывается по уравнению расхода. Однако не со
ображен ия удобства являются здесь определяющими. Напом
н им, что член hп появился в результате перехода от реальной
жидкости к идеальной и обратно, чтобы избежать трудностей
интегрирования �авнения Навье-Стокса; конкретно речь IШia
о слагаемых vV wj. Поэтому hп должен структурно включать
величины, изначально содержащиеся в отброшенных членах
уравнения Навье-Стокса - скорость и др. К тому же заключе
нию приводит рассмотрение формулы Ньютона ( 1 .9) для на
пряжения трен ия 't'т (и 't's - тоже). Наконец, скорость w масштабно связана с внутренней характеристикой течений F;rr; ,
называемой динамической скоростью (см. разд. 2.2.5), что являет
ся еще одним доводом к использованию W2 - -rs /р .
Подставив значение рассматриваемого комплекса по (и) в
выражение (з), приходим к расчетному соотношению
2
1 w ,
hп = Лг (2. 1 7)
de 2 g
называемому уравнением равномерного движения, или чаще уравнением Дарси-Вейсбаха. В практике технологических расче
тов это уравнение нередко используется в форме
--

Лрп

= hп pg =

Лг 1

� р.

de 2

(2 . 1 7а)

Для круглых труб в эти выражения вместо de входит геомет
рический диаметр d.
Коэффициент пропорциональности Лг носит название коэф
фициента rндра8JIИЧеского сопротивленИJI (или коэффициента
внутреннего трения) . Этот безразмерный коэффициент для кана
лов с конкретными значениями / и d (ил и de ) однозначно связан
с числом Эйлера. Форма связи ясна из (2. 1 7а) :
др� = Eu = Л г -1- ,
(к)
2de
pw
причем сим плекс l/de не был выя влен в ходе масштабных пре
образований, приводящих к написанию Eu, поскольку геомет
рический множитель подобия mг считается одинаковым по всем
линейным координатам.
Коэффициент гидравлического сопротивления имеет вполне
определенный физический смысл. Согласно феноменологи
ческому подходу, обусловившему появление Лг, можно записать
соответственно (и):
(л)
Л г = 8 2- .
pw 2
Это же выражение получается из физических соображений путем сопоставления потоков импульса Jll коли чества движения

141

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

(т.е. соответствующих пропускных способностей). Действитель
но, поток импульса в единицу времени, отвечающий диссипа
ции энергии за счет трения жидкости о стенки канала, равен
tsП I; количество движения массового потока жидкости G может
( p wf) w = p w 2f Из выражен ия (г) Лpnf =
быт ь зап и са но как Gw
= т5П /. Тогда по ( 2 . 1 7а ) применител ьно к круглой ( в целях п ро
=

стоты) трубе , где П = лd и f = лd 2 /4, имеем
/ w2 лd 2
p -- ,
, ts1tdl = Лг d 2
4

откуда приходим к выражению (л) .
Таким образом, п о физическому смыслу коэффициент Лг
представляет собой соотношение потока импульса к стенкам
канала (т.е. нормально к направлению движения скорости) и
количества движения жидкостного потока вдоль канала.
Ввод скоростного члена w2/2g в выражение для h п позволяет
(правда, еще не доказано, что в полной мере) установить связь
сил трения со скоростью. Но согласно уравнению Навье
Стокса ( l .20) и формуле Ньютона ( 1 .9) , в h п должно еще быть
отражено влияние вязкости µ, v (кстати, и линейного размера,
входящего в производные в указанных формулах). Пока можно
лишь предполагать, что от этих характеристик должен зависеть Аг.
Уравнение Дарси- Вейсбаха является формальным соотно
шением, широко используемым в технологических расчетах для
определения h п , ЛРп · Его формальность обусловлена принятой
заменой в форме (и), так как в общем на тех же основаниях
можно было бы предложить и другие замены, например
ts /(pg) - v/w, причем v/w тоже имеет размерность hп (м) и отве
чает отброшенному слагаемому в ( 1 .20) или формуле ( 1 .9). Но
исторически был принят путь (и) , и в гидравлике традиционно
используется именно уравнение Дарен - Вейсбаха. Закончен
ность (надежность, прогнозность) это уравнение получает, когда
удается установить физически обоснованные качественные и
количественные связи Аг с определяющими параметрами тече
ния.
2.2.3. Режимы течения жидкости
Расчетное выражение для Аг (и численное значение коэффи
циента) зависит от режима течения жидкости. Понятие о режи
мах течения утвердилось в гидравлике после исследований ан
глийского ученого О.Рейнольдса в конце XIX в.
Экспериментальная установка Рейнольдса состояла (рис. 2 .9) из прозрачно
го резервуара J, заполняемого рабочей жидкостью (уровень ее в ходе опыта
поддерживался постоянным с помощью подпитки 7 и сливного устройства 4),
прозрачной горизонтальной трубы 2 с плавным входом, регулировочного вен
тиля З и сосуда с жидкой темной краской 6. Из сосуда 6 краска по капилля р 1 42

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис.2.9. Опыт Рейнол�са:

1 - резервуар с рабочей жидхостью, 2 экспериментальная труба, З - реrулирующи й
вентиль, 4 - слив избытка жидхости , 5 - кра н , 6
- сосуд с краской ,
7 - лин ия подачи рабочей

4

жидкости

ной трубке могла подводиться в кахую
либо точку входного сечения трубы 2
(поток краски регулировали краном 5). В
1
2
ходе опытов варьировали диаметр труб 2,
скорости жидкости (их рассчитывали по
расходу) и ее свойства (плотность, вязкость). Индикатором характера течения служила краска.

3

Опыты с гладкими трубами показали, что в трубах малого
диаметра при небольших скоростях жидкости подаваемая во
входное сечение струйка краски проходила по всей длине трубы
не размываясь. Такое параллельно-струйчатое (слоистое) тече
ние было названо ламинарным (по латыни lamina - полоска,
пластинка). В трубах большого диаметра и при высоких скоро
стях частицы жидкости (а с нею и краски) перемещались хао
тически по различным траекториям - с визуально наблю
даемыми завихрениями; в результате поток интенсивно переме
шивался и на некотором расстоянии от входа в трубу равномер
но окрашивался. Такое бурное течение с нестационарным воз
никновением и разрушением жидкостных образований бъmо
названо турбулеН111ЫМ (turbulentus означает бурный, беспорядоч
ный). Рейнольдс установил, что склонность жидкости к лами
нарному течению возрастает при увеличении ее вязкости µ и
понижении плотности р, к турбулентному течению - с ростом р
и снижением µ. Позднее бьто найдено, что характер течения
определяется значением безразмерного комплекса wdp/µ = wd/v =
= Re, названного впоследствии числом Рейнольдса. При значе
ниях Re ниже некоторой критической величины (Re » течение
кi
жидкости - ламинарное; для круглых труб Rекр "" :lЗОО. При
увеличении Re (для изотермического течения в прямых круглых
трубках - сверх 1 04) течение становится существенно турбу
лентным, причем с ростом Re интенсивность турбулентности
повышается.
В гл. 1 бьто показано, что Re представляет собой соотноше
ние сил инерции и вязкости. В случае ламинарного режима
(малые значения Re) доминируют силы вязкости (они - в зна
менателе Re) , влияние сил инерции вырождается. При этом
использование числа Re, вообще говоря, теряет смысл (или
приобретает формальный характер) . В случае турбулентного
режима (высокие Re) в целом преобладают силы инерции. Од1 43

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

нако вблизи стенок канала (в очен ь тонком слое ) , где скорости
малы, течение остается близким к ламинарному; поэтому силы
вязкости продолжают оказывать некоторое влияние на характер
течения - использование Re для характеристики таких течений
сохраняет смысл . Лишь при очень высоких Re (для круглых
труб - свыше 2- 1 07 ) пристенный слой оказывается практически
сорванным - доминируют силы инерции, а влияние сил вяз
кости выроЖдается. Значит, выроЖдается и число Re - его ис
пользование становится формальным. В обоих случаях домини
рования сил вязкости либо инерции течения и менуют автомо
дельными относительно критерия Рейнольдса (см. разд. 2.2.4 и
2.2.5). При значениях Re, несколько превышающих Rекр (от
2300 до 1 0000) , сил ы инерции и вязкости сопоставимы по вели
чине: здесь уже нарушено слоистое течение, но неупорядочен
ность (хаотичность) в ы ражена еще слабо. Эти режимы течен ия
называются переходными (в зарубежной литературе - промежу
точными).
На практике возможно некоторое смещение указанных диа
пазонов. Так, при очень плавном входе жидкости в круглую
трубу и отсутствии ка ких-либо внешних возмущений удается
сохранить ламинарный режим при Re, заметно превышающих
2300. Наоборот, при неблагоприятных условиях входа (наличии
вибраци и , турбулизующих вставок, шероховатости стенок кана
ла) течение становится турбулентным при Re значительно ниже
1 04 . Особенно с ил ьное влияние внешние условия оказывают на
течение в переходном режиме - его характеристики могут сме
щаться в сторону ламинарного либо турбулентного. В этом
смысле переходный режим плохо воспроизводится, так что рас
четные формулы для различных эффектов переноса в переход
ном режиме (не только в гидравлике, в тепло- и массообменных
процессах - тоже) обычно весьма ненадежны и пригодны лишь
для определения качественных связей меЖду различными фак
торами и прибл иженной оценки численных значений характе
ристик процесса.
Физические предпосылки возни кновения и поддержания ла
минарного или турбулентного режима можно представить сле
дующим образом. В жидкостном потоке под вл иянием постоян
но действующих случайных возмущений непрерывно возникают
отклонения от характерных (для данного течения) параметров
движения жидкости. Но при доми нировании сил вязкости упо
мянутые отклонения подавляются, и движение остается упоря
доченным, т.е. ламинарным. Этого не происходит, когда преоб
ладают силы инерции: возникшие возмущения здесь развиваются ,
распространяются по объему потока (подробнее см. разд.
2.2.5) - движение становится неупорядоченным, т.е. турбулент-

l 44

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ным.

Переход к неупорядоченному течению стимулируется
внешними (по отношению к потоку жидкости) причинами:
преградами в канале, шероховатостью его стенок, вибрацией
каналов и т.п.
Проследим обшую связь коэффициента Аг с режимными ха
рактеристиками течения жидкости . Для этого в уравнении На
вье-Стокса, записанном для какой-нибудь оси, разделим все
слагаемые на силу инерции. Поскольку соотношение сил давле
ния и инерции есть Eu, внешних массовых сил и инерцион
ных - Fr, а сил инерции и вязкости - Re, то
{ Eu} = { Fr} -

�

l + { е} .

(м)

Здесь фигурные скобки означают, что речь идет не о значе
ниях Eu, Fr, Re, а о величинах, им пропорциональных (т.е. о
соотношениях сил в каком-то масштабе) . Выражение (м) не яв
ляется расчетным; оно лишь устанавливает наличие связи между
обобщенными переменными Eu, Fr и Re для группы подобных
течений:
Eu = j{Re, Fr) .
(н)
Массовые силы (реально это чаще всего силы тяжести)
обычно играют подчинен ную р ол ь в практичес ких задачах гидро
динамики , поскольку основной вклад в большинстве случаев
приходится на долю перепадов давлений, под действием кото
рых происходит движение жидкостей (тем более - газов) . В
необходимых случаях влияние силы тяжести всегда можно
учесть, заменив его соответствующим перепадом давлений (Лр =
= pgЛh
см. разд. 2. 1 .2). Поэтому выражение (н), как правило
(не всегда!) , можно упростить:
(о)
Eu = j{ Re).
Но в предьщущем разделе была показана связь (к) числа Эй
лера с коэффициентом Аг· Следовательно, Аг должен быть пред
ставлен также в зависимости от числа Рейнольдса:
(п)
Аг = /(Re).
Заметим, что применительно к конкретным технологическим
задачам в выражениях типа (о), (п) в правой их части могут по
явиться параметрические критерии (симплексы) вида //,de .
Определив Аг, можно далее по уравнению Дарси-Вейсбаха
рассчитать hп и ЛРп·
Характер и численное выражение связи (п) зависят от режи
ма течения. Ниже эта связь количественно устанавливается
применительно к изотермическому движению жидкости в пря
мой круглой трубе: это обусловлено широким практическим
применением таких труб, а в методическом отношении - про-

1 45

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

стотой анализа. В последующих разделах задача анализа постав
лена шире: рассматриваются закономерности ламинарного и
турбулентного те чен11 й , а в ходе общего анализа получаются
зависимости для определения Лг и hп.
2.2.4. Законы ламинарного течения ньютоновских жидкостей

Первоочередная задача анализа ламинарного течения - уста
новление закономерностей распределения напряжений трения и
скоростей в сечении канала. Это позволит в дальнейшем подой
ти к определению Лг и hп, ЛРп ·
В основу анализа может быть положено уравнение Навье
Стокса ( 1 .20). Записанное в цилиндрических координатах для
симметричного течения вдоль оси круглой трубы, оно, согласно
( 1 .24), при условии dp/dx = Лр/ / принимает вид
где Лр

�__O_(r dw., )
dr dr
1·

-

=

_

Лр
µ/

,

падение давлен ия на участке трубы длиной

/.

Двойное интегрирование этого уравнения (с граничными
условиями: Wл = О при r = R и d wл /dr = О при r = О) позволя
ет прийти к распределению скоростей по сечению трубы. Здесь
вполне удается справиться со сложностями решения дифферен
циального уравнения второго порядка в силу простоты
(линейности) связей между основными параметрами течения
(эти связи будут продемонстрированы ниже). Но по той же
причине здесь вполне можно обойтись без уравнения Навье Стокса, т.е. без решения дифференциальных уравнений второго
порядка, суrnественно упростив анализ. Используем этот путь
применительно к течению жидкости в круглой трубе.
Будем анализировать закономерности течения ньютоновской
жидкости на участке длиной / горизонтальной трубы постоянно
го радиуса R (рис. 2. 1 0) . Пусть жидкость движется стационарно
слева направо под действием разности давлений Лр = р 1
Р2
(р 1 > JJ2). Трубу выбрали горизонтальной, дабы исключить из
рассмотрения влияние сил тяжести (т. е. разность геометриче
ских напоров, критерий. Фруда) ; постоянство радиуса позволяет
исключить из анализа изменение скоростей вдоль трубы и появ
ление сил инерции при перемещении жидкости от точки к точ
ке. Таким образом, напор Лр целиком расходуется на преодо
ление сил трения.
Выделим внутри трубы соосный цилиндр текущим радиусом
r ; задача анализа состоит в определении текущей (локальной)
скорости wл на этом радиусе. Поскольку движение является
-

146

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 2. 10. К закономерностям ламинарного течения ньютоновской жидкости в
круrлой трубе

установившимся и равномерным, то силы давления (они дей

ствуют по торцевым площадкам 7rr2 выделенного цил и ндра - в
противоположных направлениях) уравновешиваются силам и тре
ния (по боковой поверхности цил и ндра 21trl). Тогда
= О,
(р)
Р1 ттr 2 - Р2 ттr 2 -

tт2ттr/

откуда получаем распределение (эпюру, профиль) напряжений
трения по радиусу (сечению) трубы, характерное для всех тече
ний в крутлой трубе, когда преобладают силы вязкости:
tт =

(2. 18 )

Лр r.
21

Из этого выражения следует:
- на оси трубы tт = О: приосевые слои жидкости движуrся с
одинаковой скоростью, радиальный градиент скоростей при =
= О отсугствует, так что, согласно
силы трения здесь не
возникают;
- на стенках трубы
= R) напряжение трения - наиболь-

r

( 1 .9),

(r

шее: 'tт = 'ts = Лр R;
2/
- tт линейно возрастает с радиусом r ; это обстоятельство
отражено эпюрой напряжений на рис.2. 1 0 в левой части рас
сматриваемого участка трубы.
Подставим теперь в
значение 'tт по
имея в виду,
что нормаль направлена радиально и скорость Wл изменяется
только по радиусу:

(2. 1 8)

•
т

=

-

µ

д wл
дп

-

= µ
-

d wn
dr

-

(1.9),

(с)

и

d wn

-µ -- = Лр r
dr
2/

·

(т)

Разделяем переменные и интегрируем (при µ = const - для
ньютоновских жидкостей) в пределах от = R (соответственно
концепции прилипания, на стенках трубы Wл = О) до текущего

r

1 47

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис.2. 11. Эпюра скоростей в обобщенных
координатах для ламинарного течения
жидкости в круглой трубе

радиуса
рость wл:

r,

где надо найти ско
Лр

"'JI

r

fdwл = -- f r dr.
2 µ/
R

О

Отсюда

wл = Лр/ (R 2 - ,2) = Лр R 1
4µ/
4µ

(у)

( _c_)
1-

R2

.

(2. 1 9)
Из (2. 1 9) следует, что при ламинарном течении ньютонов
ской жидкости в круглой трубе скорость в ее сечении распреде
ляется по параболоиду вращения. Параболический профиль
скоростей показан на рис. 2. 1 О в правой части прямого участка
трубы. Согласно (2. 19), на стенке трубы (при = R) закономер
но (это предопределено н ижними пределами интегрирования)
получается wл = О. При = О скорость принимает максимальное
значение

r

r

Wmax

=

Лр R2 .
4 µ/

( )

w можно записать . 7
;r
:
2
Wmax 1 - =
W
_л_ = l - л
R2
R2

С этим зна ением

И

W max

(2. 1 9а)

·

(2. 1 9б)

Последние выражения показывают (рис.2. 1 1 ) , что распреде
ление скоростей в обобщенных (безразмерных) координатах не
зависит от свойств жидкости
и параметров течения
(следовательно, и от числа Re)
для всех ламинарных течений
в круглой трубе профиль скоростей выражается единым соот
ношением (2. 1 9б). Такие течения называются автомодельными
по Re. Применительно к ламинарному течению говорят о ниж
нем автомодельном режиме, имея в виду, что оно реализуется
при низких значениях Re.
В расчетных уравнениях удобно оперировать не локальной, а
средкей скоростью w течения жидкости в трубе. Усреднение
скорости по сечению трубы можно провести непосредственно,
применяя известную из математики теорему о среднем:

-

}

f

f

}

R 2 f wл 21t rdr
w = f f wл df= 7t
о

1 48

R

о

(ф)

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

либо найти предварительно расход жидкости V, а затем сред
нюю скорость по уравнению расхода ( 1 . 1 8) . Используем здесь
второй путь.
Вьщелим в поперечном сечении трубы элементарное кольце
вое живое сечение потока d/ (см. рис. 2. 1 0) радиусом r и шири
ной dr; очевмдно: d/ = 21tr dr. Элементарный расход через это
сечение (жмдкость движется через него со скоростью wл ) соста
вит по ( 1 .2): d V = Wл df wл 2лrdr. Подставив значение Wл по
(2. 1 9б), найдем после интегрирования полный расход:
=

V=

J
о

Wл 21trdr =

J
о

Wmax

(1 -�)
R

21trdr = 21tW max

тr.Лр

J(
0

rdr

-� ) =
R

dr

21tW max R 2

4

После подстановки значения Wmax по (2. 1 9а) приходим к
уравнению Гаrена- Пуазейля :

V = 8µ/ иt.

(2.20)

Лр R2 .
тr.R 2 = 8µJ

И тогда средняя по сечению скорость жидкости
w=

v

(2.2 1 )

Сравнение выражений для скоростей - максимальной (2. 1 9а)
и средней (2.2 1 ) - показывает, что для круглой трубы при ла
минарном течении средняя скорость равна половине макси
мальной: w = Wmax/2.
Важно подчеркнуть простую линейную связь w и Лр при ла
минарном режиме течения: потеря давления пропорциональна
скорости потока в первой степени. Такого рода закономерность
присуща всем ламинарным течениям (живое сечение потока
различной формы, обтекание тел и т. п . ) : Лр w 1 .
Для горизонтального канала движущая сила равна потере
давления: Лр = Лрп; соответственно (2.2 1 )
8µ/ - 3 2 µ/
ww•
(2.2 1 а)
Лrnn
rде d = 2R

-

диаметр трубы.

- -R 2 --

-

d2

Для вертикального канала и наклонных труб необходимо вы
членить значение ЛРп из общего перепада давления , учитывая
разность уровней жидкости соотношением типа Лр = pgЛh (см.
разд. 2. 1 2) .
В случае ламинарных течений принципиально нет необходи
мости в использовании формальных выражений типа Дарси
Вейсбаха, а значит и в определении Лr. Здесь для расчета Лрп и
hn = Лрп/( рg) вполне достаточно полученных из физических пред-

149

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

уравнений: для круглой трубы - уравнения Гаrена
Пуазейля и вытекающего из него (2.2 1 а) . Однако в практиче
ских расчетах нередко традиционно пользуются именно уравне
нием Дарси-Вейсбаха не только для турбулентного, переходно
го, но и для ламинарного режима течения (в том числе - и в
круглых трубах). Поэтому (именно поэтому! - иного обоснова
ния нет) целесообразно установить выражение для Аг, но только
в такой постановке: как определять Аг, если расчет Лрn и h n вес
ти в манере уравнения Дарси-Вейсбаха?
Здесь возможны различные подходы. Можно, например,
прямо исходить из соотношения (и) в разд. 2.2.2, выразив т5 =
= - µ(dw/dr) и определив из (2. 1 9) производную dw/dr при r =
= R. Несколько проще приравнять Лрn по уравнениям (2.2 1 а) и
Дарси-Вейсбаха в форме (2. 1 7а):
w2 ,
Лрn - 32 µ/ w - Аг -/ р
d 2
d2
откуда после очевидных сокращений

посылок

_

_

--

Аг =

64

wdp l µ

= 64 _

Re

(2.22)

Подчеркнем, что такой характер зависимости: Аг = A/Re присущ всем ламинарным течениям, но значение А зависит от
конкретных условий (формы живого сечения потока, внутрен
ней или внешней задачи гидродинамики и т. п.). Вместе с тем
выражение (2.22) еще раз подчеркивает формальный характер
использования здесь уравнения Дарси-Вейсбаха. Действитель
но, при ламинарном режиме течения силы инерции подавлены (для
круглых труб - при Re < 2300) силами вязкости; поэтому крите
рий Рейнольдса, выражающий соотношение указанных сил,
физически перестает характеризовать течение. Он и не входит в
полученные теоретическим анализом выражения типа (2.2 1 ) (2.2 1 а) . Таким образом, в случае ламинарного течения использо
вание уравнения Дарси-Вейсбаха с определением Аг по форму
лам типа (2.22) - лишь расчетный прием, обусловленный даже
не удобством , а скорее традициями расчетов.
Характерный nрофиль скоростей в ламинарном потоке устанавливается не
сразу после входа жидкосm в трубу; расnределение скоростей асимптотически
приближается к параболическому, описываемому уравнением (2. 1 9). Трансфор
мация скоростного профиля от начального до характерного nроисходит на
учает&е rндродJ1118МН'1ео
СК й стабИJJН38Ц1111 . Очевидно, что его длина /сrаб, в силу
асимптотического характера nреобразования nрофиля скоростей, зависит от
приемлемой погрешности, с которой скоростной профиль можно считать
сформировавшимся.
Теоретически удается получить лишь приближенные решения, описы
вающие развитие профиля скоростей жидкости от начального (например, рав1 50

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

номерного: w" = w) до параболического. Согласно этим решениям, с погреш
ностью порядка 2% скоростной профиль можно считать сформировавшимся на
относительном расстоянии от входа в трубу:
lcrar/d "' 0,05Re.
(х)
Если ввести понятие о времени стабилизации tcraб = lcraб/w, за которое во
шедший в трубу поток деформируется до характерного профиля скоростей, и
выразить Re '"' wd/v, то
Тстаб

"'

0,05

-v .
d2

Иначе: число Жуковского Zh для участка стабилизации
Zh

Vtстаб
2- ..,
• -

d

0,05

(ц)

(ч)

при ламинарном течении равно постоянной величине, не зависяшей от значе
ния Re.
Потери напора на участке стабилизации отличаются от рассчитываемых на
стабилизированных участках по двум основным причинам:
- из-за постепенной деформации поля скоростей и их градиента от входно
го сечения до конца участка стабилизации (эдесь необходима корректировка
изменяющихся значений л.);
- из-за изменения кинетической энергии потока: переход от равномерного
профиля к параболическому сопровождается ее увеличением, а значит - сни
жением потенциальной энергии давления.
Потери напора на участке стабилизации принято представлять в виде по
луэмпирического соотношения в манере уравнения Дарси-Вейсбаха
с поправ.
кой kстаб:
h = ' lшб + k J .!C ,
(ш)
n
"г
стеб) 2g
d

(

причем по разным опытным данным kста6 находится в пределах 2-3.
2.2.S. Законы турбулентною течения

Общая картина течения

При движении жидкости в каналах, трубопроводах, техноло
гических аппаратах значения Re обычно исчисляются десятками
и сотнями тысяч, иногда - миллионами, так что течение про
исходит в условиях достаточно развитого турбулентного режима.
В отличие от ламинарного, течение здесь - неупорядоченное,
оно характеризуется пульсационным хаотическим нестационар
ным движением частиц жидкости и их образований (при сохра
нении общего направления потока) . Эти образования часто (и
не очень удачно) именуют "комками", "вихрями"; может быть,
удачнее термины "пакеты", "ансамбли". Ансамбли представляют
собой совокупности близко расположенных частиц жидкости,
совместно (т.е. с близкими скоростями) перемещающихся в ка
ком-то направлении из точки в точку. Ансамбли неустойчивы;
151

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис.2. 12.

Пульсации скорости в турбулентном потоке

время их существования и пройденный ими путь (до смешения
с другими ансамблями и остальной массой жидкости) достовер
но не фиксируется. Можно считать, что частицы жидкости, от
носящиеся к одному ансамблю, гидродинамически связаны, дви
жутся единым "комком"; за пределами его существования или
пути смешения эта связь утрачивается.
Типичная диаграмма локальных абсолютных скоростей жид
кости в направлении ее движения х представлена на рис. 2. 1 2.
Осредненное (за достаточный интервал времени t) значение
локальной скорости w в рассматриваемой точке показано
штрих-пунктиром; штриховыми линиями отмечены границы
области осредненных значений пульсационных скоростей w'
(чаще используют среднеквадратичные значения

.J

.J w ' 2 )

Отно

w ' 2 / w является показателем интенсивности турбу
•

шение
лентности. Разумеется, в турбулентном потоке существуют так
же пульсационные составляющие скоростей v' и в направлении
оси у, нормальной к х (и к стенке канала).
Из рисунка видно существование двух групп пульсаций:
крупномасштабных низкочастотных (они характеризуют пере
мещение жидкостных пакетов в целом) и мелкомасштабных
высокочастотных (они относятся к пульсациям более мелких
частиц жидкости внутри пакетов) .
Вблизи стенок канала течение жидкости является ограничен
ным, а значит и более упорядоченным: с приближением к стенке
все более гасятся пульсационные составляющие скорости ,
уменьшается и осредненная скорость (на стенке в соответствии
с концепцией прилипания она равна нулю) . Таким образом, при
турбулентном течении вблизи стенок движется достаточно тон
кая жидкостная пленка, в которой из-за влияния стенок канала
существенно подавлены пульсации - говорят о тонком упоря
доченном ламинарном слое (его толщина оценивается долями
миллиметра) . Именно здесь в условиях турбулентного режима

1 52

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 2. 13.

Модель переноса импульса в турбулентном потоке

продолжают играть роль силы вязкости. За пределами ламинар
ного слоя (часто используют термин "вязкий подслой") разви
ваются турбулентные пульсации. Разумеется, все это модельные
представления , так как реально не существует резкой границы
между ламинарным слоем и турбуленmым ядром потока . Заме
тим : ино гд а используют более сл ожн у ю - трехслойную - модел ь
течения, вводя между ламинарным слоем и турбулентным ядром
еще переходный подслой, в котором и начинается развитие тур
булентных пульсаций. С увеличением Re толщина ламинарного
слоя 8л и переходного подслоя уменьшается.
В турбулентном ядре перенос импульса осуществляется пре
имущественно за счет пульсационного движения упомянутых
выше неустойчивых ансамблей. Перемещаясь из одной области
течения в другую, они стремятся по инерции сохранить свою
первоначальную скорость в направлении движения. Смешиваясь
с остальной жидкостью, "быстрые" ансамбли увеличивают ее
скорость, медленные - уменьшают. В результате в поперечном
сечении турбулентного ядра происходит существенная нивели
ровка осредненных скоростей в направлении движения потока.
Именно в этом проявляется преобладающая роль сил инерции в
турбулентных течениях.
Модель переноса импульса в турбулентном потоке представ
лена на рис. 2. 1 3 . Пусть поток на координате у имеет осредненную скорость в направлении течения w" Ансамбль (пакет) час
тиц массой &т за счет пульсационной составляющей скорости v'
перемещается по оси у в новое положение (оно находится пра
вее благодаря направленному движению вдоль оси х). Введем
модельное представление: по пути из исходного положения пакет
перемещается как единое целое, не обмениваясь импульсом с
потоком (не смешиваясь с ним) , и попадает в новое положение,
отстоящее от исходного на расстоянии / по оси у (где осредненная скорость в направлении х равна w , + Лw). Здесь ансамбль
полностью теряет импульс (т. е. свою индивидуальность) , сме
шиваясь с окружающей жидкостью. Импульс, потерянный паке.

..

1 53

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

том массой Бт в направлении оси х, равен изменению коли чества движения отлw. Произведем подмену задачи , подагая, что
обмен количеством движения (импульсом) происходит за счет
вязкого трения при движении совокупности (пакета) частиц в
направлении у. Пусть продолжительность этого акта переноса
равна ле. Тогда изменение количества движения за единицу
времени будет трактоваться как сила трения отЛw/ле. Если
площадь, на которой действует эта сила, равна Л/, то модельное
касательное напряжение (обозначим его tи, фиксируя, что речь
идет о переносе импульса) составит

1 о тл w
(щ)
Л/ л �
Фрагмент этой формулы оm/Л0 есть приращение массового
_

'tи - -

--

расхода за счет пульсационной скорости v'. Тогда соответствен
но уравнению расхода в среднем за ле:

(э)

/ d� /

Поскольку / - мало , то, согласно правилам дифференциаль
1.
ного исчисления, Л w �
Подставив это значение Лw в (щ) , получим с учетом (э)
'tи =

-.J�
'lд.Yl .

(ю)

pv

Эту удельную (на l м2 ) поверхностную силу, обусловленную
переносом импульса, можно формально трактовать в терминах
(и в символах) касательных напряжений:
'tи = µи

дУ1
1�

ИЛИ Р = V
't и

и

l дwлl
ду

.

(я)

Здесь турбулен111ая вязкость µи = р v' / не является (в отличие
от вязкости µ) только индивидуальным свойством жидкости, а
зависит от характеристик ее пульсационного течения. Молеку
лярная вязкость µ отражает вклад теплового движения молекул в
рассеяние (диссипацию) энергии; турбулентная вязкость выра
жает вклад пакетов (ансамблей) при их пульсационном движе
нии. Отдельные молекулы переносят количество движения на
длину их свободного пробега ; турбулентные пульсации - на
значительно большие расстояния, характеризуемые длиной пути
смешения /.
1 54

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Такие предстамения позволяют выразить совместное дей
ствие вязкостных и инерционных (перенос импульса) сил в ма
нере формулы ( l .9):

'tт = ( µ + µи ) дJI

1�

ИЛИ

р=(
'tт

V

+

Vи

д)l wул 1 .
д

(2.23)

В ламинарном слое (вблизи стенки канала) , где пульсации
подамены, µи < < µ, vи < < v и доминируют силы вязкости. В
турбулентном ядре потока, наоборот, µи >> µ, vи >> v и преоб
ладают силы инерции (перенос импульса пакетами). В некото
рой области ( переходн ы й подслой) µ и и µ, v и и v
со
поставимы по величине. Очевидно, что отношения µи/µ, vи/v
имеют смысл критерия Рейнольдса, так как выражают соотно
шение конкурирующих сил инерции и вязкости.

Распределение скоростей в турбулентном потоке
Совершенно очевидно, что характер распределения скоростей
должен быть качественно различным в ламинарном слое и турбу
лентном ядре потока.
Для ламинарной (пристенноii) области те11ения характерно
v >> vи, так что выражение (2.23) может быть записано в при
вычной форме ( l .9). Поскольку речь идет о тонком пристенном
слое, можно положить, что здесь •т "" тs, и тогда
t,
(аа)
V

р

=

dwлdy

-- •

где у - нормаль к поверхности (в случае круглой трубы у = R - г) .

Разделение переменных и интегрирование дает скорость в
ламинарном слое; сначала в общем виде:

't , + С .
= -у
pv
Поскольку при у = О имеем w = О, то С =
't .
wл = - у .
wл

pv

О, так что
(аб)

F,/P

Это выражение удобно записать в безразмерной форме, введя
предстамение о динамической скорости wд =
; легко убедиться, что
чим:

((т,/р)v2)

Wл = (wд2/v)y.

=

м/с. Подставив в (аб) t/p

= wд2 , полу

В обобщенных переменных:

wд

Wл

WдУ ·

- = -- ·

v

(2.24)
1 55

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

обозначив безразмерную скорость wл/wд = w* и безразмерное
расстояние Wд.Y/v = у* в более лаконичной форме, получим
(2.24а)
w* = у* .
Таким образом, для тонкого ламинарного слоя характерен
плоский профиль скоростей Wл = ./(у) .
Для турбулентного ядра потока задача о распределении ско
ростей решается приближенно, с определенными (модельными)
допущениями. Наиболее распространенным является подход
Л . Прандтля; несмотря на известную нестрогость некоторых
допущений, получаемые результаты (скорректированн ые неко
торыми эмпирическими константами) достаточно хорошо согла
суются с экспериментальными данными.
В основе анализа - уравнение (2.23), причем для турбулент
ного ядра vи >> v. Вводим следующие основные допущения :
1) поскольку речь идет об областях течения, н е слишком да
леко отстоящих от стенки канала, то можно приближенно при
нять, что и в этой области tт = tи ::::: ts = const;
2) поскольку все же эти области находятся на известном уда
лении от стенки , то ее влияние на характеристики турбулент
ности проявляется крайне слабо, так что турбулентность вполне
можно считать изотропной ( w ' """ v') ;
3) изменение скорости л w обусловлено переносом ансамбля
(пакета) за счет пульсационной скорости v '; связь этих скоро
стей очевидна, можно считать Лw - v или Лw = k1 v ;
4) длина пути смешения / прямо пропорциональна расстоя
нию от стенки у: 1 = k2)'; при этом коэффициент k2 призван
учесть некоторую неопределенность величины /, а также неточ
ности, связанные с другими допущениями .
Согласно принятым допущениям, v =

а 1

= k2)', так что

{ ю) и п олагая < и
обы кнове н н ыми :

где к

"'

k1f

.Jk;"

kz 1
v = k.

(дw")
ду

( )

dwл
-р -- к у 2 -dy
't ,

dw" = -1-

1 56

ку

z( о;: ) ,
v

_

в

получ и м , замен и в частные производ ные

т5,

2

2
'

- коэффи циент пропорциональности,

dy

Лw =

. Подставляя это значение

F, = -1- w
�р ку

.

введенные трудноопределимые коэффи циенты .

Огсюда

�; но

д

(ав)
вобравший в себя ранее

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Разделяя переменные и интегрируя , пол уч ае м распределение
осредне н н ых скоросте й в турбулентном ядре потока; сначала в
общем в ид е :
wл

=

Wд

к

l ny + С.

(2.25)

Это выражен и е тоже удобно представить в форме связи об
обще н н ы х переме н н ых. В этих целях в правую часть добавим и
вычтем постоян ную для дан ного течения вел и ч и ну � ln � :
v
к
wл
И наче :

w,

w"
·

где С '

=

=

-(
Wд
к

w y
i 1 n ' t- + C '
"
v

= -

J

Wд
Wд
ln у + ln - - - l n
v

или w

к

•

Wд

w

w

+С .

v

= -

1

к

In y • + С ' ,

( 2 . 25а)

Wд
Wд
ln +c.
-к
v

Таким образом, для турбулентного ядра на не очен ь большом
удалении от стенки канала характерен логарифмический про
филь скоростей - соответственно выражен и ю ( 2 . 25а) , полу
ч ившему н азвание закона стенки.
Специал ьно подчеркнем , что гран ич ное условие для опреде 
ления постоян ной С' сформул ировать непросто: надо распола
гать значением скорости н а границе турбулентного ядра, а так
же тол щи н ы последнего. Теоретические оценки здесь крайне
прибл и жен ны е, и поэтому значен ия к и С' находят и з экспери 
мента; он же позволяет определить границы примени мости ло
гарифмического закона. Наиболее часто в л итературе приводят
ся значен и я к = 0,4 и С' = 5 , 5 .
Эксперимент подтверждает справедл и вость закона ( 2 . 24) ( 2 . 24а) в пристенной зон е, т.е. в области малых значен и й у* .
П р и увеличен и и у* находит подтверждение и закон стенки . Од
нако для некоторой промежуточной области значен и й у* (ее
называют буферной зоной) , где значе н ия v и и v сопоставимы по
вел и ч и н е , при качествен ном сохране н и и логарифмического за
кона требуется кол ичествен ная корректировка , отражающаяся
на числен н ых значениях коэффициентов к и С'.
П ол ны й универсал ьный профил ь скоростей при турбуле нт
ном теч е н и и по трехслойной модел и описывается следующи ми

1 57

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

соотношениями:

у* < 5

wл* = у*;

5 < у* < 30

wл* = 5,0 lny*

у* > 30

Wл* = 2,5 lny*

�

причем для круглых труб у* = w R

(Лам.)
-

3 ,05; (Буф.)

+

5,5, (Турб. )

(i �) �е (i � }
-

)

(2.26)

-

=

Заметим : приравни вая значения w * для первого и третьего выражен и й ( 2 . 26),
можно о uенить порядо к знач е н и й у* для буферной зон ы : у *= 2,5 l ny* + 5,5. Ч ис
ленное решение дает у* :::: l l ·i- 1 2, что хорошо согласуется с при нятым в (2.26)
диапазоном у * для этой зон ы .

Для основной зоны реальных течений в каналах характерно
последнее из выражений (2.26) . Опыт показывает, что оно хо
рошо работает не только около плоских стенок, но и для круг
лых труб, хотя логарифмическому профилю здесь сопутствует
"излом" на оси потока (т.е. не соблюдается физически очевидное
при r = О равенство d w /dy = 0).
Полагая, что основную долю сечения занимает турбулентное
ядро, распространим профиль (2.26 - Турб. ) на всю область
турбулентного течения и найдем среднюю скорость потока. Вос
пользуемся в этих целях выражением (ф) из разд.2.2.4, произве
дя предварительно замену: r = R - у (где у отсчитывается от
стенок трубы) . Будем искать среднюю скорость сразу в обоб
щенном виде:

� J(2,5 ln wд у + 5,5) 21t(R - yX-dy) .

j

1
w · = � = --2 w: 27trdr =
wд 7tR о
1tR

v

R

х2

При проведении операции интегрирования имеем в виду:

fln (ax)dx = х ln(ax) - х и fx \n(ax) dx =

в рассматриваемом случае а "' wлfv.

Итак,

•

:[
,

=

1 58

w

•

=

-R
2

2

R

2 1n(ax)- 4 ;

J [2,5 ln(ay) + 5,5]( R - y)dy
о

[У; - У: ]- У; ] :
i) ; ]} w(

2,5 R(y ln(ay) - у) + 5,5/о/ - 2,5

:2 {я 2 [�(

2,5 l n (aR) - 2 ,5

х2

=

5,5

ln(ay)

+

55

(аг)

=

2,5 l n

+

1 ,75 .

(ад)

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

для

Рис.2. 14. Сопоставление скоростных профилей
ламинарного (Лам.) и турбулентного
(Турб.) течений жидкости в круглой трубе

r

Так.им образом, выражение для
средней скорости w, представленное
в безразмерной форме, имеет вид
w* = � = 2,5 ln

wд

�
v--P

R + 1,75 .

�

(2.27)

v

Л ам .

Турб.

Типичный профиль скоростей в круглой трубе показан на
рис.2. 14: для ламинарного режима - по уравнению (2. 1 9) , для
турбулентного режима - по уравнениям (2.26) ; там же штрихо
вой линией обозначен уровень средней скорости w. Из сравне
ния распределений скоростей при разных режимах течения вид
но, что пристеночный градиент скоростей (в пределах ламинар
ного пограничного слоя) в случае турбулентного режима значи
тельно выше, нежели для ламинарного, а сам профиль в турбу
лентном ядре существенно выровнен (говорят: заполнен). Сред
няя скорость в круглой трубе при турбулентном режиме обычно
колеблется в пределах от 0,7 до 0,85 от максимальной (эта циф
ра, отражающая степень выравнивания скоростей в ядре потока,
возрастает с повышением Re) ; при переходе к верхнему автомо
дельному режиму ( Re � 2· 1 07) естественно w/wmax -+ 1 .
В практических расчетах обоснованное модельными представлениями

Л.Прандтля, но достаточно сложное распределение скоростей по (2.26) иногда
заменяют более простым степенным профилем. Наиболее часто используют
"закон 1/7", неплохо соответствующий логарифмическому профилю (особенно
при � > 30):
(ае)

-

где wo
скорость за пределами пограничного ламинарного слоя , близкая к
Wmax· Применительно к круглым трубам "закон 1 /7" нередко записывают в
форме

( - �)111

W = Wmax l

СущСС111уют и другие аппроксимации логарифмического

(аж)
профиля скоростей.

Коэффициент гидравлического сопротивления
Из соотношений (ад) и (2.27) можно теоретически получить
расчетную формулу для коэффициента Лr- Для этого выразим
радиус через диаметр R = d/2 и преобразуем выражение под
логарифмом:
(аз)
1 59

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Согласно формуле (л) из разд.2.2.2, Лr/8 = t/( p w2 ) = ( wJV1w) 2 .
Подставим теперь отношение wд/w =
в левую и пра
вую - преобразованные соответственно (аз) - части выражения
(2.27):

.[i:;/8

fI
�
V

=

2,s 1n

(Re (I;°)
Т Vв

+ 1,1s .

С учетом входящих в это равенство численных значений ве
личин имеем для гладких труб:

�

.,/Л г

0,88

=

( А} - 0,9 1

ln Re

·

(2.28)

Это выражение получено из логарифмического профиля ско
ростей (2.26 - Турб. ) в предположении о его справедливости по
всей области течения. Но для ламинарного слоя, градиент ско
ростей в котором существенно зависит от сил трения , этот про
филь неточен. Поэтому можно ожидать некоторого расхождения
формулы (2.28) с опытными данными. Действительно, с экспе
риментом лучше согласуется скорректированная зависимость

�

.,/Л г

=

0,87 l n( Re А} - 0,80

·

(2.28а)

Расчет Лг по трансценден111 ым теоретическим формулам mпа (2.28), (2.28а)
ведется численными методами , что не вызывает затруднений при наличии хотя
бы проrраммируемоrо калькулятора. Для упрощения расчетов можно восполь
зоваться некоторыми формулами , аппроксимирующими теореmческие форму
лы для rладких круrлых труб, что подтверждено экспериментально в оrрани
ченных диапазонах изменения числа Re:
для Re = 1 04 - 1 os - формула Блазиуса:
-

- для

Re =

l os -

= 0 , 3 1 6/Re0,25;

= 0,0032 +

3 , 4· 1 06
л.,

Лг

-

(2.28б)

формула Ннк:урад:Jе:

0, 22 1 Rе-о .ш.

( 2 . 2 8в )

Менее точна, хотя и охватывает всю практически интересную для хими
ческой технологии область турбулеН111 ых течений (вплоть до Re = 2· 1 07) , фор
мула Женеро:
( 2 . 2 8 r)
л., = 0 , 1 6/Re0 · 1 6.
Можно показать, что формула Блазиуса отвечает эмпирическому скорост
ному профилю по "закону 1/7", т.е. формулам (ае)
(аж) .
-

П р и очень высоких значениях Re > 2· 1 07 силы вязкости, как
указывалось в разд. 2.2.3, пренебрежимо малы; пограничный
ламинарный слой можно считать полностью сорванным. Здесь
модель Прандтля уже не работает, перенос импульса (коли1 60

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

чества движения) обусловлен исключительно интенсивным
движением пакетов. Поэтому диссипация энергии (значит, и
потери напора) пропорциональна количеству движения ( p wЛw,
т.е. действует квадратичный закон сопротивления: h п - w2 . При
выражении потерянного напора в форме уравнения Дарси
Вейсбаха это должно означать, что Лг перестает зависеть от Re,
он принимает постоянное значение. Профиль скоростей для
такого режима становится плоским: во всех точках поперечного
сечения скорости одинаковы и равны средней скорости w независимо от свойств жидкости и параметров течения (числа
Re и др. ) . Это верхний автомодельный (по Re) режим (термин
"верхний" означает высокие значения числа Re) .
Согласно выражениям (2.28), коэффициент гидравлического
сопротивления Лг сравнительно медленно уменьшается с ростом
Re. Соответственно уравнению Дарен-Вейсбаха это означает
увеличение потерянного напора с повышением скорости пото
ка, что обусловлено наличием квадратичного сомножителя
w2/ (2g) . Физически рост hп , Лрп со скоростью вызван возраста
нием пристеночного градиента скоростей в формуле ( 1 .9) - из
за увеличения скорости потока и одновременного уменьшения
толщины ламинарного пограничного слоя 5л , на который при
ходится наиболее значимая (см. рис. 2. 1 4) часть изменения ско
рости в сечении канала.

Приведенные выше соотношения для расчета Лr относятся к трубам с глад
кими стенками. Внутренняя поверхность большинства промышленных труб
обладает той или иной шероховатостью - в зависимости от материала труб,
способа их изготовления, условий и срока службы.
Количественная характеристика - степею. wepoxo88тocnt - представляет
собой среднее отношение высоты выступов к внутреннему диаметру трубы: Е ш =
= Бw/d.
При ламинарном течении шероховатость не влияет на потери напора, по
скольку жидкость плавно обтекает выступы . Та же картина наблюдается на
начальных стадиях турбулентного течения , когда при небольших Re толщина
ламинарного поrраничноrо слоя Бп > Бш. Однако при увеличении Re величины
Бп и Бш становятся близкими, а при дальнейшем развитии турбулентности Бш
становится больше толщины Бп, уменьшающейся с ростом Re. При достаточно
больших значениях Re (их тоже называют "критическими" и обозначают Rекр2)
роль выступов в возникновении пульсаций , образовании ансамблей и развитии
турбулентности становится оп ределяющей, а роль вязкого (ламинарного) по
граничного слоя вырождается - осуществляется переход к аатомодеm.ному
течению. Значения Rекр2• начиная с которых Лг зависит исключительно от
степени шероховатости Еш, быстро понижаются с ростом Еш. Наличие шерохо
ватости приводит к возрастанию потерь напора, что обычно отражается увели
чением значения Лг в зависимостях· типа

Лг = ./{Re, Е ш ) .

(2.29)

• См. , нап ример, (6, 1 0, 22, 25J.

161

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

l g�
-2

\ : &::�f.НЫЙ
y��'�ty
2 22
.

1
·'
1

Лам . :

\

0
�
1
,
00
� 0,00251
- 'о,l0001

,.

.,

2

�$

2 i' 2f.",ту -:...:._
1

Турб.
5

�:��

.

6

'

7

g

е

Рис.2.15. Общий график зависимости Лr от Re при различных относительных
шероховатостях &,..

Общий график зависимости Лr от Re для полного диапазона
практически интересных течений в круглых трубах приведен на
рис. 2. 1 5. График выполнен в логарифмических координатах это позволяет искусственно расширить область малых Re и про
следить характерные закономерности; для повышения нагляд
ности ось ординат дана в большем масштабе.
В области ламинарного режима ( Re < 2300) Лr следует зави
симости (2 .22) - в логарифмических координатах это падающая
прямая. В турбулентной области (Re > J 04) нижняя кривая от
носится к трубам с гладкими стенками; выше расположены кри
вые Лr = j{Re) для различных степеней шероховатости e w : для
больших значений Еш (они указаны в правой части графика) кри
в ы е рас полагаютс я в ы ш е . Жирной штр ихо в о й л и н ие й обо з на ч е
на кр и вая Rекр2; правее нее - область автомодел ьного течения (Л.,. не
зависит от Re). Вертикал ьными тонки м и штрихами ограничена
облает� переходного режим а (2300 < Re < 1 0000), где режим
неустои ч и в, плохо воспроизодится и зависимости Л.,.
f(Re) ненадежны .
=

Заметим , что п о данным разных исследователей кривые
Лr = j{ Re) для шероховатых труб различаются и не обязательно
совпадают с показанными на рис. 2. 1 5. Это объясняют различи
ем в геометрических характеристиках шероховатости (равно
мерная - неравномерная; зернистая или какая-либо иная).

В условиях турбулентноrо режима также имеется участок П\!QЮдинамической
cтa6ИJlll381UDI , на котором постепенно устанавливается характерный профиль
скоростей. Длина ero для rладких труб / "' (40+SO)d, для шероховатых несколько меньше (причем она уменьшается с ростом &w ) . Значения Лr на этом
участке примерно в 1 ,5 раза выше, чем в условиях стабилизированноrо
скоростноrо профиля .

2

1 62

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

2.2.6. Местные сопротивления

При взаимодействии потока жидкости с какой-либо распо
ложенной в канале преградой наблюдается "отрыв" потока от
стенок и возни кновение за преградой особой ("водоворотной")
зон ы с резко выраженным неупорядоченным характером тече
ния жидкости (рис. 2. 1 6, а). Направление движения отдельных
струек жидкости в этой зоне - различно (вплоть до обратного в
отдельных точ ках), а скорости изменяются по величине; пульса
ции скоростей - весьма интенсивны; зона постоянно обмени
вается количеством движения с основным потоком. Затраты
энергии на дополнительную турбулизацию в водоворотной зоне
обусловливают потери давления на участке /83 от преграды до
некоторого сечения, ограничивающего протяженность этой зо
ны (обычно /83 не более чем на порядок превышает поперечный
размер препятствия Ь) . Такие потери напора трактуются как
местные сопротивления в канале. В дальнейшем они рассматри
ваются применительно к круглым трубам, представляющим
наибольший технологический интерес.
К местным сопротивлениям относятся: внезапное расшире
ние и внезапное сужение канала; пл авный или резкий изгиб
труб (соответственно "отвод" или "колено"); дщtфрагмы ; краны,
вентили или задв ижки раз.личных типов; клапаны; распредели
тельные устройства и т.п .
Существуют два основных подхода к учету местных сопро
тивлений, позволяющие определить потери напора h м при вза
имодействии потока с препятствием .
Первый из н и х постулирует, что местное сопротивление
практически полностью турбулизует поток, так что его течение
на участке действия препятствия является автомодельным. Это
позволяет считать местное сопротивление пропорциональным
скоростному напору w2/(2g) ; коэффициент пропорциональности
� называется коэффициентом местною сопротивления:
hм

-

w2

�-·

(2. ЗОа)

2g

Рис. 2. 16. Местные сопротивления :

о - характер течения жидкости в окрестн ости пре пятствия , б
противл е ния при внезапном расширении ка н ала

-

к расчету местн ого со

1 63

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Достоинство такого подхода - простота, поскольку �

(свой

для каждого вида местных сопротивлений) в силу автомодель

ности в идеале не зависит от Re. Однако, как показывают ис
следования, принятый постулат справедлив не для всех местных
сопротивлений и не во всех диапазонах изменения числа Re; в
ряде случаев приходится учитывать зависимость � от Re, что
усложняет расчеты (заметим, что как и Лг в случае прямых кана
лов, коэффициент � уменьшается с ростом Re) .
Второй подход пытается учесть влияние Re на hм : вводится
понятие об эои88.Jlентной Д11ИНе le. Потери напора на прямом
участке такой длины соответствуют данному местному сопро
тивлению (каждому его виду отвечает свое значение le) . Такой
подход позволяет представить hм в форме уравнения Дарси Вейсбаха (2. 1 7а):
/
(2. ЗОб)
hм = Аг ..!.. - ,
d 2g
причем влияние Re отражено в Лг , который рассчитывается по
формулам, приведенным в предьщущих разделах. Однако, в силу
значительной турбулизации потока при взаимодействии с пре
пятствиями, в действительности влияние Re на hм существенно
слабее, чем это следует из формул Лг = j{ Re), поэтому и здесь
необходима коррекция.
В расчетном аспекте важно, что при изменяюшейся на
местном сопротивлении скорости потока (расширение или су
жение канала, разделение потока и др. ) коэффициенты � и le /d
в таблицах и эмпирических формулах обычно относят к зоне
большей скорости.
На практике чаще отдают предпочтение первому способу вы
ражения местных сопротивлений, так как справочные значения
величин � обычно доступнее, нежели le. Численные значения �
(а также le) для различных видов местных сопротивлений при
водятся в литературе*.В большинстве случаев они получены
экспериментально; теоретически определить � удается лишь в
некоторых наиболее простых случаях. Одним из них является
внезапное расширение потока.

wz

Пусть стационарно движущийся горизонтальный поток переходит из узкого
сечения трубы /1 в широкое .12 (рис. 2 . 1 6 , б) ; в результате внезапного увеличения
сечения поток движется в форме расширяющейся струи, окаймленной на неко
тором участке /83 кольцевой водоворотной зоной . Потери энерrии на вязкое
трение на этом участке будем считать незначимыми (вследствие преобладания
переноса импульса за счет турбулентных пульсаций ) . Выделим контур, ограни 
ченный стенками трубы и сечениями : левым 1, расположенным н а участке
большего диаметра, но в непосредственной близости к узкому сечению ft , и
правым 2 (на конце участка /83). Запишем для этоrо контура баланс количества
• См. , например, [ 1 7, 25] и особенно [ 1 2) .

1 64

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

двнжения и импульса для единицы времени, имея в виду, что массовый поток
равен pwtf1 = pw'J/2 , а Накопление равно нулю (двнжение - стационарное):
( pw:if2 )w 1 + Pih - ( p w:if2 )w2 - p:iJ2 = О .
Здесь два первых слагаемых относятся к левому сечению 1 (подчеркнем: это
сечение находится уже в широкой трубе, поэтому оно равно h. среднепотоковая
скорость в нем w2 , а давление здесь равно р1, поскольку сечение примыкает к
узкой трубе); два последних слагаемых относятся к правому сечению 2. Отсюда
реш�ьный перепад давления между сечениями 1 и 2
Брр '"' Р1 - Р2 = p w2 ( w2 - W1 ) = p ( w2 2 - w 1 w2 ).
(аи)
При отсутствии обмена импульсом и количеством двнжения между сече
ниями 1 и 2 тоже должен был бы возникать перепад давления - идеш�ьный,
обусловленный изменением скоростных напоров (силы трения на коротком
участке /аз будем считать пренебрежимо малыми). Тогда изменение пьезометри
ческих напоров в соответствии с уравнением Бернулли (2. 1 5а) для идеальной
жидкости при z1 = z2 (горизонтальная труба ) составило бы :
wi wf ;
Бри '"' Р1 - Р2" = pg wi wf
(ак )
2g 2g
2 2
индекс "и" означает mпотетическую ситуацию при двнжении идеальной жид
кости.
В разд. 2.2. 1 показано, что hп и Лрп обусловлены различием давлений Р2 при
течении по каналу реальной и идеальной жилкостей : Лрп = Р2" - Р2 · Согласно

(

_

) Р(

)

_

=

выражениям (аи ) и ( а к) :по различие равно разности перепадов давлен ий
- ОР и · И та к .
(w1 - w2 f .
p wl - W1W2 - wi /2 - wl /2
ОР
hv= Лрn f,p

ор

�

)
(ал)
2g
pg
Полученное соотношение будем сопоставлять с выражением потери напора
=

pg

по первому подходу:
w!

w2

и

_

р

h"

Е,

=

(

=

w
. При этом надо условиться , к акую из скоростей 2

(соответстве н но , какое из сече н и й - /1 и л и /2) пр и нять ·
=

2g

за расчетную
базу. Если воспользоваться уравнением pacxoдa fi w 1 = h w2 и принять в качестве
базовой скорость в малом fi или большом h сечении, то из (в) получим
w� 1 - w2 2 = w� 1 l!._ 2
hм
(ам)
2g
2g
/2
WI
или
2
h,. wi ..!!1_ 1 = wi /2 1 2
(ам')
2g W2
2g /i Сравнивая эти формулы с выражением h,.. по (2.30а), найлем значение для
расчетов на основе сечений /1 и h соответственно:
2
2
(ан)
; ; =
1
;1 = 1 ·
2
Практически удобнее основывать величину ; (и не только для внезапного
расширения) на малом сечении, где жидкость течет с большей скоростью;
поэтому в справочной литературе обычно приводится значение ;1. Очевидно,
что при безграничном расширении потока (теоретически при h � оо, практиче
ски при h > > /1) получается ;1 = 1 ; такая ситуация встречается, скажем, при
вытекании жидкости из трубопровода в резервуары больших размеров.
ил и

=

=

(

(
(

�� )

)

)

(
(

)

_

(j�

)

)

1 65

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

2.2. 7. Характер изменения напора по длине трубопровода
При движении жидкости по трубопроводу полный напор
уменьшается вследствие сопротивления движению на прямых
участках трубопровода и на местных сопротивлениях. На
рис.2 . 1 7 показаны характерные случаи изменения давления по
длине горизонтального трубопровода.
На прямом участке трубопровода постоянного сечения (а)
давление изменяется линейно, продольный его rрадиент dp/dx =
= const (здесь х - текущая координата вдоль трубопровода).
При увеличении диаметра (б, в) rрадиент dp/dx понижается. При
этом плавный переход от одного постоянного диаметра к другому
( б) сопровождается плавным переходом от одного линейного
участка падения давления к другому линейному участку (с мень
шим dp/dx, если диаметр увеличивается). Для постепенного расши
рения трубопровода (в) характерно криволинейное изменение дав
ления по длине с понижением продольного rрадиента dp/dx.
Наличие местного сопротивления (кран на вИде г) вызывает в
точке его расположения скачкообразное падение напора. Мест
ное сопротивление, возникающее при изменении диаметра тру
бопровода, характеризуется (д) изменением rрадиента dp/dx на
участке за местным сопротивлением (после скачкообразного
падения давления).
Наконец, установка на трубопроводе напорного устройства
(источник напора, например насос) сопровождается (е) скачкооб
разным повьОIIе нием давления.
Р.J -

Р./

Р./ -

Р.
/

�

-

-

-

А

а
б

8

г
д

е

р

�
р2 �
�

Pz

2

Р2
Р2

Р2

�

1

�

Рис.2. 1 7. Падение напора по длине трубопровода:

Б

Pz

Pz
Pz
Р2
Р2

Р2

/

А - схемы трубопроводов, Б - профили давлений; а - трубопровод постоянного диа
метра, 6 - д11а трубопровода разных диаметров с плавным переходом, " - трубопровод с
плавно изменяющимся диаметром, г - трубопровод с внезапным изменением диаметра, д трубопровод с напорным устройством

1 66

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Реальное производство включает не только рассмотренные
выше случаи, но и многие другие, а также их разнообразные
сочетания .
2.3. ТРУБОПРОВОДЫ

Транспортировка жидкостей (а также газов, твердых материа
лов, смесей жидкостей и газов с твердыми частицами) является
одной из наиболее распространенных технологических опера
ций. Ч аще всего ее осуществляют по закрытым каналам - тру
бопроводам - в самых различных условиях и вариантах. Под
черкнем: стоимость трубопроводов на химических предприятиях
составляет примерно 5% от общих капитальных затрат - это
немало. Отсюда - практическая важность решения задач проек
тирования (расчета, выбора) и эксплуата ции (установления па
раметров работы) трубопроводов. Н иже мы ограничимся общим
подходом к расчету трубопроводов и некоторыми типичными
примерами, иллюстрирующими общий подход.
Различают простые и сложные трубопроводы. Простым назы
вается трубопровод, соединяющий источник жидкости с ее по
треби телем и не имеющий между ними никаких дополнитель
ных Приходов и Уходов жидкости, Источников и Стоков. Мас
совый поток G (в случае несжимаемой жидкости - также и объ
емный JI) без ка ких-л ибо количественных изменений достав
ляется по простому трубопроводу от источника к потребителю.
Сложными называются одиночные трубопроводы с различным
образом организованными подводами или отводами жидкости
по пути от источника к потребителю либо сети, составленные из
каких-либо сочетаний простых трубопроводов (параллельные,
разветвленные, закольцованные и др.) . Простые и сложные тру
бопроводы включают прямые участки и местные сопротивления.
В числе основных задач гидравлического расчета трубопроводов:
- определение эксплуатационных характеристик готового
(существующего в натуре или в проекте) трубопровода с из
вестными геометрическими и конструктивными параметрами , а
также с определенными условиями на границах - это задачи
эксплуатации;

- определение геометрических характеристик трубопровода
(прежде всего его диаметра) либо конечных (начальных) пара
метров течения (напора, давления на одном из концов трубо
провода и т. п.) при заданной скорости течения жидкости в тру
бопроводе или ее расходе - это задачи проектирования.
В основе расчета трубопроводов лежат понятия и соотноше
ния, составляющие содержание предыдущих разделов. При их
использовании иногда удается выразить искомую величину в
1 67

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

явном виде (остальные составляющие расчетной формулы из
вестны) - тогда говорят о прямых задачах расчета трубопрово
дов. В других случаях в явном виде искомую величину выразить
не удается, она остается в обеих частях уравнения (иногда в
завуалированном виде) - тогда говорят об обратных задачах; их
решение часто отыскивается с помощью итерационных проце
дур.
Наименее сложными являются решения задач о простом тру
бопроводе. Методы и результаты этих решений используются
при расчете сложных трубопроводов. Поэтому первоначально
рассмотрим методы расчета простого трубопровода.
2.3. 1 . Простой трубопровод

Будем здесь анализировать течение жидкости по трубопрово
ду под действием перепада давлений, возникающего за счет раз
ницы напоров - геометрических, пьезометрических и скорост
ных (рис.2. 1 8) ; работа других побудителей движения изучается в
последующих разделах учебника. Пусть длина прямых участков
трубопровода /, сечения резервуаров и трубопровода ( соот
ветственно ft , h и / ) , вид и число местных сопротивлений известны. Требуется связать расход жидкости V (или ее скорость
в трубопроводе w) с напором и геометрическими характеристи
ками трубопровода.
Положим для определенности, что жидкость плотностью р
течет из сосуда 1 в сосуд 2. Уровень жидкости в сосуде 1 распо
ложен на расстоянии z 1 , а в сосуде 2 - на z2 от некоторой гори
зонтал ьной плоскости отсчета (на схеме не показана; ее поло
жение несущественно: для течения важна лишь разность уров
ней z1 - z2) . Давления над свободными поверхностями в сосудах
равны р 1 и Р2 · Для сечений 1 и 2, совпадающих со свободными
поверхностями в сосудах, может быть записано уравнение Бер
нулли (2. 1 6) :
р

w2

1 = Z2 +
Z1 + -1 + -

pg

где

н

1 ,2

•

z1 ,2

2g

+ Р!,2

-- +

pg

2
w 1, 2

--

2g

р

2
-

pg

+

w22 +
2g

-

hп , или

Н1

=

Н2 +

hп ,

(а)

- полные напоры на уровнях z1 ,2 в сосудах №- l

или № 2.
Заметим, что скоростные напоры в резервуарах на уровне свободных по
верхностей w12/(2g) и w2 2/(2g) , как правило, пренебрежимо малы в сравнении с
другими составляющими уравнения (а) , поскольку fj , h > > f, часто при анализе
напоры w21,2/(2g) опускают.

Соотношение (а) показывает, что разность полных напоров
(движущая сила) затрачивается на преодоление сопротивления
1 68

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

�

- №1 -

�

�w

�

�

1

Рис. 2. 18. Схема простого трубопровода

-

Н2 = hn; эту
движению жидкости по трубопроводу: Л Н = Н1
разность Л Н называют располаrаемым напором (она условно
изображена на рис. 2. 1 8 в скобках) .
Потери напора складываются из сопротивлений движению
жидкости на прямых участках трубопровода и на местных со
противлениях. Первые мoryr быть записаны в форме уравнений
Дарси - Вейсбаха, а вторые - по-разному (в зависимости от
используемого подхода - см . разд. 2.2.6) .
Если воспользоваться первым подходом, т о суммарное сопро
тивление течению жидкости со скоростью w по трубопроводу
диаметром d при общей длине прямых участков / выразится как

. -

2
w2
w2
w2
w2
w2
w2
/ w
hп - Л , -+ 1; •• - + /; , - + /; д - + С,кр .- + l; P - +. . +1; .ых
_

d 2g

2g

2g

2g

2g

2g

2g

. (б)

Здесь индекс при 1; соответствует виду местного сопротивле
ния (вход в трубу, задвижка, диафрагма, кран, расширение, . . . ,
выход из трубы) . Разумеется, при наличии прямых участков
разного диаметра необходимо фиксировать разные скорости
жидкости на этих участках (пересчет скоростей - по уравнени
ям расхода) .
В более краткой форме:

где

символом

L

(

Л Н = hп = Л г

�;

� + � �; ) ;; ,

обозначена

сумма

всех

(2.3 1 )
коэффициентов

местного сопротивления.

1 69

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

+ r lei

Если воспользоваться вторым подходом, то

L le1

причем

ЛН = h n =

Л.

r

1

i

d

2

2g

w

'

(2. 3 2 )

- сумма эквивалентных длин для всех местных

сопротивлений на трубопроводе .
При расчете простого трубопро вода необходимо установить
связь следующих характерисrик: V, w, лН; Re , Лr, Ц; (или "f. le; ) ; р,
µ. Уравнений связи - четыре:

(2.3 1 ) или ( 2 . 3 2) ;

1td2

V = w4 ;

Re =

wdp

И

-

µ

Л.r

= J{ Re).

При этом значения р и µ известны; в практических задачах
обычно задана длина трубопровода /; известен и набор местных
сопротивлений, а значит без особых затруднений о п;ределяются
суммы
лиQ<>
- нередко в форме

L1 /;1

L (leJdJ .

L1 le;

1

Задачи, чаще всего встречающиеся в практической постанов
ке, приведены ниже:
Извес:ntы
(задаИЫ)

Требусm:11

В�ц
задачи

лн и w
ЛН и d

Прямые задачи

1) d и w
2) d и V
З) V и w

определкrь
лн и v

4) лн и d
5) лн и v
6) лн и w

Vи w
dи w
dн V

Обратные задачи

Характеристи ка

решения

Прямое определение Re,
по нему - Л.,. и т.

д.

Re и Л.,. прямо не определяются
требуется итерационная
процедура

Заметим: задачи 1 -3 и 5, как правило, выступают в качестве
проектных, задача 4
в качестве эксплуатационной ; задача 6 на
пракrике встречается редко, это преимущественно учебная задача.
Расчетные соотношения в форме (2.3 1 ) , (2. 32) позволяют ре
шать прямые задачи: при известных потоках G или V и диаметре
трубопровода d легко найти (по уравнению расхода) скорость w,
далее - число Re и Л.r, отыскать значения �i или le; и рассчитать
потеря н н ый h п или равный ему располагаемый ЛН напор (при
необходимости - Н1 либо Н2 или какую-либо из составляющих
полного напора). Алгоритм расчета:
-

Известно

V,

d -. w -. Re -.Л.r

( 2.З l ) , <2- 3 2 > -. hn = ЛН.
� ; ' le;

(в)

По-иному решаются обратные задачи. Пусть, например,
нужно определить V и w при известных ЛН и d (задача эксплуа-

1 70

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

тации) или d при заданных V и ЛН (одна из задач проектирова
ния).
Попытка использовать уравнение (2. 3 1 ) , предварительно вы
разив Аг через Re (и записав выражение для Re), приводит для
турбулентных режимов к громоздким уравнениям дробных сте
пеней, аналитически не разрешимым . Рациональным представ
ляется
путь
решения
обратных
задач
сл едующий
(продемонстрируем его применительно к использованию коэф
фициентов �;; при использовании le; - подход аналогичен).
Пусть, например, необходимо определить скорость в трубо
проводе w (эксплуатационная задача) . Представим (2.3 1 ) решен
ным относительно скорости:

2gЛН

w=

(2. 3 1 а)

A . "d + :L � ;

/

Эrо выражение в скрытой форме содержит w и в правой час
ти: Аг зависит от Re, а в Re входит пока еще не известная ско
рость w. Поэтому для определения w по (2. 3 1 а) сл едует приме
нить итерационную процедуру - здесь эффективна простая
итерация, когда сначала задаются стартовым значением скорос
ти w "в разумных пределах" (некое нулевое приближение) и да
лее определяют w по (2. 3 1 а) . Алгоритм расчета:
Задались

w

1

� Re � А г �
о

-

•

�j

1

w:'

(r)

При сопоставлении ( о - • ) полученного значения w' со взят ы м
в кач естве стартового w принимается решение, является ли их
расхождение приемлемым с точки зрения точности расчета . Ес
ли ДА, то расч ет закончен ; если НЕТ, то в качестве исходного
берется теперь значение w ', и процедура расчета повторяется до тех пор, пока получаемое значение скорости с приемлемой
точностью не совпадет с исходным для последнего итерацион
ного акта. Важно: поскольку Аг для турбулентного режима весь
ма слабо изменяется с Re, итерационная процедура является
короткой - решение получается с приемлемой точностью за 35 итерационных актов.
Аналогично решается задача проектирования, когда расчету
подлежит диаметр трубопровода.
Заметим, что для ламинарных течений (на практике - нечас
тый случай) итерационных расчетных проблем нет, поскольку
прямо можно воспользоваться линейной формулой Гагена
Пуазейля.
171

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Нередко при постановке задачи в ее условии задается расход жидкости V
(или расход является определяемой величиной). Тогда наряду с выражением
(2. 3 1 а) к расче1)' привлекаются уравнения расхода ( 1 . 1 7) , ( 1 . 1 8) ; например,
V = w(11d 2/4). Можно и прямо связать расход с диаметром:
2gЛН
11d 2
(2. З l б)
у

=

--

4

._
, _____;::;..._

л., !.. + I: Е,

d
и провес1И итерационную процедуру по изложенной выше канве, сравнивая
стартовое (исходное) и рассчитанное значения V.
Иногда в целях упрощения пренебрегают слагаемым I:E,; в сравнении с
Лr(l/d) (на праК1Ике на долю I:E,; приходится обычно от 5 до 1 5 % величины
знаменателя под радикалом); в иной юrrерпр6-ации (второй подход к уче1)' месn�:ых
сопроnmлений) зrо означает, 'ПО в качесmе расчетной длины / принята сумма
геометрических /; и эквивалентных I;/�; длин. Тогда (2.3 \ б) принимает вид
У
11d 2 2gЛНd
или Л Н
(2.32а)
,
=

4

J

Л.,1

1

'
= /гУ
d'

где а " 1 6/(112 . lg) ; при использовании СИ а = 0,0827 с2/м.
На основе этих уравнений решаются прямые задачи (определение Л Н, в
редких случаях / ) и обратные (определение V и d ) . Решение обратных задач по
(2.32а) также ведется итерационными методам и .

2.3.2. Наивыrоднейwий диаметр трубопровода.

Диапазоны рекомендуемых скоростей

Проблема оптимизации диаметра трубопроводов, аппаратов и
выбора рациональных режимных характеристик их функциони
рования в химической технологии ставится и решается весьма
часто. Прежде всего с ней встречаются при проектировании
(при эксплуатации - редко) , когда задача не полностью опре
делена: не хватает значения d или w, чтобы замкнуть при реше
нии систему уравнений связи. В расчетном плане эта проблема
возникает и при осуществлении итерационных расчетов - это
вопрос о стартовых значениях параметра: скажем, в каких
"разумных пределах" целесообразно задаться скоростью, начиная
итерационную процедуру расчета трубопровода.
Подход к решению проблемы является об
щим для многих гидродинамических, тепло- и
массообменных процессов. Он базируется на
сопоставлении капитальных и эксплуатацион
ных затрат.
В основу анализа применительно к трубо
проводам положим уравнения расхода и Дарен

3

Рис. 2. 19. Подход к определению наивыгод
нейшего диаметра трубопровода:
dopt

1 72

d

З - эа1Раты , Э - э.кс плуатационн ые 3а1РЗТЬI, К ка п итал ьные ЗЗ'Ji>ЗТЫ, l: - сум мар ные 3а'Ji>ЗТЫ

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

- Вейсбаха:
V =fw

( 1 . 1 7);

w2
ЛРn= Лrd т р ·
/

G = pfw

( \ . 1 8);

(2. 1 7а)

С увеличением диаметра трубопровода возрастают капитальные затраты,
причем ускоренно: п ропорциональн о tl растет нс тол ь к о периметр трубы 11d, но,
как правило, еще и толщина ее стенок. На рис.2. 1 9 изменение ПIDП'ILllWIWX
(точнее - амортизацноннwх) затрат с d описывается некоторой кривой К. Но с
увеличением d при заданных расходах G или V по ( 1 . 1 7) , ( 1 . 1 8) снижается ско
рость потока
а с ней по (2. 1 7а) - энергия, затрачиваемая на преодоление
гидравлического сопротивления (энергия составляет значительную долю экс
плуатационных затрат) . Эксплуатацноннwм (прежде всего - энергетическим)
затратам отвечает кривая Э. Технологов интересует диаметр трубопровода, при
котором суммарнwе затраты (кривая I:) минимальны. На рисунке минимуму
кривой L отвечает точка А; значит, следует подбирать трубопровод, близкий по
диаметру к оптимальному : d0p1 = d,,..
Заметим : в учебниках иногда ошибочно определяют dopt как абсциссу точки
В; несмотря на возможную близость в каких-то случаях к dop1 . диаметр dв ,
отвечающий равенству капитальных и эксплуатационных затрат, вообще говоря ,
никакого технологического интереса не представляет.
Практика реальных расчетов показывает, что для относительно невязких
жидкостей (типа воды, низкомолекулярных углеводородов, таких как бензин и
керосин, низшие спирты, не очень концентрированные растворы и др.) при
выборе диаметра вблизи dopt скорости жидкости в трубопроводах получаются в
диапазоне 0,5 - 3 м/с. При течении rазов рекомендуете.Я брать скорости на
порядок выше - в диапазоне 5-30 м/с; при этом энергетические затраты по
(2. 1 7а) остаются приемлемыми , п оскольку у газов значения плотности р на 2 3 порядка ниже, чем у жидкостей. Именно в указанных диапазонах целесооб
разно принимать стартовые значения скоростей (или на их основе - стартовые
значения V и d) при итерационном решении обратных задач.
При проектировании аппаратов чаше всего (если нет специальных ограни
чений) скорости рекомендуется выдерживать в 3 - 5 раз ниже, чем для трубо
проводов.

w,

В качестве примеров сложного трубопровода рассмотрим:
- сеть, составленную из нескольких простых трубопроводов;
- одиночный трубопровод со спе цифическим течением жидкости .
2.3.3. Разветвленный трубопровод

Простейшая схема развеТВJJенноrо трубопровода с одной точ
кой раздачи и двумя потребителями жидкости приведена на рис.
2.20. Значения полных напоров заданы: в резервуаре - источ
нике жидкости - Н0, у потребителей в точках 1 и 2 - Н1 и Н2
соответственно; в точке раздачи М напор н. неизвестен. Пусть
для определенности Но > Н1 , Н2, так что жидкость течет из ре
зервуара по магистральному трубопроводу (его характеристики
обозначены индексом О ) к точке раздачи М и далее - к потре
бителям 1 и 2.
Будем решать наиболее интересные (практически и методи
чески) обратные задачи эксплуатации и проектирования. В обо"

"

1 73

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис . 2. 20. Схема разветаленно
rо трубопровода

их случаях необходимые
связи могуг быть заданы
либо системой уравне
ний
(для
отдельных
участков трубопровода)
типа (2.3 1 а) и соответ
ствующих им уравнений
расхода
( 1 . 1 7) ,
либо
системой
уравнений
типа (2. 32а) . Используем здесь второй путь.
Обозначив располагаемые напоры на соответствующих
участках как разности полных напоров на их концах , запишем:
2
Н о - Н. = а Л. 0 Vо
d5о
/о
Н. - Н , = а л. , v,

2

--

1,

d51

2
Н. - Н 2 = а л. 2 v2
-d52
/2

(О)

(1)

(2.33)

(2)

В зада11е эксплуатации заданы диаметры do , d1 , d2 (длины уча
стков fo, /1 , 12 будем считать также известными) и напоры у ис
точника и потребителей жидкости Н0, Н1 , Н2 . Требуется найти
расходы на отдельных участках V0, V1 и V2 ; к этим неизвестным
добавляется четвертое
н.. Чтобы замкнуть систему уравне
ний, в дополнение к (2.33) нужна четвертая связь; ее дает урав
нение материального баланса для точки раздачи М:
(2.34)
Vo = V1
V2.
-

+

Значения Л.0, Л.1 и Л. 2 тоже поначалу неизвестны , но они
должны определиться в процессе расчета. При этом полагаем ,
что методикой расчета отдельных участков мы владеем вполне:
это ведь уже рассмотренные простые трубопроводы, их надо
только состыковать.
Процедуру расчета удобно (хотя не обязательно) начать с вы
бора какого-нибудь расхода, предпочтительно в магистрали :
задавшись скоростью в н е й w0 (в разумных пределах), находим п о
уравнению расхода стартовое значение V0 . Далее, по верхнему
1 74

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

уравнению системы (2.33), решая прямую задачу для магистраль
ного трубопровода (в ходе ее решения получается А.о), находим
н. . После этого по отдельности решаем обратные задачи для
простЬ1Х трубопроводов - участков № 1 и № 2 (в ходе их реше
ния получаются Л.1 и Л.2 ) ; итерационная процедура такого реше
ния подробно рассмотрена в разд.2.3. 1 ; в результате определя
ются расходы V1 и V2. Сумма этих расходов согласно (2 . 34)
должна дать расчетный расход в магистральном трубопроводе
Vo'. Его надо сравнить со стартовым значением V0 и при непри
емлемом расхождении повторить круг расчета, приняв теперь за
стартовое значение величину Vo'. Последовательность расчета
изображена схемой ниже:
Задаемся

( l . 1 7a)
(2 .33 )(0)
Н.
wo � Vo

1

/ v, � (2 . 34)
�
-/
v,

о - •

Vo . (2. 35)
/

l

В 311iJa11e проект11рован11.11 заданы V0, V1 , V2 (длины участков /о,
11 и /2 тоже известны) и напоры Н0 , Н1 , Н2 • Требуется найти
диаметры tfo, d1 и d1. В отличие от задачи эксплуатации здесь

равенство (2.34) не является уравнением; это тождество, по
скольку Vo , V1 и V2 могут быть заданы только так, чтобы это
равенство соблюдалось. Получается, что число неизвестных (все
диаметры и Н·) на единицу больше числа уравнений . Появляет
ся одна степень свободы: один из диаметров может быть выбран
произвольно.
Продемонстрируем процедуру расчета, базируя его (в ка
честве примера) на значении d0. Это значение устанавливается
из уравнения расхода для магистрали на основе wo (скоростью
этой задаются в разумнЬIХ пределах). Последовательность расчета:
Задаем ся

( 2 .33) (0)

н.

/

�

d,

( 2 . 36)

d2

причем значения А.о, Л. 1 и л.2 определяются в ходе решения
прямой задачи (для магистрального трубопровода) и обратнЬIХ
(для уч астков № 1 и № 2).
Существенно, что в отличие от (2.35) расчет по схеме (2.3 6)
не требует каких-либо заключительных итерационных коррек
ций в связи со стартовым значением tfo: найденные диаметры
1 75
-

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

участков, вообще говоря, являются окончательными. Повторный
расчет может потребоваться в силу каких-то привходящих
(сугубо практических) обстоятельств
напри мер, отсуrствия
труб найденных диаметров tfo, d1 или d2 (в сортаменте или на
складе завода) . Тогда надо повторить расчет, приняв иное зна
чение do (получатся иные значения d1 и d2 ) . Таким образом,
задача проектирования может быть реализована при различных
наборах диаметров (но в пределах одного набора - значения d0,
d1 и d1 связаны между собой однозначно).
Специально подчеркнем, что при решении задач на развет
вленный трубопровод совсем не обязательно основываться на
усеченном уравнении (2.32а) ; к тем же результатам приводит
использование уравнения (2. З l а) совместно с уравнениями рас
ходов ( 1 . 1 8) для каждого из участков сложного трубопровода в этом случае строже учитываются местные сопротивления .
Число неизвестных и уравнений возрастает, что, однако, не вы
зывает никаких дополнительных затруднени й , поскольку итера
ционные процедуры расчета остаются прежними (последо
вательно используются те же самые расчетные связи) .
Наконец, решение возможно вести , задаваясь первоначально
полным напором н. в точке М (выбрав его, разумеется , больше
Н1 и Н2 и меньше Но) и продолжая дальше итерационную про
цедуру до приемлемой сходимости.
При разветвлении трубопровода на большее число потреби
теле й (три , четыре и т.д.) в равной мере возрастает число урав
нений и неизвестных - в процедуре расчета нет принципиаль
ных изменений. А вот при появлении каждой новой точки раз
дачи (скажем , еще одной на участке 1 ) дополнительно появляется
новая неизвестная величина - напор в упомянуrой точке. Си
стема уравнений в задаче эксплуатации, конечно, все равно бу
дет замкнуrой (добавится материальный баланс в новой точке
раздачи ) . Но в задачах проектирования будуr уже две степени
свободы , и придется произвольно задаваться двумя диаметрами
(в случае п точек раздачи - п произвольными диаметрами).
Сложные сети трубопроводов могут содержать различные
ветвления, их сочетания, закольцованные схемы и т.п. При по
нимании общих подходов к расчету простых трубопроводов и их
схем анализ сложных сетей принципиальных затруднений не
вызывает.
2.3.4. Трубопровод с путевым и транзитным расходами
-

Согласно схеме на рис . 2 . 2 1 движение жидкости по трубопро
воду происходит с постепенным (в простейшем случае - рав
номерным) отводом жидкости по мере ее течения - это ri}'Тевой
расход (для всего участка длиной / он равен Vn ) ; в общем случае

1 76

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Схема трубопровода с пуrевым
и транзитным расходами

Рис.2. 21.

из трубопровода по длине / отво
дится не весь поток, часть его
транзитный расход Jt;., - пройдя
весь трубопровод, отводится с
правого его торца. Такие схемы в
Vn
различных вариантах нередко ис/ --�
пользуются в химической технологии для устройств (или элементов
устройств) при распределении жидкости в поперечном сечении или
по длине технологического аппарата.
Рассмотрим некоторые возможные постановки задач расчета
таких трубопроводов и наметим общие подходы к их решению.
При любой постановке необходимо найти связь между падением
напора (задан обычно располагаемый напор на всей длине / ) ,
расходом и геометрическими характеристиками (размерами от
верстий и способом их распределения по длине / ) . Задача экс
плуатации состоит в установлении изменения путевого расхода
по длине трубопровода - готового или спроектированного
(часто - с равномерным распределением одинаковых отверстий
по длине участка / ) . Проектные задачи приходится решать в слу
чае заданного закона отвода жидкости по длине трубопровода
(равномерного или неравномерного): здесь необходимо устано
вить распределение отверстий по длине / (конструктивно менее
удобно варьировать размеры отверстий) . Определенную роль во
всех этих задачах играет транзитный расход; в частном случае он
может быть равен нулю.
С расчетной точки зрения основная проблема связана с пере
менным по длине потоком жидкости по трубопроводу. Это озна
чает (см.рис.2.2 1 ) , что на некотором удалении х от начала тру
бопровода поток по нему V меньше существовавшего в началь
ном сечении Vн = Vn + Jt;., причем , естественно, V = var. Поте
рянный напор на участке dx (будем считать, что этому участку
свойственны все характерные особенности трубопровода) может
быть записан в форме (2.32):
-

dh

причем

L z.;

=

п

[· ct(1 + � '-] � ·
г

d

(д)

2g

здесь относится к местным сопротивлениям в

точках отвода порций жидкости по пути ее течения (через от
верстия, насадки и подобные устройства).
1 77

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

.

Совместно с (д) будем испол ьзовать уравнение расхода в форме
( 1 1 8); важно, что в этом уравнении для рассматри ваемой задачи
расход изменяется от сечения к сечению: V V(x).
В более простой форме величина dhn ( ил и равное ей элементар
ное падение напора - dН) соответственно выражению (2.3 2а) вы
разится :
dhn
л. , v 2 _
л. '
-- = а
(е)
5 -dx .
' dh" = -dH = а dx
d5
d
=

-v2

--

Такая форма зап иси часто бы вает здесь удоб нее, поскол ьку при
постановке задачи обычно предусматри вается отыскание связи
между V и другим и характеристикам и течения в транспортном
трубопроводе. Используем в дальнейшем эту форму записи.
Поток жидкости в произвольном сечени и х найдем из матери
ал ьного баланса для элементарного участка dx в един и цу времени
(режим - стационарн ы й); согласно ОБС ( 1 . 8), в отсутств и и Источ
н и ков, Стоков и Накопления
V - ( V + d V) - V0 dx = 0 ,

0

где V - уде л ьн ы й ( на един и цу дл и н ы трубо п ро в ода) путевой р асход , в общем
сл учае - п еременн ы й .

Отсюда

d V = -V0 dx .
(ж)
Очевидно, что поток жидкости в произвол ьном сечен и и х со
ставит
V = Vн

-J
х

V0 dx ,

(з)

о

а в п ростейшем случае равномерного путевого расхода ( Vo
=

const):
V=

Vн

- V0 х = Vт + Vn - V0 х = Vт

+ V0 1 - V0 х = V

т

=

+ V0 ( / - х ) . ( и )

Подстановка значения V по ( з ) в выражен ие ( е ) дает после ин
тегрирования искомую связь в общем в иде :

1 1.,(vн

лН = hп = а J
о

J

- Vodx

d

5

)

2

dx.

(2 . 3 7)

Дал ь не й ш и е операци и с уравнен и е м (2 . 3 7) о пределя ются по
становкой задач и . В аж н о : здесь каждому значен и ю х отвечает
с вое з н аче н и е V, а знач ит, и с вои Re и А , . Реше н и е для наибо-

лее простого случая V0 = const с упрощаю щ им допуще н ие м А,
1 78

�

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

"" const приводится в л итературе * (там же рассмотрен част н ы й слу

чай V,. = О).
Установленные аналитические связи типа (2.37) позволяют
конкретизировать постановку задачи. В прямых задачах, когда
требуется рассчитать hп или необходимый напор ЛН (это задачи
проектирования) , непосредственно используется решение в
форме (2. 37) . Заметим: в простейших случаях - типа (и) - ре
шения получаются достаточно простыми. В случае обратной
эксплуатационной задачи необходимо установить закон измене
ния расхода по длине V = V(x) . В случае обратной проектной
задачи определению подлежит диаметр трубопровода d, обеспе
чивающий n ри известном ЛН значения Vn и V,., либо решается
более тонкая задача - обеспечения заданного закона отвода
жидкости по длине трубопровода. Например, при необходимос
ти равномерного путевого расхода на решение следует наложить
допол нител ьное о гран и ч е н и е : d V/dx = const = Vn/l = V0
и дал ее
искать закон распределения отверстий по длине трубопровода
(расстоян ия между отверстиями, очевидно, придется уменьшать
из-за снижения напора вдоль х).
В случае обратных задач решение уравнения (2. 37) ведется с
помощью итерационных процедур, иногда - достаточно rpoмоздких.
2.3.5. Газопровод
-

В основе расчета газопровода (прямые и обратные задачи; за
дачи эксплуатации и проектирования ) лежит уравнение Бернул
ли для реальных рабочих тел , согласно которому движение про
исходит за счет располагаемого напора, расходуемого на пре
одоление гидравлического сопротивления . При движении жид
костей изменение напора (давления) по длине трубопровода не
сопровождается изменением плотности (жидкость практически
несжимаема) , а в отсутствие дополнительных Прихода и Ухода
на рассматриваемом участке - также и объемного расхода V.
При движении газов (они сжим аемы) их плотность (а она входит
в уравнение Бернулли) изменяется в силу изменения давления;
одновременно вследствие расширения газа при уменьшении
давления в направлении движения увеличивается объемный
расход V. Эти различия в свойствах газа и жидкости должн ы
быть учтены при расчете газопровода.
Прежде всего, для газопроводов следует оперировать не объ
емным, а массовым расходом G, поскольку в отсутствие Прихо
дов и Уходов газа м ежду двумя рассматриваемыми сечениями
.цля стационарного движения именно G остается неизменным.
• См. [6, 25).

1 79

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис.2. 22.

Схема газопровода

Далее: уравнение Бернулли
для газового потока может быть
записано только в дифференци
альной форме - по типу (2. 1 4) ,
но с учетом потерь напора dhп на
элементарном участке газопрово
да. При этом плотность р пере
менна и зависит от давления р в данном сечении.
В целях иллюстрации подхода к расчету газопровода будем
рассматривать изотермическое течение газа на прямом участке
длиной /, по которому газ движется (пусть слева направо) под
действием разности давлений р 1
Р2 (рис. 2 .22) ; диаметр газо
провода обозначим D. Вьщелим на расстоянии х от входа в газо
провод элементарный участок dx, для которого характерны те
кущие значения давления р, плотности р , скорости w.
Запишем уравнение Бернулли для участка dx:
-

dz

. dp

+

-

pg

+

dw2 +

--

2g

(2.38)

dhп = О.

В этом уравнении не все слагаемые равнозначны, что обус
ловлено низкими значениями плотностей газа (обычно на 2-3
порядка ниже , чем для жидкости) . По этой причине:
- слагаемым dz можно пренебречь в сравнении с dp/pg (не
из-за горизонтального расположения газопровода на рисунке dz мало и для вертикального, и для наклонного, а из-за малого
гидростатического давления газового столба высотой dz или лz;
исключение могут составить газы с большой молярной массой при
высоких давлениях - этот случай :щесь не рассматривается);
- слагаемым d w2/(2g) можно пренебречь в сравнении с
dp/( pg) из-за малого вклада скоростного напора (исключением
являются высокоскоростные потоки тяжелых газов, когда значе
ния w далеко превосходят рекомендованн ые в ра:щ. 2.3.2; эти
случаи здесь также не рассматриваются) .
С этими предпосылками и выражением dhn на элементарном
участке dx по Дарен - Вейсбаху уравнение (2.38) принимает вид

+ dhп = О
pg
dp

dx w 2

И

-

dp = pgdh п = 'ЛrJi T р.

а/(Р 7t�2 ) ;

(2.38а)

Заменим переменную по длине газопровода скорость w через

массовый расход G согласно ( 1 . 1 7): w =
-d

1 80

lfJ

=

л.

2
' D ( rtD2 ) 2 р dx

p

4G

1

-

л.

' rt 2 D s p dx
8G

2

.

тогда

(к)

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Перенесем р в левую часть равенства (поскольку физически р
зависит от р, а не от х) и установим связь р и р. Будем считать,
что в относительно небольшом диапазоне давлений р 1 - Р2 газ
ведет себя как идеальный: pv = р/р = RT (здесь R = Ry /М, при
чем R и Ry - удельная и универсальная газовые постоянные,
М - молярная масса газа) . Отсюда р = p/(R1). Подставим это
значение р в (к):

-

р
dр = Л.
RT

г

8G2
-7t 2D s dx ·

(л )

П режде чем интегрировать выражение (л) от начального до конечного сече
ния, выясним закономерность изменения Аг по дпине газопровода. Для этого
необходимо установить закон изменения по х числа Re, поскольку Аг = j{ Re).
Вдоль оси х одновременно изменяются скорость w и его плотность р
по
одному и тому же закону (по уравнению Клапейрона - Менделеева, например,
если газ принят идеальным), но в противоположных направлениях. Поэтому
произведение wp, входящее в Re = wdp/µ, не изменяется при изменении р по
мине трубопровода. Влияние давления на динамическую вязкость газа µ чрез
вычайно мало (изменению р на десятки атмосфер сопутствует изменение µ на
единицы процентов) . Поэтому при изотермическом движении газа изменением
Re при падении давления от р 1 до Р2 вполне можно пренебречь. Значит, и Аг
можно считать постоянным (тем более, что Аг слабо изменяется с Re в практи 
чески интересной турбулентной области течения).

-

И нтегрируя теперь уравнение (л) от О до / и от р 1 до р2 , полу
чим, изба вляя с ь от знака "минус" и меняя местами пределы ин
тегрирования в левой части :
(2.39)

-

Эта формула позволяет просто решать прямые задачи проек
с определением неизвестного р 1 (или Р2 ) при за
(ил и р 1 ). Решение обратных задач требует итерацион
ных процедур, аналогичных описанным в предыдущих разделах.
Например, при необходимости определения G (задача эксплуа
тации) имеем из (2.39):

тирования
данном Р2

G

=

rtD2 (А2 - p;)D .
4

(2. 39а)

Л. , /R Т

Совместно с (2. 39а) используется уравнение расхода ( 1 . 1 7 ) :
G = pw 7tD 2 /4 . Расчет начинается с выбора скорости ( в "ра-

(

)

зумных пределах" - см. разд. 2.3.2); далее - круги итерации с со
поставлением стартовых G и рассчитанных G' значений потоков:
( 1 . 1 7)
(2.39а)
(2.40)
Задаемся w � G � Re � Л г � G ' .

t

0 - •

1

181

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

При получении приемлемой сходимости исходного G (для
данного акта итерации) и найденного G' значений расчет счи
тается законченным.
При неизотермическом течении газа выражения (2.39) (2.39а) становятся приближенными, поскольку численное зна
чение Re изменяется с изменением температуры по длине трубы
(не за счет произведения p w - оно по-прежнему остается неиз
менным, - а за счет изменения µ с температурой). В этом слу
чае придется оставить Л.r под знаком интеграла, установить за
кон изменения температуры по длине газопровода и вести инте
грирование с учетом этого закона, используя итерационную
процедуру, сходную с (2.40). Игнорирование изменения Л.r по
длине газопровода и прямое использование для этого случая
выражения (2. 39) приведет к приближенным оценкам.
2.3.6. fидраВJJический удар

На современных химических заводах существует разнообраз
ная система трубопроводов, по которым движутся - нередко с
весьма высокой скоростью - жидкости (до 3 м/с, иногда и бо
лее) и газы. В ходе производственных процессов может возник
нуть необходимость быстро перекрыть поток (аварийная ситуа
ция; специфика технологического процесса и т.п.). Такая опе
рация сопровождается возникновением больших механических
усилий - ударного давления (сверх существующего в трубопро
воде). Ч тобы не допустить разрыва трубопровода, необходимо
выявить факторы, влияющие на величину ударного давления
Руд. и установить количественные соотношения для его расчета.
Пусть на участке трубопровода длиной /, радиусом R, толщи
ной стенки о движется поток жидкости плотностью р со ско
ростью w (рис.2.23). Все необходимые свойства жидкости и ма
териала трубы известны. В какой-то момент времени мгновенно
закрывают задвижку на правом кон це участка, и скорость в тру
бе падает до нуля. При этом кинетическая энергия потока Lкин
переходит в работу деформации стенок Lдеф и сжатия жидкости
Lсж · Подчеркнем: здесь приходится учитывать эффекты, кото
рые ранее мы игнорировали: деформацию стенок трубы и сжи
маемость жидкости под действием возникающего ударного дав
ления . Значение Руд можно определить из энергетического ба
ланса - запишем его в форме ( 1 .8г) :
Lюtн = Lдеф Lсж·
(м)
·

+

Выразим каждую из составляющих баланса.
Изменение кинетической энергии потока (на участке / масса
жидкости т = р ттR2 l) п ри полном закрытии задвижки и прекра1 82

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

w

- учnсток трубопровода , 2 - задвижка

Рис. 2. 23. К расчету ударного давления при гидравлическом ударе:
1

щении движения составит

mw2 = p 7tR 2 /w 2
(н)
= 2
2
Работа деформации стенок трубы (ее материал характеризуется
модулем упругости Е) Lдеф может быть представлена как произ
ведение сил давлен ия (при развитии ударного давления от О до
fJ./д) на путь деформации (приращение радиуса лR в ходе де
L ки н

формации). Элементарная работа деформации при текущем зна
чении ударного давления р (О :S р :S Руд) запишется как dL =
= (p·2тtRl) dR. Полная работа будет выражена интегралом на всем
пути деформации, т.е. при абсолютном приращении радиуса ЛR:
Lдеф =

fp · 2тtRZdR.

(ЛR)

(о)

Найдем связь р и R. По закону Гука относительная деформация
cr
ЛR = '
R Е

(п)

crR pR 2
ЛR = - = - ·

(р)

- напряжен ие, возни кающее под действием ударного давления.
В то же время из равновесия сил (см. правый фрагмент
рис.2.23) следует: проекция равнодействующей сил давления на
левую боковую полуповерхность цилиндра (или, что то же са
мое: произведение давления на диаметральную плоскость) урав
новешивается силой , возникшей в результате появления напря
жения cr: p· 2 RZ = cr·20/. Е сли отсюда выразить cr = pR/3 и под
ставить в (п), то абсолютная деформация
где

а

Е

В дифференциальной форме

ЕЕ>

р
d R = - dp + - 2 RdR ::: - dp ;
ЕЕ>
ЕЕ>
ЕЕ>
R2

R2

(с)

второе слагаемое, очевидно, пренебрежимо мало в сравнении с
первым, так как деформация невелика (R весьма слабо изме183

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

няется с р, dJVldp � О); поэтому в конечном выражении осталось
только первое слагаемое. Подставим в (о) значение dR по (с) и
возьмем пределы в соответствии с новым параметром интегри
рования (dp). Тогда с учетом основных эффектов:

Lдеф =

[р · 2лRl Rz dp = лR3
Е&

Р"

l
Е&

р�4

·

(т)

Элементарная удельная работа сжатия рабочею тела, как из
вестно из термодинамики , составляет -pdv; элементарная работа
для массы т (н·а участке трубы длиной [) будет равна:
dLcж = т(- pdv) = - pтtR2 Z(pdv).
(у)
Связь v и р, необходимую для последующего интегрирования
выражения (у) , найдем, введЯ понятие о коэффициенте сжимае
мости kc, представляющем собой относительное изменение объ
ема при изменении давления на единицу:
dV
1 dv
(ф)
kc = - -1 = --- .
Отсюда

v dp

V dp

dv = -kcvdp и , поскольку pv = 1 , то
d Lcж = - рлR2 / (- pkcvdp) = лR2/kc/)dp.

(х)

Интегрируя по полному диапазону развития ударного давле
н ия и полагая, что в этом диапазоне kc � const, получим

f лR 2 lkcpdp

Р,,

=

тtR 2 lk

(ц)
•
2 с р�4
Записывая теперь энергетический баланс (м) с найденными
значениями его составляющих по (н), (т) и (ц) , имеем
Lсж

=

о

prtR 2 /w2

_

тсR3 /

-

Руд
2

+

тcR 2 lkc 2

Руд '

EfJ
2
откуда после сокращения на 7rR2 J и замены оставшегося радиуса
R на d/2 , окончательно:
2

Руд =

pw2

d
Е& + k с

(2.4 1 )

Анализ формулы (2.4 1 ) показывает:
- ударное давление Руд не зависит от длины выбр;э.нного
участка трубопровода /, поскольку каждая из составляющих
энергетического баланса пропорциональна /;
- наибольшее влияние на Руд оказывает исходная скорость
потока w; очевидно, если задвижку закрыть не полностью, так
1 84

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

что конечная скорость жидкости в трубе окажется

wк > О , то

Руд будет меньше, поскольку в числителе выражения (2.4 1 ) под

радикалом вместо w2 будет стоять (w2
wк2 ) ;
- чем сильнее материал стенки трубы сопротивляется де
формации (т.е. чем больше модуль упругости и толще стенка),
тем выше получается Руд ; значит, в резиновой трубе при прочих
равных условиях Руд будет заведомо ниже, чем в металлических;
- чем выше сжимаемость жидкости (т.е. чем больше kc ) , тем
ниже Руд ; поскольку для газов значения kc примерно в 1 03 - 1 04
раз больше, нежели для жидкостей , то ударное давление в газо
проводах существенно ниже, чем в жидкостных трубопроводах.
В реальных условиях ударное давление достигает десятков
атмосфер. Для уменьшения негативных воздействий гидравличе
ского удара реко м ендуется медленно закрывать задвижки на тру
бопроводах (если, конечно, речь не идет об аварийных ситуаци
ях) или устанавл ивать на трубопроводах (до задвижек) аморти
зирующие устройства (газовые полости - " колпаки " , специаль
ные клапаны с гибкими мембранами и т.п . ) .
-

2.4. ГРАВИТАЦИОННОЕ ТЕЧ ЕН ИЕ ТОНКИХ ПЛЕНОК

Пленочное течение жидкостей по поверхностям различной
конфигурации под действием сил тяжести весьма перспективно
для многих хими ко-технологических процессов, поскольку дви
жется жидкостная тонкая пленка; оно обладает рядом особен 
ностей:
- интенсивно прогревается и передает тепло, что важно для
ряда экзо- и эндотерм ичес к их реакций ;
- обеспечивает стабильное и достаточно интенсивное проте
кание ряда тепло - и м ассообменных процессов (испарения, ди
стилля ц ии , абсорбци и и др. ) ;
- обеспечивает достаточно малое время контакта с о стен кой
(например, горячей, что важно для термолабильных жидкостей);
- зани мает малый объем из-за малой толщины, что суще
ственнQ при проведен и и процессов с большими тепловыми эф
фектами , а также с взрывоопасными веществами (нитрование,
сульфирование и др. ) ; здесь в отличие от реакций в объемах
(даже с интенсивны м перемеши ванием) лучше отводится тепло
и на 2-3 поряд к а мен ьше единовременный объем реакционной
смеси в промышленно м аппарате (выше безопасность процесса) .
Среди основных задач гравитационного течения тонких пле
нок - определение расхода жид кости V, обеспечивающего задан
ную (технологическим регламентом, интенсивностью теплопере
носа и т.п.) тол щ ину плен к и о, либо расчет толщины пленки ,
1 85

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис.2. 24. Схема гравитационного
течения тонких пленок

соответствующей заданному
объемному расходу. Разу
меется , встречаются и иные
постановки задач . Во всех
этих случаях надо знать
связь между V и 8, а также их
зависимость от свойств жид
кости и условий течения.
Расчетная схема пред
ставлена на рис.2.24. Тонкая
пленка постоянной толщи
ны 8 стационарно движется
"о
под действием собственного
веса по плоской вертикаль
ной стенке - вдоль оси z
(здесь она направлена вниз).
Введем ряд упрощающих
допущений.
1 . Толщина пленки мала (практически это доли миллиметра,
редко милли метры) ; поэтому чаще всего скорость течения из-за
тормозящего де йствия бл изко расположенных стенок по всей
толщине пле н ки (на л юбом расстоян и и у от стенки ) - невели
ка . Это позволяет предположить, что течение пленки будет ла
минарным или близким к нему.
2 . В силу малой тол щины пленки ее течение можно считать
плоским, даже если поверхность искривлена по нормали к оси z
(при течении вн утри вертикальн ых труб и т. п . ) : толщина пленки
мала в сравнен и и с ради усом кривизны .
3 . Начальные участки течения, где происходит формирование
характерных толщин ы пленки и профиля скоростей, не рас
сматриваются ; это допустимо: расчеты показывают, что протя
женность этих участков не превышает 20-30 мм.
4. Будем анализировать наиболее простой случай течения
пленки - без взаимодействия ее свободной поверхности с газом ;
это правомерно, когда скорость газового потока около поверх
ности пленки невели ка либо движение газа вообще отсутствует.
Решать зад ачу можно исходя из уравнения Навье - Стокса:
как указано в разд.2.2.4, в случае ламинарных течений в силу
простоты (л инейности ) связей это уравнение часто (при нали
чии упроще н и й , подобных сфор м ул ированным выше) удается
проинте грировать.
Пуrь ре шен и я в рассматри ваемом случае до стато чн о прост:
- записы вают уравнен11е Н авье - Стокс а (2.20) для оси ;:, вдоль которой
движется пленка;

1 86

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

- выражают еди ничные массовые сил ы Р;:. = g; выделяют из лапласиана
фрагмент дlwJдyl ; остальные фрагменты лапласиана и все другие слагаемые
уравнения обрашаются в н ул ь (вдоль оси х движения нет; вдоль оси z при
постоян ном у не происходит изменен ия скоростей; движение стационарное;
давление вдоль оси z не изменяется) ;
- полученное дифференциальное уравнение 2-го порядка
(а)
dy2
µ
решают· с грани ч н ыми условиями: Wz О при у = О (концепция прилипания) и
dwJdy = О при у = Б (отсутствие взаимодействия с газовым потоком , омы
вающим пленку) .
В результате приходят к распределению скоростей wz по толщине пленки
w;:. w;:.(y) и далее - к искомой свюи V и 6 .

d 2 w.

pg

=

=

Однако для ламинарного течения можно проще сформулиро
вать задачу и свести ее к дифференциальному уравнению 1 -го
порядка. С этой целью на стабилизированном участке
(координата z) вьщели м умозрительно в пленке примыкающий к
свободной поверхности прямоугольный параллелепипед шири
ной Ь, высотой л h и толщиной (5 - у). Рассмотрим поток им 
пульса через отдельные грани (вдоль оси х такого потока, есте
ственно, нет) , записывая его соответственно ОБС ( 1 . 8) и учиты
вая, что Накопление равно нулю. При этом напряжение трения
на левой гран и ЬЛh равно tт (это составит Приход импульса) , на
правой ti; = О (это - Уход); Источ ник - на базе внешней еди
ничной массовой силы вдоль оси z: гравитационное ускорение
нет. Тогда для едини
g, масса жидкости р ЬЛh(5 - у); Стоков
цы времени
(б)
tтЬЛh - О + gр ЬЛh(5 - у) = О,
откуда после сокраще н ия на Ьлh имеем
(в)
•т + pg(5 - у) = О.
Подставим значение •т = -µ(дwJду) , замени м частные произ
водные обыкн овенными (оперируем единственной независимой
переменной у) и обозн ачим Wz = Wл , подчеркивая, что речь идет
о локШ1ьной скорости wz на расстоянии у от стенки:

dwл
dy

=

pg
µ

(5 - у) -

(г)

Разделим п еременн ые и прои нтегрируем по толщине пленки
в пределах от стенки ( где у = О, w = О) до текущей координаты
у и текущей скорости 1vл :
'"

• См . [6, 22] .

fd w

1)

1

"

pg
f<5 - y)dy ·
µ о

= -

(д)

1 87

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

В резул ьтате

л

=

w

pg
µ

(оу .L).
-

( 2 .42)

2

Отсюда нетрудно о п редел ить ма ксимал ьную скорость - оче
видно, она будет на свободной поверхности , т.е. при у = 8 :
pg 8 2
w
=
( 2 .42а)
пых

µ

2

-- ·

Таким образом , для вертикального ламинарного гравитационно
го течения пле н ки без взаимодействия с газовым потоком характе
рен парабол и ч еский скоростной профил ь жидкости с максимумом
на свободной поверхности (см . эп юру скоростей на рис. 2 . 24).
И з сопоста вления ( 2 .42) и ( 2 . 42а) видно, что в обобще н н ы х
координатах п рофил ь с коростей в пле н ке не зависит о т свойств
жидкости :

т . е . нал и цо нижний автомодельный ( п о Re) режим течения.
Для о предел ения расхода V зап и ше м поток жидкости через
элементарное сечение шириной Ь и толщиной dy соответстве н 
но уравн е н и ю расхода ( 1 1 4) : d V = wлbdy. П одставляя значение
wл по ( 2 .42) и и нтегри руя , получаем
v=

! Р: [

Окончател ь н о :

V=

.

8у

_

2
У
2

pg/) о J
µ 3

-

}dy Р: ь[ ; � 8: }
8

=

и

Vуд

=

V
ь

8

=

_

pg � .
µ 3

( 2 .4 3 )

Второе из этих вы раже н и й зап исано для удельного расхода
жидкости , т. е . приходя ще гося на еди н и цу ширины пленки ; ве 
л и ч и ну Vуд н азывают линейной плотностью орошения . Замети м :
п р и теч е н и и п л е н ки внутри кру глой верти кал ьной трубы Ь = тт.d.
И з ( 2 .43) л е гко о п редел ить средн юю скорость течения пл енки .
И мея в виду , что вел и ч и н а се ч е н и я составляет Ь8 , п олуч и м п о
уравне н и ю расхода ( 1 . 1 8 ) :
v
pg - ·
w = - = ( 2 .44)
3
µ
Ьо
Сопоставле н и е w и и111шх показы вает, что при ламинарном течении
тонких пленок (и это вообще характерно для плоских ламинарных
течений ) w/wnыx = 2/з.

02

1 88

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

При необход и мости о предел е н и я толщины пленки по зада н 
н о м у расходу V и л и Vy.'i решаем ( 2 .43 ) относител ьно & :
&

= �:;

=�Зµ�у:� .

( 2 .43а)

Есл�1 рассматри вать гравитаuионное течение пленки по наклонной плоскости
(уrол к горизонту а ) , то измен ится лишь внешняя массовая сила: вместо g в
исходном уравне н и и будет фи гурировать составляющая силы тяжести вдоль
стенки g sin1x.

П ол уч е н н ы е соотн ошения сп раведл и вы для ламинарных пле 
н о ч н ы х течен и й , соответствующих небольшим значениям ч и сла
Re . Его верхняя гра н и ца устанавл и вается эксперименто м . По
скольку реч ь идет о плоском течен и и , предварител ьно необход и 
мо установить определ я ющий л и н е й н ы й размер de, входящий в
Re . Соответстве нно вы раже н и ю (ж) из разд. 2 . 2 . 2 здесь
de =

� :

4 Ь

=

=

4&,

(ж)

поскол ьку смо ч е н н ы й пери метр для рассматриваемого фрагме н 
т а плен ки раве н Ь (с вободная поверхность пле нки , контакти
рующая с газо м , "смоч енной" не считается ) . Таким образо м , для
пленочного те ч е ния Rс пл = w(4& ) pЛt .
Оп ыты показывают . что режи м остается ламинар н ы м , а по
луч е н н ы е вы ш е выраже ния - спра ведл и вы м и при Rепл � ,,, 2 0 .
Однако качественно характер установл е н н ых связей сохраняется
и при б6л ьших значен иях Renл ' ко гда движение пле н ки стано
вится волновым (его е ще имен уют
псевдоламинарным ) . Этот
режи м , набл юдаем ы й в диапазоне 20 � Re � 1 500, отличается
образован ием продол ьных вол н на свободной поверхности
пле н ки . П оказано, что такой режи м течения оказывается энер
гетически вы годн ы м : п р и оди наковых расходах V средняя ско
рость течения повы ш ается , средняя тол щи н а пленки умен ь 
шается - в сравнении с рассчитанными по формулам для лам и 
нарного режи ма. Для указанного диапазона Renл установл е н о :
чтобы формул ы ти па ( 2 . 43 ) - ( 2 .43а) сохранили н еобходимую
точ ность , в н и х следует замен ить множител ь 3 на 2 , 4 .
При Rе пл свыше � 1 500 режим течения становится переход
ным, а при Rеп л > "' 2 000 - тур булентным. В этом случае рас
пределение скоросте й следует "закону стенки" ( 2 . 2 6 ) ; анализ
тече н и я необходимо вести по п р и веден ной выше кан ве, исходя
из этого зако н а .
Специал ь н о подч е р к н е м , что пря мая задача определения h11
при рассматр и ваемом течении тон к и х пленок не возникает; по
этому не требуется вы вода уравн е н и й типа Гагена
П уазейля
( 2 . 20) - ( 2 . 2 1 ) , не нужно ис кать зависи мости Аг = ./( Renл ) в
1 89

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

уравнении Дарси - Вейсбаха (2. 1 7) . Дело в том, что при течении
тон ких пленок вес пленки, движущейся по поверхности высотой
h, в точности уравновешивается силой взаимодействия жид
кости со стенкой (при ламинарном течении - силой трения);
поэтому изначально hп = h (для наклонной плоской стенки при
угле а с горизонтом hп = hsina).

В тех случаях, когда взаимодействием газа с о свободной поверхностью
пленки пренебречь нельзя (из-за его течения с достаточно высокими скоростя 
ми - на уровне нескольких метров в секунду) , скоростной профиль ламинарно
стекающей пленки деформируется (по-разному - в зависимости от направле
ния и скорости газового потока). Причина - появление напряжения трения t ,
на свободной поверхности пленки (при восходящем движении газа считается
t0 > О, при нисходящем
t0 < 0). Для разных значений безразмерного ком 
плекса ч/( рgБ) , выражающего соотношение сил трения на свободно й поверх
ности и веса пленки, получаются различные профили скоростей. Детально
характеристики пленочного течения при взаимодействии с газовым потоком
рассмотрены в литературе• .
Влияние возде й ствия газового потока на пленку (т.е. условие to с# О) должно
быть учтено•• :
- при решении на базе уравнения Навье - Стокса граничными условиями
на свободной поверхности пленки являются: при у = Б теперь не dw,.,ldy = О , а
dw,.,ldy = ч,/µ;
- при решении с помощью баланса импульсов Уход через правую стенку
(был равен нулю) теперь составит t0 bлh.
Решения уравнения типа (г), скорректированного с учетом этого слагае
мого, затруднени й не вызывает. Очевидно, вместо (2.42) будет получен профил ь
скоростей , учитывающий t0 :

-

-

Wл =

:

р

[{
Б

1-

;;Б ) - У2

2

]

·

(2.426)

Последующее определение w..,." w, связи V и Б ведется в и311оженной выше
последовательности.
Значения t0 определяются либо из эксперимента (в литературе приводятся
эмпирические формулы), либо на основе анализа закономерностей движения
газового потока, омывающего свободную поверхность пленки.

2.5. ТЕЧЕНИЕ НЕНЪЮТОНОВСКИХ :ЖИДКОСТЕЙ
2.5. 1 . Классификация и общие свойства
неньютоновских жидкостей

Предшествующий анализ течения жидкостей в той или иной
мере базировался на уравнении сдвиrа ( 1 .9):

tт

=

l l

дпл ·
дп = µ дw
-µ дwл

• Подробнее - см. (6) .
•• Строго говоря , при взаимодействии свободной поверхности пленки с га
зовы м потоком из-за гидравлического сопротивле ния движению последнего
уже нельзя считать др/дz = О ; надо учитывать упомянутое взаимоде й ствие не
только в граничных условиях, но и в исходных уравнениях.

1 90

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

"lL_
а

1 д 1 1/дп l

-'"
"t,....
. =
.
...._
.:...
_
__ "&,. �1,...-....:._
...
_"
1 д и1/дп l

Рис.2. 25. Диаграммы сдвига:
а - ньютоновские жидкосп1,
кости , г - дил атантные жидкости

б

-

б

в

бин гамовские жидкости ,

в

-

�

1 дw/дп l
•

г

nсевдоnластичные жид

При ламинарном режиме (преобладание сил вязкости ) коэф
фициент пропорционал ьности µ является свойством жидкости ,
не зависящим· от при меняемых усилий или (что здесь то же
самое) градиента с к оростей дwл/дп. Как было указано в
разд.2.2.4, в этом случае линейная связь •т и дwл/дп ( 1 .9) име
нуется формулой Н ьютона, µ называется динамической вяз
костью, а жид кости , следующие формуле ( 1 .9), носят название
ньютоновских. Для таких жид к остей диаграмма сдви га изобра
жена на рис. 2.25 , а, причем для данной температуры µ = tga =
= coпst . При турбулентных течен иях выраже н и е ( 1 . 9 ) п р иобретает
формальный характер, его линейность нарушается, поскол ьку
коэффициент пропорциональности становится зависящим от
характеристи к течен и я ; в раздел е 2 . 2 . 5 это было отражено заме 
ной постоянного к оэффициента µ суммой µ + µ 11 , где
"турбулентная вяз к ость" µ и была призвана в терминах и симво
лах динамичес к ой вя з кости уч есть нелинейность, вызванную
турбулентными пульсациями. Однако нелинейность связи •т и
дwл/дп может проявляться та кж е в таких течениях, когда вяз
костные силы домини руют над инерционными . Это характерно
для жидкостей , обладающих некоей внутренней структур ой,
изменяющейся под действием приложенных усилий. Такие
жидкости тоже лишь формально следуют уравнению сдвига
( 1 .9); перем енн ы й коэффициент пропорциональности в этом
случае прини мает смысл кажущейся вязкости µ к , зависящей от
величин •т и дwл/дп:

где

µ. = v ar.

'rт

=

- µ. д;, = µ.1 а;;· 1 ,

(2.45)

• Разумеется . вязкость µ, как и ряд других реологических характеристи к
жидкости , и з мею1 стся с тем 11ературой ; этот вопрос выходит за пределы анализа .
поскольку в дан ной главе р�ссматри ваются изотермические течения .
191

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Раздел гидравлики , описывающий течение таких - неньюто
новских - жидкостей , является частью более общей науч ной
дисциплины, называе мой реологией (последняя охватывает из
уче н и е механ и ч еских свойств различных рабочих тел - от газов
и ньютоновских жидкостей до твердых тел , следующих и не
следующих закону Гука). Течение неньютоновских жидкостей в
условиях преобладания сил вязкости (именно такой случай
практически и нтересен ) называется пластичным . Для него харак
терно измен е н и е . µк в поперечном сечении канала.
Неньютоновские жидкости об ы чно делят на две основные
группы:
- реологически стационарные : при снятии приложенных уси 
лий структура таких жидкостей полностью восстанавливается
(можно говорить об обратимости свойств этих жидкостей ) ; зна
чения µк здесь не зависят от продолжительности действия сил
(т.е . от "преды стории" жидкости ) ;
- реологически нестационарные: при наложении усил и й про
исходят структурные изменения, глубина которых увеличивается
при более продолжительном действии сил , так что µк зависит от
времен и ; при снятии приложенных усилий структура здесь либо
восстанавли вается пол ностью ил и н е полностью, либо вооб ще не
восстанавливается .
Для математического описания поведения неньютоновских
жидкостей уравнений ( 1 . 9) или ( 2 .45) недостаточно; необходимо
отразить воздействие основных факторов на µк либо с помощью
конкретных зависимостей выразить связи tт с дwл/дп. Такие
описания (модели: они носят феноменологический или эмпи
рический характер) относительно просты для стационарных
жидкостей (отсутствует влияние времени) и более сложны для
нестационарн ых. Н иже будут рассмотрены стационарные жид
кости , что позволит в дальнейшем установить закономерности
их пластичного течения ; нестационарные жидкости лишь каче
ственно охарактеризован ы .
Среди реологичес к и стационарных есть группа жидкостей ,
которые не движутся при относительно небольших прило
жен ных усил и я х . Дви же н ие нач и нается только при напряжени
ях, превышающих некую предельную вел ичину to, называемую
пределом теку•1ести (реже - критическим напряжением) . При tт <
< to
нет относительного сдвига слоев жидкости: дwл/дп = О .
Внутри этой группы, в свою очередь, есть жидкости , которые
при tт > to п од действи ем избытка напряжений ( tт - to) ведут
себя как н ьютоновски е . Для ни х уравнение сдвига имеет вид
tт - to
1 92

=

-11

д�,

, и л и tт

= to

+

11(- д�, )

= t0

+

Т]l д�' I

·

( 2.46)

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Такие жидкости получили название бинrамовских. К их числу
относятся, например, густые мелкодисперсные суспензии , пас
ты , некоторые шламы. масляные краски .
Диаграмма сдвига для бингамовских жидкостей изображена
на рис. 2 . 2 5 , б. (Подчеркнем : эта и другие диаграммы на
рис . 2.25 изображены вне каких-либо масштабов; кривые лишь
иллюстрируют ход зависимосте й 'т от дwл/дп. ) На диаграмме
to - отрезок , отсекаемый на оси tт при д wл/дn = О; постоянный
коэффициент ri , выражающий наклон прямой (2.46) к оси аб
сцисс (ri = tg� ) , наз ы вается коэффициентом пластической вяз
кости (кратко - пластичностью ) .
Кажущаяся вязкость, соответствующая (2.45), должна отве
чать тангенсу угла секуще й : µк = tgq>. И з рисунка видно, что с
увеличением •т и lд wл/дпl велич ина µк уменьшается. В пределе
(при tт, lдwлfдnl � оо) µк � ri = const; это означает, что при
больших приложенных усилиях бингамовская жидкость начина
ет вести себя как ньютоновская с постоянной вязкостью. Ана
литически эти эффекты легко проследить пуrем сопоставления
выражений ( 2 . 46) и (2.45):

•о +

откуда

rij a;:, j j a;:, 1
=

µ.

·

µ . = Т]
lдw,, / д� .
И з (а) ясн о : с ростом l дwл/дпl уменьшается µк ; при lд wл/дп l �
� оо будет µк � 1'1 ·
При очень высоких усилиях и l дwл/дп l начинают играть роль
+

(а)

силы инерци и ; с их нарастанием пластичный характер течения
нарушается, п отом и вырождается ; возникает турбулентное те
чение со всеми его особенностями и закономерностями .
Заметим : н ьютоновские жидкости можно трактовать как
частный случа й бингамовских (при to = О); тогда пластичность ri
приобретает смысл ди намической вязкости µ. Это означает, что
аналитические выраже ния, характеризующие пластичное тече
ние бингамовских жидкостей, при to = О (и с заменой ri на µ)
должны переходить в уже известн ые (разд . 2 . 2 .4) закономерности
ламинарного течения н ьютоновс ких жидкостей .
Среди ста ционарн ых есть группа жидкостей , уравнение
сдвига которых в области пластич ного течения может быть
представлено в виде степенной зависимости:

где k и

т

- k( дw ,)т

•т -

- дп

'

(2.47)

- эмпирически подобранные константы, характерные д11Я данной жидкосm .

1 93

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Жидкости , для которых т < 1 , носят название псевдопластич
ных; диагра м м а сдви га для них изображена на рис.2.25, в. К их
числу относятся , например, оли гомеры , низкомолекулярные
полимеры , растворы высокомолекулярных полимеров, некото
рые суспензи и с асим м етричны м и части цами.
Кажущаяся вязкость псевдопластичных жидкостей умень
шается с увел ичение м tт и lдwл/дпl - это видно из графи ка.
Аналитически это ле г ко показать сопоставлением уравнений
(2.47) при т < 1 и (2.45 ) :

откуда
µк =

kl д;:т· = µ.1 д:пл 1
k l-дwпл 1 "'- 1
д

·

при т < l .

(б)

Поскольку т < 1 , то с ростом jдwл/дnl величина µ к умень
шается . Физи ч ески это объясняется ориентацией молекул ил и
частиц свои м и больш и м и осям и в направлении течения жид
кости .
Жидкости , для которых т > 1 , носят название дилатантных;
диаграмма сдв и га для н и х изображена на рис.2.25, г. К их числу
относятся не к оторые густые суспензии, замешанные на невяз
ких жидкостях , клеи . Кажущаяся вязкость для них увеличивается
с ростом t т и lдwл/дпl - это видно из графика и из сопоставле
ния (2 .47) при т > 1 и (2 .45) :
µк =

k

д::

1 1 т-1

при т

>

1.

(в)

Дилатантн ые жид к ости менее распространены, нежели псев
допластичные и бингамовские .
Важно подчер кн уть, что уравнения сдви га (2.46) и (2.47) я вля ются эмпири 
ческими соотнош е н и я м и , справедл и в ы м и тол ько в ограниченной области плас
тичного течен и я ; за ее п ределами он и теря ют силу. На диаграммах сдвига в
области весьма высоких знаqе н и й 1т и lдwл/дnl кривые переходят в прямолиней
н ые уqастки . Кстати , по этой причине неправомерно анализировать характер
изменения кажу щ ейся вязкости при высоких lд wл/дп l по формулам (б) и (в) при таких гради е н та х скоростей значения tgq> стремятся к постоянной вел и ч и н е
(наклону пря мы х участков), и псевдопл а стичные (дилатантные) жидкости
начинают вести себя как н ьютоновски е . Кроме того, уравнения (2.46) и (2.47)
неправомерн ы и 11 непосредствен ной близости к началу координат ; это ясно
видно ю вы раже н и й ( 6 ) и (в) : nри lдwл/дпl -.. О получается , соответствен н о,
µ. -.. оо и µ , -.. О , что н е отвечает физике явле н и й и реальной ситуаци и .

Мате м ати ч еские о п и сания пластичного течения псевдоплас
тичных и дил атантн ы х жидкостей формально совпадают (раз1 94

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

личие - в ч и сл е н н ы х значениях m ) . Н ьютоновские жидкости
можно тракто вать ка к ч астн ый случай псевдопластичных и ди
латантн ых при т = 1 ; то гда коэффи циент k приобретает смысл
д и н а м и ческой вя зкости µ . Это означает, ч то выраже н ия , харак
те ризующие пл асти ч н ое теч е н и е таких жидкосте й , при т = 1
переходят в уже и з вестн ые (разд . 2 . 2 .4) зако номерности лами
нарного теч е н и я н ь юто новск их жидкосте й .
Н иже м ы о гран и ч и м ся ( н а осн ове представл е н н ых соотно 
шен и й ) изуч е н и е м закономерн осте й пластичного течения рас
смотренных в ы ше жидкосте й , хотя существуют и другие модели ,
отражающие с п е цифи ческие особенности не которых и н ы х рео
логически стационарн ых жидкосте й .
Среди наиболее часто встречающихся реологически нестационарных жид
костей выдел и м :
- тиксотропные, характеризуемые огран иченным понижен ием µ к в о време
ни под воздействием постоя н н ых приложенных усилий (к их числу аrносятся мно
гие краски , из п и щевых продуктов - простокваша); при снятии усилий структура
этих жидкостей постепенно восстанаRЛИвается , они мoryr перестать течь:
- реопектические (реопектантные) , характеризуемые повышением µк во вре
мени ( и ногда - за счет хим ического взаимодействия компонентов, толчок
котором у дает наложение механических усил и й ) , ч:�ще всего - необратим ы м ;
примером может служить смесь воды и гипса, которая после встряхиван ия
быстро затвердевает;
- вязкоуп ругие (вязкоэластичные ) , части чно возвращающиеся подобно упру
гим твердым тел;1 м в первон:�чальное состоя ние после снятия приложенных к
ним касательных напряжен и й (к их числу относятся некоторые смолы, высоко
вязкие эмульсии и суспензи и , тестообразные массы).
2 . 5 . 2 . Пластичное течение бинrамовских жидкостей

Будем анал и зировать закономерности движения б и н гамов
ских жидкосте й в кругл ы х трубах в области умере н н ых знач е н и й
t т и lд wл/дпl, когда теч е н и е я вляется пласти ч н ы м . Рассмотрим
сначала характер течения качествен но (рис . 2 . 2 6 ) . Анал и з сил для
вязких течен и й при вел (разд . 2 . 2.4) к л и нейной завис и мости
( 2 . 1 8 ) измене н и я tт по радиальной координате r
от tт = О при
r = О до наибол ьшего t т t 5 на сте н ке (r = R) . Прямол и н е й н ая
э п юра напря ж е н и й показана в левой части рисун ка.
Для жидкосте й , обл адающих пределом текучести to (урове н ь
обозначен на р и сунке ) , возможн ы д в а случая .
1 . Н аибольшее нап ряжение t 5 < t0; это означает, что на л ю 
б о м те куще м радиусе r � R также будет t т < t o · Тогда течения
жидкости не будет, в этом смысле рассматр и ваем ы й случай яв
ляется банал ьн ым и те хнологическо го интереса не представляет.
2. Н аибол ь ш е е н а п ряжение t5 > t 0 . Это означает, что для час
ти сечения трубы ( в ее кол ьцевой пристенной зоне радиусом r �
происходит
� l"o ) будет харuкте р н о н е р u в е н с т в о tт > to
зд е с ь
относител ьное пере м е щение слоев жидкости ; lд wл/дпl > О. В
-

=

-

1 95

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

�

· · · -w
Рис.2. 26. К за коно ме рностя м п л астичного те ч е ния бинга м овс кой жид к ости в
к руглой трубе
приосевой зоне r :5: r0, как видно из рисунка, tт :5: to - здесь н е

будет относител ьного перемещения слоев жидкости ; в этой об
л асти lдwл/дпl
О, и жидкость движется "стержнем" , с оди нако
вой скоростью Wст во всем сече н и и ттr0 2 (см. на рисунке с права
заштрихован ную ч асть сечения трубы ) .
Н а рис. 2 . 26 показана характерная эп юра скоростей : плас
тичное течен и е б и нгамовской жидкости представляет собой
сочетание лам и нарного движения в кол ьцевой зоне и стержне 
вого - в приосевой зо н е .
Распределение скоростей. Кол ичестве н н ы й а н ал и з закономер
ностей тече н и я б и н гамовской жидкости предусматри вает те же
эт апы, что был и реал изованы при исследовании в разд. 2 . 2 . 4 ла
минарного теч е н ия н ьютоновских жидкостей : распределение ско
ростей , расход, средняя скорость, гидравлическое сопротивление.
Особенности , присущие уравнению сдвига (2 .46) для бингамов
ских жидкосте й в отл и ч и е от формулы Н ьютона ( 1 .9 ) , приводят к
необходимости проводить начало анал иза раздельно для кольцевой
и приосевой зон .
К о л ь ц е в а я з о н а, r0 :5: r :5: R, tт � to. Для о предел е н ия
скоростного профиля подставим в ( 2 . 1 8 ) значен и е tт по ( 2 .46) ,
и мея в виду, что нормаль направлена по радиусу r, и заменяя
частн ые прои зводн ы е обыкнове н н ы м и :
=

+

t0

( d;;· )

� -

=

��

r.

( г)

Разделим перемен ные и сформулируем гранич ные условия
(пределы инте грирования) аналогич но ламинарному режиму, но
лишь для области течен ия r � r0:
".,
l
r
t о dr .
� R 2/
О

fdiv.

1 96

1

=

- -

'J ( Лр

-

-

)

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

-l [-Л4р/ (R 2 - 2 ) -

Отсюда для кольцевой зоны
wJ I =

11

г

]

t О ( R - г)

(2.48)

·

Заметим, что при to = О получается обычный параболоид
скоростей, хар а ктерн ый для ламинарного течения ньютоновских
жидкостей по (2. 1 9); при этом '1'1 приобретает смысл вязкости µ.
О с е в а я з о н а, r s ro, tт < t0. Подставив в формулу (2.48)
значение r = 1·0, получим w = wст:
wс

Лр (R - 2 ) - t (R -1 [4/

Т\

=

т

r.

2

о

. о

r.

о

]

) .

(д)

Это выражение неудобно для использования, поскольку со
держит р ад и ус 10, раз гра ни ч ивающи й осевую и кольцевую зоны;
этот радиус не задан в начале расчета (т.е. в граничных услови
ях) , его целе со о б�;>азно и сключить из расчетных соотношений.
Это делается с помощью уравнения (2. 18) с учетом, что tт = to
при r = ro:
2/t 0
Лр
.
и ro = -21
Лр
Подставив теперь (е) в (д), получи м
to

Wст =

= - ro

�[i:( - �: )
R2

(е)

� )}

(

� - t0 R - 2 0

2

Раскрывая скобки и приводя подобные члены, содержащие
lt02/лp, имеем окончательно:
w

ст

=

-• (-Лр R
'1'\

2

4/

)
Лр

t�
+--t R
/

о

Расход и сред11яя скорость бинrамовской

JКИДКОСТИ.

складывается из потоков в стержневой зоне Vст
кольцевой зоне Vк

=

(2 . 49 )

·

=

Расход V
Wcт7tr02 и в

Jw 2 n r dr ; при этом с.пособ определения

R

Vк

'"

аналогичен рассмотренному в разд.2.2.4, однако в качестве ниж
него предела и нтегрирования здесь следует брать не · r = О, а
радиус, разгранич ивающий зоны, r = ro.
Подстави м найден н ые вы ш е значения Wст и w в выражение
для расчета V:
V =.

Vст

+ Vк

=

�
'1

1f(лр
4/

R

2

+

)

/t� - т 0 R
др

2
г11 +

21[Лр4/ (R2. - r2) - t0(R - r)]гdг} ·
'•

1 97

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

После выполнения операции интегрирования, раскрытия
скобок и приведения подобных членов это весьма громоздкое
выражение упрощается :
V

=

_::11 ( ЛрR• 1 R
_

8/

3

0 3

+

/1 �

Лр

"2 +

для
11

р �r. 3 ) .

Л

8/

"4

3

_

0

°

Здесь тоже uелесообра;�но п реобразовать три последних слагаемых
в скобках, заменив по (е) неудобное
расчетов значение 'Ь:

V = _::11 ( Лp8/R 4

Лр Лр 2

/1� 22 /2 1 �
+

10 R 3

Лр 24/41�

3

V = Лр

Sril

+

81

Лр4

)

21 0 23 /31� -

3 Лр3
После при ведения подобных членов (три последних сла
гаемых) и вынесения за скобки группы величин это выражение
прин имает вид
_

+�
тtR 4 (1 - !__:L
3
3
ЛрR

1 � 14

_

Лр4 R4

)

(2. 50)

•

Отсюда в соответстви и с уравнением расхода ( 1 . 1 8) получи м
выражение для средней скорости потока:

w=

ЛрR2 (
=
тtR2 �
V

l

-

8

J

t0/

ЛрR

+

16

)

-r : / 4
3 Л 4R4 •

р

(2.5 1 )

При to = О выражения (2.50) , (2. 5 1 ) закономерно переходят в
соответствующие формулы для ламинарного течения ньютонов
ских жидкостей .
Формула (2 . 50), являющаяся аналогом уравнения Гагена Пуазейля, прямо используется при решении задачи эксплуата
ции, когда необходимо найти расход жидкости в готовом трубо
проводе при известных свойствах жидкости и параметрах тече
ния. Среди зада ч проектир ования практический интерес пред
ставляет расчет потерь давления Лрп или , что равнозначно, дви
жущей силы , необходимой для движения жидкости с заданной
средней скоростью w.
раскроем скобки в (2.5 1 ) и заменим ра
Для определения
диус R трубы более употребительным диаметром d:
Лрd 2 1 0 d + 81 � /3
(ж)

Лр

w=

_

611 З11Лр3 d 2

32ri /

Уравнение (ж) в явном виде относительно Лр не решается. Здесь
необходима итерационная процедура. l Jредставим выражение
(ж) решенным относител ьно первого слагаемого в правой части :

Лрd2 = w
3211/

--

1 98

+

10d

81 � /3

611 З11Лр3 d 2

- - ---

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

а затем и относительно Лр:

32 rilw + 1 6't 0/ 256't � /4
3d 3Лр3d4
d2

(з)
Алгоритм
итерационного
расчета очевиден: задаемся старто
вым
значением
Лр; подставляем его в третье слагаемое в правой
части,
получаем новое значение Лр ' и сравниваем его со старто
вым.
В случае неприемлемого расхождения повторяем расчет с
новым исходным значением = Лр' до разумного совпадения.
Лр

=

_

-

Лр
Заметим , что д11 я больш и нства практи ч еских случаев вел и ч ина Лр весьм а
велика и роль п оследнего слагаемого мал а ; поэтому целесообразно принять
стартовое значен ие Лр -+ ао , т.е . начинать расчет Лр , пренебрегая последним
слагаемым .

При необходимости
решения задачи
проектирования
с опре
делением
диаметра
трубопровода
решение
также
ведется
чис
ленными методами.
2.5.3. Пластичное течение псевдомастичиых
и дилатаитиых жидкостей

Закономерности
движения
псевдопластичных
изначений
дилатантныхи
жидкостей
будем
изучать
для
области
умеренных
/d wл/dn/, когда течение является пластичным. Для этих жид
костей
не существует
предела
текучести,
поэтому
анализсделано
движев
ния
ведется
для
всего
сечения
в
целом,
как
это
было
случае
ламинарного
движения ньютоновских жидкостей.
Чтобы
установить
подставим
в (2 .18)по
значение
по
(
.
4
7),
имея
в
виду,
что
нормаль
направлена
2
радиусу r, и заменяя частные производные обыкновенными:
(и)
k(- d;,л) 1 1 �� r .
Разделяемотпеременные
и интегрируем
при постоянных k и т
вприлипания)
пределах
r =
(здесь
= О соответственно концепции
значения скорости wл на текущем
радиусе до текущего
",
f ct w ( лр ) 1 1 1 'f ,1'md r .
2 kl
Отсюда
+I
I
•т

распределение скоростей,

•т

=

R

r:

.l

о

w =
л

( 2kl ) 1
Лр

=

/

-

т

Wл

( - ]
R

m+
___!!!____ R т
т+1

m

r т

.

(2.52)

1 99

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 2. 27.

''R
ИJ,Л<''·'· ----

( др )._1_ _!!!_

Оче видно, что п р и r = О ско

рость п рин и мает
зн ачен и е :

т

�w m"

m+l

Rm

2 kl
т+1
В обобщен ных переменных:

W max

обобщенных

1 - ламинарное течение ньюrоиовских
жнлкостей, 2 - пластичное течение псемоплас
тмч н ых ЖИJIКОСТе Й, з - ПЛВСПfЧНОС течение
JIИ11'1Т11 НТНЫХ ЖИJIКОСТСЙ

Q

=

Соnостааnение

профи лей с коростей:

=

( дрR)_1_ _!!!_
т

2k/

· - (�)
R

максимальное

т+1

R.

(2.52а)

nr+ 1
n/

(2. 52б)

Таким обра зом, анализ приводит к параболическому профи
лю с коросте й , однако при т � 1 парабола не является квадра
ти ч н о й . Качественно сопоставление обобщенных профилей
скоросте й представлено на р ис .2 . 2 7 в сравнении с п роф ил ем для
л аминарного течения ньютоновски х жид костей. Вид но , что для
псевдопластич н ых жидкостей (m < 1 , кр и вая Z) профиль скоро
стей является более запол ненным ( выро вн енны м в с м ысл е рас
пределения скоростей по с е че н и ю ) , а для дилатантных (m > 1 ,
кри вая .J) - менее заполненным , нежели для н ьютон о вск их
жидкостей (m = 1 , кр ивая /).
Из выраже н и я ( 2 .52б) следует вывод об оzрани11енной аетомоделъности при

ии н еныотон овских ж идкостей: обобще н н ый профиль скоростей не зави
с ит от величины коэфф и цие н та k, но остается зависящим от показателя степе
ни т. Следовател ь н о, автомодельность течения проявляется для групп жид
костей с оди на ко вы м и значе н ия м и т .

те ч е н

Определение расхода :Жllдкости V ведется уже известным
способом (см . рис.2. 1 О; элементарное сеч ен и е d/ = 27t tdr) с ис
пользованием найденного з н ач е н и я скорости по (2.52):
m+I
m+ I
R
V
f w2ntdr 27t 2k т _!!!_
f R m r - r т r dr =
l т+l о
о
=

=

=
200

2тт

( Лр )J..т
2kl

( др )_1_
т

т +

l

[

R

m+ l

т

R(

R2

Т

m+\ +2

-

R m

;1

т

+

2

J]
.

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Учитывая, что выражение в квадратных скобках равно

R

Зт + I
т

(}

_ _

2

)

m
__

( )

Зт + l

V

=

=

др
2kl

R

Зт + I
т

l /m

m+}
, имеем
2(3m + l)

З m+ l
_т_ nR ---;;;Зт + 1

=

( )

·

R _!_
т_ пR З .
др
т _
2kl
Зт + 1

(2.53)

Соответственно уравнению расхода ( 1 . 1 8) средняя скорость
выразится:
itm
т
.
V
ЛрR
(2.54)
R
w=
7tR 2
3m + 1 ·
2kl
Согласно формуле (2.54) сопротивление потоку Лр w m , т.е.
в сравнении с ламинарным течением ньютоновской жидкости
Лр медленнее возрастает со скоростью в случае псевдопластич
ной жидкости и быстрее - в случае дилатантной.
Представляет интерес соотношение средней и максимальной
скоростей по (2. 54) и (2. 52а) :
=

( )

-

w

(2.55)

т+1
3т + 1

-- = -- ·

wm••

Нетрудно заметить, что при т = 1 (k принимает смысл µ)
выражения (2. 52)-(2. 55) переходят в формулы, полученные в
разд. 2.2.4 для ламинарного течения ньютоновских жидкостей.
Формула (2.53) прямо используется при решении задачи экс
плуатации для определения расхода жидкости в готовом трубо
проводе при известных свойствах :жидкости и параметрах тече
ния . Очевидно, что с помощью этой формулы могут быть реше
ны и различные задачи проектирования - определение Лр или
d = 2R при прочих известных условиях течения.
Выше бьuю указано, что пластичное течение неньютоновских
:жидкостей существует в области умеренных значений -rт и
ldwл/dnl. Верхнюю границу пластичного течения обычно характе
ризуют приведенным числом Рейнольдса Re np• записанным на
основе параметров уравнений сдвига в предположении , что Аг в
уравнениях Дарен - Вейсбаха должен выражаться так же, как в
случае ламинарного течения ньютоновских :жидкостей: Аг =
= 64/Renp· Опуская весьма громоздкие преобразования • , приве
дем готовые выражения для Renp:
w dp
Renp
бингамовская жидкость:
d
=

• См.

(

)

t
Т) l + -о6wТ)

[6J .

20 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

псевдопластичная и дилатантная жидкости: Rеп р =
Очевидно, что при to = О (тогда 11 --+ µ) и т = 1 (тогда k --+ µ)
эти выражения приобретают обычную форму записи числа Re =

=

wdp/µ.

Опыты показали, что течение рассмотренных выше неньюто
новских жидкостей может считаться пластичным для Rеп р <
< -2000; при крайне высоких кажущихся вязкостях этих жид
костей на практике Rеп р не превосходит этой границы в очень
широких диапазонах условий течения. При существенном пре
вышении указанного граничного значения Ren p особенности
пластичного течения вырождаются, и неньютоновские жидкости
по закономерностям движения приближаются к ньютоновским.
2.6. ИСТЕЧЕНИЕ ЖИДКОСТЕЙ И ГАЗОВ

Одним из часто встречающихся практических приложений
уравнения Бернулли является истечение
явление или процесс
вытекания жидкости либо газа из сосуда через отверстие (тонкое
или снабженное насадком, соплом, участком трубопровода) в
окружающее сосуд пространство. Варианты истечения могут
быть различными: в газовую среду из заполненного жидкостью
сосуда через отверстие, находящееся достаточно глубоко под
свободно й поверхностью; через затопленное отверстие; через
преграду,
находящуюся
под
свободной
поверхностью
(водослив) ; при различных расположениях отверстия истечения;
через насадки различной формы; в стационарных и нестацио
нарных условиях; особую проблему составляет истечение газа (в
газовое пространство, в жидкую или сыпучую среду). Ниже бу
дут рассмотрены лишь отдельные случаи истечения • .
-

2.6. 1 . Истечение

жидкости

при посто.11ниом напоре

Будем анализировать истечение жидкости из закрытого сосу
да в стационарных условиях - при поддержании постоянными
в ходе процесса давлений над свободной поверхностью <Ро ) и в
среде, куда происходит истечение (р '), а также уровня жидкости
в сосуде ( h). Заметим, что форма сосуда (в частности , соотно
шение площадей поперечных сечений в его верхней и нижней
частях) роли не играет; исключение составляют крайне редкие
случаи, когда поперечные сечения отверстия /о и сосуда F соиз
меримы.
• Подробно об истечении см. ( 1 , 5 , 25) .

202

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Основная задача анализа в случае истечения при постоянном
напоре состоит в определени и расхода жидкости V в зависимос
пr от условий истечения. Разумеется, возможны постановки и
обратных задач , когда для заданного V необходимо найти те или
иные условия истечения или геометрические характеристики.
Рассмотрим отдельные варианты истечения.
Истечение через отверстие в дне сосуда

Схема истечения показана на рис. 2.28, где обозначены усло
вия процесса и геометрические характеристики. Поскольку в
отверстие жидкость из сосуда поступает не только строго верти
кально, но и из боковых соседствующих зон у дна (см . стрелки
над отверстием), то под действием инерционных сил непосред
ственно за отверстием происходит сжатие (иначе - сужение)
струи до минимальной площади сечения /с, после чего струя
вновь расширяется.
Выберем некоторую горизонтальную плоскость отсчета О - О
и запишем уравнение Бернулли для сечений - совпадающих со
свободной поверхностью жидкости (на расстоянии z1 над плос
костью отсчета) и с наиболее узким сечением струи (на рас
стоянии z2 от этой плоскости) :
2
2
w
р
р' w
(а)
Z 1 + _о_
1 = z2 + - +
+ h
+-

pg 2g

pg 2g

-

"'

причем w 1 и w - скорости жидкости в сечениях F и fc, р плотность жидкости.
П отеря н н ый напор , строго го воря , скшщыается из поте рь при
трении жидкости о стенки сосуда и при прохождении ею от
верстия. Первой составляющей, как правило, можно прене
бречь, так как w1 < < w, поскольку
по уравнению расхода ( 1 . 1 8а) w1 F ="
= wfc; и уж если !с существенно
меньше F, то подавно fc2 << F 2 .
Поэтому крайне м ал скоростной
напор, входящий в уравнение Дар
ен - Вейсбаха (2. 1 7) для движения
жидкости вдоль сосуда; при не
больших для сосуда значениях Vd
и Л г < < 1 эта составляющая hп
пренебрежимо мала. Вторую со
ставляющую учтем в форме hм =
Рис.2. 28. Схема

на п оре

истечения п ри п остоянном

203

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

w 2 , где � - коэффициент местного сопротимения при проте�2g

кании жидкости через отверстие.
Преобразуем выражение (а) , обозначив h' = z1 - z2 - раз
ность уровней, Лр = Ро р' разность дамений и выразив через
w с помощью уравнения расхода ( 1 . 1 8а) скорость w1 = w(fJF) .
Соберем слагаемые с w в одной части равенства:

- 2
h' + Лp = ( l + � - /c ) � ·
2g
pg

F2

(б)

�).

В выражении (б) величиной fc2/F 2 можно пренебречь (она
мала не только в сравнении с 1 , но обычно и с
Кроме того,
расстояние узкого сечения (шейки) струи от сечения отверстия
весьма невелико, поэтому не вполне определенную разность
уровней h ' без заметного ущерба для точности расчета можно
заменить на известную высоту жидкости в сосуде над отверс
тием: h' "" h. . Тогда

�l�� �2�h+ �) .

w=
С целью сокращения записи введем приведенную высоту h* =
= h + Лр/( рg) - она в дополнение к h включает та кж е разность
дамения Ро и противодавления р' (разумеется, при р0 = р ' будет
h* = h) . Множитель

1/�

скорости и обозначается

< 1 называется коэффициентом
Тогда
(в)
w = i.p J2g h * .

<j>.

В случае <р = 1 выражение (в) определяло бы скорость сво
бодного падения в пустоте; коэффициент скорости характеризу
ет замедление течения жидкости вследствие гидрамического
сопротивления в отверстии .
Расход жидкости найдем и з уравнения ( 1 . 1 8) : V = wfc. Такая
запись неудобна из-за неопределенности величины fc. Послед
нюю заменяют: !с = afo , где а
коэффи циент сжатия струи
(подчеркнем, что а
отношение не диаметров струи и от
верстия, а площадей их сечений) . С этой заменой получаем фор
мулу для расхода жидкости при истечении:
(г)
V = fcw = afo w = ai.pfo J2gh* .
Произведение а<р называется коэффи циентом расхода при ис
течении и обозначается символом к р · Тогда
( 2 . 56)
V = Кр /о J2gJi* .

-

204

-

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Коэффициенты <Р и а определяются, как правило, опытным пуrем; для не
которых редких случаев возможна их теоретическая оценка.
Коэффицне�п скорости зависит в основном от толщины стенки и состояния
кромок отверстия . В случае невязких (типа воды и т.п.) жидкостей для тонких
стенок, в которых расположено отверстие, когда коэффициент Е, близок к 0,06,
обычно <Р "' 0,97 ± 0,02, т.е. сравнительно мало отличается от 1 .
Коэффицне�п сжатия струи зависит от формы отверстия (для круглого от
верстия он меньше, чем для щели) и его расположения относительно стенок
сосуда. Вблизи стенок а выше (поскольку со стороны жидкости у этих стенок
действие сил инерци и при формировани и струи ослаблено); по мере удаления
от стенок а достаточно быстро приближается к своему постоян ному значению;
при удалении от стенок на расстояние трех диаметров отверстия и дальше влияния стенок уже не чувствуется. Коэффициент а также несколько возраста
ет с увеличением напора.
Более всего а зависит от толшины стенки , в которой расположено отверс
тие. В случае тонких стенок с острыми кромками при истечении невязких
жидкостей обычно а "' 0,62 + 0,64. Истечение через отверстие в толстой стенке
или через насадок (патрубок, вставленный в отверстие) увеличивает значение а ,
поскол ьку на выходе и з насадка существенно ослаблено действие сил , сужаю
щих струю. Для цилиндрических насадков, длина которых втрое и больше
превышает диаметр, а находится на уровне 0,8 - 0,85; для сужающихся кон и 
ческих - может превысить 0 , 9 , а для "коноидальных", повторяющих форму
струи , естественно, близок к \ .

Истечение в большинстве практических случаев происходит в
турбулентном режиме движения жидкости в отверстии; указан
ные выше значения q> и а приведены для этого случая. При су
щественном повышении вязкости жидкости (т.е. при пониже
нии Re) наблюдается уменьшение q> и увеличение а (скажем,
для толстых стенок и насадков при ламинарном режиме истече
ния, очевидно, а --+ 1 ) .
Особенности истечения через отверстия и насадки разной
формы и численные значения q> , а и к р для различных конкрет
ных случаев приведены в литературе • .
Истечение через отверстие в боковой стенке

При небольших размерах отверстия и достаточно большой
глубине его погружения под свободную поверхность функцио
н ирование отверстия в боковой стенке и расчет истечения прак
тически совпадают с приведенными выше для отверстия в дне
сосуда (небольшие различия возможны за счет численных зна
чений q> и а). В случае отверстий достаточно большой протя

женности в вертикальном направлении, расположенных в боковой
стенке, различие может стать существенным.

Будем рассматривать истечение из крупного отверстия про
извольной (но известной) формы в боковой стенке сосуда
(рис.2.29) . Принципиальное отличие от отверстия в дне сосуда
• См . ( 1 2, 25) .

205

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

v

Рис.2.29. Истечение жидкости при
постоянном напоре через крупное
отверстие в боковой стенке сосуда

р'

состоит в том , что здесь
различные точки по высоте
отверстия находятся под
разным напором из-за раз
ной глубины погружения
этих точек. Иначе говоря ,
движущая сила истечения
h* = h + Лр/(рg) будет пе-

ременной по высоте от
верстия вследствие изменения геометрического напора h от h1

до h 2 . Совершенно очевидно, что в разных сечениях по высоте
отверстия скорость истечения различна: из более верхних уров
ней струи жидкости выходят с мень ш ей скоростью, нежели из
нижних (на рисунке это отражено различной длиной стрелок) .
Расчет на основе некоторой средней глубины погружения
центра отверстия дает приближенные результаты (к тому же не
всегда ясно, где поместить " центр " отверстия); правда, в некото
рых случаях такое приближение вполне приемлемо.
С целью более строгого подхода к анализу вьщелим в от
верстии на текущей глубине h элементарное сечение высотой
dh; ширина отверстия х задана в виде функции х = x(h) в преде
лах от h 1 до h 2 . Элементарный расход жидкости d V через беско
нечно малое сечение dfo = xdh запи ш ем в манере полученной
ранее формулы (2.56):
(д)
d V = K p (Xdh) �2gh • ,

где h • = v ar, поскольку h =v ar.

Интегрируя (д), найдем полный расход:
,"
V=

к p fii J x#dh ·
11,

(2.57)

Конкретное выражение для V определяется формой от
верстия, т.е. конкретным видом зависимости х от h. Для просто
го случая прямоугольного отверстия постоянной ш ирины х =
= Ь = const, величина Ь выносится за знак интеграла, и после
дующее интегрирование затруднений не вызывает. В более
сложных случаях приходится выражать зависимость х = x(h),
она может оказаться непростой ; в этих случаях иногда возника
ют технические затруднения при аналитическом выражении
интеграла , и приходится прибегать к численным методам .
206

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

П роведенный анал из лрактически актуален только для вес"ма крупнwх от
вер стий достаточно большой вертикальной лротяженности (h2 - h 1 ) , соизмери 
мой с величинами налоров h 1 * , h2 * . В этом случае точное решение (2.57) мо
жет отличаться (хотя обычно и не очень значительно) от лриближенного, вы
лолненного ло формуле (2.56) с лодстановкой в нее некоей средней глубины
логружения центра отверстия hcp· Для мелких отверстий , раслоложен н ых лод
свободной ловерхностью на достаточной глубине, без сколько-нибудь суще
ственной логрешности можно лольэоваться более лростым соотношением
(2.56). Возможность ислользования этого соотношения вместо более строгого и
точного (2.57) олределяется заданной точностью технологического расчета. Так,
для лрямоугольного отверстия лри р0 = р' критерием возможности ислольэова
ния лростой формулы (2. 56) является отношение � . глубины логружения
+
центра отверстия hcp
(h1
h 2 )1 2 к высоте отверстия (h 2 - h 1 ) . При этом
лриближен ное значение V лолучается больше точно рассчитанного. Если от
верстие начинается лрямо от свободной ловерхности (тогда f, • 2), то логре ш 
ность расчета составит 6, 1 % , но уж е л р и � . = 1 (глуби на hcp равна высоте от
верстия) логрешность снижается до 1 , 1 % - в этом случае отверстие можно
считать малым (мелким) и вести расчет ло формуле (2.56) с лодстановкой в качестве
h веJD1ЧИНЫ hcp·
=

=

2 . 6 . 2 . Истечение жидкости при переменном напоре

Анализируется истечение жидкости из сосуда при изменяю
щихся во времени характеристиках процесса. В общем случае
здесь возможно изменение уровня жидкости в сосуде h и давле
н и й - над ее свободной поверхностью р0 и в среде , куда проис
ходит истечение, р '. Ограничимся рассмотрением истечения при
изменении h, практически наиболее и нтересного для хи м и 
ческой технологи и . И сследуем полное ил и частичное опорож
нение сосуда, полагая значения р0 и р ' неизменными в ходе ис
течения.
Основная задача - в определении времени истечения из сосу
да известных размеров и конфигурации при заданн ых условиях
процесса. Разумеется , возможн ы иные постановки задач и , когда
при заданном времени необходимо определить те или иные усло
вия истечения (реже - геометрические характеристики сосуда) .
Схема истечения при переменном напоре показана на рис.
2.30. И з сосуда произвольной (но известной) формы через от
верстие площадью fo вытекает жидкость, причем коэффициент
расхода равен к р· Давления р0 и р' поддерживаются постоянны
м и . Начальн ый уровен ь жидкости в сосуде обозначен hн , конеч
н ы й - hк (в частном случае полного опорожнения - hк = О). В
ходе истечения уровень жидкости изменяется ; обозначим пере
менный уровень жидкости над отверстием истечения, отсчиты
ваемый от плоскости отверстия, z, он является составляющей
напора ( и грает ту же роль, что и постоян ная величина h в слу
чае истечения при постоянном напоре ) .

207

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис.2.30. Схема истечения жидкости при
переменном напоре

В основу анализа положим фор
мулу (2. 56) . Однако в рассматри
ваемом случае эта формула при
годна лишь для описания мгновен
ной ситуации: мгновенного расхода
Vм rн при текущем значении дви
жущей силы (напора) <:* = z +
+ Лр/(рg) , где z = var. При этом
мгновенный расход можно выра
зить как об'Ьем жидкости , выте
кающей в единицу времени : Vм rн = dV/dt. Тогда
- F

Vм rн

=

dV
dt

-

=

�
K p /o "J 2 g.� ,

(е)

откуда элементарное количество жидкости , вытекающей из от
верстия за время dt (Уход), составит
(ж)
dV = к р /о �2g<:* dt.

Накопление жидкости в сосуде (это рассматриваемый про
странственный контур) за dt равно Fdz, где F
текущее попе
речное сечение сосуда на высоте z (текущая площадь зеркала
свободной поверхности ) . В случае сосуда с вертикальными
стенками F = const; в общем случае F = F(z) , причем зависи
мость эта задана геометрическими соотношениями. Используя
теперь ОБС ( 1 . 8) и учитывая, что в ходе истечения Приход жид
кости отсутствует (как и Источники и Стоки внутри контура сосуда) , запишем для времени dt материальный баланс по объе
мам жидкости , полагая ее несжимаемой :
(з)
Пр - Ух = Нак или О к р /о �2gz* dt = Fdz.
Разделяя переменные и интегрируя от О до t и от hн до hк ,
получим (принимая к р = const) связь времени истечения t с
конечным уровнем жидкости в сосуде h к :
hк F
1
t
dz ·
=
(2.58)
J
-

-

-'

к pfo fii

..Гz* '

-

hн

можно, конечно, избавиться от знака " минус " , поменяв местами
пределы интегрирования.

Заметим , что по мере истечения при переменном (падающем!) напоре
уменьшается во времени скорость движения жидкости; поэтому должно прояв
ляться действие сил инерции - они не учтены в уравнении Бернулли , на кото
ром базируется выражение ( 2 . 56). лежащее в основе анализа. Однако оценки
показывают, что ускорение этой силы во всех практически интересных случаях
на 3-4 порядка меньше ускорения силы тяжести (свободного падения ) ; поэто 
му действием сил и нерции вполне можно пренебречь.

208

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

В случае сосуда постоянного поперечного сечения при ис
пользовании ( 2 . 5 8 ) F выносится за знак интеграла, и после
дующее интегрирование затруднений не вызывает. В частности,
для простей шего случая F = const и li к = О, обознач Ив hн = h, при
Ро = р ' (так что t- = z) име е м:
2Fh
F о dz 2 Fh 112
t = ··

н

н

к p/o ..fii hн ..fi к p/o ..fii к p/o ..fiih н
J -=

=

В случае F = var необходимо предварительно выразить F в
виде функци и от z, а затем провести интегрирование · . Связь
R.z) может оказаться достаточно сложной; тогда при невозмож
ности аналитического выражения интеграла придется прибегать
к численным методам.

Не исключены ситуащ1и, когда в условиях Ро < р при некотором значении
окажется t" = О , что соответствует tкр = (р ' - Po )/(pg) . Это означает,
что при достиже11ии некоторого уровня � истечение жидкости из сосуда пре
краппся, так как геометрический напор будет скомпенсирован отр1щательной
разностью пьезометрических. В форме математической связи эдесь можно
записать: hк 2: lк р ·
t

•

tкр > О

Продемонстрированные подходы позволяют решать разнооб
разные задач и: определение необходимой формы сосуда или
величины отверстия для обеспечен ия заданного времени исте
чения т; выравнивание уровней в двух соединенных сосудах при
перетекании жидкости через отверстие в разделяющей их стен
ке; истечен11е через два отверстия , находящиеся на разных
уровнях, и т.п. В ряде случаев при этом можно прямо восполь
зоваться формулой (2.58); в других случаях приходится прово
дить полный анализ, начиная с выражений типа (е) , (Ж) , (з) и
далее - по приведенной выше канве.
2.6.3. Об истечении газов

Задача анализа - определение массового расхода газа G при
стационарном его истечении через отверстие, сопло или насадок
из сосуда с повышен ным давлением в газовую среду с более
низким.
Истечение газа можно рассматривать как адиабатный про
цесс, поскольку на коротком участке истечения потерями теп
лоты можно пренебречь. Для определения скорости выте
каю щего газа зап ишем уравнение энергетического баланса для
1 кг газа на этом участке, относя индекс " 1 " к началу участка
(сопла, патрубка) , а индекс "2" - к его концу. В отсутствие меха
нической работы в уравне н ие баланса воЙдут энтальпии i и кине•

Некоторые •1аст н ы с задачи

п р и ведены в [6, 22, 25

11

др. j .

209

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

тические энергии потоков w 2/2. Согласно ОБС в форме ( l .8в):

-

2 =0·
(и)
- i2 - 2
2
Заметим : как правило, тепловые балансы не учитывают удельной кинети
ческой энергии потоков Wl/2 (см . главы 6, 7), поскольку она мала в сравнении
с энтальпиями i и их перепадом i1 - i2 . Кинетическая энергия начинает вно
сить заметный вклад в энергетический баланс, коrда значения w исчисляются
сотнями метров в секунду . Именно такая ситуация возникает при истечении
газов , когда w2 становится соизмеримой со скоростью звука (в некоторых слу
чаях и превосходит ее) .
i1 +

2
w1

w

2

Из баланса (и) следует, что за счет падения энтальпии от i1
до i2 происходит увеличение кинетической энергии. Найдем
скорость газа на выходе из сопла:
W2 =

�2 ( i1

- i2 )

+

w:

.

Чаще всего в сосуде перед соплом скорость w1 < <

w2 ;

(2.5 9)

тогда

(2 . 59а)

Это уравнение является базовым для анализа различных слу
чаев истечения газов• . Здесь кратко рассмотрено лишь истечение
идеального rаза из короткого сопла, когда трением на его длине
можно пренебречь.
Поскольку энтальпия в рассматриваемом случае может быть
выражена как i = ср Т, то согласно (2.59а)
W2 =

�2сР(Т.

-

7; ) =

( i.) .

2сР т. 1 -

�-----

(к)

Воспользуемся далее уравнениями идеального газа p1v 1 =
= R T2 и адиабатного сжатия - расширения:
(л)
отсюда очевидно:
�
(2.60)
= Pi
т;- = 1 1 Pi

=

R T1 , P2V2

l / k (Р2) k
Р
Т2 P2V2
Р2
1
=
P V p� / k
. cp/cv -

Напомним: R
индивидуальная массовая (на 1 кг) газовая
постоянная, выражаемая через универсальную Ry: R = Ry /М;
М
показатель адиабаты, где ср
молярная масса; k =
и Cv
удельные массовые теплоемкости газа при постоянных
давлении и объеме; заметим: R = сР Cv .

--

• Детальное рассмотрение таких случаев приводится в курсах теплотехники
(3, 2 3 ) ; см. также (22) .

210

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Подставив в (к) найденное отношение Ту'Т1 и значение аб
солютной температуры Т1 = p1v iJR, имеем

[ ]

k-1
k
2
P_
= 2 ер P1 V 1 l - с р - Cv
Р1

- [ ]

k-1
k
2
P
k- V l - -_
2P1 1
k 1
Pl

=

(2.6 1 )

Массовый расход G ( в разд. 2.3.5 было показано, что для га
зов его использование предпочтительнее, нежели объемного)
через сопло сечением fo найдем из уравнения расхода ( 1 . 1 7); при
этом используем связь удельного объема и плотности (v 2 =
= 1/р 2) :
'G =

=

W2 fo
P 2 W"lfo = -- = fo
V2

После замены по (л) v 2
Ry Тi/<P 1 М) получим
G

=

fo

= /о

k

p, v2 ,
2 -- -k - l v2

[ -(-) k-1 ]
1

Р2

р1

Т

·

v 1 (p1/p2) 1 /k и v 1 = R T1/P 1

=

[

]
[(!!1._)k - ( ) k+I ]

=

!!J... (f!1._) f 1 -(f!1._) k;I =

�-----

k
2k - l V1
2

2_
k_ Р 1 М
k - l Ry T1

Р1

Р1

!!1._ k .
Р1

2

Р1

(2.62)

Анализ показывает, что расчет G по (2.62) правомерен при
сравнительно небольшом падении давления от р 1 до Р2 · Дей
ствительно, согласно (2.62) расход G зависит от относительного
снижения давления (3 = ру'р1 , причем эта зависимость носит
экстремальный характер. Проанализируем G на экстремум, взяв
производную по р от последнего выражения в квадратных скоб
ках и приравняв ее нулю:

(

д
�
pk
др

_

_

�

р k

)

=

2_,

2 Pk
k

_

-1
k 1 р�
k
-2.._
= о.
k

21 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Отсюда получается значение р в точке экстремума, называемое критическим :

�.,

·

(�:J.,�C� У" ·

(м)

По (м) можно рассчитать значения (р2fр 1 ) кр для газов разной
атомности :
- одноатомные газы
k ::::: 5/3, Ркr/Р1 ::::: 0,49;
- двухатомные газы
k ::::: 7/5, Ркr/Р 1 ::::: 0, 5 3;
- трех- и многоатомные газы
k ::::: 9/7 , Pкr/Pi ::::: 0 ,55 .
На практике нередко принимают "скопом": Ркr/Р1 0,5.
Повторное дифференцирование с установлением знака про
изводной в точке экстремума показывает, что речь идет о мак
симумах скорости wкр и расхода Gкр при рур 1 = Pкr/P I · Подставив
значение Ркр в (2.6 1 ) , найдем значение критической скорости
истечения газа:

:::::

·

Wкр =

2 -k- p v
k-1 1 1

[1-(-2-)k�lk� ] =
k+I

=

/2R Т. -k_ .
k
2p, v _
1 1 k + I 'J
1 k+I

(н)

В технической термодинамике показано, что wкр есть ско
рость звука в газовой среде.
По уже известной канве, подставив v2кр = v 1 (pкr/Pi ) l fk, получим

( )

2
/о w кр =
k _ P1 V 1 Р кр k
=
_
Gкр
/о 2 +
k 1 v�
Р1
v2 кр

Окончательно:

( )

k 2
2_ .f!.J_ _
2_ � "
= / k.
о k JV k+J
1

+

2)
рR/� Fi k(k+1
м

k+I
k-1

(2.63)

Таким образом, пока давление р2 не падает ниже критическо
го значения , определяемого формулой (м), массовый расход газа
G рассчитыва�тся по формуле (2.62) . При этом уменьшению Р2
или увеличению р 1 (в общем - уменьшению р = рур1 ) отвечает
возрастание G. Однако такое влияние Р2, р 1 , Р наблюдается
лишь до Ркр; при уменьшении, например, давления Р2 ниже Рк р

212

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

дал ьнейшего возрастания G2 не происходит, расход остается на
максимальном уровне Gк р • определяемом формулой (2. 6 3).
Причина рассматри ваемого явления связана с тем , что волна
давления распространяется в среде со скоростью звука. П ока
скорость струи газа w2 меньше скорости звука ( wкр ) , давление сре 
ды р2 передается против движения струи и устанавли вается в
устье сопла; тогда движущая сила истечения составляет р1 - Р2 ·
При скоростях струи выше скорости звука давление среды р2 не
смогло бы установиться в устье сопла: скорость передач и давле
н ия Р 2 из среды к устью сопла была бы ниже скорости движения
самой струи. Поэтому давление в устье сопла Р2 не может упасть
н иже Ркр • так что движущая сила будет оставаться равной р1 - Ркр
независимо от конкретного значения Р2, если оно ниже Ркр · Это
означает, что и скорость газа не превысит скорости звука Wкр·
П одробно эти вопросы рассмотрен ы в курсах технической
термодинамики ; там же анализируются возможности преодоле
н ия рассмотренного кризиса истечен ия.
2 . 7 . ЭЛЕМЕНТЫ ГИДРАВЛИ КИ ДИСПЕРСНЫХ СИСТЕМ

К дисперсным относят системы, содержащие дискретн ые об
разования, распределенные в сплошной среде . Дискретн ые об
разования , называемые дисперсной фазой , представляют собой
твердые зерна, частицы, не изменяющие своей формы и размера
при протекани и технологического процесса, либо капли или
газовые пузыр и , способные изменять свои размеры (дис
п ергировать, коалесцировать) и деформироваться в ходе процес
са. В качестве сплошной среды (ее еще называют дисперсионной
средой или фазой) , отделя ющей дискретные образования одно от
другого, используются жидкости или газы.
И нтерес химической технологии к дисперсным системам об
условлен высокой поверхностью контакта дисперсной и сплош
ной фаз: все контактн ые процессы благодаря развитой межфаз
ной поверхности протекают здесь с большой и нтенсивностью. В
задачу технологического расчета входит определение интенсив
ности контакта фаз - вообще и для кон кретного технологиче
ского процесса; общая задача гидр а влического расчета состоит в
установлении закономерностей переноса и мпульса при движе
нии спл ошной среды относительно элементов дискретной
фазы - это внешняя ( и ногда смешанная ) задача гидравлики.
При мерами дисперсн ых систем могут служить различ ные
суспензии (дисперсия твердых части ц в жидкости) , эмульсии
(жидкости в жидкости ) , барботажные системы и пены (газа в
жидкости ) и др.

213

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Наиболее простыми являются дисперсные системы с твердой
дискретной фазой - из-за постоянства размеров и отсуrствия
движения вещества внуrри самого зерна (тогда как в капле или
пузыре может происходить внуrренняя циркуляция) . Ниже до
статочно детально будуr рассмотрены дисперсные системы
именно с твердой фазой ; в определенном смысле они часто слу
жат упрощенной моделью для систем с жидкостями и с газовы
ми пузырями (некоторые аспекты гидравлики этих систем в
учебнике лишь затронуrы).
2.7. 1 . Общая характеристика дисперсных систем с твердой фазой

С точки зрения характера перемещения дисперсной системы
в технологическом аппарате различают следующие основные
разновидности: неподвижный слой (НС) , псевдоожиженный
слой (ПС) , движущийся слой (ДС) и транспортные системы
( ТС) . Эти системы схематически показаны на рис. 2. 3 1 .
В неподвижном слое зерна дисперсной фазы неподвижны от
носительно друг друга и стенок аппарата; через слой проходит
поток жидкости или газа (снизу - с ограниченной скоростью
или сверху). Е сли такой поток подается снизу с достаточно вы
сокой скоростью, то под его воздействием может нарушиться
контакт между зернами (частицами) , они получают возможность
перемещаться относительно друг друга и стенок аппарата возникает псевдоожиженный слой с хаотическим движением
твердых частиц и их агрегатов. Существуют системы, в которых
зерна движутся относительно стенок аппарата (под действием
собственного веса) практически без нарушения контакта друг с
другом (т.е . без взаимного перемещения) - это движущийся
слой. Наконец, часто используется перемещение дисперсной
системы (сплошной и дисперсной фаз) в канале, аппарате - это
транспортные системы (конечно, и де можно отнести к таким
системам) ; с точки зрения гидравлики анализ движения те,
строго говоря , следует относить уже не к внешней, а к смешан
ной задаче.
Основные проблемы гидравлики дисперсных систем состоят
в определении гидравлического сопротивления (при движении
сплошной среды через дисперсную фазу или дисперсной си
стемы в целом по каналу, аппарату), в установлении гидродина
мических границ между системами (скажем , диапазонов скоро
стей, в которых существует каждая из них) и выявлении некото
рых особенностей в поведении отдельных систем.
Анализу конкретных систем предпошлем рассмотрение их
общих характ ер истик.
Дисперсные системы занимают объем У, состоящий из объе
мов твердых зерен (частиц) Ут и свободного объема просветов
между ними Уев : У = Ут + Уев· Объемная доля про_светов Уев/У =
214

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис.2.31. Основные дисперсные
системы с твердой фазой :
а - неподвижный слой, б -

нс

псевдоожиженный слой, о - движу
щи йся слой , г - транспортная
систе ма

- Е называется пороз
ностью (не пугать с по
ристостью,
характери
зующей
долю
пустот
внутри твердых частиц).
Очевидно, доля твердой

пс

�

.
..." ..... .
.
:1 1 1 1:
. . ..
.... .. . . ..
..." .. .. .
.
•

а

тм

t

де

L.8..1.

б

фазы (ее объемная концентрация) составляет

в

.J =

У

г

У - Уев
у

=

l

- е. Условимся порозность и другие характеристики неподвиж
ного слоя вьщелять индексом "О": для НС Е = е0 . При наиболее
плотной регулярной укладке сферических зерен (по тетраэдру)
е0 = 0,259; при наиболее рыхлой ( кубической, без неупорядо
ченных полостей) - Ео = 0,476; в случае часто используемых
частиц округлой формы Ео обычно близка к 0,4.
Для определения массовой концентрации твердой фазы р не
обходимо знать плотность зерен Рт = mт/Vт· Тогда, учитывая,
что Ут = V/( l - Е), получаем
р =

т
1 =
-

У

т

V, / ( l

т

-

Е)

= РтО

-

Е).

(а)

Массовая концентрация твердой фазы в НС (насыпная плот
ность) составит
(б)
Р о = Рт0 - EQ).

Важной характеристикой дисперсной системы является раз
мер ее элементов (зерен, частиц). Здесь различают системы мо
нодасперсные (все частицы имеют одинаковые размеры, строго
говоря - и форму) и полидисперсные, когда наблюдается рас
пределение частиц по размерам - в небольших диапазонах раз
меров (узкие фракции) и со значительной разницей в размерах
зерен (широкие фракции) . Обычно фракцию считают узкой, если
отношение максимального размера частиц к минимальному не
превышает 2.
Если речь идет о сферических частицах, то для монодисперс
ной системы размер элементов однозначно характеризуется их
диаметром d. Для узких фракций пользуются усредненным раз
мером, причем вследствие узости фракции любые способы
215

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

усреднения дают близкие результаты. Принято использовать
среднегеометрический размер dcp = Jd 1 d2 , где d1 и d2 - наи

меньший и наибольший размеры частиц в узкой фракции . Ши
рокую фракцию рассматривают как состоящую из N узких
фракций , каждая ( i-я) из которых характеризуется своим средним размером

di =

�

i
d;m " d ;max .

фракции Х; известна (разумеется,

Пусть массовая доля каждой

L Х; =

1 ) ; тогда в гидродина-

мических задачах средний размер широкой фракции принято
определять как среднегармоническую величину:

_d1 = f d;
i=I

Х

; .

(в)

Очень часто распределение частиц по размерам (а также ка
пель, пузырей и других элементов в дисперсных системах), если
не предпринято специальных мер для их выравниван ия , следует
нормально-логарифмическому закону, что отвечает некоторым
модельным представлениям.
Заметим : усреднение размеров узких фракци й обычно не приводит к сколь 
ко-нибудь заметной погрешности в расчетах. Усреднение размеров широкой
фракци и нередко я вля ется весьма грубым расчетным приемом; для ряда техно 
логических процессов оно приводит к потере точности , так что в целях повы
шения строгости анализа расчет следует вести для отдельных узких фракци й , а
затем объединять полученные результаты.

Для характеристики зерен несферической формы указания
на их размеры недостаточно, да и сам размер d становится не
вполне определенным. Здесь вводят понятие об эквивалентном
диаметре зерен как диаметре сферы, равновеликой (по объему
частицы Уч) реальному зерну: de = V6 Уч/тt . Отклонение от
сферичности характеризуется фактором формы Ф .• =

�Sш / Sч

:S

l,

где Sч и Sw - поверхности зерна и равновеликой ему сферы.
В гидродинамических расчетах удобно пользоваться расчет
ной скоростью, определяемой из уравнения расхода ( 1 . 1 8 ) : w =
= V/f, где f - попереч ное сечение пустого ( без твердо го материа
ла) аппарата. Истинная скорость Wи будет выше, поскольку часть
сечения аппарата перекрыта твердыми частицами, так что для
прохода газа (жидкости) остается живое сечение !св < f, таким
образом , Wи > w. Реальная интенсивность технологического
процесса определяется, конечно же, величиной Wи , но скорость
w удобнее в практических расчетах.
.·

216

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

2 . 7 . 2 . Неподвижный слой

Размеры используемых в этой системе дискретных элементов
колеблются в широких пределах: от нескольких сантиметров до
долей миллиметра . П оток сплошной среды может подаваться в
НС как сверху, так и снизу; на практике встречаются Н С с
и н ы м направлением потока (через кольцевой НС и др . ) .
Основная гидродинамическая задача состоит в определении
гидра влического сопрот ивления при движении потока сплошной
среды через НС.
Анал из закономерностей течения среды ( газа, жидкости ) че
рез пол идисперсный НС, содержащий к тому же части цы раз
личной формы, - чрезвычайно сложная задача. Поэтому в це
лях ее упрощения будем рассматривать (рис. 2.32, а) идеальный
слой , составленный из одинаковых шарообразных зерен диа
метром d. П усть этот слой высотой Н0, порозностью 1:0 лежит
на поддерживающей решетке в аппарате поперечного сечения f
Однако и такой более простой сл учай весьма труден для анал и 
з а : поток, омывающий сферические зерна, движется в искрив
ленных каналах с переменным попереч ным сечением, струи газа
( ил и жидкости) постоя нно пересекаются , сл иваются , расходятся .
Сопротивление таких систем мы рассчитывать не умеем , но зато
знакомы с подходами к расчету течения в прямых каналах. П о
этому перейдем от идеал ьного слоя к некоему модел ьному фик
тивному - того же гидравлического сопротивления, сводя внеш
нюю задачу гидродинамики к внутренней: будем сч итать, что
поток (например, газа) движется по прямым каналам (их длина
/, естественно, больше высоты слоя Н0, поскольку мы мысленно
"выпрямили" искривленные канал ы ) ; диаметр каналов обозна
чим De (чтобы не смешивать с экви валентн ым диаметром час
тиц de; в рассматриваемом случае de = d) .

Рис.2. 32. К

расч ету rидраюичес коrо со п роти вл е ния н е п од вижного сл оя:

идеал ьн ы й слой . б - фикти вн ы й слой ;
J - корп ус а п парата , 2 - газорас пределител ьная ре ш етка , З
зернисты й слой
п

-

-

неподвижн ы й

217

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

На модель фиктивного слоя должны быть наложены оrраниче
ния, чтобы его гидравлическое сопротивление в самом деле бьuю
равно искомому для идеального слоя. Эrи оrраничения сформули
руем на основе уравнения Дарси - Вейсбаха в форме (2. l 7a) :

Лр =

Аг _/_
D,

w

�

2

р.

( 2 . 1 7а)

Элементы этого уравнения для фиктивного и идеального
слоев должны совпадать:
1 ) дли н ы путей газа в фиктивном и идеальном слоях должны
быть оди наковым и ;
2) свободные объем ы Уев в фиктивном и идеал ьном слоях
должны быть оди наковым и , тогда при оди наковых расчетных
скоростях w будут равными и истинные скорости wи ;
3) диаметры каналов в фиктивном слое должны соответство
вать эквивалентн ы м диаметрам De в идеал ьном; это важно и в
аспекте совпадения чисел Rе и = wиDep/µ , а значит и коэффици
ентов гидравлического сопротивления Аг в фиктивном и идеал ь
ном слоях;
4) должны быть одинаковы поверхность трения потока о
сте н ки каналов FФ в фиктивном слое и поверхность твердых
частиц Fид в идеал ьном.
При соблюдении этих условий расчет сопротивления идеал ь
ного слоя можно вести по формулам для фиктивного слоя .
В практических расчетах неудобно пол ьзоваться величинами,
входящими в уравнение Дарси - Вейсбаха для фикти вного
слоя , п оскольку в качестве исходных задаются характеристики
идеального слоя: его высота Н0 , расчетная скорость w, диаметр
зерен d. П оэтому целесообразно заменить через эти характери
сти ки вел и ч и н ы , входящие в ( 2 . 1 7а): /, Wи и De ( проводя замену,
будем снабжать характеристики фиктивного слоя и ндексом "ф'' ,
идеального - и ндексом " ид").
Замену / на Но произведем с помощью коэ ффициента изви 
листости С, > 1 , представля ющего собой отношение дл и н ы пути
газа в слое к высоте последнего:
(г)
1 = С,Но.
П о существу С, = l/cosq> , где q> - средний угол между верти 
калью и направлением потока в идеальном слое при обтекан ии
части ц (по порядку величин он близок к 45° , так что (, ,,,, Ji ).
Истинную скорость заменим на расчетную, исходя из урав
нения расхода: V = wf = Wи /св, где /св - среднее живое сечение
потока, т.е. не занятое твердыми частицами . Отсюда с учетом
сформулирован ных выше оrран ичений
С,
(д)
_l_ Н о С, = w У ид
w = w _l_
fсв /
( У св ) ф
/св
и
=

218

w

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Заметим: в литературе нередк<' представляют истинную с к орость в виде w/Eo
(или же w/E в друтих дисперсных системах); на самом деле - это вертикальная
составляющая истинной скорости Wи" (она также используется
анализа про
цессов в ряде случаев), а истинная с к орость определяется формулой (д).
дrIЯ

Эквивалентн ы й диаметр канала был введен п р и пол учении
уравнения Дарси - Вейсбаха; согласно выражению (ж) из разд.
2 . 2 . 2 , De = 4.fсв /П , где П - смоченный периметр. П реобразуем
эту запись De:
4 ( Усв ) ид
4 /св / _ 4 ( У св ) ф - ---(е)
D e - -- - П /
FФ
Fид
_

_

Для идеал ь ного слоя (Ус в ) ид = fHor.o. Б оковую поверхност ь
зерен в нем найдем и з следующих соображен и й . Поверхност ь
одной части цы равна тт d2 ; число части ц в един и це объема (т.е . в
1 м 3 ) Nуд получ и м делением их объема в 1 м З ( 1 - r.0) на объе м
одной частицы ттd3/6: Nуд = ( 1 - r.0)/(ттd3/6 ) . Тогда удел ьная по
верхность частиц в слое составит (указано в С И ) :

Fуд

- ттd

_

2

Nуд _

ттd 2 (1 - r. 0 ) = 6 (1 - r. 0 )
(м 2/м З ) .
d
rr.d 3/6

- 6( 1 - r.o) fH0 .

( 2 . 64)

П олная боковая поверхность зерен в идеал ьном слое опреде -

-

л ится как Fид - FудУид НИЯ

(Ус в ) ид

И

d

Fид в (е ) , пол учим
De

:=:

4 fHo E od
6 (1 - r. 0 ) /H 0

=

П одставив теперь значе-

3. d � .
3 1 - Е0

(ж )

Гидравл ическое сопротивление Н С будем рассч иты вать п о
формуле Дарси - Вейсбаха ( 2 . 1 7а) отдельно для ламинарного и
развитого (авто модел ь ного) турбул е нтн ого режимов теч е н ия
газа (жидкости ) в н е п одвижном слое , подставляя в эту фор
мулу н а йде н н ы е выше значения /, Wи и De , в ыраже н н ы е через
Н0, w, d и r. 0 .
Подчеркнем: режимы течения в условиях внешней задачи гид
роди намики характери зуются ч ислами Рейнольдса в написан ии
Re = wdp/µ = wd/v, базирующимися на расчетн ой скорости w и
диаметре частиц d. Для фиктивного слоя при этом остается
прежнее написание R е и = wиDe p/µ .
Л аминарны й режи м течения газа (жидкости ) в НС. Здесь Л г =
64µ
64

Re 11

=

w " D" p

219

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Тогда

Численная теоретическая оценка первого множителя в (з)
при � � J2 дает 144. Обработка многочисленных эксперимен
тальных данных разных авторов приводит к числу 1 50. С этим
значением получается:

Лрл

= 1 50

(I

Ео
3
Ео

-

)

2

wµ Но , ил и
2
d

Лрл
Н

=

о

Е
1 50 (I - о
Е3
о

)

2

wµ .

d2

Заметим: как и для всех ламинарных течений, здесь Лр

-

(2.6 5 )
w1 •

Развитой турбулентный режим. Анализ проводится по той же
канве, но при Лг = const:
2
2
3
Л /w р
р 3( 1 Е о )
Л �Н0w
Л г�__· 3 1 3е 0 w p Но .
= г
Лрт = г
= _�
(и)
_
De 2
d
4
Ео
е 2de0 . 2
·

�

б

.

t,,2

·

-

-

Обработка широкого круга экспериментальных данных при
водит к численному значению первого сомножителя в (и), рав
ному 1 , 75. Тогда

ЛРт = 1 ,75 l - 3Е о
Е0

2
w pН
d

0,

ИЛ И

Но

Лрт

=

1 ,75 I

Е

-

E Q w 2 p . (2 . 66)

�

d

Заметим: как и для всех турбулентных автомодельных (по Re)
течений, здесь Лр w2 .
-

При изучении t1нутренних задач гидродинамики (течение в трубах, каналах)
мы отмечали наличие кризиса течения: при определенных значениях числа Re
наблюдается резкое нарушение ламинарного режима. При этом диапазон пере
ходного режима был сравнительно узким: число Re изменялось при переходе от
ламинарного к турбулентному режиму примерно в 4 раза (в этом, кстати, при
чина невысокого интереса исследователей к данному диапазону) . При обтека
нии тел потоком (t1нешняя задача гидродинамики) не наблюдается резкого пере 
хода от ламинарного режима к турбулентному, переход осуществляется плавно
и постепенно. Это связано с образованием турбулентных вихрей за телом и
постепенным (плавным) перемещением области отрыва этих вихрей - от тыль
ных зон тела к лобовым по мере увеличения числа Рейнольдса. Очевидно, что в
этом случае грани цы между режимами будут условными; приближение при
низких Re к ламинарному режиму и при высоких Re
к турбулентному будет
асимптотическим. Иными словами , эти грани цы устанавливаются в известной
мере произвольно - исходя из приемлемой погрешности анализа и расчета. И
диапазон переходного режима получается весьма широким: в зависимости от
-

2 20

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

устанамиваемой погрешности расчета граничные значения чисел Re различа
ются на 2-3 порядка. Поэтому формул (2.65) и (2.66) недостаточно ; переход
ный режим представляет значительный практический интерес - нужны фор
мулы для Лр также и для этого диапазона течения.

Задача определения Лр в НС для переходного режима была
решена чрезвычайно просто - пуrем синтеза общей формулы,
охватывающей все режимы, включая ламинарный и турбулент
ный. Было постулировано: Лр = Лрл + ЛРт, причем Лрл и ЛРт за
писаны в форме (2. 6 5) и (2. 66 ) для гидравлических сопротивле
ний, приходящихся на единицу высоты слоя:
ЛРнс
НО

=

1 50

2

( 1 - & ) wµ + 1 7 1 - &

"э d2
о

"О

'

5 с- 3

"О

о

w2 р .

d

7

(2 . 6 )

Первое слагаемое отражает здесь влияние вязкостных сил
(ламинарная составляющая) , второе - инерционных (турбу
лентная составляющая).
При понижении скорости , как видно из (2.67), уменьшаются
оба слагаемых, но первое - медленнее; при уменьшении диамет
ра частиц растуr оба слагаемых, но первое - быстрее. Таким
образом, при снижении значений w и d, входящих в Re, роль
первого слагаемого возрастает, а второго - падает, доминирую
щими становятся силы вязкости, и из (2. 6 7 ) закономерно полу
чается формула (2 . 6 5 ) для ламинарного режима.
При повышении скорости возрастают оба слагаемых уравне
ния (2. 6 7), но второе - быстрее; при увеличении диаметра час
тиц уменьшаются оба слагаемых, но второе - медленнее. Таким
образом, при увеличении w и d (значит, и числа Re) роль второ
го слагаемого возрастает, вклад первого - становится малым,
доминирующими будуr сил ы инерции , и из (2.67) закономерно
получается формула (2. 66 ) для турбулентного режима.
Для числа Re = wd/v приняты (это обусловлено обычной
точностью инженерных расчетов) следующие граничные значе
ния Re: при Re < 1 течение считается ламинарным, при Re �
3
� 1 ООО - турбулентным. В диапазоне 1 < Re < 1 0 , когда силы
вязкости и инерции сопоставимы, течение считают переходным.
При этом переход от ламинарного режима к турбулентному,
согласно (2. 6 7), происходит плавно: с ростом Re постепенно
повышается вклад второго слагаемого в сравнении с первым · .
В начале 50-х годов формула, структурно совпадающая с (2.67), но с
(массивы обработанных опыт
ных данных не полностью совпадали) была опубликована М.Э. Аэровым с

н ес кол ько иными численными коэффи цие нтам и

Детал ьн ы й анализ течения сплошной среды через неподвижный слой при
веден в (2) .
'

22 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

соавт. Но эта советская работа не была замечена за рубежом. Спустя два года
формулу (2.67) независимо получил американский уч еный С.Эрrан; именно в
этом виде ее используют, называя формулой Эрrана.
Среди других задач гидродинамики неподвижного слоя важ
нейшей является определение предела устойчивости НС, т.е.
скорости потока (если он подается снизу) , при которой его воз
действие на частицы становится столь значительным, что слой
переходит в псевдоожиженное состояние. Эта скорость (ее
иногда называют первой критической) является одновременно
скоростью начала псевдоожижения. Ее удобно определять при
изучении закономерностей псевдоожиженного слоя (разд.2. 7.4. ) .
2. 7 . 3 . Движущийся слой

Использование НС предопределяет проведение процессов в
периодическом режиме по твердому материалу ( ТМ) . Это впол
не устраи вает технологов, когда процесс реализуется без ввода
твердого материала в аппарат и его вывода из аппарата: катали
тические процессы (катализатор иногда может неделями и ме
сяцами работать без замены); ТМ служит инертным контактом
(его не надо заменять) и др. Но при непосредственном участии
ТМ в технологическом процессе часто требуется его замена периодическая (с операциями загрузки и выгрузки ТМ - это
сопровождается непроизводительными затратами времени) или
непрерывная, с постоянным вводом и выводом . Такой системой ,
сходной гидродинамически с НС, является движущийся слой
(ДС) , перемещающийся в аппарате под действием собственного
веса. При этом среда (газ, жидкость) движется противотоком
или прямотоком по отношению к нисходящему потоку твердого
материала. Закономерности ДС рассматривают среди внешних, а
не смешанных задач гидродинамики , поскольку основным здесь
является взаимодействие среды с твердым материалом (большие
поверхности контакта) , а не со стенками аппарата.
На рис. 2 . 3 3 , а показано распределение скоростей твердого
материала и по сечению аппарата - идеальное ( J) с выровнен
ным профилем и реальное (2) , когда скорость у стенки на 1 01 5 % ниже, чем по оси аппарата (замети м: "концепция прилипа
ния" для движущегося ТМ не соблюдается) .
При движении ТМ п о трубе (стояку) , аппарату, при его
"вытекании" из отверстия возможно образование устойчивого
(статического) свода из зерен (рис . 2 . 3 3 , б) - тогда движение ТМ
прекращается . Это происходит п р и отношении диаметров от
верстий и зерен менее 5 . При больших отношениях (крупные
отверстия , мелкие частицы) над отверстием образуется динами
ческий свод, с которого частицы "стекают" вниз; здесь движение
ТМ не прекращается.
222

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

-

Рис.2.33.
а

Движущийся слой:

эп юры скоросте й тве рдого
м атериала - идеал ьная ( / ) и
ре ал ьная ( 1) , б - образо вание
стабильного свода (к я мен ию
завис а н ия) , в - расч етн ая схе ма
расхода твердого м атериала

2�

и

и

Объемный
расход
твердого материала Vт
через отверстие диа
метром do определяется
а
в
6
из следующих сообра
жений. Динамический
свод над круглым отверстием имеет форму, близкую к эллипсо
иду вращения; высота его
зависит от свойств материала и
отношения dr/d. Для конкретных условий
- t:fo. Истечение ТМ
с динамического свода происходит под действием напора hc;
следовательно, по условиям истечения (см. разд. 2.6. 1 )

hc

V,.

'

hc

2
2
7r.d �2ghc .. -f
7r.d �2gd0
-f
··

•

Таким образом , V,. - d02,5; значение коэффициента пропор
циональности устанавливается экспериментально.
Массовый расход ТМ получается с учетом его насыпной
плотности Gт = р0 V,.. В качестве примера приведем расчетную
формулу с эмпирическим числовым коэффициентом (все раз
мерности в С И ) :
Gт

=

�
2 Podo2 • 5 ,

tg · ye

(к)

где Уе - уrол естестаенноrо откоса (угол с горизонтальной плоскостью в основа
нии конуса, получающегося при медленном высыпании ТМ из отверстия на
горизонтальную плоскость; чаще всего Уе .., 25+40 ° ) .

Согласно представленной модели, высота Н движущегося
слоя над выпускным отверстием может влиять на объемный и
массовый расходы только в редко встречающемся и практически
малоинтересном случае Н < ho (согласно другим моделям - и
для несколько больших высот) . В реальных технологических
ситуациях влияние Н на V,. и Gт ощущается весьма слабо.
Гидравлическое сопротивление ДС определяют с помощью
формулы Эргана (2.67), имея в виду ряд обстоятельств.
1. Укладка частиц в ДС более рыхлая, нежели в НС, поэтому по
розность :щесь выше; обычно для округлых частиц :Ео "' 0,45+0,5.
2. Определяющей скоростью в ДС будет относительная ско
рость потока и твердых частиц (ее называют скоростью скольже
ния): сумма их абсолютных скоростей при противотоке (восхо223

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

дящем движении газа или жидкости и нисходящем - твердого
материала) и разность - при прямотоке (нисходящем движении
обеих фаз). Пусть средняя абсолютная скорость движения зерен ,
частиц равна и ; вертикальная составляющая истинной скорости
потока (см. разд. 2.7.2)
wje0. Тогда в формулу Эргана вместо
wfeo следует подставлять wje0 + и в случае противотока и w/to
- и в случае прямотока, ил и
3 . Расчетная высота слоя Йо не равна высоте рабочей зоны
Нр ; здесь необходимо учитывать путь, пройденный потоком в
контакте с ТМ (иначе: число слоев твердых частиц, пересечен
ных потоком при его движении в рабочей зоне) . В случае про
тивотока газ (жидкость) пройдет рабочую зону за время t =
= Hp/( w/eo) ; за это время в рабочую зону поступит дополнительно .
слой ТМ высотой ut , так что общая длина пути контакта
(расчетная для формулы Эргана) составит

-

н -н
о -

(w ±

-

Е0 и}/Е0 .

- н (НрЕ о) - н ( UEo)

p + Ut -

p + U -W

-

p J+� ·

(л)

В случае прямотока во всех выражениях, использующих форму
лу (л) , вместо суммы в скобках будет стоять разность: Но =

= Нр

( и:�)
1

_

. Таким образом, при противотоке расчетная длина

Но будет больше геометрической высоты зоны, для которой рас
считывается Лр, при прямотоке - меньше. В целом расчетная
формула для гидравлического сопротивления движущегося слоя
и меет вид
Н

р

Лрдс

-- =

[

( 1 - Е 0 ) ( w ± Е 0 и) µ +
1 50
2

Е3

о

d2

2
1 - Е 0 ( w ± Е 0 и) р
1 , 75
d
Е3
о

](

1+

-) (2
иЕ 0 .
W

. 68)

При организации процессов с ДС необходимо иметь в виду,
что в случае противотока движущийся слой прекращает свое
нисходящее движение ("зависает") при относительно невысоких
скоростях сплошной фазы, часто меньших скорости начала
псевдоожижения. Расчет скорости зависания ведется по эмпири
ческим формулам.
2. 7.4. Псевдоожиженный слой

Размер зерен, частиц в псевдоожиженном слое обычно на
порядок ниже , чем в неподвижном: от нескольких миллиметров
до десятых и сотых долей миллиметра.
Псевдоожиженный слой (ПС) возникает, когда вес частиц (за
вычетом выталкивающей силы) уравновешивается силами воз-

224

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

а

Рис.2.34.

Разновидности псевдоожиженных систем:

однородный слой; 6 - неоднородн ый слой ( киnяший слой) : 1 - газовый nузырь, 2
- шлейф nузыря , J - nл отн ая ( "неnреры вная") фа за слоя ; в - nоршневой слой:
1 - nор
шень твердого матер иала , 2 - газовая nробка; г - слой с ка н алообразованием : 1 - м ало
nодвюкный твердый м атериал , 2 - ка н ал (сви щ)
а

-

действия на них восходящего потока газа или жидкости - тогда
слой расширяется (растуг его высота Н и порозность Е ) , частицы
выходят из контакта друг с другом и получают возможность от
носительного перемещения. Газ или жидкость, способствующие
переходу слоя в псевдоожиженное состояние, в этом случае на
зывают ожижающим аrентом ( ОА) . Скорость, при которой слой
переходит в псевдоожиженное состояние, называется скоростью
начала псевдоожижения и обозначается w0 . При дальнейшем по
вышении скорости ОА сверх w0 слой продолжает расширяться,
но вес частиц и силы воздействия на них газового потока оста
ются уравновешенными , так что выноса частиц из слоя не про
исходит. Однако при наращивании скорости потока наступает
момент, когда воздействие потока превышает вес неподвижной
(зависшей ) частицы, и она будет уноситься потоком из слоя ,
аппарата. Скорость, соответствующая этому моменту, назы
ваемая скоростью уноса wy, представляет собой предел устойчи
вости псевдоожиженного слоя. Таким образом , ПС устойчив в
диапазоне скоростей w0 :S w :S wy; ему соответствует диапазон
порозностей Ео :S Е :S 1 (причем Е = 1 отвечает уносу частиц) ;
высота псевдоожижен ного слоя Н � Но .

Основные достоинства ПС: развитая межфазная поверхность , обусловлен
ная малыми размерами частиц - соответственно формуле (2.64); интенсивное
перемешивание ТМ и выравнивание свойств (температур, концентраций и др.)
по объему слоя; интенсивный теплообмен слоя с размещенной в нем поверх
ностью; простота конструктивного оформления. Основные недостатки: исти
рание и унос частиц (необходимость в ряде случаев весьма сложных улавли
вающих устройств после аппарата с пq; в ряде случаев недостатком является
перемешивание ТМ, отчасти и ОА (см. гл. 8).

На рис. 2.34 показаны разновидности псевдоожиженного
слоя . Однородное псевдоожижение (рис. 2 . 34, а) возникает, как
225

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

правило, при использовании жидкости в качестве ОА; здесь при
постепенном повышении скорости слой монотонно расширяет
ся, частицы хаотически перемещаются в нем, расстояния между
частицами статистически одинаковы. При значительно чаще
встречающемся газовом псевдоожижении возникает неоднород
ный ПС (рис. 2 . 34, 6) : при скоростях, превышающих w0 , в слое
образуются газовые пузыри, вовлекающие массы твердого мате
риала в крупномасштабное перемещение - целыми ансамблями
(агрегатами , пакетами ) . Эти пакеты движутся в горизонтальном
направлении, когда поднимающийся пузырь расталки вает псев
доожижаемый материал ; они движутся вверх вслед за пузырем
(в его шлейфе) и вниз между поднимающимися пузырями.
Именно в неоднородном ПС (он получил название кипящего
слоя) очень интенсивно перемешивание твердого материала.
В процессе подъема в псевдоожиженном слое пузыри
коалесцируют и разрушаются. При достаточной высоте слоя и
сравн ительно небольшом диаметре аппарата пузырь может за
нять все его поперечное сечение - возникает поршневой ПС
(рис . 2 . 34, в ) , когда газовые пробки перемежаются по высоте с
поршнями зернистого материала. Если материал плохо псевдо
ожижается (влажный материал; очень мелкие частицы, склон
ные к слипанию из-за большой поверхностной энергии; части
цы по форме сильно отличаются от сферических и т.п . ) , то в
слое образуются каналы (рис. 2 . 34, г). Через них и проходит
основная часть газа, а твердый материал между каналами оста
ется непсевдоожиженным; для вовлечения его в псевдоожиже
ние приходится механическим или каким-либо иным способом
разрушать эти каналы. Наконец, подвод механической энергии *
может частично или полностью замен ить воздействие ОА; при
мером здесь может служить вибропсевдоожиженный слой, когда
частицы перемещаются в аппарате в результате наложения виб
раци и , или виброкипящий - при одновременном наложении
вибрации и воздействия потока ОА.
Отдельной проблемой (она особо рассматривается в разд. 8 . 2 ,
8 . 7.2) является равномерность распределения потока ОА по по
перечному сечению слоя . При сильной неравномерности воз
можно падение скорости потока в некоторых зонах слоя ниже
w0; тогда здесь псевдоожижение прекращается, появляются за
стойные зоны, нарушается нормальное течение технологического
процесса. Для предотвращения застойных зон повышают гид
равл ическое сопротивление распределительной решетки (путем
умен ьшения жи вого сечения решетки или повышения средней

• О системах с механическим псевдоожижением см. [24) .

22 6

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

скорости потока) ; тогда потоку энергетически: выгоднее более рав
номерно перераспределиться под решеткой и на входе в слой.
В некоторых случаях в аппаратах с псевдоожиженным слоем
размещают сетки (с достаточно крупными ячейками) или насад
ку и тому подобные элементы - возникает заторможенный
псевдоожиженный слой. Движение частиц в таком слое су
ществует, но в сравнении со свободным псевдоожиженным
слоем оно затруднено , зато распределение потока ОА здесь бо
лее равномерно.

Поведение ПС во многом сходно с nоведением каnельной жидкости - го
ворят об их аналогии. · Псевдоожиженный материал текуч (легко nеремещается
nод уклон); его свободная nоверхность в nоле сил тяжести - горизонтальна;
интенсивность теплообмена с расположенной в нем nоверхностью - весьма
высока (как в жидкостных системах, в отличие от газовых); он следует законам
nлавания тел. Многие его свойства оnисываются уравнениями. установленны
ми
жидкостей. Аналогия nсевдоожиженного слоя и жидкости (в более
общем асnекте - дисnерсных систем и сплошных сред) обусловлена их статис
тичес кой общностью: в обоих случаях мы имеем дело с множеством молекул
или частиц. Если свойства жидкости изменяются с темnераrурой, то свойства
дисnерсных систем - со скоростью ОА. В этом смысле скорость начала nсев
доожижения может трактоваться как аналог темnераrуры nлавления , а скорость
уноса - как аналог темnераrуры киnения; тогда неnодвижный слой есть
"твердое тело", nсевдоожиженный - "жидкость", а унос - "nаровая фаза".
Подход к nсевдоожиженному слою и другим дисnерсным системам no аналогии
со сnлошными средами весьма плодотворен: он позволяет осуществить с nсев
доожиженным ТМ ряд nроцессов, усnешно реализованных с жид костными
системами; в свою очередь дисnерсные системы иногда могут служить удоб
ными теоретическими и эксnериментальными моделями сnлошных сред.
для

Кривые псевдоожижения
Псевдоожиженный слой характеризуют с помощью кривых
псе вдоожиже н ия , представляющих собой зависимость сопротив
ления слоя ( перепада давления) от расчетной скорости w. На
рис . 2 . 3 5 , а изображена иде альн ая кривая для аппарата постоянно
го поперечного сечения f На участке О - А, где w < wo, слой
еще неподвижен , кривая Лр = ЛРнс ( w) отвечает формуле Эргана

(2.67 ) . В точке А воздействие газового потока становится рав
ным весу ТМ в аппарате, и слой переходит в псевдоожижен ное
состояние. При дальнейшем повышении скорости в аппарате с
f = const перепад давления ЛРn с в идеале во всем диапазоне
псевдоожиженного состояния (от w0 до wy ) от скорости не зави
сит - участок А - В. При w > wy наблюдается не воспроизво
димое во времени падение Лр.
Реальная кривая псевдоожижения (рис.2.35, б) отличается от
идеал ьной:
- наличием пика давления вблизи начала псевдоожижения
(его причина - необходимость преодоления сцепления частиц
• Подробно об аналогии между дисnерсными системами и сnлошными сре
дами см. (7, 8 J .

227

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

�· · 1В

ш
А

Лр
0

С

�

Wo

а

ПС
•

ТС
Wy W

• •

Рис.2. 35.
а

-

Кривые псевдоожижения:

идеал ьная , б - реал ьные

между собой и со стенками аппарата при переходе слоя в псев
доожиженное состояние ) ;
- некоторым отклонением ЛРпс от постоянной величины н а
участке А - В; п р и росте ЛРлс с w (пунктир) это чаще всего
связано с л иквидацией застойных зон при увеличении w и более
полным вовлечением ТМ в псевдоожижение; снижение ЛРлс
(тонкие штриховые линии) часто обусловлено размещением
каких-либо деталей в ПС;
- наличием гистерезиса вблизи начала псевдоожижения и в
области неподвижного слоя , т.е. несовпадением кривых Лр( w)
прямого хода (опыт ведется при увеличении w) и обратного хода
(опыт при снижении w) . Дело в том, что при медленном пони
жени и w в области НС упаковка частиц - рыхлая (выше пороз
ность) , а согласно формуле (2. 6 7) более высоким Ео при одина
ковых w отвечает меньшее значение перепада давлений ЛРнс·
Кривые псевдоожижения позволяют наметить основные на
правления предстоящего анализа: определение сопротивления
псевдоожиженного слоя ЛРл с и значен и й граничных скоростей
Wo И Wy.

Гидравлическое сопротивление псевдоожиженного слоя

Рассмотрим первоначально (рис.2.36, а) общий случай псев
доожижения твердого материала в поле внешних массовых сил,
хара ктеризуемых ускорением а (его направление показано
стрелкой ) . Выделим в ПС элементарный участок dz, в пределах
которого эффективная (с учетом сил выталкивания) масса ТМ
равна dт3. Пусть нормальное к а сечение слоя / = var, закон его
изменения по высоте слоя известен. Баланс сил , удерживающих
массу dт3 в состоянии равновесия (псевдоожижения ) , запишет
ся (соответственно ОБС для контура, совпадающего с элемен
тарным объе мом /dz):

р/ - (р + dp)/ - (dт3)а =
228

О,

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 2. 36. К определению гидравлического сопротивления псевдоожиженного
слоя:

а - общий случай , б - nсевдоожижение в
поле сил тяжести

откуда в самом общем виде

ЛРnс Р1 - Р2
=

=

J !!:_ dтэ;

(m" ) J

(м)

а
знак "ми нус" учтен при смене
пределов и нтегрирования велич и н ы dp .
В случае аппарата с f = const при псевдоожижении в поле сил
тяжести (рис . 2 . 36, б) баланс сил может быть наглядно зап исан
для всего псевдоожиже нного слоя (слой - контур ) : ,
p i.f - p')f + Ра - Ртм = О ,

где Рт" и Р0 - вес и архимедова сила , действующие на все частицы ПС. Разу
меется, практически
архимедову силу следует учитывать лишь при псевдоож и 
жени и жидкостью ( или очень тяжелыми газами при высоких давлениях ) ; nри
псевдоожижении газами в обычных условиях вкладом выталкивающей силы
здесь в последующих соотношениях вполне можно пренебречь.
и

Из баланса

ЛРпс Р1 - Р2 = Ртм - Р. ( Ртм )э '
( 2 . 69)
f
f
где ( Ртм ) э Ртм - Ра - эффективны й вес твердых частиц в слое , т.е . их вес за
вычетом выталкивающей ( архим'едовой ) силы .
=

=

=

Совершенно очевидно, что если в общей формуле ( м ) поло
жить / = const и а = g, то придем к выражению ( 2 . 69) .
Во всем диапазоне псевдоожиженного состоян ия (от wo до
wy) эффекти вный вес ТМ не изменяется ; поэтому при постоян 
ЛРn с = const ,
ном попереч ном сечении аппарата f должно быть
что п ол ностью соответствует горизонтальному участку на кри 
вой псевдоожиже ния. Вместе с тем в аппаратах переменного
сечения f сопроти вление псевдоожижен ного слоя изменяется со
скоростью: в аппаратах с увеличивающимся снизу вверх значе
нием f величина ЛРn с снижается , с умен ьшающимся f - воз
растает. При выносе части твердых частиц из аппарата с пото
ком ОА вес части ц, поддержи ваемых во взвешенном состоян и и ,
уме н ьшается и соответственно ( 2 . 69 ) ЛРn с падает; п р и Ртм � О ,
естественно, ЛРn с � О.
Для практических расч етов формулу ( 2 . 69) удобно преобразо
вать , выразив : вес твердого материал а Ртм = РтУтg = PтdH( l - е ) ,
архи медову силу (она равна весу ожижающе го агента в объеме
всех части ц в ПС) Ра = pg(H( l - е ) . П одставив эти значен ия в
( 2 . 69 ) , получ им после сокращения на f
ЛРnс = ( Рт - p )g( l - е ) Н.
(2 . 70)
229

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

П одчер кн ем, что nри псевдоожижении в аппаратах постоянного
попереч ного сечения величины е: и Н увел и ч и ваются с ростом ско
рости, но произведение ( 1 - е:)Н о стается неизменным - соответст
венно ЛР пс = const.
Выражение (2.70) сп раведл иво для всего диапазона псевдоожи
женного состоя н ия, в том ч исле и для точки А, когда w = w0• Но
для этой точки, принадлежащей одновременно к псевдоожижен1ю му и неподвижному слоя м, е: = е:0 и Н = Н0• Тогда из (2. 70)

(2.70а)
ЛР 11 с = (Р т - p}g(l - e: o }H o .
Для дал ь н е й ш и х nреобразова11ий последнее в ы раже ние удобно
·

представить, как форму (2.67), в виде сопротивления, приходяще
Гося на еди н и цу п ерво 11ачальн о й вы с от ы сло я :

л�псо = (Р т -

р )g(l

- Ео ) .

(2.7D б)

В практических инженерных расчетах г идравли ч ес ко го сопротив
ления ПС выражения (2.70, а,б) удобнее, нежели (2 . 70), так как обыч
но известны значения пороз11ости е:о и высоты неподвижного слоя Н0•

Скорость начала псевдоожижения

На кривой псевдоожижен и я (рис. 4.35, а) точка А отн о сится как к
псевдоожижен но му, так и к не п од в иж но м у сЛою. Поэтому перепад
давления для этой точки может быть найден как по формуле Эр ган а
(2.67) дл я НС 11ри
}Vo, так и по формуле (2.70, б) для ПС:

w=

ЛРнс (wо } = ЛРпс ·
-н;
Но

(н)

Остается разрешить равенство (н) относительно w0. Дnя этого
подставим значения удельных перепадов давлений по указанным
выше формулам :

(1 - & 0 ) 2 -w0 µ + 1 7 5 ---1 - е: 0 wg p - (Рт - р)g(l - Е о )
1 50 --d2
Е�
Е� d
Сократим обе части равенства на ( 1 - е:о ) и измени м µ = vp.
1 ,7 5 wgp (р
}Vo VP + ---т
0 (1 - E o ) -=
огда 1 5 --т - Р )g .
е; �
d2
Е� d
•

·

Это равенство может быть решенQ относительно wo. Однако
решение целесообразно представить в форме зависимости обоб
щен ных переменных. С цель ю перехода к ним домножим о бе час3
ти равенства на d /(p v2 ):
.

1 50
230

(

( 1 - е: 0 ) w0 vp .!!},__

Е�

d2 p v 2

) (
+

)

1,7 5 wJ p .!!},__ = (рт р )g .!!}__ .
pv2
& � d p v2
_

(о)

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

В первом слагаемом после сокращений в скобке получаем фраг
мент, представляющий собой 'DICJIO Рейн� для начала nсе1Що
ожиже1П1Я w0d/v = Reo; во втором слагаемом - щid 2/v2 = Reo2. В
правой части стоит безразмерный коМIUiекс

gvd2з Р т р- р -= Ar,

называемый критерием Архимеда. Его смысл : соотношение сил ,
препятству ющих и способствующих взвешиванию частицы в
потоке: d3
объем части цы (с точностью до постоянных мно
жителей ) , d3 pтg
ее вес, d3( рт
p)g
эффективный ее вес (с
учетом выталкивающей силы); v и р отражают влияние сил вяз
кости и инерции потока, воздействующего на частицу.
Таким образом_,
1 75
(п)
1 50 l Е о Reo + • Re02 = Ar,
-

-

-

-

-

з
Ео

з
Ео

причем первое слагаемое в левой части - ламинарная состав
ляющая формулы, второе - турбулентная (этот смысл сла
гаемых просматривается из формулы Эргана) .
Ранее было указано . что для округлых �астиц значение по
р оз ности не подвиж н ого слоя (на пороге псевдоожижения) Ео
близко к 0,4. С этим значением Ей выражение (п) при нимает вид
1 400Re0 + 2 7 , 3 Re02 = Ar.
(п')
Величины, входящие в Ar, как правило, бывают известн ы:
это свойства ОА и ТМ. Определив Re0, далее находят wo.
Решение квадратного уравнения (п) возможно обычными ал 
ге браическими методами. Оrечественный ученый О.М.Тодес пред
ложил иной подход, позволяющий линеаризовать уравнение (п) ;
используем этот путь.
При развитом (автомодельном) турбулентном режиме первым
слагаемым в (п) можно пренебречь, так что
1 ,75 Reo2 =
Е оз

Ar и

Reo =

�

.

(р)

Подстави м это значение Re0 во второе слагаемое в левой час
ти (п) вместо одного из сомножителей :

Jлн�
/&) l!f

Е оз

1
1 50 1 Е о Reo + ,75 Re o

Полученное

з
Ео

линейное уравнение

очевидным упрощением:

1 75
Е�

'
-

о_

_

1,75

1 ,75

=

Ar.

(с)

решим относительно Reo с
=

75

Е�

'
-

. Тогда получается
23 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

расчетная формула:
Reo

=

w0d

- v

Ar

_

- 1 50 1 - <, +/'7 5 ,/Ar
f: о

з

(2.7 1 )

f: оз

называемая
конкретное численное значение
то
Если принять
формула
(2. 71) упрощается:
(2.7 1а)
5,
2
2./Ar
Первое слагаемое
в знаменателяхсоставляющую,
выражений (2.второе
7 1) и -(2.тур
7 1 а)
представляет
собой
ламинарную
булентную.
При малых
значениях Arвклад(мелкие
и легкие
частицы,
высокие
вязкости
и
т.
п
.
)
доминирует
первого
слагаемого,
при
высоких
(крупные
и
тяжелые
частицы
и
т.
п
.
)
вклад
второго.
Полученные решения, естественно, дают точные результаты при высоких
ния .

формулой Тодеса для скорости начала псевдоожиже

Reo =

1 400 +

Ar

i::o = 0,4,

значениях Ar (турбулентный режим) - это предопределено п роцедурой реше
ния: заменой по (р) и (с), правомерной именно при высоких Ar. При ламинар
ном режиме такая замена неправомерна, она вносит ошибку в турбулентную
составляющую. Но роль этой турбулентной составляющей п ри ламинарном
режиме мала, так как доминирует ламинарное слагаемое; поэтому в целом и
при этом режиме решение остается верным. Некоторое расхождение с точным
решением квадратного уравнения ( п) характерно для переходного режима
(оценки показывают, что максимальное расхождение - на уровне 20% - про
является при Ar 1 04) . Заметим, что поrре� ность расчета, обусловленная не
в значениях EQ, И11'3ет обычно бОльшую роль, поскольку i:o входит в
расчет в высок.их степенях. В общем формула Тодеса подтверждена эксперимен
тально и является в настоящее время наиболее надежным расчетным соотношени
ем; в некоторых конкретных случ она может п отребовать корректировки.
"'

точностями

аях

анализподходов
проведени терминов
на основе внутренней
формулы Эргана,
т.гидродинамики.
е.Показательно:
с использованием
задачи
результате
анализа
получен
типичный
крите
рий
внешней з адачи
Это еще раз указывает на условность
вводимых
нами классификаций.
Скорость уноса
Скорость
ожижающего агентаслоя, зависит
при которой
наступает
унос
частиц
из
псевдоожиженного
от
многих
факторов:
размера
и формы
частиц;влияния
гранулометрического
состава
(широты
фракции);
взаимного
частиц
(значения
порозности
высоты ПС; интенсивности
барботажа(в частности,
газовых пузырей;
кон
структивного
оформления
аппарата
высоты
и
фигурации надслоевого пространства). Учесть влияние дажекон
от232
В

-

Ar.

wy,

i:: ) ;

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

и

=О

о

t

11: = 1v 8
а

и

= 1111

1

l5

w=O

·1

w

б

Рис. 2.3 7.

PJ

и

в

Понятие о скорости витания единичной частицы
расчету скорости витания сферической частицы

Рис.2.38. К

дельных
факторов,
а темзадачу
болееи ихбудемсовокупности
очень труда
но.ее приближенную
Поэтому
упростимоценку:
искать не -скорость
Витанием уравновешен
будем называтьсиловым
состояниевоздействием
частицы, когдагазового
ее вес
полностью
(жидкостного)
потока.псевдоожижения,
Такая ситуация, вообще
говоря, возника
етречь
с момента
начала
т.
е
.
при
но там
идет
о
стесненном витании, когда в потоке взвешен к.омек.
тив частиц; здесь - о свободном витании единичной частицы, не
взаимодействующей
с другими
частицами
илибыть
стенками
аппарата.в
Равновесие
указанных
выше
сил
может
реализовано
различных
вариантах (рис.
а) частица поддерживается потоком в неподвижном состоя
нии, частицатогдападает
скорость
газа, жидкости равна
w8; неподвижной
в
неограниченном
объеме
среды
(газа, жидкости);
тогда скорость установившегося движе
нияв)частицы
и
различные
направления
перемещения
частицы и движущейся
среды;
тогда
скорость
частицы
и относительно потока (скорость
скольженпадает
нымисреды,
словами,то всплывает
частица вов нем)
всех
але равна
ия) в идев поток.е
Илегче
случаях
(если
она
смещен
относительной
скоростью
а направление
абсолютного пере
частицы
зависит
от
знака
разности
ия
простыхчтослучаев:
наиболеепомнить,
вести(а), дляно будем
Анализ целесообразно
(а) или
Выберем
случай
резуль
татыПусть
анализа
справедливы
и
для
всех
иных
вариантов.
под
сферическая
частицасостоянии
диаметромпотоком
и плотностью
держивается
в
неподвижном
среды,
плотность
которой
Чтобы частицана
Тогда скорость
средыравенство
равна действующих
находилась
в
равновесии,
необходимо
нее (рис.2.38): веса Р", выталкивающей (архимедовой) Ра и
3
ческой частицы w8.

wy .
скорость витания единичной сфери

w

�

w0;

2.37):

6)

и = О;

=

wв ;

w8•

w8,

(w - wв) .

(6).

р < Рт ·

d

Рт

wв .

сил

2 3

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

воздействия потока среды РРп.=ПриР Рт - О очевидно: (т)
ч
а
Здыдесьотноси
Рч = 1td3/6) Ртg, Ра = ( 1td3/ 6) pg. При движении потока сре
tельн d частицы вознЙ кает гидравлическое сопроти
вление, которое
можноw2 трактовать как местное и записать в
форме (2. ЗОа): 2g Коэффициент при обтекании тела
называют
Ввидетерминах=
перепадов
давления
это
сопротивление
запишется
в
=
а сила -сопротивления
(т.f е. сила воздействия
потока на
тело,
частицу)
как
где
- поперечное сечение
сферической
частицы. Тогда,частицы
имея вв виду,
что скорость,
необхо
димая
для
поддержания
равновесии,
есть
скорость
витания w w0, имеем d2 2 d2
7td 2
2g
2
+ Рп .

(

р>

hм = � - .

�

коэффициентом лобового сопротивления.

pghм,

= лd2/4

Лрм /,

=

р

п

=

Лр rt
м -- =

Лрм

w2
w"
rt
"' в р -- ·
рg -- = "'.., ..,

(у)

При анализе вариата (6) на рис. 2.37 возможен случай, когда частица первоначально
находкrся в неподвижном сосrоянии, затем она посrепенно разгоняется до постояннои
скорости w Если иirrepec предсrавляет движение частицы на участке разгона, то правую
часть исходного соотношения (т) нацо дополнить силами инерции:

4

•.

р

и

4

4

itd3
dw
=6
·
Рт (h

Далее этот случай не анализируется.

Подставив
сократив
на теперь значения слагаемыхdв2 формулу (т), получим,
-(Рт p)g- 2
Поделив обе(длячастиудобства
равенства
на v2p, перейдем
к обобщенным
переменным
последующих
преобразований
поме
няем местами левую и правую2 части3 равенства):
3� w ; d gd Рт - р
(ф)
4--т- = 7--рВходящий в левую часть (ф) комплекс w8d/v
представляет
со
бой
Re8;
в
правой
час
ти - критерий
(х)
сфе
от режима* ,обтекания
зависитпоказывает
начение коэффициента
что для ламиТеоретический анализ
ры Зпотоком.
л:

d3
6

_

_

w;
�р-

4

·

Аг:

число Рейнольдса мя скорости витания

�

' Выражение для с, при лами нарно м обтекан и и шара приводится без вывода
ввиду его громоздкости.
34

2

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

= 24/Re (в рассматриваемом случае Re Re8).
нарногоразвитого
режима (автомодельного)
Для
турбулентного
режима мне
но
о
величине
этой
постоянной
нет
согласованного
ния
(приводятся
значения
от 0,43(усредненное)
до 0,50); длязначение
дальнейших
выводов
примем
промежуточное
0,47. Учтем отсутствие кризиса и плавное изменение при
переходе
от ламинарного режима к турбулентному; тогда для
любого режима обтекания сферы потоком
�

=

� =

= coпst ,

�

�

=

�

� =

(u)

= � + 0,47.
Re.
Re

Очевидно:
при малых 8 доминирует первое слагаемое, при
больших
второе.
Подставим теперь значение по в выражение (х):
2
2(�
0, 4 7) Rе в = AI ,
4 Re.
или
1 8Re8 0,35 1 Re82 = AI.
этогоскорость
квадратного
уравнения позволяет найти Re8 и
далееРешение
искомую
w8• Однако и здесь возможна линеариза
уравнениявыше).
(ш) и более простое определение Re (по канве,
показанной
автомодельном
турбулентном
режиме
первое слагаемое
левойПричасти
(ш) пренебрежимо
мало,
так
что
,_-,...--0,35 1 Re82 = AI и Re8 = .JA r/0, 35 1 .
Re8 во второе слагаемое левой части
(ш)Подставим
вместо одногоэто иззначение
сомножителей:
г--,...--(щ)
1 8Re8 0,35 1 Re8 JA r/0, 35 l AI.
уравнения найдем Re8 (с оче
Из полученного
0,35 1 /.Jo,35 1 .Jo,35 1 0,59) :
упрощениемлинейного
видным
(u)

�

+

+

(ш)

ция

в

+

Rе в

=

=

w.d =

=

Ar

(щ)
=

1 8 + 0,59.JAr

(2.72)

>>
..JA.r
формулу Стокса,

В

v

Это выражениеПервое
получило
названиев знаменателе представляет
слагаемое
собой
ламинарную
составляющую,
второе -, и турбулентную.
случае
ламинарного
режима
18
0,59
тогда (2. 72)в пре
вращается
в
известную
представленную
без
размерной форме: Re8 AI/1 8.
(2 .72а)
формулы Тодеса для ско

рости витания .

=

235

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

В случае турбулентного режима 1 8 < < 0,59 .fAr , и получается

формула Ньютона :

Re8 = ( 1;1) ,59) Ji\r .
(2.72б)
Для переходного режима оба слагаемых в знаменателе (2.72)
сопоставимы по величине. При возрастании Re8 режим обтека
ния частицы потоком плавно переходит от ламинарного к тур
булентному.
Сравнение с экспериментальными данными показывает, что
формула Тодеса (2. 72) является надежным расчетным соотноше
нием для витания шарообразных (и близких к ним по форме)
частиц. Скорость витания равновеликих (того же объема и веса)
несферических частиц, зерен меньше, нежели сферических, и
зависит от формы частиц. Вычисляется она с использованием
поправочных коэффициентов (как правило - эмпирических)
типа фактора формы Фs·
-

Располагая формулами

для

w0

и

w8,

диапазон псевдоожиженного состояния.

формулами (2.7 1 а) и (2.72):
w.
Re .

можно оценить
Воспользуемся

скоростной
для

этого

1 400 + 5,22 .fAr
(2.73)
Re 0
1 8 + 0,59 ..fАё
Если витание (начало псевдоожижения - тем более) проис
ходит в условиях ламинарного режима, то wв/wo = 1400/1 8 "' 78;
если началу псевдоожижения отвечает турбулентный режим
(витанию - тем более), то wвfw0 = 5,22;1) ,59 "' 8,8. Таким обра
зом, при ламинарном режиме (мелкие и легкие частицы, соот
ветствующие свойства ОА) диапазон псевдоожиженного состоя
ния весьма широк: после начала псевдоожижения скорость
можно повышать в десятки раз, прежде чем наступит унос. Для
турбулентного режима этот диапазон существенно Уже.
=

=

Стесненное витание и расширение псевдоожиженного слоя
находятся в состоянии
слоя изменяется от i>o
:5 w :5 W8 отвечает своя
порозность i>o :5 :5 1 , зависящая, разумеется, также от свойств
твердого материала и ожижающего агента. Связь i> и w необхо
димо знать в различных технологических ситуациях; в гидроди
намическом плане знание i> необходимо для расчета высоты и
объема псевдоожиженного слоя в рабочем состоянии (по из
вестным исходным характеристикам i>o , Но , Уо ) .
23 6
В диапазоне от w0 до wy "' w8 частицы
стесненного витания, причем порозность
при wo до 1 при w8 • Каждой скорости wo
i>

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

На основе связей, установленных в разд. 2 . 7 . 1 , запишем объ
ем собственно твердого материала (при переходе от неподвижно
го состояния слоя к псевдоожиженному он, естественно, нё из
меняется):
Ут = Yo( l - Ео ) = V( l - Е) .
Отсюда рабочий объем ПС
у =

Уо

1 - to
1-t

.

Для аппаратов постоянного поперечного сечения У = fH,
= /Но , и тогда
Н = Но 1 - t o .
1-t

(э)

V0

=

(ю)

(э ) и (ю) приобретают расчетный характер, если известна рабо

При известных Уо (или Но) и Ео (например, Ео "" 0,4) формулы

чая порозность Е.

Порозность при однородном псевдоожижении . Для определения
рассмотрим совместно два выражения: (п), справедливое в мо
мент начала псевдоожижения при порозности Е = Ео = 0,4, и (ш),
записанное для скорости свободного витания, т.е. при Е = 1 :
(п')
Ео = 0,4,
1 400Re0 + 27,3Re02 = AI,
=
2
(ш)
1 8 Re8 + 0,35 1 Re8
AI, Е = 1 .
Можно констатировать сходство в структурах обеих формул,
что отражает сходство в физике рассматриваемых явлений. В
самом деле, в обоих случаях речь идет об однородных системах
(отсутствуют дискретные образования - пузыри) : неподвижный
слой - в начальный момент псевдоожижения; витание единич
ной сферической частицы. Но в случае единичной частицы мы
имеем дело со свободным витанием, а в случае псевдоожиже
ния - со стесненным, причем в момент начала псевдоожиже
ния - с самым стесненным. Сходство в предельных ситуациях
витания проявляется еще ярче (количественно!)
при сопоставлении
численных коэффициентов: 1 400/1 8 = 27,3;0,35 1 = 77,78. Если все
слагаемые в формуле (п') поделить на 77,78, то получим
(п")
1 8 Re0 + 0,35 1 Re0 2 = 0,0 1 286Ar , Ео= 0,4 .
Различие в написании правых частей формул (ш) и (п") обус
ловлено различием в порозностях. Можно предположить, что
аналогичную структуру имеют формулы в случае стесненного
витания для всех однородных псевдоожиженных систем при лю
бой порозности Е в промежутке от 0,4 до 1 . Только в правой
части в качестве множителя при Ar будет стоять некая функция

Е

237

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

и
от порозности fi.E), принимающая значения 1 при Е
0,0 1 28 6 при Е = Ео = 0 , 4 ;
(я)
1 8 Re + 0,35 1 Re = Ar fi.E) ,
где Re = wd/v базируется на скорости однородного псевдоожи
жения (стесненного витания) w, причем w0 � w � w8.
В качестве искомой функции резонно выбрать /(Е) = Еп, по
скольку в этом случае /(Е) становится равной 1 при любом зна
чении п. А численное значение п отыскивается из условия
О,4п = 0,0 1 28 6 , откуда п = 4 , 7 5 . Тогда
(аа)
1 8 Re + 0,35 1 Re 2 = ArE4,7 5 ;
из этого соотношения определяется порозность однородного
псевдоожиженного слоя с известными характеристиками твердо
го материала и ожижающего агента (критерий Ar) при заданной
скорости ожижающего агента (критерий R e: Re0 � Re � Re8):
Е

)
(
= 1 8 R e+ �:5 1 R e
2

0, 2 1

,

(2.74)

причем 0,2 1 = 1 /4,7 5 .
Формула (2.74) показала хорошее согласие с рядом эмпири
ческих формул , полученных на основе широкого эксперимента.
Выражение (аа) может быть использовано для решения об
ратной задачи - определения скорости , необходимой для под
держания заданной порозности однородной псевдоожиженной
системы с известными характеристиками твердого материала и
ожижающего агента (т.е. с известным критерием Ar ) . С этой
целью удобно провести линеаризацию квадратного уравнения
(аа) - по канве, реализованной для Reo и Re8• Предоставляем
возможность читателю проделать этот путь самостоятельно;
приведем результат:

Re

=

4 75
Arf.. ,

4 75
1 8 + 0,59 �ArE ·

------;:=
:
==

(2 . 7 5 )

Характер изменения Е с Re соот
ветственно формуле (2.75) иллю
стрируется на рис.2.39 (кривая J).
Формула (2.75) вполне при
годна для определения скорости
стесненного витания w при из
вестных размерах и других свой-

-

Рис.2.39.

слоя:

1
однородное псевдоожижение, 2
нородное псевдоожижение

238

-

Расширение псевдоожиженного
неод

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ствах частиц. Однако при необходимости определения размера
d частиц, которые будуг при известной скорости w однородно
псевдоожижены с заданной порозностью Е , возникают затрудне
ния, поскольку диаметр частиц d входит как в Re, так и в3 Ar. В
этом случае удобно безразмерное число Лященко Ly Re /Ar =
= w3p/[gv( pт р ) ) , содержащее w и не содержащее d. В общем
случае целесообразно использовать связь чисел Ly и Ar с пороз
ностью Е : тогда при известном размере твердых частиц (Ar) и Е
легко найти Ly и скорость стесненного витания w, как и наобо
рот - по Е и w ( Ly) определить Ar и размер частиц d. Аналити
ческая связь Ar, Ly и Е для однородного псевдоожижения
(стесненного витания) весьма громоздка. Графически эта связь
представлена на рис. 2.40.
Особо подчеркнем - вопреки
ошибочным указаниям в ряде
•
монографий и даже учебников : формулы (2.74) и (2.75) относятся
только к однородному псевдоожижению. Для определения расшире
ния неоднородных псевдоожиженных систем они непригодны.
Ф ормулы (2.74) , (2.75) и производные от них применяются
не только для расчета процессов с ПС; они в равной мере мoryr
быть использованы в расчетах процессов осаждения в поле мас
совых сил (см.разд.5. 1 .2).
=

-

Интересно, что скорость стесненного витания w0 (рассчитана на полное се
чение аппарата) и абсолютная скорость стесненного осаждения частиu и в
покоящейся жидкости равны между собой . Это равенство требует пояснения.
Верти кальная составляющая истинной скорости жидкости относительно ви
тающ и х частиu (скорость скольжения) запишется как wJt. Равенство w0 = и
справедливо в том случае, когда оседающие частиuы накапливаются на дне
сосуда: в своем нисходящем движении они вытесняют соответствующее коли
чество жидкости , создавая восходящий ее поток. Если рассматривать 1 м2 попе
речного сечения аппарата, то такой поток составляет и(! Е). Истинная ско
рость этого поток а в просветах между частиuами равна u( l t)/E. Тогда ско
рость скольжения (она при осаждении частиu должна оставаться равной wJt)
будет получаться как сумма скоростей нисходящего движения частиu и и вос
-

-

ходящего движения жидкости и( 1 i:)/E :
Wс
u(I - &) = u& + u - u&
= и+
,
&
&
&
откуда и = w0. Разумеется, если твердые частиuы по мере
аппарата непрерывно выводятся из него, то восходящего
-

поступления н а дно
пото ка вытесняемой
жидк ости не будет. В так ой ситуаuии, при сохранении скорости скольжения
wJt , равенство 11 = w0 неправомерно. В покоящейся жидкости при непрерыв
ном выводе из аппарата оседающих твердых частиц, очевидно, и = wJi: .

Порозность при неоднородном псевдоожижении. Для практиче
ски более интересных (чаще встречающихся) неоднородных
псевдоожиженных систем порозность, как правило, заметно
ниже, чем для однородных (см. кривую 2 на рис. 2.39).

• С м. ( 1 3 ,

1 7 , 20) и др.

239

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Ly

10

""

4

&

-

[/
,

10

�

,
1

1

1/
�

10

'(

.3

10

-4

1

1

1

1

·2

10

1

1

1

1

J
J

/

1

�

1

�
J

�

1

"

/
1/

lJ

/

1

/

"

"
,

J

""""

1

·�

О,

'/

\7

/
1
"

1/

�

/
1

�

-

,,,,.. �

,...

'
-

-

[/

�

-

0,5
�

...

&

0,4

-

,,.. "

[/�

v"""
......

.... ....

IJ

1

1
J

1

'1

10
1 04
Рис.2. 40. Кривые однородного расширения псевдоожиженного слоя

Ly = f(Ar)

Ar

Можно приближенно считать, что весь избыток газа, сверх необходимого
мя начала п с евдоожижения, п роходит через слой в виде пузырей. При этом в
подавляющем большинстве случаев газовые пузыри поднимаются в слое с за
метно большей с коростью , нежели остальной газ, движущийся в п росветах
между частицами . Это означает, что пузыри быстро " проскакивают" через неод
нородный псевдоожиженный слой , так что единовременно в нем содержитс я
меньше газа, чем в однородном при тех же объемных расходах газа, - средняя
п орозность п олу ч аетс я ниже. Для неоднородного псевдоожи ж енного слоя ,
работающего без интенсивного уноса, & редко превышает 0,7 - 0,7 5 ; только
вблизи скорости витан ия она быстро приближается к 1 .

240

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис.2. 41. Фонтанирующий слой:

1 - зона пневмотранспорта, 2
жения, З - зона движущегося слоя

-

зона псевдоожи 

Теоретически возможно получить расчетные
формулы для Е при неоднородном псевдоожи 
жении. О н и выглядят весьма просто, но содер
жат такие трудноопределимые вели ч ины, как
размеры и скорость подъема газовых пузырей,
долю газа в виде пузырей и др. Поэтому в на
стоящее время используются эмпирические
формулы. Приведем для ориентировки одну из
них (для частиц плотностью Рт � 1 000 кг/м3 ) :
Е � 1 , 2 Ео

(�)k

(2.76)

где k = 0,08 для сравнительно мелких частиц (Ar s 3- 1 03 ) ; k = 0 , 2 0 для крупных
частиц (Ar � 3 - 1 06 ) , а для частиц промежуточных размеров k = 0,08 4. 1 0- s Ar.

+

Рассмотренные выше дисперсные системы с твердой фазой
не исчерпывают многообразия их модификаций. Встречаются,
например, системы, включающие сразу несколько из рассмот
ренных выше. Примером может служить фонтанирующий слой
(рис.2.4 1 ), где сосуществуют ДС, ПС (при неудачной организа
ции процесса - больших углах конуса - и НС) , а также тран 
спортная система те (в приосевом канале), рассматриваемая в
разд.2.8.2.
2 . 7 . 5 . Образование и движение жидких капель и rазовых пузырей

Д испергирование жидкости и газа в целях увеличения меж
фазной поверхности контакта широко используется в хими
ческой технологии - при проведении процессов абсорбции,
ректификации, экстракции и др. Среди гидродинамических
проблем наиболее важными являются проблемы образования
дисперсной фазы (размера ее элементов) и движения ее в
сплошной среде (скорости подъема или падения). Ввиду слож
ности строгого анализа ниже рассмотрим некоторые упрощен
ные подходы к решению упомянутых проблем.

Оценка размеров элементов дисперсной фазы
Рассмотрим диспергируемый поток жидкости или газа п ри
истечении из сопла в сплошную среду (рис.2.42) при невысоких
скоростях истечения w. В общем случае одна жидкость (ее плот
ность Рд) должна быть диспергирована в другой (плотностью Ре);
пусть для определенности Рд > Ре и более тяжелая жидкость
диспергируется (распределяется) в более легкой - этому случаю
соответствует рис.2. 4 2,а. Диспергирование происходит при исте
чении тяжелой жидкости из сопла диаметром d, причем ско24 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

рость жидкости в нем w. Требуется определить диаметр D капли
(будем считать ее сферической) в момент отрыва от сопла.
Д иаметру D отвечает равновесие следующих сил: веса капли
Рк (разумеется, с учетом выталкивающей силы со стороны
сплошной среды Р3) , инерции движущегося потока тяжелой
жидкости Ри , сопротивления при выходе диспергируемой фазы
из сопла Pr и поверхностного натяжения Р0• Запишем баланс
сил в форме ( 1 .8в) для направленной вниз вертикальной оси:
Рк + Ри - Ра - Pr Р0 = О.
(а)
С записью двух сил - веса и архимедовой - мы уже вcтpe-

чались: Рк =

rtD 3

--

6

р�; Ра

=

rtD 3

--

6

pc,g.

Силу инерции получим как

частное от деления мощности потока дисперсной фазы (секундной кинетической энергии) в патрубке
скорость жидкости в нем
ния

Pr

w:

Ри =

Gw 2 =
2
2
w
--

nd'

-р w

4

•

'
w
-

2

на

rtd р - . Сила сопротивле-4 д 2
2

запишется соответственно уравнениям разд.2. 6 . 1 - через

Pr = Лрм

rtd 2

--

4

; в целом

Pr

=

�: hм

коэффициент местного сопротивления

= J:..,

w2

-

2

w2

2g

� - ; Лрм =

rtd 2 . Наконец,
р -д

4

сила поверхностного натяжения, если бы она действовала по
периметру среза сопла, соответственно выражению ( 1 . 7 ) соста
вила бы Р0 = crrtd. Реально вблизи отверстия перед отрывом
капли образуется более тонкая перемычка (шейка) диаметром ЧJd
(по экспериментальным данным '41 2/3)
именно здесь, а не
на срезе сопла действуют силы поверхностного натяжения в
момент отрыва. Поэтому при невысоких скоростях w вместо rrd
более точно подставлять rtdljl . Итак ,
,.,

-

w rtd
rtD- р дg + rtd . Р w - rtD
6
4 д т 6- р с g - � 2 Рд -4- - ттdчю = 0 ,
3

откуда

2

2

3

2

2

отрывной диаметр капли

(2. 77 )
242

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис.2. 42. К модели диспергирования
капель и пузырей

Аналогичным образом рас
считывается отрывной диаметр
капли при распылении снизу
более легкой жидкости (Рд < Ре)
вверх в более тяжелую сплош
d
ную (рис.2.42, б). Баланс сил
а
6
вдоль напраменной вниз верти
кальной оси :щесь имеет вид
(ав)
Подставив значения всех сил (выражения для них даны вы
ше), найдем
(2.77а)
В выражениях (2. 77) и (2. 77а) при истечении жидкости в газ
или наоборот- плотностью газа(рс в первом случае, Рд во вто
ром) можно пренебречь в сравнении с плотностью жидкости ;
расчетные формулы несколько упрощаются. Значения � при
диспергировании жидкости в газовое пространство близки к 0,5,
в другую жидкость - несколько выше. В случае очень низких w
(медленное образование капель, пузырей) вкладом инерцион
ных сил, отвечающих кинетической энергии диспергируемого
потока, можно пренебречь; невелики и потери энергии на местное сопротивление. Тогда (например, при Рд >ре)
6da'V
D
(2.77б)
-

·

=

3

(Р д

-

Ре

)g .

Выражения (2. 77), (2. 77а) правомерно использовать при
(или \j/cr) заметно больше p д w2 d/8. Если же выражения в квад
ратных скобках в упомянутых фuрмулах приближаются к нулю,
то начинают действовать иные механизмы диспергирования,
отвечающие иным физическим и математическим моделям; не
редко здесь необходимо привлечение экспериментальных дан
ных для оформления теоретических подходов в расчетные фор
мулы. Рассмотрение
этих подходов и моделей выходит за преде
·
лы курса .

cr

• См. сноску

на

следующей

стра н и це .

243

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

По найденным размерам капель, пузырей (D) легко опреде
лить их частоту отрыва fч от кромки сопла. Для секундного
объемного расхода дисперrируемой фазы V
fч

=

v
rr. D 3 /6

__ =

�
rr. D 3

·

(ar)

Рассмотренные выше подходы дают удовлетворительные
оценки при диспергировании из одиночного сопла, т.е. при
отсугствии влияния капель и пузырей, дисперrированн ых из
соседних сопел .

О скорости движения капель и пузырей в сплошной среде *
Приближенная оценка скорости движения жидких капель в
друrой жидкости (не смешивающейся с дисперrируемой) или в
газе, как и движения газовых пузырей в жидкости, возможна на
основе приведенных выше соотн ошений для твердых сфер
(см.разд.2.7.4). Однако эксперимент показывает удовлетворитель
ное согласие с такими оценками только при достаточно малых
размерах капель или газовых пузырьков. Отличие скоростей дви
жения капель и пузырей от рассчитанных по модели твердых ша
риков обусловлено двумя взаимосвязанными причинами:
- возникновением циркуляции внугри капель и пузырей;
- деформацией формы капель и пузырей, т.е. отличием
(нередко весьма существенным) их формы от сферической.
На рис . 2 .43, а демонстрируются явления, сопугствующие
всплыванию сферической капли (пузыря) в неограниченном
объеме более тяжелой сплошной среды. При трении поверх
ностньIХ слоев капли о сплошную среду они перемещаются в
направлении движен ия этой среды относительно капли, вовле
кая в циркуляционное движение жидкость внугри капли (газ
внугри пузыря), - в соответствии с направлением циркуляци
онных токов (см . рис . 2 .43 , б). Вторая причина деформации
обусловлена "стремлением" капли, пузыря двигаться в сплош
ной среде в режиме наименьшего гидравлического сопротивле
ния. В самом деле: увеличение поперечного размера капли при
деформации, конечно, повышает ее сопротивление, но сопуг
ствующее существенное уменьшение скорости движения (а сте
пень ее влияния высока - см.разд.2.7.4) в значительной мере его
снижает. В условиях деформируемости капли, пузыря на скорость
их движения в сплошной среде может оказывать заметное влия
ние поверхностное натяжение на границе дискретного элемента и
среды. Силы поверхностного натяжения стремятся мин имизиро
вать поверхность этого элемента, а значит сохранить его сфе
рическую форму. В качестве конкурирующего фактора при ма
льIХ скоростях скольжения выступают силы вязкости . Соотнесе-

•
244

Л одробно эти воп рос ы р:�ссмотре 1 1 ы

в (6, 1 1 , 1 5 , 1 6) .

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

-

-

Рис.2. 43. Движен ие капель и пузы
рей:
сферическая
а
мированная каnл я , в
ста ди и разрушен и я

-

дефор
каnля , б
круп н ая капл я в

ние сил вязкости и поверх
в
б
а
ностного натяжения приводит
к обобщенной переменной
wµ/cr. При более высоких
скоростях конкурируют силы инерции и поверхностного натя
жения, им отвечает обобщенная переменная p W2 d/cr = We, назы
ваемая критерием Вебера . (Заметим: безразмерное число wµ/cr
можно представить как отношение We/Re. )
Разумеется, при доминировании какого-либо из конкурирующих
факторов приведенные обобщенные переменные выроЖдаются.
Циркуляция слабо выражена в мелких (порядка 1 мм и ме
нее) каплях и пузырях из-за низкой относительной скорости
дисперсной и сплошной фаз, а также из-за существенного внут
реннего сопротивления циркуляции внутри мелкой капли. Д е
формация мелкой капли дополнительно подавлена еще действи
ем сил поверхностного натяжения. По указанным причинам
мелкие капли и пузыри движутся в сплошной среде со скоро
стями, достаточно близкими к рассчитанным по формуле (2.72).
Однако при увеличении размеров капель и пузырей влияние
внутренней циркуляции возрастает, деформация выражена все
заметнее. В этих случаях необходимо вносить поnравки в выра
жения для коэффициента лобового сопротивления � (см. фор
мулу (ц) в разд. 2.7.4). В результате совместного действия рас
смотренных эффектов скорость движения капель и пузырей
относительно сплошной среды возрастает - по приближенным
оценкам в "' 1 ,5 раза в сравнении с недеформируемыми твер
дыми шариками.
При движении весьма крупных капель и пузырей изменяется
механизм их обтекания сплошной · средой . Применительно к
этому случаю теоретический анализ приводит к вполне надеж
ной (подтвержденной опытами) зависимости для скорости и
подъема капель, пузырей, у которых форма их лобовой части
близка к сферической. Например, при Рд < Ре
и

=

k

gde(I - Р.1 ) ,
Р,

(2.78)

где d, - эквивалентный диаметр капли, пузыря , равный диаметру равновели
кой сферы : при объеме деформирован ного дискретного элемента У = 11d,3/6
' Анализ базируется на представлениях о потенциальном (безвихревом) тече
сплошной среды в окрестности дискретного образования . Рассмотрение
таких течений - за пределами курса (см. (4, 1 1 , 1 8, 25 J ) .
нии

245

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

d, = Vб V/rt . Коэффициент пропорциональности k теоретически
равен 0,7 1 1 ; опытам лучше соответствует k "" 0,75.

очевидно

При движении газовых пузырей в жидкости Рд < < Ре , и выра
жение (2. 78) упрощается:
(2. 7 8а)
и = k �gde .
При движении весьм а крупных капель и пузырей интенсивная
внутренняя циркуляция, обусловленная высокими скоростями
скольжения, может привести к сильной деформации и разруше
нию капли, пузыря - картина такого разрушения представлена
на рис. 2.43 , в.
Рассмотренные выше положения относятся к движению оди
ночных капель
и пузырей. При совместном движении мно 
"
жества ( коллектива") капель и пузырей наблюдается их гидро
динамическое взаимодействие. Здесь закономерности движения
изменяются, общий эффект аналогичен стесненному витанию
твердых частиц: движение капель и пузырей относительно
сплошной среды замедляется. Одновременно ситуация ослож
няется постоянной коалесценцией и разрушением дискретных
образований и их деформацией.
2.8. ДВУХФАЗНЫЕ ТЕЧЕНИЯ
2.8. 1 . Общие положения

В химической технологии многие процессы проводятся при
движении двух- и многофазных потоков в аппаратах и трубо
проводах. Здесь преследуются чисто транспортные цели или
ведется технологический процесс, либо реализуется сочетание
того и другого. При изучении и инженерных расчетах таких
систем необходимо учитывать взаимодействия как внутри пото
ка (между фазами), так и двухфазной системы со стенками ка
нала. Математические описания течения двух- и многофазных
систем - смешанная задача rидродuнамики - весьма сложны из
за необходимости одновременного учета взаимодействий между
фазами и со стенками, флуктуаций концентраций диспергиро
ванной фазы в рабочей зоне, различий в размерах, форме, а
иногда и плотности диспергированных элементов. Дополни
тельный осложняющий момент: гидродинамические характери
стики движения одной фазы зависят от характеристик движения
другой фазы (других фаз). По указанным причинам теоретиче
ское рассмотрение многофазных систем обычно п риходится
вести с существенными упрощениями ; нередко модели строятся
с при влечением экспериментальных данных; зачастую использу24 6

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ется аппарат теории размерностей, а иногда и чисто эмпириче
ские соотношения.
Взаимное перемещение фаз в аппарате возможно в одном и
том же направлении (тогда это прямоток - восходящий или нис
ходящий ) , в противоположных направлениях ( противоток ) либо
каким-нибудь иным образом (например, перекрестным током).
Все эти схемы при простейших описаниях подразумевают дви
жение фаз в режиме идеального вытеснения. Можно представить
себе течение, когда в результате интенсивнейшего перемешива
ния удельные и интенсивные характеристики выравнены по
объему рабочей зоны - говорят о движении в режиме идеально
го перемешивания (в пределах какой-либо фазы или для системы
в целом). Возможно и течение фаз с заметнь.1 м, но неполным
выравниванием характеристик - такое движение анализируется в
главе 8.
Скорости движения сплошной фазы w и стесненного витания
Wc удобно рассчитывать на поперечное сечение незаполненного
аппарата, как это было сделано при рассмотрении неподвижно
го, псевдоожиженного и движущегося слоев в разд.2.7. Д виже
ние элементов дискретной фазы характеризуют абсолютной ско
ростью " и " (относительно непОдвижного наблюдателя). Относитель
ная скорость движения фаз - скорость скольжения
в идеале
равна абсолютной скорости стесненного витания wJe (строже ее составляющей в направлении двухфазного течения). Су
ществует очевидная связь между абсолютными скоростями w/E,
и и wJe; приведем ее для случая более тяжелой дисперсной
фазы в сравнении со сплошной:
w - wr .
и= - для восходящего прямотока
-

- для нисходящего прямотока
- для противотока

Е

Е

-

Е

Е

Е

Е

w,. ,.
w +и= и = �- w

(а)

Среди характеристик проточных двухфазных систем (НС, а
также ПС без ввода и вывода твердого материала не являются
проточными по дисперсной фазе) выделим их удерживающую
способность, т.е. объемную концентрацию дисперсной фазы 13.
Удерживающая способность (еще ее называют задержкой при
диспергировании жидкости или твердой фазы в жидкости и
газосодержанием при диспергировании газа) и
порозность
связан ы одна с другой просто: 13 = 1
Величина задержки может быть оценена из следующих сооб
ражений. Пусть в аппарат с поперечным сечением f подаются
24 7
- i; .

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

массовые потоки дисперсной Gд и сплошной Gc фаз. Найдем
соотношение этих потоков, подставив их выражения из уравне
ния расхода ( 1 . 1 7):

G1, Рд и(рf) � � =Р w
=
Gc Pc Wf
Ре

(б)

Здесь в выражение Gд входит среднее живое сечение для
движения дисперсной фазы, поскольку и
абсолютная ско
рость .
Решим (б) относительно 13, имея в виду, что объемные расхо
ды фаз Vд и Vc легко выражаются через массовые ( V = G/p ) :
-

13

= Gдр,.

w = Vд w .

Gr P11 и

Vc

и

(2.79)

Подставим в (2. 79) значения и по выражениям (а) и сопоста
вим 13 с расходной объемной дол ей дисперсной фазы в потоках
Vд/( Vд + Vc ) .
Для восходящего прямотока

1-р
отсюда
(2.79а )
Для нисходящего прямотока
V

Р = V,.J\

w
w + wc
1-р

v 1= -д w,Р . ,
vc 1
---

+w

-

отсюда
(2.79б)
Для противотока

w v 1р = �' w w = __д _w__Р_ ,
V,.
Vc
c_
1-р
w 1
,. _
_
_
__

248

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

отсюда

Таким образом, при восходящем прямотоке дисперсная фаза в
своем движении отстает от сплошной, и истинная объемная
концентрация дисперсной фазы 13 превышает расходную. При
нисходящем прямотоке, наоборот, дисперсная фаза опережает
сплошную, и 13 меньше расходной объемной концентрации.
Случай 13 = Vд /( Vд + Vc) наблюдается лишь при солидарном
движении фаз, когда истинные скорости их движения одинако
вы, т.е. скорость стесненного витания Wc = О. Эrо теоретически
возможно при равных плотностях фаз, а практически - при близ
ких плотностях и(или) малых размерах дискретных элементов.
Поскольку при противотоке Wc /w > 1 , то в зависимости от
свойств дисперсной системы (величины wc) и рабочей скорости
сплошной среды ( w) возможны различные соотношения 13 и
расходной концентрации Vд /( Vд + Vc) . Солидарное движение
фаз при противотоке, разумеется, смысла не имеет, но су
ществует режим ( wc /w = 2), при котором 13 = Vд /( Vд + Vc) .
Выражения (2. 7 9) дают лишь общий подход к оценке 13 и по
зволяют проследить влияние на удерживающую способность
основных параметров процесса. Однако они не являются рас
четными , поскольку скорость Wc сложным образом зависит от
различных факторов: расхода обеих фаз, размеров диспергиро
ванных элементов и распределения их по размерам, конструк
тивных характеристик аппаратуры. Установить эту зависимость
для большинства сл уч аев удается пока только обобщением экс
периментальных данных.
Различают двухфазные течения с твердыми дискретными
элементами (их размеры и форма не изменяются в ходе движе
ния; это, например, газовзвеси, суспензии, сюда же можно от
нести и движущийся слой, рассмотренный в разд.2.7.3) и жид
костными либо газовыми элементами (здесь изменяются размеры
и форма в результате коалесценции, диспергирования, дефор
мации дискретных элементов; это эмульсии, барботажные си
стемы и др.). Ниже подробно рассмотрены некоторые течения с
твердой дисперсной фазой и затронуты отдельные аспекты те
чени й жидкость - жидкость и газ - жидкость.
249

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

2 . 8 . 2 . Транспортные системы с твердой фазой

Транспортн ые системы с твердой фазой могут быть класси 
фи цирован ы по разным признакам. Разл ичают пневмотранспорт
ные систе мы ( газовзвеси ) , когда несущей средой , переме
щающей твердые частицы , является газ , и гидротранспортные
( н есущий агент - жидкость) . По взаимному направлению движе
ния твердых части ц и несущей среды разл и чают прямоточные и
противоточные течения; существуют и разл и чного рода сложные
схемы ( перекрестное течен и е , закрученные потоки и др . ) . Для
прямотоков разл и ч ают восходящие и н и сходящие схемы движе 
н и я ; разл и ч и е здесь в знаках действующих сил , что отражается
на формирован ии скоростей скольже ния - см. формулы (а) в
разд . 2 . 8 . 1 . В зависимости от расположения транспортного кана
ла говорят о вертикальном , горизонтальном и наклонном тран 
спорте .
Важной является градация по концентрации твердой фазы в
потоке:
- при высокой ее кон це нтраци и говорят о транспорте в
плотной фазе ; здесь части цы находятся в непосредстве нной бл и 
зости одна к друго й , они постоян н о взаимоде йствуют со сте н 
ками канала;
- при н изкой кон центрации говорят о транспорте в разбав
ленной фазе ; здесь ч асти цы перемещаются в основном ядре по
тока и на некотором удалении одна от другой; их контакт друг с
другом и со стенками канала осуществляется за счет соударен и й ;
- существуют и промежуточные ситуаци и , когда твердый ма
териал транспортируется одновременно в виде плотн ых сгустко в
(ансамблей) и отдел ьных части ц.
Н иже будет рассмотрена одна из разновидностей транспортных
систем с твердой фазой : вертикальный прямоточный пневмотранспорт
в разбавленной фазе.

Общие характеристики пневмотранспортных систем
П ереч и сл и м некоторые важные особен ности таких верти 
кал ь н ых п н евмотранспортн ых систем в разбавленной фазе .
1 . Л и ней ная скорость несущего газового потока w должна
превышать скорость витания наиболее крупных части ц , состав
ляющих транспортируе мую смесь ТМ, иначе такие части цы не
будут подхваче н ы газовым потоко м . Эта особен ность предопре
деляет весьма высокие скорости w ( как правило, не менее
1 0 м/с) , так что движение газа происходит в турбулентном ре
жиме. И хотя эп юра скоростей газа при этом в достаточной сте 
п е н и выровнена, те м не менее у стенок канала существуют зон ы
с не высокой скоростью; в этих присте н н ых зонах локал ьная

250

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

скорость может быть меньше w8, и тогда частицы здесь будут
двигаться против несущего потока. Чтобы свести к минимуму
такие опрокинутые потоки ТМ, рекомендуется брать рабочую
скорость газа не ниже ( 1 ,5 - 2)w8 - в расчете на наиболее
крупные частицы.
2. Средние расстояния между частицами , транспортируемыми
в разбавленной фазе, существенно превышают их размеры (на
порядок и более). Это обусловлено крайне низкой концентра
цией ТМ в потоке (высокой порозностью
/3)
чаще
l
всего 13 менее l % .
3. Время пребывания твердых частиц в рабочей зоне очень
невелико. Действительно: частицы движутся быстро, их скорость
и лишь немного отстает от скорости несущей среды w. В резуль
тате чаще всего и - на уровне 10 м/с. Поэтому частицы проходят
рабочую зону за секунды, нередко и за доли секунды - это важно
для некоторых технологических процессов (может быть достоин
ством или ограничением в организации процесса).
Основные гидродинамические проблемы пневмотранспорт
ных систем: закономерности, связанные с массовыми расходами
газа и твердого материала, с распределением скоростей газа и
твердых частиц; определение гидравлического сопротивления
пневмотранспортных трубопроводов.
Важной эксплуатационной характеристикой пневмотран
спортных систем является номинальная концентрация твердой
фазы , представляющая собой отношение массовых потоков твер
дого материала Gт и газа G:
е

µном

=

G,
G

= - -

(кг /с).
ТМ

газа / с

(в)

(кгкг ) .

(г )

кг

Здесь в размерностях намеренно оставлены "секунды" , дабы от
личить µном от ИС1ЮПIОЙ концентрации µю представляющей собой
отношение масс твердой фазы mт и газа т, находящихся в данный
момент в транспортном трубопроводе:
µи =
-

тт
т

ТМ

газа

Е

Связь истинной концентрации с порозностью или объем
ной концентрацией твердой фазы 13 получается путем сопостав
ления количеств ТМ и газа в l мЗ пневмотранспортной системы:
р
р р.,
=
µи = (l - Е ) р =
µ 11 р . (2.80)
.,
, /3
(l р) р
ЕР
Рт + µ и р
р., + µ " р
Закономерности гидродинамики и физико-химических про
цессов в пневмотранспортных потоках определяются, конечно,
25 1

., - ИЛИ Е =

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

знач е н ием истинной кон центрации µ и ( ил и Е, р ) ; но в техноло
гических расчетах удобнее п ол ьзоваться вели ч и нами µ н ом· Связь
µ н ом и µ и найдем путем сопоставления выражен и й (в) и ( г) , опе
рируя средней расчетной скоростью газового потока w и абсо 
лютной скоростью движения твердых части ц и. П о уравне н и ю
( 1 . 1 7) G = p wf, где f - поперечное сечение трубопровода. Для
определения потока Gт необходимо учесть дол ю сечен и я , зани 
маемую твердым материалом и в среднем равную р : Gт = Рт ( Р./) и .
Отсюда, выражая вел и ч и н ы РРт и р , имеем
µ"

- РРт

-

(1 - р)р

--

G, fw
( 1 - р) fu G

- µ н о м u( I W -- µном �E µ н о м wи .
- р)
U
-

'

(2 8 1 )
.

переход к последнему выраже н и ю обусловлен тем , что в разбав
ленных пневмотранспортн ых системах р � О, Е � 1 .
П р и и � w (это практически реализуется для очень мел ких и
легких части ц, когда значения w0 очен ь мал ы ) , т . е . при солидар
ном движе н и и фаз, µ н ом � µ и . Реал ьно в случае восходя ще го
пря м отока и < w, так что исти нная массовая кон центрация µ и
всегда бол ьше рассчитанной из баланса п отоков µ н ом (при нис
ходя ще м прямотоке соотношение µ и и µном будет, естестве н н о ,
обратн ы м ) .
Распределение скорости газа в попереч 
ном сеч е н и и транспортного трубопровода ,
Газовзв е с ь
несмотря на н изкие концентраци и ТМ, су
щественно отл и чается от характерного для
однофазного газового потока.
Н ал и ч и е
твердых части ц вызы вает деформацию ско
ростного профиля газа, причем в случае
верти кального п невмотранспорта происхо
дит выравн и вание скоростей в сеч е н и и с
одновременным увеличением пристеночных
градиентов скоросте й . Экспериме нтал ьн о
доказано, что при этом изменение скоро
стей п о нормал и к поверхности в при
сутствии твердых части ц продолжает следо
вать закону сте н ки ( 2 . 25а) .
Схема транспортного трубопровода пред
ставлена на рис. 2 .44. В нижнее сечение рабо
чей зон ы (общая длина ее / ) вводится твер
дый материал. Его подхватывает газовый
поток, и твердые части цы нач и нают разго: : : : тм
.

Газ
252

.

tw

Рис . 2. 44. К о п ределе н и ю со п ротивле н ия п ри восходя
щем п ря м оточ н о м пн е в м отра н с п орте в разбавле нн ой

фазе

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

няться до некоторой равновесной скорости на некотором разгон
ном участке /Р. Далее (на стабилизированном участке Zст) части
цы движутся с постоянной (в осредненном смысле) скоростью
и. Несколько идеализируя ситуацию, обычно полагают, что они
отстают от газового потока на величину скорости витания: и :::: w
На самом деле это отставание больше из-за торможения
частиц за счет их частых (и не полностью упругих) ударов о
стенки трубопровода.
Заметим: в стационарном режиме движения газовзвеси .з на
чение µ ном одинаково во всех сечениях по длине трубопровода
(это следует из баланса по твердому материалу в единицу вре
мени для контура, ограниченного стенками трубопровода и по
перечными сечениями - нижним и произвольным). Однако µ и
выше в нижних сечениях, где частицы еще не приобрели равно
весную скорость,- это следует из выражения (2.8 1 ): скорость час
тиц и нарастает снизу вверх до примерно постоянной величины.

-

-

w8 .

Гидравлическое сопротивление
Для рассматриваемой пневмотранспортной системы общее со
противление ЛРrс складывается из трех основных составляющих:
- статической Лрст, обусловленной необходимостью поддер
жания определенной массы твердого материала mт во взвешен
ном состоянии;
- разгонной Лрр , связанной с затратами энергии на разгон
твердых частиц до постоянной скорости и;
- гидродинамической ЛРг/д • отражающей взаимодействие по
тока со стенками трубопровода:
(2.82)
ЛРтс = ЛРст + Лрр + ЛРг/д
Кроме того, в ряде случаев может оказаться существенным
вклад затрат (диссипации) энергии за счет неупругого соударе
ния частиц.
Составляющая Лрст вызвана теми же причинами, что и для
псевдоожиженного слоя; ее расчет ведется по формуле (2.70) :
ЛРст = ( Рт p )g( l
(2.83)
Е) / = ( Рт - p )g/3 /
Разумеется, в большинстве случаев р < < Рт. так что сла
гаемым р в скобках можно прен ебречь.Основная проблема здесь
в определении 13. Оценить эту величину можно с помощью со
отношений (2.80), (2.8 1 ) при известных Gт и G; более точные
значения дает · эксперимент с мгновенной отсечкой потока на
рабочем участке трубо п ровода и измерением значений mт и т.
Для определения Лрр примем, что в начальном (нижнем) се
чении вертикальная составляющая абсолютной скорости частиц
равна ин. Тогда затраты кинетической энергии в единицу време.

-

-

·

253

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

( ; и,: ) =

( и 2 ; и� )

ни на разгон частиц до скорости

Gт

и2

µ но м G

и

составят

= µ ном Р

{ и2 ; � ) ,
и

где V - объемный расход газа (в том сечении, для которого взята его плотность
р, предпочтител ь нее - в начал ь ном). Но те же затраты моrуг быть формально
записаны в в иде дрр V. Приравнивая эти величины и сокращая на V, получим
- и2
(2.84)
Лрр = р µ но м 2 "

и2

При ин = О эта формула упрощается.
Наиболее сложной является проблема определения ЛРг/д ·
Согласно формуле (2.82), эта составляющая призвана отразить
деформацию скоростного поля газа в присутствии твердых час
тиц (возросшие пристеночные градиенты скоростей вызывают
увеличение Лр в сравнении с однофазным потоком газа), а так
же затраты энергии на восполнение потерь скорости частиц из
за соударений со стенками канала. Проблема эта в настоящее
время до конца не решена. Приведем один из существующих
оценочных подходов к ее решению - на основе формулы Д ар
си - Вейсбаха в форме (2. 1 7а).
Для однофазного газового потока

_ � /тр _ _1_ w G
Р _- А г _!
d 2 р f - А г d 2/ '
тр
тр тр
тр
где /тр - се че н и е трубопровода диаметром d.,p.
л

(д)

Постулируем (феноменологически), что аналогичным обра
зом будут выражаться потери давления и при движении газо
взвеси ; только массовый поток должен быть представлен пол
G( 1 +
ностью: вместо G надо подставить G + Gт G( 1 + Gт/ G)
+ µн ом). Тогда

=

=

/ wG (l + µ ном )
ЛРг/д = А г d
2 /тр
тр
w 2 p( l + µ
= А г / w( p w/тр )( 1 + µ ном ) = А г d / T
(е)
ном ) ,
d
2 /тр
тр
тр
причем А г первоначально было предложено определять по фор

мулам для однофазных потоков. Однако такая линейная связь
и µ ном не нашла экспериментального подтверждения, по
скол ьку не учитывала деформацию скоростного поля газа в при
сутствии твердых частиц. Потребовалась замена "обычного" А г
ЛРг/д

2 54

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

на коэффициент гидравлического сопротивления для пневмо
транспортной системы "1-с = ./{ Rетр , µн 0м ) , причем Rетр базирует
ся на w и drp·

При ведем пример эм п ирической расчетной формулы дпя Лтс в случае турбу
лентного течен ия газа:
µ ом Re, -0, 20 .
Лт
(ж)
20 + О ,88 н
с
Р
'
' ( l + µ но" )2
=

[о

]

эта формула носит оценочный характер и применима в случае умеренных зна
чений µном - не выше 1 (кг ТМ/с)/(кг газа/с) .
Легко видеть , что при µном -... О формула (ж) трансформ ируется в выраже
ние, близкое к формуле Женеро ( 2 . 28 г) .
П родемонстрированный выше подход к определению ЛРг/д не является
единственно возможн ым. Влияние твердого материала иногда рекомендуют
учитывать с помощью уравнений типа (2. 1 7а), зап исанных для твердых час
тиц - с определением коэффициента гидравлического сопротивления по эм
пирическим формулам·.

2.8.3. О . двухфазных течениях типа жидкость - жидкость
..
и жидкость - газ

Постоянное изменение размера и формы дискретных образо
ваний (капель, пузырей) сопровождается изменением условий
их движения и контакта фаз. Именно эти причины, затрудняю
щие теоретический анализ, привели к распространению статис
тических подходов к описанию характеристик таких систем,
часто - с привлечением экспериментальных данных.
Д вухфазные системы используются либо при движении дис
кретной фазы через неподвижную сплошную, либо при движе
нии через аппарат обеих фаз - прямотоком, противотоком или
по какой-нибудь более сложной схеме взаимного перемещения.
В зависимости от используемых фаз, их расходов, степени дис
пергирования и других условий возникают различные режимы;
некоторые из них для вертикальных потоков показаны на рис.
2. 4 5 и обозначены в подписи к рисунку.
Связь задержки дисперсной фазы (для рассматриваемых си
стем ее чаще всего обозначают Ф - это ан алог � для систем с
твердой фазой) с параметрами процесса в общем определяется
соотношениями типа (2. 79). Однако для систем с изменяю
щимися размерами и формой элементов дискретной фазы, да
еще при соизмеримых объемных концентрациях этих фаз в ра
бочей зоне, возникают большие сложности с определением ско
ростей wc, а значит и и. Поэтому здесь весьма часто используют
ся эмпирические соотношен ия , отвечающие конкретным условиям
процесса, его конструктивному оформлению, свойствам фаз .
• См. ( 8 , 1 9 , 2 1 ) .
• • Подробнее о двух- и многофазных течениях см. [ 1 4, 1 6, 2 1 1

и

др.

255

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

о

-

о

о

о

-

о

-

о- о
-о
о -0
о -:..

-

0

_с::г

Рис. 2. 45. Режимы течения двух фазных систем:

а - дисперсн ы й , б - пузырьковы й , в
- порш н е во й , г - кол ь цево й

Для противоточных двух
фазн ых систем важной харак
теристи кой я вляется скорость
захлебывания w3 , определяе
а
в
г
мая как скорость потока
сплошной фазы , при которой
он "запирает" систему, не
позволяя дисперсной фазе дви гаться проти вотоком к сплош ной .
Я вление захлебывания может также набл юдаться в насадо ч н ы х и
пленоч ных аппаратах: например, при чрезмерно высоких скоро
стях восходя щего газового потока жидкость не может сте кать
вниз по насадке ил и по верти кальной стенке. Отметим опреде 
лен ное сходство явления захлебывания с зависанием твердой
фазы в аппаратах с движущимся слоем (см.разд. 2 . 7 . 3 ) . Скорости
захл е бывания для разл и ч н ых процессов чаще все го рассч иты
ваются по эмп ирическим формулам· ; лишь для наиболее про
стых систем (ти п а гравитационного течения тон ких пленок) они
поддаются теоретическим оцен кам••
К расчету гидравлического сопротивления двухфазн ых теч е н и й
ЛРдф предложено много подходов. Такого рода разночтения в
подходах к описан и ю какого - либо я вления часто обусл овл е н ы
отсутствием хорошей его модел и (здесь - течения) и поп ытка
м и найти луч ш и й подход. Однако в рассматр и ваемом случае
есть и и н ы е (объекти вные) при ч и н ы разл и ч и й в подходах :
многообразие режимов тече ния двухфазных систем должно най
ти с вое отражение в мн ожестве нности модел е й . Действительно,
реж и м ы тече н и я , представленные на рис . 2 .45, трудно отразить
еди ной модел ью и о п исать еди ной зависимостью . Мал о того ,
каждая из фаз может переме щаться по транспортному трубопро
воду в разл и ч н ы х режи мах (ламинарном , турбулентном и др. ) , и
здесь возможны разные сочетан ия, которым должны отвечать
разн ые расчетные формул ы .
П роде монстрируем следующие основные подходы к опреде 
ле н и ю ЛРдф при теч е н и и двухфазн ых систе м .
Расчет ЛРдф строится на формальном испол ьзован и и уравне
ния Дарси - Ве йсбаха . При этом иногда двухфазны й поток
трактуют как однофазн ый с некоторыми усредненными характе 
ристи ками ( плотн остью, скоростью и др. ) , рекомендуя те ил и
_'::;)

н а пример, [6 , 1 3 - 1 5 . 1 7 ] .
Применительно к течению тон к их плено к см. [6] .

· С
м"

••
256

в·

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

иные способы подсчета этих усредненных характеристик. В
этом случае основные трудности расчета переносят на Лг, для
которого подбирают соотношения, отвечающие эксперимен
тальным данным. В другом варианте уравнение Д арси
Вейсбаха записывают раздельно для дисперсной и сплошной
фаз - со своими параметрами (Лг, w, р и пр.). В этом случае
трудности расчета заключаются в способе объединения этих
составляющих - обычно подбирают формулу, позволяющую
учесть вклад каждой фазы в общее сопротивление движущейся
двухфазной системы.
Видимо, более перспективны и плодотворны попытки анали
за двухфазных течений с учетом режимов движения фаз, с по
строением соответствующих физических и математических мо
делей (в манере уравнения Д арси - Вейсбаха или исходя из
Рассмотрение таких моделей выходит за
других предпосылок).
•
пределы курса .
2.9. ОБ ОСОБЕННОСТЯХ МОЛЕКУЛЯРНОГО ТЕЧЕНИЯ

Выше рассматривалось течение сплошных сред, когда средняя
длина пробега молекул L была много меньше характерного раз
мера (масштаба) течения, на котором существенно изменяются
параметры последнего (скорость потока, давление, температура
и пр.). В качестве такого масштаба / в зависимости от постанов
ки задачи выступают толщина пограничной пленки Б, диаметр
канала d или его длина.

Безразмерное отношение (си мплекс) L/1, определяющее свойства среды и
характер ее течения, н азывается числом Киудсена Кn. При очен ь низких значе
ниях Кn < < I (по различным данным - при Кп < 0,00\ -0,0 1 ) среда ведет себя
как сплошная и в своем движении следует рассмотренным в предыдущих раз
делах уравнениям гидроди намики. Однако в ряде технологических ситуаций
встречаются течения, когда длина пробега L становится соизмеримой с харак
терн ым размером канала / - такие течения называют молекуЛJ11р иыми.
Установлено, что в и нтервале значений 0,0 1 < Кn < 0, 1 уравнения гидродина
мики сплошной среды тоже могут быть использованы, но только оля яора пото
ка. А непосредственно на стенке канала (или обтекаемого средuй тела) наблю·
дается явление '"проскальзывания": говорят о скачке скоростей (при теплообме
не - о скачке температур и т.д.). П ри Кn > 1 пограничный слой на стенке
канала (обтекаемого тела) не образуется , отраженн ые от стенки молекулы могут
столкнуться с другими молекулами только на удалении от стенки , так что она
практически не влияет на характеристи ки движения потока (поле скоростей и
др. ) . Такой режи м течения называется свободномолекуЛJ11р ным. В тех случаях,
когда значение Кп заметно превышает 1 (обычно полагают - при Кп > 3),
молекулярное течение рассчитывают, исходя из условия однократного столкно
вения молекул со стен кой канала. Что касается диапазона О, 1 < Кп < 1 , то в
настоящее время он изучен слабо: в этой промежуточной области надо учиты •

См. ( 1 6, 2 1 ] .

257
9-650

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

вать соударения молекул как между собой , так и со стенками канала, что созда
ет немалые теоретические трудности.
В качестве наиболее распространенного примера молекулярного течения
обычно приводят движение разреженных газов (при очень низких давлениях:
произведение давления на определяющий размер канала р/ -порядка 1 Па·м и
менее). С такими режимами течения на практике встречаются также при реали
зации некоторых процессов переноса в условиях глубокого вакуума или при дви
жении в очень узких каналах. В качестве модельных некоторые соотношения
молекулярного течения могут оказаться полезными при описании движения
разреженных двухфазных дисперсных систем в каналах.
Основная цель анализа молекулярных течений в аспекте курса ПАХТ состоит
в отыскани и выражений для скоростей и потоков в каналах и аппаратах в зави
симости от рабочих условий . Заметим, что доскональный анализ явлений здесь
весьма сложен , поэтому ниже приводятся (зачастую без подробных выводов)
предпосылки и соотношения, необходимые для описания процессов в ряде
последующих глав·.
В основе анализа лежит ряд известных соотношений молекулярной физики ;
приведем некоторые из них.
Средняя скорость движения молекул газа

;; =�8RyT ,

где Ry - универсальная газовая постоянная; Т - абсолютная температура;
молярная масса.
Вязкость газа:
1 - ,
хМ

µ=

1. р и L

М

-

(а)

(б)

где р - плотность газа.
В условиях соизмеримости длины свободного пробега молекул L и толщины
пограничной пленки S перестает оставаться справедливой "концепция прили
пания" - газ движется со а�: непосредственно у стенки его скорос1Ъ wя " ,
" О. В целях упрощения анализа примем при
ближенно (рис. 2.46), что течение газа в ядре
потока происходит с постоянной (выров
ненной) по сечению скорос1Ъю w, а все паде
ние скоростей от w до wя наблюдается в пограничном слое, толщина которого S равна
G
длине свободного пробега L. Тогда напряжение
трения на стенке 1
2

Ts =

w

( - wR ) .

µ w

s

(в)

Если подставить в (в) вязкость µ по (б) и
скорость 'ii по (а), то при S L получим
=

Рис.2. 46. К упрощенной модели молекуляр

r

ного течения газа со скольжением на стенке
канала:
1

- пограни'lная пленка, 2 - ядро nотока

• Детальный анализ различных модификаций молекулярных течений рас
смотрен , например, в монографии ( \ ) , в упрощенном варианте некоторые
аспекты этого течения изложены в [22) .
258

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

после сокрашения на
t,

L

1
= 2

p

u

2р

( w - wя) =

1

-

8 Ry T

J

(w - wя) .

--

лМ

(г)

Величину t, удобно выразить из очевидного равенства (равновесия сил) для
участка трубы длиной / и диаметром d (см . разд. 2.2.2 и 2.2.4): t,лd/ = Лр(лd2/4),
где Лр = р 1 - р2 - разность давлений на входе в трубу и на выходе из нее;
тогда t, = ( Лр/4/)d. Отсюда
2�, �
.
d � Лр
w - wя +
(д)
wя
.
P

V 8Ry T

_

+

=

2 p V SRJ l

Для определения массового потока газа следует воспользоваться уравнением
расхода ( 1 . 1 7): G = pw(лd2/4). При использовании ( 1 . 1 7) примем , что можно
пренебречь продольным потоком газа в пограничной пленке ввиду м ал ости ее
толшины б и сечен ия лd/'J, т.е. слагаемым wя в (д) , полагая , что п1з по всему
поперечному сечению трубы движется со скорост ью w:
G

=

Р

d � Лр лd2
2 р V 8RyT l -4-

G

или

� Лр

= 16 V 2 Ry T Т ·
лd3

(е)

Разумеется , более строгий анализ потребовал бы учета· изменения скорости
в ядре потока (за пределами модельной погран ичной пленки), где движение
ламинарное. Это нетрудно сделать по канве, изложенной в разд. 2. 2.4, только в
качестве значения скорости на стенке трубы (нижний предел при интегрирова
нии) надо будет подставлять не w = О, а w = wя. Такой анализ позволяет вычле
нить вклад составляюших: ламинарной и кнудсеновской (движения газа со
скольжением на стен ке канала). Но в аспекте поставленной цели здесь нам важен
характер влияния параметров течения на величину массового потока газа:
(ж)
G - ,/М ! Т (Лр//) .
Обратимся теперь к саободному молеку.uриому течению газа в длинной тру
бе круглого сечения (Кп >> 1 ). Строгий анализ, рассматриваюший отражение моле
кул, падаюших на стенки трубы, приводит" к следуюшему выражению дпя G:
G=

Подставляя
ва) , находим

/1

d

_

dp

d.x

лd

(з)

2

- - /1 - --

•

по (а) и р = pM/Ry Т (из уравнения Клапейрона - Менделее
G

=

-

:!._
3

з

4

__
J8 RyT _!!_
RY T dx

dp л d 2
4

-rr. M

.

(и)

Полагая градиент давления постоянным no дпине трубы: - (dp/dx) = (р1 - Р2)// =
= Лр//, получаем (после уnрошений) дпя изотермического течения газа выражение,
сходное по структуре с nрибпиженным (е), но с иным численным коэффициентом:
G = d3

J

2R T
лМ

Лр .

(2.85)
/
Удельный массовый поток, отнесенный к еди нице поперечного сечения / =
= лd 2/4, составляет

З

G/f = � d
3

J

y

Лр
М
.
2 л Rу Т /

• См. сноску на предыдушей странице.

(2.86)

259

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Последнее выражение можно трактовать как разность противоположных
нескомпенсированных потоков - от входа канала к выходу:
и от выхода к входу:

idJм/(2nRyT)

�

!i .
1

Из этих выражений следует, что при прочих равных условиях удельный мас
совый поток rаза (пара) пропорционален комплексу
(к)
рJМfт .
Приведенные в этом разделе положения и полученные результаты будут ис
пользованы при анализе процессов молекулярной дистилляции и мембранного
разделения .
Л ИТЕРАТУРА к главе 2

1 . Абрамов11ч Г.Н. При кладная газовая динамика. М . : Наука, 1 976. 888 с .
2. Аэров М. Э. , Тодес О.М. Гидравл ические и те мовые основы работы аппаратов с о ста
ционарным и ки пящим зернистым слоем. Л . : Химия , 1 968. 5 1 2 с.
3. Баскаков А . П. , Берz Б. В. , В11тт О. К. 11 др. Теплотехника. М . : Энергои здат, 1 982. 264 с .
4. Берд Р. , Стюарт В. , Лайтфут Е. Я вл е н и я переноса : П е р . с а н гл/ Под ред.
Н . М . Жаворонкова, В.А. М алюсова М . : Химия , 1 974. 688 с.
5. Буев11ч ЮА., Мtиtаев Г.А. С1J>УЙНое псе1111оожижение. М.: Химия, 1 984. 1 32 с.
6. Гельпер1111 Н.И. Основные процессы и аппараты химической технологии. М . : Химия ,
1 98 1 . 8 1 2 с.
7. Ге11ьпер1111 Н. И., Ай11штеi111 В. Г , Кваша В.Б. Основы техники псевдоожижен ия . М . :
Химия , 1 967. 664 с .
8. Ге11ьпер1111 Н. И. , Аti11шт�й11 В. Г Псевдоожижение, гл .Х\ "Ан ал огия между псевдоож и

женн ы м слоем и капел ьной жидкостью" / Под ред. Дэвидсона И.Ф., Харрисона Д . : Пер. с
англ/ Под ред. Н . И . Гельперина. М . : Химия , 1 974. 760 с .
9. Горб11с З. Р. Теплообмен и гидродинамика дисперсных сквозных потоков. М . : Энер
гия , 1 9 7 1 . 424 с.
1 0 . Да11юшевск111i Б. Ю. Вентиля ционные и пневмотранспортные установки в нефтя ной
пром ышленности (а эродинамические основы расчета). М . : Машиностроение, 1 976. 1 92 с.
1 1 . Дэв11дсо11 И. Ф. , Харр11со11 Д. Псевдоожижение твердых частиц: П ер. с а н гл / Под ред.
Н . И . Гельперин а . М . : Химия , 1 965. 1 84 с.
1 2. Иде11ьч11к И.Е. Справоч н и к по гидравлическим сопротивления м . М . : Машинострое
н и е , 1 975. 560 с .
1 3 . Касатк1111 А . Г. Основные процессы и аппараты химической технологи и . М . : Химия,
1 97 1 . 784 с.
14. Кафаров В. В. Основы массопередачи. М . : Высшая ш кола, 1 979. 440 с.
1 5. Koza11 В. Б. Теоретические основы типовых процессов химической технологии . Л . :
Химия , 1 977. 592 с .
1 6. Кутателадзе С. С. , Стыр11ков11ч М.А . Гидродинамика газожидкостн ых систем. М . :
Энергия , 1 976. 296 с .
1 7. Павлов К. Ф" Рома11ков П. Г. , Носков А . А . Примеры и задачи по курсу процессов и
аппаратов химичес кой технологи и . Л . : Химия, 1 987. 574 с .
1 8. Патрашев А . Н. Гидродинамика. М . : Военно-морское и:щ-во, 1 953. 720 с.
19. Разумов И.М. П невмо- и гидротранспорт в химической промышленности . М.: Хи
мия, 1 979. 248 с.
20. Саж1111 Б. С. . Саж1111 В. Б. Научные основы техники суш ки . М.: Наука , 1 977. 448 с .
2 1 . Соу С . Гидродинамика многофазных систем: П е р . с ан гл/ П о д ред. М . Е . Дейча. М . :
Мир, 1 97 1 . 536 с .
22. Ц11боравск111i Я. П роцессы химической технологии : Пер. с пол ьск/ Под ред.
П . Г. Роман кова . Л . : Госхимиздат, 1 958. 932 с.
23. Чечетют А . В. , За11емоие11 НА. Теплотехника. М.: Высшая школа, 1986. 344 с.
24. Ч11е11ов В. А . , М11хтi11ов Н. В. В иброкипя щий слой . М . : Наука, 1 972. 344 с.
25. Чуzаев Р.Р. Гидравл ика. Л . : Энергия , 1 97 1 . 552 с.

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Глава 3

ПЕРЕМЕЩЕНИЕ ЖИДКО СТЕ Й

В гл. 2 ( " Гидравлика") закономерности течения жидкостей
рассматривались безотносительно к средствам их перемещения.
В настоящей главе речь пойдет о средствах перемещения.
Как было показано в гл. 2, перемещение жидкостей по тру
бопроводу происходит лишь при наличии разности полных на
поров на его концах. Если эта разность напоров обусловлена
более высоким уровнем жидкости в исходной емкости по срав
нению с собирающей, то такое перемещение жидкости именует
ся самотеком. Скорость движения жидкости при этом, как пра
вило, невелика. Для повышения скорости подачи жидкости, а
также для транспортирования жидкости с некоторого уровня на
более. высокий используют принудительное течение за счет созда
ния дополнительного напора. Этот напор может быть обеспечен
путем увеличения давления газа на свободную поверхность жид
кости в резервуаре, из которого откачивается жидкость (назовем
его расходным), - такие устройства получили название напор
ных емкостей, или монтежю . Необходимое давление в последних
рассчитывают на основе законов гидравлики с учетом всех гид
равлических потерь в трубопроводе от монтежю до приемного
резервуара. Но чаще всего необходимый напор создают путем
передачи механической энергии от движущихся рабочих органов
(поршень, колесо и т.д.) к жидкости. В последнем случ ае преоб
разование механической энергии двигателя в энергию транспор
тируемой жидкости с помощью рабочих органов происходит в
гидравлических машинах, называемых насосами, или (чтобы
подчеркнуть наличие движущихся рабочих органов, передающих
механическую энергию к жидкости) механическими насосами.
К насосам относят также устройства без движущихся механи
ческих частей, обеспечивающие разность напоров жидкости или
ее подъем на некоторую высоту другими способами. Назовем их
немеханическими насосами .

26 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

3. 1 . КЛАССИФИКАЦИЯ НАСОСОВ .

ТИПОВАЯ СХЕМА И ОСНОВНЫЕ ХАРАКТЕРИСТИКИ
НАСОСНО Й УСТАНОВКИ
3. 1 . 1 . Классификация насосов

Как уже было сказано, насосы подразделяются на две боль
шие группы: механические и немеханические (табл. 3 . 1 )
Применяемые в химической промышленности типы механи
ческих насосов чрезвычайно многообразны, их классифицируют
по производительности и равномерности подачи, по уст
ройству, характеру и скорости перемещения рабочих органов,
Не останавли
а также по иным признакам.
ваясь на других классификациях, будем механические насосы
группировать по принципу их действия на объемные (насосы
вытеснения) , лопастные (насосы* обтекания) и вихревые (насосы
увлечения - за счет сил трения) .
.

Таблица З. /. КласснфнкаЦИ11 насосов
Вид

Разновидности

Н омер
рисун 

Оrли ч ительные ч ерты

ка

Механические

Объемные:
поршневые

3. 1 , а Движущийся рабочий орган поршень или плунжер

ротационные:
пластинчатые 3. 1 ,

б

3.1,

в

3. 1 ,
3. 1 ,

г
д

шестеренчатые
винтовые
шланговые
Лопастные:
центробежные
пропеллерные
(осевые)
Вихревые
Немеханические Газлифт
Струйные
Монтежю

Рабочий орган - ротор с выдвижными пластинами
Рабочий орган - шестерни
Рабочий орган - винты
Рабочий орган
перемещающиеся прижимы

3. 1 , е Рабочее колесо при вращении
и 3. 1 7 обеспечивает выброс жидкости
на периферию
3. 1 , Лопасти на вращающемся валу
ж
обеспечивают
перемещение
жидкости в осевом напрамении
Многократный выброс жидкости
на периферию
3.29 Создание газожидкостной смеси
с плотностью меньшей, чем у
жидкости
3.30 Большая кинетическая энергия
струи
Неподвижный газ под дамением

• Место каждой группы в общей классификации насосов видно из табл.3. 1 .

2 62

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Принцип действия объемных насосов заключается в отсече
нии рабочими органами насоса некоторого объема (порции)
жидкости, поступающего по всасывающей линии, и последую
щем его выталкивании в нагнетательную линию с изменением
при этом энергии давления.
В объемных насосах (рис. 3. 1 , а - д) рабочие органы 1 обра
зуют замкнутые объемы, в которые из всасывающего трубопро
вода 2 поступают порции жидкости за счет разрежения, созда
ваем.ого при движении этих рабочих органов. Затем упомянутые
порции жидкости под воздействием тех же рабочих органов вы
талкиваются в нагнетательный трубопровод 3. Количество пода
ваемой объемным насосом жидкости определяется геометриче
скими размерами его рабочих органов и числом актов всасыва
ния и выталкивания в единицу времени. Величина создаваемого
напора (давления) в принципе не ограничена.
В зависимости от вида совершаемого рабочими органами
движения (возвратно-поступательного или вращательного) объ
емные насосы подразделяются на поршневые, ротационные и
шланговые.
В поршневых насосах (рис. 3. 1 , а) возвратно-поступательное
движение совершает поршень или плунжер. Принцип действия,
особенности работы и расчет таких насосов подробно рассмат
риваются в разд.3.2.
К ротационным относят насосы (рис. 3. 1 , б - г) , рабочие ор
ганы которых совершают вращательное движение: пластинча
тые, шестеренчатые, винтовые.
Принцип действия пластинчатого насоса понятен из рис.
3. 1 ,б. При вращении ротора, расположенного эксцентрично по
отношению к цилиндрическому корпусу насоса, под действием
центробежной силы пластины частично выдвигаются из пазов в
роторе и прижимаются к корпусу, образуя замкнутые объемы.
За счет увеличения объема между двумя соседними пластинами
в этом пространстве создается разрежение, и жидкость из вса
сывающего трубопровода 2 заполняет замкнутый объем между
пластинами, корпусом и ротором. Затем эта порция жидкости
перемещается вместе с пластинами, рабочий объем уменьшается
и жидкость выталкивается в нагнетательный трубопровод 3.
В шестеренчатом насосе (рис.3. 1 ,в) установлены две шестерни
1, одна из которых - ведущая, а другая - ведомая. Между кор
пусом 4 и соседними зубьями шестерен 1 образуются замкнутые
объемы. При вращении шестерен в направлении, указанном
стрелками, вследствие создаваемого разрежения (за счет выхода
зубьев из зацепления) жидкость из всасывающего патрубка 2
поступает в корпус. Далее жидкость заполняет пространство
между соседними зубьями и корпусом, перемещается вдоль
263

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

3

1

2

а

б

г

в

2

1

1

д

е

ж

Рис.3. 1. Схемы механических насосов различных типов - объемных (а
поршневой , 6-д - ротационные) и лопастных (е, ж) :

-

а - поршневой: / - поршень, 2 и J - всасывающий и нагнетател ьный патрубки ; б пластин чатый н асос: / - ротор с выдвиж н ы м и пласти нами, 2 и J - всасываюший и нагне
тательн ы й патрубки; в - шестерен чатый : / - шестерн и , 2 и З - всасывающи й и нагнета 
тельный патрубки , 4 - корпус; г - винтовой: / - винты, 2 и 4 - нагнетател ьный и всасы
вающий патрубки , J - шестерни , 5 - корпус; д - шланговый : / -прижимы, 2 и J - вса
сывающий и нагнетательный патрубки, 4 - шланг, 5 - обойма (корпус ) ; е - центробеж
ный: / - лопатки , 2 - рабочее колесо; ж - пропеллерн ый: / - рабочее кол есо, 2 - кор
пус, J - направля ющий аппарат

стенки корпуса по направлению вращения шестерен и вытес
няется в нагнетательный трубопровод 3. Заметим, что насос
является реверсивным, т.е. при перемене направления вращения
шестерен области всасывания и нагнетания меняются местами .
2 64

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Винтовой насос (рис. 3 . 1 , г) по принципу действия аналогичен
шестеренчатому. Он состоит из двух винтов J, вращающихся
при помощи шестерен З в противоположных направлениях.
Винты помещены в плотно охватывающий их корпус 5 с внут
ренней гладкой цилиндрической поверхностью. Чтобы исклю
чить осевые нагрузки , жидкость подают с обоих торцов, а отво
дят - в середине насоса. Жидкость поступает в нарезку винтов
с торцов корпуса, заполняет объемы между витками винтов и
корпусом. При вращении винтов жидкость перемещается к се
редине корпуса и вытесняется в нагнетательный трубопровод 2.
К объемным насосам относятся также шланговые (рис. 3 . 1 , д) ,
в которых цилиндрические прижимы 1 (колесики) сдавл ивают
llVlaнг 4, образуя замкнутые объемы (порции) жидкости в нем.
При перекатывании прижимов порции жидкости перемещаются
от всасывающей стороны 2 к нагнетательной З по принципу
перистальтики .
В лопастных (лопаточн ых) насосах преобразование энергии
двигателя происходит в процессе обтекания лопастей (лопаток)
колеса при их силовом воздействии на поток. Они подразделя
ются на центробежные (радиальные), пропеллерные (осевые) и
диагональные.
В центробежных насосах (рис. 3 . 1 , е) при вращении рабочего
колеса возникает центробежная сила; она действует на жид
кость, находящуюся между лопатками колеса, и жидкость дви
жется от центральной его части к периферии - в целом в ради
альных направлениях.
В пропеллерных насосах (рис. 3 . 1 , ж) движение жидкости
происходит преимущественно в аксиальном (осевом) направле
нии за счет подталкивания жидкости лопастями.
В диагональных насосах осевые и радиальные составляющие
абсолютной скорости жидкости - величины одного порядка.
У вихревых насосов преобразование энергии двигателя в пе
ремещение жидкости происходит в процессе интенсивного об
разования вихрей и их последующего разрушения при взаимо
действии рабочего органа с медленно движущимися частицами
жидкости . Этот весьма сложный механизм действия вихревых
насосов
подробно изложен в специальной литературе по н асо•
сам .
Среди немеханических насосов отметим газлифт, струйные и
монтежю.
Газлифт (эрлифт) обеспечивает создание напора (и подъем
жидкости) за счет введен ия в жидкость практически неподвиж
ного газа.

' С м ., н апример, ( \ ] .

26 5

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис.3. 2. Типовая схема насосной установки :

J
4

-

расходны й резервуар, 2 - всасывающий трубопро вод, J, 5 - манометры ( в.1 куумметры ) .
насос, 6 - нагнетательн ый трубопровод, 7 - приемный резервуар

В струйных (в частности , водоструйных) насосах перепад дав
лений (напор) создается за счет подачи струи газа, жидкости
или пара с большой кинетической энергией. При использова
нии энергии струи газа (жидкости ил и пара) такой насос назы
вают инжектором (при давлениях больше атмосферного) или
эжектором (при давлениях ниже атмосферного). П ротекающие
при этом процессы преобразования кинетической энергии струи
рабочей жидкости (газа, пара) в потенциальную энергию давле
ния перекачиваемой жидкости подробно рассмотрены в гл .9.
Типовая схема насосной установки с механическим рабочим
органом показана на рис.3.2. И з расходного резервуара /, где
давление над свободной поверхностью составляет р 1 , жидкость
под действием разности напоров в сечениях ! и III по трубопро
воду 2, называемому всасывающим, поступает в насос 4. Здесь ее
давление повышается до уровня, достаточного для того, чтобы
жидкость поднялась по нагнетательному трубопроводу 6, преодо
левая его гидравлическое сопротивление и противодавление в
собирающем (приемном) резервуаре 7, где давление над свобод
ной поверхностью составляет р2 . Для измерения давления до и
после насоса устанавливаются манометры З и 5 (при абсолют
ных давлениях больше атмосферного) . Нередко давление во
всасывающем трубопроводе меньше атмосферного, тогда З
это вакуумметр .
Разность уровней установки насоса и жидкости в расходном
резервуаре 1 называется геометрической высотой всасывания hrв•
а расстояние (по высоте) между насосом и уровнем жидкости в
приемном резервуаре 7
геометрической высотой нагнетания
hгн· Соответственно Hr = hгв + hгн
полная геометрическая
высота подъема жидкости (см. рис.3.2).
-

-

-

266

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

3. 1 .2. Основные характеристики насосной установки

Основными характеристиками насосной установки являются
ее производительность, создаваемый установкой напор и мощ
ность двигателя, обеспечивающего ее работу. Рассмотрим
несколько подробнее эти характеристики .
Производительность (подача) насоса V - объем жидкости,
подаваемый насосом в нагнетательный трубопровод в единицу
времени (мЗ/с) . Массовая производительность насоса G = Vp , где
р - плотность жидкости. В задачах проектирования производи
тельность насоса задается; тогда размеры насоса для каждого его
типа определяются из геометрических соображений. В задачах
эксплуатации производительность одних насосов (например, объ
емных) определяется параметрами работы самого насоса и не
зависит от характеристик трубопровода, для других же последние
оказывают значительное влияние на производительность.
Напор, создаваемый насосом, определяют на основе уравне
ния Бернулли . В гл .2 оно было записано для реальной жидкости
в форме уравнения (2. 1 6) в отсутствие источника энергии; в
рассматриваемом случае нал ичие источника энергии (насоса)
следует учесть.
Примем за плоскость отсчета поверхность /-/ уровня жид
кости в расходном резервуаре (см. рис.3.2) и запишем полные
напоры Н1 и Н2 соответственно для сечений:
/-/, совпадающего с плоскостью отсчета, 2

w'
р'
Н1 = 0 + +-

pg 2 g
и //-//, соответствующего поверхности уровня в приемном ре
зервуаре, Н2

=

Hr

р2
+ _

+

2
w2
_
.

pg 2 g
При течении идеальной жидкости в отсутствие насоса Н 1 =
= Н2 . В случ ае те чения реальной жидкости Н2 < Н1 , и для сохра
нения равенства в правой части уравнения Бернулли (2. 1 6) учи 
тываются гидравлические потери h п в трубопроводах. Но на
сос - источник энергии, он создает дополнительный напор Н,
увеличивающий сумму слагаемых в правой части. Чтобы сохранить
знак равенства, необходимо в левую часть добавить этот напор:

2

О + li + � + Н =
pg 2g

Hr

+

Рp 2 + �2 +

Нп ,

(3. 1 )

где Hn = hn• + hnн - полные гидравлические потери , т. е. сумма потерь во
всасывающем (hп8) и нагнетательном (hпн) трубопроводах.

g

2g

267

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

В равенстве (3. 1 ) напор Н - это воспринятый жидкостью на

пор Нт за вычетом гидравлических потерь в самом насосе h�ac ,

т.е. Н = Нт - hпн ас . Из (J. l ) получаем
Н = Hr +

Р2 - Р1 + 3_

pg

2g
2

_

3._
2g

+ Hn .

2

(3.2)

Если пренебречь скоростными напорами жидкости в резерву
арах (ввиду их крайней малости в подавляющем большинстве
практических случаев) , а тем более - их разностью, по сравне
нию с другими слагаемыми уравнения (3.2), то
Н Hr + Р2 - Р1 + Hn .
(3.3)

=

pg

Таким образом, напор, развиваемый насосом и передаваемый
жидкости , затрачивается на ее подъем на высоту 111 , на преодо
ление разности давлений Р2 - р 1 и гидравлического сопротивле
ния в трубопроводах Нп .
На действующих насосных установках напор обычно опреде 
ляют по показаниям манометра (рм) и вакуумметра (рв ) , устано
вленных на нагнетательной и всасывающей линиях непосред
ственно около насоса. При этом манометр всегда показывает
избыточное (по сравнению с атмосферным) давление, а вакуум
метр - разность между атмосферным давлением и абсолютным
давлением в аппарате . В рассматриваемом случае (см . рис. 3 . 2)
манометр показывает разность между абсолютным давлением
жидкости после насоса (рн) и атмосферным (ратм ) , т.е. Рм = Рн - Ратм ; вакуумметр показывает разность между атмос ферным дав
лением (ратм) и абсолютным давлением перед насосом (рве) , т.е.
Рв

= Ратм

- Рве·

Полный напор жидкости после насоса (в месте подсоедине
ния манометра) равен
2
w" ,
р" + h rв + н 2"
pg 2g
=

а перед насосом (в месте подсоединения вакуумметра)
н 1ос

W вс
Рас + + -

где wн и w"" - скорости жидкости
водах соответственно.

в

,

2

= h rв

pg

2g

нагнетательном и всасывающем трубопро

Реальный напор Н, развиваемый насосом, есть разность напоров н;·
н 1ос
•
•

Н = н 11
2

2 68

_

Н '"'

1 _

р 11

- р ""

pg

+

w2
11

- w2

""

2g

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Вводя показания манометра Рм = Рн Рв = Ратм - Рве' получаем
+
Н = Р ,.. Р . +

pg

w" - w ""
2g
2

Ратм

и вакуумметра

2

На практике чаще всего диаметры всасывающего и нагнета
тельного трубопроводов, а следовательно и скорости жидкости в
них, оди наковы или отличаются незначительно: Wн "' w8c (да и
сами значения скоростных напоров w ,: /2g и w�,. /2g невелики ) .
Тогда

Н=

р" + Р

• .
(3 .4)
pg
Таким образом, напор насоса на действующей насосной
установке равен сумме показаний манометра и вакуумметра . За
метим, что при испол ьзовании на всасывающей и нагнетатель
ной линиях одноименных приборов (например, манометров) на
пор насоса будет равен разности их показаний.
Связь напора насоса Н с его производительностью V будем
называть характеристикой насоса Н Н( JI). Ранее было указано,
что для некоторых насосов (например, поршневых) эта связь
вырождена: V не изменяется с Н. Подчеркнем, что речь здесь
идет о том , какой напор может развивать насос при некоторой
производительности .
Работа насоса зависит от того, через какой трубопровод он
прокачивает жидкость: чем больше сопротивление трубопровода
(большая длина, малый диаметр, много местных сопротивлений
и т.д. ) , тем больший напор Нтр_ будет разви вать насос для подачи
заданного потока жидкости . Н этом случае речь идет о том , ка
кой напор при данной производительности должен в рабочих
условиях развивать насос. Такая связь Нтр (с учетом разности
уровней Hr и давлений р 1 и Р2 в расходном и приемном резерву
арах) и V называется характеристикой трубопровода (сети) . Та
ким образом, систему " насос-трубопровод", или "насос-сеть " ,
следует рассматри вать как единое целое - в о взаимосвязи рабо
ты его элементов. Поэтому насос и параметры его работы следу
ет выбирать на основании анализа совместной работы элементов
этой системы.
Напор насоса расходуется на технологически полезные эф
фекты , связанные с преодолением противодавления в приемном
резервуаре и поднятием жидкости на геометрическую высоту Hr,
а также на компенсацию потерь за счет трения в трубопроводах
Hn = hnв + hnн и потерь внутри насоса hnнac . Величина Hn зави-

=

269

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

сит от расхода V и при общей длине

/ трубопровода диаметром

drp с местными сопротивлениями I:� определяется по формуле

типа

(2.3 1 ):
Hn

(Л.г -z + I ;) -w2 = (Л. r -z + r ;) v2 2 . 42
.

=

=

lirp

2g

·drv

1t d4 ·2g

'

=

причем коэффициент гидравлического сопротивления Лг
Лг( Rе ) = Лг( JI) .
Итак, в каждом рабочем режиме насос должен преодолевать
сопротивление (развивать напор)
Нтр

или

Нтр

=

Нг +

=

Нг +

Р2 -Рg 1
p

+

Нп,

2
Р2 - Р1 + (л. r _dтl р + "'1;,) 21t42 d4g
v2
pg

=

L.J

О имеем Нтр

=

Нг +
(

( 3 .5)

р2 - р1 )/pg ,

ростом V напор Нтр зависит от V почти квадратично ( " почти " из- за слабого изменения Л " . а иногда и некоторых сопротивлений
Очевидно, что при V

а с

� . с ростом JI).
Точка пересечения двух кривых, выражающих характеристи 
ки сети и насоса, представляет собой рабочую точку насоса с
характерными рабочими значениями Н и V.
Мощность двигателя зависит от производительности и напо
ра, создаваемого насосом при работе последнего в комплекте с
всасывающим и нагнетательным трубопроводами. Расчет мощ
ности изложен в разд. 3. 1 .4.
3. 1 .3. Предельная геометрическая высота всасывания насосов

При размещении технологического оборудования и насосов,
его обслуживающих, всегда возникает вопрос о геометрической
высоте всасывания hгв · Ведь даже при правильно подобранном
насосе (способном обеспечить требуемые производительность и
напор) , но неправильно установленном (слишком большая hг8) , он
не сможет всасывать жидкость, а значит - подавать ее потреби
телю. Более того, работа в таких условиях неблагоприятно ска
жется на самом насосе. Остановимся на этой проблеме более
подробно.
При изменении геометрической в ысоты всасывания насоса
hгв изменяется давление жидкости на входе в него Рве - соответ
ственно уравнению Бернулли.

270

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Аналитическая зависимость Рас от h,8 может быть устаномена с помощью
уравнения Бернулли, записанного для сечений /-/ и на входе в насос /J/-J//
(см . рис.3.2). При прежней плоскости отсчета /-/
w 12
Рве
w вс
2
о + .!2_ + =h +
+ - + h П8 ,

pg

Рве = 12_

откуда

pg

-

2g

pg

pg

П1

+

2
�

2g

-

h

-

П1

2g

w2

�

2g

-

hпв·

Пренебрегая скоростным напором w 1 2/(2g) ввиду его малости по сравнению
с другими слагаемым и , получим

Рве
pg

=

.!!J..
pg

_

h

_

Wвс
2

2g

_

h

.

(3.6)

При установке насоса рядом с расходным резервуаром 1 (см.
рис.3.2) ( h пв
О ) и на одном с ним уровне ( h гв
О ) давление
жидкости на входе в насос Рве практически равно давлению р 1
[скоростной напор Wвe2/(2g) , как правило, значительно меньше
пьезометрического p1/(pg) ) . С увеличением hгв давление на входе
в насос Рве уменьшается и при некоторой геометрической высо
те (назовем ее предельной rеометрической высотой всасывания
hгвn ред) давление Рве понизится до упругости насыщенных паров
р, перекачиваемой жидкости при ее рабочей температуре t.
Как известно, условие кипения жидкости - это равенство
или превышение упругости ее насыщенных паров над внешним
(по отношению к ней) давлением : р, � Рве (когда Рве станет
меньше р,, жидкость закипит) . Пар, образующийся при кипении
жидкости, при повышении давления (в определенный период
времени - в объемных насосах; по мере попадания в зону по
вышенного давления - в других) будет конденсироваться. Но
объем, занимаемый одним килограммом жидкости, в сотни и
тысячи раз меньше объема пара, поэтому в зоне конденсации ,
т.е. в рабочем пространстве насоса, создается вакуум. В осво
бождающиеся при этом полости ( "пустоты" ) устремляются пор
ции жидкости , вызывая гидравлические удары и быстрый износ
рабочих органов насоса. Работа насоса в таком режиме сопро
вождается шумом и сотрясением всей машины ; за несколько
часов такой работы образуются раковины на элементах рабочих
органов, и в итоге они разрушаются.
Описанное выше явление возникновения полостей (каверн) при
вскипании в зоне пониженных давлений получило название кави
тации ("полость" по-английски - cavity) . При работе в режиме
кавитации существенно снижаются производительность насоса и
его гидравлический КПД, а сам насос быстро выходит из строя.
Явление кавитации может быть вызвано также десорбцией
растворенного газа или подсосом воздуха через неплотности

=

го

по

=

27 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

(при Рве н иже атмосферного). Поэтому не рекомендуется регу
лировать производительность насоса с помощью вентиля на
всасывающей линии.
Более подробно вопрос о " ненормальной " работе насосов и
явлении кавитации будет рассмотрен при изучении конкретных
типов насосов.
Из формулы (3.6) следует, что теоретическая (без учета раз
личных гидравлических потерь во всасывающем трубопроводе)
предельная (при условии Рве = р,) геометрическая высота всасы
вания насоса равна
ед ) р Р1 Pt ·
(3. 7)
(h пр
гв
тео
_

-

-

pg

Ее также называют максимальной " всасывающей способ
ностью насоса " . (Этот термин не вполне удачен, так как
"способность насоса" здесь не зависит от насоса, а определяется
лишь давлением р 1 в расходном резервуаре 1 и свойствами пере
качиваемой жидкости . )
С учетом гидравлических потерь в о всасывающем трубопро
воде h п в и создан ия скоростного напора Wвe2/(2g) реальная пре
дельная геометрическая высота всасывания насоса (также при
условии Рве = р,) равна

h пред _

гв

Р1

- Pt
pg

_

2
W ве
h
2g - п в

(3.8)

Из уравнения (3.8) видно, что предельная высота всасывания
уменьшается с понижением давления р 1 и увеличением р,, т.е. с
увеличением температуры жидкости. К уменьшению hгвn ред при
водят также повышенные скорости во всасывающем трубопро
воде и гидравлические потери в нем.
При перекачивании горячих жидкостей, когда давление на
сыщенных паров р, близко к р1 , возможно получение нулевого
и даже отрицательных значений hгвnред _ Это означает, что для
перекачивания горячих жидкостей насосы должны быть устано
влены на одном уровне с жидкостью в расходном резервуаре 1
или даже ниже его. В последнем случае говорят, что насос рабо
тает " под заливом" .
Методика расчета предельной высоты всасывания с помощью
формулы (3.8) справедлива для большинства типов н асосов, хотя
сами процессы всасывания для разных насосов могут суще
ственно различаться. Так, например, у объемных насосов с пе
риодическим забором жидкости в насос гидравлические потери
h п в возрастают на величину инерционных потерь, связанных с
периодическими актами перевода жидкости из неподвижного

272

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

состояния в движущееся . Эти и другие особенности расчета
hгвпред будут отражены при рассмотрении соответствующих ти
пов насосов.
Итак, для обеспече н ия нормальной работы насоса он должен
быть расположен на любой высоте hгв• меньшей hгвп ред. Под
черкнем: нужно четко различать величины h гв и hгв пред при
выполнении технологических расчетов. Например, в формуле
(3.3) для определения напора Н следует использовать реальную
высоту всасывания насоса h г8 : она может быть разной, но не
должна превышать hгвп ред _
3. 1 .4. О мощности и КПД насосов
Полезная мощность Nn при работе насосной установки рас
считывается на основе следующих рассуждений. Как известно,
работа равна произведению силы на путь. В данном случае си
ла - это вес подни маемой жидкости , а путь - ее перемещение
в направлении действия силы, т.е. расчетная высота подъема
жидкости Н. Количество перекачиваемой насосом жидкости
характеризуется массовым расходом р V (кг/с), т.е. в единицу
времени на высоту Н поднимается жидкость, вес которой р Vg.
Очевидно, произведение последнего на напор Н дает полезную
мощность в Вт:
(3.9)
Nп p VgН.

=

Мощность, потребляемая насосом (мощность на валу насоса),
N больше полез!iой вследствие потерь в самом насосе
(гидравлические потери , утечки жидкости через клапаны ввиду
невозможности их мгновенного открытия и закрытия), которые
учитываются коэффициентом полезного действия насоса ri н :

N

=

N"
'll н

=

p VgH .
11 1 1

(3 . 1 0)

Величина ri н характеризует совершенство конструкции и
экономичность эксплуатации насоса. Ее обычно представляют
как произведение трех сомножителей, каждый из которых имеет
определенный физический смысл:
(3 . 1 1 )
l"J н
1"J v1"J r1"J мex·

=
= V/

Коэффициент подачи riv
V,., где Vт
теоретическая про
изводительность насоса. Коэффициент 11 v учитывает потерю
производительности насоса за счет утечек жидкости через зазо
ры, клапаны, сальни к и и т.д. (см. разд. 3 . 3.2). При этом энер
гия , затраченная на увеличение напора потерянной жидкости ,
теряется безвозвратно. Значит, в действительности энергия за-

273

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

трачивается на перекачивание потока жидкости Vт > V, и в рас
четной формуле должна фигурировать величина V,. или равная ей
V/11v. отсюда и появление множителя 11v в знаменателе формулы
(3. 10) как составляющей 11н при использовании V вместо V,..
Гидравл ический КПД 11 r = Н/ Нт уч итывает потери напора
h п нас при движении жидкости через насос. Здесь Нт - теорети
ческий напор, он больше полезного (используемого потребите
лем) на величину h пнас . По существу,
Нт h н ас
hн ас
1 - -"
11 г =
Н п
Н
_



т

т

Строго говоря, в формуле (3. 10) должна стоять величина Нт
или равная ей величина Н/11г· Отсюда и появляется в (3. 1 1 ) со
множитель 11r как составляющая 11н·
Механический КПД 11мех характеризует потери мощности на
механическое трение в насосной установке (в подшипниках,
сальниках и т.д.).
Значение 11н зависит от производительности насоса, его кон
струкции и степени износа. Для разных насосов 11н колеблется в
весьма значительных пределах - от 0,5 до 0,95.
КПД передачи 11пер позволяет учесть при выборе электродви
гателя к насосу потери мощности из-за механических потерь в
передаче от электродвигателя к валу насоса. Величина 11пер
близка к единице и составляет 0,95 - 0,99.
Мощность, затрачиваемая двигателем, определяется в итоге
следующим образом:
Nдв =

�=
11 пер

Nn
11 н ·11 п ер

=

Nn
11

--

(3. 1 2)

КПД насосной установки 11 равен

11 = 11н11 пер·

Заметим также, что при подборе двигателя его мощность
принимают на 1 0-50% больше рассчитанной по формуле (3. 1 2)
с учетом перегрузок в момент пуска насоса, причем больший
запас берут для насосов меньшей мощности.
3.2. ПОРШНЕВЫЕ НАСОСЫ
3.2. 1 . Принцип действия и классификация насосов .

Простейший поршневой насос изображен на рис. 3.3. В ци
линдре 1, внутренняя поверхность которого хорошо обработана,
совершает возвратно-поступательное движение поршень 2, уста
новленный практически без зазора между ним и цилиндром.
274

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

4

3

2

Рис. З. З. Схема и прин ци п действия поршневого насоса :

1 - uил индр, 2 - поршень, J, 6 - трубопроводы, 4, 5- клапаны , 7 зун , 9 - шаl)'Н, 10 - кривошип , 11 - палеu кривошипа

шток, 8 - пол 

Уплотнение осуществляется с помощью уплотнительных колец,
расположенных на наружной цилиндрической поверхности
поршня; для уменьшения трения колец о внутреннюю поверх
ность рабочего цилиндра используется смазка. Преобразование
вращательного движения вала двигателя (а точнее - вала редук
тора) в возвратно-поступательное движение поршня осу
ществляется с помощью коленчатого вала либо кривошипно
шатунного механизма (как показано на рис. 3.3). Этот механизм
состоит из штока 7, ползуна 8 (он движется в направляющих
плоскостях) , шатуна 9 и кривошипа 10. Шатун 9 шарнирно сое
динен с ползуном 8 и кривошипом 10. При вращении к.ривошипа
вместе с валом ползун 8, а с ним и поршень 2 совершают воз
вратно-поступательные движения.
За один оборот кривошипа (цикл) поршень совершает ход
вправо (по рис. 3.3 - ход всасывания) и ход влево (ход нагнета
ния). В крайних положениях, где поршень меняет направление
движения, он на мгновение останавливается (так называемые
"мертвые точки " ) . Потом скорость перемещения поршня увели
чивается от нуля до максимального значения и снова умень
шается вплоть до мгновенной остановки. Далее - вновь разгон
поршня и его замедление. Затем цикл повторяется.
При таком неравномерном возвратно-поступательном движении
поршня возникает проблема компенсации больших инерцион
ных усилий, передающихся на фундамент под насосом . П о
скольку величина последних зависит от частоты вращения
(число оборотов в единицу времени) кривошипа, то закономер
но ограничение частоты вращения вала (числа ходов поршня ) ,
связанное с допустимыми нагрузками на фундамент. В случае
бетонных фундаментов, выдерживающих значительно большие
нормальные нагрузк.и (на сжатие) , чем тангенциальные (на срез) ,
применение поршневых насосов с вертик.альным перемещением
поршня (и воздействием таких же нагрузок на фу ндамент) по-

275

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Табли ц а 3. 2. Классификации порwиевwх насосов
П ризнак

Оrличительн ы е черты

Разн овидн ости

Электроприводные
(с по- Or электродвигателя с вращамощью кривошипно-шатун - тельным
движением
вал а
ного механизма или коленча- через редуктор
того вала)
Or машины (например, пароП рямодействующие
вой) с возвратно-поступательным движением штока
Ручные
Создаваемое
Н изкого давления
р < 1 МПа
давление
Среднего давления
1 < р < 2 МПа
Высокого давления
р > 2 МПа
Конструкция
S/D = 0,5 + 1 ,5
Собственно поршневые
поршня
S/D = 2 + 8
Плунжерные (скальчатые)
1 20-300 об/мин
Частота вращеБыстроходные
ния
60- 1 20 об/мин
Среднескоростные
40-60 об/мин
Тихоходные
Направление
Горизонтальные
Тангенциальная нагрузка на
движения поршфундамент
ня
Нормальная нагрузка на фунВертикальные
дамент
Кратность дейОднократного (простого) действия
равномерности
ствия
подачи
Двойного действия
жидкости
Четверного действия
Тройного действия
V < 0,005 мЗ/с
Производит�:J IJ,Малой производительности
0,005 < V < 0,08 мЗ/с
Средней производительности
ность
V > 0,08 мЗ/с
Большой производительности
Способ привода

!У-«НИ<

зволяет несколько увеличить верхний предел допускаемой час
тоты вращения кривошипа (см . табл . 3.2 и пояснения к ней ) .
В начале хода всасывания в рабочем объеме цилиндра соз
дается разрежение, под действием которого жидкость из всасы
вающего трубопровода З поступает в насос, открывая всасы
вающий клапан 4 за счет своего напора. Нагнетательный клапан
5 при этом закрыт из-за меньшего давления под поршнем, чем в
нагнетательном трубопроводе. В начале хода нагнетания
вследствие повышения давления жидкости в цилиндре под
поршнем
всасывающий клапан 4 закрывается , открывается
нагнетательный клапан 5, и жидкость выталкивается в нагнета
тельную линию 6. Затем ходы всасывания и нагнетания повто
ряются . Заметим , что при работе такого насоса в каждый дан 
ный момент он либо всасывает (нет нагнетания) , либо нагнетает
(нет всасывания).
Легко видеть, что ход поршня S связан с радиусом кривоши
па r просты м соотношением S 2r (см. рис. 3.3
крайние по-

=

27 6

-

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис.3. 4.

насос:

Прямодействующи й

1 - поршень насоса, 2
вой маш и н ы , З - шток

-

(паровой)

поршень паро-

ложения поршня при а = О и а = 7t). В самом деле, при пово
роте кривошипа от а = О (левая мертвая точка) до а = 7t
(правая мертвая точка) ползун, а следовательно и поршень, пе
ремещается на расстояние S 2r.
Четкая классификация поршневых насосов весьма затрудни
тельна ввиду значительного многообразия конструкций и приз
наков, по которым их можно подразделять. Частичная класси
фикация по некоторым признакам представлена в табл . 3.2. В
настоящее время широко используются электроприводные насо
сы - с приводом от электродвигателя посредством кривошип
но-шатунного механизма или коленчатого вала. Наряду с ними
до недавнего времени применялись прямодействующие (чаще
всего паровые) насосы , отличающиеся легкой регулировкой
производительности за счет изменения расхода пара (рис. 3.4).

=

Движение штока в прямодействующих насосах осущестВllЯ ется за счет воз
вратно-поступательного перемещения поршня в паровой машине путем пооче
редной подачи пара (с помощью золотника) то в левую (от поршня). то в пра
вую часть цилиндра. Шток жестко соединен с поршнями паровой машины и
насоса. Перемещение одного вызывает соответствующее перемещение второго.
П рямодействующие насосы широко применялись в химической промышлен
ности ввиду их взрыво- и пожаробезопасности . Использование в настоящее
время электродвигателей во взрыво- и пожаробезопасном исполнении значи
тельно сужает область при менения прямодействующих насосов из-за их гро
моздкости .

Максимальное давление в поршневых насосах ограничено
возникновением изгибающего момента, действующего на пор
шень при значительной разнице давлений с разных его сторон .
При этом возможны деформация поршня (утрированно показана
на рис. 3.5) и нарушение уплотнения между поршнем 1 и ци 
линдром 3. Это приводит к порче внутренней поверхности ци
линдра и утечке жидкости из зоны повышенного давления в
зону с меньшим давлением. Поэтому при создании давлений
более 1 МПа применяют плунжерные (иначе - скальчатые) на
сосы (рис.3.6), в которых поршень выполнен в виде продолгова
того (часто - пустотелого) цилиндра 2, называемого плунжером
(еще одно его название - скал ка) . К достоинствам плунжерных
насосов относят также их более простое изготовление: нет необ
ходимости в тщательной обработке внутренней поверхности все277

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

- поршень, 2 - шток, З - корпус

Рис.3.5. Деформация поршня :
1

- цилиндр, 2 - плунжер (скал ка), З - сальник

Рис.3.6. Схема плунжерного насоса:
1

го цилиндра, это требуется лишь в небольшой узкой части пере
хода к сальнику 3, с помощью которого обеспечивается уплот
нение.
Недостаток плунжерных насосов - худшее (по сравнению с
поршневыми) использование рабочего объема цилиндра. По
этому для получения достаточных производительностей плун
жерные насосы вытянуты в длину: отношение S/ D доходит до
5-8 против 0,5- 1 ,5 для поршневых (здесь D - диаметр поршня
или плунжера) .
Движение поршня ( плунжера), как указано ранее, сопровож
дается возни кновением инерционных сил (нагрузок на фунда
мент и детали насоса) , поэтому максимальная частота вращения
кривошипа ограничена (не более 300 об/мин)•. При этом разли
чают быстроходные насосы (
1 20+300 об/мин), обеспечи
вающие повышенную производительность и исполненные чаще
всего с вертикальным (вверх-вниз) перемещением поршня;
среднескоростные (
40+60
60+ 1 20 об/мин) и тихоходные
об/мин) . Последние применяют при перекачке жидкостей с вы
сокой вязкостью, при создании больших напоров (> 5 МПа) и
наличии дл инных трубопроводов.
Насос, изображенный на рис. 3.3, называют насосом одно
кратноrо (простоrо) действия. Для увеличения производитель
ности (подачи) применяют насосы двойноrо (двукратного) дей
ствия, у которых работают обе стороны поршня - попеременно
на всасывание и нагнетание (рис. 3.7). Уплотнение между дви
жущимся штоком и неподвижным корпусом насоса обеспечи
вают сальником 5. При движении поршня вправо жидкость че
рез левый всасывающий клапан поступает из всасывающего тру
бопровода в левую полость цилиндра (акт всасывания); при

п=

п=

(п =

• Здесь и в таблице 3.2 указана частота вращения в об/мин , как это принято
во многих справочниках и каталогах. В расчетных формулах используется час
тота вращения п в с- 1 .
278

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

6

а

Рис.З. 7. Схема работы насоса двойноrо действия:

/- цилиндр, 2 - поршень, J - всасывающие: клапан ы, 4
5 - с альник

-

нагнс:татс:льн ыс:

клапаны ,

Рис.3.8. Схема работы насосов четверного (а) и тройного (б) действия

этом из его правой полости жидкость выбрасывается через пра
вый нагнетательный клапан в нагнетательный трубопровод (акт
нагнетания) . При обратном (влево) движении поршня всасыва
ние происходит через правый всасывающий клапан , а нагнета
ние - через левый нагнетательны й . Таким образом, за один
оборот вала насос осуществляет два акта всасывания и два акта
нагнетания, т.е. можно говорить об удвоении производитель
ности . П одчеркнем, что равномерность подачи насоса двойного
действия выше, чем насоса простого действия, по крайней мере ,
нет временньiх промежутков (только мгновения - точки на оси
вре мени), когда всасывание или подача отсугствуют. Вопрос о не
равномернОС111 подачи поршневых насосов будет подробно рассмот
рен в разд.3.2.3, 3.2.4, а пока отметим, что для повышения равно
мерности подачи жидкости (см. табл. 3.2) используют насосы:
- четверного (четырехкратного) действия, представляющие
собой два насоса двойного действия, работающих на оди н тру
бопровод от одного коленчатого вала (рис. 3 . 8 , а) , но с запазды
ванием (сдвигом по фазе) на 1 /4 оборота ( 7t/2) ;
- тройного (трехкратного) действия (триплексы) , состоящие
из трех насосов простого действия с общим коленчатым валом,
кривошипы которых расположены под углом 1 20° (рис . 3 . 8 , б).
Насосы четверного и тройного действия занимают больше
места и существенно дороже простых поршневых насосов. На
сосы большей кратности действия не используются.
3.2.2. Производительность

Для насоса простого действия за один оборот кривошипа
происходит один акт всасывания и один акт нагнетания
(вытал кивания) порции жидкости. При этом объем порции
жидкости за один оборот (или ход) в идеале составляет
где F : 11JJ2/4

Уо
-

= FS,

площадь поршня или плунжера, S

-

ход.

279

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

При частоте вращения кривошипа п (в секунду! ) идеальная
производительность (подача) насоса простоrо действия составит

Vнд

= FSn.

(3. 1 3)

В реальных условиях работы поршневого насоса в самом на
чале стадии нагнетания (поршень только пошел влево, см. рис.
3.3) всасывающий клапан закрывается не мгновенно (ввиду ко
нечной скорости движения тарелки клапана), и часть уже по
павшей в цилиндр жидкости возвращается из него во всасы
вающий трубопровод. Аналогично, в момент начала всасывания
нагнетательный клапан закрывается также не мгновенно, а с
некоторой конечной скоростью. Поэтому " всасывание" некото
рого количества жидкости под поршень цилиндра происходит не
из всасывающего, а из нагнетательного трубопровода. Такая (с
запаздыванием) работа клапанов приводит к уменьшению ре
альной производительности насоса простоrо действия по сравне
нию с идеальной :
где 'lv < 1

Vi

= Vнд 1"\v = FSnriv ,

(3. 1 4)

- коэффициент подачи.

Отметим также возможные потери жидкости через неплотности , сальники и
т.д. Они, как правило, невелики и не сказываются существенно на величине
коэффи циента подачи 'lv·

Идеальная (теоретическая) производительность насоса двойноrо
действия складывается из объемов жидкости, нагнетаемых порш
нем при движении справа налево - FS и при обратном движении
- (F - f)S, где / - площадь поперечного сечения штока.
Таким образом , реальная производительность насоса двойно
го действия

Vi1 = Vнд 1"\v

= (2F - /)Snriv·

(3. 15)

Если пренебречь площадью штока, полагая / < < F, то произ
водительность насоса двойного действия будет вдвое больше,
чем насоса простого действия:

Vi1 "" 2 FSnriv·

=
=
= 0,5 i(2F -j) Snriv

(3. 1 5а)

В общем случае для насоса любой кратности действия i:
V; iFSnriv при i
1 ; 3;
V;

=

при i

= 2; 4.

(3. 1 6)
(3. 16а)

При / < < F производительность насоса V; любой кратности
действия (i
1 ; 2; 4; 3) определяется по формуле (3. 1 6).
Коэффициент подачи ll v зависит от производительности на
соса (см. табл . 3.2) и его физического состояния. Опыт эксплуа-

280

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

тации насосов позволил установить следующие примерные зна
чения коэффициентов подачи насосов при их нормальном рабочем состоянии:
малая производительность
средняя производительность
большая производительность
.

.

.
.

.

.

.

.

. .

'lv =
'lv =

, , , , 'l v =

. • .

.

.

0,85 + 0,90
0,9 + 0,95
0,95 + 0,99

Понижение коэффициента подачи ТJ v по сравнению с приве
денными значениями указывает на неисправность насоса, необ
ходимость его ремонта или замены .
3.2.3. Закон движения поршня.
Диаrрамма подачи

Производительность насоса, определяемая по формула!'rf
(3. 1 6) и (3. 1 6а), характеризует объем подаваемой жидкости за
единицу времени. Эти формулы не отражают неравномерности
ее подачи , а в случае насоса простого действия - даже преры
вистого характера подачи . Неравномерность подачи связана с
переменной скоростью движения поршня : нулевой - в крайних
( " мертвых") положениях поршня и максимальной - где-то в
середине его хода. Однако в большинстве непрерывных произ
водств технология требует равномерной подачи материалов, в
том числе и жидких. Кроме того, пульсация жидкости неблаго
приятно влияет на механическую прочность и герметичность
цилиндра насоса, трубопроводов, резервуаров и т.д. Далее будет
показано, что характер подачи жидкости во времени небезраз
личен и для работы самого насоса. Вместе с тем ряд процессов
тепломассопереноса протекает более интенсивно при пульси
рующей подаче жидкости - в силу особенностей самих процес
сов переноса ил и возн икновения сопутствующих эффектов. Так,
пульсирующую подачу жидкости направленно используют при
осуществлении процесса экстракции (см. гл. 1 3) с целью увели
чения межфазной поверхности и тем самым - эффективности
аппаратов.
В любом случае
как при использовании пульсационной
подачи жидкости, так и при осуществлении мер, направленных
на уменьшение неравномерности подачи, - необходимо знать
ее закономерности , чтобы уметь управлять ею.
·-

Закон движения поршня
Средняя

скорость движения поршня Се р рассчитывается из
простых соображени й : за 1 оборот кривошипа поршень прохо
дит путь 2S 4r ; за 1 секунду (п оборотов) этот путь, т. е. сред
няя скорость, составит Се р
2 Sп 4т (м/с) . Переменный тем п
подачи жидкости зависит от скорости (переменной в о времени!)

=

=

=

28 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис . 3. 9. К определению зависим ости перемещения поршня (х) от угла поворота
кривошипа (о.)

движения поршня с. Последняя определяется как производная
перемещения поршня х (рис.3.9) по времени t и зависит от угла
поворота кривошипа а.. Поэтому для нахождения переменной ско
рости движения поршня с(а.) надо прежде всего установить зависи
мость хода поршня х от угла поворота кривошипа
х = х( а. ) . Эту
зависимость обычно называюr "закон движения поршня".
Поворот кривошипа на угол а. (от нулевого значения, когда
шатун и кривошип расположены на одной линии А0ЕО) вызы
вает перемещение ползуна (из точки Ао в точку А, причем отре
зок АоА х) и точно такое же перемещение поршня х. Из рис.
3.9 видно, что АВ = АоЕ = l - длина шатуна; ОВ = ОЕ = г радиус кривошипа. Обозначим угол шатуна с горизонталью р и
опустим из точки В перпендикуляр BD на Ао О. Тогда из геомет
рического рассмотрения положений шатуна и кривошипа в на
чальный момент ( а. = О , прямая АоЕО) и при повороте криво
шипа на угол а. (ломаная АВО) получаем
х = АоА = АоО - АО = АоЕ + ЕО - (AD + DO) .
Так как AD = /cosp (из прямоугольного треугольника ABD) и
DO = f{;OSa. (из треугольника OBD) , то
х = / + г - (/cosp + f{;OSa.) = /( 1 - cosp) + г<. 1 - cosa.). (3. 1 7)
Поскольку обычно l : г � 5, то cosp близок к 1 . Поэтому закон
движения поршня достаточно точно предстаWIЯется зависимостью
(3. 1 8)
х = r(l
cosa.).
Теперь можно найти скорость движения поршня как произ
водную пути (перемещения) х по времени t, т.е. с = dx/dt. Так
как х = х( а. ) и а. = a.(t), то по правилам дифференцирования
сложной функции имеем
dx dx da d(r( l cos а)] da
.
=

-

С=

-

d1

=

-

-=

da d"t

-

da

d•

Производная da./dt
представляет собой угловую скорость
вращения кривошипа (в СИ - в рад/с). Заметим, что ro связана
= оо

282

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

с частотой вращения п в секунду очевидным соотношением: (1) =
2пп. Таким образом, выражение для скорости поршня имеет вид
(3. 1 9)
с = (1).rsina
Из (3. 1 9) следует, что скорость поршня изменяется с а по
синусоидальному закону от с = О при а = О и а = до
с =
=стах = (.t)Г при а = 1t/2, 31t/2.
Диаграмма подачи
Так как скорость поршня изменяется в зависимости от угла а
по закону синуса, то и подача (всасывание или нагнетание) то
же изменяется по синусоидальному закону. Эту зависимость
называют диаrраммой подачи . В любой момент работы поршне
вого насоса его мгновенная (по t) или локальная (по а) произво
дительность (подача) равна

=

п

V = Fc

[м2 . ;] или [�3 J

За время dt объем всасываемой (подаваемой) насосом жидкости равен
dV = Fcdt = F(.t)rsinadt.
Поскольку (1) = da/dt, (.t)dt = da,
(3.20)
dV = Frsinada.
Этот объем dV можно наглядно представить в виде элементар
ной площади под кривой Fr'Sina а (рис.3. 1 0) при изменении
угла поворота кривошипа на da. Тогда вся площадь под синусо
идой . должна выражать полный ·(теоретический) объем жид
кости V0 за один ход поршня:
-

х

о

Уо = J Fr sinada

=

Fr cosa l о = 2Fr = FS.
х

Для насоса простого (однократного) действия характерна
прерывистая подача жидкости, связанная с чередованием актов
всасывания и подачи. Степень
неравномерности подачи в про
Fr.siпa
стейшем варианте может быть
охарактеризована отношением
максимальной мгновенной пода
чи к средней; у насосов простого
Рис.З. 10. Диаграмма подачи поршневого
насоса простого действия

\ 41

\
r 1,.(\
da

•

2 83

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

�

Рис.3. 11.
Диаграммы
подачи
жидкости поршневыми насосами :

2 r""
h- �·

�-

о

тт

2тт

3тт

а - двойного действия , б - чет
верного действия, в - тройного дей
ствия

действия она - наиболь
шая. Равномерная за пери
а
F.
од 27t подача жидкости на
рис.3. 1 0 изобразится в ви
де прямоугольника той же
площади У0 = FS; высота
этого прямоугольника h
01t21t1i �
будет равна FS/(27t) =
.
б
= 2Fr/(27t) = Fr/1t. Макси
мальная ордината синусо
иды (при а = 7t/2 значение
sina = 1) составляет Fr.
Таким образом, отношение
О
тт
2тт
3тт
максимальной подачи к
в
средней у насосов просто
го действия равно Fr/(Fr/n)=
= 7t ::::: 3, 14.
Для насоса двойного действия (рис. 3. 1 1 , а) равномерность
подачи выше, чем у насоса простого действия, так как здесь нет
прерывистости в подаче, нулевая подача характерна только для
"мертвых" точек. Высота прямоугольника равной подачи здесь
вдвое (при /<< F) больше, и степень неравномерности в этом
случае в два раза меньше, т.е. равна 7t/2:oo l ,57.
Еще меньшей степенью неравномерности характеризуются
насосы четверного и тройного действия. Диаграмма подачи на
соса четверного действия (два насоса двойного действия со
сдвигом подачи по фазе на п/2) представлена на рис.3. 1 1 , б.
Сложение ординат здесь приводит к более равномерной подаче:
пульсации получаются чаще, но с меньшей амплитудой; нулевая
подача отсуrствует. Степень неравномерности у насосов четвер
ного действия есть отношение максимальной ординаты (она
равна удвоенной ординате одного насоса при а = 7t/4, т.е.
2Frsinn/4 = .J2 Fr) к средней (4FS/21t = 4Fr/7t):
..fi.Fr = п ..fi. ::::: 1 , 1 1 1 .
4Fr / п
4
Наибольшей равномерностью подачи отличается насос трой
ного действия (рис. 3. 1 1 , в), именно поэтому при классифика284
а

.

�
haad; _

а

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ции по кратности действия поршневых насосов принят такой
ряд: 1 ; 2; 4; 3 (см. табл . 3.2). Здесь суммируются ординаты трех
°
синусоид, сдвинутых одна по отношению к другой на 1 20
(21t/3). Площадь диаграммы, ограниченная сверху суммарной
кривой, изображает подачу всеми тремя цилиндрами . Н аиболь
шая ордината графика равна Fr - это ордината одного насоса
1t/2 (она же получается как сумма ординат для двух
при а
насосов при а = 1t/6 - в точке пересечения ординат; каждая из
них составляет Fr � i n 30 °
0,5Fr) . Средняя ордината в этом слу
чае 3FS/21t = 3Fr/1t. Тогда степень неравномерности подачи со
ставляет
Fr
1t
::::: l,047 .
=

=

=

3Fr 1

тт

J

Таким образом , насос тройного действия обеспечивает при
емлемую в большинстве практических случаев равномерность
подачи .
На практике чаще всего используют более доступные и деше
вые насосы простого и двойного действия. Для выравнивания
их подачи применяют воздушные колпаки .
3.2.4. Работа и расчет воздуwных колпаков

Подача и движение жидкости по всасывающей и нагнета
тельной линиям будут ближе к равномерным, если удастся в
ходе работы поршневого насоса поддерживать постоянной дви
жущую силу, т.е. разность напоров - между расходным резерву
аром и всасывающей стороной насоса и между нагнетательной
стороной насоса и приемным резервуаром. Этой цели и служит
установка непосредственно у поршневого насоса воздушных
колпаков (в общем случае - газовых) , аккумулирующих избыток
жидкости сверх равномерной подачи .
Пусть давление воздуха в нагнетательном колпаке составляет
Рн.к• а во всасывающем - Рв.к· Для обеспечения равномерного
движения (подачи) жидкости движущие силы процесса <Рн. к - Р2 - в нагнетательном трубопроводе и р1 - Рв . к - во всасы
вающем) должны быть практически постоянными во времени.
Но давления воздуха (газа) в колпаках Рн.к и Рв. к в принципе не
могут быть абсолютно постоянными, так как вследствие аккуму
ляции жидкости в них изменяется занятый газом объем. Задача
состоит в том, чтобы изменение давлений воздуха в колпаках
бьuю малозначимым; для этого, согласно закону Бойля
Мариотта (pV=const), объем газа в них должен меняться незна
чительно. Это возможно, когда избыток (сверх равномерной
подачи) жидкости и значительно меньше объема воздуха в кол -

285

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис.З. 12. Поршневой насос с воздушными колпаками:

1 - колпак на всасывающей линии, 2 - насос, J - колпак на нагнетательной линни

паке Vвозд · Это приведет к малым колеба
ниям разностей давлений (движущих сил)
и как следствие - потоков жидкости во
всасывающем и нагнетательном трубопро
водах.
Таким образом, размеры (объем) воз
душной части колпака связаны с объемом
избытка жидкости и и допустимой нерав
номерностью подачи (для обеспечения
абсолютно равномерной подачи потребо
вались бы воздушные колпаки бесконеч
ных размеров).
Прежде чем приступить к расчету размеров воздушных кол
паков, рассмотрим подробнее их работу. Воздушный колпак на
всасывающей линии (рис. 3. 1 2) обеспечивает практически (на
приемлемом уровне) равномерную подачу жидкости на участке
от расходного резервуара до колпака. Поршневой насос в пери
од всасывания забирает из колпака жидкость, и ее уровень в
нем понижается до минимального. В период нагнетания жид
кость из всасывающего колпака насосом не забирается, а за счет
разности давлений р1 - Рв.к "' const поддерживаются почти рав
номерное движение жидкости во всасывающем трубопроводе и
пополнение ею колпака до максимального уровня (обозначен
пунктиром). Затем цикл повторяется. Воздушный колпак на
нагнетательной линии (см. также рис. 3. 1 2) обеспечивает прак
тически равномерную подачу жидкости на линии от колпака до
приемного резервуара. При нагнетании поршневым насосом
часть жидкости (избыток) аккумулируется в колпаке
(максимальный уровень обозначен пунктиром); на стадии вса
сывания насос не подает, и этот избыток расходуется (уходит в
приемный резервуар).
Как правило, воздушный колпак на нагнетательной линии
больше, нежели на всасывающей. Д ело в том, что в нагнета
тельном колпаке давление обычно на 1 - 2 порядка выше, чем
во всасывающем. Поэтому в случае равных относительных коле
баний давлений Рв.к и Рн.к при одинаковых объемах избытка
жидкости и и колпаков Vв.квозд = Vн.квозд получились бы суще
ственно различные абсолютные колебания Рв.к и Рн . к• а с ними и
движущие силы р1 - Рв .к и Рн .к - Р2 · В результате движение
жидкости во всасывающем и нагнетательном трубопроводах
отличалось бы существенно различной неравномерностью. По286

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис.З. 13. К определению избытка жид
кости для поршневого насоса простого
действия

Frsina

этому чтобы вьщержать в каждом
из трубопроводов необходимую
равномерность течения жид
кости , значения увозд в колпа
ках делают различными.
Заметим , что хотя наличие
колпака на всасывающей линии и не влияет на равномерность
подачи жидкости потребителю, оно создает благоприятные
условия для работы насосной установки. В частности, при
большой h гв (см. рис. 3.2) наличие колпака на всасывающей ли
нии исключает возможность закипания жидкости в насосе из-за
существенного уменьшения инерционных потерь во всасы
вающем трубопроводе (см. разд. 3 . 2 . 6 ) .
Напомним: полная площадь под синусоидой (рис. 3 . 1 3) есть
объем жидкости , неравномерно подаваемой насосом за один ход.
Вертикальной штриховкой помечена равная ей площадь h· Ъr. ,
характеризующая тот же объем жидкости , н о равномерно пода
ваемой за один ход (здесь h
высота площадки) . Объем жид
кости, аккумулируемой колпаком (иначе говоря, избыток
сверх
равномерной подачи), для насоса простого действия (щ) изображен
на диа1рамме подачи площадью, помеченной косой штриховкой.
Для определения величины этой площади наЙдем "элементарный
избьrrок", т.е. разность между подаваемыми насосом элементар
ными объемами жидкости при повороте кривошипа на угол da
в случае неравномерной подачи (dV Frsinada) и в случае равно
мерной подачи h da
(Fr/7t)da. Выражение h Fr/1t получено из
h 27t
очевидного равенства V0
2r

-

и

= = P. = = · :

du

=

Fr siп ada

-

=

=

- � da F{sin -.;.) da.
=

(3.2 1 )

а

Полный избыток жидкости щ за один оборот кривошипа
(для насо
найдем инте1рированием (3.2 1 ) в пределах от
до
са простого действия) :

и� = Fr 21 (sш а - ;1 )
а 1 а2
V Frsina
Fr/1t,
а 1 = 1 8°34' а2 = 7t - а 1 = V1 6=1 °26'.
а2

•

а 1 а2

(3.22)

da.

Углы

=

и
определяются как точки пересечения синусоиды
l /7t. Отсюда
и горизонтали
так что sina
и
Расчет по (3.22) с найденны
ми пределами инте1рирования дает
=

щ =

1 , 1 02 Fr,

(3.23)

или

щ =

0,55 1 FS.

(3.23а)

287

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Следовательно , в случае насоса простого действия воздуш
ный колпак в период подачи должен аккумулировать (а в пери
од отсутствия подачи - расходовать) 55% объема жидкости ,
заполняющей рабочий цилиндр поршневого насоса.
Аналогичный расчет для насосов иной кратности действия
требует соответствующих изменений пределов интегрирования
(для насосов двойного действия) , а для насосов четверного и
тройного действия - еше и зависимостей V - а. Приведем ре
зультаты анализа для насосов разной кратности действия: и11
0,225 FS; uiv 0,042 FS; иш 0,009 FS. Можно констатировать
уменьшение избытка жидкости (неравномерности подачи) для
насосов с кратностью действия от 1 до 4 в ряду 1 ; 2; 4; 3.
Опыт проектирования и эксплуатации поршневых насосов
показывает, что для большинства технологических ситуаций
можно считать допустимыми следующие колебания давления в
колпаках (а значит, и объемов их воздушной части) :
- в о всасывающем - н а - 1 0% ,
- в нагнетательном - н а -2,5%.
Этому соответствуют следующие объемы воздушной части
колпаков:
1 Ои,
- всасывающего У "" и/О, 1
- нагнетательного У "" и/0,025 40и.
При этом разности давлений Р 1 - Рв .к и Рн. к - Р2 изменяются
в малой степени, а потоки жидкости в трубопроводах - еще в
меньшей, поскольку они пропорциональны корню квадратному
из движущей силы (см. разд.2. 3 ) .
Так, например, для всасывающего колпака объем воздуха в нем равен 1 О и
(при 1 0%-м колебании давления). Пусть в некоем конкретном колпаке в сред
нем Рв. к = О,О I МПа, а р1 = 0, 1 МПа. Тогда движущая сила в сред11е м равна 0, 1 - 0,0 1 = 0,09 МПа. За счет попадания в колпак избытка жидкости дамение в нем
изменится от Pв . к'nin до Ро.к'"ах, и эта разность составит 1 0%, т.е. Рв.к""'' = Рв.к :. О,05р8.к = 0,0095 МПа и Рв.к"'"" = Ро. к + О,05Ро.к = 0,0 1 05 МПа. Это значит, что

=

=

=

=

= =

движущая сила на кон цах всасывающего трубопровода в ходе раьоты будет
колебаться от 0, 1 - 0,0 1 05 = 0,0895 МПа до 0, 1 - 0,0095 = 0,0905 МПа, т.е .
очень мало относительно средней величины 0,09 МПа.

Конструктивно принято считать, что жидкость занищ1ет
примерно 1/3 колпака, следовательно, 2/3 колпака занимает
воздух. Тогда очевидно, что полный объем воздушного колпака
Укол п "" 1 ,5 Увозд ·
Подчеркнем, что воздушный колпак обеспечивает уменьше
ние пульсаци и в трубопроводе, но не на участках между насо
сом и колпаком. Поэтому колпаки устанавливают как можно
ближе к насосу.

288

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

3.2.5. Характеристика поршневых насосов

Зависимость между напором Н и производительностью насо
са V при постоянной частоте вращения называют частной харак
теристикой поршневоrо насоса. Как следует из самого принципа
работы поршневых насосов, их производительность не зависит
от напора, поскольку за один акт насос всасывает или выталки
вает совершенно определенный объем жидкости (в идеальном
случае V0 = FS) , а число таких актов однозначно связано с чис
лом оборотов (ходов) п в единицу времени. Поэтому теоретиче
ская характеристика поршневого насоса в координатах Н - V вертикаль с постоянной абсциссой, отвечающей производитель
ности насоса (рис. 3. 14, линия J) .
Реальная характеристика поршневого насоса обнаруживает
некоторое отклонение от вертикали (линия 2): с ростом Н про
изводительность V несколько понижается. Иногда это объяс
няют сжимаемостью жидкости при повышении напора, однако
этот эффект может сказаться лишь при очень высоких давлени
ях. Основная причина - понижение коэффициента подачи ТJ v :
с ростом Н все бdilьшая доля жидкости возвращается обратно (во
всасывающую линию из цилиндра поршневого насоса, в ци
линдр поршневого насоса из нагнетательной линии) из-за за
паздывания клапанов в период их закрытия.
В принципе, поршневой насос может развивать любой напор
(ограничение здесь связано лишь с мощностью двигателя и ме
ханической прочностью насоса - стенок корпуса, штока и т.д. ) ;
поэтому он развивает напор, определяемый характеристикой
трубопровода (линия J) : рабочая точка М насоса лежит на пере
сечении характеристик насоса (линия 2) и сети (линия 3)
(подробнее о характеристике сети см. разд. 3 . 1 .2).

Рис. 3. 14. Определение рабочей точки поршне 
вого насоса:

1 - теоретическая характеристика насоса, 2 реальная характеристика насоса, З - характеристика
сети, М - рабочая точка

о

v

289

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

3.2.6. Предельная высота всасывания

В основе расчета предельной геометрической высоты всасы
вания hгв л ред лежит формула (3.8), однако для поршневого на
соса она должна учитывать еще и затраты энергии на разгон
жидкости (преодоление и нерции - перевод ее из неподвижного
состояния в движущееся) во всасывающем трубопроводе в ходе
каждого цикла движения поршня. В геометрической и нтерпре
тации эти затраты энергии выражаются напором (высотой) hи, м
жидк. ст. (в энергетической и нтерпретации удельные затраты
выражаются произведением ghи, Дж/кг) . Следовательно, для
поршневого насоса

h гв л ред

=

Р1

-

Pt

W вс
2

- h в - hи .
п

(3.24)
pg
Для определения hи воспользуемся уже известным (разд.2.2.2)
приемом: приравняем формальное выражение, содержащее hи, к
физически обоснованному, выбрав для сопоставления силу
и нерции Fи. Формально она может быть записана в виде Fи =
= hи Рdвс • где fвс
поперечное сечение всасывающего трубопро
вода. Здесь hиpg = ЛРи - затраты энергии на преодоление инер
ционных сил , выражен ные в Н/м2 , а Лриfвс = Fи, Н. Физически
величину силы инерции можно записать в соответствии со вто
рым законом Ньютона как произведение массы жидкости m 8c во
всасывающем трубопроводе (его длина
/8с ) на ускорение а8с
этой жидкости : Fи = m8с йвс • причем m8c =
Рfвс lвс ·
Таким образом,
-

2g

-

-

=

z.c

(3 .25)
- Овс ·
g
И з уравнений расхода для потоков во всасывающем трубо
проводе и цилиндре поршневого насоса следует:
(3 .26)
/всWвс = Fc.
Отсюда, взяв производные по времен и , можно получ ить
связь ускорений поршня а и жидкости во всасывающем трубо
проводе а8с :
F
( 3 . 27 )
/вс О8с = Fa, Овс - О - ,

hи

foc

причем ускорение поршня а = dc/dt .
Выше было установлено [см. уравнение ( 3 . 1 9) ) , что с =
= w rsina; поэтому
dc d(wr sin а) da_ 1:
(3.28)
=
ro r co sа.
а=
dt
da
dt
-

290

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Подставляя в (3.25) выражение для а8с из (3.27) с учетом
(3 .28), получим
F ro 2 r cos a
(3.29)
h и = lвс

fвс

g

Для определения гидравлических потерь во всасывающем
трубопроводе h 8c по формуле (2.3 1 ) необходимо располагать
значением скорости Wвс · Последняя может быть найдена из
(3.26) с учетом ( 3 . 1 9) :

F

f

W8c = - с =

(л � :L �) F:
вс

Тогда
hп в =

F
f

dвс

вс

+

fвс

ror sшa .

.

( 3 . 30)

2 2
2
ro , s in а

2g

(3.3 1 )

Таким образом, предельная геометрическая высота всасыва
ния поршневого насоса может быть определена по (3.24) с уче
том выражений (3.29) для hи и (3.3 1 ) - для h п в ·

Формулу (3.24) иногда записывают без скоростного напора w8c2/(2g) , добав
ляя единицу к сумме местных сопротимений �);.

Из формул (3.29) и (3.3 1 ) видно, что слагаемые hи , hпв, а следо
вательно и величина hгв"ред, зависят от угла поворота кривошипа а:
2
2 2 2
2
" i: F w r sin a / F w r cos a . (3 . 3 2)
р1 - р1
h п ред =
- л - + L. '-> 2

)

--- (� doc'/К

-

pg
J;
g
f
g
Очевидно, существует некоторое положение поршня (при соответствующем
угле акр ) . при котором высота h,8п ред минимальна . Это наиболее опасное (с
точки зрения возможного закипания жидкости в цилиндре) положение поршня
(т.е. значение ак р ) можно найти путем приравнивания нулю первой производ
ной по а от выражения (3.32). Но практика и опыт расчетов позволяют суще
ственно упростить задачу.
ГВ

ок

oc

В отсутствие воздушноrо колпака на всасывающей линии в по
давляющем большинстве случаев h и > > h nв• так что величиной
h nв можно пренебречь. Тогда наиболее опасным моментом ста
новится начало хода поршня , когда а = О, cosa = 1 и инерцион
ные потери - максимальны:

hи

=

lвс

2
w r

- -- ·
F

fw::.

g

(3.29а)

Заметим , что при этом " мертвом " положении поршня W8c = О
и , соответственно, h nв = О. В этот момент
2
Р1 Pt / _!__ ro r
(3.33)
n
= --б/к
""
( hг8 ред)

-

pg

_

!"'

g

29 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис.3. 15. К расчету предельной геометрической
высоты всасывания поршневого насоса при нали
чии колпака на всасывающей линии

Предельная высота всасывания h гвпред,
определяемая по (3.33), зависит от ряда
факторов. Из-за больших инерционных
потерь при перекачке даже не очень го
рячих жидкостей (небольшие р,) , но без
колпака на всасывающей линии, воз
можно получение нулевого и даже отри
цательных значений h гвп ред. При пере
качке горячих жидкостей (высокие р,)
это тем более вероятно. Для увеличения
h гвп ред (а это расширяет возможности
монтажа насосов в технологической схе-

ме) необходимо:
- работать с жидкостью с возможно более н изкой темпера
турой , дабы понизить р, (охлаждение жидкости целесообразно,
если затем не требуется снова ее нагревать) ;
- уменьшить длину всасывающего трубопровода и увеличить
его диаметр;
- уменьшить частоту вращения п (и, следовательно, ro ,
равную 2пп) .
Заметим, что в рабочих условиях реал изация этих мер не
всегда возможна.

При заданной геометрической высоте всасывания h,. может возни кнуrь за
дача определения, например, максимально допустимой частоты вращения (в
секунду). Из (3.33) находим

-

nдоп

= 0,5

/ос g
""
/ п 2 Fr

( - р, Pt

pg

hrв\

�

·

Из этой формулы видно, что при чрезмерно большой h,. возможны ситуа
ции [ h,. � (р 1 p1)/(pg)), когда насос не будет всасывать ни при какой частоте
вращения: по формуле под радикалом получается отрицательное число.
Разумеется, возможна постановка задач определения предельных значени й
z.c . dac и других параметров системы насос - трубопровод.

При наличии воздушного колпака на всасывающей линии и нер
ционные потери сохраняются лишь на небольшом участке /о (по
сравнению с lвс) с неравномерной подачей жидкости (рис. 3 . 1 5) .
В то же время почти п о всей длине всасывающего трубопровода
lвс (за вычетом /0 ) жидкость движется равномерно с некоторой
средней скоростью w8 = const = V/fвc· По этой скорости и рас
считывают гидравлические потери во всасывающем трубопрово
де h п в - по формуле (2. 3 1 ) .

292

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

При работе поршневого насоса с воздушным колпаком также
наиболее опасен (в аспекте инерционных потерь и возможного
закипания жидкости) начальный момент хода поршня, когда
cosa
1 ; максимальные инерционные потери для этого момента
составляют
F oo 2 r
hи
lo ,
( 3 . 29б)
fo g

=

где !о

=

-

--

сечение патрубка, соединяющего колпак с насосом (часто !о = /ас ) .

Заметим, что при наличии колпака значения h п в и h и сопо
ставимы по величине. Таким образом, предельную высоту вса
сывания поршневого насоса при наличии колпака можно рас
считать по формуле

-(л.

z.c

l
o

�) �

(J.) z, .
+
(3. 33а)
L fв с •2g lo .!._
pg
dвс
fo g
Применение колпака на всасывающей линии и значительное
уменьшение при этом инерционных потерь позволяет при про
чих равных условиях существенно увеличить предельную гео
метрическую высоту всасывания.
Во избежание весьма часто н аблюдаемой путаницы в поняти
ях h гв и h гвл ред еще раз (см. с. 272) подчеркнем разницу между
ними. Предельная геометрическая высота всасывания h гвл ред
характеризует максимально допустимую высоту монтажа н асоса
по отношению к расходному резервуару. Реальная высота вса
сывания h гв может быть любой , но для нормальной работы н асо
са должно быть соблюдено условие hгв < h гвл ред_ В формул ы для
расчета н апора Н и далее - мощности N входит, естественно,
реальная геометрическая высота всасывания hгв·

(h гвл ред) к

=

Р1

-

Pt

-

-

Инерционные силы необходимо учитывать и при работе насоса с нагнета
тельным трубопроводом; здесь наиболее опасным является момент a -+ it . Под
робнее об этом можно прочитать в литературе".

3.2. 7 . Расчет мощности, потребляемой поршневым насосом

Мощность рассчитывается по формулам (3. 1 0) - (3. 1 2) . При
этом полный напор Н для проектируемой насосной установки
определяется по формуле (3.3), а в случае э ксплуатации насо
са - по показаниям манометра и вакуумметра (формула (3.4) ) .
Заметим, что при расчете мощности никак н е учитываются
инерционные потери - они не входят в Н. Дело в том, что они
энергетически компенсируются в разных фазах движения порш
ня: энергия затрачивается на разгон поршнем массы жидкости и
возвращается жидкостью поршню насоса при ее торможении.
• См . , например, [ 1 ) .

293

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

3.2.8. Регулирование производительности поршневых насосов

В соответствии с формулой (3. 1 4) производительность порш
невого н асоса может регулироваться следующими способами:
- варьирование скорости вращен ия кривошипа путем уста
новки редуктора с разными передаточными числами (коробки
передач) ; применяется на очень больших насосных установках;
- изменение хода поршня путем изменения положения
пальца кривошипа, т.е. воздействие на r (так как S 2r) ; таким
способом возможно и ступенчатое и плавное регулирование
производительности (в последнем случае - не перестановкой
пальца, а установкой винта) ;
- переброска части жидкости из нагнетательного трубопро
вода во всасывающий по обратной линии 2 с помощью задвиж
ки 3 (рис. 3 . 1 6) ; при таком способе регулирования налицо без
возвратные затраты энергии на повышение давления той части
жидкости , которая возвращается по обратной линии во всасы
вающий трубопровод; этот способ регулирования является не
выгодным в энергетическом плане и его применяют лишь при
малом изменении производительности (менее 1 0-20% ) .
Н и в коем случае не следует регулировать производительность

=

поршневого насоса задвижками на всасывающей и нагнетательной
линиях. Во-первых, потому, что этот способ не позволяет регули
ровать производительность: все равно за один акт подачи н асос
будет всасывать и выталкивать одно и то же количество жид
кости V0 = FS. Во-вторых, и это гораздо важнее, попытки регу
лировать производительность поршневого насоса с помощью
задвижки могут привести к большим неприятностям.
Действительно, при регулировании задвижкой н а всасы
вающей линии возможно понижение давлен ия под поршнем
н иже р,, а значит, и вскипание жидкости с сопутствующими
этому гидравличес ки ми ударами. Дело в том , что из-за гидрав
лического сопротивления задвижки (ЛРзадв ) давление после нее
(р'вс ) будет значительно меньше давления до нее (рве) : Р'вс
Рве - ЛРзадв; не исключено Р 'вс < р,.
При регулировании задвижкой на на
гнетательной линии возникают большие
2
давления в линии до задвижки Р'н Рн +
+ ЛРзадв • которые моrу1 11орвать линию.
При полном закрытии задвижки про-

=

=

=

3

производительности
Регулирование
Рис.З. 16.
поршневого насоса с помощью вентиля на обрат
ной лин и и :
/

-

( задвижка)

294

насос,

2

-

обратная

л и н ия ,

З

-

вентиль

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

изойдет либо остановка поршня (а значит, и электродвигателя ,
что приведет к перегоранию его предохранителей ) , либо полом
ка (разрыв) линии или насоса.
3.3. Ц ЕНТРОБЕЖНЫЕ НАСОСЫ

Среди лопастных насосов наиболее распространенными яв
ляются центробежные. Основным рабочим органом центробеж
ного насоса (рис. 3 . 1 7) является колесо 2, насаженное на вал 9 и
помещенное в улиткообразном корпусе 1. Колесо представляет
собой два диска, соединенных в единую конструкцию лопастями
( лопатками ) J, разделяющими пространство между дисками на
ряд криволинейных каналов для прохода жидкости . В одном из
дисков (на рис. 3 . 1 7 - левый) имеется отверстие для входа жид
кости в насос из всасывающего трубопровода 5. Н а входе в по
следний нередко устанавливают фильтр 7, препятствующий по
паданию в насос грубых механических примесей. Кроме того, на
всасывающей линии, как правило, ставят обратный клапан 6,
закрывающийся под действием силы тяжести при отсутствии
движения жидкости и тем самым предотвращающий опорожне
ние насоса. Перед первым пуском корпус насоса и всасываю
щий трубопровод заливают жидкостью по отдельной линии 4.
Центробежные насосы для обеспечения достаточно высоких
напоров, как прав ил о, работают с частотой вращения рабочего
колеса порядка 20 об/с (обоснование столь высоких скоростей
вращения дано в разд. 3 . 3 . 1 ) . Поэтому вал насоса соединяется
при помощи муфты непосредственно с валом электродвигателя
(чаще всего - без редуктора и других передаточных устройств) .
Герметизация места ввода вала 9 в корпус 1 осуществляется при
помощи сальникового уплотнения 10.
При быстром вращении рабочего колеса жидкость в каналах
между лопатками отбрасывается под действием центробежной
силы от оси вращения к периферии и вытекает с большой ско
ростью в улиткообразный (спиралевидный) корпус 1, а оттуда в нагнетательный трубопровод 8. При этом в приосевых зонах
насоса создается разрежение, и жидкость из расходного резерву
ара под действием внешнего давления на ее свободную поверх
ность устремляется непрерывным потоком по всасывающему
трубопроводу к входному отверстию насоса. Таким образом,
всасывание и нагнетание жидкости в центробежных насосах про
исходят непрерывно и р авномерно.
На рис. 3 . 1 7 изображен центробежный насос с односторонним
всасыванием жидкости (слева). Для увеличения производитель
ности и разгрузки вала от осевых усилий применяют центро
бежные насосы с двухсторонним всасыванием (рис. 3 . 1 8) .

295

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Jt

8

1

2

9

10

-

-

-

Рис . 3. 1 7. Центробежный насос:
1
корпус , 2
колесо, 3
ло патки , 4
л и н и я дл я зал ива насоса жидкостью, 5
всасы вающий трубопровод, 6
обратн ы й клапа н , 7
фил ьтр , 8
нагнетател ьн ы й трубо 
вал, 10
сал ьн и к
п ровод, 9
-

-

-

-

-

-

-

-

-

-

Ул иткообразная форма корпуса способствует плавному отво
ду жидкости из каналов между лопатками рабочего колеса в
нагнетател ьный трубопровод, а также постепенному пониже н и ю
скорости жидкости с целью повышения ее давления з а счет
преобразования кинетической энерги и в потенциал ьную.
Для контроля работы насоса к всасывающему патрубку при
соединяется вакуумметр , а к нагнетательному - манометр .
Кроме того, на нагнетател ьной л и н и и устанавл ивается задвиж
ка, которая служит для регул ирования подачи жидкости вплоть
до ее прекращения. Для защиты насоса от гидравл ического уда
ра при внезап ной остановке в нагнетательном трубопроводе
также иногда устанавли вают обратный
клапан.
Пуск центробежного насоса произ
водится обязател ьно под зал и вом и
при закрытой задвижке на нагнета
тел ьном трубопроводе - во избежание
Рис.3. 18. Схема uентробежного насоса с двух
сторонним всасыванием жидкости :

/ - рабочее колесо, 2 и 3 - всасывающие
тельный патрубки, 4 - корnус, 5 - вал

29 6

11

нагнета

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис.З. 19. Схема многоступенчатого центро
бежного насоса

перегрузки двигателя. Затем при
медленном открывании задвижки
насос .начинает подачу жидкости в
нагнетательный трубопровод. Чем
длиннее последний, т.е. чем боль
шую массу жидкости нужно привести в движение, тем медленнее следует открывать задвижку,
сохраняя нормальный рабочи й режим, характеризующийся от
сутствием ударов и резкого шума в трубопроводе.
Рассмотренные выше центробежные насосы, где требуемый
манометрический напор достигается при прохождении жид
кости через одно рабочее колесо, называются одноступенчатыми,
или одноколесными. Напор, создаваемый такими насосами,
обычно составляет 35-50 м жидкостного столба (в случае пере
качки воды это соответствует 0,35-0,5 МПа). Для создания бо
лее высоких напоров применяют многоступенчатые ( много
колесные) центробежные насосы, состоящие из нескольких по
следовательно соединенных одинаковых колес, вращающихся на
общем валу (рис. 3 . 1 9) . Жидкость последовательно проходит че
рез все колеса и получает напор, равный (в идеале) сумме напо
ров, создаваемых каждым колесом. В современных многосту
пенчатых насосах достигается напор до 20 МПа.
Центробежные насосы изготавливают из различных кон 
струкционных материалов - металлических (стали , чугуны,
специальные сплавы, цветные металлы) и неметаллических
(вплоть до керамических и фарфоровых) - в зависимости от
химической агрессивности перекачиваемой жидкости.
Другой разновидностью лопастных н асосов являются пропел
лерные (осевые) насосы , применяемые для перемещения боль
ших количеств жидкости (до 25 мЗ/с и более) при малых напо
рах (до 0, 1 5 МПа). Рабочее колесо осевого насоса (см. рис. 3 . 1 ,
ж) состоит из втулки с лопатками винтового профиля, за
крепленной на валу. При вращении колеса лопатки сообщают
жидкости движение не в радиальном направлении, как у цент
робежных насосов, а в осевом. Для уменьшения
окружной
(вращательной ) скорости жидкости (а следовательно, и гидрав
лических потерь) перед нагнетательным трубопроводом устана
вли вается направляющий аппарат с продольными ребрами . КПД
осевых насосов (по мощности) достигает 0,9 и выше.
При подборе лопастн ых насосов и технологическом их
расчете необходимо определ ить их напор Н и производител ь
ность V, их взаимосвязь (характеристику н асоса ) , мощность
297

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

н а валу, а также ряд других параметров и условий их работы .
Н иже эти вопросы рассмотрены применител ьно к центро
бежн ым н асоса м .
3.3. 1 . Основное уравнение. Напор

Для поршневых насосов, где замкнутые объемы жидкости
принудительно выталкиваются потребителю, вопрос о том , ка
кой напор может развивать насос, не возникает: это может
быть в принципе любой напор. В центробежных насосах рабо
чее колесо может вращаться и при закрытой задвижке на на
порной линии, создавая определенный (не беспредельный) на
пор. В рабочих режимах передаваемая механическая энергия от
лопаток рабочего колеса к жидкости (иначе: получаемый жид
костью напор) ограничена и во многом зависит от конструкции
рабочего колеса и параметров работы насоса. Поэтому для цент
робежных насосов вполне правомерен вопрос: какой напор мо
жет развивать центробежный насос?
Теоретически возможный напор Нт, создаваемый центробеж
ным насосом , определим следующим образом . Рассмотрим дви
жение жидкости между лопатками рабочего колеса (рис . 3 . 20).
При работе насоса каждая частица жидкости движется вдоль
лопатки с относительной скоростью w, перемещаясь одновре
менно вместе с рабочим колесом по касательной к окружности
(нормально к радиусу) с окружной (переносной) скоростью и.
Абсолютная скорость частицы жидкости с равна геометрической
сумме w и и . Обозначим: w 1 и w2 - относительные скорости
жидкости при входе на лопатку и на выходе с лопатки; R 1 и
R2
внутренний и внешний радиусы колеса соответственно для
окружностей входа жидкости в рабочее колесо и выхода из него;
окружные
угловая скорость вращения колеса; и 1 и и2
ro
скорости на радиусах R 1 и R2· Очевидно, и , = ro R , , и2 = ro R2. А
абсолютные скорости с 1 и с2 на входе и на выходе с лопатки
рабочего колеса определяются из параллелограммов скоростей
(см. рис . 3 . 20) .
Угол между относительной скоростью w и обратным направ
лением окружной скорости и обозначим р и назовем его кон
структивным (его величина определяется конструкцией лопат
конструктивный угол на входе; Р2
ки) . Соответственно: р 1
конструктивный угол на выходе. Угол между векторами абсо
лютной скорости с и окружной и обозначим а и назовем техно
логическим (его величина зависит от технологических пара
метров работы насоса: производительности , частоты вращения
рабочего колеса и т.д.). Соответственно: а 1
технологический
угол на входе жидкости на лопатку, а 2 - технологический угол
на выходе .
298
-

-

-

-

-

-

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 3. 20. Картина скоростей жид 
кости на входе и выходе центробеж
ного насоса

Известная теорема механи
ки гласит, что изменение мо
мента количества движения
равно
моменту
равнодей 
ствующей внешних сил в си
стеме. При массовом расходе
жидкости G (кг/с) имеем: Gc
количество движения в
какой-либо точке лопатки ;
Rcosa.
плечо, Gc Rcosa.
момент количества движения.
Тогда, согласно этой теореме,
для сечений входа жидкости в рабочее колесо и выхода из него
без учета потерь на трение между этими сечениями
(а)
Gc2 R2cosa.2 - Gc1 R1 cosa. 1 = М,
где М вращающий момент (от электродвигателя) .
-

-

-

При угловой скорости вращения колеса ro мощность, пере
данная жидкости от электродвигателя посредством лопаток ра
бочего колеса, равна N = Mro . В самом деле, момент внешней
силы на валу рабочего колеса равен произведению этой сил ы F
окруж
на радиус вала rв, так что Mro
Fro r8, причем ro r8 = и8
ная скорость на валу. А полученное произведение Fu8 (силы на
путь в единицу времени) есть работа в единицу времени, т.е.
М О ЩН ОСТЬ N.
С другой стороны, мощность может рассматриваться (см.
разд. 3 . 1 .4) как работа (в единицу времени) , затрачиваемая на
подъем G (кг/с) жидкости на высоту Нт м, т.е.

=

-

(б)
N = GgHт.
Умножим обе части равенства (а) на ro и учтем соотношение
(б), а также ro R2 = и2 и ro R1 и1 :
Gc2u2cosa.2 - Gc1 u1 cosa. 1
GgHт.

=

=

Отсюда получаем одну из форм записи основного уравнения
центробежного насоса:
1
( 3 . 34)
Нт
- ( u2c2cosa.2 - u 1 c1 cosa. 1 ) .

=g

Уравнение ( 3 . 34) может быть также получено из баланса мо
ментов для контура, охватывающего входное (на лопатки) и
выходное (с лопаток) сечения для прохода жидкости . Для фраг 299

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис.3. 21. К балансу моментов в рабочем коле
се насоса:
1 - лопатки, 2
окружность входа, З
окружность выхода
-

-

мента такого контура (между двумя
соседними лопатками на рис. 3 . 2 1 )
имеем, пренебрегая пока потерями
энергии в самом насосе :
Приход:
Уход:
Источник:
Сток:
Накопление:

Пр= Gc1 R1 cosa 1 ;
Ух= Gc2 R2 cosa 2 ;
Ис = М;
Ст= О;
Нак = О, так как рассматриваем стацио
нарную работу насоса.
Тогда по уравнению ( l .8) имеем
Gc1 R1 cosa 1 - Gc2 R2 cosa 2 + М - О = О,
откуда следуют упомянутая теорема механики и уравнение (а).
Конструкторы насосов, как и технологи , их эксплуатирую
щие, заинтересованы в получении максимального нанора. Этого
можно добиться, уменьшая второй член правой части уравнения
(3.34). Следовательно, надо стараться, чтобы угол
был близок
к 90°. К тому же при этом абсолютная скорость
будет направ
лена вдоль лопатки (см . рис.3.20), что обеспечивает плавный
(безударный) вход жидкости в рабочее колесо. На практике
обычно
= 85+88°, так что cosa 1 практически равен нулю. Тог
да основное уравнение центробежного насоса принимает вид
1
(3. 34а)
Нт - - u2 c2 cosa 2 .
g
Это соотношение не учитывает потерь напора внутри насоса
h п нас. П оэтому реальный напор насоса Н, полезно используемый
потребителем, меньше теоретического и равен
Н = Нт - h п нас = НтТ\г,
где 11 r - rидравлический К IЩ насоса.
Полные потери напора внутри насоса h п нас складываются из
потерь на трение жидкости о лопатки и диски рабочего колеса
(учитываются коэффициентом ri'г, равным 0,8-0,95) и вихреоб
разование между лопатками из-за неравномерности полей ско
ростей (учитываются коэффициентом Т\ "г, равным 0,55 - 0,85),
так что Т\ г = Т\ 'г ri "г- Обычно для насосов малой и средней произ-

с1 а 1

а1

300

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

=Чr =

водительности
0,6+0,7; для насосов большой производи
0,7+0,8.
тельности 1"\ г
Таким о бразом,

2!!:_ и1С2СОSа 2 .

(3. 34б)
g
Анализ формулы (3.34) показывает, что теоретический напор
не зависит от свойств жидкости - они не входят в уравнение.
И ными словами, насос любую жидкость (в том числе и сжи
маемую - газ) будет перекачивать на одинаковую высоту. Имен
но поэтому насос перед работой должен быть заполнен жид
костью. Если в нем воздух (его плотность - Р г) , то насос соз
даст напор Нт метров воздушного столба. Тогда жидкость под
действием этого напора поднимется по всасывающей линии
лишь на высоту Нт(Рг/Р) над уровнем в расходном резервуаре и
не попадет в рабочее колесо насоса. Вот почему центробежный
насос запускается под заливом. Чтобы при остановке насоса
жидкость не вытекала из него по всасывающей линии, на по
следней устанавливают обратны й клапан (см. рис. 3 . 1 7 , поз. 6) .
Заметим, что полезный напор насоса Н в определенной мере
зависит от свойств жидкости, в частности от вязкости : послед
няя влияет на величину потерь напора в рабочем колесе насоса
и, следовательно, на Ч г ·
Теоретический напор Нт (реальный - тоже) зависит от
окружной и2 и абсолютной с2 скоростей, причем и2
ro R2
2rtпR2. Это означает, что необходимый напор насоса Н может
быть обеспечен различными сочетаниями п и R2.
Напор, развиваемый центробежным насосом, согласно фор
муле (3.34а) зависит от технологического угла выхода а2 , следо
вательно и от конструктивного угла р2 (рис.3.22). Последний
определяется формой лопаток и их расположением . Лопатки
могут быть плоскими и радиально расположенными , так что
р2
90° (рис. 3 .22, б). Для лопаток, загнутых назад относитель
но направления вращения колеса, угол р2 < 90° (рис. 3.22, а) . И ,
Н

=

=

=

=

=

112

112

112

Рис.3. 22. Влияние угла р2 н а величину абсолютной скорости с2:
а

-

<

90°, б

-

=

90°,

11

-

>

90°

30 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

наконец, лопатки могут быть загнуты вперед (рис. 3 . 2 2 , в) . Воз
н и кает вопрос: какое расположение лопаток я вляется предпоч
тител ь н ы м с точ ки зрения формирования напора Jf?
Для ответа на этот вопрос напишем уравнение Бернулли для
сеч е н и й входа жидкости в рабочее колесо и выхода из н е го ,
уч итывая , что между сечениями есть источник напора Нт и п о 
тери в рабочем колесе h п н ас:

Z1 +

р
_!_

pg

+

_!_
cz

2g

+

Нт =

Z2 + Pz

pg

2

2g

+ С1

+

h п нас .

Здесь
= Н. Разность z2 - z1 знакоперемен н а (знак
изменяется при п овороте рабочего колеса н а 1 80°) , причем она
составляет десятые дол и метра, поэтому ею можно пренебречь
по сравн е н и ю с <Р2 - p 1 )/(pg) , и змеряемой десяткам и метров.
Тогда

Нт - h п нас
Н

=

Р - Р
с2 - с2
_
2 __
1 + _2__
1

pg

2g

Нпот + Ню� н ·

Таким образо м , развиваем ый насосом напор можно предста
вить как сумму прираще н и й поте н циального (Нп от) и ки нетиче
ского ( Ню� н ) напоров.
Назначение н асоса - создание возможно большего потенци
ального н апора. Бол ьшой кинетический напор вреден , так как
выход жидкости из насоса в трубопровод с высокой скоростью
сопряжен с бол ь ш и м и гидравлич ески м и потерям и в последнем.

, кон е чно , ситуации , тре бую щи е высо ких с коросте й жид кости на
В оз мизожны
в ыход
е ра боче го коле са (созда ни е дальнобойны х жидкостн ых струй , н а п ри 
ме р ) . Тогда вывод о направле нии лопаток рабоч е го коле са будет обратны м. Н о ,
ка к правил о , та к и е ситуации находятся за предел ам и хи м ич ес к ой те хнол огии .
И м е н н о преобразованию ки нетического напора в поте н ц и 
ал ьный служит ул иткообразная форма корпуса центробежного
насоса: посте пе н ное расширение сече н ия обеспеч и вает переход
(согласно уравне н и ю Бернулли ) кинетической энерги и в поте н 
циал ьную. Этой ж е цел и должно служить рационал ьное направ
ление лопаток рабочего колеса: надо выбрать такое , при кото 
ром доля ки нетического напора будет наименьше й .
Сопоставление скоростных диаграмм п р и разл и ч н ы х углах
выхода Р2 в условиях оди наковых знач е н и й w2 и и2 представлено
на рис. 3.22. М ожно видеть, что с точ ки зрения п олучения наи 
2
мен ьшего кинетического напора [ вел и ч и н ы c2 /(2g) ] н аилуч 
ш и м и я вляются лопатки , отогнутые назад (рис . . 3 . 2 2 , а) : Нки н =
2 - c1 2
= ( с2
)/(2g) при этом м и н и мал ьно.
Н аилуч ш и е резул ьтаты работы центробежн ых насосов полу
чаются при р 1 = 2 0 + 4 0 ° (обеспечи вается безударн ый вход жид
1 5+ 6 0 ° .
кости на лопатку) и р2
=

302

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

3.3.2. Производительность

Производительность центробежного насоса может быть рас
считана по уравнению ( 1 .3) как произведение живого сечения и
абсолютной скорости . При этом необходимо помнить, что жи
вое сечение трактуется как проекция сечения на плоскость,
нормальную к направлению скорости. Для расчета производитель
ности центробежных насосов такое представление неудобно, по
этому используют тождественное ему произведение сечения потока
и проекции скорости на направление, нормальное сечению.
Обозначим (рис. 3.23): D = 2R2
диаметр рабочего колеса; Ь
umрина лопатки на выходе; о
толщина лопатки; iп
количество
лопаток (обычно кратно 3).
Полное сечение рабочего колеса на выходе равно rt Db. Часть
его, а именно iпЬО, занята лопатками , тогда сечение / для про
хода жидкости составляет
/= rt Db iпЬО = b(rtD iп о ) = rt Dbljl ,
где lj/ 1 i,IJ/(11D) коэффициент, учИ1ъmающий стеснение потока лопатками.
-

-

-

-

=

-

-

-

-

При абсолютной скорости жидкости с2 на выходе с лопаток и
угле а2 (см. рис. 3.23) нормальная к сечению / (радиал ьная) ско
рость c R равна
cR = c2 s i na 2 .
Следовательно, теоретическая производительность центро
бежного насоса равна

v,. = fcR = rt Db1j1C2S ina2 .

(3.35)

Рис.3. 23. К расчету производительности центробежного насоса

303

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Реальная производительность центробежно го насоса будет
несколько ниже :
(3.35а)

где ТJ v - коэффициент подачи , учитывающий переток жидкости из зон нагне
тания в зоны всасывания через зазоры между рабочим колесом и корпусом (а
иногда и утечки жидкости через сальники). Величина ТJv изменяется в сравни 
тельно узких пределах - от 0,95 до 0,98, причем большее значение отвечает
насосам более высокой производительности .

3.3.3. Характеристики центробежных насосов

Одной из особенностей центробежного насоса является вза
имозависимость развиваемого им напора и производительности . В
самом деле, выражения (3.34б) и (3.35а) для напора и произво
дительности содержат абсолютную скорость с2, так что зависи 
мости Н = Н(с2) и V = V(c2) демонстрируют связь Н и V, задан
ную в параметрической форме. Зависимость между напором Н и
производительностью V для постоянной (заданной) частоты
вращения носит название частной характеристики центробежного
насоса. При выборе оптимального режима работы центробежно
го насоса целесообразно использовать его универсальную харак
теристику, которая представляет зависимости Н от V при различ
ных скоростях вращения рабочего колеса. Для технологов важно
(в плане отыскания рабочей точки центробежного насоса
см .
ниже) представить зависимость Н от V в явном виде . Связь
теоретических напора Нт и производительности V,. может быть
установлена аналитически .
-

Частная характеристика центробежного насоса

Для отыскания теоретической характеристики центробежного
насоса, т.е. зависимости Нт = Нт( V,.) , в явной форме достаточно
лишь найти выражения для с2 из формул (3. 34а) и (3.35) и при 
равнять их:
gH T

VT
тtDbl.jJ sin a 2

---- = -----

откуда

н

1

=

V1 u2 co s a 2
grrDbl.jJ s i n а 2

=

V1 u2

grrDbl.jJ

ctga 2

(в)

Полученная зависимость имеет существенный недостаток:
она содержит технологический угол а2. Выразим его через кон
структивный угол 132. Для этого рассмотрим паралл елограмм ско
ростей жидкости на выходе из рабочего колеса (см. рис. 3 . 2 3 ) .
304

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Очевидно,
ctga 2

Но ся

=

-

_

с2 cos a 2
�

-

_

--- _
- т

и2

�

-

и2 - Cя ctg p 2
�

-

_

c2s i na 2 , и из (3.35) находим

--1tDbЧJ
1tDbЧJ VT

ся =

Тогда
ctga 2

Uz

=

(

и2

�

- с t8 А
1-' 2

.

VT

ctgJ32 .

- )

Подстамяя найденное значение ctga 2 в уравнение (в), получаем
н

1

=

V1 u2

gл Db ЧJ

Н

или после преобразований
1

=

ui
g

u2 1tDb ЧJ

V1

ctg ,... 2 •
А

- Uzctg� 2 V
gлDbЧJ

.

(3. 36)

1

Эта линейная зависимость Нт от V,. представляет собой теоре
тическую характеристику центробежного насоса при заданной
постоянной частоте вращения рабочего колеса. При р 2 < 90°
(лопатки отогнуrы назад) с увеличением V,. теоретический напор
Нт падает; при р 2
90° (ctgp 2
О) теоретически й напор Нт ра
вен и1 2/(2g) и не зависит от V,.; наконец, при Р 2 > 90° (лопатки
отогнуrы вперед) Нт растет при увеличении V,.. Практически,
как было показано ранее, для химиков-технологов наиболее
важен случай р 2 < 90°. При этом теоретическая зависимость на
пора от производительности изображается прямой 1 на рис . 3 . 24.
Подчеркнем: в рассматриваемом случае увеличению производительпонижение
отвечает
ности
напора, развиваемого насосом.
Реальная частная характе
н
ристика центробежного насо
са устанавливается экспери
ментально - пуrем измере-

=

-- -

=

Частная характеристика
Рис.3. 24.
центробежного насоса:

1
теорети'lеская характеристика на
реальная характеристи ка
V) , 2
соса ( Н1
зависимость мощности
насоса ( Н- V), 3
зависи
N от производител ьности V, 4
мость КПД насоса от производител ьности V

-

1111

v

305

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ния сопряжен н ых значений напора насоса (как суммы показа
ний манометра и вакуумметра) и его производительности при
различных степенях открытия задвижки на напорной линии.
Она отклоняется от теоретической и в случае лопаток, отогну
тых назад, имеет вид кривой 2, изображенной на рис.3. 24.
Большая разница между теоретическим и реальным напорами
при малых производительностях насоса связана с потерями на
пора в самом насосе на трение и на гидравлический удар при
переходе кинетической энергии жидкости в потенциальную.
При полностью закрытой задвижке ( V = О) основные потери
напора обусловлены гидравлическим ударом ; собственно потери
на трение жидкости о лопатки рабочего колеса при этом неве
лики, поскольку жидкость не перемещается в рабочем колесе от
окружности входа к окружности выхода. Если немного приот
крыть задвижку на напорной линии ( V > О), то потери на гид
равлический удар уменьшатся, однако несколько возрастут по
тери на гидравлическое сопротивление движению жидкости
внутри насоса, но они еще существенно ниже потерь на удар.
Поэтому реальная характеристика насоса с увеличением V пона
чалу приближается к теоретической. С ростом V соотношение
упомянутых потерь (как и их сумма, обозначенная ранее ка к
hn н ac ) постепенно изменяется. При достаточно высоких произ
водительностях V потери на гидравлический удар сводятся к
минимуму (при этом вход жидкости на лопатки рабочего колеса
близок к безударному) , а потери на гидравлическое сопротивле
ние - достаточно велики. С ростом V они продолжают возрас
тать, и реальная характеристика центробежного насоса все более
отклоняется от теоретической.
С изменением производительности и напора изменяются
также мощность, потребляемая насосом (кривая З на рис.3 .24 ) ,
и коэффициент полезного действия насоса т� н (кривая 4) ,
имеющий максимальное значение при некоторой производи
тельности насоса. Заметим, что именно в этой точке суммарные
гидравлические потери в насосе hn н ac минимальны.
Рабочая точка центробежного насоса

Напомним, что насос при работе с заданным трубопроводом
должен развивать напор, равный сопротивлению этого трубо
провода. Поэтому рабочую точку центробежного насоса (точка
М1 с координатами V1 , Н1 на рис.3.25) можно определить как
точку пересечения характеристики насоса (Н
JI) и характери
стики сети [формула ( 3 . 5) ) . При этом центробежный насос
обеспечивает производител ьность, при которой сопротивление в
трубопроводе равно напору, создаваемому насосом.
-

306

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Если нужно уменьшить подачу в сеть, то следует несколько
прикрыть задвижку на нагнетательной линии. Тем самым будет
увеличиваться коэффициент местного сопротивления задвижки �з'
входящий в I:�, а значит, и множитель перед V2 в формуле (3.5). В
результате характеристика сети пойдет более круто, и рабочая точка
М2 получ ится при меньшей производительности ( V2 < V1 ) .
Этот вывод, сделанный на основе геометрических построений
на графике Н- V, находит следующее физическое объяснение.
Увеличение гидравлического сопротивления сети (за счет �з) по
требовало работы насоса с большим напором. Но росту напора на
нисходящей ветви (речь идет о насосе, в котором лопатки рабоче
го колеса отогнуты назад) отвечает уменьшение производитель
ности V. Таким образом, задвижка на напорной линии позволяет
(в отличие от поршневых насосов) регулировать производитель
ность центробежного насоса. Следует, однако, понимать, что при
таком способе регулирования производительности приходится
затрачивать энергию на преодоление дополнительного гидравли
ческого сопротивления прикрытой задвижки (вентиля).
При регулировании производительности задвижкой жела
тельно, чтобы рабочая точка характеризовалась максимальным
Тl н (или бьша вблизи этого значения Тl н ) . Поэтому если при та
ком регулировании происходит существенное снижение КПД
насоса Тl н , то этот способ следует признать нецелесообразным.
Опыт эксплуатации насосов показал , что регулирование произ
водительности задвижкой оправдывает себя, если оно осу
ществляется в пределах ±20 % .
Заметим, что рабочие точки должны находиться н а нисходящей
ветви кривой H- V (точки М1 и М2 ) . Работа центробежного насо
са на восходящей ветви является неустойчивой .
Неустойчивая работа насоса, вероятнее всего, объясняется возможностью
появления двух стационарных рабочих точек на восходящей ветви кривой Н- V
(точки Мз и М4 на рис.3.25). Два относительно устойчивых режима работы
(точки М3 и М4 ) характеризуются
разными производительностями и
напорами. При некотором изменении
(отключился
производительности
потребитель или , наоборот, подклю
чился) возможен переход из одного
устойчивого режима в другой. Такой
переход сопровождается гидравличе
скими ударами. Неустойчи вая работа
насоса, характеризуемая частой сме
ной режимов работы и гидравличе
Рис.3. 25. Определение рабочей точки
центробежного насоса:

-

1
характеристика н асоса , 2, 2' и 2"
характеристики сети

307

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

скими ударами, получила название "помпаж" . Сколько-нибудь длительная
работа центробежного насоса в режиме помпажа выводит его из строя.
Есть и иные объяснения· неустойчивой работы центробежного насоса при
рабочей точке на восходящей линии.

При необходимости более существенного изменения подачи
в трубопровод следует искать другие способы регулирования
производительности (о некоторых из них см. н иже) - вплоть до
замены насоса.
Законы пропорциональности
При необходимости существенного изменения производи 
тельности центробежного насоса идут на изменение скорости
вращения рабочего колеса путем замены электродвигателя или
передачи (редуктора). При этом изменяется не только произво
дительность насоса, но и его напор, а также потребляемая мощ
ность. И ными словами , частная характеристика насоса, сохра
нив свою форму, займет другое положение на графике H- V.
Рассмотрим влияние частоты вращения рабочего колеса на
производительность насоса V, создаваемый им напор Н и по
требляемую мощность N. Если пренебречь несущественным
изменением угла
при изменении частоты вращения насоса от
п ' до п ", то треугольники скоростей выхода жидкости могут рас
сматриваться как подобные (рис.3 .26) . Тогда, учитывая малосу
щественное изменение Т\v с V и известные соотношения оо ' =
= 2тtп ' и оо " = 2тtп ", получ им на основе формулы (3.35а)

а2

V"
V'

тtDbЧJC'i. sina 11v
rtDbЧJc]. sina 22 11v

=

c'J.
с2

-

=

и'J.
и2

-

=

oo "R2
oo 'R2

--

=

п"

-

п'

(г)

Следовательно, производительность центробежного насоса прямо
пропорциональна частоте вращения.
Для определения зависимости напора насоса от частоты вра
щения рабочего колеса воспользуемся формулой ( 3 . 34б) :

Н"
Н'

(д)

т.е. напор, развиваемый насосом, примерно прямо пропорционален
квадрату частоты вращения. Оговорка
" примерно" здесь необходима, по
скольку изменению п сопутствует из
менение производительности V, а с
ней - потерь на трение внутри цент
робежного насоса, а значит и Т\ rРис.З. 26. Треугольники скоростей при различ
ных частотах вращения рабочего колеса цент
робежного насоса (п' и n")

• См , напри мер, ( 2, 3 ) .

308

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

( ) ( )

Аналогично, в соответствии с формулой (3. 1 О) получим
N"
N'

pg V "H "11 .
11 . pg V 'H '

"'

V "H " =
V 'H '

!t:_ !t:_ 2 = !t:_ 3
п

'

п

'

п

(е)

'

т.е. мощность на валу насоса пропорциональна кубу частоты вра
щения. Это соотношение еще более приближенно, так как 11 н
заметно изменяется с числом оборотов п ; поэтому соотношение
(е) пригодно лишь для оценки влияния частоты вращения п на
мощность N.
При помощи соотношений (г) , (д) и (е), известных как зако
ны пропорциональности , можно по одной опытной характеристи
ке H- V, пол уч енной для определенной частоты вращения , при
близительно построить характеристики при других частотах
вращения. Однако для точного расчета этих характеристик не
обходимо учесть ранее проигнорированное влияние
частоты
вращения п на величины ТJ r , ТJ н , а есл и строго, то и llv ·
Поэтому более точно характеристики насоса при различных
частотах - вращения получают на специальных испытательных
стендах и для определенных конструктивных сери й приводят в
паспортах насосов или в каталогах.
Универсальная характеристика центробежного насоса

Семейство кривых Н- V при различных частотах вращен ия
(обычно они даются в об/мин) в совокупности с линиями оди
наковых КПД насоса н азывают универсальной характеристикой
(пример ее представлен на рис. 3.27). Отметим, что каждый на
сос имеет лишь один наивыгоднейший рабочий режим (при
определенных производительности и частоте вращения) ; при
любом отклонении от него КПД насоса падает. С самым высо
ким КПД (ТJ нмакс) насос работает при определенной частоте
вращения (в рассматриваемом случае - 11 н м акс = О, 70 при п =
= 1 500 об/мин) . При других п также имеются точки с наиболь
шими КПД насоса (но их значение ниже 11 н макс) . Точки с рав
ными КПД насоса дают линии одинаковых КПД (0,65; 0,60;
0,55 и 0,50 на рис. 3.27).
Выбор типа центробежного насоса (серии ) , а также опти
мальной частоты вращения рабочего колеса производится с уче
том его универсальной характеристики.
В задачах проектирования расход жидкости VP задан (требу
емая производительность насоса) . Для проектируемого трубо
провода при этой производительности рассчитывается сопроти 
вление трубопровода Нр (именно этот напор и должен развивать
насос). Если точка с требуемыми VP и Нр (точка Р) на ун ивер
сальной характеристике попадает в область сравнительно высоких
309

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

J/

р

v

Рис . З. 27. Универсальная характеристика центробежного насоса

ri н , то этот тип насоса можно считать подходящим для работы с

проектируемым трубопроводом. Поскольку значения частоты
вращения электродвигателя, а значит и рабочего колеса насоса,
как правило, можно изменять только дискретно, то выбирают
ближайшее (к упомянуrой точке) большее. Рабочей точкой
этого центробежного насоса будет точка N (см. рис. 3.27); при
этом производительность равна VP , а развиваемый напор - чуrь
больше требуемого. Дополнительное гидравлическое сопроти
вление трубопровода обеспечивается прикрытием задвижки на
нагнетательной линии (увеличивается �3).
При эксплуатации насоса с трубопроводом (характеристика
последнего N2 N3 NN1 ) изменение частоты вращения приводит к
перемещению рабочей точки по линии N2 N3 NN1 - с соответ
ствующим изменением производительности и напора. Заметим ,
что уменьшение производительности пуrем уменьшения частоты
вращения возможно лишь до определенного предела. Так, из
рис. 3 . 27 видно, что при частоте вращения 500 мин- 1 насос не
может подавать жидкость в трубопровод, так как развиваемый
им напор меньше требуемого (характеристика насоса располо
жена ниже характеристики сети: они не пересекаются и рабочей
точки не существует) .
В целом регулировать производительность центробежного
насоса пуrем изменения частоты вращения рабочего колеса це
лесообразно только в области достаточно высоких КПД насоса.
В противном случае необходимо искать иные способы: замена

3 10

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

насоса (при этом его надо подбирать так, чтобы рабочая точка
отвечала заданной производительности при возможно большем
КП Д ) , установка двух насосов (при необходимости увеличения
производител ьности) и т.д.
3.3.4. Параллельная и последовательная работа насосов

Совместная работа нескольких насосов на общий нагнета
тельный трубопровод применяется в тех случаях, когда требуе
мые значения V или Н (либо обе эти величины) не могут быть
обеспечены одним насосом. Естественной представляется парал
лельная установка насосов при необходимости увеличения про
изводительности и их последовательная работа - для увеличения
напора. Однако реально при параллельном включении несколь
ких одинаковых насосов подача не увеличивается пропорцио
нально числу насосов, а при их последовательной работе пропорционально их числу не увеличивается напор. Причины
этого становятся ясными при анализе совместной работы парал
лельно или последовательно включенных насосов. П роведем
такой анализ на примере двух центробежных насосов с одинако
выми индивидуальными характеристиками.
Допустим , что насос с характеристикой DBB 1 (рис. 3 . 2 8 , а),
нагнетая жидкость
в трубопровод с характеристикой АВС,
имеет рабочую точку В, отвечающую подаче Vi и напору Н1 .
Характеристи ка двух параллельно работающих насосов (кривая
DCC1 ) может быть построена путем удвоения производитель
ности одного насоса при каждом из рабочих напоров. Напри
мер, при Н1 производительность равна сумме Vi + Vн (в рас-

а

б

Определение рабочих точ ек при параллельной (а) и последовательной
(6) работе двух центробежных насосов (/, ![)
Рис. 3. 28.

31 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

сматр и ваемом случае оди наковых характеристик - величине
2 J1i ) . Рабочей точ кой при работе двух параллельн ых насосов с
тем же трубопроводом (его характеристика А В С) будет точка С.
Вообще говоря , характеристика трубопровода за счет коммуни 
кации второго насоса несколько изменяется . Однако из - за ма
лой дл и н ы коммуни кационных л и н и й по сравне н и ю с общей
дл иной трубопровода это изменение характеристи ки трубопро
вода можно не уч итывать.
Из рис. 3 . 2 8 , а в идно, что производительность двух н асосов
V1 + 1 1 меньше удвоенной производительности одного насоса
(2 Vj = Vi + Vj 1 ) , а развиваемый при этом обоими насосами на
пор Нн 1 1 бол ьше напора Н1 . Таки м образом , при параллельной
установке двух насосов в действител ьности происходит увеличе
н и е производительности , но все же не ее удвоен и е . Такое
удвоение н аблюдалось бы при сохране н и и напора насосной
установки на уровне Н1 . Но напор таки м не сохраняется . П р и 
ч и н а в том , что при возросшей производительности Vi + 1 1 , т.е.
увеличенном расходе жидкости по тому же трубопроводу, по
вышается ее скорость, а с н е й и гидравлическое сопроти вление.
Для преодоления последнего насосная установка должна разви 
вать больший напор, чем это было необходимо при работе одно
го насоса с меньшей производител ьностью Vj . Это означает по
вышение рабочего значения Нн 1 1 > Н1 . А поскол ьку при работе
центробежного насоса на н исходящей ветви характеристики с
увел ичением напора его производител ьность падает, то стано
вится впол н е понятн ы м неравенство V1 + 1 1 < Vj + Vн (или в рас
сматр и ваемом сл уч ае Vi + 1 1 < 2 Vj ) .
Ранее бьuю отмечено, что удвоение производител ьности
( V1 + 1 1 = 2 Vj ) все -таки возможно ( при сохране н и и напора на
уровне Н1) ; для этого нужно измен ить характеристику сети
(п роложить, например, трубопровод большего диаметра) . Однако
практически это делать нецелесообразно.
Схема последовательной работы двух оди н аковых насосов
представлена на рис. 3 .28 , б. Характеристика двух последовател ь
но работающих центробежн ых насосов ( FCG) получается при
сложе н и и (здесь - при удвоен и и ) ординат кривой DBE для
каждой рабочей производител ьности V. В трубопровод с харак
теристи кой АВС оди н насос будет подавать жидкость с произво
дител ьностью Vj при напоре Н1 ; рабочей при этом будет точка
В. При совместной работе двух насосов на тот же трубопровод
(его характеристи ка АВС) рабочей будет точка С. Значит, насос
ная установка при последовательной работе насосов действи
тел ь н о обеспечи вает увеличение напора : Н1 + 1 1 > Н1 . Однако это
увеличение не дости гает удвоения ( Н1 + 1 1 < 2Н1 ) . Дело в том , что
для удвое ния напора потребовалось бы сохран ить прежн юю

312

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

производительность V1 ; но она не сохраняется, а возрастает
( Vi +п > Jl). А при увеличении производительности уменьшается
напор Н1+ н - он стал меньше удвоенного (суммарного - при
работе пары насосов с разными характеристиками) .
Таким образом, при совместной работе двух центробежных
насосов происходит одновременное увеличение как напора, так
и производительности . Встречающиеся в литературе * суждения о
целесообразности во всех практических случаях параллельного
включения насосов при необходимости повышения производи
тельности и последовательного - при необходимости повыше
ния напора - вряд ли являются оправданными. Выбор рацио
нальной схемы их включения зависит от потребностей техноло
гической установки , а также от конкретных характеристик ис
пользуемых насосов и трубопровода (сети).
3.3.5. Предельная высота всасывания

В основе расчета предельной высоты всасывания центробеж
ного насоса лежит общая формула (3.8). При этом необходимо
также принять во внимание некоторые особенности работы
центробежных насосов. Здесь, разумеется, нет инерционных
потерь во всасывающем трубопроводе, поскольку движение в
нем - равномерное. В то же время для центробежных насосов
следует учитывать эффекты, связанные с неравномерным рас
пределением скоростей и давлений в рабочем колесе вблизи
входного сечения.
Различия в значениях абсолютных с и относительных w ско
ростей в разных точках канала между соседними лопатками
приводят к повышению (в сравнении со средним значением)
давления в зонах, где лопатки " набегают" на жидкость в рабо
чем колесе, и к понижению (именно в этом - опасность! ) там ,
где о н и " убегают " о т жидкости (т.е. з а лопаткой). Это может
повлечь за собой уменьшение давления в некоторых точках се
чения всасывания (за лопаткой) ниже давления насыщенных
паров р1, соответствующего те м пературе t перекачиваемой жид
кости , и тогда жидкость закипит. Образовавшиеся пузырьки
пара, перемещаясь вместе с жидкостью, попадают ближе к вы
ходу из колеса - в зону более высокого давления - и конден 
сируются. В освобождающиеся п р и этом полости ( " пустоты " )
устремляется жидкость и с большой силой бьет по лопаткам ,
причем с очень высокой частотой - сотни ударов в секунду.
При работе насоса в таком режиме возникает явление, полу
чившее название кавитации (см. разд. 3 . 1 .3). Работа центробеж•

См., например, (2).
313

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ного насоса в этом режиме быстро приводит к образованию рако
вин на лопатках и дисках рабочего конеса, его децентровке, бие
н и ю колеса на валу и в итоге - к его разруше11 ию.
Эффект снижения давления за счет ttеравномерности распреде
ления скоростей во входном сечении рабочего колеса обознач им
снм волом /1каа. Для обеспечения надежной работы (без кавитации)
предельную высоту всасывания умевьшают ва эту велИчиву:
2
h npcд Р 1 р, W •c - h
/1
( 3 . 3 7)
r1
2g
ПI
Kll
=

- -

-

.

Для определения ''•а• предложев ы различные расчетные соот
ношен и я . В качестве примера при ведем полуэ м п ирическую фор
мулу с безразмер н ы м м ножителем:
1
2 \2 1 3

pg

/zш

=

2,7 5g

(

Vn

J

(3 .38)

•

Значения h •••• g. V и п согласованы единой выбранной системой
един и ц (напри мер, С И ) .
·

3.4. НЕМЕХАНИЧЕСКИЕ НАСОСЫ
3.4. 1 .

Газла1фты

В газш1фтах (эрлифтах, есл и газ - воздух) подъем жидкости
(отсюда еще одно название этих насосов - " газовые подъемники")
на высоту Н (рис. 3 . 2 9) из расходного резервуара 2 в приемный 4
обеспечивается за счет меньшей плотности газожидкостной смеси
Ргж в подъем ной трубе 3, по сравнению с плотностью жидкости Рж
в резервуаре 2.
Технологический расчет предусматривает связь параметров
процесса с геометрическим и характеристикам�� системы газлифта.
Плотность газожидкостной смеси зависит от объем ной доли га
за в смеси газосодержа н ия <р :
Р rж = PrlP + Рж( l - <р),
ил и, поскол ьку обычно плотность газа Рг<<р., то
Рrж :;: Рж( 1 <р )
Обознач и м глубину погружения подъем но й трубы 3 в рас
ходном резервуаре . до сечения подач и газа н., а давления на
с вободные поверхности в обоих резервуарах P i · Согласно зако
ну сообщающихся сосудов, давление на уровне ввода газа по
трубе 2 может быть зап исано как по жидкости, так и по газожид
костному столбу; без учета гидравл ических потерь при движени и

-

- .

314

-

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис.З. 29.
1

Схема газлифта:

труба для подачи rаза, 2 - расход
ный резервуар, 3 - подъемная труба, 4 приемн ый резервуар; Г - rаз, Ж - жид 
кость
-

газожидкостной
смеси
подъемной трубе
Р 1 + РжКНж =

= Р 1 + Р гж ( Н + Нж ) .

Отсюда

4

ж

3

по

1

(б)

г

РжНж = Р гж ( Н + Нж) · (3.39)

Это соотношение поjноляет приближенно рассчитать газлифт
при различных постановках технологической задачи .
Максимальная высота подъема жидкости при известной Нж
определяется при решении (3.39) относительно Н:

Н = Нж

Рж - Р гж

(3.40)

Р гж

Необходимое заглубление подъемной трубы Нж , обеспечи
вающее требуемую высоту Н, отыскивается по формуле
Ргж

(3.4 1 )

Нж = Н
Рж - Р гж

----

Отношение ( Рж - Р гж)/ргж, входящее в формулы (3 .40) и
(3.4 1 ) , можно выразить через газосодержание <р с помощью со
отношения (а) :

В этом случае

Н = Нж

<!>_ ,
1 - <р

(3.40а)

_

Нж = Н

l - <p .
<р

(3.4 l a)

Из выражения (3 .40а) следует, что для увеличения высоты
подъема жидкости необходимо повышать газосодержание га
зожидкостной смеси .
При известных значениях Н и Нж минимальное значение га
зосодержания составляет
<р =

н

Н + Нж

---

(3 .42)

Более точный расчет параметров газлифта требует учета гид
равлических потерь при движении двухфазного (rазожидкос
тноrо) потока по трубе . Величина этих потерь зависит от расхо315

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

дов жидкости и газа, диаметра подъемной трубы, состояния ее сте
нок и т.д. С расчетом гидравлических потерь при течении двухфаз
ных потоков можно ознакомиться в специальной литературе•.
В струйных насосах (рис.3.30) рабочая жидкость (поток ее
Gp ) с большой скоростью вытекает из сопла 1 и поступает в ка
меру смешения 2. В качестве рабочей жидкости чаще всего ис
пользуют воду или водяной пар. Из-за увеличения скорости в
сечении /-/ давление в нем, соответственно уравнению Бер
нулли , падает, так что возникает разность давлений (напор)
между расходным резервуаром 4 и сечением 1- 1. Под действием
этого напора жидкость из расходного резервуара поступает
(поток ее Gп) в камеру смешения. После смешения перекачи
ваемой жидкости с рабочей эта смесь поступает в диффузор J,
переходящий в напорный трубопровод. В диффузоре (его еще
называют камерой сжатия) скорость потока уменьшается из-за
возрастания поперечного сечения, и в соответствии с уравнени
ем Бернулли кинетическая энергия движения переходит в по
тенциальную энергию давления.
Струйные насосы подразделяются на инжекторы (для созда
ния давлений выше атмосферного) и эжекторы (при меняемые
для создания вакуума в аппаратах).
Производительность струйных насосов удобно оце н и вать ко
эффициентом инжекции lj/и = (Jп / (jp · Неличина коэффициента
инжекции при заданном давлении на выходе из струйного
насоса и известных параметрах рабочей и перекачиваемой
жидкостей , а также размерах насоса может быть рассч итана
из баланса энергий и количеств движе ния потоков. Методика
такого расчета подробно изложена в специальной литерату
ре•- , а примен ительно к работе инжектора для сжатия и п е ремещен ия пара низкого дав
ления с помощью пара высо
кого давления - в разд. 9.6.7 .
При увеличении развиваемого
G p+ G11
струйным насосом напора Н
коэффициент инжекции lj/ и
уменьшается.

3.4.2. Струйные насосы

.

Рис.З.30.
/

Схема струйного насоса:

сопло, 2 - камера смешения , З
диффузор, 4 - расходн ый резервуар

• См" например, (4) .
" См" напри мер, ( 1 ) .
316

-

-

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

3.5. ДОСТОИНСТВА И НЕДОСТАТКИ НАСОСОВ
РАЗЛИЧНЫХ ТИПОВ .
ОБЛАСТИ ИХ ПРИМЕНЕНИЯ

Каждый вид насоса имеет свои предпочтительные области
применения (рис. 3 . 3 1 ), в которых с наибольшей полнотой реа
лизуются их достоинства и в наименьшей мере - присущие и м
недостатки . Перечень наиболее существенных достоинств и не
достатков различных насосов представлен в табл . 3 . 3 . Заметим,
что почти все достоинства и недостатки насосов вытекают из
специфики их работы. Так, возвратно-поступательные движения
рабочего органа (поршня) в поршневых насосах обусловливают
основные их недостатки (неравномерность подачи , большие
инерционные нагрузки на фундамент и т.д.), а наличие в них
замкнутых пространств - их достоинства, связанные с возмож
ностью получения практически любых давлений. Равномерное
движение рабочего колеса в центробежных насосах обеспечивает
непрерывную подачу жидкости и связанные с этим достоинства,
а связь напора и производительности - их недостатки .
В табл. 3 . 3 наряду с достоинствами и недостатками даны также
краткие комментарии . Из последних, как правило, ясно, чем объ
ясняется то или иное достоинство насоса или его недостаток.
Поэтому остановимся здесь кратко лишь на отдельных моментах.
П оясним специально два ограничения для центробежных на
сосов: практическую невозможность получения высоких (выше
10 МПа) напоров и нецелесообразность их конструирования на
существенно малые производительности.

Н,м
1 03

Объемные

1 02
1 01

1 0°
1 0· 3

-2
10

-1

10

Осевые

°
10

1 01

V,

с

Рис.3.3/. Предпочтитr.ль н ые области при м е не н ия насосов разли ч н ых видов
317

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Таблица 3. 3. До стоннСТ1111 и недостатки насосов различ нwх типо в
Вид насоса

\

\

Недостатки
Достоинства
1---�
-- ���������-�.�����������������п оясне ние, •
н а имен онаи менование
п ояснение , ко мментарий
ва н не
комментарии

Поршне- ВозможСоздаваемый Невозможность
вые
ность соз- насосом на- перекачки жиддания лю- пор не зави- костей, содержабых напо- сит от произ- щих твердые
ров при за- водительности частицы
данной
произ
Неравномерность
водитель
подачи
ности
Возможность
Возмож создания
лю- Необходимость
н ость перекачки вяз- бых напоров тяжелых фундаких жид- (преодоления ментов
любых проти
костей
водамений)

Наличие клапанов и
опасность нарушения
полноты их закрытия
при попадании твердых частиц под та
релку клапана
Эrо особенно сушее111енно, когда равно
мерность подачи обяза
rельна
Обусловлена большими
инерционными нагруз
ками на фундамент из
за неравномерного (с
переменной скоростью)
движения поршня
Необходимость Невозможность воз
редуктора для
вратно-поступательснижения часто- ноrо движения пор
шня с большой частоты вращения в
сравнении с
той из-за высоких
электроинерционных нагрудвигателем
зок
Металлоемкость В 4-5 раз больше, чем
у ценlрОбежных, осо
бенно при больших
производительностях
Шестерен- Равномер- Движение ра- Сложность изго- Резкое
снижение
чатые
ность (или бочего органа томения, тща- производительности и
практиче- с постоянной тельность сборки напора при увелическая равно- скоростью
нии рабочих зазоров,
мерность) (или подача
прорезей и т.п. сверх
подачи
малых порций
допустимых пределов
с большой ча- Малые произво- Малая доля объема
стотой)
дительности
заполняется
насоса
жидкостью
То же
То же
То же
Винтовые То же
То же
Пластин- То же
Сложность изго- Резкое снижение про
чатые
томения, тща- изводительности
и
тельность сборки напора при увеличении рабочих зазоров
допустимых
сверх
пределов

318

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Вид насоса

Центро 
бежные

Таблица 3.3

1

(продолжение)

\

�����..--�����+-������-,-���������
Достоинства

наименование

пояс нен ие,
.
комментарии

Недостатки

наименование

пояснен ие , комментарий

Непрерыв- Жидкость не- Взаимосвязь
Невозможность изме
ная и рав- прерывно вхо- напора и произ- НИIЪ одИН параметр
(например, производиномерная дит в насос и водительности
тельность) при неизподача;
выходит
из
безынер- неrо
менном втором (напоре)
uионность
Не требует- Оrсуrствуют
Неuелесообраз- Повышенные потери
ся 1ЯЖелых инерuионные ность конструи- на трение в рабочем
фу ндаментов �аrрузки
рования uентро- колесе насоса и поВозможБольшая часто- бежных насосов н иженный его КПД
ность не- та врашения на малую произ- при уменьшен ии ши
посредствен-рабочеrо кале- водительность
рины рабочего колеса
ноrо соеди- са насоса
Трудно сконст- Связано с ограниченруировать насос ной
механической
нения с элекконсттродвигатена высокие напо- прочностью
лем
ры (выше
1 0 рукuион н ых материаОrсуrствие Возможность МПа)
лов
клапанов перекачки
жидкостей со
взвешенными
твердыми

часпщами
Н изкая меПониженный
таллоем
КПД насоса
кость, ком
пактность
П ростота Реrулировка
Подверженность
реrулиров- осущесmляется кавитаuии
кн произ- веtf1И11ем
на
водительно. нагнетательной
сти
линии
Осевые
Большие
Малые напоры
производительности
Смешение переСтруйные Простота Оrсуrствие
устройства движущегося качиваемой жидкости с рабочей
рабочего
органа
ВозможОrсуrствие
ность пе- узких прохо
ре качки
дов для пережидкостей, качиваемой
содержащих жидкости
мелкие
твердые
частиuы

На 1 0 - 1 5 % ниже,
чем у поршневого
насоса
В особенности при
перекачивании rорячих жидкостей

Невозможность нспользования насосов,
если смешение этих
недопужидкостей
стимо

319

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Вид н асоса

1

Таблица 3. 3 (окончание)
пояснение ,
�
комментари и

\

Недостатки

Достоинства
наименова ние

н аименование

пояснение, комментари й

Газлифт

Необходимость Особенно важно учи П ростота Оrсутствие
устройства движушегося заглубления
тывать при необхорабочего
подъемной трубы димости
больших
органа
в жидкость
заглублени й
Оrсуrствие
Возмож
ность
сколько-нибудь
подъема из заметных
глубоких ограничений
скважин
высоты подъема жидкости
ВозможПри наличии
ность по- материала (для
дачи агрес- подъемной
сивных
трубы), стой
жидкостей кого к воздействию
жид
кости ; п росто
та
замены
подъемной
трубы
Монтежю П ростота Оrсутствие
Повышенн ая тол- Обусловлена
повыустройства движущегося щина стенок
шенным давлением в
рабочего
монтежю
монтежю
органа
П ервое огран и ч е н и е с вязано с н еобход и мостью увел и ч е 
н и я частоты враще н и я п рабоч е го колеса для п о в ы ш е н и я н а 
п о р а , с о гл а с н о формул е ( 3 . 34) . Одн ако це нтробежная с и л а ,
п р о п о р ц и о н ал ь н ая , как известн о , квадрату ч астоты враще 
н и я , д е йствует н е тол ько н а жидкость , но и на само рабочее
колесо. П р и оче н ь бол ь ш и х п п од действ и е м центробе ж н о й
с и л ы может произойти меха н и ч е с кое разруше н и е дисков и
л о п ато к рабо ч е го колеса. П оэтому о гра н и ч е н и е частоты вра
ще н и я , а с ним и разви вае м о го н а п ора связано прежде всего
с о гра н и ч е н н ост ь ю меха н и ч еской прочности кон струкц и о н 
н ы х м атер и ал о в . В ходе техн и ч е с ко го прогресса по мере соз
да н и я мате р и ал о в с п о в ы ш е н н о й п р о ч ностью верх няя гра н и 
ц а п ол уч а е м ы х в центробежн ых насосах н а п оров (давл е н и й )
п осте п е н н о п о в ы ш ается .
Н е целесообразн ость конструирования центробежных насосов
на малую производител ьность объясняется следующи м . Умень 320

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

шать производительность за счет уменьшения частоты вращен ия
п нельзя, так как при этом еще быстрее (пропорционально п2
см. разд.3.3.3) уменьшается развиваемый напор. Единственным
приемлемым способом уменьшения производительности остает
ся уменьшение щели Ь между дисками рабочего колеса (см.
рис.3 . 2 3 ) . Но это приводит к росту гидравлических потерь в
насосе hn н ac , а значит и к понижению КПД насоса Т\ н · Учитывая
и без того сравнительно невысокие значения Т\ н (даже у нор
мально сконструированных центробежных насосов) , констати
руем экономическую нецелесообразность центробежных насосов
с малой производительностью. Отсюда и вытекает ограничение
производительности центробежных насосов.
Рассмотрение достоинств и недостатков насосов различных
типов позволяет оконтурить предпочтительные области их при
менения (см. рис . 3 . 3 1 ) .
Обьемные насосы применяют при малых и средних произво
дительностях и больших (практически любых) напорах.
Наиболее широкое применение в химической промышлен
ности находят центробежные насосы: при средних и высоких
производительностях и не очень больших напорах.
При необходимости обеспечения весьма больших производи
тельностей при малых напорах используют осевые насосы.
Струйные насосы и газлифты выгодно применять при малых
производительностях и малых (и средних) напорах.
Простота устройства газлифтов, а также их надежность в ра
боте позволяют им в ряде случаев (при небольших производи
тельностях) конкурировать с центробежными насосами (напри
мер, при подъеме жидкостей из глубоких скважин , подаче аг
рессивных жидкостей и т. д. ) . Однако необходимость большого
заглубления подъемной трубы в жидкости и низкий КПД этих
насосов ограничивают область их применения.
Область применения монтежю (на рис. 3 . 3 1 не показана)
также ограничена невысокими значениями напоров и произво
дительностей . Увеличение напора приводит к повышению дав
ления в монтежю, что вызывает необходимость существенного
утолщения стенок. С увеличением размеров монтежю (на боль 
шие производительности) толщина их стенок также увеличи
вается.
Приведенные на рис.3 . 3 1 гран ицы предпочтител ьных об
ластей применения различных насосов являются подвижными.
По мере развития науки и техники (например, создания новых
конструкционных материалов) эти границы будут смещаться .
-

32 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

В заключение отметим, что выбор вида насоса в каждом кон
кретном случае производится на основе технико-экономического
расчета с учетом эксплуатационных и конструктивных характери
стик насоса и другого оборудования.
Л ИТЕРАТУРА

к rлаве

3

1 . Абдурошитоs С.А., Тупиченкоs А.А., Вершинин И.М., Тененгольц С.М. Насо
сы и компрессоры. М . : Недра, 1 974. 296 с.
2. Гельперин Н.И. Основные процессы и аппараты химической технологии .
М . : Химия, 1 98 1 . 8 1 2 с .
3 . Дытнерский Ю. И. Процессы и аппараты химической технологии . М . :
Химия , 1 99 5 . 7 6 8 с .
4. Соу С. ГИдРQЦИНамика мноrофа:Jных систем: Пер. с анrл./ Под ред. М.ЕДейч.
М.: Мир, 197 1 . 536 с.

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Глава 4

СЖАТИЕ

ГАЗОВ

Сжатие газов широко применяется в химической технологии
при осущестмении различных физических и химических про
uессов, протекающих под дамением, отличающимся от атмо
сферного, а также для перемещения газов и многофазных си
стем, в которых газ ямяется несущей средой. Кроме того, сжа
тие и перемещение газов используется для ряда спеuифических
(вспомогательных) uелей: передамивание и подсос жидкостей,
транспорт жидкообразных сред, распьmение жидкостей и др.
Конкретная технология может потребовать создания весьма
высоких дамений (до 1 00 МПа в промышленной практике, еще
выше - в лабораториях) или очень низких дамений (вплоть до
1 0 Па и даже ниже) . При этом потоки сжимаемого газа в ряде
производств исчисляются сотнями тысяч кубометров в час (т.е.
свыше 3 0 мЗ /с). В качестве общеизвестных примеров можно
привести: синтез аммиака или метанола (дамения порядка 1 О
МПа, объемные производительности по воздуху, сжимаемому
для ожижения в крупных установках, - более 1 20 тыс. м 3/ч);
выпаривание под вакуумом (дамение ниже 0,01 МПа) и субли
маuионную сушку (дамение на уровне 10 Па); транспортирова
ние природного газа от его месторождений к потребителю на
тысячи километров или газообразных веществ из одного аппара
та в другой в ходе технологического проuесса.
Устройства для сжатия газов (чаще всего это
машины,
имеющие движущиеся узлы) называются компрессорами. Они
сообщают газу энергию
потенциальную (дамение - в этом,
как правило, их основное назначение) и кинетическую (иногда
ее приращение существенно) .
По своему общему назначению и принuипам конструктивно
го оформления компрессоры обладают определенным сходством
с насосами - устройствами для создания напора и перекачки
жидкостей (см. гл . 3 ) . Вместе с тем надо помнить о коренном (в
аспекте курса ПАХТ) отличии в свойствах рабочих тел: газ сжи
маем, жидкость практически несжимаема. В ходе последующего
анализа проuесса сжатия газов в компрессорах используется
сходство с проuессом в насосах (нередко проводится сопостав
ление этих процессов) , но непременно учитывается сжимае
мость газов.
-

-

323

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

В задачу технолоrическоrо анализа и расчета сжатия газов в
аспекте курса ПАХТ входит ряд вопросов:
- классификация компрессоров по различным признакам;
- рассмотрение принципов функционирования компрессоров различных типов;
- расчет производительности компрессоров и (или) изменения
давления газа;
- расчет энергии на сжатие газа в компрессорах;
- анализ отдельных рабочих моментов, представляющих технологический интерес.
*
4. 1 . КЛАССИФИКАЦИЯ КОМПРЕССОРОВ

Разнообразие технологических целей, рабочих условий,
принципов действия и конструкций компрессоров затрудняет
создание единой и достаточно строгой их классификации.
Представленные ниже градации - условны, они не имеют
строгого научного обоснования, скорее носят традиционный
характер.
Приведем принятую в настоящее время классификацию ком
прессоров по некоторым срезам.
По характеру измененш� даменш� в технологических аппара
тах вьщеляют собственно компрессоры (создание повышенного
давления в аппарате) и вакуум-насосы (создание разрежения в
нем). Заметим: термин "вакуум-насос" сохранился чисто истори
чески, речь идет не о насосах (так в науке ПАХТ именуют уст
ройства для перемещения жидкостей), а о компрессорах опре
деленного назначения.
По вели11ине развиваемого напора (давленш�) различают венти
ляторы, создающие избыточное давление до 0,0 1 5 МПа, rаэодув
ки - до 0,2 МПа и компрессоры
свыше 0,2 МПа. Внутри пе
речисленных типов компрессоров нередко проводят более дроб
ную классификацию.
По производительности различают малые компрессоры - объ
емной производительностью до 0,0 1 5 мЗ/с, средние - от 0,0 1 5 до
1 ,5 мЗ/с и крупные - более 1 ,5 мЗ/с (практически - до десятков
кубометров в секунду).
В плане изучения и описания сжатия газов в компрессорах
наиболее важна классификация по принципу действш� Здесь
существуют различные подходы. Согласно наиболее простому из
них (и, вероятно, весьма удобному в плане рассмотрения в курсе
ПАХТ), все компрессоры подра:щеляют на три группы: поршневые,
центробежные и остал ьные (обычно их именуют специальными ).
-

.

• См. [ 1 , 3-5, 71.

324

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Более обоснованной в рассматриваемом аспекте представ
ляется следующая классификация:
- компрессоры объемного действи.я, принцип работы кото
рых основан на сжатии газов в результате уменьшения объема
замкнутого рабочего пространства с постоянной массой газа в
нем. К таким компрессорам относятся поршневые
с возврат
но-поступательным движением поршня, ротационные (в том
числе водо кольцевые) - с вращательным перемещением изме
няющегося рабочего объема (см. ниже) и целый ряд иных раз
новидностей;
- динамические компрессоры, для которых характерно по
вышение кинетической энергии газового потока и преобразова
ние затем значительной ее доли в потенциальную (энергию дав
ления ) . К числу таких компрессоров относятся центробежные,
или турбокомпрессоры, в которых давление создается под дей
ствием центробежных сил на газовый поток; осевые компресси
онные машины, основанные на сообщении газовому потоку
кинетической энергии (в осевом направлении) ; струйные
(инжекторы) , базирующиеся на обмене количеством движения
межцу газовыми потоками , и некоторые другие.
Кроме того, существует ряд компримирующих устройств, ис
пользующих иные физические явления.
Конструкции и принцип работы некоторых компрессоров
описаны в последующих разделах - по ходу изучения отдель
ных типов компрессионных машин.
Ниже наиболее детально рассмотрены особенности и техно
логический расчет поршневых компрессоров, отчасти - турбо
компрессоров. Для некоторых других устройств показаны прин
ципы и условия их работы, отмечены особенности; в отдельных
случаях продемонстрированы пути расчета основных (прежце
всего - энергетических) характеристик. Более подробные све
дения об устройстве, работе и расчете различных типов ком
прессоров можно найти в специальной литературе" .
-

4.2. О ТЕРМОДИНАМИЧЕСКИХ ОСНОВАХ РАБОТЫ
КОМПРЕССОРОВ

Напомним с некоторыми комментариями ряд известных тер
модинамических соотношений, необходимых для последующего
анализа. Обозначим: р - давление; v - удельный объем; Т
абсолютная температура; R = f!.y/ М
индивидуальная газовая
постоянная сжимаемого газа (М - его молярная масса, Ry -

-

• См. ( 1 , 3-5 , 7) .

325

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

универсальная газовая постоянная). Первоначально - в целях
упрощения - примем, что газ является идешzьным и подчиняет
ся уравнению Клапейрона- Менделеева:
(4. 1 )
pv = R Т.
Энергетический анализ работы компрессионных установок,
строго говоря, должен учитывать изменение (приращение) по
тенциальной и кинетической энергии газа. Однако в боль
шинстве случаев вклад кинетической составляющей невелик, и
им пренебрегают.
В основе анализа лежит 1 закон термодинамики в различных
написаниях:
du = Tds - pdv ;
(4.2)
oq = du + pdv ;
dh = o q + vdp .

(4. 3 )
(4.4)

Здесь: s - энтропия; и = cv T - внутренняя энергия; h = ср Т 
энтальпия; Cv и ер - удельные теплоемкости при постоянных
объеме и давлении соответственно; q - теплота (тепловой эф
фект) процесса.
Эrи соотношения позволяют применительно к компрессорам
анализировать различные операции над газами - изобарные (dp =
= О), адиабатические (ds = О) , иэоэнталъпические (dh = О) и друmе.
Процессы сжатия газа в компрессорах удобно изображать в
диаграмме "давление - удельный объем" (р - v) - рис. 4. 1 . Ис
ходный газ (состояние 1) давлением р1 с удельным обьемом v1
подвергается сжатию до состоян ия 2 - до давления Р2 > р 1 ; при
этом в ходе процесса сжатия удельный объем газа уменьшается до
v2 . Одновременно происходит изменение температуры от Т1 до Т2 .
Ход кривой сжатия 1-2 зависит от уСАнuй сжатия.
Процесс сжатия сопровождается повышением внутренней
энергии - разогревом газа. Чтобы удержать температуру сжи
маемого газа постоянной, необходимо организовать очень интен
сивный отвод теплоты в процессе
сжатия. В случае такого иэотермическоrо (реже применяют термин
"иэотермноrо") сжатия , когда Т2 = Т1 =
= Т = const, процесс идет по линии
1-2t. Согласно выражению (4. 1 ) ,

Р
Р2

PJ.V2 = P1V1 = pv = RT = const .

Рис.4. 1. Процессы сжатия газа
ре в диаrрамме р - v:

в

(4.5t)

компрессо

l-2t - изотерма, l-2s - адиабата, 1 -2' политропа при т < k, 1 -2" - политропа
при
m > k

326

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

в усло
происходитПриходов
газа
что сжатие
себе,изоляции
представить
Можно
отсутствие
в
.
е
(т.
тепловой
полной
его
виях
при посжатия протекает(иначе
процесс
теплоты), s.- Втогда
и Уходов энтропии
стоянной
случае
такого
бьuю бы называть
процесссжатия
идет по(точнее
линии его
1 -2s; при этом
v2k = P1V1 k = pvk = const,
(4.5s)
2
p
р/
k ""' 5/3 1,67; для двухатомных - k ""'
""' 7Для
/5В наиболее
""' одноатомных
1,4; дляобщем
трех- газов
ислучае
многоатомных
- k ""' 9/7 ""' 1 , 3 .
в
процессе
сжатия
неназывают
вьщерживают
ся условия(илиТ =политропическим).
const и s = const -Онтакой
процесс
'поли-·
описывается уравнением
(4.5m)
P2V2m = P1V1 m pvm = const,
Формулы
(4.5t) и Действительно,
можно рассматривать
как частные
случаи
выражения
при
т = 1 процесс
протекает
при соотношения:
т = k адиабатически.
Приведемизотермически,
также известные
m-k
(4.6б)
R ; ( . 6а)
т-1
адиабатическою
изоэнтропий

адиабатною)

ным)

где k = е с. называется показателем адиабаn.�.
""'

тропным

=

где т называется показателем пол1n11о пw.

(4. Ss)
(4. Sm).

-

где Ст = const

Ср - Cv =

-

ческом процессе .
В

удельная (на

4

1

кz

Ст = Cv -- ,

сжимаемоrо газа) теплоемкость газа в политропи

процессе
сжатиятеплота;
газа в компрессоре
вьщеляется
(и по воз
можности
отводится)
причины
ее
вьщеления:
-- равновесный
(обратимый)
процесс
сжатиясвязанные
газа; с диснеравновесные
(необратимые)
процессы,
сипациейоргана
(рассеянием)
энергии
(трение
движущихся
частей
рабочего
компрессора,
а
также
газа
о
его
детали).
В ходе реального процесса в компрессоре не удается удер
жать
постоянной
температуру
сжимаемого
газа,возможности
так как интен
сивность
тепловьщеления
заметно
превышает
от
вода
теплоты.
Но
часть
теплоты
все
же
отводят.
Если
при
этом
удается
полностью отвести теплоту трения и частично теплоту
сжатия,
то
1 < т < k - политропный процесс сжатия пойдет по
линии
1 -2' . Однако на практике (чаще всего - из-за ограни
ченной трения,
поверхности
теплосъема)
не удается
отвести
дажереаль
всю
теплоту
не
говоря
о
теплоте
сжатия.
Поэтому
ный процессполитропы
сжатия идет,т >какk. правило, по линии 1 -2", т.е. с
показателем
Признать
эксплуатации
при расчетах Она
- тоже)
важно
температурукомпрессоров
газа Т2 после(и компрессора.
уста327
уж

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

P2IP1

навливается в зависимости от степени сжатия
в компрес
соре. Расчетным п уrем Т2 нетрудно определить с помощью
уравнений (4. 1 ) , (4.Sm). Записав (4. l ) для начала и конца
процесса сжатия p1v 1 = R T1 и P2V2 = R T2 , получим
Tz

Р_
2 _
v_
z .
_

7; Р1 V 1
Выразив отношение удельных объемов из (4.Sm) как
_2
1/т
v.

=

(Ji)
Р2
( РР2) п:�· ,
1

=

(а)

(б)

и подставив это отношение в (а), найде м

7; =
(4.7)
Т.
причем в случае адиабатического сжатия в (4.7) вместо т будет ,
конечно, фигурировать показатель адиабаты k.
Расчет затрат энергии базируется на уравнениях (4.2)-(4.4)
- в зависимости от физических явлений в конкретных ком
прессионных устройствах• .
В случае объемных компрессоров удельные (в расчете на l кг ра
бочего тела) затраты энергии на собспе1П10 сжа111е lсж состааляют
(4.8)

где р = p(v) = var; индексы 1 и 2 относятся к начальному (перед сжатием) и
конечному (после него) состояниям газа (разумеется , v2 < v 1).

V2

Для расчета полных затрат энергии в объемных компрессорах на
до еще учесть рабоrу всасывания газа в рабочий объем от источника
и вьпалкивания (нагнетания) газа из этого объема к потребителю.
В случае динамических компрессоров полная удельная работа
на сжатие и перемещение rаза выражается формулой

Р1

(4.9)
/ = J vdp,
Р2
причем индексы при р = var имеют указанный выше смысл
(разумеется, Р2 >
Располагая связью параметров процесса р и v, например по
одной из формул (4.St) , (4.Ss) или (4.Sm), можно из (4.8) и (4.9)

р1 )

•

.•

Детально эти вопросы освещены в литературе по технической термодина
мике (см . , например, (2, 6, 8)) и по компрессорам [ ! ] . См. также [5) и ( 7 1 .

328

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 4. 2. П роцессы сжатия газа в компрессо
ре в диаграмме h - s:

1-:Zt - изотерма, 1-:ZS - nд11абата, 1-:Z' - по
литропа при т < k, 1-:Z" - политропа при т > k

h

найти выражения / для изотерми
ческого, адиабатического и поли- ·
тропического процессов в компрес
соре .
s
В условиях достаточно высоких
дамений и при температурах, су
щественно ниже критических (тем
более - приближающ И хся к температурам кипения ) , уравнение
состояния ( 4 . l ), записанное для идеального газа, становится
неточным. Уточнения вводят пугем записи более сложных урав
нений (например, Ван-дер- Ваальса) или с помощью коэффици
ента сжимаемости z, зависящего от дамения и температуры:

pv = zR Т.

(4. l ' )

Естественно, для идеального газа z = 1 ; с ростом р и пониже
нием Т коэффициент сжимаемости уменьшается (для реальных
газов он может заметно отличаться от l ) .
Использование расчетных формул, базирующихся н а уравне
нии Клапейрона-Менделеева, для области достаточно высоких
давлений может привести к заметным погрешностям. В то же
время использование более точных аналитических методов на
основе упомянутых уравнений состояния сопряжено с весьма
громоздкими расчетами .
Поэтому
переходят
к
графо
аналитическому определению параметров и характеристик про
цессов в компрессоре с помощью диаграмм состояния реальных
газов. Наиболее удобными в практическом использовании пред
s, про
ставляются энтальпийно-энтропийные диаграммы h( i)
цессы сжатия в которых изображены на рис. 4.2. Затраты энер
гии соответственно этой диаграмме получаются как разности
энтальпий сжатого и исходного газа.
При аналитическом расчете 11олитропических процессов воз
никают затруднения, связанные с неопределенностью значений
показателя политропы т; при пользовании диаграммами со
стояния - неизвестны реальное положение точки 2 и путь сжа
тия. В этих сл уч аях стадию сжатия идеализируют, полагая ее
изотермической или адиабатической: тогда для нее известны
параметры процесса и линии сжатия Т = const либо s = const. А
переход от таких идеализированных стадий к реальной (поли
тропической) стадии сжатия осущестмяется с помощью эмпи
рических поправок, называемых соответственно ".изоте рми 
"
ческим К ПД ТJ i и "адиабатическим К ПД" ТJ s компрессора. На
-

329

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

h

диаграмме р - v (менее наглядно - на - s) видно, что реаль
ная политропная работа (линия 1-2") больше адиабатной и тем
более - изотермической. Поэтому КПД компрессора, опреде
ляемый как отношение идеализированной работы к реальной ,
выражается величиной , меньшей 1 . Обычно в зависимости от
типа компрессора и условий его работы (в первую очередь - от
степени сжатия) Т\ t :::: 0,6 -7- 0,8; Т\ s :::: 0,85 -;- 0,97. Реальные затра
ты энергии получаются делением найденной работы идеального
процесса на соответствующий КПД. Конкретные расчетные
выражения, относящиеся к определению затрат энергии с ис
пользованием Т\ t и Т\ s, приводятся при р ассмотрении поршневых
и центробежных компрессионных машин.

Заметим , что термин "КПД" в расчетах энергии , потребляемой компрессо
ром, не имеет физического обоснования и сохраняется лишь в силу традиций.
В самом деле, можно себе представить достаточно хорошее охлаждение газа в
процессе его сжатия , так что / < 1,, и тогда будет fl s > 1 . Нет физического запре
та (хотя практически это трудно реализовать) на осуществление процесса сжа
тия с очень интенсивным охлаждением газа, так что будет даже / < 1,; тогда и
ri 1 > 1 . А ведь по смыслу КПД должен характеризовать степень приближения
реального процесса к идеальному, он может лишь в пределе приближаться к 1 .
Из этих рассуждений следует, что термин "КПД" - неудачен, и коэффициенты
f11 и fl s должны трактоваться как некоторые эмпирические поправочные множи
тели , связывающие не вполне определенный реальный процесс в компрессоре
с вполне определенными, чаще - с адиабатическим.

4.3. ПОРШНЕВЫЕ КОМПРЕССОРЫ

Поршневые компрессоры (ПК) являются типичными и наи
более распространенными представителями объемных компрес
сионных машин. У ПК четко выражены все стадии рабочего
цикла и наиболее наглядно прочерчиваются основные законо
мерности функционирования объемных компрессоров вообще.
4.3. 1 . Устройство и работа поршневых компрессоров

По своему устройству и принципу действия П К во многом
напоминают поршневые насосы. На рис.4.3 , а показана схема
ПК простого действия • .

В цилиндрическом корпусе 1 совершает возвратно-поступательные движе
ния поршень 2. Приводом чаще всего является электродвигатель - с редукто
ром, поскольку частота движения поршня (порядка 1 -5 с- 1 ) заметно ниже
стандартной частоты вращения ротора электродвигателя . В ращательное движе
ние электродвигателя преобразуется в возвратно-поступательное с помощью
кривошипно-шатунного механизма (принципы преобразования рассмотрены в
разд. 3 .2 . l ) , коленчатого вала или какого-либо другого устройства. На валу кри -

• Существуют и иные варианты конструктивного выполнения поршневых
компрессоров [ 1 , 3-5, 7 ) .

330

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

а

Рис. 4. 3.

б

Схема поршневых компрессоров простого (а) и двойного (б) действия :

1 - корпус, 2 - поршень, 3 - шrок, 4 - всасывающие клапаны, 5 - нагнетательные
клапаны, 6 - напрааляющие, 7 - ползун, 8 - шатун, 9 - кривошип, 10 - маховое
колесо, // - охлаждающая рубашка, 12 - уплотнение; / - газ, // - охлаждаюшая вода

воwипа у средних и крупных ПК, в особенности работающих с высокими
степенями сжатия , укреплено массивное маховое колесо 10, воспринимающее и
сглаживающее инерционные усилия . Значительно реже в . качестве привода
используют паровые машины или двигатели внутреннего сгорания .
При движении поршня 1 вправо из крайнего левого ("мертвого") положения
в рабочем пространстве цилиндра (слева от поршня - говорят: под поршнем)
возникает разрежение. Под действием разности давлений (у источника газа и в
цилиндре П К) открывается всасывающий клапан 4, и газ засасывается в рабо
чее пространство цилиндра. Нагнетательный клапан 5 при этом закрыт. Далее
поршень приходит в крайнее правое ("мертвое") положение и начинает дви 
гаться влево. При этом уменьшается рабочий объем, под поршнем повышается
давление (оно становится больше, чем у источника), и всасывающий клапан 4
закрывается. Нагнетательный клапан 5 на начальных стадиях движения поршня
влево тоже закрыт, поскольку давление в рабочем пространстве под поршнем
пока еще ниже, чем у потребителя газа. При дальнейшем движении поршня
влево давление под поршнем достигает давления у потребителя и начинает
превосходить его. Тогда открывается нагнетательный клапан , и газ из рабочего
пространства цилиндра выталкивается (нагнетается) к потребителю. После
достижения левого "мертвого" положения поршень снова начинает двигаться
вправо, нагнетательный клапан при этом закрывается , и цикл повторяется .
Таким образом, у поршневых компрессоров в отличие от поршневых насосов
рабочий цикл состоит (даже в рассмотренном упрощенном варианте) не из
двух, а из трех стадий : всасывание, сжатие, нагнетан ие.
Для эффективной работы ПК необходимо достаточно плотное соприкосно
вение поршня с внутренней поверхностью цилиндрического корпуса; в про 
тивном случае не удастся обеспечить должного повышения давления газа в
компрессоре, возможны и прямые потери (утечки) газа. По этим причинам
соприкасающиеся цилиндрические поверхности поршня (наружная) и корпуса
(внутренняя) тщательно обработаны; зазор между поршнем и цилиндром дол
жен быть минимальным. В этих целях применяют уплотняющие кольца на
поршнях и используют специальные смазочные масла, понижающие силу тре
ния движущегося поршня о стенки цилиндра в условиях их плотного контакта.

Работа П К сопровождается значительным повышением тем 
пературы Газа (эффекты сжатия; трения) , что неблагопр иятн о
сказывается на затратах энергии, посколь ку возрастают объе м 33 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

~

Рис.4.4. Схема поршневого ком
прессора (1) с 'J)'ll ИKOBЫM (а) и
проходным (6) ресивером (.2)

ные расходы сжимаемого
газа. Чтобы понизить тем
пературу сжимаемого газа
1
1
2
2
(уменьшить
его объемный
а
б
расход), используют охлаждение стенок цилиндра
с помощью установки на его боковых поверхностях (иногда и на
торцевых) теплообменных рубашек (поз. 1 1 на рис. 4.3), в кото
рые подается охлаждающий агент, как правило - вода.
С целью повышения производительности используют ПК двойного дей
ствия - см. рис. 4.3, б (устройство дЛЯ преобразования вращательного движе
ния в возвратно-поступательное на рисунке не показано). При движении
поршня , например, вправо (в направлении стрелки) в левой части рабочего
цилиндра происходит всасывание газа (левый нагнетательный клапан закрыт), а
в правой - его сжатие и выталкивание (левый всасывающий клапан закрыт) .

П К, как и поршневые насосы, подают рабочее тело неравно
мерно - пульсирующим темпом. Однако в отличие от жид
кости газ сжимаем, поэтому пульсации давления сглаживаются
по мере движения газа по газопроводу к потребителю. При ко
ротком газопроводе для сглаживания пульсаций по пути от ПК
к потребителю устанавливают ресивер - тупиковый или про
ходной (рис.4.4) - емкость достаточно большого объема. При
достаточно длинном газопроводе амплитуда пульсаций постепен
но снижается по мере удаления от компрессора, и потребитель
практически не ощущает пульсаций. Для ПК двойного действия
неравномерность подачи, естественно, выражена в меньшей
степени, нежели для ПК простого действия. В этом одно из
достоинств ПК двойного действия. Но ПК большей кратности
действия не применяют - видимо, из-за их громоздкости,
сложности и дороговизны, а также меньшей (чем для поршне
вых насосов) остроты самой проблемы неравномерности подачи .
4.3.2. Удельные затраты энергии в поршневом компрессоре

Рассмотрим первоначально затраты энергии в ПК простого
действия для упрощенного (идеализированного) варианта его
работы. Этот вариант представлен на рис.4.5, причем диаграмма
0 (ее называют индикаторной) изображена в координатах р - У ,
где У - объем газа в рабочем пространстве компрессора. Идеа
лизация процесса предполагает, что в крайнем левом положе
нии А (начало стадии всасывания) поршень подходит к крышке
компрессора вплотную, так что начальный объем газа равен
332

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис.4.5. Диаграмма р - V и схема движе
ния поршня в компрессоре:

А и В
порш ня ; 1
го тела

- край н ие левое и правое положен ия
- S - характерн ые состоя ния рабоче

р

нулю - точка 4 на рис. 4.5. Тог
1
1 1
да рабочий цикл складывается из
р1 4
1 :
следующих стадий:
2'-0 1--�--....�----...
4- 1 - всасывание газа при по
2 v:
стоянном давлении р1 , объем газа
i-.- s �--...
1
в рабочем пространстве компрес
сора изменяется от О до 1 ;
1 -2 - сжатие газа от Р1 до
1
вl
давления Ръ при этом объем газа в
А
рабочем пространстве уменьшает
ся ОТ
ДО У2 ;
2-3 - выталкивание газа при постоянном давлении р2 , объ
ем газа в рабочем пространстве компрессора изменяется от У2
Д О У3 = 0.
Для рассматриваемого Идеализированного рабочего цикла при
перемене направления движения поршня (т.е. при переходе от ста
дии вьrrалкивания газа к стадии всасывания) давление под порш
нем мгновенно падает от Р2 до .Pr (стадия 3-4 при Уз = V4 = 0).
Заметим: р1 в Идеале есть давление у источника газа, реально
- несколько ниже (на величину ГИдравлического сопротивле
ния подводящего газопровода и всасывающего клапана) ; давле
ние Р2 в Идеале равно давлению у потребителя газа, реально несколько выше (на величину ГИдравлического сопротивления
нагнетательного клапана и отводящего газопровода) .
В соответствии с представленными выше стадиями цикла
работа ПК в расчете на 1 цикл (ц.) слагается из трех составляю
щих - затрат энергии: на сжатие газа по линии 1-2; на вы
талкивание газа к потребителю по линии 2-3; приход энергии
(газ совершает работу над поршнем) при всасывании газа от
источника по линии 4- 1 . Расчетные формулы для затрат энер
гии на различных стадиях базируются на выражении (4. 8 ) :
- для стадии сжатия работа составляет в самом общем вИде

У

У1

Lс ж =

�

F &-

v.

Jp dY (Дж/ц.) и выражается площадью под линией сжа

V1

тия ( l -2-2'- l ' - l ) ;
- для стадии выталкивания ( нагнетания ) пр и Р2 = const вы
ражение (4.8) легко интегрируется: Lн = Р2 (У2 - О ) = Р2 У2
(Дж/ц. ), и работа отвечает площади (2-3-0-2'-2);
333

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

- для стадии всасывания характерен приход энергии при Р 1 =
= const; выражение (4. 8) здесь также легко интегрируется: L 0 -=
= Р 1 ( О - У 1 ) = - Р 1 У 1 (Дж/ц.), и работа отвечает площади (4- 1 1 ' - 0- 4).
Собирая составляющие затрат энергии (Уходы и Приход),
получим
v,

f p dV

L = I L; =

v,

+ Р2У2 - Р 1 У1 (Дж/ц.) .

( 4. 1 0 )

Представленное в таком виде выражение для L подчеркивает,
что в затратах энергии в ПК работа на стадии сжатия газа
(первое слагаемое в правой части) - лишь одна из составляю
щих общих затрат. Для последующего анализа
выражение
( 4. 1 О) целесообразно преобразовать. Оперируя соответству
ющими площадями (пл.), получим
L = пл.( 1-2-2'- 1 '-1)

+

пл .(2-3-0-2'-2) - пл. (4- 1-1'-0-4) =

= пл. (4- 1 -2- 3 - 4) .

(а)

Результирующая площадь (4 - 1 - 2-3-4) , очерченная жир
ной линией на рис.4.5, очевидно представляет собой интеграл:
L = J Vdp (Дж/ц.) .
Р2
Р1

(4. 1 1 )

. Таким образом, выражение для расчета затрат энергии в П К
(на все стадии, включая сжатие) совпадает с соответствующим
выражением (4.9 ) для динамических компрессоров.
Рассматривая совместно линии сжатия на рис. 4. 1 и диаграм
му рабочего цикла компрессора на рис. 4. 5, можно видеть, что
работа минимальна при изотермическом сжатии, больше - при
адиабатическом сжатии и наибольшая (поскольку реально, как
правило, т > k) - при политропическом сжатии . Ф изически
это объясняется тем, что ПК - машина объемного действия: на
сжатие одинаковых объемов газа (строго говоря, газов равной
атомности) затрачивается одинаковая энергия. Поэтому повы
шению температуры при сжатии газа, приводящему к увеличе
нию его объема, закономерно сопутствует повышение затрат
энергии. Отсюда следует вывод, что для снижения энергетиче
ских затрат надо стремиться к приближению процесса сжатия к
изотермическому или хотя бы к адиабатическому. На практике
это стремление реализуется путем охлаждения стенок компрес
сора в процессе сжатия (а также исходного газа до компрессора,
если это не противоречит требованиям технологии).
334

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

В практических расчетах неудобно оперировать затратами
энергии за цикл; поэтому под интеграл в выражение (4. 1 1 )
обычно подставляют:
- удельный объем газа (мЗ/кг) - тогда получают удельную
работу / в Дж на 1 кг сжимаемого газа
- либо объемный расход V (мЗ/с) - тогда получают затраты
энергии L в единицу времени (Дж/с = Вт).
Во всех этих случаях для вычисления интеграла (4. 1 1 ) надо
знать связь между подынтегральными величинами. Конкретное
выражение этой связи зависит от характера процесса сжатия,
т.е. от уравнения, описывающего стадию сжатия 1-2. Н иже
рассмотрены характерные режимы сжатия , причем анализ про 
водится в расчете на 1 кг сжимаемого газа с определением
удельной работы / в Дж/кг. Аналитические выражения для /
достаточно просто получаются применительно к идеальному газу.
Изотермическое сжатие. Здесь справедливо уравнение (4.St).
Домножив и разделив подынтегральное выражение на р, можно
вынести из-под интеграла произведение pv - в форме
или
=
или R T, причем
= Т.

v

JJ2V2 ,
11 =

}v dp = Jpv dp =
Pi

Р

Pi

p1 v 1 ,

Т1 Т2
P1V1 ln Р2 JJ2V2 ln Р2

= R T ln Р2
Р1

=

Р1

Р1

Адиабатическое сжатие.

(Дж/кг).

(4. 1 2)
Здесь справедливо уравнение (4.Ss);

v
pl/k,

его целесообразно переписать в форме p 1 1k = const. Домножив
и разделив подынтегральное выражение на
можно вынести
из-под интеграла произведение p 1 1k v - в форме p�'k v или
p�'k Например:

v2 .

Р2

ls = J

Р1

=

p 1 'k
1

v dp = Р2J р
Р1

v

d1 n
l / k 1Тk
r

Р

-

+

=

l

=

Политропическое

сжатие.

pl/

-

k
_k_ P1V1 [(-Р_2) k;l - 1

V 1 p�f +1_!_- p;f +1 k 1
k
k
_
k - 1 R T1 [( РР2 ) k�I - 1
1 Здесь
_

1 dp

1 / k Р2
р1 v J

1

-

·

Р1

]

Р

1

(Дж/кг).
справедливо

]

=

(4. 1 3)
уравнение

(4.Sm). Путем аналогичных (см. выше) преобразований (разу335

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

меется, с заменой k на показатель политропы т) приходим к выра
жению для удельной политропической работы компрессора:
[ =

P1V1 [(]!]:_) ]
[(]!]:_) lj

__!!!.___
т

l

-

= __!!!.___ RT1
т-1

Р1

Р1

m�I

:\

-

1

=

(4. 1 4)

(Дж/кг) .

-

Из рассмотрения выражений (4. 1 2)-(4. 14) следует, что
удельная (на 1 кг газа) затрачиваемая энергия в компрессорах
- увеличивается с повышением степени сжатия Р2/р1 ;
- возрастает при увеличении удельного объема газа v (т.е .
при уменьшении молярной массы: R = Ry/ М) ;
- возрастает п о мере удаления процесса сжатия от изотерми
ческого и адиабатического, т.е. при увеличении показателя политроп ы т, в особенности при т > k.
.
Два последних эффекта связаны с увеличением объема сжи
маемого газа.
Удельная работа компрессора может быть представлена ка к
разность энтальпий конечного и начального состояний адиабат
но сжимаемого газа. Покажем это применительно к идеальному
газу. Удельные затраты энергии, выраженные по (4. 1 3 ) , преоб
разуем с учетом приведенных в разд. 4.2 формул k = ер/ су, R =

- ТТТ k-1
- -RT1 [( P2)k;\ 1 -

= ер

су ;

/5

k

2/ 1 = (Р2 / р1 )Т , имея

изведение ср
_

k

-

1

при этом в в ид у , ч то про -

представляет собой энтальпию h:

Р1

-

-1

Т

-

С р / су

с р / Су

= ср( 2 - Т1 ) =

-

1

( ер - Су) Т1

h2 - h 1 .

[ ТТ12 - 1 ] --

(б)

Для реального газа, как указано в разд. 4.2, уравнение Кла
пейрона-Менделеева (4.l ) теряет точность, а теплоемкости ер и
Су являются функциями температуры и давления. В этом случае
аналитические выражения (4. 1 2)-(4. 14), полученные на базе
уравнения (4. 1 ) , становятся приближенными. Более строгими
будут расчеты с помощью диаграмм состояния реальных газов; в
аспекте ПАХТ наиболее удобной представляется энтальпийно336

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

энтропийная диаграмма h - s, где разность энтальпий конечного и
начального состояний выражает удельную работу компрессора:
(4. 1 5)
/ = лh = h 2 - h 1 (Дж/кг) .
Диаграмма h - s с характерными изолиниями не к оторых па
раметров состояния и изображенными на ней процессами в
компрессоре показана на рис . 4.2. Изотермический процесс
изображается на этой диаграмме линией 1 -2t , адиабатиче
ский - вертикальным отрезком 1-2s , политропические процес
сы - линиями 1-2' (при очень хорошем охлаждении газа в
процессе его сжатия) и 1 -2" (преобладающий практический
случай) . В начале расчета обычно располагают исходным со
стоянием газа в точке 1 (известны начальные давление р1 и тем 
пература t1 ) и знают конечное давление Р2 · Тогда нетрудно по
строить линию адиабатического сжатия (вертикаль от точки 1 до
линии Р2 = const) и найти удельную адиабатическую работу Л h5•
Переход к реальным затратам энергии (удельным Л / = лh и пол
ным - в единицу времени) рассмотрен в разд.4.3.6 .
4.3.3. Производительность поршневоrо компрессора

Поскольку поршневые компрессоры - машины объемного
действия, то резонно вести речь об объемной производитель
ности . Однако объемные производител ьности по исходному и
сжатому газу не совпадают: газ сжимаем. Условимся (та к приня
то в ПАХТ, если нет специальных оговорок) оперировать объ
емной производительностью по исходному (всасываемому) газу.
Рассмотрим сначала производительность ПК простого дей 
ствия в идеализированном варианте работы - поршень вплотную
подходит к торцевой крышке компрессора. По аналогии с порш
невыми насосами (см. разд. 3.3.2) теоретическая объемная произ
водительность V0 за цикл в расчете на исходный (всасываемый)
газ равна объему, описываемому движущимся поршнем: V0 = Fs,
где F и s
площадь и ход поршня. Если в единицу времени про
исходит п циклов (двойных ходов - всасывания и сжатия
нагнетания), то теоретическая объемная производительность в
единицу времени, аналогично формуле (3. 1 3) , составляет
Ут = Fsn
(4. 1 6)
С учетом коэффициента подачи 11v. отражающего запаздыва
ние клапанов (этот эффект описан в разд. 3.2.2), имеем - пока
еще в идеализированном варианте:
(4. 1 6а)
У ид = Fsn11v,
-

.

причем 11v находится обычно в пределах от 0,85 (малые ПК) до
0,95-0,98 (крупные П К) .
337

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис.4. 6. Диаграмма р
У работы поршне
вого компрессора с учетом вредного про
странства :

р

-

1

-

4 - характерные состояния рабочего тела

Применительно к поршневым
выражение (4. 1 6а)
требует принципиальной коррек
тировки. Дело в том, что в крайнем
(на рис. 4.3 , а и 4.5 - левом) по
ложении поршень не подходит
вплотную к крышке компрессора, в
рабочем пространстве всегда оста
ется некоторый промежуток. Его
наличие обусловлено необходи
вl
мостью размещения деталей клапаА
нов, а также недопустимостью уда
ров поршня о крышку - во избе
жание механического разрушения компрессора. Поэтому в кон
це хода выталкивания (в начале хода всасывания) в рабочем
пространстве компрессора остается некоторое количество сжа
того газа. На начальном этапе стадии всасывания этот газ рас
ширяется, его давление постепенно уменьшается; но пока оно
не снизится до давления источника (реально - несколько ни
же) , всасывающий клапан остается закрытым и всасывания не
происходит.
Рабочий цикл ПК с учетом стадии 3-4 расширения остатка
газа, заключенного в объеме промежутка, показан на рис. 4.6.
Из рисунка видно, что протяженность той части хода поршня
4- 1 , на которой происходит всасывание газа в компрессоре,
стала меньше, нежели в идеализированном варианте, - произ
водительность ПК понизилась. Поскольку наличие упомянутого
промежутка приводит к понижению производительности ком
прессора (уменьшается протяженность зоны всасывания газа) ,
объем этого зазора называют "вредным пространством " .
Специально подчеркнем, что в поршневых насосах поршень
тоже не подходит вплотную к крышке цилиндра . Однако
вследствие несжимаемости жидкости (идеальной - теоретиче
ски , реальной - практически) никакого расширения остатка
жидкости, разумеется, не происходит: V3 = V4. Поэтому выра
жение (3. 1 4) - аналог (4. 1 6а) - для пор ш невых насосов я вляет
ся правомерным
Для определения реальной объемной производительности П К
необходимо проанализировать эффекты, связанные со стадией
расширения остатка. Обозначим (см. р и с.4 6) : s1 - та часть хода

компрессорам

,__

l fi



.

.

338

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

-

поршня, на к оторой в действительности происходит всасывание
Е8 = Fs0/ Fs = s0/s
газа в рабочее пространство к омпрессора;
относительный объем вредного пространства. Тогда реальная
объемная производительность П К по всасываемому газу соста
вит за один цикл У0 = Fs1 . Величиной s1 оперировать неудобно,
поскольку в паспорте ПК указан полный ход поршня s. Поэтому
вводят понятие' об объемном КПД компрессора Ло = Fs1/ Fs = s1/s <
< 1 . Тогда объемная производительность П К за цикл составит
Уо = Fs1 = FsЛ.o, а за единицу времени
V = Fsпriv Л.o,
(4. 1 7)
причем все трудности расчета переносятся на нахождение Л.0.
Для ком прессоров двойного действия произ водител ь н ость, естествен но, будет вдвое бол ь ш е .
Чтобы найти Ло. рассмотрим стадию 3 - 4 расширения остат

ка, полагая, что в общем случае процесс расширения газа про
текает политропически . Тогда
р2 у3т = Р 1 у 4т ' P2l / m yз = P1l / m y4 ·
(в)
Подставим в (в) значения Уз = Fs6 и V4 = F(s6 + s - s1 ) ;
после со к ращения на F получим
l/m
V4
Sв + S - S 1
= !1..
Sв
Уз
Р1

( )

Подели м почленно величины в правой части равенства и
домножим числитель и знаменатель получившегося при этом
отношения sifs.в на s:

(f!..1.). 1/m =
Р1

l

+

�_�

S8 S

S8

-- ( ��)l/m
�� .
= +

.

В правой части последнего выражения по определению второе
s1 s
Л. о
слагаемое s/s6 = 1 /Е8 , а третье
, так что
Е8
s s6
=

[(;;( - · ]
1

l
Ев

(г)

Решая (г) относительно л.0, получим расчетное выражение
для объемного КПД поршневого компрессора:

л. � 1 -

••

(4. 1 8)

Это значение Л.0 и используется при расчете объемной произ
водительности по формуле ( 4. 1 7) .
339

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

р

Рис.4. 7. К влиянию степени сжатия
газа на объемный КПД поршнево
го компрессора (обозначения - в
тексте)

Из соотношения (4. 1 8)
следует ряд выводов отно
сительно величины объем
ного КПД ЛQ.
1 . Значение А.о понижает
ся при увеличении относи
тельного объема вредного
пространства Ев· Величина
Ев задана в паспортных дан
ных П К; обычно она нахо
дится в диапазоне 0,02-0,08
для компрессоров умерен
Р1
ного давления и может
1
1
о
несколько превышать О, 1
V
�
N
'
'
'
: Fs
-Fs1
для
компрессоров высокого
� в --:
-:"-Fs l
Fs i-:
давления.
о
---- F --�
2. Значение А.о
пониs
жается при увеличении сте
пени сжатия P2IP 1 ; этот эф
фект иллюстрируется
рис.4. 7. При относительно небольших
конечных давлениях Р2 ' (или степенях сжатия Р2 '/р 1 ) реальный
ход всасывания s' остается достаточно протяженным, так что
производительность компрессора по всасываемому газу за рабо
чий цикл сравнительно велика: Fs1 '. При больших конечных дав
лениях Р2 " (степенях сжатия Р2 ''/р 1 ) протяженность реального
хода всасывания понижается до s1 ", так что объемная произво
дительность станет меньше: Fs1 ".
Можно представить
себе столь значительные конечные давления р � и степени сжатия р �/р1 , что ход всасывания s1 0 станет равным нулю. В таких
предельных условиях ПК будет " работать на себя'', т.е. только на
сжатие газа и расширение остатка - без всасывания газа от ис
точника и выталкивания к потребителю. Если отвлечься от воз
можного различия в значениях показателя политропы т при
сжатии газа и при расширении остатка, то в рассматриваемой
предельной ситуации линии сжатия 1 -20 и расширения 30_4о
совпадают, а пары точе к 20 и зо, 1 и 4° - сливаются.
Подчеркнем: зависимость Л.0 от Р2 (или от Р2/р1 ) указывает на
то, что объемный КПД не может быть задан заранее: он опреде340

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ляется, наряду со значением конструктивной величины &8, также
условиями функционирования компрессора.
3. Значение А.о возрастает с увеличением показателя политро
пы т на стадии расширения остатка. Иными словами , наи
меньшему значению т = 1 (изотермическое расширение остат
ка) отвечали бы минимальные значения s1 и А.о, при адиабати
ческом процессе А.о был бы выше, при политропическом в слу
чае т > k
еще выше.
При работе ПК на стадии 1-2 сжимается весь газ (объемом
V1 ) под поршнем в рабочей зоне компрессора, в том числе и
находившийся ранее во вредном пространстве. Это, однако, не
должно восприниматься как бесполезные, хотя и вынужденные
потери энергии на сжатие той части газа [V4 = F(s + s8 - s 1 ) в
конце хода всасывания и
= Fs8
в конце хода нагнетания] ,
которая далее не попадает к потребителю. Конечно, на сжатие
упомянутой части газа и в самом деле затрачивается энергия; но
при расширении остатка эта энергия возвращается газом порш
ню, практически полностью компенсируя непроизводительные
затраты энергии на сжатие газа, заключенного ранее во вредном
пространстве. Выше указано " практически " , поскольку реально
возможно некоторое различие в затраченной и возвращенной
энергии в силу неполного совпадения показателей политропы
на стадиях сжатия газа и расширения остатка.
Таким образом, эффект расширения остатка понижает про
изводительность П К, но практически не влияет на затраты
энергии в расчете на цикл, на 1 кг сжимаемого газа, переда
ваемого потребителю, или перерабатываемого в единицу време 
ни при заданной производительности.
-

Уз

-

-

Диаграмма сжатия на рис. 4.6 отражает реальный эффект расширения
остатка, но тем не менее является модельной. Индикаторная диаграмма, сни
маемая на действующем компрессоре, располагается около модельной,
несколько отличаясь от нее - прежде всего конфи гурацией линий всасывания
и выталкивания. Эти отличия обусловлены особенностями работы клапанов и
темообменом газа с охлаждаемыми стенками цилиндра компрессора•.

В разд. 4.3. 1 было отмечено, что П К, как и поршневые насо
сы (см. разд. 3 . 3 . 3 ) , подают рабочее тело неравномерно
пуль
сирующим темпом: существует некое отклонение ( " избыток" ) газа
от средней (равномерной) подачи. В то же время потребителю
по условиям технологического процесса может потребоваться
существенная равномерность подачи газа Выравнивание пода
чи, как указано выше, обеспечивается установкой ресивера (см.
рис. 4.4) или естественным сглаживанием пульсаций в газопроводе.
-

.

• См. [ \ , З - 5, 7 ] .
34 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Объем ресивера должен быть достаточно большим, чтобы,
попав в него, избыток газа не изменил бы заметно давления
газа. Тогда напор (разность давлений между ресивером и потре
бителем) будет изме няться мало, пульсации сгладятся , и газовый
поток к потребител ю станет существенно равномернее. Расчет
как
объема ресивера с этих позиций ведется так же,
и объема воздушного колпака (разд.3.3.4). И с тех же позиций
можно оценить релаксирующее (снижающее амплитуду пульса
ций) воздействие участка газопровода от компрессора до потре
бителя, полагая , что объем газопровода по существу выполняет
роль ресивера.
4.3.4. Степень сжатия в поршневом компрессоре

В технологических процессах нередко используются газы,
сжимаемые от начального давления (часто близкого к атмо
сферному, т.е. к О, l МПа) до рабочего, исчисляемого сотнями
атмосфер (десятками МПа). Между тем условия функциониро
вания ПК устанавливают определенные пределы для степени
сжатия p2fp 1 . Будем рассматривать эти пределы в аспекте произ
водительности П К и конечной температуры газа Т2.
Физические пределы степени сжатия <fr2/p1 ) Ф , исходя из
производительности компрессора, определены в предьщущем
разделе : при достаточно высоких степенях сжатия Р2/р 1 объем
ный КПД компрессора Л.0 становится равным нулю, и компрес
сор перестает подавать газ потребителю ( V = О), работая "на
себя". Предельную степень сжатия находят подстановкой Ло = О
в уравнение (4. 1 8) и последующим решением его относительно
<Р2/Р 1 ) п Ф :
р

(!!..1.Р 1 ). пр
ф

=

т
1
( Е в 1)

(д)

+

Если, например, положить & в = О, 1 и принять, что расширение остатка про
исходит адиабатически (т = k) , то для двухатомных газов (k "' 1 ,4) получается
<Р2/Р � )п рФ "' 29; при Е в = 0,05 эта величина составляет "7 1 . Если бы сжатие газа
происходило изотермически (т = 1 ), то значения <Р2/Р� )п рФ составили бы соот
в етственно 1 1 и 2 1 . Заметим, что на практике расширение остатка - достаточ
но быстротечно, часто занимает сравнительно небольшую долю хода всасыва
ния и потому протекает в режиме, близком к адиабатному (изоэнтропийному).

Практический интерес для технолога представляет предельная
степень сжатия, обусловленная приемлемой производитель
ностью компрессора. Такой предел устанавли вается по некото
рому минимально приемлемому значению л.0 mi n . В этом случае
т
т
n
1 Лmi
о
(е)
!!..1..
.
+ 1
Ев
Р1 пр

( )

342

=

(

_

]

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Для л.о111i11 = 0 ,7 в условиях приведенных выше примеров получаются, есте
ственно, бо.Лее низкие предельные значения WPi )np_; в случае адиабатическоrо
расширения остатка они составляют соответствен но 7 и 1 5.

Приведенные выше численные предельные значения степени
сжатия следует оценивать как достаточно высокие; обычно не они
лимитируют, не по ним устанавливается предельное значение PJ}p 1 •
Значительно жестче пределы степени сжатия, наЙденные ис
ходя из конечной температуры rаэа Т2. Последняя определяется
по уравнению (4.7):
Т2 =

Т1

(��)

т- 1

�

(4.7а)

Ограничения по Т2 связаны прежnе всего с устойчивостью смазки.
Смазка должна бьпъ термически усrойчива к разложению (крекингу), а ее тем
пература вспышки - достаточно высока. Вязкость смазки не должна заметно изме
няться с темпераrурой, иначе смазка не удерЖИlСЯ на трущихся поверхностях.
Современные смазочные масла термически вполне устойчивы до весьма вы
соких температур и обладают высокой температурой вспышки . Кроме тоrо,
вязкость современных смазочных масел сравнительно медленно понижается с
ростом температуры. Тем не менее именно вязкостная стабильность смазки
является rлавной причиной оrраничений в температуре Т2: при чрезмерно
высоких температурах заметно понижается вязкость смазки, и она плохо удер
живается на трущихся поверхностях; приходится увеличивать ее расход, иначе
возрастут затраты энерrии на преодоление трения. В настоящее время рассмат
риваемый температурный предел определен цифрами t = 1 80+200 С
В качестве примера оценим по (4.7а) температуру Т2 при Т1 = 300 К (27 ° С)
для вполне типичных степеней сжатия, равных 4 и 5 , в случае адиабатическоrо
сжатия двухатомноrо газа (k "' 1 ,4):
°

Т2

.

�
= 300 ·(4) 1 •4 = 446 К = 1 73 С ;

Т2 =

°

300 ·(5) 1,4 = 475 К = 202 С
1 , 4 -1

°

.

Из приведенных выше численных примеров следует, что в
аспе кте устойчивости смазки степени сжатия в ПК на уровне 4-5
близки к предельным. Это означает, что ни по условиям приемле
мой производительности , ни по условия м вязкостной стабильности
смазки задача работы компрессора с высокими степенями сжатия
(на уровне десятков и сотен) не может бьrrь решена при использо
вании одноступенчатого поршневого компрессора.
4.3.S. Сжатие rаза в мноrоступенчатых компрессорах

Схема многоступенчатой компрессионной установки

Высокая результирующая степень сжатия достигается приме
нением мноrоступенчатых компрессоров с охлпщением rаза меж
ду ступенями. На рис.4.8 в качестве примера изображена схема
трехступенчатой компрессорной установки. Исходный газ дав343

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

s

Рис. 4. 8. Схема трехступенчатой компрессорной установки с охл аждением газа

между ступенями:

/ - компресс оры (рим ские цифры 1-111 - номера ступене й ) , 2 - холодил ьники , 3
в.лагоотделител и ; / - газ, /1 - охлаждающи й агент, /// - выделившаяся в.лага; 1 - 7
характерные состояния рабочего тела

-

лением р 1 и температурой Т1 (состояние 1) поступает в первую
ступень компрессора, сжимается в ней до давления р2
(состояние 2). После 1 ступени сжатия газ подается в холодиль
ник, в котором изобарически охлаждается до состояния 3
(желательно до первоначальной температуры Т1 - той же, что и
в точке 1 ) . Далее охлажденный газ подается на 1 1 ступень сжа
тия - до давления р3 (состояние 4) и затем охлаждается в холо
дильнике после 11 ступени сжатия - предпочтительно до пер
воначальной температуры (состояние 5). Охлажденный газ по
дается в следующую ступень компрессора (в рассматриваемом
примере - на 1 1 1 и последнюю) , где сжимается до давления р4
(состояние 6), после чего в случае необходимости охлаждается в
концевом холодильнике (до состояния 7 ) .
Кружкам и н а схеме изображены маrоотделиrели, уста н а вливае м ые после
каждого холодильника. Дело в том, что водяные пары , находя щиеся в исходном
газе об ы чно в ненасыщенном состоянии, в результате уменьшения объема газа
при сжати и мoryr (чаще всего так и бывает) после охлаждения примерно до
первоначальной температуры оказаться пересыщенными. Тогда избыток влаги

выпадает в виде конденсата в количестве, превышающем возможности насыще
ния, а газ остается н асы ще н н ы м водяными парами . (Эффект насыщения газа
влагой и выпадения конденсата в результате повышения давления становится
более понятным при рассмотрении свойств влажного воздуха в разд. 1 5 . 2 . 2 . )
Наличие ка пел ь но й влаги в газе неблагоприятно сказывается на работе
компрессора, поскольку з а счет вьшеления те плоты сжатия газа и трения

п роисходит исп а ре н и е капель. Это сопровождается дополнительн ым повыше
нием степени сжатия в компрессоре вследствие возрастания конечного давле
ния: при исп а рен ии капель объем рабочего тела резко увеличи вается . В рез ул ь
тате понижаются А.о и производительность компрессора. Кроме того, испарение
капел ь сопровождается возникновением локальных ( в точках испарения ка
пель) термических напряжений на стенках цилиндра - появляется усталость
металла, снижается долговечность работы компрессора. Наконец, потребитель
по условия м технологии может потребовать удаления капель из газа. Эти м
целям и служат влагоотделители (сепараторы ) , выводящие сконденсиро
вавшуюся влагу из газовой системы . Заметим , что одновременно п роисходит и
удаление к а п ел ь смазочного масла, так что эти сепараторы по существу являют

ся влаrомаслоотделителями.

344

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Оптимизация распределения степени сжатия
по ступеням компрессора
Понижение степени сжатия р;+ 1 /р; в каждой ступени много

ступенчатого компрессора в сравнении с высокой общей степе
нью сжатия Рп+1/р 1 в пс-ступенчатой компрессорной установке
позволяет успешно разрешить обе сформулированные выше
проблемы:
- в каждой отдельной ступени, где газ сжимается с умерен
ной степенью сжатия, получаются технологически приемлемые
(достаточно высокие) значения Ло;
- поскольку степень сжатия в каждой ступени ограничена и
между ступенями производят охлаждение газа, температуру в
конце стадии сжатия в любой ступени удается удерживать на
уровне , не превышающем предельных (по условиям устойчи
вости смазки) значений r2п Р .
Многоступенчатое сжатие с охлаждением газа между ступе
нями сопровождается благоприятным энергетическим эффектом.
В самом деле, при охлаждении газа уменьшается его объем
(объемный расход) , а П К - машина объемного действия; поэто
му уменьшение объема сжимаемого газа сопровождается сниже
нием энергетических затрат. Энергетические выгоды использо
вания многоступенчатых компрессоров с промежуточным
охлаждением газа в холодильниках наглядно иллюстрируются
диаграммой p-V на рис . 4.9 применительн() к идеализированному
варианту (&8 = О). Цифры на этом рисунке отвечают номерам
позиций на рис.4.8. В случае одноступенчатого сжатия от давле
ния р1 до р4 была бы затрачена энергия, выражаемая площадью
1-61-7' - l ' - l . Но в случае многоступенчатого сжатия газ, вы
толкнутый из 1 ступени компрессора в объеме У2, поступа
р
ет во 1 1 ступень после его
охлаждения - в объеме Уз < У2 .
Поэтому работа сжатия во 1 1
ступени компрессора будет вы
ражаться не площадью 2-4'5'-3'-2, а меньшей: площадью
13 ...., .. . -
3-4-5'-3'-3; выигрыш в за
1
1
тратах энергии выразится за
р_ 3•1 1
2
штрихованной площадью 3-21

1
1·: 1
.
....--, -� ....�
. --.
1
: �....'
t
1
1

Рис.4.9. Диа грамма р - V сжатия газа в
трехступенчатой компрессорной уста
новке с охлаждением газа между сту
пенями (обозначения - в тексте)

1

1

у

345

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

4'-4-3. Точно так же, в результате охлаждения газа после 1 1
ступени, выигрыш в затратах энергии на 1 1 1 ступени компрессора
отвечает заштрихованной площади S-4 '- 6'-6 - 5.

Количественно выигрыш в суммарных (по всем ступеням
компрессора) затратах энергии
зависит от распределения
промежуточных давлений р2 и
или, что то же самое, - от

r.

Рзl

распределения степени сжа'IИЯ по ступеням мноrоступенчатоrо
компрессора. Разумеется, начальное давление р 1 на входе в ком
прессор и конечное Pn +I на выходе из него (в рассматриваемом
примере Рп +I
р4)
зафиксированы условиями технологиче

-

=

lr. = l<P2, р3).

ского процесса. Таким образом,
Запишем выраже
ние для lr. применительно к удельным затратам энергии:

lr. =
+

т� 1 Р2•

[Р ]
] Рз•з [(�i' -1]

п�� 1 )
P2
(
f l; ::::: �p1v1
1 1
т 1
1= 1

{(�)

':

• ,

-1

+

+

�1

т

+ ···

•

(ж)

Из соотношения (ж) видно, что каждый из п араметров Р2 и
двояко влияет на
например, с увеличением Р2 возрастает пер
вое слагаемое в правой части (ж) , но уменьшается второе сла
гаемое. То же самое можно сказать о влиянии
на второе и
третье слагаемые в правой части (ж). Это означает, что может
существовать такое оптимальное распределение степеней сжатия
по ступеням компрессора, при котором суммарные затраты
энергии будут минимальными.
С целью определения условия
min запишем выражение для
lr., используя формулы (4. 1 3) или (ж). Для простоты положим:
- газ является идеальным;
- сжатие происходит адиабатически (s const);
- в холодильнике после каждой ступени газ удается охладить
(изобарически) до первоначальной температуры
Поскольку принято, что всасываемый газ в каждую ступень
подается при одной и той же температуре
то
P2V2 =
=
И тогда

lr.:

Рз

р3

fr. =

=

p3v3 = R T1•
1>:

346

�

k

{

� 1 R т ( �:

Т1 .
Т1 , P 1 V1 =

( (�:( (�:( - з}
+

+

(4. 1 9)

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Минимуму работы

lr. отвечают
д l r,

-

др 2

О

следующие условия выбора Р2 и Рз:
д l r,

'

др 3

-

О

.

(з)

При дифференцировании степенных функций дробного вида (х/а)п и (а/х)п,
содержащих константу а, удобной является форма записи, сохраняющая дробь
в той же степени и включающая множитель 1 /х, чтобы учесть понижение пока
зателя степени на 1 . Так,
д

.!...
.. (а/х)п =
дх

и

- (х/а) п = n (x/ a)n( l /x)
дх

-

n ( a/x)n ( l /x) . (и )

Используем этот прием - сначала для первого из условий
(з) . При этом имеем в виду, что давления р 1 и р4 существенно
постоянны, а Рз считается постоянным при отыскании частной
производной по Р2 :

дl r.
др 2

=

[

k_ R T k
1

_- 1
k

-

k

l

(.!)!.1.. ;
Р1

k I

l -

Р2

-

k

-1

k

--

(Рз)k
-

Р2

k-1

1 +
Р2

О-

о] =

О.

(к)
Согласно (к) выражение в квадратных скобках равно нулю.
Проведя очевидные сокращения
равенству

( Р2 / Р1 )

k-1

-

k

=(

Рз

/

Р2

Р2

-

)

=

Р1

( на

k-1

k
-k- и Р 2
-

1

),

придем к

-

k

, откуда следует

Рз

(л)

-

Р2

Проведя аналогичные преобразования
второй из производ
ных в выражениях (з), найдем, полагая постоянным давление Р2:

для

Рз

-

Р2

=

Р4

(м)

-

Рз

Такие же попарные равенства будут справедливы для любой
пары смежных ступеней многоступенчатого компрессора. Таким
образом,

J!.1..
Р1

= J!l = J!.j_
Р2

Рз

=

i
. . . = P +I = .
Р;

..

Pn + I = i d em .

(4.20)

Рп

Значит, для обеспечения минимума суммарных энергозатрат
во всех ступенях многоступенчатого компрессора степени ежа347

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

тия должны быть одинаковЬIМи. Суммарная удельная работа /r. в
этом случае составит

1,:

�

no RT1

[l·�;') lj .
*;'

(4.2 1 )

-

причем Р; н /Р; = P2IP 1 ·
Строго говоря, надо убедиться, что условия (з) действительно
отвечают минимуму работы lr.. Для этого следует установить знак
второй производной в точке минимума, т . е . при P2IP 1 = Рз1Р2·
Применительно к п ервой из рассматриваемых производных
(з) используем выражение (к) :

=

R Ti

::; =

k

[- -!Pi (pР21 )k;I +

� 1 R T, �2

;

' '

�(f!l__Р1 ) k;I Pi (!!i)k;I
Р2
i

l
_
P

[:,[�:) ; - :, (;:J ] =
l
+-

k

' '

i

l
+P

]

�(f!lР2 ) k;I .
k

Легко видеть, что первое и третье слагаемые в квадратных
скобках взаимно уничтожаются, а второе и четвертое - суще
ственно положительны; значит, экстремум lr. действительно есть
минимум.
Тот же знак и смысл имеет вторая производная для второго
условия (з) .
Попытка проведения анализа по той же канве в случае изотермиlfеского
сжатия дает "неожиданный" результат: суммарные затраты энергии /r. безраз
личны к распределению степеней сжатия по ступеням компрессора. В этом
гипотетическом случае газ между ступенями охлаждать незачем ( Т1
Т2
= const), так что выигрыша в работе не будет.
Пользуясь соотношением (4.20) , нетрудно решить задачу о
степени сжатия в пс-ступенчатом компрессоре при известных на
чальном р 1 и конечном Pn +I давлениях, и наоборот - о числе сту
пеней пс при выбранной степени сжатия в одной ступени. Для
этого перемножим все отношения р;+ 1 /р;, содержащиеся в (4.20):

=

f!1.._ J!l.. J!1.. .
Р 1 Р2 Рз

. .

Pi+I ... Pn+I (Pi+l) n Pn +I
=

Р;

Рп

Р;

=

Р1

(н)

Отсюда степень сжатия в произвольной ступени (при задан
ной результирующей степени сжатия в пс-ступенчатом компрес
соре) составит
(о)
348

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Из ( 4.20) получается и число ступеней компрессора при заданной степени сжатия в одной ступени :
пс

=

(
)
/
ln ( Pi + l Р; ) '

ln Pп + \ / Pt .

(п)

разумеется, рассчитанное значение пс следует округлить до це
лого числа, после чего скорректировать по формуле (о) степень
сжатия в одной ступени.
Из выражения (4.20) в соответствии с формулой (4. 1 3) следу
ет, что при равенстве степеней сжатия по ступеням компрессора
и охлаждении до Т1 газа, всасываемого в каждую ступень, затра
ты энергии во всех ступенях также будут одинаковыми:
= 1; = . . . = lnс .
(4.22)
11 = /2 = /3 =
.

.

.

Заключение о равенстве затрат энергии по ступеням ком
прессора является более общим, нежели о равенстве степеней
сжатия. Дело в том, что анализ, приведший к уравнению (4.20) ,
выполнен для идеального газа. Для реального газа при переходе в
область более высоких давлений затраты энергии при одинаковых
степенях сжатия в каждой последующей ступени возрастают: газ
при повышении давления все в большей мере сопротивляется сжа
тию. Поэтому для сохранения условия (4.22) - именно оно отвеча
ет минимуму lr. при сжатии реального газа - рабочие объемы ком
прессоров конструируют таким образом, чтобы степени сжатия
постепенно понижались от первой ступени к последней: так, чтобы
затраты энергии в разных ступенях бьmи
одинаковыми; тогда
суммарные ее затраты будут минимальными.
Многоступенчатое сжатие реальных газов с промежуточным
охлаждением между ступенями компрессора представлено в
диаграмме h - s на рис. 4. 1 0. Стадии адиабатического сжатия
изображаются вертикальными отрезками 1-2, 3-4 и 5-6, ста
дии изобарического охлаждения в холодильниках h
криволинейными участка
ми 2-3 и 4-5; если тре
буется охлаждение газа,
поступающего к потребителю, то еще и
участком
Рис. 4. 10.

Диаграмма h

-

s

сжатия

газа в трехС1)'пенчатой компрес
сорной установке с ОХ.llаждением
газа между С1)'Пенями (обозна
че н и я - в тексте)

s

349

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Минимальные суммарные затраты энергии реализуются
в случае равенства работ по ступеням компрессора: Лh1 = Лhн =

6-7.

= Лhш (причем для i-й ступени ПК /; = Лh;) и lr. = l: Л h;.
п

i=l

Реальные (политропические) затраты энергии рассчитывают
ся по адиабатической работе с использованием адиабатического
КПД компрессора (см. разд.4.3.6) .
На практике газ после очередного холодильника обычно не
удается охладить до первоначальной температуры Т1 • Например,
из холодильника после 1 ступени газ подается на 11 ступень с
температурой не Т1 , а Т! . Тогда процесс изобарного охлаждения
в холодильнике изображается участком 2-За, и далее сжатие
газа происходит по адиабате За-4а. Аналогичные построения в
диаграмме h - s могут быть выполнены и для последующих
стадий сжатия и охлаждения. Разумеется, при этом затраты
энергии несколько возрастают, поскольку приходится сжимать
увеличившиеся обьемы газа, что оЬусловлено повышением его
температуры на всасывающей стороне компрессора с Т1 до Т ' 1 .
Вывод о равенстве степеней сжатия и затрачиваемой энергии
в различных ступенях многоступенчатого компрессора справед
лив, если во всех ступенях последовательно сжимается один и
тот же (весь) массовый поток газа. На практике встречаются
случаи, когда имеются два или более потребителей: одни - на
газ конечного давления и другие - на газ промежуточных дав
лений. Здесь тоже возникает проблема оптимизации распреде
ления степеней сжатия по ступеням компрессора, дабы суммарные затраты энергии бьши
минимальными.
Оптимизация распределения степени сжатия
при промежуточном отборе части газа

Задачу оптимизации распределения степеней сжатия будем
решать применительно к двухступенчатому компрессору. Со
гласно схеме на рис.4. 1 1 , газовый поток после сжатия в первой
ступени разделяется (точка раздачи А) на два:
.
- один (его доля q> � 1 ) идет на вторую ступень компрессора
и далее под давлением р3
к первому потребителю,
- другой (его доля 1
q>) при промежуточном давлении Р2
направляется ко второму потребителю.
Задача оптимизации степеней сжатия решается в той же манере,
что и при отсутствии промежуточного отбора газового потока.
Суммарные удельные затраты энергии запишутся:
-

-

1, - 1 1 + 12 -

350

•

�

1

яr, {[(�:J ';' -}•[(�;) ';' -J

(р)

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис.4. 1 1. К распределению степе
ни сжатия по ступеням компрес
сора с промежуточным отбором
газа меЖду ступенями:

__
1 -_"'"-<р /
2

1 - комnрессоры (1, 11 - номер
сrуnени ) , 2 - холодильник, З - влаго
отдел иRль; / - газ, /1 - охлаждаю
щий а гент, 111 - выдел ившаяся влага;
1 - S - характерные состоя ния в
процессах сжатия rаза в комnрессорах
и его охлаждения в холодильниках

ш

</>

Из формулы (р) следует,
в рассматриваемом
что
случае единственной варьируемой переменной является промежуточное давление Р2. посколь
ку значения р 1 и р3 , а также <Р зафиксированы условиями техноло
гической задачи; иначе говоря, lr. = .f (p2).
Дл я решения задачи оптимизации lr. следует приравнять ну
лю производную от lr. по переменной р2 . Выполним операцию
дифференцирования по канве , изложенной в этом разделе:
дlr.
др 2

=

l

k _ R T1 k 1
k 1
k

_

-

-

(f!.1.)..
Р1

: _1_ <Р k 1

k I

-

Р2

После очевидных сокращений:

( ��)

!!.1...

откуда

Р1

k
k-1

=

q>k=l
k

=

<Р

-

( ;�)
Рз .

k

( ):
!2_

k I

Р2

k'

-·-]
Р2

= О.

k-1

Р2

(с)

Из выражения (с) следует, что при <Р < оптимальная степень
сжатия в первой ступени меньше, чем во второй. В случае увеличе
ния <Р различие в оптимальных степенях сжатия в разных ступенях
компрессора понижается. Разумеется, если газ промежуточного
давления не отводится (<Р = 1 ) , то равенство (с) переходит в вы
ражение типа (ж) . Если же устремить <Р к нулю, то теряет смысл
постановка задачи: речь пойдет об одноступенчатом компрессо
ре, а для него р2
величина постоянная.
-

4.3.6. Об охлаждении поршневых компрессоров

Отвод теплоты в компрессорах является важным объектом их
эксплуатации и технологического расчета. Полное удельное (на
1 кг сжимаемого газа) количество теплоты Qr., как указано в
35 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

разд.4.2 ,
ния qт·

складывается

из "теплоты сжатия " qc и теплоты тре

При известных начальной Т1 и конечной Т2 температурах газа суммарная
теплота t/t. может быть рассчитана по формуле
fJr. = Ст ( Т2 - Т1 ) ,

(т)

причем теплоемкость политропического процесса Ст , постоянная в условиях
политропического сжатия , определяется выражением (4.бб) .
Теплота трения lJт зависит не только от констр уктивных особенностей кон 
кретного ПК, но и от качества изготовления его рабочих узлов (цилиндра,
поршня , клапанов) , от физического их состояния (износа), а также от качества
и интенсивности подачи смазки.
Если в компрессоре нет отвода теплоты от сжимаемого газа, то его сжатие
идет с неким показателем политропы т0, и конечная температура т2° опреде
ляется по формуле (4.7) при
т = то.
Если в компрессоре удалось бы отвести всю теплоту l/f. = Qc + Qт, охлаждая
газ до первоначальной температуры ( Т2 = Т1 ) , то формально Л h = Ср( Т2° - Т1 ) = О , и согласно выражению (4.4) oq = - vdp, и

q =

Р2
Р1

f v dp. ( П ри этом

знак изменился в связи со сменой пределов интегрирования : речь идет не о
работе, совершаемой газом , а о работе над газом при изменении давления от р 1
до Р2 .) Таким образом , в рассматриваемом случае количество выдели вшейся и
отведенной теплоты совпало бы с работой, затрачиваемой в компрессоре.
На практике в ходе работы компрессора снимается часть теплоты трения
Qт, так что сжатие происходит политропически - с показателем т < т0, а ко
нечная температура Т2 < Т2°. Здесь Т2 также определяется по (4.7), но при
рабочем значении т. Удельное количество теплоты , отведенной в ходе работы
компрессора, запишется как
9к = ( Qт

+ l/т) о -

( Qт

+

Qт) = Cv

(

то - \

mo - k

- )
т-1

т- k

.

(у)

Остальная теплота (q - 9к) целиком или частично снимается в холодиль
никах после компрессора.
Основная трудность расчета - в нахоJКдении теплоты трения lJт (соот
ветственно - величины то) и теплоты, отводимой при охлаждении стенок
компрессора Qк· На практике ориентируются на допустимую конечную темпе
ратуру газа Т '2 (см. разд.4.4), организуя охлаждение компрессора таким обра
зом, чтобы воспрепятствовать превышению Т '2.

4.3. 7. Расход энерmи. Мощность

Энергия на сжатие в компрессоре G (кг) или G (кг/с) газа
рассчитывается на основе удельных затрат энергии / (Дж/кг) .
Для периодического и непрерывного процессов соответственно
(ф)
L = G I (Дж);
L
GI ( Вт);
ком
работа
непрерывная
рассматриваться
только
будет
далее
прессора.
В практических расчетах удобно базироваться на адиабати
ческом (реже - на изотермическом ) процессе сжатия газа в

=

352

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

компрессоре, оперируя удельной адиабатической работой ls или
изотермической - 11• Тогда в случае адиабатической работы
Ls = Gls

(х)

(Вт) .

Переход к политропическим затратам энергии осуществляет
ся с помощью адиабатического КПД компрессора Т\ s:
L = LJтts = GlJтt s

( Вт) .

(ц)

С учетом механических потерь энергии (трение поршня о
стенки цилиндра, в редукторе и кривошипно-шатунном меха
низме, уплотнениях и др. ) получим выражение для требуемой
мощности двигателя N:
N=

�.

(4.23)

Т\ s Т\ м

где механический КПД Т\ м находится в пределах 0,85 - 0,95.
По формуле (4.23) определяется мощность для одно- и многоступенчатых компрессоров; в последнем случае под lr. " пони
маются суммарные удельные адиабатические затраты энергии
l r.s

=

L ls
1

пс

=

L Лh 5 , где пс
1

пс

- число ступеней в многоступенча-

том компрессоре. При этом величины 15 определяются выраже
ниями, приведенными в разд.4.3.2. Значения мощности N, рас
считанные по формуле (4.23), лежат в основе подбора привода
компрессора (ныне чаще всего - электродвигателя) .
В некоторых случаях (например, при расчете мощности в
процессах получения глубокого холода - см. разд.2 1 . 3 . 1 ) удоб
нее базироваться на удельной изотермической работе 11• Тогда
расчет ведется с использованием изотермического КПД ком
прессора Т\ 1:
(ч)
L
L,/Т\ 1 = Glt!Т\ t (Вт) .

=

В этом случае расчетное выражение для мощности на валу
привода имеет вид
L 1 = -Gl1 .
- -(4.24)
NТ\ r Т\ м
Т\ 1 Т\ м
При этом величины 11 определяются выражениями, приве
денными в разд.4. 3.2.
Для многоступенчатых компрессоров l r. 1 = Lс 11 .
п

1

353

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

4.3.8. Регулирование производительности поршневых компрессоров

Регулирование производительности П К имеет целью обеспе
чить возможность изменения подачи газа потребителю соответ
ственно требованиям его технологического процесса• . Существуют
разные способы регулирования производительности; все они в той
или иной мере исходят из выражения (4. 1 7):
V=

FsnчvAo·

Рассмотрим некоторые способы регулирования производи
тельности.
Наиболее выгодно изменять производительность, варьируя
частоту ходов поршня п. Важно, что при этом не изменяются
удельные затраты энергии. Однако изменение п является доста
точно простым лишь при использовании в качестве регулируе
мого привода, например, паровых машин; кстати, в этом случае
возможно плавное регулирование производительности . Но сами
паровые машины занимают большие производственные площа
ди и не очень удобны и надежны в эксплуатации. Ныне в по
давляющем большинстве случаев в химической промы шлен
ности в качестве привода используются электродвигатели пере
менного тока с определенной частотой вращения ротора п. Спе
циальное устройство, позволяющее плавно регулировать п (а
значит - и производительность компрессора), весьма сложно,
дорого и потому используется лишь для компрессоров с высо
кой производительностью. По этим причинам приходится ис
кать другие возможности воздействия на производитель
ность v.
Вполне возможно управлять производительностью путем ре
цикла газа (рис. 4. 1 2) . Тогда часть газового потока ( 1
1j1) высо
кого давления Р2 после сжатия возвращают, регулируя потоки
задвижкой J, по обводной линии 2 на
всасывающую сторону компрессора, где
давление р 1 < Р2 · Чем бОльшую долю газа
11
(1 - ljl) возвращают на всасывающую
сторону компрессора, тем меньше газа
2
(его доля 1j1) поступает к потребителю.
&
Подчеркнем: этот способ регулирования
1
производительности энергетически невы-

Рис.4. /2. Схема компрессора с обводной линией:

1

• С м [ \ 3 5 7)
. , - , .

354

1 - компрессор, 2 - об водная л и н и я , З - задвижка; /
источник газа, /1 - потребител ь га за ; А и В - точки
0100ра и возврата циркулирующего газа
-

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

годен , поскольку безвозвратно теряется энергия, затрачиваемая
на сжатие рециркулирующего газа.
Реrулирование производительности задвижкой на всасы
вающей или нагнетательной линии привлекает своей простотой.
Однако и в этом случае возникают непроизводительные затраты
энергии - на преодоление местных гидравлических сопротив
лений в задвижке ЛРзадв· Эти потери заметно меньше , чем в слу
чае рецикла: там фиrурирует Лр = Р2 Р1 > ЛРзадв · Реrулирова
ние производительности задвижками сопровождается и другими
нежелательными эффектами.
Если прикрыть задвижку на всасывающей линии, то давление
газа р 1 после задвижки понизится, значит при том же Р2 возрас
тет степень сжатия, а с ней и затраты энергии в компрессоре.
Кроме того, на всасывающей стороне (между задвижкой и ком
прессором) давление может оказаться ниже атмосферного. Тогда
возможен подсос воздуха в компрессор из окружающей среды.
Это всегда нежелательно, а иногда (контакт кислорода воздуха с
сжимаемыми горючими газами) - просто опасно.
Если прикрыть задвижку на нагнетательной линии , то при
постоянном давлении р 1 это приведет к повышению давления
Р2 , значит и степени сжатия f12/p 1 . При этом возросшая темпера
тура Т2 может превысить предельную температуру Т • 2 , допусти
мую по условиям устойчивости смазки.
Экономичным и достаточно простым способом реrулирова
ния производительности является присоединение дополнитель
ного вредного пространства - его относительный объем равен Ед
в добавление к существующему в компрессоре Ев · Тогда в фор
мулу (4. 1 8) вместо Ев надо подставлять Ев + Ед ; при этом умень
шится л.0, а значит и производительность V Регулируемое допол
нительное вредное пространство представляет собой цилиндр, в
котором в определенном положении фиксируется неподвижный
поршень. При необходимости изменения производительности
компрессора поршень дополнительного вредного пространства
фиксируется в новом положении. Заметим, что этот способ по
зволяет реrулировать производительность без дополнительных
затрат энергии (см.разд.4.3.3).
В последнее время наиболее часто используют способ регули
рования производительности путем отжима всасывающего клапа
на на определенной (начальной) части хода поршня при сжатии.
Отжим всасывающе го клапана осуществляется специальным
кулачковым устройством - оно заметно проще и дешевле, не
жели организация дополнительного вредного пространства. При
этом на начальной части хода сжатия не происходит самого
сжатия: пока всасывающий клапан открыт, поршень просто '
выталкивает газ обратно во всасывающую линию (отрезок 1 - 1
-

355

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

р1

при давлении
на рис. 4.6). В результате реально ход всасыва
ния, а с ним и производительность компрессора уменьшаются.
З аметим, что (как и для предыдущего способа) работа компрес
сора с отжимом клапанов не сопровождается непроизводитель
ными затратами энергии.
4.4. НЕКОТОРЫЕ СПЕЦИАII ЪНЫЕ
ОБЪЕМНЫЕ КОМПРЕССОРЫ

Рассматриваемые в этом разделе специальные компрессоры
объемного действия, несмотря на наличие вращающихся дета 
лей и узлов, близки не к центробежным, а к поршневым маши
нам . Дело в том, что напор в них создается не непосредственно
центробежной силой (как у центробежных машин), а за счет
изменения объема полости (как у поршневых машин). Только
здесь движение " поршня " не возвратно-поступательное, а вра
щательное. А центробежная сила участвует в процессе не прямо,
а опосредованно - в создании этого вращающегося " поршня " .
Объемные специальные компрессоры мо гут работать на соз
дание как напора, так и вакуума.
Н иже кратко рассмотрены устройство и принцип работы
пластинчатого и водокольцевого компрессоров• .
4.4. 1 . Пластинчатые ротационные компрессоры

Пластинчатые ротационные компрессоры (вакуу м -насосы),
используемые в химической промышленности, изготовляются в
различных конструктивных вариантах - в зависимости от их
назначения и условий функционирования. Один из вариантов
такого компрессора показан на рис.4. 1 3.

Рабочий орган компрессора - помещенный в корпус 1 ротор 2 с пазами 5,
в которые вставлены пластины 4 (число их обычно превышает 20). При враще
нии ротора (на рис. 4. 1 3 , а - по часовой стрелке) под действием центробежной
силы пластины частично выходят из пазов (см. рис. 4. 1 3 , б
укрупненный
масштаб) - насколько позволяют специальные направляющие. При движении
ротора пластины трутся о стенки корпуса. При этом рабочее пространство
разделяется на отдельные перемещающиеся отсеки (полости) между ротором ,
корпусом и пластинами . Рубашка J, питаемая холодной водой , предусмотрена
для отвода теплоты сжатия и трения.
Всасwuние газа от источника (в зону всасывания 7) происходит за счет раз
режения, возникающего в зоне всасывания при увеличении объема движуще
гося отсека. Сжатие и пода ча газа к потребителю происходят при уменьшении
объема газа в этом отсеке, когда он перемещается к зоне нагнетания 6.
Проюао� ротаuионного компрессора оценим из следующих сообра
жений (рис.4. 1 3, а). В случае соосности корпуса (диаметр dк) и ротора (диаметр �)
зазор между ними составил бы е = (dк - dp)/2. В рабочем положении ротор
-

• См. ( 1 ,

356

3

- 5, 7).

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

б

а

Рис. 4. 13. Ротационный пластинчатый компрессор:
а - общая схема, б - паз и пластина; / - корпус, 2 - ротор, З - водяная рубашка, 4
- пластины, 5 - пазы , 7 и 6 - зоны всасывания и выталкивания газа; / - газ, /1 - охлаж

дающая вода

опущен вниз, в идеале - до упора, т.е . на величину е (здесь е - эксцентриси 
тет). При этом зазор в верхней части ротора становится равным 2 е, а макси
мальное живое сечение очевидно равно 2еЬ, где Ь - длина ротора по образую
щей . При известной частоте вращения ротора п скорость перемещения полости
равна лdп, причем в качестве d используется некое усредненное значение,
равное, например, средней арифметической величине (dк + dp)/2 . Тогда теоре
тическая производительность составит
V,. = 2еЬлdп.

(4. 2 5)

iл, их тол- долю рабочего объема, занимаемого лопатками (их число
щина - б): вместо лd надо писать лd - iлб;
- объемный КПД ДО: эффект расширения небольшого остатка газа при пе
ремещении газовой полости из зоны нагнетания в зону всасывания. Тогда
реальная производительность запишется как
V = V,ДО = 2 еЬ(лd - iлб)пДО ,
(4. 2 6)

Для определения реальной производительности надо учесть:

причем для ротационного пластинчатого компрессора ДО "' 0,6+0, 8 .
П роизводительность компрессора в зависимости о т частоты вращения рото
ра и его размеров составляет до 1 000 мЗ/ч (или 0,3 мЗ/с) , напор - до 0,4 МПа
(при работе на сжатие), остаточное давление - до 0,0 1 МПа (при работе на
создание вакуума) . Реrулирование производительности осуществляется измене
нием п ротора при помощи редуктора или какого-нибудь другого вариатора
либо организацией рецикла газа с помощью обводной линии, т.е. возврата
части газа с нагнетательной стороны компрессора на всасывающую.
Мощноста. на валу ротационного компрессора рассчитывается по формуле
(4. 2 3 ), причем 'ls "' 0,75+0,8 , а ri" "' 0,8+0,9. Заметим , что невысокие значения
ТJs и 'l м обусловлены затратами энергии на преодоление сил трения: для рота
цион ных компрессоров эти затраты энергии существенны.
Частота вращения ротора - от 1 0 до 2 0 с 1 ; иногда возможно непосред
ственное присоединение компрессора к электромотору.
Среди достоинств ротационных компрессоров - практически равномерная
подача газа потребителю, а так.же относительная простота конструкци и. Основ-

357

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ные недостатки: сильный шум при работе; износ пластин (хотя их изrотовляют
из износоустойчивых материалов); кроме тоrо, не исключено заклинивание
пластин при вращении ротора вследствие их перекоса.
4.4.2. Водокольцевые компрессоры

Водокольцевые компрессоры (иногда их именуют ротацион
ными мокрыми компрессорами - РМ К или водокольцевыми
вакуум-насосами - ВИН) весьма широко представлены в хими
ческой технологии и ряде других производств. Их конструк
тивное оформление также может изменяться в зависимости от
назначения и условий работы. Схема работы типичного ком
прессора приведена на рис.4. 1 4.

В цилиндрическом корпусе 1 эксцентрично расположен ротор 3, снабжен
ный небольшим числом лопаток 2 одинаковой длины (плоских или изоrнутых,
расположенных вдоль образующей). В корпус первоначально заливается жид
кость (чаще всеrо - вода) - примерно до половины. При вращении ротора
вода отбрасывается лопатками к периферии, образуя жидкостной кольцевой
слой, свободная поверхность котороrо при достаточно большой частоте враще
ния практически соосна (см. разд. 2 . 1 .3) с корпусом. В результате между рото
ром, ero пластинами и кольцевым слоем жидкости возникают замкнутые rазо 
вые полости (отсеки). Они перемещаются (на рисунке - по часовой стрелке),
изменяя при этом объем rазовой полости. При ero увеличении на всасывающей
стороне возникает разрежение, и газ засасывается в полость (положение А). На
нагнетательной стороне при перемещении газовой полости в положение Б
объем ее уменьшается, и происходит сжатие rаза. В положениях А и Б к ци
линдрическому корпусу присоединены (обычно с торцов) патрубки, ведущие
соответственно к всасывающей и нагнетательной линиям.
Производительность водокольцевого компрессора оценивается по формуле
(4.26), при этом объемный КПД А.о для водокольцевых компрессоров обычно
Превышает 0,95: вследствие ХОроШеГО УJIЛОТНеНИЯ зазоров ЖИДКОСТЬЮ МЗЛО t8.
Производительность компрессора (или вакуум -насоса) в зависимости от раз
меров и условий работы достиrает 0,3 м3/с. Создаваемый напор при работе на
нагнетание - до 0,2 МПа, остаточное давление при работе на вакуум - до 5 кПа.
Достоинства: равномерная подача газа; возможность непосредственноrо
присоединения к электродвиrателю (частота вращения - порядка 1 0 с- 1 ) ;
высокая надежность (особенно если нет
частых остановок). Эксплуатационный
недостаток - крутая характеристика:
з
А
при повышении напора или разрежения
производительность быстро понижается.
Важная особенность: из компрессо
ра вместе с газом в значительных ко
6
личествах выбрасываются капли воды
е
(поток ll на рис.4. 1 5) . Поэтому рядом
с ним устанавливают влагоотделитель
(поз.J) , из которого отделившаяся

у

Б

358

Рис.4. 14. Водокольцевой компрессор :
/ корпус , 2 - зона всасывания, 3 - ро 

тор с лопатками, 4 - rаэо в ые п олости
(отсеки ) , 5 - зона нагнетания , 6 - кольuевой
слой воды; / - газ, // - жидкость
-

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 4. 15. Схема водокольцевоrо компрессора
с водосборником :
1 - компрессор, 2 - 1J>убопровод от компрес
сора к водосборнику, J - водосборник, 4 - линия
возврата воды в компрессор; / - rаз, 11 - rазожид
костная смесь, 111 - возвратная вода

вода возвращается (поток 1//) обратно в
компрессор, а освобожденный от брызr
воды rаз (правый поток /) направляется по
назначению.
Расчет энерrе111Ческих затрат можно формально вести по выражению (4.23),
только полный КПД ri здесь весьма низок (заметно менее 0,5). Дело в том , что
для водокольцевоrо компрессора расход энерrии на сжатие rаза не является
определяющим. Вклад затрат энерrии на подъем и поддержание центра масс
жидкости соизмерим с затратами энерrии на сжатие rаза, а затраты энерrии на
перемещение жидкостноrо кольца лопатками превосходят затраты энерrии на
сжатие. Упомянуrые дополнительные затраты пока что достоверной оценке не
поддаются ; поэтому в основу кладуr затраты энерrии на сжатие rаза, а вклад
друrих составляющих учитывают низким КПД - по существу, поправочным
"коэффициентом незнания".

4.5. ЦЕНТРОБЕЖНЫЕ КОМПРЕССОРЫ

Центробежные компрессоры и газодувки (иначе - турбоком
прессоры ТК) являются наиболее распространенными предста
вителями динамических компрессоров. По своему устройству и
принципам работы (создание напора за счет непосредственного
воздействия центробежных сил) ТК близки к центробежным
насосам. Это позволяет воспользоваться некоторыми соотноше
ниями , установленными в rл.3 для центробежных насосов.
ТК по развиваемому напору условно подразделяют на соб
ственно ТК (напор свыше 0,3 МПа) , турбоrазодувки (напор от
0,0 1 до 0,3 МПа) и вентиляторы (напор не превышает 0,0 1 МПа) .
4.5. 1 . Устройство и принцип действия турбокомпрессоров
Рабочий орrан ТК (рис.4. 1 6) - насаженное на вал 1 и заключенное в кор
пус (на рисунке не показан) рабочее колесо 2, снабженное лопатками J. При
вращении колеса с лопатками rаз центробежной силой отбрасывается к пери 
ферии рабочеrо колеса и далее - в наrнетательный rазопровод к потребителю.
При этом вблизи оси рабочеrо колеса возникает разрежение, куда устремляется
rаз от источника. Газ из рабочеrо колеса выходит с большой скоростью, т.е. с
большой кинетической энерrией. Поскольку назначение компрессора состоит в
повышении давления (приросте потенциальной энс:рrии), то используются уст
ройства ' , преобразующие кинетическую энерrи ю rаза в потенциальную (в
энерrию давления): лопатки , отоrнуrые назад, улиткообразный корпус, специ 
альн ый направляющи й аппарат (система неподвижных лопаток, охватывающих
рабочее колесо) - см. разд. 3 . 3 .
' См . [ \ , 3 -

5, 7).

359

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

-

компрессора:
Схема многоколесного центробежного компрессора:
- -

Рис.4. 16. Схема центробежного
/ вал, 2 рабочее колесо, J
Рис.4. 1 7.
/

вал,

2

лопатки; /

исходный rаз, //

рабочее колесо с лопатками, З

сжатый газ

холодильник

Степень сжатия в одной ступени ТК невелика. Для ее увели
чения на валу ТК устанавливают несколько рабочих колес (рис.
4. 1 7) , через которые газ проходит последовательно, повышая
свое давление. Сжатие газа в ТК сопровоЖдается нарастанием
температуры, что приводит к увеличени ю объемного расхода
газа, а значит и затрат энергии. Поэтому в многоколесных ком
прессорах после каЖдой секции из 3-4 ступеней для снижения
затрат энергии газ направляют в выносные холодильники, после
чего подают в очередную секцию.
В задачу технолоrическоrо расчета входит определение произво
дительности ТК, развиваемого им напора (степени сжатия
и
затрат энергии (мощности).

PllP1 )

4.S.2. Производительность турбокомпрессоров

Для определения производительности ТК рассмотрим парал
лелограмм скоростей на выходе (индекс 2) из ТК (рис. 4. 1 8) по
добно тому, как это было сделано при рассмотрении центро
бежных насосов. При толщине лопаток Б и их числе iл живое
сечение газового потока равно 7t�b iлЬБ, где � = 2 R2 - диа
метр окружности выхода , Ь
ширина канала на выходе из ра
бочего колеса (см. рис.4. 1 6) . При абсолютной скорости с2я,.
нормальной к живому сечению, получим теоретическую объем
ную производительность ТК:
(а)
V = ( 7t�b
iл ЬО ) с2 я .
Для инженерных расчетов удобно ввести коэффициент стес
нения потока лопатками:
i
л Б = k1 < 1
1

-

-

-

-

rr D 2

и выразить c2 R через окружную скорость и2: с2я = c2sina2

360

= k2u2,

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 4. 18. К определени ю производи
тельности rурбокомпрессора и степени
сжатия в его рабочем колесе:
1 и 2 - окружности входа и выхода, 3
лопатки рабочего колеса

-

и2 = 2тtnR2 = тt�n, п где
число оборотов рабочего колеса
в единицу времени. Кроме то
го, следует ввести поправку kэ
на сжимаемость газа (р 2 � Р 1 ) и
учесть коэффициент подачи Т\ v .
отражающий переток через
зазор между корпусом и рабоч и м колесом небольшого коли
чества газа из зоны нагнетания в зону всасывания. Тогда (ер. с
формулой 3.35а)
V=

или

где k "' k 1 k2kзТ\v .

тt�bk1k2 u2 kзТ\v = kтt� Ьтt �п,
V = kтt 2 � 2 bn ,

(4.27)

Из (4.27) следует, что при проектировании ТК на заданную
производительность V имеется возможность варьировать его
конструктивные (�, Ь) и эксплуатационные (п) характеристики.
4.5.3. Н апор, развиваемый турбокомпрессорами

Напор, создаваемый рабоч и м колесом турбокомпрессора,
обычно записывают по аналогии с напором центробежного на
соса (см. разд. 3.4. 1 - основное уравнение центробежного насо
са) . В случае безударного входа газа в рабочее колесо (cosa 1 = О )

� и 2 = � (тt�п) 2 ,
(4.28)
g 2
g
где вместо c2 cosa 2 записано Jсои2 , причем значение коэффициен
Н=

.!.. u c2cosa2
2
g

=

та ko для ТК с лопатками, отогнутыми назад, близко к 0,5.
Полный напор Н расходуется на преодоление сопротивлений:
- гидравлического сопротивлен ия в газопроводе и противо
давления у потребителя газа Нп (это - " полезные" потери напора);
- гидравлических потерь в самом компрессоре Нк :
Н= Н + Н
(б)
к
п
Технологу важен полезный напор

. Нп

=

Н- Н =
к

l

.

н( i) =
-

Нт� ,
г

где Т\ г - rидравлический КПД турбокомпрессора, выражающий
долю полного напора, которая может быть использована по36 1

ту

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

требителем сжатого газа:
н.п

=

Hn· 1 r

= /со

11 г

(4.29)

2
- и; ·
g

Величина Нп выражается в метрах газового столба. Но плот
ность газа изменяется при его движении между лопатками в
рабочем колесе ТК. Поэтому возникает неопределенность: к
какому именно давлению следует относить Н и Нп. При не
больших степенях сжатия в ТК, т.е. при условии pgH < < р, этот
вопрос не актуален, поскольку р � const. Однако при более вы
соких степенях сжатия плотность р изменяется существенно, и
неопределенность остается. В этих случаях вместо напора Н
следует оперировать приращением давления и степенью сжатия,
связав их с конструктивными и рабочими характеристиками
турбокомпрессора.
Для выявления этой связи воспользуемся подходом, приме
ненным для определения напора центробежных насосов, но
учтем сжимаемость газа, т.е. изменение его плотности при дви
жении в рабочем колесе. С этой целью вьщелим элементарный
пространственный контур, ограниченный радиусами R и R + dR
(см.рис.4. 1 8 ) и запишем баланс по моментам количества движе
ния (импульса силы). При массовой производительности ком
прессора G имеем: Приход (нижняя стрелка на рисунке) Пр =
= GcRcosa.; Уход (верхняя стрелка на рисунке) Ух = G[cRcosa +
+ d(cRcosa)]; Источник Ис = dM0
момент импульса, переда
ваемого газу от рабочего колеса на рассматриваемом участке dR:
(в)
GcRcosa - G[cRcosa + d(cRcosa)] + dMo = О .
Раскроем квадратные скобки и произведем очевидные со
кращения:
(г)
Gd(cRcosa) = dMo .
·

-

Домножим обе части равенства на угловую скорость ro

Gd(rocRcosa)

=

d(roMo) .

Поскольку roR = и (окружная скорость) и d(roMo)
приращение мощности на участке dR, то имеем

= 27tn:

= dN -

Gd(cucosa.) = dN.
(д)
Выразим dN = GgdH и запишем dH с учетом переменной
плотности газа р: dH = dp/pg. Тогда после сокращения на G и g
получим

d(cucosa) = dp/p .

(е)

Представим текущую (переменную) плотность газа р , исходя
из уравнения Клапейрона-Менделеева: р = pM/Ry T (здесь М 362

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

молярная масса газа):

d(cucosa) = RyT dрp

(ж)

м

В выражение (ж) входит текущая температура Т, изменяю
щаяся в ходе сжатия и зависящая по (4.7) от текущего давления р:

т -1
и т = т1 (:�) т
Подставив последнее выражение в (ж) , получим
-1_ 1
m
RyTl
т
d(cucosa) = Р т-1 dp .
Р1 т
т -1
Т1 (°PiР ) т
т

=

М

[

(з)

]

Проинтегрируем (з) от сечения входа до сечения выхода:
_l

c2u2cosa2 - c1 u 1 cosa 1 = RyTI т -1 ___!!!__ p:�I P im�I
Р1 т
RyT1 ___!!!__ ( Р2) :•
Р1
М

=

М

т-1

_

[

m-1

_

l] .

_

=

(и)

Принимая теперь, как и в случае центробежных насосов, что
авыражение
вход газа в рабочее колесо ТК) , разрешим
1 ""' rt/2 (безударный
(и) относительно степени сжатия:
т
тт k
) -1 ( ouiM + 1
Р2 (c2u2 cosa2M
(4. 30)
RyT1 т
RyT1 т
Р1
В последнем выражении, как и при получении формулы
(4.28) , произведена замена: c2cosa2 = kои2 .
Степень сжатия по (4. 30) дает полный напор ТК. Потребитель
-

=

m-1

+1

=

m-l

m-I
J

(rir),

может воспользоваться лишь частью напора
поскольку
заметная его доля теряется в самом компрессоре. Для учета этих
потерь первое слагаемое в скобках выражения (4.30) следует
умножить на Тl r·
Если степень сжатия невелика (приближается к 1 ) , то первое
слагаемое в скобках мал о' в сравнении с 1 . Тогда, разлагая (4.30)
363

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

в ряд Тейлора и ограничиваясь только двумя членами ряда, най
дем:

Р2 ko-ui

-

=

Р1

1 + ---=--

М

Ry T1

(к)

В случае изотермического сжатия анализ по той же канве
приводит к следующему выражению:

!!..1..
Р1

=

exp(kouiMJ.
Ry T1

(л)

Из выражения (4.30) следует, что степень сжатия JJ]/p 1 воз
растает при увеличении частоты вращения рабочего колеса п
(соответственно - при увеличении окружной скорости и2 =
= 7tDJ_n ) и с понижением температуры Т1 • Кроме того, при прочих
равных условиях p'J!p1 выше для газов с большей плотностью (с
большей молярной массой) . Физически такое wшяние обуслов
лено увеличением центробежной силы, действующей на газ (его
масса тг, ускорение ro 2 R) :
- с ростом п возрастает центробежное ускорение, равное
ro 2 R

=

(27tn) 2 R;

- понижение температуры приводит к увеличению плот
ности газа, а значит и его массы тг в рабочем колесе ТК;
- газы с большей плотностью р (молярной массой М) сжи
маются с большей степенью сжатия, так как увеличение р озна
чает увеличение тг.
Степень сжатия JJ]/p 1 в одно м колесе современных турбоком
прессоров обычно невелика: 1 ,2 - 1 ,4; сравнительно редко она
достигает 1 ,8 . Заметим, что в пс-колесном ко мпрессоре степень
сжатия увеличивается менее чем в пс раз, так же и по тем же
причинам, что и в центробежных насосах (см . разд. 3 .4.4) .
Существенному увеличению степени сжатия в ТК препятствует ограничен 
ная прочность конструк ционных материалов . Дело в том , что центробе жн ая
сила при вращении рабочего колеса действует не только на газ, но и на само
рабочее колесо, так что оно может разрущ иться при существенном повышении
частоты вращения п . Вместе с тем это означает, что р ри повышении прочности
конструкционных материалов поя вится возможность повысить п , а с ним и
степени сжатия в 1)' рбокомпрессоре.

Мошµость на валу ТК

если
газа

рассчитывается по формулам (4.23), (4.24),
мало отличается от идеального, и по диаграммам состояния
(например, h - s), если этими отличиями пренебречь нельзя.
газ

4.5.4. Характеристики турбокомпрессоров

Уравнения для производительности V и напора Н (степени
сжатия p2fp 1 ) задают связь величин V и р в параметрической
форме: в фор мулы для обеих величин входит окружная скорость
364

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 4. 19. Частная характеристика rурбокомпрессора (ТК):

характеристика ТК, 2 и З - характеристики газопровода, 4 - КПД 1)'рбокомпрессора

1

-

Р

и2. Как и в случае центробежных
насосов, для установления рабо
чих значений р и V необходимо
построить характеристики ком
v
прессора и газопровода. Частная
характеристика задает связь 1/
(или р) и при определен ной частоте вращения рабочего коле
са, универсал ьная характеристика - связь и при различной
частоте вращения.
На рис.4. 1 9 показаны типичная частная характеристика р - V
(кривая J), а также кривая 4 изменения КПД компрессора т� в
зависимости от производительности V. Для определен ия рабо
чей точки необходим о еще построить характеристику газопро
вода (линии 2 и 3). Рабочая точка определяется как точка пере
сечения характеристик компрессора и газопровода. Приближ ен
ный пересчет характеристики компрессора на другую частоту
вращения производится, как и в случае центробежных насосов,
по законам пропорци ональности (разд. 3.4.3):

V

Н V

n1 VV21 :: �НН21 "" �N2N1 .

·!!1_ =

Более широкую и надежную информа цию о связи Н(р) и V
при разной частоте вращения рабочего колеса дает универ с аль
ная характеристика ТК (см. разд. 3.4.3).
Проблемы последовательного и параллель ного включения ТК
формулируются и решаются так же, как и в случае центробеж
ных насосов (см. разд.3 .4.4) .
4.5.5. Реrулирование производительности турбокомпрессоров

Производительность ТК возможно регулиро вать р азными
способам и. Охарактеризуем кратко некоторые из них.
Наиболее экономич ный путь - воздейств ие на частоту вра
щения п р абочего колеса. Однако этот путь конструктивно сло
жен , его целесообразно использовать в случае ТК больш ой про
изводител ьности .
Рецикл, т.е. перепуск по обводной линии некоторой доли
сжимаем ого газа с нагнетательн ой стороны компрессора на вса
сывающую. Способ неэконом ичен , поскольку энергия на сжатие
рециркулирующего газа теряется безвозвратно.
365

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Задвижка на всасывающей или нагнетательной линии. До
стоинство этого способа в его простоте. Но здесь также беспо
лезно затрачивается энергия на преодоление гидравлического
сопротивления задвижки. Однако эти потери существенно ни
же, чем в предьщущем случае, поскольку сопротивление за
движки заметно меньше полного перепада давлений Р2 - р 1 • Для
задвижки на всасывающей линии надо также иметь в виду
опасность понижения давления на входе в ТК ниже атмосфер
ного: возможен подсос воздуха через неплотности - загрязне
ние технологического газа воздухом, а в некоторых случаях образование взрывчатых газовых смесей.
4.5.6. Центробежные вентиляторы

Вентиляторы достаточно широко применяются в химической
технологии, когда необходимо обеспечить большие производи
тельности V при небольших напорах Н. По развиваемым напо
рам эти компрессоры подразделяют на вентиляторы низкого дав
ления ( Н � 1 кПа), среднего давления (от 1 до 4 кПа) и высокого
давления (от 4 до 1 0 кПа).
Отдельную группу среди вентиляторов составляют центро
бежные машины · , по конструкции сходные с турбокомпрессо
рами и турбогазодувками. Напоры, создаваемые турбовентиля
торами , сравнительно невелики, они работают с пониженными
окружными скоростями и (в 3-4 раза меньше, нежели у ТК). Про
изводительности центробежных вентиляторов, напротив, весьма
велики, поэтому лопатки в рабочем колесе вентилятора нередко
устанавливают радиально или даже несколько отгибают вперед.
Технологический расчет турбовентиляторов в общем ведется
по той же канве, что и для ТК. Поскольку напор вентилятора
Лр < < р, то степень сжатия газа в нем вполне можно определять
по формуле (4.30) , с учетом гидравлического КПД вентилятора
11г · Производительность вентилятора
оценивается по формуле (4.27).
Мощность на валу вентилятора мо
жет быть определена по формуле
(4.23). Однако в связи с малыми
напорами возможен более простой
метод расчета мощности. На рис.4.20
V V

Рис.4. 20. К расчету мощности на валу венти 
лятора

' К вентиляторам относятся не только центробежные маши ны, но и ряд
других (специальных) компримирующих устройств (осевые и т. п . ) . Их рассмот
рение выходит за рамки настоящего учебника - см. [ \ , 3-5, 7 ] .

366

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

приведена диаграмма p - V для вентилятора. Из рисунка видно,
что вследствие малости Лр затраты энергии без сколько-нибудь
заметной погрешности можно определять, игнорируя кривизну
линии сжатия газа - по ruющади прямоугольника (небольшая
ошибка при этом делается "в запас") :

N=

р
Vл
ТJ
в

(4.3 1 )

.

Значение КПД для вентилятора ТJ в ниже (на уровне 0,5), чем
для турбокомпрессоров и турбогазодувок. Это связано с более
существенным вкладом кинетической энергии газового потока и
необходимостью ее преобразования в потенциальную (из-за
потерь энергии при таком преобразовании - см. начало
разд.4.5. 1 ) .
К вентилятору прилагается его универсальная характеристи
ка, позволяющая оценить зависимость Н(Лр) от V при различ
ной частоте вращения п, а также КПД.
4.6. ДРУГИЕ ДИНАМИЧЕСКИЕ КОМПРЕССОРЫ

К динамическим компрессорам помимо центробежных отно
сятся двухроторные, осевые, струйные и другие устройства. Де
тальное рассмотрение работы и расчета таких компрессоров
можно найти в ряде учебников и специальной литературе• . В
качестве примера ниже рассмотрены и охарактеризованы только
двухроторные компрессоры: их устройство, принцип действия и
некоторые особенности.
Рабочий орган даухроторноrо atoмnpeceopa (рис. 4.2 1 ) - пара роторов "восьмерок" 2, размещенных в овальном корпусе /. Роторы вращаются в проти
воположных направлениях (на рис. 4.21 - жирные стрелки) и как бы катятся
друг по другу. При этом зазор между роторами, а также между каждым рото
ром и корпусом - очень мал (доли миллимет
ра). В целях герметизации (для уменьшения
зазоров) в рабочую зону добавляют в небольших
количествах смазочные материалы.
При вращении роторов газ захватывается и
порциями (на рисунке - заштриховано) протал
юtвается от всасывающей стороны к нагнетатель
ной. При этом в полости между ротором и корпу
сом газ не изменяет объема, сжатие происходит
Рис. 4. 21. Схема двухроторного компрессора:

1 - корпус, 1 - роторы, J
патрубок выхода газа

-

патрубок входа

rаза,

4

-

• Расчет струйных компрессоров рассматри вается в разд. 9.6.7 применитель
но к сжатию водяного пара. См. также [ 1 , 3-5 , 7) .

367

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

при сообщении полости с нагнетательным пространством, где газ принимает
давление потребителя.
Несмотря на порционную подачу, потребителем газа неравномерность подачи
практически не ощущается вследствие высокой частоты вращения роторов.
Диапазон производительностей (в зависимости от размеров газодувки и
скорости вращения роторов) - весьма широк: от 1 00 до 25000 м3/ч (от 0,3 до 7
мЗ/с) . Частота вращения роторов вполне соответствует стандартной частоте
вращения электродвигателей , что позволяет непосредственно (без редуктора)
присоединять компрессор к электродвигателю; не исключается работа и с п >
> 5 0 с- 1 (если привод не электродвигатель, а турбина или какой-либо друтой
двигатель) . Создаваемый напор достигает 0,3-0,4 МПа.
Достоинства: компактность, простота, надежность. Недостаток: шум в
процессе работы. Существенная особенность: необходимость тщательного изго
товления роторов и корпуса и точность монтажа, иначе из-за увеличения зазо
ров существенно снижаются напор и производительность.
Изготавливаются также двухроторные компрессоры с ротором более слож
ной конфигурации (три головки "восьмерок" вместо двух), что способствует
повышению равномерности подачи газа.
·

4.7. ОБЛАСТИ ПРИМЕНЕНИЯ КОМПРЕССОРОВ

Достоинства поршневых компрессоров (ПК) состоят в воз
можности создания высоких степеней сжатия (до 1 000) при не
ограниченном нижнем пределе производительности, а также в
сравнительно высоком КПД. К недостаткам относятся гро
моздкость, высокие инерционные усилия вследствие возвратно
поступательного движения поршня, загрязнение сжимаемого
газа смазкой, высокая стоимость.
Достоинства турбокомпрессоров (ТК) - компактность, рав
номерность подачи, высокий верхний предел производитель
ности (более 50 мЗ/с), отсутствие загрязнения газа смазкой, воз
можность непосредственного присоединения к электродвигате
лю. Среди недостатков
пониженный КПД, ограниченный
нижний предел производительности (около 1 ,5 м3/с).
Таким образом, П К применяются в случае высоких степеней
сжатия при умеренной производительности, а ТК - при высо
ких производительностях и не очень высокой степени сжатия.
Достоинства и недостатки специальных компрессоров, а так
же области их предпочтительного применения рассматриваются
в ряде учебников по курсу ПАХТ и в специальной литературе • .
-

4.8. ВАКУУМИРОВАНИЕ

Вакуум-насосы (ВН) служат для создания и поддержания ва
куума, перемещения газа, подсоса жидкости. Часто комприми
рующие машины могут работать на создание как повышенного
давления, так и вакуума. При этом компрессоры присоединяют• См. ( 1 , 3- 5 , 7 ) .

368

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ся к потребителю своей нагнетательной стороной, а вакуу м 
насосы - всасывающей .
Основные проблемы вакуум ирования рассматриваются ниже
на примере поршневых вакуум-насосов.
4.8. 1 . Поршневые вакуум-насосы

Устройство и принцип действия поршневых ВН в общем
аналогичны поршневым компрессорам, но есть некоторые осо
бенности, связанные с весьма высокими степенями сжатия р]/р1
( 1 0 и более). В частности , чтобы обеспечить приемлемую произ
водительность, т.е. достаточно большое значение объемного
КПД А.о, необходимо конструктивно (см. разд. 4.3.3) предусмот
реть весьма малые объемы вредного пространства (т.е. малые
е8) . Существуют и другие способы• повышения А.о.
Для создания большего разрежения (т.е. более низкого оста
точного давления в аппарате) целесообразно использовать мно
гоступенчатые В Н . Однако при этом потери давления в комму
никациях между ступенями и в клапанах ВН становятся соизме
римыми с рабочим остаточным давлением, что снижает эффект
вакуумирования. Поэтому на практике число последовательных
ступеней вакуумирования не превышает двух.
Индикаторная диаграмма в случае поршневых ВН схожа с
рассмотренной ранее для поршневых компрессоров; только об
ласть работы в этом случае располагается ниже уровня атмо
сферного давления (рис. 4.22) .
Формулы для расчета затрат энергии в принципе тоже повто
ряют полученные ранее для поршневых компрессоров:

[( ) ]

/ = _!!!_ p1 v 1 P21 m�l
т-1
Р

-1 ;

N = .!!!..._ _
·

11 м

(4. 1 4)

В Н может работать на поддержание вакуума, например на
удаление газов, подсасываемых через неплотности аппаратуры.
В этих случаях давления р 1 и Р2 - постоянны, и приведенными
выше формулами, например типа (4. 1 4) , можно воспользоваться
непосредственно. Однако нередко ВН работает на создание ваку
ума в аппарате - тогда постоянным является лишь давление Р2;
оно часто близко к атмосферному (ВН выбрасывает газ в атмо
сферу), превышая его на величину гидравлического сопротивле
ния нагнетательного клапана. А давление р 1 переменно: в ходе
процесса оно изменяется от исходного Рl н (обычно - атмосфер
ного) в начале вакуум ирования до низкого рабочего Р l к в конце
• См . ( 1 , 3-5, 7) .

369

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

�

р
р �3

,

Рис.4.22.
Индикаторная диаrрамма
вакуум
насосов (1
4
точки состояния рабочего тела)
-

1_ _

-

вакуумирования. В этом случае возникает
вопрос, на какое именно рабочее да8Аение
..."
р1 следует ориентироваться, пользуясь
формулой (4. 14).
Для разрешения возникшей пробле
4
1
Р1 - - мы удобно оперировать удельными за
тратами энергии в расчете на 1 мЗ газа
v
lv. Полные затраты энергии составляют
G/, где G - массовая производитель
ность В Н . Тогда из (4. 1 4) получается:
· - ·

L = G/

=

__!!!___ p 1 v1
m-

l

[( ) m�I 1]
P2

-

Р1

(а)

Вт ;

здесь V1 = Gv 1 - объемный расход газа на входе в ВН.
Оrнося теперь L к единице объемного расхода V1 , получим lv
в Дж/мЗ :
lv

= __!!!___ i
P
m - l

[( ) m�I l] .
P2

(б)

_

Р1

Из (б) видно, что переменное давление р1 влияет на lv двоя
ко: с одной стороны , lv падает при уменьшении р1 : множитель
перед квадратной скобкой (полное вакуумирование, нет газа нечего сжимать), а с другой - возрастает: первое слагаемое в
квадратных скобках (начало стадии вакуумирования, степень
сжатия еще равна единице) . В таких случаях возможно суще
ствование экстремума lv при изменении р 1 . Найдем этот экстре
мум, приравнивая нулю производную от lv по Р1 :

:;;

�

ф m

1 н(�:(�I 1] { 1 (�:(�1 :1
-

-

р

�

m

(в)

Здесь использован математический прием, удобный дЛЯ дифференцирова
ния степенных функций вида (х/а)п
см. разд. 4.3.5.
-

Сокращая множитель т/(т 1) перед фигурной скобкой и дав
ление р 1 в последнем слагаемом выражения (в), приходим после
раскрытия квадратных скобок к следующему соотношению:
-

(!!1...Р1 ) т
m-1

370

-

i

-

т

-

m

i

(!!1...Р1 ) т = о
m- 1

_..!_ (!!1...Р1 ) т
m- 1

или

т

-

i

= о,

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

2/Р 1:
Рзафиксировав

экстремум lv при определенном значении

Р21
Р

т m- 1 .

Р 1 или

т

=

(г)

Для оценки значения рур 1 , при котором реализуется экстре
мум lv, положим: процесс сжатия - адиабатный (т
сжи
� 1 ,05- 1 05 Па.
Тогда, сомается двухатомный газ
1 ,4 1 ) ;
гласно

(p1 )extr

�

(г) ,

(k =

Р2
искомое значение P21P i =

0,32- 1 05

Па.

kk/(k -I)

= k) ;

�

3,26 , откуда

Для определения вида экстремума ( max или min) следует
установить знак второй производной в точке экстремума. Одна
ко в рассматриваемом случае вид экстремума легко устанавли
вается из физических соображений: согласно (б) , удельная рабо
та lv равна нулю при р
(абсолютный вакуум , полное вакуу 
(начальный момент вакуум и ро
мирование) и при р 1
вания). При промежуточных значениях р1 затраты энергии на сжа
тие rаза, естественно, положительны; значит, в ходе вакуум ирова
ния lv при изменении (понижении) р 1 проходит через максимум.
Характер изменения lv в зависимости от показан на рис. 4.23.
Этот рисунок конкретизирует постановку задачи, устанавливая
некоторые ограничения.
Если по технологическим условиям приходится часто вакуу
мировать сосуд (аппарат) , то, подбирая двигатель для В Н, в це
лях преодоления "горба" lv следует ориентироваться на макси
мальную работу /� max - говорят о частом, или быстром, пуске .
При этом значения переменных давлений в сосуде (ре) и на вса
сывающей стороне ВН (р 1 ) практически одинаковы.
Однако встречаются случаи, когда операция создания вакуума в
сосуде производится редко, а после достижения в сосуде низкого
=
ВН длительное время рабо
остаточного рабочего давления
тает только на поддержание вакуума . В таких случаях нецелесооб
разно ориентироваться на максимум /у: плохо, если установленная
мощность привода (найденная на основе
заметно превышает
рабочую (требуемую - на основе p 1 J - высока реактивная мощ
ность, электродвигатель (привод ВН) перегревается, возрастают
затраты энергии. Поэтому для со:щания благоприятных условий
продолжительной работы электродвигателя надо ориентироваться
на Рl к· Но в этом случае электродвигатель обеспечит снижение
давления лишь до предельного значения . P l n p• равного
и соот
ветствующего точке А ,- далее не хватит мощности электродвигате
ля, чтобы перешагнуть через "горб" (точка В) и затем прийти в ра
бочую точку с.

= О=
=1 Р�н
Р2

р1

Ре Рlк

Plexir)

Рlк

37 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

lv

в

, - - -

1
1
1

- - -

... ,.___ к

Рис. 4. 23. Зависимость удельной работы lv от давления всасывания р1
Рис.4. 24. Схема вакуумирования сосудов:

1 - вакvvм ируемый сосуд, 2 - вакуум мС'lр, З - вакуум -насос, 4 - задвижка; V0 - объ
ем сосуда, К - контур

Здесь применяют медленный пуск, не разрешая, чтобы на вса
ВН давление р 1 превысило
Рl к · В этих це
лях между вакуумируемым сосудом и ВН устанавливают за
движку (рис.4.24, поз. 4), что позволяет за счет ее гидравлическо
го сопротивл е ния удерживать непосредственно на всасывающей
стороне ВН давление р 1 , не превышающее Рlк· Регулируют это
давление задвижкой 4, а контролируют вакуумметром 2.

сывающей стороне

Систему "ВН - сосуд" запускают (т.е. включают ВН) при закрытой задвиж
ке. Тогда в небольшом объеме (от задвижки до сосуда) на всасывающей сторо
не ВН практически сразу устанавливается малое остаточное дааление р1 < р1 • •
хотя в сосуде давление Р е пока что равно начальному. Затем задвижку чуть
приоткрывают, следя по вакуумметру, чтобы давлен ие р1 на всасывающей сто
роне ВН оставалось не выше р1 •• В сосуде по мере отсасывания газа дааление
Ре тоже понижается , но остается выше Рlк - на величину гидравлического
сопротивления приоткрытой задвижки . По мере понижения давлен ия в сосуде
Ре задвижку постепенно все более открывают , не позволяя, однако, давлению р 1
превысить Р l к · Спустя некоторое время давление в сосуде Ре понизится до целе
вого р 1 . ; тогда задвижку открывают полностью (сводя к минимуму, в идеале к нулю, ее гидравлическое сопротивление); давлен ия Ре и р1 становятся при
этом практически одинаковыми, равными Рlк· Далее ВН работает не только
при Р2 = coпst на НЗЛiет.пе.льной сrороне ВН, но и при постоянном дамении Р 1 = Рlк
на ero всасывающей сrороне. Разумеется, вакууми рование в таком режиме требует
допоmtительных ЗDmpam времени, но зато после досmжения Р1 = Рlк электродвиnrrсль
вакуум -насоса длительно работает в блаrоприяrных условиях.

4.8.2. О вакуум-насосах глубокого вакуума

Объемные вакуум-насосы мoryr обеспечить осгаточное давление
на уровне 0,05- 1 05 Па (5 кПа), в ряде случаев (двухступенчатый
ВН) - до 1 кПа и даже ниже. В то же время в химической техноло
гии встречаются процессы, проводимые при весьма глубоком вакуу
ме. В этом случае используются специальные вакуум -насосы.
372

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

�]

Рис.4.25. Диффузионный вакуум-насос:
/ - корпус, 2 - щслев�щное сопло, J - тру

ба, 4 - водя н ая рубашка, 5 - nодоfl>Сватель;
/ - газ от вакуум ируемого annapaтa , JJ - газ к
форвакуумному насосу, 111 - слой рабочей жид 
кости, JV - охлаждающая вода

Рис. 4.26. Схема глубокого вакуумирования
сосуда:
/ - вакуумируемый сосуд, 2 - насос глубо

кого вакуум ирования, J - форвакуумный насос, 4
- задllИJККа

�5
Н иже
принцип
вающего
(иногда и

�i'
47
1

�
2

3

в качестве примера • рассмотрены устройство и
действия диффузионноrо вакуум -насоса, обеспечи
остаточное давление на уровне � о - э - 1 0- 4 Па
ниже ) .

Схема диффузионного вакуум-насоса представл е н а н а рис.4.25 . В корпусе 1
смонтирована труба J, заканчивающаяся в верхней части щелеобразным соплом
2. В нижней части корпуса и трубы находится слой lll жидкого рабочего тела с
очень низким (при температурах на уровне 20 • С) давлением паров. Корпус
снабжен охлаждающей рубашкой 4, питаемой холодной водой /V. Днище кор
пуса и слой жидкого рабочего тела получают теплоту от подогревателя 5.
Диффузионный вакуум - насос работает следующим образом. ПодоJl>Сваемая
жидкость испаряется; пары рабочего тела поднимаются по трубе З и, выходя через
щелевое сопло 2, направляются на охлаждаемые стенки корпуса . Здесь они конден
сируюrся и стекают вниз - в зону жидкости /1/. При этом давление на холодных
стенках крайне низкое - соответстве нно давлениям паров рабочего тела при темпе
ратуре стенки . Пары рабочего тела от щслеобразного сопла движутся на стенки
корпуса с очень высокой скоростью, поскольку на этом участке практически отсут
ствует rидравлическое сопротивление. Высокому скоростному напору отвечает (по
уравнению Бернулли) низкое давление - ниже, чем в вакуумируемом аппарате. Под
действием этого перепада давления возникает и nодцерживается газовый поток 1 от аппарата к диффузионному вакуум - насосу. Далее газовый поток /1 выходит из
диффузионного ВН и направляется к форвакуумн ому насосу (см. ниже).
В качестве рабочего тела с низким давлением паров наиболее перспективны
жидкости на основе кремнийорганических соеди нен ий : они устойчивы и практиче
ски нетоксичны, чrо является важным преимуществом в сравн ен и и с использо
вавшимися ранее ртутью или верете н н ым маслом.

Многие В Н глубокого вакуума имеют весьма крутую харак
теристику: их производительность очень быстро падает с увели' См. также ( \ , 3 -5 , 7).

373

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

чением напора (противодавления). Поэтому их используют
совместно с форвакуумным насосом по схеме, п оказанной на
рис. 4.26.
Вначале вакуумируемый сосуд 1 присоединяется к форвакуумному насосу З:

задвижка 4 открыта, ВН глубокого вакуума 2 не работает. В результате давле
ние в сосуде постепенно снижается до уровня, отвечающего возможностям форва
куумного насоса (скажем, до 1 кПа). С этого момента включается вакуумн ый насос
глубокого вакуума и перекрывается эадВижка: теперь газ из сосуда проходит после
довательно вакуум -насос глубокого вакуума и форвакуумный насос.

Смысл такой схемы работы состоит в улучшении рабочих условий
ВН глубокого вакуума: он должен теперь развивать сравнительно
небольшой напор - от рабочего в сосуде до конечного на уровне
дамения всасывания в форвакуумном насосе (сотые доли атмо
сферы). А последующее сжатие rаза до атмосферного дааления осу
щесталяется форвакуумн ым насосом. В результате при сравнительно
малом напоре (низкое противодааление на выходе ВН глубокого
вакуума) обеспечивается приемлемая производительность системы
"сосуд - вакуум-насосы" .
4.8.3. Время вакуумирования сосудов

Среди технологических проблем вакуумирования практиче
ский интерес (особенно - при частом пуске) представляет время
•в вакуумирования сосуда, за которое с помощью вакуум-насоса
производительностью Vвн в сосуде объемом
давление пони
жается от начального Рн до конечного Рк·
Для решения задачи рассмотрим (см. рис. 4.24) промежуточный
момент времени •, когда текущее дааление в сосуде р уже ниже Рн,
но еще не достигло Рк· Выберем в качесrве пространсrвенного кон
'I)'ра " К" сам сосуд (на рисунке - шrриховая линия). Запишем ба
ланс по массе rаза для элементарного времени d•: Приход Пр = О,
Уход Ух = Vвнрd• и Накопление Нак = d(Vcp) = Vcdp . В целом:
(д)
О - VвнРd• = Ycd p .
V
Разделим переменные:
d• = - с d p

Ус

и проинтеrрируем в пределах от О до •в и соответственно от Рн до
Рк; поменяем также местами пределы интеrрирования , чтобы изба
виться от знака " минус" :
Vвн

Р

(е)

374

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Для перехода от плотностей к давлениям воспользуемся
уравнением политропическоrо сжатия , имея в виду, что v =

= 1/р :

Рн

-

и

= Рк

-

Рн =

Рк

( )
Рн

l/т

Рк

(ж)

Подставим полученные соотношения в выражение (ж):
't в

или
't в

( )
= � ( )

=

У
с 1 n Рн
V
вн
Рк

т Vвн

ln

l/т

Pн

Рк

.

(4.32)

При адиабатическом снижении давления в сосуде вместо т
подставляется показатель адиабаты k, при изотермическом т =
= 1.
Из (4. 32) следует, что при более высоких т сосуд вакуумиру
ется быстрее (в частности, при адиабатном вакуумировании
быстрее, чем при изотермическом). Это связано с понижением
температуры при уменьшении давления в сосуде: поскольку
Vс = const, то снижение температуры при адиабатическом ваку
умировании сопровоЖдается дополнительным уменьшением
давления.
-

Строго говоря, формула (4.32) является оценочной, так как производнтель
ность вакуум-насоса Vан зависит от степени сжатия (изменяется объемный
КПД Ло). Для более точного решения задачи следует учесть зависимость Ло от
степени сжатия - см. разд. 4.3.3.

ЛИТЕРАТУРА к rлаве 4

1 . Абдурашитов С.А., Тупичеюсов А.А., Вершинин И.М, Тененzольц С.М. Насосы и
компрессоры . М.: Недра, 1974. 296 с.
2. Баскаков А.П., Берг Б. В., Витт О.К. и др. Теплотехника. М.: Энергоиз
дат, 1 982. 264 с.
3 . Гельперин Н.И. Основные процессы и аппара11>1 химической технологии. М.:
Химия, 198 1 . 8 1 2 с.

375

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

4. Дытнерский Ю. И. Процессы и аппараты химической технологии . М.:
Химия, 1 995 . 768 с .
5 . Клсаткин А.Г. Основные процессы и аппара1Ъ1 химической технаnоmи. М.:
Химия, 197 1 . 784 с .
6 . Литвин А . М. Техническая термодинамика. М. - Л . : Госэнергоиэдат,
1 956. 3 1 2 с.
7. Плановский А.Н., Николаев П. И. Процессы и аппараты химической и
нефтехимической технологии. М.: Химия , 1 972. 494 с.
8 . Чечеткин А.В., Занемонец Н.А. Теплотехника. М.: Высшая школа, 1 986.
344 с.

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Глава 5

ГИДРОМЕХАНИЧЕСКИЕ ПРОЦЕССЫ

Область гидромеханических процессов весьма широка, она
включает многочисленные и достаточно разнородные процессы
(технологические приемы) - соответственно назначению и осо
бенностям объектов. Гидромеханические процессы основаны на
переносе импульса (количества движения) - именно этот приз
нак объединяет указанные процессы в отдельную группу. Ко
нечно, и другие химико-технологические процессы используют
перенос импульса, но превалирует там перенос иных субстан
ций (теплоты , вещества) . Гидромеханические процессы в своем
осуществлении и описании непосредственно базируются на зако
номерностях переноса импульса, устанавливаемых технической
гидравликой (см. гл . 2). При описании гидромеханических про
цессов рассматриваются внуrренняя , внешняя и смешанная за
дачи гидродинамики .
Перенос импульса, количества движения является предметом
также теоретической и прикладной гидравлики. Не всегда про
сто провести четкое разграничение между объектами изучения,
относящимися к теоретической гидравлике, прикладной гидрав
лике и гидромеханическим процессам, - в различных учебниках
и научных монографиях эти границы проводят по-разному. Ви
димо, к гидромеханическим процессам в самом общем плане
следует относить технологические приемы, приводящие к прак
тически важным направленным изменениям состоян ия рабо
чих тел.
В настоящем учебнике в главу ''Гидромеханические процес
сы" вошли разделы "Осаждение" , "Фильтрование" , "Перемешива
ние" и "Диспергирование жидкостей и газов" . В число объектов
изучения не включено рассмотрение гидравлических машин
(прессов, аккумуляторов, мультипликаторов): такие машины
применяются в некоторых химико-технологических процессах,
но расчет их основных технологических характеристик весьма
прост (принципы расчета гидравлических прессов изучаются в
средней ш к оле; подход к расчету а к кумуляторов практически
совпадает с рассмотренным при изучении воздушных к ол паков
поршневых насосов) .
377

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Схемы и конструкции аппаратов для осуществления отдель
ных процессов приведены в соответствующих разделах главы * .
Н иже последовател ьно рассматриваются:
- процессы разделения неоднородных систем (преимущест
венно - жидкостных) с твердой фазой: осаждение, фильтрация;
- процессы перемешивания жидкостных систем (собственно
жидкостей , суспензий и т.д.);
- процессы диспергирования.
5. 1 . ОСАЖДЕНИЕ
S. 1 . 1 . Общие положения

Процесс осаждения состоит в разделении суспензий, состав
ленных из жидкостей и твердых частиц, на осветленную жид
кость и осадок. В более общем случае речь может идти также об
эмульсиях (из несмешивающихся жидкостей) и некоторых дру
гих дисперсных системах (в частности , с газом в качестве
сruюшной среды) . В идеале осветленная жидкость не должна
содержать твердых частиц. Влажный осадок состоит из твердых
частиц, в просветах между которыми находится (остается) то
или и ное количество жидкости.
В основе процесса осаждения лежит явление отстаивания.
Это явление реализуется в поле каких-либо массовых сил : такие
силы, действующие на единицу объема твердого материала
(частиц) и жидкости , должны быть неодинаковы - в это м усло
вие разделеtDIЯ неоднородных систе м методом осаждения . Условие
разделения выполняется, когда плотности твердого материала (ТМ)
Рт и жидкости (Ж) р - различны: Рт * р, обычно Рт > р .
Состав суспензии, т.е. смеси ТМ и Ж (в общем случае возможно,- и газа) характеризуют относительной массовой кон
центрацией а. Если рассматривать 1 мЗ смеси , то при порозности
Е масса ТМ в нем равна РтО - Е ) , а масса жидкости - рЕ. Тогда
концентрация а, равная отношению этих массовых количеств,
выразится :
а

=

Рт 0 - Е ) ( кг ТМ)/<кг Ж ) .

(5. 1 )

рЕ

Отсюда по известной концентрации а нетрудно определить
рабочую порозность:
Е

=

Рт
----'Р т + ар

-

• Подробно конструкции аппаратов см. ( 1 ,
378

( 5 . l a)

-

6 , 9,

1 5 , 1 7 , 1 9 , 22) и др.

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис.5. 1. Схема потоков в отстойнике
непрерывного действия :

/ - исходная суспензия, /1 - осветленная
жидкость, ///- осадок ; К - кон тур

1

V'

а
В дальнейшем будем обозна
чать : а : а 1 и а2 - концеюрации
ТМ в исходной суспензии, в
к
осветленной жидкости и в осадке.
Производительности процесса
осаждения могут быть представлены на основе исходной суспензии или осветленной жидкости
(реже - осадка). Установим связь между этими производитель
ностями. Будем рассматривать непрерывный процесс разделения
суспензии на осветленную жидкость и осадок по схеме, пока
занной на рис.5. 1 . Пусть V', V1 и V2 - объемные производи
тельности (потоки) по собственно жидкости в исходной суспен
зии, в осветленной жидкости и в осадке (в случае периодических
процессов надо оперировать не потоками , а количествами
(объемами) жидкостей У, V1 и У2 ).
Заметим: в идеале осветленная жидкость не должна содер
жать твердых частиц ( а 1 = О , значение V1 совпадает с полным
количеством осветленной жидкости Vж); реально в случае не
полного осветления возможно а 1 > О.
Полагая, что пространственный контур "К" на рис.5. 1 охва
тывает разделяющий аппарат 1 (отстойник) , запишем для еди
ницы времени материальные балансы:
- по массовым жидкостным потокам:
'

pV ' - p V1 - p V2 = 0 ,

откуда после сокращения на р и простых преобразований
V' = V1 + V2 , V2 = V' - V1 и т.д.;
- по потокам ТМ :

(а)

p V'a ' - p V1 a1 - p V2a2 = О ,

откуда после сокращений и преобразований
(б)
Va ' = V1a1 + V2a2 и т.д.
Исключая из (б) величину Vi с помощью последнего из вы
ражений (а) , имеем
отсюда

Va ' = V1 a 1 + ( V' - V1 ) a2;

а а'
V1 = V' 2 а2 - а 1

(5.2)

Аналогичное выражение получается в случае периодического про
цесса осаждения, только вмесго потоков жидкости V в нем будут
379

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

фиrурировать ее

количества V:
'
V1 = V· a2 - а
а2 - а 1

-

(5.3)

При рациональном проведении осаждения а1 -+ О
в этом
цель процесса. Тогда выражения (5.2) и (5.3) упрощаются:

v' (1 - ;J ,

V1 =

(5.2а)

V 1 = v'

( ;J .
1-

(5.3а)

Для исходной суспензии величины а ' и V' (V') в подавляю
щем большинстве реальных задач эксплуатации и проектирова
ния заданы. Конечная концентрация ТМ в осадке (а2 ) в задачах
эксплуатации рассчитывается по известным значениям V' или V1
из выражений (5.2), (5.2а) . В задачах проектирования величина
а2 обычно выбирается на основе практических рекомендаций,
исходя из последующего использования осадка.

Часто технологи заинтересованы, чтобы осадок был возможно более сухим
(не исключено, что после осаждения его отправят на сушку); тогда стремятся
получить высокие значения а2 . В друтих случаях, например, предполагается
осадок в виде шлама (консистенция типа ила) транспортировать по трубопрово
ду с помощью специального насоса; тогда целесообразно ориентироваться на
умеренные значения а2 .

Важнейшей характеристикой рассматриваемого процесса яв
ляется скорость осаждения. В общем случае речь идет о скорости
стесненною осаждения (витания) Wc. В поле сил тяжести для
суспензии с частицами одинаковых размеров она рассчитывается
(см. разд. 2.7.4) по формуле

Rec =

А

,

(2.75 )

.1)

причем порозность е
определяется из ( 5
на основании началь
ной концентрации ТМ
в суспензии (а') .

(11)

(/)

.. .. . ...
.. . .. . ..

--- --

Рис.5.2. Схема осаждения
(разделения суспензий):

а

380

& 4,75
1 8 + 0,5 9.JAr . е 4 •75
Ar .

(/11)

б

а
монодисnерсные суспен
зии, б
суспензии, содержащие
частицы разных размеров;
/
исходная сусnензня ( /м
и /к
с мелкими н крупными
частнuамн) , /1
осветленная
жидкость, 111
осадок;
А, Б, В
начал ьная , про
межуточная н конечная фазы
осаждения соответственно

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

,.,
-

Напомним:
частиц,

v

AI

d
�
.EJ_E_
р

v

з

_

- ,1
�
l
�
l

критерий Архимеда,

кинематическая вязкость жидкости, g

d

диам тр твердых

ускорение сил тяжести.

В случае разбавленных суспензий Е � 1 , и выраж
переходит в формулу для свободного осаждения (витан

Re8 =

ие (2.75)
) w8:

Ar
.
1 8 + 0,59JAi
Ar

(2. 72)

Рассчитав Rec = wcd /v, находим искомую скорость Wc. В ходе
последующего анализа величина wc трактуется и ис льзуется
как известное свойство системы ТМ - Ж .
Реально суспензия содержит частицы разных размеров
(иногда - и плотностей); в ходе осаждения они д ижутся в
жидкости с разной скоростью: более крупные и т елые быстрее, более мелкие и легкие - медленнее. Скорое ь осажде
ния каждого сорта частиц может быть пр иближенно найдена по
формуле (2.75 ) . Приближенно потому, что в процессе саждения
частю :ы разных размеров и плотностей гидродинами ески вза
имодеиствуют друг с другом, так что скорости их д ижения в
той или иной мере выравниваются (в малой степени - в раз
бавленных суспензиях, в большей - в концентри ованных,
"густых") . Тем не менее рекомендуется вести расчет, ориенти
руясь на наиболее мелкие (и легкие) частицы в исх ной сус
пензи и . Такие частицы в своем движении все же о стают от
крупных (и тяжелых) :
- в отстойниках периодического действия, через екоторый
анице с
промежуток времени после начала процесса, на
осветленной жидкостью образуется зона (рис.5.2, 6) , в которой
находятся преимущественно мелкие (легкие) частицы; их осаж
дение происходит далее в соответствии с формулой ( 75) , при
мененной для таких частиц;
- для отстойников непрерывного действия, где эфф кт вырав
нивания скоростей стесненного осаждения может бь ть замет
ным, расчет на основе наиболее мелких (легких) част ц приво
дит к несколько заниженн ым скоростям осаждения и производи
тельностям, т.е. ошибка делается " в запас".
Разумеется, более точные значения скоростей ос
ения для
конкретных полидисперсных суспензий могут быть по учены из
эксперимен&а.
Теоретическая формула (2.75) пол учена (и приг дна) для
сферических частиц одинакового размера. Несферичность час
тиц учитывается фактором формы Фs (см . разд. 2.7. l ) Распреде
ление частиц по размерам характеризуется кривыми ануломет·

ji
1

38 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

q>(d)

х

о

а

d

I q>(d)dd
о

.....-;
...
;.__...._
.i.
____.1--_---1.__

dmin

d

d'

б

dн

dтах d

Рис.5.3. Кривые гранулометрического состава:
а

-

дифференциальная, 6 - интегральная

рическоrо состава- рис. 5.3. На рис. 5.3, а показана дифферен
циальная кривая распределения: по ординате - плотность рас

пределения q>(d); доля частиц отдельной фракции выражается
площадью под этой кривой на участке абсциссы, ограниченном
предельными размерами частиц . этой фракции d' и d". Для
удобства практических расчетов дифференциальная кривая мо
жет быть изображена в виде гистограммы - последовательности
прямоугольных площадок, равновеликих площадям под соответ
ствующими участками кривой. На рис. 5.3, б показана инте
гральная кривая распределения: по ординате - накопленная частость, т.е. доля (обычно - массовая) частиц

382

х=

J

J

q> (d)dd

раз-

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

мерами от минимального dm in до текущего d. Доля частиц в
диапазоне диаметров от d' до d" (т.е. относительное количество
данной фракции в смеси) выражается отрезком ЛХ на ординате
этой кривой . Средн ий размер узкой фракции определяют как
среднегеометрическую величину d = .Jd'd" (иногда прибли
женно - как среднеарифметическую из d ' и d ') .
С помощью кривых распределения легко найти содержание
каждой (скажем, достаточно узкой) фракции в смеси и осущест
вить пофракционный расчет процесса осаждения на основе
средних диаметров фракций .
Возможность учета полидисперсности смеси при анализе
процесса осаждения продемонстрирована в разд. 5 . 1 . 3 .
5. 1 .2. Естественное осаждение

Для разделения суспензий, содержащих сравнител ьно к руп 
ные частицы (часто - сотые доли миллиметра) , в случае невы 
сокой вязкости жидкости и не очень малой разности плотностей
твердых частиц и жидкости применяется естественное осажде
ние - процесс осуществляется в поле сил тяжести под действи 
ем движущей силы, базирующейся на величине (Рт
p )g, т.е. на
разности удельных (приходящихся на l м 3 ) сил - тяжести и
выталкивающей (архи медовой). Дело в том, что такая система
характеризуется большими значениями критерия Архимеда; это
приводит, соответственно формуле (2. 7 5) , к достаточно высоким
величинам Re c и скоростей стесненного осаждения Wc , значит, и
к приемлемым производительностям процесса.
Сущность процесса естественного осаждения ясна из рис . 5 . 2 ,
а . Примем дл я простоты , что исходная суспензия / содержит
твердые
частицы
одинакового
размера.
Первоначально
(ситуация А) суспензия заполняет верти к альный сосуд. Спустя
некоторый промежуто к времени (ситуация Ii) в результате осаж
ден ия твердых частиц в сосуде образуются (рассматривается
наиболее часто встречающийся случай Рт > р ) слой осветленной
жидкости // и осадок ///, между которыми расположена зона /
еще не разделившейся суспензии. Наконец, через определенное
время (ситуация В) в сосуде остаются лишь две зоны - // и ///,
занятые соответственно осветленной жидкостью и осадком, процесс осаждения завершен.
На рис. 5.2, б показан промежуточ ный момент (ер. с положе
нием Б на рис. 5 . 2 , а) при разделении суспензии, содержащей
твердые частицы двух разн ых размеров (в общем случае - и
плотности) . Здесь зона неразделенной суспензии состоит из
двух областей , содержащих преимущественно медленно осажда-

383

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

(1)

а

6

10

в

ll

н

г

Рис.5.4. Простейшие отстойники:

а - вертикальный отстойник периодического действия, б - верти кальный отстойник
непрерывного действия, " - горизонтальный отстой ник непрерывного действия (схемы
аппарата и процесса);
1 - цилиндрический корпус отстойника, 2 - коническое диище, З - патрубок дJIЯ от
вода осадка, 4 - транспортирующее устройство (в, с, ш - ось вала, скребки, штанга), 5 патрубок дJIЯ отвода осветленной жидкости, б - патрубок дJIЯ подачи исходной суспензи и ,
7 - круговой порог, 8 - кольцевой карман, 9 - штуцер дJIЯ отвода осветленной жидкости,
/О - прямоугольный корпус отстойника ;
1 - исходная суспензия, // - осветленная жидкость, /// - осадок

ющиеся мелкие ( /м) и быстрее оседающие крупные ( /к) части
цы. Разумеется, если разделяется полидисперсная суспензия с
широким набором непрерывно изменяющихся размеров части ц ,
то граница между областями становится размытой или даже
про сто исчезает (остается плавное распределение частиц по раз
мерам в промежуточной зоне осаждения).
Осадительные аппараты
могут работать пе 
отстойники
риодически или непрерывно, причем непрерывные отстойники
могут быть вертикальн ым и и горизонтальн ым и.
-

-

Верти кал�.нwй отстойник периодичеекоrо дейСТ8ИJ1 показан на рис. 5.4, а. Он
предстамяет собой цилиндр 1, переходящий внизу в коническое днище 2 с
большим углом в вершине. Устье конуса заканчивается патрубком З для отвода
осадка. Перемещение осадка к устью конуса (к патрубку З) осушестмяется с

384

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

помощью размещенного в отстойнике транспортирующего устройства l 4 : вал 4в со
штан гам и 4 ш ( о б ы ч но ч ислом 4--6; о н и расположены по хордам, н ес�ол ько сме
щен н ы м относительно диаметра отсто й н ика). Штанги снабжен ы с н нзу скош ен
н ы м и с кребкам и 4с. При включении это устройство медленно вращ�ется , пере
мещая образовав ш и й ся осадок к отводящему п атрубку 3. На образующей цилинд
ра / по его в ысоте размещено несколько патрубков 5 с задвижкам и lд ля в ывода
осветленной жидкости с требуемого уровня.
Отсто й н и к работает циклично. В него загружается исходная суспе1рия /; через
определенное время происходит ее разделение на слой осветленной ж мдкости /1 и
осадок ///. Ж ид кость сливают через соответствующи й патрубок 5 ( туации на
рисунке отвечает работа патрубка, в ыделенного жирной стрелкой).
алее вклю
чают транспортирующее устройство и выгружают из отстойника ос ок. Затем
останавливают это устройство, и цикл повторяется .
С рассмотренным выше сходен по устройству вертикал ь н ы й отс:rо й н и к не
п рерывного действия, показан н ы й на рис.
6. Только исходная успензия /
подается в отстойник непрерывно - через патрубок 6, а осветленная jкидкость /1
переливается через кольцевой порог 7, попадает в скошен н ы й кольцевс;>й карман 8
и R h 1 1юдится ( тоже непрерыано) ч ере"J штуцер 9. Осадок /// может отвЬдиться периоди чески и л и непрерывно:
- при н изкой кон це нтрации ТМ в исходной суспензии осадок на � апливается
медл е н но. поэтому транспорти рующее устро йство 4 включается по мере накопления осадка на короткое время ;
- п р и высокой к о н центрации ТМ в исходной суспензии быстрее н капливаю
щийся осадок отводится с помощью непрерывно работающего трансп ртирующе'
го устройства.
На рис. 5.4. в. г показана (в изометрии и на виде сбоку) схема ра
ы го р и з он
тального отстой ника непрерывного действия. Исходная суспензия / hоступает в
прямоугольный отстойник /О с левого (на схеме) торца. В ходе ее движен я вдоль от
стойника происходит постепенное выпадение твердых частиц на его дно осветление
жидкости. При достаточной продолжительности пребывания потока сус ензии в от
стой н и ке ее разделение на осветленную ж идкость /1 и осадок /// будет достаточно
полным. Осветленная жидкость вы водится из отстойника через штуцер 9 на рис. 5.4,
6 с правого торца). Осадок по мере накопления удаляется из аппарата - аще всего с
помощью специального механического устройства (на рисунке не показан .

1

t
1
[

5.4,

1

i
ооt
�

-

;J





Основные цели технологи ческого расчета отстойник в за кл ю
чаются в выявлен и и связи характерист ик суспензии и п оизводи

тельност и

(а' ,

а, V' или V1 либо

У' или У 1 ) с его

основнымu геомет

рическими размерами, а в случае периодического процесса

-т- еще и с
.
его продолжител ьностью.
отстой 
В ертик ал ьны й отсто й ни к п е риодического де й ст вия.
н и ке (рис. 5 .4 , а) площадью поперечного сечения (ее часто i!азывают
площадью осажде н ия) в ходе процесса осаждения образуете� свобод
н ы й от твердых части ц слой осветлен ной ж идкости объемом rYж = У 1
SНж. где Нж - высота этого сл оя. П р и порозности (объем:ной доле

S

�

=

жидкости) исходной суспензии

ее объеме Ус очевидно :
материала в суспензи и

Е'

[оп ределяется из (5. 1 ) при а = а' ] и

У' = Ус Е', так что Ус = У'/Е'. Объем твердого

(

)

Ут = Ус 1 - Е' = У -,- .

) - Е'
Е

(в)

В е с ь этот ТМ п р и пол ном осветл е н и и ж идкости переходит в
осадок . Пусть п орозн ость п оследнего Ео, сл едо вател ь н о, объе м-

385

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ная доля в нем твердой фазы ( 1 - &о ) . Тогда с учетом (в) получа
ем объем осадка:
V' 1 - Е'
Уо = ____!:l__ =
1 - EQ
Е' 1 - Е о

Вычитая этот объем из объема исходной суспензии , находим
объем осветленной жидкости:
V ' V ' 1 - Е ' V ' Е' - Е 0
=
(5 .4)
Уж = У 1 = Vc - Vo =
-

Е'

- --

Е' 1 - Ео

- ---

Е' 1 - Е о

В случае постоянного поперечного сечения S в зоне освет
ленной жидкости высота ее слоя составит
v· Е' - Ео .
ж
(5.4а)
Нж = У
S r.' S 1 - Е о
=

Без специальных мер механического воздействия величина &о в процессах
естественного осаждения несколько превышает обычную для неподвиж ного
слоя порозность 0 ,4.

Продолжительность осаждения to связана с высотой освет
ленной жидкости Нж условием перехода всех твердых частиц в
осадок. Это условие будет обеспечено, если в осадок перейдут
частицы, находившиеся первоначально в самом неблагоприятном
положении (у верхней границы суспензии) . Таким образом ,
расчет времени осаждения следует вести, ориентируясь именно
на эти твердые частицы. Последние в процессе осаждения
должны пройти путь Нж . Размеры частиц в суспензии невелики,
и участок их разгона (ускоренного движения) исчисляется мил
лиметрами. Поэтому можно считать, что весь путь Нж они про
ходят с постоянной скоростью стесненного осаждения wc , опре
деляемой выражением (2.75). Тогда искомая связь имеет вид
(г)
Нж � Wcto .
Знак равенства отвечает минимальной продолжительности
процесса tmin. обеспечивающей полное осветление жидкости.
Знак неравенства (" меньше" ) указывает на то, что повышение вре
мени процесса осаждения сверх минимального (to > tmin) не при
водит к увеличению высоты слоя осветленной жидкости: Нж не
может быть больше величины , определяемой выражением (5.4а).
Подставив значение Нж по (г) в выражение Vж = SНж, имеем
(5.5)
Эта связь дает решение задачи эксплуатации для периодиче
ского процесса, т.е. производительность отстойника Vж = V 1
при полном осветлении жидкости. При этом знаку равенства
отвечает максимальная производительность, когда to = tmin· Если
386

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

to < t m i n • то производительность Уж понижается. Можно бьvю
бы попьrrаться принудительно повысить производительность, от
бирая при •о < tmin объем жидкости, превышающий Swcto. В этом
случае осветление отбираемой жидкости было бы неполн ым.
Один из важнейших выводов, следующих из соотношения (5.5):
производительность периодического отстойника не зависит от его
высоты, она определяется площадью сечения отстойника.
Наиболее распространенная задача проектирования заключа
ется в расчете площади поперечного сечения отстойника S,
обеспечивающей заданную производительность Уж = У 1 при
условии осветления жидкости. Из (5.5) с учетом (5.За) следует
а' .
(5. 5а)
S > У1 = У ' 1 - а2
Wc to Wc.to
Знак равенства отвечает здесь минимальной продолжитель
ности процесса to = tmin: в этом случае S означает минимальную
площадь осаждения отстойника, которая сможет обеспечить
полное осветление жидкости при заданной производительности
У или У 1 = Уж . Попытка осуществить осветление при заданных
Уж и •о = •min в отстойнике с площадью S менее минимально
необходимой обернется неполным осветлением жидкости.
Вертикальный отстойник непрерывного действия. Технологиче
ский расчет отстойника (рис. 5.4, б) возможен на основе соот
ношений, приведенных выше для вертикального отстойника
периодического действия. Надо только вместо количеств жид
кости оперировать расходами, иначе говоря, положить to = 1 и
писать V вместо У, или (что то же самое) трактовать Y/to как
поток V (расход; производительность в единицу времени). Тогда
выражения (5.5) и (5.5а) , соответственно - для задач эксплуата
ции и проектирования, примут вид

)

-- -- (

v;

- ( -' )

v·
а .
(5.6а)
S � -1
1Wc Wc
а2
Знак равенства, как и ранее, означает максимальную произво
дительность для отстойника известного сечения S и м инимальное
поперечное сечение при заданной производительности V1 , V',
соответствующее полному осветлению жидкости.
Связь производительности и поперечного сечения для верти
кального отстойника непрерывного действия может быть полу
чена также непосредственно из уравнения расхода ( 1 . 1 8 ) . В зоне
осветления жидкость движется вверх со скоростью w (см.рис.5.4,
б) . Искомая связь имеет вид
V1 = wS.
Рабочая скорость w может быть выбрана различной, но не
любой. Ее значение не может превышать wc, иначе жидкостной

Vж = V1

�

Swc ,

(5.6)

=

387

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

поток подхватит и унесет твердые частицы, так что полного
осветления не будет. Если указанное условие w $ wc подставить
в уравнение расхода ( 1 . 1 8) , то приходим к выражению (5.6), а
следовательно и к (5.6а) .
Из полученных выражений следует, что и для вертикального
отстойника непрерывного действия производительность не зави
сит от высоты отстойника, а определяется его поперечным сече
нием (площадью осаждения).
Горизонтальный отстойник непрерывного действия. Для его
технологического расчета воспользуемся схемами, приведенны
ми на рис.5.4, в. Обозначим длину отстойника L , ширину - Ь и
высоту - Н. Тогда площадь отстойника S = Lb, а живое сечение
потока, нормальное к направлению движения жидкости, / = ЬН.
По мере движения суспензии вдоль отстойника происходит по
степенное осаждение твердых частиц. В результате в окрестности
текущего сечения / < L существуют три зоны с более или менее
четко очерченными границами: осветленная жидкость (сверху) ,
осадок (внизу - на дне отстойника) и еще не разделенная сус
пензия (между ними). При этом по мере движения жидкости высо
та зоны суспензии уменьшается, и при достаточной протяженности
отстойника L (т.е. при достаточном времени пребывания в нем
суспензии) она сводится к нулю: все частицы переходят в осадок, а
из аппарата выводится полностью осветленная жидкость.
Условие полного осветления формулируется здесь путем со
поставления времени пребывания суспензии в отстойнике tn p и
времени осаждения t0 , необходимого для осветления:
(д)
tn p 2: to ;
при этом знак равенства соответствует минимальному (для пол
ного осветления) времени пребывания жидкости в отстойнике
'tn p = 't min ·
Выразим характерные продолжительности tnp и то через соот
ветствующие пути движения и скорости. Очевидно, tn p = L /w,
где w - линейная скорость потока в направлении движения жид
кости в отстойнике, она определяется из уравнения расхода типа
( 1 . 1 8) для горизонтального потока V1 осветленной жидкости при
его живом сечении ЬН: V1 = wbH. Отсюда w = V1 /ЬН, так что
'tn p

=

L

w

-

LbH

= -- =

V1

SH

-- .

V1

Для полного осветления жидкости в осадок из суспензии
должны перейти все частицы, в том числе и первоначально на
ходившиеся в наиболее неблагоприятном положении - у верх
ней границы потока суспензии. Такие частицы в своем осажде
нии должны пройти путь Н. При скорости осаждения Wc время
388

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

осаждения составит

то =

н

Wc

Подставим найденные значения tnp и то в условие (д) :

SH

Н

- Wc

-- > .

Vi

Отсюда после сокращения на Н имеем применител ьно к за

даче эксплуатации

Vi � Swc,
применитель но к задаче проектирования

(

v;
v
а' .
S � -1 = -· I - -

Wc

Wc

а2

)

(5.7)

(5.7а)

Знаки равенства в этих выражениях, как и для вертикальны х
отстойников , отвечают максимальной производительности и ми
нимальной площади отстойника, требуемой для полного осветле
ния жидкости.
Важно: производительность горизонтального отстойника тоже не
зависит от его высоты, она определяется его поперечным сечением.
Из приведенных выше формул ясно, что при прочих равных
условиях необходимая площадь осаЖдения отстойника S обрат
но пропорционал ьна скорости осаждения Wc. Значит, для разде
ления суспензий, содержащих более мелкие частицы, более вяз
кие жидкости и при меньшей разности плотностей ТМ и жид
кости потребуется увеличивать поперечное сечение отстойника.

Заметим: анализ проведен для идеализированного случая - одинаковых
размеров частиц в суспензии, газовзвеси. Для встречающихся на практике
полидисперсных смесей расчет следует вести пофракционно, с учетом изме
няющейся порозности . Для приближенных оценок (с 01Шtбкой "в запас") можно
базироваться на более мелкой фракции.

Общий для всех отстойников вывод об отсутствии влияния
высоты аппарата Н на его производительность V, V' и об увеличе
нии производительности с ростом площади осаждения отстойника
S

используется при проектировании осадительных аппаратов:
- отстойники большой высоты изготавливать нецелесооб
разно, на производительность это не повлияет;
- для повышения производительности необходимо увеличи
вать поперечное сечение отстойника S.
На практике отстойники при небольшой высоте имеют весь
ма внушительн ые диаметры (20-30 м - не исключение ) , зани
мают большие производственные площади. Реальное соотноше
ние размеров отстойника, показанного ранее схематическ и на
рис. 5.4,б, видно из рис. 5.5.

389

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис.5.5. Вертикальный отстойник непрерывного действия (см. рис. 5 .4) :
/ - цилиндрический корпус отстойника, 2 - коническое днище, J - патрубок дл я от

вода осадка, 4 - транспортирующее устройство, 5 - кольцевой карман, 6 - патрубок для
подачи исходной суспензии, 7 - штуцер для отвода осветленной жидкости, 8 - круговой
порог;
/ - исходная суспензия, // - осветленная жидкость, /// - осадок

Уменьшить занимаемые отстойниками площади возможно
пугем конструирования мноrополочных аппаратов (рис. 5.6). В
этом случае рабочая площадь осаждения в сравнении с зани
маемой отстойником площадью, а с нею и производительность,
увеличиваются кратно количеству полок (параллельных сек
ций) . Немаловажно, что здесь не требуется больших расстояний
между полками, так как от высоты секций их производитель
ность не зависит.

На рис. 5.6,а схематично показан многололочный отстойник непрерывного
(строже - лолунепрерывного) действия для разделения жидкостных суспензий ;
н а рис . 5 . 6 , б несколько более подробно - отстойник для разделения аэросуспен
зий, т.е. запыленного rаза (пылеосадительная камера). В обоих случаях лоток /,
содержащий твердые частицы, распределяется (по возможности - равномерно)
по секциям между полками , на которые и осаждается ТМ . Освободившийся от
частиц лоток /1 отводится из отстойника. Накопленный осадок (на рисунке
показаны его фрагменты, помеченные в скобках римской цифрой 1/1) удаляет
ся - стадия очистки - из межполочного пространства. В случае жидкостных
суспензий это делается чаще механическим путем, реже кратковременной по
дачей жидкости с высокой скоростью; в случае обеспыливания газа - чаще
всего жидкостным потоком.

При очистке отстойника от осадка твердых частиц процесс
разделения в нем суспензии, запыленного газа прерывается.
Между тем производство до и после отстойника может быть
непрерывным, т.е. требуются постоянные во времени ввод в от
стойник исходного потока V' и вывод из него осветленного по
тока V1 • В этом случае устанавливают два (или более) отстойни
ка параллельно: один из них находится в режиме очистки, дру
гой (или другие) - в рабочем режиме разделения исходной сме
си . После завершения стадии очистки отстойник включают в
рабочий режим осаждения, а на очистку ставится второй
(очередной) аппарат.
390

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис.5. 6. Мноrополочные отстойники:

- отстойник д11 я ра:щеления суспензии, 6 - пылеосадительная камера;
1 - корпус, 2 - полки, J - ш�уцер ввода исходной смеси, 4 - бункер с патрубком д11 я сбора и вывода ТМ, 5 - выравнивающая перегородка, 6 - ш�уцср вывода очищенных
жидкости или газа;
1 - исходная суспензия , /1 - осветленная JКидКость, 111 - осадок

о

Обратим внимание на дее особенности пьmеосадительной камеры.
Первая связана с наличием перегородки 5. При ее отсутствии
газовые потоки в разных секциях испытывали бы разные гид
равлические сопротивления, поскольку протяженности их пути
в аппарате заметно различались бы: для верхних полок путь был
бы короче, чем для нижних. В результате газовый поток двигал
ся бы преимущественно по коротким траекториям с меньшим
гидравлическим сопротивлением (верхние секции), а поток в
нижних секциях бьш бы заметно меньше. Это привело бы к
неравномерной, а значит и менее эффективной работе отстой
ника. В самом деле, в верхних секциях (высокие скорости пото
ка) время пребывания газа мо гло бы оказаться меньше мини
мально необходимого, и газ в этих секциях был бы очищен не
полностью. А в нижних секциях (малые скорости потока) время
пребывания газа бьmо бы неоправданно велико, полное обеспы
ливание завершилось бы где-то на полпути, и хвостовые области
полок в процессе осаждения участия не принимали бы. Наличие
перегородки 5 выравнивает пути, а значит и гидравлические
сопротивления газовых потоков в разных секциях; в результате

поток равномерно распределяется по секциям.

Вторая особенность связана с изменением направления дви
жения потока при его движении над бункером 4. При повороте
потока оставшиеся в газе частицы (наиболее мелкие или легкие)
подвергаются действию инерционных сил и выпадают из пото
ка - так происходит дополнительная очистка газа. Аналогичный
метод используется для грубой очистки газа от пьши в отстой
ных газоходах.
Важно: при крутом повороте действующая на частицу инер
ционная сила может значительно превосходить силу тяжести.

39 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Это создает предпосьшки для очистки суспензий и запьшенных
газовых потоков в условиях, когда естественное осаждение не
может обеспечить приемлемую чистоту очистки или производи
тельность отстойника. Конкретно: малым размерам частиц, вы
соким вязкостям жидкостей , небольшим величинам ( Рт - р ) при
существующем значении гравитационного ускорения g = 9,8 1
м/с2 соответствуют низкие критерии Архимеда, а с ним - малые
Rec и скорости осаждения Wc . В этом случае возрастает продол
жительность процесса осаждения, понижается его производи
тельность.
Среди инерционных сил наибольший интерес для технологов
представляет центробежная, поскольку эта сила управляема.
5. 1 .3. Центробежное осаждение
в неоднородных :жидкостных системах

Осаждение под действием центробежных сил происходит в
машинах, называемых центрифуrами. Пусть суспензия вместе с
ротором центрифуги совершает вращательное движение с угловой
скоростью ro = 27tn (п - частота вращения); тогда на частицу мас
сой mч, находящуюся на расстоянии r от оси вращения, действует
центробежная сила, равная mчro2r. Это означает, что удельная (на
1 мЗ) движущая сила процесса осаждения запишется (с учетом
архимедовой силы): (Рт - p)ro 2 r. Поскольку за счет высокой часто
ты вращения п (или путем увеличения радиуса вращения r) цент
робежное ускорение ro 2 r может быть сделано значительно больше
ускорения силы тяжести g, то в поле центробежных сил наблю
дается существенное возрастание скорости осаждения, т.е. проис
ходит интенсификация процесса ра:щеления суспензии.
Для пояснения сущности центробежного осаждения
на
рис.5.7 приведены принципиальные схемы действия центрифуг.
Вертикалw1аа центрифуга (рис. 5.7 ,а) представляет собой укрепленный на
валу З цилиндрический барабан 1 (корпус, ротор) с кольцевой крышкой 2,
вращающийся с частотой вращения п (угловой скоростью ro). В барабан зали
вается суспензия ; под действием сил - центробежной и тяжести - ее свобод
ная поверхность должна принять форму параболоида вращения (см. разд. 2. 1 .3).
Но при увеличении ro вершина параболоида окажется ниже дна цилиндриче
ского барабана, а при высоких ro (именно в таком режиме работает центрифу
га) - практически сдвинется далеко вниз. Так что свободную поверхность
суспензии в центрифуге (на рисунке - сп) без сколько-нибудь заметной по
грешности можно считать не параболической, а цилиндрической , соосной с
валом и барабаном.
На некую твердую частицу 11, расположенную в н утри кольцевого слоя сус
пензии / на текущем радиусе r, действует центробежная сила, определяемая
центробежным ускорением ro 2 r. Поскольку на практике обычно плотность
частицы Рт больше, нежели жидкости р, то под воздействием движущей силы
( Рт - p)ro 2 r частица перемещается в направлении от свободной поверхности к
стенке барабана. По прошествии некоторого времени рассматриваемая частица

392

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

2

1

сп
3
1

а
Рис.5. 7.

�

\Т
(J)

1

4

-

-

3
б

1
3

в

Осаждение в поле центробежных сил:

вертикальная центрифуrа, 6 - горизонтальная центрифуrа, в - поперечное сечение
центрифуги;
1 - корпус центрифуги, 2 - кольцевая крышка, J - ось вала центрифуги, 4 - радиаль
ное ребро;
1 - суспензия , // - характерная твердая частица в текущем положен и и (сп - свободная
поверхность жидкости)
а

-

(в конечном итоге - все частицы суспензии) осядет на стенку барабана, а
ближе к оси вращения останется кольцевой слой осветленной жидкости (фу
гат) - процесс осаждения в поле центробежных сил состоялся . Далее органи
зуют раздельный вывод из центрифути осадка и футата.
Горизо�rrалW1а11 центрифута (рис. 5. 7 ,fi) предстааляет собой цилиндрический
барабан 1 с кольцевой крышкой 2, укрепленный на горизонтальном валу. При
вращении центрифути образуется цилиндрическая свободная поверхность строго говоря, не соосная с осью вращения - с эксцентриситетом g/ro2
(см.разд. 2 . 1 . 3 ) . Однако при высоких частоте вращения п и утловых скоростях ro
(именно в таком режиме работает центрифута) эксцентриситет становится
пренебрежимо малым, так что без сколько-нибудь заметной погрешности сво
бодную поверхность и здесь можно считать соосной с валом и цилиндром
барабана.
Как и в вертикальном отстойнике, некая твердая частица J/, расположенная
внутри кольцевого слоя суспензии 1 на текущем радиусе r (и другие частицы
суспензии), будет под действием центробежной силы двигаться в направлении
к стенке вращающегося цилиндра. В результате на стенке образуется осадок
ТМ, а ближе к оси вращения - кольцевой слой фугата. Осадок и футат далее
раздельно выводят из центрифути.

На рис. 5. 7 , в, иллюстрирующем процесс центробежного
осаждения, показано поперечное сечение барабана, нормальное
к оси его вращения (ось направлена перпе ндикулярно плос
кости чертежа) . Это - горизонтальное сечение в сл уч ае верти 
кальных центрифуг и вертикальное - в случае горизонтальных.
Осаждение в поле центробежных сил можно проводить в пе
риодическом, непрерывном и полунепрерывном режимах* .

На рис. 5.8 изображена верТИUJJьна11 подвесная осадНТельна11 центрнфуrа пе
рноднческоrо дейСТ8ИJ1 . На валу (ось /), соединенном с электромотором (на
рисунке не показан) , подвешен ротор З вертикальный цилиндрический бара-

' В учебнике приводятся лишь отдельные при меры устройства и работы
центрифуг (осадительных и фильтрующих). Более подробные сведения пред
ставлены в ( 1 , 9, 1 7 , 1 9 ) .
393

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

По А-А

5

Рис.5. 8. Вертикальная подвесная осадительная центрифуrа периодического
действия:

1 - 11а11 , 2 - неподвИJКНый кожух, 3 - ротор (барабан) , 4 - конус ротора, 5 - ребра, 6
фасонное днище кожуха, 7 - шrуцер для вывода фуrата, 8 - патрубок для выrруэки
оса.аха, 9 - линия подачи суспензии, 10 - отводная трубка для фуrата;
1 - суспензия, 11 - осветленная жидкость (фуrат) , 111 - осадок
-

бан, ограниченный сверху кольцевой крышкой, а снизу - коническим дни
щем, заканчивающимся патрубком 8. Подвеска ротора производится с по
мощью ребер 5, соединяющих вал (ось /) с патрубком 8 (см. сечение патрубка
А-А). Кожух 2 защищает персонал от быстро вращающегося ротора (кстати, и
ротор от нежелательного контакта с кем-то или чем-то) . Кожух заканчивается
фасонным днищем 6, позволяющим собирать и отводить (через штуuер 7)
осветленную жидкость (фуrат). На валу (ось /) расположен конус 4 - его воз
можно перемещать вдоль вала и фиксировать в определенном положении. В
отверстие в верхней крышке пропущены труба 9 для подачи суспензии и от
водная трубка 10 для вывода основной доли фуrата (предусмотрена возмож
ность радиального перемещения отводной трубки).
Центрифуrа работает в две стадии. Первая - рабочая - состоит в разделе
нии суспензии. В ротор с опушенным конусом 4 по линии 9 загружают опре
деленную порцию суспензии, после чего ротор приводят во вращение. Во вра
щающемся роторе суспензия принимает форму кольцевого слоя и происходит
(на рисунке изображена ситуация для промежуточного момента времени) по
степенное накопление осадка (заштрихованная зона J//) и осветление жидкости
(зона //). Основная доля фугата выводится на ходу центрифуrи по отводной
трубке 10-, подача суспензии при этом не прекращается. После накопления
слоя осадка необходимой толщины барабан центрифуrи останавливают начинается вторая стадия - выгрузки осадка. Для этого поднимают конус 4 и
механически выгружают осадок по патрубку 8 через просветы между ребрами 5.
Затем опускают конус 4, и цикл повторяется.

394

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Техиоло111ческий расчет осадительной центрифуги включает:

- установление связи свойств суспензии и основных геомет
рических размеров барабана центрифуги с ее производитель
ностью (в случае центрифуг п ериодического действия опреде
ляется продолжительность процесса);
- расчет затрат энергии на центрифугирование.

Связь свойств суспензий с геометрическиМи размерами центрифуги
и ее производительностью
2
Отношение ro r/g, называемое фактором разделения, в совре
менных центрифугах исчисляется сотнями и тысячами; при
ro 2 r/g > 3000 говорят о сверх(супер)центрифугах. Очень высокие

значения фактора разделения позволяют в ходе анализа центро
бежного осаждения практически без какой-либо ошибки прене
брегать влиянием силы тяжести на движение твердой частицы и

учитывать влияние только центробежной силы.

Частица в барабане совершает сложное спиралеобразное
движение
относительное (в радиальном направлении от оси
вращения к стенкам) и переносное (вместе с суспензией, вра
щающейся со скоростью вращения барабана). Траектория дви
жения частицы А, п ервоначально находившейся у свободной
поверхности, показана на рис. 5.9 штриховыми линиями (со
стрелками). В ходе движения по спирали частица проходит путь
от начального положения (точка Ан) до конечного (на стенке точка Ак) . Технолога в плане анализа процесса осаждения инте
ресует только радиальная составляющая траектории частиц
(жирная стрелка от точки Ан). Для исключения переносного
движения закрепим во вращающемся барабане систему коорди
нат у-х, как это делалось
в задачах гидростатики (разд.
2. 1 ) . Относительно такой си
у
координат,
вра
стемы
1
щающейся вместе с бараба
ном, частица будет двигаться
радиально
в дальнейшем
будем анализировать именно
это движение.
Расчетное выражение для
х
скорости стесненного осаж
дения (стесненного витания)
-

-

расчету времени центро
бежного осаждения:

Рис. 5. 9. К

1 - цилиндрическая стенка барабана
(поперечное сечение), 2 - свободная
поверхность жидкости

395

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

в поле центробежн ых сил Wc можно было бы получить, сопо
ставляя силы, действующие здесь на частицу, по канве, изло
женной в разд. 2. 7 4 , где рассматривалось стесненное витание в
поле сил тяжести. Однако проще прямо воспользоваться выве
денными там формулами (2 75 ) , а в случае свободного витания
- (2. 72).
Принадлежность этих формул к полю сил тяжести
определяется гравитационным ускорением g, входящим в крите
рий Архимеда Ar. При переходе к полю центробежных сил
(параметры осаждения для этого случая снабдим индексом "ц")
гравитационное ускорение g следует заменить на центробежное
ro 2r. В результате приходим к модифицированному начертанию
критерия Архимеда:
.

.

.

ro 2rd3 -Рт - р
- -Аrц -

(е)
v2
Р
С таким выражением критерия Архимеда остается справедли
вой формула (2.75), записанная теперь для критерия Рейнольдса
Rец в поле центробежных сил. Рассчитав Rец = wцd/v, найдем
скорость стесненного осаждения в центробежном поле wц.
В разд. 5. 1 . l время осаждения to определялось как отношение
пути Нж к скорости стесненного осаждения wc . Применительно
к центробежному осаждению полный путь частицы (в радиаль
ном направлении) равен разности радиусов (R2 - R 1 ). Однако 1
при расчете времени осаждения в поле центробежных сил •u по
формуле
'

ц

=

R2 - R1

(ж)

Wц

возникают трудности, поскольку в ходе осаждения изменяется
(возрастает) радиальная координата r, входящая в Ar и, следова
тельно, влияющая на скорость wц. Иными словами, wц
var,
поэтому не удается прямо воспользоваться выражением (ж) .
Очевидно, надо рассматривать бесконечно малый радиальный
путь dr, проходимый частицей за элементарное время dt:
=

dr ,
't - W

(з)
ц
причем скорость осаждения изменяется с радиусом, т.е. wц
= Wц(Г).
При естественном осаждении участок разгона частицы в жидкости невелик,
им пренебрегали и анализ проводили на основе постоянной скорости стеснен
ного осаждения wc . В поле центробежных с ил скорость осаждения wu п ринци
пиально переменна вследствие изменения по ходу процесса радиальной коорди
наты частицы r. Поэтому, строго говоря , анализ следует проводить с учетом
силы инерции Ри = т.(dwц /dt) (см. вывод формулы для скорости витания в
d

_

=

396

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

раэд.2.7.4). Оценим порядок ускорения d wц /dt на примере ламинарного режима
свободного осаждения для типичной модельной сиtуации : размер частиц d = 1 00
1 0-6 м2/с , р = 1 оз кг/мз, Рт = 2 · 1 03 кг/мз .
мкм = 1 0-4 м,
(J) = 1 02 с- 1 , v
По соотношению (2.72)
wц d
AI
(J) 2 Гd 3 Рт - р
Reц
=

;Е

18

=

v

откуда

=

1 8 v2

(J)2rd2

( pт 18v p

wц =

р)

р '

Обозначим среднюю радиальную координаrу для частицы в процессе цент
робежного осаждения R (грубо ее можно было бы принять равной среднеа
рифметическому из R1 и R2 ) . Тогда в последнем выражении вместо г следует
поставить R . Приближенная оценка по (ж) дает
tц

"

R2 - �

-

--- -

Wц

(R2 - � )l 8 v p

�
�
�
-

(J) 2 Rd 2 (Pт - P)

Теперь можно оценить ускорение твердой частицы в радиальном направле
нии:
Dц

"'

Лw ц

=

(J) 2 d 2 (Pт

tц

р)( R2 - R1 )(J) 2 d 2 R(Pт - р)

1 8 vp( R2 - R1 )l 8vp

-

.

Вопрос о необходимости учета силы инерции решается путем сопоставле
ния ускорений - радиального движения и центробежного:
а
а
ro 2d4 (p т - р) 2 1 0 4 · 1 0 - 1 6 · 1 0 6
_
u_ .., __
11 _ =
=
< 0,01 .
ro 2 r ro 2 R
1 8 2 ( v p) 2
324 · 1 0 - 1 2 · 1 0 6
Следовательно, радиальное ускорение (даже для сравнительно крупных час
тиц d = 1 00 мкм) более чем в 1 00 раз ниже центробежного, управляющего
процессом осаждения. Это означает, что при последующем рассмотрении силу
инерции можно не учитывать. К аналогичному выводу приводит анализ цент
робежного осаждения для турбулентного режима, а также учет стесненности
витания.
Найдем на основе (з) время центробежного осаждения •ц· С

этой цель ю запишем зависимость Rец от Аrц соответственно
(2.75):

Rец =

4
Аrц . 8 ,7 5

1 8 + 0 ,59 �Ar Е 4 •7 5

----==---.=
. ==
·

(5.8)

Подставим в комплексы Rец и Аrц входящие в них величины:
Wцd

ro 2 rd3 Рт - Р 4 7
--- Е ' 5

V2

---

р

р 4 ,75
-- Е

-- = -----'---.==========
v
Рт --

ro 2 rd3
} 8 + 0,59
.
v2

Р

397

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

и после сокращения на d/v выразим скорость стесненного
осаждения частицы в центрифуге:
ro 2 rd 2 Рт - Р 7 5
-- -- Е 4 ,
v
р
wu =
2
rd
Рт - Р Е 4 7 5
ro 3 -1 8 + 0,59 -'
Р
v2
С этим значением Wu перепишем формулу (з) и , разделив пе
ременные, получим ламинарное и турбулентное слагаемые,
поместив аргумент r в конце этих слагаемых:
dr
р
4 , 75 Гг .
2
р)Е
d(
т
ro p

(и)

Проинтегрируем почленно выражение (и) от начального момен
та времени t = О до полного времени осаждения tu - для частицы,
находившейся в начале осаждения на радиусе R 1 (положение Ан ) и
в конце осаждения на радиусе R2 (в положении Ак):
tu

= 18

+ 1,1 8

vp

ln � +

4 75
ro 2 d 2 (P т - р)Е ,

p R2
ro 2 d(p т - p)i;4 .75

(1

R1

-

,.JR;)

ГRi"\.
v�)

(5.9)

Здесь в правой части во втором слагаемом получа ю щаяся при
интегрировании разность ( /R; представлена в виде

!ii;(1 - �R1 / R2 } , а сомножитель /R;

внесен под общий ра

дикал.
Из полученной формулы следует ряд выводов.
1 . Первое слагаемое доминирует при ламинарном режиме
осаждения (достаточно частый случай), второе - при турбу
лентном (более редкий случай); в наиболее часто встре
ча ю щемся переходном режиме оба слагаемых сопоставимы.
2. Действу ю щие на частицу центробежные силы снижаются
при уменьшении радиуса r. По этой причине в центрифугах не
идут на малые R 1 , так как при этом возрастает продолжитель
ность осаждения t u.
Часто uентрифуги работают с половинным заполнением: рабочий объем
жидкости в барабане V равен половине рабочего объема барабана V6. Тогда
11R1 2 1 0 , 5 11R22 1, где / дл ина (высота) барабана. В этом случае R1/R2 Jo,5 и

398

=

-

=

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

lп(R2 /R1 ) "' 0 , 3 4 7 ;

( 1 - �R1 /R2 ) "' 0, 1 59 1 . Если учесть численные коэффициенты

в (5 .9), то эта формула приобретает вид
tu

"'

6,2 5

vp
4 75
ro2d2 (Pт - р)Е ,

+

0,1 8 8

p R2
4 75
ro 2d( pт - р)Е ,

(5 .9а)

Подобная форма записи (без lп и сомножителя в скобках, отражающих
влияние отношения R2fR1 ) иногда встречается в справочниках и расчетных
регламентах. Надо понимать, что здесь нет противоречия с формулой (5.9),
просто расчетное соотношение записано для определенного значения R2fR1 •

3. Ф ормула (5.9) может давать несколько заниженные значе
ния t ц в сравнении с наблюдаемыми на практике.

Нередко в учебной и научной литературе' выражение для t u выводится на
основе формулы Тодеса (2. 7 2) для скорости свободного витания w8, т.е. для Е =
= 1 . В этом случае продолжительность про цесса осаждения закономерно получа
ется заниженной , поскольку w8 > wc- В приведен ном выше выводе этот источ
ник занижения t u исключен: анализ базировался на рабочих значениях Е.
Друтая причина преуменьшения t u по формуле (5 .9) состоит в проскальзыва
нии подаваемой в барабан суспензии относительно его стенок: формула предпо
лагает, что вся суспензия солидарно вращается вместе с барабаном с утловой
скоростью ro. На самом же деле загруженная в барабан суспензия (при перио
дической работе центрифути) или свежие ее порции (при непрерывной работе)
не сразу приобретают эту скорость, вращаясь некоторое время с меньшими
значениями ro . Чтобы исключить эту причину, вдоль образующей барабана
устанавливают продольные (радиальные) ребра, предотвращающие проскальзы
вание. Исключить проскальзывание возможно также путем тан ген ц иальной
подачи суспензии через щелевое отверстие на свободную поверхность жидкости
в направлении ее вращения со скоростью, близкой к окружной скорости ее
движения .

4. Найденное по (5.9) значение tц может быть использовано
для расчета производительности V центрифуги непрерывного
действия в задачах эксплуатации. Здесь величина t ц трактуется
как время пребывания суспензии в барабане, минимально необ
ходимое для ее осветления. Тогда при рабочем объеме жидкости
в барабане V' очевидна связь (см. разд. 8.3; ер. размерности):
(к)
V = V'/t ц .
При необходимости решения задачи проектирования формула (к)
записывается в явном виде относительно У , и на этой основе
выбираются минимальные габариты барабана, обеспечивающие
осветление фугата.
Затраты энергии на работу центрифуги

Различают затраты энергии L (мощность на валу центрифуги
N) в пусковой период (индекс " п " ) и на рабочем ходу (индекс " р").
Рассмотрим сначала затраты энергии в период пуска (пусть его
' См . , например, ( 1 , 5 , 1 7 , 1 9 , 2 1 J .

399

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

4

5

3

сп

5

б

а

fl

К расчету затрат энергии:

- на раскручивание барабана и суспензии, 6 - на трение в подшипниках, в - на
компенсацию вентиляционных потерь (8' - овал , ". - эксцентриситет, "". - рас ч етная
схема) ;
1 - вал, 2 - нижняя крышка, З - боковая стенка барабана, 4 - верхняя крышка, 5 подшипник.и;
1 - суспензия, сп - свободная поверхность

Рис.5. 10.
о

продолжительность составляет
рех основных составля ю щих.

тп) .

Они складываются из четы

1. Энергетичес кие затраты на раскручивание барабана центри
фуrи. Пусть (рис. 5. 10,а) тело массой т, первоначально находя

щееся в покое, разгоняют до скорости w. Тогда работа на его
разгон будет равна приобретенной им кинетической энергии
L = mw2/2. . В случае вращательного движения в качестве скорос
ти w выступает окружная скорость и = ror. При массе барабана
т6 работа на раскручивание барабана 4 = т6 и62/2. = m6ro 2 r52/2..
Не установленной пока остается радиальная координата r6
центра масс барабана. Центр масс боковых его стенок находится
внугри этих стенок на радиусе %0 , промежуточном между R2 и %
(под % понимается наружный радиус барабана). Центры масс для
верхней и нижней крышек барабана находятся на меньших ради
усах - 1�· и �"соответственно. Расчет значений %0 (при известной
тол щине стенок барабана), %' и %" затруднений не вызывает. Но
обычно ограничиваются приближенной оценкой 4 , полагая, что
центр масс всего барабана расположен на радиусе Rъ иначе говоря
- масса барабана � полагается сосредоточенной на этом радиусе.
Это значение r6 = R2 несколько завышено в сравнении с точным

400

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

значением, вычисленным на основе �о. �· и �"; так что затраты
энергии, мощность получаются с некоторой поrрешностью "в за
пас" . Вклад 4 , N6 в общую мощность на валу центрифуги невелик
(основная статья затрат энергии - на раскручивание суспензии),
поэтому принятое приближение оправданно. Итак, искомая со
ставляющая затрат энергии

4=

тбrо 2 R22 .
'
2

(5. 1 0)

составляющая мощности определится как ЧV't n.

2. Энергетические затраты на раскручивание суспензии. Затра
ты на раскручивание до угловой скорости ro (рис. 5. 1 0,а) фор
мально мoryr быть определены из аналогичных соображений.
Если масса кольцевого слоя суспензии равна те, а центр масс
этого слоя находится на некотором "среднем " радиусе Rc. то
2 2
(л)
Lе = mero яе '.
2
при этом подразумевается, что первоначально суспензия нахо
дится в покое.
Здесь было бы неоправданным базироваться на каком-то
умозрительном предположении о величине Rc; необходим обос
нованный подход, учитывающий распределение массы суспензии
по толщине ее кольцевого слоя от R1 до R2 . В ыделим внутри
слоя суспензии на радиусе r кольцевой слой толщиной dr (рис.
5. 1 0,а) . Для этого элементарного слоя, вращающегося с окруж
ной скоростью ror, справедливо выражение типа (5. 1 0), посколь
ку элементарная масса суспензии в этом слое dте сосредоточена
на радиусе г. Тогда элементарные з�траты энергии на приведе
ние во вращение этой массы
2 2
dLe = ( dme )ro , .
(м)
2
Выразим элементарную массу dmc, обозначив плотность суспен
зии Ре · Площадь поперечного сечения элементарного слоя равна
2nr dr, высота - / (можно иначе: боковая цилиндрическая поверх
ность кольцевого слоя равна 2rtrl, толщина его - dr); тогда объем
элементарного слоя составит 2nr/dr, а масса содержащейся в нем
суспензии dmc = Pe2nrldr. Подставив это значение dmc в (м), получим
после сокращения на 2 и объединения одинаковых сомножителей:
dLe = rt/ro 2 pe,Зdr .
Интегрируя это выражение по всему диапазону изменения r,
т.е. от R1 до R2 , найдем работу раскручивания суспензии:
Lc =
(5. 1 1 )
(R24 - R1 4 )

rtlro: pc

и далее - соответствующую составляющую мощности Nc

= Lc /tn .

40 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Сопоставляя формулы (л) и (5 . 1 1 ) , установим расчетное значение радиаль
ной координаты цен"11>а масс суспензии Я.,, входящее в (л). Для этого полную
массу суспензии в барабане mc = p011 ( R2 2 - R 12)/ подставим в (л) и приравняем
работы L0, выраженные этими формулами:
Рс11 ( Rj - Ri2)tш 2 � 11lro 2 Pc
( R24 - R14) .
4
2
=

После очевидных сокращений имеем
2
D = R1
''с2

+

2

R22

'

(н)

т.е. среднерасчетный квадрат радиуса равен среднеарифметической величине из
квадратов граничных радиусов суспензии. С этим значением Rc2 ШIЯ расчета Lc
можно пользоваться формулой (л).
3. Затраты энерrии на преодоление трения вала центрифуrи в
подшипниках. Эти затраты удобно рассматривать применительно

к горизонтальной центрифуге (рис. 5. 1 0,б). Пусть суммарная
масса барабана и суспензии равна (fпб + те), тогда сила нор
мального давления вала на подшипники будет Рн = (т6 + тс)g.
При коэффициенте трения в подшипниках fт сила трения соста
вит Fт = fтРн. Обозначим окружную скорость вала и8 = ror8, где
r8 - радиус вала. Работа рассчитывается как произведение силы
на путь, а мощность - как работа в единицу времени; поэтому
мощность будет определяться как произведение силы на путь в
единицу времени, т.е. на скорость. Отсюда для состаВJIЯющей Nт
мощности на преодоление сил трения на валу центрифуги имеем
(5. 1 2)
Nт = Fти8, ИЛИ Nт = (тб + тс)кfтив .

4. Затраты энерrии на взаимодействие вращающегося барабана
с воздухом. В результате взаимодействия быстро вращающегося

цилиндрического барабана с окружающим его воздухом, заклю
ченным в пространстве между барабаном и кожухом, возникают
силы гидравлического сопротивления, требующие определенных
затрат энергии на их преодоление. Эти затраты называются вен
тиляционными. Вклад сил трения в общее взаимодействие вра
щающегося барабана с воздухом невелик, и его, как правило, не
учитывают. Основная составляющая вентиляционных потерь
энергии вызвана иными причинами, связанными с изготовлени
ем и монтажом барабана. Первая из них обусловлена отклоне
нием формы барабана от кругового цилиндра - всегда наблю
дается небольшая овальность (эллипсность) . Вторая связана с
невозможностью точной установки вала по оси барабана всегда есть некий (тоже небольшой) эксцентриситет е. По этим
причинам при вращении барабана возникают биения - удары
барабана о воздух в результате местного (лобового) сопротивле
ния. На рис. 5. 1 0, в эффекты овальности (Ов. - левый верхний
402

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

рисунок) и эксцентриситета (Эк. - правый верхний рисунок)
иллюстрируются в сильно утрированном виде.

Расчетная схема вентиляционных потерь представлена на нижнем рисунке
5.1 0,в. Штриховыми линиями намечена окружность барабана наружным радиу
сом /V,, жирным контуром вьшелен отклоняющийся от окружности овальный
барабан при горизонтальном положении большего радиуса, тонким - при
вертикальном его положении. С правой стороны барабана показана обуслов
ленная овальностью площадка шириной ЛR и высотой 1(, (рис. 5. 10,а); эта пло
щадка при вращении и создает местное (в данном случае - вентиляционное)
гидравлическое сопротивление. Разумеется, такие же площадка и сопротивле
ние возникают также с левой стороны овального барабана.
Потери напора на местное сопротивление (см. разд. 2.2.6) при окружной
скорости ин на наружной стенке барабана согласно формуле (2.30а) равны
и2

h8 = Е, 2; , а потери давления

др8 =

и2

h0p .g = Е, Т р8 ;

здесь Е, - коэффициент местного сопротивления, р8 - плотность воздуха.
(Заметим: Е, = const, так как вследствие высоких скоростей вращения ротора
режим - верхний автомодельный.) Тогда сила взаимодействия барабана с
окружающим его воздухом для обеих (правой и левой) площадок составит

Fв

=

Лр0· 2ЛR'6

= �

2

и
Т
2ЛR'6Рв ·

В расчетах абсолютную величину овальности барабана дR удобно выразить
через относительную овальность j "' дR//V,: ЛR = j/V,. Вентиляционная состав
ляющая мощности определяется как N. = Fаин. где ин = (J)/V,. Выражая значе
ния F. и ин и заменяя дR, приходим к расчетному выражению для вентиляци
онной составляющей мощности:
N1 =�ro3R:ljp 81(, .
(5. 1 3)
При тшательном изготовлении барабана его относительная овальность j на
ходится на уровне 0,001 . Рекомендуемые (на основе опытов) значения Е, близки
к 0,5-0,6. В целом N1, как правило, составляет не более 10% от общей мощ
ности в период пуска.
Полная пусковая мощность

Nп = N5 + Nc

+

Nт + Nв .

В выражение для мощности на валу центрифуги на рабочем
ходу, т.е. после завершения пускового периода, не входят со

ставляющие Nб и Nc; составляющие Nт и N8
остаются. Но
после выхода на режим в барабан непрерывно подается массо
вый поток суспензии Gc - на его раскручивание необходимы
затраты энергии - появляется составляющая мощности N '. Для
ее оценки примем, что исходной кинетической энергией этого
потока можно пренебречь (если это допущение и вносит неко
торую ошибку, то "в запас " ) .
Составляющую мощности N ' найдем, воспользовавшись вы
ражением (л) . Только в рассматриваемом случае речь идет не о
количестве суспензии те, а о ее потоке в единицу времени Gc;
-

403

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

поэтому в левой части выражения (л) будет стоять работа в еди

ницу времени, т.е. мощность:
N ' = Gc ro 2 R!

(5. 1 4)
2
Здесь квадрат среднерасчетного радиуса определяется по
формуле (н).
Полная мощность на рабочем ходу составит

Np = Nт + Nв + N ' .

Это выражение является более обоснованным, чем иногда
встречающиеся рекомендации - брать Np как некую (на уровне
0,3 - 0,4) долю Nп.

5.1.4.

Центробежное осаждение

а

неоднородных rазовых системах

Очистка газового потока от содержащихся в нем твердых час
тиц в пьшеосадительной камере, т.е. в поле сил тяжести, про
исходит эффективно только в случае достаточно крупных и тя
желых частиц. Промьшm енное производство часто имеет дело с
газовзвесями (запьшенными газами), несущими мелкие частицы
размерами заметно менее О , 1 мм . В этом случае используется
центробежное (инерционное) осаждение в аппаратах, назы
ваемых циклонами.
Обеспьшивание газовзвесей в циклонах, т.е. отделение газа от
пыли, производится в целях их последующего раздельного ис
пользования. В ряде производств запьшенный газ получается в
результате нежелательного уноса твердых частиц (например, из
пьшящего ТМ; из псевдоожиженного слоя) ; в этом случае выде
ляемые с помощью циклона твердые частицы возвращаются в
технологический аппарат.

Устройство и принцип работы циклонов

Принципиальная схема действия циклона приведена на рис. 5. 1 1 .

Исходный запыленный газ (поток /) подводится к циклону по цилиндри
ческой трубе 4. С помощью переходного участка 5 канал изменяет форму на
прямоугольную, и далее исходный газ поступает в циклон через прямоугольный
патрубок 6 с достаточно высокой скоростью и тангенциально. Высокая ско
рость (обычно на уровне 1 0-20 м/с) предотвращает выпадение твердых частиц
из газового потока в подводящих к циклону каналах. Тангенциальная подача
газа в циклон обеспечивает закручивание потока вокруг центральной цилиндри
ческой трубы 3. Под действием возникающей при этом центробежной силы
твердые частицы отбрасываются к стенкам циклона, а очищенный газ (поток
//) уходит из циклона через патрубок 7. Твердые частицы, осевшие на боковых
стенках циклона, под действием уже силы тяжести (собственного веса) по
пологому конусу 2 перемешаются к отводному патрубку 8 и выводятся из
циклона.
-

404

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 5. / /. С хема циклона (разрез):
1 - цил индр, 2 - конус, J - центральнu труба, 4 - цили ндр ическая входная
труба, .5 - переходное устроliство, 6 -

аходноil патрубок пр•моугольного сечения,
7 - патрубок вы вода очищенного газа. 8 патрубок вывода твердого материала;
1 - запыленныil газ /1 - очищенныil газ
111 - таердыli материал
,

,

Циклон может работать под напо
ром (газодувка, вентиляр, компрессор
перед циклоном - на линии 4) и под
разряжением (вентилятор, вакуумнасос
после циклона - на линии 7). В обоих
вариантах вывод ТМ нз циклона дол
жен быть герметизuр08ан - шнеком,
мигал ками, шлюзовым или секторным
затвором, клапанам и и т.д.' Иначе:
- в случае первого варианта: по пат
рубку 8 11ойдет не тонько ТМ, но и газ;
- в случае второго варианта: газ бу
дет засасываться не только по патрубку
4, но и по патрубку 8; этот поток под
хватит уже осевшие частицы и унесет
их нз циклона по патрубку 7.

Кол ьцевое
п ространство
корпусом
между
циклона
(диаметр
и централ ьной
'
трубой (диаметр Dвых высо
то й Н (от оси в ходного кан ал а
до н ижнего обреза централ ьной трубы) назы вается рабо ч и м объе м о м циклона; обознач и м
его Vu ( с м . р и с . 5 . 1 1 ). Очевидно: Vu = ( 7t /4) ( Dй - D� ых ) Н ;
= 2R2 ,
= 2R1 • Проходя рабочий объем, газ делает 2-3
полноценных в итка - за это время должно произойти обеспылива
ние газа. Относител ьно крупные частицьi полностью выделяются
из газового потока, достигают стенок циклона и оседают на них,
но мел кие - тол ько част и чно : успевают осесть на стенках лишь те
из н их, которые изначально находились ближе к стенкам .
Этот эффект, свидетельствующий о сепарирующих возможно
стях циклона, используется для классификации зернистых мате
риалов - см. разд. 2 3 .4 . 3 .
Удл и не н ие централ ьной трубы (для увел ич е н ия ч исла в ит
ков потока не приводит к существен ному улучшению в ыделения

Du)

Du

'

)

Dвых

Подробно устроliство и работу герметизирующих устроilств см. ( 2 , 1 3 , 1 6 ] и др.

405

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

мелких частиц. Дело в том, что по мере продвижения вниз по
кольцевому рабочему объему газовый поток, вследствие трения
о стенки корпуса и центральной трубы, теряет закрутку; поэто
му увеличение Н без специальных конструктивных мер не при
водит к улучшению очистки газа от ТМ .
Скорость вращения потока в циклонах на порядок меньше,
чем в центрифугах. Тем не менее процесс обеспыливания газа в
циклоне в значительной мере успевает закончиться: существен
но меньшие плотность и динамическая вязкость газа (в сравне
нии с жИдкостью) обусловливают заметно большую скорость
осаждения.

Практика выработала некоторые рекомендации относительно характеристик
циклонов: в оценочном плане Н ,., Df ; Dewx "" (0,4 + 0,6)Du; на каждый мЗ/с
газового потока требуется 0,4 O,S м рабочего объема циклона, иными слова
ми: время пребывания потока в рабочем обьеме далжно бьпъ близко к 0,4
O,S с.
Исходная концентрация ТМ в гаэовэвеси, подаваемой в циклон, не долж.на превы3
ша1Ъ 400 г/м (по частицам с размером свЬПIJе 10 мкм).
.
-

-

Степень очистки га�а от пьmи в циклонах 11 u зависит от гео
метрических характеристик циклона, свойств твердых частиц и
газа и скорости последнего; обычно 11 u находится в пределах
80-95% . Для повышения степени очистки иногда устанавли
вают 2-3 циклона последовательно.
В центрифугах барабан суспензии вращается с постоянной по
радиальной координате r угловой скоростью ro; поэтому при анали
зе процесса удобно пользоваться центробежным ускорением в
форме ro 2 r. Газовый поток на входе в циклон движется с большой
линейной скоростью, он в высокой степени турбулизован; его
скорость на входе в циклон (и далее - окружная скорость в рабо
чем объеме последнего) существенно выровнена по сечению, т.е. по
радиальной координате, а угловая скорость ro - переменна. Поэтому
:щесь удобнее перейти к выражению центробежного ускорения
через примерно постоянную окружную скорость и:

и = ror, ro 2r =

(�) 2

r

=

2
и .
г

(о)

Из полученного выражения следует, что центробежная сила

тч(и2/г) возрастает при уменьшении r. Это означает, что в цик

лонах малого диаметра скорость осаждения будет выше, т.е.
очистка газа от пьmи при одинаковых скоростях потока более
эффективна: 11 ц - выше. Однако такие циклоны малого диамет
ра будут иметь низкую производительность, а попытка ее по-.
вышения приведет к уменьшению времени пребывания газа в
рабочем объеме - оно станет ниже минимально необходимого.
Поэтому пармлельно устанавливают несколько десятков (ино
гда - свыше сотни) малых циклонов в общем корпусе - гово
рят о батарее циклонов, мультициклоне (рис. 5. 1 2).
406

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

tп
5
2
1

в

а
Рис. 5. 12.

6

Элементы мультициклона с закручивающим устройством:

типа "аиит", 6 - типа "розетка", 11 - схема компоновки элементов в мультициклоне;
/ - корпус, 2 - закручивающее устройство, J - опора, 4 - общий корпус, 5, 6 - пере
городки, разделяющие зоны;
1 - запыленный газ, 11 - очищенный газ, 111 - твердый материал;
А - зона газоазвеси, Б - зона очищенного газа, В - зона твердого материала
а

-

Допустимая запыленность исходного газа находится здесь на уровне 1 201 50 г/мЗ , так как превышение этой концентрации создает затруднения при
выводе твердых частиц из мультициклона.

Сравнивая центрифуги (машины) и циклоны (аппараты),
можно констатировать, что последние существенно проще и
надежнее в эксплуатации, поскольку не содержат движущихся
узлов, деталей. Циклоны неприменимы, если содержащиеся в
газовзвеси твердые частицы имеют склонность к налипанию на
стенки; в частности, циклоны плохо работают в случае высокой
влажности частиц.

Технологический расчет циклонов

При технологических расчетах приходится решать проблемы,
связанные с производительностью циклона, предельными раз
мерами улавливаемых частиц, степенью очистки газа, гидравли
ческим сопротивлением циклона. Решение первых трех проблем
407

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

нередко ведут• на основе формул типа (5.9) , иногда оставляя
лишь ламинарную составляющую. Заметим, что ошибка (к тому
же не " в запас" ) при игнорировании турбулентной составляю
щей может быть заметной, хотя обычно эта составляющая все
же уступает ламинарной.
Главная погрешность подхода заключается в неправомерности
постулата о постоянстве угловой скорости ro по радиальной ко-.
ординате r: этот постулат, вполне справедливый в случае цент
рифуг, для процесса осаждения в циклоне весьма далек от ре
альности. Его возможно трактовать как некий идеализирован
ный предельный случай, пригодный для приближенных оценок.
Другим идеализированным предельным случаем является посту
лат о постоянстве (по радиусу r) окружной скорости и = ro r,
обусловленном выравниванием скоростей в кольцевом попереч
ном сечении высокотурбулизованного газового потока. Легко
видеть, что оба идеализированных случая могут быть объедине
ны соотношением u/r s = const, причем при s = 1 получается пер
вый случай, а при s = О - второй. Экспериментально показано, что
реально для циклонов s � 0,5; тогда соответственно (о)
так что и =

и/ .Г, = const = К ,
к .г, или (.\) = к/.Г, .

(п)

Постоянную К оценим из уравнения расхода для газового потока. Для
оценки пренебрежем расширением потока в кольцевом пространстве циклона,
т.е. примем (см. рис.5. 1 1 ) наименьший радиус закрученного потока •
- 81, > R 1 • Тогдu

V= j2u dr = j2 K/idr =
Нах

Нп

R;

R;

Оrсюда
К-

2 Нвх

ЗV

КН"

R1 = R2
�3 [ Ri 12 - (R2 - 81,)3 12 ] .

[Rjl 2 - ( R2 - В1.)3 1 2 ]

.

(р)

Связь производительности циклона с ero rеометрическими ха
рактеристиками и свойствами rазовзвеси. В первом предельном

случае искомая связь задана выражениями (5.9) и (к). Заметим:
ширина потока rазовзвеси Ввх меньше полной ширины кольце
вого просвета (R2 - R 1 ), rде наименьший радиус R1 = Dвых/2
(см. рис. 5. 1 1 ,6) . Поэтому в целях уточнения рекомендуется мо
дифицировать выражение (5.9), проводя интегрирование не по
всему диапазону от R 1 до R2 , а по промежутку Ввх (т.е. от R2 - Ввх до R2 ) .
Дл я второго предельного случая в исходное уравнение (и)
следует вместо переменной ro подставить и/ r :
• См. [ 1 , 1 71 .

408

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

dt

=

р
l Svp
ldr + 0,59
JГ dr
и 2d ( р т р)& 4,75
и 2d 2 ( Р т р )& 4,75
_

_

и проинтегрировать. Если пределы интегрирования оставить
прежними, то (с учетом множителей , появляющихся при инте
грировании)
tu =

9

и

2

vp

d 2 (Рт

р

х

- р) & 4 '

15

( Ri - Rn +О , 79

х

(5. 1 5)

Если принять более обоснованную базу - соотношение (п) ,
то переменная r сокращается, и в качестве исходного выступает
выражение
dt

[

=

К 2d 2 (

lSvp
4,75 dr +
Р т р) &
_

О ' 59

интегрируя в тех же пределах, получаем

Р
dr;
2
К d( рт - р) Е 4 . 75

}я

) . (5. 1 6)
р
d (р - p)& 4,1S 2 - R 1
т
В полученном выражении разность (R2 - R 1 ) вынесена за

't ц

=

К 2 d2 (

1 8vp
- Е4,75
Р т р)

+

О,59

К

--

общие скобки; в целях уточнения вместо нее , как указано выше,
целесообразно подставить Ввх·
Искомая связь выражается формулой (к) . В задачах эксплуа
тации, когда известны геометрические размеры рабочего объема
Vu , определяется производительность циклона V. В задачах про
ектирования по заданной производительности V находят рабо
чий объем циклона Vu и, пользуясь рекомендациями по соотно
шению его основных размеров, определяют эти размеры.
Предельный размер улавливаемых частиц. Ч астицы разных
размеров осаждаются с разной скоростью; вместе с тем все они с
потоком газовзвеси находятся в рабочем объеме циклона при
мерно одинаковое время. Этого времени будет достаточно для
полного осаждения частиц крупнее некоторого предельного
размера dnp; более мелкие частицы, как указано выше, осядут
лишь частично.
В зависимости от принятой модели для отыскания dnp ис
пользуют формулы (5.9), (5. 1 5) или (5. 1 6) , решая соответствую
щее выражение относительно d dnp· При этом в формулу под
ставляют значение t u либо производительность V и рабочий
=

409

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

х

Рис.5. 13. К

расчету предельного размера улаw�иваемых частиц
расчету степени очистки газа в циклоне:

1 - стенка корпуса, 2 - стенка uентральной трубы;
1 - поrок гаэовзвеси в кольцевом пространстве uиклона

Рис.5.14. К

объем циклона Уц. Имея в виду, что dпр• как правило, сдвинут в
область достаточно мелких частиц, обычно без особой погреш
ности можно ограничиться ламинарной составляющей упомяну
тых формул.
Приведем расчетные выражен ия , базирующиеся на ламинарной
составляющей наиболее обоснованной формулы (5. 1 6):

l8vp{R 2 - R 1 )

=

l

К

l 8vp{R 2 - Ri )V
( Р т р) Е 4 75 у ц
-

,

(5. 1 7)

после раскрытия выражения для объема Vц и сокращения на

( R2 - R 1 ) :

(5. 1 7а)

В качестве порозности в эти формулы для приближенного расчета можно
подставить значение Е, найденное по исходной концентрации а0 ТМ в газовзве
си (ошибка будет " в запас" ). Для более строгого - надо знать значение пороз
ности Е" в зоне осаждения мелких частиц. Ее можно оценить исходя из пред
положения , что частицы крупнее dnp уже покинули эту зону. Тогда массовая
доля мелочи в газовзвеси равна х" (рис . 5 . 1 3 ) , а концентрация мелочи в потоке
газовзвеси а", лежащая в основе расчета порозности Е" по (5. la), может быть
определ ена как аох". Более точный анализ требует деления мелочи на несколь
ко более узких фракций (т.е. диапазона dш;11 - dnp на несколько участков) и
пофракционного расчета.
Заметим, что расчет Е" не вызывал бы затруднений при известной величине
dn p ; однако при расчете dn p по (5 . 1 7а) требуется уже знать значение Е " . Поэтому
определение dn p приходится вести методом последовательных приближений,
используя формулы (5. \ а), (5. 1 7а) и кривую гранулометрического состава .

410

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Степень очистки rаза. Газовый поток в uиклоне будет безус
ловно очищен от всех части u крупнее dnp • так что гарантиро
ванная степень очистки составит Т\nр = 1 - Хм (см. рис. 5. 1 3) . На
самом деле uиклон задерживает еще и определенную долю мел
ких частиц, оценить которую можно из следующих соображе
ний. Допустим , что в оценках можно базироваться на размере
мелких частиц dм , усредненном в промежутке размеров от dmin
до dnp (рис. 5. 1 3). Тогда, располагая величиной tu = VuJ V, можно
по формуле (5. 1 7а) найти для размера dм значение нижнего пре
дела интегрирования R ' : все мелкие частицы, находящиеся пер
воначально ближе к стенке корпуса 1 - на координатах r > R '
(рис. 5 . 1 4) , будуr улавливаться в uиклоне, а находящиеся дальше на r < R ', т.е. в промежутке (R' - R , ) - проскочат циклон и будут
унесены газовым потоком. В исходном потоке твердые частицы
всех размеров ра вномерно распределены по объему газа и по
сечению потока Ввх · Тогда доля унесенных мелких частиu, оче
видно, составит (R2 - R ' ) /В8х , а степень очистки газа от мелочи
Т\ м ""

1

-

R2 R
�
-

'

_
_

В вх

Общая степень очистки получится суммированием :

= Т\.ор

+ Т\ м ·

Т\ u

=

1 lри установке nu циклонов последовательно результирующая
степень очистки газа Т\об ш возрастает. При этом расчет степени
очистки Т\; в каждом i-м циклоне ведется по рассмотренной вы
ше методике, разумеется - с учетом для каждого циклона своих
исходной конuентрации ТМ во входящем потоке и распределе
ния частиц по размерам. После каждого циклона в газе остается
1 - Т\; доля ТМ, после nu последовательно включенных циклонов

останется доля п (1
nu

i=I

-

ТJ;) . Тогда общая степень очистки составит
Т\ общ

=1

п (1

nu

i=I
ГидpUJlll'lecкoe сооротиuенне цнклоноа.
-

-

Т\;) .

(5. 1 8)

В целях приближенной оценки со
противления циклона Лрu его рассматривают как единое местное сопротивление.
Обычно расчет ЛРu циклона ведуr на основе фиктивной скорости газа wФ , вы 
числяемой по уравнению расхода на поперечное сечение циклона диаметром
Du при производительност" V. Тогда
(5. 1 9)

Коэффициент местного сопротивления циклона 1',ц зависит от конструк
тивных характеристик циклона; обычно он не выходит· за пределы 1 00 - 300.
Более строгий расчет· предполагает раздельное нахождение местных сопро
тивлений на различных участках циклона: Лр8" ЛРвых и т.д. Определение этих
• См., например, (4 и 1 7) и особенно детально (7 ) .

41 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

величин базируется на коэффициентах местных соп ротивлений, о л ределяемых
эксл ериментально .

5. 1.5.

Некоторые друrие процессы осаждения

Процессы разделения жидких и газовых неоднородных сме
сей не исчерпываются приведенными вариантами их организа
ции. Ниже кратко охарактеризованы некоторые другие возмож
ности.
ГидрОЦИКJJОНЫ, предназначенные для разделения жидкостных
неоднородных смесей (суспензий, нестойких эмульсий), по уст
ройству и принципам работы аналогичны циклонам. Они вы
годно отличаются от центрифуг отсутствием движущихся узлов
и невысокой стоимостью. Однако скорость осаждения в них
относительно невелика: в сравнении с центрифугами здесь за
метно меньше центробежная сила (из-за более низкой угловой
скорости ro ) ; в сравнении с циклонами в них значительно ниже
Аrц (прежде всего - из-за более высокой плотности несущей
среды). Кроме того вследствие более высокого гидравлического
сопротивления, жидкостной поток в меньшей мере сохраняет
закруrку, нежели газовый. По указанным причинам степень очист
ки в rидроциклонах относительно невысока, и в химической про
мышленности они находят ограниченное применение.
Подход к технологическому расчету гидроциклонов сходен с
рассмотренным для циклонов в разд. 5. 1 . 4.
Це1Пр111UJОНЫ занимают промежуточное положение между
центрифугами и гидроциклонами. Рабочая зона центриклона
представляет собой цилиндр (или пологий конус), по оси кото
рого расположен вал с лопастями. Поток суспензии подается в
цилиндр, где вращение вала обеспечивает закручивание потока.
Возникающая центробежная сила обусловливает разделение
суспензии. Центриклоны проще центрифуг, но сложнее гидро
циклонов; они сохраняют ряд недостатков, присущих тем и
другим. Видимо, поэтому они не нашли широкого применения
в промышленности.
Пьтеосадительные камеры и циклоны не обеспечивают не
обходимой степени очистки запьтенных газов: мелкие частицы
размером до 10 мкм в значительной степени уносятся с газовым
потоком. Высокая степень очистки от мелочи достигается в
электростатическом поле - в аппаратах, называем�1х электро
фит.Трами .

Принцип действия электрофильтров заключается в следую
щем · . При разности потенциалов Л U между двумя электродами ,
• Подробнее см., например, ( 1 , 5 , 9, 14, 2 1 ) .

412

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

достигающей некоторой критической величины, в газовом про
странстве между ними возникает электрический разряд - поток
ионов. Если в этом пространстве движется запьшенный газ, то
ионы отдают свои заряды частичкам пыли (либо содержащимся
в газе капелькам жидкости) и заряжают их. Получившие заряд
частички начинают двигаться к противоположно заряженному
(осадительному) электроду и оседают на нем, а очищенный газ
покидает электрофильтр.
Технолоmческий расчет электрофильтра базируется на сопо
ставлении сил - электростатической, побуждающей заря
женную частицу двигаться к осадительному электроду, и гидрав
лического сопротивления движению твердой частицы. При этом,
вследствие малости частицы, режим ее движения к электроду сугубо ламинарный. К тому же на электрофильтр подается газ с
низкой концентрацией твердых частиц, уже прошедший другие
обеспьшивающие устройства. Таким образом, можно использо
вать ламинарный фрагмент формулы (2. 72) для скорости свобод
ного осаждения (витания):
(5.20)
Rеэ = Аrэ /1 8,
причем в "электростатический критерий Архимеда" АI·э вместо
ускорения силы тяжести входит ускорение электростатических сил.
Электрическое поле характеризуется градиентом потенциала,
называемым напряженностью этого поля Е = d U/dl. При числе z
переданных частичке зарядов величиной е сила, действующая на
частичку, равна zeE. Поделив эту силу на массу частицы тч,
найдем ускорение электростатического поля, входящее в Ar3.
Последующий анализ ведется по канве, изложенной в разд.
5. 1 .2, с определением времени осаждения частицы в электри
ческом поле (на осадительном электроде). Далее решают про
блемы, связанные с производительностью электрофильтра и его
основными размерами. Подчеркнем: в случае необходимости
учитывают переменные напряженность Е и электростатическое
ускорение, а значит и переменную скорость осаждения частицы в
направлении ее перемещения к осадительному электроду.

5.2.

ФИЛЬТРОВАНИЕ

5.2. 1.

Общие положения

Осаждение очень мелких и легких частиц из загрязненных
жидкостей (или газов) происходит крайне медленно, что огра
ничивает производительность процесса либо требует больших
производственных площадей. Переход к осаждению в центро
бежном или электростатическом поле заметно удорожает про
цесс. Разделение жидких и газовых неоднородных смесей воз413

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис.5.15. Общая

схема фильтрования:

/ - корпус филыра , 2 - ф1t11Ь1J>YIOUllUI neperopoдxa;
/ - суспензия, /1 - ф1t11 ьтрат, //1 - осадок

можно методом фильтрования, со
стоящим в пропускании загрязненно
го потока через переrородку, прони
цаемую для несущей (сплошной) сре
2
ды, но не пропускающую твердые
частицы. В результате неоднородная
смесь разделяется на осветленную
1
жидкость, называемую фильтратом, и
влажный осадок твердого материала.
Каждый из полученных продуктов
(фильтрат, осадок) может быть целе
вым; с позиций тенденции к безотходности производства пред
почтительно, чтобы целевыми бьши оба продукта.
Процесс фильтрования основан на явлении фильтрации: те
чении жидкости (газа) через пористые среды - зернистые слои,
перегородки (в частности, ткани, пористые материалы и т.п.) с
мелкими каналами.
Фильтрование по отношению к осаждению является конкури
рующим процессом. Оно сложнее в организации (если сравни
вать с естественным осаждением, то в аппаратурном оформле
нии) , но эффективнее (выше степень очистки), а в случае мел
ких и легких частиц - и интенсивнее (выше производитель
ность). Кроме того, фильтрование может оказаться ш� ьтерна
тивным методом по отношению к осаждению, когда близки
плотности сплошной и дисперсной фаз р "" Рт; в этом случае
становится невозможным отстаивание в поле каких-либо массо
вых сил: критерий Ar, а с ним Rec и скорость осаждения стре
мятся к нулю.
Схема фильтрования ясна из рис.5. 1 5. Фильтрование проис
ходит под действием разности давлений Лр = р 1 - Р2 · В общем
случае к этой разности надо еще добавить гидростатическое
давление жидкостного столба высотой h над перегородкой:
(а)
Лр = Р1 - Р2 + pgh ·
Размер пор перегородки должен быть меньше размера .задер
живаемых на ней частиц, иначе последние проскочат через пе
регородку вместе с фильтратом. На практике суспензия содер
жит частицы разных размеров, в том числе - очень мелкие.
Они поначш�у не задерживаются на фильтре, проскакивают через
него, так что первые порции фильтрата получаются мутными их собирают отдельно. По мере протекания процесса накапли
вается слой осадка - именно он является лучшим фильтром:
даже небольшой его слой задерживает самые мелкие частицы, и
414

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

фильтрат получается светлым. Первые мутные порции фильтра
та обычно повторно подвергают фильтрации - через перего
родку с осадком.
М атериал перегородки, разумеется, должен быть химически
инертен по отношению к компонентам разделяемой суспензии,
прежде всего - к жидкости (газу).

5.2.2.

Устройство и работа фильтров

Ф ил ьтры бывают п ериодического и н епрерывного действия .
Они работают при атм осферном давл ении , под повышенн ым дав
л ен ием ил и под разрежением.
П ростейший представитель фильтров периоdического дейстt11U1 - простой
фильтр - работает при атмосферном давлении над и под перегородкой , так что
такое естественное фильтрование происходит под действием гидростатического
давления столба жидкости р = pgh (пример из лабораторной практики - стек

лянная воронка с фильтровальной бумагой) . Достоинства таких фил ьтров простота конструкции и дешевизна. Но низкая производительность простых
фильтров при работе с промышленными суспензиями заставляет искать пути
повышения движущей силы процесса фильтрования .
Аппарат, работающий с повышенным (сверх атмосферного) давлением, на
зывается друк-фильтром . Вариант исполнения такого фильтра показан на
рис.5 . 1 6. Фильтр работает в две стадии - накопление осадка с получением
фильтрата; выгрузка осадка . На первой стадии в ап парат с закрытой крышкой
1, соединенной с линией 6 высокого давления р1 , подается суспензия /. Фил ь 
трат /1 проходит через перегородку 4, давление под которой Р2 - атмосферное,
и отводится из фильтра; одновременно на перегородке накапливается осадок
///. После накопления слоя осадка достаточной толщины подача суспензии
прекращается (закрывается задвижка на линии 8) и отключается высокое дав
ление р1 (перекрывается вентиль на линии 6) - первая стадия завершена. На
второй стадии открывают вентиль на линии 7 в пространстве над перегород
кой с осадком устанавливается атмосферное давление, после чего открывают
крышку 1. Далее из фильтра механически выгружают осадок. В некоторых
конструкциях друк-фильтров для облегчения выгрузки осадка предусмотрено
поворотное устройство 5, с помощью которого фильтр опрокидывается
(поворачивается на 1 80° около горизонтальной оси).
По выгрузке осадка аппарат собирают, герметизируют (закрывают вентил ь
на линии 7), соединяют с источником высокого давления р1 , после чего вклю
чают подачу суспензии - повторяется первая стадия .
Для ряда промышленных осадков характерно появление в ходе процесса
фильтрования глубоких трещин в осадке, доходящих до перегородки ; в эти
трещины устремляется суспензия , наиболее мелкие ее частицы проходят через
перегородку, так что фильтрат получается недостаточно осветленным. В закры
том друк-фильтре затруднено наблюдение за поверхностью осадка, тем более
воздействие на поя вля ющиеся трещины. Or этого недостатка свободны иуr�
фильтры, работающие с разрежением под перегородкой и атмосферным давле
нием над ней (пример из лабораторной практики - воронка Бюхнера с водо
струйным насосом) . Движущая сила при этом возрастает в сравнении с есте
ственным фильтрованием. (Заметим : иногда в нутч-фильтрах дпя увеличения
движущей силы давление над перегородкой повышают сверх атмосферного;
однако при этом пропадает доступность поверхности слоя осадка.)
Схема действия нутч-фильтра представлена на рис.5 . 1 7 . Аппарат также ра
ботает в две стадии. На первой в открытый аппарат подается суспензия /, и под
-

415

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

//

Рис.5. 16.

Схема друк-фильтра:

1 - крышка, 2 - цилиндрический корпус, J - днише, 4 - фильтруюшая перегородка,
5 - поворотное YC'IJIOЙCТllO , 6 - линия высокого дааления, 7 - линия сброса давления, 8 линия подачи суспензии;
1 - суспензия, // - фильтрат, 111 - осадок

Схема нутч-фильтра:

1 - корпус фильтра, 2 - фильтрующая перегородка, З - промежуточный сборник
фильтрата, 4 - вакуум-насос;
1 - суспензия , 11 - фильтрат, 111 - осадок, JV - поток во:щуха из вакуум-насоса

Рис.5. 1 7.

действием разрежения (давление под перегородкой Р2 ниже атмосферного)
происходит ее разделение на фильтрат lI и осадок //l. Фильтрат собирается в
приемную емкость З, соединенную с вакуум-насосом 4, создающим разреже
ние. Воздух JV от вакуум-насоса выбрасывается в атмосферу. При появлении в
ходе фильтрования трещин в осадке их "забивают" или "замазывают", механи 
чески воздействуя сверху н а слой осадка.
Рассмотренные выше фильтры отличаются сравнительно небольшой рабо
чей поверхностью фильтрования, что ограничивает их производительность.
Значительное увеличение поверхности фильтрования характерно для рамноrо
ФНЛ•тр-пресса
рис.5. 1 8. Элементами фильтр-пресса являются рамы 1 и пли 
ты 4, показанные в отдельности на виде а; на виде б изображен фрагмент
фильтра в сборке: чередующиеся рамы и плиты одинаковой высоты и ширины.
Рама 1 имеет фигурное отверстие 2, открывающееся во внутреннюю ее по
лость. Плита 4 имеет сквозное отверстие 7, совпадающее в сборке с отверстием
рамы, и фигурное отверстие 6. Форма отверстий рам и плит показана на рис.
5. 1 8,б. На вертикальных поверхностях плиты (с обеих ее сторон) выполнены
продольные утлубления
ложбин ы З , заканчивающиеся внизу на наклонных
ложбинах 5, ведущих к отверстию 6. На обеих сторонах плиты укреплена филь
трующая ткань 8 (на виде б она изображена штриховыми линиями) .
В сборке рамы и плиты монтируются попеременно; с обоих торuов сборка
закрыта сплошными крышками и стянута шпильками. Система из рам и плит
помещена над ванной (на схеме не показана).
-

-

416

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

1

2

tJi
а

1

(Ш)

7 2

6

элементы фильтр-пресса, 6 - фраrмент сборКJt:
рама, 2 - фигурное отверстие рамы, J - вертикальные ложбины, 4 - плита, 5
наклонные ложбины, 6 - фигурное отверстие плиты, 7 - сквозное отверстие плиты, 8
фильтрующая ткань, 9 - лоток;
1 - суспензия, /1 - фильтрат, 111 - осадок

1-

Рис. 5. 18.
а

Рамный фильтр-пресс:

-

На стадии накопления осадка и получения фильтрата суспензия 1 подается
под давлением и через отверстия 2 поступает в полости рам. Фильтрат прохо
дит через ткань 8, стекает по ложбинам З , подводится по ложбинам 5 к от
верстиям 6 и выводится из фильтр-пресса по лотку 9. После накопления осад
ка в полостях рам (и ero промывки в случае необходимости) наступает стадия
выrрузки осадка. Для этого рамы и плиты раздвигают (в современных фильтрах
эта операция механизирована), и осадок выrружают в ванну. После осмотра, а
при необходимости - и починки ткани фильтр-пресс вновь собирают, и цикл
повторяется.
Достоинство фильтр-пресса - развитая поверхность фильтрования и отно
сительно высокая производительность. Основной недостаток - rромоздкость
операции разборки и сборки фильтра и большие непроизводительные затраты
времени на эту операцию.
Фильтры неll/)ерw•ного действtи1 характеризуются более высокой производи
тельностью, стабильностью работы, отсутствием непроизводительных затрат
времени на стадии выrрузки осадка, возможностью автоматизации процесса.
Платить за это приходится усложнением и удорожанием аппаратуры.
Барабаннwй вакуум -фит.тр (рис. 5. 1 9, а) представляет собой медленно вра
щающийся (с частотой порядка 1 мин- • ) горизонтальный барабан /, опущен
ный в ванну 2 с суспензией. Барабан разделен радиальными стенками З на
отдельные секторы 4, в которых поддерживается разрежение. Фильтрующей
является боковая (цилиндрическая) поверхность барабана 5: чаще всего это
перфорированная металл ическая поверхность, покрытая снаружи фильтрующей
тканью. Барабан вращается (на рисунке - против часовой стрелки) на полом
валу 6, соединенном отверстиями с полостями секторов. В ванне размещено
перемешивающее устройство 8, предотвращающее выпадение в ней осадка.
Диаметр барабана достигает 3 м, длина по образующей - 4 м, поверхность
фильтрации - 40 м2 .
В барабанный вакуум-фильтр непрерывно подается (на схеме - слева) ис
ходная суспензия /. При вращении барабана на части его боковой поверхности,
опущенной в ванну, накапливается постоянно утолщающийся слой осадка
JJJ - вследствие движения фильтрата Jl через фильтрующую перегородку под
действием разрежения . Фильтрат из фильтра выводится через полый вал. Оса
док при необходимости промывают посторонней жидкостью JV.
Далее, двиrаясь вместе с боковой поверхностью барабана, он несколько
подсушивается. Выrрузка осадка происходит, когда соответствующий сектор
барабана попадает в положение А. Здесь осадок, расположенный слоем на
поверхности барабана, набегает на нож-лоток 7, срезается и отправляется (по-

417

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

а
Рис.5. 19.

Фильтры непрерывного действия:

барабанный, 6 - дисковый (фраrмент);
1 - барабан, 2 - ванна, З - радиальные стенки, 4 - секторы, 5 - фильтрующая по 
верхность, 6 - полый вал, 7 - нож-лоток, 8 - перемешивающее устройство, 9 - диск;
1 - суспензия, ll - фильтрат, /JJ - осадок, JV - промывная жидкость
о

-

ток 111) в приемную емкость (на схеме не показана). При этом с помощью
специального устройства в секторе, находя щемся в положении А, отключается
вакуум (часто даже дается небольшое избыточное давление) - это разрыхляет
осадок и облеrчает его отделение от фильтрующей поверхности. Последняя
далее при вращении барабана опять погружается в ванну с суспензией, и на
ней снова начинается накопление осадка.
В барабанном фильтре работает боковая поверхность, но торцевая в процес
се фильтрования не участвует. Основанные на тех же принципах дисковые
фИJ1�.трw (фрагмент - на рис. 5 . 1 9, 6) в качестве фильтрующей поверхности
используют торцы, выполненные в форме дисков (иногда сужающихся с рос
том радиуса). Здесь фильтрующая ткань обтягивает каркас диска - перфориро
ванный или рифленый. Осадок срезается фасонным ножом. Диаметр дисков
достигает 2-3 м, число их в одном агрегате может превышать 1 0, поверхность
фильтрации - до 1 00 м2 .
Более детальные сведения о работе рассмотренных фильтров, а также о кон
струкциях и принципе действия других приводятся в учебной и научной литера

туре• .
5.2.3.

Основные характеристики фильтрационного процесса

Процесс фильтрования, как указано в разд. 5.2. 1 , осу
ществляется под действием движущей силы Лр, определяемой
выражением (а) . Разделение суспензии на осадок и фильтрат
происходит при движении последнего через фильтрующую по
верхность (перегородку) площадью F и находящийся на ней слой
осадка. В качестве линейной скорости фильтрации используют
расчетную скорость w, отнесенную не к ·живому сечению (про-

• См.

418

( 1 , 5, 9, 1 4, 1 5 , 1 7) и др.

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

светам) пор, а к полному сечению F фильтрующей перегородки
(часто такое же сечение имеет и слой осадка). Напомним: рас
четная скорость была введена в разд. 2. 7 при изучении гидрав
лики дисперсных систем.
Если поток фильтрата через перегородку равен VФ, то
Vф/ F Процесс фильтрования часто проводится в периодическом
режиме - с переменным потоком фильтрата, поэтому в общем
плане оперируют переменным количеством фильтрата в единицу
Тогда
времени: VФ dY/dt
1 dV
(б)
.
F dt
Разумеется, в частном случае dY/dt
const анализ и расчет
процесса удобно вести на базе VФ .
Содержание твердой фазы в исходной суспензии выражают
условной концентрацией Хо, представляющей объем осадка
(твердого материала с учетом просветов между частицами), об
разующегося при пропускании (получении) 1 мЗ фильтрата че
рез перегородку. Это определение позволяет связать высоту слоя
осадка h0 с объемным количеством полученного фильтрата У. В
самом деле, объем осадка Уос. по определению х0 может быть
представлен как Ух0 либо из геометрических соображений как
Fh0• Огсюда

=

w=

=

= var.
w=

Уос, = УХо = Fho

И

=

- -

У=

Fho

хо

,

ho = Ухо .
F

(в)

Задачей технологического анализа является отыскание связи
движущей силы Лр и производительности (У и t) с основным
геометрическим размером фильтра - площадью (поверхностью)
фильтрования F Эту связь, позволяющую решать задачи экс
плуатации и проектирования, устанамивает основное уравнение
фильтрования.
5.2.4. Основное уравнение фильтрования

Движущая сила процесса фильтрования Лр расходуется на
преодоление гидравлических сопротивлений осадка Лр0 и филь
трующей перегородки Лрп:
(г)
Лр Лр0 + ЛРп .
Осадок представляет собой рассмотренный в разд.2. 7 .2 непо 
движный слой из твердых частиц, через который движется филь
трат. Поэтому для определения Лр0 можно воспользоваться
формулой Эргана (2.67). Осадок состоит из весьма мелких час
тиц (обычно - десятые и сотые доли миллиметра) , а скорости
фильтрации - весьма низкие (обычно - единицы мм/с). Вот
почему течение даже невязких фильтратов через слой осадка без
419

=

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

сколько-нибудь заметной погрешности можно считать ламинар
ным. Тогда, пренебрегая вторым слагаемым в (2.67) и перенося
высоту слоя h0 в правую часть равенства, имеем

Л.ро = 1 50 ( 1 - 3E o J2 µ2
EQ d

h W.
о

(д)

Формула Эргана выведена для сферических частиц одинако
вого диаметра d. Для полидисперсных промышленных суспен
зий с частицами произвольной (неправильной) формы необхо
димы эмпирические поправки. Чтобы обойти на данной стадии
анализа эту проблему, обозначим Ro - комплекс в правой части
перед w и назовем его фактором сопротиВJJения осадка:
о
�'о

=А

( l &o J 2 µ
EQ3 d 2
-

h

(е)

О>

где вместо 1 50 (идеальный случай) поставлен множитель А, учи
тывающий упомянутые эмпирические поправки.
Перепишем выражение (д) с учетом (е):
Лр0 = Row .
(ж)
Важно отметить, что в полном соответствии с особенностями
ламинарного движения, показанными в rл.2, сопротивление слоя
осадка прямо пропорционально скорости фильтрации: Лр0- wl .
Течение фильтрата в порах перегородки - тем более лами
нарное, так как при тех же значениях w диаметры пор в перего
родке еще меньше, чем в осадке. Тогда, обозначив фактор сопро
тивления переrородки Rn (тоже подлежит экспериментш�ьному опре
делению), полагая � - wl, по аналогии с (ж) можно записать

Лрп = Rnw .

(з)

--=-_
Лр
__

(и)

Используя выражения (ж) и (з), соответственно (г) получим
Лр = Ro w + Rnw = ( Ro + Rn )w ,
откуда

w=

Ro + R п

В учебной и научной литераrуре• выражения типа (и), как правило, запи
сываются в виде

Лр
(к)
µ(R;, + R� ) '
где µ - динамическая вязкость жидкости в суспензии, µR<; " R,, , µRп' Rп·
Такая форма записи бЫ11 а бы оправданна, если бы при переходе к жидкости
с иной вязкостью µ при прочих равных условиях характеристика осадка R,, '
w=

=

• См. [ \ , 9, 1 5, 1 7 ) и др.

420

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

оставалась бы неизменной . На самом же деле при изменении вязкости жид
кости в суспензии меняется и плотность укладки частиц в осадке, т.е. его по
розность &о , а с ней по (е) - и R,,' . В этом аспекте выделение µ в качестве
сомножителя и вынесение его за скобки в знаменателе не представляется целе 
сообразным.

В ходе процесса фильтрования сопротиаление перегородки в
идеале изменяется мало - будем считать Rr. постоянной величиной.
Напротив, фактор Ro является принципиально переменным: высота
слоя осадка ho нарастает, значит, согласно (е), увеличивается и Ro,
хотя остальные величины, входящие в выражение для Ro, - посто
янны. Обозначим постоянный комплекс этих величин
Ро

- А
=

(1

-

&0) 2 µ
& 3о
d2

и назовем его удельным (на 1 м высоты слоя) фактором сопро
тиаления осадка. Таким образом, в выражение (и) может быть
подставлен фактор сопротивления осадка Ro = p0h0.
В левой части соотношения (и) стоит скорость, выражаемая по
(б) через переменное количество полученного фильтрата У; в то же
время в знаменатель правой части (и) входит фактор Ro, выражен
ный через переменную высоту слоя осадка h0. Поскольку У и ho
связаны между собой формулой (в), то целесообразно избавиться от
h0 и далее оперировать (наряду с т) только переменной У:

Ro =

Poho =

Р о Хо

F

У.

Подставим Ro по последнему выражению в (и), записав w со:
ответственно определению (б):
1 dV
Лр
W:
(5.2 1 )
РоХо у +
F dt
R
- -

=

F

п

Это соотношение и носит название основного уравнения

фильтрования.

В ходе фильтрования нарастает количество полученного
фильтрата У, значит знаменатель в (5.2 1 ) увеличивается во вре
мени. Отсюда следует, что процесс фильтрования с накоплени
ем осадка не может протекать одновременно при постоянных
движущей силе Лр и скорости фильтрации w. Очевидно, что при
постоянной Лр в ходе процесса будет понижаться w, а чтобы
удержать постоянной w, придется по какому-то закону повы
шать Лр. На практике фильтрование ведут и при Лр = const, и
при w = const. Используют и сочетание этих режимов: сначала
поддерживают постоянной w, при этом повышаются Лр и давле
ние в фильтре; по достижении предельно допустимого давле42 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ния, на которое рассчитан фильтр, его оставляют постоянным и
работают далее при неизменном Лр и понижающейся скорости w.
В целях обеспечения работы фильтра в режиме Лр = const для подачи сус

пензии может быть использован центробежный насос с радиальным напраме
нием лопаток (см. разд. 3.3.3), а в режиме w = const - специальная модифика
ция поршневого насоса, обеспечивающая нормальную работу его клапанов (см.
разд. 3.2.5, 3.5, табл. 3.3).

5.2.S.

Оrдельные ре.жимы периодического фильтрования

В основе расчета - основное уравнение фильтрования (5.2 1 )
в различных модификациях.

Фильтрование при постоянной движущей силе
Движущая сила Лр здесь известна (задана). Перепишем (5.2 1 ) ,
избавляясь от дробей и разделяя переменные V и t :
+
PoXoVdV RnFdV =ЛpF2 !dt .
Интегрируя от начала процесса (t = О , V = О ) до промежу
точного момента с текущими значениями t и V (или до конца
процесса: t = t к , V = Vк>. получаем квадратичное выражение
у 2 + R N =ЛpF2 t .
РоХо
(5.22)
п

2

Оrсюда возможно найти решения относительно различных
интересующих технолога величин.
Продолжительность процесса, необходимая для получения на
фильтре рабочей площадью F заданного количества фильтрата
Vк при известной Лр, составляет

tк =

_I_ (PoXo2 ук2
др

2F

+

.!!д_ V к
F

).

(5.23)

Иногда требуется решить ту же задачу, но при заданном зна
чении не Ук, а накопленного в конце процесса слоя осадка
определенной высоты h0 = hк. Тогда в (5.23) Ук надо заменить
на hк по выражению (в) , естественно - для конечных значений
Ук =
l
P
(5.23а)
t к = __ o h � + R п h к .
Лрх 0 2

Fhкfxo:

(

)

Количество фильтрата, полученного на фильтре площадью F
за время t при движущей силе Лр, находим решением квадрат
ного уравнения (5.22). Перепишем его в канонической форме:
2
V2 + Rп F
2
V 2 ЛрF , = О .
_

42 2

Р о Хо

Р о Хо

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Отсюда, если вынести F из-под корня и затем - за скобки,
получим

Знак " минус" перед радикалом не отвечает физическому
смыслу процесса (V < О - невозможно). Изменив для удобства
порядок записи слагаемых, находим Vк для конца процесса (t =
= 'tк, V = Ук) :
у

к=

1(

Rn 2

РоХо

]

Rn
рt к
+ РоХо - РоХо .

)

2Л

(5.24)

Разумеется, аналогичная задача может быть решена относи
тельно высоты слоя накопленного осадка hк; в этом случае в
(5.24) в качестве множителя перед квадратной скобкой, в соот
ветствии с (в), вместо F войдет Хо ·
Поверхность фильтра F, требующаяся для получения заданно
го количества фильтрата V за время t при известном Лр, опреде
ляется записью выражения типа (5.24), решенного в явном виде
относительно F:

=== ==-( Rn ) 2

F = -;::::

+

РоХо

=
V

2Лрt

РоХо

-

-

(5.25)

Rn

РоХо

Расчет по этой формуле (замечание относится также к фор
муле 5.24 и некоторым другим) становится неточным при
2Лрt << Rп 2/( р оХ0): значения уменьшаемого (корня) и вычитае
мого близки, велика ошибка разности. Точность можно повы
сить, избавляясь от иррациональности в знаменателе (путем
умножения его и числителя на сумму величин, стоящих в знаме
нателе) , а тем самым и от разности. Тогда применительно к
концу процесса после очевидных преобразований имеем

F=

Ро Хо

2Лрt к

_

-

[(

[(

)2

�
РоХо

Rn

2Лрt к

)2

+

2Лрt к
РоХо

РоХо

+

�

Rn

Ро Хо

+ 2Лрt к + 2Лрt
к

]

у

]

к·

Vк

=

(5.25а)

423

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Определение V, Ук по (5.24) и h, hк по аналогичной формуле
относится к задачам эксплуатации. Расчет F по формулам (5.25),
(5.25а) , несомненно, - задача проектирования. Определение t, tк
по (5.23) тоже ближе к задачам проектирования.

Фильтрование при постоянной скорости фильтрации
Здесь известна скорость фильтрации w (количество фильтрата
V, пропускаемого фильтром за время t) - по практическим ре
комендациям для перегородки данного типа или по максималь
но допускаемым значениям др и рабочего давления в конце
процесса (см. ниже). Основное уравнение фильтрации (5.2 1 ) для
этого случая упрощается, поскольку dV/dt = V/t = const:

w _!._�
=

F t

=

Vф
F

=

Лр

р 0Х0 у +
Rп
F

(5.2 1 а)

причем Лр = Лр(V) или Лр = др(t ) - переменная величина.
Пусть фильтр рассчитан (или рассчитывается) по условиям
механической прочности на определенное максимальное для
данного процесса давление (т.е. максимальное Лр = Лрк ) . Тогда
по (5.2 1 а) оценивается значение w в конце, а значит и в ходе
всего процесса фильтрования.
Задача эксплуатации состоит в определении количества
фильтрата V, Ук за заданное время t, tк или потока фильтрата в
единицу времени VФ для имеющегося фильтра (F - известно) :
(5.26)
V = wFt, VФ = wF .

Задачи проектирования предусматривают определение необходи
F или продолжительности процесса tк:
F = V/Wt = VJwtк = Vф/w ; tк = YJwF .
(5.26а)
Работа в режиме w = const требует постепенного увеличения
др в ходе процесса. Закон изменения др устанавливают из вы
ражения (5.2 1 а), разрешая его относительно Лр:
х w
(5.27V)
Лр = р 0 / V + Rn w.
мой поверхности фильтра

На это выражение следует ориентироваться при регулирова
нии Лр, когда в ходе процесса легко контролировать изменяю
щиеся количества получаемого фильтрата V. Если же в процессе
фильтрования удобнее контролировать текущую высоту слоя
осадка h0, то в формуле (5.27V) фрагмент Vx0/ F целесообразно
по (в) заменить на h0:
(5.27h )
424

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Наконец, закон изменения Лр во времени получается при
подстановке в первое слагаемое в правой части выражения
(5.27V) значения V по левой формуле (5.26):
(5.27t)
Лр = PoXow2t + Rn w .

Согласно формулам (5.27), для поддержания постоянной ско
рости фильтрации w необходимо обеспечение линейного повы
шения движущей силы Лр с V, h0 и t соответственно в ходе про
цесса фильтрования. Это полностью отвечает формуле (5.2 1а):
знаменатель в ходе процесса линейно возрастает с V .

О других режимах и моделях фильтрования
При анализе режимов· фильтрования с переменны.ми во времени
скоростью фильтрации w и движущей силой Лр неоt>ходимо рас

полагать определяющей временной характеристикой . Для задач
проектирования чаще всего это - конкретная (требуемая) за
кономерность изменения во времени потока фильтрата dV/dt =
= /(t) . Тогда основное уравнение фильтрования предстанет в виде

F

w l_ f(t)
=

=

Л
�
р__

_
_

Р о Хо
F

у

+ Rп

(5.2 1 б)

причем текущее значение V к моменту времени t определится:
v

= I f(t) dt .
t

о

Подставим теперь (л) в знаменатель выражения (5.2 1 б):

F

l. /(t)

=

;l

Лр

Р о о /(t)dt +

(л)

Rn

отсюда наЙдем закономерность изменения движушей силы, обес
печивающую заданное временное изменение потока фильтрата f(t):

Лр =

/�t) [ Р о;о r /(t)dt

+

Rn] .

Рассмотрение более сложных технологических ситуаций
(фильтрование в случае сжимаемых осадков; частичное закупори
вание пор фильтрующей перегородки и др.) проводится с некото
рыми не очень строгими допущениями и требует привлечения
дополнительных экспериментальных данных. Такой анализ вы
ходит за рамки настоящего учебника* .
• См. ( 1 , 1 5, 1 7) и с бенн детальн (6) .
о
о
оо

425

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

S.2.6. Неорерыаный процесс фильтровании

на бараба1О1ом вакуум-фильтре

Расчетная схема непрерывного процесса фильтрования в ба
рабанном вакуум-фильтре представлена на рис.5.20.

Барабан 1 радиусом R и дnиной по образующей / медnенно вращается с уг
ловой скоростью ш (на рисунке - против часовой стрелки). Боковая поверх
ность 2 барабана входит в точке А в соприкосновение с суспензией /, находя
щейся в ванне J. Фильтрат /1 под действием разрежения Лр проходит через
перегородку, а на ней образуется слой осадка /1/. Толщина ero h0 постепенно
нарастает в направлении от точки А (h0 = О) к точке В выхода барабана из
соприкосновения с суспензией, rде толщина слоя осадка достиrает максималь
ной величины hк. За пределами точки В перемещающийся вместе с барабаном
слой оса,цка //1' не изменяет своей ТQ/\ЩИНЫ.

В задачу техншогu•еского рас11ета входит установление свя
зей Лр и характеристик сус пензии и осадка с основными гео
метрическими размерами барабана и скоростью его вращения.
База анализа - основное уравнение фильтрования (5.2 1 ) . За
метим: толщина слоя осадка h0, hк минимум на два порядка
меньше радиуса барабана R2, поэтому кривизной слоя осадка
вполне можно пренебречь.
Текущее время фильтрования т для некоторой точки филь
трующей перегородки М характеризуется (рис.5.20) текущим углом
а, изменяющимся от а = О (в точке А) до конечного значения а =
= ак (в точке В). Угол а связан с т очевидным соотношением
(м)
а = Ф't = 21tm,

rде п - частота вращения барабана в секунду.

Естественно, началу процесса (т = О) отвечает а = О, концу
процесса (т = тк) - значение ак = Ф'tк . Из соотношения (м)
можно выразить текущее время т = а/Ф и подставить в основное
уравнение фильтрования, тогда п оследующие связи получатся в
зависимости от а, а в конечном итоге - от ак:
l dV
Ф dV
Лр
(5.28)
F dt = F da = р 0Х0 у +

F

Rп

На практике барабанный фильтр работает с постоянным раз
режением Лр , так что дальнейший анализ проводится именно
для этого случая
по уже рассмотренному алгоритму
(разд.5.2.5, вариант Лр = const):
- разделение переменных а и V;
- интегрирование от начала (точка А) до конца (точка В)
процесса;
- запись искомых выражений для задач эксплуатации и про
ектирования.
426

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 5. 20. Расчетная схема барабанного
вакуум - фильтра:

-

1 - барабан, 2 - фильтрующая перего
родка, J
ванна ;
/ - суспензия, /J - фмь"IраТ, /JJ - ощцок

Однако здесь можно прямо
воспользоваться полученными
ранее решениями (5.22)-(5.25) ,
подставляя по (м) вместо tк
величину ак /ro и выражая про
изводительность барабана vбф =
= Vкftк = Укоо/ак·· Таким обра
зом, при известной рабо
тающей площади фильтрования
F = aкR2 l имеем решение зада

чи эксплуатации:

(н)
откуда

v.

-

бф - ОО R2 I

Rп 2
-[ ( РоХо)

Толщина слоя осадка

+

2 Лра к - -Rп
PoXoro

Р оХо

]

(5.29)

hк на выходе барабана из ванны (точка

В) получается при замене Ук по (в) для конца процесса: Ук

=

Я�кfх0.Подставив это значение Ук в (н) , находим

h.
откуда

�

х.. [ (

hк =

Rп
Р о Хо

)2

( Rп ) 2
Ро

+

+

2Лра к -

Р о Х о ОО

2 Лра к Х о

РоФ

я.

Р о Хо

Rп
Ро

]

=

'

(5.30)

Задача проектирования может заключаться в определении
площади фильтрующей перегородки F, необходимой для обес
печения заданной производительности Vбф. Здесь можно вос
пользоваться формулой (5.25а) , заменив в ней Ук и tк на па
раметры непрерывного процесса vбф и ак:
427

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

F

=

2 = [ ( )2
= [ (.&..) 2

aк R l

+

R п ro

2 Лра. к

.

2Лр

+

PoXoro

2Лро. к

Ро Хо О. к
2Лрrо

+

+

R п ro

.&__]

2 Лра. к

2Лр

V,

]

бф

Vбф

ro

а. к

=

.

(5. 3 1 )

Задачей проектирования может быть и определение необхо
димой движущей силы Лр при известных характеристиках филь
трования - ее найдем, записывая (5.22) для конца процесса и
переходя к vбф и а.к:
PoXo

2

откуда

(

)

(

aк 2 +
v.
Rп F v
бф
бф (J)

а ._ ) . а к
= ЛрРl

(2 �vF ) 2 �+R �vF .

Лр = Р о Хо

(1)

w

(J)

п

(5.32)

Разумеется, значение Лр не может превышать атмосферного
давления.
К числу задач проектирования относится также определение
угловой скорости ro или уточнение установочного угла а. к при
прочих известных величинах. Здесь целесообразно воспользо
ваться формулой (5.32), выразив сразу отношение a.� /ro: :

а.к
(J)

Лр --F 2[ Лрv2F 2 RnFvбф J .
2F2 V2бф бф
Rп

Р о Хо

" бф
и

=

_

(5.33)

Отсюда при заданном угле а.к определяется необходимая уг
ловая скорость ro , и наоборот - при известной ro уточняется ак
(обычно доля погружения в суспензию составляет 0,3-0,4 от
поверхности барабана, т.е. а.к - примерно 2-2,5 радиана) .
5.2. 7. Определение параметров процесса фильтрования

В разд.5.2.4 бьmо отмечено, что параметры процесса филь
трования р0 и Rп определяются экспериментальным путем. За
дача состоит в их нахожцении по зафиксированным в ходе опы
тов сопряженным величинам переменных У, 't , Лр при извест
ной площади F.

Поскольк у требуется определить два параметра фильтрования, то формаль
но достаточно двух опытов с фиксированием упомянутых величин. Но в этом

428

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

tN

у

6

а
Рис.5. 21.

К определению параметров процесса фильтрования:

иллюстраuия общеrо подхом в случае двух параметров, 6
тичной зависимости (S.22) для определения Ро и Rn
а

v

-

-

линеаризаuия квадра

случае на численных значениях р0 и R,. мoryr существенно сказаться погреш
ности эксперимента. Поэтому проводится несколько опытов, что позволяет
определить р0 и Rn более точно.
Подчеркнем: опыты должны быть поставлены с натурными суспензиями и
фильтрующими переrородками, которые будут использованы в реальном произ
водственном процессе (естественно, площадь переrородки F в условиях лабора
торного эксперимента может быть меньше).
Наиболее удобно определять R,. и р0 в опытах при Лр = const. В этом случае
в ходе опыта получают пары сопряженных значений V и t, отсчитанных от
начщ�а опыта.
Общий подход к определению двух параметров какого-либо процесса по
опытным данным состоит в представлении связи переменных (в случае филь
трования базирующихся на V и t) в виде линейной зависимости
+
(о)
у = kx
Ь.
Здесь у и х включают переменные, преобразованные так, чтобы зависимость,
построенная по экспериментальным точкам (рис. 5 . 2 1 ,а), был а линейной. При
этом параметры модели (в рассматриваемом случае р0 и Rn) входят в параметры
уравнения (о), т.е. в k и Ь. На рис. 5 .2 1 , а: Ь отрезок, отсекаемый на оси
ординат (при х = О), а k тангенс утла наклона 1р прямой к оси абсцисс.
В основу определения р0 и Rn положим квадратичную зависимость (5.22).
Ее линеаризация достиrается путем деления каждого слагаемого на ЛрF 2V:
Ро Хо у + R n .
�
(5.34)
-

-

-

=

V 2ЛрF 2
ЛрF
Роль переменной у здесь играет t / V, роль х V.
НаЙденные в ходе опьпа пары сопряженных величин t; и V;, отсчитанных от на
чала опьrrа, допалняются вычисленными значениями отношений t;/ V; (см. ниже):
о
t
-

/Y
v

t

о

Затем по сопряженным парам значений т; / V; и V; строится зависимость
типа (5.34), т.е. наносятся точки и через них наилучшим образом (например, по
методу наименьших квадратов) проводится прямая t /V = ft.V) см. рис. 5 . 2 1 ,б.
Отрезок, отсе каемый на оси ординат, в соответствии с уравнениями (о) и
-

(5.34) равен

Ь =

Rп
ЛрF

429

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Оrсюда при известной площади экспериментального фильтра F и зафикси
рованном в ходе опыта постоянном перепаде давления Лр рассчитываем иско
мый параметр Rn.
Тангенс k угла наклона прямой к оси абсцисс - находим из графика
(разумеется, с учетом масштабов по осям координат):
-

tg ер = k

При известных
фильтрования Ро ·

S.2.8.

х,, ,

=

РоХо

.

2ЛрF 2
Лр и F определяем второй искомый параметр процесса

Фильтрование в поле центробежных сил

Движущая сила Лр, от которой зависит интенсивность филь
трования, может быть сформирована при осуществлении про
цесса в поле центробежных сил -. в аппаратах, называемых
фильтрующими центрифугами. Устройство таких центрифуг•
сходно с устройством осадительных (см. разд. 5. 1 .2), только бо
ковая поверхность барабана в фильтрующих центрифугах долж
на быть проницаемой для фильтрата.

Вертиum.наи no.a.ecнu фнт.трующu центрнфуrа nернодическоrо дейст11ИJ11 по
устройству и принципам работы отличается от осадительной (см. рис. 5 .8) тем,
что боковая поверхность ротора выполнена не сплошной, а перфорированной;
изнутри эта поверхность покрыта фильтрующей тканью. В ходе работы цент
рифуги фильтрат (фугат) проходит через фильтрующую перегородку, а на ее
внутренней поверхности образуется слой осадка. При таком способе вывода
фильтрата в фильтрующей центрифуге (в отличие от осадительной) нет необ
ходимости в отводной трубке (поз. 10 на рис. 5.8). Рассматриваемая центрифуга,
как и осадительная, работает в две стадии - накопление осадка с получением
фильтрата; выгрузка осадка.
На рис.5.22 изображена схема rоризо11Т11аной центрифуrи nолунепрерw8Ноrо
дeйCUll.ll с но:�ке11Ой вwrрузкой осадц. На валу 1 укреплен ротор 2 (барабан) с
перфорированными боковыми стенками З и фильтрующей тканью 4. Ротор
закрыт кожухом 11, вал выводится ':lерез кожух с помощью сальникового
уплотнения 12. Суспензия 1 подается в барабан по линии 7; фильтрат 11 отво
дится через штуцер 10. Выгрузка осадка 111 производится с помощью загнутого
ножа 6 и гидравлической системы 5 (гидравлический цилиндр, работающий по
принципу поршневого насоса, и передаточные стержни), а также наклонного
лотка 8 для удаления осадка. Чтобы стимулировать транспортирование осадка
по лотку, предусмотрен вибратор 9.
Центрифуга -работает циклично, но без остановки вращения барабана. Первая
стадия накопление осадка: нож опущен к оси врашения, суспензия подается в
центрифугу, отводится фильтрат и накапливается осадок. По накоплении коль
цевого слоя осадка достаточной толщины подача суспензии прекращается первая стадия заканчивается. На второй стадии - выгрузке осадка - нож по
степенно подается вверх (по мере отвода жидкости из гидравлического ци
линдра поршень и система стержней, с которыми скреплен нож, поднимаются ) .
При этом вращающаяся масса осадка набегает на лезвие ножа и срезается тон
кими слоями; далее осадок через желоб выводится из центрифуги. После уда
ления всего осадка (нож поднят до верхнего положения) стадия выгрузки
-

• Подробнее см. [ ! , 9, 1 5) .
430

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис.5. 22. Горизонтальная фильтрую
центрифуга полунепрерывноrо
действия с ножевой выrрузкой осадка:

щая

1 - вал, Z - ротор, З - боковые пер
форированные стенки, 4 - фильтрующая
ткань, 5 - гидрамическиА uилиндр, 6 загнуrый нож, 7 - линия под;�чи суспен
зии, 8 - лоток, 9 - вибратор, 10 - шту
uер, 11 - кожух, lZ - уплотнение;
1 - qспензия, 11- филь1J18Т (фуrат), Ш
- ОС11док, JV- rипраапическая JКИдКОС'IЪ

(Ill)

3 4

11

IV

заканчивается, нож опускается к оси
вращения (под действием жидкости ,
подаваемой в гидравлический ци
линдр), и включается подача суспен
зии· - цикл повторяется.
Заметим, что осадок в центрифу
ге получается более nлотным и с
меньшим содержанием влаги, неже
ли в ранее рассмотренных фильтрах.

Технологический
расчет.
Расчет центробежного фильтрования ведется по канве, изложенной в разд. 5.2.4 и 5.2.5 с
использованием основных понятий (см. разд. 5.2.3), но с изме
нениями, обусловленными спецификой процесса. Кольцевой
слой осадка располагается в барабане центрифуги в диапазоне
от наружного радиуса R2 цилиндрической фильтровальной пере
городки до некоторого переменного во времени внутреннего ра
диуса г0; длину слоя осадка (по образующей), как и в случае
осадительной центрифуги, обозначим /.
Сuзь количества получаемою фильтрата с изменяющимся ра
диусом r0• Выразим обьем осадка в некоторый момент времени 't :
Vос = VXo = 7t(R2 2 - г02 )/.
(п)
Это ж е выражение может быть получено путем записи накоnления осадка
за элементарный промежуток времени dт:
dVос = x,,dV = 21trldr

и последующего интеrрирования от начального (т = О, V = О, г0 = R2) до теку
щего момента времени т, соответствующего V и r0•

Текущее значение г0 может изменяться от г0' = R1 в начале
процесса ( 't = О ) до некоторого значения г0" в конце его ( t = t к ) .
Видимо, минимальному значению г0" (максимальной толщине
кольцевого слоя осадка) отвечает г0" = R 1 •
Движущая сил а Лр процесса фильтрования. Для ее определе
ния вьщелим (рис. 5.23) в барабане центрифуги на текущей ра
диальной координате г элементарный кольцевой слой толщиной
dг; высота его - /. Запишем баланс для переноса импульса (или
для равновесия сил), принимая за пространственный контур
43 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис.5. 23. К определению движущей
силы фильтрования в центрифуге:

1 - барабан, 2 - фильтрующая перего
родка

ф
•

(1)

t-- r _,..___," ,

1

:....--..-R 1

�z--+.,,--....,�

объем

j

dm

элементарного

слоя

2тcr/dr с заключенной в нем
массой dm. Давление на коор
динате r равно р, на координа
те r + dr оно составляет р + dp;

внешняя (центробежная) мас
совая сила трактуется (см. ра:щ.
1 .5. l ) как источник импульса.
Тогда, пренебрегая изменением
количества движения (из-за небольших скоростей жидкости),
имеем в направлении радиальной координаты r (рис. 5.23):
р·2тсr/ - (р + dp) 2тсr/ + (dm)ro2r = О
или после сокращения на r
2n ldp = ro 2dm .

Интегрируя в полных диапазонах перепада давления
распределения массы жидкости m, находим

Лр =

mro 2

Лр и
(р)

2тс/ .

Раскрывая т = prt(R22 - R 1 2 )/, где р - плотность жидкой сре
ды в барабане, получим окончательно после сокращения на n /

Лр =

pro 2

-

2

(R2 2 - R 1 2 )

.

(5.35)

Гидравлическое сопротивление фильтрующей перегородки . По
лагая перегородку сосредоточенной на радиусе R1, а режим дви 
жения фильтрата через нее - ламинарным, запишем по (з) :
Лрп = Rn w2 , где индекс "2" указывает, что рассматривается гра 
ничная скорость в сечении 2n R2 l.
Анализируя гидравлическое сопротивление Лр0 кольцевого
слоя осадка, распределенного в диапазоне радиусов от ro до R1,
необходимо учесть изменение скорости w по толщине слоя, т.е.
по радиальной координате r. Расчет и здесь удобно вести на
основе скорости w2 , поскольку введение радиуса R1 вносит
определенность в анализ. Связь текущей (локальной) скорости
w на радиусе r с граничной w2 найдем из уравнений расхода:

l dV
w =- -

F dt '

432

(с)

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис.5.24. К выводу основного уравнения
фильтрования (перегородка /) в поле
центробежных сил:

-

/
суспензия , 11
бодная поверхность

-

слой осадка, сп - сво

откуда, имея в виду F = 2rtгl и
= 2rt R2 / :
dV
- = wF = w2 F2
d'"C

F
F

2
w = w2 -

и

1

=

F2 =

R

2 .
w2 г

(т)

Для элементарной толщины
dг слоя осадка (рис.5.24) лами
нарная составляющая формулы
Эргана запишется с учетом (т) ,
если сохранить прежнее обозначение удельного фактора сопро
тивления осадка:

dг

е: о ) 2 µ
R 2 ,.
w = p0w = p 0 2
з
г w2
d
е: о

напомним: скорость

=

w2 ('"C).

(У)

-

dp0 = 150 (1
--

w2 изменяется в ходе фильтрования w2

=

Обозначим р ' - давление на внутренней границе слоя осадка
(радиус г0 ) и р " - на внешней (радиус R2) . Разделим перемен
ные в (у) и проинтегрируем в границах кольцевого слоя осадка
для момента времени •=
R

dг
= f1 Po R 2 w 2 p
d
o
г
'
р

р"

-f

откуда находим связь
времени •=

'

ro

Лр0, г0 и w2 в некий произвольный момент

Р -Р
•

"

=

R2 .
Лро = Ро R2 w2 ln Го

(5.36)

Поскольку w2 выражается по (с) через V, целесообразно г0 за
писать тоже в зависимости от V, чтобы избавиться от одной из
переменных. Это можно сделать с помощью (п):

Го

/(

Отсюда

ln R 2 = ln R 22
Го

=

�R22

Ух о .
- --

(ф)

rt /

)

о =
R 22 - Ух
п/

[

ln 1 -

�у

п Ri l

J

- 1/2

433

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Но

nR�I = У6

-

г0 (

)-i

внутренний объем барабана центрифуги . Тогда

R2 -ln
ln = 21

Ух0

\ -V6

Это значение логарифма поставим в (5 .36). учтем фактор со
противлен ия перегородки Rn и, разреш ив полученное равенство
относительно w2 , придем к основному урав11ен и ю для центро
1 dV
F, у, •

бежного фнльтрова1111я:
w,

•

p, R,

ln(I- �: УТ'

(S/З7)

2Лр

+ 2Rn

Далее полученное уравнение может быть рассмотрено приме
к отдель н ы м режи мам фил ьтрования.
Режим Лр co nst с оответст венно ( 5 . 3 5 ) реализуется при посто
я н ной угловой скорости w и поддержании неизменным уровня R 1 •
С вязь У и t при известной F2 можно получить, разделяя в (5 .37)
переменные и и нтегрируя от начала процесса ( t
) до те
н и тел ьн о

=

кущих момента времени
до конца процесса: t t к

t

У=У

и кол ичества фильтрата V (в пределе к ):

J[•0R, 1n(i-�: vТ' ]
г0 г0
=

,

= О, У = О

+ 2Rn dv -

j

ЩF,dt

При этом для t и У су ще ст вует огран ичение, связанное с ми
нимальным значением
п о (т):
:S R1

( �: }

Тех11ические

lп 1 -

У

труд11ости

могут

v ; 11оказатель степени

•

во:ти кнуrь

при

отыскании

интеграла

"-1 " инте.гр ирования не осложняет - он вы-

11осится как м ножитель r1еред l п . Искомый интеграл является табличным · :
а + Ьх
f lп(a + bx)dx = --l n (a + Ьх) - х ,
ь
11ричем для рассматриваемого случая а = \ , Ь = -х0 / У6 . Имея в виду, что при
а = 1 и нулевом нижнем пределе интеграл обращается в нуль, получим

- f 1п ( 1 - � v)dv
11

•

434

См. (4.

V6

nоз.

620).

=

-

[ �: ( ) ·] (
-�

'-

v6

1n 1 - .3!... v
Уб

=

.

v
6
Х0

-

.

1

)1 (
n

)

1 - .3!... v + v .
Уб
.

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

- {p0R2[( v6 ) (

Окончател ьно п о сл е интегрирован и я находим решение в явном

в иде относ ител ьно t :

t=

V6 )

1

2ЛрF2

Хо

) ]

)

- v 1 11 1 - � v + v + 2R" v .
vб

F2

(5 .38)

Решен ия задач проектироваии.я для
(радиус R2 входит еще
в
и эксплуатации с определением V проводятся численными
методам и .
Р е ж и м w 2 = const поддержи вается п р и определенном законе
из мене н ия Лр , реал ьно
при программ 11ровании изменения во
времени угловой скорости барабана ro соответственно соотноше
н и ю (р), причем Лр в ы ражено по (5 .35).

-

5.2.9. П р ом ы в ка осад к а

С цел ью о чист к и осадка от нежелател ьной примеси фильтрата и
(или) более пошюго извлечен 11я фил ьтр ата в качестве целевого про
дукта после завершен ия фильтрования слой образовавшегося ТМ
под вер гают п ром ывке. Д11я этого в течение некоторого времени на
слой осадка подают 11ро."ыв11ую :жидкость, постепенно вымываю
щую фил ьтрат из rюр осадка (просветов между зернам и слоя ТМ).
Эффекти вность п ром ывки характеризуют степенью извлечения
ТJ Ф фил ьтрата из осадка; в оп ределении этой вел и ч и н ы
ос11ов11ая
задача техиологического расчета стадии промывки.

-

Подчеркнем, что для понима11 и я подхода к рассмотрению стади и пром ы в к и
осадка необходимо 11редварителыю ознаком иться с основным поняти1!11ым аппа:
ратом и м t.-тодам11 а11алнза главы 8 "Структура r1отоков", а также некоторыми ре
зультатам и , уста11оолен11ь1м11 в этой г11аве.
·
Для оцен к и 1'1Ф обычно принимают (и 11огда подразумевают без оговорок), что
жидкостно!I поток (фил ьтрат, промы в11ая жидкость) в порах осадка движется в ре
жиме либо идеального вытес11е11ия, л ибо идеального перемеш и ва1 1 и я . В обоих слу
чаях приходится прибегать к 11екоторым фе11оменологическим умозаключе11ИJ1м и
вводить ко11ста1пы. определяемые экспериментал ыю. - модель становится в значи
теJ1ыюй мере эм11ир11 ч еской. Но и 11езависимо от этого к обоим 11риведен н ы м пред
пшюжениям о структуре потока следует опюситься критически: в условиях лами
нарного д11иже1 1ия жидкости в rtopax Go11ee обо с нован но базироваться на модел и по
пере ч11ой нерав11омер11осп111 потока 11ри отсутствии обратного перемеш и ва11ия.
Кач естве1 1 н о характер вым ы вания ф и л ьтрата пром ы вноR ж идкостью из пор
осадка удоб110 1 1о я с 1 1 и т ь н а п р и мере ц и н и ндр и ч е с к о li поры . При rtодач е про
м ы в н о ll ж идкосп1 1 1 а осадо к в пер в ы li 11ер1юд времен и из поры выходит тол ь ко
ф 11 1 1 ьтрат - с 1юсто н 1 1 1ю й ( н ачал ь 1 1 о fi ) ко1ще11траци е ll С0. Так п родолжается до
тех пор, 1 ю к а 1 1 е р в ы е 11ор ц1111 пром ы о 11ой ж 11дкосп1, д в ижущие по оси поры с
11а11бол ь ш е n с коростью 1vm." не дост и п 1 ут (к н екотором у м о м е нту врем е н и

•

См.

[ 1 . 6. 1 7) и др.

435

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис.5. 25. Кривые вымывания фильтрата
из осадка промывной жидкостью
t m; n ) выходного сечения поры. С момента
t > t mi n выходное сечение будет покидать
как промывная жидкость (в приосевых
0,5
зонах поры), так и фильтрат, содержа
щийся в поре (ближе к ее боковым стен
кам); средняя концентрация фильтрата в
смеси с промывной жидкостью С < С0.
Изменение безразмерной концентрации
"t,Vшк
фильтрата С/Со в выходном сечении пор
и доли фильтрата х, остающегося в слое
осадка, в зависимости от времени, а в
более общем плане - от количества V""' поданной на осадок промывной жид
кости, иллюстрируется рис. 5.25: при t > tш;11 кривые носят гиперболический
характер (ер. с рис. 8.25). Описание этих кривых позволяет подойти к опреде
лению '1Ф:
'lф = 1 - х .
Анализ процесса промывки даже с рядом упрощающих допущений
(отсутствие адсорбции фильтрата на зернах осадка, игнорирование изменения
вязкости жидкости по радиусу поры) достаточно громоздок и выходит за рамки
учебника. Укажем только, что зависимости для определения текущего значения
С, конечного значения х и, наконец, конечный вид формулы для '1 Ф получают
ся на основе общего соотношения типа (8.8) и с использованием понятия о
плотности вероятностей распределения элементов потока qi ( t ) в поре по фор
муле типа (8.29) .

5.3. ПЕРЕМЕШИВАНИЕ
5.3. 1 . Общие положения

Процессы перемешивания жидкостных, газовых и других од
но- и многофазных сред, а также смешения пасто- и порошко
образных материалов весьма широко применяются в хими
ческой и родственных технологиях. В ряде случаев (во многих
периодических и полунепрерывных биотехнологических процес
сах, при получении композиционных материалов и т.д.) эффек
тивное перемешивание является одной из важнейших стадий про
изводства и определяет успех технологического процесса в целом.
Перемешивание состоит в многократном относительном пе
ремещении макрочастиц объема среды (элементов, ансамблей ,
пакетов) под действием импульса (количества движения), пере
даваемого ей побудителем - струей жидкости или газа, насо
сом, мешалкой и т.д.
Цели процесса перемешивания
назвать три основных цели осуществления

Можно
этого про
цесса:
1 ) получение " однородных " (равномерных) гомогенных и ге
терогенных систем - растворов, суспензий, эмульсий, твердых
436

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис.5.26. К влиянию перемешивания на
процесс растворения:

1 - раСТllОряемое твердое зерно, 11
фаза (растворитель, раствор)

-

жидкая

с

(порошкообразных) и других сме
сей - так, чтобы их составы в раз
ll
ных точках рабочей зоны аппарата
можно было
считать одинако
выми;
11
2) интенсификация тепло- и
массообменных
(диффузионных)
процессов в гомо- и гетерогенных
системах;
3) интенсификация химических превращений.
Причину интенсифицирующего воздействия перемешивания
на процессы переноса поясним на примере растворения твердо
го зерна 1 в жидкости (рис.5.26) . Растворение происходит при
возни кновении градиента концентраций d С/dп растворяемого
вещества в приповерхностной зоне: чем круче идет концентра
ционная кривая у поверхности зерна, тем быстрее растворение.
В первые моменты времени ('t' 1 ) контакта зерна с жидкостью
этот градиент достаточно велик - растворение идет быстро. С
течением времени (ч > 't' 2 > 't' 1) слои жидкости , прилегающие к
поверхности зерна, начинают насыщаться растворяемым ве
ществом - градиент понижается, и растворение замедляется .
Перемешивание жидкости способствует переносу к поверхности
зерна свежих (слабо насыщенных) порций жидкости; в резуль
тате градиент возрастает (штриховая линия, отмеченная пикто
граммой -') , а значит интенсифицируется процесс растворения.
Яаление перемешивания будет рассматриваться в гл. 8 в связи с его влияни

ем на протекание процессов переноса. Но там затрагиваются специфические
аспекты, связанные с перемешиванием (прежде всего - продольным ) , возни
кающим в потоках. Нужно видеть принципи ал ьное отличие этих аспектов
анализа от проблематики настоящего раздела: здесь рассматривается процесс
перемешивания как технологический прием направленного воздействия н:�
обрабатываемый объект.

Основные проблемы процессов перемешивания
Качество (эффективность) перемешивания. Здесь ряд вопросов.
Во -первых, следует условиться ·, что понимать под качеством
перемешивания, как его количественно характеризовать. Оче
видно, это понятие должно отражать отклонение составов в
различных точках используемой (исследуемой) смеси от средне
го его состава.
•

Некоторые подходы к понятию о качестве перемешивания приведены в

(20, 23 ) .

437

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Средний состав смеси определяется просто и однозначно из материального баланса по смешиваемым компонентам. Од
нако к определению (к формализации) отклонений возможны
различные подходы - как правило, они реализуются с привле
чением статистических методов. Так, можно условиться о спо
собе усреднения отклонений, скажем, суммируя среднеквадра
тичные их величины (определяя дисперсию) или средние из
абсолютных значений отклонений. Для некоторых процессов
вполне приемлемо характеризовать качество перемешивания
отношением такой усредненной величины к среднему составу
смеси. Но для других процессов подобная характеристика недо
статочна; надо еще, чтобы отклонение от среднего состава ни в
какой точке смеси не превышало некой предельной величины.
Иными словами, в этом случае речь идет о приемлемом распре
делении отклонений от среднего состава.
Напомним: дисперсия а2 рассчитывается как сумма квадратов отклонений
составов С; в различных точках рабочей зоны смесителя от среднего состава
смеси Сер :
т
2 ,
(а )
cr 2 - _L ( С; - Сер )

где т

- количество отобранных проб, i - текущи й номер пробы.
1=1

В целом проблему подхода к формулированию понятия
" качество перемешивания" окончательно решенной считать нельзя.
Во-вторых, рассматривая какой-нибудь конкретный процесс,
следует установить, какое именно количественное значение пока
зателя качества перемешивания приемлемо для данного процес
са. Это зависит в основном от дальнейшего использования пе
ремешанной смеси. Иначе говоря, приемлемое количественное
значение качества перемешивания задают исходя из представ
лений (часто - весьма общих) о влиянии эффективности пере
мешивания на качество конечного продукта.
В-третьих, необходимо выявить основные факторы, влияющие
на качество перемешивания, и установить характер, а затем и
закономерности влияния этих факторов. В настоящее время фак
торы выявляют чаще всего на феноменологическом уровне, а их
влияние на качество перемешивания в основном - на эмпири
ческом. Д остоверно установленным здесь можно считать, что
качество перемешивания возрастает с повышением затрат энер 
гии на эту операцию; даже более определенно: при одинаковых
удельных (на l м3 перемешиваемой смеси) затратах энергии

качество перемешивания получается примерно одинаковым.
Кинетика перемешивания . Период, требуемый для достиже
ния соответствующего качества перемешивания, называется
временем перемешивания . Заметим, что это время может служить
критерием при сравнении эффективности различных перемеши4 38

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

вающих устройств. Обычно чем меньше время перемешивания,
тем выше эффективность такого устройства.
Представления о кинетике перемешивания в настоящее вре
мя строятся на феноменологической основе с привлечением
опытных данных. Рассмотрим одну из возможных моделей тако
го рода.
Примем, что перемешивание протекает как процесс 1 порядка,
т.е. скорость процесса пропорциональна текущему значению его
движущей силы. В качестве движущей силы можно принять
текущее значение дисперсии cr2 , но точнее - избыток cr2 над
предельной величиной cr0 2 . Понятие о cr02 возникает потому, что
одновременно с перемешиванием в смесителе происходит обрат
ный процесс - сеrреrация. Дело в том, что смешиваемые ком
поненты обладают разными свойствами (плотностью, размера
ми, текучестью и т.п . ) , и под воздействием внешних сил или
движущихся рабочих органов в различных зонах возможно пре
имущественное накопление отдельных компонентов - это и
есть сегрегация. (Пример сегрегации и подход к ее описанию
для одного из конкретных процессов приведены в разд.23.4.4.)
При достаточно большой (теоретически - при бесконечно
большой) продолжительности одновременно протекающих про
цессов перемешивания и сегрегации в рабочей зоне устанавли
вается равновесие составов, отвечающее предельно достижимому
значению дисперсии cr02 .
Если в результате перемешивания получается равномерно рас
пределенный по объему рабочей зоны продукт (гомогенный или
гетерофазный), то cr02 -+ О; если неравномерно, то cr0 2 > О. Чис
ленное значение cr02 , зависящее от свойств и относительных
количеств смешиваемых веществ, устройства и режима работы
смесителя, определяется опытным путем.
Итак, с принятыми допущениями скорость изменения
(уменьшения во времени) дисперсии для периодического процес
са смешения запишется как

- dcr 2
dt = kc (cr2 - cro2 )

где kc

-

,

(б)

эмпирическая константа скорости смешения.

Разделим переменные и проинтегрируем от начального зна
чения дисперсии сrн 2 при t = О до текущего значения cr2 в момент времени t:
t
(1 2 d cr 2
J cr 2 - cr 2 = - kc J dt
О
(1 2н
о

,

(в)
439

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

откуда

(J - (J °2
ln 2
= -kct,
(J 2 - (J 2
о

(г)

н

(J 2 - (J�

или

(J 2 - (J 2
н

о

= exp(-kct) ;

(д)

в случае cr02 = О выражения (г) и (д) упрощаются.
В задачах эксплуатации по (д) при известном времени про
цесса t = tк определяется качество перемешивания , характери
зуемое дисперсией cr2 = сrк2 В задачах проектирования требуемое
·
качество конечного продукта, характеризуемое величиной сrк2,
задано; здесь п о (г) при cr2 = сrк'- рассчитывается необходимое
время перемешивания t = t к ·
Подчеркнем, что предварительно должны быть поставлены
специальные опыты для определения значений kc и cr0 приме
нительно к конкретному смесителю.
Для непрерывного процесса расчет базируется на среднем вре
мени пребывания перемешиваемой среды в смесительном аппа
рате tcp = V/ V = G/G, где V и G - объем и масса смеси в аппарате,
V и G объемная и массовая производительности по этой смеси.
На кинетические закономерности процесса перемешивания по
уравнениям (г) , (д) или по каким-то другим соотношениям,
отвечающим иным моделям смешения, должны быть наложены
характеристики продольного перемешивания в смесительном ап
парате. Методы представления этих характеристик и операция их
наложения на кинетические закономерности технологических про
цессов (:щесь - смесительного процесса) изложены в гл.8.
В задачах эксплуатации будут получены конечные значения
сrк2, в задачах проектирования (при заданной сrк2) - необходимый
объем рабочей зоны смесителя V (или G) либо максимально до
пустимая производительность V (или G).
Затраты энергии на перемешивание. Проблема определения за
трат энергии (мощности) более или менее строго решается (с
привлечением некоторых экспериментально определяемых ко
эффициентов) для жидких и жидкообразных смесей - суспен
зий , эмульсий и т.п. Для смешения сыпучих материалов
(порошков) модели менее обоснованы, и здесь превалируют
эмпирические закономерности . Видимо, причина - в слабой
разработанности представлений о переносе импульса в сыпучих
средах, да еще для весьма сложных по конфигурации рабочих
органов и зон смешения.
-

440

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Ниже проблема затрат энергии на перемешивани е рассмат
ривается применительно к жидкостным системам.

Способы перемешивания
Наибольшее распространение в промышленности получили
следующие способы перемешивания:
- пневматическое перемешивание - барботаж газа или пара
через жидкую (жидкообразную) среду;
- циркуляционное перемешивание - многократное прока
чивание жидкости (газа) через рабочую зону с помощью насосов
или вентиляторов;
- механическое перемешивание - лопастными или иными
мешалками с вращательным (реже - поступательным) их дви
жением.
Кроме того, для перемешивания сред используют и ряд дру
гих приемов• : установка неподвижных турбулизаторов в потоке
среды, подлежащей перемешиванию; взаимодействие переме
шиваемых сред (инжекция, встречные струи) ; наложение пуль
саций и др.
S.3.2. Пневматическое перемешивание
Пневматическое перемешивание применяется в случае жид
костей с не очень высокой вязкостью. Принципиальная схема
пневматического перемешивания показана на рис. 5.27 ,а.

В нижней части сосуда / расположен барботер 4 с отверстиями 9 (часто 2-3 барботера параллельно) . Барботер представляет собой трубу с располо
женными по ее длине отверстиями, обычно - парными и обращенными вниз
(рис. 5 .27, б) во избежание их забивания в случае суспензий и загрязненных
жидкостей. Труба вводится в сосуд (емкость) через люк 5 и опирается на под
порку 2. В емкости находится подлежащая перемешиванию жидкостная систе
ма /. В трубу-барботер подается поток газа 11, который диспергируется в от
верстиях и выходит в жидкостную среду. В своем восходящем движении пузы
ри интенсивно перемешивают жидкость в вертикальном и горизонтальном
направлениях. Пройдя жидкостной слой, газ попадает в сепарационное про
странство, где в значительной мере освобождается от захваченных им капель
жидкости. Далее через брызгоулавливающее устройство 8 газ выводится из
сосуда по линии 7. Предусмотрены линии подачи (6) и отвода (3) жидкости
или жидкообразной смеси.
Возможны и другие схемы пневматического перемешивания"• , в частности:
используются схемы с эрлифтом и циркуляционными трубами; применяются
иные способы диспергирования газа.

Пневматическое перемешивание наиболее эффективно в слу
чае необходимости работы с агрессивными средами, когда другие
перемешивающие устройства (насосы , мешалки) быстро выхо-

' См. ( 1 , 5 , 9) . ·
•• См. ( 1 , 9, l S j .

44 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

rp

�

rщ:.;- J::
- 9
-

(/)

4

-�

- "

--

.г

б
Рис.5. 2 7.

Схема пневматического перемеwивания:

общая схема, 6 - картина барботажа;
1 - сосуд (емкость), 2 - подпорка, З - линия слива жидкости, 4 - барботер, 5 - люк,
6 - линия залива жидкости, 7 - линия отвода газа, 8 - брызrоуловитель, 9 - отверстия
барботера;
1 - ЖИДКОСТЬ, // - газ
о

-

дят из строя. В этом случае внуrреннюю поверхность емкости
защищают от коррозии (покрывают эмалью, гуммируют, реже изготовляют из специальных материалов) ; барботер изготовляют
из нержавеющей стали или других устойчивых к коррозии мате
риалов либо предусматривают частую замену барботеров - они
относительно дешевы и просты в изготовлении.
Достоинства способа - простота схемы, высокая интенсив
ность перемешивания. Недостатки - брызгоунос и сопут
ствующие ему потери ценной жИдкости; потери возможны и в
результате ее испарения в газовые пузыри , если жид кость обла
дает достаточно высокой летучестью. Нельзя также игнориро
вать возможную коррозию трубопроводов и аппаратуры унесен
ной ЖИд костью, если она химически агрессивна, а газ использу
ется в последующем технологическом процессе. На конец, необ
ходимо учитывать экологические аспекты, если газ не использу
ется и выбрасывается из емкости в атмосферу. Во всех этих слу
чаях может потребоваться установка специальных устройств для
улавливания паров - процесс становится заметно дороже. Удо
рожание пневматичес кого перемешивания происходит, когда
ж ид кость не допускает сопри косновения с кислородом воздух а ;
приходится з�менять дешевый воздух на более дорогой газ, хи
мически инертный по отношению к перемешиваемой жИдкости.
Разумеется , возможны технологические процессы, предусматри
вающие химичес кое взаимодействие какого-либо газового ком
понента с перемешиваемой жидкостью (например, кислорода в
окислительных процесса х ) ; в этих случ аях пневматическое пе
ремешивание является , ка к правило, высокоэффективным мето
дом конта кта жидкости и газа.

442

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Объемный расход газа на перемешивание V определяется не
обходимостью приемлемого качества перемешивания , т.е. (как
указано в разд.5 . 3 . 1 ) устанавливается эмпирически для каждого
конкретного процесса. Для ориентировочной оценки можно
принять, что на 1 м2 свободной поверхности жидкости требуется
объемный расход газа на уровне 0,0 1 - 0,02 м3/с.
Гидравлическое сопротивление системы Лр складывается из
сопротивлений:
- подводящих трубопроводов (с прямыми участками и
местными сопротивлениями) от дутьевого устройства (газодувки
и т. п.) до барботера;
- самого барботера, представляющего собой газопровод с
путевым расходом;
- гидростатического столба жидкости (более точно - га
зожидкостной системы; приближенно, с некоторым запасом, просто жидкости) ;
- отводящих трубопроводов, включая брызгоулавливающее
устройство и последующие линии.
Способы расчета этих сопротивлений рассмотрены (или
подходы к их расчету намечены) в разд.2 .3.
Затраты энерrии на перемешивание рассчитываются по из
вестным величинам V и Лр (либо по степени сжатия газа) , как
это было показано в гл .4. В частности , при небольших гидрав
лических сопротивлениях Лр , значительно уступающих абсо
лютным давлениям газа, мощность компрессора (газодувки,
вентилятора) определяется по фQрмуле (4. 3 1 ) :
N = VЛр '

где р - плотность газа; ri

-

"

КПД дуrьевого устройства.

Затраты энергии на пневматическое перемешивание обычно
заметно выше, нежели для других способов перемешивания.

S.3.3.

Циркуляционное перемешивание

Циркуляционное перемешивание осуществляется с помощью
насосов (как правило, центробежных либо пропеллерных• ) , рас
положенных вне или внутри объема перемешиваемой жидкооб
разной среды - жидкости, суспензии , эмульсии и т.п . В первом
случае циркуляция именуется внешней , во втором - внутренней.
5 . 28 , а.

Схема внешнего циркуляционного перемешивания предСтавлена на рис.
Жидкость, находяшаяся в сосуде 1, забирается внешним насосом 2 и

• О некоторых иных возможностях организации циркуляционного переме
шивания см. [ \ , 5 , 1 8, 23].
443

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

а
Рис.5.28.
/

о

-

б

Схема циркуляционноrо перемешивания (стрелками - жидкость):

внешнего, б - внуrреннеrо;
сосуд, 2 - перемешивающее устройство

возвращается в тот же рабочий объем в сосуде. Схема внутренней циркуляции
представлена на рис.5.28,6. Побудитель здесь чаще всеrо - сидящее на валу
рабочее колесо центробежного насоса без корпуса с двухсторонним (сверху и
снизу) всасыванием; электродвиrатель (на схеме не показан), приводящий в
движение вал с рабочим колесом, размещается на крышке сосуда. Жидкость
засасывается в рабочее колесо по оси и выбрасывается по его периферии, во
влекая в движение весь рабочий объем жидкости. В обоих вариантах циркуля
ционноrо перемешивания многократное прокачивание жидкостной среды через
рабочий объем приводит к выравниванию свойств этой среды в различных ero
точках.
Необходимая производительность насоса V определяется при
емлемым качеством перемешивания. Обычно эмпирически для
каждого конкретного процесса rстанавливается требуемая крат
ность циркуляции kц = VfV (м /с)/мз, показывающая, сколько
раз рабочий объем системы V должен смениться в единицу вре
мени, чтобы обеспечить заданное качество перемешивания. При
известном V и принятом по опытным рекомендациям ku легко
найти производительность насоса V = kuV и подобрать подхо
дящий насос (см. разд. 3 .5).

Следует только иметь в виду, что в случае внутренней циркуляции для ра
бочего колеса центробежного насоса без корпуса, коrда области всасывания и
нагнетания свободно сообщаются, характерно пониженное значение коэффи
циента подачи 'lv· В частности, для обычного в промышленной практике отно
шения диаметров рабочего колеса и сосуда на уровне 0,5 - 0,7 значение 'lv
0,4 - 0,5 - в отличие от центробежного насоса, снабженного корпусом, где
'lv близок к 1 .
=

=

Основная составляющая напора насоса Н
высота слоя жид
кости h над сечением всасывания (см. рис. 5.28). В случае
внешней циркуляции к этому еще добавляется гидравлическое
сопротивление трубопроводов.
MoUUtocть насоса N определяется по уже известным форму
лам
на основе производительности V и напора Н
(см.разд. 3 . 1 .4) .
-

444

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Характерная особенность используемых для циркуляционно
го перемешивания центробежных и пропеллерных насосов сильная зависимость мощности от частоты вращения: N - п3. В
то же время насосы этого типа не могут функционировать с
малыми числами оборотов, так как развиваемый ими напор
пропорционален п2 (см. разд. 3 .4. 1 ) , так что при снижении п
насос не обеспечит надлежащего напора. Поэтому приходится
поддерживать достаточно высокие частоты вращения п, что
приводит к весьма большим затратам энергии N. В случае пере
мешивания вязких жидкостей и густых суспензий затраты
энергии существенно возрастают (прежде всего из-за быстрого
увеличения требуемых кратностей циркуляции kц). Это приво
дит к заметному удорожанию циркуляционного перемешивания.
5.3.4. Перемешивание лопастными мешалками

Внутреннее циркуляционное перемешивание с помощью
пропеллерных насосов или рабочего колеса центробежных насо
сов, размещенных в объеме перемешиваемой среды, иначе клас
сифицируется как быстроходное механическое перемешивание. В
рамках такой классификации перемешивание лопастными мешал
ками относится к 111Хоходному механическому перемешиванию.
Лопастные мешалки работают с умеренной частотой враще
ния п, обычно - на один-два порядка ниже, чем упомянутые
насосы при циркуляционном перемешивании. Чаще всего п
находится в диапазоне 0,5 - 2 с- (30 - 1 20 мин- 1 ), окружные
скорости и - в диапазоне 1 -6 м/с. Это позволяет осуществить
процесс перемешивания даже весьма вязких жидкообразных
сред с приемлемыми затратами энергии.

2

� �:
�з� }i�з уз �з
••

"

•••

1

2

1
2
1

.

мешалки:

б

1

2

�
-w

а

Рис.5. 29. Лопастные

;

3

i

1

в

1

2

.
.

'

г

· простая лопасть (полулопасть), б - многолопастная мешалка,
якорного типа;
1 - стенки сосуда, 2 - лопасти, J - ось вала
а -

в,г -

мешал ки

445

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

w
,l,

°'°
1

2

D;D
1

�

сЬ П!П f
4

5

()

7

Рис.5.30. Вязкостные диапазоны
применения мешалок некоторых
типов:

1 - 7 - типы мешалок: / - якор
ная , 2 - пропеллерная, J - турбинная
с плоскими лопатками, 4 - лопастная,
5 - рамная , 6 - шнековая , 7 - лен
точная

Конфигурация лопастных
мешалок отличается боль
шим разнообразием;
некото•
1 а2
рые варианты их конструктивного оформления пока
10
заны на рис. 5.29.
В простейших вариантах это
одна лопасть (или полулопасть) рис. 5 .29,а, на практике - несколько лопастей в одном сечении (скажем, три
под утлом 60°), иногда и в разных сечениях - рис. 5.29, б. Часто используются
лопастные мешалки рамного и якорного типа - рис. 5.29, в, г. В ряде случаев
мешалки повторяют форму сосуда-смесителя, особенно - его днища (рис. 5.29,
г) , дабы воспрепятствовать образованию застойных зон, а при наличии в пере
мешиваемой среде твердых частиц - их выпадению на стенки и дно сосуда.
Оrношение диаметров мешалки и сосуда редко превышает 0,7 - 0,8.
Выбор мешалки той или иной конфигурации в значительной
мере определяется вязкостью перемешиваемой среды. Рекомен
дации к выбору наиболее распространенных мешалок для раз
личных диапазонов динамических вязкостей сред представлены
на рис. 5.30. При этом в случае неньютоновских жидкостей речь
идет о кажущихся вязкостях, в случае многофазных сред - о
расчетной вязкости таких сред.

11

Движение жидкости
в окрестности вращающейся лопасти ••

В ходе перемешивания лопастной мешалкой радиусом Rм в
рабочем объеме сосуда-смесителя возникает трехмерное течение
перемешиваемой среды, которое в цилиндрических координатах
определяется
(рис.5.3 1 )
составляющими
результирующей
(абсолютной) скорости w: радиальной w,., осевой wz и окружной
(тангенциальной) w"', а также характерными углами вектора аб
солютной скорости w с вертикальной плоскостью (а) и с гори
зонтальной плоскостью (13).
Отдельные составляющие скорости w рассчитываются из пря-

' Конструкции лопастных мешалок подробно представлены в ( 1 , 5, 9. 1 4,
1 7, 20, 23).
•• В анализе этого вопроса и написании раздела принимал участие доц. Б.Г.
Варфоломеев.
446

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис.5.31.

щие;

/

Абсолюmая скорость жидкости в сечении мешалки и ее составляю

- ось вращения, 2 - лопасть, З - окружность, описываемая лопастью

моугольного параллелепипеда скоростей :

w =

'

w

�1

2
+ tg a

(�
2 '
+ tg 13

.

w=
tg=�==
Wz = -;:::==

�1 + tg 2 a + tg 2 �

wtga

(z)

разумеется, w2 = w,2 + w.,,2 + wz2 .
Картина движения жидкостной среды, перемешиваемой ло
пастными мешалками , отличается большой сложностью - раз
личным направлением скоростей в разных точках рабочей зоны,
ярко или слабо выраженными областями циркуляции :
- радиальная составляющая скорости w, направлена от оси
вращения к стенкам сосуда-смесителя в непосредственной бли
зости к лопасти-мешалке и в обратном направлении (от стенки
к оси) на удалении (вверх и вниз) от плоскости мешалки;
- осевая составляющая скорости wz направлена от плоскости
мешалки вверх и вниз - вблизи стенки сосуда; в остальном
объеме рабочей зоны существуют достаточно устойчивые цирку
ляционные потоки , к онфигурация к оторых зависит от формы
лопасти и условий работы мешалки;
- окружная (тангенциальная) составляющая с корости wчi
имеет сходные профили над и под мешалкой (по ка не сказы
вается влияние дна сосуда и свободной поверхности жидкости) .
В сечении лопасти в непосредственной бJiизости к ней при r $
$ Rм жидкость движется со скоростью вращающейся лопасти; в
остальной зоне, ограниченной радиусом r < Rм в этом же сече
нии (между лопастями , если их нес к олько), она движется при447

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

мерно с той же окружной скоростью, образуя достаточно ста
бильную вихревую зону. Важно: вихревая зона ограничена
(приближенно) радиусом мешалки Rм; за пределами этой зоны
вихрь вырождается , окружная скорость затухает по радиальной
координате из-за возрастающего влияния стенок сосуда.
Сравнение величин wr, wz и wЧ> показывает, что окружные
составляющие скорости wЧ> на порядок и более превышают со
ставляющие wr и wz. Это обстоятельство позволяет упростить
математическое описание процесса перемешивания , ограни
чившись для рассмотрения только одной составляющей скорос
ти wЧ> в систе м е уравнений Навье-Стокса.
Для сокращения записи в последующих преобразованиях
обозначим тангенциальную составляющую (т.е. окружную ско
рость) w..!e = и. Тогда в цилиндрических координатах уравнение
Навье-Lтокса ( 1 .25) для окружной скорости и имеет вид
_1_ др
pr дq>

=

[

ди
Р <р
дt

+ ) д 2 и + .!_ ди
1 дr 2

r дr

+

+

wr

ди
дr

1 д2 и
__
r 2 дq> 2

+
+

� ди

r дq>

+

� дw

иwr
r
+

r

r 2 дq>

+

д2 и
дz 2

wz

_

ди
дz

]

_!!__)
r2

+

·

( 1 .25)

Применительно к рассматриваемому случаю это уравнение
существенно упрощается:
- речь идет о стационарном движении лопасти и перемеши
ваемой жидкости , поэтому ди/дt = О;
- вдоль угловой координаты q> не действует никакая внеш
няя массовая сила, так что РЧ> = О;
- членами уравнения, содержащи м и радиальную и осевую
составляющие скорости , можно пренебречь вследствие малости
этих составляющих в сравнении с тангенциальной : wr, wz < < wЧ> ;
- окружное движение жидкости полагается осесимметричным,
поэтому производные от различных составляющих скоростей по
координате q> равны нулю;
- рассматривается плоское движение жидкости , поэтому все
производные по оси z также равны нулю.
В результате уравнение ( 1 .25) для анализируемого плоского
тангенциал ьного движения жидкости принимает вид
d 2 u 1 du
.
( 5 . 39)
- и _
- О
+ r dr r 2
dr 2
поскольку скорость и из меняется только с одной независимой
переменной r, то частные производные заменены здесь обыкно
венными.
--

-

-

,

448

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Приведенной записи Идентична более удобная для последую
щего решения:
� d(ur) = О .
(5.39а)
dr r dr

[.!. ]

·

В тождественности выражений (5.39) и (5.39а) леrко убедиться, продиффе
ренцировав последнее из них:
d( ur )
d( r) d
d
r u + и . 1 ; .!_ u = u + � ;
dr
dr
r dr
dr r
2
d u + .!_ d u � !
� ! d( ur) = � d u + �
r dr r 2
dr dr r
dr r dr
dr 2

[

] [

]

=

=

_

Проанализируем изменение окружной скорости и в горизон
тальном сечении лопасти (мешалки ) . При этом среду будем счи 
тать изотропной, е е свойства - н е зависящими о т радиальной
координаты. Разделяя переменные в (5.39а) и интегрируя первый раз, имеем
1 d( ur)
- -- = С ' = const .
r dr
Повторно разделяем переменные и интегрируем:
С2 ,
d(ur) = Cidr ; ur = C1 r 2
откуда получаем общее решение:
С2
(е)
и = c, r + -

+

r

причем С1 = Cjl.
Постоянные интегрирования С1 и С2 найдем с помощью гра
ничных условий.
Для вихревой зоны (r :S Rм): на оси потока (r = О ) окружная
скорость и = О; тогда по (е)

О=О+ �
Г -+ 0 '
что возможно лишь при С2 =
зоны

О. Таким образом, для вихревой
(ж)

Поскольку рассматривается установившееся тангенциальное
движение с неизменной скоростью u (r) по угловой координате
q>, то очевИдно, что С1 представляет собой угловую скорость ro
вращения мешалки, с которой перемещаются слои жИдкости ,
прилегающие к лопасти . Окончательно для вихревой зоны
и = ror .

(5.40)
449

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Заметим, что принятые здесь допущения о полной стабиль
ности вихревого движения жидкости и об отсутствии влияния
стенок сосуда в этой зоне должны привести к следующему:
- к некоторому завышению расчетной скорости и в сравне
нии с реальной ;
- к реальному уменьшению радиуса зоны вихря r8 в сравне
нии с радиусом мешалки Rм .
О�-ношение Ге /R" < 1 оценивается в зависимости от значения критерия
Рейнольдса для вращательного движения Reu пd•.2р/µ, где d" = 2R" - диа
метр мешалки, а произведение nd" пропорционально окружной скорости на
наружной кромке лопасти и" = roR,.. Для оценки границ вихревой области
предлагаются эмпирические рекомендации , например - формула
Reu
г8
(з)
R " = 1 03 + l,6Re u
из которой следует, что максимальное отношение Ге /R", реализуемое при вы
соких значениях Rец, составляет 1/1 ,6 .., 0,62; значит, область действия законо
мерности (5 .40) вихревого движения ограничена примерно радиусом Ге < 0,6R" .
Заметим, что на практике значения Reu обычно находятся на уровне 1 04 1 os.
"'

-

радиус аппарата, со
Для зоны вне вихря (rв < r < Ra, rде Ra
суда) влиянием стенок сосуда пренебречь нельзя, и в общем
решении (е) постоянные интегрирования С1 и С2 отыскиваются
с помощью других граничных условий.
С одной стороны, на стенках сосуда (r = Ra) в соответствии с
концепцией прилипания и = О, так что согласно (е)
-

О=

C1 Ra

откуда

+ Rа '
С2

(и)

С другой стороны, на координате r = r8 окружная скорость и
в соответствии с (5.40) должна быть равна ro rв; тоrда по (е)
ro rв

=

C1 r8

+

С2

'в
Из последнего выражения
с,

Отсюда по (и)

=

_

=

ro_r=в- =

_
_

2
R
� - r
в
гв

С1 rв

_

- Cl R

'в
ro гJ

}

____

2
Rа _ ,в2

(к)

(л)

(м)
450

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Подставив значения С1 и С2 по (л) и (м) в общее решение
(е) , получим закономерность изменения окружной скорости по
радиальной координате для области за пределами вихря:

и=

rori

Rа2 - rв2

( R;r г) .

(5.4 1 )

_

Из-за некоторого завышения расчетного по ( 5.40) значения
граничной окружной скорости жидкости и на координате r8
значения и в окрестности лопасти также могут оказаться
несколько преувеличенными в сравнении с реальными .
В некоторых учебниках и монографиях• анализ для скорости и за пределами
зоны вихря (тоже для изотропной среды) проводят вне связи с граничным
условием и = О на стенках сосуда и приходят к выражению
(н)
u = ro r,2 /r .
не отвечаюшемv �нцепции прилипания: согласно (н) получается, что на стен
ках сосуда и = ro r,2 / R, > О.
Решения (5.40) и (5.4 1 ) удобно представить в обобщенной
форме, введя безразмерные координату r/Ra и окружную ско
рость И = u/ror8• Тогда
для вихревой области :

r = О,

-----

для области вне вихря:
r
Ra
и = r
Ra .
Ra
Гв
Ra
Гв

r/Ra = О,

(5.40а)

r = r, r/Ra = r/Ra, И = l ;
r = Г8 , r/Ra = rв/R8, И = l ;
r = R8,

Из приведенных соотношений
следует, что тангенциальное течение
жидкости , перемешиваемой лопаст
ными мешалками, в сечении лопас
ти яRЛЯется автомодельным в рамках
группы подобных течений с одина
ковыми гвfR3 • Иллюстрация завиРис. 5.32. Окружные скорости в сечении
мешалки в обобщенных координатах:

-

И = О;

1
зависимость типа (н), 2 - зависимости
(5.40) и (5.4 1 )

(5.4 l a)

r/Ra = l , И = О.
и

1

0,8
0,6
0,4
0,2

о

0,2

О.4

0,6

0,8

1

r/R a

• См. (6, 1 7 , 20) .

45 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Ra

Ra

симостей (5 .40а), (5.4 l a) в обобщенных координатах для r8/ =
= 0,3 и rвf = 0,4 представлена на рис. 5.32. Там же в целях
сравнения приведена зависимость (н) для r8/ = 0,4.
Более обстоятельный анализ, точнее отражающий реальную
картину движения жидкости в сечении лопатки, должен учиты
вать неизотропность перемешиваемой среды, прежде всего (в тер
минах турбулентного течения - см. ра:щ. 2.2.5) - изменение тур
булентной вязкости по радиусу в области за пределами вихря.

Ra

ЦенmрШlьная воронка

При вращении мешалки, например лопастной, вблизи оси
сосуда-смесителя уровень жидкости понижается (образуется
воронка), у стенок - повышается. Причина этого явления детально
рассмотрена в относящемся к гидростатике ра:щ.2. 1 .3 при изучении
поведения жидкости в вертикальном вращающемся сосуде: форма
свободной поверхности представляет собой параболоид вращения,
описываемый общим уравнением (е) в указанном ра:щеле:

� =

(J) r02 .
+ 2g
2

Z•

Однако для рассматриваемого случая это уравнение справед
ливо (и то приближенно) лишь в области вихревого движения,
поскольку получено оно для постоянной угловой скорости ro во
всем диапазоне О s r s R . За пределами вихревой зоны угловая
скорость (обозначим ее ro' ) понижается с ростом r, причем закон
этого понижения можно получить исходя из известной связи и =
= ro 'r на основе , формулы (5.4 1 ) :
ro'

n2

.-- -..7'1'("., 1" 3

= иr

ro ri
Rа2 ,в2
_

( R, }2 ) .
_

1

(о)

Задача о свободной поверхности в
этой области - весьма сложна· .
Укажем лишь, что она не принадле
жит к задачам гидростатики , так как
ro' = ro '(r), т.е. налицо взаимные пе
ремещения слоев жидкости , вра
щающихся с переменной по ради
альной координате r угловой ско
ростью ro'.

- сосуд, 2 - вал мешалки, J - лопасть

Рис. 5.33.
1

Центральная воронка:

• Теория uентральной воронки представлена в (23) .
452

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Типичная форма свободной поверхности в аппарате с пря
моугольной лопастной мешалкой демонстрируется на рис.5.33,
причем п 1 > п 1 .
Наличие центральной воронки вызывает ряд неудобств при
проведении технологических процессов: неодинаковые уровни
свободной поверхности в различных ее точках, возможность
обнажения дна сосуда и перехлеста жидкости через его боковые
стенки, уменьшение интенсивности перемешивания и т.п . По
этому при перемешивании нередко используют устройства
(см.ниже) , препятствующие развитию центральной воронки.

Затраты энергии на перемешивание лопастными мешалками
В основе анализа - представления о внешнем обтекании те
ла, изложенные в разд. 2 .7.4. При обтекании тела потоком
(вообще при перемещении тела относительно жидкости) возни
кает местное сопротивление, сила которого в случае тела произ
вольной формы равна
(п)
где w
011tocиrem.нu
плотность жидкости, !;
-

скорое.... тела и жидкости (на удалении
коэффицне�rr лобо.оrо сопротиuенИJI.

от тела),

р

-

В формуле ( у) упомянутого выше раздела f = 1t d2/4 - попе
речное сечение сферического зерна. В более общем случае тела
произвольной формы f - площадь проекции тела на плоскость,
нормальную к направлению его движения в жидкости (рис.
5.34,а); f называют площадью миделева сечения.
-

б

а
Рис.5.34. К

выводу общей формулы

расчета мощности на валу мешалки:

- ПОС'J)'Пательное движение тела в ЖИдКОСТН и площадь мнделева сечен ия,
воду формулы (5.4 2 );
1 - вал мешалки, 2 - лопасть, 3 - несущий стержень
а

для

б

- к вы

453

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Вращательное движение лопасти. В настоящем разделе оно
рассматривается в отличие от поступательного, описываемого
формулой (п). Поэтому при анализе вращения лопасти в этой
формуле поступательная скорость w должна быть заменена на
окружную скорость и.
В основе расчета необходимой мощности на валу мешалки
лежат затраты энергии на преодоление силы сопротивления Pn .
НаЙдем сначала общую формулу для определения требуемой
мощности N.
Пусть полулопасть 2 произвольной (но известной) формы
(рис. 5 . 34,6) вращается около вертикальной оси 1 с постоянной
угловой скоростью ro. Протяженность полулопасти по радиаль
ной координате ограничена радиусами R1 и R2 (способ крепле
ния полулопасти на валу здесь роли не играет; пусть это, на
пример, тонкий стержень З, практически не оказывающий со
противления движению полулопасти в жидкости) . В случае по
ступательного движения использование в ходе анализа посто
янной скорости w затруднений не вызывает; в случае враща
тельного движения окружная скорость изменяется с радиусом.
Поэтому применительно к вращающейся лопасти анализ возмо
жен лишь для элементарной площадки d/, заключенной между
радиусами r и r + dr, где скорость и = ro r, с последующим инте
грированием в диапазоне изменения радиальной координаты.
Итак, элементарная сила сопротивления движению беско
нечно малой площадки d/ составляет
(1) 2 Г 2
U2
(р)
d Pn = � - p d/ = �
p d/ .
2
2
--

При этом d/ следует представить как произведение zdr, где
локальный вертикальный размер лопасти z в общем случае из
меняется (см. рис. 5 . 34,6) с радиальной координатой: z = z(r) .
Мощность есть работа в единицу времени, а работа равна
произведению силы на путь; следовательно, мощность есть про
изведение силы на путь в единицу времени, т.е. на скорость.
Применительно к рассматриваемой элементарной силе dPn речь
идет об элементарной мощности:

dN = (dРп)и =
или

(1) 2 Г 2

l; -- p z(dr)ror,
2

(1) 3

dN = l; - p z r3dr .
2
454

(с)

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Интеrрируя это выражение, получаем для самого общего случая:

N=

w зр

-

2

R1
J � z r'dr .
R1

(5 .42)

Важно: последнее выражение справедливо, когда движение
лопасти относительно жидкости характеризуется угловой ско
ростью ro. Такая ситуация наблюдалась бы при движении лопас
ти в неподвижной жидкости (если строго - то в неограничен
ном ее объеме), например, в начальный (пусковой) период вре
мени. Но в ходе перемешивания жидкость постепенно вовлека
ется лопастью во вращательное движение, и реальная относи
тельная угловая скорость лопасти станет меньше - в результате
уменьшится и потребляемая мощность N. Здесь это плохо: ведь
от затрат энергии прямо зависит качество перемешивания; при
снижении N оно тоже уменьшится.
Чтобы воспрепятствовать заметному падению качества пере
мешивания, надо не допустить значительного уменьшения ре
альной относительной угловой скорости. С этой целью на стен
ках сосуда вдоль его образующей (с небольшим зазором - во
избежание застойных зон) перпендикулярно к стенке устана
вливают две-четыре вертикальные отражательные пластины
(перегородки) шириной порядка 0,2R. Они существенно тормо
зят движение периферийных масс жидкости, что сохраняет до
статочно высокие значения угловой скорости лопасти относи
тельно жидкости в реальных условиях работы мешалки . Заме
тим: установка продольных пластин одновременно препятствует
и развитию центральной воронки при вращении лопасти.
Для вычисления интеrрала в (5.42) необходимо располагать
значением коэффициента �· Строго говоря, он различен для
разных точек лопасти, так как они движутся с разными окруж
ными скоростями и. Его среднее значение �ер обычно выносят
(соответственно теореме о среднем) за знак интеrрала и пред
ставляют в виде функции от критерия Reu, причем вид функции
зависит от типа и формы перемешивающего устройства. В наи
более интересном для практики диапазоне Reu >'"' 1 04 величина
� меняется чаще всего мало (что отвечает верхнему автомодель
ному по Reu режиму) . Здесь � может быть просто вынесен за
знак интеrрала. В обоих случаях (� = �ер и � = const) выражение
i:
(5.42) принимает вид
3

N = � RJ2z r'dr .
2

(5.42а)

R1

Последующий анализ проводится для формулы (5 .42а) ; зна
чение � полагается постоянным и известным.
455

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

�
±-R==I
а
Рис.5.35.

<j_)

� ьRJR J
6

<;?.

<;..:>

7

6

з

4

�
� f�:
1 2 3'
2

в

·

г

К расчету мощности на валу лопастных мешалок простой формы:

- сплошная полулопасть, б - сплошная лопасть, в - ОJl>аничснная полулопасть,
полулопасть фасонной формы (точки 1-9 относsm:я к кон'l)'ру мешалки)
а

z

-

Для вычисления интеграла необходимо знать конфигурацию
т.е. зависимость z( r)
Лопасти простой к:онфиrурации. Простейшей является мешал
ка, имеющая форму сплошной прямоугольной полулопасти, при
мыкающей к оси вращения (рис. 5.35,а) . Пусть ее ширина равна
Ь, радиус - R. Для получения конкретного выражения мощ
ности N в (5.42а) подставим z = Ь = const, R1 = О, R2 = R. Тогда
" 3 Ь
" 3 R
Nпл = � b f r3 dr = � � (5 .43)

лопасти,

.

2

о

8

Из полученного выражения видно, что N сильно зависит от
скорости вращения мешалки (ro , п) и еще сильнее - от ее ради
ального размера R. Ясно также, что для получения заданной
мощности N, обеспечивающей необходимое качество переме
шивания , технолог (конструктор) имеет возможность варьиро
вать значения п и R.
В случае сплошной полной прямоугольной лопасти (рис. 5.35,6)
мощность N получается простым удвоением величины, вычис
ляемой по формуле (5.43), так как работают две полулопасти :

�ro 3 p b � .
2Nпл =
(5 .44)
4
В литературе вместо !; чаще используют коэффициент Кн. формируемый на
базе выражений типа (5.44), но с заменой R на d" = 2R и выражением ширины
лопасти в виде Ь = 1j1d" , а угловой скорости - в виде (J) = 211п. Тогда (5.44)
перепишется в виде
Nл

=

(5.44а)
где Кн • !;,113'1'/1 6 - коэффициент мощности.
Использование безразмерного коэффициента Кн (как и !;) вполне отвечает
теории гидродинамического подобия , изложенной в разд.2.2.3; соответственно
приведенным там выражениям (н) и (о)
Eu = j{Re, Fr) или Eu = j{Re) .

456

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис.5.36. Типичная
= / (Reu) :

зависимость

Кн =

1 - без отражательных перегородок в
сосуде, 2 - с отражательными перегород
ками в сосуде

Применительно к вращательному
движению лопасти при перемешива
нии критерии Эйлера, Рейн0ЛW1са и
Фруда преобразуются соответсmенно:
Eu " Лр/р w2 --.. Euu " Лр/рп2 d" 2 ;
Re wdp/µ --.. Reu пd"2 р/µ ;
•

•

Fr "' w2/gd --.. Fru " n 2d" /g .

Следовательно, качественно в общем случае дQЛJКНа бьпъ правомерна запись
Euu = j{ Reu, Fru) .

В процессах перемешивания соотношение сил инерции и тяжести (т.е. Fru)
обычно учитывают только при наличии центральной воронки. Поэтому в
большинстве случаев вполне достаточно зависимости
Euu = j{Reu) .

Связь критерия Euu и коэффициента мощности Кн установим из следую
щих соображений. Мешалка, перемещающая жидкообразную среду, представ
ляет собой своеобразный насос. Поэтому для нее справедливо (см.гл.3) соот
ношение N - 1/}/ : fWt.p. Если теперь учесть принятые выше связи, то f - dw2 и
2
з
w --.. и - n d", значит N - dw (nd")Лp, откуда Лр - N/пd" . После подстановки
полученного сооmошения для Лр в Euu придем к модифицированному
критерию Эйлера для рассматриваемого процесса перемешивания:
-

Euu

,.._.

N
3 5 " Кн .

-

рп d"

Таким образом, коэффициент мощности представляет собой одно из кон
кретных выражений критерия Эйлера для вращательного движения.
Для практического использования Кн выражают• - графически и(или)
аналитически - в виде зависимостей от Reu, а если необходимо - то и от Fru.
Типичные зависимости Кн = j{ Reu) приведены на рис. 5.36 для мешалки без
отражательных перегородок в сосуде (кривая /) и при их наличии (кривая Z). В
ламинарной области (малые Reu) кривые располагаются близко; их небольшое
смещение обусловлено несколько меньшей относительной скоростью лопасти и
жидкости в отсутствие отражательных перегородок: реальные значения относи
тельной скорости (а значит, и Reu) эдесь будут меньше, потому и Кн
несколько больше.
Автомодельный режим (Кн "' const) при наличии перегородок наступает при
Reu > 1 03 - приближенно можно считать, что это соответствует движению
лопасти в неподвижной жидкости. При отсутствии перегородок и высоких Reu
жидкость вовлекается в интенсивное вращательное движение, и реальная отно
сительная скорость (а значит, и Reu> ° заметно меньше расчетной для неподвиж
ной жидкости. Здесь автомодельный режим наступает при значительно боль
ших расчетных значениях Reu - на уровне 1 0 4 и выше. На значения Кн в этом
случае оказывает влияние и образование центральной воронки, т.е. высота
• Подробные сведения о зависимостях
ских мешалок см. [ \ , 5 , 9, 14, 20, 23).

Кн

от Reu для различных механиче

457

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

уровня жидкости над лопастью; поэтому в зависимостях дЛЯ Кн появляется и
критерий Fru.
Если прямоугольная полулопасть ограничена радиусами R1 и R1
(рис. 5.35,в), то интеграл берется в пределах, обозначенных в (5.42):

з
N'1 111= � ro p b (R24 - R14) .
8

(5 .45)

Тот .же результат получается, если из мощности для сплош
ной прямоугольной полулопасти Nпл радиусом R1 = R вычесть
незатрачиваемую мощность NOnл для условной полулопасти ра
диусом R 1 :
N'пл
Прием сложения и вычитания мощностей фрагментов лопасти
позволяет оценить мощность на валу лопастной мешалЮf и не
столь простой конфигурации.
Например, площадь / полулопасти якорного типа, показанной на рис.
5.35,г, может быть разбита на составные части несколькими способами: / = ./( 1 2-3-8- 1 ) + ./(3-4-6-7-3) или / = ./( 1 -2-4-5- 1 ) + ./(8-5-6-7-8); в этих случаях резуль
тирующая мощность N палучается суммированием мощностей для составляющих
площадок палулопастей. Тот же результат получится, если из мощности для пло
щадки ..1{9-2-4-6-9) вычесть мощность нефунхционирующей площадки ..1{9- 1 -8-7-9).

Нужно только оговорить, что использование приема сложе
ния (вычитания) мощностей для фрагментов лопасти предполагает
неизменность � для различных фрагментов и лопасти в целом.
Лопасти сложной конфигурации. Здесь рассматриваются ло
пасти с изменяющимся по радиусу r вертикальным размером
z( r) = var.
Пусть имеется сплошная полукруглая лопасть радиусом R
(рис.5.37 ,а), например - повторяющая форму сферического
днища сосуда. С целью использования формулы (5.42а) лопасть
удобно рассматривать как две полулопасти; тогда R1 = О , R1 = R и
З R
i:
N = � 2 J z r'dr .
(т)

2

о

Необходимый для нахождения интеграла закон изменения z
по r установим из теоремы Пифагора; на текущей радиальной
координате r

z2 +

,:Z

=

R2 и z =

JR 2 - r2

(у)

Подставим в (т) это значение z и возьмем интеграл
I nt =

458

2j�R2 - r2 r'dr .
о

(ф)

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

б

а

в

расчету мощности на валу лопастных мешалок сложной формы:
- сплошная
полукруглая лопасть, б
полукруглая якорная лопасть,
якорная ло 

Рис. 5.37. К
а

Применим подстановку:

тогда

/1

-

пасть фасонной формы

-

s = R2 - r 2 ,

(х)

ds = -21dr. Перепишем (ф) в форме, удобной дЛЯ используемой подстановки:

R( R2 - r 2 ) 1 / 2 (

Int = J

-

r 2 ) (-2rdr) .

(ц)

о
=
Чтобы перейти к новой переменной выразим из (х) величину
Кроме того, при переходе к изменятся пределы интегрирования . соответ
ственно (х):
вместо = О будет =
вместо = будет = О .
Теперь интеграл (u) запишется в виде
l nt = J

о

-r 2 s - R2.

s,

s

s R2,
s

r R
r

s 112 (s - R2)ds = J (s 312 ds - R 2 s 1 12 ds) .
о

R2
Ri
Интегрируем почленно, предварительно поменяв местами пределы интегрирования и знак в скобке:
R2
R2 4
2
2
(ч)
J
3
5
о
15
о

( R2s112 ds - sз 12 ds) = - R2s з 1 2 - -ss 12 1 = - R s ·

�ro23p �1 5 Rs .

Окончательно, с множителем перед интегралом в (т) :

N=

(5.46)

На практике значительно чаще используются не сплошные, а
(рис. 5.37, б) с характерными ради
усами
и
Здесь также можно было бы найти закон измене
ния z(r) и прямо выполнить операцию интегрирования. Но
проще решить задачу по разности, вычитая из мощности
(для
сплошной лопасти радиусом
незатрачиваемую мощность
(для сплошной лопасти радиусом

R1 R2.

якорные полукруглые лопасти

R2 )

R 1 ):

�rо з р 4 R s R s ) .
N = N2. - N1 = 2- 15 ( 2 - 1

N2

N1

(5.47)
459

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Если лопасть имеет фасонную форму, показанную на рис.
5.37 ,в, то мощность на валу мешалки тоже может быть рассчи
тана по разности - с использованием формул (5.44) и (5.46):

)

(

ro 3 bR� - � s .
N= ; p
R
2
15
2

(5.48)

Аналогичный подход позволяет иногда рассчитать затраты
энергии на перемешивание лопастями весьма сложной формы.
5 .3.5. О перемешивании паст и сыпучих материалов
Смешение пастообразных (тестообразных) и сыпучих материалов широко
используется в химической и близких отраслях промышленности. Процесс
смешения проводится периодически (стадии заrрузки материала, перемешивания
и выrрузки) или непрерывно. В ряде случаев смешение совмещают с измельче
нием твердых компонентов. Конструкции смесителей отличаются широким
разнообразием; подробно они описаны в специальной литературе' и весьма
скупо - в учебной. Корпус смесителя может бьпъ подвижным и неподвижным; в
последНем случае перемешивание осуществляется подвижными рабочими органами,
перемещающимися внутри корпуса.
В качестве примера упомянем роторнwй смескrем., представляющий собой
горизонтальный (иноrда несколько наклоненный) барабан, внутри которого с
одинаковыми или разными скоростями в противоположных направлениях (по
и против часовой стрелки) вращается пара роторов на горизонтально располо
женных валах. На рис.5.38 показаны роторы различной формы.
Расчет смесителей для паст и сыпучих материалов (качество и время пере
мешивания, параметры работы, расходы энергии) в основном базируется на
эмпирических рекомендациях, представляемых в виде таблиц, реже - формул.

-

Рис.5.38.

а

б

-

-

г

Лопасти роторов для смешения паст и сыпучих материалов:

лопасть типа "рыбий хвост", б
нnя лопасть
а

в

• См. [ 1 4, 20, 2 ) .
3
460

лопасть типа Z,

t1

лопасть типа L,

г

-

спираль

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

5.4. ДИСПЕРГ ИРОВАН ИЕ ЖИДКОСТЕ Й И ГАЗОВ

Диспергирование в системах жидкость-жидкость, газ
жидкость применяется для создания развитых межфазных по
верхностей F, обеспечивающих высокую интенсивность тепло- и
массообменных процессов. В этом случае в пропускной способ
ности kF поверхностной стадии процесса переноса прежде всего
существенно увеличивается F; кроме того, диспергирование
часто сопровождается также повышением коэффициента тепло
или массопередачи k. Для указанных выше дисперсных систем
размер капель (пузырьков) , их распределение по размерам и
м ежфазная поверхность являются важными технологическими
факторами при организации процессов переноса и расчете теп
ло- и массообменных аппаратов.
Диаметр капель (пузырьков) D связан с удельной межфазной
поверхностью а (м2/м3 ) и объемной долей дисперсной фазы ф
[ (мЗ дисперсной фазы)/(мЗ объема системы)] . Эту связь можно
выявить из следующих соображений, например, для системы
жидкость-жидкость. Заменим неодинаковые по размерам кап
ли, находящиеся в 1 мЗ эмульсии, на п шарообразных капель с
теми же суммарной поверхностью и объемом; тогда средний об"Ь
емно - поверхностный диаметр таких капель D3 2 определяется со
отношениями

а = п(п D32 )
1 м

и

п(п D 3 / 6)
=
ф
1 м3

Выражая отсюда D3 и JJl, получим расчетную формулу для Dз2 :
откуда

-

!!}_2
D

=

Dз 2

а-

п

=

п

/

п

( 6Ф) (!!_п ) = 6аф ,

6ф = 6(1 -D31
D

з2

&)

,

(а)

где t: объемная доля сплошной (иначе - дисперсионной) среды, т.е. пороэ
ность системы.
Выражение (а) тождественно формуле (2.64) . Оно показы
вает, что удельную межфазную поверхность можно увеличивать
как пугем повышения объемной доли дисперсной фазы
(задержки) ф, так и уменьшением диаметра Dз 2 частиц (капель) в
гетерогенной (дисперсной) системе либо одновременным соот
ветствующим изменением ф и D3 2 . Отметим, что величина ф
определяется конкретным гидродинамическим режимом тепло
массообменного аппарата; подходы к ее расчету будуr рассмот
рены в дальнейшем.

46 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Диспергирование жидкостей и газов осущестмяют различ
ными способами • . Среди них: механическое диспергирование
(мешалки , вращающиеся диски); капельное и струйное (через
отверстия и сопла); потоком среды (эжекционные устройства) и
др. Некоторые из указанных способов рассмотрены ниже.
5.4. 1 . Механическое диспергирование

Диспергирование с помощью мешалок. В случае диспергирова
ния с помощью мешалок или иных механических устройств в
потоке сплошной плотностью Ре среды возникают турбулентные
пульсации скорости. Они обусловливают появление разности
динамических напоров Лр = (w 1 2 - w2 2 ) Pc /2 = w 2 Рс /2, где w 1 ,
w2 - скорости сплошной среды на противоположных концах
капли. Отношение силы результирующего динамического напо
ра, стремящегося деформировать и разорвать каплю диаметром
D, к силе поверхностного натяжения, оказывающей обратное
воздействие (т.е. направленной на сохранение капли) , оцени
вается критерием Вебера

We

_

w 2 pcD

Ом
где cr" - 1tоэффициеап поаерхнОС'Пlоrо наТ11ЖеНИJ1 на границе капли и сплошной
среды.
Повышение критерия We приводит к увеличению деформа
ции капли, и при достижении его критического значения (на
уровне We "" 1 2) капля разрывается. Следовательно при прочих
равных условиях разрыв капли определяется величиной w 2 , в
свою очередь зависящей от масштаба турбулентных пульсаций .
Если этот масштаб (обозначим его /0 ) больше диаметра капли D,
то эти крупные вихри перемещают каплю без ее разрушения.
Дробление капель наблюдается, когда масштаб мелких вихрей lп <
< D. Параметр w 2 , согласно теории локальной изотропной тур
булентности ·· , для диапазона /0 � D определяется соотношением
(б)
W - (е/п) l/З '
где е - диссипация (рассеяние) энергии в единице массы сплошной среды.

Для практического использования соотношения (б) диссипа
цию энергии выражают через мощность N, подводимую кон• Подробнее о дисперrирующих устройствах и методах их расчета см. ( 1 , 3,
1 1 , 1 4) .
• • См. ( 10, 1 2 1 .

462

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

заключенной

кретным диспергатором к массе среды,
еме У :

е

=

_!i_ .

в объ
(в)

РеУ

Величину ln полагают пропорциональной диаметру капли D.
С приведенными допущениями имеем из (б) и (в)

где

С1

- ( ND )l / З

W = C 1 --

-

РеУ

'

коэффициент пропорциональности.
Для стабилизированного режима диспергирования (устано
вившиеся скорости дробления и коалесценции капель) крите
рий Вебера имеет некое постоянное значение С2 :
e
W

откуда

..,

( ND )2 / 3

;;;; 2 pe D = с
1
0м

D=

Сз

Ре- У

0,6
Ом

PeD

0м

( N / у )О,4 Р·�, 2

'

=

С2 ,
(5.49)

причем константа Сз включает в себя постоянные С1 и С2 .
Из (5.49) следует, что размер образующихся капель уменьшается
с падением межфазного поверхностного натяжения сrм и ростом
плотности сплошной среды Ре, а также с увеличением подводимой
на диспергирование удельной мощности N/V (Вm/мЗ) .
Теория изотропной локальной турбулентности качественно
правильно отражает влияние величин ' ( N/V), сrм , Ре· Но по этой
теории при диспергировании должны получаться капли одинакового
размера D. Однако эксперимент обнаруживает распределение капель
по размерам. Эrо обусловлено рядом причин; среди них:
- капли находятся в потоке под действием вихря разное
время, подчас недостаточное для установления равновесного
размера D, отвечающего формуле (5.49) ;
- одновременно с диспергированием наблюдается и обрат
ное явление - коалесценция капель, в результате в дисперсии
появляются капли большего размера, чем это следует из теории;
- в соответствии с соотношением (б) параметр· w зависит от
lп , а величины lп в турбулентном потоке сами распределены по
размеру; это может привести к образованию и более мелких
капель в сравнении с предсказанными теоретически по средне
му значению масштаба lп .
. Таким образом, возникает проблема устаноWiения среднего раз
мера капель (пузырей) Dз2 и закона их распределения по размерам.
463

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Применение формулы (5.49) для определения среднего диа
метра D32 правомерно при введении поправок на величину за
держки ф (для систем жидкость-жидкость) и на отношение
расчетной (на полное сечение аппарата) скорости газа w к ско
рости подъема пузырей Wп (для систем газ-жидкость) . Влияние
указанных факторов в настоящее время удается установить
только экспериментально.
Для систем жидкость-жидкость рекомендуются расчетные формулы вида

дЛЯ

Dз 2

=

системы газ-жидкость :

D3 2

-

С

С

0,
Фт
а" 6
·
р
2
V)o,4
�
( N/

(J� 6
( N/V) 0 ,4 Р�, 2

•

фт ( )
W

т

Wn

Эмпирические константы С, т дЛЯ конкретных дисперсных систем и кон 
струкций тепломас сообменных аппаратов приводятся в литературе•.

Распределение капель (пузырей) по размерам следует нор
мал ьно-логарифмическому закону: вероятность логарифма доли
капель текущего размера характеризуется нормальным распре
делением. Этот закон, присущий вообще большому числу слу
чайных событий , установлен теоретически и подтвержден об
ширным экспериментом. При этом он оказался справедливым
для широкого круга дисперсий , получаемых различными спосо
бами - как при диспергировании жидкостей и газов, так и при
измельчении твердых материалов.
О дисперrировании вращающимися дисками. Схема дисперги 
рования жидкости в неподв ижн ой (малоподвижной) газовой
среде показана на рис. 5. 3 9. Жидкость / подается на диск /,
вращающийся с определенной скоростью. Под действием цент:..
робежной сил ы жидкость отбрасывается к периферии диска и
сплошной пленкой сбрасывается с его поверхности. При даль
нейшем удалении от оси вращения (r > R) толщина покинувшей
диск пленки в соответствии с урав
нением расхода уменьшается, и на
некотором расстоянии от кромки
диска пленка распадается на капли.
3
111

1v/·

11

'J

11

/11

r

' См . , например, [20) .

464

·�IV

-

-

-

Рис.5.39. Схема диспергирования
щающимся диском:

вра

.патрубок подачи
вал, 3
диск, 2
1
жидкости;
1
дисперrируемая жидкость, 11
пленка
на поверхности диска, 111
распад пленки на
капли, JV
поток капел ь

-

-

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Расчет движения пленки по диску и разрушение пленки за
его пределами - достаточно сложная задача даже с упро
щающими допущениями. В настоящее
вре мя расчет базируется
•
на эмпирических соотношениях .
5.4.2. Диспергирование при истечении из отверстий и сопел

Режим диспергирования при истечении жидкости из от
верстий и сопел может быть капельным и струйным. При ка
пельном режиме (низкие скорости истечения) капли образуются
сразу на выходе из отверстий диспергирующего устройства. При
струйном режиме (высокие скорости истечения) поверхность
струи жидкости находится под воздействием волнообразных
периодически повторяющихся колебаний, возникающих под
действием шероховатости кромок отверстий и других возму
щающих факторов; в результате струя распадается на некотором
удалении от выходного среза отверстия (сопла) - в месте ее
наибольшего сужения.
Пусть выходной диаметр сопла (отверстия) равен d, а шейки
капли - d'V ('V < 1 ) . Тогда при вертикальном направлении оси
отверстия диаметр капли D, образующейся при капельном ре
жиме диспергирования, определяется соотношением сил: веса
капли и поверхностного натяжения. Вес капли (с учетом вытал
кивающей силы, если плотности дисперсной Рд и сплошной Р е
фаз соизмеримы) равен
( Рд
Pe)g; сила поверхностного

(7tD3/6)

-

натяжения на шейке капли выразится как ттd\vсrм - см. разд.
2. 7 .5. При капельном режиме силами инерции и местным со
противлением на выходе из отверстия можно пренебречь, и об
щая формула (2.77) переходит в (2.77б):

D=

3

6cr м dЧJ
(Р д

-

(2.77б)

P e )g

Разумеется, при диспергировании жидкости в газовую фазу
или наоборот (тогда в знаменателе формулы используется раз
ность Р е - Рд ) плотностью газа в сравнении с плотностью жид
кости можно пренебречь.
При увеличении скорости истечения диспергируемой жидw2
ттd 2
кости (разд. 2. 7. 5) возрастает сила инерции струи -- р д 2 ,

4

она становится основной силой, кон к-урирующей с силой поверх-

' См . ( 1 , 14)

465

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

<р ,а, к :р �о;;;;;;:;::;�-т---т---1-=::;�;;;-,

0,9 1---т-+--=.....,-+-:7""с::;.._-+-�--+----i

0,8 l---->,....L..-4---<---1--:11----+---�

0 ,4

-�----+---<

_._..,____._,,__--:

/ ___.____....,_
...,
0,3 .___

10

1 03

1 <>2

_

1 05

1 04

Re;:

Рис.5. 40. Зависимость коэффи циентов истечения из отве рстия в тонкой стенке
от числа Рейнольдса

наступает струйный режим диспергироностного натяжения,
вания.
В этом случае диаметр капли D превышает диаметр струи dc: теоретический
анализ приводит к соотношению
D " l ,9dc .
(r)
В свою очередь, диаметр струи dc связан с диаметром
эффициент сжатия струи а (см. разд. 2.6 . 1 ) :

отве рсти

я d через ко
(д)

Зависимость коэффициентов скорости ip, сжатия струи а и расхода кр от
w� dpд /µ приведена на рис. S.40, причем теоретическая скорость истечения wит определяется здесь через напор истечения Н:
к ритерия Rеит

•

Wит

=

�2gH

(е)

.

Критическую скорость wк , при которой капельный режим
переходит в струйный, оценим, приравняв силы и нерции и по
верхностного натяжения:
w2
тt-d42- Р д 2
- 7t d
с

откуда после сокращения на
wк

тt

=

dс

J

с 'l'О"м

-

d '

•

8 cr м 'I'
Рд с

причем отличием '1' от 1 нередко пренебрегают.

466

(4.60)

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Строго говоря, величина wк по (4.60) относится к ламинарно
струи. Для развитого турбулентного режима крити
ческая скорость w'к рассчитывается по полуэмпирическим фор
мулам• . Рабочую скорость w выбирают в интервале wк < w <
< w' к ; обычно w находится в диапазоне 1 -4 м/с.
В промышленных диспергаторах распыление жидкости ведет
ся через множество отверстий. Во избежание коалесценции ка
пель (а при диспергировании газов - пузырьков) отверстия
истечения размещают на достаточном удалении одно от другого;
на практике шаг отверстий обычно превышает 1 Od.

му течению

ЛИТЕРАТУРА к главе 5

1 . Гельперин Н.И. Основные процессы и аппараты химической технологии .
М.: Химия, 1 98 1 . 8 1 2 с .
2. Гельперин Н.И" Айнштейн В. Г., Кваша В. Б. Основы техники псевдоожи
жения. М.: Химия, 1 967. 664 с.
3. Головачевский Ю.А. Оросители и форсунки скрубберов химической про
мышленности. М.: Машиностроение, 1 974. 272 с.
4. Двайт Г. Б. Таблицы интегралов и другие математические формулы: Пер.
с англ. /Под ред. К.А. Семендяева. М.: Наука, 1 969. 228 с.
5. ДЬ1mнерский Ю.И. Процессы и аппараты химической техмологии. М.:
Химия, 1 995. 768 с.
6. Жужиков В.А. Фильтрование. М.: Химия, 1 977. 440 с.
7. Идельчик И.Е. Справочник по гидравлическим сопротивлениям. М.: Ма
шиностроение, 1 975. 560 с.
8. Казакова Е.А. Гранулирование и охлаждение азотсодержащих удобрений.
М.: Химия, 1 980. 287 с.
9. Касаткин А.Г. Основные процессы и аппараты химической технологии.
М.: Химия, 1 97 1 . 784 с.
1 0. Коган В. Б. Теоретические основы типовых процессов химической тех
нологии. Л.: Химия, 1 977. 592 с.
1 1 . Кутателадзе С. С., СmЬ1рикович М.А . Гидродинамика газожидкостных
систем. М.: Энергия, 1 976. 296 с.
12. Левич В. Г. Физико-химическая гидродинамика. М.: Физматгиз, 1 959.
700 с.
1 3. Орлов С.П. Дозирующие устройства. М.: Машгиз, 1 960. 239 с.
14. Перри Дж. Справочник инженера-химика: Пер. с англ. / Под ред. Н.М.
Жавор0нкова. Л.: Химия, 1 969. 1 1 44 с. (т.1 , 640 с.; т.1 1 , 504 с.).
1 5. Плановский А.Н., Николаев П. И. Процессы и аппараты химической и
нефтехимической технологии. М.: Химия, 1 972. 494 с.
16. Разумов И. М. Пневмо- и гидротранспорт в химической промышлен
ности. М.: Химия, 1 979. 248 с.
1 7 . Романков П.Г., Курочкина М.И. Гидромеханические процессы хими
ческой технологии. Л.: Химия, 1 974. 288 с.

• См., например, (8) .

467

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

1 8 . Скобло А.И" Трегубова И.А" Молоканов Ю. К. Процессы и аппараты неф
теперерабатывающей и нефтехимической промышленности. М.: Химия, 1 982.
584 с.
19. Соколов В. И. Современные промышленные центрифуги. М.: Машгиз,
1 96 1 . 452 с.
20. Стренк Ф. Перемешивание и аппараты с мешалками: Пер. с польск. /
Под ред. И.А. Щупляка. Л . : Химия, 1 975. 384 с.
2 1 . Циборовский Я. Процессы химической технологии: Пер. с польск. / Под
ред. П . Г. Романкова. Л.: Госхимиздат, 1 958. 932 с.
22. Чернобыльский И. И., Бондарь А.Г, Гаевский Б.А. и др. Машины и аппара
ты химических производств. М.: Машиностроение, 1 975. 456 с.
23. Штербачек 3" Тауск П. Перемешивание в химической промышлен
ности: Пер. с чешек. / Под ред. И.С. Павлушенко. Л . : Госхимиздат, 1 963 . 4 1 6 с.

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Глава 6

ОСНОВЫ ТЕПЛОПЕРЕНОСА

Теплоперенос, иначе - перенос теплоты от тела к телу, от
объекта к объекту, от точки к точке занимает особое место сре
ди явлений и процессов переноса.
Во-первых, он широко распространен в химической техноло
гии (в тепловых процессах, во многих процессах разделения, в
собственно химических процессах), так что устанавливаемые в
этой и следующих главах понятия и закономерности, а также
полученные в них соотношения будут прямо использованы при
изучении ряда последующих глав (выпаривание, дистилляция и
ректификация, сушка и др. ) и учебных дисциплин (АСУ ТП,
спецтехнологии и т.д.). Этими понятиями, закономерностями,
соотношениями очень часто пользуются исследователи, проек
тировщики, производственники.
Во-вторых, несмотря на множество еще не разрешенных
проблем, описание явлений и процессов теплопереноса зача
стую проще, нежели массопереноса (во многих проявлениях
проще и переноса импульса) в силу линейности значительного
числа задач - из-за существенного постоянства входящих в них
теплофизических величин. Поэтому подХоды здесь нагляднее,
легче усваиваются, а сами задачи чаще удается довести до ана
литических решений.
И в-третьих, подходы и решения задач теплопереноса не
редко служат основой и отправной точкой при анализе более
сложных задач - переноса вещества И других субстанций.
Осн0t1ные цели теплопереноса обусловлены характером техно
логического процесса. Наиболее часто они связаны со следую
щими моментами:
- подвод теплоты к системе, рабочему телу (целевому про
дукту, теплоносителю, хладоагенту) для повышения (или от
вод - для понижения) температуры либо изменения агрегатного
состояния (плавления - затвердевания, кипения - конденса
ции и т.п . ) ; здесь цель - сам теплоперенос;
- сущность самого технологического процесса, заклю
чающегося в подводе (отводе) теплоты, иногда - в изменении
агрегатного состояния; здесь без теплопереноса процесс просто
невозможен;

469

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

з

2 1 2

з

Общая схема теплопереноса:

/ - теплопередающая стенка (поверхность), 2 - по
граничные пленки, J - области движения тепJiоносителей
ВДОЛЬ ПО8СрХ910СТИ ;
/, /1 - области горячего и холодного теплоносителей

Рис. 6. 1.

- вьщеление (поглощение) теплоты в
ходе химических превращений (экзо- и
эндотермические реакции), так что необ
ходимо обеспечивать отвод и подвод теплоты реакции либо учи
тывать влияние накопления теплоты на изменение температуры
и ход этой реакции.
Часто в осуществлении химико-технологического процесса
реализуются все или несколько из этих целей .
Нередко теплопереносу сопутствует перенос вещества (из од
ной системы в другую, из одной фазы в другую); как правило,
теплоперенос связан с переносом количества движения
(импульса) - эту связь учитывают при описании процессов
теплопереноса.
В наиболее распространенных случаях (далее будут рассмат
риваться и другие ситуации) поток теплоты передается от теп 
лоносителя с высокой температурой Т к теплоносителю с низ
кой - t через теплопередающую стенку. Принципиальная схема
такого теплопереноса для фрагмента теплообменного аппарата
представлена на рис. 6. 1 . Теплота (ее поток изображен левой
вертикальной стрелкой) вводится в исследуемый фрагмент теп
лообменника с потоком горячего теплоносителя под действием
постороннего побудителя (например, насоса). Далее поток теп
лоты через поrраничную пленку, примыкающую к поверхности со
стороны горячего теплоносителя, передается к rранице поверх
ности , проходит через поверхность (стенку) , затем через поrра
ничную пленку со стороны холодного теплоносителя (эти потоки
теплоты изображены горизонтальными стрелками). Наконец,
теплота выводится из исследуемого фрагмента с холодным теп
лоносителем (правая вертикальная стрелка) .
Происходящие в ходе переноса теплоты процессы - в целом
или на отдельных стадиях - именуются по-разному. В целях
большей четкости разrраничения понятий в учебнике принята
следующая терминология (она вьщержана и для процессов мас
сопереноса) .
Теплопереносом (иначе
тепловым процессом) именуется лю
бое явление (процесс), связанное с переносом теплоты на любой
стадии или в целом.
Элементом (видом, способом) процесса теплопереноса назы
вается стадия (акт) , относящаяся к какой-либо одной состав
ляющей теплопереноса: через поrраничную пленку - теплоот-

470

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

дача; в твердой стенке или другой среде возможен кондуктивный
перенос; теплоперенос излучением (на схеме не показан) ; пото
ковый теплоперенос с движущимся теплоносителем.
Под теплопередачей будем понимать перенос теплоты через
теплопередающую поверхность (нормально к ней); для схемы на
рис. 6 . 1 это три стадии: перенос теплоты через пограничные
пленки и через стенку.
Под теплообменом будем понимать теплоперенос в целом ,
включающий отвод (подвод) теплоты с горячим и холодным
теплоносителями; для схемы на рис. 6. 1 теплообмен включает
пять стадий: три стадии теплопередачи и две - переноса тепло
ты с потоками теплоносителей.

В главе 6 рассматри�щются явления и процессы переноса теплоты,
относящиеся к отдельным стадиям. Проблемы теплопередачи и тепло
обмена являются предметом главы 7 .

6. 1 . ОСНОВНЫЕ ПОНЯТИЯ

Основополагающим в теплопереносе является понятие темпе
ратуры. Согласно 11 закону термодинамики теплоперенос само
произвольно (без затрат механической энергии) происходит от
тела (области) с большей температурой к телу (области) с мень
шей. Именно разность температур является причиной направ
ленного переноса теплоты. Эта разность температур
темпера
турный напор - выступает в качестве движущей силы теплопере
носа. В ходе теплопереноса может происходить изменение тем
пературы (от точки к точке, во времени и т.п.). При выравнива
нии температур наступает тепловое равновесие. Совокупность
температур дает температурное поле с различными ( локальными)
температурами в различных точках пространства. Если наблю
дается изменение температур во времени, то говорят еще о
мгновенных (в данный момент) температурах. В наиболее общих
случаях оперируют локальными и мгновенными температурами; в
более простых - только локальными или только мгновенными.
Кардинальной проблемой теплопереноса является установле
ние закономерностей изменения температур в пространстве и во
времени. При ее разрешении удается решать конкретные, в том
числе - практически важные задачи, связанные с количествами
переданной теплоты в системе, в аппарате, со временем процес
са, с размерами теплопередающих поверхностей, конечными
температурами теплоносителей и др.
Температуры обычно обозна.чаются символами Т, t, е. Отсчи
тывают их (как от нуля) от температуры таяния льда (градусы
Цельсия, 0 () или от абсолютного нуля (градусы Кельвина, К) ;
другие системы измерения и отсчета температур (Реомюра, Фа-

47 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис.6.2. Изменение темпера1)'р потоков теп
лоносителей и темпера1)'рный напор

ренгейта и Ренкина) практически
вышли из употребления. Специально
подчеркнем, что шкалы Цельсия и
Кельвина лишь смещены одна относительно другой (на 273 , 1 6 градуса) ;
при этом цена деления (величина 1
градуса) в обеих системах одинакова. Поэтому разности темпера
тур и численные значения величин, приходящихся на 1 градус, в
этих шкалах совпадают.
Необходимо четко вьщелять (рис. 6.2) различные аспекты пе
реноса теплоты в технологических аппаратах:
- перенос с потоками теплоносителей (потоковый перенос);
при этом происходит изменение температур в направлении
движения теплоносителя л Т = Т'
Т" и Лt = t"- t' либо измене
ние его агрегатного состояния - это цель и результат теплопе
реноса;
- перенос между потоками теплоносителей (норммьно к их
движению); он возникает при наличии температурного напора
л = Т
t; разумеется, в различных точках рабочей зоны значе
ния л могут быть различными, их определение и усреднение
изучается в гл. 7 в связи с проблемами теплообмена.
-

-

Теплофизические свойства рабочих тел
В ходе анализа процессов теплопереноса будем оперировать
различными теплофизическими свойствами рабочих тел. Неко
торые понадобятся на начальных стадиях изложения (они пред
ставлены ниже), другие потребуются и будут введены позднее.
В разд. 1 .3.2 было введено понятие о потенциальных полях, в
том числе - о поле температур, изотермических поверхностях,
градиенте температур дt / дп , коэффициенте теплопроводности,
обусловлено противоположное направление теплового потока и
температурного градиента и представлена в форме закона
Фурье связь удельного теплового потока q и градиента дt/дп.
Понятие о теплоемкости с (с указанием ее размерности и
единиц измерения) введено в разд. 1 .2.3 как количество тепло
ты, необходимой для изменения на 1 градус единичной массы
рабочего тела (вещества). В основном при изучении теплопере
носа используют теплоемкость при постоянном давлении Ср (в
гл . 6 и 7 индекс "р" опущен). Величина с в общем случае зави
сит от температуры, хотя и не всегда существенно. Заметим, что
в практических расчетах теплоемкость выражают не только в
Дж/(кг·К), но и в кДж/(кг·К).
472

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Удельной теплотой плавления Гпл (затвердевания) называют
количество теплоты, необходимой для плаw�ения (выделя
ющейся при затвердевании) единичной массы вещества; чаще
всего Гпл слабо изменяется с температурой. Измеряется Гпл в
Дж/кг (в таблицах приводится в кДж/кг). Плаw�ение
(затвердевание) индивидуальных веществ происходит при неиз
менной температуре, называемой температурой плавления tпл.
Она зависит от даw�ения (характер зависимости в соответствии с
правилом Ле-Шателье определяется соотношением плотностей
вещества в жидком и твердом состояниях) .
Удельной теплотой конденсации r (или обратных процессов испарения, парообразования) называют количество теплоты, вы
деляющейся при конденсации (необходимой для испарения)
единичной массы вещества. Измеряется r в Дж/кг (в таблицах
приводится в кДж/кг). Конденсация или кипение индивидуаль
ных веществ происходит при неизменной температуре fкип =
= const. Она, соответственно правилу Ле- Шателье, возрастает с
повышением давления (поскольку плотность пара всегда ниже
плотности жидкости) .
Аналогичным образом вводится понятие о теплоте сублима
ции (десубJJИМации).
Значения rпл, r и проч. при ра3Личных давлениях, температу
рах приводятся в справочной литературе • .
В тепловых расчетах широко используется понятие об эн
"
"
"
тальпии ( физическом тепле , которое несет с coбoii' тело, по
ток) , обозначаемой чаще всего символами Н, h, i и измеряемой
в Дж/кг (в практических расчетах - часто в кДж/кг). Энталь
пию принято отсчитывать от некой температуры 10 (о ней услов
ливаются) , при которой принимается Н, h, i = О . Чаще всего за
начало отсчета энтальпии принимают О 0 С ; в холодильных про
цессах, дабы не оперировать отрицательными энтальпиями,
точку отсчета выбирают ниже (например, - 1 00 ° С).
При рабочей температуре t, в отсутствие изменения агрегат
ного состояния во всем диапазоне от 10 до t, энтальпию h рас
считывают по очевидной формуле :
h =

1

Jcd t .

Если изменением теплоемкости с с температурой
пренебречь ( с = const), то
h = c(t - 10),
• См., например, ( 1 , 2, 1 4, 1 5, 1 71 и разл. справочники химика.

(а)
t

можно
(б)

473

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

а при

to = О

-

еще проще:

h = ct.

(в)
Если вещество при t0 (в частности, при О 0 С) имеет иное аг
регатное состояние, нежели при рабочей температуре, то эн
тальпия определяется с учетом теплоты фазовых превращений .
Для наиболее распространенных теплоносителей значения h
приводятся в справочной литературе • .
В практических расчетах в подавляющем большинстве слу
чаев оперируют разностями энтальпий, поэтому точка отсчета
энтальпий и их абсолютные значения роли не играют. Очевид
но, в частности, что удельные теплоты представляют собой раз
ности энтальпий вещества на границах фазовых состояний
(скажем, сухого насыщенного пара и кипящей жидкости) .

Характер процессов переноса теплоты

Наиболее общими и сложными для анализа и расчета явля 
ются процессы теплопереноса, в которых температуры изменя
ются как от точки к точке, так и во времени. Среди нестацио
нарных процессов, когда t = t(t), наиболее просты безrради
екrные, в которых температура в рассматриваемой области не
изменяется в пространстве: дt / дп = О . Для другой весьма об
ширной группы процессов, называемых стационарными, харак
терно изменение температур от точки к точке, но в любой точке
отсутствует изменение температуры во времени: дt / дt О . В
дальнейшем предстоит рассмотреть примеры всех этих случаев.
Значительная доля химико-технологических процессов про
водится в непрерывных режимах, когда характеристики процесса
(в том числе и тепловые) остаются неизменными во времени. В
периодических процессах тепловые характеристики во времени
могут изменяться. В этом аспекте непрерывные процессы обыч
но отождествляют со стационарными, периодические - с не
стационарными; такое отождествление в практических целях
часто вполне оправданно". В то же время с физической точки
зрения непрерывный процесс может складываться из нестацио
нарных элементарных актов переноса теплоты, и тогда, строго
говоря, отождествление неправомерно (пример - прогрев твер
дых частиц, непрерывно движущихся вдоль теплообменной по
верхности: теплообменник может работать в стационарном ре=

• См., например, [ 1 , 2, 14, 1 5 , 17) и разл. справочники химика.
•• С позиций теории управления непрерывные · процессы, как правило,
принципиально нестационарны вследствие спорадических возмущающих и
управляющих воздействий, т.е. постоянного отклонения системы от стационар
ного режима и возврата в этот режим ..

474

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

жиме, тогда как прогрев твердых частиц - нестационарен). На
конец, иногда вьщеляют полунепрерывные процессы (в том числе
теплопереноса) : один теплоноситель подается непрерывно с
постоянной во времени начальной температурой ; по второму
теплоносителю процесс проводится периодически .
6.2. ВИДЫ ТЕПЛОПЕРЕНОСА .

ОБЩЕЕ МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ
6.2. 1 . Виды теплопереноса

Вьщеляют три вида теплопереноса: теплопроводность
(кондукцию) , конвекцию и излучение .
Теплопроводностью называют перенос теплоты при непосред
ственном соприкосновении частиц рабочего тела, имеющих раз
ную температуру, - без перемещения упомянутых частиц. При
этом под частицами здесь подразумеваются достаточно крупные
образования сплошной среды, существенно превосходящие раз
мерами микрочастицы - атомы, молекулы и т.п.
В газах кондуктивный теплоперенос осуществляется путем
диффузии атомов и молекул. В жидкостях эта составляющая
переноса теплоты играет подчиненную ро:Ль; здесь (как и в
твердых телах - диэлектриках) главный вклад в перенос тепло
ты вносят упругие волны (упругие колебания, соударения). В
металлах и эта составляющая имеет второстепенное значение; на
первый план в переносе теплоты выходит диффузия электронов.
Кон векция представляет собой перенос теплоты за счет пере
мещения масс рабочего тела (теплоносителя) - жидкого, газо
образного, в отдельных процессах и твердого - в рабочей зоне
технологического аппарата. В зависимости от причины переме
щения масс рабочего тела принято различать:
- вынужденную конвекцию, когда перенос рабочего тела вы
зван действием внешних побудителей (насосов, компрессоров,
разности давлений или уровней и т.п.);
- естественную конвекцию, когда перемещение масс обус
ловлено различием плотностей рабочего тела в разных зонах
аппарата (пространства вообще) ; часто такая разность имеет
причиной различие в температурах этих зон; разумеется, есте
ственная конвекция возможна только в поле каких-либо внеш
них массовых сил (например, силы тяжести).
На практике оба этих вида конвективного теплопереноса за
частую сопутствуют друг другу; встречаются ситуации, когда их
вообще затруднительно разделить, и напротив, в некоторых слу
чаях один из них играет определяющую роль.

475

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Необходимо подчеркнуrь, что в данной главе нас будуr инте
ресовать элементарные эффекты, связанные с нормальными (по
отношению к теплопередающей поверхности) потоками теплоты
в ходе конвективного переноса через пограничные слои
(конвективный теплоперенос в направлении движения теплоно
сителей рассматривается в гл.7).
В манере конвективного теплопереноса представляют также
теплообмен при конденсации паров и кипении жидкостей, хотя,
согласно современным воззрениям, определяющую роль здесь
играет кондуктивный перенос. В той же конвективной форме
представляют и другие процессы пристеночного переноса: при
плавлении, в дисперсных системах (например, в псевдоожи
женном слое) и др. ; некоторые из них затронуrы в данной главе.
Лучистым (теплоперенос излучением) называют перенос теп
лоты пуrем электромагнитных колебаний; он сопровождается
превращением тепловой энергии в электромагнитные волны и
обратно. Каждое тело постоянно излучает энергию, причем ин
тенсивность этого излучения, обусловленного сложными воз
мущениями на атомном и молекулярном уровнях, зависит
прежде всего от свойств излучающей поверхности и от темпера
туры. Часть излучаемой энергии при попадании на тело п огло 
щается им и вновь переходит в теплоту; другая часть отра
жается от поверхности тела или проходит сквозь тело (в конеч
ном счете она поглощается другими телами или уходит в окру
жающую среду) . В результате одновременного излучения и по
глощения телом разных количеств энергии происходит тепло
обмен; разумеется, если температура участвующих в лучистом
теплопереносе тел одинакова, то потоки излучаемой и погло
щаемой энергии одинаковы, и эффект лучистого теплопереноса
отсуrствует.
Каждому виду переноса теплоты отвечают свои понятийный
аппарат и математическое описание - в этом основное содер
жание данной главы. В расчетных целях иногда удобно один вид
теплопереноса представить в терминах и символах другого, т.е.
произвести подмену задачи - тогда говорят об эквиваленпrых
(условных, эффективных) представлениях.
На практике перенос теплоты часто происходит одновремен
но несколькими способами - это сложный теплоперенос. Каж
дый из видов теплопереноса вносит свой вклад, его не всегда
удается точно установить. Результирующий эффект сложного
теплопереноса зависит не только от интенсивности конкретных
видов переноса, но и от особенностей их взаимодействия
(например, последовательного или параллельного, стационарно
го или нестационарного). Отдельные задачи, связанные со вза
имодействием различных видов теплопереноса, рассматриваются
в гл. 7.

476

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

6.2.2. Удельные темовые потоки

В основе анализа и расчета разнообразных процессов тепло
переноса лежат понятия об удельных и полных темовых потоках,
сопротивлениях переносу и пропускных способностях, введенные в
общем виде в разд. 1 .3.2. Напомним и конкретизируем их при
менительно к переносу теплоты.
Для непрерывных (стационарных) процессов оперируют по
током темоты Q (Вт =Дж/с в СИ), для периодических (нестаци
онарных) - ее количеством Q (Дж). Удельным тепловым пото
ком q (темовым напряжением, тепловой нагрузкой) называют
поток теплоты, отнесенный к еди нице теплопередающей по
верхности F [Вт/м2 , Дж/(с,. м2 )]; для непрерывных и периоди
ческих процессов соответственно:
q = QIF и Q = qF или q = Q/Ft и Q = qFt .
( 6. 1 )
В разделе 1 .3 . 2 бьш приведен закон Фурье, устанавливающи й
связь q с градиентом температур в условиях кондуктивного теп
лопереноса:
q = -Л grad t = -Л

дt
,
дп

( 1 . 1 0 ) , (6.2)

причем множитель Л представляет собой коэффициент тепло
проводности, знак "минус" (он относится к градиенту) обуслов
лен противоположным направлением q и дt/дп.
При конвективном переносе теплоты от поверхности теплообме
на (температура 0) к потоку теплоносителя (температура t) для ха
рактеристики теплонапряжения используют формулу Ньютона:
q

=

а(0 - t) ;

(6.3)

при переносе теплоты от горячего теплоносителя к холодной
поверхности в формуле (6.3), естественно, фигурирует темпера
турный напор (t - 0).
Полные тепловые потоки (кондуктивный, конве ктивный) запи
сываются с учетом выражений (6 . 1 ); например, для непрерывного
процесса: Q = -Л Fi (дt/дп) ; Q = аFЛ, где Л = 0 - t или Л = t - 0.
В случае лучистого теплопереноса его интенсивность опреде
ляется законом Стефана-Больцмана: удельный поток энергии,
излучаемой в единицу времени с единицы поверхности абсолют
но черного тела, пропорционален четвертой степени абсолютной
температуры:
(6.4)

причем индексом "О" отмечена принадлежность лучистого по
тока Ео к абсолютно черному телу (понятие о нем детализиро
вано в разд. 6.9. 1 ) ; cro = 5,67 . 1 0-s Вт/(м2 · �) - константа излу
ченИJ1 абсолютно черною тела.

477

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Специально подчеркнем, что Т здесь (и в последующих фор
мулах теплопереноса излучением) берется в К; в других уравне
ниях теплопереноса Т чаще всего будет обозначать температуру
горячего теплоносителя (обычно в 0 С) .
Удельный поток Ео (далее Е для тел , отличающихся от абсо
лютно черного) имеет ту же размерность, что и q; однако это
еще не тепловое напряжение, а лишь база для его определения .
6.2.З. Об уравнении Фурье-Кирхгофа

Общее математическое описание переноса теплоты (без учета
излучения) представляют в виде уравнения Фурье- Кирхгофа,
решение которого должно позволить найти температуру в любой
точке рабочего пространства в заданный момент времени. Вы
вод этого уравнения и его анализ приведены в разд. 1 . 5 . 2 ; кри
терии подобия, получаемые масштабными преобразованиями
уравнения Фурье- Кирхгофа и некоторых других соотношений,
рассмотрены в разд. 1 . 8 .
В наиболее общей форме уравнение Фурье- Кирхгофа дл я
изотропной среды имеет вид
дt
+w
дt

дt

'

дх

-

+w

дt

' ду

-

+w

•

дt
Qv
,
- = а'\1 2 t + дz

ер

( l . 2 1 ) , (6. 5 )

причем смысл каждого слагаемого, теплофизических величин
а = Л./ср, удельного источника теплоты Q v и других параметров
обозначен в упомянутых разделах.
В разд. 1 .6 на примере уравнения Фурье-Кирхгофа детально
рассмотрены его модификации применительно к различным
ситуациям (стационарный процесс, отсутствие источников теп 
лоты, теплоперенос в твердом теле - изотропном и анизотроп
ном и др. ) и конфигурациям рабочего пространства (плоская ,
цилиндрическая , сферическая задачи). В разделе 1 .7 подробно
рассмотрены условия однозначности , с которыми решается
уравнение переноса: начальное и граничные.
Введенные в указанных разделах понятия и соотношения бу
дут конкретизированы в настоящей главе в аспекте переноса
теплоты. При этом последовательно будут рассмотрены основ
ные закономерности различных видов теплопереноса.
6.3. СТАЦИОНАРН Ы Й КОНДУКТИВНЫЙ
ПЕРЕНОС ТЕПЛОТЫ ЧЕРЕЗ СТЕНКИ
Закономерности стационарного переноса теплоты путем теп
лопроводности в отсутствие Источников и Стоков можно полу
чить, анализируя уравнение (6 .5) либо используя закон Фурье
(6.2). Воспользуе мся вторым путем: он проще , в особенности для неплоских стенок.

478

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

6.3.1.

Плоская однослойная стенка

Пусть на сторонах плоской однослойной стенки толщиной
&ст, теплопроводностью Лет и поверхностью F поддерживаются
постоянные температуры 0 1 и 0 2 , причем для определенности
0 1 > 0 2 , так что поток теплоты направлен слева направо (рис.
6.3,а) . Заметим, что задание 0 1 и 02 на стенках означает гранич
ные условия 1 рода. Температура 0 (отложена по вертикальной
оси) изменяется только нормально к поверхности F, т.е. по оси
х - речь идет об однонаправленном переносе теплоты вдоль
этой оси. Начало оси х удобно совместить с левой границей
стенки . Наиболее распространенная задача здесь (как и в случае
стенок иной конфигурации) заключается в установлении закона
изменения температуры внутри стенки (О � х � &ст) и определе
нии потока теплоты Q.
Для установления зависимости 0 = 0(х) запишем закон Фурье
(6.2), заменив частную производную обыкновенной, поскольку 0
изменяется только вдоль координаты х. Из (6. 1 ) и (6.2)
Q = - л.ст

d0
F dx
'

откуда после разделения переменных

d0

=

и интегрирования получаем

0

;,t - '.oi
1

=

_я_ dx
Fл. ст

_я_ х +
Fл. ст

с.

(а)

(б)

1
1
1

1 : :
о 1 i+dx
1

_

_

х

выводу уравнений кондуктивного теплопереноса через плоские стен
ки - однослойную (а) и многослойную (6)

Рис.6.3. К

479

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Постоянная интегрирования С определяется из условия 0 =
при х = О; тогда из (б) С1 = 0 1 , и выражение (6) принимает вид
0 = 01

-

_g_ x.
FА. ст

01

(в)

Это же выражение можно получить и з (а), взяв интегралы с переменными
верхними пределами: от 0 1 до 0 и от О до х.

Итак, при стационарном кондуктивном теплопереносе в
плоской стенке устанавливается линейный профиль температур.
К аналогичному выводу приходим, используя в качестве базы для анализа
уравнение Фурье- Кирхгофа, сводящееся для рассматриваемого случая к диф
ференциальному уравнению
d2 t/dx2 = О, откуда получается линейное соотноше
ние типа 0 = С1х + С2.

В практических задачах часто требуется связать тепловой по
ток Q с геометрическими размерами стенки и граничными тем
пературами 0 1 и 0 2 . С этой целью следует в (а) взять определен
ный интеграл - соответственно от 0 1 до 02 и от О до Бет либо
положить в (в) 0 1 = 0 2 при х = &ст. В обоих случаях
-

0 1 - 0 2 = л0

= _g_ &ст
FА. ет

Q=

и

Л ет

F л0.

(6.6)

Если в (в) подставить значение Q/� из (6.6), то получается профиль тем
ператур, записанный через граничные величины 0 1 и 0 2 вне связи с Q и Лет:
0

=

Б ет

х

(r)

0 1 - л0 - .

8

Для плоской стенки можно провести весь анализ и записать
конечные выражения, пользуясь вместо Q/F тепловым напряже
нием q = const.
Напомним, что величины

Q = (Лет / & ст )F
л0

и

ле
q

=

& ст

Лет

на-

зывают полным и удельным (на единицу поверхности теплопере
носа) термическими сопротивлениями; реже используют величину
/Ост - удельную кондуктивную проводимость. В курсе
· q/Л0 =
ПАХТ мы будем оперировать пропускной способностью кондук
тивного теплопереноса; для плоской стенки она выражается в виде

Лет

jl_ = Л ет F .
Л0

б ет

(д)

При достаточно больших Л0 приходится учитывать заметное изменение Лет
с температурой. В этом случае в закон Фурье необходимо подставить перемен
ную теплоемкость Лет = Лст(0) , так что интегрирование приведет к нелинейным
соотношениям, более сложным, нежели (б) - (г) и (6.6). Возможность использова
ния концепции пропускных способностей для таких случаев - проблематична.

480

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

6.3.2. Плоская мноrослойная стенка

На практике нередко приходится иметь дело с многослойными
плоскими стенками, состоящими из отдельных ПЛОПIО (без зазо
ров) прилегающих друг к другу слоев толщиной f>; с теплопровод
ностями Л;. Постановка задачи :щесь может бьrrь такой :же, как для
однослойной стенки; ра:111 ичие заключается в том, что известными,
как правило, являются лишь температуры на внешних границах
многослойной стенки - на рис. 6.3, б значения 0 1 и 04.
В случае стационарного кондуктивного теплопереноса для
каждого из слоев (в рассматриваемом примере их три) можно запи
сать выражение типа (6.6), причем поток теплоты Q, переносимой
последовательно через все эти слои, разумеется, один и тот :же:
л.
Q = -1 Fле 1
о.

=

л.
2 FЛ02

0

2

л.

= -3 F лез ,
03

(е )

где Л0 1 = 01 - 02, Л02 = 02 - 03, Л0з = 0з - 04; �ны (Л;ftJF представляюг собой
пропускные способнОС'ПI кондуюивного "Jеплопереноса каждой i-й плоской C"JeHIOI.

Чтобы исключить неизвестные промежуточные температуры
и е 3 (при большем числе слоев - и другие 0; на границах
соприкосновения) , применим общий прием, многократно ис
пользуемый ниже для анализа сходных ситуаций в процессах
тепло- и массопереноса. Решим уравнения системы (е) относи
тельно частных разностей температур и сложим эти разности;
при этом промежуточные температуры взаимно уничтожатся,
останутся лишь известные (заданные) 0 1 и 04:
02

+

= Q
где п

(

(Л 1

-

1
/ Б 1 )F

+

(Л 2

01 - 0

z

0 - 03
2

е -0
з

1
/ f> 2 ) F

+

•

(Л з

число стенок (слоев); здесь п

=

Q
F(Л 1 / f> 1 )

= --

:

�
F( Л / б 2 )
Q
= --=-F(Л з / Б з )
=

ле

) (n

1
/ бз )F

=

Q l:

i = t (Л ;

= 0 1 - 04 =

)

1
, (ж)
/ Б ; )F

3.

Отсюда поток теплоты через многослойную плоскую стенку
составляет
1
ле
(6.7)
FЛ0 =
Q=
Л. 1

Л. 2

Л. 3

.0.i_ + � + _Oi

:t

--

--

i=•

1

( Л ; / б ; )F

48 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

а пропускная способность для системы из
плоских стенок запишется как

я_ =
ле

I

п

последовательных
(з)

_
_
_
_
_

�
п

1

1 1 (Л. 1 / '6 1 ) F
Из выражений (6.7) и (з) можно видеть,

что при последова
телыюм кондуктивном переносе теплоты складываются термиче
ские сопротивления отдельных стадий, т.е. величины, обратные

пропускным способностям.

Разумеется, и в рассматриваемом случае можно п олученные выражения
представить записа нными через q = Q/F.

6.3.З. Цилиндрические стенки

Теплоперенос через цилиндрические стенки - весьма частый
случай в химической технолоmи, например при течении юрячею
и холодною теплоносителей внугри и снаружи цилиндрических
'Iруб и аrmаратов. Задача анализа сформут�:рована в разд. 6.3. 1 .
Схема стационарною кондуктивноrо переноса теплоты че
рез однослойную цилиндрическую стенку представлена на рис .
6.4: рассматривается участок цилиндра длиной /, граничные
радиусы R1 и R2 , Температуры 8 1 и 8 2 . Анализ теплопереноса
здесь ведется на базе полного теплового потока Q, поскольку
удельный поток q изменяется вдоль радиальной координаты r
из-за непостоянства поверхности теплопереноса F = 27tr/.
Общая канва анализа остается прежней. Выделим на ради
альной координате r внуrри стенки (R1 s r s R2) элементарный
цилиндрический слой толщиной dr, на котором температура
изменяется от 8 до 8 + d8, и запишем для этою слоя закон Фу
рье, учитывая, что речь идет об однонаправленном теплопереносе:

Q = -А.ст - 2rr.r/ .
d8

dr

(и)

Разделим переменные:
Q dr
d0 = - -- - .
2п/ Лет r

Для отыскания закона 8 = 8(r)
пршmтегрируем (к) с переменными

!- г .-) ,-.
1

482

dr

(к)

r

Рис. 6.4. К выводу уравнения кондуктивноrо
теruюпереноса через ЦИJIИндрическую стенку

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

верхними пределами:
0
r
Q r dr
Q
(л)
и
0 = 0 1 - -- l n - .
f d0 = - -- f R1
2п/ Л ет R1 r
2п/ Лет
01
Таким образом, для цилиндрической стенки характерен ло
гарифмический профиль температур.
Взяв теперь от (к) определенный интеграл в пределах от 8 1
до 82 и от R1 до R2, получим искомые соотношения :
0 1 - 8 2 = Л8

=

Q

1
-- l n R
2п/ Лет
1
R

·

Л0
(6.8)
Л0 = ----_l_ ln d2
2п/ Лет
d1
Замена радиусов R1 и R2 соответствующими диаметрами об
условлена большей доступностью значений d1 и d2 в расчетной
практике; произведение 2п/ Лет перенесено из числителя в зна
менатель в целях удобства последующего анализа.
При малой толщине цилиндрической стенки 8 = (d1 - d2)/2,
т.е. при 8 < < d1 , d2 формулы (6.8) путем предельного перехода
(разложением в ряд) при d1 � d2 обращаются в (6.6). Практически
это означает, 'ПО при достаточно тонких цилиндрических стенках
можно с обусловленной погреuпюстью вести расчеть1 не по (6.8),
а по более простому соотношению (6.6) для плоской стенки.
Пропускная способность кондукrивного теплопереноса для
цилиндрической стенки получается из (6.8):
2п/ Л ет
Q = ---(м)
-

и

Q_

2 п/ Лет

ln ( R2 / R1 )

Теплоперенос . через многослойные цилиндрические стенки, в
соответствии с использованным в разд. 6.3.3 приемом, анали
зируется путем записи уравнений типа (6.8) относительно част
ных разн остей температур Л8 1 = 81 - 0 ;+ 1 . сложен ия полученных
выражений и исключения (взаимн ого ун ичтожения) промежуrоч
нь�х температур . В результате этой операции приходим к очевцд
ному выражению для п-слойной цилиндрической стенки:

Q=

_l_ f

ле

(6 .9)
,
d;
_!__ ln d. 1
2 л/ ;= 1 Л ;
;
причем здесь полный температурный напор Л8 = 8 1 - 8n + l ба
зируется н а известных граничных температурах 8 1 и 811 + 1
·

483

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Пропускная способность кондукrивного теплопереноса че
рез многослойную стенку Q/Л0 легко получается из (6 .9) .
6.3.4. Сферические стенки

Сферические аппараты реже встречаются в химической тех
нологии: это обычно резервуары для жидкостей и газов; неред
ко их изолируют в тепловом отношении - тогда речь идет о
многослойных сферических стенках. Кроме того, анализ кон
дукrивного теплопереноса через сферические стенки оказы
вается полезным при модельном рассмотрении некоторых слу
чаев конвективного теплопереноса (см. разд. 6 .4.5).
Как и в случае цилиндрической стенки, анализ ведем на ба
зе постоянного полного теплового потока Q, поскольку q = var
из-за изменения (вдоль радиальной координаты r) поверхности
теплопереноса F = 47tr2 .
Выделим (рис. 6.5) на радиусе r внугри однослойной стенки (R1 s; ·
s; r s; R1) эл е м ентарны й сферический слой толщиной dr, прир аще
ние температуры составит здесь d0. Закон Фурье заmпuется как
d0
2
(н)
Q = -Л. сr dr 41t r .
Разделим переменные:

dr
= - _о_
41tЛ. cr r 2

d0

(о)

и для установления закона 0 = 0(r) возьмем интегралы с пере
менными верхними пределами, фиксируя 0 0 1 при r = R1 :

е

=

е1

(

1
- _о_ 41tЛ. cr R1

- !)
r

=

(п)

.

Таким образом , для сферической стенки характерен гипербо
лический профиль температур.
Взяв теперь от (о) определенный mrтerpaл от 8 1 до 82 и от R1 до
R2, получим

и

=_
1

е1
Q

е 2 = ле =

R1

_

R1

R1

41tЛ. cr R1

1 ле =

41tЛ.cr
_

�(-1 - -1-)

_1_ (_!_ 1 )
,
ле

_

21tЛ. cr d1

_

d2

(6. 1 0)
'

.

причем целесообразность перехода от радиусов к диаметрам и
переноса произведения, содержащего Лет в знаменатель обос
нована в разд. 6 .3.3.
484

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 6. 5. К выводу уравнения кондухтивноrо
rerutoпepeнoca через сферическую стенку

Разумеется, как и для цилиндри
ческой стенки, при о = (d2 - di)/2 < <
< < d1 , d1 формула (6 . 1 0 ) переходиг в
более простое выражение (6.6) для
плоской стенки, 'П'О нередко исполъ
зуюr в инженерных расчетах.
Пропускная способность кон
дуктивного переноса для сфери
ческой стенки записывается, исхо
дя из (6. 10), следующим образом:
Q

ле

- =

21tЛ. cr
1
1

d1

(р )

d2

Пото к теплоты через п-слойную сферическую стенку получа
ется пуrем исключения промежуточных температур уже известным приемом:
ле

1d )
(d - - L: - -

Q= l n l

Л;

l

;

(6 . 1 1 )

i+I

причем здесь ле = 0 1 - en + l
Пропускная способность кондуктивного теплопереноса че
рез многослойную сферическую стенку Q/Л0 легко получается
из (6 . 1 1 ) .
21t

;�1
·

6.4. КОНВЕКТИВНЫЙ ТЕПЛОПЕРЕНОС
6.4. 1 . Коэффициеаrr теплоотдачи и число Нуссельта

Под конве1сrивным здесь понимается поток теплоты от теп
лопередающей поверхности к рабочему телу, теплоносителю
(или в обратном направлении) нормально к этой поверхности в отличие от переноса теплоты с теплоносителем вдоль поверх
ности (его также именуют конве1сrивным); особенности такого
потокового переноса теплоты отдельно или совместно с нор
мальным теплопереносом рассматриваются в гл. 7. Заметим,
что возможны ситуации, когда теплопередающая поверхность
отсутствует и нормальный конвеIСГИвный теплоперенос осу
ществляется непосредственно от одноrо теплоносителя к другому.
Общая картина изменения температуры около теплопере
дающей поверхности рассмотрена в разд. 1 .3.2. Приповерх485

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ностная область изменения температуры, например при кон
такте горячего теплоносителя с холодной стенкой, от t в ядре
потока до е на стенке (см. рис. 1 .6) называется поrраничвым
тепловым слоем, иногда - поrравичной тепловой пленкой. Для
удобства анализа и расчета вводят понятие о модельном погра
ничном слое с четкими границами, в котором сосредоточено
е ; за пределами этого слоя
все изменение температур Лt = t
толщиной О,. (в ядре потока) температура t считается постоян
ной. Тонкий тепловой пограничный слой в чем-то аналогичен
пристенному ламинарному (вязкому) подслою в потоке .жид
кости или газа: в тепловом слое или вязком подслое невелика
роль турбулентного переноса (количества движения, теплоты , а
также вещества), и потому существен вклад кондуктивного
("молекулярного") переноса - за счет вязкого трения (перенос
импульса), теплопроводности (перенос теплоты), молекулярной
диффузии (перенос вещества).
Малая толщина пограничного слоя позволяет пренебречь
его кривизной (цаже если стенка не является плоской) и считать
темпера'JУРНЫЙ профиль в слое линейным. Эrо означает, что ко
личество переданной теплогы через модельный слой можно трак
товать как кондуктивный теплоперенос через плоскую преграду (не
твердую, конечно, а жидкую или газовую - со своей теплопро
водностью Л.), оrшсываемый выражением (6.6):
-

.!:_ FЛt .

Q ::::

(6. 12)

от

Неопределенность в значении толщины О,. не позволяет
прямо воспользоваться этим соотношением. Поэтому поток
теплоты записывают в виде формулы Ньютона - в форме кон
вективной теплоотдачи:
(6. 1 3)
Q = a.F(t
8) = a.Fдt,
-

где а
хоэффицнеtrr темоотдачи, представляющий собой поток теплоты в еди
ницу времени через единичную поверхность при единичном температурном
напоре [в СИ выражается в Вm/(м2 · К) ) .
-

Сопоставление выражений (6. 12) и (6. 13)

же потока теплоты:

.!:_ FЛt = a.FЛt

для

одного и того

15у

приводит к модельному соотношению - оно записано ранее в
разд. 1 .3.2:
а. =

.!:_ .
от

( 1 . 12), (6. 14)

Это соотношение, как правило, не является расчетным, по
скольку за редким исключением толщина пограничного слоя О,.
486

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

неизвестна (часто не поддается расчету; иногда изменяется
вдоль теплопередающей поверхности). Однако выражение (6 . 14)
позволяет модеmtровать явления конвеIСГИВноrо теплопереноса,
помогает выявигь рычаrи управления ero интенсивностью. В са
мом деле, из (6. 14) ясно, что для повышения а. надо включигь
факторы, уменьшающие толщину пограничного слоя &r.
В разд. 1 . 8 .4 пуrем масштабных преобразований выражения
( 1 . 12), (6 . 14) был получен безразмерный комплекс - число
Нуссельта Nu = а.1/Л., где / - определяющий линейный размер
(в случае цилиндрических и сферических поверхностей обычно диаметр d). Физический смысл Nu предопределен
предпосьmками получения соотношения (6 . 14): этот комплекс
характеризует теплоперенос через пограничный слой в форме
соотношения конвективною и кондуктивною тепловых пото
ков - в обоих случаях по одну сторону теплопередающей по
верхности . Определение Nu и а.
кардинальная задача кон 
вективною теплопереноса.
Пропускная способность конвективною теплопереноса на
стадии теплоотдачи записывается исходя из формулы (6 . 1 3):
Q/Лt = a.F.
( 6 . 1 5)
Величина a.F может быть использована в рамках концепции
пропускных способностей, если а. не является функцией Q и
Лt, иначе юворя - при линейной связи Q и д!. В противном
случае (нелинейная связь) возможности использования аппара
та пропускных способностей пока не определены.
-

6.4.2. Аналогия в процессах конвективноrо переноса
количества движения и теплоты, а также вещества

Связь коэффициента теплоотдачи а. с толщиной модельною
приграничною слоя &r устанавливается выражением (6. 14) .
Сходные понятия - интенсивность переноса импульса 'tт и
толщина ламинарного слоя Он - используются в гидравлике.
Это позволяет выявить аналогию в переносе соответствующих
субстанций: количества движения (импульса) и теплоты, а если
шире - то и вещества при массопереносе .
В самом деле, интенсификация конвективного теплоперено
са (повышение а.) возможна путем уменьшения толщины теп
лового пограничного слоя О,., например увеличением скорости
теплоносителя около теплопередающей поверхности. Но при
этом, как известно из гидравлики, возрастает турбулентность
потока и уменьшается толщина приповерхностною ламинарно
го слоя Он, т.е. растет градиент скоростей у поверхности, а с ним и
интенсивность переноса импульса нормально к поверхности (это
выражается ростом гидравлического сопротивления).
487

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Сходство в переносе различных субстанций илл юстрируется
аналогией в форме записи их удельных потоков с соответ
ствующими градиентами (см . разд. 1 .3 .2):
дw
дw
закон Н ьютона
't-r
- µ- =
vp
;
(а)
дп
дп
дt
дt
закон Фурье
q
-Л. - = -аср - ;
(б)
дп
дп
де
закон Фика
(в)
Чв - Dд
дп
-

=

-

=

=

- ·

Существенное сходство характерно и для дифференциаль
ньrх уравнений переноса импульса (Навье - Стокса), теплоты
(Фурье - Кирхгофа) и вещества (Фика), а также для условий
однозначности к этим уравнениям. При этом в выражениях (а) ,
(б), (в) и в дифференциальных уравнениях переноса величины
v, а и Dд характеризуют соответственно скоростное, темпера
турное и концентрационное поля .
Качественная илл юстрация сходства в переносе импульса и
теплоты может быть подкреплена количественными оценками
аналогии и связей в переносе рассматриваемьrх субстанций .
Анализ будем вести для однонаправленного (от потока к стен
ке) переноса импульса и теплоты на примере турбулентного
течения жидкости на участке круглой трубы диаметром d и
длиной l (рис . 6 .6). Цель анализа - сопоставление интенсив
ности потоков теплоты и импульса.
Полагаем, что в ядре потока существенно выровнены ско
рость w и температура t, все их изменение сосредоточено в
узкой пристеночной области (в пограничных слоях) толщиной
Он при переносе импульса и О,. при переносе теплоты (значен ия
Он и О,. в общем случае различны; на рисун ке это различие не
показано). Поэтому выражения (а) и (б) будуг применены для
характеристики скоростных
полей
и
температурных
именно в пристеночных пограничных слоях. При этом
непосредственно у стенки 't-r =
(_;_ () _.......,_
(_;
v
= t5, q = q5, Wст = О (концепция
...
��
t
прилипания), t е.
<О� -...--- \)
()
Производные в (а) и (б)
удобно заменmъ малыми при. ·

- ·

- -

-

· - ·

=

Стенка
rрубы

488

Рис. 6. 6. К аналогии в конвективном
переносе импульса и теплоты

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ращениями вблизи стенок трубы: радиуса дп � Он или Б.�- (при
переносе импульса и теплоты соответственно); дw � Лw =
= w - Wcr w; дt � Лt = t - е . Тогда

=

't s

w

= µ-

(6)

(а);

8и

Искомое соотношение удельных потоков субстанций составит
(г)

Преобразуем левую часть. Для это го выразим qs по (6. 1 3) : qs =
= Q/F = а.Лt. Величину 'ts запишем исходя из выражения (и) в
разд. 2.2.2: 4ts /pg = Л-г(w 2/2g) , так что ts = (Лг/8) р w 2 . Подставим
в (г) значения Qs и i:s :
аЛt

Лг
2
S pw

=

� Лt

µw

(�) .
От

(Он) ·

После сокращений и приведения к безразмерной форме за
писи имеем
ad Л г wdp

(д)

т - тµ �
_

Относительно толщины пограничн ых слоев Он и &i- можно
определенно уrверждать, что при одном и том же потоке суб
станции их рост отвечает увеличению, соответственно, коэф
фициентов кинематической вязкости v и температуропровод
ности а. В сугубо оценочном плане можно предположить, что
а

� =i � = Pr
8т

(е)

- так в соотношение вводится критерий Прандтля Pr. Разу
меется, точнее принять, что 8и Д есть некая функция от Pr.
Здесь пока важно подчеркнуrь, что введение Pr дает возмож
ность осуществить переход от Он к &i-.
Подставим в (д) соотношение (8и/б.�-) по (е) . Тогда, учитывая,
что а.d(Л = Nu, wdp/µ =Re, получим
Nu

8

= !::r_ Re· Pr

и

� = St
Ro �

=

�,
8

(6. 1 5)

где St "' a/(wcp) - хриrерий Crurroнa, хара�сrеризующий соо111о шение темовых
потоков: нормально к темопередающей поверхности (чис.литель) и с движу
щимся темоносите.лем (знаменатель).

489

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

В силу приближенности связи (е) выражение (6 . 1 5) иногда
записывают в более общей форме:
St

=

л.
-f
/(Pr) .

(6 . 1 5а)

Выражения (6 . 1 5), (6 . 1 5а) демонстрируют аналогию в пере
носе теплоты и количества движения. Важно подчеркнуть фи
зический смысл этой аналогии - в обоих случаях речь идет о
соотношении сходных характеристик:
- коэффициент гидравлического сопротивления представ
ляет собой (см. разд. 2.2.2) соотношение пропускных способно
стей при переносе импульса: нормально к rранице потока (ts) и
вдоль потока (pw2);
- критерий Стантона есть соотношение аналогичных теп
ловых потоков; его можно прямо получить, соотнося соответ
ствующие потоки: o.F(t - 8) и Gc(t '- t ) = wcpj(t '- t " ) .
Подобный анализ совместно с переносом вещества позволяет
распространить аналогию на процессы массопереноса: наряду с
тепловым критерием Стантона здесь появляется диффузион
ный Stд = p/w, где Р - коэффициент массоотдачи . При этом со
храняются как физический смысл критерия, так и установлен
ные выше соотношения: Stд = Sh/( Re Sc) , Sh = pd/Dд - чис
ло Шервуда (аналог Nu), Sc = v /Dд - критерий Шмидта
(аналог Pr) . В целом аналогия трактуется расширительно:
St = Stд = Лг fi ·
(6 . 1 5б)
Огдельной (важной!) проблемой являются границы (пределы)
сохранения аналогии в переносе импульса (количества движе
ния), теплоты и вещества. В общем, можно сказать, что трой
ная аналогия в процессах переноса сохраняется, пока остаются
близкими механизмы переноса различных субстанций .
"

·

6.4.3. Теплоперенос в условиях вынужденной конвекции

Интенсивность теплообмена при вынужденной конвекции
зависит от физических свойств теплоносителя, скорости его
движения около теплопередающей поверхности (в канале),
формы и размеров канала. В подавляющем большинстве случаев
эту зависимость теоретически уста.новиrъ не удается; пользуются
эмпирическими соотношен иями , базирующимися, как правило,
на понятии о тепловом поrраничном слое и обычно записы
ваемыми в безразмерной форме. Общий подход к конструирова
нию таких соотношений можно представиrь следующим образом:
- около поверхности теплопереноса при движении тепло
носителя возникает ламинарный пограничный слой, толщина ко
торого 8и определяется значением критерия Рейнольдса Re;
490

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

- интенсивность теплоотдачи (значения Nu и а. ) опреде
ляется толщиной теплового пограничного слоя От, связанного с
Он. но не тождественного ему;
- связь От с би, как показано в разд. 6 .4.2, определяется зна
чением критерия Прандтля Pr.
Из этих соображений
(6 . 1 6)
Nu /{Re, Pr, " . ) ,
причем Re устанавливает толщину ламинарного слоя Он, а Pr
переводит его в От, определяющий по (6. 1 4) интенсивность теп
лоотдачи (т.е. Nu и а.) .
Интенсивность теплообмена можно также рассчитывать по
эмпирическим формулам, основанным на числе Стантона:
(6. 17)
St = /{Re, Pr, " . ) .
=

Для химико-технологической праlСI'ИКИ характерно мноrообразие аппаратов
и схем, работающих в условиях вынужденной конвекции : движение теru10носи
телей в трубах (в разных режимах) и.ли снаружи труб (вдоль них и.ли поперек,
возможно и под углом к их оси), наружное о6rекание пучков труб (шахматных,
коридорных) и т.д. Каждому случаю отвечают конкретные зависимости типа
(6. 1 6) - они приводятся в учебниках, монографиях, справочной ЛJfтературе" . В
качестве примера приведем одну из формул для расчета а при турбулентном
течении в трубах:
(ж)
Nu = 0,023Re0,8pfl.4ц

Соответственно указаниям автора формулы, теплофизические свойства теп
лоносителя берутся здесь при среднеарифметической величине из ero температур
на входе в теплообменник и на выходе из неrо. Множитель в1 отражает эффект
тепловой стабилизации : на входном участке трубы пристеночный градиент тем
ператур (именно он определяет истинную инrенсивность теплопереноса) убывает
быстрее температурноrо напора (входящеrо в формальные выражения типа 6 . 1 3);
поэтому а снижается по ходу движения теплоносителя, постепенно приближаясь
к постоянной величине. При Vd >40+50 поправочный множитель &1 может быть
принят равным 1 , при меньших l/d он превьnпает 1 (тем больше, чем ниже Re) .
Иmорирование отличия в1 от 1 приводит при расчетах инrенсивности теплооб
мена к занижению а, т.е. к ошибке в запас.

6.4.4. Теолоперенос в условиях естественной конвекции

Интенсивность теплопереноса в условиях естественной кон 
векции зависит от теплофизических свойств среды, формы и
геометрических характеристик теплопередающей поверхности
и, конечно, от скорости движения среды около поверхности.
Однако в отличие от вынужденной конвекции эта скорость при
расчетах заранее не известна, так что критерий Re, обусловли
вающий толщину пограничного слоя 8и (в конечном итоге
От
и а.) , заранее найти нельзя; в результате расчетная цепочка
-

Re -+ Он

не реализуется.
•см " например, (3 ,

Pr

) От -+

а.

6-8, 1 1 , 1 5, 1 8 ) .

49 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 6. 7.
ция :

0

2

а

-

Естественная ко н век

1-

ляцией;

зона подоrрева среды,

зона охлаждения

t .
т

б

около вертикальной по

верхносги (расчетная схема),

-

в конrуре с естественной цирку

2-

Пограничный слой
при естественной кон 
векции возникает при
движении среды, вы
званном разностью ее
а
б
плотностей у теплопе
редающей поверхности
и на удалении от нее .
Эта разность плотностей в условиях теплопереноса обусловле
на прогревом (либо охлаждением) пристеночных слоев среды и
их термическим расumрением - понижением плотности (JШбо,
наоборот, ее повышением). Схема движения среды (газа, жид
кости) у поверхности представлена на рис. 6.7,а. В окрестности
поверхности (пусть у нее высокая температура 0) образуется на
rретьlЙ слой среды, более легкой, нежели в отдалении от по
верхности, где температура t < 0. Средняя температура прогретого
слоя может бьпь приближенно пр инята равной tm = (0 + t)/2 , тем
пература холодных слоев
t. В результате легкие слои около го
рячей поверхности поднимаются вверх (в конечном счете они
уходят от поверхности); на некотором удалении от поверхности
холодные и более тяжелые слои среды опускаются вниз, замещая
в нижних зонах поверхности нагревающиеся восходящие слои.
Возникает тяга (она особо выражена в топочных трубах), ее вели
чина определяет интенсивность движения среды около поверх
ности (в частности, модельную толщину пограничной пленюt). На
рис. 6.7, б показана естественная циркуляция, возникающая при
нагревании и (ИJШ ) охлаждении среды в замкнуrом контуре.
Критерий, контролирующий движение среды, а значит ин
тенсивность теплопереноса у поверхности при естественной
конвекции, можно получить из следующих соображений. В
гидравлике (разд. 2.7 .4) был сформирован критерий Архимеда
-

Аг =

gdз Рт - Р '
р
2

v

представляющий собой соотношение сил, препятствующих и
способствующих взвешиванию частиц в среде. Сейчас речь
идет о подъеме и опускании слоев газа (жидкости) вблизи по
верхности (пусть ее вертикальная протяженность !). Поэтому

492

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

вместо размеров частиц в формируемый критерий должна вой
ти высота столба (слоя) среды, совпадающая с вертикальной
протяженностью поверхности /: в случае вертикальной поверх
ности (пластины, цилиндра) - rеометрическая ее высота Н, в
случае rоризонтальноrо цилиндра или wapa - их диаметр D.
Вместо Л р = Рт - р должна фигурировать разность плотностей
слоев среды у поверхности (температура tm) и на удалении от
нее (температура t): Л р = Р2 - Р1 или Лр Р 1 - р2, так как при
нято Л р > О. При этом в знаменателе отношения Л р/р удобнее
ставить плотность теплоносителя на удалении от поверхности
Р2 при температуре t (она известна более точно). Дробь Л р /р 2
представим в зависимости от определяющей разности темпера
тур Лtm = tm- t с помощью температурного коэффициента объем
ного расширения Ро: Р 1 = P [ l - PoUm - t)] . Тогда
2
Лр Р 2 - Р 1 =
(з)
P o (lm - t) = Ро Лtт .
=

Р2

=

Р2

Так, из критерия AI получается критерий Грасrофа, бази
рующийся на температурном напоре Лtm:

Gr = m v 2 PoЛl m .
g/ 3

В таком написании критерий не очень удобен в расчетах,
так как требуется рассчитывать среднюю температуру присте
ночноrо слоя tm. Удобнее основывать запись критерия на тем
пературном напоре Лt = 0 - t, заданном (известном) при по
становке задачи расчета. Переход от Лtт к Лt прост:
Л1.

111

;;: ( т

-1

е-1

e+r

л1

= -- - 1 = -- == - ·
2

2

2

Опустив множитель 1/2 (он будет учтен численными значе
ниями коэффициентов в расчетных формулах), получим

Gr =

v2

g/ 3

-

р 0 ЛI.

(и)

.

Из изложенных ранее предпосылок следует, что величина

Gr определяет толщину поrраничноrо слоя 8и около поверх
ности . при естественной конвекции, а с помощью критерия Pr

осуществляется переход к 8т, а значит к Nu и

сх :

(6 . 1 8 )
Nu = f(Gr, Pr, . ")
•
В литературе имеются попытки теоретического описания
естественной конвекции в форме (6. 1 8), однако они базируют.

• См" например, (7, 9, 10 ) .

493

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ся на весьма произвольных предположен иях о температурном
профиле в пристеночном слое среды. Более надежны пока эм 
пирические зависимости ; обычно их представляют в виде степенн ых соотношений типа
(6 . 1 9)
Nu = co(Gr Рr)п.
·

Конкретн ые значения с0 и п при водятся в литературе в за ви 
си м ости от значения произведен ия Gr· Pr. В частности , для ла
минарного режима ( G r· Pr = 5 · 1 0 2 +2· 1 07) величина с0 = 0,54; п =
= 1 /4;
величина
для турбулентного (Gr· Pr = 2· 1 07+ 1 · 1 0 1 3 )
=
со
0, 1 35 , п = 1 /3 . Отсюда я сно , что пр и турбулент

ном р ежиме влияние линейного размера / на коэффициент тепло
отдачи а вырождается, так как / входит одновремен но в Nu (в

первой степени) и в Gr (в третьей степени). Дело в том , что
при турбулентном режиме длина пуrи восходящего вихря /0
около поверхности (до его отрыва) чаще всего существенно
меньше протяжен ности поверхности / (т.е. Н или D) , так что /
не может оказывать влияния на интенсивность теплообмена.
По формулам типа (6 . 1 9) на Nu влияют не Gr и Pr, а их
произведение, что означает уменьшен ие числа воздействующих
на теплообмен факторов. Это не следует ни из каких физиче
ских представлений. По-видимому, таюtе формулы базируются на
опьпах с воздухом и друrnми rазами, когда Pr изменяется мало. В
общем же множитель с0 несколько возрастает при увеличении Pr.
Концешщя пропускной способности в условиях естественной
конвекции теряет определенность, поскольку в выражениях типа
(6. 1 8) коэффициент теплоотдачи а зависит от Gr, а значит и от
температурного напора Л t- нарушается линейность Q и Л t.
На практике встречаются случаи , когда теплообмен осу 
ществляется за счет естественной и вынужденной конвекци и .
Общий вид расчетных уравнений для этого случая :

Nu = j{Re, Gr, Pr, . . . ) .

(6.20)

Такие ситуации обычно возникают при ламинарном режиме
течения теплоносителя , так как при турбулентном естественная
конвекция , как правило, подавлена вынужденною - вклад
последней доминирует.
За пределами рассмотрения остались особенности есте
ственной конвекции в стесненных условиях (т.е. в ограничен
ном пространстве : в щелях, трубах, узких каналах) . Строго го 
воря , естественная конвекция здесь уже не является свободной.
Эти вопросы детально анализируются в теплотехн ической ли
тературе и некоторых учебниках· .
' С м . [3, 6, 7, 1 1 , 1 8 , 1 9 1 .

494

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

6.4.5. Конвективная

теплоотдача

к шару

Тела сферической (или близкой к ней) формы часто фигу
рируют в задачах переноса. При расчете конвективного пере
носа теплоты или вещества необходимо располагать значения
ми коэффициента теплоотдачи а (или массоотдачи �) к шару
или от него. Последующий анализ имеет целью установить
нижнюю границу а и обосновать вид расчетных соотношений.
Будем рассматривать стационарный перенос теплоты от го
рячей среды с температурой t к находящемуся в ней холодному
шару диаметром d (рис. 6 .8). Пусть температура поверхности
шара равна е . При обтекании шара потоком среды около него
образуется тепловой пограничный слой - для простоты будем
считать его сферическим (на рисунке - штриховая линия). В
зависимости от условий движения среды диаметр этого мо
дельного слоя примет некоторое значение dc.
Поскольку, согласно принятой модели, теплота через сфериче
ский пограничный слой передается теплопроводностью, то поток
теплоть1 в соответствии с (6. 1 0) может бьпъ представлен в вще
_

Qгде Л

-

21tЛ(t - 0)
1

1

(к)

'

теruю проводность среды (поrраничноrо с.лоя).

Тот же поток в терминах и символах конвективного перено
са по (6 . 1 3) записывается в вще
(л)
Q = a1Cd2(t - е ).

/(� - 1J

Приравнивая эти выражения, получим после сокращений

2

=

ad 2 , откуда в безразмерн ой форме

ad
2
- = Nu = -- ·
л.
-�

1

(6 .2 1 )

dc

Если погранич ный слой и меет не

dc � оо
(среда неподвижна либо движется
около шара в сугубо ламинарном
режиме) , то число Нуссельта прини-

ограниченную толщину

Рис. 6. 8. К расчету интенсивности теIUJоотдачи
от шара

/

Среда

1
t
\

"\.

,... -

":з"
'

Ш ар

495

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

мает наименьшее значение
Numin = 2,

(6 .2 1а)

откуда можно найти минимальное для шара значение коэффи
циента теплоотдачи a.min.
Реально, когда толщина пограничного слоя (а значит, и dc)
конечна, теплоперенос более интенсивен ; поэтому для боль
шинства реальных задач расчет а на основе (6 .2 1а) дает ошибку
"в запас". Толщина ламинарного слоя около поверхности шара
определяется критерием Рейнольдса Re
wd/v; поэтому в рас
четной формуле для Nu должно быть отражено влияние Re. В
то же время необходимо осуществить переход от ламинарного
слоя к тепловому - это делается с помощью Pr. При этом
ограниченному диаметру пленки dWI отвечают значения Nu > 2.
Таким образом, полуэмпирические расчетные соотношения для
конвективной теплоотдачи к шару (от шара) можно предста
вить в общей форме:
(6.22)
Nu = Numin + f (Re, Pr) ;
конкретно :
Nu = 2 + a0Re '12Pr'/3,
(6.22а)
=

причем по данным разных исследователей численные значения
ао варьируются в пределах от 0,59 до 0,74.
Заметим, что аналогичным образом в конвективном массо 
переносе получают минимальн ые значе ния числа Шервуда Shmin =
реальная интенсивность массоотдачи от шара к среде
= 2;
описывается соотношением типа (6.22а) - естественно, с за
меной Pr на критерий Шмидта Sc .
6.5. ТЕПЛОПЕРЕНОС ПРИ КОНДЕНСАЦИИ ПАРА

Конденсация паров в химической технологии используется в
целях собственно теплопереноса (нагревание какого-нибудь
продукта за счет теплоты конденсации пара) либо она сопро
вождает
(является
составной
частью)
некий
процесс
(выпаривания, дистилляции и др.). Во всех этих случаях необ
ходимо уметь рассчитать интенсивность теплопереноса; в слу
чае конденсации ее представляют в терминах конвективного
переноса теплоты, определяя коэффициент теплоотдачи а..
Будем рассматривать стационарный процесс конденсащm
насыщенного пара на вертикальной поверхности - расчетная
схема представлена на рис. 6.9. Пусть температура конденси
рующегося пара равна Т, энталышя - Н. Пар контакгирует с бо
лее холодной стенкой - ее температура е1 < Т, поэтому и проис
ходит конденсация. Образование пленки конденсата начинается с
496

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 6.9. Расчетная схема теплоотдачи при конденсации паров:

1 - JCOJЩeнcar, П - поверхносrь, Ш - пар (х - просrрансrвеННЬIЙ хонrур для оосrавлеиия тспловоrо баланса)

у
-----ilr
111

верхней кромки поверхности. Пленка
стекает вниз (вдоль оси z), причем
конденсация происходит по всей вы
соте поверхности l, так что толщина
пленки постоянно нарастает сверху
вниз :(нижня я граница поверхности z =
= l на схеме не показана).
В целях упрощеlПfЯ анализа прmm
z
мается р.sщ допущений. Основные из них:
- температура поверхности 8 1 постоянна вдоль всей длины l;
- эффектом ускорения пленки за счет увеличения ее тол
щины (иначе - инерционными силами) можно пренебречь из
за малости ускорения в сравнении с гравитационным;
- температура пленки конденсата, а с ней и теплофизические свойства пленки постоянны по ее длине;
- трением пленки конденсата о пар можно пренебречь;
- пар не содержит примеси неконденсируемы:х газов;
- термическое сопроrивление при переносе теплагы от конденсирующеюся пара к пленке конденсаrа пренебрежимо мало, все тер
мическое сопрсmmление сосредоrочено в пленке конденсат;
- вследствие малой толщины пленки ее течение можно счи
тать плоским (цаже если на самом деле вертикальная поверхность
кривоmmейна) и ламинарным, так что теплота переносиrся через
пленку (от пара к стенке) пуrем теплопроводности .
Подчеркнем, что конденсация - один из немногих случаев,
когда для определения а. может бьrrь прямо использовано выра
жение (6. 14); т.е. понятие о пограничном слое из модельного здесь
становиrся реальным: толщина пленки конденсата S · и есть &r.
В основе анализа - тепловой баланс; пространственный
контур "к" ограничен сечениями z и z + dz (локальная тол
щина пленки здесь 8), стенкой и . свободной поверхностью;
ширина фрагмента поверхности (перпендикулярно плоскости
чертежа) равна Ь; временной интервал - 1 с.
При составлении баланса потребуется знание массового по
тока конденсата G в сечении z и пара dG на участке Ьdz. Они
могут быть определены из найденных в разд. 2.4 закономерно
стей течения тонких пленок, но с учетом непостоянства (по
длине поверхности) толщины пленки конденсата 8 = S(z) . Со
гласно (2.43), объемный поток Жидкости равен
pgb
v

=

µ

§.!_ '
3

497

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

откуда массовый поток (локальный - в сечении z) будет
3
0 ,
p 2gb -G = p V = -µ з

а приращение этого потока на участке высотой dz составит

d G = р 2 gьо 2

do .
(а)
µ
Здесь р и µ - плотность и динамическая вязкость конденса
та; в ходе последующего анализа в получаемых соотношениях
будуr еще фиrурировать теплопроводность конденсата Л., его
энтальпия i, а также теплота конденсации r.
Тепловой баланс в форме Пр - Ух = О записывается (см.
рис . 6 .9) как
(б)
Gi + (d G)H - (G + d G)i - d Q = О ;
при этом через фрагмент поверхности Ьdz отводится поток
теплоты d Q, прошедший через пленку конденсата толщиной 8;
в терминах кондукrивного теплопереноса

л.

d Q = 5 ( Т - 0 1 )Ьdz.

Раскрывая скобки в (б), подставляя значение d Q и учиты
вая, что Н - i = r, получим
rdG =

л

S

rp 2 g 2
о do
--

(T - 0 1)bdz ,

а после подстановки d G по (а) и сокращений на Ь:
µ

=

- (Т - 0 1 )dz ·
;.,
о

Разделим переменные 8 и z:
dz =

гр gu
2

s: )

µ (Т - 0 1 )Л.

d8

(в)

и возьмем интеграл с переменными верхними пределами; ниж
ние пределы 8 = О при z = О; тогда

rp2 g

z = -�-"---

о•

µ (Т - 01)Л 4
Решая полученное равенство относительно 8, найдем ло
кальную (на рассТоянии z от верхней кромки теплопередающей
поверхности) толщину пленки конденсата:
)Л.z
4 (
4 µ Т - 01
(г)
0
.
2
=

498

p gr

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Теперь можно рассчитать локальный коэффициент теплоотда

чи в сечении z:

(д )
В практических расчетах нас интересует средний по всей вы
соте l коэффициент теплоотдачи <Хконд:
1
1
<X кoщ = z l <X z dz = z
/

Л3pT 2-rg

4µ (

/

01 )

lz

-1 /4

dz =

4

3

rg

Окончательно для вертикальн ых (индекс "в") поверхностей:
<Х :онд

= 0 ,9 43

<Х �онд

= 0,72

л_З р 2

(6.23)

µ(Т - 0 1 ) /

Теплофизические параметры Л , р, µ здесь следовало бы
брать при средней температуре пленки конденсата lco � ( Т
Однако приступая к расчету, мы, как правило, не распо 
лагаем значением е 1 • Поэтому все физические параметры (для r
это вполне правомерно) рекомендуется брать при известной
температуре конденсации Т; вносимая при этом погрешность
невелика: малая разница ме.жду lcp и Т, корень 4-й степени.
В выражении (6.23 ) нередко перед радикалом ставится мно
житель 1 , 1 5 , что призвано отразить возможный волновой режим
течения пленки конденсата (при достаточно протяженной по
верхности и интенсивной теплоотдаче). Мы рекомендуем со
хранить множитель 0, 943 � 0 , 94 по следующим причинам:
- во-первых, термическое сопротивление на стадии кон 
денсации невелико, так что различие в величинах <Х конд • рас
считанных с множителями 0,94 или 1 , 1 5, мало скажется на об
щей интенсивности теплопереноса;
- во-вторых, более низкие значения множителя и <Х конд
моrуг в известной мере скомпенсировать принятые допущения,
поскольку обеспечивают некоторый запас в расчете интенсив
ности теплоотдачи.
В химико-технологической практике конденсация пара
весьма часто происходит на наружной поверхности zоризонталь
ных труб. В этом случае анализ должен учитывать изменение
наклона поверхности к вертикали при стекании пленки кон 
денсата. Для одиночной круглой горизонтальной трубы наруж
ным диаметром dн такой анализ приводит к формуле

+ 01)/2.

+

,

л_З р 2 rg

)

µ(Т - 0 1 d н

,

(6.24)

причем верхний индекс "г" означает "горизонтальный " .
4 99

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

О О О
О О О
О О О

&р

б

а

0
0
0
о 0 о
о
о

0,5

1
г

в

Рис. 6. 10. Конденсация на наружной поверхности труб в трубных пучхах:
б

а - увеличеЮ1е тоJПЦИНЫ плеюси конденсата в вертикальном ряду rориэонтальных труб,

(К)

(Ш)

в пучхе, г пучхов rоризонтальных труб

- коридорная компоновка труб в пучке, • - шахматная компоновка труб

коэффициент рядности для коридорных

и шахматных

Сходство формул (6.23) и (6.24) очевядно. В целях со
вместного последующего анализа удобно вьщелить комплекс
теплофизических величин в форме
Ао

=

�лз�rg '

(е)

а также более общий комплекс, не содержащий температурного
напора Т - 01 = л t, но включающий наряду с Ао множители
0,94 или 0,72 и вертикальную протяженность теплопередающей
поверхности / или dн (соответственно для вертикальных стенок
и горизонтальных труб). Тогда указанные формулы могут быть
представлены единым расчетным соотношением:
(6.25)

Интенсивность теплообмена на наружной поверхности го
ризонтальных труб может иметь определенную специфику. Она
не проявляется для одной трубы или нескольких, располо
женных в одном горизонтальном ряду. Но она играет роль при
расположении труб одна под другой (рис. 6 . 1 0, а), например в
корядорных и шахматных пучках горизонтальных тр)lб (рис .
6 . 1 0 , б, в) . Дело в том, что на поверхности любой трубы (кроме
размещенных в верхнем рцду) движется пленка коНденсата, не
только образовавшегося в результате коНденсации пара на этой
трубе, но и стекающего с расположенных выше тр)lб. Увеличение
толщины пленки приводиr, согласно (6. 14), к понижению <х.коЮI
для i-й трубы (отсчет сверху) при i > 1 , т.е. а; < а. 1 . Эrо относи500

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

тельное уменьшение коэффшtИента теплоотдачи выражаюг коэф
фициеиrом рядности Ef = а.; !а.1 � 1, причем равенство относиrся к
верхнему ряду труб ( z = 1). Оrличие Ер от 1 больше для коридор
ньIХ пучков труб, нежеJШ для шахматных (рис. 6. 10,г).
В связи с рассматриваемым эффектом в формуле (6.24) ,
применительно к трубам в i-м ряду пучка rоризонтальных труб,
должен фигурировать корректирующий множитель Е/ :
l·..3p2rg
(а.rконд)пуч = Е � 0,72 41 ---(6.24а)
µ(Т -91)dк
этот коэффициент должен быть также учтен в формуле (6.25),
если рассматриваются пучки rоризонтальных труб.
Специально подчеркнем, что значения Е / на графиках типа
приведенных на рис. 6. 10,г относятся к локальным (в i-м ряду)
коэффициентам теплоотдачи (а.rконд); для получения усреднен
НЬIХ коэффициентов по все му трубному пучку надо знать число
труб в каждом rоризонтальном ряду и рассматривать среднее
значение (а.rконд)пуч как средневзвешенную величину. Тем не
менее в ряде распространенньIХ учебников и учебньIХ пособий•
воспроизводятся графики для локальных значений Е/, но по
ним ошибочно рекомендуют отсчитывать значения Ер, средние
для всеrо пучка. Поскольку операция усреднения Ер1 весьма гро
моздка и неудобна, для расчета (с приемлемой для инженерных
задач точностью) средних значений Ер предлагается график - еди
ньIЙ для коридорных и шахматньIХ пучков. Он приведен в При
ложенюt 6 . 1 (на рис.6. 1 8) с пояснениями к использованию.
·

В случае подачи на конденсацию переrретоrо пара (с температурой Тп) к ве
личине r в соо111 ошениях (6.23) и (6.24) должна быrь добаалена теплота переrре
ва пара СпЛТ. где Сп - теплоемкость пара, ЛТ= Tn - Т. Формально это должно
привести к некоторому (чаще всего - несущественному, поскольку СпЛТ значи
тельно меньше r) увеличению аконд· Однако при этом часть теплопередающей
поверхности будет работать на охлажцение пара от Tn до Т; здесь теnлопровод
ность пограничного слоя (пара!) будет намного ниже, чем в зонах ко нденсации,
значит ниже будет и коэфф ициекr теnлоотдачи - на этих участках и в среднем.
Дабы понизить этот неrативный эффект, стараются приблизить переrретый пар
к насьпценному состоянию - путем впрыскивания конденсата либо путем бар
ботажа перегретого пара через кипящий конденсат.
Интенсивность теnлоотдачи снижается, ее.ли в конденсирующемся паре со
держатся неконденснрующнес11 raзw: поскольку их теплопроводность на порядок
и более ниже, чем у пленки конденсата, резко уменьшается числитель в формуле
(6. 14) . Это снижение весьма существенно; например, примесь воздуха к водяно
му пару в количестве 5 % снижает а в 5-7 раз. С целью поддержания теплоот
дачи на высоком уровне в ряде технологических процессов специально периоди
чески выводят неконденсирующиеся rазы из зоны конденсации (вместе с неко
торым количеством пара), восстанааливая таким способом высокую теnлоот-

•

Например, в (8, 1 4 ) .

50 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

дающую способность стад ии конденсации. Практически проводят продуму,
страмивая в атмосферу накопившийся в зоне конденсации воздух (теряя при
этом , конечно, некоторое колич еств о водяною пара).
Применяя конденсирующийся пар в качестве теruюносителя (наиболее часто
- это водяной пар), необходимо в целях э кономии полностью использовать ею
теплоту конденсации, т.е. вьmускать из теплообменника только конденсат. Для
этою на выходе конденсата из теплообменною аппарата устанами вают специ 
альное устройство - хондеисатоопод'llllt , пропускающий только ко нденсат, но
не пропускающий пар.
•

Присуrств ие в выражениях для <Хконц (6.23) - (6.25) темпера-rурно
rо напора Т - 81 нарушает m1Нейность связи ero с потоком теплаrы
Q; эrо за1J>удняет испалъзование понягия пропускной способносm в
расчетах теплопереноса с участием конденсации: паров.
6.6.

ТЕПЛОПЕРЕНОС ПРИ КИПЕНИ И ЖИДКОСТИ

Кипение жцдкосТи в химической технологии используется (как
и конденсация паров) непосредственно в целях теплопереноса
либо составляет сущность те:хнологическоrо процесса (примеры
таЮfХ процессов обозначены в разд. 6.5). Во всех этих случаях
необходимо определигь интенсивность теплопереноса; при кипе
нии ее тоже представляюг в терМIПfах конвеJсrИВной теплоагдачи.
Над свободной поверхностью любой жидкости существует
определенное давление паров, возрастающее с температурой
жидкости. Если давление паров ниже давления в пространстве
над жцдкостью, то происходит испарение жцдкости со свободной
поверхности . Если давление паров станет равным внешнему дав
лению, то испарение может происходить и BHY'IJ>И жцдкости с
образованием пузырей; такое испарение и называется кипением.
Согласно сказанному выше, кипению жидкости соответствует
температура, при которой давление паров равно внешнему давлению.
Будем рассматривать (рис. 6. 1 1) горячую теплообменную по
верхность с температурой 82 , омываемую жидкостью при тем
пературе кипения t разумеется, 82 > t, так что теплага аг стенки
передается кипяшей жцдкости. На горячей поверхн ости (стенке)
жцдкость перегревается, возникаюr паровые пузырьки; они растуr
в размерах, аrрываюrся аг стенки и уходят в объем кипящей жцд 
кости, а на стенке вновь заро:жпаюrся и растуr пузыри.
Существуют различные представления о механизме теплопе
реноса при кипении жидкостей. Простейшее из них вполне
укладывается в модель поrраничноrо слоя; с этой позиции пра
вомерно оперировать коэффициентом теплоагдачи <Хкип· Со,

• Устройство и принцип работы конденсатоотводчиков см . , например, в (3,

8, 1 6).

502

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Е

Рис. 6. 1 1. Расчетная схема теnлоотдачи при кипении жидкостей
Рис. 6. 12. Изменение коэфф ициента теnлоотдачи при кипении в зависимости от
теnловой нагрузки и температурного напора

гласно такому представлению, отрывающиеся и мигрирующие
в объем жидкости паровые пузыри турбулизируют жидкость
вблизи теплопередающей поверхности. Это приводит к значи
тельному уменьшению толщины теплового пограничного слоя
8т и, в соответствии с выражением (6. 14), к росту
На рис. 6 . 1 2 демонстрируется общий xapaicrep изменения
<Х.юm с тепловой нагрузкой q; аналогичный характер имеет зави
симость <Х.юm от температурного напора 82 t (различие будет
лишь в масштабах по оси абсцисс). На участке АВ при малых q
и (82 t) кипения нет, теплоотдача происходит за счет есте
ственной конвекции, коэффициенты теплоотдачи невелики.
Правее точки В, т.е. при более высоких q и (82 - t), жидкость
начинает кипеть, появляются пузырьки пара. На участке ВС
они возникают только на поверхности и с небольшой частотой
- это пристеночное кипение с не очень существенным ростом
СХкип · Далее, с пов1Ышением q и (02
t); частота возникновения отрыва и размеры пузырей нарастают (участок CD), и наблю
дается быстрый рост
- согласно модели пограничного
слоя (благодаря уменьшению Бт). Однако за пределами точки D
рост а.кип замедляется, интенсивность теплоотдачи проходит
через максимум, после чего наблюдается резкое падение а.кип
(участок DEF). Такой характер изменения
обусловлен
слиянием большого числа пузырей в паровую пленку, блоки
рующую (поначалу - частично, а с ростом q - все в большей
мере) тепло передающую поверхность от контакта с жидкостью.
В результате пузырьковое кипение переходит в Пленочное. А
поскольку теплопроводность пара много меньше, нежели жид
кости, то согласно (6. 14) интенсивность теплоотдачи при этом
должна понижаться. Слабый рост а.кип правее точки F вызван
a.JCIOI.

-

-

-

a. JCIOI

<Х.юm

503

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

главным образом некоторым увеличением теплопроводности
пара с температурой.
Тепловая наrрузка и темпера'l)'рный напор, отвечающие точке Е, называются
критическими: qкр и
(02 - t)кр. Определение критических величин важно для
энергетиков: превышение qкр и (02 - t)кр, сопровождающееся резким понижени
ем акип. чревато опасностью выхода из строя тепловых элементов энергетиче
ских установок (переrрев, пережог труб). В целях ориентировки: при кипении
воды под атмосферным давлением qкр "' 1оз кВт/м 2 , (02 - t)кр "' 25 •с,
а :;
"' 45·10 3 Вт/(м 2·1С). Для химической технолоm и эти моменты менее акту
п

альны, поскольку рабочая область наrрузок обычно на порЯдок ниже критиче
ских; однако во избежание падения интенсивности технолоmческоrо процесса и
здесь нужно контролировать рабочие значения q и (02 - t), дабы не выйти за
критический порог• .

Теоретическое описание теплоотдачи при кипении - весьма
сложная задача. Поэтому обычно обращаются к эмпирическим
соотношениям, ограничиваясь областью тепловых нагрузок,
интересных для той или иной практической сферы. Для хими
ческой технологии эта область лежит на участке CD, она охва
тывает диапазон q от 10 до 100 кВт/м2 (или несколько более).
Эмпирические формулы удобно представить в виде степенных
соотношений
(а)
а.КЮI = Bq"'

причем В отражает свойства кипящей жидкости. Показатель
степени п, по разным данным, колеблется чаще всего в преде
лах 0,6 - О, 75; наиболее часто встречается п = О, 7 - эта цифра
принята для последующего анализа:
(б)
а.КЮI = Bcf·7.
В расчетном плане интенсивность теплоотдачи удобнее вы
ражать в зависимости от температурного напора (02 - t). По
скольку, согласно (6. 3 ), q = а.Лt, то
а.КЮI

откуда

=

В[а.кип(02 - t)J0•7,

причем Во = Вl;{!,З = вз.зз - коэффициент, отражающий, как и
В, свойства кипящей жидкости.
Значения В и Во для каждой кипящей жидкости должны
(6.26)

определяться экспериментально. При отсугствии опытных дан 
ньIХ может быть предложен следующий прагматический пугь их
оценки . Детально изучают теплоотдачу к наиболее распростра
ненному кипящему теплоносителю - воде и получают эмпи• Сведения о qкр, (02 - t)кр и способах их оценки приводятся в у чебниках
моноrрафиях по теплопереносу (7, 9, 11, 1 9 ) и др.

504

и

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

рические формулы, позволяющие рассчитать искомые парамет 
ры для воды Вв и Вов· Затем проводят сравнительный экспери
мент, изучая теплоотдачу к кипящим воде и интересующей нас
жидкости при одинаковых тепловых нагрузках q (такой экспери 
мент достаточно прост) . В результате получают относительный

коэффициент теплоотдачи

кил
(:кил

ер:

)
в
q=idem

= q>

=

Bqo��7
Ввq

=

:в ,

(в)

причем индекс " в" здесь и в последующих расчетн ых соотно
шен ия х относится к ки пящей воде . Далее , очевидн о: В= срВв .
Поскольку практические расчеты удобнее вести на основе
температурн ых напоро в, то
3,33
2
кип
Во(82 - !) ,33
о =
=<р3,33. (r)
а.
2'33
(
)
в (02-t)=idem Вов(82 - 1)
о в
в
а.кил
Таки м образом , при известных Во в и q> нетрудно определить
Во для рабочей жид кости:
значение
Для
Во= Во в'Р3,33 И
а.кип= Во в'Р3·33(82 - t)2'33
(6 .26а)
определения величин Во в и предложены различные фор 
<р
мулы. Наиболее распространенные из них приведены ниже.
=

: (: )

·

В диапазоне давлений от 0,007 до 0,5 МПа (это практически охватывает нуж
ды химической технологии) в зависимости от давления р (выражено в барах) :
- при кипении воды в большом объеме

(д)
Во • = 4Ор0,57;
- при кипении восходящего потока воды в трубках теплообменных контуров
Во • =

46р0,57.

(е)

Значения коэффициентов <Р при кипении:
'
- индивидуальных веществ - в зависимосm от значений критических давлений
2
(ж)
<Р = ( Ркр /Ркр.в)О,5 ;
- индивидуальных веществ (в отсутствие сведений о Ркр) и их смесей

г,це

<Р=

06
( мМр. ) 0,47 ( ) 0,
.--.!!'.

µ.
µ

М - малярная масса, р - плсmюсrь жидкосm,

µ - ее динамическая вязкосrь;

�(�;)о.2з(;,)о.з'

- водных растворов неорганических веществ

q> =

'

(з )

(и)

где v - кинематическая вязкость жидкости, р - рабочее давление, Ps - давление
паров воды при температуре кипения раствора.

• Критические давления Д11Я ряда распространенных веществ по [ 1 7) приве
дены в Приложении 6.2.

505

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

В формулах для <р физичес кие свойства воды и кипящих жидкостей бер утся
при их температурах кипен ия под атмосферным давлением.

Из выражений (6 .26) и (6.26а) следует, что при кипении
жидкостей, как и при конденсации паров, связь Q и темпера
турного напора нелинейна, поскольку акип зависит от (0 2 - t).
Это приводит к затруднениям в использовании концепции
пропускных способностей.
6.7.

ТЕПЛООТДАЧА ОТ ПОВЕРХНОСТИ
В ПСЕВДООЖИЖЕННОМ СЛОЕ

Среди дисперсных систем с твердой фазой наибольший ин
терес в аспекте интенсивности теплопереноса представляет
собой псевдоожиженный слой, в особенности - при псевдо
ожижении
газами.
Химико-технологические
процессы
(массоперенос, химические реакции), проводимые в псевдо
ожиженном слое, нередко сопровождаюrся выделением или
поглощением теплоты, которую необходимо отвести из слоя
(подвести в него). С этой целью непосредственно в слое разме
щают теплопередающую поверхность: коэффициенты теплоот
дачи от слоя к поверхности апс достаточно велики, так что
удается обойтись весьма компактными поверхностями.
Подчеркнем: здесь рассматривается теплоперенос слой - по
верхность; вопросы межфазного теплообмена рассматриваюrся
в разд. 7. 1 1 .
Коэффициент теплоотдачи апс зависит прежде всего от ско
рости ожижающего агента w и его теплофизических свойств, а
также от размера псевдоожижаемых твердых частиц. Типичная
зависимость апс от w представлена на рис. 6 . 1 3 . В неподвижном
слое ( w ниже скорости начала псевдоожижения w0) интенсив
ность теплоотдачи невелика. При достижении w0 и ее превы
шении апс быстро растет. Далее с повышением w он достигает
максимального значения amax (при w = w0pt) и затем начинает
понижаться (обычно - весьма
медленно). Заметим, что индекс
апс
opt ("оптимальный") введен энергетиками; реально максимум ап с
аmах
достигается при скоростях, совсем
не обязательно оптимальных для
технологического процесса. .Ход
ИI

506

Рис. 6.13. Изменение коэффициента теплоот
дачи anc от поверхности к псевдоожиженно
му слою со скоростью газа w

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

кривой а. пс
w на рис. 6 . 1 3 характерен для газового псевдо
ожижения (неоднородный слой), при жидкостном псевдоожи
жении максимум <Х.пс выражен слабее.
-

Характер изменения апс от w качественно напоминает зависимость акип от
температурного напора 0 2
t (см. разд. 6.6). Такое сходство обусловлено анало
гией в механизме теruюотдачи в :лих системах. В аспекте представлений о по
rраничном слое после перехода в псевдоожиженное состояние начинается ин
тенсивное движение твердых частиц около теплопередающей поверхности, это
приводит к уменьшению толщины теплового пристеночного поrраничного слоя
и возрастанию апс· Однако при существенном повышении w поверхность в
значительной мере блокируется газовыми пузырями, т.е. малотеплопроводной
фазой (как и при кипении - паровой пленкой), и апс снижается.
Более современные представления о механизме теплопереноса стенка
псевдоожиженный слой базируются на "пакетной модели". В соответствии с нею
определяющую роль в переносе теплоты иrрают неустойчивые образования
твердых частиц - "пакеты". В кратковременном контакте с горячей поверх
ностью пакет проrревается (за счет его теплопроводности), забирая от поверх
ности теплоту. Газовый пузырь, подойдя к поверхности, оrtiрас ывает пакет в
ядро псевдоожиженного слоя . После ухода пузыря от поверхности на его место
приходит новый пакет частиц - так осуществляется перенос теплоты от поверх
ности к слою (или в обратном направлении). С увеличением скорости w повы
шается частота появления пузырей у поверхности (а с ней и частота смены паке
тов) и уменьшается продолжительность контакта отдельного пакета с поверх
ностью - поэтому возрастает интенсивность теплоотдачи , т.е. апс· При высоких
скоростях w > wop1 газовых пузырей становится много, растет время их контакта
с поверхностью и ее доля, занятая малотеплопроводными пузырями, - поэтому
начинается снижение апс с ростом w.
Описанный выше механизм отражает вклад кондукrивной с оставляющей
аконд в общий теплоперенос апс· Параллельно теплота передается непосредствен
но от газового потока к поверхности - конвекrивная составляющая аконв· В
целом апс = аконд + аконв·
-

В области мелких частиц (граница проходит вблизи размера
d"" 1 мм) величина <Х. пс уменьшается с увеличением d. Такой
характер зависимости а.пс от d не противоречит пакетному ме
ханизму теплопереноса.
Для мелких частиц вклад аконв мал, так как скорости газа не очень велики;
определяющую роль в апс иrрает аконд. а она уменьшается с ростом d. Для круп

ных частиц вклад акона и аконд становится соизмеримым, а аконв растет со ско
ростью (для крупных частиц она выше); здесь возможен и рост апс с d, особенно
при d > 2 - 3 мм.

Увеличение теплопроводности газа сопровождается законо
мерным возрастанием а. пс
это наглядно следует из пленочно
го механизма теплопереноса [см. выражение (6.14)).
В литературе• приводятся мн огочисленные расчетные фор
мулы для a.max, Wopt и значений <Х.пс на восходящей и нисходя
щей ветвях кривой <Х. пс
w. Ниже представлены расчетные
соотношения для W0pt и <X.max·
-

-

• См., например,

(4, 5 ) .

507

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Эксперимеmально устаномено, что при псевдоожижении мелких частиц
значения Wopt сдвинуrы в сторону скоростей витания w8, а крупных - в сторону
скоростей начала псевдоожюк ения w o. Поэr ому Д11Я оценки Wop1 оказал ось при
годным соотношение, состаменное из фраrмеmов формул Тодеса для w8 (2 . 72 )
и wo (2 .7 1 а) :
- w opt d
Ar
Reopt
(а)
-

18+5,22.fAi'
�-V

причем d здесь - диаметр частиц (не теплообменных труб и других теплопере
дающих элементов).
Достаточно полоmе максимумы на кривой апс - w (т.е. невозможность чет
кой фиксации значения Wop1) придают этой формуле оценочный харакrер ; экс
перимеm позволяет считать такую оценку вполне удометворкrельной.
Для расчета a max в области достаточно м елких части ц (велик вклад ак0нд)
наиболее надежной является формула Забродского, учитывающая вклад диаметра
частиц d и теплофизических свойств газа - р и Л. (все величины - в СИ):
a max ,,. (аконд)mах

=

35,7p0,2л_0,6tf""0,36.

(б)

В области крупных частиц заметно сказывается вклад конвеlСI'Ивной состав
ляющей• ако88, так что общий коэфф ициеm теплоотдачи будет вьпuе рассчитан
ного по формуле (б) .

6.8.

ПОРЯДОК КОЭФФИЦИЕНТОВ ТЕIUIООТДАЧИ

Инженер должен представлять себе порядок. величин коэф
фициентов теплоотдачи для различных случаев теплопереноса.
Это дает возможность:
- суметь сделать при кидочный расчет процесса, не распола
rая расчетными формулами и точными сведен иями о значениях
свойств веществ;
- оценить результаты расчетов, проведенных по теоретиче
ским или эмпирическим формулам (их правильность, соответ
ствие физическим представлен иям);
- разумно принимать стартовые значения коэффициентов
теплопереноса при итерационных расчетах (см. гл. 7).
В данном разделе приводятся диапазоны преимущественных
на
з чений а для наи более часто встречающихся ситуаций кон
вективного теплопереноса.
Для воздуха умеренной ("комнатной") температуры харакrерен следующий

диапазон значений а:

Ситуация
Естественная конвекция (например, от тепловой изоляции
аппарата при температуре ее поверхности 40-50 °С)
Выну:жценная конвекция (контакт со стенками труб и т.п.)
Вьmу:жценная конвекция (теплообмен с поверхностью)
в слое насадки, неподвижном зернистом слое
Псевдоожиженный слой - поверхность
· См . (5 ) .

508

а, Вт/(м2. К)
5-12

10-30
20-50
200-400

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

При использовании других газов (в том числе воздуха иной температуры) ко
эффицие1ПЫ теплоотдачи при прочих равных эксплуатационных условиях зави
сят прежде всего от теплопроводности газа Л . Если индексом " вэд" обозначить
воздух умеренной температуры, а индексом "r" - газ, то приближенно
2/3
(а)

)
�"(�
а.-

Лщ

Для воды (в жидком состоянии) при вынужденном ее движении внутри труб
или при наружном их обrекании со скоростью 0,3-2 м/с коэфф ициент теплоот

дачи будет в пределах

а.=

Для водных растворов

а.

1000+3000 Вт/(м2./().

зависит от концентрации растворенного вещества:
при низкой концентрации а. мало отличается от характерного для воды; при
увеличении концентрации изменение а. может бьпъ значительным . Скажем, для
водных растворов солей с ростом их концентрации а. снижается из-за увеличе
ния вязкости раствора и сопугствующего утотцения пограничной пленки.
В случае органul/еских жидкостей а. ниже, чем для воды, в 5-7 раз, посколь
ку у этих жидкостей в 4-5 раз ниже теплопроводность, к тому же примерно в 2
раза ниже теплоемкость.
Для кипящей воды в ти пичных технологических аппаратах и режимах харак
терны а. на весьма высоком уровне: а= 5000+10000 Вт/(м 2·К) .
Для кипящих водных растворов неорганических веществ а ниже, чем для во
ды, - для слабоконцентрированных снижение невелико, для высококонцентри
рованных - иноr;ца весьма существенно. Здесь все определяется значением
отиосиrельного коэффициента <р (см. разд. 6.6).
Для кипящих органul/еских жидкостей величины а ниже, чем для воды примерно на порядок - преЖде всего из-за более н изких значений теплоl!ровод
ности Л; здесь также все определяется в конечном счете значениями q1 - чаще
всего для органических жидкостей они не выше 0,4.
В случае конденсирующегося водяного пара значения а очень велики - на
уровне 7000-20000 Вт/(м2 К)
При конденсации паров органul/еских веществ а ниже, чем в случае водяного
пара, примерно на порядок. Причина ясна при рассмотрении формул (6 .23),
(6.24): у органических жидкостей (конденсата) существенно ниже, чем у воды,
теплопроводность Л и теплота конденсации r (значения р и µ - обычно сопоста
вимы); в ряде случаев на а может заметно отразиться значение вязкости µ
для
некоторых органических жидкостей оно существенно выше, чем у воды.

· .

-

Надо иметь в виду, что величины с:х. в некоторых режимах
работы мо rут выходить за пределы указанных диапазонов, но
ориентировку приводимые цифры даюг .
6.9. ТЕПЛОПЕРЕНОС ИЗЛУЧЕНИЕМ

Лучистый теплоперенос в химических и смежных областях
производства встречается реже и вносит чаще всего меньший
вклад, чем ко ндукция и ко нвекция. Он важен прежде всего в
ряде высокотемпературных процессов, а также в тех случаях,
когда другие виды теплопереноса характеризуются низкой ин 
тенсивностью - тогда вклад лучистого переноса теплоты ока
зывается ощутимым (пример : потери теплоты от стенок изоли
рованного аппарата в окружающую среду) . По указанным при509

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

чинам проблемы лучистого теплопереноса изложены в учебни
ке достаточно лаконично • , рассмотрены лишь наиболее суще
ственные моменты .

6.9.1.

Общие понятия

Из полного потока лучистой энергии Q0, падающей на тело
(рис . 6 . 1 4 , а) , часть Qл - поглощается, другая, QR,- отражается ,
третья Q D - проходит сквозь тело:
Отношение Qл/ Qo

ность тела, Qя/ Qo = R
кательную; очевидно:

=

А характеризует

-

(а)

по гл ощ а тельную

отражательную ,

А+R+ D

=

1.

Qл/ Q0 = D

-

способ

пропус

(б)

Каждая из безразмерных величин А, R, D может изменяться
от О до 1 - при соответствующем изменении других величин ,

конечно.
Если А = 1 (R = О, D = О), то тело поглощает всю падающую
на него энергию; тогда оно называется абсолютно черным. Прак
тически хорошо (не строго цеJШКом, разумеется) излучение по
глощают шероховатые поверхности (независимо от их цвета).
Если R = 1 (А = О, D = О) , то вся падающая на тело энергия
отражается ; при геометрически " правильном " полном отраже
нии тело называют зер кальным, при диффузном - абсолютно
белым. Практически хорошей отражательной способностью
обладают гладкие (в особенности - полированные) поверхно
сти - тоже независимо от их цвета.
Если D = 1 (А = О, R = О), то тело абсолютно проницаемо
для излучения - прозрачно, диатермично.
Значения А, R и D зависят от природы тела, его температу
ры и , кроме того, от длины волн излучения. Для теплового
излучения (длины волн в диапазоне от 0 , 4 до 40 мкм) твердые
тела и жидкости (исключая очень тонкие их прослойки) прак
тически непрозрачны - атермичны. Здесь

D = О,
А + R = 1.
(в)
Из последнего равенства следует, что тела, хорошо погло
щающие лучистую энергию, плохо ее отражаюr (и наоборот) .
И нтенсивность собственного излучения абсолютно черного
тела Ео определяется законом Стефана- Больцмана (6.4). Для
описания излучения реальных тел вводят понятие о сером теле,
собственное излучение которого составляет определенную до
лю Ее (если строго, то для всех длин волн - одинаковую) от
' Подробнее см. (6 , 7, 1 1 - 1 3 , 1 9] и др .

510

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

То

т

;

ни

о

-

-

А 0
Е

а
Рис.6.14. К

,

,

Е

Ео

Е1

J

,(� =Е,Е+(1- &1)Е2
Е2

(/-А)Е0

общим понятиям лучистого

1j

№1

б

в

теплопере носа:

к взаимодействию тела с падающим на неrо лучистым потоком,

черноты

и поглощательной

способности,

потоке

в

,._-

-

к

понятию об

6

-

к связи степе

эффективном

лучистом

излучения абсолютно черного тела. При этом величина &с, на
зываемая степенью черноты, зависит от природы излучающей
поверхности, ее состояния, а также в определенной мере и от
температуры. Конкретные значения &с приводятся в литературе•.
С учетом степени черноты поток энергии, излучаемой телом,
Е = &с Ео , так что
(г)
Е = &ccroT4,
причем в расчетах лучистого теплопереноса Т - в градусах аб
солютной шкалы (К).
Для установления связи &с с характеристиками взаимодей
ствия тела и лучистой энергии рассмотрим (рис. 6.14, б) две
параллельные атермичные поверхности, расположенные так
близко, что лучистый поток от одной из них обязательно попа
дает на другую. Пусть при этом одна поверхность абсолютно
черная (ее температура Т0), а другая - серая (ее температура 7).
Поток лучистой энергии от серой поверхности Е полностью
поглощается абсолютно черной поверхностью, для которой по
определению А = 1, &с = 1. В то же время часть лучистого пото
ка от абсолютно черной поверхности Е0, попадая на серую по
верхность, поглощается ею (АЕо); оставшаяся часть (1 - А)Ео
отражается (и затем поглощается абсолютно черной поверх
ностью). Если, например, Т > Т0, то для серой поверхности ба
ланс теплоты (в расчете на 1 м2) запишется как разность отда
ваемого и поглощаемого потоков:
АЕо.
q =Е
(д)
-

'

•

См., например,

-

( 1 1 , 1 2, 1 4, 1 9).

511

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Это выражение справедливо при любых значениях Т и То
от этих температур зависят величины лучистых потоков тепло
ты Е и Е0. В случае Т = То устанавливается тепловое равнове
сие между телами и q '= О . Тогда АЕо = Е, так что Е/Ео = А. Но
это отношение выше было названо степенью черноты; таким
образом, Ее = А, и в последующем анализе одинаково право
мерно оперировать символами Ее либо А.
Поверхность тела не только сама излучает энергию, но и
взаимодействует с падающим на него излучением, часть кото
рого добавляется к собственному излучению тела. Полный по
ток лучистой энергии, складывающийся из собственного и от
раженного потоков, называется эффективным излучением тела
ВэФ· Его можно найти из следующих соображений (рис. 6. 14,в).
Собственное излучение Е1 поверхности №1 определяется ее тем
пературой и физическими свойствами . Если извне на нее падает
удельный поток лучистой энергии БJ_, то отраженная часть этого
потока составит (1 - в1)ЕJ_, где в1
степень черноты поверхности
№1 . Тогда эффекгивный удельный поток от поверхности №1 со
ставит
(е)
-

-

Это выражение используется ниже для определения интен
сивности лучистого теплообмена между телами.
6.9.2. Лучистый теплоперенос между двумя телами

Задачу будем решать в наиболее простом варианте, рассмат
ривая теплоперенос (рис 6 . 1 5) между двумя равными по пло
щади параллельными пластинами №1 и №2 . Пластины обра
щены друг к другу излучающими сторонами, так что излучение
с одной из них полностью попадает на другую. Удельный по
ток энергии от поверхности №1 обозначим Е1эз�, от поверх
ности №2
ЕJ.ЭФ· Удельный (на 1 м2 ) и полныи (на всю по
верхность F) потоки лучистой энергии в единицу времени со
ставляют
(ж)
q = Е1эф - БJ.эф и Q = qF = (Е1эф - ЕJ.эФ)F.
.

-

Значения эффективных тепловых потоков определяются на
базе формулы (е), однако с учетом того, что извне на каждую
поверхность падают тоже эффективные лучистые потоки
(скажем, на поверхность № 1 поток Е2ЭФ, а не БJ_). Поэтому

{

512

Еl:ЭФ = Е1 + (1 - в1)Е2:ЭФ,
Е2:ЭФ = Е 2 +(l-в2)Е1:эф.

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

7j

а

а

б

Рис.6.15. Расч�ые схемы к формулам тennonepeнoca излучением:
плос:JСИе пар&11J1еm.ные nо.1ерхиосrи, 6 - llЬIП)'XllU и oX111nD&JOщu no11ep:llJIOCПI

Решим эту систему, например, методом подстановки. Тогда
-

откуда

Е1ЭФ = Е1 + ( 1 - &1)[ Ei, + ( 1
Е lэф -

El + Е1

-

е1Е2
&1 + &2 - &1&2

&1)Е1ЭФ],

-

Е1 + Е1

и совершенно симметрично
i;_
.и-zэф -

-

е2Е1
&1 + &2 - &1&2
-

•

Теперь возможно рассчитать q и Q по (ж); например, после
очевидных сокращений

Q=

&2Е1 -е1Е2 F.

61+&2-6162

Подсrановка сюда значений Е1 и Ei. по (г) дает

Q

=

•

61&2Co'fi•-61&2СоТ2 F.
&1+62-&162

Эrо выражение для плоских параллельных поверхностей
(F 1 = F2 = F) принято представлять в виде
Q=

а

oF('fi• - т;•)
l
l
-+--1
62
61

или в более лаконичной форме

-

с

использованием понятия о

513

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

приведенной степени черноты

где

Q=

Епр

Епр ::

Епр :

crof{T14 - T24),

(6.27)

-----

(6.28)

1

}
1
-+--1
Е1

Е2

Заметим, чrо в инженерных расчетах вместо величин Т4 часто используют
(Т/100)4, заменяя одновременно ао на Со• ао · 108. Считают, чrо такая форма
записи праlСl'ИЧески несколько удобнее.

Более общим случаем является теплообмен межцу телами
произвольной формы- первым (выпуклым) площадью F1 и
вторым, полностью его охватывающим, площадью F2. В этом
случае, если расчет базировать на поверхн ости F1, расчетная
формула записывается сходно • с (6.27), однако приведенная
степень черноты выражается иначе:
(6.27а)
Q = EпpcroF1(T14 - Т24),

Епр =

1

(__!__ _ )
2

_!_ + F1

1

(6.28а)

&1 F &2
Легко видеть, что при F1 = F2 (случай равных плоских па

ралл ельных или оче нь близких криволинейных поверхностей)
формула (6.28а) переходит в (6.28). Если же речь идет о потере
телом теплоты в окружающее пространство за счет излучения,
то>положив для этого пространства F2 _.,. оо, получим по (6.28а):
Епр = i;:1; далее расчет ведуr с использованием формулы (6.27а),
т.е. на основе поверхности F1.
На практике нередко лучистый теплоперенос происходит одновременно с
конвективным; пример: потери в окружающую среду от поверхности наrретого
техноло111ческого аппарата - излучением, а также естественной конвекцией (с
коэффициеитом теплоотдачи ак). В таких случаях иногда удобно произвести
подмену задачи, записав теплоперенос излучением в манере конвективной тепло
отдачи, т .е. ввести понятие о "коэфф ициенте теплоотдачи излучением" ал. Это
делается путем формального приравнивания тепловых потоков, записанных в
физически обоснованной форме (6.27) и в форме, принятой для конвективной
теплоотдачи (6.13):
откуда

EnpGo(7i4-Т24)
Т1-Т2

(з)

Громоздкость анализа, приводящего к формулам (6.27а), (6.28а), не позво
ляет привести его в учебнике; см. (7, 9, 11, 12J.
•

514

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Далее можно использовать в расчетах "суммарный" коэффициент теплоотда
чи О.к+ ал.
Разумеется, в таком представлении связь Q и ( Т1
Т2) остается нелинейной,
поскольку ал с.ложным образом зависиr от уровней температуры и температур
ноrо напора.
-

6.9.3. Экранирование

Экраны в химической технологии, в энергетике, в металлур
гии чаще всего устанавливают, когда нужно понизить интен
сивность лучистого теплопереноса между теплообменными по
верхностями ши от поверхности к окружающей среде. Кроме
того , иногда наличие экрана присуще самой технологической
системе. Во всех этих случаях необходимо уметь рассчитать
воздействие экрана на интенсивность теплопереноса.
Подход к расчету эффекга экранирования рассмотрим (рис .
6 . 1 6) на примере стационарного лучистого теплопереноса для
двух плоских параллельных поверхностей, между которыми
расположен тонкий экран Э - его степень черноты Еэ· Темпе
ратуры излучающих поверхностей - Т1 и Т2 (пусть Т1 > Т2);
температура обеих поверхностей экрана Т3 - одинакова (так
как экран тонкий). Согласно (6.27), лучистые потоки теплоты
от горячей поверхности №1 к экрану и от него к более холод
ной поверхности №2 составят
Qэ1

=

Еtпр cro.F(T14 - Тэ4)

и Q32 = E2пpcro.F(T34 - Т24),

(и)

причем степени черноты определены выражениями типа (6.28):
Е!пр

=

1
1
1
-+--1
EJ
Еэ

}

и

Е2пр

=

1

-

Еэ

1

+

1

--

Е2

(к)

1

В случае стационарного теплопереноса Q31 = Q32 = Q3• Ис
пользуя уже известный прием (см. разд. 6.3. 2), исключим неиз
вестную заранее величину Т3:

+

_

т4 - 4
Qэ
Тэ 1
EJпpcroF
=
Q,
Т,'
E2пpcroF

-Т,'

�

т4 - 4
Т2
1

=

..sь_ _1_ +-•

(

aoF •tnp

.)

'2п

.

Отсюда
1
--- --ao F( T1 4 - Т24)
1
1
--+-Е tпр

=

Епр.эсrо.F(Т14 - Т24). (6.29)

Е 2 пр

515

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис.6.16.

Схема экранирования (плоский экран)

Для выявления эффекта экранирова
ния следует сопоставить лучистые потоки
теплоты без экрана и с экраном. При
отсутствии экрана выражение (6.27) со
держит множитель Enp• рассчитываемый
по (6.28). Раскроем значение соответ
ствующего множителя в (6.29) при нали
чии экрана:

--

Епр.э = _1___1_ =
+ -Е1 пр Е2пр

=

---(_!_ ) (
) --1

+

Е1

_1 -

-1
_1 1 +
+
1

Еэ

Еэ

(л)

Е2

Очевидно, что Епр. э < Епр: знаменатель выражения (л) явно
больше, нежели выражения (6.28), поскольку Еэ s 1 . Это означа
ет, что наличие экрана понижает интенсивность лучистого теп
лопереноса: Qэ < Q, где Q - тепловой поток в отсутствие экра
на. Для оценки степени этого понижения примем, что Elnp =
= Е2пр = Епр· Тогда Еп р э = Епр /2, и, следовательно, Qэ=Q/2 установка одного экрана вдвое понизила интенсивность лу
чистого потока теплоты. Тот же анализ ситуации с двумя, с тре
мя, с N параллельными экранами приводит при одинаковых Е;пр
к соотношению

.

_я_ _

(м)
N+
Для системы тел, изображенных на рис. 6.15,б, с установкой
экрана между телами (он охватывает меньшее из них) анализ
усложняется. Его надо вести с учетом излучающих поверхностей
F1, F2 и экранирующей поверхности Fэ (причем F1 < Fэ < F2).
Ход анализа с использованием выражений типа (6.28а) аналоги
чен продемонстрированному выше.
QэN=

1

6.9.4. Об и3J1УЧении

rазов*

С проблемой излучения газов (значит и поглощения ими лу
чистой энергии) химическая технология встречается при осу
ществлении высокотемпературных процессов. Одно- и двух•Подробнее см. (7,
516

9,

11, 12, 1 9 ) .

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 6.17. Влияние основных
фапоров на степень черноты
СО2

атомные газы - диатермичны
(теплопрозрач
0,1
ны); однако трех- и мно
гоатомные газы и пары
0,05
обладаюr способностью
теплоизлучения
и теп
лопоглощения в опреде
0,01
ленных диапазонах длин
волн (эти диапазоны за
висят от природы газа,
0,005
его температуры и давле
н ия). Пожалуй, наиболее
0,001
часто в химической технологии приходится учи
0,001
500 1000 2000 т.к
100 200
тывать
излучение -пог
лощение в среде водяного пара и диоксида углерода, а в процессах обжига - и диоксида серы.
Для технических расчетов лучисrоrо теплопереноса межцу га
зом (чаще всеrо - rорячим , температура 7;.) и телом (температура
Т,., поверхность F, степень черноты &r) феноменологически посту
лируюr возможность использования формулы (6.27) с подстанов
кой в нее разности (7;.4 - Т,.4) и приведенной степени черноты &'пр,
отыс киваемой по соотн ошению типа (6.28):
1
(6.30)
&' пр=
1
1
- -f;r

+

f;T

1

Нахожцение &r затруднений не вызывает; проблема состоит
в определении интегральной (результирующей по всем волно
вым диапазонам) степени черноты газообразной среды &г, специ
фичной для кажцого газа, пара и существенно изменяю
щейся с температурой. Кроме того , интенсивность излучения
(поглощения) зависит от частоты взаимодействия теплового
луча с молекулами (атомами) газообразной среды, значит от
давления газа р и толщины газовой прослойки /; обычно влия
ние этих факrоров учитываюr совместно - в виде произведе
ния (р!). На рис . 6 . 1 7 (на примере СО2) иллюстрируется влия
ние основных параметров· на &r . Заметим, что для водяных
паров значения &r заметно выше, чем для СО2.
• Подробнее см . (7, 9, 1 1 , 12, 1 9 ).

517

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Степень черноты смеси газов не является адд итивной вели
чиной .
Более детальные диаграммы для определения Er приведены в
рЩ!е учебников по теплопередаче· и в справочной литературе•• .
ЛИТЕРАlУРА

к

главе 6

1 . Бретшнайдер С. Свойства газов и жидкосте й: Пер . с полъск./ Под ред.
П.Г. Романкова. М.- Л.: Х имия, 1966. 536 с.
2. Варгафтик Н.Б. Справочник по физическим свойствам газов и жид
костей. М . : Физмаn-из, 1963. 708 с.
3 . Гельперин Н.И. Основные процессы и аппараты химической технолоmи.
М.: Химия, 1 98 1 . 812 с.
4. Гельперин Н.И" Айнштейн В.Г., Кваша В.Б. Основы техники псевдоо:жи
жения. М . : Химия, 1967. 664 с.
5. Гельперин Н.И., Айнштейн В.Г. 11 Псевдоожижение, rл.Х 'Теплообмен"'/
Под ред. И . Ф . Дэвидсона, Д. Харрисона: Пер. с анrл. / Под ред. Н . И . Гельпе
рина. М . : Химия , 1 974. 760 с.
6 . Гребер Г., Эрк С., Григулль У. Основы учения о теплообмене: Пер. с нем./
Под ред. А.А. Гухмана. М . : ИЛ, 1958. 568 с.
7. Исаченко В.П., Осипова В.А., С}lхомел А.С. Теплопередача. М.: Энерmя,
1 969. 440 с.
8. Касаткин А.Г. Основные процессы и аппараты химической технолоmи .
М . : Химия, 197 1. 784 с.
9. Кутателадзе С.С. Основы теории теплообмена. М . : Атомиздат, 1979.
416 с.
10. Маньковский О.Н., Толчинский А.Р., Александров М.В. Теплообменная ап
пара'l)'ра химических производств. Л.: Химия, 1976. 368 с.
1 1 . Михеев М.А. Основы теплопередачи. М.-Л . : Госэнерrоиздат, 1956.
392 с.
12. Михеев М.А., Михеева И.М. Основы теплопередачи. М . : Энерmя, 1977.
342 с.
13. Нащокин В.В. Техническая термодинамика и теплопередача. М.: Высшая
школа, 1 980. 469 с.
14. Павлов К.Ф., Романков П.Г., Носков А.А. Примеры и задачи по курсу
процессов и аппаратов химической технолоmи. Л.: Химия, 1987. 574 с.
15. Перри Дж. Справочник инженера-химика: Пер . с анrл./ Под ред. Н . М .
Жаворонкова. Л . : Химия, 1969. 1 144 с.
16. Плановский А.Н., Николаев П.И. Процессы и аппараты химической и
нефтехимической технолоmи. М . : Химия, 1 972. 494 с.
17. Рид Р., Шер(f)'д Т. Свойства газов и жидкостей: Пер . с анrл./ Под ред.
А.Н . Плановскоrо. М.: Гостоrrrехи здат, 1 964. 334 с.
1 8 . Справочник по теплообменникам: Пер . с анrл . / Под ред. О.Г. Марты
ненко и др . М . : Энерrоатомиздат, 1987. 9 1 3 с.
19. Хоблер Т. Теплопередача и теплообменники: Пер. с полъск. / Под ред.
П .Г. Романкова. Л . : Госхимиздат, 196 1 . 820 с.
• Подробнее см. (7, 9, 1 1 , 12, 19).
•• См" например, ( 1 5, 1 8 ) .

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ПРИЛОЖЕНИЯ К ГЛАВЕ 6

Приложение 6.1. К ОПРЕДЕЛЕН ИЮ
СРЕД Н ЕГО КОЭФФИЦИЕНТА РЯДНОСТИ
ДЛЯ ПУЧКОВ ГОРИЗОНТАЛЬН ЫХ ТРУБ
Средний коэффициент рJJДНости &р для различных горизон
тальных трубных пучков из Nт труб определяется по rрафику на
рис. 6.18 в зависимости от среднего числа труб в вертикальном
РЯдУ пр.
Шахматному расположению труб отвечает их размещение в
трубных решетках по сторонам шестиугольника (или, что то же
самое, в вершинах равностороннего треугольника), т.е. по схе
ме 1 на рис. 6.19. При большом общем числе труб Nт в свобод
ном пространстве сегментов между цилиндрическим корпусом
и внешним шестиугольником размещают дополнительные тру
бы (на схеме не показаны). Коридорному расположению отвеча
ет размещение труб в углах квадрата, т.е. по схеме 2. Здесь
обычно - менее развитые поверхности теплообмена F. Реже
используется размещение труб по концентрическим окружно

стям.

При шахматном расположении труб (схема 1 ) значение пр
находят как среднеарифметическое из чисел труб на стороне
шестиугольника ( пс) и по его диагонали (пд) :
(П6.lа)
При коридорном расположении труб значение пр равно числу
труб в вертикальном рЯду, если оно в каждом РЯдУ одинаково.
В случае компоновки теплообменника с разным числом труб в
вертикальных рЯдах (как показано на схеме 2) берут средневзве-

519

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Ер

0,9
0,8

О,7�-1-1-�

0•6

ttttt±±±tlti±mrm:rm��
5

10

15

20

25

30

пр

Рис.6.18. Зависимость коэфф ициеиrа рядности Ер от среднего числа труб в вер
тикальном ряду (пр)

шенное значение пр:

(

птах + пmin

2

_

) (i

1

_

п

min
птах

)

.

( Пб. 1 6)

В табл. П6.1 приведены геометрические характеристики
пучков, необходимые для расчета среднего числа труб пр в вер
тикальном ряду для обеих схем, представле нных на рис . 6.1 9.
Там же содержатся формулы, связывающие общее число труб
Nт с характерными величинами (см. схемы 1 и 2): пс и пр, птах
и пrnin.

Схема

1

Схема2

Рис.6.19. Варианты размещения труб в теrmообменнике

520

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Таблица Л6. 1. Геометричесхне харапериСПООI пучхо• труб
•

темообмеиной аппаратуре

Число труб при шахматном их расположеюtИ
в

пучке (не
СЧJПая труб в
сеrментах)Nт

7
19
34
61
91
127
1 69
217
27 1
331
397
469
547
631
72 1
817
919
1026
1 14 1

Nт

на

стороне we- по диаrонапи

стиуrольника п,,

п.-

2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

2nc

3
5
7
9
11
13
15
17
19
21
23
25
27
29
31
33
35
37
39

-

1

Число труб при коридорном их расположев

ЮIИ

пучке Nт

5
12
21
37
52
69
97
1 20
145
185
216
264
357

вертикаль-

вертикаль

минимальное максимальное
в

в

ном ряду 11JDin ном ряду nmax

1
2
3
3
4
5
5
6
7
7
8
8
9

3
4
5
7
8
9
11
12
13
15
16
18
21
+
Nт = nminптax + 2[ (птах - 2 )
+ ( птах- 4) + ... + пminl
Наращивание
П р и м е ч а н и е.
значений вычитаемою а; = 2, 4, 6 . . .
прекращается, и р яд обрывается при
птах - а; = пmin.

= 3пс (п" - 1 ) - 1

521

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Приложение 6.2. К РАСЧ ЕТУ
ОТНОСИТЕЛЬНОГО КОЭФФИЦИЕНТА ТЕПЛООТДАЧИ
П Р И КИПЕНИ И
Таблица Пб.2, Криnt'lеские даа11енн11 для нexaropwx llllДJIJlllД)'aJU.НWX ищесв•
ВсщсСl'ВО

Аммиак
Анилин
Ацетиле н
Ацетон
Ацетонитрил
Бензол
Бромбензол
Бромэтил
Бутад иен
Вода
Гептан
Диметиловый эфир
Диоксид серы
Диэтиламин

1 �11
1 1 1,5
52, 3
6 1 ,6
46,6
47,7
48,6
44,6
61,5
42,7
2 1 8,0
27,О
53,0
77,7
36,6

ВсщеСl'ВО

Изо пропанол
п-Крезол
м-Ксилол
о-Ксилол
Метанол
Метилформиат
Оксид азота
Пиридин
Пропан
Пропанол
Сероводород
Сероуглерод
Триэтиламин

1 �11
53,0
50,8
36,0
36,9
78,5
59,2
65,0
60,0
42,О
50,2
88,9
76,0
30,О

ВсщеСl'ВО

Уксусная кис.лота
Фенол
Фреон- 12
Хлор
Хлорбензол
Хлороводород
Хлор метил
Хлороформ
Циклогексан

Тетрахлорид
углерода
Этил ацетат
Этилбензол

1�
57, 1
60, 5
39,6
76, 1
44,6
81,6
65,9
54,0
40,0
45,0
37 8
38,0
,

• Поскольку в расчетную формулу (:ж) для <р в разд. 6.6 входит отношение
критических давлений (pq,/ Pq,.8), то в переходе от физических атмосфер к единицам СИ нет необходимости.
·--· ·-·-· ··--·--·-----------"-----

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Глава 7

ТЕШIОПЕРЕДАЧА И ТЕПЛООБМЕН

Виды теплопереноса, рассмотренные в гл . 6, в реальных
теплообменных аппаратах встречаются в различных сочетаниях
в форме сложного теплопереноса. Его математическое описа
ние определяется присугствием тех или иных видов переноса
теплоты, способом их сочетания, направлением и структурой
потоков теплоносителей, их агрегатным состоянием и характе
ром изменения последнего, стационарностью или нестацио
нарностью теплопереноса (или его элементарных актов), неко
торыми особенностями теплообменных поверхностей и рЯдом
других обстоятелъств . Изучение основных закономерностей слож
ного теплопереноса является предметом настоящей главы. Перво
начально в ней дана классификация теплообменников, затем по
следовательно рассмтрены теплопередача и теплообмен.
7 . 1 . КЛАССИ ФИКАЦИЯ ТЕПЛООБМЕННИКОВ
Теплообменными аппаратами называют устройства для пере
дачи теплоты от горячих сред (теплоносителей) к холодным. О
назначении конкретных аппаратов говорят их названия: подо
греватель, холодильник, испаритель, конденсатор, кристалл и за
тор, дистиллятор и т.д. - в общем, теплообменник (в некоторых
процессах - холодообменник). Соответственно назначению
различные теплообменники имеют свои особенности; нас здесь
более всего интересуют общие моменты в их работе и методах
расчета. Однако в отдельных разделах главы будуг отмечены и
особенности, присущие различным теплообменным аппаратам.
По способам организации контакта горячего и холодного
теплоносителей различают следующие типы теплообменников.
Рекуператоры (поверхностные теплообменники). В них теп
лоносители, имеющие различные температуры, разделены теп
лообменной поверхностью. Можно сказать, что теплоносители
здесь разъед инены в пространстве, но объединены во времени.
Теплообмен в рекуператорах может осуществляться как в пе
риодическом (нестационарном) режиме, так и в непрерывном
(стационарном) . Рекуперативные теплообменники представле
ны в химической технологии наиболее широко.

523

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

q
б

�ll
п�П
в

а

г

Рис. 7.1. Кожухотрубные теnлообменники:

а
основные конструхтивные элеме1ПЫ:
1
корпус, 2 крЫШJСИ, З
трубные решепси, 4 теплообме1D1Ь1е трубх.и (Т - труб
ное пространство, М
меJIСl'рубное просrранство; / и 11 - rорячий и холоднЬ1й теплоноси
тели) ;
б-г
типичные схемы кожухотрубных аппаратов: б - одноходовой, г
двухходовой
(по трубному пространству), г
с линзовым компенсатором термических напряжений
-

-

-

-

-

-

-

-

-

К простейшим рекуператорам относятся аппараты с рубаш
ками и змеевиками (чаще всего это малопроизводительные ап
параты периодического действия). К весьма простым аппаратам
непрерывного действия относятся теплообменниЮ1 типа "труба в
трубе" , где один из теплоносителей движется по внуrренней
трубе, а другой - в кольцевом пространстве (между внутрен
ней и наружной трубами).
Наиболее распространены в химической технологии кожухо
трубнь1е теплообменники (рис. 7 1 , а) Здесь важн о четко разли
чать трубное пространство (в нем движется один теплоноситель)
и межгрубное (другой теплоноситель). Трубное пространство
отделено от межтрубного стенками труб и трубными решетка 
ми, в которых эти трубы закреплены. Трубное и межrрубное
пространства не сообщаются друг с другом.
Кожухотрубные теплообменниЮ1 могут быть вертикальными
и горизонтальными. Один из простейших вариантов
однохо
довой (по трубному и межтрубному пространствам) - схемати
чесЮf показан на рис.7. 1 ,б. С целью повышения скорости по
тока теплоносителя, а также при необходимости применения
более коротЮ1Х труб используют многоходовые теплообменни
ки; схема двухходового (по трубному пространству) теплооб
менника приведена на рис.7.1 ,в. При большой разнице темпе
ратур корпуса и труб из-за различия в их температурных удли
нениях могут возникнуrь термические напряжения, приводящие
к нарушению плотности закрепления труб в трубных решетках.
Для уменьшения этих напряжений применяют различные ком
пенсирующие устройства. Примером их могут служить линзо
вые компенсаторы, устанавливаемые на корпусе теrvюобменни.

.

-

524

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ф
а

Рис. 7.2. Оребренные трубы:

б

в

а -внуrреЮ1ее продольное ребро; 6 - нарУJКНЬlе продольные ребра,
переЧНЬiе ребра

в

- нарУJКНЬlе по

ка (рис . 7 . 1 , г) : линзы работают (как '"Гармошка") не на сжатие расширение, а на изгиб; с такого вида напряжением конструк
ция справляется легче . Существуют и другие способы компен
сации температурных напряжений, а также конструкции, во
обще свободные от них (теплообменниюt "с плавающей голов
кой", штыковые).
При необходимости интенсификации теплопередачи и соз
дания компактных теплообменников весьма широко применя
ют ребристые поверхности. На рис.7.2 показаны оребренные
трубы, используемые при продольном (вид б - прямоток, про
тивоток) и поперечном (вид в - перекрестный ток) движении
теплоносителей. Цель здесь - развитие теплопередающей по
верхности в зоне движения одного из теплоносителей - того ,
с о стороны которого интенсивность теплоотдачи ниже и под
лежит увеличению. Чаще всего применяют наружное оребрение
труб, так как внутреннее (вид а) - сложнее в изготовлении, к
тому же достигнутое здесь увеличение теплообменной поверх
ности сравнительно невелико.
При наружном оребрении внутрь трубы направляют поток
теплоносителя, харакгеризующегося в рабочих условиях более
высокой интенсивностью теплоотдачи к стенкам трубы.
Реrенераторы. В рабочей зоне теплообменника размещают
какую-либо насадку, играющую роль промежуточного аккуму
лятора теплоты (рис .7.3). Горячий и холодный теплоносители
попеременно контактируют с насадкой, то нагревая ее, то
охлаждая, при этом сами, соответственно, охлаждаясь и нагре
ваясь от нее. Можно сказать, что теплоносители здесь объеди
нены в пространстве, но разъединены во времени. В ка'{естве на
садки используют материалы, химически инертные по отноше
нию к теплоносителям. Форма и материал элементов насадки
определяются целями и особенностями теплообмена в реrене
раторе: в ряде высокотемпературных процессов это обычно
массивные, регулярно уложенные (с зазорами) кирпичи; засы525

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

.----- I

Рис. 7.3. Регенератор :
/и
//

ТtJIИ; Н

-

горячий и холодный теплоносинасадка

-

панные навалом керамические
кольца (в случае агрессивных
сред); иногда - тонкая гофри
рованная лента из высокотеп
лопроводного
материала
(например, алюминия), свер
нуrая спиралью в рулоны (в
холодильных процессах), и др.
Процесс теплообмена в регенераторе в принципе нестацио
нарен. Дабы не нарушать непрерывности технологического
процесса в аппаратах до и после регенератора, устанавливают
несколько (минимум - два) регенераторов паралле льно с по
переменным переключением потоков горячего и холодного
теплоносителей: одни из них работают в данный момент в ре
жиме нагрева насадки, другие - в режиме ее охлаждения;
спустя некоторый промежуrок времени регенераторы переклю
чают, изменяя режим работы на противоположный.
Контактные (смесительные) теплообменники. Здесь теплопе
ренос происходит при непосредственном соприкосновении
теплоносителей (рабочих тел): они объединены в пространстве и
во времени. Теплообмен возможен как в непрерывном, так и в
периодическом режиме либо в некоторых промежуrочных ре
жимах. В качестве рабочих тел мoryr быть взяты газы или вза
имно растворимые жидкости, если, конечно, в дальнейшем не
требуется их раздельное использование. Чаще всего необходи
мо последующее раздельное использование теплоносителей;
тогда мoryr быть выбраны только рабочие тела, легко отделяе
мые друг от друга: газ и жидкость, газ и твердые частицы и т.п.
В качестве примера контакгного теплообменника на рис. 7.4
показан пневможелоб - аппарат с псевдоожиженным слоем
твердого материала. Горячий исходный твердый материал по
дается в аппарат (последний слабо наклонен к горизонту). Ожи
жающий агент (он же - холодный теruюносиrель) - воздух. В
ходе процесса твердый материал охлЮI01ается, перемещаясь под
уклон; воздух нагревается и выводиrся из аппарата сверху.
Контакгные теплообменники нередко используются также в
системах жидкость-газ, пар: барботаж газа (пара) через слой
жидкости; теплообмен в скрубберах на насадке, орошаемой
сверху жидкостью при подаче газа снизу; впрыск дисперrиро
ванной жидкости в газовую среду (кстати , в среду другой жид
кости - тоже, тогда это системы жидкость-жидкость).
526

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 7. 4. Смесительный теruюобменник с
псевдоожиженным слоем:

аппарат
1
теплообменный
(пневмоJ1ССJJоб) , 2 - гаэораспределиrельная
промежуrочный сборю11с: твердого
решетха, З
материала;
1 - твердый матери ал , 11 - газ (воздух) ;
лr - JIИIOIJI гори зонта , пс - псевдоожи
женный слой

-

Более детально конструкции разнообразных теплообменных
аппаратов (упомянугых выше и других) и описание их работы
приведены в учебной и справочной литературе • .
7.2. ТЕПЛОПЕРF.дАЧА (ОСНОВ НЫЕ ПОНЯТИЯ)

В соответствии с классификацией, установленной в rл. 6,
под теплопередачей понимают перенос теплоты нормально к
поверхности контакта. Это означает, что в рамках теплопереда
чи не рассматриваюrся эффепы , связанные с переносом теплоты
вдоль теплопередающей поверхности с движущимися теплоноси
телями (or входа в теплообменник к ero выходу); такой теплопе
ренос, именуемый теплообменом, изучается в разд. 7 .5 и далее.
В процессе теплопередачи происходит взаимодействие от
дельных стадий теплопереноса, рассмотренных в гл. 6. Строrо
rоворя, последовательный кондуктивный перенос теплоты че
рез многослойные стенки (когда складываются кондуктивные
термические сопротивления) или параллельный перенос ее
пакетами частиц и конвекцией в псевдоожиженном слое (коrда
складываются проводимости <Х.конд и СХ.конв) вполне можно от
нести к теплопередаче.
Простейшие схемы стационарной последовательной и па
раллельной теплопередачи представлены на рис. 7.5.
В случае последовательного переноса один и тот же поток
теплоты Q (или отнесенный к единице теплопередающей
поверхности q = Q/F) последовательно проходит через погра
ничный слой со стороны горячего теплоносителя (его темпера
тура Т, коэффициент теплоотдачи а. 1 ) , стенку (толщина 8ст,
коэффициент теплопроводности Лет) и пограничный слой со
стороны холодного теплоносителя (температура t, коэффици
ент теплоотдачи а.2) . Разумеется, при контаJСГНой теплопередаче
кондупивный теплоперенос через стенку отсутствует, остаюrся
лишь стадии конве1СГИВного переноса через пограничные слои.
• См. (2, 5, 8, 14-16 ), а также отраслевые каталоги, нормали .

527

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Q,

q

Рис. 7. 5. Простейшие схемы теп 
лопередачи:

1
1
1

q
Q\ , l
· ---

1
1
!,

а - последовательный перенос
теплоты, б - паралл ельный перенос
теплоты

В случае параллельно
го
переноса теплота мо
.
жет передаваться различ
ными потоками Q1 и Q1
Q2,q2
под действием общего
1
1
температурного напора а
одинаковыми или разны
б
ми механизмами. Это
может быть, например,
кондуктивный поток через зоны различной теплопроводности
или же потоки теплоты одновременно за счет естественной
конвекции и излучения (теплопотери в окружающую среду от
стенок нагретого аппарата) .
Заметим, что технологические ситуации, связанные с после
довательным теплопереносом и необходимостью его расчета,
встречаются в химической технологии значительно чаще.
В основе анализа и расчета теплопереноса нормально к теп
лопередающей поверхности лежит уравнение теплопередачи ,
записываемое, как правило, в манере конвективного теплопере
носа - см. (6. 1 3):
Q = kFЛ.
(7. 1 )

Однако в отличие от (6 . 1 3) здесь используются н е частные
температурные напоры Лt' или Лt" (рис . 7 . 5, а), а полный : л = Т 
- t. Соответственно в уравнение входят не частные коэффици
енты теплоотдачи а 1 и а2 , а коэффициент теплопередачи k, зави
сящий от интенсивности теплопереноса на отдельных его ста
диях (<ч ; а2; Лет и 8ст) · Этот коэффициент k представляет собой
количество теплоты, передаваемой в единицу времени через
единицу поверхности при полном единичном температурном
напоре в 1 градус; k измеряется в Вт/(м2 . К) - в С И .
Величину k трюсrуют ка к удельную проводимость поверх
ностной теплопередачи, 1/k - удельное термическое сопроти
вление (но не для отдельной стадии, а для совокупности стадий
в целом). Пропускная способность сложного процесса теплопе
редачи вводится обычным образом:
л

Q = kF .

(7.2)

В случае отсутствия зависимости составляющих переноса
(прежде всего коэффициентов теплоотдачи, а значит и k) от
528

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

частных температурных напоров, т.е. при линейной связи Q и
д, концепция пропускных способностей для теплопередачи
получает вполне четкую трактовку (см. ниже).
Знание коэффициентов теплопередачи необходимо при ре
шении задач проектирования и эксплуатации:
- при проектировании - когда требуется найти теплооб
менную поверхность F при известных Q и Л;
- при эксплуатации - когда при известной поверхности
определяемой величиной обычно является Q или одна из тем
ператур .
Расчет коэффициента теплопередачи
одна из кар динальных задач поверхностного теплопереноса.
7.3. КОЭФФИЦИЕНТ ТЕПЛОПЕРF,ДАЧИ
7 .3. 1 . Общая концепция коэффициента теплопередачи
при последовательном теплопереносе

Будем рассматривать стационарную последовательную теп
лопередачу от горячего теплоносителя через стенку к холодно
му - в соответствии с рис . 7.5,а. Запишем поток теплоты на
каждой стадии конвективного (по формулам типа 6 . 1 3) и кон 
дуктивного (типа 6 . 6 ) теплопереноса с учетом характерных
частных температурных напоров, считая стенку плоской:
Q

= a. 1F(T - 8 1);

Q=
Л ет
8 cr

Лет

-

8 cr

F(81 - 82);

напомним, что a.1F, -- F и a. 2 F

-

Q

= a. 2F(82 - t) ;

(а)

пропускные способности

отдельных стадий теплопереноса.
Для определения коэффициента теплопередачи исключим
промежугочные температуры 81 и 8 2 (они, как правило, не из
вестны). С этой целью выразим из (а) частные разности темпе
ратур и сложим их (этот прием уже применялся в гл . 6):

k

529

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Запишем равенство (б) в форме (7. 1), решив его относи
тельно Q:
(в)

Q=

Из сопоставления выражений (в) и (7. 1 ) ясно, что
1
(7.3)
и k=
=
1
1
1
b
cr
1
1
-- +
+ --- + - + а. 1
Л сr а. 2
Физический смысл этих выражений четче выявляется при
сопоставлении обратных величин :
бет 1
1
1
1
1
1
1
- = -- +
+ -- и - = - + - + - . (7.3а)
k
Л ет

kF

l
a. 1 F P·cr / Ocr) F a.2 F

kF a.. 1 F (Л ет / б ст ) F a. 2 F

а. 1

а.2

Из (7.3а) видно, что пр и последовательном переносе теплоты
полное термическое сопротивление 1/k равно сумме частных. В

терминах пропускных способностей: величина, обратная пол
ной пропускной способности последовательного поверхностно
го теплопереноса 1/(k..F), равна сумме обратных величин про
пускных способностей стадий. Это означает, что величина,
обратная пропускной способности теплопередачи в целом,
больше любой из величин, обратных частной пропускной спо
собности стадии. Следовательно, сама полная пропускная спо

собность при последовательном переносе меньше пропускной спо
собности любой из стадий (конвективных, кондуктивной). С

позиций расчетной практики: коэффициент теплопередачи при
последовательном теплопереносе не может быть больше како
го-либо из коэффициентов теплоотдачи (или величины Лсr
Это важно и в плане выбора способа интенсификации тепло
передачи (см . разд. 7.9.2), а также для самоконтроля в практи
ческих расчетах.
В случае многослойной стенки подобный анализ, включаю
щий рассмотрение двух конвективных стадий (с а. 1 и а.2 ) и п
кондуктивных (см. разд . 6.3.2 ), приводит к формуле

�cr) .

k=

'ПО эта

1

1

п &.

�������

- + I _!_ + -1
a. I

i;J

А;

а. 2

(7.3б)

С указать,
приле
плотного
в случае
справедлмеива
формулаРеально
ждулишь
rут
существовать
стенок
мо
стенками
rанияледует
другой.
к
одна
Несмотря на малую толщину (порядка сотых, редко - десятых долей

зазоры.

530

их

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

) , при запо;шении малотеwюпроводным rазом ( воздухом, например)
метрасоздавать
мИJ111И
сопротивления, вполне соизмеримые
термические
заметные
мoryr
они
( особенно если зrи прочие сопротивления
расчет
в
введенными
прочими,
сневелики
) . При измерении температур стенок такие "контак:mые сопротивле
ния"
проявляются
rраницах стенок. (фиксируются приборами) в виде температурных скачков на
7 3 2 Расчет коэффициентов теплопередачи
.

.

.

Коэффициент теплопередачи при вынужденном движении теп
лоносителей , не изменяющих агрегатного состояния. Сохраняется
линейная связь теплового потока Q и частных тепловых напо
ров, так что последние не влияют на частные коэффициенты
теплоотдачи а. 1 и а.2 (тем более на Л�ст). Коэффициент теп
лопередачи при этом также получается не зависящим от л . В
данном и некоторых других случаях возможно прямое исполь
зование формул (7.3) для расчета k и kF.
В рассматриваемом случае а. 1 и а.2 определяются независи
мо - по эмпирическим (редко - по теоретическим) зависи
мостям, например, представленным в критериальной форме типа (6.16), (6.17); Лет - по материалу труб (его выбирают с
учетом свойств теплоносителей); 8ст
по сортаменту теплооб
менных труб.
Ф ормулы (7.3), разумеется, остаются справедливыми и при
изменении агрегатного состоян ия одного или обоих теплоноси
телей . Однако в случае конденсации паров а. 1 зависит от Лt' , а в
случае кипения жидкостей
а.2 от Лt" . При этом частные тем
пературные напоры Лt' и Лt" не заданы перед началом расчета
(их возможно найти после расчета k); известен лишь полный
температурный напор Л = Т
t. Поэтому для измен яющегося
агрегатного состояния хотя бы одного из теплоносителей при
всей правомерности формул (7.3) ими нельзя прямо воспользо
ваться, необходимо искать иные пути . Эrи соображения справед
ливы и для других случаев, когда какой-либо коэффициент тепло
отдачи зависиг от пристеночноrо температурного напора; напри
мер, при расчете теплопотерь в окружающую среду в случае есте
ственной конвекции а. зависиг от движущей силы (е2 - (), входя 
щей в критерий Грасгофа, а величина е2 для задачи эксплуатации
и ряда задач проектирования заранее не известна.
Н иже на отдельных примерах показан пугь расчета k для та
ких случаев.
Коэффициент теплопередачи от конденсирующегося пара к вы
нужденному потоку теплоносителя, не изменяющего своего агре
гатного состояния. С целью получен ия расчетного выражения
для k воспользуемся методом исключения промежугочных
-

-

-

53 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

(неизвестных!) температур. Первоначально выпишем тепловые
потоЮ1 для отдельных стадий, учитывая, что, согласно (6.25),
аконд = а 1 =

А!( Т -

8 1 ) 114 :
Q = a1 F ( T - 8 1 ) = AF ( T - 8 1 ) 314 ;
O cr

А. ст

Q = - F (8 1 - 8 2 ) ; Q = a2F (8 2 - t) .

При этом а2 определяется независимо, например н а основе
числа Нуссельта, наЙденного по соответствующей эмпири
ческой формуле .
Решаем эти равенства относительно частных температурных
напоров и исключаем промежуточные температуры 8 1 и 8 2 :
+

Т - 01 =

01

- 02

02

откуда

-

f

(А�)

4/3
Т-t
-+

= -

С?а ст
Л ст F

= --

=л=

Q
a2F

Q=

Q

(

F А

Ql /3
4/3 F1 /3

+

О
)
Л ет а 2
ст

+

+

О ст
А. ст

'

+

(r)

-

k l / 3 лl / 3
=
k
А4/З

1

------ Fл ,
Q l /3
Ocr
1
---
л4/3 pl /3
А. ст а 2

или, если п о (7. 1 ) заменить Q/F = kл, то
l
Q= l 3 l 3
Fл .
/
/
l
k л
о ст
----...,.,,.
.,.. ..- + - +
А4 /3
А. ст а 2
Сопоставляя (r) с (7. 1 ) , имеем

_!_

+

+

_1_
а2

И

k =

(

k l / 3 лl / 3
А 4/ 3

+

О ст
Лет

+

)
а2

_1_

-1

(7.4)

Первое из этих соотношений позволяет, путем его сравне
ния с (7.За) , выявить физичесЮ1й смысл первого слагаемого в
правой части : очевидно, это 1/а 1 . Заметим, что в случае пучков
горизонтальных труб в знаменателе этого слагаемого, соответ
ственно (6 .24а), дополнительно появится множитель Ер .
Значение k по (7.4) легко определяется методом простой
итерации при предварительно наЙденных л, А, а2 и известных
532

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

А.ст, 8ст. Заметим, что для отыскания А полезно предварительно
оценить F по уравнению (7 . 1 ) , задаваясь ориентировочным
значением k (ниже меньшего а., принятого по рекомендациям
раздела 6 . 8 ) . Это оценочное значение F позволяет по каталогам
взять Н или dн и найти i::p , входящие в А , а также поперечное
сечение трубного или межтрубного пространства, необходимое
для расчета критерия Рейнольдса, далее числа Нуссельта и а.2.
Принятое ориентировочное значение k целесообразно исполь
зовать в качестве стартового при итерационном расчете коэф
фициента теплопередачи по второй из формул (7.4) .
Коэффициент теплопередачи от конденсирующегося пара к ки
пящей жидкости . Подход к расчету k аналогичен предыдущему,

но коэффициент теплоотдачи а.2 выражаКУГ по (6.26) : а.КШ1 =
= а.2 = Во (82 - t)2 ·33, а если удобно, то по (6 .26а) через <р. Поток
теплоты на отдельных стадиях:

Решаем эти равенства относительно частных температурных
напоров и исключаем промежуточные 8 1 и 82:

+

Т - 01 =

( �J 4 1 3

01 - 02 =

02 - t =

QБ cr
А

cr F

( )
Q

Bo F

0, 3

--+ Т - t = Л = F

Q

l

( л4 /3 Fl// 3 3
Q

Б сr

Л сr

0
Q - ,7

вg.з F -0,1

J

+ - + ----

.

Отсюда после подстановки Q/F = kЛ получаем
Q=

1
-- FЛ .
-ст
8
----Л. сr
k l / 3 лl / 3
---А 4/3

+

k l / 3 лl / 3
л4/3

Сопоставляя (д) с (7. 1 ) , имеем
k

1

и

k -

+

k - 0,7 л-0,7
В 3
о,
о

(д)

k -0,1 л-0,1
в о, 3

8 ст
---- ----ст

(

k l / З лt / 3
А4/3

+

+

л.

+

л-0,7] -1

о

k -0,7
3 В О,

-8 ст -- +

л. ст

о

(7.5)
533

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Первое из этих соотношений при его сопоставлении с (7.За)
выявляет физический смысл третьего слагаемого в правой час
ти: очевидно, это 1/а.2. Второе из выражений (7.5) является
расчетным ; как и в предыдущем случае , k определяют методом
простой итерации - при предварительно наЙденных значениях
л , А, Во и известных А.ст, 8ст. Здесь также полезно оценить по
верхность теплопередачи F по ориентировочному значению k.
Последнее целесообразно принять в качестве стартового k при
итерационной процедуре расчета k по (7.5).
Такой же подход используется для расчета коэффициента
теплопередачи от вынужденного горячего потока (здесь уже а. 1
определяется независимо, например из уравнений типа (6. 1 6)] к
кипящей жидкости, от горячего теплоносителя к окружающей
среде, а также в других технологических ситуациях, когда ка
кой-нибудь частный коэффициент теплопереноса зависит от
частного температурного напора.

Выше бьтатеплообменниках
рассмотрена теплопередача
через
чистые поверхности. В реально
работающих
на
стенках
(с
одной
или с обеих сторон) возмож
носопротивление,
появление отложений
(загрязнения), создающих дополнительное термическое
Этот
- понижающих
коэффициент
неrативный эффеактзначит
учитывают
одним из следующих
способовтеплопередачи.
:
- физически
обоснованным введением
допоmштельноrо
термическоrо со
противления
r3 Бу?..3 (здесь Б3
толщина
отложений,
Л., - их теплопровод
ность);
некоторыевеличина
рекомендации
к величинам и (или сразу к r3) приводятся
вуравнениях
справочниках';
r3 присутствует в виде дополнительноrо слаrаемоrо в
типа (7.3) и производных от неrо (7.4), (7.5) и т.п. :
(7.3б)
k = --1
=

.S3

-

Аз

1
Бсr
&3
1
-+-++-

_
_
_

-

а.,

А3

а. 2

- формальным
уменьшением
"рабочеrо" значения k в сравнении с рассчи
танным
по полученным
выше сооnюшениям:
/сраб (О, 7 0,9) k;
этот путь оправдан лишь слабой доступностью и невысокой достоверностью
сведений о .S3 и А3•
Acr

=

+

7 3 3 Коэффициент теплопередачи
при параллельном теплопереносе
.

.

.

В случае параллельного переноса (рис. 7.5,б) тепловые пото

ки за счет разных механизмов - складываются (иногда - с

учетом доли теплопередающей поверхности, отвечающей тому
или иному механизму теплопереноса) . Так, в случае потока
теплоты от нагретой поверхности в окружающую среду одно
временно работают механизмы естественной конвещии (коэф-

• См" например, (5, 1 3 , 14) .
534

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

фициент теплоотдачи а.с.к) и излучения (эквивалентный коэф:фициент теплоотдачи а.л)· В результате

k = <Х.е.к+ <Х.л·
(7.6)
Q = Qе.к+ Qл; q = Qе.к+ Qл ;
В процессе передачи теплоты через зернистый слой, проду
ваемый газовым потоком, теплоперенос обычно представляют
в терминах и символах кондукции, оперируя эквивалентной

теплопроводностью:

(7.7)

складывающейся из параллельно работающих кондуктивного,
конвективного и лучистого механизмов переноса теплоты. Тог
да в случае плоского зернистого слоя толщиной 8 , располо
женного между параллельными пластинами, имеем
Л к �щ + Л к
Л. л
+
k = Л.
(7.7а)
8
Из приведенных примеров ясно, что в случае параллельного

;

=

�

;;в

переноса складываются проводимости, пропускные способности.
Поэтому результирующий коэффициент теплопередачи не мо
жет быть меньше любого из частных коэффициентов теплоот

дачи (частных эффектов) .

7.4. ОТДЕЛЬНЫЕ ЗАдАЧИ ТЕПЛОПЕРF.ДАЧИ

Ниже представлены некоторые характерные примеры ис
пользования рассмотренных представлений о теплопередаче
для решения отдельных химико-технологических задач .
7 .4. 1 . Распределение температур в катализаторной зоне
в круглой трубе

Среди задач
химическойреакциями,
технолоmи отличающимися
нередко встречаются
связанные
с гете
рогенными
химическими
высокими
теruювыми
эффектами
и проводимыми
вслойнепрерывном
режиме При
приэтомдвижении
rаза
(.жидкости)
через
неподвижный
зерен
катализатора.
катализатор
ная зона(с минимумом
может иметь побочных
ра:иичнуюпродуктов)
конфиrурацию.
Часто реакция
протекает
селек
тивно
и
хорошими
выходами
лишь
в
опрев
деленном
достаточно
узком
интервале
температур;
чтобы
удержать
процесс
этом температурном
интервале,
необходимо
отводить теплоту
экзотермической
реакции
(либо
подводить
в
случае
эндотермической).
Это
делается
с помощью
горячего,
кипя
теплоносителя
снаружи
катсiЛ
изаторной
трубы
холодного
или
щего или конденсирующегося.
Для
rрамотной
организации
такого
процесса
зоне, т.е.
поле вслоякатализаторной
температурное
уметь рассчитывать
необходимо интенсивность
определять
переноса
теплоты
внутри
катализатора
и межпу
этим слоемвыбрать
и стенкой,
оrраничивающей
на
зону
катализатора.
Это
позволит,
рационально организовать
трубки,
катализаторной
диаметр
пример,
теплосъем (теплоотвод) и т.п.
535

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Будем рассматривать стационарный экзотермический про
цесс в круглой трубе радиусом R, заполненной слоем катализа
тора (рис .7.6). В такой системе теплота реакции отводится че
рез стенки трубы к теплоносителю - часто кипящей воде под
давлением (величина давления позволяет воздействовать н а
уровень температур в катализаторной зоне) . Пусть тепловой
эффект в единицу времени на единицу объема катализаторного
слоя равен q v. Температуру в слое на радиальной координате 1·
обозначим Т, по оси слоя - Т0 , на его внешней гран ице
TR,
на обращенной к слою стенке трубы
8, кипящего теплоно
сителя
t.
Для простоты полагаем , что вдоль катализаторной трубЮt
температура не изменяется (иначе говоря , продольный перенос
теплоты не рассматривается) ; обсуждается только изменение
температур по радиальной координате . Теплота в сечении слоя
катализатора переносится за счет кондукции (внутри зерен и в
точках их соприкосновения) и конвекции (при движении син 
тез-газа между зернами); определенный вклад может вносить и
излучение. Интенсивность теплопереноса удобно выражать,
используя понятие эквивалентной теплопроводности - соот
ветственно формуле (7 .7). Коэффициент теплоотдачи от слоя
катализатора к стенкам трубы обозначим сх .

-

-

-

СостаR11Я ющая Лкuнд зависит' о т тешюпроводности материала зерен катали 
затора и еще более - от порозности с.лоя so и теплопроводности газа Л. Состав
ляю щую Лкuнв обычно предста R/\ЯЮТ в форме Лкuн,,/Л = В· Ре, где Ре = Re·Pr, а В
находят' в зависимости от отношения диаметров катализаторной трубки и
зерна D/d, а также формы зерен; порядок В "' О, l . СостаR11Я ющая Лп в зернистом
с.лое иrрает, как правило , подчиненную роль из-за относительно невысоких
температур и многократного взаимного экранирования зерен . Коэффициент
теплоотдачи от слоя к стенке а определяют по эмпирическим и полуэмпириче
ским соотношениям ' .

В основу анализа положим уравнение стационарного тепло
переноса в твердом теле с источником теплоты ( 1 .2 1ж'), пред
ставив лапласиан в полярных координатах по ( 1 .23б) :
аэ

(d2T
dr 2

+

)+

.!_ d T
т

dr

!I!:. = О
ер

'

(а)

причем частные производные заменен ы обыкновенными, по
скольку рассматривается (рис . 7.6) однонаправленный (по ко
ординате r) перенос теплоты .
' Зависимости типа
Л коНJV'..
дены в [ l
З J , формулы для а

536

-

=

J{�:о,л,,/Л.) , Лкuн,,/Л
в ( 1 , 2J.

=

/{ Ре) и значени я В приве

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 7. 6. К расчеrу температурн о rо
.тmзаторн о й зоне:

поля в ката

1 - слой к атализатора, 2 - сrенха тру6КJ1, З
зона кипящеrо теплоносителя

-

Раскроем значение а3 = Л.3/ср и ,
произведя в (а) очевидные сокра
щения, получим

d2 T + _! d T + !!х._ = 0 .
dr 2 r dr л. .

(7 .8)

Для решения этого дифферен 
циального уравнен ия обозначим
И = d T/dr. Тогда

d U + U + !fx_ = .
O
dr r л. .

(б)

Перенесем последнее слагаемое в правую часть и домножим
все члены равенства на rdr :

rd U+ Udr = _ J..y_ rdr.
л. э

(в)

В левой части (в) стоит полный дифференциал d ( Ur), так что

d( Ur)
И нтегрируем :

=

2
q r
Ur = _f_
_ + C1 и
_

-

л. э

!!х_ rdr.

С1 .
И = d T = - qv r + dr
r
2Л. 3
-

Л.3 2

--

(г)

Разделяя в последнем равенстве переменные и интегрируя
повторно, получаем
Т

= _ !!J:__ r 2 + C1lnr + С2.
4 Л. э

(д)

Постоянные интегрирования С1 и С2 находим из граничных
условий :
- при r = О по условию осевой симметрии температурного
поля d T/dr = О; отсюда по второму из равенств (г) тождественно
С1 = О; это ясно и из (д): при r = О, С1 = О, иначе I T I ---+ ао, что
противоречит физическому смыслу рассматриваемого процесса;
- при r = R (внешние частицы катализаторноrо слоя) дей
ствуют граничные условия 1 1 1 рода типа (о) в разд . 1. 8 .4; для
участка трубы длиной l
- Л. 3 d T 2ттR/

dr,.,

=

a.( TR -

8)2ттR/;

(е)
537

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

их

Подставим в (е) производную d T/dr по (r) и TR по (д) - в обо
случаях при r = R с уже установленным значением С1 = О

(

-лэ - _!k__
R

отсюда

2Л ,

с2 =
е

) = а.(-

qv R

2

4Л ,

}

+ С2 - е

(1

)

;

2
2Л,
- .
+a.R
4Л ,
С найденными значениями С1 и С2 уравнение (д) темпера
турного поля (профиль температур) в круглом сечении зернис
того слоя катализатора запишется как
2
2
2Л.
q R
э ,
I +(7.9)
Т = e + _v
a. R
R2
4Л.

+ qv R

--

_
_

э

(

_ _

)

_

.

Температурный перепад в . стенке трубы, как правило, оч ень мал. Есл и при
это м те пл ота реакции с н и мается кип ящей жидкостью ( высокие ко эфф ици енты
теплоотдачи с наружи трубы) , то тем пературу е без существенн о й по грешн ости
м ожн о принять равн о й тем пературе кип ящей жидкости tIOtn · . B проти вн о м случае
вел ичи ну е придется рассчитывать с по м ощью уже извеС111 ых уравнен и й тепл о 
переноса л и бо оп ер и р о вать величи н о й tIOtn вместо е и ко эфф ици енто м теплопе
редач и k вместо а .
Формула (7 .9) позволяет решать конкретны е эксплуата цион 
ные и проектны е задачи. В частности ,
- температура на оси трубюt (r = О ) :
Т0

)

(

R 2 \ + 2Л. э ·
= 8 + qv
aR '
4Л 3

(7 .9а)

- температура в слое катализатора на его границе со стен
кой (r = R) :
TR = е + Чv R ;
(7 .9 6 )
2а.

- температурный интервал в слое катализатора:
2
Л Т = Т0 - TR = qv R ;
4Л ,

(7. 9в)

температур ный скачок на границе слоя катализатора со
стен кой :
TR - е = Чv R ;
(7 .9r)
2а.

максимальн ый размер катализатор ной трубюt при макси
мально допустимо м температур ном интервале л Т:
R=

538

�4Л, ЛТ
qv

'

d = 2R.

(7.9д)

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

7 .4.2. Перенос теплоты через стержень бесконечной длины
На примере приведен ной ниже относительно простой зада
чи можно продемонстрировать подход к решению ряда более
сложных задач, встречающихся в химической технологии и
энергетике (в частности, о теплопереносе к оребренным по
верхностям при различной конфигурации ребер) .
Будем рассматривать стационарный теплоперенос через
тонкий твердый стержень известной теплопроводности Л,., по
стоянных сечения f и периметра П, закрепленный своим осно
ванием в некой стенке (рис. 7.7,а). Температура в основании
стержня То поддерживается постоянной. Стержень омывается
потоком среды постоян ной температуры t (пусть для опреде
ленности t < Т0 , значит меньше и температуры в любой точке
стержня t < Т, так что стержень отдает теплоту) . Коэффициент
теплоотдачи от стержня к среде а постоянен и известен . Стер
жень
тонкий в тепловом отношении; это означает, что в его
поперечном сечении отсугствует перепад температуры , она из
меняется только по длине стержня х. Требуется установить закон
изменения температуры стержня J(x) и потоки теплоты (через
сечение f; от стержня к среде) на любой координате х, направ
ленной IЩолъ стержня и отсчитьmаемой от его основания.
Для отыскания зависимости J(x) выделим на координате х
элемент протяженностью dx и запишем для элементарного конту
ра "к" тепловой баланс - он будет харакrеризоваться отсуrствием
Источников , Стоков и Накопления теплоть1. Приход за счет теп
Jюпроводности в левое сечение контура составиr -Л,. (d T/dxlf, Уход
- тоже за счет теплопроводности из правого сечения:
-л,....0... ( Т + d Т)/ = л,. d Т <12 Т dx /;

-

-(

dx

dx

+

dx 2

)

Уход за счет конвекции в поток среды равен а( Т - t) Пdx. В
целом

-л,. d T !
dx

- [-л.т( ddxТ

dx2 dx)1] -

2
+ d T

а( Т - t) Пdx

= о.

(ж)

В целях сокращения записи удобно обозначить Т - t = е .
(при этом из-за постоянства t очевидно d T = d 8). Тогда после
простых преобразований получим из (ж)
d2 0

_

аП е =

О·

dx 2 Л. т /
Решение этого уравнения имеет вид
е = Т t = С1 ет,х + С

-

-

= ±�аП/(Л.тЛ

·

-

ет,х ,

где т корень характеристического уравнения т22

аП/(л.J)=О ,

(з)

так что т1,2 =
539

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

б

т

Рис. 7. 7. Теruюпер едача чер ез бес ко нечно
дли нный стер жень :
ня ,

�

- расчеru ая схема: 1

- основание стерж

Значение постоянной инте
грирования С1 определяем из
граничного условия: при х � оо ,
8 "# оо ; это условие соблюдается
лишь при С1 = О.
Значение
постоянной
С2
определим из граничного усло
вия в основании стержня: при х
= О, 8 = 80 = То - t, тогда из (з)
при С1 = О имеем С2 = 80.
С найденн ыми значениями С1
и С2 выражение (з) принимает вид

а

т

а

2 - стержень, J - среда ( к - контур ) ;
б - температурный профиль

Т - t = ( То - t) e-mx ,

(7 . 1 О)

а П/(" А.т Л вид этой зависимости изображен на рис . 7.7,б.
Характерный
.
Поток теплоты вдоль стержня в любом поперечном сечении
на координате х может быть представлен в форме Прихода

где

=

(либо Ухода) : Q(x) = -Л-r

(dT�/х f.
dх

Поскольку из (7. 1 0) произ

водная d T/dx = - ( То - t)m е- тх , то
(7. 1 1 )
Q(x) = Л-�-( То - t)т е- тх f = ( То - t) �Л. та.Пf
Полное количество теплоты Q, отдаваемое стержнем среде в
единицу времени, может быть рассчитано двумя путями :
- как поток теплоты Q(x) в сечении х = О, поскольку вся
теплота, поступающая через основание стержня, в конечном
счете отдается среде; тогда по (7 . 1 1 ) при х = О
(7. l la)
Q = Qo = ( То - t) Л т а.П/ ;
как интегральный поток теплоты от стержня к среде ; на
выделенном элементарном участке:
d Q = а. ( Т - t) Пdx = а.( Т0 - t)П е- тх dx;
тогда по всей длине стержня

е-тх .

�

Q = а. ( То - t)П

f
о

e-""' dx

=

а.(Т:- с) пе-""' [ ,

и при подстановке пределов и значения т получается формула
(7 . 1 la) .

540

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Если стержень имеет конечную длину или более сложную
конфиJУРацию (трапециевидную, кольцевидную и т.д.), то при
сохранении подхода в общем - конкретные решения получа
ются значительно более сложными • .
7 4 3 Критическая и целесообразная толщина
тепловой изоляции
.

.

.

Тепловая изоляция предназначена для снижения теплопо
терь труб и аппаратов (чаще всего - цилиндрических), в холо
дильных процессах - для снижения притока теплоты к аппа
ратам извне. Смысл изоляции - в понижении пропускной
способности поверхностного теплопереноса пуrем создания
дополнительного кондуктивного термического сопротивления
за счет слоя малотеплопроводного материала на стенках аппа
рата (рис. 7.8, а). Изоляционные материалы обычно отличаются
низкой плотностью, они содержат воздушные прослойки и
полости (шлаковата, пенобетон , вспученные материалы типа
перлита, различные засыпки).

Расчет теwюпотерь для изолированною в тепловом отношении объекта ве
дется
по той же канве,
для плоской стенки (см. разд. 7 . 3 . 1), но с учетом
кривизны,
как
это
бьvю
сделано
для цилиндрических мноrослойных неплоских
стенок
(см.
разд.
поскольку
толщина слоя изоляции нередко сопоставима
6.3.3),
с радиусом ее кривизны.
Пусть
внутренний
диаметр трубы или аппарата равен d1, наружный - d1,
слоя
изоляции
dн; температура rорячеrо теплоносителя внутри трубы - Т, на
ее внутренней
стенке - 0 1, на наружной - 02, на rранице слоя изоляции со
средой
0н, в среде - t. Коэффициент теплопроводности материала стенки - Лсr,
изоляции
- Ли. Коэффициенты
теплоотдачи к внутренней и от наружной стенок
трубы
равны
и а1 известными и
а1 и а1. В целях упрощения будем считать
[расчеmые формулы типа (6.16)/;д11Я
найденными.
это
обычно
оправданно
а1 - не всегда : если в некоторых проектных задачах температур а 0 2 задана ( по
условиям
техники безопасности, например), то а1 определяется по формулам
типа
(6. 19) на основе рассчитанною критерия Gr; в других случаях мoiyr воз
никнуть
затруднения
в определении
длиной по отдельным стадиям :
Запишем
поток
теплоты
от участка трубы
- от теплоносителя к внутренней
поверхности
стенки трубы: Q а1( Т - 0 1)nd1/;
- через стенку трубы - по (6.8) : Q ln2п(d2 / di ) (0 1 - 02) ;
- через слои, изоляции (аналоmчно) : Q ln(d2пн//)..dн2) (02 _ 0и) '
- от поверхности слоя изоляции к среде: Q а1(0и - t)ndиl.
Эти в ыр е ния разрешим относительно частных температурных напоров и
См. (6, 9, 1 1 , 12 ) и др .
что н

Для а 1

а1

а1.

IЛ.cr

=

=

·

=

аж

1

=

•

54 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

а

и целесообразная
толщина тепловой изоляции:
- Критическая
-

Рис. 7.8.
а

зависимосrь тс:плопотс:рь от ТОJПЦИНЬI изоляЦЮ1;
pacчcnta11 схс:ма, 6
И30ЛЯЦИЯ
1
crc:НJCa трубы, 2

исключим промежуrочиые температуры:

-Q0 1 - 02 = _Q_ ln�
1
Т - 01 =

+

11d1 la.1

0 и - 02 = -Q- ln dи
211A cr

211А и

02 - t = -Q-

Q(_l_ +
11d1 la 1

Отсюда

d

d2

--+

Т-t=

ln(d2 / d1 ) + ln(dи / d2 ) +
11dиla2

211Acr

211А и

- )
кdи lа. 2

1- .

(7 . 1 2)

Из этоrо
уравнения не вп01ше очевиден харакrер алияния толщины с.лоя
изоляции
би (dн - d1) /2 на величину теплопотерь Q. В самом деле, с ростом би
(значит, и dи)способность
растет третьеэтойс.лаrаемое
в знаменателе,
понижая
Q, так как умень
падает
пропускная
кондукrивной
стадии;
но
одновременно
шается
пос.леднее
слагаемое,
поскольку растет пропускная способность этой
конвекrивной
стадии
а2Fи - из- за увеличения Fи 11dнl, а это повышает Q.
Ситуации,
в которых
независимаяи переменная
(здесь dи), содержащаяся
в
расчетных
с.лаrаемых,
сомножителях
т.п.,
противоположным
образом
влияет
наинтересен
функцию(иногда
(здесьопределеннее:
Q), нередки в химической технологии. В таких ситуациях
целесообразен, в ряде случаев - просто необхо
дим) анализ на экстремум. Такой анализ для выражения (7.12) облегчен тем, что
числите.ль
ненулю
зависит
от dи, поэтому можно искать экстремум знаменателя Zn.
Приравняем
dZц/d(dи); учтем при этом, что первые два с.лаrаемых в Zn от
dн не зависят; также выразим ln(dк/d2)
lndи - lnd2, тогда вычитаемое тоже не
зависит от dн. Итак,
(ж)
=

=

=

542

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Диаметр изоляции,
соответствующий
экстремуму, и отвечающая ему толщи
напреобразований,
изоляции
называются
крН111Ч есхими dкр, Окр. После сокращений и очевидных
а также
перехода от dкр к � dq/2 (так принято при написа
нии критерия Био)
получаем
(7 .13)
Анализчерез
на знак
второй значит,
производной
в точке экстремума показьшает, что
проходит
минимум;
при
dкр теплопотери проходят через макси
мум. Таким
образом,достиrая
при наращивании
слоя изоляции теплопотери Q могут
сначала
повЬШiаться,
Qmax; при дальнейшем ро сте dи они понижаются.
Такой
характер
функции
Q(dи) определяется соотношением пропускных способ 
ностей
двух
стадий
теплопереноса:
кондукции через слой изоляции и конвекции
отстадии
изоляции
к
среде.
При
малых
би, dи пропускная способность конве�сrивной
может интенсивность
бьrrь меньше, теплопередачи
нежели конду�сrивной;
тоща
конве�сrивная
стадия
контролирует
в
целом:
с
увеличением
пропускной
способности
а1 Fи (за счет роста Fи) поток теплоты Q возрастает. При больших dи
одновременно
сужеростом
а1Fи снижается пропускная способность конду�сrивной
стадии,
теперь
эта стадия - медленная, она контролирует процесс: поток
теплоты
Q в целом уже зависит от характера мияния dи именно на этой стадии.
Характер
зависимостиdи Qтеплопотери
от dи показанQ ниже,
на рис.7.8,б.
Из рисунка следует, что
неилиприаппарата
всех значениях
чем
для неиэолированной трубы
�- Чтобы rарантиро вать Q < �. необходим диаметр изоляции,
превЬШiающий
величину
du, называемую целесообразной. Значение du опреде
ляется
из
равенства
Q
�- И если цель - снижение теплопотерь (так чаще
всеюПоложение
и бывает),точки
то необходимо
вьщер:жать условие dи > du.
dкр определяется выражением (7.13). Разрешая ею относи
тельно
Rкр или dкр (проектная задача), получаем формулу dкр 2(Ли /а2), указы
вающую
на рост(высокие
dкр, бкр с Ли. Следовательно, использование плохого изоляцион
Ли) сдвиrает dкр (du - тоже) в область бО.льших значе
ною
материала
ний
dи: может потребо ваться весьма толстая изоляция для вьmолнения условия
dи > du. В то же время при низких Ли (хорошая изоляция) вполне возможно, что
dкр окажется меньше d1 - в этом случае изоляция любой толщины способствует
снижению
теплопотерь.
В выражение (7 .13) не входит диаметр аппарата, так что dкр получается неза
висимо обычно
от d1. Поэтому
вполне
возможны ситуации d1 < d и d]. > dкр. Первый
случай
характерен
для труб небольшою диаметра (d2' и на рис. 7.8,б),
второйплохая).
- для аппаратов
промышленных размеров (если, конечно, изоляция не
очень
В последнем случае проблема критической толщины изоляции
теряет
актуальность: любое наращивание изоляции сопровождается снижением
теплопотерь.
Подход к определению
целесообразной толщины изоляции указан вЬШiе:
приравниваются
выражения
Q для неизолированного и изолированною аппара
тов.
При этомметодами.
получаются весьма громоздкие соотношения, разрешимые только
численными
Задачаконкуренция
о окр, dкр представляет,
какспособностей.
правило, лишьПра�сrику
методический
интерес:
яв
ление,
пропускных
скорее
интересует
проблема
целесообразной толщины изоляции, поскольку важно понизить тепло
потери.
Собственно
величины
окр, dкр были бы интересны, если бы нужно было
стогда
помощью
покрытия
обеспечить
максимальный
тепловой поток Q (правда,
вряд
ли
остался
бы
правомерным
термин
"изоляция").
Аналогичный
анализ может бьrrь проведен применительно к сферическим ап
паратам.
Для плоских стенок проблем критической и целесообразной толщины
изоляции, разумеется, не существует, поскольку поверхность теплопереноса,
=

Zn

=

=

icp

543

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

способностью, не изменяется при нара
с конве
свя
занная
lСl'Ивной; попропускной
здесь увеличению толщины этоrо слоя всегда
ому
изоляции
слоя
нии
щи
ва
:л
сопутствует уменьшение теплопотерь.
7 .5. ТЕПЛООБМЕН
(ОСНОВНЫЕ ПРОБЛЕМЫ И ПОЛОЖЕНИЯ)
7 .5. 1 . Kpyr

задач

Теплообмен в дополнение к нормальному (к теплопере
дающей поверхн ости) переносу теплоты рассматривает (см.
рис. 6.1) еще перенос теплоты с потоками теплоносителей
вдоль этой поверхности. Теплообмен включает теплопередачу
как составную часть; самостоятельное значение (вне связи с теп
лообменом) в реальных задачах теплопередача приобретает весьма
редко. Заметим, 'ПО особенности теплообмена, связанные с дви
жением теплоносителей, МОl)Т в некоторых случаях оказывать
влиян ие на закономерн ости собственно теплопередачи.
При переносе теплоты вдоль поверхности с теплоносителя
ми возникают эффекты, связанные с характеристиками движе
ния этих теплоносителей. Поэтому на интенсивность теплооб
мена в общем случае оказывают влияние взаимное направле
ние движения теплоносителей и структура их потоков (в пре
дельных ситуациях - идеальное вытеснение И В и идеальное
перемешивание ИП). Все это существенно расширяет круг
теплообменных задач.
Цель теплообмена - изменение температуры или агрегатно
го состояния одного из рабочих тел. В ряде задач проектирова
ния рабочее тело удается полностью идентифицировать, вклю
чая величину его потока, начальные и конечные параметры; в
этом случае его часто называют целевым. Другое рабочее тело
(или другие рабочие тела), с которым целевое обменивается
теплотой, в таких задачах называют теоловосиrелем. Строго
говоря, оба потока, конечно, являются теплоносителями.
При изменении температуры массового потока G в ходе
теплообмена (вдоль поверхности ; во времени) в тепловых рас
четах участвует теплоемкость с, являющаяся составной частью
потоковой пропускной способности Gc; в задачах теплопереда
чи теплоемкость не присуrствует. Изменение температуры лю
бого из теплоносителей (или сразу обоих) сопровождается из
менением температурного напора л вдоль теплообменной по
верхности (в нестационарных процессах - и во времени). В
этих условиях теряет определенность уравнение теплопередачи
в форме (7. 1 ) , поскольку л = var. Возникает проблема усредне
ния температурного напора. В стационарных процессах речь
544

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

идет об усреднении локальных значений Л вдоль поверхности
теплообмена F; поэтому, в отличие от (7. 1 ), в уравнении тепло
обмена должна фиrурировать средняя (по поверхности F) дви
жущая сила (температурный напор); тогда поток теплоты
(7 . 14)
Q= kFЛep·
В нестационарных процессах приходится усреднять мгновен
ные значения Л по времени 't (если вдоль поверхности темпера
турный напор не изменяется) , и тогда количество теплоты
Q = kFЛep't·
(7. 1 5)
При изменении температурного напора одновременно вдоль
поверхности и во времени проблема усреднения температурно
го напора усложняется .
Операция усреднения начинается записью уравнений тепло
обмена в дифференциальной форме с использованием локаль
ного или мгновенного температурного напора Л = Т - t.
d Q = kЛdf и (или) dQ = kFЛd't.
(а)
Последующее интегрирование и приведение полученных со
отношений к виду (7. 14) и (7. 1 5) призвано дать расчетную
формулу для Лер - с усреднением по поверхности или по вре
мени соответственно. Осуществление интегрирования требует
знания ряда связей (текущих температуры и поверхности либо
времени) и граничных условий. Реализация таких операций предмет последующего изложения.
Решение задач эксплуатации и проектирования наряду с об
щими моментами имеет свою специфику. Например, в стацио
нарных проектных задачах обычно заданы начальные и конеч
ные температуры теплоносителей, так что удается рассчитать
Лер и, предварительно определив k (см. разд . 7.3), воспользо
ваться выражением (7. 14) для отыскания F:

F=

_g_ .
kЛ ср

(7. 14а)

В задачах эксплуатации чаще известны только начальные
температуры теплоносителей (F, конечно, тоже) , и Лер сразу
рассчитать не удается ; это вызывает затруднения в определе
нии Q по (7 . 1 4) , необходимо искать особые пуrи расчета.
Отдельная проблема - контактный теплообмен , в част
ности - потока теплоносителей с твердыми телами. Здесь не
редко теплоперенос весьма сложен (процесс нестационарен в
целом или в своих элементарных актах), непростым является и
математическое описание. Некоторые такие случаи будуг рас
смотрены ниже.
545

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Схемы движения теruюносителей:

Просrые: а - прямоток, 6 - противоток;
слоJ1СНЬ1е: 11 - перекреСПIЬIЙ ток, г - смешанный
ток 1-2 , д - тройной поток

Рис. 7.9.

а

В зависимости от особенностей
технологического процесса и его
"
в
конструктивного оформления воз
можно различное взаимное направ
•
ление
движения теплоносителей;
г
некоторые схемы их движения
•
демонстрируются на рис . 7.9. Пер
вые две (параллельное движение
теплоносителей), называемые простыми, моrут быть оформлены в
виде прямотока (вид а) либо проти
вотока (вид б). Остальные схемы именуют сложными: на рисун 
ке в качестве примера показаны: перекрестный ток (вид в);
смешанный ток 1 - 2 (вид г) - его индексация указывает, что
первый теплоноситель делает один ход, а второй - два; трой
ной поток (вид д), когда в одном аппарате первый теплоноси
тель обменивается теплотой сразу с двумя раздельными пото
ками. Взаимное направление движения теплоносителей важно
в технологическом и расчетном плане, в частности: при уста
новлении средних температурных напоров, конечных темпера
тур теплоносителей, количеств переданной теплоты.
Технологическая задача в процессах теплообмена - получе
ние целевого продукта в заданном количестве с необходимыми
параметрами. Величина основного параметра в уходящем из
теплообменника целевом продукте контролируется измери
тельными устройствами (если, например, параметр - темпера
тура, то в качестве датчиков используют термопары, термомет
ры сопротивления и др.). При отклонении параметра от задан
ного значения на процесс накладывают управляющее воздей
ствие, чаще всего связанное с изменением потока (количества)
теплоносителя. Способы и организация таких воздействий из
учаются в КУРСе "Авrоматические системы управления техно
логическими процессами" .

t

э

7 5 2 Потоки энтальпий и тепловые балансы
.

.

.

В ходе тепловых расчетов приходится оперировать потоками
(в стационарных процессах) или количествами (в нестационар
ных) энтальпий . Поток энтальпии записывается как произве
дение массового потока теплоносителя на его энтальпию: G h;
в СИ это (кг/с)·(Дж/кг)=Дж/с=Вт (в реальных расчетах обыч546

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

лМ, i

а

-

тешювых балансов:

непрерЬIВИЬIЙ процесс (К1 и К2 - контуры) , б - периодический процесс

Рис. 7. 10. К состамению
а

б

но кВт). Аналоrnчно записывается количество энтаЛьпии�
только G в этом случае выражается не в кг/с, а в кг, так что Gh
измеряется в Дж, кДж. Возможные способы выражения эн
тальпий Н, h, i и единиц их измерения рассмотрены в разд . 6. 1 .
Важнейшим способом (иногда - составной частью) матема
тического описания является тепловой баланс , позволяющий
анализировать теплообменные процессы и вести технолоmче
ские расчеты . Рассмотрим некоторые типичные случаи состав
ления теплового баланса.
Пусть имеется стационарный (непрерывный) процесс без
Источников и Стоков теплоты. В теплообменник подаюгся
(рис . 7. 1 0,а) потоки горячего и холодного теплоносителей (их
взаимное направле1 ще пока безразлично) G1 и G1 с энтальпия
ми на входе в теплообменник соответственно Н ' и h ' и на вы
ходе из него Н " и h " . Поток теплоты передается от горячего
теплоносителя к холодному через теплообменную поверхность
F. В качестве пространственных контуров К1 и К2 выбирают
отдельно зоны движения горячего и холодного теплоносителей
(один из них может выступать .в качестве целевого); временной
интервал равен 1 с. В соответствии с общим правилом состав
ления балансов запишем Приходы и Уходы теплоты
(Накопление для стационарного процесса отсутствует) раздель
но для К1 и К2 контуров:
G1 H' - G1 H " - Q = О и �h' + Q - G2h " = О , (7 . 16)
откуда
(7. 1 6а)
Если при неизменном агрегатном состоянии теплоносителей
энтальпии представить в форме Н = с 1 Т и h = c2t, то при по
стоянных (не зависящих от температуры) теплоемкостях с1 и с2
547

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

выражение (7. 1 6а) удобно использовать в виде
(7. 1 6б)
Q = G1 с 1 ( Т ' - Т ") = G1c2 (t " - t ') ,
причем верхние индексы ( ' ) и ( " ) относятся к входу теплоно
сителей в аппарат и выходу из него соответственно.

Строгопотоки.
говоря,Дело
в каждой
из зонприсуществуют
ещетемператур
продольные
кондуктивные
теwювые
в
том,
изменении
движущихся
теп
лоносителей
(пусть
в
режиме
ИВ) существуют отличные от нуля продольные
rрадие1ПЫ температур
d T/dxкондухтивного
и dt/dx, где х теплопереноса
- продольная координата. Однако
интенсивносrь
продольного
чаще всего
пренебре
мала
в
сравнении
с
тепловыми
потоками,
переносимыми
движущимися
жимо
теплоносителями.
Поэтому
приИВ,
анализе
процессов
теплопереноса
с теплоносите
лями,
движущимися
в
режиме
вклад
этой
кондуктивной
составляющей,
как
правило, игнорируется.
'ПО

В ходе теплообмена поток может изменять агрегатное со
стояние. Пусть, например, горячий поток входит в аппарат в
состоянии сухого насыщенного пара, а выходит из него в ре
зультате полной конденсации - в виде кипящей (а не пере
охлажденной ниже температуры насыщения Тн) жидкости.
Тогда Н ' - Н " = r1 , т.е . теплоте конденсации, так что по горя
чему теплоносителю
(7. 1 6в)
Если при этом второй теплоноситель не меняет агрегатного
состояния, то тепловой баланс (7. 1 6а) примет вид
Q = G1r1 = Chc2(t" - !'}.
(7. 1 6г)
Аналогично записывается поток теплоты, если речь идет о
подаче в аппарат кипящей жидкости и выводе из него сухого
насыщенного пара: Q = Chr2 .
В более общем случае исходный пар может быть перегрет до
температуры Т' > Тнас. а образовавшийся конденсат пере
охлажден до Т " < Тнас · Тогда первое из выражений (7. 1 6а) будет
включать фрагменты, отвечающие охлаждению пара до темпе
ратуры насыщения (конденсации, кипения), собственно кон
денсации и переохлаждения конденсата:
Q = G( Сп\ ( Т ' - Тн�) + r + Сж 1 ( Т - Т ")] ,
(7. 1 6д)

где Сп\ и Сж\ - теплоемкости горячего теплоносителя в парообразном и жидком
состояниях.

В целом возможны различные сочетания, выражающие ба
ланс тепловых потоков. Например, при переносе теплоты от
конденсирующегося пара к ' К и п я ще й жидко ст и
(7 . 1 6е)
Q = G1r1 = G1r2 .
В необходимых случаях в тепловых балансах могут быть от
ражены тепловые эффекты, а также другие фазовые превраще548

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

н ия (плавления-кристалл изации; сублимации-десублимации и
т.п.).
С помощью представленных выше и подобных соотношений
удается при прочих известных величинах рассчитать неиз
вестные поток теплоносителя, одну из температур (на входе в
теплообменник либо на выходе из него) или тепловой поток Q.
В качестве примера нестационарного (периодического) теп
лообмена рассмотрим аппарат (рис. 7. 10,6) с холодной жид
костью - ее количество М, теплоемкость еж, начальная темпе
ратура t0 . В аппарат вводят G кг горячих металлических шари
ков (их теплоемкость Ст) с температурой То, превышающей
температуру кипения жидкости lнас· В результате интенсивного
теплового конта1сrа рабочие тела (шарики и жидкость) прини
мают одинаковую конечную температуру lнас· С такой темпера
турой шарики выводятся из аппарата. Жидкость при этом на
гревается до !нас. частично испаряется; пары (их энтальпия 1)
выводятся из аппарата. Требуется найти количество испа
рившейся жидкости лМ .
Для составления теплового баланса выберем в качестве про
странственного контура весь аппарат, а за временной интервал
- весь процесс. При этом условимся для определенности
отсчет времени процесса начинать после загрузки жидкости в
аппарат, но до подачи в него горячих шариков, а заканчивать
после вывода шариков из аппарата, но до слива из него жид
кости . (Можно принять и другие условия отсчета времени: ре
зультат будет тем же.) Тогда в отсутствие Источников и Сто
ков, но с учетом Накопления тепловой баланс запишется:
(6)
Gет То - Gc.r !нас - ЛМi = (М - Л М )сж lнас - М еж fo.
Выражение (б) легко приводится к виду, четко проясняю
щему физический смысл рассматриваемого процесса:
Gc.r( To - lнас)

=

Мсж(/нас - to)

+

Л М(i - Сж !нас) ,

(в)

т.е. теплота, отдаваемая металлическими шариками при их
охлаждении от То до !нас. идет на подогрев всей жидкости до
lнас и испарение части ее; при этом (i - еж lнас) = r - теплоте
испарения жидкости.
Из выражений (6) или (в) получается решение поставленной
задачи:
(r)
Далее можно проанализировать различные ситуации . Так,
при получении в результате расчета по (r) значения О � ЛМ � М

549

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

величина ЛМ отвечает сформулированной задаче. Если расчет
дает лМ < О, это означает, что конечная температура жидкости
ниже lнас. так что испарения не происходит (т.е. реально ЛМ =
= О) . Если расчет приводит к ЛМ > М, это означает, что вся
жидкость испарилась и получился перегретый пар температурой
выше tнас. Естественно, в двух последних случаях исходный тепло
вой баланс должен отличаться от записанноrо в форме (б).
В дальнейшем предстоит мноrократно использовать различ
ные тепловые балансы, в том числе записанные первоначально
для элементарного пространственного контура, содержащего
элементарную теплообменную
поверхность d/, и для элемен'
тарного временного интервала d't.
7.6. СРFДНИ Й ТЕМПЕРАТУРНЫ Й НАПОР

Проблема заключается в определении среднего (по поверх
ности теплообмена F) температурного напора в проектных ста
ционарных задачах , когда известны (заданы) температуры теп
лоносителей - на входе в теплообменник и на выходе из него
(не исключено - постоянные по F при изменении агрегатного
состояния или идеальном перемешивании потоков) . Знание Лер
позволяет далее рассчитать необходимую теплообменную по
верхность F по формуле (7. 14а).
7.6. 1 . Характерные температурнь1е профили

Типичные температурные профили для простейших вариан
тов движения теплоносителей вдоль поверхности теплообмена
F (по текущей координате /) представлены на рис . 7. 1 1 . При
этом для каждого отдельного варианта область температурного
профиля горячего теплоносителя ( Т ) находится выше, нежели
холодного (t) . Варианты (а) и (г) илл юстрируют изменение
температур при движении горячего и холодного теплоносите
лей в режиме идеального вытеснения (И В) без изменения агре
гатного состояния. Скорость изменения температур Т и t зави
сит здесь от пропускных способностей соответствующих стадий
теплопереноса G1 c 1 и Gz_c2 : более высокому значению Gc отве
чает более медленное изменение температуры (пунктирные
кривые). При Gc � оо теплоноситель сохранил бы неизменной
свою температуру вдоль поверхности . Варианты (6) и (д) иллю
стрируют температурные профили при движении теплоносите
лей в режиме идеального перемешивания (ИП). Здесь наблю
дается скачкообразное изменение температур на входе в тепло
обменник от входных значений Т' и t' до постоянных по всей
550

Ь Ь t1_

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

т
т·

F

''--J

Т"

/

т
т·

O

_ _ _

_j

F

Т"

�
:

t

/

т
т·

O

'

!

"

F

f

(�" Ь:
b
О

'

tО

б

а

.,,,,,. --

- -А

:

F

г

/

t

(

'

O

- - -

д

F

"

/

t

t'

O

в

F
1

е

t

'

f

Харакrерные температурные профили rорячеrо (а - в) и холодного
(г - е) -теnлоносителей:
-

Рис. 7. 1 1.
а,

г

нии arperanioro сосrояния теплоносителей

ДВИJКеЮlе теплоносителей в реJ1СИме И В; б, д

в

реJ1СИМе И П ;

�. е

при измене

поверхности выходных температур Т " и t". Уровень Т " и t" и
здесь зависит от пропускных способностей потокового тепло
переноса G1 c1 и [hc2 . Наконец, варианты (в) и (е) относятся к
изменяющемуся агрегатному состоянию теплоносителей например, к конденсации горячего и кипению холодного .
Здесь температуры тоже постоянны вдоль поверхности F, но в
отличие от И П - на уровнях входных температур Т ' и f.
В реальных теплообменниках возможно сочетание этих тем
пературных профилей (возможны, конечно, и иные профили);
при этом ход температурных кривых зависит еще и от направ
ления взаимного движения теплоносителей. Ниже проблемы,
связанные с ходом температурных кривых, рассматриваются
применительно к простым схемам движения теплоносителей и
простейшим вариантам структуры потоков - И В и И П .
7 6 2 Средние температурные напоры
Стационарное прямоточное движение в ре.жиме ИВ теплоно
сителей, не изменяющих arperaтнoro состоянИJ1. Расчетная схема
и качественный ход температурных кривых показаны на рис.
7.12. Выделим элементарные контуры с поверхностью теплооб
мена d/ и запишем тепловые балансы.
Для горячего теплоносителя (контур к1 ):
G1 c1 T - Gi c 1 ( T + d T ) - d Q = О и d Q = - G1 c1 d T
(а)
Для холодного теплоносителя (контур к2 ):
G2 c2 t + dQ - G2 c2(t + dt) = О и dQ = Gic2dt.
(б)
.

.

.

551

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 7. 12. К расче'I)' среднего темпера
турного напора при прямоточном
движении теrоюносителей в режиме
ИВ:

(К1 К2,

2

и
а - расчетная схема
Kt и к конrуры) , б - температурный профиль

Т.r

о1

Т'

1

\v
а

л1

r,

о

·1

Вместе с тем для элемен
тарной поверхности d/ в соот
ветствии с (7. 1 ) можно запи
сать уравнение теплопередачи
d Q = kЛdf = k( T - t)df ; (в)
таким образом,

d Q = - G1 c1d T = G1c2dt =
(г)
= k( T - f)df

б

для
балансы
Тепловые
полного теплообменного пространства (поверхность F)
отдельно для горячего и хо
лодного теплоносителей (контуры К 1 и К2) уже бьmи записаны
ранее:
(д)
G1с1 Т' - G1c1 T 11 - Q = О и Q = G1с1 ( Т' - Т ");
�c2 f + Q - �c2t" = О и Q = G1c2(t11 - t').
(е)
Вместе с тем для всей поверхности F можно записать урав
нение теплообмена (7. 14); тогда в целом
(ж)
Q = G1с1 ( Т' - Т '� = �c2(t11 - t') = kFЛep ·
Поделим (по отдельности для каждого теплоносителя) соот
ветствующие фрагменты формул (r) и (ж) . После сокращения
на Gc и k получим

dT
Т" - Т'

= t "dt- t' = (Т - t)d/ = у,
Fл ер

(з)

причем последняя дробь обозначена у для сокращения после
дующих преобразований; знак "минус" при d T учтен измене
нием знака разности в знаменателе первой дроби.
Далее вывод формулы для Лер можно вести различными пу
тями. Один из наиболее простых реализуется следующим обра
зом. Выразим из (з) элементарные приращения температур и
вычтем одно из другого:

d T = у( Т " - Т' ), dt = y(t" - t');
d T - dt = d( T - t) = у(( Т " - Т' ) - (t" - t') ] .
552

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Группируя в последнем выражении температурные напоры
по входному и выходному сечениям Г t' = л 1 и Т " - t" = Л2 и
подставляя значение у в заключительное равенство (з), имеем
после разделения переменных и интегрирования:
T" - t"
d(T - t) (Т" - t") - (Т' - t ') F
J d/ и
J
-

T ' - f'

�

Т-t

T " - t"
Т ' - t'

=

=

FЛ ср

о

(T " - t") - (T ' - t')

FЛ ер

F.

Сокращая на F, получаем в более лаконичной записи (через

Л 1 и Л2):

Л, - Л2
(7. 17)
ln(Л 1 / Л2 )
Таким образом, средний по поверхности теплообмена тем
пературный напор рассчитывается как среднелогарифмическая
величина. Предпочтительность второго из выражений (7. 17)
обусловлена тем, что при прямотоке л 1 > л2 .
Продемонстрируем вехи еще одного простого подхода к
определению Лер · Для вывода воспользуемся одним из свойств
или лучше

Лер

=

а
производных пропорции : если имеется равенство
�

-

Ь

ется справедливым производное равенство

а - с

--

b- d

=

=

с

-

d

с

, то оста-

-

d

С этим

замечанием имеем из (з) :

d T - dt
= У·
(Т" - Т ') - (t " - t ')

(и)

------

и последующий вывод (подстановка значения у, разделение
переменных и интегрирование) проводится по изложенной
выше канве.
Аналогичный подход к определению Лер применим для про 
тивотока теплоносителей (без изменения агрегатного состоя
н ия; режим ИВ). Расчетная схема и возможный температурный
профиль изображены на рис.7 . 1 3 . Различие с прямотоком - в
тепловом балансе (контур к2 ) для холодного теплоносителя .
Соответственно расчетной схеме
(к)
G1c2(t + dt) + d Q - (hc2 t = О и d Q - G2 c2dt.
=

553

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 7. 13. К расче'I)' среднего темпера
ного напора
при противоточном
тур
теплоносителей
в режиме
движении
ИВ:
расчетная схема ( К 1 и К2 , к1 и к2 а
температурный профиль
конrуры) , б

-

7)

f

а

т·

-

Дальнейший пуrь аналоги
чен проделанному для прямо
тока. Его этапы:
dt
t' - t"

dT

---- = --- =

Т" - Т '

дj , "

FЛ е р

(T - t) qf

= У·

.

d T = у( Т " - Т'), dt = y(t' - /") ;
d T - dt = d( T - t) = у[( Т " - т ') - (/' - /")] =
= у[( Т " - /') - ( Т ' - /")] ,
6
причем Т ' - t" = л 1 и Т " - t' =
= Л2 - температурные напоры
на левом и правом концах теплообменника, отличающиеся от
Т"

сформированных в условиях прямотока.
Подстановка значения у, разделение переменных и интегри
рование дают
T " - t' d( T
/) (Т " - / ' ) - (Т' / " ) F
f Т /
f d/ и
FЛ ср
о
T' - t"
-

-

=

-

"I n Т - t'
Т'
t"

=

(Т " - t') - (Т ' t ") F .
-

FЛ

ер

После сокращения на F получаем в лаконичной форме за
писи (через Л 1 и Л2 ) выражение, формально совпадающее с
(7 . 1 7), однако с иным смыслом концевых температурных напо
ров Л 1 и Л2 . При этом в случае противотока удобным может
оказаться любое из выражений (7 . 17); первой ставится 66льшая
из величин л 1 , Л2 - это всегда температурный напор, отве
чающий выходу теплоносителя с большей пропускной способ
ностью Gc.

температурный напор меньше среднеарифметиче
rарифмический
скогоСреднело
)
(
2, причем знак равенства отвечает случаю Лt = Л2 . В
:ратур
д.р=
Л2
Лер
Л1
/
е по теплообмену обычно считают незначительным ра:иичие в Лер и д.р
лите
при
0,5 Лt/Л2 2: на rраницах этого диапазона указанное различие состааляет
4 % . Отсюда рекомендация: при небольших отличиях в Лt и Л2 вести расчеты на
основепд.р. Такая
рекомендация не учитывает, что при замене Лер на д.р поrреш
ность
олучается не "в запас "; поэтому рассчитанная поверхность теплообмена
s

554

S

s

+

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

будет несколько занижена в сравнении с реально необходимой. Лучше, незави
симо от величины д�/д2, использовать в расчетах среднелоrарифмический тем
пературный напор д:р.

Анализ задач проектирования позволяет установить соотно
шение средних температурных напоров для противотока
( Л ер ) и прямотока ( Л ер ) : Л ер � Л ер . Это означает, что при
одинаковых концевых температурах теплоносителей Т', Т11, t' и
t 11 для переноса заданноrо количества теплоты Q в случае про
тивотока можно обойтись мен.ьшей поверхностью F, чем для
прямотока, а для заданной поверхности F - передать больше
теплоты Q. Вообще при движении теплоносителей в режиме
И В из всех схем наибольший температурный напор характерен
для противотока, наименьший - для прямотока.
Однако преимущество противотока не ограничивается эко
номией капитальных затрат (возможность провести процесс с
меньшей F). Часто значительно существеннее энергетические
выrоды. Пусть заданы поток и граничные температуры целево
rо продукта (например , Т' и Т 11) и известна начальная темпера
тура теплоносителя f. При прямотоке, очевидно, всегда t 11 <
< Т11 ; при противотоке t11 < Т', что совсем не исключает t11 >
> Т 11• Значит, при противотоке теплоноситель � может быть
нагрет (в данном примере) до более высокой выходной темпе
ратуры; следовательно, для передачи заданноrо количества
теплоты Q = = G1 с1 ( Т ' - Т 11) расход теплон.осителя � будет
мен.ьше - по (д), поскольку (t11- f) стало больше.
Средний температурный напор рассчитывается как средне
логарифмический и в тех случаях, когда температура одного из
теплоносителей постоянна (кипение, конденсация, течение в
режиме И П), а второй движется вдоль теплообменной поверх
ности в режиме И В . При этом постоянная температура устана
вливается на уровне Т= Т' (конденсация), t= t' (кипение), Т =
= Т 11 или t = t 11 (для режима ИП), причем уровень Т' или t11
определяется равенствами типа (7. 1 6). Способ формирования
концевых температурных напоров для всех этих случаев очеви
ден .
Важно, что при неизменной температуре одноrо из теплоно
сителей (тем более - обоих) все схемы взаимноrо направления
движения теплоносителей (простые и сложные) с точки зрения
температурных напоров становятся равноценными.
Если температуры обоих теплоносителей Т и t постоян.н.ы по
всей поверхности, то по F не изменяется и температурный на
пор; ero надо рассчитывать просто как разность Лер = Т - t.
При конденсации и кипении значения Т= Т' и t = t' опреде555

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ляются рабочим давлением в зонах конденсации и Юfпения и
Лер = Т' t '. Значения температур Т = Т" и t = t " при движе
нии теплоносителей в режиме И П , когда Лер = Т" t ", опреде
ляются равенством типа (7. 16б) : напомним, что в задачах про
еIСГирования выходная температура одного из теплоносителей
(целевого) - известна.
Наконец, в случае равенства пропускных способностей G1 с1 =
= � с2 при движении потоков в режиме И В температуры теп
лоносителей изменяются вдоль поверхности, но л 1 = л2 . Пря
мое использование среднелоrарифмического температурного
напора по формуле (7. 1 7) приводит к неопределенности. В ее
раскрытии нет необходимости (хотя это и возможно), посколь
ку в любой точке поверхности здесь Л = Л 1 = л2 = co nst, так
что Л ер = Л1 = Л2.
Аналогичные подходы позволяют подойти к определению
средних температурных напоров в случае сложных схем движе
ния теплоносителей. Выводы формул и конечные выражения
Лер для ряда таких случаев приводятся в литературе · . Эги вы
ражения содержат пропускные способности стадий: поверх
ностной kF и потоковых G1 с1 и �с2 - в виде безразмерных
комплексов:
а = kF/( G1 c1); Ь = kF/( G2c2); Ь/а = G1 c1/( G2c2), (7. 1 8)
-

-

причем критерии а и Ь в зарубежной литературе называют чис
лами единиц переноса теплоты.
Громоздкие выражения для Лер , хараIСГерные для сложных
схем, не очень удобны для инженерных расчетов; поэтому
предлагается следующий rрафоаналитичесЮfй метод определе
ния Лер · Предварительно по входным и выходным температу
рам рассчитывают среднелоrарифмический температурный
напор Л с как для противотока, а далее отыскивают поправоч
ный множитель & 6 1 :::; 1 , чтобы перейти от противотока к рас
считываемой сложной схеме. В этих целях вводят безразмерные
температурные комплексы:
}( = Т' - Т"
t" - t'

и

р

•

t" - t'

Т' -

= ---

t'

(л)

Легко видеть, что /( = а/Ь = (hc2f(G1c1); р • также представ
ляет собой отношение пропускных способностей - процесса
теплообмена в целом и G2c2. По полученным аналитически вы-

• См. (2,

556

15).

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 7. 14. К определению средней движущей силы для смешанного тока 1-2

ражениям для Лер применительно к различным схемам движе
ния теплонос ителей построены графики Е л r = f(R • , р • ) . С помощью найденных по таким графикам значений Е Лt опреде

ляют

Лер :

Лер = Л с

(7. 1 9)

13 качестве примера на рис. 7. 14 приведен график для опре
деления Лер в случае • смешанного тока 1- 2 .
Е лt .

Средние темпераwные напоры Лер определялись выше в предположении о
независимости теплоемкостей потоков от темпера"!)'Р и постоянстве коэффици
ентов теплопередачи по поверхности F. Первое допущение часто оправдано
небольшими темпераwными интерваliами: теплоемкости изменяются мало, так
что впоJП1е можно оперировать средними их значениями . Второе допущение
правомерно (иногда прибли:женно), когда коэффициенты теплопередачи не
зависят от темпераwных напоров, меняющихся вдоль поверхности; такие си
туации нередки: вынужденное движение теплоносителей или постоянство тем
пера"!)'Р теплоносителей вдоль теплообменной поверхности. В противном случае
(скажем, конденсация или кипение с одной стороны поверхности, неизменность
агреrатного состояния при двюкении в режиме ИВ
с другой) нужно, строго
говоря, рассматривать локальные значения k и учитъшать их изменение вдоль
поверхности F вместе с температурным напором Л . Покажем, как это можно
сделать применительно к теплообмену меЖду конденсирующимся паром и теп
лоносителем, не изменяющим агреrатного состояния, - здесь k зависит от
локального л соответственно (7.4).
Запишем для элементарной поверхности d/ и полной F выражения типа (в) и
(е), ограничившись переносом теплоты с холодным теплоносителем:
-

причем для конденсирующегося пара Т = Т = const.
Поделив почленно одно выражение на другое, получим

(м)

'

dt

t"- t'

k(T - t)d/

Q

и

(н)

Соответствующие графики для других схем движения теплоносителей при
ведены, например, в ( 1 1 , 12, 16; 13 и 1 5 - особенно подробно ) .

•

557

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Для сокращения записи обозначим Т- t • л = vaJ" и представим разность t"
- t ' в виде ( Т 1) - ( Т - t') = л 1 - л2. Интеrрируем второе соотношение (н) от
Л 1 до Л2 И ОТ 0 до F.
-

-

Q=

Лг Л2 F .
Л 1 dЛ

/ -

(о)

Л 2 kЛ

В последнем из выражений (о) величина, стоящая в правой части перед F,
предстааляет собой среднее по поверхности произведение (kЛ)ср. в отличие от
Лер в (7. 14). Разумеется, при k = const выражение (о) закономерно переходит в
(7. 14).
Вычисление интеrрала в (о) принципиальных затруднений не вызывает, так
как при любом значении л в интервале от л1 до л2 локальная величина k может
быrь рассчитана по формуле (7.4).

7 .6.3. Проектный выбор теплообменника

Технологам, как правило, не приходится проектировать теп
лообменники, задача проектирования стоит перед ними обыч
но в аспекте его проектного выбора - п о каталогам. Этот вы
бор ведется в следующем порядке:
по параметрам (расходу, т.е. производительности;
свойствам; входной и выходной температурам) целевого про
дукта определяется поток теплоты Q;
- по известным температурам обоих теплоносителей на
концах теплообменника соответственно схеме их движения
рассчитывается средний температурный напор Лер;
- выбирается расчетная формула для коэффициента тепло
передачи k, отвечающая физическим процессам в теплообмен
нике (см . разд . 7.3).
При этом возможны затруднения, поскольку заранее (до
расчета и выбора теплообменника) не известны высота и диа
метр труб (они необходимы в случае теплообмена при конден
сации) , сечение трубного и (или) межтрубноrо пространства
(их нужно знать для расчета Nu и а. по Re) и т.п. Поэтому
обычно приходится выполнить предварительный расчет, за
давшись ориентировочным (см. разд. 6.8) значением kop и оце
нив ориентировочную поверхность теплообмена Fop по форму
ле (7. 14а). Это позволяет в первом приближении выбрать теп
лообменник с определенными - указанными в каталоге геометрическими характеристиками, с тем чтобы использовать
соответствующую расчетную формулу для k. Далее:
- проводят расчет k и находят расчетную поверхность теп
лообмена Fрасч ;
- окончательно выбирают по каталогу теплообменник с
подходящим значением F так, чтобы выполнялось условие:
558

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

все отклонения от расчетных величин должны давать погреш
ность "в запас " (скажем, F "?::. Fрш;ч и т.п.).

При невозможности подобрать подходящий теплообменник
расчет и выбор проводят заново, сообразуясь с опытом
предыдущеrо расчета.
7.7. ТЕПЛОВО Й ПОТОК

Эксплуатационные задачи рассматриваI<УГ ситуации, когда из
вестны потоки теплоносителей и их температуры на входе в
аппарат Т' и f, а также параметры, определяющие интенсив
ность теплопереноса между теплоносителями (через поверх
ность теплообмена в рекуператоре, например). Для задач экс
плуатации выражение (7.14), безусловно, остается справедли
вым, но для расчета тепловоrо потока Q оно не может быть
прямо использовано, так как известны лишь входные темпера
туры. На выходе из теплообменника температуры Т" и t" не за
даны, поэтому величину Лер найти нельзя (исключение - теп
лообмен между конденсирующимся паром и кипящей жид
костью, когда Лер = Т' f известна по условиям процесса). В
таких ситуациях методику расчета Q целесообразно основывать
на разности входных температур теплоносителей л. = Т' f.
Рассмотрим подход к определению Q для некоторых про
стейших случаев.

-

-

7.7. 1 . Тепловой поток при движении теплоносителей
в режиме идеальноrо перемешивания
Эта технологическая ситуация в расчетном плане - одна из
самых простых. Рассмотрим теплообменник (рис.7. 1 5) , в кото
ром оба теплоносителя движутся (без изменения arperaтнoro
состоян ия) в режиме идеальноrо перемешивания (символ И П ,
н а рисун ке - мешалки). Поэтому температуры в теплообмен
нике каждоrо теплоносителя
постоянны по поверхности теп
лообмена и равны таковым на выходе Т" и t". Подлежащий по
следующему переносу к холодному теплоносителю поток теп
лоты Q, вносимый с rорячим теплоносителем (ero пропускная
способность G1 c1 ), последовательно проходит через тепло
вой поrраничный слой с rорячей стороны (пропускная способ-

-

ность a. 1 .F), стенку

(ЛегО ет )

F , поrраничный слой с холодной сто-

роны (a.2.F) и уносится холодным теплоносителем (пропускная
способность {hc2) . Запишем выражения для Q применительно
ко всем отдельным стадиям теплопереноса [см. выражение (а)
559

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

�т .15ст

Рис. 7. 15. Расче'Пiая схема эксплуатационной задачи при идеальном смешении
темоносителей

в разд. 7.3 . 1 и (7 . 1 66) в разд. 7. 5.2) :

Q = G1c1 ( Т'
=

б ет

А. ст
(8 1 - 8 2) =

o. 1 F( T " - 8 1) =
o.2F(82 - /") = G2c2 (/" - f),
-

Т ") =

(а)

причем 8 1 и 82
температуры стенки (здесь постоянные вдоль
F) со стороны горячего и холодного теплоносителей соответ
-

ственно.
Решим равенства (а) относительно частных разностей тем
ператур и исключим все проме:жуrочные температуры, оставив
лишь известн ые Т' и /':

Оrсюда получается выражение для искомого потока теплоты:
(7.20)

560

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

или в более лаконичной записи, если все (три) поверхностные
стадии теплопереноса объединить в одну стадию теплопередачи:
- t'
(7 .20а)
=
Q

т·

1

1
+
kF

1

-- -
G2c2
G 1C1
+

Для большей общности с последующим изложением пере
пишем (7.20а), представив слагаемые в знаменателе правой
части в форме безразмерных комплексов:
(Т '

-

t ')kF

Q = kF
kF
kF
+ - + -G 1C1 kF G2c2

--

kFд.

а +1 +Ь

(7 .20б)

где символами а = kF/( G1 c 1 ) и Ь = kF/( Chc2 ) обозначены (по
формулам 7. 1 8) отношения пропускных способностей поверх
ностной и отдельных потоковых стадий теплообмена.
7. 7 2 Тепловой поток
ори прямоточном и противоточиом движении теплоносителей
.

.

В случае прямоточного движения обоих теплоносителей (без
изменения агрегатного состояния) в режиме идеального вытес
нения температуры Т и t изменяются Вдоль F, так что анализ
несколько усложняется. Выражения для Q с записью стадий
теплопередачи (в целом) принимают вид
(б)
Q = G1 с1 ( Т' - Т ") = kFЛcp= G1c2(t" f) .
Чтобы исключить из конечных формул не известные заранее
температуры Т' и t", выразим их из первого и последнего ра
венств (б):
Т " = Т,
� . t" = t' + l
G1 c1
G2 c2
и подставим в среднее равенство (6), раскрывая написание Лер:

-

-

О= •/т·-1:·1 -[(т·-�).-(1· + �)] .
( - _я_
) (
G1c1
Т'

-

r•

)

+ _я_
G

2c2

m

�� :.�J
- ( G1c1 G2c2_)

д.

1
Q --

+

1
_

kF,

Отсюда после сокращения на Q (при этом Q под знаком ln
остается)
(r)
561

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Потенцируем и разрешаем полученное равенство относи
тельно искомого потока теплоты:
л.

Q

-

Ло

е (а+Ь) '
·

1
Q G1 + G
c1
c

(

:J
-(а +Ь)
) = -1 е -1

(е <а+Ь) - l) Л •
е (а+Ь) ( 1 + 1

=

1

_

(7.2 1)

л• .

G2c2
Как и в случае ИП, знаменатель (7.2 1 ) можно привести к
безразмерному виду, домножив его (числитель - тоже) на kF:
=

G1c1

Q=Q=
• .

(

+ b)
kFл . 1 - e- (a

-G1 c1
kF

G1 c1

G2c2

)

kF
+ --

G2c2

=

kFЛ ·

+

(1 - е -(а+Ь) ) .

(7.21а)

а+Ь

В случае противотоrсноzо движения теплоносителей в режи
ме ИВ (и также без изменения агрегатного состояния) остают
ся справедливы равенства (6), но Лер формируется по-иному
(см. разд. 7.6.2). Подставим значения Т " и t" в выражение Лер
для противотока :
Q

= kF

) -(т· - G1c1 1·)
( - 1 ' - __я__
G2 c2
-- -г

1n

Т'

Т'

t'

t'

_g_

__я_
��

1n

Q

ln

_

д_

а1 с 2
Q
Л• а1 с1

--

=

�G

kF

а . с.

_

kF

а2 с2

=

а _

и разрешаем полученное
Потенцируем
тельно искомого
потока теплоты:
--=Q
_
Q-=.
л

_

Л· -

562

G2 c2

_

-G1 с 1

_

е (а-Ь) '.

л.

-

Л• -

Оrсюда (после сокращения н а Q)
Л•

- -)

1
i
rf_
G
�
G1
c1
2c2
= kF

-

Ь

__я_
��

-

,

Q

�G

(д)

равенство относи

(7.22)

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

a : kFl (G 1 c 1 ) = 0 , I

Q/Q г-::::!';:;:::::т-о:=::r-�-г..,----r--г:7!
о , 9 t------1,___....---f
.. __г-1,..._"'I:/

о ,6 t---t-+--+---+'lr--l--l+-----1
о

·б,.,.02.,.
. .1-..:-...L.
....,.
-L... -L...lilllt.
..:i -I,-..,...
..
....
....; ;.;:...
.,.,.,1 0 �. о

Рис. 7. 16. Сравнительная интенсивность теruю переноса при прямотоке и проти
вотоке в задачах эксплуатации

или с безразмерными комплексами в знаменателе :
..
l - е <Ь - а)
Q=Q=
а - Ь (Ь - а )
е

kFл.

.

(7.22а)

Заметим, что в случаях прямотока и противотока из (7.2 1а) и
(7 .22а) легко найти пропускные способности теплообмена в
целом Q/Л
Полученные выражения для потоков теплоты при прямото
ке Q и противотоке Q позволяют Провести их сопоставление в
условиях эксплуатационной задачи теплообмена. На рис. 7. 1 6
показана зависимость Q/Q от G1ci/( G2c2) = Ь/а при различных
kF/(G1 c1 ) = а. Можно констатировать, что при очень малых и
очень больших значениях комплекса G1ci/( °'2c2), а также при
малых kF/( G1c1 ) прямоток и противоток в аспекте интенсив
ности теплопереноса равноценны. Эrо объясняется малым из
менением в указанных условиях температуры одного из тепло
носителей вдоль теплообменной поверхности: например, со
гласно равенству (б), при G1ci/( °'2 c2 ) --+ О очевидно t ::::: co nst
(поскольку t" - f --. О); соответственно при 01 ci/( G2c2 ) --+ оо
будет Т ::::: co nst; наконец, при kF/( 01 с1 ) --+ О получается ( Т' - Т")/Лср --+ О, т.е. опять-таки Т ::::: co nst. · А при постоянстве
температур одного из теплоносителей, как указано в разд. 7.6.2,
взаимное направление их потоков перестает сказываться на
интенсивности теплообмена. Однако при сопоставимости зна
чений 01 с1 , °'2 с2 и kF интенсивность теплопереноса для прямо
тока всегда ниже, чем для противотока: на рис. 7 . 1 6 в этом
случае Q/Q < 1 , причем при G1 c1 = G2c2 и k >> G1 c1 , °'2 с2 •

.

F

563

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ровно вдвое. Это легко показать и пуrем прямого деления Q
на Q с последующими предельными переходами - сначала с
учетом а = Ь , а затем а � ао .
Аналогичным способом получаются выражения для Q, если
один из теплоносителей движется в режиме И В , а другой - в
режиме И П . Надо только соответственно записать выражение
для среднелогарифмического напора Лер· Еще проще получить
формулу для Q, если один из потоков изменяет агрегатное со
стояние. Например, в случае конденсации пара надо учесть
постоянство температуры Т = Т' = const, приняв пропускную
способность этой стадии бесконечно большой* : как бы G1 c1 �
� ао. �:9гда а = kF/( G1 c1 ) � О, и выражения (7.2 1а) и (7.22а)
превращаются в более простое:
1 е -Ь .
(7.2 1 б)
Q kFл . =

ь

Наконец, если оба теплоносителя изменяют агрегатное со
стояние, то проще всего воспользоваться выражением (7.20а),
положив в нем G1 c1 , G2c2 � ао, или (7.20б) с учетом а, Ь � О.
Тогда
Q = kFл . ,
(7. 14), (7.20в)
т.е. при изменении агрегатного состояния обоих теплоносите
лей задачи эксплуатации и проектирования применительно к
отысканию Лер совпадают, поскольку температуры вдоль всей
поверхности теплообмена заданы Т = Т', t = t ' - и постоян
ны, а Л • = Лер·
Для ряда более сложных схем движения теплоносителей
(смешанные токи; движение теплоносителей в режимах, про
межугочных между ИВ и ИП, и др.) также получены ·· выраже
ния для Q.
Из выражений (7.20б), (7.21а), (7.22а) легко получаются зна
чения средних температурных напоров - пуrем сопоставления
с (7. 14) для рассматриваемых случаев, соответственно:
Л ер

=

Л.

(
а + 1+ ь

Лер = Л .

( - е- ( а+ Ь)
а+ь

Лер = Л .

( - е (Ь.-а)
.(е)
а - ье<Ь.-а)

Для сложных схем движения теплоносителей тоже мoryr
быть найдены выражения, связывающие Ле� и л . с помощью
отношений пропускных способностей ( а и Ь) .
• Здес ь не следует, конечно , анализировать, чтб именно устремляется к бес
конечности - Gi или с 1; реч ь идет о математичес ком приеме, отвечающем рас
сматриваемому переходу.
•• Наиболее подробные сведения можно найти в 1 1 5).

564

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

7.8. ИЗМЕНЕНИЕ ТЕМПЕРАТУР
ВДОЛЬ TEIUIOOБMEH HO Й ПОВЕРХНОСТИ

Качественно характер изменения температур теплоносите
лей вдоль поверхности теплообмена затраmвался в разд. 7 .6. 1 .
В ряде технолоmческих задач необходимо знание локальных
температур теплоносителей Т и t в различных точках теплооб
менной поверхности, иначе rоворя - количественных законо
мерностей их изменения по F. Это позволит, в частности, най
ти конечные температуры Т " и /" в задачах эксплуатации. Для
иллюстрации подходов к отысканию упомянуrых закономерно
стей обратимся к прямотоку теплоносителей при их движении в
режиме И В и без изменения аrрегатноrо состояния.
Для этоrо случая из тепловоrо баланса для элементарной
поверхности теплообмена d/ в разд. 7.6.2 бьmи получены соот
ношения (б)-(r); представим их в несколько иной форме:

G1 c1 d T + ( T - t)df = О

k

{

и

G2c2dt - ( T - t)df = О .

k

(а)

Введем относительную координату х = f/F; тогда d/ = Fdx, и
из (а) получается система дифференциальных уравнений пер
воrо порядка:
dT
=
(Т t) -а(Т t) ,
dx
(б)
dt
(Т t) = Ь(Т t) .
dx
G2c2
=

- G1c1kF kF -

=

-

-

Эта система должна решаться с граничными условиями для
точки начала отсчета поверхности теплообмена f
(в)
Т = Т ' и t = t' при х = О.
Наиболее общий способ решения - повышение порядка
дифференциальных уравнений при сведении системы (б) к
уравнению относительно одной из переменных (здесь Т или /).
Выразим из первоrо уравнения системы (б) температуру второ1dT
и продифференцируем ее по х:
ro теплоносителя t = Т +
а dx
dt
dT 1 d2 T
2 . А теперь подставим во второе уравнение
+
dx dx 0 dx
системы найденные значения dt/dx и t :
-

=

- --

dT
dx

-

+!
а

2
d T=Ь
2
dx

[т-(т + !
а

)]

dT
dx

'

565

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

d2 T
dx 2

откуда

dT
dx

(r)

- + ( а + Ь) - = 0 ·

Решение этого однородного дифференц иального уравнения
второго порядка имеет вид
Т = Л. l ek,x + Л. 2 еk,х '
(д)
где k 1 , k1 - корни хара�сrери стического уравнения
k2 + ( а + b) k = О , так 'П'О k1

Тогда

=

О , k1

=

- ( а + Ь) .

(е)

Подставив в выражение для t это значение Т и произ
водную d T/dx :::: - Л. 2 (а + Ь) е - ( а + Ь) х , получим

(ж)
= Л,1 - Л, 2 !!.. е- ( а+ Ь)х .
а
Постоянные интегриро вания Л. 1 и Л. 2 найдем из граничных
условий (в):
l

Т' = Л 1

Отсюда
л. 1

=

где л. = Т ' - t ' .

Т'

+

Л. 2

и

а
- л. -0- :::: t' + л . -ь- , Л 2 = Л . -'
а+Ь
а+Ь
+Ь
а

(з)

Подставив значения постоянн ых интегриро вания в (е) и (ж) ,
имеем окончательно
т = Т' l :::: ! '

л . -0а+ Ь

(

b_ l - е- (а+ ь>х
+ Л. _
а+ Ь

(

)

1 - е-( а+ Ь )х ;

)

(7.23)

.

(7.24)

На входе в теплообменник (х = О) тождественно Т= Т ' и t =
= f; на выходе из него (х = 1 ) получается
Т"

=

t " ::::

566

(

0- 1 - е-( а + Ь)
Т' - л. а+Ь

t ' + л . _Ь_
а+Ь

(1 -

)

)

е - <а + Ь) .

;

(7.2За)
(7.24а)

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Найденные соотношения позволяют проследить изменение
температурного напора вдоль поверхности F; из (7.23) и (7.24)
следует
Т-t

=

Т' - t '

- (

__!!_)_ (•-

ал. +
а+Ь
а+Ь

·

е- (•+Ь)х

)

или д = Л . е-<•+Ь)х .(7.25)

Можно убедиться, что из (7 .25) по теореме о среднем непо
средственно получается известное уже выражение (7 . 17) для
среднелогарифмического температурного напора Л ер

1

=

J Лdх .

о

При этом надо учесть, что получаемые в ходе интегрирования
фрагменты имеют следующий смысл применительно к прямотоку: Л . = Л1 ; Л . е- < а+ Ь> = Л2; а + Ь = ln(Лi/Л2).
Продемонстрированный способ определения температурных
кривых пригоден также для противотока и многих сложных
схем движения теплоносителей. При этом в общем случае из
меняются исходные дифференциальные уравнения и гранич
ные условия . В литературе " приводятся и друmе (более част
ные) подходы к описанию профилей температур.
7.9. ЛИМИТИРУЮЩИ Е СТАДИ И
В П РОЦЕССАХ ТЕШIОПЕРЕНОСА
7.9. 1 . Общие понятия

Стадии, составляющие процессы переноса, мoryr быть
сложным образом связаны между собой: последовательно, па
раллельно, последовательно-параллельно. Так, при переносе
теплоты соответственно схеме на рис. 6 . 1 выделяются пять по
следовательных стадий, соответственно схеме на рис. 7.5 - три
последовательные и две параллельные. Каждой стадии отвечает
своя интенсивность; для некоторых стадий в качестве характе
ристики интенсивности выступает ее пропускная способность.
Как общий случай, интенсивность теплопереноса в целом за
висит от интенсивности составляющих его стадий, причем
конкретная форма этой зависимости обусловлена особенно
стями взаимосвязей отдельных стадий.
В ряде случаев некая стадия последовательного переноса
протекает значительно медленнее других - тогда ее называют
лимитирующей (определяющей, контролирующей) . Теоретически
можно считать, что продолжительность всех остальных стадий

• См., например, (2, 6,

1 1 , 12, 1 6) .

567

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

много меньше таковой не только для лимитирующей стадии,
но даже для погрешности в определении продолжительности
лимитирующей стадии. Практически достаточно, чтобы игно
рирование этих остальных стадий вносило ошибку, не выходя
щую за пределы приемлемой точности расчета. Это означает,
что теоретически или практически вполне можно ограничиться
анализом только лимитирующей стадии (полагая, что движущая
сила может быть целиком отнесена к этой стадии) - без
сколько-нибудь заметной потери точности расчета. Это, как
правило, существенно упрощает и обле�ает анализ, поскольку
избавляет от необходимости определения характеристик нели
митирующих стадий.
Поэтому построение необходимо начинать с анализа на ли
митирующую стадию - наличие или отсутствие, особенности
(если ее удалось выявить), способы воздействия. Без такого
анализа возможны ошибки, связанные с неосознанной подменой
задачи, а значит и с неверными рекомендациями в практи
ческом осуществлении процесса; не исключена и неграмотная
постановка научного исследования.
Ниже проблема лимитирующей стадии рассматривается в
основном для последовательного переноса (параллельный пе
ренос затронуг весьма кратко) - стационарного и нестацио
нарного. При этом по мере возможности к анализу привлека
ется концепция пропускных способностей: основная задача
формулируется как выражение пропускной способности тепло
переноса в целом Q/ Л . в зависимости от пропускных способ
ностей отдельных стадий и как упрощение соотношений для
Q/ Л . при наличии какой-либо лимитирующей стадии.
7.9.2. Пропускные способности и лимитирующие стадии
при стационарном теплоперевосе

Пусть теплообмен происходит в рекуперативном теплооб
меннике, включающем в наиболее полном варианте пять по
следовательных стадий (см. рис. 6.1): подвод теплоты в рабочую
зону с горячим теплоносителем; перенос ее через пограничный
слой от этого теплоносителя к горячей поверхности теплопере
дающей стенки; через стенку; от ее холодной поверхности че
рез пограничную пленку к холодному теплоносителю; отвод
теплоты из рабочей зоны с холодным теплоносителем.
К наиболее наглядным результатам приводит анализ тепло
переноса при .движении обоих теплоносителей в режиме иде
ального перемешивания. Воспользуемся выражением (7.20), раз568

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

решив его относительно Q/ Л . :
1
1
1 + 1 +
1
1
+ -- + -G1c1 с ч F (Лcr /8 cr)F a. 2 F G2 c2
или более лаконично:
Q

л.

--

(7.26)

--

Q

+1 +

- = -------

л.

G1 C1
1

--

kF

G2 c2

(7.26а)

1

-

либо, наконец, с безразмерными комплексами а = kFI( G1 cJ), Ь =
= kF/( °'2 c2 ) в знаменателе:
Q
1
1
kF
+ + Ь kF .
(7 .26б)
= kF + л
kF + -kF
а 1
•

=

--

G1c1

kF

G2c2

В самом общем случае у слаrаемых в знаменателе (7 .26) мо
быть разные поверхности: F1 , F2 и т.д.
В знаменателе выражений (7.26), (7.26а) стоят величины,
обратные пропускным способностям отдельных стадий. Из
этих выражений следует, что увеличение пропускной способности
любой из стадий (т.е. уменьшение отвечающей ей обратной
величины) снижает влияние этой стадии на интенсивность про
цесса в целом. Напротив, уменьшение пропускной способности
какой-либо стадии повышает ее влияние на процесс; при суще
ственном уменьшении пропускной способности стадии она
может стать лимитирующей.
Если, например, kF << G1 c1 , °'2с2 [или, что то же самое
применительно к (7.26б), а, Ь << 1 ) , то перенос те пл оты лими
тируется те пл опередачей через поверхность, поскольку вели
чина 1/(kF) значительно превосходит остальные слаrаемые в
знаменателе выражения (7 .26а). В этом случае говорят о тепло
перевосе в условиях поверхностной задачи. Для расчета теплопе
реноса здесь необходимо знание всех кинетических характери
стик (а. 1 ; а.2 ; Лет и 8ст ; F и т.п.); в то же время пропускные
способности теплопереноса с потоками теплоносителей G1 с1 и
G2c2 в этом случае роли не играют, их воздействие на процесс
пренебрежимо мало. Для интенсификации теплопереноса здесь
надо повышать kF; при этом может возникнуть вопрос, какая
из стадий поверхностно го теплообмена (а.1 или а.2 либо кон
дукция через стенку) является лимитирующей. Если, скажем,
щ F<<a.2F, (Лст/бст)F, то, как показано в разд. 1 .8.6 (анализ по
значению критерия Био), процесс контролируется теплоотдаrуг

569

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

чей со стороны горячего теплоносителя; именно ее и надо ин
тенсифицировать. Воздействовать при этом возможно на ко
эффициент теплоотдачи а. 1 (турбулизация потока с помощью
специальных устройств, увеличение скорости его движения
около теплообменной поверхности и т.п.) или на поверхность
теплообмена, развивая ее со стороны меньшей пропускной
способности, например пуrем применения оребренных поверх
ностей (см. рис. 7.2).
Если же G1 c1 << a.1F, (Л.�ст)F, a.2F и G2 c2 (т.е. а � оо), то
лимитировать теплоперенос будет подвод теплоты в рабочую
зону с горячим теплоносителем, поскольку слагаемое l/(G1 c 1 )
значительно превосходит по величине все остальные. В этом
случае говорят о теплопереносе в условиях паrоковой задачи по
горячему тепловосиrелю . Аналогично, при существенно малой
пропускной способности G2c2 (Ь � оо) задача будет паrоковой по
холодному теплоносиrелю. В случае любой из потоковых задач
технолога не интересуют кинетические характеристики тепло
переноса (типа а., А.ст , F и т.п.), поскольку расчет ведется на
основе пропускной способности Gc одного из теплоносителей
-того, что лимитирует процесс.
При движении теплоносителей в режиме идеального вытес 
нения конечные результаты не столь наглядны, хотя качествен
но они не изменяются.
Из выражений (7.2 1) и (7.21а) для прямотока имеем
л.

Q

- =

я_ =
л.

1

1

- е -(а+ Ь)

-+ -G1C1 G2 c2

- е -(а + Ь )

kF
+ --

kF

-G1 c 1

1

1

kF

=

и

1 - е -( а + Ь)

а+Ь

kF .

(7.27)

G 2 c2

Пусть подвод теплоты с горячим теплоносителем не влияет
на теплоперенос: G1 c 1 � оо, а � О. Тогда из (7.27)

;.

=

l

-

:

-Ь

kF

=

(

Ь
G1 c2 1 - е -

)

=

G1 c 2 1 - e-kF/G2 c2

(

)

(7.27а)

- интенсивность процесса определяется пропускными способ
ностями (hc2 и kF.
Симметричная ситуация - при (hc2 � оо: эта пропускная
способность перестает влиять на теплоперенос в целом:
я_ = 1 - е-а kF = GI С1 (1 - e-kF/G,c, ) .
(7.276)
д.

570

а

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

В рассмотренных случаях теruюобмен происходит в условиях
задачи: влияют поверхностный теплоперенос и одна
из потоковых стадий. Если же пропускные способности обеих
потоковых стадий велики ( G1 c1 , �с2 --+ оо, а , Ь --+ О) , то мно
житель перед kF в (7.27) дает неопределенность. Раскроем ее,
представив экспоненту в вИде ряда
смешанной

1-

z

= z

-

z2

2!

-

+

z3 - . . . ,
3!

-

имеет в данном случае смысл ( а +

малых z lim 1 где символ

е'

e-z

z

=

Ь) .

Тогда при

1, так что

.я_
= kF ;
.Л•

(7.27в)

это поверхностная задача теплопереноса, и потоковые стадии
не играют роли, так как их пропускные способности велики.
Наконец, в случае kF --+ оо ( а, Ь --+ оо) перестает играть роль
теплопередача: поверхность способна пропустить любое коли
чество теплоты, подводимой (отводимой) теплоносителями при
полном выравнивании их выходных температур ( Т " = t ) - все
определяется их пропускными способностями. Уравнение
(7 .27) в этом случае принимает ВИд, характерный для балансо
вой задачи по двум теплоносителям:
1
(7.27г)
Q
-

"

д.

=

1

Gl cl

--

1

G2 C2

+ --

Если при этом еще, например, G1 с1 < < � с2, то

.я_ = G1 c1 .

(7.27д)

. д.

К аналогичным выводам приводит анализ· противоточного
теплопереноса - на основе уравнений (7.22), (7.22а):
Q
Л•

-

=

1

--

1 - е < Ь - а)

1

- -- е (Ь-а)
G1 c1
G2c2

и

Q
Л.

1 - е <Ь - а) kF .
- Ь (Ь - а )

а

(7 .28)

е

При сопоставимости всех трех пропускных способностей

G1 с 1 , � с2 и kF ( или, как указано выше, хотя бы двух из них )

задача теплопереноса будет смешанной.

• Такой анализ выполнен в разд. 1 0 . 9. З применительно
процессу массопереноса.

к

противоточному

57 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Анализ в свете лимитирующих стадий позволяет с иных по
зиций трактовать сопоставление прямотока и противотока (см.
рис. 7 . 1 6) . При очень малых или очень больших отношениях
потоковых пропускных способностей G1 c if( � с2) теплоперенос
происходит в области потоковой задачи, соответственно по
горячему (индекс " 1 " ) или холодному (индекс "2") потоку; по
этому другие стадии (в том числе связанные с тепловым вза
имодействием теплоносителей) просто не влияюr на процесс в
целом. В области чисто поверхностной задачи [kF/( G1 c1 ) = а �
� О) также все лимпrируюr поверхностн ые эффекты ( kF) - неза
висимо от потоковых стадий G1 c1 и � с2. И только при сопо
ставимости потоковых стадий и не слишком малых значениях
kF, т.е. в условиях смешанной задачи, общая интенсивность теп
лопереноса небезразлична к взаимному направлению потоков
теплоносителей.
В учебной и научной литературе достаточно подробно ана
лизируется теплоперенос в условиях поверхностной задачи для различных схем движения теплоносителей, с выделением
лимитирующих стадий в пределах kF и т.п. Потоковые и балан
совые задачи теплопереноса, также нередко встречающиеся в
технологических процессах, как правило, не рассматриваюrся.
Это не только обедняет анализ, но иногда приводит даже к
прямо ошибочным выводам и рекомендациям, поскольку по
токовая стадия теплопереноса без оговорок трактуется в поня
тиях (т.е. в терминах и символах) поверхностной задачи - на
основе пропускной способности kF или ее составляющих a.F.
В простейшем варианте подмена потоковой задачи и ее
представление в форме поверхностной заключается в записи и
использовании выражений типа (7.27в) вместо правомерного
в рассматриваемых условиях (7.27д) или аналогичного на осно
ве �с2 . Совершенно очевидно, что пропускная способность
такого процесса, формально записанная как kF (либо a.F), ока
жется пропорциональной величине Gc. И не случайно экспе
риментаторы , неосознанно подменяющие потоковую стадию
поверхностной, закономерно получаюг коэффициенты тепло
передачи и теплоотдачи прямо пропорциональными первой
степени скорости теплоносителя и обратно пропорциональны
ми поверхности контакта F. В действительности такие зависи
мости, конечно, не связаны с особенностями кинетики тепло
обмена, это лишь результат игнорирования потокового меха
низма теплопереноса, т.е. подстановки kF или F вместо Gc,
откуда с неизбежностью следует k, а. - Gc/F.
Наглядным примером подмены задачи яаляется коJVIИзия с аппаратами воз
душного охлаждения (АВО), предназначенными для отвода теruюты холодным
воздухом от конденсирующегося или горячего продукта (рис. 7. 17) взамен водя-

572

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 7.17. Схема аппарата воздушного охлажде-

1 - корпус теплообменника, 2 - оребреННЬlе
трубы, З - вентилятор;
/ - целевой продукт, 11 - воздух

� 1
�t: : : : 1)
(1 : : : : : : : : : tj

ния:

/ 1

• .

• •

ных холодильников (с целью экономии воды:
она становится дефицитной). В корпусе 1 в
несколько рядов один над друmм расположе
ны оребренные трубы 2, внутри которых по
следовательно либо параллельно движется
продукт. Отбирающий тепло'I)' холодный воз
дух наmетается вентилятором З. Ребра на
трубах устаномены с целью икrенсификации
11
теплопереноса, поскольку со стороны воздуха
коэффициенты теплоотдачи, а с ними и пропускные способности a1F и kF без оребрения
- невелики: именно a1 F в отсуrствие ребер лимитирует теплоперенос в целом.
Для увеличения производительности АВО по целевому продуК'I)', т.е. для по
вЬШiения теплового потока Q было решено, в соответствии с концепциями теп 
лопередачи, еще более развить поверхность F со сrороны во:щушного потока. Одна
ко при реализации эrого решения было усrаноВ11ено понижение Q. Снижение ииrен
сивности теплоmдачи к ребрам может наблюдаться не талько при балее l)'CIOM ореб
рении труб, но и в случае увеличения числа их вертикальных рядов.
Такую "аномалию" можно было предвидеть при всестороннем анализе про
цесса. Дело в том, 'П'О при увеличении F за счет оребрения задача теплопереноса
перестает бьпъ поверхностной - ведь значения kF достаточно велики из-за
больших F, задача приближается к потоковой по воздуху. Поэтому дальнейшее
развитие F ничего дать не может; хуже того, из-за увеличения mдравлического
сопротимения воздушному потоку (больше рядов труб, l)'Ще их оребрение)
снижается производительность вентилятора, т.е. уменьшается пропускная способ
ность стадии, контролирующей процесс в цепом; поэтому и падает Q. Совершенно
очевидно, 'П'О для икrенсификации теплопереноса в этих условиях надо увели
чивать не kF (оно и без того достаточно велико), а пропускную способность
лимитирующей стадии - Gc для воздушного потока.

'fbl:·1

При параллельном теплопереносе одновременно разными (n)
механизмами пропускные способности стадий сющцываются, так
что при одинаковом температурном напоре пропускная способ
ность процесса в целом составляет в простейшем варианте
Q = :L
" a ;F; �
(7.29)
-

Л·

1= 1

причем в форме a1F; здесь записаны условно пропускные спо
собности любой отдельной стадии теплопереноса (не обяза
тельно конвективной).
В частности, в случае простой поверхностной задачи
Q = kF = L a F .
(7.29а)
л.

•

1=1

'

'

Очевидно, что при паралле льном переносе результирующая
пропускная способность процесса в целом будет больше (иначе:
не может быть меньше) любой частной, в том числе - самой
573

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

большой пропускной способности отдельной стадии. Таким
образом, для параллельного переноса термин "лимитирующая
стадия" приобретает смысл, противоположный характерному
для последовательного переноса. И здесь для управления про
цессом следует воздействовать прежде всего на самую быструю
стадию, имеющую наибольшую пропускную способность.
7.9.3. О пропускных способностях в нестационарных процессах
Оrличительная особенность нестационарных процессов за
ключается в появлении Накопления среди составляющих ба
ланса (исключая стадии с нулевыми пространственными кон
турами - см. разд. 1 .3. 1). При осуществлении нестационарных
процессов (периодических, полунепрерывных) также использу
ется понятие пропускных способностей; остаются правомер
ными и общие подходы к анализу теплопереноса, изложенные
в предыдущих разделах применительно к стационарным про
цессам. При этом пропускные способности типа aF, kF, как и
ранее, относятся к тепловым потокам в единицу времени. Одна
ко пропускные способности типа Gc для тех теплоносителей,
где речь Ид ет о Накоплении теплоты, относят к продолжитель
ности процесса в целом - соответственно тому, что и G здесь
уже не поток теплоносителя (кг/с), а его количество (кг).
В периодических процессах пропускные способности вооб
ще относят к продолжительности процесса в целом, оперируя
не потоками теплоты, а их количествами; это касается и коли
честв энтальпий в тепловых балансах. Предстоит оперировать
пропускными способностями Gc (если G - кг) и Get (если G кг/с), kF-t (или aF-r - в случае теплообмена с твердыми телами,
например); при необходимости эти величины записываются в
дифференциальной форме (например, a.Fd't или kFd't). Безраз
мерные комплексы (критерии) в этих случаях МОJУГ выражаться
в форме kF't/(G 1 c1 ) , если G1 - количество теплоносителя, или
G 1 c i/( � c2't), если в полунепрерывном процессе G1 - количе
ство теплоносителя ( кг), а � - поток ( кг/с) .
Особенности использования понятия пропускных способно
стей применительно к нестационарному теплопереносу и ана
лиз последнего на лимитирующую стадию - предмет после
дующего изложения.
7 .1 0. НЕСТАЦИОНАРНЫ Й ТЕПЛООБМЕН
С ТВЕРДЫМИ ТFЛАМИ
7.10. 1 . Основные понятия
Среди технологических процессов значительное место зани
мает теплообмен с твердыми телами. Такие процессы МОJУГ
осуществляться в непрерывном и периодическом режимах. В пер-

574

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

вом случае это чаще всеrо теплообменники смешения с непре
рывным вводом и выводом твердого материала (теплообмен
осуществляется с непрерывно движущейся сплошной средой газом или жидкостью) . Непрерывный теплообмен возможен
также при наличии в твердом теле Источника (Стока) тепло
ты - скажем, при проведении каталитической гетерогенной
реаЮJии с тепловым эффектом: теплота реаЮJии воспринима
ется здесь сплошной средой при постоянных локальных темпе
ратурах твердоrо материала и среды. Во втором случае
(периодические и полунепрерывные процессы) теплообмен
является нестационарным : температура твердых тел (крупные
элементы, зерна, мелкие частицы) изменяется во времени, в
уравнениях теплового баланса появляется составляющая
" Накопление"; среда обычно имеет постоянную входную тем
пературу, температура среды на выходе из рабочей зоны может
изменяться во времени. Заметим, что при осуществлении ста
ционарных (применительно к рабочей зоне теплообменника)
процессов отдельные акты теплопереноса (по отношению к
индивидуальному зерну, например) чаще всего нестационарны.
В основе расчета теплообмена с твердыми телами лежит
уравнение Фурье - Кирхгофа в форме

�
= aV 2r + !Ь...
o
ер

't

или в отсутствие Источников и Стоков теплоты:
ot
дt

- a..,2
v 1.

_

( 1 .2 1ж), (7.30)

( 1 .21ж " ), (7.ЗОа)

Эти уравнения решаются с условиями однозначности (см.
разд. 1 .7), формулируемыми в соответствии со спецификой
конкретноrо процесса теплопереноса. Среди них
начальное
условие, описывающее исходное распределение температур в
твердом теле, и rраничные условия, отражающие особенности
его взаимодействия со сплошной средой на границах (иногда и
внутри тела) в процессе теплопереноса.
Масштабные преобразования уравнения Фурье - Кирхrофа
и граничных условий приводят (разд. 1 .8) к критериям подобия
Фурье Fo = a't/R2, Био Bi = a.R/л.i:r и геометрическим симплек
сам (безразмерным координатам) типа x/l, r/R, где х и r - на
туральные координаты, l и R - определяющие размеры твердо
го тела (зерна).
Чаще всего в химико-технологических процессах зерно
омывается потоком сплошной среды, так что на его границах
осуществляется конвективный теплообмен , интенсивность ко
торого характеризуется коэффициентом теruюотдачи сх, по
t)
верхностью теплопереноса F и температурным напором (е
575
-

-

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

или ( t - е); перенос теплоты внуrри тела харакrеризуется его
теплопроводностью Л-r и внуrренним градиентом температур
(d0/dn). Соотношение этих эффектов и выражается значениями
Bi. Напомним, что среди граничных условий наиболее общими
являюгся условия 111 рода, отвечающие ограниченным значе
ниям Bi. Если теплоперенос лимитируется конвективным пе
реносом теплоты снаружи тела, то Bi -... О (практически стремится к малым значениям, определяемым допустимой по
грешностью анализа, расчета). Тогда граничные условия 111
рода вырождаюгся в безградиентный теплообмен (температура
тела постоянна по всему его объему) - говорят о теплообмене
в условиях внешней задачи. Если же теплоперенос лимитируется
распространением теплоты внутри тела, то Bi -... оо
(практически - к достаточно высоким значениям, обеспечи
вающим прие мл емую точность) и граничные условия 111 рода
вырождаюгся в условия 1 рода - говорят о теплообмене в усло
виях ввуrренней задачи.
В разд. 1 . 8 . 6 бьmо показано, что критерий Био может трак
товаться в аспекте соотношения пропускных способностей.
При этом конвективному поверхностному переносу теплоты на
границе с твердым телом отвечает пропускная способность aF
(аналог использованной в предыдуmих разделах величины kF).
Соответственно в числе критериев будет фигурировать ком
плекс "а" в написании для стационарных процессов в . форме
а :! aF/Gc (вместо kF/Gc), а для нестационарных - возможно
(в зависимости от постановки задачи), в форме a.Fт/Gc.
Ниже рассмотрены характерные случаи нестационарного
теплообмена твердого тела со сплошной средой.
7 . 1 0.2. Нестационарный безrрадие1rrный теплообмен
с твердым телом

Пусть высокотеплопроводное тело массой Gт, теплоем
костью Ст омывается (рис. 7. 1 8) потоком сплошной среды (газ ,
жидкость) постоянной температуры t. Примем для определен
ности, что начальная температура тела Во ниже t. Требуется
найти закон изменения температуры тела во времени е (t) .
Вследствие высокой теплопроводности твердого тела (в рас
четном смысле Л-r -... оо) , критерий Bi = a.R/Jvr -... О (практически
для шара в инженерных расчетах достаточно Bi :;; О , 1 --;- 0,2).
Поэтому нагрев тела можно считать безградиентным: во всех
его точках, в том числе и на поверхности, температура в каж
дый момент времени одинакова. Интенсивность нагрева опре
деляется внешним конвективным теплопереносом через по
верхность тела F; теплоотдача зависит от харакrеристик дви
жуmейся среды около поверхности, выражается она коэффици576

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 7. 18. К расчету безrрадиентноrо теплообмена с
твердым телом

-

ентом теплоотдачи а
будем считать его
известным и постоянным в ходе процесса.
В качестве пространственного контура
выберем само твердое тело (границы кон
тура - поверхность F) и запишем тепло
вой баланс для элементарного интервала
времени d-c. Приход теплоты соответственно выражению (а) из
разд. 7.5 равен dQ = a..F( t - 0)d't; Накопление составляет d(Gтer8) =
= Gтeid0. Тогда в отсуrствие Источников и Стоков, а также Ухода
теплоты получим
aF( t - 0)d't - О + О - О = Gтeid0.
Разделяя переменные и интегрируя при t = const от начального СОСТОЯНИЯ ДО текущего, получаем ИСКОМУJО С ВЯЗЬ 0 И 't:

d0
f - = - f d't
0

aF

GT

'

и

ln

-

t 0о
t-0

F't
= a.
.
G т ст

(7.3 1 )
ст о
Отсюда время, необходимое для нагрева тела до температу
ры 0 (разумеется, 0 � t), будет
(7.3 1а)
't = G т ст ln t - 0 о '

0/ - 0

aF

t-0

(- aF't ) .

а температура тела к моменту времени 't составит

0 t - (t - 0 0 ) ехр
=

GT

ст

(7.З lб)

Из выражений (7.3 1 ) и (7.3 1 б) видно, что процесс контроли
руется отношением пропускных способностей aF't/GтCr·

11 1 рода

7. 10.3. НестаЦионарный теплообмен с шаром
в граничных условиях 111 и 1 рода

Нестационарный теплообмен с телом в граничных условиях
анализируется ниже на примере симметричного нагре
ва сферы. Требуется найти закон изменения температуры тела

0

=

е

(r, 't) .

Рассмотрим первоначально процесс качественно. Шар ради
усом R (его плотность Рт , теплоемкость Ст, теплопроводность
Лт) с начальной температурой е0 (пусть для простоты она оди
накова по объему шара) помещают в среду с более высокой
температурой t (пусть в течение всего процесса она, тоже для
простоты анализа, поддерживается неизменной) . Интенсив
ность теплообмена на наружной границе шара определяется
57 7

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

l I I рода

Рис. 7. 19. К расчету нестационарного теJUJообмена с шаром в граничных условиях

коэффициентом теплоотдачи а.; внугри шара - теплопровод
ностью Л,. (пусть Л,. не зависит от 0).
Качественная картина изменения 0 по радиальной коорди
нате r и во времени • представлена на рис. 7. 1 9 . При 't = О
(начало процесса) 0 o(r) = const. В моменты времени • 1 , •2 > О
поверхностные слои шара приняли более высокую температуру
(при •2 > • i они, естественно, нагрелись больше), центральные
зоны шара пока еще сохраняют температуру 0 о . Далее
(моменты времени ч , ч, . . ) изменение температуры з ахваты
вает все точюt шара. С течением времени температура на по
верхности (а за ней - и внугри шара) все более приближается
к температуре среды t, при 't -+ оо во всех точках шара 0 -+ t.
В основе количественного анализа - уравнение Фурье Кирхгофа для твердого тела в отсугствие Источников и Стоков
теплоты в форме (7.30) с выражением лапласиана в сфериче
сюtх координатах по ( 1 .26б):

.

аэ
дt

578

=

а

а 2 е + � аэ
т дг
r дr
2

(

)

'

О < r<

R,

(7.32)

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

'ПО

Нетрудно убедиrъся,
удобной записи:

это

выражение тождественно более

) ат --)
-=

д 2 (0r
,
д2 r

д�

д (0r

О < r < R,

(7 .32а)

так что при решении будем отыскивать произведение 0r.
Запишем условия однозначности, сформулированные выше
словесно .
Начальное условие:
't = О, 0(r, О) = 0 о , О ;5; r ;5; R.
(7.33а)
Граничное условие 1 1 1 рода (оно может быть записано для
всей поверхности шара F либо для единицы поверхности):
r = R,

a.(t - 0R)F = -Л-r

Условие симметрии:

(80)
дr

r=R

F,

't

�

О .

(7.33б)

00(0 , 't )
(7.33в)
= о ' 't � о .
дr
Согласно условию (7.33б), наклон температурных кривых у
поверхности шара определяется прямыми, выходящими из
точки с координатами t ; R + Л-r/а.. Из условия (7.33в) с оче
видностью следует (см. рис . 7. 1 9): температурные кривые в
любой момент времени симметричны относительно центра
шара (абсцисса r = О ) , так что касательные к температурным
кривым (на рисунке для илл юстрации - к кривой при 't = ч) в
точке r = О параллельны оси r. Иначе: тангенсы угла наклона
касательных к оси r (т.е. производные д0/дr) в центре шара
равны нулю. Заметим, что условие (7.33в) выражает еще и
ограниченность температуры в ходе процесса: ни при каких 't не
может быть 0 � ао .
Полная процедура решения уравнений (7 .32) - (7 .32а) с
граничными условиями (7.33) приводится в литературе " . Про
демонстрируем начальные стадии анализа, позволяющие обос
новать общий вид решения.
r = О,

Наиболее наглядным яаляется решение методом "разделения переменных"
(более общие методы - за пределами • учебника). Будем искать зависимость er =
= f (r, t) в виде произведения двух функций - [, , зависящей только от r, и f." зави
сящей талько от t. Тогда (7.32а) перепишется в виде
а2
(f, f, ) = aт 2 ( /,/, )
"'
ar
а

,._

,

(а)

• См., например, (7, l O J .

579

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

и после выполнения операции дифференцирования (с учетом, чrо /r не зависит
от t, а !. - от r)

' = атf< д
1r д/
д1

2 fr

д r2

ИЛИ

Гr f,• = атf,,rr'•

J

·

Разделяя переменные, т.е. собирая в различные части равенства функции, зависящие только от r и только от t, получим

/�
/,

fr

= ат !;'

·

(б)

Левая часть равенства (б) не зависит от координаты r, следовательно значе
ние /', /!. одинаково для любого r; правая часть (б) не зависит от времени t следователь но, значение / "r //r одинаково для любого t . Такая ситуация при
соблюдении равенства (б) возможна только в том случае, когда левая и правая
части равенства постоянны - для любых r и t . Эту постоянную величину удобно
записать в виде (-a,k2) - смысл такой формы записи будет ясен из последую
щего анализа (здесь лишь заметим: k
вещественное число, так чrо k2 > О).
Таким образом,
-

-

-

fr

/ ' .!.. = ат �
/ " = т 2 = const.
___.
а k
/,

(б')

-

Из левой части (б'): f ', = (-a,k2)J., т.е. первая производная функции равна
самой функции, умноженной на некую постоянную величину. Такой функцией
является экспонента, под знаком которой перед арrументом t стоит упомянутая
постоянная (-a,k2) :
(в)
Здесь становится ясным смысл знака " минус" в написании постоянной ве
личины: при безrраничном увеличении t функция !. (а с ней и искомая темпера
тура 0) будет ограничена - в соответствии с физическим смыслом процесса и
rраничным условием (7. 33в).
Из правой части (б') - после сокращения на а,: f "r = -k2J, , т.е. вторая про
изводная функции равна самой себе (но с обраmым знаком), умноженной дваж
ды на постоянный множитель k. Такими функциями являются sin и cos, в кото
рых перед арrументом r стоит множитель k, либо их линейная комбинация:
(r)
/, = А sin(kr) + В cos ( kr) .
В результаrе на основе частных решений (в) и (r) дnя каждой переменной
можно записать
или

0r

е

=

= fгf,
e ( r , t)

=

=

[A sin(kr)

[А �

s (kr)

+ B cos( kr)j

�(kr) ]

+ Вc

2
e- a, k •

e- a,k 2, .

t

и r

(д)

Это выражение должно быть справедливо для любой точки шара при r :$ R.
Однако при приближении к его центру (r _.... О) лишь первое слагаемое в квад
раmых скобках (д) остается оrраниченным (один из "замечаrельных" пределов), а
второе - безrранично возрастаеr. Эrо проmворечие физическому смыслу и условию
об оrраниченности 0 усrраняется при В = О. Torna
sin(kr) - a,k2,
(
(е)
е
0 r, t =
r
Решение (е) является часmым: поскольку sin
функция периодическая, то
rраничное условие (7.33б) может бьrrь удов.iJетворено при ра3Личных (не любых,

) А

580

---

.

-

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

-

конечно) значениях k
каждому из них отвечает свое А. В результате общее
решение получается в виде бесконечной последовательности слагаемых типа
правой части выражения (е) :

0(r, t)

- эта

=

"'

А

l: п
n= I

sin(kпr)
е
--r

-а

•

k2t
•

(ж)

-

.

Далее определяют kп
из rраничного условия (7. 32б) и Ап
из начального
условия (7.32а); в учебнике
весьма rромоздкая процедура определения kп и
особенно Ап не приводится·. Отметим лишь, что kп удобно выразить в форме
µп / R; тогда а, kп2t = µn2 G.rt/R2 = µn2 Fo, а под знаком sin будет стоять kпr =
безразмерная величина. Поскольку kп определяются из rра
µп,r/R, причем µп
условий III рода, ro они, как и производные от них величины µп, далжнь1
зависеть от значения криrерия Bi. Величины Ап сложным образом выражаются через
µп (И1D1 через Bi).
Решение (ж) с целью повышения его общности удобно представить целиком
в безразмерной форме. Так в левой части появляется безразмерный температур
ный комплекс (/ - 0)/(1 - 0о) или (0 - 00)/(1 - 0о). Например, с устаноменным
отдельно выражением для Ап

-

ничных

0•

1

t

-0

" --- =

- 0о

sin( µn �)
R
------ --- е
µn

"' 2 sin µn - µn cos µn
l:
n = I µп - sin µп соs µ п

r

]i

-µ2р0
•

.

.

(7 34 )

При подстановке в это выражение r = О и r = R получаются соответственно
температуры в центре шара 0ц и на его поверхности 0R.
В тепловых балансах фигурирует средняя (по объему и массе шара) температура шара ё . Ее находят, записывая энтальпию элементарного шарового слоя
радиусом r, толщиной dr (фрагмент слоя показан на рис. 7 . 19) в виде CтPrd V =
= CтPr411i2dr и вычисляя (путем интеrрирования) полную энтальпию шара. Эта
же полная энтальпия может быrь записана через среднюю температуру 0 для
всей массы шара:
R

4 it R 3
I 0СтРт 4 1tr 2 dr -0СтРт 3
о

(з)

=

Отсюда
-

0

3

3

R

J 0r 2 dr ,
о

(7.35)

причем 0 под интеrралом выражается уРавнением (7.34). После вьmолнения
операции интеrрирования получается значение ё = ё ('t), не зависящее, есте
ственно, от
имеет вид••

r.

=

R

В безразмерной форме после интеrрирования выражение для ё
-•

0

=

0

---0о пz\l:.., Впе -µ"
t
t

=

2i;0

,

(7 . 36)

где безразмерные коэффициенты Вп выражаются через µп и Bi.
С помощью выражения (7. 36) определяют количество теплоты Q, восприня
той шаром при его наrревании за время t (или отданной при охлаждении). Для
• Детальные преобразования с получением kп , п и Ап приведены в ( 1 0) .
µ
• • Детальные преобразования с получением Вп приведены в ( 10 ) .

581

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 7. 20. Распределение тем ператур в

е•

шаре при теплообмене
внутрен ней задач и

в

условиях

этого вычтем из еди н и цы л евую и пра
вую ч асти равенства:

0 0
1 _ t -0
- 11
=
0
ff - 0 11

= l-fв.e-µ;Fo_
n=I

З наменател ь в левой ч асти равенст
ва и меет с м ы сл начал ь н о й движущей
силы:
Очевидно,
что
/ - 0 0 "' Л • .

Q = G т ст ( 0 - 00 ) . где G т и

'

( � ·в. е-µ; F"}
( - f. )·

ст

и теплоем кость шара. З нач ит,

а пропус кная способность

= G т ст
_Q_
Л

l

n=I

-

масса

(7.37)

Q = G , c, л • I -

•

(з)

(7.38)

B. e - µ ; Fo

Есл и теплообме н с ш аром происходит в условиях внутрен н е й зада ч и ( гран и ч 
н ы е условия 1 рода), т о и нтенси вность внеш него теплопереноса бесконеч но вел и
ка в сравне н и и с внутре н н и м , так что тем пература поверхности шара п р и н и м ает

температуру сред ы : 0 R
ся,

µ.

уже

cos nn = ( - 1 ) "• 1

не

•

= t . При этом критерий Bi

зависит

от

Bi ;

анализ

� оо

В резул ьтате из ( 7 . 3 4 ) получ ается

s i пnn = О ,

и его вл и я н и е вырождает

µ n = пп ,

дает

тогда

( 7 . 3 4 а)

а

ИЗ

(7.36)

в• "' t - ii

/ - 0о

J...2 . e -•'Fo
= �f
2
7t •= 1 п

Соответствен н о трансформ и руются выраже н и я для

Q

и

Q/л • .

( 7 . 3 6 а)

Существен но, что п р и не очень м ал ы х значениях критерия Фурье ряды быст
ро сходятся, так что вполне можно огран и ч иться первым членом разложен и я , на
пр имер :

-.
6 · • ' Fo
0 :::: -е
7t 2

( 7 . 3 6 б)

в этом случае для Fo � O, I погре ш ность не превыш ает 1 , 3 % .

Д л я илл юстрации н а р и с . 7 . 20 при веден ы тем п ературн ы е кривые д л я случая
теплообмена с шаром в условиях внутренней задач и , построе н н ы е по формуле
( 7 . 34а).

А н ал о г и ч н ы м м етод о м { разу м еетс я , с и н ы м с п осо б о м в ы р а 
же н и я л а плас и а н а и за п и с ь ю г р а н и ч н ы х усл о в и й ) п одходят к
ре ш е н и ю зада ч дл я

5 82

цил ин дра, пласт ин ,

нес к ол ь к о сло ж н е е -

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

для тел другой формы. И здесь решения получаются, как пра
вило, в виде бесконечных рядов. Продемонстрированный под
ход может, с определенными ограничениями, оказаться полез
ным и при решении некоторых задач массопереноса.
Если теплообмен с шаром происходит в условиях внешней
задачи (Bi � О и его влияние вырождается), то получаются
формулы, переходящие в решение для безградиентного тепло
переноса - типа (7.31) при подстановке F и Gт для шара. Од
нако этот переход сопряжен с весьма непростыми преобразо
ваниями, поэтому задачу безградиентноrо теплообмена проще
решать непосредственно, как это сделано в разд. 7 . 10.2.
7 . 1 1 . МЕЖФАЗНЫ Й ТЕПЛООБМЕН
В ПСЕВДООЖИЖЕННОМ СЛОЕ

В разд. 6.7 рассмотрен теплоперенос "теплопередающая по
верхность - псевдоожиженный слой" . В настоящем разделе
анализируется межфазный теплообмен - между псевдоожи
женными твердыми частицами и ожижающим агентом (пусть
для определенности - газом). Этот анализ наглядно иллюстри
рует сферу действия и соотношение внешней и потоковой
(балансовой) задач теплопереноса; сделано это применительно к
теплообменнику смешения.
Общая схема теплообменника с псевдоожиженным слоем,
работающего в стационарном режиме, представлена на
рис.7.2 1 ,а. Количество твердого материала в аппарате попереч
ным сечением !а поддерживается в ходе теплообмена посто
янным G0; порозность слоя равна е. В аппарат непрерывно
подается поток горячих частиц Gт размером d и температурой
8' и холодный газ - его поток G, температура f. Цель процесса

1

е·

о

1(

е·

е·

б

t'

Рис. 7.21. Межфазный теruюобмен в псевдоожиженном слое:
схе ма проце сса, б расчетная схема
а
-

-

583

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

- охлаждение твердых частиц до температуры 8 " . Цель анализа
- найти связь температур твердого материала и rаза с параметрами процесса и геометрическими характеристиками псев
доожиженного слоя. Расчетная схема представлена на
рис.7.2 1 , б.
7 . 1 1 . 1 . Межфазный теплообмен
в тонком псевдоожиженном слое
Пусть в тонком псевдоожиженном слое частицы полностью
доступны контакту с rазом (застойные зоны отсутствуют). Ма
лые размеры частиц и не слишком малая их теплопроводность
позволяют считать теплообмен с ними безградиентным. Псев
доожиженные частицы находятся в состоянии очень интенсив
ного движения - практически слой можно считать системой
идеального перемешивания; поэтому температура частиц по
всему объему слоя одинакова и равна температуре на выходе
их из аппарата 811 • Примем, что rаз движется в режиме И В это близко к реальности, если частицы не обладают заметными
адсорбционными свойствами по отношению к rазу.
Температуру газа на выходе из слоя t" находим из теплового
баланса (временной интервал - 1 с; пространственный кон
тур - весь псевдоожиженный слой), записанного сразу в фор
ме (7. 1 66) :
Gтст (8 ' - 8") = Gc(t" !') .
(7.39)
Для установления профиля температур в слое рассмотрим
элементарный контур "к" в зоне движения газа (рис .7.2 1 , 6) :
Gct + d Q - Gc(t + dt) = О.
При коэффициенте теплоотдачи от частиц к rазу а. элемен
тарный тепловой поток равен d Q = а.(8 " - t)dF. Тогда

-

а.(8" - t)dF = Gcdt

� = � dF .

и

8" - t

Gc

(а)

После интегрирования от О до F и от t' до t (при 8 " =
co1ist) получаем температурный профиль
газа, выражен ный через отношение пропускных способностей:
8" с
(7.40)
= a.F и 8" t ехр - a.F .
ln
Gc
8 " t'
Gc
8" - с'
Если под F понимать не текущую, а полную поверхность
контакта частиц и газа, то в (7 .40) вместо текущей темпера
туры rаза t будет стоять конечная t".
В целях наглядности и удобства практических расчетов вы
разим поверхность теплообмена (dF, F) через высоту слоя .
Удельная поверхность твердых частиц в соответствии с (2.64)
=

- -

584

-

= ( )

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

выражается (с заменой Ео на Е, поскольку здесь речь идет не о
неподвижном, а о псевдоожиженном слое): Fуд = 6( 1 - E)/d.
Полная поверхность контакта для слоя высотой Н будет F =
= FvnfaН. Тогда F = 6 ( 1 - E)faH/d, и (7.40) преобразуется к виду

ln

8 11 - f '
8 11 - ( 1 1

8 " - f"
8 11 - t '

=

=

ехр

а,

-

6(1 - Е)/а

[-!!:.._
Gc

d

Н

6(1 - E)fa
Gc
d

и

н].

(7 .40а)

Первое из этих выражений удобно использовать при реше
нии задач проектирования - для определения необходимой
высоты слоя :
.
d
8 11 - 1 '
Gc
H = - -- ln -- ·
af. 6(1 - Е) 8 11 - 1 11

(7.40б)

Важно , что при меньшей высоте слоя не удастся достигнуть
снижения температуры частиц до заданной величины 8 " , по
скольку поверхность межфазного контакта F недостаточна, и
температурные изменения (8' - 8 " ) и (t" - t') будут мен ьше не
обходимых.
В рассматриваемой ситуации интенсивность теплообмена
опреде-��я ется двумя стадиями - поверхностной (примени
тельно к твердым частицам - внешней) и потоковой
(по
сплошной среде - газу) . Поэтому и в математическом описа
нии присутствует отношение пропускных способностей этих
стадий a.F/Gc. Теплообмен здесь происходит в условиях сме
шанной задачи. Заметим: при очень больших пропускных спо
собностях Gc газового потока его температура практически не
изменялась бы при движении через тонкий псевдоожиженный
слой (ТПС); тогда задача теплопереноса бьmа бы строго внешней.
Второе из выражений (7 .40а) удобно использовать при ре
шении задач эксплуатации - для определения температуры
газа t" на выходе из псевдоожиженного слоя . Если вместо пол
ной высоты слоя Н в это уравнение подставить текушую вер
тикальную координату, отсчитанную от основания слоя , то
уравнение будет описывать температурный профиль газа в
слое , т.е. изменение t по высоте слоя .
В условиях внешней или смешанной задачи температура га
за, уходящего из псевдоожиженного слоя , t" заметно отличает
ся от температуры частиц в слое 8 " . Именно в этом смысле
слой именуется тонким .
Зависимость t" от Н представлена на начальном участке (см .
рис .7.22, область ТПС) : налицо достаточно быстрое (экспонен 
циальное) приближение кривой t"(Jf) к уровню 8 " . При этом
585

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

для более крупн ых частиц (на рисунке - пун ктир " к" ) это
при бл ижение происходит медлен нее (так как меньше Руд• зна
чит, меньше и множитель в экспоненте перед Н) , а для более
мелких - б ыстрее (пунктир " м" ; большие значения Руд) .

7.11.2.

Станем увеличивать высоту псевдоож иж енного слоя Н. П ри
этом температура уходящего газового потока !" будет все в
больше й мере при бл ижаться к 8 " . П ри некоторо й высоте слоя
Н = ha (а в случае изменения температуры газа по высоте слоя
- на некоторой координате ha внутри слоя) разн ица в темпе
ратурах 8 " и !" станет несущественной , а сами эти температуры
- просто неразличимыми . Величину ha н азывают высотой ак
тивного участка (рис . 7.22). Ее определяют, исходя из доп усти
мо й погрешности расчета: разность 8 ". - t" считается неразли
чимой , если она составляет малую долю l.JI от первонач ально й ,
t' . Чаще всего гран ицу н езначи 
т . е . на входе газа в слой 8 "
мост и раз н ости 8" - t " проводят п о величине
8" с"
(б)
' = 0 , 0 1 - 0 , 05;
l.JI = 8 "
[
иначе: остаточн ый температурный напор н а выходе из слоя со
стаRЛЯет 1 -5 % от начального (входного) . П ока l.JI превышает эту
величину, теnлообмен полагают протекающим в условиях внеш
не й или смешанно й задачи : и грает роль кон вективны й перенос
(его пропускная спосо бность a.F), t" и 8" вполне различимы - это
и есть о бласть тонкого псевдоожиженного слоя (ГПС) .
П ри нарастании высоты слоя , т .е . при Н � ha, температуры
t" и 8 " становятся неразличимыми - налицо теnловое равнове
сие (т.е . практически полная рекуперация теnлоты в условиях
идеального перемешивания одного из те п лоносителей) . Здесь с
о бусловленно й погрешностью можно считать t" = 8 " - это о б 
ласть высокого псевдоожиженного слоя ( В ПС) .
Выр ождение смешанной задачи в потоковую (балансовую)

-

-

-

Оце н ки в ысоты активного участка Н
ha по формуле (7 .40б) дr1Я частиц,
обычно используемых в практи ке псевдоожижения , приводят к величинам h"
измеряемым миллиметрами или (в случае круп н ых частиц) нескольки м и десят
ками м иллиметров. П о вышение Н сверх ha ничего не дает с точки зрения тепло
обмена (он практически завер шен в слое высото й ha) и вредно с точки зрения
энергозатрат (при увеличении Н растет сопротивление псевдоожиженного слоя ,
а знач ит и затраты энерги и на дутье) . И тем не менее в подавляющем боль
шинстве случаев межфазный теплообмен в псевдоожиженном слое протекает в
усло виях Н > h" Н > > h•. Дело в том , что в аппаратах промышленных размеров
то н кие псевдоожиженные слои структурно неустойчивы: вероятны случай н ые
выбросы твердого материала в каком-то месте в соседние участки и образование
канала (свища), не содержащего твердого материала; сюда (по пути наименьшего
сопроти влен ия) по йдет осно вная доля газа, а на других участках скорость упадет
=

586

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 7. 22. Температурные кривые при
межфазном теплообмене в псевдоожи 
женн о м сл о е ( м - мелкие частицы, к кру п н ые частицы)

и возникнуr застой н ые зо н ы . Поэто му
процесс ведуr со слоем высотой не ни.же
1 00 -200 мм, чтобы случайно возникший
свищ был туr же "засыпан " твердым
матер иалом из соседних зон .

1, 8
8'

тпс

H< ha

впс
�h a

И так, на практике межфаз
н ы й теплоо б мен осущест вляется
t'
почти исключительно в высоком
о
н
псевдоожиженном слое ( ТП С
иногда используют лишь в исПри
следовательских
целях) .
этом для тепловых расчетов не тре буется знания кинетических
характеристик типа a. F, здесь вполне достаточно уравнен ия
теплового баланса (7.39), упрощенного условием теплового
равновесия . В задачах эксплуатации при заданн ых Gт и G
определяемыми будут температуры t" = 8" ; в задачах проекти 
рования ( при заданн ых Gт и 8 " ) определению подлежит неце
лево й поток теплоносителя G (возможна и противоположная
задача: задан ы G и !", определению подлежит поток Gт) . Здесь
именно поток теплоносителя будет лимитировать теплопере
нос ; иначе говоря , задача становится п отоковой по этому теп 
лоносителю .
Таким о б разом , ко гда в тон ком псе вдоожиженном слое по
верхность теплообмена (с ней и пропускная спосо б ность a. F)
огран ичена , межфазн ы й теплоо б мен происходит в условиях
в нешней ( поверхностно й) или чаще - смешан ной задачи ; рас 
ч ет ведется по уравнениям типа (7 .40а) . Но в высоком слое
существенно нарастает F (с не й и a. F) , и внешний теплоперенос
перестает вл ияrъ на процесс в целом. И тогда смешанная задача
вырождается в бшшнсовую (потоковую); расчет ведется по уравне
нию баланса (7.39) с дополнительным условием t" = 8 " .
В литературе имеются попытки трактовать потоковую задачу
в терминах внешней . Эrо, разумеется, подмена задачи : вместо Gc (в
других сmуациях Gм) записываюг a.F. Совершенно очевидно, что
при этом получаюгся "балансовые коэфф и циенты теплоотдачи "
CJ..G
Gc/F, потерявшие сво й изначальный кин етичес кий смысл. И х
абсолюгная величина может (при малых G) оказаться на 2-4 по
рядка ниже, чем это следует из предельного значения критерия
Нуссельта Numin = 2. К практическим рекомендациям, предла
гаемым на основе "бал ансовых" коэфф и циентов теплоотдачи ,
надо относиться с большой осторожностью .
-

587

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Заметим, что неосознанная подмена потоковой задачи и
представление ее в терминах внешней, в более общем плане поверхностной, - нередкая ошибка в химической и теплотех
нической литературе при описании процессов тепло- и массо
переноса (примером могут служить некоторые процессы в тон
ких пленках).
7.12. РЕГУЛЯРНЫ Й РЕЖИМ ТЕПЛООБМЕНА ТЕЛА
СО СПЛОШНО Й СРFДО Й

При нестационарном теплоо бмене тела со средой процесс
теплопереноса проходит несколько стадий. На первой - тем
пература в разных точках тела сильно зависит от начального ее
распределения в теле - это состояние называют неупорядочен
ной стадией. При увеличении времени наступает упорядоченная
стадия , когда тело уже "не помнит" начального распределения
температур, температурное поле изменяется во времени только
в зависимости от геометрических характеристик, теплофизиче
ских свойств тела и условий теплоо бмена на его границах. Та
кой режим получил название реrулярноrо. Для некоторых тех
ноло гических ситуаций обозначают и третью стадию - практи
ческое тепловое равновесие.
При высокой теплопроводности тела и небольшой его тол
щине (точнее, при высокой температуропроводности и Fo �
� оо) режим нагревания (охлаждения) тела с самого
начала яв
ляется регулярным, стадия неупорядоченного состояния отсут
ствует. В этом случае тело называют тонким: температура его
внутренних зон в своем изменении не отстает от поверхност
ных, теплообмен является безградиентным.
Регулярный режим достаточно широко встречается в прак
тике теплопереноса - при нагревании и остывании тел раз
личной формы в среде постоянной температуры (среда при
этом может быть неподвижной либо омывать тело с опреде
ленной скоростью); в этом случае говорят о реrулярном режиме
1 -ro рода. Температура среды может изменяться во времени по
определенному закону. Если это линейное изменение, то гово
рят о реrулярном режиме 2-ro рода, если периодическое
(например, синусоидальное), то - о режиме 3-ro рода. В этих
последних случаях описание и использование регулярного ре
жима построено на отставании температуры тела е от изме
няющейся температуры среды t. Такие технологические ситуа
ции могут встретиться при термической обработке тел в случае
программированного изменения температуры среды. Наконец,
различного рода регулярные режимы используются в экспери
ментальных целях - при необходимости определения коэффи588

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

циента теплоотдачи или некоторых теплофизических свойств
тела (например, теплоемкости или теплопроводности).
Некоторые задачи и возможности реrулярного режима пока
заны ниже применительно к нагреванию (охлаждению) шаро
образного тела.
7 . 1 2. 1 . Реrулярный режим 1 -ro рода
Наиболее наглядно основные понятия и закономерности
реrулярного режима вводятся и выявляются в случае постоян
ной температуры среды.
Будем рассматривать нагрев шара радиусом R, массой Gт в
среде с температур ой t. Пусть начальная температура шара е0
постоянна по его объему, температуропроводность материала
шара - От, коэффициент теплоотдачи от среды - а.. Использу
ем общие соотношения (7.34) и (7.36), исключив из рассмотре
ния неупорядоченный нагрев, т.е. примем достаточно большие
значения времени 't и критерия Fo (для шара Fo > 0, 1). Тогда
без существенной погрешности в рассматриваемых бесконеч
ных последовательностях можно огран ичиться первым членом
ряда - получатся экспоненциальные зависимости с одинако
вой скоростью изменения температуры для любой точки внуr
ри шара, т.е. для любой координаты r/R. Скорость нагрева
(охлаждения) любой точки тела при этом определяется величи
ной µ1 , а это функция от критерия Био Bi = a.R/ "fvc.
В крайних теплообменных ситуациях · общие выражения
(7.34), (7.36) [либо (7.3 1 ) при Bi � О] в зависимости от типа
задачи принимают различный вид:
- внешняя задача теплопереноса (Bi � О, практически Bi -f
.f О, 1; безградиентный теплообмен); из формулы (7.3 1 ) с учетом F =
= 4nRL и Gт = Pr(4,l.3)7tRJ относительная избьпочная температура
е·

=

/�880 = ехр ( - G::

)

( P�: )

't = ехр -

т

R

't

;

(7.3 1 в)

внутренняя задача теплопереноса (Bi � ао, практически
Bi � 100; в ряде случаев можно ограничиться значением 40;

граничные условия 1 рода) ; из (7 .34а) относительная избыточная
температура в любой точке внуrрИ шара составляет
e· = � =
r - eо

2

sш

.

(

)

1t '
R

r
1t -

R

ex�'-7t 2 Fo ;
l'\

)

(7.37а)

• Р еrулярный режим для тел произвольной формы при промежуточных зна
чениях Bi рассмотрен в (6, 1 1 , 1 2 ) ; ряд полезных соотношений для реrулярного
режима можно получить на основе анализа , приведенного в
для по стоянной
и изменяющейся во времени температуры среды.

(1 0 )

589

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

1, 0

lne•

о

во времени при реrулярном ре
жиме:
а

р

-

Рис. 7.23. Изменение температуры

б

а

-

( Н/У

- реrулярный режим 1 -ro рода
- стадия неупорядоченноrо
изменения температур, Р - стадия
реrулярноrо режима 1 -ro рода) ;
б - реrулярный режим 2-ro рода
( Р - стадия реrулярноrо режима 2-ro
рода)

't

(

)

относительная средняя избьпочная температура будет
-.
t 0
6
2
6
7t 2 а1
(7.38а)
"t
е = -- = - ехр -n Fo = - ехр
п
t - 8 0 1t 2
R1
2
Все эти зависимости можно представить в форме

из (7.36)

(

}

- --

.

(7.4 1 )
In e " , In e · = -m't + C ,
где параметр т = дlne •;т: ( а для безградиентного теплообмена и
средней температуры т = dln в· /d"t), называемый темпом охлажде
ния, представляет собой положительный множитель перед "t (в
экспоненте), С - постоянная величина. Значения т и С опреде
ляются величиной Bi; в частности, при Bi � О, как вмдно из
(7.З l в), т = Зо./(РтСrR), С = О"а при Bi � оо, по (7.37а) и (7.38а), т =

=

n2 ar/R2

=

n2 !v.r/(CrPтR2), С = ln 2

sinn(л rR/ R)
r/

при операциях с лo-

кальным е . и с = ln 6/п2 при операциях со средним в· .
В полулогарифмических координатах зависимость (7.4 1 )
представляет собой (рис . 7.23 ,а) падающую прямую, тангенс
угла которой с осью абсцисс по абсолютной величине равен т.
При этом т одинаков для любой точки внуrри тела и для
средней его температуры; различие отражается величинами С.
Получив в ходе эксперимента прямые Ine • - "t, нетрудно опре
делить т и найти неизвестные составляющие темпа т при
остальных известных величинах, например :
- о. при Bi � О (если известны Cr, Рт и R) или Cr (при из
вестных Рт, R и о.);
- а,. и Л-г при
Bi � оо (если известны Ст, Рт и R) или Ст
(при известных Рт, Л-г и R) .
7 . 1 2.2. Регулярный режим 2-ro р ода
Будем для простоты рассматривать шар высокой теплопро
водности (Bi � О), т.е. безградиентный теплообмен . Сохраним
начальное условие для шара (температуру 80); пусть среда так-

590

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

же первоначально находится при это й температуре 80 , но с
момента времен и • = О температура ее начинает изменяться по
лине й ному закону
t =80 + s-t,
где s const.
Цель анал иза - определение закона изменения температуры
шара во времени 8 = 8 (•) .
Запишем теплово й баланс ( контур - шар) для элементарно
го п ромежутка времени d• аналогично выражению (а) в
разд . 7. 1 1 . 1 , подставив в него значение t в зависимости от •:
=

a.. F(t - 8 )d• = Gтстd8
Отсюда

a.. F(8o - 8 + s-t)d•

и

d8 + a..F (8 - 8 0 )
d -r G T ст

=

a..F

=

(а)

Gтстd8 .

sc .

ст

(6)

Неоднородное диФФ�:ренциаnьное уравнение (6) решается, например, мето 
дом варьирования произвольной постоянной; в этих целях предварительно
решают соответствующее однородное уравнение с нулевой правой частью, а
затем постоянную интегрирования представляют зависимой от аргумента. В
целом дифференциаnьное уравнение вида
(в )
у ' + Р ( )у = Q(x)
имеет решение

GT

х

=

В

рассматриваемом случае у имеет смысл 0 - 0 о ,
- смысл t;
= const; Q = (aF/(GтC,,.,) \St =
Поскольку здесь Р = const и
то решение упрощается, и выражение ( r) прин имает вид

аF/(Gтс:т)
Рх ,

[1 QePx Je-Px.
Если теперь в (д) подставить
Psx, то
[1 PsxePxd.x с0]е-Рх [Ps р�� l еРх }-Рх

=

у =

у =

Q =

=

+

- 0о

= s

(

G т Ст � t
aF G т Ст

- 1)

=

+ Со

+ Со

х

�(Рх - 1) + Со

е

хр ( -

=

=

(д )

Р х ). (е)

их физические значения и

exp{-[aF/(Gт c,,., ) ]t} St =

Р

IPd.x

dx + Со

Подставив вместо табличных переменных у и
раскрыв смысл Р , имеем
0

х

PSt.

(r)

s

G T с,.
aF

(

)

+ Соехр - � t .

G т Ст

(ж )
Для определения постоянно й интегрирования Со воспол ьз у
емся начальн ым условием: 8 = 80 при 't = О . Тогда
G ст
О s G т ст - ( 1) + С0 и
Со
т
s.
a..F
a.. F
С этим значением С0 получаем окончательное решен ие:
=

8

=

80

-

+ St

-

s

.·

=

G:;-r (1 - exp{-[aF/(Gт Ст)Jс})

·

( 7 .42)
59 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Закон изменения температур среды и шара во времен и ил
люстрируется
рис . 7 . 2 3 , б. И нтересно , что при достато ч но
больших • , когда экспонента становится прене б режимо мало й ,
разность температур среды и тела сохраняет постоянное значе
н ие , т.е . линии температур среды t и тела е становятся парал
лельн ыми (иногда такой режим назы вают квазистационар ным) :

с - 8 = (8 0 + л:) - е 0 + л: - s G т ст = s Gт с. = s p,c, R = const. (з)

(

o.F

)

o.F

Зо.

-

Легко показать, что при ино й нач ально й температуре среды
to * 8 0 для достаточно больших 't разность t
е также будет
определяться выражен ием (з) .
Вывод о постоянстве температурного напора t
е подска
зы вает спосо б достаточно простого экспериментального опре
деления коэффициента теплоотдачи - путем измерен ия темпе
ратур t и е в процессе теплоо б мена в условиях регулярного
режима 2-го рода (при известных массе тела, его теплоемкости
и поверхности) . Для тела (вообще) и шара
с.

-

p.c.R
a. = s F(c - e) ' a. = s з (r - e) ·
G

т

.

(к)

Ан ализ регулярного режима 3 -го рода выходит за пределы
учебн и ка · .

7.13. О ТЕРМОСИФОНАХ И ТЕПЛОВЫХ ТРУБАХ

Термосифоны и тепловые труб ы при званы решать про блему
переноса больших потоков теплоты . При этом температур н ые
напоры н а самих устройствах - невелики , т.е . практи ч ески
весь располагаемы й температурны й напор реализуется за пре
делами устройства - при подводе к нему теплоты и ее отводе
со сторо н ы внешних целевого продукт а и теплоносителя . Тер
мосифо н ы и тепловые тру бы наи большее применение се йчас
н аходят в энергетике и строительной индустрии (ре куперация
теплоты , разморажи вание, кондиционирование воздуха, крио
ген н ые процессы) ; в меньших масштабах их используют в хи
мической технологии и смежных отраслях промышленности
(сушка , газифи кация углей , пищевая и фармацевтическая про
мышлен ность и др . ) . Возможности этих устройств весьма вели
ки , так что можн о говорить о благоприятных перспективах их
использован ия . Н иже изложены принципы ра боты термоси фо
··
нов и тепловых труб и дана их краткая характеристика .
' См"например, [ 1 0 ) .
" Более подробные сведения о работе тепловых труб с детальным анализом и
математическим описанием см. [4, 1 5 ) .
592

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

а

А

11

Ф

Б

6

Рис. 7. 24. Термосифоны и теruювые трубы:

а - термосифон, б - тепловая труба ;
/ - JIСИДJ(ость, // - пар , /// - конденсат;
А , Б - зоны подвода и отвода теплоты, Ф - фитиль

Термосифон (рис.7.24,а) представляет собой вертикальную трубу, в которой
помещено небольшое количество рабочего тела (воды или другой жидкости);
труба вакуум ирована и ruютно закрьrrа. На нижнем конце трубы расположена
зона подвода теruюты А, на верхнем - зона отвода Б. Теплота от находящегося
снаружи термосифонной трубы горячего теплоносителя в зоне А подводится к
воде, что вызывает ее испарение; образовавшиеся пары поднимаются вверх,
попадают в зону Б, где теплота отдается холодному теплоносителю (он также
находится снаружи термосифонной трубы) . При этом пары конденсируются и
конденсат под действием силы тяжести стекает по стенкам вниз и возвращается
в зону испарения А. М ежду теплопередающими зонами А и Б находится ади
абатный участок, где отсутствует теплоперенос нормально к поверхности трубы;
на этом участке происходит продольный (по трубе) перенос теплоты с потоком
рабочего rena (пара и конденсата). Таким образом, при функционировании термоси
фона осуществляется перенос теплоты - в конечном счете от горячего теплоносителя
к холодному.
П оскольку теплота конденсации (испарения) Д11Я различных рабочих тел
(особенно Д11Я воды) весьма велика, то даже при небольших разностях темпера
тур меж:ду концами термосифона могут транспортироваться значительные коли
чества теплоты. Если оперировать терминами кондуктивного теплопереноса, то
можно констатировать, что термосифон обладает продольной эквивалентной
теплопроводностью Лс, превышающей таковую Д11Я самых теплопроводных ме
талло в ( медь, серебро, алюминий) в сотни и тысячи раз. Практически пропуск
ная способность термосифонной трубы вряд ли может явиться лимитирующим
фактором в общем переносе теплоты от горячего к холодному теплоносителю.
Существенный недостаток термосифона - возврат конденсата в зону испа
рения под действием гравитационных сил. Это диктует расположение горячей
зоны испарения обязательно ниже более холодной зоны конденсации , что огра
ничи вает возможности использования термосифона.
Теплова11 труба свободна от указанного недостатка. В общем она конструк
тивно близка к термосифону, но зоны испарения (горячий участок) и конденса
ции (холодный участок) здесь могут бьrrь расположены произвольно - в соот
ветствии с требованиями технологического процесса. Такая возможность обеспе
чивается возвратом конденсата в зону испарения под действием каnШIЛЯрных СШI
- по фитШ1ю (пористой структуре).
В качестве примера на рис.7.24,б показана горизонтальная тепловая труба.
На ее периферии расположен фитиль Ф (на рисунке заштрихован), в приосевых

593

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

зонах остамено свободное пространство. Левый участок А (зона испарения)
контактирует с горячим внешним теплоносителем, правый Б (зона конденсации)
- с холодны м ; между зонами А и Б
адиабатный участок. Пары рабо чего тела
от горя чего ко нца тепло вой трубы по свободному пространству перемещаются к
холодному ко нцу, где конденсируются; конденсат по фитилю (кольцевая
пристеночная зона) возвращается в горячую зону испарения . Таким образом, в
итоге теплота переносится от горячего теплоносителя к холодному.
Важнейшие требования к рабочему телу
высокое поверхностное натяжение
и хорошая смачиваемость фитиля, низкая вязкость (с целью обеспечения бы
строго возврата конденсата в зону испарения по фитилю), возможно б&льшие
теплопроводность конденсата и теплота конденсации (чтобы обеспечить интен
сивный теплообмен на концах трубы с горячим и холодным теплоносителями).
В качестве рабочего тела в тепловых трубах используют воду, спирты, углеводо 
роды и их производные, некоторые газы (в сжиженном состоянии) и металлы (в
расплавах) . Выбор рабочего тела зависит от рабочей температуры; тепловые
трубы могут работать близко к абсолютному нулю (несколько градусов К) и при
температурах до 2000 К.
Основные требования к фитилю: максимальный капИJUIЯрный напор (с этой
целью при прочих равных условиях следует стремиться к малому размеру пор);
минимальное Пlдравлическое сопротимение движению конденсата (здесь, на
против, надо стремиться к увеличению размера пор) - противоречие разрешает
ся в ходе технологического компромисса. В качестве фитилей используют: тка
ное волокно и войлок, мелкие сетки, спеченные пористые структуры
(керамические, металлические), засьmки мелкозернистых материалов, системы
из тон ких каналов, канавок и т. п. Размер пор в фитилях об ыч но состааляет от
0 , 0 1 до 0 , 1 мм. Фитили в зоне испарения должны плотно прилегать к стенкам
трубы (для обеспечения хорошего теплообмена со стенками). Кипение рабочего
тела в этой зоне должно бьrrь исключено ( во избежание разрушения пористой
структуры) .
Разумеется, для рабочих тел и материала фильтров общим требованием яв
ляется достаточная химическая инертность и термическая устойчивость.
Реализуемые тепловые потоки (и значения Л.0) для тепловых труб также весь
ма высоки; они в очень малой мере уступают характерным для термосифонов.
В заключение отметим, что величины тепловых потоков в термосифонах и
тепловьIХ трубах ограничены значениями относительньIХ скоростей жидкости и
пара, т.е. возможностью срыва капель конденсата с движущейся пленки встреч
ным паровым потоком ( "захлебыван ие" устройства).
-

-

7.14. ПРИБЛИЖЕННЫ Й РАСЧЕТ РЕГЕНЕРАТОРОВ
Регенераторы используются в химической технологии,
энергетике , металлургии в достаточно широком температурном
диапазоне - от высоких температур (обжиг, доменный про
цесс) до весьма н изких (процессы глубокого холода) . Сущность
работы регенераторов (см . разд. 7. 1 ) состоит в попеременной
подаче горячего и холодного газа в аппарат с насадкой, в ре
зультате горячий поток отдает теплоту холодному, а насадка, то
нагреваясь, то охлаждаясь, испол ьзуется в качестве промежу
точного теплоносителя .
Процесс в регенераторе - принципиально нестационарный,
цикличесюtй. В зависимости от его условий и выбранной на-

594

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 7.25. Температурные
регенератора:

кривые

при

работе

1 - иэменеЮ1е температуры насацки в периоды
цикла, 2 - осредненные температуры насацки по пе

риодам

,.

f

- - садки продолжительность цикла мо
жет варьироваться в широких преде
1
лах. В случае высокотемпературных
процессов, когда в качестве элементов
2
насадки используются массивные тела
(шамотный кирпич, огнеупорная ке
рамика и т.д.), время цикла составляет
десятки минут (иногда - часы) ; при
т
низкотемпературных процессах, когда
используются тонкие высокотеплопроводные элементы насадки (гофрированная лента, фольга) , время цикла
на 1 - 2 порядка меньше .
Время цикла "tц складывается из
продолжительности горячего и холодного периодов:
(а)
"tц = "tJ
"t2 .
В период "tt в регенератор подается горячий газ с постоян 
ной начальной температурой Т' = const; нагревая насадку, он
сам охлаждается до Т", причем за период "t J выходная темпера
тура газа Т" постепенно нарастает соответственно увеличению
температуры насадки е , так что Т" = var. Аналогично, в период
"t2 подачи холодного газа его входная температура t' = const, а
выходная t" = var, поскольку е за этот период постоянно по
н ижается . Характер изменения средней (по объему регенерато
ра) температуры насадки во времен и демонстрирует рис.7.25;
при этом жирным пунктиром показаны усредненные (за соот
ветствующий период) температуры насадки, тонким - усредненные температуры горячего Т и холодного l газа.
Математическое описание теплообмена в регенераторе являет
ся весьма сложным : процесс нестационарен, он протекает (в об
щем случае) в условиях сопоставимости пропускных способностей
внешнего и внутреннего (в элементах насадки) теплопереноса (т.е.
в граничных условиях 111 рода), да еще при переменных темпера
турах как во времени, так и по объему насадки. Трудности точно
го расчета привели к разработке различных приближенных инже
нерных методов", один из них изложен ниже.

+

• Строгий анализ, результаты которого мoryr бьпь положены в основу точно
го расчета регенератора, см . ( 1 0 , 1 7 1 ; некоторые приближенные подходы к расче
ту регенераторов см . (2, 6, 1 1 , 16, 1 7 ) .

595

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Произведем осознанно п одмену задачи: будем описывать
теплообмен в терминах конвективного теплопереноса (см . разд .
7 . 5 . 1 ) , используя понятие о среднем за весь цикл работы реге
нератора коэффициенте теплопередачи kц. Тогда уравнение
типа (7. 1 4) запишется как
(7.43)
Q = kцtцF( T - 1 ),

усредненные (за периоды ч и ч соответственно) темпераТУРЫ
где Т и t
горячего и холодного газовых потоков в регенераторе.

-

Это же количество теплоты может быть записано отдельно
для периодов ч и ч с использованием усредненных (за каждый
период) коэффициентов теплоотдачи а. 1 и а.2:

ё1

где

и

02

-

Q = O. \'t 1 F(T - 01 ) =

а1т2

F(82

- i) ,

(7.43а)

усредненные (за соответствующий период) темпераТУРЫ поверх

ности насадки (не станем пока акцентировать внимание на возможном суще
ственном отличии тем ператур поверхности насадки от средних по ее объему) . В
общем случае, как это следует из рис.

7. 2 5, значения 01

if

02

не совпадают.

Выразим kц в зависимости от щ и а.2. Выпишем для этого
характерные температурные напоры и сложим их :

+

т - ёl = __JL}
o.1t1F � (Т - !) - (е _ 8 ) = Q(-l- + _l_) .
1 2
Q
o.1t1F o. 2t 2F
8 2 l- 0. 2t2F
-

- --

Подставив в последнее выражение значение Q п о (7.43) и
разрешив полученное равенство относительно kцtц, получим
после сокращен ия на F

kцtц =

1
1
1
-- + --

[i

_

�1]

0�т -t

(7.44)

<X. 1 t 1 a. 2 t 2
причем kц, а. 1 и а.2 отнесены, как обычно, к единице времени.
В случае 01 = 02 регенератор называют идеальным ; для него
выражение (7 .44) упрощается:

(kц)идtц

=

1
1 ---

-- + --

(7 .44а)

a. ,t l 0. 2t 2

Это соотношение формально напоминает выражение (7 .3)
для стационарного теплопереноса, но при этом вюuочает еще
распределение времени цикла по периодам работы регенератора.
596

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Отличие реальной ситуации от идеальной выражают с по
мощью коэффициента полезного действия регенератора Т\ р :
(б)
kц = (kц)идТ\ р ;

множитель Т\ р � 1 формально представляет собой численное
значение квадратной скобки в выражении (7.44).
Физически множитель Т\ р призван учесть два основных эф
фекта. Во-первых, в процессе работы регенератора не полнос
тью используется аккумулирующая способность насадки : тем
пература ее внутренних зон (средняя по объему элемента на
садки 8ср - тоже) в своем изменении может заметно отставать
от температуры поверхности е . Этот эффект выражается с по
мощью коэффициента использования насадки к ; он определяется
соотношением количеств теплоты, которая может быть пере
дана кондукцией внутрь насадки и которая на самом деле ак
кумулируется ею. Поэтому к зависит от критерия Фурье . И во
вторых, независимо от внутреннеrо теплопереноса должны
быть учтены особенности конвективноrо теплообмена на по
верхности насадки. Здесь определяющим будет критерий, пря
мо получаемый из уравнения нестационарноrо конвективноrо
теплопереноса - типа (а) в разд. 7.10.2 - путем масштабных
преобразований: а:t/(стРт/) = \f/ , rде / - определяющий линей.:.
ный размер, выражающий соотношение объема тела и ero по
верхности . Нетрудно убедиться, что \f/ представляет собой про
изведение критериев Фурье и Био :
FО

· в J. -

ат 't а./
1 2 л. т

'

-

Элементы насадки чаще всеrо - плоские тела (ленты, плас
тины , кирпичи) толщиной 8; для таких тел в качестве опреде
ляющеrо линейноrо размера принимают полутолщину 8;2. Тоr
да, например, для первоrо периода (подача rорячеrо rаза)
FО 1

=

-

4 а 't 1
т
82

-- ,

для цикла в целом Fоц

=

\f/

1

=

-

4 а 't
т_
u
_
82

в 1· 1 FО 1

=

-

ст р т 8

2 a. 1 't 1

-- ,

Чтобы рассчитать Т\ р , необходимо уметь определять коэффи
циент к . Здесь предлаrаются полуэмпирические ero связи с
Fоц. Для идеальноrо регенератора, по определению, к = 1 .
При использовании металлической насадки (высокая тепло
проводность) можно считать с поrрешностью не более 2%, что
регенератор работает как идеальный (поскольку Fоц измеряет597

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

к

J

0 ,8
0 ,6
0 ,4 - -J
0 ,2

......! - 'Кi-

.� �/

k-

2�

1

7
I"

,lf1

V"

......

i

1

2

;
1

'2

О 0 ,2 0 ,4 0 ,6 0 ,8 1 2

,

4

6

8 1 0 2 0 40 Fo

Рис. 7.26. Коэффициеит использования насадки в регенераторе: по Руммелю ( J)
и по Грегори ( 2) .
Изломы н а кривых обусломены только изменением масuлабов шкалы н а оси абс1D1сс
при значениях Fоц, равных 1 и 1 0

ся десятками и сотнями). В случае малотеплопроводной насад
юt (в этом случае Fоц может оказаться и меньше 1) возможно
заметное отклонение реального регенератора от идеального .

Полуэмпирические связи к с Fоц в пра�сrически икrересном диапазоне из
менения Fоц показаны на рис.7.26 . Кривая 1 построена по уравнению к = ( 1 +
+ 1 / Fоц) - 1 . Кривая 2 построена применительно к синусоидальному изменению
температуры поверхности элемеита насадки; высказано предположение, что эта
кривая пригодна и дЛЯ других форм периодического изменения поверхностной
температуры (это предположение в определенной мере подкрепляется законо
мерностями реrулярного режима при не слишком малых значениях критерия
Фурье - см . разд. 7 . 12). Совпадение кривых 1 и 2 в аспекте точности инженер
ных расчетов можно считать удовлетворительным .

Для практического испол ьз ования формулы (7.43) необхо
димо условиться о способе определения Т и i . Эксперимен
тально установлено, что температура газа в регенераторе изме
няется во времени практически линейно. Это позволяет в задачах
проектирования рассчитывать осредненные по времени темпе
ратуры горячего и холодного потоков на выходе из регенерато
ра как среднеарифметические из величин для начала и конца
периодов (индексы " н" и " к") :
Т" =

Т " + Тк"
и

И

t " = -н

t"

+ t к"

__

2

(в)

Сами осредненные значения Т и i не нужны для расчетов;
согласно (7 .44), необходимо располагать только их разностью
( Т - i ). Она вычисляется как среднелогарифмическая величи598

2

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 7. 27. Коэффициеm полезного действия реrенератора

на из постоянных входных ( Т ' и t') и осредненных выходных

( Т " и t ") температур.
Зависимость Тl р от

к и 'l' I приведена на рис. 7.27 (матема
тическое описание этой зависимости из-за его rромоздкости не
приводится) . График учитывает и принятый подход к определению Т и i .
В задачах эксплуатации известны только входные температу
ры потоков Т ' и t '; определяемой величиной здесь является
количество теплоты Q , переданной за один ци кл . Анализ ве
дется по уже известной канве, продемонстрированной в
разд . 7.7.2 . Из тепловых балансов:

Q

=

G1 c 1't1 ( T1

-

Т ") = G2c2ч (t"

-

t� =

kц't�FЛcp·

(r)

Из первых двух выражений :
и

t" = !' +

Q

Раскрыв Л ер как среднелогарифмическую величину и под
ставив значен ия Т " и t ", получим (примен ительно к прямото
ку, т.е . вводу горячего и холодного газов в регенератор с одного
599

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

конца) после несложных преобразований:

(д)

rде, как и ранее, л. = Т'

-

t '.

(е)

Обозначим по аналогии с (7 . 18) отношения пропускных
способностей ао = kц'tцF/( G1 c1't1 ), Ьо = kц'tцF/( G2C2't2) и предста
вим из (е) теплоту Q в явном виде :

л.

-Q

1

( G1 c�:
1

Отсюда

Q=

)

1
+ --

G 2 c2 't 2

--G 1 C 1 't 1
1

=

1

ехР( - (а о + Ьо )] .

ехР( -(а о + Ьо

)] л

• .

(7.45)

+ ---

G2 C 2 't 2

Эта формула я вляется расчетной. К более привычному виду
она приводится умножением числителя и знаменателя на kц'tцF:

600

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Сходство формул (7 .4 5а) и (7.21а) очевидно . По существу
здесь упорядоченный нестационарный (квазистационарный)
режим работы регенератора сведен в расчетном смысле к ста
ционарному режиму работы рекуперативного теплообменн ика.
Тепловая нагрузка регенератора в един ицу времени опреде
ляется как Q = Q/tц . Отсюда нетрудно получить и выр ажение
для пропускной способности регенератора Q/ л • .
Аналогичный анализ можно провести для ввода горячего и
холодного газов в регенератор с различных его концов

(противоток).

7 . 1 5 . ОТДFЛЬНЫЕ ЗАДАЧИ ТЕПЛООБМЕНА
Н иже приведены некоторые харакгерные примеры исполь
зования рассмотренн ых представлений о теплообмене для ре
шения отдельных химико-технолоrичесЮtх задач. В отличие от
рассмотренных в разд. 7 . 5 , эти задачи включают перенос теп
лоты с потоками теплоносителей .

7 . 1 5 . 1 . Нагрев конденсирую щимся паром
интенсивно перемешиваемой жидкости
Жидкость массой G необходимо нагреть от начальной тем
пературы lн до конечной lк . Жидкость интенсивно перемеши
вается , так что в кажд ый момент времени ее температура по
всему объему одинакова. Нагрев ведется через теплообмен ную
поверхность F за счет конденсации насыщенного пара - тем
пература его Т, энтальпия Н, энтальпия конденсата h . Требует
ся найти общий расход пара G п и время нагрева жидкости •нrр ·
Для определения расхода греющего пара составим тепловой
баланс (рис . 7.28): контур - весь аппарат, временной интер
вал - про цесс нагрева в целом . В отсуrствие потерь в окру
жающую среду
(а)
откуда, имея в виду, что разность энтальпий насыщенного пара и
жидкости Н h = r (теплота конденсации), получаем

кипя щей

G c ( tк - tн )

-

G c (tк - tн )

.

(7.46)
H-h
r
С целью определен ия времени нагрева •нrр в качестве кон 
тура выберем жидкостное пространство аппарата и запишем
тепловой баланс для элементарного промежуrка времени d't.
Элементарное количество теплоты, переданной через поверх
ность за этот промежуrок, составляет dQ = k( Т - t)Fd•, где k 60 1
Gп =

=

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 7.28. К расчету теплообмена между конден 
сирующимся паром и хорошо перемешиваемой
жид костью

коэффициент теплопередачи. Оно рас
ходуется на подоrрев жцц кости Gcdt.
Итак,
dQ = k( T - t)Fd't = Gcdt,
(б)
h
причем вдоль всей поверхности F и во
времени Т = const, а t изменяется
только во времени.
Разделим переменн ы е и проинтеrрируем (с учетом знака
при t) от fн до fк и от О до 'tнrp :
t

с

1к

I

откуда

t

н

dt
kF
=
-Т-t Gc

� нrр

'tнrp

f d't
о

и

Gc

ln

Т-l
Т - tнк =

Т - tн
- - ---

_

kF

1n

Т - tк

kA нrp

(в)

Gc

(7 .47)

И тогда поток пара Gп (рис . 7 .28 ) составит Gп = Gп/•нrр ·
Разумеется, на основе (в) могут быть решен ы и другие зада
чи , например о связи текущих значений температур ы жидкости
t и времени • :
Т-t

Т - tн

kF•

= ехр(- )
Gc

,

(7.47а)

причем под знаком экспоненты стоит отношение пропускных
способностей поверхностной и потоковой стадий (для полуне
прерывного процесса ) .

7 . 1 5 .2. Нагрев псевдоожиженноrо слоя потоком rорячеrо газа
в условиях балансовой задачи
Псевдоожиженн ы й
слой
мелкодисперсного
материала
(общая его масса Gт) наrревается от начальной температур ы 8н
с помощью постоянного потока G ожижающего агента - газа
(рис .7 .29 ) . Температура газа на входе в слой t' в ходе процесса
не изменяется. Слой имеет достаточную в ы соту Н > h3, так что
теплообмен происходит в условиях балансовой задачи: в любой
момент времени температура уходящего из слоя газа t" равна
текущей температуре слоя е ; разумеется , температуры t" = е
изменяются во времени. Пусть требуется найти связь темпера
тур ы е со временем наrрева 't.
Выбрав в качестве пространствен ного контура весь аппарат
с псевдоожижен н ы м слоем, запишем тепловой баланс для эле-

602

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 7.29. К расчету нестационарного межфазного
теплообмена в псевдоожиженно м слое в условиях
балансо вой задачи

. .
ментарного промежугка времени d't. Учтем
при этом, что процесс ведется без ввода и
. . . .
вывода твердого материала, и пренебре
• Gт,Ст, 0
.
жем накоплением теплоты в газовой фазе
. . . .
(ее масса и пропускная спос обность в
. .
. . .
псевдоожиженном слое на 3 порядка ни
�---же, чем для твердого материала) . Тогда
(г)
Gct'd't - Gct"d't = Gт стd8 .
После разделения переменных (с уче том t" = 8 следует бр ать интеграл с начальным условием 8 =
= 8 н при 't = О) и переменным верхним пределом:
•

•

.

•

G,Jr'

)

J � = � Jd't .

e.

Отсюда

(

r -8

G т ст

о

для разных постановок задачи:
l n t' 8 н
� . 't = Gт Ст l n t'
=
G С '
8
t'
Gс
t'
т т
-

-

8 =

-

(

t ' - t'

) [

/(

- 8 н exp - Gct

G

т ст

8н

-

8

)] ,

(7 .48 )

причем GC't/(Gтcт) представляет собой отношение пропускных
способностей потоковых стадий для полунепрерывного процес
са, аналогичное отношению Ь/а = G1 cif( G2c2) для стационар
ного .
Легко видеть близость и вместе с тем неидентичность ана
лиза этой задачи и рассмотренной в предыдущем разделе: в усло
виях смешанной задачи определяющим критерием было отно
шение kF't/(Gc); здесь, в условиях балансовой задачи, опреде
ляющим является отношен ие GC't/(Gтcт) ·

7. 15.3. Нестационарный теплообмен
между двумя интенсивно перемешиваемыми жидкостями
В аппарате по разные стороны от разделительной перего
родки - поверхности теплообмена F
находятся (рис . 7 .30)
две жидкости масс о й G 1 и G2 с разн ыми начальн ыми темпера
турами Тн и lн. Жидкости интенсивно перемешиваются , так что
температура каждой из н их Т и t в любой м о мент времени
одинакова по соответствующему объему. Коэффициент тепло
передачи равен k. Требуется установить закон изменения тем
ператур Т и t во времени 't.
603
-

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

расчету нестационарноrо теплооб
мена меJIЩ)' ограниченными количествами
хорошо перемешиваемых жидкостей
Рис. 7.30. К

Запишем для элементарного про
межугка времени тепловые балансы
для пространств горяч его и холодн о 
го теплоносителя:
причем d Q = kF( T - t) d't.
Подставив в (д) значения

d Q,

получим систему уравнений :

dT - kF
=
(T - t) = a'(T - t) ,
d't
G 1 С1

(е)

� = � (T - t) = b'(T - t) ,
d-r

G 2 С2

где а' kF/(G1c1), Ь' kF/(G2c2) - размерные комплексы (они превратятся в
безразмерные отношения пропускных способностей, будучи умноженными на t) .
"'

"'

Эта система должна быть решена с начальным условием

(ж)
и t = lн при 't = О .
Система (е) и начальное условие (ж) по форме полностью
совпадают с запис ью для прямотока системы (б) и граничных
условий (в) в разд . 7 . 8 . Ясно, что и решения будут формально
с овпадать с (7.23) и (7.24), разумеется - с заменой координаты
х на время 't:

Т = Тн

Т = Тн t = fн +

' - 1 - е-(•' + Ь')• ,
Л : -а_
а' + Ь'
' - 1 - е-(•' + Ь')• ,
л: _Ь_
а ' + Ь'

(

(

)

)

(7.49)
(7.50)

причем Л � = Тн - fн.
Совпадение записей этого решения и наЙденного ранее вполне случайно, поскольку данный периодический процесс можно
'
не трактовать как прямоток во времени: здесь временная координата 't заменила геометрическую (поверхностную) f или х.
С помощью (7.49), (7.50) нетрудно решить ряд конкретных
задач : определить конечные значения температур Тк и fк в ко 
нечный момент времени -rк ; найти время, за которое одна из
жидкостей (целевая) примет заданную температуру ( Тк или
tк) ; установить значение текущей разности температур :

604

(a' b')
Т - t = Л �е- + t = (Тн - t н ) exp[ -(a ' + b' )'t] .

(7.5 1 )

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Получен ные выражения относятся к смешанной задаче теп
лопереноса. Продолжение анализа с сопоставлением пропуск
ных способностей стадий , т.е. оценка безразмерн ых комплек
сов a'-r, b'-r и Ь'/а' позволяет упростить эти выражения в случае
вырожд ения смешанной задачи в поверхностную (a'-r, b'-r � О) ,
потоковую или балансовую [a'-r и (или) b'-r � оо) .

7 15 4 Безrрадиеtrrное остывание тела
за счет лучистого теплообмена
.

.

.

Пусть высокотеплопроводное выпуклое тело массой Gт,
имеющее высокую начальную температуру ею помещено
(рис . 7 . 3 1 ) в большую оболочку, на поверхности которой, обра
щенной к телу, поддерживается постоянная температура t.
Примем ряд упрощающих условий : степень черноты тела будем
считать не зависящей от его температуры (поэтому и приве
денная степень черноты Епр не меняется с е); пространство
межд у телом и оболочкой полностью вакуумировано , так что
теплообмен за счет естественной конвекции можно исключит ь
- остывание тела происходит только за счет его излучения .
Требуется установить закон охлаждения тела.
Анализ ведем н а основе формулы лучистого теплообмена
(6.27); напомним , что температуры здесь выражаются в граду
сах абсолютной шкалы .
Запишем тепловой баланс для тела (оно и есть простран 
ственный контур) и бесконечно малого отрезка времени . В
отсутствие Источников , Стоков и Прихода теплоты в ходе
процесса остывания получаем выражение
(з)
О - Eп pcr0F(e 4 - t4 )d-r = Gтетdе .
Отсюда после разделения переменных и инте гр ирования (от
начал ь но го момента -r = О до текуще го -r и от 8н до текущего
значения е ) :
- �;пр

0

0н

cro F-r = GтСт f

е

4

de
-

t

4

(и)

1 х
ный: j dx 4 .!.
+ _!_ arctgx , причем для решаемой
4 ln
1-х 2
1-х
задачи х имеет смысл 0/t.

+

Икrеrрал,

входящий

=

Возьмем интеrрал:
I nt

=

J ___о
4 4 о_

1 -е

=

в

(и),

таблич- ·

d(G/t)
_!_3 1
1 1 - (е/1) 4

Рис. 7.31. К расчету безrрадиентноrо остывания тела за
счет излучения

605

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

_!__[.!_ln (i( 7))((i �))
_!__[.!..1n

Соответственно табличному выражению

lntl0

0•

=

+

4

13

=

13

е
\-t

4

-

l+

еи
l

(

)

+ .!.. arc tg � - arctg �
t
t
2

]

i

(е + t) {е и - t) .!.. arctg (е н - e)t .
ене + 1 2
(е и + t ) {е - 1 ) 2
_

(к)

С учетом (к) решение ( и ) принимает окончательный вид:
•

=

G
&пр

[

(е н - е)t
1 1 ln (e + t)(e н - t) 1
- - arctg
cr o F 1 3 4 (е н + t)(e - t) 2
8 8 + 12
н

т ст

]

. (7 . 52)

Закон изменения 8 во времени записан в явном виде отно
сительно • · Выразить эту зависимость в явном виде относи
тельно 8 не удастся, решение возможно численными методами .
Л ИТЕРАТУРА к главе

7

1 . Аэров М.Э., Тодес О.М. Гидравлические и тепловые основы работы аппа
ратов со стационарным и кипящим зернистым слоем . Л . : Химия, 1 968 . 5 1 2 с.
2. Гельперин Н.И. Основные процессы и аппараn.1 химической технолоrии . М.:
Химия, 198 1 . 8 12 с.
3. Гельперин Н. И., Айнштейн В. Г. Псевдоожижение, гл. Х "Теплообмен"/ Под
ред. И : Ф . Дэвидсона, Д. Харрисона: Пер. с англ. / Под ред. Н . И . Гельперина.
М.: Химия, 1 974. 760 с.
4. Дан П.Д. , Рей Д А . Тепловые трубы: Пер . с англ. / Под ред. Ю.А. Зей 
rарника. М . : Энергия, 1 979. 272 с.
5. Дытнерский Ю. И. Процессы и аппараты химическо й технологии. М . : Хи
мия, 1 99 5 . 76 8 с.
6 . Исаченко В. П. , Осипова В.А., ()хомел А. С. Теплопередача. М.: Э нерmя ,
1 969 . 440 с.
7 . Карташов Э.М. Аналитические методы в теории теплопроводности твер 
дых тел. М. : Высшая школа, 1985. 480 с.
8. Касаткин А .Г. Основные процессы и аппараты химической технолоrии. М . :
Химия, 197 1 . 784 с.
9. Кутателадзе С. С. Основы теории теплообмена. М.: Атоми:щат, 1979. 4 16 с.
1 0 . Лыков А.В. Теория теплопроводности. М . : Высшая школа, 1 967 . 600 с.
1 1 . Михеев М. А . Основы теплопередачи. М . -Л . : Госэнерrоиздат, 1 95 6 . 392 с.
1 2 . Михеев М.А., Михеева И.М. Основы теплопередачи. М.: Энергия, 1977. 342 с.
13. Павлов К. Ф. , Романков П.Г., Носков А.А. Примеры и задачи по курсу
процессов и аппаратов химической технологи и . Л . : Химия, 1987. 574 с.
1 4 . Перри Дж. Справочник инженера-химика: Пер. с англ./ Под ред. Н . М .
Жаворонкова. Л . : Химия, 1 969. 1 1 44 с .
1 5 . Справочник п о теплообменникам: Пер. с англ. / Под ред. О . Г. Марты
ненко и др. М . : Энерrоатомиздат, 1 987. 9 1 3 с.
16. Хоблер Т. Теплопередача и теплообменники: Пер. с польск. / П од ред.
П .Г. Романкова. Л . : Госхимиздат, 1 96 1 . 820 с.
1 7 . Шак А . Промышленная теплопередача: Пер. с нем. / Под ред. В .А. Оси
пово й . М.: Металлу ргиздат, 1 96 1 . 524 с.

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Глава 8
СТРУКТУРА ПОТОКО В

Важ нейшей проблемой бол ь шинства химико -технологи 
ческих процессов (ХТП ) является перенос субстанции
коли 
чества движения ( импул ь са) , тепл оты , вещества . В химико 
техноло гич еских аппаратах (ХТА) теплота, например , может
переноситься из одной точки рабочей зоны в другую ил и к
стенкам аппарата ; вещество , скажем , - от входа к в ыходу или
межд у разли ч н ы ми потоками . Различают продольный ( в направ 
лении движен ия потока) и поперечный перенос ы субстанции. К
первой разновидности среди приведенн ых выше примеров от
носится , в частности , перенос тепл оты или вещества от входа в
ХТА к выходу; ко второй - перенос теплоты (вещества, им 
пул ьса) между потоками фаз или , например, теплоты к стенкам
аппарата . Пр од ол ьн ы й и поперечн ы й перенос ы связаны ме жд у
собой. Так, напра вленное перемещение количества движен ия
(масс ы , энергии ) с потоком вдол ь аппарата (т . е . прод ол ь ный
перенос импул ьса ) сопрово ждается трен и ем (т . е . поперечн ы м
переносом импул ьса к стенкам аппарата) .
-

Стро го говоря, перемещение субстанции поперек основного направ.ления по
тока следует подразделять на нормал"ное и собСТ11е нно поперечное (рис. 8 . 1 ) .
Продольный поток теплоносителя вдоль теплообменной поверхности показан
стрелкой /. Направ.ление нормального (к поверхности) потока показано стрел 
ками //; именно такой перенос обусловливает интенсивность теплообмена. На
прав.ление собственно поперечного перемещения изображено стрелками ///;
наличие этого переноса обуслов.ливает выравнивание температурного поля в
различных точках поперечного сечения. При иэложении материала в настоящей
главе под поперечным перемешиванием ( переносом) будут, как правило, пони
маться оба эффекта - нормальный и собственно поперечный . П р и не о бходи
мости их р аздельного рассмотрения будут делаться оговорки .

Основной цел ь ю (содержанием) многих ХТП является ин :
тенсивн ы й п о перечн ы й (н ор м ал ьн ы й) перенос . Пример ы : пе 
ренос теплоты (к стенке аппарата или от нее) при тепл оо бмене
межд у потоками двух теплоносителей ; перено с какого -либо
в ещества, компонента пр и непосредственном конта кте ф аз
( скажем , жидкой и газовой) . Здес ь нужно интенсифицир овать
теплоперенос нормал ь но к стен кам аппарата (чтоб ы нагреть
оди н п ото к и охл ад ить д руго й ; что б ы и зменить а гр е гат н о е с о -

607

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 8. 1. Поперечный перенос
те ruю обменной поверхности :

2

11

около

1 - те плооб ме нная п о вер хно �•ь, 2 - п о 
г рани ч ный слой ;
/ - осно вное нап р авл е!Dl е пр одольного п о 
тока теп лонос ителя, // - но рмальный п ерено с ,
/// - собстве нн о п о п ер е ч ный п ерено с

стоян ие одного или о боих пото 
ков ; что б ы отвести тепло экзо терми ч еско й реакции , и т.п . ) .
И л и : н ужно интенсифицировать нормальны й перенос , что б ы
полнее передать како й -ли бо компонент из одно й ф азы в др у 
гую. Такая интенсификация переноса позволяет с больше й
производительностью и полното й ос уществлять процесс в
имеюще й ся аппаратуре ли бо при заданных производительности
и степени завершенности ХТП о бойтись бол е е компактн ым
аппаратом - с меньшей поверхностью теплоо б мена , с мен ь 
шими га баритами .
Для интенсификации норм ального попере ч ного переноса
испол ьз уют разл и ч н ые приемы технологи ч еского (повышение
скорост и потока и др . ) и конструктивного (увели ч ение по
в е р хности
контакта и т.п . ) характера . Одна ко п р и этом
п р оисходит интенси фикация и продольного переноса , что в
большинст в е сл уч аев , как будет показано н иже , нежелательно .
Это н е о з н а ч ает , что н уж но отказаться от интенси фикации
попе р е ч но го
переноса ;
просто
нео бходимо
уч итывать
од н о вр еме н н ые изменен ия в характере продольного переноса ,
в озде й ст вуя п о мере возможности на последни й в нужном
н а п р а вле н и и .
Та юt м о б р азом , реал иза ц ия важ не й ше й цели многих ХТП
(и нте н си ф и кация нормального попере ч ного переноса) с неиз
бежностью приводит к нео бходимости ан ал иза сопутствующего
явлен ия (продольного переноса) - для выявления возни
кающих при этом эффектов, возде й ствия на н их и учета их при
создан ии эффе ктивн ых ХТА . И на ч е говоря , надо из уч ать
стр у ктур у п от оков в ра бо ч ей зо н е аппарата , где происходят по 
п ере ч н ы й и продольны й переносы те плоты , вещества , коли ч ества дв иже н ия .

8.1. ОБЩИЕ ПОНЯТИЯ

Под структурой потоков понимают со вокупность р азли ч н ых
характеристик , описываю щ их гид родинами ч еское состояние
системы . Ан ал из стр уктуры потоков п р и з ван дать п р едста вле 
н ие о б осо бенностях дв ижения элементо в системы . В широком
смысле понятие стр у ктур ы п отоков охватывает след ующие про -

608

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис.8. 2. Модель ИВ (эпюра скоростей)

блемы : ламинарное и турбулент
ное течения; равномерные или
неравномерные
организованные
потоки (вспомним подачу жид
кости поршневым насосом) ; поля
w
осредненных (во времени) скор о 
сте й и мгновенные (пульсационные) скорости и т.д. Все это как-то влияет на процессы пе
реноса в ХТА, но здесь мы будем рассматривать лишь отдель
ные стороны проблемы структуры потоков.
Измерение и математическое описание изменяющегося во
времени пространствен ного поля скоросте й при движении по
тока в каком-то технологическом аппарате (или его фрагмен 
те) - сложная задача, а с учетом тепло- и массообмена, тем
более - химических превращени й , - зачастую пока неразре
шимая . Определенную (косвенную) информацию о поведении
1
потока получают из рассмотрения временных его характеристик, тем более что и сами эти характеристики существен н ы
для описания и расчета ХТП .
Пусть цель ХТП - изменение какого-либо свойства си
стемы U во времени 't, т.е . U = U('t) . При этом в качестве U
мoryr выступать : температура в случае теплообмена, концент
рация - в случае массообмена или химической реакции , ка
кое-либо свойство веществ (теплоемкость, механическая проч
ность и др .) . Разные элементы потока мoryr н аходиться в рабо
чей зоне (РЗ) системы (в теплообмен н ике, в массообменном
аппарате, в химическом реакторе) разное время ; поэтому сте
пень их обработки (конечное значение свойства - Uк) будет
различна. Естественно , результирую щая степень обработки всего
потока Uрез зависит от характера распределения элементов пото
ка по времени пребывания - именно в этом (более узком) плане
рассматривается ниже структура потоков (другие стороны про
блемы здесь практически не затрагиваются) .
Выделяют два простейших идеализированн ых представлен ия
о структуре потока - это мысленные модели, схематично от
ражающие наиболее существенные свойства системы , потока.
В некоторых случаях они в той или иной мере отвечают дви
жен ию потока в реальных ХТА. В самом общем плане понятие
об этих моделях б ыло введено в разд . 1 .2 .2 ; в настояще й главе
они будут рассмотрены подробно .
Идеаль ное вьпеснение (сокращенно - И В) , иначе - порш
невой поток, стержневой поток. Это абсолютно равномерный
(по поперечному сечению) поток (рис . 8 .2), все элементы кото-

609

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

рого движуrся с одинаковой скоростью w, а значит проходят
РЗ системы за одинаковое время 'tив ·
Идеальное перемешивание (сокращенно - И П ) . Здесь все
элементы п отока в рабочей зоне перемешивакrrся настолько ин
тенсивно, что параметры потока (температура, концентрация и
др .) выравнены по объему РЗ. В результате параметр ы потока,
покидающего рабочую зону, те же, что и в любой точке самой РЗ .
Это означает, что некий элемент потока, вошедший в рабочую
зону, в следующий момент времени может с равной вероятностью
оказаться в любой точке РЗ, в том числе и у выхода из нее .
Здесь нельзя изобразить эпюру ско ростей: стр о го говоря , в
рамках модели И П вообще не следует говорить о локальных
или мгновенных скоростях. В целях наглядности можно при
нять, что скорости бесконечно велики во всех направлениях .
Очевидно, в такой системе одни элементы (из тех, что ока
зались у выхода) быстро проскочат РЗ (почти не изменив своих
первоначальных характеристик, так как у них малое время пре
бывания 't в РЗ) , другие - надолго задержатся в ней (может
быть, бесполезно долго , так как они уже давно получили необ
ходимую степень обработки) . А поскольку время пребыван ия
элементов потока в РЗ разное, то об этом времен и нужно гово
рить в смысле его распределения.
В системах с И П (как и в системах с ограниченной интенсив
ностью перемешиван ия) нас более всего в рассматриваемом
здесь аспекте интересует перемешиван ие элементов потока в
направлении его движения , т . е . продольное перемешивание
( П р . П ) : в системах с ИП мы имеем дело с бесконечн о интен
сивным Пр . П, в системах И В интенсивность Пр. П равна нулю .
Заметим, что в общем случае для нас небезразлична и интенсив
ность поп еречного перемешивания: от него также м ожет зависеть
распределение времени пребывания элементов потока в ХТА.
Итак, в систем ах И В равномерно распределены (в попереч
ном сечении) скорости потока, и как следствие - одинаково
время пребыван ия в РЗ всех его элементов; в системах И П
равномерно распределены по объему интенсивные и удельные
свойства п отока - кон центрации, температуры, теплопровод
ности и т . п .
И В и И П - модельные представления. К системам И В в
ряде случаев близки течения внутри узких паралл ельных труб,
собранных в пучок, через неподвижный зернистый слой; к
системам И П - кипящие смеси (например , при непрерывном
выпариван ии в аппаратах с интенсивн о й естествен н о й цирку
ляцией температуры и ко нцентрации практически одинаковы в
объеме аппарата и на выходе из него) или барботажн ые си
стемы с достаточно большими расходами газа, или же движе-

610

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

а

б

Рис. 8.3. П оперечная неравномерность потока (эпюра скоростей)
Рис. 8. 4. Стержневой поток с обратным перемешиванием:

а - осредненный стер)l(}fевой поток с обра111Ь1М перемешивани ем (м rновеЮ1ая эпюра
скоростей) , б - турбулеНПfЬlе пульсации - возмоJIСИЬIЙ источник обратного перемешивания

н ие твердых частиц в односекционном псевдоожиженном слое .
Н о большинство реальных систем занимает промежугочное
положение - в них наблюдается Пр. П , но интенсивность ero

ограничена.

Обычно вьщеляют следующие основные причины Пр.П, обус
ловливающие неравномерность времен и пребывания элементов
потока в РЗ .
Поперечная неравномерность потока. Здесь характерным яв
ляется различие скоростей в различн ых точках поперечноrо
сечен ия (р ис . 8.3). В результате разные элементы потока прой
дуг РЗ за разное время . Примеры : ламинарный режим течения
жидкости в круглой трубе - параболический профиль скоро
стей; движение части газа через псевдоожиженный слой в виде
пузырей - они проходят через слой быстрее , нежели осталь
ной газ в просветах межцу псевдоожижаемыми твердыми час
тицами .
Обратное перемешивание. В этом случае на стержневой поток
(рис. 8 .4, а, жирные стрелки) накладывается изменяющееся во
времени поле мгновенных разнонаправленных скоростей (на
рис . 8 .4, а показаны их составляющие лишь вдоль движения
потока) . В результате в кажцый дан ный момент времени в
кажцой точке поперечноrо сечения формируется своя абсолют
ная скор ост ь движения элемента п ото ка как ито г сложен ия
разных локальных мгновенных скоростей с одинаковыми осред
ненными . Значит, будуг различны времена пребывания эле
ментов в рабочей зоне.
Обратное перемешивание возникает , например , при турбу
лизации потока (рис . 8.4, б) или при работе перемешивающих
устройств либо под возд ействием каких-то иных (конструк
тивных, эксплуатацион н ых) факторов.
Специально отметим , что увеличение турбулентн о сти потока
не обязательно сопровожцается усилением эффекта П р . П в

611

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ЦКМ

Рис. 8.5. Напрам енная циркуляция
ный ко нтур с мешалкой)

(ЦКМ - циркуляцион

целом . поскольку одновременно происходит
выравнивание профиля скоростей, т. е. сни
жается поперечная неравномерность потока.
Направленные циркуляционные потоки . Они
возникают в какой-то части поперечного се
чения аппарата (например , из-за н изкого ло 
кального гидравл ического сопротивления) или
специально организуются потоюt особой ин
тенсивности (рис . 8 . 5) . Здесь также нарушает
ся равномерность времени пребывания элементов в РЗ .
Заметим, что приведенные выше причины Пр . П настолько
взаимосвязаны, что между ними не всегда удается провести
четкую грань.

8.2. ВЛИЯНИ Е ПРОДОЛЬНОГО ПЕРЕМЕШИВАНИЯ
НА ЭФФЕКТИВНОСТЬ ХТП
Результирующий эффект ХТП зависит от характера распре
делен ия элементов потока по времени пребывания в РЗ . При
И В все элементы потока будуг обработаны одинаково, так как
'tив = idem. При И П (или в промежугочных случаях, в том чис
ле и в большинстве реальных систем) степень обработюt раз
н ых элементов потока будет разной из - за различий в их време
ни пребывания 't в РЗ. Предстоит выяснить, чтО лучше для
ХТП (тепло - ил и массообмена, химической реакции) - И В
или И П , в каком случае выше эффективность процесса.
Можно привести примеры положительного влияния Пр . П на
эффективность ХТП .
1 . Пусть неюtй ХТП протекает селективно только в узком
интервале температур . Если в ходе химической реакции выде
ляется большое количество теплоты , то обеспечить узкий тем
пературный интервал в зоне реакции можно лишь при интен
сивном перемешивании. Здесь Пр.П будет полезным . (Разу
меется, не менее важным здесь будет интенсивное поперечное
перемешивание , обусловливающее высоюtе коэффициенты
теплоотдачи и выравнивание температур в поперечном сечении
реакционного аппарата.)
2 . Пусть происходит автокаталитическая реакция , причем
промежуrочные продукты , резко ее ускоряющие, накапливают
ся постепенно. Тогда на начальных участках реактора (т.е. в
зоне накопления промежугочн ых продуктов) основная реакция
протекает медленно, эта зона на осно вную реакцию практиче-

612

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ски не работает. Использование объема (длины) реактора будет
эффективнее , если промежуточные продукты , катализирующие
основную реающю, перенести (забросить) в начальные участки
реакт ора ; это достигается интенсификацией Пр . П .
Н о в большинстве случаев перемешивание потока в направ
лении ero движения (т. е . Пр . П ) отрицательно сказывается на
эффективности процесса. Так, при протекании целевой хими
ческой реакции А --+ В может идти и какая-либо побочн ая, на
пример В --+ С . И тогда для элементов потока, чрезмерно долrо
нах одящихс я в реакционной зоне, ве сьма значител ь ная доля
целевоrо продукта В может превратит ься в побочн ый С. В то
же время для элементов потока с малыми < будет мала степень
превращения исходноrо вещества А в целевой продукт В. Та
ким образом , разброс во времени пребывания (из-за П р . П )
может привести к понижени ю степени превращения и селектив
ности, в итоге - доли выхода целевоrо продукта В .
Весьма существенно отри цательное воздействие Пр . П на
движущую силу процесса. Продемонстрируем это на примере

рекуперативного теплообмена.

В теплообмене изучают (см . rл. 7) различные схемы движе
ния теrtлоносителей - противоточную (наибольшая движущая
сила) , прямоточную (наименьшая ) , сложные - перекрестный
ток, смешанные токи и т . п. · (промежуточные значения дви
жущей силы) . Все эти с хемы подразумевают движение тепло
носителей в режиме И В . Рассмотрим (рис . 8 . 6 ) формирование

т

� <i
"

-

1

F

.r

Рис. 8. 6. Движущая сила (температvоный нащ>р) при тешюобмене:
1

-

прямоток (И В) ,

2

-

оrран 11чен ное продол ьное перемеши вание, 3 - И П '

613

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

движущей с илы теплоо бмена при движении тепло носителей в
режиме И П либо с огранич енным Пр. П ; анализ проведем в
сопоставлении с " наименее эффективной " схемой - прямото
ко м (в режиме И В) .
Движущая сила в случае прям отока (температурные кри
вые - спл ошные линии) рассчитывается (см . разд . 7.6.2) как
среднел огари фмическая величина Лt1n из начальн о й Л /1 и ко 
нечной Л/2 разностей тем ператур тепло носителей:

лtпр

=

Лt1 - Л/2
ln(Лt1 /Лt2 )

(а )

и по этому является промежуточн ой межд у Л /1 и Л /2 : Л /2 < Л tпр <
< Лt1 . Е сли при сохранении неизменными вели ч ин Лt1 и Лt2
потоки те плоносителей движутся в режиме И П , то вдоль всей
поверхности тепло о бмена их температуры Т и t не изменяются
(штрих - пунктирные лин и и). Поэто му вд оль поверхности F
Лt2, которая бу
остается постоянной и движущая сила ЛtШI
дет меньше , нежели Л lпр
лt1n. Это означает, что для передач и
то rо же коли ч ества теплоты Q при прочих равных условиях в
случ ае И П п отребуется ббльшая п о верхн о сть теплоо бмена, чем
при прямотоке :
=

=

F = _я_ "
kлtcp

(б)

rде k - коэффициент теruюпередачи (он условно принят здесь одинаковым для
разных схем движения теплоносителей) .

В реальн о м тепло о бменнике тепл о носители движутся с не
кото рой о гр аниченной интенсивностью Пр . П (штриховые ли
нии), так что движущая сила Л lср будет иметь пр омежуто чное
значение : лtШI � Лtср � лtив; с оответственн о, по (б) необходимая
поверхность F также будет промежуточной : FШI ;;::: F ;;::: Fив. Иг
н о рир ован ие при рас чете эффекта продольноrо перемешивания
при движении тепл оно сителей приведет к завышению Лtср• а
значит
к занNженным расчетным значениям F.
-

В литературе в настоящее время приводятся мноrочисленные эмпирические
уравнения для расчета тепло- и массообменных кинетических характеристик
процессов ( коэффициентов тепло- и массообмена и др .); точность этих уравне
ний обычно невелика (поrрешность в 20 - 30% считается вполне приемлемой).
Одна из причин разброса экспериментальных данных около расчетной зависи
мости - иrnорирование продольноrо перемешивания, различноrо в разных
изучаемых каналах , аппаратах, устройствах. Чаще всеrо исследователи постули
ровали (обычно даже не оrоваривая этоrо) движение потоков в режиме ИВ, на
этой основе определяли движущую силу (например, по (а) - Л/10) и рассчиты
вали коэффицие1пы тепло- или массообмена при разных значениях варьируе
мых факторов; в результате они приходили к эмпирическому уравнению. А
поскольку в разных аппаратах (каналах и т. п.) рассчитанная таким способом

614

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 8. 7. Химическая реакция при дви
жени и реагентов в режим�>х И В и И П :
а - реакциоЮJая зона, б - профиль
ко�щентраций комп онента А

движущая сила по-разному отличается
от реальной, то существенный разброс
оп ЬПll ЫХ данных относительно расчет
ной кривой неизбежен. Разумеется ,
учет Пр.П при определении движущей
силы дал бы лучшую сходимость и
большую достоверность расчета кине
тических характеристик.

Возвращаясь
к
влиянию
Пр. П на эффективность технологических процессов, подчеркнем, что

б

для любого ХТП, ско
рость которого
падает по мере его протекания, наиболее выгоден
В
режим И . Это ясно и из предыдущего пр имера с теплообме
ном при прямотоке ; еще более нагляден пример с химической

Рассмотрим химическую peaIO.J,ИIO 1 порядка: А � В. Просле
дим за судьбой произвольного элемента потока в РЗ, полагая, что
скорость реакции Vp завискr только от времени 't. Тогда

реакцией.

vp

=

d-c

d Uл

- --

= k Uл ;

(в)

здесь кон центрация Uл компонента А уменьшается во времени
(в этом смысл процесса) , поэтому пропорционально Uл падает
во времени скорость vP . Решение уравнения (в ) приводит после
разделения переменных и интегрирования (от О до 't и от на
чального U0 до текущего значения Uл в момент 't) к юtнети
ческому с оотношению

Uл = Uo e- k' .
(г)
Изменение концентрации Uл вдоль реакционной зон ы
(рис . 8.7, а) показано на рис . 8 . 7 , б: концентрация компонента А
U('t)

=

вдоль пуги l = Wt снижается от начальной (при l = О) до ко
нечной (при l = L). Если поток движется в режиме ИВ, то это
снижение Uл происходит постепенно - по экспоненциальной
кривой (И В), соответствующей приведенному в ы ше юtнети
ческому соотношению (r) . При движении потока в режи ме И П
падение Uл происходит скачком : вдоль всей длины реакцион 
ной трубюt устанавливается одинаковая концентрация Uл, рав
ная таков о й на выходе И� . Совершенно очевидно, что во всех
точках РЗ (исключая конечную) концентрация активного ком
понента Uл в режиме И В будет выше , нежели в режиме И П .

615

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Значит, и скорость реакции в случае И В вы ш е, чем при И П :
ип .
ив
vр > v
р '

(д)

при этом знак равенства относится только к точке на выходе
потока из РЗ, если считать, что конечные концентрации И� в

обо их случаях ( И В и И П ) - одинаковы. П о это му для заверше
н ия реакции до заданной степени превращения (заданн ой конечной концентрации

И� )

при И В потребуется меньшая дли 

на реакци о нной трубки, чем пр и И П : 4ш s L.m. Это ж е отно
сится и к объемам РЗ : Vив s VIOI·
Отно ш ение VIOI /Vив может служить мер ой снижения эф
фективности ХТ П при переходе от ИВ к И П . Это отношение
мало отличается от 1 при низ ких степенях превращения 11 ком 
понента А , но весьма существенно при высоких, как это видно
из сопоставления эффективности прото чного химического ре
актора для реакции 1 порядка при движении реагентов в режи
ме ИП и И В :
'1

Уиn /Vив

о

1

0,5
1 , 44

0,7
1 ,94

0,9
3,9 1

0,95
6, 34

0,99
21,5

0,99.9
1 45

0 , 9999
- 1 090

Сказанное выше ( И В - наиболее благоприятн ый режим) не
означает, что И П - наихудший из режимов. Во- пер в ых, в си
стемах , близких к И П , вы ш е интенсивность нормального по
перечного перемешивания (т. е. интенсивнее тепло- и массо
перенос ) , что при не очень высоких степенях превращения ил и
глубине массообмена может о казаться существеннее необходи
мого увеличения объема РЗ . А во-вторых, встречаются структу
ры потоко в (короткий байпас , застойные зоны - см. раздел
8 .7.2), приводящие иногда и к худшим результатам .
Подчеркнем, что проблема Пр . П в массообменных процес
сах (как и в химических реакциях) стоит о бычно острее , неже
ли в теплообменных. Дело в том , что в случае теплообмена
разности температур (движущая сила) на концах теплообмен
н ика не о чень малы ; для устойчивого теплообмена рекоменду
ется" поддерживать их не н иже � 1 0 градусов. Поэтому степень
использования движущей силы [в прямоточном теплообменни
ке, отвечающем схеме на рис. 8.6, это ( 1 - Лt2/Лt1 ) - аналог
степени превращения] здесь еще достаточн о далека от 1 . И ,
• Существуют исключения, когда разность температур теruюносителей под
держивается на уровне 2-3 градуса: холодообменники в циклах глубокого
охлаждения (с целью повышения полноты рекуперации холода); конденсаторы в
колоннах для разделения воздуха (чтобы избежать повышения да мения в ко
лонне) и др.

616

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

может быть, в этом случае для осуществления какого-либо
конкретного процесса теплопереноса окажется целесообразным
интенсифицировать перемешивание - поперечное (чтобы по
высить коэффициент теплопередачи k) , а с ним и продольное,
даже если это и приведет к необходимости некоторого увели
чения теплообменной поверхности F из-за снижения движущей
силы; кстати, увеличение F будет скомпенсировано (частично,
а возможно - и с избытком) возрастанием k.
В то же время массообменные процессы нередко проводятся
с очень высокими "степенями превращения" (степенями из
влечения компонента, например), приближающимися к 1
(выходные концентрации здесь близки к равновесным) даже в
большей мере, нежели это указано в приведенном выше при
мере. Поэтому потребуется весьма существенное (часто - за
пределами прие млемого) увеличение габаритов аппарата
(длины и объема ХТА) . Совершенно очевидно, что повышени
ем интенсивности поперечного (нормального) переноса не
удастся сколько-нибудь заметно скомпенсировать это увеличе
ние объема РЗ аппарата. Здесь необходимы меры, ограничи
вающие Пр. П .
При переходе о т малых (лабораторных) аппаратов к круп
ным (промышленным), т.е. при масштабировании аппаратуры,
интенсивность Пр . П обычно растет, так как возрастает попе
речная неравномерность потока (из-за трудностей его равно
мерного распределения по большому сечению) и усиливаются
обратное перемешивание и циркуляционные токи (из-за по
вышения масштабов и усложнения внуrреннего устройства
аппаратов). Эrо становится особо важным для аппаратов большой
единичной мощности: в них нередко заметно падает эффекrив 
ностъ процесса - мы говорим: при переходе к крупным аппара
там возникают масштабные осложнения. Здесь необходимо:
- стремиться уменьшить интенсивность Пр. П (улучшить га
зораспределение, ограничить турбулизацию потока вдоль его
движения и т.п.). В течение многих лет при инженерной про
работке аппаратуры проектировщики так и делали (зачастую,
правда, не формулируя для себя задачу в свете Пр.П): устана
вливали в крупных аппаратах перераспределители потока, пе
регородки, сетки, тарелки, секционируя аппараты конусами,
размещая насадку и т.д . ;
- постараться учесть интенсивность П р . П и его влияние н а
эффективность ХТП при переходе к крупным аппаратам: надо
знать, чего следует ожидать. В этих целях проводят
"гидравлическое моделирование" ХТА (см. разд. 8 .6).
617

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

8.3. СТРУКТУРА ПОТОКОВ
В СЛУЧАЕ ПРОСТЕ Й ШИХ ИДЕА/IЬНЫХ МОДF.ЛЕ Й

Поскольку свойство U = U('t), то степень завершенности
(эффективность) процесса (например, выход целевого продукта
химической реакции, степень приближения к равновесию в
массообмен ном процессе) зависит от времени пребывания •
от его величины, характера распределения. Рассмотрим перво
начально проблему распределения • применительно к идеали
зированным моделям ИВ и И П .
-

8.3. 1 . Идеальное вьпесненне

Время пребывания
длина РЗ, ее объем, масса вещества в
Обозначим: L, V, G
ней; w, V и G
скорость, объемный и массовый расходы по
тока (рис. 8.8).
При движении потока в режиме И В время пребывания всех
его элементов, перемещающихся с одинаковой скоростью w,
одинаково: • = •ив; физический смысл •ив очевиден : это время,
за которое элемент потока проходит РЗ. Значение •ив легко
найти: •ив = L/w. Это соотношение удобно представить в дру
гой форме, домножив числитель и знаменатель на поперечное
сечение потока f, тогда
L/ V
ив
•
wf v ·
Умножение на плотность р приводит к выражению
-

-

_
-

•ив =

Таким образом ,

=

Vp

Vp

=

G

G

'tив =

L v G
(8 . 1)
w v G '
причем чаще всего используют соот
ношение, содержащее V/V.
=

Рис. 8. 8. Рабочая зона и потоки

Кривые отк.лика
Движение потока в режиме ИВ можно наглядно представить
и наблюдать с помощью индикатора (трассера, метки)
ве
щества, легко определяемого химичесЮfм анализом; краски ;
порции подогретого потока и т.п . При этом трассер по своим
618
-

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 8. 9. Движение потока с трассером

по рабочей зоне в режиме ИВ при
его ступенчатом (а) и импульсном (б)
вводе

гидродинамическим характе
ристикам (плотности, вяз
кости и т.п.) во избежание
а
возмущения основного пото
ка должен быть близок к не
му, а ввод трассера не дол
жен сколько-нибудь заметно
влиять на движение самого
потока. Ввод трассера в РЗ
осуществляют
преимуще
ственно в двух вариантах.
б
1 . Пометим трассером в
начальный момент времени • =:
= О весь объем вещества V в рабочей зоне, а с момента • ;;::: О
станем подавать в нее постоянный (w, V = co n st) поток без
трассера. Тогда области меченого и немеченого потоков при их
движении в режиме ИВ будут четко разделены, граница между
ними (фронт) окажется плоской и резко очерченной (рис . 8 .9,
а). Эта граница в режиме И В будет перемещаться с постоянной
скоростью w (на рис. 8.9,а - слева направо); в момент времени
• она займет положение / = Wt. К моменту времени •ив все ме
ченые элементы покинут РЗ (L = Wtив) - рабочая зона будет
свободна от трассера. Описанный способ подачи трассера в РЗ
называют ступенчатым .
2 . Пусть по РЗ идет немеченый поток. В момент времени 't =
= О на вход в РЗ подадим небольшое (в форме короткого им
пульса) количество трассера. Эта узкая полоска (на рис . 8 .9,б заштрихована) будет в режиме ИВ, не размываясь, переме
щаться слева направо со скоростью w, так что к моменту вре
мени • она займет положение / = Wt, а к моменту времени •ив
окажется на выходе из РЗ: L = Wtив. Описанный способ подачи
трассера в РЗ называют импульсным .
Можно применить и другие варианты ввода трассера. Среди
них нередко выбирают какую-нибудь периодическую форму его
подачи , например типа прямоугольной волны или синусоиды.
В этих случаях (как и при ступенчатом и импульсном вводах)
результаты опыта достаточно просто интерпретируются мате
матически , причем в основе интерпретации - не столько ве
личина сигнала (амплитуда), сколько сдвиг по фазе; это удобно,
поскольку не требуется предварительной тарировки приборов.
619

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

С

Со ------

Рис. 8. 10. Кривые отклика на ступенчатое (а)

/ =L

и импульсное (б) возмущение при движении
потока с трассером в режиме ИВ.

Штриховыми л и ниями на виде б условно по
РЗ (/ =

казан сиmал импульсной формы на входе в
= О, " = О)

о �----t
t 11в
а

с

, ...

11
11
11
11

о

•

Существенно, что в режиме ИВ
форма возмущения потока трассе 
роJ.1 (сиrnал - ступенчатый или
какой-либо иной) не изменяется по
мере перемещен ия потока от точки
подачи сигнала (например, входа в
РЗ) до выхода из РЗ.

" l=L

Следить за движением трассера

по всей РЗ неудобно : трассер сов

б

сем не обязательно окрашен и
виден в аппарате с прозрачными
стенками, да и стенки аппарата
далеко не всегда прозрачны. Поэтому, как правило, концент
рацию трассера С фиксируют только на выходе из РЗ, подавая
на входе в нее сиrnал известной формы. Выходной сигнал C('t)
при / = L называют аrкликом, кривой аrклика, выходной функцией
ИJШ кривой. В случае ИВ кривая отклика повторяет (рис. 8. 10)
входной сиrnал без изменения формы, но с запаздыванием на
время 'Сив = L/w.
Кривые отклика при И В описываются функциональной за
висимостью, содержащей два параметра - время 'Сив и базовую
концентрацию Со, причем Со = тнfV, где ти - количество
трассера, поданного в РЗ при исследовании в ней структуры
потоков. Чаще всего при таких исследованиях используют сиг
нал импульсной формы. В этом случае функция отклика мо
жет быть охарактеризована следующим образом:
'С < •ив,

'С

= •ив,
't > •ив,

С= О ;
С = Со ;
С= О .

(8 .2)

Это означает, что до момента •ив возмущение (сиrnал) на
входе в РЗ не проявляется на выходе из нее. Выходной сиrnал
появляется в момент •ив· При этом время существования вы
ходного сиrnала Л't равно времени подачи его на вход в РЗ;
при бесконечно малом промежугке ввода трассера (идеальный
импульс) бесконечно малой будет и продолжительность выход
ного сиrnала - именно в этом случае справедливы выражения
(8 .2). После момента •ив, когда весь трассер покинул РЗ, на
выходе снова нет возмущения.
620

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Если налицо некая протяженность сигнала Л't :;; О , то выра
жен ия (8.2) подлежат очевидной корректировке скажем, С = Со
для отрезка времени 't = 'tив ± Л't/2.
Часто в целях обобщения для описания выходного сигнала
удобно пользоваться параметрическими критериями подобия
(безразмерными симплексами) 't/'tив и С/С0. Тогда характери
стика (8 .2) кривой отклика на идеальный импульсный входной
сигнал будет выглядеть следующим образом:
't/'tив < 1 , С/Со = О ;
't/'tив = 1 , С/Со = 1 ;
( 8 . 2 а)

't/'tив > 1 , С/Со = О .

В таком представлении модель не содержит параметров. Та
ким образом, И В - бесоараметрическая модель.

Результирующий эффект процесса Ирез
Каждый элемент потока в режиме И В проходит РЗ за время
'tив; поэтому степень его обработки составит· Ик = U('t ) 't= 'tиa =
= U('tив). Но поскольку все элементы потока при движении в
режиме И В будуг находиться в РЗ одинаковое время 'tив , то все
они будуг обработаны одинаково , так что результирующий эф
фект для всего ХТП запишется как

U �:З = U('tив ) .

(8.3)

Таким образом, располагая кинетическим законом измене
ния интересующего нас свойства U (концентрации, температу
ры и т.п.) во времени 't, по (8.3) легко определить значение U
на выходе из РЗ в случае И В . Для этого предварительно следу
ет отдельно - теоретически и (или) экспериментально - уста
новить кинетическую зависимость U = U('t) и затем подставить
в U('t) значение 't = 'tив ·
8.3.2. Идеальное перемешивание

Время пребывания
Разные элементы потока при его движении в режиме И П
находятся в РЗ разное время; поэтому здесь можно говорить
лишь о среднем времени пребывания 'tcp и о распределении эле
ментов потока по времени пребывания 't.
• Здесь и далее предполагается, что U зависит только о т

<t .

62 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Значение 'tcp рассчитывают (см. рис. 8 .8) из выражения ,
формально совпадающего с (8 . 1 ):

L V G
(8 .4)
-; = V = G
Важно: 'tc не аналог 'tив, т.е. формулы (8 . 1 ) и (8 .4) - не
идентичны. ействительно, 'tив
это реальное время пребыва
ния любого из элементов потока в РЗ, поэтому равенство 'tcp =
= 'tив для потоков И В тривиально; для всех других потоков 'tcp
- удобная расчетная характеристика. При одном и том же 'tcp
возможны различные Ирез - в зависимости от характера распре
деления элементов потока по 't.
Для установления закона распределения элементов по 't при
И П , т. е. функции распределения к('t) , будем базироваться на
объеме вещества V в РЗ и объемном его потоке V (см. рис . 8 . 8 ) .
Пометим мысленно все элементы потока в Р З в начальный
момент времени 't = О, как бы введя в нее (в режиме ИП
в
любую ее точку, практически - обычно на вход РЗ) определен
ное количество индикатора ти . Тогда он мгновенно (ИП!) рас
пределится в момент 't = О по всему объему рабочей зоны V,
так что его исходная (начало опыта, процесса) концентрация
составит С0 = ти / V. С момента 't � О станем подавать в рабо
чую зону постоянный поток V, не содержащий трассера. В от
личие от И В , при И П не будет четкого фронта - границы,
разделяющей меченый поток от немеченого; фронт будет раз
мыт по всей РЗ. По мере подачи немеченого потока во
входное сечение концентрация трассера в объеме РЗ будет
уменьшаться , поскольку трассер в РЗ не подается, но все время
покидает ее в смеси с немечеными порциями потока. Кон
центрация трассера С фиксируется только на выходе из РЗ
(кривая отклика), но в случае ИП (только в этом случае.� вы
ходная концентрация совпадает с концентрацией в РЗ . Иначе:
кривая отклика при И П является концентрационной характе
ристикой всей РЗ, поскольку закон изменения C('t) в выходном
сечении РЗ и в ее объеме один и тот же.
Пусть к моменту времени 't > О в РЗ осталась концентрация
трассера С < С0, так что доля первоначально помеченных час
тиц к < 1 ; при этом в случае И П к = С/С0, а С = C('t) - па
дающая во времени выходная концентрация, в каждый момент
времени равная концентрации трассера в объеме РЗ . Для опре
деления C('t) и к('t) составим материальный баланс по трассеру
для РЗ (это - пространственный контур) за время d't:
Приход трассера в РЗ
О Vd't.
CVd't.
Уход трассера из РЗ
Vd C.
Накопление трассера в РЗ

'tcp

Д

_

-

.

-

-

622

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Таким образом ,

+ О Vd't - CVd't = Vd C.
Разделяя переменные и интегрируя
с dC
tV
J - = - f - d't '
Со С
ОV

получаем, имея в виду V/V =
с
ln -

Со

=

После потенцирования
С = С0 е - t/'t cp

v

(а)

'tcp :

- - 't
V

с

= --

't

(б)

't cp

И - :к = е

- t/'t ер

Со

(8 .5)

Подчеркнем: поскольку соотношение к = С/Со справедливо
только для движения потока в режиме И П , то выражения (8.5)
характерны именно для И П .
Физический смысл к = к ('t ) применительно ко всему потоку:
это доля меченых элементов (от находившихся в РЗ в момент
времени 't О), оставшихся в РЗ к моменту времени 't ; соответ
ственно ( 1 - к ) - доля меченых элементов, покинувших РЗ к
моменту 't . С другой стороны, применительно к отдельному
элементу: к - вероятность того, что данный элемент останется
в РЗ время 't (и более), т.е. "возраст" элемента в системе ;
соответственно ( 1 - к ) - вероятность того, что данный эле
мент покинет РЗ системы к моменту времени 't.
=

Кривые отклика
Движение потока в режиме ИП
также можно наглядно проиллю
стрировать и проконтролировать с
помощью трассера. Но поскольку
здесь концентрация трассера в РЗ
и на выходе из нее в каждый мо
мент времени одна и та же, то речь
пойдет лишь об одном способе
подачи трассера. Очевидно, что
после ввода трассера в систему при
't = О его текущая концентрация С
в результате постоянной подачи

к

с

т

Рис. 8. 11. Кривые распределения (отклика) при
движении потока с трассером в режиме ИП:
а

- C(t) и к(t), б -к(t/tcp)

623

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

немеченой жидкости будет в РЗ и на выходе из нее постепенн о
умен ьшаться в о времени - о т первоначальной Со д о асимпто
тически при ближающейся к нулю при • � оо. Закон изменения
С(•), задан н ый уравнен ием ( 8 . 5 ) , показан на рис . 8 . 1 1 ; там же
даны кривые к (•) и к (•/•ср ) ·
С помощью приведен н ых зависимостей , например типа к (•) ,
нетрудно определить, какая доля элементов потока будет нахо
диться в РЗ системы в течение времен и от • t до •2 : эта доля
составит к 1 - к 2 (см . рис . 8 . 1 1 , а ) .

Результирующий эффект процесса Ирез
П родемонстрируем сначала общий подход к определению
Ирез· Эгот подход и полученные на его основе <;оотношения спра
ведливы для любых режимов течения, а не только для потоков,
движущихся в режиме И П и описываемых выражением (8.5).
Р ез ультир ую щи й эффект процесса Ирез рассчитывается с
учетом распределен ия элементов потока по •, т. е . с учетом к и
( 1 - к); в ч астности, для И П - это выражения ( 8 . 5 ) .
Если к моменту времен и • ра бочую зону покидает доля ме
ченых элементов ( 1 - к), то за время d• эта доля составит d ( l - к ) . В ведем новую функцию d ( l - к)/d• = <р (•), так что

d(l - к) =

d(l - к)
d't
dt

=

<p(•)d•;

функция <р (•) н азывается плотностью р а с п р еделения элементов
потока по времен и пре б ывания . Очевидно , <p(•)d• = d ( l - к)
та кже представляет со бо й долю элемен тов потока, находя 
щ ихся в РЗ время d• (т.е . от • до • + d•) . По определен и ю
(рис . 8 . 1 2 , а) :

f Ч>{•)d-r
t

= 1 - к;

'2

f q>{-r)d-r

Очевид но также , что при -r
так что
00

� оо

=

KJ

- к2 .

( 8 . 6а)

весь трассер покинет РЗ ,

(8 .6б)
f q{t)dt 1 ,
о
т. е . площадь под криво й <р (•) равна 1 , кривая <р (•) представляет
со бой нормированную фун кцию распределения .
Физ ически площадь под кривой <p(-r) - это все меченые
элементы потока, первоначально (в момент времени -r = О)
находившиеся в РЗ. Площадь под криво й <p(-r) от начала коор
динат до вертикали • (на рис . 8 . 1 2 , а
до -r = -ro) есть доля
мечен ых элементов, поюшувших РЗ к моменту -r = -ro . Соответ 
.
ствен но , элементарн ая площадка <p(•)d-r - это доля мечен ых
=

-

624

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

to

fqi(t)dt= l - Ко

о

t'

fqi(t)dt=

't1

о
t

q>( t)

l=L

=

к:г к 2

t+dt

о
q>(t)

а

о

б

в

Рис. 8. 12. К понятию о мотности распределения элементов потока по времени
пребывания q>(t):
а - pe)l(JtM И П , б -

общий случай, 11 - режим И В

элементов потока, покидающих РЗ за время d-c (т. е. в проме
жуrок от -с до -с + d-c) .
Понятие о q>(t) и присущие этой функции свойства справедливы не только
для движения потока в ре.жиме ИП (рис. 8 . 1 2, а), но и для друmх ре.жимов
течения. Этот тезис И.IVIюстрируется
рис. 8 . 1 2 , б для кривой отклика произ
вольной формы, полученной для некоего реального аппарата при импульсном
входном сиrnале. Смысл интеграла от О до текущего значения t = •о ·соответству
ет левому выражению (8.6а), полная мощадь под кривой равна 1 (как и должно
бьrrь для нормированной функции распределения) . Понятие о q>(t) остается
правомерным и для движения потока в режиме ИВ; отклик на импульсное воз
мущение имеет в этом случае специфический вид (рис. 8 . 1 2, в) : величина q>(t)
равна нулю при t < •и и при t > t ив А вот при t = tи8 эта функция уходит в
бесконечность. Такой вид зависимости q>(t) соответствует выражению (8.2).
Примечательно , что интеграл от q>(t)dt, взятый в определенной точке tив (т. е. от
tи8 - Лt до tи в
Лt при сколь угодно малых Лt), все равно равен 1 , как зто
должно бьrrь для нормированной фун кции распределения по (8.6б) . Такая
функциональная зависимость носит название дел•та-функцин Дирака, она для
рассматриваемого случая записывается в форме б (tив) . Эта запись означает:
функция равна нулю при всех значениях арI)'Ментов (здесь - при всех значени
ях t), кроме •ив; при •ив функция стремится к бесконечности, так что и нтеграл
(мощадь под " кри вой" бесконечно большой высоты q>(t) и бесконечно малой
ширины d t) остается равной 1. Таким образом , в случае ИВ q> (t) /
= б ( tи 1) .
t = 't и 1

в

·

+

Для рассматриваемого в данном разделе движения потока в
режиме И П значение <р (-с) может быть найдено дифференциро625

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

<P(t)
1

Рис. 8. 13. К расчету
потока в режиме ИП

tcp

l=L

ванием выражения (8.5):
=

о

Тер

Ирез при движении

t3
t2 t2+dt t3+dt

t

d(l

к) ип =

dt

-

q>(-r)ип =

�(1 - e-•/tc p) = _l_е -•/«т .
dt

t cp

(8.7)
При -r = О имеем q>(-r)ип = 1/"tcp ;
при -r � оо величина q>(-r)ип асимп
тотически стремится к нулю. В
промежугке q>(-r)ип изменяется экспоненциально.
Результирующий эффект в общем случае (не только для И П )
определяется п о адд итивности: учитывается эффект U(-r) к мо
менту времени -r и доля элементов, находящихся в РЗ в тече
ние времени от -r до -r + d-r . Иными словами (рис. 8 . 1 3 ) ,
Uрез = U(-r 1)cp(-r 1)d-r + U(-r 2 )q>(-r 2)d-r + U(ч)q>(tз)d (-r) + . . .
(б)
Суммирование ведется по всему диапазону изменения вре
мени пребывания элементов потока в РЗ - от О до оо, так что
если U зависит только от -r (заметим : так бывает не всегда), то
t1 t1+dt

«>

Ирез = J :U(-r)q>('t)d-r .

(8.8)
о .
При этом кинетическая характеристика конкретного процесса
U(-r) должна бьпъ известна заранее, а ПЛО11fОСТЬ распределения
q>(-r) соответствует струюуре потока в рассматриваемом аппарате.
При движении потока в режиме ИП выражение q>(-r) берется по
формуле (8.7). В этом случае выражение (8.8) принимает вид
.

.

.

(8.8а)
1- e-t/t cp dt -1- ju(t) e· t/tcp dt .
Ирез = ju(c) t cp
t cp O
О
Если кинетическая характеристика U(-r:) найдена и описана
=

математически, то нередко удается разрешить интеграл (8 .8а) и
получить аналитическое выражение для Ирез·
Выражение (8.8) остается правомерным и в случае движения потока в режи
ме ИВ . Дело в том, что по смыслу 15-фун кции для любой зависимости у
=
справед11И в о

f{x)

Хо
f >б(хо ) d х = f уб(хо ) d x + f >б(хо ) d х + f уб(хо ) d х =
О
О
Хо
(хо)
= О + У\х = х + О = у(хо ).
о

со

Поэтому общее выражение (8.8)
ранее ( 8 . 3 ) .

626

со

(в)

для режима ИВ превращается в полученное

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

8.3.3. Параметры кривых отклика и простейших моделей
продольного перемешивания
Кривые отклика простейших моделей продольного переме
шивания представлены соотношениями (8 .2) и (8.5). Из них
следует, что эти кривые (выходные функции) С = C('t) для мо
делей И В и И П зависят (по-разному, конечно) от двух пара
метров: Со и 'tив либо 'tcp · Это означает, что для различных ха
рактеристик процесса (количество трассера, объем РЗ, следова
тельно и Со; соотношение объема РЗ и потока V, а значит 'tив
либо 'tcp) будут получаться разные кривые отклика в натураль
ных координатах С - 't (рис. 8. 14, а). Такой разнобой в кри
вых отклика в пределах каждого из рассматриваемых режимов
течения неудобен в аспекте технологического расчета. Поэтому
переходят к безразмерным представлениям в форме связи сим
плексов С = С/Со и е = 't/'tив либо (что шире распространено,
так как выходит за пределы моделей ИВ и ИП) е = 't/'tcp · В
таком представлении кажд ая из простейших моделей описы
вается едиными зависимостями. В случае ИВ это несколько
модифицированная зависимость (8 .2а):
С = О при е < 1 ;

с

l=L

Со
о
с

't:�.

С()'
2

t�'в

3

ив

't:

С0 . С0
С'о

о

t� p
'

't:�p· t;p

't:

а

с

ив

l=L

о
с

о

0
ип

0

б

Рис. 8. 14. Кривые отклика в случае простейших моделей - И П , ИВ:

а - в натуральных координатах ( 1, 2, З
размерных координатах

-

разли чные эначеюtя Со

И· 'и••

'ер) , б

-

в без 

627

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

(8 .3б)
С = 1 при е = 1 ;
С = О при е > 1 .
В случае И П такого рода зависимость является модифика
цией второй из формул (8 .5):
(8.5а)
Таким образом , кривые отклика в натуральных координатах
(эти кривые характеризуются конкретными значениями пара
метров) сводятся к обобщенным представлениям - их называют
С-кривыми. Обобщенные зависимости (8.36) и (8.5а), показан
ные на рис . 8 . 14, б, не содержат параметров.
Итак: простейшие модели ИВ и ИП являются беспараметри
ческими. Будем именовать их моделями нулевого уровня. Отсуr
ствие параметров, обусловленное простотой самих модельных
представлений, приводит к наиболее простым расчетным соот
нош е ниям для определения Uрез (см . ниже). Однако простота
этих моделей сужает область их возможного использования
для описания стрfk'ТУJ>Ы потоков в реальных ХТА.
·

8.4. СТРУКТУРА ПОТОКОВ В РЕАЛЬНЫХ СИСТЕМАХ

В относительно редких случаях поток в реальных аппаратах
(в их РЗ) близок к И В или И П . Тогда его поведение близко к
рассмотренным ранее простейшим идеальным модельным си
стемам , и расчет ведут по полученным выше соотношениям.
Однако в большинстве реальных ХТС поток в РЗ аппарата в
той или иной мере перемешан. Наглядное представление о
структуре потока с ограниченным Пр.П можно, как и ранее,
получить с помощью трассера.
Будем на входе потока в систему подавать импульсное (это
удобнее) возмущение (сигнал), а на выходе экспериментально
снимать кривую отклика (рис. 8 . 1 5) . В зависимости от структу
ры потока в РЗ (т.е. от интенсивности в ней Пр.П) кривые
отклика будуг либо получаться ближе по форме к характерным
для И П (кривая 1) или для ИВ (кривая 2), либо существенно
отличаться от той или друтой (кривая J). По форме кривых
отклика можно качественно· (далее увидим - и количественно)
судить об интенсивности Пр . П потока в РЗ.
Возникает проблема качественного и количественного пред
ставления (описания) этих промежугочных случаев, когда Пр. П
существует, н о е го интенсивность ограничена. Можно заранее
предположить, что более сложным по форме кривым отклика
отвечают и более сложные математические описания. Здесь не
обойтись двумя параметраМii кривых ( Со и 'tив либо 'tcp) , потре628

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 8. 15. Кривые отклика:

ИВ и ИП - простейшие идеальные
модели; 1-3 - для потоков с ограни
ченным П р . П

l=L

буется большее их число . Со
ответственно и сами модели
потребуют введен ия некоторых
параметров.
Н иже рассмотрены два наи
о
't'ср ,Тив
более простых подхода к пред
ставлению таких "реальных"
систем - это тоже мысленные модели, но уже первого уровня,
они содержат по одному параметру. Эти модели призваны от
разить ограниченное Пр . П в рабочих зонах ХТА.
Модели первого уровня из-за своей относительной слож
ности рассматриваются в учебнике качественно - с анализом
подходов к их математи ческому описанию и наиболее важных
результатов, а также путей использования для технологических
расчетов. Более детально эти вопросы изложены в учебной и
научной литературе • .
8.4. 1 . Ячеечная (каскадная, ступенчатая, ... ) модель потока
с продольным перемешиванием

Сущность модели
Систему (аппарат, его РЗ) представляют (рис. 8 . 1 6) состоя

щей из ряда последовательных ячеек, ступеней (для простоты
- одинакового объема), причем в каждой из н их происходит
полное перемешивание потока, но между ступенями поток
движется только в заданном направлении.
Особо подчеркнем, что речь может идти об аппарате, дей
ствительно содержащем отдельные секции с интенсивным пе
ремешиванием потока в каждой из них; однако аппарат, канал
могут конструктивно и не содержать каких-либо ячеек, тогда
речь идет о мысленном (модельном) секционировании, призван
ном отразить конечную интенсивность Пр.П в рабочей зоне.
В представленном на рис . 8 . 1 6 аппарате бесконечно интен 
сивное Пр. П характерно для отдельных ячеек (в каждой ИП), но по всему аппарату (его РЗ) интенсивность Пр. П огра
ничена. В таком секционированном аппарате существует неко
торое распределение элементов потока по времени пребыва
ния, но здесь бdльшая (нежели в системах с ИП) доля элемен• См. например , ( 1 -5 ) .
,

629

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 8. 16. К ячеечной модели про
дольного п еремешивания:

сскциою�:рованный аппарат из
а
каскад аппаратов ячеек ИП , б
ячеек ИП
-

- i- 1 �-·�

-

тов имеет время пребыва
ния, приближающееся к
i
харакгерному для потоков
б
в режиме И В . ТаЮtм об
разом, секционирование
РЗ на ячейЮf ИП приво
а
дит к определенному выравниванию времени пре
бывания различных элементов потока в рабочей зоне аппарата
в целом. Причину такого выравнивания можно уяснить из сле
дующих соображений .
Пусть какой-то элемент потока быстро проскочит первую по
ходу ячейку РЗ: при И П в первой ячейке всегда имеется опре
деленная доля таЮtх элементов (пусть их 20%, т. е. доля 0,2).
Разумеется, с той же вероятностью (0,2) этот элемент может
быстро проскочить и вторую ячейку. Однако вероятность того ,
что и первую, и вторую ячейЮf быстро проскочит один и тот
же элемент потока, уже значительно меньше - как вероят
ность сложного события, составленного из двух независимых
простых (она равна произведению вероятностей простых собы
тий; в рассматриваемом примере это 0,2 · 0,2 = 0,04, т. е. толь
ко 4%). А вероятность того, что именно этот элемент потока
малое время задержится еще и в третьей, тем более в после
дующих ячейках, - крайне низка (для аппарата из трех ячеек
0,008, т. е. 0 , 8 %) . Скорее , элемент, быстро прошедший через
первую (тем более и через вторую) ячейку, дольше задержится
в последующих; это означает, что время его пребывания в РЗ
всего аппарата будет ближе к среднему (tcp), нежели в
"безьячеечной" рабочей зоне, т. е. с ИП по всему аппарату. Анало
гичн ые
рассуЖДения примен имы к элементу, долго задер
жавшемуся в первой (в первых) ячейке: вероятнее всего, он
быстрее пройдет последующие ячейЮf, так что время его пребы
вания в РЗ также приблизкrся к 'tcp· А выравнивание (неполное,
конечно) времени пребывания элементов потока в РЗ отвечает
постепенному переходу режима движения потока от ИП к ИВ.
Трактовка ограниченного продольного перемешивания в ас
пекте направленного движения потока через каскад ячеек И П
носит название ячеечной модели Пр . П (сокращенно Я М) .
Согласно принятым представлениям, интенсивность Пр .П в
реальном аппарате характеризуется числом расчетных ячеек п
-

630

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

(хотя в его РЗ четко вьшеленных ячеек может и не быть или же
их число , если они есть, может не совпадать с п ) . Если п = 1 ,
то м ы , очевидно, имеем дело
в режиме
с потоком
И П . При увеличении числа п режим движения потока начина
ет все более отличаться от И П , в РЗ уменьшается интенсив
ность П р . П . При п � оо (реально - можно считать, что при
достаточно больших п , например п � 50) поток движется в ре
жиме И В . В общем (промежуrочном) случае число расчетных
ячеек п, отражающее интенсивность Пр. П , есть параметр яче
ечной модели .

Ч исло расчетных ячеек п определяют с помощью специаль
но поставленных опытов (так называемое гидравлическое моде
лирование аппарата ) . Методы экспериментального определения
п применительно к конкретному аппарату и потоку в нем рас 
сматриваются в разд . 8 . 6 . 3 и 8 . 6 . 4 .
При изучении структуры потоков на основе ячеечной модели возможно
( если отмечься от наглядности ) оперировать и дробным числом ячеек: напри 
мер, п = 2,7 будет означать, что интенсивность Пр.П в РЗ выше, чем в аппарате
из трех ячеек И П, но ниже, чем в аппарате из двух таких ячеек.
Итак, согласно ячеечной модели :
при п � оо - поток движется в режиме И В ;
при п = 1 - поток движется в режиме И П ;
при 1 < п < оо - интенсивность Пр . П потока ограничена,
причем с увеличением п режим потока отдаляется от ИП и
приближается к И В .
Проиллюстрируем особенности и эффекты ячеечной модели
применительно к теплообмену (в свете примера и схемы, рас 
смотренных в разд. 8 .2 и на рис . 8 . 6 ) . При И В температурные
кривые для прямотока теплоносителей изображались жирными
линиями Т и t, а при ИП (в условиях сохранения тех же темпе
ратурных напоров - входного Л /1 и выходного Л t2 ) - штрих
пун ктирными. Пусть теплообменник теперь разделен на три
равные секции (/, 11 и 111) с поверхностями F/3 каждая , при
чем соответственно Я М в каждой секции (ячейке) потоки теп
лоносителей движуrся в режиме И П . Тогда мы получим (рис .
8 . 1 7) выравненные температуры в пределах отдельных секций со скачкообразным изменением Т и t (разумеется, и Лt;, где i номер секции) от секции к секции - пунктирные линии . При
этом лишь в 111 секции Лtш = Лtъ в двух других Лt1, Лtп > Лt2 .
Очевидно, что и средняя (для всего теплообменника) дви
жущая сила Лtср будет выше Л /2 (напомн им, что Лtср = Л /2 отве
чает И П по всему аппарату) , но останется ниже , чем при И В .
С возрастанием числа ячеек движущая сила Лtс р будет прибли
жаться к величине Лt1n, характерной для И В .
631

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

3

1

Рис. 8. 1 7. Профили температур
каждой секции:
1

-

в

II

IIl

F

/

трехсекционном теmюобменнике при ИП

И В , 2 - И П , З - Я М ; 1, 1/, 1/1 - сеl(ЦИИ (ячейки)

в

Расчетные соотношения.
Определение Ирез

Для ячеечной модели, как и для модели И П , вполне приме
нимы понятия о фун кциях распределения элементов потока
по времени пребывания к и q>. Однако если для И П к = к (t ,
•ер ) , то для ячеечной модели
к

=

к

('t , •ер• п).

(8.9)

При этом •с определяется здесь (как и для любых систем)
по формуле ( 8 .4) . Конкретные выражения для к (они различны
для разных значений параметров модели п) приводятся в лите
ратуре· . Получаются они (как и для одной ячейюt с И П пото
ка) из материальных балансов по трассеру для произвольной
ячейюt i (см . рис. 8 . 1 6 , а), где мгновен ная кон центрация трас
сера равна С;. Разница с выводом формулы (8 . 5) состоит в сле
дующем:
- в ячейку i входит поток, содержащий некоторую кон 
центрацию трассера С;-1 , тогда как в единичный аппарат (как
и в первую ячейку секционированного аппарата) входит поток
с С = О;
- объем вещества в одной ячейке теперь равен V' (в аппа
рате в целом, как и ранее в одиночном аппарате , - V) , причем
в случае одинаковых ячеек V' = V/n.

' См., например,

632

(2 ,

4,

5 ) и др .

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 8. 18. Плотность распределения

злементов потока по времени пребывания в РЗ (ячеечная модель);
цифры у кривых - число ячеек n)

Тогда для произвольной
i-й ячейЮ1, через которую
движется общий поток V,
материальный баланс по
трассеру для интервала вре
мени d't запишется так:

где при

i

+ Сн Vd't

==

<p("t)
1
tcp

tcp , t11в

1 (т.е. только для первой ячейки) первое слагаемое равно нулю.

t

(а)

Решение системы таких уравнений для всех п ячеек приво
дит (при известном 'tcp) к зависимостям С = C(i, 't), позволяю
щим определить концентрацию в i-й ячейке в произвольный
момент времени 't . Рассматривая такую зависимость примени
тельно к п-й (последней) ячейке, получим искомую выходную
функцию Cn ('t ). В дальнейшем от нее можно перейти к кон 
кретному (для заданного п) выражению типа (8.9).
Плотность распределения элементов потока по 't получается,
как обычно, дифференцированием: q>('t) = d(l - к)/d't; однако в
отличие от выражения (8.7), где для И П q> = q>('t , 'tcp), в случае
ячеечной модели, естественно, получаются формулы вида
q> = q>('t, 'tcp• п).
(8 . 1 0)
Заметим, что такие формулы возможно получить и непосредственно из
функций отклика Сп(t) . Связь к(t) и !p{t) с концентрационными зависимостя
ми C(t) устанааливается в разд. 8 .6. 1 и 8 .6 .4.

Конкретный вид выражений для q> (они тоже приводятся в
литературе по структуре потоков) определяется значением п.
Кривые q>('t) для различных значений п демонстрируются на
рис . 8 . 1 8 . Каждая из кривых q> является нормированной, ее
свойства математически и физически полностью соответствуют
выражениям (8.6).
Результирующий эффект процесса Uрез. в связи с изло
женным, определяется уже известным выражением (8.8), при
чем кинетическая характеристика рассматриваемого конкретного
процесса U('t), как обычно, должна бьrгь установлена заранее. Но
в отличие от потока с ИП, рассмотренного в разделе 8.3.2, в слу
чае ячеечной модели в качестве плотности распределения q>('t) в
интеграл (8.8) следует, разумеется, подставить выражение q> не по
формуле (8.7), а по фор муле (8. 1 0) - соответственно характерному
для данного потока числу расчетных ячеек п.
633

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

К достоинствам Я М относится ее наглядность, а также учет
секционирования, часто реально присугствующеrо в техноло
гических аппаратах. Основной недостаток - отказ от рассмот
рения реально существующего обратного перемешивания
(возвратных потоков) между секциями.
8.4.2. Диффузионная модель потока
с продольным перемешиванием

Сущность модели
Ограниченное продольное перемешивание может быть пред
ставлено по аналогии с явлениями молекулярной теплопровод
ности или диффузии . Известно (см. разд . 1 .3 .2), что количество
теплоты, перенесенной в единицу времени теплопроводностью

дt
дп

нормально к площадке f, составляет -Л. -f, а поток вещества

дС f
(здесь л. и Dд дп
коэффициенты теплопроводности и диффузии, дt/дп и дС/дп -

за счет молекулярной диффузии равен

-

Dд

градиенты температур и концентраций). В потоке с Пр .П речь
идет об эффективной теплопроводности или диффузии (их ко
эффициенты Л.3 и Е соответственно), интенсивность которых
может значительно превышать молекулярную (Л.3 > > Л. ,
Е >> Dд).
Представление ограниченного продольного перемешивания
в терминах эффективной теплопроводности или диффузии (по
аналогии с молекулярной теплопроводностью, диффузией) но
сит название диффузионной модели Пр.П (сокращенно ДМ).
Для уяснения сущности диффузионной модели удобно рас
смотреть (рис.8. 19) стационарное течение жидкости или газа
(расход V) в канале с равномерной по сечению РЗ эпюрой
осредненных во времени скоростей w (жирные стрелки на эпюре).
Это
течение
осложнено
обратным
перемешиванием
(мгновенные локальные - пульсационные
скорости , показан 
ные на эпюре тонкими стрелками), повышающим или пони
жающим в некий момент времени истинные (абсолютные) ло
кальные скорости элементов потока; в следующий момент кар
тина истинных локальных скоростей в общем случае будет
иной. Интенсивность обратного перемешивания (в данном
случае - продольного перемешивания в целом) будем характе
ризовать коэффициентом эффективной диффузии (про
дольного перемешивания) Е, так что поток вещества, по анало-

634

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

V. w

�---___....___,1- _
�·

ти

-А

а

t

·О

----

ив

-

--

----

профили ко�щеmраций
а
расчетная схема (потоки, сечеЮ1я , эпюра скоросrей) , б
трассера при ero непрерывной подаче в сечеЮ!е О - О в случае ДВИJkеНИЯ потока в режимах
ИВ, ИП и при оrраниченном продольном перемешивании (ДМ)

Рис. 8. 19. К диффузионной модели продольного перемешивания:
-

-

гни с молекулярной диффузией, составляет
-Е а с f
дп

.

Для установления параметра диффузионной модели предста
вим себе, что в сечение О - О (рис. 8 . 1 9) непрерывно подается
трассер в определенном количестве ти в единицу времени.
Полагаем, что в поперечном направлен ии (в сечении) поток
идеально перемешан .
Если бы поток двигался в режиме И В , то ниже сечения по
дачи О - О установилась бы постоянная концентрация трассера
С0 = ти / V, а выше этого сечения трассер бы отсутствовал: С =
= О. Если бы поток двигался в режиме И П , то во всем объеме
рабочей зоны установилась и непрерывно поддерживалась бы
постоянная концентрация Со = ти / V. Однако в рассматри
ваемом случае интенсивность Пр. П ограничена, так что ситуа
ция является промежуrочной между рассмотренными ранее
случаями: ниже сечения О - О при непрерывной подаче потока
V и трассера ти поддерживается постоянная концентрация С0 ,
а выше сечения О - О по мере удаления от этого сечения про 
тив потока V - концентрация С не равна нулю (вследствие
Пр .П), она постепенно понижается. В РЗ устанавливается ста
ционарный продольный профиль концентраций трассера, при
чем локальные значения С выше сечения О - О, помимо Со
(т. е. ти и V), зависят от значения Е.
В произвольном сечении А - А на некотором расстоянии l
от сечения О - О устанавливается определенная концентрация
трассера С. Она поддерживается постоянной, поскольку нисхо
дящий конвективный (продольный!) поток трассера CV пол635

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ностью уравновешивается восходящим его потоком за счет
обратного перемешивания Е( д С/д {)f Равенство этих потоков в
отсугствие Накопления трассера в сечении А - А (с учетом
уравнения расхода V = wf - после сокращения на / )
-

ас

wC = -Е -

д/

(8 . 1 1 )

позволяет определить параметр модели методом масштабных
преобразований. Реализуем метод в упрощенном варианте ,
сопоставляя левую и правую части равенства (8 . 1 1 ) в инте
гральной форме (и без учета знака "минус"):
wC .о - • Е

С .
/

(б)

Сократив на С и собрав вместе все оставшиеся входящие в
(б) величины, приходим к безразмерному комплексу - пара
метру диффузионной модели, называемому кркrерием Пекле для
продольного перемешивания, или эффективным критерием Пекле
Рез. Для всех подобных систем (течений, потоков) в сходствен
ных точках (сечениях, в аппаратах в целом)
Е

wl

Рез = - = idem.

(8 . 1 2)

Этот критерий аналогичен тепловому критерию Пекле Рет =
= wl/a (здесь а - коэффициент температуропроводности) и
диффузионному Ред = wl/Dд. Физический смысл критерия Рез
для продольного перемешивания определяется исходным урав
нением (8. 1 1 ): это соотношение потоков вещества [или про
пускных способностей соответствующих стадий wf и (Е//}/] за
счет конвективного переноса, характеризуемого скоростью w =
= V/f, и за счет обратного (продольного) перемешивания.
При высоких Рез (значит, при малой интенсивности Пр . П ,
т . е. низкой пропусююй способн ости обратного переноса; в пре
деле - при Е = О), теоретически при Ре � оо, продольным пере
мешиванием можно пренебречь: оно подавлено продольным кон
вективным переносом вещества, движущегося со скоростью w.
При малых Рез (значит, при высокой интенсивности Пр. П ,
т . е. существенно малой пропускной способности конвективно
го переноса; в пределе - при Е � оо) , теоретически при Рез =
= О, поток движется в режиме И П ; вын ужденная конвекция подавлена продольным перемешиванием.
При промежуrочных значениях О < Рез < оо интенсивность
Пр.П ограничена, причем с уменьшением Рез она возрастает.
Число Рез определяют опытным пугем (гидравлическое мо
делирование аппарата). Методы экспериментального определе636

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ния Реэ применительно к конкретному аппарату и потоку в
нем рассматриваются в разд. 8 .6.3 и 8 .6.4.
Иллюстрацией диффузионной модели применительно к теп
лопереносу в случае прямотока теплоносителей могуг служить
температурные кривые на рис. 8 .6 (пунктирные линии) . Чем
ниже интенсивность Пр.П (т.е. выше значения Ре3), тем ближе
пунктирные кривые к сплошным жирным линиям , отве
чающим движению теплоносителей в режиме И В . Соответ
ственно: средняя движущая сила Л tср при некотором конечном
значении Реэ (ограниченное Пр . П) превышает величину Л t2
(температурный напор при И П), но остается менее Лt1n
(средний температурный напор при И В). С возрастанием числа
Реэ наблюдается постепенное приближение Лtср к величине Лt1n.

Расчетные соотношения.
Определение Uрез
Значения функций распределения к и <р для диффузионной

модели могуг быть получены решением дифференциальных
уравнений переноса вещества с конвективным членом (эти
уравнения аналогичны изучаемым в курсе теплопередачи и
массопередачи уравнениям теплопроводности и диффузии) . В
случае однонаправленного переноса вещества, как это следует
из ( 1 .22) в отсутствие Источников и Стоков,

дС + w дС
a-t
az

=

Е

2
дС
az 2

(8. 1 3)

Путем сопоставления (масшгабные преобразования) конвек
тивного (второе слаrаемое в левой части) и диффузионного
(правая часть, выражает Пр.П) членов этого равенства также по
лучается параметр ДМ - критерий Ре3.
Формулируя граничные условия, соответствующие реально
му движению потока в ХТА (см., например, разд. 8 .7) , получа
ют различные конкретные решения
= C ('t, /) peэ . Положив в

С

этих

решениях l = L, приходят к искомым выходным функциям
Среэ ('t) . В дальнейшем от них можно перейти к выражениям вИда

к = к('t, 'tcp . Ре3),

а после дифференцирования по 't - к зависимостям
<р = <p('t , 'tcp, Ре3).

(8 . 1 4)

(8 . 1 5)

Заметим, чrо зависимости (8 . 1 5 ) возможно получить и непосредственно из
функци й отклика СРе ( 1 ) . Связь к(1) и <р(1) с концеmрационными зави с имо стя,

ми С( 1) устанавливается в разд. 8.6 . 1 и 8 . 6.4 .

637

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 8. 20. Плоrnость распределе
1
tcp

l=L

ния элемекrов потока по време
РЗ
в
пребывания
ни
(диффузионная модель; цифры у
кр ивых - значения Re3)

Для каждого значения
Ре3 получается своя зави
симость <p('t) . Разумеется,
при :Ре3 = О кривая <p('t)
совпадает
с характерной
о
t
tср,tив
для И П , а при Ре3 � оо с характерной для И В .
Типичные кривые <p('t) для закрытых (см. разд . 8 . 5 . 1 ) систем с
Пр. П , приведенные на рис. 8 .20, как и ранее, - нормирован
ные функции распределения со свойствами, математически и
физически отвечающими выражениям (8.6).
Результирующий эффект процесса Uрез определяется все тем
же выражением (8.8), но в качестве плотности распределения
элементов потока <p('t) под интеrралом должно фигурировать
выражение <р по (8 . 1 5) - соответственно характерному для
данного потока значению Ре3.
Достоинство диффузионной модели - в ее наглядности
(феноменологически здесь общая база с молекулярным перено
сом), а также в учете обратных потоков, как правило, реально
существующих в РЗ технологических аппаратов. Основной не
достаток применительно к некоторым типам аппаратов - иг
норирование секционирования, т.е. нарушения (затруднения)
обратного перемешивания в отдельных точках (сечениях) РЗ ,
обусловленного конструкционными особенностями аппарату
ры.
8.5. ОБЩАЯ ОЦЕНКА МОДFЛЕЙ СТРУКТУРЫ ПОТОКОВ
8.5. 1 . Сопоставление моделей продольного перемешивания
С конструктивной точки зрения при выборе моделей Пр . П
для описания структуры потоков целесообразно руководство
ваться следующими общими правилами.
К модели И В близки потоки в аппаратах с большим отноше
нием длины L к определяющему поперечному линейному раз
меру D (L/D >> 1 ) , например: аппараты с большим коли
чеством параллельных длинных и узких труб, некоторые аппа
раты с насадкой, в особенности с мелкой (неподвижный слой).
К модели И П близки односекционные аппараты с неболь
шим отношением L/D и интенсивным перемешиванием пото
ка, например : теплообменники с кипящей жидкостью (в част-

638

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ности, выпарные аппараты) ; сосуды с мешалкой; односекци
онные аппараты с псевдоожиженным слоем (если речь идет о
перемешивании твердого материала); как правило, и барботаж
ные аппараты (по жидкости) .
Ячеечной модели неплохо следует движение потока в аппа
ратах с достаточно выраженным секционированием при интен
сивном перемешивании в каждой секции; к таким относятся
(применительно к жидкой фазе) каскад смесительных аппара
тов (см . рис. 8 . 1 6 , б), тарельчатые (ректификационные, абсорб
ционные и др .) колонны (рис . 8 . 1 6 , а) и т. п.
Диффузионной модели могут близко следовать потоки в ап
паратах, не имеющих четкого секционирования и характери
зующихся ограниченным соотношением L/D; к таковым отно
сятся насадочные аппараты (с достаточно крупными элемента
ми насадки), барботажные (по rазовой фазе; по жидкой лишь при весьма низких расходах rаза) , распьmительные и не
которые другие аппараты; сюда же нередко можно отнести
структуру потока в одной ступени ХТА при не очень интен
сивном перемешивании (жидкость на тарелке и т. п.).
Для описания структуры потоков в некоторых аппаратах в
равной мере подходят ячеечная и диффузионная модели
(скажем, ХТА с нечетким секционированием). Вместе с тем
встречаются аппараты, для которых все представленные выше
модели Пр . П применимы весьма приближенно (см . разд. 8 .5.2).
Кривые, описывающие ячеечную или диффузионную мо
дель, наряду с •ер и Со содержат еще один параметр - п или
Рез. Модельные описания в обобщенной форме характеризуются
одним параметром (п или Рез). Таким образом, Я М и ДМ одно
параметрические модели, иначе - модели первого уровня.
Поскольку обе модели - ячеечная и диффузионная - при
званы охарактеризовать ограниченную интенсивность Пр . П , то
в расчетном аспекте представляет интерес переход от одной
модели к другой, т.е. связь параметров моделей п и Рез. При
этом следует учесть, что указанные модели подходят к описа
нию Пр . П потока с разных физических позиций (здесь можно
говорить об известной формальности подходов и математиче
ских описаний); поэтому полной идентичности при пересчете
(п � Рез или Рез � п) ожидать нельзя. Необходимо также
иметь в виду, что согласно ячеечной модели (см. рис . 8 . 1 6) на
границах ХТА (на входе в него, на выходе из него) полностью
отсутствует Пр. П - поток четко направлен (на рис . 8 . 1 6 , б слева направо) . Поэтому ячеечную модель правомерно при
ближенно сравнивать лишь с закрьП'ой диффузионной моде
лью, когда на обеих границах РЗ (см . рис . 8 . 19) отсутствует
Пр. П (оно есть лишь внутри РЗ) . ОrкрьП'ые или полуоткрьпые
-

639

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Второй

уровень

О О О

уровень

0�00

ypOii ёiЬ
i
Нулевой

1
1

1

.....

ям

/

..... ..... ....

/

/ '-

/
1
1
/
' .J..
1 ',

1
1

/

1
1
1

дм

t

ив

ип

Рис.В. 21. Связи моделей ра.ии чноrо уровня.

Стрелки

-

пуrи (нацписи

-

условия ) предельных переходов

(с наличием Пр. П на одной из границ) ХТА сопоставлять с
ячеечной моделью - неправомерно.
Совершенно очев Ид но, что в предельных состояниях
(простейшие модели) должно соблюдаться однозначное соответ
ствие параметров ячеечной и диффузионной моделей :
поток в режиме И В : п � оо , Рез � оо ;
(8 . 1 6)
Рез = О.
поток в режиме И П : п = 1 ,
Для режимов с ограниченной интенсивностью Пр. П реко
мендуется следующая приближенная связь параметров п и Рез,
неплохо отражающая переход от одной модели к другой и не
противоречащая предельным их соотношениям по (8 . 1 6):
Ре 3
Рез � 2(п - 1 ) ; п � + 1.
(8. 1 7)

2

Из (8 . 1 7) следует, что модели первого уровня в предельных
ситуациях переходят в модели нулевого уровня . Наглядно такие
переходы илл юстрируются
рис. 8 .2 1 : стрелки и сплошные
линии, снабженные надписями, указывают условия и пути пре
дельных переходов. Связи рассмотренных моделей с моделями
более высоких уровней (штриховые линии) будут затронуты в
разд. 8 .5.2.
8.5.2. Общая оценка моделей продольного перемешивания
Потоки в реальных ХТА весьма редко следуют основным
Идеаль ным моделям ИВ и И П . В ряде случаев поведение этих
потоков удается неплохо описать с помощью ячеечной и диф640

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис.8.22.

Некоторые
модели
продольного перемешивания:
с ко
с засrо йной зоной , б
а
с рециркуля
раnсим байпасом, г
ци ей межцу я чейками ИП
-

-

-

фузионной моделей. Од
нако на практике встре
чаются случаи,
когда
Пр. П потока не уклады
вается и в эти модельные
представления.
Тогда
приходится прибегать к
6
более сложным модель
а
ным описаниям, содер
жащим большее число
параметров (это их недо
статок), но зато лучше
отражающим
реальную
в
структуру потоков в ХТА
(это их достоинство).
Рассмотрим качественно (рис. 8 .22) некоторые из таких мо
делей более высокого уровня на примере аппаратов с псевдо
ожиженным слоем (ПС).
1. Поток с застойной зоной зернистого материала может воз
никнуrь в ПС при скоростях ожижающего агента, близких к
скорости начала псевдоожиже ния w0 . Из-за неравномерного
газораспределения в слое возникает зона (на рис . 8 .22, а
заштрихована), плохо доступная газовому потоку. Скорость
газа в ней ниже w0 , так что частицы здесь неподвижны (или
малоподвижны); обмен частицами между застойной зоной и
остальным слоем затруднен. В аспекте структуры потока твердо
го материала (ТМ), непрерывно вводимого в аппарат и выво
димого из него, в рассматриваемой ситуации на И П псевдо
ожиженного ТМ в основной области слоя наложено существо 
вание застойной зоны со слабым перемешиванием твердых час
тиц. Такая модель будет харакrеризоватъся двумя параметрами:
долей объема слоя, занятого застойной зоной, и скоростью обмена
твердьlМИ частицами между этой зоной и основным потоком ТМ .
Для потоков с застойными зонами обычно характерны
длинные хвостовые участки выходной кривой. Их появление
вызвано затрудненным обменом частицами с застойной зоной:
при использовании меченых частиц (трассера) они очень мед
ленно вымываются потоком немеченых частиц из этой зонЬ1.
При устремлении объема застойной зоны к нулю или ин
тенсивности обмена ее частицами с Ядром слоя - к бесконеч-

641

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ности двухпараметрическая модель с застойной зоной перехо
дит в модель ИП.
2. Поток с коротким байпасом может возниюtуrь в неодно
родном ПС при высоких скоростях ожижающего аrента, когда
значительная доля газа проходит (рис. 8.22, б) через ПС с вы
сокой скоростью в виде пузырей, причем в простейшем случае
газ в пузырях совсем не контаюирует с твердыми псевдоожи
женными частицами в слое. Параметром модели здесь будет
дOJIJI газа, проходящего через РЗ (т. е. через ПС) без контакта с
твердой фазой (например, с катализатором). В более сложных
случаях (они ближе к реальной ситуации) приходится вводить
еще один параметр, учитывая также интенсивность обмена газом
между пузырями и основным потоком ожижающеrо агента в ПС.
Для потока с коротким байпасом хара1СГерно быстрое появ

ление заметной концентрации трассера на выходной кривой; в
дальнейшем выходная кривая может иметь различную форму в зависимости от хара1СГера основного потока в РЗ.
При устремлении доли байпасирующего потока к нулю или
интенсивности его обмена веществом с основным газовым по
током - к бесконечности рассматриваемая двухпараметриче
ская модель переходит в модель более низкого уровня. Она в
случае псевдоожиженного слоя может перейти в модель И П ,
если газ идеально перемешан (так бывает, когда ТМ обладает
сильными адсорбционными свойствами); возможен переход и к
модели И В (когда ТМ такими свойствами не обладает). В про
межугочных ситуациях возможен переход и к ДМ.
З . Поток с рециркуляцией твердого дисперсного материала
хараюерен для многоконусного аппарата с ПС (рис. 8.22, в). В
каждой конической секции здесь твердый материал идеально
перемешивается, но между секциями он в целом движется лишь
в одном направлении (сверху вниз); кроме того, реально су
ществует обмен между секциями. Таким образом, в аппарат
сверху подается и снизу из него отводится поток G, между сек
циями вверх идет поток твердого материала Л G, а вниз G + Л G.
Здесь дополнительным (к числу секций п) является параметр
Л G/G. Очевидно, что при Л G/G ..-. О рециркуляционная модель
переходит в ячеечную.
Из приведенных примеров видно, что модели более высоко
го уровня в предельных условиях не всегда переходят в модели
следующего (более низкого) уровня. В ряде случаев при пре
дельных переходах происходит перескакивание через уровень
(например, от модели второго уровня к модели нулевого).
Разумеется, рассмотренные модели мoryr отражать струюу
РУ потоков не только в аппаратах с псевдоожиженными систе
мами. Потоки с застойными зонами (и не обязательно дискрет642

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ной фазы, но также и сплошной среды) нередко встречаются в
аппаратах с неподвижным слоем и в некоторых других, когда в
какой-то зоне аппарата затруднено движение потока, например
из-за повышенного гидравлического сопротивления . Потоки с
коротким байпасом нередки в барботажных аппаратах при несо
вершенном газораспределении, при существовании зон или
участков с пониженным гидравлическим сопротивлением. По
токи с различного рода р ециркуляцией (нередко - с весьма
сложной конфигурацией циркуляционных зон) встречаются
достаточно часто (пример - роторно-дисковые экстракцион 
ные колонны, сушильные аппараты с организованной цирку
ляцией по зонам и т. п.).
Следует особо упомянуть о двухоараметрической диффузион
ной модели. В отличие от однопараметрической (она использует
только один параметр - Ре3, базирующийся на Е), двухлара
метрическая ДМ учитывает перенос вещества не только в про
дольном, но и в поперечном направлении. Поэтому здесь наряду
с коэффициентом продольного перемешивания Е1 фигурирует
еще и коэффициент Ея, харакrеризующий интенсивность по
перечного (радиального) перемешивания. Появление двухпара
метрической ДМ обусловлено тем, что в некоторых аппаратах
распределение элементов потока по времени пребывания су
щественно зависит от интенсивности радиального переноса. И
поэтому эффективность процесса в таких ХТА в значительной
мере определяется поперечным переносом (теплоты, вещества
и т.п .). Он может быть затруднен, и тогда диффузионные (при
переносе теплоты - термические) сопротивления радиальному
переносу игнорировать нельзя; он может быть достаточно ин
тенсивен , и тогда надо учитывать выравнивание интенсивных
свойств потока (температур, концентраций и др.) в поперечном
сечении. Эти эффекты и учитываются коэффициентом Ея (в
случае теплопереноса - коэффициентом эффективной ради
альной теплопроводности А.я). Примерами здесь могут служить
химические процессы с высокими тепловыми эффектами в
трубках с неподвижным слоем катализатора (отвод теплоты
через слой и стенки трубок) или химические превращения в
ламинарно движущихся тонких жидкостных пленках (заметное
выравнивание концентраций реагентов по толщине пленки) .
Для описания реальных потоков в ХТА приходится приме
нять и более сложные -комбинированные - модели.
При выборе , создании и использовании модели необходимо иметь в виду,
что путем увеличения ч исла ее параметров почти всегда возмо жно математиче
ски описать имеющиеся экспериментальные данные - даже вне зависимости от
физическо й обо с нованности модел и (именно так нередко де йствуют экспери
ментаторы , с каж ем, при соста мении регрессионных моделей ) . Умечение мно
rопараметрическими моделями не только усложняет математичес ко е описание и
643

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

расчеты, но и может сопровождаться потерей физическою смысла явления .
Разумеется , такие модели - не про пю зны , их использование за пределами
условий проведенного эксперимента далеко не всегда правомерно, здесь вполне
вероятны ошибочные выводы и суждения. Принято считать , что в общем случае
(специфические ситуации здесь не рассматр иваются) число параметр ов модели
не должно превышать четь!рех.

8.6. ОБ ЭКСПЕРИМЕНТАЛЬНОМ ИЗУЧЕНИИ
ПРОДОЛЬНОГО ПЕРЕМЕШИВАНИЯ
8.6. 1 . Общие положения
Экспериментальное изучение структуры потоков (прежде
всего построение кривых отклика) позволяет:
- качественно судить о структуре потока, т.е. о близости его
в рабочей зоне к И В , к И П или к какому-либо иному режиму
движения;
- выбрать модель, наилучшим образом отвечающую реаль
ной структуре потока в РЗ аппарата;
- количественно оценить (иногда - найти достаточно точ
но) значения параметров моделей (например, п или Ре3), необ
ходимые для последующих расчетов ХТП, в частности - для
определения к('t), <p(t) , а затем и Upe3 ;
- количественно оценить некоторые другие характеристики
потока в РЗ (см. разд. 8.6.2).
Эксперимент для установления структуры потока обычно
проводят в "холодном" модельном аппарате, т.е. в отсутствие
тепло- или массообменного процесса либо химической реак
ции, являющихся действительной целью промышленного ХТП .
При этом варьируют масштабы аппаратуры - вплоть до габа
ритов промышленных образцов. Такое структурно-гидравли
ческое моделирование позволяет выбрать подходящую модель
Пр . П , найти значения ее параметров (или их зависимость от
габаритов аппарата) и определить функцию <p (t), с тем чтобы в
дальнейшем можно было рассчитать реальный ХТП с исполь
зованием соотношений типа (8.8). Разумеется, такой подход к
моделированию на " холодных аппаратах" правомерен , если есть
уверенность, что сам " горячий" процесс (тепломассообмен, реак
ция) не внесет существенных изменений в струкгуру потока.
Основной метод изучения структуры потоков - подача
трассера (индикатора) на вход РЗ и фиксация во времени вы
ходных кривых. Наиболее часто используют импульсный
(практически мгновенный) ввод трассера; далее анализируют
форму кривой отклика. Напомним: при вводе трассера в коли
честве ти и объеме рабочей зоны V базовую концентрацию С0
обычно рассчитывают по формуле
(а)
Со = ти / V.

644

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

а

6

в

Рис. 8. 23. Кривые отклика в на1)'ральных (а), полубезразмерных (б) и безразмер
ных (в) координатах

Кривые отклика (рис. 8 .23) представляют:
- в натуральных (размерных) координатах "концентрация
С - время 't" (достоинство - наглядность);
- в полубезразмерных координатах "приведенная концент
рация С = С/Со - время 't" (здесь начальной точке 't = О отве
чает С = 1; в ряде случаев такое представление удобнее для
анализа и расчетов) ;
- в безразмерных координатах "приведенная концентрация
'
с
п риведенное время е = 't/tс ; (здесь абсциссе 't cp отвечает е =
=
1 ; расчетные выражения в этом случае обычно получаются
проще - сравним, например, формулы 8.5 и 8.5а) .
Очевидно, при импульсном вводе трассера кривые отклика
при И В будут иметь вид короткого импульса в момент времени
't = 'tcp = 'tив (либо е = 1), а при ип - форму затухающей экс
поненты, соответственно выражению (8.5). В потоках с ограни
ченной интенсивностью Пр . П кривая отклика будет промежу
точной (см. сплошную линию на рис . 8.23) межцу выходными
кривыми ИВ и И П .
Для установления связи кривщ отклика с функциями распре
деления к и ер представим эти кривые в полубезразмерных ко
ординатах С = С/ Со - 't.
Напомним, что приведенное в разд. 8 . 3 .2 соотношение к =
= С/Со справедливо только для модели И П , когда параметры
системы в РЗ совпадают с таковыми на выходе из РЗ . В общем
же случае характеристика к относится к РЗ в целом, а концент
рация С (или q - к выходному сечению РЗ.
Связь к и ер с выходными характеристиками С, С получим из
следующих соображений. Общее количество введенного в РЗ
трассера равно C0V. К моменту времени 't в рабочей зоне ХТА
остались его доля к и количество СоVк . С другой стороны, в
момент времени 't из РЗ уходит мгновенный поток трассера
CV, а за время d't - его количество C Vd't. Тогда к моменту
-

645

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

времени 't рабочую зону покинет количество трассера, равное
't

J CVd't .

о

Материальный баланс для РЗ (это и есть пространственный
контур) по трассеру за временной интервал от 't = О до теку
щего 't запишется в общей манере ( 1 .8); в отсуrствие Источни
ков и Стоков: + Пр - Ух = Нак, так что
't

+ О - J CVd't = С0 Vк - С0 V· l .

о
Следующее из (б) равенство

(б)

't

CoV(l - к ) = J CVd't

(8 . 1 8)
о
устанавливает связь к и С для момента времени 't.
Преобразование равенства (8 . 1 8) приводит к ряду полезных
соотношений. Вынося постоянный поток V из-под интеграла и
учитывая, что V/V = 'tcp . находим
't

Co( l - к )'tср = J Cd't .
о

(в)

Отсюда для 't � оо (при этом к � О) получаем неочевидное
равенство (одна из форм полного - за время от О до оо - ма
териального баланса по трассеру для РЗ) :
ас

Co'tcp = J Cd't .

(8 . 1 9)
о
Запишем теперь (8 . 1 8), внеся под интеграл постоянный объ
ем рабочей зоны V и базовую концентрацию Со:
't c v

(r)
1 - к = J -- d't .
о Со v
Поскольку V/V = 'tcp• 't/'tcp = 8, а С/ Со = С, из ( r) находим
связь к и С(8) :
0

а также соотношение

1- к = J C(8) d8 ,
о

1- к =

f C(t) d't .

О 'tcp

(8 .20)

(8 . 2 1 )

Сравнивая это соотношение с первым из выражений (8.6а) ,
получаем связь <p('t) и C('t):
(8 .22)
<p ('t) = C('t)/'tcp ·
646

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Из (8.22) следует также, что C(8)d8 = <p ('t)d-c; соответственно
t
J C(e)de J <p(-c)d-c . Эти равенства, разумеется, справедливы и

0

о

=

при

-с,

8

о

� оо .

Заметим , чт о последняя из установленных связей позволяет представить об
щее выражение (8.8) в форме

И !>С1 = f U ( 0) C (0)d0 .
о
ао

(8.8б)

Итак, по выходным кривым можно судить о функциях распре
деления элементов потока по времени пребывания к (-с) и <р (-с).

8.6.2. О среднем времени пребывания
Среднее время "tcp пребывания элементов потока в РЗ может
быть рассчитано по приведенной выше формуле (8.4). Вместе с
тем "tcJ> можно определить по экспериментально полученной
кривои отклика. Представим ее в натуральных координатах С
- -с и выделим (рис. 8.23, а) элементарную площадку Cd-c
(заштрихована) . Момент этой площадки относительно оси ор
динат (-с = О) составит -c Cd-c. Среднее время пребывания "tcp
наЙдем, используя теорему о среднем , записанную для всего
диапазона времени от О до оо:

J -с Cd-c = "tcp f Cdt .

00

00

о

Отсюда

о

f t Cdt

00

"tcp =

,
_о00
f Cdt
_
_

(8.23)

о
причем интегралы вычисляются по экспериментальной кривой
(каким-либо известным методом - трапеций и т. д.).
Разумеется , можно воспользоваться также идентичной записью:
00

tcp = f tq>(t) dt ;

(8.23а)

о

к этому последнему выражению можно прийти адд и тивным сложением произ
ведений элементов потока q>(t;)dt на соответствующие t; в полном временном
диапазоне от О до оо - подобно тому, как это было сделано при определении
Иреэ в разд. 8 . 3 . 2 . Еще проще оно получается , если знаменатель (8.23) заменить
по (8. 19) и внести постоянные Со и tcp под знак интеrрала. С учетом (8.22) при
ходим к (8.23а):
ао

'tcp

f t Cdt
C dt = '° -=-dt
С
о
= ."f tq> ( t) dt.
= -= "'f t ft
Co t cp о Со t cp о t cp
о

647

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Выражение (8 .23) может оказаться полезным для проверк.и
материального баланса, т.е. сходимости значения "tcp с вычис
ленным по формуле (8 .4), иначе - надежности эксперимен
тальной установки и измерительной техн ики. Кроме того , вы
ражение (8 .23) может оказаться эффективным способом уста
новления "задержки" (удерживаю щей способности) в двух- и
многофазных потоках. Дело в том, что объем РЗ , занятый опре
делетюй (i-й) фазой Vi, заранее не задан (известен лишь общий
объем рабочей зоны V). Поэтому для определения среднего
времени пребывания для i-го фазового потока формула типа
(8 .4) непригодна: в выражении "tcp/ = V; / Vi известен лишь кон
тролируемый поток Vj. Кривая отклика, снятая дм поток.а i-й
фазы , позволяет по (8.23) найти "tcpi· А воспользовавшись затем
формулой (8.4), нетрудно рассчитать задержку для этой фазы: V; =
= Vi "tcp;, а если нужно, то и относительную задержку V;/V.
8.6.3. К выбору модели и определени ю ее параметров
Прежде чем рассчитывать результирующий эффект процесса
по формуле (8.8), следует установить, какая из моделей про
дольного перемешивания пригодна для описания реального
потока в данном аппарате, а если речь идет о параметрической
модели, то определить еще и численные значения этих пара
метров (например, п для Я М, Ре3 для ДМ) . Это позволит ис
пользовать к.онк.ретное - по (8.7), (8 . 1 0), (8 . 1 5) и т. п. - выра
жение для q>("t) либо С(8), необходимое для расчета Uреэ· При
этом кинетическое уравнение U = U("t) для рассматриваемого
технологического процесса устанавливается отдельно .
Выбор модели и определение ее параметров ведуr пуrем со
поставления экспериментальной кривой отклика с расчетной
по соответствующей модели - такое сопоставление удобно
вести в безразмерных координатах С - 8 (рис. 8 .24).
Будем далее для определенности оперировать однопарамет
рическими моделями . По форме полученной из опыта (сплош
ная линия) выходной кривой судят о типе модели . А далее
стремятся подобрать такие значения параметров модели ( п или
Ре3), чтобы расчетная кривая (штриховая линия) наилучшим
образом совпала с экспериментальной. Если это удалось, значит
модель выбрана удачно (говорят: модель адекватна реальному
процессу), а численное значение параметра (п, Ре3), отвечающее
рассматриваемому обьекrу, можно считать установленным.
Основная проблема здесь в том, как выбрать модель, подо
брать ее параметры, наилучшим образом отвечающие реальному
потоку, т.е. экспериментальной выходной кривой. Здесь су
ществуют разные подходы.

648

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 8.24. Сопоставление кривых отклика:
1
эксперимешальная кривая, 2
четная (модельная) кривая
-

-

рас-

С

1 . Экспериментальная и рас
четная (теоретическая - по вы
бранной модели) кривые откли
ка пересекаются в нескольких
точках. Можно взять за основу
выбора п или Рез пересечение
кривых в какой-либо обуслов
ленной отдельной точке (например , при -r = 'tcp либо в точке максимума С, и т.п.). Достоин
ство метода - простота; недостатки:
- разные точки перес�:: ч ения экспериментальной и модель
ной кривых отвечают разным значениям параметров п и Рез;
это означает, что величины п, Рез получатся различными в
зависимости от того, какая точка будет выбрана для сопостав
ления; неопределенность (субъективность) такого подхода очевидна;
- ошибка опыта для данной точки суmественно сказывается
на значениях п (или Рез), поскольку эти параметры моделей
весьма чувствительны к экспериментальным погрешностям.
2. Экспериментальная и модельная выходные кривые срав
ниваются по мноrим точкам - это сводит к минимуму погреш
ности опыта для отдельных точек. Тогда нужно подобрать та
кие значения п (или Рез), чтобы вся расчетная (модельная)
кривая совпала с опытной "наилучшим образом" . В этих целях
предварительно строят сетку теоретических кривых например ,
по · ячеечной модели для разных значений п (или по диффузи
онной модели - открытой либо закрытой - для разных Рез,
либо по какой-нибудь иной модели, физически подходящей к
рассматриваемому случаю, со своим набором параметров) . На
эту сетку накладывают экспериментальную кривую отклика,
вычерченную в том же масштабе . Если эта экспериментальная
кривая "хорошо" совпадает с какой-либо из модельных, харак
теризуемой определенными значениями параметра, то вы
бранная модель - адекватна, а ее параметры - определены. Ес
ли хорошего совпадения нет, то сравнение повторяют для
другой модели.
Недостаток метода - не столько в трудоемкости заготовки
сеток для различных моделей Пр. П , сколько в неопределен
ности суждения о "хорошем совпадении" кривых отклика экспериментальной и расчетной (модельной).
Совпадения кривых можно было бы добиваться , базируясь
на методе наименьших квадратов, т. е. минимизируя расхожде-

649

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ние экспериментальной и модельной (расчетной) кривых пуrем
подбора оптимального значения параметра принятой модели.
Однако этот метод не только трудоемок, он еще предполагает
одинаковую значимость всех точек; но ведь в действительности
экспериментальные "хвостовые" точки (при высоких 't, когда
концентрации трассера уже малы и погрешность их определе
ния велика) - менее точны . А разную значимость ("вес") раз
личных точек учесть весьма непросто.
Из изложенного следует, что нужно стремиться учитывать
всю кривую отклика (много ее точек), но делать это надо как
то иначе.
8.6.4. Определение параметров моделей
методом моментов
Сущность метода. Наиболее часто при выборе модели и
определении ее параметров прибегают к методу моментов. Этот
метод уже применялся в курсе, например при определении
координат центра давления - разд. 2 . 1 .4; при выводе основно
го уравнения центробежного насоса - разд. 3. 3.1 ; в настоящей
главе при определении 'tcp - разд. 8 .6.2. Здесь он используется
более широко, причем в основном на базе безразмерных вели
чин С(е). В самом общем плане смысл метода моментов при
менительно к задачам структуры потоков состоит в сравнении
моментов - экспериментально найденного и рассчитанного по
соответствующей модели продольного перемешивания.
Напомним необходимую для последующего анализа терми
нологию метода моментов. Начальным моментом кривой
(здесь - кривой отклика) называется полная сумма моментов
элементарных площадок C(8)d8 относительно начала координат
во всем диапазоне изменения е (в общем случае - от О до оо) .
Так, k-й начальный момент безразмерной кривой отклика за
писывается в виде

м:
При

00

k

=

мg = f C(8)d8 ;
М 10

о

00

о

О

=

00

о

f e k C(8)d8 .

получаем

при

k

=

момент

(8 .24)
нулевого

порядка

момент первого порядка

= f 8 C(0)d8 , и т. д.

Наряду с безразмерным может бьпъ записан начальный момент размерной
кривой отклика; в общем случае k-ro порядка

Mt

650

" f 1.tC(1)<:t1
о

(8.24а)

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

0

Нередко используют таюке централ"нwе моменты - размерные и безразмер 
ные, отсчитанные от t "" tcp и "" 1 :

(м.t )ц

=

r (t - t cp (C( t) dt

и

(м2 ) ц

=

r(0 - l)'t C(0)d0 ·

(8.24б )

В настоящем разделе использованы начш�ьные моменты.

Нормировка моментов. При переходе от размерных кривых
отклика C(t) к безразмерным С(е) удобно оперировать норми
рованной (к единице) функцией, как это сделано в разд. 8.3.2
для функции распределения c:p(t). В соответствии с физичесЮf
ми предпосылками (разд. 8.3.2, 8.6. 1 и 8.6.2), в последующих
преобразованиях нулевой и первый безразмерные моменты
должны быть равны единице:

мg

=

"'

J c (e) de

о

=

1 и

м�

=

"'

J e c (e) de

о

=

1.

(д)

Найдем условия нормировки. В этих целях выразим безразмерные перемен
ные через натуральные.
Для момента нулевого порядка

М00

Для

=

"' с

f0 Со

t
dtcp

=

1
-f C(t)dt
Co t c p 0
"'

момента первого порядка

1
М•
Cot cp 0

= --

=

.
1,

тогда

d -1- = -1- J1 C(1)d1 = -Co t �- м 1• = 1 ; тогда
м � fo -t c1-p �
Co t c p C0t�p o
=

1·

м 0•

= с o t cp

.

(е)

м 1• C o t � . (ж)
=

Согласно (е ) и (ж) приходим к условиям нормировки по известным
(найденным) кривым отклика и их натуральным моментам MJ и М1' :
(з)
Заметим, что полученное математическими преобразованиями первое из вы
ражений (з) совпадает с (8.23), полученным выше из физических соображени й .
Как уже указывалось, найденное по кривым отклика значение tcp следует со
постави ть с рассчитанным по (8.4). Аналогично, найденное по этим кривым
значение Ч> надо сопоставить с рассчитанным по формуле (а) . При обнаруже
нии неприемлемых расхоЖдений нужно искать причину выявленного несоответ
ствия (в работе аппаратуры и измерительной техники) .
С помощью найденных по (з) значений tcp и Ч> осуществляют переход от
натуральных величин С и t к безразмерным С и 0. Функция распределения
станет при этом нормированной , так что ее нулевой и первый моменты (д)
будут равны еди нице.

С(0)

Найдем некоторые последующие безразмерные начальные
моменты для простейших идеальных моделей продольного пе
ремешивания .
Безразмерные начальные моменты. Для модели И В определим
сразу момент произвольного (k-го) порядка, имея в виду, что в
65 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

данном случае е = 1 = co n st (см. рис . 8 .23, в):
00

00

о

о

м : = J l k C(8)d8 = l k f C(8)d8 = 1 .

(и)

Значит, для ИВ начальный момент любого порядка равен
единице.

Для модели И П можно проверить равенство единице моме1Пов нулевого и
первого порядков, используя ( 8.5а) :

1°

М8 = j e-8d0 - е-0 "' = е- 0 = 1;
00
о

м?

о

=

- е -0

1

I0 e-0d0 = 0(-e-0) \�- (-Ie-0d0)

И1Пеrрал моме1Па

=

=

М 10

=

0+1 = 1 .

взят "по частям'". и = IJ ' dv

=

)

(й)

е - 0 d0 '· du = d0 '

v =

Разумеется, проведенная проверка была необязательной, поскольку ранее
бЬVIИ введены и выполнены условия нормировки.

Для модели ИП определим начальный момент второго по
рядка, также используя интегрирование по частям, обозначив и

= е2, dv = e - 0 de ; du = 28d8, v = - е - 0 :
м� = e 2e-0 de = -e 2e- 0 - 2 - ee- 0 de = 0 + 2 = 2 .

r

1;

)

(I

(к)

поскольку последний интеграл, найденный выше [см. (й)] , ра
вен 1 .
Аналогично найдем для И П момент третьего порядка, обо
значив и = ез, тогда dи = зе2dе. Действуя в прежнем ключе
(при тех же dv и v), имеем

М! =

re 3 e -0 de = -8 3е -0 1 ; - з(-Ie2e-0 de) = о + 3 .

2 = 6 ' (л)

поскольку последний интеграл, найденный выше [см. (к)] , ра
вен 2.
Аналогичным образом, но путем более громоздких преобра
зований отыскиваются моменты различных порядков для мо
делей с одним, двумя или бОльшим числом параметров. Значе
н ия (выражения) первых четырех моментов для моделей И В ,
И П , Я М и ДМ (закрытой) приведены в табл . 8. 1 .
В литературе приводятся моменты и для других моделей .
Так, для открытой ДМ

8
2
М0 = 1 + - + р
еэ
2
Рез2
652

,

(м)

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

мя беспараме'J11ИЧеских и одиопараметрических моделей

Таблица 8. 1. HaчaJJJ.иwe безразмери�1е моме1n1о1

Моде.ль
ив
ип
ям

Мо

Мз

Моме 1пы

1

l

2

1

ДМ
(закрьпая)

6

l + � + �2

+ _!_
п

(Реэ - I + е -Р•э )
l + --2_
Ре ;
3
2 +М 20 = 1 +
2

l

+

6

3

-

п п
( Ре32 + Реэ

-

4

Ре3
+ 3Ре3 е -Р•э + 4 е -Р•э )

+

для полуоткрытой ДМ

(н)
Рез
Пуrи идентификации модели. Для выбора модели Пр.П и
определения ее параметров используем табл. 8 . 1 . Прежде всеrо
следует проверить, не подходят ли для описания структуры
потоков простейшие беспараметрические модели - И В и И П .
Достаточно точное мнение о б их пригодности можно высказать
на основании формы экспериментальной кривой отклика. При
необходимости можно представить эти кривые в безразмерных
координатах и определить значение момента второго порядка:
если
мало отличается от 1 , то поток движется в режиме,
-

Ре з

М!

М!

близком к И В ; если
приближается к 2, это указывает на
высокую интенсивность Пр .П, т.е. на близость к И П . В тех
случаях, когда форма кривой отклика явно не следует кривым
для ИВ и ИП либо расчет приводит к значениям моментов, не
характерным для простейших моделей, приходится прибегать к
однопараметрическим моделям - Я М или ДМ. В этом случае
определяется какой-то момент экспериментальной кривой от
клика и по нему рассчитывается параметр модели - на осно
вании приведенных в таблице теоретических формул , соответ
ствующих этому моменту.
Следует иметь в виду, что значения параметров моделей,
вычисленные по моментам различных порядков, не совпадают
между собой . С одной стороны, это указывает на несовершен
ство метода моментов. Но с другой стороны, это обстоятель
ство позволяет внести некоторую определенность в выбор по
рядка момента для расчета, а также в установление надежности
(адекватности) принятой модели.
653

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Н аиме нее точн о в о п ытах определяются ко н центр а ции н а
,
хво сто в ых уч астках кривых откл и ка . Следовательно погреш
ность в определен ии э кс периментал ьного момента возрастает
с увеличением его порядка: неточные зн ачения кон центраций
ум н о жаются на бол ьшие расстояния до оси о рдинат (" плечи " )
в высоких степен ях. П оэтому, что бы не вносить в расчет пара
ьз
метро в мод ели бол ьшую погрешн ость, следует испол о вать
м о менты наиболее низ ких п орядко в. Н о нуле во й и пер в ый
мо менты уже испол ьзованы для н ормиро в ки кривой отклика
при ее при вед ении к безразмерн ому виду. Знач ит, в од нопара
метри ч еских мод елях Я М и ДМ параметр ы целесообразно
определять по момента м второго порядка ; при этом будут по
луч аться ч исло расчетных яч еек п и число Пекле Ре 3 , наилуч
шим о бразом отве чающие описанию экспериментальной кри
вой откл ика в рамках Я М и ДМ с о ответственно . Предпо чтение
од н ой из этих моделей отдается путем сравнения моментов
следующего (в рассматриваемом примере - третьего) порядка : для
какой из моделей (Я М ил и ДМ) расчетный момент при найден
нь�х значениях п и Ре3 ближе к экспериментальному, та модель
лучше (аде кватнее) оп исывает струкгуру пото ка в аппарате.
Если од но п араметри ческая м одель оказывается не п риемле
мой для о п исания Пр . П в ап парате, обращаются к двухпарамет
р ической модели . Здес ь для о пределения параметро в пр идется
пользоваться моментами второго и третьего порядков , решая их
как систему двух уравнений для определения двух неизвестнь�х
параметр ов. Если при это м возможно несколько конкурирующих
модельнь�х описаний Пр. П , то адекватность будет устанавли ваться
по моментам следующего (четвеJУГОГО) порядка.
И так, конкретный анализ струкгуры потока на основании
имеющейся кривой отклика ведется в такой последо вательности :
- по экспери ментальн ы м кривым отклика в ы числяют натуи
ральные моменты
и определяют значен ия норми

М�

м:

р ующ их п араметр ов 't cp и С0 ; с о поставляют их ( п роверка на
де жности работы аппаратуры и измерительного комплекса) с
найденн ы ми по V, V и ти, V;
- с помощью найденн ых 'tcp и Со переводят кривые отклика
в безразмерную форму; р ассчиты вают безразмерные моменты
мg и

м� '

убеждаются (про вер ка правильности вычислений) ,

что о ни равн ы ед ини це ;
- по в иду кривых отклика или н а основе расчета моментов
второго порядка делают заключение о пригодности простейших
мод елей - И В и И П ;

654

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

- если упомянуrые модели не подходят (наиболее частый
случай), то рассматривают однопараметрические модели, опре
деляя по моментам второго порядка значения п и Ре3;
- по моментам третьего порядка проверяют адекватность
однопараметрических моделей и выбирают лучшую из них;
- если ни одна из однопараметрических моделей не подхо
дит, то рассматривают двухпараметрические модели, следуя тем
же принципам, и т.д.
На основании изложенного в настоящей главе общий путь
расчета ХТП с учетом Пр.П представляется следующим. На

холодной модельной установке (т.е. в отсуrствие технологиче

ского процесса) с помощью трассера снимают кривую отклика,
по которой определяют параметры модели (например, п или
Ре3). При известных значениях параметра модели записывают
конкретный вид выражения для <p('t) по (8. 1 0) или (8 . 1 5) . А да
лее, располагая заранее известной (найденной с помощью не
зависимого эксперимента) кинетической характеристикой U(t) ,
рассчитывают по уравнению (8.8) результирующий эффект тех
нологического процесса Ирез ·
Еще раз подчеркнем, что расчет Иреэ по (8.8) правомерен ,
если U зависит только от 't. В противном случае необходимо
учитывать зависимость U от ряда параметров процесса
(например, от температуры t, если U зависит от нее и t изме
няется - во времени, по длине проточного аппарата).
8.7. СТРУКТУРА ПОТОКОВ
В ТЕХНОЛОГИЧЕСКИХ РАСЧЕТАХ

В разд. 8 .2 указано, что игнорирование Пр. П приводит к
ошибочной трактовке закономерностей ХТП . И в этом одна из
причин часто отмечаемого ухудшения показателей многих
ХТП , полученных на лабораторных и пилотных установJ<ах,
при переходе к крупным промышленным аппаратам .
Часто практикуемый расчет ХТП без учета Пр. П обусловлен
двумя основными причинами.
1. Непонимание (незнание) технологами самой проблемы
структуры потоков. Это связано с пробелами в их обучении
(понятия и закономерности Пр.П стали вводить в учебные кур
сы лишь в последние годы) и с традициями (стереотипами) в
подходах к технологическим расчетам: практически проще рас
считывать ХТП вне связи с Пр.П и затем вводить найденные
из опыта эксплуатации "поправочные коэффициенты" типа
КПД или других коэффициентов незнания.
655

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

2. Объективная сложность анализа ХТП с учетом структуры
потока (такой анализ зачастую приводит к весьма громоздким
расчетным соотношениям) и одновременно недостаточная из
ученность явления Пр.П для широкого многообразия техноло
гической аппаратуры (отсутствие сведений об адекватных мо
делях Пр. П применительно к конкретным ХТА и о значении
параметров моделей в зависимости от конструктивных и ре
жимных характеристик реального аппарата).
Надо также понимать, что психологически очень непросто
отбросить многое из того (традиционные подходы, норма
тивные методы, эмпирические формулы), что было накоплено
и привычно использовалось на протяжении многих десятиле
тий. К тому же надо иметь, чем все это заменить. А наука о
ПАХТ здесь лишь в начале пути . . .
Цель настоящего раздела - иллюстрация подходов к расчету
некоторых несложных технологических ситуаций с учетом
Пр . П . Отдельные примеры таких подходов содержатся также в
ряде последующих глав.
8. 7 1 Химическая реакция в потоке
Будем рассматривать поток, движущийся со скоростью w
внутри реакционной трубки длиной L; в потоке происходит
известная объемная химическая реакция . Требуется сопоста
вить результаты процесса при движении потока в отсутствие и
при наличии Пр. П .
Обратимся сначала к движению потока в простейших режи
мах ИВ и И П . Будем считать движение и химическое превра
щение одномерными (в любом сечении потока - полное попе
речное перемешивание) .
Пусть в потоке протекает изотермически и без изменения
объема химическая реакция первого порядка; ее математическое
описание представлено в разд. 8.2 выражениями (б) и (в). Воспро
изведем здесь эти выражения, обозначив концентрацию реагента
символом С. Уравнение реакции с константой скорости k 1
.

.

dC

(а)
k1C ,
d't
откуда при концентрации во входном сечении С0 получаем
после разделения переменных и интегрирования до текущего
момента времени •
(б)
Поскольку речь идет об одномерном непрерывном процес
се, в котором поток движется по реакционной трубке с посто
янной скоростью w, то связь текущих координаты / и времени
• выразится в виде / = W't или • = l/ w.
- -

656

=

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Если движение происходит в режиме И В , то время пребы
вания элементов потока (любого и всех вместе) в реащионной
трубке
= L/w, так что конечная концентрация реагента на
выходе из трубки составит
Срез = Сое - k1 � и1 = Co e-k1 (L/w) .
(8 .25)
Если движение потока происходит в режиме И П , то соответственно (8.8) и (8 .7) либо сразу по (8.8а), с учетом 'tcp = L/w,
1 1 1qi d = Со 00f е -( k1 + l/�cv )� d 00
ре з = 00f r--(
'-"!' t ) dt - f Со е - k11 - е - /
't 't

'tив

с

О

=

_

_

О

e
't cp k 1 + 1/r. cp
Со

'tcp

1

'tcp O

k 1 't cp + 1
С0

-( k1 + 1/1cv ) � °
00

k1 (L/w) + 1
Со

. (8.2 6 )

Сопоставление значений Срез в случае И В (по 8 .25) и И П
(по 8 .26) показывает, что при одинаковой длине реащионной
( Срез)
трубки L справедливо равенство-неравенство (
Таким
обра
�
ип,
причем знак равенства отвечает ситуации L ---+
зом, при И В реащия проходит глубже, нежели при И П . Еще
нагляднее сопоставление длин реакторов при И П Lип и И В Lив
(или , что то же самое , - объемов реакторов Уип и Уив ), необхо
димых для обеспечения одинаковых степеней превращения 11 =
= 1 - Ср е з /Со . Отношение Lип /L
при задан
ив = Уип / Укв
ном значении 11 нетрудно получить из (8 .25) и (8 .26):
(в')
11 = 1 - е -k1 (Lи. /w) ; Lив = � ln -1-

с0ез)ив
•

k1

и

"=1Отсюда

1

k 1 {Lип /w) + l
L иn
L ив

= Уип

; Lип
-

=

1 - тt

тt�-

k1 1 - тt

(в")

(8 .27)
1
ln -1 - тt
Именно по этой формуле рассчитаны отношения Уип /Vив
для различных значений 11 в разд. 8 .2.
Пусть теперь установлено (опытами с трассером и расчетом,
например с помощью метода моментов), что поток в реащи
онной трубке движется с ограниченным Пр. П , причем его
структура отвечает Я М с числом ячеек п = 2. Для этого случая
в литературе приводится следующее выражение типа (8. 10):
( ) 4't е -2 �;�ср
(г)
ер 't = -V

= 1
ив

't c

p

тt

.,

n

2

657

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Определение Срез будем вести по формуле (8.8а):
с

рез

f С -ki 't Фt

00

=

О

2 е

ое

• ер

_ 4С о 00
f -(k1 + 2/'t cp)'t d
't - 2 О 't e
't .

-2't/'tcp d

(д)

Тер

Этот интеграл проще всего взять по частям, обозначив

и

=

't, dv

=

=

е -(k1 + 2 / 't )'t , так что du d't, v
-(k1 + 2 / 'tcp)'t
-1
----- е
.
k1 + 2 /
ер

=

=

'tcp

Тогда, избавляяс ь от знака "минус" и меняя местами преде
лы интегрировани я, имеем
с

рез

=

[
'�

--

4С о

Р

•

1

k1

4С0

+

2/• ср е

-(k1 + 2/'tcp)'t

't� {k1 + 2/'tcp) 2

lo

+

2 1°
00

е -(k + / 't )
1

1

k1 + 2/• ср

cp t

оо

=

Со

f -(k1 + 2/'tcp)'t d

00

О

( k1;cp

]-

• -

е

1

Степень превращения будет определена как Т\
1 - Срез /Со.
Расчеты показывают, что для одинаковых L в этом случае
значение Т\ получается промежуточным между найденными по
формулам (8 . 5) и (8 .26):
Т\ЮI � Т\ям � Т\ив·
(е)
В случае реакции иного (т-го) порядка плотность распреде
ления <р(т) должна быть наложена на кинетическую характери
стику соответствующей химической реакции, получаемую инте
грированием уравнения скорости этой реакции:
=

2

-

dC
dт

=

km C m

(ж)

Последующий путь анализа аналогичен показанному выше.
8. 7 2 Распределение элементов потока по времени пребывания
при гравитационном течении тонких пленок
.

.

Будем рассматривать проблему применительно к движению
5, плотностью р , вязкостью µ,
стекающих вдоль вертикальной плоскости под действием силы
тяжести (рис . 8 .25, а). В ламинарно движущейся пленке обрат
ное перемешивание, естественно, отсуrствует. Однако различ
ные слои жидкости (элементы потока) движутся в пленке с
·

ламинарных пленок толщиной

658

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис.8. 25. К устаноалению
функции распределения q>(1)
при rравитационном тече
нии тонких пленок:
расчетная схема, 6
а
плотность распределения эле
мешов n<лока по времени
пребывания

-

-

.

разными линейными
скоростями
здесь
налицо
в ыраженная

поперечная неравномер
ность. Поэтому эле-

L

у

dy

а

б

ментам
пленочного
потока присуще некое распределение по времени пребывания,
отвечающее характерному профилю скоростей. Его и необхо
димо учитывать при анализе и расчете технологических про
цессов в пленке, устанавливая функцию распределения q>(t).
Напомним, что в наиболее простом случае (в отсутствие
воздействия газового потока) профиль скоростей описывается
уравнением (2 .42):

-

( _ У822 ) ,

w = pg (2>6 - y 2 ) = w11 2y
8
2µ

(з)

где w, = pgli2/2µ
скорость на rранице пленки с газом , она в полтора раза пре
вышает среднюю скорость wcp.

Плотность распределения <p(t) найдем, исходя из физическо
го смысла элемента вероятностей q>(t)d't: это доля от общего
жидкостного потока V0, время пребывания которой сосредото
чено в промежутке от 't до 't + d't. Если в начальный момент ('t =
= О)
мысленно пометить элементы в верхнем (входном) се
чении пленки (это отвечает импульсному вводу трассера) , то
через отрезок времени 'ta = L/w6 рабочую зону покинут элемен
ты , движущиеся на границе пленки с газом. При увеличении
времени сверх 'ta из РЗ будут уходить элементы, движущиеся
ближе к стенке. К некоторому моменту 't РЗ покинут все эле
менты правее сечения у; при этом на расстоянии у от стенки
скорость w рассчитывается по формуле (з), так что речь идет о
моменте времени 't = L/w. Если времени дать приращение d't,
то за это время элементарный расход жидкости, покидающей
поперечное сечение РЗ толщиной dy, составит d V.
Запишем материальный баланс по меченой жидкости
(трассеру) для пространственного контура шириной Ь и тол
щиной dy (см. рис. 8 .25, а) за время d't: Прихода трассера в
этот контур нет, Уход из контура составляет d V, Накопление
659

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

выразим как долю от общего потока Тогда в отсуr
ствие Источников и Стоков соответственно общим принципам
составления балансов

Voq>('t)d't.

+о

-

d v = Vo<f> ('t)d't ,

откуда получается общее выражение для плотности распределе
ния в потоках с поперечной неравномерностью:
1

<f>('t)

=

_

dV

_

V0

d't

.

(8.29)

НаЙдем теперь конкретное выражение q>('t) для течения тон
ких пленок. Время пребывания в РЗ элементов потока, находя
L

L

щихся от стенки на расстоянии у, составляет по (з)
't = W =

w0

( : �:) ( : �:)
2

82't

ts

2

-

Отсюда возможно выразить у через
0
у 2 - 28у + --

't

=

О и у

=

(и)

-

't:

8-8 1-i

п

(к)

't

причем знак "плюс" перед радикалом при решении квадратно
го уравнения отброшен , поскольку у :s; 8.
Для дальнейшего анализа при подстановке в (8.29) величины
V потребуется знать
дифференцируем правое из выраже
ний (к):
Ots
(л )
dt .
dy

d

dy;
=

-

2t 2 Jl - t 8 /t

Далее можно найти все фрагменты формулы (8.29). Полный
расход жидкости на участке шириной Ь составляет

Vo = WсрЬ8 = 32 Ws Ь8.

(м)

Элементарный расход через бесконечно малое сечение Ьdу
равен

2у - у 2 ) Ьdу.
d V= wЬdy = w8 (8
2

(н)

8

Если здесь заменить выражение в скобках по ( 11) · и подставить
по (л), то

dy

d V -660

[

o
't Ь w0 't

O't l)

2t 2 J1 - t 0 /t

J

dt

=

- W o Ot � b

2 t 3 JI - t 0 /t

dt

·

(о)

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

С найденными выше значениями V0
тельно в соответствии с (8 .29)
<р

('t) =

4 't з

3 't �

и

d V получим оконча

�1 - 't:

(8.30)

Нетрудно убедиться, что q{t) по (8.30) представляет собой

нормированную функцию распределения :
""

""

J q>(t)d't J q>('t)d't 1 .

о

=

=

15

(п)

Вид этой функции представлен на рис. 8 .25, б. Обращаем
внимание, что на участке от О до 'ts значение функции q>('t) = О;
это полностью соответствует физике явления : при 't < 'ts ника
кие меченые элементы, введенные во входное сечение в мо
мент 't = О, рабочую зону еще не покинут.
Выражение q>('t) по (8.30) должно быть наложено на кинети
ческую характеристику U('t ) рассчитываемого процесса
(химическое превращение, тепло- или массообмен) для опре
деления его результирующего эффекта в соответствии с форму
лой (8 .8):

Ирез

=

""

J U ('t) q>(t)d't ;

15

(р)

при этом на временном отрезке от О до 't5 , как показано выше,
= О ,и потому

q>('t)

�5

J U('t)q>('t)d't = О .

о

8. 7 3 Конвективный теплообмен
при ограниченном продольном перемешивании одного
из теплоносителей
.

.

В разд. 7.6 и 7.7 рассматривался теплообмен при движении
теплоносителей в двух простейших (предельных) режимах И В и И П . Теплообмен при ограничен ном Пр.П теплоносите
лей не затрагивался из-за достаточной сложности преобразова
ний и конечных выражений. В завершение настоящей главы
проанализируем этот вопрос применительно к одной из срав
нительно простых технологических ситуаций : теплообмен меж
ду конденсирующимся паром (его температура Т - постоянна) и
холодным потоком (пропусю:�ая способность Gc), движущимся с
ограниченным продольным перемешиванием (оно характеризуется

66 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

f

т
... ----.
...- -....F I--'-..-

Рис. 8.26. К расчету теruюобмена между кон
денсирующимся паром и наrреваемым пото
ком, движущимся с оrраниченным продоль
нь�м перемешиванием

эффективным коэффициентом про
дольной
теплопроводности
Л.3) .
т
df
Пусть коэффициент теплопередачи
k известен (примем его не завися
s
щим от интенсивности Пр.П).
о .__..._--т_........
...
,,..,.
..,,
___,
..
G ,
Поставим одну из задач проекти
с
t
т
рования : необходимо найти величину теплообменной поверхности F
при заданных температурах холодного теплоносителя на входе
в аппарат (t') и на выходе из него (/") . Конкретнее: требуется
установить, как интенсивность Пр.П влияет на величину этой
поверхности .
Расчетная схема представлена на рис. 8 .26; она близка к
рассмотренной в разд. 7.6 на рис . 7.2 1 , б, но здесь налицо про
дольный ("кондуктивный") перенос теплоты за счет Пр . П .
Тепловой баланс для элементарного контура " к" с поверх
ностью теплообмена d/ при движении холодного теплоносителя
в режиме ИВ (продольный конвективный теплоперенос с про
пускной способностью Gc в отсуrствие Пр. П показан на ри
сунке простыми стрелками) запишется так:
+ Gct + d Q - Gc(t + dt) = О и d Q = Gcdt.
(с)
Величина d Q для элементарной поверхности d/ выражается
формулой
(т)
d Q = k( T - t)df
Подставим d Q по (т) в (с), разделим переменные :

k( Т - t)d/ = Gcdt, � = !5.._ d/

T - t Gc
и проинтегрируем (при Т = const) от t' до t" и от О до полной
поверхности Fo (индекс при F указывает на принадлежность
анализа к рассматриваемому режиму течения, т. е. Л.э = О):
kFo l Т - t'
Gc l Т - t'
= n
n
(8.3 1 )
и F.о =
т - t"
т - t"
k
Gc
Пусть теперь холодный теплоноситель движется с ограничен 
ным Пр.П. Тогда при составлении теплового баланса для кон
тура "к" необходимо учесть и продольный эффективный
("кондуктивный") перенос теплоты (стрелЮI с кружками на
концах) с пропускной способностью, основанной на тепловом
662

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

потоке Л. э � S' где х - координата вдоль потока,

S-

dx

его по

перечное сечение (см . рис . 8 .26). В рассматриваемом случае
тепловой бал а нс имеет вид
+

Gct + ( - Л. dt S)
dx
э

d Q - Gc(t + dt)

+

- (-Л.э

d
(t + dt) SJ =
dx

О . (у)

Для удобства последующих преобразований введем понятие
об удельной поверхности теплообмена /о, приходящейся на
единицу длины теплообменника : F = fo l, f = fox. Тогда d Q =
k( Т - t)df = k( Т - t)fodx. С этим значением d Q выражение
(у) после раскрытия скобок и очевидн ых упрощений дает диф
ференциальное уравнение второго порядка:
2
k( T -t)fodx - Gcdt + Лэ d Sdx = О
и

�

d2

dx

_

Gc �

Л э S dx

+

dx

�

kfo (Т t)

ЛэS

_

Произведем замену переменной : Т пишется так:
Gc de
d 2e
kfo 9
2
Л эS dx А. э S
dx
_

_

=

t

=

=

0 ; тогда (ф) пере

0

(х)

Решение уравнения (х) имеет вид
0 = Т - t = С 1 е <-1 х + С 2 е <- 2 х ,

где <.1 ,2 - корни характеристического уравнения

Z

2

(ф)

0.

- Gc

Л,S

z

- kfo - О ·.

(ц)

kfo

(ч)

( )2
Gc

2 A. 3 S

Л,S

+

/.. 3 5

Постоянные интегрирования определяюrся с помощью гра
ничных условий.
Формулировка граничных условий (ГУ) оказывает определяющее влияние на
соответствие получающегося решения физической сущности процесса. Матема
тики даже утверждают, что 'Т У сильнее уравнения"; иллюстрацией этого
утвержден ия может служить регулярный режим теплообмена (разд. 7 . 1 2). При
изучении Пр.П крайне сложно математически корректно описать явления на
входной и выходной границах РЗ для конкретного аппарата. Поэтому предлага
ются р�ичные модельные описания, в той или иной мере отражающие физи
ческую сущность ситуации на границах. В результате и получаемые решения
верны в той мере, в которой адекватны сформулированные ГУ.
Наиболее часто используются ГУ Данквертса, предполагающие скачок по
тенциала (температуры - и теплообмене, концентрации - в массообмене или
663

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

химической реакции) на входе в РЗ и равенство нулю продольного градиента
потенциала на выходе из нее• . Другие подходы приводят к иным ГУ и решени 
ям. В учебнике приняты упрощенные граничные условия, позволяющие тем не
менее качественно, а в известной мере и количественно , выявить влияние ин
тенсивности П р . П и некоторых других факторов на конечный результат процес
са в РЗ, здесь - применительно к рассматриваемой задаче теплопереноса.

По физическому смыслу рассматриваемого явления с ростом
х (или ./) разность Т - t уменьшается; при сравнительно боль
ших х она стремится к нулю, и задача теплопереноса из по
верхностной вырождается в потоковую. Примем (хотя это и не
вполне строго) указанное обстоятельство достаточным основа
нием, чтобы отбросить первый корень характеристического
уравнения z1 > О, дающий рост Т t с увеличением х; иначе
говоря, будем считать С1 = О. В таком предположении решению
отвечает лишь второй корень z2 < О,
и выражение (ц)
уп рощаетс я :
0 = Т - t = C2 e z 2 x .
(ш)
Для определения С2 используем ГУ на входе в РЗ: 0' = Т - t'
при х = О. Отсюда по (ш) С2 = Т - t'. Тогда
Т - t'
Т t' - X . (8.32)
т t (Т - t' ) e Z2X '. -- = e -Z2X '. ln Z2
T-t
T-t
Для поверхности теплообмена в целом (f = F, х = l и t = t")
имеем, подставив значение z2 и fo/ = F,

-

-

--

=

-т - t''

Т t'
ln -

=

-z 2 /

=

/

Gc

=

(8.33)

Соотношение пропускных способностей продольного пере
носа
конвективного Gc и продольного эффективного
Р-э / l)S
представляет собой критерий Пекле для теплового
продольного перемешивания:

-

Рез =

-

�=
/.., 3 S /l

wpSc
/.., 3 S / l

=

wl
а3 '

причем а3 = Л,3 /рс
эффективный коэффициент температуро
проводности .
Теперь (8.33) можно преобразовать, введя Ре3:
ln

Ре 3 ) 2
kF
Т - t ' = (-- +
Л, 3S /l
T - t ''
2

-

Ре 3
2

• Обоснование и формулировку ГУ Данквертса см . , например ,

664

( 1 , 5J.

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

F/Fo
4

10
5
")
-3
10
5

")
-2

10
5
2
10
5
2
1

10
Рис. 8. 27. Влияние интенсивности продольною перемешивания на величину
поверхности теплообмена в задаче проекrирования

Чтобы избавиться от иррациональности, перенесем Рез /2 в
левую часть и возведем полученное равенство в квадрат:
Ре ; +
Т - t ' + l n 2 Т - t' Ре ; + � .
Ре з l n
'
4

T - t"

T - t"

после сокращений
Ре з l n

T - t ' + ln 2 T - t '
T - t"
T - t"

=

�
/.... зS /l

=

=

4

/.... S /l
з

kF �
Gc /.... з S/l

=

kF
Gc

Ре з

l
l
kF
Т - t'
Т - t'
Т - t'
Т - t'
- = ln -- + - ln 2 -- = ln -- l + - ln -- . ( 8 . 34 )
Gc
Рез Т - t "
Т - t" Рез
Т - t"
Т - t"

(

Решим полученное равенство относительно kF/Gc:

)

Напомним, что в этом равенстве F - теплообменная по
верхность, необходимая для подогрева холодною теплоносите
ля от t' до t" при ею движении с ограниченным Пр.П. Разумеется ,
из (8 . 34) можно выразить F.
Практически важно сопоставить значения Fo и F при разных
значениях числа Рез - от соответствующею И П (Рез --. О) до
соответствующею И В (Рез --. оо). Представим такое сопоставле
ние в форме зависимости F/Fo от Рез; для этою поделим вы
ражение (8 .34) на левое из выражений (8.3 1 ) :
F
F0

-

=

l

Т t'
+ 1 ln Рез
Т - t"
--

-

665

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Если в этом соотношении заменить лоrарифм по (8.3 1), то
окончательно
.!.._ 1 _1_ kFo
(8.35)
.
Реэ Gc
Fo
Зависимость (8.35) приведена на рис . 8 .27 для различных от
ношений пропускных способностей kFo / Gc. Из формулы (8.35)
и рис . 8 .27 видно, что с увеличением интенсивности Пр.П
(уменьшением Ре3) отношение F/Fo возрастает: при наличии
Пр . П требуется большая теплообменная поверхность для пере
дачи заданноrо потока теплоты Q, т. е. для наrрева теплоноси
теля от f до t". В случае ИВ (Ре3�оо) формула (8.35) законо
мерно приводит к F = Fo.
Важно, что эффект Пр. П сильнее проявляется при больших
значениях kF0 / Gc. Дело в том, что более высокие значения
этоrо отношения отвечают более глубокому теплообмену, т.е.
существенному приближению t" к Т. Это полностью согласует
ся с данными, приведенными в разд. 8.2: более высокой степе
ни превращения (здесь - степени отработки температурноrо
напора Т t" в сравнении с первоначальным Т t') отвечает
больший необходимый объем реакционной зоны (здесь - не
обходимая поверхность теплообмена).
Формула (8.35) одновременно демонстрирует падение средней
движущей силы при наличии Пр. П . В самом деле, количество
переданной в единицу времени теплоты может быть записано
через средние температурные напоры (лt1n в случае ИВ и Лtср в
общем случае): Q = kFoлt1n = kFЛtcp· Отсюда ясно, что отноше
ние лtи/Лtср = F/Fo также выражается формулой (8.35): с пони
жением Реэ величина Лlср уменьшается.
Таким образом, наличие и усиление Пр. П при прочих рав
ных условиях понижают интенсивность теплообменного про
цесса. Аналогичные эффекты (в более сложном математи
ческом представлении) характерны для теплообменных процес
сов с переменной температурой обоих теплоносителей , а также
для других процессов (в частности - массообменных) при на
личии продольноrо перемешивания потоков.
=

+

-

-

Л ИТЕРАТУРА к

главе

8

1 . Выгон В. Г. Математическое моделирование процессов экстракции/ В кн.
Основы жидкостной экстракции. Гл.6. М . : Химия, 1 98 1 . 399 с.
2. Гельперин Н.И., Айнштейн В. Г., Кваша В.Б. Основы техники псевдоожи
жения. М . : Химия , 1967. 664 с.
3. Гельперин Н. И., Пебалк В.Л., Костанян А. Е. Структура потоков и эффек
тивность колонных аппаратов химической промьштенности . М . : Химия, 1 977.
264 с.
4 . За кгейм А. Ю. Введение в моделирование химико-технологических про
цессов. М.: Химия , 1982. 288 с.
5 . Левеншпиль О. Инженерное оформление химических процессов: Пер. с
ан гл . / Под ред. М.Г. Слинько. М . : Химия, 1969. 622 с.

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Глава 9
ВЫПАРИВАН ИЕ

По существу выпаривание представляет собой массообмен
ный процесс - с переносом компонента из жидкой фазы в

паровую. Однако на практике в ходе выпаривания в паровую
фазу переходит только растворитель; растворенное вещество
(за крайне редким исключением) полностью остается в раство
ре. При этом количество испаренного растворителя всецело
определяется количеством подведенной теплоты. Поэтому про
цесс выпаривания трактуется и рассчитывается как тепловой.
9 . 1 . СУЩНОСТЬ ПРОЦЕССА.
ЦЕЛИ И ОБЛАСТИ ПРИМЕНЕН ИЯ

Вьmариванием называI<УГ процесс частичного удаления рас
творителя из растворов путем кипения последних. В подав
ляющем большинстве случаев выпариванию подверrаI<УГ водные
растворы твердых веществ, однако растворителями мoryr быть
и другие жидкости . При этом методы инженерного расчета и
аппаратурного оформления являI<УГся общими (не зависят от
вида растворителя) .
Раствор какой-либо соли, подлежащий выпариванию, будем
называть исходным, или свежим раствором. Получаемый в про
цессе выпаривания раствор называI<УГ упаренным раствором, а
отводимый пар растворителя
вторичным паром. Вторичный
пар, как правило, практически не содержит растворенного ве
щества (унос капель с вторичным паром пока не рассматри
вается), поскольку летучесть растворенного вещества по срав
нению с летучестью растворителя за весьма редкими исключе
ниями невелика. В результате при удалении растворителя кон 
центрация растворенного вещества в растворе повышается.
Обычно удаляют лишь часть растворителя с таким расчетом,
чтобы раствор оставался в текучем состоянии и его можно бы
ло в соответствии с технологической схемой передавать в дру
гой аппарат или потребителю. Иногда при выпаривании рас
творов твердых веществ происходит насыщение раствора и
выпадение твердого вещества. В этом случае выпариванию со
путствует процесс кристаллизации.
-

667

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Таким образом, выпаривание применяют как для повыше
н ия кон центрации разбавленных растворов, так и для выделе
ния из них твердого вешества пугем кристаллизации. В данной
главе рассматриваются вопросы концентрирования растворов;
кристаллизации (в том числе с использованием выпаривания
растворителя) посвящена гл. 1 6 .
Выпаривание д о конечной концентрации может произво
диться как периодически , так и непрерывно. В последнем случае
после выхода на режим (т.е. достижения в аппарате заданной
конечной концентрации) в выпарной аппарат непрерывно вво
дят поток свежего раствора и выводят из него поток упаренно
го раствора, причем параметры ведения процесса остаются
неизменными во времени.
Концентрирование растворов методом выпаривания - один
из наиболее распространенных технологических процессов в
химической, пищевой и других отраслях промышленности .
Число действующих выпарных установок исчисляется многими
сотнями, а суммарное количество выпариваемой воды в наибо
лее крупных из них достигает миллиона тонн в год и более .
При этом на испарение 1 кг растворителя требуется подвести
теплоту, равную (оценочно) теплоте парообразования (для наи
более часто используемого растворителя - воды - это величи
на порядка 2000 кДж/кг). В результате на процессы выпарива
ния растворов расходуется огромное количество теплоты, вы
паривание - крайне энергоемкий процесс .
Выпаривание до заданной концентрации может произво
диться как в одном аппарате, так и в нескольких (в так назы
ваемой многокорпусной выпарной установке) с увеличением
концентрации раствора от корпуса к корпусу.
Необходимость передачи больших количеств (потоков) тепла
упариваемому раствору предопределяет другую отличительную
особенность процессов выпаривания - их металлоемкость: на
изготовление выпарных аппаратов расходуются десятки тысяч
тонн сталей (часто легированных), хрома, никеля и других ме
таллов. Поэтому для каждого конкретного случая выпаривания
важно научиться выбирать оптимальную схему проведения
процесса и наиболее подходящую конструющю аппарата с тем ,
чтобы обеспечить максимальную производительность установки
при фиксированных затратах энергии и металла или минималь
ные затраты - при определенной производительности.
Целью технологического расчета выпарной установки яв
ляется:
- определение расхода греющего пара на проведение про
цесса;
668

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

- определение поверхности теплообмена и основных раз
меров выпарного аппарата;
выявление
режимных
характеристик
процесса
(температуры, давления, концентрации и т.д.).
Методика расчета выпарной установки зависит от вы
бранной технологической схемы, конструкции аппарата и спо
соба ведения процесса (непрерывно или периодически).
Перед изложением методов расчета выпарных аппаратов
рассмотрим сначала их основные конструкции .
9.2. ОСНОВНЫЕ ТИПЫ ВЫПАР Н ЫХ АППАРАТОВ
9.2. 1 . Классификация вьmарных аппаратов

Множество конструкций выпарных аппаратов обусловлено
индивидуальными особенностями выпариваемых растворов,
имеющимся набором теплоносителей и желанием получить
максимальный эффект при сочетании этих факторов. Единой
классификации, охватывающей все многообразие выпарных
аппаратов, не существует; их обычно классифицируют по от
дельным признакам. Приведем наиболее существенные срезы
классификации с кратким комментарием.
По рабоrсему давлению в корпусе (в последнем корпусе, если
выпаривание производится в многокорпусной установке) вы
парные аппараты разделяются на работающие под атмосферным
давлением (или близким к нему), под повышенн ым давлением и
под разрежением. В последнем случае достигается больший пе
репад температур между греющим теплоносителем и кипящим
раствором. Однако использование теплоты отводимых вторич
Н ЬIХ паров затруднительно. При работе под повышенным дав
лением энергия вторичного пара может быть использована в
других теплоисполъзующих установках.
По степени насЬlщения раствора различают выпарные аппа
раты для повышения концентрации вещества в области ниже
состояния насыщения (без кристалл изации) и с получением на
сыщенных (и пересыщенных) растворов. В последнем случае кон
струкция выпарного аппарата отличается наличием камеры
солеотделення для образующихся кристалл о в.
Различают выпарные аппараты и по способу подаrси теплоmЬl:
через теплопередающую поверхность или путем непосредственно
го контакта греющего агента с выпариваемым раствором. По
следний вариант применяют при выпаривании агрессивных
жидкостей, разрушающих теплопередающую поверхность.
В табл .9 . 1 приведена классификация выпарных аппаратов по
характеру организации движения кипящего выпариваемого рас-

669

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Таблица 9. /. Классификаци11 вwпарu.1х аппаратов
по характеру орrанизации ДВИJКеии11 раствора в них
Вид

Разновид 
ности

Аппараты С естественс циркуля - ной циркуцией рас- ляцией
твора
С принудительной
циркуляцией

Аппараты
с выпариван и ем
жидкости
за ОДИН
проход по
аппарату

Аппараты
емкостноro типа (с
перемешиванием
жидкости
и без неrо)

670

Достоинсrва

Высокая интенсивность
теwюпередачи
Отсутствует
инкрустация
поверхности

н�достатхи

Возможность инкрустации
поверхности
ДопоJПiительный
расход
энергии на
работу насоса

Область примен�ния

Примечание

Широкая

Возможно
применение
труб вскипания
и камер для
При вьшари- солеотделения.
вании вязких По структуре
и кристалли - потоков аппазующихся
раты близки к
растворов
аппарату идеальноrо пере
мешивания

с нисходя- Фиксирован- По вышенПри малой
По структуре
щей плен- ное время
ные дnина доле отrонки потоков аппа
кой
пребывания труб и высо- растворителя раты близки к
в аппарате
та аппарата из вязких
режиму идев целом
р11створов
альноrо вьrrесс восходя- Отсутствует
При большой нения. Возщей плен- распредели
доле отrонки можность вы
кой
тель жидкос 
растворителя паривания
ти по трубам
термолабиль
Роторный
ВозможПри выпари- ных веществ
Дополнипленочный ность выпа- тельный
вании очень
испаритель ривания
вязких расрасход
творов или до
растворов до энергии.
получения
Сложность твердоrо
cyxoro
состояния
конструк
ции
остатка

Аппараты с Простота
поверхустройства
ностью теплообмена в
виде рубашки , змеевика
и т. п.
Ап параты
Большая
ко�пактноrо межфазная
поверхность
типа (без
разделяюмежду газом
щей поверх- и жидкостью
ности тепло
обмена): с
поrружной
rорелкой,
обоrрев
rорячим
газом

Возможно
Низкий
В маломаско:эффици- штабных
образование
е�п теплопе- производст- застойных зон
редачи. Or- вах
раниченная
поверхность
теплообмена
Необходи- При выпаримасть внут- вании аrресренней фу- сивных жидтеровки
костей: серная
антикорро- и соляная
зионными кислоты,
материала- растворы
ми: керами- минеральных
кой, рези- солей
ной и др .

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

твора; в таблице указаны достоинства и недостатки рассматри

ваемых аппаратов, а также области их применения и некото
рые особенности. В ней нашли отражение также разновид
ности аппаратов по перечисленным выше признакам.
9.2.2. Конструкции вьmарных аппаратов

Наиболее типичные выпарные аппараты показаны на рис .
9 . 1 и 9.2.

Bwnapнwe anпapan.i с 1U1ркул11ЦНей pacnopa (рис. 9 . 1 ) вмючают в себя
rреющу
камеру 1, циркуляционную трубу 2, сепаратор и брызгоуловитель 4 в
ючасти
верхней
последнего.
Циркуляционная
труба может
бьпъ- размещена
ваппа
осе
вой
(центральной)
части
rреющей
камеры
(отсюда
название
"выпарной

рат
с
центральной
циркуляционной
трубой",
см.
рис.
9. 1 ,а) или отдельно от
rреющей
камеры.(рис.В этом
случае последняя может бьпъ расположена либо соосно
свынесенная
сепаратором
9 . 1 ,6), либо на некотором расстоянии от оси сепаратора rреющая
камера
(рис. 9 . 1 ,в).
Подвод
теплоты
к
раствору, кипящему в трубах rреющей камеры, осу
ществляется
за счет подачи в межтрубное пространство конденсирующегося
водяного
пара. Сепаратор и в ряде случаев расположенный в нижней части
отбойник
(поз.5
на рис. 9. 1 , 6)труб,
служат
для разделения парожидкостной смеси,
выходящей
из
наrревательных
болеечасти
полнойсепаратора
очистки
на
раствор
и пар.в верхней
вторичного
пара
от
уносимых
им
капель
раствора
устанавливается
брызгоуловитель.
На рис.
9 . 1 , а показан простейший тип брыз
гоуловителя, работа
которого основана
на мно
гокраrnом изменении величины и
З

Для

2

а

Рис. 9. 1. Выпарные аппараты с естественной (а - в) и принудительной (г) цир
куляцией:
а

с це�пральной циркуляционной трубой, б

с вынесенной циркуляционной трубой,

- с вынесенной греющей камерой;
1 - греющая камера, 2 - циркуляционная труба, З - сепаратор, 4 - брыэгоуловитель, 5
- отбойник, 6 - труба вскипания, 7 - солеотделитель, 8 - насос с электродвигателем;
/ - исхоДНЬ1й раствор, // - упаренный раствор, /// - вторичный пар, JV - rреющий
в

пар, V - коuденсат

67 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

A/ I:

Lf._

2

ш

2

/

v

а

v

6

в

а - с Юlсходящей пленкой, б - с восходящей пленкой, в - роrорный пленочный испа
ритель;
1 - rреющая кам�.ра, 2 - сепаратор, З - отбойЮIК, 4 - ротор, 5 - лопасти, 6 - паро
вая рубащка.
ОбоэначеЮ1я потоков /- Vтакие же, как на рис. 9. 1

Рис. 9. 2. Пленочные выпарные аппараты:

направления скорости парового потока. Под действием инерционной силы
капли жидкости достигают поверхности сепаратора и стекают вниз либо по
стенкам, либо по специальной отводящей трубе. На рис.9. 1 , б, в представлен
брызгоуловитель циклонного типа. За счет тангенциального ввода пара в кольце
вое пространство брызгоуловителя капли жидкости под действием центробежной
силы отбрасываются к периферии, а затем стекают по трубе в основную массу
кипящего раствора.
Наличие циркуляционной трубы обеспечивает направленную естеСТ11енную
цнркулицию раствора: вниз по циркуляционной трубе и вверх - по кипятильным
трубам . Циркуляция обусловлена разностью плотностей парожидкостной смеси
(в ки пятильных трубах) и раствора (в циркуляционной трубе) . Даже при цент
ральном расположении циркуляционной трубы (внутри rреющей камеры) уста
навливается достаточно интенсивная естественная циркуляция за счет разности
плотностей. Дело в том , что удельная (приходящаяся на единицу объема раство
ра) поверхность теплопередачи /уд обратно пропорциональна диаметру трубы d:
поверхность теплопередачи одной трубы
объем жидкости в одной трубе

7t dl - 4 [м2/м3 ].
= -2
7t d / - d
-

4

П оэтому для труб с бдл ьшим диаметром удельная поверхность теплопередачи
меньше, а значит, меньше и доля паров, образующихся при кипении раствора.
Следовательно, плотность парожидкостной смеси в широкой центральной цир
куляционной трубе заметно больше, нежели в узких наrревательных трубах.
В случае необоrреваемых (расположенных вне rреющей камеры) циркуляци 
онных труб (рис. 9 . 1 , б,в) скорость циркуляции еще выше. Увеличение последней
способствует интенсификации теплообмена, в первую очередь, за счет возраста-

672

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ния коэффициента теплоотдачи со стороны кипящей жидкости . Кроме то го ,
циркуляция раствора препятствует быстрому отложению твердой фазы
(кристалло в, накипи) на стенках кипятильных труб, т.е. инкрустации поверх
ности теплообмена, повышающей термическое сопротивление, а значит, сни
жающей коэффициент теплопередачи от конденсирующегося пара к кипящему
раствору.
Скорость циркуляции (скорость движения парожидкостной смеси в кипя
тильных трубах) зависит от свойств упариваемого раствора и расположения
циркуляционной трубы: обычно это 0 , 3- 0 ,6 м/с - для аппарата с центральной
циркуляционной трубой и 0 ,5- 1 ,0 м/с - для аппаратов с циркуляционной
трубой , расположенной отдельно от греющей камеры. При таких скоростях
циркуляции поверхность теплообмена все-таки инкрустируется (хотя и с мень
шей скоростью , чем в отсутствие циркуляционной трубы) . Поэтому выпарные
аппараты подвергают периодической чистке (пассивный метод борьбы с инкрус
тацией). При этом чистку производят либо путем простого растворения солей,
отложившихся на стенках, либо каким-либо механическим способом .
П ассивный метод борьбы с и нкрустацией предполагает остановку работы ап
парата на время его чистки , а это в случае непрерывного режима работы уста
новки требует наличия резервного выпарного аппарата (точнее - греющей ка
мер ы) .
Существенное снижение отложения солей в трубах достигается п р и исполь
зовании аппаратов с вынесенной зоной кипения (рис. 9 . 1 , 6) . В таких аппаратах за
счет увеличенного гидростатического давления столба жидкости несколько по
вьШJается температура кипения раствора; поэтому кипения в трубах греющей
камеры не происходит, упариваемый раствор лишь нагревается. При выходе пере
гретого раствора из этих труб он попадает в зону пониженного гидростатическо
го давления (1J1уба вскипания 6), rде и происходит интенсивное его закипание
(высвобоЖдается теruюта перегрева) . Таким образом, уменьшается отложение
наки п и на теплообменной поверхности труб и, следовательно, увеличивается
коэффициент теплопередачи и время эксплуатации аппарата меЖду чистками
поверхности . Для обеспечения нормальной работы таких аппаратов очень важно
отделить выкристалл и зовавшиеся твердые частицы из циркулирующего потока
раствора перед его входом в нагревательную камеру. Такое отделение твердых
частиц происходит в солеотделителих, располагаемых либо в нижней части вы
парного аппарата (поз. 7 на рис. 9 . 1 , 6) , либо в верхней (рис. 9 . 1 ,г) - после
выхода парожидкостной смеси из трубы вскипания.
Метод борьбы с инкрустацией теплообменной поверхности с помощью тру
бы вскипания более эффективен, но не исключает ее полностью (ин
крустируются верхние концы нагревательных труб и труба вскипания) . Жела
тельно не допустить инкрустации поверхности на всем пути движения раствора.
Этого можно добиться применением принуднтел•иой циркуляции раствора
(активный метод борьбы с инкрустацией) с помощью пропелле рного (осевого)
или центробежного насоса 8 (рис. 9 . 1 , г) . Опьrr показывает, что при достаточно
высоких скоростях циркуляции раствора в кипятильных трубах (2, 5-3,0 м/с)
инкрустация поверхности практически полностью отсутствует даже при кон 
центрировании кристалл изующихся растворов. Причиной этого являются два
эффекта. Во- первых, быстро циркулирующий раствор просто не успевает закри
сталл и зоваться в трубах, о н лишь перегревается в них, вскипая за пределами
труб (даже при отсутствии трубы вскипания, тем более - при ее наличии). Во
вторых, свежевыпавшие кристалл ы (если таковые все же появляются на стенках
на выходе кипящего раствора из теплопередающих труб) смываются потоком
циркулирующего раствора, движущегося с большой скоростью (2-3 м/с) . Вы
парные аппараты с принудительной циркуляцией могут бьrrь выполнены с соос-

673

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ной (как показано на рис. 9. 1 ,г) или вынесенной rреющей камерой; они мoryr
иметь таюке трубу вскипания и солеотделитель (см . рис. 9 . 1 ,г). В аппаратах с
принудительной циркуляцией наиболее высокий коэффициент теплопередачи
(он достаточно высок даже при выпар ивании вязких концентрированных рас
творов). К недостаткам выпарных аппаратов с принудительной циркуляцией
следует отнести расход энергии, связанный с необходимостью работы цир куля
ционного насоса. Оrметим таюке жесткие условия работы насоса: высокие тем
пературы, нередко аrрессивные среды, повышенная опасность возн и кновения
кавитации при перекачке кипящей жидкости.
Аппараты с принудительной циркуляцией применяют в тех случаях, когда
нет другого выхода, а таюке при выпаривании дорогих растворов, когда затраты
энергии на циркуляцию не могут ощутимо увеличить себестоимость продукта
(упаренного раствора) .
Рассмотренные выше конструкции выпарных аппаратов•с циркуляцией рас
твора по структуре движения в них жидкости близки к моделям идеального
перемешивания, поэтому время пребывания отдельных частиц жидкости в аппа
рате различно (некоторых - бесконечно большое). Это не позволяет выпар ивать
в них термолабильные растворы.
Для выпар ивания термолабильных, а таюке вспенивающихся растворов ис
пользуют пленочнwе аппара11о1 (рис. 9.2), в которых выпаривание до требуемой
конечной концентрации осуществляется за один проход кипящего раствора по
кипятильным трубам. Для обеспечения заданных пределов изменения концент
раций упариваемых растворов кипятильные трубы делают длинными (6- 1 0 м) .
Жидкостная пленка раствора в пленочных аппаратах движется, как правило ,
прямоточно с образующимся вторичным паром. При этом различают нисходящий
прямоток (рис. 9.2,а) и восходящий (рис. 9.2,б). В последнем случае перемещение
жидкостной пленки вверх происходит за счет поверхностного трения вторичного
пара, движущегося с большой скоростью.
Аппарат (рис. 9. 2,б) работает следующим образом . Кипятильные трубы за
полняются поступающим снизу раствором примерно на 1/4 - 1/5 их высоты.
Подаваемый в межтрубное пространство rреющий пар вызывает и нтенсивное
кипение раствора в трубах. П одчеркнем необходимость применения здесь нагре
вательных труб малого диаметра, обеспечивающих высокую степень парообразо
вания и большую скорость пара в них.
Скорость вторичного пара внутри труб настолько велика, чrо за счет сил трения
на границе пар-жидкость он увn;екает тонкую пленку расrвора, перемещая ее вверх
до сепаратора, где происходит още.nение пара от упаренного расrвора.
Таким образом , в пленочных вьшарных аппаратах упаренный (до требуемой
концентрации) раствор получается при однократном его проходе через греющую
камеру. В этих аппаратах циркуляция отсутствует, а поэтому время пребывания
отдель ных элементов жидкости в аппарате фиксировано (особенно в аппаратах с
нисходящей пленкой, когда можно избежать большого объема свежего раствора
в распределителе). Кратковременный контакт раствора с поверхностью нагрева и
высокие значения коэффициентов теплопередачи (вследствие интенсивной теп
лоотдачи от стен ки трубок к кипящим пленкам жидкости) - основные преиму
щества пленочных выпарных аппаратов. К их недостаткам относят: большую
высоту, высокую чувствительность к изменениям нагрузок по жидкости и к
содержанию твердых частиц в ней. При слишко м малых нагрузках по жидкости
не удается достичь полной смачиваемости всей поверхности теплопередачи. Это
может приводить к местным перегревам, выделению твердых осадков.
Для выпаривания термолабильных и вязких растворов, а таюке при необхо
димости ведения процесса до получен ия сухого остатка все более широкое
применение находят роторнwе пленочнwе испарители (рис. 9.2,в) . Основным
рабочим органом в н их является ротор - верти кальный вал с насаженными на

674

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 9.3. Барботажный выпарной
аппарат с по11>ужной rорелкой:

тп

1 - форсунка, 2 - поrружная rорел 
ка, З - корпус аппарата;
/ - исходный раствор, II - упарен 
ный раствор, /J/ - топливо, IV - возд ух ,
V - дымовые rазы

/

неrо лопастями. Ротор вращается с
числом оборотов, обеспечивающим
окружную скорость на конце лопас
ти около 3 м/с. Вращающиеся ло
пасти частично срезают пленку
жидкости,
образуя
утолщение
( " валик") перед ними . Утолщенная
пленка стекает вниз с большей скоростью, нежели естественная пленка. Таким
образо м , вращающийся ротор способствует перемещению раствора вниз. Обо11>ев аппарата производится с помощью на11>евательной рубашки 6 для теплоно
сителя, а образующийся при кипении раствора вторичный пар движется вверх
(как показано на рис. 9.2,в) - противотоком к стекающей жидкости - и отво
дится через сепаратор.
Время контакта раствора с поверхностью на11>ева в роторных испарителях за
висит от многих факторов (производительность, вязкость раствора, скорость
вращения ротора и др. ) и составляет обычно
с. Важнейшими достоинства
ми этих аппаратов являются : кратковременный КОКГdКТ раствора с поверхностью
на11>ева (что очень важно при выпаривании термолабильных веществ); возмож
ность выпаривания не только высоковязких (до 0,3 мПа·с), но и кристалл и зую
щихся растворов вплоть до получения cyxoro остатка. К недостаткам относят
сложность конструкции (привода) и дополнительный расход энергии.
Кроме вышеупомянутьrх трубчатых вьmарньrх аппаратов иногда применяют
вwпарнwе аппаратw емкОС'Пlоrо 111 п а. Среди них выпарные аппараты с поверх
ностью теплообмена в виде рубашки или змеевика используются довольно редко
из-за низкоrо коэффициента теплопередачи в них. возможности образования
застойньrх зон и 0 11>аниченной теплообменной поверхности на единицу рабочего
объема. Для а11>ессивньrх растворов (серная, фосфорная, соляная кислоты, суль
фаты и хлориды некоторьrх металло в) весьма эффективными оказались аппаратw
контаКпtоrо типа : например , аппарат с поrружной rорелхой (рис. 9. 3), в котором
образующиеся при сrорании rазообразноrо топлива rорячие газы барботируют
непосредственно через жидкость. При зrом со:щаЮIСя хорошие условия (большая
межфазная поверхность) для интенсивноrо теплообмена межцу дымовыми газами и
жидкостью. Достоинством таких барботажных вьmарных аппараmв является возмож
ность их изrоmаления из обычной уmеродистой стали . Однако необходима, есте 
ственно, внутренняя футеровка такоrо аппарата антикоррозионными материалами керамикой, rрафиrом, резиной, пластмассами и т.п.
Более детально конструкции выпарньrх аппаратов (упомянутых выше и дру
гих) и описание их работы приведены в учебной и справочной литературе• .

5-2 5

9.3. ФИЗИ КО-ХИМИЧЕСКИЕ ОС Н ОВЫ
ПРОЦЕССА ВЫПАРИ ВАН ИЯ
При расчете процесса выпаривания будем использовать мас
совую абсол ютную концентраци ю вещества в растворе а ( кг
твердого вещества)/( кг раствора) ; в техн ических заданиях при
•

См . , например , (3, 4 ,

10), а также отраслевые каталоги , нор мали .
675

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

описании процессов выпаривания концентрацию нередко вы
ражают в процентах ( lOOa, %). Очевидно, что концентрация
вещества в растворе может изменяться от О до 1 (реально - до
концентрации насыщения Онас) или, в процентах, от О до 1 00
(или l ООанас, %).
Произведение количества раствора S (кг) на его концентра
цию а (кг твердого вещества)/(кг раствора) дает количество
растворенного твердого вещества Sa:
·

S (кг раствора) а

к.г

твердого вещества
=
к.г раствора

Sa (кг твердого вещества)

·

Соответственно, произведение потока раствора S (кг/с) на
его концентрацию а дает поток Sa ( кг/с) твердого вещества.
Теплоемкость раствора (смеси) ем при отсугствии экспери
ментальных (справочных) данныхС рассчитывают по правилу
адд итивности :
(а)
S
S
где
- количество раствора, полученного при растворении т• к.г твердого ве
щества в Sp к.г растворите.ля ; Сем . Сrв и ер
вещества и растворите.ля соответственно.

-

теплоемкости раствора, твердого

Поделив все члены равенства (а) на S, получим
S
S тв
S - Sтв
Sp
тв
м
=
е
=
тв
p
тв
С
S С + SC SС + S С р '
или
ем = аств + ( 1 - а) ср ,
С
где а = Sтв/S - концентрация твердого вещества в растворе.

(9. 1 )

Следует иметь в виду, что расчет п о адд итивности является приближенным ,
поскольку иrnорирует теплоту смешения (последняя не всегда пренебрежимо
мала) .

Правило адд итивности в равной мере применимо и при
смешении S 1 кг раствора концентрации а1 (с теплоемкостью с 1 )
с W кг растворителя теплоемкостью ср :
(9.2)
Soco = S 1 c1 + Wcp,

где S o = S 1
количество полученного при смешении раствора концентра
ции ао (меньшей, чем 01) ; со - его теплоемкость.

+W-

Заметим, что теплоемкости с0 и с 1 моrуг бьrrь рассчитаны по
формуле (9. 1).
Важнейшим параметром процесса выпаривания является
темпер атура кипения растворов !к. Она зависит от химической
природы растворенного твердого вещества и растворителя ,
причем tк растет с повышением давления над раствором и с
676

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

увеличением конuентраuии растворенного вещества. От темпе
ратуры кипения раствора в значительной степени зависят вы
бор теплоносителя (и его параметров), расход теплоты и теп
лоносителя, движущая сила процесса теплопередачи Лt и вели
чина необходимой поверхности теплопередачи F.
Разность между температурами кипения раствора lк и
чистого растворителя tp при одинаковом давлении получила
название температурной депрессии 8 = tк - /р для раствора дан
ной концентрации а.
В справочной литературе обычно приводятся эксперимен
тально найденные температуры кипения или депрессии рас
творов различных солей при атмосферном давлении - в виде
таблиц или графиков t = t(a), а также 8 = 8(а) ; такие темпера
туры кипения и температурные депрессии называют стандарт
ными и обозначают tr:r и 8r:r.
Совершенно очевидно, что экспериментально определить tк
или 8 для широкого набора растворов веществ при разных их
концентрациях, да еще при множестве различных давлений крайне затруднительно . Поэтому следует искать методы анали
тического пересчета tc-r, 8r:r на t, 8 при переходе к давлениям ,
существенно отличающимся от атмосферного . Заметим, что по
разным причинам (о них скажем позднее) процесс выпарива
ния зачастую выгоднее вести не при атмосферном давлении, а
под вакуумом или при избыточном давлении.
В случае рабочего давления, отличного от атмосферного,
температуры кипения раствора tк и чистого растворителя lp
отличаются от стандартных в большую (при р > 1 атм) и в
меньшую (при р < 1 атм) стороны. При этом значения /р нахо
дят по таблицам насыщенных паров для чистого растворителя
(если растворитель - вода, то по таблицам для насыщенного
водяного пара) или имеющимся расчетным соотношениям :
получают для воды fp > 1 00 ° С при р > 1 атм и /р < 100 ° С при
р < 1 атм. Если рабочее давление мало отличается от атмо
сферного (например, на 0,01-0,03 МПа ; величина такого от
клонения определяется допускаемой погрешностью расчета), то
можно приближенно принять, что рабочая депрессия близка к
стандартной: 8 � 8c-r; тогда рабочая температура кипения
lк = lp + 8 � lp + 8r;r.
(б)
Но в химической технологии процесс выпаривания нередко
проводят при давлениях над кипящим раствором в несколько
атмосфер (обычно до 5-6 ат, т.е. 0 , 5 -0 , 6 МПа) либо при су
щественном разрежении (остаточное давление, т.е . рабочее
давление, 0,02-0,0 1 МПа и даже несколько ниже). В этих слу
чаях от стандартного значения заметно отличается не только
677

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

температура кипения чистого растворителя tp , но и величина
депрессии ; поэтому выражение (б) с использованием 8ст стано
вится неточным - здесь требуется более строгая методика рас
чета tк и/или 8.
При давлениях, заметно отличающихся от атмосферного,
расчет tк и 8 следует вести на основе уравнения Кирхгофа:
dW

dQ

=

ln
R T 2 д (p/ ps )
ат

(9.3)

.

В этом уравнении dQ - количество теплоты, выделяющейся
(поглощающейся) при добавлении dW кг растворителя к рас
твору, содержащему 1 кг растворенного вещества в W кг рас
творителя ; Т - температура кипения раствора (подчеркнем:
здесь - в градусах абсолютной шкалы); R = Ry/M - газовая
постоянная для растворителя (М - его молярная масса, Ry
универсальная газовая постоянная); р - рабочее давление; Ps
-

-

упругость насыщенного пара растворит еля при температуре ки
пения раствора (естественно,
Заметим :
> р, так как
>

Ps

tк

tp ) ·

величины р и tp, р!" и t связаны термодинамическими соотно
шениями (типа Клапейрона - Клаузиуса или Антуана); эти
связи более точно заданы таблиuами насыщенных паров (в
случае воды - весьма подробными таблиuами).
Обозначим : dQ/dW = Qд - дифференuиальная теплота рас
творения. Она пракгически не зависит от температуры . Тогда
(9.3) можно переписать, разделив переменные и заменив част
ные производные обыкновенными (так как осталась един
ственная независимая переменная 7):
Qд dT
(в)
d ln .L
R Т2 =
Ps .
Интегрируя (в) от нормальных (стандартных) условий ( Тет и
Рст ) до рабочих ( Т и р)
т
Qд d T
= P
J
f d t n .L
R Т 2 Pcr
Ps
получаем
Qд 1
ln .L 1n .L
R Тст Т
Ps
Ps ст
Отсюда
Qд
1
(г)
.
ln .L 1n .L
R
Т
Т
ст
Ps
Ps cr
При известном значен ии Qд из выражения (г) может быть
наЙдена температура кипения раствора Т при любом давлении р
•

( _!_)
-

=

678

-

-

=

( )

-

( )
(_!_- )

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

над раствором - по известной температуре кипения раствора Тст
при стандартном (атмосферном) давлении.
Для разбавленных растворов, когда Qд � О, а также для неко
торых растворов, характеризующихся крайне низкими значениями
Qд (обычно это растворы с малой темп�атурной депрессией 8),
выражение (г) обращается в правwю Баоо : для раствора данной
концентрации при изменении рабочего давления р
_!!_ =

Ps

(L)
Ps

= const (константа Баба).

(9 .4)

ст

Таким образом, согласно правилу Баба, отношение давления
паров растворителя над раствором р к давлению паров над чис
тым растворителем Ps при температуре кипения раствора не
зависит от рабочего давления и температуры его кипения.
Определение температуры кипения раствора fк при любом ра
бочем давлении р не вызывает затруднений, для этого следует:
- по известной температуре Юtпения раствора в стандарт
ных условиях !ст найти величину (рs)ст и рассчитать константу
Баба ;
- при заданном рабочем давлении р рассчитать величину р5;
- по Р1> найти искомую температуру кипения раствора tк;
- если необходимо, определить депрессию в рабочих условиях: 8 = fк fp.
Алгоритм такого расчета может быть представлен схемой:
-

tст
�

по

табли це

насыщенного
пара

8

=

fк

-

(рs)ст

по

(9.4)

)1

const

по

(9.4)

)1

Ps

по

таблице

насыщенного
пара

fp .

При использовании правила Баба для концентрированных
растворов �точнее, в тех случаях, когда величина Qд суще
ственна и вторым слагаемым в правой части уравнения (г)
пренебречь нельзя) в полученный результат - величину fк по
Баба - должна быть внесена поправка Л8.
Оrыскание Qд связано со значительными техническими трудностями: значе
ния Qд известны лишь для некоторых растворов; нередко по имеющимся экспе
риментальным данным требуются громоздкие пересчеты для нахождения Qд.
Поэтому при определении рабочих температурных депрессий для концентриро
ванн ых растворов широко используются эмпирические поправки . Наибольшее
распространение для случая р < 1 атм получила таблица Стабникова, приводи
'
мая в ряде учебников и справочников . Нужно, однако, иметь в виду следующее:
- величины этих поправок основаны на экспер иментальных исследованиях
оrраниченноrо числа объектов;
' Н апример,

[ 3, 6, 8 ).

679

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

- таблица не охватывает всех практически интересных диапазонов измене
н ия отношений р/р,, рабочих дамений (в частности, дамений более 1 атм) и
концентраций ;
- в ряде случаев поправки неточны (например , для растворов с большой
темпераТурной депрессией при малых абсолютных давлениях) .
Н аконец, автор таблицы предложил ее совсем не для расчета поправок, а для
оценки максимальных погрешностей при использовании правила Бабо .

Свободен от перечисленных недостатков метод определения
поправки Л8, базирующийся непосредственно на уравнении (г) .
Согласно этому методу, температурная депрессия 8 при любом
рабочем давлении может быть вычислена по формуле

l (д)+

rде ОБ - температурная депрессия, определяемая по правилу Бабо; (
Бi:r/Ti:r) <р.Qд = М - поправка к температурной депрессии; q>. - корректи 
рующий м ножитель, зависящий от рабочих температуры и дамения:

8

+

=

8Б

-

(1 + 8cr/Tcт)<J>• Qд ,

<р . = - --- ;
r Tcr

т T - Tr:r

Т "' (tp
273,2)К и Ti:r = (t"'p
273,2)К = 373,2 К - температуры кипения
растворите.ля при рабочем и стандартном давлениях; r - теплота парообразова
н ия растворите.ля при рабочих условиях.

+

+

Знак и величина поправки Л8 зависят как от величины и
знака Qд, так и от величины и знака корректирующего множи
теля q> • • Значения дифференциальных теплот дегидратации Qд
для некоторых солей приведены в Приложении 9. 1 , а значения
q> • (с целью облегчения расчетов) - в Приложении 9.2 как по
рабочим температурам кипения растворителя lp (0 С), так и по
рабочим давлениям р (к.Па).
Температура кипения раствора по высоте нагревательных труб, строго гово
ря, не является постоянной даже в аппаратах с интенсивной циркуляцией - из
за дополнительного гидростатического давления вышерасположенных слоев
кипящей жидкости и соответствующего увеличения температуры насыщения.
Строгий расчет так называемой гидростатической депрессии затруднителен в
связи с невозможностью точного расчета протяжен ности зоны (нижняя часть
нагревательных труб), rде раствор не кипит, а только нагревается. Кипение
раствора в трубах начинается лишь при достижении раствором температуры
насыщения на некотором расстоянии от низа труб. Величина же гидростатиче
ского дамения в этом месте зависит от плотности образующейся при кипении
парожидкостной смеси . Гидростатическая депрессия, как правило, не играет
существенной роли при расчете выпарных аппаратов, поэтому ее обычно не
учитывают.

Температура вторичного пара е и его энтальпия i должны
быть известн ы при тепло вом расчете выпарного аппарата. Ре
ально она ниже температуры кипения раствора, но несколько
выше температуры кипения чистого растворителя lp, соответ
ствующей давлению над кипящим раствором. Дело в том, •по

680

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 9. 4. Диаграмма р
/ и 2
юtжняя и
-

-

h, i:

верХЮIЯ поrраии ч ные

кривые;
/ - недоrретая до темпе11атуры кипеюtя
жидJСосrь, II - парожидJСосrная смесь, III переrретый пар

р
ркр 1-------,,,-....

Prp _______.._.....

(111)

пузырьки пара, образующиеся
2
при температуре , близкой к fp,
проходят через кипящий при
температуре fк раствор и перегре
ваются, хотя и не успевают на
h, i
греться до температуры fк . Кро
ме того, различные пузырьки
пара проходят в кипящем растворе разный путь и поэтому пе
регреваются сверх fp по-разному. Это создает известную неоп 
ределенность при расчете температуры вторичного пара е . Од
нако в целом теплота перегрева сп (8 - fp ) мала в сравнении с
энтальпией i и теплотой парообразования r, и ею, как правило,
можно пренебречь. Поэтому в дальнейшем будем считать вто
ричный пар насыщенным - соответственно рабочему давле
нию в выпарном аппарате (в сепараторе), а его температуру е
равной fp. В аспекте последующей возможности использования
потенциала вторичного пара небольшая расчетная ошибка при
таком допущении идет в запас . Итак,
(9.5)
е = lк 8.
Если для выпаривания водных растворов в качестве
греющего используют водяной насыщенный пар, то в результа
те такого процесса получается тоже водяной пар, но более низ
кого потенциала (давления, температуры) . Иначе говоря, вы
парной аппарат является своеобразным трансформатором пара,
или, как его иногда называют, умформером. Причем при расхо
довании 1 кг греющего пара получается лишь 0,85-0,9 к.г вто
ричного пара. Это объясняется прежде всего увеличением зна
чений теплоты парообразования (конденсации) при уменьше
нии давления (см. диаграмму р - h, i на рис. 9.4) . На этой
диаграмме теплота конденсации (испарения , парообразования)
r при определенном давлении изображается горизонтальным
отрезком между линиями кипящей жидкости 1 и сухого насы
щенного пара 2, поэтому выделяющейся при конденсации 1 кг
грею щего пара (да вл ением Prp ) теплоты rrp недостаточно для
и с парения 1 кг растворителя при давлен и и PJТr · Из диаграммы
видно, что Гrр < rJТr , поскольку Prv > PJТr (заметим, что при кри
тическом давлении Ркр вообще Гкр = О). Естественно, если в
процессе выпаривания теплота конденсации греющего пара
расходуется еще на догрев раствора до температуры кипения, а
68 1
-

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

также частично теряется в окружающую среду, то реальное
количество образующегося пара на 1 кг греющего пара может
быть и меньше указанных выше цифр .
В процессах выпаривания иногда кипящий (или неюшя
щий) раствор попадает в область (аппарат) с пониженным дав
лением, причем это давление может быть столь низким, что
температура кипения раствора при этом давлении (t) оказы
вается ниже температуры поступающего рабочего раствора (10 ) .
Иными словами, поступающий раствор перегрет относительно
температуры кипения при пониженном давлении . Поэтому
происходит интенсивное (практически - мгновенное) испаре
ние части жидкости за счет высвобождаемой теплоты перегре
ва. Такое явление получило название самоиспарение. Доля ис
парившейся жидкости е зависит, естественно, от величины
перегрева, которая определяется начальной температурой рас
твора to и разностью давлений.
Оценим долю пара е, образующегося при самоиспарени и . Сначала опреде
лим ее для случая чистой Ж1ЩКОС111 (без растворенного в ней вещества). Пусть
l кг :жидкости (теплоемкостью со) при температуре to подан в аппарат с· пони
женным даа.1ением, при котором эта :жидкость кипит при температуре t < to. За
счет теплоты переrрева часть :жидкости (е) превратится в пар, а оставшаяся часть
( l - е) будет иметь температуру �· Тепловой баланс явления при отсутствии
потерь теплоты в окружающую среду запишется:
ei = О ,

где с - теплоемкость кипящей :жидкости при температуре t; i = r + ct - эн
тальпия пара; r - теплота парообразования :жидкости при температуре t.
Подстааляя в (е) выражение для h, после преобразовани й пuлучаем долю испарившейся :жидкости е:
coto - ct .
(:ж)
е=
l · coto

-

(1

-

e)ct

-

(е)

·

r

Ее.ли теплоемкость :жидкости мало изменяется с температурой (часто встречаю
щийся случай), то датоо испаряемой :жидкости находят по упрощенной формуле:

е=

co<to - t)
r

.

(з)

Для о пределения доли испаряющегося растворите.ля в случае растворов возь
мем при температуре t0 l кг раствора с концентрацией твердого вещества в нем
а0 и теплоемкостью с0, определяемой по формуле (9. 1), и направим этот раствор
в аппарат с пониженным давлением , при котором раствор данной концентрации
кип ит при температуре t, меньшей t0. За счет теплоты переrрева испарится е кг
растворителя, в результате концентрация раствора увеличится до значения а.
При этом соответственно повысится и температура кипения раствора - до зна
чения t. Тепловой баланс (е) в этом случае останется без изменений. Долю испа
р ившейся :жидкости здесь следует рассчитывать по формуле (ж), так как теп 
лоемкости исходного со и конечного с растворов существенно изменяются при
изменении концентраций - в ходе самоиспарения от ао до а. Концентрация а
зависит от доли самоиспарения е, а температура кипения t - от а (причем по
своему для раствора каждого вещества) . Поэтому расчет по формуле (ж) может

682

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

бьпъ вьmатmен только методом последовательных приближений: зццаваясь, напри
мер, далей 01rона е, рассчиrывая затем концеmрацию а по формуле (9.6) следующего
ра.:щела, теплоемкость с по формуле (9. 1) и проверяя е по формуле (ж).

Отметим, что в случаях большоrо самоиспарения раствора
(при большом перепаде давлений , а следовательно, и темпера
тур) возможно получение суммарно более 1 кг вторичного пара
на каждый кг греющего.
9.4. СХЕМА РАБОТЫ ВЫПАРНЫХ АППАРАТОВ.
КОЛИЧЕСТВО УДАЛЯЕМОГО РАСТВОРИТЕЛЯ
9.4. 1 . Типовая схема выпарноrо аппарата.
Обозначение параметров процесса

Независимо от конкретной конструкции и режима работы
выпарноrо аппарата представим его условно схемой, показан
ной на рис . 9.5. Пометим крестом греющую камеру, в меж
трубное пространство которой подводится насыщенный грею
щий Пар в количестве Drp при температуре Т (здесь и далее в
0 С) и с энтальпией h. После конденсации пара образующийся
конденсат (при использовании водяного пара - вода) отводится в
том же количестве Dip из нижней части этого пространства
(теruюемкость конденсата Ск при той же температуре конденса
ции 7). Исходный раствор с концентрацией а0 при температуре
t0 в количестве S 0 поступает в трубное пространство выпарноrо
аппарата. После удаления из раствора части растворителя W в
виде вторичноrо пара (ero температура е, энтальпия 1) получают
упаренный раствор в количестве S1 = S0
W при температуре
кипения t1 , соответствующей концентрации а 1 упаренного раство
ра. При выполнении тепловых расчетов вьmарноrо аппарата необ
ходимо также располагать теплоемкостями Со и с 1 исходного
и упаренного растворов.
W,0,i
Специально подчеркнем,
1//
что
харакrерной
особен
ностью большинства конст
рукций выпарных аппаратов
является интенсивное (прак
тически - идеальное) пере
мешивание кипящеrо . рас 
1
твора и, следовательно , пра
кrически полное выравнива-

Рис. 9. 5. Типовая схема выпарного
аппарата и основные потоки:

/ - выпарной аппарат, 2 - коJЩенса
тоотводчик
Обозначеюtя потоков 1 - V такие же,
как на рис.9. 1

l1

G.
v т

683

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

w

Рис. 9. 6. Расчетная схема выпарного ап

парата

ние его свойств {температуры
кипен ия , концентрации, теп
лоемкости) по всему объему.
2
Именно поэтому параметры (t,
а, с) уходящего упаренного рас
твора принимаются равными
таковым в зоне кипения рас
твора в аппарате.
Возможна организация не
прерывной работы аппарата,
представленного на рис. 9 . 5 .
При этом непрерывно подается
So кг/с исходного раствора и D
кг/с греющего пара и непрерывно отводятся потоки W кг/с вторичного пара и S1 кг/с
упаренного раствора. При перио
дической работе выпарного аппарата после заливки S0 кг исход
ного раствора и удаления из него W кг вторичного пара упа
ренный раствор в количестве S1 кг остается в аппарате. Коли
чество греющего пара и получающегося конденсата будет при
этом определяться за весь процесс выпаривания: D rp кг.
Весьма удобной для тепловых расчетов выпарного аппарата
является схема, представленная на рис.9.6, которая отражает
изменение энтальпий в потоках, разделенных поверхностью
теплообмена F. Эrа расчетная схема в равной степени справед
лива как для непрерывного процесса (здесь материальные пото
ки в кг/с), так и для периодического (тогда материальные потоки
- в кг за весь процесс). Соответственно, через поверхность теп
лообмена F от греющего пара к кипящему раствору передает
ся: либо поток теплоты Q (Вт)
для непрерывного процесса,
либо ее количество Q (Дж)
для периодического за весь пе
риод выпаривания .
-

-

-

9.4.2. Определение количества (потока) удаляемого растворителя

Независимо от способа проведения процесса (непрерывно
или периодически) поток или количество у.dаляемого раствори
теля для повышения концентрации вещества от ао до а 1 можно
найти из материальных балансов для контура К2 на рис . 9.6 (за
единицу времени для непрерывного процесса или за весь про
цесс - для периодического). Конечные расчетные выражения
(соответственно в кг/с и кr) при этом получаются одинаковы684

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ми. Поэтому н иже балансы записаны только для непрерывного
процесса:
- по общему потоку рабочего раствора
+ So - S1 W = О,
(а)

-

- по растворенному веществу
+ Soao - S1 a 1 - Wап

-

=

О,

(б)
концентрация вещества во вто
где в самом общем случае Оп
ричном паре. Так как при выпаривании твердое вещество в
подавляющем большинстве случаев практически нелетуче, то
вторичный пар, очищаемый в брызгоулавливающих уст
ройствах от капель жилкости , представляет собой пары чистого
растворителя , т.е. Оп = О.
Совместное решение (а) и (б) дает на основе производи
тельности по исходному раствору (исключается S1 )

W=

s0(1 - :�) ,

(9.6)

(;� - 1) .

(9.6а)

а по упаренному раствору (исключается S0)

W

=

S1

Таким образом, при принятом нами способе выражения
концентрации вещества в растворе количество удаляемого рас
творителя зависит не от разности концентраций (а1 - а0), а от
их отношения.
9.5. ВЫПАРНЫЕ АППАРАТЫ
ПЕРИОДИЧЕСКОГО ДЕ Й СТВИЯ

Периодическое выпаривание применяется в производствах
сравнительно небольшой производительности . По количеству
затраченной теплоты на единицу продукции периодический
процесс практически не отличается от непрерывного, а вот по
поверхности нагрева (при одинаковом времени проведения
процесса) возможна некоторая выгода. Дело в том, что в пе
риодическом процессе по мере удаления растворителя темпера
тура кипения раствора увеличивается постепенно. А вместе с
этим движущая сила процесса теплопередачи постепенно
уменьшается, достигая минимального значения лишь при ко
нечной кон центрации раствора. В аппаратах же непрерывного
действия кипит раствор конечной концентрации, и движущая
сила процесса теплопередачи всегда минимальна. К недостат685

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

кам аппаратов периодическоrо действия относят их громозд
кость (заливается весь объем исходноrо раствора или его зна
чительная часть) , невысокую производительность, а также
сложность в управлении: изменение параметров процесса во
времени, неравномерная подача греющеrо пара, необходимость
контроля текущей концентрации, меньшая стабильность в ка
честве продукта (колебания конечной концентрации от порции
к порции и др.).
В ряде технологических задач в случае периодического процес
са необходимо определить полное время -r его проведения. Есте
ственно предположить , 'ПО это время зависит от мощности под
водимого теплового потока. Последняя зависит от поверхности
теплообмена F. Таким образом, в периодических процессах
основным расчетным параметром становится произведение Ft.
Как правило, на выпаривание подается раствор при темпе
ратуре ниже точки его кипения. Поэтому весь процесс можно
(иногда условно) считать состоящим из двух разделенных во
времени стадий: стадии нагрева до температуры кипения про
должительностью "tнrp и стадии выпаривания продолжитель
ностью "tвып·
9.5. 1 . Периодическое выпаривание
с однократной заrрузкой исходного раствора в аппарат
Рассмотрим процесс выпаривания S 0 кг раствора с началь
ной температурой lн от исходной концентрации ао до конечной
0 1 с помощью теплоносителя - насыщенного греющего пара
температурой Т (рис. 9.7,а) . Весь процесс периодическоrо вы
паривания состоит из двух стадий: стадии нагрева и стадии
собственно выпаривания. Сначала обратимся к статике процес
са, т.е. определим расход теплоты на каждую из этих стадий.
На стадии наrрева температура раствора повышается от на
чальной lн до температуры кипения 1<J раствора исходной кон 
центрации а0 . Уровень жидкости в аппарате н а этой стадии
практически не изменяется. Общее количество теплоты Qнrp,
расходуемой на нагрев раствора теплоемкостью с0 от lн до !о,
очевидно, составляет
(а)
При этом требуемое количество греющеrо пара определяет
ся по формуле (7. 1 6в) :
Dн =
где rrp =

686

h

-

Q нrp

h - Ск Т

=

Q нrp
Гrр

ск Т - теплота конденсации греющего пара.

(б)

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

W,i
tн --... to
So , ао , со

,..._
...
_
_,.,.1--т-

Т._
Q-t---....P

S ,a,c, t

б

а

Рис. 9. 7. К расчеrу периодического вьmаривания при однократной загрузке
исходного раствора:

а - иэменеЮ1е уровня раствора в аппарате и параметров процесса на ст;щии выпарива
ЮIЯ, б - rрафическое определеЮ1е инте rрал а

(9. 1 0)

На стадии выпаривания от начальной концентрации а0 до
конечной а 1 необходимое количество теплоты найдем из теп
лового баланса для контура К2 (на рис. 9.6) за время 'tвып всей
этой стадии . В отсуrствие Источников и Стоков теплоты
Wi = S 1 с1 1 1 - S o с о 1о .
(в)
Qвып
Приход

Уход

Накомение

Используя правило адд итивности при определении теплоем
кости раствора, имеем из (9.2):
(г)
S1c1 = Soco - Wcp .
Подставляя выражение (г) в (в), после простых преобразований
получаем
(9.7)
Из (9.7) следует, что теплота на стадии выпаривания расходу
ется на нагрев исходного раствора (от начальной температуры
кипения 10 до конечной 11) и на испарение W = So( l - ао /а 1) кг
растворителя при температуре кипения 11 - при изменении его
энтальпии от cp1t в растворе до i в виде вторичного пара. Заме
тим, что разность (i - ср 11 ) хоть и близка к теплоте испарения
растворителя , но не равна ей (несколько меньше).
Количество греющего пара на стадии выпаривания опреде
ляетr.я из теплового баланса для контура К1 (на рис.9.6) в от
суrствие Источника и Стока теплоты :
D в ып h
D вып С к Т - Q вып =
О
'--v--'
П риход

Уход

Наком ение

687

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

откуда

Q вып
h Ск Т

Q вып
(9 . 8 )
r111
Найденные количества Q нrp и Qвып должны быть подведен ы
D вып =

-

последовательно через одну и ту же поверхность теплообмен а

F; при этом продолжительность нагрева составляет 'tнrp, а вы
паривания
'tвып· Для определения длительности этих стадий
-

рассмотрим кинетику процессов теплопереноса для каждой из
стадий в отдельности .
Для стадии нагрева запишем уравнение теплопередачи за
промежуток времени d't в произвольно выбранный момент ве
дения процесса, когда текущая температура раствора равна t

(tн

:::;

f

:::;

to) :

dQ = kнrp ( Т t)Fd't,
коэффициент теruюпередачи от конденсирую щегося пара к на111 е 
где kн rp
ваемому раствору (его приближенно можно считать неизменным во времени, т.е.
не зависящим от температуры на 111 е ваемого раствор а); F п оверхность теШJо
передачи.
Так как здесь dQ = d(Socot) = Socodt, то
S 0 с0 dt
Socodt = kнrp ( Т t)Fd't , или Fd't = --k н 111 Т t
-

-

-

-

-

Если допустить, что в процессе нагрева раствора значения

kнrp и с0 изменяются несуrnественно (т.е. что теплофизические
свойства нагреваемой жидкости слабо зависят от температуры), то

последнее выражение легко интегрируется. Проинтегрируем его в
пределах от 't = О и lн до полного времени нагрева 'tнгр и fo:

с
F'tнrp = so о � .
k н 111 fн Т t
Учитывая знак при t в знаменателе , после интегрирования по

rj

лучаем

F'tнrр

_
-

-

S 0 с0 1 Т l н
n --'-'Т to
k н 111
-

--

-

-

(9 .9)

Для стадии выпаривания уравнение теплопередачи за проме
жуток времени d't запишем аналогично тому, как это было сде
лано для стадии нагрева:
(д )
dQ = kвып( Т t)Fd't,
где t те кущая тем п ература ки пящего раствора Uo < t < 1 1 ).
Интегрирование этого уравнения осложнено тем, что в ходе
процесса наряду с изменением температуры кипения раствора t
-

-

688

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

(от t0 до t1) существенно изменяется и коэффициент теплопе
редачи kвып (за счет изменения свойств упариваемого раствора
при изменении его концентрации). В со ч етании с уменьшени
ем движущей силы процесса теплопередачи ( Т t) это приво
дит к сложной зависимости количества образующегося в еди
ницу времени вторичного пара от продолжительности проведе
ния процесса. В ходе этой стадии уровень жидкости в аппарате
понижается. Неизменными в ходе этой стадии остаются лишь
величины Т, h и i.
Будем отсчитывать время от начала стадии выпаривания и
интегрировать уравнение (д) от -r = О и Q = О до -r = 'tвып и

-

Q = Qвып:

F-rвып =

Q!ЬIП

f

О

dQ
(Т - t)

(9. 1 0)

kвып

Здесь Q8ып - полное количество теплоты на стадии выпарива
н ия по (9.7), т.е. при изменении концентрации кипящего рас
твора от исходной а0 до конечной а 1 •
Численное значение интеграла в правой части выражения
(9. 10) находят либо графически - как площадь под кривой
1/( k вып (Т - t ) ]
Q в пределах от О до Qвып (рис. 9.7,б), либо
численно. Для установления зависимости 1/[kвып( Т
t)] от Q
необходимо рассчитывать коэффициенты теплопередачи kвып
(метод расчета коэффициента теплопередачи от конденсирую
щегося пара к кипящей жидкости подробно изложен в гл. 7) и
температуру кипения t раствора при любой его текущей кон
центрации а , а также необходимое текущее значение теплоты
Q��� на стадии выпаривания при доведении концентрации
кипящего раствора от исходной ао до текущей а. Очевидно, что
для расчета Q ;:1� можно воспользоваться формулой (9. 7) с
заменой t1 на текущее значение t, а также с учетом количества
удаляемого растворителя wreк при изменении концентрации
раствора от а0 до текущей а:

-

-

wreк

( - 0: ) .

= So 1

-

Q по
Построение одной точки кривой 1/( kвып (Т - t) ]
найденным абсциссе и ординате показано на рис. 9.7, б штри
ховыми линиями .
Найденные по формулам (9.9) и (9. 1 0) значения F-rнrp и F•вып
можно использовать для определения общей продолжитель689

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

'tнrp + 'tвып· Естественно, что и
F'tобщ = F'tнrp + F'tвып ·
Располагая значением произведения F'tofiщ, можно при из
вестной поверхности теплообмена F найти время 'tобщ проведе

ности процесса 'tобщ

=

ния всеrо процесса, и наоборот: при заданной общей продол
жительности процесса можно рассчитать (задача проектирова
ния) необходимую поверхность теплопередачи F.
При сопоставлении Qнrp и Qвып видно, что, как правило, ко
личество теплоты на стадии выпаривания значительно больше,
чем на стадии нагрева. Это связано прежде всего с большими
затратами теплоты на испарение растворителя, так как
rlП > > сл t. Поэтому стадия выпаривания существенно продол
жительнее стадии нагрева.
Одним из существенных недостатков рассмотренноrо спосо
ба ведения периодического процесса является понижение
уровня раствора в аппарате и возможное в связи с этим
"оголение" части поверхности теплообмена в ходе выпарива
ния . Это приводит:
- к уменьшению работающей поверхности теплообмена;
- к инкрустации теплообменной поверхности (за счет выпаривания до сухого остатка капель раствора, попавших на
оголенную поверхность) и понижению коэффициента теплопе
редачи инкрустированной поверхности в последующих циклах
выпаривания .
9.5.2. Периодическое выпаривание
с постоянным уровнем раствора в аппарате
Для предотвращения "оголения" теплообменной поверх
ности периодическое выпаривание часто проводят с постоян
ным добавлением свежего раствора в количестве, достаточном
для поддержания первоначального уровня (объема) раствора в
аппарате. Такой процесс иноrда еще называюr полунепрерыв
ным, или дифференциальным. Кстати, такой способ периодиче
ского выпаривания является одним из основных вариантов

вывода установки на непрерывный режим работы.

Рассмотрим подробнее работу такою аппарата (рис. 9.8). В ап
парат единовременно загружается V0 м3 раствора начальной кон
центрации ао, плотностью РО и теплоемкостью с при температуре
lн . Сначала этот раствор нагревают до температуры кипения to
(стадия нагрева), после чею начинается стадия выпаривания. При
этом из аппарата постоянно отводится растворитель в виде вто
ричною пара, но 'ПОбы уровень раствора не понижался, постоянно
добавляют свежий раствор - разумеется , с первоначальной
концентрацией ао и температурой lн.
690

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

W, i

Рис. 9.8. К расчеrу периодическоrо
выпаривания при постоянном уровне
(объеме) раствора в аппарате:
на сrадии нагрева lи < t < to;
на сrадии выпаривания to < t < t1

Стадия нагрева исходного
раствора (от fн до t0) происхо
дит здесь совершенно анало
mчно рассмотренной в разд.
9.5. 1 ; расчетные зависимости
(а), (б) и (9.9) в равной степе
ни применимы и для рассматриваемой стадии процесса.
Стадия выпаривания при такой работе аппарата имеет свои
особенности. В течение всей стадии будет удалено W кг рас
творителя (вторичного пара) и добавлено дополнительно Уд м3
раствора. При этом концентрация в аппарате постепенно по
высится от о0 до о 1 . Соответственно будут изменяться парамет
ры: to � t1 , Ро � Pt , со � с1 . Таким образом, конечный раствор
при неизменном в течение всего процесса объеме У0 будет ха
рактеризоваться параметрами о 1 , р 1 , с 1 и t1 .
Количество вторичного пара, полученного за весь процесс,
найдем по формуле (9.6), учитывая, что S o = (Vo + Уд) Ро, а мас
са растворенного вещества во всем свежем растворе (S ooo ) рав
на его массе в упаренном ( S 1 01 = Уор1 0 1 ) , т . е.
(Vo + Уд) Рооо = Уор 1 01 .

Отсюда

(Vo

+

)

-1 .
Уд) ро= Уо р 1 � (е) и Уд = Уо P l 0l
Р
ооо
оо

Из (9.6) с учетом выражения (е) получаем

(

(ж)

( )

W = (V0 + Уд) Ро l - 00 = У0р1 � 1 - 00 = Уо р 1 � - 1 . (з)

( )

оо

о1

( )
о1

оо

Потребное количество теплоты Qвыл на всю стадию выпари
вания (продолжительностью 'tвы п) на йдем из теплового баланса
для контура К2 на рис . 9.6 (см. также рис. 9.8):
(и)
Приход

Уход

Накопление

Отсюда
(к)

69 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

С целью выявления физического смысла выражения (к)
преобразуем его с учетом правила адд итивности теплоемкостей
(9.2), записываемого для данного случая [см. также формулу (г)
данного раздела] в ВЦ!l.е
Уо р1 с 1 = (Vo + Уд) росо - Wcp.
После подстановки этого выражения в первое слагаемое
правой части выражения (к) получаем

Qвып
или

=

(Vo + Уд) росо /1 - Wcp/1 - Уо росо!о - Удросо!н + Wi ,

Qвып = Уо росо( /1 - !о) + Уд росо( /1 - lн ) + W(i - Ср/1 ).

(л)
Из (л) следует, что теплота на стадии выпаривания с добав
лением свежего раствора для поддержания постоянного уровня
расходуется:
- на нагрев первоначально залитого раствора (V0 p0 , кг) от на
чальной температуры кипения t0 до конечной t1 (его нагрев от
lн до !о учитывается на стадии нагревания);
- на нагрев дополнительно подаваемого раствора (Vд ро, кг) от
исходной температуры tн до конечной температуры кипения t1 ;
на испарение W кг растворителя при постоянной темпера
туре кипения t1
п ри изменении энтальпии растворителя от
ср/1 в растворе до i в ВЦ!l. е вторичного пара.
Окончательное расчетное выражение для Qвып получаем при
подстановке выражений (ж) и (з) соответственно для Уд и W:

-

-

( Роао - ) росо(/1 - lн)
+ Уо р1 ( ;� - ) - Ср/1 ).

Qвып = Уоросо( /1 - !о) + Уо Pla l
1 (i

1

+
(9. 1 1 )

Подчеркнем, что определяемое по формуле (9. 1 1 ) количе
ство теплоты отвечает концентрированию раствора от началь
ной концентрации ао до конечной а1 . Количество греющего
пара при этом определяется по (9.8).
Вопрос о продолжительности ведения процесса в этом вари
анте периодического выпаривания в принципе решается так
же, как и в предыдущем. Для стадии нагрева единовременно
залитого исходного раствора (V0 p0 кг) произведение F•нrp рас
считывают по (9.9), а интеграл в (9 . 1 0) н аходят либо графиче
ски (рис. 9.7,б), либо численным методом. При этом текущее
количество теплоты Q��п на стадии выпаривания при доведе692

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

нии кон центрации кипящего раствора от исходной ао до теку
щей а рассчитывают по формуле (9 . 1 1 ), подставляя, естествен
но, не конечные параметры процесса ( t1 , с 1 , р1 ), а текущие (t,
с, р) - соответствующие выбранной концентрации а.
Сопоставление величин Qнrp и Qвып при работе выпарного
аппарата с постоянным уровнем свИдетельствует о превали
рующем значении второй. В самом деле, единовременно нагре
вается лишь залитая порция раствора (V0 ), а на стадии выпари
вания испаряется растворитель из объема (V0 + Уд) . причем
нередко (это зависит от степени концентрирования раствора)
Уд > > Уо. Заметим также, что в Qвып входит и теплота на на
грев подпитывающего раствора Уд до температуры кипения.
Соотношение продолжительностей отдельных стадий (tнrp и
'tвып) определяется преимущественно соотношением Qнrp и
Qвып· Точный расчет 'tнrp и 'tвып здесь производят так же , как в
периодическом выпаривании с переменным уровнем.
9.6. ВЫПАРНЫЕ АППАРАТЫ НЕПРЕРЫВНОГО ДЕ Й СТВИЯ
9.6. 1 . Однокорпусный выпарной аппарат

При непрерывной работе выпарного аппарата (см. рис. 9.5)
все параметры процесса остаются неизменными во времени.
Раствор в аппарате кипит при конечной концентрации а 1
(температура кипения t1 ) и отводится из него непрерывно с
соблюдением баланса по расходам свежего раствора и вторич
ного пара. Такая работа аппарата возможна при подаче необхо
димого количества греющего пара (или другого теплоносителя)
и наличии достаточной поверхности теплообмена, способной
передавать тепловой поток от теплоносителя к раствору. Отсю
да задача расчета процесса выпаривания сводится к определе
нию необходимого теплового потока Q (индекс "вып" в вы
парных установках непрерывного действия опущен, так как
здесь нет другой стадии) и расхода теплоносителя Drp . а также
требуемой поверхности теплообмена F.
Отбор упаренного раствора (при выходе на непрерывный
режим работы) начинается с момента достижения конечной
концентрации а 1 раствора в корпусе, т.е. по завершении выхода
на режим (в ходе полунепрерывного процесса выпаривания) .
Одновременно с этим изменяется режим подачи исходного
раствора с таким расчетом, чтобы все параметры процесса вы
паривания (в том числе и объем раствора в аппарате) остава
лись неизмен ными.
693

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Продолжительность выхода на стационарный режим (полу
непрерывное выпаривание) определяется по формуле
'tнгр

+

=

'tвып

't общ

=

F-снгр + Ре вып
F

где F�н rp и F�вып находят по формулам (9.9) и (9 . 1 0) , а поверхность теплообмена
F, как правило, определяют из условий непрерывной работы выпарною аппарата.

Для расчета выпарного аппарата непрерывного действия
воспользуемся расчетной схемой передачи теплоты от
греющего пара к кипящему раствору через разделяющую их
поверхность теплообмена F (рис. 9.6).
Тепловой баланс по контуру К2 за единицу времени без уче
та потерь теплоты в окружающую среду запишется:
О .
Q + S0 c 0 t 0 - Wi - S1 c 1 t 1
..___..
Отсюда

�

"-,,.-'

Приход

Уход

Накопление

Q = S1c1 t1 - Socoto + Wi.

Выражая соответственно правилу адд итивности теплоем
кость упаренного раствора ( S1c1 ) как разность между теплоем
костями исходного раствора ( S0co ) и удаляемого растворителя
( Wcp), после преобразований получаем
Q = Soco ( /1 - to) + W(i - ср /1 ).

(9. 1 2)

Следовательно, необходимый тепловой поток расходуется на
нагрев So кг/с исходного раствора от to до /1 и на последующее
испарение растворителя W кг/с при температуре 11 .
Разумеется, возможно таюке исключить Soco с помощью (9.2); тогда прихо
дим к выражению для Q, записанному в иной форме:

Q=

W( i -

cpfo) + S1 с 1 ( 1г to).

(9. 1 2а)

Такая запись траlСl)'ется как затраты теплоты на испарение W кг/с растворителя
при темпера'l)'ре 10 и на последующий нагрев S1 кг/с упаренного раствора от to до 1, .

По рассчитанному согласно (9. 12) тепловому потоку Q мож
но найти расход греющего пара Drp из теплового баланса по
контуру К 1 за единицу времени:
Drp h - Q - Drp cк T = О,
откуда
Q
Q
(9. 1 3)
= ---

D

694

ГР

h СкТ
-

Гrр

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

и требуемую поверхность теплообмена

F = _я_ '
kЛt

(9. 14)

где k - коэффициент теплопередачи от конденсирующегося пара к кипящему
раствору; лt = Т - 11 - движущая сила процесса теплопередачи; k и лt - посто
янны по поверхности теплообмена.

Потери тепла в окружающую среду Q0 (от наружной поверх
ности аппарата) должны быть учтены при определении расхода
греющего пара по (9 . 1 3) - их добавляют в числитель формулы:
Drp

+
= Q Qo

h - ск Т

_

Q

_

+ Qo .

rrp

(9. l За)

При расчете по (9. 14) необходимой поверхности теплообме
на F труб нагревательной камеры учитывается лишь тепловой
поток на процесс выпаривания, определяемый по (9. 1 2). Поте
ри теплоты Q0 осуществляются через наружную поверхность
корпуса выпарного аппарата и, естественно, в формуле (9 . 14)
для поверхности теплообмена фиrурировать не должны.
9.6.2. Выбор рабочего давления процесса

Выбор рабочего давления связывают с экономичностью
проведения процесса. Затраты на проведение любого процесса
складываются в основном из капитальных затрат (в форме
амортизационных отчислений, конечно), т.е. из стоимости а п
парата, определяемой поверхностью теплообмена F, и энергети
ческих затрат (стоимости греющего пара) в ходе процесса.
Для уменьшения поверхности теплообмена при фиксирован
ной температуре конденсации греющего пара предпочтительнее
работа под вакуумом: при этом из-за уменьшения температуры
кипения раствора t1 увеличивается движущая сила процесса
теплопередачи Лt = Т - t1 , и согласно (9. 14) уменьшается необ
ходимая поверхность теплообмена F (заметим: при изменении
рабочего давления коэффициент теплопередачи k изменяется
значительно меньше, нежели t1 и Лt).
Максимальная величина движущей силы процесса теплопередачи не долж на
превышать -30-3 5 • с. При большей разности температур частный температур
ный напор (со стороны кипящего раствора) может превысить критическое зна
чение, при котором интенсивность теплоотдачи к кипящему раствору резко
уменьшается .

Однако более обстоятельный экономический анализ пока
зывает, что для такого энергоемкого процесса, как выпарива-

695

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ние, определяющими являюrся энергетические затраты, так что
минимум суммарных затрат находится вблизи минимальных
энергозатрат. Поэтому на первый план выходят проблемы по
нижения затрат на греющий пар и его рационального использо
вания. Получаемый при выпаривании под вакуумом вторичный
пар низкого потенциала (температура, давление), как правило,
не только не может быть использован в последующих техноло
гических операциях, но нередко требует еще и дополнительных
затрат для вывода его из технологического (в данном случае вьmарного) аппарата. В то же время при выпаривании под повы
шенным давлением (например, р = 0,2 МПа) вгоричный пар с
температурой насыщения - 120 ° С может быгь использован в по
следующих технологических операциях. Таким образом, при про
чих равных условиях целесообразно работать под давлением, так как
в этом случае наряду с упаренным раствором дополнительным
товарным продукгом будет и вгоричный пар высокого давления.
Тем не менее встречаются технологические ситуации, когда
целесообразно работать под атмосферным давлением или под
вакуумом. Назовем две такие ситуации, наиболее типичные.
С первой мы встречаемся при необходимости выпаривания
термолабильных веществ, разлагающихся выше определенной
температуры. Чтобы температура кипения
не превышала
температуру разложения, приходится понижать рабочее давле
ние в зоне кипения выпарного аппарата.
Вторая ситуация, когда следует идти на выпаривание под ваку
умом WIИ под атмосферным давлением, возникает в тех случаях,
когда на заводе имеется дешевый (подчас бросовый, просто бес
платный) теплоноситель низкого потенциала (температура 1). Его
использование возможно, если удастся создать положительную
движущую силу лt = Т t, т.е. удерживать температуру кипения
раствора t ниже невысокого значения Т Эго возможно осущест
вить, проводя процесс выпаривания под вакуумом (в некоторых
случаях - под атмосферным давлением). В результате получается
существенная экономическая выгода, даже с учетом усложнения
процесса при создании вакуума .
Если при выпаривании приходится вести процесс под ваку
умом, то стоит работать при возможно малом (технически ра
зумном) остаточном давлении
чаще всего на уровне 50001 0000 Па. В этом случае получается еще и наименьшая поверх
ность теплообмена F.

tк

-

-

9.6.3. Схема и расчет вакуумной выпарной установки
Для создания вакуум а в выпарном аппарате вторичный пар
из него направляется в конденсатор - поверхностный или
смесительный.

696

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

П оверхностные конденсаторы, представляющие собой много
ходовые кожухотрубные теплообменниЮf, охлаждаемые холод
ной водой, применяются , как правило, если нежелательно
смешение конденсата вторичного пара с охлаждающей водой .

Поверхностные конденсаторы имеют большие поверхности теплообмена, со
поставимые с таковыми для выпарного аппарата, требуют повышенных расходов
воды и настолько дoporn, 'ПО используются практически лишь тогда, когда
применение других конденсаторов невозможно . Например, при выпаривании
иеводИwХ растворов солей предпочтительны поверхностные конденсаторы, так
как в смесительных потребовалась бы дополнительная стадия ра:щеления скон
денсировавшегося вторичного пара и охлаждающего аrента .

В последние годы все чаще применяют поверхностные конден
саторы воЗ,!lуШноrо охлwtЩения, использующие в качестве охлаж
дающего агента атмосферный воздух. Последний нагнетается
мощным вентилятором. Применение аппаратов воздушного
охлаждения позволяет существенно снизить потребление воды
и соответственно загрязнение водного бассейна. "Заг
рязнение" воздуха теплотой при работе аппаратов воздушного
охлаждения пока не представляет серьезной угрозы экологии .
Однако затраты энергии н а вентилятор и достаточно дорогие
поверхности теплообмена (оребренные трубы с целью повыше
ния интенсивности теплоотдачи от стенЮf к воздуху) в извест
ной мере ограничивают область применения этих аппаратов.
С месительные конденсаторы, в которых происходит непо
средственный контакт пара и охлаждающей воды, являются
наиболее распространенными, а среди них чаще всего исполь
зуется противоточный барометрически й конденсатор сме шения . В
таком конденсаторе (рис . 9.9) поднимающиеся вверх пары кон
денсируются при прохождении через водяные завесы, созда
ваемые потоком охлаждающей воды, перетекающей с верхних
полок на нижние. Для увеличения поверхности контакта пара с
водой в полках имеются отверстия, через которые последняя
протекает, образуя струи и капли (в виде дождя). Резкое
уменьшение при конденсации пара занимаемого им объема
приводит к созданию вакуума в конденсаторе, а значит, и в сое
диненном с ним выпарном аппарате.
ТеоретичесЮf достижимый вакуум (точнее - остаточное
давление) соответствует упругости водяного пара над смесью
отработанной охлаждающей воды и образовавшегося конденса
та. Реально создается несколько меньший вакуум (остаточное
давление на уровне 5000- 1 0000 Па), так как в конденсатор
попадают неконденсирующиеся rазы (прежде всего - воздух,
при выпаривании карбонатов - диоксид углерода, образую
щийся в результате частичного разложения солей , и др .). По
следние содержатся во вторичном паре (изначально - в выпа697

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рконд

w;;, e
Бг

Vпr
lш ·

JV

5

0конд

TV

lll

Vl

4
1 - выпарной аппарат, 2 - барометрический конденсатор смеш ени я , З - барометриче
ская труба, 4 - барометрический ящик, 5 -вакуум-насос;
/ - охлаждающая вода, // - нагретая вода, /// - вторичный пар, /V - неконденсирую
щиеся газы, V - rреющий пар, V/ - конденсат

Рис.9.9. Схема выпарной установки , работающей под вакуумом:

риваемом растворе), а также выделяются (десорбируются) из
охлаждающей воды при попадании ее из сети в зону низкого
давления (в конденсатор) и повышении ее температуры от t'8
до t"8 (см. рис. 9.9). Наиболее заметный источник неконденси
рующихся газов в конденсаторе смешения - воздух, подсасы
ваемый извне через неплотности разъемных соединений уста
новки. Для поддержания заданного вакуума неконденсирую
щиеся газы (реально - парогазовая смесь) непрерывно отсасы
ваются из верхней части конденсатора вакуум -насосом 5 (см .
рис . 9 .9), чаще всего водокольцевым.

Точного метода расчета основных размеров баром етр ического конденсатора
смешения не существует. Его диаметр оценивают по расходу вторичного пара и
его скорости в свободном сечении ( 1 0- 1 5 м/с), а затем по каталогам подбирают
ближайший больший (по диаметру) конденсатор. Число каскадов принимают
равным 5 -7 - этого достаточно для полной конденсации вторичноrо пара.
Площадь сегментных вырезов для прохода парогазовой смеси с каскада на кас
кад составляет 40-5 0 % от площади сечения конденсатора.

Для нормальной работы барометрического конденсатора
смешения необходимо обеспечить требуемые расходные харак698

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

теристики : расход охлаждающей воды и объемный расход отса
сываемой пароrазовой смеси (последний необходим для подбо
ра вакуум - насоса) .
Расход охлаждающей воды Gв на конденсацию W кг/с вто
ричного пара с энтальпией i определяем из уравнения теплово
го баланса за единицу времени для контура, охватывающего
конденсатор смешения :
Wi + Gвc8 t � - (G8 + W)c 8t � - Gпrcпrlпr
О
.___..
=

"-----v---'

Приход

Уход

Накомение

Слаrаемым Gпreпrtпr, учитывающим вынос теплоты с пароrа
зовым потоком, пренебреrаем ввиду его незначительности по
сравнению с другими составляющими теплового баланса. Тогда
i - С в!�
(9. 1 5)
Gв = W

с в (t"в - t'в )

Температуру воды !'8 принимают в зависимости от географи
ческого места расположения конденсатора смешения: при ис
пользовании подземной (артезианской) воды /18 = 8+ 10 ° С, а в
случае оборотной воды - от 1 5 до 30 ° С. Последняя цифра
определяется возможностью охладить нагретую воду в градир
нях в летних условиях для данной местности .
Температура !118 жидкости, покидающей конденсатор, вооб
ще говоря , вследствие развитой поверхности контакта, может
быть принята равной температуре конденсации паров в кон
денсаторе 8конд (потоковая задача теплопереноса). Однако в
практических расчетах (для большей rарантии) ее обычно при
нимают на 2-3 градуса ниже температуры конденсации паров
в конденсаторе (8конд) . Заметим, что температура 8конд ниже
температуры насыщен ия вторичного пара 8 , покидающего вы
парной аппарат, на величину гидравлической депрессии 8r = 8 - 8конд· Причина появления 8r - понижение dавления пара р при
его транспортировании по трубопроводу от аппарата к конден
сатору: с уменьшением давления понижается и температура
насыщения (конденсации) пара - от 8 в выпарном аппарате до
8конд в конденсаторе. Из опыта работы выпарных аппаратов
установлено, что 8r ::::: 1+2 ° С.
Максимальная температура воды !"8 ограничена. Основные
причины ограничения - следующие:
- возможное отложение солей в конденсаторе и барометри
ческой трубе (особенно интенсивное при температурах выше
50-55 ° С);
- увеличение давления водяных паров с повышением тем
пературы воды !"8, что приводит к понижению парциального
699

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

давления газа в отсасываемой вакуум-насосом паро газ овой
смеси, а следовательно, к увеличению объемного потока по
следней и затрат энергии на ее сжатие (см. ниже);
- увеличение потерь оборотной воды. Нагретая в конденса
торе до !"8 вода охлажд ается, как правило , в градирнях - с
целью ее последующего использования в теплообменниках в
качестве холодного теплоносителя. Охлаждение воды в градир
нях происходит за счет ее частичного испарения. При высокой
исходной температуре воды t"8 для ее охлаждения до приемле
мой конечной температуры (до -20-25 ° С) потребуется испа
рить (т.е. потерять) значительную долю воды. Исходя из допус
каемой на практике доли потерь воды на испарение на уровне
5-7% , получают верхний предел t"в порядка 45-50 ° С.
Объемный расход парогазовой смеси, отсасываемой вакуум 
насосом, Vпr можно найти из уравнения состояния идеального
газа, записанного для сухой газовой (воздушной) части, т.е.
при парциальном давлении газа (pr) :
V.

пr

=

V.

r=

G r R Тпr
,
PrМ r

(9. 1 6)

rде R - универсальная rазовая постоянная; Мг - молярная масса сухого rаза;
Tnr = 27 3 + 1nr - температура отсасываемой смеси (в К), пр ичем 1nr - темпера
тура (в 0 С) пароrазовой смеси на выходе из конденсатора (поСJJ едняя всегда
выше температуры поступающей воды 1'1 и ниже 1"8) .

Оценим величины, входящие в формулу (9. 16).
Температура tпr определяется по эмпирическим рекоменда
циям и формулам, например:
tпr = !'в + 4 + 0, 1 (!"8 - !'в) .
Масса неконденсирующегося газа (воздуха) Gr ( кг/с) в отса
сываемой парогазовой смеси определяется как сумма двух
основных слагаемых. Первое отражает десорбцию газов
(главным образом из охлаждающей воды). Обследование дей
ствующих конденсаторов смешения показало, что из каждой
тонны смеси охл аждающей воды и конденсата десорбируется
примерно 0,025 кг неконденсирующихся газов (воздуха) . Вто
рое слагаемое - подсос воздуха в конденсатор смешения через
неплотности - оценивается сугубо приближенно: принимают,
например, что в расчете на тонну получаемого вторичного пара
подсасывается до 10 кг воздуха. Соответственно приведенным
выше сведениям, массовый поток отсасываемых сухих некон
денсирующихся газов составляет*
Gr = [0,025( W + G8) + l O Jf']- 10-3 ,
• Более то нкие эффекты, связанные с работой конденсатора смешения
(уточненный расчет подсоса, Зависимость количества десорбирующихся rазов от
температуры, источники СО2 при частичном разложении солей и др . ) , приведе
ны в специальной литературе (см " например , ( 7 J ) .

700

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

причем все потоки выражаются в кг/с. Заметим, что второе
слагаемое, выражающее подсос воздуха через неплотности ,
обычно примерно на порядок превышает первое.
Парциальное давление газа Pr находят как разность между
абсолютным (остаточным) давлением в конденсаторе (рконд) и
давлением насыщенного водяного пара (рп) при температуре
tm, т.е . Pr = Рконд Рп · При этом величина Рконд отвечает тем
пературе 8конд, т.е. учитывает небольшое понижение давления в
конденсаторе смешения в сравнении с выпарным аппаратом.
-

П о давлению в конденсаторе смешения Ркuнд и производительности
(объемный расход парогазовой смеси) подбирают вакуум -насос, чаще всего один из
типов водокальцевых. Поскальку в юrraлo rax приводиrся производительность вакуум 
насоса в н.t3/с (иноща - в н.t3/мин), то найденную по (9. 1 6) величину Vnr пересчиты
вают на нормальные условия (атмосферное давление
Ратw):

vну
пг

_
-

V.

-

Рконд

rrr --- .

Ратм

Потребляемая вакуум - насосом мощность складывается из
двух основных составляющих:
- на сжатие парогазовой смеси от давления в конденсаторе
Рконд до давления газа чугь больше атмосферного (зто неболь
шое превышение связано с гидравлическими потерями при
движении сжатой парогазовой смеси от вакуум - насоса к месту
ее выброса в окружающую среду); рассчитывается по форму
лам , приведенным в разд. 4.3.2;
- на поднятие и поддержание жидкости в водокольцевом на
сосе при его работе (центр тяжести жидкостного кольца располо
жен выше центра тяжести жидкости в неработающем аппарате).
Для нормальной работы конденсатора смешения требуется
непрерывно отводить смесь отработанной воды и образую
щегося конденсата. Проблема здесь возникает в связи с ваку
умом в конденсаторе. Принципиально возможен отвод жид
кости с помощью насоса, однако значительный расход энергии
на ее откачку делает этот способ экономически нецелесообраз
ным. Практически выгодно отводить жидкость из конденсатора
с помощью барометрической трубы (см. рис . 9.9, поз . 3). Гидро
статическое давление столба воды в барометрической трубе
( рgНб.т) вместе с давлением в конденсаторе Рконд позволяет
уравновесить атмосферное давление В (и создать при этом гид 
равлически й затвор , препятствующий проходу атмосферного
воздуха в конденсатор) .
Диаметр барометрической трубы dm определяем из уравне
ния расхода ( 1 . 1 7) жидкости в ней:

Gв + W
Рв

---

=

7tdm2

--

4

W бт

70 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

при этом скорость "естественного" течен ия wбт принимается в
пределах 0,2 5 - О, 75.м/с.
При подборе по каталоrам конденсатора смешения в ком rтекте с баромет
рической трубой технологи обычно выполняют поверочный расчет, проверяя
реальную скорость течения воды в барометрической трубе при выбранном ее
диаметре и требуемом расходе смеси охлаждающей воды и конденсата.

Высоту барометрической трубы Нбт находим из уравнения
Бернулли, записанного для сечений а-а и 6-6 (см. рис . 9.9),
приняв плоскость отсчета совпадающей с сечением 6-6:
Н

где

hп

бт

+

Р конд

+

pg

w2
бт

2g

О .!!_ +
= +
pg

w2
бт

2g

+ hn

'

(б)

- гидравлические потери при движении

=

жидкости по трубе; Л г - коэффициент гидравлического сопротивления на пря
мом участке трубы; I: � - сумма коэффициентов меС111 ых сопротивлений на
барометрической трубе (это , как правило, вход в трубу и выход из нее) .

н.

В - Р ко нд

Отсюда высота барометрической трубы
бт _

+ hп .
pg
С учетом возможных колебаний барометрического давления
(расчет ведется по среднему барометрическому давлению В в
географической точке работы выпарной установки), высоту
трубы принимают с запасом:
=

В - Р конд '

(9. 17)
+ hn + 0,5.
pg
Для определения высоты нбт надо раскрыть hп и разрешить
полученное выражение относительно Нбт. Однако при практи
ческих расчетах по формуле (9. 1 7) величиной h0 обычно прене
брегают ввиду ее малости (не более О, 1 м) по сравнению с
другими составляющими.
нбт

9.6.4.

П уrи экономии греющего пара

Ввиду значительной энергоемкости процесса выпаривания
вопросы выбора теплоносителя и его рационального использо
вания являются очень важными. Кардинально решить пробле
му экономии теплоносителя можно лишь в том случае, если за
счет кг греющего пара удалять не 0, 8-0,9 кг вторичного, а
больше . Это возможно при использовании вторичного пара в

1

7 02

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

качестве греющего. Однако непосредственно использовать вто
ричный пар в качестве греющего в том же выпарном аппарате
невозможно, так как необходимое условие теплопередачи Т > t,
а температура насыщения (конденсации вторичного пара) 8
ниже температуры кипения раствора t на величину темпера
турной депрессии . Поэтому возможны два пути:
- понизить температуру кипения раствора, т.е. использовать
вторичный пар для обогрева аппарата, работающего при пони
женном давлении с температурой кипения раствора t < 8. Эrот
пуrъ используется в многокорпусных вьmарных установках, где дав
ление от корпуса к корпусу понижается и вторичный пар из
предьщущеrо корпуса может служить греющим для последую
щего;
- повысить потенциал вторичного пара (его давление и со
ответственно температуру конденсации) до значений греющего;
такое повышение происходит при сжатии вторичного пара в
компрессоре (обычно в турбокомпрессоре) или в инжекторе.
Заметим, что простое повышение температуры вторичного па
ра за счет нагрева не дает существенной экономии греющеrо
пара, так как отдаваемая перегретым паром теплота, равная
произведению теплоемкости пара Сп на величину перегрева
л t , значительно меньше теплоты конденсации.
n ри использовании инжектора вторичный пар не весь, а
только некоторая его часть (далее этот вопрос будет рассмот
рен подробно), сжимается до давления греющего пара. Отсюда
и название - частичный тепловой насос (в отличие от сжатия в
компрессоре всего вторичного пара, получившего название
полного теплового насоса ) .

Сам термин "теwювой насос" имеет следующее происхождение. В ряде тех
нологических процессов (в часnюсти, в рассматриваемом процессе) необходима
передача теnлоты от теnлоносителя с низкой температурой (здесь - зто вrорич
ный пар) к теnлоносителю с более высокой температурой (:щесь - зrо кипящий
расrвор). Но такая передача теruюты по вrорому закону термодинамики самопроиз
вольно невозможна - так же, как и естественное течение жидкости с нижнего уровня
на более высокий или из области низкого давления в обласrь высокого. Задача пре
одоления разности напоров ЖЩIКОСТИ решаеrся с помощью Н1Jсосов; для переноса
теruюты используеrся технолоmческий прием (с затратой механической энергии),
получивший по аналогии название "теплового насоса", обеспечивающего
" перекачку" теплоты с нижнего температурного уровня на верхний .
Применительно к процессу выпаривания сжатие вторичноrо пара сопровож
дается повышением ero потенциала (давления, температуры) и , следовательно,
температуры конденсации до такой величины, при которой разность температур
(сжатоrо пара и кипящего раствора) становится положительной. При наличии
такой разности (положительной движущей силы) высвобождаемая теnлота кон 
денсации сжатоrо 11Jеющеrо пара передается кипящему раствору.

Ниже рассмотрены оба пути экономии греющего пара и об
ласти их предпочтительного использования.
703

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

9.6.5. Многокорпусные выпарн ые установки

При выпаривании раствора в нескольких аппаратах его кон
центрация повышается от корпуса к корпусу, причем для обо
грева последующих используется вторичный пар, получаемый в
предыдущих.

Схема и работа многокорпусных установок
Наиболее распространенная прямоточная схема многокор
пусной выпарной установки представлена на рис. 9 . 1 О и 9 1 1
В целях наглядности сначала рассмотрим упрощенную схему
такой установки (рис . 9. 1 0), зафиксировав характерные рабочие
давления в корпусах и температуры технологических потоков
(на примере трехкорпусной установки) . Исходный раствор с
начальной концентрацией после упаривания в первом корпусе
последовательно проходит через последующие корпуса уста
новки, постепенно увеличивая свою концентрацию до задан
ной . Примем, что первый корпус обогревается свежим
(первичным) паром давлением 620 кПа при температуре кон 
денсации 160 ° С. Пусть температура кипения раствора в пер
вом корпусе равна 135 ° С, а температура вторичного пара
130 ° С (т.е. ниже на величину депрессии в этом корпусе) . Во
втором корпусе концентрация кипящего раствора будет выше
(и депрессия - тоже). Естественно, что вторичный пар из пер
вого корпуса с температурой 130 ° С (эта температура отвечает
рабочему давлению 275 кПа) может быть использован во вто
ром корпусе в качестве греющего только в том случае , если
температура кипения раствора будет ниже 130 ° С. Этого можно
добиться путем понижения рабочего давления во втором корпусе
(в приведенном примере - до 105 ° С) . Соответственно, чтобы
вторичный пар из второго корпуса использовать для обогрева тре
тьего давление в последнем должно бьпъ еще меньше (в нашем
примере рабочее давление в третьем корпусе равно 7,4 кПа, а
температура кипения
55 ° С) . Таким образом, давление от кор
пуса к корпусу должно понижаться (в нашем примере 275; 84; 7,4
кПа) так, 'П'Обы несмотря на увеличивающиеся депрессии в кор
пусах (5 ° С
в первом, 10 ° С - во втором, 1 5 ° С
в третьем),
вторичный пар предыдущего корпуса мог обогревать после
дующий. При этом движущая сила процесса теплопередачи
(разность температур греющего пара и кипящего раствора), как
правило , растет от корпуса к корпусу в связи с умен ьшением
коэффициента теплоотдачи к кипящему раствору при увеличе
нии его концентрации (в рассматриваемом примере эта раз
ность равна 25 ° С в первом корпусе и 40 ° С - в третьем ) .
.

.

-

-

-

704

-

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

IЗd'C,

275

95'С,

кПа

11

135°С
160°С
620 кПа

105 °С

84 кПа

40°С, 7,4 кПа
К

III

кондсн�:атuру
CWCШtHJll

Упарс н н w й
раст1ор

Ис.·юднwй
расnюр

Рис. 9. 10. Типичное распределение температур и давлений
корпусной выпарной установки (упрощенная схема)

по аппаратам трех

При наличии существенной разницы давлений в корпусах
переток раствора из одного в другой регулируется вентилями
на жидкостных линиях, соединяющих эти корпуса. Такое не
принудительное (без затраты внешней работы) движение рас
твора через всю систему является одним из преимуществ пря
моточной схемы. Еще одним ее достоинством являются незна
чительные потери теплоты с уходящим упаренным раствором ,
так как температура кипения раствора в последнем корпусе ми
нимальна. Недостатком данной схемы являюrся неблагоприятные
условия теruюпередачи: самый концентрированный раствор кипиг
при наиболее низких давлении и температуре, когда его вязкость
максимальна, а теплопроводность чаще всего минимальна.
По условиям теплопередачи более выгодны многокорпусные
установки с противоточным движением раствора и паров* . Здесь
выпариваемый раствор движется по направлению от последне
го корпуса к первому, а вторичные пары - в обратном направ
лении . При этом раствор конечной концентрации (наиболее
вязкий) обогревается первичным паром и кипит при самых
высоких давлении и температуре. Существенным недостатком
такой схемы является необходимость принудительного переме
щения раствора из корпуса в корпус в сторону нарастающего
давления, что требует применения побудителей движения
(насосов, да еще работающих в жестких условиях), а значит и
затрат энергии. Вывод из первого корпуса концентрированного
раствора с высокой температурой приводит к б6льшим потерям
теплоты, нежели в предыдущем варианте схемы. По этим при
чинам чаще применяется прямоточная схема.
• См . ,

например ,

(21.
705

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

При выпаривании кристаллизующихся растворов во избежа
ние закупорки соединительных трубопроводов МОJУГ быть ис
пользованы мноrокорпусные установки с параллельным пита
нием корпусов и выпариванием раствора в каждом корпусе до
конечной концентрации. Пар, как и в предыдущих двух схемах,
движется от первоrо корпуса к последнему. В том же направ
лении снижается рабочее давление в корпусах, а следователь
но, и температура кипения растворов.
Как правило, в упомянутых выше случаях последние корпу
са выпарных установок работают под вакуумом; поэтому по
следний корпус соединяется с конденсатором - так же, как
это было сделано в случае однокорпусноrо выпарноrо аппарата
(см. рис. 9.9). Только при использовании исходноrо греющеrо
пара весьма высокого давления (порядка 1 МПа и выше) или
высокотемпературноrо теплоносителя иногда возможна орга
низация работы последнего корпуса многокорпусной установки
под атмосферным (или даже повышенным) давлением. Пре
имуществом такого режима работы является отсуrствие конденса
тора смешения, а в ряде случаев - и возможность использования
вrоричноrо пара из последнеrо корпуса; основной недостаток дороговизна греющего пара повьШiенного давления.
Поскольку наиболее часто на практике используется прямо
точная в1t111ариаJ1 установка, рассмотрим более детально ее рабо
ту (рис. 9. 1 1 ) и особенности расчета на примере трехкорпусной
выпарной установки (к вопросу об оrnимальном числе корпу
сов вернемся позднее).
Начальный раствор с концентрацией а0 и температурой t0
непрерывно пос'J)'Пает (его расход 50 к.г/с) в первый корпус, где
он выпаривается за счет теплоты конденсации первичного
( rре ющего) пара до концентрации а1 при температуре t1 . Обра
зующийся в первом корпусе вторичный пар с температурой 8 1
напраRЛ.Яется в греющую камеру второго корпуса, работающего
при меньшем давлении в зоне выпаривания, нежели в первом
корпусе. При движении вторичного пара по трубопроводу от
первого корпуса ко второму за счет гидравлического сопротив
ления дамение, а соответственно и температура насыщенных
паров несколько уменьшаются. Понижение температуры харак
теризуется гидравлической депрессией паропровода 5r 1 -2 = 8 1
- Т2 . Естественно, температура кипения раствора во втором
корпусе должна быть ниже температуры конденсации гре
ющего пара (т.е. вторичного пара из первого корпуса): t2 < т2 =
= 8 1 5rl-2·
Во втором корпусе раствор выпаривается до концентрации
а2 за счет теплоты конденсации пара и самоиспарения раствора
-

-

7()6

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

�-E z

W. -E 1

Рис.9. 1 1. К

К mидексатору

расчету прямоточной трех.корпусной установки

вследствие падения давления и понижения температуры кипе
н ия от 11 до 12 , причем доля "самоиспарившейся " жидкости
определяется соотношением (ж) раздела 9.3.
В третьем корпусе, обогреваемом вторичным паром и з вто
рого корпуса
= е 2 - 8r2_ 3) , раствор выпар ивается до требуе
мой конечной концентрации а3 при температуре кипения t3.
Вторичны й пар из третьего корпуса направляется в конденса
тор смешения с целью создания в нем вакуума.
При работе многокорпусной выпарной установки практиче
ски всегда выгодно отводить часть вторичного пара на сторону
(если только есть потребитель этого пара) . Отводимый пар (как
правило , из первых корпусов) получил название экстра-пара. В
схеме на рис. 9 . 1 1 : Е1 - экстра-пар из первого корпуса, EJ_ из второ го. Тогда при получении потоков W1 и "'2 вторичного
пара в первом и втором корпусах на обогрев последующих
корпусов направляют потоки вторичного пара Di = W1 - Е1 и

( Тз

Dз

=

�

- EJ_.

пр о
обоrрев вroporo
чала отбора

умень
Отводрасхода
экстра-пара,
например
из первого корпуса - Е1, ив дит ккорпуса.
шению
пара
DJ.
= W1 - Е1 , поС'l)'пающего на
Для
поддержания
DJ. на первоначальномьно,уровне
(до нперви
а
экстра-пара)
необходимо
увелич
и
расход
ого
ею
W1 , а следовател
чн
гр
ить
щего пара
D1 . Таким образом, отвод экстра-пара приводит к увеличению расхода гр еющего
пара,Тем неневыгодно
работы выпарной установки.
менее
экстра-пар
отводят
из ческих
выпарной
установки,- если только
его
потребитель
на
соседних
техноло
установках,
выzодно для
m
цеха, для завода в целом. Дело том, чrо последние нередко
паре
относительно
низкого
давления.
И если им не отдать экстра-пар, то они вшrуж
дены
давления
из заводского
трубопровода
(скажем,будутпариспользовать
давлением 6 , 3парат высокого
вместо вполне
приемлемого
давления
- 2,7
'ПО

для

в

это

Н}'ЖllаЮТСЯ

2,6

есть

в

707

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ат из первою корпуса - см. приведенный выше пример с численными значе
ниями темпера'I)'р). Поэтому-то и выгодно отдать такому потребителю в виде

экстра- пара часть вторичною пара, а потерю ею восполнить свежим паром
высокою давления . Тем более что этою свежею пара потребуется меньше, чем
отдано экстра-пара: ведь эффект дополнительною свежею греющею пара сказы
вается во всех корпусах установки. В результате при отдаче экстра-пара в целом
для цеха (завода) получается большая экономия.
Разумеется, наиболее выюдно бьvю бы отдавать экстра-пар из последних по
ходу пара корпусов установки. Но на пар низких параметров из этих корпусов
не часто находится потр ебитель. И поскольку на технолоmческих установках
довольно часто требуется пар давлением
то сравнительно легко
найти потребителя на экстра- пар , отбираемый из первою корпуса (реже
из
второю), нежели из последующих.

0 , 2 -0 ,4 МПа,

-

Расчет прямоточной многокорпусной установки
Материальные и тепловые потоки. Расчет сводится к опреде
лению потоков переданной теплоты по корпусам и расхода
первичного пара D 1 , поверхностей теплообмена в корпусах ( F1 ,
F2, Fз, вообще - Ff), а также к расчету конденсатора, если в
последнем корпусе создается вакуум.
Суммарный поток удаляемого растворителя
(9. 1 8)
W = W1 + JJ-2 + Wз
определяется по уравнению (9.6) при подстановке конечной
заданной концентрации ак вместо а 1 •
Тепловые нагрузки Qi корпусов определяются по выражени
ям, аналогичным (9. 1 2) и (9. 1 2а), с учетом принятых обозначе
ний на рис . 9. 1 1 . Без учета потерь в окружающую среду
Q1 = D 1 ( h1 - Ск1 Т1) = Soco(t1 - to) + Wi U1 - cpt1);
(9 . 1 9)
Q1 = ( W1 - Е1 ) (h2 - Ск2 Т2) = S1c1 (t2 - /1 ) + JJ-2(i2 - Ср/2); (9.20)
Qз = ( W2 - EJ. ) ( hз - скз Тз ) = � с2 (/з - t2) + Wз(iз - ср tз). (9.2 1 )
Заметим, что первые слагаемые в правой части приведенных
уравнений (кроме (9. 19) - для первого корпуса) отрицательны
из-за уменьшения температуры кипения растворов от корпуса
к корпусу (t2 < t1 , t3 < t2 и т.д.). Это означает, что не только не
требуется теплоты на нагрев раствора, но, напротив, раствор
отдает теплоту перегрева, и за счет этого происходит самоис
парение части растворителя.
С целью уменьшения числа неизвестных в практических
расчетах целесообразно исключить из уравнений S1c1 , �с2 (а
при большем числе корпусов - S,<:i, здесь i > О), воспользо
вавшись правилом адд итивности теплоемкости растворов
(равенствами типа (9.2)) :

S1 с 1 = S0c0 - W1 ср ,
S2c2= S1 с 1 - W2cp = Soco - W1 Ср - JJ-2cp = Soco - ( W1

708

+

JJ-2)cp;

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

вообще для i-го корпуса (при любом числе корпусов)

StCt = Soco rд е i - номер корпуса ( i =

О

(.f w;)
1=0

Ср ,

относится к исходному раствору) .

Подставим полученные выражения для S1c1 и �с2 в уравнения
(9.20) и (9.21):

Q 1 = D1 ( h1 - Ск \ Т1 ) =
=Soco (t1 - to) + W1 (i1 - cpt1) ;
(h = ( W)

(9 . 19а)

Е1 ) (h2 - Ск2 Т2) =
(9.20а)
= Soco(t2 - !1 ) - W) cp(t2 - !1 )+ W2 (i2 - cpt2);
Qз = ( W2 - �) ( hз - Скз Тз ) =
= Soco(tз - t2) - ( W1 + W2)cp(tз - t2)+ Wз ( iз ср/3). (9.2 1а)
Расчет потоков греющего пара D 1 , вторичного пара Wt и
теплоты Q1 в корпусах по приведенным выше формулам (9. 1 8)
-

-

- (9.2 1 ) затруднен , поскольку неизвестны параметры работы
корпусов - температуры кипения растворов в корпусах !; и
энтальпии h 1 и i1 (кроме Т1 и h1 в первом корпусе, где заданы
параметры греющего пара, и tз , iз в последнем корпусе, где
техническим заданием определены давление и конечная кон 
центрация раствора) . Численные значения упомянутых пара
метров связаны с потоками вторичного пара Wt и с тепловыми
нагрузками Q1• Последние, в свою очередь, зависят от:
- кинетических характеристик теплопереноса - коэффициентов теплопередачи k1;
- величин дв ижущих сил по корпусам Л 1 = 1j - t1;
- поверхностей теплообмена F1•
Таким образом, система уравнений (9. 1 8 ) - (9.2 1 ) для опре
деления Wj и Q1 должна решаться совместно с уравнениями
кинетики теплопереноса
(9 .22)
Поверхности теплообмена. Приступая к расчету многокор
пусной выпарной установки , технологи не располагают вели
чинами Л ;; обычно известны (или можно достаточно точно
определить) лишь температуры Т1 и 03 (в общем случае при
числе корпусов N - 8 н) и Л noJDI = Т1 - 0 N (в рассматриваемом
примере
8 3 ) . Эта полная разность температур
Лn oJD1 = Т1
Лn oJD1 не может оыть целиком использована в качестве движу
щей силы процессов теплопередачи в корпусах из-за темпера-

709

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

1 корпус

Рис. 9. 12. Изменение температуры по вьmарной установке в целом

f/1

турных 81 и гидравлических
депрессий (см. рис . 9. 12). Сум
марная полезная разность температур Л!: есть сумма движущих
сил в .каждом корпусе:
ЛЕ =

N

r Л ; = Л1

i=l

+ Л2 + Л 3 = ( Т1 - 11) + ( Т2 - 2 ) + ( Тз - 13) .

t

С учетом выражений для температурных (81 = - 8 t) и гид
равлических (01'1 - (t+l ) = 81 - 1i+ 1) депрессий получаем для
трехкорпусной выпарной установки:
ЛЕ = Т1 - 8 1 - 81 + 8 1 - 8r1 -2 - 8 2 - � + 8 2 - 8r2-3 - 8 з - 83 =
8 3 (8 1 + 82 + 83) - (8r 1 -2 + 15r2-з),
= Т1
или

t1

-

ЛЕ

-

_
-

3
2
Т1 - 8 3 - .r 8 ; - .r /) ir- (i + l)

1=1

1 =1

В общем случае при числе корпусов N
лЕ =

Т1 - 8 н - r б ; - r
N

N-1

i=l

i=l

.

8 f- <;+ 1> .

(9.23)

Из (9.23) видно, что суммарная полезная разность темпера
тур, обеспечивающая передачу теплоты в корпусах (от конден
сирующихся паров к кипящим растворам), равна полному тем
пературному напору ( Т1 - 8н) за вычетом температурных и
гидравлических депрессий.
710

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

9. 13. Изменение температуры
при передаче теплоты от конденси
рующегося пара при температуре Т1 к
кипящему раствору (t1) в первом
корпусе вьmарной установки
Рис.

Суммарная полезная раз
ность температур Лr; в зави
симости от свойств упари
ваемого раствора и величин
поверхностей
теплообмена
корпусов Fi распределяется
между корпусами, а в преде
лах одного корпуса - между
отдельными стадиями тепло
переноса.
Рассмотрим одновременно теплопередачу во всех корпусах и
постараемся исключить из расчета все промежуточные - не
известные в ходе расчета - температуры и температурные на
поры. На примере первого корпуса выделим (рис . 9. 1 3) отдель
ные стадии теплопередачи при общей движущей силе процесса
в нем Л 1 = Т1 - t1 • При этом воспользуемся подходами, де
тально рассмотренными в гл. 6 и 7 применительно к рекупера
тивному теплообмену между конденсирующимся паром и ки
пящей жидкостью.
Тепловой поток Q1 в первом корпусе через поверхность теп
лопередачи F1 выражается следующим образом (обозначения
см. на рис. 9. 13):
для стадии теплоотдачи от конденсирующегося пара к стенке
Q1 = а1 конд F1 Лf 1 =

� F1 Л t'1 = A1F1 (Лt'1 )314,
Vмi

rде А1 выражает теплофизические свойства конденсата и учитывает высоту теп 
лообменных труб - с м . формулу (6.25);

для стадии кондуктивного теплопереноса через стенку толщи
ной о1ст (условно - плоскую, полагая, что толщина стенки
значительно меньше диаметра трубы, т.е. пренебрегая кривиз
ной поверхности) при коэффициенте теплопроводности л.1ст
')..ст

& cr

Q1 = -1- Лt� ст F1 ;
1

для стадии теплоотдачи от стенки к кипящему раствору
Q1 = а 1 кипF1 Лt"1 = Во 1 (Л t"1 )2•33F1 Лt"1 = Во 1 F1 (Л t " 1 )3•33,

ще �1 отражает теплофизические свойства кипящего расrвора - см. формулу (6.26).

71 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Поскольку nромежугочные температуры и частные движу
щие силы ( л t( ) неизвестны, их следует исключить из анализа.
С этой целью выразим частные движущие силы отдельных ста
дий переноса теплоты в первом корпусе (аналогичные выклад
ки см. в разд. 7.3):
лt

'

1

=

(_OL.) 4/3 .
A 1 F1 '

Складывая эти частные движущие силы, получаем полный пе
репад температур (движущую силу) в первом корпусе л 1 = Т1 = t' +
+ лt"1 :

- 11 Л 1 Лtст1
Л1

=

( Q ) 4/3 + Q 8 ст
F: Л.�1т
А1�1

( Q 1 ) 0,3
Bo 1 F1

+

(9.24)

Для второго и третьего корпусов можно написать аналогич
ные равенства:
Л

_Q_2 f
F2 л_ст2
Q3 8 f
F3 3
Б

4/3 +
2 (дL_)
A2 F2
4/3 +
3 (�)
A3 F3

___

=

Л

л.ст

=

+

(9 .25)

з
(
Q
)о,
+
Воз�з

(9.26)

При расчете теплообменного аппарата (или однокорпусного
выпарного аппарата непрерывного действия) значение полной
движущей силы обычно бывает известно. В случае многокорпус
ной выпарной установки известна только сумма по всем корпу
сам - см. формулу (9.23). Поэтому в соответствии с использован
ным ранее подходом необходимо исключlfГЬ из анализа неиз
вестные значения л, для отдельных корпусов. С этой целью сум
мируем левые и правые части уравнений (9.24) - (9.26):

л1

Л1 + л

2 + Лз

=

лЕ

л1

=

L

L

i=З ( Q; ) 413 + 1=3Q1 6 �
i=I F1 Лет1
i=I A1 F1
--

- --

+

L

i=3( Q· ) о,3
1 = 1 B0t F1
' --

•

причем суммарная полезная разность температур рассчиты
вается по соотношению (9.23).
В общем виде для N-корпусной выпарной установки
Л r;

=

( Q, ) 4/3 + Q1 8 �
i=I F1
i=I A1F1
L

N

--

L

N

л.f:!

- -1

+

( Q1 ) 0,3
i=l Bo; F;
N
L

--

·

(9.27)

Для аппаратов с принудительн о й циркуляцией раство ра , а также аппарато в с
в ын ес е нн о й з о н о й кипени s� ко эффициент тепл оотдачи сч от стенки труб к рас
тво ру (ки пящему в услови s� х в ынужденн о го дв ижения или не кипящему в трубах
712

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

при наличии трубы вскипания) определяется по одной из формул типа (6.20).
Тогда, очевидно, вместо последнего слагаемого в правой части равенства (9.27)
будет стоять

так как в этом случае

N Q·
•
.
:Е -'-

i=l F;a.�

Лti' = � ·
F;a.�

При вынужденном движении раствора в трубах с заданной скоростью расчет
по (6.20) не вызывает затруднений. В случае естественной циркуляции скорость
движения раствора в трубах зависит от мноrnх факторов; ненадежны даже :эмпи
рические уравнения. В оценочных расчетах а2 при подсчете критерия Re обычно
рекомендуют принимать скорость равной 0,3-0,6 м/с.
Специально подчеркнем, что изложенный метод учитывает зависимость ин
тенсивности теплоотдачи при конденсации пара и кипении растворов (в итоге ко:эффициекга теплопередачи k;) от частных разностей ЛJ'; и ЛJ"; (в итоге - от
Л;). В ряде учебников· неоправданно предлагается метод расчета многокорпусной
вьшарной установки, игнорирующий такие зависимости, хотя в разделе о тепло
переносе :эти зависимости фиксируются.

При любом числе корпусов, N > 1 , уравнению (9.27) удо
влетворяет бесконечное множество сочетаний F;. Практический
интерес представляют две проектно-технологические ситуации :
1 ) поверхности всех корпусов одинаковы: F1 = F2 = Fз - = Fн == F = idem;
2) суммарная поверхность всех корпусов Fr. = r F; мини
N

i=l

мальна.
Первый вариант в практическом плане является более целе
сообразным по следующим причинам:
- аппараты проектируются и изготавливаются не по от
дельности, а серией, что , естественно, дешевле;
- корпуса взаимозаменяемы; возможно их переключение
(при работе с одним резервным корпусом, отключаемым для
чистки), что удобно в эксплуатации, так как не приводит к
какому-либо нарушению непрерывного технологического ре
жима процесса выпаривания.
При расчете многокорпусной выпарной установки с мини
мальной суммарной поверхностью теплообмена получается
некоторая экономия в поверхности, а следовательно, и в затра
тах металл а . Однако затраты на индивидуальное проектирова
н ие корпусов и невозможность в критических ситуациях заме
ны одного корпуса другим в значительной степени нивелируют
эту экономию. Экономия капитальных затрат (Fr. = min) стано
вится существенной при изготовлении выпарных аппаратов из
• Например, (2, 4-6 ).

713

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

дорогостоящих материалов (нержавеющая сталь, титан и др . ) так приходится поступать в случае агрессивн ых растворов. Н о в
целом в промышленной практике в подавляющем большинстве
случаев многокорпусные выпарные установюt проектируются и
эксплуатируются с равными поверхностями нагрева корпусов.
П оэтому н иже подробно рассматривается именно первая из
упомянугых ситуаций .
В случае равенства поверхностей теплообмена
отдельных
корпусов уравнение (9.27) упрощается:

[ J
{( )�/3 ( Q; ) 4/3+ !: [Q1 -1 J

( ) 4/3

лЕ - _

1

F

l

8�
( Q' ) 4/3 + -F r Q1 1
1

t 1 А
N

r =

N

;=1

А.cr

F

( ) 0,3 ( Q, ) 0,3
l

N

;=1

+ F

r

Для удобства решен ия этого уравнения
домножим его левую и правую части на

лЕ

1
F_

-

1

-

F

!:

N

t= 1

8�

А,

А.cr

-

F/Лr.:

-

Во1

относительно

0 7 ( Во;QI ) о,3

+ F ' !:

N

; 1
=

(9.28)

-

)

·

F

( 9 . 28 а )

В таком ВИде оно может быть решено относительно искомой
поверхности теплообмена
- не аналитичесюt (дробные пока
затели степени), но каюtм -либо числен н ым методом . Главная
трудность определен ия
по этой формуле состоит в невоз 
по форму
можности расчета тепловых нагрузок аппаратов (
лам (9. 1 9) - (9.2 1 ) , величин
и B0t, а также температурных
депрессий 8 1 без зн а н ия параметро в веде н ия про цесса в корпу
сах. А эти параметры моrуг быть установлен ы только после
нахоЖден ия поверхности теплообмена
и соот ветствующего ей
распределения температур , давлений и кон центраций по кор 
пусам . По указанным причинам задач а н ахождения
из урав
нения (9.28), а далее и D1 решается методом последова
тельн ых приближен и й .

F

F

Qt)

А1

F

Q1

F

Последовательность расчета многокорпусных вьmарных уста
новок. Приведем кратко алгоритм такого расчета.

1 . Определяют общее количество удаляемоrо растворителя W по формуле ти
па (9.6): W =
а�Уан). Оно распределяется по корпусам - либо поровну
( W1 = W2 = W3 = . . . = W/N), либо с учетом oroop a экстра-пара, то гда W1 :<:

So( l

-

:<: W2 � W3 � . . . � Wн.

2. По предварительно найденным W; рассчитывают концентрации а; (i =
= 1 ,2, . . . , N- 1 ) и по ним - температурные депрессии Б; в корпусах: поначалу
стандартные (так как неизвестны давления в корпусах), а для последнеrо корпуса
точ ную, так как рабочее давление в нем известно .
3. Суммарную полезную разность температур, рассчитанную по формуле
л2 =
(9.23), предварительно распределяют по корпусам - либо поровну (Л 1 =
= л3 =
= лr./ N), либо с учетом ухудшения условий теплопередачи, например Л1 :
л2 : л3 = 1 : 1 ,2 : 1,5 или каким-либо иным образом, в частности Л 1 : Л2 : Лз =
-

".

"' ( Wi/<p1):( W:i/1p2):( Wy<p3).

714

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Находят параметры ведения процесса в корпусах, используя формулы 1; =
= Т;
Л;, 0; = 1; - 11;, Т; +\ 0 ; 11r_ ( i + l) , а также энтальпии насыщенных водя
ных паров и их давления - в зависимосm от установnенных температур. Рассчиты 
вают величины А; (задавшись выоотой труб Н) и Во;.
5. Коррекrируют величины W; пуrем совмесnюrо решения системы уравне
ний тепловых балансов всех корпусов, кроме первого (уравнения (9.20), (9.2 1 ) и
т.п.), и баланса (9. 1 8) по удаленному растворителю. Заметим, <rro в тепловом
балансе первого корпуса содержится неизвестная D 1 (дополнительное уравнение
и дополнительная неизвестная); поэтому на данной стадии расчета он и не рас
сматривается.
6. Определяют тепловые наf1Jузки Q; корпусов по формулам (9. 19) - (9.2 1).
7. Находят F по (9.28а) численным методом. Далее по формулам (9.24) (9:26) с учетом найденной поверхности теплообмена F рассчитывают соответ
ствующее ей распределение Лt по корпусам, т.е. значения Л1, Л2, Лз и т.д.
8. Устанавливают параметры ведения процесса в корпусах, соотвеrствующие най
денной величине F, по формулам, приведенным в пунхrе 4 данноrо алrоритма.
9. Вновь находят тепловые Наf1Jузки Q;, предварительно опять уточнив вели
чины W; (см. пуюсrы 5 и 6).
10. Если рассчитанные по пункту 9 значения Q; для каждого корпуса отли
чаются от найденных ранее в пределах обусловленной поf1Jешности расчета
(например, до 5% при учебном расчете выпарной установки и до 2-3% - при
прое�сrном для целей производства), то расчет считают законченным. Найденные
значения поверхности F по пункту 7, потоков по пункту 9 и параметров процес
са по пункту 8 принимают как окончательные. Расход f1Jeющero пара в первом
корпусе (D1 ) определяют по формуле (9. 1 3).
При большем расхождении в значениях Q; для какоrо-либо корпуса необхо
дима корректировка параметров ведения процесса. В этом случае расчет прово
дят заново, ориентируясь на найденные в пункте 9 значения W;, установленные
в пункrе 8 параметры процесса, уточненные температурные депрессии с учетом
давлений в корпусах, а следовательно и Лt. Вычисляют новые значения ком
плексов А; и Во; и вновь решают уравнение (9. 2 8) - находят F (пункт 7). С уче
том нового значения поверхности теплообмена отыскивают распределение Лt по
корпусам (см. пункт 7). После реализации пункrов Н и 9 этого алгоритма вновь
сравнивают новые Q; с полученными в предыдущем расчете и делают вывод о
целесообразности следующего приближения.
4.

-

=

-

Не останавливаясь подробно на методе расчета многокор
пусной выпарной установЮi с минимальной поверхностью Fz:.,
заметим лишь, что он возможен с применением вариационных
методов. При этом тоже должна быть учтена зависимость ко
эффициентов теплопередачи в корпусах от распределения по
лезного температурного напора Лz:. по отдельным корпусам (см.
специальное замечание и сноску на стр . 7 1 3).
Расход первичного пара D 1 (в первом корпусе) в многокор
пусной выпарной установке значительно меньше, нежели в
однокорпусном аппарате при тех же производителъностях и
граничных концентрациях а0 и a N
за счет использования
теплоты конденсации вторичных паров. Если учесть приведен
ную ранее (см. стр . 68 1 ) оценку, что при расходе 1 кг первич
ного пара образуется около 0,9 кг вгоричного, то напрашивается
-

715

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

вывод о целесообразности увеличения числа корпусов с целью
большей экономии греющего пара.
Так, в случае трехкорпусной выпарной установки за счет 1 кг первичного
(rреющего) пара в первом корпусе получаем: 0,9 кг вторичного пара в первом
корпусе, 0,9·0,9 = 0,8 1 кz во втором и 0,8 1 · 0,9 "' 0,73 кz в третьем; всего
2,44 кz. В четырехкорпусной установке в последнем корпусе ВЫ[lаривается еще
О, 73·0,9 0,66 кz вторичного пара; всего 2,44 + 0,66 = 3, 1 кz при расходовании
1 кг rреющего пара в первом корпусе.
-

-

-

"'

Однако выше было показано (см . формулу (9.23)) , что с рос
том числа корпусов суммарная полезная разность температур
(Л!:) уменьшается за счет возрастания rБ1 и r Бr-(i+ l ) . При

этом существенно понижается и разность температур, прихо
дящаяся на один корпус, а поверхность теплообмена возраста
ет. Это приводит к увеличению размеров и стоимости установ
ки, а также затрат на ее обслуживание. Поэтому суммарный
экономический эффе.tсr при росте числа корпусов становится
менее ощутимым. Самое главное, однако, заключается в том,
что при малых разностях л1 (ниже 1 0 ° С) работа аппарата ста
новится неустойчивой. Именно из-за этого на основании опы
та эксплуатации многокорпусных выпарных установок оmи
мальное число корпусов находят из условия минимальной раз
ности температур в корпусе на уровне -10 ° С. Как правило ,
число корпусов при многокорпусном выпаривании составляет
2-4, реже 5-6.
-

Упрамение процессом на многокорпусной выпарной установке осложнено
взаимным миянием параметров работы одного аппарата на параметры соседних,
поэтому даже поддержание стабильных режимов работы вызывает значительные
технические трудности. Использование дорогостоящей реrулирующей аппарату
ры заметно понижает экономический эффект, связанный с экономией rреющего
пара при многокорпусном выпаривании.

9.6.6. Выпарной аппарат с полным тепловым насосом

Альтернативным использованию многокорпусных выпарных
установок способом экономии греющего пара является исполь
зование образующегося . при выпаривании вторичного пара в
качестве греющего в том же выпарном аппарате . Для повыше
ния потенциала пара (давления и. соответственно температуры
конденсации) его сжимают в компрессоре до давления, при
котором температура Т насыщения (конденсации) становится
на 1 О - 1 5 градусов выше температуры кипения раствора t.
Схема такого выпарного аппарата с полным (сжимается весь
вторичный пар) тепловым насосом представлена на рис. 9. 14.
716

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

W P

Рис. 9. 14. Схема выпарного аппарата с
полным тепловым насосом:
1

-

прессор

l!Ьlпарной аnларат, 2

-

турбоком

0

Сжатие вторичного пара целесооб
разно проводить в турбокомпрессорах,
так как поршневые компрессоры за
грязняют пар смазкой. Такой загряз
ненный пар становится непригодным
дальнейшего использования ввиду
значительного снижения коэффициента
теплоотдачи при его конденсации,
обусловпенного образованием на трубах
масляной IVIенки с дополнительным
(большим) термическим сопротиаnением.

для

При конденсации 1 кг греющего пара получается . меньше
1 кг вторичного (см. разд. 9.3). С учетом потерь в окружающую

среду и затрат на нагрев исходного раствора до температуры
кипения на 1 кг греющего пара получается 0,8-0,85 кг вторично
го. Поэтому для обеспечения стационарности непрерывного вы
паривания к сжатому вторичному пару ( W) добавляюr недостаю
щий поток свежего греющего пара Do, так что
D = W+ D .
(9.29)
Необходимый расход греющего пара D на процесс выпарива
ния определяется как обычно - по формуле (9. 1 3) с учетом (9. 12).
Тогда расход свежего (дополниrельного) пара составит по (9.29):

o

Do

=

D

_

W

=

_Q_
Гrр

_

W

=

S oc o (t1 - to ) + W (i - c p t1 )
Гrр

или после преобразований

Do

=

[

so co (t1 - to ) + ( 1 - ��) {i - c p t1
rrp

-

r

rp

}

]

------

_

W '

(9 _ 3 О)

(9.30а)

Из формулы (9. 3 0) видно, что расход свежего греющего пара
D0 при работе с тепловым насосом всегда меньше общего рас
хода греющего пара D. Однако при работе с тепловым насосом
дополниrельно затрачивается энергия на сжатие вторичного пара.
Потребляемую энергию определяюr по формулам , приведенным в
гл. 4. Согласно принятой в настоящей главе символике (рис. 9 . 1 5),
N

=

· -�i)
W(h_
----'

(9.3 1 )

11 ад Тl мех
rде (h• 1) работа адиабатического сжатия вторичного пара от даапения Рвт до
Prp (линия . 1-2 при s = const); h•
энтальпия сжатоl'о пара, находящегося после

- -

-

717

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 9. 15. Адиабатический ( 1 - 2 ) и
реальный ( 1 - 2 ) процессы сжатия
вторичного пара на диаграмме h - s

11

/1P 1------=-
h • 1-----.h

'

компрессора в перегретом состоянии
(поэтому h' больше энтальпии насыщен
ного пара h); (h' - 1)/11 а11 - работа поли
тропического сжатия; 11 an - адиабатичес
кий КПД компрессора; 11 мех - механичес
кий КПД компрессора.

Рвт

Напомним ,
что
реальный
процесс сжатия в компрессоре
протекает по линии 1-2 ' (с уве
личением энтропии s). При этом hP - i = (h* - 1) /11ац·
Расчеты и опыт эксплуатации показывают, что при выпари
вании с полным тепловым насосом на каждый кг свежего
греющего пара выпаривается более 5 кг вторичного. Правда,
эта экономия греющего пара в определенной степени н ивели
руется дополнительным расходом энергии на сжатие вторично
го пара в компрессоре . Поэтому вопрос о целесообразности
применения полного теплового насоса решается на основании
экономического расчета - в сравнении с многокорпусной вы
парной установкой.
Отметим , что работа выпарной установки с полным тепловым
насосом всегда экономически эффективнее, нежели без него. Но
область их применения ограничена специфичными характери
стиками р аботы турбокомпрессоров: высокими производитель
ностями при сравнительно небольших степенях сжатия.
В сравнении с многокорпусной выпарной установкой при
использован ии полного теплового насоса меньше расход ме
талл а , производственные площади, габариты установки, проще
и дешевле управление процессом.
В результате обобщения опыта эксплуатации различных вы
парных установок найдено, что выпаривание с полным тепло
вым насосом экономически оправданно, когда Prp/P � 2 , 5+3 и
производительность по вторичному пару превышает 1 , 5 м3/с.
Поскольку указанной степени сжатия вторичного пара соот
ветствует повышение температуры конденсации на 25 - 35 ° С,
то такую схему целесообразно использовать для выпаривания
растворов со сравнительно небольшими температурными де
прессиями. Именно в этих случаях движущая сила процесса
теплопередачи в выпарном аппарате ( Т - t) близка к опти
мальной величине, равной как раз 25- 3 0 ° С. При больших тем
пературных депрессиях движущая сила процесса ( Т - t) умень
шается на величину этой депрессии.
Вопрос отвода вторичного пара на сторону (экстра-пара)
решается здесь положительно при наличии потребителя. При
s

718

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

этом с целью повышения экономических показателей установ
ки предпочтительнее отбирать экстра-пар до сжатия его в
компрессоре . Оrбор экстра-пара после сжатия в компрессоре
оправдан лишь в том случае , если выгода от его использования
вне выпарной установки превышает упомянуrую многократную
(в 5 раз и более) экономию греющего пара на самой выпарной
установке.
9.6. 7. Вьmарной аппарат с частичным тепловым насосом
По этому варианту технологической схемы (рис. 9. 1 6) сжи
мается и затем используется в качестве греющею не весь вrорич
ный пар ( W) , а лишь часть ею в
количестве (в единицу времени)
Д. Сжатие осуществляется в
нижекторе за счет подачи шлока
W-D8
Do пара высокою давления Р 1
(большею, чем давление гре
2
i,0,W
ющею пара , необходимое для
обеспечения
теплопередачи).
Естественно , что такая органи
зация работы выпарной уста
новки возможна лишь при на
личии пара повышенного по
тенциала р 1 •
Рис.9. 16. Схема выпарною аппарата с
инжектором:
1

-

выпарной аппарат, 2

-

И Jl)l(exтop

Расход пара

При смешении в инжекторе паров разных давлений (р1 и
Рrл) на выходе получают требуемое давление греющего пара Prp ·
Необходимый расход последнего (D) определяют, как обычно ,
и з теплового баланса выпарного аппарата п о формуле (9. 1 3) с
учетом (9. 1 2) . Из материального баланса инжектора имеем
(9 . 32)
D Do + D8.
Обозначим: D8 /D0 = и
коэффициент инжекции, показы
вающий , сколько кг вторичного пара засасывается инжектором
за счет подачи 1 кг острого пара (высокого давления) . Тогда

=-

( ��) Do( l и),
\)
t0 ) W(i-:- c p t-'S 0c o (t1
D
�---=-,---(h -- скТ1
-)(1 + и)
D = Do l +

+

=

+

откуда расход пара высокого давления

Do

=

1+и

=

-

-

-

(9 .33)
719

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Видно, что расход острого пара D0 в значительной мере за
висит от коэффициента инжекции и: при его увеличении рас
ход острого пара Do уменьшается.

Расчет коэффициента инжекции
Для этого сначала рассмотрим подробнее устройство инжек
тора (рис . 9 . 1 7 ,а) и процессы, протекающие в нем . Изменение
основных параметров процесса (давлен ия р и скорости w) по
длине инжектора представлено на рис . 9. 1 7, б.
Заметим: на рисунке инжекrор расположен горизонтально; при вертикаль
ном его расположении продольные профили р и w пракrически не изменятся,
так как разница в величинах нивелирных высот для различных сечений инжек
тора намного меньше пьезометрических высот и скоростных напоров.

Инжектор состоит из трех основных зон : сопла 2, через ко
торое подается пар высокого давлен ия (острый пар); камеры
смешения 1, в которую через патрубок 3 засасывается вторич
ный пар и смешивается там с острым паром; диффузора 4
(камеры сжатия) , где происходит повышение давления смеси
острого и вторичного пара до Prp ·
При истечении пара высокого давления из сопла 2 в камеру
смешения (где давление близко к давлению вторичного пара)
его скорость резко возрастает, достигая на выходе из сопла в
камеру смешения 800- 1000 м/с. Столь высокая скорость (выше
скорости звука) обеспечивается формой сопла и тщательностью
обработки (полировки) его внутренней поверхности . Согласно
закону Бернулли, увеличение скорости (и скоростного напора)
сопровождается снижением давления в камере смешен ия до
значений, несколько меньших рfЛ, что и обусловливает засасы
вание вторичного пара. Резкое понижение давления и рост
скорости при истечении из сопла показаны на рис . 9. 1 7 , б вер
тикальным участком 1-2.
В камере смешения (участок 2-3) наблюдается некоторое по
н ижение скорости пара при его смешении с низкоскоростным
потоком вторичного пара - соответстве н но балансу количества
движения . Давление при этом также уменьшается - за счет гид 
равлических потерь в камере смешен ия , складывающихся
прежде всего из потерь в результате гидравлического удара при
смешении высокоскоростного и низкоскоростного потоков
пара, а также потерь на трение.
В диффузоре по ходу движения пара, т.е. по мере увеличения
площади поперечного сечения, происходит снижение скорости и
скоростного напора, а значит, преобразование кинетической
энергии в потенциальную - также согласно уравнению Бернулли.
С целью предотвращения отрыва струи пара от стенки (и образования вих
рей) угол расширения диффузора принимают небольшим (не более 7 -8°).

720

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

:
1
w :

р

1

9. 1 7.

1
1

w

1

-

:

: Ргр
�: � .::.p -::::
�-:..a--:::::-�r
.:::.
....:
-L..
�
2

б

Схема и работа

1
- ·
1

3

4

h

а - схема июкектора: 1 - ка
мера смешения , 2 - сопло, J патрубок для подачи вrоричноrо
пара, 4 - диффузор;
б - изменение давлени я и
скоросrи по длине июкектора

инжектора:

:

•
1

J1 - - - 1r.r::-

1

Рис.

а

h1

h4 t-----t---.�h--

---�-�..-----·

s

Рис. 9. 18. К расчету коэффи
циента инжекции

Анализ изменения энергетических параметров пара на вы
деленных участках инжектора (rраницы участков помечены ин
дексами) удобно проводигь с помощью диаrраммы h - .s
(энтальпия - энтропия), изображенной на рис. 9. 18.
Энергетический баланс дл я сопла. Этот баланс для участка
1-2 (от входа в сопло до выхода из него) в расчете на 1 кг ост
рого пара и в предположении об отсутствии теплообмена с
окружающей средой (адиабатический процесс) имеет вид
w 22
w 12
о
- 1.2 - h l + --

2

где h 1
w2

-

2

=

и i2 - энтальпии пара на входе и на выходе из сопла соответственно;
скорости пара до сопла и на выходе из него.

w1

и

72 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Энергетический баланс здесь состаWiен с учетом кинетической энерmи пото
ков: при больших скоростях пара она соизмерима с величинами энтальпий пара
(порядка 1 0 3 кДж/кг).

= ости

Скорость пара на входе в сопло w 1 (20-30 м/с) значительно
меньше, чем на выходе из него (w2
800+ 1000 м/с); поэтому
величиной w1 2/2 пренебреrаем ввиду ее мал
по сравнению с
другими членами. Тогда
rде Лh

"'

h1 - i2

-

"'2

= .J2лh ,

(а)

изменение энтальпии при адиабатическом разгоне пара.

Реальный процесс протекает не адиабатически : за счет тре
н ия происходит торможение пара, некоторый его подогрев и
рост энтальпии - до точки 2 . В результате перепад энтальпий
получается ниже теоретического Лh и реальная скорость пара
w'2 - также несколько ниже теоретической "'2 :
(б)
w'2 "'2q>1 '
где q>J < 1 .

Реальный запас
ставляет
где ri 1 "' !912

-

'
=

кинетической энергии 1 кг острого пара

со
(в)

КП Д

сопла.

На диаграмме h - s процесс расширения пара в сопле изоб
ражается линиями 1 -2 (адиабатический процесс) и 1 -2 '
(реальный процесс).
Энергетический баланс для камеры смешения. Здесь получае
мая смесь характеризуется точкой 3, положение которой между
точками 2' и О (состояние вторичного пара) зависит от коли
честв смешиваемых паров, а точнее - от их соотношения , т.е.
от коэффициента инжекции и. При известной величине и по
ложение точки смешения (3) находится из энергетического
баланса камеры смешения :

1

[;2 + (w�)'] + [;" + w;, ] - +3 + w!]
и

(1

+

=

О.

( г)

Теоретическую скорость w'3 на выходе из камеры смешения
можно найти из баланса (закона сохранения) количества дви
жения , записанного в расчете на 1 кг пара высокого давления :

1 · w'2

- (1

(д)
+ и) w'з = О.
кроме того , и < 1 , то вторым слагаемым

+ иwвт

Так как wвт < < w'2 и,
в левой части равенства (д) можно пренебречь.

722

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Тогда
w3

l+u

=

w2

.

(е)

Реальная конечная скорость w3 паровой смеси на выходе из
камеры смешения (на входе в диффузор) из-за rидравлического
удара при смешении (в меньшей мере - из-за гидравлического
сопротивления трению потока о стенки камеры) н иже теорети
ческой w'з:
(ж)
W3 = W'3({>2 ,
где (/)2 < 1 - коэффициент, учитывающий потери энергии в камере смешения.

Кинетическая энергия l кг смеси равна
(w 3 ) 2

(w ) ) 2

2
-2- = -2- <р 2

=

+ и) 2

(w 2 ) 2

20

2
2
Лh
Ч> 2 = (
Ч> 21 Ч> 2 •
2
+
l и)

(з)

Э нергетический баланс для диффузора. В диффузоре (камере
сжатия) происходит преобразование кинетической энергии в
потен циальную (тепловую). В отсутствие потерь теплоты в
окружающую среду энергетический баланс имеет вид
2
w 32
w4
.
h
о
- + 13 - 4
(и)
=
- -

2

2

.

Небольшой кинетической энергией пара на выходе из диф
фузора (w42/2) можно пренебречь (вследствие малости скорости
w4 - на уровне 20-30 м/с). Тогда адиабатический прирост эн
тальпии будет

w 32
2

(к)

Реальный прирост энтальпии Л i' больше адиабатического Л i
за счет теплоты, выделяющейся при трении пара о стенки
диффузора. Это ясно видно на диаграмме h - ,s для реального
процесса сжатия 3-4 ' , протекающего с увеличением энтропии,
в сравнении с идеальным процессом 3-4. Итак,

где т� з < 1 - КПД диффузора;
ТJ 1 удобна запись т�з = q» з2 •

л .,
1

для

=

Лi
1'1 3

-

(л)

последующих преобразований по аналогии с

Таки м образом , полный запас кинетической энергии 1 кг паро 
на входе в диффузор, определяемый выражением (з) ,

во й смеси

723

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

расходуется на повышение энтальпии пара в диффузоре по (л) :

Лi
Лh
<р � <р � =
2
(1 + и )
<р �

---

Огсюда

и=

�

<р 1 <р 2 <р 3 v Л h/ Лi -

�г вторичного пара]
кг острого пара ]

1 [

·

(9.34)

Расчет по формуле (9.34) затруднен тем, 'ПО прямо нельзя определить Лi, та к
как заранее не известно положение точки 3 даже при известных точках 2 (или
2 ) и О. В самом деле, при определении положения точки 3 (на изобаре Р-.л - по
энтальпии i3 , вычисляемой из энергетического баланса (r) Д1lЯ камеры смеше
ния) необходимо знать соотношение смешиваемых потоков, т.е. значение коэф
фициента инжекции и. Но он ведь и является предметом расчета. Поэтому и
находят итерационным методом, предварительно задавшись его значением в
пределах 0, 2 -0,4, по следующему алгоритму:
уравнение (r)
диаграмма h, i - s
уравнение (9.34)
'

Лj

и ------• iз

и

При этом iз определяют из уравнения энергетического баланса (r), пренебрегая
величиной скоростного напора вторичного пара по сравнению с его энтальпией
(w-.л2/2 << i8т) и используя выражения (е) и (в):
2 2
2
1. 2 + дh Ч>1 + Ul. вт
.
�-- дhq>l Ч'2
13 =
1+и
(1 + и) 2
Величины коэффициентов ср 1 , q>2 и <р з зависят от формы со
пла, тщательности обработки рабочих поверхностей и соос
ности сборки узлов инжектора (сопла, камеры смешения, диф
фузора) . Из опыта эксплуатации <р 1 :::: q>з = 0,95+0,97; qi 2
= О , 8+0,85.
И з формулы (9.34) видно, что коэффициент инжекции и
возрастает при увеличении Л h (при использовании острого па
ра с более высоким давлением) и уменьшении Лi, т.е . при
уменьшении разности давлений греющего (prp ) и вторичного
(рIП) паров. Эта разность может быть небольшой только при
упаривании растворов с малой температурной депрессией .
Опыт работы выпарных аппаратов с инжекцией вторичного
пара показал, что такой способ экономии греющего пара спо
собен конкурировать с рассмотренными ранее (много
корпусное выпаривание, использование турбокомпрессора) при
степенях сжатия вторичного пара не более 1 , 5+2,О . При этом
коэффициент инжекции может достигать значений 0, 6 (чаще
0 , 47- 0 , 5 )
-

.

724

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

9.6.8. Повышение эффективности выпарных установок
за счет уrилизации теплоты
Необходимость экономии энергетических затрат, греющего
пара стимулирует поиск и разработку вариантов утилизации
теплоты при функционировании выпарных установок. Эти ва
рианты не исчерпываются приведенными ранее схемами мно
гокорпусных выпарных установок (см . разд. 9 . 6.5) и аппаратов
с тепловыми насосами (см. разд. 9.6.6 и 9 . 6 . 7) - есть и допол
н ительные возможности. Так , независимо от схемы работы
выпарных установок , возможна непосредственная утилизация
теплоты отводимых конденсата и упарен ного раствора - для
подогрева исходного . Явление самоиспарения (см . разд . 9 .3) мо
жет быть использовано не только для упариваемого раствора, но
и для конденсата греющего пара.
На рис . 9 . 1 9 показана одна из возможных рациональных
схем утилизации теплоты применительно к выпарному аппара
ту с полным тепловым насосом . Оригинальность данной схемы
- использование самоиспарения конденсата греющего пара при
понижении давлен ия для получения пара н изкого потенциала,
добавляемого к потоку вторичного пара перед сжатием в тур
бокомпрессоре .
Конденсат греющего пара (его расход D) , покидающий меж
трубное пространство аппарата с температурой Т, дросселиру
ется в дроссельном вентиле 2 от давления Prp до рабочего давe· D + W
w
е ;

е
i

e·D

p. a 1 . l 1

D

т
с.

•

4

Dh
т

'Оo . ao
S
3

,

Prp

D(l-e) ·< · В.wх

Е

So . ao
'О , lн

t
o

1:! , D (l-e) , с�

Рис. 9. 19. Схема выпарной установки с "избьrrочным" ("сверхполным") тепловым

насосом и утилизацией теплоты конденсата и упаренного раствора:
турбокомпрессор.
4
J - выпарной аппарат, 2 - дроссельный венrиль, 3
5, 6 - поверхностные теплообме ЮDtки

-

сепаратор,

-

725

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ления р кипящего раствора в трубном пространстве . При этом
конденсат, попадая после дросселирования в сепаратор 3, ока
зывается перегретым относительно температуры кипения воды
0 при давлении р, поскольку Т > 0 . В результате за счет само
испарения конденсата образуется смесь (при температуре 0)
конденсата и пара низкого (рабочего) давления р. Пусть доля
пара в этой смеси составляет е; тогда его поток равен eD. Пос
ле отделения от оставшегося конденсата образовавш ийся пар
смешивается с потоком вторичного пара W и сжимается в турбо
компрессоре. Суммарный поток сжимаемого в турбокомпрес
соре пара ( W + eD) может даже превысить необходимый расход
D греющего пара в нагревательной камере выпарного аппарата .
Получение избытка пара Е (Е <!: О) возможно при следующем общем условии :
W + eD

<!:

w
е � 1 - li

D, или

;

<м>

при этом знак равенства отвечает условию Е = О , т.е. замкнутой по теплопото
кам схеме работы выпарной установки.
В соответствии с формулой (з) раздела 9.3 доля е пара, образующегося при
самоиспарении конденсата, зависит от разности температур конденсатов
rреющего пара ( 7) и вторичного (0), а таюке от теплоемкостей конденсатов (ск и
с'к соответственно) и теплоты конденсации r при давлении р. Поскольку теп
лоемкость водного конденсата слабо зависит от температуры (с'к "' ск), то

е=

ск ( Т - 0)
r

.

Подставляя это выражение в общее условие (м), нетрудно получить необходи
мую разность температур, обеспечивающую избыток пара (Е > О) сверх потреб
но го для обоrрева выпарного аппарата:
т

-

0

>

.!_(1 w)
'к

-

D

·

(н)

Строго терминолоmчески здесь следует говорить о выпар
ном аппарате уже не с полным, а со "сверхполн ым "
( "избыточным") тепловым насосом, поскольку н а сжатие в
турбокомпрессор подается избыточное количество пара в срав
нении с покидающим аппарат вторичным паром.
Для случаев, когда суммарный расход сжимаемого в турбо
компрессоре пара ( W + eD) меньше требуемого расхода D
греющего пара, необходимо компенсировать эту разницу до
полнительным потоком Do свежего греющего пара:
(о)
D0 = D - I W + eD) = D( 1 - e) - W.
В отсутствие дросселирования конденсата греющего пара (е =
О) фор мула (о) полностью соответствует формуле (9.29) .
Избыток пара высокого давления Е = W + De - D = W - D( l - е) может быть отведен из установки в качестве экстра-

=

726

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

пара (сплошная линия на рис. 9 . 1 9) с большой экономической
выгодой. Подчеркнем: отвод экстра-пара до сжатия в турбо
компрессоре (пунктирная · линия Е) чаще всего менее вы го 
ден - из-за меньшей ценности (пригодности для использова
ния) пара низкого потенциала: р < Prp, е < Т.
Избыточный поток пара Е может быть, разумеется , направ
лен на нагрев исходного раствора S0 с концентрацией а0 и
температурой fн . Экономически выгоднее , однако, отдавать
экстра-пар Е на сторону для более квалифицированного ис
пользования (см. раздел 9.6.5), а исходный раствор нагревать в
теплообменн иках-рекуператорах 6 и 5 - последовательно горячи
ми пото ками конденсата и упаренного раствора (как показано на
рис. 9. 19). Температура упаренного раствора (t1) больше, чем тем
пература конденсации после дросселирования. Поэтому конденсат
uелесообразно использовать на первом этапе (в теплообменнике
6 ) , а упаренный раствор - на последнем этапе (в теплообменнике
5) нагревания исходного раствора от температуры fн до �В заключение раздела укажем, что перегрев растворов при
понижении давлен ия и связанный с этим эффект самоиспаре
н ия раствора (см. уравнение (ж) раздела 9.3) широко использу
ется в современных многоступенчатых установках.
Так, этот эффект был рассмотрен (среди других) в разд . 9 . 6 . 5
п р и изучении многокорпусных выпарных установок. Заметим:
здесь тоже возможно дросселирование конденсата, отводимого
из какого-либо корпуса, до рабочего давления кипящего в том
же корпусе раствора и присоединение пара , образующегося за
счет самоиспарения, к вторичному, направляемому на обогрев
последующего корпуса.
Еще более последовательно эффект самоиспарения раствора
·
применяется в многоступенчатых адиабатных испарителях , по
лучивших также название установок мmовенноrо вскипания:
образующиеся при самоиспарении раствора пары растворителя
используются здесь для нагревания (перегрева) исходного рас
твора. Ввиду отсуrствия поверхностей теплообмена в зоне ки
пения растворов и связанной с этим инкрустации поверхно
стей работа таких установок остается стабильной в течение
длительного периода их эксплуатации .

9.7. ШIЕНОЧНЫЕ ВЫПАРНЫЕ АППАРАТЫ
Отличительной особенностью пленочн ых аппаратов, как от
мечалось ранее, является отсуrствие циркуляции раствора, т.е .
его упаривание до конечной концентрации за один проход. Это
означает, что концентрация раствора и соответствующие ей
•

Подробнее об этом см.

в

учебной и специальной литера1)'ре (2, 3, 9).

727

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 9.20. Схема процесса выпа
ривания · в пленочном аппарате
со стекающей пленкой:
1 - пленка конденсата,
стенка, 3 - пленка раствора

L

� d Q -.--,...A1

к,

+-'---+---;.;:-:;.:i:

-

физико-химические свой
ства изменяются по по

S. a, t, c

1 -+d W
S+dS, a + da

3

2

t + dt,c+ dc
d

верхности

теплообмена ,

оставаясь неизменными во
времени в каждой ее точ
ке . Напомним, что в
выпарных аппаратах пе
риодического
действия
параметры ведения про
цесса изменяются во времени, оставаясь при ин
тенсивном перемешива

нии раствора практически одинаковыми во всех то чках поверх
Напротив , в пленочных аппаратах непре
рывного действия ситуация обратная - наблюдается рассредо
точение параметров по поверхности, но в каждой точке про
странства они постоянны во времени. Отсюда - общность
(переменность параметров) и отличия (во времени или в про
странстве) в методиках расчета выпарных аппаратов периоди
ческого действия и пленочных непрерывного действия .
Рассмотрим подробнее процесс выпаривания в пленочном
аппарате (рис . 9.2 и 9.20) с н исходящей пленкой внуrри труб,
обогреваемых конденсирующимся водяным паром постоянной
температуры Т. Обозначим (см. рис . 9 .20): а.ко нд
коэффици
ент теплоотдачи при конденсации пара; 8п и "-п - толщина и
коэффициент теплопроводности стенки ; a.WI - коэффициент
теплоотдачи от стенки к упариваемому (кипящему) раствору
(плен ке) ; S0 - поток раствора в начальном (z
О) сечении ; а0,
со и to его концентрация, теплоемкость и температура кипе
ния; S - текуший (в сечении z) поток раствора; а, с и t
его
концентрация , теплоемкость и температура кипения;
S0 (1 - а0/а)
количество растворителя , удаляемого в еди
ницу времени на участке протяженностью z, так что d
(S0ao/a2)da -: количество растворителя, удаляемого в едини
цу времени на элементарном участке dz; d - диаметр трубы ; п
число труб в аппарате .
С учетом а.к0 нд , а.11л и термического сопротивления стенки
'бп/"-п коэффициент теплопередачи от конденсирующегося

ности теплообмена.

-

=

-

=
=

-

728

W=
W=

-

-

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

пара к выпариваемому раствору

kвып

-------

=

8 cr

+

а конд

--

+

На элементарном участке поверхности высотой
трубного выпарного аппарата тепловой поток

d Q = kвып( Т - t)1tdndz

dz п
(9.35)

через левую грань контура к 1 на рис . 9.20 расходуется в соот
°
ветствии с выражением (9.7) на увеличение теплосодержания
раствора d(Sct) и испарение d W растворителя с повышением
кон центрации вещества в растворе от а до а + da, т.е.

d Q = d(Sct) + (i - Cp/)d W,

где ер теruюемкость растворителя; i - энтальпия его паров.
Полный тепловой поток (через всю поверхность теплопередачи
F = 7tdnL) определяется выражением (9.7), получаемым при инте
rрировании (9.36) от О до F, от .SOCofo дo S1 c1 t1 и от О до W
Проинтегрировав уравнение (9.35), находим необходимое
число труб п (длиной L) пленочного аппарата:
-

1

Qвыл

п = 7tdL
или

п=

1

QВЬIП

1tdL

J
о

(9.36)

J
о

dQ
k вып (Т - t) '

1

---

· ако н.п

+

8 cr

--

Л ст

Т-t

+

1

--

а пл

dQ

(9 .37)

Значение интеrрала в правой части выражения (9 .37) нахо
дят так же , как и при периодическом процессе выпаривания
(например, численными методами, предварительно установив
зависимости всех величин , входящих в подынтеrральное выра
жение (9.37), от текущей концентрации а) . Тепловые потоки
Q :�� через поверхность теплообмена, обеспечивающие выпа
ривание до текущей (локальной) концентрации а, находят по
формуле (9.7), подставляя вместо t1 текущую температуру t и
вместо W соответственно w тек = So ( l - ао/а). Коэффициент
теплоотдачи от стенки к кипящим жидкостным пленкам (a/UI)
находят по формулам , приведенным в различных учебниках и
монографиях · .
• См., например, ( 1 , 3) .

729

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Выбор размеров труб (d и L) должен быть произведен таким
образом, чтобы при данном расходе исходноrо раствора и за
данной степени концентрирования растворов не происходило
их "оrоление" из-за разрыва жидкостных пленок. Из опыта
установлено, что минимальн ая толщина пленЮt, при которой
обеспечивается полное смачивание всей поверхности, состав
ляет 0 , 1 мм.
9.8. В ЫБОР РАЗМЕРОВ СЕПАРАЦИОННОГО
ПРОСТРАНСТВА ВЫПАРНЫХ АППАРАТОВ

При нормальной работе выпарноrо аппарата отводимый
вторичный пар не должен содержать капель упариваемоrо рас
твора по ряду причин . Прежде всего, унос капель вторичным
паром приводит к безвозвратным потерям самоrо раствора.
Капли аrрессивных жидкостей вызываюг коррозию аппарату
ры, к которой ведуг паропроводы. Кроме тоrо, капли заrряз
няют вторичный пар, затрудняя использование ero конденсата
для питания паровых котлов. Наконец, капли в паре являются
причиной инкрустации обоrреваемых им поверхностей.
Отделение вторичноrо пара от капель жидкости в выпарном
аппарате происходит в надрастворном (сепарационном) про
странстве. Из-за неопределенности в интенсивности уноса и в
распределении образующихся капель по размерам до сих пор
не разработаны точные методы расчета необходимоrо объема
сепарационноrо пространства. В настоящее время ero объем
принято определять по максимально допустимому объемному
напряжению паровоrо пространства R0 , зависящему прежде всего
от давления в аппарате . Величина R0 представляет собой пре
дельно допустимый удельный (приходящийся на 1 м3 сепара
ционноrо пространства) расход вторичноrо пара (м3/с), при
котором гарантировано достаточно полное отделение капель
(их осаждение) в сепарационном пространстве. При большем
расходе вторичноrо пара наблюдается повышенный унос ка
пель из-за роста скорости пара в этом пространстве .
Рекомендуемая зависимость максимально допустимого объ
емноrо напряжения паровоrо пространства от рабочеrо давле
ния в аппарате при Юtпении многих водных растворов солей и
Юtслот приведена на рис. 9 .2 1 . Для растворов солей, характери
зующихся малым пенообразованием, допустимое напряжение
паровоrо пространства может быть увеличено вдвое. Величина
R0 резко уменьшается при увеличении рабочеrо давления в
аппарате до 1 00 кПа, затем падение замедляется, и при давле
ниях выше 300 кПа значение R0 стабилизируется на уровне
0 ,45 - 0 , 50
730

(мЗ/с) /мЗ.

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 9.21. Зависимость мак
симально допустимого объ
емного напряжения парово
го пространства Rп от рабо
чего давления р

Если в аппарате
образуется
W
кг/с
вторичного пара плот
ностью Рп кг/м3 , то
требуемый обьем сепа
рационного
прост
ранства V (м3 ) равен

,..,�..."";:...
�1
с
Q::;

1 ,2

0,8

\

\

\

\

'

'"

......

0,4

о

1

2

w
V = --

--

3

4

.5

p · JO , Па

Р п Rп

При этом диаметр сепарационного пространства dc (м) (или
сепаратора - если он расположен отдельно от греющей каме
ры) находят из формулы объема цилиндра:
dc =

�л�

·

Высоту сепарационного пространства Нс (м) принимают в
зависимости от свойств кипящего раствора: для растворов с
высокой вязкостью и низким поверхностным натяжением,
склонных к образованию пены при кипении, Нс = 2 , 5+3 , О м, а
для невспенивающихся Нс не менее 1 , 6 м.
Отметим, что диаметр сепаратора dc нередко превышает
диаметр греющей камеры (см. рис. 9. 1 и 9.2).
При больших скоростях выброса парожидкостной смеси из
труб в сепарационное пространство с целью погашения ее ки 
нетической энерmи над трубной плитой устанавливают отбой
ник (см . рис. 9 . 1 , б и 9.2,б) с к р и в ол и н е й н ы м и n о в е р х н о ст я м И ,
обеспечивающими возврат жидкости в основную массу раство
ра. При раздельном расположении греющей камеры и сепара
тора подачу парожидкостной смеси в неrо часто осуществляют
танrенциально (см. рис . 9 . 1 , в) . За счет возникающей при этом
центробежной силы основная масса жццкости эффекrивно отде
ляется от пара: отбрасывается к стенкам сепаратора и стекает по
ним. Применение отбойников и орrанизация танrенциалъноrо
ввода позволяюr существенно понизlfГЬ нагрузку на сепарацион
ное пространство и брызrоулавливающие устройства, устанавли
ваемые на выходе вторичною пара из сепаратора.
Даже при наличии отбойников и сепарационного прост
ранства необходимых размеров уходящий вторичный пар несет
73 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

а

б

в

- инерционны й , б - волнистый, s - циклонный;
1 - труба для сrока улоWJеННЬ\Х брызr, 2 - опора для брызrоуловителя

Рис. 9.22. Брызrоуловители выпарных аппаратов:
а

с собой очень мелкие капли раствора , которые также следует
улавливать . Для этой цели и используются брызгоуловители,
упомянутые выше и при описании конструкций на рис. 9. 1 .
Работа брызгоуловителей основана на различии в инерционных
силах, действующих на капли (плотность порядка 1 01 кг/м3 ) и
пар (плотность порядка 1 0-1 - 1 0 кг/м3 - в зависимости от дав
ления) . Наиболее широко используются брызrоулавливающие
устройства в двух основных вариантах (рис. 9 .22):
- многократное резкое изменение скорости и направления
вторичного пара (рис . 9 .22,а и б);
- использование центробежной силы (циклонный брызго
уловитель , рис. 9.22, в) .
Сток уловленных брызr осуществляется либо по трубам 1 небольшого диа
метра, опущенным в раствор (см. таюке рис. 9 . 1 , б - г), или с помощью rидроза
твора (рис. 9.22,а), либо по тем же каналам, rде движется пар (волнистый
брызrоуловитель на рис. 9 . 22 ,б) В последнем случае скорость пара в волнистых
каналах доmкна быть ниже скорости захлебывания, при которой пленки или
струйки :жидкости, образующиеся при коалесценции уловленных капель, пере
стают стекать. Величину этой скорости можно рассчитать по формулам, характе
ризующим течение жидкостных пленок (см. rл. 2) с учетом противоточноrо
движения rаза (пара). На практике эта скорость пара находится в пределах 2 5 м/с при давлении в аппарате свыше 1 00 кПа и 4-8 м/с при давлении до
.

90 кПа.

732

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

В циклонных брызrоуловителях за счет танrенциальноrо входа пара через
щели, образуемые отоmуrыми внутрь пластинами, эффекrивность очистки пара
от

капель

наибольшая. Поэrому эrот тип брызrоуловителя широко применяется

при выпаривании вспенивающихся и кристаллизующихся растворов. Суще
ственным недостатком тахих брызrоуловите.лей является большое гидравлическое
сопротивление, приводящее к повышению давления в корпусе и ухудшению
ус.ловий теплообмена. При скорости входа пара в щели брызrоулавливающеrо
устройства 20-70 м/с перепад давления в циклонном брызrоуловите.ле составля
ет 2-9 кПа.

ЛИТЕРАТУРА
1. Воронцов Е.Г., Тананайко Ю.М.
Технi.ка, 1972. 194 с.

к главе

9

Теплообмен в :жидкостных пленках. Киев:

2. Гельперин Н.И. Выпарные аппараты. М.-Л.: Госхимиздат, 1947. 380 с.
3. Гельперин Н.И. Основные процессы и аппараты химической технологии.
М.: Химия, 1981. 812 с.
4. Дытнерский Ю И.
мия, 1995. 768 с.
.

Процессы и аппараты химической технологии. М.: Хи

5. Касаткин А.Г. Основные процессы и аппараты химической технологии.
М.: Химия, 1971. 784 с.
6. Павлов К.Ф., Романков П.Г., Носков А.А. Примеры и задачи по курсу про
цессов и аппаратов химической технологии. Л.: Химия, 1987. 574 с.
7. Перри Дж. Справочник инженера-химика: Пер. с aнrn. / Под ред. Н.М.
Жаворонкова. Л.: Химия, 1969. 1144 с.
8. Справочник химика, т.V. М.-Л.: Химия, 1966. 974 с.
9. Таубман Е.Н., Пастушенков Б.Л.
Процессы и установки мmовенноrо
вскипания. М.: Энерrоатомиздат, 1990. 185 с.
10. Удыма П.Г. Аппараты с поrружными rорелками. М.: Машиностроение,
1973. 271 с.

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ПРИЛОЖЕНИЯ К ГЛАВЕ 9

Приложение 9. 1. ДИФФЕРЕН ЦИАЛЬНЫЕ ТЕПЛОТЫ
ДЕГИДРАТАЦИ И Qд (кДж/кг РАСТВОРИТЕЛЯ)
ДЛЯ ВОД Н ЫХ РАСТВОРОВ
Н ЕКОТОРЫХ РАСП РОСТРАНЕН Н ЫХ
Н ЕОРГАН ИЧ ЕСКИХ ВЕЩЕСТВ
РАЗЛ ИЧ Н ЫХ КОН Ц ЕНТРАЦИ Й а [ % (МАС .)] ,
Растворенное
вещество

Значен и я
5

N H 4NOз
CaC l2
NaCI
CuS04
N H4CI
NaOH

Qд

при различных а

10

15

20

25

30

35

40

4
- 2
3
- 0,5

7

12

18

26

37

51

6

8

4
4

1
26
13

4
80
30

1 74
62

308
1 16

198

кон

Приложение 9.2. ЗНАЧ ЕН ИЯ
ПОПРАВОЧНОГО МНОЖИТЕЛЯ (j) .
(К.кг РАСТВОРИТЕЛЯ/кДж)
В ЗАВИСИ МОСТИ ОТ РАБОЧ ИХ ТЕМ П ЕРАТУР КИ П Е Н ИЯ
РАСТВОРИТЕЛЯ /р (0 () И дАВЛ ЕНИ Й р (кПа)
fp

30
35
40
45
50
55
60
65
70
75
80
85
90
95
1 00

-

Ч"'

0,0234
0 , 0222
0 ,0209
0,0 1 96
0,0 1 82
0,0 1 67
0 ,0 1 5 1
0 , 0 1 35
0 ,0 1 1 8
0,0 1 00
0 , 0082
0,006 3
0,0043
0,0022
о

fp

105
1 10
1 15
1 20
125
1 30
1 35
140
145
1 50
155
1 60
1 65
1 70
175

+
+
+
+
+
+

+
+
+
+
+
+
+
+
+

q>•

р

0 , 0023
0,0046
0,0070
0,0096
0,0 1 22
0,0 1 49
0,0177
0,0206
0,0237
0,0268
0,030 1
0,0335
0,0369
0 ,0406
0 , 0443

4
6
8
10
15
20
26
30
40
50
60
70
80
90
100

q>•
-

0,0236
0,02 1 9
0,0205
0,0 1 94
0,0 1 70
0 ,0 1 5 1
0,0 1 35
0,0 1 2 1
0 ,0097
0,0077
0,0059
0 , 0043
0,0028
0,00 1 4
0,0002

�

р
1 50
200
250
300
350
400
450
500
550
600
65 0
700
750
800
850

+
+
+
+

+
+

+
+
+
+
+
+
+
+

+

Ч"'
0,0053
0 , 0097
0,0 1 35
0,0 1 69
0 ,0200
0,0228
0,0255
0,0280
0,0304
0,0327
0 ,0348
0,0369
0,0 384
0,0409
0,0428

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Глава 10
ОСНО В Ы МАССОП Е РЕ НОСА

К массообменным относят процессы преимущественного

переноса какого-либо компонента
в другую. Явление массообмена

(компонентов) из одной фазы
сопровождается изменением
кон центраций компонентов в фазах и потому лежит в основе
процессов разделения. Вместе с тем термины "разделение" и
" массообмен" не тождественны: рассмотренные в главе 5 про
цессы гидромеханического разделения не относят к массооб
менным, поскольку там разделение фаз происходит без обмена
компонентами между фазами.
Химичесюtе производства вкл ючаюг три основных этапа:
подготовка сырья ( 1 ) , химичесюtе превращен ия (2) , разделение
продуктов (3). Массообмен в значительной степени обеспечи 
вает первую стадию, когда требуется подготовить сырье опреде
ленного состава (с заданным содержанием компонентов) . Он
обычно играет определяющую роль на третьей стадии. Дело в
том , что процессы происходят не со 1 00-процентными выхода
ми и не с идеальной селективностью - остаюгся непрореаги
ровавшие вещества, появляюгся побочные продукты . Поэтому
из гаммы полученных компонентов необходимо вьщелить це
левые , хорошо бы разделить и остальные с целью их разумного
использования. Но и на второй стадии собственно химическое
превращение сопровождается массопереносом. Например, ге
терогенный катализ вкл ючает адсорбцию исходных компонен
тов на зерне катализатора, собственно химическое взаимодей
ствие и десорбцию продуктов с поверхности зерна ; в рЯде случаев
именно адсорбция или десорбция (а это - массообменные эффек
ты ) являюгся наиболее медленной стадией процесса и потому
определяюг скорость технолоmческого процесса в целом.
В качестве основных целей разделения смесей с помощью
массообменных процессов обычно указываюг:
- получен ие чистого (либо достаточно концентрированно
го) целевого компонента из смеси;
- удаление нежелательных примесей из смеси .
Разумеется, с целью утилизации всех продуктов производ
ства (безотходные : технологии; экологичесюtе проблемы , а в
735

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

долговременном плане - и экономические аспекты) целесооб
разно совмещение ук азанных целей.
В химической технологии и ряде смежных отраслей про 
цессы массообмена используются весьма широко . На проекти 
рование и изготовление массообменной аппаратуры, оснаще
ние ее приборами и т.п. в химических производствах затрачи
вается до 50% капитальн ых вложений.
Ранее уже рассматривался один из массообменных процес
сов
выпаривание, обладающий характерными признаками
массопереноса - переходом компонента (растворителя, часто
- воды) из жидкой фазы в паровую. Однако этот массообмен 
ный процесс всецело определяется подводом теплоты, и по
этому его рассчитывают как тепловой процесс . Н иже будут ис
пользованы некоторые подходы и понятия , введенные при
изучении теплопереноса; но в целом для рассматриваемых ни
же массообменных процессов ситуация значительно сложнее.
В настоящей главе анализируются общие вопросы массопе
реноса, излагаются общие понятия и подходы к расчету групп
различных массообменных процессов. Конкретизация эти х
понятий и подходов применительно к отдельным (наиболее
распространенн ым) технологическим приемам составляет со
держание последующих глав.
-

1 0. 1 . ОБЩАЯ ХАРАКТЕРИСТИКА МАССОПЕРЕНОСА
1 0. 1 . 1 . Классификация массообменных процессов
Классификация массообменных процессов может прово
диться по разным признакам .
Наибольшее распространение получила традиционная клас 
сификация - по технологическим приемам (процессам - в ши
роком поним ании этого термина) . Ее возникновение и распро
странение в значительной мере обусловлено тем , что различ
ные группы исследователей занимались в основном отдельны
ми технологическими приемами; связи этих групп зачастую
были весьм а слабыми , и потому методы и инструм ентарий ана
лиза разных приемов (процессов) также были разрозненными ,
специфичными для каждой группы исследователей . В послед
нее время в учебной (отчасти и в научной) литературе все чаще
выступает стремление выявить общие м оменты в различн ы х
процессах. Реализация этого стремления в сочетании с сохра
нен ием специфических черт отдельных приемов и привела к
созданию "традиционной классификации" .
Рассматривают фазы - жидкую (Ж) , газовую ( Г) либо паро
вую (П) и твердую (Т) . Вьщеляют две группы процессов. Пе р
-

736

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

вая (1) - процессы с непосредствен ным соприкосновением фаз,
обменивающихся веществом (компонентами) ; сюда относится
подавляющее большинство технологических приемов. Здесь две
подгруппы:
1А - процессы с изменяющимися границами раздела фаз
(поверхность их контакта не фиксирована);
IБ процессы с фиксированной границей раздела фаз.
К подгруппе 1А относятся процессы в системах:
- Жидкость - Пар; массообмен здесь основан на переносе
при кипении-конденсации из фазы в фазу нескольких компо
нентов с разной интенсивностью; это процессы дистилляции ,
ректификации , парциальной конденсации ;
- Жидкость - Газ; массообмен основан на растворении од
ного из (или нескольких) компонентов газовой смеси жидким
растворителем; это абсорбция (либо обратный процесс - де
сорбция);
- Жидкость - Жидкость; массообмен базируется на раство
рении отдельных компонентов жидкой смеси в другой жид
кости, которая не должна смешиваться полностью с исходной
жидкой смесью; это жидкостная экстракuия.
В большинстве случаев элементы контактирующих фаз
(часто это дискретная фаза - капли , пузыри, - распределен
ная в сruюшной ; иногда - пленки и струи) в ходе процесса
изменяют свои размеры и форму. Например, мелкие капли в
результате действия сил поверхностного натяжения близки к
сферам , крупные - мoryr быть существенно деформированы .
Кроме того , происходят постоянное разрушение капель и пу
зырей и их коалесценция. В расчете поверхности контакта фаз
здесь чаще всего нет определенности, используются прибли
женные модельные представления или качественные оценки.
К подгруппе IБ относят процессы с твердой фазой, обла
дающей фиксированной, часто неизменной и в принципе под
дающейся расчету межфазной поверхностью контакта. Это
процессы в системах:
- Газ - Твердое и Жидкость - Твердое; здесь рассматри
вается выделение из газовой или жидкой смеси какого-либо
компонента (компонентов) с помощью твердого поглотителя ;
это процессы адсорбции (либо десорбции) и основанные на
ней практически важн ые хроматография , ионообмен ная сорб
ция. Один из десорбционных процессов Г Т (сушка) выде
ляется особо - в силу его распространенности и специфи
ческой методики расчета;
Жидкость - Твердое; это растворение твердых веществ
(или компонентов твердых веществ) - собственно растворе-

-

737

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

г

т

г

процессы

Мембранные

ж

Фаза - источник

Дисmи.:1/1.Яция

Десорбция
( Выпаривание )

1

т

Десорбц ия

Субли.нация
Сушка

А бсорбция

Жидкостная
экстракция
Мембранные
процессы

Десорбция
( Выщелачи-

Адсорбция
Десублимация

А дсорбция

Фазовые
превращения
// рода

вание ) 2

1 - Процесс выпаривания обычно рассматриваtтся в теплообменны х, а н е в массообмен
ных процессах (см. rл.9). 2 - Выщелачивание нер едко лишь формально моJКНо оmести к
массообменным процессам

Рис. 10. 1. К традиционной классификации массообменных процессов�

ние; выщелачивание, когда жидким растворителем поглощает
ся компонент (компоненты) из его (из их) смеси с твердым
веществом, нерастворимым в растворителе; к этим же системам
относят и процессы кристалл и зации из растворов и расплавов;
- Газ - Твердое; здесь происходит испарение твердого ком
понента в газовую фазу, минуя жидкое состояние (или конден 
сация из газовой фазы сразу в твердое состояние) ; это процес
сы сублимации (возгонки) или десублимации .
Ко второй (11) группе относят процессы массопереноса, про
текающие без непосредственного соприкосновения фаз. В на
стоящее время это лишь один , но весьма перспективный тех
нологический прием - мембранные процессы. Сущность его - в
переносе компонента из фазы в фазу через полупроницаемую
перегородку (мембрану) , через которую компоненты проходят с
разной скоростью (а некоторые совсем не проходят) .
На рис . 1 0 . 1 традиционная классификация представлена в
виде диаграммы с указанием фазового состояния исходной
смеси (фаза-источник) и продукта (фаза-приемник) . Такое
представление достаточно наглядно, но лишь для однонаправ
ленных массообменных процессов; ректификация, экстракция
при ограниченной взаимной растворимости разбавителя и экс
трагента здесь не представлены, да и выщелачивание можно
лишь условно поместить в ячейку Т -+ Ж. Массообмен Г -+ Г

738

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

возможен лишь при наличии полупрон ицаемой перегородки
(мембраны). В ячейку Т --+ Т могуг быть помещены фазовые
превращения 11 рода (изменен ия в кристалл и ческой решетке и
др .), в курсе ПАХТ не рассматриваемые .
К недостаткам традиционной классификации относится ее
неоднозначность, что ясно видно из рис . 1 0 . 1 . Еще суще
ственнее, что эта классификация не выявляет в должной мере
общности в осуществлении и описании рассматриваемых тех
нологических процессов. Вероятнее всего , использование гро
моздкой традиционной классификации обусловлено, в первую
очередь, стремлением сохранить устоявшиеся специфические
подходы к анализу отдельных технологических приемов.
Подчеркнем уиа.ность традиционной классификации (как и всякой дру
rой - см. разд. 1 .2.3). В самом деле, конечной цепью ряда процессов подrруппы
IБ является изменение размеров твердых частиц (растворение, кристалл изация), а
значит и межфазной поверхности. Следовательно, здесь требуется уточнение:
rоворя о фиксированной или изменяющейся межфазной поверхности, СJiедует
подразумевать скоротечные (почти "мгновенные") явления разрушения и коалес
ценции пузырей или капель - в противовес протекающему относительно мед
ленно целевому изменению размеров элемекrов твердой фазы. Кроме тоrо, надо
иметь в виду, что в ряде процессов типа Ж - Г (скажем, при массообмене rазо
вой фазы с тонкими пленками, движущимися по внутренней стенке труб) по
верхность межфазноrо кокrакта определяется достаточно точно.
Более обоснованной с позиций методов анализа и расчета
(т.е. в аспекте курса ПАХТ) представляется классификация по
числу фаз и компонентов, в том числе перенесенных из фазы в
фазу, - будем называть такую классификацию компонентно
фазной, или КФ-классификацией. Введем численное обозначе
ние: a(b-c)d, где а - общее число компонентов в системе; Ь и
с - числа компонентов в каждой фазе (отдающей и получающей
компонент) ; число d - число компонентов, переходящих из
фазы в фазу. Заметим: компонент здесь - не обязательно ин 
див идуальное вещество; это может быть и группа веществ, вы
полняющих одинаковую роль (т.е. неразличимых в смысле мас 
сопереноса) . В такой символике некоторые двухфазные про
цессы, выделенные выше в традиционной манере, будут отне
сены к определенным классам; они представлены в табл . 1 0 . 1
применительно к простейшим вариантам для минимально воз
можного числа компонентов.
Возможности этой классификации выходят за пределы соб
ственно массообменных процессов. В нижних строках таблицы
обозначены процесс выпаривания , а также фазовый переход 1
рода для однокомпонентной системы (например, испарение) . В
принятой символике может быть представлен и трехфазный
процесс , например кипение бинарной смеси двух несмеши
вающихся ж ид костей (две жидкие фазы и одна паровая) : 2( 1 - 1 -

739

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Таблица

10. 1.

Технолопtческие приемw

Процесс в традициоюJОм
наименовании

ДисТИJUIЯция, ректифика
ция
Абсорбция
Экстракция
Экстракция

Адсорбция
Сушка твердых материа
лов
Вьuцелачивание
Мембранные процессы

КФ
класси
фи хация

в

КФ-классификации

Компоненты и фазы

2(2-2)2 Bcero 2 компонента и 2 фазы, в каждой по 2 компонента; оба переходят из фазы в
фазу
3(2-2) 1 Bcero 3 компонента и 2 фазы, в каждой по 2 компонента; l переходящий компо
нент
3(2-2) l То же (обе ЖИдкости полностью нераство
римы одна в друrой)
3(3-3)3 Bcero 3 компонента и 2 фазы, в каждой - по
3 компонента; все 3 переходят из фазы в фазу
(жидкосrи оrраниченно распюримы друг в
друге)
3(2-2) 1 РассмоТРено выше
3(2-2) 1 То же
3(3-2)2 Всеrо 3 компонента и 2 фазы, в одной 3
компонента, в друrой - 2; переходящих
компонентов 2
2(2-2)2 Bcero 2 компонента и 2 фазы (по разные
или
стороны мембраны), в общем случае
по
2(2- 1) l 2 компонента в фазе и оба переходят из
фазы в фазу; в Идеале - 1 компонент в
одной из фаз, тогда l компонент - пере
ходящий
2(2- 1 ) l Всеrо 2 компонента и 2 фазы, в одной 2
компонента, в друrой - l; переходящий
компонент - 1
l ( l - l ) l Любой двухфазный переход 1 рода (испаIUJавление-затвердерение-конденсация,
ванне и т.п.)
-

-

Выпаривание
Фазовый переход в одно
компонентной системе

2)2; в скобках указано , что две фазы содержат по одному ком 
поненту, а третья (паровая) - два, причем оба компонента
переходят в паровую фазу.
Важно подчеркнуть, что многие технологические приемы,
обособленные в традиционной классификации , здесь объедине
ны в общие группы , для которых моrут быть использованы оди 
наковые (по меньшей мере - сходные) подходы к анализу и
расчету. Так, в КФ -классификации к общей группе отнесен ы
Абсорбция и Десорбция, Экстракция (при взаимной нераство
римости жидких фаз), в некоторых технологических ситуациях
- Адсорбция и т.п . В других случаях расчетные методы весьма
близки : жидкостная экстракция при ограниченной взаимной
растворимости жидких фаз и выщелачивание (совпадает число
компонентов и их максимальное число в одной из фаз). Не740

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

трудно видеть , что степень обобщения в КФ-классификации
з аметно выше , нежели в традиционной.
(
Нередко различают процессы с однонаправленным одно 
сторонним) переносом вещества) из одной фазы в дрУJУЮ и с
двунаправленным (двусторонним встречн ы м переносом - и з
первой фазы во вторую и из второй в первую. Ч аще всего эти
ситуации легко разл ичимы в р амках КФ-классификации : про
цессы с одним переходящим компонентом (цифра правее
скобки) относятся к однонаправленному массопереносу. При
большем числе переходящих компонентов процесс может быть
как однонаправленным (например , дистилляция или много
компонентн ая абсорбция) , так и двунаправленным (например ,
ректификация , противоточная экстракция при ограниченной
вза имной растворимости жидких фаз ) . Для различения этих
ситуаций целесообразно заменить дефис в скобках двунаправ
ленной стрелкой , скажем , для ректификации бинарной смеси:

2(2 � 2)2.

Иной срез классификации - по типу структурно -конфи
гурационного комплекса ( СК К) :
- по нап равлению взаимного движения фаз : прямоточн ые ,
противоточн ые и другие схемы движения ;
- течение фазы в режиме идеального вытеснения (И В) ,
ид еально го перемешивания ( И П ) или в другом режиме;
- комбинация р азличных схем взаимно го перемещения фаз
и режи мов продольного перемешивания в каждой из них.
Различа ют процессы непрерывные (иногда их отождествляют
со стационарными · ) , когда входные, выходные и промежуточ
ные потоки и параметры (темпе ратуры , концентрации, другие
свойства) статистически неизменны во времени, и периодические
(они принципиально нестацион арны), когда параметры изме
няются во времени. Нередко среди периодических процессов
выделяют группу полунепрерывных, когда один или несколько
потоков сохраняют во времени неизменными свои входные ха
рактеристики (расходы , температуры и пр.), а остальные
(например , выходные) характеристики этих и других рабочих
тел претерпевают изменен ия во времени.
Наконец , возможно рассмотрение функционирования оди
ночных аппаратов (массообменных устро й ств с оп ределенными
С К К) и их сетей, т.е. комбинаций устройств с одинаковыми
ил и раз ными СКК в отдельных аппаратах.
• Непрерывные процессы обычно не строго стационарны; возмущающие во з 
действия откrю няют их от регламентированного состояния, в которое они воз
вращаются в силу собственной устойчивости или с помощью упраR11Я ю щих
воздействий. Стационарность процесса здесь соблюдается лишь статистически .
74 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Выбор варианта осуществления массообменного процесса за
висит от многих факторов:
- свойства рабо ч их тел (бывает, что эти свойства диктуют
однозначное обрашение к тому или иному приему) ;
- производительность (расходные поI01Затели): при высоких
производительностях предпочтительнее непрерывные процессы;
- заданный уровень конечных концентраций: наибольший
эффект здесь обычно дает противоток фаз ;
- особенности оформл.ения аппаратов и схем: одиночный
аппарат проще сети аппаратов, сеть зачастую эффективнее
одиночного устройства ; периодические процессы часто исполь
зуют для малотоннажных производств (особенно если в одной
и той же аппаратуре попеременно проводятся различные мас
сообменные процессы);
- экономическая эффективность (технико-экономический
анализ позволяет выбрать оптимальный вариант) и т.д .
Некоторые сравнительные характеристики вариантов и ре
комендации по выбору наиболее эффективных из них содер
жатся в последуюших главах при рассмотрении кон кретных
технологических приемов.

1 0 . 1 .2. Составляющие описания массопереноса
Перенос вешества из фазы в фазу сопровоЖдается измене
нием его концентрации как в исходной, так и в принимающей
фазе (эти концентрации далее обозначаюrся, например, х, у, )
Поэтому описание массопереноса связано с выражением состава
фаз (концентраций переносимого и друmх компонентов).
Для представления и реализации любого процесса переноса
(не только вещества) необходимо проанализировать его в трех
основных направлен иях : равновесие, кинетика, баланс .
Перенос субстанции в системе происходит под действием
разности потенциалов в различных ее точках. В науке о ПАХТ
в качестве потенциалов чаще всего рассматривают давление р,
температуру Т и химический потенциал µ1 каЖдого из i компо
нентов сИстемы . Изолированная система с течением времени
приходит в равновесие - тогда в ней не происходит никаких
качествен ных и количественных изменений во времени, т.е.
переноса субстанции нет. Это наблюдается, если в системе (во
всех ее точках, в разных фазах) выравнены потенциалы р, Т, µi;
иногда записывают dp = О , d T = О , dµi = О .
В теплопереносе (когда речь не идет об изменении давления
и переносе вещества) равновесие означает равенство темпера
тур рабочих тел , составляюших систему (для двух рабочих тел
- Т и t) . В диаграмме Т - t теruювое равновесие выражается
" .

742

.

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 10. 2. Фазовое равновесие: равенство хими
ческих потенциалов фаз (температур теruюно
сителей)

(при равных масштабах по осям Т и
t) прямой линией , выходящей из
начала координат и проходящей под
углом 45° (рис . 1 0.2, символы в скобО
µx (l)
ках). В массопереносе при выравненн ых давлениях и температурах равновесие столь же просто выражается
на основе химических потенциалов µ1 . Для класса 3(2-2) 1 на
рис . 1 0 .2 в тех же декартовых координатах µх = µу , где индексы
х и у относятся к кон центрациям каждого переносимого ком
понента i в пределах любой из фаз и в разных фазах. Однако
химические потенциалы невозможно померить и весьма слож
но рассчитать" . Поэтому используют более наглядные, доступ
н ые измерению и расчету концентрации компонента х1, у1, тем
более что материальные балансы по компоненту (они - в
основе технологических расчетов) базируются на его концент
рациях в фазах. Но концентрации сложным образом (чаще
всего - нелинейно) связаны с химическим потенциалом µ1. В
результате равновесная диаграмма в кон центрационном пред
ставлении трансформируется чаще всего в кривую линию, про
ходящую через начало координат; конфигурация этой кривой
зависит от природы компонентов, составляющих фазы, и усло
вий (температур, давлений).
В основе кинетических соотношений лежат закон Ф ика
(разд. 1 .5.3) и уравнение массоотдачи (разд . 1 .3.2). Эти соотно
шения будуr использованы в интегральном написании
для
1 с, для всего процесса, для всей поверхности контакта фаз, или
в dифференциальн.ом
для t>есконечно малых временн ого ин
тервала d't и (или) поверхности контакта dF. Общий подход к
получению кинетических соотношений аналогичен принятому
в главах 6 и 7 для переноса теплоты . При независимости кине
тических коэффициентов (диффузии D, массоотдачи �) от
уровня кон центраций и движущей силы процесса кинетические
уравнения линейны, что существенно упрощает их решение и
применение.
Балансовые соотношения используются в данной главе на
основе общих предпосылок (разд. 1 .3 . 1 ) . Проблема здесь заклю
чается в выборе подходящей формы записи, чтобы эти соот-

-

• О подходах к расчету µ; см" например, ( 14), учебники и монографии по
химической термодинамике.

743

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ношения по возможности тоже оказались линейными - это
упрощает последующую работу с ними .
Если все три составляющие удается выразить линейными
соотношениями , то и описание массообменного процесса в
целом будет линейным. В этом случае в полной мере приме
н има концепция пропускных способностей, и решение задач
массообмена часто удается довести до конечных аналитических
выражений, обычно разрешимых в явном виде относительно
искомых величин . Из этих выражений ясен характер влияния
основных параметров; здесь возможны количественные про
гнозы и оптимизация процесса. Однако необходимо четко
представлять себе границы линейных соотношений ; за преде
лами этих границ использование линейных представлений мо
жет привести к ошибочным результатам в количественном
плане (если эффект нелинейности невелик) и в качественном
(если нелинейность существен на) . Вместе с тем сведение не
линейных представлений к линейным создает иногда неплохие
возможности для анализа на уровне качественных аспектов:
больше - меньше, лучше - хуже.

1 0 . 1 .3. Массообменные устройства
Устройства для осуществления массообменн ых процессов
отличаются широким разнообразием. Оно обусловлено разли
чием в агрегатных состояниях контактирующих фаз и в
свойствах участвующих в процессе компонентов и их смесей.
Отсюда слажности в общих рекомендациях по конструирова
нию и выбору подходящих массообменных устройств - они во
многом определя ются спецификой конкретного процесса.
При организации переноса вещества из фазы в фазу техно 
л о г должен стремиться улучшить межфазный контакт - з а счет
увеличения межфазной поверхности, более полного использо
вания движущей силы и повышения интенсивности переноса
на единицу поверхности. Движущую силу повышают, реализуя
благоприятную схему движения контактирующих фаз, предпоч 
тительно - противоточную. Интенсивность переноса вещества
через единицу межфазной поверхности повышают путем турбу
лизации потоков контактирующих фаз . Наиболее действенным
и относительно просто реализуемым обычно является увеличе
ние поверхности межфазного контакта F; поэтому создание
массообменных устройств направлено прежде всего на разви
тие поверхности массопереноса.
Множество конструкций массо о бменных устройств можно условно ЮJасси
фицировать следующим образом: пленочн•1е, насадочн•1е, барботажн•1е (чаще
всего
для систем Г, П - Ж) , дисперrнрующне (дrIЯ систем Г - Ж и Ж - Ж);
отдельн о следует рассматривать устройства д11 11 контакта потоков Г и Ж с твердой
-

744

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

фазой. Классификация названа условной, поскольку не всегда можно четко раз
граничить классы устройств из-за сложности отдельных конструкций и неодно
значности (пересечения) достигаемых эффектов . Одиночные массообменные
устройства нередко комбинируют в сети аппаратов, развивая поверхность кон
такта, повышая движущую силу (за счет организации эффективных схем движе
ния фаз).
Н иже дана самая общая характеристика упомянутых контактных устройств;
более детально они рассмотрены в последующих главах при изложении конкрет
НЬIХ технологических приемов.
Пленочнwе устройства (рис. 1 0.3,а) предполагают контакт жидкой и газовой
фаз (не исключаются и системы Ж - Ж), причем жидкость стекает nленкой по
внутренней поверхности трубы или множества параллельных труб либо со
бранньIХ в пакеты параллельньIХ вертикальньIХ пла1..'ТИ Н. В верхней части труб
обычно размещают устройство, организующее пленочное движение жидкости
(иногда - закрученное). Газ при этом преимущественно подается снизу - про
тивотоком к жидкости. Скорость его ограничивают, стремясь обычно не допус
тить срыва капель с поверхности менки и их уноса с газом (обратного переме
шивания - в терминах структуры потоков), а также опрокинутого движения
жидкости на границе с газом. Заметим: при высоких мотностях орошения (а
также расходах газа) возможно заполнение жидкостью контактного объема тогда массообмен происходит в эмульгированном режиме: газ становится дисперс
ной фазой (пузыри), движущейся в смошной жидкой (см. распьиивающие
массообменные устройства) .
К меночным аппаратам примыкают полочнwе; они отличаются небольшим
гидравлическим сопротивлением и одновременно невысокой эффективностью.
Поэтому их целесообразно применять, когда не требуется высокая степень раз
деления.
Насадочнwе устройства шире применяются в массообменньIХ процессах; при
этом используются элементы насадки разного вида (рис. 10.3,6). В простейшем
случае это куски правильной или неправильной формы; часто используются
кольца (иногда - фасонные: с перегородками, с отверстиями и т.п.), седла либо
элементы более сложной конфюурации. В отдельньIХ случаях применяют xopдo
l!)IIO насадку - из поставленньIХ на ребро рядов досок, собранных в решетки.
Разумеется, материал насадки должен быrь химически инертен к участвующим в
массообмене веществам.
По элементам насадки 1..-текает жидкая менка, омываемая восходящим газо
вым потоком. Скорость газа в насадочном аппарате ограничена явлением захле
бwвани•: при больших скоростях восходящего газового потока жидкость не
может стекать вниз, она оказывается "запертой". Поэтому подаваемая
(например, насосом) жидкость накамивается над слоем насадки; когда ее вес
станет достаточно большим, она "провалится" через слой насадки - без эффек
тивного контакта с газом (далее жидкость снова будет накамиваться над насад
кой). Такой режим работы неэффективен, поэтому скорость газа в насадочном
аппарате должна быrь ограничена неким пределом, называемым "скоростью
захлебывания".
Насадку обычно загружают в аппарат навалом (типичное исключение - хор
довая насадка). Реrулярная укладка используется р е ж е по ряду причин: боль
шие затраты времени (особенно для крупньIХ промышленньIХ аппаратов); про
воцирование существенной неравномерности потоков (вмоть до байпасирова
ния фаз вследствие пониженного гидравлического сопротивления). При загрузке
навалом эти эффекты выражены слабее. Однако и в этом случае вблизи стенок
аппарата упаковка насадки - более рьIХЛая (непосредственно у стенок доля
свободного объема выше порозности слоя насадки). Поэтому жидкость (она вы
бирает путь наименьшего гидравлического сопротивления) имеет тенденцию
.

745

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

о

�11

о

8-9�

-O-=�o-

i11 t1 i11

6

а

2

в

г

11'

11"

д

� 11
� ///
1

е

а - пленочные и ·полочные усrройсrва: 1 - трубчатое с распределителем, 2 - полочное
(фраrмент);
б - насацки: 1 - кольца Рашиrа, 2 - кольца с переrородкой , З - седло, 4 - хордовая
насадка, 5 - сеJСШ{Я с псевдоожюкеЮJой насадкой;
в - барботажные усrройсrва (фраrменты тapeJIJQf): 1 - колпачковое, 2 - клапанно е, З
- ситчатое непровальное, 4 - ситчатое провальное;
г - дисперrирующие усrройсrва: 1 - распылительное , 2 - роторно-дисковое;
д - аппараты для массообмена с твердой фазой (примеры): 1 - прямоточный , 2 - про
тивоточный, З - с перекреСПIЬIМ двюкеЮ1см фаз, 4 - периодическоrо дейсrвия, 5 - полу
непрерывноrо действия;
е - соединеЮ\е аппаратов в сети: 1 - сrупенчатый противоток; 2 - сrупенчатый пере
кресrный ток;
/ - rаз, // - JJСИдlСОСТЬ, /// - твердая фаза

Рис. 10.З. Основные массообменные устройства:

746

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

двигаться преимущественно в пристеночных зонах, остааляя газовому потоку приосевые. Дабы понизить эту поперечную неравномерность потоков, приводя 
щую к ухудшению контакrа жидкой и газовой фаз, слой насадки разбивают на
несколько (высота каждого из них близка к диаметру аппарата) с установкой
между слоям и перераспределительных устройств, направляющих жидкость
несколько ближе к осевым зонам аппарата, что обеспечивает в среднем более
равномерное распределение потоков по его поперечному сечению .
Кусковую, кольцевую, седnообразную насадки обычно загружают в аппарат,
заполненный для этой цели водой - во избежание деформации элементов на
садки (ее.ли они металл ические) или разрушения (если керамические).
Поперечная неравномер ность потоков существенно снижается при использо 
вании псевдоожиженной насадки - это полые шары; их объемная плотность
ниже, чем у жидкости. Шары подаваемым снизу rазом (паром) приводятся в
псевдоожиженное состояние. Интенсивно перемещающимися шарами жидкость
разносится по всему поперечному сечению секции - пракrическое отсутствие
поперечной неравномерности значительно повышает эффекrивность массопере
носа. Одновременно может бьпъ повьШiена и ero икrенсивность (производительность
аппарата), поскольку скорость захлебывания смещается :щесь в сторону б&льших вели
чин, а унос капель заметно снижается из-за mfuйнoro действия смоченных жид
костью псе�щоожиженных шаров.
Барботажи•1е устройства (рис. 1 0 . 3 , в) используются в процессах массоперено
са наиболее часто . Такое устройство предстааляет собой секцию , заполненную до
определенной высоты жидкой фазой ; в нижней части секции размещено газо
устройство ( "тарелка") - колпачковое, ситчатое,
(паро- )распределительное
клапанное или другое (на рисунке эти конструкции показаны схематически).
Газовая фаза дисперrируется в этом устройстве (это приводит к увеличению
поверхности межфазного контакrа) и барботирует через слой жидкости. Число
колпачков и клапанов на тарелке достигает десятков (в крупных аппаратах сотен) . Ситчатые устройства обычно отличаются меньшим rидрамическим со
протимением газовому потоку; они, однако, весьма чувствительны к загрязне
ниям. Над жидкостью расположена сепарационная зо на, снижающая унос капель
газовым (паровым) потоком, т.е. перемещение жидкости в направлении, проти 
воположном движению е е основного потока (обратное перемешивание в терм и 
нах струкrуры потоков). Жидкость организованно, через сливные трубки ил и
карманы, транспортируется н а расположенную ниже секцию ( непровальные та
релки) либо - в отсутствие сливных устройств - уходит с тарелки за счет про
вала через отверстия по законам истечения (ситчатые провальные тарелки). Ско
рость газа в барботажных устройствах ограничена возникновением заметноrо
уноса капель газовым (паровым) потоком.
Диспер111рующие контактные устройства (рис. 1 0 . 3 ,г) отличаются широким
разнообразием .
В некоторых из них диспергирование фазы про изводят на одном из концов
устройства: сверху, ее.ли жидкость дисперrируется в газовую фазу; снизу, ее.ли
газ дисперrируется в жидкость; сверху и (или) снизу, ее.ли одна жидкая фаза
дисперrируется в друrую, не смешивающуюся с ней полностью. С целью увели
чения поверхности контакrа об ычно (ее.ли это возможно) стараются дисперrиро
вать ту фазу, объем которой больше. Распьиивающие устройства достаточно
просты, но обладают рядом недостатков:
- сравнительно небольшие объемные концентрации дисперсной фазы (во
избежание коалесценции капель и пузырей, что привело бы к уменьшению
поверхности межфазноrо контакrа);
- достаточно выраженные эффекrы продольного перемешивания (за счет
поперечной неравномерности потоков, направленной циркуляции и обратноrо
перемешивания);

747

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

- слабое "обновление поверхности контакта", особенно в системах Ж - Ж
(из-за малых скоростей взаимного движения фаз), значит, падение rрадиентов
концентраций у поверхности раздела и снижение скорости массопереноса.
В другой rруппе устройств диспергирование ведется по всей высоте рабочей
зоны с помощью принудительного движения рабочего орrана (вращающегося
диска, перемещающейся ситчатой тарелки и т.д .). Такие устройства чаще всего
применяются при малой разнице в плотностях фаз, преимущественно в системах
Ж - Ж, когда без механических диспергирующих устройств по высоте аппарата
контакт фаз не эффективен.
Производительность диспергирующих устройств оrраничена скоростью за
хлебывания (в основе ее расчета - скорость стесненного витания злементов
дисперсной фазы).
Конструкции устройств для массообмена газов и жидкостей с пердwми тела
ми типизировать сложно, поскольку они в значительной мере зависят от разме
ров, формы, физико-химических свойств самих твердых тел, их концентрации в
сплошной среде, а также принятого способа контакта (в неподвижном, движу
щемся или псевдоожиженном слое, в потоке сплошной среды и т.д.). При этом
твердая фаза нередко выполняет роль насадки, но не инертной (как в насадоч
ном аппарате), а активной, участвующей в массообмене. На рис. 10.3,д в качестве
примера приведены контактные устройства для прямотока фаз (например, пнев
мо- или mдротранспорта), противотока фаз (пример - движущийся слой) ,
перекрестного тока (аэрожелоб, в котором псевдоожиженный твердый материал,
пронизываемый газовым потоком, перемещается под уклон), аппараты периоди
ческого (4) и полунепрерывного (.5) процессов (например, для экстрагирования
ценного компонента из твердого материала).
Каждое из приведенных выше устройств может рассматриваться как само
стоятельный массообменный аппарат. Комбинация таких устройств представляет
собой сеп. аппаратов (хотя конструктивно они мoryr быrь объединены общим
корпусом). Сети различаются способом соединения отдельных устройств
(аппаратов) потоками фаз. Очень часто в целях повышения движущей силы
процесса реализуют противоточное движение фаз между устройствами
(рис. 10.3,е- J), хотя в каждом отдельном устройстве возможен иной СКК
(прямоток, идеальное перемешивание фаз и др.); в результате получается С'J)'Пен
чатwй прО111 вотох фаз. Встречаются также сети аппаратов со С1)'Пенчато
перехреС111wм движением фаз (рис. 10.3,е-2).
В ряде массообменных процессов массоперенос сопровождается положи
тельным или отрицательным тепловым эффе ктом. В этих случаях массообмен
ные аппараты снабжают теплообменными устройствами - встроенными или
вынесенными .
Конструкции массообменных аппаратов (в виде отдельных устройств или се
тей), а также основных узлов рассматриваются при изучении конкретных техно
логических приемов - там можно в большей мере учесть специфику приема и
ее влияние на аппаратурное оформление. Более подробно конструктивные осо
бенности массообменных аппаратов приведены в ряде учебников и моноrра
фий", в специальной литературе.

1 0- 1 .4. Порядок последующего изложения
Порядок последующеrо изложения ясен из оглавления.
Особо укажем, что существенное внимание в настоящей главе
уделено системам класса 3 (2-2) 1 по КФ -классификации,
поскольку они служат удобной и поучительной моделью:
• См " например, (8, 10, 12, 16, 1 7, 23) и др.
748

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

- они образуюг широкую группу реальных процессов (см .
табл . 1 0 . 1 ) ;
- принципы и х организации и расчета (аналитического ,
графического) наиболее просты ;
- для их аналитического расчета наиболее подробно разра
ботан математический аппарат.
Указанные системы изучаюrся не только безотносительно к
конкретным производствам (это общий принцип построения
современных курсов ПАХТ) , но и безотносительно к техноло
mческому приему. Например , процессы абсорбции и десорб
ции , экстракции при взаимной нерастворимости жидких фаз
(разбавителя и экстрагента) , при определенных условиях - и
некоторые другие (адсорбция и т.п.) - мoryr рассматриваться
совместно в пределах указанной классификации , поскольку

математическое описание для всех процессов данного класса идентично.

Технологическая ситуация анализируется применительно к
простейшим С КК ( идеальное вытеснение , идеальное переме
шивание; прямоток и противоток фаз) - сначала в отдельном
аппарате , а затем при их соединении в простые сети; кратко
затронуты и другие С КК. Основное внимание уделено непре
рывным (стационарным) процессам , менее детально анализи
руюгся периодические и полунепрерывные (некоторые из них
подробнее рассмотрены в последующих главах) . Итогом анали
за должно быть установление необходимых связей концентра
ций компонентов, потоков переносимых веществ и т.п. с пара
метрами процесса и использование этих связей для инженер
ного расчета задач эксплуатации и проектирования.
Процессы, относящиеся к другим группам по КФ 
классификации , кратко рассматриваюrся в конечных разделах
главы . Подчеркнем, что при решении многих вопросов анализа
и расчета массопереноса для систем , относящихся к этим
группам процессов , удается сохранить подходы , модели и рас
четные приемы , справедливые для систем класса 3 (2-2) 1 .
Завершается глава изучением особенностей массообмена с
твердыми телами .
З а пределами рассмотрения данной главы остаюrся весьма
сложные проблемы одновременного протекания массопереноса
и химической реакции . В определенном аспекте эти проблемы
находят отражение в гл . 24, отдельные моменты затронуты в
других главах при изучении конкретных технологических при
емов. Детальная проработка проблемы содержится в специаль
ной литературе , в отдельных курсах массопереноса· .
' См. , например, ( 1 , 5, 18, 23).

749

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

1 0.2. КОНЦЕНТРАЦИИ
Концентрацией называется величина, выражающая

ние какого-либо компонента в смеси

содержа 

(в фазе, в системе из
нескольких фаз, в том или ином сече н ии технологического
аппарата, в части аппарата или в аппарате в целом) . Концен т
рация ко м понента задается отношением его количества к ко 
личеству какого -л и бо другого компонен та смеси , нес кольки х
или всех ее компонентов. Концентрации классифицируют по
разным признакам :
- по размерностям : одн ородн ые (кг/кг и т.п.) и смешанн ы е
(кмоль/м3 и др .);
- по базе, к которой отнесена концентрация компонен та :
абсолютные (за базу прин ята с ум ма всех компонентов смеси) и
относительные (база - какой - н и будь один компонент);
- по принятой единице экстенсивно го свойства : массовые
( кг/кг), мольные (км оль/км оль), объемные (мЗ/мЗ ) и т.д.
Размерность концентрации, записанная полностью, обнажа 
ет физический смысл принятого ее пред ставления; пример : (кг
низкокипящего компонента)/( кг смеси); здесь не следует со 
кращать кг в числителе и знаменателе (это " разные" кг) , и н аче
физический смысл затуш евывается .
Концентрации чаще всего обозначают первыми буквами латинского алфавита
(а, Ь, с, d . . . ) или, наоборот, последними (х, у, .. . ) - строчными или заглавны
ми. Нередко Д11Я различения компонентов, к которым относятся концентрации,
вводят и ндексы : х 1 , х2, хз, . , ХА, хв . . . . Прин адr1еж ность концентрации к том у
или иному способу ее выражения каждый раз будем оговаривать специально.
"

Совокупность всех концентраций смеси дает ее состав. Если
мы работаем с бинарн о й смесью, то достаточно зафиксировать
концентрацию одного из компонентов - пусть она равна х в
одной фазе и у - в другой . Если смесь содержит п компонен 
тов, то фи ксировать н ад о концентрации п - 1 компоне нтов : х 1 ,
хъ . . . , Хп- 1 и У1 , J12 , . . . , Уп- 1 · Тогда состав фазы "х" задается
этим набором концентраций , т.е. состав Х (х1 , х2 , . . . , Хп-1 ) есть
вектор концентраций ; аналогично - по фазе "у". В по следую 
щих расчетах мы будем чаще всего оперировать бинарными
смесями как наиболее простыми.
В тех ниче с кой литературе , заводских регламентах концен т
рации неред ко задают в процентах - в силу привычки ; др уги х
ар гум ентов в пользу процентов нет. Вместе с тем это более
громоздко и сопровождается потерей физического смысла
(либо приходится дополнительно писать % а бс . ; % мае . и т.п . ) .
В учебн и ке последующие анализ и расчет базируются на выра 
жении концентраций " в долях " , т.е . в форме отношения соот
ветст вующи х единичны х количеств : кг/кг, м ол ь/кг, кг/м 3 и т . п .

750

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

10.2. 1 . Способы выражения и пересчета концентраций
Абсолютны е и относительные концентрации различаются
базой расчета: вся смесь (в первом случае) или какой-либо из
компонентов (во втором).
Поскольку абсолютные концентрации выражаются в долях
от всей смеси, то сумма всех однородных кон центраций ком
понентов равна единице. Так, если концентрация компонента
№ 1 есть х, (кг комп . 1 )/(кг см.) , где "см ." означает смесь, а №2
- х2 (кг комп .2)/(кг с м . ) и т.д . , то
(а)
Х1 + Х2 + . . . = 1 .
Из (а) следует, что абсолютная кон центрация любого из
компонентов может изменяться от О (отсутствие компонента)
до 1 (чистый компонент) . Поэтому концентрационные шкалы
для любого компонента ограничены здесь нулем и единицей, а
расчетные диаграммы - замкнуты : квадрат для бинарных сме
сей, треугольник (например, равносторонний) - для тройных
и т.д . Можно говорить, что 1 кг смеси содержит, например, хА
долей кг компонента А.
Для бинарной смеси ситуация проще: достаточно указать
содержание одного компонента (надо условиться, какого) - и
концентрация второго определяется однозначно: хА + хв = 1 ,
Хв = 1 - ХА .
При выражении относительных концентраций примем
(например , для смеси А, В, С, D) за базу, скажем, компонент
D - его концентрация считается равной 1 . Тогда кон центрация
первого компонента ХА будет выражена в (кг А)/(кг D), второ
го - в (кг В)/(кг D) и т.д. Сумма всех компонентов п-ком понентной смеси составит 1 + !: Xi . Нижняя граница конп- 1

i=I

центраций i-ro компонента в этом случае также О, но верхняя
- не ограничена единицей, так как на 1 кг компонента D мо
жет приходиться и несколько кг компонента i. И расчетные
диаграммы ограничены лишь с одной стороны - началом ко
ординат (например , для бинарной смеси это чаще всего откры
тые декартовы координаты на плоскости) . Можно говорить,
что здесь 1 кг компонента D несет с собой ХА кг компонента А.
Для бинарных смесей ситуация упрощается: достаточно указать
лишь ХА , так как Хв = 1 .
Разумеется, все сказанное справедливо и при выражении
концентраций в каких-либо иных абсолютных или относитель
ных единицах, например в моль/моль.
Пересчет концентраций• ведется исходя из принятой базы
Это т подход правомерен и для пересчета разл ичн ых удел ьн ых вел ичин,
определяемых на основе концентраций ( см . ниже ) .

•

751

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

выражения заданной концентрации , т.е. смысла и размерности
ее знаменателя. Метод пересчета состоит в сопоставлении за
данного и требуемого способов выражения концентраций; на
основе этого сопоставления формируется конкретный пуrь
пересчета. Продемонстрируем метод на примерах.
Пусть задана массовая относительная концентрация компо
нента ( " комп .") А в смеси: Хл (кг А)/(кг N) , причем в качестве
базы принят компонент N. Требуется найти абсолютную массо
вую кон центрацию хл (кг А)/(кг см.). Значит, на 1 кг компонен
та N (это знаменатель размерности исходной концентрации)
так что

п- 1

I Xi кг остальных компонентов,
i=l
о бщее количество к.г смеси (на 1 к.г комп . N) составит I +

приходится

Хл кг

комп.

А

и

л ; ДЛЯ бинарной
+ L xi . Отсюда по определению Хл = -��п-1
i=l
l + I Xi
i=l
п-1

Х

смеси проще:

хл=

Хл
1 + Хл

---

Пусть, наоборот , задана абсолютная концентрация хл
(кг А)/(кг см.); требуется найти относительную концентрацию
Хл (кг А)/(кг N). Здесь исходная база 1 кг смеси; в нем масса
комп. А равна хл кг (долей кг, конечно) , а комп. N (эта масса
-

должна быть базой относительной концентрации)
п- 1

I xi . Отсюда по определению Хл =
i= l

смеси проще:

Хл = ----2L_ .

хА

n- 1

i= I

состdвляет 1 -

; для бинарной

1 - Z: x;

1 - ХА
В курсе ПАХТ нередко встречаются расчеты, оперирующие
молярными массами компонентов и их смесей. При этом в С И
молярная масса некоего индивuдуального компонента А изме
ряется в (кг А)/(моль А), а смеси - в (кг см.)/(моль см.)
(Подчеркнем: под молем здесь и далее соответственно С И по
н имается киломоль.) Число молей комп . А в 1 кг смеси при
известной его абсолютной массовой концентрации а (кг А)/(кг
см.)

752

и

молярной

массе

Мл

рассчитать

просто :

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

(

кг

кг

А моль А
кг А

)

или

( моль А) . В
кг

расчетах приходится иметь

дело и с числом кг, приходящихся на 1 моль смеси,
эту вели
чину легко получить исходя из мольных абсолютных конuентсм .

раuий

хА: ХАМА

( моль

МО.!Ъ

см.

-

)

см.

кг А
А моль А

или

( мо.т, А )
кг

.

см .
Переход от мольных конuентраuий к массовым и обратно
ведется на сформулированной выше основе . Пусть смесь зада
на абсолютными массовы.ми конuентрациями а (кг А/кг см.), Ь, с
" . ; требуется определить абсолютные мольные кон центрации хА
(моль А/моль см .) и др . Здесь нужно от исходной базы "кг с м . "
перейти к базе "моль см . " . Эrот переход реализуется с по
мощью молярн ых масс . Общее количество молей в 1 кг смеси
равно

а
МА

--

+

Ь
с
+
+
МВ МС

--

--

выразится :
ХА =

. Тогда мольная доля комп. А

".

а/ Мл
С
Ь
а
-- + -- + -- + . . .
Мл Мв Мс

Для бинарных смесей проще :
хл

=

х

=

(6)

Ь = 1 - а, так что

а/М А
а/М А + (1 - а)/Мв

Если же смесь задана абсолютными мольными долями ХА, хв,
" . , то за базу пересчета берется
1 моль смеси: общее
число кг в нем составляет ХАМА + хвМв + хсМс +
Тогда
абсолютная массовая конuентраuия комп. А равна:

хе,

а
Для

=

бинарных

ХА
МА
.;..;____;,,;;

�
�
�
�
�

(в)

�
�
�
�
-

х.4 МА + Хв Мв + Хс Мс +" .

смесей,

где

ХА - х,

проще:

а

=

хМА
хМА + ( 1 - х) М8

В случае относительных конuентраuий формулы пересчета
конструируются исходя из размерности знаменателя базового
компонента. При заданной относительной массовой конuент
раuии а компонента А количество его молей в расчете на 1 кг
базового компонента комп . N составляет а/МА, а самог6 базово 
го компоне н та
1/Мм Тогда относительная мольная конuент -

753

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

рация компонента

А запишется:
=

ХА

а / мА
1 / MN

=

а мN .
МА

(г)

Обратн ый пересчет очевиден : а = ХАМл/Мм
Среди других однородных концентраций наиболее часто ис
пользуются абсолюгные обьемные, например а. (м3 А)/(м3 см.).
В случае газовых смесей эти концентрации совпадают с моль
ными (следствие закона Авогадро). В случае жидких или каких
либо других смесей использование объемных концентраций
зачастую неудобно: в природе нет " закона сохранения объема " ,
и з а редким ис ключен ием (идеальные растворы, например)
адд итивное сложение объемов компонентов неправомерно, для
расчета объемов смеси приход ится привлекать данн ые экспе
римента . Это обстоятельство надо учитывать : операции с объ
емными концентрациями (или смешанными, содержащими в
единицах измерения м3 ), как и с удельными свойствами веществ
на основе объемных концентраций, в общем случае являюrся
приближенными. Они оправданы лишь отсуrствием достоверных
экспериментальных данных и точн ых методов расчета.
С указанными оговорками связь объемной концентрации а.
(м3 А/ м3 см.) с массовой а (кг А)/(кг см.) устанавливается, как
и ранее, на базе знаменателя размерности а. - 1 м3 см. Произ
веден ие а. на плотность компонента А РА (кг А)/(м3 А) имеет
размерность : а.рА

( мм33см . м 3 АА)
А

кг

или

(кг А)/(м3 см.),

т.е . это мас-

са компонента А в 1 м 3 смеси . Общая масса всех компонентов
l м3 см ес и выразится суммой произведений: а. рА + РР в + crp c +
+
( где 13 , cr . . . - о бъе м н ы е кон центрации других компонен
тов, а р 9, Р е . - их плотности) . Тогда
в

. . .

"

а=

а.рл

(д)

------ ----

ар А + Р Р в + crp c +" .

Обратный пересчет - массовых концентраций в объемные
- ведется на основе частных типа _!!____
РА

( м3 А) ,
кг

см .

кг

кг

м3 А
см . кг А
А

)

или

т.е . объемов, занимаемых отдельными компонента

ми, входящими в

7 54

(

1 кг

смеси . Полный объем

1 кг

смеси равен

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

+

+

..

и тогда объемная концентрация
с/ре + . ,
а / РА
а 1 Р А + Ь 1 Р в + с 1 Р е +. . .

а/рл

Ь/рв

а.

=

Аналоrnчный подход реализуется и в других случаях
(смешанные концентрации ; более сложн ые пересчеты и т . п . ) .
Приведем без подробных пояснений некоторые примеры ( в це
лях упрощения - для бинарных смесей и в предположении об
адд итивности объемов компонентов).
1 . Задана относительная объемная конценrрация компонента а (мз А)/(мЗ В);
требуется найти массовую абсолютную концентрацию а ( кг А)/(кг см.). Пересчет:
одному м3 комп. В ставится в соответствие (символ 0 • ) а м3 комп. А:
Переход к массам на 1 мЗ комп.

В-.

а

а: РА кг А

-

l · rв кг

в0

+ l · рв кг см.

ар А
apA + l ·рв

Q = --�-

Расчет абсолютной массовой конценrрации:

-

м3 А о -• 1 мЗ В.

0-•

• а: rA +

(;c�J

2 . Задана абсолютная объемная конценrрация компонента а (мЗ А)/(мЗ см.);
требуется найти мольную относительную конценrрацию ХА. Пересчет требует
1 мЗ
ввода понятия о мольном объеме компонента v; (мз 1)/(мол ь 1); база
смеси, ему ставятся в соответствие
1 мз см. • • а м3 А • - • ( 1
а) м3 В.
Переход к молям на 1 мЗ см.: a/v,1. мол ь А 0-• ( 1 - а)/(vв мол ь В) .
.моль А
a / vA
- .
---8
Расчет относительной мольной конценrрации: ХА
/

-

-

=

( 1 - а)

VВ

-

(

.МОЛ Ь •

)

На практике прямой пересчет может бьлъ затруднен отсутствием сведений о
значениях мольных объемов v;. Тогда, если доступны сведения о мотностях
компонентов р;, возможен "обходной" путь:
1 мЗ см. •-• мз А • • (1 - а) мЗ В.
Переход к массам на 1 мЗ см.: ар,1. кг А • • ( 1 а)рв кг В.
Переход к молям на 1 мЗ см.: apAf(M,1. моль А) 0 • ( 1 - а)рв /(Мв моль В) .
Расчет
относительной
мольной
концентрации:
ХА

=

ар А / М А
(1 - а)р В / М D

-

(МОЛЬ )

А
.
моль В

- --

1 0 .2.2. Расчет некоторых свойств смесей
с использованием концентраций
Аналитический расчет некоторых свойств смесей по аддитивности, строго ГО ·
воря, возможен лишь в рамках предположения об отсутствии физико
химического взаимодействия компонентов. Это правомерно далеко не всеrд<1,
часто адцитивный расчет дает лишь приближенные оценки; более точные значе
ния свойств получаются опьrrным путем. Ниже показаны пути расчета некото
рых удельных свойств смесей при допущении об их аддитивности. В основе
подхода - размерность знаменателя известной величины (см. разд. 1 0 2 1 )
755

.. .

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

мо.л

Пусrь необходимо наЙIИ
ярную массу смеси М по известным малярным массам
компонентов и их абсолютным мальны.м кoнцempal.DUIM ХА, хв
База расчета - 1
маль смеси (знаменшето. в размерности концеmраi.Diй). В ра;щ. 10.2. 1 показано, 'ПО
произведения ХАМА, хвМв и т.д. выражаюr коJDfЧества кг от,цельных компонентов А,
В и др. в 1 маль смеси; вместе с тем М по определению
общая масса всех компо
нентов в 1 маль смеси. Следовательно, М = ХАМА + хвМв + ... .

.

есть

.

"

Пусть теперь молярную массу смеси надо определить по заданным абсолют
ным массовым долям компонентов: а, Ь, с . . . База расчета - 1 кг смеси
(знаменатель в размерности концентраi.Diй). В разделе 10.2. 1 показано, что дроби
а/МА, Ь/Мв выражают количества молей отдельных компонентов в 1 кг смеси;
вместе с тем 1/М по определению есть общее количество молей в 1 кг смеси.
1
а
Ь +
Следовательно,
+

--м = -м"
Мв

-

-

Для бинарной смеси (хв = 1 ХА = 1 х, Ь = 1 - а) полученные выражения
упрощаются.
Аналогичным образом рассчитывается М для смеси по заданным относитель
ным концентрациям. Только надо учитывать, что для п-компонентной смеси
суммарное число молей или

кг

1 + L Х;
п-1

будет не 1, а соответственно

i=l

1 + L а; . Тогда с учетом сказанного выше
п-1
i=I

(

1+

)
t;:x; М = �Х;М; + l · Мн
•- 1

•- 1

и

i+

•- 1

L a1

и

1

� а;
1

Мн >
--М = �М; + -1=1

....

i=I

откуда легко выразить значение М.
Теплоемко� смеси Сем в идеале (в отсутствие химических превращений и
тепловых эффектов смешения) определяется по теплоемкостям компонентов сА,
св и т.д. и их абсолюmым массовым долям а, Ь, . . . исходя из базы - знаменатекг
А
ля концентраций ( 1 кг смеси). Произведение сА а
Дж
или
кг
кг А · К см.

(

Дж

)

( кг ) предстаlilIЯет собой вклад компонента А в общую теплоемкость сме
СМ. · К

+ свЬ + . . . .

си; аналогично учитывается вклад остальных компонентов, так что
ПлоП!о� смеси

тов

РА,

произведение типа
ность смеси.

756

Сем = С.АО

.

(ж )

по объемным концентрациям а, 13, . . и плоmостям компонен
РВ также рассчитывается по адд и тивности; база расчета
1 м3 смеси,
В

арА

целом

(

)

-

�3 � А дает вклад компонента А в общую ruютм см. м А
А

Рем = РАа

+ Рв13 +

··· ·

(з)

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ляющие расчетной формулы тогда имеют вид �

(�
Л)
см .
РА
).

ва (для идеальных смесей, конечно) аддитивность обратных величин; состав

(---) , а результат получается в виде --l ( м3 А
кг СМ .

Pcw

Значит,

l

а

мз А

-

кг

м3
кг А

кг

-

СМ .

Ь

(и)

-- = - + - +" .

РА

Р сы

или

РВ

- Рсы рассчитывается по массовым концентрациям как среднегармоническая вели
чина.
В качестве примера ниже схематично показан путь расчета средней моляр
ной массы и плотности р бинарной смеси с обьемной относительной концент
рацией компонекrа А, равной а мЗ А/мз В. С этой целью одному мЗ компонен
та В будем ставить в соответствие фрагменты, необходимые для выражения ис
комых величин:
l мЗ В о-• а мЗ А о-• ( 1 + а) мЗ см.
Масса в расчете на l мЗ В:
1 · р кг В о-• арА кг А о-• ( 1 + а)р кг см.

М

Число молей в расчете на 1 мЗ В:

в
1·Р
Мв
�
В

0-·

Расчет плотности смеси:

1 ·рв +

моль В о-•

МАА

ар

моль А о-•

МQЛЬ С М .

арА = ( 1 + а)р или

в

Р=

арА + l · Рв
1+а

Разумеется, можно не 11ыписывать левое равенство, а сразу получить р как
частное от деления суммарной массы (арА + l · р ) на суммарный объем (1 + а).
Расчет средней молярной массы смеси:

Мв МА М

М

1 ·рв + ар А = (l + a ) p = l·рв + ар А

в

М
( МАА 1МРвв) .

Здесь также можно сразу получить
(арА + l р ) на общее число молей ар
·

или

+

арА + l · рв
М = арА
-- + l ·рв

МА Мв

--

путем деления общей массы смеси
·

Подход к расчету других средних удельных величин (например, энтальпий,
удельных объемов) - аналогичен. Он, разумеется, правомерен в пределах ука
занных О11Jаничений. Надо иметь в в иду, что некоторые характеристики смесей
не поддаются аддитивному расчету. Иногда (коэффи циент диффузии идеальных
газов, вязкость идеальных жидкостей) удается использовать специфические
формы адд итивных усреднений. В других случаях (например, теплопроводность
жидкостей) приходится разрабатывать иные подходы (например, аддитивность с
полуэмпирическими поправками). Нередко достаточно достоверные сведения о
свойствах смеси в зависимости от концентраций компонентов дает только
опъrr.

757

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

1 0 .2.З. О концентрациях

в

технологических расчетах

В случае бинарных смесей для отсчета концентрации, незави
симо от выбранной основы, достаточно линейной шкалы (рис.
1 0.4, а) , - оrраниченной, если используются абсолютные концент
рации (на этом рисунке - х), или полуоrраниченной, если речь
идет об относительных
концентрациях (здесь - Х). По шкале
отсчитывается концентрация первого компонента (какого именно
- надо условиrься); концентрация второго берется как 1 - х
(абсолютные концентрации) или 1 (относительные).
В случае многокомпонентных смесей расчеты, как правило ,
ведут на основе абсолютных концентраций ; поэтому концент
рационные диаграммы должны ограничивать изменение со
держания любого компонента диапазоном от О до 1 , а сумма
концентраций всех компонентов должна быть равна 1 . При
этом состав смеси задается концентрациями п - 1 компонен 
тов, для п-го компонента она получается по разности .
Для часто встречающихся трехкомпонентных смесей необхо
димо зафиксировать концентрации двух - х1 и х2, третья выра
1 - х 1 - х2• Поэтому здесь нужны две шкалы зится как х3
оси , т.е . диаграмма на плоскости. Обычно в этих целях выби
рают косоугольную систему координат, замыкая ее в равносто
рон ний треугольник (рис. 1 0 .4,6). При этом используют извест
ное свойство последнего: сумма внутренних перпендикуляров
на стороны из любой точюt равностороннего треугольника есть
величина постоянная, равная его высоте , - ее принимают за
единицу. Это позволяет трактовать отрезок перпендикуляра от
точюt до стороны как концентрацию компонента, обозначен 
ного в противоположной вершине. В таком представлении : в
вершинах
чистые компоненты (обозначенные там символами
А , В или С либо цифрами 1 , 2 или 3); на сторонах
бинарные
смеси компонентов, указанных на ее концах (в вершинах); в поле
внутри треугольника - тройные смеси. Линия , параллельная
какому-либо основанию, отвечает постоянству концентрации
компонента, проставленного в противоположной вершине.
Точке за пределами треугольника не отвечает реально су
ществующая смесь, так как внешний перпендикуляр на какую
либо сторону - отрицателен .
Определение концентрации по длине перпендикуляра на
сторону неудобно . Поэтому линии постоянных концентраций
сносят (рис . 1 0 .4, в) на соответствующие стороны, располагая
там шкалы отсчета. Так, шкалу отсчета компонента А удобно
расположить на левой стороне треугольника, В - на правой , С
- на основании . Отсчет концентрации компонента А ведут с
помощью линии, паралл ельной стороне ВС, В - с помощью
горизонтали, С - с помощью линии, параллельной А В.

=

-

-

758

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

в
о

о

о, 2

0,4 0,6 0,8

0,2 0,4 0,6 0,8

х

1,2 х

А

а

б

с

0,2 0,4 0,6
х� хе
в

а - шкалы для абсол ютны х (х) и О'ПIОСИТСЛЬНЫХ (Х) кщще�праций в случае бинарных
смесей , б - треуrольная диаrрамма для тройных смесей : физический смысл, лини и посrоян
коЮiеtпраци й , г - треуrольная диаrрамма: отсчет ко�щешраций компонешов

Рис. 10. 4. Концентрационные шкалы и диаграммы:

ных

Нетрудно догадаться, что для четырехкомпонентной смеси по
требуется пространственная диаграмма в форме правильного
тетраэдра, а при большем числе компонентов - построения в
многомерном пространстве. В этих случаях оперируют векrо
рами составов Х (х 1 , хъ х3 , . . . ) и аналитичесЮfМИ соотноше
ниями , сопровождая их для наглядности фрагментами rеомет
ричесЮfх построений для бинарных и тройных смесей, состав
ляющих п-компонентную систему.

1 0.2.4. Правило рычага
Концентрационные шкалы и диаграммы помогают сформу
лировать и наглядно изобразить правило смешения (разделения)
веществ - компонентов и их смесей, известное как "правило
рычага".
Пусть имеются бинарны е системы 1 (концентрация рассмат
риваемого компонента х1 ) в количестве т 1 и 2 (концентрация того
же компонента х2) в количестве т2 • Требуется определигь кон
центрацию вещества х, при смешении этих систем. Запишем ма
териальные балансы для систем в целом и для рассматриваемого
компоненrа (в отсутствие ero Источников и Стоков):
(к)
Отсюда, исключив
rеометричесЮf:

т 1 (х, - х 1 )

=

т,

=

т1(х2

т 1 + тъ
-

имеем аналитичесЮf и

Хе) ; т 1 ( lС ) = т1 ( 2С )

(л)

Геометрическая интерпретация соотношения (л) приведена
на рис . 1 0 . 5 , а-J, где процесс смешения представлен на кон
центрационной шкале в вИде находящегося в равновесии рыча
га 1 рода. Роль сил здесь играют массовые количества взятых
759

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

в

о

о

Х] Х
Х1

х

А

а

с

fi

Рие . 10. 5. Правило рычага: к выводу расчеrных формул; интерпретация результа
тов анализа (обозначение позиций и точек - в тексте):
а

-

для бинарных смесей , б - для трой НЬIХ сме сей

веществ т1 и т2 , а место приложения сил (точка опоры, величина
плеч рычага) определено с учетом х1 и х2 соотношением (л).
Чаще удобно располагать точку опоры в точке 1 или 2 (рис .
10.5,а-11). Тогда надо во второй из формул (к) исключить мас
су, отвечающую точке опоры; по рисунку т2 = те - т 1 • В ре
зультате
(м)
т1 (Х2 - Х1 ) = те(Х2 - Хе) ; т1 (i2) = те( 2С )
Это соотношение можно представить в виде находящегося в
равновесии рычага 1 1 рода с характерными "силами" - коли
чествами веществ т 1 и те , точкой опоры и плечами .
Выражения (л) и (м) можно объединигъ в обобщенное правило
рычаrа - в аналитическом и геометрическом представлениях:

т1 ----'- =

т2
Хе - Х1

те
Х2 - Х1

т 1 = т2 = те

-== .
(н)
IC 1 2
2С
Х2 Хе
В случае тройных смесей правило рычага должно быть реа
лизовано применительно к треугольной диаграмме (рис . 10.5,6).
Здесь придется записать материальные балансы для порций
(потоков) в целом и для двух компонентов (для третьего баланс
получается по разности):
-

и

=

т 1 + т2 - те = О; т 1 х 1 8 + т2х28 - тс.JС/ = О ;

т1х1А + т2х2А - тс.JСеА = О .

(о)

Отсюда - координаты точки смеси:

т 1 Х 1В

т 1 Х 1 + т2 Х2
(п)
т 1 + т2
т1 + т2
Из (п) видно , что положение точки смеси зависит от взятых
количеств веществ т1 и т2 (точнее - от их соотно ш ения) .
в

Хе =

760

+

т2Х2В .

•

А
Хе --

А

А

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Таким образом , в общем плане речь идет не о точке , а о гео
т.е. о зависимости х/ = f(xcA) .
Если в правых выражениях (о) подставить Щ : = т 1 + т2 и раз
решить полученные формулы относительно тJ/т 1 , то прихо
дим к двум равенствам , в которых кон центрации точек 1 и 2
известны (заданы) :

метрическом месте точек смеси,

ХеВ - Х }В

ХА
= е
Х2В - Х еВ
Х2А

- Х }А
- Х еА

=

т2

(р)

Равенство первых двух отношений дает уравнение линии сме
f(xcA) . Легко видеть , что при т2 = О (в смеси со
держится только вещество /) получается Хсв = х1 в, хсА = х1А линия смешения проходит через точку 1 . Аналоrnчно: при т 1 =
= О (в смеси только вещество 2) имеем хс8= х2 8, хсА = х2А - ли
н ия смешения проходит через точку 2. По форме соотношения
(р) видно, что это уравнение прямой х/ = f(xcA) ; в этом можно
убедиться , перемножив наперекрест разности концентраций:
после сокращений остаются только слагаемые , содержащие х/
и хсА в первой степени. Таким образом , линия смешения в
треугольной диаграмме есть прямая , проходящая через точки
исходных веществ, взятых для смешения .
Для отыскания положения точки смеси С воспользуемся ле
вым и правым фрагментами соотношения (р) и изображенны
ми в кон центрационном треугольнике соответствующими раз
ностями кон центраций (рис. 1 0.5 , б). Из полученных подобных
треугольников следует

шения хсВ =

хев - х1в т1
= 1С = х2в - х ев 2 С т1

(с)

Можно видеть , что и здесь смешение трактуется в аспекте
правила рычага I рода: т 1 ( lC ) = т2 ( 2С ) , что полностью согла
суется с (л) и рисунком 1 0 . 5 ,а-1. Добавление по 1 во все части
равенства (с) дает после приведения к общему знаменателю

х8 - х 8 1 2 т
1 =
2
= е
8
8
2С т1
х2 - х е

(т)

Это отвечает правилу рычага 1 1 рода с опорой в точке 2:
т1 (1 2) = те ( 2С ) , - 'ПО rакже согласуется с выражен ием (м) для
бинарных смесей .
В обобщенной форме правило рычага для тройных смесей
имеет вид соотношения (н) .

76 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Таким образом, смешение веществ (математически - их
сложение) или обратная операция - разделение смеси на со
ставляющие (математически - вычитание) - происходит в
соответствии с правилом рычага. В зависимости от кон кретной
постановки задачи используюг правило рычага 1 рода или
(чаще) 1 1 рода. Заметим, что правило рычага используется не
только применительно к концентрационным диаrраммам, но и
для диаrрамм типа " состав - свойство " ; такие ситуации будут
рассмотрены в некоторых последующих главах.

10.3. РАВНОВЕСИЕ
10.3. 1 . Общие положения
В разд. 1 0 . 1 .2 сформулирована сущность равновесного со
стояния для массообменных процессов: практически речь идет
о концентрационном равновесии в фазах. В системе устанавли
вается динамическое равновесие: обмен субстанциями (в част
ности , веществом) через фазовые границы осуществляется в
эквивалентных количествах (в частности , сколько молекул ка
кого-либо вещества переходит из фазы 1 в фазу 2, столько же
переходит и обратно). Для достижения фазового равновесия
необходимо обеспечить тесный контакт фаз (увеличить поверх
ность контакта, например путем диспергирования фаз; повы
сить интенсивность переноса вещества из фазы в фазу, напри 
мер за счет перемешивания) и (или) достаточно длительное
время контакта. Равновесие считается практически достигну
тым , если последовательные измерения состава фаз (разу
меется, температур и давлений - тоже) не обнаруживают из
менений - на уровне чувствительности имеющейся измери
тельной техн ики, соответственно задаче и приемлемой по
rрешности исследован ия .
В основе анализа равновесия лежит правило фаз - оно для
к-компонентных и ф-фазных систем позволяет установить чис
ло степеней свободы q>, иначе
интенсивных свойств
(фактически - управляющих воздействий) , которые могут быть
выбраны произвольно, т.е . навязаны системе извне. В случае
систем, для которых 1 1 закон термодинамики включает в ка
честве потен циалов температуру ( Т, t) , давление (р) и химиче
ский потенциал (µ) , правило фаз записывается в виде •

q> = к - ф + 2.

(10. 1 )

В такой форме правило фаз приводится в многочисленных учебниках по
ПАХТ (8, 10, 12, 22 и др . J; вывод правила фаз см. ( 1 41 и ра:�личные учебники по
термодинамике.

•

762

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Соответственно этому правилу, например для индивидуально
компонента ( к = 1 ) в системе жидкость - пар (ф = 2) полу
чается <р = 1 ; это означает, что произвольно может быть вы
бран один параметр , например температура, а давление паров
будет уже определенным, отвечающим этой температуре. Пра
вило фаз показывает, что для индивидуального вещества харак
терна одна тройная точка, в которой сосуществуют три фазы
- жидкая, паровая и твердая : <р = 1 - 3 +2 = О, здесь система
инвариантна (нонвариантна) . Для юшящих бинарных смесей
(процессы дистилля ц ии , ректификации) класса 2(2-2)2 получа
ется <р = 2 ; значит, произвольно можно выбрать, например,
давление и состав одной из фаз; температура Юtпения и состав
другой фазы будут определенными. Аналогичный тест соответ
ст в и я
правилу фаз целесообразен и для других систем на
начальных стадиях организации массообменных процессов.
В стационарных массообменных процессах кон центрация (а
также t и р) в любой точке аппарата тоже не изменяются во
времени . Однако при проведении таЮfх процессов система
обменивается субстанцией (в аспекте массообмена - прежде
всего веществом) с внешней средой ; в результате в системе
возникает поле концентраций. Эти обстоятельства устанавли
вают неравновесность фазовых составов в системе, а отклоне
н ие от равновесия является предпосылкой массообмена.
Каждая фаза задается совокупностью - вектором - кон 
центраци й ; пусть для фазы "х" характерен состав Х (х1 , хъ х3
. ) , для фазы "у" - У (у1 , Уъ Уз . . . ) , причем одинаковые индек 
сы при х и у указывают на принадлежность концентрации к
одному компоненту. Тогда в условиях равновесия Х и У - рав
новесные составы: концентрации любого компонента х1 и у1
равновесны. Линия (реально проведенная или мысленная ) ,
соединяющая эти составы (точЮt в фазах), называется равно
весной нодой (иногда
конодой); это тоже вектор, его обычно
считают направленным в сторону преимущественного перехода
компонентов при неравновесных составах фаз.
Эти представления существенно упрощаются при переходе к
таЮt м двухфазным системам , когда каждая фаза содержит не
более двух компонентов, т.е . к классам 3 (2-2) 1 , 2(2 - 2)2 и некото
рым другим . В этих случаях диаграмма фазового равновесия
изображается на плоскости , чаще всего - в декартовых коор
динатах (рис . 1 0 6 , а) . Работать с нодами неудобно: приходится
то и дело строить дополнительные (необходимые для расчета)
ноды по огран иченному числу экспериментально найденных .
Поэтому по равновесным концентрациям у1 , х1 ; У2, х2; . в по
ле диаграммы строят соответствующие равновесные точЮt J, 2,

го

. .

-

-

.

"

763

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

А

у

а

б

а - для систем с двумя компоненrами в каждой фазе, б
стем (JJСИрные uприховы е ЛИЮIИ - равновесные ноды )

Рис. 10. 6. Равновесные диаграммы:

-

для треххомпоненrных си 

. . . и проводят из начала координат через них плавную кривую:
на рисунке - сплошная линия равновесия 0- 1 -2-3. Теперь для
любого значения концентрации в фазе "х" легко найти равно
весную ей концентрацию в фазе "у" (и наоборот) . Положение
и конфигурация линии равновесия зависят от природы компо
нентов, составляющих фазы , а также от температуры и давле
ния (если обе фазы жидкие или твердые, т.е. практически не
сжимаемые, то влияние давления, естественно, становится ис
чезающе малым). Поэтому равновесные линии привязывают к
определенной температуре (тогда эта линия - изотерма) или
давлению (тогда это изобара).
В случае двухфазн ых трехкомпонентных систем, вообще го
воря , необходимо использовать две треугольные диаграммы ,
где определенным (не всегда - любым) точкам одной из них
поставлены в соответствие равновесные точки другой . Работать
с двумя диаграммами неудобно, и поэтому равновесие в фазах
изображается в одной общей треугольной диаграмме (рис .
10.6,6). Равновесные точки при этом соединяются нодами ,
кон цы которых принадлежат разным фазам. В ряде случаев
удается найти для нод геометрические места их концов в раз
ных фазах, в других случаях - только признаки (параметры,
например температуры), позволяющие установить концы нод
отрезков. Детально такое представление равновесия рассматри
вается в некоторых последующих главах ( 12, 13, 17).
Для многокомпонентных систем , когда число компонентов в
какой-либо фазе больше трех, геометрические представления
теряют наглядность; в этом случае прибегают к векторным
представлениям · .
· см. ( 1 1 ) .
764

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 10. 7. Рабочая область массообмен
ноrо процесса

у

Поскольку
при
анализе
у
процессов массопереноса осу
ществлен переход от химиче
ских потенциалов к концент
рациям (именно последние
используются в диаграммах
у < уР
уР
типа у - х, вообще при пред
1
ставлении потенциальных по
1
лей), то прямое сравнение
'
у
концентраций (их сложение,
х
хР Х
вычитание , использование их
разности в качестве движущей
силы) допустимо только в пределах одной фазы. В общем случае · нельзя судить о направле
нии переноса компонента, сопоставляя уровни концентраций у
и х.или выражать движущую силу в форме (у
х) . В массооб
мене численные значения концентраций (они играют роль по
тенциалов) в разных фазах впрямую несопоставимы, нередко у
них и разные размерности (потому что разные базы выражения
кон центраций : кг А/кг Г и кг А/кг Ж, где Г И Ж - rазовая и
жид кая фазы). Здесь для сопоставления концентраций исполь
зуются разные подходы.
Пусть фаза "х" с концентрацией переходящего компонента
х вводится в контакт с фазой "у'' , в которой концентрация
этого компонента у. Концентрации контактирующих фаз (в
точке, в сечении, в некоторых процессах - в объеме аппарата)
наз ываются сопряженными (рис . 1 0.7, точка А). В этой точке при
некотором значении х концентрация у превышает равновесную
уР. Согласно 1 1 закону термодинамики, субстанция самопроиз
вольно переносится от большего потенциала к меньшему; по
скольку у > уР, то рассматриваемый компонент под действием
движущей силы у уР будет переходить от у к уР (иначе - к х) ,
т.е. из фазы "у" в фазу "х" . К аналогичному выводу приходим
при сопоставлении хР и х для данного у: поскольку хР > х, то
компонент под действием движущей силы хР
х будет перехо
дить от хР (иначе - от у) к х, т.е. опять-таки из "у'' в фазу "х" .
Если смысл конкретного технологического процесса отвечает
переносу компонента в этом направлении, значит поле диа
граммы у - х выше линии равновесия представляет собой рабо
чую область процесса. Если же необходим перенос компонента
-

-

-

• Имеются частичные исключения для систем, в которых все компоненты со
держатся в обеих фазах, - классы типа 2(2-2)2, 3(3-3)3.
765

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

из фазы " х" в фазу " у" , то рабочая область располагается ниже
равновесной кривой, где � > у, хР < х, движущими силами
являются разности �
у и х хР. Для осуществления массо
обмена в этом случае в контакт с фазой состава х надо ввести
другую фазу с более низкой концентрацией у ' (на рисунке со
пряженная точка А ') .
В рассматриваемом смысле процессы массообмена можно
считать обратимыми, все определяется положением точки со
пряженных концентраций относительно линии равновесия.
Массообмен становится практически необратимым, если пере
носимый компонент переходит (в результате химической реак
ции) в другую фазу, выводимую из зоны межфазного контакта
(простой пример для системы газ - жидкость: химическое свя 
зывание компонента и выпадение полученного химического
соединения в осадок).
Описание равновесия имеет конкретные особенности в пре
делах каждой группы процессов по КФ-классификации , иногда
оно специфично для отдельных технологических приемов. Это
может быть связано с некоторыми особенностями, присущими
группе технологических приемов ил и отдельному приему, либо
с недостаточной проработанностью (теоретической, экспери
ментальной) самого технологического приема или равновесно
го состояния . В отдельных случаях описание равновесного со
стояния пока остается обособленным и не включено в общую
систему представлений о равновесии , в основном - в силу
традиций и психологического сопротивления (здесь просто
нужно время . . . ) .
Способы предстамения равновесия детализируются в главах,
посвященных анализу конкретных технологических приемов.
-

-

1 0.3.2. Равновесие в системах класса 3(2-2) 1
Системы, принадлежащие к этому классу, содержат по два
компонента в каждой фазе, причем лишь один из этих компо
нентов переходит из одной фазы в другую. Этот компонент
называют " веществом" В или " переходящим компонентом"
П К. Остальные компоненты из фазы в фазу не переходят, они
являются носителями вещества и в смысле массообмена инертами ( " ин . " ) . Количества (в периодических процессах) и
потоЮt (в непрерывных) инертов остаются неизменными в
ходе массообменного процесса. Именно поэтому концентрации
П К здесь удобно выражать в относительных единицах, прихо
дящихся, например, на 1 кг того или другого инерта. И на осях
концентрационных диаграмм откладываются относительные
кон центрации ; например , в случае абсорбции : у (кг П К)/(кг
инерта-газа) , х (кг П К)/(кг инерта-жидкости) . Естественно,
фазовая диаграмма здесь является полуоткрытой.

766

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Согласно правилу фаз, при к = 3 и ф = 2 получается q> = 3 .
Это означает, что равновесие в системе определяется тремя
независимыми параметрами , например давлением, температу
рой и составом одной из фаз (скажем, концентрацией х) ; кон 
центрация вещества в о второй фазе (у) примет определенное
значение. В случае работы при постоянном давлении равно
весная связь у и х определяется температурой. Такие ситуации
для класса 3(2-2) 1 встречаются наиболее часто ; поэтому равно
весие изображают в виде изобарической (в целом) диаграммы с
семейством линий равновесия - изотерм (для различных тем
ператур). Разумеется , можно построить и изотермическую
диаграмму с семейством изобарических линий равновесия .
В общем случае линии равновесия в диаграмме у
х - кри
вые, выходящие из начала координат. Для отдельных смесей
кривизна равновесных линий невелика, и в рабочем диапазоне
процесса их можно приближенно (без существенной погреш
ности) представить в виде прямых. Такое спрямление
(линеаризация) упрощает последующий анализ и расчеты .
Отношение равновесн ых концентраций у и х называют ко
эффициентом распределения т = (у/х)Р. Этот коэффициент
представляет собой тангенс угла наклона секущей• к линии
равновесия - из начала координат в точку с равновесными
кон центрациями у, х. Для кривой линии равновесия т изме
няется с концентрациями, для прямой - остается постоянным .
Постоянство т
одно из условий линейности массообменного
процесса в целом и возможности его аналитического описания.
В противном случае, как правило, приходится обращаться к
графическим построениям или численным методам расчета.
Заметим, что процессы массообмена нередко реализуются в
области малых значений концентраций (например, в случае
глубоких степеней разделения) , т.е. весьма близко к началу
координат концентрационной диаграммы . Но на начальных
участках кривую равновесия можно без существенной погреш
ности трактовать как прямую (с постоянным углом наклона: т
= const) и использовать в пределах этих участков линейное
представление равновесия уР = тх.
Анализ массообменных процессов с линейным равновесием
достаточно широко представлен н иже для систем рассматри
ваемого класса.
-

-

=

Подчеркиваем эrо специально, поскольку в рsще и:щаний (даже в учебниках)
нередко т траюуется как тангенс yrna касательной к линии равновесия в точках (у, х)
см" например, [ 1 2 J .

•

-

767

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

1 0.4. КИНЕТИКА МАССОПЕРЕНОСА В ФАЗЕ
10.4. 1 . Общие положения
В случае непосредствен ного контакта фаз (именно такие си
туации преобладают в массообменных процессах) перенос ве
щества осуществляется по схеме, изображенной на рис . 1 0 . 8 для
фрагмента массообменного аппарата. В пределах каждой фазы
у границы их раздела формируются диффузионные погранич
ные пленки, в которых происходит плавное изменение кон 
центраций переносимого вещества - от значений в ядре фазы
(потока) до значений на границе раздела. В модельном пред
ставлении пограничные пленки полагают (как И в случае теп
лопереноса) резко очерченными, а весь концентрационный
напор - сосредоточенным в пределах этих пленок.
Примем для определенности, что процесс ведется в непре
рывном режиме и вещество переходит из фазы " у" в фазу "х" .
Тогда оно с фазой "у" (его поток показан левой вертикальной
стрелкой - см. рис . 1 0 . 8 ) под действием внешнего побудителя
(насос , компрессор) вносится в рассматриваемый фрагмент
массообменного аппарата. Далее под действием частной разно
сти кон центраций в фазе "у'' (в ядре потока и на границе раз 
дела) вещество транспортируется (горизонтальная левая стрел
ка) к фазовой границе . Затем от нее вещество переносится
(горизонтальная правая стрелка) в фазу "х" - также под дей
ствием своей частной разности концентраций (на границе и в
ядре этой фазы). Наконец, оно выводится из аппарата с пото
ком фазы "х" (правая вертикальная стрелка) . Разумеется, при
переносе вещества из фазы "х" в фазу "у" стрелки примут
противоположное направление. Естественно, некоторый поток
вещества выносится с фазой "у" из аппарата и может также
вноситься с фазой "х" в аппарат. Поэтому подчеркнем , что при
рассмотрении потока вещества с фазами "у" и "х" речь идет
только о той его части М, которая передается из фазы в фазу.
При осуществлении мембранного массопереноса фазы будут
разграничены проницаемой перегородкой; тогда схема по сущест
ву совпадает с рассмотренной для теплопереноса (см. рис.6. 1 ) .
Наименование процессов и их стадий при переносе вещества
согласуем с приняrыми ранее при изучении переноса теплоты.
Массопереносом именуется любое явление (процесс), связан 
ное с переносом вещества на отдельной стадии или в целом .
Элементом процесса массопереноса называется стадия (акт) ,
относящаяся к какой-либо одной составляющей этого про
цесса. Соответственно схеме на рис . 1 0 . 8 : массоперенос нор
мально к поверхности раздела фаз через пограничную пленку

768

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 10. 8. Общая схема контакrного массопереноса
(фрагмент массообменного аппарата):

1 - rрающа раздела фаз, 2
фазах х и у, З - фазы х и у

-

поrраничные плеюси в

у

- массоотдача; перемещение вещества
с потоком фазы - потоковый массопе
ренос . В случае массопереноса в твер
дом теле (частный случай - через мем
брану) говорят о массопроводвости
(диффузии в твердом теле). Диффузионный массоперенос, ко
нечно, наблюдается также в жидкостях и rазах. Каждой из
этих элементарных стадий соответствует определенный аналог
в теплопереносе; аналога лучисто му переносу теплоты в массо
переносе нет.
Массопередачей называется перенос вещества из одной фазы
в другую нормально к межфазной границе. Для схемы на рис .
1 0 . 8 - это перенос вещества через пограничные слои (две ста
дии); в случае мембранного процесса массопередача насчиты
вала бы три стадии: добавляется перенос вещества через мем
брану. Под массообменом будем понимать массоперенос в це
лом, включая подвод и отвод вещества с потоками фаз. Для
схемы на рис . 1 0 . 8 массообмен насчитывает четыре стадии (для
мембранного процесса их бьmо бы пять).
Кардинальная проблема массопереноса - установление рас
пределения концентраций в системе (рабочей зоне аппарата) в
пространстве и во времени. С разрешением Этой проблемы по
существу связано (прямо или косвенно) решение многочислен
ных конкретных теоретичесюvс и прикладных задач переноса
вещества.
Наиболее общими и сложными для анализа и расчета явля
ются процессы, в которых концентрация вещества (обозначим
ее здесь С) изменяется как от точки к точке, так и во времени
't. Среди нестационарных процессов, когда С = C('t), наиболее
просты безградиентн.ые, в которых концентрация не изменяется
в исследуемом пространстве: дС/дп = О (п - нормаль к по
верхности раздела фаз). Для стационарных процессов чаще
всего характерно изменение концентраций от точки к точке,
но в любой точке технологического пространства концентра
ция не изменяется во времени: дС/д't = О. Особняком стоят
процессы переноса в твердой фазе (зерно, пластина и т.п.).
Если исключить из рассмотрения стационарный перенос ве
щества через проницаемые перегородки, то с позиции твердого
тела (зерна, например) в отсутствие химических превращений
массообменный процесс принципиально нестационарен., по-

769

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

скольку сопровождается изменением во времени концентрации
вещества в различных точках тела. Тем не менее при регуляр
ном (направленном или беспорядочном) перемещении тела
(скажем, коллектива зерен) внуrри аппарата концентрация в
зерне в данной точке рабочего пространства может оставаться
неизменной. Следовательно, с позиции аппарата массообмен
будет протекать в стационарном режиме. В этом аспекте массо
обменный процесс с твердыми телами формально может счи
таться отвечающим схеме на рис. 1 0 . 8 ; при безградиентном
массопереносе в зерне такая трактовка становится физически
оправданной.
В технических расчетах оперируют полным количеством или
потоком (в единицу времени) вещества М, чаще всего массо
вым или мольным, измеряемым в кг, моль - для периодиче
ских (нестационарных) процессов или их стадий, в кг/с, моль/с
- для непрерывных (стационарных). УдельньIМ называется по
ток вещества q9, отнесенный к единице поверхности фазового
контакта - в кг/(м2 · с) , моль/(м2 · с) . Очевидно, М = qвF't - для
периодических процессов и их стадий, М = qвF - для непре
рывных стадий и процессов.
10.4.2. Виды массопереноса.
Об уравнении Фика

Под диффузией (массопроводиостью) понимаюг перенос ве
щества без перемещения частиц рабочего тела (газа, жидкости,
твердого), причем частицы здесь трактуются как образования
сплошной среды, существенно превышающие размеры атомов
или молекул. В разд. 1 . 3 .2 было введено понятие о потенциаль
ных полях, в том числе - о поле концентраций, градиенте кон
центраций дС/дп, коэффициенте диффузии Dд (применительно к
твердым телам его называют коэффициентом массопроводиости
Dм )· Там же было обосновано противоположное направление
диффузионного потока вещества и концентрационного гради
ента и представлена их связь в форме закона Фика:
qв

ас
= -Dд - .
дп

( 1 . 1 1 ) , ( 1 0.2)

Коэффициент диффузии, характеризующий интенсивность
массопереноса, формально выражается в м2/с; физически это
означает
мз

м 2 . с (Л С

где (ЛС = 1 )/м

770

=

1)/м

'

есть единичный градиент концентраций.

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Диффузионный перенос вещества может выступать как от
дельная стадия массопереноса.
Конвективный массоперенос в широком смысле понимается
как перенос вещества с крупными образованиями сплошной
среды (газом, жидкостью, в определенных ситуациях - и твер
дой фазой) в любом направлении. Здесь (и далее) под конвек
тивным будем понимать перенос вещества нормально к поверх
ности раздела фаз как результат сложного взаимодействия ме
ханизмов переноса вещества: собственно конвективного (в яд
ре потока) и молекулярно-диффузионного (в пограничном
слое). Такой вид массопереноса, именуемый массоотдачей,
также может выступать в качестве отдельной стадии. Интен
сивность его, аналогично переносу теплоты, выражают ко
эффициентом массоотдачи р , причем
qв =

рл с ;

м=

рFл С ,

( 1 0.3)

где Л С - даижущая сила массоотдачи: разность концентраций переносимого
вещества в ядре фазы и на границе раздела (со стороны этой фазы). Размерность
р определяется размерностью величин, входящих в уравнение массоотдачи (10.3).
Но в любом случае зrо поrок вещесrва (он может измерJПЪСя в массовом, мольном
И1D1 друrом выражении) в единицу времени через един ицу межфазной поверхности ,
отнесенный к еди нице движущей сИIПd . Произведение P F предсrавляет пропускную
способносn. конвективной стадии массо переноса - массоощачи.

О бщее математическое описание переноса вещества пред
ставляется уравнением Фика:
- + W x - + Wy - + W z д-t
дz
дх
ду

дС

дС

дС

дС

=

D"V 2 С + к ( 1 .22), (10.4)

Вывод этого уравнения , его модификации применительно к
различным ситуациям, начальное и граничные условия, крите
рии диффузионного подобия, полученные масштабными пре
образованиями уравнения (10.4) и граничных условий , рас
смотрены в разд. 1 .5 - 1 .8. Решение уравнения ( 1 0.4) с гра
ничными условиями, отвечающими определенным случаям
массопереноса, призвано дать концентрацию С в любой точке
рабочего пространства в заданный момент времени.
Рассмотренные понятия и соотношения ниже будут анали
зироваться применительно к достаточно простым технологиче
ским ситуациям : отсутствие химических превращений (а зна
чит, Источников и Стоков вещества к); стационарные и про
стейшие нестационарные (например, безградиентные) процес
сы; некоторые твердые тела правильной формы (т.е. Wx, у, z =
= О) , пото ки фаз в режимах идеального вытеснения (И В) и иде ...
ального перемешивания (ИП) и т.п.
77 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

10.4.3. Диффузионный массоперенос
В основе расчета диффузионного переноса вещества в пределах
фазы лежиг закон Фика ( 10.2). Для его практического использова
ния необходимо располагать коэффициентами диффузии Dд, Dм;
способы их определения и значения ШIЯ различных рабочих тел

приведены в mrrepaтype" - в моноrрафиях по термодинамике,
справочн иках, приложениях к техническим изданиям.

-

Коэффициенты диффузии для газов уменьшаются с ростом давления р (в
диапазоне до 2 , 5 3, 0 МПа изменяются практически обратно пропорционально
р) и достаточно быстро растуr с температурой t; для данного компонента они
снижаются с ростом его концентрации в смеси (при малой концентрации ком
понента ее влияние на Dд несущественно). Для жидкостей Dд растет с t ; харак
тер влияния концентрации зависит от природы компонентов (возможны мини
мумы и максимумы с изменением концентрации). Для твердых тел D..., также
растет с t ; характер его изменения с концентрацией диффундирующего вещества
С и :щесь зависит от природы этого вещества и твердого тела. В области малых
концентраций они весьма с.лабо влияют на D..., , так что можно принимать D..., =
= const; при более высоких С часто наблюдается заметный рост D..., с С.

Пугь решения задач стационарного массопереноса через те
ла различной формы (плоские стенки или прослойки, стенки
другой формы - одно- и многослойные) полностью повторяет
рассмотренный в разд. 6.3 для переноса теплоты: аналогичные
предпосылки - закон Фика взамен закона Фурье; та же канва
анализа - с заменой t на С и Л на Dм - Поэтому и результаты
выглядят идентично.
Так, для плоской стенки или прослойки толщиной 8 [см.
формулу (6.6)) количество переданной в единицу времени мас
сы при Dм = const составляет

М=

Dм
Fл С,
8

( 1 0.5)

причем пропускная способность диффузионного переноса вещест
ва представлена фрагментом
Dм
F.
8

(а)

Для сферической стенки [обозначение характерных д н аметров d1 и d2 то же, 'ПО и в формуле (6. 1 0))
лс
( 1 0 .6)
М=
'
1 (1 -1 )
-27tD м d1 d 2

• Сведения о коэффициентах диффузии, особенно для многокомпонентных
систем и твердых тел, разбросаны в научной литературе и концентрированно не
приводятся. Сведения для однокомпонентных (самодиффузия) и бинарных
жидких и газовых смесей см. (5-7, 9, 19 и др.J, для некоторых веществ в твердых
телах �м. ( 1 5 , 2 1 и дрJ .

772

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

причем пропускная способность составляет
М

лс

2 1t D

(б)

м

1

1

d1

d2

Написание результирующих соотношений для других случаев
(по аналогии с кондукrивным теплопереносом) - очевидно.
СоО111о шения типа ( 10.5). ( 10.6) получены (или записаны) в предположении
о постоянстве коэффициеJПа диффузии, т.е. его независимости от уровня кон
центраций. Это часто справедливо для прослоек rазов и жидкостей (Dд "' const),
но далеко не всеrда для капилляр но-пористых твердых тел . При заметной зави
симости D" от С надо для приближенных оценок пользоваться усредненными
значениями коэффициентов диффузии, а для более точных расчетов (при из
вестной зависимости D" от С) - численными методами расчета (см. заключи
тельный абзац разд.6.3 . 1).

Закон Фика в форме ( 1 0 .2) достаточно хорошо работает при
умеренных значениях rрадиентов температур и давлений . При
высоких дt/дп и др/дп ero приходится дополнять слагаемыми,
отражающими перенос вещества за счет rрадиента температур
- термодиффузия и давлений - бародиффузия. Обычно это
делают в форме, аналогичной переносу вещества за счет rради
ента концентраций:
qв = -

(Dд дп
дС

+

Dт

)

дt + Dp др .
дп
дп

( 1 0.2а)

Заметим, что вклад термо- и бародиффузии обычно невелик,
он становится заметным только при высоких дt/дп и др/дп.
Устройства,
использующие
эти
эффекгы,
существуют
(например , бародиффузия - в суперцентрифугах).
Наряду с отмеченными эффекгами дополнительные диффу
зионные потоки появляются при наложении на систему поля
каких-нибудь внешних сил (например, элекгрическоrо поля). В
этом случае соотношение типа ( 1 0.2а) дополняют слагаемыми,
учитывающими соответствующие коэффициенты диффузии и
rрадиенты внешних сил.
Детальное рассмотрение термо- и бародиффузии и других
подобных эффектов находится за пределами учебника. В нем
анализ ведется на основе концентрационной диффузии; это
означает, что в основе изложения - закон Фика в форме ( 1 0 .2)
и уравнение Фика в записи (10.4) при к = О.
10.4.4. Конвективный массоперенос

Рассмотрим массоотдачу - перенос вещества через поrра
ничную пленку нормально к поверхности раздела фаз . Потоко
вый перенос вещества с движущейся фазой вдоль межфазной
773

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 10. 9. К модели диффузионной поrраничной

1 rраница раздела фаз, 11 - поток
эа - по нормали к плоскости рисунка

пленки:
-

Сп

JIОlдКОСТИ или

rа

границы (его тоже именуют конвек
тивным) будем изучать отдельно или
совместно с диффузией и конвекцией в
разделах, посвященных массообмену.
Подход к анализу массоотдачи ведем в
соответствии с концепцией диффузион ной пограничной пленки - аналогич
ные подходы к переносу теплоты изло-

жены в разд.6.4. 1 .
На рис. 1 0.9 изображено изменение концентрации вещества
С в одной из фаз (явления в другой фазе пока не рассматри
ваются; взаимодействие фаз - предмет массопередачи). При
мыкающая к границе (J) фазового раздела область, в которой
наблюдается изменение С нормально к границе, называется
диффузионным пограничным слоем. Изменение концентрации от
значения Сп на границе до С в ядре фазы происходит плавно.
Для удобства анализа и расчета вводят понятие о модельной
пограничной пленке с четкими границами и определенной
толщиной од ; считают, что в этой пленке сосредоточено все
изменение концентрации от Сп до С, а за пределами пленки (в
ядре) концентрация постоянна. Диффузионная пограничная
пленка аналогична тепловой (ее толщина 8.r) и ламинарному
пристеночному слою (Ом): во всех этих пленках невелика роль
турбулентного переноса (количества движения, теплоты, ве
щества), доминирует вклад молекулярного переноса - вяз
кость, кондукция, а в изучаемых здесь явлениях - диффузия . В
общем случае толщина диффузионной пленки Од не совпадает с
Он и &r; количественная оценка связи между ними дана в разд.
6.4.2. Разумеется, значения Од (как и 8.r) за редким исключени
ем (течен ие тонких пленок, например) не известны, эти вели
чины имеют модельный смысл и мoryr быть использованы для
качественной оценки ситуации.
Малая толщина пограничной пленюt часто позволяет от
влечься от ее возможной кривизны и считать пленку плоской, а
кон центрационный профиль в пленке - линейным. Это озна
чает, что поток вещества через пленку можно рассматривать
как диффузионный перенос (массопроводность) через плоскую
прослойку (газовую, жидкостную) с характерным коэффициен
том диффузии Dд . Такой перенос описывается выражением
(1 0.5). Однако неопределенность в значении Од не позволяет
774

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

прямо воспользоваться им для расчета М. Поэтому вводят (как
и при переносе теплоты) понятие о коэффициенте массоотдачи
и записывают формулу для М в форме ( 1 0.3). Сопоставление
выражений для М ( 1 0.3) и ( 1 0 .5)
( Dд/8д)FЛ С = рFл С
(в)
приводит к модельному соотношению (оно записано ранее
в
разд. 1 .3 .2)
( 1 . 1 3), ( 1 0 .7)
-

Как и для коэффициента теплоотдачи а , это выражение не яв
ляется расчетным, но оно позволяет качественно анализировать
процесс массоотдачи. В частности, ясно, что для интенсифика
ции конвективного массопереноса надо включить факторы,
уменьшающие толщину пограничной пленки 8д , например за
счет повышения скорости движения фазы относительно меж
фазной границы.
В разделе 1 .8 .4 путем масштабных преобразований соотно
шения типа (в) или выражения ( 1 . 13), ( 1 0.7) было получено
безразмерное число Шервуда Sh = pl/Dд , rде l - определяющий
линейный размер (в случае шара или цилиндра - диаметр d) .
Физический смысл Sh вытекает из равенства (в): это соотно
шение потоков вещества по одну сторону границы раздела фаз;
речь идет об одном и том же потоке вещества, но выраженном
в терминах конвекции и диффузии.
Значения р определяются из опыта на основе формул типа
( 1 0.3) - путем измерения в разных условиях процесса геомет
рических характеристик, движущей силы и количества пере
данного вещества. Результаты эксперимента чаще всего пред
ставляют в виде критериальных уравнений, формируемых из
следующих общих соображений:
- при движении рассматриваемой фазы около границы раз
дела возникает ламинарная пограничная пленка толщиной 8и;
- толщина 8и определяется значением критерия Рейнольдса
Re - значит, интенсивность массоотдачи будет зависеть от Re;
- интенсивность массоотдачи определяется толщиной диффу
зионной пограничной пленки бд - значит, надо от 8ir перейrи к 8д;
переход от 8и к 8д определяется (это ПJ�Одемонстрировано
в разд.6.4.2) критерием Шмидта Sc = v/Dд, полученным в
разд. 1 . 8 . 3 .
Таким образом, критериальное уравнение, отражающее ин 
тенсивность переноса вещества Sh (а значит, и р ) , должно быть
представлено в форме
( 1 0.8)
Sh = j{Re, Sc, . ),
причем Re устанавливает толщину ламинарной пленки 8ю а S c
обеспечивает переход от нее к толщине 8д, определяющей ин-

.

.

775

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

тенсивность массоотдачи:

Re --+ 8и

Sc

Реже для харакrерисrик конвекmвной маwют,цачи используют диффузионный
криrерий Сгакrона Stд "' Sh/(Re-Sc) " �/w - см. ра:щ.6.4.2. Эмпирическая формула в
:ло м случае имеет вид
Stд = /{Re, Sc, . . . ) .

( 10.9)

Значения р , входящие в Sh, однозначно должны иметь раз
мерность [Sh(D;/l)J = м/с, или в полном написании: мЗ ВЛм2 х
3 В/м3 )] . Вместе с тем в выражения типа ( 10.3) коэффи
х с · (м
циент массоотдачи (обозначим его Р') может входить в другой
размерности . Пусть, например, М выражается в кг В/с, а л С в ( кг В)/( кг ин.) - именно в таких единицах часто выражаюrся
концентрации и движущая сила для систем класса 3(2-2) 1 . Тог
да из уравнения массоотдачи

М = Р'FЛ С
получаем размерность [ ,_,А ')

кг ин.

= -2-- .
М

·С

с

[М]

=

[F] [ЛС]

( 10.3а)

=

кг в

с · м (кг В/кг ин. )
2

v

равнение размерностеи Р' и р показывает различия в

числителях: кг ин . и м3 [причем для систем 3(2-2) 1 - это м3
инерта] . Оrсюда вполне очевидно: для рассматриваемой ситуа
ции Р' = рр, где р - плотность инерта. Теперь уравнение мас
соотдачи, записанное на основе р, находимого из критериаль
ной формулы, примет вид

М = ррFЛ С.

( 1 0.3 6)

Конкретные эмпирические соотношения для определения

Sh и р приводятся в литературе • . Теоретические соотношения

удается получить для весьма ограниченного числа случаев и ,
как правило, для предельнь1х ситуаций. Так, для шара, исполь
зуя канву анализа конвективного теriлопереноса (разд.6.4.5),
нетрудно установить минимальное значение числа Шервуда.
Для этого следует рассмотреть пограничную пленку (ее диаметр
dпл) около шара диаметром d и уравнять потоки вещества М,
записанные в форме (10.6) как диффузионный (d1 = d, d2 = dпл,
коэффициент диффузии Dд) и в форме (10.3) - как конвектив
ный (причем F = 7Т.d2):

21t Dд Л С

1 1

=

р7Т.d2Л С.

(г)

См. учебники по ПАХТ и массопередаче, например (8, 10, 12, 1 3 , 22, 23), а
также учебники и монографии по конкретным технологическим приемам.

•

776

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Отсюда, аналогично (6.2 1),

Sh " � =

2

(д)
1-�
dпл
при неоrраниченном возрастании толщины (диаметра) поrра
ничной пленки dпл --.. оо (неподвижная среда или сугубо лами
нарный режим) получаем Shmin = 2. Реально значение dпл ко
нечно, и поэтому Sh > 2. При этом толщина ламинарной плен
ки 8и зависит от Re, а переход от 8и к 8д осуществляется с по
мощью числа Sc. В результате, аналогично теплопереносу и в
полном соответствии с ( 10.8),
Sh = Shmin + j( Re, Sc) .
( 1 0 . 8а)

Dц

Примечательно, что и конкретный вид зависимости полностью, вnлоть до
ч.исленных коэффициентов, совпадает с (6.22а) для те1111о обмена:
Sh = 2 + a0Rel/2 Scl/З,
( 10.86)
где ао варьируется (по данным разных исследований) в том же диапазоне - от
0,59 до 0,74.

При отсуrствии эмпирических уравнений типа ( 1 0.8) вели
чину р можно оценить, базируясь на аналогии конвективного
тепло- и массопереноса (см . разд.6.4.2). Дело в том, что тепло
обмен изучен для значительно более широкого круга техноло
гических ситуаций, нежели массообмен , так что значения Nu и
а. доступны (есть эмпирические формулы) чаще, чем Sh и р .
Воспользуемся равенством (6. 1 5б), подставив значения S t и Stц:
р
а.
=
(д)
St .
Stд,
wcp

-

w

-

Отсюда получается формула Льюиса - связь а. и р, позво
ляющая по известному а. рассчитать р :
( 1 0 . 10)
Р = а/ер , РР = а/с .
Достоверность найденного таким пуrем р определяется диапа
зоном условий, в котором рассматриваемая аналогия соблюдается.
Установление rраниц аналогии - самостоятельная проблема.
На практике приходится встречаться с одновременным кон 
вективным массопереносом нескольких ("многих") компонентов
к rранице раздела фаз или от нее. Здесь в самом общем плане
сохраняются подходы и модельные представления (например, о
поrраничной пленке), удается сформировать безразмерные
критерии для описания конвективного массопереноса. Но
диффузия через поrраничную пленку и другие явления ослож
нены здесь взаимным влиянием компонентов; учесть это влияние
очень сложно. Поэтому при сохранении общих подходов для
777

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

определения р (применительно к отдельному компоненту или к
их группе) здесь пока чаще всего ограничиваются эмпириче•
скими корреляциями .

В литературе встречаются попьпки использования "коэффициентов массоот
дачи", отнесенных не к единице поверхности контакта фаз, а к единице объема
фазы или даже к единице поперечноrо сечения аппарата. Такие попьrrки
"обосновывают" недостаточностью сведений о величине поверхности в массооб
менном устройстве. Из.лишне rоворить, что это уход от физической сущности
ямений, фактически - грубая подмена задачи. Эмпирические зависимости,
построенные на таких предпосылках, работоспособны лишь в очень узкой об
ласти проведенноrо эксперимента; они не обладают пропюзностью; к практиче
ским рекомендациям здесь следует относиться крайне осторожно. Эти подходы
моrут бьпъ терпимы лишь на определенной стадии исследования и инженерной
практики, пока не разработаны более правомерные подходы и методы расчета (в
частности, пока не разработаны достоверные методы определения поверхности
контакта). В учебнике использование таких коэффициентов массоотдачи прак
тикуется лишь в единичных случаях .

1 0.5. ЭЛЕМЕНТЫ МАТЕРИАЛЬНОГО БАЛАНСА ДЛЯ ФАЗ Ы

При составлении материальных балансов массообменных
процессов оперируют количествами и потоками фаз - массо
выми, мольными и др . Ниже анализ ведется на примере массо
вых единиц.
Количества и потоки фаз мoryr быть выражены:
- для всей смеси (фазы) в целом; это абсолютные коли
чества или потоки; они выражаются в (кг см.) и (кг см.)/с и
чаще всего изменяются в ходе технологического процесса;
- для компонента (или группы компонентов), предпочти
тельно для того (или тех), количества (потоки) которого не
изменяются в ходе процесса (их называют "инертами"); эти
относительиые количества (потоки) выражаются в (кг ин .) и
(кг ин .)/с.
Для обозначения количеств и потоков фаз обычно используют заглавные
буквы латинскоrо алфавита, чаще всеrо это D, L, G, S. Иногда символы стремят
ся обусловить смысловым содержанием (названием потока по-латыни, по
немецки, по-английски). Это не всегда удобно из-за ра:lllи чий в названиях рабо
чих тел на разных языках и пересечения названий, например: L - liquid
(жидкость, англ.) и L - Luft (воздух, нем.); S - solid (твердое, англ.) и S solution (раствор, англ.). Кроме тоrо, в процессе моrут участвовать две одинако
вые фазы, их пришлось бы ра:�личать индексами, а последние заняты в других
целях. Попыrка назначить символику в зависимости от тоrо, отдает фаза перено
симый компонент или получает, тоже не может быть одобрена: при описании едино
rо технолоrическоrо 1IНК111l (скажем, абсорбции и десорбции) прИIWiось бы изменять
симюлику при переходе ar одной сrадии к друrой. По зmм причинам:
- в данной общей главе нам безра:lЛИЧНО обозначение количеств и потоков
(будем усломиваться о них);

• Вопросы мноrокомпонеитноrо межфазного переноса см. (5, 1 3 , 23).

778

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 10. 10. К составлению матери
ального баланса по фазе и перено
симому компонекrу (К и к - кон
туры)
- в конкретных технолоrnче
ски.х главах будем придерживаться
определенных обозначений.

x+ dx

о
Количества и потоки не
F
f f + df
f
коего компонента записы
ваются как произведение количества или потока фазы (L, D, G и т.п.) на концентрацию
этого компонента (х, у, С и т.п.). Это справедливо как для аб
солютных, так и для относительных величин, хотя смысл со
множителей - различен . Смысл произведения следует пони
мать следующим образом.
Применительно к абсолютным величинам: каждый кг (или
кг/с) фазы содержит С долей кг данного компонента (вещества
В); G кг (или кг/с) фазы переносят в G раз больше. По размер
ностям (например, для непрерывных процессов) :
кг в
G кг см . . С кг в = GC с
кг см.
с
Применительно к относительным величинам: на каждый кг
инерта приходится С кг вещества, а этих кг (или кг/с) инерта
идет G; поэтому количество (поток) вещества будет в G раз
больше. По размерностям (тоже в единицу времени) :
= GC кг В
G � . с кг В
с
кг ин .
с
Разумеется, недопустимо умножать абсолютные потоки на
относительные концентрации (как и мольные потоки на мас
совые концентрации) . В ходе материальных балансов нам при
дется постоянно использовать количества и потоки фаз L, D,
G, . . . и компонентов Lx, Dy, GC и т.п.
В составлении материальных балансов реализуем общий
подход, изложенный в разд. 1 .3 . 1 . На рис. 10. 10 изображен
фрагмент массообменного аппарата: рабочая зона фазы "х" ,
потоки L ; от другой фазы она мысленно отделена поверх
ностью контакта F. Станем отсчитывать поверхность слева на
право (стрелка на шкале /). Положим, что химических превра
щений (значит ,Источников и Стоков вещества) нет и что мас
сообменный процесс - непрерывен. Выберем пространствен
ные контуры - для всей рабочей зоны фазы (К) и для беско
нечно малой поверхности контакта (к) . Наконец, примем для
определенности, что фаза "х'' отдает вещество. Материальные
балансы (МБ) для абсолютных и относительных величин будуг
несколько различаться .
779

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Абсолютные потоки и концентрации.
Для потоков фазы:
контур К : L1 - LJ, М = О , М = L 1 LJ,;
(10. 1 1 )
контур к: L - (L + dL) - dM = О, dM = dL .
Для потоков компонентов:
контур К : L1x1 LJ.x2 - М = О, М = L1x1 - LJ.x2 ;
контур к: Lx - [Lx + d(Lx)] - dM = О , dM = -d(Lx).(10. 12 )
Оrносительные потоки и концентрации.
Материальный баланс для потоков фазы выражается:
контур К: L1 LJ. = О, L1 = L1 = L = const;
(10.1 3)
контур к: L - (L + dL) = О , d L = О , L = const .
Для потоков компонента (L = const):
контур К : Lx 1 - Lx1 - М = О, М = L(x1 х2) ;
контур к: Lx - L(x + dx) - dM = О , dM = - Ldx. (10. 14)
-

-

-

-

-

-

Сопоставление полученных выражений показывает, что при
постоянных потоках фаз балансы записываются проще. Поэто
му во всех случаях, когда только можно выделить поток, не из
меняющийся в ходе процесса, следует пользоваться относи
тельными потоками и концентрациями. Именно с такой ситуа
цией мы встречаемся в случае систем класса 3(2-2) 1 , детально
рассматриваемых ниже. Исключение составляют некоторые
процессы (типа выпаривания), где в силу традиций и удобства
выражения некоторых количественных характеристик техноло
ги продолжают использовать абсолютные потоки и концентра
ции. Заметим также, что в случае двунаправленной диффузии
при эквивалентных встречных потоках компонентов (из фазы
"х" в "у" и обратно) потоки фаз получаются постоянными при
использовании абсолютных величин (с такой ситуацией мы
встретимся при изучении процессов ректификации) .
В тех случаях, когда фаза содержит п компонентов, . материальный баланс
(МБ) по компонентам составляется для ка:ждоrо из них. Но при представлении
состава фазы всегда вводится концентрационное ограничение: сумма концентра
ций компонентов равна 1 либо одни из компонентов принят за 1 ; поэтому до
1 МБ, а для поСJJеднеrо компонента баланс получается по разности
статочно п
(с учетом МБ по фазам). В аспекте массопереноса технолоrов часто интересует
МБ только по переходящему компоненту (компонентам).
-

10.6. МАССОПЕРFДАЧА И БАЛАНС
ДJIЯ ПРОЦЕССОВ КЛАССА 3(2-2) 1
1 0.6. 1 . Массопередача
В соответствии с терминологией, введенной в разд .
10.4. 1 ,
под массопередачей понимается межфазный перенос вещества
(переходящего компонента) нормально к поверхности контакта.

780

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Иначе говоря, в задачах массопередачи вычленены поверхност
ные стадии переноса; при этом не рассматриваются эффекты ,
связанные с движением фаз вдоль поверхности контакта, - эти
вопросы анализируются ниже в рамках изучения массообмена.
Таким образом, предметом изучения здесь должна явиться со
вокупность двух стадий массоотдачи - последовательный пе
ренос вещества через поrраничные пленки, примыкающие к
rранице раздела фаз.

Составление уравнения массопередачи
В основе анализа и расчета лежит уравнение массопередачи,
аналогичное уравнению теплопередачи (7. 1 ) ; для непрерывных
процессов оно имеет вид
( 1 0. 1 5)
М = kFЛ .
Охарактеризуем величины, входящие в (10. 15). Пусть речь
идет о переносе вещества из фазы "у" в фазу "х" (рабочая об
ласть процесса над линией равновесия). Тогда М
поток (в
единицу времени) компонента , вещества (В), передаваемого из
фазы "у" в фазу "х" ; примем для определенности, что М выра
жается в кг В/с; F - поверхность .контакта фаз (м2 ). Здесь на
лицо сходство в описании переноса вещества и теплоты; далее
возникают различия. В теплопереносе движущей силой бьmа
разность температур теплоносителей, и не возникало вопроса о
способе ее выражения: л = Т - t. В массопереносе движущая
сила может быть выражена в концентрациях любой из фаз
"х" или "у" . Соответственно рис . 10.7, в терминах фазы ".х" : л =
= л.х = .х Р - х, в терминах фазы "у'': Л = Лу = у - уР. Поэтому
и коэффициент массопередачи должен быть выражен в расчете
на ЛХ (это будет kx) или в расчете на Лу (ky). Уравнение массо
передачи при этом запишется в терминах ("на языке") какой
либо одной фазы:
(10. 1 5у)
M = kxFЛX ( 10. 15.х) или M = kyFЛy .
Подчеркнем, что х и у (соответственно лх и Лу) - величины
разных размерностей (поскольку они отнесены к разным инер
там). Поэтому kx и ky также имеют разные размерности, при
чем соотношение размерностей kx и ky обратнЬ таковому для х
и у, ЛХ и Лу. Приступая к анализу и расчету, надо предвари
тельно определиться, по какой из фаз их предполагается вести.
Как и при переносе теплоты, важнейшая проблема массопе
редачи состоит в определении kx и/или ky по частным коэффи
циентам массоотдачи Рх и Ру·
-

-

Двухпленочная модель массопередачи
Для определения kx, ky используют двухпленочную модель
она наглядна и позволяет подойти к определению коэффици
ентов массопередачи с тех же общих позиций, что были приня78 1

-

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

х, у

т, t

у

у - уР

-

�

��
Го р .

а

бу

Ф аз а " у "

Хол .

Бх

Ф аз а " х"

б

Рис. 10. 1 1. Двухпленочная модепь коmакпюrо переноса тeIUIO'IЪI (а)

о

и вещесrва ( б)

ты при рассмотрении теплопередачи (разд.7.3. 1). Модельные
схемы применительно к переносу теплоты в отсутствие тепло
передающей стенки (контактная теплопередача) и вещества
представлены на рис. 10. 1 1 .
Н а виде (а) изображена модельная схема контактной тепло
передачи: тепловые пограничные пленки 871 и 872, коэффициен
ты те плопередачи а 1 и а2 , частные (Лf и Лt") и полный ( Т - t)
температурные напоры. Здесь все соответствует схеме на
рис.7.5, только для случая 8c-r = О. Важно: температуры Т и t
отсчитываются по общей температурной шкале; в ядре потоков
температуры теплоносителей различны ( Т и t); на поверхности
контакта температуры выравнены.: Т = t = е. Очевидно, что ана
лиз по канве, принятой в разделе 7.3 . 1 , должен привести к вы
ражению коэффициента теплопередачи (обозначим его здесь
kr), анало ги чному (7.3), но при 8c-r = О :
1 1 _
1
_
(7.3в)
+ 1
kr =
'
k
<Х 2
1
1
<Х 1
т
=

-

а1

+-

а2

На виде (6) изображена модельная схема контактной массо
передачи: диффузионные пограничные пленки 8х и 8у, коэффи
циенты массоотдачи �х и �У' частные концентрационные напо
разные для разных
ры Лх. ' = Хп - х и Лу' = у Уп и полные
фаз: лх = хР х и Лу = у уР. Важно: в отличие от теплопере
носа, здесь концентрационные шкалы не совпадают (по мас
штабам и численным значениям концентраций); на границе
-

-

782

-

-

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

фазово го контакта концентрации Хп и Уп не равны, а равновес
ны. Если воспользоваться понятием коэффициента распределе
ния т = (у/х)Р, то в условиях равновесия т = Уп /Хп = у/хР =
= уР/х (эти равенства иллюстрируюгся на рисунке подобными
треугольниками). При этом смысл и взаимозависимость вели
чин х, у, х Р, у Р ясны из рис. 10.7 (в предположении о т =
= const). В практических задачах массопереноса концентрации х
и у определены; концентрации Хп и Уп важны для понимания
модели и механизма массопереноса, в технологических расче 
тах их, ка1< правило, не используюг.
Согласно двухпленочной модели вещество из ядра фазы "у"
движется к границе раздела фаз под действием частной разности
концентраций Лу' и далее в ядро фазы "х' под действием частною
концентрационного напора ЛХ'. Двухпленочная модель массопере
носа базируется на двух основных постулатах:
- все изменение концентраций в пределах каждой из фаз со
средоточено в пограничных пленках, за их границами (8х и 8у со
ответстве н но) концеН1рации вещества в каждой фазе выравнены
(см. горизонтальные линии х = const и у = const на рис. 10. 1 1 ,6);
- на границе раздела фаз отсутствует сопротивление пе
реносу вещества, именно поэтому концентрации Уп и Хп
равно весны.
Коэффициенты массопередачи не могут быть представлены
(исходя из примитивно понимаемой аналогии с теплопереда
чей) в форме
1
1
1
(?!).
(а)
-=-+k
Рх Р у
Применительно к системам класса 3(2-2) 1 , а также ряду
других систем, f3x и [3у величины разных размерностей (они
отнесены к движущим силам, базирующимся на разных инер
тах); для систем с формально одинаковыми размерностями
[типа 2(2-2)2, например] формула (а) тоже неправомерна из-за
несовпадения понятий равенства и равновесия концентраций:
при равенстве концентраций нет равенства химических потен
циалов компонента в разных фазах.
По указанным причинам определение коэффициентов мас
сопередачи можно вести по той же канве, что и в случае теп
лопередачи, но обязательно с учетом отличительных особенно
стей массопереноса. При этом определению подлежат оба ко
эффициента - kx и ky , так что анализ придется проводить раз
дельно - в терминах (на языке) каждой из фаз.
Представим потоки вещества на основе частных движущих
сил - уравнения массоотдачи:
(б)
М = [3у(у Уп)F, М = f3х(Хп - x)F;
-

-

-

783

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

у

у

Рис. 10. 12. Массоперенос в контексrе двухменочной модели

произведения PyF и PxF представляют собой пропускные спо
собности стадий поверхностного непрерывного массопереноса
(массоотдачи) в фазах у и "х" соответственно.
Связи и соотношения между величинами у, х, Уп . Хп . Ру, Рх
наглядно высвечиваются при графической интерпретации двух
последовательных стадий - массоотдачи в фазах. Пусть кон
тактируют фазы с концентрациями вещества у, х (точка А на
рис. 10. 12). Значения Ру он Рх будем считать известными. Тогда
точку равновесных концентраций В легко найти, приравнивая
правые части выражений (б); после сокращения на F
Рх
У - Уп
(10. 16)
.
АУ(у - Уп ) - 1-'АХ(Хп - Х) И
1-'
Ру
Хп - Х
Следовательно, при известных точке А (концентрации х, у
заданы) и коэффициентах Ру, Рх легко найти точку В(уп . Хп ) ,
проведя из точки А прямую:
- под углом qi, тангенс которого (см. рисунок) равен Рх /Ру;
- до пересечения с линией равновесия, поскольку, согласно
постулату двухфазной модели, концентрации Уп и Хп - равно
весны.
Отрезок АВ будем называть вектором массопередачи. Он бе
рет свое начало в точке сопряженных концентраций А(у, х),
всегда направлен к линии равновесия и заканчивается на ней.
Вектор ориентирован (см. рис.10. 12) под углом (n - qi) к поло
жительному направлению оси абсцисс. Все эти подходы пра"

'

=

-

• О пропускных способностях периодических и полунепрерывных процессов,
включающих временн/iе хара�сrеристики, см. разд. 10. 14, 10. 16.

784

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

вомерны и в тех случаях, когда рабочая область расположена
под линией равновесия; векторы массопередачи здесь будуг
изображаться направленными отрезками типа А'В'. Рассмот
ренные положения справедливы безотносительно к тому, пря
мой или кривой является линия равновесия.
Расчет коэффициентов массопередачи
На базе полных движущих сил (они также показаны на
рис. 10. 12) тот же поток вещества записывается соответственно
выражению ( 10. 15):
{в)
М = ky(y - y P) F; М = kт.(_х Р - x)F,
причем произведения kyF и kxF представляют собой пропуск
ные
способности
поверхностной стадии
в
целом
(массопередачи), записанные на языках фаз "у" и "х" соответ
ственно. Здесь две частные стадии массоотдачи объединены в
одну общую стадию массопередачи, которая может быть пред
ставлена в терминах фазы "у" либо фазы "х''.
Оrвлечемся от возможности изменения коэффициента рас
пределения т с концентрацией {этот момент важен в аспекте
массообмена, но не массопередачи). Определим сначала ky,
затем kx.
Коэффициекr массопередачи на языке фазы у Используем
первое из выражений (в). Весь анализ будем вести в терминах
фазы "у"; в этих целях избавимся от концентраций фазы "х" во
втором из выражений (б): Хтt = упfт, х = у Р/т. Тогда это выра
жение перепишется в вИде
"

".

h (yn

(б')
- Y') F.
т
Теперь в целях исключения Уп решим первое из выражений
(б) и (б') относительно разностей концентраций и сложим по
лученные разности:

М=

у - уп =

+
откуда

Yn

м

lJ3 у

-у = М
F(Рх/ т)
р

1

� у - уР

=

Лу = м

1

М = ----,-1---1.,--- Лу = 1
+
13у
13 y F Px F / т
--

---

-

1
+

(-1 + Рх 1 /т)
13y F

у
т FЛ
Рх

F

, ( г)

(д)

-

785

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Сопоставляя (д) с первым из выражений (в), находим
т .(10.17у)
1 ::; 1 + 1
1 - иk =
kyF = -1--y
'
1
1
- + !!!__ ky
Р у Рх
+
Py F P xF / т
Ру Рх
Величина РхF/т, как и PxF, представляет собой пропускную
способность массоотдачи в фазе "х" , но только РхF/т записано
теперь на языке фазы "у'', т.е. в размерностях, характерных для
этой фазы.
Коэффициент массопередачи на языке фазы "х". Определение
kx ведется анало гичным образом ; только замене здесь подлежат
концентрации вещества в фазе "у'': Уп = mхп , у = тх Р. Первое
из выражений (б) при этом принимает вид
(б")
М = т ру(хР Хп) F.
Используя (б ") и второе из выражений (б), исключим неиз
вестное Хп:
-

--

-

---

-

(е)

+

откуда
М=

1

-----

1
1
-- + --

ЛХ ::;

1
1

--

+

1

-

Fлх

(ж)

т Ру F PxF
т ру Рх
Из сопоставления (ж) со вторым из выражений (в) ясно:
1 ::; 1
1
1
1
_ __ + - . ( 10. 1 7.х)
=
kxF =
1 + 1 И kx _1_ + -1- ' kx т ру Р х
т р у F Px F
т ру Рх
------

--

Величина т руF, как и PyF, выражает пропускную способ
ность массоотдачи в фазе "у'', только т руF записано на языке
фазы "х" , в ее характерных размерностях.
Из сопоставления выражений (10.17у) и (10.17.х) прямо сле
дует соотношение между коэффициентами массопередачи:
(з )
kx/ky = т ; kx = тkу , ky = kх /т.
786

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Полученные выражения для k; и k;F позволяют провести
Пусть интенсивность массо
переноса (иначе - пропускная способность) в фазе "у" значи
тельно выше, чем в фазе " х", т.е. pyF >> PxF/m, или (что то же
самое) mpyF >> PxF. Тогда слагаемые 1/{PyF) или 1/(mpyF) в
знаменателях формул (10. 17) пренебрежимо малы (разумеется,
сопоставление можно проводить не только по пропускным
способностям, но и по величинам Рх. Ру, т). В этом случае вы
ражения для k1 упрощаются: ky = Рх/т, kx = Рх· При обратном
неравенстве (PyF << PxF/m) очевидно ky = Ру, kx = mPy·

анализ на лимитирующую стадию .

Проблема выбора языка, на котором целесообразно вести расчет, вообще го
воря, возникает при переходе от массопередачи к массообмену. В случае прямой
линии равновесия безразлично, язык какой фазы выбрать: здесь нет затруднений
с т = const. В случае кривой равновесной линии (т = var) расчеrnая ситуация
усложняется. Дело в том, что при заменах типа у = :16'/т и Уп = х.� /т здесь,
строго говоря, надо брать разные т, что не позволяет по приведенной выше
канве выразить движущую силу у - )А'. В этих условиях теряет определенность
само понятие коэффициента массопередачи. Но других приемлемых инженер
ных подходов пока нет, по:л-ому в не очень широких диапазонах концентраций
линию равновесия искусственно спрямляют и пользуются неким усредненным
( "постоянным") значением т. Если же диапазон рабочих концентраций широк,
то использование "средних" коэффициентов распределения может привести к
ошибкам. Существует ряд рекомендаций о способах усреднения т; видимо,
наиболее строгий способ состоит в записи уравнений массопереноса для элемен
тарной поверхности контакта dF с последующим интеrрированием (как правило,
численным) по всей поверхности F и нахождением полного потока вещества М.
Затруднения с т = var снимаются при наличии лимитирующей стадии мас
соотдачи: достаточно вести расчет на языке той фазы, которая лимитирует мас
соперенос. В самом деле, пусть, например, массоперенос лимитируется массоот
дачей в фазе "у". Тогда ky "' /3у, поскольку слагаемое т/13х пренебрежимо мало.
Значит, т не будет входить в расчет, если его вести в терминах фазы "у".

Линейность равновесия (т = const) и кинетики
(независимость kxF, kyF от уровня концентраций и движущих
сил) создает предпосылки для аналитического расчета процес
сов массообмена, учитывающего продольные потоки фаз и
компонентов.
Достоинство двухпленочной модели - в ее относительной
простоте. Вместе с тем надо понимать ее приближенность, по
скольку:
- возможно диффузионное сопротивление на границе раз
дела фаз;
- возможны нелинейные эффекты даже при линейной ки
нетике в отдельных фазах (за счет взаимного влияния массоот
дачи по разные стороны межфазной границы);
- Рх и Ру могут изменяться с уровнем концентраций, так
как будут непостоянны Dд х,у (да и Dx,y) и т.д.
787

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

1 0.6.2. Материальный баланс аппарата

Общая схема непрерывного массообменного процесса пока
зана на рис. 10.13: фазовые потоки D и L, несущие переходя
щее вещество В, движугся через аппарат, причем взаимное
направление потоков здесь для описания процесса несуще
ственно. Входные концентрации вещества (для процессов рас
сматриваемого класса
относительные) обозначим индексом
" 1 " , вьi:ходные - индексом 2 Для определенности принято
(см. на рисунке стрелку М, пересекающую границу раздела
фаз), что В переходит из фазы "у'' в фазу "х", так что у1 > у2 ,
Х2 > XJ .
Материальный баланс по потокам фаз составлять не станем:
очевидно (и это показано в разд. 10.5), что он вырождается в
тривиальные равенства типа L - L О и L = const.
Материальный баланс (МБ) аппарата по потокам компонен
та В призван связать концентрации вне (на концах) аппарата и
потоки фаз. Для составления МБ (применительно к 1 с, так как
процесс непрерывный) выд елим контуры К1 и К2 и поочередно
запишем балансы (в отсутствие Источников и Стоков вещест
ва), обозначив поток В из фазы в фазу символом М:
+ Dy1 - DY1. - М = О, откуда М = D(y1 - У2 ) ; (10. 1 8у)
+ Lx1 + М - Lx1
откуда М = L(x2 - х1 ) . (10. 18х)
О
В этих соотношениях пропускные
способности потоковых ста
ди й равны М/(у1 - У2 ) = D и М/(х2 - х 1 ) = L; заметим, что L
и D выражены на языках разных фаз - в обоих случаях (кг
ин .)/с, но инерты - разные. При т = const пропускные спо
собности одной фазы нетрудно выразить в размерностях дру
гой. Например, от выражения (10. 1 8х) перейдем к записи на
языке фазы "у'', подставив х1 у1 Р/т и х2 У2Р/т:
у
L
(и)
� =т
М = L(x2 - Х1 )
уР1 - уР2 .
т т
Тогда пропускная способность стадии отвода вещества из ап
парата с фазой "х" будет на языке фазы "у" выражена как L/т.
Соответственно пропускная способность стадии подвода В в ап
парат с фазой "у" запишется на языке фазы "х" в форме тD.
Материальный баланс возможно составить для контура (на
рис . 1 0 . 1 3 не показан), охватывающего аппарат в целом:
+ Dyl + Lx1 - Dy2 - Lx2 о ,
откуда
(10. 1 8)
-

"

".

=

=

,

=

=

L[yf ]
-

=

(

=

788

)

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

х

Рис. 10.13. К материальному
балансу массообменноrо аппара
та ( К1 и К2 - КО1f1УРЫ)

Рис. 10.14. Балансовые линии
массообменноrо процесса Д11Я
ТСХllОЛОПIЧССКИХ
различных
ситуаций:
о, б - прямоток или идеальное
перемешивание фаэ, • - д- проти

воток

о,

фаз;

11, г -

перенос вещесrва иэ

фаэу "Х', б, д - перенос
вещества иэ фазы "Х' в фазу 'У"
фазы 'У"

а

х

х

г

д

В пол уч енное выражение, естественно, не входит поток ве
щества М через межфазную поверхность, поскольку эта по
верхность не пересекается общим контуром.
Материальные балансы ти п а ( 10 . 1 8) правомерны н с толь ко Д11Я сисrсм кпасса
3(2-2) 1 , но и для друmх классов, ее.ли потоки фаз постоянны. Далее увмдим, что

такие выражения описывают и МБ ряда периодических процессов с постоянным
количеством инертов; разумеется, входные н выходные концентрации в этих
случаях заменяются на на'lальные и конnные.

Баланс ( 1 0. 1 8) связывает 6 величин: 2 потока фаз и 4 кон
центрации, так что по пяти известным величинам можно опре
делить одну неизвестную. В прапичес ки х задачах часто выде
ляюr целевой поток - очистка или насыще н ие именно этоrо
потока является целью конкретного технологического процес
са. Пусть для определенности здесь - это поток фазы "у"; тог
да для него обычно (в зада'}ах прое пирования) задан расход
( п рои з водительность) D , входн ая у1 и выходн ая У2 концентра
ции. В качестве неизвестн ого выступает поток нецелевой фазы
(в п р и н ятом примере - L) или одна из концентраций х1 или
(чаще) х2• Разумеется, при известных D, у1 и У2 по (10. 1 8у) лег
ко определить поток переносимого вещества М.
На рис . 1 0 . 1 4 представлена графическая интерпретация ба-

789

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

лансовых соотношений. Эти соотношения, конечно, не зависят
от формы кривой равновесия, и на рисунке показан общий
случай - кривые равновесные линии. Отрезок 1-2 (показан
жирным штрих-пунктиром) будем называть вектором баланса
[строго говоря, следует рассматривать не отрезок, а только на
чальную ( J) и конечную (2) точки] . Направление вектора ба
ланса определяется из выражения (10. 1 8):
L
Yt - У2
(10. 1 8а)

Из графика ясно, что положение отрезка 1-2, т.е. угол \jl ,
устанавливается - по (10. 18а) - отношением фазовых потоков:
tg\j/ = L/D. Поскольку приращение концентрации в одной фазе
сопровождается уменьшением ее в другой, то вектор баланса
всегда направлен из точки 1 (у1 , х1 ) к равновесной линии, при
чем с осью абсцисс этот вектор составляет тупой угол (п \j/ ) .
В случае прямотока и при идеальном перемешивании фаз
балансовая линия не может пересекать равновесную (рис.
10. 14,а, б); в случае противотока - может (вид г, д), хотя при
небольших изменениях концентраций в фазах это не обяза
тельно (вид в).
Построение балансовой линии при известных потоках L и
D, входных концентрациях у1 и х1 и выходной концентрации
целевого компонента (в принятом примере - У2) ведется в сле
дующем порядке:
- определяется направление вектора баланса, т.е. тангенс
угла \jl из условия tg\j/ = L/D;
- из точки 1 (у1 , х1 ) проводится прямая под углом \jl до пе
ресечения с линией конечной концентрации (в при
нятом примере - с горизонталью Y.z) , фиксируется точ
ка 2;
- на оси х отсчитывается х2 - абсцисса точки 2.
Разумеется, можно предварительно найти х2 из материаль
ного баланса (10. 1 8) и построить балансовую линию по точкам
(у1 , х1 ) и (У2, х2 ), при этом определится и угол \jl.
При неизвестном потоке одной из фаз (в примере - неце
левой L) и заданных входных и выходных концентрациях сна
чала строят точки 1 и 2, по ним - балансовую линию, а по ее
положению определяют угол \jl; далее при известном целевом
потоке D рассчитывают L из равенства tg\j/ = L/D. Разумеется,
и в этом случае неизвестный поток L может быть наЙден непо
средственно из баланса ( 1 0 . 1 8).
-

Для процессов теплопереноса также может бьпъ построен rрафик с балансо
вой линией, отвечающей тепловому балансу. Этоrо не было сделано в главе 7

790

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

только потому, что при описании теплообмена не принято пользоваться диа
rраммами Т - t.

Векторы массопередачи и баланса начинаются в точке 1 ; оба
вектора ориентированы от этой точки к линии равновесия под
тупым углом к оси абсцисс (7t - q> и 7t - Ч' соответственно) .
Подчеркнем, что рассматриваемые векторы характеризуют сов
сем разные стороны явления массопереноса - различать эти
стороны совершенно необходимо.
1 0.6.3. Пропускные способности массообменноrо процесса

Для схемы массопереноса, изображенной на рис . 1 0 . 8 , ха
ракrерны четыре стадии. Если две стадии массоотдачи объеди
нить в одну - поверхностную, то процесс можно трактовать
как трехстадийный: стадии подвода и отвода вещества с фаза
ми и стадия массопередачи. При этом каждая стадия может
быть описана на языке фазы "у'' или фазы "х". В случае ли
нейной равновесной зависимости (у/х) Р = т = const переход от
одного языка к другому осуществляется с помощью постоянно
го множителя т, выраженного в

(кг В)/ (кг L)
(кг В)/ (кг D)

=

(кг L)/(кг D) .

Как показано в разд. 10.6. 1 и 1 0.6.2, пропускные способ
ности отдельных стадий записываются так:
- в терминах и символах фазы "у' ' : D (потоковая стадия), kyF
(поверхностная);
- в терминах и символах фазы "х" : L (потоковая стадия) ,
kxF (поверхностная).
Для сопоставления и совместного использования потоковых
стадий, выраженных на разных языках, необходим переход к
записи в терминах другой фазы. Так, пропускная способность
L на языке фазы "у'' записывается как L/m, а D на языке фазы
"х'' - как mD. Правомерность такой записи обоснована в разд.
1 0 . 6 . 1 и подтверждается анализом размерностей, например:
/ ] кг L кг L кг D
.
=
[L т

=

с

; кг D

с

Переход от символики одной фазы к другой при выражении
поверхностной стадии задан выражением (з) в разд. 1 0.6. 1 .
Пропускная способность массообменного процесса в целом
определяется (как и в случае теплообмена) отношением потока
М переносимого (из фазы в фазу) вещества к входной разности
концентраций. Последняя при записи по фазе "у'' равна Лу• =

79 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

= У1 - у1 Р, где у1 Р - концентрация, равновесн ая с входной Х1
для фазы "х" . При анализе в терминах фазы "х'' входная раз
ность концентраций лх. = х1 Р - х1 , где х1 Р - концентрация,
равновесная с у1 . Пропускная способность массообменного
процесса записывается как М/ лу . или М/ ЛХ• .
При описании массообмена (как и в случае теплообмена см. разд. 7 .9) удобно использовать безразмерные комплексы,
представляющие собой оrношения пропускных способностей.
При выражении этих комплексов будем прцдерживатъся обозна
чений, введенных в ходе изучения процессов теплопереноса:
- отношения пропускных способностей поверхностной и
потоковых стадий:
ky F kx F
= -- = а '·
(10.19)
D
mD
- отношения пропускных способностей потоковых стадий:
� = с и mD =
( 1 0.20)
.
L
mD
Величины а и Ь называют числами еди ниц переноса; в отече
ственной литературе их обычно обозначают соответственно Sy
и Sx. Это безразмерные критерии, и поэтому численные их зна
чения не зависят от того (при т = const, конечно), в терминах
какой фазы (через ky или kx) они представлены.
При линейном описании процессов удобно оперировать об
общенным отношением пропускных способностей - системы в
целом и поверхностной стадии. Это отношение может быть
записано на языке любой из фаз:
м
м
(10.2 1 )
--

с'

В случае линейных равновесия, кинетики и баланса (для
многих процессов класса 3(2-2) 1 это характерно или может
бьпъ приняrо с известн ым приближением) аппарат пропускных
способностей - весьма плодотворен. Он позволяет достаточно
просто решать некоторые эксплуатационные задачи ; кроме того, с
его помощью выявляется и обосновывается смысл рЯда понятий и
соотношений, введенных ранее технологами без обоснования
(зачастую - интуигивно) в практику инженерных расчетов.
10.7. РАБОЧИЕ ЛИНИИ В АППАРАТЕ
ДЛЯ НЕПРЕРЫВНОГО ПРОЦЕССА КЛАССА 3(2-2) 1

Цель массообменного процесса - перенос вещества (В) из
фазы в фазу: одна из фаз отдает В, другая его получает. В ходе
процесса по мере движения потоков в аппарате вдоль поверх
ности контакга происходит изменение концентраций В - по792

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

нижение в отдающей фазе, повышение - в принимающей.
Поэтому в разных точках, сечениях аппарата контактируют
фазы с разными концентрациями; эти концентрации в точке
или сечении контакта называются сопряженными.
10.6 . 1 массоперенос рассматривался безотносиВ разд .
тельно к изменению сопряженных концентраций, так что в
уравнении массопередачи (10. 1 5) фигурирует движущая сила л
(Лу или ЛХ) для некоторой пары сопряженных концентраций
(у, х). Поскольку в процессах массообмена сопряженные кон
центрации изменяются, движущая сила в общем случае также
изменяется вдоль поверхности межфазного контакта. Поэтому
в уравнениях массообмена должна фигурировать средняя (по
поверхности F) движущая сила:
(10.22)
М = kxF!!.xcp , М = kyFЛycp
Эти выражения с очевидностью вьrrе кают из уравнений массообмена (а по
существу - массопередачи), записанных для злементарной поверхности dP.
(10.22а)
dM = k,,лxdF , dM = kyЛydF .
Интегрирование по поверхности F при условии постоянства kx, ky дает (с ис
пользованием теоремы о среднем):
.

М = J kx ЛXdF = kx J ЛХ dF = kxF!!.xcp ;

аналогично:

F

F

М = f k y ЛydF = kyFЛycp .
F

Для определения ЛХср • ЛУср необходимо располагать законом
изменения сопряженных концентраций; иногда говорят определить геометрическое место точек этих концентраций .
Зависимость сопряженных концентраций у = ft.x) в рабочем
диапазоне их изменения носит название рабочей линии процес
са. Она выражает материальный баланс по потоку вещества
внутри массообменного аппарата (напомним, что балансовая ли
ния выражает МБ на концах последнего). В отличие от векторов
массопередачи и баланса рабочая линия направления не имеет.
Определение уравнений рабочих линий, их положения в
диаграмме у - х и построение для различных структурно
конфигурационных комплексов (СКК) и технологических си
туаций является предметом настоящего раздела.
1 0.7. 1 . Уравнения и положение рабочих линий

Рассмотрим пять наиболее простых вариантов оргdнизации
массообменного процесса в аппарате: прямоток фаз; противо
ток фаз (в обоих случаях подразумевается, что потоки движутся
в режиме Идеального вытеснения), Идеальное перемешивание
(ИП) только одной фазы - "у' или "х" ; ИП обеих фаз. Для опре793

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 10. 15. Рабочая линия в

- расчетная схема,
ди аrрамма у - х

случае
а

прямотока фаз:

б -

деленности примем, 'ПО
вещество переходпг из
т.е.
фазы 'У' в фазу
рабочая область процес
са - над линией равновесия.
D,у2
L.x2
х1
-Х1
х
Уравнение и поло6
а
жение рабочей линии
не связаны с формой
линии равновесия; поэтому будем рассматривать общий случай
кривой равновесной линии (разумеется, все выводы остаются
справедливыми и в случае линейного равновесия т = const) .
Для всех СКК вывод уравнений рабочих линий базируется
на материальном балансе, причем пространственный контур
ограничивается сечениями : с текущими значениями сопря
женных концентраций; с известными концентрациями на од
ном из кон цов аппарата.
Прямоток фаз . Расчетная схема показана на рис . 10. 1 5,а: оба
фазовых потока с известными концентрациями вещества У1 и
х1 входят в аппарат с одного конца и выходят с другого <.У2, х2).
При этом в процессах класса 3(2-2) 1 , как и для некоторых
друтих классов, потоЮI фаз D и L постоянны. Для установле
ния связи у = j(x) выделим контур, проходящий через началь
ное и произвольное сечения; в последнем текущие концентра
ции равны у и х. Запишем МБ по веществу (в отсутствие Ис
точников и Стоков, а также Накопления, поскольку процесс непрерывный):

"х",

+ Dy1 + Lx1

-

Dy - Lx = О , откуда у =

Dyl ;

Lxi

-

� х .( 1 0.23)

При постоянных D и L это уравнение прямой линии, обра
зующей с осью абсцисс угол о. , причем tgo. = - L/D (тангенс
дополнительного угла р = 7t - о. равен L/D). Легко убедиться ,
что прямая проходит через точку с координатами (у 1 , х1 ): по
ложив в ( 1 0 .23 ) х = х1 , получим у = Yl · Такой результат можно
бьmо предвидеть, поскольку в качестве концевого взято сече
ние контура, характеризуемое концентрациями У1 , х1 . Отрезок
прямой (см. рис . 1 0. 1 5,6) между точками (у1 , х1 ) и <.У2, х2 ) и но
сит название рабочей линии. Легко видеть, что в случае прямо
тока рабочая линия совпадает с балансовой. Рабочая линия не
может пересечь равновесную; в самой благоприятной ситуации

794

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

линия в случае
расчtтНая схема, 6, 11

Рис. 10. 16. Рабочая
а -

противотока фаз:

-

диаrраммы у

-

х

(бесконечно большая интенсивность массопереноса - kF -.+оо,
т.е. контакт фаз - идеальный) рабочая линия заканчивается на
линии равновесия, т.е. точка (yz, х2) расположена на ней.
Противоток фаз. Расчетная схема показана на р и с . 1 0 . 16 , а :
потоки фаз с известными концентрациями у1 и х1 входят в ап
парат с разных концов. При этом потоки D и L остаются по
стоянными в ходе массообмена. Для установления связи теку
щих сопряженных концентраций выделим, как и в случае пря
мотока, контур так, чтобы одно из ero сечений было произ
вольным, характеризуемым текущими концентрациями у и х. В
качестве второго выберем сечение, в котором известны обе кон
центрации - входная (она известна для любой из фаз) и вы
ходная (обычно задана для целевой фазы); на схеме это х1 и Уъ
т.е. верхнее сечение аппарата. Если была бы задана концентра
ция хъ а не Уъ то контур замкнули бы на нижнее сечение.
Для схемы на рис . 1 0 . 16 , а запишем МБ по веществу:

+Dy +Lx1 - DYl. -Lx = О , откуда у =

Dy2 D- Lxi + �D х .(1 0.24)

При постоянных D и L это уравнение прямой линии (см.
рис. 10. 16,б), проходящей через точку (она соответствует вы
бранному концевому сечению) с концентрациями (yz, х 1). Пря
мая наклонена к оси абсцисс под углом а., причем tga. = L/D.
Рабочая линия и в этом случае не может пересечь равновесную
(хотя балансовая линия - может, она в целях сопоставления
показана на рисунке тонким штрих-пунктиром). В предельном
гипотетическом случае (kF --+ оо) рабочая линия может закон
читься на кривой равновесия.
На рис . 10.16,в показано положение рабочей линии для про
тивоточноrо процесса при переносе вещества из фазы "х" в
фазу " у " .

795

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис.

10. 1 7. Рабочие линии в случае
идеальноrо перемешивания одной
или обеих фаз:

расчеmая схема, б
г
диа
а
граммы у
х для идеального переме
шивания фазы )>" (б), фазы 'х " (1r) и
обеих фаз (г)
-

-

-

-

х

Идеальное перемешива
ние одной или обеих фаз. На
рис. 1 0 . 17, а
представлена
расчетная схема для движе
ния фазы "у' ' в режиме
идеального перемешивания
а
(ИП), а фазы "х'' - в ре
жиме идеального вытесне
ния (ИВ). в ЭТОМ случае
(см. гл. 8) концентрация у
выровнена по всей поверх
ности контакта F и равна
концентрации
уходящего
компонента в этой фазе У2 ·
Следовательно,
рабочая
линия (жирная сплошная
пойдет
прямая)
(рис. 10. 17,6) по горизонта
ли У2 = const; она будет ограничена концентрациями х 1 и х2.
На рис. 10. 17,в изображена рабочая линия в случае И П потока
(жирная сruюшная линия): это вертикальный отрезок по
линии х2 = const, ограниченный концентрациями У1 и Yl ·
На рис . 10. 17,г представлена ситуация для И П обеих фаз . В
этом случае рабочая линия вырождается в точку с координата
ми (У2, х2) , поскольку вдоль всей поверхности массообмена
концентрации в фазах выровнены и равны соответствующим
выходным значениям х2 и У2·
Разумеется, и в этих случаях рабочие линии не могут пере
сечь равновесную (при И П обеих фаз рабочая точка не может
оказаться ниже линии равновесия для рассматриваемого на
правления переноса вещества) . Лишь в случае идеального кон 
такта
рабочая линия заканчивается (рабочая точ
ка при И П обеих фаз - располагается) на равновесной линии.
С понятием рабочих линий и идеального контакта фаз свя
зана концепция теоретической ступени (иногда говорят: теоре
тической тарелки) . Под теоретической ступенью понимается
контактное устройство, из которого потоки фаз уходят с равно
весными концентрациями. В случае прямотока, а также И П од
ной или обеих фаз это означает бесконечно интенсивный кон-

фазы "х"

фаз (kF -.. ао)

796

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

такт фаз в аппарате " , т.е. kF � оо, так что точка (уъ х2), соот
ветствующая уходящим концентрациям, лежит на линии рав
новесия . В случае противотока теоретическая ступень может
быть реализована и при конечном значении kF - этот случай
отвечает вектору баланса, заканчивающемуся на линии равно
весия . А при векторе баланса, пересекающем эту линию, оди
ночное противоточное массообменное устройство при доста
точно больших kF может оказаться даже эффективнее теорети
ческой ступени.
Из сопоставления рис. 10. 17,б-г с рис . 1 0 . 1 5, б и 10. 1 6,б мож
но видеть, что перемешивание потоков фаз смещает рабочую
линию ближе к линии равновесия. Этому сопуrствует пониже
ние движущей силы массообменноrо процесса, а значит (при
прочих равных условиях) уменьшение потока М переносимого
компонента; для сохранен ия М придется увеличивать интен
сивность массопереноса kF, например развивая поверхность
контакта F.
1 0.7.2. Построение рабочих линий
Будем и здесь анализировать процесс на примере переноса
вещества из фазы "у" в фазу "х" . Рабочая линия связывает 6
переменных: 2 потока (D и L) и 4 концентрации.
Если задано пять переменных из шести, то неизвестная ве
личина находится однозначно по уравнению материальною
баланса (10. 1 8) или по рабочей линии, а она полностью опре
делена уравнениями типа ( 10.23), (10.24).
Пусть, например, фазы в аппарате движутся противотоком, при этом заданы
потоки D, L и три концентрации: у1 , х1 и У2 · Недостающую концентрацию х2
найдем одним из следующих способов:
- из баланса ( 1 0 . 1 8);
- из уравнения ( 10.24), положив в нем у = У1;
- построением рабочей линии (рис. 10. 1 8,а): через точку (У2, х1 ) проведем
прямую под углом а так, чтобы tga = L/D, продолжим эту прямую до пересече
ния с горизонталью YI - абсцисса точки пересечения будет равна х2 .

Пять переменных мoryr быть заданы таким образом (рис .
что возможно осуществить процесс как с прямотоком
(отрезок /), так и с противотоком (//) фаз. В этом случае ба
лансовая линия, совпадающая с рабочей в случае прямотока, не
пересекает линию равновесия. Но переменные мoryr быть за
даны и таким образом, что балансовая линия пересекает рав
новесную. В этом случае осуществим только противоточный
процесс (как это показано на рис. 10.18,а) либо осуществление
процесса вообще невозможно (рис. 10. 1 8,в), поскольку задан 
ные условия проведения процесса несовместны.

10. 1 8,6),

• В случае периодического процесса

-

kFt

-... со

(см. разд. 10. 14).

797

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

а - определение ко1Ще1Праuии х2, б - осущесrвимосrь прямоточноrо (/) и ПJЮТИВ<ЛОЧ
ноrо (11) процессов, /1 - неосущесrвимосrь процесса

Рис. 10. 18. К построению рабочей линии при пяти известных переменных:

Если заданы четыре переменные и есть связывающее их
уравнение рабочей линии, то появляется одна степень сво
боды, и рабочая линия может быть построена по-разному. Что
бы построить конкретную рабочую линию, надо использовать
имеющуюся степень свободы - принять значение какой-либо
из неизвестных переменных. Это делается с помощью технико
экономическоrо расчета (ТЭР).
ТЭР чаще всего заключается в определении каnкrал•нwх 381]1&Т (точнее амортизационных расходов) и эксмуатациоJОtwх 381)18Т (прежде всего - энерге
тических). Первые обычно возрастают с ростом поверхности контакта F, а вто
рые - с увеличением потоков фаз. При этом возрастанию F при прочих равных
ус.ловнях сопутствует, как правило, уменьшение эксплуатационных затрат. Такой
характер изменения этих двух видов затрат обус.ловливает экстремальное изме 
нение суммарнwх 381]18Т с изменением поверхности контакта или фазовых пото
ков. Поскольку безrр аничному увеличению F либо L(D) отвечают бесконечно
большие затраты, то экстремум яаляется минимумом при некотором определен
ном значении F или потоков L, D. Задача ТЭР состоит в определении оптималь
ного значения F или L (либо D), отвечающего минимуму суммарных затрат.
Такого рода оптимизация бьта продемонстрирована в разд . 2.3.2 (см. рис. 2. 19)
на примере наивыгоднейшего диаметра трубопровода. Более конкретное воruю
щение анализ на оптимальные характеристики процесса наЙдет при изучении
ряда отдельных технологических приемов.

Рассмотрим некоторые из типовых ситуаций .
Прямоток. Пусть заданы потоки D, L и входные концентра
ции у 1 , х1 - типичная задача эксплуатации. Тогда известны
точка исходных сопряженных концентраций (см. рис . 10. 1 9 , а) и
наклон рабочей линии (по величине отношения L/D). Однако
где заканчивается рабочая линия - неизвестно.
Определим сначала предельные варианты . Если поверхность
контакта фаз kF -+ О, то массообмена не происходит, и рабочая
линия вырождается в точку с координатами У1 , х1 ; иначе: У2 =
= у 1 , х2 = х1 • Если наоборот - kF -+ оо, то будет теоретическая
ступень: рабочая линия доходит до равновесной, т.е. точка с
координатами Уъ х2 лежит на кривой равновесия. Положение
конечной точки (У2, х2) рабочей линии в реальной ситуации О <

798

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

r.� ����
Xi

а

х

б

х

х,

в

х

Рис. 10. 19. Семейства рабочих линий в случае прямотока фаз (условия процесса

см. в тексте)

< kF < оо зависит от конкретной величины kxF, kyF (смотря по
какой фазе ведется расчет). В результате получается семейство
рабочих линий - отрезки разной длины, выходящие из точки
(у1 , х1 ) под одним и тем же углом � · При известном · коли 
честве перенесенного вещества М с помощью (10 . 1 8)
отыскиваются У2 и х2 , т.е. конечная точка рабочей линии.
Пусть теперь заданы потоки фаз, а также входная и выход
н ая концентрации вещества в одной из них, скажем у1 и У2 (см.
рис. 10. 19,6). Это одна из задач проектирования. Здесь известен
наклон рабочей линии (по отношению L/D) и границы изме
нения концентраций фазы "у'' . Семейство рабочих линий
представлено параллельными отрезками между горизонталями
у1 и У2· При этом крайнему левому положению отвечает чистая
фаза "х" на входе в аппарат (х1 = О), а крайнему правому равновесие выходных потоков: точка (.У2, х2) на линии равнове
сия, что могло бы быть достиmуто при kF � оо.
Пусть, наконец, известен поток фазы (например, D) и кон
центрации у 1 , х1 и У2
тоже задача проектирования, именно
она встречается чаще всеrо. Тогда в диаграмме у - х (рис.
10.1 9,в) задана точка входных (сопряженных) концентраций (у 1 ,
х1 ) и уровень выходной концентрации у2 . Семейство рабочих
линий будет представлено веером, расходящимся из точки (у1 ,
х1 ). Крайнее левое (вертикальное) положение рабочей линии
отвечает бесконечному потоку L (tga. = L/D � оо, а. � 7t/4): при
бесконечном потоке фазы изменение концентрации в ней в
ходе массообмена не ощущается, так что х2 = Х1 . Крайнее пра
вое положение харакrеризуется конечной точкой на линии равно
весия: здесь при необходимости выдержать заданное значение У2
поток фазы L - минимален; естественно, еще и kF � оо.
Конкретное (в том числе - оптимальное) положение рабо
чей линии в рассматриваемых случаях определяется выбором F
(строже kF) и (или) L либо D.
-

-

• О подходе

к

расчету М в рассматриваемом случае см. разд. 10.9.2.

799

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

у

У,

У,

IY2

а

{Х2 Х

�1

�

У2

у

б

1
1

{Х2 Х

У,

2

у
у

в

{Х2 Х

;,ос
У2

1
1

Х1 {Х2 )

г

Х

Рис. 10. 20. Семейства рабочих линий в случае противотока фаз (условия процес
са см. в тексте)

Противоток. Пусть, как и в случае прямотока, заданы пото
ки D, L и начальные концентрации в них у 1 , х1 - типичная
задача эксплуатации. Однако здесь не задана ни одна из со
пряженных точек, известны лишь (рис. 10.20,а) вертикальная
(х1 ) и горизонтальная (у1 ) границы рабочей линии и ее наклон
(tga. = L/ D) .
В предельной ситуации kF = О рабочая линия
тоже вырождается в точку (у1 , х1 ), посколь i<у массопереноса не
происходпг и х2 = х1 , У2 = у1 . J В противоположно й ситуации kF �
� оо, и точка на одном из концов массообменного аппарата (у2 ,
х1 ) либо (у1 , х2 ) должна находиться на линии равновесия; в
рассматриваемом на рис. 10.20,а примере это вторая из на
званных выше точек. Семейство рабочих линий - паралл е ль
ные отрезки, ограниченные упомянутыми выше линиями Yt =
= const и х 1 = const. Конкретное положение рабочей линии
здесь также определяется величиной kyF или kxF (в зависимос
ти от того, по какой фазе ведется расчет). При известном * по
токе вещества М с помощью (10. 1 8) отыскивают У2 и х2, т.е.
концевые точки рабочей линии.
Пусть теперь заданы D, L и концентрации целевого потока
у1 и У2 - одна из задач проектирования. Семейство рабочих
линий будет представлено также паралл ельными отрезками с
известным углом наклона а. к оси абсцисс (tga. = L/D), заклю
ченными между горизонталями у1 и У2 (рис. 1 0.20,6). Семейство
ограничено слева линией, отвечающей чистой нецелевой фазе
(х1 = О), а справа - отрезком, один конец которого находится
на линии равновесия (случай kF � оо) . Какой из концов рабо
чей линии попадет на равновесную, зависит от конфигурации
последней и наклона рабочей линии.
Пусть, наконец, известны поток целевой фазы (например,
D) и концентрации у 1 , х1 и У2 - наиболее часто встречающаяся
проектная задача. Тогда заданы точка (У2 , х1 ) и уровень входной
концентрации у1 • Семейством рабочих линий (см. рис. 10.20,в)
• О подходе к расчету М в рассматриваемом случае см. разд. 10.9.2.

800

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

будет веер , расходящийся из заданной точки. Крайнее левое
положение займет вертикаль, отвечающая бесконечному потоку
второй фазы L � оо, иначе : L/D � оо, так что а. = тт/4. Крайнее
правое положен ие займет отрезок, оканчивающийся в точке
пересечен ия горизонтали у 1 с линией равновесия; для этой
ситуации характерно kF � оо. Важно , что такое положение ра
бочей линии отвечает наименьшему возможному углу, значит и
минимальному потоку L; при меньшем потоке в заданных усло
виях понижение у в диапазоне от у 1 до У2 невозможно. На
практике не исключена такая конфиrурация кривой равнове
сия, при которой минимальный поток L определяется не точ
кой пересечения, а точкой касания рабочей линии к кривой
равновесия (рис. 10.20,г) ; разумеется, в таком случае условие
kF � оо относится к этой точке касания .
Оптимальное положение рабочей линии в рассматриваемых
случаях определяется выбором F (точнее - kF) или L (либо D)
на основе ТЭР.
Аналогичным образом мoryr быть проанализированы другие
ситуации: с противоположным направлен ием переноса вещест
ва; с перемешиванием одной или обеих фаз; с иными из
вестными переменными - потоками и концентрациями.

10.7.3. Рабочие линии

в

некоторых специфических случаях

На практике приходится встречаться с ситуациями , когда
часть потока одной из фаз (иногда - обеих фаз) движетс я вне
аппарата без контакта с другой фазой . В тех случаях, когда
часть фазового потока, выходящего из аппарата, возвращается и
присоединяется к входному потоку этой фазы, говорят о ре1щкле
(рис. 10.2 1 ,а). Если же часть исходного потока фазы минует аппа
рат и присоединяется далее к уходящему из него потоку этой
фазы, то говорят о байпасе (см. рис . 10.22,а) . Рассмотрим пооче
редно трансформацию рабочих линий при наложении на процесс
рецикла и байпаса на примере противотока фаз.
Пусть в отсутствие рецикла рабочая линия занимает (рис .
10.2 1 , 6) положение 1. Осуществим рецикл фазы "х'', причем
исходн ые кон центрации обеих фаз у 1 и х 1 остаются неизмен
ными, выходные У2 и х2 (качество продуктов!) - тоже . Однако
возврат некоторого количества Lц фазы с кон центрацией х2 и
его присоединение к исходному потоку L с концентрацией Х 1
приведет к изменению концентрации вещества на входе в ап 
парат до величины х( Эта входная концентрация определится
по прав илу рычага: смешиваются пото ки L со става х 1 и Li1 со
става х2 . Заметим , что операция смешения происходит здесь в
пределах фазы "х", т.е. не на концентрацион ном уровне У2. а
801

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

D. y2

х1' L , x 1

Рис. 10. 21. Рецикл фазы (а
схема процесса, б рабочие
линии)

у

-

-

У1

на оси абсцисс. Рабочая
линия при сохранении
Lц
х2 и наличии рецикла
займет положение 2,
т.е.
пойдет круче, под
f
х
большим углом к оси
Х2 L
D,y1
абсцисс. Это полностью
а
соответствует уравнениям рабочих линий: в
tga2 = (L +
отсуrствие рецикла tg<ч = L/D, в присугствии
+ Lц)/D. Из рис. 10.2 1 ,б ясно, что доля потока, возвращаемого
на рецикл, ограничена предельным значением концентрации
х1 ' , получающимся при смешении свежего и возвращаемого
потоков: точка сопряженных концентраций 6'2, х1') не может
оказаться правее (ниже) линии равновесия.
Аналоmчный подход позволяет проанализировать транс
формацию рабочей линии при рецикле другой фазы, а также
обеих фаз.
Существенно, что рецикл приближает рабочую линию к рав
новесной кривой, т.е. сопровождается понижением движущей
силы массообменного процесса - значит, и интенсивности
процесса в целом. А чтобы в условиях рецикла сохранить эф
фективность процесса (т.е. необходимое значение выходной
концентрации У2), придется увеличивать поверхность контакта
фаз (например, пугем увеличения габаритов аппарата) . И тем
не менее возможны технологические ситуации, когда рецикл
целесообразен . Чаще всего это связано с плохим межфазным
контактом при малых потоках одной из фаз или обеих фаз :
плохая смачиваемость жидкостью насадки в насадочном или
стенки в пленочном аппарате, вь1сокая поперечная нерав
номерность потока в барботажном аппарате и т.п. Рецикл спо
-

·

с обствует п о в ы ш е н и ю и н те н с и в н о с т и м ас с ообм е н а и п о в е р.х н о с -

ти ко н т а кта ф а з . Н е р ед ко с п о м о щ ь ю р е u и кл а удаетс я с н и з и т ь
температурный перепад вдоль аппарата и приблизиться к изо
термическому проведению процесса, что может положительно
сказаться на его селективности. В общем, при организации
рецикла необходимо сопоставить его положительное и отрица
тельное влияние на процесс и оценить эффект в целом. В тер
минах структуры потоков рецикл представляет собой одно из
проявлений обратного перемешивани я (не распределенно го по
длине аппарата, а сосредоточенного ).

802

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

D . y2

L, x 1
Lб

D, y

Рис.

l

xi_
а

L , x2

у

У1

у�
У2

о

х,

х1

б

Х2

xi х

10.22. Байпас фазы (а - схема процесса, б - рабочие линии)

Пусть в отсутствие байпаса рабочая линия занимает
(рис . 1 0.22,6) положение J: выходные концентрации равны х2 и
У2· Примем: часть L6 исходного потока фазы "х" идет мимо
массообменноrо аппарата. Байпасный поток L6 (концентрация
х 1 ) и поЮtдающий аппарат L - Lб (концентрация х2' ) смеши
ваются. Получается поток L с концентрацией х2" на выходе из
системы. При этом х2" определяется по правилу рычага.
Рабочая линия 2 процесса с байпасом проходит с меньшим
(чем без байпаса) углом наклона к оси абсцисс, поскольку (L - Lб)/D < L/D. Эта линия, как и раньше, ограничена вертика
лью х1 и горизонталью у1 . Но уменьшение потока фазы "х" в ап
парате сопровождается, согласно материальному балансу типа
( 1 0 . 1 8), уменьшением потока переданного вещества М, так как
(см. рис. 1 0.22, 6) повышается выходная концентрация фазы
"у" и пон ижается фазы "х": У2' > J12 ; х2" < х . Иначе: при появ
лении байп:�са ухудшаюгся результаты массообменноrо процесса.
В отличие от рецикла байпас в подавляющем большинстве
случаев не используется технологами для управления процес
сом, а возникает внутри (весьма редко - снаружи) аппарата
самопроизвольно. Причина - крайняя степень поперечной
неравномерности потока, появление преимущественных зон
движения отдельных фаз; это и есть байпас с нарушением
межфазного контакта, уменьшением реальной ("активной")
поверхности массопереноса F.
Аналоmчный подход позволяет проанализировать транс
формацию рабочей линии при байпасе другой фазы или обеих
фаз. Качественно модель байпаса (в ее простейшей или более
сложных модификациях) затронута в главе 8 .
Построение рабочих линий 2 в случае рецикла и байпаса является в некото
ром аспекте формальной операцией: внешний (относительно аппарата) поток
совместно с внуrренним траК'I)'ется как целиком внутренний относительно си
стемы "аппарат - рецик.л (или байпас)".

803

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 10. 23. Отвод части пото

ка одной из фаз из промежу
точного сечения аппарата (а
- схема процесса, б - рабо
чие линии)

Самостоятельный
интерес представляет
рабочих
построение
линий для процессов с
отводом или подводом
6
а
потока
какой-нибудь
фазы в произвольное
сечение аппарата. Про
стейшие примеры такой ситуации рассмотрены ниже.
Пусть из промежуrочноrо сечения массообменного аппарата
отводится (рис . 1 0 .23 ,а) часть потока L* фазы "х" ; концентра
ция вещества в этом сечении равна х* . Очевидно, для рабочих
линий на участках аппарата до и после отвода L* характерны
разные углы наклона (см. рис. 10.23 ,6): больший с ч - соответ
ственно отношению L/D для верхней части аппарата до отвода
(это нижняя часть диаграммы у - х); меньший а.2 - соответ
ственно (L - L* )/D для нижней части аппарата после отвода L*
(это верхняя часть диаграммы). Сечению отвода L* на диа
грамме отвечает излом рабочей линии , но не разрыв, так как
потоки - приходящий в это сечение и уходящий из него, как
и отводимый здесь из аппарата, - имеют одинаковую кон
центрацию х* .
Пусть теперь поток L* фазы " " с концентрацией х· подается
в некоторое промежуrочное сечение аппарата (рис. 10.24,а).
Здесь возможны два случая : в сечении аппарата та же кон
центрация Х • , что и в подводимом потоке (х" ); в сечении иная
концентрация, Х • * х· .
В первом случае (рис . 1 0 .24,6) подход к построению рабочей
линии тот же, что и при отводе части фазы из аппарата. До
точки подвода (верхней части аппарата отвечает отрезок рабо
чей линии АВ на нижней диаграмме у
х) наклон рабочей
линии соответствует отношению L/D (это меньший угол а.1 );
после этой точки рабочая линия (отрезок ВС) пойдет под боль
шим углом а.2 - соответственно увеличившейся величине дроби
(L + L*)/D.
Абсцисса точки излома В характеризуется кон
центрацией х• = Х • = х� .
Во втором случае (рис. 10.24,в) остаются справедливыми все
рассуждения относительно наклонов рабочих линий - отрезки
АВ и CD. Однако х" * Х • , поэтому в сечении подпитки потоком
L" наблюдается разрыв ВС рабочих линий - он отвечает сме804

х

-

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

у
х.

б
Рис. 10. 24. Подвод дополнительного потока одной из фаз в промежуrочное
сечение аппарата (а - схема процесса, б, в - рабочие линии)

шению (по правилу рычага) потоков фазы ".х": L и L* . При
этом концентрации .х. и .х• являются сопряженными с одной
и той же промежуrочной концентрацией вещества в фазе "у" в
сечении дополнительного питания.
Концентрация вещества в дополнительном потоке (.х* ) мо
жет оказаться весьма высокой, и тогда при достаточно больших
значениях L* (точнее - отношения L*/L) точка смеси может
оказаться правее (ниже) линии равновесия . Принятое направ
ление массопереноса (напомним: рассматривается перенос ве
щества из фазы "у" в фазу "х'' ) запрещает такое положение
рабочей линии.
Аналогичный подход позволяет установить положения рабо
чих линий для различных технологических ситуаций: отвод или
подвод в промежуrочное сечение аппарата фазы "у" или обеих
фаз; отвод или дополнительное питание какой-либо из фаз в
нескольких точках; те же ситуации, но при переносе вещества
из фазы "х'' в фазу "у" и т. д.
Отвод части потока фазы из промежуrочного сечения или
подвод фазы в такое сечение может трактоваться как простей
ший вариант разделения одного аппарата на два, для каждого
из которых характерно свое соотношение фазовых потоков. В
этом аспекте рассмотренные выше ситуации являются переход
ными от работы одного аппарата к работе сетей, рассмотрен
ных в разд. 10. 1 1-10.13.
СРЕДНЯЯ ДВИЖУЩАЯ СИЛА
ДЛЯ ПРОЦЕССОВ КЛАССА 3(2-2) 1

10.8.

Проблема заключается в определении средней (по поверх
ности массообмена) движущей силы Лер (иначе - среднего
концентрационного напора) в проектных стационарных задачах

805

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

массообмена. Это возможно сделать, поскольку в задачах про
ектирования заданы: поток целевой фазы, поток второй фазы
(известен или найден с помощью ТЭ Р), входные концентрации
вещества в обеих фазах и выходная концентрация в целевой
фазе; тогда недостающая концентрация определяется из
( 10. 1 8), а при известных входных и выходных концентрациях и
равновесной зависимости, заданной аналитичесЮf или графи
чесЮt, можно определить и среднюю движущую силу.
Общий подход к расчету Лер аналогичен продемонстриро
ванному для теплообмена (разд.7.6), однако есть и некоторые
отличия. Во-первых, "линия равновесия" в диаграмме Т t
прямая ( Т = f), она выходит из начала координат и идет под
углом 45°; здесь Лtер выражается аналитичесЮf как среднелога
рифмическая величина. В случае массообмена равновесная
линия может быть прямой (тогда также возможен аналитиче
сЮtй расчет) и кривой - это более общий случай, здесь прихо
дится искать иные методы определения Лер · Во-вторых, в слу
чае теплообмена анализ ведется на единственном языке - в
терминах температур. В массообмене анализ, а значит и выра
жение Лер • возможен на языке любой из фаз - "у" или "х" .
Если рассмотрение ЮtнетиЮt позволяет установить, в какой из
фаз массообмен протекает медленнее, то анализ предпочтитель
нее вести на языке этой фазы. Это особенно существенно в
случае кривой линии равновесия: в пограничной пленке упомяну
той фазы сосредоточена основная доля концентрационного напо
ра; кроме того, в ряде случаев удается избежать сложностей, свя
занных с переменным коэффициентом распределения т.
Определение средней движущей силы ниже рассматривается
для стационарных процессов массопереноса применительно к
различным структурно-конфигурационным комплексам. В этих
разделах анализ ведется на языке фазы "х" на примере перено
са вещества из этой фазы в фазу "у" (рабочая область процесса
- под линией равновесия) .
-

-

10.8. 1 . Идеальное перемешивание обеих фаз

На рис. 10.25,а представлена схема массообменного процес
са с И П обеих фаз (место ввода и вывода потоков здесь роли
не играет), на рис . 10.25,б - диаграммы у - х: штриховые ли
нии - векторы массопередачи, штрих-пунктирные - векторы
баланса. Диаграмма 1 иллюстрирует общий случай: линия рав
новесия - кривая. Точка А(у1 , х 1 ) отвечает входным (сопря 
женным) концентрациям потоков; точка В - рабочая точка
процесса; АВ - вектор баланса (строже здесь следовало бы
говорить не об отрезке АВ, а о его крайних точках А и В);

8 06

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

а

б

Рис. 1 0. 25. К расчету движущей силы массообмена при идеальном перемешива
нии обеих фаз:

расчетная схема, б - диаrрамма у - х;
общий случай: смешанная :�адача массоперсноса; 11 - поверхностная задача; IП потоковая задача; IV - смешанная задача массопереноса при L --. ао; V - то же при D --. оо
а -

1

ВС - векrор массопередачи. Соответственно ( 1 0 . 1 6) tgcp =
Рх/Ру, соответственно ( 1 0. 1 8а) tg'I' = L/D. ПодчерJQfем, что
вдоль всей массообменной поверхности концентрации вещест
ва в каждой из фаз постоянны (ИП!) и равны выходным х2 и
У2 · Значит, и полная средняя движущая сила равна выходному
концентрационному напору дхср = лх2 = х2 - х2Р , где х2Р рав
новесно с У2· Аналогичным образом определится и ЛУср ·
В частном случае, когда пропускная способность поверх
ностной стадии массообмена значительно больше, нежели по
токовых (kxF >> L, kyF >> D), точка В будет находиться на ли
нии равновесия: х2 = XiJ = х2Р , У2 = Уп = У2Р - диаграмма 1 1 ,
поверхностный перенос уже не контролирует процесс - задача
становится потоковой. В этом случае массообмен теряет кине
тический харакrер и в определении движущей силы нет необ
ходимости (очевидно, ЛХср = О).
В обратном (тоже частном) случае, когда лимиrирует поверх
ностная пропускная способность (kxF < < L, kyF < < D), задача яв 
ляется поверхностной. Здесь вследствие больших потоков фаз из
менение концентраций в них становится малозначимым: х2 =
= х1 , У2 = у1 - диаграмма 111 . В этом . случае ЛХср = х1 - х1 Р .
Если доминирует поток одной из фаз (например , L >> D),
то диаграмма 1 для общего случая трансформируется в диа
грамму IV: точки А и В будут на одной вертикали, х2 = х1 , так
что ЛХср = х1 - х2Р . А если, наоборот, L << D, то точки А и В
будут на одной горизонтали (диаграмма V), и ЛХср выражается
общей формулой: ЛХср = х2 - х1 Р .
=

807

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

1 0.8.2. Прямоточное движение фаз в режиме И В
Расчетная схема процесса приведена на рис. 10.26,а, где
принято направление координат
х, у) снизу вверх. Рабочая
(она же - балансовая) линия прямоточного процесса и пере
мещение векrора массопередачи в ходе этого процесса показа
ны на рис. 10.26,б. Там же обозначена движущая сила лх = х - х Р для промежуточного сечения аппарата. Применительно к
бесконечно малой поверхности dF (контур к1 на вuде а) мате
риальный баланс по веществу для фазы "х" имеет вuд
(а)
La - dM - L(x + dx) = O и dM = - Ldx.
Для зоны движения фазы "х" в целом (контур К 1 на вuде а)
Lx1 - М Lx1 = О и М = L(x1 - х2).
(б)
Материальные балансы по фазе "у " , записанные для эле
ментарного контура к2 (пунпир) и зоны движения этой фазы в
целом (контур К2), имеют В Ид
(в)
Dy + dM - D(y + dy) = О и dM = Dy,
(г)
Dyl + М - DYl = О и М = D<Yl - У1 ).
Кроме того, надо заrшсатъ уравнение массопередачи для эле
ментарной dF и полной поверхности межфазного контакта:
(д)
dM =kx dFЛX и М =
причем лх = х - хР.
Таюtм образом,
dM = - Ldx = Ddy = kx (x - xP )dF,
(е)
D<Y-2
(ж)
L(x1
)
=
=
х2) =
М
- У1
Поделим по отдельности фрагменты равенств (е) и (ж) для
имеем
и
после сокращений (соответственно на L, D и
(с учетом знака)
dx
dy _ - х Р dF
(з)

(F,

-

F

kxFЛXcp•

-

dF F;

k;кЛхсрF.

(х

kx)

)

- ЛХ.ср F
Способ определения движущей силы на основе выражения
Х2

=

Х1

У2 - У1

(з) зависит от формы равновесной линии.
Прямая линия равновесия . Здесь дальнейший анализ сходен с
рассмотренным в разд. 7.7.2 для теплопереноса. Надо только
последовательно вести его на языке одной из фаз. В этих целях
выразим концентрации фазы "у", входящие в равенство (з),
через концентрации фазы "х" : у = тхР , У2 = mx2P , У1 = mx1P
Тогда равенство (з) перепишется (с учетом сокращения на m):
d.x

х 2 - х1

808

.

xr - Xf

---

=

(х - xP)dF
ЛХ ср F

=r ·

(и)

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

L, X 2

D , y2

К1

К2
y + dy
dM
К2
F
dF
о

x+dx
к,

х- хР

1

У2

У,
L, x 1

а

в

- расчеrnая схема, б - днаrрамма у - х, s - к определеЮIЮ ЧЕП; К1 и К2, к1 и к2 -

Рис. 10.26. К
а

у

расчету движущей силы массообмена при прямотоке фаз:

ошуры
Используем один из рассмотренных в главе 7 способов ре
шения . Введем для обозначения отношений символ у; тогда
d.x = у(х2 - х 1 ), dxP = у(х2Р - х1 Р) ;
(к)
d.x - dxP = d(x - хР) = у[(х2 - х1 ) - (х2Р - х1 Р)] .
Группируем слагаемые в квадратной скобке, выражая
концентрационные напоры во входном и выходном сечениях:
х, - х1Р = лх, , х2 - х2Р = лх2 . Запишем теперь значение у = d(x - х Р)/(ЛХ2 - лх1 ) и приравняем ero последнему слагаемому в
(и). После разделения переменных и интегрирования имеем
x2 - xr �f x - х Р
лх - лх F
х2 - хР2
лх 2
1 f
1 F (л )
2
- лх
.
dF и ln
f \
ЛХср F о
ЛХср F
х - хР
xi - xr
х1 - xf

к

)

=

=

Сокращая на F и меняя местами разности концентраций ,
чтобы иметь дело с положительными величинами (при прямо
токе лх1 > лх2 ), получим в более лаконичной записи
ЛХ 1 - ЛХ2
( 10.26х)

д.Хср - l n(ЛХ / ЛХ .
1
2)
_

Таким образом, средняя движущая сила массоперевоса в слу
чае прямой линии равновесия рассчитывается как среднелоrа
рифмическая величина из входного и выходного концентраци
онных напоров ЛХ 1 и ЛХ2 .
Кривая равновесная лини.я. В этом общем случае связать у и х
простым соотношением не удается, поэтому фрагмент dy/(.Yl - у1 ) из последующего анализа исключают. В оставшемся ра
венстве (и) разделим переменные и. · проинтегрируем по всей
809

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

поверхности F:

d.x
f -- =

Х2

х1 х - х Р

F

Х2 - Х 1

ИЛИ

f dF

Fо

ЛХср

ЛХср

=

Х 1 - Х2

7�-

(м)

Х2 Х - х Р

Изменение пределов интегрирования и знака разности (х2 - х1 ) вызвано желанием видеть в числителе и знаменателе по

ложительные величины.
Из (м) следует, что интеграл
Int

=

d.x

Х1

f

х2

Х1 - Х2

ЛХср

х - хР

Но согласно (з), (х1 - х2)/ЛХср

= kxF/L - справа стоит от
ношение пропускных способностей поверхностной и потоковой
стадий по фазе "х". Это отношение в теплопереносе (разд .

7.7. 1) для отдельного теплоносителя было обозначено симво
лом а, сохраним здесь это обозначение. Его называют (см .
разд. 10.6.3) числом единиц переноса Ч ЕП ( в данном случае по фазе "х" ) и в учебной и научной литературе обозначают еще
Для расчета а ==
в случае кривой равновесной линии на
ходят значение интеграла Int - графичесЮ1 (см . рис . 1 0.26,в)
или численными методами. Разумеется, при переносе вещества
из фазы "у" в фазу "х" тоже удобно оперировать положитель
ными значениями числителя и знаменателя, поэтому здесь
=

Sx

Sx.

=

Х2

d.x

Sx

f -X1 х Р - Х

TaIOIM образом, в общем случае (кривая линия равновесия,
т = var) среднюю движущую силу определяют из соотношения

- Х2 .
ДХСр = Xt S
x

(J0.27x)

Разумеется, при линейной связи равновесных у и х величину
Int =
можно найти аналитичесЮ1; в результате получится
среднелоп1рифмическая величина ЛХср по ( \ 0.26 х).
Аналогичные преобразования могут быть выполнены на
языке фазы " у" . Для прямой линии равновесия также получает
ся среднелоrарифмическая движущая сила:

Sx

Л�ер

=

ЛУ1 - ЛУ2
ln( ЛУ1 /ЛУ2) '

(10.26у)

для криволинейной равновесной зависимости

ЛУср

810

=

У2

-

Sy

Yi

(10.2 7у)

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

При этом в случае переноса вещества из фазы "х" в фазу
У2 dy
, при обратном на"у" Ч Е П вычисляется как Sy = f
У1

У1

правлении переноса Sy = f

dy

уР

-

У

а в числителе выражения

уР
типа (10.2 7у) будет разность (у1 - У2). Физический смысл Sy : Ь
(см. разд. 7.7. 1 ) определится как отношение пропускных спо
собностей стадий массопереноса :р терминах фазы "у": Sy = Ь =
У2 У

-

= kyF/D.
1 0.8.3. Противоточное движение фаз в режиме И В
Расчетная схема процесса приведена н а рис. 10.27,а; на
правление отсчета координат (F, х, у) принято снизу вверх.
Рабочая линия и перемещающиеся в ходе массообмена векторы
массопередачи показаны на рис. 10.27,б. Для бесконечно малой
dF и полной F поверхности контакта (контуры к1 и К 1 ) мате
риальные балансы по веществу для фазы "х' записываются так
же, как для прямотока; результат - тот же:
(б)
dM = - Ldx (а); М = L(x1 х2).
По фазе "у" есть отличие (при сохранении подхода), по
скольку здесь - противоположное направление потока относи
тельно принятой системы отсчета. Для контура к2
(элементарная поверхность d.F)
(н)
+ D(y + dy) + dM - Dy = О и dM = - Ddy.
-

расчетная схема, б - диаграмма у

Ри с . 1 0. 2 7. К
а

-

кокrуры

расчету движущей силы массообмена при противотоке фаз:
-

х, в

-

к определению Ч Е П ; К1 и К2 , к 1 и к2

-

81 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Для зоны движения фазы "у' ' в целом (контур
баланса сохраняется; результат:
М=

К2)

запись

D<Yl - У1).

(г)
Уравнения массопередачи и массообмена (е) также сохра
няют свой вид. Таким образом, для dF и имеем
(о)
Ldx = -Ddy = kx (x - xP )dF
и аналогично прямотоку
(ж)
=
М = L(
=
Поделим по отдельности фрагменты равенств (о) и (ж); пос
получаем (с уче
ле сокращений (соответственно на L, D и
том знаков)
P F
dy
dx
(п)
Х2
ЛХср F

dM =
x1 - х2)

F

-

-

D(y2 - У1) kxЛxcpF.
kx)
(х - x )d
Х1 У1 - У2

Далее анализ ведется по той же канве, 'ПО и для противотока.
Прямая линия равновесия. При т = const концентрации
фазы "у" выражаются : у =
Тогда
у =
У2
равенства (п) после сокращения на т примут вид
dx

Х2 - Х\

тхР, 1 тх1Р,
(х - xP)dF
ЛХср F
Xf - xf

= тх2Р.

(р)

Воспользуемся далее (для разнообразия) методом производ
ных пропорций (см. разд. 7.6.2):

(х - х Р �F
(х2 - х1 ) - (xf - xr ) ЛХср F
dx - dx P

--

Объединяем сумму дифференциалов (числитель в левой час
ти) в дифференциал суммы; группируем знаменатель, вычленяя
в нем концевые движущие силы - они формируются иначе,
Тогда
=
=
нежели в прямотоке:
и

ЛХ1 х1 - х2Р ЛХ2 х2 - х1 Р .
х - х Р �р
хР )
(х2 - ) - {х1 - х� ) - ЛХср F

d{x (
xf
d(x - х Р ) = ЛХ2 ЛХ1 J
_

После разделения переменных и интегрирования:
хг хf
F
dF и
J
О
хг хf
_

х - хР

812

ЛХср F

(с)

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

=

{х2 - xf ) - (x1

F,
ЛХср - 1nЛХ2
( -/ЛХ1 )
ЛХ2 ЛХ1

-

ЛХср F

получим выражения для
Сократив на
вотока (в зависимости от того , что больше
_

или

х�

)F.

(т)

-ЛХсЛХ1р или ЛХ2) :

в случае проти

1 -/ЛХ2 ) .
ЛХср - lnЛХ(ЛХ1
ЛХ2
_

( 10.28х)

Таким образом, и при противотоке среДНJ1я движущая сила в
случае прямой линии равновесия рассчитывается как среднело
rарифмическая величина из концентрационных напоров на кон
цах аппарата.
В случае т = const при противоrо ке фаз возможна СИ'l)'ация лх1 = ЛХ2
(равновесная
и рабочая линии параллельны). Тогда выражение (10. 2 8х) дает
неопределенность. Ее раскрывают по правилу Лопиталя либо введя параметр &
. Тогда ( 1 0. 2 8х) можно переписать в виде ЛХср = &ЛХ2 ;1n( I + &) .
- ЛХ2в)/ЛХ2рассматриваемой
Очевидно,
СИ'l)'ации О . Разлагая ln в степенной ряд и
ограничиваясь
вследствие
& < < 1) первым членом разложения ln ( l + &)
(
получаем
- ЛХ1 - ЛХ2 - &ЛХ2 ЛХср (10. 2 8а)
ЛХср = ЛХ2 = ЛХ1 ЛХ.
ln (ЛXi /ЛX2 ) & - ....2.

= (ЛХ1

&

А�

=

-+

"' & ,

И

=

Кривая линия равновесия. В этом общем случае концентра
ции у и х не удается связать простыми соотношениями, по
скольку т = var. Поэтому, как и для прямотока, анализ ведут,
исключая из рассмотрения в (п) отношение
)2). В
оставшемся равенстве разделим переменные и проинтегрируем
по всей поверхности (с учетом того, что по условию
>
поскольку вещество по кидает фазу
dx
dx
'
И
=
= - Х1
= Х1

dy/(y1

F

"х" ) :

- Х2 F
7
Х2 JdF jl
х1 х - х Р ЛХср F о
х1 х - х Р ЛХср F
= Х 1 - Х2
Х\

dx

�I x - x P

-

х1 х2 ,

ЛХср

(у)

--

Согласно (у) интеграл в знаменателе
Х\
dx
ХI Х
Int = I

-2
ЛХ
Р
ср
х1 х - х
Но из (ж) следует, что (х1 - х2)/ЛХср = kxF/L . Это отношение
пропускных способностей стадий - поверхностной и потоковой
по фазе "х", - как уже указывалось, именуется числом единиц
813

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

переноса ЧЕП и обозначается: в учебнике а, в отечественной
литературе обычно
Способ определения Sx = а ясен из рис .
10.27,в. С этой символикой средняя движущая сила для общего
случая т = var запишется:

Sx.

- Х1 - Х2
ЛХср
S

(10.29х)

-

х

Разумеется, при т = const выражение для I nt = Sx можно
найти аналитически; в результате придем к среднелогарифми
ческой величине дХср по ( 10.28х).
Аналогичные преобразования мoryr быть выполнены на
языке фазы "у" . В результате получатся среднелоrарифмическая
движущая сила в случае прямой линии равновесия:
д 11
=
J CP

Лу 1 - Лу 2
l n (ЛУ1 / ЛУ2 )

д 11

J CP

или

=

ЛУ2 - ЛУ1
l n (ЛУ2 / ЛУ1 )

( 1 0 . 2 Sy)

и выражение, подобное ( 1 0.27у), в случае кривой равновесной
линии:

ЛУср

=

У2 - У1

( 1 0.29у)

Sy

При этом для переноса вещества из фазы "х" в фазу "у"
Ч ЕП будет вычисляться как
Sy

=

У2

f

У1

dy

---

уР

-

У

и

У1

Sy = f

У2

dy

У - уР

(для обратного направления

переноса),
а в числитель (10.29у) войдет разность (у1
смысл Ч ЕП тот же, что и в случае прямотока: y
-

У2) . Физический
S Ь kyF/D =

=

это отношение пропускных способностей поверхностной и пото
ковой стадий массообмена.
Оставшаяся простейшая схема движения фаз - перекрест
ный ток - применительно к отдельному массообмен ному уст
ройству весьма сложна для анализа. Этот случай затронут в
разд . 10. 1 3 .
10.8.4. Основные размеры массообменных аппаратов

Определение основных размеров массообменных аппара
тов - один из важнейших практических результатов решения
проектных задач. К таким размерам относятся прежде всего
поперечное сечение fa и высота Н (либо длина) аппарата.
814

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Ниже рассматриваются простые массообменные устройства,
в которых фазы движутся стационарно прямотоком или проти
вотоком (в режиме ИВ) либо проходят рабочую зону в режиме
И П . Более сложные системы, состоящие из совокупности про
стых, т.е. сети аппаратов непрерывного действия, аппараты для
периодических и полунепрерывных процессов, для иных СКК
рассматриваются в других главах при изложении конкретных
технологических приемов.
Поперечное сечение аппарата !а Расчет !а ведется на базе
уравнений расхода (1 . 17), ( 1 . 1 8):
V
G
.

!а =

-

pw

=

-

w

(10.30)

Выбор фазы, по которой ведется расчет Д11Я двухфазного массообменного
процесса, прост, если объемный расход одной из фаз V; яаляется преобла
дающим: скажем, в случае Vy >> Vx расчет /а ведется по объемному расходу Vy.
Ситуация с выбором фазы чаще всего бывает ясной Д11Я систем газ (пар) - жид
кость и газ (пар) - твердое, когда объемный поток газовой фазы значительно
больше, нежели жидкой или твердой, из-за ра:111 ичия в плотностях на 2-3 по
рядка. Для систем жидкость - жидкость и жидкость - твердое требуется специ
альный анализ.
Четкие рекомендации к выбору рабочей скорое111 w расчетной фазы сформу
лировать вряд ли возможно из-за разнообразия физико-химических, механиче
ских и других свойств участвующих в массообмене рабочих тел, а также специ
фики (конструктивных особенностей, например) рассчитываемых массообмен
ных аппаратов. Поэтому здесь рассматриваются лишь самые общие аспекты.
При прямотоке скорость сплошной фазы w должна быть достаточной Д11Я
транспортирования дисперсной фазы. Поэтому устанавливается нижний предел
скорости Wmin· В случае восходящих транспортных систем (например, пневмо
транспортных) такой физической границей яаляется скорость стесненного вита
ния wc; практически Д11Я устойчивого транспорта рекомендуется Wmin ;:: 2wc. При
противотоке, наоборот, скорость сплошной среды обычно ограничивается верх
ним пределом Wmax, дабы предотвратить унос дисперсной фазы с потоком
сплошной, а в ряде случаев - избежать образования и срыва капель со сте
кающей вниз жидкостной пленки и их уноса газовым потоком. Эти максималь
ные скорости чаще всего рассчитываются по эмпирическим формулам. В неко
торых аппаратах (пленочных и насадочных, например) в качестве Wmax выступает
"скорость захлебывания" или "скорость зависания" - они также определяются
по эмпирическим соотношениям.
Более сложным яаляется выбор рабочей скорости при противоточном дви
жении фаз Д11Я систем с близкими объемными расходами - это обычно системы
Ж - Ж и Ж
Т. База расчета Д11Я них та же - скорость стесненного витания
Wc. Но Д11Я систем с близкими плотностями фаз величина Wc очень чувствительна
к объемной концентрации дискретной фазы в сплошной среде и потому должна
определяться (и вьщерживаться в ходе процесса) весьма тщательно.
Встречаются ситуации, когда на скорость w накладывается несколько ограни
чений. Так, при работе с псевдоожиженной твердой фазой величина w сни зу
ограничена скоростью начала псевдоожижения, а сверху - скоростью уноса. А
для движущегося слоя в случае противотока имеются два ограничения снизу: w
должна быть ниже скорости начала псевдоожижения и скорО'-'ТИ зависания
(чтобы не было псевдоожижения и чтобы слой не прекратил своего нисходящего
-

815

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

движения). Здесь приходится определять оба ограничения и выбирать из них
более жесткое.

После расчета !а находят габаритные размеры сечения: диа
метр da, если сечение круглое (fa = 7tda2/4) или длину l и шири
ну Ь (скажем, в случае прямоугольного сечения !а = bl).
Высота простого массообменвоrо устройства Н. Расчет Н для
процессов, протекающих в условиях поверхностной или смешанной
задачи, проводиrся по предварительно найденной величиНе по
верхности межфазного ко нтакга F. В основе расчета - уравнение
массообмена ( 10.22) с известными значениями М и ЛХср, ЛУср:
М = kxFЛXcp = kyFЛYcp• откуда F =

М

kх ЛХ ср

М

kу ЛУ ср

;

( 10.3 1 )

при этом М найдено из уравнений материального баланса
( 10 . 1 8).
Далее должна быть установлена связь найденного F и иско
мого Н
в зависимости от конструкции массообменного уст
ройства. Например, для пленочных устройств в виде п парал
лельных труб, по внутренней поверхности которых течет плен 
ка жидкости толщиной 8, а вдоль оси движется газ:
F = 7tп(dвн - 28)Н.
(ф)
-

Для насадочного аппарата с удельной поверхностью насадки
Руд :
F = Fуд{аН,
(х)
причем поперечное сечение !а уже рассчитано (см. выше), а
значение Fуд взято по справочной литературе в зависимости от
типоразмера насадки.
В проектной практике высоту рабочей зоны Н часто определяют по высоте
единицы переноса. Суrъ метода проилл юстрируем на примере насадочного аппа
рата в терминах фазы "х', последовательно подстаWIЯя значения Н, F, М и ЛХq,
по (х), (10 . 3 1 ), ( 1 0. \ &х) и ( 1 0.27х):
F_
М
Н
= _

_
_
_
= _

Fуд/а

k х ЛХср rуд/а

Окончательно:

Н=
=

L
Sx .
kx Fyд fa

( 10.32)

К (10.32) можно также прийти, последовательно расшифровьmая смысл Sx

kxF/L.

•

=

Комплекс L/(kxFyдfa) получил название llWC011'1 единнцw переноса (ВЕП); и з
(10. 32) ясно, что он равен H/Sx (отсюда и название комплекса). Рассчкrав по
эмпирическим формулам этот комплекс (через kx или по отдельным соотноше
ниям - они приводятся в литературе) и определив (см. разд. 10.8.3) значение Sx,
находим Н по ( 10.32).

816

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Из приведенноrо должно бьпь эrо
ясно,-чrориакr
"методрасчета
ВЕП" не является отдельным
уравнения
св помощью
существу
По
ва
массообмена,
видимо,
вариакr
менее
удачный,
поскольку
ВЕП "спрятан" ряд
физически ясных харакrеристик процесса.

методом расчета

Н.

В случае потоковой ( балансовой) задачи величина F, а с ней
и Н, роли не играет; высота рабочей зоны выбирается здесь из
конструкrивных соображений . Надо только в ходе проектиро
вания (конструирования) устройства взять достаточные значе
ния Н и F, поскольку при чрезмерно малых их значениях зада
ча перестанет быть потоковой.
Некоторые общие оценки расчета и выбора Н применитель
но к составным противоточным аппаратам (сетям, цепям аппа
ратов) даны в разд. 10. 12.
1 0.9. ПОТОК ВЕЩЕСfВА В П РОЦЕССАХ КЛАССА 3(2-2) 1

В эксплуатационных задачах рассматривается rотовый аппа
рат с известными габаритами. Здесь считаются известными:
- потоки фаз;
- концентрации вещества в фазовых потоках на входе в аппарат;
- поверхность межфазноrо контакта· F;
- коэффициент массопередачи.
Определению подлежат поток М переносимого вещества и
его концентрации в фазах на выходе из аппарата.
Уравнение ( 10.22 ) в задачах эксплуатации остается, конечно,
справедливым, но воспользоваться им впрямую для расчета М
нельзя, так как невозможно определить ЛХср . поскольку не из
вестны выходные концентрации .
В случае линейного описания всех составляющих массопере
носа (прежде всеrо - равновесия, остальные составляющие
обычно принимают линейными) задачу относительно М удает
ся решить прямо, базируясь на входных концентрациях фаз для
любых СКК. В случае кривой линии равновесия задачу опреде
ления М приходится, как правило, решать как обратную, сводя
ее к проектной. По существу это метод подбора: задаемся по
ложением рабочей линии, решаем задачу проектирования с
определением поверхности контакта F, сравниваем найденные
F с заданными по условию задачи. При совпадении этих F за
дача считается решенной, в противном случае подбор положе
ния рабочей линии продолжается до совпадения. Зная F, нахо-

Поверхность
кокrаJСГ
d зависиr
от конструкции и параметров
работы аппа
рата,
точно
она
может
быrь
неизвес
Сегодня
пробпему
F зачастую приходит
тна.
ся решать на эмпирическом уровне.
*

817

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

дим М по ( 1 0 .22), а после определения М легко будет по урав
нениям материального баланса (10. 1 8) найти выходные кон
центрации х2 и У2·
Ниже рассмотрены некоторые простые технологические си
туации. Как и при определении средней движущей силы, ана
лиз ведется в терминах фазы "х' для переноса вещества из нее
в фазу " у" .
10.9. 1 . Идеальное перемешивание обеих· фаз
Расчетная схема процесса представлена на рис . 10.25. Кон 
центрации вещества в каждой из обеих фаз выравнены вдоль
поверхности фазного контакта и равны х2 и У2 ; последние не
известны - их надо в ходе анализа исключить из конечных
(расчетных) выражений. Это удается сделать, если линия рав
новесия
прямая, у = mx P.
Выразим в терминах и символах фазы "х" потоки вещества
М через пропускные способности:
М = L(x1 - х2 ); М = kxF<x2 - х2Р);
М = D(Yl - У1 ) = mD(x2P х1Р ).
( а)
Чтобы исключить конечные концентрации, решим ра
венства (а) относительно частных разностей концентраций и
сложим эти разности:

-

-

Х 1 - Х2

м
=L

- x f _!i__
kxF
х 2р - x lр = м
mD

+ Х2

=

�

Х1

- х1Р
-

=

(

)

м _!_ + _l_ _l_ .
L

kx F

+

mD

Оrсюда получается выражение для искомого потока вещества:

м

1

L

1

x

f

1

-
k
mD

XJ

-+

+

(10.33)

xF
Эта формула может быть записана и более детально, если
выразить kxF пo ( 1 0 17х) через РхF и pyF:

.

-Px F

М = -1 + 1
L

х1

- xf

1 +
+ -mPyF

mD
1

(10.33 а)

Аналогичный подход позволяет получить расчетное выраже
ние для М в терминах и символах фазы "у" :
818

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

у

У1

или

у
Уп

. К"
\. К'
�

_

__13:_'V� A
Х1

а

У2
У1

х

Хп Xz

Х1

6

Х

решению задачи эксWJУатации при идеальном перемешивании фаз
их- прямотоке:
-

Рис. 10. 28. К
а

метод подбора, б

М=

прямое решеЮ1е

Yf - У1

-

l

1

1

ky F

D

-- + -- + _

L/

т

=

f - У1
Y�

-

-

1

1

- + -- + -- + L PxF PyF
т

т

( 1 0 .33б)

D

В случае кривой линии равновесия возникают упомянутые в
начале раздела 10.9 трудности в определении М. Если следо
вать общему подходу к их разрешению, надо придерживаться
такой последовательности действий (рис. 10.28,а) :
- на балансовой линии (ее начальная точка А и угол накло
на ЧJ , определяемый отношением L/D, - известны) выбирается
некая точка К ';
- эта точка принимается за рабочую K'(h' , х2' );
- решается задача проектирования на базе К', т.е. определяется ЛХср' = ЛХ ' и рассчитывается F ';
- наЙденное F ' сравнивается с заданным F; при их недопу
стимом расхождении выбирается новая рабочая точка К" - и
т.д. до совпадения .F(t) и F.
Для процессов с идеальным перемешиванием фаз ( только в
этом случае) можно избежать итеративной процедуры, прису
щей обратным задачам, и решить задачу прямо даже при нели
нейном равновесии. С этой целью выпишем, подобно (а), но
более подробно, выражения для М:

2

М = L(x1 - х2); М = PxF(x2 - Хп);
М = Ру F(уп - У:2); М = D(y2 - У1);

(б)
здесь х0 и
- равновесные концентрации на границе раздела
фаз (см. разд . 10.6. 1 - постулаты двухпленочной модели).
819

Уп

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Исключим конечные концентрации х2 и
вестны :
У2 - У1

+

Уп - У2

Уп - У1

Отсюда

1

1

--

-+
D /3 y F

Уп - У1

1

1

- + -/3 x F
L

Х1 - Хп

=

У2

- они неиз

м

= 

=

м ( _!_
D

D
м

-

/3y F

)
/3 F

1
+ -- .

(в)

y

(г)

Легко видеть· (рис. 10.28,6), что в диаграмме у - х соотно
шение (г) выражает отрезок прямой от начальной точки А(у1 ,
х1) до линии равновесия - точка С(уп, Хп), причем тангенс угла
наклона у отрезка А С равен
1

tgy

=

1

- + -D /3 y F

--

1
1
-+
L

(д)

/3 x F

Заметим, что в случае поверхностной задачи, когда /3/ << D
и /3xF < < L, первые слагаемые в числителе и знаменателе пра
вой части пропадают, и выражение (г) трансформируется в
(10. 16), а у = <р. В случае потоковой задачи, когда /3yF >> D и
/3xF > > L. пропадают вторые слагаемые, и выражение (г) пере
ходит в ( 1 0. \ 8а), а у = 'V ·
Способ определения рабочей точки В иллюстрируется на
рис . 10.28,б:
- из начальной точки А (у1 х1) проводится прямая под уг
лом у [в задаче эксплуатации все величины в правой части (г),
(д) - заданы] ;
- отыскивается точка пересечения этой прямой с линией
равновесия С(уп, Хп);
- из точки А проводится балансовая линия под углом '1' •. так
что tg'I' = L/D , .
- из точки С проводится линия массопередачи под углом <р,
так что tg<p = /3х/ /3у ;
- определяется точка пересечения двух последних прямых
- точка В(У2, х2) .

,

820

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Точка В я вл я ется рабочей при ИП обеих фаз . Последующее
отыс кание движущей силы
н и й не вызы вают.

х2 - хР

и расчет М по

( 1 0.22)

затрудне

Прямоточ ное движение фаз в режиме ИВ

Расходная схема процесса п редставлена на рис. 1 0.26,а. В отл и
чие от И П фаз их концентраци и изме няю тся вдоль поверхности и

1 0.9.2.

рабочей л и н и и от известн ых значе н и й у1 , х1 (точка
до пока не
известн ых У2, Х2. Последние можно определ ить аналитически в
случае прямой л и н и и равновесия, предварител ьно рассч итав поток
вещества М. В этих цел я х воспол ьзуемся соотношен и я м и (а) и вы
раз и м неиз вестн ые конечные ко н це нтраци и :

А)

м.
м
Х2 = Х1 - , Х2р = Х1р + --

Раскроем теперь нап исание Лх ср:

/,

М

= k х FЛХ ер = k

х

(е)

mD

F I ЛХ 2 - ЛХ � = k F (х 2 - х о
n (ЛХ/ЛХ 1 ) х
x 2 - X 2р
ln

м
Х1 - у
- Х 1р - mD
м - X i + Х1р

Х1

.:..;,;
-
= kx F --=----....:.�M
Х1 - - - Х iР M
L

ln

х1 - x r

P
- XI

(ж)

mD

Пере п и ш е м (ж) более лакон ично, проведя ряд сокраще н и й и
обознач и в ( на язы ке фазы "х") разность входных кон це нтраций
х 1 - xr = дх • :

I )
+_
м (l
L mD
М = -k x F -----,----� .
l )
ЛХ • -М _!_ + _

(

ln

L

ЛХ •

(з)

mD

После сокращения на М и перехода (в числ ителе) к отношениям
пропускных способностей kx F / L = a и kx F / mD = k y F / D = b получи м

+

kx F kx F
L

--

1=

ln

--

(

mD
L

)
mD

I
ЛХ • -М _!__ + _

и

1n[ 1 - � ( l + 1 )] = -(а + Ь)

ЛХ •

L

mD

(и)

82 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Потенцируем (и), обозначив здесь и ниже поток вещества
при прямото чном движении фаз М :
1

_

)
_
_1
.
(..!.
= е -(а + Ь) .
тD
лх. L
М

(к)

+

Отсюда находим поток переносимого при прямотоке ве
щества в разных формах записи:
1 е -(а + Ь)
1 е-(а + Ь)
=
лх. ;
М =
k x Fлx. ;
k F k F
М
1
1
- +
+
L тD
mD
L
•

-

--

1 - е -( а + Ь)
,
М=
ь
kx Fлx.,,, ;
а+

Х Х
k
1 - ехр [ - ( x F kx F) ]
L mD
М=
k x F kx F
-тD
L
•

_
_

•

_
_

+

+ --

kx Fлx • .
( 1 0.34)

Далее в случае необходимости по (10. 1 8) рассчитываем х2 и У2 ·
В случае кривой линии равновесия поток вещества М опре
деляют подбором (см. рис. 10.28,а) . В отличие от режима И П
теперь речь идет не о рабочей точке В(У2, х2), а о рабочей линии
АВ, поэтому однозначное определение конечной точки В(У2, х2)
здесь невозможно. Неизвестную точку В ищем, сводя эксплуа
тационную задачу с известной поверхностью контакта F к про
ектной (см. рис. 1 0.28,а) :
- из начальной точки А(у1 , х1) проводится балансовая ли
ния (ее направление совпадает с направлением рабочей линии,
.L P = = L \jl, tgp = tg\j/ = L/D);
- на этой линии выбирается некая точка К', предполагает
ся, что это и есть конечная точка рабочей линии В;
- по присущим точке К' концентрациям .У2, х2 (это еще не
окончательно найденные выходные концентрации) рассчитывается поток вещества М ' ;
- по рабочей линии АК' решается задача проектирования,
т.е. определяется ЛХср по ( 10.27х) и с предварительно найден
ным потоком М' рассчитывается F' по ( 1 0. 3 1 ) ;
- найденное значение F 1 сравнивается с заданным F; при
их совпадении задача считается решенной; при недопустимом
их расхождении выбирается новая конечная точка рабочей ли
нии К", и расчет повторяется сначала - до совпадения.
Установленной окончательно точке В(у2 , х2) отвечает найденное в ходе расчета значение М ' .
822

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

10.9.3. Противоточное движение фаз в режиме И В

Расчетная схема процесса представлена на рис. 10.27 . Для
противоточного процесса, как и для прямоточного, харакrерно
постепенное изменение концентраций в фазах вдоль поверхности
F и рабочей линии. При это м наююн рабочей линии (угол а., от
вечающий отношению L/D) и ограничивающие ее вертикаль х1 и
горизонталь у1 в задачах эксплуатации заданы (рис. 10.29), но кон
кретное положение рабочей линии - неизвестно.
В случае прямой линии равновесия задача определения по
тока вещества М (далее - У1 и х2) решается аналитически.
Воспользуемся опять соотношениями (�) и выразим неиз
вестные конечные концентрации, как и в случае прямотока, в
форме (е) . Раскроем написание ЛХср - оно будет иным, нежели
в прямотоке, поскольку здесь лх 1 = х1 - х2Р, лх2 = х2 - х1Р; с
использованием выражения (е):
Х2 - xr - Х1 + xr
М = kx FЛXcp = kx F дх2
( /дх1 ) = kxF
Jn

ЛХ 2 ЛХ1

Jn

Х2 - х1Р
х 1 - xr

м
Х1 - - Х1р - Х1 + Х р м
L
mD --k x F -M
р
Х1 - - - Х
+ -

ln

Х1

L
м
-mD

1

(л)

- Х 1р

Перепишем (л) более лаконично, проведя ряд сокращений и
обозначив разность входных концентраций (в терминах фазы
"х" ) х1 - х1 Р = лх. :
М - kх F

м(� - м±) ·

ln

(м)

дх. - L

лх . -

м

тD

После сокращения на М и перехода к отношениям про
пускных способностей kxF/L = а и kxF/mD = Ь полУчим
ln

дх.

лх .

м
-L

_

М

mD

=

k F
mD

k F
-

х
х
__
- _

L

= Ь-

а .

(н)

823

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

решению задачи эксплуатации при
проmвотоке фаз
Рис. 10. 29. К

у

У1

��

Потенцируем (н), обозначив здесь
и ниже поток вещества при противоточном движении фаз М :
м
лх .
--�f:.,,_
_ = е Ь -а .

Xi х

лх .

м

(о)

--

mD
Отсюда находим поток переносимого вещества в разных
формах записи:
е Ь- а - 1 лх . "
еЬ-а - 1
м=
k x FЛX . ;
1 Ь-а
1
• '
kх F Ь k
F
х
_
__ е а
е
-mD
L
L
mD
"
Ь -а 1
kx FЛX. ;
= е ь-

М=

------

_

М

_

-

(
(

Ье а

-

а

)
)

k x F kx F
ехр -- - -- - 1
mD
L
( 1 0.35)
=
kx Fлx • .
kx F
�
x F kx F _ k x F
exp
mD
mD
L
L
Далее, если это необходимо, по ( 1 0. 1 8) рассчитываем х2 и .У2 ·
В случае кривой линии равновесия поток вещества
может
быть определен подбором. В этих целях между ограничи
вающими прямыми х 1 и Yt проводят произвольную рабочую
линию, например PQ (см. рис . 1 0.29), под заданным в эксплуа
тационных задачах углом се., так что tgcc. = L/D. А далее решают
проектную задачу:
- по значениям У2 или х2, отвечающим принятой рабочей
линии PQ, рассчитывают М ' с помощью ( 10. 1 8) ;
- по (1 0.2 9х) рассчитывают ЛХср;
- по ( 1 0.3 1 ) с промежуточным М ' вычисляют массообменную поверхность F ' , соответствующую принятому положению
рабочей линии PQ;
- сравнивают это .F ' с заданной: по условиям эксплуатаци
онной задачи величиной F : при их совпадении с приемлемой
точностью задачу считают решенной, при неприемлемом рас
хождении выбирают новое положение рабочей линии и повто
ряют расчет, пока не добьются совпадения.
824
"
М

_

М

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Установленному окончательно положению рабочей линии
отвечает найденное в ходе расчета значен и е М .
10.10. ПРОПУСКНЫЕ СПОСОБНОСТИ
И ЛИМИТИРУЮЩИЕ СТАДИИ
ДJ1Я ПРОЦЕССОВ КЛАССА 3(2-2) 1

Н иже анализ проводится применительно к стационарным
процессам массопереноса (для нестационарных процессов про
блема рассматривается в разд. 10. 14). Анализ может быть дове
ден до аналитических соотношений лишь при линейном описа
нии всех составляющих массопереноса (практически это в наи
большей мере относится к описанию равновесия у = тх при
т = const). Однако качественно (на уровне "лучше-хуже" , а
иногда и "больше-меньше") получаемые результаты приложи
мы ко многим нелинейным процессам рассматриваемого клас
са, а также к другим процессам по КФ-классификации - ли
нейным и нелинейным.
10.10. 1 . Пропускная способность массообменноrо аппарата

Пропускная способность массообменного аппарата в целом
М/ д . легко получается из уже найденных (при решении задач
эксмуатации) выражений для потока вещества М. Запишем
для
пропускные способности (например, на языке фазы
различных случаев применительно к переносу вещества из
фазы
в фазу "у''.
Идеальное перемешивание обеих фаз. В основе - выражения
( 1 0 .33), ( 10.33а) , ( 1 0 .33б). Обозначим в целях сокращения запи
си: х 1 - х 1 Р = лх. , у1 Р - у1 = ду • . Тогда для аппарата в целом;
на языке фазы "х''
м
м
. ( 10.36)
=

"х'' )

"х''

лх.

1
-+

1

--

L . kx F

+

1

лх .



mD

1
1
1
1
-+
+ -- +
L Px F mf3 y F mD
--



Для большей общности с процессами теплопереноса
(разд.7.7) перепишем первое из выражений ( 1 0.36) в форме
м
1
1 k
( 1 0 . 3 6 а)
=
лх.

-----

kx F
L

+

1

+

kx F
mD

kx F

а+

1+Ь

xF ,

причем отношения пропускных способностей а = kxF/L и Ь =

= kxF/mD = kyF/D введены ранее .

Аналогичное выражение на языке фазы "у'' (подход к его
825

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

выводу - тот же) имеет вид

М

лу .

1 k F.
1
k F=
mkyF
kyF У
а+1+Ь У
+ l + -L
D

--

( 1 0.36б)

Из сопоставления разных форм записи М - ( 1 0.22) и
силы через
( 10.33), ( 1 0.36 ) - нетрудно выразить движущие
лх. , лу. :
л.

М = kFЛcp =

a+l+b

kF и Лер =

л.

l
+
а 1+Ь

(а)

Здесь
k = kx, ky; Лер = ЛХср, Луср; Л • = лх. , Лу. соответственно.
Обобщенное отношение пропусЮfЫХ способностей аппарата
выражается одинаковой записью в терминах обеих фаз:

м

r.

м

= --- = ---

kxFлx.

(1 0.37)

ky FЛy.

Прямоточное движение фаз. В основе - выражения ( 1 0.34).
ПропусЮ1ая способность прямоточного аппарата в целом на
языке фазы " х" равна:

М·

- =

лх.

1

[ ( kxF + kxF
)]
mD

- ехр -

L

-L
kх F

kх F
+ --

-

- а+
kx F = 1 е ( ь) kx F . ( 1 0.38)

mD

а+Ь

Аналоmчным образом получаемое выражение на языке
фазы "у" имеет вид
1 - е- ( а + Ь)
=
( 1 0.38а)
ky F .

а+Ь

Лу.

Связь Лер и л . определяется на тех же основаниях, что и
для И П фаз:

---
Ь

1 - е- ( а + Ь)
Ле р = Л .

а+

(б)

Обобщенное отношение пропусЮ1ых способностей аппарата
имеет одинаковое численное значение на языке обеих фаз:
r.

=

м

kx Fлx.

м

= ---

ky Fлy.

( 1 0.39)

Противоточное движение фаз. В основе - выражения (10.35).
ПропусЮ1ая способность противоточноrо аппарата в целом пред-

826

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

( k F kx F ) 1
( kтDx F - kx F) - kx F kx F

ставляется по фазе "х " как
М
лх .

=

x
ехр -;;Jj

-

k F
ехр
тD

_х
_

L

-

=

ь
е -а - 1 F .
kx
ь
Ье - а а
-

( 1 0 .4U )
L
L
Аналогичное выражение (способ ero получения - тот же) на
языке фазы "у" запишется в виде
М
еЬ а - 1
=
ky F .
( 1 0.40а)
ь а
-

Лу.

Ье

-

-

а

Связь Лер определяется на тех же основаниях, что для И П фаз
и прямотока:

Л ер =

л.

еЬ-а - 1 .
Ье Ь -а - а

(в)

Обобщенное отношение пропускных способностей аппарата
может быть записано в терминах обеих фаз:
м
м
r. = --- = --( 1 0.4 1 )

kx Fлx.

ky FЛy.
Влияние пропускных способностей стадий н а пропускную
способность аппарата в целом нагляднее всего высвечивается

при анализе процессов с идеальным перемешиванием обеих
фаз - см. соотношения ( 1 0 .36). В знаменателе стоят выраже
ния, обратные пропускным способностям отдельных стадий, это диффузионные сопротивления массопереносу на соответ
ствующих стадиях. Можно констатировать: увели чение пропуск

ной способности любой из стадий приводит к возрастанию про
пускной способности (интенсивности массообмена) аппарата в
целом. Но при этом чем выше пропускная способность какой-либо
стадии, тем .меньше отвечающая ей обратная вели ч ина, а зна ч ит
и влиян ие этой стадии на общую интенсивност ь массопереноса. И
наоборот, уменьшение пропускной способности какой-либо стадии
повышает ее значимость для массопереноса в целом.

Эти общие выводы позволяют технологу грамотно выбрать
способ воздействия на массоперенос , на процессы переноса
вообще : надо , если это возможно, воздействовать прежде всего
на фактор, в наибольшей мере влияющий на процесс , т.е. для
последовательного переноса - на наиболее медленную стадию
(с наименьшей пропускной способностью).
При сушественном понижении пропускной способности ка
кой-либо стадии массопереноса эта стадия может стать лими

тирующей.

827

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

10.10.2. Лимитирующие стадии процесса
Лимитирую щей будем называть стадию, протекающую суще
ственно медленнее всех остальных, которые в сравнении с ней
протекают " мmовенно " . Продолжительность любой из этих
остальных стадий значительно меньше не только продолжи
тельности лимитирующей, но (при строгом понимании послед
ней) и погрешности, с которой она определена. Поэтому при
наличии лимитирующей стадии при расчете интенсивности
массообменноrо процесса следует рассматривать только эту
стадию. Наиболее нагляден анализ в случае И П обеих фаз.
Пусть, например, kxF < < L, mD; применительно к выраже
нию ( 1 0.36а) зто означает а, Ь << 1 . Тогда массоперенос лими
тируется массопередачей через поверхность контакта, посколь
ку дробь 1/kxF значительно превышает остальные слагаемые в
знаменателе. Для расчета массообмена здесь необходимо распо
лагать значениями кинетических характеристик Рх и Ру (а так
же m) или сразу коэффициента kx (либо ky) и величиной F;
пропускные способности L и mD в такой ситуации роли не
играют. В этом случае говорят о массообмене в условиях поверх
ностной задачи. И для интенсификации массопереноса в целом
нужно увеличивать F, повышать kx. При этом может возник
нуть вопрос, какая из стадий массопередачи контролирует
процесс - перенос вещества через пограничную пленку со
стороны фазы "у" или фазы "х". Разумеется, следует увеличи
вать в первую очередь ту из стадий PxF или mpyF, которая
медленнее (скажем, при PxF < mpl'F принять меры для допол
нительной турбулизации фазы "х" с целью уменьшения тол
щины диффузионной пограничной пленки в этой фазе).
Пусть теперь L < < mD, PxF
лимитирующей становится
стадия подвода вещества с фазой "х" в рабочую зону массооб
менноrо устройства; тогда в рассмотрении остальных стадий
необходимости нет. В этом случае задача называется потоковой
по фазе "х" . Для повышения интенсивности массопереноса в
целом здесь нужно увеличивать фазовый поток L; поток фазы
"у", как и кинетическая характеристика kxF, в этих условиях
роли не играет. Разумеется, при mD << L, PxF лимитировать
будет отвод вещества из аппарата с фазой "у" , т.е. поток D.
Аналоmчные выводы могут быть сделаны также для прямо
точных, противоточных и друmх процессов переноса вещества
(любой субстанции вообще). Такой анализ применительно к
некоторым случаям теплопереноса при движении фаз в режиме
ИВ приведен в разд.7.9.2.
Выявление лим итирующей стадии существенно в различных
аспектах:
управления процессом переноса (здесь - массообмена) :
надо интенсифицировать лимитирующую стадию - может
-

828

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

статься, что в результате интенсификации она перестанет быть
лимитирующей;
- расчета процесса массопереноса: надо вести расчет толь
ко лимитирующей стадии процесса.
При сопоставимости н.ескольких пропускн.ых способн.остей
(хотя бы двух из них) задача массопереноса именуется смешан
ной. Это означает, что в расчетах придется учитывать влияние
пропускных способностей нескольких стадий, в наиболее об
щем случае массопереноса в процессах класса 3(2-2) 1 - всех
трех (L, kxF, тD) или четырех (если в пропускной способности
kxF выделить f3xF и /3yF) . При выборе способа воздействия на
процесс надо будет сопоставить пропускные способности раз
ных стадий и установить, какая или какие из них вносят боль
ший вклад в массоперенос - на них и воздействовать в первую
очередь.
10.1 0.3. О подмене задачи в массопереносе
В практике химической технологии при теоретическом ис
следовании процессов и обобщении экспериментальных дан
ных не всегда проводится сопоставительный анализ пропуск
ных способностей различных стадий массопереноса с целью
установления лимитирующей стадии или вывода об отсутствии
такой стадии. При этом способ описания процесса нередко
обусловлен не столько научным его анализом, сколько тради
циями, многолетней привычкой использовать устоявшиеся
подходы. В результате достаточно часто ипюрируется наличие
лимитирующей стадии, и массоперенос описывается в поняти
ях (символах и терминах) совсем иной стадии - происходит
подмена задачи. К математическим описаниям и практичесюiм
рекомендациям, сделанным на такой основе, надо относиться
критически, дабы не прийти к ошибочным решениям. Спен:и
ально подчеркнем, что подмена задачи иногда бывает вын.уж 
ден.н.ой: мы порой просто не умеем количественно оценивать
эффект и вклад некоторых стадий массопереноса, приходится
идти на подмену задачи, вводя некие коэффициен.ты н.езн.ан.ия.
служ ить

Примером подменызадачи
задачи,
чаще всеrорамках
- неосознанной, может
трактовка
принимается
в
привычных
(чаще
всеrо
без
оговорок),
что
процесс
может
бьпъ
описан
на
основе
коэффици
ентов
массообмена
Рх, j3y, kx и т.д ., тогда как в действительности он лимитирует
подводом в аппарат вещества с фазой Факrически здесь про
ся,
например,
пускная
способность
лимитирующей
стадии
L подменяется величиной, скажем,
L
(аподменяюзадачая одной,
смешанная,
то
две
стадии
с
пропускными. Вспособностями
PPxF
случае
потоковой
харакrеризуемойполучаются
величиною
xзадачи
F в тсситуациях "неожиданно"
Pxf)
эмпирические или теорети
ческие
уравнения,
в
которых
Рх - L/F, поскольку Рх входит в Shx РэVDд, а L в Re, то длязадач
Sh - Re1 . В случае
предлаrаемых
смешанных
расчетныерасчетных
уравненияуравнений
типа Sh харакrерно
/{Re) выглядят более пристойп оверхностной:

потоковой

"х' .

если

этих

=

и

=

829

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

но: кривые
отклоняются вниз от линейной зависимости, и пока.1атель степени
при
Re получается ниже 1 .
Более осознанно смешанную поверхноС'Пlо-потокоаую 38,Дачу подменяют сме
шанной потоковой: исключают из рассмотрения поверхносrnую стадию массопе
реноса.
При этомспособность
понимают,составляет
что на самом
деле поверхносrnый перенос (пусть
его пропускная
13xf) в какой-то степени влияет на массо
обмен.
Но величина 13х13xF(и(или13у);kxF
и т.п.) достовернов значениях
не извесrnа:т виз-за
неточно
стей
в
определении
неопределенности
случае
нелив
нейного
равновесия;
в
наибольшей
мере
из-за
объективных
трудностей
определении
F (особенно в процессах с изменяющейся поверхностью контакта
фаз).
Поэтому
мысленно полаrают
величины
13xF, kxF достаточно большими,
чтобы
фазы
в
массообменном
устройстве
пришли
в равновесие, - говорят об
идеал•ном коюакте фаз. Если в качестве примера рассматривать прямоточный
10.28,а, характеризующая уходящие потоки фаз,
процесс,
то точкамежфазном
Хе на рис.контакте
при
идеальном
будет лежать на линии равновесия (при
этом
начальная
точка
А и наклон линии АКс при извесrnых потоках L и D
Но в действительности нет идеального контакта фаз, так что ре
определены).
ально
конечная
точкаможет,
В рабочей линии АВ лежит на прямой АКс где-то правее и
ниже
точки
Хе
(это
например,
бьпъ
точка К') . Отличие реального про
цесса
от
идеального
обычно
учитывают
коэффнциеюом полезного дейСТllИ Я аппа
рата,
характеризующим
"степень
приближения
процесса
к идеальному".
Этот
КПД
и
есть
"коэффициент
незнания"
поверхности
контакта
F и пропускной
способности
13xF или kxF.
Поясним
смысл КПДдляна этого
примере
процесса
с идеальным
перемешиванием
обеих
фаз.
Сопоставим
описание
процесса
с
учетом
реальной про
пускной
способности
kxF и без ее учета (идеальный контакт фаз, kxF -+оо ); КПД
выразится
отношениепроцессах
пропускных способностей массообменного устройства
в реальномкак
и идеальном
:
-

1
1 / L + l / kx F + l / mD
=
----�
11
1
_
_
__

1 / L + l / mD

1

1

- + -
L mD
1
1- + -1 +
L kx F mD

( 10.42)

Кстати,
из ( 10.42) способность
при извесrnыхповерхносrnой
по опьrrным стадии
даннымkxF,значениям
11 можно оце
нить
пропускную
а
при
извесrnых
kx
трудноопределимую истинную поверхность межфазного контакта
1
kxF = � --1 - 11 ..!.. + _1_
L тD

Р.

-

( 10.42а)

Соответствующие
выражения
можно
получить
и для других
схемв взаимного
движения
фаз,
других
СКК.
Здесь
возникают
трудности
не
только
определе
нии
величины
F, но и в оценке структуры потоков фаз, если речь не идет о
простейшихвыrеснение
предельныхфазовых
моделяхпотоков,
ИП и ИВ. этих случаях часто постулируют
идеальное
а незнание
истинной
структуры пото
ков также учитывают с помощью КПД, усложняя
его смысл
и выражение.
В

1 0. 1 1 . СЕТИ АППАРАТОВ (ОБЩАЯ ХАРАКТЕРИСТИКА)

Ранее анализировалась работа оди ночных массообменных
устройств (аппаратов) . Такие устройства мо rуг функциониро
вать в различных комбинациях, образуя сети устройств. Есл и
при этом аппараты вытянуты в одну цепочку, то такие сети
830

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

У

х

У

1

:::():()::
:::():()::
п

х

у
х
У

У

х

=я;-

х

у

х-

у

~

у

х

х

v

у

у

х

Простейшие сети аппаратов:

1- прямоток, 11 - противоток, UI - перекрестный ток при раэбиеюtи фазы ')> ", IV
же при разбиеЮ1и фазы 'Х", V - разбиеЮ1е обеих фаз
Рис.

1 0.30.

-

то

называют одномерными. Если же аппараты связаны в сеть
нескольюtми цепочками, то говорят о двумерных сетях; нетруд
но представить себе и трехмерные сети. Предметом последую
щего изучения являются простейшие одномерные сети
це
почки аппаратов, принадлежащих классу 3 (2-2) 1 ; функциониро
вание цепочек для некоторых других классов рассматривается
при изучении отдельных технолоmчесюtх приемов. Заметим,
что цепочка аппаратов весьма часто конструктивно оформляет
ся в виде одного общего аппарата - системы (например, ко
лонного типа).
Массообменный эффект сети аппаратов при прочих равных
условиях зависит от того , каким образом аппараты собраны в
сеть. Покажем возможности соединения в сеть простейшей
системы из двух аппаратов; таких вариантов - пять (рис . 1 0.30).
При этом в каждом варианте внутри отдельного устройства
возможны различные СКК - прямоток, противоток, И П од
ной или обеих фаз.
При соединении аппаратов в цепи возникает ступенчатый
контакт фаз. Чаще всего это ступен чатый противоток, нередко
используют перекрестное соединение аппаратов. Ступен чатый
прямоток эффективен только в смысле наращивания поверх
ности контакта фаз, его использование обусловлено лишь кон 
структивными соображениями либо спецификой технологиче
ского процесса, лежащей, как правило, вне массопереноса.
Каждому способу соединения аппаратов в сеть отвечает своя
рабочая линия в диаграмме у
х, учитывающая как этот спо
соб, так и СКК внутри каждого аппарата.
-

-

В качестве
примера
нанихрис.- 10.31,а-1
изображена
цепочкаонииз двух
аппаратов,
причем
в
каждом
из
прямоток,
а
соединены
по
С'I)'пенчато
проmвоточной
схеме.
у х построены (рис. 1 0.31,а-11, 111) для про
2 -2 )1. Диаrраммы
цессов
класса
3(
Входные
концентрации
переносимого вещества в фазах
обозначены
у1 и х1 , выходные - У2 и х2 , промежуточные (между аппаратами) у' и
аппарата входными концентрациями я R11Яются и х', выход
Для
ными
у' и х2 . В соответствии с проведенным ранее анализом (разд.10.7) рабочая
линия для этого аппарата представлена нижним левым отрезком на рис. 10.31,а-

х'.

л евого

YI

83 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

1

'

����
у

х

Х1

У1

у

У2
У1

у

У2

у
у

У1

х

а

'

У1

Рис. 1 0. 31. Рабочие линии для простейших цепочек из двух аппаратов:
а - сrупенчатый противоток с прямотоком фаз в каждом аIШарате: 1 - схема потоков,
11 - диаrрамма у - х (общий случай), 1П - диаграмма у - х (идеальный кошахr фаз);
6 - сrупенчато-перекресmое двЮ1СеЮ1е фаз с раэбиеЮ1ем фазы 'Х " при противото�се фаз
в первом 81Шарате и прямотоке во втором: 1 - схема потоков , П - диаграмма у - х (общий

случай)

11 в диаrрамме у - х, наклоненным под углом (3 (tg(3 = L/D). Для правого аппа
рата входными будут концентрации у ' и х1, выходными - У2 и х'. Этому аппарату
отвечает верхняя правая рабочая линия, ее угол наклона тоже равен (3, поскольку
потоки L и D - те же.
Таким же образом будет обозначен ступенчато- противоточный процесс при
ИП обеих фаз в КЗJl<дом аппарате. Только здесь рабочие линии вырш1щаются в
рабочие точки с координатами: у ', х2 для левого аппарата и }'2, х' - для правого.
Чем больше пропускная способность поверхностной стадии (т.е. величины а
и Ь), тем ближе к линии равновесия заканчивается рабочая линия . Если в от
дельных массообменных устройствах ко1Пакт фаз происходит идеально (kxF -+ оо,
потоковая задача переноса), то фазы из КЗJl<дой ступени уходят в равновесии .
Поэтому рабочие линии должны заканчиваться н а равновесной кривой, ка к это
показано на рис. 1 0 . 3 1 ,а-IП. Рассмотренные ситуации часто встречаются на прак
тике; именно они фИ1урируют в последующем анализе.
На рис. 1 0 . 3 1 ,6- 1 приведена цепочка аппаратов, где в левом аппарате - про
тивоток, в правом -- прямоток, аппараты соединены в ступенчато-перекрестную
схему с разбиением фазы х Диаrрамма у - х для этого случая - тоже приме
нительно к процессам класса 3(2-2) 1 - представлена на рис. 1 0 . 3 1 , 6- 11. Положе
ние рабочих линий (их начальные и конечные точки, углы наклона) отвечает
правилам, выявленным при анализе работы одиночных аппаратов. Фазу ";('
разбивают совсем не обязательно поровну; впоJD1е возможно, 'ПО ее потоки в
левом и правом аппаратах не одинаковы, пусть для определенности Lr < Lп. В
этом случае углы а и (3 не равны, причем а < (3, поскольку tga = Lr/D < tg(3 =
"

832

'.

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

= L1 1/D. Процесс может завершаться смешением потоков фазы
дающих аппараты (так показано на схеме):
Xl �
_..::,
Xu

.

Xl·

" х' ,

поки -

Сам акт смешения изображается на оси х и рассчитывается по

правилу р ыча r.1; поскольку в рассматриваемом примере
результирую ща я точка х2 расположена ближе к х н , нежели к х1 .

L11

Li ,

>

В предыдущих разделах рассматривались аппараты с непре
рывным контактом фаз. Сети аппаратов реализуют дискретный
(ступенчатый) контакт фаз. Ранее было установлено, что при
непрерывном контакте наиболее эффективно противото чное
движение фазовых потоков. Однако в одиночном аппарате
обеспечить такое движение удается далеко не всегда: из-за не
обходимости диспергирования фаз для увеличения поверхности
контакта; из-за особенностей конструкции, обусловливающих
поперечную неравномерность и обратное перемешивание по
токов; из-за специфических требований конкретной техноло
гии. Поэтому в одиночном аппарате СКК может соответство
вать прямотоку либо И П одной или обеих фаз. Соединение
таких одиночных аппаратов в цепочку с противото чн ым пере
мещением фаз от аппарата к аппарату позволяет приблизиться к
противотоку, т.е. использовать достоинства этой схемы.
Разумеется, соединение противоточных одиночных аппаратов в ступенчато
противоточную схему дает просто суммирующий эффект: пропусю1ые способ 
ности поверхносn1ых стадий отдельных аппаратов k,/; складываются в общую
пропускную способность kxF (причем в случае одинаковых kx здесь F = 2: /; ) .
Н иже этот тривиальный случай отдельно не рассматривается.

j

Далее сети наиболее подробно анализируются применитель
но к цепочке аппаратов с противоточным движением фаз меж
ду аппаратами, менее детально - применительно к ступенчато
перекрестной схеме. В случае кривых линий равновесия расчет
сетей ведется графически; при т = const сети для процессов
класса 3 (2-2) 1 поддаются аналитическому расчету.
1 0 . 1 2. СТУПЕНЧАТЫ Й ПРОТИ ВОТОК
ДЛЯ ПРОЦЕССОВ КЛАССА 3(2-2) 1

Схема ступенчатого противотока представлена на рис . 1 0.32,
где концентрации вещества в одном сечении (между ступенями)
обознач ены в фазах одинаковыми индексами: Yt и Х1 , У; и х;.
Условимся анализировать ступенчатый противоток на языке
фазы "х'' применительно к переносу вещества из этой фазы в
фазу " у" . Проблема расчета ступенчатого противотока связана
с числом ступеней - известных (задача эксплуатации) или ис
комых (задача проектирования).
833

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

D , уп

1

i У;
1

+1 .....__
..
_...._

-

...._..
...,._
.

п - 1 , � -J
_ _

Рис. 10.32.

ji

_j

Ступенчатый противоток: цепочка из п аппаратов

10. 12. 1 . Общие положения.
Графоаналитический расчет

На практике чаще всего в каждом массообменном уст
ройстве (ступени) осуществляют идеальное перемешивание
обеих фаз, их прямоток либо И П одной из фаз и движение
другой в режиме, приближенном к И В . Во всех этих случаях,
как показано в разд. 1 0.7, рабочая линия строится формально
одинаково (при И П обеих фаз она вырождается в рабочую точ
ку, но последняя находится на рабочей линии, характерной для
прямотока фаз). Построенная в упомянутом разделе рабочая
линия воспроизведена применительно к i-й ступени на рис .
10.33,а для общего случая - кривой линии равновесия. Началу
рабочей линии отвечает точка с концентрациями У;+ 1 , х;, концу
(или рабочей точке при И П обеих фаз) - с концентрациями У;,
Х;+ 1 ; угол наклона рабочей линии р определяется потоками фаз:
tgp = L/D. Такое представление рабочей линии (она показана
жирными штрихами), вполне приемлемое для единичной сту834

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

у

у

У;

а

X;+ J

Рис. 10.33.
а

Ступенчатый

Х; х

пр011t воток

6
-

реальные ступени

в диаrрамме у - х:

- юперпретация реальной ступени , б - построение реальных ступеней

пени, не очень удобно для изображения n-С1)'Пенчатой цепочки
аппаратов, так как требует громоздких пошаrовых операций при
переходе от ступени к ступени. Поэтому принято изменять базу
построения, существенно упрощая и 1рафические процедуры.
Очертим около рабочей линии прямоугольник (рис. 10.33,а),
ограниченный упомянугыми выше концентрациями, - рабочая
линия является для неrо диаrональю. Проведем вторую диаrо
наль - она пройдет через середину рабочей линии под утлом а
к оси абсцисс , причем а. = р ; концы второй диагонали характе
ризуются точками с координатами У;, х1 и Yt+1 , Xt+I · Тогда сту
пень, т.е. переход от одного сечения к другому, можно изобразить
(жирные линии на рисунке) прямоутольным треугольником,
опирающимся своей гипотенузой на эту вторую диагональ.
Последняя при этом представляет собой фраrмент рабочей ли
нии ступенчато-противоточной цепочки аппаратов (см. ниже).
Такой подход позволяет сформулировать принципы по
строения ступеней в противоточной цепочке из п аппаратов
(рис . 10.33,6). Отрезки рабочих линий для каждой ступени в
такой цепочке составляют продолжение один другого, так как
начало одного отрезка совпадает с концом другого, а утлы их
наклона а.
одинаковы (как и р), причем tga. = L/D. Положе
ние рабочей линии для цепочки в целом определено входными
и выходными концентрациями - точками Уо, Хп и Уп. Х{). В этом
смысле цепочка аналогична единичному противоточному мас
сообменному устройству, поэтому и уравнение рабочей линии
для цепочки будет по существу таким же, как и для противо
точного устройства, т.е. повторит ( 1 0 .24). С обозначениями,
принятыми на рис . 10.32, такое уравнение получают из матери
ального баланса для контура, показанного штрих-пунктиром ,
замкнугого на сечение п (низ цепочки) и текущее сечение i, где
-

835

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

у = у1 и х = х1• Для стационарного процесса
+Dyo +Lx - Dy - Lхп = О,
откуда

( 1 0 .43)
Контур выше приведен на базе сечения "п" , это обусловле
но предположением, что наряду с входными концентрациями
Уо и Хо известна также выходная Хп, так что начальная точка
рабочей линии Уо, Хп задана. Если же известна выходная кон 
центрация Уп, то уравнение типа ( 1 0 .43) будет получено и з ма
териального баланса для контура, замЮfуrого на концевое се
чение "О".
Для построенной рабочей линии характерны все особен
ности и ограничения, рассмотренные в разд . 1 0.7 применитель
но к одиночному противоточному устройству. В частности,
остается правомерным понятие о минимальном потоке второй
(нецелевой) фазы.
На рабочей линии, ограниченной точками Уо, Хп и Уп, Хо ,
располагается определенное число ступеней, соединенных в
противоточную схему. Отдельные ступени этой цепочЮI на
диаграмме у - х предстанут в вnде последовательно располо
женных прямоугольных треугольников, опираюшихся своими
гипотенузами на рабочую линию (рис . 10.33,6). При этом для
реальной ситуации размеры этих треугольников могут быть
определены аналитичесЮI (в случае прямой линии равновесия
- по материальным балансам и пропусЮfЫМ способностям
каждой ступени) или графичесЮ1 (в случае кривой равновесной
линии - методика расчета для ИП и прямотока фаз изложена
в разд. 10.8 . 1 и 1 0 . 8 .2). Это весьма громоздкая процедура, тре
бующая знан ия коэффициентов массопередачи kx или ky и по
верхности межфазного контакта в каждой i-й ступени !t (при
этом k; и ft могут различаться от ступени к ступени, потому и
размеры треугольников могут быть разными - см. рис . 10.33 , 6) .
Отсутств ие достоверных сведений о б этих величинах заставляет
технологов Идеализировать ситуацию - рассматривать теорети
ческие ступени с Идеальным контактом и равновесными выход
ными концентрациями на каждой, т.е. полагать kx;f; � ао, а
затем вводить поправку на отличие реального процесса от идеаль

ного - потокового.

Построение теоретичесЮIХ ступеней демонстрируется на
рис. 1 0.34 применительно к кривой линии равновесия (общий
случай). Переход от некой i-й ступени к (i + 1)-й трактуется
следующим образом (рис . 1 0.34,а) . Будем вести построение от
точЮ1 М (сечение с концентрацией х;) в несколько этапов соответственно схеме на рис . 1 0.32:
836

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

)'

у

у1.

X;+ I

Х; Х

а

- юперпретация теоретической cryneIOI,

Рис. 10.34.
а

Хп

б

- х:

б - nocrpoeIOfe теоретиче ских сrупеней

Ступенчатый проmвоток: теореmческие ступени в диаrрамме у

- находим (пересечением с вертикалью х1) на рабочей ли
нии цепочки начальную точку линии сопряженных концентра
ций для i-го сечения А (у1, х1), причем концентрации у1 отвечает
точка Р на оси у;
- находим равновесную с у1 выходную концентрацию хн 1 ,
она соответствует точке В, лежащей на равновесной кривой, и
точке N на оси х;
- устанавливаем конечную то чку сопряженных концентраций
в сечении (i + 1 ) : С(у1+1 , Х1+ 1 ) .
Последовательный переход М � А � Р � В � N � С и есть
построение одной теоретической ступени, иначе - переход от
сечения i (точка А) к сечению i + 1 (точка С). Разумеется, нет
необходимости фиксировать точки М, Р и N - достаточно
просто построить треугольник АВС между рабочей и равновес
ной линиями. Переход к следующему сечению (построение
следующей теоретической ступени) обозначится треугольником
CQS. Число таких прямоугольных треугольников в заданном
диапазоне изменения концентраций от Хо до Хп и есть число
теоретических ступеней nr, необходимых для обеспечения про
цесса. В зада чах проектирования при построении может полу
читься "дробное" значение nr; его следует округлить в сторону
ближайшего большего, чтобы гарантировать некоторый запас.
В задачах эксплуатации известны наклон рабочей линии, ее
границы (вертикаль .хо, горизонталь Уо) и число ступеней nr
(будем пока считать известным число теоретических ступеней).
В случае кривой линии равновесия положение рабочей линии (с
определением выходных концентраций Уп и Хп) можно устано
вить лишь подбором. Проводится произвольно, но с заданны
ми ограничениями (tga. = L/D; у0 и .хо) рабочая линия; строятся
теоретические ступени. Если их число совпадает с заданным fir ,
то задача решена; если нет, то проводится новая рабочая ли837

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

н ия ,

и так - до совпадения построенного и заданного значе
ний fir · В случае прямой линии равновесия задача решается
аналитически.
1 0 . 1 2.2. Аиалиrическнй расчет идеального процесса

Расчетная схема процесса с прямой линией равновесия (угол
ее наклона е отвечает tg е = т) и рабочей линией (угол сх, при
чем tgcx = L/D) представлена на рис . 10.35. Крайние точки ра
бочей линии соответствуют парам концевых концентраций Уп ,
Хо и Уо,
Между равновесной и рабочей линиями построены
теоретические ступени - треугольники, их счет условимся вес
ти от точки с координатами (у .хо) : 1, 2, ... , i, i + 1, . . . , п. Со
ответственно пометим отрезки - от ЛХ1 до ЛХп и ЛХп+ 1 = п -.хоР (последний отрезок не входит в счет числа ступеней, он
лишь характеризует движущую силу на нижнем конце системы,
изображенной на рис . 1 0.32). Пометим также отрезок Лу1 именно он послужит базой для установления соотношения
между соседними отрезками ЛХ1+ 1 и ЛХ1• Из треугольника i:
Лу1 = ЛX1tga = ЛX;(L/D); из треугольника, расположенного над
ступенью
1 : Лу; = ЛХ1+ � tge = ЛХ1+ � т. Приравняем выра
жения для Лу; :

Хп.

п,

Х

i+

L
ЛХt D = ЛХ1+1 т и

L
ЛХ; 1
(а)
тD
ЛХ;
причем с = а/Ь представляет собой безразмерное отношение про
пускных способностей потоковых стадий массопереноса (символы
введены в разд. 7.7 и 1 0.6); иногда с называют фактором массо

+ = -- = С ,
---

переноса.
Соотношение (а) справедливо для двух любых соседних сту
пеней. Поэтому, начиная с движущей силы в первом сечении
запишем
ЛХ1 = Хо -

ХпР,

ЛХ1 = ЛХ1 с о
ЛХ2 = ЛХ1 с l
(б)

Последовательность (б) позволяет подойти к решению задач

проектирования (определение числа теоретических ступеней п =
= nr) и эксплуатации (определение неизвестных выходных кон

центраций при заданном nr).
838

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

у

Рис. 10.35. К аналитическому расчету ступенчато- противоточноrо процесса при
идеальном контакте фаз

Задача проектирования решается на базе последней строки
последовательности (б) :

ln ЛХп + l

nr =

ЛХ1

ln с

Хп хоР
хе =
= In(LХо/-mD)
ln

-

Р
-х

п
Хп - Хор

ln х о

( 1 0 .44)

In(mD / L) '

причем в проектной задаче параметры рабочей линии (как и
равновесной) заданы, поэтому все величины в правой части
известны.
На практике ступенчатый противоток нередко применяется
для массообмен ных процессов с очень высокой степенью за
вершенности (извлечения, очистки и т.п .). В этом случае це
почка, как правило, состоит из большого числа аппаратов п
а потоки фаз удобно выбрать так, чтобы рабочая линия
была примерно параллельна равновесной. Тогда с 1 , посколь
const.
ку L/D
т; при этом
ЛХ
=
Правая часть формулы ( 1 0 .44) дает неопределенность типа O;t>,
но в математическом раскрытии ее нет необходимости: сумма п
одинаковых отрезков равна (см. рис . 10.35) полному диапазону
концентраций Х{) Следовательно, при с = 1

=

= nr,

=

=
лх1 = ЛХ2 ЛХ1 = ЛХп+I =

Хп·
nr = Хо лх- Хп Хо -- хХеп ХоХ-о Yn- Хfп m
Хо
--

---

=

--=----:.:.-

=

( 1 0.44а)

839

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Задача эксплуатации решается пугем сложения последова
тельности (б), кроме последнего слагаемого. Получается гео
метрическая прогрессия, ее сумма определяется по известной
формуле:
п
с" - 1
� ЛХ; = XQ Хп = ЛХ1 (1 + с + с2 + " . +
= ЛХ 1 -- ; (в)

cn- I )

-

i= l

с

-1

разумеется, при с < 1 величины в числителе и в знаменателе
следует поменять местами.
Чтобы найти х11 , используем связь ЛХп+I = Хп X{f = ЛХ1 с" и
подставим в (в) величину ЛХ1 = (х11 .хоР)/с" :
-

-

с" - 1
с-1
откуда

хп = хО

с"+ 1 - сп
сп - 1
vд
+ "'tГ
n+l
с
сn+l - 1
-1

(10 . 45)

_
_
_

Задачу эксIUiуатации можно считать решенной, поскольку Уп
теперь легко определяется из материального баланса (10. 1 8).
Решение задачи эксплуатации целесообразно представить через пропускные
способности Сl)'Пенчато-противоточной цепочки аппаратов М/Л х. где М =
= L(�
X{f. С этой целью вычтем из � левую и правую части
Хп), а х. = �
равенства ( 1 0 .45):

-

,

-

Умножив теперь обе части равенства на L, получим в привычной форме для

М -- ·
=
L
ЛХ• 1 -

1 - сп+\
сп

с > l или с < l

или
Межфазный поток вещества составляет

М=

с

с

"

п+

t

l

Lлх
-

l

( 1 0.46)

( 10.4ба)

• .

В случае с = 1 формулы ( 10.45), ( 10.46) содержат неопреде
ленность. Чтобы раскрыть ее, используем правило Лопиталя ,
беря производные по с и затем устремляя с к 1 . Тогда
_ сп

c n+ I
lim n + I
с _. 1
с

840

l

.

= l1m
с_. 1

d { n+l п }
{c n +l - 1 )

d

n
d

dn

с

- с

=

(п + l) c n - пс " - 1 =
l1 m
с--. 1 (п + l)c n - О
.

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

(п + 1) - п

1
(д')
= -- ,
п+l
п+1
соответственно (опуская аналогичные промежуrочные преобра
зования)
-1
п
(д " )
1.lffi n l _ = -
=

C-+ l

п
с
C +

l

п+l

С учетом (д) формула (10.45) принимает вид
Хп =

Xo_
l_
п+1

п

+ Х<JР -- '
п+1

( 1 0 .45а)

а формулы ( 1 0 .46) и ( 1 0.46а) п
п
М
= -- L и М = __ Lлх • .
( 1 0.46а)
лх. п + 1
п+1
Таким образом, используя понятие о пропускных способно
стях, можно в задачах эксплуатации найти межфазный поток
переносимого вещества (далее - и выходные концентрации
фазовых потоков), причем без предварительного определения
профиля концентраций по цепочке аппаратов.
10.12.3. Аналитический расчет реального процесса

Ступенчато-противоточные процессы класса 3 (2-2) 1 подда
ются аналитическому расчету в случае линейности составляю
щих, в том числе и равновесия (т = const). С помощью полу
чаемых соотношений возможно решать задачи эксплуатации и
проектирования. Ниже вехи и результаты такого расчета пред
ставлены для простейшей цепочки из двух одинаковых аппара
тов и далее обобщены на ступенчато-противоточную схему с
числом ступеней п.

Ступенчатый противоток для цепочки из двух аппаратов
В целях общности с последующим изложением входные
концентрации потоков в цепочку (рис . 1 0.36) .снабдим индексами
"О", выходные - индексами "п " (для цепочки из двух аппара
тов п = 2). Пvсть и в этом случае вещество переходит из фазы
"х" в фазу "у". Анализ будем вести в терминах фазы " х" . Тогда
поток фазы "у" составляет тD, а концентрация вещества, соот
ветствующая у1, запишется xf.
'ПО аппараты

Примем (эта с итуация весьма близка к широко встречающейся на практике),
одинаковы: в них идентичны СКК (хотя тип их - ИП фаз, прямо
ток и т.д. - для анализа безразличен) и равны пропускные способности, в част
ности kxJ!r = kx1i/i1 "' kxf, индексы при kx и / - номера аппаратов. Очевидно, 'ПО

841

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 10. 36. К аналитическому расчету реальноrо Сl)'Пенчато-противоточноrо
процесса: цепочка из двух аппаратов (1 и 11)

в случае двух аппаратов k,/ = k"F/2, где / и F - поверхности межфазноrо контак
та в одном и во всех (здесь - двух) аппаратах цепочки. Этот простейший вари
ант Сl)'Пенчатоrо противотока характеризуется одинаковыми обобщенными
пропускными способностями отдельных аппаратов r. 1
r. п "' r. , базирую
щимися по ( 1 0.37) на разных входных концентрациях для каждоrо из них:
=

r.

М1

Мп

(хо - xr)k"f (х1 - xg�"f

-

_

_

эти

( 1 0.47)

.

Разумеется, в зависимости от СКК в аппаратах величина r. будет выражать
ся по-разному; здесь важно, что
выражения одинаковы для всех (при п =
= 2
д11Я обоих) аппаргrов.цепочки.
В ( 1 0 .47) содержатся промежуточные (с позиций цепочки аппаратов) кон
центрации х1 и х1Р; их надо исключить, оставив лишь входные
для цепочки
концентрации � и x{f. Сделать
можно с помощью материальных балансов
для каждоrо из аппаратов:
(е)
М1 = Ц� х1 ), так
х1 = � - Мi /L;
Мн = .D(y1 - Уо) = mD(x1P - x<f), так что х1Р = x<f Мн /mD.
Выразим М1 и
из ( 1 0 .47) и подставим значения Х\ и х1Р:

-

это

-

-

что

Мн

М1 = (Х\1

-

(ж)

- x1P)k,/r. = (x0 - x8 - :�)k"fr. ,

(з)

М1 1 = (х1

- x<f) k,/r. = хо -

(и)

( �1 - x8)k"[r. .
чтоk"F/mDF/2,

В более лаконичной форме, учить1вая,
щая сила для цепочки аппаратов, k"F/L • а,
М1

м11

=

=

лx . k" fr. -

�

x<f

�;. Мн]
:s

•

,лх.

Ь и/=

входная движу
запишем
(к)

лx. k xfr. - 2 r. M1

Решая систему (к) относительно М1
ки), получаем

и М11 (например, методом подстанов

лх . r.

t

лх . r. .

842

-

(л)

(м)

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

М = М1 + Мн; тогда из (л), (м) с учетом k:xf = kxF/l имеем

Полный межфазный поток вещества в цепочке из двух аппаратов составляет

М

лх.

_

2kx f

-

- 1 ( a)kxfr.
2
l4 r.
2 Ь+
аЬ

1 - ( + ) �4
1 - 4 ,2
Ь

r =
•

•

аЬ

а

kxF

r,

(10.48)

•

- это полная пропусхна1 способносn. цепочки из д11ух аппаратов.
Как и в случае одиночных массообменных устройств, удобно ввести понятие
об обобщенной пропускной способностн се111 (здесь - цепочки) R. , представ-

М/ лх. и поверх

ляющей собой отношение пропускных способностей - полной
ностной стадий kxF'.

М

R. " --- =
лx. kx F

(

1 - Ь + а) �
1

_

аЬ 2
r.

4

r'

4 - (b + a)r..
4 - abr.2

�
�
= -

r•

.

(10.49)

4
В таком же виде обобщенная пропускная способность записывается на языке
фазы "у" : R. • M лy.ky F . С помощью ( 10.49) решаются задачи эксплуатации

/(

)

и проектирования для двухступенчатой цепочки. Пути таких решений показаны
ниже для противоточной цепочки из п аппаратов.

Ступенчаты й противоток
для цепочки из п одинаковых аппаратов
Анализ процесса для п аппаратов является весьма громозд

ким, поэтому ограничимся в учебнике результирующей форму
лой для обобщенной пропускной способности цепочки :

R.

=

М

п

п

( � ) ( � )
а (1 - � ) ь (1 - � )

---- = -----

лx. kxF

� -

г.

г.

п

-

l -

г.

r.

-

п

( 10.50)

Легко убедиться (пуrем подстановки соответствующих значе
ний п), чrо R· по (10.50) при п = 1 тождественно превращается в
r. , а при п = 2 - в R· по (10.49).

Из общих соображений очевидно, что при наращивании числа аппаратов в
цепочке поток переносимого вещества М будет возрастать из-за увеличения
общей поверхности контакта F и пропускной способности kxF.
Представляет интерес трансформация формулы
при п --. оо, если уве
личение числа аппаратов происходит не за счет их наращивания, а при сохранении
общей поверхности контакта F путем ее дробления на п частей. В этом случае
поверхностная пропускная способность отдельной ступени k:xf = kxF/п будет
стремиться к нулю при kxF = const. Но при малых k:xf поверхностная стадия
становится лимитирующей в массопереносе, так что пропускная способность

(I0.50)

отдельного аппарата - обозначим ее

(М / лх. )

0

- будет равна пропускной

843

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

способности его поверхносrной стадии k,/. Поэтому при п
r. •

(м / лх.)
k,,J

-(1-�)·
! (1-�)·
(1--) { )

0 = 1 . Значит, соmасно ( 10.50), при п --.
R· =

���

ь "

п

а

Входящие в (н) фрагменты типа

-

( �)

Тогда

(1 - �)"

М

и

лх.

- =

n

R.

R. k x F

=

lim
ln/ Ьj -+ oo

"

е - Ь - е -а

=

а - Ье Ь - а

J

(н)

при переходе к пределу п

lim (1 + !t ) ' = е:

1-+ <О

(1 -ь)<-п l

ае-Ь - ье -0
1 - еЬ- а

получится

оо дпя всей цепочки аппаратов

\-п

1-

+

оо

а " '

упрощаются на основе замечатель ного предела

lim
n -+ oo

--.

Ь

n

оо

Ь
)(- ) = е- ь .

l - e b-a

(о)

а - Ье Ь - а
kx F =

--.

еЬ -а - 1

Ье Ь - а - а

(п)

kx F,

что совпадает с ( 1 0 .40) Д11Я противотока в отдельном массообменном устройстве.
Таким образом, дробление ступеней в ступенчато -противоточной схеме в предел е

тождественно переходу к чисто противоточному процессу
в отдельных аппаратах цепочки.

-

независимо

от

СКК

Пропускную способность ступенчато-противоточной цепоч
ки М / лх. при конечном числе аппаратов п тоже удобно выра
зить через пропускные способности отдельных аппаратов
(М / ЛХ• ) 0 . Подчеркнем, что индекс "О" указывает, что М и
ЛХ· в скобках при наличии этого индекса относятся к отдель
ному аппарату. Раскроем смысл некоторых величин, входящих
в ( 1 0.50): а = kxF/L и а/п = kxf/L, Ь = kxF/mD и Ь/п = kxf/mD;
r• . =

,

/ ЛХ·)о .
(М kxf

а

- r

п

•

=

L

(М / ЛХ·)о .

формула ( 1 0 . 50) преобразуется к виду
- "' R . kx F
лх.

М

844

=

ь r•
п

-

=

(М / ЛХ·)о
mD

[1 - {М::п·)о]" -[1 - {М/�·)о]"
_!_[) - {М/ЛХ·)о]" 1 ·[1 - {М/ЛХ·)о]"

Тогда

-"' ----�- . ( 1 0 . 5 1 )
-=-------=------

-

_

L

mD

_

mD

L

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Это выражение является базовым для решения задач экс
плуатации и проектирования применительно к прямой линии
равновесия (т = const).
Задача эксплуатации решается прямо на основе формулы
( 1 0 . 5 1 ) : в правой части стоят известные величины, поскольку
потоки фаз и D - известны, число аппаратов в цепочке п
тоже ,
пропускные
способности
отдельных
аппаратов
(М / лх. ) уже найдены (см. разд . 1 0. 10). При известном лх. =
0
= Хо
.хоР определяется поток вещества М, а с помощью мате
риальных балансов (1 0. 1 8) - выходные концентрации Хп и Уп ·
Путь решения задачи проектирования зависm· от ее конкретной
постан овки. Чаще всего заданы поток и концентрации (входная и
выходная) целевой фазы и входная концентрация второй фазы.
Тогда технико-экономический анализ (сопоставление капиталь
ных и эксплуатационных затрат и нахождение условий минимума
суммарных затрат - см. разд. 10.7.2) позволяет найги поток второй
(нецелевой) фазы и рассчитать из материального баланса (10. 1 8)
выходную концентрацию вещества в ней. Определению здесь под
лежиr необходимое число аппаратов п (реальных!) в ступенчато
противоточной цепочке.
Для разрешения уравнения (10.51) относительно п обозначим
(в целях сокращения записи) первое и второе слагаемые в числи
теле соответственно В и А; тогда

L

-

-

м

лх .

=

В

В-А

-

L

-

А
mD

-

Выразим отсюда отношение В / А =

м 1 в м 1
в
--- - =--1
лх. L А лх. mD А
Таким образом,
1-

м; лх.
mD

1 _ м; лх.
L

=

( 1 0 . 5 1 а)

----

[

[ 1 -(М(М
1-

1

В 1
А =

и

лх.
{М_
)о
/ _�
_
mD
М лх. ) 0
1-{ /

1-

L

]n

_

]

лх. ) / mD n
0
/ лх. ) / L
0

/

м; лх .

mD

_

м ; лх .

L

'
845

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

откуда искомое (необходимое для осуществления процесса)
число ступеней составляет
In

1

_

м; лх.
mD

м;лх.

п = ------=L�)
1 (М/ЛХ• о
mD
ln
1 - (М/ЛХ• )о
1

_

( 10.52)

-

L

Подчеркнем, что формула ( 1 0 . 52) дает необходимое число
реальных ступеней (аппаратов, тарелок и т.п. индивидуальных
массообменных устройств).
Числитель формулы (10.52) удобно выразить через входные
и выходные концентрации для цепочки аппаратов - в задачах
проекrирования они известны . Преобразуем фрагменты числи
теля с учетом материальных балансов - см. выражения (а) в
разд. 10.9. 1 :
l _

М/ЛХ•

mD

=

тDлх. М тDлх. - D(У п - У о )
тDлх.
тDлх.
mD x o - хе - mD xc - хе Хо - хе
лх.
тDлх.
-

=

(

)

и более коротко:
1-

м;лх.
L

=

Lлх. - М
Lлх.

=

=

=

(

(

)

)

- хп ) Хп - хе

L x o - xC - L xo
(
Lлх.

=

лх.

(о)

•

(п)

Подставляя (о) и (п) в ( 1 0.52), получаем после сокращений
п

хо - хпР
Х п - х8
1 - ( М/ЛХ •) о
mD
ln
1 - ( М/ЛХ •) о
ln

=

----:--�,..--

( 1 0.52а)

L

Это выражение справедливо для любых СКК в отдельных
ступенях (напомним: одинаковых для разных аппаратов в це
почке). Знаменатель Zn в ( 1 0.52) и ( 1 0 . 52а) харакrеризует СКК
в ступенях: конкретное выражение Zn будет своим для каждого

846

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

из С КК в ступенях ( И П фаз, прямоток, противоток и др.).
Наиболее просто Zn выражается в случае И П фаз - соответ
ственно формуле ( 10.36). В этом случае фрагменты знаменателя
запишутся:
1

-

)о
_
(М_/_
лх_.�
mD

=

и
1-

(М/ЛХ•) о
L

=

1-

(�

1

)

1_ + l
+_
__ mD
k x f mD
L

(�

)

1
1 - --+ -1- + l L
k xf mD
L

_
_
_
_
_

1
1
-- + 
k xf L
1
1 + 1
+
kxf mD
L

--

1
1
-- + 
kxf . mD
1
1
1
+
+
kxf mD
L

-

--

(р)

(с)



В результате для ИП фаз знаменатель, после очевидных со
кращений, принимает вид
Zn

-= ln

Окончательно:

1
1
+kx f L
1
_
1_
+ __
k xf m D

n =

(

)

= ln m D L + kx f
L mD + kx f

.

(т)

х
хР
ln о - п

- тD
ln

----...._
.:;.... _

L

Хп

- xg

L + kx f

(1 0.53)

тD + kx f

Заметим, что под знак логарифма в знаменателе входит без
размерное отношение потоковых пропускных способностей
тD/L = а/Ь = с'; второй сомножитель также может быть пред
ставлен в виде соответствующих отношений а и Ь, но уже с
участием пропускной способности поверхностной стадии kxf.
Если ступени характеризуюrся крайне малыми поверхностями
контакта kxf, то они не эффективны, так что для обеспечения
процесса, т.е. получения заданных выходных концентраций, по
требуется много ступеней. При kxf --+ О подлогарифменное выра
жение в знаменателе стремится к единице, а Zn = ln l --+ О; чис
ло необходимых ступеней устремляется к бесконечн ости .
Если, наоборот, контакт фаз в каждой ступени очень эф
фективен, kxf --+ оо, то :
- фазы из каждой ступени буду�· уходить в равновесии
(ступени будут теоретическими, или идеальными);

847

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

- под знаком ln в знаменателе выражения ( 1 0.53) остается
безразмерное отношение потоков тD/L! т.е. задача потеряет
поверхностный xapaJcrep ;
- для обеспечения процесса в заданном диапазоне кон
центраций (от Хо до Хп) при фиксированном отношении тD/L
потребуется наименьшее число ступеней:

Р
ln х о - х.!!._
р
___

Хп - Хо

ln(тD / L) ·

( 1 0 . 53а)

Это выражение справедливо для ступенчато-противоточных
цепочек при всех рассмотренных СКК в отдельных массооб
менных устройствах с непрерывным контаJСГом фаз, кроме
противоточных.
1 0 . 1 2.4. Оценка эффективности функционирования
ступенчато-противоточной це1ючки
реальных массообменных аппаратов

В разд. 10. 12. l и 10. 12.2 изложены применяемые на праJСГике
методы определения числа теоретических ступеней nr при за
данных концевых концентрациях (задачи проеJСГирования) ,
потока переданного вещества и выходных концентраций при
известном nr (задача эксплуатации). Между тем при проеJСГи
ровании и эксплуатации технолоmческих схем в конечном сче
те необходимо оперировать реальн ым числом ступеней п. В
разд. 1 0. 12.З даны необходимые для этого соотношения; однако
они имеют ограничения:
- справедливы только для линейных процессов, примени
тельно к классу 3 (2-2) 1
для прямой линии равновесия
(добавим: и для одинаковых СКК в аппарате цепочки);
- предполагают знание кинетических поверхностных харак
теристик массопереноса типа kxf, kxF.
Первое обстоятельство ограничивает круг технологических
процессов, для которых возможен аналитический расчет. Вто
рое (для мноmх реальных ситуаций, когда поверхность меж
фазного контаJСГа неизвестна) - делает такие расчеты либо
невозможными, либо приближенными. Здесь достоверно лишь
число теоретических ступеней fir. Переход от fir к числу реаль
ных ступеней п осуmествляют с помощью коэффициента полез
ного действия сети аппаратов '11 с · Этот КПД определяется как
отношение теоретического и реального числа ступеней при
одинаковой эффеJСГивности сети (цепочки):
( 1 0 .54)
'11 с = nr/n , откуда п = nr/'11 c .
848
-

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Ч исленные значения 11с устанавливают эмпирически - с
помощью специального эксперимента или обследования мно
гочисленных работающих аппаратов. В наиболее тщательных
исследованиях устанавливают зависимость 11с от конструк
тивных особенностей аппарата (или группы аппаратов) и пара
метров процесса.
Подчеркнем, что понятие о КПД сети, цепочки аппаратов
или , что то же самое, в случае линейного описания процесса отдельного массообменного устройства является вынужденным
шагом, обусловленным прежде всего незнанием (неточным
знанием) величины поверхности конт-акга /, F
В науке ПАХТ исторически сложилось, что процессы массообмена в оди
ночном устройстве с непрерывным кокrапом фаз принято преимущественно
рассчитывать в терминах поверхностной задачи, т.е. на основе поверхности кон
таJСrа фаз (по величине типа kxF или методами, связанными с определением kx и
F). В то .же время массообмен в сетях аппаратов (прежде всего в ступенчато
противоточных цепочках) рассчитывают в терминах смешанной потоковой задачи
(по величинам типа L и D, тD) - на основе теоретических ступеней с использо
ванием КПД, призванного отразить степень приближения к равновесию. Связи
этих двух подходов не прослеживаются.

Сопоставление аналитических выражений для nr и п позво
ляет установить количественную связь между 11с и пропускной
способностью kxF. Важно: эта связь предполагает полную сег
регацию фазовых потоков, т.е. отделение одной фазы от дру
гой, и движение их между аппаратами в строго заданном про
тивоточном направлении (без обратного перемешивания за
счет захвата некоторого количества другой фазы), как это по
казано на рис . 1 0.32 и 10.36. Используя выражения ( 1 0.44) и
( 1 0 .53), найдем связь 11с и kxF для наиболее простого случая
И П обеих фаз:
mD L + kxf
__!:____ mD + kxf
+
ln
ln
ln
ь
+ k xf
mD
L
�
ftr
+
__
L
--.,.
_
m_
D
_
x
f
+
k
l
a . ( 1 0.55)
-,.-=
'11 с =
=

1

п

С ростом kxf пo ( 1 0.55) 11с увеличивается, и при kxf �оо полу
чается 11 с � 1 , что соответствует физическому смыслу КПД.
ln(mD/ L)

ln c

In(L/mD)

Не представляет трудностей выразить kxf в зависимости о т ТJ с в явном виде.
Из ( 10.55), имея в виду L/mD " с, получим из предпоследнего фрагмента

ТJ с1nс _
-

1nс

+ kxf
+ kxf

mD
L

-+

mD + kxf
с · ·· = с ---=�
L + kxf
n

-+

L с '1

'

+ kxfс '1

<

= т Dс + kх/с.

Отсюда, с учетом c(mD/L) " 1 , имеем

mDc - Lc'l• = L 1 - c'lc L c'l• - 1
( 10.56)
= -c'l c - с
с - c'lc
c 'lc - с
ТJ с = 1 соответствует kxf -+ оо (для этого следует раскрыть

kxf =

--

Легко показать, что
неопределенность в правой части, например по Лопиталю).

849

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

В случае
кроем ее:

с=1

выражения ( 1 0. 5 5 ) и ( 1 0. 56) содержат неопределенность. Рас

,,

• � l c - c''

i_(
c '' 1 )
l1, c = 11,_
dc
- lim
,
J - n c•· - 1
r�I d {
l - 11
- \С - С )
dc
-

lim � = lim

С учетом ( 1 0.56)

k, f = L �
l - 11,

r

и

r�l

k, f " а = � .
L
1 - 11,

"· - 1

·1 с

-

'

а- = _
11 = ь_
'
l +a
l +b·

(у)

(ф)

В ыражение ( 1 0. 56) позволяет по опытн ы м значениям 'lc оценить по верхность
контакта ступени ( м ассообменноrо устройства), точнее - величину k,f. Особо
просто это сделать. подобрав смесь с прямой линией равновесия и выдержав та
кое отношение фазовых потоков, чтобы LlmD = 1 .

В случае кр ивой л и н и и равновесия представленные выше сооб

ражения п риобретают оценоч н ы й характер.

т = const

Кроме того, и при

непол нота сегрегаци и фаз (скажем , унос о пределен ного
кол ичества капел ь дискретной фазы потоком сплошной) нарушает

бл иже н н ы м . Именно поэтому п рактически найден н ы е значения Тl с

при нятую модел ь ступенчатого проти вотока и делает анализ при

нередко отражают не тол ько вскрытую выше связь с k,/( ил и kx F ) ,
но и другие трудноопредел имые эффекты . По существу, КПД вы
ступает в качестве "коэффициента незнания", но степень этого не

k,/, L,

знания при установлении е го связи с пропускны м и с пособностям и

mD и их отношениями а, с становится значительно меньше .
На п ракти ке весьма часто встречаются технологические ситуа
ц и и , когда поверхностн ы й массоперенос и в самом деле не л и м и
ти рует п роцесс м ассооб мена. И н ы м и сл овам и , рабочая л и н ия пря

Ь,

мото ч ного акта м ассообмена заканчи вается (либо рабочая точ ка в
аппарате с ИП фаз располагается ) достаточно бл изко к л и н и и рав
новесия . Тогда кон це п ци ю КПД можно сч итать п рагматически оп
равдан ной : наиболее медленные стадии - потоков ы й перенос ве

надо вести расчет. А поверхностны й перенос "почти" завершен,
некую е го незавершенность позвол ител ь но учитывать с помощью
КПД, достаточно бл изкого к 1 (скажем , на уровне
и выше в
щества; эти стад и и в основном контроли руют процесс, п о н и м и

0,7-0,8

некоторых э кстракцион н ы х аппаратах) .
Но встречаются ситуации , когда КПД далек от 1 ( в некоторых
абсорбцион н ы х а ппаратах, например, о н н иже
1 ) Это означает,
что про цесс контрол ируется в основном поверхностн ы м и стадия
м и м ассопереноса; поэтому подменять задачу, испол ьзуя кон це п 
цию КПД, здесь в р я д л и оправданно . В эти х случаях нужно опре

О,

.

делять и класть в основу расчета поверхностные характеристики
м ассопереноса - kx иf, F.

850

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

1 0 . 1 2.5. О расчете противоточных аппаратов
"
и их цепочек по методу ВЭТС"

При расчете массообменных противоточных устройств с не
прерывным контактом фаз (см. разд. 10.8 .4) нередко возникают

затруднения, связанные с определением поверхности контакта
F Их пытаются разрешить, подменяя поверхностную либо
смешанную задачу практичес� удобными представлениями ,
имеющими отдаленное отношение к потоковой задаче .

Отклонение реальноrо процесса от идеалъноrо учитывается затем с помощью
понятия о Высоте рабочей зоны, Эквивалентной (по эффекrу массопереноса,
т.е. изменению концентрации в фазе) одной Теоретической Сrупени (ВЭТС) .
Тогда, определив (по диаграмме у
х в случае кривой линии равновесия и
аналитически - в случае прямой) число теоретических С'I)'Пеней nr, далее просто
рассчитывают высоту рабочей зоны аппарата Н:
-

Н = ВЭТСпr .

( 1 0.57)

Все трудности расчета здесь переносятся на определение ВЭТС, которую вы
ражают в виде эмпирической зависимости от параметров процесса и конструк
тивных характеристик аппарата.
Метод ВЭТС внешне напоминает определение Н по ВЕП . Однако там учте 
ны характерные особенности контаJсrНоrо массообмена, здесь они игнорируются
путем отказа от реальной поверхностной моде.ли. Иначе rоворя, математиче
ское описание по методу ВЭТС (ступенчатая модель массопереноса) не соответ 
стеует физике процесса (непрерывному контакrу фаз). Попьпки чисто эмпири
ческоrо (вне физической модели) учета кинетики процесса в расчетных форму
лах Д11Я ВЭТС
малопродукrивны, сами формулы - ненадежны и непрогнозны
при выходе за исследованные в эксперименте диапазоны изменения натуральных
параметров процесса и конструкrивных характеристик аппаратуры.
-

К результатам расчетов высоты рабочей зоны аппаратов с
непрерывным контактом фаз по методу ВЭТС надо относиться
с осторожностью.
·

10. 13. ПЕРЕКРЕСТНОЕ СОFДИ НЕНИЕ АППАРАТОВ
В СЕТИ ДЛЯ ПРОЦЕССОВ КЛАССА 3(2-2) 1

Типичные схемы перекрестных массообменных процессов
были приведены в разд. 1 0. 1 1 (см. рис . 10.30 - 111 , IV, V). При
этом возможно разбиение потоков любой из фаз или обеих
фаз. Расчетная схема ступенчато-перекрестного процесса с
разбиением (в качестве примера) фазы "у'' представлена на
рис . 10.37. Потоки фаз имеют исходные концентрации Хо и Уо·
Поток фазы " х" с постоянным расходом L (в расчете на инерт)
последовательно проходит через каскад массообменных аппа
ратов. Фаза " у" отдельными потоками D1 , � • • • • , Dn (в общем
случае - различными) проходит через отдельные аппараты,
контактируя в каждом с фазой "х" . Из сети (цепочки) аппара851

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

у

Уо

Рис. 10. 3 7. Типовая схема ступенча
того ( 1, 2, . . . , п) перекресnюrо про
цесса с разбиением одной фазы

Ступенчатый перекрест
ный ток: реальные ступени в диа
rрамме у - х

Рис. 10. 38.

тов выходят один поток фазы "х'' с концентрацией Хп и п по
токов фазы "у" , каждый со своей выходной концентрацией у1 ,
У2, . . . , Уп; эти потоки при необходимости моiуГ бьпъ объединены
в общий поток (их смешение на схеме не показано).
Диаграмма у - х для реального ступенчатого перекрестного
процесса, соответствующего приведенной выше схеме, изобра
жена на рис. 1 0 . 3 8 . Исходные точки рабочих линий для каждой
ступени (аппарата) характеризуются одинаковой входной кон
центрацией Уо фазы "у" (в случае "чистой" фазы, первоначаль
но свободной от переносимого компонента, Уо = О). В то же
время входные концентрации фазы "х'' для разных ступеней
различны: Хо , х1 , . . . , Xn- I • причем входная концентрация i-й
ступ ени есть выходная концентрация предыдущей (i - 1 )-й.
Определение конечной точки рабочей линии (при прямо
точном движении фаз в режиме ИВ либо при таком движении
одной из фаз, а другой - в режиме ИП) или рабочей точки
(при И П обеих фаз) подробно рассмотрено в разд. 1 0 .7 приме
нительно к одиночному аппарату. Для ступенчатых пере
крестных схем эти точки отыскиваюгся соответственно пара
метрам работы каждого аппарата:
- направление линии (угол Р д отвечает tg/3; = L/D;, D; поток фазы "у" в i-й ступени;
852

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

- положение конечной (или рабочей) точки на этой линии
соответствует отношениям пропускных способностей поверх
ностной и потоковой стадий в данной ступени.
Разумеется, при одинаковых потоках фазы "у'' (D1 = fh =
= ... = D1 = ... = Dп) рабочие линии будуг параллельны вследст
вие равенства углов Р 1 = Р 2 = ... = Р 1 = ... = Рп · Чем выше про
пускные способности поверхностных стадий в аппаратах, тем
ближе к равновесной линии располагаются конечные точки для
каждой ступ ени.
Основное затруднение при построении реального процесса в
случае кривой линии равновесия при известных кинетических
характеристиках массопереноса kxtft состоит в rромоздкости
процедуры определения конечных (при И П обеих фаз - рабо
чих) точек. Это затруднение снимается в случае прямой равно
весной линии, когда становится возможным аналитический
расчет. Однако на практике часто неизвестны поверхностные
пропусЮ1ые способности kxtft; тогда приходится принимать
процесс идеальным (полагая kxtft ....+ оо), осуществляемым в
условиях потоковой задачи, а далее учитывать отклонение от
реальности с помощью КПД ступени или каких-либо иных
поправочных коэффициентов.
Ниже рассмотрен сначала расчет перекрестных схем с иде
альным контактом фаз в каждой ступени, а затем продемон 
стрированы возможности аналитического расчета реального
процесса для случая т = const.
10.13. 1 . Массоперенос при идеальном контакте фаз в ступенях
Кривая линия равновесия. Расчет ступенчатого перекрестного
процесса в случае т = var ведется rрафоаналитически. Диа
rрамма у - х для идеального процесса применительно к разбие
нию на порции фазы "у" и переходу в нее вещества изображе
на на рис . 1 0 .39,а. Точки сопряженных выходных концентра
ций фаз для каждой ступени лежат здесь на линии равновесия.
Направления рабочих линий характеризуются углом наклона
р 1, так что tgp 1 = L/D1• Эти углы для любой ступени больше,
нежели для одноступенчатого процесса с подачей в аппарат
всей фазы "у'' : D = Di + fh + . + Dn > Di , /h, .. " Dn (рабочая
линия для такого одноступенчатого процесса для сравнения
проведена на диаrрамме штрих-пунктиром, конечная концент
рация вещества в фазе "х" равна х1 ) . Построение показывает (а
расчет для прямой линии равновесия это подтверждает - см.
ниже), что эффект в случае разбиения какой-либо фазы выше,
чем при контакте обеих фаз в одном аппарате: Хп < х1, т.е. фаза
" х" здесь в большей мере очищается от переносимого ве
щества.
853
"

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

у

у

Уп
Уп - 1
У2

У1
У2
Уп

У1
Уо

Уо

х

а

разбиение фазы ')> ", б - разбиение фазы 'х"

Рис. 10.39. Сtупенчато-перекресmая схема: диаJраммы д11Я идеальноrо контакта фаз:
а

-

При разбиении фазы "х" расчетная схема аналогична приве
денной на рис. 1 0.37, только здесь уже фаза "у" неизменным
потоком последовательно проходит через все аппараты, а фаза
" х" делится на потоки L1 , Lz., . . . , Ln , подаваемые в отдельные
аппараты. Рабочие линии для этоrо варианта изображены на
рис. 10.39,б. Здесь углы наклона рабочей линии меньше, чем
при подаче обеих фаз в один аппарат (рабочая линия тоже по
казана штрих-пунктиром) : L = L 1 + Lz. + .. + Ln > L 1 , Lz., . . . ,
Ln , а tgp, = L1 /D. Результирующий эффект и здесь выше, чем
при контакте потоков L и D в одном аппарате: Уп > YJ, фаза "у"
в большей мере насыщается переносимым веществом.
За пределами анализа остаются пока две проблемы:
- какую из фаз целесообразно распределить (разбить);
- каким образом разбиваемую фазу целесообразно распределять между аппаратами (ступенями) .
Эти проблемы строrо решаются аналитически в случае пря
мой линии равновесия; при т = var однозначноrо ответа нет,
так что для каждоrо конкретноrо случая к решениям приходят
методом проб и ошибок. В оценочном плане можно воспользо
ваться рекомендациями, вытекающими из анализа для т =
= const, но точное решение здесь зависит от конфиrурации
кривой равновесия и рабочеrо диапазона концентраций .
Прямая линия равновесия. Рассмотрим для т = const сначала
процесс в первой ступени, для чеrо воспользуемся выражением
( 1 0.36) для пропускной способности, только применительно к
схеме и обозначениям на рис . 1 0.37. Для И П обеих фаз и иде
альноrо их контакта (kxf � оо)
м
м
м
(а)
1
1
лх.
т
/
-+
L mD1
.

-

854

хо - Уо

-

х0 - х8

---

-

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Нетрудно убедиться, что при kxf --+ оо такое же выражение
получается и в случае прямотока фаз.
Подставив в (а) поток вещества М = L(x1 - X<J), найдем зна
чение концентрации х1 в фазе "х' на выходе из первой ступени:

- xi) _- 1
х0 - х1 _- 1
1
хо - Уо/т _!_ + __ XQ - Уо /т 1 + �
L mD1
mDi
хо + хо �
mDi - х1 (1 + �
mDi ) = хо - Уо/т ;
L (xo

XfJ

окончательно:

Х1 =

D1
+ Уо у
1 + mDi
L

(10.58)

=

Значение выходной концентрации вещества в фазе "у" составит
L
У1

+ D - Yo + xo D1
l+�
mDi

= mx1 = Lxo 1Yo
L / m + D1

1

( 0 . 58 а)

Выражения длJ1 х1 и У1 можно получить непосредственно из материального
баланса длJ1 первого аппарата (он представит собой пространственный контур) :
Dl)'o + /..хо

- D1Y1 - Lx 1 = О.

(б)

Подставив длJ1 первой ступени YI = тх1, имеем

D 1Yo + /..хо = m D 1x1 + Lx1 ,

(в)

откуда сразу получается х1 по ( 1 0.58) и затем У1 по ( 1 0 .58а) .

В задачу эксплуатации входит определение всех выходных
концентраций вещества в обеих фазах по заданным потокам L
и
и входным концентрациям и Х{) для первой ступени,
и
Х;- 1 для i-й ступени. При этом входная концентрация Х;- 1 опре
деляется как выходная для предыдущей ступени; такой пошаговый
расчет позволяет поочередно найти все выходные концентрации.
Значение х1 определяется выражением (10.58). Аналогично
получается и записывается выражение для
из материального
баланса второй ступени при идеальном контакте фаз � =
имеем
- D2Y2 = О, Lx 1 + �о =
Lx1 + �о
(r)
=
+�=
+

D1

Уо

Уо

х2;

- Lx2

Lx2

тх2)

Lx2 mDx2,

855

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

откуда
D

Х1 + Уо 2
у

( 1 0.58б)
т�
L
Здесь надо заменить х1 в ( 10.58б) через Хо по ( 1 0 .58) - полу
чится х2 в зависимости от .хо, у0 и потоков фаз L, D1 и �Далее аналогичные преобразования проводятся для третьей
и последующих ступеней. Эта процедура достаточно проста,
если в процесс массообмена вводится чистая фаза "у" , не со
держащая вещества: Уо = О. Чтобы осуществить анализ в таком
простом варианте, сохранив при этом общность с реальной
ситуацией (у0 * О), перенесем начало отсчета концентраций в
точку А (у0 , .хоР)
см. рис . 1 0 .40. Тогда сохранится угол накло
на равновесной линии е, так что tg8 = т, а новые
("приведенные") концентрации составят У = у у0, Х = х X(f ,
причем .хоР = yr/m.
В приведенных концентрациях Уо = Уо - Уо = О, и выраже
ние ( 10.58) принимает вид
1+

.

--

-

-

..
Х1 =

-

Хо

(д)

D
1+m 1
L

--

Приведенная концентрация после второй ступени записывается аналогично (с учетом Уо = О ) :
Х1
(е)
Х2 =
l + т�
L

-

Подстановка значения Х1 по (д) позволяет избавиться от Х1 :
Х2 =
.

Хо

( z )( � )
1+m 1

2
1+т

.

(ж)

После п-й ступени путем таких же подстановок получим

п =- Хп - х0Р

Х

.

- 1

-

ХО

p
XQ - X

О

( + m�1)(i + mz2 ) · · · (i + mzп ) 1�Ji + mi1)
=

( 1 0.59х)

Концентрация вещества в фазе "х" после промежуrочной j-й
ступени рассчитывается по идентичному выражению, только
верхний индекс произведения будет не " п " , а " i" .
856

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 10. 40. К преобразованию координат для
анапитическоrо расчета перекрестноrо ступенчатоrо массообмена

У

у

Концентрация вещества в фазе
у'' после j-й ступени при идеальном
контакте фаз выразится:
У; = тХ1; Yt Уо = т(х1 - X{f);
Yt = Уо + т(х1 - уа/т). (1 0.59у)
"

х

-

х

Полученные решения позволяют
поставить ряд задач оптимизации
ступенчато-перекрестною массообмена - их следует относить
к проектным или проектно-эксплуатационным задачам.
10. 13.2. Оптимизация ступенчато-перекрестных процессов
при идеальном контакте фаз

Решение задач оптимизации доводится до простых аналити
ческих выражений только при линейном описании процесса, в
частности, в случае т = const (прямая линия равновесия).

Оптимизация потоков распределяемой фазы
Задача легко решается на примере двух ступеней; здесь � =
= D - D1, где D - полный поток фазы "у" (см. рис. 10.37), так

что выходная концентрация по (ж) будет функцией одной пе
ременной
Хо
(з)
Х2 =
-

D1 :

(t mzi )[t
+

+

m (D

� Di )

J

.

D1 ,

Цель анализа - в установлении такой величины
при ко
торой массообмен происходит с наибольшей полнотой; иначе:
надо найти такое значение
которое обеспечивает минимум
при данном (определенном, постоянном) полном потоке
Рассмотрение выражения (з) показывает, что согласно пер
вому сомножителю в знаменателе (Zn) рост
вызывает
уменьшение Хъ а согласно второму - увеличение; значит,
=
функция
может иметь экстремум. Для проверки его
существования и определения значения
в точке экстремума
надо приравнять нулю производную:
= О. Операцию
дифференцирования можно упростить, так как числитель от
не зависит, и вполне достаточно взять производную знаменате
ля (при этом изменится тип экстремума):

D1,

Х2

D.

D1

Х2 X2 (D1 )

D1
dXi/d D1

:� = d� [(1 + mi) (1 + : mi)] 7(1 + : mi) + (-7)(1 + mi)
т

-

=

т

-

D1

= О.

857

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

После сокращения на т/L, раскрытия скобок и очевидных
упрощений получаем
D
D
(и)
D - 2D1 = О, D1 = 2 , значит, D1 = fh = 2 .

Анализ на тип экстремума (приравнивание нулю второй
производной и проверка ее знака в точке D1 = D/2) показы
вает, что в точке экстремума Zn проходит через максимум.
Значит, при делении общего потока D поровну на D1 и fh вы
ходная концентрация Х2 (а с ней и х2) минимальна, а процесс
массообмена наиболее эффективен . Полученный результат од
новременно показывает, что разбиение потока D на D1 и fh
выгоднее подачи всего потока фазы "у" в один аппарат для кон
такта с фазой "х'' : в противном случае анализ на минимум Х2
привел бы к результату D1 = D или D1 = О.
Замеmм, 'ПО цель анализа может б ыrь сформулирована иначе: надо найти
такое распределение потоков разбиваемой фазы между ступенями , 'Побы до
С11t ЧЬ заданного значения Х2 при минимальном общем потоке D. В этом случае
необходимо выразить D в виде функции от D 1 при п остоянном Х2 и найm зна
чение D 1 в точке минимума D. Результат получается тот же: D1 = Di = D/2.

Аналогичный подход позволяет определить оптимальное
распределение фазы "у" в случае трех ступеней. Только конеч
ная концентрация Х3 является функцией уже двух перемен 
ных
D1 и /h , поток в третьей ступени будет взят по разно
сти: Dз = D - D1 - fh. Далее придется приравнивать нулю уже
две производные: дХудD1 = О и дХуд/h = О
и решать полу
ченную систему уравнений. Решение ее приводит к результату
-

-

� = fh = � =

�.

w

В случае большего числа ступеней анализ можно вести ана
логичным образом; результат - тот же; наиболее выгодно рас
пределять разбиваемый поток между ступенями поровну:
D
(л)
D1 = D1 = ... = Dt = ... = Dп =
-

п

Тогда сомножители в знаменателе ( 10.59х) становятся оди
наковыми по величине, так что
Хп

=

+

Хо п =

+

Хо п .

(1 m�t) (1 ��)

( 1 0 .60)

Отсюда можно найти число ступеней п, необходимых для
осуществления процесса с заданной эффективностью (от х до
Хп ) при известных L, D и т.
858

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Оптимизация числа ступеней
Выше показано, что разбиение фазы выгоднее подачи пол
ного потока в один аппарат. Можно предположить, что вообще
увеличение числа ступеней п будет сопровождаться повышени
ем эффективности процесса. Чтобы проверить это предполо
жение, попытаемся найти экстремум функции ( 10.60) Хп =
= Хп(п), для чего приравняем нулю производную Хп по п. Как и
ранее, здесь проще искать dZn/dп, поскольку числитель Хо от п
не зависит.
Для дифференцирования с.ложноrо Zn ( 10.60) возьмем сначала ero ло1'арифм :
= nln( l + I/cn), те с "' L/mD. Продифференцируем теперь lnZn по п:

lnZn

10(1 ...!.)._ :

и

+

сп

-1- .
l

п+
с

(м)

Последнее равенство удоалетворяется при п -+ ""

Таким образом, анализ показывает, что эффективность сту
пенчато-перекрестной схемы возрастает с увеличением п, при
чем наибольшая эффективность достигается при п � оо . Пред
ставляет интерес определить Хп при бесконечном п
это будет
характеристика
наибольших
возможностей
ступенчато
перекрестной схемы. На основе (10.60)
-

.
11m

n -+ oo

(

1+

Хо

)

mD
Lп

поскольку liш

f -+ oo

n

=

(i !)f
+

.
lim

n -+ oo
t

(

l
1+-

= е

Окончательно: при п

Хо

сп

-

� оо

)

п

=

.
lim

n -+ oo

(

1
1+-

)

Х0

сп

Х0

(сп)/с

= --

e l /c

'

"замечательный предел" .

(10.61 )
859

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 1 0. 4 1. Эффективность ступенча
то-перекрестной цепочки массооб
менных аппаратов

Хп
Хо

0 ,5

0,4

2

з

4

Зависимость типа ( 1 0 .60)
приведена на рис. 10.41 для
значения с = L/mD = 1 .

5

Полученные соотношения позво
ляют записать выражение для про
пускной способности
отдельного
аппарата с перекрестным током в
условиях идеального контакта фаз, поскольку "чистый" перекрестный ток отве
чает п _... оо. Поскольку М = /.,(Хо
Х..) , а ЛХ• = Хо
XrJ' = Хо (так как при
переносе координат XrJ' = x(f - x(f = О), то

6 7

п

8

-

_!!_ =
лх.

r(xо -

х e- l / c

o

Хо

-

) (

} (

)

= L 1 - e- l l c = L 1 - e-mD ! L ·

(10.62)

Заметим, что прямой вывод этого соотношения требует весьма rромоздкого
анализа.

Выбор распределяемой фазы
Проблема состоит в том, какую из фаз целесообразно после

довательно пропустить через все аппараты ступенчато
противоточной цепочюt, а какую следует распределить (уже
доказано: поровну при т = const) между аппаратами - при
заданных общих потоках фаз и известном числе аппаратов.
Упростим задачу, решая ее для п � оо; очевидно, что получаемые
выводы будуг качественно справедливы для люfюго п > 1 .
Будем сравнивать пропускные способности цепочек аппара
тов при разбиении потоков различных фаз. Выше было полу
чено выражение ( 1 0 .62), относящееся к разбиению фазы "у''.
Симметричное выражение при разбиении фазы "х" (тоже на ее
языке) запишется:
( 1 0.62а)
= mD e-L /mD mD - е- с .

(

:;,.,

I

-

)

{

=

I

)

В качестве характеристики относительной эффективности
разбиения Z примем отношение пропускных способностей про
цессов по ( 1 0.62) и ( 1 0.62а):
Z=

с ) 1 е- 1 / с
-с = C 1 - е - с
mD (I - е )
(

L1

-

е- 1 1

_

----

( 10.63)

Если получится Z > 1, то выгоднее разбиение фазы "у" , если
Z < 1 , то фазы "х " ; при Z = 1 разбиения равноценны. Из фор
мулы ( 1 0.63) следует, что при с = 1 (т.е. при L = m D) тожде860

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ственно Z = 1 , т.е. оба способа разбиения равноценны . Анализ
показывает, что при с -1; 1 выгоднее разбивать ту фазу, приведен

ный поток которой больше.

10.13.З. Массоперенос в реальных ступенях контакта
в случае прямой линии равновесия

Реальный контакт фаз в общем случае происходит в услови
ях смешанной задачи, поэтому надо учитывать кинетические
характеристики kxf, kxF. Анализ при этом существенно услож
няется. Для случая кривых линий равновесия подход к по
строению реальных ступеней при ступенчато-перекрестном
движении фаз кратко затронут в начале разд. 1 0 . 1 3 ; процедура
построения ступеней весьма громоздка, а для ряда технологи
ческих задач приходится действовать подбором. Для прямых
линий равновесия (т = const) анализ удается довести до ко
нечных соотношений. Однако сложность преобразований
оставляет этот анализ вне учебника; в нем даны лишь некото
рые конечные соотношения и вытекающие из них качествен 
ные заключения.
Выражение дтIЯ пропускных способностей ступенчато-перекрестной схемы
имеет вид (при разбиении фазы "у" )
М
ЛХ .

rде

l- (-

- L l- 1_

(М/ЛХ• )1

(M/лx.)1,2,",i .",n

L

-

)(

1-

( М/лх.)2
L

) -] [ (
" .

=

L l

-

п
П

i=I

l

-

( М/ЛХ• );
L

пропускные способности отдельных ( l -ro,

)]

( 10.64)

•

2-ro,

"

. , i-ro,

" . , n-ro) аппаратов; именно в этих пропускных способностях }"Пено влияние
кинетических харакrеристик (kxf);.
Анализ показывает, что при равных k,/ на разных ступенях и при одинако
ВЬIХ СКК в них максимуму пропускной способности цепочки, как и при иде
альном ко�пакте фаз, отвечает разбиение распределяемой фазы на равные потоки
по ступеням. Тогда и пропускные способности
) ; по ступеням одинаковы, ниже они обозначены
ки преобразуется к виду

( М/ лх.
(М/ лх. )о. При этом формула (10.64) дтIЯ всей цепоч

( 1 0.64а)
В часnюсти, при идеальном перемешивании фаз на каждой ступени, с уче
том kxf = k"F/n и формулы (10. 3 6), имеем

.!!__
лх.

=

[[

l- l

1J -[l
n

_

1

1
1

1

+ - + -kxFfn L mD/n
-

=

L

1

_

l+n

(

1
1

-

а

]ь)

n

·

( 1 О . 64б)

+а

-

861

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

для осущесТR11е ния процесса с заданной эффекrивностью (задача проеJсrИрова
ния, величина М/ дх. известна) потребуется следующее количество реальных

Из ( 10.64а) следует, что при одинаковых (в массообменном аспекrе) ступенях

ступеней:

( 1 0.65)

Приведенные формулы мoryr бьrrь проанализированы на предельные ситуа
ции. При k,/ � оо они закономерно переходят в приведенные выше соотноше
ния для идеального контакrа фаз. При п � оо выражение ( 1 0.646) принимает вид

( -a/(l+b))

.!!..._ L 1 - е
дх.

=

=

[

kx f 1 L
1 + �flтD

[- (
( /:1 ) J

=

L l

L l - ехр -

1/kx

ехр -

)]

=

( 1 0 .64в)

/тD

Это - общее описание перекрестного тока в одной peflllьнoii ступени непрерыв
ного контакта фаз. При k,/ � оо оно закономерно переходит в ( 1 0.62).

10. 14. ПЕРИОДИЧЕСКИЕ И ПОЛУНЕПРЕРЫВНЫЕ
ПРОЦЕССЫ КЛАССА 3(2-2) 1

В разд. 1 0 . 1 были выделены массообменные процессы, про
водимые в периодическом и полунепрерывном режимах. В пер
вом случае в аппарат загружаются определенные количества
фаз с начальными концентрациями хн и Ун, причем эти исход
ные концентрации - неравновесны. В результате во времени 't
происходит изменение концентрации вещества в обеих фазах, и
по истечении определенного промежугка времени 'tк фазы выrру
жаюrся из аппарата с конечными концентрациями Хх и Ук· В слу
чае полунепрерывного процесса (ero иногда называют
"дифференциальным") одна из фаз (например, ".х'') загружается в
аппарат и пребывает там в ходе всею процесса; концентрация ве
щества в этой фазе изменяется от � до Хх · А вrорая (здесь - фаза
"у") непрерывно подается в аппарат с неизменной концентрацией
Ун и непрерывно выводится из него с переменной во времени
(вследствие протекающего массообмена с фазой ".х'', в которой
концентрация х = var) выходной концентрацией Ук·
В отличие от непрерывных процессов здесь приходится опе
рировать не потоками, а количест6ами фаз (в периодических
процессах) , количествами и потоками (в полунепрерывных).
Н иже последовательно рассмотрены основные подходы к
расчету простейших схем периодических и полунепрерывных
862

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

процессов класса 3 (2-2) 1 . Для определенности принято, что и
здесь вещество переходит из фазы "х" в фазу "у" . Анализ ве
дется на языке фазы "х" .
10. 14. 1 . Периодические процессы

В случае периодических процессов в качестве пропускных
способностей потоковых стадий выступают количества фазы .
Будем обозначать их теми же символами, но полужирным пря
мым шрифтом. Пропускная способность поверхностной стадии
в целом выразится в форме kхFт.к (или kxFт для текущеrо мо
мента времени, kxFdт - для бесконечно малоrо) .
Общая расчетная схема массообменноrо периодического
процесса с обозначенной на ней поверхностью раздела фаз
представлена на рис. 10.42. Количества фаз постоянны и равны
L и D. В задачу анализа входит установление связи текущих
концентраций вещества в фазах х и у (в итоге - конечных Хк и
yJ с текущим временем процесса т (в итоге - с конечным •к) ·
Для анализа процесса очертим для отдельных фаз простран
ственные контуры, проходящие через поверхность раздела фаз
F. Концентрации вещества в фазах в промежуточный момент
времени т равны х и у; дадим времени приращение d• и запи
шем для этого бесконечно малоrо промежутка времени матери
альные балансы.
Для контура К1 :
(а)
+ О dM = d(Lx) = l..dx, откуда dM = 1..dx
Для контура К2:
(б)
+ dM О = d(Dy) = Ddy, откуда dM = Ddy.
Вместе с тем
(в)
dM = kxF(x - .xP)d• ,
-

-

.

-

где J6'

равновесная с у концентрация: она берется по равновесной зависимос
из графика (ее.ли линия равновесия - кривая, т = var) либо аналитически
(если т = const) .

ти

-

-

В целях упрощения анализа примем,
что фазы идеально перемешаны, так
что х и у вдоль поверхности контакта не
изменяются, они являются функциями
времени.
Из выражений (а) - (в)
dM = 1..dx = Ddy = kxF(x - .хР)dт . (г)
-

Проинтегрируем

по

отдельности

L,x

D ,y

F
К2

10. 42. Расчетная схема периодического про
ко нтуры)
цесса (К1 и К 2

Рис.

-

863

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

выражения (r):
М

f
О

или

М = L (хн -

d M = -L

Хк

J dx

=

Хн

tк

Ук

D J dy

= kxF J

О

Ун

(x - xP)d• ,

D(ук - Ун) = kxF (x - .хР)ср•к = kхFЛХср•к , ( 1 0 .66)
причем ЛХr,р - средняя во времени движущая сила для всего
массообменного процесса продолжительностью 'tк .
xJ

=

Поделим почленно выражения (r) и ( 1 0.66); с учетом знака
по (а)
--- =

dx

Хк - Хн

dy
--Ун - Ук

= --- --

Х - хР

d't
't
ЛХс р к

(д)

Примечательно, что выражение (д) для периодического про
цесса математически идентично выражению (и) в разд . 1 0. 8 .2
для непрерывного стационарного прямоточного процесса. Только
вместо dF/Fк (для прямотока) в случае периодического процес
са в правом выражении стоит d't/•к · Физическое различие за
ключается в том, что в случае непрерывных прямоточных про
цессов рассматривается изменение концентраций вдоль массо
обменной поверхности, т.е. оси F (для фиксированного проме
жуrка времени, например - 1 с), а в случае периодических
процессов - изменение концентраций вдоль оси времени (для
фиксированной поверхности контакта F, если речь идет о И П
фаз). Именно поэтому в периодическом процессе дВюt..")'Щая
сила усредняется по времени (в стационарном противотоке она
усредняется по поверхности контакта).
Таким образом, математически периодический процесс может
трактоваться как прямоточный во времени.
Продемонстрируем идентичность выражений для ЛХср (этой
величиной оперируют в задачах проектирования). В случае кри
вой линии равновесия расчет ведется графически. С этой целью
используются только первое и третье из выражений (д); разде
лим переменные и проинтегрируем:

�

J

Х

н

dx
х-

хР

=

Х - Хн
к

ЛХср 't к

t

{d't ; Sx =

о

Хн - Хк

ЛХср

;

ЛХср =

х

н - к ' (1 0.67)

х

Sx

поскольку интеграл в левой части равен Sx - числу единиц
переноса по фазе " х" . Правое выражение ( 10.67) совпадает с
( 1 0 .27 х).
В случае прямой линии равновесия (т = const) надо
полностью повторить анализ, выполнен ный в разд . 1 0 . 8 . 2 . И
Н64

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

тогда, естественно, приходим к формуле, совпадающей с
( 1 0.26 х):
( 1 0 .68)
где ЛХн = хн - х,.Р (вычитаемое равновесно с
равновесно с ук).

Ун), ЛХк

= Хк

-

� (вычитаемое

Решение задачи эксплуатации для периодических процессов
на основе определения пропусююй способности периодически
работающего аппарата также ведется аналогично продемон
стрированному ранее (разд . 10.9) для непрерывного прямотока,
только с заменой оси f на ось -r. Конечные выражения для
прямотока типа ( 1 0 .34), ( 1 0.38), ( 10.39) сохраняют силу, но в
качестве пропускной способности поверхностной стадии в них
фигурирует не kxF, а kxF't; и все отношения пропускных спо
собностей ( а, Ь и др.) понимаются как отношения не потоков
(например, кг/с или моль/с) , а количеств (кг, моль и т.п.).
Разумеется, в повторном написании здесь математических
преобразований, выполненных для прямотока в разд. 10.8 и
10.9, нет необходимости.
10. 14.2. Полунепрерывные процессы

Пусть в аппарат непрерывно подается фаза "у", ее поток
D - постоянен ; фаза "х" в количестве L (в ходе процесса не
изменяется) находится в аппарате. В самом общем случае в
аппарате может находиться также некоторое постоянное коли
чество D o фазы "у". Пропускными способностями потоковых
стадий для постоянных количеств фаз будут величины L и D0 ,
для стадии непрерывного подвода и отвода фазы "у" количе
ство Dк = Dtк для всего процесса (соответственно: D = Dt для
текущего времени 't, dD = .Dd't - для элементарного промежут
ка времени d't) . Пропускная способность п оверхностной стадии
выражается , как и для периодического процесса, величиной
kxF'tк (kxF't; kxFd't). Соответственным образом выражаются вве
ден ные ранее отношения пропускных способностей а, Ь, с.
Общая расчетная схема полунепрерывного массообменного
процесса приведена на рис. 10.43 , где показаны: граница меж
фазной поверхности , количества фаз L и D0 , непрерывный
поток фазы D. Начальная концентрация вещества в непрерыв
но подаваемом потоке Ун в ходе процесса не изменяется; на
чальная кон центрация фазы "х" составляет Хн· Примем (это не
обязательно), что фаза "у" , постоянно находящаяся в аппарате
в количестве D0 , первоначал ыю находится в равновесии с xti,
т.е. ее концентрация yJ'.
Расчет реального полунепрерывного процесса весьма сло865

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

у

у

)(

Рис.

а
10. 43. К

а -

Ук

Ун

_l_

1
1
1
1 у - ун 1
1
1
-1
-т

у�

Хк

х

б

у - ун

1

х

Хн

Хк

в

Хн Х

расчету полунепрерывноrо процесса:

расчетная схема, б - днаrрамм а у

-

х,

г -

к расчету нmеrрала Int 1

жен , поэтому анализ проведем применительно к упрощенному
его варианту:
.
- величина RxF-r � ао (фазы в аппарате в каждый момент
времени, включая конечный, - в равновесии);
- поток D движется через аппарат, а фаза "х'' пребывает в
нем в режиме И П (т.е. фазы "у" и "х" имеют выравненные каждая по своему объему - концентрации в аппарате); поэто
му в каждый момент времени концентрации у в обьеме аппара
та и на выходе из него одинаковы.
Очертим пространственный контур, охватывающий весь ап
парат. Выберем промежугочный момент времени 't (текущие
концентрации вещества в фазах х и у равновесны; последняя
равна выходной концентрации фазы "у"). Дадим времени при
ращение d't и для этого элементарного отрезка времени запи
шем материальный баланс по веществу:

+ Dyнd't - Dyd't

= Ldx

+ D odY .

(е)
Разделим переменные и проинтегрируем по всему процессу
(от О до 'tx). Изменив знаки и пределы интегрирования, полу
чим связь продолжительности процесса 'tx с конечными кон
и
центрациями
·

Хх Ух:

"l: к

Хн

dx

О

Хк

У - Ун

D J d't = Dtx = L J
у�

+ Do I

dУ

У - Ун
Ук

=

+

Llnt 1 + Do Int2 .

(10.69)

Способ нахождения интеграла lnt 1 с использованием диа
граммы у - х в случае кривой линии равновесия ясен из рис .

866

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

10.43, б, в. Интеграл Int2 определяется аналитически (напом
ним: Ун = const):
=

Yf �н

=

1n

У Е - Ун
Ух - Ун

=

1n

тхн - Ун .

(ж)
У х - Ун
У -У
Связь текущих значений •, х, у будет получена, если эти
значения подставить в качестве пределов вместо 'tx , Хк, Ух ·
При практической организации полунепрерывных процес
сов весьма часто Do мало, так что Накоплением (изменением
количества вещества) в зоне Do можно пренебречь. Тогда вы
ражение ( 1 0.69) упрощается:

I nt2

Ук

н
Dtx = L Хf dx
У - Ун
Хк

( 1 0.69а)

В случае прямой равновесной линии возможен аналитиче
ский расчет с использованием постоянного коэффициента рас
пределения т. Проведем такой анализ применительно к упро
щенному варианту, описываемому уравнением ( 1 0.69а). Для
этого выразим концентрации фазы "у" на языке фазы "х'': у =
= тх и Ун = mxJ', причем x.t = const , поскольку в холе массо
обмена Ун остается неизменным. Преобразуем теперь ( \ 0.69а):

Dtк = L

x

Г

dx
..!:_ ln xн - x�
=
Р т хк - хнР
х " тх - тхн

( 1 0 .70)

в результате наЙдена аналитическая связь продол:жиrелъности
процесса •к и конечной концентрации .хк; при этом Ук = 1'11Хк ·
Представляет интерес сопоставление выражений для полуне
прерывного процесса с наЙденными ранее для непрерывного
массообмена. В этих целях перенесем L/т в ( 1 0.70) в левую
часть равенства; при этом сохраним введенное ранее обозначе
ние отношения пропускных способностей применительно к
полунепрерывному процессу: тDtк/L = с' = 1/с. Тогда

Х н - х�
Хк - х�

=

emD t к / L

=

e l / c ; Хк

- x.f = (хн - x.t) e- l /c . ( 1 0 .70а)

При отсчете концентраций не от нуля , а от Ун и x.f , т.е. при
замене Хн - x.f = Хн и Хк - x.t = Хк , получаем
ХJХн = e- l /c• Хк = Хн е-l / с .
( 1 0.70б)
Последние выражения совпадают с соотношением ( 1 0 . 6 1 ) ,
установленным для стационарного массопереноса в аппарате с
непрерывным контактом фаз при их перекрестном движении.
Таким образом, полунеnрерывный массоперенос математически
может трактоваться в аспеi<те перекрестного процесса.
867

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

10.15. О РАСЧЕТЕ МАС С ООБМЕННЫХ ПРОЦЕССОВ
ИНЫХ КЛАССОВ, НЕЖЕЛИ 3(2-2) 1

В предьщущих разделах главы основное внимание было уде
лено массообменным процессам класса 3(2-2) 1 , характеризуе
мого наличием двух фаз, инертом (носителем) в каждой из них
и одн им переносимым веществом (компонентом). Вместе с тем
по ходу изложен ия были затронуты некоторые общие положе
ния, справедливые и для процессов иных классов, предусмот
ренн ых КФ-классификацией.
Процессам класса 3(2-2) 1 в пределах рассмотренных схем
движения фазовых потоков присуща линейность балансовых
соотношений - она обусловлена постоянством этих потоков L
и D, их независимостью от концентраций. В упрощенных под
ходах к процессам упомянутого класса приписывается и линей
ность кинетики - независимость пропускных способностей
типа kxF от уровня концентраций и движущей силы. Равновесие
рассматривалось как в линейном варианте ( т = const), так и в
нелинейном ( т = var) . Основное качественное отличие боль
шинства процессов, принадлежащих к другим классам, - от
сутствие (невозможность вьщеления) инерта и как результат
принципиальная нелинейность балансов. Это может привести к
существенным осложнениям при математической интерпрета
ции. В наибольшей мере такие затруднения относятся к описа
нию и построению рабочих линий, например для широко рас
пространенных противоточных процессов - даже достаточно
простых, двухфазных, представляемых в диаграмме у - х
(двухкомпонентные смеси в каждой из фаз): Дело в том, что
фазовые потоки L и D здесь обычно изменяются при движении
вдоль поверхности межфазного контакта, т.е. с изменением
концентраций х и у. Поэтому рабочая линия становится кривой,
неудобной для построения.
Существуют различные пути преодоления возниюиих за
труднений.
Первый из н их заключается в выборе такого способа выра
жения концентраций , чтобы потоки фаз оставались постоян 
ными, хотя эти фазы и н е являются инертами. Это возможно
для процессов, характеризующихся эквивалентной разнонаправ
ленной диффузией. Пусть из фазы "х" в фазу " у" и в обратном
направлении переносится в единицу времени одинаковое коли
чество молей (или килограммов) компонентов. Тогда мольные
(соответственно - массовые) потоки фаз будут оставаться не
изменными. При этом, разумеется, надо оперировать абсолют
ными потоками фаз и абсолютными концентрациями компонен
тов в фазах. С такой ситуацией мы встречаемся, например , в

868

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 10. 44. Типичная равновесная диаrрамма
"состав (х, у)
свойство (F)"
-

F

процессах рекгификации. Заметим,
что при слабо выраженной (в ка
кой-то мере - сохраняющейся)
кривизне рабочей линии ее отли
чием от прямой нередко пренебре
гают, если возникающие при этом
погрешности не нарушают приемо 0 , 2 0 ,4 0 ,6 0 , 8 1 х , у
лемой точности расчета.
Второй путь состоит в следова
нии обстоятельствам - построении
кривой рабочей линии. Дело в том, что в некоторых случаях
удается достаточно достоверно выявить причины нарушения
линейности баланса и математически связать (количественно!)
сопугствующие эффекгы с изменением концентрации. Это
могуг быть эффекгы , связанные с тепловьщелением (испа
рение-конденсация, плавление-затвердевание и т.п .), взаим
ной растворимостью и др. Тогда в диаrрамме у - х удается по
строигь кривую рабочую линию, хотя сама процедура ее построе
ния является весьма rромоздкой. Последующие расчеты осу
ществляюrся rрафоаналитически либо численными методами;
чисто анал итические методы здесь, как правило, неприменимы.
Третий путь - более радикальный - состоит в отказе от
расчетов в концентрацион ных диаграммах (например, типа у х) и переходе к диаграммам типа " состав - свойство" . При этом
выбирается именно то свойство рабочих тел (F), которое яви
лось причиной нарушения линейности рабочей лин ии. Ска
жем , для двухкомпонентных систем в декартовых координатах
составляют диаграмму "Свойство F" - х, у (рис . 1 0 .44) : строят
две кривые F - х и F
у. Равновесные точки на кривых сое
диняют водами (на рисунке - штриховые линии). Для трех
компонентных систем такого рода диаграммы строятся в кон
центрационном треугольнике, где также проводятся линии
свойств (например, растворимости) и равновесные ноды. По
нятие "рабочая линия" в этих случаях не используется, но по
нятия сопряженных и равновесных концентраций, теоретической
ступени и т.п. остаются в силе. Одновременно вводятся некото
рые необходимые для расчета дополнительные понятия - они
будуг рассмотрены при изучении конкретных технологических
приемов (рекгификации, жидкостной экстращии, выщелачи
вания и др .).
Проблема нелинейности кинетики может быть связана с
определением пропускных способностей и движущих сил.
-

869

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Проблема линейности-нелинейности пропускных способностей,
строго говоря, крайне сложна. Эта сложность обусловлена дву
мя основными причинами :
- возможной (даже - вероятной) зависимостью коэффици
ентов диффузии и толщины пограничных пленок от уровня
концентраций (с изменением последних изменяются и
свойства фазы); следовательно, и коэффициенты массоотдачи
(с ними - и массопередачи) МОJУГ оказаться существенно пе
ременными в рабочем диапазоне изменения концентраций;
- приближенностью принятой для расчета двухпленочной
модели, как в плане отдельных ее постулатов (например , о
равновесии на границе раздела фаз), так и в аспекте правомер
ности самого подхода (игнорирование нестационарных элемен 
тарных актов массопереноса).
Поскольку отмеченные моменты не учитываются , то юrне
тичесюrе характеристиюr (kxF, kyF и т.п.) получаются (в экспе
риментах, где определяются �х. �у) зависящими от уровня кон
центраций, иногда - от движущей силы. Свой вклад может
внести и неопределенность процедуры усреднеf{ия коэффици
ента распределения т в случае т "# const.
Нелинейность движущей силы может быть обусловлена эф
фектами продольного перемешивания (см . главу 8). Такая не
линейность не вызывает осложнений лишь в простейших
("крайних") ситуациях - в режимах И В (где ее нет) и И П
обеих фаз (где е е часто удается весьма просто учесть, посколь
ку рабочая линия вырождается в рабочую точку) . Ограниченное
продольное перемешивание сказывается на локальных движу
щих силах лх, Лу и на средних по поверхности контакта ЛХср.
ЛУср· Упомянутые эффекты МОJУГ быть учтены при составлении
балансовых
соотношений,
приводящих
к
описанию
(построению) кривых рабочих линий.
ПодчерЮiем, что нелинейность пропусЮiых способностей
поверхностных стадий не играет роли при идеальном контакте
фаз (потоковая задача). Нелинейность движущей силы оказы
вает влияние на процесс и в этом случае; характер такого
влияния в общем плане рассмотрен в разд. 8.2.
В целом отклонения от сравнительно простых расчетных
процедур, присущих процессам класса 3(2-2) 1 , как правило,
специфичны для различных технолоrичесюrх приемов. Поэтому
при сохранении изложенных выше общих подходов к расчету
процессов массопереноса особенности расчета конкретных
приемов рассмотрены в соответствующих главах курса.

870

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

1 0 . 1 6. МАССООБМЕН С ТВЕРДЫМИ ТF.ЛАМИ
1 0 . 1 6 . 1 . Общие положения

Массообмен с твердыми телами широко распространен в
химической технологии. Это, например, процессы адсорбции и
десорбции (в частности, сушки), растворения, выщелачивания,
кристаллизации, сублимации и т.д. Кроме того, в качестве од
ной или нескольких стадий он может играть существенную
роль в ряде химических процессов - каталитических и неката
литических. Чаще всего твердая фаза в таких процессах ис
пользуется в виде не очень крупных зерен (их размеры редко
превышают несколько сантиметров) или мелких частиц (доли
милл и метра) . Эти зерна, частицы (дискретная фаза) контакти
руют со сплошной средой (газ, жидкость), и nроисходит nеренос
какого-либо компонента (компонентов) от среды к твердой
фазе или в обратном направлении.
Процесс массообмена с твердой фазой может быть органи
зован в непрерывном, периодическом или полунепрерывном
варианте . Однако относительно единичного зерна массообмен
с твердым телом (например, округлым; в друrих случаях речь
может идти о цилиндрических или плоских телах) , как прави
ло , представляет собой нестационарный акт с характерной ки
нетикой переноса вещества внутри зерна и вне его (в сплош
ной среде около зерна) . Известным исключением из этого пра
вила являются стационарные каталитические процессы с по
стоянным Источником или Стоком переносимого вещества.
Процессы массопереноса с участием твердой фазы проходят
в несколько стадий. В отсутствие химической реакции это
(рис. 10.45) ввод вещества в рабочую зону процесса с потоком
сплошной фазы; диффузия вещества нз обьема этой фазы через
пограничную пленку к поверхности зерна (внешняя диффузия);
миграция вещества внутри зерна (внутреин.яя диффузия); вывод
вещества нз рабочей зоны с твердой фазой. Разумеется, в случае
переноса вещества из твердой фазы в
газ, жидкость порядок стадий будет
обратным.
При протекающ в зерне химиче
ских превращений с выделением (по
глощением) переносимого компонента
к перечисленным выше добавляется
еще стадия химической
реакции с о
Рис. 10. 45. К стад иям массопереноса с участием
твердой фазы:
1 - rраница рабочей ЭО НЬI , 2 - С!LЧОUJНаЯ среда, 3
диффузионная nо11>аничная nлеюса, 4 - твердое зерно

-

871

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

своими кинетическими характеристиками . Если они неблаго
приятны (реакция протекает существенно медленнее массопе
реноса), то массообменные стадии для анализа и расчета ин
тенсивности технологического процесса не представляют инте
реса - расчет следует вести на основе кинетики самой хими
ческой реакции. Если , наоборот, химическая реакция в сравне
н ии с други ми стадиями протекает практически мгновенно, то
влияние химической кинетики на технологический процесс
вырождается, и расчет ведется на основе закономерностей мас
сопереноса. При сопоставимости этих стадий приходится со
вместно рассматривать кинетические характеристики массопе
реноса и химической реакции - говорят о макрокинетических
закономерностях химических превращений. Проблемы макро
кинетики находятся за пределами учебника: в нем рассматри
ваются процессы массопереноса только в отсутствие хими
ческой реакции (или при наличии быстрых превращений, когда
вклад кинетики исчезающе мал из-за ее высокой пропусююй
способности) .
В основе расчета массоqбмена с твердым телом лежит урав
нение Фика (1 .22), записываемое для твердого тела без конвек
тивных членов:
дС
- = D v2 c + к
(1 .23), ( 1 0 .7 1 )
дt

м

или в отсутствие Источников или Стоков переносимого ве
щества (к = О):
ас
дt

= Dмv2 c'

( 1 0 . 7 1а)

причем Dм - коэффициент диффузии переносимого вещества
в твердом теле.
Если речь идет о сферическом зерне, то эти уравнения за
писываются в сферических координатах.
Уравнения Фика решаются с условиями однозначности (см.
разд. 1 .7), формулируемыми в соответствии со спецификой
конкретного процесса. При этом начальные условия описывают
распределение концентраций в начальный момент времени, а
граничные - отражают особенности массопереноса на границе
сплошной среды с твердым телом. Результаты решения урав
нений ( 10 . 7 1 ) позволяют установить распределение концентра
ций по объему зерна в любой момент времени. Сочетая это
решение с подробно рассмотренными выше закономерностями
переноса в сплошной среде, получают решение технологи
ческой задачи в целом - для сплошной и дискретной фаз, т.е.
для массообменного процесса.

8 72

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Масштабные преобразования уравнения Фика и граничных
условий позволяют (разд. 1 .8) сформулировать ряд критериев
подобия . Среди них - диффузионный критерий Био Вiд =
= pRm/Dм, выражающий отношение пропускных способностей
стадий внешнего (в пограничной пленке сплошной среды) и
внутреннего (в твердой фазе) массопереноса.
Если стадия внешней диффузии является существенно мед
ленной (ее продолжительность гораздо больше, нежели любой
другой стадии, Вiд ---.. О), то эта стадия контролирует массопе
ренос в целом - ее называют лимитирующей и говорят, что
массообмен протекает в условиях внешней задачи. В этом случае
проще прямо использовать уравнения конвективного массопе
реноса, не обращаясь к уравнению Фика. Если в качестве ли
митирующей стадии выступает миграция вещества внутри зер
на (тогда Вiд ---.. ао) , то говорят о внутренней задаче массопере
носа. Однако возможны технологические ситуации , когда усло
вия внешнего и внутреннего массопереноса весьма благопри
ятны, а существенно медленной стадией является п одвод ве
щества в рабочую зону со сплошной средой Или же ее отвод из
рабочей зоны с твердой фазой. Тогда массообмен в рабочей
зоне будет практически завершен, контакт фаз считается иде
альным, фазы уходят с равновесными концентрациями перено
симого компонента. Это означает, что массоперенос происхо
дит в условиях потоковой задачи по одной из фаз - той, что
лимитирует массоперенос в целом.
При наличии лимитирующей стадии расчет процессов мас
сопереноса относительно прост. В отсутствие лимитирующей
стадии, когда хотя бы две контролирующие процесс стадии сопо
ставимы по интенсивности, расчет обычно значительно сложнее;
в этом случае говорят о смешанной задаче массопереноса.
Ниже в общем плане рассматрИВ' •�::Уrся процессы массопере
носа, протекающие при наличии различных лимитирующих ста
дий. При этом концентрация переносимого вещества в сплош
ной среде обозначена символом у, ее поток - символом L (или
количество - L); для твердой (дискретной фазы) использованы
символы: С - концентрация, G - поток или G - количество
(при изучении массообмена в других главах возможно отступ
ление от этой символики) . В целях определенности будем счи
тать, что перенос вещества происходит из сплошной фазы "у"
в дискретную " С " .
1 0 . 1 6.2. Внешняя задача массопереноса

Составляющие внешнего массопереноса
В основе расчета конвективного переноса вещества из
сплошной среды к поверхности твердого тела лежат понятия и
подходы, изложенные в разд. 10.4.4.
873

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

�Fo
� �fo
1

11

а

Рис. 10. 46. К расчету поверхности
контакrа при омывании сплошной
средой (поток /) засыпки твердых
зерен (1/) :

а - схема протекания процесса, б модельная полусфера и ее rеометрические
характеристики

6

Коэффициеиrы массооrдачи редко удается установиrь теорети
чески; чаще всего их находят из эмпирических уравнений внеш
него массопереноса, представленных в криrериальной форме:
( 1 0.8)
Sh = Pv'Dд = j{Re, Sc, . . . ) ,

При этом за определяющий линейный размер / для твердых
тел сферической или цил индрической формы принимают диа
метр d, для тел другой формы - эквивалентный диаметр, для
пластины - толщину (или полутолщину) .
Располагая значениями Re и Sc, рассчитывают число Шер
вуда Sh и находят массообменный коэффициент р или рр, вхо
дящий в основное уравнение массообмена типа ( 1 0 .22). Следу
ет, однако, подчеркнуть сушественное отличие выражения
(10.8) от ( 1 0 .22), справедливого для двухфазного массообмена
при контакте двух сплошных фаз. В массообмене с твердыми
телами представление о "пограничной пленке", примыкающей
к межфазной границе со стороны твердого тела, - некоррект
но, так что понятие о коэффициенте массопередачи k теряет
смысл. Здесь физически обоснованно вместо kx (или ky) исполь
зовать коэффициент массоотдачи р :
М = P 'Ftv - уР)ср = Р'FЛУср• ИЛИ М = ррFЛУср·
( 1 0 .72)
Конкретный вид расчетных формул для р типа ( 1 0.8) зави
сит от специфики рассматриваемого массообменного процесса;
они приводятся в учебной, научной, справочной лиrературе• . В
качестве примера такого уравнения для одиночной сферической
частицы в разделе 10.4.4 приведено выражение ( 10.8б).
Как и в случае двух сплошных фаз, здесь также иногда в
чисто прагматических целях вводят "объемные коэффициенты
массоотдачи" Pv (см. разд. 10.4.4) .
где Dд

- коэффициент диффузии переносимого вещества в сплошной среде.

тел

правильной формы определяется из

Для тел , беспорядочно насыпанных н а какой-либо площади /, при движении
сплошной среды над засыпкой (рис. 10.46,а) поверхность контакта F находят из
модельного представления: вьщеляют элемент твердого тела и принимают
(рис . 1 0 .46,6), что поверхность его контакта с потоком близка к полусфере (пусть
Поверхносп. межфазною контакта
геометрических соображений .

• См., например, f2, 8,

874

F

9, 10, 1 3, 20, 23).

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ее диаметр d). Тогда поверхность контакrа составляет .,.,cfl/l, а ruющадь, на кото 
рую опирается зга полусфера, равна .,.,d2/4. Таким образом, поверхность контакта
зерна Fo вдвое превышает площадку /о основания полусферического зерна. И
ее.ли площадка / полностью покрьrrа насьmным материалом, то общая поверх
ность контакта F "' 2/, поскольку контакrу доступен только верхний слой зерен
(жирная 11>аница на рис. 1 0.46,а).
В случае движения сплошной среды сквозь слой зерен (неподвижный, дви
жущийся или псевдоожиженный и т.п.) поверхность контакта определяют через
удельную поверхность (см . разд.2.7): Fуд = 6 ( 1
E)/d, где Е - порозность. Оче
видно, что для объема рабочей зоны V
-

F = FудУ.
(а)
Следует, однако, иметь в виду, что по (а) рассчить1вается полная поверхность
твердых тел в рабочей зоне ; реально в массообмене может принимать участие
меньшая ( "активная") поверхность Fa < F. Задача технолога - на стадии проек
тирования и эксплуатации - обеспечить возможно более поmюе раскрьrrие
поверхности контакта, т.е. постараться приблизить Fa к F.

Средн юю (по поверхности контакта) движущую силу массо
обменного процесса ЛУсу чаще всего определяют, используя
путь, принятый в разд . lU.8:
- записывают уравнение массоотдачи для элементарной по
верхности контакта dF:
(б)
dM = �р(у p>)dF = �pЛ}dF;
- устанавливают связь у и р> с М или F;
- интеrрируюr в полном диапазоне изменения переменных в
ходе процесса;
- получен ное выражение представляют в форме (10.72).
Тогда слева в этом выражении фигурирует М, а справа - �р,
F и фрагмент, найденный в результате интеrрирования. Этот
фрагмент и будет представлять собой ЛУср·
-

Массообмен в псевдоожиженном слое в условиях внешней задачи
Проиллюстрируем путь расчета для непрерывного стацио
нарного процесса массообмена с идеальным перемешиванием
твердых зерен , находящихся, например, в псевдоожиженном
состоянии. Расчетная схема процесса изображена на рис. 10.47 :
поток сплошной фазы L, входная и выходная концентрации у1 и J12 ; поток твердой фазы (псевдоожиженные зерна) равен G,
входная концентрация - С1 ; в результате И П вся масса зерен
Gт имеет одинаковую концентрацию вещества, равную выход
ной С2 . Запишем материальный баланс по переносимому ком
поненту в сплошной среде для элементарной поверхности кон
такта dF (контур к):
(в)
Ly - dM - L (y +dy) = О, dM = -Ldy.
Вместе с тем dM выражается соотношением (6). Приравня
ем (6) и (в), разделим переменные и проинтеrрируем, учиты-

875

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Gт
F

у

ип

F

о

Рис. 10. 47. К определению средней дви
жущей силы массообмена с твердыми
телами

вая, что равновесная концент
рация в сплошной фазе уР =
= const по всей массе Gт и по
верхности контаюа F, посколь
ку С = С2 = const:
-L I

У2

dy

·
р

--

У1 У - У

-у

=

F
о

/3p f dF

и

Р = ppF.
(r)
У2 - у Р
Отсюда находим L и домножаем его на (у1 - У2), чтобы по
Lln Y l

лучить М:

L(y1

-

у2 ) = М = ppF

У

ln

1 - У2

У1

Y2

-

- --

=

(д)

- уР

--

Сравнивая теперь (д) и ( 10.72), видим:

ЛУср = У1 - У2 Р
ln У1 - у Р
У2 - у

- уР

--

(Yi - у Р ) - (У2 - у Р ) = ЛУ1 - Лу2
Р

ln(ЛY 1 / Лу2 ) . ( 10.73)

-у
ln У1
У2 - у Р

---

получается столь
Разумеется, не для всех процессов
просто и выражается как среднелогарифмическая величина. В
обшем случае основная трудность состоит в установлении за
при уР = var.
кономерности изменения уР (с F или с
Пропускная способность стадии внешнего массопереноса
записывается как P'F = ppF; существенно, что вместо ky здесь
фиrурирует Р', рр. В условиях внешней задачи именно эта про
пускная способность контролирует процесс массопереноса в
целом.
В условиях внешней задачи (только в этих условиях!) прак
тически оправданно для некоторых процессов массообмена
между дискретной (твердой) и сплошной фазами использова
ние уже рассмотренных представлений о непрерывных стацио
нарных (например, противоточных) процессах. При этом мас
соперенос относительно каждой перемещающейся частицы,
конечно, остается нестационарным, но по отношению к вы
бранному сечению аппарата (т.е. - к неподвижному наблюда
телю) стационарность процесса нарушена не будет. В аспекте

ЛУср

у)

876

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

нестационарною массопереноса в твердой фазе такой подход
означает замену временн 6 й координаты 't на поверхностную f
При описании ряда процессов нередко удается представить
потоки контактирующих фаз постоянными (т.е. потоками
инертов - носителей переходящею вещества). Тогда для расчета
приюдны подходы, понятия и математический аппарат, приме
ненные для процессов класса 3(2-2)1 - естестве нно, с заменой
коэффшщентов массопередачи на коэффициенты массоотдачи.
Заметим: строю юворя, выражения типа (в) - (д) описы
вают смешанную (потоково-внешнюю) задачу массопереноса,
поскольку в этих выражениях присутствует поток L. Чтобы
задача была чисто внешней, этот поток должен быть бесконеч
но большим; при L � оо и конечном М будет У2 = у1 • Иначе
говоря , внешняя задача массообмена означает ее сведение к
массопередаче (здесь - к массоотдаче ).
1 0 . 1 6.З. Внуrренняя задача массопереноса
1 рода:

В основе анализа - уравнение Фика с граничными условиями

задается концентрация вещества на межфазной границе,
в простейшем случае - постоянная во времени и одинаковая
вдоль всей поверхности тела.
Качественно картина изменения концентрации во времени в
случае симметричною массопереноса применительно к беско
нечной пластине толщиной 28 показана на рис. 10.48 . До нача
ла массообмена концентрация по толщине пластины одинакова
и равна С0 . Как только пластину помещают в рабочую зону, на
ее границах х = ±Б мгновенно (поскольку стадия массоотдачи
здесь бесконечно интенсивна, f3pF � оо ) устанавливается и под
держивается постоянной концентрация вещества, равновесная
с кон центрацией у в сплошной среде, С6 = С Р . Сначала массо
обмен захватывает приграничные зоны пластины, практически
не затрагивая внутренних ее областей. Постепенно повышение
концентрации захватывает и внутренние области. Через беско
нечно долюе время концентрация по толщине пластины вы
равнивается и становится равной С Р .
Приведенное качественное описание массообменного процесса
математически представляется следующим образом. Закономер
ность изменения концентрации вещества в пластин е С = С(х, 't)
должна явmъся решением уравнения Фика для одномерной
(ццоль оси х) диффузии, поскольку в бесконечной пластине гради
енты концентраций в направлении других осей н ичтожны:
ас
т

-

=

а2с

Dм 2 , -Б < х < +Б .
ах

(10.74)
877

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис.

10. 48. Общая картина изменения
концентрации вещества во времени по
толщине Wiоской бесконечной Wiастины в
rраничных условиях 1 рода.

Yt.

�
у

Цифры у кривых 1 ,2, ... , оо отвечают на
расrающим моменrам времени процесса, отсчи
танным от � = О

Начальное условие:
С(х, О) = С0, 't = О,
- о � х � +о . ( 1 0.75а)
Граничное условие 1 рода:
. ( 1 О.75б)
С(о, 't) = СР ,
Условие симметрии и ограни
х
ченности концентрации (данное
специфическое условие тоже яв
ляется граничным):
( ,
( 1 0.75в)
= , • О.
дС
д С хО
't) О
;:::
х х= О =
д
д
Это условие утверждает, что касательные к концентрационным
кривым (см. рис. 10.48) в любой момент времени в точке х = О
паралл ельны оси х.
Подобные задачи для шара (тоже симметричные, одномер
ные) были рассмотрены в разд. 7. 10.3 применительно к перено
су теплоты. В массопереносе при коэффициенте диффузии
вещества внутри твердой фазы Dм = const решение = С(х, •)
С
также получается в виде бесконечного рЯда.
Решение практических задач обычно требует усреднения
концентрации вещества по толщине пластины: именно усредненные концентрации С (• ) фигурируют в материальных ба
лансах. Переходя от бесконечно тонкого слоя dx к конечному
о , имеем

'(;::: о

I

-

C ('t)

=

1 Б
- f C('t, x) d.x .

80

( 1 0 .76)

Далее по уравнению материального баланса нетрудно рас
считать количество вещества, воспринятого участком пластины
длиной / и шириной Ь за время 't . Если С - массовая концент
рация и Pr - плотность материала пластины, то
м=

/b·2orr[c ('t) - С0 ] .

(е)

В целях большей общности выражения С(х, • ) и С (•) пред-

878

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ставляют в критериальной форме:
С Р - C(x" t)
= fi (Foд, х/О)
СР - Со
и
СР - C('t)
= f.2 (Foд) ,
СР - Со
где Fод • D,... �/Б 2 - диффузионный хриrернй Фур"е, его

( 1 0.77)

( 1 0.78)
часто еще называют

хриrерием Фика.

В качестве примера приведем конкретный вид формулы для
С в случае плоской пластины при Dм = const:
С Р - C(t)
с Р - Со

где

=

�

L..

� е - µ�Fод '

n = l µ п2

( 1 0.78а)

2п - 1
-2- л .
(ж)
При не очень малых значениях Fод ряд ( 1 0 .78а) быстро схо
дится, так что можно ограничиться одним членом ряда (в
частности, при Fод ;;:::: 0, 12 ошибка не превысит 1 %). При малых
значениях Fод приходится рассчитывать сумму нескольких чле
нов ряда.
Относя количество переданного вещества М к начальной
движущей силе л С. = с Р - С0, получим пропускную способ
ность стадии внутреннего переноса вещества М/Л с• .
Аналогичным образом ставятся задачи для твердых тел дру
гой формы - цилиндрической, сферической и т.п. Разумеется,
при этом лапласиан имеет иное написание, и решения C(r, 't) и
С ('t ) имеют иной вид. Операция усреднения концентраций для
этих случаев также имеет свои особенности; для сферы такая
операция бьmа продемонстрирована в разд. 7. 1 0.3 примени
тельно к переносу теплоты - формула (7 .35).
Решение можно считать законченным, если все элементы
твердой фазы находятся в рабочей зоне одинаковое время. Од
нако в системах с продольным перемешиванием это условие не
выполняется. Скажем, частицы в псевдоожиженном слое ха
рактеризуются широким спектром времени пребывания в зоне
массообмена ('t изменяется от О до ех> , поскольку псевдоожи
женный слой очень близок по твердой фазе к системам И П).
Здесь требуется усреднение по времени пребывания элементов в
рабочей зоне; предварительно надо установить закон их расµп

=

879

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

пределения по времени пребывания (см. главу 8). Такая опера
ция усреднения выполнена в разд. 1 5 . 8 .4 применительно к
псевдоожиженным сферическим частицам, высушиваемым в
условиях внуrренней задачи.
Строго говоря, зерна, как правило, на практике неодинако
вы также и по размерам, так что надо учитывать их распреде
ление (и проводить их усреднение) еще и по размерам - зада
ча усложняется . Но, пожалуй, наибольшие сложности вызывает
расчет процесса массообмена, если коэффициент диффузии
вещества в твердом материале Dм оказывается непостоянным,
зависящим от уровня концентраций. В этом случае предвари
тельно потребуется установить зависимость Dм = Dм( С). Задача
переноса здесь стан овится существенно нелинейной, так 'ffO ее
решение возможно, как правило, только численными методами.

10. 16.4. Потоковая задача массопереноса
Задача массопереноса является внешней, когда лимитирует
перенос вещества из объема сплошной среды к поверхности
твердого тела, и внутренней, когда превалирует диффузионное
сопротивление внуrри тела. Нередко встречаются технологиче
ские ситуации, когда эти стадии протекают в благоприятных
условиях и не являются лимитирующими:
- высокие коэффициенты массоотдачи и развитые поверх
ности контакта: мелЮ1е частицы, когда Shmin � 2 и получаются
высокие р ; кроме того, малым d отвечают еще и большие Fуд;
- высокие коэффициенты диффузии Dм внуrри твердого
тела: мелкие частицы, тонкие нити или пленки высокой порис
тости - при сравнительно крупных и преимущественно
сквозных порах, специфических физико-химических свойствах
вещества и твердого тела.
Тогда внешняя и внуrренняя стадии протекают с высоЮ1ми
скоростями, так что нестационарный акт массопереноса бы
стро завершается: фазы приходят в равновесие. В этих случаях
массообмен в целом может лимитироваться одной из потоко
вых стадий - подводом вещества в рабочую зону (в рас
сматриваемом примере - с потоком сплошной среды) или его
отводом из рабочей зоны (с твердым телом; с потоком твердых
зерен, например). Это означает, что массоперенос протекает в
условиях потоковой задачи, а контакт фаз является идеальным.
При этом кинетичесЮ1е характеристиЮ1 внешней (р , F) и
внуrренней (Dм, d) задач перестают влиять на интенсивность
процесса в целом.
Массоперенос в условиях потоковой задачи описывается
уравнением материального баланса типа ( 1 0 . 1 8), дополненным

880

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

у

с

а
Рис. 10.49. Идеальный массо перенос с твердыми rелами в условиях пmuковой задачи:

а - рабочая лиюtя (точка) при прямотоке или ИП обеих фаз , б - рабочие ЛИЮIИ при
пр отивотоке фаз: лимитирует п <>Ток сплошной среды ( /) или твердой дискретной фазы (2)

равновесной зависимостью у = f Р (С) , причем для рассматри

ваемой задачи с Сп с (где Cii - концентрация на поверхности
тела). Поскольку фазы уходят из системы в равновесии, то в ба
лансовом уравнении (записано для непрерывного процесса)
L(y, У2 ) = G( C2 С1 )
( 1 0 .79)
=

=

-

-

выходные концентрации У2 и С2 - равновесны.
-

-

В рассматриваемом случае пропускные способности потоковых
стадий равны L и G; одна из них может быть лимитирующей .
Рабочая линия при идеальном контакте фаз заканчивается (а
рабочая точка при И П фаз - располагается) на линии равно
весия . Иными словами (рис . 10.49,а), при ИЛ одной wiи обеих
фаз либо при их прямотоке точка выходных концентраций (У2,
С2) лежит на равновесной линии. В случае противотока (рис .
10.49, 6) на линии равновесия будет лежать один из концов ра
бочей линии. Если лимитирующим является поток L фазы "у" ,
то рабочая линия занимает положение 1 (при заданном С2 она
выше пойти не может из условий материального баланса), и
равновесной будет точка с координатами у1 , С2 . Если же лими
тирует поток G (в терминах фазы "у" - поток тG), то рабочая
линия занимает положение 2 (при заданном у2 левее она пойти
не может по условиям материального баланса), а равновесной
будет точка (у2 , С1 ).
Решение эксплуатационных и проектных задач примени
тельно к непрерывным процессам массообмена с твердыми
телами при идеа;�ьном контакте фаз не отличается от рассмот
ренных в разд. 10.7 (и последующих) для отдельных аппаратов и
в разд. 10. 12 и 10. 1 3 для их сетей. В случае прямой линии рав
новесия (у = т С, т = const) задачи решаются аналитически.
Изложенный подход к решению потоковьtх задач использо
ван в последующих главах при рассмотрении конкретн ых тех
нологических приемов.
88 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

1 0 . 1 6.5. О смешанных задачах массопереноса
Массообмен нередко протекает в отсуrствие лимитирующей
стадии: две медленные стадии (или больше) имеют сопостави
мые пропусЮiые способности . В этих случаях расчет процесса,
как правило, заметно усложняется . Исключением в этом смыс
ле является идеальный контакт фаз - смешанная потоковая
задача. Здесь подходы к расчету остаются качественно незави
симыми от соотношения потоков L и G (в сопоставимых едини
цах при т = const - от соотношения величин L и тG); это соот
ношение G/L (или тG/L) отражается лишь на количественных
результатах, поскольку определяет наклон рабочих линий.
В тех случаях, когда по величине сопоставимы пропусЮiые
способности внешней и внуrренней стадий, уравнение Фика
должно решаться в граничных условиях 1 1 1 рода - одна из
смешанных задач массопереноса. Эти условия выражают равен
ство потоков вещества, подводимых конвекцией из сплошной
фазы к границе с твердым телом и отводимых диффузией
(массопроводностью)· от границы внугрь тела:
·

f3p(y -

ас F
yP)F = -Dм дп
.

1

rp ;

.

( 1 0.80)

здесь символ "гр" означает принадлежность к границе раздела
фаз .
Масштабные преобразования этого соотношения приводят к
диффузионному критерию Био Вiд = рRт/Dм, разграничи
вающему внешнюю (Вiд --.. О, практически - к достаточно ма
лым величинам) или внуrреннюю (Вiд --.. оо, практически - к
достаточно большим величинам) задачу - и смешанную (когда
Вiд ограничен, практически не более чем на порядок больше
или меньше 1).
Общая картина изменения во времени концентрации ве
щества в твердой плоской пластине при симметричном массо
переносе приведена на рис . 1 0.50 для простейшего варианта
задачи : концентрация вещества в потоке постоянна во времени
и одинакова во всех точках около поверхности пластины. От
личие от внугренней задачи состоит в том, что здесь задана
концентрация вещества в сплошной среде, а его концентрация
на поверхности твердого тела С5 переменна - она с течением
времени и по мере насыщения твердого тела изменяется, при
ближаясь к равновесной СР . При этом и приповерхностный
градиент концентраций 1 дС/дх 1 rp понижается во времени: на
клоны линий С = С(х) 1 rp в каждый момент времени отвечают
выражению ( 1 0.80), т.е. эти линии выходят из точки с ордина
той С Р и абсциссой l од 1 = р/Dм (см. рис . 1 0.50).
882

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис.

1 0. 50.
Общая картина изменения
концентрации вещества во времени по
толщине плоской бесконечной пластины в
rраничных условиях 1 1 1 рода.

Цифры у крИВЬIХ 1,2, . " , «> отвечают на
расrающим моменrам времени п роцесса, отсчи
танным от t = О

Решение задачи массопереноса
в граничных условиях 1 1 1 рода (в
отличие от внугренней задачи см. разд. 10. 1 6.З) должно в ка
честве независимой переменной
включать критерий Вiд:
СР - C(x, t,f3,Dм . · · · > = '- ( F
JЗ
Од, X.1};:u , в l·д)

СР - Со

и

СР - C(t, /3, Dм • · · · )
С Р - Со

(10.8 1)

Конкретные решения ( 1 0 . 8 1) сходны с получаемыми для
внутренней задачи, например в форме ( 1 0.78а). Однако в слу
чае граничных условий 1 1 1 рода корни µп выражаются через
Вiд, формула (ж) теряет силу. Вид функции µп = µп (Вiд) разли
чен для разных задач массопереноса, например для пластины,
цилиндра или шара.
В предельных ситуациях
(Bi � О, оо) решения типа (10.8 1 )
закономерно переходят в выражения для внешнего и внутрен 
него массопереноса.
Пусть теперь сопоставимы пропускные способности внешней
и одной из потоковых стадий переноса вещества - тоже одна
из смешанных задач. Здесь анализ массопереноса аналоmчен
рассмотренному в разд. 10.8- 10. 1 0 для двух сплошных фаз :
процесс определяется отношениями пропускных способностей
а = /3pF/L и (или) Ь = j3pF/m G.
Смешанная задача при сопоставимости пропускных способ
ностей потоковой н внутренней стадий массопереноса требует
представления отношений их пропускных способностей. Чтобы
конкретно записать соответствующее отношение, необходимо
предварительно выразить градиент дС/дп в ( 1 0 . 80) и пропуск
ную способность внутреннего переноса. Выражения получаКУГ
ся различными для тел разной формы (см. разд. 6.3). Для теку
щих и конечных значений пропускных способностей стадии
внутреннего переноса должна быть учтена специфика неста
ционарного процесса (время t , 'tк и т.п.).

883

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Подходы к анализу и расчету массообмена с твердыми тела
ми, изложенные в разд. 10. 16, могуг оказаться полезными и
при анализе процессов массообмена с каплями, пузырями, т.е.
с дискретными образованиями с изменяющейся конфигурацией
элементов. Однако в этом случае все процессы переноса про
текают значительно сложнее, поскольку на молекулярную
диффузию внутри элемента дискретной фазы (теплопро
водности в случае теплопереноса, молекулярной вязкости при
переносе импульса) накладывается внутренняя циркуляция жид
кости, газа. Она вызвана взаимным перемещением сплош1:юй и
дискретной фаз - см. рис. 2.4 3 . Эта циркуляция слабо выра
жена в случае мелких капель, пузырей (скажем, размером ме
нее 1 мм) , но ее интенсивность быстро нарастает при увеличе
нии размера элемента дискретной фазы. Циркуляционный и
диффузионный переносы протекают параллельно. Для мелких
элементов превалирует диффузионный механизм переноса, так
что здесь в значительной мере работают подходы и справедли
вы выводы и оценки, полученные в разделе 1 0 . 1 6. Для крупных
элементов дискретной фазы доминирующим становится цирку
ляционный перенос, требующий особого анализа; эти сложные
вопросы - за пределами учебника.
10.17. К ОЦЕНКЕ КАЧЕСТВА РАЗДFЛЕНИЯ

В результате процессов разделения из исходной смеси раз
ных компонентов, находящихся в ней в каком-либо опреде
ленном соотношении , получаются два или более продуктов
(фракций, классов и т.п.), содержащих эти компоненты в иных
соотношениях. Практически важно количественно оценить ка
чество разделения смеси на эти продукты, имея в виду техноло 
гическую эффективность - в плане их пригодности для исполь
зования в виде конечных продуктов или полупродуктов, мало
отходности, экономичности, экологичности . Такая оценка по
зволяет сопоставлять различные процессы (схемы) разделения
и выбирать оптимальные - с позиций принятого критерия
оптимальности.
Будем р ассматривать один из наиболее простых процессов
разделения исходной бинарной смеси (ИС) класса 2(2-2)2 на два
продукта - L и Н (рис . 10.5 1). Смеси (исходная и продукты)
состоят из компонентов, отличающихся друг от друга каким
либо приз наком (признаками): химическим строением, физи
ко-химическими свойствами, размерами. Пусть в рассматри
ваемом случае компоненты различаются , например, плот
ностью - назовем их легким / (light) и тяжелым h (heavy) .
Количества компонентов будем выражать в массовых, моль
ных или каких-либо иных величинах, подчиняющихся закону
884

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис.

1 0. 51. К оценке качества разделе
ния исходной бинарной смеси ИС на
два продукта - L и Н

сохранения . Обозначим: коли
чества легкого и тяжелого
компонентов (скажем, массо
вые - в кг) в исходной смеси
/о и ho . соответственно. Пусть
продукт L в результате разде
ления обогащается легким компонентом, а продукт Н - тяже
лым; при этом доля получающегося продукта L составляет
(L/ИС) = <р, тогда доля продукта Н будет (Н/ИС) = 1 - <р.
Процесс разделения соответственно рисунку может быть пред
ставлен схемой:
(а)

В идеале продукт L должен содержать только легкий компо
нент /, а продукт Н - только тяжелый h . Реально каждый про
дукт из-за несовершенства процесса разделения содержит еще
нежелательную примесь другого компонента. Пусть (см. рис .
10.5 1 ) в продукте L содержится /L кг целевого (легкого) компо
нента и h L кг примеси (тяжелого компонента); соответственно
в продукте Н содержится hн кг целевого (тяжелого) компонен
та и /н кг примеси (легкого). По закону сохранения вещества
материальные балансы типа (1 .8 б-г) запишутся для отдельных
компонентов в виде
(б)
/о = /L + /н , ho = h н + h L.
Качество каждого из продуктов может быть, с одной сторо
ны, охарактеризовано его чистотой:
ЧL =

JL
IL + h
L

'

Чн =

_h
-'н
"--_
hн + lн

(в)

С другой стороны, качество процесса может быть охаракте
ризовано выходом целевых компонентов (от их содержания в
ИС) в каждый из продуктов:

BL = IL //o, В н = h н /ho.

(г)

Для практических расчетов полезны также соотношения,
прямо следующие из схемы (а) или рис . 1 0 .5 1 :
/L + h L = <р(/о + ho ); h н + /н = ( l - <р ) (/о + ho ).
(д)
С позиций современных технологических требований в про
цессах разделения обычно желательно увеличение как чистоты
885

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Ч продуктов, так и выходов В целевых компонентов в продук
ты; в свете тенденции современных производств к безотход
ности в ряде случаев требования к В и Ч весьма высоюt; эти
величины приближаются к 1 . Ограничения в увеличении В и Ч
на данной стадии развития промышленности носят чаще всего
экономичесюtй характер: повышение В и Ч сопровождается
дополнительными затратами .

Величины /о и ho обычно заданы. Для определения пяти искомых величин IL,
hL, hн, /н (или производных от них ЧL, Ч н, B L, Вн) и ч� необходимы пять свя
зей; три из н их предстаалены выражениями (б), а также любым из выражений
(д). Следовательно, еще две определяемые величины должны бьпъ заданы до 
полнительно, остальные будуr получены расчетным пуrем. Например, заданы
значения B L и Вн; требуется определить ЧL, Чн и Ч'· Тогда из (r) находят /L и
hн, далее по (б) рассчитывают /н и hL и по (в) определяют искомые ЧL и Чн .
Наконец, доля ч� продукта L вычисляется по любому из выражений (д).

Из изложенного следует, что даже в рассматриваемом про
стейшем случае разделения бинарной смеси на два продукта
приходится характеризовать качество разделения четырьмя
числами (пусть - взаимосвязанными) : Ч L. Ч н , B L , В н - это
весьма громоздко. Желательно располагать более лаконичным
способом оценюt качества разделения - с меньшим числом
показателей. В этих целях предложены технологи'lеские крите
рии разделения Е, характеризующие одновременно чистоту и
выход, - они представляют собой разность выходов в данный
продукт целевого компонента и примеси. Для продуктов L и Н
соответственно:
hL
h
EL = �
( 1 0 . 82)
; Ен = н 2L .
10 h 0
ho
10
Рассмотрим иекаrорые свойства этих критериев разделения
бинарной смеси на два продукта (фракции, класса).
1 . Численные значения критериев разделения для обоих
продуктов - одинаковы:
EL = Ен .
(е)
Для доказательства этого утверждения запишем сначала оче
видное тождество :
lc/10 = hc/ho = 1 ,
откуда согласно (б)
/
/ н hн h L
/ L + lн h н + h L
=
или, что то же самое, L + +- .
h0
h0
10
ho
10
10
Собирая теперь стоящие в числителях компоненты / и h с
одинаковыми индексами в левую и правую части равенства со
ответственно, приходим к постулату (е) :
EL = Ен = Е .
(ж)
Эrо означает, чrо использование криrериев разделения EL и Ен равноценно; в дальнейшем криrерий Е прюленяется без индекса.
886
-

-

-

-

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

2. Пусть исходную смесь делят формально (чисто механиче
ски) на два продукта, не отличающиеся от нее по составу.
Иными словами, отсутствует обогащение продуктов соответ
ствующими компонентами. В этом случае (на примере продук
та L) : /L = q> lo, h L = qih0 (аналогично можно было бы выразить
hн и /н , но с использованием доли 1 - qi ). Тогда
q> lo - q>h o = q> - q> = о .
EL = Е = !1-. - h L
(з)

10

h0

=

10

h0

Такая ситуация полностью соответствует "процессу разделе
ния" без обогащения продуктов.
Тот же результат получится при попадании всей исходной
смеси (q> = О или q> = 1) в один из продуктов.
З. При идеальном разделении компонент / целиком переходит
в продукт L (/L = lo, BL = 1), а примесь в этот продукт не по
падает совсем ( h L = О). Тогда
EL = Е = !1-. - ht
lo

ho

=

/о - _о_ = 1
!JL
ho

(или 100%),

(и)

что отвечает смыслу идеального разделения.
Таким образом, в полном диапазоне реального разделитель
ного процесса (от формального деления исходной смеси на пор
ции без обогащения продуктов - до идеального разделения) кри
терий Е изменяется в диапазоне от О до 1 . Возрастание критерия
Е означает повышение качества разделения; поэтому увеличение
Е в общем плане технологически целесообразно. Надо иметь в
виду, 'fГО несмотря на дополнительные энерrетические и прочие
затраты, сопуrствующие, как правило, повышению Е, требования
к величине критерия разделения в рЯде случаев носят харакrер
жестких ограничений (подчас - просто вето ) не только в техноло
гическом аспекrе (последующее использование продуктов), но и в
плане экологической чистоты .
На практике значительно чаще технология имеет дело с раз
делением многокомпонентных исходных смесей на несколько
продуктов с доминирующим содержанием какого-нибудь одно
го (иногда - нескольких) компонента в каждом . В этих случа
ях оценка качества разделения с помощью критериев, сформи
рованных на изложенной выше основе , приводит к значитель
но более сложным выражениям для Е.
Более наглЯдной, хотя пока и менее привычной, является
оценка качества разделения исходной смеси с произвольным
количеством компонентов на несколько продуктов - на базе
энтропийного критерия разделения Es. Для п-компонентной сме
си при разделении ее на N продуктов критерий Es представляет
собой разность Sн - Sк полных энтропий - начальной и конеч
ной . Эти энтропии, базирующиеся на информационных энтропи
ях компонентов, вычисляются на основе мольных (в случае раз-

887

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

деления сыпучих материалов - на основе " частичечных" ) кон 
uентраuий компонентов (х) .
Для каждого i-го компонента удельная энтропия опреде
ляется как s1 = x1Inx1• Тогда полная энтропия для G молей ис
ходной смеси составляет

G L: x1 lnx1 .
п

(к)
1=1
Э нтропия j- го продукта (его мольное количество равно �' а
число продуктов - N) вычисляется как сумма энтропий соДерSн =

в нем компонентов: � L: х1 I nx1, причем L: G j = G.
1= 1
}=\
Тогда полная суммарная энтропия конечных продуктов состаRЛЯет
п

жащихся

N

Sк = L G L: x; I nx1 .
j
N

j=I

п

i=l

(л)

Существуюr и другие формы заmtси энтроmtйных критериев· .
Каждому разделительному процессу отвечает (в задачах экс
плуатации) или должно отвечать (в задачах проекrирования)
конкретное значение критерия разделения, определяемое наз
начением и ограничениями производства.
ЛИТЕРАТУРА к rл�

10

Астарита Дж. Массопередача с химической реакuией: Пер. с англ./ Под ред. Л.А. Серафимова. Л . :
Химия, 197 1 . 224 с.
2. Азроt1 М.Э., Тодес О.М. Гидрамические и тепловые основы работы аппаратов со стационарным и
кипящим зернисrым слоем. Л.: Хииия , 1968. 512 с.
3. Барашй Л.А., Пла�«:ин И.Н. Критерии О1ПЮ1изацни ра:щслиrелышх npoцe<:<m. М.: Hayica, 1967 г. 118 с.
4. Барский МД., Рини•цt<J В. И. , Соколкин Ю.В. Гравитационная J(J)асснфиющия зернисrых материа·
лов. М.: Недра, 1974. 232 с.
5. &рд Р" Стюарт В" Лайтфут Е. Явлени• переноса: Пер. с англ./ Под ред. Н . М . Жаворонкова,
В.А. Малюсова. М.: Химия, 1974. 688 с.
6. Бретшнайдер С. Свойсrва газов и жидкосrей: Пер. с польск./ Под ред. П.Г. Романкоиа. М . - Л.:
Химия, 1966. 536 с.
7. Варюфтик Н.Б. Справочник по физическим CllOilcrвaм rii:юв и ЖИJD<О<,7СЙ. М.: Физизпиз, 1963. 708 с.
8. Гельперин Н. И. Основные процессы и аппараты химической технuлогии. М . : Химия, 1981. 812 с.
9. Гельмрин Н.И., 11.йнштеiiн В.Г., kаша В.Б. Основы техники ПССl\llОЖЮl<ения.
О
М.: Химия, 1967. 664 с.
1 0. Дытнерсхий Ю.И. Процесс.ы и аппараты химичес�wil технологии. М.: Химия, 1995. 768 с.
1 1. Жаро• В. Т., Сq>афимо• Л.А. Физикu-химические основы дисr11JIЛ•ции и ректификации. Л.: Хими•, 1975. 240 с.
12. Касаткин А.Г. Основные процессы и аппараты химической технологии. М . : Химия, 1971. 784 с.
1 3. Кафаро• В.В. Основы массопередачи. М.: Высшая шкuла, 1979. 440 с.
14. Коюн В.Б. Теоретические основы типовых процеах>11 химической технологии. Л.: Химия, 1977. 592 с.
15. Хришtр О. Научные ocHOllЬI техники сушки: Пер. с нем/ Под ред. АС. Гинзбурrа. М.: ИЛ, 196 1 . 540 с.
16. Основные процессы и аппараты химической технологии./ Под ред. Ю.И. Дытнерскоrо. М.: Химия,

1.

1991. 496 с.
17. Перри Дж. Справочник инженера-химика: П ер. с англ./ Под ред. Н.М. Жаворонкова. Л.: Химия,
1969. 1 144 с. (т.1, 640 с . ; т.11. 51)4 с. ) .
1 8. Рамм В.М. Абсорбция газов. М.: Химия , 1976. 656 с.
19. Рид Р., Шеrжуд Т. С.ойсrва газов и жидкосrей: Пер. с англ./ Под ред. А. Н. Плановского. М . : Гос
топтехиздат " 1964. ·3j4 с.
20. Ромони:(ul П.r., Фролог В. Ф. Массообмснные проц(ссы химической тсхнолоrnи (си1..."Темы с дис·
персной твердой фазой). Л.: Хииия, 1990. 384 с.
2 1 . Рудобашта С.П. Массоперенос в сисrемах с твердой фазой . М . : Химия, 1980. 248 с.
22. Циборо•ский Я. Процессы химической технологии: nep. с пuльск./ Под ред. П.Г. Романкова. Л.:
Госхимиздат, 1958. 932 с.
23. Шероуд Т. , Пигфорд Р., Уилки Ч. Массопередача: Пер. с англ/ Под ред. В.А. Малюсuва. М.: Химия,
1982. 696 с.
' О требованиях к критериям разделения , способах их консrруирования и о сопосrаале 
нии различных критериев см. ( З , 41 и др.

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Книга 2

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ОГЛАВЛЕНИЕ
Книга 1
Предисловие
Предисловие

к
к

пятому изданию
первому изданию

13
14

Основные условные обозначения

26

Оглавление

3

Глава 1. ОСНОВНЫЕ ПОНЯТИЯ И СООТНОШЕНИЯ

31

Глава 2. ГИДРАВЛИКА
Глава 3. ПЕРЕМЕЩЕНИЕ ЖИДКОСТЕЙ
Глава 4. СЖАТИЕ ГАЗОВ

119
261
323
377

Глава 5. ГИДРОМЕХАНИЧЕСКИЕ ПРОЦЕССЫ
Глава
Глава
Глава
Глава
Глава

469

6. ОСНОВЫ ТЕПЛОПЕРЕНОСА
7. ТЕШIОПЕРFДАЧА И ТЕШIООБМЕН
8. СТРУКТУРА ПОТОКОВ
9. ВЬШАРИВАНИЕ
10. ОСНОВЫ МАССОПЕРЕНОСА

523
607
667
735

Книга 2
Основные условные обозначения .""".."".."..""....""."."""""".". """"".".

901

Глава 11
АБСОРБЦИЯ
11.1.
11.2.

11.3.

11.4.

" ..............................."...........

907

Общие сведения о процессе абсорбции """"""""""""""""""" . "..

907
911
912
917
920
922
922

.

КонСJрукции абсорбционных аппаратов """"""""""""""""""
"
11.2.1. Пленочные и насадочные абсорберы""""""""""""""""""
11.2.2. Барботажные абсорберы """"""""""""""""""""""""""""
11.2.3. Распылительные абсорберы""""""""""""""""""""""""".
....

Фазовое равновесие в системе газ-жидкость""""""""""""""""""

11.3.1. Фазовое равновесие при физической абсорбции""""""""..
11.3.2. Фазовое равновесие при абсорбции, сопровождаемой химической реакцией """ ....."" """" ..""""""""" "." """".""".
11.3.3. Фазовое равновесие в некоторых специальных случаях" ... "
Технологический расчет абсорберов """""""""""""""""""""""".

11.4.1.
11.4.2.
11.4.3.
11.4.4.
11.5.

...............................................

Поперечное сечение абсорбера...."""...."..".".""""..".."..""
Высота абсорберов с непрерывным контактом фаз"""""""
Высота абсорберов со ступенчатым контактом фаз"""" ""
О целесообразности рециркуляции рабочих потоков""""".
..

Особенности расчета некоторых специальных случаев абсорбции "

11.5.1. Неизотермическая абсорбция""""""""""""""""""""""""
11.5.2. Абсорбция нескольких компонентов из газовой смеси""""
11.5.3. Абсорбция при химическом взаимодействии поглощаемого компонента с абсорбентом""""""""""""""""""""""""

11.6.

11.5.4. Абсорбция летучим поглотителем """"""""."""""""""".."
О процессах десорбции . ""......""... "...".......".................................
..

Десорбция в потоке инертного газа или водяного пара"...........

926
926
928
929
932
935
935
938
938
943
945
95 1
959
959

891

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Наrревание абсорбента ................................................................
Понижение дааления над абсорбеmом". ...... .. ". ..""...... ".."" ... ..

11.7.

Гидравлическое сопротивление абсорберов..." .... ... ". .... """ "....."""

Литература

к

главе 11 .""".. """ ......""...."" .. ...".. ..."". " . "" ". .... .......... """ ."

960
960
964
967

Глава 12
ДИСТИЛЛЯЦИЯ И РЕКТИФИКАЦИЯ ............. ".... ....... ............ ......

969

12.1.
12.2.

969
970
970
972
973
979
979
981
983
985
986
988
988
990
990
996

Общие сведения ....... .... ............. ...... .. .. ....... .. ... .... ... .... .. . ... .. .. ...... .... ....
Физико -хи мически е основы процессов переrонки ". .. " """ . . ..". "... .

12.2.1.
12.2.2.
12.2.3.
12.2.4.

Состав и свойства смесей ...." "....... ..... " . .. ."" ... ". ..........". .... .
Правило

фаз

и равновесие в системах жидкость-пар.""".".

Равновесие для идеальных смесей.. .""... "".... "....... ... " .. ."""
Равновесие для реальных бинарных смесей .."" " . . "." " ... .. " "
Малые отклонения от идеальности ........."..." ". .. ...... ."" ".. .... ... ..
Большие отклонения от идеальности ..... ..... ................. ... .... .... ....

Смеси взаимно нерастворимых компонеtПОв.."""..... ..... ... .. .."..
Гетероазеотропные смеси ..... ".... ".. ."."..... .. .. .." "......... ....... ........

12.3.

12.2.5. Равновесие для мноrокомпонентных систем " ....." "....." ". . ..
Дистилля ц ия ......... " . . . ...... ....... ...... ..".."...... ...". .. ...."... ... .... ... ...... ... ...
12.3.1. Общие положения .................................................................
12.3.2. Простая дистИJUIЯция .............................................................
Постепенная дистилляция ...........................................................
Однократная дистилляция ...........................................................

12.3.3.
12.3.4.
12.3.5.
12.3.6.
12.4.

12.5.
12.6.
12.7.

О д истилляци и в токе инертноrо rаза."""."..""" ..""""" "" .
О молекулярной дистилляции" ....." ... .. ."" ."..."..... .. "...... "" .
О некоторых друmх дистилляционных процессах.""".... "."
Общая оценка процессов дистилляции.""... ""."."" .""" " . ."

Ректификация ....................................................................................

12.4.1. Сущность процесса." .. ...". ". .. ........ .........""..... ...... ...... .. .....".
12.4.2. Типовая схема, потоки, терминолоmя..." ... ....".. .......... ..... ".
Об аппаратурном оформлении и работе ректификационных установок... " .........."... .. " . ... .. .. " " .. . . "" ... .. " .... ............".". ..... .."" .. ...... ...."
Материальные и тепловые потоки в ректи фикацио нной колонне "
Непрерывная ректификация бин арных смесей . ." ... ". "..... ""...."" ".
12.7.1. Статика процесса ректификации..."..... "".. . ...". .. ".. ". .. .." ". ..
Укрепляющая часть колонны .."" .. ..."... .." . . . ........... . ........."........
Отгонная часть колонны. ... ... .. ........ ....... ........... .. .. ..... ..... .... .... .. ...
Последовательность расчета ректификационной колонны.."" ...
12.7.2. Осно вные раз меры ректификационных колонн ..". ......".... ..
Высота ректи фикационной колонны .... """. .."." .. ......"... ."". .....
Диаметр ректификационной колонны . ..........". "".. ........... ........ .
12.7.3. Тепло вой расчет колонны ....................".......... ... ...... .. . .......".
12.7.4. Воздействие на эффективность работы колонны""....."" ..."
12.7.5. В лияние arperaтнoro состояния исходной смеси на работу
ректи фикаци онно й колонны .................................................

12.7.6. Некоторые ос обенности работы ректификационных колонн........................................................................................

12.8.

1015
1018
1021
1021
1023
1028
1030
1031
1032
1033
1035
1037
1039
1044

Расчет ректификации бинарных смесей с помощью эmальпийной
диаrраммы..........................................................................................
Укрепляющая колонна " ..... " ........................ " ..... " ....".........".....
Отrонная колонна ......... ......".............."".... " .............. "."......... ".
Общая

последовательность

1045
1046
1051

расчета ректификационной ко-

лонны...........................................................................................

892

999
1002
1005
1009
1010
1010
1013

1059

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

12.9.

Ректификация би на рн ых
areкra...

смесей

с применением разделяющею

... .................. ... .. ........ ........... ............. ...... ,..............................

Экстрактивная ректификация..."."......"......"..............................
Азеотропная ректификация""."...."..............."""""""....""".....
О с оле в ой ректификации ............"..............................................
12.10. Периодическая ректификация бин а рн ых смесей ....."."...."..."........
12.10.1. Общие положения................................................................
12.10.2. Ректификация при по сто янн ом составе дистиллята.".....""
12.10.3. Ректификация п ри постоянном флеrмовом числе ...... ..".".
12.11. О расчете ректифика ци и мноrокомпонентных смесей....... ....... .. ... ..
12.11.1. Разделение трехком по нентн ых смесей................................
Укрепляющая колонна ....... .... ..... . . ...... .. ... .......... ....."............."...
Отгонная колонна........................................................................
Полная ректифи к ац ионная колонна ............".............................
12.11.2. Разделение мн оrо ком по нентных смесей ....................."......
Укрепляющая к олонн а .........".....................................................
Отгонная кало нна . .. ..... .......... ...... ... . ... .................. ....... ......... .......

1063
1063
1066
1070
1071
1071
1074
1077
1082
1084
1085
1089
1092
1093
1095
1098

12 .." ..................... ".................................."..."........... "..

1101

Литература

к главе

Глава 13
ЖИДКОСТНАЯ ЭКСТРАКЦИЯ..........................................................
13.1.
О б щ ая ха рактеристи ка п роцессо в жидк остно й экстр акции ........ .....
13.2.
Основные конструкции э кстр акцион ных аппаратов ...." .......... ........
13.2.1. Экстракторы с н епрерыв ным кокrаIСГом фаз...." ..................
Экстракционные колонны без подвода внешней энерmи ........ .
ЭкстраIСГоры с подводом внешней энерmи .""......"... . . ........ ......

13.3.
13.4.
13.5.

13.2.2. ЭкстраIСГоры со ступенчатым контаIСГом фаз........................
Секционированные колонн ы ...... ............................... . ................
Ступен чатые смесительно-отстойные экстракторы .... .. ......... .....
13.2.3. О выводе фаз из экстрактора ....... ................................... .......
Основные схемы экстракции. ........
" ................ .. .....
Выбор экстраrеша и подходы к анализу ЭКСIJ>акциоЮIЫХ процессов....
Расчет п роц ессо в экстракции " ...... .... .. ... ... ..." .. ." ". ..."" ............ ........
13.5.1. Экстракция при палной взаимной нерастворимости экстраrекrа и разбавителя· ........................................................... .
Однокраmая эк стр акция ." ............. ... ......". ."" .."" .." .." .. .. ..... .. ...
П орци он ная эк стракци я"" ..... ." .... . .. .... .. .... . ...... ............ ......... .... .
Неп рерывная противоточная экстракция..." ...."""" .".......... . .....
13.5.2. Эк"тракция при частичной взаимной растворимости экстрагента и разбавителя .............. . . .. ...... ... ............... .... . .......... .......
Фаз ов ое р авно ве си е " ." .."" ." .."" ...... ..... ..... . " ." "" ." .." ".... .. ........
Некоторые особенности треу rол ьн ой диагр амм ы для п роцес ...........................
·

1103
1103
1106
1107
1108
1109
1113
1114
1114
1116
1118
1121
1122
1122
1123
1124
1127
1137
1137

сов экстракции."..................".."...."......."........"...""..................
Однокраmая экстракция ......".................."...".....".......""".."""
Порционная экстракция."" .. .""....."...................""......."."........
Непрерывная противоточная экстракция.. ".""."""""" ....""..""

1141
1143
1145
1147

13"".. .... .. .. .. ..... .... ...".".............""..............."................

1156

Глава 14
А,ЦСОРБЦИЯ.............................................................................................

1157

Литература

14.1.
14.2.

к главе

Адсорбенты........................................................................................
Физико-химические основы адсорбционных процессов .. ....... . ... ."..

1158
1161

893

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

14.2.1. О механизме мсорбции . " .."". ."". . .""
. " .. " "
14.2.2. Равновесие при адсорбции . """ .""""""
""" "
""""
Адсорберы .......
. ... . . .
.. ..
.
. .. .. .
.
. . . ..... .
14.3.1. Адсорберы непрерывного действия с псевдоожиженным
слоем сорбента ......................................................................
14.3.2. Адсорберы непрерывного действия с движущимся слоем
сорбента.................................................................................
.

..

..

...

.

14.3.

14.4.
14.5.

, ...

..

.

.

.

..........

.

.

...

...

.....

.......

.....

.....

..

...

...

....

.

...

..

. . ..

.

"

.....

..

...

.

...

.

1167

.

1171

14.3.3. Адсорберы полунепрерывного действия с неподвижным
слоем сорбента ......................................................................
О технологическом расчете адсорбционных процессов"."."
. . .. .
Расчет непрерывных процессов адсорбции в псевдоожиженном
слое сорбента .....................................................................................
14.5.1. Односекционный адсорбер с псевдоожиженным слоем"" ..
Адсорбция в условиях потоковой задачи.""."""
"
"
.. .
Адсорбция в условиях внутренней задачи"..........................."""
14.5.2. Ступенчато-противоточный адсорбер с псевдоожюкенным
слоем
Адсорбция в условиях потоковой задачи................................."
Об адсорбции в условиях внутренней задачи ..." .". ..."" .. . . .
Расчет непрерывного процесса противоточной адсорбции в движущемся слое сорбента.. .
.
.
.
.
..
. ...
Адсорбция в условиях внешней задачи ....."
..
""" " ."""
Адсорбция в условиях внутренней задачи."""" .."""."""""" "
Об адсорбции в условиях смешанной задачи ...... ""
""""".
Расчет полунепрерывного процесса адсорбции в неподвижном
слое сорбента ....................................................................................
14.7.1. Качественные представления о полунепрерывной адсорб-

.

....

.

.

.

.

....

............................................

....

......

.

.

.

..........................................

.

14.б.

.

.

...........

.......

......

.........

."

...........

......

.

.

..........

....

...

.

.

..

.

14.7.

.

.

"

"

" ....

.

ции. Задачи расчета .. "
. .. "" . ""
" ".
" ....
Некоторые общие понятия.." " """" ".. .." ". ". ." "...
Идеальная адсорбция ...."" ....... . ."... .".
.. " " """"" .... . ..
Реальная адсорбция .....................................................................
Статическая и динамическая емкости сорбента.." .. """ . .
.
Задачи технологического расчета ".""
""
"" . """ " . """
14.7.2. Расчет процесса идеальной адсорбции""""".".""""""""""
14.7.3. Уравнение связи 'tпр и L для процесса реальной адсорбции
14.7.4. Об эксперимеНТ'dЛЪНом определении параметров уравнения Шилова ..........................................................................
14.7.5. Расчеnюе определение параметров формулы Шилова"""".
Расчет скорости движения фронта и и коэффициента защитного действия к .........." " .
. ".
. ". " . ".
." "
".
Оценка времени массопередачи tм "". ".. "" ""
. " """"""""
Определение потерянного времени t0"""""
"""""""""""" "" " .
14.7.б. Определение динамической емкости сорбеJПа"""""""""".
14.7.7. Расчет количесТ11а десорбируемого поглощенного компонента.
. ."............"".............. ""......"....... ".........""".......
.

........

..

...

..

.

...

.

..

.

...

"

.

.........

...

.

...

...

. . ..

.

.

....

.

.....

..

.

. ...

.

.

..

..

.

.

.

... "

.

...

..

.

. .

..

.

....

..

.

.

..

......

...

.

.....

.

.

.

.......

Литература

к главе

..

..

...

" "

....

.

.

.....

.

".

.

..

14"" .. . "."...".."......"" ........."..."...".....".."....... """".
..

.

.

1161
1163
1167

1174
1175
1176
1177
1177
1179
1184
1184
1186
1187
1187
1189
1190
1191
1192
1192
1192
1194
1198
1199
1199
1201
1202
1203
1203
1205
1208
1210
1211
1212

Глава 15
СУШКА ТВЕРДЫХ МАТЕРИАЛОВ.""""."."""
15.1.

".."""""""""""""

1213

Устройство и принцип работы сушильных аппаратов """""""""""
15.1.1. Конвективные сушильные аппараты"""""""."""""""""""
15.1.2. Специальные сушильные аппараты"".""" .""""".".. """"."
Физико-химические основы процесса конвективной сушки "".....

1215
1216
1225
1229

..

.

15.2.

894

..

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

15.2.1. Условие сушки ...................................................................... .
15.2.2. Свойства мажноrо воздуха...................................................

.

Концентрация маги в воздухе ...................................................
Объемный поток мажноrо воздуха ........................................"

.

...

Относительная энтальпия мажноrо воздуха.........................." ..
Диаграмма

/-х .............................................................................

.

.

15.2.3. Свойства мажноrо твердого материала................................
15.2.4. Об адиабатном испарении маги .. . . .............."".... ... .. .. .
15.2.5. Равновесие ........................................................................".
Простая сушилка .....................".... ..".. ........ . ........ ..... ........... . ..
15.3.1. Основные потоки в простой сушке"................................ "
Материальные потоки .........................................".. . . ... .
. .
Теruювые потоки ..................................................................." ...
15.3.2. Простая идеальная сушилха ......." . .... .. ... ... .. ... . .."" ".
15.3.3. Простая реальная сушилка ... ...
..... .... .. .... ...... ......"".
Простая сушилка при неизвестной точке 2 " ................ ........."
Простая сушилка при неизвестной точке 1 ...............................
15.3.4. О распределении в простой сушилке подводимой теплоты
между калорифером и сушильной камерой...................." ..
Мноrозональная сушилка ........................................"........ .... " .
15.4.1. Мноrозональная идеальная сушилка."..........."
."
15.4.2. Мноrозональная реальная сушилка..." . ... " .
..
.

.

.

.

...

..

..

..

15.3.

.

.

.

.

.

.

.

.

.

.

....

"

.

..

..

.

..

"

.....

..

"

.

.

.

.

.

.

.

.

.

.

..

"

. "

.

.. .

1255
1258
1260
1261
1265
1267
1269
1271
1273
1275
1275
1278
1284
1284
1289
1293
1295
1295
1299

. "........................................... "....................

1305

.

15.4.

.

.

.. .

...........

....

15.5.

...

...

.

.

.

... .

..... .

......

" ......

Сушилка с частичным возвратом отработанноrо воздуха""............

.

15.5.1. Смешение свежеrо и отработанноrо воздуха ........................
15.5.2. Идеальная сушилка с частичной рециркуляцией.................
15.5.3. Реальная сушилка с частичной рециркуляцией ...... : ."" .."
О некоторых других вариантах сушильноrо процесса"....." ..." .
Сушка топочными п1зами ...................................." .. ..."...... . . . .
15.7.1. Общие положения.""...." ".. . ".... . . ..." .." . "... .. . .
15.7.2. Приближенный аналитический расчет".." ".....
..."."... "
К.И нетика сушки .......................................................". ... . ... . . ..
15.8.1. Общие положения ............" .... ". . .....
...... ...."". . .
15.8.2. Сушка в условиях внешней задачи......... ."..."..."..... " . ..
15.8.3. Сушка в условиях потоковой задачи............"........" "
15.8.4. Сушка в условиях внутренней задачи ......." "". ...." " ."
.
Постановка задачи ..........................................................
.
Решение задачи............................." . . .. .. . ... . .... "
.

.

15.6.
15.7.

...

...

..

.

15.8.

...

.

.

.

.

.

.

....

.

.

.....

.

""

..

.

.

"" ..

.

.

.

.

"

".

"

....

..

.

....

...

.

.

.

."

..

..

....

"

..

....

.

.

.

.

...

.

.

..... "

.".

" ....... " .

.

Литература

к

zлаве 15 . .
..

.

....... . .

.

1229
1230
1230
1234
1235
.1236
1239
1241
1243
1245
1246
1246
1247
1249
1251
1252
1254

...

..

...

...

.

..

......

..

.

Глава 16
КРИСТАJIЛИЗАЦИЯ
16.1.
16.2.

. . " .................................. ".... ".................. ".......

.....

.

Основные особенности процесса кристаллизации".".""."... " "
Фазовое равновесие ..................................................................
"

"

....

" ... . ...

16.2.1. Однокомпонентные системы .........."... ..... ." . . ...
""
16.2.2. Бинарные системы ...............................................". .. .... . .
16.2.3. Тройные системы ..............................................................." .
Кинетика процесса кристаллизации ..........." . ...... ..... """ . . .
16.3.1. Создание пересыщения .."
. . .."
... ." .... . . . .
16.3.2. Зарождение кристаллов ........................................................
16.3.3. Рост кристаллов .".................................................................
16.3.4. Переход расплава индивидуальных веществ в твердое сос..

..

"

.

...

.

......

.

..

.

...

.

16.3.

.

...........

....

..

..

...

..

.....

.

.

...

....

.

..

.

.

.

...

.

.

тояние

.
... . . . . ...... . . . .................... . ...............................................

16.3.5. Кристаллизация бинарных и мноrокомпонентных смесей ..
16.3.6. Форма кристаллов ..................................................................

1307
1308
1311
1311
1313
1317
1324
1324
1325
1329
1332
1337
1338

895

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Отверждение расплавов " . .."......""....."".""."....."......... "..............
16.4.1. Отверждение в формах"""""""""""""""""""""""""""""
16.4.2. Отверждение в тонком слое""""""""""""""" . """"""""".
Фракционная кристаллизация. . . "......"........"......."...... ".".".........

1341
1341
1343
1344

16.5.1. Основные особенности фракционной кристаллизации""""
16.5.2. Массовая кристаллизация с отводом теплоты через охлаждаемые поверхн()сти ... .. . . . .. .. .."......".."....""..................
16.5.3. Массовая кристаллизация при непосредственном контакте
с хладоаrентом
16.5.4. Кристаллизация с частичной отrонкой растворителя"""";"
16.5.5. Кристаллизация на охлаждаемых поверхностях""""""""""
16.5.6. Противоточная кристаллизация""""""""""""""""""""""
16.5.7. Фракционное плавление." . .... ...."......"""....""..."..........
16.5.8. Направленная кристаллизация""""""""""""""""""""""..
16.5.9. Зонная плавка""""""""""""""""""""""""""""""""""""
Схемы перекристаллизации .
... . "......""....."""......""."............
16.6.1. Перекристаллизация без использования растворителей""".
16.6.2. Перекристаллизация с использованием растворителей """"

1345

Литература к главе 16.""......... ""......"..............."".....""........"..........".......

1391

16.4.

..

.

.

16.5.

...

.

.

..

.

.

.

.

.

.

. . . . ............. . . .. . . ...... ............................... . . . . . . . . . . .

..

16.6.

..

....

..

. ..

..

..

1352
1360
1365
1369
1372
1377
1382
1384
1386
1386
1389

Глава 17
РАСТВОРЕНИЕ И ВЫЩЕЛАЧИВАНИЕ""""""""""""""."".""".

1393

17.1.
17.2.
17.3.
17.4.
17.5.

1393
1395
1402
1410
1413
1416
1416
1419
1426
1428

17.6.

17.7.

Основные особенности процессов растворения твердых веществ""
Аппаратурное оформление процессов растворения""""""""""".".
Физико-химические основы растворения твердых веществ"".""""
О кинетике процессов растворения""""""""""""""""""".""""".
Способы и схемы прощ:ссов растворения"""""""""""""""""."".
Расчет процессов растворения""."""""""""""""""""""""""""""
17.6.1. Полное растворение веществ"""""""""""""".:""""""""".

17.6.2. Частичное растворение веществ с инерrnым компонентом
17.6.3. Фракционное растворение веществ""""""""""""""""""".
Отдельные задачи растворения и выщелачивания"""""""""".""".
17.7.1. Растворение неподвижного сферического зерна в неогра-

1428

ниченном объеме покоящейся жидкости""""""""""".""".
17.7.2. Выщелачивание в потоке растворителя в условиях балансовой задачи . . ......... . . . . . .. .. "................".".................
17.7.3. Протяженность рабочей зоны для процесса противоточного выщелачивания с непрерывным контактом фаз""."""""

1430

Литература к главе 17." ..................... "................"......"."..."".........."".......

1434

. . .

.

..

.

.

...

. .

. .

1432

Глава 18
СУБЛИМАЦИЯ И ДЕСУБЛИМАЦИЯ """""""""""""""""" """."

1435

18.1.
18.2.
18.3.

1436
1440

Физико-химические основы сублимации и десублимации """"."."
Основные особенности процессов сублимации и десублимации .....
Возможные вариа1rrы организации процессов сублимации и де-

...." ... .

Технологический расчет процессов сублимации и десублимации ."

1444
1448
1458
1463

Литература к главе 18"""." "."""""""".""""""""""".""""""."""."""."

1468

суб.лимации ..""

18.4.
18.5.
18.6.

...... . .

..

Сублимационная сушка...""

. .

896

.. . .

..

.. . . " ... . " ... ."" .. "" ." .

...

..

.

.

.

.

.

..

..

.

..

. . .

..."

.

Аппаратурное оформление сублимационных процессов"""""""""

.. ." .. .. ." ..

...

.

.

.

.

...

" .... . ..." .. . ..." ..... ..... .. .. ....

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Глава 19
ГРАНУЛИРОВАНИЕ....... ....................... ...... ........ ".................................

1469

19.1.

1469
1470
1472
1474

Основные понятия.............................................................................

19.1.1.
19.1.2.
19.1.3.
19.1.4.

Стадии гранулообразования .... ."..."."....." ..""""."""......"...
Основны е механизмы взаимодействия частиц в грануле......
Классификация процессов гранулирования.. " ......... """.......
Элеме1rrы типовой технологической схемы гранулирования... ""....".............................................................................

19.2.

19.3.

Аппаратурное оформление процессов гранулирования""..... "."...".
19.2.1. Гранулирование окатыванием и агломерацией"...... """"..".

19.2.2. Гранулирование прессованием и формованием....... "....."."
19.2.3. Гранулирование кристаллизацией капель расШiава"......... ".
Гранулирование мелкодисперсных материалов"........ ".""..."""......
19.3.1. Физико-механические свойства дисперсных материалов... "
19.3.2. Материальные и теШiовые балансы гранулятора ."........ . .....
19.3.3. Кинетика и расчет гранулирования окатыванием и агло.

мерацией ................................................................................
Кинетика образования зародышей и роста гранул".. "............".
Расчет процесса гранулирования"". .. "".....".............""...."........

19.4.

19.5.
19.6.

19.3.4. Расчет гранулирования прессованием.. ."""."""........".........
19.3.5. Расчет гранулирования формованием.. "."..."" ......".."".......
Гранулирование расплавов""".". .""..."...".."".....""............"..........
19.4.1. Материальные и теШiовые балансы гранулятора ... "..".........
19.4.2. Кинетика криспuиизации капель расШiава """"""" ..""."".
19.4.3. Кристаллизация расплава на поверхности растущих гранул
Гранулирование кристаллизацией из растворов и паровой фазы....
О капсулировании гранулированных продуктов .. .. "....."..".............

Литература

к

главе 19"." ..............".".".""" ....".""".".".""....."""".....".....

1477
1478
1479
1484
1486
1490
1490
1491
1496
1496
1500
1504
1507
1508
1508
1510
1515
1515
1516
1518

Глава 20
МЕМБРАННЫЕ ПРОЦЕССЫ РАЗДЕЛЕНИЯ.... ".......""..............

1519

20.1.
20.2.

1519
1521
1522
1524
1526

Общие понятия"............................". ..... ................. ............".... ........
.

Основные механизмы переноса вещества через мембраны ..............

20.2.1. Механизм переноса вещества через непористы е мембраны
20.2.2. Механизм переноса вещества через пористые мембраны"...
20.3.

Мембранные процессы разделения и способы их организации.......

20.3.1. Процессы

разделения

без

химическоrо

взаимодействия

проникающеrо компоне1rrа и материала мембраны"""." .. "

20.3.2. Процессы

разделения

с

химическим

проникающих компоне1rrов и материала мембраны ".".......

20.4.
20.5.

1526

взаимодействием

Основные конструкции мембранных ячеек."........"". ..." "" .. " . .....
.

"

Основы расчета процесwв разделения в мембранных ячейках...... "
20.5.1. Идеальное перемешивание потоков в надмембранном и
подмембранном пространствах..............................................

1529
1530
1533
1533

20.5.2. Идеальное вьrrеснение потока в надмембранном прост
раН(,'ТВе с отводом пермеата от поверхности

мембраны в

подмембранном пространстве .................................. ...........
"

1537

20.5.3. Идеальное вьrrеснение потока в надмембранном и иде
альное перемешивание потока

в подмембранном прост-

ранствах.....................". ................. .. .. ...... .. ........... ...... ... ... ....
.

.

1539

20.5.4. Перепад давления в потоках, движущихся в подмембранном и надмембранном пространствах................".....""..

..

""

1542

897

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

20.6.

Простейшие каскадные схемы разделения """""""""""."" .. """""
20.6.1. Разомкнуrый каскад с выводом проходящего потока из

20.6.2.

к

1544

ячеек .......................................................................................
касющ с возвратом проходящего потока на
предьШУIЦУю ступень ...".... .. ""..............".. ".... ........ ....... . .....

1546

главе 20 ...................................................................................

1550

Замкнутый

.

Литература

1543

Глава 21
УМЕРЕННОЕ И ГЛУБОКОЕ ОХЛАЖДЕНИЕ""""""."""""""""

1551

21.l.
21.2.

1551
1553
1553
1556
1563

Общая харакrеристика холодильных процессов".""""""""""""""

21.2.1.
21.2.2.
21.2.3.
21.2.4.

21.3.

".. .. .. ".......""..... ". "..............
машина ...." """.. .. ................... ...... ..

Процессы умеренного охлцщения ..
Идеальная холодильная

"

.

.

Реальная паровая компрессионная холодильная машина .. "
О воздушной компрессионной холодильной машине.. """"

паровая компрессионная холодильная
машина...................................................................................
21.2.5. Абсорбционная холодильная машина""""""."""""... .. ."""
21.2.6. О некоторых других холодильных машинах умеренного

1566
1574

охлцщения.............................................................................

1577

Двухступенчатая

21.2.7. Рабочие тела, охлцщающие и охлцщаемые среды, промежуточные хладоагенты . "".."."."""...""""."""".........."""
21.2.8. Об аппаратурном оформлении процессов умеренного охлцщения """..."""".."....".""."........."............"............"."".
Процессы глубокого охлцщения ."...."..".."""...."".....""""...".."".
21.3.l. Термодинамические основы процессов глубокого охлаждения ..... "........".".........""....."................"....".".........."."....
Дросселирование..........................................................................
Адиабатическое расширение с отдачей внешней работы.".. ""."
Сопоставление ah и as . """ "" """..."""""""""""""".""""""""
Технологические харакrеристики процесса ".."."................."""
21.3.2. Простой регенеративный цикл"""".""""""" ..."..""""""""
Харакrеристика, схема и диаrрамма T-s """" ""..""""""""""."
Технологический расчет цикла...... "....".""""..""""""""""".....
21.3.3. Усовершенствованные циклы с дросселированием "" ..""""
Пути совершенствования цикла""""""""".""""""""" .. ".""""
Схема и диаrрамма T-s"""""""""""""""."..."""".".".""."."".
Технологический расчет цикла."...... .""..""""".""""............"".
21.3.4. Циклы с поршневыми детандерами"".""" .."."..........""."".
Основные варианты циклов .. """..."""".""""""".""""."."""".
Схема цикла Гейландта и диаrрамма T-s... """"".""""""""".."
"".""""".."."" """""
Технологический расчет цикла
21.3.5. Циклы с турбодетандерами.".""""".""".""""""."""""".""
Схема цикла Капицы и диаrрамма T-s"""""""""""".""".""".
Технологический расчет цикла".... "......."""."."""..."..""""......
21.3.6. Об аппаратурном оформлении процессов глубокого охлаждения....................................................................................

1580
1582
1584
1585
1585
1588
1588
1591
1592
1592
1594
1596
1596
1598
1599
1602
1602
1603
1604
1605
1606
1608
1610

21.3.7. Двухколонный ректификационный arperaт для разделения
воздуха....................................................................................
Устройство и принцип работы arperaтa " """"""""""" ..."."".
"

.

Особенности работы arperaтa . """"".."."""""".""."""".".""....

Литература

898

к

главе 21"""". .. .""."..."."""..."""..".."......"".".".".""""".""

1612
1613
1615
1617

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Глава 22
ИЗМЕЛЬЧЕНИЕ ТВЕРДЫХ МАТЕРИАIIОВ.......................................

1619

22.1.

Общие положения..................................................................................
22.1.1. Классификация размольных машин .......................................
22.1.2. О затратах энергии на и:1мельчение........................................
22.1.3. Основные требования к размольным машинам. Типовые
схемы размольных установок...................................................
Щековые дробилки................................................................................
22.2.1. Устройство и принципы работы щековых дробилок............
22.2.2. Основы технологическоrо расчета...........................................
Угол захвата твердого материала в щековой дробилке ...............
Производительность щековой дробилки и et регулирование....
О расчете затрат энергии на измельчение в щековой дробилке
Валковые дробилки................................................................................
22.3.1. Устройство и принципы работы валковых др6билок ...........
22.3.2. Основы технолоrическоrо расчета...........................................
Захват валковой дробилкой кусков твердого материала.............
Производительность валковой дробилки и ее регулирование ...
О расчете затрат энергии на измельчение в валковых дробилках......................................................................................................
Барабанные мельницы ................. ............................. ... ........... ..........
22.4.1. Устройство и принципы работы барабанных мельниц ........
22.4.2. Основные режимы движения насадки в барабанной мельнице (качественный анализ)....................................................
22.4.3. Основы технолоrическоrо расчета...........................................
Некоторые геометрические характеристики слоя дробящей
насадки..............................................................................................
Границы технологических режимов ..............................................
Некоторые эксплуатационные характеристики барабанных
мельниц.............................................................................................
О затратах энергии на измельчение в барабанных мельницах..
Коллоидные мельницы мокрого помола ............................................

1619
1619
1621

главе 22.... .................. ................. " ........................... "..... "........

1654

22.2.

22.3.

22.4.

22.5.

.

Литература

к

.

.

.

.

.

.

1623
1625
1626
1628
1628
1630
1633
1634
1634
1635
1635
1638
1639
1639
1639
1642
1643
1643
1645
1651
1652
1653

Глава 23
КЛАССИФИКАЦИЯ ЗЕРНИСТЫХ МАТЕРИАЛОВ ........................"

1655

Общие сведения ............... .............................. . .."....... ".........................
Грохочение..............................................................................................
23.2.1. Общая характеристика метода ................................ "...............
23.2.2. Устройство и работа грохотов .............. ..... " .........................".
23.2.3. Элементы технологического расчета.......................................
Классификация в тяжелых средах.......................................................
23.3.1. Описание процесса................... ....................................... ......"
23.3.2. Элементы технологичес"оrо расчета.......................................
Гидравлическая и пневматичесJ(ая классификация...........................
23.4.1. Общие положения ...""." ......."..".".."..........." ......""...""......."
23.4.2. Классификация в поле сил тяжести. . ""........"...."".........".....
Типовые конструкции и пр•1нципы работы классификаторов"
К инженерному расчету кла.;сификаторов, работающих в поле
сил тяжести.......................................................................................
23.4.3. Классификация с испол1.зованием инерционных сил . .. ""..
Устройство и работа инерционных воздушных сепараторов ."..
Основы технологического расчета ...... "..."..."."... ""................. "..

1655
1657
1657
1660
1663
1667
1667
1669
1673
1673
1675
1675

23.1.
23.2.

.

.

23.3.

.

23.4.

.

.

1677
1679
1679
1683

899

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

23.4.4. Классификация псевдоожижаемых твердых частиц..............
Гидродинамическая дистилляция и гидродинамическая ректификация ......... ............................................................ ...... ..........
Сепарация на основе сегрегации в псевдоожиженном слое......
О некоторых других возможностях классификации твердых материалов......................................................................................................
Фрикционные сепараторы..............................................................
Флотация ................................................................ .........................
Электромагнитные методы классификации .................................

1685

глаt1е 23............................. .................. : .........."......"".................

1696

.

.

23.5.

.

.

Литература

к

.

1686
1689
1691
1692
1693
1694

Глава 24
СОПРЯЖЕННЫЕ И СОВМЕЩЕННЫЕ ПРОЦЕССЫ...................

1697

24.1.
24.2.

1698
1701
1702

24.3.

Основные типы и особенности комбинированных процессов ........
Сопряженные процессы ....... ...... . ...... "...............................................
24.2.1. Процессы с рекуперацией импульса и теплоты....................
24.2.2. Ректификация азеотропообразующих смесей в двух колоннах, работающих по,11 разными давлениями . . ..................
24.2.3. Дистилляция-кристалли:sация" ................"...".".....................
24.2.4. Ректификация-кристалл�tзация ...............................................
24.2.5. Экстракция-кристаллизация ......................"".........."..............
24.2.6. Адсорбция-десорбция ........ "...............".."".......".....................
24.2.7. Некоторые другие сопряженные процессы............................
Совмещенные процессы .... "....... " ................ " ........... "....... "................
24.3.1. Реакционно-массообменные процессы"" .... """....................
Реакционно-ректификационные процессы..................................
Реакционно-кристаллизаци(lнные процессы ......... "....................
Реакционно-десублимационные процессы...................................
24.3.2. Массообменно-массообменные процессы............................"
ЭкстрахЦионно-кристаллизационные процессы .........................
Сушильно-rрануляционные процессы ....... ".................................
24.3.3. Процессы, включающие механические или гидромеханические операции ........ .... ... ........
.... ......... ................

1730

главе 24.............. ........ "............ ....... . ......................... . .... ....... ... . .

1732

.

.

Литература

к

.

..

..

.. .....•.......

.

. .

1703
1705
1708
1713
1716
1717
1719
1720
1721
1724
1726
1728
1728
1729

Перечень учебников по общему курсу ПАХТ на русском языке.................

1733

Предметный указатель .............................................. ........ ".......".....................

1735

.

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ОСНОВНЫЕ УСЛОВНЫЕ ОБОЗНАЧ Е Н ИЯ
ника) отнестись к этому разделу с

Настоятельно рекомендуем студентам (вообще - читателям учеб

ним поможет лучшему усвоению изложенного в учебнике материала.

большим вниманием:

ознакомление с

Выбор символики (условных обозначений) в учебнике основан на

следующих положе ниях и подходах:

- число используемых в учебнике поюrгий больше количества
имеющихся символов; при совпадающей символике смысл разных

величин различается с помощью индексов;
- потоки, силы , геометрические размеры и прочие величины обо 
значаются

латинскими

символами

(исключения

-

единичны ) ;

при

выборе символов исходили из латинского, английского или немецко

го корня соответствующего по нятия либо из установившихся тради 
ций ;

- расходы, потоки (теплоты, вещества) и другие величины , обо
значенные латинскими символами, изображены наклонным шрифтом,
количества (в редких случаях - другие характеристики) - прямым;

ми; они обычно соответствуют начальным буквам поясняющего поня
- индексы при величинах обозначены чаще всего

русскими

буква

тия.

В

НеКОТОрЫХ

Для

случаях

ВОЗМОЖНЫ

6ЬlНуЖденные

отступле ния

ОТ

сформулированных выше подходов.
облегчения работы с материалом учебника (иногда - и для

уточнения) смысл обозначений , содержащихся в при1юдимом ниже

перечне (и, естественно, дополнительно вводимых) , поясняется также

С целью сокращения записей и акцентирования внимания читате

в каждой главе .

ля в ряде глав прописными буквами выделены ключевые CJJ o вa,

В

смысл специально пояснен
шрифтов. В

в

их

тексте.

заголовках разделов и подразделов учебника выдержана иерархия
тексте учебника тоже используются различные шрифто

вые выделения, что способствует смысловой рубрикации материала и
расстановке акцентов.
Ниже последовательно приведены (где возможно - в алфавитном
порядке) основные уСJJ о вные обозначения, используемые в учебнике :
понятийная символика, аббревиатура ключевых слов (тех, что приме
няются в учебнике широко) и другие сокращения, некоторые матема
тичес кие с имволы , виды шрифтовых выделений в тексте.

901

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

символы
а

температуропроводность;
поверхность;
удельная
концентрация (преиму
щественно - массовая)
линейный размер, umри
ь
на
с
константа
излучения;
концентрация
компо
нента (вещества) в пото
ке, в одной из фаз
с
скорость;
абсолютная
теплоемкость
диаметр;
коэффициент
D
диффузии
D и D
количество и поток пара
d
диаметр
Е
WIОТНОСТЬ лучистого ПО'Ю
ка; энерrия; эффеюивнОСIЬ;
коэффициент эффе КПIВ
ной диффузии (продоль
ного перемешивания)
F
сила; поверхность темо
обмена или контакта фаз
площадь
поперечного
1
сечения; частота
G и G - массовые количество и
расход вещества, твердой
фазы
ускорение
свободного
g
падения
н
высота
h
высота; экrальпия (удель
ная)
ус.ловное темосодержа
1
ние
воздуха;
М()Мент
инерции
энтальпия (удельная)
k
коэффициенты теIL'!опе 
редачи или массопереда
чи; показатель адиабаты;
консrанта скорости хи
мической реакции
L
расход воздуха (в расчете
на абсолютно сухой);
удельный (на 1 кг топли
расход
воздуха;
удельная работа
работа
L

ва)

902

расход
и
количество
жидкости
линейный размер, дли
на; удельный (на 1 кг
удаляемой влаm) расход
воздуха
молярная масса
М
М и М
межфазные количество и
поток переданного ве
щества
т
масса; показатель политропы;
коэффициент
распределения
мощность; чис.ло ячеек
N
полного перемешивания;
чис.ло ступеней
чис.ло оборотов; крат
п
ность циркуляции; чис.ло
ступеней
Р
сила
парциальное
давление,
р
давление
поток
Q и Q
и
количество
темоты
удельные поrоки - темо
q
ты (напряжение rемовоrо
потока) или вещества
(массы, компонента)
радиус; rазовая постоянR
(индивидуальная,
ная
универсальная)
радиус, радиальная ко
r
ордината; те1U1ота паро
образования (конденса
ции)
поперечное сечение
s
поток
и
количество
S и S
раствора
энтропия (удельная)
s
температура
т, t
относкrельная влажность
и
твердого материала
скорость
и, v
объем
у
объемный расход
V
удельный объем
v
и W - межфазные количество и
поток удаленной влаm
Lи L

-

W

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

w

х
х

у

у

х, у,
а.

z

г

'У
л

·

скорость
относительная концеm
рация вещества в фазе х;
степень сухости влажно
го пара
влагосодержание возду
ха; мольная (или какая
либо иная) концентра
ция вещества в фазе х;
степень ожижения воз
духа
относительная концент
рация вещества в фазе у
мольная (или какая-либо
иная) концентрация ве
щества в фазе у
координаты
коэффициент теплоотда
чи; относительная лету
честь; угол
коэфф и циент объемного
расширения; коэффи циент массоотдачи
плотность орошения
угол
движущая сила про цесса
( ЛI, Л С, ЛХ, . . . )
линейный размер, тол
щина стенки или пленки
степень
порозность;
черноты; холодильный
коэффициент
пластикоэффициеm
ческой вязкости

(пластичность); коэффи
циеm полезного дей
ствия , эффективность
температура, безразмер
ная температура; безраз
мерное время
коэффициент расхода
коэффициент rnдравличе
ского сопротивления; теп
лопроводность;
теплота
(затвердева
плавления
ния)
динамическая вязкость;
номинальная (расходная)
твердой
концентрация
фазы
кинематическая вязкость
коэффициент местного
сопротивления
периметр
осмотическое давление
плотность; абсолютная
ко нцентра
массо вая
ция
поверхностное натяже
ние
время ; напряжение тре
ния
плотность распределеотносительная
ния;
влажность; доля; угол
угловая скорость; абсо
лютная влажность твер
дого материала

8
к

µ
v

п
7t

р

CJ

(J)

И НДЕКСЫ

кр
р
л
т

а

вл

критический
равновесное значение
ламинарный
турбулентный
начало, на входе

аппарат
алажный

Верхние
•

конец, на выходе
знак безразмер ной величины

Н ижние

вх
вых

средний, усредненный (над
символом )

на входе
на выходе

903

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

r

rp
д

газ, газообразный
rраничный; rреющий
диффузионный, дисперсная фаза
эквивалекrный

пл
пп

истинный
идеальный
инерт, инертный
конечный
кипение
конденсация
легкий, локальный
местный; материал
начальный
начальный,
исходный;
нулевой
пар

св
см
ер
ст
т

р
с

ЖИДКО СТЬ, ЖИДКИЙ

е

)К

и
ид
ин
к
кип
конд
л
м
н
о

п

плавление
продольное перемеши ванне
реальный
сплошная среда; сухой;
стесненный
свободный
смеси
средний
стенка
твердый; тяжелый; трення
условный
удельный
частица
эффехrивный
поверхностиый
объемный

у
уд
ч
э

F

v

А Б Б Р Е В И АТ У РА КЛ Ю Ч Е В ЫХ СЛ О В
и ТИ П О В Ы Е С О К РАЩ Е Н ИЯ

ГУ
ив
ип

ПАХТ - процессы

rраничное условие
идеальное вытеснение
идеальное перемешивание
коэффициекr полезного
действия
кеподвюкный слой
начальное условие
основное
балансовое
соотношение

КПД
нс

НУ
ОБС

и аппараты
химической технолоmи
псевдоожиженный слой .
твердый материал
источник
накопление
приход
результат
сток
уход

пс
тм

Ис
Нак

Пр
Ст

Рез
Ух

О БОБЩЕННЫЕ ПЕРЕМЕННЫЕ:
критерии

р

d Py - p
Ar• !._
2
з

v

а, Sx "
8.1

{

k

а/ , Е -

Ь, Sy

904

А.у

aR
А.у

kyF

= --

D

п одобия

- критери й
Архимеда
- число еди ниц
переноса
- критери й Био
- число едини ц
переноса

и

други е

ко мпле ксы

С • � C' • mD
L
mD '

Eu

F1"

Fo

• _!!!2 !._
pw

Dt Dt
" -;z . """;;!"
R
1
=

O't

O't

12 · В!

- факторы
массопереноса
- число Эйлера
- критерий
Фиха
- критерий
Фурье

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Fr

Gr

,.. �2
w

dз
"' �
ры
v

Nu = а/ ad
�, л
w/

Ред

и-

Рет

s-

Рез

w/
а

idem

1im

max
min

opt
var

Sc

- чис.по Нуссельта

w/

- критерий
Пекле для
продольного
перемешивания (эффекти н н ый)

Е

одинаковый ( - ая, -ое,
- ые)
предел
максимум
минимум
оптимум
переменная величина

µ

wdp
µ

,

v
· -

D

D

D

а

St

· --

Stд

• w

We

р

а

v2
п
1:

л

11

о-•

"

wd

- криrерий
v
Рейнот,цса

- критерий
Шмидта
- критерий
Шервуда
- число Стантона теruювое

cpw

2

· --

gp .•. 1

И З Н А К О ВАЯ

постоянная величина
экспонента: ехр у означает еУ

w/p

Sh " Pl ' pd

- критерий
Пекле тема вой

Е-

const

Re =

- критери й
Пекле
диффузионный

D

- критерий
Прандтля

а

- критерий
Грасrофа

М АТ Е М АТ И Ч Е С КАЯ

ехр

Pr ,.. �

- критери й
Фруда

- число Стантона диффузионное
- критерий
Вебера

С И М В ОЛ И КА

разность, приращение
ламасиан
произведение
сумма
абсолютная величина
операция сопоставления
знак тождества; обозначение
пропорциональность
приближенное равенство

905

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ШРИФТОВЫЕ ВЫДЕЛЕНИЯ
В тексте
1. Полужирный прямой - рубрикационные выделения (в начале
строки), новые, принципиальные для данного текста понятия, терми
ны; для некоторых обобщающих понятий используется полужирный
курсив.
2. Светлый прямой в разрядку - рубрикационные выделения (в
начале строки; подчинены полужирному прямому).
3. Светлый курсив - смысловые акценты;

определения, формули

ровки законов, правил.
4. Прописные буквы - аббревиатура ключевых слов и наиболее
распространенных понятий.
5. С прописной буквы - составляющие балансовых соотноше
ний

(в обобщенном виде,

безотносительно к переносимой суб

станции).
6. Мелкий шрифт - конструкции аппаратов;

фраrменты, иногда

- элементы текста (углубление анализа), без проработки которых не
нарушаются связность изложения и понимание последующего мате
риала, а также подписи к рисункам и сноски.
На р и с у н ках
!, ll, ...

потоки веществ, рабочих тел (символы снабжены на рисун

(1), (11), ...

те

ках стрелками)

же

вещесrва,

рабочие

(обласrи, зоны аппарата)

rела,

занимающие

пространСI'Вll

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Глава 1 1
АБ СОРБЦ И Я

Абсорбцией начинается рассмотрение конкретных массооб
менных процессов. В самом простейшем исполнении абсорб
ция является одним из наиболее наглядных процессов
класса 3 (2-2) 1 .
1 1 . 1 . ОБЩИЕ СВFДЕНИЯ О ПРО Ц ЕССЕ АБСОРБЦИИ
Абсорбцией называют процесс избирательного извлечения
одного или нескольких компонентов из газовой смеси жидким
поглотителем (абсорбентом). Обратный процесс - выделение
из абсорбента растворенных в нем газов (паров) носит назва
ние десорбции·.
В абсорбционных процессах (абсорбция, десорбция) уча
ствуют две фазы - жидкая и газовая. При их контактировании
один компонент (либо несколько) переходит из одной фазы в
другую. При наличии в газовой фазе компонента (ком
понентов), практически (часто абсолютно) не растворяющегося
в жидкой фазе, его называют ивертом, или газом-носителем .
Растворяющийся компонент - это абсорбируемый компонент,
или поrлощаемый компонент.
Таким образом, газовая фаза состоит из газа-носителя (ГН)
и поглощаемого компонента ( П К), а жидкая - из абсорбента
(А) и поrлощаемого компонента ( П К) .
При отсуrствии химического взаимодействия между погло
щаемым компонентом и абсорбентом процесс называют физи
ческой абсорбцией, а при наличии такого взаимодействия хемосорбцией. В последнем случае поглотитель представляет
собой химически активный компонент или раствор химически
активного компонента , вступающего в химическую реакцию с
поглощаемым компонентом; при этом вещество , в котором
растворен активный компонент, называют растворителем.
' В более широком плане под десорбцией понимают также ряд других техно
логичес ки х приемов, состоящих в вьщелении из сорбента (не обязательно жид
кого) какого-либо ком понента (ком п онентов) в сплошную среду - жидкую или
газовую. Примером мor:yr служить про цессы сушки, а также выщt:.лачивания .
реэкстракnии и др. (см . гл. 1 3- 1 5 , 16).

907

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

При отсуrствии испарения абсорбента в газовую фазу и рас
творения газа-носителя в абсорбенте процесс физической аб
сорбции одного компонента газовой смеси поглотителем (или
обратный процесс - десорбция), согласно приведен ной в гл .
1 О классификации массообменных процессов, относится к
классу 3 (2-2) 1 . Для таких процессов, в которых каждая фаза
состоит из двух компонентов - П К и инерта (газа-носителя в газовой фазе и чистого абсорбента - в жидкой) , - концент
рации ПК в фазах удобно выражать в кг П К /кг инерта: х кг
П К /кг А - в жидкой фазе и у кг П К /кг ГН - в газовой.
Абсорбция весьма широко применяется в химической и
смежных отраслях промышленности. При этом преследуются
две главные цели: извлечение ценных (целевых) компонентов из
газовой смеси; очистка газовых смесей от примесей перед их
использованием в технологических процессах или перед их
выбросом в атмосферу. В современной промышленной практи
ке возрастает значение безотходных технологий, поэтому на
званные выше две цели все чаще объединяют в одну.
Укажем на некоторые конкретные области · применения
процессов абсорбции:
- получение готовых продуктов в виде насыщенных абсор
бентов. Это, например, абсорбция хлороводорода водой с по
лучением соляной кислоты, абсорбция серного ангидрида в
производстве серной кислоты , абсорбция нитрозных газов во
дой в производстве азотной кислоты или щелочными раство
рами - для получения нитратов;
- разделение газовых смесей при помоши селективных по
глотителей . Например, извлечение бензола из коксовых газов,
ацетилена - из газов крекинга, буrадиена - из контактного
газа после разложен ия этилового спирта;
- очистка газов от нежелательных примесей . Например,
очистка нефтяных и коксовых газов от сероводорода, очистка
азотоводородной смеси от диоксида углерода при синтезе ам
миака. (Отметим здесь удачные варианты развития безотходной
технолоГии: из сероводорода получают товарный продукт серу; уловлен ный при очистке азотоводородной смеси диоксид
углерода после десорбции используют вместе с аммиаком для
получения карбамида - ценного удобрения);
- обезвреживание производственных газовых выбросов.
Сюда относятся очистка топочных газов от сернистого ангид
рида, улавливание хлора, фтористых соединений и т.д.
Разделение газовых смесей в ряде случаев возможно пуrем и х ожижения
(например, при повышении давления) и выделения отдельных составляющих
смеси методом реК111 фикацин (см. гл. 1 2) . Однако из-за высоких энергозатрат на
ректификацию Д1lЯ большинства процессов разделения газовых смесей предпоч
тительней оказывается абсорбция. Затраты в последнем случае связаны со стон-

908

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

мостью абсорбента (восп01mение его потерь), с подачей газового и жидкостного
потоков в абсорбционный аппарат и созданием необходимых условий для их
кoJПaicra, а также с затратами теwюты при последующем вьщелении (десорбции)
поглощаемого компонеJПа. Но несмотря на большое число статей расхода, сум
марные затраты на проведение процесса абсорбции-десорбции, как правило,
значительно меньше, нежели на реIСГИфикацию.

Основные проблемы при осуществлении абсорбции связаны
с подбором абсорбента и созданием рациональных условий
контактирования газа и жидкости. Подходы к решению этих
проблем рассматриваются в настоящей главе.
При выборе абсорбента к нему предъявляется ряд требова
ний:
- селективность, т.е. способность избирательного поглоще
ния извлекаемого (целевого) компонента при возможно малой
растворимости в нем газа-носителя, это позволяет перевести в
жид кую фазу только поглощаемый компонент (П К), оставляя
газ-носитель - в газовой;
- большая поглотительная способность, иначе - высокая
растворимость поглощаемого компонента в жидкой фазе в ра
бочих условиях; при выполнении этого требования умень
шаются затраты, связанные с расходом абсорбента (затраты на
его подачу в абсорбер, затраты теплоты на его наrрев при де
сорбции и т.д.);
- возможно более низкая летучесть (в идеале - нулевая),
т.е . малая упругость паров абсорбента при рабочей температур е
во избежание его потерь с уходящим газом и связанных с этим
трудностей при его отделени и от газа-носителя;
- устойчивость в работе, т.е. абсорбент не должен подверrатъ
ся изменениям - разложению, окислению, осмолению и т.п.;
- удобство в работе нетоксичность, негорючесть, малое
коррозионное воздействие на аппаратуру;
- доступность и дешевизна;
- легкая регенерируемость при десорбции или каком-либо
другом процессе регенерации.
В подавляющем большинстве случаев промышленные аб
сорбенты не удовлетворяют в полной мере одновременно всем
перечисленным требованиям. Поэтому на практике приходится
идти на компромисс, определяя при выборе абсорбента для
каждого конкретного случая основные требования в зависи
мости от условий проведения процесса (свойств и состава газо
вой смеси, температуры и давления газа, требуемой степени
очистки и т.д.).
Отработанный абсорбент (абсорбент с раст1tоренным в нем
П К) должен быть подвергнуг обработке, при которой из него
выделяют растворенный П К. Чаще всего это делают пугем де
сорбции ПК из абсорбента. Получаемый при этом абсорбент с
-

909

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

II

ш

4

v

Vl
2

1 - абсорбер, 2 - десорбер, 3 - реJС)'Перативный теJVJообменюо:, 4 - холодилыlИХ ре
генерированного абсорбеша, 5 - подогреватель отработанного абсорбеша, 6 - насос, 7 реrулируюЩИЙ венгиль;
1 - загрязненный газ (ГН + ПК), 11 - очюцеННЬIЙ газ (ГН) , 111 - регенерированный
абсорбент, JV - отработанный абсорбент (абсорбент с ПК) , V - поток свежего абсорбента
для компенсации его потерь, V1 - поток извлеченного компонента (ПК)

Рис. 11. 1. Схема абсорбционно-десорбционной установки:

малым содержанием в нем П К (регенерированный абсорбент)
может быть вновь использован в качестве абсорбента.
Схема абсорбционно-десорбционного агрегата, в котором
газовая смесь разделяется на два потока (поглощаемый компо
нент и газ-носитель), представлена на рис. 1 1 . 1 . Непременным
условием работы такого агрегата является наличие абсорбера 1
и десорбера 2. Поскольку десорбция - процесс, обратный ·аб
сорбции, то благоприятные условия (давление и температура)
для его проведения противоположны условиям, способствую
щим абсорбции .
Собственно очистка газа-носителя от поглощаемого компо
нента происходит в абсорбере 1, где сверху подается абсорбент
(11[) с малым содержанием П К, а навстречу ему поднимается
газовый поток. При его контакте с жидкость10 поглощаемый
компонент растворяется в абсорбенте, а очищенный газ (J[)
выводится из установки . Отработанн ый абсорбент (IV), выхо
дящий из абсорбера снизу, подается на регенерацию в десорбер
2. Здесь из насыщенного абсорбента выделяется П К, а регене
рированный абсорбент из нижней части десорбера вновь по
дается в абсорбер J. При такой замкнугой по абсорбенту схеме
он практически не расходуется; на самом же деле, из-за нали
чия его (хотя и в малых количествах) в очищенном газе и ухо
дящем .из десорбера 2 потоке поглощаемого компонента, а
также из-за возможных протечек через неплотности, есть поте
ри поглотителя; они компенсируются дополнительным пото
ком v.
910

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

В разд. 1 1 .3 . 1 будет показано, что абсорбцию целесообразно
проводить при низкой температуре и высоком давлении, а де
сорбцию - при высокой температуре и низком давлении. Для
повышения температуры процесса десорбции в нижнюю часть
десорбера 2 подводится теплота Q, а абсорбент перед его пода
чей в десорбер еще и нагревается в подогревателе 5. С целью
улучшения процесса абсорбции реге н ерированный абсорбент
перед его подачей в абсорбер 1 охлаждают в холодильнике 4
(например, холодной водой).
Для экономии расхода теплоносителей в теплообменниках 4
и 5 устанавливают рекуперативный теплообменник 3, где отра
ботанный абсорбент подогревается (перед его подачей в десор
бер) за счет теплоты, отдаваемой горячим регенерированным
абсорбентом при одновременном понижении температуры по
следнего - в идеале до рабочей в абсорбере 1 (в этом случае
отпала бы необходимость установки холодильника 4). Подача в
десорбер 2 нагретого (в теплообменниках 3 и .5) абсорбента
уменьшает расход теплоты Q в нижней части десорбера 2.
Давление в абсорбере 1 выше, чем в десорбере 2. Поэтому
жидкость из абсорбера в десорбер движется самотеком; для
регулирования потока на линии отработанного абсорбента ста
вят вентиль 7. Для подачи регенерированного абсорбента из
десорбера в абсорбер необходим насос 6; его целесообразно
ставить после охлаждения регенерированного абсорбента в теп
лообменнике 3, чтобы избежать осложнений, связанных с ка
витацией (см. разд. 3.3.5).
1 1 .2. КОНСТРУКЦИИ АБСОРБЦИОННЫХ АППАРАТОВ

Различия в свойствах газовых смесей и поглотителей, а так
же в связанных с ними механизмах переноса вещества из фазы
в фазу обусловливают весьма широкое разнообразие конструк
ций применяемых аппаратов. Интенсификация абсорбционных
аппаратов связана с развитием поверхности контакта F между
жидкой и газовой фазами, а также с увеличением интенсив
ности массопереноса в каждой из фаз и в первую очередь - в
той фазе, интенсивность массопереноса в которой является
лимитирующей (определяющей интенсивность всего процесса
массообмена) . Из опыта работы абсорбционных аппаратов с
различными газожидкостными системами известно, что лими
тирующей стадией чаще всего оказывается �тадия переноса
вещества от границы раздела фаз в жидкость. Поэтому при
абсорбции и десорбции используют (в большей мере, чем в
других массообменных процессах) аппараты, в которых жид
кость движется в виде текущих тонких пленок (в разных на
правлениях - вниз, вверх, под углом). Но применяются и ап91 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

параты, в которых поверхность контакта создается за счет пу
зырьков газа, распределенных в жидкости (барботаж), или за
счет мелких капель жидкости, распределенных в газовой среде
(распыление жидкости). В соответствии с этими способами соз
дания межфазной поверхности можно выделить три основные
rруппы абсорберов:
- пленочные и насадочные;
- барботажные;
- распьmительные.
1 1.2. 1 . Пленочные и насадочные абсорберь1

Пленочнwе абсорберw подразделяют на аппараты:
- с орrаннзо111111НWМ течением менкн: свободное стекание пленки по внуr
ренней или наружной поверхности труб вниз или течение при взаимодействии с
rазовым потоком вверх или вниз (в обоих с.лучаях по вертикальным или на
клонным поверхностям);
- с неорrаннзо8аННWМ течением J11ИДКОС111WХ менок в насадочных абсорберах.
Еще раз подчеркнем условность любой классификации. Так, во мноmх учеб
никах" (в этом учебнике тоже - в гл. 10) насадочные и пленочные аппараты
выделены в отдельные группы, хотя основным способом кокгакта фаз в наса
дочных аппаратах, как и в пленочных с орrанизованным течением пленки, яв
ляется обтекание rазом :жидкостных пленок, перемещающихся по элемекгам
насадки.
Простейшими пленочными аппаратами с орrанизованным течением пленки
являются xacк8Дllwe nолочнwе (рис. 1 1 .2, а) и с системой конусов (рис. 1 1 .2, б) .
Жидкость, перетекая с верхних элемеlП'Ов внуrренних устройств на нижние,
образует пленочные завесы. Проходя через эти жидкостные завесы, rаз кокгак
тирует с :жидкостью. Иногда внуrренние конусы (поз. З на рис. 1 1 .2, б), укреп
ленные на валу 4, вращают для получения тонкой пленки одинаковой толщины.
Прорыв rаза через такие пленки приводит к образованию пены; за счет этого
улучшается эффективность контакта.
Тип ичным пленочным ап п аратом с организованным течением пленки яв
ляется трубчатwй абсорбер (рис. 1 1 . 3 , а), устроенный анало iично ко:жухотрубно
му теплообменнику. Абсорбент lll поступает на верхнюю трубную реu1етку З,
распределяется по трубам 2 (как показано на рис. 1 1 .3, а, узел А) и стекает по их
внуrренней поверхности в виде пленки. При большом числе труб для равномер
ного распределения :жидкости по трубам применяют специальные распредели тельные устройства. Газ движется по трубам снизу вверх противотоком к сте
кающей :жидкостной пленке. Для отвода теплоты абсорбции (когда она суще
ственна) в межтрубное пространство абсорбера подают охлаждающий аrент V
(чаще всего - воду).
При больших расходах rаза, ко гда скорость его в трубах превышает 10 1 5 м/с, противоток. становится невозможным (см. разд. 2.4); то гда орrанизуют
режим восходящего прямоток.а абсорбента и rазовой смеси (рис. 1 1 .3, б). Газ,
движущийся в трубах с большой скоростью, увлекает за собой :жидкостную
пленку (см. узел Б на рис. 1 1 . 3, б). Газожидкостная смесь при выходе из труб
ударяется о брызгоотбойники 4 (см. узел В на рис. 1 1 .3, б); rаз отделяется от
:жидкости и движется вверх, а жидкость собирается на трубной решетке З и
отводится на следующую (расположенную ниже) ступень (или - из аппарата).
В с.лучае восходящего прямотока могут бьrгь получены высокие коэффициен
ты массоотдачи в rазовой фазе (за счет уменьшения толщины пограничного слоя

• См. (3, 4, 7 ) .

91 2

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 1 1. 2. Пленочные абсорберы:

а - полочиый каскадный: 1 - корпус, 2 - rоризошальная полка;
t5 - абсорбер с сисrемой конусов: 1 - корпус, 2 - наружный конус, З - внуrрешmй
конус, 4 - вал;
1 - заrрязненный rаз, 1/ - очищенный rаз, III - свежий абсорбсш, IV - отработан

ный абсорбеш

�Жид

� '"'"""'
Узел Б

з*Жид-

5

а

б

t

-

-

-

Гиэ

=-

2

кисть

а - противоточный односrупенчатый, t5 - противоточиый двухсrупенчатый с прямото
ком фаз в каждой сrупени;
1 - корпус, 2 - трубы, 3 - трубные решетки, 4 - брызrооrбоЙНИJСИ, 5 - щели для
ввода абсорбеша в трубы;
1 - заrрязненный rаз, Il - очищенный rаз, III - свежий абсорбеш, IV - отработан
ный абсорбент , V - охлаждающий аrент.
УЗЛЬ1: А - ввод жидкосrи в трубу при ее течении вниз. Б - движение фаз на входе в
трубу при восходящем течении пленки, В - двюкение фаз на выходе из трубы

Рис. 1 1.З. Трубчатые абсорберы:

913

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

1Il

_д_
1
Ci)

1 - ЛИ СТЬI насадки, 2 - распределительное усrройсrво;
/ - заrрязненньdi rаз, /1 - очищенньdi rаз, 1/1 - свежий абсорбеш, /V - отработанный

Рис. 11.4. Пленочный абсорбер с плоскопараллель ной (листовой) насадкой:
абсорбеш

1 - корпус колонны, 2 - слой насадки, 3 - распределитель жидкосm, 4 - опорная ре
ШtтКа, 5 - перераспределитель жидкосm;
/ - вход rаза, // - очищенный rаз, //1 - свежий абсорбеш, /V - отработанный абсор
беш

Рис. 11.5. Насадочный абсорбер:

при высоких скоростях газа) и отчасти - в жидкой (за счет уменьшения толщи
ны пленки и повьпuения ее турбулизации) , следовательно и повьпuенные общие
коэффициекrы массопередачи. Но при прямоточном движении невозможно
получить эффект разделения более, чем в одну теоретическую ступень; поэтому
для лучшего использования движущей силы процесса и получения большего
эффекта разделения применяют многоступенчатые трубчатые пленочные аппара
ты (на рис. 1 1 .3, б показан двухступенчатый абсорбер). В Ю1Х реализуюrся как пре
имущества противоточной схемы от ступени к ступени, так и преимущества высоко
скоростною восходящею прямотока в каждой ступени. Для снюкения вьmоса капель
газовым потоком между ступенями установлены брызrоо'Iбойники 4.
Весьма прост по конструкции абсорбер с плосхопараллет.ной насадКой (рис.
1 1 .4), в котором размещены вертикальные листы / из различных материалов
(металл , пластмасса, натянутые на каркас ткань, пленка и т. п.). Для орrанизации
равномерного смачивания листовой насадки с обеих сторон используют распре
делительные устройства 2. Прорези в верхних краях конических лотков (см. рис.
1 1 .4) обеспечивают достаточно высокую равномерность орошения по периметру
листов. Жидкость через нижние части треугольных отверстий 2 вытекает в виде
струй по обе стороны пластины. На некотором расстоянии от верхнего сечения
эти струи сливаются в единую , образуя жидкостные пленки по обеим сторонам
пластин 1.
Насадочнwе абсорберы (рис. 1 1 .5) получили наибольшее· применение в про
мышленности из-за отсутствия необходимости в устройствах для распределения
жидкости по каждому контактному элемекrу. Жидкость стекает по поверхности

9 14

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 11. 6. Трансформация эпюры скоростей жид

кости по мере стекания ее по насадке с большой
высотой слоя
жутках межцу ними - в виде струй и капель.

насадочных теп в виде тонкой IUiенки, а в проме

Затем она вновь растекается в виде IUieнoк по
Q
поверхности злеме�пов насадки. При достаточной
ПЛО111 0С111
О ОUJеННИ,
характеризуемой раСХОДОМ
жидкости (м '/с) на единицу IUiощади поперечноrо
сечения аппарата (м2), пракrически вся поверх
ность злеме�пов насадки покрьrrа жидкостными
IUiенками, так что поверхность массопередачи близ
ка к суммарной поверхности насадочных тел . В
ряде случаев (при хорошей смачиваемости насад
ки, отсутствии застойных зон) поверхность массо
передачи между газовой и жидкой фазами может
превьпuать rеометрическую поверхность всех
злеме1ПОв насадки за счет наличия капель и струй
между ними.
Требования к насадкам, а также наиболее часто применяемые в массообмен
нь�х процессах (в том числе при абсорбции) типы насадок приведены в разд.
10. 1 . 3. Основные характеристики широко используемь�х в промьпuленности
насадок
удепьная поверхность насадки Fуд (м2/мЗ) и порозность Ен (мЗ/мЗ) .
приведены в учебной и справочной литературе• . Значительное мноrообразие
типоразмеров применяемой насадки связано с приоритетом вьmолнения тоrо
или иноrо требования к ней. Так, если требуется насадка с большой удельной
поверхностью контакта, то предпочтительнее мелкая насадка (с малыми разме
рами злеме�пов насадки). При этом порозность насадки, как правило, меньше
и, следовательно , больше ее rидраWIИЧеское сопротивление при тех же расходах
газовой и жидкой фаз. Если первоочередным требованием к насадке является
малое гидравлическое сопротивление, то целесообразно применять насадку с
высокой порозностью. Увеличение последней возможно за счет уменьшения
толщины злеме�пов насадки (например, толщины стенок колец Рашига) при
сохранении габаритнь�х размеров ее злеме1ПОв.
В ряде случаев на первый IUiaн выдвигаются и друп1е требования к насадке,
например ее химическая стойкость по отношению к аrрессивному воздействию
рабочей среды.
В насадочнь�х абсорберах орошающую жидкость (абс9рбе�п) равномерно
распределяют по сечению аппарата с помощью различнь�х оросителей З (на рис.
1 1 . 5 показан простейший - выполненный в виде части сферы с отверстиями и
работающий по принципу душа). Однако, как отмечалось в гл. 10, одним из
недостатков насадочнь�х абсорберов является неравномерность стекания жид
кости по сечению колонны, обусловленная пристеночным эффектом. По мере
движения вниз по аппарату эrа неравномерность усиливаеrся (рис. 1 1 .6), и из-за
малоrо потока жидкосm в приосевь�х зо нах эффеIСIИВность абсорбера замеmо ухуд
шаеrся. Для уменьшения поперечной неравномерносm потока ЖЮIКОСТИ насщхку
заrружают слоями 2 (на рис. 1 1 .5 их два), а в промежутках между ними размещают
перераспределительные устройства 5, которые собираюr жидкость к центру и обеспе
чиваюr более равномерное орошение насадки по сечению armapani.
Простейшим распределите11е м жидкости является собирающий конус 5, по
казанный на рис. 1 1 .5 . Степень выравнивания орошения по сечению аппарата в
этом случае невелика. Более равномерное перераспределение жидкости достита-

f

-

-

·

• См " например, (5 , 6, 8 ) .

915

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

3

1 - тарелка, 2 - патрубок, 3
в патрубке

Puc. 1 1. 7. Распреде.Jiительн ая тарелка:
-

прорези

ется с помощью распределительных
тарелок 1 (рис. 1 1 .7), в которых жид
кость, стекая по всем патрубкам 2,
равномерно орошает практически всю
насадку. Для включения в работу всех
патрубков и создания Wiенки по всему
их внутреннему периметру в них де
лают вертикальные прорези J. В отсуr
ствие этих прорезей:
- возможно "отключение" от ра
боты части патрубков, верхние срезы
которых вЬШiе, нежели у других (или
при не строго горизонтальном поло
жении тарелки);
- не будет устойчивого Wiеночно
го стекания жидкости по всему внутреннему периметру патрубков, что также
приведет к некоторому ухудшению равномерности орошения, а значит, к сни
жению эффективности работы абсорбера.
Насадку с размером элементов до 50 мм заrружают в абсорбер навалом. Вы
сота слоя насадки в каждой секции обычно равна 4 - 5 диаметрам колонны, но
не более 2 - 3 м. Расстояние между слоями насадки опреде.i�яется конструкцией
распределительного устройства.
Отличительной особенностью работы насадочных колонн с заrрузкой эле
ментов насадки навалом яаляется образование застойных зон - с неподвижной
(малоподвижной) жидкостью в местах более Wiотной упаковки насадки.
Кольца Рашига, Памя, с перегороiJк.ой и друmе размером более 50 мм иногда
размещают правильными рядами со смещением их в соседних рядах; такое рас
положение элементов насадки называется регулярным. К регулярным насадкам
относятся также хордовая и блочная.
Хордовая насаiJк.а (см . рис. 10.3, б) состоит из поставленных на ребро досок /,
скреWiенных шrырями 2 и образующих решетку. Решетки укладывают одна на
друтую с поворотом на 90° (как показано на рисунке) или на 45°. Такая кон
струкция позволя ет организовать достаточно равномерное IUiеночное течение по
всем элементам насадки. Таким образом, насадочные абсорберы с хордовой
насадкой вполне можно отнести к Wiеночным аппаратам с организованным
течением Wiенки, что еще раз свидетельствует об условности классификации.
Хордовую насадку изготавливают из rрафита, IUiacтм acc, металла и чаще всего из дерева, пропитанного специальными растворами, препятствующими его бы
строму гниению. Во избежание значительного давления на нижние решетки
укладку насадки производят ярусами ( по 15 - 20 решеТок в каждом).
Блочная насаiJк.а (рис. 1 1 .8) состоит из IUiастмассовых или керамических бло
ков, укладываемых регулярно - рядами. Отсуrствие специальных устройств для
распределения жидкости в каждом ниже.лежащем ряду приводит к значительной
неравномерности орошения и низкой ее эффективности. Блочную насадку при
меняют при больших скоростях газового потока и невысоких требованиях к
очистке газовой смеси.
Для обеспечения высокой эффективности абсорберов требуются насадки с
большой удельной поверхностью (м2/м 3). Последняя может бьrrь существенно
увеличена при использовании элементов насадки малых размеров. Однако из-за
повышенного гидравлического сопротивления абсорбера с такой насадкой газо
вому потоку существенно возрастают затраты энергии на дуrье. Поэтому про
блема создания насадки, обладающей высокой эффективностью при низком rиz

лL

916

_-11

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

а

б

Рис. 11.8. Блочная насадка
а

р

б

Рис. 11.9. Насадка высокой эффективности при низком mдраалическом сопро
розетхи Теллера, б

тивлении:
а -

насацхи)

-

сетчатая насl\дlСа " Спрейnак" (h и р

-

хараrrерные размеры

драRЛИЧеском сопротивлении, и впредь будет оставаться аlСl)'алъной. К числу
таких насадок оnюсятся проволочные спирали (например, диаметром 30 мм из
проволоки тотциной 3 мм и расстоянием ме:жцу спиралями 5 мм), розетки
Теллера (рис. 1 1 .9, а) и металлические се�чатые насадки, в частности насадка
" Спрейпак" (рис. 1 1 .9, б).

1 1 .2.2. Барботажные абсорберы
Среди барботажных простейшими являются абсорберы со сплошным барбо
слоем (рис. 1 1 . 10, а) . Здесь газ, проходя через распределительную ре
шетку 1, дробится на пузырьки, которые поднимаются в слое жидкости. Недо
статком этих аппаратов является интенсивная циркуляция жидкости (см . разд.
5 . 3 .2) в вертикальном направлении (продольное перемешивание), приводящая к
снижению движущей силы процесса массообмена (подробнее - см. разд. 8.2).

тажным

917

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ш
о

о

о
о
о
о
о

о

о

о

о

о

о
о

о

о

о

о

о
о

о

о

о

о

о
о
о

о

о

о

о

о

о
о

о

о

о
о

б

а

Рис. 1 1. 1 О. Барботажные абсорберы:

- проrивоточный односекционный, б - проrивоточный секционированный ;
1 - решепса (тареmса), 2 - переливная труба, J - rазовый слой;
1 - заrрязненный rаз, /l - очищенный rаз, lll - свежий абсорбент, lV - отработан

а

ный абсорбент

Вредное влияние продольного перемешивания уменьшают путем секциониро
вания аппарата (рис. 1 1 . 1 0, б) тарелхами 1, обеспечивая небольшую высоту бар

ботажного слоя в отдельной секции. При этом пузырьки rаза собираются под
каждой тарелкой, образуя сплошную газовую фазу J. Давление в газовой фазе
должно бьпъ достаточным, чтобы газ барботировал через слой жидкости на
расположенной вьпuе тарелке. Жидкость уходит с тарелки либо через те же
отверстия, что и газ, либо (что бывает чаще) через переливные трубы 2 круглого
или иного сечения, устанавливаемые внутри абсорбера (как показано на рисун
ке) или вне его.
Последний вариант применяют при необходимости промежуточного охлаж
дения жидкости (абсорбента) или по другим причинам . С целью понижения
температуры в абсорбере охлаждать следует именно жидкос'rь, а не газ, так как
коэффициент теплоотдачи от жидкости к теплопередающей поверхности на
один-два порядка выше, чем от rаза Следовательно, для отвода теплоты абсорб
ции необходимая поверхность теплообмена в случае охлаждения жидкости на
много меньше, чем при охлаждении rаза
Некоторые (основные) конструкции
тарелок рассмотрены в разд. 10. 1 . 3 (см.
рис. 1 0 . 3). КПД таких тарелок при про
ведении большинства абсорбционных
процессов крайне низок - на уровне 5
.

.

Рис. 1 1. 1 1.

Схема

колпачково-ситчатой

1 - патрубок, 2 тый элемент тареmси

тар елки:

918

колпачок, J

-

ситча

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 1 1. 12. Абсорбер с псевдоожиженной шаро
вой насадкой:

1 - опорные �шепси, 2 - оrранич:ительная ре
шетка, З - шаровая насадJСа, 4 - распределитель
жидкосrи ;
J - заrрязненный rаз, lI - очищенный rаз, /11
- свежкй абсорбенr, IV - отработанный абсорбенr

�11�'1..f==*===fr�

-

- 10% . Это можно объяснить малой пропуск
ной способностью (kxF или kyF) процесса
оrраниченные поверхности
массопередачи:
массопередачи F и невысокие скорости массо
передачи /сх, ky. Дело в том, что из-за большой
разницы в IШотностях жидкости и rзза время
прохождения rззовым пузырьком слоя жид
кости мал6 (по сравнению с временем про
хождения капель одной жидкости в другой экстракции).
процессов
проведении
при
Вследствие малого времени контактирования
жидкости и пузырей rзза, а т-.tкже оrраничен
ной массообменной поверхности всех пузырей
F количество передаваемого из фазы в фазу
вещества мало по сравнению с возможным при
достижении равновесия (F -+ оо или ,; -+ оо).
Для увеличения поверхности кокrактирования F используют тарелки с двух
кратным дисперmрованием rззо вого потока, на.п ример хоJJПачхово-СИ1'181Wе
тарелхи (рис. 1 1 . 1 1) . Здесь rззовый поток проходит через патрубки 1 и, выходя
из-под коJDiачка 2, барботирует в слой жидкости. Образовавшиеся при этом
пузыри затем дополиительно дисперmруются при прохождении через ситчатые
элементы З тарелки. Однако даже Д11Я таких комбинированных тарелок с увели
ченной и обноменной (при допОJU1ительном дисперmровании) поверхностью
массопередачи КПД редко достигает 20 % . Поэтому Д11Я абсорбции чаще, чем в
случае друmх массообменных процессов, испОЛЪ3уюТ IШеночные (насадочные)
аппараты с развитой поверхностью контакта фаз. Однако оrраниченные (из-за
уноса капель и захлебывания) скорости газа в противоточных насадочных аппа
ратах предопределяют невысокие значения коэффициентов массоотдачи в rззо 
вой фазе и, следовательно, коэффициекrов массопередачи.
Весьма эффективным и сравнительно простым яRТIЯется тарельчатый абсор
бер с псе�щоожижеиной насадкой на тарелках (рис. 1 1 . 12). В качестве насадки,
помещаемой на опорные решетки 1, используют тела различной формы (чаще
всего - шаровые) с кажущейся IШотностью Рк. меньшей IШотности жидкости р.
Насадку (шары диаметром от 10 до 30 мм - полые или сIШошные) изготаRТIИ
вают из полиэтилена, полипропилена и друmх полимеров, а также из металла
или резины. При скоростях r.tзa, превышающих некоторое критическое значе
ние, на тарелках образуется слой жидкости, а насадка переходит в псевдоожи
женное состояние. С ростом скорости газа высота слоя насадки и, следователь
но, порозность слоя увеличиваются. При интенсивном перемешивании насадки
хорошо перемешивается и жидкость на тарелке. Это уменьшает поперечную не
равномерность потока жидкости и увеличивает эффективность аппарата.
Образующиеся и подхватьmаемые rззовым потоком капли жидкости в значи
тельной степени уламиваются смоченными псевдоожиженными шарами и вновь
возвращаются в слой жидкости при попадании шаров в нижнюю часть секции,
оrраниченной двумя соседними тарелками. Для предотвращения уноса шаров из
самой верхней секции устаноалена оrраничительная решетка 2 (см . рис. 1 1 . 12) .
Все это позволяет работать при повЬШiенных ( в сравнении с насадочными аппа
ратами, у которых скорость rзза оrраничена скоростью захлебывания неподвиж-

919

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

1 - опорная реш етка, 2 - насадJСа, З - rидрав
лический затвор, 4 - распределитель JIСИдКОСТИ;
1 - загрязненный rаэ, /1 - очищенный rаэ, 111 свеJIСНЙ абсорбеш, JV - отрабоrанный абсорбеш

Рис. 1 1. 1З. Эмульгсtционный насадочный аб

сорбер:

111

3

ной насадки) скоростях газового потока. Рабо
чая скорость газа достигает здесь 4-5 м/с при
ruюnюстях орошения до 0,05 м3/(м2 . с).
Переток жидкости с тарелки на тарелку
происходит здесь через те же отверстия, через
которые проходит и газ .
Достоинствами этих аппаратов являются:
- высокая эффективность (КПД) одной
ступени за счет развитой поверхности массо
обмена (это поверхность менок на шарах и
поверхность капель) и высоких значений
коэффициентов массоотдачи вс.ледствие малых
толщин жидкостной пленки и поrраничного
слоя со стороны газа при больших скоростях
газового потока. Высоким КПД способствует
также отсутствие поперечной неравномерности
за счет хорошего перемешивания жидкости по объему секции (как в виде ме
нок жидкости на элементах подви:жной насадки, движущихся в различных на
правлениях, так и в виде капе.ль, брызг);
- увеличение иигенсивности абсорберов: в 4-6 раз по газовому потоку и
еще больше - по жидкостному;
- возможность работы с заrрязненными :жидкостями и газами.
Один из главных недостатков этих аппаратов - выравнивание концентраций
в продольном направлении и уменьшение за счет этого средней движущей силы
процесса массопередачи (см. разд. 8.2 и 10.8). Эффективным средством борьбы с
продольным перемешиванием является секционирование аппарата - на рис.
1 1 . 1 2 показан трехсекционный абсорбер.
Более сложным по поддержанию устойчивого режима работы является наса
дочный эмул•rациониwй абсорбер (рис. 1 1 . 1 3) . Это насадочный абсорбер, рабо
тающий в режиме эмульгирования, т.е. в начале его захлебывания - с поддержа
нием в нем постоянного объема жидкости с помощью гидравлического затвора.
По механизму взаимодействия фаз такой абсорбер относится к числу барботаж
ных, хотя по конструктивным признакам является типичным насадочным.

1 1 .2.3. Распылительвь1е абсорберы
В простейших распылительных абсорберах восходящий поток газа движется
навстречу абсорбенту, распыленному в виде м елких капель. Распыление
(диспергирование) производится чаще всего механическими форсунками такие абсорберы получили название форсуночнwх. Форсуночные абсорберы
работают при небольших скоростях газа ( 1 - 1 , 5 м/с) и плотностях орошения не
ниже 0,003 м 3/(м2 с). Несмотря на простоту устройства и низкую стоимость,
небольшое гидравлическое сопротивление и возможность работы с загрязнен
ными газами, форсуночные абсорберы имеют оrраниченное применение из-за
низкой эффективности. Этот недостаток вызван ииrенсивным продольным
перемешиванием в обеих фазах и уменьшением вследствие этого движущей силы
процесса. Некоторое увеличение эффективности достигается при повышении
скорости газа до 5 м/с и плотности орошения до 0,0 1 - 0,0 1 5 м3/(м2 с), но при
этом заметно увеличивается унос газом капель жидкости .

·

·

920

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

а

Рис. 1 1. 14.
а -

Абсорберы Вентури:

б

односrупенчатый абсорбер с пленочным вводом жид1юсrи, б - сrупенчато-противо
точиый абсорбер с эжеJЩИеЙ JIСИДКосrи;
1 - конфузор, 2 - rорлоВJП1а, З - диффузор, 4 - сепарационное пространсrво, 5 цирку11ЯШ1онная труба в одной сrупени, 6 - переливная труба (от сrупени к сrупени), 7 брызrоотбойних, 8 - корпус аппарата;
/ - вход rаза, // - выход rаза, /J/ - вход JКИДКОСТИ, /У - выход JКИДКОСТИ

Более эффе�сrивны абсорберw ВеlП)'ри, встречающиеся в различных конструк
тивных вариантах (рис. 1 1 . 14), но при обязательном прямотоке жидкости и газа
в конфузоре-диффузоре.
На рис. 1 1 . 1 4, а представлен одноступенчатый абсорбер Вентури с пленоч
ным вводом жидкости. Жидкостная пленка в горловине дисперrируется газовым
потоком /, движущимся здесь с большой скоростью (более 20 - 30 м/с). Разде
ление газа и жидкости происходит в сепарационном пространстве 4. Обладая
высокой производительностью , такие абсорберы имеют оrраниченную массооб
менную способность, обусловленную прямотоком фаз.
Применение ступенчатого противотока в абсорбере Вентури (при сохранении
прямотока газа и жидкости в одной ступени) возможно при эжекции жидкости
(рис. 1 1 . 14, б). Здесь газ, проходя в каждой секции по узкой щели между по
верхностью жидкости и нижним обрезом конфузора 1, увлекает за собой жид
костную пленку. Последняя, как и в предыдущем случае, в горловине 2 дробится
газовым потоком на мелкие капли, создавая развитую поверхность массопереда
чи. Организация противотока жидкой и газовой фаз между секциями
(ступенями) дает возможность увеличить массообменную способность в сравне
нии с прямотоком за счет повышения движущей силы процесса.
можно
С другими конструкциями распьтительных и иных абсорберов
ознакомиться в специальной литературе по абсорбции•.
•

См. ( 1 , 10 1 .

92 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

1 1 .З. ФАЗОВОЕ РАВНОВЕСИЕ
В СИСТЕМЕ ГАЗ-ЖИДКОСТЬ
1 1 .З . 1 . Фазовое равновесие при физической абсорбции

В процессах физической абсорбции участвуют как минимум
три компонента: два вещества-носителя (газ и жидкость) и
компонент, переходящий из одной фазы в друrую. Система из
двух фаз (ф = 2) при общем числе компонентов к = 3 согласно
правилу фаз ( 1 0 . 1 ) имеет применительно к равновесному со
стоянию три степени свободы: <р = к - ф + 2 = 3 - 2 + 2 = 3 .
При полной нерастворимости инерта в абсорбенте и малой
летучести последнего (когда можно пренебречь его содержани
ем в газовой фазе) составы фаз будуr полностью характеризо
ваться концентрациями поглощаемого компонента в каждой
из фаз: х (кг П К /кг А) - в жидкой фазе и у (кг П К /кг ГН)
- в газовой фазе. Параметрами равновесного состояния си
стемы также являются температура и давление, при котором
находится эта система.
Таким образом, общее число переменн ых равновесной си
стемы равно 4. При <р = 3 три переменные мoryr быть выбраны
произвольно - соответственно условиям технологического
процесса, а четвертая будет зависимой. Например, можно про
извольно выбрать температуру и давление, а также концентра
цию П К в жидкости (х) . Тогда для такой системы равновесная
концентрация этого компонента в газовой фазе (у Р) будет
вполне определенной . При другой концентраnии П К в жид
кости (х ' ) в равновесной системе другой будет и концентрация
у 'Р, при х" будет у "Р и т.д. Такая зависимость у от х при опре
деленных температуре и давлении называется равновесной, в
геометрической интерпретации - линией равновесия, или кри
вой равновесия (рис. 1 1 . 1 5) .
Пусть некая точка А (рис. 1 1 . 1 5 , а) ( с концентрациями П К в
фазах х и у), характеризующая рабочее (неравновесное) состоя
ние контактирующих фаз, лежит выше линии равновесия; тог
да при приближении системы к равновесию (по стрелке J)
концентрация поглощаемого компонента в газовой фазе будет
уменьшаться, а в жидкой - увеличиваться. Такой характер
изменения концентраций П К в фазах отвечает именно процес
су абсорбции. Эго означает, что все точки, лежащие выше и
левее линии равновесия , составляют область абсорбции. Пусть
теперь рабочее состояние системы характеризуется точкой D
(концентрации х ' и у '), расположенной ниже линии равнове
сия . Здесь, наоборот, при стремлении (по стрелке 2) к равно
весному состоянию происходит уменьшение концентрации
поглощаемого компонента в жидкой фазе и уве-!Jичение его - в

922

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

у
у

У1

Область
аб сорб ции

у

P=const
t1

yf

Р

'

'Р
ур
У,
Р
у
у

t=const

•1

х' х Р

х

а

Область
дес орбции

х Рt

6

х

при р = const, б - при t - const

Рис. 11. 15. Диаграммы фазовоrо равновесия газ-жидкость:
а

-

газовой, т.е. идет процесс десорбции. Рабочая область, распо
ложенная ниже и правее равновесной линии, называется об
Приведенная на рис. 1 1 . 1 5 кривая 3 харакгеризует равновес
ные концентрации в фазах при некоторой постоянной темпе
ратуре t, отсюда еще одно название этой кривой - изотерма
абсорбции. Если температуру системы t изменить до t1 , то
прежней кон центрации ПК в жидкости х будет соответствовать
новое значение у1Р, величине х '
значение у1 'Р и т.д. При этом
с увеличением температуры ( t1 > t) растворимость поглощае
мого компонента (газа) в жидкости, как правило, понижается:
xfi < xf при одной и той же концентрации ПК в газовой фазе .

ластью десорбции.

-

Именно этим объясняется необходимость проведения процесса
абсорбции при пониженной температуре (см . разд . 1 1 . 1) - в
таких условиях абсорбент обладает большей . поглотительной
способностью, а значит, его расход при прочих равных услови
ях будет меньше . При десорбции же с целью более полного
выделения поглощаемого компонента из жидкой фазы необхо
димо повышать температуру процесса (см. схему на рис . 1 1 . 1).
Если точка, харакrеризующая рабочее состояние системы,
лежит меЖду двумя изотермами 3 и 4, например точка Е (см.
рис . 1 1 . 1 5, а), то в такой системе будет происходить абсорб
ция - при температуре t (область абсорбции при изотерме 3)
или десорбция - при температуре t1 (область десорбции при
изотерме 4). Поэтому" воздействуя на температуру системы,
можно изменять направление процесса "абсорбция-десорб
ция" .
923

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рассмотрим теперь влияние полного давления р в системе
газ-жидкость на равновесное распределение компонента меж
ду фазами. Для газовой фазы, состоящей из П К и ГН и близ
кой по свойствам к идеальному газу, применимо уравнение
состояния идеального газа (4. 1). Напишем его отдельно для П К
и для всей газовой смеси, содержащей nпх молей П К в nсм мо
лях смеси при температуре Т и объеме V:
РпхV = nпxRy T, pV = ncм Ry T,
где Рпк

-

парциальное давление поглощаемого компонента.

Поделим одно уравнение на другое:
Р пх
Р

=

n пк
nсм

Обозначив мольную концентрацию поглощаемого компо
нента в газовой фазе nmr/ncм = у, имеем:
у=

Р пх

-

.

р
Отсюда следует, что для газовой фазы:
- при постоянном поmюм давлении р равнозначно использо
вание мольной концентрации у и парциального давления П К Рпх.;
при постоянной концентрации у парциальное давление
ПК Упх изменяется пропорционально полному давлению р, т.е .
Рпк = УР·
В рабочем диапазоне изменения концентраций равновесная
зависимость Рпх от мольной доли компонента в жидкой фазе х
может быть линейной; тогда говорят, что система подчиняется
закону Генри (как правило, это бывает при не очень высоких
значениях х):
(1 1.1)
Рпк = Ех,
-

где

Е

-

константа Генри.

Разделим левую и правую части равенства ( 1 1 . 1 ) на р:
Р пк
Е
х;
=у =р
р
обозначив Е/р =
коэффициент распределения П К между
газовой и жидкойтфазами, получим:
--

-

т

=

(�) Р .

( 1 1 . la)

Для систем, подчиняющихся закону Генри, отношение рав
новесных концентраций ПК в газовой и жидкой фазах не зави
сит от уровня концентраций.
924

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Уравнение ( 1 1 . la) часто записывают в виде

уР =

mx,

( 1 1 . l б)
подразумевая, что любому содержанию ПК в жидкости (х) со
ответствует определенная равновесная (у Р) концентрация ПК в
газовой фазе .
Иногда удобнее зависимость ( 1 1 . l a) представить в виде

хР

=

у/т,

( 1 1 . l в)

где х Р
концентрация ПК в жидкости, находя щейся в равновесии с газовой
фазой (кон uе нч> аuия П К в ней равна у).
-

Из приведенных зависимостей следует, что при постоянном
значении кон центрации ПК в жидкой фазе (например, при
х = хз на рис . 1 1 . 1 5 , 6) равновесная концентрация ПК в газовой
фазе уменьшается (у1 Р < У2Р < у3Р) при увеличении давления
(pl > Р2 > р3 ). Кривые равновесия (при отклонении системы от
закона Генри) при постоянной температуре t и различных дав
лениях (р 1 > Р2 > Рз) показаны на рис . 1 1 . 1 5, б (при х � хз от
резки кривых можно считать прямыми) .
При неизменной концентрации П К в газовой фазе е го рас
творимость в жидкости с повышением давления увеличивается
(х1 > х2 > хз при Р1 > Р2 > р3 ). Поэтому абсорбцию (см. рис .
1 1 . 1 ) выгодно проводить при повышенном давлении, а десорб
цию - при пониженном (при атмосферном или под вакуумом).
Работу проводят под вакуумом в том случае, если десорбция
при атмосферном давлении - недостаточно полная. При по
н ижении давления газовой смеси в газовых турбинах высво
боЖдаемую энергию используют либо для последующей подачи
регенерированного абсорбента (JJJ на рис . 1 1 . 1 ) в колонну под
давлением, либо на другие НУЖдЫ.
Равновесные зависимости строят, как пра�ило, на основе
опытных данных. Если распределение ПК меЖду фазами под
чиняется закону Генри, то по формулам ( 1 1 . 1) возможен ана
литичесЮ1й расчет равновесных концентраций ПК в фазах.
В случае многокомпонентных идеальных (подчиняющихся за
кону Генри) газовых смесей равновесное распределение каЖдо
го поглощаемого компонента меЖду фазами также может быть
рассчитано аналитически по формулам ( 1 1 . 1 ).
В случае многокомпонентных реальных газовых смесей рас
пределение каЖдого поглощаемого компонента меЖду фазами
зависит от содержания в системе других поглощаемых компо
нентов, т.е. происходит искривление линий равновесия. Ана
литичесЮIЙ расчет равновесных концентраций отдельных ком
понентов в фазах становится затруднительным, а порой - не
возможным. Тогда равновесные зависимости устанавливаются
опытным путем.
925

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

1 1 .З.2. Фазовое равновесие при абсорбции ,
сопровождаемой химической реакцией

При протекании необратимой химической реакции между
поглощаемым компонентом и абсорбентом (или его активной
частью) для равновесного состояния характерно нулевое содер
жание компонента в газовой фазе (линия 1 на рис . 1 1 . 1 6)
до
тех пор, пока количество поглощаемого компонента меньше
требуемого по стехиометрии количества поглотителя. При пол
ном связывании поглотителя (или его активной части) погло
щаемый компонент будет распределяться между фазами, как и
в случае физической абсорбции, в соответствии с линиями
равновесия .
Для обратимой химической реакции между поглощаемым
компонентом и абсорбентом (или его активной частью) содер
жание компонента в газовой фазе (уобр ) определяется констан
той равновесия химической реакции, а при его избытке он
также будет перераспределяться между фазами по законам фи
зической абсорбции (линия 2 на рис . 1 1 . 16).
Наличие горизонтального участка на линии · равновесия по
зволяет использовать хемосорбцию для
глубокой
очистки газа-носителя от
у
поглощаемого компонента. В случае
необратимой химической реакции та
кая очистка может быть практически
. полной.
-

х

Рис. 11. 16. Линии равновесия rаз-жидкость в
случае хемосорбции:
1

-

необратимая реакция, 2

-

обратимая реакция

1 1 .З.З. Фазовое равновесие в некоторых специальных случаях
К числу таких случаев отнесем равновесие при ощугимой
летучести абсорбента , а также при некоторой (тоже ощугимой)
растворимости газа-носителя в абсорбенте. В обоих случаях по
крайней мере одна из фаз будет содержать все три компонента:
ГН , П К и А. Составы таких смесей представляют в треуголь
ной диаграмме (о ее свойствах см. разд. 10.2.3).
Применительно к процессу абсорбции в вершинах треуголь
ника (чистые компоненты) расположим ГН , ПК и А. Тогда
бинарные газовые смеси (ГН + П К) , в том числе и исходная
газовая смесь, лежат на стороне ГН- П К треугольника, а би
нарные жидкие (П К+А) - на стороне П К-А. Здесь абсолют
ные концентрации отдельных компонентов характеризуются
длинами перпендикуляров, опущенных из точек соответствую
щих смесей на стороны треугольника, или отрезками на сторо
нах треугольника (см. разд. 1 0 .2.3).

926

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

пк

rн

а

б

пк

А
г

Рис. 1 1. 1 7. Треугольные диаграммы фазового р авновес ия :

а - Г Н нер аство рим в абсор бенrе А, абсор бе нr нелетуч : б - ГН нерастворим в абсор 
бенrе, летучий абс ор бе нr; в - ГН частично раство ри м в абс о рбенrе , абсорбенr нелетуч ; г ГН частично растворим в абсор бенr е , летучий абсорбе нr

При абсолютной нерастворимости ГН в абсорбенте и нелету
чести абсорбента А их смесь (любая точка на линии ГН-А)
разделяется на чистый газ-носитель ГН и чистый абсорбент А.

Введенный в систему поглощаемый компонент распределяется
между газовой и жидкой фазами , образуя равновесные бинар
ные смеси, лежащие на сторонах ГН- П К (газовая фаза) и
П К-А (жидкая фаза) . В треугольной диаграмме равновесие
таких смесей может быть представлено семейством нод, соеди
няющих равновесные составы фаз при фиксированн ых темпе
ратуре и давлении (рис . 1 1 . 1 7, а) . Здесь точка Е соответствует
максимальной растворимости П К в абсорбенте А в реальных
условиях. При увеличен ии растворимости (в результате повы
шения давления , понижения температуры) точка Е смещается
в сторону П К.
В отсуrствие тройных смесей (простейший случай) равновесие таких систем
проще и удобнее представлять в диаграмме у-х, что и бьuю сделано в разд.
1 1 . 3 . 1 . Кстати, диаграмму у-х можно рассматривать как частный случай тре
угольной диаграммы с прямым углом между сторонами П К-ГН и П К-А (при
переходе к относительным концентрациям).

Рассмотрим последовательно возможные варианты диаграмм
фазового равновесия .
При ощутимой летучести абсорбента, когда содержание его
паров в газовой фазе сопоставимо с содержанием других ком
понентов, составы газовой фазы будут характеризоваться точ
ками на линии О С (рис . 1 1 . 1 7, 6) . Здесь отрезок ГН-0 характе
ризует содержание паров абсорбента в газе-носителе , а
отрезок П К-С - содержание паров абсорбента в поглощае
мом компоненте (газе) . При этом точки О и С отвечают насы
щению парами абсорбента газа-носителя и газа-поглощаемого
компонента соответственно. Ноды, соединяющие в этом случае
равновесные составы газовой и жидкой фаз , заканчиваются на
линии О С . Область ГН- П К-С-0 на рис . 1 1 . 1 7 , б
это об
ласть гомогенной газовой смеси. Область C OAJ:: C
гетероген-

927

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ная область, все точ.ки которой при расслаивании даюr две равно
весные фазы: газовую на линии СО и жидкую - на линии ЕА.

При частичной растворимости газа-носителя в нелетучем аб
сорбенте в равновесном треугольнике существует область рас

творов П К и ГН (и их смесей) вблизи вершины А (рис .
1 1 . 17, в) . Здесь ноды "упираются" в линию FE, отвечающую
трехкомпонентным смесям в жидкой фазе. Отрезок FA харак
теризует максимальную растворимость газа-носителя в абсор
бенте (при фиксированных температуре и давлении), а область
FEA является областью гомогенных растворов.
При частичной растворимости газа-носителя в летучем аб
сорбенте (наиболее общий случай) ноды, соединяющие равно
весные составы газовой и жидкой фаз, ограничены линиями
ОС и F E (рис. 1 1 . 1 7, г) . Любой точке У состава газовой фазы
отвечает равновесная точка Х состава жидкой фазы, лежащая на
другом конце ноды, проходящей через точку У: Любая тройная
смесь компонентов, характеризуемая точкой в гетерогенной
области OCEF (это может быть механическая смесь всех трех
компонентов), разделяется на две тройные смеси - газовую и
жидкую фазы. При достаточно интенсивном ко нтактировании фаз
разделение происходиг по ноде, т.е. с образованием равновесных
составов. Так, гетерогенная смесь состава М 1 разделяется (по пра
вилу рычага, разумеется, - см. разд. 10.2.4) на газовую смесь со
става У 1 и раствор ПК и ГН в абсорбенте состава Х 1 .
Представленные на рис . 1 1 . 1 7 диаграммы фазового равнове
сия являются изотермами-изобарами, т.е. относятся к конкрет
ным температуре и давлению. При повышении температуры
летучесть абсорбента увеличивается, и кривая ОС смещается
вправо. Растворимость газа-носителя в абсорбенте при возрас
тании температуры пон ижается, и, следовательно, кривая FE
также смещается вправо. Соответственно, при понижении тем
пературы кривые ОС и FE смещаюrся влево, и при некоторой
температуре tнл кр ивая ОС совпадает со стороной ГН-П К тре
угольника; летучесть абсорбента в этом случае пренебрежимо ма
ла, т.е. его можно с•nrгать практически нелетучим. С ростом пол
ного давления р в системе летучесть абсорбента уменьшается. По
этому при увеличении р линия О С приближается к стороне ГН
ПК треугольника; при этом линия FE также смещается влево, так
как растворимость ГН в абсорбенте (точка F) и ПК в абсорбенте
(точка Е) увеличиваются при повышении давления.
1 1 .4. ТЕХНОЛОГИЧЕСКИ Й РАСЧЕТ АБСОРБЕРОВ

Технологический расчет абсорбера конкретизируется в зави
симости от постановки задачи. В наиболее часто встре
чающихся в инженерной практике зада чах проектирования он
обычно включает расчет необходимого расхода абсорбента и
928

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

геометрических размеров абсорбера (высоты, диаметра и т.п.),
при которых обеспечиваются необходимая степень разделения
газовой смеси и заданная производительность по газовой фазе
или по поглощаемому компоненту. Реже технолОiу приходится
решать задачу эксплуатации, когда для абсорбера известных
размеров с конкретными внутренними контактирующими уст
ройствами требуется определить конечную концентрацию по
глощаемого компонента в газовой смеси при известных пото
ках фаз и их начальных составах.
Методы решения обеих задач (проектирования и эксплуата
ции) для массообменных процессов класса 3(2-2) 1 - для раз
личных схем движения потока (противоток, прямоток, пере
крестный ток по ступеням) с идеальным перемешиванием
фаз или в режиме идеального вытеснения в каждой ступенц,
а также с непрерывным контактом фаз - подробно изложены в
гл . 10. Именно к таким процессам относится абсорбция неле
тучим поглотителем при отсутствии растворимости в нем га
за-носителя . В настоящей главе отметим лишь некоторые осо
бенности расчета процессов абсорбции, связанные:
- с выделением теплоты при абсорбции (неизотермическая
абсорбция);
- с летучестью поглотителя, т.е. частичным переходом его в
газовую фазу;
- с протеканием химической реакции между поглощаемым
компонентом и абсорбентом;
- с поглощением нескольких компонентов из газовой сме
си.
Предварительно рассмотрим общие подходы (для всех слу
чаев абсорбции) к определению основных размеров аппаратов:
его поперечного сечения (диаметра - в случае колонных аппа
ратов) и высоты.
Будем рассчитывать абсорберы непрерывного действия, так
как периодические процессы абсорбции, как правило, малоэф
фективны, труднее в управлении и поэтому драктически не
используются в промышленности.
1 1 .4. 1 . Поперечное сечение абсорбера

Необходимую площадь поперечного сечения абсорбера не
прерывного действия в задаче проектирования находят на
основе уравнений расхода ( 1 . 1 7), ( 1 . 1 8) по формуле ( 1 0 .30):

!а =

G =V
'
pw
w

-

-

( 1 1 .2)

где G и V массовый и объемный расходы той сплошной фазы, которая лими
тирует пропускные способности абсорбера; w скорость движения этой фазы в
расчете на полное сечение аппарата.
-

-

929

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

В подавляющем большинстве случаев объемный расход га
зовой фазы существенно больше, нежели жидкой, поскольку
плотность газа на 2-3 порядка ниже, чем у жидкости . Поэтому
поперечное сечение абсорберов рассчитывают по потоку V га
зовой фазы. Очевидным исключением являются барботажные
абсорберы со сплошной жидкой фазой (см. рис . 1 1 . 1 0).
Входящая в формулу ( 1 1 .2) рабочая скорость сплошной фазы
должна выбираться из условий обеспечения оптимальных ре
жимов работы с учетом направления движения фаз
(противоток или прямоток).
При противоточном движении фаз скорость сплошной фазы
должна быть несколько ниже критической Wкр' при которой
нарушается или совсем прекращается противоток (переходя в
прямоток). Так, в пленочных аппаратах и в насадочных колоннах
с противоточным движением фаз такой критической скоростью
является "скорость захлебывания" Wзахл (см . разд. 10. 1 .3). Ино
гда максимальную скорость сплошной фазы ограничивают до
пустимым уносом капель из аппарата.
Максимальная скорость сплошной жидкой фазы в полых
барботажных аппаратах (см. рис. 1 1 . 1 0, а - здесь также проти
воток) ограничена скоростью подъема газовых пузырей в непо
движной среде . При бОльших скоростях течения жидкой фазы
газовые пузыри будуг з ахватываться жидкостным потоком.
В тарельчатых барботажных аппаратах противоточного типа
(см . рис . 1 1 . 1 0 , б) максимальная рабочая скорость газовой фазы
определяется допустимым уносом капель жидкости на распо
ложенную выше тарелку. Напомним, что брызгоунос приводит
к нарушению противотока и, следовательно, к уменьшению
движущей силы процесса.
Наоборот, в пленочных абсорберах с восходящим прямото
ком, а также в распьmительных абсорберах с прямотоком в
каждой ступени (см. рис . 1 1 . 14, а, б) скорость газа должна быть
достаточной, чтобы при наличии жидкости газ увлекал ее за
собой.
При нисходящем прямотоке в пленочных и насадочных аб
сорберах упомянугых ограничений в скорости газового потока
не существует. Пракгически она лимитируется повышенным
выносом капель жидкости и гидравлическим сопротивлением
газовому потоку.
Отметим, что теоретический подход к определению крити
ческих (граничных) скоростей пока возможен лишь в простей
шем случае - для пленочных аппаратов с организованным
течением пленки - на основе закономерностей течения жид
•
ЮIХ пленок в присугствии газового потока .
•

930

См., например, (3) .

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Во всех других случаях пользуются эмпиричесюtми зависи 
мостями · для критической скорости , учитывающими физиче
сюtе свойства газа и жидкости, соотношения их потоков и ха
рактеристиюt аппаратуры (в насадочных аппаратах - характе
ристиюt насадюt) .
В качестве примера приведем широко применяемую д11Я процессов абсорб
ции и ректификации эмпирическую формулу д11Я определения расчетной (на
сечение незаполненного аппарата) скорости W захл газа (пара), соответствующей
предельной нагрузке насадочного аппарата (началу захлебывания). Пусть Ен свободный объем (порозность) насадки " , Fуд - удельная поверхность насад
ки •• , Pr и Рж - плотности газа (пара) и жидкости, µ"' - вя:жость жидкости, L и
G - массовые расходы жидкости и газа (пара) . При принятьIХ обозначениях
формула д11Я Wзахл имеет вид

w�зFуд
!:Е н

Pr

Рж

µ�16

=

A exp[-в(i=.) t/4(ELJt/8 ] '
G

Рж

причем все величины берутся в СИ; g - ускорение силы тяжести; А и В - ко
эффициенть1.
Значения безразмерного коэффициента В во всех формулах, приводим ьIХ в
учебниках и справочной литературе, равны 4. Значения же размерного коэффи
циента А различны д11Я разньIХ типов насадки: д11Я колец Рашиrа он почти в 2
раза ниже, чем д11Я седел Берля. Кроме того, из-за нечеткости в терминологии
при определении критической скорости приводятся различные значения этого
коэффициента: А = 0,348 д11Я скорости захлебывания и А = 0,397 - д11Я близ
кой к ней скорости эмульгирования. Труднообъяснимым является понижение
коэффициента А до 0,249 при прохождении пара (вместо газа) через слой оро
шаемой насадки в случае ректификационных насадочных аппаратов (см . гл. 12).
Такие расхожден ия в значениях коэффициента А связаны, по-видимому, с не
вполне обоснованным набором параметров в левой и правой частях приведенно
го вьШiе уравнения и с ограниченной его точностью. Критическую скорость газа
понимают или в аспекте целесообразного рабочего режима, или как предельно
допустимую физически, выше которой начинается захлебывание аппарата. По
этому при использовании различньIХ формул необходимо внимательно отслежи
вать их назначение.
-

При выборе рабочей скорости газа заметно ниже скорости
захлебывания, во-первых, увеличится поперечное сечение ап
парата согласно уравнению ( 1 1 .2) и, во-вторых, снизится эф
фективность массопередачи за счет уменьшения коэффициента
массоотдачи в газовой фазе, зависящего от скорости движения
газового потока относительно жидкостных пленок на элемен 
тах насадюt. Поэтому рабочую скорость газа в насадочных аб
сорберах рекомендуется принимать достаточно близкой к ско
рости захлебывания :

w = (0, 8

+

О, ?)wзахл·

' См. (3, 7, 8, 10 и др . ] .
• • Для принятого типоразмера насадки значения
пример , в ( 1 , 6, 1 1 ) .

( 1 1 .3)

Ен

и Fуд приводятся, на

93 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

1 1 .4.2. Высота абсорберов с непрерывным контактом фаз

При непрерывном контакте газа и жидкости высота рабочей
зоны абс орбера Н зависит от необходимой поверхности массо
обмена F.
В условиях поверхностной задачи величина F определяется
по количеству передаваемого вещества, скорости и движущей
силе процесса массопередачи. Расчет F и Н основан на уравне-·
нии (10.22). Обозначим (рис. 1 1 . 1 8 , а): G - расход газовой
фазы (по инертной ее части), кг ГН/с; L - расход чистого аб
сорбента, кг А/с; Ун и Ук - начальная и конечная относитель
ные концентрации поглощаемого компонента в газе, кг П К/кг
ГН; Хн и Хк - относительные концентрации поглощаемого
компонента в исходном абсорбенте (в случае чистого абсорбен
та Хн = О) и насыщенном (отработанном). Поверхность массо
передачи F условно представим в виде вертикальной линии,
разделяющей газовую и жид кую фазы.
Поток М компонента, переходящего за единицу времени из
газовой фазы в жидкую , можно найти из ура�нений матери
ального баланса по поглощаемому компоненту для контуров К1
и К2 :
для контура К 1
Gун - Gук - М = О, откуда
( 1 1 .4)
М = G(ун - ук) ;
Lx.. + М - Lхк = О, откуда
для контура К2
( 1 1 .4а)
М = L (Xx -- Хн) .
В гл. 1 0 показано, что при таком выражении расходов фаз (L и
G неизменны по высоте абсорбера) и концеmраций уравнения
рабочих mmий представляют собой прямые, проходящие:
- через точки (Хн, ук) и (хк, Ун) - при противотоке фаз (как
показано на рис . 1 1 . 1 8 , 6) ;
- через точки (Хн, Ун) и (Хх., ук) - при прямотоке.
( Подробнее - см. разд. 1 0.7. 1 : уравнения ( 1 0.23), ( 1 0.24) и
рис . 10. 1 5 и 1 0 . 16.)
Согласно КФ-классификации рассматриваемый процесс аб
сорбции относится к классу 3(2-2) 1 . Полученные в гл. 10 фор
мулы для расчета массообменных процессов класса 3 (2-2) 1
полностью применимы к абсорбции нелетучиМ поглотителем.
Так, поверхность массопередачи F может быть найдена по од
ной из формул ( 10.3 1):
=

м

---

kу ЛУср '

(1 1 .5)

где kx и ky - коэффициенты массопередачи на языке фазы " х ' и "у" соответ
ственно; ЛХср и Луср - средние движущие силы процесса абсорбции также на
языке соответствующей фазы.

932

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

у
м

а

К2 У

у� -------
уР1--�,.__�"
у "t---+--71'�

Х�

у� �__;_--1�.i...-'. �.J.......
.,.. .--..L.
6

Xк

Х

У

упрощеЮJая схема аппарата, б - диаrрамма у-х;
рабочая линия, 2 - ЛЮIИЯ равновесия

Рис. 11. 18. К расчету противоточных абсорберов с непрерывным контакrом фаз:
а -

1

-

Для общего случая физической абсорбции с кривой линией
равновесия при противотоке фаз средние движущие силы ЛХср и
Луср находят по формулам, аналогичным (10.29). Соответственно
=

ДХСр =

Х к - Хн

Хк

J

xн

--У�к�
ЛУс = _У�н�
р
Sy

=

dx

-

хР

-Х

У н - Ук

Ун

dy
f
р
Ук у - у

( 1 1 .6)

О физическом смысле чисел единиц переноса Sx и Sy (как об
отношении пропускных способностей поверхностной и пото
ковой стадий массообмена) и методах их расчета см. разд.
10.8.3.
Для частного случая абсорбции с

прямой линией равновесия
(т = const) среднюю движущую силу вычисляют как среднело
гарифмическую величину из движущих сил на концах аппарата:
лх1 и лх2 или Лу1 и ЛJ12. Применительно к противотоку спра
ведливы формулы ( 1 0 .28); в рассматриваемом случае: лх1 =
= xJ' - Хк = унfт - Хк; ЛХ2 = ХкР - Хн = укfт- Хн; Лу1 = Ун - У� = Ун - тхк; Лу2 = Ук - У� = Ук - тхн .

Рассчитав необходимую поверхность массопередачи F наса

дочных абсорберов, находят высоту слоя насадки:
Н=

�
'
Р
уд /а

( 1 1 .7)

причем поперечное сечение абсорбера /а уже найдено по ( 1 1 .2);
см. также разд. 1 1 .4. 1 .
933

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Для плено чных устройств в виде п паралл ельных труб, по
внутренней поверхности которых течет пленка жидкости тол
щиной 8 , а вдоль оси движется газ, поверхность массопередачи
F равна
F = 1tn(dвн - 2 8) Н;
отсюда может быть найдена высота труб Н
В условиях потоковой (балансовой) задачи массопереноса ве
личина поверхности F, а также высота рабочей зоны Н роли не
играют. В этом случае Н выбирается либо из условий гидроди
намики (приемлемое гидравлическое сопротивление абсорбе
ра), либо из условия обеспечения теплоотвода, либо из опыта
проектирования и эксплуатации подобных абсорберов. Необхо
димо лишь в ходе проектирования принять достаточные значе
ния Н, чтобы задача оставалась потоковой.
В с.лучае собственно меночных аппаратов (трубчатые, листовые) потоковая
задача (поток поглощаемого компоне нта прямо пропорционален расходу абсор
бента) реализуется тоща, коrда коэффициент массоотдачи в жидкой фазе Рх.
(м/с) в несколько раз больше отношения Г/Н, где Г
nлотность орошения в
м3/(м· с). Практически уже при f3x = 2( Г/Н) расчет по балансовым соотношениям
дает ошибку не более 1 0% по сравнению с точным решением. При значениях Pxl
/(Г/Н) > 2 скорость диффузии компонента в менке настолько велика, а время
завершения диффузии настолько мало, что последним можно пренебречь по
сравнению с продолжительностью стадии подвода вещества в абсорбер с газом
или, что как раз xapaicrepнo для абсорбции, отвода вещества из абсорбера с
потоком абсорбента .
-

Расчет высоты насадочных (и других абсорберов) по методу
ВЕП (см. разд . 1 0 8 . 4 ) здесь также правомерен , причем для рас
чета В Е П тоже используются эмпирические соотношения, а
подсчет числа единиц переноса Sx и Sy производится, как пра
вило, графическим или численными методами. Заметим, что
при равенстве углов наклона рабочей и равновесной (при
т = const, естественно) линий, т.е. при их параллельности,
числа единиц переноса Sx и Sy одинаковы и совпадают с чис
лом теоретических тарелок.
Весьма приближенным и не соответствующим физическим
процессам в реальных пленочных абсорберах (подмена задачи!)
является метод расчета абсорберов на основе высоты, эквива
лентной теоретической ступени (ВЭТС). Величина последней
находится по эмпирическим формулам, имеющим крайне
ограниченную область достоверного применения . Этим мето
дом можно воспользоваться лишь в тех случаях, когда для ра
бочих условий конкретного рассчитываемого процесса абсорб
ции с приемлемой точностью известны ВЭТС или метод ее
расчета. Некорректность и ненадежность этого метода обсуж
дены в разд. 10. 12.5.
.

934

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

1 1 .4.3. Высота абсорберов со ступенчатым контактом фаз

Высоту тарельчатой части абсорберов (Нт) �о ступенчатым
контактом фаз на тарелках (рис. 1 1 . 19) определяют по формуле
Нт = kr(n - 1 ) ,
( 1 1 . 8)

rде п - необходимое число реальных тарелок в проектируемом аппарате; hт расстояние между двумя соседними тарелками; в зависимости от диаметра аппа
рата величину hт принимают от 0,2 до 0,8 м.

При расчете полной высоты аппарата Н необходимо также
учесть высоту зоны аппарата над верхней тарелкой Н0 и высоту
ее под нижней тарелкой Нн. Высота Н0 должна обеспечивать
хорошую сепарацию газового потока от брызг, уносимых с
верхней тарелки; как правило, она в 1 , 5 - 2 раза больше рас
стояния между тарелками kr и составляет 0,6 - 1 ,2 м. Высота
Нн определяется в соответствии с конструктивными решения
ми отвода абсорбента и ввода газового потока в аппарат. На
практике эта величина также превышает kr и составляет обыч
но 1 - 1 , 5 м.
Число реальных тарелок п рассчитывают с помощью КПД
тарелки '11т , базируясь на требуемом числе теоретических таре
лок nт, они связаны соотношением п = nrf'l1т· Расчет числа тео
ретических ступеней (тарелок) nт может быть вьшолнен графи
чески в диаграмме у-х путем построения "ступенек" между
рабочей и равновесной линиями в случае, если последняя - кривая (рис.
1 0.34). При прямой линии равновесия
::rf
возможен аналитический расчет числа
теоретических тарелок - см. формулы
( 1 0 .44) и ( 1 0 .44а), записанные на языке
фазы ".х'' ; аналогичные выражения мож
но получить и на языке фазы "у" - по
i
схеме, использованной в разд. 10. 12.2.
Подчеркнем, что незнание точных зна
чений КПД тарелок делает этот метод
расчета высоты тарельчатых аппаратов
сугубо приближенным.
- - -

Рис. 11. 19. К расчету аппаратов со ступенчатым кон

тактом фаз

1 1 .4.4. О целесообразности рециркуляции раб!)ЧИХ потоков

Рециркуляция потоков в абсорбере возможна в различных
вариантах:
- возврат части абсорбента с конечной концентрацией по
глощаемого компонента Хк и присоединение его к потоку исхо935

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Ук

•

Хн

Ук

Хн

Х см

Хк

у

Ni

Усы

-

Хк

Ун �--------:::11

Хк Х

а

у

Ун

Усм �---___,,,..__,..
Ук

t------

б

Хк Х

рециркуляция абсорбс�па, б рециркуляция газа.
Рабочи е ли нии : сплошны е - при рециркуля ции потоков, пунктирные - в отсутствие
рециркуляции
Рис. 1 1. 20.
а

-

Схемы работы абсорберов с рециркуляцией потоков и дИаfl'аммы у-х:
-

дного абсорбента, подаваемого сверху в абсор€iционный аппа
рат (рис . 1 1 .20, а);
- возврат части газового потока с конечной концентрацией
Ук и присоединение его к потоку исходного газа, подаваемого
снизу в абсорбционный аппарат (рис. 1 1 .20, б);
- возврат части обоих уходящих потоков - газового и жид
костного - и присоединение их к исходным газовому и жид
костному потокам соответственно.
Схемы работы абсорберов с рециркуляцией потоков абсор
бента и газа, а также диаграммы у-х представлены на рис.
1 1 .20. При смешении отработанного абсорбента (концентрация
xJ со свежим (концентрация Хн) получается абсорбент с про
межуrочной концентрацией Хсм . определяемой по правилу ры
чага, а рабочая точка для верхнего сечения (рис . 1 1 .20,а) имеет
координаты Хсм , Ук· Аналогично > при смешении газов с кон
центрацией поглощаемого компонента в них Ун и Ук получается
некоторая промежуrочная концентрация Уем • которая вместе с
936

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

концентрацией Хк определяет положение рабочей точки для
нижнего сечения аппарата на рис. 1 1 .20, б.
Из рисунков видно, что рабочие линии процесса при нали
чии рецикла (сплошные линии) расположены ближе к равно
весной кривой, чем без рецикла (штриховые линии). Степень
рециркуляции (количество возвращаемого потока на единицу
исходного) в задачах проектирования (с фиксированными гра
ничными концентрациями П К в потоках фаз) ограничена зна
чением, при котором рабочая линия пересечет линию равнове
сия; движущая сила массопередачи в этом случае становится
равной нулю - процесс прекратится . При увеличении степени
рециркуляции (в пределах возможного) уменьшается движущая
сила процесса массопередачи, а следовательно, увеличиваются
необходимые размеры аппарата (см. разд. 1 1 .4.2 и 1 1 .4.3). Здесь
вполне правомерен вопрос : для чего же тогда нужна рецирку
ляция?
Рециркуляция абсорбента. При малых расходах L , т.е. при
низких плотностях орошения L/(fap ) абсорбента, жидкости мо
жет оказаться недостаточно для хорошего смачивания элемен
тов насадки. В этом случае в массообмене участвует лишь часть
("активная") поверхности насадочных тел Fa < F. Отсюда низкая эффективность работы аппарата в целом. При рецирку
ляции абсорбента в работу включается дополнительная поверх
ность контактирования жидкости и газа, так что Fa � F. Кроме
того, растет коэффициент массоотдачи в жидкой фазе Рх за
счет турбулизации пленочного течения; такой рост особенно
эффективен в случае низкой пропускной способности PxF. Ес
ли при этом увеличение пропускной способности стадии массоот
дачи PxF и массопередачи в целом kxF (или kyF) компенсирует
уменьшение движущей силы и дополнительные затраты энергии
на перекачку абсорбента снизу вверх, то рециркуляция абсор
бента оправдывает себя . Ее применение также целесообразно
при необходимости отвода большой теплоты абсорбции: на
линии возврата абсорбента устанавливают холодильник (на
рис. 1 1 .20, а не показан) . О необходимости поддержания рабо
чей температуры процесса за счет охлаждения жидкости под
робнее см. в разд. 1 1 .2.2.
Рециркуляция газа. Увеличение скорости газа в аппарате
приводит к росту коэффициента массоотдачи в газовой фазе, а
вместе с ним - коэффициентов массопередачи ky , kx. Одно
временно происходит некоторое увеличение поверхности мас
сопередачи - за счет утончения жидкостной пленки на эле
ментах насадки и дополнительного каплеобразования между
ними. На рециркуляцию газа идут при малых расходах газовой
фазы в случаях, когда положительные эффекты от ее использо
вания перевешивают негативные, связанные с уменьшением
937

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

движущей силы и увеличением rидравлического сопротивления
орошаемой насадки . Степень рециркуляции газа ограничена не
только уменьшением (до нулевого значения) движущей силы
процесса, но и скоростью захлебывания; при этом ограничение
по скорости захлебывания может сказаться раньше .
Расчет основных размеров абсорберов при известных рабо
чих и равновесных линиях в случае рециркуляции потоков не
отличается от изложенного выше; необходимо лишь учесть
увеличение потока фазы, по которой берется определяющая
скорость w.

Метод построения рабочих линий и проектного расчета абсорбера при ре
остается прежним. Подчеркнем, 'П'О на этот крайне
редкий вариант работы абсорбера следует идти лишь в том случае, когда увели
чение плотности орошения и скорости газа не может бьпь достиrnуто простым
уменьшением поперечного сечения аппарата.
При эксмуатации действующего абсорбера на рециркуляцию обоих потоков
следует идти, если расход исходных потоков существенно уменьшился
(например, производительность по исходному rазу). В соответствии с матери
альным балансом должен быrь уменьшен и расход исходного абсорбента. Это
приводит к неблагоприятной (в гидродинамическом плане) обстановке дЛЯ про
цесса массопередачи: большие толщины поq>аничных пленок из-за малой турбу
лизации потоков и низкие коэффициенты массоотдачи Рх и Ру· В этом случае
рециркуляция обоих потоков приведет к увеличению Рх и Ру и, следовательно,
циркуляции обоих потоков

k,,, ky.

Не вызывает затруднений и расчет других схем с рециркуля
цией потоков, например многоступенчатой противоточной аб
сорбции с рециркуляцией жидкости в каждой ступени . Подход
к построению рабочих линий и расчету размеров абсорбера
остается прежним.
1 1 .5. ОСОБЕННОСТИ РАСЧЕТА НЕКОТОРЫХ
СПЕЦИАJIЬНЬIХ СЛУЧАЕВ АБСОРБЦИИ
1 1 .5. 1 . Неизотермическая абсорбция

В случае адиабатной абсорбции (отсутствие отвода теплоты,
выделяющейся при поглощении П К) температура газа и жид
кости повышается по мере увеличения в последней концентра
ции поглощаемого компонента (х). Если изменение температу
ры ощутимо сказывается на положении линии равновесия, то
такую абсорбцию называют неизотермической. Зависимость
температур газа е и жидкости t от концентрации в ней погло
щаемого компонента можно получить путем совместного рас
смотрения материальных и тепловых балансов, а также уравне
ний тепло- и массообмена между газом и жидкостью.
Обозначим (рис . 1 1 .2 1 , а) : L - поток абсоР.бента; lн - ero
начальная температура; Хн - концентрация поглощаемого ком938

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

о

!

а

у

Ун

�
р
;/2

Кур1

t3
t1
Хн

Х1

Х2

Х3

б

Хк

lн
х

- упрощеЮ1ая схема работы абсорбера, б - диаграмма у-х;
1 - кривая равновесия при перемеЮ1ой по высоте aJDiapaтa температуре процесса, 2 рабочая JIИНИJI , З - линия равновесия после охлЗJ1ЩеЮ1Я жидкости с концешрацией х3 до
первоначальной температуры 18

Рис. 1 1. 21. К расчету неизотермической абсорбции:
а

понента в исходном абсорбенте (для чистого исходного абсор
бента Хн = О); G - поток газа-носителя; Ун - концентрация
П К в исходном газе; 0н - его начальная температура; t и е соответственно температуры абсорбента и газа в произвольном
сечении с концентрацией х поглощаемого компонента в жид
кости и у - в газе.
Введем понятие относительной теплоемкости абсорбента с;
это теплоемкость смеси абсорбента и поглощаемого компонента в расчете на 1 кг чистого абсорбента: с = l ·сл + хс :.К , где

ел - теплоемкость чистого абсорбента, а

•

С пк -

поглощаемого

компонента в конденсированной фазе (ждд кости).
Аналогично для газовой фазы введем понятие относительной
теплоемкости газа c r ; это теплоемкость смеси газа-носителя и
поглощаемого компонента в расчете на 1 кг газа-носителя:
cr = I · cm + у сик, где Cm - теплоемкость чистого газа-носителя,
а Спк - теплоемкость поглощаемого компонента в неконденси
рованной фазе (газе). Соответственно, Си и снr - относитель
ные теплоемкости абсорбента и газа на входе в аппарат, а Ск и
с/ - на выходе из аппарата.
Тепловой эффект абсорбции характеризуется удельной диф
ференциальной теплотой абсорбции (растворения) q3 компонен
та, поглощенного ждд кой фазой. Величина qa зависит от кон 939

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

центрации П К в абсорбенте (строго говоря - и от его темпера
Qa (и ее зависимость от концентрации х) нахо
дят в справочниках и специальной литературе . по абсорбции * .
При малых концентрациях х величина Qa может быть принята
постоянной.
Материальный баланс по ПК для бесконечно малого жид
костного пространственного контура К 1 (рис . 1 1 .2 1 , а) за еди
ницу времени в соответствии с основным балансовым соотно
шением ( 1 .8) может быть записан как
dM + Lx - L(x + dx) = О,
откуда межфазный поток поглощаемого компонента через по
верхность массопередачи d/ составляет
(а)
dM = Ldx.
Такой же баланс для элементарного газового контура К2
туры). Величину

G(y + dy) - Gy - dM = О

дает

dM = Gdy.

(б)
Полная теплота абсорбции, выделяющаяся в жидкости (при
поглощении ею П К), расходуется на нагрев как жидкости, так
и газа. Это означает, что существует тепловой поток d Q через
поверхность d/ из жидкости в газ. Величину этого теплового
потока найдем из теплового баланса по контуру К2 за единицу
времени :
ac r (8 + de) + d Q - Gc re = О,
откуда
d Q = - Gc rde .
Тепловой баланс по элементарному пространству, объеди
няющему контуры К 1 и К2 , за единицу времени с учетом ис
точника теплоты при растворении П К в абсорбенте имеет вид
Gc r (e + d8 ) + Lct - Gc re - Lc(t + dt) + QadM = О.
Огсюда после сокращений и с учетом выражения (а) имеем
(в)
Gc rde Lcdt + QaLdx = О.
Уравнение передачи теплоты от жидкости к газу через
межфазную поверхность d/:
d Q = k(t 8 )df,
или
-

-

- Gc rde = k(t - e)df,

где k
газа и

ЖИДКО СТИ .
-

(r)

коэффициент теплопередачи при непосредственном контактировании

• См., например, ( 1 0 , 1 2 ).
940

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Уравнение передачи вещества ( П К) через поверхность df :
dM = ky(y Yp)d/,
или с учетом выражения (а)
(д}
Ldx = ky(y - Yp)d/,

-

где ky - коэффициенг массопередачи (на языке фазы "у").

Система уравнений (а)-(д) описывает процессы тепло- и
массопередачи в системах газ-жидкость при наличии теплоты
абсорбции. Для определения выходных параметров процесса
эта система уравнений должна быть решена .при следующих
граничных условиях:
f = F, е = ею у = Ун ·
f = о, t = tю х = Хн.
В общем случае решение такой системы возможно только чис
ленными методами.
Для осушествления анализа и количественной оценюt влия
ния неизотермичности процесса на массообмен примем допу
щение о столь интенсивном теплообмене между газом и жид
костью, что в любом сечении аппарата е = t. Тогда уравнение
(в) приобретает вид
( c r - Lc)dt + qaLdx = О.
Разделим переменные

G

dt

=

Lql\
dx
Lc - Gc r

и проинтегрируем в пределах от начального (вход абсорбента)
до произвольного сечения, т.е. от Хн до х и от tн до t.
t

J

fн

dt

=

х

J

Хн

Lqа

Lc

- Gc r

dx .

Поделим на L числитель и знаменатель подынтегрального
выражения правой части равенства и запишем с и c r как функ
ции концентраций ПК в жидкости и в газе:

t=

lн +

J

хн

( 1 · Сл

+

)

qa

хс :�к - (G/L)(l

·

С гн + УС пк

)

dx.

Концентрация П К в газе (у) связана с концентрацией П К в
.жццкости (х) уравнением рабочей mmии противоточноrо процесса
(10.24). Подставим это выражение для у в знаменатель подьmте
rралъного выражения и преобразуем его; в результате получим:
t

=

t.i +

j

х6

Ча

(l · cл+Xн Cп� - (G/L)(l · C111 + УкСпк ) + (с �к - спк )х

dx

. ( 1 1 . 9)
9 41

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

При несложной зависимости qa от х иногда возможно ана
литическое нахождение интеграла в ( 1 1 .9); при произвольной
зависимости qa от х температура 1 в любом сечении аппарата
может быть найдена численными методами.
В простейшем случае qa = const (как отмечалось ранее, это
справедливо при малых концентрациях х) интегрирование
( 1 1 .9) приводит к выражению
1 = 1н +
где + = ( 1 сл

·

+ С пк хн)

-

(

)

ф + с � к - с пк х
ln -�,..:,_----,-'-с пк - Спк
Ф + с � к - Спк хн
•

qa

( G/L)(l

·

C111

+ Спк.Ук).

{

)

( 1 1 . 1 0)

Итак, температура 1 в любом сечении аппарата в случае не
изотермической абсорбции при принятых ранее допущениях
может быть рассчитана по уравнению ( 1 1 . 10).
ОчевИдно, 'ПО конечная температура 1к на выходе абсорбента
из аппарата получится, если вместо х подставить значение Хк·

Во многих учебниках· для расчета температуры t жидкости в любом сечении
аппарата предлагается формула
t = fи

+ � (х - Хн),
Си

(е)

полученная из теплового баланса в предположении малой теплоемкости газа по
сравнению с теплоемкостью жидкости. Но в действительности пренебрежимо
мала (разница - в 3 порядка) объемная, но не массовая теплоемкость газа по
сравнению с теплоемкостью :жидкости, а расчет ведется по массовым (или моль
ным) потокам. Кроме тоrо, входящая в формулу (е) теплоемкость Си принципи
ально изменяется с х, что не учитывается при выводе этой формулы.

На рис . 1 1 . 1 5, а были показаны лишь две изотермы: при 1 и
11 ; в принципе такие изотермы можно построить (расчетным пу
тем или из опъпа) для любых температур. Базируясь на изотермах
у-х при различных температурах, для произвольных концентра
ций Х1 , х2 , хз ... по ( 1 1 .9) или ( 1 1 . 10) можно рассчитать температу
ры 11 , 1ъ 13 . • . и по соответствующим изотермам найти равновес
ные значения у1 Р, )21', у3Р . . . . Соединив точки х1 , у1 Р; х2 , )21'; х3 , у3Р
. .. , получим изобарную линию равновесия (кривая 1 на рис.
1 1 .2 1 , б) при неизотермическом процессе абсорбции.
Из рис . 1 1 .2 1 , б в Ид но, что при неизотермической абсорбции
может значительно уменьшиться движущая сила процесса, так
как линия равновесия 1 приближается к рабочей (линия 2).
Уменьшение движущей силы процесса требует повышенной
поверхности массопередачи, а следовательно, и размеров аппа
рата. Расчет последних при известных рабочей и равновесной
линиях остается прежним.
• См. (3, 4, 7 , 9) .
942

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

С целью повышения эффективности процесса абсорбции с
выделением теплоты растворения П К жидкость охлаждают
одним из двух способов:
- размещая поверхность теплообмена прямо в рабочем объ
еме абсорбента (с подводом в теплообменник охлаждающего
агента);
- выводя абсорбент из аппарата и охлаждая его в выносном
холодильнике, а затем возвращая в абсорбер.
Предположим, что после повышения концентрации П К в
жидкости до уровня х3 ее направляют в теплообменник, в ко
тором она охлаждается до первоначальной температуры tн; затем
жидкость вновь нагревается за счет теплотъ1 абсорбции - при
повышении концентрации теперь уже от х3 до Хк· Тогда изобара
равновесия на участке х3 -.хк изобразиrся штриховой линией 3 (см.
рис. 1 1 .2 1 , б), расположенной ниже линии равновесия J.
Наличие скачка (при х = х3 ) на линии равновесия , отве
чающего понижению температур ы в теплообменнике , делает
расчет числа теоретичесюtх ступеней еще более неточным. Де
ло в том, что горизонталь очередной ступени может либо
пройти над " горбом", либо в него упереться, а это сказывается
на числе теоретических ступеней. Здесь рекомендуется рассчи
тывать поверхность массопередачи отдельно для каждой из зон
(на рисунке - две зоны, в общем случае - любое число зон)
по уравнению ( 1 1 .5). Кроме того, предпочтительнее вести рас
чет на языке фазы "у" , поскольку из-за наличия "горба" в об
ласти рабочих концентраций у < у3 Р отсчет движущей силы на
языке фазы "х'' становится неопределенным: то ли до линии 1,
ТО ЛИ ДО ЛИНИИ J.
1 1 .5.2. Абсорбция нескольких компонентов из газовой смеси

В ряде случаев из газовой смеси необходимо поглощать не
один, а несколько компонентов. При этом требования к извле
чению отдельных компонентов мо:rут быть различными. Расчет
необходимых размеров абсорбера должен быть выполнен с уче
том требований по всем извлекаемым компонентам.
Ввиду сложного влияния прочих компонентов на распреде
ление каждого из них между газовой и жидкой фазами, равно
весная зависимость Yt = j{xt) для любого i-го компонента чаще
всего нелинейна, т.е . не подчиняется закону Генри . Будучи
представленной в общей диаграмме у-х, каждая из этих рав
новесных зависимостей характеризуется своей линией : на
рис . 1 1 .22 каждая такая линия помечена буквами, соответ
ствующими отдельным компонентам: А, В или С (компоненты
здесь выстроены в порядке уменьшения раСТ.f!Оримости в аб
сорбенте).
943

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

у

1

х

Рис. 11.22. К расчету высоты абсорбера при поr.лощении из газа нескольких ком

понеmов:
1, 2, З - равновесные зависимости;

l,

� 3' - рабочие линии

При использовании относительных концентраций (на 1 кг
инерта - газа-носителя или чистого абсорбента) для каждого
компонента получаются прямые рабочие линии, связывающие
сопряженные концентрации этого компонента в газовой и
жидкой фазах. Поскольку потоки инертов L и G по колонне
постоянны и не зависят от содержания в них извлекаемых
компонентов, то рабочие линии по каждому компонен:гr имеют
одинаковый угол наклона, тангенс которого равен L/G. Место
их расположения зависит от заданных концентраций, напри
мер начальных У н i и конечных Укi в газовой фазе. В случае
чистого исходного абсорбента (Х н ; = О для любого i-го компо
нента) рабочие линии начинаются от оси ординат и заканчи
ваются при их пересечении с горизонталью начального содер
жания i-ro компонента в газовой смеси (У н i ) .
Высота абсорбера должна быть выбрана такой, чтобы обес
печить заданную степень извлечения по каждому компоненту.
Иными словами, по каждому из н их необходимо рассчитать
высоту абсорбера, базируясь, как обычно, на отвечающих ему
рабочей и равновесной линиях, и выбрать наибольшую, соот
ветствующую самому трудному разделению.
В приведенном на рис. 1 1 .22 примере наиболее жесткие
условия - по извлечению компонента В : здесь требуется наи
большее число теоретических ступеней - четыре. Реальное
число тарелок в абсорбере по извлечению каждого компонента
зависит от КПД. Если КПД тарелки по компонентам не оди944

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

наков, то число реальных тарелок в абсорбере устанавливается
по компоненту, требующему максимального их числа. Заметим:
расчет высоты абсорбера через число теоретических ступеней
выбран здесь лишь для большей наглядности . Подробнее о
расчете высоты абсорберов см. разд. 1 1 .4.2 и 1 1 .4.3.
1 1 .5.3. Абсорбция при химическом взаимодействии
поглощаемого компонента с абсорбентом

Во многих практически важных процессах абсорбции по
глощение rаза жидкостью сопровождается химическим взаимо
действием фаз. При этом поглощаемый компонент, достигнув
границы раздела фаз, вступает в химическую реакцию с абсор
бентом или с его активной частью. В этом случае концентра
ция П К в фазе х по нормали п от межфазной границы к ядру
жидкостного потока будет уменьшаться более интенсивно, чем
при физической абсорбции. На рис . 1 1 .23, а представлены кри
вые распределения концентраций ПК в диффузионных погранич
ных пленках со стороны rаза толщиной 8i и со стороны жидкости
(8д) как для физической абсорбции (кр ивая 1 штриховая ли
ния), так и для хемосорбции (кривая 2 сплошная).
Отметим сразу, что в случае хемосорбции кqнцентрация П К
в жидкости н а границе раздела фаз (хп2) ниже, чем в случае
физической абсорбции (Хл 1 ) . При определенных условиях
(значениях скорости химической реакции, концентраций) она
может быть равна нулю, и тогда, естественно, и концентрация
П К в rазе на границе раздела (уп2) в соответствии с двухплено-

-

-

Абсорбент

п

х= о

/J

Рис. 11.23. Распределение концентрации поглощаемого компонента вблизи гра

ницы раздела фаз (гр.):
а - реальное, б - в соответствии с двухпленочной моделью массопередачи ;
1 - при физической абсорбции , 2 - при хемосорбции

945

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

чной моделью массопередачи также равна нулю. В этом случае
основное сопротивление массопередаче будет сосредоточено в
газовой фазе , а скорость абсорбции в целом будет определяться
скоростью диффузии П К через пограничный слой 8[ Как и
для двухлл е ночной модели массопередачи при физической аб
сорбции (разд. 10.6 . 1), здесь также будем считать линейным из
менение концентраций в диффузионных пограничных пленках
'&i со стороны газа и '&де со стороны жидкости (рис . 1 1 .23, б) .
Уменьшение толщины пленки (8/ < '&д) , в которой концентра
ция П К в жидкости уменьшается от Хп до О, пµиводит к увели
чению коэффициента массоотдачи при хемосорбции, опреде
ляемого соответственно уравнениям ( 1 . 13) и (10.7) как
-

рех = �
8 де

( 1 1 . 12)

по аналогии с коэффициентом массоотдачи при физической
абсорбции Рх = D/8д .
Подчеркнем, что введением эквивалентного коэффициента
массоотдачи производится осознанная подмена задачи: при со
хранении формы уравнения конвективного массопереноса эквивалентный коэффициент массоотдачи р� учитывает не толь
ко скорость самой конвективной массоотдачи, но и скорость
химической реакции.
В основе расчета основных размеров аппарата формально
лежат все те же уравнения конвективной массоотдачи:
- для поверхности ЛF
ЛМ =
= Хп

р� лхлF,
а при х = О значение ЛХ
х = Хп, и
ЛМ = Р� .хплF;
- для поверхности F
М = р� хпF.
-

( 1 1 . 1 3)

( 1 1 . 1 3а)
В общем случае скорость хемосорбции зависит как от ско
рости химической реакции, так и от скорости массопередачи
между фазами . В зависимости от того , какая скорость опреде
ляет общую интенсивность процесса переноса вещества, разли
чают кинетическую и диффузионную области протекания про
цессов хемосорбции .
В кинетической области скорость собственно химического
взаимодействия существенно меньше скорости массопередачи,
и потому именно химическая реакция лимитирует скорость
всего процесса. Расчет необходимых размеров аппарата в этом
случае производится с учетом только кинетики химических
реакций.
946

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

р 1. с .

Рис. 11.24. Профили концентраций по

глощаемого компоне�па (у) и а�сrивноrо
компоне�па абсорбе�па (ел) вблизи гра
ницы раздела фаз для мгновенной реак
ции (гр. - граница раздела фаз; р.с. реакционное сечение)

1

В диффузионной области ли
митирующей стадией является
диффузия компонентов в зону
реакции; скорость этой стадии
зависит от их физических
свойств и гидродинамической
обстановки вблизи границы раздела фаз. Размеры абсорбера в
этом случае определяются с использованием основного урав
нения массообмена ( 1 0 .22).
Если скорости химической реакции и массопередачи сопо
ставимы по величине, то говорят о смешанной задаче переноса,
или о его протекании в диффузионно-кинетической области.
Если в случае смешанной задачи обе скорости (химической
реакции и массопередачи) велики, то лимитирующей стадией
может стать стадия подвода П К в аппарат (или его отвода из
аппарата). В этом случае говорят о потоковом характере пере
носа вещества, а задача расчета
потоковая (подробнее о по
токовых задачах см. разд . 10. 1 0).
В случаях диффузионной и смешанной задач переноса, ког
да скорость химической реакции интенсифицирует как массо
отдачу в жидкой фазе , так и в целом массопередачу из одной
'
фазы в друrую, вводят понятие о коэффициенте ускорения абсорбции ф = �� /�х за счет химической реакции. Величина этого
коэффициента зависит от скорости и порядка химической ре
акции, ее константы равновесия · .
В качестве примера рассмотрим определение коэффициента
ускорения ф для быстрой (с позиций сопоставимости пропуск
ных способностей) необратимой реакции между поглощаемым
компонентом В и активным компонентом А абсорбента с обра
зованием нелетучего продукта S:
( 1 1 . 14)
В + пА = S.
Обозначим здесь (рис . 1 1 .24), как и ранее (см . рис . 1 1 .23),
толщины газовой и жидкостной пленок соответственно 8i и 8д,
причем коэффициент массоотдачи при физической абсорбции
(�х) связан с 8д через коэффициент диффузии D поглощаемого
компонента В в жидкости : �х = D/бд . В процессе хемосорбции
-

• Подробнее об этом см. (2, 1 0).

947

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

поглощаемый компо нент В и ак:гивн ый компо нент А абсорбен
та будуг диффундировать навстречу друт друту. При мгнове н
ной реакции компон енты В и А не могуr существовать со
вместно в свободн ом состояни и. Поэтому на некотор ом удале
нии от границы раздела фаз (8де) - в "реакционном сечении "
- концентрации В и А равны нулю: в этом сечении молекул ы
В и А встречаются друт с друтом и вступ ают в химическую ре
акцию. В соответствии со стехиометрией реакции мольные
потоки, диффундирующие к "реакцион ному сечению", связаны
соотношение м

Мв = М,/п.

Мл = пМв,

через который диффун 
Пусть z
дирует ак:гивный компонент А абсорбента; ед - его концент
рация ; Dл - коэффициент диффузии компонента А в жид
костной пленке. Тогда удельные (отнесенные к 1 м2 межфазной
поверхности) потоки этих веществ можно выразить по закону
Фика (см. рис. 1 1 .24); в интегральной форме, постулируя ли
нейное изменение концентраций в модельных пограничных
пленках, имеем:
D
М
(ж)
__!!_ = - (х - О) '·
= 8д -

8де - толщина слоя,

F 8 де п
Мл = Dл (ел - 0) .
z
F
-

-

Поскольку

Рх

то

= D = D ,
8 д 8� + z
-

---

8� z
1
= +D D
Рх
-

(з)
(и)

(к)

Первое слагаемое в правой части уравнения (к) найдем из (ж):

8�

D

= Fхп

Мв '

(л)

а второе - с помощью (з); при этом

Z_

DлFсл
Мл

'

и

z

л Fсл
= DDM
D
л

Подставляя (л) и (м) в выражени е (к), получаем
Dл -Fсл .
Fхп 1
-

Рх

94 8

=

--

Мв

+ D Мл

(м)

(н)

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

В последнее уравнение входят два взаимосвязанных потока:
Мл и Мв. Поскольку интенсивность массопереноса харакгери
зуется потоком поглощаемого компонента Мв, то последний в
уравнении (н) оставляем, а Мл выражаем через Мв. Получаем:

_1_
Рх

=

Fx 0
Мв

или

+ D л Fсл
D Мв п

м�
F

=

=

Fx 0

Мв

1-'А Х п ( 1 + с п
х

(

)

е D
1+ л л
nx0 D '

)

л Dл
D . .

пх

( 1 1 . 1 5)

Сравнивая выражения ( 1 1 . 1 5) и ( 1 1 . 1 За), находим :

Р�

=

(

)

D
Рх 1 + ::" ; ;

отсюда коэффицие нт ускорения абсорбции

D
Ф = Р � = l + сл л _
( 1 1 . 1 6)
nx0 D
Рх
Неизвестная концентрация Xii на границе раздела фаз может
быть рассчитана при известных коэффициентах массоотдачи Рх
и Ру из равенства удельных потоков Мв/F поглощаемого ком
понента (В) через пограничные диффузионные пленки со сто
роны rаза и жидкости:
Ру(у - Уп) = Р : (х - О) = Px<Xii - 0) 1 + ел Dл .
(о)
п
nx0 D

(

)

Положим в целях упрощения, что система подчиняется за
кону Генри. Тогда Уп = mxu, и из правой и левой частей выра
жения (о) следует
ел Dл
- Р
Ру
Ру
+ Р
У
mхп - �
�п D '
nхп откуда после сокращений и очевядных преобразован ий получа
ется:
р у - р л Dл
хс
у
пр D
Xii =
( 1 1 . 1 7)
Рх + т у
Из формулы ( 1 1 . 17) вядно, что в случае фиксированной
концентрации поглощаемого компонента в газе (у = coпst) зна
чение х0 уменьшается при увеличении концентрации ел ак
тивного компонента абсорбента. Это приводит к уменьшению
�

949

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

гр.

Рис. 11.25. Профили концентраций погло
щаемого компонента (у) и активного ком
понента абсорбента (сА) вблизи границы
раздела фаз при различных концентрациях
последнего в основной массе:
J - сл = сл"4',

2 - сл > сл"4'

толщины пограничной пленки 8де
(т.е. приближению "реакционного
сечения" к границе раздела фаз) и,
следовательно, к увеличению скорости абсорбции; согласно
( 1 1 . 1 2) увеличивается р� . Максимальная скорость абсорбции
будет при некоторой критической концентрации слкР,
когд�_
Хп = О . В этом случае числитель выражения ( 1 1 .7) становится
равным нулю:

откуда

с;;:

=

D
Dл

п -- 1 у .
р

Рх

( 1 1 . 1 8)

На рис. 1 1 .25 сплошными линиями показаны профили кон 
центраций П К в газовой пленке и активного компонента ел в
абсорбенте вблизи границы раздела фаз при Хп · = Уп = О , когда
"реакционное сечение" совпадает с границей раздела фаз.
При концентрации активного компонента ел > слкр скорость
абсорбции такая же, как и при ел = слкР. В обоих случаях она
определяется скоростью диффузии поглощаемого компонента
через пленку в газовой фазе. " Реакционное сечение" при
ел > слкр также совпадает с границей раздела фаз, но концент
рация активного компонента на границе раздела фаз больше
нуля (см. точку пересечения линии 2 с границей раздела на
рис . 1 1 .25). Это означает, что на границе раздела фаз имеется
избыток активного компонента абсорбента.
Итак, проведенный анализ позволяет установить оптималь
ную концентрацию активного компонента поглотителя ( сл0m =
= слкР ) , соответствующую максимальной скорости абсорбции
при данной концентрации ПК в газовой фазе (у).
Таким же образом можно решить и обратную задачу: для аб
сорбента с заданной концентрацией ел активного компонента
найти максимальную концентрацию ПК в газовой фазе Ymax•
при которой абсорбция будет протекать с максимальной ско
ростью. Из ( 1 1 . 1 8) следует:
Ymax

950

=

л х

D -Р ел.
-nD Р
у

( 1 1 . 1 9)

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

1 1 .5.4. Абсорбция летучим поrлотителем

При абсорбции летучим поглотителем (абсорбентом) фазо
вое равновесие систем газ-жидкость удобно представлять в
треугольной диаграмме (см. рис. 1 1 . 1 7, б, г). Расчет размеров
аппарата выполним с помощью треугольной диаграммы для
общеrо случая абсорбции летучим поглотителем и при некото
рой растворимости газа-носителя в абсорбенте (см . рис .
1 1 . 1 7, г).
Рассмотрим работу противоточноrо абсорбера. Обозначим
(см. рис. 1 1 .26): L и G - жидкостный и газовый потоки в про
извольном сечении аппарата; хпк , хЛ, xrn - абсолютные (на 1
кг фазы абсорбента) концентрации П К, чистоrо компонента А
и газа-носителя ГН в жидкостном потоке в произвольном се
чении; упк , у л, yrn - концентрации П К, А и ГН в газовом по
токе в произвольном сечении; индексами "н" и "к" помечены
кон центрации компонентов в потоках на входе (начальные) и
выходе (конечные) соответственно.
В отличие от массообменных процессов класса 3 (2-2) 1 здесь
нет компонентов, потоки которых по высоте аппарата остава
лись бы постоянными. Потоки газовой ( G) и жидкой (L) фаз
также переменны по высоте аппарата, так как в каждой из фаз
изменяются потоки всех трех компонентов. Здесь рабочие ли
нии процесса массопередачи, связывающие концентрации ка
коrо-либо компонента в газовой и жидкой фазах, в диаграмме
у-х не бы.ли бы прямыми , так как отношение L/G по высоте
аппарата не остается постоянным. Нужен какой-то иной споуК (уПк�УtУ�Н)

Gк

------

У (у "�у �у

-ё

-

--

к

.
L
Х(� п�х �х r'

/ nк А ГН \
ун 1У
·Ун ·Ун /

н

Gн

Рис. 1 1.26. Обозначения и концентрации потоков при абсорбции летучим абсор

бентом

95 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

соб представления зависимости сопряженных (рабочих) соста
вов жидкой Х(хпк, хА, x rn ) и газовой У(упк, ул, yrn) фаз . Общий
подход к установлению зависимостей рабочих составов фаз
оставим прежним.
Возьмем произвольное сечение аппарата с. составами фаз
X(xnx, хл, xrn) и У(УП<-, ул, yrn) и выделим контур К (см . рис .
1 1 .26), охватывающий это сечение и верхнюю часть аппарата.
Выбор с пособа замыкания контура на верхнее или нижнее се
чение аппарата зависит от того , где известны составы обеих
фаз ; выбранный нами контур соответствует наиболее часто
встречающемуся на практике случаю задания исходных соста
вов абсорбента Хн и газа Ун. а также уходящего газового потока
Ук. Составим материальный баланс для выделенного простран 
ствен ного контура К по общим массовым потокам фаз за еди 
ницу времени :
G + Lн - G - L О ,
к
откуда
L - G = Lн - G .
=

к

Следовательно , потоки жидкой и газовой фаз могут изме
няться от сечения к сечению, но в любом сечении разность
между жидкостн ым и газовым потоками фаз одна и та же:
(п)
L - G = idem = S.
Физический смысл S: это расчетный поток (здесь - массо

вый), получаемый при вычитании газового потока из жидкост
ного в любом сечении аппарата.
Материальный баланс по поглощаемому компоненту для того
же контура К (см . рис . 1 1 .26) за единицу времени:

Gу"к + L х "к
�

о

._____,

Нак

Пр

откуда

Lхпк - Gупк

=

Lнхнпк - GкУ пк
к

=

idem

=

S.хsпк.

(р)

Следовательно, потоки ПК с жи дкой и газовой фазами из
меняются от сечения к сечению, но разность потоков П К, пе
реносимого этими фазами, во всех сечениях одна и та же .
Эта постоянная для всех сечений аппарата разность потоков
П К представлена по аналогии с другими составляющими в
равенстве-тождестве (р) как произведение полного массового
расчетного разностного потока S на кон центрацию П К в нем

Хsпк.

Из (р) с учетом (п) получаем :

Хsпк =
952

1..,х, п к Gу " к
L-G
_

-----

(с)

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

пк

D

А

а

s

х�"= const

б

s

Рис. 1 1. 27. К расче-rу непрерывной противоточной абсорбции летучим абсорбен

том:

а

-

доказательство наличия п олюса, б - лучи полюса

Поскольку числитель и знаменатель в (с) , как видно из (п) и
(р) , одинаковы для любого сечения абсорбера, то и Хsпх - не
которая постоянная для всех сечений аппарата концентрация
П К. В поле треугольной диаграммы линии постоянных кон 
центраций (хпх = const) параллельны стороне ГН-А треуголь
н ика. Характерная для конкретного аппарата линия Хsпх = const
может быть расположена как выше, так и ниже стороны ГН
А. Предположим, что она находится выше стороны треуголь
ника (как показано на рис . 1 1 .27, а).
Аналогичный материальный баланс для того же контура К
(см . рис . 1 1 .26) за единицу времени может быть составлен по
другому компоненту, например по газу-носителю (ГН):
Gy rн + Lнхнrн - GкУкrн - Lx rн = О,
откуда
Lх ГН - Gу ГН = LнХнrн - GкУ rн = idem = s.xsrн .
(т)
к
Следовательно , и потоЮI ГН с жидкой и газовой фазами
изменяются от сечения к сечению, но разность потоков ГН ,
переносимого этими фазами, также одна и та )J(e во всех сече
ниях. Сочетая (п) и (т) , получаем :
Xsrн

=

Lx rн

Gy rn
L-G
-

=

const.

(у)

Линия , отвечающая постоянной концентрации Хsгн , парал
лельна стороне П К-А треугольника и может быть расположе
на по одну и другую стороны от нее (на рис . 1 1 .27, а она рас
положена правее и выше) .
Разумеется, аналогичный материальный баланс может бьпъ состамен и ДIIЯ
третьего компонента. В этом, однако, нет необходимости, так как концентрация
этого компонента в тройной смеси однозначно определяется остальными двумя .
953

Пересечение двух линий (Хsпк = const и Xsrn = const) дает
точку S в поле треугольной диаrраммы (внугри треугольника
или вне его) с концентрациями Хsпк, Xsrn и Хsл = 1 Хsпк Xsrn ·
Эта точка S называется полюсом; через нее проходит прямая
(луч), соединяющая точки сопряженных составов газовой и
жидкой фаз в любом сечении аппарата (рис . 1 1 .27, б).
Таким образом, если рабочие (сопряженные) концентрации
отдельных компонентов в газовой и жидкой фазах для процес
сов класса 3(2-2) 1 в диаrрамме у-х бьти связаны рабочей ли
нией, то для тройных смесей в треугольной диаrрамме эта
связь реализуется с помощью полюса. При известном составе
одной из фаз (например, точка Х3 на поrраничной кривой
жидкой фазы - см. рис. 1 1 .27, б) можно найти состав другой
фазы в том же сечении абсорбера, проведя луч через эту точку
и полюс до пересечения с поrрfiничной кривой второй фазы
(точка Уз) .
В соответствии с правилом рычага 1 1 рода при закреплении
"опоры" в точке S имеем:

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

-

-

L SX = G SY.
Отсюда можно найти переменное (по высоте аппарата) отноше
ние L/G - в отличие от постоянного L/G для процессов клас
са 3 (2-2) 1 . При равенстве расходов фаз ( G = L) полюс, соответ

ствующий выражениям (с) и (у), лежит на бесконечном удале
нии от треугольника, а � и параллельны друг дрУJУ. При
уменьшении отношения L/G полюс смещается влево . Проана
лизируем, как смещение полюса отражается на· движущей силе
процесса массопередачи.
Обозначим (рис . 1 1 .28) точками У и Х сопряженные составы
газовой и жидкой фаз; они находятся на линиях ОС и FE со
ответственно. Концентрации ПК в них
упк = у и хпк = х.
Составу Х жидкой фазы отвечает (по ноде - штриховая линия)
равновесный состав газовой фазы УР, причем концентрацию
П К в ней обозначим уР. Разность (у уР) является движущей
силой процесса массопередачи ПК из газовой в жидкую фазы.
При смещении полюса S влево точка У перемещается вверх по
линии ОС, и движущая сила процесса (у - Ур ) увеличивается .
Об оrраничении роста движущей силы поговорим чугь позже.
При смещении полюса S вправо точка У приближается к
точке УР, и движущая сила уменьшается . Для некоторого от
ношения ( L/G)пUn луч и нода совпадают: движущая сила (у
- уР) в этом случае равна нулю, и массоперенос отсутствует. Это
соответствует минимальному расходу абсорбента LпUn при из
вестной производительности по газу G.
-

-

-

При расположении полюса правее точки, отвечающей минимальному расхо
ду aбcopбeirra, происходит десорбция ПК из жидкой фазы в газовую.

954

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 1 1 . 28. Рабочие и равновесные составы газовой и жидкой фаз при непрерыв

ной абсорбции летучим абсорбентом

Рис. 11.29. К нахождению полюса при абсорбции летучим поглотителем

Оптимальный расход абсорбента Lн определяется , как и в
случае других процессов, в том числе и класса 3(2-2) 1 , на осно
вании экономического расчета, учитывающего как капиталь
ные расходы (стоимость аппарата), так и эксплуатационные
(стоимость абсорбента, затраты на его подачу и т.д . ) :

( 1 1 .20)
где Oopt > 1
оrrrи мальный коэффициент избыrка абсорбента сверх минималь
ного, соответствующий минимуму суммарных затрат.
-

В реально работающих и проектируемых абсорберах коэф
фициент избытка абсорбента cr может по ра:,зным причинам
отличаться от cro pt ·
Для расчета необходимых размеров аппарата требуется знать
локал ьн ые движущие силы. Последние легко определить (см .
выше) при наличии полюса S - его месторасположение нахо
дится из следующих соображений . В точке S пересекаюrся все
лучи, в том числе и относящиеся к верхнему и н ижнему сече
н ия м - соответственно , прямые, проходящие через точки Хн.
Ук и Хк, Ун (см . рис . 1 1 .26). Графически положение полюса S в
треугольной диаграмме при известных составах фаз на входе в
аппарат (точки Хн и Ун) и на выходе из него (точки Хк и У11:)
находят как точку пересечен ия прямых (лучей), проходящих
через указанные пары точек (рис . 1 1 .29).
Положение точки Хн определяется составом исходного
(обычно - регенерированного) абсорбента; при использовании
чистого абсорбента точка Хн совпадает с вершиной А треуголь
ника. Исходная газовая смесь состоит из газа-носителя (ГН) и
поглощаемого компонента ( П К) ; ее состав характеризуется
точкой Ун на стороне ГН- П К треугольн ика. Состав уходящей
из абсорбера газовой смеси (точка Ук) чаще всего задан ; он
обусловлен приемлемой (технологически, экономически, эко955

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

логически) остаточной концентрацией поглощаемого компо
нента в газовой фазе, в рассматриваемом случае - при некото
ром содержании в ней паров летучего абсорбента. Отработан
ный абсорбент (точка Хк) наряду с растворенным в нем погло
щаемым компонентом содержит также некоторое количество
растворенного газа-носителя; точка Хк лежит на линии FE на
сыщенных растворов абсорбента.
В некоторых задачах проектирования могут быть заданы все
четыре состава - четыре точки : Ую Ук, Хн, Хк. Тогда оба гра
ничных луча (ХкУн и ХнУк) известны, и положен ие полюса
устанавливается простым нахождением точки пересечения этих
лучей. Одновременно определяются рабочие потоки фаз исходный Lн ( Gн
задан) и конечные Gк и Lк_. С этой целью
попарно соединяют прямыми точки Ун и Хю Ук и Хк. Точка
пересечения прямых (N) представляет собой точку материаль
ного баланса, т.е. сложения входящих в абсорбер смесей или
уходящих из него. По характерным измеренным отрезкам УнN,
NХн и другим и известной производительности по исходному
газу Gн определяют все остальные граничные потоки. Напри
мер, поток абсорбента Lн, обеспечивающий заданные составы
уходящих газовых и жидких смесей, находят по правилу рычага
1 рода:
Gн · Ун N Lн · NХн -

=

Чаще в задачах проектирования состав Хк не задан; о н зави
сит от принятого расхода абсорбента. При известном, наЙден
ном по ( 1 1 .20), расходе исходного абсорбента Lн конечный со
став Х11: можно найти из системы уравнений материального
баланса (как по общим потокам, так и по отдельным компо
нентам) абсорбера в целом.
Удобнее, однако, определить точку xl[ путем графического
представления материального баланса с использованием пра
вила рычага при сложении и вычитании растворов. Суммарно в
абсорбер в единицу времени поступают свежий газ (точка Ун) в
количестве Gн и абсорбент (точка Хн) в количестве Lн. Точка N
материального баланса такой расчетной (р·е ально не су
ществующей в абсорбере) смеси определяется сложением Gн и
Lн по правилу рычага (лучше - 1 1 рода) . Но уходящие потоки
4 и Gк при суммировании должны давать ту же расчетную
смесь N . Поэтому из заданной точки Ук надо провести прямую
через уже наЙденную точку N до пересечения с линией насы
щенных растворов абсорбента; точка пересечения даст иско
мый конечный состав Хк. По физическому смыслу - это опе
рация вычитания растворов: из N вычитаем Ук и получаем Хк.
Кстати, с помощью правила рычага по точкам N , Хк и У11: мож
но определить конечные потоки 4 и Gк .
956

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 1 1.30. К расчету поверхности мас
сопередачи противоточноrо абсорбера
ХнУн и ХкУк представляют со

Подчеркнем,

что

прямые
к

бой линии результирующего
смешения и разделен ия ; к ли
н иям р а вновесного разделения
(нодам) они никакого отноше

F

-��·- - - -

о
Lx

"\,f---'� --1---1---�--1 /
dM

/
y + d(Gy) Lx +d(Lx)
Точка N должна находиться
в гетерогенной области DCEF,
соответствующей наличию двух
Lк Хк
фаз . При весьма малых расхоGн у"
дах абсорбента точка N может
занять положение N 1 (или даже левее нее) , соответствующее полному переходу абсорбента в
газовую фазу; второй (жидкой) фазы при этом не существует.
Наоборот, при весьма больших расходах абсорбента получим
точку N2 (или правее) , что соответствует полному растворению
газовой смеси в жидкости с образованием насыщенного (в слу
чае получения точки N2) или ненасыщенного (справа от точки
N2) гомогенного раствора.
Таким образом , при известном расходе исходной газовой
смеси Gн расход абсорбента Lн должен быть больше наимень
шего, определяемого по точке N 1 , но меньше наибольшего ,
соответствующего точке N2 (см . рис . 1 1 .29).
С целью расчета необходимой поверхности массопередачи F
противоточного абсорбера (рис . 1 1 .30) для рассматриваемого
общего случая составим материальный баланс по поглоща емому
компоненту для элементарного контура К для тазовой фазы за
единицу времени, учитывая, что переменными здесь являются
как у, так и G :
ния не имею т .

Gy + d(Gy)

'--v--'

Пр

Gy - dM

'------v--'

Ух

о

�

Нак

отсюда после сокращения

dM = d(Gy) .
Уравнение массопередачи на языке фазы
тарной поверхности df остается прежним :

"у"

для элемен 

dM = ky (y - y P) df
Приравнивая правые ч асти двух последних равенств, имеем:

d( Gy) = ky(y - yP) df
957

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

l
__

к/у-у�
1

Ку (у-у�
1

Gy

ЧJk Gy

Рис. 11.31. Графическое вычисление интеrрала в формуле ( 1 1 .2 1 )

Разделяем переменные и интегрируем от О до F и от GкУх
до GнУн:
G нУн d(Gy)
F=
( 1 1 .2 1 )
J
G "y " ky (Y - У р )

Вычисление интеrрала в уравнении ( 1 1 .2 1 ) возможно лишь численными ме
тодами. Коэффициент массопередачи ky и произведение Gy беруr при соответ
ствующей концентрации ПК в rазовой фазе (у). Последней отвечает сопряжен
ная концентрация х - в жидкой фазе; определяется она с помощью треуrольной
диаrраммы. В соответствии с правилом рычага L(x - х."") = G(y - у,"") . Учиты
вая, что L - G = S = Lн - Gн, можно найти непосредственную связь G с у:
откуда
и

( G + S) (х - х."")

=

G(y - х.""),

G(y - х."") - G(x - х."")

G= S

= S(x - х."")

х-х ""
у- х

-•- .

Более наглядно rрафическое интеrрирование (рис. 1 1 .31). Здесь площадь под
кривой 1/[ky(y - у Р) ) - Gy в пределах от GкJк до GнУн равна интеrралу в правой
часrи уравнения ( 1 1 .21), а значит, и требуемой поверхности массопередачи F.

В случае постоянного по высоте абсорбера коэффициента
массопередачи ky его можно вынести за знак интеграла. Если
при этом постоянен и газовый поток G [такой процесс отно
сится к классу 3(2-2) 1 ) , то из ( 1 1 .2 1 ) получаем:

ky F У н dy
= Sy ,
-= J
Р
G
Ух у - у
т.е. приходим к известному для этого случая выражению [см.
пояснения к формуле ( 1 0.27)) .

958

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

1 1 .6. О ПРОЦЕССАХ ДЕСОРБЦИИ

Десорбцию проводят с целью выделения абсорбированных
компонентов и регенерации отработанного абсорбента для его
последующего использования . Этот процесс можно проводить
различными способами:
- пуrем взаимодействия встречных потоков регенерируе
мого абсорбента и десорбирующеrо аrевта (обычно - воздуха
или водяного пара, реже - инертного газа);
- наrреванием абсорбента (растворимость в нем П К падает
с ростом температуры);
- понижением рабочего давления над абсорбентом.
На практике широко применяются комбинированные ме
тоды десорбции (например, десор бция при снижении давления
над абсорбентом и одновременном его наrреве).

Десорбция в потоке инертного газа или водяного пара
Если температуры инертного газа и поступающего на де
сорбцию абсорбента близки, а теплотой абсорбции (при де
сорбции эта теплота поглощается) можно пренебречь, то про
цесс можно считать изотермическим. Рабочая линия такого
процесса десорбции расположена ниже равновесной зависи
мости (см. область десорбции на рис. 1 1 . 1 5, а). Если абсорбент
нелетуч, а десорбирующий агент в нем нерастворим, то в расче
тах удобны относительные концентрации поглощаемого компо
нента на 1 кг инерта: х (кг ПК/кг абсорбента) - в жидкой фазе
и у (кг П К/кг десорбирующего агента) - в газовой; при этом
рабочие линии - прямые (рис. 1 1 .32). Тангенс угла наклона
рабочей линии процесса десорбции, как и в случае абсорбции,
зависит от соотношения потоков жидкой и газа.в ой фаз (L/G).
у

с

у

с

В'

б

Рис. 1 1.32. Расположение рабочей линии при десорбции:

пересечеЮ1е рабочей JDDllDI с равновесной, б - хасание рабочей JDDllDI с равновесной
рабочая линия, ОС - линия равновесия (изотерма сорбции), АВ' - положеЮ1е ра
бочей линии при минимальном расходе десорбирующеrо аrеюа
а -

АВ

-

959

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

G

Расход десорбирующего газа
чаще всего не задан
(известны обычно расход абсорбента, а также начальная и ко
нечная концентрации П К в нем); поэтому
определяют на
основании технико-экономического расчета - так же, как и
расход абсорбента при абсорбции:
- находят минимальный расход десорбирующего агента
(концентрация П К в уходящем газ овом потоке Укд макси
мальна), при котором рабочая mmия пересекает равновесную в
точке с абсциссой Xif (рис. 1 1 .32, а) и.ли касается линии равнове
сия (рис. 1 1 .32, б). Здесь движущая сила процесса равна нулю,
размеры и стоимость аппарата cтamt: бы бесконечно большими ;
- устанавливают оптимальный (рабочий) расход десорби
рующего агента, соответствующий минимальным суммарным
эксплуатационным и капитальным затратам;
= cropt Gmin ;
здесь cropt > 1 - оптимальный коэффициент избытка десорби
рующего агента.
Расчет основных размеров десорбера производится в той же
последовательности, что и расчет абсорбера (см . разд. 1 1 .4).
Движущая сила на языке фазы "у'' при десорбции будет, есте 
ственно, (уР - у) вместо (у - уР) при абсорбции, а на языке
фазы "х" - (.х - .хР) вместо (.хР - .х).
Отметим широкое использование водяного пара в качестве
десорбирующего агента - особенно в тех случаях, когда выде
ляемый компонент ( П К) нерастворим в воде. Последнее усло
вие обеспечивает легкость отделения ПК из парогазовой смеси
пуrем ее конденсации и поочередного слива (декантации) от
дельных .жидкостных слоев.

G

Gmin

G

Нагревание абсорбента
Этот метод десорбции получил наибольшее распростране
ние в технике вследствие своей простоты.
Часто десорбцию осуществляют, подводя теплоту к абсор
бенту через теплопередающую поверхность (десорбция глухим
паром) . В этом случае вместе с десорбируемым компонентом
нередко испаряется часть абсорбента. Для разделения такой
смеси используют процесс перегонки: образующуюся смесь
паров направляют в ректификационную колонну для разделе
ния ее на чистые компоненты. Подробнее о процессах пере
гонки см. гл. 12.
Понижение давления над абсорбентом
Этот способ десорбции технологически является одним из
наиболее простых. Он особенно выгоден в тех случаях, когда
абсорбцию проводят при повышенных давлениях. Десорбция

960

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

2

L Рабс

Х1

Р
дес

у2=

D

1 Мдес
1

у

t

L-Мдес Ун
.Х2

а

1
1
1
1
1
1
'

1
у2=

Е

'

'

Xz

б

XI

с
-х

- схема аппарата, 6 -изображеЮl.е процесса в диаrрамме у -х;
1 - десорбер, 2 - дроссельный ве1ПИJ1Ь;
ОС - равновесная линия при Рабе, OD - равновесная линия при Рдес• А - точха, харах
теризующая состояЮl.е систеМЬJ в ко1Ще процесса абсорбции (при противотоке фаз), ED рабочая линия процесса десорбции

Рис. 11.33. Десорбция за счет снижения давления жидкости:
а

здесь может быть реализована пугем снижения давления до
атмосферного. Можно проводить десорбцию и под вакуум ом,
однако в этом случае возникают дополнительные затраты на
отсасывание десорбированноrо компонента вакуум-насосом.
Схема процесса десорбции при снижении давления показа
на на рис . 1 1 .33, а. Абсорбент с относительной концентрацией
поглощаемого компонента х1' (и абсолютной - х1 ) после аб
сорбции подается в десорбер 1, где рабочее давление Рдес за
метно ниже, чем Рабе при абсорбции; сброс давления от Рабе до
Рдес осуществляется с помощью дроссельного вентиля 2. Из
потока абсорбента L' (в расчете на инерт) получают потоки П К
в газовой фазе (Мдес) и регенерированного абсорбента [L' (1 +
+ х1) - Мдес ] с низкой концентрацией х2' Разумеется, х1' равна
конечной концентрации ПК в абсорбенте· после абсорбции Хк ,
а х2' - начальной его концентрации в абсорбенте, подаваемом
на абсорбцию, Хн·
Задача технологического расчета состоит в определении
концентрации х2' при сбросе давления от Рабе до Рдес• а также
уходящих из десорбера потоков.
Поскольку рассматриваемый процесс десорбции протекает с
изменением материальн ых потоков (инерт отсуrствует) , то от
относительных концентраций и потоков инертов целесообразно
перейти к абсолютным. Переход к абсолютной концентрации х1

96 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

осуществляется (см. разд. 10.2. 1 ) по формуле
xi

х·' = --'1 + х;1 '

соответственно, абсолютный поток смеси на десорбцию состав
ляет L = L ' ( l + х1').
Идеализируем процесс десорбции, приняв упрощающие до
пущения:
- абсорбент абсолютно нелетуч, следовательно, абсолютная
концентрация П К в газовом потоке Мдсс составляет У2 = 1
(здесь Рпх = Рдсс);
- теruювыми эффектами, сопровождающими процесс де
сорбции, пренебрегаем;
- в десорбере-сепараторе происходит полное (равновесное)
разделение чистого П К и абсорбента с концентрацией, равной х2.

Отказ от идеализации процесса потребовал бы учета летучести абсорбента,
так что стало бы Yl' < 1 . Кроме тоrо, пришлось бы учесть тепловые эффе кrы ,
обусловленные дросселированием и переходом ПК из жидкой фазы в газовую
(явление, обратное неизотермическому по г.лощению ПК абсорбентом) - все это
связано с изменением температуры процесса десорбции.

Процесс десорбции удобно строить в диаграмме у-х (рис .
1 1 .3 3 , б), где у и х
абсолютные концентрации П К в газовой
и жидкой фазах соответственно (О ::;; у � 1 ; О � х ::;; 1 ) . Допустим,
что точка А здесь соответствует насыщенному абсорбенту
(концентрация П К в нем Хк), по кидающему абсорбер в контакте
с исходным газом (при противотоке) состава Ун· Естественно,
что точка А расположена выше линии равновесия ОС дЛЯ ра
бочего давления Рабе·
При десорбции путем сброса давления концентрация П К в
газовой фазе У2 = 1 , т.е. линия равновесия
совпадает с
верхней стороной квадрата.
-

Процесс десорбции П К из абсорбента при резком (с помощью дроссельно ю
веНТИ71Я) сбросе давления во мноrом сходен с процессом самоиспарения жид
кости при ее дросселировании до давлений ниже упруrости насыщенных паров
для рабочей температуры (см. разд . 9. 3) . В случае абсолютной нел етучести аб
сорбента при сн ижении давления жидкости из нее десорбируется ("самоиспа
ряется " ) только П К . Процесс протекает пракrически м rновенно, жидкость после
дросселирования необход имо направ ить в десорбер (он иrрает рол ь сепаратора),
где и происход ит отделение газово ю потока от абсорбента.

Концентрация П К в жидкости при этом уменьшается до
значения хъ равновесного с его содержанием в газовой фазе
для рабочих давления в десорбере Рдес и температуры. Связь
равновесных концентраций П К в фазах устанавливается с по
мощью коэффициента распределения т = (у/х)р · В исследуе
мом случае у = У2 = 1 , и т приобретает смысл показателя рас
творимости ПК в абсорбирующей жидкости.
962

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Пусть коэффициент распределения П К между фазами т не
зависит от уровня концентраций - это часто характерно для
не очень больших значений х2 и Рдес· Тогда линия О D
(штриховая линия на рис . 1 1 .33, б) , определяющая раствори
мость ПК в жидкой фазе при рабочих условиях десорбции, прямая . Ее положение характеризуется значением т и углом а :
т = у�х2 = 1/х2 = tga .
Отсюда в условиях равновесной сепарации остаточная кон 
центрация П К в жидкой фазе составит:

х2 = 1/т.
(а)
Коэффициент распределения т связан с константой Генри
Е и рабочим давлением р соотношением т = Е/р, так что по
ложение прямой OD в диаграмме у-х, а значит, и остаточная
кон центрация х2 (абсцисса рабочей точки десорбции) зависят
от рабочего давления в десорбере р = Рдес:
(а')
Х2 = Рде с/Е.

Для установления степени извлечения (доли отгона) П К в
десорбере е = Мде с /L составим материальный баланс по пото
кам поглощаемого компонента для контура, охватывающего де
сорбер (см . рис . 1 1 .33, а) :
Lx1 - Мде сУ2 - ( L - Мдес)х2 = О .
Отсюда при У2 = 1
и

е=

Х1 - Х2 .
1 - х2

(б)

Используя выражение (а) и связь т и Е, получаем для
в случае прямой линии равновесия :

р = Рдес

е=

т Х1 - Рдос. / Е
1 - 1 / т = 1 - Рдос / Е

х1 - 1 /

'

или

е=

Х1 Е - Рдос.
Е - Рдос.

( 1 1 .22)

----

Из ( 1 1 .22) следует, что при снижении давления десорбции
Рдес степень отгона е увеличивается, но она не может превы
сить абсолютную долю (х 1 ) поглощаемого компонента в абсор
бенте , поступающем на десорбцию.
Давление десорбции Рдес подбирают таким, чтобы остаточ
ная (абсолютная) концентрация ПК в абсорбенте после десорб-

963

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рабе

L

М�ес

М';,ес

L-М'де с

Рис. 11.34. Схема десорбции при ступенчатом понижении давления

ции х2 отвечала требованиям к исходному абсорбенту при аб
сорбци 17, т.е. чтобы х2' = Хн, rде относительная концентрация

х2' = х11 (1

-

х2 ).

Иногда десорбцию проводят при снижении давления жидкости в несколько
ступеней (рис. 1 1 .34). В первой ступени давление жидкости снижают от давле
ния абсорбции (рабе) до некотороrо проме:жуточноrо давления р1. При этом
десорбируется некоторое количество rаза Мд.,, . Оставшаяся жидкость (L
- Мдес) поступает во вторую ступень, где давление снижается до Р2 и вьщеляется
М'д•с rаза, и т.д. При мноrоступенчатом снижении давления часть десорбирован
ноrо rаза имеет повьпnенное давление, что в ряде случаев оказывается блаrопри
ятны:м фактором при ero дальнейшем использовании. Если при абсорбции было
извлечено из исходноrо газа несколько компонентов, то многоступенчатое сни
жение давления жидкости позволяет в некоторой степени разделить вьщеляемые
при десорбции компоненты, так как в первой ступени в газовую фазу вьщеляют
ся наименее растворимые компоненты, во второй ступени - более растворимые
-

И Т.Д.

1 1 .7. ГИДРАВЛИ ЧЕСКОЕ СОПРОТИВЛЕНИЕ АБСОРБЕРОВ

Жидкость в абсорбер подается, как правило, сверху и стекает самотеком по
элементам насадки или по сливным трубам, организующим перелив жидкости с
тарелки на тарелку. Поэтому вопрос о потере напора для жидкости при прохож··
дении ее через абсорбер не рассматривается; достаточно лишь подать ее в аппа
рат сверху и соответствующим образом распределить в абсорбере.
Для обеспечения требуемоrо газовоrо потока G через абсорбер нужен напор ,
достаточный для компенсации всех гидравлических потерь, связанных с прохож
дением rаза по аппарату. ПовьШJение давления rаза (ero сжатие) сопровождается
затратами энергии, иногда - весьма существенными. Необходимая мощность
дутьевоrо устройства зависит от скорости газовоrо потока; поэтому выбор опти
мальной скорости газа в аппарате производится с помощью технико
экономическоrо расчета, учитывающеrо этот расход энергии.
Н иже рассмотрим по отдельности расчет необходимоrо перепада давления в
абсорберах со ступенчатым контактом фаз - на тарелках и с непрерывным при прохождении rаза в пленочных и насадочных аппаратах. Расчет мощности
при со:щании необходимоrо перепада давления газового потока приведен в разд.
4.3.2.
Тарет.ча1Wе абс:орберw. Полное гидравлическое сопротивление одной тарел
ки (Л/1;) любой конструкции складывается из статического сопротивления слоя
жидкости на тарелке (Лр.,), потерь напора на преодоление местных сопротивле -

964

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 1 1.35. К определению высоты слоя жид
1 - 11:орпус 11:олоЮ1Ь1,
псрсrородка

2-

-

кости на тарелках с переливными устройства
ми:
тарелхи, З

3

сливная

ний на сухой (неорошаемой) тарелке (Лрс) и
сопротивления, вызьшаемого силами поверх
ностного натяжения (Лро) :
Лр; = ЛJlж + Л/lс + Л/lо·
( 1 1 .23)
В еmrчину ЛJJж , зависящую от высоты hx
слоя жидкости ruютностью Рж на тарелке (рис. 1 1 . 35), определяют по формуле
гидростатического давления (2.6):
Л/lж = Ржвсnghж,
( 1 1 .24)
rде Рж..всп - плотность вспененной жидкости (точнее
газожидкостной смеси)
на тарелке, причем р,,,•сп = (0,5 + О,7)р... .

На тар елках непровального типа полиая высота слоя жидкости hж. в формуле
( 1 1 .24) формируется (см. рис. 1 1 . 35) высотой сливной перегородки hсл и вели
чиной подпора жидкости над перегородкой hcл00JJЛ: hж. = hсл + hcл00JJЛ. Значение
hcл00JJЛ зависит от массового расхода жидкостного потока L( l + х) и, по опьrr
ным данным, принимается обычно равным hcл00JJЛ = (0,65 + 0,7)1,,.2/3. Плотность
орошения 4 (объемный расход жидкости, отнесенный к единице длины В слив
ной перегородки) связана с массо вым расходом абсорбента L соотношением 4
= L( l + x)/(r>ж..l/) .
Потерю напора rаза при прохождеЮIИ ero через месrные сопротивления (прорези
КОJПiачка, отверстия ситчатых тарелок и т.п.) определяют по формуле (2.30а):
=

2

-

r:це Warв - скорость газа в отвер стиях (прорезях и т.п.) тарелки . При известной
скорости газа w в колонне величина Warв находится из уравнения расхода с уче
том доли свободного сечения отверстий тарелки <J>св: War1 = w <J>cв·
Л/Jс - ; WC7111 p/l ,

( 1 1 .25)

Коэффициенты местных сопротивлений !; для тарелок различных конструк
ций приведены в справочной литературе• . Влияние уровня жидкости на тарелке
на коэффициент местного сопротивления !; при этом, как правило, не учиты
вается.
Сопротивление, обусловленное силами поверхностного натяжения, получим,
обозначив: а - коэффициент поверхностного натяжения на границе газ
жидкость; dc - эквивалентный диаметр каналов для прохода газа через от
верстия тарелки ( dc = do в случае круглых отверстий диаметром do) . Приравняем
теперь формальное и физически обоснованное выражения для сил поверхност
ного натяжения в отверстии: Лр0 · d 2/4 = 11d.a. Отсюда

/

11 c

( 1 1 .26)
Лр0 = 4a/d0•
Полное сопротивление абсорбционной колонны, сод�ржащей п тарелок,
складывается из сопротивления всех тарелок:
11

Лр = r. Лр; .
i=l

Если в ходе процесса (т.е. п о высоте колонны) физические свойства абсор
бента (р... , а) изменя ются незначительно, а гидродинамические характеристики
• См., например, ( 1 , 6 ) .

965

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

тарелок (hсл, hcлno11t1 и h...) остаются неизменными, то потери напора на отдель
ных тарелках близки между собой (др1 "' др 1 ), и полное сопротивление колонны
др можно найти как произведение ЛJ11п.
Н а тарелках провального типа слой жидкости создается и поддерживается при
скоростях rаза, превЬШiающих некоторое минимальное значение, ниже которою
вся жидкость протекает через отверстия тарелхи. Наоборот, при очень больших
скоростях rаза все сечение отверстий тарелки занято газовым потоком, и жид
кость не может перетекать с тарелки на тарелку - это режим захлебывания колон
ны. Рабочая скорость газовою потока должна бьпъ ниже скорости захлебьmания.
Ее принимают такой, чтобы на тарелке образовывался слой :жидкости высотой
0,05 - 0, 10 м, соответствующий величине Лр... = 250 + 350 Па. При этом через
одни и те :же отверстия тарелок поочередно или одновременно проходят и газ, и
жидкость. Доля отверстий, занятая стекающей :жидкостью, зависит от сооnюше
ния расходов газовой и жидкой фаз и составляет обычно 10 - 20 % от площади
всех отверстий.
ДопоJDfительные сведения о расчете mдравлическою сопротивления тарелок
провальною типа и оптимальной скорости rаза можно найти в специальной и
справочной литературе•.
Гидравлическое сопротивление меночнwх и нас:адочнwх аппаратов с большей
(в случае пленочных абсорберов) или меньшей (для насадочных) точностью
можно определить с использованием традиционно применяемою уравнения
Дарси-Вейсбаха (2. 17). Трудность здесь - в определении ;эквивалентною диа
метра d0 каналов для прохода rаза и в неточности определения коэффициентов
mдравлическою сопротивления в присуrствии :жидкостиою потока.
Трубчатwе мeнo"lllWe aJDJapan.a. Эквивалентный диаметр d0 каналов для про
хода газа здесь меньше внутреннею диаметра труб d на две толщины (2li) сте
кающей жидкостиой пленки. Из-за значительного срыва и выноса капе.ль из
пленки и допОJD1ительных затрат энерmи на поддержание в потоке rаза их во
взвешенном состоянии mдравлическое сопротивление пленочных аппаратов
превьпuает расчетное значение для mадких труб. Для учета влияния капель в
расчетные зависимости для коэффициента mдравлического сопротивления вво
дят эмпирические поправки. Наиболее распространенной поправкой является
множитель ( 1 + ЗOOli/d) к уравнению Дарси-Вейсбаха для mадких труб внут
ренним диаметром d - 2li.
Hac:aдo"lllW e aJDJapaтw. В этих аппаратах, заполненных насадкой с известиыми
значениями Fуд и &к. эквивалентный диаметр канала для газовою потока может
быть наЙден с помощью формулы (:ж) разд. 2.2.2, в которой: / = fc8 - площадь
поперечною сечения потока, П - смоченный периметр канала. Домножим
числитель и знаменатель правой части этой формулы на высоту слоя насадки Н
и ее объем V:
Учитьmая, что

d• =

4

/са
п

lN

lN .

&н •VcвfV = /c8H/V и Fуд • F00ж/V = ПН/V, получаем:
4fc8 H V
4Ус8 V
4& н
-- .
d0 = -V ПН
V Fб<ж Fуд
-

=

--

=

( 1 1 .27)

Наряду с затруднениями в определении d0 (здесь каналы неправильной фор
мы и переменного сечения) возникают большие дополнительные проблемы при
расчете длины каналов. Реальное сечение последних для прохода rаза, кроме
тою, в значительной степени зависит от плотности орошения (в данном случае это объемный расход на единицу площади поперечного сечения аппарата) . С
увеличением последней величина d0 уменьшается.
•

966

См. ( 1 , 10, 1 1 ) .

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Расчет rидраWIИческоrо сопротивления орошаемой насадочной колонны Лрор
чаще всеrо базируют на гидравлическом сопротивлении неорошаемой (сухой)
насадЮI Лрсух:
( 1 1 .28)
Лрор = kЛрсух ,

где k - коэффициент, учитывающий увеличение сопротивления орошаемой
насадки по сравнению с неорошаемой.

Гидравлическое сопротивление сухой насадЮI Лрсух находят с помощью
уравнения типа (2. 1 7а) . Более резонно было бы использов�ть формулу Эрrана
(2.67) для сопротивления слоя неподвижной насадЮ1; следуя, однако, устано 
вившейся традиции, для расчета Лрсух будем использовать формулу Дарси
Вейсбаха (2. 17). Положим 1 = Ннас. а также учтем, что вертикальная составляю
щая истинной скорости rаза в каналах насадЮI ( wк8) больше расчетной w, а
именно Wи8 = w/f::н (ще &н - доля свободноrо сечения насадки).
Тогда расчетная формула (2 . 17а) примет вид
( 1 1 . 29)

Коэффициент rидравлическоrо сопротивления Лг учитывает искривление ка
налов, суммарные потери давления на трение и местные сопротивления насадхи• .
В зависимости от типоразмера насадки и величины критерия Рейнольдса для
rазовоrо потока коэффициент л. определяют по тем или иным эмпиричесЮ1м
соотношениям " .
Величина коэффициента k в формуле ( 1 1 .28) зависит как от вида насадЮI и
ее размера, так и от плотности орошения и физических свойств абсорбента
(k > 1 ) . Здесь тоже пока отсутствуют кaI01e-JD160 установившиеся теоретичесЮ1е
подходы к расчету; в настоящее время k определяют на сугубо эмпирической
основе " .
Л ИТЕРАТУРА

к главе

11

1 . Александров И.А. Рекrификационные и абсорбционные аппараты. Методы
расчета и основы конструирования. М . : Химия, 1978. 280 с.
2 . Астарита Дж. Массопередача с химической реакцией: Пер . с англ./ Под
ред. Л .А. Серафимова. Л . : Химия, 197 1 . 224 с.
3. Гел ьперин Н.И. Основные процессы и аппараты химической технологии .
М . : Химия, 1 98 1 . 8 1 2 с.
4. Дытнерский Ю.И. Процессы и аппараты химической технологии . М . : Хи
мия, 1995. 768 с. (т. 1 , 400с.; т.2, 368 с.).
5 . Жаворонков Н.М. ГидраWIИческие основы скрубберноrо процесса и тепло
передача в скрубберах. М . : Советская наука, 1 944. 224 с.
6. Идельчик И.Е. Справочник по гидравлическим сопротивлениям. М . : Ма
шиностроение, 1 97 5 . 560 с.
7 . Касаткин А.Г. Основные процессы и аппараты химической технологии.
М . : Химия, 1 97 1 . 784 с.

•• См. (1, 6, l IJ.
• См. ( 5 ) .

967

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

8. Павлов К. Ф., Романков П.Г., Ноское А.А. Примеры и задачи по курсу про
цессов и аппаратов химической технолоmи. Л.: Химия, 1987 574 с.
9. Планоеский А.Н., Никмаее П.И. Процессы и аппараты химической и нефтехимической технолоmи. М . : Химия, 1972. 494 с.
10. Ромм В.М. Абсорбция газов. М . : Химия, 1976. 656 с.
1 1 . Справочник химика, т.V. М.-Л . : Химия, 1 966. 974 с.
12. HandЬook of Chemistry and Physics. / Ed. Ьу Hodgman C.D. Cleveland, Ohio:
Chemical RubЬer PuЫishing Со" 1955 (37 copyright). 3 1 56 р .
•.

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Глава 12
ДИСТИJШЯЦИЯ И РЕКТИФИКАЦИЯ

В хи м ич еской технологии, нефтехимической и ряде других
отраслей промышленности (пищевой, фармацевтической вплоть до металлур гической) исполъзуюг широкое многообра
зие жидких и газовых смесей, подлежащих разделению на до
статочно чистые компоненты или фракции различного состава.
Разделение таких смесей при контакте ЖИд кой и паровой фаз,
сопровождающееся перераспределением компонентов между фа
зами, называется перегонкой.
12. 1 . ОБЩИ Е СВЕДЕНИЯ

В основе перегонки лежит различная летучесть составляю
щих смесь компонентов (иногда - компонентов и их особых
образований), т.е . разная их склонность к переходу из жИд кой
фазы в паровую или в обратном направлении.
Пусть, например, в сосуде находится жиiJкая смесь метанола и воды с кон
ценrрацией метанола 40 % . Если 'Л'f смесь нагреть до кипенИя и подвести неко
торое дополнительное количество теплоты, то образовавшаяся (в небольшом
коJП1Честве) паровая фаза, находящаяся в контакте с оставшейся жидкой смесью,
будет содержать -73 % метанола, т.е. обогатится метанолом.
Пусть теперь от парообразной смеси бензола и толуола, содержащей 40 % бен
зола и находящейся при температуре конденсации, отводится некоторое количе
ство теплоты. Тогда образовавшийся (в небольшом коJП1Честве) ко нденсат, нахо
дящийся в контакте с оставшейся паровой фазой, будет содержать - 1 9 % бензола,
т.е. обогатится толуолом .
Разная склонность компонентов смеси к переходу в парообразное (JD1бo
жидкое) состояние обусловлена разницей их температур кипения (конденсации).
Так, при атмосферном давлении температура кипения метанола равна 64,5 с а
воды - 100 с; бензола - 80,2 с а толуола - 1 1 0,6 с Очевидно, что метанол
в первой из смесей и бензол - во второй будут прояRIIЯТЬ большее стремление
перейти из жидкой фазы в паровую, а вода и толуол - из паровой в жидкую.
•

•

•

,

•

,

.

Приведенные примеры иллюстрируюг лишь явление разде
ления, т.е. возможность обогащения паровой или жидкой фазы
каки м -либо компонентом. Но именно это явление лежит в
основе про ц ессов разделения методами дистилляции и ректифи 
кации, о бъединенных общим названием : процессы перегонки.
Такое объединение (в одной главе учебника) обусловлено общ
ностью физик.о -химическ. их основ дистилляции и ректификации
969

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

(см. разд. 1 2 .2): основных законов и правил, способов пред
ставления равновесия и т.п. Разумеется, при более детсlЛьном и
глубоком изучении дистилля ции и ректификации выявляются и
рассматриваются также специфические термодинамические
закономерности, присущие каждому из этих процессов" .
При весьма обширных и в чем-то пересекающихся областях
применения процессы дистилля ц ии и ректификации имеют и
различия. Можно говорить, что разделение методами дистил
ляции часто осуществляют, когда не требуется высокой чисто
ты разделения компонентов, а методами ректификации - ког
да продукты должны быть более чистыми, и что дистилляци
онные процессы (особенно в периодических и полунепрерыв
ных режимах) обычно реализуют в случае малотоннажных про
изводств, а ректификационные - в случае крупнотоннажных.
Можно указать также на определенные различия в аппаратур
ном офор мл ении. Однако все это - сопугствующие, но далеко
не всегда обязательные признаки и различия дистилляц ии и
ректификации . Основное и существенное (кардинальное) раз
личие, на наш взгляд, состоит в следующем: дистилляция процесс непротивоточный, ректификация - принципиально
противоточный. Заметим: в учебной и научной литературе это
различие не всегда подчеркивается; более того, нечеткость в
терминологии подчас размывает границы между этими двумя
процессами перегонки.
Далее в главе последовательно рассматриваются: физико
.химические основы перегонки; процессы дистилляции (анализ
и расчет основных технологических схем) ; процессы ректифи
кации (более подробно).
1 2.2. ФИЗИ КО-ХИМИЧЕСКИЕ ОСНОВЫ
ПРОЦЕССОВ ПЕРЕГОНКИ
12.2. 1 . Состав и свойства смесей

в системах, подвергаемых перегонке, как правило, отсуr
ствует инерт, не переходящий из фазы в фазу: все компоненты
смеси участвуют (в разной мере, естественно, иначе не будет
разделения) в межфазном обмене. Поэтому здесь нет основа
ний для использования относительных концентраций , опи
рающихся на постоянные потоки (количества) инерта; приме
мольные и массовые. Уелоняют абсолютные концентрации
-

• См., например, (9, 26 ) .
970"

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

вимся обозначать символами х и а мольные и массовые ' кон 
центрации компонентов в жидкой фазе, символами у и а - в
паровой. Способы взаимноrо пересчета мольных и массовых
кон центраций изложены в разд. 1 0 .2 . 1 .
Дистилляции и ректификации на практике .в общем случае
подвергаются мноrокомпоне�пные смеси, причем каждый из
компонентов выделяется соответствующим символом и/или
индексом : хл, хв, ул.; а, Ь, а ' и т.д . Разумеется, сумма концент
раций всех компонентов любой жидкой ил и паровой смеси в
мольном либо массовом представлении равна единице (или
1 0 0 % при выражении концентраций в процентах), например

L, x; = 1 ,
где i =

А , В,

i

...

- обозначение компонеmов.

Н иже дистилляция и ректификация в целях простоты и на
глядности рассматриваюгся в основном на примере бинарных
смесей. Тогда ХА + хв = 1 , УА + Ув = 1 , а + ь = 1 , а ' + ь · = 1 .
При этом нет необходимости указывать кон центрации обоих
концентрацию одноrо из
компонентов, достаточно указать
ХА и Ув = 1 - УА· И в
них, скажем хА и ул, поскольку х8 = 1
последующем изложении для бинарных смесей указывается
кон центрация лишь одноrо компонента; индекс при х и у в
Нужно только условиться, на базе
этом случае опускается .
кон центраций какого именно компонента ведется анализ , и тог
да можно опустить индекс у концентрации этоrо компонента:
ХА = х. Для процессов переrонки за базу принимают леrколету
чнй (иначе - низкокипящий) компонент (Н КК) , т.е. имеющий
более н изкую температуру кипения . И в названии смеси он
фигурирует первым: например , смесь "метанол-вода" (но не
"вода-метанол"). Высококипящий компонент (В КК) указывают
вторым (последним). Такой порядок перечисления компонен
тов соблюдается и для мноrокомпонентных смесей .
Физико-химические (в том числе теплофизические) свойства
жидких и паровых смесей, необходимые для анализа и техно
лоmческоrо расчета процессов дистилля ц ии и ректификации,
определяюгся свойствами составляющих смесь индивидуальных
компонентов и зависят от состава смеси. Наиболее надежные
сведен ия о таких свойствах дает эксперимент. В ряде случаев
удается построить модели, позволяющие учесть взаимодействие
компонентов в фазах и с приемлемой точностью рассчитать
свойства смеси по свойствам индивидуальных компонентов и
их концентрациям . При слабом взаимодействии компонентов
свойства смеси с точностью, достаточной для инженерных рас
четов, иногда могут быть наЙдены по адд итивности (см . разд.
1 0 .2.2).
-

97 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Согласно введенной в разд. 1 0 . 1 . 1 КФ-классификации, про
цессы перегонки к-компонентной смеси относятся к классу
к(к - к)к. Для бинарной смеси (к = 2) - это процессы класса

2(2-2)2.

1 2.2.2. Правило фаз и равновесие в системах жидкость-пар

При достаточно длительном (теоретически - при бесконеч
но длительном) контакге жидкой и паровой фаз между ними в
изолированной системе устанавливается равновесие. При этом
в сосуществующих фазах выравниваются два интенсивных па
раметра - температура и давление (упругость паров), а также
химические потенциалы каждого из компонентов. Поскольку
этими потенциалами для практических целей пользоваться не
удобно, то от них переходят к концентрациям: вместо равных
химических потенциалов компонентов оперируют их равновес
ными концентрациями в жидкой и паровой фазах.
Для качественного анализа равновесия привлекают приве
денное в разд. 1 0 .3 . 1 правило фаз ( 1 0 . 1 ) , связывающее вариа
тивность q> (число степеней свободы) системы с числом компо
нентов к и фаз ф ; в случае равновесия "жидкость-пар"
"

( 1 0. 1 )
- ф + 2.
Правило фаз позволяет получить ряд полезных выводов
применительно к рассматриваемым системам в состоянии рав
новесия .
Пусть компоненты смеси полностью взаимно смешиваются
в каждой из фаз, так что общее число фаз ф = 2 (одна жидкая
и одна паровая). Тогда для бинарной смеси (к = 2), согласно
( 1 0 . 1 ) , q> = 2 - 2 + 2 = 2. Значит, в общем случае возможно
ввести (задать) два ограничения, например давление и состав
жидкой смеси; остальные величины (в данном примере - тем
пература кипения и состав паровой смеси) варьировать невоз
можно: они примут определенные значения, отвечающие приня
тым ограничениям. Это также означает, что при заданных дав
лении и температуре кипения жидкая и паровая фазы имеют
вполне определенные составы.
А вот для тройной смеси (к = 3) в принятых условиях (ф =
2)
= получается q> = 3 - 2 + 2 = 3. Следовательно, здесь произ
вольно могут быть заданы три величины (например, давление,
температура кипения и концентрация какого-либо компонента
в одной из фаз); остальные характеристики системы однознач
но примут определенные значения . Это также означает, что
при заданном давлении определенную температуру кипения
могут иметь жидкие смеси разных составов. Последний вывод
тем более справедлив для многокомпонентных смесей (к > 3).
q> =

972

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Пусть теперь компоненты бинарной смеси в жидкой фазе аб
солютно взаимно нерастворимы; тогда число фаз ф = 3: две
жидкие и одна паровая. В этом случае <р = 2 - 3 + 2 = 1 . Эrо
значит, что, например, при заданном давлении температура
кипения смеси и состав паровой фазы определены однознач
но - независимо от состава жидкой кипяшей смеси.
Качественный анализ равновесных состояний по приведен
ной выше схеме возможен также для других равновесных усло
вий и систем.
12.2.3. Равновесие для идеальных смесей

Первоначально рассмотрим фазовое равновесие "жидкость
пар" в идеальных системах: это проще и в то же время позволя
ет проследить основные тенденции и ввести ряд понятий, ис
пользуемых при дальнейшем анализе.
Идеальными называют смеси, компоненты которых при сме
шении не изменяют объема, а само смешение происходит без теп
ловых эффектов взаимодействия компонентов. Иногда считают,
что в идеальных смесях отсутствует взаимодействие молекул.
Такое представление в известной мере правомерно для паровой
фазы, когда молекулы достаточно удалены друг от друга; в
этом случае паровые смеси следуют уравнению Клапейрона
Менделеева. Применительно к жидким идеальным смесям,
видимо, правильнее говорить об одинаковом взаимодействии
друг с другом молекул как одного и того же, так и разных ком
понентов. К идеальным часто близки жидкие смеси, состоящие
из компонентов, сходных по химическому строению; пример смеси органических соединений одного гомологического ряда,
мало различаю щихся молярно й l\laccoй ( сю1жс м , бе нзол 

то луол , н - rексан-н-ге птан , метанол - этанол , фенол-крез ол ,
многие изомеры ) .
В силу отсутствия теплового эффекта смешения теплофизи

ческие свойства идеальных смесей (теплоемкость, теплота па
рообразования и т.д.) могут быть рассчитаны аддитивно по
свойствам и концентрациям составляющих смесь компонентов.
Идеальные смеси подчиняются закону Рауля, согласно ко
торому равновесное парциальное давление (упругость пара) како
го-либо i-го компонента над смесью при определенной температу
ре (pJ равно произведению его упругости пара над чистым компо 
нентом при той же температуре (Р/) на его мольную долю в
жидкой смеси (xJ:
( 12. 1 )
Заметим: по своему написанию закон Рауля сходен с законом Генри (см .
разд. 1 1 . 3 . 1 ) . Различие состоит в том, что закон Генри используется при темпе
ратурах t, превышающих критическую fкр , а закон Рауля - при докритических

973

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

температурах. Именно поэтому коэффициент пропорциональности Е в законе
Генри при t > tкр имеет некий условный смысл; в то же время физический
смысл аналоmчноrо коэффициента РР в законе Рауля ( 12 . l ) определен вполне
четко.

Сумма парциальных давлений всех компонентов паровой
смеси равна полному (рабочему, внешнему) давлению Р.
( 1 2 .2)
Р = L P; = r P;°x; .
В случае бинарной смеси
Рл = Рлох и Рв
= хл. Зависимости Рл и Рв от х, а также
i

i

=

Pвu(l - х),

где

х=

Р = Рл + Р в = Рл0х + Рв0 ( 1 - х)
( 1 2.2а)
при некоторой постоянной температуре в полном диапазоне
изменения О :::; х :::; 1 представлены на рис . 1 2. 1 : это прямые восходящая для Рл и нисходящая для РВ · В принятом способе
назначения Н КК Рл > Рв , поэтому прямая Р(х) по ( 1 2.2а) тоже
является восходящей.
Из ( 1 2.2а) можно выразить х = хл:
Х
Р - Р. о
=
( 1 2 .2б)
О
В
рА
Согласно ( 1 2.2а) и ( 1 2.2б) величине х = 1 отвечает Р = Рл0
(чистый низкокипящий компонент А), а х = О отвечает Р = Рв0
(чистый высококипящий компонент В).
Связь полного давления Р с составом паровой фазы наЙдем,
воспользовавшись уравнением идеального газа. Запишем урав
нение Клапейрона-Менделеева для i-го компонента и для
всей смеси в целом:
(а)
PN = ntRyT; PV = пRу Т;
здесь п1 и п - число молей компонента i и общее число молей
всех компонентов многокомпонентной смеси соответственно в
ее объеме V .
Поделим первое выражение на второе и произведем сокра
щение на объем V , универсальную газовую постоянную Ry и
абсолютную температуру Т. Тогда, имея в виду, что отношение
п /п равно у1 - мольной абсолютной концентрации i-го ком
понента в паровой смеси, - получим:

_

Р;

-

Р

_

-

n;

-

п

-

_

у

(,

;
о

уi _

Р;

-

Р

_

-

Р;

-- .

( 1 2.3)

L P;
i

Для бинарной смеси (i = А, В) с учетом (12.2б) имеем:
рА - Р х Р р - Р
- -- - Ул -= У -- р
р
р рАО Р.ВО

1

974

1

_

3

·

( 1 2 .За)

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

о

Х - :У

х ,у

Рис. 12. 1. К закону Рауля для идеальных бинарных систем

Рис. 12. 2. Зависимости Р(х) и Р(у) и равновесные концентрации для идеальных
бинарных систем

Из выражения ( 1 2.3а) в форме у

= Pi х/Р следует, что у ;;:: х,

Р, причем знак равенства относится к чистым
компонентам - низкокипящему (Р = Pi , х = у = 1 ) или вы

так как

Pi

;;::

сококипящему (х = у = О). Вывод о преимущественном перехо
де в паровую фазу низкокипящего компонента является част
ным выражением более общего первого закона Коновалова для
бинарных систем, гласящего :
в условиях равновесия паровая фаза в сравнении с жидкой обо
гащена тем компонентом, добавление которого к жидкости по
нижает ее температуру кипения (в другой формулировке "повышает полное давление паров ').

Более г.лубокое осмысление первого закона Коновалова позволяет трактовать
его как одно из проявлений принципа Ле-Шателъе.

Р:

Зависимость ( 1 2.3а) может быть представлена решенной от
носительно
р Pi у - р р� у = р Pi - Pi р� '
откуда
О О
рА Р,В

( 1 2 .3б)
Р = - (Р о Р. о \ " ·
рО
B f'
Гиперболическая связь Р(у) совместно с ранее найценной ли
нейной зависимостью Р(х) изображена на рис. 12.2. Разумеется, и
здесь ве
е у = 1 отвечает Р = Pi , а у = О - Р = Р� .
_

А

А

личин

Зависимости типа (12.2), (12.3) записаны для постоянной тем
пературы, так 'ПО диаrраммы на рис. 12. 1 и 12.2 - изаrермы.

975

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Для определения равновесных составов х и у нужно в соот
ветствии с правилом фаз уравнять в жидкой и паровой фазах
оба хара�сrерных параметра - давление и температуру. В изо
термической диаграмме Р - х, у для бинарной смеси темпера
туры уравнены по определению. Равновесные конuентраuии
при некотором полном давлении Р. найдем (см. рис . 1 2.2),
уравняв в фазах также и давления. Для этого следует пересечь
кривые Р(х) и Р(у) горизонталью Р. , тогда абсuиссы точек пересечен ия будут равновесными значениями х и у. При друrом
полном давлении PI получилась бы иная пара равновесных
конuентраций - х' и у '.
Реально в подавляющем большинстве случаев процессы ди
стилляции и ре�сrификации проводят при постоянном (или
примерно постоянном) давлении. Поэтому технолога больше
интересуют изобарные зависимости и диаграммы - типа t(x) и
t(y), а также некоторые другие.
С целью построения зависимости температур кипения иде
альных смесей от их состава обратимся к выражениям ( 1 2 .2б) и
( 1 2.3б). Для принятого рабочего давления Р = const будем по
очередно задаваться температурами в полном диапазоне темпе
ратур кипения чистых компонентов - высо кокипящего 18 и
низкокипящего tл:, естественно, 18 > tл. При t = t8 по ( 1 2 .2б) и
( 1 2.3б) имеем Р = Р� и получаем х, у = О - чистый ВКК. При
t = tл имеем

Р = Р�

и по тем ж:е уравнениям х, у = 1 - чис
тый Н КК. Для промежуточных температур 18 > t > tл по ука
занным выражениям при Р = const получаклся промежуточные
значения О < х < 1 и О < у < 1 - свои для каждого значения t в
диапазоне от t8 до lл. Соединив соответствующие точки, полу
чим изображенные на рис. 12.3 зависимости температур кипе
н ия (конденсации) от концентраций Н КК в жидкой (х) и паро
вой (у) фазах - кривые t(x) и t(y) при давлении Р.
Для определения равновесных составов фаз с помощью изо
барной диаграммы t - х, у (давления в фазах по определению
выравнены) необходимо уравнять еще и температуры. Для не
кой температуры t. (соответствующая горизонталь на рис .
1 2 .3) равновесные концентрации х и у получаются как абсцис
сы точек пересечения этой горизонтали с кривыми t(x) и t(y) .
При друrой температуре r: получилась бы иная пара равновесных значений х' и у '.
976

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

P = const

о

х --- у
х, у

Рис. 12.З. Зависимости t(x) и t(y) и равновес
ные концентрации для идеальных бинарных
систем

Рис. 12. 4. Влияние давления на положение
зависимостей t(x) и t(y) и равновесные кон

центрации для идеальных бинарных систем

Влияние давления на положение кривых t
х,у для бинар
ной смеси иллюстрируется на рис . 1 2.4: с повышением давле
ния возрастаюг температуры кипения обоих компонентов, так
что вся диаграмма t
х,у смещается в область более высоких
температур . При этом уменьшается расстояние между кривыми
t(x) и t(y), что приводит к ухудшению возможностей разделения:
одному и тому же х с ростом Р отвечаюr меньшие равновесные
значения у. На рисунке видно: при Р' > Р" > Р"' некоторой кон
центрашm Н КК в жидкой фазе (х) отвечаюr различные ero кон
центрации в паровой фазе, причем у ' < у" < у"'.
-

-

Понижение разделяющих возможностей с ростом давления, видимо, связано
с характером зависимости температур кипения компоне�пов от давления. По
уравнению Клаузиуса-Клапейрона•

InP 0 = a - !!_

т '

так чrо Т =

ь

a - \n P

0 ,

(б)

т.е. температура кипения с ростом давления увеличивается весьма медленно,
поскольку Р о стоит под знаком логарифма (причем для подавляющеrо боль
шинства реальных процессов переrонки а >> InP 0) . Это приводит к уменьше
нию разности температур кипения компонентов при повышении давления, а
значит, и к понижению разделяющей способности.

Продемонстрированное качественно влияние давления на
характеристики разделения бинарной смеси находит количе
ственное выражение при представлении равновесия в замкну• См. (22 ) .

977

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Puc. 12. 5. Равновесные кривые в диаrрамме

для идеальных бинарных систем при
разных коэффициеmах nазделения

у-х

х

на

Р� ,

той квадратной диаграмме у - х
пуrем введения понятия об отно
сительной летучести, иначе - о
коэффицнеmе
разделения
а.о = Р,/Рв � 1 . С этой целью в
промежуточном выражении ( 1 2.За)
у = Р� х/Р запишем Р по ( 1 2.2а) и
поделим числитель и знаменатель

вводя а.о:
( 1 2 .4)

Кривые равновесия у = f(x) по ( 1 2 .4) при постоянных а.о
представляют собой равнобочные гиперболы, симметричные
относительно диагонали , проведенной из левого верхнего угла
в правый нижний (на рис. 12.5 эта диагональ не показана). Из
выражения ( 1 2 .4) следует, что при а.0 = 1 (равные упругости
паров компонентов, а значит, и одинаковые их температуры
кипения) получается у = х, т. е. состав паровой смеси тот же,
что и жидкой - разделения не происходит. В этом случае кри
вая ( 1 2 .4) совпадает с диагональю, соединяющей левый ниж
ний угол с правым верхним, - она показана на диаграмме.
При а.0 --+ оо (летучесть Н КК бесконечно велика в сравнении с
летучестью В КК) получается у = 1 , т.е. в паровой фазе - толь
ко один Н КК. Кривая (12.4) в этом случае совпадает с верхней
горизонтальной стороной квадрата. С такой ситуацией мы
встречались в гл. 9 - растворенный компонент был абсолютно
нелетуч, и в парах присутствовал только растворитель.
На практике разделению чаще всего подвергаются смеси с
сопоставимы.ми (но не равными) температурами кипения
(значит, и уnругостями паров чистых компонентов), что отве
чает конечному значению а.о > 1 . В этом случае кривые ( 1 2 .4)
располагаются выше диагонали, причем тем дальше от нее
(лучше возможности разделения), чем больше а.0. Это означает,
что при прочих равных условиях . обогащение паровой фазы
низкокипящим компонентом выше для смесей, характеризую
щихся большей разницей в температурах кипения . А для дан
ной бинарной смеси обогащение выше при более низких дав
лениях Р, так как по указанным ранее причинам а.о возрастает
с понижением Р.

978

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Строго говоря, коэффициенты разделения щ� для идеальных смесей необяза
тельно должны оставаться постоянными в поJШом диапазоне концентраций, так
как при изменении температур кипения с изменением х упругости паров чистьIХ
компонеmов

Р�

и

Р�

мoryr изменяться в разной мере. Тогда кривые у(х)

будуr для идеальньIХ смесей несколько отличаться от равнобочньIХ гипербол. На
практике такое отличие обычно невелико.

Ранее бьmо принято, что технологический расчет процессов
перегонки бинарных смесей ведется на базе Н КК. Направлен
ный перенос НК К из жидкой фазы в паровую реализуется,
когда
равновесная
концентрация
превышает рабочую
(сопряженную). Поэтому рабочая область процессов дистилля 
ции и ректификации располагается ниже кривой равновесия. Но
концентрация Н К К в паровой смеси больше, чем в жидкой;
поэтому одновременно рабочая область
выше диагонали.
-

12.2.4. Равновесие

для

реальных бинарных смесей

В реальных системах существует взаимодействие компонен
тов - обычно слабое в паровой фазе и зачастую существен 
ное - в жидкой (различное для одно- и разноименных моле
кул). Это взаимодействие сказывается на равновесии, приводя
к отклонению от идеальности (в частности, от закона Рауля) .
Такие системы на практике встречаются значительно чаще, чем
близкие к идеальным.
Рассчитать взаимодействие между парой компонентов смеси
весьма сложно, поэтому равновесие в реальных бинарных си
стемах устанавливается экспериментально .
Различают "малые" и "большие" отклонения бинарных си
стем от идеальности.

Малые отклонения от идеальности
В случае малых отклонений от идеальности линии Р(х) пе
рестают следовать линейной (адцитивной) зависимости ( 1 2.2а).
При этом кривые Р(х) могут проходить ниже прямой (см. рис .
1 2 . 1 ), отвечающей закону Рауля (отрицательное отклонение),
или выше (положительное отклонение) , но во всем диапазоне
изменения х от О до 1 они остаются восходящ ими, как показано
на рис . 12.6. Иначе: касательная к КР.ИВОЙ Р(х) здесь всегда
образует острый угол с осью х, т.е. d P/dx > О . Такие смеси на
зываются зеотропными.
Растворы (жидкие смеси) первого типа образуются и з смешиваемьIХ компо
неmов с выделением теплоты, так 'ПО теплота парообразования смеси превышает
рассчитанную аддитивно по составу смеси. Значит, образование паров из такой
жидкой смеси затруднено. Иными с.ловами, в этих растворах связи межцу моле
кулами разньIХ компонеmов сильнее, нежели межцу одинаковыми молекулами ,
поэтому упругость паров над смесью понижена в сравнении с рассчитанной по
аддити вности.

979

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 12. 6. Диаrраммы Р(х) для реальных бинар

i, h

о

1 - прямая, сл11дующая закону Рауля; (-) и (+)
- отрицательное и полоJ1СJПСЛЪное ОТJСJ1он11юrя от

ных смесей :

закона Рауля

Рис. 12. 7. Диаrраммы
температура-состав

энтальпия-состав

и

о

а ,а'

--

Растворы второrо типа образуются с поглощением теплоты , так <по теплота
парообразования смеси меньше рассчитанной по аддитивности. Значит, образова
ние паров из такой жидкой смеси облеrчено. Иными словами, в этих растворах,
наоборот, связи между молекулами разных компонентов слабее, нежели между
одинаковыми молекулами, - поэтому упруrость паров над смесью вьпuе рассчи
танной по аддити вности.

Кривые Р(х) и Р(у) для реальных смесей определяКУГСя из
эксперимента.
Кривые t(x) и t(y) тоже определяются экспериментально;
они качествен но сходны с приведенными на рис . 12.З
(являются нисходящими в полном концентрационном диапазо
не), но их конкретная форма зависит от свойств компонентов.
Кривые равновесия в диаграмме у-х мoryr отличаться от сим
метричных (относительно нисходящей диагонали) гипербол,
иначе говоря , ао = ао(х).
Первый закон Коновалова сохраняет смысл, характерный
для идеальных смесей: в равновесном состоянии паровая фаза
в сравнении с жидкой обогащена низкокипящим компонентом.
Равновесные составы фаз с помощью диаграмм t-x, у и у-х
определяют графически - таким же построением , как и для
идеальных бинарных смесей.
В ряде случаев удобно представить равновесие в диаграммах
типа свойство-состав, конкретно - в диаграмме энтальпии
концентрации. При этом в качестве концентраций используют
мольные абсолютные величины х и у либо (чаще - см. разд.
12.8) массовые абсолютные а и а ' - для жидкой и паровой фаз
соответственно. Обозначим энтальпию паровых смесей h =
980

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

= h(a') а жид ки х - i = i( a) . Тогда упомянугая диа грамма и меет
вид , п'оказанный на рис . 1 2 .7 совместно с д иагра ммой t - а, а �

Энталъпийные кривые Д11Я пара h(a ) и жидкости i(a) строятся по экспери
ментальным данным; как правило, это кривые, выпуклость которых зависит
преЖде всего от формы температур ных кривых t-a, а ', знака разности теruюем
костей компонентов (ел - св) и теплот парообразования смесей. Приближенно
энтальпии могут бьпъ аддитивно рассчитаны Д11Я отдельных концентраций (см .
разд. 6. 1 , 9. 3 и 1 0 .2.2); далее по найденным значениям можно построить упомя
нутые энтальпийные кривые. Строже - должны бьrrь )"Пены теплоты смешения
компонентов, а также изменение теплоемкостей и теплот парообразования с
температурой·.

Равновесные точки на энтальпийных кривых соединяются
нодами (здесь - изотермами); способ их r:остроения с привле
чением диаграммы t - а, а ' (ил и t - х,у - при испол ьзовании
мольных концентраций) ясен из рис . 1 2 .7 . Изотермы, соеди
няющие пары равновесных концентраций, изображены на ри
сунке штриховыми линиями . Это - вертикали для чистых
компонентов (х, у = О; 1 ) и наклонные (непара.ллельные) прямые
в промежугочной области О < х, у < 1 ; наклон изотерм зависит
от формы кривых t-x, у, т.е. от свойств компонентов и их сме
сей . Таюtм образом , энтальпийная диаграмма включает кривые
h(a ) , i(a) и поле изотерм (равновесных над).
В энтальпийной диаграмме, разумеется , может быть отраже
но наличие азеотропа или гетероазеотропа (см . н иже) .
Большие отклонения от идеальности
Для некоторых смесей отклонения от идеальности бывают
столь велиюt, что кривые Р(,х) проходят через экстремум. Кон 
кретное значение х для точюt экстремума зависит о т свойств
компонентов. Диаграммы Р(х) с экстрем}rмом давления
(максимумом или минимумом) показан ы на рис . 1 2 . 8 , а, г.
Смеси с экстремальн ым отклонением от идеальности следуют
второму закону Коновалова (см. рис . 1 2 . 8 , а, б, г, д) : максимуму

на кривой давления отвечает минимум на кривой температур
кипения; минимуму на кривой давления отвечает максимум на
кривой температур кипения.
Рассмотрим несколько подробнее системы с максимумом
давления и минимумом температуры кипения (он и встречаются
чаще). На кривой Р!.х) налицо две ветви (рис . 1 2 . 8 , а ) - восхо
дящая (для нее d P/d.x > О) и нисходящая (d P/d.x < О), а также
точка максимума, где касательная горизонтальна и d P/d.x = О.
На диаграмме t-x, у (рис . 1 2 . 8 , 6) первая область, как и в случае
зеотропных смесе й , в состоянии равновесия характеризуется
неравенством у > х. Однако для второй области у < х, т.е. па• См. (22 ] .

98 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

р

р
р�

d P/dx = O

о

х

�

О

-

у>х

А

А

1

tв

б

о

Х

О

х,у

-

в

Рис. 12. 8. Диаrраммы Р-х (а,г), t-x,y (б,д) и

смесей

р�

г

tд

,
r.-

о

Р1

а

tв

lаз

dP/dx> O

х,у

-

Хе

у-х

1

А

tд

А

(в,е) для азеотропообразующих

ровая фаза в сравнении с жидкой обогащена высококипящим
компонентом. Если для dP/dx > О справедливо у > х, а для
dP/dx < О верно у < х, то резонно предположить, что равенству
dP/dx = О отвечает у = х, т.е. равенство равновесных концент
раций в жидкой и паровой фазах при определенном составе
жидкой смеси Хаз. Смесь такого состава называют азеотропной
(или нераздельно кипящей), а смесь компонентов, имеющую
азеотропную точку А при некоторой концентрации Хаз, - азео
тропообразующей. На диаграмме у-х (рис . 1 2.8, в) для такой
смеси также существуют области у > х и у < х; азеотропу (у =
= х) соответствует то ч ка пересечени я линии равновесия с
диагональю.

982

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Обогащение паровой фазы во второй области высококипящим компонентом
не с.ледует тракrовать как нарушение первого закона Коновалова. Просто азео
тропная смесь в приведенном примере рассматривается как "отдельный компо
нент" - более летучий (низкокипящий), чем оба чистых компонента. И паровая
фаза в сравнении с жидкой в обеих областях обогащена именно этим лет)l'fим
"компонентом" - в строгом соответствии с первым законом Коновалова в его
полной формулировке (см. разд. 1 2.2.3).

Физический смысл второго закона Коновало.ва поясним, со
поставляя фрагменты рис. 12.8, а, б. Азеотропная смесь с кон
центрацией Хаз кипит при некоторой температуре t = lаз. Это
означает, что при !аз упругость паров азеотропной смеси Раз
равна внешнему давлению. Смесь любого иного состава (х > Хаз
и х < Хаз) при температуре !аз, как видно из диаграммы Р-х на
рис. 12.8, а, дает более низкую упругость паров Р < Раз ; такая
смесь при данном внешнем давлении кипеть не будет. Чтобы
она закипела, необходимо повысить упругость ее паров до
внешнего давления - это можно сделать, увеличивая ее темпе
ратуру сверх !аз. Значит, температура кипения любой смеси,
отличающейся по составу от азеотропной, будет выше !аз.
Иными словами, именно для смеси азеотропного состава (ему
отвечает максимум давления Раз) температура кипения !аз будет
минимальной.
Аналогичный анализ можно провести для азеотропных сме
сей с минимумом давления и максимумом температуры кипения.
В энтальпийной диа11>амме существование азеотропа отражается наличием
вертикальной изотермы в азеотропной точке - тогда здесь у = х; при работе с
массовыми концентрация ми а = а '.

Составы азеотропных точек, зависящие от свойств компо
нентов, смещаются при изменении давления в соответствии с
правилом Вревского: в случае смесей с минимумом температур
кипения при повышении давления увеличивается концентрация
компонента с большей мольной теплотой парообразования, а в
случае смесей с максимумом температур кипения - с меньшей.
Смещение точки азеотропа с изменением давления может
быть использовано для разделен ия азеотропообразующих сме
сей, в том числе смесей азеотропного состава, на весьма чис
тые компоненты.
Смеси взаимно нерастворимых компонентов
Согласно правилу фаз, как показано в разд. 1 2 .2 . 2 , в случае
взаимно нерастворимых в жидкой фазе компонентов равновес
ный пар имеет постоянный состав - независимо от состава
жидкой смеси. Это утверждение справедливо для всего диапа
зона концентраций жидкой смеси, разумеется,исключая чистые
В КК и Н КК (х = О ; х = 1 ). Тогда в пар ах - тоже чистые ком
поненты (у = О ; у = 1 ) . Именно поэтому в дщ lграмме Р(х) на

983

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

р

Р&
t

о
о
Р = Рд + Рв

Р1

о

Р&

рис. 12.9, а (и на других фрагментах
этого рисунка) линии Р1 и Р�
условно не доведены до вертикалей,
отвечающих чистым компонентам.
Обозначим мольную концентра
цию Н КК в паре Ys. массовую - as ' и
найдем состав пара. В рассматри
ваемом случае поведение каждого
компонента не зависит от присут
ствия другого; их парциальные дав
ления РА или Рв пр\1 определенной
температуре для смесей любого со
става равны соответственно упру
гостям паров чистых компонентов
Р1 или Р� при той же температуре .
Значит, полное давление над смесью
(в отсутствие инерта, конечно) по
закону Дальтона Р = РА + РВ в рас
сматриваемом случае составит:

рО

А

--х--

а

tв

tл
о

Y·t

Рис. 12.9. Диаrраммы Р-х (а), t-x,y (б) и у-х
(в) для взаимно нерасrворимых компоне�по в

о

х,у

-

б

Ys

Р = Р1

+

Р�

(в)
По ( 12.3) УА = рлfР. Тогда для со
стояния равновесия (ул = Ys) получа
ются мольные составы пара - по
Н КК и В КК:

х

в

рО
рО
А
У.1 = _л_ =
'
р
р о + Р,Во
А

1

-

Ys =
'

Р,ВО

рАО + Р,Во

·

.

( 1 2 . 5)

рассчитывается по У.1·
согласно формуле пересчета, приведенной в разд. 1 0.2. 1 :
Массовая концентрация Н КК в паре
аs ' =

as

Ys MA
.
)М
У
(1
+
- s
в '
YsMA

после подстановки значения Ys по ( 1 2 . 5) и сокращения на
( Р1 + Р� ) имеем:
аs ' =
984

( 1 2 . 5а)

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Напомним: жидкость кипит, когда упругость паров равна
внешнему да вл ению, а упругость паров растет с температурой .
Для жидких смесей из взаимно нерастворимых компонентов
упругость паров согласно (в) всегда выше, чем для любого из
компонентов: Р > Р , Р . Поэтому температура кипения рас
сматриваемых смесеи всегда ниже, чем для ИНдИВидуальных ком
понентов: t < tл, tв. И поскольку во всем диапазоне концентраций
(исключая х = О; 1) суммарная упругость паров Р = const, то в
этом концентрационном диапазоне и температура кипения смесей
t = const - см. рис. 12.9, б, где приведены также кривые t(y). В
этом диапазоне у = Ys = const - см. рис. 12.9, в.
Абсолютно взаимно нерастворимых компонентов теоретиче
ски не существует. К таковым относят компоненты, раствори
мость которых друг в друге ничтожно мала, так что практиче
ски ее можно игнорировать.

� �

Гетероазеотропные смеси

Гетероазеотрооными называют смеси компонентов, ограни
ченно растворимых друг в друге. Если к жидкому высококипя

щему компоненту добавить небольшое количество низкокипя
щего, то образуется раствор Н КК в В КК. Однако при даль
нейшем добавлении Н КК может наступить насыщение - пусть
оно характеризуется абсолютной мольной концентрацией Н КК
в смеси х/ Аналогично: при небольшом количестве высококи
пящего компонента, добавленного к низкокипящему, образу
ются растворы В КК в Н КК, пока не возникнет насыщение;
обозначим концентрацию Н КК в такой насыщенной смеси xs "·
Таким образом, диапазоны О - Xs ' и Xs " - 1 характеризуются
взаимной растворимостью компонентов - это rомоrенные сме
си; напротив, в гетерогенной области концентраций Н КК от х� '
до Xs " компоненты взаимно нерастворимы: любая жидкая смесь
в этой области расслаивается на насыщенные растворы с кон
центрациями Xs ' и Xs ".
Диаграммы Р-х, t-x, y и у-х для рассматриваемых смесей
приведены на рис. 12. 1 0. На диаграммах имеются области пере
менных упругостей паров, температур кипения и составов па
ров - в диапазоне гомогенных растворов, и область постоян
ных суммарной упругости пара, температуры кипения и состава
пара (горизонтальные плато) - в гетерогенном диапазоне. В
последнем суммарная упругость паров Р выше, а температура
кипения t ниже, чем для обоих чистых компонентов.
Гетероазеотропные смеси мoryr считаться общим случаем,
включающим в качестве частных смеси как с а�еотропом, так и
из взаимно нерастворимых компонентов. В самом деле :
- при смещении точек S' и S" к точке S (т.е. при стягива
нии горизонтального плато S'S" в точку) получается азео
тропная смесь;
985

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

р

о

Рис. 12. 10. Диаrраммы Р-х (а), t-x,y ( 6) и у-х
( в) для смесей с оrраниченной взаимной рас

о

творимостью компонекrов

Р=Рл + Рв
РХ

Р&
t

о

tв

Xs

х

а

Xs

- при смещении точки s· к верти
кали х = О и точки S" к вертикали х =
= 1 приходим к смеси взаимно нераст
вори мых комп онентов.
для

12.2.5. Равновесие
мноrокомпонентных систем

Мноrокомпонентные ( к > 2) двух
фазные (ф = 2) системы хара:ктери
зуются векторами (наборами) кон 
tл
центраций в каждой фазе: состав
жидкой фазы Х(хл, хв, . . . , хк) , состав
паровой фазы У(ул, Ув, . . . , Ук.) . Условимся в дальнейшем именовать ком
поненты А, В , . . . , К
в порядке
нарастания их температур кипения: tл<
< tв < . . . < tк. Каждому составу мно
гокомпонентной жидкой фазы Х отвечает определенный равновесный
состав паровой фазы У (и наоборот) .
В случае тройных смесей для пред
ставления равновесия (и для техноло
гических расчетов) удобно воспользо
ваться треугольной диаграммой (см .
разд. 1 0 .2). В вершинах равносторон 
него треугольника (рис . 1 2 . 1 1 ) - индивидуальные компоненты А, В и С,
на сторонах - бинарные смеси АВ , ВС и АС, внутри треуголь
ника - тройные смеси АБС . На рисунке также приведены
диаграммы t-x, у для каждой из упомянутых бинарных смесей .
Равновесные составы отдельных бинарных смесей , как по
казано в разд. 12.2.2, получаются при проведении в этих диа
граммах прямых t = const и фиксации их точек пересечения с
кривыми t(x) и t(y). Пусть надо знать равновесие при некото
рой температуре tъ причем lл < t2 < tв. Тогда равновесные со
ставы могут быть зафиксированы для двух бинарных смесей :
АВ и АС; спроецировав эти составы на соответствующие сто
роны треугольника - АВ и АС, - получим на них точки
(отдельно для жидкой и паровой фаз), отвечающие температуре
t2. Очевидно, изотермы t2 для тройных смесей АБС есть линии
внутри треугольника, соединяющие упомянутые пары точек на
его сторонах. Аналогичным образом строятся изотермы для

уt

986

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 12. 1 1. Равновесие в идеальных трехкомпонеН"Пii.iх системах

других температур, например t1 и /3 (на рисунке /1 < t2 < /3 );
полная диаграмма содержит семейства изотерм (для жидкости
и пара) в диапазоне от /л до tc.
Для идеальных систем изотермы
прямые; на рис . 12 . 1 1 они
показаны полужирными линиями применительно к паровой
фазе и жирными - применительно к жидкой . Равновесные
составы жидкой и паровой фаз характеризуются точками (для t2
L и S), делящими одноименные изотермы в одинаковом
соотношении. Для реальных смесей изотермы пара и жидкости
- кривые линии; равновесные составы фаз для каждой пары
изотерм точнее всего определяюrся экспериментально. Су
ществуюr и расчетные методы * , · позволяющие по равновесию
бинарных смесей оценить равновесие тройных; часто это
удается сделать достаточно точно, поскольку именно бинарные
взаимодействия вносят основной вклад в поведение тройных
систем.
В случае к > 3 концентрационные и равновесные представ
ления теряют наглядность: для четырехкомпонентной смеси
требуются построения в правильном тетраэдре, т.е. в трехмер
в многомерном пространстве.
ном пространстве, а для к > 4
Здесь многокомпонентные системы представляюr как набор
тройных смесей, каждая из которых изображается (изотерми-

-

-

• См. (9, 20, 26 J .

987

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ческие линии, равновесные составы фаз) в своем концентра
Детально эти вопросы изложены в специонном треугольнике.
циальнои литературе • .
Выше рассмотрены зеотропные см еси В трех- и многоком
понентных смесях мoryr существовать азеотропы и гетероазео
тропы
бинарные, тройные, многокомпонентные; их рассмот
рение выходит за пределы учебника.
В настоящее время разработаны непростые; но достаточно
надежные модельные подходы • , позволяющие по своиствам
бинарных и тройных смесей предсказывать свойства весьма
сложных многокомпонентных систем и рассчитывать их равно
весие.
u

.

-

u

1 2.3. ДИСТИJUIЯЦИЯ
1 2.3. 1 . Общие положения

Под дистилляцией понимают процессы переноса компонента
(компонентов), осуществляемые между жидкой и паровой фа
зами в отсуrствие противотока этих фаз. Дистилля ция представ
ляет собой частичное испарение (при температуре кипения)
жидкой смеси; пар при этом в соответствии с первым законом
Коновалова обогащается низкокипящим (Н КК) компонентом
(или азеотропом с минимумом температуры кипения), а жид
кий остаток - высококипящим (ВКК) компонентом (или азео
тропом с максимумом температуры кипения). В этом и состоит
эффект разделения. Полное испарение жидкой смеси к разде
лению не приводит, так как пар получается того же состава,
что и исходная жидкость. Такой процесс имеет практический
смысл, когда исходная жид кая смесь содержит нежелательные
малолетучие примеси (скажем, смолистые вещества) , не пере
ходящие в паровую фазу, - в этом случае полная дистилляция
позволяет от них избавиться.
Процесс, обратный дистилля ц ии, состоящий в частичной
конденсации паровой смеси, называется парциальной конденса
цией. В ходе такого процесса, также в соответствии с первым
законом Коновалова, в конденсат преимущественно переходит
В КК, так что конденсат в сравнении с исходной паровой
смесью обогащается высококипящим компонентом, а нескон
денсировавшийся пар - низкокипящим.
Если отслеживать общее направление межфазного переноса
какого-либо из компонентов исходной смеси, то дистилляцию
и парциальную конденсацию следует трактовать как однона
правленные процессы переноса.

•

988

См. (3, 9, 20, 24, 26 ) .

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Процесс дистилляции (в меньшей мере - парциальной кон
денсации) достаточно широко представлен в химической тех
нологии и близких к ней отраслях промышленности (пищевой,
фармацевтической и др .), прежде всего:
в относительно малотоннажных производствах, осу
ществляемых преимущественно в периодическом и полунепре
рывном режимах;
- в процессах, не требующих получения высокочистых ко
нечных продукrов.

Основные элеме1пы 1'онструкm11•н020 оформ.сешUI • процессов дИСТИ/lЛЯЦИИ и
парЦиальной конденсации - это дистИJVIЯционные кубы, снабженные обогре
вающими устройствами, обеспечивающими нагрев и кипение жидкой смеси ;
конденсаторы; при необходимости - дополнительные теплообменники; ем
кости; насосы.
ДиС111JJJJ 11ЦИоннwй куб представляет собой сосуд с теплообменным устрой
ством в нижней части - встроенным или выносным . Возможные конструкции
'
этих теплообменников (кипятильников) - от паровых рубашек и змеевиков до
кожухотрубных аппаратов - рассмотрены в rл.7; они в общем сходны с тепло
обменными устройствами, используемыми в процессах вьmаривания, прежде
всего - периодического (см. rл. 9). Отличительная особенность диСТИ11ЛЯ цион
ного куба - паровое пространство над поверхностью жидкой смеси.
Конструкции конденсаторов и допол111ПеJ11онwх теплообменников (подогре
вателей, холодильников), вьmолненных в различных вариа1ПЗХ в зависимости
от особенностей диСТИ/lЛЯционного процесса, также приводятся в rл. 7 .

Технологические схемы процессов дистилля ц ии весьма раз
нообразны. В учебнике подробно рассмотрен инженерный рас
чет лишь некоторых из них· , ряд схем только упомянут
(пояснена их сущность).
В целях простоты изложения ниже анализ и расчет процес
сов проводятся на примере дистилля ции бинарных смесей. По
КФ-классификации такие смеси относятся к классу 2(2-2)2. В
ходе анализа с равным основанием мо rут быть использованы
мольные (х, у) и массовые (а, а ) концентрации Н КК в жидкой
и паровой фазах. Поскольку равновесные данные в литературе
представлены в основном для мольных концентраций, то мате
риальные расчеты чаше всего ведут в мольных величинах
(потоках, концентрациях). Вместе с тем удельные теплофизи
ческие свойства компонентов и фаз в справочниках обычно
отнесены к единице массы; поэтому тепловые расчеты чаще
ведут на основе массовых величин . Подчеркнем: в подавляю
щем большинстве процессов дистилляции отсутствует инерт;
поэтому расчеты ведут на всю смесь, т.е. используют абсолют
ные концентрации.

•

Сведения о таких элементах, а также других схемах дистИJVIЯции и их тех
нолоmческом расчете содержатся в учебной и научной литературе ( 1 , 2, 6, 7, 12,
19, 2 1 и др. ) .

989

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

При анализе процессов дистилляции используется следую
щая терминология:
- исходная смесь в жидком (реже - в парообразном) состоя
нии;
- дистиллят (или дистиллат) - отводимые при кипении
жидкости парообразные продукгы; так же именуются жидкие
продукгы, получаемые после конденсации паров;
- кубовый остаток - жидкость, остающаяся в кубе в ходе и
в результате процесса дистилля ции.
При проведении парциальной конденсации вместо термина
"кубовый остаток" иногда используют термин "конденсат" .
12.3.2. Простая дистилляция

К процессам простой дистилля ции относятся постепенная
(иногда - с отбором отдельных фракций) и однократная.

Постепенная дистилля ц ия

Техволо111Ческая схема периодическоrо процесса. Схема пока
зана на рис. 1 2 . 1 2 . В дистилля ционный куб 1 с теплообменным
устройством (кипятильником) заливается исходная бинарная
смесь в количестве 4. молей с начальной концентрацией Н КК
Хн при температуре fo. Через теплообменную поверхность под
водится теплота Q. Сначала жидкость, как видfю из рис. 1 2 . 1 3 ,
нагревается до начальной температуры кипения lн (стадия на
грева без изменения агрегатного состояния), а затем происхо
дит испарение части жидкости с понижением в ней кон цент
рации Н КК и повышением температуры кипения (стадия ди
стилляции) . Образующиеся пары отводятся из дистилля ционно
го куба немедленно - в момент их образования. Пары поступа
ют в конденсатор-холодильник 2, после которого в виде жид
кого дистиллята собираются в приемнике 3. В конце стадии
дистилля ц ии количество оставшейся в кубе жидкости равно Lк,
концентрация Н КК в ней - Хх., а конечная температура кипе
ния - tx ; концентрация Н КК в дистилляте составля ет Хд, а
количество последнего - П . Постепенному изменению кон
центрации Н КК х в кубовой жидкости сопутствует изменение
его концентрации у в паровой фазе. Идеализируя процесс ди
стилля ции, будем считать, что в каждый момент стадии ди
стилля ц ии текушие концентрации Н КК в жидкой и паровой
фазах равновесны. Такое допущение отвечает медленной ди
стилляции или очень большой поверхности контакта паровой и
жидкой фаз - тогда успевает установиться межфазное равно
весие, и массообмен происходит в условиях потоковой задачи.
Материальный расчет. В задачу материального расчета вхо
дит выявление связи между характерными количествами фаз и
990

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 12. 12. Схема простой постепенной дистил

ляции:

дисrилляционный куб, 2
1
холодилыnпс:, З присмиих дисrиллята
-

-

коНдснсатор 

-

Рис. 12. 13. К расчету простой постепенной ди

стилля ции

их концентрациями, в частности - определение хд. Для
отыскания указанной связи составим материальные балансы
для контура К (см. рис. 1 2 . 1 2) за весь процесс дистилляц ии,
начиная отсчет времени после загрузки исходной смеси в куб и
заканчивая его до выгрузки кубового остатка. При этом коли
чеством паровой фазы (мольным, массовым) в кубе над жид
костью пренебрегаем, поскольку плотность пара на 2-3 поряд
ка ниже, чем жидкости. Тогда
по количествам исходной смеси и продуктов (Пр = О ,
Ух = П , Нак = Lк Lн):
(а)
О П = Lк Lн, ил и П = Lн Lк;
по количеству Н К К ( Пр = О, Ух = Пхд, Нак = Lк.Хк - Lнхн):
О Пхд = Lк.Хк Lнхн. или Пхд = LнХн lкХк·
(6)
выразить
хд:
частности,
в
Из (б) и (а) можно,
-

-

-

-

-

-

-

( 1 2.6)

Последнее уравнение, однако, нельзя еще считать расчет
ным, так как в условиях задачи, как правило, известны обе
начальные величины Lн и Хн , но лишь одна из конечных - Lк
либо Хк· Поэтому задача дистилля ции обычно формулируется в
одной из двух постановок: надо вести процесс до тех пор, пока:
- концентрация Н КК в кубе не понизится до заданной ве
личины .xic;

99 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

- количество остающейся в кубе жидкости не упадет до Lк
молей .

Разумеется, возможны и иные постановки задач дистилля ц ии, например
связанные с получением дистиллята заданного состава хд; тогда определению
подлежат обе конечные величины - Lx и Хк·

В любом случае для решения задачи в дополнение к ( 1 2 .6)
необходима еще связь Lк и Хк . Эту связь установим тоже из
материальных балансов для контура К (см. рис. 1 2 . 12), но за
бесконечно малое время d't и с привлечением равновесных
данных (рис. 12. 1 3) .
По количествам смесей (фаз):
(в)
d П = dL, или d П = dL;
О
по количествам Н КК [Уход его с паровым потоком dП равен
уdП; при текущем (к моменту времени 't) количестве НКК в
кубовой жидкости Lx его Накопление за время d't составит
d(Lx)] :
(г)
О уdП = d(Lx),
причем у изменяется соответственно х, оставаясь равновесным
с ним.
Раскроем в (г) дифференциал произведения и разделим пе
ременные, подставив -dL вместо d П :
dL
dx
+ ydL = Ldx + xdL и
(д )
L
у-х
Интегрируя в пределах от начала до конца стадии дистилля
ции, получим для процесса в целом:
-

-

-

-

Lк

Хfк

=

--

ln---1L Хн dx

L
dx
( 1 2 .7)
,
, или
J
Lк х у - х
хн у - х
Lн
к
причем пределы интегрирования поменяли местами, чтобы
оперировать положительными величинами.
Если интеграл взять не до конца процесса, а до некоторого
текущего момента стадии дистилляции, когда количество жид
кости в кубе равно L, а концентрация Н КК в ней - х (Lн >
> L > Lк, Хн > Х > Хк ), то
Х н dx
L
( 1 2.7а)
Jn ---1L J
.
L
х у - х
f

dL
L

-

=

=

--

=

--

--

Выражение ( 12.7) дает искомую связь Lк и Хк· При этом ин
теграл вычисляем (графически или численными методами),
задаваясь поочередно некоторыми значениями х в промежутке
от Хк до Хн (х ', х " и т.д.) и отсчитывая для каждого х по диа
грамме у-х равновесные значения у (у ', у" и т.д.) - см. рис .
992

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

1 2 . 1 3 . Если по условиям задачи задана концентрация .хк, то
первоначально вычисляют значение интеграла в правой части,
а затем при известном � находят Lк. Если же задано Lк
(нечастый случай), то приходится подбирать . такой нижний
предел интегрирования .хк, чтобы интеграл в правой части
( 1 2 . 7 ) оказался равным известной левой части.
Заметим: если дистиллируемая смесь является идеальной, то
интеграл в правой части ( 1 2 .7) удается взять в квадратурах, т.е.
получить аналитическую связь Lк и Хк·
Подставляя теперь в ( 12 .6) отвечающие друг другу значения
Lк и .хк, находим концентрацию Хд.
Тепловой расчет. Он включает в себя определение количеств
теплоты Q и теплоносителей. В качестве греющего аrента чаще
всего применяют водяной пар под давлением - обозначим его
энтальпию hrp, температуру конденсации Т. Тепловой расчет
ведется раздельно для разных стадий.
Расчет стадии нагрева кубовой жидкости полностью анало
гичен подробно изложенному в разд. 7. 1 5 . 1 1 и 9. 5 . 1 для перио
дического нагрева жидкости. Приведем здесь кратко основные
вехи и результаты анализа. Затраты теплоты на этой стадии
при теплоемкости исходной жидкой смеси с8 и изменении ее
температуры от to до /8 составляют
( 12.8)

причем о способах вычисления теплофизических свойств жид
ких и паровых смесей (по их составу), входящих в это и после
дующие соотношения, сказано в разд. 6 . 1 , 1 0 .2.2 и 1 2.2. 1 .
Если теплоемкость конденсата греющего пара равна с ; , то
расход его на стадии нагрева
Dн

где rrp

-

=

Q=н'°'---

_
_

*

=

Q_
н
_

hrp - с к Т

( 1 2 . 9)

теплота конденсации rреющеrо пара.

Поверхность нагрева F определим из уравнения теплопере
дачи для кубовой жидкости. Поскольку ее температура t пере
менна, то тепловой баланс записывается для элементарного
промежугка времени d't, за который температура нагреваемой
жидкости изменится на dt:
dQ = �cнdt = kн,( Т - t)Fd't,
где kн
ко эффициент тепло передачи от rреющеrо пара к наrреваемой исходной
смеси (далее kн приближенно принят неизменным в ходе рассматриваемой ста
дии) ; температура конденсации rреющеrо пара Т = const определяется по задан
ному ero дамению.
-

993

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Оrсюда

�=
Т-t

kн F

L н Си

d't ,

и после интегрирования (с учетом знака "минус" у температуры
t в знаменателе) от О до конца стадии нагрева ('t = 'tн ) и от t0 до
1н имеем:
ln

Т - to
Т - fн

= Lkн FtС
н

и

и

F't = L н С и
kн

ln Т - to .
Т - lн

(12. 1 0)

Расчет стадии дист и.лл.я ц ии более сложен , так как теплофи
зические свойства фаз, зависящие от их состава, изменяются
во времени вслед за изменением состава. Запишем тепловой
баланс для разделяемой смеси, заключенной в контуре К, разумеется, в дифференциальной форме (для временного ин
тервала d't). Здесь Приход теплоты от теплообменной поверх
ности составляет dQ, Уход ее с парами ( их текущая энтальпия
h зависит от кон центрации Н КК в парах у) равен hdП , Накоп
ление при текущих теплоемкости с и температуре кипения t
будет d(Lct). Тогда после замены d П = -dL :
d Q - hd П = d( Lct) и d Q = -hdL + d(Lct) .
Интегрируя от начала до конца стадии дистилля ции, полу
чим затраты теплоты на эту стадию (для первого интеграла в
правой части поме няем местами пределы интегрирования, что
бы избавиться от знака "минус"):

Qд

Lн

= J h dL

+

( Lкскtк - Lнсн tн ) ·

( 1 2. 1 1 )

Lк

Икrеrрал, входящий в ( 12. 1 1 ) , берется графически или численными метода
ми. Для этоrо задаются некоторым текущим значением состава кипящей жид
кости х ' в промежутке ме.жду Хк и Хн · Далее, с одной стороны, по уравнению
( 1 2.7а) рассчитывают отвечающее ему количество кубовой жидкости L; с другой
стороны, по х ' находят равновесное ему значение у ' и по этой концентрации
определяют текущую энтальпию пара h '. В результате получают сопряженные
значения h ' и L '. Повторяя эту операцию для друrой текущей концентрации х ",
находят друтую пару сопряженных значений h " и L" и т.д. - в полном диапазо
не х от Хк до Хн, т.е. от Lк до Lн. А располагая связью h и L в указанном диапа
зоне, отыскивают значение икrеrрала.

Для последующего расчета шлребуется знать текущее значение
Q; в этом случае интеграл надо брать до текущего значения L :

Q

Lн

=

J h dL + (Lct - Lн сн tн) .

L

·

( 1 2 . l la)

Определение поверхности теплообмена на стадии дистилля 
ции требует записи уравнения теплопередачи для контура К за
994

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

бесконечно малый интервал времени:
dQд = kд( Т - t)Fd-r:,
где коэффициент теплопередачи на стадии дистилляции kд яв
ляется в принципе переменным, поскольку изменяется состав
кубовой жидкости .
Решая последнее уравнение относительно Fdc и интегрируя
по всей стадии дистилля ц ии (ее продолжительность обозначим
'tд) , имеем:
dQ
Fdc =
( 1 2 . 12)
и
kд (Т - t)

Интеrрал в ( 1 2 . 1 2) также беруr, задаваясь промежуrочными значениями х и
определяя соответствующие им значения Q и 1/[kд( Т - t)) . Текущему значению
х = х' отвечает текущее количество теплоты Q', найденное по ( 1 2 . l la). Этому же
значению х соответствует текущая температура кипения t '. Текущее значение
коэффициента теплопередачи k ' определяется способами, изложенными в
разд.7. 3.2, а необходимые д11Я этого теплофизические свойства расс'Df!Ъmаются
по составу смеси х'. Такие операции повторяют д11Я х·: х"' и т.д. и находят иско
мое значение интеrрала - rрафически или численными методами.

Очевидно, что величина F на стадиях нагрева и дистилляции
одна и та же, а величины 'tн и 'tд - различны (-�:д > 'tн , посколь
ку на испарение требуется существенно больше теплоты, неже
ли на нагрев). В задачах эксплуатации при известной F опреде
лению подлежат 'tн и 'tд. В задачах проектирования технолог
имеет возможность варьировать F и 'tю 'tд , так как расчет по
( 1 2 . 1 0) и ( 1 2 . 1 2) дает их произведения .
Определение расхода хладоагента G н а конденсацию пара
покажем на примере охлаждающей воды (ее теплоемкость Св ) · Пусть вода входит в конденсатор с температурой tв ' и выхо
дит из него с tв ". Количество теплоты Qконд• забираемой водой
от конденсирующегося пара за весь процесс, получается из
теплового баланса для конденсирующихся паров. По их резуль
тирующему составу хд определим теплоту конденсации паров
rд , и тогда можно записать сразу:
( 1 2 . 13)
Qконд = Пrд.
Расход охлаждающей воды наЙдем из теплового баланса:
G

=

Q конд
. ( 1 2 . 14)
с в (t"в - t'в )

Поверхность теплообмена конденсатора Fконд определяется
тем же путем, что и F для дистилляционного куба на стадии
собственно дистилляции .
Дистиллят при постепенной дистилляции можно по ходу
процесса собирать в разные приемники З, составы дистиллятов
995

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

в них будуr, естественно, различными: первые отобранные
фракции - богаче низкокипящим компонентом, нежели по
следующие. Такой процесс постепенной дистилляции называют
фракционированной дистилляцией. Расчет этого процесса ведет
ся по изложенной выше канве, но пофракционнд.

Однократная дистил.л.яция
Технологическая схема. Схема непрерывного процесса пред
ставлена на рис. 1 2 . 14. Поток исходной смеси Lн состава Хн
проходит подогреватель-испаритель 1, где нагревается от на
чальной температуры to до парожидкостного состояния при
конечной (рабочей) температуре tк (т.е. выше начальной темпе
ратуры кипения этой смеси fн)· При температуре fк парожид
костная смесь подается в сепаратор 2, и там в изотермических
условиях происходит равновесное разделение жидкости (точка
М на рис. 12. 1 5 , а) состава Хк и пара (точка N) состава Ук·
Жидкостной поток Lк отводится снизу сепаратора, а паровой
поток П н аправляется в конденсатор-холодильник 3, после
которого в жидком состоянии при темпер атуре tд собирается в
промежуrочной емкости 4, откуда отправляется к потребителю.
Схематически ход процесса показан на рис. 12. 15, а, где в
диаграмме t-x, у точка А (неюmящая жидкость) отвечает исход
ной смеси до подогрева, а точка В - этой смеси в парожидкост
ном состоянии. Из рисунка видно, что в результате разделения
жидкая фаза оказывается обогащенной высококипящим компо
нентом (Хк < Хн), а дистиллят - низкоКИПЯIЦИМ (ук > Хн).
Предельные возможности р азделения ясны из рис . 12. 1 5 , б:
это наибольшее обогащение жидкости высококипящим компо
нентом - до Хк"Р, а пара (дистиллята) - - низкокипящим до
Ук"Р. Поэтому, ставя задачу разделения смеси методом одно
кратной дистилля ц ии, нельзя пьпаться получить кубовую жид
кость с Хк < Хк"Р, а дистиллят с Ук > Ук"Р.
Материальный расчет. Задача материального расчета может
быть сформулирована в различных постановках. В подавляю
щем большинстве случаев известны поток Lн и состав Хн ис
ходной смеси, а также ее н ачальная температур а to. Далее тре
буется найти связь р абочей температуры t с потоками Lж_, П и
составами Хк, Ук конечных продуктов - это позволит решать
задачи эксплуатации и проектирования. Пусть, например, за
дана температура tк; тогда в диаграмме t- x,y•_ (рис . 12. 1 5 , а)
определяется точка В (вертикаль АВ
нагрев и получение
парожидкостной смеси). В сепараторе происходит равновесное
разделение жидкости и пара:
-

./' N

в�

996

м

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

1
подогреватель-испаритель, 2
емних дистиллята

сепаратор, З

коНденсатор-холодильних, 4

Рис. 12. 14. Схема простой однократной непрерьmной дистшщяции:
-

-

-

-

при

Для определения конечных потоков и составов фаз (4 неиз
вестные величины) запишем материальные балансы сепаратора
(контур К 1 на рис. 1 2 . 14) :
- п о потокам фаз
(е)
Lн - 4. П = О и П = Lн - 4., Lн = П + 4.;
-

fк t-��+-�.;..
fн t--t__.....,.,__
Хк

б

Хн

Ук
Ун

yt

Хк

Хн

а

расчет процесса в диаграммах t-x,y и у-х; б - предельные возможности разделения

Рис. 12. 15. К расчету простой одно кратной непрерывной дистилляции:
а

-

997

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Lнхн - Lкхк - Пук = О И Пук = Lнхн - Lкхк ,
(ж)
Lнхн = Пук + Lкхк.
Кроме того, располагая диаграммой t-x,y или у-х, мы
имеем равновесные связи величин lк, Хк и Ук ·
В случае задачи эксплуатации по tк определяются (рис.
1 2 . 1 5 , а) кон центрации Хк и Ук, а из системы уравнений (е)
(ж) - потоки Lк и П:
Lк Lн Ук - Х н
П = Lн Х н - Хк '
=
У к - Хк
Ук - Хк
Ук - Х н Lк
( 1 2 . 1 5)
или
Х н - Хк П
- по потокам НКК

·

=

-

Н апомним, 'ПО все выражения ( 1 2. 1 5) представляют собой записанные в
разной форме пр ав ила рычага: первые два
11 рода, третье - 1 рода.

-

Пусть теперь технологическая задача состоит в получении
определенного потока какой-либо фазы или необходимого ее
состава (задачи проектирования) ; требуется найти оставшиеся
неизвестные величины. Продемонстрируем последовательность
расчета, если, например, требуется получить дистиллят задан
ного состава Ук · Тогда в диаграмме t-x, у на линии t(y) по Ук
находим точку N , отсчитываем по ее ординате температуру
разделения lк и на линии t(x) определяем концентрацию кубо
вой жидкости Хк (точку М) . Далее по ( 1 2 . 1 5) находим конечные
потоки фаз. Если же задан один из уходящих потоков, то вто
рой по разности рассчитывается из (е), а составы фаз удобно
определять с помощью диаграммы у-х (рис . 1 2 . 1 5, а). Для
этого из точки В пересечения вертикали Хн с диагональю про
водим до пересечения с линией равновесия (точка С) прямую
под углом к горизонту 13 , так что tgf3 = Lк/П. Легко видеть, что
в то же время tgf3 = (ук - .хн)/<хн - Хк)· Таким образом, соблю
ден материальный баланс, выраженный в форме третьего соот
ношения в ( 1 2 . 1 5) . Рабочую температуру tк находим, проецируя
точку С на линию t(x) в диаграмме t-x, у.
На составы продуктов Хк и Ук можно воздействовать с по
мощью рабочей температуры tк (т.е. нагревом смеси в подогре
вателе-испарителе): из выражений ( 1 2 . 1 5) следует, что с повы
шением tк (точка В перемещается вверх по вертикали хн):
- возрастает выход дистилл ята и уменьшается - кубовой
жидкости;
понижается концентрация Н КК в дистилляте и кубовой
жидкости.
Тепловой расчет . Uн предусматривает определение тепловых
потоков и теплоносителей в подогревателе-испарителе и кон·-

998

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

денсаторе-холодильнике. Такого рода задачи для теплообмен
ников непрерывного действия в эксплуатационной и проектной
постановках достаточно подробно рассмотрены в разд. 7.5-7.7.
Здесь приведем без выводов лишь расчетные формулы, подоб
ные полученным в этих разделах - с учетом символиюt, при
сущей однократной непрерывной дистилляц ии (обозначения см. рис. 1 2 . 14):

Qn

=

Пh + Lк.ск tк - Lнсн to ; D =
Qконд = П(h F.ко

нд

=

Сд/д);

Qn

Qn

;
hrp - с � Т rrp
Q нд
G = ( ко ) ,
=

Св /� - /�

Q конд
k конд Лt хонд

( 1 2 . 1 6)

Здесь k и л t - коэффициенты теплопередачи и температур
ные напоры, их принадлежность к соответствующим теплооб
менникам указана индексами.
Заметим: тепловой поток Qii найден из тепловоrо баланса по проС1ранствен
ному контуру К2 , вхлючающему рабочие зоны разделяемой смеси Д11Я цепочки
из двух аппаратов
1 и 2 (см. рис. 12. 14).

-

Процесс, обратный рассмотренному, называется непрерыв
ной однократной парциальной конденсацией. Для его изображе
ния также подходит технологическая схема на рис . 1 2 . 1 4 - с
изменениями, отвечающими состоянию исходной смеси и те
чению процесса. Исходная смесь в перегретом парообразном
состоянии (ее температура - to') поступает в холодильник
конденсатор 1, откуда выходит в парожидкостном состоянии
при определенной температуре tк. В сепараторе 2 происходит
равновесное разделение жидкости и пара, отводимых раздель
но. Далее пар в случае необходимости может быть сконденси
рован .
Изображение процесса парциальной конденсации в диа
грамме t-x,y сходно с рассмотренным ранее для непрерывной
однократной дистилляции, только исходная смесь на рис .
1 2 . 1 5 ,а отвечает точке . А' в области перегретого пара (для рас
смотрения принят случай, когда состав исходной смеси тоже
равен хн ) . Последующий анализ повторяет изложенный для
однократной непрерывной дистилля ц ии.
1 2.3.3. О дистилляции

в

токе инертного газа

Процесс простой дистилля ц ии ряда смесей невозможен при
атмосферном давлении, если составляющие их компоненты
термичесюt нестабильны при температуре юtпения . Кроме то999

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

го , в случае высоких температур кипения приходится исполь
зовать дороmе высокотемпературные теплоносители, для кото
рых характерны невысокие коэффициенты теплопередачи
(значит, потребуются развитые теплообменные поверхности).
Для понижения рабочей температуры дистилляции следует
уменьшать парциальные давления компонентов смеси. Это
возможно осушествить, проводя дистилляц ию под вакуумом,
что, однако, удорожает процесс из-за дополнительных капи
тальных и энергетических затрат, связанных с вакуумировани
ем. Альтернативой процессу под вакуум о м является дистилл я 
ция при атмосферном давлении в токе инертного газа: на его
долю приходится часть общего давления газовой (паровой)
фазы, так что дистилляция компонентов смеси происходит под
более низким остаточным давлением, а значит, и при более
низкой температуре кипения . Важно, что дистилляцию в токе
инертного газа можно проводить вообще не при температуре
кипения, а при испарении жидкой смеси ниже ее температуры
кипения. Изменяя расход инертного газа, можно воздейство
вать на рабочую температуру процесса - обеспечение опреде
ленного ее значения является одной из задач организации тех
нолоmческого процесса.
Расчет дистилляц ии с потоком инертного газа в принципе
не должен отличаться от расчета при атмосферном давлении.
Скажем, в случае постепенной или однократной непрерывной
дистилля ц ии он ведется по канве, изложенной для этих про
цессов в разд. 12.3.2; только равновесные данные следует брать
не для полного давления газовой фазы, а для приходящегося
на долю дистиллируемой смеси. В идеале (при полном насы
щении инертного газа компонентами дистиллируемой смеси при бесконечно большой интенсивности контакта) парциаль
ные давления компонентов определяются по данным об упру
гости их паров при рабочей температуре, а давление, приходя
щееся в паровой фазе на долю дистиллируемой смеси, - сум
мированием этих парциальных давлений. Сложность заключа
ется в том, что реально контакт инертного газа и дистиллируе
мой смеси далек от совершенного, так что степень насыщения
инертного газа парами ер < 1 . При этом величина ер обычно
колеблется от 0,65 до 0,95, возрастая с увеличением высоты
жидкостного слоя, через который барботирует инертный газ, и
с уменьшением диаметра газовых пузырьков, а также с при
ближением к температуре кипения. В настоящее время вели
чина ер рассчитывается по полуэмпирическим зависимостям · .
Основой расчета дистилляц ии в токе инертного газа являет
ся соотношение потоков инерта (индекс "ин") и дистиллируе• См. (6, 7, 27 ) .

1 000

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

мой смеси (индекс "де") в газовой фазе. НаЙдем их мольное
(или что для газов то же самое , - объемное) отношение
QVдc· По закону Дальтона рабочее давление в газовой фазе Р
складывается из парциаль ных давлений компонен тов. Обозна
чим равновесные (отвечающие рабочей температуре) парциаль
ные давления бинарной дистиллируемой смеси компонентов А
и В соответственно Рл и РВ· Тогда в идеале

Р =Рин + Рл + Рв =Рин + Рдс•
а с учетом неполноты насыщения инертного газа

Р =Рин+ �Рдс =Рин+ �(рл + Рв),

откуда

Рин = Р

(з)
Концентрация (мольная, обьемная) инерта в газовой фазе,
равная доле инерта в парогазовом потоке, согласно ( 12.3) составляет
V

ин

----

V

Из

этого

ин

+ Vдс

равенства

-

=

�(рл+ Рв).

Р- �(Р л - Рв )

--�---�

Р

определим

искомое

соотношение

Vиц/Vдс:
_vи_
н

V дс

=

_Р_-� �-("'- Р_л_-_�Рв_._)
�(Рл - Рв)

=

Р
�(Рл - Рв)

_

1

·

(и)

Оrсюда получается требуемый поток инертного газа Vин,
обеспечивающий заданную производительностБ Vдс по парово
му потоку дистиллируемой смеси, т.е. по дистилляту.
Для идеальных смесей парциальные давления Рл и Рв выра
жаются по закону Рауля, что позволяет аналитически связать
отношение Vиц/Vдс с концентрациями компонентов в жидкой
фазе.
В случае непрерывного осуществления дистилля ции с инерт
ным газом отношение Vю/Vдс остается неизменным в ходе
процесса. В случае же периодического процесса нужно посте
пенно уменьшать парциальное давление паров дистиллируемой
смеси Рдс• чтобы в ходе процесса поддерживать постоянной
рабочую температуру. Поэтому вслед за уменьшен ием кон 
центрации Н КК в кубовой жидкости и увеличением е е темпе
ратуры кипения приходится увеличивать парциальное давление
инерта Рин, а значит, и отношение Vю/Vдс· Заметим, что и сте
пень насыщения инертного газа парами дистиллируемой смеси
� тоже , строго говоря, не остается постоянной при изменении
состава кубовой жидкости, что дополнительно осложняет рас
чет процесса.
1 001

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

При дистилляции с инертным rазом рабочая температура
процесса не зависит жестко от полного давления. Увеличивая
поток инертного rаза Vин, т.е. понижая парциальное давление
дистиллируемой смеси Рдс• можно обеспечить весьма низкую
рабочую температуру, что важно при дистилляции термола
бш�ьных веществ. Однако из инертного rаза трудно полностью
извлечь пары дистиллируемых компонентов. К тому же низкие
коэффициенты теплопередачи приводят здесь к необходимости
использования громоздких теплообменников с большими по
верхностями .
В качестве инертного rаза может быть использован перегре
тый или насыщенный водяной пар. Если после конденсации
получаемая при дистилляции смесь и вода взаимно нераствори
мы, то они легко отделяются друг от друга декантацией . Следу
ет, однако, указать, что дистилляция с водяным паром требует
значительно более высоких энергетических затрат, нежели с
инертным rазом . Кроме того, при некоторой (пусть - неболь
шой) взаимной растворимости воды и дистиллята процесс бу
дет происходить с обводнением (чаще всего нежелательным)
дистиллята и с некоторыми его потерями с водным слоем.
Коэффициенты '(еПЛоотдачи при дистилляц ии с водяным
паром относительно высоки, и потому поверхности теплообме
на - достаточно компактны.
Некоторые подходы к более детальному технологическому
расчету дистилляции в токе инертного rаза и с водяным паром
приводятся в учебной и научной литературе * .
1 2.3.4. О молекулярной дистилляции

Молекулярная дистилля ция стоит особняком в ряду дистил
ляционнъIХ процессов: разделение здесь проводится при очень
низких рабочих давлениях (порядка 1 0- 1 50 мПа) и основано
на специфических эффектах молекулярного течения (см . разд.
2.9). Низкое давление позволяет вести процесс при низких ра
бочих температурах (еще и за счет испарения при температурах
ниже точки кипения); в сочетании с малым временем контакта
разделяемой жидкой смеси с поверхностью нагрева это важно
для разделения термолабильных смесей. Речь идет о химических
соединениях, имеющих высокие температуры кипения и разла
гающихся при дистилляц ии под атмосферным давлением, о
биологически активнъIХ веществах (лекарственные препараты,
некоторые пищевые продукты), вообще не выдерживающих
температуры свыше 40-50 °С.

•
1 002

См., например, ( 3, 6, 7).

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 12. 16. Аппарат для молекулярной дистилля ции:

1 - подоrреватель, 2 - rреющая поверхносrь, 3 охлаждающая рубашха, 4 - охлаждающая поверхносrь, 5 распределиrель исходной J1СИД1Сосrи, 6 - устройство вывода
дистиллята, 7 - шrуцер отвода кубовоrо остатка;
1 - исходная смесь, /1 - дистиллят, 111 - кубовый
остаток, IV- хладоаrеtп, V - rаэы х вакуум-насосу

v

Схема аппарата• для проведения мо
лекулярной дистилляции показана на
рис . 1 2 . 1 6 .

3

/
5

IV
4

2

Процесс осущесТRЛЯется в кольцевом про
1
странстве межцу обоrревающей 2 и охлю�щающей 4
ЦИ!Пfндрическими поверхностями. Обоrрев произ
7
водкгся подоrревате.лем 1 (злекrрически м или с
помощью теплоносителя), охлю�щение - хладоаrен
том , подаваемым в охлаждающую рубашку J. Ди
СТИJVIИруемую жидкость / через распределительный
узел 5 подают на rреющую поверхность, по кото
рой жидкость стекает в виде тонкой пленки. За счет
подвода теплоты она частично испаряется (при
температуре ниже точки кипения). Молекулы компонентов испаряемой смеси
конденсируются на охлаждаемой поверхности, температура которой значигельно
(на 50° и более) ниже, чем rреющей; этого впоJU1е достаточно, чтобы обратный
поток молекул компонентов от охлю�щающей поверхности к rреющей считать
несущественным и в последующем анализе не учитывать, тра�сrуя молекулярную
дистилляцию как одионапрuлениwй массоперенос. Конденс�т, образующийся на
холодной стенке и стекающий по ней тонкой пленкой, отводкгся из аппарата в
виде дистиллята //, а неиспарившаяся жидкость - в виде кубового остатка ///.
Вакуу м в рабочем (кольцевом) пространстве создается и поддерживается вакуум 
насосом (на рисунке показан поток V отсасываемых газов).
При осуществлении молекулярной дистилляции моrут возникнуть затрудне
ния, связанные с нарушением вакуум а из-за десорбции растворенных в жид
кости газов и термического р11311о.жения составляющих смеси. Поэтому дистил
лируемую смесь подвергают предварительной дегазации, а р11311 о.жения смеси
избегают nцате.льным подбором рабочей температуры.

Эффекг разделения при молекулярной дистилляции оцени
вают, как и в других дистилля ционных процессах, определяя
соотношение мольных потоков отдельных компонентов, равное
отношению их парциальных давлений Pi· В случае процессов
дистилля ц ии и рекгификации бинарных смесей для такой
оценки используют коэффициент разделения, равный отноше
нию упруrостей паров чистых компонентов р о при рабочей
температуре: а.о =
(см. разд. 12.2.3). Отношение моль

Р1 / Р�

ных потоков (применительно к бинарным идеальным смесям,

•

Подробнее об аппаратурном оформлении процессов молекулярной ди
стилля ции см. (6, 7, 16, 19).

1003

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

подчиняющимся закону Рауля ) составляет:

Рл
Рв

-

rде

х = хл

-

Р1 хл
Р.в0 хв

--=

=

х
ао-1 х.

(к)

-

мольная конце11трация НКК в жидкости.

В случае молекулярной дистилляции в основе оценки эф
фекта разделения лежат выражение (2.86) и вытекающий из
него вывод, что массовый поток какого-либо компонента (с
парциальным давлением р и молярной массой М) пропорционален комплексу

р�М/Т ,

причем рабочая температура

Т бе

рется в К. Переход к мольному потоку осуществляется делением
массового потока на молярную массу; таким образом, мольный
поток компонента пропорционален компл е ксу
Если
речь Идет об Идеальной бинарной смеси (р1 = PPxt), то отноше
ние мольных потоков составит:

p/J},fT

.

(л)
Здесь

амд

=

Р1 �},fв / Р� �},f

л

имеет смысл

коэффициента раз

в процессе м олекулярной дистилляции.
Сопоставление коэффициентов раздел ения
по (л) иd0по
(к) показывает, что о.мд
МА .Это означает, что:

деления

=ао�Мв/

а.мд

- при разделении смесей, для которых низкокипящему
компоненту отвечает меньшая молярная масса (наприм ер , сме
сей углеводородов какого-то гомологического· ряда), молекулярная дистилляция дает в
л раз более высокий эф

�},f8/},f

фект, нежели простая дистилля ция;
- молекулярной дистилля цией могут быть разделены смеси
компонентов с одинаковыми температурами кипения и азео
тропные смеси, если составляющие их компоненты имеют раз
ные молярные массы.
Из выражения (л) следует, что разделяющий эффект при
молекулярной дистилляции постепенно понижается по мере
удаления от сечения ввода исходной смеси, поскольку при
преимущественном испарении летучего компонента его кон
центрация х в нисходящем потоке жилкости уменьшается .
Ухудшение процесса возможно таюке из-за обратного потока
компонентов от холодной поверхности к горячей .

1004

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Обоснованность игнорирования обратного потока какото-либо компонента
от холодной поверхности продемонстрируем на типичном числовом примере.
Пусть температура горячей пленки равна Т1 = 300 К, а холодной Т2 = 250 К
(ЛТ = Т1 - Т2 = 50°); мольная теплота испарения = 40· 106 Дж/моль. С целью
оцен ки воспользуемся уравнением Клапейрона дляr упругостей паров Pl,2 при
менительно к температурам Т1 и Т2 , пренебрегая некоторым изменением r в
этом температурном диапазоне:
r _; ln Р2 = А __
r ,
ln PI
А
_
R T
R T

-

=

где Ry

=

y 1

-

y 2

- универсальная газовая постоянная.
из второго выражения первое и потенцируя, получаем:
и
( rЛТ )
р; = ехр -

8314 Дж/(моль·К)

Вычитая

-

Р2

RyT1T2

.

Отсюда ясно, что чем ниже рабочие температуры Т1 и Т2 и чем больше раз
ность ме.жду ними ЛТ, тем меньшую долю Р2 составляет от р1 и с тем большим
основанием можно пренебречь обратным молекулярным пото ком от охлаждае
мой поверхности.
е-з,2"
Для приведенного числового примера rлT/< RyT1 Т2) = 3,2 и JJ7/p1
" 0,04, т.е. обратный пото к составляет " 4% от потока с горячей пленки. Для
Т2 = 200 К и лт = 100° получается еще меньшее отношение: рур1 0,0003.
=

"

12.З.5. О некоторых других дистилляционных процессах•

В ходе периодического процесса простой постепенной ди
стилля ции количество жидкости в кубе уменьшается от Lн до
Lx. Это может привести к обнажению части теплообменной
поверхности, что сопровождается понижением эффективности
процесса, а в ряде случаев - и разложением продуктов дистил
ляции: из-за низких коэффициентов теплоотдачи к паровой
фазе возможно заметное возрастание температуры поверх
ности нагрева.
Полунепрерывная дистилляция. Этот процесс (аналог диффе
ренциального процесса - см. разд. 1 0 . 14.2) позволяет избежать
упомянуrого выше обнажения теплообменной поверхности . Он
отличается от простой постепенной дистилляцйи подачей в
дистилля ционный куб жидкой смеси исходного состава в тече
ние всего процесса. Это позволяет удерживать жидкость в кубе
на уровне, полностью покрывающем греющую поверхность,
что обеспечивает интенсивный теплообмен и потому - прием
лемую температуру этой поверхности .
Схема полунепрерывной дистилляции представлена на рис.
1 2 . 1 7 . В дистилляционный куб заливается некоторое начальное
количество жидкости Lн состава хн; она доводится до кипения,
после чего в куб начинают подавать жидкость (поток 1) того же

•

зrих

Более подробно описание
и ряда других диСТИЛ11Яц ионнь�х процессов
и методов их технологического расчета см., например, (3, 6, 7, 1 1, 1 2, 1 9 ) .
1 005

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Puc. 12. 17.

Схема полунепрерывной

ДИСТИJVIЯЦИИ:
1

D

ДИСТИЛJJЯЦИОЮIЬIЙ куб, 2

сатор-холодильник, З

II

/ll

-

-

лята;

I

-

сат,

исходная смесь, II
IV хладоаrент

-

конден
приемник дистил
пар, lll

-

-

конден

-

состава Хн, отводя одновре
менно поток пара JJ. Эти по
токи жидкостй и пара сохра
няются в ходе всего процесса;
соответственно схеме на ри
сунке к моменту времени 't в куб подано L моль жидкости (или
L кг при расчете в массовых величинах) и отведено из аппа
рата 1 D моль пара (после конденсации он собирается в виде
дистиллята в приемнике 3 в количестве П = D). Если подача
жидкости и отвод пара производятся равномерно (потоки в
единицу времени L' и D' соответственно), то отвечающие им
количества к указанному моменту составят L = L'-r. и D = D'-r..
В ходе процесса изменяется (хотя и медленнее, чем при по
степенной дистИJUIЯ ции) состав кубовой жидкости, а с ним и
состав пара : содержание в них Н КК понижается. При большом
количестве жидкой смеси L (теоретически - при бесконечно
большом) состав пара у стремится к начальной концентрации
жидкой смеси Хн·
Постепенная дистилляция и парциальная конденсация. Схема
последовательного осуществления этих процессов приведена на
рис . 1 2 . 1 8 . Отличие от рассмотренной в разд. 1 2 . 3 . 2 постепен
ной дистИJUIЯции заключается в том, что в конденсаторе 2 кон 
денсируется лишь некая доля пара 'i', причем конденсат воз
вращается в дистИJUIЯ ционный куб J. Оставшаяся в парообраз
ном состоянии доля пара ( 1 - '!') полностью конденсируется и
охлаждается в ко нд енсаторе-холодильнике 3, после чего соби
рается в приемнике 4. Установка парциального конденсатора 2
позволяет за счет частичной конденсации дополнительно обо
гатить пар D(l - '!') низкокипящим компонентом в сравнении
с паром D: в соответствии с первым законом Коновалова в
сконденсированную жидкость Dljl преимущественно переходит
ВКК. В результате дистиллят П в большей мере обогащен низ
кокипящим компонентом, нежели при простой постепенной
дистИJUIЯ ции. Плата за более высокую эффективность разделе
ния - повышенные затраты теплоты на повторное испарение в
кубе сконденсированной жидкости Dljl.
Конденсат, полученный в парциальном конденсаторе 2,
иногда не вполне строго именуют флегмой, а сам рассматри
ваемый процесс
простой дист илляцией с дефлегмацией, т.е . с
-

-

1006

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 12. 18. Схема дистилляции с
частичной конденсацией пара:

1

ДИСТИЛЛЯЦИОЮIЫЙ куб, 2 - пар
ко�щенсатор, З - ко�щенсатор
холодильник, 4 - приемник дистиллята:'
/, 11 - хладоаrенты
-

циальный

вьщелением из пара неко
торой доли жидкости пугем
ее конденсации . Эту долю "'
регулируют, воздействуя на
работу парциального кон
денсатора 2 (на количество
и температуру потока 1 охлаждающего агента); от величины l.jl
зависит степень дополнительного обогащен ия низкокипящим
компонентом пара D(l
\j/), а значит, и дистиллята П .
Дополнительное обогащение дистиллята возможно и в слу
чае непрерывной однократной дистилляции . Для этого после
сепаратора 2 на паровой линии (см . рис . 12.14) следует устано
вить парциальный конденсатор; образующийся в нем поток
конденсата может быть присоединен к потоку исходной смеси .
Дистилляция смеси взаимно нерастворимых компонентов. Она
применяется , когда необходима очистка термолабильных ве
ществ, разлагающихся при кипении под атмосферным давле
нием, от содержащихся в н их высококипящих, практически
нелетучих (смолистых и др .) примесей. Для понижения рабочей
температуры , наряду с дистилля цией под вакуумом и с инерт
ным газом, возможно добавление к целевому веществу компо
нента, не смешивающегося с ним в жидком состоянии, напри
мер воды к углеводородам с относительно высокой молярной
массой . Разумеется , на практике могуг встретиться и исходные
смеси, состоящие из взаимно нерастворимых компонентов.
Отметим особенности перегонки таких смесей до тех пор ,
пока в жидкой фазе остаются оба компонента:
- независимость состава пара от состава жидкости - соот
ветственно формуле (12.5);
- понижение температур кипения смеси в сравнении с
температурами кипения обоих индивидуальных·компонентов.
П одчеркнем, что обе эти особенности теряют силу, как
только в дистиллируемой жидкой смеси оказывается исчерпан 
н ым какой- нибудь из компонентов. И одна из проблем техно
логического анализа - определение предельной доли Ч1 испа
ренной жидкости (от исходной дистиллируемой смеси), при
которой упомянугые особенности еще сохраняют силу. Моль
ное соотношение НКК и ВКК в исходной жидкости равно
хнf (1 - Хн), в уходящем паре - у/( 1 - у). Очевидно , что при хн/
/( 1 - Хн) = у/( 1 - у) (т.е. ПрИ Хн = у) оба КОМПОНеНТа ИСЧер-

1 007

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис.12. 19. К расчету предельной доли дистил
лята в случае взаимно нерастворимых компо 
нентов
пываются одновременно, так что ди

У,"1'

к
вкк

стю1ляцию можно вести до полного
исчерпания жидкости в кубе ("1' = 1 )
при сохранении указанных особен
ностей процесса. Если .хц/( 1 - Хн) >
> у/(1 - у), то быстрее исчерпы
вается (полностью удаляется из кубовой жидкости) ВКК, а при
Хн /( 1 - Хн ) < у/( 1 - у) - НКК.
Расчетная схема процесса приведена на рис . 1 2 . 1 9
(поверхность теплообмена в кубе, конденсатор и приемник
продукта на схеме не показаны) . Будем решать задачу опреде
ления "1' в общем виде примен ительно к 1 моль исходной сме
си. Содержание НКК в ней обозначено хн; в конце процесса в
кубовой жидкости оно будет Хк ; состав пара, неизменный в
ходе процесса, у = Р�/ (Р� + Pi�), причем упр утости паров ин нкк

дивидуальн ых компонентов

}'�

и

Р�

берутся при рабочей

температуре Ю1пения. При мольной доле испаренной жидкости
"1' материальный баланс по НКК для контура К (см. рис . 1 2 . 1 9)
в отсуrствие Источников и Стоков запишется в виде:

-Хн
у

- Хк .
(м)
- Хк
Последнее равенство подтверждает сделанный ранее вывод
об условии полного испарения дистиллируемой смеси: при "1' =
= 1 получается Хн = у. Если в кубе в конечном итоrе остается
только ВКК, т.е. Хк = О, то из (м) следует "1' = Хн /у. Если же в
кон це про 13есса в кубе остается только Н КК, т.е. Хк = 1 , то "1' =
= ( 1 - Хн)/( 1 - у).
Для повышения чистоты получаемых компонентов используют
схемы многократной дистилляц ии и парциальной конденсации.
Мноrократная дистилляция. Она осуществляется следующим
образом (рис . 1 2 .20, а) . В левом дистилляционном кубе 1 про
водят постепенную дистилля цию, конденсирукrг в конденсато
ре 2 весь образовавшийся пар и собирают полученный дистил
лят - в нем концентрация НКК, естественно, выше, нежели в
исходной жидкости в первом кубе . Этот дистиллят снова под
вергают постепенной дистиллнции во втором кубе 1 и после
полной конденсации получают новый дистиллят с еще более
высокой кон центрацией НКК. Его опять дистиллируют, и т.д . В
результате многократных операций частичного испарения и поло

1 008

- 'f'y =

(1 -

'f')Хк

-

1 ·Хн И

'"
т

-

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

4

а

4

б

Рис.12.20. Схема мноrокраmой дисТИ1VIЯции (а) и парциальной конденсации (6):
1 - дистилляциоЮ1Ые кубы, 2 - коRЦенсаторы, З - греющие элеме1ПЪ1, 4
приемники
целевого npoдYJCfa
-

в хвостовом (правом) приемнике 4 собирают
некоторое количество ЖИдкости с достаточно высоким содер
жанием Н КК.
М ногократная парциальная конденсация. Она проводится при
необходимости получения достаточно чистого В КК. Здесь
многократно повторяются операции частичной конденсации и
полного испарения (рис . 12.20, б) . В результате каждого акта
парциальной конденсации в получаемой ЖИдкости нарастает
содержание ВКК; в итоrе в хвостовом приемнике 4 собирают
жидкость с достаточно высоким содержанием В КК.
Процессы многократной дистилляции и парциальной кон 
денсации характеризуются низким выходом Н КК или ВКК : зна
чительные их количества в смесях невысокой чистоты остаются
в промежуточных приемниках 1. Поэтому данные процессы
находят применение преимущественно в лабораторной практи
ке , когда можно удовольствоваться малыми количествами
весьма чистых компонентов в целях их препаративного исполь
зования или Идентификации (т.е. установления индивИдуаль
ных свойств типа плотности, вязкости, температур плавления и
кипения и т.д.).

ной конденсации

12.3.6. Общая оценка процессов дистилляции

С помощью процессов дистилляц ии (это относится и к пар
циальной конденсации) обычно не удается получить продукты
(дистиллят, кубовый остаток) достаточно высокой чистоты .
Этот тезис иллюстрируется на рис . 1 2 . 2 1 : при изменении кон 1009

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 12.21. К оценке эффективности процес
сов дистилляции :
1
равновесная кривая при невысоком коэф
фициеше разделения С!{), Z
то же при весьма
высоком С!{)
-

-

центрации Н КК в кубе от Хн до Хк
концентрация его в паре, а значит
и
в
дистилляте,
изменяется
(кривая равновесия /) в интервале
относительно невысоких концентХк
хн
раций - от Ун' до Ук' · Высокие
концентрации Н КК в дистилля те
(ун ", Ук") получаются лишь при большой разнице в температурах кипения компонентов: тогда линия равновесия (кривая 2)
располагается далеко от диагонали, и прирашение концентраl..ЩЙ
Н КК в паре по сравнению с жидкостью достаточно велико.
Чаще всего дистилля ц ию применяют в промышленности в
тех случаях, когда не требуется высокой чистоты продукта (или
полупродукта для последующих стадий производства) .
Правда, многократная дистилля ция или парциальная кон
денсация позволяют получать достаточно чистые компоненты .
Однако помимо очень низких выходов чистых продуктов эти
процессы крайне невыгодны энер гетически. В самом деле,
здесь приходится многократно испарять уже однажды испарен 
ную жидкость, затрачивая большое количество теплоты и теп
лоносителя. Одновременно приходится затрачивать хладоаrент
на неоднократную (повторную) конденсацию паров.
Разумеется, при разделении смесей в условиях фазового пе
рехода жидкость-пар принципиально не обойтись без испарения
жидкости и конденсации пара. И технолог готов к затратам
энергии на такие операции, если каждая из них осуществляет
ся однократно. Кроме того, выходы продуктов приемлемой
чистоты должны быть близки к количественным, отвечающим
содержанию компонентов в исходной смеси. Эrи задачи ре
шаются при реализации процессов перегонки в противоточных
схемах разделения .
12.4. РЕКТИФИКАЦИЯ

12.4. 1 . Сущность процесса

Ректификацией называется процесс перенQса компонента
(компонентов) между кипящей жидкой и насыщенной конден 
сирующейся паровой фазами при противотоке этих фаз. При
чередовании по схеме противотока операций частичной кон
денсации паровой и испарения (дистилляции) жидкой смесей

1010

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

D
Non
1

№3

№2

• t

. .
-

[J

п
хш,у
XN,y

"'

N

tв
t�,t�
t�,t�
t"
)1(

2

а

Q Хо

,

-

х х,у

1

tл

б

Рис. 12.22.
Противоточное
коJПактирование
паровой
и
жидкой
фаз
(идеализированный процесс):
а - схема ректифихациошюrо агрегата (1 - колонна, 2 - кипятилъЮ1к, 3 - ко�щенса
тор), 6 - процесс ректифихации в диаграмме t- XJI

можно получить выходы Н КК и В КК, примерно соответ
ствующие их содержанию в исходной смеси.
И ными словами, ректификацию можно трактовать как со
вмещение процессов многократной дистилля ции и многократ
ной парциальной конденсации при противоточном контакти
ровании потоков пара и жидкости. При таком проведении
процесса перегонюt появляется возможность использования
при каждой упомянуrой операции теплоты конденсации пара
для испарения жидкости - пуrем непосредственного контакти
рования конденсирующейся паровой и юtпяще� жидкой фаз.
В процессе ректификации подводимая извне теплота затра
чивается только в юtпятильнике - в низу колонны однократно
для частичного испарения жидкой смеси с получением началь
ного потока пара в обогревающем устройстве в нижней части
ректификационного аппарата (чаще всего - колонны). Теплота
конденсации паров также отводится только в конденсирующем
устройстве - в верхней части ректификационного аппарата.
Сущность ректификации как явления удобно рассмотреть на
примере пуска колонны применительно к разделению бинар
ной смеси. Схема ректификационного агрегата показана на
рис. 12.22, а, ей соответствует диаграмма t-x,y для разделяемой
смеси (рис. 12.22, б) . Колонну 1 будем считать адиабатической :
она хорошо изолирована в тепловом отношении, так что поте
ри теплоты в окружающую среду отсуrствуют. В нижней части
IOl l

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

колонны находится куб 2 с обогревающим устройством, анало
гичным рассмотренному выше для дистилляционнь�х проuессов.
На вь�ходе паров сверху колонны расположен коцденсатор 3.
Схематизируем явления, происходящие при ректификаuии.
Пусть в куб залита бинарная жидкая смесь с содержанием
Н КК х1 ; нагреем ее до температуры кипения tж.0 и начнем ис
парять. Пары, обогащенные Н КК, состава у (примем для про
стоты , что они равновесны кубовой жидкости , их температуры
одинаковы, т.е. tп' = tж.0) поднимаются вверх, выходят из ко
лонны и полностью конденсируются в конденсаторе до состоя
ния кипящей жидкости . Эта жидкость, естественно, имеет со
став х' = у', но ее температура кипения tж' < tп' (см . рис .
12.22, б) . Она возвращается в колонну, стекает вниз и на та
релке № 1 контактирует с восходящим потоком пара того же
состава. Пар имеет более высокую температуру, чем жидкость;
поэтому на тарелке № 1 происходит интенсивный теплообмен
(прямой контакт, высокие коэффициенты теплоотдачи при
конденсации и кипении), сопровождающийся массообменом
между жидкой и паровой фазами. В результате пар конденси
руется (реально - частично), выделяется теплота конденсации,
и за ее счет частично испаряется жидкость.
Подчеркнем: на тарелке No 1 (см . рис. 12.22, а) жидкость
обогащена Н КК в сравнении с кубовой жидкостью (х' > х1 );
поэтому при ее испарении (принимаем, что равновесном) по
лучается пар, еще более обогащенный Н КК (у" > у', его темпе
ратура tп" < tп'). Образовавшийся пар поднимается вверх, кон 
денсируется в конденсаторе, откуда жидкость состава х" = у"
при температуре кипения tж" возвращается в колонну. На та
релке № 2 (рис . 12 .22, а) жидкость встречается с паром того
же состава. И поскольку температура пара выше, нежели жид
кости, то и здесь происходит акт конденсации - испарения с
получением пара с более высоким содержанием Н КК: у '" > у " .
Так постепенно за счет противоточного контакта фаз на та
релках (в случае насадочной колонны - на поверхности насад
ки) снизу вверх нарастают концентрации НКК в паре и жид
кости - устанавливается некий профиль концентраций; этот
эффект и лежит в основе процесса ректификаuии . Чистота
Н КК на верху колонны (значит, и на выходе из нее) опреде
ляется в рамках рассматриваемой схемы числом тарелок (или
высотой слоя насадки).
После установлен ия необходимого концентрационного про
филя, т.е. требуемой концентрации Н КК (чистоты) на верху
колонны, верхний продую' может отбираться в качестве целе
вого. Но если отбирать весь верхний продую', то жидкая фаза
перестанет стекать по колонне противотоком к пару, и процесс
ректификаuии будет нарушен . Поэтому после конденсации
1 012

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

верхний продукт отбирается лишь частично; предусматривается
возврат определенной части конденсата на орошение колонны
для поддержания противоточного контакта фаз .
Заметим, что представленная выше картина является идеа
лизированной. В действительности при неполном орошении
колонны (отбор части конденсата в виде верхнего продукта)
обогащен ие пара НКК на тарелке понижается (по условиям
материального баланса - см. разд . 1 2 . 6) . Кроме того, при кон 
такте фаз не успевает установиться равновесие. Поэтому коли 
чественно картина будет иной (нарастание концентрации НКК
снизу вверх будет не столь быстрым). Однако качественно все
рассмотренные эффекты сохранятся.
Важно : в отличие от дистилляции и парциальной конденса
ции при ректификации имеет место двунаправленн ый процесс
переноса компонентов: НКК из жидкой фазы в паровую и
В К К - в обратном направлении.
В дальнейшем процесс ректификации весьма подробно ана
лизируется преимуrnественно для наиболее простого разделе
н ия бинарных смесей. Более сложные случаи рассматриваются
менее детально - со ссылками на научную, учебную и иную
литературу.
12.4.2. Типовая схема, потоки, терминология

Приведенная на рис. 1 2 .22, а схема илл юстрирует лишь эф
фект ректификации; она ограничена получением только высо
коконцентрированного НКК. Реальный ректификационный
процесс позволяет получать оба компонента высокой концент
рации.
Принципиальная схема процесса непрерывной ректифика
ции бинарных смесей показана на рис. 12 .23. Исходная смесь 1
подогревается в подогревателе 2 (предпочтительно до темпера
туры кипения или близкой к ней) и через гребенку З
(обеспечивающую возможность варьирования места подачи)
подается в ректификацион ную колонну 1, внутри которой раз
мешены контактные устройства (тарелки, насадка) . Источни
ком парового потока является кипятильник 4, источником
жидкого потока - конденсатор 5. В схеме предусмотрены хо
лодильники 6 и 7 продуктов, отбираемых сверху (поток //) и
снизу (поток JJJ), а также емкости исходной смеси и продуктов
8-10. Перекачивающие насосы на рисун ке не показаны .
Принята следующая терминология основн ых потоков и узлов ректификационной установIGf :
- поток 1 носит естественное название
исходная смесь;
- поток II именуют дистиллятом (или дистиллатом);
- поток JJJ называют кубовым остатком (или кубовой жидкостью);
1013
-

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Jl

1
8

9

Рис. 12. 23. Принципиальная схема непр ерывнодейсrвующей ректифюсационной
установки для разделения бинарных смесей:

1 - колоЮfа, 2 - подоrреватель исходной смеси, З - rребешс:а, 4 - юmяrильник, 5 конденсатор, 6, 7 - холодильники, 8 - 10 - сборШ!ки;
/ - исходная смесь, // - дистиллят , /// - кубовая жидх:осrъ, /V - пар, V - флегма, VI
- теплоноситель, Vl/ - охлаждающий аrент

- восходящий паровой поток IV так и называют: поток пара
(иногда просто "пар");
- нисходящий жидкостной поток V (в том числе - возвра
щаемый сверху в колонну на орошение) именуют флегмой
(иногда просто "жидкостью") .
Тарелку, находящуюся в сечении подачи исходной смеси в
колонну 1, называют тарелкой питания. Часть колонны, нахо
дящаяся выше тарелки питания (на выходе из нее получается
"крепкий" НКК) , носит название укрепляющей части колонны
(иногда - укрепляющей колон ны). Часть колонны , находя
щаяся ниже тарелки питания (в ней НКК отгоняется из жид
кости, исчерпывается), носит название отгонной (реже - ис
черпывающей) части колонны (иногда - отгонной или исчер
пывающей колонны). Генератор пара называют кипятильником ,
источник флегмы (чаще всего - и дистиллята) - конденсато
ром.
1014

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

1

а

б

Рис. 12. 24. Схемы конденсации уходящего из колонны пара и возврата в нее
части образовавшейся жидкости:
а
полная конденсация пара в конденсаторе, б
частичная конденсация пара в дефлегматоре;
1
колоЮJа, 2 конденсатор, З дефлегматор, 4 rидроэатвор;
1- исходная смесь, // - дисrиллят, /// - кубовая JКИДКосrь
-

-

-

-

-

-

КонденсаI.ЩЯ пара в конденсаторе, mбор дистиллята и возврат флеn.fы в колонну
осущестмяют двумя способами, схематично изображенными на рис. 12.24.
По первому способу (рис. 12.24, а) уходящий из колонны 1 пар полностью
конденсируется в конденсаторе 2, откуда часть жидкости возвращается в колон
ну, а остаток выводится из системы в виде жидкого продукта. Очевидно, в дан
ном случае составы всех трех потоков (пара, поступающего в конденсатор, флег
мы, возвращаемой в колонну, и отводимого жидкого дистиллята) оди наковы.
По второму способу (рис. 12. 24, б) уходящий из колонны 1 пар лишь час
тично конденсируется в конденсаторе 3, и вся образующаяся жидкость возвра
щается в колонну 1. Дистиллят же отводится в виде пара и при необходимости
полностью конденсируется в дополнительном конденсаторе 2. В этом случае
парциальный конденсатор 3 часто называют дефле1111атором, а сам процесс выде
ления флегмы из пара - дефле1111ацней. Здесь отводимый из системы продукт
богаче ИК.К, чем выходящий из колонны пар и тем более - возвращаемая в
колонну жидкость. Заметим, что дополнительное обогащение дистиллята при
этом обычно невелико. Дефлегмацию целесообразно применять, когда в после
дующем технологическом процессе дистиллят используется в виде пара.

12.5. ОБ АППАРАТУРНОМ ОФОРМЛЕНИИ
И РАБОТЕ РЕКТИФИКАЦИОННЫХ УСТАНОВОК*
Для проведения процессов ректификации применяются почти исключитель
но аппараты колонною nша. По характеру взаимодействия паровой и жидкой
фаз ректификационные колонны можно разделить на две основные группы:
- со ступенчатым (дискретным) контактом фаз;
- с непрерывным контактом фаз.
•Более подробно см. (1, 5, 6, 8, 12, 19, 21, 25).

1015

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

П ервую группу составляют тарел�.чатые колонны, вторую - насадочные, пле
ночн�.1е и роторно-пленочные.
Ректификацноннwе кoлomJJ.1 со С1)'11енчат�.1м хо1rrактом фаз. В наиболее рас
пространенных тарел�.чатwх ректификационных колоннах паровая фаза барбо ти 
рует (проходит в виде пузырьков или струек) через слой жидкости на тарелке,
поэтому их часто называют также барботажи�.1ми колоннами. Эти аппараты ста
бильно работают в широком диапазоне изменения нагрузок по паровой и жид
кой фазам . Их применяют в мало- и крупнотоннажных производствах Д11Я чет
кого разделения смесей .
К недостаткам тарельчатых колонн относится сравнительно высокое гидрав
лическое сопротивление движению парового п отока, что приводит к увеличению
давления и , соответственно, температур кипения жидкости в отгонной части и
кубе колонны. Это обстоятельство приобретает особое значение для процессов
ректификации под вакуумо м, когда необходимо обеспечить низкие температуры
кипения . Поэто�1у тарельчатые аппараты для ректификации под вакуумом при
меняются обычно при остаточном давлении не менее 3-5 кПа.
Конструкции тарелок, применяемых в ректификационных колоннах (как и
большинства внутренних устройств других типов), аналогичны применя.емым в
абсорбционных аппаратах. Они кратко о писаны в разд. 10. 1.3 и более подроб
но - в разд. 1 1 . 2 . 2 . Здесь лишь отмети м, что в настоящее время на практике
используются ра:l11и чные типы тарелок - от простейших ситчатых до клапан
ных, клапанно-ситчатых и разнообразных колпачковых.
В колоннах с провал�.ными тарелками жидкость переливается (проваливается)
в виде струй и капель ("дождя") с вышележащей тарелки на нижележащую через
отверстия тарелки (по законам истечения). В колоннах с непровал�.н�.1ми тарел
ками жидкость поступает с верхней тарелки на нижнюю по переточным трубкам
или карманам. В первом случае высота барботажноrо слоя на тарелке зависит от
нагрузок по потокам фаз, во втором она определяется высотой переливноrо
порога (высотой переточных трубок над тарелкой) и в широком диапазон е на
грузо к изменяется мало . В обоих случаях с увеличением нагрузок возрастает
унос капель жидкости паровым потоком.
В идеале провальные тарелки должны обеспечить равномерное распределение
жидкостноrо и паровоrо потоков за счет попеременноrо прохождения фаз через
каждое отверстие. Однако реально по сечению провальной тарелки устанавливакm:я
зоны преимущественноrо движения отдельных фаз - поперечная неравномерность
паровоrо и жидкостноrо потоков на такой тарелке достаточно высока. По:лому не
смотря на большую простоту они применяются реже непровальных.
В колоннах с переливными устройствами существует (а с ростом диаметра аппа
рата dк - увеличивается) перепад высот барботажноrо слоя по дmrne пути движения
жидкости (от точки поступления ее с вьШJележащей тарелки к месту слива на ниже
лежащую). Это приводит к увеличению разницы в локальных гидростатических дав
лениях и как следствие - также к появлению (и возрастанию с ростом dк) попереч
ной неравномерности потока паровой фазы.
целью снижения отрицательных (для
массообмена) последствий эroro явления рекомендуется:
- диаметральный подвод-отвод жидкости заменять на радиальный (переливные
устройства устанавливать попеременно по центру и по периферии тарелок);
- использовать секционированные тарелки и тарелки с транспортированием
жидкости паром (движение жидкости по тарелке обеспечивается не за счет пере
пада высот барботажноrо слоя, а благодаря направленному входу пара в барбо
тажный слой).
Заметим, что на непровальных тарелках (в отличие от провальных), как пра
вило, имеет место перекрестный ток паровой и жидкой фаз:
- жидкость движется в гор изонтальном направлении по тарелке от rидроза
твора (образуемого путем погружения нижней части переливноrо устро йства в
слой жидкости на тарелке), через который она поступает на тарелку, к переливу
на нижележащую тарелку;

С

1016

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

- пар проходит (поднимается) в вертикальном напрамении через тарелку и
слой движущейся на ней жидкости.
РектификаЦJtониые коло1111ы с иепрерыв11ым контактом фаз. В этих колоннах
жидкость стекает в виде пленки - либо по поверхности насадки (насадочные
колонны), либо по внуrренней или наружной поверхности вертикальных труб
(плеиочн"ае и роторно-пленочные аппараты), а пар в виде сплошного потока
поднимается вверх через свободный объем насадки или внуrри вертикальных
труб. Несмотря на пленочный режим течения жидкости в обоих случаях, колон
ные аппараты принято называть в первом случае - насадочными, а во втором пленочными.
В насадочных колоннах применяют множество разнообразных типов насадок
(см. разд. 10.1.3 и 11.2.1).
По способу размещения насадки выделяют две группы: неупорядоченная
(или нерегулярная) насадка и упорядоченная (реr;лярная) насадка. Нереrулярная
насадка (например, кольца Рашига) загружается в аппарат навалом и располап1ется в нем случайным образом: укладка элементов насадки относительно друг
друга и стенок колонны имеет в общем неупорядоченный (случайный) характер.
Реrулярная насадка характеризуется вполне определенным упорядоченным распо
ложением элементов. Она обычно изготамивается в виде пакетов с сотовой
структурой из перфорированных металлических или - реже - неметаллических
полос либо из сеток с каналами различной формы. Такие пакеты укладываются
в колонне друг на друга в 0ИJ1е отдельных слоев, занимающих все поперечное
сечение аппарата.
Таким образом, каналы ДJЫ прохождения паровой фазы в нерегулярной на
садке имеют хаотичную, а в регулярной - правильную (упорядоченную) струк
туру. Во втором случае достигается более равномерное распределение потоков фаз
по сечению колонны.
На эффективность работы насадочных колонн значительное мияние оказы
вает первоначальное распределение потоков фаз по сечению аппарата. Для рас
пределения жидкости обычно применяют м1юrоточечн"1е распределители. Их
используют также для промежуточного перераспределения потока после отдельных
слоев насадки с целью снижения поперечной неравномерности (см. разд. 10.1.3)
- не реже, чем через каждые 2-3 м оысоты слоя насадки. Как правило, их
устанамивают в случае нерегулярной насадки.
Достоинством колонн с регулярной насадкой яаляется низкое rидрамиче
ское сопротимение. Это относится также к пленочным и роторно-пленочным
колоннам.
Пленочные аппараты описаны в разд. 11.2.1. Ротсрно-пленочный ректифика
тор предстааляет собой колонну, внуrри которой вращается ротор - вертикаль
ный цилиндр или вал с закрепленными на нем элементами (лопасти, диски,
ленточная спираль, набор коаксиальных цилиндров и т.п.), создающими разви
тую поверхность для пленки жидкости.
В колоннах с охлаждаемы.м ротором и обогреваемым корпусом проводятся
процессы термической ректификации. Пар поднимается вверх по колонне и
частично конденсируется на поверхности охлаждаемого ротора, с которого жид
кость центробежной силой сбрасывается на стенку корпуса, где происходит ее
частичное испарение. Эти акты конденсации и испарения многократно повто
ряются по высоте колонны.
Пленочные и роторно-плсночные аппараты применяются для переработки
продуктов с ограниченной или низкой термостойкостью. В них обеспечиваются
низкие рабочие температуры нроцесса и малое время пребывания продуктов в
зоне повышенных температур.
Расчет гидродинамических характеристик колонн ра:l/IИЧНЫХ конструкций подо
бен расчету этих аппаратов для процессов абсорбции, приведенному в разд. 11.7 .

1017

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Различные применяемые в ре!СI'Ификационных агрегатах конструкции тепло
обменной аппаратуры (кипятильники, конденсаторы, подогреватели, холодильни
ки) описаны в разд. 7.1.
Кипятильники колонн бывают встроенными в куб или (чаще) выносными.
Для колонн больших диаметров обьNНо применяют несколько установленных
параллельно выносных кипятильников. Естественная циркуляция жидкости
через кипятильник (кипятильники) происходит благодаря разности плоrnостей
парожидкосrnой смеси в трубках выносного кипятильника и жидкости внизу
колонны и в вертикальной трубе, соединяющей нижние части колонны и кипя
тклъника.
В качестве теплоносителя 11 кипятильниках чаще всего используют водяной
пар различного давления (обычно до 2,0-2,5 МПа). Для более высоких темпера
тур в кубе (более 170-200 °С) применяют высокотемпературные органические и
неорганические (плавы металлов и их солей) теплоносители.
В качестве хладоаrента в конденсаторах и холодильниках обьNНо применяют
обороrnую воду комнаrnой температуры или захоложенную до 5-10 °С либо
рассолы. Весьма перспе!СI'Ивны и экономичны в качестве конденсаторов также
теплообменники воздушного охлаждения. Низкие коэффициенты теплоотдачи и
теплопередачи компенсируются в них большой поверхностью теплообмена
(оребрсние, пластинчатые теruюобменники и т.п.).
Конденсатор может бьпъ расположен выше колонны; тогда флегма возвра
щается в колонну самотеком. Чтобы предотвратить попадание парового потока в
линию возврата флегмы, последнюю подают в колонну через rидрозатвор (поз. 4
на рис. 12.24). В крупных рекrификационных установках конденсатор чаще
всего устанавливают на площадке у основания колонны, а флегму на верх ко
лонны подают насосом (т.е. принудительно). В этом С."I}'Чае в rидрозатворе нет
необходимости.
Процессы рекrификации проводят в непрерывном или периодическом
(преимущественно в малотоннажных производствах) режиме. Рабочие давления
процесса мoryr бьпъ различными:
- атмосферное - наиболее простой и дешевый вариант реализации процесса;
- вакуум - для понижения температур процесса (разделение высококипя
щих или термолабильных жидкостей);
- повышенное
для увеличения температур процесса (разделение смесей,
являющихся газообразными при нормальных температурах).
Соответственно рабочим условиям вносятся изменения в конструкцию рек
тификационных колонн и сопутствующей аппаратуры.
-

12.6. МАТЕРИАJIЬНЫЕ И ТЕПЛОВЫЕ ПОТОКИ
В РЕКТИФИКАЦИОННОЙ КОЛОННЕ
В ходе материального и теплового расчета ректификацио н 
н ы х установок (материальные и тепловые балансы, рабочая
линия процесса и т.п .) приходится оперировать потоками фаз и
компонентов по высоте колонны. В расчетном плане удобно,
когда эти пото!Оf не изменяются по высоте колонны : в этом
случае упомянутые балансы проще, а рабочие линии
прямые.
В отличие от процессов класса 3 (2-2) 1 в процессе ректифи
кации нельзя вьщелить инерт, поток которого постоянен: все
компоненты (в бинарной смеси - оба компонента) участвуют в
переносе вещества между фазами . Поэтому здесь нецелесооб-

1018

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 12. 25. Схема материальных и
теrшовых потоков в укрепляющей
части ректификационной колонны

разно использовать относи
кон центрации
тельные
компонентов. Такая ситуа
к
D
L
ция в общем плане рас
х
смотрена в разд . 1 0 . 1 5; для
линеаризации
расчетов
процесса
ректификации
удается реализовать первый
из указанн ых там путей
решения проблемы : выбор
способа выражения кон центраци й , приводящего к постоянству
потоков фаз по высоте аппарата .
Рассмотрим непрерывный процесс, протекающий в контуре
К, охватывающем верхнее сечение ректификационной колон
ны и произвольное сечение ее укрепляющей части (рис . 12.25) .
Будем оперировать абсолютными концентрациями и потоками
фаз; способ их выражения (массовые или мольные) пока без
различен . Обозначим : L и D - потоки жидкой и паровой фаз ,
х и у - концентрации НКК в них. Параметры процесса в
верхнем сечении снабдим индексом "в", в произвольном сече
нии - оставим без индекса.
Материальны й баланс для выделенного контура К (см . рис .
12 .25) по потокам фаз:

Lв +
откуда

D- L

-

Dв = О ,

= Dв - Lв = jdem .
разность потоков фаз (а
D

-

L

(а)

сами потоЮf могут
Таким образом,
изменяться по высоте ректификационной колонны) во всех
сечениях колонны - одна и та же : она равна разности потоков
в верхнем ее сечении . Л егко видеть (из материального баланса
для точки разделения потоков на флегму и дистиллят) , что эта
разность Dв - Lв = П; значит, и для любого сечения колонны
D - L = П.
Разумеется , аналогичный материальный баланс можно со
ставить для контура, охватывающего нижнее сечение колонны
и произвольное сечен ие ее отгонной части : вывод будет тот же,
но величина разности потоков фаз будет другой:
L' - D

=

idem = Lo ,

rде L' и Lo - потоки ж идкой фазы в произвольном сечении и на выходе из
колонны (отвод кубового про дукта) соответственно.

1019

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Тепловой баланс для выделенного контура К (см. рис . 12.25)
составим , пренебрегая потерями теплоты в окружающую среду
и обозначив h и i - энтальпии пара и жид кости:

Lвiв + Dh - Li - Dвhв = О ,

откуда

(6)

Dh - Li = Dвhв - Lвiв = idem.

Таким образом, потоки теплоты с паровой и жид кой фазами
(Dh и Lz) могуг изменяться по высоте колонны, но их разность
для любого сечения колонны - одинакова.
Если энтальпии компонентов, а значит и их смесей, неиз
мен ны (на практике - близки), т.е. не зависят от состава фаз

hл "" hв :::: h

const и iл :::: iв :::: i "" const ,
то фазовые потоки будут постоянными по высоте колонны.
Это положение легко доказывается с помощью соотношения
(6) с учетом, что h = i + r, где r - теплота испарения :
::::

Dh - Li = idem

или

= D(r

+ z) - Li

Dr + i(D - L) = idem.
Поскольку D
L = idem, i = const и r = h - i =
D = idem, а следовательно, и L = D П = idem.
-

(в)

const, то и

-

Заметим, что в выражении (в) в подавляющем большинстве
случаев первое слагаемое значительно превосходит второе. Это
означает, что для постоянства фазовых потоков по высоте ко
лонны (отдельно - для укрепляющей и отгонной ее частей)
важно преЖде всего равенство теплот испарения rл :::: rв :::: r.
На практике весьма часто мольные теплоты испарения разде
ляемых компонентов достаточно близки. Это обстоятельство
объясняют· близостью мольных энтропий парообразования для
разных веществ.
Например , ДJIЯ воды и этанола массовые теплоты испарения различаются
2 , 5 раза, а мольные - менее, чем на 2 , 5 % :
Вещество
вода
этанол

r

(кДж/кг)

2260
907

М (кг/моль)
18
46

r

в

( кДж/моль)
40700
41700

На практике мольные потоки фаз D и L с приемлемой по
грешностью принято считать неизменными по высоте колон
ны, если мольные теплоты парообразования r различаются не
более, чем на 10%, а разница температур кипения н е превы
шает 20-30°. Можно сказать, что при постоянстве мольных
энтальпий пара и жидкости конденсация в каком-либо сечении
• См. (10, 22 ) .

1020

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

(на тарелке) 1 кмоль пара должна приводить за счет вьщеле н ия
теплоты конденсации к испарению 1 кмоль жидкости.
Целесообразность (в расчетном плане) использования моль
ных потоков и концентраций для получения постоянных фазо
вь�х потоков очевидна.
Постоянство абсолютных потоков фаз при наличии меж
фазного переноса компонентов указывает на существование
эквивалентного (здесь - эквимолярного) разнонаправленного
массообмена: сколько молей Н КК переходит из жидкой фазы в
паровую, столько же молей ВКК переходит из паровой фазы в
жид кую .
Подобно зависимостям (а) и (б) для того же контура К (см . рис. 12. 25) мож
но записать уравнения материального баланса по поток.ом НКК:
L,,x8

откуда

Dy

-

+

Lx

Dy - Lx -

=

DвУв

-

D.y8 = О,

L,,x. = idem.

Иными словами: потоки компонента, переносимые паром и жидкостью,
мoryr изменяться по высоте колонны, но разность потоков компонента с от
дельными фазами для всех сечений (в пределах укрепляющей или отгонной
части ректификационной колонны) - одна и та же. Величину эrой разности для
укрепляющей части колонны легко определить из материального баланса для
точки разделения конденсата на дистиллят и фле гму :
- L,,x. = Пх2, а значит,
Dy Пх2; дпя отгонной части колонны такая разность L'x - Dy
l.-()X{J
В случае постоянных потоков
и L можно записать для соседних тарелок
(сечений):
= Dy;+ 1 - Lx;+ 1 ·
Dy; Отсюда
Yi + I - У;
(r)
.!::... idem.

Lx

D.:y8

=

=

=

•

D
Lx;

х;. 1

=

- х;

D

=

D

Из (r) следует, что при постоянстве потоков L и
на всех тарелках оnюше
ние приращений концентраций в фазах - одно и то же. При этом величины
самих приращений лх и Лу мoryr быть разными.

В дальнейшем детально анализируются процессы ре�сrифи
кации с постоянными по высоте колонны мольными потоками
паровой и жидкой фаз .
1 2.7. Н ЕПР Е РЫВНАЯ Р Е КТИФИКАЦИЯ
Б И НАРНЫХ СМ ЕСЕ Й
1 2.7. 1 . Статика процесса ректификации

Расчет процессов ректификации, как и других массообменных
процессов, сводиrся к решению задач двух основных nmoв:
- проектирования - определения условий проведения про
цесса и основных констру�сrивных характеристик аппарата,
обеспечивающих требуемую степень разделения компонентов;
- эксплуатации - нахожден ия достижимой степени разде-

102 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ления для заданных условий процесса (имеющийся аппарат,
известные входные параметры и режимы работы).
При решении обеих задач вначале необходимо количествен 
н о оценить эффективность процесса массообмена: в первом
случае требуемую для достижения заданного качества разделе
ния, во втором - обеспечиваемую существующей ректификаци
онной установкой.
Для оценI01 эффективности массообмена широко использу
ют один из двух параметров - число теоретических ступеней
(или тарелок) rtr или число единиц переноса (см . разд. 1 0.71 0 . 9 и 1 0. 1 2).
Напомним, что н а теоретической ступени достигается иде
альный контакт фаз, т.е. из контактного устройства (например,
барботажной тарелки) потоки взаимодействующих фаз уходят с
равновесными концентрациями.
Число единиц переноса (Ч Е П) представляет собой отноше
н ие пропускных способностей поверхностной и потоковой
стадий массопередачи по одной из фаз (см . разд. 1 0.8). Обозна
чим : kx - коэффициент массопередачи при выр ажении дви
жущей силы в терминах фазы "х"; F - полная поверхность
массообмена, т.е. суммарная поверхность межфазного контакта
в аппарате (в данном случае в ректификационной колонне).
Тогда на языке жидкой фазы (фазы "х" )

Ч ЕП

=

а

=

kx F

L =

xf"
х'

dx

х - хР

'

(а)

причем при питании колонн ы кипящей исходной смесью для
укрепляющей части колонны х ' = х1 , х " = х2 , а для отгонной
х ' = Хо, х " = xi ; в процессах ректификации х > х Р .
В результате решения проектных задач по величине ftr или а
может быть определена высота ректификационной колонны
как противоточного массообменного аппарата (см . разд . 10.8.4
и 10. 12). Расчет поперечного сечения колонны ведется по
уравнению расхода - на основе потока паровой (газовой) фазы
- идентично расчету абсорбцион н ых аппаратов (разд . 1 1 .4 . 1 ) .
Для определения числа теоретических ступеней ftr и числа
единиц переноса а надо располагать линией равновесия и
знать закон изменения сопряженных концентраций х и у по
высоте колонны (в рабочем диапазоне их изменения) . В диа
грамме х-у зависимость сопряженных концентраций представ
ляет собой рабочую линию процесса (см . разд. 10.7). Выведем ее
уравнение для ректификации, как это бьmо сделано в разд. 10.7
для противоточноrо массообмена.
Ректификац ионная колонна непрерывного действия состоит
из двух частей : верхней (укрепляющей) - от тарелки питания
до конденсатора и н ижней (отгонной) - от куба до тарелю1

1022

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

питания. В этих частях колонны различны фазовые потоюt,
поскольку на тарелку питания подается исходная смесь. По
этому при описании процесса непрерывной ректификации для
каждой части колонны характерна своя рабочая линия .
Первоначально будем считать, что в ректификационную ко
лонну подается исходная смесь при температуре кипения .

Укрепляющая часть колонны
Схема укрепляющей части показана на рис. 1 2.26. Выделим
контур К 1 , проходящий через произвольное сечение с потока
ми D, L, сопряженными концентрациями у, х и верхнее сече
ние, где отводится низкокипящий продукт - дистиллят (его
поток П с концентрацией х2 ). Запишем для этого контура ма
териальные балансы:
- по мольным потокам НКК
Dy - Пх2 - Lx = О;
(б)
- по мольным потокам фаз
D - П - L = О.
(в)
Совместное решение (б) и (в) дает уравнение рабочей линии:

L Х.
П Х + -У = -2
П+L
П+L
Разумеется, тот же результат получится, если материальный
записать для контура К2:
Dy + Lx2 - DJ2 - Lx = о,

( 1 2 . 17)
баланс по Н КК

откуда

(12. 17а)
При полной ко нден сации пара в конденсаторе У2 = х2, и числитель первоrо
слаrаемоrо принимает вид (D - L)x2 . Материальный баланс для то чки разделе
ния дистиллята П и флеl'МЫ L дает: D - L = П. Так что выражения ( 1 2 . 17) и
( 1 2 .17а) идентичны.
Поскольку в этом разделе рассматриваются процессы рек
тификации с постоянными потоками фаз D и L по высоте
укр епляющей части колонны (а П для каждого процесса величина фиксированная), то зависимость сопряженных кон 
центраций ( 1 2 . 1 7) представляет уравнение прямой линии .
Для анализа ректификационных процессов принято исполь
зовать приведенные фазовые потоки . Обозначим L/П = R и на
зовем это отношение флеrмовым числом; оно представляет со
бой количество к.моль флегмы, возвращаемой в колонну в рас
чете на один к.моль отводимого дистиллята. В дальнейшем ис
пользуются соотношения:
(r)
L = ПR и D = L + П = П(R + 1).

1023

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 12.26.
Рис. 12. 27.
диаграмме

Расчетная схема у креWIЯющей части колонны
Рабочая ли н ия укреWIЯюще й части ректификационно й коло нны

у

-х

в

Уравнение ( 1 2 . 1 7) после деления числителей и знаменателей
слагаемых в правой части на П с учетом (r) принимает вид:

R х.
Х2 + -у = -R+1 R+l

( 1 2 . 1 8)

Прямая по ( 1 2 . 1 8 ) образует с осью абсцисс угол сх. , причем
= R /(R + 1 ) , и отсекает на оси ординат (при х = О) отрезок
у. = x2 /<R + 1) (рис . 1 2 .27) . По известной точке ( У • , х = О ) и
углу сх. можно построить рабочую линию. Но удобнее строить ее
по двум точкам; поэтому найдем вторую харакгерную точку
рабочей лин ии, отвечающую ее пересечению с диагональю.
Если ( 1 2 . 1 8) решить совместно с уравнением диагонали у = х,
то, исключив у, получим абсциссу точки пересечения :
tgcx.

R х
Х2 + -у = х = -R+l R+l '

откуда х = х2 , причем при полной конденсации пара в конден
саторе х2 = У2 · Значит, в. диаграмме у-х рабочая линия проходит
через точку В с координатами х2, Уъ лежащую на диагонали.
Располагая рабочей линией, можно построить теоретические
ступени (см. разд. 1 0 . 1 2 и рис. 1 0.34) между нею и кривой рав
новесия в виде ряда прямоугольных треугольников, опи
рающихся своими гипотенузами на рабочую линию (см. рис .
1 2 .27) . Так находят число теоретичес ких ступене й, необходи
мь�х для повышения концентрации Н КК в укрепляющей части
колонны от х1 до х2 . В случае непрерывного контакта фаз с
помощью рабоче й линии по формулам типа (а ) находят Ч ЕП в
терминах и символах фазы "х'' или "у" (см . разд. 1 0 . 8 . 3 ) .
Положение ра6о чей линии, как следует и з уравнения
( 1 2 . 1 8) , определяется флегмовым числом R и составом дистил1 024

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 12. 28.

Предельные

рабочей линии
колонны

положения

укреw�я ющей

части

1 ..-------,,,"

У2

yt

лята х2. Состав дистиллята в
случае проектной задачи из
вестен (задается при ее поста
новке). Основную проблему
составляет выбор флеrмовоrо
числа .
----
х
Рассмотрим сначала каче
ственно влиян ие положения
рабочей лин ии на процесс ректификации . С ростом R рабочая линия, проходящая через точ
ку на диагонали с абсциссой х2, располагается ближе к диаго
нали, так как уменьшается отрезок У• . В результате с ростом R
уменьшается число теоретических тарелок, необходимое для
достижения заданной степени разделения в укрепляющей час
ти колонны. Одновременно при постоянном потоке отбирае
мого верхнего продукта П (дистиллята) с ростом R увеличи
ваются потоки (затраты) теплоты в кубе и конденсаторе колон
ны: рост R при постоянном П означает увеличение потока
флегмы L. Ее надо JiСПарять в кипятильнике, а образовавшийся
пар - конденсировать в конденсаторе . Поэтому с повышением
R возрастают расходы теплоносителя (чаще всего - греющего
пара) в кипятильнике и охлаждающего агента (скажем, воды
или воздуха) - в конденсаторе.
Рассмотрим пределы возможного изменения флегмового
числа. При заданной концентрации дистиллята х2 величина
отрезка У• = х2 /(R + 1 ) (см . рис . 1 2 .27) , отсекаемого рабочей
линией на оси ординат, зависит только от флеrмового числа R.
С увеличением R упомянутый отрезок уменьшается, и рабочая
линия поворачивается вокруг точки В , приближаясь к диагона
ли и удаляясь от кривой равновесия . Очевидно, в нижнем пре
дельном своем положении рабочая линия совпадает с диагона
лью и представляет собой участок АВ на рис. 1 2. 2 8 . При этом
отрезок У• = О , что соответствует R � оо. Этот же вывод следует
из анализа изменения угла а. и tga. = R /(R + 1 ) (см . рис. 1 2 .27) :
для диагонали а. = 45° и tga. = 1 , что означает R � оо. Так как
R = L/П, то (при физической не в озможности L � оо ) устрем 
ление R к оо означает П � О , т.е. нет отбора дистW1ЛЯта, и вся
жидкость, полученная в результате полной конденсации пара,
возвращается в колонну в виде флегмы. В таких случаях гово
рят, что колонна работает "с полным орошением·; или "на се
бя'; - без выдачи продукта.
Этот реж и м работы ректификаци о н н о й коло н н ы применяется в исследова
тельских целях

-

для

оце н ки эффе.кти в ности коло н н ы , для сравнения эффек -

1 025

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

тивносте й колонн р азличных констру кци й . Кроме того, полн ое орошение рек
тифи кацио нно й коло нны используется в некоторых специ аль н ых случаях, когда
ректификация н е имеет цел ью разделение ком поненто в , а применяется в иных
целях, например для обеспечения определе н ного профиля температур по высоте
техн оло гического аппарата . Н а конец , полн ы й возврат фле гмы я вля ется непр е 
менной стадие й выхода на н епрер ывн ы й режим раб оты ректифи кацио нн о й
колонны - спер ва устанамива ется необходимый проф иль кон це нтр аци й , толь ко
после этого начи н ают отбор дистиллята .

(линия 1 на рис . 1 2.28) достигается макси 
и поэтому заданная степень
разделения обеспечивается, как видно из рисунка, минималь
н ым числом теоретическ их ступеней, т.е. nг = rir min · Очевидно, и
число реальных ступеней (тарелок) п = п/Т\ т в этом случае
будет наименьшим (здесь Т\т - средний по колонне КПД таре
лок) . Однако в режиме R � оо испаряется максимальное коли
чество жидкости в кубе (кипятильнике) колонны и конденси
руется максимальное количество пара в конденсаторе; следова
тельно , расходы греющего пара и охлаждающего агента в этом
случае будут наибольшими.
С уменьшением R отрезок У • увеличивается, и рабочая линия
поворачивается около точки В, отдаляясь от диагонали и при
ближаясь к равновесной линии. Если она при этом пересекает
кривую равновесия в ы ш е точки А' (х 1 , yf ), то при данном сос
таве питания х1 процесс невозможен даже при бесконечном
числе тарелок (линия 2 на рис. 12.28). Предельный случай рабочая линия проходит через точку А' (линия 3 на рис . 1 2.28).
Тогда в точке А' движущая сила (уР - у) равна нулю, и для прове
дения процесса разделения в заданном диапазоне составов от х 1
(на тарелке питания) до х2 (в дистилляте ) потребуется бесконечно
большое число теоретических ступ'еней. Заметим: в случае массо
обмена с непрерьmным контактом фаз значение (уР - у) = О на
одном из концов массообменноrо аппарата (здесь - укрепляющей
части колонны) приводит к бесконечному возрастанию Ч ЕП, к
нулевой средней движущей силе и как следствие - к необходи
мости бесконечно большой поверхности контакга фаз, а значит, и
высоты коло н н ы . Эrо предельное положение рабочей линии соот
ветствует максимальной величине отрезка У • и, следовательно,
минимальному флеrмовому числу Rmin.
Для определения Rmin воспользуемся уравнением рабочей
линии ( 1 2 . 1 8 ) . При R = Rmin рабочая линия проходит через
точку А' с коо рдината м и х1 и yf (см . рис. 1 2 .28). Подставив
В режиме R

�

оо

мальная движущая сила процесса,

эти значения в ( 1 2 . 1 8) , получим :

У 1Р
1 026

=

Х2

Rmin

+

1

+

Rmin
х
Rmin + 1 l '

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

откуда

Rnuн

=

Р
Х2 - у1Р - У2 - у1
yf - Х1 yf - Х1

( 1 2 . 1 9)

При R = Rmin разделение возможно только в колонне беско
н ечно большой высоты . При этом расходы теплоты в кубе и
конденсаторе , а с н ими и расходы греющего пара и охлаж
дающего агента, будуr наименьшими .
Таким образом, с увеличением флегмовоrо числа капитальные
затраты, связанные с габаритами ректификацион ной колон н ы
(строже - с амортизационными отчислен иями , зависящими
еще и от нормативного срока ее функционирования), умень 
шаются, а эксплуатационные затраты (их главную часть со
ставляют энергозатраты) - возрастают.
Рабочее флегмовое число R, при котором может работать
колонна, находится в пределах Rmin < R � R = оо.
Выбор оптимального флегмового числа определяется техни
ко-экономическим расчетом. Общий подход заключается в ми
нимизации суммарных затрат. Для процесса ректификации
капитальные (амортизационные) затраты пропорциональны
высоте колон н ы (числу тарелок п; высоте слоя н асадки Нн) , а
также зависят от диаметра колонны dк. Последняя зависимость
неоднозначна: если "начинка" колонн ы - дешевая, то стои
мость пропорциональна периметру колонны, т.е. ее диаметру
dк; если дорогая, - то поперечному сечению колонны, т.е. dк2 .
А величина dк по уравнению расхода определяется паровым
потоком D
П(R + 1 ) : при кон кретной скорости пара в ко
лон н е D - dк2 . Итак, капитальные затраты пропорциональны
произведению п [ П( R + l ))S, где s изменяется в интервале от 0 , 5
до 1 (при этом росту R сопуrствует уменьшение п ) . Эксплуата
ционные (энергетические) затраты пропорциональны паровому
потоку D (его испаряют в кипятильнике и конден сируют в
конденсаторе), а значит, величине П(R + 1 ) . Суммарные затра
ты 3 составляют:
3 = A· n [П(R + 1 ) ) 5 + Э·Л(R + 1 ) .
Здесь удельные коэффициенты амортизацион н ых А и эксплуа
тационн ых Э затрат зависят от складывающихся цен на мате
риалы и оборудование и на энергию, а также от конструк
тивных характеристик аппаратуры.
Задача технико-экономического анализа
минимизация
функции 3 в зависимости от R: минимуму 3 отвечает опти
мальное рабочее значение R (см . разд . 1 0 . 7) .
Трудности технико-экономического расчета (они заключа
ются прежде всего в определении А и Э) стимулируют доста=

1 02 7

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

точно широкое использование эмпирических оценок и практи
ческих рекомендаций.
Существует ряд приближенных подходов к определению щпималъноrо зна
чения R. Приведем некоторые из них.
Наиболее _ПJ'ОСТОЙ подход базируется на понятии о коэффици енте нз61J11(8
значение а установлено, то рабочее флеrмовое
флеnw с • R/Rmin > 1 .
число рассчитывается как R = aRmin· Рекомендуемые диапазоны с по разным
источникам заметно расходятся: нижний предел - от 1,05 до 1 , 3, верхний - от
2 до 1 0.
В последние rоды все чаще обращаются к расчету оJПИмальноrо R, минуя а .
Так, приводятся • формулы типа R
+ k)Rmin + k с диапазонами значений k,
а иногда - с численными значениями (обычно на уровне 0, 3).
Более физически обоснованным является подход, учитывающий отклонения
от минимальных значений (R - Rтш) и (п, - п, min). Приведем в модифициро
ванном виде некоторые соотношения с рекомендуемыми диапазонами пара
метров:

Если

=

R- R

---"m=ш�
R
·

m;n + l

Если

взять

=

(1

nт -nт min
ао ( ао = 0, 1 +0,5); --nт min + 1

=

Ьо (Ьо

=

0,4+ 1) .

(д)

произведение этих комплексов

R - Rтm nт - nт min
Rmin + 1
+1

-'=,..
-'-----'
---===- -nт
min

=

а о Ьо ,

то оно вполне отвечает физич�скому смыслу: если R _. оо, то необходимо п, _.
-+ п, min так как произведение аоЬо - конечно; из этих .же соображений R -+ Rmin
•
при п, ...,. оо.
Выражение (д) легко преобразуется к виду

R+l

Rmin

nт + l

+1 nт min +1

---

=

(1

+

ao)(l

+

Ьо)

"' const.

(е)

Анализ показываеr, чrо в рекомендуемых диапазонах численное значение
правой части выражения (е) изменяется мало, оно близко к 2,2 (естественно,
наибольшему значению ао отвечает наименьшее значение Ьо). Задавшись, на
пример, приемлемой величиной комплекса (п, + 1 )/(п, min + 1) или практически
совпадающей с ней величиной п,/п, min (конечн о, более 1 и менее 2, 2), получа
ем оJПИмальное рабочее флеrмовое число R.
Существуют и иные подходы к оценке оmимальноrо флеrмовоrо числа•• .

Отгонная часть колонны
Схема отгонной части колонны показана на рис . 1 2 .29. По
ток жидкости L' в этой части колонны больше потока флегмы
L, стекающей из укре пляющей части, на величину потока ис
ходной смеси L 1 , поступающей на тарелку питания в виде ки
пящей жидкости. Для вывода уравнения рабочей линии выде
лим контур К, проходящий через промежуточное сечение с
потоками D, L' и сопряженными концентрациями у, х и через

[!, 14, 18).

• См.
• • С м . , например,

1 028

(8, 27 ) .

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 12. 29.
колон н ы

Расчетная

схем<�

отго н н о й

части

н ижнее сечение, где отводится вы
сококипящий поток L0 - кубовая
жидкость с кон центрацией Н КК .хо .
Запишем для этого контура уравне
н ия материального баланса:
- по мольным потокам Н КК
L 'x - Dy
Lo.xo = О ,
(ж)
- по мольным потокам фаз
L' - L0 = О .
(з)
Решая совместно (ж) и (з) , полу
чаем уравнение рабочей линии отгонной части колонны:

к

-

D

D

У =

Lo
D

- - Хо +

D + Lo Х .
D

( 1 2 .20)

Поскольку
и L0 постоянны, то это - уравнение прямой.
Зафиксируем ее положение на диаграмме у-х. Это можно бы
ло бы сделать по тангенсу утла наклона и отрезку, отсекаемому
на какой-либо оси координат. Но, как и для укрепляющей час
ти колон н ы , проще построить эту прямую по двум точкам ,
через которые она проходит, - пересечения ее с диагональю и
с рабочей линией укрепляющей части колон н ы . С помощью
уравнений ( 1 2 .20) и диагонали у = х найдем первую точку пе
ресечения, приравнивая ординаты :
у = х =

_

L
+L
o x + D
o x.
o

D

D

'

отсюда находим абсциссу точки пересечения: х = Хо · На диагонали
.хо, поэтому составы отводимой из куба жидкости и образую
щегося в нем пара одинаковы. Заметим: равенство Уо = Хо означа
ет, что ректификационное действие куба не учитывается .
Для нахождения точки пересечен ия рабочих линий необхо
димо совместно решить уравнения ( 1 2 . 1 8) и ( 1 2 .20) . Приравняв
их правые части, получим, сократив на
Уо =

D:

откуда

Пх1 + Lx = - LQXo + L'x,
Пх1 + Lo.xo = (L' - L)x.

(и)

Из материального балан са по потоку Н КК для контура К, ох 
ватывающего всю колон ну (рис . 1 2 . 30 ) ,
L 1x1 -

получаем выражение для

Пх1

левой

Лх1

- Lo.xo = О

части (и) :
+ Lo.xo = L 1 x 1 .

(к)
1 02 9

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 12. 3 0. К расчету граничн ы:>. потоко в в ректификаци о н н о й колонне

Рис. 12. 3 1 . П о строение рабочих ли ний укрепляющей ( J) и отго н н о й ( 2) частей
ректификаци о н н о й колонны

Если, как нами принято , исходная смесь поступает на та
релку питан ия при температуре кипения, то L' =
+
Тогда
правая часть (и) прини мает вид:
(л)
- L)x =
Из (к) и (л) следует:

L L1 •

(L'

L 1 x.

L 1 x1 L 1 x,

=
т.е. х = х 1 •
Это означает, что при подаче исходной жидкости при тем пера
туре кипения рабочие л инии обеих частей колонн ы пересека
ются в точке с абсциссой
Таким образом, построив рабочую линию укрепляющей час
ти по точке В (х2, У2) и ординате У * при = О (см . рис . 1 2 .27),
находим точку ее пересечения с вертикалью
= х1 (рис. 12.3 1 ) .
Соединив эту точку с ранее наЙденной точкой на диагонали (с
абсциссой хо), построим рабочую линию отгонной части колонны.

х1 .

х

х

Последователыюсть расчета ректификационной колонны

Теперь можно сфор м улировать последовательность расчета
ректификационной колонны в целом :
- построение (по экспериментальным данным или расчет
ным путем) кривой фазового равновесия ;
- нанесен ие на диаграмме у-х заданных кон центраци й
и хо ;
- определение Rmin и на его основе - рабочего флегмового
числа R;
- построение р а бо •шх лини й укрепля ю щей и отгонно й
частей коло н н ы ;
- граф ическое определение числа теоретических ступеней
(тарелок) В укрепляюще й И ОТГО Н НОЙ частях КОЛОН Н Ы rtrY И rtr0
(на рис. 1 2 .3 1 rtrY = 2 , fir" = 4).

х2

1030

х1,

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

В случае получен ия дробных чисел теоретических тарелок в задачах проекти
р о вания их окр угляют до ближ а й шего большего цело го, т. е. "в запас " .

Такова же последовательность расчета колон н ы в случае не
контакта фаз , только вместо числа теоретических
ступеней обычно используют число единиц переноса а. Здесь
последним этапом является (см. разд. 1 0 . 8 . 3 , рис . 1 0.27) вычис
ление соответствующих интегралов для укрепляющей и отгон 
ной частей колонны:

прерывного

Х2
аУ = J
х1

dx

х хР

и

--
-

Х1

ао = J

Xo

dx

х - хР

--

Заметим : расчет на осно ве числа теоретических тарело к иногда применя ют и
в случае непрер ывно го ко нтакта фаз, используя понятие высоты, эквивалентной
теоретическо й ступени или тарелке ВЭТГ. Ограниченность такого подхода рас
смотрена в разд.

10.1 2.5.

Материальный расчет процесса ректификации предполагает
определение всех граничных потоков в ректификационной
установке - входящих в колонну и выходящих их нее. С этой
целью н а рис. 1 2 . 3 0 выделен пространственный контур К, ох
ватывающий входящий и уходящие потоки. Материальный
баланс для этого контура по мольным потокам фаз имеет вид:
L 1 - П - Lo = О .
Решая (м) совместно с балансом (к) по Н КК, находим :

П=

L1

х1 - х о
Х2 - Х о

;

(12.21)

(м)

( 1 2.22)

Зависимости ( 1 2 . 2 1 ) , ( 1 2 .22) отвечают правилу рычага (см . разд.
1 0 . 2 .4) .
Далее определяем потоки флегмы L = RП и пара D = (R +
+ l)П, а также жидкостной поток в отгонной части колон н ы
L ' = D + L0; в случае питания колон н ы кипящей исходной
смесью он равен также L ' = L + L 1 •
Подчеркнем: в полученных формулах для граничных пото
ков могут фигурировать и массовые величины - потоки фаз и
кон центрации . Кстати, при полной конденсации пара в кон 
денсаторе значения флегмового числа R в мольных и массовых
единицах совпадают, так как составы, а значит, и мольные
массы дистиллята и флегмы одинаковы.
12.7.2. Основные размеры ректификационных колонн

К основным размерам ректификацион ной колонны относят
прежде всего ее высоту и диаметр .
103 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Высота ректификациоююй колонны
В ысоту тарельчатой колон н ы рассчитывают на основе числа
или высоты
На реальн ых тарелках ректификационной колон н ы не до
стигается состояние равновесия уходящих с тарелки потоков
фаз :
для
достижения
равн овесия
требуются
большие
(теоретически - бесконечные) время или поверхность контак
*
та фаз . Поэтому с тарелки уходит пар состава у < уР (рис .
1 2.32): кон центрация Н КК в нем меньше равновесн о й , т . е .
меньше, ч е м в паре, уходящем с теоретической тарелки . Дви 
жущая сила процесса (выразим ее, к примеру, на языке фазы
"у") при этом реализуется не полн остью :

реальных тарелок п

слоя насадки Ни.

у* - у < уР - у.

*
Отношение этих разностей, трактуемое как КПД тарелки Т\т ,
характеризует степень приближения к равновесию уходящих с
тарелки фаз , иначе - степень приближения (по использовани ю
движущей с ил ы ) реальной тарелки к теоретическо й :
•

*
у
.,,' IT =
уР

-у
•

-у

*
Знание Т\т позволяет построить реальную ступень , т.е . устано
вить реальное приращен ие кон центраций Н КК в фазах.
КПД может оказаться разным для различных тарелок, по
скольку от тарелки к тарелке изменяются составы фаз (а с н и 
ми и
свойства
рабочих
тел)
и
условия
процесса
(температура, с корость движения фаз и т .д . ) . Технолога интере 
сует не локальное значение Т\/, а среднее значение КПД таре
лок
Т\т; при этом величину Т\т обычно усредняют от
дельно для укрепляющей и для отгонной частей колон н ы .
Вел ичи н а llт сложн ы м образ ом за вис ит от скорости пара : с по
вышением скорости пара увеличивается поверхность контакта на
тарелке , а следовательно , и Т\т, но одновременно возрастает унос
капель с н ижней тарелки на вышележащую (интенсифицируется
продольное перемешивание в терми н ах структуры потоков - см .
разд. 8.2 и 8.5), 'fГО приводит к понижению движущей силы про
цесса, т.е. его эффективности Т\т (см. разд. 8 .2). На КПД оказывает
сн ижается
влияние расстояние между тарелками
с ростом
унос капель жидкости с паром, и Т\т растет. КПД завис ит также от
конструкции тарелок и, разумеется , от физ ических свойств ком
понентов. Значение Т\т определяется эмпирически , обычно оно
находится в диапазоне Т\т � 0,3+0 , 8 .
Некоторые практические рекомендации п о определению Т\т
приводятся в учебной , н аучной и справочной литературе· .

в колонне

Лh:

• См " например, ( 1 ,

1 032

7,

1 4 , 1 8, 1 9 ) .

Лh

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 12. 32.

К

определению

КПД

р еально й

тар елки
Замети м : вели чина ТJт д11Я тарелок ректи
фикационных колонн значительно выш е , че м
для анало ги чных по ко нструкции абсорбцион
ных. Это связано с актами конденсаци и 
тарелке ,
испарения
на
ректификационной
обусловливающи ми более тесный контакт фаз,
нежели пр и бар ботаже газа через слой жид
кости на абсорбционной тарел ке (в отсутствие
фазовых переходо в) .

уР

у•
у

х

Зная fLrY, fLr0 и располагая значениями 11т, н аходят число реальных тарелок в каждой из частей
колонны ny = fLrY/11тУ и п0 = fLr0/11т0 и далее - общее число
ре ал ьных тарелок п = ny + п0 .
Высота тарельчатой части колонны (рабочей зоны) при из
вестном расстоянии между тарелками Лh определяется как

Нт = (п - l)Лh.

Величину Лh выбирают из условия обеспечения сепарирую
щего эффекта в паровом пространстве тарелки - для предот
вращения уноса капель жидкости потоком пара на вышележа
щую тарелку. Обычно Лh � 0 , 2+0 , 5 м.
В случае ректификаци онных колонн с непрерывным контак
том фаз (например, насадочных) высота рабочей зоны равна
высоте слоя насадки Нн. Расчет Нн изложен в разд. 1 0 . 8 .4 и
1 1 .4.2. Если слой насадки разделен перераспределительными
устройствами на несколько слоев, то общая высота рабочей
зоны должна определяться с учетом высот этих устройств.
Полная высота р ектификационной колонны складывается из
высоты рабочей зоны и высот верхней и нижней зон колонны.
Ввод в последние флегмы и парожидкостного потоков увели
чивает здесь образование капель. Чтобы избежать повышенною
брызrоуноса, высоту этих участков колонны вьmолняюг заметно
превышающей Лh. Она при прочих равных условиях растет с уве
личением диаметра колонны; порядок ее величин ы
1 м . Заме
тим, что по этим же причинам высота пространства над тарелкой
пита ния также берется несколько больше Лh. Разумеется, если куб
колонны содержит встроенный кипяrилъник, то высота нижней
зоны сообразуется с ero конструктивными размерами.
-

Диаметр ректификационной колонны
Как уже отмечалось , диаметр колонны dк рассчитывается по
потоку пара, поскольку скорость пара (линейная ил и объемная)
на несколько порядков выше скорости жидкости .
Объемный расход пара пр и мольном его потоке D в нор
мальных условиях Uн = О 0 С, Т = 2 7 3 К; Рн = 105 Па) составляет
1 033

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

D-22,4 нмЗ/с; в рабочих условиях (при температуре t и давлении
р) он, соответственно уравнениям Гей-Люссака и Бойля
Мариотта, равен :

22

5
D t + 27 3 1 0
'
273 р
4

(мЗ lc) .
;•

По уравнению расхода при скорости парового потока
величина выразится как (7tdк2/4)wп. Отсюда

4
р 1tWп

dк = 22 '4D 2 7 3 + t 1 0
273

Wп

эта

5

( 1 2 .23)

Проще диаметр колонны выразить через массовый поток пара
Dм; если рабочая плотность пара Рп, то по уравнению расхода
Dм 1td� w

Рп

--

откуда

dк =

-

4

--

п'

�

(12.24)

В формуле ( 12.23) мольный паровой поток постоянен по вы
соте колон н ы (преимущество этой формулы) . Массовый поток
пара Dм изменяется по высоте колонны; при известном составе
пара он определяется по мольному потоку: Dм = DM. Способ
расчета средней (в данном сечении) молярной массы паровой
смеси М изложен в разд. 10.2. 1 . Плотность пара может быть
оценена по уравнению Клапейрона-Менделеева (заметим , что
она будет необходима для последующих расчетов) .
Температура t (в мен ьшей мере и давление р - из-за гид
равлического сопротивления паровому потоку) изменяется по
высоте колон н ы . К тому же налицо различия в скорости пара
Wп в различных сечениях (см . н иже) . По этим причинам dк рас
считъIВаюr для ряда сечений колонны . ЕсJШ при расчете величины
dк получаюrся близкими, то колонну делаюr одного диаметра
(ориентируясь на большее расчетное значение dк). Если различие
в расчетных значениях dк велико, то секции колонны из готавли 
ваюr разного диаметра; чаще всего в этом случае укрепляющая
колонна имеет один диаметр, а отгонная - другой.
Расчет диаметра колонны предполагает выбор скорости пара
Wп. О на должна быть ниже некоторой предельной (крити
ческой) величины , соответствующей значительному уносу ка
пель жидкости (если процесс ведется под атмосферным и из
быточным давлением) или перепаду давлен ия по высоте (если
колонна работает под существенным разрежением) . Расчет Wп

1 034

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ведуг на основе эмпир ических или полуэмпирических реко 
мендаций и формул * . В них для тарельчатых колон н Wп выра
жают в зависимости от относительной плотности жидкости и
пара ржfрп, а также промежугка Лh, а для насадочных - на
основе скорости захлебывания w 3 (см . разд . 1 1 .4.2).
12. 7 .3. Тепловой расчет колонны

Схема, иллюстрирую щая тепловой расчет ректификацио н 
н о й колонн ы , представлена на рис . 1 2 . 3 3 . Поскольку теплофи
зические кон станты , приводимые в литературе, обычно отне
сены к единице массы, то тепловые расчеты предпочтительно
проводить в массовых величинах.
В колонну вносится теплота:
Qк - в кипятильнике (чаще всего - конденсирующимся во
дян ым паром);
L 1 c 1 t 1 - с исходно й смесью ( с 1 и t1 - ее теплоемкость и
температура) ;
Lc2t2 - с флегмой ( с2 и t2 - теплоемкость и температура
флегмы, равн ые соответствующим параметрам дистиллята) .
Из колонны выводится теплота:
- теплосо
- с паром, поступающим в конденсатор
держание в ыходящего ю колонны пара) ;
Locoto - с кубовым пр одукт о м
и to - его теплоемкость и
температура) .
Для определен ия расхода теплоты в кипятильни ке запишем,
пренебрегая тепловыми потерями в окружающую среду, урав
нение теплового баланса для контура К 1 (см . рис. 1 2.33), про
ходящего через теплообменную поверхность кипятильника:
(н)
Qк + L 1 c1 t1 + Lc2t2 - Dh2 - Locoto = О.

Dh2

(h2

(со

ПR и D = П(R + 1 ), выразим Qк:
ПR(h2 c2t2) + Пh2 + Locoto - L 1 c1 t1 ,

Подставляя в (н ) L

Qк =

=

-

или , учитывая , что с крытая теплота испарения дистиллята
(флегм ы) r2 = h2 ( 12.25)
+
+ Locoto - L1 c1 !1 .
Qк =

с2 !2 ,
П(Rr2 h2)

Определив количество теплоты Qк, подводимой в кипятиль
нике колон н ы , можно рассчитать расход греющего пара дrр •
составив тепловой балан с для контура Кз (см . рис . 12.33). Обо
значим:
- энтальпю1 греющего пара, Тк
его температура
в 0 С, ск - теплоемкость конденсата. Тогда

hгр

-

дгр h гр - дrр Ск Тк
•

-

Qк = О ,

Более подробно с м . литературу в сноске на с. 1 0 32 .

1 035

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 12. 33. К теruювому расчету ре ктификацион но й
1
кипятильних, 2 колонна, З коццснсатор
-

и

-

колон н ы:

-

( 1 2 .26)
где rrp

=

hrp

-

Ск Тк

-

теплота конденсаци и греющею пара.

Поверхность кипятильника Fк находим по многократно ис
пользованной формуле (см. разд . 7 . 6 ) :
F=
где

k

-

коэффициент тепло передачи;

_я_
'
kЛ

Лер

(7. 1 4а)

ср

-

средни й температурны й напор .

Применительно к кипятильнику ректификационной колон
ны k = kк
коэффициент теплопередачи от конденсирую
щегося пара к кипящей жидкости ; метод его расчета изложен в
разд. 7 . 3 .2; Лер = Лк = Тк to . Тогда
-

-

Fк =
1 036

Q

kк( Тк

к
-

to )

( 1 2.27)

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Поток теплоты, отводимой в конденсаторе
теплового баланса для контура �:
откуда

Dh2 - Dc2t2 -

Qконд•

найдем из

Qконд = О ,

( 1 2.28)
Поток охлаждающей воды G8 с начальной температурой !8' ,
конечной 18 " и теплоем костью с8 определим из теплового ба
ланса для контура Ks :
так что

GвСвfв' + Qконд - Gвсв tв "
Gв

=

Q КОНД

с в (tв" - t'в )

= О,

.

( 1 2 .29)

Поверхность конденсатора рассчитывается по формуле
(7 . 14а), где для конденсатора k = kконд - коэффициент тепло
передачи от конденсирующегося пара к потоку, не изменяю
щему агрегатного состояния (метод его расчета дан в разд.
7.3 .2); Лер = Лконд - среднелогарифмическая разность темпера
тур , вычисляемая по формуле

В результате

F.

КОJ Щ

=

Qконд

k конд

( 12.30)

Л конд

Представляет интерес сопоставление тепловых потоков

Qк

и

Qконд· В этих целях на рис. 1 2 . 3 3 выделим контур К2 и запишем

для

него тепловой баланс :

Qк + L1c1 !1 - Qконд - Пс2t2 - Locoto =

О.

(о)

Теплоты , подводимые и отводимые жидкостными потоками,
примерно одинаковы : L 1 c1 t1 � Пс2!2 + Locoto . Тогда из равенства
(о) получаем : Qк � Qко�щ · Физически это надо понимать так:
именно флегму, получаемую в конденсаторе, и надо испарять в
кипятильнике ; поэтому теплоты (подводимые и отводимые) в
этих аппаратах примерно равны .
1 2 . 7 .4. Воздействие на эффективность работы колонны

Важнейшая технологическая задача при реализации процес 
сов ректификации - воздействие на их протекание с целью
получения продуктов необходимой чистоты .
1 037

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

В ходе проектирования ректификационной колонн ы такое
воздействие возможно пугем увеличения числа тарелок или
высоты слоя насадки, а также использован ия наиболее эффек
тивных конструщий тарелки или типа и размеров элементов
насадки .
В ходе эксплуатации ректификационной колонн ы повысить
чистоту продуктов можн о , повышая флегмовое число
- увеличением потока флегмы (при сохранении отборов ди
стиллята
и кубового остатка L0 ) , если кипятильник и кон 
денсатор рассчитаны с некоторым запасом и позволяют повы
сить тепловую нагрузку ;
- умен ьшен ием производительности колонн ы по исходной
смеси , а значит, и по продуктам ; при этом, сохраняя поток
флегмы L и пон ижая П, получают более высокие
Повысить флегмовое число можно также пугем захолажива
ния флегмь/, т.е. возвращения ее в колонну при температуре
н иже t2 : холодная флегма будет нагреваться в верхних зонах
колонн ы до температур ы кипения за счет конденсации части
парового потока, и пото к флегмы по колонне возрастет.
Увеличивая число тарелок п (высоту слоя насадки Ин) , а
также флегмовое число
можно в принципе получить сколь
угодн о чистые дистиллят
� 1 ) и кубовый остаток (х � О) , но
абсолютно чистые Н КК и В К К методом ректификации (вообще
- массообмена) получить невозможно. Ведь точки чистых
компонентов располагаются в правом верхнем и левом н ижнем
углах диаграммы
где движущая сила равна нулю; это
означает необходимость безграиичного увеличения п (или Ин) даже при бес конечном
(что , кстати, тоже невозможно при
отборе продуктов) .
Еще одн а возможность воздействия на ч истоту продуктов смещение точки подачи исходной смеси по высоте колон н ы .
Так, если подать исходн ую смесь в колонну пониже , то увели
чится протяженность укрепляющей части , и дистиллят станет
чище; при этом уменьшится протяжен ность отгонной части
колон н ы , так что кубовый остаток будет больше загрязнен
н изкокипящим компонентом. Изменение точки питания рек
тификацион ной колон н ы может оказаться полезным в двух
основных случаях:
1) только один из продуктов должен быть весьма чистым (во
втором допускается заметное содержание примеси) ; тогда сле
дует увеличивать протяжен ность той части колонны, на выходе
из которой нужно получать чистый продукт;
2) по како й-то причине изменился состав исходной бинар
но й смеси. Например : содержание Н КК в исходной смеси по-

R:

П

R.

R,

(х

у-х,

R

' П одробнее с м . 17 1 ·

1 038

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

низилось; для сохранениs� прежней чистоты дистиллята теперь в
укрепляющей •1асти колонны потребуется большее число тарелок

(или бо льшая высота слоя насадки ) , чем раньше , а для сохра
нения чистоты кубового остатка
меньшее число тарелок в
отгонной части колонн ы . Поэтому исходную смесь нового со
става следует подавать в колонну на более низкую тарелку. Кон 
кретно : е е надо подавать в то сечение колонны, в котором этот
состав равен составу исходной смеси.
-

Для реализации этого метода н а практике предусматр и вают вводы и сходной
смеси на разные тарелки по высоте колон н ы ( "гребенку" со штуцерами и венти
ля м и - поз. З на рис. 1 2 . 2 3 ) .

Отдельный вопрос
контроль нормального течения процес
са рекrификации . В общем случае любого массообменного
процесса контроль осуществляется путем анализа состава продук
тов. Но при рсктификаuии бинарных смесей температура на та
релках однозначно связана с составом фаз. Поэтому составы от
водимых потоков вполне можно контролировать по температуре с
помощью термопар, термометров сопротивления и других датчи
ков измерительных устройств, устанавливаемых (предпочтительно
- в жидкости) вблизи выхода потоков из колонны. Показания
приборов позволяюr правильно воздействовать на потоки в ко
лонне, а значит, и на контролируемые составы.
-

Пример. Предполож и м , •rro п р и разделен ии смеси метанол-вода температура
на верху коло н н ы в р абочем режиме составляет 65 ° С (температура ки пения

чистого метанола равна 64,5 ° С) . Пусть теперь п о како й - то причине эта темпера
тура по высилась до 66 °С. Следовательно, в отводимом сверху паре ( в дистилля 
те - тоже) возросло содержан ие ВКК ( воды) - такой продукт некондиционен.
Чтобы до вести е го до заданно й чистоты, надо увеличить флеrм о вое число . При
сохране н и и п р о из водител ь н о сти по и сходно й смеси L1, дистилляту П и кубо во
му остатку Ц, это можно сделать, повысив расход греющего пара в кипятильнике
( и , ко нечно , - расход охлаждающего агента в конденсаторе): увеличится поток
пар о в D разделя емой смеси в колонне,
значит, и пото к флегмы
= D - П, а с
н и м и флеrмоnое число

R

=

/

L

L П.

12.7.5. Влияние агрегатного состояния исходной смеси
на работу ректи ф икационной колонны

В предшествующих разделах расс матривалась работа рекrи
фикационно й коло н н ы , питаемой исходной с месью при темпе
ратуре кипен ия . Реально возможны и другие технологические
ситуации : исходная смесь может быть не догрета до температу
ры кипения либо находиться в парожидкостном или даже в
парообраз ном состоя н и и . Важно знать, как такие отклонения
от ранее расс мотренного режима питания отразятся на работе
рекrификационной колонны.
П ри подаче в колонну исходной кипящей жидкости состава
х1 с температурой кипения t1 на тарелке питания кипит жид 
кость того же состава х 1 , а следовательно, п р и той ж е темпера-

1 039

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 12. 34. К материальному балансу тарелки пита
ния

туре t1 • В этом случ ае конденсация од
ного моля пара на тарелке питания
приводит к испарению одного моля
жидкости
; значит, если снизу на pacL,
D
сматриваемую тарелку в единицу вре'tx1·
.у
мени поступает D моль пара, то сверху
уходит такой же его поток. При откло
нениях от подачи в колонну кипящей
ж1щкости на тарелке питания происходят изменения, характе
ризуемые удельным потоком пара Е.
Если на тарелку питания подается недоr"Ретая исходная жид
кая смесь при температуре to < t1 , то часть теплоты конденса
ции пара затрачивается на подогрев поступающей жидкости от
to до t1 • Поэтому для нагрева и испарения 1 моля исходной жид
кости на тарелке питания сконденсируется Е моль пара, причем
Е > 1 . При этом в расчете на каждый моль исходной смеси с
тарелки питания уходит вниз ЛL = Е - 1 моль дополнителыюй
жидкости, образующейся при дополнительной конденсации
пара, а вверх - на ЛD = Е - 1 моль меньше пара, нежели при
питании колонны кипящей исходной смесью.
Для количественного анализа представим (рис. 1 2.34) схему
потоков на тарелке питания. В целях упрощения здесь и далее
пренебрегаем ректифицирующим действием тарелки питания
- это приводит к некоторой погрешности при расчете числа
теоретических тарелок (не более чем на 1 тарелку и "'в запас 't)
С таким допущением составы фаз (а с ними и теплота испаре
н ия смеси r) н а тарелке питания не изменяются . Из определе
н ия Е следует:
(п)
E-r = l · [c(/ 1 - to ) + r] ,
причем в правой част и равенства представлена теплота, необ
ходимая для подогрева L моль исходной смеси до температуры
кипения и его полного испарен ия, а в левой - теплота, выде
ляющаяся при конденсации необходимых для этого Е моль пара.
Из (п) находим удельное количество пара Е (моль конденси
рующегося пара/моль исходной смеси):

+ t

Е

=

(t
1 + с 1

- to )
r

>

1.

Отсюда следует, что дополнительное количество флегмы , обра
зующейся на тарелке пнтания , Е - 1 = c( t1 - t0 )/r , и такое же
количество пара теряет здесь паровой поток. При !о = !1 есте
ственным образом получаем: Е = 1 , или Е - 1 = О
.

1 040

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Если на тарелку питания исходная смесь подается в паро
жидкостном состоянии при степени сухости \\f (\\f - доля пара,
1 - \\f - доля жидкости), то по определени ю Е для тарелЮt пи
тания характерно равенство :

Er = ( 1

-

\\f)r.

В правой части теперь - количество теплоты, необходимой для
испарения 1 моль исходной парожидкостной смеси . Отсюда
Е = 1 - \\f < 1 , т.е. для образования пара из 1 моль исходной
парожидкостной смеси на тарелке питания требуется сконден 
сировать Е < 1 моль поступающего снизу пара (поскольку часть
исходной смеси поступает уже в виде пара) . Если \\f = О
(исходная смесь - I01ш1щая жидкость) , то Е = 1 . Если \\f = 1
(исходная смесь вся подается в виде сухого насыщенного пара) ,
то Е = О . Если, наконец, исходная смесь подается в виде пара,
перегретого до !п > t, , то Е = спUп - t1 ) < О, где Сп - теп 
лоемкость пара.
В последующем анализе удельный поток пара Е использует
ся (независимо от состоян ия исходной смеси) для получения
необходимых связей в общем виде .
Запишем уравнения материального баланса для тарелЮt пи
тан ия (см. рис. 12 .3 4 ) Учитывая приращения потоков жидкости
Л L и пара ЛD на каждый моль исходной смеси, нетрудно внести
изменения в баланс потоков на тарелке питания. Для питания
колонны кипящей жидкостью бьто справеД1ШВо (см. разд. 12.7. 1 )
D' = D = const и L' = + L 1 • В рассматриваемом общем случае (см.
рис . 12.34) баланс тарелки питания запишется так:
- по потокам фаз
L' = + L1 + Л L = L + + 1 ( E - 1 ) = L + EL, ,
(р)
-

.

L

L

L1 L
D' = D - ЛD = D - (Е

-

l)L1 ;

(с)

1

- по потокам Н КК (сразу в форме " П риход = Уход") с уче
том (р) и (с)
Lx + L1 x 1 + Dy = L 'x + D'y = ( L + EL1 )x + [D (Е - l)L1 ]Y,
а после раскрытия скобок и очевидн ых сокращений:
-

Отсюда получается

Х1

=

Ех

-

(Е - l )y.

(т)

уравнение тарел к и питания :

у=

Е
х
Е-1

--

Х1

E-l

- -- .

(12.3 1 )

Зависимость (12.3 1 ) в диаграмме у-х описывает прямую , на
которой лежат сопряженные кон центрации фаз на тарелке пи
тания. Эту прямую называют линией тарелки питания. Постро
им ее по двум характерным точкам . Первая - точка пересече-

1 04 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

г

д

Рис. 1 2 . 35. Влияние состояния исходной смеси на расположение тарелки питания
в колонне при R = const:
а - Е > 1 , б - Е < 1, в - Е = О , г - Е < О , д - к определеш1ю предельной степеюt су

хо сти пара

ния М этой линии с диагональю. Решая совместно уравнения
диагонали у = х и ( 1 2 . 3 1 ) , т.е.
Е
у=х=
х Х1
Е-1'
Е-1
получим абсциссу точI01 М: х = хм = х1 • Вторую точку, N , най
дем на оси абсцисс, решая совместно уравнения абсциссы у = О
и ( 1 2 . 3 1 ) , т.е .
--

-

--

О = � x - __l_

Е-1
Е-1 '
откуда х = XN = x i/E .
В зависимости от значения XN линия тарелI01 питания мо
жет занимать различн ые положения.
При Е = 1 (исходная смесь - I01пящая жидкость) абсцисса
точки N равна х 1 - этот случай рассмотрен в предыдущих раз
делах .
При Е > 1 (исходная смесь не догрета до ее температуры
кипения) XN < х 1 , и точка N располагается левее х1 на положи 
тельной оси абсцисс (р ис . 1 2 . 3 5 , а) .
При Е < 1 (исходная смесь подается в парожидкостном со
стоянии) XN > х 1 , и то ч ка N л ежит правее х 1 на оси абсцисс
(рис . 1 2 .3 5 , 6) .
1 042

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

При Е = О (исходная смесь подается в виде насыщенного
пара) отрезок 1/Е � ао, т.е. линия MN пересекается с осью в
бесконечности , иначе говоря, она параллельна оси абсцисс
(рис . 1 2 . 3 5 , в) .
При Е < О (исходн;�я смесь - перегретый пар) точка N о ка
зывается в об:шсти XN < О (рис . 1 2 . 3 5 , г).
Тарелка п итания одн овременно принадлежит укрепляющей
и отгонной частям коло н н ы : ее место - на пересечен и и рабо
чих линий этих частей коло н н ы . В то же время сопряже н н ые
кон центрации для тарелки питания лежат на линии MN . Сле
довательно, точка С пересечения упомянугых рабочих лин ий
лежит на линии тарелки питания (рис . 12.35, а- г) . Замети м :
этот факт для питания колонн ы кипящей жидкостью (Е = 1 )
был установл е н ранее : XN =
=
Про веденный анал из позволяет зафиксировать три основ
ных эффекта.
1 . П ри сохранении неизменным флегмового числа R (т.е.
положен ия рабочей лин ии укрепляющей части колон н ы ) пере
ход от питан ия недогретой исходной смесью к питанию паро
жидкостной смесью сопровождается перемещением точки пи
тания С влево . При этом увеличивается число тарелок, необ
ходимых для обеспечения заданной степени разделения
(чистоты получаемых продуктов) , иногда - весьма заметн о
(если рабочая линия удалена от диагонали) . Подчеркнем, что
состав жидкости на тарелке питания (абсцисса точки С) равен
составу исходной смеси тол ысо при подаче ее в колонну в ки
пящем состоянии.
2 . Следует внести изменения в тепловой баланс (н). Вместо
прихода теплоты L1 c1 t 1 с кипящей исходной смесью надо будет
подставить:
- при подаче недогретой жидкости с температурой to - ве
личину L 1 с 1 to ;
- п р и подаче парожидкостной смеси с о степенью сухости
'V - величину L 1 ( c1 t1 + 'Vr) , причем возможно изменение \\f от
о до 1 ;
- при подаче перегретого пара с температурой lп - величи
ну L 1 [с, !1 + r + спUп - t1 )] , где Сп и !п - теплоемкость пара и
его температура соответственно.
3 . Задача определения минимального флегмового числа Rmin
становится более сложной . Дело в том , что при переходе от
питания недогретой жидкостью к паровой смеси в случае со
хранения рабочего значения
(положения рабочей линии
укрепляющей части колонны) возможно попадание точки пе
ресечения С в нерабочую область над линией равновесия (с м .
рис . 1 2 . 3 5 , д) . Поэтому для каждого состояния исходной смеси
следует пред в арительно найти свое значение Rmin - по точке К

х

х

х1/Е х1 •

R

1 043

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

пересечения линии тарелЮ1 питания с кривой равновесия (см .
рис . 1 2.35). А затем можно определить рабочее значение флег
мового числа и положение рабочей линии укрепляющей части
колонны - оно будет разным в зависимости от состояния ис
ходной смеси .
На практике может вознию{уrь задача определения максимально допустимо й
степени сухости парожидкостной смеси lj/max при заданном рабочем значении R.
Решение задачи ясно из рис. 1 2 . 3 5 , д: по точке
(она соответствует значению
Rmin) и точке М находят точку N ; из XN =
рассчитывают Е = 1 - ljl и далее

lj/

=

lj/max·

xi/E

К

Более просто и наглядно все эффекты и особенности расче
та процесса ректификации в зависимости от состояния исход
ной смеси выявляются при использовании энталъпийной диа
граммы (см . разд. 1 2 . 8 ) .
12. 7 6 Некоторые особенности работы ректификационных колонн
.

.

Н иже рассмотрены некоторые специфичесЮ1е
функционирования ректификационных установок.

аспекты

Ранее рассматривалась работа колонны в адиабатных условиях. Такие усло
вия подразумевают хорошую ее изоляцию, дабы свести к минимуму потери теп
лоты в окружающую среду и затраты энерги и в кипятиль нике. Но ведь наличие
теплопотерь пр и водит к частичной конденсации поднимающихся по колонне
пар о в смеси, а значит - к увел ичению (сверху вниз) потока флегмы . Это сопро
вождается повышением чистоты продукто в . Такой эффект в свое время послу
жил поводом к ошибочной рекомендаци и снять изоляцию с ректификационно й
коло нны. Ош ибочность легко обосновать следующим образом . В кипятильнике
пр идется испарять весь возросший поток флегмы, хотя в верхних зонах колонны
ее пото к меньше. Н о чистота продукrов была бы еще вьШJе, если бы большо й
поток флегмы шел по всей колонне, а не только в нижней ее части . И если уж
решено по йти на дополнитель ные затраты теплоты в кипятильнике, то резонно
дать большой (полн ый) пото к флегмы по всей высоте колонны, а саму колонну
заизолировать самым тщательн ым образом .
В ряде случаев серьезно й проблемо й при осущест!lJlении про цессов ректи 
фикации может стать орга н изация (получение) флегмы . С этим встречаются ,
когда в ыходя щие из колонны пары имеют низкую температуру конденсации
(скажем , ниже 20 • с или даже ниже О 0 С); тогда нельзя воспользоваться деше
вым и и доступн ыми тепло носителя ми - х олодно й водо й или атмосферным
воздухом . Если пр и этом тем пература ко нденсаци и паров не очень низка (на
20-50 градусо в н иже нуля), то используют два основных приема.
Первый закmочается в применении для конденсации паров в конденсаторе како
rо-либо низкотемпературноrо хнадоагента (аммиак, холодильные смеси - см. ра.:щ.
2 1 .2.7). Второй - в повьШJении рабочеrо дамения , а с ним и температуры конденса
ции паров, так что становитсн возможным исп ользовать воду или во�.
Н апр имер , ректификаци и подвергается пропан-бутановая смесь . П р и атмо 
сферн ом давлени и температура конденсации паров, выходящих сверху из ко 

ло н н ы, заметно н иже О 0 С. Процесс ведут под давлением 1 0-20 ат ( 1 -2 МПа);
пр и тако м да м ен ии темперюура конденсаци и выходя щих сверху паро в состав
ляет 50-70 ° С, что позволяет для их ко нденсаци и использовать холодную воду.
Проблема орга низации фле.гмы существенно усложняется, если рабочая тем 
пература процесса и темпера1ура ко нденсаци и паров значительно н иже нуля

1044

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

-200

(например , на уровне
° С; встречаются промышленные процессы, где она
еще ниже) . В этих случаях приходится прибегать к специальным (как правило,
весьма энергоемким) методам; один из них рассмотрен в разд.

2 1 .3.7.

12.8. РАСЧЕТ РЕКТИФИ КАЦИ И Б И НАРНЫХ СМЕСЕЙ

С ПОМОЩЬЮ Э НТАЛЬПИЙНО Й ДИАГРАММЫ

В предыдущих разделах рассматривалась рекrификация сме
сей , состоящих из компонентов с равными (близкими) мольны
ми теплотами парообразования . На пракrике встречаются сме
си компонентов с близкими массовы.ми теплотами парообразо
вания (например, углеводороды одного гомологического ряда,
содержащиеся в нефти) - тогда расчет ведуг с помощью диа
грамм а'-а и t - а , а'. При разделении смесей компонентов, у
которых мольные или массовые теплоты испарения сильно раз 
личаются (скажем , н а 20 % - цифра зависит от требуемой точ
ности расчетов), потоки пара D и флегмы L уже нельзя прини
мать постоянными по высоте укрепляющей и отгонной частей
колонны . Соответственно усложняются материальные балансы,
а рабочие линии - уравнения типа ( 1 2. 1 7) и ( 1 2 .20) - пере
стают быть прямыми . Построение кривых рабочих линий со
пряжено с большими трудностями: здесь необходимо учитывать
изменение энтальпий пара (h) и жидкости (1) с изменением их
составов. В этом случае переходят к энтальпийным диаграммам
(см . рис . 1 2 .7), представление о которых дано в разд. 1 2 .2.4.
Н иже изложен метод расчета процесса рекrификации с по
мощью энтальпийной диаграммы i, h - а , а ' (в равной мере
вместо массо вых концентраций а, а' могуr быть использованы
мольные - х и у). В этой связи построение кривых i(a) и h(a')
рассмотрим более подробно.
Зависимость энтальпии кипящей при температуре t жидкости
от ее состава - i(a) - можно, базируясь на теплоемкости сме
си, представить в виде:
rде

ел и

св

(а)
i = ct = [ асл + ( 1 - а)св] t,
- теплоемкости чистых компонентов при температуре кипения t

смеси, содержащей а массо вых ;1олей НКК. Аzщитивный расчет теплоемкосrи смеси
(выражение в ющцратных скобках), строrо rоворя, яВТIЯется приближенным; более
точный расчет требует учитывать теплооу смешеиия компоне1ПОв.

Поскольку температура кипения ВКК (tв) больше, чем Н КК
св tв , как правило, превышает iл = слtл (различие в
(tл) , то iв
теплоемкостях св и ел обычно невелико) . При точном расчете
кривой i(a) надо учитывать нелинейное изменение температу
ры кипения смеси с ко н центрацией, теплоту смешения , а так
же изменение теплоемкостей с температурой . Чаще всего кри
вая i-a имеет вид, представленный на рис . 1 2.7.
=

1045

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Энтальпия насыщенного пара h определенного состава при
температуре конденсаци и рассчитывается как сумма энтальпии
ки пящей жид кости с1!1 и теплоты парообразования r' , взятых
при кон центрации Н К К в паре (а') . Температура кипен ия жид 
кости t' определяется при концентрации а ' п о кривой !(а) так
же , как в тепловом расчете процесса простой дистилляции при
вычислении энтальпии пара. Наиболее точные значения с ' и r'
дает эксперимент; при отсутствии экспериментальных данн ых
эти величины рассчитывают по адд и тивности :

h

=

c't' + r'

=

[ а 'сл

+

( 1 - a')cв J t' +

(а 'rл

+ (1

-

a') rв J .

(б)

Форма кривой h-a' в наибольшей степени зависит от соотно
шения и изменения с температурой величин rл и rв .
Напомним (разд. 1 2.2 .4): равновесные концентрации Н КК в
жидкости и паре лежат на концах изотерм , которые строятся с
помощью диаграммы t а, а ' (см. рис . 1 2 . 7 ) .
В энтальп и йной диаграмме предстоит построить теоретиче
ские тарел ки , не используя понятие о рабочих линиях, т.е.
иным путем устанавливая связь между сопряженными кон 
центрациями компонента А в жидкости и паре . С этой целью
составим материальные и тепловые балансы за единицу време
ни для пространственных контуров, проходящих через произ
вольные сечен ия колон ны . Сделаем это разделыю для укреп
ляющей и отгон ной частей, так как потоки фаз в н их различны
из-за подачи на тарелку питания потока исходной смеси L1 •
Напомним, что в гл. 1 1 установление связи между сопря
жен н ым и составами газовой и жидкой фаз (при наличии трех
компонентов в каждой из н их) привело к понятию полюса
некоторой общей для всех сечений точ ки , которая лежит на
линии (луче) , соединяющей сопряженные составы контакти
рующих фаз .
Анализ про цесса буде м вести применительно к непрерывной
ректификации со ступенчатым контактом фаз, полагая снача
ла, что искомая смесь подается в колонну при температуре
ки пения .
-

-

Укрепляющая

колоuна

Обозначим для произаольного сечения укрепляющей колонны
(рис . 1 2.36): D
пото к пара, а'
концентрация Н КК в паре,
энтальпия пара, L
поток жидкости , а - кон центрация
h
Н КК в жидкости, i
ее энтальпия . В верхнем сечении колон 
для жид
н ы имеем соответствен н о : для пара
а0' и
кости
Lв, а8 и i8 . Используем некоторые фрагменты анализа,
рассмотрен ного в разд . 1 2 .6 , оперируя массовым и кон центра
циями, потою1ми и энтальпиями .
Составим материальный баланс для контура К1 (см . рис .
-

-

-

-

-

-

-

1 046

D0,

h0,

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 12.36. Схема

и

обозначения потоков в укрепляющей части колонны

12.36)

по общим потокам фаз:
1 - Dв - L = О '·
D + -'-'&
отсюда
Л - L = Dв - 4.

Поскольку для непреры вно работающей колонны потоЮJ D8 и
Lв фиксированы , а сечение выбрано произвольно, то разность
массовых расходов пара и жидкости для любого сечения колон
ны есть величина постщшная :
D - L = D8 - 4 = ideш.
(в)
Иными словами: массовые потоЮJ пара и жидкости могуг ме
няться по высоте колон ны, но их разность в каждом сечении
- одна и та же .
Материальный баланс для того же контура К1 по потокам
компонента А:
Da ' + Lвав - D0a0' - La = О ;
отсюда
(г)
Da' - - La = D0a0 ' - Lo a8 •
Правая часть равенст ва (г) равна некоторой конкретной ве
личине; следовательн о , и разность потоков компонента А в
паре (Da') и в жидкости (La) - неизмен на, хотя сами потоки
Da ' и La переменны по высоте колонны:
(г')
Da ' - La = Да0 ' - Loa0 = idem.
1 047

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Выражения типа ( в) , ( r ' ) характерны вообще для противо
точных массообменных процессов (например , для абсорбции
при постоянн ых потоках фаз - см. разд. 1 1 .5.4).
Поделив друг на друга левые части выражений (г') и (в), по
лучим одинаковую для любого сечения величину

Da' - La
D-L

_

.
1 d em ,

имеющую размерность и смысл некоторой массовой кон цент
рации компонента А. Обозначим:

Da' - La
в.
D - L = as

(д)

Dh - Li _ . в
D - L = ls '

(ж)

_

Тепловой баланс для контура К 1 (см. рис. 12.36) за единицу
времени в отсутствие потерь теплоты в окружающую среду
записывается в виде:
Dh + 4iв - Dвhв - Li = О .
Отсюда
(е)
Dh - Li = Dвhв - 4iв = idem.
Значит, разности энтальпий парового и жидкостного потоков
для любого сечения адиабатной колонны - одинаковы .
Очевидно, что соотношение
---

имеющее размерность и смысл энтальпии, также одинаково
для любого сечения коло нны.
Две координаты а58 и i58 определяют в поле диаграммы i,h а,а ' (рис . 12.37) некую точку, характерную для любого сечения
колонны (в рассматриваемом случае - укрепляющей) . Эту точ
ку назовем полюсом s в ( as8 , i58 ) укрепляющей части колонны.
Для построения полюса sв необходимо уметь определять а58
и i58 через известные исходные или заданные (требуемые) ве
личины . Найдем постоянные по высоте колонны разности D -L, Dd - La и Dh - Li из материальных и теплового балансов
контура К2 (см. рис. 12.36).
Материальный баланс по массовым потокам фаз
дает
Материальный

D - L - П= O
D - L = П.
баланс по массов ым потокам компонента
Da' - La - Па2 = О

приводит к равенству
1 048

Da' - La = Па2 .

(з)
А

(и)

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 12. 3 7. Верхний полюс s•
пийной диаграмме

в знталь 

Тепловой баланс для того же
контура К2 имеет вид:
Dh Li Пi2 QКОНД = о .
-

-

i, h

h (a ')

-

Отсюда

Dh - Li = Лi2 + Qконд·

(к)
Подставляя (з) и (и) в (д) ,
н а.ходим:

О

1
а �
а . а а ' а2

( 1 2 .32)
Таким образом, для верхней (укрепляюшей) части колонны
абсцисса а58 полюса равна концентрации компонента А в ди
стилляте а1.
Согласно выражению (ж), с учетом (к) и (з) получаем:

.

1sв

=

fl j2 + Q KOllД
п

( 1 2.33)

Значит, ордината i58 полюса для укрепляюшей части колонны
равна сумме энтальпии получаемого дистиллята и удельного (в
расчете на 1 кг дистиллята) потока теплоты, отводимой в кон 
денсаторе (qконд = Qконл/П).
Итак, полюс укрепляю шс й колонны sв имеет координаты а2
и i2 + qконд (см . рис. 1 2.37). Абсцисса полюса а1 задана; ордина
ту найдем по ( 12.33), если определим qконд• поскольку энталь
пия кипящего дистиллята i2 при его составе а1 известна - она
отсчитывается по диаграмме или вычисляется по формуле (а) .
Подчеркнем: материальные балансы (в) , (г) и (е) характери
зуют некоторое (произвольное) сечение, значит, и полюс яв
ляется характеристикой этого сечения и одновремен но каждого
иного сечения колонны. Линия, проведенная через полюс s в и
пересекающая энтальпийные кривые h(a') и i(a), называется
лучом. Абсциссы точек пересечения луча с линиями h(a') и i(a)
дают сопряженные (характерные для некоторого сечения ко
лонны) составы жидкости (а) и пара (а ').
Проведем и з полюса некий луч S8N M (см. рис . 1 2.37). Точка
пересечения N соответствует составу пара а', а точка М - со
пряженному составу жидкости а. В соответствии с выражения
ми (з) и (и) поток дистил.лята П получается при вычитании
потока жидкости L из потока пара D, а поток компонента А с
дистиллятом (Па2) - при вычитании потока компонента А в
жидкости (La) из потока компонента А в паре (Da'). Поэтому,
1 049

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

применяя правило рыча га 1 1 рода (см. разд. 10.2 .4) с опорой в
точке S0, можно найти отношение массовых расходов жид
кости и пара в рассматриваемом сечении:

L
D

-

=

а 2 - а'
а2 - а

�
-

Отношение разностей -концентраций
заменим равнозначным
-отношением отрезков N S 8 и M S 8 , так что

L NS8
D = мsв .

(12.34)

Очевидно, что при другой концентрации компонента А в
жидкости (в другом сечении колонны) с помощью соответ
ствующего луча получим другой сопряженный с нею состав
пара и иное соотношение потоков жидкой и паровой фаз L/D.
В любом случае для укрепляющей части колонны L/D < 1 .
Расчет величины qконд• необходимой при построении по
люса sв , требует предварительного рассмотрения метода опре
деления числа теоретических тарелок, достаточного для кон 
центрирования исходной смеси о т а1 д о а2 .
При полной конденсации паров, выходящих из колонны,
получаем конденсат того же состава (применительно к рис.
12.36 а8' = а8 = а2 ). Следовательно, верхнему сечению колонны
1 - 1' отвечает вертикальный луч 1- 1 ' (рис. 12.38). Уходящая с
первой (самой верхней) теоретической тарелки жидкость нахо
дится в равновесии с паром состава а2 • Для отыскания этого
состава жидкости (точка 2) проводим изотерму 1'-2. Луч, про
ходящий через точку 2, пересекает линию h(a� в точке 2'. Се
чение 2- 2 ' характеризуется сопряженными составами жид
кости и пара. Пару состава 2 ' отвечает равновесная (на общей
изотерме 2 ' -3) концентрация НКК в жидкости (точка 3). Сно
ва проводим луч 3-3' с получением сопряженного пара (точка
3 ' ) - и так до тех пор, пока очередная изотерма не пройдет
через точку И (или левее нее) . Требуемое число теоретических
тарелок определяется по количеству проведенных изотерм, а
крайний левый луч соответствует сечению подачи жидкости
(тарелке питания) .
Из рис. 12.38 видно, что при фиксированных а 1 и а2 число
теоретических тарелок зависит от ординаты (i2 + qконд) точки
S8• Поскольку i2 определено свойствами жидкой смеси, то на
положение полюса S8 можно воздействовать за счет изменения
qконд · При увеличении qконд полюс S8 перемещается вверх; тог
да потребуется меньшее число теоретических тарелок. Наобо
рот, при уменьшении qхонд число теоретических тарелок увели
чивается .
1 050

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

i,h

sв
_+-----.-

S�р ед
. qкопд
q nun
КОНД

Рис. 12.38. Построение теоретических тарелок в укреrтяющей колонне

Если полюс s в сместится в точку пересечения продолжен ия
изотермы И - 4' с вертикалью а2 = const, то луч совпадет с изо
термой, и число теоретических тарелок устремится к бесконеч
ности. Отвечающая этому предельному положению полюса
min
min
(sвпред) ордината определяется как 12 + q конд
, здесь q конд
·

.

удел ьн ый теплоотвод в конденсаторе, он соответ
ствует минимальному флегмовому числу Rmin при расчете числа
теоретических тарелок в диаграмме у-х.
Бесконечному флегмовому числу отвечает qконд � оо. При
этом лучи вертикальны, а число тарелок - минимально.
Следуя общему подходу, при определении оптимального
значения qконд необходимо q �fiл.
умножить на коэффициент
минимальный

избытка а (в данном случае это избыток теплоотвода в конден
саторе по сравнению с минимально необходимым):
m in
q канд ·

( 1 2 . 3 5)

Qконд = qконд П.

( 1 2.36)

qканд

_
-

а

Величину коэффициента избытка а выбирают как обычно - на
основании технико-экономического расчета.
Полный поток теплоты, отводимой в конденсаторе, соглас
но определению qко нд • составляет

Отгонная колонна
Отгонная колонна отличается от укрепляющей увеличением
потока жидкости за счет подачи кипящей исходной смеси на
тарелку питан ия: L' = L + L 1 , причем L' > D.
105 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

iL

Рис. 12. 39. Схема и обо значения пото ко в в отго н н о й части колонны

Для определен ия разности потоков жидкости L' и пара D в
отгонной колонне составим материальный баланс по массовым
потокам фаз для контура К1 (рис. 1 2 .39), охватывающего н иж
нюю часть колон н ы до произвольного сечения:
L ' + Dн - 4'
D = О.
Отсюда
D = 4' - Dн.
L'
Поскольку потоЮI Dн и 4' фиксированы , а сечение выбрано
произволыю, то разность массовых расходов жидкости и пара
одинакова для любого сечения колонны:
(л)
L' - D = 4'
Dн = idem .
И н ыми словами , массовые потоЮ1 жидкости и пара могут ме
няться по высоте отгонной колонны, но их разность в каждом
сечении - одна и та же .
Материальный баланс для того же контура К1 по массовым
потокам компонента А:
L'a + Dн ан - Lн'ан
Da' = О;
отсюда
-

-

-

'

1 052

-

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Правая часть этого равенства равна некоторой конкретной
величине; следовательно , и разность в потоках компонента А в
жидкости (L'a) и в паре (Da� есть величина неизменная, хотя
сами потоЮ1 L'a и Da' - переменны по высоте колонны:
L'a - Da ' = Lн'ан - Dн ан' = idem.
(м)
Подеmm друr на другс:1 левые части выражений (м) и (л), полу
чим одинаковую для любого сечения отгонной колонны величину

L'a - Da '
= idem,
L' - D
имеющую размерность и смысл некоторой массовой концент
рации компонента А. Обозначим
L'a - Da '
----L, _ D

-

аsн ·

(н)

Тепловой баланс для контура К 1 (рис . 1 2.39) за единицу вре
мени в отсутствие потерь теплоты в окружающую среду запи
сывается в виде:
L'
откуда

i + Dнhн - Lн'iн -

Dh = О,

L' i Dli = Lн 'iн - Dн hн = idem.
(о)
Значит, разности энтальпий жидкостного и парового потоков
для любого сечения адиабатной колонны одинаковы по высоте
отгонной колонны.
Очевидно, что отношение
L 'i - Dh
·н
(п)
- ls '
L1 - D
имеющее размерность и смысл энтальпии , также одинаково
для любого сечения колонны.
Две координаты а5н и ;5н определяют в поле диаграммы i,h
- а, а' некую точку, харакrерную для любого сечения отгонной
части колонны. Она получила название полюса sн (а5н , isн ) от
гонной (нижней) части колонны.
Для построения полюса sн (рис. 1 2 .40) необходимо выразить
аsн и ;5н через исходные или заданные (требуемые) величины .
Найдем постоянные разности L' - D, L'a - Da' и L'i - Dh из
материальных и теплового балансов для контура К2 (см. рис .
1 2 .39).
Материальный баланс по массовым потокам фаз
L' - D - Lo = O
дает:
L' - D = Lo.
(р)
-

1 053

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

i, h

i, h

i(a)
а

'

____.
'
а,а

Рис. 12. 40. Нижний п олюс sн в энталъ п ий
ной диаrрамме
Рис. 12. 41. Построение числа теоретических тарелок в отгонной колонне

по массовым потокам компонента А
L 'a - Da ' - Loao = О

Материальный баланс
приводит к равенству

L 'a - Da' = Loao.

(с)

Тепловой баланс для того же контура К2 имеет вид:
L ' i + Qк - Dh - Loio = О,

откуда

L' i - Dh

=

Loio - QK.

(т)

Подставляя (с) и (р) в (н) , находим:

as"

=

L'a - Da'
J,' - D

=

Loт aо
"-1)
-

=

ао.

( 1 2 . 37)

Таким образом, для нижней (отгонной) части колонны аб
сцисса аsн полюса равн а концентрации компонента А в кубо
вом остатке ао .
Согласно выражению (п), с учетом (т) и (р) получаем:

.н

ls

_
-

L'i - Dh Lo io Q к '.о - !;;
Q к zo.
L' - D
Lo
_

-

_

_

_

qк.

( 12.38)

Значит, ордината isн полюса отгонной части колонны равна раз
н ости энтальпии кубового остатка и удельного (в расчете на 1 кг
кубового остатка) теплоподвода в кипятильнике (l/x = QJLo).
Итак, полюс отгонной колонны sн имеет координаты а0 и
io qк (см. рис. 1 2 .40) . Как правило, qк > io, так что нижний
полюс s н располагается ниже оси абсцисс (см. рис . 1 2 .40). По
люс s н относится к любому сечению отгонной колонны . Луч,
-

1 054

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

проведенный в диаrрамме из точки s н , пересекает линии i(a) и
h(a') в точках Е и F, абсциссы которых являются сопряженными
(в некотором сечении) концентрациями компонента А в жид
кости
( а)
и
в
паре
(а') . Отношение отрезков

s н р/s н Е характеризует

отношение L'/D (доказательство этого
соотношения идентично приведенному выше для укрепляющей
колонны) . Очевидно , что в случае отгонной колонны отноше-

S"F/S"E

ние L'/D =
> 1.
Ч исло теоретических тарелок в отгонной колонне опреде
ляется, как и для укрепляющей колонны, путем поочередного
построения изотерм и лучей, но уже в диапазоне концентраций
от ао до а 1 (рис. 1 2 .4 1 ) . Вертикальный луч 1- 1 ' характеризует
н ижнее сечен ие колонны (в предположении об отсутствии раз
деляющего действия куба) . Через точку 1 проводим изотерму
1- 2 ' (штриховая линия); луч S"-2: проведенный через точку
2 ' (состав пара), дает точку 2 (сопряженный состав жидкости) .
Далее - снова изотерма 2- 3' , луч S"-3' с получением точки 3
и т.д . - пока очередная изотерма не пересечет крайний луч,
проходящий через сечение питания И И' (или попадет точно в
точку И ' ) . Число изотерм соответствует числу теоретических
тарелок.
Крайний правый луч отгонной колонны, связывающий со
пряженные концентрации в жидкости а 1 и в паре а 1 ' на тарелке
пиrания, совпадает с крайним левым лучом укрепляющей ко
лонны, также связывающей сопряженные концентрации на этой
тарелке. Поэтому для получения нижнего полюса sн достаточно
лишь продолжить прямую sв и до пересечения с вертикалью ао.
По найденному с помощью диаrраммы (рис. 1 2.42) отрезку
qк находят необходимый тепловой поток в кипятильнике :
( 1 2 .39)
Qк = qкLo.
В

целях сопостамения различных режимов процесса удобно оперировать

удельными теruютами (в расчете на

1

кг

исходной смеси) в конденсаторе

q;,,1\11 =

= Qкoiц/L1 = qк011J1П/L1 и в ки пятильнике qк•
Q-4'L1 = qкц/L1 . Для нахоЖZ1е
ния этих величин запишем сначала характерн ые оmошения П/L 1 и 4/L 1 . Со
гласно материальным балансам дrIЯ всей колонны, эти отношения выражаются
формулами типа ( 12.21) и ( 1 2.22). Оперируя здесь массовыми потоками и концентрациями, имеем:
=

(у)
Заменим отношения разностей концентращ� й (абсцисс) отношениями соответствующих отрезков
01 - ао

S"И

П

а2 - а о "' s "s;-"' L 1

и

(ф)

1 055

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

i, h

•

определению удельных пото ков теruюты в конденсаторе q: конд и в
кипятильнике qк' в расчете на 1 исходной смеси
Окончательно (см. рис. 1 2 .42) :

Рис. 12. 42.

К

кг

•

qКt>llД = qКt>НД

s"и

S"S"

=

(х)

Величина Qк при подаче исходной смеси в виде кипящей
жидкости (точка И с координатами а1 и i1 лежит на линии i
а) целиком определяется величиной Qконд · Чем больше Qконд ,
тем больше Qк · Рост значений Qк и qконд соответствует повыше
нию флеrмового числа по колонне, а это обеспечивает разде
ление смеси состава а1 на а0 и а2 при мен.ьшем числе теоретиче
ских тарелок. Соответственно, мин.имш�ьн.ому теплоотводу в
конденсаторе q��
отвечает мин.имш�ьн.ый теплоподвод в ки
пятильнике qктШ (рис . 1 2 .43); при эrо м заданное разделение
возможно лишь при бесконечно большом числе теоретических
тарелок.
Энтальпийная диаграмма позволяет СУШественно упростить
тепловой расчет ректификационной колонны. При установлен
ных положениях полюсов потоки теплоты Qко нд и Qк рассчи
тываются по формулам ( 1 2.36) и ( 1 2 .39). При подаче на тарелку
питания кипящей смеси положение полюсов базируется на изо
терме, проходящей через точку И кипящей жидкости исходно
го состава а1 . Не вызывает особых затруднений теrщовой рас
чет и при питании ректификационной колонны некипящей
жидкостью. Здесь могут быть рассмотрены два варианта.
П ервый вариант отвечает найденному и зафиксированному
верхнему полюсу. Тогда при подаче в колонну исходной смеси, н.е
догретой до температуры кипения (точка Ин на рис. 12.44),
1 056
-

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

i, h

Рис. 12. 43. К полному расчету ректификационной колонны непрерывного дей
ствия в энтальпийной диаrрамме

i, 11

-
'
а, а

s�
Рис. 12. 44. Влия н и е аrрегdтного состояния исходной смеси на удельный расход
тсIШоты в кипятильнике при 1 1остоянном удельном теIШоотводе в конденсаторе
(при фиксированном положении верхнего полюса)

1 057

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

полюс s н для н ижней колон ны смещается вн из (точка S � ) .
Удельный тепловой поток в ки пятильнике Qкн в этом случае
закономерно возрастает на величину (qкн - Qк), компенсируя
затраты теплоты на подогрев исходной смеси до температуры
кипения . Мин имальн ый удельн ый теплоотвод в конденсаторе
при п итан ии колонны недогретой исходной смесью ( q:�д ) н
находится по продолжению изотермы, проходящей через точку
Ин, до пересечения с вертикалью а2 . Эта величина ( q:� ) н
меньше, чем

q:�д

для кипящей исходной смеси, так как час

тично теплота отводится самой недоrретой исходной смесью.
При п итан ии колон н ы парожидкостной смесью (точка Ипж
на рис . 1 2 .44) удельный тепловой поток в кипятильнике
уменьшается, так как больше теплоты в колонну приносит ис
ходная смесь: Qкпж < Qк · Минимальн ый удельный теплоотвод в
конденсаторе при этом, естественно, увеличивается : на рис .
1 2 .44 ( q:�д )пж > q:�д ; пусть он как раз отвечает точке S 8 .

Посл еднее совпадение означает, что при питании колон ны
парожидкостной смесью принятый теплоотвод Qконд является
минимальным, а требуе м ое число теоретических тарелок в этом
случае стремится к бесконечности .
При питан ии колон н ы насыщенным паром (точка Ип) и тем
более
перегретым (точка Ипп) величина Qк уменьшается еще
значительнее. В этих случаях (в предыдущем - тоже) возмож
но уменьшение Qк до нулевого значения и даже до отрицатель
ного . Это означает, что избыточная теплота должна быть отве
дена в "кипятильнике". При этом луч проходит так, что равно
весная кон центрация Н КК в сечении оказывается меньше со
пряженной. Последне е противоречит физическому смыслу
процесса и указывает на невозможность такого варианта рабо
ты колон н ы .
Второй вариант, базирующийся на устаномении минималь
н ых значен ий Qконд и Qк, более обоснован . При подаче исход
ной смеси состава а 1 через точку И;, отвечающую любому со
стоянию этой смеси, проводится секущая (крайний луч укреп
ляющей или отгонной ч астей колонны), совпадающая с соот
ветствующей изотермой (рис . 1 2 .45). Точки пересечен ия секу
щей с вертикалями а2 и а0 дают предельные положен ия полю
сов, отвечающие минимальным удельным тепловым потокам
q:� и qкrrUп· Технико -экономический расчет позволяет опре
-

делить рабочие значен ия тепловых потоков Qконд и
мощью коэффициентов типа а - см . формулу ( 1 2 . 3 5) .

1 058

Qк

с по

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

i, h

(q��)"

-а,а·

Рис. 12. 45.

а2 1

Влияни е arperaтнoro <.:0сrояния исходной
смеси н а минимальные значения
.
m1n
потоков в конденсаторе q�':д
в юmятильнике q к
и

удеrп,ных теruюв ых

Из рис. 12.45 следует, что значения минимальных удельных
тепловых потоков определяются по положению рабочих лучей
для тарелки питания, совпадающи х с изотермой для пода
ваемой исходной смес и . Как правило, чем меньше теплоты
несет с собой исходная смесь, тем ниже значение q �� и вы
ше - qктШ· Если изотерма сильно изменяет свое направление,
то возможны исключен ия из этого правила. Так, на рис. 12.45
показано, что в случае п итан и я паром (точка ип) значения
qктШ' п > qктШ, пж. Кроме того, из р и с. 12.45 в идно, что составы
жидкости на тарелке питан ия (абсци ссы точек пересечения
крайних лучей с кр и вой i-a) отл ичаются от состава исходной
смеси; они совпадают только в случае подачи исходной смеси
при температуре кипения.

Общая последователыюсть расчета
ректификационной колонны
Последовательность расчета колонны непрерывного дей
ствия (проиллюстрируем ее на пр и мере питания колонны ки
пящей исходной смесью) такова:
- строят диаграммы t а,а' и i,h а,а ';
- из точки И исходной смеси (а1 , i1 ) проводят изотерму до
-

-

1 059

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

пересечения с верти кал ь ю

а2 ;

определяют q�� (см. рис . 1 2 .43)

как ординату точки пересечения за вычетом i2;
- проводят технико-экономический расчет (или пользуются
практичес ю1 ми рекомендациями) и устанавливают значение
коэффициента избытка cr;
- рассчитывают qконд по ( 1 2 .35) и находят положение верх
него полюса s в (см. рис . 1 2.43);
- продолжают луч S8И до пересечен ия с вертикалью а0 и
фи ксируют точку нижнего полюса sн (см. рис . 12.43);
- определяют (из диаграммы рис . 1 2 .43) значение qк;
- строят (предпочтительно - из точки питания И ) число
теоретических тарелок в отгонной и укрепляющей частях ко
лонны, отсчитывая их по числу изотерм (как показано на рис .
1 2 . 3 8 и 1 2 .4 1 ); далее находят (с помощью КПД тарелки) число
реальных тарелок;
- рассчитывают полную тепловую нагрузку конденсатора рек
тификащюнной колонны по формуле (12.36): Qконд = qконд П;
- рассчитывают полный тепловой поток в кипятильнике
ректификационной колонны по формуле ( 1 2 . 39): Qк = qкLo·
Рассмотренный выше расчет представляет собой решение зада
чи проектирован.ия. Задача эксппуатации решается сложнее (в пер
вую очередь - из-за нешmейности равновесия). Общая ее поста
новка: при заданных исходн ых параметрах (L1 , а 1 ) и известн.ом
числе тарелок требуется опредетrrъ конечные параметры процес
са (П, аъ Lo, ао). Конкретно: надо найти такое положение полю
сов в э нтальпийной диаграмме (она для разделяемой смеси из
вестна), чтобы при построении тарелок в диаграмме получилось
заданное их число lir · Задача решается подбором. Решение
несколько облеrчается, если принять определенное значение t/конд;
тогда в ходе поиска решения верхний полюс перемещают эквиди
стантно линии i(a), проверяя для каждого положения полюса чис
ло построенных тарелок отдельно в укрепляющей и отгонной
частях колонны - до совпадения с заданным lir·
Энтальпийную диаграмму в принципе можно использовать
также для расчета ректификации с непрерывным контактом
фаз. Необходимую для этого связь равновесных и сопряженных
концентраций (на языке одной из фаз) найти легко ; затрудне
ния возникают в связи с переменными потоками фаз при вы
числении чисел единиц переноса.
Продемонстрируем пути решения задачи на примере укреп
ляющей части колонны (рис . 1 2 .46) . В нижнем сечении колон
ны , граничащем с сечением питания, потоки паровой и жид
кой фаз обозначим D1 и L1 ' ; в верхнем, граничащем с ко нд ен 
сатором, - Dв и 4. По колонне потоки D и L переменны.
Анализ будем вести в терминах и символах паровой фазы.

1 060

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 12. 46. К расчету размеров
укре1L11Я ющей части колонны с
непрерывным контакrом фаз с
помощью диаграммы i, h-a, а'
Рис. 12. 47. К определению со
пряженной (а') и равновесной
(а')Р концентраций НКК в паро
вой фазе

Da' + d(Da')
df

к

к

dM

D а

D1
о

L1, a 1

i, h

м

sв

f

'
а1

--

О �
а,а

а а
1

а' a 2 l
(а ) Р

Материальны й баланс по НКК в зоне парового потока для
( контур К )
D 1 a 1 ' + М - D8 a2' = О
приводит к выражению
(ц)
М = Dва2' - D 1 а {
Материальный баланс для элементарной поверхности кон 
такта d/ (контур к) :
Da' + dM - [Da' + d(Da)] = О
дает выражение
(ч)
d M = d(Da') .
Согласно уравнению массопередачи (см. разд. 1 0 .6) dM =
= ky [(a)P - a'] d/; тогда
ky [ (a)P - a') d/ = d( Da) .
(ш)
Разделяя переменные в (ш) и инте гр и руя полученное выоа

всей колонны

укрепляющей
при
лагая коэффициент массопередачи Ку постоянным
жеюtе

по

всей

высоте

(а' = а1 • и D = D1 при I = U; a' = а]_

kyF _- v.�
f

и D = П0
d(Da ' )

части

колонны
получаем (по
усредне нным ):

I = Р) ,
или

( 1 2 .40)
.
(а ')Р - а '
Для вычисления интеграла необходимо располагать связью
между текущими значения ми D и а '. Она устанавливается из
следующих соображений (см . рис . 1 2 .46 и 1 2 .47) :
- разность D - L п о всей укрепля ющей колонне постоянна,
она равна D8 - Lв = П;
1061
Diиi

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

- отношен ие D/L для текущего сечения с концентрацией
Н КК в жидкости а и в паре а' беруг по соотношению харак
у
терных отрезков луча
- см. соотношение ( 1 2 .34);
- зная разность D - L и отношение этих величин D/L, на
ходят D для текущего значения а ;
- величину (а')Р определяют по изотерме, проходящей через
точку, отвечающую концентрации а , сопряженной с а' (см . рис .
1 2 .47) .
Найдя интеграл, п о ( 1 2 .40) рассчитывают необходимую по
верхность контакта фаз (например , поверхность насадки) для
укрепляющей части колонны.
Если расчет поверхности контакта фаз F вести по уравне
нию массопередачи ( 1 0 . 1Р5у), то фигурирующую при этом сред 
н юю движущую силу процесса массопередачи Лер = Ла'ср мож
но найти следующим образом . Домножим на Ла'ср обе части
равенства ( 1 2 .40) :
Р
k

F

Л а 'с

=

Ла'с

Dafai ( d(Da ' )
'
Di ai а ) Р - а ,

Слева - поток переданной массы М. Подставляя этот поток по
(ц), имеем :

Отсюда
( 1 2 .4 1 )

Очевидно , что при D = const выражение ( 1 2 .4 1 ) приобретает
вид, характерный для расчета с помощью числа единиц пере
носа Ч ЕП (см . разд . 1 0 .8).
Аналогичн ы м образом ведется расчет поверхности контакта
для отгонной части колон н ы .
С помощью энтальпийной диаграммы i, h - а , а' может бьпъ
вьmолнен и расчет ректификационных колонн периодического
действия, работающих с а2 = const или с Qконд = const. Канва рас
чета здесь общая с изложенной в разд. 12. 1 0 применительно к
диаграмме у-х. Подробно с методами расчета колонн периодиче
ского действия в энтальпийной диаграмме можно ознакомиться в
специальной литературе по ректификации * .
•

1 062

См . , напр имер , (6 ) .

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

12.9. Р Е КТИФ И КАЦИ Я БИ НАР Н ЫХ СМ ЕС Е Й

С ПРИ МЕН Е Н И ЕМ РАЗД ЕЛЯЮЩ ЕГО АГЕНТА

Для разделения смесей, состоящих из компонентов с близ
кими температурами кипения и характеризующихся небольшим
зtt ач ение м ко эфф иuиента отно с ительной летуч ести о.да =
/ Р�
(кривая 1 на рис . 1 2 .48), потребуется большое
=
число тарелок в колонне (или большая высота слоя насадки).
При разделении таких смесей велиЮf будуг и флегмовые числа
(рабочая линия пройдет под линией равновесия, т.е. близко к
диагонали), а значит и расход энергии - теплоты в кубе,
охлаждающей жидкости в конденсаторе. Еще хуже, если смесь
образует азеотроп (кривая 2 на рис . 1 2 .48), - здесь разделение
исходной смеси (пусть - состава х1 ) на практически чистые
компоненты методом обычной ректификаuии становится не
возможным (возможно лишь получение одного из компонентов
(Хо) и смеси, близкой к составу азеотропа .хаз).
Разделение таЮfХ смесей может быть облегчено под ваку
умом. При этом наряду с увеличением коэффициента относи
тельной летучести а смещается (по правилу Вревского - см.
разд. 12.2) состав азеотропа Хаз, иногда вплоть до его исчезно
вения. Но использование вакуума не всегда существенно по
вышает а. Кроме того, его создание и поддержание связано с
дополнительной затратой энергии и неизбежными потерями
ценных продуктов (или созданием дорогостоящей системы
улавливания паров перед вакуум-насосом). Значительно эко
номичнее методы, основанные на
введении в разделяемую смесь до
полнительного - "разделяющего" компонента (аrента) . Здесь исполь
зуюгся два основных технолоmче
СЮfХ подхода, получивших название
экстрактивной и азеотропной ре:кти
фикации.

РХ

Рис. 12. 48. Кривые равновесия для труднораз
делимых смесей:
1 - при малой относиrельной летучести компо 
нешов, 2 - при наличии азеотропа в смеси

О Хо Х 1

Х-

Хаз

Экстрактивная ректификация
Пусть нео бходимо разделить на достаточно чистые компо
ненты трудноразделимую бинарную смесь (а --. 1 или су
ществует азеотроп). К такой смеси добавляют специально по
добранный компонент (обычно - труднолетучий), избиратель
но растворяющий один из компонентов исходной смеси (на1 063

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 12. 49. Диаrрамма равновесия и по
строение теоретических ступеней в при
суrствии экстрагирующего агента:

1 - участок линии равновесия в укрепляю 
щей части колонны , 2 - то же в отrонной части ,
З- рабочая линия в укрепляющей части колон
ны, 4 - то же в отrонной части , 5 - теоретиче
сКJ1е тарелКJI (ступени)

пример, компонент В) и мало
растворяющий
другой
(ком
понент А) . Иными словами , вве
0 Хо
дение в систему третьего компонента заметно понижает упру
гость паров
растворяемого
компонента бинарной смеси, увеличивая тем самым коэффи
циент относительной летучести: а.'лв > а. лв разделяемой смеси.
Этот метод ректификации и получил название экстрактивной
ректификации, а дополн ительный компонент - разделяющего,
или экстрагирующего агента .
Линия равновесия бинарной смеси при наличии разделяю
щего компонента представлена на рис. 1 2.49 (сплошная линия)
в сравнении с равновесием без него (штриховая линия). Оче
видно, что количественный эффект разделяющего компонента
при прочих равных условиях определяется его концентрацией в
разделяемой смеси. Поэтому в случае непрерывной ректифи
кации на линии равновесия наблюдается скачок концентраций
в паровой фазе (в точке с абсциссой х1 ), обусловленный изме
нением концентрации экстрагирующего агента в жидкости при
подаче в колонну исходной смеси.
К экстрагирующему агенту предъявляется ряд требований
помимо избирательного растворения одного из компонентов
разделяемой смеси; основные из этих требований следующие:
- он не должен образовывать азеотропов с компонентами
исходной смеси (чтобы его можно было без затруднений впо
следствии отделить от них с целью его регенерации и получе
н ия чистых компонентов) ;
- он должен существенно отличаться от компонентов ис
ходной смеси по температуре кипения, т.е. быть значительно
более труднолетучим , чем ВКК исходной смеси, или (это бы
вает реже) значительно более легколетучим, чем Н КК исход
ной смеси (что позволяет его выделять без больших энергети
ческих и капитальных затрат) .
На рис . 1 2 .50 представлена схема разделения исходной сме
си А + В методом экстрактивной ректификации с добавлением
труднолетучего разделяющего агента С , хорошо растворяющего
компонент В . Компонент С подается на одну из верхних таре
лок колонны 1 и вместе с флегмой стекает вниз по колонне.

Р�

1 064

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

I IV
1

Рис. 12. 50. Схема установки для экстракrивной рекrификации :
1, 2
ректификационные колонны, J, 4 - насосы, 5 - кипятильники, 6 - конденса
торы;
1- охлаждающая вода, /1
rреющий пар, lll - конденсат, /V восполнение потерь
эксrраrирующеrо аrента
-

-

-

Растворяя в себе компонент В, разделяющий агент С понижает
тем самым упругость его паров и способствует разделению А и
В . Верхний продукт колонны 1 представляет собой компонент
А заданной чистоты , а нижний продукт - смесь В + С . Насо
сом З эта смесь подается в колонну 2, где методом обычной
ректификации получают компоненты В (верхний продукт) и С
(нижний продукт) . При этом колонна 2, как правило, отлича
ется небольшой высотой и работает с небольшим флегмовым
числом , поскольку компоненты В и С существенно различают
ся по температуре кипения (см . второе требован ие к экстраги 
рующему агенту) . Экстрагирующий агент С насосом 4 подают в
колонну 1, замыкая цикл по компоненту С . Результатом рабо
ты по такой схеме является разделение исходной смеси А + В
на отдельные компоненты А и В , причем некоторые потери
разделяющего компонента С с этими продуктами восполняют
ся - см . дополнительный поток IV, показан ный на схеме
штриховой линией.
В том случае , если экстрагирующий агент является легколе
тучим, т.е. отличается н аиболее низкой температурой кипения
(tc < tA) , в колонну 1 он подается снизу, а выводится вместе с
1 065

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

н изкокипящим компонентом А - сверху. Высококипящий
компонент В отводится снизу колонны 1, а смесь А + С разде
ляется в колонне 2.

Э кстрактивная ректификация является наглядной илл юстрацией тезиса (см .
разд. 1 . 1 . 3) об условности классификаций и подчеркивает отсуrствие четких
границ между некоторыми разделительными процессами . В самом деле, по
скольку речь идет о процессе разделения в системе жидкость-пар, то налицо
все признаки ректификационного процесса. Но одновременно происходит пре
имущественное растворение одного из компонентов разделяемой смеси в экстра
гирующем аrенте - это характерно для процесса экстракции (см. гл. 13). Нако 
нец, некипящий экстрагирующий аrент преимущественно поглощает пары одно
го из компонентов разделяемой смеси , а это - признак абсорбционного процес
са (см. гл. 1 1 ) . Очевидно, в экстрактивной ректификации присуrствуют призна
ки различных разделительных процессов.

Азеотропная ректификация •
Метод азеотропной ректификации применим как для смесей
с малым коэффициентом относительной летучести, так и для
азеотропообразующих смесей (в том числе при составах, близ
ких к азеотропному) . В отличие от экстрактивной, при азео
тропной ректификации разделяющий агент С образует с каким
либо компонентом разделяемой смеси азеотроп с иным соот
ношением компонентов, нежели в исходной смеси, если по
следняя является азеотропообразующей. В качестве разделяю
щих агентов могуг применяться вещества, образующие гомоазе
отропы с компонентами А или В (это могуг быть азеотропы с
минимумом или максимумом температур кипения), либо rете
р оазеотропы, представляющие собой тройные смеси разделяе
мьIХ компонентов А и В с разделяющим агентом С . Во всех
случаях один из компонентов разделяемой смеси в колонне
азеотропной ректификации может быть получен в практически
чистом виде .
На рис . 1 2 . 5 1 изображена принципиальная схема установки
азеотропной ректификации при работе с разделяющим агентом
С, образующим с компонентом А rомоазеотроп с минимумом
температуры кипения. Разделяющий (азеотропообразующий)
агент С подается в колонну 1 не выше точки подачи исходной
смеси А + В , чаще всего - вместе с исходной смесью. Сверху
колонны в виде rомоазеотропа отводятся пары смеси А + С ,
конденсируемые в конденсаторе 3, а снизу - в качестве кубо
вого остатка - практически чистый компонент В . Гомоазео• Азеотро пную ректификацию не следует смешивать с ректификацией азео 
тропообразующих (в частности, азеотрqпных) смесей, осущеСТRЛЯемой, напри
мер, с помощью экстрагирующего аrента (см . выше) или при реализации сопря
женных процессов в паре колонн, работающих под разными давлениями (см .
разд. 24 . 2.2).

1 066

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 12. 51. Схема установки для
азеотропной ректификации :
1
колоЮ1а для азеотропной )JеКТИ
фикации , 2
узел разделеЮtя компо
конденсатор, 4
ненrов А и С, З
-

-

КИПЯТИЛЬЮIК;

-

-

I
охлаждающая вода, //
rрею
щий пар, III конденсат, IV воспол
неЮtе потерь разделяющеrо areнra
-

-

А+С

-

-

А+С

троп из колонны азеотропной ректификации подле
с
жит разделению (в особом
узле 2 на рис. 1 2 . 5 1 ) на
l 1v
компонент А необходимой
1
чистоты и разделяющий
4
агент С. Последний вновь
lI
колонну
возвращается в
в
азеотропной ректификации .
потери
Незначительные
разделяющего агента С с
выделенными продуктами А
и В восполняются - см. дополнительный поток JV, показан ный на схеме штриховой линией .
Заметим, что наиболее сложным и энергоемким в схемах
азеотропной ректификации является узел 2 разделения азео
тропной смеси . Если разделение последней ведется методом
ректификации , то он включает в себя две колонны с сопут
ствующими аппаратами (см. сноску на с. 1 066 ) . Для разделения
образующейся азеотропной смеси возможно использование и
других разделительных приемов (в схемах сопряженных про
цессов - см. разд. 24.2).
Анапоrnчная схема разделения с получен ием практически чистоrо компонен
та А внизу колонны реапизуется при образовании rомоазеотропа В + С с темпера
турой кипения смеси меньшей. чем температура кипения чистоrо компонента А.
При образовании rомоазеотропов А + С или В + С с максимумом температуры
кипения они должны отводиться снизу колонны, а второй ком понент необходи
мой чистоты забирается сверху колонны.

Несколько проще разделение смеси А + В с помощью раз
деляющего агента, образующего гетероазеотроп · . Последний
после его конденсации образует два жидких слоя с разными
соотношениями разделяемых компонентов в них. Это различие
в составах двух слоев сопровожцается уменьшением требуемой
разделительной способности самой ректификационной колон 
ны (и ее высоты) по сравнению с образованием гомоазеотропа.
Подчеркнем : температура кипения гетероазеотропа ниже, чем у
компонентов А и В .
• Подробнее см. (9) .

1 067

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

б

а

Y1 v

(J

>iv

Y1 v

А

..t

у;//
Уш
Y1i1

А

Ут

Уш
Xv

х

Рис. 12. 52. К о п р еделен и ю

числа

х--

теоретических тарелок при rетероазеотро п н о й

ректификаци и :

а - подача исходной смеси (х1 < xv) в колонну 1 . б - подача исходной смеси ( x v < х ; <
<xv1) во флорентийский сосуд, в - п одача исходной смеси (xf > х�1) в колонну 2,
1, 2 - колоЮiЫ , .1, .1' - ко�-щен саторы, 4, 5 ПЯтильники, 6 - флорентийский сосуд ,
7 - рабочие л и ни и отгонных ч�стей колонн, 8, 8 - рабочие линии укрепляющих частей
KOЛ O IOfbl ;

КIJ

l - исходная см есь; о , Il - кубовые остатки в колоннах 1 и 2 соответственно;
составы паров из колонн 1 и 2, V, Vl - составы равновесных слоев ЖИJ (хости

111, IV -

Расслаиван ие и декантацию гетероазеотропной смеси осу
ществляют во флоренти йском сосуде , позволяющем раздельно
выводить слои легкой и тяжелой жидкости . Подробнее прин 
ципы его работы и гидравлический расчет изложены в разд .

1 3 .2 . 3 .

Возможны различные схемы установок для гетероазеотроп
ной ректифи каци и . На рис . 1 2 . 52 представлены некоторые из
них; в качестве флегмы здесь используется слой жидкости п осле
расслаивания конденсата во флорентийском сосуде. Исходная
смесь А + В (поток 1) может быть и азеотропообразующей лю
бого состава, в том числе и близкого к азеотропному; она по
дается в коло н ну 1. Есл и соотношение А/В в парах гетероазео
тропной смеси больше, чем в исходной, то снизу из этой ко
лон н ы в качестве кубового продукта отводится высококипящий
компонент В с кон центрацией компонента А в нем, равной хо .
Уходящие с верху коло н ны парь� тройного гетероазеотропа кон 
денсируются в конде нсаторе З. Расслоен ие конденсата проис
ходит во флорентийско м сосуде 6; составы равновесн ых слоев
с разными ко н центраци ями компонента А в них (x v и xv1) от-

1 068

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

личаются от состава отбираемого сверху rетероазеотропа. Это
равновесное расслаивание наряду с ректификацией дает значи
тельный вклад в общий процесс разделения бинарной смеси на
чистые компоненты .
Один слой (на р ис 1 2 . 52 - верхний, с меньшим содержан и
ем компонента А) во з вр ащаетс я в колонну 1 в качестве флег
мы. Второй слой (на схе ме - нижний, с большим содержанием
компонента А) направляется в колонну 2. Поскольку темпера
тура кипения rетероазеотропа меньше, нежели компонента А,
то сверху колонны 2 буд уг уходить пар Ьl rетероазеотропа. Он и
направляются в конде н с ато р 3 '
нередко он общий для двух
колон н . Сн изу колонны 2 отводится пр од у кт А зад ан ной
чистоты; последняя зависит от высоты колонны 2, представ
ляющей собой по суги отгонную колонну, в которой из жид
кости отгоняется легколетучий гетероазеотроп.
Процесс разделения методом rетероазеотропной ректифика
ции удобно анализировать в диаграмме у-х с условно
абсолютными кон це нтра ци ями компонента А
.

-

в паре у = улf(ул + УВ ) и в жидкости х = хлf(хл + .хв);
присугствие компонента С учитывается видом диаграмм равно
весия .
Обозначим: х1 - содержание н изкокипящего компонента А
в исходной смеси; .хо и х11 - его содержание в кубовых продук
кон центрации
тах колонн 1 и 2 соответственно; xv и x v1
компонента А в ра в н овесн ых жидких фазах после их рассдое
н ия во флорентийском сосуде; Уш и Y1v - составы паров, по
кидающих колонны 1 и 2.
Заметим: если состав исходной смеси находится в области
между xv и xv1, то ее н уж но п од а вать во флорентийский сосуд
для разделения на два слоя . Здесь обе колонны будуг отгонн ы 
ми (рис . 1 2.52, б) .
Исходная смесь с концентрацией компонента А х1 < x v по
дается в колонну 1, где разд еля ется на кубовый остаток (Хо) и
пары у1п, состав которых зависит от разделяющей способности
(флегмового числа и числа тарелок) укрепляющей части ко
лонны 1. При увеличении числа тарелок в укрепляющей части
колонны (см . штриховую линию 8') повы ш ается кон центрация
компонента А в паре ( Уiп > Уш) , и рабочей точкой для верх-

него сечения будет точка З' с координатами у;11 и x v. Очевид
но, что минимальная высота (минимальное число тарелок)
укрепляющей части колон н ы 1 может быть рассчитана из усло 
вия получен ия пара с конце нтр а ц ией У/11 = x v (в этом случае
при его конденсации воз можно образование отдельной капли

1 069

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

второй фазы на поверхности первой). При конденсации паров
с концентрацией YJJJ > у;;1 получается жидкость, расслаи
вающаяся на два слоя .
Высота колонны 2 зависит от требуемой чистоты компонента
А. При этом рабочая линия колонны 2 пересекает диагональ квад
рата (диагр амма у-х) в точке с абсциссой хп и имеет угол накло
на, тангенс которого равен отношению потоков жидкости и пара.
При кон центрации х/ > xv1 содержание НКК (компонента
А) в гетероазеотропе меньше, чем в исходной смеси. Поэтому
она должна подаваться в колон ну 2 (рис. 12.52, в), где в ка
честве нижнего продукта получается практически чистый ком
понент А. Сверху колонны 2 отводятся пары состава Y!V· Оче
в ид но, схема "в" здесь совпадает со схемой "а", если в одной из
них поменять местами номера колонн и компоненты А и В .

О солевой ректификации
Иногда в качестве разделяющего агента используют твердые
вещества (например , соли), преимущественно растворимые в
одном из компонентов разделяемой смеси и потому понижаю
щие его упругость паров. Такой процесс разделения называют
солевой ректификацией • .
Для выяснения рассматриваемого эффекта применим идеа
лизированную модель с рядом упрощающих допущений. В от
сутствие соли коэффициент разделения бинарной смеси обо
значим а.о= Рл0/Р8°. Пусть соль растворяется только в одном из
компонентов, например в В ; ее мольную абсолютную концент
рацию в этом растворе обозначим z. Тогда концентрация са
мого компонента В в растворе составит (1 - z) . Положим, что
упругость паров этого компонента следует закону Рауля, т.е. в
присутствии соли она равна Рв " = Рв0 ( 1 - z) . В этом случае
коэффициент разделения бинарной смеси в присутствии соли
запишется так: а.. = Рл0/Рв" = Рл0/ [ Рв0( 1 - z) ] = а.о /( 1 - z) .
Отсюда а../ а.о = 1/( 1 - z) .
В целях уп рощения последующего анализа прологарифмиру
ем полученное соотношение и разложим правую часть в сте
пенной ряд " :
а. •

1 11 -

а.о

здесь

•
ное

п

-

=

1
I n --

1

-

z

=

00 z"
}:; -

n=l

п

2

=

z

3

z
++z +
2
3
-

...

'

индекс суммирования.

Краткое и:uюжение процесса солевой ректификации - см. (7), более пол

-

( 2 8J.

• • Разложение в ряд различ ных функций приведено в справочниках по мате
матике, в частности (4 ) .

1 070

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Поскольку на практике концентрация соли z исчисляется
процентами , т.е. сотыми долями , то вполне можно ограничить
ся первым членом разложения ; тогда в линейном приближении

ln(a.• /а.о) :::: z .

(а)

Согласно этому выраже нию коэффициент разделения а.. воз
растает с увеличением концентрации соли z.
Выражение (а) отвечает идеализированным представлениям ;
отказ от упрощающих допущений не изменяет качествен н ых
эффектов, однако требует количественной корректировЮ1, т.е.
введения поправочного множителя с. , специфичного для каждой конкретной системы:

ln(a.. /•а.о) =

с. z

.

(б)
•
Выражение (б) подтверждено экспериментально .
Подачу соли в ректификационную колонну производят пуrем
ее предварительноrо растворения в потоке флегмы или исходной
смеси, а регенерацию - пуrем вьmаривания кубовоrо остатка.
При использовании методов экстрактивной, азеотропной и
солевой ректификации наиболее трудным является выбор раз
деляющего ком понента. Имеющиеся теоретичесЮ1е подходы ··
к решению этого вопроса разработаны недостаточно; чаще
всего в настоящее время разделяющий компонент выбирают с
учетом практичесЮtх рекомендаций ***
12. 10. ПЕРИОДИЧЕСКАЯ РЕКТИФИКАЦИЯ

БИ НАРН ЫХ СМЕСЕ Й

12. 10.1 . Общие

положения

Ректификационные установЮf периодического действия ис
пользуются преимущественно в малотоннажных производствах.
Установка состоит из дистилляционного куба (часто весьма
большого объема), снабженного нагревательными устройствами
в виде рубашЮ1, змеевика, трубчатЮ1 или выносного теплооб
менника ; колонны с тарелками или насадкой ; конденсатора
или дефлегматора, а также емкостей для исходной смеси и
продуктов, насосов и другого вспомоrательного оборудования .
Исходную смесь загружают в куб и подогревают до Юtпения .
Образующийся в кубе пар, поднимаясь по колонне, обоrащает• См., например, (7, 2 8 ) .
: • Подробнее о выборе разделяющего аrента с м . ( 15, 23).
•••
Некоторые практические рекомендации имеются в (7, 15, 19) .

107 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ся Н К К в результате контакта со стекающей вниз флегмой, кото
рая по мере движения к кубу обогащается ВКК. Пары из колонны
D отводят в конденсатор, где они, как и в случае непрерывной
рекгификации, полностью или частично конденсируются. Часть
конденсата L возвращают на орошение в колонну в качестве
флегмы, а остальной конденсат П отводят через холодильник в
сборник дистилляга (верхнего продукта). Жидкость в кубе посте
пенно обогащается ВКК, теряя Н КК, который уносигся паром в
колонну, к конденсатору, и выводигся с дистиллято м . После до
стижения заданного состава кубовой жцдкости (что можн о уста
новиrь по температуре кипения) ее сливают, а в куб загружают
новую порцию исходной смеси, и операция повторяется.
Таким образом , колонна работает в режиме укрепляющей
части, роль отгонной части играет куб.
Технологическая задача периодической ректификации мо
жет формулироваться по-разному. Н иже рассмотрены лишь
некоторые из постаново к задачи .
Заметим (это существенно для последующего анализа), что
масса жидкости в кубе в случае периодических процессов, как
правило, значительно превышает ее массу, находящуюся на
тарелках (или в слое насадки) ректификационной колонны .
Кроме того, принято , что изменения (перестройка, релаксация)
кон центраций и температур на тарелках колонны вполне успе
вают за сравнительно медленным течением процесса.
Процессы периодической ректификации проводят в двух
основных режимах: с получением дист иллят а постоянного со
става или с постоянны.м флегмовым числом . Основа материаль
ного и теплового расчета этих режимов
едина .
Материальный расчет периодической ректификации. Матери
альн ый (а в дальнейшем - и тепловой) расчет требует уста
новления связи текущих (и конечных) концентрации кубового
остатка Хо и количества оставшейся (с начала процесса) жид
кости в кубе Lo либо ото бранного дистиллята П . С этой целью
выделим на схеме колонны (рис . 1 2.53 , а) контур К и запишем
материальный баланс для элементарного промежутка времени
d't. Напомн и м : массы фаз на тарелках (или в просветах насад
ки ) существенно меньше, нежели жидкости в кубе; поэтому
вкладом изменения составов фаз (количеств Н КК) на тарелках
при составлен ии балансов пренебрегаем . Тогда материальные
балансы будут иметь следующий вид .
По количеству фаз в отсутствие Источников и Стоко в:
Пр = О , Ух = dП, Нак dLo; в итоге
-

=

О

d П = dLo,

или

dП

=

d Lo.

(а)
И нтегр ирован ие (а) от начала до конца процесса (от О до П к и
от Lн до Lк) приводит к очевидным соотношениям:
Пк
Lн -- Lк; Lн = Lк + П к; Lк = Lн Пк. (12.42)
=

1 072

-

-

-

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

б

а

Рис. 12. 53. К материальному (а) и теwювому (б) расчету периодической ректифи
каци и

Интеrрирование до промежуточного момента времени, когда от
начала процесса отобрано П молей дистиллята, а в кубе осталось
Lo молей жидкости, дает сходные соотношения, например:
п =

Lн

-

Lo = Lн

Lo;

-

п

и т. л .

( 1 2.42а)

По количеству НКК для тех же пространственного контура и
временн 6 го интервала: Пр = О , Ух = х2dП, Нак = d (�); тогда
(б)
0 х2dП = d ( �) .
Интеrрирование (б) имеет особенности для упомянутых режи
мов и далее рассматрива ется раздельно для каждого из них.
Тепловой расчет периодической ректификации . Он основан на
тепловом балансе, первоначально записанном для контура К,
охватывающего всю колонну (рис . 12.53 , б) , и для бесконечно
малого промежутка времени . Вкладом изменения энтальпий
фаз на тарелках по ука:1анным выше причинам при составле
нии баланса пренебрегаем. Тогда
-

dQк + c2 t2dL

-

h1d D =

d (Locoto).

(в)

Здесь в правой части - накопление теплоты в кубе, т.е. в рас
сматриваемом контуре . В левой части для уменьшения числа
переменных целесообраэны подстановки: dL = Rd П , dD = (R +
+ l )dП. Тогда
(г)
dQк + c2t2 Rd П h1(R + l)dП = d (Locoto).
-

Ниже последователь н о изложен расчет периодической рек
тификации для режимов х2 = coпst и R = const.
1 073

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

1 2 . 1 0.2. Ректификация при постоянном составе дистиллята

С позиций потребителя дистиллята удобнее получать про
дукт постоянного (стабильного) состава. Такой процесс можно
осуществить несмотря на непрерывное уменьшение содержа
ния Н КК в кубовой жидкости, если в ходе ректификации по
степенно повышать флеrмовое число .
Задачу технологического расчета сформулируем следующим
образом : известны состав Хн и количество Lн исходной смеси,
заданы составы получаемого дистиллята х2 и кубовой жидкости
Хк, остающейся в конце процесса ; требуется определить коли
чества дистиллята и кубового остатка, а также выполнить теп
ловой расчет процесса.
Материальный расчет. Расчет рассматриваемого процесса
использует формулы ( 1 2.42) и ( 1 2 .42а) . Интегрирование выра
жения (б) затруднений не вызывает, так как х2 = const. Для
процесса в целом (от его начала П = О, 1-oXQ = Lнхн до конца
П = Пк, 1-oXQ = Lкхк) имеем:

О

-

х2Пк = Lкхк - Lнхн .

Избавляясь от отрицательных величин и заменяя
Lк с Хк:

му из выражений ( 1 2 .42) , получаем связь

х2 (Lн - LJ

откуда

=

Пк по перво

Lнхн - Lкхк,

(д)
( 1 2 .43)

последнее выражение наЙдено пугем подстановки в первое
Пк = Lн - Lк по ( 1 2.42) .
Если рассматривать процесс до некоторого промежуточного
момента времени, когда концентрация Н КК в кубе равна XQ, а
количества дистиллята и кубовой жидкости - П и Lo, то ана
лоmчные преобразования приводят к связи текущих величин:
П

= Lн Х н - Хо
Х2 - Хо

;

н
Lo = Lн Х2 - Х .

Х2 - Хо
случае х2 = co11st

( 1 2 .43а)

К формулам ( 1 2 .43) и ( 1 2.4За) в
можно
прийти и сразу, составляя материальные балансы для проме
жугка времени от начал ьного момента до конечного или теку
щего . Эти соотношения , естественно, идентичны полученным
в разд . 1 2 . 3 .2 для процесса постепенной дистилляции.
Расчет необходимого числа тарелок в ректификационной
колонне связан с определением минимального флегмового
числа Rmin, теоретически обеспечивающего отбор дистиллята
заданного состава х2 = t:oпst (при бесконечном числе тарелок) .
Оно изменяется в ходе периодического процесса вслед за изме1 074

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

б

а

Рис. 12.54. К установлению чисrrа теоретических тарелок в начале и в конце про
цесса (а) и связи текущих знач�ний R и Х() дтrя процесса с х2
const (б)

=

нением состава кубовой жидкости. Для любого момента време
Р
ни от начала процесса текущее (мгновенное)
значение Rmin
можно определить по формуле ( 1 2 . 19), заменив в ней кон цент
рации фаз на тарелке пнтанил х1 и у1 на текущие и равновес
ные концентрации жидкости в кубе Хо и пара над ней ycf :
R

пun
.

=

Х2

- у8

У8

- Хо

(е)

Концентрация Хо непрерывно понижается в процессе пе
риодической ректификации, поэтому величина предельного
отрезка на оси ординат х2 /( Rmin + 1 ) тоже уменьшается, так
что значение Rmin долж но постепенно возрастать. Если в куб
колонны загружается исходная жидкость состава Хю а после
завершения процесса получается кубовый остаток состава Хю
то минимальные флегмовые числа для начала и конца процесса
выразятся соответственно (е) :
(ж)
ще yJ' и у.}' - равновесные коннентрации пара в кубе в начале и конце процесса .

Рабочие значения флегмовых чисел для начала и конца про
цесса Rн и Rк (их превышение над Rmin) дает технико
экономический расчет; укажем, что коэффициенты избытка
флегмы для начала и конца процесса в общем случае мо гут
различаться .
Из рис. 1 2 . 54, а видно, что в ходе процесса рабочая линия
поворачивается около точки на диагонали х2 = У.!, переходя из
начального крайнего положения (отвечающего Хо = Хн) в ко
нечное (Хо = .xic); при этом она постепенно приближается к
1 075

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

диагонали соответственно постепенному возрастанию R и
уменьшению отрезка x2 /<R + 1).
Располагая рабочими значениями Rн и Rк, строят рабочие
линии для начала и кон ца процесса. Далее, зная начальный н
Х
и конечный Хк составы кубовой жидкости, графическим по
строением определяют числа теоретических тарелок, необхо
димые для разделения в начале и конце процесса (рис .
12.54, а) . В последующих расчетах ориентируются на большее
число необходимых тарелок n.r, соответствующее более трудно
му разделен ию (в примере на рисунке - это крайнее положе
ние рабочей линии, отвечающее концу процесса) .
Связь текущих значений R и состава жидкости в кубе Хо
устанавливают путем построения принятого числа теоретиче
ских тарелок nr при каждом текущем положении рабочей ли
нии, т.е . при известном текущем R (рис . 12.54, 6). Заметим:
второе крайнее положение рабочей линии (а следовательно, и
значение R) приходится устанавливать подбором - так, 'fl'Обы при
числе теоретических тарелок nr в кубе получалась вторая крайняя
концен1Рация Н КК (в расс.ма1Риваемом примере - .хн).
Тепловой расчет. Расчет периодической ректификации при
х2 = const предусматривает интегрирование выражения (г) . Ин
тегрируя от начала до конца процесса, получаем :
Пх

Qк + c2t2 f R d П
о

-

h2

Пх

f (R

о

+

1) d П = Lкскtк - Lнсн fн .

Затраты теплоты в к убе за весь процесс находим из этого
уравнения :
Qк =

Lкскtк - Lнсн f11

+ h2

Пх

f R dП

о

Пх

+ h2Пк - c2t2 f R dП .
о

После очевидных преобразований (с учетом 112 - c2t2 = r2
скрытая теплота парообразования дистиллята, флегмы) имеем:

Qк = Lкскtк

--

Lнсн fн

+

h2Пк

ll x

+ r2 f R d П .
о

( 12.44)

Величину интеграла в (12.44) можно по теореме о среднем
записать как Rср П к, где Rcp - среднее за процесс (строже среднее по количеству дистиллята П к ) значение флегмового
числа. Окончательно:

(12.45)
И нтегрирование до nромежуточного момента времени, ко
гда затраты теплоты в кипятильнике составляют Q к"Р, при1 076

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

водит к формуле:

Q кпр = Locolo

причем R �р П

п

-

Lнсн!н

+

(r2 R.;p' + h2 ) П ,

( 1 2 .45а)

= J R dП .
о

Обращаем внимание на сходство выражения ( 1 2 .45) с полу
ченным ранее ( 1 2 .25) для непрерывной ректификации.
Величину среднего флегмового числа рассчитывают по его
определению:

1 Пк
R.;p = J R dП.
Пк

о

Связь текущих R и П , необходимую для вычисления инте
грала, устанавливают с помощью диаграммы у-х: проводят в
ней произвольную рабочую линию при промежуточном (фик
сируемом) значении R, строят принятое число теоретических
тарелок и получают теJ...'}'Щую кон центрацию Н КК в кубе Хо ·
Затем по первой из формул ( 12.43а) рассчитывают текущее зна
чение П. Эту операцию повторяют для полного диапазона из
менения П от О до Пк и находят искомое значение интеграла.
Количество теплоты , отводимой в конденсаторе за весь про
цесс, рассчитывают по формуле, получаемой из теплового ба
ланса конденсатора (приводим ее без вывода) :

Qко�щ

Dr2 = ( R.;p + l )Пкr2.

( 1 2 .46)
Расходы теплоносителей в кубе-кипятильнике и конденса
торе определяют по тем же формулам ( 1 2 .26) и ( 1 2 .29), что и
для непрерывного процесса. Разница лишь в том, что здесь это
не потоки теплоносителей в единицу времени, а их количества
за весь процесс .
Поверхности теплообмена кипятильника и конденсатора на
ходят по канве, изложенной в разд. 1 2 . 3 .2 применительно к
простой постепенной дистилля ц ии. При вычислении интеграла
типа ( 1 2 . 1 2) для определения текущего значения Qкпр пользу
ются формулой ( 1 2 .45а) .
=

12. 1 0.3. Ректификация при

постоянном

флеrмовом числе

Получение дистиллята постоянного состава в процессе пе
риодической ректификации с непрерывным увеличением
флегмового числа требует очень тонкого и сложного реrулиро
вания работы кипятильника и конденсатора. Поэтому чаще
периодическую ректификацию проводят с постоянным (на
протяжении всего процесса) флегмовым числом R = const . В
этом случае концентрация Н КК в дистилляте постепенно
1077

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

уменьшается соответственно непрерывному падению его со
держания в кубовой жидкости .
В процессе ректификации при R = const, согласно зависи
мости ( 1 2 . 1 8) , tga = R /1 R + 1 ) = coпst; поэтому рабочая лини я
в ходе процесса, т.е. по мере снижения концентрации Н КК в
кубовой жидкости и д истилляте, перемещается вниз парал
лельно самой себе. При этом число тарелок в колонне, есте
ственно, не изменяется .
Задачу технологического расчета сформулируем следующим
образом : известны состав Хн и количество � исходной смеси и
задан конечный состав J...-убовой жидкости хк ; требуется опреде
лить состав и количество дистиллята и провести тепловой рас
чет процесса·. При этом для потребителя состав дистиллята
должен быть приемлем, ориентировочное его значение - из
вестно.
Материальный расчет периодической ректификации в этом
режиме проводится тоже с использованием формул ( 1 2 .42) и
( 1 2 .42а) . Интеграл в правой части выражения (б) берется так
же, как и в разд. 1 2 . 1 0 .2. Однако при интегрировании левой
части выражен ия (б) необходимо учитывать, что х2 = х2(П) =
= var. Воспользуемся теоремой о среднем:
Пк

,i Х2 d П = Х2 к П к ,

1)

где черта н ад х2 означает усреднение концентрации Н КК в
дистилляте по его количеству. Здесь подчеркивается, что в ходе
процесса дистиллят изменяет свой состав; к концу процесса
состав накопленного (но не отводимого в данный момент!) ди
стиллята равен х2 к . И значит, с этой средней концентрацией
формально справедливы выражения типа (д), ( 1 2 .43) и ( 1 2.43а)
для процесса в целом .
В свете поставленной технологической задачи наЙдем .Х2 к .
И з выражения типа ( 1 2 .42) следует:
Х2" =

L н Хн - L к Хк
L н - Lк

( 1 2 .47)

Это соотношение полностью совпадает с полученным в
разд. 1 2 . 3 .2 для постепенной дистилляции. Здесь, как и там,
заданы либо конечный состав кубовой жидкости Хк (так приня
то при постановке задаqи), либо количество кубового остатка
Lк. Для расчета х2к необходимо найти зависимость между величинами Хк и Lк- Это можно сделать, установив связь мгно
венного (текущего) состава дистиллята х2 с накопленным
1078

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

(отобранным) с начала процесса текущим количеством дистил
лята П или же с текущим (находящимся в кубе) количеством
кубовой жидкости Lo . Искомую связь установим с помощью
того же материального баланса (б), раскрыв дифференциал
произведения в правой части:
(з)
о
Х1d П = XQd Lo + LodXQ .
-

Заменяя в выражении (з) dП по (а) и разделяя переменные,
находим:
d Lo
dxo
(х2 - XQ)d lo LodXQ , и
(и)
Lo
х2 - хо
==

=

Выражение (и) проинтегрируем (меняя местами пределы, чтобы
оперировать положиrельными величинами) от начала процесса,
ко гда Lo = Lн, XQ = Хн, до конца процесса ( Lo = Lк, XQ = Хх):
( 1 2 .48)
а также до промежуточного момента времени (Lo, XQ) :
L
Lo

ln __..!!..

=

хн

f

хо

dxo

�
-

х2 - хо

( 1 2.48а)

Подчеркнем: в знаменателе под интегралом переменны по ходу
процесса обе концентрации
х2 и XQ.
Полученные соотношения призваны дать искомую связь Lк
(или Пк) и Хк , Lo (или П) и XQ. Они сходны с выражениями
( 1 2 .7) и ( 1 2 .7а) для процесса простой постепенной дистилля
ции . Разница в том, что текущие значения х2 = У2 и XQ, необхо
димые для расчета текущих и конечных количеств фаз, не яв
ляюгся здесь равновес ными, поскольку разделены в про
странстве тарелками (насадкой) ректификационной колонны.
Расчет числа тарелок в режиме R = const отличается боль
шей неопределенностью (можно сказать: большей свободой в
варьировании переменных), нежели в режиме х2 = const.
Для определения числа теоретических тарелок зададимся
начальным содержанием НКК в дистилляте х2н; оно должно
быть больше ориентировочно приемлемого .Х2 к . При этом чем
выше выбранное х2н. тем больше потребуется тарелок в колон 
н е и выше будет флеrмовое число R . Зафиксировав в диаграм
ме у-х на диагонали для начала процесса точку с абсциссой
х2н. найдем по первому из выражений (ж) начальное значение
Rrnin и далее
R. После этого проведем рабочую линию для
начала процесса и построим теоретические тарелки - пусть их
-

-

1 079

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

О

хк

х0 хо х2к х2 хн х2
-х

Рис. 12. 55. К расчету п е р и одическо й ректиф икаци и

Х-2 к х2н 1

в р ежим е

R=

coпst

число nг (на рис . 1 2 . 5 5 nг = 4) . В ходе процесса рабочая линия
перемещается параллельно самой себе при уменьшении теку
щих кон центраций Н КК в дистилляте х2 и в кубовой жидкости
Хо· Для любого текущего значения х2 можно с тем же наклоном
провести рабочую линию и , сохраняя nг, найти текущую вели
чину Хо , а по ( 1 2 .48а) - - текущие количества кубового остатка
Lo и дистиллята П = Li.i - L0. Заметим, что для момента завер
шения процесса положение рабочей линии придется отыскивать
подбором , останавливаясь на таком конечном Х2к, которое при
принятом числе теоретических тарелок nг приведет к получению
· заданной конечной концентрации Н КК в кубе Хк.
Таки м образом , иско мая связь Lo и Хо установлена, что по
зволяет найти (графиче<.:ки или числен ными методами) значе
н ия инте грала в правой части ( 1 2.48), рассчитать Lк и далее состав получаемого дистиллята по ( 1 2 .47).
Тепловой расчет для рассматриваемого режима также базиру
ется на выражении (r) . Проинтегрируем его от начала до конца
процесса:
Пк

J h1 ( R

о

1 080

+ l ) d П = Lкскlк

-

Li.icнfн.

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Отсюда затраты тепла
будуг равн ы

Qк

=

в

кубе (кипятильнике) за весь процесс
Пк

Пк

о

о

Lкскfк - Lнснfн + J h2 (R + l )d П - J С2

После объединения интегралов (с учетом h2
Qк

=

Lкскfк

Пк

- c2t2

=

t2Rd П .

r2) получаем :

- Lнсн!н + J ( Rr2 + h2 ) d П .
о

( 1 2 .49)

Эту формулу полезно сошоставить с выражен ием ( 1 2 . 2 5 ) для непрерывного
процесса, и м ея в виду, что роль Lнснfн там иrрает состаWIЯющая L 1 c 1 t1 , а роль
L.:скtк состаWIЯ ющая Locoto.

-

Аналогичным образом получается формула для текущего ко
личества затраченной в кубе теплоты :
п

Q кпр = Lo coto - l,.1 снfн + f (Rr2 + h2 ) d П .
о

( 1 2 .49а)

Стоящие под интегралом в ( 12 .49) теплофизические характе
ристи ки п ара , уходяще го из колонны в конденсатор, т.е. r2 и
h2, изменяются по мере отбора дистиллята. Эти свойства опре
деляются текущим составом пара (дистиллята) У2 = х2 и , строго
говоря, зависят от тем пературы, т.е. требуют использования
диаграммы t-x, у. Связь х2 с количеством отобранного дистил
лята П уже установлена - с помощью построения числа теоре
тических тарелок nr и формулы ( 1 2 .48а) ; поэтому вычисление
интеграла принципиал ь н ых трудностей не вызывает, хотя и
весьма трудоемко .
Заметим, что при близких мольных теплотах парообразова
ния компонентов и их смесей rл ::::: rв ::::: 12 ::::: const вычисление
интеграла в ( 1 2 .49) упрощается :
Пк

Пк

f ( Rr2 + h1 ) d П = J (Rr2 + r2 + c2 t2 ) dП =
о
о
Пк

Тогда

= ( R + l )r2Пк + f с2 t2dП .
о

Qк = Lкскtк - Li1cн lн

+ (R

+ l )r2Пк

+

Пк

f С2 !2dП .
о

( 1 2 .50)

Количество теплоты , отводимой в конденсаторе за весь про
цесс, рассчитывается на основе теплового баланса конденсато
ра за бесконечно малый промежуток времени :

h2d D - c2!2dD - dQконд = О.
1 08 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Отсюда, подставляя d D = (R + l )d П и интегрируя получен
ное выр ажени е от н ача.1а процесса до его конца с учетом h2 - С2!2 = /"2 > П ол учим :

Qконд =

(R + 1 )

либо

Qконд =

Пк

J r2 d П
о

r2(R + l )Пк;

последнее вы ражение относится к случаю r2

( 1 2.5 1 )
( 1 2 . 5 1 а)
:::.

const.

1 2. 1 1 . О расчете ректификации многокомпонентных смесей

Процесс ректификац ии многокомпонентных смесей, как и
бинарных, может проводиться периодически и непрерывно .
Периодическая ректификация осуществляется в одной ректи
фикационной колонне путем последовательного (во времени)
получения в виде дистиллята сначала наиболее летучего ком
понента смес и , а затем -- компонентов с более высокими тем
пературами кипения . Компонент смеси с самой высокой тем
пературой кипения остается в кубе колонны в виде кубового
остатка. Разумеется , реально получают не отдельные компо
ненты , а фракции (порции) с преимущественным их содержа
н ием. Управление таким периодическим процессом существенно
сложнее, нежели непрерывным, когда параметры процесса не
изменяются в ходе работы установки .
Непрерывная ректификация многокомпонентных смесей
осуществляется в установках, состоящих из ряда ректификаци
онных колонн непрер ывного действия, соединение которых в
общую схему может быть различным. Каждая из колонн разде
ляет поступающую в нее смесь на два продукта, один из кото
рых - дистиллят, а второй - кубовый остаток. Поэтому при
наличии хотя бы трех компонентов в исходной смеси их разде
ление на три продукта в одной колонне невозможно . В этом
случае нужны две колою1ы, причем их работа может быть орга
н изована в двух вариантах (рис . 1 2 . 56).
В варианте (а) смесь трех компонентов А, В , С (компоненты
указаны в порядке возрастания их температур кипения) разде
ляется в первой колон не на дистиллят (компонент А требуемой
чистоты) и кубовый остаток, содержащий преимущественно
компоненты В и С (рис . 1 2 . 56 , а). Эту бинарную смесь разде
ляют во второй колонне на В (дистиллят) и С (кубовый оста
ток) . Кипящая кубовая жидкость из первой колонны во вторую
подается насосом.
В варианте (6) дистиллятом первой колонны является кон 
центрирован ная смесь двух компонентов (А+ В), а кубовый ос
таток содержит преимущественно компонент С (рис. 1 2 .56, 6).
1 082

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

А
А +В + С

1

А+ В+С

4

А+В

2

4

б

а

Рис. 12. 56. Схемы разделения 111 ехкомпоне1Пной смеси :
дистиллят - бинарная
а - кубовый остаток - бинарная смесь , б
1, 2 - колонны, З
конденсатор, 4 - кипятильник, 5 - насос
-

смесь ;

-

Бинарная смесь А+ В самотеком направляется во вторую ко
лонну, где разделяется н а А и В .

Отсутствие насоса для перr.качивания ки пящей жидкости (во избежание ка
витации насос надо устанавливать ниже уровня жидкости в колонне) как будто
бы делает вариант (б) более привлекательным, чем (а) . Однако (и это более
важно) вариант (б) характеризуется повышенным расходом фтiеrмы (здесь это смесь А + В) по сравнению с (а), где расход флегмы определяется возвратом на
орошение лишь одного ком понеJПа А. Поэтому для варианта (б) характерн ы
более высокие расходы теnпоносителей и увеличенные теnпообменные поверх
ности кипятильника и конденсатора. Оценки показывают, что вариант ( б) по
энергетическим затратам становится равноценным (а), если конденсатор первой
колонны по схеме (б) использ<'вать в качестве дефлегматора, т.е. конденсировать
в нем только флегму, а дистит�ят направлять во вторую колонну в парообразном
состоянии. О кончательно вопрос о преимуществе той или иной схемы разделе
ния может бьпъ решен при сопоставлении их технико - экономических показа
телей.

Для непрерывного разделен ия четырехкомпонентной смеси
(A+ B+C+ D ) ректификационная установка должна состоять
уже из трех колонн. Так, например, в первой колонне в виде
дистиллята получают практически чистый компонент А, во
второй (разделяющей кубовый остаток первой колон н ы
В+ С+ D) - компонент В необходимой чистоты . В третьей ( в
данном случае - последней) колонне получают два компонента
С и D . Возможны и другие варианты (пример - на рис . 1 2 . 57),
когда во второй колонне в виде дистиллята получают смесь
В+С . Ее разделяют в третьей колонне на компоненты В и С
требуемой чистоты.
1 083

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

в

А
2

A+B+C+D

В+С

3

B + C +D

Рис. 12. 5 7. Возможная cxe.\fa разделения четырехкомпонентной смеси:
1

-

3

-

колонны, 4 - насос

Очевидно, если смесь содержит к компонентов, то для ее
непрерывного разделения на отдельные компоненты приемле
мой чистоты потребуется установка из к
1 ректификацион 
ных колон н . Ч исло вариантов возможных схем соединения
колонн с увеличением к быстро возрастает. Так, в случае четы
рехкомпонентной смеси число вариантов схем равно 5 , для
пятикомпонентной смес и - 1 4 , для шестикомпонентной - 42
и т.д . Выбор рационал ьной схемы компоновки колонн при
разделении многокомпонентной смеси является сложной тех
нологической задачей ; к тому же некоторые схемы мoryr ока
заться нереализуемыми из-за термодинамических ограничений
(условий фазового равновесия) для реальных смесей, особенно
в случ аях с сильными отклонениями от закона Рауля . Методы
выбора оптимальных схем разделения подробно изложены в
специальной литературе".
-

12. 1 1 . 1. Разделение трехкомпонентных смесей

Расчет второй колонны, где бинарнШl (практически) смесь
разделяется на компоне нты требуемой чистоты, не отличается
от рассмотрен ного ранее. Однако в первой колонне в ощути
мых количествах присугствуют все три компонента - как в
паровой, так и в жидкой фазах. Составы таких смесей (пусть в мольных долях) и фазовое равновесие удобно представлять в
треугольной диаграмме (см . рис . 1 2 . 1 1 и пояснения к нему в
разд . 1 2 .2 . 5 ) .
Будем рассматривать непрерывную работу первой колонны п о
варианту, в котором в качестве дистиллята получают практиче•

См. (9, 24, 26), а

1 084

также

статьи авторов этих монографий.

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 12. 58. К определен ию составов
дистиллята и кубового остатка при
ректификации тройной смеси

А

ски чистый ("целевой") низко
кипящий компонент А (см.
рис. 1 2 . 56 , а) . Точно известен
только состав исходной трой
ной смеси (точка Х1 на
рис . 1 2 . 5 8 ) . Точка Хъ характе
ризующая состав дистиллята,
лежит вблизи вершин ы А тре
уrольника (рис . 1 2 . 5 8 ) . Но в
дистилляте задана лишь кон центрация ХА2 целевого компонента А; концентрации осталь
НЬIХ компонентов в дистилляте х8 2 и .хс2 малы (особенно по
следняя) и точно не известны; поэтому положение точ ки Х2
пока не определено.
По правилу разделен ия смесей - исходной (Х1 ) на дистил
лят (Х2) и кубовый остаток (Хо) - в соответствии с материаль
ным балансом (правилом рычага) точка кубового остатка ( Х о)
должна лежать на прямой, проходящей через точки Х 1 и Х2.
Для фиксации точки Хо необходимо зафиксировать положен ие
точки Х2 и задать кон центрацию какого-либо одного компо
нента в кубовой жидкости . Обычно это - содержание целевого
компонента А в кубовом остатке хл0• Тогда, продолжив прямую
Х 2 Х 1 до пересечения с го ризонталью хл0 = const, получаем Хо.
Заметим, что положение точки Х0 изменяется в некотором
весьма узком диапазоне в зависимости от принимаемого поло
жения точки Х2 (см . штриховые линии на рис . 1 2 . 58).
Расчет необходимого числа тарелок (сначала - теоретиче
ских, далее - реальных) будем вести отдельно для укрепляю
щей и отгонной частей колонны. С этой целью установим для
каждой из колонн связь сопряженных (рабочих) составов контак
тирующих фаз - жидкой Х (хл, хв, хе) и паровой У (ул, .Ув , Ус).

Укрепляющая колонна
произвольного сечения этой

Обозначим для
части колон н ы
(рис . 1 2 . 59) L и D - мольные потоки жидкости и пара; кон 
центрации в верхнем се'lении колонны снабдим индексом "2" .
Материальный баланс по потокам фаз для контура К1 (рис .
1 2 . 59)

+ D- L - П= O

дает

D-

L

= П=

ideш.

(а)

1 085

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 12. 59. Схема потоков в рекrификационной колонне для разделения трех
компонентных смесей

Согласно (а) , разность потоков пара и жидкости по высоте
укрепляющей части колонны остается неизменной, хотя сами
потоки D и L в общем случае мoryr и изменяться от сечения к
сечению. Далее в целях упрощения примем их постоянными по
высоте укрепляющей колонны , полагая близкими мольные
теплоты парообразован ия компонентов.
Материальный баланс по потокам компонента А для того же
контура
+ DyA Lхл - ПхА2 = о
приводит к выводу о постоянстве (no высоте укрепляющей
части колонны) разности потоков компонента А с паровой
(Dул) и жидкой (Lхл) фазами :
(б)
Dул - Lхл = ПхА2 = idem;
при этом сами потоки компонента А с каждой из фаз мoryr
быть переменными по высоте.
Поделим (б) на (а) :
Пх л 2
Dул Lхл ---Л- хл2 ,
D L
т.е. для любого сечения укрепляющей части колонны отноше
ние характерных разностей равно одной и той же величине хю.
-

-

=

-

1 086

=

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 12. 60. К расчету числа теоре
тических тарелок в укреШIЯющей
части колонны при разделении
тройн ых смесей

А

В поле треугольной диа
граммы этой
величине
горизонтальная
отвечает
прямая ХА2 = const, парал
лельная стороне ВС.
Материальный баланс
по потокам компонеита В
для того же контура К1

+ DУВ - L.хв - П.хв2 = О
указывает на постоянство (по высоте укрепляющей части ко
лонны) разности потоков компонента В с паровой (DУВ ) и
жидкой ( L.хв) фазами :

Lхв

=

Dу в Lхв
D-L

=

DУВ
Поделим (в) на (а) :

-

-

П.хв2
П х8 2
п

=

--

idem.

(в)

= хв 2.

Концентрация .ХВ2 также характеризует любое сечение
укрепляющей колонны . В плоскости треугольной диаграммы
этой величине отвечает прямая .ХВ2 = coнst, параллельная сто
роне АС.
Пересечение прямых ХА2 = const и .хв2 = const дает точку Хъ
отвечающую составу дистиллята, причем она характерна для
любого сечения укрепляющей части колонны. По аналогии с
другими массообменн ыми процессами (абсорбцией, ректифи
кацией при расчете в энтальпийной диаграмме, экстракцией и
др.) эта точка получила название полюса. Полюс Х2 позволяет
связать сопряжениые составы потоков пара и жидкости в про
извольном сечении укре пляющей части колонны.
Расчет числа теоретических тарелок в укрепляющей части
колонны производим путем поочередного нахождения равно
весных и сопряженных составов контактирующих фаз (рис .
1 2 .60) . Расчет выполним для случая полной конденсации паров
в конденсаторе ; тогда состав дистиллята (флегмы) Х2 совпадает
с составом пара У2, по кидающего верхнюю тарелку и уходя
щего из колонны (см . рис. 1 2 . 59). Жидкость, уходящая вниз с
верхней теоретической тарелки , равиовесна с У2. Точка, харак
теризующая се состав
лежит на соответствующей изотерме
(нижний индекс "у" указывает на принадлежность к укрепляю
щей части колонны). Эту точку находят на изотерме жидкости ,

Ху',

1 087

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

деля ее в том же соотн ошении, что и точка У2 делит однои
менную изотерму пара, - для идеальных смесей (см . разд .
1 2 .2 . 5) , либо по опытн ы м данным или расчетным моделям для реальных смесей . П ар состава Уу' , сопряженного с Ху ', располагается на луче Х 2 Х у , деля его в соответствии с правилом
рычага 1 1 рода (с опорой

в

точке Х2) :

L · X 2 Xy = D· X 2 Yy ,
---

откуда

---

( 1 2 . 52)

Ху".

С паром состава Уу ' равновесна жидкость состава
Точку
Ху" находят на изотерме жидкости , соответствующей изотерме
пара состава Уу', таким же способом, как указано выше. Состав
жидкости Х./ сопряжен с составом пара Уу". Точка Уу" лежит
Х� , ее положение находят по соотношению, анало
на луче
гичному ( 1 2 . )2):

Х2

X2 Y:j = X 2 Xy ·

�·

Снова находят соста в жидкости - теперь это состав Ху"',
равновесный составу пара Уу", и т.д . Построение продолжают
до тех пор , пока не достигнут уровня концентрации компонен
та А в исходной смеси (хл1 ) . Число теоретических тарелок в
укрепляющей части колонны равно числу актов сепарации па
ра и жидкости , т.е . равновесных переходов (изотерм).
Линия
характеризует ход изменения состава
жидкости от тарелки к тарелке; она получила название траек
тории ректификации. Направление траекторий ректификации
зависит от особенностей фазового равновесия разделяемой
смеси (расстояния между одноименными изотермами пара и
жидкости) и отношения L/D. При постоянных по высоте ко
лонны потоках D и L их отношение может быть выражено че
рез флегмовое число R = L/П:
D П (R + 1) R + 1 1 + _!_
.
R
ПR
L
R
Тогда выражение ( 1 2 . 52) для любой j-й тарелки (точнее
j
го сечения колонны) может быть записано так:

Х2Ху'Ху"Ху"'

=

=

=

-

Х yj

2

у

_

-

Х2 Х � .

Из ( 1 2 . 52а) следует, • 1то при R

=D) отрезки
1 088

Х

Х 2 � равн ы

( 1 2 . 52а)

1 + 1/R

� ао

отрезкам

(что соответствует

Х 2 У� ,

L=

и, следовательно ,

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Х? У1

совпадают; траектория ректификации получает
и
точки
ся наиболее короткой и круго н исходящей . Число теоретиче
ских тарелок, необход имых для повышения концентрации
компонента А от хл1 до ХА2, в этом случае минимальн о . Наоборот, чем меньше R, тем меньше отношение отрезков Х 2
и Х2

Х? .

У/

В этих случаях меньше приращение концентрации

компонента А на ка.ждой теоретической тарелке, их необходи
мое число увеличивается , а трае Ктории ректификации становятся длиннее. При определенном (минимальном" ) флегмовом

Yjy

х? ,

числе Rmin точки
располагаются так высоко на лучах Х 2
что прекращается движение составов
вниз от Х2 к Х 1 . При
R < Rmin даже бесконечное число теоретических тарелок в
укрепляющей колонне не приведет к увеличению концентра
ции компонента А от хл1 до ХА2. Очевидно, что рабочее флег
мовое число должно быть больше Rmin , причем рабочее значе
ние R определяется технико-экономическим расчетом - по
минимальным суммарным затратам (см. разд. 1 2 .7 . 1 ) .

х?

Отгонная колонна
произвольного сечения

Обозначим для
этой части колонны
(см. рис. 1 2 . 59) L' и D - мольн ые потоки жидкости и пара;
концентрации компонентов в уходящем кубовом остатке снаб
дим индексом "о" .
Материальный баланс по потокам фаз для контура К2 (см .
рис . 1 2 . 59), проходящего через произвольное сечение отгонной
части колонны ,
+ L ' - D - L0 = 0
дает
L ' - D = L0 = idem.
(г)
Согласно (г) , разность потоков пара и жидкости по высоте
отгонной части колонны остается неизменной (сами потоки D
и L ' в общем случае могуг изменяться от с ечения к сечению) .
Далее в целях упрощения примем их неизменн ыми по высоте
отгонной части колон н ы .
Материальный баланс по потокам компонента А для того же
контура

• Некоторые методы расчета минимального флеrмового числа при ректифи
кации многокомпонентных смесей приведены в (19) .

1 089

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

фиксирует неизменность (по высоте отгонной части колонны)
разности потоков компонента А с жидкой ( L хл) и паровой
( Dул) фазами :
(д)
L хл - Dул = LoXAo = idem;

при этом сами потоки компонента А с каждой из фаз не обяза
тельно постоянны по высоте .
Поделим (д) на (г) :

т.е. для любого сечения отгонной части колонны отношение
характерных разностей составляет одну и ту же величину Хло · В
поле концентрационного треугольника этой величине отвечает
горизонтальная прямая Хло = coпst, параллельная стороне ВС.
Материальный баланс по потокам компонента В для того же
контура К2
+ L хв - DУВ - LоХВо = О

приводит к неизменной (по высоте отгонной части колонны)
разности потоков компонента В с жидкой ( L Хв) и паровой
(DУВ) фазами :
L Хв - DУВ = LоХВо = idem.
(е)
Поделим (е) на (г) :

L'хв - Dув
L' - D

-�-�

=

LаХво
L0

. m.
= ХВо = 1de

Кон центрация ХВо также характерна для любого сечения отгон
ной колонн ы . В плоскости треугольной диаграммы ей отвечает
прямая ХВо = const, паралл ельная стороне АС .
Пересечение прямых хл0 = const и ХВо = const дает точку
Х0, отвечающую составу кубового остатка и характерную для
любого сечения отгонной части колонны. Как и в случае укреп
ляющей части колон н ы . эта точка получила название полюса .
Полюс Х0 позволяет связать сопря:J1сенные составы потоков пара
и жидкости в произвольном сечении отгонной части колонны .
Расчет числа теоретических тарелок в отгонной части ко
лонны ведем от точки Х0 снизу вверх путем поочередного на
хождения равновесных и сопряженных составов контактирую
щих фаз (рис. 1 2 . 6 1 ) .
Ки пящей кубовой жидкости (соста в Х 0 ) отвечает равновесный
состав пара У0' ; его находят на соответствующей изотерме
пара, причем н ижний индекс "о" здесь указы вает на принад
лежность к отгонной части колон н ы (подробнее об
отыскан ии равновесных кон центраций см. расчет ч исла та1 090

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 12. 61. К расчету числа теоретических
тарелок в отгонной части колонны при
разделении тройных смесей

релок в укрепляющей части
колонны). Состав жидкости Х0',
сопряженный с составом пара
У0 ', лежит на прямой, проходя
щей через полюс Хо. Местопо
ложение точки Хо' можно найти
из материального баланса - по
правилу рычаrа 11 рода (с опо
рой в точке Хо) :

А

в -----1---- с

У� х�

отсюда

D
L'

( 12.53)

Таким образом, построена одна теоретическая тарелка: осу
ществлен переход от Х0 к Х0 ' .
Равновесный с Хо' состав пара У0" лежит в определенной
(известной - см. выше)
точке на соответствующей изотерме .
"
Сопряженный с У0 состав жидкости Хо " находим на прямой
У0"Х0 по соотношению, аналогичному ( 1 2 . 53 ) :

Х � Х0

=

У;; Х 0 ·(D/L')

- таким образом, построена вторая теоретическая тарелка.
Для третьей теоретической ступени характерный переход от
Х0" к Хо"' реализуется по той же канве. Построение продол
жается до тех пор, пока не пересечем горизонталь хл1 (или по
ка не достигнем ее, как показано на рис . 12.6 1 ) . Число теоре
тических тарелок равно числу актов сепарации пара и жид
кости, т.е. равновесных изотермических переходов; в рассматриваемом примере на рис . 1 2 . 6 1 - это Х0 У� , Х� У;; и Х�У:,''.
Третье разделение фаз дает точку Х0"' , лежащую на уровне Х 1 ,
знач ит, здесь трех теоретических тарелок в отгонной части ко 
лонны достаточно.
Заметим, 'ПО приведенный выше метод расчета числа теоретических тарелок
правомерен и для D, L, L ' = var. В этом случае при использовании зависимостей
типа ( 1 2 .52) и ( 1 2 . 5 3) надо в каждом сечении знать свои отношения L/D и D/L '.
Они моrут бьrrь найдены с учетом тепловых балансов тарелок, проще - с по
мощью заранее построенной энтальпийной дюн]Jаммы для тройных смесей.

1 09 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Полная рек.тифик.ационная к.олонна
Задача расчета числа теоретических тарелок в ректификаци
онной колон не является пока недоопределенной, поскольку оста
ется произвол в местоположении точки Х2 (обоснованно при
н имается лишь кон центрация ХА2) , а значит и Х 0 (здесь задана
лишь кон центрация хд0). Необходим некий критерий , исклю
чающий отмеченную неопределенность и приводящий к одно
значному решению при з аданных Х 1 и рабочих параметрах
процесса (флегмовом числе R) . В качестве такого критерия
выступает сходимость материального баланса для тарелки пи
тания .
Предлаrается следующий путь расчета полного числа теоре
тических тарелок в колонне (рис. 1 2 . 62):
- задаемся некоторы м составом дистиллята Х2 (на горизон
тали ХА2) и находим Х0 (на горизонтали хл0);
- строим теоретические тарелки для укрепляющей части
колонны, получая составы жидкости и пара на тарелках вплоть
до уровня хл1 (на рис . 1 2.62 - это точка Ху"' на третьей сверху
теоретической тарелке) ;
- строим теоретичесЮfе тарелки для нижней части колонны
от точки Хо до получения пара с концентрацией компонента в
нем, превышающей хл 1 (точка У0 "' на рис . 1 2 .62);
- проверяем материальные балансы для контура К1 на рис .
1 2 .63 по любым двум компонентам:

LXy"'

+

L1X1 = DY0"'

+

L0X0 ;

(ж)

- если условие (ж) не соблюдается, то необходимо задаться
новым значением Х2 (при том же ХА2)Расчет числа теоретических тарелок повторяют до тех пор ,
пока с приемлемой погр ешностью не выполнится условие (ж) .
Заметим, чrо материальный баланс по потокам фаз Д11Я указанного контура
при подаче кипящей исходной смеси очевиден: L + L1 = D + L,,. При подаче
исходной смеси в другом состоянии придется скоррекrироватъ паровой и :жид
костной потоки D и L + L1 = /, ' с учетом п араметра типа Е (см. разд.

1 2 .7.5) .

Ч исло реальных тарелок определяется по числу теоретиче
ских и по значениям с р едних КПД тарелок.
Выше была рассмотрена проек.тная задача - определение
необходимого числа тарелок, когда заданы составы исходной
смеси (точно), дистиллята и кубового остатка (по целевому
компоненту) . Значительно более трудоемким является решение
задачи эк.сплуатации - определен ие составов дистиллята и ку
бового остатка при известн ых составе исходной смеси и числе
тарелок. Решение здесь отыскивается подбором . Фактически
его сводят к решению з<щачи проектирования, задаваясь соста
вами дистиллята и кубового остатка и проверяя числа теорети1 092

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

А

v� х �

Хо

Lo

Рис. 12. 62. Расчет общего числа теоретических тарелок в колонне при ректифика
ции трехкомпонеН111 ы:х смесей
Рис. 12. 63. Потоки и кон центрации в нижней части колонны (включая тарелку
питания) при р е кти ф и каци и тр ехкомпоне нтн ых смесей

ческих тарелок в укр епляющей и отгонной частях колонны на
совпадение с заданными. При несовпадении задаются новыми
составами дистиллята и кубово го остатка и повторяют расчет вплоть до сходимости полученного и заданно го числа тарелок.
Особенности вычислительных операций ЭВМ мoryr продиктовать и другие
пути решения проектных и экс плуатаци о н н о й задач· .

12. 1 1 .2. Разделение многокомпонентных смесей

Материальный и тепловой р асчеты рекrификационных ко
лонн при разделении в н их мно гокомпонентных смесей анало
гич ны р ассмотренным ранее для бинарных смесей. Они бази
руются на мате р иальных (по потокам фаз и каждого и з комп о
нентов) и тепловых балансах.
Расчет необходимого числа та р елок в колонне (ее высоты)
при разделении многокомпонентных смесей, подобно расчетам
для бинарных и тройных смесей, может быrь выполнен пуrе м
поочередного нахождения равновесн ых и сопряженн ых концент
раций. Однако графичес ки е пр едставления с увеличением числа
компонентов в смеси стан овяrся менее наглsщными . Так, фазо вая
диаграмма для четырехкомпонентной смеси изображается в пра
вильном тетраэдре, а для смеси из пяти и более компонентов тре
буюrся представления о многомерных пространствах .
Стро гие методы р асчета рекrификации многокомпонентных
смесей (нап р име р , " от тар елки к тарелке " ) отличались громо зд• См" например, ( I 4 J .

1 093

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

костью и большой трудоемкостью. Поэтому весьма широкqе
распростр анение получили различные приближенные методы ,
основанные на упрощающих допущениях, но зато более нагляд
ные и простые. Однако с разработкой модельных представлений о
равновесии в многокомпонентных системах и с развитием вычис
лительной техники ·· зна•шмость приближенных методов утрачи
вается, а строПIХ, наоборот, - восстанавливается.
Рассмотрим основные положения метода "от тарелки к та
релке " примен ительно к непрерывной реIСГификации к-компо
нентной смеси - необязательно идеальной, но не образующей
азеотропов и гетероазеотропов. Примем для простоты полную
конденсацию пара в конденсаторе и подачу в колонну исход
ной смеси при температуре кипения; постулируем также по
стоянство мольных потоков по высоте каждой из частей ко
лонны - укрепляющей и отгонной. Расчет будем базировать на

теоретической тарелке.
Состав исходной многокомпонентной смеси (А; В;
К) известен полностью : Х1 (хл 1 , хв 1 , . . . , х11 , . . , хк 1 ) ,

" 1; . . . ;
как и ее
поток L1 (производительность). Требуемое качество отбирае
мого дистиллята выражают назначением концентрации целевого
компонента хА2, если дистилл ят содержит компонент А высо
кой чистоты , или суммы кон центраций целевых компонентов
(хА2 + хв2 + . . . ) , если в дистилляте содержится несколько
компонентов . Кон центрации остальных компонентов в дистил
ляте не могут быть задан ы произвольно : они зависят как от
особенностей фазового равновесия разделяемой смеси, так и от
режима реIСГификации (флегмового числа и т.п. ) . Тем не менее
состав дистиллята должен быть выбран полностью, а в кубовой
жидкости принято содержание целевого компонента. Тогда из
материального баланса (правило рычага - см. разд. 1 0.2.4)
можно найти полный состав кубовой жидкости Х 0 (хл0, ХВо, :
хк0). Заметим: Хо мож но определить и не задаваясь содержа
н ием целевого компонента в кубовом остатке, если известен
его поток L0 (или поток дистиллята П) .
Для расчета числа теоретических тарелок необходимы рав
новесн ые зависимости и связи сопряженных концентраций по
каждому компоненту разделяемой смеси.
Пусть рабочее давление процесса равно Р. Равновесные кон 
центрации в фазах для произвольного (i-го) компонента связа
ны эмпирическим или модельным уравнением
( 1 2 . 54)
у Р1 = f;(хл, . . . ,XJ , . . . , хк),
причем эта функция зависит от температуры . Для идеальных
многокомпонентных смесей, подчиняющихся закону Рауля, за.

.

· · ·

• См . (8, 1 1 , 1 5 , 27 и др. ] .
• • С м . , например , (9 , 1 4 , 2 0 , 26 ] .

1 094

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

висимость равновесных концентраций ( 1 2 . 54) имеет вид :
y P I = k i Xl .

Константа фазового равновесия k; = РР/Р для i-ro компо
нента при Р = const изменяется с уровнем концентрации компо
нента, так как упругость паров чистого компонента РР есть функ
ция температуры кипеню1 t, а последняя завискг от сосrава смеси.
И только в случае t
const величина РР была бы постоянной,
тогда и k; = coпst; подчер кнем: это не рабочая скгуация.
Связи сопряженных концентраций жидкой и паровой фаз
устанавливаются (как и в случае бинарных и тройных смесей)
из материальных балансов - по потокам фаз и каждого компо
нента. Найденные из этих балансов связи сопряженных концент
раций (рабочие линии ) различаются для укрепляющей и отгонной
частей колонны, поскольку в них различны потоки фаз.
=

Укрепляющая колонна
Обозначим (рис . 1 2 . 64) для произвольного сечения укреп
ляющей части колонн ы : L и D - жидкостной и паровой пото
ки ; А, хв , . . . , .:q , . . . , хк и УА , УВ , . . . , YI , . . . , ж - мольные
Х
кон центрации компонентов А, В, . . . , 1, . . . , К в этих потоках
соответственно. Концентрации компонентов в дистилляте (его
мольный поток П) снабдим индексом "2" (например, ХА2).
Материальные балансы по потокам компонентов для контура
К1 запишутся :

DyA -

- ПхА2 = О ;
DУВ - Lхв - Пхв 2 = О ;
LxA

DYI - L.:q - П.:q2

Dж - Lхк. -

= О ;

ЛХК2 = О .

Отсюда находим связи между сопряженн ыми кон центрациями
для каждого компонента смеси :
УА =
У13 =

L

D ХА
L
D хв

L

УК = - хк

D

П

+

D ХА2 ;

+

D ХВ 2 ;

+

- ХК2

П

П
D

( 1 2 . 55)

·

1 095

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

У2

К1

Ул ·Ув , ".у! , " . у к

+
--·
у-·+ -+х
Y "t + х "
D

L

ХА 2 •
ХВ 2 •

L

XJ2

•

п ХК2

хл , х8 , " . х1 , " . х к

Хл 1 , хв 1 , . " х1 1 , " . хк 1

Li

Рис. 1 2. 64. Схема потоков в ректификационной коло нн е для
компонентных смесей

разделения много

При постоянных по высоте колонны потоках L и D уравне
н ия ( 1 2 .55) описывают прямые линии. Эти рабочие линии для
всех компонентов имеют один и тот же угол наклона, опреде
ляемый отношением L/D, но им отвечают разные точки на
диагоналях и отрезки , отсекаемые на осях ординат, - соответ
с тв ен но раз н ы м кон центрациям компонентов в дистилляте .
При изменяющихся по высоте колонны потоках L и D уравнения ( 1 2.55) вы
линии. Связь между сопряженными конце�прациями в этом
случае устанаwшвается с привлечением тепловых балансов типа (е) в разд. 12.8.

ражают кривые рабочие

Сугь метода "от тарелки к тарелке" продемонстрируем на
примере постоян н ых по высоте колонны потоков L и D. Для
каждого компонента строится диаграмма у-х; связь сопря
женн ых кон центраций изображается в н их прямыми рабочими
лин иями по ( 1 2 . 55). На рис . 1 2 .65 такие диаграммы представле
н ы для компонентов А, 1 и К. При полной конденсации выхо
дящего из колонны пара его состав У2 (уА2, УВ2, ". , У1 2 , " . ,
1 096

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

УА 2 �--------.....�
..

УД -1------....,..-.,"7
у�

Ут
't------7''#"
У! -....--...�

У12

о

а

б

--
Хк

в
Рис. 12. 65. К расче'I)' числа теоретических тарелок в укрепляющей части колонны

при разделении многокомпонентных смесей:
а,

б, е - диаграммы для компонентов А , 1 и К соответственно

УК2) идентичен составу получаемого конденсата, флегмы, ди
стиллята Х2 (хА2 , .хв 2 , . . . , xr 2, . . . , ХК2); это соответствует точ
кам пересечения рабочих линий с диаrоналями квадратов у-х.
Разделяющий эффект колонны существенно зависит от флег
мового числа R = L/П. Оптимальное значение R, как и в слу
чае бинарных смесей, определяется здесь технико - эконо
мическим расчетом на базе минимально \'<> флегмового числа
Rmin · Для расчета последнего в литературе приводятся различ
ные методики .
Как и все рассмотренные ранее, метод "от тарелки к тарел
ке " баз ируется на поочередном учете условий равновесия - по
• См., например, ( 12, 19, 20).

1 097

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

( 1 2 . 54) и связей сопряжен н ых концентраций - согласно урав
нениям ( 1 2.55). Так, для верхней тарелки, с которой уходит пар
состава Уъ надо найти равновесный с ним состав жидкости Х' ,
покидающей эту теоретическую тарелку. Но равновесные со
ставы фаз зависят от температуры, а температура t ' на верхней
тарелке априори не известна.
Очев идно, что сумма концентраций всех компонентов смеси
должна быть равна един ице :

i=K
I xi
i=A

= 1.

(з)

Поэтому температура t' должна быть подобрана таким образом,
чтобы удовлетворялось условие (з) . Пусть этой подобранной
температуре на рис . 1 2 .65 отвечают концентрации отдельных
компонентов хл', . . . , XJ ' , . . . , хк ' . Теперь согласно связям
( 1 2.55), т.е. с помощью рабочих линий, можно найти полный
состав сопряженной (встречающейся с жидкость ю в этом сече
нии) паровой фазы У (ул', . . ., у ( , . . . , ж').
Далее рассмотрим вторую (сверху) теоретическую тарелку.
По составу пара У , покидающего эту тарелку, находим равно
весный состав Х" уходящей с нее жидкости, подбирая темпера
туру t " на этой тарелке так, чтобы соблюдалось условие (з ) .
Затем по рабочим лин иям ( 1 2 . 55) находим сопряженный с Х"
состав пара У' .
П остроен ие теоретических тарелок продолжают до тех пор,
пока концентрация целевого компонента (в данном случае А) не уменьшится до его концентрации в исходной смеси хл 1 .
Так получают число теоретических тарелок nrY в укрепляющей
части колонны.

Отгонная колонна

Сохраним обозначения сопряжен ных концентраций компо
нентов (см . р ис . 1 2 .64) ; концентрациям компонентов в кубовой
жидкости (ее мольный поток L0 ) присвоим индекс " о " (напри
мер , хл0 ) ; D и L ' - потоки пара и жидкости (L ' = L + L0) в
отгонной части колонны.
Материальные балансы по потокам отдельных компонентов
для контура К2 (см . рис . 1 2 .64) имеют вид:

L 'хл - Dул - LоХло
L Хв - D.УВ - LоХВо
L 'XJ -

DYI -

= О ;

= О ;

LoXIo = О ;

L 'хк. - Dж - Lохк.о = О .
1 098

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Уi ч....----
у�

а

б

Ук �---�
Ук

в
Рис. 12. 66. К расчету числа теоретических тармок в опонной части колонны при
раздмении мноrокомпоне1n11 ых смесей:
диаrраммы для компонешов А, I и К соответствеШiо
а, б, •
-

Оrсюда получаем уравнения рабочих линий для кажцоrо компо
нента смеси:
L' X
L

УА = jj A +

УВ

=

/у ХАо j
L'
L
jj XВ + /у ХВо ;

YI

= Ii xr

+ /у xro ;

Ж

L'
= D хк

+

L'

L

( 1 2. 56)

L

_о_ ХК.о

D

·

1099

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

В рассматриваемом случае постоянных L ' и D по высоте ко
лонны - это прямые линии. Они пересекают, как и для бинар
ных смесей , диагонали квадратов в точках Х;о· Вторые точки ,
необходимые для построения рабочих линий, удобно фиксиро
вать на осях координат, задаваясь в ( 1 2 . 56) значен иями Xf = О ,
Xf = 1 , Yl = О или YJ = 1 либо используя известный ( и одинако
вый для диаграмм у-х всех компонентов) наклон рабочей ли
нии с тангенсом, равным L '/D (рис . 1 2 .66).
Теоретические тарелки для отгон ной части колонны строят
тоже путем поочередного использования условий равновесия
( 1 2 . 54) и связей сопряженных концентраций ( 12 . 56).
Рассмотрим сначала сечение отгонной части колонны под
нижней тарелкой - в нем поток пара состава Ун' (уд' , Ув' , . . . , YI ' ,
. . . , Ук' )ра&новесен с кубовой жидкостью состава Х0 • Для опре
делен ия Ун' надо подобрать такую температуру, что бы при
определении равновесных концентраций по ( 12 .54) со блюда
лось очевидное условие'

i=K
L Yi
i =A

=

1.

(и)

Н аЙден ному таким об разом составу пара Ун' отвечает сопря
женный с ним состав жидкости, стекающей с н ижней тарелки ,
Хн ' (хл', .хв' , . . . , xi ' , . . . , хк'). Состав этот лежит на рабочих ли
н иях; на рис . 1 2.66 построение показано для компонентов А, 1 и
К. Далее находят равноаесный состав уходящего с нижней та
релки пара Ун" , так подбирая температуру tн", чтобы удовлетво
рить условию (и) . Затем определяют сопряженный состав жид
кости Хн", стекающей с вышележащей тарелки, и т.д. - до
превышения концентрации целевого компонента в паре над
его содержан ием в исходной смеси . Так получают число теоре
тических тарел о к 1ir0 в отгонной части колонны.
Далее оценивают результаты расчета для колонны в целом .
Критерием сходимости расчета служит удовлетворен ие матери
альных балансов по каждому компоненту на тарелке питания,
как это было показано в разд . 1 2 . 1 1 . 1 - формула (ж) . При не
соблюдении (с обусловленной погрешностью) балансов по
каждому из компонентов расчет числа тарелок повторяют,
приняв новый состав дист иллята Х2 (изменяя в нем кон цент
рации любых компонентов, кроме целевого).

1 1 00

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Л ИТЕРАТУРА

к главе

12

1 . Александров И.А. Ректификационные и абсорбционные аппараты. Методы
расчета и основы конструирования . М . : Химия, 1 978. 280 с.
2 . Александров И.А . Перегонка и ректификация в нефrепереработке. М.: Хи
мия, 198 1 . 352 с.
3 . Багатуров С. А. Теория и расчет перегонки и ректификации. М.: Гостоп
техиздат, 1 96 1 . 436 с.
4 . Бронштейн И. Н. , Семендяев К.А. Справочник по математике. М.: Наука ФМ, 1 986. 544 с.
5 . Вихман ГЛ. , Круглов С.А. Основы конструирования аппаратов и машин
нефrеперерабатывающих заводов. М.: Гостоптехиздат, 1 962. 294 с.
6 . Гельперин Н. И. ДистИЛJUщия и ректификация . М . -Л . : Госхимиздат, 1 947 .
3 1 2 с.
7. Гельперин Н. И. Основные процессы и аппараты химической технолоrии .
М . : Химия, 1 98 1 . 8 1 2 с.
8. Дытнерский Ю. И. Процессы и аппараты химической технологии. М.: Хи
мия, 1995. 768 с. (ч. 1 , 400с . ; ч.2, 368 с.)
9 . Жаров В.
Серафимов Л.А. Физико-химические основы дистИJUJЯции и
ректификации. Л . : Химия , 1 9 7 5 . 240 с.
1 0 . Карапетьянц М.Х Химическая термодинамика. М . -Л . : Госхимиздат,
1 9 5 3 . 6 1 2 с.
1 1 . Касаткин А . Г Основные процессы и аппараты химической технологии .
М . : Госхимиздат, 1 9 5 5 . 7 5 6 с.
12. Касаткин А . Г Основные процессы и аппараn,1 химической технологии .
М . : Химия, 1 97 1 . 784 с.
13. Кафаров В. В. Основы массо передачи . М . : В ысшая ш кола . 1 9 7 2 .
494 с.
1 4 . Кафаров В. В. , Ветохин В. Н., Бояринов А.И. Программирование и вычис
лительные методы в химии и химической технологии. М . : Наука, 1 972.
487 с.
1 5 . Коган В. Б. Азеотропная и экстрактивная ректификация. М.: Госхимиз
дат, 1 96 1 . 3 1 5 с.
1 6 . Матрозов В. И. Аппаратура для молекулярной диСТИJVIЯции. М.: Машгиз,
1954. 146 с.

Т.,

17. Основные процессы и
Ю.И. Дьrгнерского. М . : Химия ,
1 8 . Павлов К. Ф. , Романков
су процессо в и аппарато в
5 7 4 с.

/

аппараты химической технологии
Под ред.
1 99 1 . 496 с.
П.Г., Носков А.А. Примеры и задачи по кур 
химическо й технологи и . Л . : Химия, 1 9 8 7 .

/

19. Перри Дж. Справочник инженера-химика: Пер. с англ.
Под ред. Н . М .
Жаворонкова.Л . : Химия, 1 969. 1 1 44 с. (т. 1 , 640 с,; т. 1 1 , 504 с.).
20. Петлюк Ф.Б. , Серафимпв Л.А. Многокомпонентная ректификация. Тео
рия и расчет. М . : Химия, 1 993. 393 с.
2 1 . Плановский А . Н" Николаев П. И. Процессы и аппараты химической и
нефrехимической технологии . М . : Химия, 1972. 494 с.

/

22. Рид Р" Шернуд
Свойства газов и жидкостей: Пер . с англ. Под ред.
А.Н . Плановского . М.: Гостоптехиздат, 1 964. 334 с.
2 3 . Свентославский В. В. Азеотропия и полиазеотропия. М . : Химия, 1968 .
244 с.
24. Серафимов Л.А., Тимофеев В. С" Писаренко Ю.А., Солохин А.В. Технология
основного органического синтеза. Совмещенные процессы. М . : Химия, 1993.
420 с .

Т.

1 101

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

25. Скобло А.И., Трегубова И.А., Молоканов Ю.К. Процессы и аппараты неф
теперерабатывающей и нефтехимической промышленносrи. М.: Химия, 1982.
584 с.
26. Тимофеев В.С., Серафимов Л.А. Принципы технологии основного орга
нического и нефтехимического синтеза. М.: Химия, 1992. 431 с.
27. Циборовский Я.

Процессы химической технологии: Пер. с польск. /Под

ред. П.Г. Романкова.Л.: Госхимиздат, 1958. 932 с.

28. Ципарис И.Н., Доброседов Л.Л., Коган В.Б.
Химия, 1969. 162 с.

Солевая ректификация. Л.:

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Глава 13
ЖИДКОСТНАЯ ЭКСТРАКЦИЯ

Жидкостная экстракция
это избирательное извлечение
компонента (компонентов) из жидкой смеси с помощью жид 
кого растворителя. Жидкостная экстракция предусматривает
две технологические операции:
- контактирования исходной смеси с растворителем, в ходе
которого осуществляется собственно массообменный процесс,
т.е. переход (перенос) компонента (или группы компонентов)
через границу раздела из одной фазы в другую;
- отделения полученного раствора от оставшейся жидкой
смеси.
Таким образом, жидкостная экстракция предполагает не
полную взаимную растворимость исходной смеси и раствори
теля - в противном случае вторая операция неосуществима.
Операция контактирования фаз обычно проводится путем
распределения (дробления) одной фазы в виде капель в объеме
другой.
-

13. 1 . ОБIЦАЯ ХАРАКТЕРИСТИКА П РОЦЕССОВ
ЖИДКОСТНОЙ ЭКСТРАКЦИИ

Дискретную (капельную) фазу называют дисперсной (или
сплошной (или дис
дисперrируемой) фазой, а непрерывную
персионной) средой. В самом общем случае взаимодействующие
фазы являются растворами, состоящими из растворителей и
одного или нескольких растворенных в них веществ. Фазу,
которая в процессе экстракции обедняется переходящим ком
понентом, называют исходным раствором (до взаимодействия со
второй фазой) и фазой рафината или маточника (после начала
соприкосновения фаз). Растворитель в этой фазе именуют раз
бавителем. Фазу, обогащающуюся переходящим компонентом,
называют экстрагентом, или исходным растворителем (до кон 
тактирования) и экстрактом (после взаимодействия фаз). Для
обозначения фаз в ходе процесса экстракции используют также
термины : фаза экстракта и фаза рафината . В простейшем слу
чае исходный раствор и рафинат состоят из разбавителя и од
ного переходящего компонента, экстрагент является чистым
растворителем, а экстракт - его смесью с переходящим ком
понентом.
-

1 1 03

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Собствен но процесс экстракции включает в себя две уnомя
нугые стадии - смешения и разделения фаз . Однако полная
технологическая схема экстракции предусматривает еще стадии
вьщеления целевых компонентов из экстракта с возвращением
экстрагента на экстракцию (иногда экстрагент частично или
полностью подвергается регенерации - очистке от накапли
вающихся примесей), а также вьщеления экстрагента из рафи
ната. При этом под регенерацией экстрагента в общем случае
понимают все операции по его возвращению в процесс экс
тракции. Чаще всего для вьщеления целевых компонентов из
экстракта и регенерации экстрагента применяют ректифика
цию или отгонку с водяным паром; иногда соответствующие
компоненты вьщеляют пугем реэкстракции (обратной экстрак
ции), кристалл изации и другими методами .
Сопряженные процессы экстракции органическим экстрагентом целевоrо
компонента из исходноrо водноrо раствора и последующей ero реэкстракции из
органическоrо экстракта вторым (водным) экстрагентом применяют для двойной
очистки продукта (например, в производстве капролактама) и для вьщеления и
концентрирования ценных компонентов из разбавленных растворов ( например ,
в mдрометаллу рrии). В последнем случае процесс массообмена обычно сопро
вождается химическим взаимодействием переходящеrо компонента и реагентов,
содержащихся в фазах экстракта и реэкстракта, т.е. имеют место не чисто физи
ческие процессы экстракци и , а так называемые процессы реактивной экстрак
ции.

Экстракция в системах жидкость-жидкость применяется
для разделен ия смесей, трудно разделяемых или вообще не
разделимых пугем ректификации или иными широкодоступ
ными методами. Экстракция в отличие от ряда других процес
сов разделения обычно проводится при невысокой (часто комнатной) рабочей температуре. Это обстоятельство играет
решающую роль при работе с термолабильными веществами,
чувствительными к повышенным температурам, например в
фармацевтических производствах.
Жидкостная экстракция обычно оказывается энергетически
более выгодным процессом, чем ректификация, - особенно
для вьщеления веществ из растворов с низкой концентрацией
целевого компонента. Примером может служить получение
уксусной кислоты из разбавлен н ых растворов пугем экстрак
ции ее этилацетатом с последующей ректификацией экстракта
(это - один из первых промышленных процессов применения
экстракции). Экстракция выгоднее ректификации при разделе
нии:
- высококипящих смесей, ректификационное разделение
которых без разложения возможно лишь в условиях глубокого
вакуум а ;
- смесей , состоящих из близкокипящих компонентов или
обладающих малой относительной летучестью.
1 1 04

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Экстракцией при соответствующем подборе экстраrента не
редко удается разделить азеотропные смеси. Например, смесь
вода-пиридин нельзя разделить ректификацией : она образует
азеотроп с содержанием воды 75% (мол.). При добавлении к
смеси бензола практически весь пиридин переходит в бензол ,
от которого он легко отделяется ректификацией.
Выделение органических веществ экстракцией бьvю издавна известно хими
кам. Позднее бьv1а открьrrа способность некоторых органических растворителей
(простых эфиров) селективно изалекать из водных растворов различные неорга
нические вещества.
Процессы экстракции в кр уп ных мacurraбax впервые начали использовать в
нефrехимни для Извлечения ароматических соединений в процессах переработки
нефrи, дизелъноrо топлива и см азочн ых масел.
Мощный импульс дальнейшему развитию и практическому использованию
процессов экстракции дала ядерная технология.

В настоящее время жидкостная экстракция применяется в
химической технологии, гидрометаллургии и аналитической
химии для извлечения, разделения, концентрирования и
очистки веществ. Экстракционные процессы используются в
производствах органических продуктов, антибиотиков, пище
вьхх продуктов, редкоземельных элементов, ряда редких, цвет
ньхх и благородньхх металл о в (примерно три четверти мирового
производства меди получаюr методом реактивной экстракции
из водньхх растворов), в технологии ядерного горючего, при
очистке сточных вод.
Жидкостная экстракция представляет собой перенос ве
щества в системах жидкость-жидкость, т.е. охватывает процес
сы массообмена между двумя взаимно нерастворимыми или же
частично взаимно растворимыми жидкостями. По компонентно
фазной (КФ) классификации (см. табл. 1 0. 1 ) в случае полной
взаимной нерастворимости жидкостей (экстраrента и разбави
теля) эта технологическая операция обозначается кодом 3(22) 1 , а при частичной взаимной растворимости - 3 (3-3)3. В
первом случае происходит однонаправленный перенос вещества
- из фазы рафината в фазу экстракта, во втором
разнона
правленный (встречный) перенос экстрагируемого компонента и
разбавителя из фазы рафината в фазу экстракта и экстраrента
из фазы экстракта в фазу рафината.
Разнонаправленный перенос компонентов имеет место и
при экстракции двумя растворителями, когда исходная смесь
разделяется путем распределения ее компонентов между двумя
взаимно несмешивающимися экстраrентами, а также при проти
воточной экстракции с флегмой, когда часть экстракта после уда
ления из него экстраrенrа возвращается в процесс в виде флегмы.
Оба этих процесса относятся к специфическим методам жидкост
ной экстракции, используемым для достижения высоких степеней
разделения" ; в учебнике они не рассматриваюrся.
-

•

См. , например , (2 , 4, 5, 7 -9 ) .

1 1 05

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Наличие двух технологических ситуаций - практически
полной взаимной нерастворимости разбавителя и экстрагента
или частичной (ограниченной) взаимной растворимости разбави
теля и экстрагента - предопределяет различие в подходах к
описанию равновесия и к технологическим расчетам (при
общности основных схем и аппаратурного оформления экс
тракционных процессов) .
13.2. ОСНОВНЫЕ КОНСТРУКЦИ И
Э КСТРАКЦИОННЫХ АППАРАТОВ

Процесс экстракции , как отмечено выше, включает две
основные
стадии
(операции) .
На
стадии
смешения
(контактирования) исходного раствора с экстрагентом проис
ходит образование гетерогенной двухфазной смеси в форме
эмульсии: одна жидкость в виде капель распределена в другой.
На стадии расслоения гетерогенной смеси пуrем отстаивания и
и
коалесценции капель производят отделение
(сепарацию)
раздельный отвод фаз рафината и экстракта. В зависимости от
конкретной технологической задачи возможны различные ап
паратурные варианты осуществления этих операций.
Экстракционные аппараты * классифицируют по разным
признакам .
По принципу взаимодействия контактирующих фаз экстрак
ционные аппараты можно разделить на два больших класса:
работающие с непрерывным или со ступенчатым контактом фаз .
В первом случае состав фаз изменяется непрерывно по пуrи
контактирования фаз - по высоте (колонны) или диаметру
(центробежн ые аппараты) экстрактора. Здесь имеется лишь
одна граница раздела фаз - на выходе дисперсной фазы. Во
втором случае составы фаз изменяются скачкообразно
(прерывисто) при переходе из ступени в ступень. При этом на
каждой ступени происходит смешение (эмульгирование) и раз
деление (расслаивание) фаз, т.е. в каждой ступени имеется
своя граница раздела фаз .
·

В некоторых технолоrnческих процессах на rранице раздела фаз со временем
накаwmваются примеси с образованием третьей фазы, которая периодически
удаляется из аппарата. Очевидно, что для таких процессов желательно иметь
минимальное количество rраниц раздела.

По расположению аппарата экстракторы подразделяются на
вертикальные, горизонтальные и другие (к последним можно
отнести и центробежные ) . Заметим, что вертикальные аппараты
занимают малую площадь, но требуют высоких помещений.
• Устройство и работа различных типов экстракторов описаны в 1 (2-8 ) и др.

1 1 06

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Важнейшим признаком классификации экстракторов яв
ляется отсутствие или наличие подвода энергии извне.
В экстракторах, работающих без подвода механической энер
гии извне, диспергирование одной из фаз ограничено, как пра
вило, величиной внугренней потенциальной энергии, обуслов
ленной разностью плотностей фаз . Иногда диспергирование
производится также за счет кинетической энергии потока дис
персной фазы с помощью специальных устройств (барботеры ,
форсунки), т.е . подвод энергии имеется только на входе. До
стоинствами подобных экстракторов являются простота, низ
кие капитальные и эксплуатационные затраты и высокая про
изводительность. Но для таких аппаратов характерна неболь
шая величина поверхности межфазного контакта и, как след
ствие, невысокая эффективность массообмена. Они обычно
применяются в тех случаях, когда для разделения (экстракции)
не требуется особо развитой поверхности контакта.
В экстракторах с подводом механической энерrни извне степень
диспергирования и, следовательно, поверхность межфазного
контакта сушественно повышаются за счет сравнительно не
больших затрат механической энергии. Эта энергия обычно
сообщается смеси жидкостей или посредством вращающихся
либо вибрирующих (колеблющихся) мешалок различных кон 
струкций, или наложением пульсаций (пульсационное переме
шивание), или же с помощью центробежных сил (центро
бежные экстракторы) . В последнем варианте поле центробеж
ных сил используется одновременно также для движения и
(или) разделения фаз .
Колонные экстракторы, в которых противоточное движение
и сепарация фаз осуществляются под воздействием сил тя
жести, часто называют гравитационными.
Аппараты с подводом механической энергии извне назы
вают интенсифицированными экстракторами.
Удельный полезный расход энергии представляет собой об
щие затраты энергии за вычетом потерь, связанных с движу
щимися механическими элементами конструкции - на трение
в приводе и сальниках, инерционные потери; он количествен
но равен диссипации (рассеянию) энергии в единице массы
сплошной среды (см . разд. 5.4 ) . Удельный полезный расход
энергии во многом определяет рабочие характеристики процес
са и является одним из основных параметров масштабирования
экстракторов с внешним подводом энергии.
13.2. 1 . Экстракторы с непрерывным контактом фаз
Эти аппараты называют также дифференциально-контакт
ными экстракторами. Впервые они были применены в нефте
химической промышлен ности в неинтенсифицированном вари1 1 07

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

анте, т.е. в виде колонн без подвода внешней механической
энергии. В колоннах тяжелая фаза вводится сверху, легкая
снизу.

Экстракционные колонны без подвода внешней энергии
Простейшим типом
колонны (рис . 1 3 . 1 , а).

э кстра кторо в являются

распьтительные

В полую вертикальную цилиндрическую колонну 2, запОJD1енную сплошной
фазой, с помощью дисперrnрующеrо УС'Jl>ойства 1 распределяется (здесь - сни
зу) в виде капель дисперсная фаза. С дpyroro конца (здесь - сверху) в колонну
вводится сплошная фаза. В качестве диспергаторов обычно используют сопла и
перфорированные распределители. Противоточное двюкение фаз обеспечивается
силой тяжести, т.е. различием плотностей фаз. Образовавшиеся в диспергаторе
кawm проходят по колонне через сплошную фазу и коалесцируют в отстойной
зоне З на поверхности раздела фаз 4; за пределами этой зоны находится сплош
ной слой дисперсной (здесь - легкой) фазы. В зависимости от тоrо, какая фаза
(тяжелая - ТФ или легкая - ЛФ) дисперrnруется, rраница (поверхность) разде
ла фаз располагается в нюкней или верхней части колонны. Наряду с отстойной
зоной, rде находится rраница раздела фаз, ЭКС'Jl>акдионная колонна обычно
имеет таюке вторую сепарационную зону 5 (иноrда таюке называемую отстой
ной) на выходе сплошной фазы - для предотвращения захвата ею капель дис
персной фазы.
В распылительной колонне поток дисперсной фазы двюкется преимуще
ственно по центральной части поперечноrо сечения, что приводит к возникно
вению rрадиекrа плотности эмульсии по сечению и, как следствие, к образова
нию циркуляционноrо контура, охватывающеrо весь рабочий объем экстракrора.
При этом С'Jl>уктура потока сплошной фазы приблюкается к ПOJDfoмy перемеши
вани ю (см. разд. 8 . 2 . 3 ) . Поэтому эффеJсrИвность распылительных ЭКС'Jl>акrоров
обычно не превышает 1 -2 теоретических ступеней.
Усовершенствованные конструкции распылительных колонн снабжены попе
речными переrородками, направляющими поток дисперсной фазы в чередую
щейся последовательности - от одной стенки к другой или от центра к стенке и
обратно. Б.лаrодаря устранению при этом циркуляции сплошной фазы и при
блюкению течения фаз к противоточному эффеJсrИвность таких колон н повы
шается, хотя полностью избежать поперечной неравномерности потока все же не
удается .
Снижение гидродинамических неоднородностей достигается таюке путем за
полнения колонны насадкой. Насадочи•1е экстракторы по простоте КОНС'Jl>УКUИИ
стоят вслед за распылительными. В рабочей зоне 2 ЭКС'Jl>актора (область колон
ны мс.жду двумя концевыми сепарационными зонами) на опорных решетках 6
располагаются слои насадки 7 (рис. 1 3 . 1 ,6) . Материал насадки должен предпоч
тительно смачиваться сплошной фазой; в противном случае вместо потока ка
пе..'IЬ дисперсной фазы может возникнуть пленочное ее течение по насадке, и
поверхность контакта фаз будет оrраничена геометрической поверхностью на
садки.
Размещение насадки в виде отдельных слоев 7 с безнасадо'lными промежут 
ками 8 межцу ними способствует уменьшению поперечной неравномерности в
потоке сплошной фазы за счет выравнивания в этих промежутках потоков и
концентраций вещества по сечению колонны. Снюкение отрицательноrо влия
ния продольноrо перемешивания наблюдается таюке при использовании эффек
тивных КОНС'Jl>УКUИЙ диспергаторов (распьтителей) 1, создающих равномерное
первоначальное распределение дисперсной фазы по сечению колонны. Для этой
же цели в ЭКС'Jl>акторе размещают распределители 9 сплошной, а таюке перерас
пределители дисперсной фаз.

1 1 08

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

2

а
Рис. 13. 1. Э кстракционные колонны без подвода внешней энергии:
расПЫJJ ительная JСолонна, 6 насадочная колонна;
а
1
диспергатор, 2
рабочан зона, 3, J
ко1Щевые отстоЙЮ!ки, 4
поверхность
(граница) раздела фаз, б
опорны� решетки, 7 слои насадки, 8
беэнасадочные проме
жупси, 9
распределитель сплошной фазы;
1 тяжелая фаза, II легкая фаЗа
-

-

-

-

-

-

-

-

-

-

-

-

Эффекrивность массообмена в насадочных экстракторах выше, чем в распы
лительных, однако их удельная производительность ниже.

Экстракторы с подводом внешней энергии
Эту группу аппаратов разделяют на три основные подгруп
пы - все они нашли применение в промышленности :
- колонны с вращающимися мешалками;
- пулъсационные колонны и колонны с вибрирующими
перфорированн ыми тарелками;
- центробежные экстракторы.
Общим для аппаратов данной группы является непрерыв
ный (без промежуrочных зон расслаивания) противоточный
контакт фаз и интенсификация массообмена путем подвода
извне механической энерmи. И нтенсификация массопереноса
достигается в основном благодаря росту поверхности контакта
фаз из-за уменьшения р азмера капель.
Из различных вариаmов колонн с вращающимися элементами наибольшее
распространение наIШIИ роторно-дисков.1е экстрахторw (РДЭ). В этом экстракrо
ре (рис. 1 3 .2) внутри цилиндрическоrо корпуса 1 на равном расстоянии непо
двюкно установлены кольцевые переrородки 2. По оси колонны проходит вер
тикальный вал З с rоризонтальными дисками 4
ротор аппарата. Диски ротора
обычно располагаются в середине секций, образованных двумя соседними коль
цами 2. К рабочей зоне экстракrора сверху и снизу примыкают отстойные
(сепарационные) зоны, диаметр которых равен
диаметру рабочей части (или
больше ero) .
-

1 1 09

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ЛФ

а

Рис. JЗ. 2. Роторно-дисковый э к страктор (РДЭ):
1
корпус, 2
кольцевые пeperopoдIOI, З
(барботер) дисперсной фазы
-

-

-

б
вал, 4

-

диски, 5

-

распределитель

Рис. 13. 3. Пульсационные колонны:
насадочная, б сJПЧатая;
а
1
колонна, 2 пульсатор;
ЛФ
леrкая фаза, ТФ тяжмая фаза
-

-

-

-

-

-

Дисперсная фаза через распределитель (обычно кольцевой барботер 5) по
дается с одноrо конца в рабочую зону колонны; с друтоrо конца поступает
сплошная фаза. Дисперсная фаза, двиrаясь по колонне противоточно к сплош
ной, дробится вращающимися дисками ротора на мелкие капли и, пройдя через
всю рабочую зону, коалесцируt:Т на поверхности раздела фаз в соответствующей
отстойной зоне.
Роторно-дисковая колонна фактически предстааляет собой каскад нечетко
разделенных контак:mых ступеней, через которые противотоком движутся пото
ки рафината и экстракта в виде сплошной и дисперсной фаз. Интенсивное пе
ремешивание дисками создает в каждой секции (ступени) режим, близкий к
идеальному перемешиванию для сплошной фазы, так что аппарат может рас
сматриваться как каскад ячеек полного перемешивания (или идеальных ступе
ней), между которыми происходит циркуляционное обратное перемешивание
(см . рециркуляционную модель продольноrо перемешивания - разд. 8.5). Ин
тенсивность межсекционной циркуляции, вызванной работой вращающихся
дисков, возрастает пропорционально доле свободноrо сечения секционирующих
колец. Поэтому с уменьшением последней снижается и продольное перемеши
вание; однако при этом, естественно, снижается и производительность экстрак
тора.
В промьШU1енности нашли применение как усовершенствованные конструк
ции РДЭ (многороторные экстракторы, колонна с асимметрично располо
женным ротором) , так и другие типы секционированных калонн, ра:�личающихся
в основном устройством вращающихся элементов (открьпые турбинные мешал
ки, лопастные капсулированные и др.). Эти колонны изrотавливают до 3 м диа
метром; высота их достигает 20 м (с ростом высоты заметно усложняется кон
струкция ротора) .
В пул.с:ационной колонне
насадочной (рис. 1 3. 3,о) или с ситчатыми тарел
ками (рис. 1 3 . 3 , 6) на потоки жидкостей с помощью пневматического или порш
невого пульсатора 2, находящеrося вне экстрактора, накладывается возвратно-

1 1 10

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

поступательное движение, обеспечивающее тонкое дробление капель и интен
сивный контакт фаз.
В мировой практике применяются СИ1Чатые пульсационные колонны диа
метром до 3 м и насадочные диаметром до 2 м. Отличительная особенность этих
аппаратов - отсутствие движущихся внутренних деталей обусловливает специ
фические области их применения: коrда требуется полная герметизация обору
дования и недопустим контакт обслуживающего персонала с обрабатываемыми
ЖJ1Дкостями (радиоактивные и ядовитые растворы) . К недостаткам пульсацион
ных колонн можно оmести динамические наI])узки на днище и высокие энерго
затраты.
Наиболее проI])ессивным типом колонных экстракторов с внешним подво
дом энергии на настоящий момент являются колонны с 11Ибрирую11U1ми nерфори
ро118НН1dМИ тарелками. Они экономичнее пульсационных экстракторов по энерго
затратам; в них в отличие от пульсационных аппаратов колебательное движение
совершает пакет (или пакеты) перфорированных тарелок, а не столб жидкости .
Если учесть, что в аппаратах промышленных размеров вес столба жидкости на
порядок больше веса пакета тарелок, то станет очевидным, что инерционные
наI])узки в вибрационном экстракторе значительно меньше, нежели в пульсаци
онном. (Разработаны и применяются в промьШJЛенности более сложные кон 
струкции
пульсационных
и
вибрационных
колонн
с
пониженными
( компенсируемыми) инерционным и наI])узками.)
Еще одно важное преимущество экстракторов с вибрирующими тарелками
(по сравнению с остальными типами колонн с внешним подводом энергии) сочетание высокой производительности и массообменной эффективности.
Производительность противоточных колонн лимитируется размером капель
дисперсной фазы и свободным сечением секционирующих (поперечных) пере
городок. При одинаковом размере капель производительность вибрационных
экстракторов примерно вдвое превЬШiает производительность колонн типа РДЭ .
Секционирующие кольца занимают примерно половину сечения РДЭ; отсюда
можно сделать вывод, что колеблющиеся в вертикальном направлении перфори
рованные тарелки в отличие от неподвижных не тормозят движение капель
дисперсной фазы.
При равной эффективности механического перемешивания (одинаковом
подводе внешней энергии) эффективный коэффициент продольного перемеши 
вания в потоках ф аз Е;,Ф практически одинаков в обоих типах колонн (РДЭ и
виброэкстракторе) . Однако при оценке влияния продольного перемешивания на
эффективность массообменноrо процесса следует оперировать не сами м коэф
фициентом ВэФ, а его оmошением к средней скорости потока соответствующей
фазы. (Эти оmошения можно рассматривать упрощенно как диффузионные
добавки на продольное перемешивание в фазах в эффективную высоту единицы
переноса.) В соответствии с изложенным вьnuе степень продольного перемеши
вания для вибрационного экстрактора примерно вдвое ниже, чем для колонны
типа РДЭ того же диаметра. И менно поэтому наряду с высокой производитель
ностью промышленные виброэкстракторы обладают также более высокой по
сравнению с РДЭ массообменной эффективностью.
На рис. 1 3 . 4 изображен типичный колонный экстрактор с вибрирующими та
релками. Цилиндрический корпус 1 представляет собой рабочую зону. Она
соединена с верхним отстойником 2, имеющим распределитель 3 тяжелой фазы
(кольцевой барботер) и перелив 5 для вывода скоалесцировавшей легкой диспер
гируемой фазы. Н ижняя часть экстрактора состоит из отстойника 6 со штуцером
вывода тяжелой фазы 7 и распределителем легкой фазы 8. В рабочей зоне 1
размещен пакет (в промышленных аппаратах - пакеты) перфорированных таре
лок 9, жестко закрепленных на штанге 10, которая соединена посредством ша
тунно-кривошипного механизма с приводом 4, обеспечивающим возвраmо
поступательное (вверх-вниз) движение штанги с тарелками. Амплитуду колеба-

1111

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

5

3

Рис. 13. 4. Колонна с вибрирующими тарелками:
1 - корпус, 2 - верХЮIЙ отсrоЙЮIК, З - распре
делитель ТФ, 4 - привод с шатунно-кривошипным
механизмом, 5 - перелив для вывода скоал есциро
вавшей леrкой дисперсной фазы, 6 - НИЖЮ!Й отсrой
нюс:, 7 - вывод ТФ, 8 - распределитель ЛФ, 9 перфорированны е таретси, 10 - штанrа

ний регулируют изменением эксцентриситета
кривошипа, частоту - изменением числа его
оборотов.
2
Тарелки 9 могут иметь круглые (мелкие или
крупные) либо прямоугольные отверстия. В
последнем случае отверстия тарелок снабжены
напрааляющими . лопатками. Они создают на
клонные каналы, проходя через которые, рабо
чие среды приобретают горизонтальную состав
ляющую скорости движения. Возникающее при
этом поперечное перемешивание снижает отри
цательный эффект поперечной неравномерно
сти, предотвращая уменьшение эффективности
массообмена с ростом диаметра аппарата. По
добные тарелки применяются и в пульсацион
ных экстракторах.
В отличие от ранее рассмотренных аппара
тов эффективность массообмена в тарельчатых
пульсационны:х экстракторах и в колоннах с
вибрирующими тарелками с увеличением диа
метра от 0,2-0,3 м до 1 , 5-2 м снижается не
значительно.
Центробежнwе экстрахторw (ЦЭ) представ
ляют собой особую группу аппаратов, включающую в себя ряд существенно различающихся
6
конструкций: вертикальные и горизонтальные,
напорные и безнапорные, многоступенчатые
экстракторы и др. П одробно они описаны в
специальной литературе" .
В этих экстракторах дробление дисперсной
фазы, противоточное движение и сепарация фаз
происходят под действием центробежных сил,
возникающих при быстром вращении ротора.
Простейnmй ЦЭ (рис. 13.5) предстаВТIЯет собой ухреплею1ый на валу 1 ротор 2,
размещенный в неподвижном корпусе З и сосrоящий из пакега перфорированных
ко�щентрически расположеЮfых ЦИЛИJЩров 4, зажатых боковыми стенками 5. Подача
и вывод фаз производятся через имеющиеся в валу 1 каналы. Герметичность достиrа
ется с помощью сальников 6. Тяжелая фаза подаеrся в центральную часть ротора, а
леПWI - в периферийную. Под действием центробежной силы ЖJЩКОСТИ движутся
противотоком, дисперmруясь при прохожцении через отверстия ци.лющров, коиrак
тируя и ра:щеляясь в кольцевых ющалах межцу ними. Тяже.лая фаза отводится с пе
риферии ротора, а леПWI - вбlmзи ero оси. Обе фазы уда/IЯЮТСЯ •1ерез ра:щельные
отводные каналь1 вала.
Достоинства ЦЭ - компактность и сочетание высоких производительности и
интенсивности массообмена; они особенно эффективны для жидкостных систем
с небольшой разностью плотностей фаз. ЦЭ отличаются малым временем пре• См., например, ( 1 0 ) .

1 1 12

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

2
/
;3

-

'
'

+1

�

,

· - · - · - ·

6/

//////

.,.,1

- · -

� 1// / / / / / / /

�

�

�

ТФ

('1\.�
. .
��

"77i v///."

'

-

!

-

.

ЛФ

�
�

'

�

"-- 4
'5

Рис. 13. 5. Центробежный экстракто р :
1 - вал , 2 - ротор, З - неnодвюкный
боковые стенки цилиндров, 6 - сальники

корnус,

4

-

nерфорированны е цилиндры ,

5

-

б ьmан ия фаз в а п п арате, что обуслоали вает успешное их применение при обра
ботке н есто й ких веществ,
время

эти

в

частности в производстве антибиотико в .

В

то же

ап параты непр и год н ы , ко гда требуется дrштельное время контакта фаз

(например ,

при

экстракци и , л и м итируе м о й недо статочно быстрой х и м ическо й

реакци е й ) .

В

п р отивоточ н о й коло н н е п о верхностью , пер пенди куля р н о й движе н и ю п о 

токо в ф аз , я вля ется ее по перечное сечение; в ЦЭ - это по верхность цилиндра .
Рассто я н и е ,

проходимое фаза м и , в коло н н е о п р еделяется е е высото й , а в Ц Э -

его радиусо м . П о это му п р о и зводительность ЦЭ увеличи вается с ростом ш и р и н ы
р отора, а дости гаемая сте п е н ь 11залече н и я (разделения) - с ростом его диаметра.

Если
ней

в процессе э кстракции требуется большое число теоретических ступе

разделе н и я

противоточный

К

или

большая

поверхность

каскад центробежных

межфазного

контаr.rа,

п р и меняют

экстракторов.

недостаткам ЦЭ следует отнести

сравн ительно высокие кап итал ь н ые

и

эксплуатаци о н н ы е затраты.

1 3 . 2 . 2 . Экстракторы со ступенчатым контактом фаз

Экстрактор ы со ступенчатым контактом фаз состоят из сек
ций или соединенных в каскад (батарею) ступеней, в каждой
из которых происходит смешение и расслаивание фаз . По ан
парату или каскаду ступеней в целом потоки фаз обычно дви
жутся противоточно, но в секциях или ступенях возможен так
же их прямоток или 'Iаще - идеальное перемешивание. Ино
гда экстрактор ы или система экстракторов работают по порци
онной (перекрестной) схеме .

1 1 13

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Все аппараты данного класса можн о разделигъ на две rруппы:
- секционированные колонн ы ;
- ступ ен ч атые смесительно - отстойные экстракторы.

Секционированные колонны
Среди м н ожества конструкций се кционированных колонных
экстракторов лишь некоторые нашли пракrическое применение.
Простейший тип таких экстраJсrОров - С:И1Чатwе колонны, иначе - колонны
с ситчатыми тарелками . Они работают в смесительно-отстойном режиме: дис
персная фаза, проходя через отверстия ситчатых таре.пак, дробится на струи и
каrши; после контакrа в межтарельчатом пространстве со сrшошной фазой каrши
коалесцируют с образованием сrшошноrо слоя у соседней тарелки, и далее про
цесс повторяется .
Толщина слоя скоалесцировавшейся дисперсной фазы (под или над тарел
кой - в зависимости от rшотностей фаз) должна бьпъ достаточной, чтобы ее
гидростатического давления хватало для преодоления сопротивления отверстий
тарелки ( при и стечении из них дисперсной фазы) и межфазного поверхностного
натяжения.
Конструкти вно ситчатый экстрактор (рис. 1 3.6) в принципе сходен с абсорб
ционными и ректификационными колоннами с ситчатыми тарелками. Отличие
- в более коротких перето<1ньIХ устройствах (в виде карманов или труб) для
транспорта сrшошной фазы (СФ) из секции в секцию.
Ситчатые тарелки устанавливают на расстоянии 0,2-0,6 м. Свободное сече
ние тарелок обычно составляет 40-60% , диаметр
отверстий 2-6 мм.
С итчатые экстракторы наиболее эффективны
среди аппаратов, работающих без подвода внешней
энерrnи. Их достаточно высокая разделительная
способность объясняется близостью к противоточ
ному режиму движения фаз; они особенно зффективны для жидкостньIХ систем с небольшим меж
2
фазным поверхностным натяжением.
Недостаток ситчатьIХ экстраJсrОров - низкая
интенсивность массопередачи, обусловленная ма3
лой поверхностью контакта фаз. Дело в том, что
для систем жидкость-жидкость разность rшотностей
фаз зна'ПIТеЛЬно ниже, чем ШIЯ систем rаз (пар)
жидкость; за исюпочением систем с ЮIЗКИМ межфаз
ным натяжеЮ1ем, она обычно недосгаточна ШIЯ тонкого дисперrnрования одной жидкосrn в другой.
4

tлФ

Рис. 13. 6. Ситчатый колонный экстрактор:

1 - корпус , 2 - ситчатые тарелки, З - перетоки ТФ ,
- дисперrатор

4

Ступен чатые смесительно - отстойные экстракторы
С месительно - отстойные экстракторы ( СОЭ ) относятся к
числу наиболее распространенных экстракционн ых аппаратов.
Кажд ая ступ ень такого экстрактора состоит из смесителя и
отстойн ика. При этом имеется больше воз можн остей для варь 1 1 14

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ЛФ -------.

г-�-;:з==::::;-.-�--;:::J
- - - -- - -

ЛФ

1

2

ТФ

Рис. / 3. 7. Насосно- отстойный ЭКС11>актор :
1 - отстойиихи , 2- цеmробежные насосы

ирования конструктивных элементов, чем в ранее рассмотрен 
ных аппаратах. Поэтому число предложенных конструкци й , в
том числе и пр и меняемых в промышленности, весьма велико .
Разные С ОЭ различаюrся конструкцией перемешивающих уст
ройств (мешалки, насосы, инжеЮJ.ионные и пульсационные
смесители); принципом работы отстойников (гравитационные
и центробежн ые); формой корпуса (цилиндрические и прямо
угольные
ящичные) ; размещением ступ еней (горизонтальные
и вертикальные); взаимным расположением смесителей и от
стойников.
-

Простейшим многоступенчатым экстрактором может служить каскад
(рис. 1 3.7), состоящий из отстойников 1 и цеН11> обе:ж:ных насосов 2. В таком
насосно-отстойном экстракторе все отстойники расположены на одном уровне, а
смесителями и дисперrnрующими устройствами служат центробежные насосы.
Ввиду полного перемешивания фаз объемная доля дисперсной фазы (задержка
- удерживающая способность) в таком смесителе определяется сооnюшением
потоков фаз. Несмотря на короткое время пребывания фаз в смесителе, в этом
экстракторе мoryr бьпъ достигнуты высокие эффективности ступеней. Однако
здесь иногда образуются очень тонкие, а значит. и плохо расслаивающиеся
эмульсии, что приводит к уносу мелких капель с потоком сплошной фазы.
Тон кое дробление дисперсной фазы - характерная особенность смеситель
но- отстойных экстракторов. В самом деле, в колоннах без внешнего подвода
энерrnи средний размер капель составляет примерно 3-6 мм, в колоннах с
подводом энерrnи - порядка 1 мм, а в СОЭ средний размер капель - порядка
О, 1 мм. Благодаря 1..толь тонкому дисперrnрованию и обусловленной им большой
поверхности коmакта фаз, в каждой ступени достигается межфазное распределение
концентраций переходящего компонеmа, близкое к равновесному. Поэrому в первом
приближении каждую ступень экстракrора можно рассматривать как теоретическую
ступень ра.:щеления. Реально КПД ступени здесь состааnяет 80-90% .
Основную долю объема ступени СОЭ, как правило, занимает отстойник. 0 1 1
и лимитирует производительность аппарата.
Смесительная и отстойная камеры чаще всего размещаются в одном корпусе.
В одном общем корпусе мoryr располагаться также и все ступени экстрактора.
На рис. 1 3 . 8 показана схема горизонтального 11>ехступенчатого ящнчноrо экс111актора , ступени которого 2, 3, 5, размещенные в общем корпусе прямо утоль
ного сечения, отделены друг от друга вертикальными перегородками 4. В смеси
тельных камерах 6 ступеней фазы перемешиваются турбинными мешалками 1 и
поступают в отстойные камеры 7. Из отстойных камер легкая (ЛФ) и тяжелая
(ТФ) фазы вьmодятся соответственно сверху или снизу и за счет насосного эф
фекта мешалок подаются в смесительные камеры предьщущей и последующей
ступеней (или выводятся из каскада). Таким образом, исходный раствор и экс-

1 1 15

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 13. 8. Ящичный смесительно-отстойный
экстракrор:
ступени
1 - турбинные мешалки, 2, З, 5
эксrрахтора, 4
вертикал ьные переrородки,
разделяющие ступени, 6
смесительные каме
ры , 7 - отсrойные кам еры
-

-

-

тparem, один из которых явля.лся тяжелой
фазой, а друrой - легкой, движутся через
ТФ
ступени противотоком, последовательно
перемешиваясь и расслаиваясь. При этом
режим движения в смесителях близок к
идеальному перемешиванию, а в каждом
отстойнике - к противотоку.
Смесительно-отстойные
экстракторы
применяются для процессов, требующих
большого числа теоретических ступеней (в
некоторых mдрометаллур гических процес
сах число ступеней экстрактора доходит до
с.отен). Они могут работать практически
при любом соотно шении потоков фаз и с желаемым (реrуJmруемым) временем
пребывания их в ступенях, что играет большую роль в ряде процессов экстрак
ции, сопряженной с химической реакцией. Для регулирования сооrnошения фаз
иногда используют частичную рециркуляцию одной из них из отстойника в
смеситель той же ступени .
Достоинствами рассматриваемых аппаратов является также сохранение рабо
чих концентраций в фазах при продолжительных остановках (значит, и быстрый
выход на режим при возобновлении работы), простота и надежность масштаби
рования. Последнее обусловлено тем, что, как уже отмечалось, в смесительной
камере происходит практически идеальное перемешивание потоков фаз. Услови
ем одинаково1'0 rидродинамическоrо режима и одинаковоrо р3змера капель в
смесителях разного масштаба является постоянство удельного полезноrо расхода
внешней энергии.
Н едостатки СОЭ в значительной степени связаны с проблемами расслаива
ния эмульсий в отстойных камерах. За иmенсивный массообмен, достигаемый
тон ким диспергированием одной из фаз, приходится расплачиваться значитель
ными размерами отстойников и уносом мелких капель. Большое число поверх
ностей раздела фаз также усложняет эксплуатацию экстрактора (образование
третьей фазы - см. разд. 1 3. 1 ) . В целом, как правило, капитальные и эксплуата
ционные расходы для этих экстракционных аппаратов выше, чем для колонн с
внешним подводом энергии.
Выбор типа экстрактора обусловлен весьма многочисленными факторами .
Обычно если требуемое число теоретических ступеней разделения не превышает
1 0 , чаще всеrо применяют колонные экстракторы, при большем числе ступе
ней - преимущестl!енно СОЭ. Заметим : такая практика, обусловленная сло
жившимися традициями, не всегда согласуется с технико-экономическими сооб
ражениями.

1 3 .2.З. О выводе фаз из экстрактора

Вывод легкой фазы Л из верхней отстойной з оны колонного
экстрактора ил и верхне й части отстойной камеры СОЭ не вы
зывает затруднений : расположенный здес ь горизонтал ьн ый
патрубок (штуцер - перелив) защищает аппарат от переполне
н ия , избыток жидкости сливается через патрубок. Однако вы -

1 1 16

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

2

/

//

lll

л
т

т

а

1

б

Рис. 13. 9. Флорентийский сосуд:
а - с переrородкой, б - с сифоном;
1 - сосуд, 2 - 11ереrородка, J - поверхносrь раэдма фаз, 4 - выравнивающая линия, 5
- сифон;
1 - исходная reтeporeIOfaя смесь, 1/ - леrкая фаза, 11/ - тяжелая фаза

вод тяжелой фазы Т из нижней части экстрактора требует спе
циальной регулировки; в противном случае через нижний пат
рубок может вылиться из аппарата вся жидкость - легкая и
тяжелая.
Наиболее простым устройством, обеспечивающим раздельный вывод фаз,
предотвращая попадание Л в л инию тяжелой жидкости (кстати, и Т - в линию
легкой жидкости). и поддержи1Jающим на определенном уровне rраницу раздела
фаз, является флорентийский сосуд. Его исполнение в двух вариантах показано на
рис. 1 3.9,а и 1 3 .9,б. Исходная гетерогенная смесь /, состоящая из фаз Л
(плотностью Рл) и Т (плотностью Pr) в некотором сооrnошении, подается в сосуд
1, снабженный перегородкой 2 или сифоном 5. В сосуде при расслаивании
устанаRЛИвается rраница 3 между легкой и тяжелой фазами. Легкая фаза Л вы
водится (поток //) с верхнего уровня; тяжелая фаза Т выводится (поток lll) с
уровня, обеспечивающего гидростатическое равновесие фаз (но не с самого
нижнего уровня сосуда) . Этот уровень под11е:жит расчету.
Принцип работы флорентийского сосуда заключается в уравновешивании
столбов жидкостей, вьmодимых потоками ll и J//. Если в исходной смеси /
возрастает доля, например, тяжелой фазы Т, то при этом увеличивается давление
столба жидкостей Л и Т в левой части сосуда, находящегося в гидростатическом
равновесии со столбом тяжелой жидкости Т в правой ero части (или в сифоне) .
Тогда при фиксированном положении точ ки вывода фазы Т должна по условию
гидростатического равновесия понизиться суммарная высота столбов жидкостей
в левой части сосуда; поэтому rраница раздела фаз 3 переместится вниз, а из
патрубка вывода легкой жидкости фаза Л уходить не будет. К противоположно
му результату (прекращению в ывода фазы Т из точки вывода тяжелой жидкости
и перемещению rраницы раздела фаз 3 вверх) приводкr возрастание в исходной
смеси / доли легкой фазы.
Заметим : в сосуде с сифоном на последнем предусмотрен вертикальный пат
рубок, чтобы при избьrrке в исходной смеси легкой жидкости струя в сифоне
могла быть разорвана; тогда поток JII прекратится .
Флорентийские сосуды часто работают под атмосферным давлением, так что
давления в точках вывода легкой и тяжелой фаз выравнены. Если рабочее давле
ние отличается от атмосферного, то сосуд за крыг, а выравнивание давлений в
случае сосуда с сифоном дости гается с помощью специальной линии (позиция 4
на рис. 1 3.9,б).

1 1 17

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Расчет флоренти йского сосуда будем вести на примере сосуда с сифоном .
Поставим задачу следующим образом: заданы точка вывода легкой жидкости
( высота hл + hr) и п оложение гр аницы раздела фаз (hл и hr в отдельности) ; тре
буется рассчитать высоту сифона h , т.е. уровень (точку) вывода тяжелой жид
кости .
В ходе анализа пренебрегаем гидравлическим и сопротивлениями движению
жидкостей (небольшие протяженности каналов, невысокие скорости). Тогда
можно базироваться на соотношениях гидростатики, конкретно - на законе
сообщающихся сосудов (выражение (з) в разд. 2 . 1 .2 для уравновешенных давле
н и й в разных сосудах). Применительно к обозначениям на рис. 1 3 .9,б для са
мого н ижнего сечения сосуда справедливо:
(а)
где g

-

ускорение силы тяжести .

Отсюда иско мая высота сифона:

h

=

Р л hл

+

Р т hт

Рт

( б)

Возможны и иные постановки задачи . Например , при заданных точках вы
вода фаз (известны hл + hr н h) может потребоваться установить по.1ожение
границы раздела, т.е. найти hл и h,. Тогда равенство (а) надо будет решать отно
сительно hл или hт, имея в виду, что сумма этих высот задана.

13.3. ОСНОВНЫЕ СХЕМЫ ЭКСТРАКЦИИ

В зависимости от технологического процесса, где использу
ется экстращия, возможн ы различные способы ее осуществле
н ия . Наиболее простой является схема однократной экстракции
(рис . 1 3 . 1 0 , а) . Процесс экстракции здесь может проводиться
как периодически, так и непрерывно. Исходный раствор, состоя
щий из разбавителя Р и переходящего компонента В, смеши
вается с экстрагентом Э в смесителе 1, а затем смесь разде
ляется на два слоя в отстойнике 2. При периодическом процес
се обе операции могут проводиться в одном аппарате - тогда
они разделены во времени . В случае непрерывного процесса
операции смешения и расслаивания проводятся в разных аппа
ратах (например, в насосно-отстойном экстракrоре) или в раз
ных зонах одного аппарата (СОЭ), т.е. они разделены в про
странстве .
На рис. 1 3 . 1 0 , б схема однократной экстракции представлена
в стилизованном виде, удобном для техноло гического анализа.
Однократная (или одноступенчатая) экстра кция применяет
ся на пракrике лишь в тех случаях, когда коэффициент распре
деления (отношение равновесных концентраций в фазах) в
пользу экстрагента очен ь высок или когда допустимы невысо 
кие концентрации извлекаемого вещества в экстракrе . Пример :
экстракция применяется для очистки продукrа, причем экс
трагент не регенерируется, а используется в другом процессе.

1 1 18

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 13. 10. Однокраrnая экстракция:
а - схе м а процесса, б - расчеrnая
схема;
1 - смесиrель, 2 - отсrойник

Эффективность процесса
повышается , если он по
строен по схеме порционной
экстракции (рис . 1 3 . 1 1 ) . Ее
а
еще не совсем строго назы
вают перекрестной экстрак
цией или многоступенч атой экстракцией при перекрестном то
ке. Схема включает ряд последовательно-параллельных опера
ций смешения и сепарации фаз . Процесс проводится в каскаде
ступеней, через которые последовательно перемещается, на
пример, исходный раствор . Общее количество (или поток) све
жего экстрагента Э в этом случае паршzлельно распределяется
межлу ступенями - в каждую ступень подается определенная
порция свежего экстрагента. Соответственно из каждой ступе
ни выводятся свои экстракт и рафинат. При этом для всех сту
пеней, начиная со второй, исходным раствором является ра
финат с предыд ущей ступени . Количество экстрагента, пода
ваемое в каждую ступен ь, может быть одинаковым (Э 1 = Э2 =
= . . . = Эп) либо различным (Э 1 * Э2 *- . . . *- Эп).
Концентрация переходящего компонента В в экстрактах, ес
тественно, понижается от первой ступени к последней, по
скольку в этом направлении понижается его концентрация в
растворах, подаваемых на очередную (последующую) ступень
экстракции.
Рассмотренная схема при большом числе ступеней позволя
ет из исходного раствора получить весьма чистый разбавитель ;
она применяется, когда необходимо получать достаточно чис
тый разбавитель с помощью дешевого экстрагента, не требую
щего регенерации .
Возможна также обращенная схема порционной экстракции,
когда исходный раствор паралл е льно распределяется межлу
ступенями, через которые последовательно перемещается экстэ

11
11
11
11
11
11

1

R 1 : .--:

Рис. 13. 1 1. Схема порционной экстракции :
1

- смеситсnи, 2 - отстойникн

J l 19

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. / 3. 12. Схема н епрерывной противоточной
а
в каскаде СОЭ, б в колонне;
1
смескrелн, 2 отсrойникн
-

-

экстракци и:

-

-

раrент. При такой схеме достигается максимальная концентра
ция извлекаемого компонента в экстракте.
Периодические процессы однократной и порционной экс
тракции часто применяются в малотоннажных производствах.
Он и используются также в лабораторной практике, rде прово
дятся обычно в делительных воронках.
Наибольшей эффективностью в аспекте полноты разделения
обладает схема противоточной экстракции , показанная на
рис. 1 3 . 12 . По этой схеме процесс в подавляющем большинстве
случаев организуют в непрерывном варианте. Процесс противо
точной экстракции может проводиться :
- со стуленчато-противоточным контактом фаз, т.е. в касступеней
экстрактора
смесительно-отстойноrо
каде
(рис . 1 3 . 1 2 , а) ;
- с непрерывным контактом фаз , т.е. в противоточной ко
лонне (рис . 1 3 . 1 2 , 6) или центробежном экстракторе.
Исходный раствор и экстрагент вводятся с противополож
нь�х концов установки - в первую и последнюю ступени кас
када СОЭ, в верхнюю и нижнюю части колонны, в централь
ную и периферийную зоны ЦЭ - и движугся противотоком
друг к другу. Экстракт и рафинат выводятся с противополож
ных концов установки .
Как было показано в разд . 1 0 . 8 , в противоточном процессе
максимально используется движущая сила массообмена, так
что данная схема экстракции является наиболее эффективной
(экономичной) и потому чаще других применяется в много
тоннажной промышленности. В таком процессе наиболее
обедненная переходящим (экстрагируемым) компонентом фаза
1 1 20

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

рафината на выходе из установки встречается со свежим э кс
трагентом , а наиболее богатая этим компонентом фаза экс
тракта на выходе контактирует с концентрированным исход
ным раствором. Благодаря этому достигаются:
- наиболее высокая средняя дв ижущая сила процесса;
- максимальн ая степень разделения при заданном расходе
экстрагента;
- наименьший расход экстрагента при заданной степени
разделения.
13.4. ВЫ Б ОР Э КСТРАГЕНТА И ПОДХОДЫ
К АНАЛИЗУ ЭКСТРАКЦИОННЫХ П РОЦЕССОВ

Успех процесса э кстракции в з начительной степени опреде
ляется подбором экстрагента : от него зависит н е только эко
номичность процесса, но и методика его расчета. Оптималь
ным является экстрагент, обеспечивающий минимум капиталь
ных и эксплуатационных затрат на обеих техноло гических ста
диях процесса экстракц и и - собственно экстракции и регене
рации экстрагента.
Основные требовани я к экстрагенту:
- миним альная в за имная растворимость (в идеале - полная
нерастворимость) с р азбавителем ;
- высокая селективность (избирательность), т.е . способ
ность извлекать из смеси преимушественно целевой ко мпо нент;
высокий коэффици е нт распределения (в пользу экс
трагента) и большая емкость (растворимость в экстрагенте пе
реходящего компонента) .
Эти показатели влияют на работу обеих стадий; они о преде
ляют качество разделения, потоки фаз, затраты на р егенерацию
экстрагента и другие показатели процесса. Однако наряду с
отмеченным и надо учитывать и целый ряд других требований :
достаточно большая р азность плотностей фаз (влияет на про
изводительность экстра ктора); доступность, дешевизна и лег
кость регенерации экстрагента, его нетоксичность и взрыво
безопасность, малое коррозион ное воздействие на аппаратуру и
некоторые другие свойства, определяемые конкретным произ
водством . Я сно, что в реальных технологических ситуациях не
все требования мо гут быть удовлетворены .
В зависимости о т выполнения первого основного требова
ния при расчете различных технологических вариантов экс
тракции различают два случая :
- полная взаимная нерастворимость экстрагента (Э) и раз
бавителя (Р) ;
- частич н ая взаимн ая растворимость Э и Р .
1 121

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Далее эти случаи будут рассмотрены последовательно. В пер
вом из них расчет экстракции ведется по схеме, подробно изло
женной в гл . 10 для массообменных процессов класса 3(2-2) 1 ; во
втором - экстракция должна рассматриваться как процесс класса
3(3-3)3 . В первом случае нередко представляется возможным ли
нейное описание и как следствие - анал итический расчет про
цесса массообмена; во втором - таких ситуаций прак:гически не
бывает, так 'П'О расчет приходится вести графоан алитически. При
технолоЛfЧеских расчетах решаются обе задачи: эксплуатации и
проек:гирования (см. разд . 10.8, 10 .9).
Особенности кон центрацион ного равновесия в фазах рафи
ната и экстрак:rа в значительной степени определяют аппара
турное и технологическое решение кон кретного процесса раз
деления: конструщию и размеры аппаратов, выбор экстрагента
и соотношение потоков фаз, схему - метод проведения про
цессов э кстракции и регенерации экстрагента.
Сущн ость равновесного состоян ия для массообмен н ых про
цессов и общие положения, касающиеся описания фазового
равновесия и его влиян ия на массообмен , сформулированы в
разд . 1 0 . 1 .2 и 1 0 . 3 .
Поскольку влиянием давлен ия на равновесие в системах
жидкость-жидкость можно пренебречь (жидкости несжи
маемы), то диаграммы фазового равновесия изображаюгся в
виде изотерм экстракци и . Формы этих изотерм и способы их
графического отображения различны для первого и второго
случаев, н о в обоих случаях рабочая область экстракции распо
лагается под изотермой экстракции (линией равновесия) .
1 3 . 5 . РАСЧ ЕТ П РОЦЕССОВ ЭКСТРАКЦИ И

1 3 . 5 . 1 . Экстракция п р и полной взаимной нерастворимости
экстрагента и разбавителя

При полной взаимной нерастворимости Р и Э потоЮf (или
количества в случае периодического процесса) экстрагента и
разбавителя не изменяются в ходе процесса - они постоян н ы
вдоль поверхности массопередачи (вдоль аппарата) . Это делает
возможным линейную запись балансов с использованием отно
сительных концентраций . Допуская независимость коэффици
ентов массоотдачи и массопередачи от кон центраций и посто
янство удельной поверхности контак:га фаз (или оперируя их
усредненными значениями), получаем возможность линейного
описания и кинетической составляющей массопереноса. А если
и линию равновесия можно представить в виде прямой, то весь
процесс массопереноса описывается линейными соотноше
н иями, и расчетные зависимости получаюгся в аналитической

1 1 22

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

форме. TaIOle соотноше ния и расчетные зависимости, а также
графоаналитичесЮlе методы расчета в случае кривой линии
равновесия для процессов класса 3 (2-2) 1 применительно к раз
личным структурно-конфигурационным комплексам (техноло
rичесЮ1м вариантам реализации) подробно обсуждены в гл . 1 0 .
Ниже результаты и выводы гл . 10 используются для анализа
процессов жидкостной экстракции . Приняты следующие обо
значения потоков и концентраций:
L и L - массовые количество и поток фазы рафината в рас
чете на инерт - чистый разбавитель;
D и D - массовые количество и поток фазы экстракта в
расчете на другой инерт - чистый экстрагент;
х - относительная массовая концентрация переходящего
компонента (вещества В) в фазе рафината (кг В/кг Р), а у его относительная концентрация в фазе экстракта (кг В/кг Э);
т = (у/х)Р - коэффициент распределения .
Введенные обозначен ия совпадают с принятыми в гл . 1 0 для
переноса вещества из фазы "х' в фазу "у", когда на диаграмме у-х
рабочая область процесса находиrся под линией равновесия. Опи
сание массообмена условимся вести в терминах фазы "х'.

Однократная экстракция

Однократная экстракция обычно проводится в условиях ин
тенсивного перемешивания в смесителе, так что вполне можно
принять идеальное перемешивание обеих фаз .
Стационарным условиям данного процесса соответствуют
схема, представленная н а рис. 1 0.25,а и 1 3 . 1 3 , и диаграмма у-х
на рис . 1 0.25,б. Анализ проектной задачи (определение средней
движущей силы) приведен в разд. 1 0 .8 . 1 . Эксплуатационная за
дача
(определение
потока вещества)
анализируется
в
разд. 1 0 . 9 . 1 и иллюстрируется на рис . 1 0 . 2 8 , б.
При идеальном контакте фаз из материального баланса не
прерывного процесса дл я контура, охватывающего весь одно
ступенчатый аппарат (см . рис . 1 3 . 1 3 ) , имеем:

х2) = D<Yl

- У1 ),
причем фазы уходят в равновесии, т.е. х2 и У2 - равновесные
концентрации . Если при этом линия равновесия - прямая, то,
подставив сюда

L(xi

-

У2 = тх2 ,

концентрации получаем ых рафината и экстракта можно найти
аналитичесЮI:
D
D
Х 1 + У1
Xi + У 1
L
L
-=-=(13.1)
Х2 =
тD
1 + с'
l+
L
-

=

-

l 1 23

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. JЗ. 13. Расчетная схема процесса однокраnюй экс
трак.цюt при полной взаимной нерастворимости экс
трагента и раз б авителя

У1 = тх1 =

тх

1 + у1 с '

1 + с'

( 1 3 . la)

Величина с ' = mD/L, представляющая со
бой отношение пропускных способностей
потоковых стадий по экстрагенту (на языке фазы "х" это mD) и
по разбавителю (L) , называется фактором экстракции (часто так
называют и обратную величину с = 1 /с').
Достигаемая степень извлечения, или степень экстракции:
q>

=

L (x 1 - х2 )

=

Lx 1

1-

Х2
Х1

c' + �

D

Х1 L

=

( 1 3 .2)

1 + с'

В случае периодического процесса в выражениях ( 1 3 . 1), ( 1 3 .2) и
последующих вместо фазовых потоков L и D будуr входить L и D .
Из выражений ( 1 3 . l a) и ( 1 3 .2) видно, что остаточная кон
центрация в рафинате падает, а степень извлечен ия растет с
увеличением коэффициента распределения и соотношения
потоков D/L, а также с уменьшением начальной концентрации
извлекаемого ве щества в экстрагенте у1 • Огмеченная закономер
ность справедлива для всех схем экстракцио н н ых процессов.
Если на экстракцию подается чистый экстрагент (у1 = О) , то
зависимости ( 1 3 . 1 ) и ( 1 3 .2) упрощаются :
mx

l
; ( 1 3 3б)
1 + с'
с'
mD
( 1 3 .3в)
q> = -- =
1 + с'
L + mD
Приведен н ые зависимости показывают, что полного извле
чен ия (х2 = О , q> = 1) одноступ енчатой экстракцией можн о до 
стичь при с ' � оо, т.е. когда соотношение потоков D/L � оо ил и
коэффициент распределения т � оо. Практически это возмож
но, когда проводится отмывка разбавителя от вещества В боль 
шим количеством экстрагента при большой величине т или
когда в фазе экстрагента вещество В вступает в достаточно
быструю и необратимую реакцию с содержащимся в ней реа
гентом. В последнем СЛУ'Iае концентрация В в экстрагенте
у � О , что можно трактовать как т � оо .

Х1 = -2!_ ·, ( 1 3 .3)

1 + с'

Yl =

·

Порционная экстракция
Этот технологический вариант массообменного процесса
подробно проанализирован в разд. 1 0 . 1 3 . Расчетная схема пред1 1 24

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Puc. J 3. 14. Расчетная схема процесса порционной эксТракции

ставлена на рис. 10.37. Диаграмма у-х для реально.го процесса
показана на рис . 1 0 . 3 8 . Диаграмма у-х для идеального контак
та фаз в случае кривой линии равновесия изображена на
рис . 1 0.39,а. В разд. 1 0 . 1 3 . 2 установлено, что оптимальному
распределению полного потока (количества) экстрагента D
между п ступенями при т = co11st отвечает деление его на рав
ные порции D1 = fh = . = Dn = D/n (рис. 1 3 . 14). При этом
достигается минимальная выходная концентрация Р.афината
для заданного общего соотношен ия потоков фаз D/L, а значит,
и максимальная степень извлечения
= 1
/Хо, rде Хо входная концентрация исходного раствора (см . рис . 1 3 . 14). При
идеальном контакте фаз и т = const выходную концентрацию
для оптим ал ьного распределения экстрагента можно полу
чить из выражения
подставив D1 = D/n, или из зави
их
симости
заменив приведенные концентрации
и

Хп

"

</>п

Хп

-

Хп

(10.60), (10. 5 9х),
Хп Хо
значениями Хп = Хп
x (f и Хо = Хо х б :
Хп хб хо хб
(1 + ��) п
Оrсюда после подстановки mD/L = с ' и хб = у</т получаем:
-

-

-

=

-

( 1 3 .4)

Степень извлечения после

п-й

ступени составляет:
( 1 3 .5)

1 1 25

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

При отсугствии извлекаемого компонента в исходном экс
трагенте (у0 = О)
1
Хо
( 1 3 . 5а)
Хп =
; ( 1 3 .4а) <i' n 1 п .
1+
=

(1 + �) п

( �)

Из этих выражений следует, что полное извлечение вещества
В, как и в первой схеме, возможно лишь при с ' ----+ оо. Степень
извлечения повышается с ростом п, однако из рис . 10.41 видно,
что при п > (4 + 6) дальнейшее увеличение числа ступеней
приводит лишь к очень небольшому понижению концентрации
вещества В в рафинате, т.е. к весьма малому росту <i'n·
Выражение для максимальной степени извлечения получа
ется при п ----+ ао; из зависимости ( 1 0.6 1 ) вытекает :
<i' m ax

При Уо

=О

-1
_

-

имеем :
<i' m ax

=

1

-Хо
X m in

-

е-

-

-

( - )(l
l - Уо-

- е-с

mx o

с'
=

'

).

( т::) .

1 - ехр -

Среднюю концентрацию у в объединенном экстракте мож
но найти из баланса для всей схемы (рис . 1 3 . 1 4)

D( y
откуда с учетом ( 1 3 .4)

- Уо) = L(X{) - Хп) ,

Используя выражения ( 1 3.За) и ( 1 3 .4а), можно сравнить эффек
тивности однократной и порционной схем экстракции - в случае
идеального конта:кrа фаз при т = const. С этой целью для обеих
схем обозначим одинаковыми символами входные (х1) и выход
ные (х2) концентрации: в выражении ( 1 3.4а) Х{) = х1 и Хп = х{
Соотношение остаточных (выходных) концентраций в ра
финате для первой и второй схем выразится так:
xz

х:2

(1 + �) п
1 + с'

Правая часть этой зависимости всегда больше единицы, следо
вательно, вторая схема эффективнее первой.

1 1 26

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

В самом деле, разложение
'

(1+-)
с

п

11

правой части

числителя

в

ряд Тейлора дает:

2
(с')
=1+11 -+ --п(п

с'

- 1) - + ." >l+c'·

2!

п

п

Сравнение эффективностей обеих схем при т = var прове
дено в разд. 10.13.1 и на рис. 10.39,а. Оно еще раз показывает,
что эффекrивность порционной подачи экстраrента в ряд сту
пеней всегда выше, нежели для одноступенчатого процесса с
подачей в аппарат всего э:кстраrента.

Непрерывная противоточная экстракция
Процесс реализуют со ступенчатым или непрерывным кон
такrом фаз, соответственно - ступенчатым или непрерывным
изменением концентраций компонента В по ходу процесса в
потоках фаз. Особенности обоих процессов рассмотрены в
разд. 13.2 и 13.3.
Противоточная многоступенчатая экстракция. Этот процесс
осуществляется по схеме, изображенной на рис. 10.32 и 13.15.
Анализ массообмена по этой схеме для различных технолоm
ческих ситуаций проведен в разд. 10.12: графоаналитический
расчет для случая кривой линии равновесия (m = var) изложен в
разд. 10.12.1 и проиллюстрирован на рис. 10.33, 10.34, аналити
ческие
расчеты
для
случая
прямой
линии
равновесия
(m = const) - в разд. 1 0 12.2 и 10.12.3.
Для данного процесса аналитические методы расчета имеют
особое значение. Дело в том, что в противоточной экстракции
часто достигается весьма низкая концентрация извлекаемого
вещества в конечном рафинате. При изображении процесса в
диаграмме у-х его завершающая (по рафинату) стадия сме
щается в левый н ижн ий угол диаграммы, где графическое
определение числа те оретически х ступеней довольно неточно.
По этой причине предпочтение отдается аналитическим мето
дам расчета (где это возможно).
Применительно к идеальному контакrу фаз в ступенях си
стемы, показанной на рис. 10.32, 13.15, степень извлечения
можно определить из выражения (10.45):

.

'Рп
те

с

При

=

L /(тD)

Уо = О

=

Хп
сп -1
=1 --=
Хо
cn+l -1
1/с'.

Уо )
( -тх
1-

о

'

(13.6)

данная зависимость упрощается:
'Рп

=

сп -1
cn+l

-1

.

(13.ба)

Напомним: условия, близкие к идеальным, на пракrике реа
лизуются в каскадах смесительно-отстойных экстракrоров.

1127

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. JJ. 15. Расчетная схема ступенчатой
противоточной экстракции
1, 0
0, 9

0, 8

Рис. 13. 1 6. Зависимость степени измече
ния IPn от числа равновесных ступеней п:
1
nротивоrочная схема, зависимость
( 1 3.6а) ; 1
порционная схема, зависимость
( 1 3.5а)

0. 7

-

-·

На рис. 1 3 . 1 6 сопоставлены степени извлечения, получаемые
при использовании двух многоступенчатых схем - порционной
и противоточной - в условиях идеального контакта фаз . Вели
чины <J> n рассчитаны по зависимостям ( 1 3 . 5а) и ( 1 3 .6а); одно
кратной экстракции отвечает значение <J> n = qi 1 при п = 1 . Как
видно из рис. 1 3 . 1 6 , из трех рассмотренных схем экстракции
самой эффективной является противоточная.
Рассмотрим возможности аналигическоrо решения некоторых
задач эксплуатации и проектирования. При этом воспользуемся
анаmrrическими зависимостями, установленными в гл. 10.
Пусть ступени каскада на рис. 1 0.32, 1 3 . 1 5 характеризуются
полным перемешиван ием фаз, а mпенсивностъ массопередачи в
каждой ступени - пропускной способностью поверхностной ста
дии kxf. Тогда степень извлечения q> найдем из формулы ( 1 0.53).
Избавившись от лоrарифмов, преобразуем Э1У формулу к виду:

п

XQ

- хС
� х оР

=

( mD mDL ++kxkxff)
у

n

[

mD

kX /
1 + -L

mD + kxf
= L -L

]п

--L

Учитывая (см . рис. 1 0 .35), что хпР = Ук /т и Х# = Уо /т, и обо
значив (см . разд. 1 0 . 8 .2) отношение пропускных способностей
поверхн остной и потоковой стадий (или число единиц перено
са в ступени по фазе рафината)
t =

1 1 28

kx f
-L

kx F
nL

а
п

= -- = - ,

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

имеем:

где

Л=(l + ct)/(l+t) .

Хо - У к /
Хп - У о /

m

( 1 t)п
+

m
=

+

1

Ct

1

Л,п '

=

(13 .7)

Пусть необходимо выразить в явном виде выходные кон
центрации, т.е. решить эксплуатационную задачу. Запишем ма
териальный баланс для всего каскада ступеней - для контура,
замкнугоrо на сечение О и сечение п (рис . 10.32, 1 3 . 1 5):

- Lхп = О ,

Lxo + Dyo - Dук

откуда

(13 .8)
Подставим

это

значение Ук в
/...п (х

о

Уо

_

т

п

(13.7) и избавимся от знаменателей:

_ Lx o
Dm

+

Lхп = Х
)

Dm
(13.9)

_

Уо

т

.

( l 3 .9)

Добавим теперь к правой части
величины +X{J и -X{J и с
учетом с = L/(mD) сгруппируем члены в полученном уравнении
в виде
л_п (Х{) yt/m) - ct..,n(X{J - Хп) = X{J yt/m - (X{J - Хп)
и далее

-

-

Отсюда
Ч' п

Из

(13. 10)

находим:

_

=

= X{J а Ук определяется из (13.8).
Задача проектироваиия Хп

п слп

х0 - Х
Хо - Уо /

т

Ч'п (Х{)

=

1 - л1 п

---

1-

(13. 10)

- yt/m) ,

определение числа реальных сту
пеней, обеспечивающих требуемую степень извлечения,
также решается с помощью уравнения (13. 10):
далее:

и окончател ь но :

п=

In[{l - Ч' п )/(1 - С\\1 п ))
ln /....

1 1 29

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Величина Ч'п, называемая степенью экстракции, представляет
собой отношение достигнуrоrо извлечения к максимально воз
можному теоретичесЮt , когда конечная концентрация рафина
та равновесна с начальной концентрацией экстрагента:
Хп = :хоР = Уо /т. Величина Ч'п также представляет собой (см.
разд . 1 0 . 10) отношение пропускных способностей аппарата в
целом и стадии подвода вещества с исходным раствором
(потоковой стадии по фазе рафината) . Действительно, количе
ство передаваемого вещества в единицу времени М = L(Xo -хп), а характерная разность исходных концентраций в терми
нах фазы "х" выражается как д . = Хо - yafm. Значит,
L М
( 1 3 . 1 1)
Ч'n = х0 - Хп /
т
L д .L
хо Уо
=

q> и Ч' связаны соотношением
о - хРо
q> = \j/ Х

Очевидно, что величины

При Уо

= О Хор = О ,

XQ

так что

q> = \j/ .
(13. 10) позволяют

Зависимости ( 13.8) и
решать проектную и
эксплуатационную задачи для реального процесса в кас каде
СОЭ. Их считают применимыми и к колонному экстрактору,
если структура двухфазного потока в нем отвечает каскаду сту
пеней идеального перемешивания ( И П ) - когда отклонения
движения потоков от противотока описываются ячеечной мо
делью продольного перемешивания · . Эти зависимости в той же
мере применимы для практичес Юt х расчетов экстракционных
колонн с внешним подводом энергии. Дело в том, что в ко
лоннах промышленных масштабов суммарный эффект про
дольного перемешивания вещества в обеих фазах обычно экви 
валентен числу ячеек идеального перемешивания п � 10. При
таких п расчет по более сложным моделям (диффузионной,
рециркуляционной) дает практичес Юt те же результаты, что и
по значительно более простой - по зависимостям (10.53) и

( 1 3 . 1 0) *.•

В ЬШi е рассматривался аналити ческий расчет в случае прям ой ли нии равнове
сия . Ан алитичес ки й метод применим та кж е, ее.ли кри(f)lю равновес ия удается
представ ить в виде ломаной ли нии . Обыч но с достаточной Д11Я пра 1С111 ки то ч
ностью равновесную линию в рабочем диапазоне мо жн о разбить на два или три
прямолинейных уч астка.
Пусть кривая равновесия в области рабочих концентраций �. Уп и хп, Уо

•

Строго говоря, здесь необходимо оговорить, что при таком подходе расчет
ное чис.ло ячеек в коло нн е пр и нимается одинаковым Д11Я обеих фаз.
•• п одробнее см. ( 3 ) .

1 1 30

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис . 13. 1 7. Ап п роксимация
кривой
равновесия двумя прямыми :
1, 2 - спрямле1щые учасrки линии
равновесия (см. уравнения ( 1 3 . 12)) ; J линия равновесия; 4 - рабочая линия

У

(рис. 1 3 . 1 7) приближенн о изобра
жается двумя прямыми, разделенны
ми горизонталью у':
1) У' = т1х ,
О s; у :S у';( 1 3 . 1 2)
2) У' = Ь2 + т 2х , у � у' .
Для каждого из участков можно
записать зависимость типа ( 1 3. 1 0):
'VI

=

'1'2 =

"

1 - л. 11
Х ' - Хп
=
; ( 1 3 . 1 3)
х ' - Уо 1 "'1
1 - с1 Л.�1

1 - л."22
х0 - х'
=
Хо - (У' - Ь�) / mi
1 - с2Л'f

х"

=--

х

( 1 3 . 1 3а)
Здесь n1 и n2 - числа ступеней ИП, приходящиеся на пер вый и второй
участки рабочего диапазона; общее число ступеней

,1
11.

_

_

1 + c1t ,
l+t

,2
11.

п = n1 n2 ;
+

_
_

1 + c2t ,
l+t

( 1 3 . 1 4)

С1 =

L
--

m1D

• С2 =

L
--

m2D

·

( 1 3 . 1 5)

Разrраничивающую концентрацию х' находим из баланса для части
системы, включающей n1 ступеней (первый участок рабочего диапазона) :
L(x' - Хп)
D(y' - Уо) .
( 1 3. 1 6)
Отсюда
( 1 3 . 1 6а)
(у ' - Yo) D/L .
х' - Хп
""

""

По зависимостям ( 1 3 . 1 2) - ( 1 3. 1 6) можно рассчитать:
- для имеющихся колонны или каскада неидеальных (конечные значения
kxf) смесителей-отстойников (задача эксплуатации) - выходные концентрации
вещества В в фазах Хп и Уп ;
для требуемой степени извлечения (задача проектирования) - необходи
мое число ступеней и высоту колонны.
В эксмуатационной задаче извесmы: общее число ступеней ИП п, величины с1 и
с2 (определяются по кривой равновесия - см. рис. 13. 17 - и извесmым потокам
фаз), Л. 1 и Л.2 (рассчитываютяс по извесrn ым с1 , с2 и f) и у' (находится по кривой
равновесия). Неизвестными являются выходная концеmрация х,,, концеmрация х',
сопряженная с у', и числа ступеней n 1 или n2, приходящиеся на первый или второй
участки рабочеrо диапазона концеmраЦИЙ (один из них может быrь выражен по
( 1 3 . 14) через друrой). Для определения трех неизвесrnых имеем три уравнения:
( 1 3 . 1 3), ( 1 3 В а) и ( 1 3 . 16). Возможен следующий путь расч�.
Подставив з н аче ния х - Хп из ( 1 3 . 1 6а) и п1 из ( 1 3 . 14) в ( 1 3 . 1 3) , получим:
-

.

'

l

л_n - п2

1
У' - Уо
( 1 3. 17)
=
L х ' - Уо / m1
1 - с1 л';_ - "2
Уравнения ( 1 3 . l За) и ( 1 3 . 1 7) решаются rрафически или методом последова
тельных приближен ий . В итоru находим х' и
и далее по ( 1 3 . 1 3) рассчитываем

D

_

п2

1131

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

выходную концеlf!'Рацию рафината Хп · Выходную концеlf!'Рацию экстракrа опре
деляем из общеrо баланса для всей системы п ступеней ИП:

Уп = Уо + (Хо - Xп)L/D .

Проектная задача решается проще. Здесь известны концеlf!'Рации
у'; по
зависимости ( 1 3 . 16) находим х'; по левым частям уравнений ( 1 3 . 1 3) рассчиты
ваем lj/t и lj/2 · Далее в зависимости от аппаратурноrо оформления процесса мо
жет быть два варианта продолжения расчета.
1 . Каскад С1)'11 еней ИП. Здесь известны коэффициент массопередачи kx и по
верхность коmакта фаз в одной ступени f, а следовательно, и число единиц
переноса ступени
По зависимостям ( 1 3 . 1 5) рассчитываем величины с1
и с2 , Л. 1 и Л.2 и далее по уже определенным значениям lj/t и lj/2 с помощью ( 1 3 . 1 3)
и ( 1 3 . 1 3а) - числа ступеней для первоrо и второrо участков рабочей области
КОНЦеlf!'Раций:
l( 1 3 . 1 8)
1j1 1 ln Л. 1 •
п 1 ln
1 - Ct lj/ J

Хп,

t = k.,//L.

=

f .

Затем по ( 1 3 . 14) находим необходимое для достижения заданной степени извле
чения общее чис.ло ступеней .
2. Колонн•1й экстрактор. Известны kx, поверхность контакrа фаз в единице
рабочеrо объема Fуд и количественный эффект продольноrо перемешивания в
потоках фаз, оцениваемый высотой ячейки И П Ня (см. rл .8) , а также попереч
но� сечение колонны /" определенное по расходам фаз. Ч исло единиц переноса
в ячейке ИП можно рассчитать из выражения
t "'

k,,.f

=

L

kxFyд

L

fаНя .

Далее расчет проводится так ЖР., как в первом случае, и по найленному общему
числу ячеек ИП определяется требуемая высота колонны Н:
Н = пНя .

Для условий идеального контакrа фаз в ступенях каскада

оо) аналитиче
ский расчет (концентраций или числа ступеней) nри нелинейной зависимости
равновесных концеlf!'Раций сходен с изложенным выше. Расчетные формулы для
этоrо случая легко получить из зависимостей ( 1 3 . 1 3) и ( 1 3 . I За), переходя в них к
пределу
оо ; при этом Л. 1 = с 1 и Л.2 с2 . С этими значениями Л. 1 и Л.2 остаются
в силе несколько упрощенные процедуры расчета по зависимостям ( 1 3 . 1 3) ( 1 3 . 1 8) .

t -+

(k.,/ -+

=

Противоточная экстракция с непрерывным ко нтактом фаз .
При анализе противоточной многоступенчатой экстракции уже
отмечалось, что реальный процесс экстракции в колоннах с
непрерывным контактом фаз при движении их потоков в ре
жиме, отличающемся от идеального вытеснения (ИВ), нередко
удобно рассматривать как процесс в цепочке (каскаде) ступе
ней идеального перемешивания (ИП). При этом не происходит
подмены поверхностной либо смешанной задачи, как при рас
чете по "методу ВЭТС" (см. р азд. 10. 12.5), поскольку здесь ис
пользуется ступенчатая модель структуры потока, а не массо 
переноса (как в "методе ВЭТС"); т.е. здесь можно говорить о
подмене задачи структуры потока. Расчет на основе непрерыв
ной диффузионной модели структуры потока значительно
сложнее, а при Ре � 20 (что характерно для промышленных ко-

1 1 32

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 13. 18. Определ ен и е локальной
движущей силы при расчете числа
единиц переноса а:
JIИНИЯ равновесия, 2
рабочая

�

-

у

-

Yz 1-------:::11-='"--:81

лонн с внешним подводом
энергии) приводит практиче
ски к тем же результатам, что
и расчет по ступенчатой мо
дели · .
хР
х
Для противоточной экс
тракции с движением фаз в
режиме И В полностью применимы расчетная схема рис . 10.27
и результаты анализа проекгной и эксплуатационной задач,
полученные в разд. 10.8.3 и 10.9.3 в предположении полной
сегрегации (раздельного течения) фаз .
Высоту Н экстракционного аппарата, работающего с непре
рывным контактом фаз, можно определить на основе уравне
ний массопередачи (см . разд. 10.8.3, 10.8.4) либо по методу
В Е П . В последнем случае по результатам экспериментов оце
н ивают значение высоты единицы переноса he и, определив чис
ло единиц переноса (Ч Е П) а, необходимое для достижения за
данной степени извлечения (по известной кривой равновесия и
построенной рабочей линии ) , рассчитывают высаrу (протя
женность) рабочей зоны экстрактора:

Н=

hea .
При расчете в терминах фазы "х" величина а вычисляется с
помощью диаграммы у-х (рис . 1 3 . 1 8) на основе локальных
значений дв ижуЩей силы процесса массопереноса (х - .хР):

k F --
Х

1
а = х - = f dx
L х2 х - х Р

(13.19)

Интеграл находится графически или численными методами .
Рассмотрим некоторые частные случаи, вытекающие и з об
щего аналитического решения задачи определения потока ве
щества при пр.ямой лин ии равновесия. Для этого выражение
(10.35) перепишем в виде:

exp( kxmDF kxF) _ ( )
L
L(x1 - х2 ) = .
х1 - х1Р L ,
kx
kx
L
F
F
)
- ехр -- - -- - 1
L
mD ( mD
_

1

• См . (3).

1 1 33

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

откуда
'1' 2 =

Х1
Х1

- Х2 = ееа(а(сс--11)) - 1
- xf с - 1

( 1 3 .20)

При одинаковых пр опускных способностях пот оковых стади й
с � 1 , так что выражение ( 1 3 .20) дает неопределенность. Рас
кроем ее, используя правило Лопиталя:

с�lim1 '112

=

__O__dc (ea(c - I) - 1]
ае а(с - 1)
-��_
:с (сеа(с - 1) - 1] c �I еа(с - 1) саеа(с�- 1)
=

Окончательно при с

lim

+

-

_
_

= 1:

а
kxF
.
(13.21)
=
-1+а
L kxF
В случае поток9вой зада'JН массообмена а = kxF L �
тог
да в ( 1 3 .20) ea(c-I) , cea(c-IJ > > 1 , так что после сокращений,
раскрывая смысл с L/<тD), получим:
lj/ 2

=

+

/

оо

;

=

1

В то же время по ( 1 3 . 1 1 )

ljl

тD

=� =Т.

'11 2

=

м
л.

( 1 3 .22)

М / (Л . L) . Оrсюда
( 1 3 .23)

= тD .

Это означает, что в рассматриваемом случае пропускная спо
собность экстрактора в целом определяется потоковой стадией
по фазе экстракта, т.е. массоперенос лимитируется стадией
отвода вещества из аппарата с потоком экстрагента.
Для с > 1 уже при а(с
1 ) � 5 экспоненциальные члены в
выражении ( 1 3 .20) становятся такими большими, что позволя
ют пренебречь единицей в числителе и знаменателе, и тогда
1
.
lj/2 � с
Значит, поверхностная стадия в этих условиях перестает ока
зывать влияние на массообменный процесс в экстракторе.
Зависимость ( 1 3 .20) можно получить и непосредственно решением дифференциальных уравнений (о) баланса и массо
передачи, приведенных в разд . 1 0 . 8 . 3 :
( 1 3 .24)
Ldx = .Ddy = kx(x xP)dF .
Бесконечно малую поверхность межфазного контакта d F мож
но выразить через удельную поверхность контакта Fуд• попе-

-

-

1 1 34

-

-

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

речное сечение колонны fa и элементарную высоту колонны dz:
dF =
Уравнение

(13.24)

Fyд{adz .

при этом перепишется следующим образом:
dx

dy
dz
дифференциальных

L - = - kxFyд/a(x - .хР) = D- .

(13.25)

dz
Граничные условия для
уравнений
(13.25) запишутся (рис . 10.27,а):
- для сечения входа исходного раствора и выхода экстракта

z = O:

х = х1 , у = У2 ;

(13.26)

- для сечения входа экстрагента и выхода рафината

Z = Н: Х = хъ У = YI ,

( 1 3.26а)

г.це Н - протяженность раб очей (массоо б менной) зоны аппарата.

Заметим: применительно к выражениям (13 .25), (13 .26) и
на рис . 10.27,а координата F заменена на z.
Из материального баланса по переносимому компоненту В
для участка колонны между нижним (Z = О) и промежуточным
(z < Н) сечениями следует:

(13.26а)

D(y2 - у) = L(x1 - х) .
(13.26б)
Переходя к безразмерной форме записи уравнений, заменя
ем переменные их безразмерными эквивалентами :
ljl

=

Х1 - х
х1 -

xf

'

г

=

у - У1 D
х1 - x f L

'

z=

_!_ .
Н

С учетом этих и принятых ранее обозначений с = L/(mD),
а = kxF/L = kxFyд{aH/L зависимости (13.25) - (13.26б) можно
привести к виду:
d1j1
dГ ·
(13 .27)
= a(\JI + сГ - 1) = - '
dZ
dZ
-

Z=

О:
Z = 1:

'i' =

О,

'i'

'i'Ъ

=

Г
Г

=

Г2 ;

= О;

= '1'2 - \j/ .
(13 .27) в граничных

г

(13.28)
1 3.28а)
(13 .29)
( 1 3 .28)

И нтегрируя уравнения
условиях
можно получить выражения, описывающие измене
ние концентраций компонента В в обеих фазах по высоте ко
лонны, - профили концентраций . Знание (хотя бы оценочное)
профилей концентраций необходимо, когда одна из фаз (или
обе) вводится в колонну в виде нескольких потоков с различ
ным содержанием переходящего вещества (см . н иже).

- (13 .29),

1 1 35

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Найдем профили кон центраций В в фазах. Для этого доста
точно решить одно из дифференциальных уравнений ( 1 3 .27) ,
например
d
'v
- dZ

= a('V + сГ - 1) .

(1 3 . 30 )

Подставив значение Г из (13 .29) в (13 .30), получ им после не
сложных преобразований неоднородное линейное дифферен
циальное уравнение:

d\j/
dZ

+

-

'Va(l

с) = a( l - C\V 2 )

( 13.3 1 )

.

Вначале решаем уравнение ( 1 3. 3 1 ) как однородное ·- без правой части:
d \j/

dZ

·

разделения переменных, интегрирования и потенцирования имеем:

Пос.ле
где л1

+ \j/O(l - с) = 0

-

-l ) Z
Ч' = A i ea (c
,
постоянная интегрирования.

Решение с правой частью ищем в виде:
'V

Подставив это выражение

для

А 1а(с - 1) ea(c-l) Z

=

А 1 ea(c- l ) Z + А2 .

( 1 3. 32)

Ч' в ( 1 3 . 3 1) , находим:

+

(А 1 ea(c -l)Z

+

A2)a( l - с) = a( l - СЧ12).

Отсюда пос.ле сокращения на а и приведения подобных членов получаем:
А2 =

При этом значени и А2
Ч'

==

1 - СЧ12
.

--1-с

A i e a( c - l) Z

+

( 1 3 . 3 3)

1 - СЧ' 2
.
1-с

( 1 3. 34)

Из граничного условия ( 1 3 .28) определяем постоянную А 1 :
1
А1
- - СЧ1 2 .
1-с

( 1 3. 35)

=

Решая совместно ( 1 3.34) и ( 1 3 . 35) для Z = 1 (при этом согласно ( 1 3 .28а) будет
Ч'
Ч'2) , выразим Ч'2:
l еа(с-1)
.
( 1 3 .20)
Ч'2 =
1 - сеа (с- 1)
=

_

Из ( 1 3 .34), (13 .35)
рафината :
\jl =

1 J 36

х1 - х
Х1 -

xf

=

определяем профиль концентраций в фазе

\j/(Z) =

l - e a( c - l ) Z

1 се0 ( с -1)
-

'

или

e a( c - l)Z
( с - 1)

се0

_1
-

1

'

( 1 3 .36)

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

а из ( 1 3 .29) и ( 1 3 .36) - в фазе

Г

=

(у Yl ) D
х1 x f) L
_

( -

=

с

экстракта:

Г(Z)

=

e a ( c - l)Z

е а ( 1)
(
- се а с - 1)
_

--

--- ----

1

е а (с - 1) ea ( c - 1)Z
сеа ( с - 1 ) - 1
_

или

( 1 3 .37)

С помощью зависимостей ( 1 3 .36) и (13 .37) можно оценигь оп
тимальные сечения колонны для ввода дополнительных потоков
фаз - сечен ия, в которых концентрации вещества В в соответ
ствующей фазе равны его концентрации во вводимом потоке.
По зависимости ( 1 3 .20) решается эксплуатационная задача определение результирующей эффективности работы имею
щейся колонны при допущении о противоточном движении в
ней фаз в режиме И В . С помощью той же зависимости ре
шается и проектная задача - определение высоты колонны Н,
необходимой для обеспечения заданной эффективности \Jl2 из
уравнения :
1 - \Jl 2
kxF kx Fyдfa H
1
.
а = --ln
L
L
с - 1 1 "V 2
=

=

-

В случае кривой линии равновесия обе задачи можно решить
аналитически, используя прием линеаризации, описанный вы
ше для ступенчатого процесса.
13.5.2. Экстракция при частичной взаимной растворимости
экстрагента и разбавителя

Фазовое равновесие
Ранее рассматривались равновесие и расчет процесса в экс
тракционных системах класса 3 (2-2) 1 , когда в каждой фазе со
держится по два компонента ( Р и В, Э и В) и лишь один из
них (В) переходит из одной фазы в другую.
В техноло гических процессах экстракции не всегда удается
подобрать экстрагент Э , полностью взаимно нерастворимый в
раз бавителе Р; то гда приходится оперировать жидкостными
системами с частичной (ограниченной) взаимной раствори
мостью Э и Р . (Заметим : чаще всего одна из фаз - водная,
другая - органическая .) В этом случае в контакт вступают:
- исходный раствор, состоящий из разбавителя Р и компо
нента В ;
- экстрагент Э, который в общем случае может также
(после регенерации) содержать небольшие количества перехо
дящеrо компонента В и разбавителя Р.
1 1 37

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

В результате разделения фаз путем отстаиван ия образуется два
жидкосrn ых слоя, каждый из которых содержиг все три компо
нента - В, Р и Э. Таким образом, по КФ - классификации в этом
случае экстракционная система относится к классу 3(3-3)3.
По правилу фаз ( 1 0 . 1 ) для таких систем (к = 3 , ф = 2), как и
для ранее рассмотренного случая , число степеней свободы
q> = 3 , причем независимыми управляющими параметрами яв
ляются температура, давление и состав одной из фаз . Так как в
жидкостных системах влиянием давления , как правило, можно
пренебречь, то при задан ных температуре и составе одной из
фаз состав второй фазы определяется однозначно.
Отсутствие постоян.н ых потоков (количеств) инерта делает
нецелесообразным использование относительных концентра
ций компонентов - переходят к абсолютным концентрациям и
потокам фаз . При этом диапазоны изменения концентраций
каждого компонента ограничены (от О до 1 ) , так что концент
рационная диаграмма должна быть замкнутой (см . разд . 1 0 .2 . 1 ) .
Составы трехкомпонентных систем удобно изображать в
треугольной диаграмме (см . разд . 1 0 . 2 . 3 , рис . 1 0.4, б, в), вершины
которой соответствуют чистым переходящему веществу В, раз
бавителю Р и экстрагенту Э . На рис . 13.19,а приведена типич
ная треугольная диаграмма для экстракционных систем класса
3(3-3)3. В рассматриваемом случае компоненты Р и В, В и Э
обладают неограниченной взаимной растворимостью и образуют
соответствующие бинарные смеси, составы которых определя
ются точками на сторонах РВ и В Э . Компоненты Р и Э час
тично растворимы друг в друге, и составы их бинарных смесей
выражаются точками на стороне треугольника РЭ.
Если к чистому разбавителю Р добавить небольшие количества
экстрагента Э, то образуются гомогенные растворы экстрагента в
разбавителе, изображаемые точками вблизи вершины Р на сторо
не РЭ. При увеличении количества добавляемого экстрагента на
ступает насьпцение. Точка Q отвечает насьпценному раствору экс
трагента в разбавителе. Анало гичн ая картина наблюдается при
растворении разбавителя в экстрагенте: здесь отрезок ЭD соответ
ствует области гомогенных растворов, причем насьпценный рас
твор Р в Э изображается точкой D. Отрезок QD - гетерогенные
смеси растворов Q и D : так,смесь произвольного состава А рас
слаивается на насыщенн ые растворы Q и D. Количества обра
зующихся фаз определяются по правилу рычага - в зависимости
от состава гетерогенной смеси А (см. разд. 10.2.4). При этом
D ·AD = Q ·QA .
-

-

Смеси Р и Э составов G1 и G 2 расслаиваются на те же насы
щенные растворы Q и D , но, естественно, в другом количе
ственном соотношении.

1 1 38

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

R

р
а

б

Рис. 13. 19. Треугольные диаграммы для смеси с одной парой оrраничецно рас
творимых ком п онекrов:
постросаm е биноды, б- т рансформация тре уrольной диаrраммы в кривую распре
а
делеЮIЯ (равновесную)
-

Тройные смеси, характеризуемые точками внутри треуголь
н ика РВЭ, моrуг быть гомогенными и гетерогенными. Если к
гетерогенной бинарной смеси состава А добавлять постепенно
вещество В , то вначале (при небольших количествах В) обра
зующиеся трехкомпонентные смеси А 1 , А2 будут гетерогенными.
При дальнейшем добавлении вещества В тройная смесь станет
гомогенной. Граничное состояние смеси, отвечающее исчезнове
нию rраницы раздела фаз, т.е. переход от гомогенной системы к
гетерогенной, изображается rраничной точкой !>( на линии ВА.
Можно взять и другие бинарные смеси на отрезке QD (G1 , G2 и
Т .д.), проделать ту Же оп ерацию И ПОJIУ'ШТЪ rр аничн ые ТОЧКИ G 1 ' ,
G2' и т.д. Соединив все rраничные точки, получим бииодальную
кривую (биноду, бииодаль), которая отделяет гетерогенную область
(под ней) диаrраммы от гомогенной (над ней). Все смеси в гетеро
генной области расслаиваются на две фазы: экстракr Е и рафинат
R
это рабочая область экстракции.
Положение биноды определяется природой компонентов Р,
Э и В и температурой . Бинодаль обычно строят по экспери
ментально наЙденным равновесным составам сосуществующих
фаз при постоянной температуре, т.е. бинодальная кривая яв
ляется изотермой растворимости.
Гетерогенные смеси при достаточной продолжительности
контакта фаз в результате расслоения дают определен ные рав
новесные составы фаз , расположенные на левой и правой вет
вях биноды. Прямые отрезки, соединяющие равновесные со
ставы получающихся фаз, называются конодами ( их называют
также хордами равновесия или кодами). Все смеси, составы ко
торых лежат на какой-либо коноде, расслаиваются на одни и
те же равновесные фазы на концах коноды; количества фаз
зависят от точки расположен ия конкретной гетеро генной сме
си и определяются по п р а вил у рычага. Разные коноды в преде-

1 1 39

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

лах рабочей области, разумеется, не пересекаются. Смесь со
става М (см . рис . 1 3 . 1 9 , а) при равновесном расслоении дает
экстракт Е и рафинат R, лежащие на пересечении коноды
(проходящей через точку М) и биноды. Такой же состав R и Е
получится и из смеси М1 , но количества R и Е будуr иными .
Через точку N проходит другая конода, поэтому рафинат R 1 и
экстракт Е1 имеют другие составы.
Протяженность конод в рассматриваемом случае (см .
рис . 1 3 . 1 9, а) уменьшается с повышением концентрации ве
щества В; в точке К на бинодалъной кривой, называемой кри
тической точкой растворимости или вершиной биноды, коноды
стяrnваются в точку: оба слоя жидкости (экстракт и рафинат)
имеют одинаковый состав. Обычно бинодальная кривая не
симметрична относительно вершин треугольника, а ее вершина
не обязательно совпадает с rеометрической вершиной биноды.
Ветвь биноды KQ, расположенная ближе к вершине Р, назы
вается ливней рафинатов; ветвь KD , находящаяся ближе к вер
шине Э, - линией экстрактов.
В rетерогенной области диаграммы располагается бесчис 
ленное множество конод, причем в общем случае они не па
раллельны, а изменяют свой наклон по мере изменения кон 
центрации вещества В в rетеjюгенной смеси.
Равновесные данные для тройных систем изображают также
в диаграмме у-х как зависимость между концентрациями В в
равновесных растворах. На рис. 1 3 . 1 9, б показана трансформа
ция треугольной диаграммы в диаграмму у-х: каждой паре
точек R и Е на кон цах коноды в треугольной диаграмме соот
ветствует одна точка Р на кривой равновесия в диаграмме у-х .
Равновесная кривая строится по экспериментально найденным
конодам . С помощью этой кривой по заданной точке на линии
экстрактов (или рафинатов) легко найти равновесную точку на
линии рафинатов (или экстрактов), т.е. построить промежуточ
ную коноду.
Ниже рассматриваются только трехкомпонентные системы
типа показанных на рис . 1 3 . 1 9 , а,б - с одной парой ограничен
но растворимых компонентов Р и Э . На практике встречаются
также системы с иной конфигурацией бинод · . На рис . 1 3 .20, а,б
в качестве примера показаны бинодальные кривые для систем
с двумя парами ограниченно растворимых компонентов. Здесь
имеются две гомоrенные области, разделенные одной гетеро
rенной (рис. 1 3 .20, а) , ил и две отделенные одна от другой rете
роrенн ые и одна гомогенная области (рис . 1 3 .20, 6) .
С изменением температуры вид диаграмм фазового равнове
сия меняется, при этом возможен переход диаграмм от одного
-

•

Подробнее см. (2, 4, 7-9 ) .

1 140

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

в

э
Рис. 13. 20. Типы равновесных диаrрамм для систем с двумя парами оrраниченно
растворимых компонентов:
а
с двумя гомоrсННЬ1Ми и одной rcтeporetn1oй обласrями, б с двумя rетсроrсННЬIМИ
и опной ГОМОГСШ!ОЙ обласrями
-

-

вида к другому. С увеличением температуры обычно увеличи
вается взаимная растворимость растворителя и экстрагента,
следовательно, уменьшается гетерогенная , т.е. рабочая, об
ласть экстракции. При этом снижаются возможности достиже
ния высокой степени извлечения в процессе экстра кц ии и воз
растают расходы на регенерацию экстрагента. Поэтому процес
сы экстракции стремятся проводить при невысоких (умерен 
ных) температурах.

Некоторые особенности треугольной диаграмм ы
для процессов экстракции
С помощью треугольной диаграммы ведуг расчет процессов
однократной, порцион ной и противоточной экстракции при
ограниченной взаимной растворимости разбавителя и экс
трагента. Нелинейность двух составляющих массопереноса равновесия и материального баланса (изменяющиеся абсолют
ные количества или потоки фаз) - предопределяет в данном
случае графоаналитический метод расчета.
Хотя экстрагент может после регенерации содержать не
большие количества вещества В и разбавителя Р, далее для
простоты будем рассматривать случай, когда исходный раствор
обрабатывается чистым экстрагентом (точка Э).
Как методы , так и результаты расчета во многом сходны для
периодического и непрерывного проведения процессов; но в
первом случае оперируем количествами, а во втором - пото
ками фаз и компонентов. В дальнейшем анализ ведется на
примере непрерывного процесса.
Во всех случаях предполагается идеальный контакт фаз, а
также полная их сегрега ция (при ступенчатом исполнении экс
тракционной аппаратуры - полное расслоение уходящих фазо
ВЬIХ потоков) .
Исходные растворы (некоторая точка М на рис . 1 3 . 2 1 ) ,
представляющие собой смеси разбавителя Р и вещества В , ле-

1 141

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

в

Рис. 13. 21. Изображение операций сме
шен ия и равновесного расслаивания в
треугольной диаrрамме

жат на стороне РВ концентра
ционного
треугольника.
Из
свойств треугольной диаграммы
(см . разд. 1 0 .2 . 3 , 1 0 .2 .4) следует,
что составу смеси, получаемой
при смешивании исходного раствора М с чистым экстрагентом
о э
Р Q
Э, отвечает точка N на прямой ,
соединяющей вершину Э с точ
кой М. Положение точки N на прямой МЭ определяется соот
ношением масс (потоков) исходного раствора и экстрагента в соответствии с правилом р ычага 1 или 1 1 рода:

Э · NЭ = м.мN и м.мэ = (М + Э) -NЭ .
( 1 3 .38)
В ( 1 3 .38) символы Э и М обозначают состав (положение точек) ,
а Э и М - массовые потоки экстрагента и исходной смеси.
Полученная гетерогенная смесь (точка N) находится на ка
кой -то коноде (RE) и потому расслаивается на равновесные
фазы экстракта Е и рафината R.
Очевидно, что для осуществления процесса экстракции
смесь N при смешении исходного раствора и экстрагента
должна попасть в гетерогенную область диаграммы, т.е. прямая
МЭ должна пересекать эту область. Этому условию отвечают
лишь те исходные растворы, для которых линия смешения М Э
лежит ниже касательной к бинодальной кривой из вершины
треугольника Э. Для расположен ных выше линий смешения
МЭ экстракция невозможна при добавлении любых количеств
экстрагента к исходной смеси : не будет стадии расслаивания .
Кроме того , как следует из диаграммы, для реализации про
цесса экстракции из исходного раствора М количество добав
ляемого экстрагента должно быть таким , чтобы смесь N попала
в гетерогенную область - в промежуток между точками N 1 и
N2 на отрезке М Э . В точке N2 (пересечение прямой смешения
М Э с левой ветвью би ноды - линией рафинатов) получится
раствор экстрагента в исходной смеси; этой точке соответству
ет наименьший (н/м) расход экстрагента:
Эн;м = М ·

MN 2
=-

N2Э

Точка N 1 (пересечение МЭ с правой ветвью биноды - линией
экстрактов) представляет собой раствор исходной смеси в экс
трагенте, этой точке соответствует наибольший (н/б) расход
1 1 42

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

экстрагента:

Эн/б

= М·

MN 1
N 1Э

В обоих этих предельных случаях образуются гомогенные сме
си, так что процесс экстракции невозможен . Для осуществле
ния экстракции поток Э, добавляемый к потоку исходного рас
твора М, должен соответствовать некоторому промежугочному
значению Эн;м < Э < Эн/б .

Однократная экстракция
Процесс однократной экстракции в треугольной диаграмме
показан на рис . 1 3 .22, стилизован ная схема - на рис . 1 3 .23 .
Jipи смешении М кг/с исходного раствора с Э кг/с экс
трагента образуется N кг/с гетерогенной смеси, из которой
после равновесного расслаивания (ко нтакr фаз полагаем идеаль
. ным) получаются R кг/с рафината и Е кг/с экстракrа:

N= M+ Э = R + E.

Условиями задачи заданы исходный раствор (состав и по
ток) и треугольная диаграмма (бинода, поле конод).
В проекrной задаче чаще всего дополнительно известен тре
буемый состав рафината (концентрация в нем компонента В);
надо рассчитать необходимый поток экстрагента. В эксплуата
ционной задаче заданы потоки исходного раствора и э кс
трагента; надо определить составы экстракrа и рафината.
В задаче проектироваиия поток Э (для непрерывного процес
са) находится из следующих соображений. Точка смеси N ле
жит на прямой МЭ. Точка R (она задана) получается из пока
неизвестной точки N при расслоении по коноде RE, значит,
точка N лежит и на этой коноде. Таким образом, точку N
можно найти как точку пересечения прямых МЭ и RE. А те
перь по правилу рычага I рода при известном потоке исходной
смеси М легко отыскать поток Э :

Э-NЭ = M-MN ,

и Э = м.

МN

NЭ

.

Далее определяются потоки рафината R и экстракrа
почтительнее по правилу рычага I I рода:

E-RE = N N R ;

R · RE

= NNE

.

( 1 3 .39)

Е-

пред
( 1 3 .40)

В задаче эксплуатации первоначально находим точку N, по
скольку составы (и потоки) М и Э известны . Затем через точку
N проводим коноду, которая дает составы R и Е на биноде;
потоюt R и Е определяются по ( 1 3 .40) .
1 1 43

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Puc. 1З. 22. Изображение процессов одно

в

краnюй экстракции и реrенерашш экс
ч>аrеmа в ч>еуrолъной диаграмме

Рис. 1.1. 23. Стилизов анная схема одн о 
кратной экстракции п р и частичной
взаимной растворимо сти экстрагента и
р азбавителя

Заметим , что задан ие состава R в проектной задаче и потока
Э - в экс riлуатационной ведется с учетом экономических со

ображений, в том числ е - затрат на регенерацию экстра гента
из рафината и экстракта .
При полной отгонке (например, в ректификационной ко
лонне) экстрагента из экстракта Е получается чистый экс
трагент (его массовый поток - Э ') и сконцентрированный
раствор М' вещества В в разбавителе . При полной очистке ра
фината R от экстрагента получается чистый экстрагент Э " и
обедненный извлекаемым компонентом В раствор М " . Составы
полученных растворов М' и М" находятся по правилу разделе
н ия (вычитан ия) смесей - проведением прямых из вершины Э
через точки R и Е до пересечения со стороной РВ концентра
ционного треугольника (см . рис . 1 3 . 2 1 ) . Количества отогнанн ых
экстрагента Э ' и Э " и полученных растворов М ' и М " можно
определить из соотношений типа ( 1 3 .38) в соответствии с пра
вилом рычага. Здесь удобнее использовать рычаг 1 1 рода:
М'· М ' Э

=

Е- Е Э , и М'

=

ЕЭ
Е- М

'Э

'

Э
М " · М " Э = R· RЭ , и М " = R· R
.
М"Э
В итоге в результате эк<..-тракции и реrенерации экстрагента произ
водится разделение исходной смеси М на конечные смеси - обога
щенную м· и обедненную М" КОМПОНе}ffОМ в. При этом потоки ко
нечных и исходной смесей также связаны правилом рычага:

М '· М ' М " = М· М М "

м. М М ' . ( 1 3 .4 1 )
и М "· М " М '
Легко проверить, что из зависимостей ( 1 3 .4 1 ) вытекает общий
баланс :
М = М' + М " .

1 144

=

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Количества (потоки) экстрагента, которые необход имо из
влечь (например, отоmать) из экстракта Э ' = Е М' и рафината
Э " R М " , моrут бьпь также найдены по правилу рычаrа из
соотношения соответствующих отрезков на линиях ЭМ' и ЭМ" .
Обычно однократная экстраКция не дает веществ высокой
чистоты - достаточно концентрированного раствора вещества
В в разбавителе М' и достаточно чистого (свободного от В)
разбавителя М " .
Порционная экстракция
Для более эффективного разделщшя применяют порцион
ную экстракцию. Стилизованная схема процесса приведена на
рис. 13.24, расчетная процедура в треугольной диаграмме пока
зана на рис . 1 3 .25.
Пусть требуется получить максимально чистый разбавитель.
Для этого процесс проводится ступенчато, и имеющийся ис
ходный (например, свежий) экстрагент с расходом Э разде
ляется на порции Э1 , � . . , Эп, которые последовательно
контактируют с исходным раствором и далее - с рабочими
рафинатами.
Последовательность технологических операций и расчетных
процедур будем рассматривать на примере трехпорционного
(трехступенчатого) процесса (п 3). Напомним: в каждой сту
пени предполагается идеальный контахт фаз.
Первая порция экстрагента Э1 (точка Э) смешивается
(контактирует) с исходным раствором. Состав гетерогенной
смеси в первой ступени определяется точкой N 1 (см.
рис. 13.25). После расслоения получаются равновесные экс
тракт Е 1 и рафинат R1 , к которому добавляется вторая порция
экстрагента Э2 (та же точка Э). Получаемая во второй ступени
смесь N2 расслаивается на равновесные фазы экстракта Е2 и
рафината R2. Рафинат R2 контахтирует с третьей порцией экс
трагента Э3 (также точка Э) с образованием гетерогенной сме-

=

-

"

=

Рис. 13.24. Стилизованная схема порционной экстракции

1 1 45

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

в

р

э

Puc. JJ. 25. Изображение процессов порционной экстракции и регенерации экс
траrеIТТа в треугольной диаграмме

си Nз, при расслаивании которой получаются равновесные
экстракт Ез и конечн ый рафинат Rз
Rк.
После отгонки экстрагента из конечного рафината получа
ется разбавитель М" с малым содержанием компонента В. Из
каждого экстракта Е 1 , Е1 и Ез извлекается экстрагент Э; оста
ются бинарные смеси М 1 ' , М2' и Мз' . При их объединении по
лучается смесь В и Р, отвечающая точке М' (на рисунке не по
казана) . Альтернативный вариант: предварительно объединя
ются экстракты Е 1 , Е1 , Ез и после выделен ия экстрагента из
этой смеси получают раствор М', обогащенный компонентом В .
Задача эксплуатации для рассматриваемой схемы решается
просто : известны исходный раствор М и число ступеней экс
тракции с определенн ыми порциями экстрагента Э1 , Э2 и Эз .
Положение точек N 1 , N2 и N3 определяется из соотношения
потоков фаз по правилу рычага. Потоки растворов (фаз) и ге
терогенных смесей, получаемых в каждой ступени экстракции ,
находятся по зависимостям типа ( 1 3 .40) :
=

R1

R1

Rз

=

=

=

N 1 E1
R 1 E1

N1 · = , Е1

N1 E2
�
R 1 E2

N1 ·

= ,

Nз ·

=

N3 E 3
R3E3

,

Ез

=

=

=

N1R1
R 1 E1

N1 ·

= ,

N1 ·

N1R2
R 1 E2

Nз ·

= ,

N3 R 3
R 3 E3

N1

=

Э1 + М;

.
, N1 - Э2 + R1 ,

Nз

=

Эз + R1 .

Далее аналогичным образом определяются потоки получаемых

1 1 46

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

в итоге экстракции растворов М' и Лf:
R зЭ
М' = Rз .
'
М"Э

М1 ' = Е1 ·

Е �Э
МiЭ

,

М2'

=

Е;,

·

Е 2Э

м2 э

,

Мз'

=

Ез ·

ЕзЭ

мзэ

.

Очев идно, что М = М1' + М2' + Мз'·
Решение задачи проектирования - отыскание числа ступе
ней (разбиение определенного количества экстрагента на пор
ции) , например, для получения требуемого конечного состава
М" - сложнее. Для этого используют метод подбора: задав
шись числом ступеней и распределением экстрагента ( Э 1 ,
� ' " . , Эп) , на концентрационной диаграмме проводят по
строения, характерные для эксплуатационной задачи, и нахо
дят состав М 1 " . Этот состав сравниваI<УГ с заданным М " : если
кон центрация вещества В в М 1 " не превышает требуемой
(отвечает М " ) , то принятое число порций и выбранные потоки
Э1 , Э2 , " . , Эп - приемлемы . Если нет, то увеличиваI<УГ число
порций, на которое делится весь поток экстрагента
( Э = Э1 + Э2 + " . +, Эп) , и находят новый состав М2 " . Такие
операции продолжают до получен ия требуемого М". При этом
может оказаться, что заданный общий поток экстрагента Э не
позволяет получить требуемый состав М" ни при каком числе
порций при любом его разбиении на Э;. В этом случае следует
увеличить общий поток экстрагента Э или перейти к противо
точной схеме экстракц ии.
Если требуется получить максимально чистый компонент В ,
то разбиению на порции подвергаI<УГ исходн ый раствор , и эти
порции последовательно контактируют с экстрагентом.
Порционная экстракция выгоднее однократной: при одина
ковом общем количестве экстрагента деление его на порции
приводит к более высокой степени извлечения .

Непрерывная противоточная экстракция
Этот процесс является самым выгодным с точки зрения ис
пользования движущей силы и повышения степени извлече
н ия . Его проводят в колонных аппаратах или батарее смеси
тельно - отстойных экстракторов. Схемы противоточного про
цесса экстракц ии со ступенчатым и непрерывным контактом
фаз показаны на рис . 1 3 .26.
П остроение полюса . При полной взаимной нераствор им ости
экстрагента и разбавителя (см. разд . 13.5. 1) по ступеням или
высоте экстрактора изменялась лишь концентрация вещества В
в фазах экстрагента и разбавителя, а их потоки •( Э и Р) остава-

1 147

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

а

R.x

Е,у

б
Рис. 13. 26. Расчетные схемы противоточной экстракции со ступенчатым (а) и
непрерывным (6) кошактом фаз

лись неизменными. При этом геометрическое место точек со
пряженных концентраций вещества В в фазах в различных се
чениях (ступенях) аппарата в диаграмме у-х описывалось пря
мой рабочей линией. Эта прямая вкупе с линией равновесия
использовалась при решении технологических задач (проект
ной и эксплуатационной).
При ограниченной взаимной растворимости экстрагента и
разбавителя в ходе процесса происходит изменение (от ступени
к ступени или по высоте экстрактора) потоков и содержания
всех трех компонентов в фазах: переходящего В, разбавителя Р
и экстрагента Э . Здесь для решения проектной и эксплуатаци
онной задач тоже наряду с равновесными данными (бинода и
поле конод) необходимо располагать связью сопряженных
концентраций. Эта связь необходима при технологическом
расчете непрерывной противоточной экстракции как со сту
пенчатым, так и с непрерывным контакто м фаз .
Для установления указанной связи рассмотрим каскад сту
пеней СОЭ (рис . 1 3 .26 , а), в котором с одного конца подводит
ся исходный раствор Rii и выводится э кстракт Ек, а с друго
го - подводится экстрагент � и выводится рафинат Rк · Разу
меется, с тем же успехом можно рассмотреть экстракционную
колонну (рис . 1 3 .26,6) с подачей легкой фазы снизу и тяже
лой - сверху (на рисунке это исходный раствор) .
Материальные балансы составим для контура, ограниченно
го с одной стороны произвольным (промежуrочным) сечением
колонны или каскада (текущие потоки и концентрации R, х и
Е, у), а с другой - те м концевым сечением, в котором из
вестны концентрации в обеих фазах. Концентрации в любом
сечении (лромежуrочном, концевых) и будут сопряженными;
1 148

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

р

Рис. 13. 27. Доказательство наличия полюса для противоточной ЭКС1ракции

связь между ними для экстракционного процесса при оrрани
ченной взаимной растворимости Р и Э предстоит установить.
Начальные кон центрации известны для обоих входных пото
ков; одна из конечных концентраций задана - чаще всего для
выходящего рафината. В этом случае контур замыкается на
концевое сечение с потоками E.i и Rк. Тогда для выбранного
контура:
- по потокам фаз
1;' + R - Rк Е = О·'
-'-'}-[
- по потокам переходящего вещества В
-

ЕнУн + Rx
Отсюда:

1;'
-ин

ЕнУн

-

-

-

Еу = О .

= Е R = const = S
RкХк = Еу Rx = const = sXsв '

-

Rк

где S
некий расчетный поток; xsB
чающая соотношению ( 1 3 .43).
-

RкХк

-

-

-

'

( 1 3 .42)
( 1 3 .43)

гипотетическая концентрация В, отве

Таким образом, величины Е и R, Еу и Rx изменяются от се
чения к сечению (от ступени к ступени), но их разности оста
ются неизменными. Это означает, что в установившемся
(стационарном) процессе не может происходить уменьшения
или увеличения суммарного потока фаз или компонентов в
каком-либо сечении или в какой-либо ступен и экстра:кrора.
Через некую пару точек (скажем, Е1 и R1 на рис. 1 3 .27) со
пряженных концентраций, т.е. относящихся к потокам в каком
либо сечении колонны или в сечении между ступенями каскада
СОЭ, может быть проведена прямая, именуемая лучом . Лучи
можно провести для любого сечения экстра:кrора (например ,
1 1 49

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

отмеченного точками Е2 и R2 на рис . 1 3 .27) , в том числе и для
крайних (концевых ) , замыкающих экстращионную установку.
Поделив ( 1 3 .43) на ( 1 3 .42) и принимая во внимание посто
янство числителя и знаменателя, имеем:

здесь у и х -

Еу - Rx
E-R

=

Sx�
S

=

хв
s

=

const '·

( 1 3 .44)

концентрации компонента В .
Линия постоянных концентраций компонента В
Хs в =
= const - прямая, параллельная основанию треугольника РЭ
(см. рис . 1 3 .27) . На этой линии, согласно ( 1 3 .44), заканчиваются
лучи, проходящие через любую пару сопряженных концентраций;
пусть это
линия 1
(о ее расположении - см. ниже).
Выражение ( 1 3 .42) записано безотносительно к конкретному
компоненту ( В , Р или Э), а зависимость типа ( 1 3 .43) справед
лива для любого компонента смеси - отнесем ее теперь к раз
бавителю Р . Тогда•
-

Ey - Rx
E-R

--- = const =

у_р.·

( 1 3 .44а)

�

здесь у и х -

концентрации уже компонента Р.
Линия Xs P = const - прямая, параллельная стороне ВЭ;
пусть она находится в положении 2
(см . рис . 1 3 .27). На этой
линии тоже заканчиваются лучи, проходящие через любую пару
сопряженных концентраций.
Это означает, что лучи, проходящие через точюt сопря
женных кон центраций на ветвях рафинатов и экстрактов (R 1 и
Е1 ; Ri и Е2 и т.д.), одновременно принадлежат линиям 1
и
возможно только для точюt пересечения этих ли
2. Такое
ний; точка S (Xs 8 , Xs P , Хsэ) называется полюсом (см . рис . 1 3 .27).
Расположен ие его зависит от составов и потоков фаз.
Разумеется, анализ можно выпОJШить и для компонента Э. Однако в :этом
нет необходимости , поскольку х.э = l
х. в
х.Р определяется однозначно по
XsB и х.Р .

-

-

Для геометрического толкования зависимостей ( 1 3 .42)
( 1 3 .44) рассмотрим противоточную экстращию на кон центра
ционной диаграмме. Из ( 1 3 .42) следует:

Rк + S, Е = R + S, Е1 = R1 + S, � =
= R2 + S и Ек = Rн + S.
( 1 3 .45)
Значит, если смешать потоюt Rк и S, то получим поток смеси
состава Ен, смешение nотоков S и R дает поток Е и т.д . И в
каждом сечении сопряженные потоки фаз связаны зависиЕн =

• Аналогичный вывод для разных концентраций
разд. 1 1 .5.4.

l l 50

: подробно

приведен

в

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

мостью ( 1 3 .45), в которую наряду с двумя переменными реальны
фаз входит третий постоянный расчетный поток S.
Со гласно правилу смешения все три точки Е , R и S для любого
произвольного сечения лежат на одной прямой . По высоте
(ступеням) экстрактора сопряженные величины Е, у и R, х из
мен.яются ; но поскольку значение S и точка S неизменн ы для
всех сечений аппарата, то все прямые, на которых лежат упо
мянутые точки, являются лучами , исходящими из одной точки
S
полюса. А проведенный анализ по своей сути является
доказательством существования полюса.
Выражения ( 1 3 .42) и ( 1 3 .43) можно трактовать в аспекте раз
деления смесей в некотором рабочем сечении: экстракт состава
у (поток Е) разделяется на ра шнат состава х (поток R) и неко
торый продукт состава S (Xs , XsP, Хsэ) - поток S. Со гласно
правилу рычага 1 1 рода (если "точку опоры " разместить в полю
се S), справедлива связь:

ми потоками

-

�

E- ES

=

R· R S .
поток Е больше,

( 1 3 .46)
На рис . 1 3 .27 ES < RS , з начит,
нежели R. Не
равенство Е > R отвечает расположению полюса справа от тОч
ки экстракта. При обратном соотношении (Е < R) будет ES > RS ,
и полюс расположится слева от точки рафШiата. В этом случае
соотношения типа ( 1 3.44) следует представлять в виде
Rx - Ev

--'-0)'

R-E

= const

=

Xs

.

( 1 3 .44б)

Наконец, при Е = R в соответствии с ( 1 3 .44) полюс (т.е. точка
пересечения лучей) уходит в бесконечность. Эrо означает, что
все лучи параллельны меЖду собой.
Итак, на концентрационной диаграмме сопряженные соста
вы фаз изображаются точками, лежащими на биноде и лучах,
пересекающихся в точке (полюсе) S. На этом свойстве диа
граммы основано решение технологических задач. В рассматри
ваемом случае проще решается задача проектирования - опреде
ление необходимого числа ступеней каскада СОЭ или высоты
колонны. Эксплуатационная задача решается подбором.
Определение полюса . Для решения обеих задач предвари
тельно необходимо найти полюс . Для этого требуется провести
два любых луча и зафиксировать точку их пересечения . В обоих
и экс
случаях заданы концентрации исходной смеси (т. М )
трагента (т. Э) , а также поток исходной смеси (рис . 1 3 .28). Пусть
известен и поток экстрагента (задан в задачах эксплуатации;
находится с помощью техн ико-экономических расчетов в зада
чах проектирования) . В задаче проектирования чаще всего еще
задан состав конечной смеси - рафината после выделения из
него экстрагента М" (или Rк) . Тогда один луч определен : он
1 151

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

в

s

Рис. 13. 28. К

определению состава конечного экстракта (точка

Ек)

проходит через то концевое сечение экстрактора, где встреча
ются потоки фаз Rк и Э. Второй луч отвечает другому конце
вому сечению, где проходят потоки фаз М и Ек; для определе
ния этоrо луча следует установить состав конечноrо экстракта
(точка Ек, концентрация компонента В
Ук)·
Определим этот состав из следующих соображений. В соот
ветствии с правилом рычага наЙдем точку материальноrо ба
ланса N по потокам фаз М и Э, поступающим с противопо
ложн ых концов в колонну (или каскад СОЭ) . Но та же точка N
(смесь входных растворов) должна характеризовать и потоки,
выходящие (тоже с противоположных сторон) из экстракцион н о й установки:
-

N = М + Э = Rк + Ех

и

И ными словами, смесь N , получаемая результирующим смеше
нием М и Э, должна в конечном итоге разделиться на Rк и Ек.
Значит, точка N, лежащая на прямой МЭ, в то же время при
надлежит и прямой Rк Ек, т.е. является точкой пересечения
этих прямых. Тогда дл я отыскания точки Ек достаточно про
вести прямую RкN и продолжить ее до линии экстрактов: точка
пересечения с бинодой и дает концентрацию Ук, отвечающую
потоку Ек. А теперь через точки М и Ек можно провести вто
рой луч, и полюс построен (рис. 1 3 .28).
Потоки Rк и Ех мoryr быть наЙдены по правилу рычага
по отрезкам внутри биноды:

Rк
или

1 1 52

вне ее :

·

R к Е к = N · N E к и .Ех · R к Е к = N · NR к

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

в

s

Рис. 13. 29.

тракции

Определение числа теоретических ступеней при противоточной экс

Подчеркнем : отрезок R к Е к представляет собой линию ре
зультирующего разделения. Он не имеет никакого отношения к
конодам - линиям равповесного разделения: ведь потоки, ухо
дящие с разных концов противоточной экстракционной уста
новки, не находятся в непосредственном контакте, значит, не
могут быть равновесными.
Не исключена ситуация, когда одновременно заданы концентрации компо
некrа В в фаза.х - Хк и Ук· Тогда поЛIОс сразу находят как точку пересечения
двух известных лучей. Но линии резулътирующеrо смешения МЭ и результи
рующеrо разделения RкЕк все равно необходимы - для определения не заданно
rо в этом случае потока экстраrекrа.
Определение числа теоретических ступеней. После нахожде
ния полюса можно приступить к определению числа теорети
ческих ступеней . Примем, что в каждой ступени батареи СОЭ
(см . рис. 13 .26,а) достигается идеальный контакт фаз и затем
происходит полное (равновесное) расслаивание.
Уходящий из экстракционной установки экстракт Ек (точка
на ветви экстрактов биноды) находится в равновесии с поки
дающим эту (последнюю по ходу движения фазы экстракта)
ступень рафинатом R1 (х1 ), а значит, лежит (рис . 13 .29 ) на
другом конце коноды (точка на ветви рафинатов - фиксируем
ее). Сопряженный с R1 состав экстракта Е 1 (у1 ) лежит на ветви
экстрактов биноды и на луче, проходящем через полюс и точку
состава R1 , - фиксируем точку Е 1 .
П оток рафината R2 (см. рис. 13.26,а) уходит с предпоследней
(по ходу фазы экстракта) ступени в равновесии с Е 1 ; состав
этого рафината находится на другом конце коноды E1 R2, про
ходящей через точку Е1 (см. рис . 13 .29). Сопряженный с R1 со-

1 153

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

в

Рис . JЗ.ЗО. К

определению минимального потока экстраrе!ffа

став экстракта Е2 (см . рис. 13.26, а) есть точка пересечения лу
ча, начинающегося в точке R2, и ветви экстракrов биноды (см .
рис . 1 3 .29).
Построения конода-луч-конода-луч- ... продолжаем до
тех пор, пока очередная конода не пересечет крайний луч
Rк - Э - S (либо случайно попадет в точку конечного рафи
ната Rк). Число конод соответствует числу операций расслаива
ния - это и есть число теоретических ступеней.
Для заданной степени разделения количество ступеней за
висит от соотношения потоков экстрагента и исходного рас
твора. Это соотношение согласно правилу рычага (1 рода) вы
ражается отношением отрезков:

Э

М

MN

= NЭ

С умень ш ением расхода экстрагента (точка материального ба
ланса N перемещается по прямой МЭ влево) растет концент
рация экстракта (точка Ек перемещается по линии экстрактов
вверх); но при этом увеличивается число ступеней, необходи
МЬIХ для получения рафината заданного состава.
Как и в случае полной взаимной нерастворимости разбави
теля и экстрагента, сушествует некий минимальный поток экс
трагента, при котором заданная концентрация Хк может быть
достигнуга при бесконечном числе ступеней. Минимальному
удельному расходу экстрагента (соотношению потоков Э/М)
соответствует такое положение точки N , при котором кон ода
fкR1 совпадает с лучом MS: сопряженные концентрации в сече
нии входа исходного раствора - равновесны. Тогда построение
луч-конода-луч- . . . не сдвинется с верхнего луча MS, и для
достижения необходимого состава рафината потребуется бес
конечное число ступеней. Описанная ситуация иллюстрируется
на рис . 1 3.30.
С увеличением расхода экстрагента (точка N перемещается
по прямой МЭ вправо) падает концентрация экстракrа (точка

1 1 54

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

в

Рис. 13. 31. Определение локальной движущей силы в треугольной диаrрамме при
расчете числа единиц переноса а

Ек перемещается по линии экстрактов вниз и вправо) и
уменьшается необходимое число теоретических ступеней.
Рабочий расход экстраrевта выбирается на основе мини
мального с помощью технико-экономического расчета - пуrем
минимизации суммарных (капитальных и эксплуатационных)
затрат (см . разд. 1 0.7.2). При этом должны быть учтены затраты
на всех технологических стадиях - экстракции, регенерации
экстрагента из экстракта и рафината.
После определения числа теоретических ступеней (11т) мож
но найти требуемое число реальных ступеней смесительно
отстойного экстрактора (п) - с учетом поправки на отличие
реального процесса от идеального . Переход от 11т к п проводит
ся с помощью экспериментально устанавливаемого коэффици
ента полезного дейстния ступени Т\ с (см . разд. 1 0 . 1 2 .4) :

п = 11т /Т\с ·

Для смесительно-отстойных экстракторов обычно
с ситчатыми тарелками Т\с " О, 1 + 0,3.

Т\с

"

0,8

+

0,9

; Д1IЯ

колонн

Высота колонного экстрактора с непрерывным контактом фаз .
Для расчета высоты колонного экстрактора с непрерывным
контактом фаз необходимо знать высоту h3, эквивалентную
теоретической ступени · (ВЭТС), или высоту единицы переноса
(ВЕП) he. Расчет по ВЭТС базируется на lfт. Расчет с помощью
ВЕП требует определения числа единиц переноса а, обеспечи
вающего необходимое разделение. Далее: высота рабочей зоны
колонны н = 11тhэ или н = ahe.
Число единиц переноса в принципе определяется тем же
способом, что и в случае полной взаимной нерастворимости
экстрагента и разбавителя, - в предположении о полной сег
регации фаз при противоточной непрерывной экстракции .
Техника расчета а, естественно, модифицируется соответствен-

• Оrраниченность и недостатки метода

ВЭТС

обсУЖ11е ны в разд. 10. 12.5.
1 1 55

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

но переходу от диаграммы у-х к треугольной, но в основе рас
чета остается локальная движущая сила (х - .хР) .
В концентрационном треугольнике (рис . 1 3 . 3 1 ) концентрация
х изменяется от Хн до Хк . Любому произвольному значению х
отвечает сопряженное (находящееся на данном луче) значение
равновесное (на одной коноде) значение .хР < х.
у, а тому
Проведя произвольно несколько лучей в диапазоне от Хн до Хк
(включая и оба крайних луча) , с помощью соответствующих
конод получаем достаточное количество пар взаимосвязанных
величин х и .хР. По локальным разностям (х - .хР) наЙдем зна
чение а, используя зависимость ( 1 3 . 1 9) .
-

Л ИТЕРАТУРА к главе 1 3
1 . Броунштейн Б. И., Железняк. А. С. Физико-химические основы жидкостной
экстракции. Л . : Химия, 1966. 3 1 8 с.
2. Гельперин Н. И. Основные процессы и аппараты химической технологи и .
М . : Химия, 1 9 8 1 . 8 1 2 с.
3 . Гельперин Н. И., Пебалк. В.Л. , Костанян А.Е. Структура потоков и эффек
тивность колонных аппаратов химической промьШIЛенности. М . : Химия, 1977.
264 с.
4 . Зюлк.овск.ий З. Жидкостная экстракция в химической промьшшенности :
Пер . с польск Под ред. П . Г. Романкова. Л . : Госхимиздат, 1963. 480 с.
5. Касаткин А.Г. Основные процессы и аппараты химической технологии.
М.: Химия, 1 97 1 . 784 с.
6 . Логсдейл Д.Х., Лоуэс Л. Последние достижения в области жидкостной экс
тракции, гл. 3 "Промьшшен ное экстракционное оборудование" Под ред.
А. Хансона: П ер . с англ. М.: Химия, 1974. 448 с.
7 . Пратт Г. Р. К. Экстракция жидкость -жидкость в теории и практике В
кн . : Жидкостная экстракция : Пер. с англ Под ред. А.Г. Касаткина. М . :
Гос
химиздат, 1 9 5 8 . 1 5 5 с.
8 . Трейбал Р. Жидкостная э кстракция: Пер. с англ. П од ред. С.З. Кагана. М . :
Химия, 1966. 724 с .
9. Фрэнсис А. Равновесие жидкость-жидкость: П ер . с англ. П од ред.
Д.С. Циклиса. М.: Химия, 1 969. 238 с.
1 0 . Шк.оропад Д Е., Лыск.овцев И. В. Центробежные жидкостные экстракторы.
М.: Машгиз, 1 962. 2 1 6 с.

/

/

/

/

/

/

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Глава 14
АДС ОРБ ЦИЯ

Ад сорбцией называется избирательное по глощение одного
или нескольких компонентов из газовой или жидкостной смеси
твердым поглотителем - адсорбентом (ин огда используюг более
широкий термин - сорбент). П оглощаемый компонент (ПК) ,
содержащийся в сплошной среде (газе, жидкости) именуется
адсорбтивом, содержащийся в сорбенте - адсорбатом. Адсорб
ция чаще всего (не всегда) применяется при малых концентра
циях адсорбтива в и сходной смеси, ко гда требуется возможно
более полное его поглощение. При высоких исходных кон
центрациях адсорбти ва процессу адсорбции нередко предше
ствуют другие поглотительные процессы (например, абсорб
ция), с помощью которых концентрация ПК в сплошной среде
снижается до достаточно низкой величины, после чего и ведет
ся глубо кая доочистка газа, жидкости методом адсорбции.
Адсорбция используется для очистки газовых (жидких) сме
сей от . нежелательной примеси или для вЫделения этой приме
си в качестве целевого продукга; оптимальной является реали
зация совместно обеих целей, т.е. приближение технологии к
безотходной. Благодаря селе :ктивности поглощения р азличных
компонентов адсорбция является одним из эффе:ктивных про
цессов разделения. Вместе с тем она составляет одну из стадий
проведения гетероге нной химической реакции - каталити
ческой или некаталитической. В тех случаях, когда сама реак
ция идет быстро, а пропускная способность адсорбционно
десорбционной стадии мала, адсорбция (или десорбция) может
выступать в роли лимитирующей стадии процесса химического
превращения в целом.
После осуществления адсорбции, как правило, производят
десорбцию адсорбата. Это позволяет извлечь из сорбента П К
(нередко - целевой продукг) и в новь использовать освобож
денный от него сорбент: промышленные сорбенты чаще всего
очень дороги , так что одноразовое их использование экономи
чески невыгодно, иногда - просто недопустимо. После де
сорбции обычно необходимо провести активацию сорбента,
чтобы восстановить его адсорбционные свойства. Стадии де
сорбции и активации адсорбента (вместе) представляюr собой
1 1 57

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

его реrеверацию : после нее сорбент готов к повторному исполь
зованию в процессе адсорбции .
Процессы адсорбции, десорбции, активации могут осущест
вляться в непрерывном режиме . - тогда каждый из них прово
дится в отдельном аппарате, а адсорбент перемещается из ад
сорбера в десорбер, далее - в регенератор (активатор) и снова
в адсорбер. Адсорбция - один из немногих процессов, когда
полунепрерывные режимы (неподвижный слой сорбента и дви
жение через него потока сплошной среды) вполне конкуренто
способны с непрерывными. Целиком периодические процессы в
промышленности используются нечасто (преимущественно при
сорбции ПК из отдельных порций жидкости) . В полунепре
рывных и периодических процессах стадии адсорбции, десорб
ции и активации обычно проводят поэтапно в одном и том же
аппарате.
Адсорбция широко применяется в химической технологии:
для осушки газов и их очистки с выделением ценных
компонентов;
для извлечения (регенерации) растворителей из газовых
(паровых) или жидких смесей;
для осветления растворов;
для очистки газовых выбросов и сточных вод;
- в аналитических целях (например, методы хроматографии
основаны на сорбционных эффектах), а также для других слу
чаев.
-

-

-

-

14. 1 . АДСОРБЕНТЫ

Успех процесса адсорбции во многом определяется выбором
адсорбента. Основные требования к адсорбентам :
- селективность (способность поглощать заданный компо
нент, не затрагивая других компонентов смеси);
- возможно большая поглотительная способность (емкость
по адсорба1)'), что позволяет обойтись меньпmм количеством сор
бента; это важн о для увеличения концентрации адсорбата и сни
жения затрат (пре�е всего - энер гетических) при десорбции ;
- приемлемая стоимость и доступность;
- легкость десорбции и регенерации;
- высокая механическая прочность;
- удобство в работе: негорючесть, малое эрозионное воздействие на элементы аппаратуры и т.п.
На практике в полной мере удовлетворить все требования (в
ряде случаев они противоречивы) не удается, приходится вы
бирать компромиссные варианты .
Соответственно требованию высокой поглотительной спо
собности, адсорбенты чаще всего - высокопористые твердые
1 1 58

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

вещества, используемые, как правило, в виде зерен размером от
долей миллиметра до нескольких миллиметров. Пористость
зерен обеспечивает внутреннюю поверхность в сотни и даже
тысячи квадратных метров на один грамм сорбента, что на
несколько порядков выше его наружной поверхности. Именно
благодаря столь развитой внугренней поверхности некоторые
сорбенты моrуг по глощать адсорбат в количествах, соизмери
мых с собственной массой.
В зависимости от размеров различают микропоры, промежу
точные поры (мезопоры) и макропоры.
К микропорам относят поры с радиусом до 20 А (1 А =
= io- 1 0 м); они соизмеримы с размерами молекул П К. Именно для
микропористых сорбентов характерны крайне развитые внут
ренние поверхности - от нескольких сотен до 2000 м2/г сор
бента (эта цифра приведена для сравнительной оценки, так как
понятие геометрической поверхности к микропорам, строго
говоря, неприменимо) . Промежуrочными считают поры радиу
сом от 20 до 1000 - 2000 А; удельные поверхности здесь от 10
д о 500 м2/г. Полагают, что мезопоры выполняют две роли: соб
ственно адсорбционную (на внуrрен ней поверхности пор сор
бируется П К) и транспортную (перенос молекул П К к микро
порам, где и сорбируется основное его количество) . Макропоры
(их радиус превышает 2000 А) отличаются небольшой удельной
поверхностью (до нескольких квадратных метров на 1 г), их
вкладом в общую сорбционную емкость сорбента обычно мож
но пренебречь. Основная их роль - транспортная: перенос П К
к микро- и мезопорам .
Промышленные сорбенты моrуг содержать поры разных
размеров. Соответственно преобладанию пор тех или иных
типов говорят о микропористых, мезопористых и макропорис
ТЬIХ сорбентах. При наличии в зернах сорбента различньIХ пор
в соизмеримых долях сорбенты относят к смешанным.
Приведем и кратко охарактеризуем наиболее распростра
ненные промышленные сорбенты .
Alrnulнwe (или акпDИроааннwе) угли (АУ) получаются термической обработ
кой без доС'!)'Па воздуха (или с ограниченным ero доступом) ра:щичных углерод
содержащих веществ: древесины, утлей, плодовых косточек - с последующей
аtсrИвацией. В зависимости от назначения (и соответствующего ему исходного
сырья и способа приготовления) в АУ могут преобладать микропоры либо, на
ряду с ними, и мезопоры. Будучи приrотовленными из неполярного материала,
АУ хорошо сорбируют неполярные вещества (например, многие органические
соединения, в час11ю сти углеводороды) и значительно хуже - полярные. Чаще
всего АУ отличаются невысокой механической прочностью.
Силнхаrели и алюмоrели представляют собой продукты термической обработ
ки (обезвоживания) rелей кремниевой и алюминиевой (гидроксид алюминия)
кислот. Эrи сорбенть1 хорошо поrлощают полярные вещества, в частности воду,
1 1 59

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

и потому часто используются для осушки газов. Механическая прочность сили
каrелей и алюмоrелей значительно выше, нежели АУ.
Акrивные угли, силикаrели и алюмоrели хараIСГеризуются весьма широким
набором пор раЗ11 ичных размеров. Поэтому они могут поглощать сразу несколько
компоне1Пов из газовой (жидкостной) смеси.
ЦеоJ11П1о1
природные, а в последнее время все в большей степени синтети
ческие алюмосиликаты - ·слабополярные сорбенты, пригодные для сорбции как
полярных, так и неполярных вещесrв; их, в частности, используют для сорбции
слабополярных органических соединений с двойной связью. Цеолиты отличают
ся высокой однородностью пор, а потому и высокой селекrивностью, т.е. способ
ностью адсорбировать из сплошной среды молекулы определенного размера
(более крупные молекулы в поры проникнуть не могут). Это позволяет исполь
зовать набор цеолитов с различными размерами пор для поочередной сорбции
различных (от мелких молекул к крупным) поглощаемых компонентов из ис
ходной смеси (принцип "молекулярного сита").
Несколько особняком в ряду сорбентов стоят ноннn.� - природные или
(чаще) си1ПетИческие ионообменные смолы (аниониты и катиониты); пример сульфированный полистирол, содержащий rруппы - SO)". Чаще всего их при
меняют в виде зерен (округлой или неправильной формы) размером до 1 ,0 1 ,5 мм . Сущность действия ионитов - в обменных реакциях (в приведенных
примерах стехиометрические коэффициенты не уравнены):
для катионитов (обмен катионами):
Na+[R-) + CaCl2 � CaR2 + Naa ;
-

-

...- �

тв

-

для анионитов (обмен анионами):

[R+]c1тв

+

Na2S04

;:::::!

тв

,R2S04
тв

,

+

NaCI .

Здесь R - органическая основа ионита с какой-либо заряженной (положительно
или отрицательно) функциональной rруппой (rруппами).
Реакция ионообмена происходит пракrически мmовенно и, как правило, не
является лимитирующей стадией. Однако проникновение ПК внутрь зерна ио
нита представляет собой медленную стадию, что хараIСГерно для обычных сор
бе1Пов. В этом смысле нас здесь ИIПересует не сам ионообмен, а ионообменная
сорбция.
С целью повышения поглотительной способности сорбента
стре мятся развить его внуrреннюю поверхность, что, однако,
снижает его механическую прочность - налицо противоречие.
С другой стороны, попытки повысить механическую прочность
сорбента привели бы к существенной эрозии аппаратуры, если
он перемещается внуrри аппарата (непрерывные процессы
адсорбции) . На практике определяющим чаще всего является
требование большой поглотительной способности сорбента,
что приводит к использованию сорбентов невысокой механи
ческой прочности. Очевидно, что непрерывные процессы ад
сорбции с такими перемещающимися в аппарате сорбентами (в
движущемся, тем более - в псевдоожиженном слое) будуr со
провождаться механическим разрушением зерен и значитель
ным пьmеобразованием (возникнуr осложнения с пьmеулавли
ванием, расходом и приготовлением свежего сорбента и т.п. ) .
Именно поэтому, в отличие о т большинства технологических

1 1 60

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

процессов, непрерывному осуществлению адсорбции (со всеми
его достоинствами : стабильностью режима, простотой управле
ния и др .) нередко предпочитают полунепрерывные процессы
сорбции в аппаратах с неподвижным слоем сорбента: здесь
проблема механической прочности зерен сорбента стоит не
столь жестко .
14.2. ФИЗИКО-ХИ М И ЧЕС КИЕ О С НОВЫ
АДС ОРБЦИОННЫХ ПРОЦ ЕССОВ
14.2. 1 . О механизме адсорбции

На поверхности любого твердого тела возникают неуравно
вешенные (направленные внугрь тела) силы , взаимодействие
которых с внешней средой обусловливает притяжение ее моле
кул к поверхности. Однако наружная поверхность твердых тел
невелика; поэтому для н аправленного использования этих не
уравновешенных сил с целью притяжения и выделения опреде
ленных (целевых) компонентов из сплошной среды применяют
сорбенты , обладающие развитой внуrренней поверхностью.
Несмотря на широкое многообразие адсорбционных сил ,
явления адсорбции обычно разделяют н а две основные группы:
физическая адсорбция и хемосорбция. В первом случае адсорб
ция вызывается силами межмолекулярного взаимодействия П К
и сорбента. При этом адсорбат и сорбент сохран.яют свои инди
видуальные свойства. Во втором случае речь идет о химическом
взаимодействии с образованием химических соединений адсор
бата и сорбента; разумеется, оба они в процессе сорбции теря
ют свою индивидуальность. Процессы физической адсорбции обратимы; процессы хемосорбции чаще всего необратимы.
Именно поэтому в целях многократного использования сор
бента в промышленности предпочитают использовать физи
ческую адсорбцию.
При физической адсорбции неполярных веществ основной
вклад приходится на долю дисперсионных сил, возникающих в
результате согласованного движения элекгронов сближаю
щихся молекул адсорбата и сорбента. Дисперсионные силы не
специфичны, т.е. мало зависят от природы ПК и сорбента. В
случае полярных веществ дисперсионные силы дополняются
электростатическими, специфичными для конкретных П К и
сорбента. В некоторых случаях (например, Гидратированная
поверхность сорбента) электростатические эффекты усили
ваются в результате возникновения водородных связей между
гидроксильной группой поверхности сорбента и молекулой
адсорбата. При физической адсорбции молекулы адсорбата в
одних случаях могуг быть зафиксированы в определенном по
ложении на поверхности сорбента, в других - мoryr переме1 161

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

щаться по поверхности . С ростом температуры склонность к
перемещению усиливается.
К физической адсорбции относится особое явление, харак
капил
терное для микропор и в известной мере для мезопор
лярная конденсация. Это явление связано с влиянием кривизны
поверхности жидкостного мениска на давление паров вещества
над ним. Если обозначить rк
радиус капилля р а (поры), е
угол смачивания, v0
мольный объем жидкости, cr
ее по
верхностное натяжение, то связь между давлением паров над
мениском (р) и над плоской поверхностью жидкости (р0) запи
шется, согласно формуле Томпсона, как

-

- -

-

(

где Ry

-

)'

2crv о cos е
Ро
- = ехр ---RyTrк
Р
универсальная газовая постоянная,

Т

-

(а)

абсолюmая температура.

Из (а) следует, что в случае хорошего смачивания жид 
костью стенок капилля ра (cos е > О) при уменьшении rx давле
ние паров над криволинейным мениском снижается. Иными
словами, вещество над мениском становится низколетучим , т.е.
высококипящим. Значит, вещество ( П К) , находящееся над
плоской поверхностью при некотором давлении (например ,
атмосферном) и температуре Т в газообразном состоянии, над
криволинейной поверхностью вогнутого мениска может в тех же
условиях стать жидкостью. Следовательно, в мелких порах
(капиллярах) возможна конденсация адсорбата, хотя адсорбтив
находится в rазообразном состоянии . Конденсация адсорбата в
ходе адсорбции получила название "кап илляр ная конденсация".
При ее возникновении поглотительная способность сорбента
(если ее выражать в виде массовых концентраций), естествен 
но, значительно возрастает. Разумеется, при температурах,
превышающих критические для П К, кап илляр ная конденсация
невозможна.
При хемосорби,ии в определенной точке сорбционной по
верхности образуется химическое соединение адсорбата и сор
бента. Здесь положение сорбированной молекулы, конечно,
является фиксированным.

Термодинамически самопроизвольное явление адсорбции
должно сопровождаться уменьшением свободной энергии G
системы адсорбтив-сорбент: Л G < О. Кроме того, переход П К
из сплошной среды (газ, жидкость) н а поверхность сорбента
означает потерю степени свободы (одной, если положение мо
лекулы адсорбата на сорбенте не фиксировано, или большего
1 1 62

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

числа, если фиксировано); следовательно, понижается и эн
тропия системы: ЛS < О . Отсюда, согласно термодинамическо
му соотношению
(б)
ЛН = Л G + ТЛS ,
при адсорбции изменение энтальпии ЛН < О, система теряет
теплоту, т.е. адсорбция сопровождается тепловыделением. Вели
чина его при физической адсорбции обычно соизмерима с теп
лотой конденсации r (в случае капиллярной конденсации превышает r на соизмеримую с ней величину) и может дости
гать 8 5- 1 25 кДж/моль П К. В случае хемосорбции тепловыде
ление соизмеримо с теплотой, характерной для экзотермиче
ских реакций, и потому может быть на порядок выше r.
Ацсорбат может располагаться на поверхности пор сорбента
в виде отдельных молекул, в пределе покрывая всю поверх
ность мономолекулярным слоем . При высоких концентрациях
адсорбтива в случае достаточно крупных пор сорбента возмож
на полимолекулярная сорбция: поверхность сорбента удержи
вает несколько слоев адсорбата.
В дальнейшем рассмотрение процесса ведется, в основном
применительно к простейшим случаям адсорбции (физической,
мономолекулярной и т.п.).
14.2.2. Равновесие при адсорбции
В соответствии с общими положениями, приведенными в
разд . 1 0 .3 . 1 , равновесие при адсорбции будем представлять в
диаграмме у - х. В качестве концентv.ации адсорбтива (у) ис
пользуем относительную долю: кг П к/(кг остальной части газа
или жидкости); это позволит в ходе расчетов оперировать по
стоянными потоками инерта
сплошной среды
D
(количествами D). В качестве концентрации адсорбата х также
используем относительную величину: кг Пк/(кг чистого сор
бента); это позволит оперировать постоянными потоками твер
дого инерта - сорбента G (в непрерывных процессах) или ко
личествами G (в полунепрерывных и периодических) . В этом
смысле процессы адсорбции принадлежат к классу 3 (2-2) 1 .
Типичная равновесная диаграмма изображена на рис. 14. 1 ,а.
Обращаем внимание, что на оси ординат отложена концентра
ция у, а на оси абсцисс - х, по аналогии со сходным (по це
лям, постановке технологических задач, иногда и по подходу к
расчетам) процессом абсорбции . При адсорбции из газов вмес
то концентрации адсорбтива у нередко используют его парци
альное давление р (или отношение р/рю где Рн - давление
насыщенных паров адсорбтива) . При этом р однозначно связано
с у (см . разд . 1 2 .2): у = р/Р, где Р - полное давление . Область
адсорбции (как и абсорбции) находится выше линии равнове
сия , поскольку П К переходит из фазы "у" в фазу "х" .

1 1 63

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

х

у,р

а
Рис. 14. 1.
а

х

б

у,р

Предстамение равновесия при адсорбции:

- диаrрамма в манере, принятой в учебнихе ; б - обращенная диаграмма

Специально отметим (и здесь необходимо бьrrь внимательным!), чrо в лите 
ратуре по адсорбции очень часто применяют обращенную равновесную диаграм
му: у и р (иногда p/p.J откладывают на оси абсцисс, а х - на оси ординат (см.
рис. 14. 1 , б).

Равновесные кривые чаще всего снимают в эксперименте
при постоянной температуре, поэтому они представляют собой
изаrермы сорбции. Конфигурация равновесных линий зависит,
в первую очередь, от природы П К и сорбента, а при сорбции
из жидкостных смесей - еще и жидкого инерта. На форму и
положение равновесной кривой для данного
П К влияет при•
суrствие других поглощаемых компонентов . Кроме того , может оказывать влияние и взаимодействие адсорбатов на по
верхности сорбента.
Типичная равновесная кривая в случае физи'lеской адсорбции
на сорбенте с однородными по размеру порами изображена на
рис. 14.2,а. При наличии в сорбенте пор разных размеров мо
жет нарушиться плавность линии равновесия - мoryr появить
ся перегибы, подобные показанным на рис. 14. 1 , - их положе
ние и величина зависят от распределения пор по размерам.
Отклонения от плавной кривой мoryr быть следствием и вза
имодействия молекул адсорбата (обусловленного, скажем, по
явлением водородных связей), если оно заметно сильнее вза
имодействия молекул адсорбата и сорбента. В рабочем
(ограниченном) диапазоне концентраций, достаточно удален
ном от насыщения сорбента адсорбатом, кривые равновесия
мoryr оказаться и выпуклыми. На рис. 14.2,б изображены изо
термы сорбции при разных температурах. Поскольку адсорбция
сопровоЖдается выделением теплоты , то, согласно правилу Ле
Шателье, при одинаковых концентрациях адсорбтива в газе

более высокой температуре t2 > t1 отвечает меньшая поглоти
тельная способность сорбента х2 < х1 •
• Адсорбция мноrокомпоне1П11 ых смесей в учебнике не рассматривается. Не
которые ее аспекты содержатся в (5).
] 1 64

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

у

у(р)

12

11

р(у)

у

у

Р
хо
а

Х2 Х 1

х

х

б

у

в

у

х

1
1

__;!
г

Рис. 14.2.

а

х

д

а

Хадс

х

е

Хдсс х

Типичные кривые адсорбционноrо равновесия:

физическая адсорбция (изотерма сорбции ) , б
к влиянюо температуры на адсорб
ционное равновесие, 11
равновесная кривая, отвечающая уравнеюоо ЛэШ"МJОра, г
хемо
сорбция, д капиллярная коцпенсация , е к явлению rисrерезиса при адсорбции
а

-

-

-

-

-

-

Математическое описание плавных равновесных кривых при
физической адсорбции чаще всего представляют в виде одной
из трех зависимостей у = f (х) ил и р = f (х).
Наиболее простое представление - линейное у = тх, где
т постоянный коэффициент распределения . Это представ
ление оправдано тем, что в области малых рабочих концентра
ций (частый случай на практике) равновесная зависимость в
самом деле близка к линейной (начальный участок лин1m равно
весия на рис. 14.2,а) . Использование такого представления позво
ляет в ряде случаев получmъ достаточно простые аналитические
решения при расчете некоторых процессов адсорбции.
Степенная зависимость у = Ах", называемая уравнением
Фрейндлиха, первоначально бьmа предложена для жидкостных
сплошных сред; позднее ее распространили и на газовые. Это
чисто эмпирическое описание равновесия с подбором пара
метров кривой А и п для каждой системы П К-сорбент при
данной температуре . Определенные достоинства уравнения
усматривают в простоте метода определения А и п по опытн ым
данным (линеаризация уравнения путем его логарифмирова
ния) и неплохом описании этих данных в ограниченном диапа
зоне изменения концентраций (см . рис . 14.2,а) .
Гиперболическое - уравнение Лэнrмюра
наилучшим обра
зом отражает некоторые специфические особенности физичес-

-

1 1 65

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

кой сорбции из газовой фазы (см. рис. 14.2,в) :
х

=

_(!р_ .

(в)

Ь+р

Оно получено из простых физических представлений. Если рассматривать
поверхности и положить, что его доля Ф занята адсорбатом, то
скорость адсорбции , пропорциональная парциальному давлению адсорбтива и
Ф ) , где k. - константа
незанятой доле поверхности, запишется так: k. p( l

1 м2 сорбционной

-

k.p(lk• -

скорости сорбционного процесса. А скорость обратного (десорбционного) про
цесса пропорциональна доле поверхности , занятой адсорбатом: k•Ф, где
константа скорости десорбци И . Очевидно, в условиях равновесия

- о1)

=

k• Ф , откуда легко найти Ф

=

k.pj(k.p+k0} .

Разделив Ф на площадь, за

н имаемую одной молекулой, найдем число молекул, адсорбированных единицей
поверхности. Отсюда, зная удельную поверхность сорбента, нетрудно перейти к
массовой концентрации адсорбата х, представив ее в виде выражения (в) .

Особенности выражения (в) отражены на рис . 14.2,в:
- в области малых концентраций адсорбтива (р << Ь) полу
чается линейная зависимость на начальном участке равновес
ной кривой, причем отношение Ь/а отвечает постоянному ко
эффициенту распределения т;
- в области высоких концентраций адсорбтива (р >> Ь) кон
центрация его в сорбенте стремится к предельному значению
а, отражая полное (при р, у � оо) насыщение сорбента погло
щаемым компонентом;
- в области промежуточных концентраций осуществляется
плавный переход от линейной зависимости к предельному на
сыщению.
В случае хемосорбции на поверхности пор сорбента образу
ются достаточно устойчивые химические соединения его с ад
сорбатом, что приводит к значительному падению концентра
ции адсорбтива над сорбентом; только при достаточно больших
х (поверхность пор сорбента уже в значительной мере химиче
ски связана с адсорбатом) в сплошной среде (газ, жидкость),
находящейся в контакте с сорбентом, наблюдается заметная
концентрация (давление паров) адсорбтива (рис . 14.2,г).
В случае капиллярной конденсации на кривой равновесия су
ществует участок, близкий к горизонтальному (рис. 14.2,д) : с
началом конденсации количество П К в порах сорбента быстро
нарастает при малых изменениях парциального давления П К в
смеси.
Строго говоря, нарастание х при одинаковых размерах пор в сорбенте должно
происходить при практически постоянной концентрации адсорбтива у. Но ре
ально сорбент имеет некий набор размеров пор. Капилляр ная конденсация
начинается в порах самого малого радиуса, а при постепенном повышении
парциального давления адсорбтива (у, р) ею захватываются и более крупные

1 1 66

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

поры. Поэтому концентрация
несколько повышающихся у, р.

х

в самом деле растет быстро, но все же при

При наличии капиллярной конденсации нередко наблю
дается явление гистерезиса адсорбционного равновесия : несов
падение равновесных за висимостей при адсорбции и десорб
ции (рис . 1 4 . 2 , е) . Полагают, что при адсорбции часть внугрен 
ней поверхности пор блокирована посторонними примесями
(воздухом, например), препятствующими смачиванию стенок
капилляров, так что требуется достаточно высокая концентра
ция адсорбтива (у, р), чтобы вытеснить эту примесь из пор
поглощаемым компонентом . При десорбции на внугренней
поверхности пор примеси нет (или нет в таких количествах) ;
поэтому при тех же р, у содержание адсорбата выше
(Хдес > Хадс) .
В дальнейшем рассмотрение процесса ведется . в основном
применительно к процессам физической сорбции, характери
зуемым плавными изотермами - типа линейной, Фрейндлиха,
Лэнгмюра.
14.3. АДСОРБЕРЫ

Н иже рассмотрены конструкции некоторых адсорбционных
аппаратов и принципы их работы. Представлены отдельные
адсорберы непрерывного действия (с псевдоожиженным слоем
сорбента - одно- и многосекционные и с движущимся слоем),
а также эти аппараты в составе адсорбционно-десорбционно
регенерационных агрегатов. В заключение показана конструк
ция и работа адсорбера полунепрерывноrо действия .
14.3. 1 . Адсорберы непрерывиоrо действия
с псевдоожиженным слоем сорбента

Адсорберы (десорберы, активаторы) с псевдоожиженным
слоем сорбента могуг работать при непрерывных подаче и вы
воде, а также перемещении адсорбента из аппарата в аппарат.
Это позволяет проводить сопряженные (см. разд. 24.2.6) про
цессы адсорбции П К - регенерации сорбента в стабильном и
легко управляемом непрерывном режиме .
Одмосехционнwй адсорбер с псевдоожиженным слоем мелкодисперсного сор
бекrа показан на рис. 14.3. Поток исходного газа /, содержащего адсорбтив,
яаляется ожижающим агентом: пройдя газораспределите.лъное устройство 7, он
приводит в псевдоожиженное состояние мелкозернистый сорбент lI и покидает
слой через сепарационное пространство З и систему циклонов 4. Расширенное
сепарационное пространство уменьшает пьтеунос благодаря понижению рабо
чей скорости газа. Последовательно расположенные два-три циклона (их чаще
всего размещают внутри аппарата с псевдоожиженным слоем) существенно по
вышают степень обеспьVIИвания газа; тем не менее за аппаратом, как правило,
1 1 67

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 14. 3. Односекционный адсорбер непрерывного действия с псевдоожи 
женным слоем сорбента:
1 - аппарат с псевдоожиженным слоем, 2 - стояки, 3 - сепарационная зона, 4 - цик
лоны, 5
холодильное устройство. 6
подрешеточная камера, 7
rаэораспределительная
решетка;
/ - rаэ, // - псевдооJЮ1женный слой сорбента, //с - свсж:ий сорбент, //н
насышен
ный сорбент, /// - хладоаrент
-

-

-

-

устанаWIИвают дополнительные пыпеулаwrnвающие устройства (рукавные
фильтры, злектрофилътры и т. п . ) . Сорбент, отделенный в циклонах от газового
потока, возвращается в псевдоожиженный слой по о пускным стоякам 2. П оток
свежего сорбента Пс постоянно подается в аппарат питателем (на схеме не пока
зан). П оток насыщенного адсорбатом сорбента l/н непрер ывно отводится из
аппарата. При высоких теruювых эффектах адсорбции, если газ не обеспечивает
необходимого отвода теплоты, в псевдоожиженном слое размещают холодильные
устройства 5 (змеевики , трубные пучки , штыковые теплообменники), позво
ляющие поддерживать температуру процесса на должном уровне.
Достоинство односекционного адсорбера с псевдоожиженным слоем - в
простоте его конструктивного оформления и развитой поверхности межфазного
контакта. Основной недостаток (помимо пыпеобразования • ) - в плохом защит
ном действии из-за и нтенсивного перемешивания сорбента: аппарат не позволя
ет добиться высокой очистки газа. В самом деле, пусть в нижних зонах псевдо
ожиженного слоя частица сорбента, контактируя с высококонцентрированным
газом, в значительной мере насыщается адсорбатом, а концентрация адсорбтива
в газе существенно снижается. Но вследствие интенсивного перемешивания
насыщенная частица сорбента в следующее мrnовение может попасть в верхние
зоны слоя, где окажется в контакте с обедненным газом (т.е. в области десорб
ции). И тогда частица вернет часть сорбированного П К, так что глубокой очист•
Заметим, что при осуще(;твлении адсорбции при жидкостном псевдоожи
жении сорбента его механи<1еское разрушение происходит значительно медлен
нее.

1 1 68

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 14. 4. Многосекционный противоточный
адсорбер непрерьmного действия с псевдо
ожиженным слоем сорбента:

1 - мноrосекциоЮIЬIЙ аппарат, 2 - стояхи, З
- rазораспределительные решетки, 4 - ЦИJU1он, 5
- сепарационная зона, 6 - холодильные устройства, 7 - хоничесхое ДЮ1Ще ;
/ - rаз, II - сиJIСИЙ и насыщенный сорбент,
III - хладоаrент, lV - nсеl\ЦоожижеЮIЬIЙ сорбент

tI
5

11
-

ки газа не получится. (Количественное вы
ражение этого эффекrа рассмотрено в разд.
14. 5. 1 .) По изложенным причинам односек
ционньхй аппарат с псевдоожиженным слоем
сорбенrа редко используется для адсорбции ,
чаще - для десорбции при повьШiе1mых тем
перlПУРах, коща круrая равновесная кривая (см.
рис. 14.2,б) расumряет обласrь десор6Ш1и и
обеспечивает достаточную ее полнmу.
Достоинства метода псевдоожижения
(при одновременном устранении его недо
статков) моrут бьrrь реализованы в мноrосех
цнонном аппарате с псевдоожиженным слоем
сорбента, работающем по принципу ступен
чатого противотока. На рис. 1 4 .4 показан
трехступенчатый адсорбер. Поток / исходно
го газа подается снизу, очищенньхй газ ухо
дит сверху. Поток П свежего сорбента по
дается сверху и насыщенный адсорбатом отводится снизу. По мере движения по ап
парату сорбент поддерживается на тарелках в
псевдоожиженном состоянии 1V за счет
восходящего газового потока; с тарелки на
тарелку сорбент перемещается плотным
У• п
слоем по стоякам 2. При необходимости в
секциях (не обязательно во всех) устанавливаются теплосъемные устройства 6. Назначение остальных узлов ясно из подпи
си к рисунку.
ПосколькУ интенсивное перемешивание сорбента ограничено здесь отдель
ными сехциями, общая эффективность (глубина очистки газа) в многосекцион
ном противоточном адсорбере может быrь значительно вьпuе, чем в односекци
онном; разумеется, она возрастает с увеличением числа секций.
Отдельной проблемой для многосекционных аппаратов является устойчи
вость работы переточных устройств (стояков): они склонны к "захлебыванию" и
нарушению транспортной функции при не очень значительных отклонениях от
заданного режима. Эта проблема рассматривается в специальной литературе".
На рис. 1 4. 5 демонстрируется адсорбцнонно-десорбцноннwй (реrенерацноннwй)
arperaт для осушки газов - с псевдоожиженными слоями сорбента и его тран
спортом по опускным стоякам и в восходящем пневмотранспортном потоке.
Основные аппараты: многосекционный ступенчато-противоточный адсорбер 1 с
провальными решетками J(}, односекционный десорбер 4; регенератор
(ахтиватор) 7 с холодильником 8. Поток исходного газа /, подлежащего осушке,
подается в адсорбер снизу, пссвдоожижая находящийся в секциях сорбент. По
ток осушенного газа П уходит сверху. Поток регенерированного сорбента 11' по•

См., например,

(2 , 6 ) .

] 1 69

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

IV

Рис. 14. 5. Адсорбционно-десорбционно-реrенерационный агрегат для непрерыв
ной осушки газа:
цихлоны, З - веJПИЛЯТоры, 4 - десорбер, .5 1 - мноrосекдиоННЬ\Й адсорбер, 2
сrояки, 6 rаэораспределитель типа "паух", 7 - реr-енератор, 8 - охлаждающее усrройство
реrенератора, 9 - охлаждающие усrройства, 10 - провальные распределительные рещетхи;
/ - исходный В.ЛаJКНЬIЙ rаэ, // - осушенный rаэ, ///
rорячий воздух, IV - алаJКНЬIЙ
воздух, V - псевдоожиженный слой сорбента в адсорбере ( Vи - насыщенный сорбент, J'\J реrенерированный сорбент), VI - то же, в десорбере, VII - то же, в реrенераторе, V/// насыщенный алаrой сорбент
-

-

-

дается сверху; по мере накопления на газораспределительной решетке с доста
точно крупными отверстиями, сорбент проваливается, постепенно перемещаясь
с верхних секций в нижние; поток насьпценного сорбента И1 отводится снизу.
Он подхватывается потоком rорЯчего воздуха /J/ и пневмотранспортом VIII.
перемещается в десорбер 4 через газораспределителъ 6 типа "паук" ; горнчий
воздух поддерживает сорбент 11 десорбере в псевдоожиженном состоянии. Про
цесс десорбции, начинающийся в пневмотранспортиом трубопроводе, завер
шается в десорбере; воздух, содержащий водяные пары, отводится из десорбера
4 с помощью вентилятора. Высушенный горячий сорбент по стоякам 5 пере
мещается в реrенератор-активатор. Активация состоит в охлаждении сорбента (за
счет холодного rаза /l и охлаждающего устройства 8), после чего сорбент пнев
мотранспортом возвращается ( Vp) в адсорбер. В качестве холодного газа не

1 1 70

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

не воздух, то это
следует брать атмосферный воздух. Если осушаемый газ /
вообще недопустимо: в верхней часrи адсорбера получится смесь осушенною газа и
во:щуха. Но даже если осушке подвергается воздух (/), то и в эrом случае атмосфер
ный воздух в качестве охлаждающею потока // нежелателен. Дело в том, что в атмо
сферном воздухе содержиrся влаrа; ее воспримет транспортируемый сорбент, так что
в адсорбер будет подаваться влажный исходный сорбент - глубина осушки rаза
понизится. По зmм причинам в качестве охлаждающеrо потока // в регенератор
подают часrь осушенною холодноrо rаза после адсорбера. В ходе работы arperaтa
необходимо постоянно поддерживать в аппаратах заданный nщравлический режим,
чтобы не нарушалась устоЙ'mвая циркуляция сорбента.
Оценивая работу различных адсорберов и сопутствующих аппаратов непре
рывноrо действия с псевдоожиженным слоем, следует отметить их общий недо
статок: интенсивное перемеши вание частиц сорбента и, как результат, соударе
ния, трение частиц друг о друга и о внутренние устройства аппарата. Это приво
дит к значительному пылеобразованию, необходимости установки мощных си
стем пьиеулавливания и, что не менее существенно, к немалым затратам на
производство свежею сорбента взамен превратившеюся в пъть. Именно эти
обстоятельства сдерживают использование адсорберов с псевдоожиженным
слоем сорбента и заставляют обращаться к друmм технологическим схемам,
обеспечивающим противоток фаз и. вместе с тем большую механическую устой
чивость сорбента.
-

1 4.3.2. Адсорберы непрерывного действия
с движущимся слоем сорбента

В аппаратах с движущимся слоем з ёрна сорбента совместно
перемещаются вдоль ап парата и не испытывают столь значи
тельного механического воздействия, как в псевдоожиженном
слое; поэтому и разрушаются они здесь в меньшей степени . В
зарубежн ой литературе процессы адсорбции в аппаратах с дви
жущимся слоем (приме н ительно к разделению углеводородных
газов) именуют гиперсор бцией.
Типичный адсорбер с движущимся слоем сорбента показан на рис. 1 4. 6 . Под
лежащий очистке газ движется восходящим потоком (простые стрелки) сквозь
слой опускающихся (стрелки с кружками) под действием силы тяжести зерен
сорбента. Эти зерна (на рисунке условно вьщелены некоторые из них) движутся
сплошным потоком. Для ввода газа ./' в нижней части аппарата используется
особая конструкция: "газораспределительная решетка 3 со стояками 2 - глухая
переюродка 4; для вывода газа //, из верхнеЧ части адсорбера используется
глухая перегородка 4 со стояками 2. При необходимости адсорбер снабжают
теплоотводящим устройством 6. Ввод сорбента в аппарат l/l и вывод из него
/V осуществляются · питателями 5. Заметим: работа питателей в аппаратах с
движущимся слоем создает серьезные проблемы, поскольку именно здесь наи
более существенно механическое воздействие на зерна сорбента (возникают
трещины, происходит разрушение). Адсорбер с движушимся слоем чаще всего
не нуждается в пылеулавливаю щих устройствах, так как сам слой обладает пыле
улавливающими (фильтрующими) свойствами.
На рис. 1 4 .7 представлен адсорбционно-десорбционнwй (реrенерационнwй) arpe
raт для разделения углеводородных газов; в нем стадии адсорбции и десорбции
происходят в движущемся слое сорбента (активированного угля) . Основные
аппараты: адсорбер-десорбер J. подъемный стояк 2, регенератор (активатор) J, а
также система циркуляции транспортирующего аrента 4.
Сорбент движущимся слоем опускается в адсорбере-десорбере J, проходит
ряд секций, разделенных газораспределительными устройствами со стояками 1 . 2.

1171

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 14. 6.

Противоточный адсорбер с движущимся
слоем сорбента:

1 - №Сорбер, 2 - стояки, З - rазораспределительная
4 - rлухие переrородки, 5 - питатели , 6 - тепло
отводящее устройсrво;
l - исходный rаз, 11 - очищенный rаз, 111 - свеJ1СИй
сорбеш, IV- насыщеННЬ1й сорбеш, V - ХЛ№оаrеш
решетка,

В верхней части в холодильнике 1.3 сорбекr охлаж
дается до необходимой (для адсорбции) температуры.
С потоком сорбекrа встречается восходящий поток
исходного газа - смесь углеводородов. Сорбекr
поглощает ряд компонентов газовой смеси, исключая
тощий газ (он проходит в сепарационное простран
ство 1. J) и наиболее легкую фракцию - она вьrгес
няется из сорбента более тяжелыми фракциями и
выводится из аппарата (поток /lл). Сорбекr с более
тяжелыми ПК движется вниз; в конечном итоге он
попадает· в десорбционное устройство 1.4, ще при
повышении температуры освобожцается от адсорби
рованных ранее углеводородов. Десорбции способ
ствует подача голого водяного пара VJ/, понижаю
щего парциальное давление углеводородов. Освобож
денный от углеводородов сорбекr по стояку 1. 6 пе
ремещается в распределительную коробку 2. 1, а смесь
4
десорбированных углеводородов движется в аппарате
1 навстречу нисходящему потоку сорбента. При этом
более тяжелые фракции, обладающие бот.шей
склонностью к сорбции, постепенно вьпесняют из
сорбента более легкие (промежуточные). Вытеснен
ные промежуточные фракции выводятся из аппарата
(поток /lп) в более высоком сечении, нежели тяже
лые вместе с водяным паром (поток /lr).
Горячий сорбент из коробки 2. 1 пневмотранспор
том (предпочтительно - тощим газом, в некоторых
системах - воздухом) поднимается по трубе 2 в приемник-амортизатор 2.2,
откуда сползает к холодильнику 1.3, и далее возвращается в рабочую зону.
Сорбент, отводимый в коробку 2. 1 из зоны десорбции, может содержать ве
щества, которые не удается десорбировать с его поверхности. В ходе работы они
накапливаются в сорбенте, постепенно снижая его сорбционную емкость. По
этому часть сорбекrа постоянно или время от времени подается в регенератор
3 - реактор, состоящий из зоны подоrрева высокотемпературным теплоносите
лем (часто топочными газами - поток Х), двух псевдоо.жи.ж:енных слоев VJ на
провальных решетках 3.2 и барботера 3.5, питаемого голым паром (поток VJI).
Наличие псевдоо.ж:и.ж:енных слоев позволяет увеличить время контакта зерен
сорбента с гоm.rм паром и rорнчей поверхностью, упомянутые слои работают на
унос сорбента. Продукты реакции (термического ра3Ложения, конверсии) и
водяной пар выводятся из системы (поток Х/), а активированный сорбент пнев
мотранспортом перемещается в сборник-амортизатор 2. 2.
Потерянный в результате разрушения сорбент компенсируется добавлением
свежего. Можно констатировать, что для адсорбера с движущимся слоем про
блемы разрушения сорбента и пылеулавливания стоят не стоm. .жестко, как в
случае псевдоо.ж:и.ж:енноrо слоя. Заметим: в движущемся слое зёрна сорбента
обычно в 10-30 раз крупнее, нежели в псевдоожиженном; это приводит к сни
жению интенсивности массопереноса, а значит - к необходимости увеличения
масштабов аппаратуры при той .же производитр1ьности.

1 1 72

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

111/

х

-

'Г
1
1
1
1
1
1

Vll

-

4.4 1/11 1
lII

4. 2

1
1
1

tш

1

-

4. 1

Лцсорбционно-десорбционно-реrенерационный arperaт для разделения
rазов с движущимся слоем и пневмотранспортом сорбента:

Рис. 14. 7.

1 - адсорбер: 1. 1 - сепарационное пространсrво, 1. 2 - распределиrельная решетка со
стояхами, 1.3 - охлаждающее устр()йсrво, 1. 4 - наrревающее устройсrво, 1. 5 - барботер, 1. 6
- опусJСНой стояк;
2 - 1D1евмотранспорnшя труба: 2 1 - распределиrельная коробка, 22 - сборНИIС
амортизатор;
3 - реrенератор: 3. 1 - наrревающее устройсrво, 3.2 - распределиrельные решетки, 3.3
- трубопровод для пневмотранспорта сорбента после реrенерации , 3. 4 - то же, до pereнepa
JUIИ, 3.5 - барботер;
4 - циркуляционная система: 4. 1 - транспортный трубопровод, 4. 2 - вентилятор;
/ - исходная rазовая смесь, Пл - леnсая фракция, //п - промежуточная фракция, /lr
- тяжелая фракция, /// - неадсорбирующиеся {тощие) rазы, /V - нисходящий поток
сорбента, V - ВОСХ()ДЯЩИЙ пнеl!мотранспорт сорбента, V/ - псевдооJ1СИJКенный слой сорбен
та, VII - острый пар, Vl/I - хладоаrент, IX - теплоноситель, Х - высокотемпераТУРНЬIЙ
теплоноситель, Х/ - rазы после реrенерации

1 1 73

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

14.3.3. Адсорберы полунепрерывноrо действня
с неподвижным слоем сорбеита

Ранее бъmа указана основная причина, побуждающая техно
логов вести сорбцион ные процессы в полунепрерывном
(реже - в периодическом) режиме - с неподвижным слоем
зерен сорбента, чтобы п редотвратить их разрушение . Это ответ
на вопрос, почему нужно проводить адсорбцию в неподвижном
слое сорбента.
Целесообразность адсорбции в неподвижном слое обусловлена еще и тем,
'По исходная концентрация П К в газовой (жидкой) смеси, как правило, очень
невелика (если велика, то часто предварительно используют другие методы по
глощения П К (абсорбцию, экстракцию и др .), а на адсорбцию направляют сме
си, обедненные поглощаемым компонентом). Поэтому сама активная стадия
процесса - адсорбция (продолжительность ее часто составляет часы) - занимает
достаточно большую долю времени от полного цикла процесса (он включает еще
"непроизводительные" стадии десорбции и активации сорбента). Это ответ на
вопрос, почему адсорбцию можно проводить в неподвижном слое.
Типичный аппарат Д11Я по,'J)'непрерывной (циклической) сорбции углеводо
родов неподвижным слоем активированного угля представлен на рис. 1 4 . 8 . В
корпусе 1 смонтированы опорная решетка 2, поддерживающая слой сорбента IV,
и барботер J; аппарат сверху закрьп крышкой 5, а снизу заканчивается диффу
зором 4. Сорбент представляет собой зерна неправильной формы размером от
2 - 5 до 6 - 10 мм.
Процесс проводится в четыре стадии:
1. Собсn�енно адсорбция. Ч ерез штуцер в крышке на слой холодного сорбента
подается исходная смесь la (газ, содержащий ПК - смесь углеводородов) . Сор
бент поглощает П К и постепенно насыщается им. Процесс ведуr до тех пор,
пока слой сорбента не насьпится до определенной степени и содержание ад
сорбтива в очищенном газе (выходной поток Па) не дости111 ет предельно допу
стимой величины Упр - с этого момента стадия адсорбции считается закончен
ной и подача исходной смеси прекращается.
2. Десорбция. Через барботер 3 начинают подавать перегретый водяной пар
(поток Ill) с целью нагревания сорбента и понижения парциального давления
адсорбтива (оба эффекта способствуют десорбции адсорбата) . В первые моменты
подачи пара (пока идет нагрев слоя и аппарата) некоторая часть его конденсиру
ется, конденсат удаляется снизу (поток V); затем смесь перегретого пара и де
сорбированного ПК отводится сверху (поток Vl). Далее ПК отделяется от пара (в
случае углеводородов, нерастворимых в воде, - просто конденсацией и деканта
цией; в других случаях мoryr потребоваться дистилля ция, ректификация и т.п.).
3. Сушка сорбента. После десорбции сорбент содержит влагу и подлежит
сушке. Она проводится горячим воздухом , подаваемым по линии исходной
смеси ( поток /б) и выводимым снизу через нижний штуцер (по линии потока
Пб) . В результате сорбент освобождается от влаги; однако он еще не полностью
готов к следующему циклу сорбции, поскольку остается горячим .
4. Охлаждение сорбента. Через тот же ШТУцер исходной смеси подается хо
лодный воздух (поток Iв) , выводится он - по линии потока l/fJ.
На этом (стадии 2, 3 и 4) завершается регенерация сорбента, после чего цикл
"адсорбция-регенерация" повторяется .
На практике используются аппараты полунепрерывного действия (с непо 
'
движным слоем сорбента) и несколько иной конструкции (среди них адсорберы
с кольцевым слоем сорбента и др .).
' См" например , (1 -

1 1 74

5).

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 14. 8. Адсорбер полунепрерывноrо дей
ствия с неподвижным слоем сорбента:
1 - аJП1арат (корпус), 2 - распределительная
(поддерJ1СИ11а1Ощая) решетка, З - барботер, 4 диффузор, 5 хрышха;
I -входящие rаэы: /а - исходная смесь, 1б rорячий воздух Jв - холодный воздух;
IJ -уходящие rаэы: Па - rаэ, очищеННЬJЙ от
ПК, /lб - воздух после сушки и охлаждеюtя сор
беша;
IJI - водяной пар, JV - ненодвюкный слой
сорбеша, V
хо�щенсат, VI - десорбироваННЬJ Й
ПК с водяным паром
-

,

5

\

1

18888��t " �v

ш

-

Поскольку технолоmческие операции до
и после адсорбера с неподвижным слоем
сорбента мoiyr осущесТR11ЯТься в непрерывном
режиме, то ставят обычно два (иногда больше двух) адсорбера полунепрерывноrо действия. Их переключают (в одном
происходит сорбция, в другом в это время - десорбция и регенерация) так, что
периодически действующий адсорбер с неподвижным слоем сорбента не нару
шает непрерывности технолоmческоrо процесса в целом .

14.4. О ТЕХН ОЛОГИЧЕСКОМ РАСЧЕТЕ
АДСОРБЦИОННЫХ ПРОЦЕССОВ

Расчет процессов адсорбции весьма сложен , поскольку сло
жен сам процесс: здесь присуrствуют акты массообмена при
менительно и к отдельному зерну сорбента, и к коллективу зе
рен; на явление адсорбции накладывается еще перенос тепло
ты. Строгие расчеты возможны лишь для самых простых тех
нологических ситуаций , поэтому идуr на существенное упро
щение моделей процессов, описывающих их уравнений, усло
вий. Но даже и в этом случае чаще всеrо необходим достаточно
rромоздкий математический аппарат. В этой связи зачастую
используют более простые эмпирические и полуэмпирические
методы расчета. Отмеченные обстоятельства придется неодно
кратно подчеркивать при изложении методов расчета различ
ных сорбционных аппаратов.
В учебнике рассмотрены подходы к анализу и расчету наи
более простых случаев адсорбции. При этом в основе расче
та - общие теоретические представления, изложенные в
разд . 1 0 . 1 6 . В отдельных случаях придется прибегать к феноме
нологическим представлениям и эмпирическим сведениям о
значениях некоторых характеристик процесса.
Как показано в разд . 1 0 . 1 6 , в случае массообмена с твер
дыми телами (в частности, в процессах адсорбции) можно вы
делить ряд стадий. В отсутствие химических превращений это :
подвод вещества ( П К, адсорбтива) в рабочую зону с потоком газа
(или жидкости) ; перенос ПК к поверхности зерна сорбента; диф1 175

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

фузия адсорбата внутрь зерна; отвод адсорбата (ПК) из рабочей
зоны с сорбентом. Разумеется, такая последовательность свой
ственна непрерывным процессам ; в случае полунепрерывных про
цессов последняя стадия не реализуется, сразу переходят к
процессу десорбции с обратной последовательностью стадий от внутренней диффузии до вывода П К из рабочей зоны .
Если одна и з стадий протекает значительно медленнее
остальных, то ее именуют лимитирующей. При существенно
медленном переносе ПК из 96ъема газа (жидкости) к внешней
поверхности зерна сорбента говорят, что массообмен (здесь адсорбция) протекает в условиях внешней задачи. Если внут
ренняя диффузия ПК в зерне происходит много медленнее
других стадий , то говорят о внугренней задаче адсорбции. Если
лимитирующими являются подвод адсорбтива в аппарат (с по
током сплошной среды) или отвод адсорбата из него (с сорбен
том), то задачу массообмена (здесь - адсорбции) называют
потоковой, соответственно по сплошной среде или по сорбенту.
При сопоставимости скоростей переноса на нескольких (хотя
бы на двух) стадиях говорят о сорбции в условиях смешанной
задачи.
Расчет процесса при наличии лимитирующей стадии проще :
достаточно математического описания этой отдельной стадии
переноса ; в учете сложного взаимодействия нескольких стадий,
характерного для смешанных задач, нет необходимости. Н иже
последовательно рассматриваются подходы к расчету отдель
ньхх процессов адсорбции при наличии лимитирующей стадии.
Эти подходы излагаются в упрощенных вариантах.

14.5. РАСЧЕТ НЕПРЕРЫВНЫХ ПРОЦЕССОВ АДСОРБЦИИ
В ПСЕВДООЖИЖЕННОМ СЛОЕ СОРБЕНТА

Для псевдоожижен н ого слоя характерно использование мел
ких частиц сорбента (как правило , доли милли метра, редко более 1 мм) . Поэтому даже внешняя поверхность контакта F, а
с ней и пропускная способность стадии внешнего массопере
носа pF (или ppF) весьма велики. При этом и коэффициент
массоотдачи р характер изуется достаточно большими величи
нами: он получается на основе числа Шервуда Sh = pd/Dд
(причем Sh � 2), а диаметр частиц сорбента d очень мал . По
этим причинам в псевдоожиженном слое внешняя стадия мас
сопереноса практичесЮf никогда не является лимитирующей надо рассматривать адсорбцию лишь в условиях потоковой или
внутренней задачи. Именно эти технологические ситуации
анализируются ниже.
1 1 76

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

14.5. 1 . Односекционный адсорбер с псевдоожиженным слоем

Аппарат для сорбци и псевдоожиженным слоем сорбента
изображен на рис. 14.3, расчетная схема - на рис. 14.9. В связи
с тем . что сорбент движется через адсорбционную зону
(псевдоожиженный слой) в режиме идеального перемешива
ния, направление потоков сорбента и газа (или жидкости) на
расчетной схеме безразл ично.

Адсорбция в условиях потоковой задачи
Ацсорбция, не осложненная внутренним диффузионным со
противлением, может быть отнесена к процессам класса 3(2-2) 1
по КФ-классификации . Поэтому ее расчет в общем базируется
на положениях, рассмотренных в гл . 1 0 для систем данного
класса. Это касается способов выражения концентраций
(относительные величины; примем: массовые концентрации у и
х, инерты - сплошная среда без П К и чистый сорбент), диа
грамм у-х (с рабочей областью над линией равновесия), урав
нений материальных балансов. Ниже используется подход к
расчету, изложенный в разд. 10.16.4.
Запишем материальн ый баланс по ПК для контуров К 1 и
Къ проходящих (рис. 14.9) через границу раздела фаз и
входное и выходное сечения адсорбера; наЙдем М - количе
ство П К, передаваемого от газа к сорбенту в единицу времени:

Dy1

-

М - Dy2 = О

и

М = D(y1 - .У2),

( 14

l y)
(14. lx)
.

Объединяя эти выражения или составляя баланс по П К от
дельно для адсорбера в целом (контур · К ), получим анало
гично (10.79):

(14. 1 )
В условиях потоковой задачи это выражение дополняется
уравнением линии равновесия, поскольку потоки газа
(жидкости) и сорбента покидают адсорбер с равновесными кон 
центрациями У2 и х2
точка с координатами (.У2, х2) лежит на
равновесной кривой.
Сформулированные положения позволяют весьма просто
решать задачи эксплуатации и проектирования. Пусть целевым
является газовый (жидкостной) поток; это означает, что задана
его величина D и исходная (входная) концентрация адсорбтива
у1 . Кроме того , известн ы равновесная зависимость у = f (х) и
входная концентрация адсорбата х1 (вполне возможно , что ис
ходный сорбент - чистый, не содержит П К; тогда х 1 = О ).
Цель процесса - извлечение П К из газового потока.
-

J l 77

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 14. 9. К расчету непрерьшной адсорбции в односекционном псевдоожи
женном слое (К, К 1, К2
ко нтуры

)

-

Рис. 14. 10. К решению задач эксплуатации и проекrирования при адсорбции в
односекционном псевдоожиженном слое

В задаче эксплуатации известен еще поток сорбента G; необ
ходимо найти выходные концентрации адсорбтива (v.i) и адсор
бата (х2 ). Уравнения ( 14.1) и равновесной зависимости доста
точно для решения задачи по канве, изложенной в разд. 10.9.
Перепишем уравнение ( 14. 1) :

У1 - У 2 G
( 14. la)
- Х1 = D .
Зафиксируем теперь в диаграмме у-х (рис . 14. 10) точку со
пряженных (входных) концентраций (у1 , х1 ) и проведем из нее
до линии равновесия (так как задача - потоковая) прямую под
углом так, чтобы tga. = G/D. Точка с координатами (v.i, х2 ) на
Х2

а.

равновесной кривой будет искомой - она отвечает обоим по
ставленным условиям: находится на линии равновесия; соот
ветствует выражению ( 14. l a), так как tga. равен отношению
разностей концентраций .
В процессах типа адсорбции нередко оперируют понятием
степени извлечения 11извл, представляющей собой долю извле
ченного адсорбтива от первоначально содержавшегося в потоке
сплошной среды:
1l извл =

М

Dy1

=

D (Y 1 - У 2 ) l У2
.
Dy1
У1
и у2 позволяет в ходе
=

_

(а)

Однозначная связь Т) извл
расчетов пе
реходить от выходной концентрации к степени извлечения и
1 1 78

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

обратно. В задачах эксплуатации по найденной величине У2
легко отыскать Тlиэвл ·
В задаче проектирования не задан поток G, но обусловлена
выходная концентрация У2 или степень извлечения Тlиэвл· Здесь
алгоритм расчета еще проще: по заданному (или найденному
по Тlиэвл) значению у2 в диаграмме у-х определяется равновес
ная (она же - выходная) концентрация х2, а далее по уравне
нию ( 14. 1 ) отыскивается необходимый поток сорбента G.
Подчеркнем, что количество сорбента в псевдоожиженном
слое Gт (оно в ходе процесса не изменяется), определяющее
величину поверхности межфазного контакта F, в потоковых
задачах не существенно. Важно лишь, чтобы Gт не оказалось
чрезмерно малым, иначе задача массопереноса просто переста
нет быть потоковой - станет смешанной или внешней .
Из приведенного анализа и построения ясно: чтобы умень
шить У2 (повысить Тlиэнл) , нужно увеличить угол а (штрих
пунктирная прямая на рис. 14. 1 0) . При заданной производи
тельности D это означает повышение потока сорбента G; до
биться достаточно низкой выходной концентрации У2 (в этом
цель процесса) можно лишь при существенном увеличении G.
Но за понижение У2 путем повышения G приходится платить
снижением степени насыщения сорбента, т.е. уменьшением х2.
Это сопровождается возрастанием энергетических затрат при
десорбции (да и пылеобразование с ростом G увеличивается, а
это затраты на восполнение утраченного сорбента) .
В случае прямой линии равновесия у = тх (это реально , если
адсорбция проводится в узком диапазоне низких концентра
ций) возможен аналитический расчет задач эксплуатации и
проектирования (см . разд. 1 0 . 1 6 .4) .

Адсорбция в усл_овиях внутренней задачи
Несмотря на малый размер частиц сорбента (малую протя
женность пуги адсорбата внуrри зерна), внутренний перенос
вполне может оказаться лимитирующей стадией при сорбции в
псевдоожиженном слое из-за крайне низких значений коэф
0
фициента внутренней д иффузии Dм (нередко - менее 10- 1 2
1
м2/с).
10
Основные вехи расчета внутренней диффузии в зерне даны
в разд . 1 0 . 1 6 . 3 . Применительно к процессу адсорбции расчет во
многих случаях облегчен примерным постоянством Dм , по
скольку рабочий диапа.зон кон центраций достаточно узок и
приходится на область весьма малых значений х и у.
Для единичного сферического зерна радиусом R уравнение
Фика для симметричного массопереноса удобно записать в
1 1 79

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

сферических координатах (см . разд. 1 .6 .2) :
дх
д2 х 2
Dм -- + - - , "t > О, О < r <
д"t
r дr
дr 2
-

(

=

дх)

R,

( 14.2)

где � - время, отсчитываемое от момеJПа внесения зерна в зону адсорбции; r радиальная координата.

Решение этого уравнения х = х (r, -i:) дает локальную (на
координате r) и мгновенную (в момент времени -i:) концентра
цию адсорбата. Конкретный вид решения определяется усло
виями однозначности ; сформулируем их в наиболее простом
варианте:
- начальное условие: по всему объему зерна одинаковая на
чальная концентрация адсорбата Хн = х1 ; возможно Хн = О:
О s: r s: R;
(14.3а)
Хн = х (r, О) х1 = const;
- граничное условие J рода (внутренняя задача) : во всех
точках поверхности зерна в ходе процесса адсорбции поддер
живается постоянная концентрация адсорбата хя, равновесная
с концентрацией адсорбтива у в потоке сплошной среды:

't

= О,

=

(R, 't) = хя = »> = const;
't � О; ( 14.3б)
граничное условие симметрии массопереноса (од
новременно оно выражает и ограниченность в изменении кон 
центрации адсорбата) :
дх(О, 't )
·
( 14.3в)
r = О, -- - О ' 't ;::: О .
дr
Решение уравнения ( 14.2) с условиями ( 1 4.3) приводит к вы
ражению • типа х = х ( r, 't), которое удобно представить в фор
ме зависимости обобщенных переменных. Для процесса ад
сорбции это безразмерное время
критерий Фика
(диффузионный критерий Фурье) Fод = Dм't/R2, безразмерная

r=

R,

координата r/R
х Р - x(r 't )
х•

=

'

хР

- хн

х

и

безразмерная

концентрация

адсорбата

. В общем виде решение
х · = Ji ( Foд, r/R)

( 14.4)

получается в виде бесконечного ряда, весьма быстро сходяще
гося при не очень малых значениях Fод.
•
Решения уравнения Фика в сходных начальных и граничных условиях с
более подробными преобразованиями, включающими операции усреднения,
приведены в разд. 1 5 .8.4 применительно к десорбционному процессу сушки
влажных материалов.

1 1 80

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Технолога в большинстве случаев интересуют не локальные ,
а средние (по объему зерна) концентрации адсорбата - имен
но они фигурируют в исходных условиях процесса и в его ре
зультатах, в материальных балансах, являются показателями
эффективности процесса. Поэтому концентрация x(r, 't) или
Х 0(Fод, r/R) должна быть усреднена по объему зерна. Операция
усреднения температуры применительно к переносу теплоты в
сферическом зерне показана в разд. 7 . 1 0 .3 [выражение (7.35)) ;
аналогичным способом в рассматриваемом случае усредняется
концентрация. Средняя концентрация адсорбата:

-•

Х ( Fо д )

и

=

R

3
J x(r, 't)r 2 dr
R
хР - X('t)
3 R •(
r)
J
Fо д , - r dr = h ( Foд) , ( 14.5)
R
хР Rз
.X ('t)

3

=

о

=

о

Хн

Х

2

причем черта над символами х и х · означает усреднение по
объему зерна.
Конкретная запись зависимости типа h(Fo) для теплоперено
са приведена в разд. 7 . 1 0*. 3 . В терминах и символах массоперено
са для Dм = const имеем :
-•
6 00 1 -n 2n 2 Fo
( 14. 5а)
д .
Х =� -е
7t 2 n = l п 2
Различные частицы сорбента находятся в адсорбционной
псевдоожижен ной зоне разное время, так что выходят из нее с
разной концентрацией адсорбата. Средняя его концентрация в
покидающих адсорбер частицах рассчитывается с учетом плот
ности распределения их по времени пребывания q>('t) , как это по
казано в разд . 8 .3.2. Поскольку в псевдоожиженном слое части
цы сорбента движуrся в режиме, близком к идеальному перет.
мешиванию, то cp('t) = (1/'tср) е - / т. ср , где среднее время пребы
вания 'tcp = Gт/G. Тогда, в соответствии с формулой (8.8), вы
ходная концентрация адсорбата (результирующий эффект про
цесса)
ОС>

Х2
-•

где
•

.

И Х2
' Focp

См.

�

=

х Р - х2
---"-хР 2
Хн

Dмт.с/R .

сноску

на

J X ('t) q> ('t )d't

=

о

оо _ •
=

J Х (Fo д )q>('t)d't = /з(Fоср),

о

( 1 4.6)

стр . 1 1 80.

1 18 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Конкретная запись зависимости fз(Focp) в случае постоянно
коэффициента диффузии Dм представляет собой• медленно
сходящийся бесконечный ряд:
го

-·

6

со

1

X2 = 2
L п2
7t
n=l

1
( 2 п 2 Focp
).
+l
7t

( 14.6а)

Разумеется, если частицы сорбента имеют разные размеры R,
то придется вводить еще операцию усреднения по R с учетом
функции распределения частиц по размерам cp(R) .
Соотношения ( 14.6), ( 14.6а) являются расчетными, пригод
ными для решения задач эксплуатации и проектирования.
Решение задачи эксплуатации, когда заданы потоки D и G и
начальные концентрации адсорбтива у1 и адсорбата х1 = Хн ,
ведется в следующем порядке:
а) рассчитывают среднее время пребывания зерен сорбента
в рабочей зоне 'tcp = Gт/G;
б) по (14�• (14.6а) вычисляют значение концентрационного
комплекса Х2 , беря определенное количество членов ряда,
отвечающее приемлемой точности расчета;
в) задаются усредненной концентрацией адсорбтива в псев
доожиженном слое Уср ( практически она обычно близка к вы
ходной концентрации у2); по кривой равновесия находят равновесную концентрацию адсорбата хР;
--:-.
r) по найденной безразмерной концентрации Х рассчиты
2
вают натуральную концентрацию х2 .
После этого необходимо проверить правильность принятых
величин Усе ::::: У2 и »'. Здесь исполъзуюr итерационный путь: по
(14.1) с наиденным значением х 2 вычисляют У2; при несовпа
дении с принятым в пункrе (в) значением У2 расчет, начиная с
этого пункта, повторяют до совпадения.
Решение задачи проектирования не требует итерационных
процедур, но имеет свои трудности (о них - далее). Здесь
обычно задана выходная концентрация У2, поэтому определе
ние »' по кривой равновесия и х 2 по уравнению материально
го баланса ( 14. 1 ) затруднений не вызывает. Последовательность
дальнейшего расчета:
--:-.
а) по х1 , х2 и хР находят комплекс Х2 ;
б) по уравнению (14.6), (14.6а) вычисляют значение Focp и по
нему - среднее время пребывания частиц сорбента в слое 'tcp;
в) по 'tc = G;/G и известной производительности (потоку
сорбента &) рассчитывают массу сорбента Gт, необходимую для
обеспечения процесса;
• См.
1 1 82

сноску на стр.

1 180.

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

г) выражают Gт = py( l
e)faH и при найденном отдельно
поперечном сечении слоя !а (см. ниже) рассчитывают рабочую
высоту псевдоожиженного слоя Н или высоту насыпного слоя
Но, связанную с Н известным из гидравлики (разд. 2.7.4) соот
ношением: H( l е) = Ho(l ео) .
При решении задачи возникают технические осложнения на
этапе (б) - это обратная задача, требующая определения числа
Focp• входящего в каждое слагаемое ряда (14.6а). Затруднение
преодолевается либо табулированием этой функции в ее пря
мом решении по канве эксплуатационной задачи (е2П!f необхо
димо, то с построением графической зависимости Х2 Focp),
либо расчетом на ЭВМ, или же просто подбором.
Заметим: при решении задачи прое1сrирования поток сор
бента G выбирают с учетом экономических соображений.
Поперечное сечение адсорбера определяют по уравнению
расхода, причем объемный поток V сплошной среды при из
вестной ее плотности р рассчитывается по величине массового
потока: V = D/p. Рабочая скорость газа (ЖИдкости) w имеет
н ижн ее ограничение - скорость начала псевдоо:ж:ижения:
w > wo. На пра1сrике во избежание застойных зон рекомендуют
w � 2wo. Верхнее значение w при адсорбции из газовых смесей
ограничено не столько уносом, сколько интенсивным истира
нием частиц сорбента при их бурном перемешивании в случае
высоких w. Поэтому при работе с адсорбентами рекомендуют
рабочий диапазон скоростей газа Зw0 � w � 7w0. При адсорбции
из ЖИдКИХ смесей, когда истирание сорбента невелико, рабо
чий диапазон скоростей может быть расширен. Определив по
перечное сечение !а = V/w, находят его габаритные размеры диаметр, если сечение круглое; длину и ширину, если оно
прямоугольное.
При адсорбции в условиях внутренней задачи конечный ре
зультат, естественно, получается хуже, чем в случае потоковой:
фазы уходят из адсорбера, не достигая равновесия (в состоя
нии, отвечаюшем некоей точке N на рис. 14. 10 - с большим У2
и меньшим х2) . В целом односекционный псевдоожиженный
слой обладает плохим защитным действием, он не пригоден для
глубокой очистки газа (ЖИдкости). Такую систему для адсорб
ции целесообразно применять только в особых случаях, напри
мер:
- не требуется тонкой очистки сплошной среды от адсорбти
ва (т.е. допустимы относительно высокие выходные концент
рации У2) ;
- приемлемы больш ие расходы сорбента при низкой степени
его насыщения;
- очень благоприятная линия равновесия, она расположена
близко к оси абсцисс: тогда равновесная концентрация уР, а в
-

-

-

-

1 1 83

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

случае потоковой задачи - и совпадающая с нею выходная У2,
будуг весьма низкими.
Односекционный псевдоожиженный слой может оказаться
полезным при осуществлении десорбции, когда за счет повыше
ния температуры (если это допустимо) линия равновесия рас
полагается близко к ординате, что обусловит высокую движу
щую силу и достаточную эффективность десорбционного про
цесса.
Итак, для большинства адсорбционных процессов односек
ционный псевдоожиженный слой не эффективен с точки зре
ния глубины очистки, несмотря на благоприятные условия
массопереноса (прежде всего - высокие значения �F). Для
сохранения этих достоинств псевдоожиженных систем, приме
нительно к адсорбционным процессам, необходимо использо
вать другие схемы движения потоков. К их числу относится
ступенчатый противоток.
14.5.2. Ступенчато-пр отивоточный адсорбер
с псевдоожиженным слоем

В случае многосекционных аппаратов процесс адсорбции в
псевдоожиженном слое сорбента также протекает в условиях
потоковой или внугренней задачи, поскольку поверхность мас
сообмена в каждой отдельной секции (ступени) достаточно ве
лика и условия внешнего массопереноса весьма благопрИЯ'Пiы.
Многоступенчатый адсорбер с псевдоожиженным слоем по
казан на рис. 14.4. Ступенчатый противоток фаз при достаточ
ном числе секций может обеспечить тонкую очистку и высо
кую степень извлечения, а также хорошее насыщение сорбента.

Адсорбция в условиях потоковой задачи
Для потоковой задачи, не осложненной внугридиффузион
ным сопротивлением переносу, вполне применимы методы
расчета, подробно рассмотренные в разд. 10.12 для процессов
IOiacca 3(2-2) 1. Поэтому здесь не воспроизводятся в деталях изло
женные ранее под:ходы и методы. Напомним JПШIЬ, 'ПО в случае
линейности математического описания (в первую очередь для
прямой линии равновесия - это условие нарушается чаще всего)
задачи эксплуата.J..ОШ и проектирования решаюrся аналитически; в
противном случае прибегаюг к графическим методам. В качестве
примера в данном разделе рассматривается только проектная за
дача адсорбции в.случае кривой JШНИИ равновесия.
Расчетная схема аппарата с потоками и концентрациями ра
бочих тел показана на рис. 14. 1 1 ,а. Уравнение рабочей линии
получается из материального баланса по ПК для простран
ственного контура · К , проходящего через промежугочное се·

1 1 84

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

D

G
к

Puc. 14. J l. К расчету ступенчато-противоточной адсорбции с псевдоожи:ж:енным
слоем сорбента (К - контур) :
расче111ая схема, б диаrрамма у-х
а
-

-

чение с текущими концентрациями у и х, а также через то гра
ничное сечение, в котором известны обе концентрации ПК.
Технологи в начале расчета знают входные концентрации у1 и
х1 . Чаще всего ставится проектная задача в расчете на обеспе
чение определенной степени извлечения или конечной кон
центрации у2 . Поэтому в качестве граничного выберем сечение
с известными концентрациями У2, х1 • Производительность по
газовому (жидкостному) потоку D известна; поток сорбента G
определяется на основе технико-экономического расчета (разд.
10.7, 10.8).
Для вьщеленного пространственного контура:
Gx = О и у = Dy2 - Gxi + G х . ( 14.7)
D
D
При постоянных D и G это уравнение описывает прямую,
проходящую через точку (У2, х1 ) под углом
таким, что
tga. = G/D. Удобно по уравнению (14. 1) определить пока неиз
вестную концентрацию х2 и провести рабочую линию по двум
точкам: (У2, х1) и (у1 , х2) - см. рис. 14. 1 1 ,б. Располагая рабочей
и равновесной линиями, нетрудно построить теоретические
ступени и зафиксировать их число l'lт; на рисунке их более 3 ,
поэтому с некоторым запасом принимаем 1'1т = 4 . Далее пола
гается установить КПД ступени Т'lст и найти число реальных
ступеней п:
(б)
п = п/т�ст ·

Dy + Gx1

-

DY2

-

а.,

1 1 85

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Однако рассмотрение массообмена в условиях потоковой
задачи (�F � оо) принципиально означает Т\ст = 1, так что здесь
п = п,.. На практике, дабы учесть возможные негативные эф
фекты типа байпаса, застойных зон, рециркуляции между сту
пенями (иначе - отклонения от ступенчатоrо противотока),
обычно принимают Т\ст = 0 , 8 +- 0 , 9 . Тогда с некоторым запасом
получают согласно (б) п > п,..

Об адсорбции в условиях внутренней задачи
Точное решение задачи в данном случае требует чрезвычай
но rромоздкоrо математическоrо аппарата. Дело в том, что
решения типа ( 14.6) должны быть получены для каждой секции
в отдельности с учетом следующих элементов:
- материальноrо баланса в каждой секции, базирующеrося
на средней концентрации адсорбата;
- уравнений массопереноса (в обшем случае - в rраничных
условиях 111 рода, где требуется знание поверхностной кон
центрации xR; в случае rраничных условий 1 рода - XR = хР),
связанных с распределением концентраций адсорбата в зерне и
по секциям ;
- скачкообразного изменения концентраций адсорбтива
при переходе сплошной среды из секции в секцию.
Эrи решения (они получаются в виде бесконечных рядов с
двойными и тройными суммами) - за пределами учебноrо
курса. В учебнике приведен формальный подход, базирующийся
на уже известных понятиях: определение числа теоретических
ступеней в диаrрамме у-х. Таюtм образом, вся сложность пе
рехода от теоретических ступеней к реальным переносится на
КПД Т\ст· Эта величина в условиях внуrренней задачи может
заметно отличаться от 1 . Будем считать, что Т\ст берется по экс
периментальным данным или на основе эмпирических реко
мендаций; приближенную оценку можно получить пуrем тео
ретическоrо расчета отдельной секции в неЮIХ усредненных
условиях. При известной величине Т\ст число реальных ступе
ней п определяется выражением (б).
Поперечное сечение мноrосекционного адсорбера с псевдо
ожиженным слоем определяется на тех же основаниях, что и
для односекционноrо.
Общим недостатком всех адсорберов с псевдоожиженным
слоем является значительное истирание сорбента и ero потери
(вывод из процесса адсорбции) в виде пыли. Эrо является наи
более сушественной причиной стремления перехода к более
"спокойному" противоточному процессу адсорбции - в дви
жущемся слое сорбента.
1 1 86

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

14.6. РАСЧЕТ НЕПРЕРЫВНОГО ПРОЦЕССА

ПРОТИ В ОТОЧНО Й АДСОРБЦИ И
В ДВИЖУЩЕМСЯ СЛОЕ СОРБЕНТА

Аппарат с движущимся слоем показан на рис. 14.6. В таком
аппарате исполъзуюrся зерна сорбента на 1 ,0-1 , 5 порядка
крупнее, чем в псевдоо жиженном слое. В результате контапи
рующие фазы из-за ограниченной внешней поверхности кон
тапа F и меньшего коэффициента массоотдачи р не успевают
прийти в равновесие. Поэтому в движущемся слое не реализу
ется потоковая задача массопереноса, он протекает в условиях
внешней либо внугренней задачи, или же массообмен проис
ходит в условиях смешанной задачи. Ниже рассмотрены подхо
ды к приближенному расчету адсорбции при наличии одной из
упомянуrых лимитирующих стадий.

Адсорбция в условиях внешней задачи
Расчет адсорберов с движущимся слоем удобно вести по
аналоmи с расчетом массообменных процессов в насадочных
аппаратах. Принципиальное отличие в том, что переме
щающаяся вниз насадка - зерна сорбента - не инертна к П К,
а апивно участвует в массообменном процессе в качестве од
ной из фаз.
В основе расчета лежат уравнения внешнего массопереноса
и способы их применения, приведенные в гл. 10, в частности в
разд. 10. 16.2:
- на основе поверхности контапа фаз
(14. 8 })
М = р рFЛУср 1
на основе рабочего объема
( 14. 8 V)
М = PvpVЛYcp·
Такое написание предполаrает, что поток переносимого
компонента М выражается в кг П К/с, коэффициенты массоот
дачи определяются (теоретически или по эмпирическим фор
мулам) из безразмерных чисел Шервуда Sh = pd/Dд и
Shv = Pvd2/Dд, а средняя движущая сила ЛУср базируется на
относительных концентрациях адсорбтива в кг ПК / кг rаза
или жидкости . Согласование размерностей левой и правой
частей равенств (14.8) потребовало ввода плотности сплошной
среды р в уравнения массообмена.
Для определения ЛУс.v. необходимо располаrать линией равнове
сия и рабочей линией. Уравнение последней получается из тех же
соображений, что и для многосекционного аппарата с псеJЩо
ожиженным слоем (разд. 14.5.2) и n<лому совпадает с ( 14.7).
-

1 1 87

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Задачи эксплуатации требуют определения выходных кон
центраций У2 и х2 при известных потоках фаз D, G и начальных
концентрациях адсор бтива у1 и адсорбата Х1 - на основе из
вестных либо V. Здесь положение рабочей линии заранее не
определено (нет значений у2 и х2) , так что среднюю разность
концентраций ЛУср рассчитать нельзя. Количество переда
ваемого в единицу времени вещества (М), а далее по (14. 1 ) выходные концентрации У2 и х2 в этом случае (см. разд. 10.9.3)
определяются двумя способами:
- аналитически - при линейном описании составляющих
переноса (в том числе - при линейной равновесной зависи
мости) - ер. с (10.35):

F

[� (1 - �) ] - 1
(
_!_ exp[ P yF ( 1 - mD) ] - _1_
G
G/m
D
D
ехр

=
М

·

}

.

У1 - У 1Р '

(14.9)

- методом подбора положения рабочей линии в области ее
существования, ограниченной значениями концентраций у1 и
х 1 , - в случае кривой линии равновесия.
Задачи проектиро�ания, требующие расчета основных разме
ров адсорбера, решаются на базе уравнений (14.8). При этом
выходная концентрация целевого потока У2 задана, а поток
сорбента G устанавливается технико-экономическим расчетом.
Определив предварительно по формулам типа ( 14. 1) количество
П К, переносимого из сплошной среды в фазу сорбента в еди
ницу времени (М), и рассчитав (см. разд. 10.8.3) среднюю дви
жущую силу ЛУср . получ ают :
F= м , V= м
(14. 1 0 )
р рЛу ср
Рv РЛУ ср
причем коэффициент массоотдачи р или
находят отдельно
(см. разд. 10.16.2).
Далее определяют требуемую высоту зоны адсорбции с дви
жущимся слоем сорбента Н:
·
F = F.удV = 6(l - в о ) J;аН и Н =
(14. l l F)
6(1 во ) /3 '
V = fаН и Н = V/fa,
(14. l l V)
причем порозность движущегося слоя е0 (она близка к 0,45 ) и
размер зерен сорбента d известны.
Необходимое (само по себе; для нахождения 11) поперечное
сечение адсорбера fa рассчитывается по уравнению расхода:
1 1 88

----

Pv

d

-

F-d
-

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

/а = V/w; при этом определение объемного расхода газа
(жидкости) V по известному массовому потоку D и плотности р
затруднений не вызывает. Основная проблема - в выборе ра
бочей скорости сплошной среды w. Эта скорость в противо
точном процессе имеет два верхних оrраничения. Во-первых,
она не может превышать скорость начала псевдоожижения wo,
чтобы движушийся слой не перешел в псевдоожиженное со
стояние. Во-вторых, она должна быть ниже скорости зависания
w3, иначе слой прекратит свое нисходящее движение (см. разд.
2.7.3). Определив значения w0 и
ориентируются на более
жесткое оrраничение, выбирая рабочую скорость газа
(жидкости) из условия iv < min {w0, w3} .
w3,

Адсорбция в условиях внутренней задачи
В основе строгого решения задачи должны лежать уравне
ния внутренней диффузии для единичного зерна типа (14.2). В
этом уравнении переменную 't целесообразно заменить : 't = z/ v,
где z - расстояние от входа зерна сорбента в адсорбцион ную
зону (О s z $ Н), v
скорость нисходящего движения этого
зерна. Начальное условие при 't = О, z = О и условие симметрии
(при r = О) формулируются аналогично ( 14.3а) и (14.3в) соот
ветственно. Однако в формулировке rраничного условия 1 рода
(14.3б) появляются принципиальные изменения, существенно
осложняющие решение задачи: значение х (R, 't) или заменяю
щее его х (R, z) - величина переменная во времени 't движения
зерна или по мере его перемещения сверху вниз вдоль коорди
наты z. Это обусловлено изменением концентрации адсор бтива
у по высоте z адсорбционной зоны с движущимся слоем, сле
довательно и равновесной с ней концентрацией адсорбата
х:Р = XR = х ( R, z). Закономерность изменения XR по z весьма
сложна, она устанавливается с учетом связи XR со средней по
объему концентрацией х ; на эту закономерность, кроме того,
влияет характер равновесной зависимости у = f (х) . Чаще всего
аналитически: решить задачу не удается, привлекают численные
методы. В результате приходят к выражениям типа
-

х•

=

хР

-

-р

x(r, z)

Х - Хн

=

/.4 (Foд ' �) '
R

(14. 12)

причем х Р - равновесная концентрация, каким-то обуслов
ленным способом усредненная по высоте рабочей зоны Н
(возможно, равновесная с У1), Fод = Dм't/R2 = Dмz!vR2 - крите
рий Фика (диффузионный критерий Фурье), Хн = х1
входная
концентрация адсорбата.
Усреднение концентрации адсорбата по объему зерна
(способ усреднения продемонстрирован в разд. 14.5. 1) приво-

1 1 89

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

дит к выражению
х
-·

=

-

_х Р

-

x(z) -- f5 (

_х Р - Х н
а на выходе из адсорбционной зоны

х;
где Fон •

D"H/vR2,

=

Н)

х Р - х(
_х Р - Х н

=

с
г

од )

( 14. 1 3)

'

(z = 1/)
/s (Fo н ) ,

( 14. 1 4)

х(Н) = х2.

Поскольку все зерна сорбента в движущемся слое имеюг прак
тически одинаковые скорости v (т.е. твердая фаза движется в ре
жиме ИВ), то дальнейшего усреднения по времени пребывания не
требуется, так 'ПО выражение (14. 14) является расчетным.
Решение задач эксплуатации и проектирования ведется по
той же канве, что и для односекционного аппарата с псевдо
ожиженным слоем (см. разд. 14.5 . 1 ) .
В задаче эксплуатации п о времени пребывания 'tив =
= Gт/G = H/v вычисляюг значение Fон и далее по ( 14. 14) концентрационный комплекс 1'; , а по нему и выходную кон
центрацию адсорбата х2 = .Х(Н) . Поток поглощаемого компонен
та М и выходную концентрацию адсорбrива Yl находят из уравне
ния материального баланса ( 14. 1). При возникновении затрудне
ний с определением х Р прибегают к иrераi.щонньrм процедурам.
В задаче проектирования по производительности D и гранич
ным концентрациям адсорбтива у1 и У2 находят М а далее - х2
и безразмерный концентрационный комплекс
. Затем по
( 14. 14) вычисляюг Fон = Dм H/v 2 откуда рассчитываКУГ необ
ходимую высоту адсорбционной зоны Н

�

R,

Об адсорбции в условиях смешанной задачи
Для движущегося слоя речь идет о сопоставимости стадий
внешнего и внугреннего массопереноса. Строгий расчет пред
полагает решение уравнения ( 14.2) с заменой граничных усло
вий - 1 рода на 1 1 1 рода (см . разд. 1 0 . 1 6.5):
рр(у - р>) =

-Dм дx(R , z )

.
дr

( 1 0 . 80), (14. 1 5)

Решение получается еще более сложным, нежели для внуг
ренней задачи : в число аргументов наряду с Fод и / входит
еще диффузионный критерий Био Вiд = pRm/Dм .
В связи со сложностью С'Jl!ОГОГО решения нередко используются р азличные
полуэмпирические методы расчета. Чаще всего• идуr на подмену задачи, решая
• См" например, ( 6, 7 ) .

1 1 90

rR

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ее в терминах конвекrивного массопереноса, как это сделано в разд. 10.4.9 для
систем класса 3 (2-2) 1 . Пр и этом оперируют эквивалентным коэффициентом
массопередачи kэ, учитывающим интенсивность как внешнего, так и внутренне
го массопереноса. В этом случае формально получаются известные из гл. 1 0
сооrnошения и решения, а всн трудность расчета переносится на kэ - с введе
нием понятий (и расчеrnых сооrnошений) о глубине насьпценных слоев в зерне
сорбента, степени обработки зерна и т. п.

14.7. РАСЧЕТ ПОЛУНЕПРЕРЫВНОГО

ПРОЦЕССА АДСОРБЦИИ
В НЕПОДВ ИЖНОМ СЛОЕ СОРБЕНТА

Строгий расчет требует совместного решения уравнений ти
па ( 14.2) для единичного зерна и уравнений Фика типа ( 1 .22а,
б) для слоя, причем последнее записывается применительно к
однонаправленному перемещению П К (1Щоль неподвижного
слоя - по координате [) :

ас
т

+ w ас
i az

=

2
Dэ а с
az2

( 14. 1 6)

Уравнение ( 14. 1 6) должно быть записано (с учетом е0 - по
розности неподвижного слоя) отдельно для фазы сорбента
(тогда под С подразумевается х) и сплошной среды - газа или
жидкости (тогда в роли С выступает у). Решения в самом об
щем плане должны получиться в виде у = у (/, Ь, 't ) и х = х (r, /,
Ь, 't ) , где Ь - поперечная, перпендикулярная
направлению /,
координата в неподвижном слое. Для отыскания решений не
обходимы дополнительные уравнения: равновесная зависи
мость, начальное и гран ичные условия (по отдельному зерну и
по слою сорбента).
Без существенных упрощений такая задача не решается. Ряд упрощений
вполне оправдан и очевиден. Так, из ( 14 . 16) для твердой фазы вьmадает слагае
мое с WJ. Для потока сплошной среды поС'J)'лируется поперечная равномерность
потока, поэтому игнорируется изменение у и х по поперечной координате Ь.
Эффекr продольного перемешивания учитывается: множитель перед cfl C/дfl
выступает как эффекrивный коэффициент диффузии (аналог Е) .
Объединяя уравнения ( 1 4. 1 6) д л я обеих фаз, с перечисленными допущениями
и при игнорировании продольного перемешивания газового (жидкостного)
потока, приходим к выражению:
в0

ду

т(1 - во ) дх
t7t

ду

82У .

( 1 4 . l ба)
д/2
Здесь т - коэффициент распределения ; член De отражает эквивалентную
диффузию ПК вдоль слоя сорбента, обусловленную продольным . градиентом
концентраций .
Далее - эффекты в отдельном зерне рассматриваются лишь косвенно : вво
дятся различные коэффициенты, отражающие степень насьпцения зерна адсор
батом. Массообмен межлу зернами сорбента и сплошной фазой описывается
целиком в терминах внешней задачи - с помощью эмпирически наЙденных
Ut

+

+ w1

д/

=

D

е

1 191

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

коэфф и циеmов массопереноса . С этими и некоторыми другими допущениями
( например, D0
О) удается получить зависимости изменения концеmраций
адсорбтива и адсорбата по Д11И 1 1е адсорбера 1 и во времени t
в виде хоюtекrра
циоииой JIOJlllW . Такие решения приводятся в литературе• для наиболее просrых
технологических сmуаций.
=

-

В учебнике эти сложные методы решения не приводятся .
Здесь используюrся феноменологические подходы, базирую
щиеся на достаточно обоснованных уравнениях. Подчеркнем,
что эти подходы для большинства практических задач приводят
к тем же решениям, что и более строгий анализ . Ниже рас
смотрены модели процессов, называемых идеальной адсорбцией
и (условно , в целях отличия от уже упомянутой Идеализации)
реальной адсорбцией.
14.7 . 1 . Качественные представления
о по.iJувепрерывной адсорбции. Задачи расчета

Некоторые общие понятия
Будем рассматривать неподвижный слой сорбента высотой
поперечным сечением /, в который сверху поступает поток
(например, газовый) с расчетной (на полное поперечное сече
ние слоя) скоростью w при исходной концентрации адсорбтива
УО· Начальная концентр ация адсорбата Хн равна нулю (свежий
сорбент) либо несколько больше нуля (сорбент после регенера
ции). В ходе адсорбции слой сорбента постепенно (начиная с
верхних участков) насыщается поглощаемым компонентом,
очищая газовый поток. При этом на выходе из слоя сорбента
концентрация адсорбтива ( П К в потоке) Ук не должна превы
шать некоторой предельно допустимой величины Упр . назы
ваемой "проскоковой концентрацией" . Считают: пока Ук � Упр •
слой защищает потребителя от проскока П К; как только на
выходе из слоя Ук превысит Упр , наступает проскок. Продолжи
тельность работы слоя сорбента до проскока называют време
нем проскока или временем защитного действия 'tпр · ОчевИдно,
что 'tпр - предельная продолжительность .стадии адсорбции.
Пусть линия равновесия задана, т.е. для любой концентра
ции адсорбтива можно определить равновесную ей концентра
цию адсорбата (и наоборот); например, для Уо равновесная
концентрация равна х<}' (см. рис. 14.2,а).

L,

Идеальная адсорбция
Если поток с П К движется в режиме Идеального вытеснения
и (это главное!) массообмен в ходе сорбции происходит мгно
венно, то говорят об идеальной адсорбции . Проследим качест•

См., например, (5

1 192

-

7 ) , л итературу по хроматографии.

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

о

't

�

-

а

't np
-

'

6

в

Рис. 14. 12. К анализу идеальной адсорбции:
слой сорбенrа и хонrур (К) материальноrо баланса; б, 11
изменение хо�щенrрации
а
ПК во времени по высаrе слоя в сорбенrс и в потоке соотвстствснно
-

-

венно изменения в системе поток газа - слой сорбента для
такой модели адсорбции. Изобразим (рис. 14. 12) слой сорбента
и отвечающие ему профили концентраций х и у в разные мо
менты времени, причем под J будем понимать текущую верти
кальную координату, отсчитанную от верхнего (входного) сече
ния слоя.
Примем, что в начальный момент 't = О слой сорбента не со
держит П К (это упрощающее допущение - не обязательно;
можно рассматривать ситуацию, когда при 't = О концентрация
адсорбата мала и равна Хн по всей высоте слоя L). Концентра
ция адсорбтива на входе в слой равна у0 ; во всех более низких
участках слоя в промежугках между зернами сорбента ПК еще
отсуrствует: с момента -r = О только начнется подача в систему
газа, содержащего ПК.
В условиях идеальной сорбции (массоперенос ПК из потока
инерта к сорбенту здесь протекает бесконечно быстро , т.е . за
вершается мгновенно) спустя некоторое время 'tJ > О первые
(верхние) участки сорбента окажутся насыщенными погло
щаемым компонентом - в соответствии с условиями равнове
сия до концентрации X{)J> (см. рис. 14.2,а). Иными словами, эти
участки к моменту 'tt не пропускают П К, пока не насытятся до
концентрации Х{/'. Ниже участка слоя, насыщенного к этому
моменту, находится исходный (свежий) сорбент с концентра
цией адсорбата Хн = О (рис. 14. 12,б). Поток проходит насыщен
ные участки сорбента, не отдавая ему П К, т.е. минует их без
1 1 93

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

изменения концентрации у0 (рис. 14.12,в). Процесс сорбции
происходит на rранице насыщенных и ненасыщенных уча
стков; на этой rранице концентрация П К в сорбенте падает от
.хоР до О , а в потоке - от у0 до О (рис . 14. 12,б, в).
Упомянуrая rраница со скачками концентраций П К в слое
сорбента и в потоке называется фронтом сорбции. В случае иде
альной сорбции фронт плоский, четкий.
Спустя промежуrок времени 't2 > 'tJ (время отсчитывается от
начала адсорбции) фронт окажется ниже (ПК насытит еще
некоторый участок слоя) - рис. 14. 12,б, в. С течением времени
фронт будет перемещаться вниз с постоянной скоростью и
(поскольку условия сорбции на всех участках слоя одинаковы) .
В некоторый промежуточный момент 't фронт окажется на те
кущем расстоянии / от входа в слой (см. рис. 14. 12, а - в). К
этому моменту концентрация адсорбата выше сечения / равна
Х()Р, т.е. равновесна с Уо (см. рис. 14.2,а); _ иначе говоря, сорбент
здесь насыщен (заштрихованная область на рис . 14. 12,а). Ниже
сечения / сорбент свободен от П К, т.е. там х = Хн = О (Хн > О
при более общем подходе); это незаштрихованная область на
рис . 14. 12,а.
При продолжении подачи газа с адсорбтивом фронт будет
перемещаться к нижней rранице слоя сорбента (/ __,. L). Пере
мещение плоского фронта ццолъ слоя сорбента в случае идеальной
сорбции представляет собой концентрационную волну. До тех пор,
пока фронт будет еще оставаться выше этой rрающы (т.е. в пре
делах слоя сорбента), концентрация ПК в потоке, выходящем из
слоя, допустима (в рассматриваемом примере равна О), и стадия
адсорбции может продолжаться. Однако как только фронт до
стшнет нижней rрающы слоя (момент 'tпр), весь сорбент будет
насьпцен (соответственно условиям равновесия с Уо), его защиг
ное действие будет исчерпано, так что П К больше не может сор
бироваться из потока. Наступит проскок, при идеальной адсорб
полh Ый проскок: в выходящем потоке концентрация П К
ции
будет равна Уо · Далее сорбция невозможна.
Подчеркнем, что фронт сорбции перемещается по слою
медленно, его скорость и, как правило, значительно ниже w
(см . разд. 14.7.3).
Понятие об идеальной адсорбции дает весьма упрощенное
представление о процессе; оно оправдано тем, что позволяет
ввести и осмыслить некоторые понятия: постепенная отрабаrка
участков слоя сорбента; фронт сорбции; ковцевтрациоввая волна;
проскок; время защиrного действия; скорость движения фронта.
-

Реальная адсорбция
В реальных условиях адсорбция происходит сложнее: воз
можно продольное перемешивание потока при движении через
1 1 94

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

w vo
(1)

t1

_<=>

xg

(2)

-Q

ljl xg

�----J

а

6

в

Рис. 14. 13. К анализу реальной адсорбции (смысл фрагментов а

рис. 14. 1 2) .

-

в

-

см.

Учасrхи с.поя сорбеиrа в моменr 't : ( 1) - ПOJUIOC насыщение; (2) - часrичное насыщение
(зова массопередачи, фроиr сорбции) ; (J) - отсутсrвие ПК в спое (х - х,, , у s У11р)

слой сорбента (хотя в неподвижном слое оно, как правило,
невелико), но главное - массообмен при сорбции протекает во
времени, не мгновенно. Эrо означает, что в слое не существует
четкой границы отработанного и свежего сорбента, фронт
сорбции размыт, так что массообмен происходит (начинается
и заканчивается) на некотором участке протяженностью /о, на
зываемом зоной массопередачи.
Аналогично идеальной адсорбции представим графическое
изменение кон центрации П К (в сорбенте и потоке) во времени
(рис. 14. 1 3 ) для реального полунепрерывиоrо процесса адсорбции.
В начальный момент • = О состояние системы (слой - поток)
полностью соответствует рассмотренному ранее для идеальной
адсорбции. С этого момента станем подавать в слой поток с
постоянными скоростью w (в расчете на сечение пустого ад
сорбера) и исходной концентрацией адсорбтива Уо
начинает
ся сорбция, т.е. постепенное насыщение сорбента и падение
концентрации ПК в потоке.
Сначала в наибольшей мере насыщаются первые (верхние)
участки слоя сорбента: здесь выше концентрация ПК в потоке,
р>, .хР
х). Степень
а значит, и движущая сила процесса (у
-

-

-

1 1 95

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

насыщения этих лобовых участков слоя сорбента постепенно
(моменты времени •i , •2) нарастает, кон центрация адсорбата х
с течением времени становится ближе к равновесной X{f; по
ходу потока (с ростом l) она закономерно понижается . Кон 
центрация адсорбтива у п о мере прохождения этих слоев сор
бента, естественно, пон ижается; но с течением времени в опре
деленном сечении она растет, сопутствуя возрастанию х.
В некоторый момент времени 'tф первый слой зерен сорбента
в верхнем сечении слоя можно считать полностью насыщен
ным адсорбатом - до концентрации X{f, соответственно рав
новесию с кон центрацией адсорбтива у0 в этом сечении. Одна
ко в н ижележащих сечениях сорбент насыщен еще не полнос
тью, кон центрация адсорбтива здесь ниже Уо · Итак, в момент 'Ф
образовался начальный участок. слоя протяженностью /0 с харак
терным постепенным понижением (сверху вниз) кон центрации
адсорбата от .хоР до О (в общем случае - до хн ) . Поскольку зер
на сорбента в лобовом (самом верхнем) сечении слоя насыще
ны, поток минует их (только их!) без снижения кон центрации
П К, которая далее (сверху вниз) постепенно понижается от у0
до О (или до некоторой малой величины - см. ниже) .
При увеличении времени сверх 'Ф зона с этим характерным
понижением кон центрации ПК станет перемещаться вниз по
слою. Будем считать, что участок протяженностью /0 переме
щается с неизменным распределением в нем кон центраций П К
(в слое сорбента; в потоке) и с постоянной скоростью и, по
скольку условия массообмена на разных участках слоя сорбента
одинаковы. Характерное время 'Ф называется временем форми
рования фронта сорбци11, а перемещение кон центрацион н ых
кривых представляет собой концентрационную волну в условиях
реальной сорбции. Движущийся вниз участок длиной /0 пред
ставляет собой размьпый фронт сорбции, иными словами зону массопередачи.
Теоретически й анализ показывает, 'ПО в действительности скорость переме
щения ра:щ:ичных участков концентрационной кривой не одинакова, она зависит
от уровня концентрации. Если кривая равновесия вьшукла по отношению к оси
у, р (см . , например, рис. 1 4 . 2 , а, в) , то участки с большей концентрацией движуr
ся быстрее (рис. 1 4 . 1 4 , а) , и по мере перемещения вдоль слоя фронт становится
более крутьrм, т.е. менее размьпъrм: его протяженность /о уменьшается. При
линейной изотерме сорбции все точки концентрационной кривой движутся с
одинаковой скоростью (рис. 1 4 . 1 4 , 6) , сама кривая не деформируется; именно
этот случай отвечает принятом у выше постулату /о
const. Наконец, при вогну
той к оси у линии равновесин быстрее перемещаются участки кривой с мень
шими концентрациями (рис. 1 4 . 1 4 , в) , фронт по мере его движения по r.Jюю
сорбента все более размывается .
Н иже будем рассматривап. перемещение фронта сорбции с постоянной ско 
ростью и для всех участков концентрационной кривой, при этом /о
const.
Такое допущение обусловлено следующими обстоятельствами:
- встречаются системы с прямыми линиями равновесия;
=

=

1 1 96

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

а

б

в

Рис. 14. 14. Деформация концентрационной волны в зависимости от вида кон
цекrрационной кривой:
а - m.myicлaя ( к оси у) равновесная кривая, б - прям ОJD1Нейная равновесная зависи
мосrь (постоJIННЬIЙ коэффициею расnределеЮ1я) , в - воmуrая (к оси у) равновесная кривая

- очень часто процессы адсорбции ведуrся в области малых концекrраций ,
r:д е равновесие вполне может считаться линейным;
- в случае вьmуклой линии равновесия сжатию фронта сорбции противо
стоит обратный эффекr - его расширение за счет продольного перемешивания;
в конечном итоге оба эффекrа уравновешивают друг друга, и далее форма кон
цекrрационной кривой пракrически не изменяется.
Перечисленные случаи охватывают большинство реальных адсорбционных
процессов; случай с воmуrой линией равновесия, таким образом, из рассмотре
ния исключается.

К некоторому промежуточному моменту врем_ени 't > 'tф
фронт (зона массопередачи) займет какое-то текущее положе
ние в слое (см. рис . 14. 13). Выше этой зоны мы условились
считать слой сорбента (на рис. 14. 1 3 , а он заштрихован) насы
щенным до концентра uии XQP, массообмен здесь практичесЮf
завершен . Поэтому сплошная фаза проходит этот слой без из
менения исходной концентрации адсорбтива Уо· Ниже рассмат
риваемой зоны (на рис . 14. 1 3 , а здесь нет штриховки), где сор
бент не содержиr ПК (в общем случае - содерЖJП в малых кон
центрациях Хн), массообмен еще не начинался. Концентрация ПК
в потоке, омывающем зерна сорбента, здесь близка к нулю (по
крайней мере, она не выше предельно допустимой, т.е. проскоко
вой концентрации Упр), так как массообмен практически закон
ЧWIСЯ вьпuе. Таким образом, можно счиrать, 'ПО массообмен про
исходиr и завершается в зоне массопередачи, постепенно движу
щейся сверху вниз с постоянной скоростью и. Время, за кcrropoe
фронт сорбции проходит со скоростью и путь, равный протяжен
ности зоны массопередачи /о, называется временем массопередачи и
обозначается -см. Очевидно: 'tм = 1</и.
С течением времени фронт сорбции перемещается к нижней
границе слоя. Стадия адсорбции может продолжаться лишь до
тех пор, пока на . выходе из слоя концентрация адсорбтива
1 1 97

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

останется менее Упр · Время, соответствующее поямению на
выходе из слоя потока с концентрацией Ук = Упр . называется
временем заш,итноrо действия tпр в случае реальной адсорбции,
так что 'tпр - предельная продолжительность стадии адсорбции.
Фронт сорбции в этот момент занимает крайнее нижнее поло
жение (см . рис . 14. 1 3 ) . Продолжение стадии адсорбции за пре
делы 'tпр привело бы к превышению проскоковой концентра
ции Упр в выходящем из слоя потоке (см. пуюсrирный профиль
на рис. 14. 1 3 , в) , что, конечно, недопустимо.
В самой зоне массопередачи протяженностью /0 в промежу
точный момент времени 't (он лежит в интервале между 'tф и
'tпр) первые по движению потока (на рис . 14. 1 3 - верхн ие)
слои сорбента близки к насыщению, т.е. концентрация адсор
бата близка к Х(}'. Далее (вниз по координате /) концентрация
адсорбата, а значит, и степень насыщения сорбента понижают
ся. На выходе потока из зоны массопередачи (на рисунке - в
нижних ее участках) концентрация адсорбата близка к нулю
(если исходный сорбент не содержал ПК) или к начальной Хн ·
Такой характер уменьшения концентрации адсорбата отражен
на рис. 14. 1 3 , а переменной плотностью штриховки в пределах
зоны массопередачи.
Средняя концентрация адсорбата в rраницах зоны массопе
редачи, промежуточная между Х(}' и Хн, остается постоянной в
процессе перемещения зоны вниз по слою во всем диапазоне
времени от 'tф до 'tпр · Эта средняя по зоне концентрация адсор
бата записывается в виде произведения 'VX#, причем '1' име
нуется средней степенью насыщения зоны массопередачи (по
отношению к полному насыщению, т.е. к кон центрации Х(}',
равновесной с у0). Разумеется, '1' < 1 .
Заметим: в момент tпр участки сорбента, расположенные
выше фронта сорбции, насыщены полностью (до Х(}'); однако
нижний участок (т.е. сама зона массопередачи) протяжен
ностью /о насыщен лишь частично (см. рис. 14. 13,б, момент
проскока 'tпр )·

Статическая и динамическая емкости сорбента
Предельную концентрацию П К в сорбенте (насыщение, со
ответствующее равновесию с потоком исходной концентрации)
называют его статической емкостью хст; в принятых обозначе
ниях Хст = Хор . Эта емкость реализуется к концу стадии адсорб
ции в случае идеального процесса; в реальных условиях эта
емкость достижима, если процесс сорбции продолжать сверх
'tпр (не обращая внимания на проскок), что бы зона массопере
дачи целиком переместилась за пределы слоя сорбента. Однако
на пракгике стадия адсорбции должна быть прервана в момент
'tпр , когда последние участки сорбента (по схеме рис. 14. 1 3 -

1 1 98

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

нижние) насыщены лишь частично. Поэтому средняя емкость
(включая не полностью насыщенную зону
массопередачи) будет меньше Хст · Эта средняя концентрация
П К во всем слое сорбента, соответствующая моменту 'tпр• на
зывается динамической емкостью сорбента хдин. Очевидно,
практически Хдин < Хст·
Понятие динамической емкости используется при сравни
тельной оценке характеристик слоя сорбента в различных ап
паратах. В расчетном плане она необходима, например, при
сведении материального баланса процесса по П К, при расчете
стадии десорбции (определение количества десорбированного
П К) и т.д.

всего слоя сорбента

Задачи технологического расчета
Основная цель анализа и расчета полунепрерывной адсорб
ции состоит в установлении связи между высотой слоя сорбен
та L и временем защитного действия 'tпр· Располагая такой
связью, можно при известных параметрах процесса решать за
дачи:
а) эксплуатации (прежде всего, определять 'tпр для слоя из
вестной высоты L);
б) проектирования (прежде всего, определять высоту слоя
сорбента L, обеспечивающую заданное 'tп р).
Разумеется , наличие связи 'tпр и L позволяет решать и ряд
других эксплуатационных и проектных задач: определение при
заданных 'tпр и L некоторых условий (параметров) процесса максимально допустимой производигельности (скорости потока
w) ; максимальной исходной концентрации адсорбrива у0 ; выход 
ной его концентрации в некоторый момент времени и др.
К числу практически важных задач относится также нахо
ждение динамической емкости сорбента Хдин (статическая ем
кость определяется по равновесной зависимости и известной
концентрации Уо).
14. 7 2 Расчет процесса идеальной адсорбции
.

.

Связь 'tпр и L устанавливается здесь весьма просто : за время
фронт сорбции, перемещаясь с постоянной скоростью и,
проходит путь L. Отсюда
( 14. 17)
L = и'tпр ; 'tпр = L/и.

'tпр

В уравнении (14. 17) необходимо знать единственный пара
метр, представля ющий собой динамическую характеристику
системы, - скорость движения фронта сорбции и. Теоретиче
ский анализ позволяет найти скорость и достаточно точно - с
помощью материального баланса. Запишем такой баланс для
контура К (рис . 14. 12,а), ограниченного входным сечением
1 1 99

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

слоя сорбента и текущи м сечением l фронта сорбции в произ
вольный момент времени 't. Материальный баланс по ад
со � бтиву для промежутка времен и от О до 't представим в фор
ме : сколько ПК потерял газ за это время, столько приобрел
сорбент.
Обозначим : D - массовый поток газа, y.f - концентрация
адсорбтива, равновесная с начальной концентрацией адсорбата
.хн; определяется она по равновесной зависимости у - х (в слу
чае свежего сорбента Хн = О, очевидно, y.f = О; практически в
процессах адсорбции Ун Р < < Уо , и этой малой кон центрацией
обычно можно пренебречь). Тогда газ к моменту 't потерял сле
дующее количество П К ( кг) :

(а)
= wfp't (yo - y.f) .
Слой сорбента (его лорозность в0) за время 't получШI ПК в
сорбированном виде (в зернах сорбента) и в газовой фазе (в
просветах между зернами сорбента):
Dt(yo

- y.f)

fl(l - во)Рr(.х# - Хн) + flвop(yo - у.;>),

(б)

где Pr и р - шюrnости сорбента (здесь - кажущаяся) и потока; заметим: как
правило, Хн << x;f.
Кажущейс11 пл011t осn.ю твердого материала называют его плоrnостъ с учетом
пористости е: Pr = р"( 1 - е), где р" - плоrnостъ монолитного твердого материа
ла ("матрицы") .

Приравнивая выражения (а) и (б) и решая полученное ра
венство относительно l/'t = и, найдем искомое значение ско
рости движения фронта. Проделаем эту процедуру, пренебре
гая в целях упрощения значениями Ур" в сравнении с Уо и Хн в
сравнении с X{f:
pwftyo = /l( l - во) Рr.х# + flвoPYo ,
откуда

и

=

-l
't

=

w

РУо
__.:;_
----'-

_
___

(1 - Ео ) РтХб + Е о РУо

( 14. 1 8)

Подчеркнем, что в случае идеальной адсорбции найденное
значение и остается неизменным в ходе всей стадии сорбции ОТ 't
0 ДО 't = 'tпр ·
Из полученного выражения следует, что скорость движения
фронта и растет пропорционально скорости потока w, посколь
ку количество П К, внесенного в адсорбер с потоком инерта,
при прочих равных условиях пропорционально w. По этим же
=

• Разумеется. материальныii баланс можно записать и в общей форме (в от
суrствие здесь Источников и Стоков) : + Приход - Уход = Накопление, причем
для 't � 'tпр Уход = О.

1200

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

причинам и возрастает с ростом Уо · Если бы твердый матер иал
не обладал сорбционными свойствами (.xol' = О) , то и = w/Eo скорость фронта была бы равна вертикальной составляющей
истинной скорости потока ( wи8 = w/Eo ) в просветах зерен. Прак
тически же - первое слагаемое в знаменателе значительно
больше второго ; поэтому и обычно существенно меньше, неже
ли w или w/E0. Чем больше емкость сорбента X(f, тем меньше и
и тем дольше слой может работать без проскока (будет больше
'tпр ) или тем меньшая высота слоя L потребуется для обеспече
ния заданного 'tпр ·
Проблема определения Х.шш для идеальной адсорбции при
менительно к моменту 'tпр не возникает, поскольку к этому
моменту весь слой насы щен (в смысле равновесия адсорбата с
концентрацией .хоР и адсорбтива с концентрацией у0 ) , так что
здесь можно говорить только о статической емкости сорбента
Хст = X(f.
14.7.З. Уравнение связи 'tпр и L
Д11J1 процесса реальной адсорбции
Принятая (см . разд . 14.7 . 1 ) модель реальной адсорбции
предполагает, что фронт сорбции протяженностью /о переме
щается вдоль слоя сорбента с постоянной скоростью и, начи
ная с момента формирования фронта 'tф (само формирование
фронта происходит по специфическим законам , учитывающим
свойства рабочих тел и интенсивность массообмена). Поэтому
расчетное уравнение, связывающее 'tпр и L с помощью скорос
ти и [аналогично уравнению ( 14. 1 7) для идеальной сорбции] ,
может быть здесь записано только для 't > 'tф , т.е . для участков
слоя (см . рис. 14. 1 3 ) , находящихся ниже изначально сформиро
вавшегося фронта (/ > fo). Иными словами, уравнение связи 'tпр и
L, аналогичное формуле ( 14. 17), можно записать, есJШ исключить
из рассмотрения начальный промежугок времени 'tф и соответ
ствующий ему начальный участок слоя протяженностью fo:
'tпр

L - 10

- 'tф = -и

(14. 1 9)

Это соотношение удобно преобразовать, решив его относительно 'tпр :
'tnp

=

� - ('� -

't

ф) .

(в)

Величина 1/ и = К называется коэффициеJПом защитного дей
ствия слоя сорбента. Дробь lr/и представляет собой время 'tм , за
которое фронт сорбции проходит со скоростью и участок слоя
протяженностью /0 . Выражение в скобках (lr/и) - 'tф = 'tO пред
ставляет собой потерю времени защитного действия [в сравне120 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

T np
tgo. =

Рис. 14. 15. Графическая инrерпретация
связи 1np и L:
1 - кривая по эксперименrальным точкам
при оnределеюm связи 1пр и L (к расчету
парам етров уравнения Шилова - см. разд.
14.7.5), 2 - линия идеальной сорбЦЮI - урав
нение (14. 17)

4- = к

L

нии с идеальной адсорбцией см. уравнение (14. 17)] и называет
ся пслерявным временем.
Наиболее часто соотношение
(в ) представляют в форме урав
нения Шилова:

-спр =

КL

- -со .

(14.20)

Заметим, что чаще всего
процесс адсорбции ведуг при
достаточно больших 'tпр и L, так что роль второго слагаемого в
правой части уравнения ( 14.20) не очень велика. Однако пре
небрегать вычитаемым 'to не следует: ошибка может оказаться
заметной (и кстати - это ошибка не "в запас").
На рис. 14. 1 5 представлена графическая интерпретация за
висимости L и 'tпр · Линейный участок кривой отвечает уравне
нию Шилова. Отклонение от линейности в областях малых 'tпр и
L соответствует формированию фронта на начальных стадиях
адсорбции, завершающемуся в момент 'tф , коrда протяженность
фронта на участках, примыкающих к верхней границе слоя,
равна /0. Тангенс угла наклона прямой (разумеется, с учетом
масштабов по осям координат) равен К; отрезок, отсекаемый
на оси ординат продолжением прямой в области 'tпр < О, дает
'to. Очевидно, 'tO + 'tф = К/о = 1</и = 'tм ·
14. 7 .4. Об экспериментальном определении
пара м етров уравнения Шилова

Параметры уравнения (14.20): К и -с0 мoryr быть найдены
эмпирически . При этом эксперимент должен быть поставлен с
реальными рабочими телами (сорбент, поток с ПК) и в реальных
условиях (рабочие значения w, у0 и др .). Измеряя для слоев
сорбента различной высоты L время проскока 'tпр • на график
'tпр - L наносят точки сопряженных экспериментальных зна
чений "tпр и L (см. рис . 1 4. 1 5). Прямая , проведенная наилучшим
образом (например, по методу наименьших квадратов) через
точки на линейном участке зависимости -Спр - L, соответствует
уравнению ( 14.20). Расположение прямой позволяет определить
К = 1/и и -со (см. разд. 14.7.3).

1 202

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Особо следует подче ркнуть, что при изменении рабочих
условий эксперимент необходимо провести заново, так как из
менившимся условиям будут соответствовать иные значения
параметров. Это обстоятельство приводит к необходимости
разработки расчетных методов определения параметров К и •о
со следующими целями :
- установление влияния условий процесса адсорбции на
параметры уравнения Шилова;
- корректировка параметров применительно к изменив
шимся рабочим условиям процесса;
- независимое (без эксперимента) определение (или хотя
бы приближенная оценка) параметров уравнения .
14. 7 5 Расчетное определение параметров формулы Шилова
.

.

Расчет скорости движения фронта и
и коэффициента защитного действия К

Определение динамических характеристик системы (и, К)
возможно с помощью материальных балансов. Такого рода
балансы просты для массообменных аппаратов, функциони
рую �их в непрерывном режиме . Если в первой фазе (поток ее D кг/с) концентрация переносимого вещества понижается от У1
до .У2, то во второй ( G кг/с) - повышается от х1 до х2 . Матери
альный баланс для аппарата в целом по потоку вещества в
единицу времени из одной фазы в другую можно записать в
виде ( 14. 1 ) :
(г)
В рассматриваемом случае мы имеем дело с полунепрерывным
процессом; сведем его умозрительно к непрерывному. С этой
целью рассмотрим положение зоны массопередачи (фронта
сорбции) в произвольный момент времени •, отвечающий
оrраничению 'Ф ::;; • ::;;•np· Динамический характер полунепре
рывного процесса отражается перемещением зоны сверху вниз
со скоростью и. Закрепим систему координат в переме
щающейся зоне массопередачи . Тогда относительно этой си
стемы координат зона (фронт) неподвижна, а "поток сорбента"
будет "двигаться" вверх через эту " неподвижную" зону со
скоростью и (рис. 14. 1 6) . Поток газа, содержащего П К, физи
чески движется через слой сорбента сверху вниз с расчетной
скоростью w или с истин ной (точнее - с ее вертикальной со
ставляющей) wи8 = w/i::0 . Однако зона массопередачи "убегает"
от потока со скоростью и. Поэтому относительно принятой
системы координат в зону массопередачи поток будет входить
со скоростью wи8 - и (в подавляющем большинстве практичес1 203

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 14. 16. К расчету скорости дв ижения
фронта сорбции.

3 .М .

Фраrм енr с.лоя сорбенrа с зоной м ассопере
дачи (З . М) в пром ежуrочный мом енr времени � ;
К - конrур м атериального баланса

ких случаев и << wив ). Концент
рация адсорбтива на входе в зону
массопередачи равна Уо, на выхо
и , х.,
де - Упр· На "входе" сорбента в
зону (в нижнем ее сечении) кон 
центрация адсорбата близка к
нулю (реально может быть равна
хн); на "выходе" (в верхнем сечении зоны) сорбент насыщен (в
соответствии с условиями равновесия с Уо) , концентрация П К
в нем принимается равной x<f.
В таком представлении в любой момент времени (но обяза
тельно в промежутке от •ф до •пр) зона массопередачи анало
гична противоточному аппарату непрерывного действия, для
которого несложно составить уравнение материального баланса
типа (г) . Здесь для выделенного контура (см . рис . 14. 1 6) вместо
У1 следует подставить Уо , вместо У2 - концентрацию Упр; исход
ная концентрация в "потоке" сорбента - Хн вместо х1 , конеч
ная - x<f вместо х2. Поток сплошной фазы D = (wив - и)./Еор,
поток сорбента G = uf{ 1 - s0 ) rr. Тогда, соответственно выраже
нию (г) , масса П К, отдаваемая потоком газа (или жидкости) и
воспринимаемая "движущимся" сорбентом в зоне массопере
дачи в единицу времени , составляет
(д)
Мо' = ( wив - и)/sор (уо - Упр) = и.1{ 1 - so) Pr(x<f - Хн) .
Это уравнение нетрудно решить относительно и. Сделаем
это , как и в случае идеальной адсорбции, в упрощенном вари
анте, учитывая, что, как правило, Упр << Уо и Хн << Х</', и имея
в виду, что Wивьо = w:
к

и=

w ----Y_o"""P

_
_
_
_

xg (l - s о ) Р т + Yosop

Разумеется, НИ'По н е мешает решать уравнение (д) с учетом величин
х{}' и
фИiур ировать разности (;х{}' - Хн) и (уо - Упр) соответственно.

в этом случае в выражении ( 1 4.2 1) и далее - в ( 14.22) в место

( 14.2 1)

Хн

Уо

и Упр ;
будут

Выражение ( 14.21) формально совпадает с формулой (14. 1 8)
для случая идеальной адсорбции . Различие в том, что формула
( 14. 1 8) справедлива для всего временного диапазона от • = О до
•пр (причем •пр отвечает полному насыщению всего слоя по
глощаемым компонентом); выражение же (14.2 1) справедливо в
интервале времени от тФ до •пр (пр �чем здесь •l!P устанавли
вается значением Упр • так как нижнии участок сорЬента - про
тяженностью 10 - насыщен не полностью).

1204

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Коэффициент защитноrо действия определяется по найден
ному значению и; возможна и непосредственная ero запись:
К =

1

и

-

=

1
w

-

[е0 +

Рт х8]

(1 е0 ) Р Уо
-

--

.

( 14.22)

Из анализа выражений (14.2 1 ) и ( 14.22) следует ряд выводов
[частично они повторяют результаты анализа формулы (14. 1 8)] ,
позволяющих корректировать значения и и К при изменении
условий процесса адсорбции.
Скорость движения фронта и прямо пропорциональна (а
коэффициент защитного действия К обратно пропорционален)
скорости потока w (объемному ero расходу w/), т.е. количеству
П К, подаваемому с газовым потоком в единицу времени. Ско
рость и возрастает с увеличением исходной концентрации П К
в потоке Уо , причем практически тоже прямо пропорциональ
но, поскольку в знаменателе выражения ( 14.2 1 ) второе слагае
мое (оно пропорционально количеству П К в просветах между
зернами сорбента) обычно мноrо меньше первоrо (про
порциональноrо количеству сорбированноrо П К) . Физическое
влияние Уо аналогично влиянию w: увеличение у0 означает воз
растание количества П К, подаваемоrо в систему за единицу
времени с потоком. Вместе с тем скорость движения фронта
закономерно снижается (коэффициент К повышается) при уве
личении сорбционной емкости сорбента x{f.

Оценка времени массопередачи 'tм

Потерянное время 'tQ, входящее в уравнение Шилова ( 14.20),
формируется на основе /о , 'tф и является кинетической характе
ристикой, связанной с условиями (в том числе интенсив
ностью) массообмена в зоне массопередачи. Поэтому оно
должно рассчитываться с использованием уравнения массооб
мена, включающеrо время массопередачи 'tм . Как указано вы
ше, строгий расчет требует весьма громоздкоrо математическо
rо аппарата (в настоящее время такие попытки еще не нашли
достаточно точной реализации) . Поэтому будем базироваться
на упрощенном подходе к определению 'to на основе 'tм , при
вле кая известные подходы к описанию массообмена в условиях
внешней задачи . Отмеченные обстоятельства предопределяют:
- эмпирический характер некоторых величин, необходимых
для нахожден ия 'tм и 'to ;
- приближенность получаемых значений 'tм и 'to.
Запишем количество адсорбата, поrлощаемоrо зоной массо
передачи при ее насыщении от Хн до x{f:
(е)
Мо " = flo( l
ео) Рт(х<f Хн),
причем flo
объем зоны массопередачи, flo( l - ео) - объем
сорбента в ней, fl0( 1
ео)Рт - масса сорбента в этой зоне.
1205
-

-

-

-

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Поскольку дальнейший анализ ведется в понятиях
(терминах) внешней задачи, удобно представить Мо" на основе
концентрации не адсорбата, а адсорбтива. Сделать это нетруд
но с помощью соотношения (д):
8

f{ l

И

-

Eo) Pr(XoP

-

Хн) = /еор(уо

-

-

W
Упр ) и
и

U

;.;_
___;-

тогда из (е)
м. " = l'-r. '"
о
UtPEo vo

-

Упр )

Wив - и
и

(ж)

---

То же количество перенесенного П К можно выразить на
основе уравнения массообмена (см . разд. 10.4.4, 10.1 6.2, 14.6),
записанного для зоны массопередачи с учетом продолжитель
ности процесса в ней •м:
(з)
Мо" = kvp /ofЛYcp•м·
Здесь kvP - объемный коэффициент массопередачи, учиты
вающий реальную интенсивность массопереноса П К из потока
газа в сорбент, т.е. подмену смешанной задачи массопередачи
внешнею (необходимость введения множителя р обоснована в
разд. 10.4.4); ЛУср - средняя движущая сила процесса в зоне
массопередачи ; •м - время массообмена (он происходит только
в зоне массопередачи) , за которое фронт сорбции минует учас
ток протяженностью /0, где концентрация П К в сорбенте изме
няется от О (или от Хн) до насыщения (практически до XQP).
Поскольку принято , что на границах зоны массопередачи
концентрация адсорбтива изменяется от Уо до Упр . то в общем
случае (см . разд. 10.8.З) для этой зоны

ЛУср

=

Уо

-

У пр

Sу

(и)

'

где в знаменателе стоиr число единиц переноса Sy по фазе у (т.е. по потоку
сплошной среды).

ЛУср в выражение
Уо - у
kvp lof
пр •м .

Подставляя это значение

Мо"

=

Sу

(з) , имеем
(к)

Приравнивая выражения (ж) и (к), получаем после сокра
щений и подстановки Wи8Ео = w:
'С

м=

W

-

EQU

kv U

SУ ·

(14.23)

Из этой формулы следует, что •м определенным образом
связана с другими параметрами процесса:

1206

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

у

з.м.

J

:: 1 :: :: : : :
г
�- ---- � 00

�

х

б

а

Рис. 14. 1 7. К определению числа единиц переноса:
а - слой сорбе�па бесконечной высоты (З. М - зона массопередачи) , б
кривая ( !) и рабочая линия процесса (2)

-

равновесная

- уменьшается при увеличении интенсивности массообмена
(при kv � оо будет 'tм �о, что соответствует идеальной адсорб
ции);
- не зависит от скорости w в плане влияния фрагмента
формулы (w - &о и)/и , поскольку с изменением w пропорцио
нально изменяется и (см. разд. 14.7 .2); однако увеличение w
может приводить к возрастанию kv , и в этом плане w влияет на
'tм (с ростом w возможно уменьшение 'tм) ;
- зависит от Sy, и здесь требуется специальный анализ.
Число единиц переноса

Sy =

YI

dy

f -,
у-у Р

У2

входящее в выражение ДТIЯ движущей силы в процессах массообмена типа сорб
ции, содержит у и у(> - сопряженную (рабочую) и равновесную (с х) концентра
ции адсорбтива, У2 и У1 - рабочие концентрации адсорбтива на выходе газа из
слоя и на входе в него. Для установления пределов интеrрирования У2 и у1 при
менительно к зоне массопередаrtи рассмотрим слой сорбента бесконеrtной протя
женности с мmовенным расположением фронта сорбции (зоны массопередачи)
где-то в положении, доступном наблюдению (рис. 14. 17). Для данных сорбеита
(будем Д11Я простоты считать его первоначально свежим) и газового потока с П К
располагаем линией равновесия 1, показанной н а рис. 14. 17,б. Рабочая линия 2
на этом рисунке по строена из следующих соображений. На бесконечно удален
ных нижних участках слоя сорбеит не содержит П К, газовый поток - тоже
(поскольку весь ПК сорбируется на более верхних участках); поэтому точка
сопряженных концентраций для бесконечно удаленных нижних сечений слоя
имеет координаты у = О, х = О (т.е. рабочая линия проходит через начало коор
динат). На бесконечно удаленных верхних участках слоя сорбеит полностью
насьпцен соответственно условиям равновесия (не только практически, но и
теоретически: пока фроит сорбции дошел до рассматриваемого положения зоны

1 207

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

массопередачи, сорбция на бесконечно удаленных верхних участках продолжа
лась бесконечно долrо); поэтому точка сопряженных концентраций для беско
нечно удаленных верхних сечений слоя имеет равновесные координаты у = Уо;
x= x<f. Рабочая линия представляет собой отрезок, лежащий на прямой (поток
сплошной среды D и "поток" сорбента через зону массопередачи G - постоян 
ны) , проходящей через указанные точки сопряженных концентраций .
Возвращаясь теперь к рассмотрению зоны массопередачи, установим ниж
ний предел интеrрирования, соответствующий выходу потока из зоны: согласно
разд. 14.7 .6, это - проскоковая концентрация У2 = Упр; при этом пределе инте
rрирования движущая сила имеет определенное конечное значение, равное
вертикальному отрезку между рабочей и равновесной линиями.
Сложнее ситуация с верхним пределом интеrрирования У1, соответствующим
входу потока в зону массопередачи. Во всех предьщущих рассуJ1<Цениях мы при
нимали у1 = Уо; такое представление, строго говоря, неоправданно:
- e CJDI бы во входном сечении зоны массопередачи концентрация П К в сор
бенте соответствовала полному насьпцению x<f, а в потоке - Уо, то движущая
сила в этом сечении у - ?' бьиа бы равна нулю (знаменатель в Sy - тоже), так
что Sy � оо; это делало бы бессмысленным вычисление tм по ( 1 4.23) и после
дующие операции с tм;
- равенство концентрации адсорбтива на входе в зону массопередачи исход
ной величине Уо означало бы, чrо все предьщущие (лежащие вьШJе) слои сорбен
та поJШостью насыщены. Между тем реально сорбция происходит во времени,
и для полноrо насыщения (для достижения R сорбенте концентрации Х{/', равно
весной с Уо) требуются бесконечно большие время или поверхность контакта;
такое можно представить для гипотетического слоя сорбента бесконечно боль
шой высоты, но не для реального слоя оrраниченной протяженности L. По этим
причинам физически концентрация адсорбата на входе в зону массопередачи
будет несколько ниже X{f, так что сорбция на входном участке в зону хотя и
весьма медленно (из-за близости х к X{f), но все же продолжается; значит, У! <
< Уо и разность у - Ур тоже не равна нулю.
Способ задания У! в известной мере субъективен (произволен), фактически
он определяется требуемой точностью представления о завершенности процесса
сорбции на участках сорбента, расположенных вьШ1е зоны массопередачи. На
практике иногда задают у1 = (О,95 + О,97)уо, т.е. считают, что массообмен вьШJе
зоны массопередачи завершился на 95-97% . Резонно также, исходя из симмет
рии расчета (одинаковое отличие от предельных ситуаций на rраницах зон),
принять У! = Уо - Упр· С этим доп ущением вели чина

Sy =

УО - У пр

J

Упр

-°L_
у - уР

может бьrrь определена обычными rрафоаналитическими
методами. Далее по ( 14.23) рассчитывается tм .

или численными

Определение потерянного времени •о
Потерянное время •о найдем на основе •м из следующих со
ображений. В слой сорбента поступает неизменное количество
П К в единицу времени, поскольку скорость газового потока w
и исходная концентрация адсорбтива в нем в ходе сорбции не
изменяются . Пока время сорбции • ::;;;; •пр • весь ПК (с погреш
ностью, не превышающей малой величины Упр ) улавливается
слоем сорбента. Поэтому количество адсорбированного П К

пропорционально времени рабоmы слоя сорбента.
1208

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

- - · - i-

-· -

а
Рис. 14. 18. К определению потерянного времени.
Профили ко1Щешраций адсорбата в моме1ПЫ времеЮ1 "tф (а) и "tф + <t w (б)

Для определения 'to рассмотрим два момента времени, от
считанных от начала процесса адсорбции и относящихся к на
чальным его стадиям: 'tф и 'tф + 'tм (рис . 14. 18).
К моменту 'tф завершено формирование фронта, и зона мас
сопередачи протяженностью /0 занимает верхнее положение
(рис . 14. 1 8,а) . Количество ПК в слое сорбента (поперечное
сечение адсорбера - /) пропорционально 'tф и равно произве
дению массы сорбента в зоне массопередачи lof (1 - &o) Pr на
концентрацию ПК в нем 'VXpo (напомним: 'V - степень насы
щения зоны массопередачи).
Спустя время 'tм после завершения формирования фронта
зона массопередачи переместится вниз на расстояние /0 и зай
мет положение, показанное на рис. 14. 1 8 , б: верхний и нижний
участки протяженностью по 1о каждый. Количество П К в слое
сорбента к этому моменту будет пропорционально ('tФ + 'tм) и
равно сумме количеств П К в верхнем (полностью насыщенном
по условиям равновесия) участке и в следующем за ним ниж
нем (частично насыщен ном - соответственно степени насы
щения), т.е. в зоне
массопередачи:
lof (l - &o) PJXp0 +

+ lof ( 1 - &o) PrЧJXp0 .

Запишем теперь сформулированное выше положение про
порциональности в форме соотношения масс сорбированного
ПК за время 'tф и 'tф + 'tм; сократив числитель и знаменатель
правой части на /of(l - Eo)Pr, имеем:
'tф

't ф

+ 't м

-

ЧJXg

xg + ЧJXg

Оrсюда 'tф = 'tмЧJ· Поскольку
формулу (в) и рис. 14. 1 5 ) , то

'tм

=

.

'to + 'tф

(л)
[см . разд. 14.7.З,

= 'tм(l - ЧJ) .

(14.24)
Величина 'V уменьшается с ростом отношения У<IУпр · По
этому на практике не следует стремиться к чрезмерно малым
"СО

1 209

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

величинам Упр. выходящим за пределы экономичесюtх или эко
лоrичесюtХ требований .
Физичесюt 'V < 1 , практичесюt 'V < 0,5. Из опыта эксплуата
ции адсорберов известно , что чаще всего 'V находится в преде
лах 0, 1 -0,4. Оценить значение 'V можно с помощью полуэмпи
ричесюtХ соотношений
'V •

l/S,;

'V •

(1п[;:J ,

(м)

дающих неплохое согласие с экспериментом при У</Упр � 10
(такое соотношение характерно для подавляющего боль
шинства реальных процессов полунепрерывной адсорбции) .
Первое из этих выражений точнее; оно, кроме того , удобно,
так как значение Sy уже найдено в ходе оценюt -rм. Сдержи
вающим моментом в его использовании является отчасти про
извольное установлен ие верхнего предела интегрирования при
вычислении Sy. Второе выражение проще, оно наглядно высве
чивает влиян ие Упр на величину IJ.I ·
Итак, при известных значениях и (К) и -r0, найденных для
кон кретных условий процесса, можно пользоваться уравнением
Шилова для решения задач эксплуатации и проектирования в
случае полунепрерывной адсорбции. Подчеркнем, что неточ
ности (результат упрощающих допущений) при вычислении -r0
практичесюt не приводят к существенным погрешностям в
расчетах 'tпр (при известных L) или L (при заданных 'tпр); ведь
реально процесс проводится при достаточно больших -Спр• так
что -со в уравнении (14.20 ) обычно заметно меньше КL.
14.7.6. Определение динамической емкости сорбента

Располагая приближенным значением -rм, можно с той же
погрешностью оценить протяжен ность зоны массопередачи
lo = и-см, причем скорость движения фронта и рассчитана до
статочно точно. Заметим , что умен ьшение значения Упр и при
ближение У1 к Уо повышает -rм, а с ним и /о.
Динамическую емкость сорбента хдин при известной стати
ческой (хст = X{f) можно найти следующим образом . В завер
шающий момент процесса адсорбции (-с = -rпl! ) слой сорбента
можно разделить на два участка (рис . 14. 1�): н а основной
(верхний) протяженностью L - /0, где концентрация адсорбата
.хоР соответствует практичесюt полному насыщению (равновесию
с потоком исходной кон центрации у0 ) , и на нижний (зона мас
сопередачи) протяжен ностью /0, где насыщение неполное (на

1210

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 14. 19. К расче"!)' динамической емкости сорбента.
На рисунке для наrлядности прочерчен профиль кон
цеиrра.ций адсорбтива в момент 'пр

верхней границе зоны концентрация Х{!;
на нижней - Хн, не исключено Хн = О) .
При этом степень насыщения н ижнеrо
участка поглощаемым компонентом рав
на IV · Тогда средняя концентрация ад
сорбата на нижнем участке (в зоне мас
сопередачи) составляет \VXfl ·
Среднюю концентрацию адсорбата во
всем слое сорбента (т.е. хдин) найдем по
аддитивности:
хдин =

(L -

l0 )xg + 10 \Vxg

(н)

L

или после очевидных преобразований:
Хдин =

xg 1 - ( l - 1V )

[

�].

(14.25)

Из этой формулы следует, что хдин возрастает с увеличением
статической емкости: при прочих равных условиях предпочти
тельнее выбирать сорбент с большей Х{!. Важно, что Хдин растет
(приближается к Xf?) при повышении интенсивности массооб
мена (т.е. при уменьшении /0) . В наиболее благоприятном слу
чае /о = О имеем Хдин = Х{!, что отвечает идеальной полунепре
рывной адсорбции. В неблагоприятных случаях, ко гда fo при
ближается к L, имеем: Хдин � IVX{)P . В реальных ситуациях О <
< lo/L < 1 ; оценка /0 позволяет найти отношение k/L и далее
Хдин по формуле (14.25). Наконец, хдин возрастает при увеличе
нии IV· В наиболее неблаrоприятном случае IV = О получается
хдин

= х8

(1 - lc/L);

при неизвестной величине

IV

такая оценка

дает хдин с погрешностью в сторону преуменьшения (т.е. с
ошибкой "в запас"). Случай IV � 1 практически невозможен в
реальном процессе адсорбции ; он отвечал бы идеальному про
цессу (здесь хдин = Х{)Р) .
14. 7 . 7. Расчет количества
десорбируем ого поглощенного компонента

На стадии десорбции выделяют П К, поглощенный сорбен
том в ходе адсорбции. Применительно к одному циклу
(адсорбция-десорбция) количество М десорбированноrо П К

121 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

нетрудно рассчитать, располагая значением Хдин и зная, до ка
кой остаточной концентрации адсорбата (это начальная кон
центрация хн для стадии адсорбции) ведется процесс десорб
ции . Из материального баланса по П К в слое сорбента (способ
его составления - очевиден) имеем:

М=

Lf(l

-

Ео) Рт(Хдин

-

.хн).

( 1 4 .26)

Входящее в ( 14.26) поперечное сечение адсорбе,Р а / опреде
ляют из уравнения расхода V = /w, причем V = D/p. Расчетн ая
скорость w, фигурирующая также в выражениях ( 1 4 .2 1), ( 14.22),
( 14.23), при подаче газового потока в адсорбер сверху не огра
ничивается никакими физическими пределами, при подаче
снизу - ограничена скоростью н ачала псевдоожижения (при
б6льших скоростях слой должен бьпъ зажат сверху какой-нибудь
сеткой). Однако из экономических соображений скорость w
выбирают небольшой , дабы не бьmо высокого гидравлического
сопротивления слоя, а с н им и значительных затрат на дутье
(или на подачу жидкости) . Обычно скорость потока составляет
десятые доли метра в секунду при адсорбции из rазовых смесей
и на 1 - 2 порядка ниже - при адсорбции из жидкостей.

Л ИТЕРАТУРА к главе

14

1 . Гельперин Н.И. Основные процессы и аппараты химической технолоmи.
М . : Химия, 198 1 . 812 с.
2. Гельперин Н.И., Аiiнштейн в.r., Кваша В.Б. Основы техники псевдоожи
:ж:ения. М . : Химия, 1967. 664 с.
3. Дытнерский Ю. И. Процессы и аппараты химической технолоmи. М . : Хи
мия, 1 99 . 768 с.
4. Касаткин А.Г. Основные процессы и аппараты химической технолоmи.
М.: Химия, 197 1 . 784 с.
5. Кельuев Н В Основы адсорбционной техники. М . : Химия, 1976.
с.
6. Рачинский В. В. Введение в общую теорию динамики сорбции и хромато
rрафии . м . : Наука, 1964. 136 с.
7. Романков П.Г., Фролов В. Ф. Массообменные процессы химической техно
лоmи (системы с дисперсной твердой фазой). Л . : Химия, 1990. 384 с.

5

.

.

512

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Глава 15
СУШКА ТВЕРДЫХ МАТЕРИАЛОВ

Сушка (высушивание) твердых материалов (сокращенно
состо ит в удален ии влаги (более или менее полном) из
влажных материалов путем ее д и ффузии из твердого материала
и испарения . Необходимость удаления влаги из материала мо
жет быть обусловлена разными пр и чинами, например:
- влажный продукт может портиться при хранении, так как
влага вредно воздействует на товарные свойства некоторых
материалов: слеживан и е; смерзание в зимнее время; образова
ние плесени (на поверхности пищевых и других продуктов);
- влажность полупродуктов может быть вредна на после
дующих стад иях их переработки: действовать как каталитиче
ский яд; ухудшать качество конечных продуктов (например,
влага в волокнообразующих полимерах существенно сн ижает
качество н ити при продавливании расплавов полимеров через
отверстия фильеры);
- перевозки высушенного материала потребителю, особен 
но на дальн и е расстоян и я, обходятся дешевле, нежели влажно
го - более тяжелого.
Сушке подвергают не только твердые влажные материалы; в
химической и ряде с м ежных отраслей промышленности влаrу
нередко удаляют также из суспенз ий и растворов.
Пр и большом содержании влаги в и сходном материале час
тичное ее удаление возможно механическими методами осаждением, фильтраци ей, центр и фугированием (см. начало
гл. 5); экономически (по затратам энергии) они значительно
выгоднее сушки и, где возможно, их следует применять. Одна
ко достаточно полного удаления влаги с их помощью добиться
не удается, более глубокое удаление влаги требует использова
ния сушки с большим и затратами теплоты на испарен и е влаги.
Сушка влажных материалов - энергоемкий процесс: на
удаление 1 кг влаги требуется затратить по крайней мере теп
лоту ее испарения (далее увид и м, что обычно в 1 , 5-2,0 раза
больше). В стране 12- 1 3 % топл и ва расходуется на высушива
ние твердых матер и алов. Чтобы осуществить процесс сушки с
максимальной эффективностью, в том числе - с приемлемыми
затратами и получением конечного продукта заданной влаж
ности, необходимо знать физико -химические основы процесса,

ТМ)

1213

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

представлять себе принципы работы сушильных аппаратов ,
владеть методами технологического расчета.
В химической технологии наиболее широко распространено
высушивание материалов от воды. Поэтому в дальнейшем рас
смотрение сушильных процессов строится на примере обезво
живания твердых материалов; переход к построению схемы
процесса и к расчету удаления какой-либо иной влаги принци
пиальн ых затруднений не вызывает. Объектом последующего
изложен ия являются в основном непрерывные процессы сушки :
они более производительны, проще в управлении, позволяют
получать стабильный конечный продукт.
Сушка твердых материалов - один из наиболее распростра
нен н ых десорбцио н н ых процессов . Разработка методи ки ее
расчета первоначально велась вне связи с технологическими
расчетами других массообменных процессов. И по настоящее
время материальные и тепловые расчеты, определение расход
н ых показателей (то , что традиционно именуется статикой
сушки) базируется на специфической основе, не используемой
при рассмотрении других процессов переноса вещества, неред
ко даже с символико й , отличающейся от общепринятой в мас
сообменных процессах. Такой подход сохраняется в известной
степени потому, что в большинстве сушильных процессов речь
идет о переносе одного и того же вещества - воды и сушиль
ный агент один и тот же - воздух. Расчет кинетических харак
теристик процесса (здесь проблемы, связанн ые со скоростью и
продолжительностью сушки) ведется на общей основе, изло
женной в разд . 1 0 . 1 6 .
Различают две группы методов сушки. Первая
конвек
тивные методы - основана на контакте высушиваемого мате
риала с потоком газа - сушильного агента (СА) и переносе
теплоты от СА к Т М испарении влаги и переходе ее из ТМ в
СА. При этом в качестве сушильного агента чаще всего ис
пользуется нагретый воздух или топочные газы , реже - другие
СА. На долю конвективных методов приходится свыше 90%
промышле н н ых сушильных процессов. В некоторых случаях
материал не допускает длительного контакта с горячим СА
тогда используют иные методы сушки, объединяемые общим
термином
специальные. Они отличаются от конвективных
способами подвода теплоты на испарение влаги и характеризу
ются обычно повышенн ыми энергетическими затратами и
(или) сложностью аппаратурного оформления . Применяются
специальные методы сушки, как правило , в малотоннажных
производствах для высушиван ия дорогостоящих ТМ, чаще
всего - как вынужденная мера при неприемлемости кон век
тивных методов (напр и мер, для термолабильных материалов) .
Специальные методы сушки нередко используют в пищевой и
фармацевтической пром ышленности , вообще в биотехнологи и .
-

,

-

-

1214

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Н иже расс м отрены устройство и прин цип действия типовых
сушильных аппаратов для конвективных и специальных мето
дов сушЮf . Рассмотре н ие ф изико-хими чес ЮIХ основ и методов
технологического расчета представлено в учебнике для конвек 
тивной суш Юf - наи более распространенной в хими ческой
технологии и смежных с ней отраслях промышленности . Для
знакомства с м етодам и расчета специальной суш ЮI следует об
ратиться к лите ратуре • по сушильны м процессам .
1 5. 1 . УСТРОЙСТВО И ПРИНЦИП РАБОТЫ
СУШИЛЬНЫХ АППАРАТОВ

Конструкции сушил ьных аппаратов (сушилок) крайне раз
нообразны. Можно назвать две основные прич и ны такого раз
нообразия: различ и е в с войствах выс уш и ваемых материалов и в
постановке технологи ч еской задачи ; недостаточные успехи
проекти ровщ иков в разработке единой опти мальной конструк
ции . В случае суш ильных аппаратов определенно преобладает
первая причина. Это является следствием широкого разнообра
зия определяющих факторов:
- консисте нция высуш иваемого исходного сырья ( изделия ;
ленты ; плен Юt; нити ; зерн истые матер иалы, хорошо и плохо
сыпучие ; пасты ; суспензии и даже растворы) ;
- размер и форма Т М (крупные и мел Юf е ; сферические и
бл из Юf е к ни м либо сильно отличающиеся от шарообразных;
дробленые, игольчатые , чешуйчатые и т.п.);
- устойчи вость к высоким те мп ературам : стабил ьность к
очень высоки м (на уровне топочных газов) или достаточно
высо Юf м те м пература м л и бо , наоборот, термолабил ьность и
потому ограниченность температур при сушке ;
- виды св я зи влаги с м атериалом и необходимая глубина вы 
сушивания ;
- скорость сушки ( существуют материалы, портящиеся при
быстрой сушке) ;
- механиче ская прочность (устойчивость к сжатию и истира
нию) и т.п.
Ниже приведены отдельные •• (наиболее распространенные и
интересные в методическом отношении) сушильные аппараты
и рассмотре н ы прин ци п ы их работы . Изложение ведется в со
ответств ии с градацией методов с уш ки : конвекти вные суш ил 
ки; специальн ые сушилки.
• См., например, (9, 1 0) , менее детально (2 1 ) .
"Ряд других сушильных аппаратов рассмотрен в учебниках и монографиях
( 1 , 2, 4, 6, 10, 1 5 , 1 6, 19, 22 ) .

1215

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

1 5. 1 . 1 . Конвективные сушильные аппараты

На рис .

15.1

показан фрагмент полочной (камерной) сушилки

полунепрерывного действия.

В ысушиваемый ТМ (на п ример, зернистый ) размещают на полках 2, распо
ложенных в камерах 4. Н иже и вьпuе камер находятся воздушные короба J: по
нижнему подается rорячий СА ([), по верхнему отводится СА (/[) с парами
влаrи, вьщелившимися из ТМ . Равномерное распределение СА ме:жду полками в
камере обеспечивается косыми переrородками 3, выравнивающими гидравличе
ское сопротивление движению сушильноrо агента; распределение потока СА
между камерами обеспечиваетсн поворотными заслонками 5.

Достоинство полоч н ой сушилки - простота. Среди недо
статков:
- периодичность действия и как следствие - невысокая
производиrельность, в частности из-за затрат времени на извле
чение полок из камер , выгрузку высушенного материала и за
грузку новых порций влажного, возврат полок в камеру; этот
недостаток частично устраняется в вагонеточном варианте :
полки размещаются в вагонетках, и непроизводительная стадия
разгрузки-загрузки заметно ускоряется - вагонетки с высу
шенным материалом вывозятся из камер, а туда ввозятся ваго
нетки с заблаговременно подготовленным влажным ТМ;
- неравномерность сушки: лучше высушиваюrся области ТМ
(зерна, слои и т.п.), непосредственно соприкасающиеся с СА,
хуже - внутренние зо н ы ТМ (скажем, зерна в глубине засып
ки), не контактирующи е или плохо контактирующие с потоком
СА; это ухудшает качество продукта либо заставляет увеличи
вать продолжительность сушки (снижает производительность);
- затраты теплоты на наrрев транспортных устройств: полки ,
вагонетки вводятся в процесс холодными, а выводятся горячи
ми; в технологических расчетах они будут трактоваться как
потери теплоты с транспортными приспособлениями Qтр ·
На рис . 15.2 показана туннельная сушилка.
В туннеле 4 находятся ваrонетки 2 с полками 3, на которых размещается
высушиваемый ТМ Ваrонетки медленно перемещаются по рельсам 6 (иногда непрерывно, чаще - толчками ) , на рисунке - слева направо ( стрелка с попе
речной чертой на конце) . Высушиваемый материал контактирует с потоком СА,
подаваемым преимущественно противотоком к движению ваrонеток (см . потоки
СА 1 и /[), чтобы повысить глубину сушки ТМ и степень насыщения сушильно
rо агента влаrой . По мере сушки температура rорячеrо ([) СА понижается; не
редко по ходу движения СА ставят дополнительные нагреватели, повьпuающие
ero температуру. Ваrонетки с ТМ вводятся в туннель и выводятся из неrо через
шлюзы 1, ограниченные периодически открывающимися дверьми 5. Протяжен
ность туннеля достиrает десятков метров, в туннеле может одновременно нахо
диться несколько десятков вагонеток.
.

Туннельные сушилки достаточно производительны, но
весьма громоздки, занимают большие производственные пло
щади . Для них, как и для полочных сушилок, характерн ы перав-

1216

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

1

3

2

1

4

5

4

Рис. 15. 1. Камерная (полочная) сушилка:
1
rазоходы , 2
пoJIICJI с ТМ, З
косые переrородхи,
-

-

-

ЗЗСJIОНJСИ;

/

-

rорячий СА, /1

-

4

-

отходящ11й СА

камеры, 5

-

поворотные

н.омерн.ость . сушки и значительные потери теплоты с тран.
спортн.ы.ми приспособлениями.

На рис . 1 5 . 3 , а представлена конструкция одной из конвейер
ных сушилок, применительно к сушке зернистых материалов ее
чаще называют ленточной.

В сушильной камере 1 находится транспортирующее устройство - два вра
щающихся барабана 2, на которых натянута "бесконечная" лента 6. Исходный
влажный ТМ из бункера 7 питателем 3 подается на ленту и перемещается по ней
противотоком к потоку СА. В сушильной камере расположены пластины 4 и 5,
направляющие ТМ на ленту и СА (/) в пространство над лентой.

Ленточная сушилка работает непрерывно, ее производи
тельность достаточно высока. В приведенном варианте в су
шилке нет потерь теплоты с транспортными приспособлениями
(поскольку они целиком размещены внутри сушильной каме
ры). Однако н.еравн.омерпость сушки здесь н.е устранен.а. Поэто
му используют мноrоленточвые сушилки, принцип работы кото
рых ясен из рис . 1 5 . 3 , 6. Эти сушилЮf дороже, но " перетря
хивание" высушиваемого материала при его переходе с ленты
на ленту существенно повышает равномерность сушки . Число
последовательно расположенных лент в таЮfХ сушилках дости
гает десятка.

6

5

Рис. 15. 2. Туннельная сушилка:
1
шлюзы , 2
ваrонетха, .1
полки с ТМ ,
рельсы;
1 rорячий СА, /1 отходящ11й СА
-

-

-

-

6
4

-

туннель, 5

-

1

6

шлюзовые двери,

6

-

-

1217

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

3

3

6

4

5
2

1vl

а

4

1

3

5

2

4

5

3

б

!

JV

Рис. 15. З. Ленточные сушилки :
а
одноленrочная сушилка, /5 мноrоленrочная сушилка;
1
сушильная камера, 2
вращающиеся барабаны, З
шпатели, 4
направляющие
переrородки для ТМ, 5 то же, для СА, 6 ленты, 7 заrрузоЧНЬIЙ бункер;
1
rорячий СА, 11 отходящий СА, 111 мажный ТМ, JV- высушенный ТМ
-

-

-

-

-

-

-

-

-

-

-

-

Во всех рассмотренных сушильных аппаратах СА контакти
рует с ТМ, проходя над слоем последнего . При такой органи
зации процесса неравномерность сушки неизбежна. Дв ижение
СА сквозь слой высушиваемого ТМ с омыванием (в идеале)
каждого отдельного зерна призвано существенно повысить
равномерность, а значит и эффективность сушки . Примером
здесь
являются
шахтные
сушилки
с
неподвижным
(полунепрерывный процесс) или с движущимся (непрерывный
процесс) слоем высуши ваемого ТМ и движением СА через
слой. Эти сушилки просты, однако для них характерна замет
ная поперечная неравномерность потока СА (особенно в случае
слипающихся материалов), так что неравномерности сушки
избежать не удается. Для этого необходимо использовать кон
струкции и режимы, в которых зерна (частицы) высушиваемого
ТМ отделены одна от другой.
На рис. 1 5 .4 изображена барабанная сушилка.
Основной ее элемент - цилиндрический барабан 1 (с отношением длины к
диаметру на уровне 5 - 10, при этом диаметр может доходить до 3 м) . На барабан
надеты бандажи 2, опирающиеся на опорные ролики 6. Барабан, наклоненный к
горизонту на 1 -5°, приводитсн во вращение с помощью надетого на него зубча
того венца JJ и шестерни 7, соединенной с э.лекrродвигателем через редукrор,
так что скорость (частота) вращения барабана 3-6 мин-1 • Чтобы барабан не
смещался вдоль оси, около одн ого из бандажей установлена пара упорных роли-

1218

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

По А - В

2�
�
6

Рис. 15. 4. Барабанная сушилка:
а - общий вид, б - сечеЮtе (no опорной станции) ;
1 - барабан, 2 - бацnажи, З - уплотнеЮtя , 4 - приемная камера, 5 - подпорное коль
цо, 6 - опорные ролиJСИ, 7 - шесrерня, 8 - упорные ролиJСИ, 9 - дуrьевая камера, 10 стояк, 11 - питатель, 12 - бункер для исходноrо ТМ, 13 - зубчатый венец;
/ - rорячий СА, // - rазовзвесь (в nылеулааливающие устройсrва), /// - исходный ТМ ,
/V - высушеЮIЫЙ ТМ

ков 8. Влажный ТМ (/11) подается (из бункера 12 питателем 1 1) с одного торца
аппарата и отводится с дpyro1u в приемную камеру 4 и далее (/V) в сборник
высушенного ТМ. Внутри барабана расположена наса.цка (на рис. 1 5 .4, б показана
наиболее простая - лопастна я), она захватывает ТМ поднимая его по мере
вращен ия барабана. Падая с одного элемента насадки на другой (или просто
просьшаясь сверху вниз), масса частиц пронизывается потоком СА. Для поддер
жания определенной степени заполнения барабана материалом (обычно порядка
20% по объему) на выходном торце устанавливается подпорное кольцо 5.
Горячий СА подается в барабан - нередко прямотоком через дутьевую каме
ру 9. Дело в том , что высуше н ный ТМ не всегда допускает контакт с горячим
исходным воздуХом, тем более с топочными газами, - из-за опасности разложе
ния, размягчения, стшания и т.п. Между тем. влажный исходный материал
часто "не боится" такого контакта: при наличии свободной (см. разд. 1 5.2) влаги
температура материала не может подняться выше 1 00 ° С (при атмосферном
давлении). Но при необходимости глубокой сушки материала (до малой оста
точной влажности) и в случае достаточной устойчивости ТМ к высоким темпера
турам предпочтительнее протиr10ток СА и ТМ
Запьтенный газ из приемной камеры 4 отводится в пьтеулааливающие уст
ройства (циклоны, фильтры, электрофильтры, аппараты мокрой очистки - на
рисунке не показаны) . Дутьевая и приемная камеры снабжены уплотняющими
устройствами З, препятствующими контакту СА и окружающего барабан атмо
сферного пространства.
,

.

Досто инство суш ильного барабана - в высокой производи
тельности и надежности . Среди недостатков : громоздкость,
большие производстве нн ые площади , шум, а также плохое ис
пользование рабочего объема сушилки.
Отличител ь ная особенность суш илок с псевдоожиженным
слоем состоит в широких возможностях эффективного высуши
ван ия материалов с раз нообразным и свойствами (от хорошо
сыпучих зере н до растворов) и услов иям и процессов (высокие
и умеренные температуры , непрерывные и полун епрерывные

1219

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

3
9

8

а

6

10

9 8

б

Рис. 15.5. Сушилки с псевдоожиженным слоем:
а

- аппарат для сушхи зернистых материалов:
1 - сушильная хамера, 2 - сеnарациоЮfая зона, J - бункер исходноrо ТМ, 4 - IШiехо
вый питатель, 5 - rаэораспрсделительная решетка, 6 - дуrьевые камеры, 7 - повоJКУПIЫе
заслонхи, 8 - rаэоход (холлехтор) , 9 - хороб для вывода высушеЮJоrо ТМ, 10 - С!DIВНОЙ
пороr;
l - горячий СА, 11 - отработанный запыленный СА, 111 - исходный ТМ, lV - высу
шенный ТМ;
б - аппарат для обезвоживания растворов или суспензий:
1 - хамера хи пяшеrо слоя, 2 - сспарациоЮfая зона, З - раэбрызrиватсль, 4 - труба
для вывода ТМ, 5 - питатель, 6 - газораспределительное устройство," 7 - хамера смсшеНИ.11 ,
8 - кольцевой ханал, 9 - топха, 10 - форсунка;
l - топливо (rаэ, JКИДХосrь), П - воздух на сжиrание, 111 - вторичный воздух, lV пылеrаэовая смесь, V - раствор, суспензия, Vl - высушеЮfЫЙ ТМ

режимы, равномерная и пулъсирующая подача СА и др.). Соот

ветственно этим свойствам и условиям аппараты с псеJЩоожи
женным слоем констр)'Ю"lmно оформляются по-разному. Во всех
случаях в этих аппаратах СА служит ожижающим аrентом.
Особенностью и достоинством сушилок с псевдоожи
женным слоем является выравнивание температур в объеме
слоя, поскольку псевдоожиженный ТМ движется в сушилке в
режиме, близком к идеальному перемешиванию. Это означает,
что в основание слоя можно подавать СА с достаточно высо
кой температурой, но во всем его объеме температура может
поддерживаться (если необходимо - с помощью теплообмен
н ых устройств в слое) на уровне, приемлемом для ТМ и необ
ходимом для сушки - соответственно тепловому балансу.
На рис . 1 5 . 5 , а показа н а прямоуrольная сушильная камера 1 с
находящейся над ней расширенной сепарационной зоной 2.

Исходный ТМ из бункера J подается (//[) питателем 4 на псевдоожиженный
слой (существуют вариакrы с подачей ТМ под уровень слоя) . Сушильный агент
поступает ([) в аппарат из коллектора 8 через дутьевые камеры 6; ero подачу
можно регулировать по зонам с помощью поворотных заслонок 7: нередко в

1 220

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

зону ввода влажного ТМ целе<.:ообразно (во избежание образования там застой 
ных зон) подавать повьШiенное количество СА. И з аппарата отработанный СА
отводится (//) к пьmеулавливающим устройствам . Материал в псевдоожиженном
состоянии перемещается к выходу, "переливается" через порог 1 0 и по коробу 9
отводится (JJI) в приемный бун кер .
Иногда приходится сушить липкие материалы, плохо поддающиеся псевдо
ожижению, образующие каналы (через них газ проходит без достаточного кон
такта с ТМ
байпас в терминах структуры потока). Разрушению каналов спо
собствует повышение скорости СА, но тогда возрастает унос ТМ Поэтому для
разрушения каналов непосредственно над решеткой 5 размещают механический
побудитель (на рисунке отсуrствует), например решетчатое устройство, разру
шающее каналы и застойные зоны при своем возврапю-поступательном движе
нии в горизонтальной плоскости и вовлекающее в псевдоожюкение весь зернис
тый материал.
На рис. 1 5. 5 , б представлен аппарат для обезвоЖ1111811Н я растворов: в нем соче
таются процессы выпаривания и сушки. В топку 9 через форсунку 10 подается
топливо (/) и первичный воздух (//) на его сжигание. Вторичный воздух (JI/) через
кольцевой зазор 8 (для снижения потерь теплоты) поступает в камеру 7, где
смешивается с ГdЗами из топки с целью понижения температуры до требуемой
величины (обычно 500-700 • С); эта смесь служит исходным сушильным аген
том . Через газораспределитель н ое устройство 6 горячий СА поступает в находя
щийся в сушильной камере 1 псевдоожиженный слой , образующийся при обез
воживании капель жидкости (или суспензии), подаваемой ( JI) в аппарат через
разбрызгиватель J. Сушественно: капельная завеса над слоем значительно пони
жает унос мелочи с отходящи м (/JI) сушильным агентом, направляемым в си
стему пылеулавливания . Высу шенный ТМ по опускной трубе 4 питателем 5
вьшодится ( V/) из аппарата.
-

.

Конструкци и сушило к с псевдоожиженным слоем далеко не
исчерпываются • представленными на рис . 1 5.5. Существуют
аппараты с подвижным и газораспределительными решетками ,
устраняющими каналы и застойные зоны , они обеспечивают
высокую поперечную ра вномерность потока СА. Для глубокой
сушки пр и меняют вертикальные последовательно секцион и ро
ванные аппараты с проти вотоком ТМ и СА (проблема здесь в
организации регулируемого перетока матер и ала и з секции в
секцию). Используют конические аппараты - для них харак
терна направленная циркуляция ТМ в о бъеме слоя . Существу
ют аппараты с псевдоожиженным слоем нагретых частиц: при
соприкосновении с ними влажного материала последний теря
ет влагу. Наконец, техн ика псевдоожижен ия применяется для
сушки в комбинации с другим и способами обезвоживания.
При рациональной орган изации движения ТМ и нтенсив
ность массообмена в псевдоожиженном слое в расчете на еди
н и цу рабочего объема на порядок и более выше, чем в бара
банных и некоторых других сушилках.
Встречаются диспер<:ные материалы, плохо поддающиеся
псевдоожижен и ю даже в сухом состоян ии; это относится, на
пр и мер, к материалам с пластинчатой, игольчатой и некоторой
•

См. (2, 1 0, 1 2, 16).

122 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 15. 6. Виброаэросушилка:
1 - сушильная камера, 2 - газораспредели
тельная решетха, .1 - основание, 4 - амортизи
рующи е п ружины , 5 - виброnривод, 6 - дутьевая
камера;

1 - rорячий СА, 11 - отходящий СА,
исходный Т М , IV -высушеЮihlЙ Т М

5

4

3

111 -

другой формой зерен (скажем,
пшеница) . В этом случае пр и бега
ют к ряду модификаций псевдо
о жижения (кстати, он и пригодн ы
и для хорошо псевдоожижаемых

ТМ) - см. ниже .
На рис . 1 5.6 изобр ажена схема виброаэросушилки.

Горячи й СА через дуrьевую коробку 6 и решt-'ТКУ 2 по с�упает (/) в сушильную
камеру 1 аппарата, в которой исходн ый мажный ТМ (/11) транспо)УП!руется (слоем)
вдоль rазорасnределительной решетки 2 и в высушенном состоянии выводится
( I V) из камеры. Горячий воздух (СА) подают в сушильную камеру в количестве,
недостаточном д11Я псевдоожижения, - это позволяет существенно уменьшИТh
унос пьmи с отработанным СА ( J f) . Дополнительная (н едоста ю щая) энергия д11Я
псе вдо ожижен и я ТМ подводится к слою за счет механи•1еской вибрации : си
стемы пружин-амортизаторов 4 (они соединяют сушильный аппарат 1 с непо
движным основанием З) и вибратора 5. Вибронсевдоожижению (в присутствии
rазового потока и в его отсутствие) п од вержен ы ТМ с различной формой частиц.

Механ ичес кое воздействие на слой способствует разруше
нию каналов и застойных зон , препятствует комкованию ТМ все это расширяет возможный диапазон использования вибро
сушилок. Недостатки : усложнение аппарата, небезвредные ме
ханические воздействия на его узлы , быстрое гашение вибра
ции в псевдоожиженном слое (т.е. необход и мость работы с
вес ьма тонкими слоя м и) .
На рис . 1 5 . 7 , а показана коническая аэрофонтанная сушилка.

Исходный ТМ подается (1 !/) из бункера З питателем 4 в трубопровод, где
подхватывается потоком (/) сушильного аrента и пневмотранспортом вносится в
сушильную камеру 1. В ней устанавливается направленная циркуляция ТМ :
восходящий пневмотранспорт в относительно узком центральном канале (и
. фонтан над ним), нисходящий движущийся слой у .стенок камеры, ино гда еще
- псевдоожиженный слой в кольцевом пространстве меЖдУ этими зонами. От
работанный СА выводится ( //) из сушилки к пьmеулавливающим устройствам ,
ТМ выводится (/V) через наююнную трубу 5 и питатель 4. В некоторых кон
струкциях аэрофонтанных суш илок в основании конуса устанавливают rазорас
пределительные решетки; тогда влажный ТМ подают непосредственно в сушиль
ную камеру - в зону движущегося слоя .

В аэрофонтанных сушилках сравнительно крупные зерна
(размером не сколь ко милл иметров) вовлекаются в достаточно
при
интенсивное
умеренных расходах СА
движе н и е
(псевдоожижение потребовало бы чрезмерно высоких его рас
ходов) . Причина: площадь поперечного сечения центрального
канала много мен ь ше площади сечения аппарата над фонтани1 222

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

1

Рис. 15. 7. Аэрофонтанные сушилки:
а - коническая, 6 - приэмати•rеская;
1 - суш1U1Ъная камера, 2 - воздухопровод, 3 - бункер исходноrо ТМ, 4 - питатель, 5
- опускнаи труба, 6 - щелевой ввод газа или rазоювеси;
/ - горячий СА, 11 - отходяший СА, 111 - исходный ТМ, /V - высушенный ТМ, V rnt>ячий СА или 1·аэоювесь ero с исходным ТМ

рующим слоем. Значит, для восходящего транспорта зерен в
канале потребуются при емлемые расходы СА, так как его ско
рость в канале значител ьно выше, чем над слоем . По этим же
причинам в аэрофонтанн ых сушилках возможна работа с поли
дисперсными материала ми, причем - без существенного уноса
мелочи (пыли) .
Аэрофонтанная сушилка обычно близка к аппаратам Иде
ального перемешивания . Дело в том , что продолжительность
одного оборота зерна (т.е. цикла "восходящий пневмотранспорт
в канале - нисходящее движение у стенок - восходящий
пневмотранспорт в канале"), как правило , значительно меньше
среднего времени пребывания зерна в фонтанирующем слое.
Аэрофонтанная сушка может быть организована в цилиндро
коническом варианте, а также в призматическом аппарате . Схе
матически (без узлов литания и вывода ТМ) призматическая
сушилка с щелевым вводом СА (или СА, несущего исходный
ТМ) показана на рис . 1 5 .7,б.
Для удаления свободной влаги в химической и фармацевти
ческой промышленности широко используются пневмаrран
спортиые сушилки (иначе - трубы-сушилки) (рис. 1 5 . 8 ) .

Горячий воздух ( /) , движущийся со скоростью, превьШiающей скорость ви
тания твердых ч�1стиц w8, подх ватывает мелкоизмельченный ТМ, о пускающийся
( VI) по наклонной трубе 9. В ысушивание происходит при движении (//) rазо
взвеси по трубе /. Далее rазоnзвесь попадает в расширительную камеру 2, откуда
ТМ по наклонной трубе З движется совместно с воздухом в циклон 4 и далее

1 223

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Пневмотранспортная
Рис. 15. 8.
сушилка:
1 - пневмотранспортная труба, 2
- распределительная камера, 3 наклоtn1ая труба, 4 - циклон, 5 бункер исходноrо ТМ, 6, 7, 9 - тран
спортные трубы, 8 - шнековый
питатель-транспортер;
1 - rорячий СА, Il - rаэовзвесь,
Ill - отходящий запЬ1ЛеННЫЙ СА, lV
- исходный ТМ, V - возврат недо
статочно высушеtn1оrо ТМ, VI смесь исходноrо и возвращаемоrо ТМ

ш

г

4

5

(///) - на мультициклоны и
фильтры (на схеме не показаны)
для отделения высушенных твер
дых частиц. Осевшие в циклоне 4
более крупные частицы вьmодят
ся ( V) из него и мщуr быrь
собраны в приемнике высушен
ного материала. Однако часто
(такой случай и представлен на
рисунке) эти крупные частицы
(или агломераты мелких частиц)
оказываются не высушенными до
приемлемой остаточной влаж
ности; тоrда их по стоякам 7 и 9
возвращают в трубу-сушилку,
присоединяя к потоку (IV) ис
ходного влажного материала из
бункера 5.

Скорость газа в пневмотранспортной сушилке обычно н ахо
дится в диапазоне 1 0-30 м/с. Почти с такой же скоростью
(отставая на величину w8) движутся твердые частицы. Поэтому
время их пребывания в трубе 1 (ее высота чаще всего несколько метров) исчи сляется долями секунды (редко превы
шает 1 с) . За столь короткое время частица может потерять
влагу, но не успевает "испортиться" , даже есл и температура СА
относительно высока, а материал - термолабилен . К недостат
кам ·пневмотранспортных сушилок относигся малая степень на
сыщения СА влагой, а потому повышенный его расход . Кроме
того , возн и кает сопутствующая проблема, связанная со стати
ческим электр ичеством, возникающим при соударении частиц
со стенкам и трубы (здесь необходимы меры, препятствующие
его накоплению: заземление узлов сушилки и т.п.) .
Рассмотрение конвективных аппаратов завершим распыли
тельной суш ил кой, используемой для обезвоживания растворов
и суспензий (рис . 1 5 . 9 ) .

Раствор (суспензия) под<1ется (///) п о трубе 4 н а быстро вращающийся диск
З, дробящий жидкостной поток и разбрызгивающий каrmи. Они падают в ши
рокой (иногда диаметром до дt:сятка метров) сушильной камере /, куда подается

1224

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 15. 9. Распылительная сушилка:

1
сушильная камера, 2
коллек
тор СА, З
вал с диском, 4
трубка
для подачи раствора (суспензии), 5
вводы СА по окружносrи аппарата, 6
rребковое устройство, 7
шнек, 8
фильтры ;
1
rорячий СА, 11
ОТХОJ\ЯЩИЙ
СА, 111
раствор или суспензия, JV
высушеШ1Ый ТМ
-

-

-

-

-

-

-

-

-

-

-

-

1-1
1 1
1 1
1 1
1 1
1 1
1 1

�

8

(/) из колле�сrора 2 по нескольким
(по окружности камеры 1) вводам 5
rорячий СА. Высушенный сыпучий
ТМ транспортируется
медненно
вращающимся rребковым устрой
6
ством 6 к отверстию вывода, откуда
с помощью шнековоrо питателя 7
выводится (/JI) из сушилки. Отра
ботанный СА, несущий мелкую
пь11IЬ ТМ, проходит через фильтры 8, расположенные в кольцевом пространстве
аппарата, и выводится (//) из неrо. Уловленный в фильтрах материал собирается
и присоединяется к основному потоку IV высушенноrо ТМ .

В распылительных сушилках тоже невелико время контакта
ТМ с горячим СА, и потому их также можно и спользовать для
сушки термолабильных матер иалов. Для распьmительных су
шилок, как и для пневмотранспортных, характерны высокие
расходы СА.
1 5 . 1 .2. Спе циальные сушильные аппараты

Использован и е специальных сушилок связано , как правило,
со специфическими свойствами высушиваемых материалов, в
первую очередь - с их термолаб ильностью либо нежелатель
ностью контакта с кислородом воздуха. Поэтому для получения
качественного продукта технологи вынуждены идти на повы
шенные энергозатраты и использовать сложное оборудова
ние - это характерно для специальных сушилок. Ниже рас
смотрены устройство и принц ип работы лишь отдельных спе
циальных сушильных ап паратов.
На рис. 1 5. l U демонстрируются к0trl'8X11lble сушилки. Теплота на
удаление влаги здесь передается за счет непосредственного кон
такта высушиваемых матер иалов с горячими поверхностями.
На рис. 1 5 . 1 0 , а показана полочная конта�сrная сушилка (в простейшем вари
анте
вахуум-сушнльнwй шкаф), rде ТМ лежит на противнях 2, положенных на
поверхности J, обоrреnаемые теплонос и телем 11 (паром, rорячей водой). Для
понижения температуры процесса в сушильной камере 1 создается вакуум: смесь
воздуха и водяных паров отво;1ится (/) через конденсатор к вакуум -насосу. Эти
сушилки хара�сrеризуются ни �кой производительностью: необходимо немало
времени для создания вакуу м а и проrрева материала (ero теплопроводность чаще
всеrо невелика), а также на за� рузку и выrрузку ТМ. Вакуум-сушильные шкафы
достаточно широко применяются в лабораториях и малотоннажных произ
водствах.
-

1 225

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

1

1

2

3

1
2

._________,;:J....._ 3

а

6

в

Рис. 15. 10. Контактные сушилю 1 :
а - вакуум-сушильный шкаф: 1 - сушильная камера, 2 - полки с ТМ, J - обоrре
вающие поверхности; / - водяные пары, II - теплоносиrелъ;
б - цилиццрическая сушилка (фраrмент, схема): 1 - вращающиеся обоrреваемые ци
линдры, 2 - движущаяся лента; / -- w�ажная лента (пленка, ткань, юпь) , II - высушеШJая
лсша;
в - двухвальцовая сушилка: 1 - сушильная камера, 2 - обоrреваемые вращающиеся
вальцы, J - устройство подвода и распределеЮIЯ :жидкости, 4 - ножи, 5 - наклоюше
стеюси, 6 - шнек; / - исходный раствор (суспензия) , l/ - высушеЮIЬ1Й ТМ, III - вывод
водяных паров
На рис. 1 5 . 1 0 , б схемати чес ки показан фрагмент цилиндрической контактной
сушилки, предназначенной ш �я сушки пленок, лент, тканей, бумаги, нитей.
Основной рабочий орган - вращающиеся цилиндрические барабаны 1, обогре
ваемые внутри каким-либо горячим теплоносителем. Эти барабаны приводят в
движение ленту 2, которая по переменно контактирует с горячей поверхностью
то одной, то другой стороной - происходит ее высуши вание от исходного со
стояния (вход /) до конечного (выход //).
На рис. 1 5 . 1 0 , в дана схема двухвальцовой контilктной сушилки. Исходные
раствор или суспензия (/) разбрызгиваются с помощью устройства 3 (в других
конструкциях - просто подается по трубе в зоне устройства 3) на поверхность
валков 2, обогреваемых изнутри. Валки медл енно вращаются навстречу друг
друту, жидкость смачивает горячую наружную поверхность валков, получает от
нее теплоту и обезвоживается. Образовавшаяся пленка высушенного материала
срезается ножами 4 и по наклонным стенкам 5 перемещается в нижнюю часть
аппарата, откуда ТМ шнековым питателем 6 выводится из сушилки в приемник.
Сушилка может работать под атмосферным давлением и под вакуумо м . В по
следнем случае паровоздушная смесь отводится (111) через конденсатор к ваку
ум-насосу.

Заметим: в контактных сушилках теплота в идеале расходу
ется только на испарение влаm (реально, конечно, и на потери
в окр ужающую среду) - - в отличие от конвективных сушилок,
где соизмеримое количество теплоты расходуется еще и на
подогрев СА К недостаткам контактных сушилок относятся
ограничения в температуре горячей поверхности (при сушке
термолабильных материалов), возможная неплотность прилега
ния высушиваемого материала к этой поверхности, длитель1 226

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 15. 1 1. Схема терморадиаuионной сушки :

1 - поверхность с высуши11аем ым ТМ , 2 - ТЭН'ы, .1 - от

ражатели

ность прогрева малотеnлопроводных мате
риалов, а также высокая металлоемкость
большинства контактн ых сушилок.
Рис . 1 5 . 1 1 иллюстрирует принцип работы
терморадиационной сушилЮI .

3

6
�,

Рабочий орпш - излучатели 2, работающие в диапазоне инфракрасного
(теплового) из.лучения. Оно на nрааляется (непосредственно от излучателей 2 и с
помощью отражателей J) на ТМ, находящийся на поверхности 1. Применение
лампы в качестве излучателя приводит к образованию на поверхности материала
светового пятна с неравномерной интенсивностью теплового потока. Поэтому
предпочтительнее использование трубчатых злектронаrревателей (ТЭН'ов): внут
ри ЦИJDfндрических труб - <:пираль из нихрома или какого-нибудь другого
материала с высоким злектрич�ским сопротивлением; изоляция от стенок трубы
обеспечивается наполнителем - злектроизолятором (кварцевый песок, MgO,
А12Оз и т.п.). ТЭ Н ' ы дают более равномерные полосы тепловых потоков. Су
ществуют и другие способы организации направленного ИК-из.лучения
(злектронаrрев керамических блоков; обоrрев излучателей газовым пламенем).
Поверхность 1 может предстаалять собой ленту конвейера, тоrда процесс
можно проводить как непрерывный. Возможно также движение высушиваемого
материала по наклонным плоскостям с излучателем над ними.

Особенность терморадиационной сушЮI - слабая проницае
вглубь высушиваемого материала. Поэтому их
чаще всего применя ют для термического воздействия
(высушивания) на поверхностную влагу и тонкие прослойки
сыпучих материалов. Терморадиационные сушилки достаточно
производительны и ком пактны, однако их энергетичесЮ1е ха
рактеристики весьма неблагоприятны : затраты энергии в 3-4
раза превышают теплоту испарения жидкости.
Сушка токами высокой частоты представлена на рис . 1 5 . 12,
причем на виде (а) иллюстрируется принцип ее работы.

мость излучения

Между обкладками конденсатора 2, присоединенными к злектроrенератору
высокой частоты 3, находится зона высушиваемого материала 1. Пусть в данный
момент времени верхняя пластина конденсатора заряжена положительно, ниж
няя - отрицательно. Тоrда соответствующим образом ориентируются полярные
молекулы материала и влаги. Спустя м а1D,1й промежуt"<Ж времени (порядка 10 -4 с)
пластин изменяется на противоположный, вслед за этим происходит
заряд
переориеНТЗJ..QiЯ молекул. В результате многократной переориентации молекул в
единицу времени происходит rепловьщеление, причем достаточно равномерное по
объему твердого материала. За счет зrой теплоты влага удаляется из материала.
На рис. 1 5 . 1 2 , б демонстрируется работа сушильной установки, сконструиро
ванной по принuипу ленто<1ной сушилки . Отличительная особенность здесь отсутствие СА и наличие обкладок конденсатора. Потоки и основные узлы ясны
из рисунка (разумеется, предусмотрен и отвод водяных паров - на рисунке не
показан).
·

.·

В заключение - сублимационная сушилка ' (рис .
15.13).
Смысл процесса - в замораживании влаги и возгонке льда без
1 227

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

1

2

3

�
+<->М<
-(+)
�

а

1
3

б

Рис. 15. 12. Сушка токами высокой частоты:
а - к прющипу рабоrы: 1 - зона высушиваемого ТМ, 2 - обхладюr (JVIастины) кон
денсатора, J - генератор высокой часrоты;
6 - схема сушилхи: 1 - сушиnная )(аМера, 2 - лента коН111й
1 ера и вращающиеся бара
баны , 3 - направляющая JVIocкocтa. , 4 - пластины коJЩенсатора; 1 - исходный ТМ , ll высушенный ТМ

перевода в жидкое со стояние. Метод осо бе нно актуален для
лекарственных препаратов и ряда п ищевых проду1сr0в, отJШЧаю
щихся высокой чувствительностью к повышению температур ы .
Чтобы обеспечить сублимацию льда без ero таяния, необходимо весrи про
цесс сушки в весьма mубоком вакуум е (остаточное давление на уровне 5200 Па). В сушильной камере 1 располагаются обогреваемые (часто - теплой
водой lll-IY) полости 2, на которых размещают противни З с замороженным
высушиваемым материалом. Температуру сублимации при указанном давлении
удается вьщержать в пределах 1 5-50 • с ниже нуля. Водяные пары отilодятся (/)
через конденсатор 4, охлаждаемый ( V, VI) низкотемпературным хладоаrентом
(например, рассолом - см.разд.21 .2.7); сконденсировавшаяся влага отводится
(//) из аппарата. Вакуум создается и поддерживается вакуум - насосом 5; вакуу
мируемые газы выбрасываются в атмосферу.
Затраты те плоты в сублимацио нной сушилке невелики , тем бо 
лее чrо используется сравнительно дешевый теплоноситель , да
еще низкоrо потен циала - теплая вода. Основные энергетические
затраты приходятся на
(повакуумирование
/
скольку вакуум - доста/
точно глубокий) и холод
в конденсаторе .
з
Рис. 15. 13. Сушка с заморажи
ванием влаm и сублимацией
льда:

2

1

t IlI
1228

2

3

1 - сушильная камера, 2 обогреваемые полости, 3 - про 
ТИВЮI с высушиваемым ТМ, 4 коJЩенсатор, .5 - вакуум -насос;
1 - паровоздушная смесь,
JJ - коJЩенсат, lll, JV - теплая
вода (теплоноситель) , V, V1 хладоаrент

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

15.2. ФИЗ И КО-ХИ МИЧЕСКИ Е ОСНОВЫ ПРОЦЕССА
КОН В ЕКТИ ВНОЙ СУШКИ
1 5.2. 1 . Условие сушки

Рассмотрим в общем плане конвективную сушку материала,
расположенного на некоторой поверхности (рис . 15. 14). Влаж
ность ТМ будем обозначать символами ro или U (см.разд .
1 5 .2.3). Над материалом движется поток сушильного агента,
парциальное давление nаров влаги в нем равно Рп · Он отдает
материалу теплоту, за счет которой испаряется влага, перехо
дящая в поток СА. Непосредственно над влажным ТМ давле
н ие паров влаги равновесно с ее концентрацией в материале
•
(ro , И) и составляет рМ. Выдели м в потоке СА модельный по
гранич н ый слой 1/1 - в нем происходит падение концентра
ции влаги от равновесного значения рМ до величины Рю харак
терной для ядра потока СА. Разность рМ - Рп может тракто
ваться как одно из выражений движущей силы процесса сушки .
В зависимости от знака этой движущей силы (или, что то же
самое, знака равенства-неравенства рМ < Рп ) перенос влаги
может кдти от ТМ к СА или в обратном напрамении.
Если рМ > Рп , рМ - Рп > О, то происходит высушивание маж
ного материала - этот процесс составляет предмет рассмотре
н ия в настоящей главе, а само неравенство есть условие сушки.

Рис. 15. 14. Условие сушки:
1 - высушиваемый твердый материал, П сушильный arem, П/ - пограничная пленка в пото
ке сушильного arema над твердым матери алом

Рп

СА

-п
-

�
ппрп'>!(.пп

о

/ (ТМ) И, rо

Если рМ < Рю Рп - рМ > О, то происходит адсорбция влаги из
СА и увлажнение ТМ. Этот процесс , обратный сушке ТМ ,
имеет вполне определе нный технологический смысл : осушка
газов. Его основы рассмотрены в гл . 14.
Случай рМ = Рп , рМ - Рп = О означает динамическое равнове
сие влаги в системе ТМ-СА, процесс межфазного переноса
влаги в целом не Идет.
• Индекс " м " , традицион но используемый при рассмотрении процессов
сушки , означает " непосредственно над материалом"; он абсолютно идентичен
верхнему индексу "р", означающему "равновесный" при изучении друrих мас
сообменных процессов.

1229

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Из изложенного следует, что для процесса сушки ТМ необ
ходимо создать и поддерживать в технологическом аппарате
условие рМ > Рп ·
В дальнейшем нам придется оперировать величинами с ука
занием их принадлежности к о пределенному рабочему телу. В
целях сокращения зап иси введем следующие обозначения :
АСВ - абсолютно сухой воздух, вл . В - влажный воздух,
С М - сухой материал , вл . М - влажный материал , Вл - влаrа,
уд. Вл - удаляемая (удаленная) влага.
1 5.2.2. Снойства влажного воздуха

Последующее изложение ведется применительно к исполь
зованию воздуха в качестве СА (переход к другому газу, как
будет показано н иже, затруднений не вызывает) .
Воздух трактуется ка к смесь его абсолютно сухой части и
содержащихся в нем водян ых паров . Поэтому общее давление
воздуха В, согласно закону Дальтона, есть сумма парциальн ых
давлений сухой его части Рв и водяных паров Рп :

В = Рв + Рп ·

(а)

На практике чаще всего кон вективная сушка ведется под
атмосферным давлениеl\ 1 , так что для европейской части стра
ны в среднем В = 750 мм рт. ст. = i os Па = 1 б (бар ) .
Величина Рп м о ж ет изменяться о т нуля (абсолютно сухой
воздух или другой СА) до максимально возможного значения
Рн . отвечающего давлению насыщенных паров при данной тем 
пературе СА.
При Рп > Рн (пересыщенные пары) система нестабильна; при каком -либо не
большом возмущении избьrrок влаги выпадает в виде конденсата, а в газовой
фазе устанавливается равенство Рп Рн ·
=

Значения Рн в зависимости от температуры приводятся в
таблицах насыщенн ых паров .
Концентрация влаги в воздухе

Кон центрация влаги в воздухе может быть представлена в
форме абсолютной влажности Рп, выражаемой количеством во
дяных паров ( В П ) в 1 мз влажного воздуха: кг В П/м3 . Очевидно
(это ясно и из размерн ости) Рп есть плотность водяных паров
при их парциальном давлении Рп · Естествен н о , в том же 1 м3
при своем парциальноr-1 давлении Рв находится и абсолютно
сухая часть воздуха (далее обозначе но
АС В) - его плот
ность Рв ·

1 23 0

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 15. 15. Влияние температуры на абсолютную
алажность в насыщенном состС1янии

Величина Р п может изменяться от
нуля (когда воздух не содержит водя
н ых паров) до максимально возмож
ного значения Рн, отвечающего насы
щению воздуха водян ыми парами при
данной температуре:
О ::::; Рп ::::; Рн ·

(б)

\

\

Е?:

--------

,---

1
1
1
1
1
1
1

1

tA
1

Состояние Рп > Рн неус1ойчиво : избы
(
точная сверх Рн влага выпадает в виде
конденсата.
Значения Рн при различн ых температурах приводятся в
справочниках. Изменен ие Рн с температурой, соответственно
уравнению Клапейрона·- Клаузиуса, носит экспоненциальный
характер; качественно оно иллюстрируется на рис . 1 5 . 1 5 . Для
t" > t' характерно Рн " > Рн' · Пусть температуре t' отвечает мак
симальная абсолютная влажность Рн' ; очевидно, что при темпе
ратур е t " эта влага (точка А) находится в перегретом состоянии
(относительно температуры своего насыщения t') . Пусть темпе
ратуре t" отвечает максимальная абсолютная влажность Рн " ;
очевидно, что эта влага (точка А) при любой температуре t < t "
(в том числе и при t') будет находиться в ненасыщенном состоя 
нии (относительно абсолютной влажности при насыщении Рн" ) .
Таким образом , ненасыщенные пары - перегреты.
Использование абсол ютной влажности не вполне наглядно ,
поскольку по названной цифре Рп трудно судить о близости
системы В П -АСВ к насыщению. Поэтому вводится понятие о
степени насыщения q>, называемой относительной влажностью
воздуха:
q> == Р r/Р ю О ::::; q> ::::; 1 .
(в)
Значение q> = О отвечает отсутствию влаги в воздухе ,
q> = 1 - полному его насыщению водяными парами при дан
ной температуре. В случае q> > 1 избыток влаги выпадает в виде
конденсата, после чего состояние воздуха соответствует

<р =

1.

На практике <р нередко указывают в % ; в технологических расчетах следует
пользоваться ( это вьщержа но в дальнейшем н:иожении ) выражением <р в до
лях - соответственно левому и з соотношений (в) .

При увеличении тем пературы ер достаточно быстро пони
жается - не столько из-за медленного уменьшения Рп (рост
объема влажного воздуха) , сколько из-за существенного воз
растания Рн ·
1 23 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Относительную влажность можно выразить через давления
паров Рп и Рн· Воспользуемся для этого уравнением Клапейро
на- Менделеева:
pV

Здесь

р

=

G рМ п
G
.
( г)
Rу Т и р = - =
У
Ry T
Мп
при давлении р и абсолютной температуре

nRy T =

- плотность

--

Т, Мп - молярная масса влаги (воды для системы "вода

воздух"); смысл остальных символов очевиден .
Зап и шем правое из выражений (г) при мен ительно к воздуху,
не насыщенному и насыщенному водяными парами при одной
и той же температуре:
р

п

=

!п М п .
Rу Т

'

Поделив первое выражение на второе, получи м соотноше
ния, полезные для последующего анализа:

.!:..!!_
Рн

=

Рп
Рн

= q>

И

п

Р

=

(д)

<J>Рн ·

В ходе процесса сушки влага переходит из ТМ в СА; поэтому
поток последнего не остается постоянным, он возрастает от
входа СА в с уш илку к выходу из нее. С целью перехода к по
стоянному потоку газовой фазы (это удобно в технологических
расчетах - см. гл. 10) следует, как показано в разд. 10.2, опе
рировать относительны.ми концентрациями влаги в СА. Такие
концентрации в процессах сушки именуются влагосодержавием,
обозначаются символом х и имеют размерность кг Вл/кг АСВ
(для СА сокращения " Вл" и " В П " - тождественны). При та
ком подходе в качестве потока СА в расчетах ф и гурирует его
абсолютно сухая часть L (кг АСВ/с), остающаяся неизменной в
ходе процесса сушки . П ринятое выражение концентраци й сле
дует пон и мать так: 1 кг АСВ несет с собой х долей кг В л (в виде
паров); общее кол и чество влажного воздуха в расчете на 1 кг
АСВ составляет 1 + х. При этом поток L (кг АСВ/с) несет с
кг АС В кг Вл
= кг Вл; с
.
и поток
собои поток влаги L · x
v

(

кг АС В
L(l + .х) кг вл В/с. В таком
с

,

/

)

.
представлении кон
влажного воздуха
центраций и потоков уравнения материальных балансов и ряд
других расчетных выражен и й получаюгся достаточно простыми.
Расчет влагосодержания х ведется на основе уравнения Кла
пейрона- Менделеева, эаписанного для паров влаги (индекс

1 232

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

"п") и сухого СА (индекс " СА"):

РпV =

G

_
n_

Мн

Ry Т, РслV

=

L Ry T .

М ел

--

(е)

Поделив одно выражение на другое, после сокращения на
и
(поскольку речь идет об одном и том же объеме
(потоке) V и одинаковой температуре Т для пароrазовой смеси)
получим

V, Т

Ry

Мп
Gn =
-x = Р п -L
Р е л Мел

(15.1)

--

Для рассматриваемой в учебнике системы "вода-воздух"
молярные массы М11 = I H кг/моль, Мел = 29 кг/моль, так что при
Рсл = Рв имеем с учетом (а) :
х = 11{_ Р п =
29

Рв

0,622

Рп
Рп

В-

окончательно , используя (д) , получаем:

х = О 622
'

Ч'Р н
В - Ч'Рн

( 1 5 . la)

Из последнего выражения следует:
- влагосодержание х возрастает с ростом относительной
влажности qJ ;
- предельное (максимальное) значение х получается при
qJ = 1 :
Х

Влагосодержание

max =

Рн
Рн

О 622
'

х может изменяться
В

-

O :;;; x :;;; xmax .

( 1 5 . l б)
в пределах
(ж)

При этом значению х = О (при Ч' = О) отвечает абсолютно
сухой воздух, значению х = х тах (при Ч' = 1 ) - полностью на
сыщенный водяными парами. При х > х max избыток влаги вы
падает в виде конденсата.
Из формулы ( 1 5 . l б) ясно: х тах повышается с ростом темпе
ратуры благодаря возрастанию Рн · Вместе с тем х max понижает
ся с увеличением давления сушки В. Это обстоятельство не
часто становится актуал ьным при реализации сушильных про
цессов, но важно для работы компрессоров: при сжатии влаж
ного rаза вполне возможно при повышении В возникновение
ситуации х > х тах, тогда необходимо предусмотреть устройство
для отделения сконденсировавшейся влаги.
1 233

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Обьемный поток. влажного воздуха
Подача СА в сушил ьную установку осуществляется с по
мощью вентиляторов, газодувок; это машины объемного дей
ствия, и подбираются о н и по объемной производительности V
Между тем в технологнчесюtх расчетах фигурирует массовый
поток сушильного агента L. Связь объемного ( JI) и абсолютно
го массового ( G) потоков устанавливается с помощью удельно
го объема v (см . разд . 1 .2.2): V = G· v, где v выражается в мЗ на
1 к.г смеси, т.е. влажного воздуха. Однако здесь важна связь
объемного потока V с относительным массовым потоком L:
V Lvo , где v o
относ11тельный удельный объем, выражающий
объемное количество воздуха, приходящееся на 1 кг сухого воз
духа, - В мЗ/кг АСВ .
Расчетные выражения для v0 составим также на основе
уравнения Клапейрона-- Менделеева, записанного для влажно
го воздуха, т.е. для смеси водяных паров и сухого воздуха. С
этой целью найдем число молей, приходящихся на 1 кг АС В: это
1/М8 молей сухой части и х/Мп молей водяных паров. Сумма этих
=

-

Рис. 15. 16. Номо11>амма для определения относительного удельного объема си
стемы "вода - воздух" при атмосферном давлении.
Прим�р: t 80 ° С, х = 0,040 и Вл/и АСВ; результат: v0 1 ,07 мЗ/кz АСВ
=

1 234

=

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

величин есть число молей, движущихся с 1 кг АСВ, а с
АСВ/с - в L раз больше. Тогда при общем давлении В:

В· V
Отсюда определим

v0 =

=
=

1- +
L М

(

в

L

кг

�) Ry T .
М

п

V/L:

Vo =

(_l + �) R Т
М

М

в

в

У

п

( 1 5.2)

По этой формуле построена номограмма (рис . 1 5 . 16), позво
ляющая по известным х и t (t = Т
273,2) определить v0 для
системы "водяные пары-воздух" в наиболее часто встре
чающемся случае сушки под атмосферным давлением

-

(В = 105 Па) .
Отпосительная энтальпия влажного воздуха

Технологические расчеты сушильного процесса требуют
знания тепловых характеристик влажного воздуха. Использова
ние энтальпии влажного воздуха (абсолютной
на 1 кг вл . В ,
т.е. в Дж/кг вл. В) здесь неудобно п о указанным выше причи
нам : поток влажного воздуха изменяется в ходе процесса. По
этому в тепловых расчетах, как и в материальных, целесооб
разно оперировать величинами, приходящимися на 1 кг АС В .
Эти величины называют относительными энтальпиями и обозна
чают заглавным символом 1; соответственно физическому
смыслу их единица измерения - Дж/кг АСВ . Поскольку эн
тальпия влажного воздуха iвл.в отнесена к 1 кг смеси (т.е. влаж 
ного воздуха) , а относительная энтальпия 1 - к 1 кг АСВ , то
1 = iвл.в(l + х) . В дальнейших расчетах будем оперировать ве
личинами 1; тогда поток тР.плоты запишется в виде Ll

-

( кг АСс В кгД ж

= Дж/с =

\

Вт 1

причем в ходе сушки L = const.
АС В
J
Расчет 1 при температуре t и маrосодержании х ведется по
формуле, прямо следующей физическому смыслу этой величины:

( 1 5 .З)
где с8

-

теплоемкость cyxoro воздуха, iп

-

энтальпия паров влаrn .

В ( 1 5.З) первое слаrаемое представляет собой энтальпию су
хого воздуха, а второе -- вклад энтальпии водяного пара в 1 с
учетом его доли х, приходящейся на 1 кг АСВ .

1235

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

В широком диапазоне темn ера'fУР. можно (с поrрешностью не более 2-3% до
500 • q считать с8 = 1 , 0 1 7 1 ,02 кдЖ/<кг АСВ· К) . Энтальпию napa iп можно пред
ставить как сумму теплоты и спарения при О • с (при этой температуре вода
принимается в жидком состоянии) и теплоты наrрева ,в одяных паров до рабочей
температуры t: in = 2490 + l ,�17t, где с0 = 1 ,97 кДж/(кг ВП·К) - теплоемкость
водяноrо пара в весьма широком диапазоне температур.

Диаграмма 1-х

Определение величи н х и 1 по достаточно простым форму
лам (15. la) и ( 1 5.3) затруднений не вызывает. Однако в ходе
расчета сушильного процесса ими приходится пользоваться
многократно. Для облегчения расчетных операций по этим
формулам построена диа1'J)амма 1-х. В отечественной литера
туре используется диаграмма Рамзина, изображенная на рис.
1 5 . 1 7 в косоугольных прямолинейных координатах: вертикаль
ная - !, наклонная (под 135°) - х. Диаrрамма построена для
давления В = 750 мм рт.ст.= 105 Па . Естественно, линии посто
янных значений координат расположены параллельно соответ
ствующим осям : линии х = const вертикальны (параллельны оси
ординат /, т.е. линии х = О), линии 1 = const - наклонны
(параллельны оси абсцисс х, т.е. линии 1 = О). Значения 1 от
ложены на вертикальной оси; значения х должны быть отло
жен ы на наклонной оси, для удобства они перенесены на го
ризонтальную линию.
Линии постоянных температур t в диаrрамме 1-х - прямые,
что следует из линейной связи 1 и х при t = const; это ясно из
уравнений ( 1 5 . l a), ( 1 5 .3) и выражения для iп. Эги линии прак
тически параллельны друг другу (они были бы строго парал
лельными при независимости Св и Сп от t) . Для более высоких
температур линии t = const располагаются выше, отвечая более
высоким значениям 1 при одинаковых х.
Линии постоянных относительных влажностей <р - кривые ,
так как х, а значит, и 1 нелинейно зависят от <р. Верхней rра
нице <р = 1 соответствует нижняя кривая <р = 1 00% , ниже этой
линии - нерабочая область диаграммы. Для более низких зна
чений относительной влажности линии <р = const располагают
ся выше.
Автор диаrраммы допустил поrрешность, воспроизведенную впоследствии в
ряде учебных пособий и моноrрафий•: при достижении температуры кипения
влаги для давления В (в диаграмме Рамзина - чуrь ниже 100 •с при 750 мм
рт. ст "' 1 0 5 Па) линии i:p = co11�t претерпевают излом и направляются вертикаль
но вверх (показано вертикал ьным пунктиром на рис. 1 5 . 17). Приводим ые
объяснения весьма неубедительны. В действительности излома линий <:р = const
при t "' 1 00 • С бьrrь не должно, эти линии остаются плавными и выше t = 1 00 • с
при давлении сушки , асимптотически приближаясь к определенным тем• См., например, 1 , 6, 1 0 , l З , 1 4 ) .
(

1236

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

о
""

..:'1
0

�-'()

�'О

"'"о

".D
o

,.._,.о

""'о

""'о

iD'

""'о

:::::-

f.!

.D
o

....:

..>о

�

�

-'О
"'о

-'о

"о
0,04

х,

0,05

0,06

(кгВл) /(к<! АСВ)

0,07

Рис. 15. 1 7. Диаграмма 1-х JJJ1Я влажного воздуха

пературным прямым . Так, ли ния qi = 1 ( 1 00 % ) в бесконечности (х -+ оо, 1 -+ оо)
стремится к лини и температур ы кипения воды l к "' 99,6 ° С, линия <р = 0, 5 (50% )
асимптотически приближается в бесконечности к температурной кривой, отве
чающей удвоенному значению В (t "' 1 20,2 ° С) , линия <р = 0,2 (20 %) - к темпе
1 5 1 , 8 ° С. Вообще, линия <р = const асимrтrоrnчески стре
ратурной прямой fк
мится к той температуре, отвечающей давлению В/<р, при которой обращается в
нуль знамеюпель выражения ( 1 5 . \ а), т.е. х и / одновременно стремятся к беско
нечности .
"'

Диаграмма 1-х вычерчена в косоугольных координатах с
целью удобства ее использован ия . В декартовых координатах
линии <р = coпst пошли бы гораздо круче, и вся расчетная об
ласть расположилась бы в левой верхней части диаграммы; ее
середина и правое н ижнее поле оказались бы пустыми . Кроме
того, линии с различн ыми <р сблизились бы, их стало бы трудно
1237

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

различать, что тоже неудобно при расчетах. Косоугольная
диаграмма лишена этих недостатков.
В оригинальной диаграмме Рамзина из начала координат
проведена прямая , показывающая изменение парциального
давления водян ых паров Рп в зависимости от х. В практических
расчетах величина Рп используется весьма редко, поэтому сво
бодное правое нижнее поле целесообразно занять номограм
мой для определения v0, т.е. рисун ком 1 5 . 1 6 (так и сделано
нами в учебных диаграм мах 1-х).
Из четырех параметров t, <р , х и 1 достаточно знать два, что
бы определить положен ие точки в диаграмме 1-х и отсчитать
по ней значения осталь н ых двух параметров. На практике чаще
всего задают температуру (измеряется термометром, термопа
рой и т.п.) и относительную влажность (измеряется психромет
ром или каким-то други м влагомером); по t и <р находят точку
на диаграмме и определяют х (по вертикали х = const) и 1 (по
наклонной линии 1 = coпst) .
С помощью диаграммы 1-х весьма просто решается ряд
технологических задач; приведем два простых примера (рис.

1 5. 1 8).
Первый:

пусть имеется влажный воздух известных пара
метров, например t0, <ро (точка А, рис . 1 5 . 1 8,а). Требуется опре
делить точку росы, п редставляющую собой температуру, при
которой влажн ый газ (здесь - воздух) в процессе его охлажде
ния становится насыщенным. В ходе охлаждения воздуха при
отсутствии конденсации влаги в нем не изменяется ни количе
ство влаги, ни количество абсолютно сухой части; поэтому
процесс охлаждения идет при х
const и в диаграмме 1-х
изображается нисходящей вертикальной прямой. Для определе
н ия точки росы необходимо из исходной точки (точка А) про
вести вертикаль до линии насыщения <р
1 (100%) и в точке
пересечения отсчитать температуру - это и будет точка росы
/р . Охлаждение до более низкой температуры пойдет по линии
<р = 100 % (воздух будет оставаться насыщенным) с понижением
влагосодержания х - влаrа будет выпадать в виде конденсата.
Второй пример: требуется определить количество теплоты в
расчете на 1 кг абсолютно сухого воздуха, необходимой для
нагрева исходного воздуха заданных параметров (точка В на
рис . 1 5. 1 8, б, найденная по известным <р 1 и t1 ) до температуры
t2 . Нагрев влажного воздуха, как и его охлаждение, изображает
ся в диаграмме 1-х вертикальной прямой (разумеется, здесь
восходящей) . Конечная точка получается пересечением этой
вертикали с температу р н ой линией t2: точка С . Отсчитав значе
ния относительных энтальпий в начальной и конечной точках
/8 и lc, найдем искомое количество теплоты : ЛJ
/с 1в
Дж/кг АС В (реально в диаграмме не Дж, а кДж).
=

=

-

-

1 238

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

[

[

х

х

б

а

Рис. 15. 18. Решение про..:тей ших
а
<>ЛределеЮ1е T<>'II01 росы, б

-

задач

х

с помощью диаграммы /-х:

- <>nределеЮ1е расхода теплоты

Диаграммы 1-х для влажного воздуха в наиболее распро
страненных вариантах изготовлены для умеренных темпера
тур - до 1 50, до 200 ° С или несколько выше. В ряде случаев
сушка проводится при .значительно более высо Юfх температу
рах - до 400 и даже до 700 ° С. В таких случаях пользуются
диаграммами 1-х для высоких температур. Эти диаграмм ы
вполне пригодны для расчетов процесса сушЮf топочными
газами, поскольку основной составляющей как воздуха, так и
топочных газов является азот - примерно в одинаковых коли
чествах (70- 80%), а остальные составляющие (по крайней ме
ре - основные) мало различаются по своим теплофизичес Юf М
свойствам.
1 5 .2.3. Свойства влажного твердого материала

Кон центрация влаги во влажном материале может быть
представлена в абсолютных и относительных величинах (см .
разд. 1 0 .2. 1 ) .
Абсол ютные концентрации ro выражают содержание влаги в
расчете на 1 кг влажного материала (вл . М ) И измеряются в (кг
Вл)/(кг вл . М) . Величина ro может изменяться в диапазоне
О

�

ro

�

1,

(з )

причем значению ro = О отвечает абсолютно сухой ТМ , значе
ние ro = 1 соответствует влаге в отсутствие твердого материала.
Здесь база - 1 кг смеси (сухой части ТМ и влаги). Очевидно ,
доля сухой части составляет 1 - ro . Если поток (в периодиче
ских процессах - количество) влажного материала обозначить
1 239

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Gвл. то поток (либо количество) влаги с влажным материалом
кг вл. М кг Вл
.
- кг Вл.1/с) .
составит Gвл·оо (по размерностям :
кг вл. М
с
Поток сухой части раве н Gвл( l - оо) .
Расчеты в абсолютных концентрациях и потоках неудобны
из-за непостоянства (уменьшения в процессе сушЮt) потока
влажного материала Gвл · Поэтому предпочтительнее использо
вать относительные концентрации И, выражающие содержание
влаги в расчете на 1 кг сухой части материала (СМ) и измеряе
мые в (кг Вл )/< кг СМ). Диапазон возможного изменения U:
о � и�

оо ,

(и)

причем значение U = О отвечает абсолютно сухому ТМ, U = оо
соответствует влаге в отсутствие ТМ. Здесь база - 1 кг сухого
материала, он несет с собой U кг (или долей кг) влаги.
Обозначим поток (в периодических процессах - количество) ТМ в расчете на е го сухую часть - G кг СМ/с; тогда по
ток
(либо
количе ство)
влаги
с
ним
составит

кг С М кг Вл
. /.с) , а поток влажного материала = кг Вл;
.
кг С М
с
+ U) . Величина G в ходе сушильного процесса не изменяет

G- U(

G( l
ся (уменьшается лишь lf), что существенно упрощает преобра
зования и расчетные формулы .

В литературе по сушке величины (J) и U "для большей наrтщности" нередко
выражают в % (абсолютных или относительных). Это делает громоздкими рас
четные формулы и ЯВ/IЯется одной из причин ошибок в расчетах. В учебни ке
концентрации последовательно выражаются в долях.

Технологические расчеты удобнее вести в относительных
потоках и влажностях ; практикам привычнее абсолютные
влажности . Пересчет одних концентраций в другие рассмотрен
в разд. 10.2. 1 . Применительно к величинам оо и U формулы
пересчета легко устанавливаются приравниванием потоков
влаги : Gвлоо = GU; если теперь выразить Gвл = G( l + U) или же
G = Gвл( l - ю ) и подставить одно из этих выражений в форму
лу для потоков влаги, то получается :
(1)

и

U = -- ' оо = -l+U
1 - оо

(к)

Тепловые расчеты сушильных процессов ведутся с исполь
зованием теплофизичесЮfх характеристик ТМ. Как и в случае
влажного воздуха, здесь неудобно пользоваться энтальпией
влажного материала, поскольку о н а отнесена к 1 кг влажного
материала, а его поток Gвл изменяется в ходе сушЮf . Удобнее
1 240

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

оперировать относительной энтальпией материала i

(в расчете

на 1 кг сухой части ТМ). В этом понимании Т представляет
собой "физическую теплоту'', переносимую таким количеством
( l + U) влажного материала, в котором содержится 1 кг абсо
лютно сухого. Если энтальпию отсчитывать (так условились) от
О 0 С, то при температуре е имеем:

Т

=

се ,

(л)

где ё - отмосителW188 теплое111 1:ост. ТМ, учитывающая теruюемкости сухой
части (cr) и содержащейся в материале алаm (СВл) - с учето м ее дали, ко нечно :

с = 1 · cr + ИсВл .

Gi

(м)

Поток теплоты с влажным ТМ в таком представлении равен
кг С М
Дж
= GCe
(по размерностям:
К = Дж1. /с =
с
(кг С М) - К

= Вт).

Выражение в разд. 1 5.2.2 и 1 5.2.3 концентраций влаги в СА
и ТМ в относительных единицах, т.е. выделение потоков инер
тов (АСВ и С М), позволяет отнести процесс сушки к классу
3 (2-2) 1 по КФ-классификации и воспользоваться рЯдом подхо
дов и соотношений, присущих процессам этого класса.

15.2.4. Об

адиабатном испарении ВJiarи

Реальные процессы сушки протекают в условиях весьма
сложного взаимодействия как между участвующими фазами,
так и системы "влага-воздух" с внешней средой. Одним из
способов упрощения (идеализации) процесса является рас
смотрение адиабатвоrо испарения влаги, когда оно осу
ществляется за счет теплоты сушиль ного агента (он при этом
охлаждается), а тепловое взаимодействие с внешней средой
отсутствует.
Рассматривается ограниченный объем алаж:ного во здуха, содержащий L кг
абсолютно сухого и достаточно большое ко.rшчество алаm - тако е, 'ПО оно не
может перейти целиком в газовую фазу. По истечении длительного отрезка
времени (или за небольшое время, но при развитой поверхности контакта алаm
с воздухом) во здух примет не кую температуру lw и станет насыщен ным при это й
температуре - процесс испарения алаm прекратится. Установившаяся темпера
тура lw называется температурой мокрого термометра (или те111 пературоl васuще

).
иu Процесс адиабатного испарения ( насЬШJ.ения) может бьпь посrроен в диа
грамме /-х на основе матери�UIЬного баланса для контура, охватывающего рас
сматриваемый ограниченный объем, и отрезка времени, достаточного для за

вершения процесса насыщения. Обозначим количество испаренной алаm W, ее
теплоемкость - свп. начальные алагосодержание во здуха х1 и относительную
энтальпию /1, а в условиях насьпцения ссстветственно х,. и lw. Тогда в отсуrст-

1241

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 15. 19. Линия мокрого термометра в диа
грамме 1-х

вне Источни ков и Стоков материальный баланс
по влаге дru1 воздуха (периодический процесс)
запишется:
W = Lхм - Lx1, откуда W = Цх.. - х1), (н)
а тепловой баланс:
Wcвл tw = L/м - L/1 ,
W=

откуда

Хм - Х1

= /w

L

св л tм

--

Uм - /1 ) .

(о)

Приравнивая левые части равенств (н) и (о)
и сокращая L, приходим к следующему соотношению :

11
Свлtw
-

•

или

/1 = Uw - свлtмхм>

+

СВлfмХ1 .

(п)

Если теперь исходную точку 1 считать произвольной, но связанной с точкой
насьпцения М(/м. х.. ; tw) , то последнее выражение превращается в урuнение
лвввв адвабатнческоrо ucwщeнu в диаграмме /-х (иначе - линии адиабатной
сушки при данной конечной температуре мокрого термометра tw):
l = (/" - СВлfмХ.. )

+

СВлlwХ·

Для построения этой прямой линии в диаграмме /-х

( 1 5.4)

заданной
температуре мокроrо термометра (точке М на кривой <р = 1) достаточно принять
произвольное значение х (Л}"Ш!е х < х,..) и по ( 1 5 .4) рассчитать сопряженное ему
значение /. Прямая, проведенная через точки М и N(/, х), изобразит процесс
адиабатного испарения - жирная штриховая ли ния с надписью (t.п) на рис.
1 5 . 1 9 В некоторых диаграммах 1-х в дополнение к ли ниям постоянных t и <р
проведено семейство линий адиабатного испарения дru1 разных температур
мокрого термометра.
Разность рабочей температуры СА в некоторой точке А и в отвечающей ей
точке М (точки А и М лежат на одной линии адиабатного испарения) либо
соответствующая им разность магосодержаний, т.е. (IA - tw) или (Хм - хл) мoryr
трактоваться как движущие силы, определяющие скорость адиабатного процесса
сушки.
Модель адиабатного испарения влаrn применима к сушке влажных материа
лов при достаточно высокой их влажности, когда влага в ТМ ведет себя так же,
как влага в отсуrствие материала (см . разд. 1 5 .2.5). В этом случае ТМ вместе с
содержащейся в нем влагой в ходе адиабатной сушки, как и сушильный агент,
стремится приобрести температуру мокрого термометра; выше этого уровня
температура влажного материала подняться не может.
Специально подчеркнем:
- в случае адиабатного испарения влаги из ТМ при достаточной продолжи
тельности процесса (или при развитой поверхности межфазного контакта) рав
новесная концентрация .xN не 11сеrда отвечает точке, лежащей на линии насыще
ния ер = 1; при удалении связанной влаrn (см. следующий раздел) эта точка будет
лежать на некоторой линии <р < 1 ; в такой ситуации термины "адиабатное испа
рение" и "адиабатное насыщение" не совпадают; соответственно, дви:жушая сила
будет выражаться разностью .xN - хл � Хм - хд;
- в случае реального (не адиабатного) процесса движущая сила также будет
выражаться разностью .xN
хл, но линия процесса пойдет не по прямой Uwт), а
в общем случае по иной линии реального процесса (см . разд. 1 5 . 3.4); при этом
.

-

1242

ори любой

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

конечная точка с влажностью хМ (при полном завершении массообмена: 't --. ос,
j}F -.оо) будет лежать на линии ер = 1 при удалении свободной: влаги (тогда
х..) и на друтой линии q> < 1 при удалении связанной: влаги (тогда хМ < Хм).
хМ
=

15.2.5.

Равновесие

Равновесие по влаге в системе "сушильный агент-твердый
материал" в общем плане характеризуется положениями, рас
смотренными в разд. 1 0 .3, в частности - для систем класса
3(2 - 2) 1 , а более конкретно - положениями разд. 14.2.2. Однако
применительно к процессам сушки выявляются особенности ,
•
обусловленные природой связи влаги с материалом . Различаюг
свободную и связанную влагу в ТМ.
Свободной (иногда - поверхностной) называюг влагу, удер
живаемую материалом только в результате механического
сце пления . По существу такая влага в ТМ ничем не отличается
от разлитой на какой -нибудь поверхности. Равновесное давле
ние паров рМ непосредственно над материалом со свободной
влагой (см. рис. 1 5 . 14) независимо от ее концентрации в ТМ
таково же, как над чистой :жидкостью (если влага - вода, то
как над чистой водой) при той же температур е; иначе говоря это давление насыщенных паров: рМ = Рн · Затраты энерmи при
испарении 1 кг свободной влаm отвечаюг (при изотермическом
испарении - равны) теплоте испарения чистой :жидкости.
Связанной называется влага, удерживаемая материалом ка
кими -либо дополнительными (помимо механического сце пле
ния) силами : физической адсорбции, капилляр ными, mгроско
пическими (влага в виде кристаллогидратов) и др. Эгу влагу
при сушке надо оторвать от материала, затратив дополнитель
ную энерmю , так что ее затраты на испарение 1 кг связанной
влаm превышаюг теплоту испарения. Более прочная связь та
кой влаm с ТМ приводит к понижению давления ее паров над
материалом: рМ < Рн, причем рМ зависит от влажности материа
ла U, Ф. Скорость испарения связанной влаm меньше, нежели
свободной.
Существуют материалы, практически не содержащие свя
занной влаm (пример - стеклянные шарики) . Но в общем
случае ТМ может содержать свободную и связанную влагу. При
сушке сначала удаляется свобод ная влага, затем связанная.
Границу между свобод ной и связанной влагой называюг крити
ческой влажностью материала ( l./kP) .
Равновесие для системы СА-ТМ представляюг в декарто
вых координатах, как это показано в разд. 10.3 .2.
На рис. 15.20,а приведены равновесные зависимости в диа
грамме q>'d- U. Рабочая область сушки располагается под лини• См нап
"
rн ч ер,

(9, 1 9 ) .

1243

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

с

б
Рис. 15. 20. Ра в новесие при сушке:
о

-

диаrрамма ч>"

-

U, 6 - диаrрамма Jl!I

-

U

ей равновесия (символ С ); над равновесной кривой - область
увлажнения твердого материала (т.е . сушки газа) . Нижняя кри
вая (например , экспериментально снятая) отвечает постоян 
ной температуре t1 - это изотерма равновесия . В области сво
бодной влаги , т.е. при и � и кр , относительная влажность
<р = 1 , что соответствует рМ = Рн· В области связанной влаги,
т.е. при и < CJl<P , величина <р < 1 , что отвечает р м < Рн· Для
другой температуры t2 > t1 изотерма равновесия располагается
выше, поскольку давлен ие паров влаги возрастает с температу
рой . Это означает, что при одинаковой влажности материала и
справедливо 'Р2 > 'P l . С другой стороны, при одинаковых отно
сительных влажностях воздуха <р более высокой температуре
отвечает меньшая равновесная влажность материала и2 < и1 ;
значит, при повышенных температурах возможна более глубокая
сушка ТМ . Из сопоставления кривых равновесия при разных
температурах видно, что величина и кр при повышении темпе
ратуры уменьшается.
Поскольку последующие технологически:е расчеты ведутся с
использованием диаграммы 1-х, представим равновесие в ко
ординатах ri- и (рис . 1 5 .20,б). В этой диаграмме при и � икр
соответственно ер = 1 величина х м = x max , причем для !2 > 11
характерно x2max > x1 max .

1244

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

1 5.3. ПРО СТАЯ СУШИЛКА

Изучение процесса сушюs начнем с простой сушильной
установюs - ее схема представлена на рис. 15.2 1 . Рассмотрение
этого варианта сушильного процесса позволяет сформулиро
вать основные понятия и подходы к расчету параметров работы
аппаратов, составляющих установку.

Пос.ледняя включает паровой или элекrрический калорифер 1 Д11Я подоrрева
СА и сушильную камеру 2, где происходит процесс обезвоживания (сушки) ТМ .
В качестве дутьевого устройС11 1а, обеспечивающего движение С А через калори
фер и сушильную камеру, используется вентилятор .1. Исходный влажный мате
риал подается в сушильную камеру, высушенный - выводится из нее. Сушиль
ный агент пос.ледовательно проходит калорифер и сушильную камеру, в ней он
забирает влаrу у ТМ - с потоком СА она выбрасывается в атмосферу. Материал
перемещается в сушильной ка мере противотоком к СА (так показано на рис.
1 5 . 2 1 ) либо прямотоком; возможны и друmе схемы взаимного направления
потоков фаз.
С точки зрения процессов сушки место расположения веJПИЛЯТОра (в голове
или на хвосте процесса либо между калорифером и сушильной камерой) безраз
лично. Дело в том, что mдрав.ническое сопротивление системы невелико в срав
нении с давлением процесса сушки В, и можно считать, что в любом с.лучае
сушка ведется под давлением В (чаще всего - при атмосферном) . Но место
размещения вентилятора важн о в ином аспекте: при установке веJПИЛЯТОра в
голове процесса в сушильной камере возникает небольшое избьпочное давление,
соответствующее ее mдравлическому сопротивлению, при установке на хвосте небольшое разрежение. В пер1юм с.лучае через неплотности аппаратуры неболь
шое- количество СА выходит из сушильной камеры в о кружающую среду, во
втором - происходит подсос воздуха в сушилку извне. Ее.ли высушиваемый
материал пылит или пары удаляемой влаm токсичны, то при установке вентиля
тора в голове схемы около сушилки возникает неблагоприятная санитарная
обстановка (запыленность, вредные выбросы). При установке вентилятора на
хвосте схемы этого не происходит. Поэтому при прочих равных ус.ловиях векrи
лятор предпочтительно усrdнаRЛИвать на хвосте процесса, как это показано на
рис. 1 5 .2 1 . Однако если высушиваемый материал не допускает соприкосновения
с кис.лородом воздуха и сушка ведется каким- нибудь " инертным" газом, то во
избежание подсоса необходимо поддерживать в сушилке некоторое избьпочное
давление. Тогда вентилятор устанавливают в голове процесса. Разумеется, его

о

Jl

G

0'

И'

2

3

Рис. 15. 21. Принципиаш.ная схема простой сушильной установки :
1 - калорифер, 2 - сушильная камtра, З - вtнrилятор;
/ -сушильный areиr, 11 - высушиваемый материал

1 245

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

размещение межцу калорифер о м и суш ильной камерой нецелесообразно из-за
жестких условий работы (высо кие температуры). Наконец, при больших гидрав
лических сопротивлениях установки, когда напора одноrо веlПИЛЯТОра не хвата
ет, устанавливают два - в rоло ве и на хвосте процесса.

На схеме обозначены состояния рабочих тел. Поток СА бе
рется в расчете на абсолютно сухую часть, поэтому во всех
точках схемы идет одинаковый поток L. Параметры сушильно
го агента до калорифер а (точка О) отмечены и ндексом " О " : t0 ,
q>o, .хо, 1о. На выходе из калорифера - точка 1 , параметры t1 ,
С/>1 , х1 , 11 . После сушильной камеры (точка 2): t2, q>2, хъ 12 . По
ток высушиваемого ТМ берется в расчете на его сухую часть,
поэтому в ходе сушки его поток G = const. Параметры ТМ на
входе в сушильную камеру отмечены верхним штрихом: U', 8 1,
с ' ; параметры высушен н ого ТМ на выходе из нее - двумя
штрихами: U11, 8 " , с " . В общем приведенные обозначения (с
некоторыми изменениями, дополнениями) сохранены и при
рассмотрении более сложных схем сушильного процес с а .
В задачу технологического расчета статики процесса входит
определение по заданным исходным условиям материальных и
тепловых потоков - полных (в единицу времени) и удельных
(они дают сравнительную характеристику процесса) .
1 5.3. 1 . Основные пото к и

в

простой сушке

Материальные потоки
К числу основных определяемых материальных потоков от
носят количество удаляемой в едини цу времени влаги W и рас
ход сушильного аге нта L. Поток твердого материала G, как
правило, задан условиями задачи. Для определения W и L рас
смотрим расчетную схему сушильной камеры (рис. 15.22), на
которой зафиксированы зоны ТМ и СА, разделенные поверх
ностью межфазного контакта, а также обозначены потоки L и G
(для рассматриваемых целей их направление безразлично). Через
поверхность контакта от ТМ к СА идет поток влаги W. Входные и
выходные концентрации влаги в ТМ и СА отмечены индексами,
соответствующими принципиальной схеме на рис. 15.21.
Для определения потока удаляемой влаги рассмотрим про
странственный контур ТМ, проходящий через поверхность
раздела фаз F и охватывающий зону высушиваемого материала.
В случае непрерывного процесса в отсутствие Источников и
Стоков материальный баланс по влаге в ТМ имеет вид:
GU' - W -

1 246

GU" = О

и W=

G( U'- U") .

(1 5.5)

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 15. 22. К определению основных матери
альных потоков
Ес:.ли в условиях задачи заданы абсолют
ные потоки ( G'м или G"u) и абсолюmые
•
'
концекrрации ( ю и ю" ) , то рекомендуется
первоначально пересчитать по (к) абсолюmые
величины Ф(iJ в оmосите.льные lfl) и выра
зить
заданную
производительность
G",/iJ
через G по выражению, предшествующему
(к), а затем определять W по ( 1 5.5).

GU
тм

Для определения потока СА, обеспечивающего удаление W

кг/с влаги,

рассмотрим контур СА на рис.
баланс п о влаге для СА зап ишется:

Lx1

+ W-

Lx1 = О

и W=

15.22.

L(x2 - х 1 ); L =

Материальный
w
--- .

(15.6)

Х2 - Х1

В целях сравнения и сопоставительной оценки различных
сушилок представляет интерес удельный - на 1 кг удаляемой
влаги (уд. Вл) - расход сушильного аrевта l (кг АСВ)/(кг
уд . Вл) :

L
l=-=
w

1
Х2 - Xt

1
= ---

(15.7)

Х2 - Хо

поскольку в простой сушилке х1 = Хо· При этом разности (х2 - xi) = (х2 - .хо) представляют собой uаrоемв:ости СА в (кг
уд. Вл)/(кг АСВ).

Тепловые потоки

К основным тепл овым потокам относят расходы теплоты в
калорифере и сушильной камере. Определяются эти п отоки с
помощью те пловых балансов.
Расчетная схема калорифера применительно к паровому
обогреву представлена на рис. 15.23,а. Поток теПJJоты в нем Qк
(в Дж/с или в Вт) найдем из теплового баланса для зоны су
шильного агента (контур СА, ограниченный поверхностью теп
лообмена Fт):
( 15.8)
Llo + Qк - L/1 = О и Qк = L(/1 - /о) .
Удельный расход теПJJоты, приходящийся
на 1 кг уда
ляемой влаги , обозначим (как и другие величины, отнесен 
ные к 1 кг уд . Вл) строчной буквой Qк = Q./W (Дж/кг уд . Вл).
•

Возможно, конечно,
"

и

непосредственно рассчитать W п о G'м или G"м и

концекrрациям ю' и ю , но рш:чеmые
rромоздко - см . , например, ( 1 ,
14).

6,

формулы

в этом случае выглядят

более

1247

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

гп

Д ,h

L

L J2

Д ,с",Т L J 1

L J1

Jo

СА
б

а

Рис. 15. 23. К определению тепловых потоков (расчетные схемы) :
а - дл я калорифера, б - для сушильной камеры

По о пределению
qк

=

L(l1

w

1

О

)

ИЛ И qк = 1(11 - J.о) '

( 15.9)

причем 11 - lo = Лlк представляет собой затрату теплоты в ка
лорифере в расчете на l кг абсолютно сухого воздуха.
Расход греющего пара Д определяется из теплового баланса
для зоны греющего пара (контур ГП). Если энтальпия пода
ваемого греющего пара (чаще всего это водяной пар под дав
лением) равна h, а отводимого конденсата - произведению его
теплоемкости Ск на темnературу Т, то

(15. 1 0)
где

rrp

- теwюта конденсации rреющеrо пара.

Расчетная схема сущильной камеры представлена на рис .
без вьщеления зон ТМ и СА. При этом здесь в целях
большей общности обозначен ряд тепловых потоков, не пока
занн ых на принципиальной схеме (рис. 1 5.21). Эrо потери теп
лоты в окружающую среду Q0 и с транспортными приспособле
ниями Qтр . а также подвод теплоты непосредственно в сушиль
ную камеру Qc (заметим , что в реальных условиях нередко теп
ловые потери QTP • а еще чаще подвод теплоты Qc - отсутству
ют). Тепловой баланс для контура ' К запишется в случае не
прерывного процесса:
(а)
Ll1 + G c ' 8' + Q(, - Ll2 - G c " 8" - Qo - Qтр = О
Обозначим для сокращения записи затраты теплоты на на
грев материала Gё 118 11 - Gё 18 1 = Qм , а сумму потерь Qo + Qтр +

1 5.23,б

.

+

Qм

124 8

=

L Q. Тогда из (а) для еди11ицы времени
L(l2 - 11 ) = Qc - L Q,

(б)

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

а

на 1 кг удаляемой влаги

(с обозначением Q;

LU2 - l1 ) = Qc _ :E Q
w

w

w

=

Q/Jt'):

и l(l2 - I1 ) = qс - :E q'

(в)

причем "f,q = Qo + Qтр + Qм ·
Разность в правой части (в) именуется параметром сушки
Лq· = Qc - "f,q. Тогда изменение относительных энтальпий, т.е .
процесс в сушильной камере, окончательно выразится соотно
шениями - на 1 кг уд . Вл и на 1 кг АСВ :
/(/2 - /1 ) =

Лq.

и 12 - /1 =

Лq./l.

( 1 5. 1 1)

И з (15. 1 1) следует, что характер изменения относительной
энтальпии в сушильной камере определяется знаком параметра
сушки дq • .
Технологический расчет начинают с определения потоков удаляемой влаги в сушильной установке по формуле ( 1 5.5) и
сушильного агента по формуле ( 15.6). В общем плане в задачу
расчета входит идентификация (определение местоположения
и установление значений всех параметров) трех точек: О ; 1 и 2.
Каждая из них определяется двумя параметрами, следовательно
всего необходимо знать (по условиям или найти в ходе расчета)
шесть параметров. Некоторые из точек моrуг быть заданы
(любой парой параметров из t, ер, х, [), для других известен
лишь один из параметров или не задан ни один из них - эти
точки нужно найти в ходе расчета. Обычно в условиях задачи
задаются четыре параметра; поэтому для определения неиз
вестных параметров необходимы два уравнения связи. В ка
честве первого из них выступает соотношение х = const при
нагреве СА в калорифере, в каче стве второго - выражение
( 1 5. 1 1) для процесса в сушильной камере.
1 5 .3.2. П110стая идеальная сушилка

Рассмотрение простой сушильной установки начнем с идеа
лизированного варианта, позволяющего выявить основные
принципы - построения процесса в диаграмме 1-х и техноло
гического расчета с использованием этой диаграммы.
Идеальной (иногда используют термин теоретическая ) назы
вается сушилка, в которой каждая составляющая параметра
сушки равна нулю. Такое упрощенное представление не проти
воречит физическому см ыслу:
- большинство суш илок работает без подвода теплоты в
сушильную камеру, что соответствует Qc = О;

1249

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 15. 24. Диафамма 1-х дЛЯ простой
Идеальной сушильной усrановки

[

- во многих сушилках
нет потерь теплоты с тран 
спортными
приспособле
ниями (нет этих приспособ
лений либо они целиком
размещены внугри сушиль
ной камеры), т.е. qтр = О ;
- вполне можно предста
1
вить себе ситуацию (хотя на
<р
практике она, как правило,
не реализуется) , когда отно
сительные энтальпии входя
щего и выходящего материала
х
одинаковы, так что qм = О ;
- предполаrается совер
шенная тепловая изоляция
сушильной камеры, исключающая теплопотери в окружающую
среду: qo = О .
В таких условиях "'L.q = qo + qтр + qм = О и Л q. = qc - L.q = О .
Это означает, что теплота, отдаваемая сушильным агентом в
суш ил ьной камере, затрачивается только на испарение влаги из
материала. Поскольку лq . = О , то, согласно ( 1 5 . 1 1 ) , для иде
альной сушилЮ1
( 1 5 . l la)
=

т.е. процесс сушЮ1 в сушильной камере идет по линии посто
энтальпии 1 = const - это второе уравне
ние связи в случае идеальной сушки . Объяснение возможности
суш ки с /1 = /2 состоит в следующем: поток СА отдает свою
теплоту (это должно сопровождаться снижением /), но она
здесь идет исключительно на испарение влаги, а влаrа эта в виде
паров присоединяется к потоку СА, возвращая тем самым за
траченную теплоту; в ре.зультате процесс идеальной сушки про
текает с неизменной относительной энтальпией 1.
Таким образом, для идеальной сушилки характерны уравне
ния связи: в калорифере х = Х{) = х1 = const, в сушильной ка
мере / = 11 = 12 = const .
Диаграмма 1-х для п ростой идеальной сушильной установЮI
представлена на рис. 1 5 .24, причем индексация точек и параметров
процесса соответствует приведенной ранее на рис. 1 5 .2 1 .
Пусть в услов иях з адачи заданы четыре параметра: q>o, to , t1 и
q>2• ТаЮ1м образом, исходное состояние влажного воздуха из
вестно, это точка О ( t0 , q>o ). В калорифере воздух нагревается по
вертикальной линии х = Х{) = х 1 до заданной температуры t1 ,

янной относительной

1250

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

так что точка l определяется пересечением вертикали х1 = Хо и
линии t1. Далее в сушил ьной камере процесс идеальной сушюt
идет по линии 1 = 11 = 12 - до заданного значен ия <1>2; реже
вместо q>2 задают выходную температуру t2. (Дело в том, что
задание q>2 < 1 гарантирует построение процесса в рабочей об
ласти - выше кривой q> = 1; при задании t2 конечная точка 2
может попасть в нерабочую область q> > 1 .) Пересечением ли
ний 11 = 12 = 1 и q>2 (либо t2) определяется точка 2.
Пусть теперь заданы другие четыре параметра влажного воз
духа: нар яду с исходной точкой О (to, q>o) указаны параметры t2
и <f>2, т.е. определена точка 2. Тогда точка 1 устанавливается
пересечением вертикали .хо = х1 (проводится из точюt О) и ли
нии 11 = 12 (проводится из точюt 2).
Для заданных ИJШ найценных точек О, 1 и 2 по диаграмме от
считываюrся все необходимые параметры ti, с:р1, х1, ft, где i = О, 1 , 2.
При известных параметрах точек определяюrся значения l по
(15.7) и fk по (15.9) и далее L и Qк - для варианта L,q = О.
В ходе технологической проработюt процесса (задачи эксплуа
тащm или проектирования) может возникнуть необходимость
понижения температуры сушки (например, из-за неустойчивости
материала при контакте с высокотемпературным СА). В рамках
простой сушилки это может бьrгь достигнуrо увеличением потока
СА: то же количество теплоты будет внесено в процесс при нагре
ве КЮIЩОГО кг воздуха до меньшей температуры (11). Разумеется,
при этом на выходе из сушилки будет получен (см. иприх
пунктирную ЛШIИЮ сушки на рис. 15.24) отработанный СА с
меньшим влаrосодержанием х2, поскольку возрастанию l = l/(x2
- .хо) при фиксиро ванном .хо со путствует понижение х2.
Специально подчеркнем, что в идеальной сушилке, когда
нет никаюtх теплопотерь и Qc = О, удельный расход теплоты в
калорифере превышает (причем заметно) теплоту испарения
влаги: Qк > r. Дело в том , что в сушильной камере теплота в са
мом деле идет лишь на испарение влаги, но для сушильной
установки в целом надо еще учитывать затраты теплоты на на
грев СА. Ведь в точке О его температура, как правило, заметно
н иже, чем в точке 2, а на каждый кг удаляемой влаги обычно
затрачивается 10-20 и более кг воздуха. По этой причине даже
в экономичных конвективных сушилках величина Qк обычно
примерно в 1 , 5 раза превышает теплоту испарения.
-

1 5.3.3. Простая реальная сушилка

В основе технологического расчета и построения в диаграм
1-х процесса в простой реальной сушилке лежит выражение
(15. 1 1). Здесь возможны различные случаи :
лq. > О, т.е. Qc > l,q - подвод теплоты в сушильной камере с
избытком компенсирует суммарные теплопотери . Тогда проме

1 25 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

цесс сушки идет с повышением относительной энтальпии:
> 11;
лq. < О , т. е. qc < 'f,q - подвод теплоты в сушильной камере
недостаточен (может быть, он вообще отсугствует) для компен
сации суммы теплопотерь. Тогда процесс сушки идет с пони
жением относительной энтальпии: 12 < 11;
Лq. = О, т.е. qc и отдельные теплопо тери q1, входящие в 'f.q, су
ществуюr, но в точности компенсируюr друг друга (qc = L.q) . Тогда
реальный процесс идет по линии идеального 1 = const и 12 = 11.
В последнем случае построение в диаграмме 1-х и расчет
реального процесса ничем не отличаются от рассмотренных
выше для идеального процесса. Поэтому далее рассматривают
ся лишь случаи Лq. > О и Лq. < О.
Как и для идеальной сушилки , в исходных условиях задают
ся четыре параметра - чаще всего в одном из двух вариантов:
- известны to и <ро, t1, <fJ2 (или t2); здесь наряду с точкой О
(исходный воздух) легко определяется точка 1, т.е. параметры
СА на входе в сушильную камеру; точка выхода СА (точка 2) не
известна, задан лишь один ее параметр <р2 (или t2) ;
- известны to и <ро, t2 и <fJ2; здесь наряду с точкой О задана
точка 2, т.е. параметры воздуха, покидающего сушилку; не из
вестна точка 1.
Ниже последовательно рассмотрены оба этих варианта, в
кажд ом из них - случаи Лq. > О и Лq. < О. Уравнение процесса
в калорифере - прежнее (х = const) ; процесс в сушильной ка
мере определяется выражением ( 1 5 . 1 1). При этом значение Лq.
считается найденным; предварительно принято qc и рассчитана
каждая из составляющих 'f,q.

12

-

Простая сушилка при неизвестной точке 2
С целью получения и использования уvавнения связи 1 =
= 1(х) для процесса в сушильной камере преобразуем выражение
(15.11), заменив /по (15.7):
(г)
При этом 11 и х1 - известны : х1 = Х{), 11 определяется при
нахоЖдении точки 1 пугем пересечения вертикали х1 = Х{) с те м
пературной линией t1• Неизвестными являюrся 12 и х2, но в зада
нии оговорено, что точка 2 (12, х2) расположена на линии <f'2· Не
которому промежуточному значению х > х1 отвечает промежуточ
ное значение 1 :1= 11• При этом уравнение связи для сушильной
камеры 1 = 1(х), в соответствии с (r), принимает вид:
( 1 5 . 1 2)
1 - 11 = Лq. (х - х1).
Очевидно, что прямая, описываемая уравнением (15.12), про
ходит через точку 1, так как при х = х1 получается 1 = 11• А при
1252

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Диаrрамма /-х для про
стой реальной сушильной установ
ки при неизвестном состоя нии
во:щуха на выходе из нее

Рис. 15.25.

1

х = х2 должно получаться
1 = 12, причем точка 2 (12,
х2) лежит на линии <f>2· Для

нахождения точки 2 следует
задаться произвольным зна
чением х (луч ше х > х1) и
рассчитать по ( 1 5 . 12) отве
=1
чающее ему значение 1;
далее проводится прямая
через точки (11 , х1) и (J, х) и
отыскивается точка 2 н а
пересечении этой прямой и
х
линии <1>2·
Расположение
прямой
1(х) выше или ниже линии
11 = const определяется знаком Лq• (рис. 15.25). При Лq• > О в
соответствии с ( 15. 12) для х > х1 получается 1, 12 > 11. При
дq. < О для х > х1 пол учается 1, 12 < 11 .
В обоих рассматриваемых случаях потери теплоты "f,q долж
ны быть чем-то скомпенсированы. П ри этом здесь компенсация
невозможна за счет большего нагрева воздуха в калорифере:
точки О и 1 фиксированы, так что в обоих случаях, как и в
идеальной сушилке, каждый килогр амм воздуха (в расчете на
абсолюrно сухой) получает в калорифере одно и то же количе 
ство теплоты Л1к = 11 - 1о.
Компенсация теплопотерь в случае дq. > О происходит за
счет подвода теплоты qc в сушильную камеру. При достаточно
больших значениях qc эта теплота с избытком компенсирует "f,q,
так что можно даже о бойтись меньшим количеством СА, неже
ли в идеальном процессе. В самом деле, точка 2 реального
процесса получается правее точки 2ид (см. рис. 1 5 .25), т.е . х2 >
> х2 ид, и по ( 15.7) удельный расход воздуха / (кг АСВ/кг уд.Вл )
будет меньше, чем для идеально го процесса lн.
В случае лq. < О теплопотери "f,q не мш:уг бьпь скомпенсиро
ваны за счет qc, поскольку qc < "f.q (возможно, qc = О). Как можно
видеть из рис. 1 5.25, в этом случае точка 2 для реального процесса
лежит левее, чем для идеального (точка 2IOI), т.е. х2 < х2Ю1. Эrо
означает, что для реального процесса / должно бьпь больше, чем
для идеальн о го lи; иначе говоря, компенсация потерь "f.q осу
ществляется пугем увеличения расхода СА (воздуха).
Из (15.11) следует, что приращение относительных энтальпий в сушильной
камере Л/ = /2 - 11 Лq. /1. Казалось бы: можно построить идеальный процесс,
=

1253

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

определить точку 2ид, а затем при заранее найденном параметре Лq. - в зави
симости от ero знака добавИ1-ь к значению /2ид = /1 (или отнять) величину
лq.
- будет на йдено искомое значение /2 для реально rо процесса. Нахо жде 
ние далее точки 2 затруднений не вызывает. Однако такое построение возможно
лишь при известном / ( Лq. - найдено), тогда как в рассматриваемом случае
просто (по х2"д) определяется лишь lи, а / - не известно до тех пор, пока не
найдено вла rосо держа ние ре ально rо процесса х2. Поэтому без использования
уравнения ( 15. 1 2) здесь не обо йтись.

/1

при неизвестной точк.е 1
уравнения связи 1 = 1( х ) в этом случае

Простая сушилк.а

Для получения
воз
можен сходный подход, только в выражении типа (r) в ка
честве фикс ированных следует при н ять параметры /2 и х2, от
веч а ющие заданной точке 2, а значения /1 и х1 заменить пере
мен ными :
12 - / = Лq. (х2 - х).
(15. 1 3)
Эта линия, очевидно, проходит через точку 2, так как при
х = х2 получается 1 = 12. Точка 1 определяется пересечением
прямой по уравнению ( 1 5 . 1 3) с вертикалью х = Х() = х1. Кон
кретное расположение линии процесса в сушильной камере
/ = /( х ) - выше или н иже линии 12 = const - определяется
знаком Лq• (рис . 1 5.26).
Линию / = /(х) здесь можно построить, также задавшись произвольным зна
чением х (лучше х < х2), рассчитав по (15.13) сопряженное с этим х значение/ и
зафиксировав в диаrрамме промежуточную точку (/, х). Линия, проведенная
через эту точку из точки 2, и будет JШнией ре ально rо процесса; ее следует довес
ти до вертикали Х() = х1 и наЙ11i точку 1 .

Существенное отличие от предыдущего варианта состоит в
том , что при заданной точке 2 (а точка О тоже известна) мы
располагаем значениями Х() = х1 и х2, одинаковыми для идеаль
ного и реального процессов. Поэтому здесь по (1 5.7) можно
однозначно найти l = lи, а следовательно и отношение
Лq. /1 = 12 - 11. Дальнейшее построение линии реального про
цесса здесь проще, чем для предыдущего варианта, поскольку
нет необходимости в использовании уравнения ( 1 5 . 1 3) и
отыскании промежуточной точюt ( / , х). Надо просто провести
очевидное построение на вертикали Х() = х1 (рис . 15.26):
- величину Лq./l следует добавить к / 1ид = 12 (либо от точ
ки )ид отложить вверх отрезок, отвечающий лq ./!) при
Л q . <О, когда 11 > 12 - будет получена точка 1 реального про
цесса;
- величину Лq./l следует вычесть из J1ид = 12 (либо отло
жить от точюt Jид вниз соответствующий отрезок) при лq. > О,
когда 11 < 12 - также будет получена точка 1 реальной сушюt.
Затраты теплоты в калорифере, как и в идеальной сушилке ,
на 1 к.г АС В Лfк = 11 - 1о, а на 1 к.г уд. Вл qк = /(/1 - lo). Отли-

1254

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 1 5. 26. Диаграмма /-х для про
стой реальной сушильной установки
при неизвестном состоянии воздуха
на входе в нее

чие от идеальной сушилки в
том, что в качестве 11 берется
относительная
энтальпия
реальной точки 1.
В обоих случаях Лq. > О и
Лq. < О потери теплоты L,q
должны быть скомпенсирова
ны. При этом компенсация
здесь невозможна за счет
lj> =1
изменения потока СА: точки
О и 2 фиксированы, значения
l и L (при данном W') опре
деляются однозначно, в ре
х
альном и идеальном процес
сах они одинаковы .
Компенсация теплопотерь
в случае Лq• > О обеспечивается за счет подвода теплоты в су
шшzьную камеру Чс· При достаточно высоких значениях Чс поте
ри L.q компенсируются с избытком, так что каждый килоrрамм
СА можно наrревать в калорифере до меньшей (чем в идеаль
ном процессе) температуры: из расположения точек lид и 1 на
рис . 1 5 .26 ясно, что /1 < t1ид.
Потери в случае лq. < О не могут быть скомпенсированы за
счет чс : этой теплоты недостаточно (может быть вообще
Чс = О), поскольку Чс < L.q. В этом случае компенсировать теп
лопотери приходится за счет нагрева СА в калорифере до более
высокой (нежели в идеальном процессе) температуры: из рас
положения точек lид и 1 на рисунке ясно, что здесь t1 > t1ид.
15.3.4. О распределении в простой сушилке подводимой теплоты
между калорифером и сушильной камерой

В сушильную установку теплота (например, через поверх
ность теплообмена) под1юдится как в калорифер (Qк, Чк) , так и
в сушильную камеру (Qc, Чс)· В зависимости от величины Чс ,
как показано в конце предыдущего раздела для заданных точек
О и 2, получаются положите.IIь ные или отрицательные значения
параметра сушки Лq•. А это влияет на необходимую теплоту Чк
подоrрева СА в калорифере и определяет линию реального
процесса сушки в сушильной камере . В целом теплота, подво
димая в единицу времени, равна Qr. = Qк + Qc, а в расчете на 1
кг удаляемой влаги Чr. = Чк + Чс· Распределение полного по-

1 255

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

тока теплоты {h и удельного qz:. между калорифером и сушиль
ной камерой является важной технологической проблемой как для само й простой сушилки , так и в плане связи ее с дру
гими схемами сушки.
Будем вести анализ для удельных потоков теплоты - на 1 кг
АС В или на 1 кг уд . Вл. Перепишем уравнение ( 1 5 . 1 1 ) , раскрыв
смысл параметра Лq.; в расчете на 1 кг АС В (в таком пред
ставлении можно оперировать диаграммой 1-х):

12
откуда

- 11 = Лq.l = !!s_l -

"i.

l

q

'
(д)

-

Сумма,р ное количество теплоты
( 1 5 . 9 ) qкf l 11
10:
=

qL.

l

= !!.ь_

l

+

!!s_

l

=

(11 - 1 о)

-

+

( 12 - 1 1

qцlz
+

найдем, выразив по

)

L. q =
l

-

12 - 1 0

+

L. q

( е)

l .
идеаль

Поскольку в случае идеальной сушки 12 = 11, то для
разность 12
11 10 может трактоваться как
10
удельный расход теплоты в калорифере; 12
1о = qкил/z. Тогда
выражение (е) принимает вид :

ного процесса

qL.

или в расчете на 1

=

!!.ь_ + qc = q�

-

+

L. q

l
l
l
1
l
кг удаляемой влаги:
lft = qк + qc = qкид + L.q.
=

( 1 5 . 14)

( 1 5 . 14а)

Таким образом, полный расход теплоты , необходимой для
проведения реального процесса сушки , складывается из тепло
ты, затраченной на идеальный процесс и необходимой для
восполнения всех теплопотерь - qo, qт р , qм. На диаграмме 1-х
(рис . 1 5 .27) полное количество теплоты на 1 кг АСВ qz:. /l изоб
ражается в соответствии с ( 1 5. 1 4) отрезком 0-1', полу
чающимся как сумма отрезков 0-lид (отвечает величине q кид/[)
и 1ил-1• (выражает теплопотери L.q/[). При этом величина от
резка 0-1' не зависит от того, как суммарное количество теп
лоты (qz:. или qz:. /[)распределено между калорифером и сушильной

камерой.

Если qc
О ( час тый случай в технологии сушки) , то , со
гласно ( 1 5. 1 4) и ( 1 5 . 1 4а) , qz:. = qк - все тепло на сушильный
процесс должно быть подано в калорифере . Тогда отрезок 0-1'
изображает процесс нагрева СА в калорифере, а 1 '-2 - про=

1256

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 1 5. 27. К распределению теплоты в
простой сушильной установке ме�у
калорифером и сушильной камерой

1

/1

" ... 1'

...
цесс сушюt в сушильной каме
ре (линия qc = О) . Если же
часть теплоты подводится в
сушильной камере, т.е. qc :t:- О,
то при сохранении суммар ного
расхода теплоты (f/r,, tJrf l, от
0-1 )
резок
потребуется
меньше теплоты подавать в
калорифере : qк = flr. qc. При
=1
небольших qc, не компенси
рующих полностью теплопоте
ри '[.q, на диаграмме 1-х под
вод теплоты в калорифере qJl
изобразится отрезком 0-1",
х
заканчивающимся выше точюt
идеального процесса 1ид; рас
ходу теплоты в сушильной
камере qc/l будет отве•1ать отрезок 1"-1'. Процесс сушки в
этом случае изобразится линией 1"-2. Пусть теперь подвод
теплоты в сушильную камеру в точности компенсирует тепло
потери: qc = '[.q. Тогда нагрев СА в калорифере изобразится
отрезком 0-lид, а сушка в сушильной камере - линией иде
ального процесса lид-2; величине qc/l будет отвечать отрезок
1ид_1 •. В сушильную камеру может быть подведена теплота,
превосходящая теплопотери: qc > '[.q. Тогда, в полном соот
ветствии со сказанным в предыдущем раз.qеле, потребуется
меньше теплоты в калорифере. Величина qкfl изобразится от
резком 0-1"', qc/l - отрезком 1'"-1', а процесс в сушильной
камере - линией 1'"-2; отрезок 0-1' по-прежнему будет
изображать полное количество теплоты fft/l. Наконец, в су
шильную камеру можно подводить всю теплоту, необходимую
для сушильного процесса: f/r. = qc. Тогда, согласно (1 5.14) и
( 15. 14а), qк = О, весь отрезок 0-1' отвечает величине qc/l, а
процесс в сушильной камере изображается линией 0-2 (на
рисунке - линия qк = О).
Из приведенного анализа видно, что увеличение qc приводит
(при фиксированной для конкретного процесса величине flr.) к
уменьшению qк. Иначе говоря, повышение qc позволяет нагре
вать СА (воздух) в калорифере до меньшей температуры. Сни
жение температуры СА на входе в сушильную камеру - суще
ственный технологический фактор, поскольку ряд материалов
(их называют термолабильными) не выдерживает высоюtх тем'

-

1 257

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ператур. К числу таких ТМ относятся многие полимерные ма
териалы, пищевые продукты, тем более лекарственные и дру
гие биологически активные препараты - они не допускают
контакта с горячим СА. Пусть для данного конкретного высу
шиваемого материала известна предельно допустимая температу
ра !пр (линия !пр обозначена на рис. 1 5 .27; на вертикали Хо =х
ей отвечает точка А). Тогда воздух в калорифере допустимо
нагревать только до этой температуры, и процесс нагрева в
диа грамме 1-х изображается отрезком О-А. Остальное количе
ство теплоты, соответствующее отрезку А-1', должно быть
подведено в сушильную камеру. Процесс сушки в ней изобра
зится отрезком А-2, так что ни в какой точке сушилки темпе
ратура СА не превысит предельного значения !пр· Таким обра
зом, распределение (перераспределение) общего количества
теплоты Qr.. между калорифером и сушильной камерой позволя
ет обеспечить необходимую технологическую обстановку в
процессе сушки .
В разд. 15.3.3 бьто показано, что в случае идеальной сушЮf
подводимая в калорифере теплота qк не может быть меньше
теплоты испарения влаги r. В сушилках с подводом теплоты в
сушильную камеру (qc) вполне возможно qк < r, поскольку при
увеличении qc величина qк понижается (в пределе до нуля ) .
Здесь необходимо говорить о безусловном неравенстве Qr.. > r,
поскольку qхид > r, а Qr.. = qкид + '"f.q > qкид·

15.4.

МНОГОЗОНАЛЬНАЯ СУШИЛКА

Выше показано, что в случае термолабильных материалов
температура СА может быть понижена до необходимой вели
чины !пр путем подвода части теплоты Qc (qc, qc /!) непосред
ственно в сушильную камеру. Технически это не составляет
затруднений для некоторых конструкций сушилок, например с
псевдоожиженным слоем или пневмотранспортных. Однако
для других сушилок (скажем, барабанных, отчасти - туннель
ных или ленточных) подача теплоты в сушильную камеру со
пряжена со значительными констр уктивными трудностями или
неудобствами . В этом случае распределенную подачу теплоты в
сушильную камеру (предпочтительно - равномерно
по дли 
н е ) можно заменить сосредоточенной е е подачей в отдельные
точки камеры. По существу это означает разделение сушиль
ной камеры на несколько зон; в эти зоны теплота не подается ,
но перед каждой зоной устанавливается калорифер , повышаю
щий температуру СА (разумеется, не выше заданного предела
!пр). В результате ни в какой из точек сушильной установки
температура СА не превышает предельную.
1258

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

3

1

калориферы, 2 - сушильные камеры, 3 � венrилятор;
/-сушильный аrеш, 1/ - высушиваемый маrериал

Рис. 1 5.28.

Принципи альная схема мноrозональной сушилки:

-

Принципиальная схе ма многозональной (иногда применяют
термин "многозонная") установки (на примере трехзональной)
с промежуrочным подогревом СА между зонами представлена на
рис . 1 5.28. Здесь принято противоточное движение сушильного
агента (его поток L последовательно проходит все зоны - от
первой до третьей) и высушиваемого материала (его поток G
движется от третьей зоны к первой). Относительные (в кг
АСВ/с и кг СМ/с) потоки L и G, естественно, постоянны и
одинаковы для всех зо н. На рисунке обозначены расчетные
точки и отвечающие им параметры СА, а также параметры ТМ
на входе в многозональную сушильную установку и выходе из
нее.
Для определения основных материальных потоков W и L
необходимо записать материальные балансы для единицы вре
мени (рассматриваются непрерывные процессы) и простран
ственного контура, охватывающего всю многозональную уста
новку (разумеется, по отдельности для зон ТМ и СА, как это
сделано в разд. 1 5 . 3 . 1
см. рис . 1 5 .22) . Совершенно очевидно ,
что запись материальных балансов для многозональной сушил
ки н ичем не отличается от рассмотренной ранее для простой
сушилки . Поэтому общее количество влаги W, удаляемой в
единицу времени , и расход сушильного агента L определяются
для многозональной сушилки по тем же формулам ( 1 5.5) и
( 1 5.6), что и для простой. При одинаковых производительности
G по высушиваемому ТМ и его влажностях U' и И" величина W
получается такой же, что и в простой сушилке. Аналогично: при
одинаковых входном и выходном влаrосодержаниях Хо и х2 расход
СА (воздуха) будет таким же, что и для простой сушилки.
Ниже рассмотрены построение процесса в диаграмме 1-х и
техноло гич еский расчет для многозональной :идеальной су
шильной установки и продемонстрирован подход к расчету
реальной сушилки.
1 259
-

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

15.4.1. Многозональная идеальная сушилка

Диаграмма 1-х для идеальной сушилки приведена на рис .
1 5 .29; обозначения точек и параметров процесса соответ�;твуют
указанным на принцип иальной схеме . Вместо одной стадии
нагрева и одной стадии сушки здесь нагрев СА в калорифере
предшествует каждой зоне сушки, причем температура .нагрева
ограничена
предельной
величиной
tпр .
обусловленной
свойствами конкретного высушиваемого материала. Эrа темпе
ратура, как видно из диаграммы, заметно ниже (t1) - темпера
туры, до которой пришлось бы нагревать СА, чтобы обеспечить
необходимый подвод теплоты при работе по схеме простой
сушилки . На диаграмме принято (выполнение этого условия не
обязательно), что на выходе из каждой зоны относительные
влажности СА одинаковы и равны 'Р2·
Рассматриваемый сушильный процесс включает по три че
редующиеся стадии нагрева и сушки . Стадии нагрева СА в ка
лорифере изображаются в диаграмме 1-х вертикальными (х =
= const) отрезками: 0-1' ; 2'- 1" и 2"-1'". Стадии идеальной
сушки идут по 1 = coпst, линии : 1'-2'; 1"-2" и 1"'-2 .
Количество теплоты в калорифере какой-либо зоны опреде
ляется из теплового баланса (контур - данный калорифер) для
сушильного агента (см . разд. 1 5 . 3 .2); получаемые расчетные
выражения построены по типу (15.8). Для единицы времени , в
расчете на 1 кг АСВ и на 1 кг уд. Вл, соответственно:

( 1 5 . 1 5)
Тогда для отдельных зон рассматриваемой трехзональной
сушильной установки , например в расчете на 1 кг удаляемой
влаги, имеем (см. рис. 1 5.28 и 15.29):

qк(l) =

1(1' - 1о);

qк(2)

= /(1'1 - 1');

qк(З) =

/(12 - 1"), ( 1 5 . 1 6)

rде верхние индексы - номера зон, перед которыми устаноалены калориферы.

Общий расход теплоты в калориферах сушильной установки:
= qк(l) +

qx(2) + qк(З) =
( 1 5 . 1 7)
1(1' - lo) + 1(1" - J') + /(12 - 1") = /( 12 - 1о).
Поскольку при идеальной сушке 12 = 11 , можно констатиро
qк

=

вать, что выражение (15.17) совпадает с ( 1 5.9), полученным
ранее для простой идеальной сушилки. К этому же выводу
можно прийти , рассматривая на рис . 1 5 .29 вертикальные отрез
ки, характеризующие нагрев СА в калориферах в расчете на 1
кг АСВ : (0-1') +·(2'-1") + (2"-1"') = 0-(1). Напомним, что
1 260

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Диаграмма /-х дня
идеальной многозональной су
шилки

Рис. 15.29.

/

отрезок 0-(1) отвечает,
как показано в разд.
1 5 . 3 . 3 , нагреву СА в ка 
лорифере простой иде
альной сушилки.
Из изложенного сле
дует, что переход от про

стой сушилки к многозо
нальной не отражается
на расходе теплоты в
расчете на 1 кг АСВ ил и
1 кг уд. Вл (имеется в

виду: при одних и тех же
и
входных
выходных
параметрах воздуха) . По
скольку для простой и
многозональной сушилок
"
'
сравниваются процессы с
х
х
одинаковыми значения
ми х2 и .хо, то, согласно
формуле ( 1 5.7), изменение варианта сушильного процесса не
отражается и на удельном (в расчете на 1 кг уд. Вл) расходе воз

духа /.

Удельные затраты теwюты на 1 кг влаги, удаляемой в сушильной установке,
для калорифера отдельной зоны определяются по формуле ( 1 5 . 1 5):

Qк(•)

=

1(1;

-

11-1)

Х2

1· - 1,
=

/

1

Хо
-

-

·

(б)

Представляет интерес выяснение физического смысла выражения, где в зна
менателе стояла бы разность в.лагосодержаний СА в данной зоне:
Х; -Х/-1

1; - 1,_,

=?

(в)

Здесь целесообразно сопоставить размерности числителя н знаменателя. Полная
запись единиц измерения числителя: (Дж в i- м калорифере)/<кг АСВ); знамена
теля: (кг уд.Вл в i-й зоне) (кг АСВ). Тогда отношение (в) получает (после со
кращения "кг АСВ") следующий смысл: затраты теплоты в i-м калорифере на
1 кг влаги, удаляемой в этой i-й зоне,. но не во всей сушильной установке - в
отличие от выражения (б) .

/

1 5.4.2. Мноrозовальная реальная сушилка

В основе расчета реальной сушилки лежит уравнение
( 1 5 . 1 1 ) , учитывающее потери теплоты '2:,q и оперирующее пара
метром сушки лq • . Применительно к многозональным сушил126 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

кам здесь есть одна особенность : они возникли как альтерна
сушилкам с распределенным подводом те ruюты в су
шильную камеру. Поэтому в многозональных сушилках Qc = О ,
так что всегда Лq. < О .
Рассмотрен ию, как и для простой сушилки, подлежат два
варианта: определены (при построении идеальной сушилки)
либо точки (состоян ия СА) на входе в зоны: 1' ; 1"; 1"', либо
точки на выходе из н их: 2'; 2"; 2. Далее будем рассматривать
один из этих вариантов; примем в качестве примера последний
из н их.
Общий путь построения реального процесса в диаграмме 1х такой же, как и в случае простой сушилки, только построе
ния надо проводить длн каждой из зон . Точный расчет здесь
осложняется отсутствием достоверных сведений о составляю
щих суммы теплопотерь r,<t>q по отдельным зонам. Если потери
в окружающую среду для i-й зоны q0(i) еще можно как-то оце
нить, то величины Qтр и Qм по зонам рассчитать трудно, по
скольку неизвестны промежуточные температуры транспорт
ньrх приспособлений и материала при переходе из зоны в зону.
Поэтому обычно используют приближенный подход, дающий,
тем не менее , хорошие результаты . Сущность подхода:
- определяют составляющие L,q для сушильной установки в
целом (входные и выходные параметры составляющих из
вестны), рассчитывают общие теплопотери L,q, значит, и пара
метр сушки лq. = -L,q;
- распределяют Лq. (по существу - теплопотери) по зонам
пропорционально удаляемой в них влаге;
- строят реальный процесс по зонам, находят все необхо
димые параметры СА и проводят технологический расчет.
При
реализации подхода необходимо найти параметры

тива

сушки для отдельньrх зон

лq!1>, Лqр> и Лqр>,

лq!1> + лq!2> + Лqр> лq.
=

<

о и

причем

л q !; > <

Согласно принятому подходу, в расчете на 1
влаги:

лq!1>

=

Лq.

i:;; ' лq!2>

=

Лq.

� ' лq!3>

где W1, W2, Wз - количества wiarn, удаляемой
зонах; естественно, W1 + W2 + Wз
W

в

единицу

=

О.

(r)

кг

удаляемой

Лq.

7;; '

вр ем ени в

(д)

отдельных

=

При известных в диаграмме 1-х точках на выходе из зон
(рассматривается именно этот вариант) определение отноше
ний W; /W не вызывает затруднений. В самом деле, имея в
виду, что х 1 =хо, соответственно (15.6) W= L(x2 - xo) , а для i-й
зоны
из материального баланса СА по влаге с очевидностью
1262

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

1

х

Рис. 1 5. 3 0.

получается:

'

х

"

Диаrрамма Z·-x для реальной мноrозональной сушилки

Wj

- Х;-1)/(х2 - Х()).

лq!1>

= L(xi - х1-1) . Следовательно, Wj /W = (х;
Отсюда конкретно дл я зон :

=

лq.

х' х
_:___о_; лq!2>
х2 -хо

_

Лqр>

=

=

-

х" -х'
лq. --х2 - хо

2- "

Х Х
Лq. --Х2 - Х о

(е)

Чтобы воспользоваться найденными значениями Лqу> для
построений в диаграмме. 1-х, надо представить затраты тепло
ты в калориферах п расчете на 1 кг �.бсолютно . сухого воздуха,
Лq.(1> (х1 - Х;-1):
т.е . перейти от Лq.(1> к величинам Лq �i) /1
=

Лq.(х' -х0); лq!2> / / = лq.(х" - х' ) ;
Лqр> / / лq.(х2 -х").
(ж)
Отрезки, соответствующие величинам Лqу>/1 (как и в про
стой сушилке, но » пределах отдельных зон), откладываются
вверх (так как Лq.( 1> /1 < О) от точек идеального процесса (1'),
( 1") и (1"')
(рис . 1 5 . 3 0) . В результате определяются точки
лq!1> / /

=

=

реального процесса 1', 1" и 1"'. Жирные линии 1'-2', 1"-2" и
1"'-2 изображают реал�.ный процесс сушки по зонам; эти ли
нии расположены выше соответствующих линий . \идеальной
(
сушки (тонкие линии 11 = const) , поскольку при Лq.''
< О спра
ведливо J1fi) > J/iJ. Иными словами, в отсуrствие подвода теп
лоты в зоны сушки (q/I) = О) компенсация теплопотерь по зо
нам ''i/iJq осуществляется за счет подвода большего количества
теплоты в калориферы : приходится нагревать в них СА
несколько выше, чем в случае идеального процесса.
1263

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

По рис . 15.30 в резул ьтате построения получается, что СА в
калориферах реально нагревается выше предельно допустимой
температуры !п р · Это надо предусмотреть в начале расчета,
приняв при построении идеального процесса ограничивающую
температуру Uп р Р) на нес колько гр адусов ниже !пр· Не ис кл юче
но, что в ходе технологического расчета придется пару раз по
вторить построения, добиваясь, чтобы на входе в любую из зон
температур а СА не превышала максимально допустимую tпр ·
Зам етим, 'ПО необходимости в этих итерацио нных операциях не возникает,
ее.ли отrалкиваются от идеального процесса при заданных точках (а точнее уровня температур) на входе СА в зоны. Однако тогда смещаются в сравнении с
идеальным процессом точки на выходе из зон, что сказывается на значении /,
следовательно и на величине отрезков
В результате и здесь расчет может
приобрести итерационный характер, но уже не по входным температурам, а по /.
Итерации здесь можно избежать, если сообразовать построения с mпотети 
ческой простой сушилкой, хар актеризуемой тем же значением Лq
Расходы теплоты в калориферах по зонам qк(i) и в целом по
установке qк
L.qк(t) рассчитываются на той же основе, что и в
случае простой реальной сушилки:
qк(l) = l(l' lo); qк<2> = 1(1" N);

лq�> /1.

•. .

=

-

-

( 1 5 . 1 8)
в отличие от выражений ( 1 5. 1 7) в качестве относительных эн 
тальпий 1', 1" и 1111 здесь берутся величины, характерные для
реального процесса сушки.

Практически может возникнуть проектная задача об определе
нии числа зон, необходимых для обеспечения процесса много
зональной сушки. При этом могут быть заданы входная и вы
ходная точки О и 2 и ограничивающие условия, например оди
наковые температуры воздуха t1 на входе в зоны и его относи
тельные влажности <р2 на выходе из них. Упомянутые точки и
ограничения показаны на рис . 15.3 1 . В целях упрощения опре
деление числа зон на рисунке иллюстрируется на примере иде
альной сушилки: попере.менно строятся стадии нагрева СА в
калориферах и сушки в сушильных
камерах. По рисунку получается, что в
заданных условиях необходимо более 4
зон ; с некоторым запасом принимаем
к проектированию сушильную уста
новку с 5 зонами .

��
0�=1

<

•
�������

1 264

Рис. 15.31. К

определению числа необходимых зон

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

15.5. СУШИЛКА С ЧАСТИЧНЫМ ВОЗВРАТОМ
ОТРАБОТАННОГО ВОЗДУХА

Процессы сушки протекают с большей скоростью при более
высокой движущей силе , иначе - при повышенных температу
рах и пониженных влажностях сушильного агента. Как прави
ло, технологи заинтересованы именно в увеличении интенсив
ности процесса, что позволяет nри эксплуатации повысить
производительность сушилки, а при ее проектировании на за
данную производительн ость - уменьшить необходимую по
верхность межфазного контакта, а значит, габариты и стои
мость установЮI. Однако на практике встречаются технологи
ческие ситуации, когда необходимо вести процесс сушки мед
лен.но, в более мягких условиях. Так, на поверхности некоторых
паст при быстрой их сушке образуется плотная корка, препят
ствующая удалению влаги из внутренних зон, - сушка резко
замедляется. В ходе быстрой суш Ю1 продукт нередко оказы
вается высушенным неравномерно : чрезмерно у поверхности
контакта с сушильным ;�гентом и недостаточно во внутренних
зонах. Отдельные гранулированные материалы при быстрой
сушке растрескиваются, иногда просто рассыпаются. А, ска
жем, при быстром обезвоживании древесины происходит раз
рыв волокон, и из такой древесины не изготовить высококаче
ственных изделий. Дерево для музыкальных инструментов,
например, сушат очень медленно - годами и даже десятиле
тиями.
В целях замедления сушки возможно понизить температуру
процесса - выше показано, что этого можно добиться увели
чением потока СА в простой сушилке, подачей части теплоты в
сушильную камеру либо переходом к многозональной сушилке .
Но есть и другой путь
увеличение влажности исходного су
шильного агента. Добавление к исходному СА некоторого коли
чества водяного пара нсэкономично, поскольку связано с до
полнительным расходом ценного теплоносителя - пара. Ис
пользуется иной путь: к потоку свежего СА добавляется часть
отработанного, покидающего сушилку с большей концентраци
ей влаги, нежели у свежего СА. В результате на вход в сушиль
ную камеру подается СА более влажный в сравнении со све
жим. Такой вариант процесса называется сушкой с частичным
возвратом (рекуперацией) отработанного воздуха. Поставленная
цель, таЮ1м образом, достигнута: как показано в разд . 1 0.7. 3 ,
рециркуляция в самом деле сопровождается понижением дви
жущей силы процесса.
Принципиальная схема сушил Ю1 с частичной рециркуляцией
представлена (в расчетном варианте) на рис . 1 5 . 32, где показа
ны основные потоЮI и обозначены параметры СА и ТМ.
-

1 265

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

'

\ (J+n)
' ...

кг
'

1

11 кг

Рис. 1 5.32. Принципиальная схема сушилки с частичной рециркуляцией сушиль
ного аrента:

1 - веИП1JIЯТор, 2- задвижхи, J - калорифер, 4 - сушильная камера;
1- сушЮJышй arem, 11- иысушиваемый материал

Движение сушильного аrента обеспечивается вентилятором 1, распределение
воздуха (выброс в атмосферу, 1юзврат на рециркуляцию, ввод свежего) реrулиру
ется системой задвижек 2. Поскольку установка работает в непрерывном ре.жи
ме, то поток свежего воздуха (конечно, в расчете на абсолютно сухой), подводи
мого в установку извне (состояние О), должен быть равен потоку, выбрасы
ваемому в атмосферу (состояние 2) . Возвращаемый на рециркуляцию воздух
(то.же состояние 2) носит название обра111оrо. Пос.ле его присоединения к потоку
свежего воздуха получается смес• (состояние С, параметры отмечены индексом
"с"). Эта смесь наrревается в калорифере З (до состояния 1) и направляется в
сушильную камеру 4; пос.ле контакrа с твердым материалом смесь покидает ее в
состоянии 2.

Количество обратного воздуха, приходящегося на 1 кг све
жего (выбрасываемого) обозначается символом п и называется
степенью рециркуляции (на практике чаще всего п < 1 кг/кг).
Таким образом, при потоке свежего воздуха L (или на 1 кг уда
ляемой влаги - [) поток обратного воздуха составляет Ln кг
АСВ/с (или ln кг АСВ/кг уд. Вл). ОчевИдно, в калорифере и
сушильной камере движется циркулирующий СА, т.е. смесь
свежего и обратного воздуха - поток (кг АСВ/с):
(а)
Lц L + Ln = L( l + п),
а на 1 кг удаляемой влаги:
=

lц

==

l + l·n = /( 1 + п) .

Анализ процесса удобно вести на базе 1
1 266

(б)

кг свежего

(или, что

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

то же самое, выбрасываемого) сушильного агента, п кг - об
ратного и (1 + п) кг
u иркулирующего.
Количество удаляемо й в единицу времени влаги получается
из материального баланса по влаге для высушиваемого мате
риала (контур ТМ, проведенный по поверхности F контакта
ТМ и СА) . Легко видет1., что этот баланс ничем не отличается
от рассмотренного в разд. 1 5 .3 . 1 . Поэтому и расчетная формула
для W повторяет выражение ( 1 5.5).
Потоки воздуха L, l и Lц, lц найдем из материальнь1х балан
сов по влаге для сушилъного агента. Рассмотрим сначала кон 
тур СА1, охватывающий зону сушильного агента для всей уста
новки. Потоки влаги, пересекающие границы этого контура,
те же, что были в случае простой сушильной установки (разд .
1 5. 3 . 1 ) . Поэтому и формулы для расчета потока свежего (и рав
ного ему - выбрасываемого в атмосферу) воздуха совпадают с
( 1 5 .6) для L и с ( 1 5 .7) для /. Чтобы отыскать поток uиркули
рующего воздуха, возможно взять контур СА2 (штрих-пунктир
на рис . 1 5 .32), исключив узел смешения свежего и отработан 
ного воздуха. Баланс по влаге в зоне СА для контура СА2 за
пишется так:
-

Lцхс + W -· Lцх2 = О и Lц =

w

( 1 5 . 1 9)
Х2 - Хе
Эту формулу можно было записать сразу - по аналогии с
( 1 5.6). Действительно, фрагмент сушильной установки, охва
ченный контуром САъ есть "простая сушилка" с входным
влагосодержанием Хе (выесто Хо в обычной простой сушилке) и
ВЫХОДНЫМ Х2.

Соответственно, удельный (на 1
циркулирующего СА составит:

Lц

=

кг удаляемой

влаги) расход

1

( 1 5 .20)
Х2 -Х е
Согласно схеме рециркуляционной сушильной установки на
рис. 1 5 .32, процесс, наряду с рассматриваемыми ранее стадия
ми нагрева СА в калорифере и сушки в сушильной камере ,
включает еще одну стад ию ( в рассмотренных выше схемах она
отсутствовала) - смешения свежего и отработанного воздуха.
lц

=

w

15.5.1. Смешение свежего и отработанного воздуха

Задача заключается R определении точки смеси С при из
вестных потоках (точнее - их соотношения) и параметрах
смешиваемых потоков
в состояниях О и 2. Анализ ведется по
общей канве , изложенной в разд. 1 0 .2.4: точка смеси опреде
ляется по правилу рычага, в рассматриваемом случае - не в
-·

1 267

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

концентрационной диаграмме, а в диаграмме "состав (х) свойство (J) " .
Точку смеси будем искать для 1 кг свежего и п кг обратного
воздуха (в расчете на абсолютно сухой) . Составим материаль
ный (по влаге) и тешювой балансы для контура, охваты
вающего вентилятор (штриховой контур на рис . 1 5 .32):
l·XQ
1 . /о

+

+

nx2 - (1

+

n)Xc =

О

и

+ п) Ic = О и

n/2 - ( 1

l ·х о

+ пх2
1+п
1 · 10 + п/2
1+п

Хе =
lc

_
_

(в)
(r)

Точка с параметрами Uc, Хе) представляет собой точку смеси
С. Из выражений (в) и (r) видно, что ее положение зависит от
степени рециркуляции п; таким образом, в общем плане речь
идет не о точке смеси, а о геометрическом месте точек смеси
(т.е. о линии смешения ) в зависимости от соотношения п пото
ков обратного и свежего воздуха.
Практически точку смеси в ходе технологического расчета удобно определять
с использованием диаrраммы 1-х. Пусть (рис. 15.33) заданы точки О (свежий
воздух) и 2 (отработанный во:щух). Требуется найти mtнию их смешения и на
ней зафиксировать точку смесн при известных количествах свежего и отработан
ного воздуха - 1 кг и п кг соответственно.
Чтобы найти линию смешения /с = lc(Xc), используем левые выражения ба
лансов ( в) и (r):
1 +п

=

хо+ nx2

1

'

Хе

+

п

=

/о+ п/2
Ie

1_
l+n

и

_

=

Ie
Io +п/2

Хе

Хо +пх2

(д)

Из (д) следует линейность связи /с и Хе, т.е. точка С лежит на некоторой
прямой в диаrрамме 1-х, причем ее положение при заданных точках О (/о, хо) и
2 (/2, х 2) зависит от величины п. При п = О (отсутствие в смеси обратного возду
ха), согласно (в) и (r), Хе Хо и /с = /о, т.е. точка С совпадает с точкой О свежего
воздуха. А при п ..,.. оо (в смеси отсутствует свежий воздух) получается Хе = х 2 и
/с = /2 (для этого числите.ли и знаменатели правой части равенств надо предва
рительно поделить на п); значит,в этом случае точка С совмещается с точкой 2
=

отработанного воздуха. Таким образом, линия смешения есть прямая, соеди
няющая точки свежего и отработанного воздуха: точка С лежит на отрезке 0-2.
Для последующего анализа полезно выразить степень рециркуляции через
концентрации и относительные энтальпии. Раскроем скобки в левых выражени
ях (в) и (r) и найдем п:
Хе - Хо и
(е)
Ie - Io.
п
п
=

х2-Хе

=

12-Ic

Отсюда леrко получаются также характерные удельные потоки (1 + п):

1

+

п

=

1+

х,,

-�

х0
х2 - х0
---- --

х2-хе

=

х2-Хс

и

1 +п

12- 10 .
1 2-Ie

= ---

(ж)

Построение точки смеси демонстрируется на рис. 15.33,а. Для обоснования
положения точки С (она нахоцится на прямой 0-2) .пl)Qведем_ горизонтальные
линии, построив подобные треугольники на отрезках (0 -С) и (с=2 )как на rи-

1 268

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

с
о11 Тд-7.
'о

-

с

о
Хо

а

2

б

1с ',

Рис. 15.33. К

111

Х2

х
с

а

1-х, б,

-

1

1+11

х

в
1

11

расчеtу точюf смеси при частичной рециркуляции воздуха:

диаrрамма

в

рычаrи

и

рода

потенузах. Отношение горизонтальных катетов этих треугольников, согласно (е) ,
равно п, а поскольку треугольн ики подобны, то
_с
__ =

х

хо

�-�

71

= 0- С
С-2

=

, или

п

-(С
- 2)= 1 (0 - С)

(з)

-

·

·

- точка С определяется по правилу рычага (в данном случ�iе - 1 рода), "точка
опоры" находится в точке С.
Рассмgтnение д ных треугольников, построенных как на гипотенузах на
(ж) аналоотрезках (0 - 2) и - , и одновременное использование выражений
гичным образом приводит к правилу рычага 11 рода:

с1

Х2 - Хо = 1
Х2 - Хе

+

п= О -l
С-1

, ИЛИ
·

(1 + n) (С - 2)1= 1 (0- 2),
·

(и)

·

"точка опоры" здесь расположена в точке 2.
Иллюстрация правила рычага 1 и 11 рода приведена на рис. 1 5 . 33,б,в. Заме
тим, что в практических расчетах чаще более удобным оказывается правило
рычага 11 рода. Разумеется, правило рычага для смешения свежего и отработан
ного воздуха может бьпъ представлено и в обобщенной форме (см. разд. 1 0 .2.4).

15.5.2. Идеальная сушилка с частичной рециркуляцией

За стадией смешения свежего и отработанного воздуха сле
дуют стадии нагрева смеси в калорифере и сушки в сушильной
камере. Для идеальной сушилки все три стадии построены в
диаграмме 1-х на рис. 1 5.34 (для наглядности направления
процесса на отдельных стадиях показаны стрелками) . Здесь
о---.

2 / С;
идеальной сушки (по ликии 11

стадия смешения

стадия нагрева

=

12

=

СА: С

const): 1

--+

2.

--+

1; стадия

1 269

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

1
11 ,�

Рис. 15. 34. Диаrрамма 1-х Д11Я идеальн ой
сушилки с частичн о й
рециркуляцией
воздуха

�(!)
.,

На диаграмме в целях сопо
ставлен ия
штрих-пун ктирной
1
1
линией намечен процесс в про
стой идеальной сушилке. Можно
видеть, что при сушке с частич
ным возвратом отработанного
воздуха исходный СА поступает в
2
сушильную камеру с более высо
ко й влажностью, нежели в про
стой сушилке : Хе > Хо· Одновре
менно происходит и снижение
температуры СА на входе в зону
сушки : t1 < t( I ) , так что и темпе
ратурный режим здесь мягче (это
важно для сушки термолабильн ых материалов) . Заметим , что понижение температуры на
входе в сушильные камеры может быть обеспечено и в ранее
рассмотренных схемах (в простой сушилке - путем увеличения
потока СА; в многозональной - делением на зоны с промежу
точным подогревом СА) ; а вот повышение исходной влажности
СА - особен ность именно сушки с рециркуляцией .
При практической постановке задач технологического рас
чета чаще всего задается (наряду с точками О ; 1 или 2) не сте
пень рециркуляции п (как раз для этого случая выше рассмот
рен путь построения диаграммы 1-х) , а влажность (хе) или
температура (!1 ) воздуха на входе в сушильную камеру. П о 
строение процесса в диаграмме 1-х и определение необходи
мой величины п в этих случаях затруднений не вызывает.
В н ачале разд . 1 5 . 5 приведены выражения (а), (б) , а также
( 1 5 . 19) и ( 1 5 . 20) для определения потоков циркулирующего
воздуха (для калорифера и сушильной камеры они одинаковы
и постоян ны) - в единицу времени Lц и на 1 кг удаляемой
влаги lц . Ис пользуя соотношения (ж) и (и) , нетрудно показать,
что эти выражения идентичн ы . Например , для lц :
1
1
Х2 Х о
(к)
lц
1( 1 + п)
.

Х2 - Х о Х2 - Хе
-

=

=

Эффективность идеального процесса сушки определяется
удельными затратами теплоты в калорифере qк . П олный расход
теплоты есть произведение ее затрат в расчете на 1 кг циркули
рующего сухого воздуха Л1к = 11 - 1с и потока этого воздуха Lц

( 1 5 .2 1 )

1 270

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Удельный (на
рифере:

1 кг удаляемой

влаги) расход теплоты в кало

( 15.22)
Сравнение этого расхода теплоты с характерным для про
стой идеальной сушилки удобно проводить с помощью диа
граммы 1-х. Будем сравнивать подобные тр�ьники 2- 1-С
и 2-(1)-0 на рис . 15.34, причем отрезок С - 1 соответствует
затратам теплоты на 1 кг АСВ (11 - 1с) в калорифере сушилки с
рециркуляцией, а o=(i) - в калорифере простой сушилки.
Из подобных треугольников с учетом соотношений (и) имеем:
1( 1) - 1 0
1 1 - 1с

---

= 0

-

(1)

С-1

= 0-

2
С-2

--

=

Х 2 - Хо
Х2 - Хе

=1+п.

Теперь, преобразуя выражение (15.22), находим :
qк = lц (11 - lc ) = /(1 + п)( J1 - lc) = /(!(! ) - lo) ,

что

(л)

(м)

с выражением ( 1 5.9) для простой иде
(в отсуrствие qc и L,q) .
Из изложенного следует, что при переходе от простой су
шилки к рециркуляцион ной (как и ранее - к многозональной)
удельные расходы свежего сушильного агента и теплоты в рас
чете на 1 кг удаляемой влаги не изменяются. В рассмотренных
конкретных примерах проявляется общее правило: при одинако
вых входных (точка О) и выходных (точка 2) параметрах сушиль
ного агента удельные расходы свежего воздуха (/) и теплоты (q,J
не зависят от варианта сушильного процесса Между тем из
диаграммы 1-х ясно видно, что в случае сушки с частичным
возвратом отработанного воздуха в калорифере на подогрев
одного его килограмма теплоты затрачивается меньше, чем в
простой сушилке: С - 1 < 0-(1) ; из сравнения подобных тре
угольников ясно даже, во сколько раз меньше: в ( 1 + п) раз .
Но количество циркулирующего воздуха на 1 кг удаляемой
влаги в сушилке с рециркуляцией ровно во столько же раз
бол ь ше : lц = ( 1 + п)/. Поэтому произведения l(lт - 10) и lц(11 - lc), выражающие qк (на 1 кг уд . Вл), в обо их случаях одинако вы.
полностью

альной сушилки

совпадает

.

15.5.3. Реальная сушилка с частичной рециркуляцией

В реальной сушилке процесс в сушильной камере идет с из
меняющейся относительной энтальпией 1 = var. Для сушилки с
рециркуляцией такой процесс может трактоваться по аналогии
с простой сушилкой, если оперировать (см. рис. 1 5.32) штрих
пунктирным контуром СА2 . При этом, в отличие от простой

127 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Puc. 1 5. 3 5. Диаrрамма 1-х для реальной
сушилки с частичной рециркуляцией
воздуха

l

сушилки, потоки СА составят
не L и l (полный и удельный) ,
а Lц и lц; в остальном пути
анализа и расчета совпадают.
Для сушки с частичной ре
циркуляцией, как и для про
стой, мoryr быть проанализи 
рованы два варианта: не зада
:z
на точка 2 (определено со
1
: q>
стояние воздуха в точке 1 на
входе в сушильную камеру); не
задана точка 1 (определено
состояние воздуха на выходе
Хе
х
из сушильной камеры, т.е . в
х
1
точке 2) . В пределах каждого
из этих вариантов следует рас
смотреть два случая: Лq• > О и Лq • < О . Подходы к анализу и
расчету этих вариантов и случаев подробно рассмотрены для
простой сушилки (разд . 15. 3 . 3 ) , поэтому здесь выберем один из
вариантов (пусть задана точка 2) и чаще встречающийся случай
Лq. < О (рис. 1 5 .35): процесс сушки в сушильной камере идет с
понижением 1, так что 12 < 11 .
Как и для простой сушилки, при Лq• < О компенсация тепло
потерь производится за счет дополнительного подогрева возду
ха в калорифере; поэтому точка 1 реального процесса после
калорифера на диаграмме 1-х будет расположена выше точки
1 ' идеального процесса. Отрезок 1' 1 соответствует величине
Лq./lц . Таким образом, стадия нагрева СА в калорифере изоб
ражается линией С 1 , процесс реальной сушки в сушильной
камере
.линией: 1 2 .
=

1

-

-

-

-

В целях сопоставления на рис. 1 5 .35 шrрих- пунктиром показаны идеальный
и реальный процессы для простой сушилки . Нетрудно видеть (из подобных
треугольников), что отрезок ( J ' ) -(1) в (1 + 11) раз больше отрезка 1 - 1 ' ; следо-

вательно ,

отрезок

( 1 ' ) - (1 )

(лq•/lц) (1 + 11) лq./1 , как

и

равен

(в

масштабе)

величине

в случае простой сушилки. Таким образом, при

построении реального процесса для сушилки с частичным возвратом отработан 
ного воздуха можно действовать по-разному:
- добавить к теплосодержанию 12 = 1'1 величину
или, что то же са
мое, отложить на вертикали С-1' от точки 1' вверх отрезок, отвечающий
Линия реальной сушки изобразится отрезком 1 -2;
или, что то же
- добавить к теплосодержа нию 1'( 1 ) = /'
12 величину
самое, отложить на вертикали 0-( 1 ') от точки ( 1 ' ) вверх отрезок, соответствую=

Лq* /lц.

1272

лq./lц

=

лq./1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

/1.

Л иния реальной сушки здесь на прямой ( 1 )-2: тот же отрезок
щий лq.
1-2.
В rmaнe понимания метода расчета проще первый путь; в аспекте точности
построений - второй, поскольку больший отрезок ( 1' ) - (1 ) можно отложить

точнее, чем меньший 1 ' - 1 .

Оценивая процесс с частичной рециркуляцией СА, необхо
димо иметь в виду, что при равенстве (в сравнении с другими
вариантами сушки) затрат свежего воздуха и теплоты здесь
будуг выше затраты энергии на дугье, поскольку общий расход
СА увеличивается в ( 1 + п) раз.
15.6. О НЕКОТОРЫХ ДРУГИХ ВАРИАНТАХ
СУШИЛЬНОГО ПРОЦЕССА

На практике процессы конвективной сушки осуществляются
не только в трех рассмотренных основных вариантах, их множество; еще больше разновидностей можно представить
умозрительно. Каждому варианту сушильноI'О процесса отве
чают свои построения в диаграмме 1-х. Ниже в качестве при
мера рассмотрены две схемы сушильных установок и соответ
ствующие им диаграммы - рис . 1 5 .36 (вентиляторы на схемах
не показаны). Построения выполнены применительно к иде
альным процессам; стрелками условно показаны направления
процесса по стадиям (потоков СА) .
На рис . 1 5. 3 6 , а показана схема с частичной рециркуляцией
отработанного воздуха, где вместо подогрева смеси в калори
фере наrревается отработанный воздух. В диаграмме 1-х эта

стадия изображается линией 2 1 Обратный воздух, нагретый
до высокой температуры t1 , смешивается с холодным свежим
воздухом (точка О); стадии смешен ия отвечает линия О 1 с
получением точки С. Смесь (т. С) направляется в сушильную
камеру: стадия сушки С 2 . Степею. рециркуляции в данном
случае представляет собой отношение отрезков: п
= (О С) / (С - 1) . Типичная постан овка задачи для рассматри
ваемой схемы: при известных состояниях потоков воздуха -

.

-

-

-

свежего (точка О) и отработанного (точка 2) - и заданной сте
пени рециркуляции п надо определить температуру t1, до кото
рой следует нагревать воздух в калорифере. Пугь решения :
- по выражению (в) в разд. 1 5.5. 1 определяем координату х.с;
из точки 2 проводим (идеальная сушка!) линию
12 = lc = const до пересечения с вертикалью хе; определяется
точка С ;
1 273

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

1

б

сушилка с подоrревом обратноrо воздуха, б
сушильного areкra
Рис. 15. 36.
а

-

Некоторые схемы сушильных установок и диаграммы 1-х:
-

сушилка с полной рециркуляцией

- из точки О через точку С проводим прямую (линия сме
шения) до пересечения с вертикалью х2 = х 1 ; определяется
точка 1 и соответствующая ей температура t1 •
На рис . 1 5 .36,б представлена схема с полной рециркуляцией
СА Такая ситуация встречается в химической технолоmи , ког
да высушиваемый материал не допускает соприкосновения с
кислородом воздуха и в качестве сушильного агента должен
использоваться газ, химически инертный к ТМ (азот, диоксид
углерода и т.п.). В этом случае экономически нецелесообразно
выбрасывать в атмосферу дорого стоящий СА, поэтому органи
зуется замкнуты й цикл с полным возвратом отработанного СА
Однако в рассмотренных ранее схемах выделившаяся из высу
шиваемого материала влага выводилась из системы с отработан
ным сушильным агентом, выбрасываемым в атмосферу. При
полной рециркуляции влага будет с течением времени накапли
ваться в цик.ле, станет расти влагосодержание СА, оно до
стигнет равновесного значения , и процесс сушки прекратится .
Чтобы этого не произошло, удаляемую влагу нужно непрерывно
выводить из системы. С этой целью отработанный сушильный
агент (точка 2) направля ют в холодильник-конденсатор. Там он
сначала охлаждается до насыщения (до точки росы - состоя
ние 3), а затем происходит конденсация влаm: сушильный
агент (инерт) сохраняет насыщенное состояние ер = 1 , процесс
идет с понижением тем пературы и влагосодержания по линии
3 -4. Выделяющаяся в 11иде конденсата влага W выводится из
цикла в брызгоулавливающем устройстве (на схеме показ ано
кружком) . Насыщенный влагой инерт (СА) в состоянии 4 (с

1 274

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

низким влагосодержанисм) подается в калорифер, где нагрева
ется до состояния 1 и н аправляется в сушильную камеру: про
цесс сушки 1 -2.
Заметим : при замене воздуха на азот можно без существен 
ной погрешности пользоваться диаграммой 1-х для воздуха
(поскольку в нем ""' 7 3 % азота, а теплофизические свойства
кислорода мало отличаются от таковых для азота) . При исполь
зовании других инертов необходимо специально построить
диаграмму 1-х для соответствующего ГdЗа.
Некоторые другие схемы и отвечающие им построения в
*
диаграмме 1-х приводятся в учебной и научной литературе .
15.7. СУШКА ТОПОЧНЫМИ ГАЗАМИ
15.7 . 1 . Общие положения

В качестве источника теплоты в калориферах чаще всего
используется водяной пар под давлением примерно до 1 , 6-2,0
МПа, температурный уровень - примерно д о 200 ° (пар более
высокого давления доро г) . В этом случае нагретый СА, направ
ляемый в сушильную камеру, получается в результате ряда по
следовательных операций: сжигание топлива с образованием
топочных газов; теплообмен в котельной установке с получе
нием водяного пара высокого давления; передача теплоты от
конденсирующегося пара к сушильному агенту в калорифере . В
случае электрического обогрева добавляется еще одна стадия:
подача водяного пара в турбину с выработкой электроэнергии
и подогрев СА в электрокалорифере. На каждой из упомянутых
операций происходят потери теплоты и снижение потенциала
теплоносителя . Температура СА на выходе из парового кало
рифера как правило не превышает 1 50- 1 8 0 ° С; в случае элек
трообогрева она может быть выше, но электрическая энергия
дороже паровой. Между тем технологически выгоднее пользо
ваться сушильным агентом высокой температуры: больше ко
личество теплоты, которое несет и может отдать каждый кило
грамм СА, и выше его влагоемкость, быстрее идут процессы
удаления влаги (как диффузия ее внугри материала, так и испаре
ние с поверхности). По этим причинам выгодно, отказавшись от
калорифера, исполъзоваn. в качестве сушильного агента непосред
ственно топочные газы - либо отбросные (после их квалифици
рованного использования в котельных установках или других тех
нолоrичесЮfХ аппаратах), либо от топок, специально предназна
ченных для обслуживания сушильных установок.

С

• Многозональная сушка с рециркуляцией СА между зонами рассмотрена
( 1 ) , аналогичная схема с более сложным циркуляционным контуром - в (6 ) .

н

1275

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Vlll
Рис. 1 5. 3 7. Сушильная установка с использованием топочных газов в качестве
сушильного аrента:

1 - топха, 2 - камера смешеI01я, З - сушильная камера, 4 - веНJИJJятор;
1 - топливо, II - первичный воздух, III - топочные rазы, JV - вторичный воздух, V смесь rазов (сушильный areнr), VI - отработанный rаз, VII - исходный влаJJСИЫй материал,
Vlll - высушеННЬIЙ материал

Применение топочных газов в качестве сушильного агента
имеет ряд 1 оrраничений.. Основное из них - температурные
пределы: топочные газы моrут быть использованы только для
сушки материалов, усто йчивых к высоким температурам. Сле
дует иметь в виду и термическую устойчивость конструкцион
н ых материалов сушильной камеры (даже защищенной футе
ровкой от непосредственного контакта с топочными газами) .
Другое ограничение св.нзано с последующим использованием
высушенного материала. Дело в том, что топочные газы моrут
быть загрязнены образующимися в топке частицами сажи или
запылены (частицы золы или несrоревwего топлива) . При вы
сушивании пищевых продуктов (например, столовой соли), тем
более лекарственных препаратов (даже если они термически
стабильны), это, естественно, недопустимо.
Принципиальная схема сушки топочными газами с индиви
дуальным топочным агр е гатом представлена на рис . 1 5 .37.

В топку 1 подается топливо (поток [) в количестве Fт в единицу времени и
поток ll первичною воwха L1 на сжигание топлива (здесь и далее все потоки L;
- в расчете на абсолюnю сухой воздух). В результате образуются топочные газы
(lll) с высокой температурой fт. (Эта температура должна обеспечить полное
сгорание топлива; для твердого топлива она обычно не ниже 1100-1200 ° С, для
жидкого - не менее 1 000 ° С, JUIЯ газообразного обычно не ниже 900 ° С.) Далее
топочные газы подаются в камеру смешения 2, где смешиваются с потоком /V
холодного аторичноrо воwха L 2 - в результате получается смесь ( JI), т.е. су
шильный агент требуемой температуры t1 . Он поступает в сушильную камеру J,
куда подается поток VJJ алажн ого материала G (в расчете на абсолютно сухой);
из камеры выходят потоки отработанного сушильного аrента ( Vl) и высушенного
материала ( Vlll) . Движение газов через систему обеспечивается вентилятором 4.

Важно: нельзя подать в топ ку весь воздух L1 + �' чтобы без
всякой камеры смешения сразу получить на выходе из топки
газы с температурой 11 , поскольку значение 11 - ниже темпера1 276

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

туры, необходимой для полного сгорания топлива (tr) . Именно
поэтому в топку подается лишь холодный первичный воздух
L1, тогда там поддержи вается достаточно высокая температура
tr- А затем в камере смешения эти горячие газы разбавляются
холодным вторичным воздухом L2; таким образом обеспечи
вается приемлемая температура СА на входе в сушильную ка
меру.
С целью интенсификации сушки высушиваемый материал
направляют противотоком к сушильному аrенту: выше движу
щая сила процесса, лучше используется влагоемкость газа. Ес
ли при этом из ТМ удаляется свободная влага (см. разд. 1 5.2.5),
то температура материала не может подняться выше темпера
туры кипения (при удалении воды - выше 1 00 ° С) , так что
материал по сушеству защищен от воздействия высоЮfХ темпе
ратур . Однако если на конечных стадиях сушки удаляется
связанная влага, то высушиваемый материал, контактируя с
высокотемпературным сушильным агентом на входе его в су
шилку, может нагреться и выше 1 00 ° С. Это не всегда допусти
мо: мoryr ухудшиться товарные качества ТМ (вплоть до час
тичного его разложения ) . В этом случае следует организовать
прямоточное движение высушиваемого материала и смеси га
зов - этот вариант и показан на рис . 1 5 .37. Тогда с высоко
температурным СА контактирует материал, содержащий сво
бодную влагу> - он сушественно перегреться не может. А мате
риал с оставшейся в нем связанной влагой находится в контак
те с газами, температура которых заметно понизилась в ходе
сушки, так что порчи материала не произойдет.
В реальной сушильной установке топка, камера смешения и
сушильная камера непосредственно примыкают друг к другу это снижает гидравлическое сопротивление газовому потоку и
потери теплоты в окружающую среду. На схеме элементы уста
новки отделены один от другого с целью фиксации температур
и физических свойств газов на границах этих элементов
(аппаратов) - это нужно для анализа процесса.
Диаграмма 1-х для сушки топочными газами представлена
на рис. 1 5 . 3 8 . В отличие от рассмотренных ранее сушильных
установок, повышение температуры СА в топке (стадия О � 1)
не идет по линии х = coпst; здесь х 1 > .хо . Дело в том, что в
состав топлива входит водород, при его сгорании образуются
пары воды, и в сравнен ии с исходным воздухом (точка О) вла
госодержание топочных газов (точка Т) возрастает. Далее в
камере смешения эти газы смешиваются со свежим вторичным
воздухом (точка О); стадия смешения:

т --.....
/ 1.
о

в сушильной камере происходит процесс сушки 1

Наконец,
�

2

- по
1 277

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

1

Диаграмма 1-х процесса сушки то 
почными газами

Рис. 15. 38.

линии 1 = const, если это была бы
идеальная сушка; с изменяющимся
(почти всегда - понижающимся) 1 в
реальной технологической ситуации.
В задачу технологического расчета
входит определение (при заданной
производительности
высуши
по
2
ваемому материалу G и его исходной
1
<р
U' и конечной U" влажностям) расхо
да топлива Рт, потоков первичного L1
и вторичного L}. воздуха, а также
установление
входных, промежуточ
х
ных и выходных параметров процесса
(в частности, температур) и свойств
рабочих тел (воздуха, топочных газов, высушиваемого материала).
Технологический расчет может быть выполнен с использо
ванием диаграммы 1-х для воздуха (разумеется, вычерченной
для области высок их температур), поскольку теплофизические
свойства топочных газов мало отличаются от свойств воздуха: в
обоих случаях основной компонент - азот (его концентрация
близка к 75%), а для остальных компонентов эти свойства
близки к характерным для азота. Однако в случае сушки то
почными газами возможен и аналитический расчет, в ходе ко
торого определяются искомые потоки и технологические пара
метры работы установки . Заметим : топочные газы мoiyr иметь
разный состав (в зависимости от состава топлива и расходов
воздуха) ; на некоторых этапах расчета возможное различие в
составе газов игнорируют, что предопределяет приближенность
расчета. Вносимая при этом погрешность п о указанным выше
причинам (преобладание в газах азота) - невелика.
=

1 5 . 7.2. Приближенный аналитический расчет

Наметим предварительно общую схему расчета. Определить
сразу потоки первичного L 1 и вторичного L}. воздуха не пред
ставляется возможным, так как они зависят от расхода топлива
Рт, а он устанавливается только в результате полного расчета
сушильной установки . Поэтому сначала определяют удел ь 
ные - на 1 кг топлива - потоки первичноrо Z1 .и вторичноrо
� воздуха (в кг АС В на кг топл.), а затем после нахождения
Рт, их полные потоки 1,1 и L}. (в кг АСВ ). Расчет ведется с
помощью материальных и телловых балансов аппаратов, вхо
дящих в сушильную установку. Этапы расчета охарактеризовц
ны в табл . 1 5 . 1 .

/с

1 278

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Таблица

1 5. 1. Этапw

2

Этап

Удельный
расход первичноrо воз
духа на 1 кг

Удельный
расход 1rrо
ричноrо
воздуха на
1 кг то плива

к г АС В
кг топл .

к г АС В
к г тоrи.

Показа
тель

Определяемая
величи
на

Удельное
теоретичес
кое количество воздуха
на СЖИГdНИе
1 кг топлива
кг ле в

Метод
рас'Iета

Z1 ,

TOIVIИBa

Zrooo ,

кг

расчета сушки топочными

тоrи.

СтехиометТеrиовой
рия реакций баланс
сгорания
топки

Z2,

Тепло вой
баланс.:
камеры
смешеню1

rазамн

4

1 Расход

5

1

топ- Полные по
лива в еди- токи
пер
ницу време- вичноrо
и
вторичноrо
ни F1,
воздуха L 1 ,
кг тоrи.
с

L1 ,

кг АС В
с

Тепловой
баланс
сушильной
камеры

Связь
удельн ых
и полных
потоков

Отличительная особенность рассматриваемого ниже анали
тического расчета состоит в использовании абсолютных эн
тальпий i газов вместо относительных /, принятых в
предыдущих разделах главы. Иными словами, тепловые потоки
будуг выражены произведениями абсолютных массовых пото
ков (не кг АС В/с, а кг нл. Г/с) на э нтальпию газа c/ti, где cr теплоемкость газа при температуре ti. Эта теплоемкость приво
дится в справочной литературе• ; она мало зависит от состава
топочных газов и близка к теплоемкости воздуха, поскольку в
составе этих газов и воздуха превалирует азот. Однако она за
метно изменяется с температурой (напомним, что в
предыдущих разделах влияние температуры на теплоемкость
воздуха принималось несущественным), так как здесь речь идет
об изменениях температуры в очень широких диапазонах
(сотни градусов) .
Н иже представлен расчет по этапам - соответственно
табл. 1 5. 1 .
1 . Определение удельного теоретического количества воздуха
на сжиrание 1 кr топлива. В состав топлива входят различные
химические элементы и компоненты; они перечислены ниже
(перечень, разумеется, можно дополнить) . При этом под хими
ческими и другими символами понимается не только каче
ственное
указание
на
присуrствие данного
элемента
(компонента) в топливе, но и его содержание в расчете на 1 кг
топлива. Например, символ С обозначает содержание углерода
в топливе в кг С/кг топл. Тогда сумма всех элементов и компо• См" нап ри м ер
,

( 1 1 ).

1 279

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

(кг топл . ) :
+S+N+О+

нентов топлива равна 1

С+

Н

.

+

АРб

+

rо Рб =

1,

( 1 5.22)

где АРб - содержа н ие золы в тоШiиве (оно равно нулю, если тоШiиво - rаз ,
н евелико - если жидкость, и может бьrrь значительным в случае твердого топ
лива), rорб - влажность тоШiива; индекс "рб" означает " в расчете на 1 кг рабоче
ю топлива", т .е. включающего золу и влагу.
"

Реакция сгорания углерода: С + 02 = СО2 ; на 12 кг С тре
буется 32 кг Оъ значит, удельный расход кислорода на 1 кг
углерода составляет 32/1 2 = 2,67 кг О/кг С. При концентрации
углерода в топливе С (кг С/кг топл.) получим расход кислорода

на сжигание всего углерода в 1 кг топлива:
кг о
кг с

2 , 67 - С -

кг с
к.г топл.

= 2, 67С

кг О/кг топл .

(а)

Подобный расчет для водорода : 4 Н + 02 = 2 Н 2 0 ; на 4 кг Н
требуется 32 кг 02, значит, удельный расход кислорода на 1 кг
водорода равен 3i/4 = 8 кг О/кг Н . Тогда расход кислорода на

сжигание всего водорода 1 кг топлива составляет:
кг о
кг н
= 8 - Н кг О/кг топл.
8·Н
кг н кг топл .
fl

--·

(б)

Точно так же для серы: S + 02 = S02; на 32 кг S уходит 32
кг 02, значит, удельный расход кислорода на 1 кг серы равен
32/32 = 1 кг О/кг S. А дл.я сжuгания всей серы, содержаЩейся в 1
кг топлива, требуется кислорода:
l ·S кг О/кг топл.
(в)
Аналогично мо гут быть записаны удельные расходы кисло
рода для других химических элементов, если они содержатся в
топливе и сгорают в кислороде.
Азот топлива не горит, он переходит в топочные rазы в виде
молекул N2 · Вода топлива дает водяные пары. Зола, если она
присутствует в топливе, как правило, состоит из негорючих
соединений, так что на ее сгорание кислорода не требуется
(если в золе есть горючие компоненты, то для них надо будет
записать реакции горения и подсчитать потребное количество
кислорода) .
Полный удельный расход кислорода воздуха на сжигание 1
кг топлива запишется :
Ко = 2,67·С + 8 ·Н + l·S + . - О,
(г)

2

"

причем вычитаемое О учитывает, что на связывание горючих
элементов топлива в оксиды будет использовано и то неболь1280

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

шое количество свободного юtслорода, которое содержится в
некоторых топливах; это несколько уменьшает потребность в
юtслороде воздуха.
В воздухе (в расчете на абсолютно сухой) содержится 23,2%
(мае.) кислорода, т.е. 0,232 кг О/кг АСВ . Следовательно, теоре
тический удельный расход сухого воздуха (теор. В) на сжигание
1 кг топлива составит:
Zreop

=

Ко
2

/ 0,232

=

4,3 1 · Ко2 кг АСВ/кг топл. ( 1 5 .23)

2. Определение уделt.вого количества первичного воздуха. Что
бы гарантировать полное сгорание топлива, первичный воздух
(перв. В) надо подавать в топку в количестве Z1, несколь
ко превышающем теоретическое. Отношение Zi/Zreop =
кг перв.в.
называется коэффициентом избt.пка воздуха в
= a.r
кг теор.в.
топке.
В топках котельных усrановок, г,це в высокотемпературных ("' 1 500 ° С) ради
антных зонах получают переrретый пар, величина o.r обычно незначительно
превьпnает 1 (находиrся в пределах 1,05-1, 1 5). В индивидуальных топках для
сушильных усrановок нет необходимости в столь высоких температурах, Здесь
можно подать на сгорание больше холодного первичного воздуха; важно только,
чгобы температура tт обеСпечивала полноту сгорания топлива. Поэтому избыток
воздуха (холодноrо!) здесь больше: o.r = 1,5 + 2 .

Массовый удельный поток вл ажн ых топочных газов на вы
ходе из топки есть сумма первичного воздуха с учетом внесен
ной им влаги Z1 (1 + .хь) и той части топлива "'' которая в ре
зультате его сгорания пepenma в газовую фазу: '11 = С + Н +
Арб . Очевидно, при использова
+ S + N + О + . . . + rо рб = 1
нии газообразного топлива '11 = 1 , ЖИдкого - '11 достаточно
близко к 1 ; в случае твердого топлива '11 может существенно
отличаться от 1 (например, в горючих сланцах возможно
Арб = 0,3+0, 5) .
При составлении теплового баланса топки наряду с Прихо
дами и Уходами теплоты будем учитывать и ее Источник теплотворную способвостt. топлива Qрн (она приводится в спра
вочниках для топлив различных месторождений или подсчиты
вается по элементарному составу топлива и теплотам сгорания
элементов).
В качестве пространственного контура выбирается топка
(контур ТК на рис. 1 5 . 37). Тогда в расчете на 1 кг топлива
-

cx.i-Zreop (l + .хь)соГ/о + 1 ·с,.8'т - Арбсэ8"э (д)
- [ '1' + <X.rZreop( l + XQ))C,.Чr + Qpliriт :;::: О .
Здесь первое слагаемое - Приход теплоты с первичным возду
хом , второе - Приход ее с самим топливом при температуре

128 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

0т'· Третье слагаемое - Уход (знак " минус") теплоты с золой ,
если она присуrствует в топливе, причем температура уходя
щей золы 03" обычно близка к температуре в топке (и на выходе
из нее) tr. Основная составляющая Ухода теплоты (с топочными
газами) - величина, содержащая квадратные скобки. Символы
с! - теплоемкости газов, н ижний индекс при с! указывает, при
какой температуре берется теплоемкость. Индекс при темпера
туре указывает ее принадлежность к определенной точке на
схеме (рис . 15.37). Наконец, последнее слагаемое - Источник
теплоты: теплотворная способность, теплота сгорания.
В ходе осуществления процесса в топочной камере есть по
тери теплоты: в окружающую среду, с химическим недожогом
(от неполноты сгорания топлива), с механическим недожогом
(провал несrоревших частиц топлива вместе с золой при сжи
гании твердого топлива) . Эти потери можно оценить для еди
н ицы времени, но затруднительно в расчете на 1 кг топлива.
Поэтому величина Qрн берется с множителем 11т < 1 , назы
ваемым коэффи циентом полезного действия топки. Из пра:кrики
работы топок для сушильных установок 11т i:::: 0,9070,95. Таким
образом, произведение Qр�т представляет собой часть источ
ника теплоты Qрн , полезно используемую для нагрева топоч
ных газов.
Выражение (д) нетрудно разрешить относительно a.r, рас
крыв квадратные скобки:
Qрн 11 т + 1 · Ст е т· - А рб Сз е "з - 'V Стr tт
( 1 5 .24)
a.r г
г
Zreo p (1 + хо )(ст tт - c0to )
_

Величину a.r определяют, предварительно приняв необходи
мое значение tr, гарантирующее достаточную полноту сгорания
топлива. Далее рассчитывают искомое удельное (на 1 кг топли
ва) количество первичного воздуха:

( 1 5.25 )
Z1 = <X-i-Zreo p .
Величину Z1 можно найти и сразу, перенеся Zreop из знаменателя (15.24) в
левую часть эrого равенства. Тем не менее, во избежание технических ошибок
при вычис.лениях, рекомендуется все же снача/lа определить а..- и, убедившись,
что эrот коэффициент находится в указанных выше пределах, затем рассчитать
Z1 по (15.25).
Для последующего анализа удобно отдельно записать удель
ный поток теплоты, уносимой из топки топочными газами:
Qт

= [ 'V + Z1 ( l + Xo) ] c/tr (Дж/кг топл.).

(е)

3. Определение удельного количества вторичного воздуха. Со
ставим тепловой баланс для камеры смешения (контур КС на
рис. 1 5.37) в расчете на 1 кг топлива, имея в виду, что из кон 1282

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ту ра уходит сумма потоков поступ ивших в него газа из топки
'1 ' + Z1 (1 + х0) и вторичного воздуха Z1( 1 + хо) :

QтТ\кс + �( 1 + Хо) соЧо - [\11 + (Z1 +� )(1 + Xo)]c1ft1 = О . (ж)
Здесь КПД камеры смешения Т\кс учитывает неполноту исполь
зования поступающего из топки теплового потока Qт в резуль
тате потерь в окружающую среду. В камере смешения темпера
тура ниже, чем в топке, и нет теплопотерь с недожогом ; по
этому Т\кс ближе к 1, чем Т\т: Т\кс ::::: 0, 97-7- 0 ,99.
Раскрывая квадратные скобки и решая балансовое соотно
шение (ж) относительно � . получаем:

�

-

_

- [\11 + Z1 (1 + Xo ) Jc[t1
.
(1 + х0 )(с 1 t1 c0 t0 )

QтТ\ кс

r

-

r

(15.26)

Величину � определяюr, предварительно приняв (исходя из
свойств высушиваемого материала и других технологических
сообр ажений) температуру t1 на входе СА в сушильную камеру.
В последующем анализе придется оперировать удельным по
током теплоты, вносимой с сушильным агентом в сушильную ка
меру. Соответственно (ж) :
Q 1 = [\11 + (Z1 + � )(1 + Хо ) ] с 1Ч1
(з)
(Дж/кг топл .).
4. Определение расхода топлива. Составим тепловой баланс
для сушильной камеры (контур СК на рис. 1 5.37) - теперь
применительно к единице времени. В этом случае Приход тепло
ты с потоком СА запишется как произведение Fт Q 1 . Итак, с
учетом теплопотерь в окружающую среду Qo и с транспортны
ми приспособлениями Qтр :

Fт[\11 + (Z1 + �)(1 + Xo)] c{t2 Qo - Qтр = О.
(и)
Здесь второе и третье слагаемые - Приход и Уход теплоты с
исходным и высушенным материалом соответственно (расчет
относительных теплоемкостей ё - см. разд. 15.2.3). Четвертое
слагаемое - Уход теплоты с отработанн ым сушильным аген 
том. Важно: в это слагаемое не включен поток теплоты с водя
ными парами, вьщелившимися из ТМ при его высушивании и
присоединяющимися к отработанному СА. Эта теплота учтена
пятым слагаемым, где iп - энтальпия водяных паров при тем
пературе t2 (способ расчета iп приведен в разд. 15.2.2).
Из баланса (и) наЙдем расход топлива в единицу времени ,
раскрыв смысл Q 1 п о (з) :

FтQ1 + Gё' 0' - G ё" 0" - W1п -

F:

т=

G(ё"0 " - с'0 ') + Qo + Qт р
[\11 + (Z1 + Z2 ) (1 + х 0 )] (с1 t1 - c2 t2 )
Wi п +

r

r

(15.27)
1283

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

5. Паrоки (р асходы) первичиоrо и вторичвоrо ВОЗJJУХ8 . Расхо
ды первичного и вторичного воздуха определяются очевид
ными соотношениями:

(15.28)
Для подбора вентиляторов и расчета некоторых типов рас
ходомеров необходимы объемные расходы газовых потоков J'f.
Их нетрудно найти, располагая массовыми потоками L1, пред
варительно рассчитав относительные удельные объемы v0:

(15.29)

При этом определение v о; для расчета объемных поrоков пер
вичного и вrоричноrо воздуха затруднений не вызывает (см. разд.
15.2.2), так как Хо и � известны. Для определения v02 на выходе
из установки (именно там чаще всего ставят вентиляrор) необхо
димо специально найти влаrосодержание х2 отработанноrо СА
Для этой цели следует выразить в расчете на 1 кг топmmа :
- количество влаги: внесенной с исходным воздухом
(Z1 + �) .хо; образовавшейся при сгорании топлива 9 Н; содер
жащейся в исходном топливе оо рб и удаленной из высуши
ваемого материала W/Fт;
- удельный расход абсолютно сухого воздуха (Z1 + �) и су
хой части газов, образовавшихся из топлива, '1' - Н - оо рб.
Тогда
{Z1 + Z2 )х0 + 9Н + оо рб + W / Рт
� w
б
.
(Z1 + Z2 ) + '1' - H - 00 P

-

_

{

)

Расчет v0 ведется по номоrрамме (рис. 15.16), а если значения х
и t выходят за пределы шкал номоrраммы, то по формуле (15.2).
Попьrrка проведения аналитического (или фафоаналитическоrо) расчета на
основе относительных энтальпий /; вместо абсолютных c{t; приводит на этапе
расчета топки к получению нелинейных связей Xr, а,. и lт. Для расчета этих
величин требуются итерационные процедуры JD16o выражение относительной
энтальпии на выходе из топки /т по ( 15.3), т.е. снова обращение к абсолютным
энтальпиям. Использование в одном расчете одновременно относительных (/о и
др.) и абсолютных с{tт энтальпий предстаRЛЯется непоследовательным в методи
ческом отношении и потоыу здесь не приводится.
15.8. КИНЕТИКА СУШКИ
15.8. 1. Общие положения

В предыдущих разделах рассмотрена статика сушки. Про
блемы скорости и продолжительности высушивания, состав
ляющие предмет кинети ки процесса, пока не затрагивались.
МеЖду тем владение кинетикой необходимо при решении
практических задач. Скажем, в з ад аче эксплуатации необходи-

1284

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Puc. 15.39. Кривая сушки (внуrри
rрафика - иллюстрация проrрева
высушиваемого материала в на
чальные момеlПЬI времени)

и

и

мо установить значения
выходных влажностей х2 для
СА и U" для ТМ - при из
ложении статики они счи
t
о
тались известными, тогда
как на самом деле зависят
от кинетических характери
стик процесса, например от
p
U
величины p p F. А в задачах
проектирования для непре
0
рывных процессов часто
необходимо найти поверхность контакта F, обеспечивающую проведение процесса с за
данной производительностью до
обусловленной выходной
влажности ТМ.
Скорость процесса сушки зависит от множества факторов:
природы высушиваемого материала и влаги (в общем случае и сушильного агента), температуры, скорости движения СА над
поверхностью высушиваемого материала, его размеров и фор
мы, а также внугренней структуры и диапазона влажности. Как
указано в разд . 15.2.5, в высушиваемом материале в общем слу
чае содержится свободная и связанная влага. Удаление влаги
различных форм имеет свои особенности, которые выявляются
при построении •кинетических кривых процесса.
Кривая сушки представляет собой зависимость изменяю
щейся относительной влажности материала U во времени -r в
процессе сушки (рис . 1 5.39). Эта кривая снимается экспери
ментально при постоянной температуре. (Заметим: ранее такой
эксперимент был практически единственным способом опреде
ления продолжительности сушки.) Сначала влага удаляется
равномерно во времени, т.е. с постоянной скоростью, - гово
рят о сушке в 1 периоде (или в периоде постоянной скорости) . На
кривой этому периоду отвечает прямолинейный участок - от
точки с начальной концентрацией Ин до точки с критической
влажностью U кр . Далее влага удаляется медленнее - говорят о
11 периоде сушки (или о периоде падающей скорости) , когда с
течением времени влажность материала асимптотически при
ближается к равновесной (с влагосодержанием СА) величине
UP. Строго говоря, на небольшом начальном участке кривой
сушки первоначально скорость удаления влаги меньше, нежели
в 1 периоде (этот участок указан стрелкой на внугреннем гра
фике рис. 15.39). Это объясняется существованием непродолж:и· - ·-· - · - · - · - · - · - · - · - · - · - · - · - · -

1285

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

l . dU

F dt

Рис. 15. 40.

Кривая скорости сушки

тельной стадии прогрева вы
сушиваемого материала, далее
сушка идет в типичных 1 и 1 1
периодах.
Эксперимент и анализ яв
лений показывает, что в 1 пе
риоде скорость удаления влаги
из материала такая же, как и
испарения со свободно разли
Ин U
той на поверхности - в тех
же условиях (в частности, при
одинаковых поверхностях контакта ТМ и СА). Это означает,
что в 1 периоде удаляется свободная влаrа. На этом участке
кривые сушки в одинаковых условиях совпадают для разных
материалов. Во 1 1 периоде удаляется связанная влаrа. Форма
кривой сушки для этого периода зависит от природы материа
ла; общим является лишь асимптотическое стремление к UP
при большой продолжительности процесса.
Более наглядными являются кривые скорости сушки. Под
скоростью сушки понимается количество влаги, удаляемой в
единицу
времени
с
единицы
поверхности
контакта:

1 dU

/

- - -- (знак "минус" обусловлен тем, что d U/d't < О). Кривая
F d't
скорости сушки , построенная при известной поверхности кон
такта по данным кривой сушки , представлена на рис. 15.40.
Первому периоду здесь соответствует горизонтальный участок
в диапазоне Ин- U КР (эффект прогрева материала на начальной
стадии сушЮf изображен жирной штриховой линией и указан
стрелкой) . Скорость удаления влаги в этом периоде отвечает
интенсивности теплоподвода. Температура высушиваемого ма
териала в пределе (и в идеале) может достигать температуры
мокрого термометра. Во 1 1 периоде кривые скорости сушЮf в
зависимости от свойств материала (в общем случае - и влаги)
могуг идти различно (на рисунке - различные линии при
U < U КР) . Здесь возможны перегибы и даже изломы, отве
чающие, например, различной степени гидратации (числу мо
лекул кристаллизационной влаги). Общим является устремле
ние этих линий к абсциссе U Р при бесконечно долгой сушке,
хотя сами значения U Р для разных систем "влага-ТМ" будут,
естественно, разными. Скорость испарения влаги в этом пери
оде может лимитироваться как внешней диффузией влаги от
поверхности ТМ в СА, так и внутренней ее диффузией в мате-

1286

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

риале (разумеется, возможно и конкурирующее влияние этих
стадий).
Сложность кинетических расчетов сушильных процессов об
условлена сложностью наблюдаемых явлений: внутренняя миг
рация влаги в материале, диффузия ее с поверхности в поток
сушильного агента, сопутствующие физико-химические пре
вращения (дегидратация , преодоление капилля р ных сил, фазо
вые переходы), одновременное протекание теплопереноса, по
ведение единичного зерна в
высушиваемых зерен .
массе
По этой причине до настоящего времени сохраняет свое зна
чение экспериментальное изучение сушильных процессов. Од
нако по мере проникновения в физическую сущность процесса
возрастает роль теоретических построений. Они позволяют:
- грамотно поставить эксперимент;
- судить о механизме процесса, построить его физическую
модель;
- в отдельных (достаточно простых) случаях - математиче
ски описать и рассчитать процесс сушки.
Кинетические расчеты сушильных процессов строят и про
водят на основе общих положений, изложенных в разд . 1 0 . 1 6 .
Согласно этим положениям (они использованы при рассмотре
нии процессов адсорбции разд. 14.4 - 1 4.6), в отсутствие химиче
ских превращений процесс кон вективной сушки (десорбции
влаги) включает четыре стадии:
- подвод влаги в зону сушки с влажным материалом;
- диффузия влаги внутри ТМ из его внутренних областей к
поверхности контакта с СА;
- диффузия влаги с поверхности ТМ в поток (в обьем) су
шильного агента;
- вывод влаги из рабочей (сушильной) зоны с сушильным
агентом.
Результирующая скорость сушки зависит от интенсивности
каждой из этих стадий . Однако, если скорость на какой-либо
одной из стадий значительно меньше, чем на остальных
(иначе: продолжительность данной стадии знач ительно больше) ,
то эта медленная стадия является лимитирующей . В таком случае
расчету подлежит только эта стадия процесса, так как осталь
ные в сравнении с ней протекают практически мгновенно.
Если в качестве лимитирующей стадии выступает диффузия
влаги от Поверхности ТМ в поток СА, то говорят о сушке в
условиях внешней задачи, если диффузия влаги внутри ТМ - то
о сушке в условиях внутренней задачи. Если лимитирует подвод
влаги в рабочую зону с твердым материалом, то речь идет о
сушке в условиях потоковой задачи по ТМ, если отвод влаrn из
этой зоны с сушильным агентом, - то о сушке в условиях по
токовой задачи по СА. При сопоставимости скоростей хотя бы
-

1287

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 15. 41.
Принципиальная схема су
шильной установки с псевдоожюкенным
слоем высушиваемого материала:

1
корпус аппарата, 2
газораспредели
тельная решетка;
/, п
входящий и выходящий потоки су
шильного areнra, ///, 1У
входящий и выходя
щий потоки высушиваемого материала, V
ПСеlЩООЖИJКеЮIЬIЙ СЛОЙ
-

1

-

-

-

-

двух каких-либо медленных ста
дий задача именуется смешанной,
ее расчет усложняется.
Далее последовательно рас
сматриваются процессы сушки
при наличии отдельных лимити
рующих стадий. При этом при
н имается, что подвод теплоты не
лимитирует процесса, так как
происходит быстрее переноса влаги (иначе: подвод теплоты в
соответствии с расчетами статики процесса достаточен для
осуществления сушки) .
В качестве объекта последующего анализа принят непре
рывный процесс сушки в псевдоожиженном
слое высуши•
ваемоrо материала, поскольку эта система
достаточно показательна:
- имеет большое распространение в хймической технологии
и ряде других отраслей промышленности;
- очень удобна в методическом отношении своей просто
той , наглядностью и возможностью довести анализ до расчет
н ых выражений.
В ходе изложен ия будут затронуты и некоторые общие мо
менты, выходящие за пределы специфики псевдоожиженных
систем.
Принципиальная схема сушилки с псевдоожиженным слоем
( П С) представлена на рис. 1 5 .4 1 . В аппарат 1 с зернистым ма
териалом непрерывно через газораспределительную решетку 2
подается горячий сушильный агент (его расход L) с исходным
влаrосодержанием х1 , псевдоожижая зернистый материал .
Увлажненный СА уходит из аппарата с влаrосодержанием х2 .
Исходный влажный материал (его лоток G) входит в аппарат с
влажностью И' и выходит с влажностью И". Потоки L и G
представлены как ннерты (в кг АС В/с и кг СМ/с) и потому в
ходе сушки не изменяются . Высота П С равна Н, поперечное
сечение - Sa; масса ТМ в аппарате (в расчете на абсолютно
v

•

Ряд

1 288

других систем интенсивной сушки рассмотрен

в

(19).

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

сухую часть) Gт и отвечающая ей поверхность межфазного кон
такта F - постоянны. Порозность ПС в рабочих условиях со
ставляет &, размер твердых частиц (в целях упрощения анализа
они приняты сферическими и одинаковыми) равен d. Сушиль
ный аrент движется через слой в режиме идеального вытесне
ния, так что его в.лаrосодержание изменяется в слое по верти
кальной координате z. Псевдоожиженный ТМ находится прак
тически в состоянии идеального перемешивания, и потому его
влажность по объему слоя одинакова и равна влажности выхо
дящего высушенного материала U".
При наличии любой лимитирующей стадии и в ее отсут
ствие остается справедливым выражение, получаемое совме
щением соотношений ( 1 5.5) и ( 1 5.6):

W = L(x2

-

х1 )

=

G( U' - U'�

( 1 5 .30)

и совпадающее с уравнениями материального баланса типа
( 1 0 . 1 3), ( 1 0 . 14).
15.8.2. Сушка в условиях внешней задачи

Сушка в условиях внешней задачи протекает при удалении
свободной в.лаги и может происходить при удалении связанной
в.лаги - преимущественно вблизи влажности f.JКP, если силы
сцепления влаги с ТМ не очень велиюt , а условия ее диффузии
с поверхности в объем СА
неблагоприятны.
Основное уравнение внешнего массопереноса для непре
рывного процесса имеет вид:
-

( 1 0 . 72) , ( 1 5 . 3 1 )
Применительно к сушке массовый поток переносимого ве
щества (влаги) М = W; р
плотность инерта (сухого СА); ве
личины коэффициента массоотдачи р и поверхности контакта
F сохраняют свой смысл; средняя по F движущая сила выра
жается через влаrосодержания сушильного аrен та: Лер = ЛХср =
(хМ
х)ср, хм равновес ное (с U влажностью ТМ, . в рас 
сматриваемом случае
в псевдоо жиженном слое) влагосодер
жан ие СА. Таким образом, для сушки в условиях внешней за
дачи выражение ( 1 5 .3 1 ) запишется в виде:
-

=

-

-

-

-

W = ррFЛХср .

( 1 5.З lа)

Обоснование формы уравнения ( 1 5 . 3 1 ) , а с ним и ( 1 5.3 1а), и
подходы к расчету входящих в них величин даны в разд . 1 0 . 1 6 . 2 .
Наличие в формулах плотности СА обусловлено принятыми
единицами измерения W кг Вл/с и х кг Вл/кг АСВ. Коэффи 
циент массоотдачи р определяется п о эмпирическим соотно1289

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 15.42. К анализу сушки в псевдоо.жюкенном слое

в условиях внешней задачи: расче111ая схема процесса
(к - контур )

� х
IL
х1

\ \U'

СА

шениям (их примеры приведены в ука
занном разделе) . Поверхность конта�сrа F
находят с помощью формул типа (2.64) :
F=

ТМ

6(l - e)

d

SаH

- при известных размере частиц d (он
задан) и порозности & (ее оценивают из
гидродинамических соотношений - см. разд.2.7.4). Наконец,
концентрацию х!4 определяют по диаграмме равновесия
(рис . 1 5 .20б) как величину, равновесную с U"; поскольку
вследствие интенсивного перемешивания ТМ его влажность
постоянна по объему ПС ( U = U" = const), то и х!4 = const.
Цель последующего анализа - определение средней движу
щей силы ЛХср и связи конечного влагосодержания х2 с высо
той слоя Н. При достижении этой цели можно будет сформу
лировать пути решения эксплуатационной и проектной задач.
Расчетная схема представлена на рис . 1 5 .42. На расстоянии z
от входного (для СА) сечения, совпадающего с распредели
тельной решеткой, выделим фрагмент ПС, содержащий неко
торый объем с зонами сушильного агента (СА) и твердого ма
териала (ТМ). Для бесконечно малого пространственного кон 
тур а к · (поверхность контакта фаз здесь равна d/ ) в зоне дви
жения сушильного агента запишем материальный баланс по
влаге:

Lx + d W -

L(x

+ dx)

= О и d W = Ldx .

(а)

Для рассматриваемой бесконечно малой поверхности кон
та�сrа df выражение типа ( 1 5.З l а) запишется с локальной (на dj)
движущей силой:
(б)
d W = j3 p(x!" - x)df .
Из (а) и (6) :
(в)
Ldx = j3 p(x!" - x)d/ .

Применительно к псевдоожиженному слою это уравнение
после разделения переменных легко интегрируется (в пределах
соответственно от х1 до х2 и от О до F), так как для ПС х!4 =
= const по всей поверхности контакта F:

j2х1 х Mdx- х
1290

=

j3 p

fdf .

L o

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

С учетом знака при х в знаменателе левого интеграла и меем :
( 1 5 . 3 2)
ность материала И, а с ней и равновесное влагосодержание хм из
меняются по объему систе м ы ( координате z, поверхности контакта

Дnя бол ь ш и нства других систем, где в отличие от ПС влаж

Л. интегрирование приводит к более сложным выражениям либо

вообще провести его аналитически не удается .
И з вы ражения ( 1 5 . 3 2) в идно, что в случае внешней задачи зако
номерности изменения влагосодержания сушил ьного агента о пре
дел я ются "числом един и ц переноса", т.е. отношением пропуск н ы х
способностей поверхностной ( иначе - внешней) стадии

( pp F )

и

потоковой стадии (L).
Дnя нахождения средней движущей с ил ы реш и м левое из
урав н ен и й ( 1 5 . 3 2 ) относител ьно

L

и домножим обе части равен

ства на (х 2 - х 1 ) , чтобы получ ить слева кол и чество передавае м о й
в л а г и W:

L = Pp F

1n

х

Х

м

м

-х

(г)

.
- Х2

Сравни вая последнее выражение с ( 1 5 .3 1 ,а), находи м :
ЛХср

-_

х2 - х1
м
1 n х - х.
м
Х - Х2

ил и ЛХс р

-_

х

(

м

м
- х2
- х1 - х
м
х
- х.
1n
м
Х
- х2

) (

)

( 1 5 .33)

- средняя движущая сила п р и сушке в П С в условиях внешней за
дачи выч исляется как

среднелогарифмическая

вел и ч ина.

Соотношением ( 1 5 .32) установлена связь х2 и F. В расчетах
удобно оперировать не поверхностью контракта F, а рабочей вы
сотой слоя Н. Выражая для ПС поверхность контакта F через Н,
как показано в начале раздела, получае м из ( 1 5 . 3 2 ) :

( 1 5 . 3 4)

1 29 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

В задачах эксплуатации известны Н, а также Sa и рЯд других
характеристик процесса; требуется определить хъ U" и произ
водительность по влаге W Это удобно сделать, используя вто
рое из выражений ( 1 5 .34). По найденному х2 с помощью урав
нения баланса ( 1 5 .30) определяются конечная влажность мате
риала U" и поток передаваемой влаrи W Расчет осложняется
тем, что при первоначально неизвестной конечной влажности
U" нельзя точно взять равновесное значение �. входящее в
( 1 5 .34). Поэтому приходится прибегать к итерационной проце
дуре, задаваясь "в нулевом приближении" некоторым значе
нием U" и добиваясь в ходе итерации приемлемой сходимости
этой величины:
U"

1

-----

равновесие

�

ур-е ( 1 5 .34)

Х2

-----+

ур-е ( 1 5.30)

U"

сопоставление

В тех случаях, когда равновесие при сушке является (или его
можно принять) линейным, задача эксплуатации поддается
аналитическому решению на основании методики и соотноше
ний, приведенных в разд. 10 . 9 для процессов класса 3(2-2) 1 по
КФ-классификации.
В типичной задаче проектирования обычно задана произво
дительность по высушиваемому материалу G и его влажности
- входная U' и выходная U". По материальному балансу ( 1 5 . 30)
определяется выходное влагосодержание сушильного агента х2
и далее (при других известных величинах) по п ерво м у из выра
жений ( 1 5 .34) - искомая высота слоя Н, обеспечивающая за
данную глубину сушки (конечную влажность U") . При этом
рабочий поток сушильного агента L определяется из условий
статики процесса, а при неизвестном на начальных стадиях
расчета значении х2 - уточняется с помощью технико
экономического анализа .
Входящее в расчетные уравнения поперечное сечение аппа
рата Sa рассчитывается по уравнению расхода V = Saw, где
V = Lv0. Здесь скорость сушильного (ожижающего) агента w
выбирается из технологических соображений - обычно во из
бежание значительного уноса мелких частиц на уровне (3 7)wo, где wo - скорость начала псевдоожижения.
Уравнение ( 1 5.34) связывает влагосодержание уходящего СА
х2 с высотой слоя Н Эта связь иллюстрируется на рис . 1 5 .43 .
Частицы в ПС невелики по размерам: чаще всего d изменяется
долями миллиметра, реже - несколькими миллиметрами . Это
означает, что выражение под знаком экспоненты ехр в ( 1 5 .34)
весьма велико (при не очень малых Н). Поэтому в пределах не1 292

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 15.43. Связь влаrосодержания сушильноrо
покидающеrо тонкий псевдоожижен

areкra,

ный с.лой, с ero рабочей высотой

больших высот слоя с увеличением
Н разность х!" - х2 быстро умень
шается. Кривая х2 = x2( J/), показан
ная на рис . 15.43, хараперна для
слоя .
псевдоожиженною
товкоrо
Заметим, что эта же кривая харапе
ризует изменение текущего влагосо
держания х по высоте слоя z.
1 5.8.З. Сушка

в

х"

· - · -· - · - · - · - · - · - · - · - ·

условиях потоковой

Н(z)
задачи

Будем увеличивать высоту псевдоожиженного слоя Н, а с
ней и поверхность контакrа F. Очевидно, при достаточном
возрастании F внешний массоперенос уже не будет лимитиро
вать процесс сушки , так как станет большой пропускная спо
собность �pF. Тогда выходное влагосодержание х2 приблизится
к х!" - это следует из уравнения (15.34): при Н � оо
(практически - при достаточно большой величине Н) х!" - х2 �
� О, т.е. х2 � х!". Такая ситуация показана на рис . 1 5 .44: если
высота слоя Н превышает некоторую величину ha (ее называют
активным участком псевдоожиж енною слоя), то без сколько
нибудь заметной погрешности можно практически считать, что
х2 :.:::: х!". При этом допустимая погрешность устанавливается
технологом, обычно ее выбирают на уровне 1-5%; иначе гово
ря, отношение разностей концентраций в левой части выраже
ния (15.34) полагают равным 0,01-0,05. Это означает, что с
точностью 95-99% массообмен в псевдоожиженном слое на
участке Н = ha можно считать завершенным. При увеличении
Н сверх ha массообмен (сушка) может считаться законченным с еще
х2 (х)
большим основанием (меньшей погрешностью) .
Расчеты по уравнению (15.34) по
казывают, что при указанных значе
11
1
ниях концентрационною комплекса
11
11
величины Н = ha получаются обычно
11
на уровне нескольких миллиметров,
1
для крупных частиц
порядка
1: н _
> hа
Н < ha 11
нескольких сантиметров. При Н < ha
Рис. 15. 44. К выро)!Щению внешней
сушки в потоковую

задачи

1 293

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

псевдоожиженный слой в смысле внешнего массообмена трак
туется как тонкий, и тогда справедливы все положен ия и соот
ношения предыдущего раздела. Однако со столь тонюtми псев
доожиженными слоями работают только в исследовательсюtх
целях в лабораториях. На производстве используют ПС значи
тельно большей высоты , так как тонкий слой в аппарате про
мышленных размеров структурно неустойчив из-за образования
в слое "свищей" , в которые устремляется основная доля газа
(см . разд.7. 1 1 .2 , 14.3 .2). Поэтому в промышленн ых аппаратах,
как правило, Н >> h3• А при Н � ha независим о от кинетических
характеристик внешнего массопереноса х2 � ХЫ; тогда можно
утверждать, что внешняя задача сушюt выродилась в потоковую
- чаще по СА (т.е. по потоку L) , реже по ТМ (по потоку G) . В
этих случаях для расчета процесса сушюt достаточно уравнения
материального баланса ( 1 5 .30), дополненного условием равно
весия в форме равновесного соотношения .ХЫ = .ХЫ( U) или гра
фической зависимости типа показанной на рис . 1 5 .20,6. И ными
словами :
( 1 5 .35)
L (x2 - х1 ) = G( U' - И") .

J

р ав но вес и е

J

Задачи эксплуатаци и и проектирования при линейном
описании равновесия (или при х м = х т ах = const) решаются
аналитически , как это показано в разд . 1 0 . 8 и 1 0 .9 для про
цессов класса 3 (2-2) 1 . При произвольной форме кривой рав
н овесия (именно этот случай чаще всего встречается при
удалении связанной влаги) расчет ведется графоаналитиче
с ки (ри с . 1 5 .45) .
Для решения задачи эксплуатации, т.е. отыскания выходных
кон центраций х2 и И" при заданных входн ых Х1 и И' и из
вестных потоках L и G, перепишем выражение ( 1 5.35):

Х2 - Х1 = G
L

U 1 - U 11

--=---=-

( 1 5 . 3 5а)

Из точюt ( И', х 1 ) под углом а. , так что tg a. = G/L , проводим
прямую. Точка ее пересечен ия с линией равновесия представ
ляет собой точку выходных концентраций х2 и И", поскольку
удовлетворяются оба поставленных условия:
- уравнение ( 1 5.35), ( 1 5.35а) - это видно из графика, так
как отношение (х2 - х 1 )/( И' - И") = tg a. ;
- потоковый характер массопереноса, так как точка ( И", х2 )
лежит на линии равновесия.
1294

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Р ешение задач эксnлуата
ции и проектирования при сушке в
псевдоожиженном с.лое в ус.ловиях
потоковой задачи
Рис. 15. 45.

Типичная задача проекти
(чаще всего заданы
концентрации U' и U", х1 )
решается еще проще: при
известном значении
U" по

рования

равн ове с н о й
ч ал е

хм

диаграм ме

о п р е д е л я ет с я

и

в н а

=

х2 ;

далее из материального баланса ( 15.30), (1 5.35) отыскивается
неизвестный поток (обычно L, обеспечивающий заданную
производительность по высушиваемому материалу G) .
При решении задач эксплуатации и проеюирования в усло
виях потоковой задачи нет необходимости в определении ки
нетических харакrеристик внешнего массопереноса типа 13, F и
др. (а также внугреннего массопереноса - Dм и др . - см. сле
дующий раздел). Надо только быть уверенным, что процесс
ведется при Н � ha,, т.е. при достаточно высоких значениях по
верхности контакrа (строже: при достаточно высоких пропускных
способностях внешнего массопереноса j3pF > > L, G).
Сушка в условиях потоковой задачи может происходить при
удалении как свободной, так и связанной влаm.
1 5 . 8 .4. Сушка в условиях внуrренней задачи

Постановка задачи
Суш.ка в условиях внугренней задачи может протекать толь
удалении связанной влаm. Зерна (частицы) материала в
ПС очень невелики по размерам, поэтому протяженность пути
диффундирующей влаги внугри зерна мала; можно было бы
предположить, что рассматриваемая стадия - быстрая и не
может стать лимитирующей. Однако для ряда ТМ коэффици
ент внугренней диффузии влаm Dм крайне низок (скажем, для
воды в полимерных материалах он находится на уровне 10 - 1 2
- 10 - 13 м2/с); поэтому внугренняя диффузия вполне может
о казаться лимитирующей стадией несмотря на малые размеры
частиц.
.
Про Цесс сушки в условиях внугренней задачи сначала рас-

ко при

с м от р и м

кt1 ч е с т в е п н о .

к о н це нтра ци е й

влаги

в

Буде м

о п е р и р о в ат ь

м а те р и ал е

с

=
-

1 1Р

u1

т

см еш ан но й

( ккг Вл

г см

кг С М
мз

1295

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 15.46. К анализу симметричной сушки сферического зерна в условиях внуr
ренней задачи

Вл/м3 ) . Проследим за процессом в единичном зерне, при
няв его в целях упрощения сферичесюtм, а процесс сушюt симметричным (рис. 1 5 .46) . Пусть исходная влажность мате
риала С0 постоянна по объему зерна, а равновесная (с потоком
СА) составляет С Р. После внесения зерна в зону сушюt на его
поверхности мгновенно (в условиях внутренней задачи внеш
ний массообмен подразумевается бесконечно интенсивным)
устанавливается и в ходе всего процесса поддерживается рав
новесная концентрация С Р. Спустя небольшой промежуток
времени -с1 приповерхностные области зерна теряют влагу
(глубинные - еще не затронуты сушкой). К моменту -с2 неза
тронутыми остаются лишь центральные зоны, в остальных
влажность заметно меньше . А к моменту -с3 концентрация влаги
меньше исходной уже во всем объеме зерна; в момент ч обез
воживание зерна еще глубже : влажность понижена, она стала
ближе к равновесной. Если сушка ведется долго (теоретичесюt
- бесконечно долго), то влажность во всем объеме зерна стре
мится к равновесной.

= кг

1296

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Задача анализа применительно к единичному зерну состоит в
определении влажности в произвольной точке внутри зерна (на
радиальной координате r) в произвольный момент . времени • :
С = C(r, •) .
Задача анализа применительно к псевдоожиж:евиому слою за
ключается в учете поведения единичного зерна . в массе
зерен.
Для ПС анализ облегчается тем, что зерна (частицы) в нем
прапически находятся в режиме Идеального перемешивания,
для которого распределение их по времени пребывания выра
жается относительно просто.
Представленная качественная картина должна быть интер
претирована колll'Сественно. В основе анализа лежит уравнение
Фика (см. разд. 1 .5.3, 1 0 . 1 6.3). Для единичного сферического
зерна радиусом R при симметричной сушке в случае постоян
ного коэффициента диффузии влаги в материале (Dм) в отсуr
ствие химических превращений (Источников и Стоков) оно
записывается в сферических координатах:

ас (а-2 с2- + - ас)
аг

- =

а.

Dм

2
- ; О � r < R,
r дr

't

> О .

( 1 5 .36)

Как показано в разд. 7 . 1 0 применительно к теплопереносу,
для анализа и решения это уравнение более удобно в форме:

( 1 5 .36а)
Коэффициент диффузии влаги в материале Dм нередко существенно зависит
от ее концентрации в нем: при изменении С мoryr изменяться физическое со
стояние влаги в материале и характеристики ее диффузии. В этом случае Dм
нельзя считать постоянным в ходе процесса сушки (по объему зерна - тоже).
Тогда усложняется написание уравнения Фика - получаются выражения типа
рассмотренных в разд. 1 .6.З; даже при достаточно простых зависимостях Dw =
= Dм( С) решение такоrо нелинейного уравнения Фика возможно, как правило,
только численными методами. Дополнительное затруднение - в установлении и
математическом выражении зависимости Dw от С.

Уравнению ( 1 5 .36а) должны сопуrствовать три условия од
нозначности (поскольку в него входит первая производная по •
и вторая - по r):
- начальное условие (чтобы подчеркнугь, что речь Идет о
ситуации до начала процесса, иногда вместо 't = О пишут
• = - О): исходная концентрация влаги в объеме зерна (на лю
бой радиальной координате r) равна С0 , так что
't

= - О; C(r, 't), = 0

=

C( r,

О)

=

С0 ; О

�

r � R;

( 1 5.37)
1 297

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

- граничное условие 1 рода (оно отвечает внуrренней зада
че): в любой момент времени кон центрация влаги на поверх
ности зерна есть равновесная концентрация, тогда

r = R; C( r, 't)r=R = C(R, 't) С Р ; 't � О ;
=

( 15.38 )

условие симметрии сушки и ограниченности изменения
концентрации влаги (по существу это тоже rраничное условие) :

( r, 't)
r = О; дСдr

r=O

=

о С (О, 't)
дr

=

О; 't � О .

(15.39)

Справедливость последнего условия ясна из рис. 15.46: касательная к ЛIОбой
кривой изменения концекrраuий C('t), проведенная в центре сферического зер
на, горизоJrrаЛЬ на, т.е. параллельна оси r; иначе: танrенс утла наклона касатель
ной к оси абсцисс (производная) равен нулю. Это условие xapaicrepнo для сим
метричной сушки, в противном случае экстремум пришелся бы на какую-нибудь
точку с r " О. Одновременно это условие запрещает безrраничное (в том числе
симметричное) возрасrание концекrрации в ходе процесса, например при
асимптотическом приб.люкении тший C(r) к вертикали r = О (urrр их овые JПIНИИ
на рис. 1 5.46).

Зависимость С = C( r, 't) целесообразно для большей общ
ности представить в критериальной форме. Критерии подобия
формируются методом масштабных преобразований (см.
разд . 1 . 8 .2, 1 . 8 .3); проведем их в упрощенном варианте, сопо
ставив величины в левой и правой частях уравнения Фика:

С

Dм С

- о - • -- .

't

r2

(д)

После сокращения на С и переноса всех оставшихся вели
чин в одну часть равенства-сопоставления (д) получим безраз
мерный комплекс Dм't/12. Эrот комплекс неудобен : он содер
жит сразу две независимые переменн ые - r и 't. Поэтому его
преобразуют:
(е)
Каждая из полученных безразмерных величин Dм't/R2 и r/R
содержит по одной переменной . Комплекс Dм't/R2 = Fод = Fi
выр ажает соотношение количеств вещества (влаги), переноси
мого диффузией и аккумулированного зерном ; его называют
диффузионным критерием Фурье или критерием Фика ; иногда
его трактуют как безразмерное время. Симплекс r/R представля1298

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ет собой безразмерную координату ; он может изменяться от О до
1 . Таким образом, в результате решения уравнения Фика кон
центрация получается в виде функции от Fод и r/R. Очевидно,
концентрацию также резонно представить в безразмерной
форме. Анализ (см. для сравнения разд. 7. 10.3) приводит к об
общен ному
концеmрацнонному коммексу с · ==" ( С - СР)/( Со - СР), изменяющемуся от 1 в на•1але процесса сушки зерна
(когда С
Со) до О, если сушка ведется бесконечно долго
(тогда С � С Р ). Итак, решение уравнения Фика для симмет
ричной сушки сферического зерна должно привести к зависи
мости в обобщенной форме:
с•
C(r> t) С Р
=
= f (Fод, r/R).
(15.40)
=

-

Со - С Р

Подчеркнем, что

(15.40)

подлежит конкретизации .

Решение задачи
Единичное зерно. Подход к получению конкретной формы
зависимости типа (15.40) для сферы (зерна) в случае постоян
ного коэффициента диффузии Dм был продемонстрирован в
разд. 7. 10.3 применительно к переносу теплоты. Для переноса
•
вещества (влаги) при сушке такая зависимость имеет вид бесконечного ряда:

с· =

(15.41)

где п - индекс суммирования.

Для наглядности выпишем первые члены рассматриваемого
разложения:
c•

.
2 SШ
=

( R' )
1t -

r
1t -

е -112 Fод

-

R

ПОJПIЫЙ вывод такого рода выражений (он весьма
громоздок и в учебник
не включен), а также модификации подхода к расче'J)' нестационарного массо
обмена при сушке твердых тел р азличной формы приведены в специальной
литературе - см. , например, (3, 5, 7, 8, 1 2 , 1 7 - 20 и др. ) .
•

1299

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

( �)

( )

2 sin 37t
2 sin 21t �
R е -3 2 112 Foд
R е -2 2 11 2 Foд +
31t �
21t �
R
R
-----

-

(е)

Ряд ( 1 5 .4 1 ) быстро сходится (при не очень малых значениях
Fод), так как от слаrаемоrо к слагаемому быстро нарастает ве
личина n2 , стоящая в экспоненте.
Технолоrов интересует не столько распределение концентра
ции влаги по радиусу r (обьему зерна), сколько средняя влаж
ность зерна: именно она входит в материальные балансы, опре
деляет необходимые затраты теплоты на процесс сушки и во
обще устанавливается с течением времени в высушенном зерне
при ero хранении с целью последующеrо использования .
Усреднение концентраций ведется по канве, представлен
ной в разд.7. 1 0.3, 1 0 . 1 6 . 3 . В сферическом зерне на текушей ра
диальной координате r выделяется (см. рис. 1 5 .46) сферический
слой бесконечно малой толщины dr. Количество влаги в этом
шаровом слое обьемом 47tt2dr равно C(r, 't)-47tt2dr, а в зерне в
целом - интегралу от этой величины по объему зерна. С дру
rой стороны, полное количество влаги в зеnне выражается как
произведение средней ее концентрации с ('t) на объем зерна
4/31tR3. Приравнивая количества влаги в зерне, записанные
различным образом, получаем:
R

J C(r, 't) · 41tr dr
о
и C ('t)

2

=

3

3

-

R

R

- ('t) 4 1tR 3
=C
3

2

J C(r , 't)r dr .
о

( 1 5 .42 )

При этом средняя концентрация С получается как функция
времени; зависимость от r уrрачивается при интегрировании по
параметру r и подстановке пределов.
Усреднение концентрации влаги в зерне удобно проводить в
безразмерных переменных, отыскивая не С ('t), а комплекс
-•
-·
C ('t) - С Р
С =
. Эrо правомерно, поскольку С и С одноСо - С Р
значно и линейно связаны между собой. Таким образом, в ма
нере ( 1 5 .42) имеем:

1 300

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

-.

С

=

3

R

3 f •
C (r; t)r 2 dr .

R

( 1 5 .42а)

о

Для выпол нения операции интегрирования надо под инте
грал в ( 1 5.42а) подставить значение с · по ( 1 5.41):

6 � 1 l n+l е -n27C2 Fод Rf r sш
.
= -( - )
2
R n = I mt
о
k

где

(rт -' ) d
R

Входящий в (ж) икгеrрал берется по частям. Обозначим
а•

mc/R:, тогда du = dr,

v = _ ..!..
cos(ar).
а

В целом:

и •

r

(ж)

r, dv • sin(a7'dr,

ar)I

R r cos(ar) R
R R
R R 1
sin
R
r
cos(ar'\I11 о - о/ - f u d v = u� - оf v d u = - cos(ar) d r = (2 о =
а
а
а
о

о

а

поскольку sin О = О, при п - целом sin(7Cn) =
ных скобках содержит множителем нуль.

О,

I

о

а последнее слагаемое в фиrур

Подставим значение интеграла (з) в выражение (ж), внеся знак
"минус " в ( - l) n+ l пол им в нем мно.жиrель ( - l п + 2 . В целом:
уч
;
)
-•
с

_

1 (- l) n+2 е -n 2 1C2 Fод R 2 соs(mt) 6 � -k
mt
R 2 n=t mt
� �k 1 -n 21C 2 Fо д (-l) n+ 2 соs(rт) .
(и )
�
2
1t n=l п
При п четном ( - l)n+ 2 = 1 и cos ( n1t) = 1 , так что фрагмент
(- l)n+ 2 cos(rт) = 1 . При п нечетном (- l)n + 2 = -1 и cos(mt) = -1,
_

=

так 'ПО

указанный фрагмент тоже равен 1 . Поэтому окончательно
-.

С

=

с

- СР
- СР

(t)

Со

=

00

F

2 2
е-п 7С 0.11 ;
2 n=l
L 2
п
6

1

( 1 5 .43)

1t

1 30 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

такого рода выражение уже п ри водилось в уче бнике при из
учении теплообмена с шаром в условиях внутренней задачи
(разд. 7. 1 0 .3).
Для наглядно сти в ы п ишем нес колько первых членов разло
жения ( 1 5 .43):

(

6 1 -тr.2ро
С =1
е
2
1
-•

7t

д

+

-

1 -2 2 2ро
1
е тr. д + 2 е
2
3
2

)

32 2ро д + . . . .
тr.

(к)

Этот ряд при не очень малых значениях Fo4 быстро сходится, так как при
увеличении номера члена ряда показатель степени быстро растет. Например, при
Fo4 = О, 1 второе слаrаемое состаRЛЯет от первого лишь 1,3%, а сумма всех по
следующих не превышает 0,005%. Поэтому при Fo4 <: 0, 1
технических расче
тов впОJП1е можно оrраничиться первым членом ра311о:ж:ения, т.е. вместо ( 1 5 .43)
записать:

-·
С
=

ш

6

7r. 2

Д1lЯ

e- "2Fo� .

( 1 5 .43а)

Д1lЯ

При мен ь их значениях Fo4 второй и последующие члены ряда ( 1 5 .43), (к)
становятся со измеримыми с первым, и
расчета приходится брать больше

слаrаемых: их число при опрgеленном значении Fo4 < О, 1 зависит от требуемой
точности расчета. Значения С в зависимости от Fo4 (или от Fод) табулированы
в специальной литературе• .

Псевдоожиженный слой. Разн ые зерна в не прерывно р або
тающем ПС (т.е. с постоянным вводом и выводом твердого
материала) имеюг различное время пребЫВ!ЦIНЯ в зоне сушки ;
них будуr
поэтому и значения средней влажности С (t)
р азными. Что б ы определить получ ающуюся усредненную влаж
но сть зерен на выходе из псевдоожиженного слоя Сп с , необ
ходимо уче сть их распр еделение по времени пребывания
с оот
ветственно выражению (8 .8), п риведенному в разд. 8 . 3 .2:

для

Сре з = С п с
И

-.

С

пс

с
=

пс
Со

-

= J С (t)q>(t)d't

- СР

СР

оо _

о

00 - .

= J C ('t)q>('t)d't .
о

(л)

Поскольку перемешивание з ерен (частиц) в ПС чрезвычай
но интенсивное, то в качестве плотности распределен ия ис
пользуется формула (8 . 7 )
систем идеального перемешива1 ния : q>('t) =
здесь среднее вр емя пре бывания зерен
't c
Р

-- е 111 0 Р ; для

• См" например,
1 302

(8).

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

в зоне сушки 'tcp = Gт/G (смы сл Gт и G определен в разд .
1 5 .8 . 1 , о н также ясен и з рис . 1 5 .4 1 ). Подставив во второе из
•
выражений (л) значение С по ( 1 5 . 43) , имеем :
с•

aof 6

�

1

- п2
n2
_

п с

6

о

ао

L
=1t2 n : l

,L.,
n :l

1

_

п2

е

-n2 11 2 Fод

1

f e -n

оо

't c р

О

__

1

-'t c
p

- t
tcp d 't
е

2 11 2 Foд - /
e t tc p

=

d 't

(м)

Возьмем интеграл Iпt, содержащийся в (м), рас крыв запись
Fод = Dм't/R2 и изменив знак (и пределы интегрирования) в
ходе преобразований:
Int

00

= Je

2 2

- п lt

о

D"t - �
R2 е

-

00

t c p d 't

=J e
о

-

(n 2 2
11

)

Dw + -1- t
2
R
t p

c

d 't =

=

Подставив теперь значение Int в (м) и внеся множитель 'tcp в
знаменатель, получим:

-. = 6 I:00
с
пс

-----

1
7t 2 n : l п 2

1

-

п

2 7t 2 D м 't c p
R2

(о)

+1

Обозначим Dм'tcr/R2 = Focp и будем трактовать этот ком
плекс как усредненный диффузионный критерий Фурье
(Фика), базир ую щи йся на среднем времени пребывания з ере н
в рабочей зо н е ('tcp) · Тогда окончательно:
-.
с

пс

-

=

Сп с - С Р
С0 - С Р

=

6

00

(

1

)

..
o ___...,.
F_
__
_2
_7t
� :- 1 _n_2....,_2
cp + l
n

""'

п

(1 5

.44)

Это решение представляет собой медленно сходящийся ряд (даже при высо
ких значениях Focp): в самых блаrоприятных условиях второе с.лаrаемое состав
ляет более 6% от первоrо, а третье - более 1 ,2%. Здесь даже для технических
1 303

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

расчеrов пр иходится брать нес колько чле нов ряда ( их число определяеrся необ
ходимо й точн остью расчето в) .

Формула ( 1 5.44) позволя ет решать задачи эксплуатации и
прое�сrирован ия.
В задаче эксплуатации известны массовая производитель
ность по высушиваемому материалу G и масса материала в слое
Gт . Эrо позволяет рассчитать •ер = Gт/G и найти величину
Focp· Далее по ( 1 5.44) определяют значение кон центрационного
комплекса с; с и для известных С0 и СР - искомую концент
рацию С п с . Затем по материальному балансу ( 1 5.30) при
известных L и х1 расс ч итывают выходное влагосодержание х2 .
Трудный момент здесь - в неопределенности величины СР,
поскольку в начале расчета неизвестно х2 (кон центра цию СР
обычно без существенной погрешности можно считать равно
весно й с х2 ) . Эrо затруднение разрешается пуrем применения
итерационно й процедуры - до приемлемой сходимости равно
весн ых величин СР , х2•
В задачах проектирования заданы значения G, С0 (или U') и
Сп с (или U'�; неизвестна масса твердого материала Gт в ПС ,

обеспечивающая получение заданного значения С 0 с· Сначала

определяют концентрационный
комплекс с; с , причем
сложностей с концентра цией СР нет , так как х2 (при 'Известном
потоке L) отыскивается из материальною баланса ( 1 5.30). Да
лее по ( 1 5.44) находят Focp · Здесь возможны чисто технические
затруднения, так как Focp входит в несколько слагаемых в пра
части . Эти затруднения разрешаются использованием
во й
ЭВМ или предварительным табулированием функции ( 1 5.44) :
с; с = f ( Focp) , Focp = <р( с; с ) . П о наЙденному Focp рассчиты
вают •ер и при известно й производительности G вычисляют
искомое Gт = G· •cp · П ри меньших з начениях Gт не удастся по 
лучить высушенный материал с обусловленной выходной
влажностью С 0 с (или U'') - вл ажн о сть будет выше.
На пра�сrике удобно оперировать не массой Gт, а необходи
мой высотой псевдоожиженного слоя Н. Ее определяют на
основе очевид ного соотношения:
(п)
Gт = Pr (l - е) SаН;
ПС
ме
не
высоту
езультата
принимают
качестве
конечного
в
р
нее рассчитан н о й по (л) : при меньших Н глубина сушки будет
недостаточной.
П одход к определению сечения аппарата Sa изложен в разд.
1 5 . 8 .2.
1 3 04

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Проблемы разграничения задач массопереноса при сушке,
существования той или иной лимитирующей стадии либо про
текания процесса в условиях смешанной задачи, формирования
разграничивающих критериев (типа диффузионного критерия
Био и других) разрешаются на основе общих положений, из
ложенных в разд . 1 0. 10.5 .
Л ИТЕРАТУРА к главе 1 5
1 . Гельперин Н. И. Основные процессы и аппараты химической технологии .
М . : Хим ия , 1 9 8 1 8 12 с.
2. Гельперин Н. И., Айнштеiiн В.Г., Кваша В.Б. Основы техники псевдоожи
жения. М . : Химия, 1967. 664 с.
3. Гребер Г., Эрк С., Григулл ь У. Основы учения о теплообмене: Пер . с нем. /
Под ред. А.А. Гухмана. М.: ИЛ , 1958. 568 с.
4. Дытнерский Ю. И. Процессы и аппараты химической технологии . М . : Хи
мия, 1 995. 768 с.
5. Исаченко В.П., Осипова В.А., Сухомел А. С. Теплопередача. М.: Энергия,
19 69 . 440 с.
6 . Касаткин А.Г. Основные процессы и аппараты химической технологии .
М.: Химия, 197 1 . 784 с .
7. Кутателадэе С. С. Основы теории теплообмена. М.: Атомиздат, 1 9 79 .
416 с.
8. Лыков А . В. Теория тепло проводности . М . : Высшая школа, 1 9 6 7 .
600 с.
9. Лыков А.В. Теория сушки. М . : Энергия, 1968. 472 с.
10. Лыков М.В. Сушка в химической промышленности. М. : Химия, 1 970.
430 с.
1 1 . Михеев М.А. Основы теплопередачи. М.-Л . : Госэнерrоиздат, 1 956. 392 с.
.

1 2 . Муштаев В.И., Тимонин А. С., Лебедев В.Я. Конструирование и расчет ап
паратов со взвешенным слоем . М.: Химия, 199 1 . 344 с.
13. Основные процессы и аппараты химической технологии Под ред. Ю.И.
ДЬПlfерскоrо. М. : Химия, 1 99 1 . 496 с.
14. Павлов К. Ф. , Романков П. Г. , Носков А.А. Пр имер ы и задачи по
курсу процессо в и аппаратов химической технологии . Л . : Химия, 1987.
574 с.
1 5 . Перри Дж. Справо•1ник инженера-химика: Пер. с анг.л. Под ред.
Н . М.Жаворонкова. Л.: Химия, 1969. 1 144 с. (т. 1 , 640 с; т.11, 504 с.).
16. Романков П.Г. , Рашковская Н.Б. Сушка во взвешенном состоянии . Л. :
Химия, 1979. 272 с.
17 . Романков П.f., Фролов В. Ф. Массообменные процессы химичес
кой технологи и (системы с дисперсной твердой фазой). Л . : Химия, 1 99 0 .

/

/

3 84

с.

1 8 . Рудобашта С. П.

1980. 248 с.

Массоперенос в системах с твердой фазой. М . : Химия,

1 305

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

1 9 . Сажин Б. С., Сажин В. Б.
1977. 448 с.
20. Хоблер Т. Теru10передача

Научные основы техники сушки. М . : Наука,

и теплообменники: Пер. с п ольск./ Под ред.
П.Г. Романкова. Л.: Госхимиздат, 196 1 . 820 с.
2 1 . Циборовский Я. Процессы химической технолоmи: Пер. с польск./ Под
ред. П.Г.Романкова. Л.: Госхиыиздат, 1958. 932 с.
22. Членов В.А., Михайлов Н.В. Виброкипящий слой. М . : Наука, 19 72 .
344 с.

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

rлава 1 6
КРИСТАJШИЗАЦИЯ

Кристаллизация пред ставля ет с о бо й процесс о бразования
кристалличес кой фазы из расплавов, растворов и газ овой ф азы .
Эrот процесс ис пользуется в химичес ко й , нефтехи м иче с ко й ,
коксохимичес кой, металлур гичес кой, пищево й , фармацевти
ческой и других отраслях промышленности. С помощью кри
сталлизации решаются следующие задачи:
- получение твердых продуктов в виде блоков, rр анул , че
шуек и т.п. ;
- разделение различных смесей на фракции, обо гащенные
тем или иным компонентом ;
- вьщеление различных веще ств из технических и природ
ньrх растворов ;
- глубо кая очистка ве ществ от примес е й ;
- кон центриро вание разбавленньrх растворов пугем вымо р аживан ия растворителя;
- выращивание монокристаллов ;
- получение веще ств с опред еленным и физи ко - механи ческим и сво й ствами ;
- нанес ение на пове рхность твердых тел различньrх по кры
тий и др. •
Кристалл изация отличается чрезвычайно большим коли
чество м м етодов и прие мов ее реализации, которые можн о
разделить на пять ОСНО ВНЬIХ rрупп :
- кристаллизация из расплава ;
- кр исталл изация из раствора;
- кр исталл изация из паровой ( газо во й) фазы ** ;
- кристалл изация в твердом состоянии ;
- кр исталл изация при химическом взаимодействии веществ.
Закономерности процесса кристаллизации зависят от целого
ряда фаlСЮров, важн е йшими из которых являются: с о став ис
ходного веще ства (с_м еси, раствора), его физико -химические
с во йства, вид (характер) диаrр аммы равновес ия ф аз рас с матри • Более подробные сведен ия о практическом использовании процесса кри
сталлизации содержатся в (2 -6, 1 0 -12, 14 - 16).
•• Процесс кристаллизации из rазовой фазы обычно называют десублимацией
или "твердофазной" конденсацией. Он рассмотрен в гл. 1 8 .
1 307

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ваемой системы , способ создания пе ресыщения, интенсивность
подвода и отвода теплоты, интенсивность перемешивания.
Изложенные в настоящей главе сведения в значительно й
мере носят общи й хар актер. Они имеют непосредственное от
ношение к описанным в гл. 1 7 и 1 8 п роцессам растворения ,
сублимации и десублима ции ве ществ.
16.1. ОСНОВНЫЕ ОСОБЕННОСfИ
ПРОЦЕССА КРИСТАJUIИЗАЦИИ

Твердые тела по своей структуре моrуг быть кристалл иче
скими и аморфными.
Кристаллы моrуг состоять из ионов, атомов, ионных ради
кал ов , молекул и даже из жи вых организмов ( вирусов) . Так,
кристалл ы металл о в и многих неорганических соединений
(соли , щелочи) построены из атомов и ионов, а большинства
органичесюtх веществ - из молекул. Кристаллы строятся по
принципу наиболее пл отно й упако вюt частиц, слои которых
строго повторяются через определенные интервалы, - говорят,
что кристаллическая фаза обладает как ближним, так и даль
ним порядком расположения элементарных частиц в твердом
теле. П р и этом расположение их в пространственной решетке
кристалло в спе цифично для каждого вещества. Оrличительным
признаком кристаJVIического состояния является наличие четко
выраженной температуры плавления вещества.
Аморфные тела подобно жидкостям обладают лишь ближ
ним порядком расположения части ц . Они характеризуются
отсутствием четко выраженно й точюt плавления . При повыше
нии температуры аморфные тела постепенно переходят в жид
кое состояние благодаря возрастанию интенсивности колеба
ний атомов (молекул). К аморфным телам относится большое
число высокомолекулярных соединений (пластичесюtе массы ,
смолы и др : ) , а также многие силикатные вещества (например,
стекла).
Аморфные вещества , подобно газам и жидкостям, вследст
вие беспорядочн ого р асположен ия молекул изотропны. Кри
сталл ы же обычно анизотропны: их физичесюtе свойства не
одинаковы в различных направлениях.
Существуют вещества, которые моrут нахощrrься в ЖltlU(окристаJJJ1Нческом co
CТOlllllDI (ЖJtlU(Иe кpиcтaJJJW) . В некотором интервале темпера'I)'р таким вещест
вам одновременно присущи свойства как жидкостей (высокая текучесть), так и
кристаллических тел (анизотропия). При определенной темпераwе они перехо
дят в обычное жидкое состояние.
Температура , при которой происходит переход вещества из
жидкого состояния в кристалл ическое, н азывается температу-

1308

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Температура обратного перехода - из
твердого состояния в жидкое - называется температурой плав
ления. Часто эти температуры не совпадают друг с другом, что
связано с особенностями кинетики образования твердой фазы.
Наиболее низкую температуру плавления имеют молекуляр
ные кристалл ы , для которых характерна весьма слабая связь
между частицами, образующими кристаллическую решетку.
Температура плавления таких веществ редко превышает 300 " С.
Кристаллические вещества, построенные из ионов или атомов,
имеют более высокие температуры плавления.
Температура кристаллизации индивидуальных веществ по
стоянна при определенном давлении. Эrа температура зависит
от природы жидкой и возникающей твердой фазы. Некоторые
вещества могуг образовывать несколько кристаллических фаз,
имеющих различное строение решетки (явление полиморфиз
ма), плавление которых может происходить при разных темпе
ратурах. Так, сера моноклинной стру�сrуры плавится при
1 14 С а ромбической стру�сrуры - при 1 19 С
Внугренняя энергия жидкости выше, чем упорядоченного
твердого тела, поэтому переход из одного состояния в другое
сопровождается выделением или поглощением энерrnи. Тепло
та, вьщеляющаяся при переходе жидкости в твердое тело, т.е.
теплота кристаллизации rкр равна и противоположна по знаку
рой кристаллизации.

"

,

"

теплоте плавления

rIVJ .

.

•

Переход кристалли ческой фазы в жидкое состояние
(плавление) связан со значительно меньшими изменениями в
степени упорядоченности частиц, чем переход из жидкого со
стояния в газообразное. Поэтому теплота плавления значи
тельно (в 4- 7 раз) меньше теплоты испарения.
При температуре кристаллизации имеет место равенство
энерrnй Гиббса• жидкой Gж. и твердой Gт фаз :
(16. 1)

В свою очередь величины Gж. и Gт можно представить в виде
( 16 .2)
Gж. Нж. - ТSж. и Gт Нт TSy ,
=

=

-

�де Н.. и Sa, Нт и Sr - экrальпия и эmропия сооnеrствеюю жидкой и твердой фаз.

При температуре кристалл изации Ткр разность энтальпий
фаз представляет собой скрытую теплоту фазового перехода.
При этом с учетом зависимостей ( 1 6 . 1 ) и ( 1 6.2) имеем:
rWI Нж. - Нт = Ткр(Sж - Sy) ТкрЛS'кр . ( 1 6.З)
Гкр
Мольное изменение энтропии при кристаллизации различ
ных веществ не столь постоянно, как при парообразовании.
=

-

=

=

• Изобарно-изотермический потенциал ("свободная" энергия).

1 309

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Это не позволяет сформировать однозначное полуэмпириче
ское соотношение, аналогичное правилу Трутона, связы
вающему теплоту и температуру фазовою перехода. Имею
щиеся экспериментальные данные показывают, что в порядке
. грубою приближения при кристаллизации можно принять: для
элементарных веществ ЛSкl' = 8+ 12 Дж/(моль·К), для неоргани
ческих соединений - 2 1 -29, для органических - 38-46 .
Зависимость температуры кристаллизации Ткр индивидуаль
ньrх веществ от давления р можно описать уравнением . Клау
зиуса-Клапейрона :
( 16 .4)
где

Vк, Vж

-

удельные объемы кристаллической и :жидкой фаз.

Удельный объем жидкой фазы может бьпь больше или
меньше удельною объема твердой фазы. Для большинства ве
ществ Vж > vк , поэтому для них температура кристаллизации
возрастает при увеличении давления. Аномальный случай
Vж < vк наблюдается, например, у воды и висмуrа, для которЬIХ
Ткр падает с ростом давления.
При постепенном охлаждении расплавов индивидуальных
веществ температура t = tкр в точке кристаллизации в идеале
остается постоянной во времени - до тех пор, пока весь рас
плав не закристаллизуется (рис. 16. 1 , а). Дальнейший отвод теп
лоты вызывает, естественно, понижение температуры. Такое
поведение расплава наблюдается в тех случаях, когда при тем
пературе кристаллизации в нем сразу появляются центры кри
сталлизации или когда в расплав при tкр вводят ютовые центры
кристаллизации (затравку).
Однако на практике ход температурной кривой часто отсту
пает от идеальною из-за переохлаждения жидкой фазы ниже
точки кристаллизации на величину лt (рис. 1 6 . 1 , 6) . Если пере
охлаждение Лt невелико, то при появлении центров кристалли 
зации начнется процесс кристаллизации, и за счет выделяю
щейся теплоты температура вещества может повыситься до
температуры кристаллизации tкр· При сильном переохлаждении
жидкой фазы выделившейся теплоты может оказаться недоста
точно для повышения температуры до равновесною значения
lxp (рис. 1 6 . 1 ,в) . Способность жидкой фазы к переохлаждению
связана с заро.)IЩением и ростом кристалло в (эти вопросы рас
сматриваются ниже). При охлаждении расплавов аморфных
веществ не происходит выделения теплоты фазовою перехода,
поэтому в данном случае температура системы монотонно из
меняется во времени (рис. 1 6 . 1 , г).
При плавлении твердьrх тел получаются кривые, сходные с
кривыми охлаждения. Однако существует и различие межцу
1310

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

t
t'ltfl

t

1

� � � -� ~
lкр

--

а

Puc. 16. J.
а

t

б

t

в

t

г

t

Кривые охлаждения расплавов:

Jфисrаллизация в отсуrсrвие переохлаждения, 6, • - JСрисrаnлизация при неболь
шом и значительном персохлаJ1ЩеЮ1ЯХ, г - затвердевание аиорфноrо всщесrва
-

процессами плавления и затвердевания: кристаллическую фазу
практически н ельзя перегреть. Плавление всегда начинается
при достижении температуры плавления .

16.2. ФАЗОВОЕ РАВНОВЕСИЕ
При анализе диаграммы состояния k- компонентных систем
широко используется приведенное в разд. 10.З.1 правило фаз
Гиббса
(10. 1)
rp = k - ф + 2 ,
r,це ip - число степеней свободы, ф - число фаз.
Эrо правило позволяет предсказать появление или исчезно
вен ие тех или иных фаз в данной системе при различных усло
виях; оно показывает также пуги управления процессами фаз о 
ВЬIХ превращений. Рас с мотрим основные особенности ф аз овых
превращений в с и стемах с : р азл ичным числом компонентов
применительно к про це ссу кристаллизации.

16.2. 1 . Однокомпонентные системы

В общем случае для однокомпонентной системы (k = 1 )
возможно сосуществование фаз : газообраз ной, жидкой, жидко
кристаллической и одной ил и нескольких кристаллич еских
модификаций .
В качестве независим ых переменных для однокомпонентно й
системы вы ступают температура t и давление р. Согласно вы
ражению (1 0. 1 ) максимально возможное число одновременно
сосуществующих фаз в однокомпонентной равновесной систе
ме равно трем. При этом число степеней свободы rp = О
(система нонвариантна: значения параметров t и р жестко фик
сированы). В этом случае изменение любой из независимых
переменных (t или р) приводит к исчезновению одной из фаз.
131 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

р

D
Жидкость

Тt1ердая

фаза

р

с

Пар
а

б

Диаграмма состояния однокомпонеmной системы при отсутствии
п ри на.'lИЧИИ (б) п олиморфных модификаций
Рис. 1 6. 2.

(а) и

Если одновременно в равновесии находятся две различные
фазы, то число степеней свободы q> = 1 , и равновесие будет
моновариантным. Это означает, что одну из независимых пе
ременных (t или р) можно изменять в определенных диапазо
нах при сосуществовании упомянуrых фаз. В области суще
ствования одной фазы число степеней свободы q> = 2, и систе
ма будет бивариантна.
Равновесие однокомпонентной системы может быть пред
ставлено в виде диаграммы фазового состояния. При этом
каждому состоянию системы на диаграмме соответствует точка,
отвечающая определенным значениям температуры и давления.
Для однокомпонентных систем, имеющих только одну твер
дую фазу и не образующих жидкокристаллических фаз, на
диаграмме состояния нонвариантному равновесию отвечает так
называемая тройная точка А (рис. 1 6.2,а). В этой точке одно �
временно при фиксированных для каждого вещества значениях
температуры и давления моrут находиться 11 равновесии три
фазы: газообразная, жидкая и твердая. Моновариантным равно
весиям на диаграмме отвечают линии ВА, СА и DA. Линию ВА
часто называют еще кривой возгонки (десублимации), линию
СА
кривой испарения (конденсации), а линию DA - кривой
плавления (кристаллизации). При этом наибольшими угловыми
коэффициентами отличается кривая плавления (из-за очень
малой сжимаемости жидкой и твердой фаз), а наименьшими кривая испарения. Участки, заключенные между линиями мо
новариантных равновесий, представляют собой области бивари
антного равновесия, где в определенных пределах можно изме
нять температуру и давление без исчезновения рассматри
ваемой фазы.
Если вещество в твердом состоянии претерпевает поли
морфное превращение, то диаграмма состояния усложняется,
так как каждой модификации твердого вещества соответствует
собственная область. В данном случае появляются линии мо1 3 12
-

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

новариантных равновесий, разграничивающие различные мо
дификации вещества, а также дополнительные тройные точки .
Диаграмма состояния вещества, имеющего две полиморфные
модификации, показана на рис. 1 6 .2, б. С увеличением числа
модификаций фазовые диаграммы еще более усложняюгся.
Так, существованию шести полиморфных модификаций льда
отвечают семь тройных точек на диаграмме состояния воды.
16.2.2. Бинарные системы

Диаграммы состояния бинарных систем изображают зави
симость между тремя переменными: составом (концентрацией
одного из компонентов смеси), давлением и температурой.
Соответственно, эта зависимость может быть представлена в
пространственной системе координат. Построение полных
диаграмм состояния бинарных систем сопряжено с большими
экспериментальными трудностями и пока осуществлено для
немногих систем.
В процессе кристаллизации из расплавов и растворов обыч
но участвуют только жидкие и твердые фазы, т.е. мы имеем
дело с конденсированными системами, удельные объемы которых
мало зависят от давления. Поэтому изучение равновесия в та
ких системах часто проводят при постоянном давлении (чаще
всего - при атмосферном). В результате получают функцио
нальные зависимости между составом и температурой, которые
можно графически изобразить на плоскости.
Если система состоит только из одной жидкой фазы, то при
постоянном давлении она бивариантна и допускает произволь
ное изменение в определенном интервале независимых пере
менных - температуры и состава. При наличии двух фаз си
стема будет моновариантной, и ее равновесное состояние
изображается линией. Такие линии ограничивают области су
ществования отдельных фаз. Точка пересечения двух линий
соответствует одновременному существованию трех фаз. В
этом случае система нонвариантна, и изменение любого пара
метра (температуры ил и состава) приводит к исчезновению
одной из фаз .
Бинарные системы обладают большим разнообразием диа
грамм фазового равновесия; наиболее часто встречающиеся из
них показаны на рис. 1 6.3. Процесс кристаллизации бинарных
смесей, как правило, происходит в диапазоне температур. Он
начинается при достижении в системе температуры ликвидуса tл
(температуры начала кристалл изации), а заканчивается при
температуре сол идуса fc (температуре полной кристаллизации ).
Геометрическое место точек, соответствующих температурам
начала кристалл изации lл смесей различного состава, называет1313

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

А

х

А+В

-

'л
ХЕ

в

а

А

в

-

х

б

а

tp

А

в

в

А

в

-

х

г

'в
/А
tв
,
А

х
Е,

х

с

--

д

ХЕ

2

в

А

А+С

х

-

е

с

в

а - нс образующей твердых расrворов, б - с нсоrраничснной взаимной расrворимостью
хомпонсшов в твердом сосrоЯЮ1и; в, 2 - с оrраничснной расrворимостью хомпонешов в
твердом сосrоЯЮ1и (в - эвrеnичесхая, 2 - псритсJСТИчесхая), д - с образованием хонrру
эшно nлавящеrося соединения, е - с образованием инхонrруэJПНо nлавящеrося соединения

Рис. 16.З. Диаграммы фазового равновесия бинарных сисrем:

1 3 14

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ся линией ликвидуса, а точек, соответствующих температурам
-

tc ,

линией солидуса .
На рис. 1 6 . 3 , а показана

диаграмма равновесия фаз бинарной
системы, не образующей твердых растворов. Данная диаграмма
построена в координатах температура-состав (концентрация)
смеси. Линии ликвидуса для данной смеси - кривые аЕ и ЬЕ.
Линия солидуса здесь представляет собой прямую cd, прохо
дящую через эвтектическую точку Е, в которой система нахо
дится в нонвариантном состоянии. Участок линии ликвидуса
аЕ по суги дела является линией насыщения системы компо
нентом А, а участок ЬЕ - линией насыщения компонентом В.
Выще линии ликвидуса система находится в ЖJlдКОМ со
стоянии L. При охлаждении расплавов с концентрацией х < ХЕ
ниже линии ликвидуса начинается образование кристалл о в
компонента А, масса которых растет с понижением температу
ры. При этом состав жидкой фазы (маточника) изменяется по
линии ликвидуса аЕ до эвте:кrической точЮI Е, соответствую
щей температуре кристаллизации эвте:кrиЮI tв = tc. При охлаж
дении расплавов с концентрацией х > ХЕ первоначально обра
зуются кристаллы чистого компонента В , и состав ЖJ1дкой
фазы изменяется по линии ЬЕ. Ниже температуры tв система
полностью переходит в кристаллическое состояние с образова
нием механической смеси кристаллов компонентов А и В. При
х = ХЕ система кристаллизуется при постоянной температуре
1Е = fc .

Для описания линии ликвидуса рассматриваемых систем часто используют
уравнение Шредера, п олученное для идеальных растворов:
1rn: = ь

-

а/т ,

( 1 6 . 5)

где х - мольная равновесная концентрация компонента А в жидкой фазе при
273 + t; rпл,л мольная теплота
температуре t; Ь
rпл .А/R Тл; а = rпл .А/R; Т
плавления компонента А; R
универсальная газовая постоянная; Тл = 273 + tл;
tл - температура плавления компонента, в фазовом поле которою происходит
кристаллизация .
=

=

-

-

Для систем, отличающихся от идеальных, линию ликвидуса описывают раз
личными эмпирическими зависимостями .

Весьма часто встречаются системы с неограниченной взаимной
в твердом состоянии, т.е. обра
зующие непрерывный ряд твердых растворов. Температурам нача
ла кристалли зации таЮiх систем на диаграмме фазового равно
весия (рис. 1 6.3,б) соответствует кривая ликвидуса tл = f(x), а
температурам полной кристаллизации - линия солидуса !с =
= f(x) . Выше линии ликвидуса система находится в жидком со
стоянии L, ниже линии солидуса - в твердом состоянии S. В
области, заключенной между кривыми ликвидуса и солидуса,
система rетероrенна: она состоит из твердой и жидкой фаз,
1315

растворимост ью комп он ентов

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

причем состав равновесных фаз Хк и Хм зависит от температу
ры t.
Для описания фазового равновесия систем, образующих не
прерывный ряд твердых растворов, близких к идеальным,
•
можно использовать теоретическое уравнение Ван-Лаара .

Функциональную связь между концентрациями кристаллической Хк и жид
кой х,,. фаз для рассматриваемых систем можно также установить с помощью
равновесною коэффициента распределения т:
т =

Х к (l - х м ) .
Хм (l - Х к )

( 1 6.6)

Дл я разбавленных систем (х,.. , Хк < < 1) зависимость ( 1 6 .6) упрощается:
( 16 .7)

Системы с ограниченной растворимостью компонентов в
твердом состоянии бываюг двух типов: эвтектического и пери
тектического .
Для систем эвтектического типа (рис . 1 6.З , в) точка нонва
риантноrо состояния Е находится ниже температур кристалли
зации чистых компонентов tл и t8. Как и для других диаграмм,
выше линии ликвидуса аЕЬ располагается область жидкой
фазы. Ниже линии солидуса acEdb система находится в твер
дом состоянии. Область acfA соответствует ограниченным
твердым растворам а , образованн ым на базе компонента А, а
область bdhB
ограниченным растворам /3 на базе компонента
В . В области асЕ система состоит из двух фаз: твердой а, со
став которой с понижением температуры изменяется по кривой
ас, и жидкой, состав которой изменяется по отрезку линии
ликвидуса аЕ. В области bdE система состоит из жидкой фазы
и кристаллов твердого раствора /3 , а в области fcdh система
представляет собой смесь кристаллов твердьIХ растворов а и 13 .
Бинодальные кривые fc и dh н а диаграмме показывают изме
нение взаимной растворимости компонентов в твердом со
стоянии при различных температурах.
На диаграмме перитектического типа (рис. 1 6.З, г) точка
нонвариантного равновесия Р находится межлу температурами
кристалл изации чистых компонентов. Области acfA и bdhB
соответствуют твердым растворам а и 13 . В области аРс из жид
кой фазы вьщеляются кристаллы твердого раствора а , а в об
ласти b Pd - кристалл ы твердого раствора /3.
При охлажлении бинарных систем нередко наблюдается
кристалл изация с образованием химических соединений, устойчи
вьIХ лишь в твердом состоянии. Состав последних соответству
целые числа. Примером таких
ет формуле АпВт, где п и т
-

-

• См. ( 1 ) .

1316

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

соединений являются кристаллогидраты солей. Данные си
стемы подразделяются на два вида: с конгруэнтно плавящимися
соединениями - они устойчивы вплоть до температуры их плав
ления (рис . 1 6 . 3 , д) ; с инконгруэнтно плавящимися соединениями
- они разлагаются н иже точки их плавления (рис. 1 6 . 3 , е) .
Конгруэнтно плавящиеся соединения могуr рассматриваться
как индивидуальные компоненты . При образовании такого
соединения С диаграмма равновесия фаз как бы распадается на
две сопряженные диаграммы, из которых одна характеризует
равновесие в системе компонент А-соединение С, а вторая равновесие в системе компонент В-соединение С . При этом
точка М соответствует температуре плавления соединения С .
Инконгруэнтно плавящееся соединение при температуре /р
распадается на жид кую фазу Р и твердую фазу, представляю
щую собой кристалл ы одного из компонентов смеси .
Для разделения и очистки веществ часто применяют про
цесс кристаллизации нз раствора. Сущность его заключается в
том, что для понижения температуры кристалл изации или для
повышения эффективности разделения к исходной смеси (или
к очищаемому веществу) добавляют низкоплавкий компонент
(растворитель). С термодинамической точки зрения процесс
кристаллизации из раствора не отличается от процесса кри
сталлизации из расплавов. Любой расплав, содержащий более
одного компонента, независимо от температуры его кристалл и 
зации, представляет собой раствор . Поэтому существующие
разграничения процессов кристаллизации из расплава и рас
твора являются условными .
При организации процесса кристаллизации с применением
растворителей, а также при анализе его результатов используют
так называемые "кривые растворимости", которые описывают
функциональную зависимость растворимости вещества в том
или ином растворителе от температуры (см. гл. 1 7) . Под
черкнем, что кривые растворимости представляют собой част
ный случай диаграмм фазового равновесия; они являются
участками кривых ликвидуса.
1 6.2.3. Тройные снстемь1
В общем случае фазовое равновесие трехкомпонентных систем
определяется четырьмя независимыми переменными: темпера
турой , давлением и концентрациями любых двух компонентов.
Поэтому графическое представление равновесия в таких систе
мах требует изображен ия в "четырехмерном пространстве" и
может бьпъ реализовано с использованием специальных гра
фических методов. Для практических целей обычно используют
более простые изобарические диаграммы фазового равновесия

1317

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

тройных систем: они представляют собой трехгранную призму,
основанием которой служит треугольник составов, а по орди
нате отложены значения температуры. Рассмотрим некоторые
из таких диаграмм.
Изобарическая диаграмма равновесия системы, не образую
щей твердых растворов, показана на рис. 16.4,а. Точки а, Ь и с
соответствуют температурам плавления индивuдуальных ком
понентов. На боковых гранях призмы нанесены линии ликви
дуса аЕ 1 Ь, ЬЕ2с и сЕ3 а бинарных систем соответственно АВ, ВС
и АС с точками бинарн ых эвтектик Е 1 , Е2 и Е3 . При добавле
нии третьего компонента к бинарным смесям температура на
чала кристалл изации понижается, поэтому наряду с двойными
эвтектическими точками в тройной системе существует еще
одна - тройная эвтектическая точка Е. Совокупность точек
начала кристалл изации тройных смесей образует поверхности
ликвидуса. При этом поверхность аЕ1 ЕЕз соответствует первич
номv выделению (насыщению) компонента А; поверхность
ЬЕ 1 ЕЕ2 - выделению В; поверхность с Е2ЕЕз - выделению С.
При взаимном пересечении этих поверхностей образуются ли
нии вторичных выделений Е 1 Е, Е2Е и ЕзЕ. Линия Е 1 Е показы
вает изменение положения точек двойных эвтектик А + В под
влиянием компонента С; линия Е2Е - точек двойных эвтепик
В + С под влиянием компонента А; линия Е,Е - эвтектик А +
+ С под влиянием комп онента В. Эти три линии пересекаются в
точке тройной эвтектиюf Е самой низкой точки поверхности
ликвидуса. В точке Е поверхность ликвидуса системы касается
поверхности солидуса, представляющей собой горизонтальную
плоскость А'В'С'.
Тройной расплав, изображаемый некоторой точкой G, при
охлаждении будет оставаться жидким, пока его температура не
снизится до точки ликвидуса lл. После этого начнется первич
ная кристалл изация компонента А, так как фигуративная точка расплава G в рассматриваемом случае находится над поверхностью ликвnдуса именно этого компонента. Выделение
твердой фазы (кристаллов компонента А) вызывает, естествен
но, изменение состава жuдкой фазы. Так, при охлаждении
смеси до температуры t1 состав жидкой фазы будет соответ
ствовать точке М, лежащей на поверхности ликвидуса компо
нента А.
При охлаждении смеси G от tл до t2 состав маточника будет
изменяться по линии GлК. После достижения кривой вторич
ных выделений Е 1 Е (точка К) совместно будут выделяться кри
сталлы компонентов А и В. При этом состав маточников будет
изменяться по линии КЕ.
-

•

• Точка, хар актер и зую щая н араметры системы (температуру и ее состав) .
1318

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

а

с

в

б
Рис. 16. 4. Пространственная (а) и плоская (б) диаrраммы фазовоrо равновесия
тройной системы; не обр азующей твердых растворов

1319

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Для определения состава и массы фаз в процессе охлажде
ния удобно использовать плоскую диаграмму тройной системы,
представляющую собой проекцию точек пространственной
диаграммы на ее основание (рис . 1 6.4,6) . На этой диаграмме
исходная смесь показана точкой G. В процессе первичной кри
сталлизации точка, соответствующая составу жидкой фазы,
перемещается по прямой AG по направлению к точке К, по
скольку в системе идет образование кристалл о в компонента А.
Если при некоторой тем пературе фигуративная точка жидкости
займет положение М, то по "правилу рычага" отношен ие мас
сы выделившихся кристаллов компонента А к массе жидкой
фазы выразится отношением отрезков MG и GA. Отношение
же количеств выделившегося твердого вещества в конце пер
вичной кристаллизации и оставшейся жидкости выразится от
ношением отрезков G К и GA.
При вторичной кристаллизации состав жидкой фазы изме
няется по кривой КЕ, а состав твердой фазы - по прямой АН .
Для промежуточного состояния системы, в котором состав
жидкой фазы будет соответствовать точке N, отношение коли 
чества твердой фазы к количеству жидкости равно отношению
отрезков GN и GF. Отношение же количеств твердой и жид
кой фаз при заверш е нии вторичной кристалл изации, когда в
системе будет достигнута температура кристалл изации тройной
эвтектики, выразится отношением отрезков GE и G H .
Таким образом, для рассматриваемого расплава характерны
три стадии кристаллизации : первичная (одного компонента) ,
вторичная (двух компонентов) и затвердевание тройной эвтек
тики .
Если фигуративная точка исходного расплава лежит на вер
тикали, проходящей через кривую вторичных выделений
(например , точка D на рис. 1 6 .4 , б) , то при охлаждении распла
ва до этой кривой сразу начнется вторичная кристаллизация ( в
данном случае компонентов А и С). Если же проекция точки
исходной смеси находится на прямой, соединяющей точку
тройной эвтектики с какой-либо вершиной треугольника, то
после первичной сразу наступает кристаллизация тройной эв
тектики. Наконец, если исходный расплав соответствует соста
ву тройной эвтектики, то отсутствуют процессы первичной и
вторичной кристаллизации и сразу кристаллизуется смесь со
става Е.
Для анализа фазовых превращений в тройных системах
часто используют изотермические сечения пространственной
диаграммы плоскостями, параллельными ее основанию. На
рис. 1 6 . 5 показаны несколько таких сечений пространственной
диаграммы (см . рис . 1 6 .4,а) .
1 320

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

с

с

с

с

В А

А

в

Рис. 16. 5. Изотермические сечения диаrраммы фазового равновесия тройной
системы, не образующей твердых растворов

Сечение 1 отвеч ает температуре несколько ниже точек IUiав
лен ия компонентов В и С, но выше точки плавления компо
нента А. Здесь имеются три области, из которых одна соответ
ствует однофазному (гомогенному) состоянию L, а две другие
- гетерогенным областнм равновесия первично выделившихся
кристаллов В и С и жидкой фазы. Линии nm и ef являются
изотермами, а прямые, соед иняющие вершины треугольника с
точками на изотермах,
конод а ми
Сечение 1 1 проведено на уровне температуры кристалл и за
ции двойной эвтектики Еъ здесь видна одна жидкая гомоген ная область L и три гетеро генные области . Сечение 1 1 1 , отве
чающее температуре двойной эвтектики: Е3 , содержит еще две
гетерогенные области трехфазного равновесия L+A+ B и
L+ B+C. Наконец, се ч е н ие IV соответствует температуре н иже
точки существования двойных эвтектик. Здесь имеются уже
три трехфазные области, три двухфазные и одна однофазная .
Рассекая диаграмму рядом паралл е льных плоскостей , прохо
дящих через определенные тем п ературные интервалы, и орто
гонально проецируя получаемые изотермы на основание диаг-

.

1321

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

п-Эвгенол
- J 0, 2 ° C

°
J З, 5 С
о-Эвгенол

8, 5 ° С
м-Эвгенол

Рис. 16. 6. Плоская диаrрамма фазовоrо равновесия 1JIОЙной системы (изомеров
эвгенола); tЕ = 60, 5 • с
-

раммы, получают плоскую диаграмму равновесия фаз с семей
ством изотерм (рис. 16.6). Подобные диаграммы дают нагляд
ное представление о характере поверхности ликвидуса и позво
ляют провести графичес Ю1е построения процесса кристаллиза
ции тройных смесей при различных температурах.
При анализе превращений в тройных системах используют
ся также различные вертикальные
(политермические) сечения
•
диаграммы равновесия фаз .
На рис . 16.7,а показана пространственная диаграмма фазо
вого равновесия тройной системы с неограниченной раствори
мостью компонентов в жидком и твердом состояниях. На гра
нях диаграммы нанесены кривые равновесия бинарных систем,
через которые проход я т поверхности ликвидуса и солидуса
тройной системы. Эти поверхности пересекаются в точках,
отвечающих температурам плавления индивидуальных компо
нентов.
В точках, лежащих выше поверхности ликвидуса, все рас
плавы находятся в жидком состоянии, а в точках ниже поверх
ности солидуса система состоит из кристаллов твердого рас
твора. Между поверхностями ликвидуса и солидуса (рис . 16.7,6)
система находится в гетерогенном состоянии и состоит из
жидкой фазы Ч и кристалло в твердого раствора а. . Превраще
ния , происходящие при переходе тройной системы в твердое
состояние, протекают подобно превращениям в бинарных си
стемах, кристалл изующихся с образованием непрерывного ряда
• См. ( 1 , 5 J .

1 322

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

В'

а

б

Рис. 16. 7. Пространственная диаграмма фазового равновесия тройной системы,
образующей непрерывный ряд твердых растворов (а) , и ее изотермическое сече
ние (б)

твердых растворов. Разница между кристаллизацией бинарных
и тройных расплавов заключается в хара:к:rере изменения со
става фаз . В первом случае это изменение протекает по линиям
ликвидуса и солидуса, расположенным в одной плоскости, а во
втором - по пространственным поверхностям ликвидуса и
солидуса.
Кристалл изация охлаждаемого тройного расплава исходного
состава G начинается по достижении точки L1 , лежащей на
поверхности ликвидуса. При этом состав первых образующихся
кристаллов твердого раствора соответствует точке S 1 на по
верхности солидуса при той же температуре. При дальнейшем
понижении температуры состав жидкой фазы изменяется по
кривой L1 L3 на поверхности ликвидуса, а состав кристалл о в
твердого раствора
по кривой S 1 S3 на поверхности солидуса.
Процесс кристалли зации заканчивается в точке S 3 .
Проекции линий L1 L3 и S 1 S3 на основание диаграммы по
зволяют определить соотношение количеств твердой и жидкой
фаз в процессе кристаллизации. Так, при промежуточной тем
пературе, соответствующей точке n , отношение масс выделив
шихся кристаллов и жидкой фазы равно отношению отрезков
�'G' и S2'G'.
Для анализа фазовых превращений рассматриваемой си
стемы также используют политермические и изотермические
разрезы диаграммы равновесия . На рис . 16.7,б показано одно
из изотермических сечений диаграммы горизонтальной плос
костью, проходящей ниже температуры плавления компонента
-

1 323

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

с

Рис. 16. 8. Плоская диаrрамма фазово
го равновесия тройной системы,
образующей непрерывный ряд твер
дых растворов:
спл ошНЬi е Л ИЮIИ - из отермы ликви 
дуса , nприхо выс линии
- и зотермы
солидуса

С . На этом сечении имеется
три области: жидкой фазы L,
твердого раствора а. и гете
рогенной смеси жидкой и
твердой фаз . В гетерогенной
В
области обычно проводятся
А
коноды, соединяющие со
ставы равновесных фаз.
Выполнив ряд последовательных сечений и спроецировав их
на основание диаграммы, можно получить плоскую диаграмму
с семейством изотерм, позволяющих судить о характере по
верхностей ликвмдуса и солмдуса рассматриваемой системы
(рис . 1 6 . 8 ) .
Более подробные сведения о диаграммах различных бинар
ных, тройных
и четверных систем содержатся в специальной
*
литературе .
1 6.З. КИ НЕТИ КА ПРОЦЕССА КРИСТАЛЛ И ЗАЦИИ

Вьщеляют три основные стадии процесса кристалл и зации:
создание пересыщения исходной системы, зарождение центров
кристалл и зации и рост кристалл о в.
16.3. 1 . Создан и е пересыщения

Для того чтобы начался процесс кристаллизации, в системе
необходимо создать определенное пересыщение.
Для однокомпонентных с и стем пересыщения можно до
стичь пуrем изменения давления или температуры . Так как
температура кристаллизации веществ слабо зависит от давле
ния, то для таких систем пересыщение обычно создается пуrем
охлаждения расплавов.
Для бинарных и многокомпонентных систем пересыщение
можно создать следующими способами:
- охлаждением смеси через теплообменные поверхности или
в результате ее непосредственного контакта с различными хла
доагентами;
.

• С м . ( 1 , 6, 1 3 ) .

1 324

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

- частичным испарением легколетучего компонента смеси
(чаще всего - раствор ителя);
- изменением давления в системе;
- изменением взаимной растворимости компонентов пуrем
введен ия дополнительного ("высаливающего") компонента;
- добавлением к разделяемой смеси химических реагентов, обра
зующих с одним или несколькими комnонентами смеси химиче
ское соединение, вьmадающее в виде кристаллического осадка.
1 6.3.2. Зарождение кристаллов

Интенсивность зарождения кристалло в характеризуют ско
ростью их зарождения , под которой понимают количество цент
ров кристалл изации (зародышей), возникающих в единице
объема за единицу времени. Различают гомогенное и гетеро
генное зарождение . Гомоrенное за рождение происходит при
отсуrствии в расплаве (растворе) посторонних твердых приме
сей (частиц), на которых могли бы образоваться кристалл ы .
Процесс зарождения в данном случае определяется флуктуациями
свободной энергии системы (энергии Гиббса). Геrероrенное зарож
дение происходиг на твердых поверхностях, а также на взвешен
НЬIХ в расплаве мельчайших инородньIХ частицах.
Направлен ие фазового превращения в системе определяет
ся, как уже отмечалось выше, изменением свободной энергии
системы. Из двух фазовьхх состояний устойчивым является то,
которое обладает меньшей свободной энергией. Поэтому кри
сталл изация происходит в слу•1аях, когда переход вещества из
жидкого состояния в кристалл и ческое сопровождается умень
шением свободной энергии.
При температуре Т выше точки плавления (кристаллизации)
вещества ТWI = Ткр удельная свободная энергия жидкой фазы
ниже, чем кристаллической, а при Т < TWI наблюдается обрат
ная картина (рис . 1 6 . 9). Поэтому при температурах Т > TWI бо
лее устойчива жидкая фаза, а при Т < TWI - кристалл и ческая .
При Т = Тrui свободные энергии кристаллич еской и жидкой
фаз равны между собой, так что в устойчивом состоянии мoryr
находиться обе фазы.
Процесс кристалл иза ции происходит при температурах ниже
точки плавления, т.е. при наличии некоторого переохлаждения
л Т = Trui - Т .
(а)

Движущей силой процесса кристаллизации при температуре
•
Т является разность удельных свободных энергий жидкой Gж
и кристаллической Gт фаз:
(б)
Л G = Gж - Gт .
• Пр иходя щихся на еди н ицу массы вещества .

1 325

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

G

Рис. 16. 9. Изменение свободной энергии жидкой

G.._ и

кристалл ической Gr фаз с температурой

Образование в системе кристалличе
ского зародыша объемом V3 сопровож
дается выделением свободной э нергии
(в)
Л Gv = ( Gж - Gт)VэРк ,
- IШотность кристаллической фазы.
Если образующийся зародыш имеет
сферическую форму с радиусом r, то
о

т

т

где Рк

4
Л Gv = 3 7tr1( Gж - Gт)Рк .

(г)

С учетом зависимостей (16.2) и ( 1 6.3) разность удельных
свободных энергий фаз можно представить как
Л G = Gж - Gт = (Нж

-

Т

Нт ) - (Sж - Sy) T =
Ткр - Т
Ткр

- Гкр - -- Гкр - Гкр
_

_

Ткр

(д)

Так как Ткр = TWI, а Гкр = -rw1> то выражение (д ) можно
представить также в виде
ЛТ
Т. - Т
Л G = - 'пл п л
= - rWI -- ,
Т
пл

(ж)

Тп л

причем Л Т = Тпл - Т есть величина переохлаждения расплава
относительно точки его плавления .
Подставляя зависимость (ж) в формулу (г) , получим значе
н ие энергии, выделившейся при образовании зародыша радиу
сом /�
4
лт
(з)
Л Gv = - - пr1ркrпл

3

--

Тпл

.

При возникновении зародыша часть энергии Л GF затрачи
вается на образование поверхности раздела фаз . Для сфериче
ского зародыша эти затраты энергии составляют
Л GF = 4пr2сrп ,

(и)

где сrп - удельная поверхностная свободная энергия (поверхностное натяжение
на границе кристаллическая фаза - расмав) .

Общее изменение свободной энергии при образовании кри
сталлического зародыша выразится соотношением
4
лт
(к)
Л Gr. = Л G v + Л GF = - - 1t1.1р кrпл -- + 4nr2crn
Т
3
пл
.

1 326

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 16. 1 О.

ЛG от радиуса зародыша r

ЛG

Зависимость свободной энерrnи

Зависимость величин Л Gv, Л GF .
и Л G-r, от радиуса зародыша при
ведена на рис . 1 6 . 1 0 . Анализ
уравнения (к) показывает, что
при некотором критическом зна
чении радиуса зародыша rк вели
чина Л G-r_ проходит через макси
мум . Дифференцируя (к) и при
равнивая производную нулю, по
лучим

о

r

откуда следует выражение для оценки значения критического
радиуса зародыша:
( 16.8)

rк

Любой зародыш с радиусом более
является центром кри
сталлизации , способным к росту, так как по мере его роста
происходит понижение свободной энергии системы Л Gr,. При
r < зародыш неустойчив, поскольку при его росте Л Gr. уве
личивается.
Анализ выражения ( 1 6 . 8 ) показывает, что с возрастанием
переохлаждения Л Т величина rк уменьшается, что повышает
вероятность образования центров кристаллизации. При Т � Тпл
величина
� оо, поэтому при малых переохлаждениях зарож
дения кристаллов практически не происходит.
Для образования зародыша радиусом
при данном пере
охлаждении Л Т необходимо преодолеть энергетический барьер
Л Gкр (см. рис . 1 6 . 10), равный
4
лт + 4п r 2cr з
ЛG
n3
Тnл

rк

rк

rк

кр - --пrк Ркr!Щ-r (-.!.rпл Рк Т
=

4

п к2

3

к

)

Л
rк + сrп .
Тnл

Подставляя в это выражение значение
1 6псr� Т�л
Л Gкр =

З р� r�iл ( л ) 2
Т

rк

(л)

из ( 1 6 . 8), получим:
( 1 6 . 9)

1 327

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 1 6. 1 1.

Зависимость скорости за
рождения кристаJL1ов w3 от переохлаж 
ден ия л т

возникновения
Процесс
кристаллических
зародышей
является флуктуационным и
подчиняется общим законо
мерностям
статистической
физики, согласно которым
вероятность образования цен 
тра кристаллизации равна

= Со ехр

-

где k
станта.

постоянн ая Больцман а ; В

=

[

-

Т (всr:,
Л Т)2

1 бп Тпл2/(Зkрк2rпл2); Ч>

-

],

(м)

некоторая ко н 

Скорость зарождения кристаллов w3 определяется , с одной
сторон ы , вероятностью процесса зарождения , а с другой сто
раны ,
подвижностью
молекул . Согласно молекулярно*
кинетическои теории
�

w3

где U

(

) ехр [ -

= С ехр - !!_
RT

- энер гия активации молекул.

Всr �

Т (л т) 2

],

(16. 1 0)

Из выражен ия ( 1 6 . 1 0) следует, что с увеличением пере
охлаждения л Т вероятность зарожден ия кристалл о в возрастает
(рис . 1 6. 1 1 ). Но при увеличении Л Т одновременно снижается
температура системы Т, что приводит к уменьшению интен
сивности
движен ия
молекул
[пониже ние
величины
exp( - U/R7)) . В рез ультате конкурен ции эти х э ф фектов ско
рость зарожден и я iv3 с ростом Л Т п роходит ч е рез максимум ,
что часто согласуется с опытн ыми дан ными .
При гетерогенном зарожден и и процесс в значительной мере
ускоряется , так как наличие в расплаве твердых частиц способ
ствует образованию на их поверхности кристаллической фазы,
снижая величину энергетического барьера , связанного с воз
н икновением центров кристаллизации. Последний в условиях
гетерогенного зарожден и я (Л G'кр) можно выразить через барьер
Л Gкр гомоге н н ого зарождения :
(н)
Л G'кр срЛ Gкр ,
·

где <р $ l
го тела.

- коэффициент, за в и сящий о т физических свойств расплава и твердо =

• П одробнее анализ пронесса зарожден и я кристалл о 11 см. в / 9 , 1 7 ] .

1 3 28

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Значение коэффицие нта q> определяется сродством свойстu
твердого тела (подложки) и возникающей кристаллической
фазы. Установлено , что q> сильно зависит от угла смачиван ия
расплавом поверхности твердого тела е . При е
О коэффици
ент q> � О , а при е
1 8 0° q> � 1 . В последнем случае подложка
практически не влияет на скорость зарождения кристаллов.
На процесс зарождения кристаллов оказывает воздействие
большое число внешних факторов: вибрация , перемешивание ,
ультразвуковые колебан ия, электрические и магнитные поля ,
*
радиация и др. Как правило, действие этих факторов повы
шает скорость зарождения.
В случае кристаллизации бинарн ых и многокомпонентных
систем скорость зарождения зависит также от состава смеси.
При этом в качестве движущей силы процесса зарождения
часто используют разность концентраций .
=

=

1 6 .3 . 3 . Рост кристаллов

Предложено несколь ко теорий роста кристаллов; рассмот
рим некоторые из них.
Теория поверхностного натяжения, предложен ная Гиббсом ,
постулирует, что кристалл при своем росте стремится к форме,
соответствующей мин имуму поверхностной энергии при дан 
ном объеме . По этой теории скорости роста отдельных граней
пропорциональн ы свободным энергиям этих граней. В то же
время удельные свободные энергии пропорциональны длинам
нормалей к граням из центра кристалла. Так как эти длин ы
обычно неодинаковы , то разные гран и кристалла должны расти
с различной скоростью. Теория поверхностного натяжения
позволяет объяснить форму кристаллов, однако она не раскры
вает механизма их роста .
Диффузионная теор1т роста представляет кристаллизацию
как массообменный процесс. Обозначим: т - масса кристал
лов; 't - время ; f - поверхность раздела фаз; Рм - коэффици
ент массообмена; х
концентрация кристаллизующегося ком 
понента в основном об1,еме фазы; Хр - равновесная кон цент
рация . Тогда скорость образования кристаллической фазы
можно выразить как
--

dm
- =

d't

Рм/{х

-

Хр ) .

(16. 1 1)

Использование коэффициента массоотдачи Р м предполаr-ает,
что на границе раздела фаз (фронте кристаллизации) имеется
пограничная пленка толщиной 'i5D, через которую перенос ве• Подробнее о

миянии эти х

факrоров с м .

1 5 , 9, 1 1 , 1 8].
1 329

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

щества происходит за счет молекулярной диффузии, интенсив
ность которой определнется коэффициентом диффузии D. В
этом случае уравнение ( 1 6. 1 1 ) можно представить в виде

dm D
=
х - Хр) .
dt -!
8D (

-

( 1 6 . 1 2)

Однако с этих позиций процесс кристаллизации плохо объ
ясним, если принять, что его скорость определяется одной
лишь диффузией . Элементарные частицы (атомы, молекулы и
т.д.), подходящие к поверхности растущего кристалла, должны
еще определенным образом ориентироваться, чтобы присоеди
ниться к растущей гран и . Скорость такого процесса построе
ния грани для многих веществ может определять скорость ро
ста кристаллов в целом . В связи с этим в более поздних вари
антах диффузионной теории рост кристалло в представляется в
виде двух последовательных стадий: диффузии молекул к по
верхности раздела фаз и "поверхностной реакции" встраивания
элементарных частиц в кристаллическую решетку. При этом
стадия диффузионного переноса описывается, как обычно,
уравнением
(о)
dm/d't = р nf(x - Хп) ,
а стадия построения грани - уравнением

dm/dt = pпf(xn

-

Хр ) .

(п)

где Xn - концентрация кристаллизующегося компонента в пограничной rтенке;
Pv - коэффициент массопередачи диффузией; Рп - константа скорости поверх
ное111 о й реакции .

Чтобы освободиться о т трудно определяемой величины Хп ,
вводится понятие об общем (эффективном) ко э ффициенте
массопередачи (см. разд . 1 0 .6. 1 ) :
Рм

1

= 1/PD + l/ ri п

(р)

При Р п >> P D процесс кристаллизации контролируется диф
фузией в жидкой фазе , а при Р п << PD
поверхностной реак
цией.
Экспериментально установлено , что величина Р м может из
меняться от грани к гр ани кристалла. Поэтому при расчете
процесса кристаллизаци и обычно используют средние значе
-

ния Р м·

Заметим, что диффузионная теория роста кристаллов при
мени ма лишь к бинарн ы м или многокомпонентным системам
Кроме того , она не объясняет существования различных форм
роста кристаллов.
1 330
.

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 1 6. 12.

Схем а роста грани кристама

Молекулярно-кинетич.еская meoptt.R
роста кристаллов в настоящее время
является
наиболее
разработанной.
Согласно этой теории, рост кристал
лов рассматривается как последова
тельное образование слоев элемен
тарных частиц на гранях растущего кристалла. При росте кри
сталлов выделяется поверхностная энергия, количество кото
рой зависит от условий присоединения элементарн ых частиц
(атомов, молекул или "двумерных" зародышей) к грани .
Возможны три варианта присоединения элементарн ых час
тиц к растущему кристаллу : 1 ) в торец ряда; 2) образование
нового ряда; 3) на поверхности гран и (рис . 1 6 . 12). Наибольшее
количество энергии выделяется в варианте 1 , а наименьшее в варианте 3 . Как уже отмечалось выше (в разд. 1 6 . 3 .2), при
росте кристалла преимущество имеет вариант, соответствую
щий выделению наибольшего количества энергии. Исходя из
этого вероятным представляется следующий механизм роста.
Первоначально на гладкой грани оседает отдельная элементар
ная частица, а затем идет построение р ядов. При этом каждый
новый р яд образуется в основном лишь после построения
предьщущего . После застройки всей грани слоем элементарн ых
частиц процесс повторяется.
Согласно молекуляр но-юшетической теории, • линейная ско
рость роста кристалл о в описывается уравнением

-

Vл

(

)
-

( На; ]

= А ехр - � ехр RT

где А и Н
постоянные величины;
д вумер ных зародышей .

а1

ТЛ Т

'

( 1 6 . 1 3)

по верхностное натяжение на гранях

Как следует из уравнения ( 1 6 . 1 3) , зависимость линейной
скорости роста кристаллов Vл от переохлаждения Л Т, как и
w3 = f (Л 'J) , имеет экстр ем ум .
Представление об идеальном строении кристаллов, лежащее
в основе молекулярно-кинетической теории роста, не всегда
подтверждается . Реальные кристаллы часто имеют различные
дефекты (нарушения, дислокации), которые могут повлиять на
механизм роста. Как правило, кристалл ы с дефектами способ
н ы расти при значительно меньших переохлаждениях с образо
ванием спиральных фро нтов pocra на поверхности кристаллов.
Более подробно особенно сти молекулярно- кинетическо й теории рассмот
рены в ( 9 ) .
•

133 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Такой процесс описывается так называемой дислокационной
.
теориеи роста .
На скорость pocr.1 кристалло в сильное мияние оказываюг фи
зико-химические свойства вещества, его состав, наличие приме
сей, а также различные физико - механические воздействия.
�

16.3.4. Переход расплава индивидуальных веществ
в

твердое состояние

Кристаллизация (отверждение) расплавов обычно произво
дится пугем их охлаждения через теплопередающие стенки или
же в результате их не посредственного контакта с потоком
охлаждающего агента. При этом кристаллизация является ти
пичным нестационарны м процессом, скорость которого в об
щем случае зависит ка к от интенсивности теплопереноса в
системе, так и от скоростей зарождения w3 и роста Ул кристал
лов. Для различных веществ соотношение этих факторов про
является по-разному.
При отверждении рас плавов веществ с высокими скоростями
W3 и Ул (почти все металлы и большая часть н изкомолекуляр
н ых орган ических веществ) лимитирующей стадией процесса
обычно является интенсивность отвода теплоты от растущих
кристаллов к охлаждающему агенту. Для таких веществ процесс
протекает следующим образом. Первоначально на охлаждаемой
стенке, где достигается наибольшее переохлаждение расплава,
происходит зарожден ие центров кристаллизации, образующих
при своем росте приповерхностный кристалличесЮfй слой. С
течением времени фронт кристаллизации (граница раздела кри
сталлической и жидкой фаз) постепенно перемещается в глубь
расплава (рис . 1 6 . 1 3) со скоростью, обусловленной интенсив
ностью отвода теплоты от границы раздела фаз. При этом тем
пература на фронте кри сталлизации ts ниже равновесной тем
пературы кристаллизаци и вещества lк р на величину переохлаж
дения Лts fкр - ts.
Величина переохлаждения Лfs, с одной сторон ы , зависит от
интенсивности отвода теплоты от границы раздела фаз, а с
другой - от скоростей \V3 и Ул. Для веществ с большими значе
н иями w3 и Ул величина Ms близка к нулю. Здесь процесс кри
сталл и зации полностью определяется интенсивностью неста
ционарного теплоотвода от границы раздела к охлаждающему
агенту, имеющему тем пературу fc· При этом реализуются две
возможности menлonepelloca в расплаве - пугем теплопровод
ности либо кон векцией .
Рассмотрим процесс кристаллизации полуограниченного
массива перегретого рас плава вещества с высокими скоростями
Ул и w3 , примыкающе го к плоской охлаждаемой стенке , для
=

• Подробнее с м . (5 , 9 ) .

1 332

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Кристаллизация
pacJUiaвa
на
плоской стен к е при высо1шх скоростях за
роЖдения и роста кристалл о в :
Рис. 1 6. 13.

1

-

сте нка

к ристал л ический слой , 2

-

расплав, J

-

случая , когда перенос теплоты в
расплаве прои с ходит за счет теп
лопроводности. Пусть за время 't на
стенке толщиной 8ст, изготовлен 
ной из матери ал а с те плопровод 
ностью Лет , образуетс я кристалли
чески й слой толщиной 8 . Интен 
х
сивность внешнего охлаждения
характеризуется
коэффициентом
теплоотдачи а.с . Кри стал ли ч ес кая фаза им еет плотность Рк , ко
эффициент те плопровод ности Лк и коэффициент температуро
проводности ах, а жидкая фаза (расплав) - соответственно Рж·
Л.ж и аж. В этом случае распределение температуры в кристал 
лич еской t1 (х) и жидкой t2(x) фазах по нормальной к стенке
координате х описыва ет ся уравнениями Фурье- Кирхгофа (см .
разд . 1 . 5 .2) для однонаправленного потока:
для твердой фазы

дt1 (х , ) д't 't

�
�
-

а

к

д2 t1 (х, 't ) (
дх2

't

> О; О

<

х

<

8) ;

(с)

a2 t2 ( X,
't) ('t
2
дх

> О ·, б-

<

х

< оо) .

(т)

для жидкой фазы

дt2 (x , 't)
д't

=

аж

Исходный расплав перегрет относительно температуры кр и 
температура fp > fкр ·
Начальные условия рассматриваемой задачи имеют вид:

сталл и заци и : его

при

't

= О t2(x, О) = /р, 8 = О .

(т)

f1 (x, )

(у)

Граничные условия :
при

х=

О

т

= tn;

(ф)
(х)
где tn - температура кристаю1ической фазы на охлаЖдаемой стенке.

Наряду с этим на перемещающейся границе раздела фаз
должно выполняться граничное условие IV рода с сосредото1 33 3

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ченным (на этой границе) источником теплоты фазового превращения (граничное условие Стефана) :
Л

к

Л

дt1 (8, ) =
дх

т

d8

+ ,.,

дt2 (8 ; t)

кр Р к d-r

дх

ж

(ц)

·

Решение уравнений (с) и (т) с учетом краевых условий (т)
(х) дает распределение температуры в кристаллической и жид
*
кой фазах :

--'t1'-(x__, •_)_-_t-"-c

/р

Ь

=

+ Jпак •

e

rf

2_J;:.а_... к_•_

_

х

_
_

_
_
_
_
_
_

Ь + Jпак• erf ---

8

- lz (X , 't)

t;"=-�

erfc

-

_

erfc

х

2Jaк•

(16. 14)

'

2ra;;;

�'

(16. 1 5)

2 Ож 't

где Ь
Л ( l ас + Ocr Лсr) - коэффициент, характе;� изующий термическое со
проршление со стороны охлаждающего агента 1/ ас и охлаждающей стенки

/

=

Бcrf'Лcr .

Символом

2

erf(z) = - J

z

1t о

/

2

erf

обозначается

е - и du , п ричем

er1{0)

нение интеграла ошибок до l :

e1fc(<:)

=

1

=О и

инте11>ал

erf(ao)

- eif{<:)

2

=

ошибок

= 1 . Символ

- ос:1 е - и
11

z

2

dи

(вероятностей):

erfc означает допол-

.

В этих выражениях z - аргумент, стоящий под знаком функций
Значения
и
т<�булированы•• .

erf e1fc

erf и erfc.

Дифферен цируя зависимости ( 1 6 . 14) и ( 1 6. 1 5) при х = 8 и
подставляя полученные производные в уравнение (ц) , наЙд ем
скорость перемещения фронта кристаллизации, т.е. скорость
изменения толщины кристаллического слоя:
dб

dt =
/'кр Р к -

"- к (tк р - tc ) ехр

• Подробнее решение данной задачи см .

•• См. (20 ) .

1 334

(5 ] .

( �)
-

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Jrtaж't e i-fc

h
2 Ож't

(16.16)

Дифференциальное уравнение ( 1 6 . 1 6) позволяет определить
скорость кристаллизации при достаточно общей постановке
рассматриваемой задачи. Это уравнение относительно функции
8 = j('t) решают численными методами. При определенных до
пущениях из уравнения (16 .1 6) можно получить ряд более про
стых частных зависимостей . Так, если теплообмен охлаждае
мого образца с окружающей средой осУ.J.Цествляется в rранич
НЬIХ условиях 1 рода, когда
� оо , Л.ст/8ст � оо и tп = const, то
уравнение (16.16) приобретает вид
8 = /3 ..г.
(16. 1 7 )
а.с

где � - корень трансценденnюrо ур авнени я
Гкр Р к

2

�

)

{

=

'

( LJ

Л- к tкр - tc exp 4а к
/3 J;a; erf - к

2 Га;

Jп аж

e1"fc _/3_

2JQ;;

Если перенос теплоты в расплаве происходит за счет кон
векции, что обычно имеет место при охлаждении интенсивно

перемешиваемого расплава, то на перемещающемся фронте
кристаллизации реализуются граничные условия 1 1 1 рода, ко
торые с учетом теплоты фазового превращения имеют вид
rде ар

Гк Рк
р
-

d8 дt1 (8, 't ) a.p(lp
к
А
't
дх
d

-

(ч)

lкр),

коэффициекr теплоотдачи от расплава к границе раздела фаз.

В этом случае при ре шении уравнения (с) с учетом услови й
(т)-(х) и (ч ) для ско рости кристаллизации в общем случае по
лучается выражение

d8
ГкрРк
d't

=

А к (fк р - tc ) ехр

•такие з<� висим ости

Ь

+ .;;а;:;.
к

приведен ы

в

(- �)
4ак't

erf -8--(5).

2 Jaк 't

- a.

p (tp - lкр )

.

(1 6 . 1 8)

1 335

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 16. 14.

ОтверЖдение

р ас м ав а

1 - расплав, 2 - переходная
-- отвержде1Шое вешество

низки м и скоростя м и w1 и vл:

зона.

с
.1

Из ур авн е н и я ( 1 6 . 1 8) тоже
может
быть
получен
ряд
ч астн ых зависимосте й .
Пусть теперь интенсив
н ость охл ажд ения р ас плав а
достаточно велика , а с корос
3
ти зарождения w3 и роста Ул
о
х
относительно
малы .
Тогда
расплав при охлаждении за
конечное время закристалл изуется л ишь частично; оставшаяся
часть вещества будет находиться в амор ф н о м состоянии. Эrо ха
рактерно для ве ществ, у которых при переохлаждении происходит
знач ительно е повыше н и е вязкости pacIUiaвa. П р име р о м таких
веществ являются кристаллизующиеся полимеры ( п оли э т ил е н ,
полиамид и д р . ) . В это м случае при охлаждении образуется так
называемая " п е реходная " зо н а (р и с . 1 6 . 14), в кото рой происходит
зарождение и рост кристаллических обр азо ваний. Однако вследст
вие увеличения вязкости расплава с корость массообмена в систе
ме снижается . В результате рост кристалл ич еских о браз о ваний
постепенно замедляется, а при определенной температуре !i:r
- вообще прекращается.

(температуре стеклованw1)

П р и отверЖде н и и pacruшno в таких веществ в фор м ах п р и достаточно и нте н 
с и в н о м охлажден и и обычно нолучаются продукты (изделия ) с неоднородной
струкrуро й . Дело в том , 'ПО в ц
е фор м ы скорость охлажден ия вещества
ниже (процесс охлаждения идет более медлен н о) , чем в перифер и й н ых слоях .
П о этому полнота превращения расплава в кристаллич ескую фазу, характеризуе
мая степенью кристалл ичносп111 , в центре образца, как правило, выше, чем в
наружных слоях. П р и понижении интенсивности внешнего охлажден и я средняя
степень кр исталл и чности обычно возрастает, так как увеличивается продолж и 
тельность пребывания вещества в температур н о м интер вале, благопр иятн о м
образовани я и роста кристалл о в . Это я вление, в частности, и м еет место при
переработке к и сталл и зую щихся пол и ме о в и целого ряда оргаНИ'lеских ве
ществ, и меющих высокую вязкость расмав<� .

ентр

р

для

р

Д ля полной кр исталлизац ии вещества с н изкими скоростями
о хлажде н ие следует производ ить медленно или же про
изводить его в квазиизотермическо м режиме , когда про цесс
кристаллизации происходит при практически постоян ном пе
реохл ажд ении расплава .
Изменение степе н и кристалличности вещества </>к =
- объемы кристаллической фаЗЬJ и исходного рас
(где к и
плава) во в р еме н и 't о п исывается уравнением
v
1
( 1 6 . 1 9)
1 - ехр (- 7tWз Ул3't4)
к=
w3 и vл

Vк/Vo

V Vo

</>

•

П одробнее см.

1 336

(5 ) .

V�

J

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 1 6. 15. П ереход вещества в кристалл и ческое
с остояние в кваз и и зотер м ичес.ком реж име <�n врем я полной кр исталл и зации)

<D
'1<
1

Дифференцируя уравнение ( 1 6 . 1 9) ,
можно определить с ко р ость превраще
н ия (объемной кристаллизации) :
.
d V:
1
tп
t
О
- 7tWзvлЗ't3 Vo exp ( - - nwзvл3't4) .
d't
3
3
( 1 6 .20)
Анализ зависимости ( 1 6 . 1 9) показывает, что степень фазово
го превращения срк монотонно увеличивается во времени от О
при 't � О до 1 при 't � oc:i (рис . 1 6 . 1 5) . Решая уравнение ( 1 6 . 1 9)
относительно 't, получ и м зависимость для расчета продолжи
тельности выдержки , обеспечивающей заданную степень пере
хода вещества в кристаллическое состояние

к=4

__

t =

4

1
1 - q> K

З ln -1tW3 Vл

3

( 1 6.2 1 )

Существует целый ряд веществ ( стекло , полистирол, раз
личные смолы), обладающих столь низкими скоростями зарож
дения и роста кристаллов, что п ри их охлаждении с конечной
интенсивностью криста:шическая фаза вообще не образуется .
Охлаждение таких веще ств сопровождается постепенным по
вышением вязкости - 1шлоть до их превращен ия в затвердев
шие аморфные тела. Для расчета процесса отверждения таки х
веществ можно использовать обычные уравнения нестационар
ной теплопроводности без источников теплоты.

16.3.5.
и

Кристаллизация бинарных
смесей

многокомпонентных

Как указывалось в разд . 1 6 .2.2, при охлаждении бинарных и
многокомпонентных р ас пл аво в (растворов) переход из жидкого
состояния в кристалли ч е ско е обычно происходит в определен 
ном диапазоне температур . Процесс кристаллизации начинает
ся по достижении температуры ликвидуса tл и заканчивается
при тем пературе сол идуса tc . Исключение составляют лишь
расплавы эвтектического состава, для которых tл = tc .
В зави с имо сти от и н тенсивн о ст и внешнего охлаждения воз
можны два варианта процесса - с высокой и низкой интен
сивностью охлаждения.
При высокой интенсивности отвода теплоты в объеме ве
щества имеет м есто значительный градиент температуры. В

1 3 37

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

:о · •о· оо· �• -о�
о •- 1
оО• о О
•
•
о
•
•·
а
.
о
о
о . о оО• .
О •• • 0 1
о
о. а• о t < t < о
оО•'
t
л Оо 0
о с
•
о· о
. о. о
о
•0 о.о
_о .
0 0 0 0
. 0 0
о ,о о о о .о �о о0 1
.
.

0 0.
ln

•

ln
о

1

.

а

1
'\'
1

o'J=J.o o .Or:Ь
�
�� o_o_ t-o·cU.o� �J
.

х

о

3

б

х

Рис. 1 6. 1 6. Кристаmшзация бинарных расплавов при высоко й ( а) и низкой ( б)
интенсивности в н ешнего охлаждения:
l
расплав, 2
кристалличсосий сл ой .1 - nepe xoдHЭJI область
-

-

,

этом случае в системе можно вьщелить три характер ные облас 
ти : 1 ) расплав, 2) полностью затвердевшее вещество и 3) пере
ходная область (рис . 1 6 . 1 6 , а) . При этом на границе переходной
области и рас плава п р и t = tл начинается процесс кристаллиза
ции , а на границе переходной области и кристаллического слоя
при t = tc этот процесс закан чивается. Ш ирина переход ной
области 8п зависит о т ющ а диаграммы состояния системы , с о 
става смес и, е е теплофизических свойств, а также о т интенсив
ности внешнего охлаждения. С пон ижением последней протя 
жен ность переходной области растет. При увеличении продол 
жительности процесса гран ицы начала 8л и кон ца 8с кристалли
зации постепен но перемещаются вглубь рас плава. Такой про
цесс часто называют направленной кристаллизацией .
При малой интенс11вности охлаждения смеси температура во
всем ее объеме изменяется примерно одинаково . Здесь проис
ходит так называемая массовая кристаллизация (рис . 1 6 . 1 6 , б) . В
этом случае кристаллы возникают и растут во всем объеме
охлаждаемой смеси; можно сказать , что переходная область
зан имает весь объем с меси (рабочей зоны аппарата) . Такой вид
кристаллизации особенно часто наблюдается при охлаждении
различных растворов. Аналогичная картина наблюдается при
кристаллизации перемешиваемых смесей.

16. 3 . 6. Форма кристаллов

Форма отдельн ых кристалл о в, а также структура кристалли 
ческой фазы зависят о т целого ряда факторов: физико
химических и теплофиз ических свойств вещества, метода соз1 33 8

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

дан ия пересыщения, интенсивности охлаждения, состава ве 
щества, природы раство рителя , наличия примесей и Т ..1]. Разли 
чают равновесную и ре<lГ!ЬНую форму роста кристалл о в .
Форма равновесных кристаллов определяется строением кри 
сталлической решетки , а также силами связи между ее элеме н
тар н ыми частицами (ионами , атомам и, молекулами и т.д . ) .
Кристаллы равновесной формы имеют грани с наименьшей
поверхностной энергиеii и , как правило , отличаются относи
тельной простото й . Н :�ходясь сколь угодно долго в маточной
среде при равновесной температуре, такие кристаллы не изме
няют своей формы.
Форма реальных кристаллов обычно изменяется во време н и
и сильно зависит о т внешних факторов. Ч е м медленнее растут
кристалл ы , тем ближе о н и к своей равновесной форме . При
малых переохлажден и ях кристаллы растут, как правило , сохра
няя правильную форму, соответствующую их внутрен нему
строен и ю . При увел и чении переохлаждения скорость роста
раз н ых граней может повышаться не в одинаковой мере . По
этому изменению пересыщен ия часто сопутствует изменение
формы кристаллов; могут исчезать одн и гран и и появляться
другие. При больших пересыщениях кристаллы часто приобре
тают форму дендритов, скелетов, сферолитов, спиральных и
других несоверше н н ых образован и й . Известн о , что быстрое
охлажден ие расплавов и растворов обычно приводит к образо
ван ию игол ьчатых кр исталлов : такая форма способствует луч 
шему отводу теплоты от фронта кристаллизации во внешнюю
среду.
Под воздействием внешних факторов в кристаллах нередко
возн и кают различные дефекты структур ы, что отражается на их
форме и физико-меха н и ческих свойствах.
Форма и размеры кристаллов с ильно зависят от условий
охлажден ия расплавов 1 1 растворо в. При охлажден и и переме
шиваемых растворов , как уже отмечалось выше , происходит
массовая кр исталлизация, сопровождающаяся образованием
отдельных кристаллов в маточной среде. Так как центры кри
сталлизации обычно воз н икают в раз ные моменты време н и и,
соответстве н н о , продолжительн ость их роста различна, т о по
лучаемый кр и сталли ч е с ки й продукт, как правило , имеет поли 
дисперсный состав.
При охлажден и и неперемешивас мых расплавов в системе
практически всегда наблюдаются градиенты тем пературы . В
этом случае кристалл ическая фаза образуется в в ид е с плошного
или пористого слоя , который обыч но состоит из кристалло в
различн ых размеров и формы .
• П одробнее

см.

( 1 1 , 191.
1 339

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

v.,
l �':i

Лt

Рис.

1 6. 1 7. Влияние переохлажцения расплава на струкrуру кристаллической

фаз ы

При отверждении расплавов часто возникает задача получе
н ия отвержденных продуктов (гранул , чешуек, блоков, отливок
и т.д . ) , имеющих определенную кристалл и ческую структуру.
Последняя , как и форма кристаллов, зависит от теплофизиче
ских свойств вещества, интенсивности внешнего охлажден ия ,
размеров отливки, наличия примесей и ряда других факторов.
Определяющее влияние на структуру получаемого продукта
оказывает соотношен ие скоростей зарожден ия w3 и роста Vл
кристаллов. Рассмотр и м влияние этих скоростей на структуру
продукта для случая квазиизотермической кристаллизации
(рис. 1 6 . 17).
Обычно положения максимумов на кривых зависимостей w3
и Vл от переохлажден ия Лt не совпадают. При кристаллизации с
небольшим переохлажде нием Л t1 скорость зарождения w3 мала,
а линейная с корость роста Vл достаточно велика. В силу этого
при кристаллизации возникает о граниченное количество заро
дышей, быстрый рост которых приводит к образованию круп
нокристалл и ческой структуры. При Л t2 скорость w3 возрастает,
а Vл снижается, поэтому средний размер кристалло в умень
шается . При больших переохлажден иях Лtз возн икает значи
тельное число медлен н о растущих кристаллов, благодаря чему
образуется мелкокристаллическая структура.
В случае реальной кристаллизации расплавов в формах ве
личина переохлажден ия расплава изменяется по сечению фор
м ы , что, естественно, отражается на структуре отвержденного
продукта. Обычно на поверхности отливок, где имеются значи
тельные Л t, вещество состоит из мелких кристаллов, а в центре
(малые Л t) образуются более крупные кристаллы .

1 340

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

1 6.4. ОТВЕРЖДЕНИ Е РАСШIАВОВ

Отвержден ие расплавов является одним из весьма распро
страненных видов процесса кристаллизации . С ним мы встре
чаемся при получен и и минеральных удобрений, нафталина,
дифен ила, парафина, серы, гидроксида натрия, пищевого льда,
а также при переработке полимерных матери алов, металлов и
многих других продуктов химической , пищевой, коксохими
ческой, нефтехимической и других отраслей промышленности .
При отверждении расплавов п ол учаютс я продукты в виде отли
вок, блоков, пластинок, чешуек, гранул и т.п.
Отве ржд е н и ю поднергаюrся расплавы как индивид уальных
веществ, так и многоко мпонентных смесей . В последнем слу
чае при отверждени и расплава возможно нер ав н о ме р ное рас
пределение компонентов по объему отвержденного продукта.
Это обстоятельство может оказывать заметное влияние на
структурные, механичес кие , физичесюtе и други е свойства п о 
лучаемых продуктов .
1 6.4. 1 . Оrверждение в формах

При отверждении расплавов в формах пр одукты получаюrся
в виде отдельных блоков той или иной конфигурации.
В простейшем случае форма представляет собой конический
сосуд, охлаждение которого производится путем естествениого
теплообмена с окружающей средой (р ис . 1 6 . 1 8 , а) или подачи
хладоагента в о хлажд а ю щую рубашку (рис. 1 6 . 1 8 , б) . Таюtе
формы часто используют для получения продуктов в виде
крупных блоков. Н ап р имер , при получен ии блочного льда
применяются формы объемом до 500 л. При этом в про мыш 
ленных ледо генерато рах одновременно охлаждается до 1 000
та юtх форм . Продолжительность процесса зависит от объема
формы и нередко достигает 1 0-20 ч .
При п ол уч ен и и продуктов в виде плит (пластин ) использу
ются различн ые ф ор мы , состоящие из отдельных охлаждаемых
пластин (рис. 1 6 . 1 8 , в). П ер ед заливкой расплава в пространство
между пластинами последние стягиваются с помощью гидрав
лического или винтового механизма. После отвержден ия ком 
плект охлаждающих элементов разъединяют и продукт удаляют
из ф о р м . Толщина плит обычно составляет 40- 1 00 мм, про
должи тел ьность процесса отверждения - 1 -4 ч.
Весьма производительными аппаратами для отверждения
расплавов являются трубчатые охладители (р и с . 1 6 . 1 8 , г) , напо
минающие по с во е й конструкции обычные кожухотрубные
тепл.о обмен н и юt . Рас плав заливают в трубное пространство , а
охлаждающий агент подают в межгрубное . После отверждения

1341

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

а

в

б

г
б - отдельные формы . R - разъемные форм ы , г - трубч атый криста.1лизатор, д охлаждающий конвейер;
1 - и сходный расплав, 11 - оп�срЖденный п р ; щухт , 111 - хладоаrеm
Рис.

1 6. 18. Отверждени е рас1LЛаво в в формах:

а,

открывают н ижнюю крышку, и продукт удаляется из трубок. В
ряде случаев для облегчения этой операции производят час
тичное подплавление отвержден н ых стержней путем подачи в
межтрубное пространство нагретого теплоносителя . Иногда под
трубчаткой р;.�змещается дробилка для измельчения полученно
го продукта. В некоторых конструкuиях удаление отвержденно
го п родукта производится при по вороте трубчатки вокруг гори 
зонтальной оси на 1 8 0 ° . Продолжительность процесса отверж
дения в трубчатых аппаратах составляет о коло ч .
В многотон нажных производствах применяют разливочные
конвейеры, состоящие из удлинен н ых металлических форм
(рис. 1 6 . 1 8 , д) . Заливка расплава производится с помощью дози
руюшего устройства, охлаждение расплава происходит при
движении форм в ван н е с холодной (проточной) водой . От
вержде нны й продукт удаляется при опрокидывании форм на
н ижней ветви кон вейера .
Процесс отверждения расплавов в формах можно разделить на
две С'ГdДИИ . На первой происходит кристаллизация, на второй доохлаждение кристалл ич еской фазы до заданной температуры.
Расчет стад и и крист:l'lлизации производят с использованием
теоретических зависи мостей, полученных при рассмотрении
процесса кр исталлиза ци и расплавов на охлаждаемых поверхно
стях соответствующей форм ы . Для расчета стадии доохлажде*
н ия используют уравн е н ия нестационарнои теплопроводности .

1

v

6

М етодика

•

гл .

и 7.

1 342

та ких

расчсто n приведе н а в

1 5 1 . П одходы к расчету И:lrюже н ы в

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

16.4.2. Отверждение в тонком слое
Отвержден ие рас плавов в тон ком слое позволяет получать
продукты в виде тон ких пластинок (плиток) , чешуек и полу
сфер . Для осушествлен ня такого процесса используются лен 
точные, барабанные и дисковые кристаллизаторы .
Ленточные кристалл11заторы (рис . 1 6 . 1 9 , а) обеспечивают
охлаждение расплаво в в тон ком слое на медлен но движущейся
металлической ленте . При этом охлаждение может произво
диться несколькими с пособам и : путе м орошения хладоагентом
(обычно водой) н ижней поверхности ленты ; за счет естествен 
ного теплообмена с окружающей средой или обдува продукта
газообразным .хладоагентом; непосредственным орошением
продукта холодной водо й или погружен ием ленты с продуктом
в ванну с проточной водой . Последние два способа применимы,
конечно, для водонерастворимых веществ (например, для серы,
эпоксидных смол, пека и др .). Полученный отвержденный про
дукт удаляется с ленты при ее изгибе на приводном барабане.
Толщина слоя расплава на ленте составляет 1 - 1 0 м.м . Скорость
движения ленты 0, 1 -0 , 3 м/с. Длина охлаждаемой части ленты
зависиr от толщины отверждаемого слоя и скорости ее движения ;
обычно она составляет от 4 до 30 м . Иногда расплав подаюг н а
ленту через с пециальные дозирующие устройства в виде уз ких
полосок или капель. В последнем случае п ри отвержден ии полу
чается продукт в виде полусферических гранул.

а

2

3

в

г

ленrочный кристалли 1ато р : б, в, г - барабанные кристалл и затор ы с НИJКНИМ, верх
ним и боковым питанием соответс-rвеШ10, д - кристаллизатор с двумя барабанами ;
1 - ленrа, 2 - щ1иводнъ1е барабаны , 3 - манна для рас пл
, 4 - охлаждаемый барабан.
5 - нож, 6 - калибрующий роли к ;
1 - исходны И расплав, 11 - отнержденный 11 родукт . 111 - хл адоаrе нт

Рис. 1 6. 19. Схем ы аппаратов
а

-

/1.IUI

отверждения расплавов в то нком слое:

ава

1 343

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Барабанные кристаллизаторы отличаются разнообразием
конструкций . На рис . l б . 1 9,б показана схема барабанного кри
сталлизатора с нижии.м питанием. Исходный расплав 1 подается
непрерывно в ванну З кристаллизатора. При вращении бараба
на 4 на его поверхности в результате охлаждения образуется
кристалличесЮtй слой , который непрерывно снимается непо
движным ножом 5. Охлаждение барабана производится путем
орошения его внутренней полости холодной водой или испа
ряющимся хладоагентом (например, жидЮtм аммиаком).
В барабанных кристаллизаторах с верхним питанием (рис.
1 6 . 1 9 , в) ванна отсутствует, а расплав подается из п итающего
бункера непосредственн о на поверхность вращающихся бара
банов. При этом толщина слоя регулируется с помощью специ
альной подвижной план ки .
При боковом питапuu расплав подается в поливной лоток З,
откуда он захватывается поверхностью вращающегося барабана
(рис. 1 6 1 9 , г) Толщина захватываемого слоя обычно регулиру
ется специальным калибрующим роликом 6.
В кристаллизаторах с двумя охлаждающими барабанами (рис.
1 6 . 1 9 , д) расплав подается в пространство между барабанами,
вращающимися в противоположные стороны.
Барабанные кристал.1изаторы являются высокопроизводи
тельными аппаратами . Их диаметр достигает 2 м, длина - до 4
м. Толщина чешуек отвержденного продукта обычно составляет
0 , 5-3 .м.м. Скорость вращения барабанов находится в пределах
0 , 0 1 -0 , 1 5 об/с; для аппаратов с боковым и верхним питанием
она иногда достигает 0, 5 об/с.
Дисковые кристаллизаторы бывают вертикального и горизон 
тального типов. В таких аппаратах отвержден ие расплава про
изводят на поверхностях вращающихся, охлаждаемых изнутри
дисков. Отвержденный продукт снимается неподвижными но
жами . По сравнению с ленточными и барабанными аппаратами
они используются реже из-за более сложной конструкции .
Более подробно конструкции ленточных и барабар н ых кри
сталл и заторов описаны в с пециальной литературе ; там же
приведены и методиЮt их расчета .
.

.

16.5. ФРАКЦИ ОННАЯ КРИ СТАIIЛ И ЗАЦИЯ

Фракцион ную кристi:lллизацию используют с целью разделе
н ия различн ых смесей на фракции, обогащенные тем или
иным компонентом, дш1 кон центрирования разбавленных рас
творов путем частичного вымораживания растворителя, а также
для глубокой очистЮt веществ от примесей . Данный процесс
•

См . , напри м ер ,

1 344

(5 ) .

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

характеризуется относительно низкими энергетическими затра
тами и достаточно высокими коэффициентами разделения .
Фращион н ая кристаллизация отличается от других массо 
обменных процессов большим раз нообразием технологических
методов, из которых основными являются :
- массовая кристаллизация с отводом теплоты через охлаж
даемые поверхности;
- массовая кристалл и зация при непосредственном контакте
с хладоагентами ;
- кристаллизация при частичном упаривани и растворителя;
- кристаллизация на охлаждаемых поверхностях;
- противоточная кри сталл и зация;
- направленная кристалл и зация ;
- фракционное плавление;
- зонная плавка;
- экстрактивная кристалл и зация ;
- адд укт ивная кристаллизацияi
- селективная кристалл и зация .
Большая часть этих методов может осуществляться в перио
дическом, полунепрерывном и непрерывном режимах.
16.5. 1 . Основные особенности фракционной кристаллизации

Большинство методов фращИонной кристалл и зации реали
зуется в две последовательные стадии : образования кристалли 
ческой суспензии и отделения (сепарации) кристалл и ческой
фазы от маточника.
В случае массовой кристаллизации обычно создают по воз
можности равномерное пересыщение во всем объеме смеси .
Такой процес с чаще все го осуществляют в аппаратах с механи
ческим перемешиванием смеси при достаточно медленном ее
охлаждении. При этом твердая фаза выделяется в виде отдель
Н ЬIХ кристаллов, средний размер которых зависит от свойств
вещества и режимов процесса кристалл и зации .
Эффективность разделения смесей и очистки веществ от
примесей в процессе фращионной кристалл и зации сильно
зависит от полноты отделения маточника от кристаллической
фазы на сrадии сепарации полученной суспензии. В реальных
условиях количество остающейся маточной жидкости может со
ставлягъ от 2 до 50% массы крисrалл ической фращии. Для сепа
рации крисrаллических суспензий используюг процессы осажде
ния, фильтрования и центрифугирования, а также прессования .
Осаждение (сгущение) суспензий обычно осуществляется в
самом кристаллизаторе в термостатированных условиях. Чаще
• Подробнее

см.

[6 J .

1 345

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

все го этот проuесс предшествует фильтрованию. Как правило ,
при отстаивании в твердой фазе остается много маточника, что
значительно снижает эффективность разделения проuесса в
uелом. При малой разности плотностей фаз , высокой вязкости
маточн ика и малых размерах кристаллов осаждение становится
медленным, а потому малоэффективным проuессом .
Значительно чаще для разделен ия суспензий применяют
фильтрование и центрифугирование. Заметим, что при использо
вании фильтров захват маточника кристаллической фазой
обычно составляет 1 0 -20 % . Использование фильтрующих
uентрифуг позволяет со кратить остаточное содержан ие маточ
ника в кристаллическом продукте до 2- 5 % .
Процесс прессования сводится к уплотнению кристаллов и
механическому вытеснению маточн ика при давлениях 1 0 60 МПа. Для этого применяют поршневые и шнековые уст
ройства. П р и прессовании кристаллическая фаза обычно пре
вращается в плотную массу (брикет), остаточное содержание
маточника в которой составляет от до 3 % .
Выход и состав кристаллического продукта зависит не толь 
к о о т полноты удален ия маточн ика и з кристаллизата, но и от
температуры е го сепарации.
Если в ходе сепараuии температура смеси понижается, то
выход кристаллической фракuии возрастает в результате до
полнительной кристалл:изаuии маточника. Такой эффект обыч
н о характерен для сепараuии высокоплавк их смесей , когда про
uесс сопровождается потерями теплоты в окружающую среду.
При фракционирован ии низкопл авких смесей наблюдается об
ратная картина: в резул ьтате притока теплоты из окружающей
среды часть твердой фа:1ы может подплавляться . При этом по
н ижается выход кристаллического продукта; одновременно в
нем, как правило , возрастает содержание высокоплавкого ком
понента.
Механизмы захвата м аточника кристаллической фазой могут
быть разными. При фильтраuии суспензий образуется порис
тый кристалличесI01й слой, в котором маточник может удержи
ваться за счет капилляр ных сил . Маточник может также удер
живаться на поверхности кристаллов адсорбuионными силами
в виде тонкого слоя, уд <Ui ения которого при фильтраuии прак
тичесI01 не происходит. Основн ым с пособом удаления остаточ
ного маточника из кристалл и ческого слоя является его про
мывка различными растворителями или расплавом уже очи
щенного вещества.
В процессе роста кристаллы часто срастаются между собой ,
образуя так называемые "кристалличесI01е агрегаты". Внутри
этих агрегатоu могут н аходиться зам Юfутые полости , заполнен
ные маточн иком . К тому же реал ь н ые кристаллы нередко со-

1

1 346

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

держuт трещи н ы и пор ы , в которых также может удерживатьсs1
маточник. Для удален ия маточн ика из агрегатов их подвергают
механ ическому разрушению либо частичному подплавлению
или растворен ию.
Промывку кристалл ической фазы можно проводить непо
средствен н о на поверхности фильтр;�. Иногда ее осуществляют
путем репульпации (механического с мешивания) кристалли
ческой фраКliИИ с растворителем и л и ж е в специальных про
мывных колоннах, работающих в противоточно:м режиме.
В случае направленной кристаллизации структура образую
щегося слоя кристаллов в значительной мере определяется
скоростью перемеще н и я фронта кристаллизации, интенсив
н остью перемешивания жидкой фазы , исходным составом .
Направлен н ый рост кристаллов наблюдается при фраJ<liион 
н о й кристаллизации н а охлаждаем ых поверхностях, зонной
плавке , а также при кристаллизации в тон I01х слоях, контакти
рующих со стекающей жидкой пленкой расплава.
При направленном перемещении фронта кристаллизации ,
как и при массовой кристаллизаци и , происходит межфазное
перераспределение ко мпонентов, зависящее от величины к о 
эффициента распределе1-1ия компонентов между жидко й и твердой
фазами. Различают равн овесн ый т и эффективный тэФ коэф
фициенты распределения.
Значение т = хJхм, где Хк и Хм - равновесные концентра
ции рассматр иваемого компонента в кристаллической и жид
кой фазах. Величину т можно оп ределить по диаграмме фазо
вого равновесия, а также испол ьзуя зависимости ( 1 6 . 6) и ( 1 6 . 7) .
Однако равновесное распределение компонентов между фаза
ми возможно лишь при бесконечно малой скорости кристалли
заци и . В реальн ых условиях равновесие устанавливаться не
успевает, и процесс н аправленной кристаллизации протекает с
более низко й эффективностью.
Под эффективным коэффициентом распределения fпэф обычно
подразумевают отношен ие реальных концентраций рассматри
ваемого компонента в кристалл ической (xs) и жидкой (XL) фазах :

тэФ

= xs /xi .

( 1 6 .22)

Коэффи циент тэФ зависит от скорости кристаллизации , ин 
тенсивности перемешивания жидко й фазы, формы гран ицы
раздела фаз 11 ряда других факторов. Значение тэф чаще всего
определяется опытн ым путем . О� нако имеются попытI01 теоре 
тического подхода к его расчету .
Для о це н ки сте п е н н приближе н ия реального процесса
к равновес н о м у ис пол ьзуют также к оэффициент эффек -

' См .

[3, 6, 8 1 .

1 347

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

т ивности

разделения:

Е = xs xL
Хк - хм
-

( 1 6.23)

.

Для оценки полноты отделения кристаллической фазы от
маточника применяют 1<:оэ фф ициент захвата А маточника кри 
сталл изатом. Если обозначить массу захватываемого маточника
М', а массу кристаллической фазы К, то
А

=

М'
К

=

Xs

_хк

-

Xs

- хм

.

.

( 16.2 4)

Если принять, что состав отделенной жидкой фазы XL = Хм,
то между коэффициентами Е и А существует следующая оче
видная связь:

А = (1

-

Е)/Е .

( 16.25)

Фракционная кристалл изация может быть реализована в ви
де однократного, последовательного и многоступенчатого про
цессов. Рассмотрим таю1е процессы применительно к разделе
нию бинарных смесей.
При однократнолr фракционировании (см. рис. 16.20 , а) ис
ходную смесь F с концентрацией XF высокоплавкого компонен
та А на стадии кристаллизации Кр охлаждают до температуры
фракционирования tФ, лежащей в интервале между температу
рами ликвидуса tл и солидуса tc смеси (рис . 16.20,б, в). Полу
ченную при этом суспензию, состоящую из кристалл и ческой К
и жидкой М фаз, направляют на стадию сепарации Ф . В ре
зультате получают кристаллическую фракцию S с концентраци
ей xs и жидкую фракцию L с кон центрацией XL ·
В условиях равновесной кристаллизации составы кристалли 
ческой Хк и жидкой Хм фаз можно определить п о диаграмме
фазового равновесия (рис . 16 .20,6). Составы же xs и XL зависят
от степени прибл иженин реального процесса кристаллизации к
равновесному и от усло вий сепарации суспензии. При сепара
ции суспензии в изотермических условиях концентрация XL
обычно близка к равновесному составу жидкой фазы Хм· Вели
чина же xs, как правило . заметно отличается от Хк из-за захвата
маточника кристаллизатом.
Для стадии кристалл изации справедливы следующие урав
нения материальных балансов для массовых потоков фаз и
компонента А:

Решая совместно

1 348

F= К+ М ;
F.ц = Кхк + Мхм
уравнения ( 1 6 .26)

( 16.26)
( 1 6 .27)
и

(16.27),

получим вы-

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

а

tл

�-��--�/С----� / ф

в

x" =xL

XF

А

Хк

Х5

х

tв

в

ХЕ

6

x" =xL

х

F

в

Х5

Xf'f
А

:
Рис. 16. 20. Однократная фракци онная кристаллизация бинарных смесей й ряд твер

разде>лени е> смеси , образующей непрерывны
а - прющипиал ьная сх е>ма, б
дых растворов , в - разделени е> см еси , не образующей твердых растворов
·-

ражения для выхода кристалл и ческой и жидкой фаз :
К
Х F - Хм
<vк

=

м

-

F

=

( 16.28)

Хк - Хм

( 1 6.29)

Для смесей , не образующих твердых растворов (см . рис .
1 6 . 20, в), при хр > ХЕ получаются кристаллы чистого компонента
А. При этом Хк = 1 , и уравнение ( 1 6.28) примет вид:
<t>к

=

X F - Хм
1 - Хм

( 1 6 . 3 0)

Из уравне ний матери ального баланса всего процес са в це
лом аналоги чным образом находим выходы конечн ых продук
тов разделен ия:
L xs - хр
xF - xr .
S
( 16.3 1)
- - - -- , <J' L = <v s
F xs - xL
F xs - xL
Если принят ь, что х1, :::: хм, то с учето м коэфф ициента эф
фектив ности раздел ения Е уравне ние для выхода кристалличе
ского продукга будет иметь вид:
_

_

=

=

( 1 6.32)
1 349

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 1 6 . 2 1 . К расчету п р о цесс<! п о сл е 

фракци о н н о й криста;1люаци и бю1<1р н о й с м ес и , обр<1зу ю 
щеfi н е п р е р ы в н ы й ряд твердых р<1с
тво р о в (р<шно вес ный п р о цесс)

до в<1те,1 ь н о й

а

П р и последовательной ( п о 
кристалл изации

с те п е н н о й )

образ ующаяся

А

в

кр и сталл и ч е 

с к;�я ф ;� з а туг же

в ы в од ит с я

из кр и с тал л и з атора ( и л и о н а

н аход ится

тако м

в

с о с то я 

н и и , что практически не уча
ствует в дальне й шем массооб
м е н е ) . Такой вид фракци о н и 

рования реализуется при кри 
стаплизации

на

по верхн остях ,

охлаждаемых
также

а

направлен ной
ци и .

В
Хм

-

-

в

·
1

ход е отбора кр и сталл и 

ч е с ко й

фазы

н ие

нем

К

кол и ч ество

маточника М, остающееся в
к р и с тал л и з атор е , и с од ер ж а 

1
1

1��
'

в

ум е н ь ш аются .
но

и

ко н це н т р а 

отбирае м о й

кристалл и 

(р и с .

1 6 .2 1 , а ,

полу•�ается

од и н

ч е с ко й фаз ы
б) .

п о с те п е н н о

Соответстве н 

с н ижается

ция
Хм

Хм

в ы с о ко плавко го

ко м п о н ента

о

при

кристалл иза

В

Хк

резул ьтате тако го раз -

дел е н ия

м ато•1 н и к с остава Хм и набор
кри сталл и ч е с ки х фр а к ц и й , ко н ц е н трации которых и з м е н я ются
от н а ч ал ь н о й Хко до ко н е ч н о й Хк .

При

усл о в и я х

п о сл едо вател ь н о й

исход н о й с м е с и
м ато ч н и ка

Л1,

Р,

к р и стал л из а ц и и ,

о т о б р а н н о го

равн овесия

фаз ,

а та кже

их

соотн о ш е н ия

п роте кающей

между

кристалл и ч е с ко го п р од укт а К

ко н це нтрац и я м и ,

в

кол и ч е ства м и

ка к и

и

п р и од н о -·

крат н о м п р о цессе , в ы р ажаются ур <t в н е н и я м и ( 1 6 . 2 6 ) и ( 1 6 2 7 )

переменн ый
.

Так ка к отб и р а е м ая
с л едует

к р и сталл и ч е с ка я

фаза

и м еет

.

с ос т а в , т о п р и расчете ныхода п р од укт о в раздел е н и я в урав н е 

н ие

( 1 6 .27)

уравн е н и й ( 1 6 . 2 6 ) и
сталл и ч е с к о й

н е о бход и м а

фаз ы .

п одставлять

срсд11юю

ко н це н тр а ц и ю

кр и 

П о э то м у в да н н о м случае бала н с о в ы х
( 1 6 . 2 7 ) н ед о с т а т о ч н о для р е ш е н и я задач и :

ка кая -то

д о п о л н ител ь н ая

з а в и с и м о сть

,

с вя з ы 

в а ю щая и з м е н е н и я ко н ц е н т р а ц и й фаз в п р о ц е с с е разделен и я .

1 3 50

В

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

качестве такой зависимости можно использовать дифференци
альное уравнение матер иального баланса по одному из компо
нентов смеси, аналогичное используемому в расчете простой
постепенной дистилляции (см . разд . 1 2. 3 .2) :
--хкdК = d(Мхм) ,

или

ХкdК + Мdхм + ХмdМ = О .
Учитывая , что dK
dM, из (б) имеем:
(Хк
Хм)dМ = Мdхм .
=

(а)

(б)

-

-

(в)

Разделяя перемен н ы е и интегрируя уравнение (в) в пределах
от F до текущего значен ия М и от XF до текущего хм, н аходим :

М
F

111

-

=

х"

dхм
Хм

J ---'-'--

Хр

Хк

( 1 6.33)

--

В кон це процесса М и Хм принимаюг свои конечные значения .
В общем случае уравнение ( 1 6 . 3 3) решается численными ме
тодами или путем графического интегрирования на основе
диаграммы равновесия фаз (рис. 1 6 .2 1 , б, в) . Если известна
фун кциональная зависи мость между кон центрациями Хк и Хм ,
то уравнение ( 1 6 . 3 3 ) иногда удается решить аналитически .
Так, если линии .т иквидуса и солидуса близки к прямым
(обычно без существен ной погрешн ости это можно принять
для кон цевых областей диаграмм ы равновесия фаз), то связь
между кон центрациями Хк и Хм может быть описана с исполь
зованием равновесного коэффициента распределен ия т. В
частности , для смесей , обог.�щен н ых высокоплавким компо
нентом, можно испол ьзовать зависимость
Хк

=

1

-

m( l

-

Хм)

( 1 6 . 34)

.

Решая уравнение ( 1 6 . 3 3 ) с учетом ( 1 6 .34), получим зависи 
мость, описы вающую изменен ие кон центраций жидкой фазы в
процессе разделения :
Хм

=

1

-

(1

-

ц)

(м)т-1
F

.

( 1 6.35)

Зная величину хм и з ( 1 6 . 34) , можно определить значение Хк·
Многоступенчатая фракционная кристаллизация рассмотре
на н иже (см . разд . 1 6 . 6 . 1 ) .
Процесс обычной фракцион ной кристаллизации (без ис
пользования растворителей) о казывается невозможным или
экономически невыrодн ым в следующих случаях:
- при разделении nы с окоплавких веществ, когда требуется
1351

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

поддерживать высокие температуры в кристаллизаторах и во
вспомогательном оборудовании;
- при разделении вязких смесей, когда обычная кристалли 
зация сопровождается значительным переохлаждением и про
текает при н изких скоростях тепломассообмена;
- если исходная смесь содержит большое количество смо
листых веществ, затрудняющих процесс разделения, и др .
Для предотвращения подобн ых затруднений можно реко
мендовать фракционную кристаллизацию с использованием низ
коплавких растворителей . Однако в этом случае возникает не
обходимость в ряде дополнительных операций: растворения
смеси, отгонки растворителя от продуктов разделения, регене
рации растворителя .
При фракционировании неорганических веществ в качестве
растворителя чаще всего используют воду, а при разделении
органических смесей - спирты, кетоны, эфиры, хлорорганиче
ские соединения, циклические углеводороды, н изкокипящие
продукты перегонки нефти и др .
К растворителям предъявляют следующие требования:
- достаточно высокая растворимость очищаемого вещества;
- существен ное изменение растворимости вещества с изменением температуры;
- обеспечен ие проведен ия процесса в умеренном темпера
турном интервале;
- нетоксичность и химическая инертность по отношению к
разделяемой смеси;
- слабое коррозионное воздействие на оборудование.
1 6.5.2. Массовая кристаллизация с отводом теплоты
через охлаждаемые поверхности

Для осуществления данного процесса применяют аппараты
*
разнообразных конструкций с охлаждающими рубашками или
различными
погружными
теплообменными
элементами
(змеевиками , трубчатками, дисками и т.п. ) . Охлаждающими
агентами служат жидкости, сохраняющие неизменным свое
агрегатное состояние (вода, рассолы , органические вещества с
низкой температурой плавления и др.), а также испаряющиеся
жидкости (аммиак, фреоны, пропан , ЭТ'ан и др.). Последние
обычно используюг при фракционировании низкоплавких смесей.
Наиболее простыми аппаратами для проведен ия рассматри
ваемого процесса являются ем к остн ые кристаллизаторы с
охлаждающей рубашкой (рис . 1 6 .22 , а) , в которых кристалли
зующаяся смесь перемешивается рамными, якорными, лопает•

П одробнее о писание этих констру кций см. (2,

1 3 52

5 , 6, 10, 1 1 , 14 ).

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

6

/[

Рис. 16. 22. Схем ы кристалли заторов с внеш н и м охлаждением:
- с охлаждающей рубашкой , б - трубчатоrо типа;
1 - корпус, 2 - рубашха, З - мешалка, 4 - шнек со скребками ;
/ - исходная смесь, l/ - суспензия, l// - охлаждающий аrеш

а

н ыми или пропеллерными мешалками . Перемешивание под 
держивает растущие кристаллы в о взвешенном состоянии и
интенсифицирует процессы тепломассообмена. Объем таких
аппаратов может достигать нескольких кубических метров. Ча
ще всего емкостные кристаллизаторы работают периодически .
Режим охлаждения устанавливают с учетом особенностей кри
сталл и зации конкретных смесей , в большинстве случаев плавно
понижая температуру в аппарате по определенной программе.
В случае кристалл и зации смесей, склонных к переохлаждению,
при достижении насыщения в смесь вводят затравочные кри 
сталл ы .
Недостатком емкостных кристаллизаторов является неболь
шая поверхность теплообмена. Для ее увеличения внутри аппа
ратов часто размещают дополнительные охлаждающие элемен 
ты: змеевию1 , трубчатки , а также различные вращающиеся
элементы (барабаны , диски и др . ) .
Получаемую кристаллическую суспензию II (см . рис . 1 6.22 , а)
выгружают через н ижний спускной штуцер . Во избежание за
бивки спускн ые штуцера обычно подогревают паром или горя
чей водой .
Для непрерывной кристаллизации часто используют гори
зонтальные трубчатые аппараты (рис. 1 6 .22,6) с наружной
охлаждающей рубашкой, снабженные шнеком или валом со
скребками . И сходная смесь 1 непрерывно подается с одного
1 3 53

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

1

: = : =1 : = : = :

ш

1

L._

3

\

2

1 - вал . 2 - скребок, З - диски;
/ - исходная смесь, // - суспензия, /l/ - хладоаrенг

Рис. 1 6. 23. Схе м а диско вого кр исталл изатора:

кон ца кристалл изатора, а суспензия 11 выводится с противопо
ложного конца. Содержание твердой фазы в суспензии обычно
не превышает 40 % . Длина трубчатых кристаллизаторов нередко
достигает 30-40 .м, причем их разбивают на отдельные соеди
ненные последовательно секции длиной по 6-8 м. Секци и ,
охваченные общей руба шко й охлажден ия , мoryr располаrdться
друг над другом или по углам шестиугольника. Скребки
(лопасти шнека) предотвращают образование кристалл о в на
теплопередающей пове рхности , а также интенсифицируют
процессы теnломассообмена.
К аппаратам непрер ывного действия относятся также диско
вые кристаллизаторы вертикального и горизонтального типов .
Вертикальн ые кристаллизаторы (рис . 1 6 .23) состоят из пустоте
лых дисков, в которых no кольцевым каналам движется хладоа
гент. Диски собраны в пакет, стягиваемый болтами , и имеют
1 3 54

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 1 6. 24.
Схема кристаru1изатора с
uир куляuией осветленного м аточника:
1
кристаллорастворитель, 2
тепло
обм еюm к , З
насос, 4
центра.1ьная труба,
5
uиркуляuиою!Ый контур ;
l
и сходнLIЙ раствор, 11
сrущенная
суспензин, lll
осветлешwй м аточник, IV
-

-

-

-

-

-

-

-

-

хладоаrент

отверстия для перето ка кри
сталл изующейся смеси. Каж
5
дый диск сн абжен двум я шту
церами - для подвод;� и отво
да хладоагента . Через цент
ральное отверстие в дисках
проходит вал , на котором закреплены скребки для очистки охлаждающих поверхностей и
для перемешивания кристаллизата.
И сходная смесь 1 поступает в междисковое пространство
через верхний питающий штуцер , проходит через все меж
дисковые пространства и выгружается в виде суспензии 11 че
рез н ижн ий штуцер . Хладоагент 111 обычно направляют проти
вотоком к охлаждаемой смеси.
Для кристалл и зации неорган ических солей из водн ых рас
творов используют цир куляционные кристаллизаторы . Кристал
лизатор с циркуляцией осветлен ного маточника (рис. 1 6 .24)
включает кристаллорастворитель 1, теплообменник 2 и цирку
ляцион н ый насос З. Исходный раствор 1 смешивается с цирку
лирующим маточн иком и подается в теплообмен ник, где смесь
охлаждается на 1 -2 °С ниже точки насыщения. Далее пересы
щенный раствор поступает по центральной трубе 4 в н ижнюю
часть кристаллорастворителя . Образующиеся кристаллы взве 
шены в восходящем потоке маточн ика. Пройдя через псевдо
ожиженн ый слой кристаллов, маточник осветляется и по цир
куляционному контуру 5 возвращается в теплообменник 2.
В кристаллорастворителе происходит частичная классифи
кация кристалл о в по размерам . Сгущенная суспензия 11 отво
дится чере.з штуцер в донной части аппарата, а часть осветлен 
ного маточн и ка 111 отб ирается через штуцер в верхней части
кристаллорастворителя . Для обеспечения циркуляции маточни
ка используют осевые или центробежные насосы .
При охлаждении циркулирующего маточника возможна ин
крустация внутренних поверхностей теплообменника. С целью
удаления осевших кристаллов теплообменник периодически
промывают или пропар и вают.
Для н епрерывной кр исталлизаци и растворов часто исполь
зуют барабан н ые кристалл изаторы с внешней охлаждающей
рубашко й , конструкuия которых напоминает вращающиеся
барабанные сушилки (c l\I . разд . 1 5 . 1 . 1 ) .
1 3 55

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

К, М

tn t

б

а

tn t

схема процесса , б - изменение во времени температуры смеси , в
времени массы к ри сталл иче ско й К и жидкой М фаз

Рис. 1 6. 25.
а

Периодическая массовая кристалл изация в емкостном аппарате:

-

-

изменение во

Методики расчета процесса массовой кристаллизации в ап
паратах с внешним охлаждением определяются режимом рабо
ты, способом охлажден ия, свойствами кристалл изующегося
вещества, а также структурой потоков, зависящей от конструк
ции аппарата. Все это пока затрудняет создание единого под
хода к расчетам аппаратов различной конструкции . В литерату
ре приводится ряд моделей, описывающих рассматриваемый
•
процесс кристаллизации при различных постановках задачи .
Рассмотри м в качестве примера периоди'tеский процесс фрак
ционной кристаллизации бинарно й смеси в аппарате идеального
перемешивания для случая, когда лимитирующей стадией про
цесса является отвод тепла от кристаллизующейся смеси к
охлаждающему агенту (рис. 1 6 .25,а). Примем, что температура
охлаждающего агента е в процессе охлаждения остается неиз
мен ной (это справедливо, н апример , при использовании испа
ряющихся хладоагентов) . В общем случае охлаждения перегре
того исходного расплава tp > tл кристаллизация состоит из двух
последовательных стадий (рис . 1 6 .2 5 , б, в) : охлаждения исходной
смеси F от температуры lp до ее насыщения (температуры лик
видуса !л) и кристалл изации при понижении температуры от tл
до конечной температур ы фракционирования 'Ф·
Н а стадии простого охлаждения от смеси отводится следую
щее количество теплоты :
( 1 6 . 36)
гд е cF

•

-

тешюемкость исходно й смеси .

Подробнее о моделях мас..:овой кр исталл и зации

1 3 56

см. (6,

8,

1 1 , 1 4, 1 6 ) .

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

С целью определен ин продолжительности данной стадии • 1
запишем уравнение теплового баланса для контура, совпа
дающего с объемом жидкой смеси, и элементарного промежут
ка времен и d't, за который температура смеси снижается на
величину dt. При этом от смеси отводится элементарное коли
чество теплоты Fcplt - это накопление теплоты . Прихода теп
лоты нет, а Уход ее через поверхность теплообмена кристалли
затора составляет k J(t
8 ) d• , где k 1 - коэффициент теплопе
редачи на стадии простого охлаждения.
Тепловой баланс в отсутствие Источников и Стоков теплоты
запишется
О - k1 (t - e )/d• = Fcplt .
(г)
-·

Разделяя перемен ные и интегрируя уравнение (г) в пределах
от tр до tл и от О до • i , получаем

-'r �
1/ - 8

откуда

't J

=

kif fl d. ,
Fcp о

Fcp
tp - е
= -- 111 -- .
k1 f
tл - е

( 1 6 .37)

На стадии кристалл и зации образуются кристаллическая фаза
К с теплоемкостью Ск и маточник М с теплоемкостью См. При
этом от кристаллизующейся смеси отводится количество теп 
лоты Q2, для определен ия которого составим тепловой баланс
данной стадии для всей смеси:

FcF tл - Кск t,I> - Мск tф -

откуда

Q1

+

Кrкр

=

О

,

( 1 6 . 3 8)
С целью определения продолжительности стадии кристалли 
зац ии •2 = •п - • i , где •п - общая продолжительность процес 
са, запишем уравнение теплового баланса для бесконечно ма
лого отрезка времени d•:
- Скd(Кt) - смд ( Мt) - d Q + Гкрd К = О .
(д)
Отсюда, раскрывая d ( К/) и d ( Mt) , получаем :

dQ

=

ГкрdК - I<cкdt - CкtdK - Mcмdt - См tdM .

(е)

=

- d M, уравнение (е) примет вид:
(ж)
dQ
ГкрdК - Kcкdt - Mcмdt - (ск - Cм)td K .
Если теплоемкости кристаллической и жидкой фаз близки ,
то уравнение (ж) можно упростить:
dQ
/"крdК - Kcкdt - Mcмdt .
(з)
С учетом того, что dK
=

=

1 3 57

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

С друго й сто р о н ы ,

можно
где k2

количество отводимого тепла за время dт

пр ед с та вить ка к

dQ

kJ.l(t - e ) d i: ,

=

- коэфф и циент rеruюперt•дачи от кр истdJU!Изующейся смеси

Расс матр и вая с о вм е с т н о

kz!( t - 8 ) d т

урав н е н и я (з)

rк p d K

(и)
к хладоагеюу.

и ( и ) , получае м :

- Kcкd t - Mcмd t

( к)

.

В ур ав н е н и е ( к) вхою1т п е р е ме н н ы е К, М, t и i:, поэто м у для
решения задач и н еобходимы дополн ител ьные уравнен ия с вязи .
В качестве таковых мож н о использо вать уравн ен ия материаль
н о го баланса ( 1 6 . 26) - ( 1 6 .29), связы вающие величи н ы К и М с
текущ и м и ко н це нтраци я ми ф а з Хк и хм . Есл и принять, что л и 
мити рую щ е й с тад ие й п р о цесса я вляется с ко рость отвода те пл о 
ты от крист алл и з ую ще й с я смес и , т о с вя.зь между кон центра
ция м и Хк и х м и тем п е р атуро й t можно установить и з условий
фазового равновес ия .
В общем случае рас с ы атриваемую задачу м ожн о решить чис
лен н ы м и методам и .
=

В частн о м случае, ко гда л и н и и солидуса и л и кв идуса бл и з ки к пря м ы м ( этот
случай часто реали зуется в о бл а ст и м ал ых ко н це н тр а ц и й ) , связь м ежду ко нцент
о писана ура в н е н и е м

( 1 6 . 34),

р а ци я м и Хк и Хм м ожет бьггь в ыражена с о о тн о ш е н и е м

где

tл -

Хм

1

- (tд - t)/N ,

а

линия ликвидуса

те м п ература кр и сталл изаци и высокоnлавко го ко м п о н е нта смес и ; N
=

(л)

-

п о стоя н н ый коэф ф и ц и е нт, • 1 и сл е н н о рав н ый тан ге н су угла наклона л и н и и л и к
в идуса к о с и абс1 111сс.
Рассм атр и пая с о в м естно ура в н е н и я ( l ti . 2 8 ) , ( 1 6 . 2 9 ) , ( 1 6 . 34) и (л) , и м е е м :

K ,= __!_[
1 _ ( 1 tд- xF)N]:
1-т
-1
__!_[(\
- т]
1-т
ц)N

Л1 "

tл - t

(м)
(н)

·

П р о л и ффе р е 1 щируе м ура n н е н и е ( м ) :

dK =

FN ( l - x F )

(1 - т)(tд - 1) 2

П одста вля я в ура в н е н и е ( к) н айд е н н ы е з н а ч е н и я

в п р едел а х от

О

по tк и от fп до

и з :-.1 е н е н и е те м 1 е µ атур ы

ся

в

про цессе

1

частн о го случ а я :

1Ф

разделе н и я

tФ

К, М и
и и нтегр и руя е го
п р и допущен и и , 'fТО те пл о е м кост и фаз остают
п олуч и м

dK

пр о це с с е кр и стаruш заци и для рассм атр и ва е м о го

п о сто я н н ы м и ,
в

(о)

dt.

выраже н и е ,

о п и с ы ва ю щее

1·._ r FN ( l - xFXtл - tФ)
F(с._ - т см ) 1,, - е
+
tк = k2f(1 - m ) lп �;-=u k2f( I - т Хtл - е Хtл - tФХtл - tл )
flV(t - xF )[(c._ -- cм Xtл - 0) - rк r ]
+

1 3 58

k2f ( 1 - тХtл - е )

2

1

n

-+--'--..L..Т---'-

+

( 1 6 . 3 9)

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

F.1:1

�2

: � � tф

-- ·
::::::1!::,..!

fGx ,01

а
К, М

6

M=:f(I)

F

'"

/

-

'r
в

/ / ---t�>---- /] ---,п _____

Рис. 1 6. 26. М ассо вая кр и сталл и::ация в ап парате ид еально го вьrrеснени я :
а - схема rют<жов, б - измене ние потоков ф аз , в - изменение температур t и

не аппарата

е по

дли 

Рассмотр и м теперь при тех же допущениях непрерывный про
цесс фраки,ионной кристаллизаиµи в кристаллизаторах идеального
вытеснения (к н им можн о отнести аппараты шнековоrо и скреб
ковоrо типа - рис . 1 6 .26). В таком кристалл изаторе с одноrо кон 

ц а аппарата непрерывно подается исходная смесь, а с дpyroro
выводится образующаяс.н суспензия . По длине аппарата диа
метром D можно вьщел итъ участки: /1 - простоrо охлажден ия
смеси до ее насыщения и /2 - охлаждения, сопрово:ждающеrося
кристаллиз ацией смеси . Общая длина аппарата составляет

11 + 12

(п)
.
На участке простого охлаждения температура исходной сме
си изменяется от IF до температуры ликвидуса tл. Для элеме н 
тарноrо отрезка d/ п р и простом охла:ждении справедливо урав
нение тепловоrо баланса

ln

=

(р)
О - k 1 nD(t - 0)d/ Fcpjt .
Разделяя переменн ые и и нтегрируя уравнение (р) в пределах
от IF до tл и от О до 1 1 при 8
co нst, имеем:
=

=

-'

r�

1·F t

-

8

=

f

nk1 D dl .

Fc F

0

1 3 59

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Отсюда получаем выражение для расчета длины участка
простого о хл ;�жден и я :

( 1 6 .40)

Количество отвод и �ю й на это м участке теплоты Q1 можно
рассчитать по уравнен ию ( 1 6 . 3 6) .
Н а участке кристаллизации темпе р атур а смеси изменяется от
lл до tФ . При этом тепловой баланс для элементарного участка
дл ин о й d/ (с принятыми ра нее доп ущен и ями) описывается
урав н е н ие м (з) . С друго й сторон ы , количество теплоты , отво 
димой на дан ном участке , равно

dQ

При с о в местн о м

=

k2nD(t - 8 )d/ .

р а сс м о тр ении ура внений

(с)
(з) и (с) имеем:

(т)
Гкр dК - Kcкd t - Mcм d t .
П одставляя в (т) значения К, М и dK из уравнений (м), (н) и
(о) и и нтегр и р уя получ е н ное выраже н и е в пределах от О до /2 и
от tл до tФ, н а йд ем в ыр а жение для расч ета длины уч а ст ка кри
с талл и за ц ии :
k2

nD( t -

G)d /

=

т
/2 Р(ск - см ) l n tл - 0- +
n k2 D (l
+

)

- т

--

'Ф

-

О

Frкp N (l - xp )(tл - tФ )
nk2 D (1 т)(tл - 8 )(tл - tФ ) (tл - tл )

FN(l - Хр Жс к см )(tд - 8 ) - Гкр ] (tФ - е ) (tл - tл )
nk2D(l т)(tд 8) 2
l n {tл - tФ )( tл 8 )
-

-

+

-

-

-

Количество отвод и м о й те плоты Q2 н а
считать по урав нен и ю ( 1 6 . 3 8 ) .

участке /2

. ( 1 6 .4 1 )

м о жн о рас 

1 6.5.3. Массовая кристалл изация
при непосредстRенном контакте с хладоаrентом
Этот метод отли ч ается высокой интенсивностью тепломас 
с оо бмена, обусловлен н о й развитой м еж ф азн о й поверхн остью и
ин тенс и вн ы м перемеши ван ием фаз , возможн остью про веде н ия
п р о ц есс а при незначительной разности температур между кри
сталлизующейся смес ью и хлад о а гс н то м (порядка 0 , 5-2 ° С) , ;i
также отс уrствием в крнсталлизатор;�х те плообмен н ых поверх
ностей, что исключает их и н крустацию и существенно упро
щает ко нструкц и ю аппаратов. Появляется возможность изго 
то влени я а п п а рато в из материал о в с н изкой тепло провод 
н о стью (пол и м е р ы , сте кл о , керам и к:.1 и т.д . ) . Ра ссм атр ив а ем о му
п р о цесс у п р и сущи и н едо стат ки : возможность .загря з н е н и я

1 3 60

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

продуктов разделения хладоагентом; появлен ие дополнитель
ной операции отделения отработанного хладоаrента от продук
тов разделения.
В качестве хладоаге нтов используют охлажденн ые жидкости
и газы , сжижен ные rазы , переходящие при контакте с кристал
лизующейся смесью в rd зообразное состояние, а также твердые
вещества, плавящиеся в процессе контактной кристаллизации .
Хладоаrенты должны быть химически инертны к разделяемой
смеси и полностью нерастворимы в ней .
При контактно й кристаллизации органических веществ в ка
честве жидкого хладоагента обычно используют воду или вод
ные растворы различн ых неорrанических солей. При кристал
лизации неорганических веществ применяют различные органи
ческие жидкости . В качестве газообразных хладоагентов ис
пользуют воздух или инертные rазы, в качестве испаряющихся
хладоаrентов - бутан , бутилен , бутан -бутиленовые смеси, ме
тилхлорид , а также различные фрео н ы .
В зависимости о т соотношен ия потоков разделяемой смеси
и хладоагента, их физ ико-химических свойств и рабочих усло
вий процесса кристалл и эация может происходить в дисперсной
или сплошной фазе .
При кристалл изации в дисперсной фазе исходная смесь дис
перrируется в виде капель в потоке сплошной фазы хладоаrен
та. Такой процесс чаще применяют при кристаллизации орга
н ических веществ из расплавов.
Кристаллизация в сплошной фазе осуществляется путем дис
пергирования хладоагента в кристаллизующейся смеси. Такой
процесс обычно применяют при кристалли зации неорганиче
ских солей из водных растворов и при концентрировании вод
н ых растворов методом вымораживания.
Контактная кристаллизация может осуществляться
как в пе
•
риодическо м , так и в не п рерывном режимах .
Периодический процесс чаще всего проводят в емкостных ап
паратах. При этом исходную смесь заливают в аппарат в
несколько перегретом состоянии. Далее при непрерывном пе
ремешивании в аппарат постепенно вводят хладоаrент до до 
стижения заданной температуры фракционирования . После
некоторой выдержки полученная гетерогенная смесь подается
на разделение. Крист<umическая фаза отделяется методом
фильтрации, а хладоагент от маточн ика - методом отстаива
н ия (декантации). Хладоаrенты обычно подают через распреде
лительные коллекторы или через сопла.
Непрерывный процесс контактной кристаллизации имеет бо
лее разнообразное аппаратурное оформление.
• Более подробно данный 11роцесс и его аппаратурное оформление представ
лены в (2, 5 , 6 ) .

1 36 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

VI

1

Рис. 1 6. 2 7. Схема н епрер ы вн о й ко н 
такrной кристалл изации с использова

нием жидкого хладоаrента:
1 - кристаллизатор, 2 - фильтр, 3 -

сборник кристалл и че скоrо продукта, 4 отстойник, 5 - теплообменник;
/ - исходный расплав, // - жидкая
фракция п осл е промывки . /// - р асплав на
п ромы вку, JV - rотовый продукт, V маточная жидхость, VJ - хладоаrеtп

Одна из схем установки с исполь
зованием непрерывного емкоС'Пlоrо
кристалли:штора п о каза н а на рис.
1 6.27. Здес ь исходную смесь / и хла
доа1-ент V/ непрер ы в н о подают в кр и 
сталл и зато р 1, откуда также непрерыв
н о в ы rр ужается получаемая суспензия.
П о с.пе фильтрации кристалл ы промывают и выrружают в сборник 3, где их
расплавляют. Ча1.:ть р ас плава выводят в виде готового высоко плавкого п р одукта ,
оставшуюся часть и сп ол ьз у ют для пр о м ыв ки кристалло в. В промывной жид
кости ( фр а кци я /1) обычно содержится значительное количество высокоплавко го
ко мпонента , поэтому ее п р и с о еди няю т к исходной смеси. П ос.пе расс.поения
фильтрата мато•1 ную жид ко ст1 . отводят в качестве низкоплавкого пр одукта , а
хладоаrент охлажда ют в те ш ю о б м е н н и ке 5 и с н о ва подают в кристалл и затор .

Для непрерывной контактной кристаллизации применяют
также аппараты колонного типа с противотоком хладоаrента и
кристаллизующейся смеси. По кон струкции такие кристаллиза
торы напоминают жидкостные экстракторы .
На рис. 1 6 . 2 8 п о казан роторнwй колонный кристаллизатор, в котором кр и 
стаJИизация пр о и с ход ит в дисперсной фазе. П р и этом кр и сталл и зу ю щая ся смесь
и м еет более н изкую плотность, че м хладоаrент. Аппарат снабжен вало м 2, на
котором размещены лопастньн.> м еш алки J. Для снижени я продольного переме

шивани я фаз аппарат по высс>те секционирован кольцевыми перегородками 4.
В низу кристалл и зато р а расноложен ы секции э м уль гир о ва н ия 8 и отста и в а ния 9
отработа н н о го хrшд о а rе нта , а вверху - сбор н и к 6 кр и сталл и ческой суспензи и .
Исходная смесь / п о сту п а ет в н иж н юю часть аппарата и в д ис п ер rи р о ван н о м
виде поднимается вверх. Хл ал о а rе н т II п од ается в одну из верхних секций и

движется проти uото ком к кристалл и зующейся смес и . В верхней секции , где
отсутствует перемешивание, кристалл ическая суспензия отделяется от хладоаrен
та и посту п а ет в сб о р н и к 6, он.-уда направляется н а филыраци ю .
На рис. 1 6.29 п о каза н а одн а из конструкций рас11•шител•ноrо колонноrо кри
сталлизатора, в котором п р о цесс кри сталл и за ции п ро и сх одит в сплошной фазе.
Исх од н ы й раствор / подаетс я в аппарат через коллектор 4, р ас п ол о женн ы й в
верхней части секции ко нтакт и р о ва н ия, а хл адоа rе нт l/, более легкий, неж ел и
кр исталл и чес ки й раствор , - '!(•рез коллектор 5 в нижней части секци и . П ро ходя
через сопла 6, ХЛ <tдоа rе нт дисперrируется и в виде капель п одн и м ается проти во 
то ко м к о п ус ка ю щей ся кр истаю1изующейся смеси . В секции сгущения 2 пр о и с 
ходит осветление маточни ка. Сгущенную суспензию l// отводят через нижн и й
штуцер, сн абж е н ны й п ульсирующим клапано м , а о с в етлен н ый маточник IV из в ерхн ей части се кци и сгущени я . Капли отр аботан н ого хладоаrента с о б ир а ют 
ся в секции отста и вания J, 111 е они коалесцируют и сплошным потоком V в ы в о 
дятся из аппар<1та.

1 3 62

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

6

1

2 - вал , З - меш алк а , 4 - секционирующие пер еrородки , 5 скребковая мешалка, 6 - приемник сусп ензи и , 7 - перфорированн ая пер еrородка, 8 секция эмульrировани н , 9 - секцин отстаивания:
1 - исходная см е сь , 11- исходный хладоаrенr, lll - криста,1лическая суспензи я , JV отработанный хлааоаrенr
1

Рис. 1 6. 28.

Схема колонного кристаллизатора роторного типа:

- корпус алларата,

1 - секция противоточноrо

КС1н rактироваии я , 2 - секция сгущения суспензии , З - сек
ция отстаивания хладоаrенrа, 4 и 5 - коллекторы ввода исходной смеси и хладоаrенrа
соответственно, 6 - с опла ;
1 - исходная смесь, 11 - исхониый хладоаrенr, 111 - сrушенная суспензия , JV - освет
ленный м аточЮt к . �, - отработа� ощй хладоаrснт

Рис. 1 6. 29.

Схема распьmительного кристалл изатора:

К достои нствам колон н ых кристаллизаторов следует отнести
отсуrствие н еобходимости в специальном оборудовании для
отделения хладоагенти от кристаллизующейся смеси.
Этим также отличается процесс контактной кристаллизации
с использованием испаряющихся хладоаген,тов. Здесь образую
щиеся при испарении (кипении) хладоаrента пары обычно со
бираются в верхней части кристаллизатора, откуда они отво
дятся, сжимаются компрессором, охлаждаются и после их кон 
денсации снова возвращаются в кристаллизатор.
Определим выход кристаллической фазы для случая , когда
охлаждение производится жидким хладоагентом (не меняющим
агрегатное состоян ие) . В аппарат подается исходная смесь F (с
1 3 63

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

теплоемкостью cF) при температуре tF, при охлаждении кото
рой до температуры tФ образуются кристаллическая фаза К с
теплоемкостью Ск и маточник М с теплоемкостью См. Хладоа
гент Gx имеет теплоемко сть Сх . В процессе кристалл и зации его
температура изменяется от 8 1 до 8 2 . При этом в результате ин
тенсивного межфазного теплообмена в аппаратах полного пе
ремешивания конечная температура смеси tФ становится прак
тически равной 82 .
Тепловой баланс для всего процесса (контур - весь аппа
рат) имеет вид:
=

FciJF + Gxcx8 1 - Кскtф - Мсм tф - Gxcx82 + ГкрК О .
=
=
Отсюда при 82
/Ф и М F - К получим зависимость

(у)

для
расчета массового потока образующейся кристаллической фазы
(задача эксплуатации):
К=

Gx cx ( tф - 8 1 ) - F(c F t F - См tф )
.
Гкр - (с к С м ) tф

( 1 6 .42)

-

Задаваясь величиной К, из ( 1 6 .42) легко определить необхо
димый расход хладоа ге нта Gx на процесс кристаллизации (одна
из задач проектирован ия) .
П р и использован ии испаряющегося хладоагента конечная
температура смеси tФ практически будет равна температуре
кипения хладоагента 8КJ1п· При этом тепловой баланс для всего
процесса имеет вид:
=

(ф)
FciJF + Gxcx8 1 Кскtф - Мсмlф - Gxhx + ГкрК О .
=
=
Учитывая , что М }' - К, Вкип
tФ , а энтальпия паров хла
доагента hx
rx + Сх8КЮJ (где rx - его скрытая теплота парооб
-

=

разования) , из уравнени я (ф) найдем необходимый расход хла
доагента (проектная задача) :

Gx

=

к[rкр - (ск См )!ф ] + F(cF tF - См tф )
.
Гх + сх ( tф - 8 1 )
-

( 1 6 .43)

При кристалл и зации из раствора с использованием газооб
может происходить частичное испарение
раствориrеля. При этом целесообразно использовать относиrель
ные энтальпии исходного 11 и отработанного 12 хладоаrента, рас
считанные на 1 кг абсолюrно сухой его ча<..-ти (см. гл. 1 5) . В этом
случае расход хладоаrенrа можно определигь по выражению

разных хладоагентов

Gx
1 364

=

к[ rкр - (Ск

-

См )tф ] + F (c F t F - См tф )
12 - 11

( 1 6 .44)

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Заметим, что значения 11 и 12 определяются температурой и
влагосодержанием х хладоаrента и мo.ryr быть определены по
диаграмме 1-х (см . гл. 1 5) , построенной для используемого
:хладоаrента.
16.5.4. Кристаллизащ1я с частичной отгонкой растворителя

Этот метод кристаллизации широко используется для выде
ления растворенных веществ из различных водных растворов.
Его проводят в двух вариантах.
По первому
варианту пересыщение создается за счет частичного удален ия растворителя (воды) при упаривании раство
ра с подводом тепла из внешней среды. Такой процесс часто
называют изотермической кристаллизацией (или вьmарной кри
сталлизацией ) , поскольку выпаривание насыщенного раствора
происходит при практически постоянной температуре кипения .
По второму варианту процесс кристалл и зации осуществляют
без подвода тепла, производя адиабатическое испарение части
растворителя путем пон ижения давления , т.е. за счет самоис
парения (см . разд . 9 .3). При этом на испарение растворителя
расходуется физическое тепло самого раствора, что приводит к
его охлаждению до температуры кипения раствора при оста
точном давлении . В этом случае пересыщение достигается
как вследствие повыше н ия кон центрации раствора, так и за
счет пон ижения температуры. Количество испаряющегося рас
творителя составляет 8- 1 0 % от общей массы раствора. Такой
процесс называют вакуум-вьmарной кристаллизацией (или ваку
умной кристаллизацией ) .
Кристаллизацию с частичной отгонкой растворителя выгод
но применять для веществ, растворимость которых мало зависит от темп � ратуры.
•
П о своеи конструкции выпарные кристаллизаторы напо
минают обычные выпар ные аппараты (см. гл. 9), дополненные
узлом вывода кристаллической суспензии . Выпарные кристал
лизаторы могуг иметь внуrреннюю или выносную греющую
камеру.
Одна из конструкций выпарного кристаллизатора с вынос11ой
греющей камерой показана на рис. 1 6 .30. Циркулирующий рас
твор нагревается в греющей камере 1 до температуры кипения .
Образующаяся парожидкостная смесь поступает в сепаратор 2,
где происходит отделение вторичных паров 11 от раствора,
благодаря чему достигается его пересыщение. Из сепаратора
растущие кристалл ы вместе с маточным раствором направля
ются в секцию отделен ия кристаллов 4, откуда сгущенная сус• Подробнее конструкции выпарных кристаллизаторов описаны в [2, 10, 1 1 ,
14, 16 ) .

1 365

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Выпарной кристмлизатор с выносной
греющей камерой:

Рис. 1 6. 3 0.

1 - rреющая каме ра, 2 - сеnаратор, З - циркуляцион
ная труба, 4 - отделитель криспvщов;
1 - исходный расrвор, 11 - втор ичный пар , 111 - хри
сrаллизат

1 - сепаратор, 2 - цирхуляuи<>нная труба, .1 - барометри ческая труба, 4 - rидрозатвор :
/ - исходный расrвор, 11 - вторичный пар, 111 - хрисrаллиэат

Рис. 16. 3 1.

Вакуум -кристалл изатор с естественной циркуляцией раствора:

пензия (кристаллизат 111) выводится на стадию фильтрации , а
осветленный маточник направляется в rреющую камеру.
Для предотвращения инкрустации теплообменных поверх
ностей скорость движен ия раствора в �:-реющей камере должна
быть достаточно велика (не менее 2 м/с). Для обеспечения та
ких скоростей используют принудительную циркуляцию рас
твора с помощью осевых или центробежных н асосов (на ри
сунке насос не показан ) .
Недостатком выпарных кристаллизаторов являются относи
тельно большие затраты энергии на проведен ие процесса. Бо
лее экономичны вакуум -выпарные кристаллизаторы. Они могут
быть периодического и непрерывного действия, с естественной
и принудительной циркуляцией раствора.
Одна из конструщий вакуум -кристаллизатора с естественным
контуром цщ) куляции показана на рис. 1 6 .3 1 . Исходный раствор
1 подается в н ижн юю часть циркуляционной трубы 2 и вместе
с циркулирующим раствором поднимается вверх, где в резуль
тате понижен ия гидростатического давления вскипает. Обра
зующиеся при этом вторичные пары 11 выводятся из сепарато
ра 1 и подаются на конденсацию. Пересыщенный раствор
движется вн из по кольцевой барометрической трубе J. В про
цессе циркуляционного движения раствора в нем происходит
1 366

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

IV

1 - кристалл юаторы ( корп у с а ) . 2 - барометрическая труба, 3 - rидраалический затвор.

Рис. 1 6. 32. Схема
4

многокорпусн ой вакуу м - кристалл изационной установки:

- ко�щенсаторы;
1 - исходный раство р, 11 - крнсталлизат, 111 - охлЗJ1Щающая вода, JV- ко�щенсат

образование и рост кристаллов. Из барометрической трубы
кристаллы с частью маточника выводятся в гидрозатвор 4 и
далее (поток 111) - н а фильтр . Для поддержания вакуум а
вакуум -насосы
или пароструй
испол ьзуются обычн ые
н ые инжекторы.
Вакуум - кристаллизаторы имеют большую производитель
ность. К их достоинствам можно отнести также равномерное
пересыщение раствора во всем рабочем объеме. Это резко
снижает вероятность и н крустации внутренних поверхностей
аппарата. Ап парат может быть сделан из любых конструкцион 
н ь�х материалов.
В многотоннажных производствах используются многокор
пусные вакуум - кристаллизационные установки с числом корпу
сов от 3 до 24 (рис. 1 6 . 3 2 ) . При этом давление в корпусах посте
пенно пон ижается от первого корпуса к последнему. В верхней
части каждого корпуса установлен ы поверхностные конденса
торы. Нагретый исход н ый раствор 1 подается в первый корпус ,
где он вскипает и за счет самоиспарения охлаждается до тем
пературы, соответствующей остаточному давлению в этом кор
пусе. Образующаяся при этом суспензия самотеком (за счет
разности давлений в корпусах) перетекает во второй корпус ,
где вновь частично упаривается , и так далее . Образовавшийся
кристаллизат выводится из последнего корпуса через баромет1 367

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

рическую трубу 2 в гидрозатвор 3. Конденсация паров осу
ществляется холодной водой III, которая последовательно про
ходит через все конденсаторы корпусов. В ряде случаев обра
зующиеся пары используют для нагрева исходного раствора.
Это позволяет существенно сократить расход энергии и охлаж
дающей воды на проведение процесса кристаллизации .
Технологический расчет выпарных и вакуум -выпарных кри
сталлизаторов методически близок к рассмотрен ному в гл . 9
расчету обычных выпар ных аппаратов. Основное различие за
ключается в необходимости учета влияния образования кри
сталл и ческой фазы на ход процесса разделен ия .
Материальный баланс процесса выпарной кристалл изации от
личается от материального баланса обычной кристаллизации
по ( 1 6.27) наличием потока выпаренного растворителя П. При
отсутствии уноса капеш, раствора вторичным паром концент
рация растворенного ве щества в нем Хп = О. Тогда уравнения
материального баланса всего процесса в целом будут иметь вид:
- по потокам
F = К + М + П;
(х)
- по растворенному веществу
Fц = Кхк

+

Мхм

(ц)

.

Если кристаллизующееся вещество не образует с раствори
телем твердых растворов и молекулярных соединений
(кристалл о гидратов) , то кон центрация кристалли ческой фазы
будет равна Хк = 1 ; в противном случае .хж < 1. При образова
нии кристаллогидратов значение Хк можно представить как
отношение молекулярных масс безводной соли М и кристалл о 
гидрата Мг:

Хк = М/Мг.
Решая совместно уравнения (х) и (ц) , получим выражение
для расчета массового нотока кристаллической фазы при вы
парной кристаллизации :
К=

F(xp - хм ) + Пхм .
Хк - Х м

(16.45)

Как уже указывалось выше, при осуществлении " изо
термическо й " выпарной кристаллизации затрачивается опреде
ленное количество теплоты Q на упаривание раствора, сопро
вождающееся образован ием вторичных паров П с энтальпией
iп . Уравнение теплового баланса всего процесса в данном слу
чае имеет вид:

FcflF +

1 368

Q+

�·к рК - Кскlк

-

Мсмlк

-

Лiп

= О

.

(ч)

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

При этом температура кипен ия раствора tк зависит от дав
ления и температурной депрессии упариваемого раствора
(маточника) .
Из уравнения (ч) найдем расход теплоты на проведение
процесса:
( 1 6 .46)
Материальный баланс процесса вакуумной кристалл изации
имеет тот же вид, что и для выпарной кристаллизаци и . Урав
нение же теплового баланса записывается проще, так как в
адиабатном процессе Q О :
=

(ш)
Совместное решение уравнений (х), (ц) и (ш) позволяет свя
зать выход кристаллической фазы и поток выпариваемого рас
творителя.
1 6.5.5. Кристаллизация на охлаждаемых поверхностях

При проведении фракционной кристаллизации на охлаж
даемых поверхностях, как правило, наблюдаются весьма высо
кие градиенты температуры в разделяемой смеси. При этом
кристаллы первоначально зарождаются на охлаждаемой по
верхности, где достигается наибольшее переохлаждение смеси.
Далее они растуг, обра:�уя на охлаждаемой поверхности ком
пактный кристалличесю1й сло й . Чтобы исключить зарождение
и рост кристаллов во всем объеме разделяемой смеси, ее
обычно поддерживают в перегретом состоянии .
В результате перераспределения компонентов между фазами
кристалл и ческий слой обогащается высокоплавким компонен
том . Степень разделения зависит от доли закристаллизо
вавшейся смеси, режима охлаждения, состава и величин
ы пе*
регрева смеси , конструктивных и других факторов .
Фракцион н ая кристаллизация на охлаждаемых поверхностях
протекает в известной мере сходно с процессом направленной
кристаллизации . Отличие состоит лишь в том, что в данном
процессе фронт кристалл и зации перемещается в результате
направленного отвода теплоты, а не принудительного движе
н ия контейнера или холодильника.
Процесс образования кристаллической фазы на охлаж
даемых поверхностях по своей природе нестационарен , поэто 
му чаще всего он осуществляется в периодическом режиме. В
отличие от массовой кристаллизации в рассматриваемом про 
цессе не требуется отдельной стадии сепарации фаз, что яв• Влияние различных параме'lров на
рассмотрено в [ 5 , 6 \ .

данный

процесс разделения подробно
1 369

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ляется ero достоинством. Однако при кристалл и зации на
охлаждаемых поверхностях обычно наблюдается значительный
захват маточн ика кристаллической фазой , что снижает эффек
тивность разделения. Поэтому для достижения высокой степе
н и очистки веществ от примесей часто производят мноrосту
пенчатую перекр исталли зацию.
Для осуществления рассматриваемого процесса используют
барабанные кр и сталл и з а тор ы с нижним питанием. Исходную
смесь загружают в ванну кристаллизатора. Образующийся на
поверхности барабана кристаллический слой снимают ножом и
отбирают в качестве высокоплавкой фракции . После отбора
определенного количества кристаллической фазы процесс пре
кращают, оставшийся маточник, обогащенный низкоплавкими
примесями, сливают, и процесс повторяется .
Для проведен ия про цесса используются также аппараты с
трубчатыми охлаждаемыми элементами. В этих аппаратах про
цесс кристаллизации может быть реализован как при непо
движном состоянии кристаллизующейся смеси, так и при цирку
ляции жидкой фазы вдоль теплообменных поверхностей.
В первом случае исходную смесь заливают в несколько пе
регретом виде в трубное пространство кристаллизатора, а в
межтрубное подают хладоагент. Кристаллизацию обычно осу
ществляют в режиме программированного охлажден ия . В кон 
це процесса производят слив оставшеrося маточника и затем
выплавление кристалли• 1еской фазы. И ногда после частичного
подплавления из аппарата выгружается суспензия , которую
направляют на ф ил ьтр для ее разделения .
Во втором случае жидкая фаза в течение всего процесса
кристаллизации принудительно циркулирует в замкнутом кон 
туре. П р и этом поддерж ивается определенный е е перегрев. Это
способствует образован ию более плотноrо кристалл и ческого
слоя и повышает эффективность разделения .
Еще более высокая эффективность разделения достигается в
процессе кристалл и зации на охлаждаемых поверхностях при
стекан ии по ним ж ид кой пленки разделяемой смеси . Дело в
том , что при пленочном течении и нтенсифицируются процес
сы тепломассообмена между фазами. Кристалл и зацию со сте
кающей жидкой пленкой проводят обычно в вертикальных труб
чатых аппаратах , в которых высота труб достигает 1 2 м, а их
число - нескольких тысяч.
Для глубокой очистки веществ от примесей часто использу
ется многостадийный процесс разделения, который может осу
ществляться в одном или нескольких кристалл изаторах.
Принципиаш,ная схема установки дпя четырехступенчатой перекристалл и за
ции показана н а рис. 1 6 . 3 3 . Она состоит из кристалл изатора Кр, теплообменни
ков Т1 и Т2, емкостей Е1 и Е1, насосов Н1, Н2 и Нз, а также сборников фракций
Со, С 1 . . . Ск.
1 370

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Кр

Принципиальная схема установки для мноrосгадийной фракционной
кристалл и зации со стекающей пленко й :

Рис. 1 6. 33.

К р - кристаллизатор; Т 1 , Т2 - теплообменники; Е1, � - промежуrочные емкости; Н 1 ,
Н 2 , Нз - насосы; Со, С 1 , С2, С 3, С4, С" - сборники фракций

Процесс разделения осущеt..1W1Яется в циклическом режиме. Исходная смесь
F подается в сборник С 1 , откуда она насосом Н 1 через кристалл изатор Кр зака
чивается в емкость Е 1 . На стадии кристалли зации разделяемая смесь непрерывно
циркулирует в замкнутом ко нтуре. При этом теплообменник Т1 обеспечивает
заданную тем пературу смеси , подаваемой в кристалл изатор. В нем смесь стекает
по внутренней поверхности трубок в виде тонкой пленки . Охлаждение произво 
дится хладоаrентом, который непрерывно цир кулирует с помощью насоса Н 2
через теплообменник Т2 и промежуточную емкость Е1. В процессе кристалли за
ции температура хладоаrент<1 изменяется по определенной программе. В кон це
процесса охлаждения оставшиiiся маточник сливают в сборник Со, а кристалл и 
ческую фазу выплаWIЯют и сли вают в сборн и к С 2.
В ыплавление кристалл ичес кой фазы можно производить двумя способами :
путем нагрева теruю носителя, циркулирующего в контуре охлаждения, с по
мощью теплообмен ника Т2 ил и путем подачи нагретой обогащенной фракции из
сборника С2 насосом Н з в кр исталли затор. После расплавления кристалл ической
фазы полученный расплав возвращается в сборник С2.
Аналоmчно осущесгвляе�'Ся ра.:щеление и на друrих ступенях. При :лом низко
плавкая фракция W с п-й С1)'Пени подаеrся в сборник (п
1)-й ступени, а высоко
плавкая фракция П
в сборни к (п + 1)-й С1)'Пени. Цикл начинаеrся с ра:щеления
самой низкоплавкой фракции, а заканчивается разделением наиболее высокоплавкой.
При зrом может бьпъ реализована схема противоточной кристаллизации.
-

-

Расчет материальных потоков и их составов при фракцион 
ной кри сталлизации н а охлаждаемых поверхностях произво1371

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

дится с использованием уравнений последовательной фракци
онной кристаллизации ( 1 6.33) и др.
1 6.5.6. Противоточная кристаллизация

Противоточная непрерывная фракционная кристаллизация
является одним из наиболее перспективных методов разделения
•
и очистки веществ . Она позволяет достигать высоких степеней
разделения при значительной производительности. В настоящее
время данный метод успешно используется, в часmости, для про
мышленного разделения ряда углеводородных смесей.
Создать противоток лри кристаллизации значительно труд
нее, чем в других про 11ессах разделения (ректификации, аб
сорбции) - вследствие малой разности плотностей кристалли
ческой и жидкой фаз : обычно их плотности различаются менее
чем в 1 , 1 - 1 , 3 раза. Поэтому противоток фаз в кристаллизато
рах чаще всего осуществляют принудительно - с помощью
различных механических устройств (шнеков, поршней, скреб
ков, враща ю щихся барабанов и др .) или путем использования
центробежных сил .
По принципу действия противоточные кристалл изаторы
можно разделить на две группы - со ступенчатым и непре
рывным контактом фаз (массообменом).
Особенностью ступенчатых кристаллизаторов является от
сутствие четко выражен ных секций (зон) охлаждения и разде
ления . В таких аппаратах в каждой ступени происходит плав
ление кристаллической фазы , поступающей с предыдущей сту
пен и , и образование новой кристалл и ческой фазы с более вы
сокой кон центрацией в ысокоплавкого компонента. Ступенча
тые противоточные крж:таллизаторы по принципу работы ана
логичн ы другим ступенчатым массообменным аппаратам . При
ме�ом
является многоступенчатый барабанный крнсталлиза••
тор . Каждая ступень такого аппарата снабжена охлаждающим
барабаном и обогреваемой ванной . Образующиеся на барабанах
кристаллические слои снимаются ножами и поступают в ванну
последующей ступени , где полностью расплавляются . Между
ваннами имеются переточные трубки. При этом расплав пере
текает из ван н ы в ван ну противотоком относительно движения
кристалл и ческой фазы .
Для глубокой очистки небольших количеств вещества от
примесей часто используют различные шнековые кристаллиза
торы периодического и непрерывного действия .
На рис . 16.34,а показана схема непрерывного шнекового кри
сталлизатора с центральным питанием. В верхней части аппа• Более подробные сведен и я с м . (5, 6 ] .
• • Подробнее конС'Jl)ук.ции nротивоточных

1 372

кристалл изаторов с м . ( 5 , 6).

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

а

Некоторые

б

поршневой , г - п ульсационный;
1 - секция ра.1делеЮ1я , 2 - с�кция охлаждеЮ1я, З шень, 6 - фильтр, 7 - п ульсато р

Рис. 1 6. 34.
а

- штковый. б -

в

конструкции противоточных кристалл изаторов:
пла.витель, 4

-

шнек ,

5-

пор

рата расположена секция ' (зона) охлаждения 2, где происходит
образование кристаллической фазы (охлаждение производится
хладоаrентом Gx) . Транспортировка кристалло в в аппарате
осуществляется шнеком 4. Внизу колонны (в плавителе З) кри 
сталл ы расплавл�ются. Часть получаемого расплава отбирается
в виде высокоплавкоrо продукта П, а другая часть возвращает
ся в зону разделения , где движется противотоком к опус
кающимся кристаллам . Н изкоплавкий продукт W выводится из
верхней части колонн ы .
В противоточн ых кристаллизаторах поршневоrо типа (рис .
1 6 .34, 6) исходный расплав F подается первоначально в секцию
охлаждения 2. Из нее образовавшаяся кристаллическая суспен 
зия поступает в секцию разделения 1, где кристалл и ческая фаза
перемещается к плавитслю З с помощью поршня 5. Высоко
плавкий продукт П выводится из зоны плавления 3, а н изко
плавкий W - через фил ьтр 6, расположенный в верхней части
секции разделения 1.
В кристаллизаторах пульсацнонного типа (рис . 1 6 . 34 , в) проти
воток фаз осуществляется благодаря пульсатору. С этой целью
на линиях подвода и с ходной смеси и отбора продуктов разде
ления установлены обратные клапаны.
Поршневые и пульсационные кристаллизаторы обладают значительной про
изводительностыо (до нескольких тонн разделяемой смеси в час ) и используются
1 373

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

1

М'

а

з м

4

>ft
�t:

�

х

-

6

х ••

Xn

1

Рис. 1 6. 35. Непрерывная противоточная криста.тurизация:
а - схема потоков ф аз , б - раздел ение смеси , образующей непрерывный ряд твердых
растворов;
1 - секция ниэкоплавхоrо продукта, 2 - секция питания, J - секция высокоплавхоrо
продукта, 4 - секция плавления

в промьШUiенности JJJJЯ ра:щелен ия углеводородных смесей (в частности, JJJJЯ выделе
ния 99,9% п-ксилола из ero смеси с друrnми изомерами) . Диаметр таких аппаратов
достигает 1000 мм, а высота сею{Ии противоточноrо массообмена - 2-{) м.

Схема потоков фаз в многоступенчатом кристаллизаторе по
казана на рис . 16.35,а. Весь аппарат можно разбить по длине
на четыре хара:�сrерные секции: низкоплавкоrо продукта 1, п и
тания 2, высокоплавкоrо продукта З и плавления 4.
Исходный расплав F с концентрацией высокоплавкоrо ком 
понента х р подают в секцию питания, являющуюся одной и з
промежуrочных ступеней аппарата. Обедненный высокоплав
ким компонентом продукт W с кон центрацией x w выводят из
первой секции в расплавленном в�ще. Обогащенная высокоплав
ким компонентом крисnuиическая фаза К по выходе из третьей
секции поступает в четвертую, где полностью расплавляется. При
этом часть полученноrо расплава отбирается в в�ще конечноrо
высокоплавкого продукта П с концентрацией Хл, а другая часть М - возвращается в секцию З в качестве флегмы.
Рассмотрим расчет мноrоступенчатых противоточных кри
сталл изаторов применительно к разделен ию бинарной смеси,
образующей непрерывный ряд твердых растворов (ри с . 16.35 ,б).
Запишем уравнения материального баланса для всеrо аппарата
в целом:
для потоков фаз
(щ)
F= П+ W,
для потоков высокоплавкого компонента

Fxp = Пхп + Wx w .

(э)

При совместном решении уравнений (щ) и (э) получим вы
ход высокоплавкоrо продукта:

(16.47)
1 374

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Уравнения рабочих линий, представляющих собой геомет
рическое место точек сопряженных концентраций кристалл и 
ческой (хк) и жидкой (хм) фаз , как и для других противоточных
процессов, можно получить из уравнений материального ба
ланса соответствующих секций .
Для контура к1 с потоками К, П и М (см . р ис . 16.35,а) урав
нение материального баланса высокоплавкого компонента
имеет вид
Кхк = Пхп + Мхм ,
откуда получаем :
Хк

=

п
К

м

Хп + К Хм .

( 16.48)

Уравнение (16.48) описывает рабочую линию секции высо
коплавкого продукта.
Рассматривая контур к2 с потоками М', К' и W (см. рис .
16.35, а), имее м :
М'хм = К'хк + Wx w ,
откуда
Хк

=

W

- - x iv

К'

М'
+ -К ' Хм .

(16.49)

Зависимость ( 1 6.49) представляет собой уравнение рабочей
линии секции н изкоплавкого продукта. При этом К' и М' потоки кристалл и ческой и жидкой фаз в данной секции.
Заметим, что ход рабочих линий зависит от соотношения
потоков фаз в отдельных ступенях и эффекта продольного пе
ремешивания . Если массовые потоки фаз одинаковы во всех
ступенях и исключено продольное перемешивание между сту
пенями , то рабочие линии являются прямыми .
Необходимое число ступеней разделения здесь определяется
теми же методами , что и для ректификации, абсорбции и жид
костной экстракции . Проводя графические построения в диа
Хм (см . рис . 16.35,6), определяют необходимое чис
грамме Хк
ло теоретических ступеней для достижения заданных кон цент
раций продуктов разделения Хп и x w. Зная найденные из опыта
коэффициенты эффективности разделения (КПД ступеней) ,
находят число реальных ступеней разделения.
Противоточные кристаллизаторы с непрерывным массообме
ном (шнековые, поршневые, пульсационные) по принципу
действия и в расчетном плане аналогичны насадочным и пле
ночным абсорбционным и ректификационным колоннам. Со
став фаз по длине таю1х аппаратов изменяется плавно . При
этом исходная смесь может подаваться либо в центральную ,
либо в торцевую часть кристаллизатора.
-

1 375

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

1

Рис. 16.36. Схема противоточной кристалли зации
с непрерывным массообменом:

а - питание подается в центр аппарата, б - питание
подастся в торец аппарата;
1 - секция охлаждсюtя, 2 - секция противоточноrо
раэдСЛСЮIЯ, з - секция ПЛЗВЛСЮIЯ, 4 - ССIСЦИЯ фильтра
ции

Аппар аты с подачей питания в цент
ральную часть (рис . 16.36,а) состоят из
трех секций: охлаждения 1, противо 
F
точного массообмена 2 и плавления 3.
км
км
2
Секция охлаждения обычно снабжена
рубашкой для образования кристалли 
ческой фазы. Длина этой секции зави
сит от производительности аппарата,
физико-химичесЮIХ свойств смеси,
температуры охлаждающего агента и
других факторов. Отметим , что в сек
ции охлаждения, где происходит одно
а
кратная кристаллизация, достигается
дополнительный эффект разделен ия ,
который, одн ако , меньше эффекта одной ступени разделения.
При питании в центральную часть колонны в секцию
охлаждения из секции противоточноrо массообмена поступает
маточник М1 с концентрацией высокоплавкоrо компонента хм ,
а уходят из нее ПОТОЮI кристаллической фазы К1 с кон центрациdй
хк 1 и низкоплавкоrо продукта W с концентрацией x w- Матери
альный баланс данной секции описывается уравнениями:

it

if

it

М1 = К1 + W;

(ю)
(я)

Из уравнений (ю) и (я) легко найти поток кристаллической
фазы, поступающий из секции охлаждения в секцию противо
точного массообмена:
к,

=

w

хм 1 - xw
хк1 - хм1

•

( 16.50)

Основной эффект разделения достигается в секции противо
точного массообмена, длина которой зависит от требуемой
степени разделения , физико-химических свойств разделяемой
смеси, характера взаимодействия
, скорости движения фаз и
•
ряда других факторов .
Для н ижней части секции массообмена справедливо уравне
ние рабочей линии (1 6 .48), для верхней - уравнение ( 1 6 .49) .
·

' Подробнее см. [5, 6).

1 376

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Если процесс перекристаллиза ции в секции массообмена
происходит в адиабатических условиях и теплоты кристалл и за
ции обоих компонентов близки, то поток кристалло в остается
неизменным по высоте секции массообмена, и рабочие линии
будут прямыми. В случае неадиабатных условий потоки фаз
изменяются по длине данной секции . При дополнительном
подводе теплоты поток кристаллов по мере его движения в
секции уменьшается , а при отводе теплоты - увеличивается.
Рабочие линии в этом случае, естественно, будут кривыми .
Аппараты с подачей шrrания в тор цевую часть (рис. 1 6 . 3 6 , 6)
обычно состоят и з четырех характерных секций: охлаждения 1,
массообмена 2, плавления З и фильтрации 4. Примерами таких
аппаратов мoryr служить пульсационные и поршневые кри
сталлизаторы . Исходную смесь F подают в секцию охлаждения ,
где она частично кристаллизуется . Образовавшаяся суспензия
направляется в секцию фильтрации и там смешивается с ма
точником, поступающим из секции массообмена. В секции
фильтрации происходит отделение кристаллической фазы от
жидкой, выводимой из аппарата в качестве н изкоплавкого про
дукта W Из секции фильтрации кристаллическая фаза направ
ляется в секцию массообмена, где при противотоке с жидкой
фазой обогащается высокоплавким компонентом. Далее кри
сталлы попадают в секцию плавления, где полностью расплав
ляются. Как и в предыдущих случаях, часть образующегося
расплава - высокоплавкий продукт П - выводится из аппара
та, а часть М2 возвращается в зону массообмена в качестве
флегмы.
Для аппаратов с подачей питания в торцевую часть харак
терно наличие только одной рабочей линии, описываемой
уравнением (16.48).
Высота секции противоточного массообмена определяется
теми же методами, что и для других массообменных аппара
тов,- с использованием положений теории массопередачи,
числа теоретических ступеней и ВЭТС, числа единиц переноса
и ВЕП (см. гл. 10). Для описания процесса противоточной кри 
сталл изации (распределения концентрации компонентов п о
высоте аппарата,
фактора разделения) предложен р яд теорети•
ческих моделеи
u

16.5.7. Фракционное плавление

Известно несколько вариантов данного процесса" , из кото
рых наиболее часто используются однократное и последова
тельное фракционное плавление.
• Подробно они изложены

в

[6 J .

1 377

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

t"

fн
tв

в

х...

xf

-

х

Хк

а

А

в

мl

xf

"кi

-

х

Хк2

А

б

Рис. 1 6. 3 7. Разделение бинарной смеси с использованием однократного фракци
онного плавления:

а
просrой процесс, б
оЮJоrо JИавлеюtЯ
-

-

сочетание процессов фракциоЮJоЙ крисrаллизации и фракци

Процесс однократного фракционного плавления чаще всего
проводят в вертикальных кожухотрубных теплообменниках или
в емкостных аппаратах с внутренними теплообменными эле
ментами (змеевиками, трубчатками и т.п.).
Рассмотрим данный процесс применительно к разделению
бинарной смеси, образующей непрерывный ряд твердых рас
творов (рис. 1 6.37,а). Исходную смесь F с концентрацией XF
загружают в аппарат в несколько перегретом состоянии. Далее
ее медленно (со скоростью 1-5 ° С/ч) охлаждают до температу
ры tк н иже ее полной кристалл и зации. При таком режиме
охлажден ия на теплообменных элементах образуются сравни 
тельно крупные кристаллы, что способствует на последующей
стадии плавлен ия образованию крупнокристаллической суспен
зии и более эффективному отделению маточника от кристал
лической фазы на стадии сепарации.
Затем образующуюс.н кристалл и ческую массу постепенно
нагревают от температуры tx до температуры фракционирова
ния t"' промежуточной между температурами солидуса и лик
видуса системы. При этом кристаллическая масса частично
расплавляется . Получен ная суспензия после некоторой вы
держки (для более полного приближения к равновесию) при
температуре tн подверг-ается сепарации . В результате получают
маточн ик М и кристаллическую фазу К, обогащенную высоко
плавким компонентом.
Стадия сепарации Ф может осуществляться двумя способа
ми: без выгрузки и с выгрузкой суспензии из аппарата.

1 378

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

По первому варианту отделение маточника от кристаллов
производится путем его свободного стекания . Для предотвра
щен ия уноса кристалло в маточником в н ижней части аппарата
обычно устан авливают опорную (фильтрующую) перегородку .
Кристалличе с кую фракцию после сепарации расплавляют и
спускают в соответствующий сборник.
По второму варианту суспензию выгружаюг из аппарата и се
парируюr с помощью фильтра или фильтрующей центрифуги .
Если при проведении процесса достигается равновесие фаз
и образующаяся жидкая фаза полностью отделяется от кри
сталлов, то выход кристаллической фракции , как и при одно
кратной кристалл и заци и, можно рассчитать по уравнению
( 1 6 .28). Однако в реальном процессе равновесие фаз из-за ко
нечной продолжительности процесса достигается не всегда.
Кроме того , часть образ овавше гося маточника на стадии сепа
рации удерживается кристаллической фазой вследствие дей
ствия капиллярных и адсорбционных сил. В результате реаль
ная степень разделения оказывается ниже теоретической. Сте
пень приближения к последней можно оценить с помощью
коэффициента эффективности разделения Е, определяемого
опытным путем. Зная Е, выход кристаллической фракции
можно рассчитать по ур а внению ( 1 6 .32) .
Для повышения разделяющей способности процесса одно
кратное фракционированное плавление иногда используют в
комбинации с обычно й фракционной кристалли зацией (рис .
1 6.37,6). При этом первоначально п р оводят стадию фракцион 
ной кристаллизации Кр исходной смеси F, в результате кото
рой получают маточник М1 и кристалл и ческую фазу К1 • Ма
точник М1 отбирают в качестве низкопл авкого продукта, а кри 
сталл и ческую фазу К1 направляют на стадию фракционного
плавления П. При фракционном плавлен ии получают кристал
лическую фракцию Къ которую отбирают в качестве высоко
плавкого продукта, а маточник М2 возвращают в кристаллиза
тор Кр , присоединяя к исходной смеси F.
При последовательном фракционном плавлении исходную
смесь F, как и при однократном процессе, первоначально мед
лен но охлаждают до ее полной кристаллизации (рис . 1 6 . 3 8 , а) , а
затем медленно нагр е вают. Часть кристаллической фазы
(преимуществен н о низкоплавкого компонента) плавится и от
деляется от остающихся кристалл о в. При этом, естественно,
постепенно возрастает концентрация высокоплавкого компо
нента - как в кристалл ической, так и в жидкой фаз ах . В ходе
равновесного процесса состав кристаллической фазы изменяет
ся по линии солидуса от исходной кон центрации хр до конеч
ной Хк (участок аЬ) , а состав жидкой фазы - по линии ли кв и 
дуса от начальной ко н центрации образующе гося маточника
Х мF до конечной Хм ( уч асток cd) .
1 379

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

а

в

Хм !

F

кl

Хм

х

б

А

к

Рис. 1 6. 38. Раздел е н ие бинарноii смеси методо м последователъно rо фракционного
JUiавления при полном (а) и частичном (б) отвержлении исходной смеси

Теоретически при последовательном фракционном плавле
нии можно получить в конце процесса сколь угодно чистый
высокоплавкий компонент, но с очень малым выходом, так как
по мере удаления жидкой фазы масса оставшихся кристаллов
постепенно уменьшается. На практике обычно процесс пре
кращают после достижения заданного обогащения кристалл и 
ческой фазы высокоплавким компонентом.
В ряде случаев исходную смесь первоначально подвергают лишь частичной
кристаллизации (рис. 16.38,б) путе м охл�ения до некоторой температуры fк,
лежащей между точками ликвидуса и солидуса исходной смеси. В результате
образуются твердая фаза с о ста ва хк 1 и жидю1я фаза состава х м\ После слива
п ер в и чно rо маточника процес<: разделения протекает так же, как в предьщущем
.

варианте. Фракционное плавление с частичным отвержлением исходной смеси
позволяет несколько сократить общую продолжительность процесса разделения ,
но при этом выход о чи щенно го продукта снижается по сравнению с фракцион
ным JUiавлением при полном отвержлении исходной смеси.

Последовательное фракционное плавление, как и однократ
ный процесс, проводят в аппаратах с развитой теплообменной
поверхностью. На р и с 16.39 приведена схема установки , ис
пользуемой для промышленной очистки ряда органических
веществ (нафталина, бензола, дихлорбензолов и др .). Исходную
смесь F в несколько перегретом состоянии заливают в емкост
ный кристаллизатор 7, снабженный ребристыми охлаж
дающими эл ементам и , и медленно охлаждают хладоаrентом ,
циркулирующим в охлаждающем контуре. По достижении за
данной конечной температуры смесь выдерживают 1 -2 ч. Пос
ле этого начинают медленный нагрев системы, в процессе ко
торого осуществляют отбор образующихся жидких фракций .
По достижении задан ного состава кристаллической фазы про
изводят быстрое ее выплавление . Затем процесс повторяется.
Скорость охлаждения и нагрева в промышленных установ
ках обычно составляет J -3 ° С /ч. Объемы промышленных ап
паратов достигают 40 мз .
.

1 380

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

4

3

Рис. 1 6. 39. Схема установки для разделения смесей методом последовательного
фракционного мавления:
1

-

кристаллизатор, 2

-

нас{)с, 3

-

теплообмеюnпс, 4

-

буферная емкость

Обычно выма вляемые жидкие фракции разделяют на три части. Первая М1 ,
наиболее обедненная высокоJUJавким компонентом, выводится из системы как низ
коплавкий продукr. Промежуrочная фракция М2 возвращшm:я на повторное разделе
ние. Пос.леДНJ1Я фракция К оrоираеrся в качестве высокоплавкоrо продукrа.

Достоинства процесса фракционного плавления - простота
аппаратурного оформления , герметичность оборудования, воз
можность полной автоматизации процесса. К недостаткам
можно отнести большую длительность процесса.
Соотношение между массами образующихся фаз и их соста
вами при последовател ьном фракционном плавлении можно
выразить с помощью дифференциального уравнения матери
ального баланса по высокоплавкому компоненту:
(аа)
--хмdМ = d (хк К)
Учитывая , что изменение массы кристалл и ческой фазы dK =
-dM, из (аа) имеем :
.

=

dK
к

(аб)

=

Интегрируя последнее выражение в пределах от
Хк , н аходим :

XF до

К
111 -

F

=

-

Хк

dх к
Хм
xF Х к
J

F до

К и от
(16.5 1)

-

В общем случае уравнение ( 1 6 . 5 1 ) решается численными ме
тодами с использованием линий ликвидуса и солидуса. Если же
известна фун кциональная связь между Хк и _хм, то иногда воз
можно его аналитическое решение .
1381

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Для случая , когда концентрации Хк и Хм связаны между со
бой выражен ием ( 1 6.34) , при решении уравнения (16.51) полу
чается зависимость
Хк

где

т - коэффициент

=

1 -

(1

-

XF)

распредмения.

(K)(l-m)/
F

т

,

(1 6.52)

1 6.5.8. Направленная кристаллизация

Направлен ную кри ст;uшизацию широко используют для глу
бокой очистки небольших количеств вещества от примесей .
Обычно процесс осуществляется в вертикальных или горизон
тальных контейнерах (рис. 16.40,а, б) . В ходе процесса контей
нер 1 с исходным расплавом медленно перемещают из зоны
нагрева 2 в зону охлаждения З. На границе этих зон происхо
дит процесс кристалл и зации, фронт которой в контейнере пе
ремещается со скоростью его движения .
В процессе направленной кристалли зации (рис. 16.41 ,а)
происходит перераспределение компонентов (примесей) по
длине образца (рис. 1 6 . 4 1 ,б) . Если при этом коэффициент рас
пределения т = хJ.хм < 1 , то в начале образца будет происхо
дить понижение концентрации примеси в кристалл и ческой
фазе Хк по отношению к исходной концентрации XF, а в кон це
образца кон центрация Хк будет боль ш е XF. При т > 1 набл ю 
дается обратная картина (рис. 1 6 .41 ,в).
После окончания процесса кристалл и зации очищенная
часть образца отделяется, а оставшаяся подвергается повторной
очистке . Скорость движения контейнера имеет порядок 10-3-

1 0 -2 мм/с.

Кон струкци и контейнеров (см. рис. 1 6.40,в) весьма разнообразны. В е рти 
кальные конте й н еры обычно имеют круглое сечение диаметром от 5 до 30 мм.
Горизонтальные контейнеры выполняются в виде лодочек с различной формой
поперечного сечения. Материал контейнера зависит от свойств очищаемого

вещества. При очистке органических веществ обычно используют термостойкое
стекло или кварц, при очистке тугоWJавких веществ - графит и керамику.
Для расчета процесса направленной кристалл и зации можно
использовать уравнение ( 1 6 .33), полученное для последователь
ной кристаллизации.
Пусть поперечное сечение образ ца f не изменяется по его
длине; тогда М = flмРм, F = flпPF, где Zп - длина образца, Zм длина зоны р асплава, р F и Рм - плотности исходной смеси и
расплава М соответстве нно. Если принять PF :;,,, Рм . то в этом
случае уравнение ( 1 6.33) примет вид :
Jп 2!...

/

lп

1 3 82

х
= J"

XF

d.х м

Х к - Хм

( 1 6.53)

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

1
11

1!1

в
- иртикальный, б - rоризоmальный, в - сечеШ1Я коmейнеров;
1 - коmейнер, 2 - зона наrрева, З - зона охлаждения;
/ - расплав, // - кристаллическая фаза, 111 - хла.цоаrеm

Рис. 1 6. 40.
а

Схема аппаратов направленной кристалл и зации :

Если для области малых значений Хк и Хм принять Хк = тхм ,
то при решении ( 1 6.53) легко получается зависимость, описы
вающая распределение примеси в кристаллической фазе при
направленной кристаллизации :
Хк = т:ц

-1 .
m
�:
( )

�- '·Щ
а

х
х кF

( 1 6 . 54)

tA

о

Хк

Хм

х

о

х"

Хк

х

XF

хк F

о

б

-

lк

'"

в

а - схема процесса, б - распределение примеси по длине образца в кристаллической фазе, в
- учаспси диаrрамм фазовоrо рав!Юl!t'СИЯ в обпасrи малых конценrраций при т < и т >

Рис. 16. 41. Процесс направленной кристалли зации:

1

1

1 3 83

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

*

1 6 . 5 . 9 . Зонная плавка

Зонная плавка , как и направленная кристаллизация , применяется в основном дл я глубокой очистки различных веществ
от примесей . Процесс n роизводится в удлиненных контейне
рах , медленно двигающихся вдоль одного или нескольких на
гревателей, с помощью которых в предварительно закристалли 
зовавшемся образце создаются расплавленные зоны (рис .
1 6 .42,а) . В некоторых установках производят перемещение на
гревателей вдоль неподnижного контейнера. Скорость переме
щен ия зон обычно составляет � о-з- 1 0-2 мм/с. Контейнеры для
зонной плавки по своей конструкции аналогичны контейнерам
для направленной кристалл и зации .
П р и движении расплавленной зоны происходит перераспре
деление примесей (компонентов) по длине образца. Если ко
эффициент распределен ия т < 1 , то примесь переходит в рас
плавленную зону и переносится с ней в конец образца (рис .
1 6 .42,б). При т > 1 при месь кон центрируется в начале слитка.
Распределение примеси вдоль образца зависит от числа прохо
да зон п: с увеличением п степень разделения (градиент кон 
центрации) возрастает.
Рассмотрим распределение примеси по длине образца пло
щадью поперечного сечен ия f после одного прохода расплав
ленной зоны длиной /3 (см . рис . 1 6 .42,а). Если исходный рас
плав (образец) имел кон центрацию XF, то при перемещении
зоны за бесконечно малое время d-r на длину d/ в расплавлен
ную зону поступает примесь в количестве xifdl. Часть этой
примеси /зfdхм остается в зоне, а другая часть xкfd/ переходит
во вновь образующуюся кристаллическую фазу. В результате
имеем следующее уравнение материального баланса:
(ав)
- x,Jdl = lзfdxм - xifdl .
Проинтегрируем уравнение (ав) в пределах изменения дли 
н ы прохода от О д о текущего значения / и концентрации при
меси в расплаве - от X f до хм :

f/ (\/
-

о

-

Хм

f

d Xм_

(аг)
Хк - X F
Если принять, что в процессе разделения устанавливается рав
новесие и в расплавленной зоне расплав полностью перемешан ,
то концентрацию кристаллической фазы можно представить как
(ад)
Хк = mхм
Тогда при интегрировании уравнения (аг) приходим к зако 
номерности изменения концентрации примеси в зоне в про-

/з

=

_
_
_

XF

.

• Более подробные сведен и я об аппаратурном оформлении данного процесса
и методах его расчета содержатся в ( 3 , 4, 6, 1 5 ( .

1 384

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

а

-

о

-

l

б

схема процесса, 6 - распределе1D1е концешраций примеси по длине образца при
различном числе проходов зон п;
1 - кошейнер, 2 - наrреватели;
1
расплавлеННЬ1е зоны, l/ кристаллическая фаза

Рис. 16.42.
а

Очистка вещества зо нной rтавкой :

x;- [1 - (l - m)exp(-m 1:J J·

цессе ее перемещения по координате /:
Хм =

( 16.55)

Подставляя значение Хм из ( 1 6.55) в уравнение (ад) , получа
ем зависимость, описьшающую распределение примеси вдоль
кристалл и ческоrо образца при одном проходе зоны :
Хк

=

[ (1 -

хр 1 -

( �)].

т ) ехр - т

( 16.56)

нескольких проходах зон
Методика расчета процесса пv.и
•
описана в специальнои литературе
w

• См., например, (3, 1 5 ) .

1 385

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Достоинство зонной плавки состоит в высокой степени
очистки и относительной простоте метода, недостаток - в
н изкой производительности.
1 6.6. СХЕМЫ ПЕРЕКРИСТАШIИЗАЦИ И

Для получен ия продуктов высокой чистоты или для дости
жения задан ной степени извлечения целевого компонента од
ной стадии кристаллизации часто оказывается недостаточно. В
этих случаях применяют многоступенчатую перекристаллиза
.
цию без использованин или с использованием растворителей .
1 6.6. 1 . Перекристаллизация без использования растворителей

В данном случае разделен ие производят пугем многократ
ной перекристалл и зации вещества из расплавленного состоя 
ния. Наиболее простыми вариантами такого разделения явля
ютс я последовательная перекристаллизация по линии маточни
ка или то же - по лин и и кристаллической фазы.
Перекристаллизация по линиu маточника применяется для
увеличения степени извлечения целевого компонента из ко
нечного маточн ика. В этом случае (рис . 1 6 .43) исходная смесь
F поступает в кристаллизатор первой ступени, где получается
кристаллическая фракция К1 и маточник М1 • Последний под
вергается вторичной кр исталлизации во второй ступени . При
этом образуются маточн ик М2 и кристаллическая фаза К2. Ма
точник М2 подвергается последующей перекр исталл и зации .
При наличии п ступеней получается п кристалл и ческих фрак
ций и оди н конечный маточник Мп, как правило, с н изким
содержанием высокоплавкого компонента. Рассматриваемая
схема перекристаллизации часто применяется для разделения
эвтектикообразующих смесей с полной взаимной нераствори
мостью компонентов в твердом состоянии, когда однократный
процесс фракционирования затруднен из-за высокого содер
жания твердой фазы в образующейся суспензии .
Для получения кристалл и ческой фазы высокой чистоты
применяется последовательная перекристаллизация по линии
кристаллов с отбором маточников после каждой ступени. В
результате такого разделения в п ступенях получается п маточ
ников различного состава и одна кристаллическая фаза, суще
ственно обогащенная высокоплавким компонентом.
Недостатком описанн ых выше схем перекристалл и зации яв
ляется получение при их реализации целого ряда промежугочБолее подробные сведснш1 о ра.:�личных вариантах перекристалл изации со
держатся в (2, 4, S [ .
· •

1 3 86

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

а
tл

lл

4
в

х

б

А

tE -------i

в

х

в

А

схема процесса; б, в - раэделеЮ!е би нарной смеси с неоrраЮ1ЧеЮ1ой расrвор и 
мостью (6) и полной нерасrворимостью (в) компоненrов в твердом сосrояЮ1и ;
1 - 4 - сrупени крисrаллюац1 1и
Рис. 1 6. 43.
а -

Последовательная перекристалл изация по линии маточника:

ных кристаллических ил и жидких фракций различного состава.
Этого можно избежать при использовании схем перекристалл и 
зации с рециркуляцией фаз.
В случае многократной перекристалл и зации маточника с ре
циркуляцией кристалл и ческой фазы маточник последовательно
проходит через все ступени (рис. 1 6.44). Кристаллическая фаза
из первой ступени К1 выводится в виде готового продукта;
кристалл ы из второй ступени после их расплавления возвра
щаются в первую ступень, из третьей - во вторую и т.д . В ре
зультате такой перекристаллизации получают одну кристалли
ческую фазу, обогащен ную высокоплавким компонентом, и
один маточник, обогащенный низкоплавким компонентом.
При низком содержа нии высокоплавкого компонента в ис
ходной смеси целесообразно применять схему многократной
перекристалл и зации с рециркуляцией маточника. Эта схема осо
бенно выгодна, когда в первой ступени достигается требуемая
степень очистки маточн ика от высоко плавкого компонента, н о
необходимо повысить содержан ие этого компонента в кристал
лической фазе.
При необходимости одновременного получения обоих ком
понентов смеси в чистом виде выгодно применять схему про
тивоточной многоступе11чатоu перекристаллизации (рис . 16.45).
Здесь исходная смесь подается в одну из промежугочных сту1 387

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

а

tв
в

х

б

А

Рис. 1 6. 44. Мноrоступенчат<�я перекристалл из<�ция маточника с рециркуляцией
кристалли ческой фазы:

а - схема процесса, б - р �щел ени е смеси с неоrраничею1Ой растворимосrью компонен
тов в твердом СОСТОЯЮ!И ;
1 - 4 - ступени кристаллизащ1и

а

в
Рис. 1 6. 45.

х

б

А

Многоступенчатая n ротивоточная перекристаллизация:

- схема процесса, б - ра.щелени е смеси с неоrраниченной растворимостью компонен
тов в твердом СОСТОЯЮ!И;
1 - 5 - ступени кристаллизации
а

1388

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

пеней, кристалл и ческая фраю..tи я выводится с одного конца, а
жидкая фращия (маточник М1 ) - с противоположного . В ряде
случаев для повышения эффективности разделения противо
точную перекристаллизацию проводят с частичным возвратом
той или иной фращии в виде флегмы. Такой возврат позволяет
ре гулировать потоюt ф а:1 в ступенях разделения , а также суще
ственно повысить эффе1...-тивность разделения.
16.6.2. Перекристаллизация
с использованием растворителей

Разделение веществ с использованием растворителей про
водят пугем однократной или многократной перекристаллиза
ции.
Одно1'ратная пере1'ристаллизация используется, когда за
один акт кристалл и зации достигается требуемая степень очист
юt вещества. Наиболее простой здесь является схема однократ
ной перекристаллизации без возврата маточника (рис . 1 6 .46, а) .
Исходное вещество F н а стадии растворения Н смешивается с
растворителем Р. Полученный раствор N подается на кристал
лизацию, в результате которой образуюrся кристалл и чесюtй
продукт К и маточник М. Недостаток такой схемы - большие
потери вещества с маточником.

а

6

в

без возврата маточЮ1ка; б, в - с полным и частичным возврато:-.� маточЮ1ка соот
ветсrвеюю, г - с упариванием мат11чЮ1ка;
Н, Кр, В - сrадии расrворения , крисrаллизации и выпаривания соответсrвеЮ!о
Рис. 1 6. 46.
а

Схемы однократной кристалл изации с использованием растворителя :

-

1 3 89

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

а

Рис. 1 6. 4 7.

Схемы многократно й перекристалл изации с использованием раство

рителя :
а

-

без

возврата маточни ка,

б - с возвратом м аточни ка на предыдущую ступень

Если содержание примесей в маточнике невелико, то после
первой кристалл и зации он может быть возвращен в процесс
для растворения исходноrо вещества (рис. 16.46,6). Такая опе
рация может быть повторена несколько раз, пока концентра
ция примеси в маточнике не повысится до предельно допусти
мой величин ы . Далее в установку подается новая порция све
жего растворителя . Эта схема позволяет сократить расход рас
творителя и потери вещества с маточником. Если примесь бы
стро накаruшвается в м аточн ике, то применяют схему с час 
тичным возвратом мато•тика (рис. 16.46,в).
Еще более экономичной является схема с частичным упари
ванием маточника М1 и повторной кристалли зацией упаренноrо
раствора М1 ' (рис . 16.46,г). При этом кристаллы Kz, полученн ые
после вторичной кристаллизации, присоединяются к исходно
му веществу F.
Многократная кpucmatl./luзau,uя используется для повыше
ния степени очистки вещества от примесей . Применяются
различные схемы многократной перекристаллизации , из ко 
торых н аи более простой является схема последователь н о й
перекр исталлизации без возврата маточника (рис . 1 6 .47,а) .
Здесь н а каждой ступ е н и перекристаллизации · применяется
чистый растворитель . При этом получается оди н очищен н ы й
3)
кристаллический продукт Кп (в приведенном примере п
и несколько маточников разл ичного состава . Рассматри
ваемая схема обычно характеризуется невысоким выходом
очищенного продукта Кп и большими затратами на регене 
рацию растворителя .
=

1 390

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Более выгодны схемы с рециркуляцией потоков. Так, в схеме ,
показанной на рис . 1 6 .4 7 , б, чистый растворитель используется
лишь на последней ступени перекристалл и заци и . Исходное
вещество F растворяется в маточнике второй ступен и М2 , кри
сталл и ческая фаза первой ступени К1 - в маточнике третьей
ступен и М3 и т.д . В результате получаются очищенный кри
сталлический продукт К" и маточник М1 , обогащенный приме
сям и .
Л ИТ Е РАТУРА к главе 1 6
1 . Аносов В.Я., Погодин С.А. Основные начала физико-химического
ан ал и з а. М . : АН СССР, 1 947. 876 с.
2. Бэмфорд А . В. Промьшmенная кристалл и зация: Пер. с англ. / Под
ред. Л . Н . Матусевича. М . : Химия, 1 969. 240 с.
3. Вигдорович В. Н. , Вольпян А. Е. , Курдюмов Г. М. Направле нная
кристаллизация и физико -химический анализ. М . : Химия, 1 976.
200 с.
4. Вильке К. Т. Методы f\Ыращивания кристаллов: Пер. с не м. / Под
ред. Т. Г. Петрова. Л . : Недра, 1 968. 424 с.
5. Гельперин Н И. , HocOfJ Г.А. Основы техники кристаллизации рас 
плавов. М . : Химия, 1 97 5 . 3 5 2 с.
6. Гельперин НИ., Носов Г.А. Основы техники фракционной кри 
сталлизации. М . : Химия , 1 986. 303 с.
7. Захаров А . М. Диаграммы состояний четверных систем. М.: М е 
талл ургия, 1 964. 240 с.
8 . Кафаров В. В. , Дорпхов И. Н. , Кол ьцова Э. М. Системный ана
лиз процессов
химической технологи и . Процессы массовой
кристаллизаци и из растворов и газовой фазы. М . : Наука, 1 9 8 3 .
368 с.
9 . Кидяров Б. И. Кинетика образования кристалл о в из жидкой фазы.
Новосибирск: Наука, 1 979. 1 34 с.
1 0. Мамин Д. У Кристалл и зация: Пер. с англ. / Под ред. В.Н.
Вигдоровича. М . : Металлур гия, 1 96 5 . 342 с.
1 1 . Матусевич Л. Н Кrисталл и зация из растворов в химической
промьшm енности. М . : Хим ия, 1 968. 304 с.
1 2. Пап Л. Концентрирование вымораживанием: П ер . с венгр. /
Под ред. 0 . Г . Комякова. М . : Легкая и пищевая промышленность,
1 982. 96 с .
1 3 . Петров ДА. Тройные системы. М . : АН СССР, 1 95 3 . 3 1 5 с.
1 4 . Пономаренко В. Г" Ткаченко К. П. , Курлянд Ю.А. Кристалл и зация
в псевдоожиженном слое. Киев: Техника, 1 972. 1 3 1 с.
1 5 . Пфанн В. Зонная плавка: Пер. с англ. / Под ред. В.Н. Вигдоро
вича. М . : Мир, 1 970. 3 6 6 с.
1 6. Тодес О. М. , Себамо В.А., Гольцикер А.Д. Массовая кристалл и за
ция из растворов. Л . : Хими я, 1 984. 232 с.

1391

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

1 7 . Френкель Я.И. Кинетическая теория жидкости. М . : АН СССР,
1 945. 430 с.
18. Хамский Е.В. Кристатшзация в химической промышленности .
М . : Химия, 1 979. 344 с.
19. Хонигман Б . Рост и форма кристаллов: П ер . с англ. / Под ред.
Н.Н. Шефталя . М . : ИЛ, 1 9 6 1 . 2 1 2 с.
20. Янке Е. , Эмде Ф. , Лt·ш Ф. Специальные функции: Пер. с нем. /
Под ред. Л . И . Седова. М . : Наука, 1 977. 343 с.

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Глава 1 7
РАСТВОРЕНИЕ И ВЫЩЕЛАЧИВАНИЕ

Процесс растворен ия твердых веществ в жидкостях широко
используется в химичес кой и родственных ей отраслях про
мышленности (металлургической, пищевой, текстильной, фар
мацевтической и др .). Чаще всего он предшествует проведению
других технологических процессов.
1 7 . 1 . ОСНОВНЫЕ ОСОБЕННОСТИ
ПРОЦЕССОВ РАСТВОРЕН ИЯ ТВЕРДЫХ ВЕЩЕСТВ

*
Известны три варианта процесса растворения : полное, час
тичное и химическое.
При полном раств оре н ии исходное твердое вещество пол
ностью переходит в растворенное состояние . При этом полу
чают гомогенный жидкий раствор вещества в том или ином
растворителе.
В результате частичного растворения получается гетерогенная
смесь, состоящая из жидкого раствора и остатков твердого ве
щества. Частичное растворение обычно применяют для изби
рател ьного (селективного) извлечения из твердых смесей одного
или нескольких компонентов. Часто данный процесс называюr
еще выщелачиванием , или экстракцией в системе твердое тело
жидкость. Здесь наряду с раствором (экстрактом) получаюr твер
дый осТ'аток, который называюг рафинатом, или нижним продук 
том. Экстракт rакже часто называюr верхним продуктом.
При химическом растворении все вещество или какие-то его
компоненты вступают в химическое взаимодействие с раство
рителем (ж ид ким реагентом) , в результате чего образуются
продукты, которые мoryr полностью или частично растворяться в
жидкой фазе. Химическое растворение нередко сопровождается
выделением газообразных продуктов химической реакции .
Растворяемое вещество может представлять собой индивиду
альный компонент, бин арную или многокомпонентную смесь
твердых веществ. При этом оно может находиться в кристал
лическом или аморфноr.1 состоян ии. Бинарные и многокомпо-

• Более П OJUf aя информаwffi о процессе растворения содержится в ( 1,

2 , 4--{}).
1 393

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

нентные твердые вещества нередко представляют собой меха
ническую смесь крист:uшов отдельных компонентов. Такие
системы часто образуются при кристаллизации смесей , компо
ненты которых не обра:1уют твердых растворов (см . разд . 1 6. 2 ).
Исходное растворяемое вещество может также представлять
собой твердый раствор двух или нескольких компонентов.
Иногда твердые вещества состоят из компонентов, одн и из
которых растворимы , а другие нерастворимы в выбранном рас
творителе. Иногда таки е вещества содержат некоторое количе
ство жидкой фазы. Наконец, исходное вещество может пред
ставлять собой смесь кристаллической фазы одного компонен 
та с аморфной фазой другого компонента.
Однокомпонентные твердые вещества обычно имеют одно
родную структуру, многокомпонентн ые же обладают большим
разнообразием структур образующих их фаз . При этом твердые
фазы могут быть достаточно равномерно распределены по объ
ему вещества в виде отдельных дисперсн ых включений при
мерно одинаковых размеров. Часто одна фаза образует ден 
дритный скелет, между ветвями которого располагаются другие
твердые фаз ы . Иногда твердое вещество имеет анизотропное
(слоистое) строение .
Структура твердых тел и размеры дисперсных включений
отдельных фаз оказывают существенное влияние на кинетику
процесса растворения . Скорость растворения сильно зависит
также от размера твердых частиц исходного вещества. Учиты
вая это, твердые вещества обычно подают на стадию растворе 
н ия в раздробленном виде . Это увеличивает межфазную по
верхность контакга твердого вещества с растворителем и зна
чительно ускоряет процесс растворения .
В качестве растворителей (экстрагентов) обычно используют
низкоплавкие индивидуальные вещества (воду, спирты , кето
ны, кислоты и др .) или различные жидкие смеси веществ
(например, водные растворы неорганических или орган ических
кислот, щелочей, спиртов, нефтяные фракции и др. ) .
К растворителям твердых веществ предъявляются примерно
такие же требования , как и к экстрагентам в процессе жид
костной экстракции (см . разд. 1 3 .4). Они должны обеспечивать
хорошую растворимость, обладать н изкой вязкостью, доступ
ностью и дешевизно й , нетоксичностью, легкостью их регене
раци и . При частичном растворен ии (выщелачивании) раство
ритель кроме этого должен обес печивать высокую селекгив
ность разделения. Обыч но подбор растворителей производится
опытным путем.
Полное растворение твердых веществ возможно при выпол
нении следующих двух основных условий :
-отсутствие в исход ном веществе компонентов, нераство
римых в использованном растворителе;

1 394

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

- достаточный расход растворителя - такой, чтобы все ве
щество могло растворит ься при выбранной температуре прове
дения процесса.
Частичное растворение твердых веществ имеет место, когда
указанн ые выше условия не выполняюrся. Обычно частичное
растворение состоит из двух стадий (операций) : растворения и
сепарации, т.е. отделения остатка твердой фазы от полученного
раствора. Здесь, как и при фракционной кристалл и зации, на
стадии сепарации не удается полностью отделить полученный
раствор от твердой фазы. Захват раствора твердой фазой про
исходит за счет действия капиллярных и адсорбционных сил .
Стадию сепарации производят с использованием процессов от
стаивания, фильтрации, центр ифугирования, а иногда и пуrем
отжатия твердого остатка с помощью специальных прессующих
устройств. Заметим , 'ПО на общую эффе ктивность процесса вы
щелачивания мoryr сильно WIИЯТь режимы работы сепарирующего
оборудования. Для коли чественной характеристики стадии сепа
рации можно использовать коэффициент захвата раствора твердой
фазой (см. разд. 16.5. 1). Величина этого коэффициента зависит от
способа сепарации и ее режимов. Для извлечения из твердой фазы
захваченного раствора иногда ее промывают чистым растворите
лем или какой-либо друrой ЖИдкостью, которая вьпесняет захва
ченный раствор из пор твердого остатка.
Процессы полного и частичного растворения твердых ве
ществ нередко совмещают с процессами дробления, растира
ния, кипения и др.
При осуществлении процессов растворения и выщелачива
н ия часто возн икает задача регенерации растворителей. Ее ре
шают так же, как и в процессе жидкостной экстракции (см. гл .
1 3), применяя процессы выпаривания, ректификации , кристал
лизации, ионообмена и др. Часто возникает также задача из
влечения растворителей из твердых остатков . Здесь используют
сушку твердых остатков или отпаривание с последующим улав
ливанием образующихся паров растворителя .
17 .2. АППАРАТУРНОЕ ОФОРМЛЕН И Е

ПРОЦЕССОВ РАСТВОРЕНИЯ

Для проведения процессов полного и частичного растворе
•
н ия используют аппараты разнообразной конструкции . При
этом они должны по возможности удовлетворять следующим
основным требованиям :
- обеспечивать высокую степень извлечен ия целевых ком
понентов;
Более подробные сведениs� об аппаратур ном оформлении процессов рас
творения см. (2 ( .
•

1 395

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

- обеспечивать макс имально высокую концентрацию полу
чаемого раствора;
- обладать высокой удельной производительностью;
- характеризоваться н изкими удельными затратами энерги и .
По принципу действия все аппараты-растворители можно
разделить на аппараты периодического , полунепрерывного и
непрерывного действия .
В аппаратах перио дического действия процесс растворен ия
обычно состоит из ряда последовательных операций : загрузки
исходного вещества и экстрагента, растворения вещества; от
деления раствора от нерастворенного остатка, выгрузки рас
твора и остатка, подготовки аппарата к следующему циклу.
Периодическое растворение обычно используют в малотон
нажных производствах при значительном ассортименте раство
ряемых веществ.
В простейшем случае растворение можно производить в по
лых емкостн ых аппарата х , куда загружают измельченный твер
дый материал и залива ют растворитель. После определенной
выдержки производят слив раствора и выгрузку твердого остат
ка. Такой процесс используют, например , для извлечения цен 
н ых компонентов из ра:1личного растительного сырья . В лите
ратуре этот процесс часто называют еще настаиванием. Однако
данный процесс отличается малой эффективностью.
Для повышения скорости процесс растворения часто осу
ществляют в емкостных аппаратах с механическим или пневма
тическим перемешиванием .

На рис. 1 7 . 1 , а покuзан емкостной аппарат с лопастно й ме
шал ко й 3. Исходный мuтериал 1 и растворитель 11 загружаются
через штуцеры в крышке аппарата. После растворения раствор
вместе с остатками не растворившейся твердой фазы выгру
жается через спускной штуцер в днище аппарата. Для поддер
жания определенного температурного режима аппарат снабжа
ют греющей рубашкой 2. В таких аппаратах могут также раз
мещать пропеллерные, турбинные и другие мешал ки . Иногда
для интенсификации процесса растворен ия на внутрен ней по
верхности емкостных ап паратов располагают ребра или специ 
альные направляющие н асадки .
Интенсифицировать процесс растворения твердых веществ в
емкостных аппаратах можно и путем возбуждения в жидкой
фазе колебан ий или пульсаций различной частоты и амплиту
ды. Это достигается с помощью различных вибромешалок,
пневматических и акустических пульсаторов, вибраторов и т . п .
Ускорить процесс растворения можно также, организуя
внутренние или внешние контуры циркуляции суспензии. На
рис . 1 7 . 1 , 6 показан емкостно й аппарат с внешним контуром цир
куляции сус пензии, в который вкл ючен центробе:нсный насос 4.
1 3 96

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

l1 -Ь.п

1 1

+ш
5

" _."
-4
-

- -

��
�

'
' " -,
" - ...
'
'
�
"'
-

" ,.:.. "

1
6

+

��4
г

в
1

а - с механической мtшалкой, б - с внешним конrуром цирку11ЯЦИИ , 11 - с внуrреЮ1ей
IП1евма111Ческой циркуляцией суспенэlОI, l - с фильтрацией через неподвIОIСНЫЙ слой рас
творяемоrо вещесrва;
1 - корпус аппарата, 2 - rреющая рубашка, З - мешалха, 4 - насос, 5 - циркуляци
ОЮ!&Я труба, б - опорная решетка, 7 - слой инертной насадки;
l - исходное вещеСI'ВО, JJ - раСI"ВОритель, JJJ - конечная суспензия, JV - воздух

Рис. 1 7. 1. Схемы емх.оС'J11ЫХ растворителей периодического действия:

Внугреннюю циркуляцию суспензии можно реализовать с
помощью эрлифта (рис . 17. 1 , в) . При этом в аппарате обычно
размещают внугреннюю циркуляционную трубу 5, в н ижнюю
часть которой подают воздух I V. Циркуляция суспензии проис
ходит за счет разности плотностей гетерогенных систем в цир
куляционной трубе и в кольцевом зазоре между корпусом ап
парата 1 и циркуляционной трубой . Интенсивность циркуля
ции здесь зависит прежде всего от расхода воздуха, высоты
трубы и эффективной вязкости суспензии.
Периодическое растворение иногда производят в автоклавах
под избыточным давлением. Это позволяет поднять температуру
процесса, что ускоряет растворение, способствует получению
более концентрированных растворов и снижает потери раство
рителя из-за подавления его юtпения.
Для растворения веществ в вязюtх жидкостях используются
периодичесюtе аппараты с одной или двумя лопастными
(ленточными) мешалками. Конструкции таЮIХ растворителей
напоминают бетономешалюt.
Большинство растворителей периодического действия отно
сятся к аппаратам идеального (полного) перемешивания. При
1 397

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Экстрактор-отстойник
процессов выщелачивания :

Рис. 1 7. 2.

Ш (ВП
VJ

для

1
корпус, 2
заrруэочная труба, 3
rребковая мешалка, 4
приемный карман, 5
сепаратор фаз;
расrвори·
/
исходный материал, II
расrвор (эксrракт), JV
тель, III
пульпа
(сrущенная суспензия), V
твердый осrаток
(рафинат), VI отделенный расrвор.
-

-

-

-

-

-

-

-

-

-

-

этом движущая сила (примерно
постоянная по объему рабочей
зоны) постепенно изменяется в
ходе процесса растворения.
На рис . 17. 1 ,г показан емкостной аппарат-растворитель по
лунепрерывного действия, в котором процесс растворения про
исходит при фильтрации раствора через неподвижный слой
твердого вещества. В нижней части аппарата располаrается
опорная решетка 6, на которой размещен слой инертного дис
персного материала 7 (например, кварцевого песка). Исходный
материал 1 загружается периодически, растворитель 11 поступа
ет в аппарат непрерывно. Раствор, проходя через слой твердого
материала, насыщается растворяемым компонентом , проходит
через слой инертного материала и выводится из аппарата. Та
кой аппарат целесообразно использовать для полного раство
рения веществ, когда в аппарате не происходит накопления
твердых остатков.
Непрерывное растворение может осуществляться в одном или
в нескольких соединенных меЖду собой аппаратах. В послед
нем случае отдельные а ппараты (устройства) служат для вы
полнения операций дозирования, загрузки, растворения и се
парации полученной гетерогенной смеси (суспензии, пульпы).
При этом непрерывно действующие аппараты мoryr работать в
режимах прямоточного, противоточного и смешанного движе
ния жидкой и твердой фаз. Такие аппараты в основном ис
пользуются в многотоннажных производствах и отличаются
большим разнообразием конструкций .
Одним и з первых аппаратов для выщелачивания бьm цилин
дроковический экстрактор-отстойник, показанный на рис. 17.2.
По своей конструкции он повторяет вертикальный отстойник,
подробно рассмотренный в разд.5 . 12. В аппарат через входную
трубу 2 подаются измельченный твердый материал 1 и раство
ритель 11. В процессе их контакта происходит выщелачивание.
Раствор (экстракг, маточник) попадает в кольцевой карман 4 и
выводится из аппарата сверху; поэтому экстракг носит название
верхвеrо продукта (ВП) . Влажный твердый остаток, полученный
при разделении в сепараторе пульпы, выводимой из нижней
части аппарата, именуется н ижн им продуктом (НП) . Заметим,
что термины В П и Н П используются в процессах выщелачива1 398

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

2

прямоточный, б противоточный, •
треххолонный;
1
корпус аппарата, 2
шнек, J рубашка, 4 фильтрующая повсрхиосrь;
I
исходное вещество, II
растворитель, /[/
твердый остаток, IV
конечный рас
твор (экстракт)
Рис. 1 7. З.
а

-

-

-

Шнековые растворители:
-

-

-

-

-

-

-

-

н ия применительно к экстрапу и твердому остатку соответ
ственно - безотносительно к тому, в каких точках они выво
дятся из аппаратов других конструкций.
Для непрерывного растворения может быть использован ап
парат с пневматической циркуляцией (рис. 1 7 . 1 , в) . В этом случае
потоки / и // подают в него непрерывно, а на уровне свобод
ной поверхности предусматривается штуцер в боковой стенке
корпуса, через который непрерывно выводят раствор или сус
пензию на стад ию разделения жидкой и твердой фаз.
Для проведен ия непрерывного растворения твердых веществ
часто используют различные шнековые аппараты-растворители
некоторые из них показаны на рис . 17.3. Эги аппараты моrуг
работать в прямоточном и противоточном режимах.
На рис . 1 7 . 3 , а показан шнековый растворитель, работающий
по прямоточной схеме . Он представляет собой удлиненное на
клонное корыто 1, в котором вращаются один или два шнека
2. С одного конца в аппарат поступают исходное вещество / и
растворитель //. При этом питание возможно в виде пульпы,
заранее приготовленной в отдельном смесителе, или в виде
раздельных потоков / и J/. ПродУJСГЫ растворения (конечный
раствор IV и твердый остаток J//) выводятся в виде суспензии с
противоположною конца аппарата. Для обеспечения подогрева
смеси аппарат может бьпь снабжен греющими рубашками 3. Фазы
здесь движуrся в режиме, близком к идеалыюму вытеснению.
Шнековый растворитель, работающий по схеме противото
ка, показан на рис . 17 . 3 , б. Здесь с одною конца в аппарат по1 399
-

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

дается исходное вещество /, а с другого - растворитель JJ. При
этом твердая фаза с помощью шнека 2 перемещается навстречу
раствору. Конечный раствор JV выводится через фильтрующую
поверхность 4 во избежание захвата твердых частиц. Благодаря
наклону аппарата в верхней части происходит отделение жид
кой фазы от твердого остатка JJI.
Иногда на выходе нижнего продукта в шнековых аппаратах
устанавливают специальный элеватор для вывода из аппарата
твердого остатка. В этом случае нет необходимости в наклон
ном расположении корыта растворителя. Шнеки обычно изго
тавливают в ВИде набора спиральных лопастей.
Для непрерывного противоточного растворения твердых ве
ществ используют также трехколонные шнековые аппараты
растворители (рис . 1 7 .3 , в) . Они состоят из двух вертикальных и
одной горизонтальной секций, снабженных транспортирую
щими шнеками 2. Исходное вещество 1 подают в секцию за
грузки твердого материала, а растворитель II - в секцию вы
грузки твердого остатка. Движение твердой фазы обеспечивает
ся шнеками , а жидкой фазы - разностью уровней ее ввода и
вывода. При противоточном контакте фаз происходит посте
пенное насыщение раствора. Отбор конечного раствора IV
(экстракта) производят через перфорированную (фильтрую
щую) перегородку 4 в корпусе секции загрузки твердого мате
риала. Для улучшения контакта твердых частиц с растворите
лем лопасти шнека изготавливают из перфорированн ых плас
тин .
Шнековые растворители отличаются большой производи
тельностью. Однако он и представляют собой ве сьма громозд 
дкие сооружения, обладают большой металлоемкостью и тре
буют мощного привода.
Более компактными являются колонные раствориrели с дви
жущимся (падающим) слоем, а также аппараты с псевдоожи
женным слоем твердого материала.
На рис. 17.4,а представлена схема колонного аппарата с па
дающим слоем твердой фазы, используемого, например, для
растворения сильвинитовой руды. Исходная руда 1 с размером
частиц до 5 мм загружается в колонну через трубу 2, а раство
ритель II подается через коллектор 5, расположенный в н иж
ней части колонны. Иногда для лучшего распределения руды
по сечению колонны часть растворителя (примерно одна чет
верть) подается вместе с исходной рудой . Растворение проис
ходит при стесненном осаждении частиц руды в подни
мающемся потоке растворителя. Насыщенный раствор IV вы
водится из зоны отстаивания. Остаток твердой руды попадает в
отстойник 4, откуда он периодически отводится в вИде сгу
щенной пульпы JJJ. Степень извлечения ценн ых компонентов

1400

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

1

1

5
JII

-

6

а

б

Рис. 1 7. 4. Колонные растворители с падающим (а) и псевдоожиженным (6) слоем
твердого материала:

1 - хорпус аппарата, 2 - загрузочная труба, J - секция осветления раствора, 4 - от
стойних твердой фазы, 5 - холлектор, 6 - распределительная решетха;
/ - исходное вещество, II - растворитель, /l/ - твердый осадок, JV- хонечный раствор

в таком аппарате составляет 96-97% , а производwrельность по
исходной руде может превышать 1 00 т/ч.
Одна из конструкций колонного растворителя с псевдоожи
женным слоем твердой фазы показана на рис . 17.4,б. Он пред
ставляет собой вертикальный цилиндр, в нижней части которо
го размещена распределительная решетка 6. В верхней части
колонны размещена секция осветления раствора 3. Исходный
твердый материал 1 подают через загрузочную трубу 2 непо
средственно в псевдоожиженный слой. Растворитель 11 п()сту
пает в аппарат снизу через распределительную решетку 6 и
псевдоожижает частицы твердого материала. При этом проис
ходит интенсивное перемешивание твердой фазы. Пройдя
псевдоожиженный слой, насыщенный раствор поступает в сек
цию осветления, где в результате снижения скорости потока
раствора происходит сепарация (осаждение) мелких частиц.
140 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Осветленный раствор 1v· непрерывно отводится сверху секции
ос ветлен ия . Остаток твердой фазы lll периодически спускается
через штуцер, расположенный над распределительной решет
кой . Такой аппарат целесообразно использовать для полного
распюрения вещества л ибо в случае �ебольшою выхода твер
дою остатка. Имеюrся конструкции растворителей с псевдо
ожиженным слоем, в которых твердые остатки выводят через
специальн ый rидрозатвор или через трубу, расположенную в
центре распределительной решетки .
Для непрерывного растворен ия крупных частиц часто ис
пользуют вращающиеся наклонные барабанные растворители,
которые по своей конструкции напоминают барабанн ые су
шилки. Такие растворители могут работать по схемам как пря
мотока, так и противотока. При прямоточном расnорении ис
ходный материал и растворитель подают с одною конца, а с
дpyroro производится выгрузка суспензии. За счет вращения
барабана достигается хорошее перемешивание материала. При
проти воточиом растворении исходный материал подается с
одною кон ца, а растворитель с другою. В ывод раствора произ
водится в этом случае через перфорированную поверхность.
Для растворения мелких частиц иногда используют трубча
тые аппараты, в которых суспензия прокачивается центробеж
ным или осевым насосом по обогреваемой трубе. Р�створение
происходит в процессе движения суспензии.
Процесс растворен ия твердых веществ можно производить с
использованием ленточных и· карусельных фильтров При этом ис
ходный матер иал помещается на движуЩуюся фильтрующую
поверхность и сверху орошается растворителем или циркули
рующим ненасыщен н ым раствором. Растворение происходит
при фильтрации жидкости через зернистый слой твердою ма
териала. После стадии растворения остаток твердою материала
промывается чистым растворителем, отжимается
(осушается)
и удаляется с фильтрующей поверхности.
Иногда в одном аппарате не удается достичь заданной сте
пен и извлечения целевых компонентов или же требуется зна
чительный расход растворителя . В этих случаях для растворе
ния используют несколько аппаратов, соединяя их в последо
вательные или противоточные каскады.
.

17.З. ФИЗИКО-ХИМИЧЕСКИЕ ОСНОВЫ
РАСfВОРЕНИЯ ТВЕРДЫХ ВЕЩЕСfВ

Закономерности процесса растворения твердых веществ
сильно
зависят от равновесия в системе твердая фаза
жидкость - оно подробно было рассмотрено в разд. 16.2. При
растворении веществ с истема состоит как минимум из двух

140 2

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 1 7. 5. Изображение процесса раство
рения однокомпонекmоrо вещества А
чистым растворителем В в диаrрамме
фазового равновесия

1.

компонентов
растворяемого
вещества и растворителя. При
КА+МА
растворении двухкомпонентного
---твердого вещества с использо
а ----. tE
ванием чистого растворителя
о
ХЕ
х" , Хн
/
речь идет уже о трехкомпонент
В
А
---Хной системе. С такой же системой мы имеем дело при растворении индивидуального вещества бинарным растворителем.
Рассмотрим сначала особенности растворения одноком
понентнЪlХ веществ в чucm6lX растворителях. В общем случае
такой процесс может быть изображен в диаграмме фазового
равновесия "твердая фаза-жидкость" (рис . 17.5) , где компонент
А представляет собой растворяемое вещество, а компонент В
- растворитель. На этой диаграмме выше линии ликвидуса (она
состоит из двух ветвей - аЕ и ЬЕ) располагается область L
гомогенных ненасыщенных растворов, а ниже этой линии области гетерогенного равновесия аЕа' и Ь ЕЬ'. При этом в об
ласти аЕа' в равновесии находятся кристалл ы растворяемого
вещества Кл и насыщенный им раствор (маточник) Мд. В об
ласти же ЬЕЬ' в равновесии находятся кристаллы растворителя
Кв и маточник Мв.
Если процесс растворения производится при постоянной
температуре fp , то линия смешен ия растворителя В с ве
ществом А представляет собой изотерму PF, на которой
(согласно правилу смешения) находится точка смеси М . П оло
жение данной точки на изотерме PF, естественно, зависит от
соотношения масс смешиваемых потоков растворителя В и
растворяемого вещества А.
Если точка получаемой смеси М 1 попадает в гомогенную
область L, то все вещество полностью растворится и получится
ненасыщенный раствор с концентрацией растворенного ком
понента Хм 1 . Последнюю можно определить, используя пра
вило рычага 1 1 рода (см . разд. 10.2.4):
-

Хм !

=

РМ 1

(а)

PF

Если же точка смеси М2 попадает в гетерогенную область,
то часть ве щества А останется в твердом состоянии (хл
1), т.е.
произойцет частичное растворение. Жидкая же фаза будет пред
ставлять собой насьпценный раствор Мн с концентрацией Хн·
=

1 403

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Для полного растворения вещества А с получением насы
щенного раствора необходимо взять такие количества раство
ряемого вещества F и растворителя Р, чтобы выполнялось
условие
1-х
М F
Р
н
н
(б)

F=

РМ н

=�

Из рис . 1 7 . 5 видно, что с понижением температуры раство
рения область существования гомогенных растворов сокра
щается из-за снижения растворимости компонента А в раство
рителе В. Поэтому для получения более концентрированных
растворов процесс растворения проводят при повышенных
температурах (вплоть до температуры плавления растворяемого
вещества tл) .
Для анализа и расчетов процесса растворения веществ ши
роко используют кривые растворимости - их строят в коорди
натах "температура - состав раствора". Как уже указывалось в
разд . 1 6 .2.2, эти кривые являются участками (фрагментами)
линий ликвидуса диаграммы равновесия фаз.

Для характеристики состава раствора пользуются конце1Прациями, выра
женными: мольными и массовыми процентами; числом молей в 1 л раствора,
числом молей в 1 кг распюриrеля; массой расmоренноrо вещесrва на НЮ г расmори
rеля и др. Применение сrолъ lilllpoкoro разнообразия способов выражения ко1Щент
рации расrвора затрудняеr технолоIЯЧесхие расчеrы процесса расrворения, а также
ero rрафическое изображение на диаrраммах фазовою равновесия Наиболее рацио
нально - выражать сосrавы растворов в массовых или мальных долях.
.

Для большинства веществ, растворение которых сопровож
дается поглощением теплоты, растворимость с увеличением
температуры растет. У веществ, растворение которых сопро
воЖдается вьщелением теплоты, растворимость с повышением
температуры снижается . В этом случае принято говорить о ве
ществах с обратной растворимостью.
Если вещество при охлаждении раствора не образует кри
сталлогидратов или молекулярных соединений, то кривая рас
творимости, как правило, представляет собой плавную линию
(рис . 17.6, кривые 1-3) . В противном случае на кривой раство
римости появляются характерные изломы при температурах,
соответствующих перитектическим переходам, связанным с
образованием хи мических соединений или кристаллогидратов
(рис . 17.6, кривая 4).
Влияние температуры н а растворимость веществ проявляется по-разному.
Так, в интервале от О до 100 ос растворимость КNОз в воде увеличивается более
чем в 1 8 раз, Ва(NОз)2 - в 4,3 раза, а NaCl - всего на 10%.

Для анализа процесса растворения бинарных твердых сме
сей индивидуальными растворителями, а также растворения
1404

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

250
200
с::>

'.:::"':. 1 50
�
�
"'
�

....- 1 00

1

50
о
1

20

40

60

t •0с

80

100

- NaCI; 2 - Ва(NОэ)2; З - КNОэ; 4 - Na2�03 (1), N32�0э·2Н2О (11} и N32�0э·SH20

Рис. 1 7. 6. Кривые растворимости солей в воде:
(111)

однокомпонентных веществ бинарными растворителями можно
использовать пространственную диаграмму равновесия соот
ветствующих трехкомпоиентных смесей или же их проекции на
плоскость концентрационноrо треугольника (см. рис. 1 6 .2.3).
Часто процесс растворения изображают в так называемых изо
термических диаграммах растворимости, которые являются изо
термическими сечениями пространственной диаграммы равно
весия фаз (см . рис. 16.5).
Для тройных систем полное растворение компонентов на
блюдается в rомогенной области равновесия фаз, располо
женной над поверхностями ликвидуса рассматриваемой си
стемы. Если же фигуративная точка смеси попадет в любую из
гетерогенных областей, то произойдет лишь частичное (фрак
ционное) растворение .
Рассмотрим в качестве примера растворение бинарной твер
дой смеси F в чистом растворителе. Пусть бинарная смесь со
стоит из компонентов А и С, а в качестве растворителя исполь
зуется низкоплавкий компонент В (рис . 17.7,а) . Примем, что
рассматриваемая система не образует твердых растворов. При
добавлении к исходной смеси F растворителя В состав полу
чаемой смеси (точка смеси М) будет находиться на прямой
смешения FB. Пусть растворение происходит при температуре
tp, которой на диаграмме равновесия фаз соответствует изотер
ма растворимости nmp.
В случае малоrо расхода растворителя точка смеси М 1 попа
дает в гетерогенную область сосуществования двух твердых фаз
А и С . При этом получаемый раствор L будет насыщенным как
компонентом А, так и компонентом С.
1405

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

в

в

а

Рис. 1 7. 7. Изображение процесса растворения бинарной смеси в диаrрамме рав

новесия фаз:

а
ВJIИЯНИе СООПIОШеЮIЯ потоков расrвориrеля и расrворяемой смеси, б
температуры расrвореЮIЯ
-

-

ВJIИЯНИе

При увеличении расхода растворителя точка смеси М2 попа
дает в гетерогенную область существования твердой фазы ком
понента А. Для данного соотношения количеств (или потоков)
растворителя В и исходной смеси F и выбранной температуры
растворения tp компонент С полностью растворится. Получен
ный при этом раствор будет насыщен компонентом А, но не
насыщен компонентом С . Состав полученного раствора Ч
можно определить, проводя коноду (хорду) через точку смеси
М2 и точку чистого компонента А до пересечения ее с изотер
мой растворимости tp . Соотношение между массами получае
мого раствора Ч и остатка твердой фазы Кл можно установить
по правилу рычага. как отношение соответствующих отрезков
коноды ЧА:
L2
А
= М2
(в)
Кл L2M2
При соотношении количеств (потоков) В и F, соответ
ствующем смеси М 3 , лежащей на изотерме растворения , ис
ходная смесь F полностью растворится с получением раствора,
насыщенного компонентом А.
Дальнейшее увеличение расхода растворителя приведет к
образованию ненасыщенного раствора по отношению к обоим
растворяемым компонентам (точка М4), так как точка смеси
М4 попадает в область гомогенных растворов L.
На растворимость бинарных твердых смесей, как и индиви
дуальных веществ, оказывает влияние температура процесса
1 406

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

растворения. Проанализируем это влияние для постоянного
соотношения масс растворяемой смеси F и растворителя В , со
ответствующего точке смеси М (рис . 17.7,б).
Как известно (см. разд. 16.2.3), минимальная температура,
при которой в рассматриваемой системе существует жидкая
фаза, равна температуре кристалл изации тройной эвтектики tr.
Если проводить растворение при температуре tr, то произойдет
частичное растворение смеси F. Заметим, что в данном случае
преимущественно будет растворяться компонент С, так как
точка смеси М попадает в кристалл изационное (фазовое) поле
компонента А. При этом состав получаемого раствора Lr будет
совпадать с составом тройной эвтектики, а состав оставшейся
твердой фазы будет находиться на стороне СА треугольника
(точка Sт) . Соотношение между массами раствора Lr и твердой
фазы�можно найти по правилу рычага как отношение отрез
ков Sт М и М L т .
При повышении температуры растворения состав полу
чаемых растворов будет перемещаться по линии начала кри
сталл и зации (насыщения) двойных эвтектик ЕтЕсл, а состав
твердой фазы - по линии S1A. Например, при температуре t1 >
> 1т состав раствора отвечает точке L 1 , а состав твердой фазы точке S 1 . Такое перемещение точек смеси с ростом температу
ры будет продолжаться до тех пор, пока весь компонент С не
растворится. Это произойдет при температуре t2, когда твердая
фаза S2 будет представлять собой чистый компонент А, а со
став насыщенного раствора - соответствовать точке у.
При дальнейшем повышении температуры растворения мас
са компонента А в твердом состоянии уменьшается, а состав
раствора перемещается по коноде L2A. Так, при температуре tз
получается раствор состава L3 . При температуре t4 изотерма
растворения пройдет через точку М - произойдет полное рас
творение твердой фазы с получением раствора, насыщенного
компонентом А. При температурах выше t4 будет происходить
полное растворение твердой смеси F с образованием ненасы
щенных растворов. Такой процесс, например, будет наблю
даться при температуре !5 .
Рассмотрим теперь растворение однокомпонентного вещества
А бинарнЬIМ растворителем Р, представляющим собой смесь
низкоплавких компонентов С и В (рис . 17.8). Такой процесс
осуществляют, например , при растворении сахарозы водным
раствором этилового спирта. Для соотношения количеств
(потоков) А и Р, соответствующего точке М, при температуре /1
образуется насыщенный компонентом А раствор L1 • Далее по
мере повышения температуры t3 > t2 > t1 содержание компо
нента А в растворе будет закономерно возрастать (растворы у
и L3) , а масса твердого компонента А - соответственно умень1407

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

в

Растворение вещества с
использованием бинарного раство

Рис. 1 7. 8.

р ителя

шаться. При температуре t4
компонент А полностью
растворится, и для вы
бранного соотношения по
токов А и Р получится пре
дельно насыщенный ком
понентом А раствор М .
П р и дальнейшем повыше
нии температуры (напри
мер, до ts ) раствор станет
с
А
уже ненасыщенным.
Нередко исходное веще
ство представляет собой твердую смесь растворимых компо
нентов с инертными примесями, нерастворимыми в исполь
зуемом растворителе. Ставится задача извлечения растворимых
компонентов из этой смеси. С такого рода процессами мы
встречаемся, например, при извлечении ценных компонентов
из руды или из растител ьного сырья.
Применительно к такой задаче рассмотрим равновесие фаз в
трехкомпонентной системе, состоящей из растворимого ком
понента А, инертного компонента С и растворителя В (рис .
1 7 .9). На рис. 17.9,а показана диаграмма равновесия фаз для
бинарной системы, состоящей из компонента А и растворителя
В . На диаграмме нанесено семейство изотерм (t1
14), что по
зволяет определить состав насыщенных растворов при разных
температурах.
Добавление инертного компонента С к смеси А-В не изме
няет температуры фазовых превращений этой смеси, происхо
дит только разбавление данной смеси инертом. Поэтому на
тройной диаграмме (рис . 17.9,6) изотермы растворения изобра
жаются в виде лучей, сходящихся в точке С : эти лучи по суги
дела есть линии изотермического смешения инерта с соответ
ствующим насыщенным раствором. Предельная температура,
при которой в тройной системе еще существует жидкая фаза,
равна температуре двойной эвтектики tE.
Заметим, что рассматриваемая трехкомпонентная система
при всех температурах будет гетерогенной, т.е. она всегда со
держит одну или несколько твердых фаз и одну жидкую фазу.
Жидкое rомоrенное состоян ие (rомоrенные растворы) здесь воз
можно JПШIЬ в бинарной системе А-В при температурах выше
насыщения. Поэтому в рассматриваемой трехкомпонентной си
стеме возможно лишь частичное (фракционное) растворение.
-

1 408

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

а

/4

А

Е

n

в

'э ---"

12 1--+--�'lllo.

с

с

Рис. 1 7.9. Равновесие в тройной системе с инерmым компонскrом:

-

а
диаrрамма равновесия фаз би11ар11ой сисrемы "расrворяемое вещес:rво
растворнтель" ; 6
1111 оскц диаr11амма рав11овеси11 фаз тройной сисrемы "рас111Оряемое
вещество- растворитель-инерт11 ы J1 ком11оне1п"; •, l - изоrермичесJСИе сечени.t диаrрамNЫ
равновесия фаз системы А-В-С п ри температурах lэ (•) и '2 (l)

-

Для расчетов проuесса фракционноrо растворения (выще
лачивания) при наличии в исходн о й смеси инертного компо
нента обычно используют изотермические сечения тройной
диаrрамм ы равновесия фаз . На рис . 11.9,в показано такое сече
н ие при температуре tз > tв. В фазовом п оле ACn существует
гетероген ная система, состоящая из твердых компонентов А и
С, а также насыщенного компонентом А расТвора L. В поле
СВн располагается гетеро ге н ная смесь ненасыщенного раство
ра L с и н ертн ы м компонентом С .
При п он ижении температуры р астворе ния область rетсро
rенного рав н ове с ия A+C+L расширяется , а область существо
ван ия равновесия L+C сокращается (р ис . 17.9,г). Кроме этого
при t2 < tn появляется область rетероrенноrо равно весия
B + C + L.
Раство рение веществ практически всегда сопро вождается
тепловым э фф ектом : чаще всего по гло щением теплоты, реже ее в ыдел ени е м . Под термином теплота растворения понимают
количество теплоты, поглощенной (или вьщеленной) при рас
творении ед и н ицы масс ы вещества в определен ном раствор и 
теле. Теплота растворе н ия зависит от природы растворителя и
растворяемого вещества, их составов, а также от конuе нтраци и
получаемоrо раствора. О бычн о ее определяют опытным путем .

1409

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Теплота растворения Гр складывается из теплоты г1 , затрачи
ваемой на разрушение кристаллической решетки, и теплоты гъ
вьшеляющейся в результате взаимодействия растворяемого ве
щества с растворителем :
Гр = г1 + г2 .

Величина г1 < О , так как на разрушение кристалл и ческой
решетки всегда затрачивается энергия. Величина г2 > О; она
связана с процессами сольватации и гидратации, проте
кающими в растворе. Для большинства веществ г1 > г2, и их
растворение сопровождается поглощением теплоты. Если
г2 > г1 , то растворение сопровождается выделением теплоты,
что часто наблюдается при растворении в воде солей, склон 
ных к гидратации и образованию кристалло гидратов.
1 7 .4. О КИНЕТИКЕ ПРОЦЕССОВ РАСТВОРЕНИЯ

Процесс растворения твердых веществ происходит в гетеро
генной системе твердая фаза-жидкость. При этом в качестве
дисперсной фазы здесь практически всегда выступают частицы
твердого материала.
Несмотря на близость физико-химических основ процессов
простого и частичного растворения, их кинетические законо
мерности мoryr заметно различаться.
При растворении однокомпонентных веществ твердая фаза
имеет более или менее однородную структуру. Процесс просто
го растворения таких веществ в отсуrствие хи мических пре
вращений можно представить состоящим из следующих основ
н ых стадий:
- подвод растворителя к поверхности раздела фаз;
- переход вещества из твердой фазы в растворенное состояние (протекает на границе раздела фаз);
- диффузионн ый
перенос растворенного компонента
(вещества) от поверхности раздела фаз в основную массу раствора.
Анализ этих стадий показывает, что кинетика растворения
однокомпонентных веществ чаще всего определяется интен
сивностью третьей стадии
внешнего массопереноса
(массоотдачи), протекающего в пограничной пленке жидкой
фазы около поверхности растворяемого твердого вещества.
При химическом растворении однокомпонентных веществ
наряду с интенсивностью внешнего массопереноса на скорость
процесса растворения может оказывать существенное влияние
скорость хи мической реакции, происходящей на границе раз
дела фаз.
Процесс частичного (фракционного) растворения бинарных и
многокомпонентных твердых смесей по сравнению с растворе1410

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

нием однокомпонентных веществ протекает более сложно из-за наличия в системе нерастворенных твердых компонентов.
В этом случае на скорость растворения мoryr оказывать влия
ние следующие факторы: состав и структура исходной твердой
фазы; свойства растворителя; форма и размеры частиц (зерен)
твердого материала; размеры, расположение и вид пор в твер
дой фазе; температура и др.
Процесс фращионного растворения твердых веществ вклю
чает в себя следующие стадии:
- подвод растворителя к поверхности раздела твердой и
жидкой фаз ;
- прониюювение жидкой фазы в поры твердого тела
(частиц);
- растворение извлекаемого компонента или химическое
взаимодействие с ним;
- диффузия растворенного компонента в порах твердого
тела к его внешней поверхности;
- переход растворенного вещества или продуктов хи ми
ческой реащии с поверхности твердого тела в основную массу
(в ядро) жидкой фазы (раствора) .
Естественно, общая скорость массопереноса в такой системе
в общем случае зависит от скоростей всех отдельных стадий .
Как и в случае других массообменных процессов, здесь также
может существовать лимитирующая стадия, протекающая зна
чительно медленнее остальных. При частичном растворении
твердых материалов чаше всего такой стадией является перенос
(внутрен 11яя диффузия) растворенного вещества в порах твер
дого тела . Кинетика частичного растворения зависит также от
того , в каком фазовом состоянии (жидком или твердом) нахо
дится извлекаемый компонент в исходном твердом веществе, а
в последнем случае и от того, образует ли он с другими компо
нентами твердые растворы. Особенности массообмена в систе
мах с твердой фазой рассмотрены в разд. 10. 1 6 .
Истинной движущей силой процесса растворения, как и
любого другого массообменноrо процесса, является разность
химических потенциалов жидкой и твердой фаз. Их непосред
ственный расчет или экспериментальное определение в реаль
нь�х системах затруднены ; поэтому на практике движущую силу
процесса растворения обычно выражают через разность рабо
чих и равновесных концентраций в растворе, сводя таким об
разом задачу массообмена к внешней. Эrо часто оправдано в
случае простого растворения. При этом, как правило, прини 
мают, что н а поверхности твердой фазы раствор достигает на
сыщенного состояния , т.е. его кон центрация равна Хн· В ос• Подробнее см. ( 1 , 3-8 ) .

141 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

новной же массе (в ядре потока) раствор ненасыщен, и его
концентрация х < Хн·
При растворении однокомпонентного вещества в условиях
внешней задачи скорость процесса (изменение массы твердого
вещества М во времени ) можно представить в виде уравнения
массоотдачи:
t

где f - текущая межфазная поверхность в моменr времени 't; р· = рр; р
ность жидкой фазы.

(17.1)
-

IUIОТ

Величину коэффициента массоотдачи в жидкой фазе J3 мож
но определить, используя обобщенные критериальные зависи
мости вида (10. 10), приводимые в специальной литературе*.
Значение межфазной поверхности f зависит от дисперсного
состава исходной твердой фазы и в периодическом процессе
является переменной величиной, что затрудняет решение урав
нения (17. 1). При непрерывном растворении, когда массу твер
дой фазы и межфазную поверхность в аппарате можно принять
постоянными, массу растворяемого вещества можно опреде
лить по уравнению массоотдачи:
(17.2)
F = М = J3j{ЛX) cp ,
где (ЛХ)ср

-

средняя (по поверхности Л движущая сила процесса растворения.

Расчет процесса выщелачивания (частичного растворения),
если массообмен протекает в условиях внутренней задачи, бази
руется на уравнении Фика и граничных условиях 1 рода (разд.
10.16.3). При этом чаще всего рассматривается диффузия ве
щества из внутренних зон твердого зерна к его поверхности,
так как пропитка зерна растворителем обычно происходит за
метно быстрее. Осложняющим расчет обстоятельством являет
ся значимое изменение коэффициента диффузии D с концент
рацией вещества в растворе х: как правило, D растет при
уменьшении х. Анализ становится еще сложнее при отсутствии
лимитирующей стадии, если процесс протекает в условиях сме
шанной задачи массопереноса.
На практике нередко обходят расчетные трудности, прибе
гая к построению упрощенных моделей (например, послойной
отработки зерна). Иногда производят подмену задачи, исполь
зуя уравнения внешнего массообмена типа (17.2) и придавая
при этом коэффициенту массоотдачи J3' эффективный характер:
полагаюг, что он учитывает не только конвективный массопе
ренос, но и другие эффекты. Достаточно широкое распростра
нение получили также эмпирические зависимости - для опре• См. [ 1 , 2, 4, 6, 8) .

1412

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

деления параметров предлагаемых моделей, а подчас (при от
для описания процесса в целом; так
суrствии моделей)
иногда поступают применительно к промышленным аппара
там, где на процесс существенно вл ияет структура потоков, не
всегда достаточно изученная и описанная.
Теоретические построения, некоторые модельные представ
ления, сведения эмпирического характера и ряд примеров рас
чета процессов выщелачивания приводятся в специальной ли
тературе .
-

•

17.5. СПОСОБЫ И СХЕМЫ ПРОЦЕССОВ РАСТВОРЕНИЯ

Процессы полного и частичного растворения мoryr осу
ществляться в периодическом, полунепрерывном и непрерыв
ном режимах.
Периодический процесс полного растворения чаще всего про
водят в аппаратах с механическим перемешиванием дисперс
ной системы (суспензии), состоящей из частиц твердого мате
риала и ненасыщенного раствора. При этом движущая сила
процесса растворения постепенно снижается во времени в ре
зультате повышения концентрации раствора. Иногда процесс
растворения реализуют пуrем фильтрации растворителя или
циркулирующего раствора через неподвижный слой твердого
вещества, расположенного на фильтрующей перегородке. Та
кой процесс продолжают до растворения всего загруженного
твердого материала.
Непрерывное полное растворение твердых веществ можно вес
ти в аппаратах прямоточного или противоточного типов. При
прямоточном движении твердой и жидкой фаз концентрация
раствора постепенно увеличивается по длине (или высоте) ап
парата, а масса твердой фазы соответственно уменьшается
вплоть до нуля. Очевидно, в данном случае длина аппарата
определяется продолжительностью растворения наиболее
крупных исходных частиц твердого вещества. При прямоточ
ном движении фаз движущая сила процесса по ходу движения
потоков фаз в аппарате (как и в периодическом процессе - во
времени) падает. Противоточное движение может быть органи
зовано пуrем механического перемещения твердой фазы на
встречу потоку ненасыщенного раствора или же пугем филь
трации восходящего потока раствора через опускающийся слой
твердой фазы.
В ряде аппаратов имеет место смешанный режим движения
потоков. Так, например, в колонных растворителях крупные
• См., например, ( 1 , 6, 8 ) .

14 1 3

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

частицы первоначально могуг двигаться вниз (осаждаться) в
восходящем потоке раствора в режиме противотока. Однако
при растворении масса частиц уменьшается, и их скорость
стесненного осаждения снижается . По достижении определен 
ного размера частиц с корость их осаждения может оказаться
меньше скорости потока жидкой фазы, и такие частицы начнуr
двигаться вместе с потоком раствора, т.е. в прямоточном ре
жиме .
Непрерывное полное растворение твердых веществ можно
осуществить в аппаратах полного перемешивания, соединяя их
в прямоточный (или противоточный) каскад либо устанавли
вая в аппарате специал ьное фильтрующее устройство для за
держки частиц твердой фазы.
Процесс частичного растворения твердых материалов по
принципам его орган изации в значительной мере напоминает
жидкостную экстракцию (см . разд. 1 3 . 1 , 1 3 . 3 ) . Как уже указы 
валось выше, такой процесс включает в себя две стадии: рас
творение переходящих в раствор компонентов и сепарацию
продуктов растворения . В периодическом процессе эти операции
производятся в одном или в различных аппаратах, но в любом
случае они разделены во времени. При непрерывном выщелачи
вании стадии растворен ия и сепарации разделены в про
странстве - они производятся одновременно в отдельных ап
паратах или же в разных зонах одного аппарата.
Частичное растворение (выщелачивание) , как и процесс
жидкостной экстракции , может осуществляться в виде одно
кратного или многоступенчатого процесса.
При однократном непрерывном выщелачивании поток твердого
вещества F с кон центрацией растворяемого компонента хр на
стадии растворения Н смешивается (рис . 1 7 . 1 0, а) с растворите
лем Р, имеющим концентрацию Хр (в случае использования
чистого растворителя Хр = О) . Полученная суспензия (пульпа)
поступает на стадию сепарации Ф ; в результате получают рас
твор L с кон центрацией XL и твердую фазу (рафинат S) с кон 
центрацией xs. Такой п роцесс , как правило , характеризуется
низкой эффективностью: малым коэффициентом извлечен ия ,
з начительным расходом растворителя и существенным захва
том целевых компонентов твердой фазой.
Существенно повысить эффективность разделения можно
при использовании разл ичных схем многоступенчатого разделе
ния, одна из которых показана на рис. 1 7 . 1 0 , б. Здесь исходное
вещество F поступает на первую ступень разделения, куда по
дают часть (первую порцию) растворителя Р1 • Полученный
раствор (экстракт) L1 отводят, а нижний продукт (рафинат) S1
передают на вторую ступень разделения , где разделение осу
ществляется с использованием второй порции растворителя Р2 .

1 4 14

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

б

в

Схемы потоков при однокра111 о м (а), порционном (6) и противоточ
ном (в) частичном растворении
Рис. 1 7. 10.

Рафинат второй ступени S2 передают на третью ступень и т.д.
В результате такого разделения получают один конечный ниж
ний продУКI' Sn с низким содержанием растворяемых компо
нентов и ряд экстрактов (маточников) различных концентра
ций. Подобный процесс в литературе часто еще называют пор
ционным или перекрестиым выщелачиванием. Порционное вы
щелачивание позволяет достичь высокой степени из влечения
целевых компонентов из исходной твердой смеси; однако та
кой процесс требует значительного расхода растворителя, по
скольку концентрация растворяемого вещества в получаемых
экстрактах с увеличением числа ступеней быстро снижается.
Заметим, что перемещение твердой фазы из одной ступени в друrую часто
сопряжено с определенными трудностями. Обойти их можно, орrанизуя процесс
пepeкpecruoro выщелачивания во времени, т.е. подавая поо11ередно порции рас
творите.ля в аппарат с твердым материалом.
Возможны и другие схемы мноrоступенчатоrо вьпцелачивания. Например :
исходное вещество делят на порции и подают их на каждую ступень, а раствори
тель последовательно проходит через все ступени . В ряде схем орrанизуют ре
циркуляцию твердой или :жидкой фазы. Многоступенчатое фракционное раство
рение можно реализовать также с использованием различных каскадных схем
разделения.

Наиболее эффективным способом извлечения ценных ком
понентов из твердых материалов является непрерывное проти
воточное растворение (выщелачивание). Принципиальная схема
ступенчатого противотока показана на рис. 17. 10,в. Здесь ис1415

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ходное вещество F подают с одного кон ца схемы (аппарата) , а
с другого . Между ступенями органи
свежий растворитель Р
зовано противоточное движение жидкой L и твердой S фаз .
Противоточное выщелачивание может быть также организова
но и с непрерывным контактом твердой и жидкой фаз . Такие
схемы разделения позволяют максимально использовать дви
жущую силу процесса, достигать высоких степеней извлечен ия
целевых компонентов и насыщения экстрактов, а значит, обхо
диться умерен ными расходами растворителей (экстрагентов) .
-

Как уже упоми налось в rл . 1 6, полное и частичное растворение часто исполь
зуют дr1Я разделения и очистюt веществ в сочетании с процессом фракционной
кристалли зации. При этом раствор со стадии растворения поступает на стадию
кристалли зации , где при его охлаждении происходит образование кристалло в
целевого компонента. Обедненный целевым компонентом маточни к со стадии
кристалли зации возвращается на стадию растворения, где он используется в
качестве растворителя исходного вещества. Для предотвращения накопления
примесей в циркулирующем маточнике производят его частичный отбор с по
следующей регенерацией и возвратом в цикл или же перед стадией растворения
маточник дополнительно очищают от примесей методами адсорбции , химиче
ского осаждения , с помощью мембран и т.д.

Ранее уже указывалось, что процесс растворения твердых
веществ может сопровождаться выделением или поглощением
теплоты фазового превращения . Подвод (или отвод) теплоты
на стадии растворения может быть осуществлен за счет внеш
него теплообмена. При этом аппараты-растворители должны
иметь теплообменные поверхности в виде рубашек, змеевиков,
трубчаток и т.п. Подвод (или отвод) теплоты фазового превра
щен ия в зону растворения или в аппарат можно также осу
ществить за счет выбора соответствующей температуры раство
рителя. Так, при поглощении теплоты на стадии растворения
растворитель предварительно нужно нагреть, а при выделении
теплоты - охладить до определенной температуры.
17.6. РАСЧЕТ ПРОЦЕССОВ РАСТВОРЕНИЯ

Методики расчета процессов полного и частичного раство
рения заметно различаются . Рассмотрим последовательно осо
бен ности их расчета.
17.6. 1 . Полное растворение веществ

При полном растворении веществ получают гомогенный
жидкий раствор . Схема п отоков фаз для такого процесса пока
зана на рис . 1 7 . 1 1 . В аппарат Н поступает поток исходного
твердого вещества F с кон центрацией растворяемого компо
нента хр и растворитель Р с его концентрацией .хр. В результате

1416

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 1 7. 1 1.

вещества

Схема процесса полного растворения

растворения получается раствор L с
концентрацией XL· Ур авнения матери
ального баланса процесса имеют вид:
- по потокам (или массе) фаз
F+ P- L = O ;
(а)
- по потокам (или массе) целевого (основного) компонента
Fц + Рхр - LxL = О .
(б)
При совместном решении уравнений (а) и (6) находим кон
центрацию получаемого раствора:
XL

=

Fxp + Рх р
F+P

При растворении чистого вещества
примет вид:

( 17.3)

XL

=

F + Рх р
F+P

( 17.3)
хр

=

1,

и уравнение
( 1 7 .4)

Если к тому же используют чистый растворитель (Хр = О), то
из уравнения ( 1 7.3) получается:
XL =

F
.
F+P

--

( 17 . 5)

При осуществлении процесса полного растворения часто
возникает задача определения минимального расхода раствори
теля . Очевидно, что такой расход растворителя Рн соответству
ет получению насыщенного раствора. Если в уравнении ( 17.3)
положить концентрацию XL равной концентрации насыщения
Хн , то из него можно получить значение Р = Рн:
( 1 7.6)

Заметим, что соотн о шения ( 1 7 .3) - ( 1 7 .6) соответствуют
правилу рыча га в различных его представлениях.
При полном растворении однокомпонентного вещества его
концентрацию в насыщенном растворе Хн можно определить из
диаграммы равновесия фаз (см. рис. 17.5) или по кривой рас
творимости вещества (рис. 1 7 . 1 2) .
Расчет процесса полной растворимости бинарных смесей
удобно производить с использованием проекций диаграммы
равновесия фаз на плоскость концентрационного треугольника
1417

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

х

в

/р

t

Рис. 1 7. 12. Изотермическое полное растворе

ние однокомпоне1rпюго вещества

Рис. 1 7. 13. Полное растворение бинарного твердого вещества

(см. разд. 17.3). На рис. 17. 13 показан процесс полного рас
творения бинарной смеси F, состоящей из компонентов А и С,
с использованием растворителя Р (в случае чистого растворите
ля точка Р совпадает с точкой В). Состав насыщенного раство
ра Lн находится на пересечении линии смешения
(растворения) P F с изотермой растворения IL· Расход раствори
теля для получения насыщенного раствора легко определить по
правилу рычага 1 рода :
Lн

rде FL,, и �

-

= F

FL

н
РL н

(в)

длины отрезков линии смешения .

Выше указывалось, что растворение твердых веществ может
сопровождаться поглощением или выделением теплоты фазо
вого превращения. Количество подводимой (или отводимой)
теплоты можно найти нз теплового баланса. Пусть поток ис
ходного вещества F (его теплоемкость ер, теплота растворения
rp ) поступает на стадию растворения с температурой tp, а рас
творитель Р (теплоемкость ер) подается с температурой lp. Рас
творение производится при температуре ti, теплоемкость полу
чаемого раствора равна сL·
Если процесс растворения вещества сопровождается погло
щением теплоты, то уравнение теплового баланса процесса
полного растворения имеет вид:
(17.7)
Оrсюда наЙдем необходимое количество подводимой теплоты:
( 17.8)
Если же в процессе растворения происходит выделение теп
лоты фазового превращения, то в уравнение (17.7) член с r�
воЙдет со знаком "плюс"; соответственно в уравнение (17.8)
1418

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

значение r!'. следует подставлять со знаком u " минус " . При этом
величина {..! может оказаться отрицательнои, что указывает на
необходимость отвода теплоты от получаемого раствора.
Иногда при незначительных тепловых выделениях процесс
растворения проводят без внешнего теплообмена ( Q = О). При
этом заданная температура процесса обеспечивается за счет
выбора соответствующей исходной температуры растворителя,
подаваемого на стадию растворения (растворитель предвари
тельно нагревают или охлаждают до определенной температу
ры). В этом случае тепловой баланс процесса растворения опи
сывается уравнением
(17.9)
Fcptp + Pcplp - LcL tL - rpF = О ,
откуда можно найти значение исходной температуры раствори
теля tp, обеспечивающее проведение процесса растворения при
заданной рабочей температуре tL :
_ F(rp - cptp ) + LcLtL .
(17.10)
/р РсР
17 6 2 Части чное растворение веществ с инертным компонентом
.

.

.

Частичное растворение твердых смесей при наличии инерт
ного компонента (выщелачивание) может быть осуществл ено
по схемам однократного, порционно го (перекрестного) и про
тивоточного процессов.
Рассмотрим эти процессы применительно к растворению
твердого вещества бинарного состава. В данном случае ис
ходное вещество F представляет собой смесь растворимого А и
инертного С компонентов. Концентрацию компонента А в
данной смеси обозначим хр. В качестве растворителя Р может
использоваться низкоплавкое вещество В или же разбавленный
раствор компонента А в растворителе В (скажем, полученный
после регенерации растнорителя). Содержание компонента А в
растворителе Р соответствует � (в случае чистого растворителя
Хр = О, и точка Р совпадает с В).
На рис. 17. 14 показаны схема однократного частичного рас
творения (выщелачивания) и изображение этого процесса на
изотермической проею.щи диаграммы равновесия фаз рассмат
риваемой системы. Линия Cn на этой проекции есть изотерма
насыщенных растворов А в В (в смеси с С): область ACn соот
ветствует гетерогенной смеси твердых компонентов А, С и на
сыщенных растворов компонента А в растворителе В .
Заметим, что в ряде случаев извлекаемый компонеm А может находиться в
жидком состоянии. Тогда все точки в треугольнике АВС будут соответствовать
rетероrенной смеси твердого компонеmа С и жидкой фазы L, представляющей
собой растворы компонеmа А в В .

1419

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

А

а

б
Рис. 1 7. 14. Схема потоков в процессе частичного растворения бинарной смеси с
инертным компонентом (а) и изображение этого процесса в диаrрамме равнове
сия фаз (б)

На стадии растворен ия
Н исходное вещество F смешивается с растворителем Р. Для полного растворения компонен
та А расход растворителя Р должен быть таким, чтобы точка
смеси М (лежащая на линии смешения FP) находилась в гете
рогенном поле CnB . В результате растворения получается гете
рогенная смесь, состоящая из ненасыщенного раствора (экс
тракrа) L с концентрацией XL компонента А и чистого твердого
инертного компонента С. Однако при разделении полученной
суспензии на стадии сепарации Ф, как уже отмечалось, не
удается полностью отделить жидкую фазу от инертного компо
нента С. В результате из смеси М получаем экстракr L и твер
дый остаток S с концентрацией компонента А, равной xs. За
метим, что точки L и S, соответствующие составам получаемых
продукrов разделения, лежат на линии сепарации CL, прохо
дящей через точку смешения М . Линию разделения (сепара
ции) LS называют хордой.
Уравнения материального баланса однократного растворе
ния рассматриваемой смеси по потокам фаз и компонента А
соответственно имеют вид:

F+ P- L - S= O ;

(г)

(д)
FxF + Рхр - LxL - Sxs = О .
Выр ажая S из (г) и подставляя его в (д), получим зависимость для расчета выхода экстракта L:

L=
1420

F(xF - xs) - P(xs - xp )
XL - Xs

(17. 1 1)

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Зная величину L, из (r) можно определить выход твердого
остатка (рафината) S.
Для определения L и S необходимо располагать значением
концентрации компонента А в твердом остатке xs, которая
зависит от количества жидкой фазы L', захватываемой инерт
ным компонентом. Для определения величины L' можно ис
пользовать коэффициент захвата жидкой фазы инертным
(твердым) компонентом Аз (см. разд. 1 6.5), который в рассмат
риваемом случае (с использованием правила рычага) можно
представить в следующем виде:
L'

где Cs и SL

Аз = С =
-

xs
CS
=
L
S
xL - xs

(17. 12)

длины соответствующих отрезков линии сепарации на рис. 1 7 . 14.

Величину коэффициента захвата Аз обычно определяют опыrным путем: она
может бьпь описана эмпирическими зависимостями, учитывающими физико
химические свойства растворителя и твердой фазы, а также способ и параметры
стадии сепарации.
Зная величину А" из уравнения ( 17. 12) можно найти значение концеmрации
xs. Используя коэффициент А:" можно также на диаrрамме равновесия фаз по
строить линию нижнего продукта
составов твердых остатков (рафинатов) N H .
Ч е м меньше п р и сепарации ф аз захватывается жидкой фазы (экстракта), тем
ближе линия нижнего продукrа к вершине С. Если коэффициент А3 не зависит
от концеmрации получаемых растворов, то линия NH будет прямой, параллель
ной стороне треугольника АВ. Часто с увеличением концеmрации компонента А
в растворе повьШiается его вязкость, а с ней и захват раствора инертным компо
нентом. В этом случае линия NH приближается к стороне АВ при перемещении
от точки N к точке Н .
-

Выход продуюов частичного растворения можно определить
и по диаграмме равновесия фаз, используя правило рычага.
При этом соотношения между потоками исходных продуюов F
и Р, а также потоками продуктов разделения L и S можно
представить в виде отношений соответствующих отрезков линий смешения и сепарации:
F

р

МР
МР
F
F
= -= или
=
=�
F+P м
FP
MF

мs
L
MS
L
L
�
= -= или
=-=
м
L +S
s ML
LS
--ML
s
= -=м
LS
-

(ж)
(з)
(и)

В зависимости от заданных величин (задачи эксплуатации
или проектирования) удобнее использовать те или иные из
приведенных соотношений.
142 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

При проведении процесса частичного растворения часто
возникает задача извлечения (регенерации) растворителя из
твердого остатка S. Регенерацию обычно осуществляют мето
дами сушки или выпаривания (отгонки). Последний процесс
показан на рис. 17. 14. Стадия отгонки О происходит по линии
WP, проходящей через точку S . В результате полного из вл ече
ния растворителя из влажного нижнего продукта S мы получа
ем сухой твердый остаток W с концентрацией x w компонента
А и растворитель Р, содержащий некоторое количество компо
нента А. Соотношение между потоками W и Р можно опреде
лить по правилу рычага:
w
р

SP

sw

(к)

При полной нелетучести компонента А линия регенерации
(отгонки) растворителя будет выходить не из точки Р, а из точ

кИ в .

Степень из влечения компонента А при однократном выще
лачивании из исходной смеси F составляет:
ri =

LxL

FxF



( 17. 13)

Однократный процесс выщелачивания часто не обеспечи
вает заданной степени извлечения целевого компонента А из
исходной смеси F из-за значительных его потерь с твердой
фазой (рафинатом) S или с сухим продуктом W. Для снижения
потерь компонента А можно использовать процесс многосту
пенчатого перекрестного выщелачивания, схема которого приве
дена на рис. 1 7 . 10,б, а его построение в диаграмме равновесия
фаз показано на рис. 17. 15. Примем, что растворение в данном
случае производится чистым растворителем (.хр = О), поэтому
точка растворителя Р совпадает с точкой В.
На первой ступени разделения исходное вещество F смеши
вают с частью (первой порцией) растворителя Р1 • Здесь полу
чают раствор L1 и рафинат S1 ; последний передают на вторую
ступень разделения. Там он смешивается со следующей порци
ей растворителя Р2 • В результате на второй ступени получают
раствор � и рафинат S21 который передаюr на третью ступень,
и т.д. В ходе расчета здесь приходится определять потоки фаз,
уходящих с соответствующих ступеней, L1 и S1, а также точки
материальных балансов (составы смесей) на этих ступенях
М;. Делается это с использованием правила рычага. Такой про
цесс позволяет существенно снизить остаточное содержание
целевого компонента А в конечном твердом остатке (рафи
нате ) : точка W здесь заметно ближе к вершине С, чем на рис.
-

1422

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

А

Рис. 1 7. 15. Процесс перекрестноrо мноrоС'l)"Пенчатоrо растворения бинарной
смеси с инертным компонентом

17. 14. Недостаток этою процесса - получение целою набора
жидких фракций (экстраiсrОв) различной концентрации.
Более совершенным процессом является непрерывное сту
пенчато-противоточное вwщиачивание, схема которою приве
дена на рис . 1 7 . 1 0, в, а ею построение в диаграмме равновесия
фаз - на рис. 17.16.
Материальные балансы для схемы в целом запишуrся так:
- по потокам фаз
(л)
F + Р Sп
L1 = О ;
- по потокам компонента А
(м)
Fxp + Рх.р
SnXsn Lxu = О ,
-

-

г,це S" и xs"
поток нижнеrо продую-а (твердоrо остатка) и концентрация в нем
компонента А на выходе из 11-й ( последней) С'l)"Пени.
-

-

-

А

п

Рис. 1 7. 16. Процесс противоточноrо растворения бинарной смеси с инертным
компонентом

1423

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Совместное решение уравнений (л) и (м) при известных ко
нечных кон центрациях xi1 и Xsn позволяет, исключив Sn, найти
поток отводимого экстракта L1 :
-

L1

_

F(xp - Хsп ) - P(xsn - хР }
XL1 - Хsп

( 1 7 . 1 4)

Для заданн ых начальных потоков, зная величину L1 , из (л)
легко рассчитать поток Sn. Если же задан расход одного из ко
нечных продуктов, то из уравнений материального баланса
можно найти одну из неизвестных концентраций .
Методика расчета числа необходимых ступеней противоточ
ного выщелачивания в значительной мере совпадает с изло
женной для противоточной жидкостной экстракции (см . разд .
1 3 . 1 5.2). Для пространственного контура, охватывающего одно
из крайних (например п-е) и произвольное (i-e) сечения, за
пишем уравнение материального баланса:
(н)
Р + S1 - Sп - L;+ 1 = О .
Отсюда следует, что в любом произвольном сечен ии раз
ность между сопряженн ыми потоками фаз одинакова и равна
разности потоков в крайнем сечении - обозначим ее П:
=

S2 - L з = . . .

S - Р = F - L1 = S1 - Li_ =
= S1 - L 1+ 1 =
= Sп - 1 - Ln = П = idem . (о)
. . .

Эту разность можно трактовать как некоторый гипотетиче
ский поток фазы П.
Для того же контура материальный баланс по потоку ком
понента А запишется:
(п)
РХр + S;Xs; - SnXsn - L;+ 1хц;+ 1) = О ,
откуда для произвольного i-го сечения

(р)
S;Xs; - L;+1XL(1+ I) = SnXsn - РХр = idem ,
причем возможность Хр = О сути анализа не затрагивает.
Из (р) следует, что разности между сопряженными потока
ми компонента тоже одинаковы .
Поделим друr на др уга разности для произвольного сечения
по (о) и (р) и обозначим частное символом хп:
-'---�

SixSi - Li + 1XL(i + I)

-

S; - 4 + 1

=

s" xsi

-

4 + 1XL( i + l) - 1" d em .
= Хп -

П

(с)

Величина хп имеет смысл некой условной кон центрации ,
одинаковой для всех сечений ступенчато-противоточного аппа
рата. Если составить материальный баланс для любого другого
компонента, то придем к аналогичному результату: условная
кон центрация этого другого компонента хп' = idem. Две посто-

1 424

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

янные концентрации разных компонентов в треугольной диа
грамме дают точку П (полюс), одну и ту же для любого сечения
ступенчато-противоточного аппарата, в том числе и для край
них сечений (см. рис . 1 7 . 1 6) . Последнее заключение представ
ляет собой доказательство существования полюса, находяще
гося на пересечении прямых (лучей) , проходящих через любые
пары сопряженных потоков экстрапа и нижнего продУJсrа.
При этом из (р) следует, что SpcSi
L1+1xL(f+\) = Пхп. Это ра
венство можно траповать как операцию вычитания потока
компонента с экстрапом из его потока с нижним продУJсrОМ,
иначе го воря, - как разделение н ижнего продУJсrа на экстрап
и некий гипотетический продУJсr (его поток П, концентрация
хп) . Разделение, разумеется, следует правилу рычаrа (здесь
удобнее применить рычаг 11 рода с опорой в точке П):
-

П L ;+i
L;+1
П S;
и внешний отрезки соответствующего луча.
S;

-- = ---==�

где ПLн1 и ПS;

-

ПОJПIЫЙ

(т)

Равенство (т) дает соотношение потоков нижнего продУJсrа
и маточника в произвольном сечении; это соотношение, ко
нечно, справедливо и для крайних сечений, включающих кон 
цевые потоки Р или F.
Для определения числа необходимых ступеней (задача про
ектирования) необходимо сначала найти полюс .
Полюс П будем строить как точку пересечения крайних лу
чей, соответствующих концевым потокам F, L1 , Р и Sn. Чаще
всего заданы исходные потоки F и Р и их составы (xF, .хр), а
также концентрация компонента А в нижнем продупе (точка
Sп) либо в сухом продУJсrе после регенерации растворителя
(точка Wп) · Тогда один из крайн их лучей, проходящий через
точки В(Р) и Sn (или Wп), может быть проведен сразу. Для по
строения второго луча мы первоначально располагаем лишь
точкой F, точку L1 надо найти. С этой целью сначала отыщем
точку материального баланса М по известным потокам
F и
Р, по правилу рычаrа 1 1 рода:
МВ
F
=
F+P
FB '
-

откуда определяем отрезок МВ и-откладываем его на лин ии BF.
Ту же точку М даст смешение уходящих потоков L 1 и Sn;
значит, точки L 1 , Sn и М лежат на одной прямой. Положение
точки Sn известно (она лежит на линии нижнего продУJсrа, а ее
концентрация в проепной задаче задана) . Относительно точки
L 1 известно, что она лежит на линии экстрактов АВ . Продол
жив прямую SпМ за М, найдем точку ее пересечения со сторо1425

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ной АВ - получим точку L1 . Теперь можно построить и второй
крайний луч, проходящий через точки F и L1 . Полюс П полу
чаем как точку пересечения двух крайних лучей.
Лучи П L1 и П Р ограничивают область возможного разделе
ния при заданных концентрациях исходных и концевых пото
ков. На промежуточных лучах S 1 L2 , S2 Lз , Sз L4 . находятся
сопряженные концентрации в соответствующих сечениях, а на
хордах S 1 L1 , S2L.z, S з Lз ". лежат концентрации потоков, поки
дающих соответствующую ступень. Число ступеней разделения
определяется путем графического построения и равно числу
хорд (стадий сепарации ) . Заметим: чем эффективнее сепарация
фаз (линия нижнего продукта N H ближе к вершине треуголь
ника С), тем меньшее число ступеней требуется для осущест
вления процесса разделения.
Подчеркнем, что в данном случае в результате построения
(в отличие от других массообменных процессов) мы сразу по
лучаем реальное число ступеней разделения. Дело в том, что
построение процесса разделения здесь базируется не на равно
весных концентрациях, а на реальных составах твердой фазы,
определяемых с помощью линии рафинатов N H . Напомним,
что данная линия строится на основании опытных данных; она
учитывает влияние на процесс разделения кинетики стадии
растворения и эффективности стадии сепарации.
В ряде аппаратов (на пример, в шнековых) процесс выщела
чивания протекает с непрерывным контактом фаз. Высоту
(протяженность) рабочей зоны аппарата в данном случае нахо
дят так же, как и для других массообменных аппаратов с не
прерывным массообменом.
"

17 6 3 Фракционное растворение веществ
.

.

.

Данный процесс может быть использован для разделения
различных веществ на фракции, обогащенные тем или иным
компонентом, а также для глубокой очистки веществ от приме
сей. Возможны различные варианты процесса: однократное,
порционное и противоточное растворение. Однако эти процес
сы разработаны пока слабо. Ч асто фракционное растворение
используется в сочетании с фракционной кристаллизацией.
Рассмотрим простейший вариант однократного фракцион
ного растворения применительно к разделению бинарной эв
тектикообразующей смеси, состоящей из компонентов А и С ; в
качестве растворителя Р используется низкоплавкий компонент
В. Процесс (рис. 1 7 . 1 7 , а) состоит из четырех стадий: частично
го растворения Н, сепарации Ф и двух стадий отгонки
(регенерации) растворителя из конечных продуктов разделения
Оs и O i.
1426

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

В,Р

а

б

Схема потоков в процессе однократного фракционного растворения
(а) и изображение этого процесса в диаграмме равновесия фаз (б)

Рис. 1 7. 1 7.

Сначала исходная смесь F с концентрацией компонента А,
равной Хр, при температуре tp подается в твердом состоянии на
стадию частичною растворения Н; там она смешивается с рас
творителем Р, поступающим при температуре tp . Процесс сме
шения изображается на диаграмме равновесия фаз (рис .
1 7 . 17,6) линией FP (или FB, если растворитель чистый) . Состав
полученной тройной смеси соответствует точке N .
Подвод тепла (или е ю отвод) здесь, как и при полном рас
творении, можно осуществлять двумя способами: с потоком
растворителя либо пуrем теплообмена с внешней средой
(теплоносителями). В первом случае теплообмен между пото
ками F и Р происходит при их непосредственном контакте, что
существенно упрощает аппаратурное оформление процесса
растворения.
Для успешной реализации фракционною разделения рабо
чая температура на стадии растворения tФ должна быть не ни
же температуры начала кристалл изации двойной эвтектики tm .
В рассматриваемом случае исходная смесь F лежит в кри
сталлизационном поле компонента А, поэтому при температуре
tФ произойдет полное растворение компонента В и частичное
- компонента А. В результате такою растворения получаем
кристалли ческую фазу, представляющую собой чистый компо
нент А, и маточник М. На диаграмме равновесия сосущество
вание этих фаз изображается линией А М, проходящей через
точку смешения N. При этом точка М лежит на пересечении
коноды (хорды) тА с изотермой tФ.
Полученную на стадии растворения кристалли ческую сус
пензию N подают на стадию сепарации Ф, где производится ее
1427

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

разделение. В результате сепарации получают кристаллическую
S и жидкую L фракции . Состав кристалл изата S зависит от
количества захваченного им маточника.
После отгонки растворителя из фракций L и S н а стадиях
Os (лин ия PW) и OL (линия PV) получают конечные продукты
разделения - соответственно W и V. При этом продукт W обога
щен (по сравнен ию с исходной смесью F) компонентом А, а про
компонентом С. Отогнанные (регенерированные)
дукт V
фракции раствор ителя Ps и PL возвращают на стадию растворе
ния. Неизбежные в ходе процесса разделения потери растворителя
компенсируют потоком Р' (см. рис. 17. 17,а).
Выход продуктов разделения W и V и их состав зависят от
состава исходной смеси F, массы добавляемого растворителя ,
температуры фракционирования и режимов стадии сепарации.
Положение точки N на линии смешения потоков F и Р
устанавливается по правилу рычага:
-

F
NP
NP
F
- = = или -- = =
Р

NF

P+F

FP

(у)

Состав получаемого маточника Хм = XL можн о определить
по положению точки М на диаграмме равновесия фаз . Соот
ношение между потоками S и L определяется отношением со
ответствующих отрезков линии растворения :

S NL
S
NL
(ф)
- = = или
=� .
L NS
S + L SL
Положение точки твердой фракции S можно определить,
располагая величиной коэффициента захвата маточника кри 
сталл ической фазой.
Если качество продукта W не удовлетворяет заданным тре
бованиям (велико содержание примеси С), то можно приме
н ить двухступенчатое фракцион ное растворение.
--

17.7. ОТДFЛЬНЫЕ ЗАДАЧИ
РАСТВОРЕН ИЯ И В ЫЩFЛАЧИВАНИЯ

Ниже рассмотрены некоторые простые задачи, иллюстрирую
щие общие подходы и методики расчета. Примеры и р �шения
ряда более сложных задач содержатся в научной лиrературе .
17. 7 . 1 . Растворение неподвижного сферического зерна
в неограниченном ofu.eмe покоящейся жидкости

Процесс протекает в периодическом режиме. Схема его
изображена на рис . 17. 1 8 . Сферическое зерно плотностью Pr и
начальным радиусом R помещено в неподвижную жИдкость
• См. ( 1 ,

1428

6, 7 ] .

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 1 7. 18. К расчету растворения сферического
зерна в неподвижной :жидкости

плотностью р; коэффициент диффузии
Хн
растворяемого вещества в жидкости
равен D. Требуется установить связь
текущего радиуса зерна r и времени
растворения 't.
Формулировка задачи позволяет ре
шить ее аналитически, поскольку:
- неоrраниченность объема жидкости позволяет допустить,
что концентрация в ней растворенного вещества х равна на
чальной х1 и не изменяется при растворении зерна;
- неподвижность зерна и жидкости означает отсутствие
кон ве.к:rивной составляющей массопереноса: процесс растворе
ния происходит только за счет диффузионного механизма;
- сферическая форма зерна в сочетании с предьщущим
условием позволяет воспользоваться (см . разд. 10.16.2) теорети
ческим выражением Sh = �d/D = �·2r/D = 2 (здесь d = 2r диаметр зерна; � = D/r).
Будем считать зерно непористым, так что растворитель не
пропитывает объем зерна, его растворение происходит только с
поверхности.
Расчет ведем по уравнению ( 1 7. 1 ) , в котором М = (4/3)7t,ЗРт,
dM = 47t,J. Pтdr, f = 47t,J. . Подставим получен ные величины в
выражение ( 1 7 . 1 ) :
- 47t,J.Pт

dr

-

d't

=

D
r

-

"

__

р4пт-(Хн

-

х) ,

причем, естественно, величина концентрации насыщения Хн
const.
После очевидных сокращений и разделения переменных по
лучим:
=

=

- rdr =

_!?_ D(хн

Рт

- x)d't

.

(а)

И нтеrрируя (а) в общем случае от R до текущего значения r и
от О до текущего 't, находим искомую связь (с учетом знака
"минус"):

R2 -

,J. =

2 _!?_ D(Хн - X)'t .
Рт

(17. 1 5)

Из (17. 1 5) определяем:
- значение r к моменту времени 't, конечно, с оrраничени
ем r � О; если получится r < О, это означает, что зерно полнос
тью растворилось за меньший, нежели заданное 't, промежуrок
времени;
1 429

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

- значение 't, необходимое для уменьшения размера зерна
до заданной величины r.
В частности, время полного растворения зерна 'tп (r = О) со
ставляет, согласно (17. 1 5):
2рD (хн - х)

(17. 1 6)

Если объем жидкости V ограничен, то решение задачи суще
ственно усложняется, поскольку в ходе растворения изменяет
ся концентрация растворенного вешества в жидкости: х = var.
В этом случае понадобится использовать материальный баланс
для текущего промежуrка времени, чтобы связать изменение
массы ЛМ и объема Л V зерна (от начала процесса) с текущей
концентрацией растворяемого компонента х (в сравнении с
начальной х 1 ) . Очевидно: ЛМ = РтЛ V = (4/3 )7tPт ( R3 - ,.З). Тогда
Х = Х\

+

рТ л v
p V + Рт Л V

( 1 7. 1 7)

Подстановка в (а) этого значения х (при выражении Л V че
рез r) приводит к достаточно сложному дифференциальному
уравнению, решение которого - непросто. Заметим: при ре
шении надо будет дополнительно иметь в виду ограничение х :::;
� хн ; при растворении вещества в ограничен ном объеме вполне
возможно получение насы щ енного раствора при неполном рас
творении зерна - тогда равенству х = Хн отвечает минималь
ный размер зерна.
1 7.7.2. В ыщела чивание в потоке растворителя
в условиях балансовой задачи

Процесс протекает в полунепрерывном режиме. Схема его
показана на рис . 1 7 . 1 9 . В аппарат, где находятся интенсивно
перемешиваемые постоянные количества подлежащего выще
лачиванию твердого материала и первоначально залитого рас
творителя, непрерывно подается исходный растворитель и от
водится раствор вещества. Раствор в аппарате после первона
чального залива растворителя будем считать ненасыщенным.
Требуется найти связь остаточной концентрации вещества в
аппарате (в твердом остатке) с количеством поданного раство
рителя.
В целях упрощения задачи положим, что внуrренняя и
внешняя стадии массообмена протекают весьма интенсивно
(крупные поры, высокие коэффициенты внуrренней и внеш
ней диффузии, развитая поверхность контакта), так что харак
терные концентрации устанавливаются практически мrновен -

1430

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 1 7. 19.

чивания

Схема полунепрерьш ного выщела

но. В этом случае процесс опреде
dL .
ляется количествами контакти
Х '=О
х
рующих фаз, т.е. протекает в усло
виях · балансово й задачи.
Обозначим: F и Xf - количество
загруженного в аппарат твердого
материала и концентрация в нем растворяемого компонента;
L0 - количество первоначально залитой жидкости, а L рас
творителя, поданного в аппарат к текущему моменту времени.
Анализ процесса удобно вести в относительных концентра
циях :
Х= х
(б)
1 х
в этом случае можно будет оперировать постоянными коли
чествами и пото ками фаз. Тогда количество инерта в твердой
фазе F. = F( 1 хр) = const; текущее количество поданного и
отведенного растворителя в расчете на чистый экстрагент
(штрихом отмечены входные параметры) в общем случае L. =
L' ( l
О , чистый раствори
xL' ) coпst, в частности (п р и xL'
тель), L. = L1; соответственно L� = Lu( l - xL') = const или же
r.:. = L ' (при xL' = О).
В дальнейшем для простоты будем счиrать исходный раствори
тель (экстрагент) чистым. Тогда начальная (после залива в armapaт
растворителя в количестве L0) абсолюrная концентрация вещества
в armapaтe составит Хо = Fxp /(F + LO), она по соотношению (б)
легко переводится в относительную концентрацию Х0 .
Для пространственного контура, совпадающего с аппаратом,
запишем материальный баланс по веществу применительно к
элементарному промежутку времени, за который в аппарат по
дается (и отводится из него) растворитель в количестве d L
При этом имеем в виду, что при интенсивном перемешивании
смеси в каждый момент времени выходная концентрация ве
щества в экстракте Х раJ�на концентрации в аппарате. Итак,
-

-

-

-

=

.

=

=

о

• .

(в)
причем в левой части стоят Приход и Уход вещества, в правой
- его Накопление. Заметим, что при подаче экстрагента с на
чальной концентрацией вещества Х' ':f; О в левой части Приход
будет равен не О, а Ха L . ; никаЮfх дополнительных затрудне
ний в анализ это не вносит.
143 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Разделим переменные и проинтегрируем в пределах от начальных их значений до текущих:
L.
о

J

d L.

F. + L�

Х

dX

.
= - х0J Х

Избавляя с ь от знака "-" и меняя местами пределы Хо и Х,
получаем:
L.
Хо
.
- ln
о Х
F. + r.;.
Огсюда для определен ия L. при заданном значении Х рас
четную формулу удобно представить в впде

( 17. 18)
а

для

-

Х при известном количестве поданного растворителя L .
В ВИде
Х = Х0ехр

[ 0] .
L.

(17.19)

F. + L .
Если растворитель подается равномерно, т.е. задан расход
растворителя в единицу времени /. , то , подставляя L. l•'t ,
находим по (17. 1 8) и (17. 19) связь текущей (или конечной)
концентрации Х с продолжительностью процесса 't .
По завершении расчета относительную концентрацию Х при
необходимости переводят в абсолютную: х = Х/(1 + Х). Расчет
остаточной концентрации растворяемого вещества в твердом
остатке после сепарации при известном коэффициенте захвата
затруднений не вызывает.
=

для

1 7 . 7 .3. Протяженность рабочей зоны
процесса противоточноrо вьпцелачивания
с непрерывным контактом фаз

Противоточный процесс выщелачивания с непрерывным
контактом фаз (непрерывный процесс) осуществляется в ко
лонных аппаратах с движущимся или падающим слоем твердой
фазы либо в шнековом аппарате . Требуется определить протя 
женность рабочей зоны Н (задача проектирования).
Величина Н связана с другими характеристиками рабочей
зоны - поверхностью контакта /, попер е чным сечением аппа
рата sa, удельной поверхностью твердой фазы �д· Поперечное
сечение sa определяется по уравнению расхода �исходя из пре-

1432

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

I�

+lx

L

dМ

а

df

S x+d(S x)

К

п

б

В(Р)

Рис. 1 7. 20. К расчету процесса противоточного вьпцелачивания с непрерывным
контактом фаз:
а

- схема потоков для элсжшарноrо коиrура

"равновесия" фаз

К , 6 - иэобрwксюtе

на диаrрамме

дельных скоростей - уноса, зависания твердой фазы или по
ворота вспять жидкостного потока) . Удельная поверхность /уд
рассчитывается (см. разд. 2.7) по среднему размеру твердых
частиц и их объемной концентрации в рабочей зоне. Поверх
ность контакта f подлежит определению.
Рассмотрим фрагмент рабочей зоны (рис. 17.20,а), разrрани
чив в ней схематически (поверхностью контакта) области дви
жения разных фаз. Выделим в области движения нижнего про
дукта пространственный контур К с элементарной поверх
ностью контакта d/, направив ось f вниз. На рисунке примени
тельно к выделенному контуру показаны потоки нижнего про
дукта S и концентрации в нем растворяемого вещества х, а
также поток последнего dM из контура (в экстракг). Матери
альный баланс по растворяемому веществу имеет вид:
откуда

Sx - [ Sx + d(Sx)] - dM = О ,

(г)
dM = - d(Sx) .
Согласно уравнению массопередачи, записанному для бес
конечно малой поверхности контакта d/,
(д)
dM = k(x - x )df ,

где х' - аналог равновесной концентрации . Под k понимается коэффициент
массопередачи, хара�сrеризующий интенсивность массопереноса с учетом ско
рости процесса на всех составляющих его стадиях (будем считать k известным,
например найденным экспер иментально ил и рассчитанн ым по имеющимся
эмпирическим формулам) .

Приравнивая (г) и (д) , получаем:
dM = k(x - x 'df = -d(Sx) ;
отсюда после разделения переменных и интеrрирования (со
сменой пределов, чтобы избавиться от знака "минус") находим

1433

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ис комую

поверхность контапа:

/=

7

d(Sx)
k(x
- х' )
s, \

( 1 7.20)

х

Для расчета по верхности контакта f необходимо вычислить
интеграл в правой части ( 1 7 . 20) . Это делается с помо щью фазо
вой диаграммы (рис. 1 7 . 20 , 6) . Крайн и е лучи и полюс постро 
ены обычным способом - с м . разд . 1 7 .6.2. Проведем из полюса
П произвольный луч П Si - I Li и из точки Li - хорду L i S i .
Тогда кон центра ци я вещества в жидкости для i-го сечения
С опря енной с ней
равна
L i- I .
ко н центра ц ии в твердом
ж
остатке x's ; отве ч ает то чк а Si .
точ к а s i соответствует а н ало 
"
гу "равно ве сной с x L,i- J ко н це нтра ции - смеси твердого
инерта с жидкостью
состава xr ; , т.е . абсолютной
кон центрации xs , ; . Текущее знач ен ие S, сод ержащееся под ин те1ралом, определяеrся с помощью правила рычага по соотноше-

х

А

того же

П S / ПL в рассматриваемом сечении (rак как раз
ность потоков S - L одинакова для всех сечений armapara и извест
на - см. разд. 17.6.2). Такая же связь кон цеmраций (сопряженной и
"равновесной") и потока нижн его продую'а характерн а для тобого се 
нию аrрезков

чения аппарата, т.е. для множесrва лучей, расположенных межцу
крайними - ПL1 и ПВ. Это позволнет найти значение инте1рала
(1рафически или <mсленными методами) .
Определение протяже н ности рабочей зон ы Н ведется н а
основе известн ого (см . р азд . 1 0 . 8 .4) соотношения

откуд а

Н = _L
.
/yrr5a

Л ИТЕРАТУРА

к главе

( 17.2 1 )
17

1 . Ахсельруд Г.А. Массообмен в системе твердое тело - :жидкость. Львов: Изд.
.
Львовского университета, 1 970. 188 с.
2. Ахсельруд Г.А., Молчанов А.Д. Растворение твердых веществ. М. : Химия,
1977. 272 с.
3. Броунштейн Б.И., Фишбейн Г.А. Гидродинамика, массо- и теIVIообмен в
дисперсных системах. Л.: Химия, 1977. 279 с.
4. Вигдорчик Е.М., Шейнин А.Б. Математическое моделирование непрерывных
процессов растворения. Л.: Химия, 197 1 . 248 с.
5. Зелик.ман А.Н., Вольдман Г.М., Белявская Л. В. Теория гидрометаллургиче
ских процессов. М.: Металлур rия, 1975. 504 с.
6. Романков П.Г., Фролов В. Ф. Массообменные процессы химической техно
логии. Л.: Химия, 1990. 385 с.
7. Рудобашта С. П., Карташов Э.М. Диффузия в химико-технологических
процессах. М.: Химия, 1993. 209 с.
8. Рудобашта С. П.

1980. 248 с.

Массоперенос в системах с твердой фазой. М . : Химия,

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Глава 18
СУБЛИМАЦИЯ И ДЕСУБЛИМАЦИЯ

Под термином сублимация понимают процесс перехода ве
щества непосредственно из твердого состояния в газообразное,
а под термином десублимация - обратный процесс перехода
вещества из газообразного в твердое состояние. Сублимацию
часто также н аз ывают испарением или возгонкой твердой фазы, а
десублимацию - твердофазной конденсацией или кристалл иза

цией из паровой фазы.

Процессы сублимации и десублимации широко используют
ся в химической, пищевой, медицинской, металлур гической,
электронной, текстильной и других отраслях промышл енности .
С помощью этих процессов решаются следующие задачи:
- выделение ценных (или вредных) компонентов из пароrа
зовьrх смесей ;
- разделение и глубо кая очистка веществ от примесей;
- получение мелкодисперсных порошков (красителей, ле карств, различных реагентов) ;
- извлечение ценных компонентов из твердых смесей путем
газовой экстракции ;
- н анесение различных покрьпий на поверхность твердых ма
териалов (готовые изделия, фолыу, пленки, бума�у, ткан и и т.д.) ;
- реагентная обработка твердых: тел с целью протравлива
ния или придания особых свойств поверхности та ких тел;
- получение твердых продуктов в результате хи мических
реакций ме жду исходными газообразными реагентами ;
- выращивание монокристалл ов ;
- газовая полимеризация;
- концентрирование и аккумулирование различных газов
металло rидридами ;
- термохимическое аккумулирование теплоты.
Процесс сублимации сопровождается значительным э ндо
термическим эффе кrо м при переходе вещества из твердого в па
рообразное состояние. Поэто му некоторые сублим:ирующиеся
вещества исполъзуюrся в качестве теплозащитных агентов, нано
симых на поверхности тел, подверrающих:ся мощным тепловым
воздействиям (напр имер, корпуса космичес ких аппаратов).
Процессы сублимации и десублимации обычно тесно связа
ны между собой и часто реализуются в виде последовател ьно
1 43 5

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

осуществляемых стадий . В технической литературе в последние
rоды даже появился специальный термин сублимационно
десублимационная технология. Однако эти процессы мoryr ис
пользоваться и раздельно.
В химической технологии процессы сублимации и десубли
мации используются при промышленном получении и перера
ботке большоrо числа различных веществ: антрацена, антрахи
нона, аценафтена, малеиновоrо и фталевоrо ангидридов, сали
циловой и терефталевой ки слот, нафталина, фталимида, кам
форы, серы, иода, хлоридов алюминия и железа, техническоrо
углерода (сажи) и многих других веществ. В криогенной техни
ке эти процессы применяются для вымораживания паров воды
и диоксида углерода из воздуха, поступающеrо на разделение .
Данные процессы широко используются также для получения
чистых металлов, при производстве ядерноrо rорючеrо, очистке
полупроводниковых материалов, получении твердь.qс веществ с
определенными физико-механическими свойствами .
1 8 . 1 . ФИЗИКО-ХИ МИЧЕСКИ Е ОСНОВЫ
СУБЛИ МАЦИИ И ДЕСУБЛИМАЦИ И

Как уже отмечалось в разд. 1 6.2, процессы сублимации и де
сублимации происходят при параметрах системы ниже тройной
точки. На диаграмме состояния фаз одноко1нпонентного
(чистоrо) вещества (см . рис. 1 6 2 , а) моновариантному равнове
сию "твердая фаза - пар" соответствует линия АВ. Направле
ние фазовоrо превращения в данном случае определяется ве
личинами химическоrо потенциала твердой /Ат и паровой µп
фаз. Если эти потенциалы равны между собой (/Ат = µл), то с и 
стема находится в равновесном состоянии . Если окажется, что
при рассматриваемых параметрах /Ат > µю то в системе будет
происходить процесс испарения твердой фазы, а при µп > /Ат
будет наблюдаться обратный фазовый переход - конденсация
пара с образованием твердой фазы.
Как известно, состояние равновесия фаз в однокомпонент
ной системе определяется двумя параметрами: давлением р и
температурой Т. Для большинства веществ зависимость между
давлением и температурой насыщенноrо пара можно достаточ
но точно описать уравнением Клаузиуса- Клапейрона:
.

в
lg р = А - Т ,

( 1 8 . 1)

где Т абсолюrnая темпер11тура; А и В - п остоянные коэфф ициенты, харакrер
ные для отдельных веществ • • .
-

• •з начения этих коэффициенто11 для многих uеществ приведены в литерату

• Подробнее см. ( 1 , 4, 5 ).
ре - см. , например, (4) .
1 4 36

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Внуrренняя энергия пара выше, чем кристаллической фазы.
Поэтому сублимация веществ сопровождается поглощением
энергии, а при десублимации происходит выделение энергии
(теплоты) фазового превращения.
Зависимость между скрытой теплотой сублимации Гсуб , дав
лением паров р , температурой и мольными объемами паровой
Vп и твердой Vт фаз описывается уравнением Клапейрона

rсуб = const.

dp
dT

Гсуб
= Тд
v=Т

'суб

(vп - v т )

( 1 8 .2)

Заметим, что уравнение ( 1 8 . 1 ) получается из ( 1 8.2),

ее.ли

принять

vn

>> vт и

В свою очередь, скрытую теплоту сублимации можно пред
ставить в виде суммы теплот испарения 'исп и плавления 'пл
вещества:
/'суб = Гисп + Гпл
( 1 8 .3)
•

Заметим, что адцитивное уравнение ( 1 8 . 3 ) применимо толь
ко при данной температуре. Зависимость теплоты сублимации
вещества от температуры можно установить, используя уравне
ние Клаузиуса:

d Гсуб Гсуб
= Сп - Ст
d T - -Т

--

'

( 1 8 .4)

где Cr и Сп - теплоемкости твердой фазы и насыщенного пара при температуре
испарения.

Мольный объем твердой фазы Vт гораздо меньше мольного
объема пара vп. так что уравнение ( 1 8 .2) можно упростить:

dp
dT

= ТГсуб
vп

( 1 8 .5)

Ry T
р

( 1 8 .6)

Для идеальных газов мольный объем паровой фазы равен
Vп

=

-

При подстановке значения Vп из уравнения ( 1 8 .6) в
получается уравнение Клаузиуса- Клапейрона:

др = � d T .
2
Р

Rу Т

( 1 8.5)
( 1 8 .7)

Если принять, что в небольшом интервале изменения тем
пературы от Т1 до Т2 скрытая теплота сублимации изменяется
незначительно, то при интегрировании уравнения ( 1 8 .7) полу
чается зависимость
( 1 8 . 8)
1 437

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Уравнение ( 1 8.8) может применяться для определения скрьrrой теruюты суб
лимации в диапазоне температур Л Т
Т2 - Т1 , если имеются данные о б упру
гости паров вещества при определенных температурах. Это уравнение может
бьrrь использовано также для определения упругости паров вещества при раз
личных температурах, если известна скр ьrrая теплота сублимации (Гсуб = / ( 1)).
=

Для бинарных и многокомпонентных систем равновесие
между твердой и паровой фазами зависит от давления, темпе
ратуры и состава системы (смеси) . Данное равновесие, как и
для фазовых переходов "твердая фаза- жидкость" и "жидкость
пар", можно представить в виде диаграмм равновесия фаз .
Здесь, как и в случае равновесия "твердая фаза-расплав", воз
можно большое разнообразие типов диаграмм состояния фаз .
Правда, в литературе пракrически отсутствуют полные диа
граммы такого равновесия; это , видимо, связано с большими
экспериментальными трудностями его изучения . Обычно в
литературе приводятся
данные изобарического или изотерми•
ческого равновесия .
В качестве примера рассмотрим равновесие бинарной эвтек
тикообразующей системы при различных давлениях (рис. 1 8 . 1 ) .
Пусть для данной системы летучесть компонента В выше, чем
компонента А ; соответственно, температура кипения lкв ком
понента В будет ниже температуры кипения tкА компонента А.
С другой стороны, температура кристаллизации tв чистого
компонента В выше температуры кристаллизации tл компонен
та А. К тому же давление тройной точки Ртв компонента В
больше давления тройной точки Ртл компонента А.
При давлении в системе р1 выше давлен ий тройных точек
чистых компонентов (рис . 1 8 . 1 ,а) диаграмма фазового равнове
сия разделяется линиями моновариантного равновесия
(ликвидуса, солидуса, юшения и конденсации) на шесть фазо
ВЬIХ полей. Выше линии конденсации (полного испарения)
располагается поле гомогенной паровой фазы П. Между ли
ниями конденсации и кипения находится гетерогенное поле, в
котором сосуществуют жидкая Ж и паровая П фазы. Между
линиями ликвидуса и кипения располагается поле гомогенной
жидкой фазы Ж, а между линиями ликвидуса и солидуса гетерогенные поля жидкой и твердой фаз (Кв + Ж и Ж + Кл) .
Ниже линии солидуса, проходящей через эвтекrическую точку
Е, находится область твердьIХ фаз Кл и Кв.
Как известно, равновесие в конденсированных системах (с
участием жидкой и твердой фаз) мало зависит от давления, так
как они пракrичес ки несжимаемы. В то же время равновесие с
участием паровой фаз ы ("жидкость - пар" и "твердая фаза
пар") существенно изменяется с давлением. Поэтому при по• Подробные сведения о равновесии с участием твердой, жидкой и паровой
фаз см., например , в \ 1 , 3 \ .

1 438

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ж

КА+ Кв

в

а

х

/А

А

в

(Е

в

Х-

А

/А
---. /аА

A�-"""'!!f"°--t tм
А

А

(fA < tв, Рrв > р,А):

Рис. 18. 1.

Диаrраммы равновес11я фаз бинарной смеси при раз.личных дааленнях

а - Р1 > Рrв

и PrA

;

6 - Рrв • P"l

> PrA

;

• - Рrв > Р3 >

PrA ; l - Р4 < Prl и PrA ; д - Ps - Р4ф

нижении давления область парожидкостного равновесия (П +
+ Ж) прибл ижается к линия м ликвидуса системы. При этом об
ласть существования жидкой фазы Ж сокращается (см.
рис . 1 8 . 1 ,6), а температуры кипения чис.:rых компонентов при
ближаются ·к температурам кристаллизации: tкл � tл и lхв � tв.
При определенном давлении ( в нашем примере при P'J., отве
чающем тройной точке Ртв компонента В) температуры кипе
н ия lхв и кристаллизации t8 становятся равными температуре
тройной точюi компонента В .
При дальнейшем понижении давления до Рз ниже Ртв на
диаграмме появляется дополнительная область (поле) гетеро
генного равновесия "кристалл ическая фаза Кв - пар П" (рис.
1 8 . 1 ,в) . Выше линии H N происходит полное испарение кри1 439

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

сталл о в Кв в рассматриваемой бинарной системе при давлении
Точка N соответствует нонвариантному равновесию трех
фаз (Кв-Ж- П) .
При давлении в системе р4 ниже тройных точек обоих ком
понентов (рис. 1 8 . 1 , г) на диаграмме появляются еще одна гете
рогенная область равновесия П - Кл и точка М нонвариантного
равновесия трех фаз ( Кд-Ж-П) .
Наконец, при определенном давлении Ps = Р4ф в нонвари
антном равновесии будуг находиться четыре фазы (Кл-Кв
Ж-П). При э том состав жидкой фазы отвечает эвтектической
точке Е (рис. 18. 1,д) . При давлении же ниже Р4ф полностью
исчезнет жидкая фаза, и в равновесии будуг находиться две
твердые фазы Кв и Кл и одна паровая.
Имея таки е диаграммы, можно , установив параметры, при
которых существует та или иная фаза, определить ее состав, а
также выход в процессе разделения .
Исходные вещества (смеси) моiуГ содержать твердые приме
си с очень низкой летучестью паров. Такие примеси, как и в
процессах растворения и кристаллизации, практически не
влияют на равновесие в системе, так что их можно рассматри
вать в качестве нелетучего компонента (как это делается, на
пример, в процессах выпаривания и выщелачивания) .
Многие вещества имеют весьма низкое давление в тройной
точке, поэтому проведение процессов сублимации и десубли
мации таких веществ требует глубокого вакуума. Это суще
ственно затрудняет реализацию рассматриваемых процессов, а
в целом ряде случаев их осуществление на современном техни 
ческом уровне пока практически невозможно. П р и проведении
процессов сублимации и десублимации веществ с низкими дав
лениями в тройных точках в систему часто дополнительно вво
дят инертный газообразный компонент ( газ-носитель)
для
понижения парциального давления основных компонентов.
Использование инертного газа-носителя позволяет процессы
сублимации и десублимации многих веществ проводить при
атмосферном давлении или при умеренном вакууме. Этот при
ем аналогичен перегонке высококипящих веществ в потоке
инертного газа (см. разд. 12.3.3 ) . В качестве инертных газов
носителей используют воздух, азот, аргон и другие газы.

р3 .

-

1 8.2. ОСНОВНЫЕ ОСОБЕННОСТИ ПРОЦЕССОВ

СУБЛИМАЦИИ И ДЕСУБЛИ МАЦ И И

Для протекания любого фазового превращения необходимо
чтобы система находилась в пересыщенном состоянии. Это
обеспечивает движущую силу любого массообменноrо и хими
ческою процесса. Для однокомпонентных систем их пересы1 440

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

щения можно достичь изменением двух основных параметров
- давления и температуры. Для бинарных и многокомпонент
нь�х смесей пересыщения помимо этого достигают пуrем изме
нения состава систем , например , разбавляя смесь инертным
компонентом . В соответствии с этим сублимацию твердь�х ве
ществ можно проводить тремя способами : повышая температу
ру, снижая давление или добавляя к исходному веществу
инертный газообразный компонент (либо сочетая два или все
три способа) . Десублимацию паров, соответственно, можно
осуществлять путем охлаждения , сжатия паров и изменяя со
став паров. Последний вариант десублимации реализуют, на
пример, проводя адсорбционное поглощение одноrо из компо
нентов смеси или посредством его химического связывания.
Скорость фазовых превращений "твердая фаза-пар" и
"пар-твердая фаза", подобно скоростям друrих фазовых пре
вращений, зависит от скорости создания пересыщения и ки
нетики самого фазового превращения. Для процессов сублима
ции и десублимации, как и для процессов растворения и кри
сталлизации , влияние этих факторов проявляется по-разному.
При сублимации веществ кинетика фазового перехода обыч
но не лимитирует скорость процесса в целом. Лимитирующим
фактором здесь чаще всего является интенсивность тепломас
сообмена в системе. Поэтому скорость сублимации определяет
ся обычно скоростью подвода теплоты из внешней среды. Если
теплота подводится через твердую фазу, то скорость сублима
ции сильно зависит от теплопроводности твердого вещества и
его дисперсного состава. Поэтому твердые вещества часто пе
ред их испарением дробят, а в самом сублиматоре организуют
перемешивание твердой фазы. Необходимую теплоту можно
также подавать в сублиматор с инертным газом-носителем ли
бо организуя индукционный или радиационный наrрев.
При десублимации веществ ки нетика фазового превращения
оказывает более существенное влияние на ход процесса. Так
же, как и при кристалл изации из расплавов и растворов, при
десублимации необходимо, чтобы в пересыщенной пар� вой
фазе происходило образование центров кристаллизации . В
зависимости от условий процесса и состава исходной парогазо
вой смеси при десублимации , как и при кристаллизации из
жидкой фазы, может происходить rомоrенное или rетероrенное
зарожцение центров кристалл и зации (зародышей) . Гомогенное
зарождение кристалло в чаще реализуется при десублимации
чисть�х паров; оно определяется флуктуациями энерrии в си
стеме. При анализе данного процесса также используется поня• Более подробно кинетик:� и механизмы заро�ения и роста кристалло в в
паровой фазе рассмотрены в ( 1 , 2) .
1 44 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

тие кр1ПИЧеского размера зародыша. Гетерогенное зарождение воз
можно при н аличии в паровой фазе готовых твердых частиц, на
поверхности которых и начинается процесс кристаллизации.
Рост кристаллов в паровой или парогазовой фазе может
происходить пуrем непосредственного присоединения элемен
тарных частиц к поверхности растущего кристалл а . При анали
зе данной стадии используюг те же теории роста, что и для
обычной кристаллизации (см. разд . 16.3). Рост кристалло в в
паровой фазе может также происходить пуrем коагуляции мел
ких кристалл и ческих фрагментов, находящихся в паровой фазе .
Скорости зарождения и роста кристаллов в паровой фазе,
как и при обычной кристаллизации, зависят от физико
химическ:их свойств вещества, способа и скорости создания
пересыщения, состава исходной паровой фазы, скорости ее
движения и других факторов.
В зависимости от условий десублимация может осущест
вляться в двух вариантах: в объеме газовой фазы либо на теп
лообменных поверхностях или стенках десублиматоров. С точ
ки зрения термодинамики принципиального различия между
этими двумя вариантами нет, поскольку основной процесс де
сублимации в каждом из этих случаев происходит на поверх
ности кристалл ической фазы. Обьемная десублимация является
аналогом массовой криста.riлизации из раствора, а поверхност
ная десублимация
аналогом направленной кристаллизации
жидкой фазы.
Однако следует отметить и некоторые различия между объ
емной и поверхностной десублимацией . В случае обоемной де
сублимации паровая фаза всегда пересыщена по отношению к
равновесной концентрации, которая устанавливается на по
верхности твердой фазы. При этом теплообмен твердой фазы с
внешней средой происходит через паровую или парогазовую
фазу - конвекцией либо излучением. При поверхностной де
сублимации теплота фазового превращения обычно отводится в
результате контакта десублимата (твердой фазы) с охлаждаемой
поверхностью. При это м охлаждаемая поверхность, как прави
ло, имеет температуру существенно н иже, чем паровая фаза.
Более того , паровая фаза может даже находиться в перегретом
(ненасыщенном) состо я нии ; насыщение достигается только
вблизи поверхности твердой фазы.
Размеры и форма кристаллов, образующихся в процессе де
сублимации, как и при обычной кристаллизации , зависят от
большого числа факторов: физико-химических и теплофизиче
ских свойств вещества в различных фазах, состава исходной
парогазовой смеси, способа и скорости создания пересыщения ,
температуры, давления, наличия примесей, интенсивности
перемешивания паровой фазы и др .
-

1 442

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Чем выше скорость создания пересыщения, тем больше об
разуется центров кристаллизации и тем меньше получается
средний размер кристалл о в десублимата.
При кристалл изации из паровой фазы обычно наблюдается образование кри
сталло в с развитой поверхностью (иголок, дендритов, снежинок и т.п.). Такая
форма кристалло в способствует более быстрому рассеиванию теплоты. Заметим ,
что при десублимации в ыделяется значительное количество теплоты фазового
превращения. В то же время паровая фаза является плохим проводником тепла.
дендРитны:й рост кристалло в особенно характерен для процесса десублимации
вещесrв в неподвижной паровой среде на охлаждаемых поверхностях. При де
сублимации хорошо перемешиваемой паровой фазы на охлаждаемых поверхно
стях часто наблюдается образование "плоских" дендритных кристалло в. Типич
ным примером такой десублимации является образование дендритных узоров на
оконных стеклах.

При десублимации веществ на охлаждаемых поверхностях,
как правило, образуется пористый слой кристалло в, толщина и
структура которого изменяются в ходе процесса. В начале про
цесса на охлаждаемой поверхности обычно образуется кристал
лический слой в виде инея, состоящего из игольчатых или ден 
дритных кристаллов. Толщина такого слоя сначала быстро рас
тет, однако затем скорость роста слоя снижается - вплоть до
нуля. Одновременно с ростом толщины слоя идет его уплотне
ние - в результате проникн овения пара в слой и его после
дующей кристалл изации там. Одновременно с этим в слое де
сублимата происходит перекристалл изация вещества: первично
образовавшиеся неравновесные формы кристалло в превра
щаются в более устойчивые формы. Все это постепенно приво
дит к уменьшению порозности слоя десублимата, вплоть до
образования монолитного слоя.
В ходе процесса десублимации происходит изменение сил
сцеплен ия (адгезии) кристаллов с охлаждаемой поверхностью.
Обычно с увеличением продолжительности процесса десубли
мации адгезия кристалл ической фазы к охлаждаемым поверх
ностям растет. Это следует учитывать при выборе режимов
работы десублиматоров.
С увеличением концентрации конденсирующегося компо
нента в исходной парогазовой смеси обычно снижается пороз
ностъ слоя и увеличивается его адгезия к охлаждаемым поверх
ностям. В ряде случаев при десублимации чистых паров может
происходить сразу обр азование монолитного кристалли ческого
слоя .
Образование пористого слоя и рост его толщины, есте
ственно, снижают интенсивность теплообмена между паровой
фазой и охлаждаемыми поверхностями. Поэтому при поверх
ностной десублимации величины коэффициентов теплоотдачи
3 - 1 0 Вт/(м2 ·К).
невелики
-

1 443

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

18.3. ВОЗМОЖН ЫЕ ВАРИАНТЫ
ОРГАНИЗАЦИИ ПРОЦЕССОВ
СУБЛИ МА ЦИИ И ДЕСУБЛИМАЦИ И

Существует значительное число вариантов (способов, мето
дов) проведения процессов сублимации и десублимации ве
ществ. Их используют для решения различных технологичесЮ1х
задач. Рассмотрим кратко некоторые из них.
В зависимости от состава исходного вещества и технологи
чесЮIХ параметров (температуры и давления) при сублимации
может происходить полное или частичное испарение вещества.
Целью полной сублимации (испарения) является получение чис
тых паров испаряемого вещества или парогазовой смеси (ПГС).
Полученные таЮ1м образом пары или П ГС в дальнейшем моrуг
быть использованы для нанесения различных покрытий на
твердые тела, реагентной обработЮ1 различн ых материалов,
дезинсекции, проведения химических реакций и т.д .
Полное испарение обычно имеет место при переработке ин
дивидуальных (чистых) веществ. Оно может осуществляться без
использования или с использованием инертного газа-носителя.
В первом варианте (рис.18.2,а) исходное твердое вещество /
полностью испаряется в сублиматоре С. Для этого в последнем,
естественно, должно быrъ подведено необходимое количество
теплоты для наrрева вещества до температуры испарения и ком
пенсации теплоты фазового перехода "твердая фаза-пар". В целях
предотвращения проскока мелких частиц, уносимых потоком пара
//, после сублиматора обычно устанавливаюr ловушку Л .
Во втором варианте (рис. 1 8 .2,6) в сублиматор может пода
ваться холодный или нагретый инертный газ-носитель ///. В
результате получают смесь паров вещества с инертным газом.
Ч астичная (фракцион11ая) сублимация имеет место при пере
работке многокомпонентных твердых смесей. Целью фракци
онной сублимации может быть выделение ценных или вредных
компонентов из исходной смеси, глубокая очистка вещества от
примесей. Данный процесс широко используется также для
обезвоживания различных продуктов. В технической литерату
ре такой процесс обычн о обозначается термином сублимацион
ная сушка и будет достаточно подробно рассмотрен ниже .
Фракционная сублимация также может быть осуществлена
без использования (рис. 1 8 .2,в) и с использованием (рис. 1 8 .2 , г)
инертного газа-носителя. Последний процесс в литературе
иногда называют газовой экстракцией. Состав получаемых при
частичной сублимации твердой VI и паровой V фракций зави
сит от физико-химических свойств и состава исходной смеси ,
технологичесЮIХ параметров про цесса, расхода газа-носителя и
других факторов.
1 444

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

б

а

г

в

а и 11 - полная и часrичная сублимация без rаза-носиrеля, б и г - полная и часrичная
сублимация с rазом-носиrелем;
/ - исходное вещество, /I - чисrые пары, //I - rаз-носиrель, IV - пароrазовая смесь, V
паровая фрахция, VI - твердый осrатох

Рис. 18.2. Принципиальные схемы процессов сублимации:

-

При десублимации чистых паров 1 может происходить пракrи
чески полная твердофазная конденсация вещества с получением
твердого вещества 11
десублимата (рис. 18.3,а). Некоторые
потери возможны лишь за счет проскока мельчайших частиц
твердой фазы через ловушку Л и потерь с парами, отводимыми
при вакуумировании десублиматора Д с помощью вакуум
насоса В Н . При конденсации чистых паров пуrем их непос
редственного смешения с газообразным или испаряющимся
-

в
а и б - десублимация без использования и с использованием rаза-носиrеля, 11 - десуб
лимация с рециркуляцией rаза-носнтеля;
/ - исходные пары или пrс, /Т - десублимат, /Il - отводимая пароrазовая смесь, /V 
rаз-носиrель; V, VI - рециркулирующий и отводимый потоJСИ rаза-носиrеля

Рис. 18.3. Принципиальные схемы процессов десублимации :

1 445

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

а

б

Рис. 18. 4. Принципиальные схемы сублимационно-десублимационной перекри
сталли зации без использования (а) и с использованием (6) газа-носителя:

/ - исходное твердое вещесrво, II - пар или ПГС, III - десублимат, IV - отходнщие
пар или ПГС, V - газ-носитель

хладоаrентом 1V (рис. 1 8 .3 , 6) некоторое количество целевого
компонента будет теряться с отходящей парогазовой смесью
111. Это количество зависит от парциального давления паров
конденсирующегося вещества в отходящей П ГС.
Десублимацию с использованием газообразного хладоаrента
можно осуществлять с частичной или полной рециркуляцией
хладоаrента (рис . 1 8 .3 , в) . При этом отработанный хладоаrент V
охлаждают в теплообменнике Т и снова подают на стадию де
сублимации.
При десублимации многокомпонентных П ГС обычно прово
дится лишь частичная твердофазная конденсация . Здесь из ис
ходной П ГС выделяют один или несколько компонентов. Та
кой процесс часто называют фракционной десублимацией.
Простую и фракцион ную десублимацию широко используют
для выделения компоне нтов из реакционных и других парога
зовых смесей, получения мелкодисперсных порошков, нанесе
ния различных покрытий, выращивания монокристаллов и т.д .
Процессы сублимации и десублимации часто осуществляют
ся в комбинации друг с другом (рис . 1 8 .4) .
На рис. 1 8 .4,а показана одна из схем, часто используемая
для перекристалл изации веществ с целью получения твердых
продуктов с заданными свойствами (например, в виде продукrа
с определенным дисперсным составом, кристалло в определен
ной формы или в монокристаллическом виде). В данном слу
чае перекристаллизация проводится под вакуумо м без использо
вания газа-носителя. При этом исходное твердое вещество 1 на
стадии сублимации С полностью испаряется. Полученные при
этом пары 11 поступают на стадию десублимации Д, где они
практически полностью десублимируются с образованием кри
сталл о в 111 нужных формы и качества. Вакуумирование осу
ществляется с помощью вакуум - насоса В Н .
Н а рис . 1 8 .4,б приведена принципиальная схема аналогично
го процесса перекристаллизации с использованием инертного
газа-носителя. Данный процесс можно осуществлять при атмо
сферном давлении.
1 446

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

б

а

Рис. 18. 5. Принципиальная схема разделения смесей пугем сочетания процессов
сублимации и десублимации без использования (а) и с использованием (б) rаза
носителя:

1
исходное вещество, 11
пар или ПГС, 111
отходящая ПГС, VJ rаз-иосит�ль
-

-

-

-

-

твердый осrатох, lV

-

десублимат, V

Сочетание процессов сублимации и десублимации широко
используется с целью разделения технолоrических смесей на
фракции, обогащенные тем или иным компонентом (рис. 1 8 .5),
для очистки веществ от примесей, а также для обезвоживания
различных продуюов. При этом число различных вариантов
такоrо сочетания весьма велико . На рис. 1 8 . 5 , а показана схема
разделения, в которой на стадии сублимации производится
частичное испарение вещества, а на стадии десублимации практически полная конденсация паров. При этом процессы
сублимации и десублимации проводятся под вакуумом. Данная
схема широко применяется при проведении процесса сублима
ционной сушки.
Схема, в которой процесс полноrо испарения сочетается с
фракционной десублим:щией , показана на рис . 1 8 .5 , б. Здесь
разделение осуществляется с использованием газа-носителя .
Эта схема часто приме няется при разделении и очистке ве
ществ. В единой технолоrической схеме возможно сочетание
процессов фракционной сублимации и фракционной десубли
мации.
Иногда процесс полной или частичной десублимации соче
тают с процессом испарения жидкой фазы. Здесь стадия испа
рения жидкости выступает в качестве генератора паров для по
следующей стадии десублимации. Такой процесс в литературе
часто называют псевдосублимацней. Ero также широко исполь
зуют для получения продуюов с заданными свойствами и для
разделения веществ. При этом испарение можно производить,
нагревая жидкости при атмосферном давлении или под ваку
умом. Высокоплавкие вещества предварительно расплавляют.
Такой процесс существенно упрощает аппаратурное оформле
ние и интенсифицирует стадию испарения.
Процессы сублимации и десублимации часто сочетаюrся с хи
мическими процессами. При этом особенно часто используются
так называемые "газотранспортные" реакции. Эrи комбинирован
ные процессы будуr рассмотрены ниже (см. разд. 24.3. 1).
1 447

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

1 8 .4. АППАРАТУРНОЕ ОФОРМЛЕНИЕ
СУБЛИ МАЦИОННЫХ ПРОЦЕССОВ

Для проведения процессов сублимации и десублимации ис
пользуется разнообразное оборудование : испарители твердой
фазы (сублиматоры); конденсаторы паv ов (десублиматоры);
вакуум-насосы, фильтры, ловушки и др . Конструкции этого
оборудования зависят прежде всего от масштаба производства,
способов проведения процессов, состава и физико-химических
свойств веществ, требований к конечным продуктам перера
ботки .
Как уже указывалось, процессы сублимации и десублимации
могут проводиться с использованием и без использования
инертного газа-носителя .
Процесс сублимации веществ без использования газа-носиrеля
чаще всего проводят в аппаратах, снабженных различными
теплообменными устройствами : рубашками, змеевиками, обо
греваемыми полками, дисками и т.п. Для ускорения (интен 
сификации) процесса испарения исходный материал обычно
загружается в аппарат в раздробленном виде. Если производит
ся частичное испарение материала, то в сублиматоре необхо
димо предусмотреть устройство для выгрузки твердого остатка.
Для большинства веществ процесс сублимации проводится под
вакуум о м, что сушестве нно затрудняет операции загрузки ис
ходного вещества и выгрузки твердого остатка из аппарата.
Поэтому в большинстве случаев процесс сублимации ведут в
периодическом режиме.
В простейшем случае сублимацию можно осушествить в
обычном емкостном аппарате, снабженном греющей рубашкой.
После загрузки исходного материала аппарат вакуум ируют и
при нагреве производится частичное или полное испарение
вещества. Образующиеся пары непрерывно отводятся из аппа
рата. С целью интенсификации теплообмена твердая фаза
(материал) в аппарате обычно перемешивается с помощью ме
шалок, скребков или специальных ворошителей. После отгон
ки легколетучих компонентов ва куум сбрасывают, и . если оста
ется твердый остаток, е го выгружают. Далее процесс повторя
ется.
Для проведения процесса сублимации часто используют
удлиненные горизонтальные аппараты, снабженные греющими
рубашками . Перемешивание твердого материала в таких аппа
ратах обеспечивается ш неками или различными скребками . В
прин ципе такие аппараты могут работать и в непрерывном
• Более подробно об аппаратурном оформлении рассматриваемых процессов
см. ( 1 , 4, 5 ) .
1 448

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

режиме , если их снабдить специальными шлюзовыми камерами
(устройствами) для непрерывной или порционной загрузки
исходноrо материала и выгрузки твердоrо остатка.
Часто также процесс сублимации проводят в вакуумируемых
камерах, снабженных этажерками с обогреваемыми полками;
на них устанавливают противни, лотки, флаконы и другие со
суды с исходным материалом. Именно такие камеры широко
применяются при сублимационной сушке различных продуктов
(см . разд. 1 8 . 5).
Процессы сублимации осушествляют нередко в вертикаль
Н ЬIХ аппаратах, секционированных обогреваемыми полыми
переrородками. По конструкции эти аппараты напоминают
полочные (камерные) сушилки (см . разд. 1 5 . 1 . 1) и дисковые
кристалл изаторы (см . разд. 1 6 . 5 .2). Обогреваемые полки имеют
сегментные переточные отверстия. Перемешивание твердоrо
материала осушествляется скребками, укрепленными на цент
ральном валу. Исходный материал подается сверху аппарата и в
процессе сублимации пересыпается с полюt на полку. Твердый
остаток выгружается снизу аппарата.
При сублимации высокоплав ЮIХ материалов часто исполь
зуют индукционный или радиационный нагрев.
Процесс сублимации с использованием инертного rаза
носиrеля осушествляют двумя способами: подводя необходимое
тепло через теплопередающие поверхности и путем непосред
ственноrо контакта твердоrо материала с предварительно на
гретым газом. В последнем случае сушественно интенсифици
руется тепломассообмен в системе и в значительной мере
упрощается аппаратурное оформление процесса.
Сублимацию с использованием нагретоrо газа-носителя
можно проводить в аппарате с псевдоожиженным слоем твердоrо
материала. Таюtе аппараты особенно удобны для проведения
полноrо испарения вещества. Здесь исходный материал подает
ся шнеком в псевдоожиженный слой, псевдоожижение произ
водится газом-носителем. При необходимости в псевдоожи
женном слое можно разместить дополнительные теплообмен
ные элементы. Уносимые мелюtе частицы материала улавли
ваются циклонами и возвращаются в псевдоожиженный слой.
Сублимацию вещества можно проводить при фильтрации
нагретоrо газа - носителя через неподвижный или движущийся
(опускающийся) слой твердоrо материала. Наконец, испарение
мелкодисперсных материалов можно осушествлять при их
пневмотранспорте в потоке нагретоrо газа-носителя.
Весьма часто процесс десублимации проводят в сочетании с
обычным испарением жидкости (см. разд. 1 8 .3), т.е. выше
тройной точки (процесс псевдосублимации). Если такой про
цесс осушествляется без газа - носителя, то стадию испарения
1 449

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ведуr в емкостных аппаратах, снабженных греющей рубашкой,
или в трубчатых теплообменниках - нагревая вещество до его
Юtпения. Испарение высокоплавЮtх веществ обычно осу
ществляют в тиглях, помещенных в муфельные печи. TaIOte
вещества часто испаряют также с использованием индукцион
ного нагрева.
Жидкости можно испарять путем барботажа нагретого rаза
носителя через слой жидкости . При этом происходит насыще
ние газа-носителя парами испаряемого вещества.
Аппаратурное оформление процесса десублимации отличает
ся еще большим разнообразием конструкций. Все десублима
торы (твердофазные конденсаторы) по принципу их действия
разделяют на две групп ы : объемные и поверхностные. Заметим,
что такое деление часто носит условный характер.
В объемных десублиматорах образование и рост кристалл о в
происходит в объеме пересыщенного пара. При этом выде
ляющаяся теплота фазового превращения рассеивается (пере
дается) в газообразную фазу.
В поверхностных десублиматорах образование и рост кри
сталло в происходиr на охлажцаемых поверхностях, где достигается
максимальное пересыщение. Основная масса паровой или парога
зовой фазы может находиться в ненасыщенном состоянии.
Ранее для десублимации многих веществ (нафталина, антра
хинона, салициловой кислоты, хлоридов алюминия и железа и
др .) широко использовали емкостные (ящичные, камерные)
десублиматоры. Их рабочие объемы нередко достигали несколь
ЮtХ десятков кубичесЮ1х метров (на некоторых производствах
они используются и в настоящее время) . TaIOfe десублиматоры
обычно представляют собой полые сосуды, охлаждение парога
зовой смеси в которых осуществляется за счет внешнего тепло
обмена с окружающей средой . При этом образование кристал
лов может происходить как в объеме паровой фазы, так и на
стенках аппарата. Парогазовая смесь в таЮtе аппараты подает
ся из внешнего испарителя или же испаритель (сублиматор)
располагается в самом десублиматоре.
Процесс охлаждения пара или парогазовой смеси в емкост
ных десублиматорах происходит довольно медленно, поэтому
десублимация в таЮtх аппаратах осуществляется при незначи
тельном пересыщении. В результате такого процесса получают
ся относительно крупные кристалл ы , которые обычно имеют
слабое сцепление (адrе.зию) с твердыми поверхностями: при
постуЮtвании по стенкам аппарата кристаллы, как правило,
легко отделяются и осаждаются на днище аппарата, откуда они
выгружаются через люю1 или течЮf. Для снятия кристаллов со
стенок в емкостных десублиматорах иногда размещают различ
ные вибрирующие механизмы .
1 450

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

1
сепаратор, 2
камера роста
кристаллов, З
цешральная труба, 4
камера смешения, 5 транспортер:
1 исходная 11ароrазовая смесь, 1I
rазообразИЬIЙ хладоаrеш, lll
десубли
иат , lV
отработанная пароrазовая
смесь

Рис. 18. 6. Объемный десублиматор:
-

-

-

-

-

-

-

-

-

Емкостные десублимато
ры просты в изготовлении,
А -А
не требУJ<УГ квалифициро
ванного обслуживания . Од
нако их производительность
крайне мала, а эксплуата
ция связана с большими
затратами ручного труда. В
силу этого в настоящее
время такие десублиматоры
А
уступают место более со
вершенным аппаратам .
Попытки интенсифици
ровать процесс десублима
ции в емкостных аппаратах
путем использования ох
лаждающих рубашек приво
дят обычно к образован ию достаточно плотных слоев десубли
мата, обладающих значительной адгезией к охлаждаемым по
верхностям. Это существенно затрудняет очистку поверхностей
от кристалло в десублимата.
Объемные десублиматоры сравнительно широко использУJ<УГ
при десублимации паров пуrем их непосредственного смеше
ния с газообразными хладоаrентами, например с воздухом .
Однако при такой десублимации часто образуются мелкие кри
сталл ы , что затрудняет их отделение от отработанной парогазо
вой смеси. Контактную десублимацию целесообразно приме
нять для выделения веществ из концентрированных парогазо
вых смесей при рециркуляции хладоаrента (газа-носителя). В
этом случае уносимые мелкие кристаллы возвращаются в зону
роста кристалло в.
На рис. 1 8 .6 показана одна из конструкций объемного де
сублиматора, в котором камера смешения 4 потоков исходной
парогазовой смеси 1 и газообразного хладоаrента 11 выполнена
в виде двух соосных циклонов. В результате смешения этих
потоков создается пересыщение, что приводит к образованию
кристалло в в объеме полученной парогазовой смеси. Восходя
щим парогазовым потоком кристалл ы выносятся в камеру 2,
где вследствие увеличения диаметра аппарата снижается ско-

w

1 45 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

рость парогазового потока. В этой камере кристалл ы задержи
ваются и растуr, пока не достиrают определенного размера
(скорость их стесненного витания wc) , зависящего от скорости
восходящего потока w. При Wc > w кристалл ы падают вниз,
через центральную трубу З попадают в шнековый транспортер
5 и выводятся из аппарата. Для снижения уноса мелких кри
сталлов десублиматор сн абжен сепарационной камерой J.
Десублимацию с непосредственным контактом паров с газо
образным хладоаrентом можно также проводить, смешивая
потоки в трубе Вентури с последующей подачей парогазовой
смеси в сепарационную камеру.
В качестве эффективного хладоаrента при объемной десуб
лимации можно использовать испаряющиеся жидкости, на
пример воду. Такой хладоаrент впрыскивают с помощью фор
сунки в поток пара или парогазовой смеси. При контакте тон
кодисперmрованных капель жидкости с нагретой парогазовой
смесью происходит испарение жидкости, сопровождающееся
интенсивным охлаждением и пересыщением парогазовой сме
си. По конструкции такие десублиматоры напоминают распы
лительные сушилки. Расход жидкого хладоаrента легко опреде
ляется из уравнения теплового баланса аппарата.
К объемной десублимации можно отнести также процесс
выделен ия веществ из парогазовых смесей путем их непосред
ственного контакта с жидким хладоагентом. При такой десуб
лимации образуется суспензия из кристалло в и отработанного
жидкого хладоагента; дшtее ее подают на фильтрацию. Отде
ленный хладоагент про пускают через холодильник и возвра
щают на стадию десубли мации. Естественно, что такой процесс
применим только для дссублимации веществ, нерастворимых в
выбранном хладоагенте. Обычно этот процесс осуществляют в
полых или секционированных колонных аппаратах. Его иногда
используют в конденсаторах сублимационных сушилок.
Объемные десублиматоры с контактным охлажден ием по
своей конструкции относительно просты. Однако их общим
недостатком является необходимость установки улавливающих
устройств (фильтров, ловушек, циклонов, скрубберов и т.п.).
Пересыщения парогазовой смеси можно достичь при ее
адиабатическом расширении. Такое расширение можно осу
ществить в сопле Лаваля (см. разд. 2.6.3). При этом скорость
истечения может достиrать сверхзвуковых значений . В резуль
тате такого расширения снижаются как температура, так и дав
ление, и парогазовая смесь переходит в пересыщенное состоя
ние. Недостатком данного процесса является образование мел
ких кристаллов.
В настоящее время в промышленности большее распростра
нение получили десублиматоры поверхностного типа с различ1 452

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

1 - секции десублимашut , 2 - охлаждаюшие
рубашхи, .1 - бункер, 4 - вал, 5 - скребки;
/ - исходная парогазовая смесь, II - отра
ботанная ПГС, JJ/ - десублимат
Рис. 18. 7.

Схема скребковою десублиматора:

1 - корпус аIПJарата, 2 - охлаждаемый ба
рабан, 3 - нож;
/ - исходная ПГС, II - отработанная
ПГС, J// -десублимат

Рис. 18.8.

Схема барабанною десублиматора:

/

ными теплообменными элементами. При поверхностной десуб
лимации необходимо периодически или непрерывно произво
дить очистку охлаждаемых поверхн остей от образующихся кри
сталло в. Это делается в основном двумя методами : механиче
ским съемом десублимата или путем его расплавления.
Механический съем производят с использованием различных
устройств: ножей, скребков, шнеков, цепей, щеток и др.
Одна из конструкций скребкового десублиматора показана на
рис . 1 8 .7 . Он имеет две вертикальные секции 1, снабженные
охлаждающими рубашками 2. Секции расположены над общим
бункером готового продукта 3. Внугри охлаждающих секций
размещены валы 4, на которых укреплены скребки 5 для съема
десублимата с охлаждаемых поверхностей. Исходная парогазо
вая смесь 1 подается в одну секцию, а отработанная парогазо
вая смесь II выводится из другой секции.

Такие аппараты используют, например, для десублимации паров хлорида
алюминия . При этом внуrренний диаметр секций равен 0, 5
а их высота 6 м.
Удельн ая
производительность составляет примерно 15

м,
кг/(м2·ч).

-

Процесс десублимации удобно проводить на наружной по
верхности вращающихся, охлаждаемых изнугри барабанов.
Одна из конструкций барабанного десублиматора показана на
рис . 1 8 . 8 . Барабан 2 может охлаждаться холодной жидкостью,
не изменяющей своего агрегатного состояния, или испаряю
щимся хладоагентом, например аммиаком. Образующийся де1 453

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

сублимат снимается с барабана неподвижным ножом 3. Ско
рость вращения барабана составляет 1 - 8 об/мин.
Для удаления десублимата с охлаждаемых поверхностей
можно использовать подвижные пластины (решетки) с от
верстиями, через которые проходят трубчатые охлаждающие
элементы . Пластины периодически приводят в возвратно
поступательное движение, благодаря чему и происходит съем
кристаллов с охлаждающих элементов.
Достоинством десублиматоров с механическим удалением
кристаллов с охлаждающих поверхностей является поддержа
ние в процессе десубли м ации практически постоянных условий
теплообмена. Недостатки : относительно небольшая удельная
теплопередающая поверхность, плохое использование рабочего
объема аппарата. Кроме того , при значительной адгезии кри
сталлов к охлаждаемой поверхности резко возрастают затраты
энерmи на удаление десублимата с охлаждаемых элементов.
По указанным причинам в настоящее время в промышлен 
ности преимущественно используются поверхностные десубли
маторы с оплавлением десублимата, снабженные трубчатыми
охлаждающими элементами. При этом процесс десублимации
может производиться внутри охлаждаемых горизонтальных или
вертикальных труб либо на их внешней поверхности.
Десублиматоры с конденсацией паров на внутренн их поверх
ностях труб по своей конструкции практически ничем не от
личаются от обычных кожухотрубных теплообменников. В этом
случае парогазовая смесь подается в трубное пространство, а
хладоагент - в межтрубное . Недостатком таких десублимато
ров является неравномерное (по длине труб) отложение десуб
лимата. Скорость роста слоя десублимата обычно на входных
участках труб значительно выше, чем на концевых. Это связано
с падением концентрации конденсирующихся компонентов в
парогазовой смеси по мере ее движения в трубах. Неравномер
ное выпадение десублимата снижает общую эффективность
процесса и часто приводит к зарастанию входн ых участков
труб. Для улучшения степени использования охлаждающих
поверхностей иногда применяют ступенчатое или постепенное
изменение уровня кипящего хладоагента в межтрубном про
странстве. Такой прие м , в частности, используется в верти
кальных трубчатых конденсаторах сублимационных сушилок.
При десублимации веществ на наружных поверхностях труб
легче избежать зарастания поперечного сечения аппарата де
сублиматом. Поэтому десублиматоры с наружным наморажива
нием кристалло в получили более широкое распространение.
На рис . 1 8 .9 показана схема одного из десублиматоров с
конденсацией паров на горизонтальных трубчатых элементах. В
призматическом ко р пусе аппарата 1 размещены секции трубча1 454

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 18.9. ПоверхноС111 ый десублиматор с
трубчатыми охлаждающими элементами:

1
корпус, 2
охлаждаемые орсбрсННЬiс
трубы ;
1
исходная ПГС, II
<>тработанная
ПГС , III десублимат
-

-

-

-

-

тых охлаждаемых элементов 2.
Для повышения интенсивности
(пропус кн ой способности) теп
лообмена трубы снабжены на
ружными поперечными ребра
ми . После стадии десублимации
в трубчатые элементы подаюr нагретый теплоноситель и про
изводят расплавление десублимата. Образующийся плав выво
дят из аппарата и подаюr на стадию отверждения, которую
обычно осуществляюг на вальцевых кристаллизаторах. Такие ап
параты urnpoкo исполъзуюrся для десублимации фrалевоrо и ма
леинового ангидридов из реакционных парогазовых смесей. Сте
пень измечения целевых продукгов из ПГС достигает 98 - 99 % .
В десублиматорах с nаружным намораживанием также может
наблюдаться неравномерное распределение твердой фазы по
длине труб и месту их расположения в рабочем пространстве
десублиматора. Такая неравномерность особенно проявляется в
аппаратах большой производительности со значительным чис
лом труб. Поэтому при конструировании таЮIХ десублиматоров
ставятся две задачи : максимальное использование рабочего
объема аппарата и обеспечение по возможности равномерного
роста слоя десублимата. Последняя задача обычно решается
пуrем определенного расположения труб в пространстве десуб
лиматора и установкой различных секционирующих перегоро
док. Иногда равномерность роста слоя десублимата достигается
постепенным уменьшением шага между трубами по ходу паро
газовой смеси .
Заметим, что при рас плавлении десублимата перенос тепло
ты в ero слое происходит в основном за счет теплопровод
ности. Но десублимат обычно имеет пористую структуру, так
что эффективность теплопереноса мала, и для полного плавле
ния десублимата требуется значительное время. Поэтому для
сокращения продолжительности стадии регенерации теплооб
менных поверхностей предусматриваюrся различные меры.
Так, для ускорения стадии регенерации часто применяют
штыковые теплообменные элементы. При нагреве происходит
частичное подплавление поверхностных слоев десублимата, он
легко соскальзывает с таких элементов и быстро расплавляется
в обогреваемом бункере . Иногда после частичного подплавле
ния теплообменные элементы подвергают вибрационному воз
действию, способствующему очистке теплообменных поверхно
стей от оплавившегося десублимата.
1 455

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Имеются конструкции десублиматоров с вертикальными
В сублимационных сушилках часто
конденсаторы располагают непосредственно в сублимационной
камере. Такие аппараты отличаются малыми гидравлическими
сопротивлен иями движе нию парогазовых смесей.

пластинчатыми элементами.

В криоrенных установках возникает задача вьшеления воды и диоксида угле
рода из воздуха перед его сжатием (см. разд. 2 1 .3.6 и 2 1 . 3 .7) . Эта задача часто
решается
с
испаrо.зованием
пластинчатых
оребренных
десублиматоров
(рекуператоров). Стадия вымораживания в таких аппаратах сосrавляеr порJЩК.а 20-30
мин. Очисrку охлаждающих поверхносrей проводят пуrем возгонки lфисталло в лм.а и
диоксида yrnepoдa при продувке десублиматоров reWIЫМ во::щухом.
Для этой же цели в криогенных установках часто используют насадочные
реrенераторы. Первоначально насадку охлаждают пуrем продувки реrенератора
холодным отходящим газом. Далее в реrенератор подают воЗдух. При этом влага
и диоксид углерода вымораживаются на поверхности охлажденной насадки.
Десублимат удаляют с насадки возгонкой при продувке отходящими газами.

Поверхностную десублимацию можно также проводить в
аппаратах с шаровой насадкой, перемещающейся во вра
щающемся барабане, снабженном охлаждающей рубашкой.
Такие аппараты напоминают барабанные сушилки. Внутри
барабана засыпана шаровая насадка, на поверхности которой
идет образование десублимата. При перекатывании шаров про
исходит очистка их поверхности . Десублимат выносится из
аппарата потоком отработанной парогазовой смеси. Такой
процесс можно также проводить на гранулированных частицах
конденсирующегося вещества, выполняющих роль подвижной
насадки. В этом случае на выходе из аппарата производится
отбор дисперсной фазы, после сортировки которой часть твер
дого продукта возвращается в десублиматор в виде ретурноrо
потока.
Высокопроизводительными являются десублиматоры с псев
доожиженным слоем инертной насадки или твердых дисперсных
частиц десублимируемоrо вещества. В первом случае стараются
подобрать такой режим, чтобы десублимат удалял ся с поверх
ности инертной насадю1 за счет его истирания и выносился с
парогазовой смесью, во втором - десублимацию проводят на
поверхности частиц самого десублимируемоrо продукта. Такие
десублиматоры могут работать как с внешним, так и с внут
ренним ретуром . Охлаждение парогазовой смеси в псевдоожи
женном слое может быть осуществлено тремя способами: с
использованием охлаждающих поверхностей, путем непосред
ственного смешения с холодным инертным газом и при
впрыскивании в слой испаряющегося хладоаrента. В последнем
случае достигается наиболее высокая удельная производитель
ность аппаратов.
Недостатком всех десублиматоров с псевдоожиженным
слоем является унос мелких частиц десублимата отработанной
парогазовой смесью.
1 456

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 18. 10. Фракционирующий субли

1 и 2 - секции сублимации и лесубли
мации, 3 - бункер, 4 - nmex;
1 - исходное всщесrво, 11 - твердый
осrатох, 111 - очищенный десублимат

матор:

Рис. 18. 1 1. Аппарат

для

но-десублимационной
ществ :

сублимацион
очистки ве

1 - ампула; 2 и З - сеJЩии сублима
и десублимации;
1 - исходное вещесrво, 11 - пары, 111
очищенный десублимат

ции
-

2

1

з

ш

При очистке и фракционировании веществ, а также при
сублимационной сушке часто стадии сублимации и десублима
ции проводят в одном аппарате. Одна из конструкций фракци
онного сублиматора показана на рис . 18. 10. Аппарат имеет сек
ции сублимации 1 и десублимации 2. Исходное вещество / за
гружается в бункер З и далее поступает в секцию сублимации,
где оно нагревается до заданной температуры. Транспортиров
ка твердого вещества осуществляется шнеком 4. При нагреве
происходит частичная возгонка вещества. Твердый остаток //
выводится из аппарата, а пары легколетучих компонентов по
ступают в секцию десублимации. Там пары десублимируются
на охлаждаемых стенках. Шнек снимает десублимат со стенок
и выгружает из аппарата в ВИде фракции ///.
Очистку небольших количеств вещества часто проводят в
удлиненных запаянных ампулах (рис. 1 8. 1 1 ) . Исходное веще
ство / загружают в один из концов ампулы. Далее ампулу
обычно вакуум ируют и помещают одним концом в трубчатый
нагреватель 2, а другим - в охлаждающую секцию З. При на
греве часть вещества возгоняется, образующиеся пары чистого
вещества поступают в зону охлаждения и там десублимируются.
Такой процесс часто называют сублимаи,ионно-десублимаи,ионной
перегонкой.
1 457

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

18.5. СУБЛИМАЦИОННАЯ СУШКА

Сублимационная сушка является типичным комбинирован
ным сублимационно-десублимационным процессом (кратко
она затронута в разд . 1 5 . 1 .2) . Данный метод сушюt широко
используется в химической, пи щевой, фармацевтической и
других отраслях промышленности. Сублимационная сушка по
сравнению с обычной имеет ряд достоинств* :
- возможность проведения процесса обезвоживания при
низких температурах, что особенно важн о при сушке термола
бильных веществ;
- практическое отсутствие изменения компонентного со
става и структуры высушиваемого вещества, что особенно важ
но для пищевых продуктов;
- возможность достижения весьма низкой конечной влаж
ности продукта, так как процесс осуществляется при достаточ
но глубоком вакууме;
использование дешевого низкопотенциального тепла
(например, теплой воды) .
Однако данный процесс имеет и свои недостатюt, среди ко
торых следует отметить более высокую по сравнению с обыч
ной сушкой энергоемкость (на замораживание продуктов и
создание вакуума) и более сложное аппаратурное оформление.
Сублимационная сушка осуществляется следующим обра
зом . Исходный влажный продукт первоначально охлаждаl<УГ до
полного замораживания влаги. Далее под вакуумо м производят
испарение льда (МJmуя жццкую фазу). Эrа стадия протекает при
параметрах ниже тройной точки замораживаемого раствора.
Сублимацион ному высушиванию МОJУГ подвергаться влаж
ные дисперсные материалы, жидюtе растворы, эмульсии, сус
пензии, растительное и животное сырье . В большинстве этих
продуктов влага находится в виде раствора. Чтобы эти раство
ры полностью заморозить, их необходимо охладить ниже тем
пературы солидуса fc (см. разд. 1 6.2) . Для эвтектикообразующих
смесей охлаждение проводят ниже температуры кристаллиза
ции эвтектию1 tE = fc. Температуру полной кристаллизации
раствора можно определить по диаграмме равновесия фаз "вода
- растворенное ве щество". Для разбавленных недиссоциирую
щих растворов с мольной концентрацией растворенного ве
щества х температуру их полной кристаллизации fc можно
определить по полуэмпирической формуле
( 1 8 .9)
tc = tв - kx ,
где ta - температура кристалл изации (плавления) чистого растворителя (воды);
k
криоскопическая константа (значения констант k для многих веществ при
ведены в специальной литературе • • ) .
-

• Подробнее с м ( 4 , 5 ] .

* • См. , нап р име р , 1 4 1 .
.

1 458

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Скорость охлаждени.н исходного продукта на стадии замо
раживания должна быть такой, чтобы не происходило разру
шения структуры высушиваемого продукта образующимися
кристалла ми льда. Разрушение часто наблюдается при медлен
ном замораживании, когда в затвердевшем продукте происхо
дит образование крупных кристалло в льда. Режим заморажива
ния особенно важен при сублимационной сушке пищевых про
дуктов растительного или животного происхождения, а также
при сушке живых микроорганизмов (например , дрожжевых
клеток) . Обычно скорость охлаждения продуктов на стадии их
замораживан ия подбирают опытным путем. Она зависит от
состава прод укта, его теплофизических свойств, способа
охлаждения и других факторов.
Замораживание продуктов осуществляют несколькими спо
собами. Наиболее часто его проводят путем отвода теплоты
через охлаждаемые стенки. Иногда замораживание производят
путем непосредственного контакта продукта с газообразным
хладоагентом, например, распыляя жидкий продукт в поток
холодного воздуха или другого инертного газа (азота, диоксида
углерода и др.). Продукты можно замораживать также в самой
камере сушки при вакуум ировании. В последнем случае в ре
зультате понижения давления происходит интенсивное практи
чески адиабатное испарение влаги. При этом за счет отвода
теплоты испарения наблюдается самоохлаждение продукта вплоть до его полного замораживания . При осуществлении
такого процесса обычно удаляется до 1 5-20% влаги.
Стадия испарения (сублимации) влаги, как указано выше,
реализуется ниже тройной точки на диаграмме равновесия
"вода-растворенное вещество". Параметры данной точки
(температура и давление) зависят от свойств растворителя и
растворенного вещества, а также от состава раствора.
Для чистой воды Э111 параметры составляют: р = 6 1 0 Па и 1 = 0,0076 °с. Суб

лимационную сушку обычно проводят при остаточном давлении 1 0- 150 Па и
температуре минус 20-30 о с.

На стадии испарения теплоту, затрачиваемую на испарение
(сублимацию) льда, к продукту подводят путем теплопровод
ности или от источника инфракрасного излучения. В разд. 1 8 . 1
отмечалось, что удельная теплота сублимации веществ Гсуб
примерно равна сумме их удельных теплот плавления r� и
испарения Гисп · Для воды величина Гсуб достигает - З МДж;к.г,
а Гпл составляет - 0, 34 МДж/кг.
Обычно с понижением мажности материала интенсивность
парообразования падает; соответственно этому следует снижать
количество подводимой теплотъ1. Если же этого не делать, то из
ЛJШJек теплоты может привести к нагреву материала - вплоть до
пламения льда, 'П'О нарушит режим сублимационной сушки.
1 459

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Для поддержания вакуума в процессе сублимационной суш
ки необходимо обеспечить непрерывный отвод паров влаги из
сушильной камеры (сублиматора) . Это можно сделать несколь
кими способами . В принципе поддерживать необходимый ва
куум можно , используя прямой отсос образующихся паров из
сушильной камеры с помощью пароструйных, эжекторных или
других вакуум н ых насосов. Однако это экономически невыгод
но: такой отсос требует значительных энергетических затрат.
Поддерживать вакуум в сушильной камере можно также пугем
адсорбционного поглощения паров воды цеолитами или же
другими адсорбентами . Данный прием также не нашел широ
кого промышленного применения (из-за дороговизны адсор
бентов и необходимости их регенерации).
Более радикальным является удаление паров влаги пугем их
конденсации. По сути дела в данном процессе, как и в процес
се вакуумного выпаривания (см . разд.9.6.3), конденсатор играет
роль насоса для откачки пара. Величина создаваемого разреже
н ия определяется температурой хладоагента, применяемого для
конденсации пара.
Конденсатор присоединяется к системе перед вакуум 
насосом . При этом большая часть откачиваемого пара в кон
денсаторе переходит в жидкое или твердое состояние,
оставшаяся несконденсированная парогазовая смесь удаляется
вакуум-насосом. Давление пара в конденсаторе обычно близко
к давлению насыщенного водяного пара при температуре
охлаждающих поверхностей конденсатора.
Процесс сублимационной сушки осуществляется при доста
точно высоком вакуум е (низком остаточном давлении), поэто
му в конденсаторе обычно происходит твердофазная конденса
ция (десублимация) паров воды. Данный процесс можно про
водить с использованием не только поверхностных, но и кон 
тактных конденсаторов.
При поверхностной конденса ции обычно используют трубча
тые десублиматоры периодического действия. которые охлаж
даются хладоагентом с температурой от - 30 до -40 ° С.
Образующийся слой льда удаляют с охлаждаемых поверхностей
путем плавления .
В контактных конденсаторах пары непосредственно контак
тируют с жидким хладоагентом. Образующиеся при этом кри
сталлы льда выводятся из конденсатора вместе с отработанн ым
хладоагентом . Далее лед отделяется от хладоагента.
СубJШМационную сушку можно проводить в периодическом
ИJШ непрерывном режиме. В настоящее время в промышленности
и в лабораторной практике используются преимущественно уста
новки периодического действия. Эrо связано с трудностями загруз
ки и вьпрузки продукrов из вакуумных аIПiаратов.
1 460

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

к
ск

Рис. 18. 12. Схема установки периодической субmtмационной сушки мажных

материалов

Принципиальная схема типичной сублимационной сушильной установки
периодического действия показана на рис. 18. 12. Она состоит из сушШIЬной
камеры СК, холодильников Х 1 и Х2, теплообменников Т1 и Т2, конденсатора
пара К и ва.кууы - насоса ВН. Сушильная камера представляет собой герметичный
аппарат, в котором размещена этажерка из полых полок. Последние охлаждают
ся на стадии замораживания с помощью хладоагента Х41, поступающего из
холодильной установки Х 1 . Высушиваемый материал заrружают во флаконы,
ампулы ИJП1 специальные противни, устанавливаемые на охлаждаемых полках.
Иног,ца замораживание производят в отдельном аппарате, и тогда в сушильную
камеру заrружают уже замороженный исходный материал.
Пос.ле замораживания сушильную камеру ва.кууы ируют, и начинается стадия
испарения маги. Образующиеся при сублимации льда пары воды П поступают
в конденсатор К, где происходит их десублимация на поверхностях, охлаж
даемых хладоагентом Х42 из холодильной установки Х2. Пары воды десубmtми
руются в виде льда или снега (инея). Несконденсированная парогазовая смесь
(ПГС) отво.zпrrся из конденсатора с помощью ва.кууы -насоса ВН.
Для подвода теплоты к материалу на стадии испарения в СК используется
теплообменник Т1, а для распламения льда в конденсаторе К после окончания
стадии сушки - теплообменник Т2. Образующийся при пламении льда конден
сат В отводят из конденсатора• . Время сушки обычно составляет 40 - 120 мин.
Иногда процесс сушки проводят в две стадии. На первой мага удаляется при
фазовом переходе льда в пар . При этом достигается влажность материала 1 -2 % .
На второй стадии материал постепенно подоrревают д о температуры наrревате
ля, и окончательное досушивание материала ведется уже выше криогенной точ
ки (температуры пламения раствора). В результате такого процесса достигается
весьма низкая конечная мажность продукта (-0,5% и меньше).

В обычных сублимационных сушилках операции загрузки
исходного и выгрузки конечного продуктов весьма трудоемки,
• Более подробно аппаратурное оформление процесса субmtмационной суш
ки представлено в (4, 5 ) .

1 46 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

1
сушильная камера, 2
лекrочный транспортер, J
форсунка, 4
наrреватель, 5
ножевое устройство, 6
шлюзовая камера, 7
бункер, 8
коцценсатор, 9
вакуум 
насос;
1 исходный жидкий продукт, II сухой продукт, /ll пары (ПГС), JV хладоаrент,
V отработанный хладоаrент с кристаллами льда, VJ оrходящая ПГС

Рис. 18. 13. Схема установки непрерывной сублимационной сушки:
-

-

-

-

-

-

-

-

-

-

-

-

-

-

-

поэтому при разработке более совершенных установок ста
раются максимально механизировать и даже автоматизировать
эти опера ции . Механизации стадии заrрузюt наиболее легко
достичь при сушке исходных жидЮIХ продуктов, так как они
хорошо транспортируются по трубам. В этом случае в сушиль
ных камерах можно устанавливать стационарные пол юt, на
которые исходный продукт поступает самотеком из питателя .
При этом уровень жидкости на полках регулируется перелив
н ыми устройствами. Для выrрузЮ1 сухих продуктов используют
различные механизмы, снабженные ножами, скребками и т.п.
Конечно , наиболее удобными в эксплуатации и экономич
ными являются сушильные установюt непрерывного действия, в
которых загрузка продуктов и выгрузка производятся без на
рушен ия вакуума в сушильной камере. Однако таюtе установЮ1
конструктивно сложнее, так как они должны иметь спе циаль
ные шлюзовые камеры, накопительные бункеры и другие
вспомогательные устройства.
Одна из конструкций сублимационной сушилки непрерывною действия по
казана на рис. 1 8 . 1 3. В сушильной камере 1 располагается транспортер с непре
рывно движущейся металлической лентой 2. Исходный жидкий продукт 1 с
помощью форсунки З наносится тонким слоем на движущуюся ленту. За счет
частичною испарения влаги под вакуум о м исходный продукт (раствор) самоза
моражиеается. П одвод теruюты в процессе сушки производится с помощью
нагревателя 4. Высушенный продукт // снимается с ленты ножевым устройством
5 и поступает через шлюзовый затвор 6 в приемный бункер 7, который перио
дически разгружается при закрьпом затворе. Образующиеся пары 11/ поступают
в конта�сrный конденсатор 8, куда подается жидкий хладоаrент /V. Из конденса
тора отводится отработанный хладоаrент с кристалла ми льда V и подается на
стадию ею реrенерации .. Несконденсированные пары с примесью воздуха Vl

1 46 2

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

(подсос через неплоnюсти аппарата) из конденсатора отсасываются вакуум 
насосом 9. Продолжительность сушки в такой установке составляет несколько
минут.

И меются промышленные туннельные сушилюt, в которых
сушка производится непрерывно на движущихся поддонах
(этажерках), а операции загрузки и выгрузки конечного про
дукга осуществляются периодически с использованием специ
альных шлюзовых камер .
Процесс сублимационной сушки можно использовать для получения мелко
дисперсных порошков. При этом исходное вещество растворяют в воде. Полу
ченный раствор (обычно эвтектического состава) быстро замораживают и высу
шивают сублимационным способом. При такой сушке из твердой эвтектической
смеси удаляются кристаллы льда. Полученный таким образом продукr состоит
из мельчайших кристалло в растворенного вещества.

18.6. ТЕХНОЛОГИЧЕСКИ Й РАСЧЕТ ПРОЦЕССОВ
СУБЛ И МАЦИИ И Д ЕСУБЛ И МАЦ И И

Сублимационно-десублимационная переработка веществ в
общем случае может состоять из нескольких последовательных
стадий :
- замораживания (полной кристалли зации) исходного ве
щества перед его сублимацией;
- частичного или полного испарения (сублимации) твердой
фазы;
- частичной или полной десублимации парогазовой смеси;
- плавления десублимата.
Естественно, что в зависимости от цели проведения процес
са, фазового состояния исходного вещества, а также требова
ний к конечным продукгам переработюt - в кон кретном слу
чае - та или иная стадия может отсутствовать.
Стадия замораживания. Процесс замораживания исходного
продукга проводят перед его подачей на следующую стадию сублимации. При этом исходное вещество может поступать на
стадию замораживания в виде раствора либо смеси твердой и
жидкой фаз (например , при проведении сублимационной суш
юt влажных материалов) .
При замораживании растворов их охлаждают до температу
ры lз, которая должна быть равна или несколько ниже темпе
ратуры солидуса раствора lc· Последнюю можно определить по
диаграмме равновесия "твердая фаза-жидкость" либо рассчи
тать по теоретичесюtм или эмпирическим зависимостям, на
пример используя формулу ( 1 8 .9).
Количество теплоты, отводимой при замораживании, Qз
можно определить из теплового баланса данной стадии. Пусть
на замораживание поступает раствор в количестве F с темпера1 46 3

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

турой tF. Исходный раствор имеет те ruюемкость cFp , а полнос
тью замороженный - СF т . Тепловой баланс (пространс
твенный контур охватывает весь материал) рассматриваемой
стадии с учетом выделяющейся теплоты фазового превращения
rкр = -rlDI имеет вид:
для непрерывного процесса
(а)
Fcpp tF - Fсрт tэ - Q3 + Frкp = О ;
-

-

для

периодического процесса (за всю стадию)
- Q3 + Frxp = Fсрт 13 - Fcpp tF .

(б)

Из уравнений (а) и (6) в обоих случаях получается следующая
зависимость для расчета отводимой при замораживании теплоты:
(1 8 . 1 0)
Qэ = F(rкp + Срр tF - Срт /3)
•

Значения теплофизических свойств смесей ricp, с Fp и сF т при отсуrствии
эксперимеJПаЛЪных данных М<1ЖНо оценить по аддитив ности, исходя из тепло
физических свойств компонентов и концентрации раствора.

Пусть теперь замораживается продукт, состоящий из твер
с массовой долей последней <1>ж.; теплоем
кости твердой и жидкой фаз исходного продукта равны Cr и еж.
Тогда уравнение теплового баланса при полном замораживании
жидкости имеет вид (например, для непрерывного процесса):

дой и жидкой фаз

.F(l

-

</>ж.)Сr IF + F<1>жсж IF - Fc Рт /3 - Q3

+

F<1>ж.rкр = О ;

отсюда получаем:
Q3 = F [ <1>ж.(rкр + Cж.IF) + (1 - </>ж)Crlp - Срт /3]
( 1 8. 1 1)
При сублимационной сушке величина 'Рж. представляет со
бой абсолюrную влажность исходного материала.
СтадиJI сублимации. При частичной сублимации исходного
вещества F с концентрацией легколетучего компонента XF без
использования газа-носителя (рис. 18. 14,а) получаюrся пар П с
кон центрацией Хп и твердый остаток G с кон центрацией Xr· В
этом случае материальные балансы по массовым потокам фаз и
легколетучего компонента для контура, охватывающего субли
матор С, можно записать в виде системы уравнений:
•

(в)
F- П- G = O ;
Fx1· - ЛХп - G.xr = О .
(г)
При совместном решении (в) и (г) получаюrся формулы
(составленные с использованием правила рычага) для расчета
выхода продуктов разделения. Так, выход паровой фазы

(18. 12)
1 46 4

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 18. 14. К расчету стадии сублимации без использования (а) и с испоЛЬ3ова
нием (б) инерrnого газа-носителя

Заметим, что концентрации Хп и Xr мoiyr быть найдены из
условий фазового равновесия рассматриваемой системы.
Если при сублимации образуются чистые пары легколетуче
го компонента (Хп = 1 ), то из уравнения ( 1 8 . 12) имеем:
П=

p xF

- Хт .
1 - Хт

Если к тому же в т вердом остатке G
компонентов (Xr = О), то выход паров

( 1 8 . 1 3)

не остается

П = Fц .

летучих
( 1 8 . 14)

При полной сублимации исходного вещества П = F и, соот
ветственно, Хп = хр.
На стадии сублимации к продукту необходимо подводить
определенное количество теплоты Qc для компенсации теплоты
фазового перехода. Величину Qc определим из уравнения теп
лового баланса данной стадии . В сублиматор поступает ис
ходное вещество F с температурой fз, а уходят насьпценные пары
П с энтальпией hп и твердый остаток G с температурой tr (см. рис.
1 8 . 14,а). Теплоемкость исходного вещества равна сF т , а твердоrо
остатка
Cr· Уравнение тепловоrо баланса имеет вид:
-

FcF т fз + Qc

-

Пhп

-

Gertr = О .

(д)

При этом энтальпию паров можно представить как

hн =

Гсуб

+ Сm lкон ,

(ж)

где Cm
теплоемкость сконден с ированных паров при температуре их конденса
ции fКDн = fт.
-

Из уравнения (д) с учетом (ж) получим зависимость для рас
чета Qc:
( 1 8 . 1 5)

Если принять, что теплоемкости с р т , Ст и Cr близки между
собой, а температура продукта на стадии сублимации остается
постоянной tr = /3, то из уравнения ( 1 8 . 1 5) с учетом (в) можно
1 465

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

получить приближенную зависимость
Qc

�

Лrсуб

( 1 8 . 16)

·

При сублимации с использованием инертного газа-носителя L
из исходного материала F получаем твердый остаток G с кон 
центрацией легколетучего компонента Xr и парогазовую смесь
W с кон центрацией легколетучего компонента xw (рис . 1 8 . 14, 6).
В этом случае уравнения материального баланса по потокам
фаз и легколетучему компоненту применительно к непрерыв
ному процессу будут иметь вид:

F + L - W- G О
Fxp + Lч - Wxw - G.xr
=

;

=

(з)
О

(и)

,

rде XL - концентрация (содержание) леrколетучеrо компонента в исходном
инертном газе-носителе (при рециркуляции последнего и в некоторых других
случаях XL � О).

При совместном решении (з) и (и) получается зависимость
для расчета выхода паро газовой смеси:

W

=

F (xF - Хт ) + L(x L - хт )
x w - хт

.

( 1 8 . 1 7)

Если концентрация легколетучеrо компонента в свежем исход
ном газе - носителе XL = О, то уравнение ( 1 8 . 17) принимает вид

W

=

FxF - (F + L)хт
x w - хт

( 1 8 . 1 8)

Если же при сублимации происходит полное извлечение лег
колетучего компонента из твердого остатка (Xr = О), то выход
парогазовой смеси

W=

FxF - Lx L .
xw

( 1 8 . 1 9)

Как уже указывалось выше, процесс сублимации с исполь
зованием газа-носителя можно проводить двумя способами:
путем подвода теплоты через теплообменные поверхности или
с потоком предварительно нагретого газа-носителя. В первом
случае количество подводимой теплоты Qc находим из уравне
ния теплового баланса сублиматора С:
(к)
ще hL и hw - энтальпии Гdза- носителя и получаемой насыщенной парогазовой
смеси.
Значения ЭНТ'dЛЬпий hL и hw можно определить, используя правило адди 
тивности. Обозначим: Сп и Спт - теплоемкости леrколетучеrо компонента в па-

1 466

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

К расче'I)' стадии десублимации
парогазовой смеси

Рис. 18. 15.

рообразном и твердом состояниях при
темпера'J)'ре насьпцения парогазовой сме
си; fL - исходная темпер а'J)'ра rаза
носителя; fк
температура насыщения
газа- носителя с концекграцией XL леrколе
тучего компонента; tw темпсра'J)'ра отво
димой парогазовой смеси. Тогда
hL = ХL/Гсуб + Cn(tL tк) + Cmfк) + ( 1
-

-

-

h w = хн-{rсуб + cmtw) + ( 1

-

-

XL)CLfL ;

xw) cLfw .

Из уравнения (к) найдем значение Qc:
Qc = Wh w + Gertr - F cFт 13

}

(л)

LhL .

( 1 8 .20)
В случае подвода необходимой для сублимации теплоты с
нагретым газом-носителем ( Qc = О ) из ( 1 8 .20) можно рассчи
тать расход нагретого газа-носителя:
Whw + Gс т tт Fc F т lз
L
(18.21)

=

-

-

hL

Если задано значение L, то из уравнений (л) и ( 1 8 .2 1 ) мож
но определить начальн ую температуру газа-носителя IL, обес
печивающую необходимый выход парогазовой фракции
(степень сублимации) .
Стадия десублимации. При десублимации (рис. 1 8 . 1 5) из па
рогазовой смеси W с концентрацией x w получают твердую фазу
(десублимат) Н с кон це нтрацией легколетучего компонента Хн
и остаточную парогазовую смесь V с концентрацией xv. Мате
риальный баланс данного процесса по потокам фаз и легколе
тучего компонента для контура, охватывающего десублиматор
Д, описывается уравнениями:
(м)
W- V- Н= О ;
(н)
Wx�v - Vxv - Нхн = О .
Рассматривая эти уравнения совместно, можно получить за
висимости (с использованием правила рычага) для расчета вы
хода продукrов разделен ия . В частности, выход десублимата
Н= w

xw

Ху .
( 1 8 .22)
Х н - Ху
Количество теплоты Qд, которую необходимо отводить на
стадии десублимации, определим из уравнения теплового ба
ланса десублиматора. Обозначим: lн
конечная температура
охлаждения на стадии д есублимации; Сн
теплоемкость десуб
лимата; h v - энтальпия отходящей парогазовой смеси. Тогда
-

-

-

Wh w -

Vhv - Нснlн -

Qд

=

О

,

1 46 7

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

откуда

( 1 8 .23)

Если принять, что отходящая парогазовая смесь V уходит из
десублиматора в насыщенном состоянии, соответствующем ее
температуре tv = tн, то с учетом Cm ::::: Си
h v = xi-<rcyб + Crnfн) - ( 1 - xv)citн .
Заметим, что для расчета процессов сублимации и десублимации веществ с
применением инерmоrо rаза- носителя можно использовать энтальпийную диа
грамму, аналогичную применяемой для процесса сушки. При этом вводятся
понятия абсолюmо сухого инерmого rаза, приведенного (условного) теruюсо
держания пароrазовой смеси, 0111о сительноrо ее насьпцения и др. С помощью
такой диаrраммы легко определить параметры пароrазовой смеси на раз.личных
стадиях и движущую силу процесса.

Стадия плавления десублимата. Как уже отмечалось, стадия
плавления десублимата используется для ero удаления с тепло
обменных поверхностей . Иногда плавление десублимата произ
водят с целью ero последующеrо гранулирования.
Поступающий на стадию плавления десублимат Н обычно
имеет температуру tн ниже точки ero плавления tпл, а получен 
ный расплав отводится в несколько перегретом состоянии (при
температуре tp > tпл). Тепловой баланс данной стадии с учетом
поглощаемой (сток) теплоты фазовоrо перехода rпл описывает
ся уравнением :
(о)
Нснtн + Qп - Hcptp - Нrпл = О ,

где

Ср

- теплоемкость расплав.ненного десублимата.

Из (о) найдем количество теплоты Qп, которую необходимо
подвести для полного плавления десублимата и нагрева распла
ва до заданной температуры tp :
Qп

=

Н(rпл + Cptp - Снtн) .

( 1 8 .24)

Особенности тепломассообмена и кинетика процессов, проте
кающих на различных стадиях сублимационно-десублимационной
•
переработки веществ, рассмотрены в специальной литературе .
ЛИТЕРАТУРА

к главе

18

1 . Горелик А.Г., Амитин А. В. Десублимация в химической промышленности.
М. : Химия, 1986. 272 с.
2. Кафаров В. В., Дорохов И. Н., Кольцова Э. М. Системный анализ процессов
химической технологии. Процессы массовой кристаллизации из растворов и
rазовой фазы. М . : Наука, 1983 . 388 с.
3. Левинский Ю. В. р- Т-диаrраммы состояния двухкомпонентных систем. М .:
Металrтурrи я ,
1982. 1 12 с.
4. Шумский К. П. , Мялкин А. И., Максимовская И. С. Основы расчета вакуум н ой
сублимационной аппаратуры. М . : Машиностроение, 1967. 224 с.
5. Шумский К.П. Вакуум ные аппараты и приборы химического машино
строения. М.: Машиностроение, 1974. 576 с .
·

• См . , например, (1, 2, 4 , 5 1 .

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Глава 19
ГРАНУЛИРОВАНИЕ

для

Процессы гранулирования широко применяюrся в хи ми
прида
ческой и смежных с не й отраслях промышлен ности
ния твердофазным продукrам необходимых потребительских
свойств и улучшения их товарного вида. Выпуск этих продук
тов в гранулированном виде уменьшает их потери при тран
спортировке, хранении и переработке, улучшает техноло гич е
с кие, экономические и экологические по казатели их дальней
шего использования .

19. 1. ОСНОВНЫЕ ПОНЯТИЯ
называется процесс придания твердофаз
Гранулированием
ным продуктам определенной (требуемой) формы и необходи
мь�х потребительских свойств. Получаемые в результате грану
лирования частицы твердой фазы называюrся гранулами . Гра
нулы представляюr собой чаще всего двухфазные, иногда трехфазные агрегаты , имеющие сложную (нередко - пори
стук>) структуру. Гранулы мо гут либо состоять исключительно
из гранулируемого веще ства (или веществ), либо включать на
ряду с ним еще и вещество, скрепляющее исходные частицы
гранулируемо го продукrа в агрегат (гранулу) . Это вещество
называ юr связующим . Частицы гранулируемого продукта в гра
нуле мо гут быть связан ы между собой за счет образования кри 
сталл ических "мостиков " , возникающих при кристаллизации
расплава (раствора) связующего или при десублимации послед
него, при перекристаллизации и полиморфных превращениях в
твердой фазе под давлением. Упомянутая выше связь может
возникнуть за счет вязких, кап иллярн ых, электростатических и
других поверхностных сил различной физической природы. Она
может также образоваться при химическом взаимодействии свя
зующего или компонентов связующего с гранулируемым мате
риалом.
Основными характеристиками гранулированных продуктов
явля юrся:
- их гранулометрический (фра IО.1 ионный) состав (см. разд.

2.7. 1) ;

1469

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

- статическая прочность, определяемая статическим усилием
(отнесенным к миделеву сечению гранулы), необходимым для
разрушения гранулы;
- пористость гранулы (см. разд. 14. 1);
- слежнваемость, определяемая статическим усилием, необ ходимым для разрушения слежавшегося (обычно цилиндри 
ческой формы) образца - при фиксированных усилии прессо
вания, температуре и влажности гранулированного материала.
Ряд требований предъявляют только к отдельным видам гра
нулированных продуктов. Это :
- mrроскопичность гранулированного материала (способ
ность последнего поглощать влагу);
- устойчивость гранул к термическим ци клам наrрев
охлаждение (обычно для веществ, претерпевающих в опреде
ленном диапазоне температур полиморфное превращение, на
пример N H4NOз); устойчивость определяется числом термиче
ских циклов, предшествующих появлению первых разрушен
ньrх гранул;
- впитывающая способность гранул (обычно для веществ,
гранулы которьrх для придания им потребительских свойств
" пропитывают" жидкими компонентами, например промыш
ленные взрывчатые вещества на основе аммиачной селитры);
такая способность определяется объемной (массовой) долей
впитавшегося жидкого компонента;
- статическая (обменная) емкость гранулированньrх адсор
бентов (ионообменных смол) (см. разд. 14.7. 1 ) и ряд других по
каз ателей.
19. 1 . 1 . Стадии rранулообразования

Гранулообразование включает в себя два этапа: формование
и структурирование гранулы. На этапе формования исходному
гранулируемому материалу придают форму, которую он должен
иметь в гранулированном виде. На этапе стру ктурирования в
теле гранулы окончательно формируются связи между обра
зующими ее частицами (кристаллами), и возникает rетерофаз
ная структура, обеспечивающая требуемые потребительские
свойства гранулированного продукта. В различных процессах
гранулирования эти этапы могут протекать последовательно и
паралл ельно во времени .
Типичными примерами последовательного протекания этапов
являются процессы гранулирования кристаллизацией капель
расплава в потоке хладоаrента или на охлаждаемых поверхно
стях либо гранулирование паст и влажных порошков экструзи
ей. В первом случае на этапе формования расплав дисперrиру
ют в поток хладоаrента или на охлаждаемую поверхность в
виде капель требуемого размера. Во втором случае подбирают
1470

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

необходимый диаметр профилированных отверстий (фильер) и
частоту вращен ия ножа для получения цилиндрических агрега
тов необходимоrо размера, из которых после сушки (прока
ливания) будуr получены гранулы. На этапе структур ирования,
завершающем процесс гранулообразования, в первом случае в
ходе кристалл изации кап ель расплава за счет отвода теплоты к
хладоагенту образуется кристаллическая и пористая стр уктур ы
гранулы. Во втором случае в ходе высушивания цилиндричес ких
агрегатов формируюrся струкrурирующие гранулу связи - часто в
виде кристалличес ких (твердофазных) " мостиков " ме:жду частица
ми агрегата (гранулы), а также ее пористая струкrура.
Типичными примерами параллельн.ого протекания этапов
формования и структур ирования гранул являются процессы
гранулирован ия порошков агломерацией с использованием,
например, кристаллизующеrося связующеrо, а также гранули
рование кристалли зацией расплавов (растворов) веществ на
растущих частицах гранулируемо го проду�сrа. В ходе этих процес
сов изменение размеров и формы гран ул (их рост) и формирова
ние струюур ы (н апример, за счет кр исталлизации связующего или
гранулируемо го вещества) происходят одновременно .
Принципиальные отличия в организации процесса грануло
образования п о двум названным выше схемам подразумевают
различия и в аппаратурно-технологическом оформл ении про
цесса. В первом варианте процессы формования и структуро
образования п роводят либо в разн.ых аппаратах, либо в разн.ых
зон.ах одноrо и тоrо же аппарата (например, зоны гранулирова
ния и сушки :гранул в БГС - барабанном грануляторе
сушилке ). На стадии формования обычно не требуется подвода
теплоносителя (хладоагента). В то же время именно на этой
стадии продукт находится в наиболее неблаrоприятном состоя
нии с точки зрения ун. оса (порошок, капли диспергированноrо
расплава или раствора) . На стадии же структурирования необ
ходим подвод теплоносителя, однако здесь агломерированный
(сформованный) прод укт менее подвержен уносу. По этим
причинам схема с последовательным протеканием стадий фор
мования и структур ирования может оказаться более экологиче
ски чистой, чем гранулирование с совмещением стадий
(следовательно,
и зон ) формования и структурирования про
ду�сrа. Пониз ить унос пыли при реализации такого варианта мож
но, осуществляя опосредо ванный перенос теплоты к теплоносите
с помощью rранулированноrо проду�сrа , который
лю
" пере:rреваеrся " ( " пересуnnmается " ) теплоносителем вн.е зоны
гранулирования, а пото м вводиrся в нее и о беспечивает ход про
цесса за счет своих тепломассоаккумулирующих свойств .
Повышенное внимание к экологической проблеме п ылеуно
са объясняется тем, что в современных техноло гич еских схемах
147 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

гранулирования стоимость системы очистки газовых выбро
сов и ее эксплуатации достигает 50% от общей стоимости про
цесса.
1 9 . 1 .2. Основные механизмы взаимодействия частиц в грануле

Для реализации стадий формования и структурирования не
обходимо обеспечить взаимодействие частиц гранулируемого
вещества - чаще всего это делается за счет подвода механи 
ческой энергии
в гранулируемый слой . Она сообщается слою
гранулируемого вещества:
- рабочими органами грануляторов (лопастями, тарелками,
движущимися частями барабанов, лент, дисков, валками , бегу
нами и т.д.),
- теплоносителями в виде кинетической и потенциальной
энергии (гранулирование в псевдоожиженном, вихревом , фон
танирующем и других слоях - см. разд. 2.7. 1 ) ,
- либо аккумулируется в виде потенциальной или кинети
ческой энергии rранулируемоrо вещества, вводимого в грануля
тор (при диспергировании капель расплавов, растворов в поток
теплоносителя или в гранулируемый слой) .
Взаимодействие частиц гранулируемого вещества между со
бой необходимо, но не достаточно для гранулообразования .
Нужно еще, чтобы силы межчастичноrо сцепления бьmи боль
ше сил разрушения агрегатов (гранул). В целом процесс грану
лирования представляет собой последовательность множества
элементарных актов присоединения и отрыва частиц гранули
руемого вещества от образующегося агрегата. При этом чем
больше силы . межчастичного сцепления и меньше силы раз
рушения агрегатов, тем выше вероятность элементарных актов
присоединения и ниже - отрыва частиц гранулируемого ве
щества от гранулы. Разумеется, при превалировании сил сцеп
ления возрастает интенсивность процесса гранулирования. В
противном случае может начаться обратный процесс - дробле
ние или истирание зерен материала.
Рост вели'«ины удельной (на единицу объема гранулируемого
материала) механи'«еской энергии, рассеиваемой в слое, повы
шает, с одной стороны, частоту взаимодействия частиц грану
лируемого материала с растущим агрегатом, что способствует
интенсификации процесса гранулообразования, а с другой. увеличивает силы разрушения агрегатов, следовательно, и ве
роятность отрыва частиц от гранулы, что снижает интенсив
ность гранулообразован ия. Поэтому интенсивность процесса
гранулообразования экстремалыю зависит от подводимой
удельной энергии .
Другим важн ейшим фактором, определяющим ход и резуль
тат процесса гранулирования, являются силы межчасmи'«ноzо
·

1472

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

сцепления. Связи между частицами при формовании и струкгу
рировании гранул можно подразделить на три основных клас
са: твердофазные мостики; жидкофазные мостики; механиче
ские связи и притяжение между твердыми частицами.
Твердофазные мостики возникают за счет:
- диффузии молекул или атомов в точках контакта между
частицами ;
- плавления и затвердевания вещества в этих точках;
- кристаллизации растворенных веществ при сушке;
- химической реакции.
Скорость диффузии, как правило, увеличивается с повыше
нием температуры. Вещества с низкой температурой плавления
(органические соединения, термопласты, некоторые неоргани
ческие продукты - сера, карбамuд) в процессе гранулирования
с подводом тепла или при его выделении за счет внутрен него
трения в точках контакта между частицами легко переходят в
расплавленное состояние за счет понижения температуры
плавления при уменьшении положительного радиуса кривизны
поверхности. Возможна также подача исходного расплава в
слой в качестве связующего - при его кристаллизации образу
ются твердофазные мостики. В случае гранулирования увлаж
ненных продуктов и последующей сушки гранул выкристалли 
зовываются твердофазные мостики в местах контакга твердых
Час'ПЩ. При химическом взаимодействии компонентов с вязую
щего друг с другом или с rранулируемым веществом образуются
мостики ново го вещества или комплексного соединения.
Жидкофазные мостики возникают за счет:
- поверхностного натяжения пленки жидкости;
- вязких свойств связующего;
- молекулярного
притяжения в адсорбированных тонких
слоях.
В качестве связующего, образующего жидкофазные мостики,
на практике часто используют воду. В связующее для улучше
ния его смачивающих свойств и увеличения поверхностного
натяжения нередко добавляют поверхностно-активные вещества (ПАВ).
Предложено несколько механизмов связывающего действия
жидкофазных мостиков за счет поверхностного натяжения.
При малом количестве связующего жидкость заполняет лишь
часть пространства между частицами, не образуя сплошной
пленки на поверхности агрегата. В точках соприкосновения
твердых частиц образуются жидкофазные мостики, внутри ко
торых понижено капиллярное давление вследствие отрицатель
ного радиуса кривизны межфазных поверхностей. Оценить это
давление, а значит, и усилие "сцепления" частиц можно по
формуле Том псона (см . формулу (а) в разд. 14.2). Если же меж1473

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

частичные промежуrЮI целиком заполнены жидЮIМ связующим ,
образующим пленку на поверхности агрегата, то п р и оценке
сил "сцепления" нужно учесть еще поверхностное натяжение в
системе твердое-жидкость-газ на внешней границе агрегата.
При большом избытке связующего (гранулирование суспензий)
частицы твердой фазы "плавают" в капле связующего . Устойчи
вость такого агрегата определяется силами поверхностного на
тяжен ия и вязкостью суспензии . Для оценок в этом случае ис
пользуют формулы, описывающие диспергирование жидкостей.
Пластичные связующие вещества с большой вязкостью со
храняют иногда заданную форму поверхности, ибо энергия их
деформации намного превышает поверхностную энергию. В
этом случае наряду с поверхностными силами сцепления нуж
но учитывать также силы молекулярного взаимодействия по
верхности частиц и связующего.
Ацсорбционные тон Ю1 е слои (толщиной менее 3 . 1 0 -9 м)
обеспечивают молекулярную связь между частицами в местах
их контакта. Активному проявлен ию действия этих сил может
способствовать повышение давления в местах контакта
(например, при гранулировании прессованием).
ПрlfГяжение между твердыми частицами возникает у мелко
дисперсных порошков за счет молекулярного взаимодействия
контактирующих тверд ых поверхностей (силы Ван-дер
Ваальса) или электростатического воздействия. Силы Ван-дер
Ваальса начинают проявляться, когда расстояние между части
цами не превышает 1 0 -s м . Особенно заметны они при взаимо
действии свежесколотых поверхностей - сразу же после про
ведения тонкого размола. При движении частиц вследствие их
трения возникают электростатические заряды, величина кото
рых зависит от свойств материала, условий гранулирования и
отвода электричества.
М еханические связи возникают за счет сцепления шерохова
ТЬIХ поверхностей.
На практике при гранулировании на этапах формования и
структурирования гранул силы сцепления мoryr действовать
одновременно за счет нескольких описаннь�х выше механиз
мов. Причем на этапах формования и структурирования эти
механизмы мoryr быть различны. Например, при формовании
гранул из влажнь�х порошков преобладает сцепление за счет
жидкофазных мостиков и механичесЮ1х связей, а пр и структу
рировании таЮ1х гранул на стадии сушЮI и в сухом грануляте
- за счет твердофазных мостиков.
1 9. 1 .3. Классификация процессов гранулирования
Классификация процессов гранулирования возможна по
разным признакам.
Прежде всего, все процессы гранулирования подразделяются
на непрерывные и периодические .

1474

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

По способу формирования гранул выдел яют:
- гранулирование окатываt1ием, когда процесс гранулообра
зования происходит за счет :качения зерна при подводе меха
н ической энергии - с послойным наращиванием поверхности
за счет гранулируемого продукта (или за счет истирания высту
пов в "полирующих" грануляторах) . Для данного процесса ха
ракrерно получение сферических гранул с гладкой поверх
ностью и высокопрочной структур ой. В этом случае легко
можно получить многослойные (или капсулированные - см.
разд . 19.6) гранулы требуемого состава и структуры. Процесс
проводят в барабанных, тарельчатых, дисковых, ленточных,
чашеобразных, конических, :качающихся, скоростных, вихре
вых, виброгрануляторах, в конических аппаратах с фонтани
рующим слоем, в аппаратах тип а "пьяная бочка" (емкостной
аппарат, при вращении которого материал перемещается в трех
плоскостях) ;
- гранулирование диспергирован ием расплавов в потоке хла
доагевта ; оно состоит из двух стадий - диспергирования распла
ва на :капли (формование) и кристалл изации (отверждения)
образовавшихся :капель (структурирование). Отвод тепла от
кристаллизующихся гранул осущестмяют с помощью газооб
разного, жидкого, кипящего, газокапельного (тумана), пыле
видного или возгоняющегося потоков хладоагента. В ходе про
цесса образуются сферические гранулы с гладкой поверх
ностью. Недостатками процесса являются с вязь высоты аппа
рата с временем кристаллизации капель расплава и сложность
получения многослойных гранул и гранул заданной структуры .
Процесс проводят в грануляционных башнях в потоке воздуха
и в колонных аппаратах различн ых конструкций;
- гранулирование кристаллизацией на поверхности частиц;
расплав (раствор) или суспензию гранулируемого вещества
дисперrируюr на капли в гранулируе мом слое или н;щ ним. По
следний находится чаще всего в псевдоожиженном состоянии
либо движется в режимах пересыпания или уноса, например в
барабанных грануляторах. Капли расплава (раствора), суспен
зии попадают на растущие гранулы и смачивают их, а гранули
руемое вещество кристаллизуется на таких гранулах при дви
жении хлада- или сушильного агента через слой. Аналогично
реализуется процесс гранулирования десублимацией из паро
вой фазы, пропускаемой через слой, в который подается, на
пример, испаряющийся хладоагент. В ходе процесса получают
прочные гранулы, поверхность которых, однако, не столь глад
кая, а форма не столь сферическая, :как в описанных ранее
процессах. Достоинство процесса состоит в совмещении стадий
формования и структурирования, недостаток - повышенный
пьmеунос ;

1475

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

- rранулировавие агломерацией порошков ; его проводят, свя
зывая мелкие частицы гранулируемого порошка в агре rаты
(гранулы) путем введения связующего . Последнее дисперrиру
ют в слой порошка или получают подплавлением из исходного
продукта. Указанный способ особенно эффективен с позиций
повышения экологической чистоты процесса. Например, при
гранулировании расплавов экологически чистым методом
(кр исталл и зацией на охлЮl<даемых поверхностях) отверждают
бОльшую часть расплава; затем охлЮ1<денные чешуики окомко
вывают в сферические гранулы, используя оставшийся расплав
в качестве связующего . Подобный прием позволяет избежать
непосредственного контакта хладоагента и гранул, а следова
тельно, и необходимости очистки хладоагента. Эrот прием ис
пользуется для увеличения размера имеющихся гранул, для
получения многослойных гранул и т.д .;
- rравулирование прессованием и формованием ; в процессах
прессования гранулы мо гут быть получены путем дробления
плиток (прессовок) и рассева. Продукт имеет неправильную
форму и часто требует дальнейшей обработки. Процесс прово
дят обычно на валковых прессах с гладкой поверхностью вал
ков. Главное достоинство этих процессов - высокая произво
дительность при малых rа баритах грануляторов; однако необ
ходимость обширного вспомо rательного оборудования (сит,
транспортеров, дробилок, полировочных барабанов и т.д.) мо
жет свести на нет это преимущество .
В процессах формования гранулируемому материалу путем
прессования придают зццанную форму, чаще всего - цилин
дрическую или чечевицеобразную. Если сформованные грану
лы имеют строго одинаковые форму и размеры, то такой про
цесс называется таблеmрованием , а полученные гранулы - таб 
летками. Обязательным элементом таблетирующих машин яв
ляется наличие пресс-формы требуемых rабаритов и дозирую
щего устройства.
Некоторые дополнительные сведения приводятся в разд.
1 9 .2.2.
В грануляторах формования основными элементами явля
ются система подачи гранулируемого материала, обеспечи
вающая его прессование (шнеки, валки, бегуны, плунжеры и
т.д.), и перфорированная поверхность, формующая (в результа
те силового воздействия ) материал в виде цилиндров. Иногда
после перфорированной поверхности устанавливают нож,
обеспечивающий нарезание цилиндров (гранул) равной длины.
Процесс гранулирования прессованием проводят как с исполь
зованием, так и без использован ия связующего .
В зависимости от способов контакта с теплоносителем
(сушильным агентом) процессы гранулирования можно подраз
дел ить на:
_

1476

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

- гранулирование без использования теплоносителя (суmиль
ноrо аrеита) - в основном это процессы гранулирования прес
сованием. Достоинство этих процессов - отсутствие системы
отделения хладоаrента от мелкодисперсных частиц гранули
руемого вещества;
- гранулирование при отсутствии контакта теплоносителя
(сушильноrо агента) н гранулируемого вещества - это процессы
гранулирования на поверхностях, разделяющих две названные
среды. Здесь то же достоинство, что и в предыдущем случае;
- гранулирование при контакте с теплоносиrелем (сушильным
агентом) - к этим процессам относиrся оолъшая часть оrmсанных
вьШiе способов гранулирования. Их преимущество - высокая ин
тенсивность, низкая удельная материалоемкость и стоимость гра
нуляторов. Недостаток - необходимость создания системы отде
ления те плоносителя от частиц гранулируемого вещества.
В зависимости от физико-механического состояния гранули
руемого вещества и связующего различают:
- гранулирование порошков с использованием связующего ,
изменяющего или не изменяющего агрегатное состояние, либо
без свнзующе го ;
- гранулирование расплавов кристаллизацией капель в пото
ке хладоаrента на охлаждаемых поверхностях или частицах,
вводимых извне либо содержащихся в возвращаемом гранули
рованном продукте (ретуре) . Сюда же относят комбинирован
ные методы - получение мелких гранул (порошка, мелкого
ретура) кристаллизацией капель расплава в потоке хладоаrента
или отверждением на охлаждаемых поверхностях, а далее использование схемы гранулирования порошков;
- гранулирование обезвоживанием растворов или суспензий варианты организации процесса анало гич ны изложенным для
гранулирования расплавов;
- гранулирование десублимацией целевого компонеиrа из паровой
фазы проводят на частицах ретура с использованием теплоносите
лей, изменяющих и не изменяющих агрегатное состояние;
- гранулирование с выделением целевоrо компонента за счет
химическоrо взаимодействия компонентов связующего или гра
нулируемого вещества и связующего. Процесс чаще всего прово
дят на частицах мелкого ретура при химическом взаимодействии в
паровой или жидкой (в том числе в суспензии) фазах.
·

19. 1 .4. Элементы типовой технологической схемы гранулирования

Типовая технологическая схема процесса гранулирования
(рис. 19.1) обычно включает в себя следующие узлы:
- приема и подготовки гранулируемого продукта ( /), со
стоящий из бункерного (емкостного), транспортирующего (тру-

1477

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Типовая технологическая схема
гранулирования:

Рис. 19. 1.

1 - узел приема и подrотовхи гранулируе
мого материала, 2 - узел гранулироВЗЮ!я, 3 узел подrотовхи и подачи связующего, 4 узел подачи теплоносителя и его отделения от
частиц гранулируемого материала;
1 - исходный гранулируемый материал , lI
исходные компонеlПЫ связующего, l/1 исходный поток теплоносителя, IV - поток
отработанного теплоносителя, V - гранулиро
ванный продухт

бопроводного), размольного, кл ассифицирующего, смеситель
ного и дозирующего оборудования;
- собственно гранулирования (2), имеющий в зависимости
от способа гранулообразования отдельные или совмещенные
зоны (аппараты) формования и структурирования гранул, их
рассева, дробления крупных кусков и возврата мелкого ретура;
- подготовЮf и подачи связующего (3), состоящий из ем
костного, смесительного , запорного оборудования и дисперги
рующих устройств;
- подачи теплоносителя (сушильного агента) и его отделе
н ия от частиц гранулируемого материала ( 4), состоящий из
побудителей потока теплоносителя, теплообменного оборудо
вания, различного рода аппаратуры для отделения теплоноси
теля от частиц гранулируемого материала.
Заметим, что узел З может отсутствовать при гранулирова
нии прессованием и при получении связующего за счет плав
ления исходного продукта, а узел 4 отсутствует при гранулиро
вании прессованием (на рис. 19 . 1 эти узлы оконтурены штри
ховой линией).
Можно предположить, что узел собственно гранулирования
далеко не всегда является самой дорогой и энергоемкой частью
технологической схемы гранулирования. Поэтому при выборе
способа гранулирования необходимо оценивать эффективность
технологической схемы в целом.

19.2. АППАРАТУРНОЕ

ОФОРМЛЕНИЕ
П РОЦЕССОВ ГРАНУЛИРОВАНИЯ

Производительность гранулятора по готовому продукту Gг
обусловливается конструктивным оформлением и технолоrиче
СЮfМИ параметрами его работы, а также необходимым для гра
нулообразования временем 'tк , определяемым Юfнетикой пре
вращения . Связь производительности с этими факторами уста
навливается в зависимости от типа гранулятора и структуры
движения сплошной и д исперсной фаз (см. гл. 8).
Многообразие грануляционной аппаратуры и сложность
протекающих в ней процессов не позволяюг конкретизировать
1478

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

*
эту связь в рамках данного курса . Решающее влияние на ап
паратурное оформление процесса и способ его расчета оказы
вает механизм гранулообразования . С учетом этого фактора
аппаратуру для гранулирования можно подразделить на грану
ляторы для окатывания и агломерации; прессования, формова
ния (таблетирования); кристаллизации дисперrированных ка
пель расплава.
19.2. 1 . Гранулирование окатыванием и агломерацией

Для гранулирования окатыванием используют грануляторы
барабанного, тарельчатого, ленточного, дискового и других
типов. В них гранулируемый материал "катится" по образую
щей поверхности гранулятора. Для гранулирования агломераци
ей используют аппараты с псевдоожиженным слоем, в которых
формирование гран ул происходит за счет соударений частиц
порошка с гранулами и между собой.
Разумеетс я , для конкретного гранулятора следует говорить
лишь о превалирующем влиянии указанных выше механизмов. В
аппаратах некоторых типов гранулообразование происходит за
счет обоих механизмов: виброгрануляторы, аппараты с механи
ческим взвешенным слоем (скоростные грануляторы), с на
правленным движением "взвешенной" дисперсной фазы (фон 
танирующий , вихревой слои) .
Внутри указанных классов аппаратуру можно разделить на
монофункциональную и полифункциональную • • . В первом случае
в аппарате осуществляется лишь стадия гранулообразования,
остальные стадии протекают в других аппаратах; во втором
случае в том же аппарате происходит и дальнейшая обработка
получен ного продукта (сушка, охлаждение, классификация ,
дробление, "полировка" (окатывание) поверхности гранул , на
несение капсул из других веществ (капсулирование) и др . ) .
Ниже рассматриваются устройство и принципы работы не
которых из названн ых выше аппаратов.
Барабаниwе 1ранулпорw, работающие на принципе ок11mы•он11.11, выпускают в
монофункциональном и полифункционалъном исполнении. Барабанный грану
лятор, показанный на рис. 1 9 .2, предстааляет собой медленно вращающийся
цилиндр 1 с закрепленными на нем бандажами 2, катящимися по роликовым
опорам 3. Для уменьшения налипания влажного материала на внутреннюю
стенку барабана ее футеруют резиной, тефлоном и т.д. ГрануJП1рованный мате
риал выводят из гранулятора через разгрузочный узел 4. Orcoc паров и пьmи
производят с помощью вентилятора, присоединенного к патрубку в верхней
части у311а выгрузки. Шихту увлажняют связующим с помощью форсунки, уста
новленной в 1 - 1 , 5 м от загрузочного устройства гранулятора.

• Некоторые сведения о влиянии основных фапоров на процесс гранулооб
разования приведены в специальной литературе, например (2-4).

•• С м . ( 3 , 4 ) .

1479

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

v
//

1 - обечайка (корпус) , 2 - б андаж,
З - опорная сrа:нция, 4 - узел выrруэк.и;
1 - rранулируемый продуrr , 11 - св11эующи, 111 - rранулы; /V - исходный
теплоноситель, V - отработанный тепло

Рис. 19.2. Гранулятор барабанною типа:

носитель

JV

4

Достоинство rрануляторов такою
типа - их простота и большая про
изводительность, недостаток - по
rранулометрический
лндисперсный
состав продую'а.
От этою недостатка свобод�н барабанный rранулятор с встроенным /(.// ассифи
цилиндрическим ситом. Мелкий отсеянный ретур может транспор
катором
тироваться расположенным вне барабана транспортером к входному устройству
rранулятора. Данный аппарат 11вляется уже полифункциональным. Главный ею
недостаток - внешний трансп ортер ретура, не исК11Ючающий пылеобразования
и потерь при транспортировке.
Преодолеть этот недостаток позволяет внутренний (встроенный) обратный
шнек 6 (рис. 19.3). Он представляет собой закрьrrый винтовой короб, закреплен
ный на внутренней стенке барабана J. При вращении барабана этот шнек тран
спортирует мелкий ретур от перфорированною, встроенною внутри обечайки
конуса 4, расположенною на выходе из барабана, к ею входу, где мелкий поро
шок орошается связующим с помощью форсунки 8. Представленный на рис. 19.З
барабанный rранулятор вьmолняет таюке роль сушилки, удаляющей испаряю 
щееся связующее. Такой полифункциональный аппарат называют барабаниwм
rраву.uторо111 -сушилкоl-uассифиuтором. В аппаратах этою типа возможны
различные конструкции встроенных классифицирующих устройств, в том числе
с псевдоожиженным слоем · .
Модификация этою аппарата - дополнение ею шаровой мельницей за клас
сифицирующим устройством (для дробления крупных кусков в мелкий ретур) и
наличие зоны охлаждения, расположенной после зоны rранулирования и сушки
по ходу продукrа. Такой полифункциональный аппарат называют барабанвwм
-

rраву.uтором-суwилкоl-uассифнuтором-холодИJJ .,.. ком.

Рис. 19.3. Барабанный rранулятор-сушилка с встроенным обратным шнеком и

1 - барабан, 2 - усrройсrво, обеспечивающее вращение барабана, З - выrруэочная ка
мера, 4 - классифицирующий конус, 5 - поД"Ьемно-лопастная насадка, 6 - обраПIЬIЙ nmeк,
7 - приемная насадка, 8 - форсунка;
1 - rранулируемый продукт, // - связующее , 11/ - rранулы, /V - исходный теплоноси
тель, V - отработанный теплоноситель

коническим классификатором:

• См. (4) .

1 480

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

1

1

1 - тареmс:а, 2 - кожух, З - форсунка, 4 - штуцер ввода гранулируемого продукта, 5 приводной вал, 6 - регулятор;
1 - гранулируемый продукт, Il - связующее, Ill - гранулы, /V - исходный теплоноси
тель, V - отработанный теплоноситель

Рис. 19.4. Тарельчатый I])анулятор:

1 - леша, 2 - направляющие борта, З - ролики ;
1 - гранулируемый продукт, /l - связующее, 111 - гранулы, /V - исходный теплоноси
тель, V - отработанный теплоносю·ель

Рис. 19.5. Лекrочный rранулятор:

Иэ.ложенные консrруктивные решения позволяют сделать установку более
компактиой, уменьшить потери теплоты и выбросы пьти в окружающую среду.
Как уже отмечалось, пьmеобразование происходит в основном в зоне дисперги
рования связующего форсункой и ввода порошкообразного исходного продукrа.
Июкенерные решения направлены на исключение подачи теплоносителя в эту
зону. Сушку и охлаждение проводят в зоне уже сформированных rранул, 'По
достиrается промежуточным отводом воздуха из барабана и вводом его в зону
выгрузки . Иногда в барабан со стороны входа продукrа всrраивают циклон или
батарею циклонов, через которые перед выходом из барабана пропускают су
шильный аrент, а собранную пыль в качестве мелкого ретура возвращают для
rранулирования .
Тарет.чатwе rранул1ПОр•1 (рис. 19.4) также реализуют механизм rранулообра
зования tжаmы•анием. На станине установлена тарелка /, закрьrrая кожухом 2 с
форсункой З. При работе rранулятора порошок / через заrрузочный штуцер 4
подают на наклонную вращающуюся тарелку 1, где он увлажняется из форсунок
З и окатывается до rранул заданной величины. Угол наклона тарелки можно
реrуJПtровать с помощью устройства 6. Тарельчатые rрануляторы отJПtчают высо
кая удельная производительноt;ть и хороший классифицирующий эффекr. Одна
ко это в основном монофункциональные аппараты: в н их с.ложно орrанизовать
сопутствующие тепломассоо б менные процессы.
Основной раб очий орrан леJПОчнwх rранул1ПОров (рис. 19.5) - движущаяся
бесконечная отбортованная ле нта 1, расположенная под уг.лом к горизонту. И
здесь за счет пересьmания порошка по движущейся ленте реаJПtзуется rрануJПt
рование tжаты•анием. Главное достоинство аппарата - простота консrрукции и
доступность слоя материала для обработки связующим. Недостатки - низкая
производиrеrIЬность, сложность герметизации , трудность орrанизации сопуrствующих
тепломассом
об енных процессо в. Эrи rрануляторы имеют значиrельно меньшее рас
пространение в промьШVIенносш, нежели барабанные и тарельчатые.
Гранулообразование t1211омерацией происходит в раэ.личного рода аппаратах с
п сеuоожюкен н•1м сл оем (ПС). Эти аппар аты, как правило, изначально поли
функциональны: ожижающий агент обеспечивает сущесгвование псевдоожюкен-

148 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

VI

а

+1

б

б - с подачей раствора или расплава
а - с подачей раствора на п<>верхность слоя,
внуrрь слоя;
1 - 0JКИJК111Ощи й аrеш, JJ - rранулируемое вещество, lll - распыливающий аrеш, JV rранулированны й продукт, V - ретур, Vl - отработанны й воздух

Рис. 19. 6. Аппараты для rранулирования в псевдоожюкенном слое:

ного слоя, следовательно, режим икrенсивной "нуклеации" (кинетического вза
имодействия частиц) и одновременно протекание сопуrствующих тепломассооб
менных процессов (сушки, на1ревания, охлаждения). Кроме того, в псевдоожи
женном слое без труда реализуются процессы классификации rранул. Для осу
ществления процесса rранулирования в слой, содержащий rранулы, подают
связующее (часто в виде суспензии-пульпы) и порошок rранулируемого продук
та. Нередко rранулируемый продукт подают в виде расплава (раствора).
Грануляторы с ПС различаются в основном • способом подачи пульпы в слой
(рис. 19.6) :
- н о поверхность слоя (рис. 19.6,о) часто с обдувом факела распьияемого
раствора rранулируемого вещества высокотемпературным теплоносителем для
икrенсификации испарения связующего в распьте. Достоинство - сравнитель
но равномерный rранулометрический состав. Недостаток - повышенный пьте
унос и высокая шероховатость rранул;
- в С11 ой форсунками, установленными в боковой части аппарата (рис.
19.6,6) с организацией горизонтального факела распьта или установленными
вертикально в прирешеточной зоне. Достоинство - меньший пылеунос и более
гладкая поверхность rранул. Недостаток - сложность регулировки процесса.
Теплоноситель чаще всего подают в П С в виде горячего ожюкающего или
распьтнвающего агента при диспергировании пульпы либо комбинацией этих
двух способов. Теплоту также подводят в слой П()rруж:ными горелками или раз
мещением в нем теплообменных поверхностей. Пульпу обычно диспергируют
форсунками, являющимися одновременно и эффективными тепломассообмен
ными устройствами.
Псевдоожижение позволяет в одном аппарате совместить процессы rранули
рования и классификации (рис. 19.7). Исходный продуКТ в виде пульпы подают
форсункой 1 в зону rранулирования 5, отделенную от зоны классификации 7
наклонной перегородкой 6 с переточными окнами. Гранулированный продукт
постепенно перетекает в зону классификации, сужающуюся по высоте. В над
слоевом пространстве зоны классификации происходит разделение полидис
персной смеси на два продукта: верхний - мелкий внутренний ретур и нижний
- достигшие заданных размеров rранулы (готовый продуКТ). Верхний продукт
вьщувается из зоны классификации и поступает для наращивания размеров в
зону rранулирования, нижний - выводится через разrрузочную течку аппарата.
Для rранулирования предложены различные конструкции аппаратов с фон
танирующим слоем (рис. 19.8). Среди них - rрануляторы конической или ци• Подробнее см. (2) .

1482

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 19. 7. Гранулятор-классификатор с

1 - форсунка, 2 и З - подпорная и rазо
распредеmпельная решсnси, 4 - корпус
аппарата, 5 - зона rранулирования, 6 наклоЮ1ая персrороДJСа, 7 - зона классифи
кации ;
1 - исходный (rранулируемый) продукт ,
11 - rранулироваЮ1Ый продукт, J/J - ожи
J1UUОщий аrент, IV - распыливаюший аrе нт,
V - отработаЮIЫй воздух, VJ - воздух,
подаваемый в классификатор

псевдоожиженным слоем:

VJ

линдроконической формы с подачей пульпы по оси аппарата - сверху на слой
(рис. 19.8,а) и снизу в слой (рис. 19.8,6). Недостатками эmх аппаратов являются
унос пыли и истирание материала. В дальнейшем распространение получили
аппараты с несимметричным (щелевым) вводом ожюкающеrо агента (рис.
19.8,в), обеспечивающие бол�.шую интенсивность циркуляции и надежность
рабо1ЪI. Недостатками этих аппаратов являются неравномерносТh газораспреде
ления по периметру и большое 111Дравлическое сопротиаление.
Общий недостаток аппаратов с псевдоожиженным слоем - повышенный
пылеунос, в том числе из-за совмещения стадий rранулообразования, сушки и
охлаждения. Частично проблема решается за счет использования rоанvлятоuов с
механическим азвеwеннwм слоем - вибро- и скоростных - rранулы в них обра 
зуются как за счет аrломерации частиц порошка, так и за счет окатывания.
Виброrрануляторы обеспечивают образование rранул ("нуклеаци ю" и пере
мещение частиц в слое) за счет вибрации рабочих орrанов (чаще всеrо корпуса
или ero части). Преобладание тоrо или иноrо механизма rранулообразования
определяется конструктивно-тсхнолоrическими параметрами аппарата. Изобра
женный на рис. 19.9 виброrранулятор представляет собой комбинацию вибро
формователя З и виброокаТhmателя /. Виброформователь состоит из наклонноrо
1

а

1

6

в

Рис. 19.8. Грануляторы-сушилки с фонтанирующим слоем:

а - ц илиндроконический аппарат с подачей материала на слой, б - то же с подачей
материала в слой , в - мноrосекционный щелевой аппарат с тангенциальным подводом газа;
1 - исходный продухт, 11 - r11анулиро&аЮ1Ый продухт, 111 - оJIООкаlОщий аrеш, IV расПЪVD<ВаЮщий агент, V - отработаЮIЫЙ воздух

1483

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

1 - виброокатыватель, 1 - лоток, 3 - виб
роформователъ, 4 - питатель, 5 - капельница, 6
- вибратор;
1 - rранулируемый продукт, 11 - связующее,
111 - rранулы

Рис. 19. 9. Виброгранулятор :

1 - буюс:ер, 1 - вибратор, .1 - шнековые питатели, 4 - емкосrь свяэующеrо, 5 - на
сос -дозатор , 6 - скоросn1ОЙ rранул ятор;
1 - rранул и рvемый mюдvкт, 11 - связующее, 111 - rранулы

Рис. 19. 1 0. Схема скоросnюго гранулятора:

прямоугольного лотка 2, установленного на вибраторе 6 дебалансного типа
(привод - от электродвигателя). Амплитуду колебаний вибратора можно реrу
лнровать набором съемных дебалансов. Исходная смесь 1 секrорным питателем 4
подается на вибрирующий лоток 2, образуя виброюшящий слой. Связующая
жидкость поступает на слой из капельницы 5. Сформированные таким способом
гранулы для сглаживания их поверхности и придания сферической формы пе
ремещают в виброокаты:ватель 1.
Друтие конструкции виброгрануля:rоров приводятся в специальной тперюуре• .
СкорОС111W е 111 анул1ПОрW обеспечивают нуклеацию и перемещение частиц по
рошка за счет движения (чаше всего - вращательного) рабочих органов аппарата
- лопастей, мешалок и т.д. Эти грануляторы представляют собой обычно верти
кальный или горизонтальный цилиндрический корпус со скоростными
(окружная скорость лопастей - 3-10 м/с) вращающимися механическими пе
ремешивающими устройствами различной формы. Последние иногда для на
правленного перемещения продукrа располагаются по винтовым линиям. Ти
пичная схема скоростного гран улятора представлена на рис. 1 9 . 1 0 .
Достоинство грануляторов этою типа - компактность и высокая производи
тельность. Особенность и главный недостаток - повышенная по сравнению с
другими типами грануляторов вероятность раскалывания и агломерации гранул,
что ухудшает качество продукта.
Отичительная черта аппаратов механическоrо взвешенноrо слоя - последова
тельное проведение в ра:щельных аппаратах стадий rранулообра:.ювания и сопут
ствующею тепломассообмена пр и сушке (охлажцении) гранулированных материалов.
Это позваляет снизить унос пыли, поскалъку на стадИЮ rранулообразования, наибо
лее опасную с точки зрения образования пыли, теплоноситель не подаеrся.

1 9.2.2. Гранулирование прессованием и формованием
При гранулировании прессованием и формованием процесс
агрегирования частиц ос уществляется под действием сил давле
ния, создаваемого рабочими ор га нами гранулятора. Удержание
частиц в агрегированно м состоянии происходит за счет " сухого"
•

См. (3, 4 ) .

1 484

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

1

q>;

1

1

а

6

1 - прессующие валки , 2 - подпрессовыватель;
I - исходный порош ок , 11 - продукт (плитка, куски, леюа);
а - вид кусков после дробления

Рис. 19. 1 1. Схема валкового пресса для yIVIomeния сухих продуктов:

- роликовый, б - валковый;
1 - перфорированная обечайка (матрица) , 2 - бегун;
1 - rранулируемый материал, II - продукт

Рис. 19. 12. Принципиальные схемы роторных экструдеров:
а

(в отсуrствие связующего) взаимодействия твердых частиц ,(сил ы
Ван -дер - В аалъса, эле ктростатическое взаимодействие, механ иче
ские связи, твердофазные мостики ) или за счет использования свя
зующего (жидкофазные мостики , адсорбционн ы е тонкие слои) .

Чаще всего процесс прессованu проводят на прессах нenpepW1111 oro дейСТllИfl с
гладкими вращающимися цилиндрическими валками (рис. 19. 1 1). Реже исполь

зуют валки с профилированной поверхностью. Прессующее усилие в валковых
прессах создается за счет пружин, прижимающих валки 1 друт к друrу, или за
счет специальных гидравлических (реже - других) прижимных устройств. Кон
струю{Ии и принцип действия этих rрануляторов во многом сходен с валковыми
дробилками (разд. 22 . 3 . 1). Отличительной особенностью таких rрануляторов
является наличие подпрессовывателя 2, который предварительно (с небольшим
усилием прессования) уплотняет исходный порошкообразный продукт, увеличи
вая его насьmную IVIomocть. Этот прием позволяет замеmо повысить массовую
производительность rранулято р а. Спрессованный продукт в виде IVIиток, ленть1,
кусков поступает в дробилку, а далее - на рассев. Товарная фракция выводится
из аппарата; мелкая фракция возвращается в бункер пресса, а крупная - на
дробление. Достоинства данного rранулятора - его большая производитель
ность при малых габаритах и оmосительная простота конструкции . Кроме того,
выбросы пьии из аппаратов такого типа невелики. Недостатки - неправильная
форма и посредственный товарный вид rранул, а также rромоздкая вспомога
тельная часть схемы rранулиро вания - дробление, рассев, возврат ретура.
Гранулирование формованием реализуется на практике в процессах экструэии
(продавливания материала через круглые или профилированные отверстия фильеры), формования на профилированных валках и таблетироаанни. Как и в
случае прессования, ра311Ичают формование со связующим и "сухое".
По способу создания усилия формования экструдеры делят на шнековые,
плунжерн ые и роторные.
Для UDtexo&IX экструдеро в характерно создание больших давлений прессова
н ия, что обеспечивает хорошую гомоrенизацию ШИХ'IЪI и прочность rранул.
Недостаток - повышенная энергоемкость.

1485

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Плунжернwе экструдеры ис пользуют для формования мастичных веществ. К
недостаткам аппаратов этого типа оmосится периодичность работы и необходи
мость очистки рабочих поверхностей перед новой загруз кой .
П овышение производительности обеспечивают роторнwе экструдеры - роли
ко111о1 е (рис. 1 9 . 12,а), в которых усилие прессования развивается за счет качения
ролика ("беrуна") по внутренней пе р ф орир ованной поверхности валка
( цил и ндрической о бечайки ) , и более про и з водительные JWJкo111o1e (рис . 19. 1 2 , 6) ,
гд е такое усилие возникает между вращающимися пер фор иро в анным и валкам и .
Таблnирующие маwинw представляют собой ра311Ичн ые вариаlПЪI комбина
ции дозирующих устройств, пресс-форм и подвижных или неподвижных пуас
сонов (поршневидных стt.: р ж н ей ) . Эти грануляторы малопроизводительны, кон
структи вно сложны, энергоемки . Поэтому их исп ользование оправдано только
тогда, когда к продукту предъsrвляют особые требования по его форме, составу,
массе, физико-химическим свойствам и возможности уп ако в ки . Основной по
требитель этих гр а нулятор ов - фармацевтическая промышленность, в меньшей
мере - бытовая химия, пищевая промышленность и производство катализато
ров. Конструкции этих аппаратов приведены в специальной литературе• .

1 9.2.3. Гранулирование кристаллизацией капель расплава

Процессы гранулирования кристаллизацией расплавов, ког
да стадии формования и структурирования гранул разделены в
пространстве и во вре м ени, проводят при непосредственном
контакте кристаллизую щихся гр анул с хладоагентом или на
охлаждаемых поверхностях.

При гранулировании • потtже иадоагента диспергирование расплава на
капли осуществляется с помощью специальных устройств - дисперrаторов, уста
навливаемых в верхней части гранулятора, если моmость расплава Р:а: больше
мотности хладоаrента Рх, и в нижней части - при Р:а: < Рх· Ре.жим диспергиро
вания бывает капельным, когда кaIVIИ расмава образуются сразу на выходе из
отверстий дисперrатора, и струйным, когда струя расплава распадается на капли
за счет воmюобразных колебаний ее поверхности, обусловленных шерохова
тостями кромки отверстий и други ми возмущающими воздействиями. Распад
струи происходит на некотором расстоянии от выхода из отверстий дисперrато
ра - в местах максимальных сужений, периодически повторяющихся по ее
длине. Именно в этих местах при разрыве струи неизбежно образуются мелкие
(и разною размера) капли - с путники . Для уменьшения полидисперсности на
поток расплава накладывают гармонические колебания с частотой, равной часто
те собственных колебаний струи. Наложенные колебания, резонируя с собствен
ными, способствуют разрыву струи на кaIVIИ одинакового размера.
Дисперrаторы по принципу действия делят на центробежные, статические и
ви браци онные .
Цеmробежн"1й дисперrатор (рис. 1 9 . 1 3,а) представляет собой вращающиеся с
частотой 3-10 об/с перфориро ванные конус или цилиндр (иногда с распредели
тельными или скребковыми устройствами внутри), в который подается расмав.
Под действием центр обежной силы (в меньшей степени - статическою напора)
струйки расплава вытекают из отверстий и дробятся на капли.
Отличительной чертой таких дисперrаторов является малый (не более 0 , 3)
коэффициент сжатия струи в отверстиях. Это обусловлено проскальзыванием
расплава над отверстиями перфорированной поверхности. В результате при
отверстиях относительно большого размера можно получать мелкие капли. С
• См. (4) .

1486

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

7!&
.

,......
,......
,......
, , 1 ,......
,� ...... /[

,,
,,

,,

/

а

б

в

г

а - цешробеJКНЫЙ полый коничесЮtй ( 1 - коничесЮIЙ перфорированный вращающий
ся корпус) ;
б - сrатичесЮtй леечный ( 1 - корпус, 2 - перфорированное эллиптическое днище);
е - вибрационный акусrичесЮtй (1 - корпус, 2 - перфорированное днище, З - вибри
рующий элемеш, 4 - сопло);
г - сrатичесЮtй трубчатый ( 1 - неподвижная труба, 2 - щелевое отверстие, З - пер
форированная вращающаяся цили1t11 рическая обечайка, 4 - охлаждаемая поверхносrь);
/ - исходный поток расплава, // - дисперrироваиный поток расплава

Рис. 19. 13. Схемы дисперrаторо о:

ростом окружной скорости эффект проскальзывания возрастает. Поэтому Д1lЯ
получения капель приблизительно одинаковоrо размера в конических дисперrа
торах (у них разная окружная скорость по высоте конуса) по мере увеличения
радиуса надо делать отверстия болъшеrо диаметра. Более равномерный rрануло
метрический состав капель дают цилиндрические оболочки, но они менее рав
номерно орошают сечение ап парата. Чтобы .жидкость не проскальзывала над
отверстиями, конусы (цили ндры) секционируют радиальными переrородками .
Для очистки отверстий в центробежных rрануляторах применяют неподвижно
закрепленные скребки. Для улучшения распределения расплава в дисперrаторе
используют неподвижно закр епленные распределительные каналы (переrо
родки). Достоинство дисперrатора заключается в возможности использования
e ro для разбрызrnвания суспензий и заrрязненных механическими примесями
расплавов. Основной недостаток - небольшая (0,02-0,05 кг/(м2·с)) и весьма
неравномерная плоmость орошения.
Указанный недостаток в меньшей мере выражен у ста111ческих (леечных)
дисперrаторов (р и с. 19. 1 3,6). Истечение расплава здесь происходит под действи
ем статическоrо напора столба .жидкости (и/или внешнеrо давления) . Однако
для этих дисперrаторов характерны сильная зависимость качества дисперrnрова
ния от величины статическоrо напора и чувствительность к механическим при
месям в .жидкости, а значит, необходимость ее предварительной фильтрации .
Оба рассмотренных дисперrатора дают неравномерный rранулометрический
состав продукта. Резко улучшить последний удается наложением на жидкость
резонансных (с собственной частотой колебаний струи) вибраций. Эта идея
реализуется в вибрационных дисперrаторах (р и с. 19. 1 3,в) . Причем для возбужде
ния колебаний на практике используют электродинамическое, механическое или
акустическое воздействие.
При rранулнровании кристаллизацией капель расплава но ОХАождоемых no
•epxнocm.tlX избе.жать появления капель-"спутников" можно, используя ротацнон
нwе ста111ческие rранул1ПОрь1 (рис. 19. 1 3 ,г) - с неподвижной трубой 1 и вра
щающейся перфорированной коаксиально расположенной цилиндрической
обечайкой 3. Окружная скорость движения отверстий последней равна скорости
движения охлаждаемой поверхности 4. Поэтому разрыв "шейки" капли происхо
дит над каплей, уже расположенной на охлаждаемой поверхности. Все капли
"спутники" при этом "втяrnваются" в каплю расплава, превращающуюся после
кристаллизации в rранулу.

1487

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Диаметр капель dк, образующихся при капельном режиме истечения, опре
деля ется по формуле (2 . 77б ) при Рж >> Pr· Подробно расчет процесса дисперги
рования истекающей из отверстия струи см . в разд.5.4.2.
При rранулировании кристаллизацией капель расплава на охлаждаемых по
верхностях используют известные (см. разд. 16.4.2) конструкции кристаллизато
ров (леIПОчные, валковые, дисковые). Иногда организуют дополнительный
контакr с хладоаrентом той части поверхности rранулы, которая соприкасается с
охлаждаемой поверхностью . Достоинство таких rрануляторов - экологическая
чистота процесса, недостаток
малая удельная производительность.
Аппараты для rранулирования при контакте капель расплава с хладоаrентом
можно разделить на колонные и емкостные.
Колоннwе аппараты наибоJ1ее распространены в промышленности; процесс
rранулирования в них происходит, как правило, в противотоке хладоаrента и
капель расплава (rранул). Эти аппараты по аrрегатному состоянию хладоаrента
классифицируют на rрануляторы с использованием:
- газообразного хладоаrента (обычно - воздуха) - rрануляционные башни;
- испаряющегося хладоаrента - аппараты с хладоаrеIПОм в виде потока испаряющейся газокапе.льной смеси (если последняя не представляет собой туман
типа воздух-вода, организуют замкнутый цикл с конденсацией испарившегося
хладоаrента и возвратом его в нроцесс);
- кипящего хладоаrента; обычно такие rрануляторы также работают в замк
нуrом цикле, обеспечивают высокие интенсивность теплообмена и удельную
производительность;
- жидкого хладоаrента - также аппараты с высокой удельной производи
тельностью .
Реже используют rрануляторы с хладоаrентом в виде псевдоо:жюкенного слоя
пылевидных частиц или возгоняющихся хлопьев (например , твердого диоксида
углерода с замкнутым циклом по СО2).
Грануляторы eмxocn1oro ти па обычно снабжены мешалкой и теплообменны
ми поверхностями (рубашки, змеевики) . В емкость заrру:жают хладоаrент, пода
ют rранулируемое вещество, причем на этой стадии температура хладоаrента
должна бьпь выше температуры кристалли зации rранулируемого вещества. Затем
с помощью мешалки получают эмульсию rранулируемого расплава в хладоаrенте
и при перемешивании охлаждают ее ниже температуры кристаллизации. Образо
вавшиеся в ходе процесса rранулы отделяют от хладоаrента.
При проектном расчете описанной вьпuе аппаратуры определяют габариты
rранулятора, обеспечивающие время пребывания в нем кристаллизующихся
rранул, требуемое для достижения степени кристалличн ости, которая исключала
бы деформацию rранул при ударе о дно аппарата или о псевдоожиженный слой
продукrа на нем, а также необходимую температуру продукrа на выходе из ап
парата.
Более подробно рассмотрим одну из конструкций rрануляционных башен •
(это наиболее широко применяемые и типичные rрануляторы данного класса) . В
верхней части башни (рис. 1 9 . 1 4) расположена напорная емкость для расплава
(на рисунке не показана) и дисперrирующие устройства 2 центробежного, стати
ческого или вибрационного типа. Капли расплава подают навстречу восходяще
му потоку воздуха, при этом о ни охлаждаются, кристаллизуются и переохлажда
ются ниже температуры кристатmизации . Воздух в башню засасывается вентиля
торами J, чаще всего устанамиваемыми на ее крыше. Воздушные выбросы /V из
башни подвергают очистке от пьти. Смягчения удара rранул (во избежание их
разрушения) и более rлубокоrо их охлаждения удалось достичь, располагая на
дне башни псевдоо:жюкенный слой rранул 4. Иноr;ца охладите.ль rранул с псев
доожиженным слоем продукrа выносят за пределы башни.
-

• Различные конструкции rрануляционных башен подробно описаны в (3 ).

1488

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

1

2

З - векrилиrор
4 - псевдооJКИ

Рис. 19. 14. Схема rрануляционной башни :
- корпус башЮ1,

- дисперrаторы,

жеЮIЫЙ слой rранул, 5 - rаэораспределительная решетка, 6
- устройсrво для перетока rранул, 7 - ленточный тран
спортер;
/ - rранулируемый расплав, // - rранулы, /// - исход
ный воздух, IV - отработанный воздух

для создания потока хладоаrенrа (11Оздуха) ,

о - с двюкущимся слоем rранул, 6 - с псевдооJКИ
женным слоем rранул ;
1 - корпус, 2 - распределительная насадка, З - ве!П'И
лятор, 4 - rаэораспределительная решетка, 5 - сито;
/ - rорячие rранулы, // - охлшкдеЮIЫе rранулы, /// исходный воздух, IV - отработанн ый запылеЮ1Ый и наrре
тый воздух, v - комки

Рис. 19. 15. Схемы охладителей 1ранул:

а

v

б

Используемые в настоящее время конструкции охладителей rранул можно
подразделить на две rруппы. В первой из них охлаждение происходит в проду
ваемом охлаждающим воздухо м пересыпающемся слое rранул (рис. 19. 1 5,а) . До 
стоинство таких охладителей - малые истираемость rранул и пылеунос, а также
отсуrствие термических циклов наrрев-охлаждение, наблюдаемых при переме
щении rранул по высоте псевдоожиженного слоя. Недостаток - сложность
конструкции и невысокая интенсивность охлаждения. К другой rруппе относят
ся разнообразные охладители с псевдоожиженным слоем продукта (рис. 19 . 1 5 , 6) .
В них очень интенсивен теплnобмен меЖ11у воздухом и rранулами, однако по
ВЬШ1ено истирание последних и мщуr иметь место термические циклы наrрев
охлаждение, а значит, вероятно растрескивание rранул и возникают проблемы с
улавливанием пы11и .
Аппараты для rранулирования кристаллизацией расплавов с совмещением
стадий формования и структурирования представляют собой описанные в разд.
19.2. 1 rрануляторы с формированием rранул окатыванием (барабаны, тарелки,
виброrрануляторы и т.д.). Кроме того, эдесь применяют также rранулирование в
псевдоожиженном и фонтанирующем слоях, коrда расплав дисперrируется фор
сунками на слой (в слой) растущих rранул. Основным недостатком подобного
рода аппаратуры является повышенное образование пыли. Избежать этого удает-

1489

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ся, охлцщая гранулы в выносных холодильниках (см., например, рис. 19. 1 5),
вводя их затем в гранулятор , работающий без подачи хладоагента, а отвод тепло
ты кристаллизации осуществляя за счет теплоаккумулирующих свойств ретура,
циркулирующего межцу холодильником и гранулятором.

1 9 .3. ГРАНУЛИРОВАНИЕ
МЕЛКОДИСПЕРСНЫХ МАТЕРИАЛОВ

Мелкодисперсные материалы (порошки) гранулируют ока
тыванием, агломерацией и п рессован ием .
Процесс гранулооб
разования порошков существенно зависит от их физико
механических свойств.
1 9.3. 1 . Физико-механические свойства дисперсных материалов

Рассмотрим наиболее важн ые свойства порошков,
опреде
•
ляющие эффективность процесса гранулирования .
Коэффициент внуrреннеrо трения fт' представляет собой ко
эффициент пропорциональности, устанавливающий связь меж
ду величиной касательн ых 'tт и нормальных Рн напряжений в
слое порошкообразного материала:
где

Ссц

'tт =

-

напряжени е сцеплен ия.

fт'Рн

+ Ссц ,

(а)

Увеличение fт' способствует интенсификации перемешива
ния и гранулообразования в порошках. При прочих равных
условиях fт' существенно зависит от концентрации связ,.УК>щего ,
причем эта зависимость носит экстремальный характер .
Сыпучесть характеризуется углом естествен ного откоса по
рошка �о ( с м . разд. 23 .2.3), а иногда рядом других параметров.
С ростом сыпучести повышаюrся скорость прессования порошка
на вальцевых прессах и качество прессовки. Увеличение сыпу
чести способствует повышению качества rранулообразования.
Смачиваемость порошка связующими характеризуют величи
ной угла смачивания ее. Различают три способа смачивания :
адсорбционное, пропиткой и растеканием по поверхности гра
нулы. С ростом смачиваемости эффективность гранулообразо
вания возрастает.
Диффузия связующего (часто - влаm) в частицах порошка и
в гранулах - ее интенсивность выражают эффективным коэф
фициентом диффузии D3• Эта характеристика определяет ди
намику увлажнения пористых дисперсных материалов связую
щим. С ростом Dэ интенсивность агломерации порошков пада
ет, а качество поверхности гранул растет.
• Более подробно см. (3, 4 ) .

1490

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Адrезионные свойства характеризуются нормальным напря
жением отрыва Рад двух приведенных во взаимодействие твер
дьrх поверхностей . Рост силы адгезии увеличивает интенсив
ность гранулообразован ия, однако затрудняет работу с мате
риалом из-за налипания ero на стенки аппаратов. При прочих
равных условиях Рад существенно зависит от концентрации
связующего, причем эта зависимость носит экстремальный
характер.
Пластическая прочность порошка выражает "сопротив
ляемость" сыпучей среды действию механической нагрузки и
измеряется глубиной по гружения стандартного конуса в иссле
дуемую среду под действием постоянной нагрузки. Данный
параметр тоже экстремально изменяется с влажностью. БОль
шая его величина приводит к получению прессовок более вы
сокого качества.
Разумеется, на процесс гранулирования оказывают влияние
также теплофизические параметры (теплопроводность, теп
лоемкость, теплоты превращения) связующего и гранулируе
мого материала.
1 9 .3.2. Материальные и тепловые балансы гранулятора

Процесс непрерывного гранулирования, как бьmо сказано
выше, часто проводят с использованием связующего в виде
раствора или расплава.
Для первого случая схема материальньrх и тепловых потоков
приведена на рис. 19. 1 6 , а. Исходный порошок с массовым рас
ходом Gn (в расчете на сухую массу), концентрацией в нем
связующего иu . теплоемкостью Сп (теплоемкость влажного ма
териала в расчете на сухую массу) и температурой !п поступает
в гранулятор . Туда же подается "внешний" ретур, полученный
при дроблении крупных гранул и возвращаемый на вход грану
лятора "внешними" транспортирующими устройствами, с соот
ветствующими параметрами Gp , и,Е, Ср , !р , а также мелкий
"вн утренний" ретур с параметрами (jрвнут, ur, cr, tr. В гранулятор
подается связующее с массовым расходом Gсв . теплоемкостью
Сев и температурой !св
оно может содержать в виде раствора
с
или суспензии гранулируемый продукт с параметрами Gп в , Сю
п
п
!св , Lж,р (где 4Р
теплота кристаллизации гранулируемого
продукта, растворенного в связующем). Из гранулятора выхо
дит гранулированный продукт с параметрами (после отбора
вн утреннего ретура) Gr, Ur, Cr, !r. Для удаления связующего
(сушки гранулируемого продукта) в гранулятор подают су
шильный агент
е го м ассовый расход L1 (в расчете на абсо
лютно сухой), влагосодержание по связующему Х{), температура
to, относительная энтальпия 10, относительная влажность q>o
(см . разд. 1 5 .2.2) и концентрация пылевидного гранулируемого
-

-

-

149 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

�-------....1 ,- - ----

Lj ,x0, t1 .11 , <р1
.
Q
<.

"

- - - -

�-- ---- .

:
:
1

1
--•

�·(�п lca+�p)

' Gclt' fta• t

- - - - ·

Ц. , ur , Cr , tr

1 .

i Lj ,x0,10 ,10 .<р�
.

с• !

"

L\,xo .t о .lо . Ч>о . а со
· - · - · - · - · -

б

/

/

х

х

в

г

Рис. 19. 16. Схемы материа11 ь ных и темовых потоков при rранулировании:
а

-

-

11ри использовании испаряющеrося с11яэующеrо,

зующеrося связующего, е

распыливающеrо с11язующее теплоносиrеля, г

1492

-

6-

изобрюкение процесса (б) в дИ

аrрамме

/-х

случае <Уrсуrствия

при испот.эоваюtи крисrалл и 
в

то же,дрli наличии последИеrо

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

aG0 Часть сушильного агента с параметрами L1 ", Хо " ,
<ро" , 10" может подаваться в форсунку для диспергирования

продукта
to" ,

•

связующего или растворенного в нем исходного гранулируе
мого продукта (либо суспензии) . Сушильный агент подогрева
ют в калорифере (или используют топочные rазы), где ему со
общается теплота Qк (см. разд. 15.2.2). После калорифера он
имеет параметры L1', .хо. t1 , 11 , <р 1 , а на выходе из гранулятора
LJ., х2 , t2, 12 , <р2, aG2 , где aG2 - концентрация в нем пыли
(гранулируемого материала) в расчете на абсолютно сухой су
шильный агент. Иногда по эколо гическим соображениям суш
ку осуществляют в замкнугом цикле (штрих-пунктирная ли
н ия). Тогда поток LJ. "осушают" конденсацией из него в холо
дильнике части паров связующего Gсв . отбирая теплоту Qко ·
Здесь происходит обеспыливание газового потока за счет, по
существу, его "мокрой" очистки; выделенный при этом раствор
(или суспензию) связующего можно возвратить в гранулятор .
Иногда в гранулятор в том или ином виде подают дополни
тельное количество теплоты Qc.
Огличительная черта схемы на рис . 19. 16,б - использование
в качестве связующего практически не испаряющегося кри
сталлизующегося расплава, при этом сушильный агент
(скажем, воздух) несет пары другого вещества (например, во
ды). Теплоту Qко от теплоносителя отбирают в холодильнике .
Иногда организуют дополнительный отвод теплоты из грануля
тора - Qc. Одним из способов увеличения количества отводи
мой теплоты является испарение впрыскиваемой в хладоагент
капельной влаги с пара метрами Gx, сх, rx, tx.
Материальные и тепловые балансы процесса гранулирова
ния записывают по общим правилам, изложенным в разд. 1 . 3 . 1 ,
- с вьщелением пространственного контура, фиксацией времен
ного интервала (для непрерьmных процессов - это единица вре
мени) и записью Приходов и Уходов ве щества или теплоты, а при
н аличии химических процессов - еще и Источников, Стоков
(Накопление для непрерьmных процессов равно нулю).
Материальный балан с по потоку целевого компонента без
учета связующего записывается для контура К (см. рис . 19. 16,а,
б) и единицы времени (процесс предполагается непрерывным) :

(19.1)
Gп + Gp + Li' aGo + Gпсв - Gr - LJ. aG2 = О .
И з уравнения (19.1) можно определить производительность
гранулятора по исходному порошку Gп или гранулируемому
продукту Gr.
Материальный баланс по потоку связующего для этого же
контура при игнорирОJ1ании переноса связующего с пьmью
имеет вид:
GpUp + Gп Uп + Gсв + L1'Xo + Li "Xo" - GrUr - LJ.x2 = О . (19.2)
1493

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Из уравнения ( 1 9.2) определяют расход связующего.
При сушке в замкнугом цикле, когда Li = L1' + L1 " и .хо" =
= .хо, количество конденсируемого связующего Gсв получается
из материального баланса по связующему для холодильника:
Lix2

- L1'Xo - L1"Xo - Gсв = О .
Тепловой баланс процесса с испарением связующего для конту

ра К (см. рис. 1 9 . 1 6,а) имеет вид:

Qк + L1' lo + GпСпtп
rде Qo
п ыль ю).

-

п
+ Gpcplp + GсвСсв lсв + Gпс8(Спlсв + Lкр ) +

потери темоты

( 19.3)
в окружающую среду ( вЮIЮчая перенос темоты

Пусть параметры воздуха после калорифера и подаваемого
на форсун ку близки, т.е. Хо = .хо"; t1 = to" ; 11 = 10" . В этом слу
чае, поделив почленно уравнение ( 1 9.3) на расход растворителя
/о), получим выражение, по су
Gсв и раскрыв Qк = L1'(/1
ществу совпадающее с известным уравнением простой реаль
ной сушилки (см. разд . 1 5 .3 .4):
-

L2
(б)
или

/2(/2 -

11 ) = gп сп tп + gpcp/p + gпс8 (Спlсв + LкрП) +
+ Ссвlсв + qc

- grCrtr

-

qo = Лq

·

( 19 .4)

Далее расчет по уравнению ( 1 9 .4) для системы воздух-вода
можно проводить с использованием диаграммы 1-х по мето
дике, принятой для процесса сушки (см. гл. 15).
Расход теплоты в конденсаторе определяется из теплового
баланса для него:
(в)
Qко = О ,
Lil2 - Lilo
откуда
( 1 9 .5)
Qко = LiU2 - lo) .
-

Материальный баланс по испаряющемуся в грануляторе ком
поненту х.ладоагента записывается в виде:
(r)
L1'Xo + L1 "Хо" + Gx Lix2 = О .
Для удельного (на 1 кг испаряющегося хладоагента) потока
абсолютно сухого воздуха /ц при Хо = .хо " (памятуя , что L1' +
-

1 494

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

+

L 1 11

=

L2) или при

L1 11

=

О из уравнения (г) получим:
Х2

1

-

Хо

(д)

Тепл о вой бала н с для кон тура К (с м . рис . 1 9 . 1 6 , 6) с кристалл и 
за ц ией связующего имеет вид:
св
Gпсп tп + Gpcp tp + L1'1o + L1 111011 + Gсв (Ссвlсв + Lк,р ) +
+ Gп свhпсв + GxCxlx - Grcrtr - � 12 - Qc - Qo = О , (19.6)

rде для суспензии исходного вещества в связующем hпсв
исходною вещества в связующем hпса Спfсв + Lq,n .
=

=

Cnfc8, для раствора

Тепловой баланс для удельных (на 1 кг испаряющегося хла
доагента) потоков запишем, поделив в уравнении (19.6) КЗJ1Щое
слагаемое на Gx и обозначив все удельные потоки малыми
(строчными) символами :
gпСпtп + gpcplp + 1210' + gсв ( Ссвlсв + Lк,рсв) +
(е)
+ gпсвhпсв + Cxtx - grertr - /2/2 - Qo - Qc = О
·

Огсюда

'2( 12 - 1о') = gпCntп + gpCp/p + gс8 (Ссвfсв + Lк,рсв) +

(19.7)
здесь 16 - усредненная относительная энтальпия входящего в
гранулятор влажного воздуха:
1'

о

-

�

1 1 1о
L{

+

L1"1о"
.
+ Li'

Далее расчет по уравнению ( 19.7) можно проводить с ис
пользованием диаграммы 1-х по методике, принятой для суш
ки . Приведем два примера такого расчета.
Для замкнутого по хладоагенту цикла и использования испари
тельного охлаждения построение процесса в диаграмме 1-х
представлено на рис. 19. 16,в при XQ " = XQ. На участке 0-2 про
исходит повышение температуры хладоагента в грануляторе за
счет отвода им теплоты кристаллизации связующего. Участок
2- 1 отвечает охлаждению хладоагента (воздуха) в холодильни
ке - конденсаторе, а участок 1-0 - конденсации там же части
хладоагента. Отводимая теплота рассчитывается аналоmчно
уравнению (19.5):

( 1 9.8)

В более общем случае параметры воздуха, подаваемого на
(точка 0 "), отличаются от параметров воздуха, пода-

фор сунку

1495

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ваемоrо в качестве хладоаrевта (точка О) - рис . 1 9 . 16,г. Стадия
смешения этих потоков в грануляторе изображается отрезком
0"-0. При отсутствии испарительною охлаждения линия,
изображающая изменен ие состояния хладоаrента в процессе
гранулирования, представляет собой вертикальную линию (Хо =
х2
const) .
=

=

1 9 .3.3. Кинетика и расчет гранулирования

окатыванием и аrломерацией

Кинетика образования зародышей и роста гранул
В процессе гранулообразования в порошках за счет обработ
ки связующим или воздействия дpyrnx факторов возникают
поверхностные силы, способные обеспечить слипание сталки
вающихся частиц, движущихся в условиях случайною распре
деления энерпш, подводимой извне в объем материала. Такой
процесс можно формально трактовать как фазовое превращение,
основанное на структурной перестройке дисперсной системы.
При этом за фазу с "неупорядоченным" строением принимает
ся исходный порошок, а за фазу с "упорядоченным" строением
- гранулы. Механическая энергия, рассеиваемая в объеме по
рошка и обеспечивающая присоединение частиц друr к друrу,
подводится рабочими органами грануляторов. В такой трактов
ке процесс гранулирования порошков, как и любой друrой
процесс фазовою превращения (кристалл изация, конденсация,
десублимация и др.), происходит за счет образования и роста
центров новой фазы . Отношение объема новой фазы - гранул
(Vr') - к объему исходной фазы - порошка (Vп) - называется
степенью превращения 1"\ = V 'r /vп ; в ходе гранулирования 1"\
изменяется от О до макс имальной величины 1"\max � 1 .
При гранулировании в порошках аrломерацией и окатыва
нием каждая гранула является результатом большою числа
актов присоединения-отрыва при взаимодействии частиц по
рошка и агрегатов (гранул) между собой. Гранулообразование в
этом случае является типичным случайным процессом, скорость
зародьпоеобразования w3 в котором по анало гии с классической
теорией кристаллизации (см. разд. 1 6 .2) трактуется как наибо
лее вероятное число центров гранулообразования M('t), возни
кающих в объеме "неупорядоченной" фазы (порошка) Vп в
единицу времени 't:
1 dM('t)
( 1 9. 8)
_
}Уз = _
vп
d't
Друrой кинетической характеристикой процесса является
(см. разд. 1 6 .2) линейная скорость роста гранул Vл. Ее можно
выразить через изменение во времени объема гранулы Vr , по1496

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

стоянную, зависящую от формы гранулы р, и параметр роста
агрегата п:
/n
1 dVrl
( 1 9 .9)
Vл =
l/п
d't
p

Для шара р = 4/3 7t; для куба р = 8 ; для диска толщиной 8
р = 7t8; для "иглы" сечением s р = 2s и т.д. ; п = З - для трех

мерного роста гранулы, п = 2 для двухмерного и п = 1 - для
одномерного.
Согласно ( 1 9.9) объем растущей гранулы к моменту оконча
ния процесса 'tк определяется выражением:
( 1 9 . 1 0)
Поскольку скорость зарождения центров гранулообразова
н ия конечна, то появлению первого центра предшествует ин
дукционный период 'tинд, величина которого определяется инте
гральным соотношением, связанным с ( 1 9.8):

При подстановке

w3

1иид
Уп f w3 d't = 1 .
о

( 1 9. 1 1 )

по ( 1 9.8) получается, что
1 инд
f d M('t)
о

=

1,

т.е. з а время 'tинд зарождается один (первый) центр гранулооб
разования . В случае w3 = const
1
( 1 9 . l l a)
'tинд =
.
Уп w з
Для практического использования кинетических зависимо
стей гранулообразования необходимы данные о скоростях за
рождения и роста гранул .
Вероятность P( k, 1) возникновения з а время 1 числа k ценrров rранулообра
зования следует распределению Пуассона:
P( k, 1)

=

r Mf "\

�)l k"' ехр (-М(1)] ,

(ж)

хорошо описывающему случайные процессы, у которых вероятность самого
собьпия мала, а число актов, в результате которых оно наступает, велико·. Это
• См. ( 1 ) .

1497

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

вполне отвечает механизму процесса зарождения центров гранулообразования в
порошках, описанному выше.
ВероЯ111ость образования одноrо и более центров превращения (k � l );т.е. 1
- Р(О, 't), выражается зависимостью, полученной из (ж) при k = О:

P(k, t) =

1

-

-

(з)

exp [-M('t)) .

Эта вероЯ111 остъ может бьrrь экспериментально определена по данным о числе
опьrrов n('t), в которых ко времени t гранулирование началось, оmесенным к
общему числу опьrrов ni; (плюс 1, как это принято в теории вероЯ111остей0):
n('t)
P(k, t) = 1 =
ni; +
-

1

-

1

exp [-M('t) ), k � .

(и)

Выражая M(t) из уравнения (и) и подставляя ero в ( 1 9.8), получаем зависи
мость для расчета скорости зарождения гранул w3 по фиксируемым в экспери
ментах моментам появления первой гранулы в объеме порошка (с набором
соответствующей статистики: ni; " 20+50 опьrrов):

Wз

=

1

Yn

d{1n[1 - �J}
dt

(к)

Переходя в уравнении (к) от бесконечно малых к конечным приращениям л,
перепишем (к) в виде:
n( t )
1 л
ni; +l
( 1 9 12)
W3 =
Yn
Лt

1 n[ 1 -

]

.

Скорость зарождения центров rранулообразовавия существен 
но зависит от технологических параметров процесса. Так, эта
скорость возрастает с ростом концентрации связующего,
уменьшением эквивалентного диаметра частиц порошка, экс
тремально зависит от скорости движения рабочего органа гра
нулятора и слабо - от типа гранулятора и массы загрузки (при
обеспечении хорошего перемешивания порошка и равномерно
сти подведения энергии к этой массе) . Иными словами: все,
что способствует превышению вероятности присоединения
частиц порошка над вероятностью их отрыва от агрегата, уве
личивает частоту и э ф феJСГивность нуклеации частиц порошка
в гранулируемом слое и приводит к росту скорости зарождения
центров гранулообразования .
Линейная скорость роста rранул зависит от режима гранули
рования и свойств гранулируемого материала. Продолжая
пользоваться формальной аналогией между процессами грану
лообразования в порошках и кристаллизации , напомним, что в
последнем случае известны (см. разд. 1 6 .2) три основных меха
низма роста кристаллов - нормальный, послойный, а также
дислокационный (последний здесь не рассматривается) .
Нормальный рост хараJСГеризуется равновероятным присоеди
нением элементарных "кирпичиков" роста (кластеров при кри-

1498

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

сталлизации и частиц порошка при гранулировании) к любой
точке растущей поверхности. При гранулировании порошков
такой механизм роста гранул с наибольшей вероятностью реа
лизуется в грануляторах с псевдоожиженным слоем без органи
зации направленного движения дисперсной фазы. Косвенным
свидетельством этого является образование в таких аппаратах
гранул, по форме напоминающих плоды малины. Иными сло
вами, такой механизм роста гранул реализуется при гранулиро
вании порошков агломерацией.
Причиной нормального механизма роста является высокая
вероятность присоединения части ц порошка к грануле и низ
кая - их отрыва. При этом частичка порошка присоединяется
к любой точке поверхности гранулы, с которой она столкну
лась. Скорость роста гранулы в этом случае максимальна, а
поверхность гранулы - шероховата. Прочность агрегатов дале
ка от максимальной, а товарный вид оставляет желать лучшего .
Его улучшают, используя полировочные барабаны и тарельча
тые грануляторы.
Послойный рост характеризуется последовательны.ми актами
присоединения друг к другу "кирпичиков" роста с приращени
ем линейного размера гранулы или кристалла . При гранулиро
вании порошков такой механизм роста обычно наблюдается в
режиме окатывания гр анул . Косвенным свидетельством его
реализации служит образование в этом режиме округлых гра
нул с достаточно гладкой поверхностью.
Послойный рост гранул, как правило, имеет место, когда
вероятность присоединения частиц порошка, из которых стро
ится поверхность гранулы, хотя и превышает вероятность и х
отрыва, однако в общем соизмерима с ней. В результате по
верхность гранулы образуется за счет цепи элементарных актов
присоединения-отрыва кирпичиков роста, когда каждый кир
пичик ищет наиболее выгодное (в аспекте малой вероятности
его отрыва) место, иными словами, - такое, где поверхность
его контакта с гранью гранулы максимальна. У гранулы
(кристалла), растущей по такому механизму, это - выступы
растущей грани . Подобный механизм роста граней кристаллов
хорошо изучен в теории кристаллизации и имеет достоверное
математическое описание (см. разд. 1 6.2). Самая медленная ста
дия при таком механизме роста - появление двухмерного за
родыша нового слоя на гладкой поверхности выросшего слоя .
В этом случае линейная скорость роста пропорциональна ско 
рости двухмерного "гетерогенного" зародышеобразования .
Прочность получаемых агрегатов здесь близка к максимально
возможной для данных вещества и связующего. Л инейную ско
рость роста гранул устанавливают экспериментально .
Линейная скорость роста гранул наряду со скоростью их за
рождения определяет нс только качество гранулируемого про1 499

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

дукга, но и удельную производительность гранулятора. Соот
ветствующая кривая зависимости степени превращения от вре
мени Т\ = ft..т.к) по внешнему виду напоминает изопотенциаль
ные кривые - объемной изотермической кристалл изации , изо
термического полиморфного превращения, изобарической де
сублимации (см. разд. 1 6 . 3 .4 и 1 8 .3), описываемые уравнением
типа Колмогорова-Авраами.
Отметим характерную особенность гранулирования порош
ков: максимально возможная степень превращения здесь может
быть меньше единицы . Дело в том, что при определенной сте
пени превращения достигается динамическое равновесие в
актах присоединения частиц к грануле и отрыва их от нее, сле
довательно, равновесие между количествами гранул и порошка.
Линейная скорость роста гранул зависит от техноло гич еских
параметров гранулирования. Она повышается с увеличением
кон центрации связующего и эквивалентного диаметра частиц
порошка, экстремально зависит от скорости движения рабочего
органа гранулятора. Иными словами, факторы, повышающие
частоту и эффективность "нуклеации" частиц порошка, приво
дят к увеличению линейной скорости роста гранул.

Расчет процесса гранулирования
Пусть гранулирование происходит в изотропных по объему
гранулятора условиях, например при постоянной концентра
ции связующего в объеме исходного порошка и равномерной
интенсивности перемешивания . Тогда динамика превращения
порошка в гранулы может быть описана по анало гии с изопо
тенциальным объемным фазовым превращением (например,
изотермической объемной кристалл изацией - см. разд . 1 6 .3).
Процесс гранулирования по аналогии с процессом объемной
кристалл изации (см. разд. 1 6 .2) проводят при самопроизволь
ном (rомогенном) зарождении центров гранулообразования в
объеме порошка в ходе гранулирования либо с введением ис
ходных центров гранулообразования - затравки,
на которых
происходит дальнейший рост гранул, или же при сочетании
этих эффектов. В первом случае , разумеется, получают наибо
лее равномерный гранулометрический состав, во втором наибольшую полидисперсность гранулированного продукга.
Первоначально рассмотрим процесс гранулообразования без
введенШI. в исходный порошок центров гранулообразоваНШI.. Здесь
бесконечно малое приращение количества гранул, образую
щихся за время dт.' в остающемся к моменту времени т. объеме
порошка Vп - Vr', равно dNr = w3(Vп - Vr')dт.' . Объем гранулы
данной фракции, образовавшейся при ее росте от текущего
момента ее появления т.' до окончания процесса гранулирова-

1 500

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

н ия 'tк, в соответствии с

(19. 10) равен:
·
V, � р vл(<)d•

[!. J

Тогда бесконечно малое изменение объема dVr всех dNr rра
нул, образовавшихся за промежугок времени d't', можно пред
ставить в виде произведения dNr на Vr:

dV,'

�

V,dN,

�

р

[!. J
vл(<)d•

w,

(Vп - V,')d< .

(19. 13)

Поделив обе части уравнения (19. 13) н а Vп, получим прира
щение степени превращения за время dt':
dч

��

[!. ]"
vл (<)d•

w,[ 1- ч(<)]d<

(19.14)

.

Степен ь превращения определяется после интеrрирования
от момента появления первого центра rранулообразова
ния 'tинд до момента окончания процесса 'tк:

(19.14)

(19. 1 5)
При больших степенях превращения увеличивающиеся в
размерах rранулы моrут влиять на взаимный рост (аналог объ
емной кристаллизации при больших степенях превращения см. разд. 1 6.2). При этом скорость Vл максимальна при нестес
ненном превращении; с ростом 'У\ она чаще всего п адает.
На начальной стадии превращения (обычно при 'У\ � 0,2)
р астущие rранулы еще не влияют на рост друг друга. В таких
условиях величины w3, vл, � можно считать постоянными. Это
позволяет выразить аналитически некоторые интеrралы в урав
нении (19. 15):

{ [(

Т'\('tк) = р Vлп W з

't

К

·'tинд

n+l

-

\n+l
.

�
-

! 'Y\('t')('t к - 't') d't'
к

� нд

п

]}

.(19.16)

Заметим, что при р, vл, w3 = const и 'tинд --.. О интеrрирование
зависимости (19. 14) приводит к уравнению Колмогорова
Авраами :
(л)

1501

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

отсюда
11 = 1

- (ехр

А
..,

1

п + w з vлn
1

'tn+1)
к

.

(19.17)

Это выражение широко используется для описания , например,
изотермической объемной кристалл и зации (см. разд . 16.2 ) .
При "стесненном" гранулировании (когда 11 > 0,2) скорости
зарожден ия и роста центров гранулообразования переменны.
Тогда уравнение (19.15) решают численно.
Ч асто центры гранулообразованил вносят в исходный поро
шок извне перед началом гранулирования. Число этих центров
N, отнесенное к объему порошка Уп, именуют их удельным
количеством :
N
Nуд = у ·
п

(м)

Н азовем отношение общего объема центров гранулообразо
вания VР• представляющих собой частицы мелкого ретура, к
объему порошка Vп коэффициентом рециркуляции R. Тогда,
учитывая, что объем одного центра гранулообразования,
имеющего линейный раз мер r, р авен р r п , получим связь между
R и Nуд:
V
Nprn
R = P = -- =NyдPr".
(19.18)
Vп
Уп

-

Коэффициент рециркуляции R может задаваться либо он
определяется режимом гранулирования и его аппаратурным
оформлением.
В отличие от описанного выше безреrурвоrо процесса рас
сматриваемый процесс гранулирования называется реrурньIМ и
является аналогом гетерогенной объемной кристаллизации (см.
разд.16.2) .
В ретурном процессе образовавшийся к данному моменту
времени 'tк объем гранулированного продукта Vr"'('tк) склады
вается из объема Vr" ( к ) гранул, выросших на частицах ретура

't

Vr"(tк)

( Tvл('t')d'tJn,

= УпNудР r +

(н)

Vr'(tк) гранул, обр азовавшихся за счет "гомогенного"
зарождения центров rранулообраз ования в порошке . Таким
и объема

образом :

Объем

Vr"'('tк)
вносимых

=

Уг'('tк) + Уг"('tк) .

центров

rран улообразования

(о)
равен

УпNудР r"; уменьшающийся в ходе гранулирования объем
1502

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

остающегося порошка опр еделя етс я выраже нием Уп - [Yr"'('t')

-

Тогда объем Уг' (tк) , если следовать канве вывода
выражений ( 1 9 . 1 3)-( 1 9 . 1 5), может быть описан формулой:

- УпNудрrп].
У,' (<.) =

.L {!.

vл (')d'

Г

w,

(v - [v;· (<' ) - Vп NyдPr" ]J d,' ,(n)
л

или с учетом ( 1 9 . 1 8):

V,'('x) =

.L Р[!.

{

vл (<)d

w,

{v.- [V;'(,') - V п RJ} d'' .

(р)

Очевцдно, что степень превращения порошка в гранулы в этом
случае не должна включать объем исходных частиц ретура УпR:
_

'll ('tк) -

УГ'('tк) - УпR
Vп

=

УГ'('tк) - УпNудРrп
Vп

.

(с)

Если в выражение (с) для степени превращения к моменту
времени 'tк для ретурноrо процесса подставить Yr"'('tк) по (о) и
использовать выражения (н) и (п), то получим более общее
соотношение:

"('><) = NудР

{[r ! ]" r•}
+

Vл (')d'

-

+

( 1 9 . 1 9)
Выражение ( 1 9 . 1 9) при отсугствии ретура (Nуд = О) перехо
дит в уравнение ( 1 9 . 1 5) для безретурноrо гранулирования и в
последующие более простые зависимости ( 1 9 . 1 6) , (19. 1 7) . Если
же гранулирование цдет только на частицах затравки, получае
мой из ретура, а зародышеобразование в объеме порошка в
ходе процесса исключено, то можно полагать w3 = О, и в пра
вой части выражения ( 1 9 . 1 9) останется лишь первое слагаемое.
Такой режим гранулирования часто применяют для уменьше
ния полцдисперсности продукта. Уравнение ( 1 9 . 19), как и
уравнение ( 1 9 . 1 5), позволяет рассчитать не только динамику
изменения во времени степени превращения, но и грануломет
рический состав продукта.
Представленное математическое описание процесса грану
лирования игнорирует процессы агломерации и раскалывания
агрегатов. Это допустимо, когда в процессах гранулирования
режим удается подобрать так, чтобы исключить эти явления; в
противном случае образуются гранулы неправильной формы.
1 503

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

19.3.4. Расчет rравулирования прессованием

В процессе гранулирования порошков прессованием (см .
рис . 1 9 . 1 2) и х кажушаяся плотность изменяется о т насыпной Рн
в питающем бункере аппарата до плотности плитки (ленты) Рл
на выходе из пресса (перед поступлением в дробилку) . По мере
движения порошка в сужающемся зазоре между валками дав
ление в прессуемом материале возрастает до максимального
значения, определяющего в основном качество гранулирован
ного материала.
Механизм уплотнения порошков в валковом прессе изучен
недостаточно; математ�;�еское описание тех или иных его мо
дельных представлении весьма громоздко. М ожно лишь счи
тать установленным, что плотность ленты Рл прямо пропор
циональна плотности материала порошка Pr и насыпной плот
ности Рн; кроме того, она зависит от гранулометрического со
става порошка (существует состав, обусловливающий макси
мальную Рл) и я вляетс я сложной функцией crc
среднего
нормального напряжения в слое: Рл = Pнf{crc). Если порозность
слоя исходного порошка равна s0, а пористость плитки е0, то из
приведенного в разд. 2.7. 1 соотношения Рн = Pr(l
so) и ана
ло гичного ему Рл = Pr( l
ео) получается (п утем приравнивания
и исключения Pr) зависимость:
-

-

-

Pr

=

--1:!!_
1

-

s0

=

_Ед_ .
1

-

(т)

е0

Величина s0 обычно известна, так что выражение (т) фактиче
ски однозначно устанавливает соотношение между Рл и ео.
Производительность гранулятора Gr при прочих равных
условиях зависит от скорости вращения валков и может изме
няться в пределах от максимально возможной Grmax до мини
мальной Grrnin ( Grrnin < Gr < Grmax) . Если длина валков Ь, шири
на зазора между ними 2е, то при отсуrствии проскальзывания
плитки относительно валка на выходе из гранулятора линейная
скорость и8 движения поверхности валка радиусом R связана с
массовой производительностью гранулятора Gr уравнением
расхода:
( 1 9 .20)

В свою очередь, и8 = 01R = R ·21tn, где п
частота вращения
валков, об с.
.
Минимальная производительность гранулятора Gr'nm опре
деляется условием просыпания порошка из бункера аппарата
через зазор между неподвижными валками площадью Ь·2е. Удель
ный массовый расход порошка gп в этом случае является непрос-

/

• См. (2 ).

1 504

-

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис.19.17. Расче'Пlая схема валкового пресса

той функцией критерия Ar, пrnрины зазора
ме:жду валками 2е, уrла <р, образованною
стенками бункера и валками, соотношения
пrnрины зазора и диаметра drr. частиц по
рошка
(у)
8п = / (Ar, 2е, <р,

2e/d0:

2e/d0)

.

С учетом изложенного производитель
ность Gr min равна:
Grmin = b ·2e·gпmin .
Непрерывное уплотнение порошка ( е0 < Ео) на валковых
прессах вызывает интенсивное "выдавливание" газа из просве
тов ме)!Щу частицами и его фильтрацию в слой порошка, за
полняющего зазор между валками , в направлении, противопо
ложном движению порошка. Таким образом, возникает рас
смотренная в разд. 2.7 проблема течения сплошной среды
(газа) через слой дисперсного материала. До определенных
пределов увеличение скорости потока газа полезно, так как
при этом разрушается свод, образующийся в бункере аппарата
при истечении порошка. Однако при больших встречных пото
ках газа истечение порошка в зазор ме)!Щу валками может во
обще прекратиться. Поэтому существует критическая скорость
фильтрации газа через слой порошка, ограничивающая произ
водительность гранулятора Grmax . В самом деле, при весьма
высоких скоростях прессования пороiuков в канале ме)!Щу вал
ками (в зоне уплотнения) материал может переходить в псев
доожиженное состояние, хотя выше он находится в неподвиж
ном состоянии. Максимальную производительность гранулято
ра оценивают по скорости начала псевдоожижения в зоне
уплотнения между валками.
В дальнейших рассуждениях примем, что зазор узла "валки
бункерное устройство" (см. рис. 1 9 . 1 1) имеет форму, изобра
женную на рис. 1 9.17.
Для расчета максимальной производительности необходимо
определить скорость начала псевдоожижения w0 на границе
валки-стенки бункера на радиусе r (см. разд.
Объемный
расход газа Vr, "выдавливаемого" при прессовании с макси
мальной скоростью (при u 8 = u8max), определяется из условия
постоянства массовою расхода твердой фазы. Объемный рас
ход порошка, подаваемою на прессование, складывается из
объемного расхода выдавливаемого из него газа Vr и объемного
расхода спрессованного материала, проходящего через щель
между вращающимися валками, который в условиях отсуrствия
проскальзывания материала относительно валков равен

(19.21)

2.7.4).

1 505

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

2ebиumax.. Если сумму этих расходов умножить на Рн, то получим
массовый расход твердой фазы, который, с другой стороны,
равен 2еЬи8mахрл:
( Уг + 2еЬи5mах)Рн = 2еЬивmах.Рл ,
откуда
Vr =

В то же время

-

Е е о 2еЬи5mах. .
1 2еЬи8mах = о
:
Ео
( )
1 _

Р
р

Vr

(ф)

-
d

= wo·2eb = Reo 2еЬv

где d
диаметр частиц порошка, а Reo - критерий Рейнольдса для 'скорости
начала ero псевдоо:жюкения.

Тогда максимально допустимая линейная скорость движе
ния поверхности валка и8mах. равна

и8лшх =

Reo

�

(Рл/Рн-l)d'

(19.22)

а максимал ьная производительность пресса Grmax по гранули
рованному продукту определяется уравнением расхода:

(19.23)
Проведенный анализ позволяет сделать ряд прапически
выводов:
- для увеличения массовой производительности пресса сле
дует увеличивать Рн, т.е. производить "подпрессовку" шихты,
поступающей на валки;
- в тех же целях (во избежание выдувания мелких фракций)
на прессование должна поступать шихта по возможности более
крупного гранулометрического состава, близкого к монодис
персному;
- из бункера с порошком целесообразно организовать эва
куацию газа (вакуумирование) .
На качество прессуемых продУIСГОВ решающее влияние ока
зывают: давление прессования, время выдержки прессовок,
температура прессования. Изменение прочности и плотности
прессовок с повышением давления прессовавИJ1 хараперизуется
восходящей кривой. С ростом времени выдер1КК11 прессовок их
прочность возрастает за счет явлений перекристаллизации; со
ответствующие зависимости также хара:�сrеризуются восходя
щими кривыми. С увеличением температуры прессования
прочность прессовок возрастает быстрее их плотности, так как
с увеличением температуры особенно интенсивно протекают
процессы перекристаллизации (см. разд . 16.2) и формирование
твердофазных, а иногда и жидкофазных мостиков - в резульважн ых

1506

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

тате плавления вещества в областях концентрации механиче
ских напряжений. Существенное влияние на качество прессо
вок оказывает ковце1Прация связующего: с ее ростом прочность
прессовок и производительность пресса проходят через макси
мум . Часть порошка просыпается (особенно при сухом прессо
вании) между валками, не успевая превратиться в прессовки ,
либо образуется за счет их истирания при дроблении. Этот
порошок называют просыпью .
Приведен н ые выше выражения для производительности
валкового пресса непрерывного действия описывают массовый
расход проходящего через пресс .материала Gr1nin < Gr < Grmax.
Производительность
же по прессованному прод укrу Gr'
харакrеризуется, как уже отмечалось ранее, величиной Gr и
степенью превращения исходного порошка 11, которая даже
при "сухом" прессовании обычно не менее 90 % :

Gг'

= 11 Gr .

( 1 9 .24)
Выход же товарного гранулированного продукrа G? зависит
от требований к его гранулометрическому составу и условий
работы узла дробления прессовок. Прессованный продукт, не
удовлетворяющий требованиям товарной фракции, вместе с
просыпъю возвращается в процесс в качестве внешнего ретура
Gp: G? = Gг' - Gp.
19.3.5. Расчет rравулирования формованием

Гранулирование формованием реализуется на пракrике в
процессах экструзии
продавливания материала через круглые
или профилированные отверстия (фильеры) в рабочей поверх
ности (матрице), формования на профилированных валках и
таблегирования.
Плунжерные экструдеры используют обычно для формования
пластичных материалов. К недостаткам аппаратов этого типа
относятся периодичность работы и необходимость очистки
рабочих поверхностей перед новой загрузкой .
Если рабочая площадь матрицы с отверстиями, через кото
рые продавливается материал, равна F, средняя скорость тече
v , а доля поверх
ния гранулируемого материала в фильерах
ности матрицы, занятая отверстиями,
'V, то производительн ость
экструдера из уравнения массовоrо расхода составляет:
-

-

-

Gr = FЧJ v Рл .

( 1 9.25)
Конструктивными параметрами матрицы являются удельное
(на 1 м 2 ее площади) количество отверстий пуд и диаметр от
верстий do. Очевидно, 'V = ттd02пуд/4. На практике толщина
матрицы больше диаметра отверстий . Формуемые продукты
обычно являются сплошными средами, для которых длина
1 507

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

участка гидродинамической стабилизации не превышает /� :::::
z d0. При этом условии среднюю ско рость течения среды в кана
лах можно рассчитывать по уравнениям , полученным в разд .
2.5 для течения неньютоновских жидкостей по трубам.
Производительность роторных экструдеров (см. рис . 1 9 . 12)
определяется уравнением, аналогичным ( 1 9 .25):

Gr =

F'+''+'' V Р л

,

( 1 9 .26)

где ljl' - доля площади матрицы, nо крьпой продавливаемым через отверстие
материалом.

19.4. ГРАНУЛИРОВАНИЕ PACIUIAВOB

Среди процессов гранулирования расплавов выделяют сле
дующие:
- с раздельно (в пространстве и времени) протекающими
стадиями формования и структурирования (кристаллизация
капель расплавов при непосредственном контакте с хладоаrен
тами или на охлаждаемых поверхностях);
- с одновременно протекающими стадиями формования и
структурирования (кристаллизация мелких капель расплава,
растекающихся по поверхности растущих гранул);
- процессы, совмещающие оба варианта (в них мелкий ретур
образуется за счет кристалли зации капель расплава, а затем
полученные мелкие гранулы наращиваются дисперmрованием
на них расплава) .
При контакте гранулированного материала с хладоаrентом
обеспечиваются высокая производительность и интенсивность
процесса, при контакте с охлаждаемыми поверхностями экологическая чистота.
19.4. 1 . Материальные и тепловые балансы rранулятора

В гранулятор 1 (рис. 1 9.1 8) поступает массовый поток рас
плава Gp с температурой tp, теплоемкостью ер и энтапъпией hp. В
общем случае охлаждаемый расплав кристаллизуется при темпера
туре /хр, отдавая теплоту перегрева cp(fp - fкр) и теплоту кристал.ли 
защm Lк,р. Поэтому энтал ьпия исходного расплава hp равна:

hp = Cp(tp -

fк )
р

+ Lк,р +

Ск fкр

.

(а)

На выходе из гранулятора массовый расход гранул Gr < Gp,
так как часть продукта уносится с потоком хладоаrента Gx в
виде пылевидных частиц, относительная (на 1 кг абсолютно
сухого хладоаrента) кон центрация которых в выходящем
потоке составляет ак п . Энтальпия гранулированного про1 508

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 19. 18. Схема материальных и теruювых потоков при rранулировании из
расплавов в случае неизменного arperarnoro состояния хладоагента:
1
rранулятор, 2 ПЬVJсосадительное усrройсrво, 3 холодильюrх
-

дукта

-

-

hr равна:
(б)

Здесь YJ( - средняя температура потока гранул на выходе из
гранулятора. Она определяется при решении задачи о динами
ке кристалли зации и охлаждения гранул в аппарате.
Используемый в качестве хладоагента массовый поток Gx в
ходе процесса не может изменять своего агрегатного состоя
ния. Поэтому его энтальпия на выходе из аппарата при темпе
ратуре � равна hхк = Сх 7х , где Сх - теплоемкость хладоаrента.
При изменении агрегатного состояния хладоагента (например,
при его юtпении), полагая массовый расход испарившегося
хладоагента ЛGх, а теплоту испарения rx, энтальпию хладоаген
та на выходе из аппарата можно представить в виде

hк
х

-

Cxlюm +

ЛGх
Гх.
Gx

--

Наконец, возможно в качестве хладоагента использовать
частично испаряющийся газокапельный поток. Пусть расход
испаряющейся жидкости - ЛGж, теплота ее испарения - rж., а
теплоемкости газообразной и жидкой составляющих - Сх и еж
соответственно. Здесь при абсолютной исходной массовой
концентрации жидкости в потоке аж энтальпия хладоаrента на
выходе из аппарата равна:

hхк = [cx(l

-

- ЛGж
аж) + Сжаж.] l x + ---а- Гж·
х

Схема гранулирования может быть замкнута по хладоагенту;
тогда после узла пьmеочистки 2, где в единицу времени улав1 509

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ливается массовое количество пьши Gхапк, необходимо пред
усмотреть узел охлаждения хладоагента 3, а возможно - и
конденсации испарившейся его части Л Gх . В этом случае в хо
лодильнике отводится теплота Q0хл = Gx ( hxк - hхн), где hхн энтальпия хладоагента н а входе в гранулятор. При разомкнутой
по хладоагенту схеме предусматривают лишь узел пьшеочистки .
Материальный баланс непрерывно действующей установки
по гранулируемому веществу (контур К на рис. 1 9 . 1 8) при от
сутствии его Источников, Стоков и Накопления, а также вве
дения пьшевидного продукта с хладоагентом имеет вид:

Gp - Gr

-

Gх апк = О .

( 1 9 .27)

Уравнение ( 1 9 .27) позволяет определить массовый расход гра
нулируемого продукта Gr при эксплуатационной постановке
задачи или расход расплава Gp - при проектной.
Тепловой баланс гранулятора для того же контура К составим,
полаrая, что уносимая пьmь принимает температуру хладоагента
на выходе из аппарата У,,_ и имеет энталыrnю hr,x = Cxfx:

Gphp + Gxhxн - Grhг - Gxhxк - Gxaпкhr,x = О .
( 1 9 .28)
Из уравнения (19.28) определяюr энтальmпо hхк, а следователь

но, и температуру хладоагента

tx на выходе из гранулятора.

19.4.2. Кинетика кристаллизации капель расплава
Капли расплава превращаюгся в гранулы в результате весьма
сложного процесса их кристаллизации. Поэтому его приходится
анализировать при существенных упрощающих допущениях:
- капли имеют форму сферы;
- условия теплообмена неизменны по поверхности гранулы;
- температура хладоагента изменяется только по высоте armapaтa (в поперечном сечении хладоаrент идеально перемешан);
- процесс кристаллизации в капле происходит за счет по
следовательного перемещения вглубь последней четкой сфери
ческой межфазной границы "расплав-кристаллы";
- циркуляция расплава в формирующейся грануле отсут
ствует, так что перенос тепла в фазах является кондуктивным;
- термическая усадка гранулы за счет изменения плотности
с температурой игнорируется;
- теплота полиморфных превращений (см. разд . 1 6. 1) игно
рируется;
- из-за разности плотностей расплава Рж и кристалл и ческой
фазы Рк (при Рк > Рж) в центре гранулы на самом деле образу
ется усадочная полость и возникает кон вективный поток теп
лоты, переносимый "натекающим" на межфазную границу рас
плавом; эти явлен ия также игнорируются.

1510

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Напомним , что теплота кри сталлизации, приводимая в справочной литераrу 
ре и определяемая экспериментально, включает в себя тепло rу , возникаю щую
при фазовом превращении за счет различия теплоемкостей расплава и кристал
лической фазы ( еж и с" соответственно) .

Приняты е допущения наиболее близки к условиям процесса
кристалли зации капель расплава в потоке хладоагента. При кри
сталлизации же на охлаждаемых поверmостях капли расплава те
ряюr сферическую форму, приобретая чечевицеобразную; кроме
того, здесь ярко выражена неравномерность интенсивности
охлаждения по поверхности капли. Эrо делает задачу многомер
ной и еще более усложняет ее строl)'Ю формулировку и решение.
С учетом изложенных упрощающих допущений рассмотрим
для простоты процесс кристаллизации одиночной капли расплава
внешним радиусом �. движущейся с потоком аналогичных ка
пель противотоком к хладоаrенту. Огсчет времени 't
О начнем с
момента вылета капли из отверстия диспергатора. В этот момент
кристаллическая фаза в капле отсугствует, а расплав переrрет до
температуры !ж,н >
причем температура кристаллизации
неизменна по всей радиальной координате капли: О s; s; �·
При противотоке капель и хладоагента последний с началь
ной температурой tnt подается в колонный аппарат высотой Н,
которую условимся отсчитывать сверху - от диспергатора:
tx(Jf) tnt. На этой основе сформулируем начальные условия
математического описания процесса:
(в)
О) =
О s; s; Rr;
1юt
При падении в потоке хладоаrента капля расплава охлаждается
с поверхности. При температуропроводности расплава аж для
симметричного нестационарного теплопереноса в сферической
системе координат справедливо выражение (см. разд. 1.6.2):

=

fкр.

r

r

fкр

=

t(r,

tжн;

r

tx(lf) = .

дt(r,'t) aж[д2t(r,'t) +� дt(r,'t)]
дr2 r дr ·
дt

(r)

=

Наконец, температура расплава на поверхности капли ста
новится равной, а затем и ниже температуры кристаллизации:
t(Rr, 't) s;
Здесь появляется возможность зарождения кри
сталлической фазы. Известно (см. разд. 1 6.2), что скорость за
рождения центров кристаллизации
зависит от переохлажде
ния
t( , 't) расплава относительно равновесной тем
пературы кристаллизации
В то же время
т.е.
изменяется по текущим и
т.е.
Эrо позволяет
представить
в зависимости от текущих значений и
't ) . Время начала кристаллизации 'tнк можно определить из
=
условия появления первого центра кристаллизации в области
существования переохлажденного расплава, ограниченной сфе
опредерическими поверхностями радиусами Rr и r'('t), rде

w

lкр·
Лts = lкр - r
3(1-, w3

w3
r fкр•'t, w3=
Лts =w3(Лts
Лts()r,. 't). r 't: w3Лts=
r'('t)

1511

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Время начала пребывания си
т) =
ляется из условия
стемы в метастабильном состоянии отсчитывается от -с', опре
с поверхностью
деляемого из условия совпадения изотермы
опре
капли радиусом Rг, т.е. «..Rг, -с' ) =
Таким образом,
деляется из решения интегрального уравнения :

lкр·

t(_r',

lкр

fкр·

tнк

4 7t f

Rr

f

w3(r,-c)r2 drd-c = 1

t' r'(t)

•нк

(д)

.

Интеграл в левой части уравнения (д) представляет собой по
существу "накопление" во времени вероятности появления пер
вого центра кристалл изации в подвижном объеме переохлаж
денного (метастабильного ) расплава, заключенного между сфе
В момент времени
рическими оболочками радиусами Rг и
когда вероятность этого события станет равной единице,
появится первый центр и начнется процесс кристалл и зации. С
этого момента в капле расплава появляется кристалл и ческая
фаза. Будем полагать, что она образует на поверхности гранулы
сферическую симметричную оболочку с внутренней подвижной
перемещающейся к центру капли.
границей радиусом
и ческой фазе, разумеется, кон 
кристалл
в
теплоты
Перенос
дуктивный. При температуропроводности кристаллической
фазы ак для симметричного нестационарного переноса тепла в
сферической системе координат имеем выражение:

r'(-c).

•нх,

rк(•),

дt( , -с)

r

m

=

ак

д2t(r, -с )

[ ar2

+

� дt(r, )

r дr

•

]

.

(ж)

Для получения однозначного решения систему (в)-(ж) за
мыкаем следующими граничными условиями :
- в центре капли из-за симметрии задачи теплопереноса и
ограниченности значения температуры
дt(О, -с)

дr

=

О .'

(з)

- на границе кристалл и зации линейная скорость роста кри
-с )] , т.е. Vл =
сталл о в зависит от переохлаждения Лt5 = [tкр
= vл(Лfs). Кроме того, соблюдается условие баланса потоков теп
лоты на межфазной границе, а именно: поток теплоты, отводt(rк• -с)
), равен сумме двух
димои в кристалл ическую фазу
-

v

Р·к

«..rк,

дr

тепловых потоков - подводимого к границе кристаллизац ии из
дt(rк , -с)
) и выделяюрасплава при кондуктивном переносе (Л.ж
дr

щегося за счет приращения объема кристалли ческой фазы при
1512

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

перемещении с линейной скоростью
межфазной поверхности (.lхр Рк Vл):
л. к

Vл = dl;/d•

единичной

дt(rк , ) =
LхрРк Vл;
ж дr
зависимости vл(Лts) определяется

дt(rк , )
дr
-r:

-

-r:

�
"'

(и)

вид функциональной
обычно
экспериментально (см. разд. 1 6.2) . Соотношение (и) называется
условием Стефана (см. разд. 1 6.3);
- полагаем, что на внешней границе капли или твердой
гранулы теплообмен с хладоагентом переменной по высоте
аппарата z температуры tx(z) происходит в граничных условиях
111 рода. Отметим, что для падающей капли текущая координа
та z связана через скорость падения с текущим временем паде
ния •, поэтому справедлива замена переменной tx(z) на lx(•):
-

Л. i

дt(R r,•)

дr

= (1 х

(t; (R r> 't)

-

tх ('t) ) '

i = ж,

к.

(к)

В дальнейших рассуждениях будем иrnорировать поток
тепла, переносимого содержащейся в хладоагенте пьmью, ввиду
малой ее концентрации и, следовательно, малой погрешности
данного упрощения.
Температура хладоагента lx(•) на расстоянии z от дисперга
тора в элементарном объеме dVa = Fadz аппарата сечением Fa
определяется интенсивностью теплообмена с кристаллизую
щимися каплями, гранулами. Время пребывания d't гранул в
объеме аппарата dVa при порозности s и движении фаз в ре
жиме идеального вытеснения составляет:
d-r:
dVa (1 в)рж .
(л)
=
-

Gr

Для сферических частиq удельная поверхность (см. разд.
2.7.2) равна Fуд = 3( 1 - в)/Rr. Тогда поверхность гранул dFr в
объеме dVa запишется:

dF.r - F.удdV

а

-

3 Gr d't .
--

R Р
r ж

(м)

Поток теплоты, передаваемой от элементарной поверхности
гранул, dQ = ax[t,{Rr, -r:) - /x('t)]dFr, согласно граничному усло
вию 111 рода (уравнение (к)), приводит к бесконечно малому
изменению температуры хладоагента d!x за счет аккумулирова
ния им отдаваемой гранулами теплоты dQ = - Gx cxdlx Соответ
ствующее уравнение теплового баланса имеет вид:
.

dQ = <Xx[tt(Rr, •) - tx('t)]dFr =
= _2._ Gr <Xx(t1(Rr, ) - lx(•))d't = -Gxcxdlx

Rr

Рж

-r:

.

(н)

1513

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Уравнение (н) при совместном решении с уравнениями (в)
- (к) позволяет определить изменение температуры хладоаrен
та fx('t) в зависимости от времени пребывания его в аппарате за
счет отбора им теплоты от кристалл изующихся и охлаж
дающихся гранул.
Высота аппарата Н связана со скоростью стесненного вита
ния гранул
скоростью хладоаrента Wx (в расчете на неза
полненный аппарат) и временем пребывания гранул в аппарате
'tк зависимостью:

wc,

(о)
Текущие значения высоты аппарата z и времени 't также связа
ны уравнением типа (о), где вместо "'к и Н фигурируют 't и z.
Коэффициент теплоотдачи от сферических гранул к хладоа
rенту определяется по эмпирическим и полуэмпирическим
формулам (см . разд. 6.4.5) типа
(п)
Nu = J{Re, Pr) .
Среди н их можно выделить зависимость:

k = 0 , 59 + 0,74 ,
N u = 2 + kRc0•5P�·33 ,
(р)
причем Re базируется на скорости
/s потока сплошной сре
ды относительно поверхности гранулы.
Система (в)-(п) замкнута и может быть решена численны
ми и приближенными аналитическими методами.
Порозность i:: в аппарате можно определить из соотноше
ния, связывающего массо в ы е количества гранул Gr' = Н!а РжО
- s) и хладоаrента Gx' = HFaPxl': в аппарате с их расходами Gr =
f'..1 (1 - E:)(Wc - Wx)Pж/s и Gx = .F>vxPx соответствен но . Отно 
шение м ас с о вых количеств гранул и х..1 адо агента равно:

Wc

-

=

GJ:.=Pж(l-e)

G�

(с)

Рх&

Из уравнений для массовых расходов гранул можно получить
выражение, стоящее в правой части уравнения (с) :

Рж (1- Е:)
Рх&

=

0s_
Gx

Wx
&

1

(Wc :Wx )

;

(l - е) Рж = 0s_
Рх

Gx

Wx
(Wc :Wx)

.

(т)

Уравнение (т) позволяет найти порозность s, если известна
скорость падения (стесненного осаждения) гранул в хладоаrен
те Wc. Методика ее расчета приведена в разд. 2.7.4. Остальные
величины, входящие в уравнение (т), заданы либо имеются в
справочной литературе. Для гранулирования, например, кри
сталлизацией капель расплава в грануляционных башнях или
высушиванием растворов в распылительных сушилках (см.
разд.1 5.1 . 1 ) характерны высокие зн ачения пороз и ости s = 0 ,99 +

1 5 14

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

0 ,998.
В этих случаях скорость хладоагента, рассчитанную на
пустой аппарат Wx, мо ж но пола гать равной истинной скорости
сплошной фазы w�e. При этом уравнение (т) для расчета по
розности упрощается и принимает вид:
&

=

l

_

!!.L_ Рх

Wx
Gx Рж Wc -Wx

(у)

Решение системы уравнений (в)-(у) позволяет рассчигать ди
намику крисrаллизации капель расплава в потоке хладоагента.
19.4. 3. Кристаллизация расплава;
на поверхности рас тущих гранул

При гранулировании расплавов стадии формования и струк
турирования мшуr быть объединены в пространстве и времени.
Расплав в этом случае диспергируется на поверхность растущих
частиц ретура или затравки . При этом в перемешиваемом объ
еме гранул параллел ьно происходят образование центров грану
лирования и их рост, а также рост частиц затравки или мелкого
ретура. Детальное математическое описание этого процесса
весьма затруднительно. Приближенное описание при игнори
ровании раскалывания и агломерации растущих гранул воз
можно в рамках модельных представлений, изложенных в разд.
19.3.3 - уравнения (и) - (т), ( 1 9 . 17), ( 1 9 . 1 8) .
19.5. ГРАНУЛИРОВАНИЕ КРИСТАЛЛ И ЗАЦИЕЙ
ИЗ РАСТВОРОВ И ПАРОВО Й ФАЗ Ы

Гранулирование кристаллизацией нз растворов осущестмяют,
дисперrируя раствор или суспензию гранулируемого вещества на
перемешиваемый слой частиц мелкого ретура или на затравочные
гранулы. При этом процесс вьmар иван ия раствора происходит как
при диспергировании его пневматическими форсунками , так и за
счет обдува влажной поверхности растущих гранул сушильным
агентом. Тепловой и материальный балансы процессов такого
рода подробно рассмотрены в разд. 19.3.2 - они описываюrся
уравнениями (19. 1)- (19.4) при Gп О (см. рис. 19. 16).
Механизм образован ия и роста гранул в этом случае во
многом аналогичен наблюдаемому при гранулировании распла
вов, ко гда совмещены стадии формования и структурирования
гранул . Здесь в перемешиваемом объеме гранул также происхо
дят гомогенное зарождение центров гранулообразования, рост
этих центров и паралле льно - рост мелких частиц затравки "гетерогенных центров зарождения" гранул . Детальное матема
тическое описание этого процесса затруднительно из-за боль
шого числа трудноучитываемых факторов. Приближенное опи
сание при игнорировании раскалывания и агломерации расту
щих гранул возможно в рамках модельных представлений =

1515

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

см. разд. 19.3.3, уравнения (и)-(т) , ( 1 9. 17), ( 1 9. 1 8) , относя
щиеся к кинетике гранулообразования и гранулометрическому
составу образующегося продукта.
Аппараты для гранулирования кристалли зацией из раство
ров обычно совмещают стадии формования и структурирова
ния гранул . Они представляют собой описанные в разд. 1 9.2 . 1
гран уляторы с формированием гран ул окатыванием (барабан
ные, тарельчатые, вибрационные грануляторы), а также с псев
доожиженным и фонтанирующим слоями. Основной недоста
ток здесь - повышенное образование пьmи. Уменьшить пьmе
образование удается, высушивая влажные гранулы в отдельном
аппарате и перемещая их в зону нанесения на них раствора без
подачи сушильного аген та.
Процессы гранулирования н з паровой фазы значительно ре
же встречаются на практике . Съем теплоты десублимацией
гранулируемого вещества обычно проводят за счет испаряю
щегося хладоаrента или расширения газового потока в сопле .
Уравнения материального и теплового балансов в этом случае
могуr быть записаны по аналогии с приведенными в разд.
1 9.3.2 . Кинетику гранулообразования десублимируемого про
дукта описывают в рамках приближенных модельных представ
лений, изложенных в разд. 1 9 . 3 . 3 : уравнения (и)-(т), ( 1 9 . 1 7),
( 1 9 . 1 8). Для организации этого процесса применяют гранулято
ры с псевдоожиженным, фонтанирующим или движущимся
слоями гранул, охарактеризованные в разд. 1 9.2. 1 .
19.6. О КАПСУЛИ РОВАНИИ
ГРАНУЛ ИРОВАННЫХ ПРОДУКТОВ
Капсулирование - это нанесение на поверхность какого
либо тела, содержащего целевой компонент (в частности, на
гранулы), инородного вещества, образующего сплошную (замк
нутую) оболочку.
Целью капсулирования является замедленное или управляе
мое вь1деление целевого компонента в окружающую его среду,
защита поверхности целевого компонента от воздействия
окружающей среды и организация селективного взаимодей
ствия целевого компонента с окружающей средой .
По размеру обрабатываемых частиц процессы капсулирова
ния подразделяют на микрокапсулирование (при размере час
тиц менее нескольких десятков микрометров) и макрокапсули
рование (при большем размере частиц) .
Мнкрокапсулнрование обычно проводят в растворе капсули
рующего вещества (капсулянта), создавая в последнем эмуль
сию или суспензию капсулируемого вещества с добавлением
ил и без добавления поверхностно- активны х- веществ. Затем
вводят (или п редварительно наносят на капсулируемые части
цы) иющиатор полимеризации капсулирующего агента, который

1516

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

чаще всего находиrся в растворе в виде мономера. За счет изме
нения температуры, подвода в систему энергии ультрафиолетово
го, гамма-, ультразвукового или иных видов излучения создаюг
опrималъный режим полимеризации капсулирующего аrента на
поверхности капсулируемых частиц. При этом толщина капсули
рующего покрьП'ИЯ часто не превышает 10-{) м. Далее образо
вавшуюся суспензию капсулированных rранул филътруюr, отделяя
раствор капсулянта от продукта, и сушат последний.
Другим перспективным методом микрокапсулирования являет
ся капсулирование частиц (гранул) в пар ах мономера капсулянта с
инш.щированием процесса полимеризации химическим способом
или за счет облучения. Данный способ позволяет получать наибо
лее равномерные по толщине покрьП'ИЯ и капсулироватъ часnщы
со сложной формой шероховатой поверхности .
Процессы макрокапсулироваиия подразделяют в зависимости
от толщины капсулирующего покрытия на капсулирование
тонкими (не более 6% (об.)) оболочками (обычно из полимер
ных материалов) и толстыми (более 6% (об.)) оболочками. В
последнем случае материал оболочки или его компоненты
должны бьrrь выбраны так, чтобы их можно было использовать
в качестве целевых компонентов (капсулы в этом случае назы
вают спавсулами). Например, при капсулировании гранул ми
неральных удобрений толстыми ( 1 0-30% (об.)) оболочками из
неорганических материалов последние полностью или частично
используются как удобрения, ростовые вещества, структури
рующие либо раскисляющие почву аrенты.
Макрокапсулирование проводят расплавами и растворами
капсулянта или с использованием паровой фазы мономера кап
сулирующего покрытия (по описанной выше технологии) . При
капсулировании неорганическими покрьrrиями применяют
порошок капсулянта со связующим или суспензию капсулянта.
При высушивании или кристалл изации связующего оно
вместе с порошком капсулянта создает на поверхности гранулы
капсулирующее покрытие. Обычно оболочки, полученные по
такой технологии, являются толстыми (более 1 0 % (об.)).
При капсулировании раствором капсулянта его диспергиру
на поверхность гранул, по которой он растекается. Это воз
можно лишь тогда, когда раствор хорошо смачивает капсули
р уемvю поверхность. При высушивании растворителя на кап
сулируемой поверхности остается обычно тонкая (менее 6%
(об.)) сплошная пленка капсулянта. Такой процесс наиболее
перспективен при кристалл изации капель расплава гранули
руемого вещества в растворе капсулянта, который используется
в качестве хладоагента. При отделении гранул от хладоагента
(раствора капсулянта) последний захватывается потоком гранул
и служит для их последующего капсулирования. Теплота, акку
мулированная еще не остывшим потоком гранул, обеспечивает
испарение растворителя. Последний при капсулировании рас-

ют

1517

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

твором капсулянта регенерируется (например, конденсацией,
реже - адсорбцией) в замкнутом цикле и возвращается на ста
дию растворения капсулирующего вещества.
При капсулировании расплавами капсулянта их наносят
обычно на поверхность гранул, нагретую выше температуры
кристаллизации капсулянта. Поэтому перспективным также
явля ется гранулирование кристаJVIИ зацией капель расплава грану
лируемого вещества в расплаве капсулянта. Капсулирующее по
крыгие образуется при этом за счет кристалл изации захваты 
ваемого гранулами расплава капсулянта. После образования на
поверхности гранул равномерно распределенного слоя расплава
капсулянта температуру в аппарате постепенно снижаюr (или пе
реводят капсулируемый поток в более холодные зоны аппарата).
При этом капсулирующее покрыгие отвер:Jl\дается и охла:Jl\дается.
По этой технологии получаюr продукты с содержанием капсули
рующего покрьпия не менее 6- 1 0% (об.).
Поскольку стоимость капсулирующего покрытия часто
имеет решающее значение, перспективным представляется
многослойное капсулирование, когда первый (грубый) капсу
лирующий слой наносят с использованием дешевых капсулян
тов. Он выполняет роль армирующей подложки, на которую
затем наносится тонкая (0, 5-2% (об.)) пленка эффективного ,
хотя часто и дорогого капсулирующего вещества.
Капсулирование формально можно трактовать как много
слойное (по крайней мере двухслойное) гранулирование, и
потому аппаратурное оформление такого процесса аналогично
описанному выше. Это относится и к составлению материаль
нь�х и тепловых балансов процесса. Кинетика процесса описы
вается приведенными выше зависимостями для гранулирова
ния на частицах затравки, в качестве которой в данном случае
выступают капсулируемые гранулы.
В данном разделе рассмотрены лишь приемы получения
капсулированнь�х гранул и подходы к расчету этих процессов.
Выделение целевых компонентов из капсул представляет собой
самостоятельные задачи массопередачи, которые во многом
аналогичны нестационарному переносу целевых компонентов
через мембраны (см. разд. 20. 3 . 1 ) .
ЛИТЕРАТУРА к главе

19

1. Бронштейн И.Н., Семендяев К.А. Справочник п о математике д11Я инжене
ров и учащихся вузов. М.: Наука (ФМ), 1986. 544 с.
2. Казакова Е.А. Гранулирование и охлаждение азотсодержащих удобрений.
М.: Химия , 1980 . 287 с.
3. Классен П.В., Гришаев И.Г. Основы техники гранулирования. М.: Химия ,
1982. 272 с.
4. Классен П.В., Гришаев И.Г., Шомин И.П. Гранулирование. М . : Химия,
1991. 240 с.

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Глава 20
МЕМБРАННЫЕ

ПРОЦЕССЫ

РАЗДЕЛЕНИЯ

От других процессов разделения
с межфазным
переносом
вещества
отличает
наличие
перегородЮi
(мембраны),массообмена.
отделяющейМетоды
в пространстве
фазы,разделения
участвующиесмев
процессе
мембранного
сей
основаны
на различной
проницаемости
мембран для раз
ныхПроцессы
компонентов
разделяемой
смеси.
мембранного
разделения
широко
применяютсясмев
промышленности
при
разделении
жидЮiХ
и
газообразных
сей, Юfслорода
концентрировании
растворов, опреснении
воды,
выделе
нии
из
воды
(искусственные
жабры),
очистке
атмов
сферы
гермоотсеков
с
биологическими
объектами
и
людьми,
медицинена (искусственные
леГЮfе,
почка,
печень,
разделение
крови
компоненты
и
др.),
в
металлур
ги
и
и
биохимии
(обогащенное
Юfслородом
дуrье),
в
пищевой
пром
енности
(при
создании
атмосферы,
п
епятствующей
порче
пищевых
р
продуктов)
и долядругих
отрасляхразделения
.
Основная
процессов
в объектах
живойЭтопри
роды
происходит
с
помощью
биологических
мембран.
нане
водит
на
мысль,
что
мембранные
процессы
разделения
только
высокоэффективны
(практичесЮf - Последний
селективны),показа
но и
обладают
малой
удельной
энергоемкостью.
тель
особенно важен при выборе метода разделения разбавлен
ныхГлавным
систем.
недостатком использовать
процессов мембранного
разделения
является
необходимость
большие
поверхности
мембраны,
ибо в последней
преобладают
процессы молекулярного
переноса
массы. весьма медленные
мембранные процессы

ьши

в

20.1. ОБЩИЕ ПОНЯТИЯ

это твердаявсе илиилижидкая
перегородка, через
ко
торую
мoryr
проникать
часть
компонентов
смеси.
первом случае мембрана называется
во втором
Мембрана

-

В

проницаемой,

-

полупроницаемой.

• Подробнее см. (1

-

3 ).

1519

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Wн

l

•

.хн

Рис. 20. 1.

1

ки:

Схема мембранной ячей-

1
надмембранное пространство, 2
подмембранное пространство, З
мембрана;
1
проходящий поток, /1
пер
меат, /// поток вещества через мем
б рану
-

-

-

-

-

-

аппаратразделения
или его элемент
длясостоящий
осущест
вления
процесса
мембранного
смесей,
(рис. из двух1 инеподмембранной
сообщающихся между
собой полостей
надмембранной
разделенных
мембраной
Поток
1, подаваемый
на разделение
и называемый
движется
вдоль
мембраны;
поток
отводимый
из ячей
киникающим
(в рассматриваемой
схеме
он
совпадает
с
потоком
про
через
мембрану),
называется
Перемеще
ние пространства
проходящего впотока
через мембрану
из надмем
бранного
подмембранное,
как
и
пермеата,
естественно,
исключаетпо процесс
разделения.
Мембраны
классифицируют
разным признакам.
а)
- мембраны живых организмов и
полученные
на
их
основе;
б)
- органические и неорганические;
- полимерные
неорганическиепленки
аморфные
и кри
сталлические
стекла,
фольга;
аморфные
и со смешанной
аморфно-кристаллической
структурой;
жидкие
пленки
(обычно
поверхностно-активные
вещества)
на
границе
раздела
жидкость-жидкость- или
жидкость-газ;мембраны с диа
микропористые
6)
метром порсеребра
d3 и других м(прессованные
поро изкерамика;
стекла,
вольфрама,
о
в);
микропористая
полимерныемембраны
струкгурыс (ацетилцеллюлоза,
нуклеопоры и
др.пористые
)
;
макропористые
диаметром
пор
dз
(ультрафильтры, ипоровские фильтры и др.);
а)б)
- испарение
черезжидкостью
мембрану;газа,
се
лективная
дегазация
жидкостей;
поглощение
проникающего
через мембрану
(например,
насыщениеаэрозолей
крови кисот
лородом
и
выделение
из
нее
СО2);
отделение
газового
потока на волоЮiистых мембранах
- войлоках;
осмос; электролиз;
диализ;
в)
электроосмос; термодиффузия; диффузия с химическими
реакМембранная ячейка

-

20. 1)

2,

З.

щим,

проходя

11,

111,

пермеатом.

всего

отсутствие

1 . По природе мембраны:
природные мембраны

сиJrrеТические мембраны
2 . По структуре мембраны:
а) непористые мембраны

пористые мембраны
::;;

0,5-10-6 м

еталл

шки
�

милл

3. По областям применения мембраны:
rазо(паро)фазные процессы разделения;
системы газ-жидкость

жидких

системы жидкость-жидкость

1 520

0,5-10-6 м

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

циями
в мембране,
например
облегченная
диффузия, активный
массоперенос
"против
градиента
концентрации"
(метабо
лический
насос);
разрушение
устойчивых
эмульсий
на
волок
нистых
мембранах
войлоках;
г) аэрозольных твердыхволокнистые
мембраныПетрянова
для улав
ливания
частиц
(фильтры
Соколова); самоочищающиеся
волокнистые
мембраны
для
улавливания
растворимых
твердых
аэрозольных
частиц;
мем
браны
длянанесения
селективной
десублимациипокрыгий
через перегородку;
мембра
ны
для
эпитаксиальных
и
выращивания
кри
с д) ов из газовой фазы, проникающейразличные
через мембрану;
типы
фильтро
вальных
перегородок;
капсулирующие
покрытия
для
управляе
мого
растворениякристаллов
(выщелачивания)
капсулированных
веществ;
выращивание
из
растворенных
веществ,
прони
кающих через мембрану.
системы газ -твердое

талл

-

системы жидкость-твердое

-

20.2. ОСНОВНЫЕ М ЕХАНИЗМЫ ПЕРЕНОСА ВЕЩЕСТВА
Ч Е РЕЗ МЕМБРАНЫ

Проницаемость
отдельных
компонентов
через мембрану за
висит
при
прочих
равных
условиях
от
физико-химической
природы
мембраны.мембран это связано, как правило, с раз
Для
личной
скоростью адсорбции
компонентов
поверхностью
мем
браны,
различной
растворимостью
компонентов
в
материале
мембраны (иногда
с образованием
химическихдиффузии
соединенийэтихс
материалом
мембраны),
разной
скоростью
компонентов
в мембране
и разной
скоростью десорбционных
явлений
на
обратной
стороне
мембраны.
Для
мембранразных
это связано
с различной
скоростью
молекулярного
течения
компонентов
(кнудсеновская
диффузия)
в порах
мембраны,
а прив вязком
течении
-с
"застреванием"
крупных
частиц
потока
пористой
перегородке
мембраны
(или перед
ней). выше явлений различной физи
Совокупность
названных
ческой
природы формально
объединяется
понятием "прони
цание
(проникновение)
через
мембрану".
Для определения
потока
(потоков)
"проникающих"
компо
нентов
используется
основное
уравнение
массопередачи
(см.
разд.10.6,
0.8,
10.13).
Согласно
этому
уравнению
количество
1
М1 (поток М;условиях
) перенесенного
через мембрану
неизменных
пропорционально
площадикомпонента
мембраныприF,
152 1
непористых

пористых

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

i

продолжительности
номер
переносимого процесса
компонента:и его движущей силе Лi, где
Л
Л
(20.1)
Л i - символ осреднения движущей силы по
причем
над
поверхности
мембраны.
Коэффициент
пропорциональности К называется ф
для i-гонашекомпонента.
этоммеханизма
коэффи
циенте
"спрятано"
все
незнание
"проницания". Численное значение К р; определяется чаще
всего
экспериментально.
По формальному
подходуКк решению
проблемы
переноса коэффициент
проницаемости
- аналог
теплопередачи (в теплообмене) и массопе
редачикоэффициентов
(в массообмене).
20.2.1.
Рассмотрим
ст ационарный перенос компонента через непо
ристую
мембрану,
используя
подходы пленочной модели мас
сопереноса
(см.
разд.10.
6
).
Обозначим
(рис.20. 2 ): т С1 , Хп т С2 ;
пара рав
новесных
с
С 1 и С2 концентраций компонента - в пермеате и
проходящем
потоке;
С1 С2"растворенного"
соответствующие
концентрации
переносимого
компонента,
в
материале
мем
браны;
т - константа растворимости (по смыслу - коэффи
циент распределения) этого компонента материале мембраны;
D - среднеинтегральный по диапазону концентраций
(согласно
теореме о всреднем)
коэффициент
диффузиимембраны
перено
симого
компонента
мембране.
Тогда
для
элемента
площадью dFвыражениями:
массовый поток dM переносимого компонента
определяется
•

М; = К р ; F ; • ;

М; = К р ; F ; ,

-

• = l,

ч е ртu

pi

коэ -

В

фициентом проницаемости

pi

Механизм переноса вещества через непористые мембраны

и

Уп� Xit

=

Уп =

-

-

в

dM = � 1 (y-yn)dF = D ( C1 - C2)dF = D (уп-хп)dF = �2(xп-x)dF.
-

-

В

Вт

(20.2)
С
другой
стороны,
из
основного
уравнения
стационарного
массопереноса
поток переносимого компонента dM
через
площадкумассовый
d F равен :
(20. 3 )
dM = Кр(у x) d F ,
-

rде (у х) - разность концентраций пер еносимого компонента в пото ках, р аз
деленных мембраной.
-

Следуя методам,
изложенным концентрации
в разд.10.6.1, исключаем
рассмотрения
трудноопределимые
целевого ком-из
1522

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

· -г · 
Р2 1

-т
1 ll 1
1

1

1

·

Уп

С1

3�

1
1
М; 1
_...,
Ру

___J_, .

Рис. 20. 2. Расчетная схема nроцесса переноса компонента смеси М1 через непори
в стационарных уСJювиях - в рамках меночной модели массо11сре11оса:
1 - мембрана; 2 и J - rра�ощы пограничных слоев в 11рохоД11ЩСМ 11аrокс и лермсаrе

стую мембрану

·

понента на поверхности мембраны Хп и Уп · В этих целях выра
зим из уравнения (20.2) частные движущие силы для отдельных
стадий переноса и сложим полученные выражения:

dM
- Yn = P
1 dF
dM · 8m
Уп - Хн =
dF
d
X
Хn p 2 dF

У

+

=

Jf

--

Из совместно го решения формул (а) и (20.3) следует:

dM
KpdF

у - х = -- .

(б)

Отсюда коэффициент прон ицаемости мембраны (через ее
поверхность F) по переносимому компоненту Кр равен:
кр =

1
1 бт
1
- + -=- + -

Р1

D

. , (20.4)

Р2

Из уравнения (20.4) ясно, что коэффициент проницаемости
Кр, строго говоря , не является характеристикой только свойств
компонента и
мембраны ( D , 8, m). Он зависит
также от гидродинамики потоков в ячейке, так как связан с
массоотдачи р1
р 2 на обеих границах по
ток-мембрана.
1 523

параметров
коэффи�.iиентами

и

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Отношение коэффициентов проницаемости а для пары ком по
нентов смеси (i-го и s-го) называется селективностью разделения
этой пары ком понентов:

a = a;, = Kp; / Kps ·

(20.5)

В подавляющем большинстве случаев технологи заинтересова
ны в увел ичении селективности а: тогда при прочих равн ых усло
виях выше частота разделения. Из уравнения (20.4 ) следует важ
н ы й вы вод : пол ное сопроти вление массопереносу каждого ком понента сосредоточено

1.

вне мембраны

[-1- Б_!!!) ,
Р 1 .2

»

D

то согласно

уравнению (20 . 5 ) она не будет обладать селективностью, так как
а;, �
С увеличен ием коэффициентов массоотдач и 131 и 132 селек
тивность а;, возрастает. Таки м образом , для увел ичения селектив
ности мембраны надо максимально турбул изировать потоки в
надмембранном и подмембранном пространствах (т.е. увеличи вать
131 , 132 ) , поскол ьку при прочих равных условиях а;, принимает мак
симал ьное значение при 13 1 .2 � оо .
Изложенный выше подход к описанию диффузии компонента в
мембране, базирующийся на постулате о линейной связи потоков
и движущих сил, справедл и в лишь для МШIЫХ концентраций диф
фундирующих ком понентов в материале мембраны и для неболь
ших средних скоростей проникающего через мембрану потока.
Такая ситуация нередко встречается в практике процессов мем
бранного разделения.

20.2.2. Механизм переноса вещества через пористые мембраны

При использовании пористых мембран выделяют два механизма
"проницания" - с ними связаны механизмы разделения смесей. Пе
ренос вещества в порах мембраны может осуществляться за счет
свободного молекулярного течения или за счет вязкого течения.
Первый механизм реализуется, если диаметр пор мембраны м но
го меньше длины свободного пробега молекул компонента - обыч
но это наблюдается при радиусе пор r < 0,25 · 1 0-{j м, т.е. для микро
пористых мембран (см . выше классификацию мембранных методов
разделен ия). В этом случае вероятность стол кновения молекул друг
с другом м ного меньше вероятности их столкновения со стенкой
канала (поры) и отражен ия от нее (под углом, равным в идеале углу
падения). Разли чие в длине свободного пробега молекул ( из-за раз
ных молярных масс проникающих компонентов) приводит к разнице
в скоростях движения компонеtп0в в пористом теле мембраны и яв-

1 524

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

послед
селективности
от единицы
отличной
причиной
ляется
диф
молекулярной
"свободной
называется
течение
Такое
ней.
фузией",
или
"кнудсеновским
течением".
Пусть
компонент
молярнойчерез
массой
движется
изотермиче
ски
в
условиях
разрежения
тонкий
капилляр
длиной
lи
радиусом
под
действием
разности
давлений
на
его
концах (р1 - Р2) ; его мольный поток М'
составляет (см.
разд.
М

r0

= G/M

2.9):

Р1 - Р2

( 20.6)

/
где G - массовый поток компонекrа;

Ry

-

универсальная газовая постоянная.

Применительно
к
кнудсеновскому течению
теле
мембраны,
в пористом
пронизанном
[) , расчетные выражения для мольного
иплощади
массо
потоков
через
бесконечно
малый
элемент
мембраны dF имеют вид: dF
изотермическому

рами ( 2ro
ВQГО G

короткими капилля
М'

�

dM' =

dG =

J21t Ry MT

� <Р 1
v�

(р1 - Р2)

'·

(в )

(г)
Из уравнения
(г) ясно,черезчтомембрану
движущейявляется
силой процесса
массопе
реноса
компонента
разность
парци
альных
давлений
компонента
на
противоположных
сторонах
мембраны.
Примембрану процесс кнудсеновском
течениинекомпонентов
через
переноса
происходит
только про
под
действием
перепада
давлений
в
надподмембранном
странстве элемента dF, но и в условиях разных температур:
J (_!!l_
..J!]_J dF кр(д..J!]_J dF . (д)
JТi ,JТ;
JТi ,JТ;
Из уравнений (г, д) видно, что .t(Ш), значит, мембрана
селективна
массой: по отношению к компонентам с разной молярной
-

P2) dF =

Kp(pl

-

P2 )d F.

неизотермическом

и

dG

=

М

_

21tRy

=

Кр

.
N
"' IS

=

Kpi

Kps

=

-

�Mi

Ms

'

( 20 . 7)

Из уравнений
(г, д) следует
также,в еечтопорах
селективность
браны
при кнудсеновском
течении
не зависитмемот
1 52 5

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

способа
создания движущей силы процесса и определяется
выражением
Второйс механизм
переноса
характерен
для макропористых
мембран
эквивалентным
диаметром
пор
(dэ
сул .
щественно
превышающим
длину
свободного
пробега
молеку'
перенос
компонентов
через
мембраны
происходит
обыч
ноЗдесь
за
счет
вязкого
течения
субстанции
через
сквозные
поры.
Массовый
поток
компонентов
через
бесконечно
малый
эле
мент
площади
мембраны
dF в этом случае можно рассчитать,
используя уравнение
для ламинарного
течения
в каналах килипов
зернистом
слое
(см.
и
Применительно
следнему
случаю обозначим:
dи
диаметр поры
и пороз
ность
мембраны;
и
вязкость
и
плотность
проникающей
субстанции; толщина мембраны
(длина канала). Тогда
з
2
d
dG - е
Р ЛpdF = KpЛpdF .
(е)
150 (I
)
Из уравнения
(е) следует,
что дляравна
компонентов,
движущихся
вэффекта
порах
мембраны,
селективность
единице.
Отсуrствие
разделения
вязком
потоке
объясняется
тем, сво
что
здесь
эквивалентный
диаметр
пор
много
больше
длины
бодного
пробега молекул.
Разделение
потокапроисходить
на компоненты
при
использовании
таких
мембран
будет
лишь
тогда,
когда
один
компонент
проникает
через
поры
мембраны,
а другой(К"застревает"
в них. Селективность мембраны в этом
случае
О) равна бесконечности.
(20 .7).

�

разд.2.2.4

µ

8 -

2.7.2).

ео -

р-

о

l

=

_

ео

2

0,5-10-6 м) ,

µо

в

ps

----.

20.3. МЕМБРАН НЫЕ ПРОЦЕССЫ РАЗДЕЛЕНИЯ
И СПОСОБЫ ИХ ОРГАНИЗАЦИИ

Массоперенос
через мембрану
-феноменологического
типичный необратимый
процесс,
анализируемый
(с
позиций
под
хода)
в
соответствии
принципами
неравновесной
термодина
мики
см. разд.рассмотрим
На основе
представлений,
изложенных
впроцессов
этом- разделе,
подходы
к
описанию
некоторых
мембранного разделения·.
с

1 .3 . 2 .

20.3. 1 . Процессы разделения без химического взаимодействия
проникающего компонента и материала мембраны

- это процесс диффузионного проникновения ком
счет разности
через
смеси
понентов
надмеми Уу -заобъемы
Пусть мембрану
= концентраций Лм(раствора)
Диализ

Х;

•

Более подробно

1 526

см.

( 1 ).

у1.

Ух

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Ух < < Уу

бранного
ипоток
подмембранного
пространств.
Тогда приповерхности
массовый
i-го
компонента
через
элемент
мембраны
площадью dF определяется основным уравнением
массопереноса:
(а)
dM; =
Y;)dF,
Км. (х;
1

-

где К М; коэффицие нт про н ицаемости мембран ы по i-му компо н енту за счет
раз ности кон центраци й .
-

это процесс
диффузионного
прониюювения
раствора
через
мембрану
за
счет
разности
давлений
- обычно
в
сторону
оольших
концентраций
компонента
в
растворе
(в
отли
чие
откомпонентов
диализа). Дляраствора
увеличения
интенсивности
процесса
разде
ления
проникающий
через
мембрану
поток
может
бьrгь
направлен
и
сторону
меньших
концентраций
и
дав(за
лений.
Тогда
обе
движущие
силы
процесса
переноса
массы
счет
разности
концентраций
и для
разности
давлений)
действуют
в
одном
направлении.
Уравнения
расчета
потоков
компонента,
через элемент
переносимого
мембраны,
тоже мoryr
бьrrь записаны
на основе
уравнений
переноса
под
действием
различных
движу
сил (см. разд.1. 3 .2):
(б)
dM; = [Кмм (хi - У i ) + К мр ( Рх - Py )] dF .
это процесс,
аналогичный
пьезодиализу,
носкихвместо
перепада
давлений
организуют
перепад
электриче
потенциалов
на
различных
сторонах
мембраны.
При этом
величина
наложенной
на
мембрану
разности
потенциалов
по
зволяет управлять
потоками
переносимых
компонентов.
это процесс
диффузионного
проникновения мем
(ниже
индекс
"2")
через
полупроницаемую
брану
из(у) области
меньшей
концентрации
растворенного ве
щества
в
область
большей
концентрации
Допустим,
что перенос массы через элемент площади мем
браны
dF осуществляется под действием двух движущих сил:
перепадов
концентраций и давлений. Тогда расчетное уравне
ние имеет вид:
(в)
d M2 = [к мм ( х2 У2 ) + К Мр ( Рх - Py )) d F ,
П ьезоднализ

-

в

щих

Электродиализ

-

ра с

Осмос
творителя

-

ero

(х) .

-

ко эффи ци енты п ере но са массы за счет разно сти концент
где К и К
раций растворителя и разности дамений .
Mv

мм

-

Движущие
силы процесса
переносанавстречу
веществадругмогутдругу.вызывать
потоки
компонента,
направленные
Тогда
несимого
исключен;�
ситуация,
когда
результирующий
поток
перено
веществачторавен нулю:атмосферное
dM; = О , при этом > >
Возможно,
давление. Тогда вели
оно
чину
= pgh называют
х2

Ру

-

Ра = тт

Рх

=

Ра

У2 ·

-

осмотическим давлением;

1 527

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

возникает за счет проникновения растворителя через мембрану
- из надмембранного пространства в подмембранное. При
этом уровень растворителя в подмембранном пространстве
поднимается на высоту h, а проникновение растворителя через
мембрану прекращается :
(г)
К мм (х 2 - У 2 ) = К мр ( Ру - Р х ) = К мр 1t ·
Для разбавленного (у2 � 1 ) идеалыюго раствора 7t =
= (Rу/М) Ту 1 , а для разбавленного неидеального раствора, со
гласно закону Вант- Гоффа, осмотическое давление равно: п =
= П (Rу/М) Ту 1 , где П - осмотический коэффициент, отличный
от 1; индекс " 1 " обозначает растворенное вещество.
Обратный осмос - это процесс диффузионного проникнове
н ия растворителя через полупроницаемую мембрану из области
большей кон центрации растворенного вещества в область
меньшей его концентрации.
Процесс применяется в целях "обессоливания" растворителя.
Для осуществления процесса надо в надмембранной зоне (т.е. в
области более концентрированного раствора) поддерживать
давление р, превышаюшее осмотическое: р > п + Ра· Тогда мас
совый поток растворителя, проникающего при Ру = р через
площадку d F, будет равен:
d M2 = К Мр [р -(ра + n) ]dF = К Мр [ру - (ра + 1t)] dF . (д)
При обратном осмосе при р > Ра + 7t встречный поток раство
рителя за счет разности давлений (р - ра) не только компенсирует
поток растворителя за счет разности концентраций, но и превос
ходит его на величину, пропорциональную [р - (ра + п) ] .
Аномальный осмос - это осмотический процесс в электроли
тах, при котором й ре з ультате м ассопереноса компонента про
тивоположные поверхности мембран ы получают разноименные
заряды, и в теле мембраны проходит ток 1.
Это явление, как следует из уравнений переноса под дей
ствием различных движущих сил (см. разд . 1 .3 .2), может уско
рять или тормозить массоперенос: наблюдается положительный
или отрицательный аномальный осмос соответственно . Здесь
качественно все определяется знаком второго слагаемого в
уравнении (ж):

dM2 =

dl =

( К (х2 - У2 ) + К ми (U - U у )] dF,
[ К IМ (х2 - у 2 ) + Кю (U х - U y )] dF ,
мм

(ж)

х

(з)

где КММ , Кми - ко эффици енты п ереноса р аствор ителя за счет р азности
кон центраци й и раз ности эл е ктри ческих п отенциалов соответственно ; К К
- ко эффи ци енты пер ен оса электрического зар яда через ме мбр ану п од действ и 
ем р аз носm концентраци й и п отенци ало в со ответствен н о ; их. иу - эле ктричеIM ,

1 528

ю

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

с кие поте нци алы ме мбраны со стороны надм ембранноrо
пространств.

и

подм ембранноrо

Уравнение (з) позволяет определить силу тока 1 в замкнутой
цепи, соединяющей над- и подмембранные пространства, не
обходимую для организации этого процесса. Включение в эту
цепь источн и ка тока, согласно уравнениям (ж) и (з), позволяет
управлять процессом переноса растворителя через мембрану.
Электроосмос - это аналог процесса обратного осмоса в
электролитах, но в этом случае на мембране вместо перепада
давлений организуют разность потенциалов, эквивалентную
перепаду давлений - сверх осмотического, т.е. сверх величины
Ру - (п + Ра) . Расчетн ые выражения для потоков, переносимых
через элемент мембраны dF, могут быть записаны на основе
уравнений (ж) и (з) .
Ультрафильтрация - это процесс мембранного разделения
смесей на компоненты, отличающийся от рассмотренных выше
размером пор в мембране и, естественно, механизмом прони
цания. Обычно это сочетание кнудсеновской диффузии и ад
сорбционного течения в порах мембраны . Под последним по
нимают "течение" адсорбированного компонента по поверх
ности адсорбента (стен ке поры) под действием движущей силы
- разности концентраций, поверхностного натяжения, элек
трического, магнитного и других полей.
Комбинируя движущие силы процессов переноса субстанций
различной физической природы, можно предложить широкий
спектр и друш:х процессов разделения с помощью мембран.
20.3.2. Процессы разделения

с химическим взаимодействием
проникающих компонентов и материала мембраны

В

описанных выше п роцессах в ходе переноса компонентов
через мембрану не происходит химического взаимодействия
переносимых компонентов между собой и с материалом мем
браны . Если процессу переноса целевых компонентов в мем
бране сопутствует химическое превращение, то процесс
"транспорта" вещества через мембрану значительно облегчает
ся. Процессы с химическим взаимодействием переносимых
компонентов между собой и с м атериалом мембраны являются
превалирующими в природных биологических мембранах. Рас
смотрим некоторые из вышеназванных механизмов.
Облегченная диффузия - это процесс диффузионного пере
носа целевого компонента в мембране с "повышенным" коэф
фициентом диффузии за счет наличия в мембране вещества
носителя. В этом случае целевой компонент "передается" по
цепочке молекул носителя (например, кислород в крови с ис
пользованием носителя - гемоглобина)* .

• Более подробно см.

[3).

1 529

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

· - · - ·

Низкая

Высокая

конuентраuия

конuентраuия
компонента А

А

в
+

----- в

А

н

()

компонента А

+

А

н

лв � лв

Рис. 20.З. Схем а перено са комп о нента А по м ехани з му "акти вноrо массоперено
са" в мембран е

Активный перенос (метаболический насос) - это процесс
диффузионного переноса вещества "против градиента его кон 
центрации" (иными словами, и з области низкой концентрации
- в область высокой концентрации этого вещества) за счет
химического взаимодействия компонентов между собой внутри
мембраны при каталитическом воздействии ее материала.
Для реализации переноса компонента А из области низкой
концентрации в область его высокой концентрации необходи
мо наличие транспортирующего вещества В у поверхности
мембраны и ферментов: Ф 1 - ускоряющего прямую реакцию А +
+ В � АВ; Ф2 - ускоряющего обратную реакцию АВ � А + В .
В этом случае реализуется показанный н а рис. 20.3 транспорт
веществ АВ и В "по градиенту концентраций" (иными словами,
из области высокой концентрации этих веществ - в область их
низкой концентрации), обеспечивающий перенос вещества А
из области н изкой концентрации в область его высокой кон
центрации (якобы "против градиента концентраций").

20.4. ОСНОВНЫЕ КОНСТРУКЦИИ
МЕМБРАННЫХ ЯЧЕЕК

Мембранная ячейка состоит

из:

- надмембранноrо пространства , куда подается разделяемая

смесь и откуда выходит обедненный вьщеляемым компонентом
проходящий поток, не проникший через мембрану, и
- подмембранноrо пространства, куда через мембрану прони
кает поток пермеата, обогащенный выделяемым компонентом .
Подмембранное и надмембранное цространства разделены
между собой мембраной , через которую происходит перенос
1 530

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 20.4.
1

-

Устройство плоского мембр анного м одуля:

фланцы, 2 -

корпус, 3

-

мембранный модуль, 4

-

в ид

с торца

компонентов разделяемой смеси - согласно описанным выше
основным механизмам массопереноса.
В целях увеличения механической прочности мембраны по
следняя располагается обычно на подложке или между подлож
ками - механически прочными материалами, внешне напоми
нающими мембрану, но практически не представляющими со
противления переносу массы и не обладающими селектив
ностью (обычно это сетки или крупнопористые фильтры из
различных материалов) . Иногда подложку в целях увеличения
механической прочности мембраны располагают внугри мате
риала мембраны или материал мембраны тонким (до несколь
ких микрометров) слоем наносят на поверхность подложки .
Такие мембраны иногда называют армированными . Достоин
ством таких конструкций наряду с повышенной механической
прочностью является более высокая проницаемость (из-за
малой толщины мембранного слоя) мембраны при практически
неизменной ее селективности. Конструктивные варианты рас
положения мембраны и подмембранного и надмембранного
пространств разнообразны. Однако на практике наиболее рас
пространены мембранные ячейки трех типов· .
Плоские пакеты (кассеты) мембран (рис. 20.4) . Достоинства
этих ячеек - простота изготовления, контроля в случае по
вреждения мембраны и малое гидравлическое сопротивление
проходящему потоку. Недостаток - малая удельная поверх
ность (порядка лишь сотен м2 в 1 мЗ мембран.ной ячейки) .
Мембранные ячейки рулонного типа (рис. 20 . 5) . Ячейки пред
ставляют собой "сэндвич" с наружными непроницаемыми стен
ками. Между ними закладывается мембрана на двух пористых

• Детальное оп и сани е ячее к пр иведено в ( 1 ,

3).

1 53 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 20. 5.
/

воды ,

З

-

1-

Кон струкция ме мбр анного модуля с пирального типа:

пространство со стороны ко�щекrрированноrо раствора, 2 дренаж для очищенной
тело мембраны;
ко�щекrрированный ра<.;вор, ll очищаемая вода, lll очищенная вода
-

-

-

Рис. 20. 6.

-

Ми крофотоrрафия полого волокна

Рис. 20. 7. Схе ма конструкци и трубчатого модуля с и спользовани е м с мол ы в
честве связую щего :
/

-

фла�ща

1 532

корпус,

2

-

фланец,

.1

-

1

рубчатые мембраны, 4

-

пористая смола,

5

-

ка

прокладка

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

подложках (с обеих ее сторон), которые образуют надмем
бранное и подмембранное пространства. Этот "сэндвич" свер
нуr в рулон , что делает его компактным. Потоки разделяемых
веществ движуrся перекрестным током. Достоинство rаких
ячеек - простота их изготомения; недостаток - небольшая
удельная поверхность (порядка 1000 м2 в 1 м3 мембран.ной ячейки).
Мембранные ячейки из полых полимерных волокон (рис . 20.6,
20.7). Они конструктивно оформлены аналогично некото
рым видам кожу.хотрубных теплообменников. Диаметр волокон
- 3 . 1 0-4 м, толщина стенок (0,7 + 1 , 0)· 1 0-4 м. Основное досто
инство - развитая удельная поверхность - до 4- 1 04 м2/мз .
Мембранная аппаратура на основе rаких ячеек (модулей) наибо
лее современна и широко используется в промышленности. Глав
ный недостаток - сложность определения места разрыва мем
бранного волокна. Из-за этого при разрыве отдельного волокна
обычно приходиrся заменять весь мембранный модуль.
20.5. ОСН ОВЫ РАСЧ ЕТА ПРОЦЕССОВ РАЗДЕЛЕНИЯ
В МЕМБРАННЫХ ЯЧЕ Й КАХ

Основные проблемы расчета мембранных ячеек состоят:
- в определении потоков, выходящих из над- и подмем
бранного пространств и концентраций компонентов в них
(задача эксплуатации) ;

- в определении необходимой поверхности мембраны и со
ответствующего перепада дамения, возникающего при движе
нии материальных потоков в ячейке (задача проектирования) .
Разумеется, получаемые соотношения остаются справедливыми
в рамках соответствующих модельных представлений о структуре
потоков в над- и подмембранном простран<.."'J'ВаХ ячейки.
Ниже при выводе расчетных соотношений будем пользо
ваться абсолютными кон центрациями компонентов и потоками
их смеси.
20.5. 1 . Идеальное перемешивание потоков
в надмембранном и подмембранном пространствах

Будем рассматривать процесс мембранного разделения при
менительно к газовым смесям. Каждый из потоков в над- и
подмембранном пространствах идеально перемешан (рис . 20. 8) ;
поэтому концентрации любого из компонентов в каждом из
этих пространств ячейю1 постоянны и равны соответствующим
концентрациям на выходе из ячейки .
Обозначим дамения в над- · и подмембранном пространствах
Рх и Ру. Средней движущей силой процесса Л; в этом случае
1 533

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

к

L+ Q

Q

Рис.20. 8. Расч н я схема мембранной я•1е й ки потоками ид еального п ер е м е ши
вания в надмембр анном и подм ембранн о м пространствах
ет

а

с

является разность парциальных давлений i-го компонента в
надмембран �ом (pxi = P;iXt) и подмембранном (pyi = Pyyt) про
странствах: Л; = Pxi - Ру; ; напомним, что х1 < YI ·
Движущую силу процесса переноса вещества через мембрану
из надмембранного пространства (концентрация компонента xt) в подмембранное (концентрация - yt) в этом случае можно
создать за счет:
- перепада давлен ий в над- и подмембранном про
странствах Рх > Ру;
- использования (пр и Рх = Ру) потока инертного разбавите
ля
не взаимодействующего с проникающим потоком пер
меата
и легко отделяющегося от него (например, водяной
пар в случае разделения углеводородных газов) ;
- использования обоих этих факторов.
Если смесь является бинарной и идеальной, то выражения
для движущих сил (средних по поверхности мембраны F) при
различных способах ее создания имеют вид:
- для первого компо нента

Q,

L

Л1

=

Рх1 - Ру 1

=

- для второго компонента
Л2 =

Рх2 - Ру 2 =

Px( l

PiX 1 - Ру

( LL�iQ)
[ Li : �!)] .

- Х1 ) - Ру

;

(а)
(6)

Для расчета мембранной ячейки необходимо составить
уравнения для:
- определения выходящих из нее потоков и концентраций в
них (здесь три неизвестн ых, так как одним из "выходных" пара
метров обычно задаются по технологическим соображениям);
- расчета необходимой поверхности мембраны F.
Решение этой задачи применительно к бинарной смеси тре
бует записи четырех независимых уравнений:
- материальных балансов по потокам и компоненту, при
чем контуром является мембранная ячейка (два уравнения) ;
1 534

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

- " поперечного " массопереноса для расчета потока L ком
понента, проникшего сквозь мембрану (одно уравнение);
- связи (аналог уравнения равновесия) концентраций ком
понента в потоках на выходе из мембранной ячейки (одно
уравнение) .
Обозначим проходящие потоки на входе в надмембранное
пространство и на выходе из него Wн и W1 . соответственно .
При неизменном потоке Q инертного разбавителя искомые
уравнения для контура К запишутся в виде:
Wн

- W1 - - L

О; .

=

(20 . 8)
(20 .9)

F=

(20 . 1 0)

(20. 1 1 )

При известной "равновесной" зависимости (20 . 1 1 ) система
уравнений (20. 8 )-(20 . 1 1 ) является замкнутой, и расчет мем
бранной ячейки в эксплуатационной или проектной постанов
ке в принципе можно считать состоявшимся .
Для отыскания зависимости у1 = fix1 ) запишем уравнения
массопередачи для обо их компонентов, проникающих через
мембрану. При идеал ьном перемешивании потоков вследствие
постоянства кон центраций в рабочих объемах (следовательно ,
и вдоль поверхности массопередачи) эти уравнения записы
ваются весьма просто :
(в)
LY1 Кр 1 Л1 F ;

L( J

=

- У1 ) =

(г)

Кр2 Л 2 F .

Поделим выражен ие (в) на (г) ; после очевидных преобразо
ваний получим для бинарной смеси:

----

а.Л 1
У1 = а.
Л1 + Л2

или

(20 . 1 2)

Подставив в (20 . 1 2) выражения движущих сил из (в) и (г) ,
получим функциональную зависимость у1 = Л:х1):
<t

У1

=

(а.

- l)(x 1 -

(

Х1

-

Ру

-

L

.

-·

Рх L + Q

Ру
_f_
Рх L + Q

YI

)

У1) + - РРух _L+_Q
1

(20 . 1 3)

L

1 53 5

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Если движущая сила процесса создается за счет разности дав
и Р. в над- и подмембранном пространствах, т.е. Рх > Р," а
Q = О , то уравнение (20. 1 3 ) преобразуется к виду :

лений Р"

а( � )
х1 -

У1

(20. 1 4)

Есл и же движущая сила процесса создается л и ш ь за счет ис
пол ьзования инертного разбавителя, т.е. Q > О, а Рх = Ру, то урав
нение ( 2 0 1 3 ) преобразуется к виду :

.

У1 =

(

L У1
а х1 - _
L+Q

)

( -- ) --

( а - 1 ) х1 -

L

у1

+1-

L

(20 . 1 5 )

L+Q
L+Q
Сопоставление уравнений ( 20 . 1 4) и (20. 1 5 ) показы вает, что о н и

идентич н ы при

_

L_

L+Q

=

Ру
рх

=

В.

(д)

В явном виде зависимость у1 /{х1 ) определяется как положи
тельный корень общего квадратного уравнения (20. 1 3 ) л ибо част
ных его выражений (20. 1 4) и (20. 1 5).
Выражение (д) дает возможность кол ичественной оценки пере
хода от одного способа создания движущей сил ы процесса к дру
гому. Это особенно ценно при экономическом и э нергетическом
сравнении различных способов создания движущих сил .
При Рх � оо л ибо Q � оо , или Ру � О, когда движущая сила
процесса я вляется максимально возможной, из уравнений (20. 1 3 )
(20. 1 5 ) следует выражен ие, аналогич
ное по структуре уравнению равнове
сия для идеал ьной бинарной с истем ы
"жидкость - пар"( с м . разд. 1 2.2.3):
=

-

Рис. 20.9.

о

1 536

ах1
Y1 = --�(a - l)x1 + 1

(20. 1 6)

Связь концентраций комnонента в
nотоках, отводимых из надмембран ного и
nодмембранного nространства мембран ной
ячейки, n р и идеальном nерем е ш и ван и и обоих
n отоков

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Эта зависимость изображена на рис. 20.9 применительно к
различным селективностям мембраны а.. Если полаrать за
висимость (20 . 1 6) аналогом уравнения равновесия, то результат
процесса разделения бинарной газовой смеси в мембранной
ячейке с идеальным смешением потоков аналогичен эффекту
одной теоретической ступени.
20.5.2. Идеальное вьпеснение потока
в надмембранном пространстве с отводом пермеата
от поверхности мембраны в подмембранном пространстве

Надмембранное пространство может быть конструктивно
устроено так, что поток в нем движется в режиме идеального
вытеснения . Это обычно имеет место на практике при движе
нии потока внутри полил1ерных волокон и в мембранных модулях

рулонного типа.

Подмембранное пространство обычно присоединено ко вса
сывающей линии побудителя расхода - насоса, компрессора
(вакуум - насоса). В этом случае говорят об "отсосе" пермеата из
подмембранного пространства, подразумевая отвод пермеата
по нормали к мембране - без его взаимодействия вдоль мем
браны с соседними порциями пермеата. Уравнение материаль
ного баланса по потокам в целом (20 .8) остается в этом случае
правомерным. Однако концентрации рассматриваемого компо
нента х, у в потоках (са.ми потоки - тоже) изменяются по дли
не (поверхности) ячейки. Поэтому материальные балансы по
потоку переносимого компонента (а в целях упрощения записи
- и по потоку смеси) приходится записывать для элементарно 
го пространственного контура К (рис. 20. 1 0) с бесконечно ма
лой площадью мембраны dF. При этом поверхность мембраны
отсчитывают от сечения входа потока Wн по направлению
движения последнего .
Для потока смеси:
W - ( W + d W) - dL = О,
(е)
откуда с использован ием формулы (е) получим:
dL = -d W .
(ж)
Для потока компонента:
(з)
Wx - [ IVx + d( Wx)] - }dL = О ,
откуда с использованием формулы (ж) получим:
-d( IVx) = }dL = -}d W .
(и)
Преобразуем уравнен ие (и) к виду:
(к)
xd W + Wd:x = }d W .
1 537

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

о

F

к

'----���-._....-�--_./

tL1 .Y1

Рис. 20. 10. Расчетная схема мембранной ячейки с идеiiЛьным вьпеснением потока
в надмембранном пространстве и отводом пермеата от поверхности мембраны в
подмембранном пространстве

Разделим переменные н уравнении (к) и проинтегрируем от
н ачального сечения (F О) до конечного - выходного по про
ходящему потоку сечения (F = F1 ) . При этом получим
(поменяв пределы интегрирования для перехода к положитель
ным величинам):
=

W:н d W Хн dx
1 - = J -- '·

(л)

Хн dx
= J -- .
W1
Х1 у - х

(20 . 1 7 )

U'1

w

Х\

у-х

W

н
1 11 -

Интегрируя уравнение типа (20. 1 7) не до конечных значений

W\ и х1 , а до текущих И/ и х, получим уравнение (20 . 1 8), связы

вающее текущие значения потоков W и концентраций х или у.
111

WH
W

=

Х н dx
I -- .
х

у-х

(20. 1 8)

Нередко вместо текущего потока W удобно оперировать теку
щим (интегральным вдоль поверхности мембраны от F = О до
рассматриваемого текущего сечен ия }) значением потока ото
бранного пермеата L. Найдем его из материального баланса по
смеси для контура К 1 (см . рис .20 . 1 0) :
Wн - W - L = О, откуда W = Wн - L .
(м)
Сочетая уравнения (м) и (20 . 1 8), имеем:

Wн

l п -JV

и

-

L

=

х н dx
.
У -Х
хf --

(20. 1 8а)

Интегралы в уравнен иях (20 . 1 7) и (20. 1 8) или (20. 1 8а) берут
численными методами с использованием (в качестве функцио1 53 8

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

концентраций х
=
=

нальных связей
и у) уравнений "равновесия"
(20 . 1 3) - (20 . 16).
Выражения (20 . 1 8) и (20 . 1 8а) позволяют найти зависимости
fl..x) и L
W
.f<x) . Отсюда, располагая уравнениями
"равновесия" (20 . 1 3) - (20 . 1 6) , возможно получить зависимос
ти W J(y) и L J(y) . И спользуя последние, рассчкrывают необ
ходимую поверхность мембраны F. С этой целью запишем урав
нение баланса - массопередачи для элемента поверхности

=

=

dF:

dM = ydL = Кр1Рх(х - � y) dF .
Отсюда:

F1
J dF

о

=

F1

=

L1
ydL -J ---'---

о

К pl

Рх

Рх (х - � у)

(20 . 1 9)

= const получим:
F1 = Кр11 Рх LiоJ ydРLу
х - -у
Рх

В частности, при Кр1 ,

(м)

(20.20)

Интеграл в (20. 19) и (20.20) определяется с использованием урав
нений "равновесия" (20.13) - (20. 1 6) и функциональных зависи
мостей L ft.y) или L =
Если уравнения (20.19) и (20.20) запи
саны для текущей вел ичины поверхности мембраны F � F1 , то
можно установкгь закономерность изменения потоков L и W, а
также концентраций
и у вдоль поверхн ости мембраны:


=

F= J
о

./(х).

х

К р 1 Рх

ydL

[- ]
Х

Ру
-· У
рх

=

К

l

pl

J

Рх о

ydL

Х

-

Ру
-у
рх

Kp , Px = const

(н)

Рассмотренные в разд.20.5 . 1 и 20.5.2 случаи мембранного
разделения можно трактовать как предельные. Реальная эф
фективность переноса в мембранной ячейке с учетом конечной
интенсивности продольного перемешивания находится в про
межутке между ними .
20.5.3. Идеальное вьпеснение потока в надмембранном
и идеальное перемешивание потока
в подмембранном пространствах

Более сложным явл.нется случай , когда в надмембранном
пространстве поток движется в режиме идеального вытесне
ния, а в подмембранном - в режиме идеального перемешива1 539

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

В качестве примера рассмотрим процесс мембранного
ния.
потока> Руразбавителя
с использованием
разделения
Q > О при
. Тогда потоки компо
мембране
на
давления
перепаде
нентов
бинарноймoryrсмеси,
прошедшие
через
элемент мембраны
площадью
быть
определены
с
использованием
урав
нений (а) - (г) :
[х - + Q ]
yd L (о)
[ х) + Q ] . (п)
при
этом перемешанном
средняя концентрация
переносимого
компонента
в
идеально
потоке
пермеата
согласно
теореме
о
среднем равна
У! = L1 L1J
Поделим уравнение
(о) текущие
на (п); после
сокращенийконцентра
получим
выражение,
связывающее
"равновесные"
ции и х:
L1
х-У1
Q
(20.2 1)
L1
- х) - - --- (1 - У1 )
Рх

dF,

_

(1

Кр 1 Рх

_

- y)dL - Кр2 Рх

(1 -

Ру

Рх L

Ру

1

Рх

у

где

а =

К pl / К Р 2

у

Ру

(1

dF ,

У1

L1

(1 - У 1 )

Рх L 1

Ру

-- = а

L1

--

1 о

у

i

Рх

dF;

y (L)dL .

L

1 +

L

1 + Q

- селективно сть мембран ы .

'

Уравнения
материальногоприбаланса
для ячейки
по потокамперв
целом
и
по
компонентам
идеальном
перемешивании
меатаМатериальный
бьmи полученыбалансразд.по2 0.переносимому
5 .1 - формулы компоненту
(20. 8 ), (20.9). для
элементарного
объема
надмембранного
пространства,
т. е . для
бесконечно
малой
площади
мембраны
запишется
(см.
вы
вод формул (е) - (и)) виде:
d ( W ) -yd W; xd W + Wdx yd W,
(р)
откуда
результате
разделения переменных и интегрирования
по всейвячейке
получим:
Wн
Wн
ln J -- .
(с )
Wн W1
уравнений (20.
материального
баланса пообразом
потокамзаписме
си помощью
(20. 8 ) и компонента
9) можно следующим
1540
в

-

x

в

=

=

=

С

d F,

111

L1

Хн

=

х1

у

dx

х

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

сать нижний предел интегрального уравнения (с):
(т)
=

При
заданном
и при отсуrствии
разбавителя
(Q О) по
ток
пермеата
L
находится
численным
решением
интегрально
1
гонения
ft..x) -вычис
урав
уравнения
(т)Последняя
с привлечением
зависимостии простоты
(20.21).
для
наглядности
лений
может
быть представлена графически "равновесной"
кривой
в
координатах
разбавителя
(итерационно.
Q > О) система уравнений
(20.При
2При1) ииспользовании
(с),
(т)
может
быть
решена
решении
системызначения
(20. 2 1)-(с),вместо
(т) свыходной
использованием
в
уравнении
(с)
текущего
концент
рации
и текущего значения
L вместо L1 получаем функцио
х1 зависимость
нальную
L
ft..
x
).
Поверхность
уравнение
(о): мембраны можно определить, интегрируя
(20.22)
или при Кр, Рх
ydL
(у)
F = К р 1 Рх Lf1 ---'----Ру Li
у1

у

=

у--х.

х

=

=

const:

1

в

1

F1

о

х-

-

Рх L1 + Q У1

Интегралы уравнениях
(20. 22) и (у) беруrся
численно
с т.исе .
пользованием
известных
зависимостей
L
ft..
x
),
ft..
x
),
уравнений
(20.яют2 1 ) наи аналогичного
(с), когда конечные значения
L 1 Закон
и х1 замен
щие
L
и
те
х.
ку
изменения
потока
пермеата
вдоль поверхности
мем
ft..
F)
можно
получить
из
уравнений
(20.
2
2)
и
(у),
за
браны
L
менив
в
них
конечные
значения
1
и
L1
на
текущие
значения
F
ивыражению
L. Располагая зависимостями
L ft..F) и L ft..x), приходим
ft.. F) , а с использованием уравнения "равно
весия"
- и расчеты
ft..F) . по трем описанным моделям дают су
Численные
щественные
расхождения
при
значительной
долевариантах
пермеата.струк
Разумеется,
возможны
расчеты
при
других
туры
в расчетные
над- подмембранном
пространствах
ячейки.
Вболее
этихпотоков
случаях
выражения
получаются
значительно
громоздкими.
1541
=

у =

=

=

х =
к

у=

и

=

F

к

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

20.5.4. Перепад давления в потоках, движущихся
в подмембранном и надмембранном пространствах

Данные о иперепаде
давленияпространствах,
в потоке, движущемся
в под
мембранном
надмембранном
необходимы
для
подбора
побудителей
расхода
(насосов,
компрессоров).
Данные
об изменениивеличины
давления попотока
длинепермеата,
этих каналов
необходимы
для
определения
так
как
они
опреде
ляют
закон
изменения движущей силы процесса вдоль поверх
ности
мембраны.
Перепад
давления
движущемся
по бьrгъ
каналамнайденмембранной
ячейки
потоке
с
живым
сечением
fк
может
рованием дифференциала Бернулли реальной жидкостиинтегри
(газа):
(ф)
d ( � ;; h п ) О .
Течениеобычно
в канале из-за малой
величины
его характерного
размера
Поэтому
коэффициент
ческого сопротивления Л.r (см. разд. 2 . 2 . 2 и равен:гидравли
w = - - -- '
Л.r = Р к pdJJ'
в

для

Z +

+

+

=

ламииарное.

2 . 2.4)

64
Re '

G
f

- -

4G

= -

rде массо вые пото ки G = W для надмембран ноrо пространства и G L для
п одмембранно rо пространства; / и d3 дли н а и эквивалентный диаметр кан ала;
П с м очен н ый п ериметр пото ка .

-

Тогда уравнение (ф) перепишется в виде:
2
2
/
dz dp d w
d / dz dp d w
' (х)
pg 2g pgd�
pg 2 g р 2 gd ; л d
где - н ивелир ная высота.
В общем случае текущее значение потока
G(l) изме
няется
по
длине
канала
(аналог
трубопровода
с
пугевым
расхо
дом).Для несжимаемой жидкости при стационарном изотерми
ческом теченииуравнение:
из уравнения (х) получаем следующее диффе
ренциальное
(ц)
d (z � ;;) - 2�ds;
G(l) d l '
P
причем текушее значение длины канала (изменяется от О до
После(индекс
интегрирования
(ц) мембранной
от входного ячейки
(индекс получим
"н") до вы
ходного
сечений
вестное уравнение для расчета ламинарного течения жидкостииз
1542
+

+

+

3 2 µ�

=

+

+

+

1 28 µ G

z

G

+

/-

+

=

=

0

=

п

/1 ) .

" 1 ")

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

по каналу с пугевым расходом G(/):
w н2 - w 2
Р
128µ f G(l) d/ . (20. 2 3)
+ н
2g р gd3 П
pg
Это частный
случай более общего решения, приведенного в
разд.2.
3
.
4
.
В случае течения газов, следуя допущениям, сделанным при
расчете
газопровода (см. разд. 2 .3.5), упрощаем уравнение (в):
1 2 8 µ G(/) d /.
(ч)
d3 П р
дифференциального
уравнения
(ч)
ведется численны
миРешение
методами
с
учетом
(р).
р
В случае изотермического течения близкого к идеальному
газа
интегрирование
выражениярасходом:
(ч) приводит к следующему
уравнению
течения с пуrевым
256 µ Ry /j G(/) d /.
(20.24)
Р � Р 12
d; п
В пракrических расчетах длину канала /1 разбиваюг на ряд уча
стков
Л/ с давлением в начале и конце каждого участка и со
ответственно,
в сопределах
которыхизменением
расход потокауча G принимаюг
постоянным,
но
ступенч
к участку.
Тогда разностный аналог уравнения (20.24) залmnется в виде:
256 µRyT GЛ/
Р' 2
(20. 2 5)
d ПМ
Zн

_

Zt

-

1

Pt +

dp

=

2

3

l

о

_

э

р

=

_

=

м

о

р"

р'

атым

-

где

G

-

р"

2

=

от

стка

3

3
массовый поток, осрсдненный на участке дl.

мембранного элемента
ведуг итерационными
мето
дамиРасчет
- предпочтительно
с использованием
ЭВМ.
20.6. П РОСТЕ Й Ш И Е КАСКАДН Ы Е СХЕМЫ РАЗДЕЛЕНИЯ

Целью
процессов
мембранноготребуемой
разделения
является
получе
ние
вьщеляемых
компонентов
чистоты.
Однако
се
лективность
мембран
ограничена
их
природой,
механизмом
проницания
компонентов, физико-химическими
свойствами
последних,
конструктивными
особенностями
мембранной
ячейки.
Требуемой
степени
обоrdщения потока целевым мем
ком
понентом
достигают
пуrем
бранных
соединенияаппаратуру
мембранных- ячеек
называют ячеек. Такие а схемы
соответствующую
1543
последовательного соединения

каскадными ,

каска-

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

дом мембранных ячеек . Как и при расчете любого процесса, в
данном случае возможны две постановюt задачи - проектная и
эксплуатациопная. В первом случ:�с заданы поток и концентра
ция исходной смеси и , чаще всего, концентрация получаемого
целевого ком понента. Требуется определить необходимое число
ячеек (ступен ей) каскада, поверхность их мембран , значения
потоков и кон центраций во всех ячейках каскада. При экс
плуатационной постано вке задачи, напротив, число ступеней
каскада и их поверхность известны , а требуется определить
значен ия потоков и концентраций на всех ступенях каскада
(включая и значения на выходе каскадной схемы).
Ниже в качестве примера рассмотрены две простейшие кас
кадные схемы .

20.6 .1. Разомкнуrый каскад
с выводом проходящего потока из ячеек

Если мембранные ячейки соединены последовательно, т.е .
пермеат из последующей ячейки подается в надмембранное
пространство предыду�цей, и отсутствует рециркуляция непро
диффундировавшего через мембрану потока, то каскад назы
вают разомкнуrым с выводом проходящих потоков из ячеек кас
када (рис. 20 . 1 1 ). Такая схема обеспечивает последовательное
концентрирование пермеата от ячейки к ячейке и в конечном
итоге - требуемую чистоту целевого компонента.
Для определения значений потоков смеси и концентраций
целевого компонента для всех ячеек каскада запишем уравне
ния материального баланса по потокам смеси и компонента
для п-й ступени каскада (контур К на рис . 20. 1 1 , а):
L"._1 - W
(а)
п Lп = О ;
(б)
L"_ 1 Y11- \ - WnXn - LпУп = о .
Введ я понятие о дол е проникаю щего потока 'Рп = Ln / Ln - 1 ,
из (а) и (б) получим уравнение перехода от концентрации
-

Уп- 1

К

Уп :

(20 .26)

При этом концентрации Уп и Хп связаны "равновесным" со
отношением - например, по уравнениям (20. 13), (20 . 1 6),
(20.2 1 ),
ему отвечает штриховая линия на рис.20. 1 1 ,б. Урав
нению (20.26) на этом рисунке соответствует сплошная линия.
Очевидно, что этих двух линий, как и двух уравнений (связи
(20.26) и "равновесия") , достаточно для определения всех кон 
центраций в потоках к:�скада .
-

Если параметр ы ступ ени (я че йки) ка скада - разные (наприм ер, из - за раз
ли чных по сту пе ня м давлений, селекти вн о стей м е м бр ан, доле й про никающе го
1 544

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

у" =f(хп)

Уз

- - - - -

L_V- l · Y N - 1
о Х1

Хи х2

У1

У2

Х3

Х4

�

Уз

У4

б

а

Рис. 20. 1 1. Разо м кнутый каскад с выводо м проходящего п отока из каждо й ячейки
( 11Jафически й м етод расчета ) :
а

-

б

технологическая схе ма,

расчетная д и аграмма

-

потока '!' и т.д . ) , то для расч ета ко н центраци й каскада н адо стро ить соответ
ствующее число "ли н и й равн овесия " и уравн е н и й связи (20 . 26).

Потоки в ячейках кас када можно найти из соотношений :
L

Легко видеть, что
причем для '-11 i

где

п

и N

W�

� = '-112 ;

L

(в)

п

(r)

П '-11;

=

i=l

idem

Ln

wн

-

L

= '-11 1 ;

=

l.Jl n

( 20. 27)

и

теку щt:е и ко нечное числа ячеек в каскаде:

п $

N.

Выражения (в) , (r) и (20.27) связываюг величины потоков, вхо
дящего в каскад и в каждую ячейку и выходящего из него и из
каждой ячейки, число ступеней и долю проникающего через мем
браны потока. В простейшем случае l.Jli = idem число ступеней
каскада N определяется по уравнению, следующему из (20 .27) :
N

=

l n( Lк /Wн )
1 11 Ч'

(20 . 2 8)
1 54 5

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Достоинство рассматриваемой схемы состоит в отсутствии
необходимости повышен ия давлен и я в отводимых потоках, так
как последние не возвращаются в процесс разделен ия . Глав
ным недостатком является вывод из надмембранн ых про
странств каскада, т.е. из процесса разделен ия, потоков Wn,
содержащих еще достаточно высокую кон центрацию вьхделяе
мого компонента Хп. По этой причине эффективность процесса
разделения в таком кас каде невысока.

20.6.2. Замкнутый каскад с возвратом проходящего потока
на предьщущую ступень

Проходящий поток с предьхдущей ступени с весьма высокой
еще кон центрацией переносимого компонента целесообразно
возвратить на вход предьхдущей ступен и . Схема такого каскада
приведена на рис. 2 0 . 1 2 , а. Материальные балансы по потокам
смесей и компонента для контура к, включающего ступени от п
до N, имеют вид :
(д)
Ln = Wn + J + 4. ;

LпУп = Wn+ ]Xn + J

+

4.Ук

(е)

·

Тогда сопряженные (текущие , находящиеся в одном сечен ии)
кон центрации переноси мого ко мпонента Уп и Хп+ 1 связывает
уравнение рабочей л и н и и :

Уп

где R =

=

Wп +I
-т;:- Хп + l

wn + 1 / Lк

-

ДОЛЯ

+

Lк
n
L

Ук

=

R

R

+

Х
1 п+\

+

1

R + 1

У к ' (20 . 29)

во:1вращаемого (рецир кулирующего) потока (это -

а налог флеrмово го числа в ректификации); ком пл екс R/( R + 1 ) есть тангенс угла
н акло н а ра бочей ли н и и - уравнени е (20 . 2 9 ) .

Уравнение (20.29) при постоянном R связывает текущие
кон центрации Уп и Хп + 1 линейной зависимостью, для построения
которой в диаграмме у-х (рис .20 . 1 2 , 6) достаточно располагать
двумя точками . Найдем параметры этих точек.
Прямая , описываемая уравнением (20 .29) , отсекает на оси
ординат (х = О ) отрезок:

Уп =

Ук

R

+

1

(ж)

Объединяющая масс и в точек диагонал ь

Уп = Xn + J

(з)

пересекает прямую (20 .29) в точке, определяемой совместн ым
решен ием ур;�внений (20 . 29) и (з) . Приравнивая Уп по (20 .29) и
1 546

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

б

а
''

Рис. 20. 12. Замкнуrый каскад
возвратом проходящеrо потока на предыдущую
ступень (rрафический метод расчета при R const и одинаковых
всех ячеек
условиях "равновесия"):
дт1Я

=

а -

технологическая схема,

б-

расчеrnая диаграмма

(з) , получаем абсциссу второй искомой точки на диагонали:
откуда при

п

= N

(R + l )Xп+J = Rxп+J + Ук
Xn+ l = Ух ·

,

(и)

Минимальные поток (см . разд . 1 0.7 .2) или доля рециркули
рующего потока RпШ1 (аналог минимального потока второй
фазы) определяются так же, как и в других массообменных
процессах: требуемая степень обогащен ия пермеата Ук достига
ется при бесконечном числе мембран н ых ячеек (аналогов тео
ретических ступеней ) . Для этого необходимо, чтобы рабочая
линия, соответствующая мин имальн оii доле р � циркулирующеrо
потока, пересекалась с "линией равновесия", найденной, на
пример, по уравнениям (20 . 1 3 ) - (20 . 1 6) и (20.2 1 ) , в точке с
координатами у 1 Р и х1 ,
где кон центрация в пермеате у1 Р
"равновесна" с х1 • Тогда Rmin получаем и з уравнения (20.29)
подстановкой Xn +l .::: х1 , Уп = У1 Р , R = Rrnin:
R min

+1

У к - yf
Ук

-

Х1

1 547

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

так что
RШU. \

к
= У
р
У1

-

y

f

(к)

- Х1

С использованием балансовых уравнений (д) и (е) , записанных
для входн ых и выходных параметров каскада (контур К) ,
имеем :
(л)
Wн - W1 - 4. = О ;
Отсюда, исключая

Wнхн - W1 X1 - 4Ук = О .
Wн, п олучае м :
W1 У к - Х н
Lк

Приравняв (к) к

(н),

Хн - Х 1

(м)

(н)

н аходим :

f

У_
-_
_
к_
- У
__

=

откуда следует:
YJ P

_У_к�
-_х_н_
= Хн ·

=

W1

Lк '
(о)

Располагая значением Rrnin, из экономических соображений
(по аналоги и с другим и массообмен ными процессами - рек
тификацией , абсорбциеii, экстракцией и т.д . ) определим опти 
мальное значение коэффициента избытка рециркулирующего
потока cr = R/Rmin и получим рабочее значен ие доли рецирку
лируемого потока R = crRrnin. Далее построим рабочую линию,
теоретические ступен и , найдем их число , кон центрации пере
носимого компонента в потоках Хп и Уп и потоки Wn и Ln.
П о установлен н ы м nотокам и кон центрациям в ячей ках
кас када последовательно от ячейки к ячейке рассчитаем пло 
щади мембра н ы Fn для ступеней (ячеек) каскада:
(20 . 3 0 )

Возможен случай , когда каждая ступен ь каскада фун кцио
н ирует со своей "лин ией равновесия" (например , от ступени к
ступен и изме н яется селективность мембран ы) ил и же со своим
значен ием доли рецир кулирующего потока Rn. Тогда для каж1 548

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

а

о

б

Хн

Ук

1

Рис. 20. 13. К расчету замкнуrо го каскада с рециркуля цией проходящего потока на
предыдущую сту11ен ь (rраф и •1е<:ки й метод расчета) :
а

-

(R

var) ,

- 1 1 р и п е р е м е нны х
( R = var)

п р и постои нных для всех н ч е е к условиях " "ривновесия" и п е р е м енной доле р е ц и р к у 

л и руемоrо п о т о к а

=

б

долях реци р кул ируемоrо потока

д л я в с е х я ч е е к у с л о в и я х ""равновесия"

и

дай стуnени аналогично изложен ному выше строится

своя в
первом случае "линия равновесия", а во втором - рабочая ли
н ия . П р имер подобного построения для второго случая приве
ден на рис . 20 . 1 3 , а.
Наконеu, воз мож н о , •по для каЖдой стуnени кас када харак
терн ы как своя "лин и я равновесия " , так и свое значение доли

1 549

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

рециркулируемого потока Rn (т.е. своя рабочая линия). В этом
случае по изложенному выше алгоритму строят (рис . 20. 1 3 , 6)
"линию равновесия" для первой ячейки каскада и соответственно
выбранному значению R1 - рабочую линию. Затем фиксируют
первую теоретическую ступень и определяюr кон центрацию ком
понента в потоках первой ступени . Для второй ступени вновь
строят уже свои (дpyrne) линии - "равновесную" и рабочую; после
построения второй теоретической ступени фиксируют кон центра
ции в потоках второй ступени. Аналогичный графоаналитический
метод построения хода процесса реализуют до достижения тре
буемых выходных кон центраций (см . рис. 20. 1 3 , 6) . Обычно подоб
ного рода расчеты проводят на Э В М .
ЛИТЕРАТУРА к главе 20

1 . Дытнерскиii Ю.И. Про цессы и аппараты химичес ко й техноло гии . М . : Х и 
м и я , 1 99 5 . 768 с .
2 . Технологически е процессы с применением мембран : П е р . с англ . / П од
ред. Ю.А. М азито ва. М . : М и р , 1976. 369 с.
3 . Хванг С. - Т , Каммермеiiер К. Мембранные процессы разделени я : П ер . с
ан гл . / Под ред. Ю . И . Дьпнерс коrо . М . : Х и м и я , 1 98 1 . 464 с.

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Глава 21
УМЕРЕННОЕ

И

ГЛУБОКОЕ ОХЛАЖДЕНИЕ

Ряд химико-технолоrичесюrх и других процессов проводится
при температурах ниже, чем у окружающей среды. Диапазон
н изких температур, необходимых для реализации разнообраз
НЪIХ технологий в различных отраслях промышленности, чрез
вычайно широк: от температуры окружающей среды до темпе
ратуры, приближающейся к абсол ютному нулю . Осуществление
такого рода процессов связано с производством искусственного
холода . Потребность технологических установок в холоде до
стигает десятков тысяч киловатт и требует применения высо
копроизводительного ко мпрессионного оборудования.
Специально подчеркнем: в данной главе рассматриваются
технологические проблемы производства искусственного холода
и излагаются они с позиций инженерной химии . Термодинш.t и 
ческие аспекты этих проблем более строго и детально освещены
в учебной и научной литературе по термодинамике• .
21 . 1 . ОБШ,АЯ ХАРАКТЕРИСТИ КА

ХОЛОДИЛЬНЫХ П РОЦЕССОВ

К числу протекающих при искусственном охлаждении отно
сятся процессы кристаллизации, сублимационной сушки, неко
торые процессы абсорбции и адсорбции, отдельные реакцион 
ные процессы ( например, полимеризации). Все большее рас
пространение холодильные процессы приобретают в электро
технике, электронике , ядерной, ракетной, строительной про
мышленности, в пище вой, фармацевтической и во многих
других технологиях.
В техн оло гически х процесс<1 х н ефтяной , r.�зовой и х и мической пром ышлен 
н о сти применяется и скусствен н ый холод в дианазоне примерно д о -200 ° с,
иногда и ниже.
В нефтехи мическо й про м ы шленности искусствен ное охлажде н ие исполь зуют
в системах непосредственного кипен и я р<tбочи х тел в по вер х ностных теплооб
менн ых аппар<tта х . Здесь Ч<tст<> применяют про изводные углеводородо в с высо 
ко й моляр н о й массо й , при год н ые поэто му к сжати ю центр о б еж н ы ми ком прес
сора ми .
• См. , например , 1 1 , 2, 8, 9 . 14, 1 5 ) .

1551

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

В газ ово й пр ом ьшшен но сти ис кусств е н н ы й холод требу ется при под готовке

газа к транспорт ировани ю и п р и переработке газ ов - природных, по путн ых и
нефтя ных и з газо ко нденсатн ых м есторо ждени й .

Химическая и смежные отрасли промышленности (получе
н ие этилена, фармацевтических и биохимических препаратов,
производство синтетического каучука, хлора и др .) отличаются
многообразием систем холодоснабжсния с различными типами
холодильных машин .
Потребность техноло гических установок в холоде достигает
десятков тысяч киловатт и требует применения высокопроиз
водительного компрессионного оборудования .
Холодильный процесс заключается в передаче теплоты от объ
екта с меньшей температурой к объекту с большей температу
рой. Согласно второму н ачалу термодинамики такой процесс не
может происходить самопроизвольно , он осуществим только с
затратами подводимой извне механической (или других вИдов)
энергии, т.е. с затратой работы в явной или неявной форме .
Способы производства искусственного холода в значитель
ной степени определяются требуемой температурой охлажде
н ия и масштабами устан овки.
В настоящее время различают два основных типа холодиль
ных процессов - получение умеренного и глубокого холода. Как
показывают названия, в основе такой классификации лежат
температурные уровни охлаждения . Сегодня принято считать,
что умеренное охлаждение оперирует температурами до - 1 00
0 С, а глубокое охлаждение - н иже - 1 00 ° С.
Однако классификация по температуре охлаждения подвиж
на (граничная температура постепенно снижается) , она условна
и все более приобретает историческую окраску. Сейчас глав
ное различие глубокого и умеренного охлаждения формулиру
ют в зависимости от типа технологических схем получения низ
ких температур . При производстве умеренного холода для пере
дачи его охлаждаемой среде используются посторонние (не рас
ходуемые) рабочие тела (нагреваемые ЖИдКости и газы) , и по
этому холодильные циклы умеренного холода полностью замкну
ты по рабочему телу. А при производстве глубокого холода
охлаждаемая среда сама служит рабочим телом, она отбирается
из холодильного цикла для технологических нужд; поэтому
циклы глубокого холода замкнуты по рабочему телу не nолностью.
В последующем изложении указанные различия в холодильных
циклах будут проиллюстрированы предметно .
Далее последовательно рассмотрены основные способы и
технологические схемы получения низких температур в про
цессах умерен ного и глубокого охлаждения , а также методы их
расчета.
1 552

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

21 .2. П РОЦЕССЫ УМЕРЕН НОГО ОХЛАЖДЕНИЯ
21 .2. 1 . Идеальная холодильная машина
Идеальная холодильная машина умеренноrо охлаждения тео
ретичесюt неµеализуема. Но ее рассмотрение позволяет уяснигь
принципы организации циклов умеренного охлаждения , осмыс
лигь их стадии и ввести основные характеристиюt процесса.
Узел , в котором от объекта н изкой температуры передается
(отводится) теплота к рабочему телу, будем называть нижним
теl\tпературным источ1шком ; узел , в котором к объекту высокой
температуры передается (подводится) теплота от рабочеrо те
ла, - верхним температурным источником .
Охлаждение веществ до температур, более низких, чем тем
пература окружающей среды, связанное с переносом теплоты
от нижнего температур н ого источника к верхнему, как отмеча
лось выше, требует затраты внешней работы. Здесь уместна
аналогия с перекачкой жидкости из области низкоrо давления
(потен циала) 11асосом в область высокого давления: Поэтому
схему передач и теплоты из зоны н изкого температурного по
тен циала в зону высоко го (вообще и в холодильных процессах
- в частности) именуют тепловым насосом.
Н аиболее совершен ным ( идеальным) является процесс
охлажден ия, обеспечивающий передачу максимального коли
чества теплоты (производства максимальноrо количества холо
да) на единицу затраченной работы. Этому условию удовлетво
ряет рабочий процесс , проводимый по обратному циклу Карно.
Напомним, что этот цикл предусматривает две изотермиче
ские и две адиабатические операции: изотермический отвод
теплоты от рабочего тела (РТ) в верхнем температурном источ
ни ке (холодильнике-конденсаторе Х К) , адиабатическое пони
жение температуры РТ в расширительной машине (детандере
Д), изотермическое нагревание РТ в нижнем температурном
источнике (испарит�ле И) и адиабатическое повышение темпе
ратуры РТ в компрессоре ( К) . При этом в нижнем источнике
РТ получает теплоту от охлаждаемой среды, т.е. последняя
охлаждается - в этом цель про цесса.
Подчеркнем, что РТ здесь не расходуется, так что цикл по
рабочему телу в самом деле замкнут.
Отвод теплоты от РТ и подвод теплоты к нему в изотерми
ческих условиях осуществимы только при конденсации и ки
пении РТ, поэтому ци клы Карно (прямые и интересующие н ас
здесь - обратн ые) могут быть реализованы в области влажного
пара. Соответственно указан ным выше операциям строится
идеальный циi<.л умерен ного охлаждения (рис. 21 .1, а) . В ком 
прессоре
происходит адиабатическое сжатие рабочего тела

К

1 553

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

т

lJ

Рис.21. 1.

а

lJ

6

б

s

Идеальная машина умеренноrо охлаждения:

принципимьная схема, б - диаrрамма Т-s;
/ - рабочее тело, // - охлаждаемая среда, /// - охлаждающая среда;
К - компрессор, ХК - холодильних-конденсатор, Д - детандер, И - испаритель
а -

1-2; в холодильнике (здесь это конденсатор) ХК - изотерми
ческий отвод теплоты от РТ (конденсация) 2-3; в детандере Д
- адиабатическое расширение 3-4; в испарителе И - изотер
мический подвод к РТ теплоты (кипен ие) 4-1.
Установим первоначально характерные температуры РТ.
Пусть исходная температура охлаждаемой (целевой) среды рав
на t0'; среду надо охладить до t0" (см. рис. 2 1 . 1 , а) . Очевидно ,
что температура испарения рабочего тела Тн при его рабочем
давлении Рн = р1 в испарителе И должна быть ниже температу
ры охлаждаемой среды t0" , чтобы теплота Q0 отнималась от
последней и передавалась РТ. Пусть теперь исходная темпера
тура имеющегося на производстве хладоаrента, т.е . охлаж
дающей среды (например, воды), равна /8', а приемлемая ко
нечная - !в" · Тогда температура конденсации рабочего тела Тв
при рабочем давлении Рв = Р2 в холодильнике-конденсаторе
ХК должна быть выше температуры хладоаrента lв", чтобы теп
лота Qx отнималась от Р Т и переходила к хладоагенту.

Приведенные выш е рассуждения о выборе температур Тн и Т8 носят сугубо
инженерный характер и относ1rrся к некоему "теоретическому" циклу, но они не
являются термодинамически строгими. Дело в том, что в идеальном цикле холо
дильной маш ины все процессы - равновесны (тогда они обратимы), а это воз
можно только при совпадении температур верхнеrо или нижнеrо источников и
соответствующих каждому из них температур внешних объектов (сред) .
Температуру рабочего тела Тн называют температурой ниж

неrо источ ника,
В

1 554

Тв

-

темпе р атур ой верхнего источника.

компрессионной холодильной машине, работающей по

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

идеальному циклу (см . рис . 2 1 . 1 , а) , пapt-J РТ сжимаются в
компрессоре от давлен и я р 1 до Р2 (затраты энергии) . П осле
сжижения в холодильнике-конденсаторе РТ расширяется в
детандере (отдача энергии) , давлен ие снижается от Р2 до пер
воначального р 1 , и РТ подается в испаритель.
Идеальный цикл удобно изображать в диаграмме T-s (рис .
2 1 . 1 , б). Стадии цикла (они соответствуюr схеме на рис . 2 1 . 1 , а):
1 -2 - адиабатическое сжатие РТ в компрессоре (s = const) ;
2-3 - изотермическая и изобарическая конденсация паров
РТ в конденсаторе ( 7;1 = const, Рв = const) ;
3-4
адиабатическое расширение РТ в детандере
(s = const) ;
4- 1 - изотермическое и изобарическое испарен ие РТ в ис 
парителе ( Тн = const; Рн = const) .
Диаграмма T-s отнесена к 1 кг рабочего тела (s - в
Дж/( кг· К)] , поэтому затраты энергии (работа) и количества
теплоты также являютсн удельными, т.е. рассчитан н ыми на 1
кг РТ, циркулирующего в цикле . В диаграмме T-s удельная
работа, затрачиваемая в компрессоре, измеряется площадью
1 235 1 , а удельная работа, получаемая (возвращаемая) в детан 
дере, - площадью 3453 . Следовательно , безвозвратный расход
энергии (удельная адиабатическая работа цикла) , измеряемый
площадью 1 234 1 , составляет /ад = ( Тв - Тн)Лs. Площадь 23672
выражает удельное количество теплоты qконд = ТвЛs, отводимой
хладоагентом от РТ в конденсаторе , а площадь 1 467 1 - удель
ное кол ичество теплот ы q0 = Тн Лs , получаемой в испарител е
рабочим телом от охлаждаемой среды, т.е . удельное количество
произведенного холода.
Расчеты и опыт эксплуатации показываюr, что основную долю
(до двух третей) расходов при получении холода составляюr затра
ты энерrnи. Для их оцен ки и сопоставления эффективности раз
личных циклов вводят понятие о холодильном коэффициенте Ех ,
выражающем количество холода, производимого в испарителе,
приходящееся на единицу затраченной адиабатической работы:
Ех = qo/ lал·
( а)
Холодильн ы й коэффициент Ех в определенном смысле оце
н ивает термодинамическое совершенство рабочего цикла: чем
выше Ех, тем выгоднее цикл , так как тем больше рабочее тело
передает холода охлаждаемой среде (забирает от нее теплоты)
за счет еди н и цы затраче н ной работы .
Для идеального цикла общее выражение (а) при подстановке
значений q0 и /ад приобретает вид :
Ех

=

Тн ЛS
(Тв - Тн )Лs

=

Тн
Тв - Тн

(б)
1 5 55

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Как видно из (б) , для идеального цикла холодильный коэф
фициент не зависит от физических свойств РТ, а целиком
определяется температурой верхнего и нижнего источн иков.
На величину Ех можно воздействовать, выбирая уровни тем 
ператур Тн и Тв. С понижением Тн коэффициент Ех уменьшает
ся , и производство хо.1ода удорожается; значит, не следует
стремиться к чрезмерному (ниже необходимого технологиче
ского уровня) понижен и ю температуры Тн. С понижением Тв
коэффициент Ех возрастает; однако возможности снижения Тв
обычно огран ичены, та к как ограничен диапазон температур
охлаждающей среды в конденсаторе (это чаще всего - холод
н ый воздух или холодная вода) .

2 1 . 2.2. Реальная паровая компрессионная холодильная машина
Практическое осуществление холодильного процесса требует
модификации идеальной схемы (цикла). Реальная компресси
онная холодильная машина имеет три существенных отличия
от идеальной:
1) вместо расширительной машины (детандера) в схеме ис
пользуется дроссельны й вентиль;
2) компрессор реальной холодильной машины всасывает су 
хой насыщенный пар (при сжатии последний становится пере
гретым);
3 ) жидкость после конденсации несколько переохлаждается
перед дросселированием .
Первые два отличия являются вынужденными (надо выяс
нить - почему): они негативно сказываюrся на эффективности
процесса. Третье отличие вводят намеренно (надо выяснить - за
чем). П редметная оценка указанных изменений дана при рас
смотрении диаграммы T--s для реальной холодильной машины .
Напомни м , что в дроссельном вентиле происходит адиа бат 
ны й процесс сброса давления без отдачи работы на сторону.
Небольшие размеры ве нтиля (значит, и малая его наружная
поверхность) при весьма значительных потоках рабочего тела
через вентиль позволяют игнорировать теплообмен с окру
жающей средой ; заметнм : в холодильных процессах вентиль
часто покрыт естественной изоляцией - "шубой" инея из за
мерзшей влаги атмосферного воздуха. Смысл процесса состоит
в прохождении потока через узкий канал, обладающий суще
ственным гидравличесю1м сопротивлением .
Принцип работы дроссельного вентиля иллюстрируется схе
мой на рис . 2 1 . 2 . П оток движется через узкий канал А под дей
ствием перепада давлен ий Рн
Рк · равного гидравлическому
сопротивлению канала, обусловленному трен ием потока о его
стенки. При этом энтал1>пия потока должна бы понижаться от
-

1 556

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 21. 2. К п р и н ципу работы ;1россельно rо вентиля
уз кий ка н ал )

(А

-

начальной величины iн до конечной iк. Но
затраты энергии на тре н ие переходят в теп
лоту, а последняя целиком (устройство изоли 
ровано в тепловом отн ошении) возвращается
потоку. Поэтому на выходе энтальпия потока
iк · та же ,
что и на входе iн . Результат
А
процесса в сужающем устройстве А следует
записывать в форме iк = iн; часто его запи
сывают (не совсем строго) в форме i = const.
Рассмотренный процесс падения давления
потока в сужающем устройстве пр и сохра
нении его энтальпии именуют дросселирова
нием . Некоторые допол нительные моменты,
с вязанн ые с процессом дросселирования,
рассмотрен ы в разд . 2 1 . 3 . 1 .
Замена детандера дроссел ьн ым вентилем обусловлена отсут
ствием расшир ительных машин для жидкости . Использование
энергии "сжатой" (но практически несжимаемой) жидкости
потребовало бы создания расширительной машины с крайне ма
лым ходом поршня, что технически неосуществимо . Образование
капель в детандере при адиабатическом расширении в нем жид
кости (см. рис . 2 1 . 1 , 6 - точка 4 в области влажного пара) нежела
тельно из-за эрозии стенок цилиндра, затруднений при выводе
двухфазного потока, гидравлических ударов в пространстве под
поршнем на стадиях неизобарической работы машины .
П р и всасывании компрессором влажного пара (парожид 
костной смеси) происходит испарение капель жидкости за счет
теплоты сжатия . При этом увеличивается количество паровой
фазы и дополн ительно повышается давление, значит, падает
объемн ый К ПД компресL:ора (см . разд. 4.3.3), а с ним и произво
дительность холодильной машины. Кроме того, при испарении
капель РТ возникают локальные термические напряжения в точ
ках их контакта с поверхностью цилиндра компрессора, материал
его "устает", что отрицательно сказывается на долговечности ком
прессора. Этим и обусловлен переход к (.у.wму сжатию.
Схема реальной одн оступенчатой компрессион ной холо
дильной маш и н ы показана на рис . 2 1 . 3 , а . Компрессор К сжи
мает пары РТ, поступающие из испарителя И , от давления р 1
д о давления Р2 и подает и х в холодильник-конденсатор Х К
(вместо конденсатора в схеме идеального цикла) . Из него жид
кое РТ направляется на дросселирование в дроссельном венти 
ле Др , где давление падает от р2 до р 1 , и далее - в испарител ь .
Регулирован ием степе н и открытия дроссельного вентиля мож'

"

1 557

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

т

1

о

а
Рис. 21.З. Реальная

одноС1)'пен чатая

паровая

7 6 " 6 6'

б

1' 7

компрессионная

s

холодильная

- принщшимьная схема. б - диаrрамма T-s;
1 - рабоче е тело, /1 - охлажда�мая среда, 111 - охлаж,цающц среда;
К - компрессор, ХК - холодильник-коJШенсатор, Др - дроссмьНЪIА
парит ель

ма

ш и на:

а

ве11ТИJJЬ ,

И

-

ис

но при заданной производиrельности компрессора (потоке РТ в
цикле) измеюпъ в некото р ых пределах перепад давления Р2 - р1 и
сами Р2,Р1 , а значкг, соответственно, и те мператур ы Т8 и Т11•
Вопрос " где в холод ильной машине производится холод?" не
имеет одн означного ответа . С позиции потребителя охлаждае
мой среды - несомненно, в испар ителе И , где происходит
,v
охлаждение целевого потока, т.е. отбор теплоты от самои
охлаждаемой среды. Но с позиций технолога, обслуживающего
холодильный цикл , холод производится там, где РТ отдает теп
лоту, т.е. в холодильнике-конденсаторе .
Диаrрамма T-s при переходе к реальной машине умеренного
охлаждения п ретерпевает изменения (рис . 2 1 .З, б), отвечающие
схеме процесса на рис. 2 1 .З, а. СтdДИИ реального цикла:
1 - 2 - ад иа батическое (s = co11st) сжатие сухого (перегре
того) пара;
2-3'-3"-3 - изобарическое <Р2 = co11st) охлаждение паров
до точки ко н де нса ц и и , конденсация пара и переохлаждение
полученной ж •щ кости ;
3-4 - изоэнтальпичсское (i = coнst) дросселирование;
4-1 - испарение до состояния сухого насыщенного пара.
Диаграмма T-s позволяет наглядно оценить выгодность или
невыгодность изменений, внесенных в цикл при переходе от
меальной холодильной машины к реальной.
Переход к "сухому" сжатию, т.е. сжатие паров в перегретой
области, является термодинамичесI01 невыгодным: на участке

1 558

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

2-3 возрастает удельная работа f:w - на величину площади
1 ' 1 23' 1 в сравнен ии с идеальным uи клом , где сжимается влаж
ный пар (то ч ка 1) . П равда, при этом увеличивается и удельная

теплота q0 (на велич и н у площади 1 ' 1 7 7 ' 1 '); но это увеличен ие
компенсировало бы возрастание' /ал , если дополн ительная рабо
та выражалась еы площадью 1 ' 1 2'3'1 ', а она в действительности
больше (на величину площади Z'23'2.') . ТаКим образом, затраты
энергии /ад рuстут в большей мере, нежели q0, и согласно (а)
холодильныii коэффиuиснт Ех пон ижается .
Переход к дросселиt1ованню ухудшает энергетичесюtе харак
теристики uикла по двум при•шю1м . Во-первых, нет возврата
энергии в детандере , что приводит к увеличению удельной. ра
боты цикла f:w (на вели•шну площади 3"4"53", если бы рабрп
велась без п ереохлажде н и я жидкости перед · дросселем) . Во
вторых, умен ьшается теплота q0, получаемая рабочим телом от
охлажд ае мо й среды в испарителе (поскольку при дросселиро
ван ии точка 4' смещается впрuво в сравнении с адиабатиче
ским расширением РТ в детандере) . В результате в выражении
(а) возрастает знаменuтсль и уменьшается числитель - холо
дильный коэффициент, характеризующий эффекrивность цик...:
ла, падает.
А вот 11ереохлажде1111е РТ после е го конденсации (подстадия
3"-3) благоприятно с казы вается на э ффе ктивности холодиль
ного цикла: не затрагивая затрат энергии на сжатие РТ в ком
прессоре, мы уnеличиnаем удельную холодопроизводиrельностъ qo
на величину, измеряемую площадью 4'466'4' . В результате повы
шается значение Ех - uикл ст.ш о шrгся более экономичным.
Построение диаграммы T-s ведется , как и для идеальной
машин ы , на основе заданных температур целевой (охлаж
даемой) среды и хладоагента (охлаждающей среды) . Только
надо иметь в виду, что в рассматриваемом случае температура
РТ после переохлаждеиия ( Тз) должна оставаться выше темпера
туры хладоагснта на соответствующем конце холодильника
конденсатора (rю схе ме на рис . 2 1 . З , а - выше t8') .
Диаграмма T-s хорошо иллюстрирует различные эффе кты
холодильного цикла, н о она не оче н ь удобна для технологиче
ских расчетов, так как п риходится оперировать площадями или
определять н еобходимые энтальпии рабочего тела h по криво
л и н е й н о й с ет ке на диаграмме. Поэтому предпочитают пользо
ваться д и а гр ам м а м и сос rоя н ия РТ в координатах p-i (реально
для более точ ного отсч ета давле н ия в области невысоких р - в
координатах lg р-1). В этой диаграмме все расчеты ведутся в
отрезках абсшн:сы, а кр ивой лин ией изображается только ста
дия сжатия пара в компрессоре.
На рис . 2 1 .4 п р и веде н а дииграммu p- i для реальн ой одн о
ступенчатой ком прессионной холодильной машины. В целях

1 559

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 2 1 . 4. Диаrрамма p-i. К расЧе'I)' ре

lg p

альной односrупенчатой парово й ком
прессионной холодильной машины

иллюстрации на диаграмме п о 
казан ход температурных кри
вых - они необходимы при
построен ии цикла.
Рас полаrая входной и выход
ной тем п е р атурам и хладоаrента
18' и /0 " , принимают температуры
О
рабочего тел а Тз и Тз· несколько
° С) ; тогда известен
выше (на
уро вень давления Р2· Зная необ
ходим ую ко н е ч н ую тем п ер атур у о хлаждае мой сред ы t0" , устана вливают тем пературу ко нденсации рабочего тела Т4 = Т1 ниже
· . Дал ее из точки 1 (на
на
° С; тогда известн о давл ен и е Pt ·
пересечен ии горизонтм и р1 с линией сухого насы щенного па
ра) проводят адиабату с жатия д о горизонтали р2 (с етка л и н и й
s = coпst есть н а диаграм ме р-1). Точку 3 находят на линии Р2 по
температуре переохлажде н ия РТ. Из этой точки по вертикальной
пря м ой i = coнst строят п роцесс в дроссельн ом вентиле.
Стадии цикла:
1 -2 - адиабатическое (s = coпst) сжатие от Р1 до Р2;
2 - 3 ' - и з обар ичес ко е (р2 = coпst) охлаждение перегретого
пара;
3'-3" - и з обар и че с кая (р2 = const) и и зотер м и че с кая
( Т = coпst) ко нде н сация РТ;
3"-3 - и з обариче с ко е <Р2 = coнst) переохлаждение конден 
сата;
3-4 - изоэнтальпичсское (i = coнst) дросселирование с па
ден ием давления от Р2 до Р 1 ;
4-1
изо ба р и ч ес кое (р 1 = const) и изотермическое
( Т4 = Т1 = coпst) испаре н и е РТ.
Заметим : цикл замкнvг по РТ.
В диаграмме p-i хар а кте р н ы е удельные (на l кг РТ) величи
н ы , необходимые для тех н ологи ч е с ких расчетов, выражаются
следующим образом:
- удельная холодопроизводительность цикла
(в)
- удельная ад и а батич ес кая работ-а сжатия РТ в компрессоре

5-10

5-10

·

·

lал =

(г)
- удельная теплота охлаждения перегретых паров РТ, их
конденсаци и и п ерео хл а жд е н и я полученной жидкости
(д)
Qx = i2 - i3 .

1 560

i2

- i1 ;

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

В задачу технологичес кого расчета входит определение по
тока РТ и затрат энер ги и . При этом в качестве расчетной базы
задается производительность по охлаждаемой среде Go и ее
начальная t0' и конечная t0" температуры.
Первоначально получают холодопроизводительность цикла
Q0 - поток теплоты, отбираемой в единицу времени от охлаж
даемой среды . С этой нелью составляют тепловой баланс для
контура К 1 (см. рис . 2 1 . 3 , а) :
G0c0t11' - G0c0t0" - Q0 = О,
где со

-

теплоемкость охлаждаемой среды. Отсюда:

Qo = Goco(to' - !о").

(2 1 . 1 )

Если охлаждаемая среда должна быть сконденсирована, то очевидно:
(2 1 . l a)
где 11>

-

теплота конденсации о хлаJ1Щаемо й

среды .

Зная теперь требуемый расход холода Qo и параметры цик
ла, можно определить поток G циркулирующего в цикле РТ - из
теплового баланса для контура К2 (см . рис. 2 1 .3 , а) :
Gi4 + Qo - Gi1 = О;
отсюда, имея в виду, что i1 - i4 = q0 , получаем:
и = _Оо__ Qo .
(2 1 .2)
i1 - i4 qo
=

Расход теплоты в холодильнике-конденсаторе Qx найдем из
теплового баланса для контура К 1 (см . рис. 2 1 . 1 , а) :
Gi2 - Qx - Giз = О,
откуда

(2 1 .3)
Расход охлаждающей среды в холодильнике-конденсаторе (при
известных температурах ее входа !8' , выхода !8" и теплоемкости
с8) определим на основании теплового баланса для контура К2
(см. рис. 2 1 . 1 , а) :
G8c8!11' + Qx G8c8!8" = О .
Подставив Qx из (2 1 .3 ) , получим :
-

Gв -

_

G ( i2 - iз )
(
.
С8 f�
!� )

(2 1 .4)

-

Мощность компрессо11а (при и з вестных КПД - адиабати
11 ад и механическом 11 м ) найдем по известной (см. разд.

ческом

1 56 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

4.2 и 4.3 .7) формуле:

N=

(2 1 .5)

Т\ ад Т\ м
причем адиабатический КПД ( Т\а.п < 1) позволяет учесть откло

нение реального (политропического) процесса сжатия РТ в
компрессоре от адиабатического .
Последнюю формулу удобно использовать в модифициро
ванном виде. Заменим в (2 1 . 5) G по (2 1 .2) через Qr/q0:
N=

Qo laд
----

вместо чо//а.п по (а) запишем ех ; тогда
N=

Q-=-o-

(2 1 .6)

_
_

Е х Т\ ад Т\ м

Здесь ех , разумеется , определяют не из формулы (б) для иде
ального процесса, а из общей формулы (а).
Достаточно большой разности температур верхнего и ниж
него источников Т2 - Т1 = Л Т сопутствует большая результи
рующая степень сжатия в компрессоре JJ2/p1 (подчас недо
пустимая по объемному КПД и температуре на выходе . пара из
компрессора - см. разд.4.3. 4) ; здесь р2 отвечает температуре Т2 ,
а р1 - температуре Т1 . Поставим вопрос: можно ли для реали
зации заданного диапазона ЛТ подбором рабочего тела обеспе
чить умеренную степень сжатия?
Для ответа на этот вопрос выполним оценочный анализ .
Связь давлен ия (упругости паров) р с температурой Т описы
вается уравнением Клаузиуса-Клапейрона• , интегрирование
которого в предположении о постоянстве теплоты парообразо
вания r приводит к выражению

lnp = А

r

-.
Ry T

(е)

Мольные теплоты парообразования r примерно одинаковы
для различных веществ (см. разд. 1 2 .6) ; значит, частное от де
ления r на универсальную газовую постоянную Ry тоже одина
ково для разных рабочих тел. Величина А определяет различие
температурных уровней для разных РТ.
Пусть потребителю холода требуется обеспечить некоторый
температурный диапазон Л Т на определенном уровне темпера
тур Т1 и Т2. Для этих уровней, согласно (е), имеем :
1 = _!___ Л Т .
(ж)
l пр')- IПPI = J n Р 2 = _!___
2
1
Ry
Т1
Т
Ry Т1 Т2
Р

-

• См .
1 562

(3 , 9) .

(_!__ - - )
-

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Огсюда следует, что при заданном л Т по (ж) для разных РТ
будут одинаковыми степени сжатия P21Pi (хотя сами значения
р2 и р 1 мо гут быть разными - в зависимости от свойств РТ) .
Следовательно, одинаковыми будут и удельные ( н а 1 моль РТ)
затраты энергии на сжатие. Одновременно при равенстве
мольных теплот парообразования r удельные (здесь - моль
ные) холодопроизводительности q0 для разных РТ тоже будут
примерно одинаковыми. Эго означает, что сущесtьенного вы
и гр ыша в Ех = qo/laд за счет подбора РТ получ ить не удастся .
Но подбором РТ можно воздействовать на уровни температур
ных диапазонов Л Т, смещая их вверх или вниз по температур
ной шкале, или предотвратить, например, замерзание РТ.
Общий вывод из приведенной выше количественной оцен
ки : требуемому в некоторых производствах расширению темпе
ратурного диапазона Л Т сопутствует неизбежное повышение
степени сжатия P21Pi , почти одинаковое для любого применяе
мого РТ. Поэтому для увеличения Л Т, сопровождающегося
неприемлемым повышением степени сжатия паров в компрес
соре, недостаточно подобрать РТ с подходящими свойствами ;
здесь придется идти н а изменение схемы (цикла) паровой ком
прессионной холодильной машины. Но прежде чем перейти к
анализу работы таких машин, кратко рассмотрим одноступен
чатую компрессионную холодильную машину, в которой в ка
честве РТ циркулирует неконденсирующийся газ.
2 1 .2.3. О воздушной компрессионной холодильной машине

Двухфазные (жидкость-пар) циклы, как показано в
предыдущих разделах, исключают по техническим соображени
ям применение детандеров, уменьшающих общие затраты
энергии. Детандеры применяют лишь в однофазных газовых
циклах. Примером тако10 процесса в области умеренного холо
да является воздушная компрессион ная холодильная машина,
призванная использовать доступное и дешевое рабочее тело воздух и возвратить в цикл энергию расширяющегося в детан
дере газа. Эта машина отличается от парокомпрессионных тем,
что РТ в рабочем цикле не конденсируется и не испаряется.
Схема цикла и его изображение в диаграмме T-s представ
лены на рис . 2 1 . 5. В схеме на рис . 2 1 . 5 , а вместо холодильника
конденсатора и испарителя (см . рис. 2 1 .3, а) функционируют
два теплообменника
хол одильник Х и наrреватель Н . Воздух
(поток /) сжимается компрессором К (условно - адиабатиче
ски) от р 1 до р2 1 тем п ер атура его повышается от Т1 до Т2 (рис .
2 1 .5, б) . Далее он изобарически (при давлении Р2 = coнst)
охлаждается (скажем, холодной водой - поток lll) в холодиль
нике Х до температуры Т3. Сжатый и охлажденный воздух
расширяется в детандере Д, при этом его давление падает до
-

-

1 563

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

т

Т2 1----� "

о

б

а

Рис. 21.5.

"

Во здуш ная компрессионная холодильная машина:

nрющипиальная схема, б диаrрамма T-s;
- воздух, // - охлаJКДаемая среда, J// - охлаждающая среда;
Х - холодиЛЬНИК. Н - наrреватсль, К
компрессор, Д - дст�щдер
а -

-

/

-

р 1 , а температура снижается до Т4. Из детандера охлажденный
газ

поступает в теплообменник Н, где изобарически (р1 =

= const)

нагревается до

Т1 ,

отнимая теплоту у потока

1/ - целе

вой охлаждаемой среды. Стадии цикла по рабочему телу:
1-2 - адиабатическое (s = coпst) расширение;
2-3 - изобарическое (р2 = coпst) охлаждение;
3-4 - адиабатическое (s = coпst) расширение ;
4- 1 - изобарическое (р 1 = coпst) нагревание.
Таким образом, в воздушном цикле изобары-изотермы
конденсации и испарения РТ (рис . 2 1 .2, б) заменены изобарами
охлаждения сжатого и нагревания расширившегося воздуха при
давлениях Р 1 и Р2 (рис . 2 1 .5, б).

ХолоДИJJьный коэ ффицие11т 11оздуu.о1оrо цикла &х8 определя ется по общей фор
муле (а). Обо значим массо в у ю удельную те плоемкость воздуха
ер (она м ало
меняется с изменением дамения и температуры) . Удельная теплота , получаемая
РТ в нагр евателе Н, равна qo = Ср( Т1 Т4). Удельная теплота, отнимаемая от РТ
Тз). Наконец, удельн ые затр аты
в холодильни ке Х , составля ет qx = ер( Т2
энер m и /ад = qx - qo. Тогда для воздушно й холодильной машин ы:
-

-

-

&х

PI

r.

=

q0

lм.

=

с р ( Т1 - Т4 )
ср ( Т2 - Тз ) - ср ( Т1 - Т4 )

(е)

Холодильный коэффициент газового цикла удобно выражать через дамения
и Р2· С этой целью преобразуем зн ам е нател ь в ыражения (е):
(ж)

1 564

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Согласно формуле (4 .7), учитывая, что здесь 7i
(воздуха), имеем:

-

абсолютные температуры газа

(з)
здесь

k

- показатель адиабаты; тогда
8
Ех

Т1

(ж)

преобразуется к виду:
(и)

[( �:) k - 1 ] - [( ��) k -1 - ]
-1
Т

·-

Т4

1

Т

1

Если произвеt-"ТИ обратную замену по (з), то приходим к выражению :
1
Т
( к)
8
€ х = -- = --- ,
Т2 - 1 Т2 Т1
Т1
формально (только!) совпадаю щему с (б) для обратного идеального цикла Кар
но, в котором Т1
Тн и Т2 Т8. Однако для идеального цикла в действитель
ности Т8 Т1 Т4 const и Т8 Т2 Тз const. При этом в воздушной ма
шине темпер атурный урове н ь РТ определяется (по условиям теплообмена с
на
о хл аждаемой и охлаждаю щей средами) коне•1ными темпер атурами Т1 и Тз
выходе РТ из теплообменных апп аратов Н и Х соответственно. Естественно,
Т4 < Т1, а Т2 > Тз. Э то озн ачает, что в воздушном цикле средняя темпер атур а
нижнего источника Тн < Т1 , а средняя темпер атура верхнего источника Т8 > Тз.
Согласно формуле (а), п онижение Тн и повьШJение Та приводят к уменьшению
холодильного коэффициента. Поэтому &х1 получается значительно меньше, не
жели &х для обратного цикла Карно.
=

=

=

=

=

=

=

=

-

Из изложен ного выше следует, что воздушная холодильная
машина энергетически значительно менее выгодна, чем иде
альная; ее эффективность также ниже, чем у компрессионных
машин, работающих по nарожидкостным циклам.
Воздушная холодильная машина обладает и другими недо
статками; основные из них:
- малые объемные теплоемкости и разности энтальпий воз
духа, а следовательно, и малые тепловые потоюt на единицу его
объема в сочсrании с небольшой его ruютностъю требуют боль
ших объемных потоков РТ для обеспечения заданной холодопро
изводителъности Q0, значит - больших затрат энергии и приме
нения крупногабаритных компрессоров и другой аппаратуры;
- невысокая молярная масса воздуха затрудняет (хотя, конеч
но, и не исключает) использование высокопроизводительных тур
бокомпрессоров при степенях сжатия порЯдка 1 0 - см. разд. 4.5.З ;
низкие коэффициенты теплоотдачи для воздуха приводят
к необходимости применения теплообменников (Х и Н) с
весьма развитыми поверхностями.
В связи с указанны.ми недостатками воздушных холодиль
н ых машин , несмотря н а дешевизну и экологическую безопас
ность РТ, на практике применяют преимущественно двухфаз-

-

1 565

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ные компрессионны е циклы , т.е. используют холодильн ые
установки с фазовыми переходами РТ типа жидкость-пар . Это
не означает полного отказа от использования расширительных
машин в газовых холодильн ых циклах, работающих в друrих
диапазонах температур и давлений, - см. разд. 2 1 .3 .
21 .2.4. Двухступенчатая паровая компрессионная
холодиль ная машина
Ряд технологических процессов требует достижения весьма
н изких температур охлаждаемой среды, а значит, и рабочего
тела в испариrеле цикла умеренного охлаждения. При этом тем
пературный уровень в холодильнике-конденсаторе, определяемый
температурами охлаждающего агента (воды, воздуха), остается
прежним. В такой ситуации вслед за увеличением различия тем
ператур РТ в конденсаторе и испаригеле будет расти и разница
давлений в этих теплообменниках. Следовательно, будет повы
шаться (часто - весьма заметно) и необходимая степень сжатия
РТ от давления в испариrеле до давления в холодилънике
конденсаторе. Но работ-а с высокими степенями сжатия, как пока
зано в разд. 4.3 .4-4.3.5, приводит к недопустимым
- возрастанию температур газа в конце стадии сжатия ;
- понижен ию объем ного КПД компрессора, а с ним - к
падению его производительности, значит, и всего цикла.
В этом случае, соответственно результатам оценочного ана
лиза в кон це разд. 2 1 .2 .2 , целесообразно изменить схему ц икла:
перейти от одноступенчатых холодильных машин к многосту
пенчатым, реально чаще всего - к двухступенчатым, с охлаж
ден ием сжимаемого РТ между ступенями компрессора. Это
позволяет уменьшить затраты энергии в холодильном цикле и
повысить его общий холодильный коэффициент.
Кроме того, при умен ьшении степени сжатия в каждой сту
пени ком прессора возрастает его объемный КПД, а с ним производительность цикла.
Применение двухстут1енчатых (в общем случае - многосту
пенчатых) компрессион н ых машин позволяет получать холод
на двух разных температурных уровнях в одной машин е . Эти
температурные уровни соответствуют давлен иям всасывания
ступеней компрессора.
П усть, например, цех расrютш1ет охлаждающей водой с начальной темпера'I)'рой
20 • с, а конечная ее тем п ера'I)'ра tв''
зо-;.. з s • с; требуется охладиrь среду №
до -40 • с и среду № 2
до -5 • с. Тоща темпера'I)'ра РТ на выходе из холодильни
ка-коцденсатора должна находmъся на уровне 40 • с, в испариrеле для среды № 1
tв'

=

1

=

-

на уровне -SO • с, а в испарителе

для среды №

2

-

на уровне

- 1 5 • с.

-

Схема двухступенчатой компрессионной холодильной ма
шины приведена на р и с . 2 1 .6 . При этом в рассматриваемой
1 566

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

а

lgp

б

Двухступенчатая п ар овая компрессионная холодильная машина с пол
ным внуrренним охлаждени е м:
Рис. 21. 6.

- прющипимьная схема. б диаrрамма р-1;
К1 и К2 - первая и вrорая cтyneIOI компрессора; ХК - холодильЮ1к-конденсатор; дРt ·
дР2 - дроссельные вентили; И1 и И2 - испарители первоrо и вroporo уровней холода; ПХ
- промежуточный холодильЮ1к; С сепаратор
а

-

-

схеме холод получают на двух уровнях: теплота от охлаждаемых
сред забирается в испар ителе И 1 (среда № 1 с холодопроизво
дителъностъю Q 1 ) и И2 (среда № 2; Q1 ).
Пары РТ при давле нии р 1 (поток G1 ) из испарителя И 1
(состояние 1 ) поступают в первую ступен ь компрессора К1 , где
1 567

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 21. 7. Фрагмент диа гр а м м ы p-i.
н о rо о хлаждения

К

расчету двухступенчато й маши н ы умерен 

сжимаются до промежуrочного давления Р2 (состояние 2). Да
лее они перед сжатием во второй ступени компрессора К2
должны быть охлаждены - предпочтительно до наиболее низ
кой возможной температуры, здесь - до состоян ия 3 сухого
насыщенного пара. Обсудим такую возможность и сопут
ствующие ей аспекты , используя приведенный выше пример с
конкретными (в числах) температурными уровнями.
На рис . 2 1 .7 представлен фрагмент диаграммы p-i с кривой
сухого насыщенного пара (С И П ) и уровнями давлений Р2
(после первой ступени компрессора К 1 ) и р3 (после второй сту
пени компрессора К2 ) . Состояние рабочего тела после первой
ступени изображается то чко й 2 в области перегретого пара.
Изобарическое <Р2 = const) охлаждение происходит по горизон
тали - влево от точI01 2, желательно до состоян ия 3 на линии
сухого насыщенного пара. В этом случае удельная (на 1 кг РТ)
адиабатическая работа сжатия 3-4 в К2 составит i4 - iз = Лiс.
Если же охладить РТ удается только до состоян ия 3' в области
перегретого пара, то сжатие 3'-4' приведет к повышенным
адиабатическим затратам энергии i4' - iз' = Лiп > Лiс. Дело в
том , что при изобарическом удалении вправо от линии С И П
адиабаты ид ут все более полого, потому и затраты энергии н а
сжатие газа от Р2 д о Р з возрастают. Причина: п о мере переме
щения вправо по изобар е Р2 увеличивается температура пара, а
с ней и объем газа, засасываемого в ступень К2 . Поскольку
компрессор
машина объемного действия, то рост засасы
ваемого объема газа сопровоЖдается увеличением энергии на
его сжатие . Поэтому и следует стремиться к возможно больше
му охлаждению пара пе ред его сжатием в К2 (лучше бы - до
состоян ия 3 ) .
-

1 568

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

П р 1шле•1ем n р и nсдс н н ый в ы ш е ч исловой пример . Тем пера
тура РТ в соишш шt 2 после сжат11я в К1 на практике обычно
н аход 11тся н а уровне от 80 до 120 ° С. Охлаждение РТ холод н о й
водой ил и холод н ы м воздухо м в н е котором промежуrочном
те плообме н н н ке (холод и л ьн и ке) воз можно до температур ы 3040 ° С, тогда ка к в • ш сло 1юм п р имере точке 3 отвечает темпера
тура РТ - 1 5 ° С. И н а • 1 е го воря , РТ после е го охлажден ия в хо 
лодил ь н и ке остается пе р егреты м - в состоянии З'. Если в К2
сжимается перегрет ы й п а р , то rо ворит о двухступенчатой маши
не с не1юл н ы м в11уr11е111111м охлажде11 и е м . Если удается , ис поль
зова в в н уr ре 1 1 н и е воз l\южн ости цнкш1, охладить РТ до состоя 
сухого //асыще//щfго 1 1 ара (то ч ка 3), то говорят о двухступен
чатой маш и 11 е с пол �1 ым в11уrре11 1ш м охлаждением . П оследняя
отл ичается н ес колько более сложной схемой , но она эконо
м ичнее; поэто м у п р �• высокой холодопроизводительности ей
отдают ЩJсд гю • 1тс н и с . Н иже подробtю б удем рассматр и вать
( п родол жа я о п исан и е схемы) ма ш и н у с полным внутренним
0Х.11ажде11ием (с м . р ис . 2 1 . 6 ,
К с 1 юсобу охлаждс юн1 РТ ( п о сле сжатия в К1 ) до состоян и я
3 вер н емся поздн е е . П ол н ы й пото к
сух.ого н асыще н н о го п а 
ра с ж и м ается в о второ i i ступен и ко м прессора К2 д о давления р3
11
в холод 1 1л ь н и к - кондснсатор , где пар ы охлаж
даются , ко ндс 11 с ируютс н и п ереохлаждаются . Жидкое пере
охлажде н н ое РТ щюссст 1 р уется через дроссельн ый вентил ь
Др2; п р и это м давле н и е шщает от Рз до
и РТ попадает в об
ласть uлаж н о го пара - состоян ие 8 .
изобаричесю1
(р2
co11st) ра1дел s1етсн в сепараторе С на
(поток G3) и кипящую жидкост ь. Последнюю , в свою оче
ред ь , раздел н ют н а д в а п отока . Оди н (
поступает из сепара
то ра 11 HCJJX li l l ii ИС ГIЩНПСЛ u
и с п аряется (до СОСТОSI Н ИЯ 3 ) ,
отн им ая те плоту у охл аждаемой с р еды № 2 , и пары направл я 
дроссел и р ус тся в д р ос
ютс я в ко м п р ессо р К 2 . Д р у го й по т ок
сел ь н о м ве нтиле
до давлен и я р1 и поступает в нижний ис 
пар 1пел ь И 1 . Та м этот поток , испаряясь, отводит теплоту от
охлаждаемой сред ы № 1 - на бол ее н и з ком температурном
у ро в н е , • 1 е м в испар ителе И ъ та к ка к
< р2 . Образо вав ш и йся
с ухой . нас ы ще н н ы й п а р (состо я н ие 1 ) засасы вается в первую
ступен ь ком п рессора
rдс сжим ается до давления
Далее
е го по возмож11ост1 1 охлажда ют в пра межуrочном холодильнике
ПХ (до СОСТО S I Н ИЯ 3') .
Чтобы зам.t..-н уrь холодильн ы й цнкл, остается рассмотреть
д ва вопроса . Первый: что происход ит с паро м , отделен н ым от
ж и д кости в сепараторе С? Этот с ух о й пар уже получил теплоту
парообр азо ва н ш•
и е го нецелесообраз н о использовать для
о хл ажд е н и я с р ед ы № 2 в и сп а р и те ле И 2 . П о это м у е го ср аз у
нап равл я ют 1 1 а вс ас ы ва ю щую сто р о н у ко мпрессора К2 (как

н ю1

а) .

G

напрант1 стсн

Ръ

Влажный пар
сухой uасыщеuuый

=

пар

И2,

G2)

G1

Др 1

р1

К1 ,

р2.

1 569

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

правило, мимо испарителя Иъ чтобы не увеличивать габариты
последнего ) . Второй во прос : как охладить переrретый пар пос
ле компрессора К1 и промежугочного холодильника ПХ
(состояние 3') до состоя н ия 3 сухого насыщенного пара? Пере
гретый паровой пото к G1 направляют в сепаратор С , где он
барботирует через слой кипящего жидкого РТ; при этом пар
отдает свою теплоту перегрева и охлаждается до состояния 3 .
Снятие теплоты перегрева происходит з а счет испарения неко
торого количества кипящей жидкости (поток Л G); образовав
шийся поток ( G1 + Л G) сухого насыщенного пара присоеди
няется к потоку G3 и направляется на всасывание во вторую
ступень компрессора К2 .
Важно: охлаждаем ую среду No 2 нужных параметров можно
получить и с помощью низкотемпературного РТ после его
дросселирования в вентиле Др 1 • Однако тогда температура
нижнего источника Тн для среды № 2 будет меньше, чем в
рассматриваемой схеме - в испарителе И 2 до дросселирования
в Др 1 . В результате пон изится холодильный коэффициент, т. е .
холод для среды № 2 станет дороже (см . разд . 2 1 .2 . 1 ) . Разу
меется, если в охлаждении сред ы № 2 (РТ при давле н ии р2)
вообще нет необходимости, то испаритель И 2 в схеме двухсту
пенчатой холодильной машин ы отсутствует.
Паровой поток G, сжимаемый во второй ступени компрес
сора К2 , складывается и:J потоков:
- G1 - после компрессора К1 ;
- Л G - из испарившейся жидкости в сепараторе при снятии теплоты перегрева с потока G1 ;
- Gз - при дросселировании переохлажденного РТ через
вентиль Др 2 ;
- G2 - после испар ителя И 2 .
На рис. 2 1 .6, 6 цикл двухступенчатой холодильной машины с
полным внутренним охлаждением изображен в диаrрамме p- i:
1-2 - адиабатическое (s = coпst) сжатие от р1 до Р2 потока
G1 сухих паров РТ в пер вой ступени компрессора;
2-3' - изобарическое <Р2 = coлst) охлаждение потока G1
переrретого РТ в промежугочном холодильнике ;
3'-3 - изобарическое <Р2 = coлst) охлаждение потока G1
перегретого РТ с одновременным ис парением части (Л G) жид
кости в сепараторе и получением сухого насыщенного пара
(поток G1 + Л G) ;
3-4 - адиабатическое (s = co п st ) сжатие от Р2 до р3 потока
G сухих паров РТ во второй ступени компрессора;
4- 7 - изобарические (р3 = co л st) процессы с потоком G в
холодильнике-конденсаторе: 4-5
охлаждение переrретых
паров РТ, 5-6 -изотермическая ( Т = coлst) конденсация па
ров, 6- 7
переохлаждение жидкого РТ;
-

-

1 570

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

7-8 - дросселирование (i = co11st) переохлажденного жид
кого потока G в вентиле Др 2 с паден ием давления от Рз до Р2 ;
..?' 3

8�

9

-

изобарическая (р2

=

co11st) и и зоте рмическ ая ( Т =

= co11st) сепарация на паровую (точка 3, поток Gз ) и жидкую
(точка 9) фазы;
9-3 - изобарическое <Р2 = co11st) и изотермическое ( Т =

const) испарение жидкостного потока G2 в испарителе И 2 ;
9 - 1 0 - дросселирование (i = co11st) жидкостного потока G1
в вентиле Др 1 с падение м давления от р2 до р 1 ;
10-1 - изобарическое (р1 = coпst) и изотермическое ( Т =
= const) и спар е ние потока G1 в и с п ар ителе И 1 .
Заметим : жидкостно й поток в состоянии 9 (перед дроссели
рованием в вентиле Др 1 ) не переохлаждают - нечем.
При расчете двухступенчатой холодильной машины с пол
ным внуrрен ним охлаждением по диаграмме p-i отсчитывают
энтальпии характерн ых состояний РТ (они обусловлены
свойствами выбранного РТ) . Значения р1 , Р2 и р3 известны , так
как заданы соответствующие температурные уровни . Холодо
производит ельности Q 1 и Q2 диктуются потребителями холода и
рассчитываются исходя из потоков охлаждаемых сред и диапа
зонов изменения их температур (см. разд. 2 1 .2.2). Определению
подлежат потоки РТ в различных точках цикла (значит, и про
изводительности ступеней компрессора), мощности на первой
и второй ступенях ком прессора, расходы охлаждающей среды
(чаще всего - воды) в холодильн иках.
Потоки РТ определяются из тепловых балансов, аналогич 
ных рассмотренным в разд . 2 1 . 2 . 2 . Не повторяя детально все
стадии анализа, приведе м результаты - там, где они очевидны :
Q,
(2 1 . 8)
G2 =
с, = .
.
=

11 -

А
.
1 3 - 19

110

(21 .9)

Поток Л G наЙдем из теплового баланса для стадии отвода теп
лоты перегрева потока G1 за счет испарения Л G кипящей жид
кости в сепараторе ; запишем баланс сразу в форме Пр = Ух:

откуда

G 1 (iJ1 - iз)

=

л G - G1
сы
К,

Л G(iз - i9),

iз · - iз
.
13

- 19.

.

(2 1 . 1 0)

С целью отыскания остальных потоков РТ тепловые балан 
дополним матер иальными . Применительно к контуру
на
р и с . 2 1 . 6 , а , кото р ый охватывает
пока занному

1 57 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

сепаратор, имеем :

1G + G 1 - G1 - G1 - л G - Gз - �

=

О.

(н)
Для дальнейших преобразований целесообразно ввести по
нятие о степени сухости Х влажного пара, понимая под ней
долю сухого пара в его смеси с кипящей жидкостью. На линии
кипящей жидкости Х = О, на линии сухого насыщенного пара
Х = 1 . При полной ;щиабатической сепарации 1 кг влажного
пара (состояние 8 на рис. 2 1 . 8 , б) получается Х кг сухого насы
щенного пара (состояние 3) и (1 - Х) кг кипящей жидкости
(состояние 9); разность 1 - Х иногда называют степенью влаж
ности. Тепловой баланс стадии сепарации запишется :
l · is
отсюда

- Xi3 -

(1

- X)-i9 = О ;

is - i9
13. - 19.

Х=

(о)

'

что отвечает правилу рычага 11 рода с опорой в точке 9 .
Понятие о степен и сухости позволяет найти поток пара
после дросселирования потока G в вентиле д Р2 от Р з до Р2 =

G3

Gз = GX.
(2 1 . 1 1 )
Заменим теперь в (н) G3 по (2 1 . 1 1 ) и найлем полный поток G
рабочего тела (производительность нгорой ступени компрессора):

G = G1

+ Л G + G2 .
1 -Х

(2 1 . 1 2)

Заметим , что формулу (2 1 . 1 2 ) можно получить проще, опе
рируя долей кипящей жидкости 1 - Х после дросселирования в
вентиле дР2 · Общий поток жидкости после сепаратора (с учетом
необходимого для испарения при снятии теплоты перегрева с
потока G1 ) равен G1 + Л G + G2 . Тогда
G( 1 - Х) = G2 + Gi + Л G,
откуда прямо следует выражение (2 1 . 1 2) .
Расход охлаждающей воды в холодильнике-конденсаторе
рассчитывается идентично рассмотренному в разд. 2 1 . 2.2 - см.
формулу (2 1 .4) :
Gв

=

G (i4 - i7 )
с в (t"в - !'в ) .

(2 1 . 1 3 )

Расход охлаждающей воды в промежуrочном холодильнике
определяется по сходной формуле , но базируется, естественно,
на потоке G1 и присущей ему разности энтальпий :

G'=
0

1 572

G1 (i2 - iз· )
с в (!� - !�) ·

(2 1 . 1 4)

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

За м ет и м : з н ач е н и я в ходных тем ператур 18' , как п р авило ,
оди на ковы для раз н ых холодиль н и ков машины; значен ия вы
ход н ы х те м пср uту р 10" м o ryr нес кол ь ко ра зл и чаться .
Мощ1юсть ком11рессо11а состuвляст (см . разд . 4.2 и 4.3 .7):
- для ступ е н и н изкого давлен ия К1

G 1 (i2

N1 =
- для ступени

Общий

i1 )

11ад 11 м

высокого давления

холодильн ы й

(2 1 . 1 5)

;

К2

_ G (i4 - iз)

N1 п ро цессо в

-

11 ад 11 м

.

коэффициент (для

(2 1 . 1 6)
двухступенчатых

он нос и т усло в н ы й характер и использ уется для со 

поставле н и я р а з н ы х

ци клов)

з u п и ш с м ни основе

производ11телыюстей и затрат энергии:
_

-

Ех

Q1 + Q1
N
( 1 } + (N2 }

=

полных холодо

G 1 (i1 - i 10) + G2 (iз - i9)
G 1 ( i2 - i1 } + G (i4 - iз }

(п)

·

Д вухступ е н чатая холодильная машина с неполным внутрен
ним охлаждением ис п ол ьз уется преимуmественно при н евы со

ких холодо производительностях, когда повышен н ы й расход
энергии в о п р едел е н н о й мере ко мпенсируется большей просто
той цикла. Схема это й машин ы (в упрощенном начертании) и
диаграмма p- i представлены на рис. 2 1 . 8 .
Основное отличие этого цикла от предь�дуmего заключается
в то м , что после промежуточного холодильника ГdЗообразное
(перегретые п ар ы ) р а бо чее тело (состо я ние 3') не направляюг в
се п арато р дл я охлажде ния до с о стоя н ия 3" с ухо го насыще н н о го
п ара. П ото к G1 п е р е гр ет ы х пupon РТ сме ши ва ют с потокам и
с у х ого н а с ы щ е н 1 1 ого п а р а

И2

G2

и

Gз ,

п о л у ч а е м ы м и в и с парит еле

п ар аци и . Н результате получается поток G 1 + (h + G3 перегре
того п ар а в с остоян и и 3, пр и ч е м положение точки 3 о п р еде 
ляется из те п ло во rо баланса для ст<ЩИИ и з о бар и ч е с ко го <Р2 =
= coпst) с м е ш е н ия упомянутых потоков. Перегретый пар сжи
маетс я во второй ступен и ко м п р е сс о ра К2 - адиабата 3-4.
Удел ьные зат р ат ы энергии на сжатие здесь меньше, нежели
при сжат и и исходного перегретого лара (штр и хо вая линия 3'4' н а р и с . 2 1 .8 , б), н о n1.:c же больше, чем при сжатии сухого
н ас ы щенного пара (штр 11хо вая л ин ия 3"-4"), - см. также рис .
и

2 1 .7

п осле дро с с е л и р о в а юr я жидк о сти (в в ентиле Др 2)

и

се 

и пояс н е н ия к н е м у .

1573

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

а

б

Рис.21. 8. ДвухС1)'п енчатая холодильная машина с неполным внуrренним охлаж

дением:
а

-

прющипиальная схема.

б

-

диаграмма p-i

К достоинствам цикла следует отнести отсутствие испарения
части рабочего тела Л G, так как перегретый поток G1 вообще
не попадает в сепаратор .
Расчет цикла прин ципиально не отличается от приведенного
для машин с полным внуrренним охлаждением .
2 1 .2.5. Абсорбционная холодильная машина
В абсорбционной холодильной машине холод получается за
счет использования теплоты невысокого потенциала, тогда как в
компрессионной холодильной машине - за счет затрат меха
нической энергии.

1 574

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

11
Jf

11

2

ir;·

){4

з

11

'(

IV

llI

- -

Рис.21. 9.
1

- - -- - -

Абсорбционная холодильная машина:

-

колонна с кипятильннком. 2 конденсатор; J, 8 дроссельные веJПИЛи; 4 ис
паритель, 5 абсорбер, 6 насос, 7 теплообменник;
1
охлаждаемая среда, /1 аммиак, /// водно-аммиачный расrвор, /V разбавлен
ный раствор аммиака в воде, V охлаждающая вода, V/ rреющий пар

-

Принцип действия абсорбционной холодильной машин ы
основан на поглошении паров Р Т каким-либо абсорбентом при
невысоком давлении Рн в абсорбере и последующем выделении
их в генераторе при достаточно высоком давлении Рв · Иными
словами, сжатие паров РТ в компрессоре заменено в абсорбци
онной холодильной установке выделением (десорбцией) и кон 
центрирован ием паров РТ и з смеси абсорбентом - с получе
нием этих паров под избыточным давлением.
Наибольшее применение для получения холода на уровне
абсорбци о нн ые уста
- 1 0 +-30 ° С находят водно-аммиачные
новки, в которых рабочими телами служат аммиак и ero вод
ные растворы разной ко н центрации .
Аммиак активно абсорбируется водой: при комнатной тем
пературе в единице объема воды растворяется свыше 1 000 объ
емов парообразного аммиака. Абсорбция аммиака сопровож
дается значительным вьщелением теплоты .
Схема абсорбционной холодильной машины показана на
рис . 2 1 .9 . Генератором аммиака (потоки /1) является куб 1,
снабженный кипятильн иком и колонной (тарельчатой или на
садочной) . В кубе происходит десорбция аммиака (из водно
аммиачноrо раствора - поток /11) , в колонне - более тща
тельная его очистка от примеси воды .

1 575

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Газообразный аммиак с кон центрацией, превышающей 99%
NH3, при высоком давлении Рв (на уровне 0 , 5- 1 , 5 МПа) по
ступает в конденсатор 2. Там аммиак конденсируется при от
носительно высокой температуре, отдавая теплоту парообразо
ван ия и абсорбции охлажденной воде (поток V). Небольшая
часть сжижен ного аммиака возвращается на орошение в ко
лонну, основная же часть - дросселируется в дроссельном
вентиле 3, где давление падает до Р н· При этом давлении ам
миак испаряется в испарителе 4, воспринимая теплоту на низ
ком температурном уровне от потока 1 охлаждаемой среды. Да
лее газообразный аммиак направляется в абсорбер 5, где при
охлаждении (отводе теплоты конденсации и абсорбции) он
поглощается водой (поток JV) с образованием концентриро
ванного раствора (поток Ill) - � 50% NН з .
Полученный раствор (поток IIJ) через теплообменник 7 на
сосом 6 питает колонну 1. Там в результате подвода теплоты в
кипятильник куба (греющим паром невысокого давления или
другим теплоносителем - поток Vl) бdльшая часть аммиака
испаряется и в виде пара направляется в конденсатор 2. О бед
ненный водно-аммиачн ый раствор с концентрацией N Н з на
уровне � 20% уходит (поток JV) из кипятильника через тепло
обменник 7 и дроссельн ый вентиль 8 в абсорбер 5, где исполь
зуется в качестве абсорбента для поглощения газообразного
аммиака. Заметим: здесь в принципе можно бьmо бы обойтись
и без теплообменника 7, но он выполняет роль рекуператора
теплоты, повышая экономичность цикла.
Таким образом, в рассматриваемой схеме роль компрессора
выполняет агрегат, включающий в себя кипятильник, абсорбер
и насос ; иногда этот агрегат именуют термохимическим ком
прессором.
Цикл абсорбционной холодильной машины в диаграммах
состояния обычно не изображают, поскольку на разных
участках установки циркулируют различные рабочие тела - га
зообразный аммиак и его водные растворы.
Расчет абсорбционной холодильной машины · исходит из хо
лодопроизводительиости Q0 , определяемой (см . разд. 2 1 .2.2) по
потоку и теплоемкости охлаждаемой среды. База расчета материальные и тепловые балансы отдельных аппаратов.
Энергетическая эффективность цикла абсорбционной холо
дильной установки оценивается холодильным коэффициентом
'
Ех (его еще называют тепловым коэффициентом) - в общем это
аналог Ех · Величина Ех' определяется отношением :
'
(р)
Ех = Qo/Qк ,
где Qк теплота, подведенная в ки пятильнике генер атор а амм и ака .
-

• Подр обнее
1 576

см.

(3,

8, 1 0 ,

1 1,

17).

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Более строго - в знаменателе (р) следует добавить затраты
энергии на работу насоса 6.
Величина ех' абсорбционной холодильной машины находит
ся на уровне 0 ,4-0 , 7 , т . е . в несколько раз ниже, чем Ех для
компрессионных машин - это считают основным недостатком
абсорбцион н ых холодил ьных машин по сравнению с компрес
сионными · . К недостаткам абсорбционных холодильных ма
шин следует отнести также большие капитальные затраты
(повышенную металл о емкость) .
Следует отметить, что приведен ное сопоставление Ех и Ех'
является не вполне правомерным, поскольку сравниваются
разные виды энергии - электрическая (или механическая) и
тепловая, а стоимость первой - выше . Правомернее проводить
сопоставление по приведенному холодильному коэффициенту:
Ех

=

Qo / Qт ,

rде Q. - расход подведенной в цикл тешюты.

Сопоставление по величине Ех показывает, что в боль
шинстве случаев и n o этому параметру абсорбционная холо
дильная установка уступает компрессионной.
Испол ьзование абсорбционной холодильной машины стано
вится выгодным при наличии "отбросных" источников теплоты
низкого температурного потенциала (отходящих газов печных и
котельных установок, вторичного пара и т.д . ) .
21 .2. 6 . О некоторых других холодильных машинах
умеренного охлаждения

Возможные способы получения умеренного холода не огра
ничиваются приведен ными ранее. Н иже упомянуrы некоторые
другие схемы (циклы) холодильных установок. Более подробно
их описание и расчет приводятся в учебной и специальной
литературе * * .
Каскадные циклы. Они применяются для получения весьма
низких температур охлаждаемой среды. В разд. 2 1 .2.2 была
продемонстрирована невозможность получения таких темпера
тур и значительных температурных перепадов Л Т с сохранени
ем умеренных степеней сжатия в компрессионных холодиль
ных машинах, использ ую щих какое-либо одно рабочее тело .
В каскадных холодильных циклах используются разные РТ с
различными свойствами (строением молекул, упруrостями па
ров или температурами кипения). Основная идея такого цикла:
в теплообмен нике одно РТ, кипящее при более низкой темпе•

См. (3, 5, 8 , 9, 1 1 ) .
См. ( 3 , 6 , 9 , 1 1 ).

••

1 577

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 21. 1 0.

Каскадная компрессионная холо

дильная машина;
1, 2 - компрессоры; J, 4 - ко�щенсаторы; 5, 6 испариrели; 7, 8 - д1юсселы1Ь1� l!Снrили

ратуре в зоне испарения, отнимает
теплоту от другого РТ, охлаж
дающегося и конденсирующегося
при более высокой температуре в
зоне конденсации .
Каскадные
циклы
являются
определен ной альтернативой двух
ступенчатым циклам умеренного
охлаждения , отличаясь в то же
время большими возможностями в
достижен и и н изких температур (до
- 1 00 ° С) .
А
Схема простейшей каскадной
компрессионной машин ы приве
дена на рис . 2 1 . 1 0 . Два одноступенчатых цикла А и В объеди
нены общими теплообменником (испарителем .5) и холодиль
н иком (конденсатором 4) . Аппараты и машин ы низкотемпера
турного цикла далее помечены нечетн ыми цифрами, высоко
температурного цикла - четными . Каждый холодильный цикл
состоит из компрессора ( 1, 2), конденсатора (J, 4), испарителя
(5, 6) и дроссельного вентиля ( 7, 8) .
цикле А применяется рабочее тело No 1 , в цикле
ра
бочее тело No 2. Теплообмен между ними происходит в тепло
обменнике 4- 5: испаря ющееся (кипящее) РТ2 служит охлаж
дающей средой для конденсирующегося (охлаждающегося, пе
реохлаждающегося) PTl . В конденсаторе 4 РТ2 отдает теплоту
(конденсируется, охлаждается, переохлаждается) холодной во
дой или холодным воздухом . В испарителе 5 кипящее PTl за
бирает теплоту от охлажд.аемой среды .
Каждый цикл работает с умеренной степенью сжатия и по
зволяет реализовать свой перепад температур Л Тл и Л Тв. Ре
зультирующий перепад температур л т < Л Тл + Л Тв, поскольку
часть температурного напора затрачивается в испарителе
конденсаторе 3 для обеспечения теплового потока от PTl к
РТ2 . Однако в целом в каскадном цикле Л Т > Л Тл, Л Тв, что
позволяет обеспечить весьма низкие температуры охлаждаемой
среды. Разумеется, возможна орrанизация и большего числа
каскадов.
Недостаток каскадного цикла состоит в увеличен и и коли 
чества действующих машин и аппаратов.
Совсем коротко остановимся н а некоторых других холо
дильных циклах.

В

1 578

В

-

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Пароэжекторная холодильная машина. Работа такой машины
основана на эффекте понижен ия температуры при самоиспа
рении воды , используемой в качестве РТ.
Для получен ия насыщенноrо водяноrо пара в области доста
точно н изких тем ператур необходимо создание очень низких
давлений ( порядка 100 Па). С такими давлениями не рабо
тают обычн ые поршне вые компрессоры: большие удельные
объемы водяноrо пара потребовали бы огромных размеров
компрессора и больших затрат энергии. Поэтому компрессоры
в цикле заменяют прото'lными пароструйными эжекторами. Про
исходящее при дросселировании сжатоrо в эжекторе влажноrо
пара част ичи ое самоиспарение воды сопровождается понижени
ем температуры (см . разд. 9.3).
Пароэжекторные холодильн ые установки, позволяющие по
лучить охлаждаемую среду с температурой 4-5 ° С, применяют
ся для охлаждения водн ых растворов солей в процессах кри
сталл и зации, а также при кондицион ировании воздуха в поме
щениях.
Основное достоинство метода - дешевое, доступное и эко
логически чистое РТ. Основной недостаток - большой расход
охлаждающей воды в конденсаторе: наряду с эжеюируемым
паром, являющимся РТ, необходимо еще конденсировать
эжектирующий пар, под водимый к эжектору.
Вихревые трубы. В н их, располаrая исходным газом опр еде
ленной температуры, получают потоки газов с разными конеч
н ыми температурами. Сжатый rаз, танrенциально введенный в
гладкостен ную трубу с большой скоростью (до 200 - 400 м/с),
перемещается по ней одновременно винтовым и осевым дви
жен ием . В результате сложн ых термодинамических явлений
пристеночн ые (закручен н ые) слои газовоrо потока забирают
теплоту от поступательно движущихся приосевых слоев. При
этом первые - нагреваются, а вторые - охлаждаются (в срав
н еюш с тем пературой исходного п отока) . Горячие и холодные
потоки выводятся раздельно: холодный поток используется
непосредствен но для понижения температуры иной охлаждае
мой сред ы .
В и хревые трубы применяются п р и кратковременных рабо
тах, при получении холода в малых количествах, при наличии
даро в ых пр иродных источников сжатоrо газа. Основной недо 
статок метода - невысокая термодинамическая эффектив
н ость .
Термоэлектрические холод.ильные уста н овки . Они состоят из
последовательно соединенных элементов - полупровод н и ко в
дыро ч ной и электрон ной проводимости , зажатых в электро
проводящих коммутирующих пластин ах . При прохожде н ии
постоянного электричсс коrо тока по этой термоэлектрическо й
·

1579

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

батарее на коммугирующих пластинах возникает разность тем 
ператур Л Т, причем на одн их пластинах температура повы
шается , на других - пон ижается . Величина Л Т зависит от чис
ла полупроводниковых элементов в батарее . В термоэлектриче
СЮfХ батареях достигается ЛТ до нескольЮfх десятков градусов.
Эти установЮf обычно применяются в широком температурном
диапазоне - вплоть до области температур порядка - 1 00 ° С. До 
стоинство термоэлектрических холодильных установок - ком
пактность, недостаток - низЮfЙ холодильный коэффициент.
21 .2.7. Рабочие тела, охлаждающие и охлаждаемые среды,
промежуrочные хладоаrенты
В литературе примен яют различные термины для обозначе
н ия веществ, циркулирующих в рабочем контуре холодильной
машины, и внешних теплоносителей . Это не способствует яс
ности изложения, зачастую приводит к пуган ице и даже к раз
ночтению. В целях большей однозначности понятий, исполь
зуемых в дан ной главе, еще раз специально акцентируем вни
мание н а принятой терм инологи и .
Теплоноситель, циркулирующий в цикле, именуется рабочим
телом ( РТ) . Теплоноситель, отбирающий теплоту у РТ в холо
дильниках и конденсаторах, будем называть охлаждающей сре
дой или хладоаrентом. Целевой поток, подлежащий охлаждению
и отдающий теплоту (в испарителях, в холодильниках) , назовем
охлаждаемой средой
это потребитель холода.
Рабочие тела* . От свойств РТ зависят тип холодильной ма
шин ы , ее размеры, конструкционн ые материалы, условия ра
боты , наконец, - величина холодильного коэффициента для
реального цикла.
К РТ предъявляется ряд требований:
- достаточно низкая температура замерзания (в противном
случае ограничены пределы применения РТ) ;
- малый удельный объем паров при рабочих условиях (это
позволяет уменьшить габариты некоторых узлов холодильной
машины, а значит, и сто имость аппаратуры);
- высокие значения коэффициентов теплоотдачи (приводит
к уменьшению теплообменн ых поверхностей испарителей ,
конденсаторов и прочих теплообмен ников) ;
- умерен ное давление при конденсации паров (чтобы избе
жать удорожания аппаратуры при высоких давлениях) ;
- давлен и е кипящего РТ в испарителе должно (желательно!)
превышать атмосферное : легче предотвратить угечку, чем под-

' Весьма детальные сведения о р а:ll! и ч н ых рабочих телах
холодильных процессов приведены в ( 3, 9, 1 1 , 16, 1 7 1 .

1 580

и

миянии их на ход

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

сос воздуха извне (это - ухудшение теплопередачи в конденса
торе и испарителе, внесение в систему воздуха, а с ним - и
водян ых паров, повышение рабочего давления, иногда - обра
зование взрывоопасных смесей РТ и воздуха) .
Специально остановимся н а часто формулируемом требова
нии · : большая теплота парообразования РТ для уменьшения его
расхода и затрат энергии на сжатие в компрессоре. Выполнение
этого "очевидного" требования чаще всего не приводит к суще
ственной экономической выгоде . Дело в том , что мольные теп
лоты парообразования близки у всех РТ (см. разд . 1 2 .6), и, сле
довательно, мольные потоки различн ых РТ для обеспечения
заданной холодопроизводительности Q0 примерно одинаковы .
Значит, примерно одинаковыми будут и обьемные потоки заса
сываемых компрессорами РТ, а с н ими и затраты энергии .
Еще ряд требований: хладоагент должен бьпь по возможности
- экологичесю1 приемлемым, в частности - безвредным
для человека;
- химически инертн ым к конструкционным материалам ,
смазочным маслам;
- негорючим и взрьшобезопасным;
- доступным и дешевым.
Подобрать РТ, в пол ной мере удовлетворяющее всем пере
численным требованиям, не удается; практически всегда РТ
выбирают в рамках технологического компромисса.
По совокупности свойств в наибольшей мере указанным
требованиям отвечают аммиак и фреоны (хлор- и фторзаме
щенн ые предельных н изших углеводородов) .
Акrивн о п р именяемые на протяжен ии де сятилетий фреоны (широкие диапа
зо н ы н и зких те м п ератур , неrор ю честь и нето ксичность) теряют свои позиции
из соображени й экологическо й безо пасности : фрео ны ( в иди м о , их хлорсодер 
жащие "осколки " ) разрушают озоно вый слой Земли .
В качестве РТ примен яют также диоксид углерода и диоксид
сер ы .
В табл. 2 1 . 1 приведены основные харакгеристики (при атмо
сферном давлении) некоторых РТ, используемых в настоящее
время.
Таблица 21. 1. О сновн w е физические свойства

Хладоаrенr

Температура затверде11аН11 11 ,

Воздух

о

Н2О
NН з
СО2
S02
CF2Cl2
• См.,

напри м ер ,

-77,7
-56,6

-75,2
- 1 55,0
(3, 6 ) .

0С

иехотор"1 х РТ

Предельно допустимая конценrрация паров в воздухе, %

0,5 - 0,8
25 - 30
0,5 - 0,8
25 - 30

1 58 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

В последние годы наряду с индивилуальными хладоаrентами
начинаюг использовать их бинарные с.меси. Эrо позволяет расши
риrь температурный диапазон ( Тв - Тн ) , а в случае смесей взаим
но нерастворимых компо нентов - еще и понизигь значение Тн.
Охлаждающие среды (хладоаrенты) . При их выборе предпо
читаюг доступные и дешевые холодную воду и воздух. При
необходимости отнимать теплоту у РТ в конденсаторе на срав
н ительно низких температурн ых уровнях приходится приме
н ять более дорогие низкотемпературные хладоаrенты .
Охлаждаемые среды. Свойства целевых продуктов процесса
производителями холода не регламентируются, они целиком
определяются требован иями заказчика.
Промежуточные хладоаrенты. После получения РТ низкой
температуры необходимо от него передать холод потребителю .
Если холодильная маши на находится близко к потребителю (а
иногда она создается п рямо для конкретного потребителя) , то
отвод теплоты в испарителе производится рабочим телом непо
средственно от охлаждае мой среды . Но иногда на заводе име
ются несколько потребителей холода, и их обслуживает общая
холодильная машина. Устанавливать отдельные испарители
около каждого потребителя холода, особенно если они удалены
один от другого , невыrодно: будут велики потери теплоты и
напора РТ в протяжен н ых коммуникациях от холодильной ма
шин ы до потребиrелей, сопровожцающиеся нарушением тепловых
режимов. В этих случаях применяюг промежуrочные хладоаrекrы,
забирающие холод в ис nариrеле холодильной устан овки (здесь
они выполняют роль охла:ждаемой среды) и передающие его раз
личным потребиrелям (здесь они - хладоаrенты).
В качестве промежуrочных х1адоаrенrов, разносящих холод по системе трубопро
водов ПО'IребитеJIЯМ, используют водные расrворы солей. У таких веществ - высокая
теwюемкостъ (так как расrворитель - вода), а значит, и высокая аккумулирующая
способностъ по rеплоте. Наиболее распространены так называемые paccOJJW - кон
центрированные растворы NaCI, СаО2, MgCl2. Их темпt1ратура замерзания зависит от
концентрации. Выбор рассола и ero концентрации определяется требуемой темпера
турой охлаждения (она доmкна бьпъ ВЬШ!е температуры замерзания рассола). Так, в
виде 22%-ro расrвора Naa используют до температуры около -20 • с (не ниже!),
растворы Саа2 - при бол ее низких температурах.
Основной недостаток рассолов - коррозионное воздt1йствие на мt1талл ы .
Для ослабления коррозии в рассолы добамяются ингибиторы (например, 2%-й
раствор Na2Cr207).

2 1 . 2 . 8 . Об а ппа 1 1 атурно м оформлении процессов
уме р е нно го охлаждения
В процессах умеренного охлаждения используются в основном аппараты и
машины, рассмотренные в предыдущих главах. Поэтому ниже их описание дано
весьма лаконично·. При необ�одимости болеt1 детального знакомства и анализа
следует обратиться к соответстнующим главам .
• Достаточно подробные сведения приведены в [8, 1 1 ) .

1 58 2

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 21. 1 1. Барабанный вертика 1ьный испаритель:
1
нижний б ир абан 2
верший барабан, 3
ши
рокие опускные труб ы , 4 узкие nодъемНЪ1е трубки;
1
рабочее тел о 11 охлаждаемая среда
-

,

-

-

-

-

,

2

-

Компрессор�.�. Чаще всего - это машины объ 
емного действия, преимущественно - nласт1шча
тые или коловратные либо nopuo1eвi.1e (в последнем

4

4

случае, как правило, - l'Оризонтальные, двойного
действия). Реже используются многоколесные
турбокомпрессоры (ТК) - см. разд. 4 . 5 . Если рабо
чее тело обладает высокой молярной массой
3
(значит, и плотностью), то степень сжатия в од
ном колесе ТК достаточно высока, так что резуль
1
тирующая степень сжатия - приемлема. Кроме
того, применение ТК оrраничено нижним преде
лом его производительности : 0 , 1 5 - 0,20 мЗ/с.
Холодил�.иики-коиденсаторы .
Весьма редко
применяют поrружн�.1е теплообменники (в основ
ном - змеевики) - из-за их низкой теплопроизводительности. Значительно чаще используются злементные и оросительные
теплообменники, а также аппараты воздушного охлаждения (АВО).
ЭлемеН111 �.1е теплообменники представляют собой кожухотрубные аппараты
типа "труба в трубе". Внутри труб - охлаждающая вода, снаружи - РТ
(охлаждение его паров, их конденсация и переохлаждение конденсата) . Элемен
ты при необходимости увели• 1ения теплообменной поверхности соединяются в
секции последовательно и (илн) параллельно . Переохлажденное жидкое рабочее
тело вьmодится из межтрубно го пространства нижнего злемента.
ОросНПЛЬНJ.1е rеплообменники различных конструкций получили наиболее ши
рокое распространение. Эrо вертикальные кожухотрубные аппараты, в трубное про
странство которых сверху полаt..'ТСЯ охлаждающая вода. Подача ее в трубы осу
ществляется через специальныt: направляющие вставки, со:щающие закрученное
пленочное течение воды по вну�ренней поверхности труб. В верхние зоны межтруб
но rо пространства подают пары РТ, конденсат РТ отводят из нижних его зон.
Конденсаторы типа АВО привлекают доступностью и дешевизной охлаж
дающего агента и благоприятными его экологическими характеристиками : ис
пользование воздуха вместо во;хы, все более дефицитной и требующей специаль
ной подготовки . Работа АВО о писана в разд. 7 . 9 .2 (см. рис. 7 . 17).
Испарители . Наиболее широко используются теплообменники вертикально
трубные барабанные и горизонтальные кожухотрубные.
Секция вертикал�.нотрубноrо б арабанн ого испаритеш1 (рис. 2 1 . 1 1 ) состоит из
двух горизонтальных (или слегка наклонных) барабанов 1, 2, соединенных
- рядом широких вертикальных труб З (на рисунке показаны стенки труб);
- множеством узких труб ./ (показаны жирными линиями).
Охлаждаемая среда находится снаружи барабанов и труб. Подлежащее испа
рению жидкое РТ подается в нижний барабан; испаряясь в тонких трубках,
парожидкостная смесь РТ поднимается в верхний барабан, где пары сепариру
ются от жидкости . Сухой п<1р в дальнейшем направляется в компрессор, а ки
пящая жидкость по широким сливным трубам возвращается в нижний барабан.
Такое направление циркуляции РТ обусловлено существенно большей удельной
поверхностью узких труб в сравнении с широкими: поэтому в узких трубах
парожидкостная смесь значительно легче жидкости в широких - возникает
эффект термосифона (см . р<!зд. 6.4.4).
При необходимости повышения холодопроизводительности arperaтa устана
вливают несколько секций ш1раллел ьно. Вертикальнотрубные барабанные испа
рители применяются в случае газообразной охлаждаемой среды.
-

-

1 58 3

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

2

9

Рис. 21. 12. Игольчатый дроссельный вентиль:
J
составной корпус, 2 нарезное отверстие, 3
vплотнение, 4 коническое седло, 5 входное отверс
тие, 6 иrла, 7 выходное отверстие, 8 стержень, 9
рукоятка-маховик;
А
зона дросселирования
-

-

-

-

-

-

-

-

-

-

испарители
Горизонтмьные кожухотрубныс
предстаWIЯЮТ собой обычные кожухотрубные
теплообменники , в межтрубном пространстве
8
которых кипит РТ, а в трубном - течет пода
ваемая насосом жидкая охлаждаемая среда. В ка
7
честве последней моrут выступать различные
целевые жидкости, в том числе и с не очень
низкой температурой замерзания (например,
"рассолы") . В этом случае пояWIЯется опасность
4
выпадения "льда" охлаждаемой среды на внутрен
ней поверхности труб - не только при остановке
6
насоса, но и при недостаточно высоких скоростях
5
ее течения. Для предотвращения замерзания уве
А
личивают скорость потока в трубах, применяя
РТ из Х
многоходовые (по трубному пространству) тепло
обменники (см . разд. 7. 1 и рис. 7 . 1 , в) .
Испарители тщательно изолируют во избежа
ние "потерь холода в окружающую среду" (притока теплоты извне).
Детандерw .
Их применя1от исключительно в газовых (воздушных и др.)
циклах. Как правило, в циклах умеренного охлаждения предусматривают ис
пользование поршневых детандеров. По своей конструIО.IИИ они сходны с порш
невыми компрессорами; только клапаны у детандеров открываются и закры
ваются принудительно (от привода).
Наиболее распространенный способ oroopa энергии от детандера - присое
динение его к электроrенератору с выработкой электроэнергии.
Дроссел�.нwе веJП11Ли . Конструкция одной из модификаций показана на рис.
2 1 . 12. Составной корпус 1 (сборка - на резьбе с у1щотнением J) имеет сверху
отверстие с мелкой резьбой 2, а снизу - пологое коническое седло 4, ведущее к
входному отверстию 5. Выход ное отверстие 7 находится сбоку. В корпус на
резьбе 2 встамен стержень 8 с иглой 6, при•1ем уюл иmы 6 равен углу конуса 4;
сверху стержень заканчивается маховичком 9. Присоединение вентиля к трубам,
по которым движется поток в установке, осущесТWJЯется с помощью накидных
гаек (резьба у зон входа и выхода потока) . Рабочее тело из холодильника
конденсатора Х при высоком дамении Рн подается под иглу, теряет напор (в
узком зазоре А между иглой и седлом) и при низком дамении Рк выводится
(сбоку) к испарителю И. Связанные друг с другом расход РТ
(производительность) и перепад дамения в вентиле определяются величиной
зазора между иглой и седлом; этот зазор тонко (резьба - мелкая!) регулируется
поворотом маховичка.

2 1 .3. П РОЦЕССЫ ГЛУБОКОГО ОХЛАЖДЕНИЯ
Процессы глубокого охлаждения применяются для достиже
ния низких температур , получения сжиженных газов и rазовых
смесей; в последнем с.1учае таюке - для разделения их н а
компоненты .
Получен ие температур ниже - 1 00 ° С иногда классифицируют
следующим образом:
- техни ка глубокого охлажден ия (от 1 75 до 55 К) ;
1 584

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

- криоген ная техни ка (от 55 до 0 , 3 К) ;
- техника сверхн изю1х температур (д о 2 . 1 0-s К) .
Температуры н иже 2 К применяются пока лишь в лаборатор
н ых условиях .
Далее глубокое охлаждение рассматривается на примере воз
душных циклов с частичным ожижением воздуха.
При рассмотрении ул �еренного холода были указаны два пути
пон ижен ия температуры (оба связаны с уменьшением давления
рабочего тела) :
1 ) дросселирование (энтальпия h = const);
2) адиабатическое расширение с отдачей внешней работы
(энтропия s = const) .
Второй вариант для процессов умерен ного охлажден ия оказал
ся неприемлемым по чисто техническим причинам: трудности
конструирования машиJ-1 для расширения жидкостей . При рас
ширении же газов это препятствие отпадает, так что в процес
сах глубокого охлажден и я могут быть использованы оба пути .
21 .3. 1 . Термодинамические основы процессов
глубокого охлаждения
В общем случае скорость изменен ия температуры с пон иже
н ием давления р характеризуют дифференциальным эффектом
а. = d T/dp . П р и получении н изких температур интерес пред
ставляет случай а. > О, отвечающий уменьшению температуры
(d T < О) при пон ижении давлен ия (dp < О как при дроссели
ровании, так и при адиабатическом расширении) . На практике
под дифференциальным эффектом обычно понимают измене
ние температуры (в гр:щусах) при уменьшении давления на
1 бар (1 бар = 1 0 5 Па) : CLдp=J ат = л т/лр град/бар.
Полное изменение температуры Л Т от начальной Тн до ко
нечной Тк при умен ьшении давления от Рн до Рк носит назва
ние нвтегральноrо эффекта:
-

л Т := Тн

Рн

-

Тк = f a. dp .
Рк

Дифферен циальн ы й и интегральн ый эффекты для упомяну
тых выше двух путей получения низкой температуры форми
руются по-разному.
Дросселирование

Процесс дросселиро вания в общих чертах охарактеризован в
разд . 2 1 .2 . 1 . Рассмотрим его подробнее. Это изоэнтальп ийный
процесс расширения га:1а без отдачи внешней работы, сопро
вождающийся изменением температуры. Количественная харак
теристика процесса
д11фференциальный дроссельный эффект:
(а)
a.h = (д Т/др)h·
-

1 58 5

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

т
Тн1�

Тк h

�r
�

t:::J.':l:.

t:::J.>r..

<1

-

?� -

�J't

•
f....
<1

"о

Рис. 21. 13. К расчету интеrральных дроссельных эффекrов
Для возду]Са в практически интересном диапазоне и зменения давлений

"" 0,2+0,4 град/бар.

a.h "'

При изменении давления в полном диапазоне от Рн до Рх.
получаем интегральный дроссельный эффект:

Рн
л тh = тнh - ткh = f a. h dp = (о.h)ср (рн
Рх

-

рк) .

(6)

Последнее выражение записано в соответствии с теоремой о
среднем. Поскольку закон изменения a.h с давлением р, как
правило, неизвестен, то эффект л тh не вычисляют аналитиче
ски, а определяют по диаграмме T-s (рис . 2 1 . 1 3) .

П опуrnо заметим: в диаrрамме T-s для воздуха (т.е. для смеси компонентов с
разными темпер атурами кипения) линии р
const в обпасти влажноrо пара не
совпадают с изотермами - см. наклонную штриховую линию на рис. 2 1 . 1 3 . Де
тально этот эффек:r анализируется в разд. 1 2.2. Для индивидуального компонента
JПtнии Т const и р = const в области влажноrо пара, конечно, совпадают.
=

=

Для выяснения физического смысла и знака эффекта дрос
селирования воспользуемся записью выражения (определени
ем) энтальпии:
(в)
h = и + pv;
здесь и - удельная внутренняя энергия; pv - удельная потен
циальная энергия давления ; v - удельный объем . При этом
и = Су Т, где Су - теruюемкость при постоянном объе ме .
При h =
выражение (в) может бьпъ переписано в форме:
(r)
Ин + РнVн = ик + РкVк.
Отсюда следует, что изменение величины pv будет сопро
вождаться определенн ым изменением внутренней энергии газа
и, а значит, и температуры Т.

const

1 586

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Т, К

300
250

т�
/1

200
1 50

s

Рис.21. 14. К

явлению инверсии для воздуха

Если РкVк > РнVн, то llк < ин. т.е. с падением давления вели
чина и уменьшится, так что Т
упадет; здесь дифференци
альный дроссельный эффе�сr положителен (a.h > О) , что соот
ветствует целям холодильного процесса.
Если же РкVк < РнVн. то Uк > ин. т.е. и и Т возрастают и a..h <
< О . Здесь падение давления при дросселировании сопровождает
ся повышением температуры; этот случай не может быть ис
пользован для получения холода.
При РнVн = РкVк имеем и и Т = const. Здесь газ ведет себя
как идеальный.
Xapaicrep неравенства
зави
РкVк > РнVн или РкVк < РнVн
сит от природы газа, а также уровней температур и давлений.
Иначе говоря , в разных диапазонах температур и давлений при
дросселировании температура газа может повышаться ми по
нижаться.
Например, при температурах, близких к 300 К, дросселирование воздуха дав
лением 20 МПа приводиr к понижению температуры, а водор ода или rелия - к
повьШiению. С другой стороны, дросселирование воздуха давлением >50 МПа
при температурах ниже 200 К сопровожцается повышением температуры.
-

-

-

Явление изменения знака a..h при изменении температур и
давлений носит название инверсии
она для различных газов
наблюдается при разных давлениях и температурах, ей в диа
граммах состояния (например, в диаграмме T-s) соответствует
кривая инверсии. Эффект инверсии для воздуха иллюстрируется
-

1 58 7

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

на рис . 2 1 . 1 4: можно видеть, что в области высоких давлений и
низких температур при падении давления кривые h = const
являются восходящими - температура возрастает.
Таким образом, не всякий газ в любом диапазоне температур и
давлений можно охладить дросселированием. Предварительно надо
оценить знак дифференциального дроссельного эффекга o.h.

Адиабатическое расш ирение с отдачей внешней работы
Здесь также различают эффекты :
- ади абат и ый ди фференциальный

O.s = (д Т/др)s,

(д)

- адиаб атный и нтегр ал ьный

(е)

Рк

Для определен ия знака о.5 запишем 1 закон термодинамики
в форме
dq = d и + d /,
(ж)
где

d/

- удельная работа, производимая рабочим телом .

В адиабатном процессе поток теплоты d q = О, так что dи =
= -d/. Это означает, что в отличие от дроссельного эффекта

адиабатное расширение РТ с отдачей внешней работы (d/ > 0 )
всегда сопровождается уменьU1ением внутренней энергии РТ
(du < О) , а значит, и понижением температуры . Здесь всегда о.5 > О.
На практике величину о.5, как и �'}' выражают в разностной
форме O.s = л т/лр и измеряют в гра д/бар.

В праК'111ч ески интересных диапазонах темпераlУJ' и даалений воздуха вели
чина а , достигает 1 град/бар.

Поскольку закон изменения о.5 с давлением, как правило, не
известен, то Л Тs не вычисляют аналитически , а определяют по
диаграмме T-s (рис . 2 1 . 1 3) .

Сопоставление o. h и

о.5

При изучении умеренного охлажден ия было показано (разд .
2 1 .2.2) , что переход от адиабатического расширения к дроссе
лированию отрицательно сказывается на количестве получае
мого холода и на экономичности процесса (на Ех) · Следова
тельно, о.5 > o.h, и при одинаковых перепадах давления (рн - Рк)
всегда Л Тs > Л Th . Этот вывод прямо следует из сопоставления
интегральн ых эффектов в диаграмме T-s н а р ис. 2 1 . 1 3 ; его
можно подтвердить и математическим анализом . Тем не менее
' См., например, (3 ) .

1 58 8

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

для получения холода и сжиженных газов используют оба пуги
- по двум основным причинам .
Первая связана с получением жидкого рабочего тела. Обра
зование капель в детандере нежелательно (см. разд. 2 1 .2.2) расширительная машина даже при незначительном их содер
жании в РТ быстро выходит из строя . Поэтому детандеры ра
ботаюг на производство холода, а при необходимости сжижения
газа в цикле наряду с детандерами используют (в области па
рож:идкостной смеси) дроссельные вентили. Разумеется, в
циклах глубокого холода без получения сжиженных газов сопро
вождение детандеров дроссельными вентилями не обязательно.
Вторая причина связана со степенью реальной близости рас
ширительного процесса в детандере с отдачей внешней рабо
ты - к адиабатическому: все зависит от того, в какой мере
удается воспользоваться этой работой, т.с . от адиабатического
КПД расширительной машины.
Под адиабатическим КПД детандера 11ац' понимаюг отноше
ние реально отдаваемой работы к адиабатической:
(з)
= L/Lац = l/laц < 1 .
Специально укажем , что величина 11 ац' по способу формиро
вания обратна адиабатическому КПД компрессора 11ац = L;;/L
11 ад'

(см . разд. 4.2 и 4.3 .7).
Неравенство 11ац' < 1 вызвано трением поршня о стенки ци
линдра в поршневых детандерах и внуrренним трением расши
ряющегося газообразного РТ - в турбодетандерах. Кроме того,
при работе в области низ ки х температур неизбежен приток
теплоты из окружающей среды к рабочему телу в детандере. В
результате реальная конечная температура газа Тк получается
выше, чем при адиабатическом расширении.
Итак, реальное расширение газа в детандере идет не адиаба
тичес ки , а политропически , при этом 11ац' < 1 , что снижает эф
фект охлаждения. Поэтому на практике оба пуги получения
низких температур конкурентоспособны.
Можно так примерно оценить сравнительную эффектив
ность различных процессов расширения газа в детандере (см .
рис. 2 1 . 1 3 ) :
при 11ац' = 40+50% будет (аs)практ < ah - процесс расширения
газа в детандере изображается кривой, проходящей выше линии
h = const, так что интегральный эффект расширения Л Т' < л Th;
при 11ад' = 6U+70% получается (аs)практ ::::: a h - кривая расши
рения газа в детандере располагается где-то близко к линии
дросселирования, и интегральный эффект расширения в де
тандере близок к дроссельному Л Th;
при 11ад' = 80 + 85 % будет (а,1)практ > ah
процесс расшире
н ия в детандере изображается кривой, проходящей ниже линии
-

1 589

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис.21. 15. К расчету /min: диаrрамма
обратного эталонного цикла

т

T-s

дросселирования , так что инте
гральный эффект расширения в
з оок
детандере л т· > л тh.
Для оценюt и сопоставления
эффективности различных цик
лов глубокого охла:ждения по
лезно понятие о минимальной
удельной рабаrе /min, необходи
мо й для полного ожижения 1 кг
исходного газа. На рис.2 1 . 1 5
s
представлена диаграмма T-s
цикла,
обратного
эталонного
отвечающего /min. В отличие от
цикла Карно адиабатическое сжатие газа в компрессоре здесь
заменено изотермич е с юtм . При этом точка 1 соответствует
исходному состоянию газа, точка О - полному его ожижению.
Стадии цикла:
1 -2* - изотермическое ( Т1 = Т2 = const) сжатие газа в ком
прессоре от давления р1 до Р2• - с отбором теплоты для обес
печения изотермичности сжатия;
2*-О - адиабатическое (s = const) расширение газа в детандере
при падении давления от Р2 • до р1 - с понижением температуры и
полным ожижением rаза (точка О - кипяwая :жидкость);
0-3-1 - изобарическое (р1 =const) испарение всей жид
кости до состояния сухого насыщенного пара (точка 3) и его
нагревание до исходного газообраз но го состояния 1 .
Чтобы 1 кг исходного (точка 1 ) газа обратить в жидкость,
требуется отвести от него теплоту в количестве q. = h1 - h0.
При этом удельные (на ожижение 1 кг газа) затраты энергии
/min на диаграмме выражаются площадью 12 031 . Расчеты · по
казывают, что для воздуха при атмосферном давлении и начальной
температуре 300 К величина q. = 4 1 9 кДж/кг, а /min =
= 7 1 0 кДЖ/кг.
Изображенный на рис. 2 1 . 1 5 цикл, обусловливающий /min,
техничесюt неосуществим, так как требует давле н ия в точке 2*
на уровне 50000 МПа. В производстве глубокого холода приме
няются давления Р2 < < fl2• , причем Р2 редко превышает 20
МПа. Поэтому в реальных циклах удельные затраты энергии lж
в несколько раз превышают /min·
химикобольшинстве
в
подчеркнем:
Специально
технологических процессов энергетические затраты составляют

• Подходы
1 590

к

определен ию lmin см. (4, 5, 8).

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

определяющую долю в стоимости продукции. В производстве
же глубокого холода и ряда сжиженных газов заметная доля
приходится на капитальные затраты
из-за применения
весьма дорогих конструкционных материалов (см. разд. 2 1 .3.6).
Поэтому в данном случае для полной оцен ки и сравнения эко
номичности различных холодильных процессов величина /rnin
необходима, но не всегда достаточна.
-

Технологические характеристики процесса
В ходе технологического расчета холодильных процессов
надлежит определить следующие величины:
степень ожижения х; специально подчеркнем: х не является
степенью влажности парожидкостной смеси после дросселиро
вания, это доля сжиженного воздуха по отношению к исход
ному, сжимаемому в компрессоре; [х] = (кг жидкого возду
ха)/(кг сжимаемого воздуха);
удельный расход энергии
- на 1 кг сжимаемого газа (воздуха) lк; [/к] = кДж/< кг сжи
маемого воздуха);
- возвращаемой детандером, lд, в расчете на 1 кг газа, сжи
маемого в компрессоре; очевидно, что (/д] = [/к] ; разумеется,
величина /д рассчитывается только для циклов с детандерами;
- в расчете на 1 кг получаемого жидкого воздуха lж; [ lж] =
= кДж/(кг жидкого возду}(а) ; именно этот параме'Гр является важ
нейшей характеристикой энерrетической эффе ктивн ости цикла;
мощность компрессора Nк; [Nк] = кВт.
Величины х рассчитываются с помощью тепловых балансов.
При этом пространственные контуры для составления балансов
выбираются в зависимости от конкретного холодильного цик
ла. Общим моментом является исключение из контура всех холо
допроизводящих агрегатов, поскольку тепловые потоки в н их,
как правило, не известны.
Потребитель задает производительность цикла по исходному
(сжимаемому) воздуху G или по жидкому воздуху Gж. Связь
между этими производительностями следует из физического
смысла степени ожижения х:

Gж =

Gx,

G = Gж /х.

(2 1 . 1 7)

Удельная энергия lк рассчитывается по формулам для изо
термической работы - см. разд. 4.2, формулы (4. 12), (4.24) .
Если Ry - ун иверсальная газовая постоянная , а М - молярная
масса газа, то

(2 1 . 1 8)
где 1'Jиз и 'lw

-

изотермический и механический КПД компрессора.

1 59 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Возвращаемая детандером удельная работа в случае адиабати
ческоrо процесса в расчете на 1 кг расширяемоrо Гi1За состави
ла бы Л hад = (hн - hк)s. Пусть в детандере расширяется опреде
ленная доля Ч' от исходноrо газа, сжатоrо в компрессоре . Тогда
с учетом отклонения процесса в детандере от адиабатноrо и
механических потерь в нем
rде 'lм

lд = \j/ЛhадТ\ ад'ТJ м ,

(2 1 . 19)

- механический КПД детандера.

Удельная энерПUI lж. определяется исходя из lк и /д:

lж. =

(/к

- lд)/х.

(2 1 .20)

Здесь в скобках - результирующие удельные затраты энер
гии на 1 кг газа, сжимаемоrо в компрессоре.
Мощность воздушного компрессора:
Nк =

Glк .

(2 1 .21)

Ниже последовательно рассмотрены циклы глубокоrо
охлаждения с частичным ожижением воздуха, сначала - ис
пользующие только дросселирование, а затем - работающие с
применением расширительных машин " .
СпеЩ1фика отдельных циклов глубокою охлаждения потребует
расчета некоторых параметров работы дополниrельно. Такие рас
четы вьmолняются по ходу рассмотрения этих циклов.
21 .3.2. Простой регенеративный цикл

Характеристика, схема и диаграмма

T-s

Это - наиболее простой из циклов, использующих только
дросселирование. Чтобы получить приемлемо низкую темпера
туру, надо подвергать дросселирован ию по возможности охлаж
денный сжатый газ. Для этоrо процесс сжатия в мноrоступен
чатом компрессионном агрегате проводят условно изотермиче
ски, охлаждая газ (воздух) после каждой ступени в холодиль
никах до температуры перед сжатием. Но этоrо недостаточно,
поэтому сжатый газ направляют в теплообменный аппарат (в
процессах глубокоrо охлаждения его называют холодообменнн
ком), где он дополнительно охлаждается . В этом случае после
дросселирования воздух попадает в область влажного пара, что
позволяет после сепарации выделить:
- жид кую составляющую, используемую как конечный про
дукт (выводится из цикла);
- холодный пар (газ)
он используется в цикле для охлаж
дения встречноrо потока в холодообменнике.
-

•

Некоторые другие циклы приведены

1592

в

(2 ,

3 , 5, 1 3 ).

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

т

s

б

а

Рис. 21. 16. Простой регенеративный цикл Линде:
а - принципиальная схема, б - диаrрамма T-s;
К - компрессионный arperaт, Х - холодообмеИНИJС, Др - дроссельный

сепаратор

Анализ удобно вести в расчете на

компрессоре.
На рис. 2 1 . 16, а изображена

1 кг

газа,

венrиль,

С

-

сжимаемого в

принципиальная схема простого
реrенеративного цикла (цикл Линде) . Исходный воздух изотер
мически сжимается от давления р1 до Р2 в компрессионном
агрегате К и охлаждается в холодообменнике Х при постоян 
ном давлен ии Р2 (за счет обратного потока холодного воздуха) .
Затем сжатый воздух дросселируется в вентиле Др до давления
р1 . Полученная парожидкостная смесь поступает в сепаратор С,
откуда жидкость (сжиженный газ ) отводится из системы в ко
личестве х, а газ в количестве ( 1 - х) возвращается в холодооб
менник Х, забирая теплоту у потока сжатого газа, идущего на
дросселирование.
Заметим: давление р 1 , как правило, - атмосферное: свежий
воздух забирается из атмосферы; жид ки й воздух хранится и
транспортируется в сосудах Дьюара, где зона хранения соедине
на с атмосферой.
В связи с р 1 = 1 бар может возникнуть вопрос: зачем долю
( 1 - х) возвращать в цикл, не проще ли направлять на сжатие в
компрессор весь воздух (1 кг) из атмосферы, а не небольшую
ero долю х? Дело в том, что воздух в циклах глубокою охлаж
дения проходит специальную подrотовку (очистку от воды,
1 593

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

диоксида углерода и других примесей - см. разд . 2 1 .3 .6, 2 1 .3 .7) .
Очистка воздушного потока Gx дешевле, чем полного потока
G. Поэтому поток воздуха G(l - х) , ранее уже прошедшего
очистку, возвращают в цикл.
В диаграмме T-s (рис . 2 1 . 1 6, б) стадии процесса изобража
ются следующим образом:
1 -2 - изотермическое ( Т1 = Т2 = const) сжатие 1 кг воздуха;
2-3 - изобарическое <Р2 = const) охлаждение в холодооб
меннике;
3-4 - дросселирование (h = co11st);
/о

4�

5

- изобарическая (р 1

=

const) сепарация (с выводом

потока х жидкого воздуха);
5- 1 - изобарическое (р 1 = const) нагревание потока ( 1 - х)
воздуха (с присоединением потока х свежего воздуха и направ
лением 1 кг смеси на сжатие в компрессор).
Далее стадии повторяются. Вследствие отбора и восполне
н ия количества (х) рабочего тела (воздуха) цикл по РТ не замк
нут, и его можно трактовать как замкнутый только условно.

Технологический расчет ц икла
Связь производительностей по сжимаемому G и жидкому Gж
воздуху определяется формулой (2 1 . 1 7) .
Степень ожижения называется теор етичес кой .хт , если она
определяется в предположении об отсутствии потерь холода в
окружаю щую среду и о п ол ной рекуперации теплоты в холодооб
мевиике ( Т1 = Т2 ) . Значение .хт наЙдем из теплового баланса для
контура 1 (см . на рис . 2 1 . 1 6 , а), отсекающего холодопроизво
дящий агрегат. Заметим: дроссельный вентиль не является хо
лодопроизводящим устройством, так как процесс в нем проис
ходит без изменения э нтальпии.
В расчете на 1 кг РТ (воздуха, сжимаемого в компрессоре) :
откуда

l · h2 - .хтhо - ( 1 - .хт) h 1 = О,
Xr

=

h1 - hz
h1 - �

(2 1 .22)

В числителе выражения (2 1 .22) - удельная холодопроизводи
(теплота, отбираемая у 1 кг изотермически
сжимаемого РТ в компрессионном агрегате К с холодильника
ми), а в знаменателе - количество холода (отнимаемой тепло
ты) , необходимого для полного ожижения 1 кг исходного воз
духа.

тельность установки

1 594

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Реальная степень ожижения х отличается от теоретической Xr
по двум основным причинам .
Во-первых, существует приток теплоты и з окружающей сре
ды к холодному РТ, хотя установка самым тщательным обра
зом изолирована. Его трактуют как потери холода в окружаю
щую среду, обозначают символом q0 и относят к 1 кг исходного
сжимаемого в компрессоре газа.
Во-вторых, предположение о выравнивании температур Т1 и
Т2 в холодообменнике Х может быть реализовано только при
его бесконечно большой пропусююй способности kF � CXJ , т.е.
в случае балансовой задачи теплообмена. На практике холодо
обменники и в самом деле отличаются развитыми теплообмен
ными поверхностями F, но, разумеется, не бесконечно боль
шими . По этому холодный воздух нагревается не до температу
ры Т1 (точка 1 ) , а до несколько меньшей Т1', соответствующей
точке 1 ' на рис. 2 1 . 1 6 , б. Это означает, что холодный
(нагреваемый) поток не весь свой холод отдает встречному
(охлаждаемому) потоку, т.е. в холодообменнике не происходит
полной рекуперации теплоты . Такой эффект называется недо
рекуперацией и обозначается символом qp ; его также относят к
1 кг сжимаемого воздуха. Очевидно, что каждый килограмм
холодного потока недодает (h 1
h1 ') холода. Но удельный холод
ньIЙ поток равен ( 1 х); поэтому в расчете на каждый килограмм
сжимаемого воздуха охлаждаемый поток недополучает от холодно
го Qp = (h1 h 1 ' )(1 х) холода (недоотнимает те ruюты) .
При расчетах в С И величины qo и qp выражаются в Дж/(кг исходного возду
ха); реально вместо Дж обычно используют кДж.

-

-

-

-

В результате потерь холода q0 и qp реальный цикл не может
быть полностью замкнут в тепловом отношении. Обычно
(q0 + qp) :о:: 7+ 1 2 кДж/<кг сжимаемого газа) . Наличие потерь
холода в окружающую среду и от недорекуперации приводит к
уменьшению удельной холодопроизводительности, т.е. к
уменьшению числителя в выражении (2 1 .22); реальная степень
ожижения составляет:
h1 � - qo + qP
(2 1 .23)
х
.
h1 - ho
опредеУдельный расход энергии на сжатие 1 1а воздуха
ляется по формуле (2 1 . 1 8).
Основная э нергетическая характеристика цикла
удельная
работа, приходящаяся на 1 кг жидкого воздуха , - lж.
рассчиты
вается соответственно по (2 1 .20) при /д = О:
=

-

(

)

-

4к = zJx.

(2 1 .20а)

Мощность на валу компрессора Nк рассчитывается по форму
ле (2 1 .2 1 ) .
1 595

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

В расчеrные формулы не вошли параме1ры точек 3 и 4. При необходимосrи
для коmура 11):
можно найm из тепловоrо баланса сепаратора (на рис. 2 1 . 16, а
так что

l ·h4 - xho

h4

=

hз

=

-

( 1 - x)hs

hs - x(hs

-

=

О,

-

ho).

их

(2 1 .24)

При зrом энтальпии РТ (воздуха) для точек О и S при заданном давлении Р1 ИЗВеС111 Ы .

Характеристики простого реzенеративноzо ЦUIUa при температуре исходного воздуха Т1 = 300 К и Р2 =
МПа: х :::: 0,05;
"

20

14· 103

lж. ::::
кДж/(кг жидкого воздуха). Важно: для этого цикла
lж. почти в 20 раз превышает lтт. Это указывает на малую эф
фективность цикла и заставляет искать пуги ее повышения.
Тем не менее рассмотрение данного цикла оправдано методи
чес ки , так как позволяет осмыслить ряд понятий и приемов
анализа (расчета) основных величин .
21 .3.3. Усовершенствованные

циклы

с дросселированием

Пути совершенствования ц ик.ла
С целью совершенствования крайне энергоемкого цикла
Линде используются два основных пуги.
Первый состоит в понижении температуры газа перед дрос
селированием . Это должно благоприятно сказаться на удель
НЬIХ (на 1 к г жидкого воздуха) энергетичес ких затратах lж. прежде всего за счет увеличения степени ожижения.
Возрастание эффективности цикла в общем плане здесь об
условлено уменьшением температуры верхнего источника Тв
(см . разд. 2 1 .2 . 1 ), ростом &х - по соотношению (б) в разд. 2 1 .2 .
Конкретно: при более низкой температуре исходного воздуха
для полного ожижения потребуется отвести от него меньше
теплоты q • . Кроме того, несколько увеличится удельная холо
допроизводительность (разность энтальпий) в сравнении с
фиксируемой при более высоких температурах (см. ниже) . По
нижение температуры газа перед дросселированием осу
ществляется в испарителе машины умеренного охлаждения .
Так строится цикл с предваркrельным охлаQеннем воздуха.
Второй пуrь связан с различным характером влияния рабо
чих давлений р1 и Р2 на затраты энергии в компрессоре и на
интегральный эффект охлаждения при дросселировании. В
самом деле: величина lк, согласно
определяется отно 
шением fJ1/p 1 , в то время как л тh , согласно выражению (б), их разностью (Р2- р 1 ) . Поэтому если дросселировать газ , на
пример, с давлением Р2 =
МПа до Р1 = 2 МПа, то Л Тh пони-

(21.18),

20

• Характеристики этого и других циклов при различных параметрах процесса
приводятся, например, в [6) и подробнее - в ( 1 3 ) .

1 596

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

(1)

т

а

б

s

Рис.21. 1 7. Усовершенствованный ЦИЮJ с пuепваоительным охлаждением в маши
не умер енного холода, двукрат ным дросселиро ванием и циркуляцией rаза сред
него давления:
К1, К2 - компрессиоШIЬlй arperaт (ступени ниэкоrо и высокого давлеШIЙ); ПХ - пред
варительный холодильюп:; Ку, Ху, ДРу, Иу - компрессор, холодильюп:, дроссельный вен
тиль, испаритель машины yмepeIOJoro охлаждения; ОХ - основной холодильник ; дР1 . дР2
- дроссельные вентили ; С1, С2 - сепараторы

1 597

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

11ез1 1 а • ш т ел ыt0
в с р ав не н и и с дросселирован ием до Р 1 =
МПа ; в п е р в о м CЛ)"l:lC Л Т11 о прtдt:J 1нется п ереп адом давле н И й :
\ 9.9- М11а, во втором - 1 8 МПа. П о н н ж ен 1 1е Л Т1, ( п римерно н а l Oo/o),

з ится

= О, 1

будет с о п р о вождаться уме н ьшением х; это в соответствии с
фор м ул о й ( 2 1 .23а) долж н о п р и водит ь к н ежелател ьному
чеиию lж .
Н о поскол ьку газ давлен и я P t потом сжи мается в
ц и кле до р2 , то lк за.ме111110 умеиьшается: степе н ь сжатия в ко м 
п р ессо р е р2/р 1 1.1 расс м ат р и вае м ом п р и мере уменьш итсн в 20 раз
( 200 и 1 0 соответстве н н о), а удел ь н ые затраты э н е р г и и lк - 1.1
3 раза. Этот эффе кт с избытком ко м п е н с ирует п о н иже н ие х.
З н а•нп, э н с �н·ети•1ески в ы годно дроссслиро�ть шз до некоторого
промежуrо • 1 н о го да.влеюu1 (в пр имере - это 2 М а ) . Н о продукт
(жидкий воздух долже н быть получен при атмосферном давле 
н и и . Поэто му н е которую дол ю РТ. (обычно порядка 20-50%) вес
же д р оссел и р уют от п роJ\Jсжуто • 1 ного давлени51 до атмосферн о го .
Так строится ц и кл с двухкра111ым дросселированием и циркуляцией
воздуха промежу�·о•11юго (срсднсrо) давления .
Наибол ь ш нй эффект дает сочета н ие первого и второго п уrей
м одиф и ка ц юt ц и кл о в . На р ис . 2 1 . 1 7 представ.лен усовершен
ствованныii цикл , нспол ъзующнй предварительное охлаждение в
машине у м е 11е ююго охлажден11я и двухкратное дросселирование
с цирку.л яциеit воздуха с11еднеrо давления.

увели

П

)

·

Схема

Схе ма

и

д

р

иаг а.мма

Т-s

устано1.1ю1 п р и веде н а на р и с . 2 1 . 1 7 , а. Она включает:
м н о гоступе н ч атый ко м п рессио н н ы й агрегат (на рисун ке пока
зан ы ступ е н и н из ю 1 х-сред н их давл е н и й К1 и сред н их
высоких давлений К2) , пред ва р ител ь н ы й ПХ и основной ОХ
холодообме н н и ю1 , м а ш и н у у мере н н о го охлажден ия (содер
жащую и с п а р ител ь
ком прессор
холодильник-кон 
де н с ато р Ху , дроссел ь н ы й вентиль
дв а дроссельн ых вен 
тиля д Р 1 и
два с е п а р атора
и
Анал из ведется в расчете на 1 кг в о зд уха , сжимаемого в сту
п е н ях
в о здух , н ах одя щийся под давлением
П осле
последовательно охлаждается в ПХ, И у (до состояния , соответ
ствующего то•1 кс 5) и ОХ. П р н этом тем пература Т5
шшtы
о:хлажiJеи ия о пределяется природой циркул и 
р ющего там РТ л ибо д и ктуетс я требованиями цикла глубокого
о хлажде н и я (тогда утю �1 янутое РТ пр и ход итс я подбирать) . В
вентиле Др 1 воздух дросселируется до среднего давления JJ2, в
резул ьтате • 1 с го п олучается парожид костная смесь (состояние в
точ ке 7 ) . П осле сепарации в сосуде С 1 ж ид ко сть (се д ол я 1 - <р)
подвергается повтор н ому дросселированию в вентиле дР2 до
давл е н и я р1 и н а правляется на следующую сепарацию в сосуд
Отс юда выводятся продукт (жидкий возд ух ) в количестве х
и газ в кол и честве ( 1 - (Р - х) . Потоки q> при давлении
и

Иу,

Др 2 ,

К2 .

у

С2.

1 598

умереююго

К2

Ку,

Д ру),
С 1 С 2.

р3,

после ма

Р2

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

( 1 - <Р - х) п р и давл е н и и Р 1 н агре ваются в холод ообме н н и ках
о хлаждая встре ч н ы й п оток воздуха. П о сле ПХ поток ( l - <Р �
- х) смешива етс я с о с вежи м во щухом (поток х) , и с м е с ь в коли 
чест ве ( l - q>) с жи м аетс я в первых ступ е нях ком пре сси о н но го
а гр егата К 1 от Р 1 д о Р2 ; к не й присо еди н яют поток q>, и с м е с ь
( l кг) направл я ется на сжати е от р2 до р3 во вторые ступ е ни
компре ссо ра К2 . Разум е ется , вследстви е от вода из ц ию:rа про
дукта и вос п ол н е н ия с вежего возд ух а цикл ли ш ь усл овно может
с ч и тат ь с я з<1 м кнуты м .

Н а рис .

2 1 . 1 7, б в диаграмме T-s даны стадии цикла:
( Т1 = Т2 = const) сжатие части ( 1

1-2 - изотермическое

- <р ) воздуха;
2-3 - изотермическое ( 12 = Тз = const) сжатие 1 кг воздуха;
3-4 - изобарическое (р3 = coпst) предварительное охлаж
дение;
4-5 - изобарическое (р3 = const) охлаждение воздуха в ма
шине умерен ною охлаждения ;
5 - 6 - изобарическое (р3 = const) охлаждение воздуха в
основном холодообменнике;
6-7 - первое дросселирование (h6 = h7 = const) газа до
промежуточною давления Р2;
./'

7�

8

- изобарическая (р2 = const) сепарация жидкости 9
доля ( 1 - rp) и газа (сухою насыщенною пара) - доля q>;
8 - 1 0 - второе дросселирование (hs = h1 o = co n st) жидкости
до низкою давления Р 1 ;
./'
10�

о

-

изобарическая

(р1

=

const) сепарация

жидкости и

11
выводом из цикла жидкой доли х;
1 1 - 13 и 9 - 1 2 - изобарическое (р1 = const и Р2 = const)
нагревание различных потоков воздуха - (1 - q> - х) и <р соот
ветственно - в основном холодообменнике;
13-1 и 1 2-2 - изобарическое (р 1 = const и Р2 = const) на
гревание указанных потоков в предварительном холодообмен
н ике.
пара с

Технологический расчет цик.ла
производительностей G и Gж. задана формулой (2 1 . 1 8).

Связь
Остальные потоки определяются на базе производительности
G. Например , поток газа из сепаратора С 1 (доля этою потока
- rp) равен G<p и т.п.
Определение степени ожижения проводим на базе теплового
баланса для контура 1 (см. рис. 2 1 . 17, а), охватывающею фраг-

1 599

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

мент схемы ниже испарителя И у , н е включающий холодопро
изводящие компрессионный агрегат и машину умеренного
охлаждения:
(и)
1 -hs - qih12 - (1 - <р - Хт)h1 3 - Хтhо = О .
Огсюда, добавляя и вычитая h 12, находим теоретическую сте
пень ожижения:

Хт = 1 (h12 - h5 ) + ( 1 - <p)(h13 - h12 ) .
(2 1 . 25 )
h1з - ho
Реальная степень ожижения запишется с учетом q0 и qp:
1 · (h1 2 - hs ) + (1 - <р) (h1з - h12 ) - (qo + qP ) .
х=
(21 .26)
h1з - ho
·

При отсуrствии машины умеренного холода не было бы необходимости раз
биения холодообменниха на ПХ и ОХ. В этом случае пространственный контур
охватил бы единый холодообменник на уровне Т1 = Т2 = Тз: в числителе формул
типа
стояли бы разности (h2 - hз) и (h1 - h2), а в знаменателе
fh. =

(21.25), (2 1 .26)
h1 - ho. Это - ЦИКJJ с даума JЧККселированиllМИ

и

ЩlpltfJJlllOleй

-

во:щуха еред

При <р = О получим -.uui с OJIЖЖPIП1IWlll щнкселироминем от Рз до Р 1 <Р2 вообще
1Ие во:щvх.а • М111181Не умереююrо ХОJЮда.
отсутсrвует) и пpeдмpиre.JJWIWМ 0ХJW11Де1м

неrо да11J1 еииа.

Итак,
рассматриваемый усовершенствованный
цикл
"спустился " с уровня температур Т1 = Т2 = Тз на более низкий
уровень Ts = Т1 2 = Т1 з за счет машины умеренного охлажде
ния. Степень ожижения х в этом цикле в 2-2,5 раза больше;
чем в простом регенеративном цикле.
Пр ич и н д в е. Пер_вая: а н ал из п о к аз ы вает , что ( h 1 2 - h5) > (h2 - hз ) и ( h в - h 12) > (h 1 - h1), поэтому несколько вырос числи
тель в (2 1 .26). Вторая: ( h 1 з - h0) < (h 1 - ho), поэтому заметно
уменьшился знаменатель. Правда, появились затраты энергии,
связанные с работой машины умеренного охлаждения, но эти
затраты невелики; скажем, мощность компрессора К у этой
машины редко превышает 5% от мощности воздушных ком
прессоров К 1 и К2 .
Холод "получается" в обеих ступенях компрессора, но в К1
сжимается лишь часть газа (1 - <р), поэтому и холодопроизводи
телъностъ этой ступени составляет долю (1 - <р) от (h в - h1 2) . Хо
лод "получается" и в испарителе машины умеренного охлаждения.
При этом каждый кг воздуха теряет там теплоту (/у = h4 - hs .
В целом удельный расход энергии lr. с учетом затрат энергии
в компрессоре машины умеренного холода ly составляет:
lr. = lк + ly =
RyT1(ln(Pз /P2 ) + ( l - <p) ln(p2 /P1)) h4 - h5 .
(2 1 .27)
=
+ & 11 11
М
11 из 1l м

1 600

х ад

м

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

При этом последнее слагаемое ly в ( 2 1 .27 ) записано в соот
ветствии с формулой (2 1 .6 ) , но в расчете на 1 кг воздуха, сжи
маемого во вторых ступенях компрессионного агрегата К2 .
Величина /"Е. здесь существенно ниже, чем в простом регенера
тивном ЦИЮiе: часть газа не нужно сжимать в первой ступени К 1 .
Удельные затраты энерrнн на 1 кг жндкоrо воздуха формиру
ются аналогично рассмотренным в цикле Линде:
lж

( 2 1 .206)

= zJx,

но lк и х рассчитываются по иным формулам.
Поскольку lк меньше, а х больше, нежели в простом регене
ративном цикле, то величина lж получается значительно ниже,
а сам цикл - экономичнее.
Мощность, потребляемая воздушным компрессором, рассчиты.
вается по ( 2 1 .2 1 ) , причем lк берется без учета ly.
Следует обсудить 1несто машины умеренного 0Х1U1Жденuя в
цикле. В /.r. к lк добавилось слагаемое (хотя и относиrелъно не
большое), отражающее вклад (работу) компрессора установки уме
ревноrо охлаждения (см. рис. 2 1 . 17, а). В расчете на 1 кг воздуха,
сжимаемого в воздушном компрессоре К2 , в испариrеле машин ы
умеренного охлаждения отнимается теплота Qy· Тогда холодопро
изводиrелъностъ машины умеренного охлаждения состаWIЯет
(2 1 .28)
Qo = Gqy = G( h4 - hs).
На основе Q0 рассчитывается мощность компрессора Ny . В
частности, для одноступенчатой машины умеренного охлажде
ния Ny определяется по формуле (2 1 .6). Расчеты не вызывают
затруднений, если известны энтальпии h4 и hs, причем знать hs
нужно еще и при нахождении х. С величиной hs - все просто,
так как температура воздуха в точке 5 (рис. 2 1 . 1 7, б) опреде
ляется возможностями самого цикла умеренного охлаждения :
например, если это аммиачный цикл, то ниже t "'
45 ° С н е
работают. Значение h 4 найдем из теплового баланса предвари
тельного холодообменника ПХ (см . рис . 2 1 . 17, а - контур II);
запишем баланс в форме Приход = Уходу:
(к)
q> ( h 2 - h 1 2 ) + ( 1 - q> - x)( h 1 - h1 з ) = l · (hз - h4) ·
-

Если пренебречь недорекуперацией в ОХ, то , полагая Ts "'
"' Т1 2 "' Т1 3 , м ожно опр едел ить по д иа гр амме T-s значения h 1 2 ,
h 1 з и найти единствен ную неизвестную величину h4.
Далее находят Qy , Q0 и по параметрам цикла умеренного
охлаждения - потоки рабочего тела и охлаждающей среды (см.
разд. 2 1 .2.2).
Характеристики усовершенствованного цикла при Т 1 = 300 К,
Т5 = 233 К, Р2 = 5 МПа, Р з = 20 МПа, ч> = 0 , 8 :
х = U , 1 1 + О, 12 ( кг жидкого воздуха)/(кг сжимаемого воздуха);
1 60 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

lж = 2750 2800 кДж/< кг жидкого воздуха).
Это в 5 раз экономичнее в сравнении с простым регенера
тивным циклом и менее чем вчетверо превышает /min.
+

2 1 .3.4. Циклы с поршневыми детандерами

Основные варианты циклов

В циклах с поршневыми детандерами холод получают в двух
основных вариантах - а и б. В обоих случаях вместо одного
холодообменника последовательно устанавливают два - высо
котемпературный 1 и низкотемпературный 2 (рис. 2 1 . 1 8). По
варианту а (принцип Гейландта, рис. 2 1 . 18, а) определенную
долю '1' воздуха сразу после сжатия до Р2 в компрессионном
агрегате (точка А) направляют в детандер, где давление пони
жается от Р2 до р1 ; далее воздух присоединяется к потоку низ
кого давления (в точке В). По варианту б (принцип Клода, рис.
2 1 . 18, б) сжатый до Р2 воздух сначала охлаждают в холодообмен 
нике 1, после чего (точка С ) его долю '1' направляют в детандер,
а затем присоединяют к потоку низкого давления (в точке D).
Эффективность вариантов удобно сопоставлять в диаграмме
h -s (рис. 2 1 . 18, в) . Можно видеть , что качество холода выше
h

1
1

1 - (j)

2

а

б

s

в

Рис. 21. 18. К ци клам mубоко rо о хлаждения с расширением в поршневых детан

дер ах:

- ЦИJОJ Гей.лаццта, б - цихл Клода, в - диаrрамма h-s;
1 - высокотемпературный холодообмеШD!к, 2 - низкотемпературный холодообмеШD!К,

а

J - детаJЩер

1602

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

для варианта б: после детандера здесь получается поток более
низкой температуры: t0 < t 8. Однако количество холода больше
в случае варианта а: Лh0 > лh6. Чтобы использовать выгоды
принципа Гейландта и в то же время попасть в область низких
температур, следует сжимать воздух в компрессионном агрегате
до более высоюtХ давлений Р2 ' > р2 (см. рис. 2 1 . 18, в, точка А') .
Циклы Клода работают в области средних давлений (2-6
МПа), циклы Гейландта - в области высоких давлений ( 1220 МПа). Установки, базирующиеся на принципе Гейландта,
как это следует из рис. 2 1 . 1 8 , в, позволяют получать низкие
температуры (отвечающие точке D) с высокими холодопроиз
водительностями: Лh0' > Лh0 > Лhб. Цикл Гейландта требует,
конечно, увеличения затрат энергии в компрессионном агрега
те, но в целом он на 8-10% экономичнее цикла Клода. В оте
чественных технологиях при умеренных производительноспiях
применяют цикл Гейландта.
Схема цикла Гейландта и диаграмма

T-s
Из рис. 2 1 . 1 9 , а видно, что этот цикл отличается от простого
регенеративного тем, что в точке 2 часть сжатого до давления
р2 воздуха (его доля Ч1
0,3+0,6) отводят на адиабатическое
(реально - политропическое) расширение в детандере, где
давление падает от Р2 до р1 • При этом в идеале получают и хо
лод, и энергию. Остальной газ (его доля 1 ЧJ) направляется
на дросселирование.
Стадии цикла Гейландта ясны из диаграммы T-s на рис.
2 1 1 9 , б:
1 -2 - изотермическое ( Т1 = Т2 ) сжатие газа ( 1 кг);
2-3 - изобарическое (Р2 = coнst) охлаждение
части газа
:::::

-

.

(1

-

ljl);

- адиабатическое (s = coнst) расширение части газа ЧJ ;
- изоэнтальпийное (h4 = h5 = const) дросселирование
части газа ( 1 ЧJ );
2-6
3-4

4

/
�

5

0

-

-

изобарическая

стной смеси на жидкую часть
- чi -

5

=

(р 1

х

const)

сепарация

парожидко -

и пар (газ) в количестве

х);

�
7
/
6'

-

изобарическое

(р 1

еле детандера Ч1 (т.6, реально - т.6 ' )
7-1

- изобарическое (р 1 =
тока (1 х) газа.

=
и

const)

(1

-

смешение потоков п о -

сепаратора 1 - Ч' - х (т.5);

coнst)

нагревание обратного по

-

1 603

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

т

6

s

б

а

Рис. 21. 1.9. Цихл Гейландта:

- прющипимьная схема, б - диаrрамм а T-s;
arperaт , Х - холодильЮIJС, Др - дроссельный ве!ПИЛЬ, С - сепа
ратор, Д - детандер
а

К - �сомпрессионный

.Технол оги ч ески й расчет цикл а,

Связь производительностей G и Gж определена формулой
Поток газа, отводимого на детандер, равен °'J!, а на
дросселирование - G( l - \11 ) .
Теоретическую степень ожижения найдем на базе теплового
баланса для контура 1 (см. рис. 2 1 . 19, а), отсекающего холодо
производящие агрегаты - компрессор и детандер.
Напомним : в действительности расширение в детандере процесс политропический (линия 2-6' на рис. 2 1 . 1 9 , б), но в
расчетах удобнее использовать адиабатический процесс (линия
2-6 на рис. 2 1 . 1 9 , б)
с поправкой на адиабатический коэф
фициент т� ад'.
Тепловой баланс для контура 1 :
l · h2 + \jl h 6 - ( 1 - Xr )h 1 - Xrho - \ll h2 = О ,
(л)
откуда
l {h1 - � ) + \11 (� - �) .
(2 1 .29 )
Xr =
(2 1 . 1 8) .

-

h1

-

ho

В числителе формулы (2 1 .29 ) стоят удельные холодопроизво
диrельности компрессора и детандера (для последнего - с уче

том доли \11 направляемого в него воздуха).
1 604

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Отличие реального процесса в детандере от ад иабатическо
как было показано в разд. 2 1 .3 . 1 , уменьшает холодопроиз
водительность д етандера :
го ,

(м)

Учитывая

q0, qP
х =

и Т\ ,щ' , получим р еал ь ную степен ь ожижения :

1 · (h1

-·

h2 ) + '1' (h2

- �)Т\:�д - (q0
,. h1 - ho

+

qP

).

(2 1 .30)

Удел ьный расход энерrии в к ом п р е с соре рассчитывается по
( 2 1 . 1 8).
Механ ичес ю1е потери дополнительно понижают работу,
возвращаемую в цикл. По этому удел ьная работа детандера /д
должна уч ит ы вать механический КПД Т\м:

lд =

'1' ( h2 - hб)Т\ <\/t'Т\ м ·

(2 1 . 1 9а)

Удельныii р а сх од э11ергнн в цикле на 1 кг .жидкого воздуха
формально определяется по (2 1 .20). Заметим , что возврат
эиергии поршневым детандером в цикле Гейландта обычно не
велик (величина /д не превышает 1 0 % от lк)· Это обусловлено
относительно невысокими значениями Тl<\lt' и '1'· По указанной
причине на практике в цикле Гейландта часто не используют
энергию детандера для э кономи и механической работы (см .
разд . 2 1 .3 .6) . При этом вклад детандера в холодопроизводитель
иост ь ц икла значителен . Поэтому при расчете степени ожиже
ния вклад детu н д е ра учитывают о бя зательн о , а при расчете lж. только при возврате э нергии от детанд ера в цикл. В противном
случае lж, = zJx.
Характери стики цикла Гейландта при Т1 = 3 00 К, P l =
= О, 1 МПа, р2 = 20 МПа, '1' = 0, 35:
х = 0 , 26+0, 28 ( кг жидкого воздуха)/(кг сжи маемо го возду
ха) ;
lж. = 2200+2500 кДж/<кг жидкого воздуха).
Это наилучшие характеристики сред и циклов, работающих
на получение жидкого воздуха.

2 1 .3.5. Циклы с турбодетандерами

В этих ци кл ах эксплуатируется идея П Л . Капицы, разрабо
тавше го цеитробежную расширительную машину - турбодетан
дер (ТД), - способную использовать относительно небольшой
перепад давлений: от 0 , 6 -0 , 8 до О, 1 МПа. Достоинство ТД за
ключается не только в о чен ь высоюtх производительностях по
расширяемому rазу, но и в повышенных адиабатических КПД
Тl<\lt' · Дело в том , что в противоп ол ожность поршневым детан
дерам здесь нет тако rо источ н и ка теплоты, как трение поршnя
1 605

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

поэтому отличие ri aл' о т 1 обусловлено лишь
притоком теплоты из окружающей среды к расширяемому ра
бочему телу и внутренним трен ием газа в ТД . Замети м :
вследствие очень высою1х производительностей ТД удельные (в
расчете на 1 кг газа) потери холода в окружающую среду здесь
невелики , и отличие от 1 обусловлено в основном внутрен ним
трен ием расширяющегося в детандере rаза.
Величины 'll aд' уже в первых ТД были на уровне 0 , 8 ; в со
време н н ых машинах они составляют 0 , 8 5 и даже несколько
более . Повышенные значения 'll aд' делают целесообразным по
дачу в ТД большей дол и газа IJl, нежели в циклах с поршневы
ми детандерами . Правда, невысокие давления Р2 заставляют
брать газообразное РТ для расширения в турбодетандере обяза
тельно после предварительного холодообменника (это несколь
ко понижает перепад э нтальпий Л h в детандере - см. разд .
2 1 . 3 .4), иначе в результате расширен ия в ТД не получить при
емлемо н из ких температур .
Работа в области сравн ительно низких давлений Р2 позволя 
ет для сжатия РТ использовать турбокомпрессоры (ТК) , также
обладающие высокой производительностью .

о стен к и ц ил индра ;

Схема цикла Капицы и диаграмма T-s

Схема цикла Ка пицы показана на рис . 2 1 .20, а. И сходный
воздух (состояние 1 ) изотермически сжимается в ТК от давле
н ия р1 до Р2 (состоян ие 2) и подается в предварительный холо
дообменник П Х , где он изобарически охлаждается до состоя
н ия 3 . Здесь воздух разделяют на два потока:
- некоторую его долю IJ1 (обычно 0 , 6- 0 , 8 ) направляют в
турбодетандер , где давление адиабатически с нижается до р1 и
происходит охлаждение воздуха (теоретически - до состояния
6 , реально - до 6');
- оставшуюся его долю (1
IJl) подают в межтрубное про
странство основного холодообменника
ожижителя (О), пред
ставляющего собой кожухотрубный аппарат (см . разд . 7 . 1 ) .
В межтрубном пространстве ожижителя, где давлен ие равно
Ръ происходит охлажде11ие воздуха до состоян ия сухого насы
щенного пара и последующая полная его конденсация (сос
тоя н ие 4 - кипящая жидкость , температура Т4) . Теплота
охлаждения и конденсации отдается более холодной среде,
н аходящейся в трубном пространстве ожижителя О (см . н иже) .
Жидкий воздух из межтрубного пространства дросселируется в
вентиле Др до давлен ия р1 . Образовавшийся парожидкостно й
поток (состоян ие 5) нап равляют в н ижн юю зону трубного про
странства ожижителя ; туда же подают холодный воздух после
ТД. Получающаяся смесь (влажн ый пар - состояние 7) час
тичн о сепарируется в упомянутой зоне, и определенная (в рас-

-

1 606

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

т

д

а

s

б

Рис. 21. 20. Цикп Капицы:

а - 11риш11ш имы 1ая схема, 6 - диаrраииа T-s;
Т К - коипрессиошшй arperaт. ПХ - предварительный холодообиеННИJС, Д - детuщер,
О - ожижиrель, Др - дроссельный венrил"

чете на исходный воздух) доля х жидкого воздуха (состояние О)
выводится из цикла. Остальной поток (его доля 1
х; состоя
ние 8 , темпе р атур а Т8 ) и я вля ется той самой холодной средой в
труб ном пространстве ожижителя, которая отнимает теплоту от
воздуха, о хл ажда юще гося и конденсирующегося в его межтруб
ном пространстве. Условие переноса теплоты из межтрубного
пространства в трубное - Т8 < Т4 - обеспечивается разницей
давлений в этих зонах: р1 < Р2 · Воздух, прошедший трубное
пространство ожижителя и нагретый до состояния 10, поступа
ет в проме:жуrочны й холодообмен н ик ПХ, где отдает теплоту
встречному воздушному потоку, нагреваясь при этом в идеале
до исходного состояния 1 . Далее он подается (вместе с некото
рым количеством х свежего воздуха) на всасывание в ТК, и
цикл условно за мы кается .
Диаграмма T-s для цикла Капицы представлена на рис.
2 1 .20, б. Стадии процесс а с потоками в расчете на 1 кг воздуха,
сжимаемого в ТК:
изотермическое ( Т1 = Т2 = const) сжатие воздуха в
1-2
ТК от Р1 до Р2;
2-3 - изобарическое (/>]. = const) охлаждение 1 кг воздуха в
ПХ ;
3-6 - адиабатическое (s = const) расширение части \jl воз
духа в ТД с падением да вл ения от Р2 до Р1 ;
3-4 - изобариЧеские (J>2 = const) охлюrщение и конденсация
часm 1 '1' воздуха в ме:жтрубном пространстве ожижиrеля;
-

-

-

1607

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

4-5 - дросселирование
духа до давления Р 1 ;
5�
7
?

-

и зо б ар и ч еск о е

(h4
(р

1

=

=

hs = const) потока l
const) смешение газа

-

\11

п о сл е

воз
ТД

6
(поток \11 ) и влажного п ара посл е Др (поток 1 - \11 ) ;
7

?о

и зо б ар и ч е ская ( р 1 = const) частичная се п ара ци я
8
парожидкостной с меси на жидко сть (О) и влажный пар (8) с
последующи м в ы водом доли х жи д кого воздуха (0) из холодил ь
ного цикла;
8-10 - и зобарическое (р 1 = co11st) на гр евание воздушного
потока 1-х в трубках о ж ижител я;
10 - 1 - изобарическое (р1 = coпst) нагревание воздушного
потока 1 -х в предварительном холодообменнике.
Далее к п отоку 1 -х добавляют поток х свежего воздуха
(замыкание цикла) и сум марный поток ( l кг) подают на сжатие
в тк.
Для реал изации ци кла важн ы два обстоятельства:
- поток воздух а после дета ндера должен быть холоднее (не
только теоретически - точка 6 , но и реально - точка б') , чем
конденсат в межтрубном пространстве ожижителя;
- поток воздуха, поступающи й в трубки ожижителя , должен
обеспечить полную конденсацию воздуха в межтрубном про
странстве; п оэтому в трубках ( там давление р 1 ) должны проис
ходить не только нагрев воздуха, но и испарение части паро
жидкостной смеси ; таким образом , на стади и сепараци и полу
чают жидкость (точка 0) и вла ж ный (не сухой насыщенный точка 9) пар , состояние которо го изображается точ кой 8, распо
ложенной между 7 и 9.
�

-

Технологи•1еск ий расчет цикла

Расчет базируется на тепловых балансах. Для контура 1 (на
рис. 2 1 .20, а ), не вкл юча ющего холодопроизводящие агрегаты компрессорную установку и детандер, - в идеале тепловой ба
лан с и меет вид:
(н )
откуда теоретическая степень ожижения

(2 1 .3 1 )
1 608

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Заметим, что формулу (2 1 .3 1 ) можно было бы, базируясь на
смысле величин и аналогии с циклом Гейландта, записать сра
зу: в числ ителе стоит сумма холодопроизводительностей ком
прессион ного агрегата и детандера, а в знаменателе - количе
ство теплоты q. , которую нужно отобрать от 1 кг исходного
воздуха для полного его ожижения .
Реальная степень ожижения х будет н иже Xr из-за потерь хо
лода q0 в о к р ужающую среду (в де йствительности - пр итока
теruюты из нее) и от недорекупераци и q , а также неполной ади
P
абатиости расширения воздуха в детандере (учитывается ади
абатическим К ПД Т\ аа' ) . Способ учета указанных отклонений от
идеальности процесса иде нтичен рассмотренному для цикла
Гейландта (см. разд. 2 1 .3.4). Тогда реальная степень ожижения
х выразится :
х

=

1 · (h1 - h2 >

+ "' <hз - hб )Т\:�д - (qo + q p )
h 1 - ho

(2 1 . З l а)

Для определен ия .xr, х требуется располагать значениями
этпальпии hз и однозначно связанной с ней (процессом ади
абатного расширения воздуха в детандере) энтальпии h6 . Кста
ти , такого же рода проблема возникает и при расчете других
циклов с отбором РТ на детандер после предварительного хо
лодообмен ника (например, для цикла Клода). Покажем путь
решения задачи применительно к определеJJию Xr ·
Для нахожден ия hз необходимы дополиительные связи. С
это й целью можно попытаться составить, например , тепловой
баланс промежуточного холодообменника (контур 11 на рис .
2 1 .20, а) без учета потерь q0 и qp :

l · h2 + ( 1 - x.-)ll1 0 - l · hз - ( 1 - Хт) h 1

=

О.

(о)

Здесь h 1 и h2 известны . Однако появилась дополнительная
неизвестная переменная h 1 0 , так что к н ахоЖдению hз прибли 
зиться не удалось.
Тепловой баланс для контура, охватывающего основной хо
лодообме н н и к О с сепаратором,
дополнительных связей не
дает, так как представляет собой разность тепловых балансов
(н) и (о) . Анализ показывает, что составление тепловых балан
сов для других промежуточн ых контуров (для собственно О;
для то•1ек разделения потоков воздуха, направляемых в О и
деrандер Д, J I Л И смешен ия потоков из д и О) также не приво
дит к однозначной ф11 ксации точ ки З (определению h3). Дело в
том, что наращиванию числа уравнений связи сопутствует та
кое же уnет1•1 е н ие чнсла переменных (неизвестных энтальпий).
В р ез ул ьтате с исте ма ур авнен и й свнзи остается незамкнуто й :
число свнзей на един и цу меньше числа переменных. Оста1 609

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ющаяся степень свободы должна быть заполнена из феномено
логических соображен ий. Целесообразно, например, положить,
что в результате р_еального процесса расширения в детандере
должен пол�аться воздух с температурой, близкой к насыще
нию (точ ка 9 ) при давлении р 1 ; для гарантии от каплеобразова
н ия в детандере - на несколько градусов выше. Таким образом
фиксируются т оч ка 6' и энтальпия hб' . При известном адиабати
ческом КП Д детандера Т\:W это позволяет найти h3, поскольку
по определен и ю Т\�
J.�
Т\ 'ад
h "
(!
(п)
и
h
3
1 - Т\ ад
/
1 - Т\ /ад

6·

В еличину hз отыскиваем (используя упомянутую ее связь с
hб) с помощью итера ц ионных про цедур . А тепловые балансы
типа (о ) для промежуrочных контуров позволяют (при уже
найденн ых .хт. х) определить в случае необходимости значения
промежуточн ы х энтал ь п и й (h 10 и др . ) .
Удельные р асходы э 11ерrии и моuщость компр ессора выража
ются так же, как в ци кл е Гейландта:
/

к

/д

=

= Ч'

Ry T1

ln(P2 /P1 ) .

(2 1 . 1 8)

hб) Т\ ад1Т\м;

(2 1 . 1 9а)

мТ\ из Т\ м

(hз

-

'

lж = (/к - /д)/х;

(2 1 . 20)

Glк.

(2 1 . 2 1 )
=
Хараюперистики цикла п р и Р2 = 0 , 6 МПа, Т 300 К и 'V = 0,8:
х = 0,05 (кг жидкого возд уха )/( кг исходного воздуха); не
бол ьшие х обусловле н ы м ал ым перепадом давл ения Р2 - Pt ;
при этом невелики и затраты энер гии lij
lж. = 4200 кДж/<кг жидкого воздуха); это заметно больше,
нежели в цикле Гейландта. Но н и з ки е значения Р2 приводят к
значительному удешевлению аппаратуры, что для циклов глу
бокого охлаждения существен но влияет на общую экономич
ность процесса (см . также разд . 2 1 .3 .6) .
Высокопроизводительные отечественные установки глубоко
го холода с получением жидкого воздуха базируюrся на прин
цип ах цикла Капицы .
Nк

=

2 1 .3.6. Об аппаратурном оформлении процессов

rлубокоrо охлаждения

Ниже кратко охарактеризо ваны машинw и аппарат ы, приме
няемые в циклах глубо кого охлаждения·.
•

Более подробные сведения приводятся в

1 6 10

1 2,

1 1 ).

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Компрессоры. В случае ум еренной производите.пьности (до 1 м 3/с) приме
няют мноrоС1)'11 енчатwе nopumcвwe компрессора.1; при этом давления на выходе
иногда превышают 20 МПа (200 бар). В зависимости от конечного давления (а
начальное - близко к атмосферному) компрессор содержит до 6 ступеней . При
высоких дамен иях газ далек от идеального; поэтому степень сжатия снижается
от ступени к ступени: в пер вых ступенях она на уровне 4, в последних несколько превышает 2. Как п равило, используют горизонтальные компрессоры
(первая ступень - двойного действия, остальные - простого ) с поршнями,
находящимися на общем шrоке; компрессор снабжен массивным маховым коле
сом . Между ступенями газ охлаждается в холодильниках.
В случае высокой производительности (порядка 30 м3/с) и невысоких конеч
ных дамений (до 0,6-0,8 МПа) применяют многоколесные турбокомпрессоры с
мощным (до 6000 кВт) электромотором в качестве привода. Число колес дости
гает 1 2, степень сжатия в одном колесе не превышает 1 ,2; после 2-3 ступеней
сжимаемый газ охлаждается в холодильниках.
Детандерw. В циклах высокого ( 1 0-20 МПа) и среднего (2-6 МПа) даме
ния используют nop11D1eвwe детандерw. Их основная роль - получение холода
при расширении газа. В идеале они должны еще и возвращать энергию в цикл;
но этот возврат невелик - как в абсолютных цифрах (невысокая производитель
ность) , так и относительно . - он составляет несколько процентов от затрат
энергии на сжатие газа (из-за низких адиабатических КПД) . А устройство для
съема энергии с детандера требует определенных капитальных затрат, поэтому
часто поршневой детандер работает без возврата энергии в цикл.
В высокопроизводительных циклах низкого дамения используются турбоде
тандерw - они дешеме и компактнее поршневых. Наиболее распространены
одноступенчатые радиальные центростремительные детандеры, работающие с
очень высокой частотой вращения рабочего колеса (иногда - свыше 1 000 с- 1 ) .
Здесь отказ от возврата весьма значительных количеств энергии в цикл - недо
пустим: велики потоки расширяющегося газа, к тому же машина работает с
высоким адиабатическим КПД. Энергию от турбодетандера чаще всего отводят с
помощью посаженной на его вал динамомаumнw (электрогенератора) ; не исклю
чено и расположение турбодетандера на одном валу с турбокомпрессором, хотя
технически это менее удобно.
Теплообменные аппаратw (холодообменники) . В циклах глубокого охлаждения
используют рекуператоры и регенераторы (см. разд. 7 . 1) . Общие проблемы
здесь: подготовка воздуха (предотвращение замерзания содержащихся в нем
паров воды и диоксида углерода), обеспечение достаточной интенсивности теп
лообмена ( газам , в том числе - воздуху, присущи невысокие коэффициенты
теruюотдачи к стенкам) и выдерживание повышенных дамений теплообменной
аппаратурой. А для рекуператоров - еще и проблема термических напряжений
(вследствие значительных диапазонов температур при пуске и работе установки).
В качестве рекуператоров наиболее широко применяются внп.1е теплообмен
ники, в которых узкие трубы навиты (с зазорами ) в несколько слоев на полый
заглушенный сердечник. Эти холодообменники отличаются большой теплопере
дающей поверхностью в единице объема. Заметим, что для витых теплообмен
ников в значительной мере снимается проблема термических напряжений, так
как навить1е на сердечник трубки обладают возможностью более или менее
свободного термического расширения. В качестве реrенераторов используются
аппараты с насадкой - чаще всего в виде дисков из тонкой (доли миллим етра)
гофрированной металлической (например, алюминиевой ) ленты либо в виде
металли ческих сеток. Регенераторы дешеме рекуператоров.
В случае рекуператоров необходима предварительная очистка воздуха от па
ров Н20 и СО2, причем до весьма низких остаточных концентраций - иначе
лед забьет коммvникации. Очистка ведется в специальных установках методами
абсорбции и адсо рбции. В (;Лучае реrенераторов происходит вымораживание Н2О
и СО2 на элементах насадки на стадии охлаждения потока и их испарение

161 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

(сублимация ) на стадии его н а гревания (с выносом Н 2 О и СО 2 из теплообмен
ника); здесь не требуется предварительной тонкой очистки исходного воздуха.
BИJWe холодообмеJ111111U1 -рекуператорw с развитой поверхностью обеспечивают
достаточно интенсивный теплообмен rаза (воздуха) с внутренними стенками
труб, в которых он движется с высокими скоростями. А в меж.трубном про
странстве скорость rаза заметно ниже, и коэффициенты теплоотд а ч и здесь в 57 раз меньше, чем внутри труб. Для повышения интенсивности теплообмена в
этой зоне трубы снабжают наружным оребрением, увеличивающим пропускную
способность теплопереноса o.F за счет F. В реrенераторах интенсивный теплооб
мен обусловлен очень большой удельной и общей поверхностью насадки . По
этой причине потери холода от недорекуперацни здесь ниже, чем в рекупера
тивных холодообменниках. Однако в регенераторах, применяемых в процессах
разделения воздуха, его компоненты (N 2 , 02) получаются недостаточно чистыми:
они загрязняются примесью воздуха при смене горячего и холодного потоков.
Проблему прочности в витых рекуперативных холодообменниках решают,
направляя сжатый газ по трубкам, а газ низкого давления (практически атмо
сферного) - по межтрубному пространсm(f)'. В этом случае трубки даже при
тонких стенках легко выдерживают высокое давление, а корпус теплообменника
избыточного давления не испьrrывает. Корпус реrенератора в циклах высокого и
среднего давления приходится делать толстостенным, чтобы он смог противосто
ять большим усилиям; повышенная металло емкость удорожает аппарат. Стои
мость регенераторов невысока только в циклах низкого давления - в этом одно
из достоинств циклов типа Капицы.
Конструкционные материалы аппаратов глубокого холода должны бьпъ до
статочно пластичными и прочными при низких температурах. Наиболее широко
в технике глубокого холода применяются медь и ее сплавы (латуни, бронзы),
сварка (пайка) ведется сплавами (припоями) на основе серебра. В неответствен
ных у:�лах применяются алюми ниевые сплавы, редко - нержавеющая сталь. Эти
обстоятельства значительно удорожают аппаратурное оформление процессов
глубокого охлаждения: капитальные затраты вносят здесь более существенный
вклад в общую стоимость, нежtти в других областях химической технологии .
Во избежание притока теплоты и з окружающей среды к холодному РТ
("потери холода в окружающую среду") необходима тщатмьная темоизОАRЦUR
всех машин и аппаратов, функционирующих в области низких тем ператур . В
противном случае стоимость процесса резко возрастает.

2 1 .3 . 7 . Двухколо нн ый ректификационный arperaт
для разделения воздуха

Жид кий воздух , пол учаемый в ци клах глубо кого холода ,
применяют для создан ия и подд ержания низких температур .
Но основная его часть и спользуется для разделения возд уха на
азот и кислород методо м ректи ф и кац ии .
Получаемый азот достаточно высокой чистоты идет в дальнейшем на синтез
аммиака; далее N Н з используют непосредственно (например , как рабочее тело в
циклах умеренного охлаждения) либо в качестве реагента: окисляют до оксидов
азота (производство азотной кислоты и ее солей); направляют на синтез
(например, карбамида) и т.д. Кроме того, азот в жидком состоянии, как и жид
кий воздух, применяют для создания низких температур, а в rазообразном - в
качестве защитной атмосферы при работе с пирофорными (самовоспла
меняющимися) веществами и как "инерт" при необходимости "погасить" какую
то химическую реакцию.
Получаемый кислород в химической технологии широко используют как
окислитель (нередко - в смеси с воздухом), например в процессах конверсии

1612

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

метана, в rазификации, а Тdкже в металлур mи (дуrье), в медицине, при прове
дении сварочных работ и в друmх случаях, зачастую весьма далеких от хими
ческой технолоmи ( при этом очень часто высокой чистоты кислорода не тре
буется) .

Воздух предстамяет собой бинарную (практически) смесь
низкокипящего компонента (Н КК) - азота N 2 и высококипя
щего (ВКК) - кислорода 0 2. Основная проблема при ректи
фикации жидкого воздуха состоит (см. разд. 12.7 .6) в оргаииза 
ции потока флегмы: в обычных колоннах пары Н КК (с при
месью В К К) конденсируют в конденсаторах с помощью холод
ной воды, холодного воздуха или иного хладоагента; здесь же
(в области температур на уровне -200 ° С) мы не располагаем
хладоагентом необходимой (более низкой, чем жидкий азот)
температуры. Проблема может быть решена пугем использова
ния двухколонного ректификационного агрегата, включенного в
общий холодильный цикл .
Устройство и принцип работы агрегата

Агрегат (рис . 2 1 .2 1 , а) состоит из двух колонн : нижней 5
(работает под дамением 0 , 5-0, 7 МПа) и верхней 1 (давление
чугь выше атмосферного - на 0,02-0 , 04 МПа) . Исходная
смесь / предстамяет собой сжатый и предварительно охлаж
денный воздух - его давление зависит от используемого цикла
глубокого холода и может превышать 1 0 МПа, температура на
уровне -(90 + 1 50) 0 С; обычно это газ (не исключено, что и
мажный пар). Исходная смесь служит теплоносителем, обогре
вающим кубовую жидкость нижней колонны. Будучи более
"горячей", нежели кипящая в кубе жидкость, исходная смесь
отдает в кипятильнике 4 свою теплоту перегрева и конденса
ции и превращается в жидкость. Далее ее давление сбрасывает
ся в дроссельном вентиле А до 0,5-0, 7 МПа, и смесь подается
на тарелку питания н ижней кол он ны (ТП Н) - чаще всего в виде
парожидкостной смеси. В этой колонне происходит ректифи
кация , устанавливается характерный профиль концентраций с
нарастанием Н КК (N 2 ) снизу вверх. В результате в кубе 4 по
лучается воздух (промежуточный кубовый остаток /V), обога
щенный кислородом (е го концентрация в кубе - на уровне
40-60 % ) , а наверху колонны - существенно обогащенный
азот (его концентрация - от 94 до 98%).
Разумеется , обогащение возможно только при наличии
флегмы, получаемой в конденсаторе 2 наверху нижней колон
ны 5 - в результате конденсации паров смеси (с высокой кон
центрацией N 2 ) в трубном пространстве конденсатора 2. Оче
видно, что при этом в межтрубном пространстве конденсатора
должно находиться более холодное рабочее тело (см . ниже).
Образующийся конденсат частично стекает вниз (это флегма,
1613

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

а

б
аrрег.п для разделения воздуха:
- аrрегат, б - фраrменr агрегата: конденсатор-кипятильних;
1 - верхняя колонна, 2 - конденсатор-кипятилыmк, .1 - азотные карманы, 4 - куб
ШIJIСНеЙ колонны с КИПЯТИЛЬШIКОМ, 5 - ШIJIСНЯЯ колонна, 6 - ХОЛОДИЛЬШIК JIQЩКОГО азота, 7
- JС:рЬIШХа конденсатора-кипяпtлып�ка;
1 - исходный сжатый холодный воздух, II - смесь, питающая ШIJIClllOIO колонну, J// промежутоЧНЬIЙ дистиллят , флегма. JV - промежуточный кубовый остаток, V - отводимый
газообразный кубовый остаток, V/ - холодный поток азота сверху колонны 1, VJJ - отводи
мый газообразный дистиллят ;
Не, Ne, Ах, Кr и Хе - точки отбора фрахций, богатых соответствующими инертными
газами

Рис.21.21. Двухколонный
а

1614

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

обеспечивающая процесс ректификации), а частично собирает
ся в кольцевом кармане 3 и отбирается в виде промежуточного
дистиллята 111. Некоторую часть его (поток Jlla) иногда отби
рают в качестве продукта (жидкий азот), транспортируемого и
хранимого в сосудах Дьюара.
Кубовый остаток JV и дистиллят 111 (самотеком, за счет раз
ности давлений) поступают в верхнюю колонну 1. При этом
кубовый остаток нижней колонны, подаваемый через дрос
сельный вентиль Б, является исходной смесью Д11Я верхней ко
лонны (подается на ее тарелку питания ТП В), а дистиллят из
азотных карманов нижней колонн ы (в виде парожидкостной
смеси после дросселирования в вентиле В) служит флегмой Д11Я
верхней колонны. В нижней части колонны 2 накапливается
кипящий кубовый остаток, значительно обогащенный кислоро
дом (до кон центрации 80-95% - в зависимости от требований
потребителя); его обычно отводят в газообразном состоянии поток V. Теплота на его кипение берется за счет конденсации
паров дистиллята в конденсаторе н ижней колонны 5. Из верх
ней части колонны 1 отводят газообразный азот со следами
(доли %) кислорода, поскольку в последующем синтезе N Н з
присутствие 0 2 нежелательно . Чистота уходящих продуктов ( N 2
и 02 ) обеспечивается необходимыми кол ичествами тарелок и
флеrмовыми числами в колоннах 5 и 1.
Заметим , что конденс<iтор 2 на рис. 2 1 .2 1 , а показан схематич
но. В действиrелъности это
кожухотрубный аппарат с трубной
решеткой и крышкой (рис. 2 1 .2 1 , б); в трубках конденсируюrся
пары (нижняя колонна), в межrрубном пространстве - кипит
жидкость (кубовый остаток верхней колонны).
-

Особенности работы агрегата

Для понимания и реализации устойчивой работы агрегата
весьма важны тепловые режимы теплообменных устройств.
Дело в том , что исходный воздух содержит больше Н КК
(приблизительно 77 % мае.), нежели жидкость, находящаяся в
кубе нижней колонны 4. Чтобы температура конденсации ис
ходного воздуха в кипятильных трубках была здесь выше тем
пературы кипения кубовой жидкости (а без этого теплообмен
неосуществим) , необходимо более высокое давление исходной
смеси в сравнении с давлением в нижней колонне 5. Это по
ложение иллюстрируется на рис . 2 1 .22 диаграммами t-x,y для
воздуха при разных давлениях (диаграммы 1 и 11; средние тем
пературы конденсации 1 и кипения Z). Точно так же темпера
тура кипения кубовой жидкости в колонне 1 (высокий % ВКК)
должна быть ниже температуры конденсации паров в конден
саторе колонны 5 (высокое содержание Н КК). Эrо обеспечи
вается различием давлений в колоннах 5 и 1 (см. рис . 2 1 .2 1 , а),
1615

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис.21. 22. Диаграммы t-x,
при разных дамениях:

у

для

воздуха

! - высоко е , ! ! - 5-7 бар (нижняя колонна) ,
Ш - "' 1 бар (верхняя колонна) ;
температуры: 1 - конденсации в кипятильни
ке нижней колонны, 2 - кипения в кубе нижней
колонны , З - конденсации в конденсаторе нижней
колонны , 4 - кипения в кубе верхней колонны

как видно на диаграммах 1 1 и 1 1 1
(см . рис . 2 1 .22); сравните темпера
туры фазовых превращений смесей
З и 4.
Отметим также ряд других осо0
х:у-бенн остей работы ректификаци
онного агрегата (см . рис. 2 1 .2 1 ) .
С целью увеличения потока
флегмы в верхней колонне целесообразно по возможностQ
охладить поток дистиллята III из н ижней колонны в верхн юю
- перед его дросселированием . Для этого холодный поток VI
(N2), отводимый сверху из колон н ы 1, направляют в холодиль
ник б промежуточного дистиллята, установленный перед дрос
сельным вентилем В.
Холодные потоЮ:t газообразн ых N2 и 02 направляются
(раздельно) в холодообменниЮ:t (см . схемы получения глубоко
го холода - разд. 2 1 . 3 .2-2 1 . 3 . 5) для охлаждения встречного
потока исходного воздуха: рекуперация холода повышает эко
номичность процесса. П осле холодообменников N2 и 02 соби
рают в отдельные газгольдеры (давление в н их, как правило ,
атмосферное) . Поскольку движение газов по системе сопро
вождается потерями напора (на преодоление гидравличесЮ:tх
сопротивлений), то давление в верхней колонне несколько
выше атмосферного .
Воздух содержит не только N2 и 02, но и ряд других компо
нентов. От воды и диоксида углерода избавляются до подачи
исходного воздуха в холодильную установку и колон ну; в про
тивном случае лед (Н 2 О, С О 2 ) просто забьет все коммуника
ции . Но воздух содержит еще небольшие количества инертных
газов (по крайней мере, от гелия до криптона), они постоянно
накапливаются в агрегате, преимущественно - в определенн ых
зонах колонн ы . Так, фракции, обогащенные Не и Ne, в основ
ном кон центрируются под крышкой 7 (см . рис . 2 1 .2 1 , а) кон 
денсатора нижней колонны 5; фракции, обогащенные Ar , чуть ниже тарелЮ:t питан ия верхней колонны (ТП В), а фрак
ции, содержащие Кr и Хе, - над кубовой жидкостью верхней
колонн ы 1. Из упомянутых зон (см . рис . 2 1 .2 1 ) эти фракции
1616

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

забираI<УГ и направляют в отдельные колонн ы для выделен ия
индивндуальных компонентов· .
На практике достаточно серьезна проблема безопасности работы ректифика
ционного arperaтa, особенно - в связи с применяемыми конструкционными
материалами на основе меди и серебра (см. разд. 2 1 . 3 .6) . Дело в том, что в
атмосфере химического завода всегда есть орrанические соединения (из-за суще
ствования других производств) , в их числе - и ацетилен (технологические про
цессы с ним, сварочные работы). Эти вещества попадают через системы трубо
проводов в колонну. Наиболее опасно их присутствие в кубе верхней колонны:
контак:r почrи чистого 02 с орrаническими веществами; опасность усугубляется
при наличии С2Н2, поскольку моrут образовываться взрывчатые ацетилениды
меди и серебра. Поэтому исходный воздух тщательно очищают от примесей
орrанических соединений (нередко забор воздуха вообще выносят с территории
завода подальше о т него и с учетом розы ветров). Кроме того, время о т времени
производят слив части кубовой жидкости из верхней колонны, чтобы избавиться
от орrанических соединений , если они попали в колонну ("орrаника" обычно
плавает в жидком киСJiороде хлопьями).

Сходные схемы разделения мoryr использоваться и для по
лучения других компо н ентов или их смесей (фракций ) , кипя
щих при н изких температурах"
Л ИТЕРАТУРА

к rлаве

21

1 . Б азаров И.П. Термодинамика. М . : Высшая школа, 199 1 . 375 с.
2. Беляков В. П. Криогенная техника и технология . М.: Госэнергоиздат, 1982.
270 с.
3 . Гельперин Н. И. Основные процессы и аппараты химической технологии.
М . : Химня, 1 98 1 . 812 с.
4 . Карапетьянц М.Х.
Химическая термодинамика. М . -Л . : Госхимиздат,
1953. 6 1 2 с.
5. Касаткин А. Г. Основные процессы и аппараты химической технологии.
М.: Госхимиздат, 1955. 756 с.
6. Касаткин А. Г. Основные процессы и аппараты химической технологии.
М.: Химня, 1 97 1 . 784 с.
7. KypЬllleв Е. С., Герасимов Н.А. Холодильные установки. Л.: Машинострое
ние, 1 980. 622 с.
8. Лебедев П.Д. Теплообменные, сушильные и холодильные установки. М . :
Энергия, 1972. 320 с .
9 . Литвин А.М. Техническая термодинамика. М.- Л . : Госэнергоиздат, 1956.
312 с.
1 0 . Основные процессы и аппараты химической технолоrииjtl од ред.
Ю.И. Дытнерского. М . : Химия, 199 1 . 494 с.
1 1 . Промышленная теплоэнергетика и теплотехника. Справочни к;tl од ред.
В .А. Григорьева, В.М. Зорина. М . : Энергоатомиздат, 1983. 55 1 с.
1 2 . Рид Р., Шерf!Уд Т. Свойства rазов и жидкостей: Пер . с aнrл.jtl oд ред.
А.Н . Плановскоrо. М . : Гостоmехиздат, 1964. 334 с.

• См. ( 1 3 ) .
•• С м . ( 2 , 3, 1 1 , 1 3 ) .

1617

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

1 3 . Справочник по р азделен ию rазо в ых смесей методом глубокого охлажде
ния;tiод ред. И.И. Гельпери на. М. -Л.: Госхимиздат, 1953. 39 1 с .
14. Тепло физические основы получения искусственного холода;tlод ред.
И.М. Калниня. М.: Пищ. пром., 1980. 23 1 с.
1 5 . Хей�д Р. Термодинамика равновесных процессов: Пер. с аиrл.;tlод ред.
Ю.А. Чиз мадж:ева. М.: Мир, 1983. 492 с.
16. Холодильные компрессоры. Справочник;!Iод ред. А.В . Быкова. М.: Ко
лос, 1992. 302 с .
1 7 . Холодильные маш ины . Справочиик;!Iод ред . И.М. Калииня. М.: Легкая
пром., 1 982. 223 с.

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Глава 22
И ЗМЕЛЬЧЕНИЕ ТВЕРДЫХ МАТЕРИАЛОВ

Под измельчением твердых материалов (ТМ) понимают на
прааленное уменьшение их размеров пуrем механического
(реже - какого -либо иного) воздействия на ТМ. Ниже рас
сматриваются основные инженерные проблемы измельчения
на примере
некоторых типичных представителей размольных
•
машин .
22. 1 . ОБЩИЕ ПОЛОЖЕНИЯ

Общее назначение процессов из иел ьчения :
- увеличеиие поверхности контакта измельчаемого ТМ для
осущесталения ряда химических, физических, физико-хими
ческих процессов, если именно поверхность межфазного кон
та�сrа определяет интенсивность процесса в целом (многие ка
талитические и некаталитические гетерогенные процессы и
т.д.);
- применение ТМ в последующих конкретных технологиче
ских процессах, если их возможно осуществить с ТМ только в
тонкоизмельченном
состоянии (состааление композиций и
др .);
- выделение ("вскрытие") целевого компонента, изначально
существующего в твердой породе в смеси с ней (например ,
процессы выщелачивания в rnдрометаллурrии или полимерных
технологиях) .
22. 1 . 1 . Классификация размольных машин

Процессы измельчения формально и условно классифици
руют по размерам (начальному dн и конечному dJ зерен, ку
сков, частиц ТМ, иногда дополнительно и по степени измельче-

• Подробнее п роблемы измельчения, р абота и расчет разнообразных раз
м ольн ых м аши н рассм атр и ваются в ряде учебников по курсу ПАХТ ( 1, 2, 5, 7) и
в специальной литературе [ З , 4, 6).

1619

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ния - линейной

Zи

=

dн /dк или объемной

Vи

=

Vн /Vк:

Размер кусков d,, и d,,., мм

Класс НЗМСJIЬЧе НИЯ

ДО llЗМСJIЬЧеюtЯ

Дробление :
крупно е
среднее
мелкое
Помол :
rрубый
средний
мелкий

КОJUIОИДНЫЙ

после ИЗМ&ЛЬЧСЮIЯ d"

d.,.

1 000
250
20

250
20
1 -5

1 -5
0, 1 -0,04
0, 1 -0,04
< 0,1

0 , 1 -0,04
0,005-0,0 1 5
0,00 1 -0,005
< 0,001

Рассмотрение таблицы обнаруЖивает достаточно четкую
тенденцию возрастания степени измельчения Zи по мере
уменьшения размеров зерен (кусков, частиц) ТМ.
Условность приведенной классификации - не только в
субьеIСI'ивности (произвольности) установления границ между
классами , но еще и в объеlСl'ивных различиях:
- получение одних и тех же классов ТМ в разных размоль
НЬIХ машинах;
- применение одних и тех же размольньIХ машин для раз 
НЬIХ классов ТМ.
Более обоснованной является классификация по способам
измелъ"ения. Основные из этих способов представлены на рис .
22 . 1 : раздавливание ( а) ; изrиб, и наче - разламывание (6) ; раска
лывание ( в) ; удар ( г) и истирание ( д) . В размольн ых машинах
разрушение ТМ, как правило, происходит одновременно
нескольЮ1ми способами, так что следует говорить о комбиниро
ванном воздействии на ТМ, может бьпь - с преобладанием
какого-либо одного или двух-трех способов. При этом выбор
способа (соответственно - типа размольной машины) опреде-

а

б

Рис. 22. 1. Основные способы измельчения:
а - раздавливаиие , б - разламывание (изгиб),
раюtе
1 620

д

г

в
г

-

рш:калываиие ,

г

- удар , д

-

и сrи 

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ляется свойствами ТМ и отчасти исходным и конечным разме
рами кусков. Так, для твердых и хрупких ТМ применяют раз
давливание в сочетании с раскалыванием и (или) изгибом, а
для мягких и вязких ТМ предпочитают истирание в сочетании
с раздавливанием и (или) ударом либо изгибом.
Сравнивая две приведенные выше классификации, отметим
нечетко выраженную тенденцию: чаще всего для крупного и
среднего измельчения применяют машины, использующие
преимущественно раздавливание, раскалывание, изгиб и удар,
а для мелкого измельчения и помола - истирание и удар.
22. 1 .2. О затратах энергии на измельчение

Затраты энергии на измельчение (разрушение) ТМ зависят
от производительности размольной машины, а также от сле
дующих характеристик:
- физико-механические свойства твердого материала (предел
прочности материала ар , его модуль упругости Е) ;
- геометрические параметры разрушаемого куска ТМ (его
объем или линейный размер);
- степень измельчения;
- выбранный способ измельчения этот фaJcrOp чаще всего
является определяющим.
Строго говоря, каждому способу измельчения должны отве
чать своя физическая модель разрушения куска (своя "теория
прочности") и соответствующее ей математическое описание.
В настоящее время в оценке затрат энергии при разрушении
ТМ господствуют две гипотезы.
При измельчении способами раздавливания, раскалывания,
удара затраты энергии L на разрушение куска до конечного
размера dк. при степени измельчения Zи качественно следуют
гипотезе Кнр пичева , согласно которой:
na 2 d3
L = l;Eк
(а)
- 1 (Дж).

-

(z� )

При измельчении способом истирания (и некоторыми ины
ми) затраты энергии L на разрушение куска начального разме
ра d8 при степени измельчения Zи согласно гипотезе Рнтrи нrера
пропорциональны вновь образованной поверхности:
L = Кр�2 (Zи 1) (Дж),
(б)
причем эмпирический коэффициент Кр (в Дж/м2) оценить
теоретически пока не удается. Он подлежит эксперименталь
ному определению для каждых ТМ и размольной машины, что,
конечно, снижает инженерную ценность этой гипотезы для
технолога.

-

1621

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Оценивая упомянутые mпотезы (и ряд других более частных
моделей), при их практическом использовании необходимо
учитывать следующие обстоятельства:
- прочностные характеристиЮt конкретного ТМ, подлежа
щего измельчению (минерала, породы и т.п.), бывают различ
ными для разных месторождений и размеров куска: сказывают
ся структурные дефекты в ТМ (плохо воспроизводимые по вели
чине и распределению в куске), влияющие на прочность мате
риала и затраты энергии на его разрушение ;
- даже в случае абсолютной строгости модели разрушения
ТМ и ее математического описания для каждого способа из
мельчения в силу комбииированного воздействия рабочего органа
размольной машины на ТМ невозможно количественно оце
нить вклад различных способов измельчения, присущих кон
кретной размольной машине; отсюда - невозможность точно
го расчета затрат энергии на измельчение в реальной размоль
ной установке;
- но и в случае успешного разрешения указанных выше
проблем возникают расчетные затруднения, связанные с необ
ходимостью оценЮt затрат энерmи на перемещение массивных
рабочих органов на холостом ходу размольной машины (т.е. в
отсутствие измельчаемого материала); эти затраты обычно
вполне соизмер имы с затратами на собственно измельчение, а
для некоторых размольных машин и превосходят их. Заметим:
чаще всего затраты энерmи холостого хода размольных машин
пока что не поддаются теоретическому анализу.
В настоящее время используются два основных конкури
рующих пути преодолен ия сформулированных выше расчетных
осложнений .
Первый опирается на теоретичесЮtе формулы типа (а) и (б),
правильно отражающие доминирующий способ разрушения
ТМ . Но в затраты энергии вносят свой вклад и друmе способы
измельчения, а также перемещение рабочих органов самой
размольной машины. Поэтому в теоретичесЮtе формулы вно
сят корректирующие эмпиричесЮtе поправЮt, призванные от
разить реальные затраты энергии. Авторы таких формул с эм
пирическими поправками фактичесЮt предлагают следующий
подход: теоретичесЮtе фрагменты формул учитывают влияние
основных факторов (в этом достоинство расчетной формулы),
а согласие с реальными затратами энерmи достигается за счет
эмпиричесЮtх поправочных коэффициентов незнания (явный
недостаток формул, так как теоретичесЮtе фрагменты далеко
не всегда базируются на основных эффекгах реального процесса
разрушения ТМ).
Второй путь базируется на обследованиях лабораторных и
промышленных размольных машин; в результате формируются
1 622

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

расчетные соотношения сугубо эмпирического характера. Досто
инство такого расчетного метода - надежность в тех рабочих
диапазонах, в которых были проведены эксперименты и обсле
дования реально функционирующих размольных машин . Недо
статок - отсуrствие (в лучшем случае - ослабление) связи
затрат энергии со свойствами измельчаемого материала.
В силу указанных причин предлагаемые в литературе фор
мулы для расчета энергетических затрат в размольных машинах
зачастую не обладают приемлемой надежностью. Поэтому в
настоящем учебнике они не приводятся (или же в отдельных
случаях приводятся, но лишь для иллюстрации сформулированых выше положении ) .
v

•

22. 1 .3. Основные требования к размольным машинам.
Типовые схемы размольных установок

В размольных машинах получается смесь кусков ТМ разных
размеров (даже при достаточно однородном - по крупности исходном материале). Основной принцип работы размольных
машин - измельчать ТМ только до требуемых размеров, не за
трачивая энергию на излишнее измельчение. Исходя из этого
принципа формулируется большинство требований к размоль
ным машинам:
- получение измельченного ТМ заданного гранулометриче
ского состава (частный случай - равномерность измельчения,
конечные зерна одинакового размера);
- возможность реrулирования степени измельчения;
- минимум пылеобразования;
- немедленное удаление из рабочей зоны зерен, уже достиПIIих заданного размера (т.е. недопустимость их дальней
шего измельчения - бесполезного, а для ряда потребителей просто неприемлемого).
Есть и другие требования, не имеющие прямого отношения
к основному принципу. Одно из них связано с износом узлов и
деталей размольной машины, поскольку в рабочих условиях
большие усилия действуют не только на измельчаемый ТМ, но
и на упомянуrые узлы и детали. Поэтому необходимо предо
хранить от поломки наиболее ответственные и трудносменяе
мые узлы, а для некоторых размольных машин - даже прово
цировать поломки определенных (быстро изнашиваемых и легко
доступных для замены) узлов и деталей при возниюювении
особо жестких условий работы.
И еще одно очевидное требование, относящееся и к другим
технологическим аппаратам: минимальные затраты энергии
при заданной производительности или максимальная произво
дительность при заданных затратах энергии.
• Подробнее о затратах энерmи см. ( 1 , 3, 6 ) .

1 623

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

3

Gp

G

( 1 -х)

Gu

Gи

Gи
1

1

Gi)'
3

2

2

б

а

Рис. 22.2. Типичн ые схемы размольных установок с умеренной (а) и высоко й (б)
степенью измель•1е11ия:
1

-

раэмольна.>1 машина,

2-

сортируюшее устройство,

J-

линия рецик.ла

ТМ

С учетом перечислен ных требований строятся типовые схе
мы размольных установок, в которых исходный ТМ должен
быть измельчен до зерен (кусков, частиц) заданного размера.
Умеренные требуемые степени измельчения. Типовая схема в
этом случае имеет вид, показан ный н а рис 2 2 . 2 а В размоль
ную установку непрерывного действия подается исходный мас
совый поток твердого материала Gи . Однако за оди н проход до
заданного размера dк в размольной машине 1 измельчается не
весь ТМ, а лишь его некая доля х. Полученная в дробилке
смесь кусков разных размеров направляется н а сортировку в
классификатор 2, где целевой продукт Gц = Gи , содержащий
достаточно мелкие (приемлемые по размеру) зерна, отделяется
от потока Gp с более крупными зернами. Поток Gp - рецикл
возвращается по линии 3 на вход размольной установки , где
присоединяется к исходному потоку Gи . Так что полная (общая)
производительность размольной машины составляет:
.

,

.

-

G

= Gи

+

Gr

=

Gц

+

Gp .

(в)

Разумеется , в размольной .машине можно бьmо бы обеспе
чить требуемое измельчение за один проход
тогда не было бы
потребности в сортиро вке и рецикле: Gp = О . Но в этом случае
продукт содержал бы много мелочи - был бы нарушен основ
ной принцип измельчения, возникли осложнения при после
дующем использован и и измельченного ТМ , ухудшились техн и
ко-экономические показатели размольной установки . И менно
по этой причине организуют сопряжение процессов в размоль
ной машине 1 и классификаторе 2 - с рециклом потока Gp
твердого материала по л инии J.
-

1 624

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Взаимозависи мость потоков ТМ найдем из материального
баланса для классифи катора ( п оз. 2 на рис. 22.2,а). При доле х
целевого продукта Gu от общей прои зводительности G размоль
ной установки доля реuикла Gp, естественно, составит ( 1 - х).
Тогда легко зап исываются два равноценных балансовых соот
ношения:

Gц =

Gx = ( Gц + Gp)x и

Gp

=

G( l

- х) = ( Gц + Gp)( l - х).

Используя л юбое и з этих соотношен и й , находим искомые
связи:
G

=

Gц /х = Gи/х и Gp = Gц( l - х)/х = Gи( l - х)/х .

(22 . l )

Высокие степени измельчения. В этом случае получ ить целе
вой продукт с хороши м выходом в одной размол ьной машине
(т.е . обеспеч ить собл юде ние основного принципа измел ьчения)
не удается : образуется много мелочи (пыл и ) . Поэтому исполь
зуют более сложную технологнческую схему (рис. 22.2, 6) , со
стоящую и з нескольких последовательно расположенных раз
мольных маши н
со своим рециклом ( l - х) недоизмел ьченного
ТМ для каждой из маш и н .
-

Объектом инженерного анализа размольной маш и н ы являют
ся прочностные и технологические характеристики ; несколько
особняком стоят энергетически е проблемы.
Прочностные расчеты
дело конструктора, науч ная база рас
сматривается в курсе " П рикла;(ной механики " ; курс ПАХТ эти
моменты не затрагивает.
Технологические вопросы
предмет анал иза в курсе ПАХТ:
они важны при эксплуатации размол ьных установок и при их
проектирован и и . В посл еднем случае технолог зачастую высту
пает в роли заказчи ка в д иалоге с конструктором.
Затраты энерrии при измел ьчен и и важны как для технолога,
так и для п роектировщика. Слабость теоретической базы и
сложность вл ия н ия м н о гочислен ных факторов, как показано в
разд. 22. 1 .2, пока преп ятствуют достаточно строгому анал изу и
разработке н адежных расчетн ых формул .
Н иже рассматри ваются не которые технологические моменты ,
характерные для отдел ьн ых размольн ых маш и н .
-

-

22.2. ЩЕКОВЫЕ ДРОБИЛКИ

Щековые дробилки ( lЦД) относятся к размольным машинам
с преобладан и ем и змел ьчения сп особами разламыван и я , раска
л ывания и раздавл и ва н 11 я . Чаще всего lЦД испол ьзуются при
крупном и среднем дроблени и .

1 625

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

22.2. 1 . Устройство и принцип ы работы щековых дробилок

Общий вид и кинематическая схема 1l1Д показаны на рис.
22.3,а.
Основными рабочими органами lllд являются смокrированные на станине 1
стальная или чугунная неподвижная щека 2 и подвижная щека 4, защищенные
плитами, изготоаленными из очень прочного (износоустойчивого) материала.
Рабочий объем lllд - пространство между плитами, называемое пастью. С
торцов пасть закрыта гладкими плитами 3.
lllд работает циклично - в две стадии : измельчение ТМ; загрузка- выгрузка
ТМ. На стадии измел•чения подвижная щека перемещается мево, плиты сбли
жаются и происходит разрушение ТМ. На стадКИ 381}1узхи-11WI'рузки подвижная
щека перемещается вправо ; при этом измельченный материал выгружается из
lllд через нижнее сечение пасти (шпальт), и одновременно в рабочий объем
через верхнее сечение пасти (зев) подается свежая порция исходного ТМ .
Поверхность плит может бьпъ гладкой (работа на раздавливание ТМ ) , н о она
может бьпъ рифтте ной или зубчатой (работа на изгиб, отчасти - на раскалыва
ние ТМ).
Возвратно- поступательное (а точнее - качательное) перемещение подвиж
ной щеки около оси 5 обеспечивается подъемно-опускным движением шатуна
8, сидящего на эксцентриковом валу 7, и распорными плитами 9, шарнирно
соединяющими шатун с подвижной щекой (левая плита 9) и клиньями 12
(правая плита 9) . При подъеме шатуна распорные плиты располагаются почти в
одну m1нию, так что подвижная щека идет алево (измельчение ТМ в пасти). При
опускании шатуна распорные плиты располагаются в ломаную линию так, что
подвижная щека идет вправо (разгрузка ТМ через ш пальт и загрузка свежих его
порций через зев). На стадии загрузки- выгрузки под действием собственного
веса и веса ТМ в рабочей зоне подвижная щека весьма медленно перемещается
вправо ; чтобы частота этого перемещения соответствовала режиму lllд , пред
усмотрен принудительный возврат подвижной щеки в крайнее правое положе
ние с помощью тяг 10 и пружин 11.
Для восприятия значительных инерционных усилий на эксцентриковом валу
7 устанааливается массивное маховое колесо 6.
Конечный размер куска измельченного ТМ регулируется шириной щели
(нижнего сечения) шпальта за счет фиксации КJШньев 12 в о пределенном поло
жении.
При работе lllд возможно случайное попадание в рабочий объем (в пасть)
очень прочного куска какого-либо постороннего ТМ . Чтобы избежать поломки
дорогостоящих узлов и деталей lllд , на этот случай предусмотрена преднамерен
ная поломка какой-нибудь дешевой и легко заменяемой детали, чаще всего специально ослабленной правой распорной плиты 9: она выполняет роль
"предохранительного клапана·· - при поломке ее легко заменить на новую.

Крепление подвижной щеки может быть различным (см. рис .
22.4) . Применяемое чаще всего верхнее крепление (рис. 22.3,а и
22.4,а) обеспечивает надежную выгрузку ТМ. Однако из-за пе

ременной ширины шпальта в этом случае продукт состоит из
кусков, заметно различающихся своими размерами. Нижнее
крепление подвижной щеки (рис. 22 .4,6) обеспечивает большую
однородность в размере кусков измельченного ТМ . Но в этом
случае возможно зависание измельченного ТМ при его выгруз
ке через шпал ът. В обоих рассмотренных случаях различные
участки подвижной щеки при ее качании перемещаются на
1 626

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

11

а

Рис. 22.З. Щековая дробилка:

а - процессуальная схема, б - кинематическая схема;
1 - стаюmа, 2 - неподвижная щека с защиn�ой плиrой, З - боковая плита, 4 пoДllIOl(}faя щека с защитной плитой, 5 - ось качания поДВIОКНой щеки, 6 - маховое колесо,
7 - эксцентриковый вал, 8 - шатун, 9 - распорные плиты, 10 - тяги, 11 - пружина, 12 -

КJIИИЬЯ

а

6

в

г

Рис. 22. 4. Варианты креrтения подвижной щеки:

а - верхняя подвеска, 6 - нижняя подвеска, в - параллельное перемещение подвиж
ной щеки, г - сложное перемешение;
1 - неподвижная щека, 2 - подвJIJОfаЯ щека, З - ось качания подви:жной щеки

1627

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

разные расстояния и потому испытывают неодинаковые меха
нические нагрузки (наибольшие - в области максимального
перемещения участков подвижной щеки) . Or этого недостатка
свободны lllД с параллельным перемещением подвижной щеки
(рис. 22.4,в) ; платить за это улучшение приходится значитель
ным усложнением кинематической схемы ll.IД. Наконец, су
ществуют lllД со сложным перемещением подвижной щеки
(см . рис.22.4,г) - влево и вниз на стадии измельчения. В этом
случае облегчается выгрузка измельченного ТМ; кроме того , к
указанным выше способам измельчения в lllД добавляется еще
истирание, что важн о при разрушении мягких и вязких ТМ .
Разумеется , кинематическая схема перемещения подвижной
щеки здесь тоже весьма сложная.
Диапазон размеров lllД весьма широк: от лабораторных дро �
билок (с размером в зеве 1 50х 1 00 мм) до пилотных (укруп
ненных лабораторных) и промышленных (размер в зеве
2000х3000 мм ) . Щековые дробилки мoryr развивать очень
большие усилия.
Достоин ства ll.IД: простота; надежность; легкость обслужи
вания; относительная компактность (см . рис. 22. 3 , а) . Недостат
кu ll.IД: периодичность цикла работы и, как следствие, нерав
номерность нагрузки на рабочий орган в процессе измельчения
(от высоких на стадии измельчения до почти нулевых на ста
дии загрузки-выгрузки) ; поломки и необходимость замены рас
порной плиты ; шум.
22.2.2. Основы технологического расчета

Угол захвата твердого материала в щековой дробилке
Углом захвата в lllД называется угол сх. (рис. 22. 5 , а) между
неподвижной и подвижной щеками . Если рассматривается lllД
с паралл ельным перемещением подвижной щеки (рис . 22 .4, в) ,
то угол захвата в процессе работъ1 llIД остается постоянным. Ес
JШ же в ходе измельчения ТМ этот угол несколько (на практике весьма слабо) изменяется (например, при верхней или н ижней
подвеске подвижной щеки - см . рис. 22.4,а,6), то при анализе
проблемы захвата речь идет об угле сх. в начале стадии измельче
ния: подвижная щека - в крайнем правом положении.
С позиций технолога обычно следует стремиться к увеличе
нию угла захвата сх. , так как с ростом сх. повышается степень
измельчения Zи - как правило, это желательно . Но при чрез
мерном увеличении сх. кусок ·ТМ , подлежащего измельчению,
не будет захвачен щеками, а выскользнет ("эффект мыла") вверх
из рабочей зоны, но не будет разрушен .
На кусок ТМ, находящийся в рабочей зоне (в пасти) , дей
ствует сила F8 (рис . 22.5,а), стремящаяся вытолкнуть его из

1 628

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

р

о

а

б

Рис.22.5. К расчету предельного угла захвата щековой дробилки:

а - схема действия сил, б - к определеЮtю уrла внешнеrо треЮtЯ (Т - тело,
верхносrь треЮtЯ)

П

- по

пасти. Одновременно на кусок действуют силы трения Fт ,
удерживающие его в пасти, что необходимо для последующего
его разрушения. С ро стом а. увеличиваются силы, выталЮ1вающие кусок, и уменьшаются силы, удерживающие кусок в
рабочей зоне.
Очевидно, существует некий предельный уrол захвата а.пр'
при котором упомянутые силы находятся в равновесии; рабо
чий уrол захвата а. должен быть меньше предельного О.Пр · Вели
чину предельного угла захвата а.пр определим путем сопостав
ле н ия (рис. 22. 5 , а) сил, действующих на кусок вдоль оси О-А .
Для упрощения будем рассматривать шарообразный кусок ТМ.
Выразим составляющие конкурирующих сил.
Нормально к неподвижной и подвижной щекам действуют
сдавливающие силы Р - разложим их на составляющие: вдоль
оси О-А и нормально к ней. При работе дробилки на измель
чение ТМ важны нор м ал ьные составляющие сил Р - именно
они разрушают ТМ. Но при о п р еделен ии предельного угла
захвата важны вьпалкивающие составляющие сил, действующие
вдоль оси. Из рассмотрения рис. 22.5,а следует, что характер
ные углы при проецировании сил на ось О-А равны половине
угла захвата щековой д робилЮI (как углы с взаимно перпенди
кvляоными сторонами). Тогда проекция выталЮ1вающей силы

на ось О-А составляет P si n ( a / 2) , а поскольку этих сил две (одна
для неподвижной и другая для подвижной щеки), то в итоге
Fв

2Psin(a / 2) .
Удерживают кусок в рабочей зоне составляющие сил трения
Fт , действующих вдоль щек в точках их касания с шаром. Эти
силы также разложим на нормальную к оси О-А и тангенци
альную вдоль оси. Нормальная составляющая добавляется к
=

1 629

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

разрушающей нагрузке (см. выше), а тангенциальная F3 важна
при решении задачи об удержании куска в рабочей зоне. Из
технической механики известно, что сила трения вдоль щеки
Fт может быть представлена в вИде произведения нормальной
силы Р и коэффициента трения fт: Fт Рfт; поскольку этих сил
тоже две (по поверхностям неподвижной и подвижной щек), то
результирующая сила трения равна 2Рfт. Проекция сил трения,
удерживающих кусок в рабочей зоне, на ось О-А равна F3
2Pfтcos(a/2).
=

=

=

Рис. 22.5,б ИЛЛ Ю С11J Ирует связь нормальной с клы Р и силы, обеспечивающей
движение тела Т по поверхности П: эта движущая сила численно равна силе
трения Fт и противоположна ей по направлению. Из рисунка следует: Fт = Ptgqi,
rде уrол qi называется уrлом 1111 е1Ш1еrо 1J1еиия (трения тела Т о постороннюю
поверхность П). Сравнение формул для силы трения Fт = Р/т и Fт = Ptgqi приво
дит к выражению: fт = tgqi.

Предельный угол трения <х.пр найдем, приравнивая дей
ствующие вдоль оси О-А силы, выталкивающие кусок из ра
бочей зоны и удерживающие кусок в ней:
2Аiн(а./2) 2Pfтcos(a./2)
Отсюда после очевИдных сокращений:
sin(a. / 2)
tg(a./:2) 1т tgq> .
cos(a. / 2)
Равенство тангенсов означает равенство углов. Окончатель
но для предельного и рабочего углов захвата:
(22.2)
<Хпр
2q>
< 2q> .
К аналогичным результатам приходят , рассматривая равенство проекций сил на вертикальную и горизонтальную оси.
=

=

=

=

' а.

=

•

ПракrичесЮI для многих ТМ угол qi находится в диапазоне 1 5 -20°, так что
30740°. Рабочие утлы захвата принимаются обычно с достаточным запасом
на возможные изменения рабочих условий (увлажнение ТМ и др.) - в пределах
1 5-25°.

Оtпр "'

Производительность щековой дробилки и ее регулирование
Произ1юдительность ПJД.·. Она определяется геометрически
ми характеристиками llJД и частотой качания подвижной ще
ки. Расчетная схема на рис. 22.6 представлена применительно к
параллельному перемещению подвижной щеки (это несколько
упрощает анализ). Обоjначим: е
ширина щели в шпальте;
Ь - длина щеки (перпендикулярно плоскости чертежа) ; s ход подвижной щеки ; п - рабочая частота качаний щеки или,
что то же самое, число оборотов эксцентрикового вала в еди-

• См " например, ( 1 ) .

1630

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 22.6.

-

К расчету производительности щековой

дробилки:

-

1
неподвижная щека, 2
подвижная щека в
крайних левом (сплошная линия) и правом (шrриховая
ЛЮDIЯ) положениях

ницу времени: один оборот склады/
вается из одного качания влево
(стадия измельчения) и одного вправо (стадия загрузки-выгрузки).
Точками на рисунке помечено попе
речное сечение призматического объ
ема твердого материала, измельченно
го до заданного максимального конечного размера куска dкм,; он отвечает (см. рис. 22.6) наибольшей ширине щели . (е + s). Средний
конечный размер куска dк принимается (тот же рисунок) рав
ным полусумме верхнего и нижнего оснований помеченного
сечения измельченного ТМ: dк [е + (е + s)]/2. Размеры ку
сков ТМ, расположенного над помеченным объемом, моrуг
превышать заданные (dкм,) ; такие куски не будуг выгружаться
через шпалът.
За одно качание щеки вправо происходит выгрузка призма
тического (основание призмы - h(2e + s)/2, ее длина - Ь)
объема V0 измельченного ТМ:
Уо
2е + s
= hЬ
::::

2

За п качаний в
вость IЦД составит:

единицу времени

объемная производиrе.ilь

2е + s
V = V0n = hb -- n .

(а)
2
В выражение (а) входят конструктивные величины
е, s и
Ь, эксплуатационная харакrеристика п, а также расчетная вы
сота h, не заданная в паспорте IЦД. В расчетных целях h целе
сообразно выразить через известные конструктивные характе
ристики: из геометрических соображений h = s/tga.. Тогда
а.,

V=

_!_ Ь 2е + s

tga.

2

п .

(б)

Массовая производиrельвость дробилки .G (в кг ТМ/с) полу
чается как произведение объемной производительности на
массовую концентрацию ТМ в измельченном материале: G =
Vpт( l - Е). Здесь Рт - кажущаяся плотность (см. разд. 14.7.3)
ТМ, (1 - Е) - его объемная доля в выгружаемом ТМ, Е - по
розность. Заметим: в технологии измельчения величина ( 1 - Е )

=

1 63 1

·

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

именуется коэффициентом разрыхления и обозначается щ�. На
пракrике обычно щ� = 0,4 -:- 0,6. Окончательно:
s
2е + s
G
Ь
(22 .3)
п р т µо
2
a.
tg
Реrулирование производительности UЩ. С этой целью следу
ет воздействовать на величины, входящие в формулу (22.3).
=

-

--

Ширину е зазора в шпальте можно изменять перемещением клиньев (поз. 1 2
на рис. 2 2 . 3 ) . Надо только иметь в виду, что одновременно изменится и конеч
ный размер разрушенноrо куска ТМ (допустимо ли это с позиций заказчика?) .
Ход s подвижной щеки в наибольшей степени зависит от эксцентриситета вала,
на котором установлен шатун . Воздействие на эксцентриситет - громоздкая
процедура, на праlСl'Ике она не применяется. Заметим также, что величина s
изменяется в весьма узких пределах, и потому вряд ли целесообразно использо
вать s для реl)'лирования V и G. Воздействие на длину щеки Ь в процессе дроб
ления, конечно , невозможно, на уrол захвата а - праlСl'Ически тоже
("прак:rически" п отому, что изменение е в некоторой - малой - мере сказы
вается и на а) . Плотность Рт - свойство измельчаемоrо ТМ (справочная величи
на). Степень разрыхления µо зависит от режима работы IЦД, но харакrер этой
зависимости (не rоворя уже о количественном ее выражении) изучен недоста
точно.

Наиболее простым и действенным способом регулирования
производительностей V и G щековой дробилки является изме
нение частоты п качаний подвижной щеки (числа оборотов экс
центрикового вала в единицу времени): согласно формулам (б)
и (22 . 3), производительности V и G пропорциональны п.
В конце стадии измельчения твердый материал, находящийся в
рабочей зоне IIJД, подразделяется на две части (см. рис. 22.6):
- нижнюю объемом V0 , помеченную точками, где ТМ уже
измельчен до заданного размера куска;
- верхнюю, где размер многих кусков ТМ может превышать
максимальную ширину щели (е + s); высыпание этой части
материала через щель в шпальте затруднено или просто невоз
можно, она продвинется вниз и займет место V0 в следующем
цикле измельчения.
Подчеркнем, что в конце стадии выгрузки (подвижная щека
- в крайнем правом положении) должен полностью высыпать
ся через шпал ът весь и з мельченны й ТМ в объеме V0 ; в про
тивном случае будет происходить дополнительное (чрезмерное!)
измельчение материала - в нарушение основного принципа
измельчения. Это означает, что продолжительность стадии вы
грузки должна быть достаточной для высыпания всего измельчен 
ного ТМ, занимающего обьем V0 высотой h. Следовательно, при
чрезмерно высоюtх частотах качания щеки п время стадии вы
грузки окажется недостаточным для высыпания всего объема V0
измельченного ТМ.
Это обстоятельство ставит предел увеличению п: для 1ЦД
существует некая максимальная частота качаний подвижной
1 632

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

щеки птах, превышать которую нельзя из-за недопустимого
уменьшения времени хода (вправо) подвижной щеки.
В целях оценки птах обозначим: 'tx - время перемещения
подвижной щеки на стадии загрузки-выгрузки, 'tвыс - полная
продолжительность высы пания всего ТМ, заключенного в объе
ме V0, помеченном точками на рис.22.6. Основной принцип
измельчения соблюдается при
(в)
'tx �
Время одного оборота эксцентрикового вала составляет 1/п ;
продолжительность стадии выгрузки ТМ (одного качания) за
нимает половину времени полного оборота: 'tx = 1/(2п) .
Время 'tвыс найдем исходя из допущения, что высыпание из
мельченного (помеченного) ТМ через шпальт происходит по
законам свободного падения - без учета rидравлического сопро
тивления воздуха. Такое допущение вполне оправдано: rидрав
лическое сопротивление на стадии высыпания ТМ очень неве
лико из-за малых скоростей падения кусков ТМ на участке
небольшой высоты h (рис. 22.6 } . Тогда по законам свободного
падения (ускорение g = 9, 8 1 м/СJ.) при нулевой начальной ско
рости движения ТМ справедлива формула: h = g-с;мс/2. Отсюда с учетом h s/t a имеем: t в ы с J2h/ g = J2s/(gtga) .
Подставим выражения для и t с в условие (в):
1
/2S откуда п 1 gtg
(22.4)
�
2п V
::;;; 2 2s" .
'С в ы е

g

=

·

=

gtga

tx

� a

вы

'

Знаку равенства в последней формуле отвечает предельное
(максимальное) число качаний (оборотов вала) в единицу времен и:
п

max

=

]_Jgtga
.
2 2s

(22.4а)

Определение производительности llJД по (22.З ) и числа ка
чаний щеки по (22.4 ) относится к задаче эксплуатации. Типич
ная проектная задача - расчет длины щеки Ь по (22.3 ) при
заданной производительности G с учетом ограничения п по
(22.4).
О расчете затрат энергии на измельчение в щековой дробилке

Приведем одну из эмпирических формул для расчета затрат
энергии, полученную из анализа реальных (по каталогам)
мощностей приводов ще. ковой дробилки.
При ее массо вой производительности G мощность привода NШд составляет:
NШд

=

2G

NШд

=

0,55 G

кВт
+

в с.лучае G � 20725

2 5 кВт

/

т ч;

в случае G � 20-7-25

/

т ч .

(r)

(д)

1 633

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Заметим: в формулы (r), (д) не входят физико-механические свойства ТМ .
Видимо, Д11Я щековой дробШ1ки затраты энергии на собственно измельчение ТМ не
яаляются значимыми, тем более определяющими в общих затратах энергии (см.
разд. 22. 1 .2).

22.З. ВАЛКОВЫЕ ДРОБИЛКИ

Валковые дробилки (ВД) чаще всего используются при
среднем и мелком измельчении. В зависимости от формы вал
ков (точнее - бандажей) преобладающим способом измельче
ния может быть раздавливание (в случае гладких валков) либо
разламывание и раскалывание (если поверхность бандажей
снабжена рифами или шипами). Ниже принципы работы и
технологические расчеты будуг рассмотрены применительно к
rладковалковой дробилке.
22.З . 1 . Устройство и принципы работы валковых дробилок

Общий вид и кинематическая схема валковой дробилки по
казаны на рис. 22.7.

Основным рабочим органом ВД яаляется пара 1А11Хов / , 2 с бандажами, изю
товленными из износоустойчивою материала. Валки установлены с некоторым
зазором и вращаются навстречу друг друrу: левый - по часовой стрелке, правый
- против нее. Ус.ловимся : здесь и далее будем юворить о "'валхах", подразумевая
валки вместе с бандажами . Кусок ТМ попавший в зазор (щель) меЖду валками,
должен быrь захвачен ими и разрушен (измельчен). Ш ирина щели меЖду валка
ми, значит и конечный размер куска ТМ после измельчения, реrулируется фик
сацией щитка 5 с помощью упорных ботов.
При попадании в зазор куска постороннею очень прочною ТМ валки
(бандажи) могут разрушиться под действием возникающих высоких нагрузок.
Чтобы этою не произошло, один из валков (на рисунке - левый) установлен в
неподвижных подшипниках, друrой (правый) - в скользящих. Ее.ли валки не
смогут разрушить упомянутый прочный кусок ТМ то подвижн ый валок 2 ото
двинется вправо и ВД пропустит этот кусок ТМ неразрушенным, предохраняя
ВД от поломок. А затем под действием пары пружин 4 подвижный валок воз
вратится в исходное положение.
Оба валка чаще всею (например, при измельчении твердою, подчас - хруп
кою матер иала) вращаются со строго одинаковыми числами оборотов в единицу
времени, обеспечивая работу на раwмивание подлежащею измельчению ТМ .
Если ТМ яаляется мягким и вязким, то надо обеспечить истирающее воздей
ствие; в этих случ аях предус матюи вают несколько различ�� ющиеся (обычно на
- 2 0%) скорости вра щен ия вал ков.
,

,

Достоинства ВД: надежность; "автоматическое" выполнение
основного принципа измельчения, так как разрушение ТМ
происходит за один проход (нежелательного повторного измель
чения ТМ здесь нет); возможность регулирования ширины
щели между валками, а значит и размера кусков измельченного
ТМ . Основной недостаток: возможность перекоса валков из-за
неодинаковой затяжки пружин и неравномерной подачи ТМ в
дробилку по ее длине.
1 634

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 22. 7.

Схема

rладковалковой дробилки:

1 - валок в НСПОДВНJIСИЫХ ПОДIUИПЮIКЗХ, 2 - то JКС, в ПОДВЮIСНЬIХ , J - рама, 4 - пру
JКИНЬI, 5 - щиток, 6 - загрузочный бункер, 7 - ПЬIJ!сзащитная nласrина, 8 - привод

(шкив)

22.3.2. Основы технологического расчета

Захват валковой дробилкой кусков твердого материала
Угол захвата. Для валковых дробилок, как и для щековых,
существует проблема захвата кусков измельчаемого ТМ. Со
стороны левого валка 1 на кусок 2 исходного ТМ в точках их
касания действуют (рис .22.8) силы: Р
по линии центров вал
нормально к линии центров, т.е . по
ка и куска; трения Fт
касательной к окружностям валка и куска ТМ (будем для про
стоты считать кусок сферическим) . Разложим эти силы на со
ставляющие вдоль горизонтальной и вертикальной осей. Для
разрушения ТМ важны горизонтальные составляющие, а для
захвата куска
вертикальные: вьпалкнвающая Р8 и обусловли
вающая захват куска F3• Угол а. между горизонтальной осью и
линией центров будем именовать уrлом захвата. (Заметим:
иногда углом захвата называют и другие характерные углы
результаты анализа от выбора угла, разумеется, не зависят.)
З апишем условие захвата куска ТМ:
-

-

-

P8 s; Fэ .

(е)

Выразим эти силы (Р8 = Aina., F3 = Fт cosa. = Pfrcosa.) и под
ставим их значения в условие захвата (е), учитывая, что со сто
роны правого валка на кусок ТМ действуют такие же силы:

2 .A>ina. s; 2Pfr cosa. ,

rде fт - ко:эффи1D1екr внешнеrо трения, равный тангенсу угла ip внешнеrо ч>ения.

(ж)

Знаку равенства в (ж) отвечает предельное (максимальное)
значение угла захвата а.1 1 , знаку неравенства - рабочие режи
мы измельчения в ВД . Найдем из (ж) предельный угол захвата;
1635

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 22.8. Критические
диаметра валков ( J)

угол

захвата и соотно шение размеров кусков

ТМ (Z) и

после очевидных сокращений:

sin

а

пр

COS <X np

= tgetпp = fт = tgq> ,

откуда, соответственно предельному и рабочему режимам ВД,
(22.5)
(�пр = q>, а. < q>
Для щековых дробило к угол захвата является конструктивной
характеристикой: технолог сообщает конструктору предельную
величину этого угла (ап = 2ср) , и данное ограничение
(а. < 2ср - см. разд. 22.2.2 учитывается при проекrировании
IЦД. Для валковых дробилок значение Сtпр = ер является рабочей
(функциональной) харакrеристикой; оно самопроизвольно
устанавливается и выдерживается в процессе измельчения. При
а. < q> куски . исходного ТМ захватываются валками и разру
шаюгся; при а. > ер куски исходн ого ТМ не захватываются вал
ками и выталкиваюгся из рабочей зоны дробилки.
Предельное соотношение размеров куска и валка. Из рис . 22. 8
следует, что более крупному куску измельчаемого Т М сопут
ствует большее значен ие угла захвата, а предельному значению
угла Сtпр - больший предельный (т.е. максимальный) размер
исходного куска dпр · Все куски ТМ крупнее предельного не
будут захвачен ы валкам и, а мельче предельного - будут ими
захвачены и разрушен ы . Таким образом , задача о предельном
угле захвата здесь идентична задаче о предельном размере кус
ка исходного ТМ (или диаметре валка - см. ниже) либо о пре
дельном соотношении размеров куска и диаметра валка.
Найдем это предельное для ВД соотношение . Обозначим
(рис . 22.9): r и d = 2r, R и D - радиусы и диаметры соответ
ственно куска исходного ТМ и валка (предельные значения
будем выделять индексом "пр"); 2е - ширина щели (зазора)
между валками. Рассмотрим равновесную для ВД ситуацию: со•

f

1636

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис.22.9. К определению производительности валковой дробилки

отношения r/R = d/D равны предельным. Тогда из геометри
ческих соображений:

(R + е)пр = (R + r)пр соsапр .
(з)
Полуширина щели е обычно составляет 2-3% от R; для ин
женерного расчета отношения r/R величиной е в левой части
равенства (з) вполне можно пренебречь в сравнении с R
(физически это означает, что валки расположены вплотную
без зазора) . Решаем (з) относительно искомого предельного
соотношения:
1
1 - co s а п р
1
(и)
со s а п р
с оs а п р
-

_

=

Переходя от радиусов к чаще используемым в инженерных
расчетах диаметрам, получим:

(d)
D

Для многих ТМ

билок:

<р =

1 - соs а пр
пр

16-7- 17°.

(d/D)пp "' 1/20

=

Тогда из
=

(22 .6)

СОS <Х п р

(22.6)

следует д11Я

rладко11аJJковwх

0,05; dmax = D/20; Dmm = 20dн .

дро

(22.7)

В случае рифленой или зубчатой поверхности бандажей валковых дробилок
захватываются заметно более крупные куски : отношение (d/D)np там превышает

0,25-0,3.

Разумеется, можно решать задачу о предельном отношении
брегая величиной е.

d/D,

н е прене

В задачах эксплуатации (задан диаметр валков D) необходи
определить максимально допустимый размер куска
dпр = dmax исходного ТМ . Если рабочий размер куска d превы
шает dmax , то такой ТМ следует подвергнугь предварительному
измельчению (в других размольн ых машинах), чтобы ТМ, по1 637

мо

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

даваемый в валковую дробилку, не содержал кусков крупнее
dmax . В задачах проектирования (известен исходный размер dн
наиболее крупных кусков ТМ) необходимо определить мини
мально допустимый диаметр валка Dпр = Dmin, так как ВД с
меньшим размером валка D < Dmin не захватывает ТМ для из
мельчения .
Производительность валковой дробилки и ее регулирование
Производительность ВД. Она определяется в расчетах задач
эксплуатации; будем ее рассчитывать (см . рис . 22.9 ) в предпо
ложении, что захваченный дробилкой кусок ТМ движется вмес
те с валками без проскальзывания, т.е. с окружной скоростью
валков ФR = 2ппR, где й> - угловая скорость валка При длине
валка (и щели) Ь обьемный поток твердого материала V через жи
вое сечение Ь-2е, согласно уравнению расхода ( 1 . 1 8), составиг
.

V = 2Ье-2ппR

а массовый -

G=

Рт( l

- в

(м3/с)

,

) V = 4пРтЬепRµо (кг ТМ/с) ;

(к)
( 22 . 8 )

для ВД кон центрация измельчаемого ТМ в рабочем сечении
Ь-2е заметно меньше, нежели в щековых дробилках; поэтому
коэффициент разрыхлен ия µо = ( 1 - в ) здесь невелик (на уров
не 0,2-0,3) .
Реrулирование производительности ВД. При фиксированных
размерах Ь и R (т.е. для данной дробилки) регулирование воз
можно путем воздействия на е и п. При этом надо учитывать,
что изменению е сопутствует изменение размера кусков из
мельченного ТМ - это не всегда приемлемо с точки зрения
последующего использования измельченного ТМ. Основной
способ регулирования производительности ВД - изменение
частоты вращения (числа оборотов) валков п с помощью спе
циального вариатора.
Чаще всего рабочая окружная скорость валка находится на
уровне 2 , 0-4 , 5 м/с (но не выше 6-7 м/с) . Однако необходимо
иметь в виду ограничение по частоте вращения п: при чрезмер
ном увеличении п (сверх максимально допустимого птах) куски
исходного ТМ перестают двигаться с окружной скоростью вал
ка; они отстают, даже если исходный размер кусков не пре
вышает предельного значения по (22 .7). В результате:
- производительность ВД остается ниже рассчитанной по
выражениям (к) и (22 . 8 ) ;
- в нарушение осно вного принципа измельчения происходит повышен ное истирание ТМ, образование пыли;
- усиливается износ бандажей;
- возникает вибрация ВД;
- повышаются затраты энергии.
1638

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Теоретическое определение пПW< в настоящее время возможно только с
большими (и не всегда убедительно обоснованными) допущениями. В результате
приходят к формуле:
(22.9)

где dн - наибольший размер куска ТМ , подаваемого на измельчение.
Важно: коэффициент А - размерный, так •rro не следует требовать согласова
ния размерностей левой и праной частей равенства (22 .9).
Значение коэффициента А зависит от ряда трудно определимых факторов;
поэтому его устанавливают опьrrным путем, усредняя данные для различных ТМ
(используемых не только в химической промышленности, но и в строительной
индустрии, металлур гии и т.п. ) . Применительно к материалам, измельчаемым в
химической промышленности, усредненное значение множите.ля А "' 60, если в
правой части формулы (22 .9) все величины подставлены в СИ; тогда п получает
ся в ,- 1 .

Одна из задач проектирования состоит в расчете длины валка
Ь по формуле (22.8) при заданной производительности G с уче
том ограничений по п .
О расчете

затрат энергии на измельчение в валковых дробилках

Валковые дробилки являются нечастым примером размоль
нъ�х машин, для которых удается
структурировать и прибли*
женно описать затраты энергии : она расходуется на измельчение ТМ, преодоление сил трения при движении ТМ и трения в
подшипниках. Однако предлагаемая на этой основе теоретиче
ская формула для Nвд требует значительной корреJСГировки с
помощью КПД валковой дробилки: 't'lвд = 0,32-7-0, 3 8 . Суще
ственное отличие 't'l вд от единицы свидетельствует о том, что
пока не удалось устано вить и удовлетворительно описать со
ставляющие расхода энергии на измельчение в ВД.
22.4. БАРАБАН Н ЫЕ МЕЛЬНИЦЫ
22.4. 1 . Устройство

и п рин ци п ы

работы барабанных мельниц

Барабанные мельн ицы (БМ) чаще всего используются для
мелкого измельчения ТМ .
Общий вид одной из барабанных (здесь - шаровой) мельниц представлен в
разрезе на рис. 22 . 1 0, а. Во нращающемся цили ндрокон ическом барабане 1,
установленном под малым углом к горизонту, находится измельчающая
(дробящая) насадка из твердого износоустойчивого материала (в рассматри
ваемом случае - шары) . При вращении б<1рабана с достаточной скоростью
(частотой) шары (см. рис. 22. 10,6) поднимаются (под действием центробежной
силы), на некоторой высоте отрываются (под действием силы тяжести) от стенок
барабана и падают на слой насадки и измельчаемого материала. Траектория
падения шаров зависит прежде всего от соотношения действующих на шары сил
• П одробнее о затратах энер гии см. [ ! , 3 , 6 1 .

1 63 9

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

6

а

Рис. 22. 10. Uили ндроко н и ческая шаровая мельница:

процессуальная схема, б схема движеЮtя элемеmов насадки;
подшипЮtки, 2 броневые ПЛIПЫ, З - корпус (барабан), 4 зубчатый венец,
фундамеm, 6 заrрузочно-разrрузочный люх;
1 исходный ТМ, П - измельченный ТМ;
ШН
шаровая наС1111Ха
а

1

-

-

-

-

-

-

5

-

-

-

- центробежных и тяжести . Для защиты от разрушающего воздействия внутрен
няя цилиндрическая поверхность барабана футерована броневыми плитами 2.
Если в рабочей зоне (барабан с шарами) находится подлежащий измельчению
твердый материал, то падающая шаровая насадка измельчает его в результате
ударного воздействия. Одновременно часть шаров перекатывается в слое насадки
и измельчаемого ТМ; здесь измельчение происходит за счет истирающеrо, а
отчасти и раэдааливающеrо в оздействия шаров. Частицы ТМ , измельченного до
заданного размера, выводятся из мельницы. Назначение остальных узлов и дета
лей мельницы, изображенной на рис. 22. 1 0 , а , ясно из подрисуночной подписи .

В химической технологии используются БМ разных видов в зависимости от физико-механических свойств ТМ, степен и
измельчения , распределения измельченных частиц по времени
пребывания в рабочей зоне и по размерам . Соответственно
этим условиям и целям практически удобна следующая клас
сификация Б М по различным признакам .
1 . По типу насадки: шаровая , стержневая, галечная . Шары
(обычно диаметром 30- 1 70 мм) проще в изготовлении, зато их
воздействие на ТМ
точечное. Для стержней (их диаметр 3080 мм , длина - на 25-50 мм мен ьше длины барабана) харак
терно более эффективное воздействие
по линии. Шары чаще
применяют, когда нужн о усилить вклад ударного воздействия
на ТМ , стержни - вклад истирающего и раздавливающего воз
действия. Шары и стержни изгото вляются из специальной ста
ли или керамики (в частности, из фарфора) . В Б М использует
ся также природная окатанная (речная или морская) галька -

-

1 640

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

она значительно дешевле шаров и стержней, но по твердости и
механической прочности заметно уступает и м . Она быстрее
изнашивается (измельчается) , так что ее приходится чаще об
новлять ; кроме того , из мельчен н ая галька в большей мере за
грязняет целевой измельченный ТМ.
2 . По конфигурации: короткие (отношение длины
мельни
= 3+
цы к ее диаметру
составляет 1 , 5-2) ; трубчатые
6); цилиндрокониче ские. Короткие мельницы - дешевле, но в
н их велико перемеш и ва н ие измел ьчаемого ТМ и н иже одно
родность помола. В дли н н ых трубчатых мельницах заметно
сужен диапазон време н и пребыван ия ТМ в рабочей зоне , а
значит, меньше разброс в размерах измельчен н ых части ц .
Иногда трубчатые мельн ицы разделяют п о длине перфориро
ванными поперечными перегородками (непроницаемыми для
дробящей насадки, но проницаемыми для измельчаемого ТМ)
н а несколько рабочих зон , причем размер элементов н асадки
(шаров) умен ьшается от зоны к зоне (в направлении от входа
ТМ в барабан ную мельн ицу к его выходу) . В результате получа
ется еще более высокая однородность измельченного ТМ по
раз мерам . Корпус цилиндроконических
мельниц состоит из
двух конусов (обычно кругоrо со сторон ы подачи исходного
ТМ и полого го со стороны выгрузки ТМ), соединенных цилин 
дрической обечайко й . Основная часть рабочей зоны приходит
ся на цилиндр и пологи й конус . Пр и вращении барабана наи
более крупные шары сосредоточиваются в цилиндрической
части , более мелкие - в кон ическо й . Здесь два эффекта :
- ТМ последовательно измельчается первоначально в ц и 
линдрической з о н е (до некоторого промежуточного размера
частиц) и дополнительно - в кон ической зоне (до требуемого
конечного размера) . В результате получается измельченный
ТМ, более однородный по размерам ;
- значительная доля насадки функцион ирует в коническо й
части , что уменьшает затраты энергии (см . разд . 22.4 . 3 ) .
3 . По режиму функционирования Б М : периодического (чаще в
случае
малотоннажных производств)
или
непрерывного
(крупн отоннажные производства) действия .
4. По месту вывода измельченного ТМ : с торца БМ (как пока
зано на рис . 22. 1 0 , а ) или с ее боковой поверхности.
По среде, в которой ведется измельчение : сухой помол
(проще орган изация процесса измельчен ия) и мокрый помол
(мягче условия измельчения, более однородный гранулометр и 
чес ки й состав измельчен н ых частиц) .
6 . По характеру движения среды (газа или жидкости) в рабо 
чей зоне мельн ицы : непроточные (проще в изготовлении и э кс 
плуатации) и проточные (выше однородность в размерах частиц
измельчен н о го ТМ ; воз можно изменение конечн ых размеров

D6

Ь
(Ь/Dб

5.

1 64 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

частиц "на ходу" - путем "подхватывания" регулируемым пото
ком и выноса из рабочей зоны БМ частиц мельче определенно
го rраничного размер<i) .
22.4.2. Основные режимы движения насадки
барабанной мельнице (качественный анализ)

в

При вращении барабана разрушающее воздействие дробя
щей насадки на измельчаемый ТМ происходит благодаря вза
имному перемещению ее элементов. Это перемещение обуслов
лено сшzами (или их составляющими) , действующими на от
дельный элемент насадЮf (иногда - и на слой насадки в це
лом) : тяжести , центробежных , трения : внешнего - о стенки ба
рабана"- и (или) внутреннего - между элементами насадки. В
зависимости от решаемой задачи и режима движения элемен
тов насадки упомянутые силы могут оставаться постоянными
или изменяться от точки к точке во вращающемся барабане .
Условно можно выделить четыре основных режима движе
ния насадки во вращающемся барабане .
Режим 1 ре ал изуется при малых скоростях (частотах п) вра
щения барабана. Можно считать, что в этом случае элементы
насадки образуют связный сегмент, перемещающийся как одно
целое (рис. 22 . 1 1 , штриховка крест-накрест). Перемещение
сегмента (слоя насадю1) происходит за счет сил трения Т
(уточним: трения трогания) между наружной цилиндрической
поверхностью сегмента и внутренней цилиндрической поверх
ностью барабана - без проскальзывания (зазор между сегмен
том и цилиндром в нижней части пос�леднеrо на рис. 22. 1 1
ут
рирован). В результате поднимается центр масс сегмента Е и воз
никает (а по мере подъема точки Е - увеличи вается) составляю
щая Ре CWIЫ тяжести сегмента с насадкой, стремящаяся возвратигь
поднимающийся сегмент в более низкое положение. Когда эта
состаRЛЯющая превысит силу трения,
произойдет обрушение
связного сегмента. Далее ЦИЮI (подъем сегмента и ero обрушение
- без потери связности элементов насадки) повторяется.
Поскольку взаимное расположение элементов насадки в
пределах связного сегмента не изменяется, то их воздействие
на измельчаемый ТМ сведено к минимуму . Поэтому режим 1
движения насадки явл я ется для БМ нерабочим.
Режим 2 осуществляется при более высокой частоте вращения
барабана (п) . Здесь нарушается связность сегмента, и элементы
насадки получают возможность взаимного перемещения. Под
нявшись в верхние зо н ы сегмента, они скатываются (см. рис .
22. 1 1 ) вдоль наклонной плоскости сегмента - по ней и под
ней (при достаточном ее угле с горизонтом) - и измельчают
ТМ путем истирания и раздавливания.
1 642

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Реж:и.11 1

Рис. 22. 1 1.

Режим 2
К

основным

Режимы 3 , 4

режи м а м движения насадки в

БМ ( 1)

Данный режим - рабочий. Его используют, когда физико
механические свойства ТМ требуют применения такого спосо
ба измельчения (см . разд. 22.4. 1 ) , нередко - в стержневых
мельницах.
При дальнейшем увеличении п возникает и поддерживается
режим 3: элементы насадки под действием центробежной силы
поднимаются более высоко и под действием силы тяжести от
рываются от поверхности барабана (см. рис . 22. 1 1 ) . Падая на
насадку с ТМ, они измельчают материал пугем удара . Заметим ,
что в этом режиме продолжается перекатывание элементов
насадки по наклонной плоскости сегмента (в соответствии с
режимом 2) ; в зависимости от рабочих условий могуr превали
ровать ударное либо истирающее и раздавливающее воздействия .
Режим 3 является ра бочим. Его используют при измельчении
ТМ с различными физико-механическими свойствами (см.
разд. 22.4. 1 ) .
Наконец, при чрезмерно высоких п наступает режим 4: эле
менты насадки будут без отрыва от стенок барабана подни
маться до верхней предельной точки С. Достигнув этой точки,
они далее уже не отрываются от внутренней стенки барабана и
продолжают двигаться вместе с вращающимся барабаном (как
бы "прилипнув" к его внутренней поверхности). Измельчающее
воздействие элементов насадки в таком режиме опять сводится
к минимуму; этот режим - нерабочий.
22.4.3. Основы технологического расчета

Некоторые геометрические характеристики слоя дробящей насадки

На рис. 22. 1 2 схематично показан барабан внутренним ради
усом � и длиной Ь с н асадкой в рабочем положении (на ри
сунке она помечена штриховкой) . Барабан вращается по часо1 643

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 22. 12. Схема барабана с сегментом измельчающей насадки

вой стрелке. Схематизация заключается в допущении о плос
кой (на рисунке - слегка волнистой) rранице а сегмента
(заполненного измельчающей насадкой, например шаровой) с
остальным пространством барабана. Введем ряд геометрических

-

параметров и соотношений:

F площадь поперечного сечения барабана;
S - сечение барабана, занятое дробящей насадкой ;
'V - центральный угол (в радианах) сегмента с насадкой ;
р = Sb/Fb = S/F - степень заполнения барабана слоем насад
ки (именно слоем , а не насадкой, - с учетом просветов между
ее элементами).
Величину S найдем как разность площадей сектора S', охва
тывающего сегмент, и треугольника S " основанием а и высотой
h. Очевидно:
S' =

� 1tR 2 ; S "
б
21t

=

ah

2

=

( ) � cos( 2 )

2� sin �
2

"'

·

2

при записи вычитаемого применена формула
ного угла.
Площадь сегмента
'V
S = S' S " = R 'V sin

-

-

2

6

2

=

для

sin '1'

2

R2 ;
б

синуса двой
(а)

объем, занимаемый слоем насадки, определится как Sb.
Относя теперь S к F = 7tRe,2 , после сокращения числителя и
знаменателя на Ri2 получим (в принятом приближении о форме
слоя насадки) степень заполнения:
'V
S' S"
sin '1'
=
(б)
р = ---'-�
F
21t

-

1 644

-

--

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

причем физически допустимо О ::;; � ::;; 1 ; практически р , есте
ственно, заметно мен ьше 1 . Отметим : р выражается в зависи
мости от '1' в явном виде; утол '1' при заданном р приходится
отыскивать численными методами .
Масса насадки (плотность ее материала - Рн) в сегменте
т
( е) при средней его порозности &н определяется как
1tD б2
т
е = Рн( l - f.н)Sb = Рн( l - &н) -- р Ь =
4
2
D
= РнО - &н)
b('I' - Sll1\j/) .
(в)

Т

Центр масс сегмента с насадкой (точка Е) находится на рас
стоянии Гц от оси вращения барабана:
гц
i я sin з ('I' / 2)
=
(г)
б
3
'1' - sin '1'

Границы технологических режимов

·

Ранее было отмечено, что основными способами измельче
ния ТМ в мельницах являются удар и истира ние (а также раздавливание) .
В задачу технологического анализа и расчета входят* оценки
границ упомянутых режимов, а для рабочих режимов - еще и
установление связей геометрических харакrеристик барабана и
дробящей насадки с параметрами работы БМ. Среди основных
технологиче ских факгоров:
- степень заполнения р дробящей насадкой рабочего объе
ма БМ;
- частота вращения п ;
- утол а.е зоны перекатывающейся насадки при истирающем и раздавливающ ем ее воздействии;
- утол отрыва а.0 эле ментов насадки от поверхности барабана при ударном воздействии .
В целях упрощения последующего анализа примем:
- насадка - шары диаметром dш ;
- для режимов 2 - 4 рассматривается поведение единичного элемента насадки;
- насадка до момента отрыва находится в контакте с ци
линдрической поверхностью барабана;
- в момент отрыва шар теряет контакт с корпусом барабана;
- диаметр шара dw знач ительно меньше , нежели барабан а

• Подробно проблемы технолоmческоrо анализа барабанных мельниц см.

(1,

3, 6] .

1 645

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

D6, так что вполне можно считать, что шар находится на ради
усе � (а не � - dш fl) .
Режим 1 . Расчет сводится к определению предельного
(максимального) угла (а.�)пр. на который без обрушения можно
повернуть связный сегмент дробяшей насадки (см. рис . 22. 1 1 ) .
Равновесие сегмента массой те (непосредственно перед обру
шением) означает равенство противоположно направленных
моментов сил - трения Т и составляюшей Ре веса Р = те�: на
садки в сегменте .
Сила трения записывается как произведение коэффициента
внешнего трения fт и силы нормального давления; последняя
формируется как сумма центробежной силы тero 2 r и радиаль
ной составляюшей силы тяжести щ;gcos(a.i)пp · Плечо силы тре
н ия - �. Врашаюшая составляюшая силы Ре выражается как
Ре = щ;gsin(a,i )пp; ме чо - ОЕ = rц (рис. 22. 1 2). Равенство указаннь1х М()
ментов, связываюших предельный (максимальный) угол подъе
ма цельного сегмента (а.�)пр и частоту врашения п, имеет вид:
h[ тero 2 rц + тс�:· соs(щ )пр ] � = щgsin (<ч )пp rц .
После сокрашения на те и запис};?: ro = 21tn получим связь
(а,�)пр и п при заданной степени заполнения барабана р, по
скольку rц записывается через центральный угол "'' а тот, в
свою очередь, по (б) связан с р - см . рис . 22. 1 2 и 22 . 1 3 .
Режим 2 . Основным в е го расчете является установление
условий работы БМ в режиме истирания и раздавливания. По
скольку здесь элементы насадки в рабочем се гменте теряют
связность, то анализ приближенно ведется для единичного эле
мента массой т3• На рис. 22. 13 изображено поперечное сечение
БМ радиусом �. вращаюшейся по часовой стрелке (направ
ление врашения показано в правом нижнем квадранте). Пусть
элемент находится в точке К1 , характеризуюшейся углом а,,
отсчитываемым от верхней· вертикальной оси (или а,' = 7t - а, от нижней вертикальной оси). Тогда на элемент по касатель
ной к окружности барабана действуют конкурируюшие силы:
скатывающая Ре и трения Т. Разлагая силу тяжести (вес элемен
та Рэ = т"ЭК) на составляюшие, получим :
- танген циальную скатывающую силу, препятствуюшую
подъему элемента насадки: Ре = т"ЭКSinа,' = т"ЭКSinа,;
- тангенциальную силу трения Т, способствуюшую подъему
элемента насадки: она рассчитывается как произведение суммы
центробежной силы m3ro 2 � и нормальной составляюшей N
силы тяжести элемента N = т"ЭКСОS<Х-' = -т"ЭКСОS<Х- на коэффици
ент внешнего трения fт:
(д)
Т = (т3rо 2 � - т"ЭКСОSа.)fт .
Заметим, что выраже ние для Т в равной мере справедливо
для а. < 1t/l и для а. > nfl - скажется знак тригонометрической
функции .
1 646

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 22. 13. К расчету режимов движения насадки в барабанной мельнице

В точке К1 возможно различное соотношение Действующих
сил Ре и Т. Очевидно, при Ре ::;; Т элементы насадки у стенки
барабана будут подниматься безотрывно с ero окружной ско
ростью roR , при Ре > Т - отставать от вращающейся стенки
барабана, сползая или с�а.тываясь по ней. По мере подъема
элемента насадки (роста
понижения ) на участке А-В
происходит увеличение скатывающей силы Ре (в точке А Ре =
= О , в точ к е В Ре = т�) и уменьшение силы трения Т (за счет
уменьшения нормальной составляющей N силы тяжести: в точ
ке А N = т�, в точке В N = О); центробежная сила при безот
рывном движении элемента насадки одинакова во всех точках
поверхности барабана: w � .
В рассматриваемых идеализированных условиях возможность
сдвига элеменrа насадки по поверхности барабана (иначе рав
новесие элемента около этой поверхности) реализуется в некото
рой точке К2 (рис.22. 13) и определяется равенством сил Ре = Т
После подстановки значений этих сил и сокращения на т3 имеем:
(е)
gsiнa. = (ro p2 �
gcosa.)fт ,
-

'
а. ,

а.

-

-

где угловая скорость

шр

отве'1ает равновесию элемента насадки .

Значение равновесной частоты вращения барабана пр
в рассматри ваемом идеализированном случае найдем , под 1 647

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

п =
Р

g (sin о. + fт cos o.)
2п

(22 . 1 0)

fт %

Для определения по формуле (22 . 10) равновесного угла о.р
при рабочей частоте вращения барабана п используют числен
ные методы.
*
В технической литературе выражения типа (22. 1 О) иногда
упрощают, сокращая численно практически равные g п2 Это
справедливо, например, для единиц СИ (принята в настоящем
учебнике) или М КС .
На участке А - В элемент насадки в точке К1 (рис . 22 . 1 3) у
внутренней цилиндрической поверхности барабана не может
оторваться от нее: действующая на элемент радиальная резуль
тирующая сила, стоящая в скобках выражения (е), направлена
от оси вращения . На участке В- С нормальная составляющая
веса элемента направлена к оси вращения; поэтому здесь воз
можно неравенство 2R;:, < gcoso., приводящее к отрыву эле
мента от поверхности барабана.
Указанные расхождения в идеализированных ситуан,иях на
участках А- В и В- С вряд ли позволяют сопоставлять пове
дение элементов насадки в точках В и С. Тем более неправо
мерно использовать формулу (22 . 1 0) для анализа некоторых
реальных предельных ситуаций вследствие существенных разли
чий в реальных и идеализированных условиях работы БМ.
Во-первых, рассматриваемый элемент насадки сложным об
разом взаимодействует с другими элементами. Он не может
сползать вниз даже при благоприятном для этого соотношении
сил, так как вслед за этим элементом движутся и его
"подталкивают" находящиеся ниже элементы. При этом рас
сматриваемый элемент может потерять контакт с поверхностью
барабана - тогда сила внешнего трения Т падает до нуля. И
если плоская поверхность сегмента (штрих-пунктир на рис
22. 1 3) расположена достаточно круто (ее угол с горизонтом
равен углу естественного откоса Уе или превышает Уе), то рас
сматриваемый элемент насадки будет сползать (частично перекатываться) по плоскости сегмента, осуществляя исти
рающие и раздавливающие воздействия на измельчаемый ТМ .
�

.

й)

Уrлом естественноrо откоса Уе называется угол, образуемый сыпучим материа
лом (здесь - дробящей насад кой) с горизонтальной плоскостью при высьmании
из воронки (рис. 22. 14). Этот угол близок к углу внутреннего трения сьmучего
материала.

•

См"например, ( 1 ,

2,

6).

•• Как это сделано в (6 ) .
1 648

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 22. 14. Уrол естественноrо откоса сыпучеrо
материала

Из геометрических соображений
следует, что углу Уе отвечает централь
НЬIЙ уrол сегмента с насадкой <:х.е = 7t
ЧJ/2, причем угол 'V связан со сте
- уе
пенью заполнения барабана /3, так что
<Х.е = <:х.е(Уе, /3) .
(22. 1 1)
Во-вторых, только внешний ряд дробящих элементов нахо
дится на радиусе �. другие элементы насадки - на радиусах
r < �· Для элементов, находящихся и двигающихся на этих
меньших радиусах r, характерны количественно иные значения
скатывающих и центробежных сил (и их соотношений), а так
же нормальных с ил , способствующих (в левом верхнем квад 
ранте) отрыву элементов насадки.
Приближенно можно считать, что режим 2 реализуется при
определенном (характерном) положении сегмента с дробящей
насадкой - угол его плоскости с горизонтом равен Уе (или чугь
превышает Уе) . Минимальную частоту вращения п2' , при кото
рой наступает режим 2, можно оценить по формуле (22. 10),
полагая п' "" пр при а = а.е; в свою очередь, <:х.е отыскивается по
(22. 1 1). Повышение п сверх n' не изменяет существенно поло
жения сегмента, увеличивается лишь интенсивность движения
элементов дробящей насадки, а значит, истирания и раздавли
вания измельчаемого ТМ. Максимальная частота вращения п "
ограничена переходом к режиму З - см. ниже формулу (22. 1 3 )
при а.о "" а.е.
Разумеется, реальные технологические задачи могуr потре
бовать определения и других параметров процесса, например
определения при заданном п степени заполнения барабана
насадкой (/3).
Режим 3 . Здесь ударное воздействие дробящей насадки реа
лизуется при ее падении на верхнюю границу рабочего сегмен
та, занятого перекатывающейся насадкой и измельчаемым
твердым материалом. Технологическая проблема состоит в
обеспечении условий для отрыва элемента насадки от внут
ренней стенки вращающегося барабана в зоне В- С. ОчевИдно,
что при низкой частоте вращения барабана в единицу времени
(п) отрыва шара, а значит и удара, не произойдет: элементы
насадки будуг перекатываться в сегментной зоне (см. выше). А
при чрезмерно высоких значениях п шары достиmуг точки С
("приmmнув" к стенке барабана под действием центробежной си
лы) и далее будуг двигаться вниз вместе со стенкой вращающегося
барабана без проскальзывания. В такой ситуации отрыв насадки
от барабана просто не соt.-тоится режим 4 (см. ниже).
-

-

-

1 649

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Ударное воздействие шаров на ТМ в режиме 3 обеспечи
вается расположением точки К3 отрыва на участке В- С внут
ренней цилиндрической поверхности (рис . 22. 13). Будем харак
теризовать положение точки Кз угл ом о тры ва а.о . Оценим с
принятыми допущениями связь числа оборотов п с углом а.о и
геометрическими характеристиками барабана.
На шар массой т3 у поверхности барабана вдоль радиуса
действует центробежная сила т3m 2 �' препятствующая отрыву
шара и не зависящая от положения точки отрыва К3 . Одновре
менно на шар действует сила тяжести т�; ее радиальная со
ставляющая N = т�· с о sа. способствует отрыву шара. Состав
ляющая N увеличивается при перемещении точки отрыва К3 по
внутренней поверхности барабана от положения В к положе
нию С, поскольку cosa. возрастает с уменьшением а.. В момент
отрыва шара от поверхности барабана силы, способствующие
и препятствующие отрыву, уравн иваются :
т�· со sа.о = m3ю 2 � .
(е)
Отсюда, сокращая на т3 и выражая

мую связь а.0, � и п:

2
cosa.o - (2пп)
g
_

0_
''О

_

(J)

через п, имеем иско

2(пп) 2 D
б
g

.

(22 . 1 2)

Из (22 . 1 2) прямо определяется угол отрыва а.0 элементов на
садки, находящихся в контакте с поверхностью, т.е. при r = �
(задача эксплуата ции) . Для шаров, находящихся ближе к оси
барабана (r < �), угол отрыва будет отличаться от найденного
из выражения (22 . 1 2) для r = �. Физически это объясняется
уменьшением (при r < �) центробежной силы, препятствую
щей отрыву. Элементы, находящиеся ближе к оси вращения
барабана, тоже участвуют в измельчении материала. Если счи
тать, что эти элементы вращаются с такой же угловой ско
ростью (ffi , п), то угол их отрыва будет больше (так как косинус
- меньше) найденного по формуле (22. 12).
Решая (22. 1 2) относительно п и л и � (либо D6 ) п р и заданном
угле отрыва а.о (задача проектирования), находим:

п

=

и

J

_1_ g cos a.0
2п

Rб

=

J

_1_ g cos a. o
п

.fi.

Dб

(22 . 1 3)

g cos a. 0 .
g cos a. 0
(22. 14)
, D6 =
2
(2пп)
2(пп) 2
Ф ормулы (22 . 1 2)-(22 . 1 4) позволяют проследить связь основ
ных факторов - п, а.0 и D6. Так, при увеличении частоты вра1650
�

=

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

щения п угол отрыва а.о в барабане данного диаметра D5
уменьшается, и точка отрыва К3 смещается к точке С. В бара
банах большего диаметра D6 пр и сохранении п угол отрыва а.о
тоже становится меньше. В обоих этих случаях возрастает дей
ствующая на шар центробежная сила, и для ее компенсации
требуется увеличить нормальную составляющую N силы тя
жести, т.е. уменьшить а0. При переходе к барабанам большего
диаметра для сохранения угла отрыва потребуется снизить час
тоту вращения п . (Анализ взаимного влияния параметров рабо
ты мельницы можно продолжить.)
Из уравнения (22.13) можно найти предельное (максималь
ное) значение п = птах (нижняя граница режима 4), при кото
ром отрыв шара в барабане диаметром D6 должен произойти в
верхней точке С (а.о = О, cosao = 1 ):
п

тах

=

тt� J_;6 .

(22. 1 5)

При таких и больших частотах вращения п ;;:: птах элемент
насадки (шар), без отрыва пройдя верхнюю точку С, далее
(точка 14 на рис. 22. 1 3) оторваться от поверхности барабана
уже не может: центробежная сила остается постоянной, а со
ставляющая N веса шара уменьшается .
Анализ может быть выполнен и для элементов насадки, находящихся в момент отрыва ближе к оси барабана - на ради
усах r < ilf,.
Наибольшему ударному воздействию отвечает опrимальная
частота вращения барабuна по рt· Для оценки порt теоретически
исследуют* траекторию падения элемента насадки и отыскива
ют угол отр ы ва, соответствующий максимальным высотам и
скоростям падения этого элемента. Обычно принимают:
по рt (0,6 -;- О, 75)птах .
(ж)
Режим 4. Этот режим, возникающий и существующий при
> птах, как указывалось выше, является нерабочим.
п
•

�

НекоторЫе эксплуатационные характеристики барабанных мельниц

Степень заполнения барабана дробящей насадкой (13) колеб
лется в весьма широких пределах: от 0,2 до 0,6 (чаще всего
0 ,3 � р � 0,5).
Отдельная проблема - выбор размера элементов насадки.
Здесь используются эмпирические рекомендации, базирую
щиеся на двух феноменологических подходах, - продемон
стрируем их применительно к шаровой насадке.
• С м. ( 1 , 3, 6 ) .

1 65 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Первый подход ориентирован на ударное воздействие насадки и исходит из
организации движения шаров в БМ. П оэтому он базируется на отношении диаметров шара dw и барабана D6: dw /Dб "' О/20- 1/30); приводятся и несколько
иные соотношения. Второй подход ориентирован на истирание ТМ и потому
dmax измельчаемоrо
исходит из максимальноrо на•1альноrо размера кусков d
твердоrо материала: ( dш.) max "' (25 7 30) �dmax. ; здесь максимальные диаметры
шаров ( dш.)max и исходно rо ТМ ( dmax) выр ажены в м илли м етрах.
=

В ходе работы мельницы измельчается не только целевой
ТМ, но и сама дробящая насадка (шары) - конечно , много
медленнее . При этом отдельные шары измельчаются по
разному, так что в рабо•1ем пространстве БМ содержатся шары
разных размеров. Поэто му периодически насадку восполняют,
добавляя в БМ наиболее крупные шары - их размер соответ
ствует приведенным выше практическим рекомендация м .
О затратах энергии н а измельчение в барабанных мельницах
БМ представляют собой размольные машины , для которых
затраты энергии (см . разд . 22. 1 .2) на перемещение рабочих ор
ганов (барабана с насадкой) значительно выше , нежели на соб
ственно измельчение ТМ. Нагляднее всего это иллюстрируется
формулой Барта, в которую не входят физико-механические
свойства ТМ , так как здесь доминирует расход энергии
"холостого хода" :

(22 . 1 6)
Мощность NБм получается в кВт, если вес барабана с на
садкой GБн подставляется в т, а диаметр барабана Dб выражен
в метрах. Размерный коэффициент С0 при частотах вращения
барабана, близких к n0p1 , зависит от степени заполнения бара
бана дробящей насадкой р :
р . . . 0,2
С11 . . . 8

0, 3

7

0,4
6

Вид формулы (22 . 1 6) и м еет определенные теоретические основания. Ч ислен
ные значения Со при разных р автор получил эмпирически - в результате об
следования (при разных услониях) многочисленных мельниц для измельчения
цемента. В случае измельчения других материалов (в том числе превосходящих
цемент по прочности) он рекомендует - скорее всеrо из осторожности (!?) увеличивать рассчитанное по (22. 16) значение NБм на 10%.
Если быrь последовательным, резонно было бы включить в G Бн еще и вес
измельчаемоrо материала G т м в рабочей зоне БМ . Но посколь ку Gтм << G i; м ,
то и эта поправка несущественна.

1 652

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

22.5 .КОЛЛОИДНЫЕ МЕЛЬНИЦЫ МОКРОГО ПОМОЛА

Коллоидными мельницами (КМ) называются размольные
машины, измельчающие ТМ от начальных размеров (обычно
это доли миллиметра) до конечных - порядка 10-4- 1 0-6 мм .
Столь мелкие частицы имеют склонность к слипанию (из-за
высокой поверхностной свободной энергии); поэтому их как
правило подают в мельницу в виде суспензии ("мокрый по
мол " ). В качестве дисперсионной (сплошной) среды использу
ются нейтральные к ТМ жидкости, причем объемная концент
рация ТМ в суспензиях обычно колеблется в диапазоне от 1 5
до 3 5 % (абс.).
Механизм коллоидного измельчения в настоящее время изучен
слабо, поэтому ограничимся рассмотрс::нием устройства и принци
пов работы одной из размольных машин данного IOiacca.
На рис. 22. 1 5 , а предстаалена коллоидная мельница мокрого помола. В кор
пусе 1 с коническим mездом Ja вращается с высокими скоростями (n
300-7500 с- 1 , окружная скорость - 30-125 м/с) ротор 2. Межцу mездом корпуса и
ротором имеется малый зазор Б (десятые, иногда и сотые доля милли метра) .
Величину Б реl)'лируют микрометрическим винтом J. Исходную суспензию
подают в КМ через входное отверстие (поток /), образующийся коллоидный
раствор выводят через отверсти е (поток //) .
=

Доминирующий в КМ способ воздействия на ТМ - истира
целью рассмотрения на качественном уровне влияния
основных факторов, воздействующих на измельчаемую частицу
111, на рис. 22. 1 5,б в укрупненном масштабе показан фрагмент
ние. С

5
ш
la

дХ

а

б

Рис.22. 15. Коллоидная мельница мокрого помола:
5-

- устройство мельницы,
б - к механизму измельчения;
1 - корпус, Ja - коническое rнездо, 2 - ротор, З - микровинr, 4 - приводной шкив.
рабочая зона мельницы (зазор) :
1 - исходная суспензия, JI - коллоидный раствор, Jll - измельчаемая частица

а

1 653

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

рабочей зоны (на рис. 22. 1 5,а он обозначен символом ф ) Для
удобства анализа стенI01 корпуса и ротора изображены верти
кально, зазор 8 - горизонтально.
Согласно "концепции прилипания" (разд. 1.3.2), скорость
жидкости у поверхности равна скорости движения самой по
верхности. Обозначим: х - текущая горизонтальная координа
та, и - окружная скорость. Тогда относительно неподвижного
"

"

.

наблюдателя:

- скорость жидкости у неподвижной стенки корпуса (т.е. при
О) равна нулю;
- ее скорость у стенки вращающегося ротора (при х = 8)
совпадает с окружной скоростью движения ротора и, т.е. очень
высока - на уровне 1 00 м/с.
Большие перепады скоростей на малых расстояниях
(порядка толщины зазора) означают очень высокие градиенты
скоростей в рабочей зоне. Применительно к измельчаемой час
ти�е градиент скоростей можно записать (см. рис. 22. 1 5,6):
ди/дх ::;; ли/лх, где Ли - разность скоростей на боковых по
верхностях частицы, ЛХ - оценка ее поперечного размера. А
высокий градиент скоростей приводит по формуле ( 1 .9) к боль
шим тангенциальным (срезающим) ус илиям 'tт на боковых по
верхностях разрушаемой частицы: 'tт - ли/лх. В результате в
рабочей зоне происход ит дисперmрование ТМ - отщепление
от частицы 111 мельчайших частичек коллопдных размеров.

х=

Л ИТЕРАТУРА

к главе 2 2

1 . Гельперин Н.И. Основные процессы и аппараты химической технологии.
М . : Химия, 1 98 1 . 812 с.
2. Касаткин А. Г. Основные процессы и аппараты химической технологии.
М . : Химия, 1 97 1 . 784 с.
3. Левенсон Л. Б. Маш и н ы для обогащения полезных ископаемых. М . -Л . :
Госмашметиздат, 1 9 3 3 . 8 0 3 с.
4 . Левенсон Л. Б. , Цигел ьный П. М. Дробильно-сортировочные машины и
установки для переработки каменных материалов. М . : Сrройиздат, 1952. 428 с .
5 . Плановский А.Н., Николаев П.И. Процессы и аппараты химической и неф
техимической технологии . М . : Химия, 1972. 494 с.
6. Сиденко П. М. Измельчение в химической промьШUiенности. М.: Химия,
1 977. 368 с.
7 . Циборовский Я. Процес.сы химической технологии: Пер . с польск. Под
ред. П .Г. Романкова. Л . : Госхи миздат, 1958. 932 с.

/

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Глава 23
КЛАСС И Ф ИКАЦИЯ ЗЕРНИ СТЫХ МАТЕРИАЛ ОВ

23. 1 . О Б ЩИЕ CBFJJ;EHИЯ

Исходные зернистые (сьmучие) материалы, с которыми имеюr
дело в химической и смежных технологиях, как правило, пред
ставляюг собой смеси зерен (кусков, часпщ и т.п.), существенно
различающихся по свойствам: размерам, плоrностям, форме, хи
мическому составу, смачиваемости, цвету (блеску) - перечень
таких свойств (признаков) можно продолжиrъ . Между тем кон
кретное производство зачастую оперирует наборами зерен, имею
щими ограничения по каким-либо из этих свойств. Тогда из ис
ходной смеси необходи мо выделить отдельные классы, обла
дающие требуемыми свойствами или совокупностями свойств
(разумеется, · в идеале надо стремиться к ·тому, чтобы и друmе
Юiассы нашли свое технолоmческое применение).
Разделение исходной смеси сыпучих материалов, содержащей
разнородные зерна, на отдельные классы (фракции) по какому
то признаку называется классификацией (иногда применяют
термин сепарация) .
Общие цели классификации:
- разделение исходной смеси зернистых материалов с раз
ными свойствами на отдельные классы - такие процессы име
нуют собственно классификацией;
- отделение от исходной смеси зерен, обладающих (или не
обладающих) необходимыми свойствами - такие процессы
называюr сортировкой .
Примером собственно классификации может служить разде
ление полидисперсной смеси на различные классы по круп
ности зерен с последующим использованием этих классов
(скажем, более крупных - для осуществления процессов в не
подвижном слое, а более мелких - в псевдоожиженном слое
или в пневмотранспортных системах). Примером сортировки
является отделение недопустимо крупных кусков после дро
билки с целью их возврата (рецикла) на повторное измельчение
(см. разд. 22. 1 .З).
Общее назначение классификации:
- выделение узких классов зернистых материалов, облада1 655

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ющих определенными признаками, и последующее использо
вание каждого такого однородного класса (на пракгике часто
- лишь некоторых из них);
- приrотовление достаточно узких классов, а затем из них смесей (например, заданного гранулометрического состава), в
наибольшей степени отвечающих: оптимальным условиям про
ведения последующего технологического процесса.
Укажем, что классификация зернистых материалов приме
няется не только в технологических (промышленных) целях, но
и как метод анализа , позволяющий установить распределение
зерен в смеси по исследуемому признаку (например, по разме
ру зерен).
Существуют различные методы классификации сыпучих ма
териалов"; для химичес кой технологии будем считать основными
три из них: грохочение, классификацию в тяжелых средах, гид
равлическую (пневматическую) классификацию.
Грохочением называется разделение зерен по размерам (в
определенной мере - и по форме) на сите, решете - грохоте.
Принцип грохочения - провал зерен через отверстия (про
светы) определенных размеров: мелкие зерна проваливаются
через отверстия, крупные - остаются на сите. Набор сит по
зволяет получать несколько классов, каждый - в диапазоне
определенных граничных размеров.
В промышленности грохочение используют для классифи
кации зерен размером от 250 до 1 мм (иногда - несколько ме
нее), в лаборатории - до 0,05 мм Более мелкие частицы на
сите разделить не удается: они обладают очень большими
внешними поверхностями и поверхностными (свободными)
энергиями, поэтому образуют устойчивые агломераты непосто
янного (значит, неопределенного) размера.
Разделение в тяжелых средах ведется в поле массовых сил
(преимущественно - сил тяжести) в зависимости от плотно
стей зерен. Тяжелая среда подбирается промежуточной плот
ности, так что более тяжелые зерна в ней тонут, а более легкие
- всплывают. Разделение в тяжелых средах оперирует относи
тельно крупными зернами (чаще всего 1 мм и более), так
как мелкие частицы тонут и всплывают в тяжелой среде мед
ленно, и процесс становится малопроизводительным.
Гидравлическая и пневматическая классификации построены
на взаимодействии зерен твердого материала (ТМ) с жидкост
ным или газовым потоком в поле массовых сил. Здесь исполь
зуется несолидарное движение зерен в потоке: они движутся с
отставанием от потока (в более редких случаях - с опережени.

• Подробно сведен ия о р азнообразных методах классификации, устро йствах
для их реализации и подход<1х к технологическому расчету см. (7-9 , 1 1 )
.

1656

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ем). При этом зерна разных размеров, плотностей , формы от 
стают от потока в разной мере, что позволяет отделить их друг
от друга, т.е. произвести классификацию.
Гидравлическая и пневматическая классификации отлича
ются большим разнообразием конкретных исполнений. Приз
нак, по которому здесь происходит классификация, базируется
на скоростях витания или на инерционных свойствах частиц,
иногда - на сочетании этих факторов.
В промышленности методами гидравлической (пневмати
ческой) классификации разделяются смеси с размерами зерен
от 5 до 0,05 мм, в лаборатории нижний предел размеров удает
ся ПОН ИЗИТЬ ПОЧТИ ДО 1 МКМ.
Нередко использован ие какого-либо одного метода класси
фикации не дает приемлемых результатов; должный технологи
ческий эффекг достигается при сочетании (последовательном
применении) разных ме юдов.

Ниже рассмотрены основные методы классификации и обо
значены некоторые другие возможности разделения сыпучих
материалов.
23.2. ГРОХОЧЕНИЕ

23.2. 1 . Общая характеристика метода

Процесс грохочения предназначен для разделения твердого
материала на фракции, различающиеся размерами кусков, зе
рен, частиц с целью:
- раздельного технологического использования разных
фракций;
- составления композиций разного гранулометрического
состава;
- ситового (гранулометрического) анализа смесей сыпучих
материалов.
Для классификации методом грохочения применяют рассеи
вающие устройства
грохоты: решетки из параллельных
стержней (колосников); решетки из металлических листов со
штампованными отверстиями; плетеные или тканые сита.
Колосники, применяемые при классификации крупных
(десятки и сотни миллиметров) кусков, представляют собой
металл и ческие стержни (обычно трапеце идального сечения) ,
иногда - трубы . Трапециевидная форма колосников облегчает
проход кусков материал а через расширяющиеся книзу зазоры
между колосниками .
-

1 657

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Решета из готавли вают из металл ических листов толщиной
2- 1 2 мм, в которых штампуют круглые или продолговатые
отверстия размером от 3 до 30 мм. Чтобы отверстия не заби
вали сь, их иногда выполняют расширяющимися книзу. На ре
шетах классифицируют мелкие куски, зерна среднего размера.
Сита изготавливают с квадратными или прямоугольными
отверстиями. Плетеные сита, изготавливаемые из металли
ческой проволоки, . имеют отверстия от нескольких миллимет
ров до долей миллиметра; они предназначены для рассеивания
относительно крупных частиц. Тканые сита, предназначенные
для классификации мелких частиц, имеют отверстия в десятые
и сотые доли миллиметра. Ткань сита изготавливают из корро
зионно-стойких материалов (нержавеющей стали, латуни , ка
прона и т.п.).
Размеры отверстий сит регламентированы стандартом, их
суммарная площадь составляет 36% от всей площади сита; ми
нимальный размер стороны .квадратного отверстия равен
50 мкм. Пло щад и двух последовательных отверстий сит в оте
чественном стандартном их наборе (i-го и i+ l -гo, считая свер
ху) различаются в 2 раза, т.е. изменение линейных размеров
отверстий d1/d1+1 = J2
это отношение называют модулем
сита.
-

Для проведения 111анулометрическоrо анализа просеивают среднюю пробу сы
пучего материала и взвешивают остатки материала на кццо м из сит. Отношение
полученных масс к массе материала, взятого д11Я анализа, дает содержание раз
.личн ых фракций частиц в материале, т.е. частиц, ограниченных по размеру
определенными верхним и н ижним пределами d1 и d;+t·
П олученные в результате просеивания на грохоте сьmучие материалы чис
ленно характеризуются размером отверстий сита (в мм), поJШостью пропус
кающего их (со знаком " ) и размером отверстий сита, поJШостью задержи
вающего их (со знаком "+"). Так, сьmучий материал, прошедший сито с от
верстиями 2 мм, обозначается как -2, а оставшийся на сите - как +2. Фракции
(классы) сыпучих материалов обозначаются размерами сит, соответствующих
предельным размерам зерен данного класса. Например, ее.ли класс получен
последовательно просеиванием на ситах с отверстиями 4 и 2 мм, то его обозна
чают так: -4+2. Это означает, 'ПО в данном классе нет (знак
) зерен крупнее
4 мм, но остались (знак "+") все зерна крупнее 2 мм.
В результате ситового анализа получают характеристику сыпучего материа
ла - его фракционный (111анулометрический) состu.
-"

,

"_"

Грохочение сыпучих материалов осуществляется при движе
отн о с ительно рабочей поверхности rрохота. Огноси
движение материала создают либо на неподвижном
rрохоте, установленном под углом к горизонту, превышающем
угол внешне го трения материала о сито, либо на движущихся
различным образом рабочих поверхностях rрохота.
В рез ультате грохочения на одном сите получают два про
дуюа: зерна, прошедшие через рассеивающее устройство, -

нии их
тельное

1 658

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

1

-60 +30.м.w

- 1 5мм

б

а

- 1 5мм
в

Рис.23. 1.

-60 +) 0Al.Af

- 1 5.м.w

-30 + 15мм
г

С п особы мноrокраmоrо rрохочения:

- ar мemc:oro к круmюму, б - ar крупноrо к меmс:ому, 1, г - комбИЮ1рованные ;
1 - поверхность rрохочеЮtя, 2 - корпус rрохота, З - усrройсrва (бункеры) вывода
фра�сцЮt ;
1 - исходная смесь ТМ, J/- V - отдельные фраJС:ШОI ТМ (с yвeJDAcIOtcM размера эсрен
ar фр&JЩИИ 1/ к фр акции JI)
а

отсев (или нижний продукт), и не прошедшие через рассеи
вающее устройство, - отход (или верхний продукт) .
Эффективность f1Jохочения характеризуют на общих для про
цессов разделения основаниях (см . разд. 1 0. 1 7).
Грохочение проводится через одно сито (решето, колосники)
или последовательно через несколько сит - мвоrократиое flJОХо
чевие. Последний вариант реализуют тремя способами:
- от мелкоrо к крупному (рис . 23 . 1 , а) - через сита, распо1 659

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ложенные в одной плоскости, причем размеры отверстий сит
от каждоrо
увеличиваются по ходу перемещения ТМ
предьщущеrо сита к последующему;
- ел крупноrо к мелкому (рис . 23 . 1 , б) - через сита, распо
ложенные одно под другим, причем размеры отверстий сит
.уменьшаются по ходу перемещения ТМ - от верхнеrо сита к
нижнему;
- комбивироваввым способом (рис. 23 . 1 , в, г) .
Грохочение ел мелкого к крупному имеет ряд достоинств: до
ступность поверхности сита, а значит, удобство обслуживания,
ремонта и смены сит; небольшая высота грохота; удобство вы
вода и распределения отдельных фракций продукта по сборни
кам . К недостаткам этоrо. способа относятся: невысокое каче
ство грохочения, так как отверстия мелких сит перекрываюrся
крупными кусками; кроме тоrо, последние мо�уг транспорти
ровать на себе некоторое количество мелких частиц; значи
тельная длина грохота (большие производственные площади).
Достоинства грохочения ел крупноrо к мелкому: лучшее ка
чество грохочения вследствие отсева в первую очередь наибо
лее крупных кусков; меньший износ сит; меньшая производ
ствен ная площадь. Недостатки: сложность осмотра, ремонта и
смены сит из-за худшей доступности их поверхности; большая
высота грохотов, неудобный отвод rотовоrо продукта.
Недостатки первых двух способов грохочения удается в из
вестной мере преодолеть при грохочении комбивироваввыми
способами.
23.2.2. Устройство и рабаrа rpoxaroв

В химической и смежных отраслях промышленности
(rорной, строительной и др.) применяюrся барабанные и пло
ские грохоты.
Барабаннwй rpoxcrr предстаRЛЯет собой (рис.23 .2) отхрыrый с торцов наклон
ный барабан цилиндрической или конической (реже - мноrоrранной) формы,
снабженный сетчатыми или перфорированными стальными листами. Он устана
В1Dfвается под утлом 4 -7° к rоризокrу и медпенно вращается вокрут своей оси с
окружной скоростью (на периферии) от 0,6 до 1 ,2
Барабан 1 вращается
либо на центральн<'м RaЛV. vстановленном на выносных подшипниках, либо на
опорн ых рол иках. Враще н и е барабана обыч но осуществляется с помощью
зубчатой пе редачи , причем одна и з ш естерен укре пля ется н а вал у , а у
больших rрохотов - непосредственно на барабане (в общем, аналогично приме
няемым в барабанных сушилках и мельницах). В конических барабанах свобод
ное перемещение происходит блаrодаря самой форме барабана, так что ось ero
вращения может бьпъ rоризо нтальной.
В большинстве случаев барабаны работают по способу rрохочения от мелкоrо
к крупному, как показано на рис. 23.2; при работе от крупноrо к мелкому сита
в барабане устанавливаются концентричн о .
Мноrоrранные rрохоты, ил и буратw, применяются дпя сравнительно тонкого
rрохочения. Бурат имеет ш ест и rр анный барабан, каждая rрань котороrо пред
ставляет собой съемное плоское сито . Барабан закрывается кожухом, из котороrо

м/с.

1 660

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

б

а

Рис. 23. 2. Барабанный 11>охот:

- схема rрохота, б - сеrмею барабанноrо rрохота;
1 - коопvс (баоабан), 2 - поверхности rрохочеюtя, З - раздеmпельная
подпорное кольцо;
1 - исходная смесь ТМ, JJ-!V - отдельные ф ракции ТМ
а

4

-

: переrородка,

при работе 11>охота отводится ньmъ. Иногда бураты вьmолняются с горизонталь
ными барабанами пирамидальной формы, расширяющимися к раз11>узочному
концу. В буратах возможна быстрая смена каждого из сит, составляющих лишь
часть рабочей поверхности барабана.
· Достоинства барабанного 11>охота: непрерывность работы, как следствие высокая производительность; · относительная простота конструкции; легкость
обслуживания. К недостаткам относятся: 11>омоздкость и металло емкость; пло
хое использование рабочей поверхности сита (в работе единовременно находится
лишь 1/8 - 1/6 поверхности - рис. 23.2, б); пЬVIеобразование из-за истирания
ТМ (как в барабанных мельницах; только здесь нет специальной насадки, так
что происходит самонстирание ) .
В связи с указанными недостатками (а они весьма существенны) барабанные
11>охоты постепенно уступают место плоским.
Неnод11ИЖИwй нахлоннwй rpoxar (рис. 23.3) представляет собой плоское сито
(:жирная штриховая линия), на клоненное так, что уrол его к горизонту а превы
шает yr.лw вне!Шfеrо трения Ч' и естественноrо antoca твердою материала у,
(последний устанааливается при медленном высьmании твердого материала на
горизонтальную шюскость - рис. 22. 14). Основные достоинства этого 11>охо
та - простота и дешевизна. Однако он не всегда пригоден из-за низкой эффек
тивности . Его используют в слt.:дующих случаях:
- нет необходимости в большой четкости разделения (часто - при сорти
ровке);
- исходная смесь состоит из классов, резко отличающихся по размерам
(например, 11>авий и песок) , так что эффективность разделения будет вполне
приемлема.
Повышение эффективности классификации
удается обеспечить на плоских грохотах более
1
сложной конструкции. На последующих рисун
ках для простоты рассматр ивается разделение
исходной смес и / на два к;шсса: мел кую М и
круп ную К .

получили весь
ма широкое распространение в химической проПлоские качающиеся rpoxoТld

Рис. 23.3. Неподвижный наклонный 11>охот:
1

исходная сшсь ТМ,
фр акции ТМ
-

If

-

III

-

отдельные

-;:-+

'

'

М�Пl��'ii',. к
1 66 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

1

1

:J1

lII
к

Рис. 23.4. Качающийся rрохот:
1 - короб с ситом, 2 - опоры, 3 - привод;
1 - исходная смесь ТМ, П - J/l - отдельные фракции ТМ
·

МЫIШ1енности. Качающийся грохот (рис. 23.4) представляет собой наклонный
короб 1, в котором устаноалено сито. Классифицируемый ТМ перемещается под
уклон. В рассматриваемой конструкции привод - шкив З с тягой (крепления
шарнирные); вместо шкива можно использовать коленчатый вал. При вращении
шкива короб с ситом, устано аленный на плоских пружинных опорах 2, совер
шает возвратно-поступательное движение.
Н аклон сита к горизонту 5 - 1 5°; амплитуда качаний (определяется радиусом
точки крепления тяm к шки11у) 1 0-30 мм, частота качаний 3-8 с- 1 . Грохот
может работать как в непрерывном, так и в периодическом режиме.
Достоинства плоских качающихся rрохотов: относительная простота кон
струкции; достаточно высокая производИтель ность; компактность; удобство
обслуживания и ремонта. Недостатками этих rрохотов я вляются: существенные
инерционные наrрузки, обус.лоаленные возвратно-поступательным движением;
несколько пониженная эффекrивность разделения (мелкие частицы моrут зале
живаться на крупных, а характер перемещения твердого материала не способ
ствует их стряхиванию); пьmеобразование, обуслоаленное истиранием твердого
материала при его танrенциаль ном движени и по ситу.
Гирацио1П1Wй rрохот (рис. 23.5) отличается от предыдущего приводом: колен
чатый вал J, пропущенный через втулки 5 короба /; для разrрузки от чрезмер
ных усилий вал снабжен противовесами 4. Такой привод обус.лоаливает нормаль
ные перемещения короба (плоскости сита) относительно напрааления движения
ТМ а значит, подбрасывание зерен и стряхивание мелких частиц с более круп
ных. Опоры здесь - вить1е пружины 2. Характеристики работы (амплитуда,
частота, наклон сита) - такие же, как у предыдущего rрохота.
К достоинствам mрационны:х rрохотов относятся: нормальные наrрузки . (на
опоры, фундамент и т.п.); более высокая эффективность разделения вследствие
подбрасывания твердого материала; малое пьmеобразование (поскольку нет
танrенциальных наrрузок, истирание невелико). Основной недостаток: забива
ние отверстий частицами в результате их падения на сито после подбрасывания
(отсюда - необходимость пери одической очистки сита) .
Вибрационн•1й rрохот (рис. 23.6) предста вляет собой короб /, на котором
устаноален вибратор J. В простейшем вар ианте - это электродвигатель, на вал
которого насажен дебалансированный шкив (с асимметричным rрузом). При
вращении вала со шкивом rруз занимает то верхнее, то нижнее положение,
изменяя их с большой частото й ( 1 0-5G cl) при амплитуде 10-50 мм. Система
"короб с ситом - электродвигатель со шкивом" стремится сохранить положение
своего центра масс; поэтому с той же частотой при подъеме rруза короб будет
опускаться, а при опускании rруза подниматься. Пружинные витые опоры 2
обеспечивают возможность вертикального (нормального к поверхности сита)
перемещения короба. А поск()льку масса короба значительно больше, нежели
rруза на шкиве, то амплитуда вибрации короба с ситом будет очень малой - от
,

1 66 2

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

3

Рис.23.5. Гирационный rрохот:

1 - короб, 2 - опоры, J - привод, 4 - противовесы, 5 / - исходная смесь ТМ, 11-111 - отдельные фракции ТМ

. i\

вrулки, 6 - сито;

Рис. 23. 6. Вибрационный rрохот:

1 - короб с ситом, 2 - опоры , J - привод с дебалаисированным ШJСИВОМ, 4 - сито ;
/ - исходная смесь ТМ, 11-111 - отдельные фракции ТМ

долей мИJVIИметра до нескольких мИJVIиметров. Грохот может работать в непре
рывном и периодическом режимах.
Следует отметить, чrо у виброrрохотов по.лносrью или часmчно отсутсrвует жест
кая связь между злеменrами. Полому ампmnуды колебаний сита в различных точках
ero поверхноеm неодинаковы и зависят от числа колебаний, yпpyrocrn опорных
пружин, движущейся массы �рохота с материалом и друmх факrоров.
В настоящее время виброrрохоты получают широкое распространение благо
даря следующим преимуществам: отсутствие забивания отверстий сит из-за ма
лой амплитуды вибрации и небольших высот подбрасывания частиц; более вы
сокая производительность и эффективность �рохочения, чем у грохотов других
типов; пригодность для �рохочения влажных материалов; компактность; относи
тельная легкость реrулировани я и простота смены сит; широкий диапазон раз
меров зерен исходного ТМ (от десятков МИJVIИМетров до долей милли метра) ;
меньший, чем для других rрохотов, расход энерmи (фактически это энерmя
холостого хода эле1С1родвигателя со шкивом на его валу).

23. 2.3. Элементы технолоrическоrо расчета

Основной вопрос технологического расчета - фор м ул и ро 
вание условий провала м ел кой частицы через отверстие грохота.
Анализ здесь не столько сложен, сколько громоздок; поэтому
он рассматривается для наиболее простого варианта - rоризон
тальвоrо грохота: этого вполне достаточно для уяснения подхода.
Схема провала мелко й частицы (з е р н а) через отверстие гро
хота представлена на рис. 23.7, а. Частица 2 ' (примем ее для
простоты сф ерич е ско й ) радиусом r, находящая ся на левой
верхней кромке отверстия диаметром d0, движется со ско
ростью w вдоль гор из о н тальн о й оси х (источник движения пока
без р азл иче н ) . Отор вав ш и с ь от кромЮt, частица начинает па
дать, т.е. перемещаться также вдоль оси у (направим ось у
вниз, это позволит о п е р иро вать положительны.ми отрез кам и и
ско р остям и ) . Скорости движения частицы малы, п о это м у rид
равличесЮtм сопротивле н ием среды п рене бр егаем .
1 66 3

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

а

6
сита:

- к определению критического уrла встречи, б - уrлы встречи больше и меньше кри
тического;
1 - кромхи отверсrия сита, :z' - зерно в начальном (стартовом) положении , J" - зерно
в конечном положении (момент конrапа)
Рис. 23. 7. К анализу провала зерна через отверстие rоризонталъноrо
а

В общем случае падающая частица придет в конта:�сr с пра
вой кромкой отверстия - положение 2". Назовем "углом встре
"
чи и обозначим <р угол , образуемый с осью х касательной к
трае:�сrории частицы в момент ее конта:�сrа с кромкой. Су
ществует некоторое критическое значение q> = q>o, при котором
происходит прямой удар зерна о кромку отверстия; тогда угол
ме.ж:ду горизонтом и линией, соединяющей центр частицы и
точку контакта, совпадает с критическим - именно такая си
туация показана на рис . 23.7, а. Угол встречи <р может оказать
ся больше критического <ро (на р ис . 23.7, б - крупные штрихо
вые линии) ; тогда частица после удара о правую кромку от
верстия гарантированно провалится через отверстие под дей
ствием собственного веса. Однако угол встречи <р может ока
заться и меньше критического <ро (мелкий пун:�сrир на рис .
23.7, 6); тогда частица продолжит свое движение по поверх
ности грохота, если она сумеет подняться над кромкой, н о
провалится , если не с мо жет подняться над кромкой отверстия .
Критическое значение уг.ла встречи <ро наЙдем из следующих
соображений . Текущи е (ко времени 't ) координаты частицы,
отсчитанные от точки ее отрыва, составят:
у = gt2/2 ;
х = Wt,
следовательно , траектор ия движения частицы (исключаем вре
мя 't ) описывается уравн ением :
у = � х2 .
(а)
2w2
В момент конта:�сrа частицы с кромкой отверстия, согласно
геометрическим связям (рис . 23.7, а) ,
Хо = do - rc os<p0,
1 66 4

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

так что

_L·
x5
\V 2

Уо =

_
g_ (do - r cos <p 0 )

2

.
(б)
2iv 2
Дш1 кр11п1ческоii ситуации траектория частицы в момент .
контакта отвечает углу встречи <р = qi0; значит, по (а):

2

dy

dx

l

=

-

=

Х = Хо

tg<po

=

.

g

2 хо
W

.

Это выражение 11оз1юляет исключить из (б) фрагмент

= tg<pt(xu:

.

Уо

tg

1p 0
2хо

=

=

t <

g po
- (do - 1-cos<po) .
2

g/Wl =
(в)

Всртика.11 ы 1 ы й путь YCI до момента контакта может быть Т"dК
11 шщс (см . рис. 23 .7, а) :
(r)
Уо = 1· - 1�iнqio = 1'( 1 - siнq>o) .
Пр11равшшан теперь (n) и (r) , получим выражение, позво
ш1ющее подоiiт11 к определению <ро:

жс записан

�

tg

o

(d0

- n: os<po)

=

1'(1

- s iti<po) .

Поделим обе •шстн раnевства на d0 и обозначим
щеюш заш1сн r/d0 = у s 0 , 5 ; раскроем скобки:
t gi p

2

llpcдcr.iшuш

o - у t g<po co sqi0

tg<Po = si

tgipo

2

шrt/coSiPQ,

для

сокра

= у - ys iнqi0.

имеем после умножения на 2:

- ysiн<po = 2у - 2ysi11<p o.
В результате 0•1ешщн ых прсобразован11й приходим к расчетному nыраже1шю для <р0:
(23 . 1)
tgip0 = у ( 2 - siнqi0) .
Дl�я 01щс 1 п 1 1 1 1 0 1 1 КJ 1 : •111е.11с1 1 1 юс реш е н и е этого ураn11с1шя nоказы 11ает, 'ПО при
·

·

JIЗMCIJCJ l lJ И у

35,5

до

от

1 11 , 5°) .

() , 5 ДО 0,2

з 1 н 1• 1 е 1 1 ия

!j1\)

l l O l l llJIШIOTCЯ от

.

0,6 1 2 ДО 0,324 рад (т.е. ОТ

Итак, безуслоаиой гара 11т11еii провала частицы, т.е. рассева на
с1пе (грохоте), яwшстсн нср:шснство <р . > <pu в момент контакта
частицы с кро м кой с нта в положснш1 2 " . Чтобы это неравен
спю выполю1110с ь, скорость iv движе11ш1 частицы не должна
превышать н скоторо ii 11ределыюй 11сл1 1ч11 н ы щ,11. Значение W11p
онределнетсн нз (б) дю1 момента контакта (х = хо, у = Уо):
"" ''

�

{;r
v�

•

(do - r cos 'Р О )

2r

(l

к.

- Stn <po

)

.

(23 . 2)
1665

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

В
Frпp

безразмерной

=

форме,

введя

критерий

Фруда

2(1 sin <р о}
(1 / у COS <po ) 2

(2 3 . 2 а)

gr/(wпp)2, имеем для гарантированноrо провала частиц

учетом (а) для момента контакта:
Frпp

_
-

2y0r

--

х�

2r2 (1 sin <р о)
(do - Г СОS <ро) 2
-

=

-

=

-

с

Рабочее значение F1· = gr/Wl- должно превышать предельное .
При <р < <РО наличие или отсутствие провала связано с упругими свойствами
часnщ и материала rрохота. Можно полагать, что при абсолютно упругом кон
такте частица не провалится, а п родолжит движение п о поверхности сита. На
о борот, пр и полностью неупругом контакте частица, остановившись, затем уп адет
в отверстие сита. Реально контакт частицы с кромкой отверстия - не п ол ностью
упругий, и здесь исход ко нтакта о пределяется численными значениями показате
лей упругости коэффициента восстановления и т.п.
Для устойчивой работы грохота необходимо основываться на
сформулированной выше гарантии безусловного провала частиц:
-

<р

>

<ро .

В случае наклонных грохотов (сито - под некоторым углом
а к rоризонту) общий подход к анализу провала сохраняется · ,
но преобразования и получаемые соотношения значительно
усложняются .
Реальные величины скорости зерен w относительно поверх
ности сита определяются кинематическими характеристиками
грохота (частотой и амплитудой его качаний, углом наклона к
rоризонту), а также особенностями движения зерна по поверх
ности сита (скольжение, качение) .
Сушествуют подходы • к приближенной оценке скорости w
движения зерна по поверхности грохота. Однако эти подходы
не учитывают явление подбрасывания зерна над поверхностью.
Экспериментальные данные показывают, что фактическая
скорость движения частицы в 2-3 раза превышает рассчитан
ную на основе упомян угых подходов. Поэто му в настоящее
время скорость w (включая и ее оmималъное значение) устана
вливается экспериментально - в зависимости от производитель
ности грохота и необходимой эффективности грохочен � Е.
Чем больше скорость движения (подачи) материала по гро
хоту, тем больше производительность грохота по исходному
материалу, но тем мен ьше эффективность просеивания при
прочих равных условиях. Для наклонных инерционных грохо
тов рекомендуется прин имать скорость подачи в пределах 0,60,8 м/с.

• И ные подходы к про валу зерна, а также способы о ценки скорости движе
ния частиц при водятся в учебной и научной литературе - см" наприм ер, ( 3 , 7 ,
1 1 ).

1 6 66

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

23.3. КЛАССИФИ КАЦИЯ В ТЯЖЕЛЫХ СРF.ДАХ
23 .3 . 1 . Описание процесса

Пусть исходная смесь состоит из леrких (плотность р11) и тя
рт) твердых материалов - кусков, зерен.
Технолоmческая задача их разделения состоит в подборе жид
кообразной "тяжелой среды" промежуrочной плотности Рте так,
чтобы рт > Рте > р11 . В такой среде легкий ТМ всплывет, тяже
лый - уrонет.

желых (плотность

Примерами поД11ежащих разделению смесей мoiyr служить:
- уюль (плоrnость на уровне 800-950 кг/мз) и порода (плоrnость 20002500 �/мЗ);
- руда (плотность порядка 5000 кг/мЗ) и порода (упомянуrой выше плот
ности).
Пусть последующая технология переработки ТМ требует щделення полезных
компонентов (угля, руды) из смеси с бал.,астом (породой) или хотя бы концент
рирования полезною компоне1rrа, т.е. обогащения смеси углем, рудой - с целью
проведения дальнейших опера ций с ними - с большей эффективностью и ин
тенсивностью. Чаще всею предварительным условием разделения является дроб
ление исходных твердых материалов для получения раздельно ('"вскрьrrия" ) зерен
полезноrо хомпонеmа и балласта.

Принципиальная схема обогащения в тяжелых средах пока
зана на рис. 23 . 8 . Исходная смесь может состоять из ле гких и
тяжелых зерен , подаваемых в классификатор, заполненный
жидкостью (тяжелой средой) . Нередко для лучшей смачивае
мости смесь зерен и тяжелой среды для подачи на разделение
готовят заранее .

Исходная смесь разделяемых компонентов II подается в классификатор 1,
заполненный тяжелой средой . Распределительная переюродка 2 позволяет регу
лировать стартовый уровень (глубину подачи) смеси. Тяжелые зерна (на рисунке
- темные кружки) тонут, легкие (светлые кружки) - всплывают. Одновременно
эти зерна перемещаются к выходному сечению (на рисунке оно справа) под
действием какою-либо механ ическою побудителя и слабою потока тяжелой
среды. Этот пото к возникает, поскольку некоторое количество тяжелой среды
неизбежно выводится вместе с легким (J//) и тяжелым (JJI) продуктами. Тяже
лую среду отделяют от продукrов и возвращают (поток /) во входное сечение;
одновременно восполняют ее потери. Легкий и
тяжелый продукть1 отводятся чаще всею с
помощью механических устройств (на схеме не
показаны) .
Рис. 23.8. Типовая
тяжелых средах:

схема

классификации

в

1 - классификатор, 2 - регулирующая переrо
род1Са;
1 - тяжелая среда, II - разделяемый твердый ма
териал, lll - смесь продукта юtзкой плотности с
тюкелой средой, IV - смесь продукта высокой плот
ности с тяжелой средой

п1 •
/
to
j
2

III

о - =--о11 0 о• /оо
1
• ._

••

- " ·

-

•

IV

1 66 7

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

В качестве тяжелых сред могут быть использованы жид
кости , суспензии и аэросуспензии .
При использовании жидкосте й Prc = р, где р - плотность
жидкости . Достоинство жидкой тяжелой среды - высокое ка
чество разделения; немаловажна и простота процесса.
Основные проблемы состоят здесь в следующем :
- трудности подбора подходящей жидкости;
- необходимость последующей суш ки разделенных материалов;
- потери жидкости и сопуrствующее загрязнение окру
жающей среды.

С целью ИЛЛ ЮС1J!ации воспользуемся приведенными вьпuе примерами . Для
р азделен ия угля и породы подходит вода (плотность р = 1 000
Но вода
непригодна для отделения породы от руды. В подобных случаях при шл ось бы
искать жидкость более высокоii плотности - водные растворы некоторых солей ,
более тяжелые индивидуальньн: жидкости. Это н е всегда удается, а если и удает
ся, то удорожает процесс разделения, повышает эколоmческую напряженность и
вряд JDI приемлемо для массовых производств.

кг/мз).

Переход к применению суспензий (как правило - водных) в
качестве тяжелых сред технологически решает первую из упо
мянуrых проблем. В самом деле, плотность Prc тяжелой среды,
представляющей собой смесь жидкости плотностью р с тяже
лым тонкоизмельченным ТМ (уrяжел ителем) плотностью Ру.
при порозности суспензии s составит:
(а)
Prc = Py(l - s) + ре.

В качестве взвешенной д ис п ерсной фазы (утяжелителя) используют дешевые
(массовые) твердые материмы типа тонкоизмельченных кварцевого песка, маг
нетита, ферросилиция. В з а ви симости от кон центр аци и ( 1 - е:) утяжелителя в
суспензии удается получить тнжелые среды с плотностями в диап азоне 12003500
Такие среды при годны для р азделения по плотностям ком понентов
широкого круга ТМ.

кг/м3.

Использование суспе нзии в качестве тяжелой среды не из
бавляет от необходимости решения двух оставшихся (см . выше)
проблем . Кроме того, здесь появляются дополнительные затра
ты на приготовление суспензии.
Термином аэросуспе11зия обогатители обозначают псевдо
ожиженный слой (ПС) с газом (воздухом) в качестве ожижаю
щего агента. Относительно крупные тела в ПС дисперсного
материала подчиняются законам плавания, поэтому его вполне
можно использовать в качестве тяжелой среды . Плотность ПС
в этом случае может быть рассчитана по формуле (а) . Но по
скольку для газа р < < Ру· то формула упрощается:
(б)
Prc � Py( l - Е ) .
Заметим: в классификаторах при использовани и П С, естественно, пред
усмотрена распр еделитель н ая решетка, под которую подается поток газа (на рис.
2 3 . 8 эта решетка не показана) .

1 66 8

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Разделение материалов по плотностям в ПС - сухой метод,
исключающий потери жидкости и затраты энергии на сушку
ТМ . Нет также особых проблем с составлением и поддержани
ем определен ной плотности тяжелой среды. Просто решается и
проблема возврата частиц, составляющих ПС и выводимых из
классификатора вместе с верхним и нижним продуктами: псев
доожижаемые частицы на несколько порядков мельче зерен
(кусков) разделяемых ТМ , так что частицы легко и полно отде
ляются от них на грохотах.
Ш ирокое применение метода тормозится трудностями полу
чения достато чно однородного газового ПС:
- в неоднородной псевдоожиженной системе восходящие
газовые пузыри выносят наверх (в основном, в своем шлейфе)
зерна тяжелого ТМ , при этом зерна ле гкого ТМ затягиваются
вниз опускными потоками псевдоожиженных твердых частиц
ме�у поднимающимис,1 пузырями;
- снижение рабочей скорости газа до величин , близЮfХ к ско
рости начала псевдоожижения, с целью получения "спокойных"
(достаточно однородных) псевдоожиженных систем сопровож
дается нарушением равномерности газораспределения и появле
нием застойных зон: они не обладают свойствами псевдожид
кости, и Юiассификация н них происходить не может.
23 .3.2. Элементы технологического расчета

Процессы разделения в тяжелых средах сопрово�аются ря
дом эффектов, зависящих от свойств разделяемых компонентов
и их содержания в смеси; эти эффекты зачастую трудно под
даются математическому описанию. На практике для расчета
процесса обычно привлекают экспериментальные данные и
используют опыт эксплуатации действующих установок. Ниже
представлены упрощенные подходы к технологическому расчету.
Идеальная классификация в тяжелых средах. Идеализация
состоит в допущении о взаимной независимости движения
ле гких и тяжелых зерен (кусков) в тяжелой среде.
Пусть классификатор 1 представляет собой (рис. 23 .9) пря
моугольный аппарат дли ной l и шириной Ь. Исходная смесь III
подается во входное (левое) сечение на уровне 2, характери
зующемся высотами Н1 и Н2• Будем считать, что легкие и тя
желые зерна равномерно распределены в объеме тяжелой сре
ды вблизи входного сече11ия. В результате процесса классифика
ции при приближении к выходному (правому) сечению в зоне
высотой Н1 не должно оставаться тяжелых зерен , а в зоне вы
сотой Н2 - легких. Скорости витания легких и тяжелых частиц
(в оценочном варианте расчета - свободного, в более точном стесненного ) обозначим соответственно w1 и w:z .
1 669

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

н,

ш

л,т

l

h1

л

-

Н2

2

1

Рис.23.9. К расчету идеальной классификации в тяжелых средах:
1

-

/-

J(Jlассификатор, 2 - разделяющий уровень;

лепсий продукт, /I - тяжеllЬIЙ продую, П/ - исходJlаЯ смесь лепсих и тяжелых зерен

Рабочий объем классификатора, занятый тяжелой средой и
разделяемым твердым материалом, равен :
Ук =

(Н1

+

Н2 ) Ы.

(23 .3)

Объемная производительность по каждому твердому продукту
составляет Vi, где индекс i = 1 ; 2 обозначает принадлежность к
легкому или тяжелому продукту соответственно . Массовая
производител ь ность по i- му: твердо му продукту равна G1 = р 1 Vf.
Соотношения Vi/V2 и Gi/G2 определяются составом исходной
смеси.
Протяженность пуги осаждения тяжелого продукга состав
ляет Н1 - в этом случае выше разделяющего уровня 2 (см. рис .
23 .9) не останется тяжелых зерен . Очевидно, Н1 = W2't, где 't минимальная продолжительность классификации (вре мя пребы
вания разделяемого ТМ в аппарате). Протяженность пуrи
осаждения легкого продукrа составляет Н2 - в этом случае ни
же разделяющего уровня не останется легких зерен . Очевидно,
Н2 = w1't. Исключая 't, находим:

(23 .4)

Объемная доля (1 - i:.t) каждого сорта зерен в тяжелой среде
должна быть невелика (не более 1 -2%), чтобы их движение
оставалось близким к н езависимому. При этом начальное и
рабочее (в зоне разделе н ия) соотношение ( 1 - е1)/( 1 - е2) за
дано в первом приближении составом исходной смеси .
Принятые объемные доли ( "задержки" ) зерен (1 - et) позво
ляют подойти к определению необходимого рабочего объема
классификатора. Суммарная объемная доля ТМ в классифика
торе составляет:

1 -е=

1 6 70

(1 -

i:: 1 ) + ( 1 - i::2)

= 2

- (е 1 + i::2).

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Тогда объем ТМ в ра бочей зоне равен :
Утм

=

Ук ( l

-

е)

И

Ук

= Vтм/(1

-

е).

(23 .5)

Связь Vтм и объемной производительности по разделяемому
материалу V = V1 + J'2 определяется (см. разд. 8.3) необходи
мым временем разделения 't = Vтм/V, где 't = Hi/'W1 = H'J/w1 •
В задачах проектирования по заданной производительности
V и выбран ным целесообразным значениям Н1 и Н2 определя
ют объем классификатора Ук и значения l и Ь. В задачах экс
плуатации (Vк - известно) определяют допустимую (макси 
мальную) производительность V, а при ее превышении (т.е.
при уменьшении 't) - ре ал ьную высоту зон классификаци и h 1 =
= 'W2't и h1 = WJ't (см. рис . 23.9).

Реал•на11 классификация в тяжелых средах . Здесь следует учитывать взаимное
алияние разделяемых компонентов (зерен). При этом возможен кризис класси
фик.ации , когда процесс нельзя осуществить с высокой четкостью разделения.
Это яаление возникает, когда поднимающиеся легкие зерна уалекают за собой
тяжелые, не позволяя последним осаждаться на дно аппарата (или, наоборот, тяжелые увлекают за собой легкие) . Попьrrаемся оценить условия возникнове
ния такой ситуации на примере запирания тяжелых зерен легкими.
Число сферических зерен i-го продукТа в единице объема равно (см . разд.
2.7 .2):

(в)
Постулируем для простоты кубическое расположение (в рабочем объеме
классификатора) зерен i-го продукта. Найлем объемную долю · его в суспензии
( 1 - t:;) . О боз н ачи м расстоя ние между uентрами зере н z;; тогда куб со сторон о й z;
содержит фрагментов сфер диаметром d;, причем на долю каждого фрагмента
приходится
шара (рис. 23. 10). Общий объем фрагментов зерна в рассматриваемом кубе, равный полному объему шара, составляет
Отсюда

8

1/8

1

-

с; =

( d з ) /z,3
�....!..._
6

Zi =

и

d;

пd[!/6.

[

11

6(1

-

&;)

]1;з

·

(r)

Оценивая соударения легких и тяжелых зерен, будем принимать упро
щающие допущения с по гр ешностью в запас, дабы гарантировать надежность
предлагаемого метода расчета процесса классификации.
Найлем количество легких зерен 1, взаимодействующих с одним тяжелым
зерном 2 (рис. 2 3 . 1 0 , б). Для этого необходимо предварительно определить пло
щадь /, "занимаемую" тяжелым зерном, т.е. перекрывающую свободное всплытие
легких зерен.
Из рис. 23. 1 0 ясно, 'ПО для шара диаметром � перекрываемая им площадь кон
такrа с шарами диаметром d1 (в пределах круга 4 на рис. 23. 10, б ) составляеr:

f = � (d2

4

+

2d1 ) 2 .

(д)

Ее.ли в единице о бъема содержится N1 ;tе rких равномерно распределенных
зереµ, то на единицу длины придется N1 Vз зерен, а на единицу площади N1113. Тогда на площадь /, щ:рекрываемую одним тяжелым зерном, приходится
число легких зерен п1 = [N1113. Подставим значения N1 по (в) для i = 1 и / по

1 67 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

б

а

-

-

Рис. 23. 10. К оценке кризиса классификации в тяжелых средах:
характерное распределение зерен, б
а
JVJощадь взаимодействия тЯJКелоrо зерна с

лепсими;
1
лепсие зерна, 2

-

тЯJКелые зерна, З

-

среда, 4

-

rрающа области взаимодействия

(д); после сокращений:

n1

=

[

]

6 ( l - E 1 ) 2 / 3 .!:.. (d
+ 2d1) = 6 2/3 n l/3 ( 1
2
4 2
�

- Ei)2/3 (.!.2 d�1 +1) 2
1 /3
п_ ]

(е)

Промежуток между двумя ударами легкой частицы по тяжелой равен:

Лt

"" Z1 /w 1 =

di
W1 6 ( l - E1 )

[

(ж)

_
_

В течение этого промежутка тяжелое зерно стремится уrонуrь (под действием
собственного веса за вычетом вьrrалхи вающей силы), а в конце промежуrка
удары легких зерен препятстт1уют этому, побуждая тяжелое зерно всru1ывать.
Равновесное состояние ("поко й") тяжелого зерна определяется сопостамением
импульса (количества движеню1) элементов системы при равном нулю результи
рующем ее количестве движения (удар легких зерен о тяжелое подразумеваем
неупругим ) .
Опускающая сила, дейсn1ующая на тяжелое зерно, записы вается как
пd�
6 (р2 p)g; подъемная сила со стороны легких зерен соответствует
ко(

/)

-

личеству движения

n1p1 ( ndf

их

/ti) w1. Тогда для промежуrка времени Л't условия

равновесия тяжелого зерна выразятся так:

nd 3
(р
6 2

2
--

-

p)gЛ't

""

nd13
n1P1 -w1.
6

П одставим сюда полученные вьппе значения Л't по (ж) и

[

nd
1t
i ( Р p)g !!l_
W l 6 (1 - E l )
6 2-

]

1/З

=

n1

по (е) :

2
6 2/З п l/3 ( 1 - Е 1 ) 2 / З .!._ d1 + 1 P l nd6 f W 1 .
2 d1

(

)

Это выражение после сокращения на п/6 и пVЗ и перегруппировки некото
рых сомножителей предсr.1вим решенным оmосительно равновесного (кри-

1 67 2

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

= ( dd12) 2 gwd22 P2 - P 6l d 2
( 2 _l_d1 + l)

тическою) значения ( 1 - &1):

(l - Et �

кр

1

Р1

1

1

_

Скорость w1 существенно завискr от &1 ; эта зависимость для жидких сред
описывается формулой Тодеса ( 2. ) . В целях упрощения представим згу зави
симость в виде степенной функции w1 = w18&111 где W1a - скорость свободного
виrания легких частиц. Из сравнения этой зависимости с
следует, что для
ламинарною режима п =
для турбулеН111 ою п =
а для переходною
- показатель степени п имеет промежуточное значение. Таким образом:

74

4,75 ,

,

(2 .74)
4,75/2 ,

(23.6)

Из :лою выражения наход им критическое значение порозносrи & 1 : при более
низких & 1 , т.е. при более высо кой концентрации ( 1 - & i ) легких зерен, послед
ние препятствуют осаждению тяжелых зерен, подхватывая их и вынося наверх.
При организации разделения в тяжелых средах необходимо, чтобы концентрация
легких зерен не превЬШiала кршической, найденной из выражения (23.6).
Аналогичная оценка может бьrrь проведена применкrельно к кр итической
концентрации тяжелых зерен: при чрезмерно высоких значениях ( 1 - &2) тяже
лые зерна в своем нисходящем движении будут захватывать легкие зерна и опус
кать их на дно аппарата.
Строmй анализ взаимодействия легких и тяжелых зерен потребует:
- учета нестационарносm движения зерен в результате соударений;
- рассмотрения косого (не прямою) ударною взаимодействия легких и тяжелых зерен;
- отказа от допущения о 11еупруrом ударе и использования упругих свойств
легких и тяжелых зерен;
- отказа от степенной зависимости &11 и перехода к общей формуле типа

(2.74);

- возможной модификации формул для расчета скоростей виrания в специ
фических условиях JIC1lleчиoro J1вижения зерен .
Такой анализ выходит за рамки учебника.

23.4. ГИДРАВЛИЧЕСКАЯ И ПНЕВМАТИЧЕСКАЯ
ЮJАССИФИ КАЦИЯ
23 .4. 1 . Общие положения

Гидравлическую (пневматическую) классификацию зернис
тых материалов часто организуют в поле сил тяжести. Прин
ципы такой классификации удобно рассмотреть на примере
разделения смеси зерен (частиц) двух сортов: № 1 - мелких и
(или) легких, со сравнительно малыми скоростями стесненного
витания Wc' в некоторой (пусть - более легкой) среде и No 2
- крупн ых и (или) тяжелых зерен , с большими скоростями
стесненного витания wc " в той же среде.
1 67 3

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 23. 11. Гидраалическая (пневматическая) класси

фикация

в

поле сил тяжести

Поместим эти зерна в поток среды
(рис . 23 . 1 1 ) , движущийся со скоростью w,
w
так что w ' < w < w ". Тогда зерна каждого
и·�
сорта отстают от потока среды , т.е. па
дают относительно потока со скорост ью
скольжен ия wc/e (если движение зерна ста билизированное). В результате проис
ходит разделение зерен - см. разд. 2 . 8 . 1 ,
формулы (а) :
- зерно сорта No 1 подхватывается потоком среды и уносится им вверх
относ ительно неподвижного наблюдателя со
скоростью и 1 =

w
w'
- - ___f_ ;

&

&

- зерно сорта No 2 движется вниз, против потока
среды
по отношению к неподвижному наблюдателю,со скоростью и2 =
=- w

&

wс"

_

&

(ось скоростей направлена вверх), или, если опери

ровать абсолютными величинами скоростей , - со скоростью
wс"
w
· и2 =
_

&

-

&

Таким образом, разделение зерен разных сортов здесь про
исходит по скоростям витания.
Если разделению подвергается п олиди сперсная смесь с непре
р ывн ым распределением зерен по скоростям витания, то поток
среды, движущийся со скоростью w, должен в идеале уносить с
собой все частицы, скорость витания которых меньше w; на
оборот: зерна, имеющие скорость витания BЫ}Ile w, будут дви
гаться против потока среды. Реально же унос всегда содержит
некоторую примесь крупных (тяжелых) частиц, увлеченных
мелкими (легкими); аналогично: выпавшие из потока крупные
(тяжелые) частицы загрязнены захваченными ими мелкими
(легкими).
Скорости витания определяются по формулам (2.72) и (2.74) .
В целях ка ч ественно й оценки воспользуемся первой из них:
Rев

=

18 + 0,59/Ai

(2 .72)

·

В случае витания в ламинарном режиме Re8 ... Ar, или, если
раскрыть смысл критериев, w8 - d 2 <Рт - р )/µ. В случае витания
в турбулентном режиме Re8
1 67 4

- JAi ,

или W8

�

�d{Рт - р) / р .

От-

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

сюда следует возможность разделения методом гидравлической
(пневматической) классификации "равнопадающих" частиц, т.е .
обладающих одинаковыми скоростями витания: для этого надо
сменить среду, воздействуя на ее свойства ( µ , р) и на режим
витания.
Приведенные выше положения остаются качественно спра
ведливыми при переходе к классификации в поле других массо
вых cwi (например, центробежных).
Некоторые особенности характерны для использования
инерционных сил при гидравлической (пневматической) клас
сификации . В этом случае сила, сопротивляющаяся изменению
скорости и направления движения зерна, пропорциональна
d3 Рт. Поэтому при разделении по размерам смесей зерен одина
ковой плотности (весьма распространенный практический слу
чай) включение в процесс инерцион ных сил дает дополнитель
ный эффект в сравнен и и с классификацией по скоростям ви
тания в ламинарном (тем более - в турбулентном) режиме.
23 .4.2. Классификация

в

поле сил тяжести

Типов ые конструкции и принципы работы к.лассификаторов
Введем некоторые условные обозначения: мелкие и легкие
частицы - МЛЧ ; крупные и тяжелые - КТЧ; скорость стес
ненного витания мелю1х и легких частиц - wсмл; скорость
стесненного витания крупных и тяжелых частиц - wскт; рабо
чая скорость газа или ж1щкости - w.

Оrстойних-классифнкатор нenpepWJ111 oro дейСТ1111 и. Аппарат (рис. 2 3 . 1 2) состо
ит из двух частей 1 и 2 различ ною диаметра, соединенных конической переход
ной зоной 7. Исходная смесь / (суспензия частиц, характеризующихся различны
ми скоростями витания wci ) поступает в переходную зону по стояку 9. Снизу
подается дополн ительный поток жидкости //; при этом поперечные сечения в
зонах 1 и 2 и потоки жидкости (чаще всего - воды) - с суспензией / и снизу //
- согласованы так, чтобы рабочие скорости w в обеих зонах были одинаковы. В
таких ус.ловиях в идеале все МЛЧ (их скорость витания wсмл < w) должны быrь
унесены потоком жидкости, а все КТЧ (для них wcicr > w) должны утонуть в
потоке. Классы МЛЧ и КТЧ раздельно (потоки /// и ГV) выводятся из классифн
катора. Реально абсолютно четкой классификации не происходит: класс МЛЧ
несколько загрязнен КТ-частицами, а класс КТЧ - МЛ-частица ми . Управление
граничной скоростью витанин, по которой происходит разделение исходной
полидисперсной смеси на кл а ссы (все, что мельче и легче , - в поток ///, что
крупнее и тяжелее - в поток Л'), ведется воздейсrвием на рабочую скорость w; на
пример, ее повьШiение привощп к уветrnчению граничной скороСПI В\П'ЗНИЯ (т.е.
уносятся потоком уже более крунные и тяжелые части1щ, чем при меньшей w).
Аппарат позволяет разделить исходную смесь на два класса. При необходи
мости ее разделения на N классов потребуется N - 1 классификаторов, в каждом
из которых будет вестись разделение на два класса.

Пневматические классификаторы непрерывного действия. Они
построены подобно рассмотренному выше гидравлическому
1 675

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

е о /

//Т
9
8

1
2

7

3
6
4

-- - 1
- -2
� -з

5

Рис. 23. 12. Оrстойник- классификатор непрерывноrо действия:

1 - верхняя зона, 2 - Ю1J1СНЯЯ зона, З - патрубок вывода КТЧ N, 4 - диффузор, J патрубок подачи (нижней) JКИДХосrи П, 6 - распределительная решетка, 7 - переходная
зона, 8 - патрубок вывода МЛЧ l lI, 9 - сrояк для ввода исходной смеси, 10 - патрубок
подачи исходной смеси 1, 11 - сбо)IНИК МЛ;
1 - паrок JКИДХости, 2 - движение МЛЧ, 3 - движение КТЧ

Рис. 23. 13. Воздушный классификатор резина-тканевых смесей:

1 - конический корпус, 2 - r11ynna верХЮ\х конусов, З - rpynna НИJ1СНИХ конусов, 4 воздухораспределительный короб, J - патрубок вывода резиновой крошхи N, 6 - патрубок
подачи воздуха П, 7 - бункер исходной смеси 1 с питателем, 8 - патрубок вывода воздуха с
ВOJIOICНOM IП

классификатору и работают с н изкой четкостью разделения
вследствие существован ия поперечной неравномерности газо
вого потока и склонности твердых частиц к агломерации в та
ких потоках. Поэтому гравитацион ные пневматические клас
сификаторы либо используют несколько иные принципы (см.
ниже), либо в той или иной мере подключают инерционные
силы (см. разд. 23.4.3).
Работу пневматических классификаторов покажем н а примере аппарата для
разделения резинотканевых с.+rесей. Проблема состоит в реrенерации резины из
резинотканевых смесей (шины, рукава, другие изделия) и возврате полученной
резины в производство резиновых и рез инотканев ых изделий. Актуальность
проблемы обус.ломена прежде всеrо мноrотоннажностью резинотканевоrо
производства.
Для отделения резины от ткани необходимо предварительно измельчить ис
ходный материал (это делается путем охлаждения материа.11а до температур ниже
- 100 •с для придания ему хрункости с пос.ледующим измельчением, например в

1 676

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

молотковых дробилках). Измельченная смесь состоит из 60-70% резины в виде
крошки размером 1 -5 мм (это КТЧ) и 30-40% ткани в виде волокон длиной до
2 мм (это МЛЧ).
Использование классификации на IJ>OXoтax к успеху не приводит: осrающиеся на
сиrе волокна захватывают до 20% резиновой крошки (высокие потери), прошедшая
через сито крошка содержит до 1 0% во.локон (низкая чисrота).
Классификатор МИТХТ (рис. 23. 1 3) предстааляет собой полый конический
корпус 1 с верхней (2) и ннжней (J) rруппами конусов, между которыми в
аппарат вводится измельченная исходная смесь 1 (из бункера 7 с питателем).
Воздух для классификации П подается в распределительный короб 4. Суще
ственно, что диаметры (поперечные сечения ) устьев конусов уменьшаются свер
ху вниз, так что скорости воздуха в них в этом направлении увеличиваются. В
конусах происходит псевдоожижение смеси (при невысоких концентрациях
твердоrо материала) с обменом частицами между конусами. При этом КТЧ
резины стремятся вниз, так как в верхних зонах аппарата (в устьях конусов 2 также) скорости воздуха недоt.-таточны для их уноса. Наоборот, МЛЧ волокна
стремятся двигаться вверх, так как в нижних зонах (тем более - в устьях кону
сов 3) скорости воздуха вЬШiе скоростей витания - волоконца не мoiyr пройти
вниз (не дает воздушный поток).
Снизу из классификатора через патрубок 5 выводится крошка IV с выходом
до 98%, практически не содержащая волокна. Она вполне может быrь использо
вана (иноrда в смеси со свежим каучуком) для производства ряда резино
технических изделий. Конце�rrрация крошки, отводимой сверху с волокном в
потоке /// через патрубок 8, не превьnиает 5%. Основное препятствие широко
му использованию данноrо классификатора - необходимость замораживания
исходных резинотканевых изделий перед измельчением (холод - дорог) .

К инженерному расчету классификаторов,
работающих в поле сил тяжести

Гидравлический отстойник-классификатор. Технологический
расчет предполагает прежде всего установление связи расход
Н ЬIХ характеристик и площадей поперечного сечения верхней и
нижней зон . В основе расчета - формулы (2.79) для восходя
щего прямотока (верхняя зона) и противотока (нижняя зона) .
Обозначим (см. рис. 23. 12) поток жидкости в исходной сус
пензии I символом V1 , а дополнительный ее поток // снизу
аппарата - J/2. Рассмотрим сначала верхнюю зону классифика
тора. Используем формулу (2.79а), выразив задержку через по
розность р = 1
е и представив скорость ст есненного витания
Wc не по формуле Тодеса (2.74), а упрощенно: Wc = wвеп. Здесь
скорость свободного витания Wв определяется формулой (2.72), а
п зависит от режима витания: согласно (2 .74), для ламинарного
режима п = 4, 75, для турбулентного п = 2 , 3 8 . Отношение пото
ков дисперсной и сплошной фаз для сокращения записи обо
значим V;/ Vc = vp. Тогда при расчетной скорости жидкости в
верхней зоне w имеем:
-

1 677

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Избавляясь от дроби и производя очевидные сокращения,
получаем :
w
wв
1 - _ &п - Vp& - & + --1t &&п О
w
w
или
=

(а)
Задаваясь приемлемым (высоЮfм - не менее 0,97 - 0,98)
рабочим значением &, из (а) находят решение задач проектиро
вания:
- необходимое отношение объемных производителъностей
при принятой рабочей скорости жидкостного потока w:
Vp

=

Vд
Vc

-

(1
=

-&

>(1 - : &п)

---

--

&

(23 .7а)

- рабочую скорость, обеспечивающую принятую порозность

& при заданном

vp :

w = w8

&n (l - &)

(Vp 1) .
+

1-&

(23 .7б)

Поперечное сечение верхней зоны fi рассчитывают по урав
нению расхода сплошной среды на основе суммарного потока
ЖИДКОСТИ Vc = J/i + J'2: fi = Vc/ W
При необходимости решения эксплуатационной задачи
(определение & при известных vp и w) придется использовать
численные методы, так как из уравнения (а) в явном виде по
розностъ & не выражается.
Аналогичным способом находят основные характеристиЮf
нижней зоны - исходя из формулы (2.79в). Опуская сходные
преобразования, приведем конечнь1е проектные решения:
·

(б)

(23 . 8а)

w = w8
1 67 8

&n (l - &)
& Vp + } - &

---

(23 .8б)

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Поперечное сечение нижней зоны h также определяется из
уравнения расхода, но н а основе объемного жидкостного потока Vc = lf2.
Основы подходов к расчету пневматического классификатора
рассмотренного выше типа изложены в разделе 23 .4.4. База
расчета - данные о равновесии разделяемых компонентов
(МЛЧ и КТЧ) в "фазах" провала и уноса. Заметим: соотноше
ние поперечных сечений устьев верхнего и н ижнего конусов
должно быть обратно пропорциональным скоростям витания
разделяемых компонентов. С увеличением числа конусов чет
кость разделения повышается.
23.4.З. Классификация с использованием инерционных сил

Работа рассмотренных выше гидравлических и пневматиче
ских классификаторов базируется в основном на различии в
скоростях в итан ия Л wс = lwc' - wc"I частиц разных сортов
(классов, фракций). Между тем различие в скоростях движения
Ли = l и ' - и"! разных частиц можно заметно увеличить, если
использовать инерционные свойства частиц, т.е. вести процесс
классификации не в стационарном режиме дв ижения частиц, а
на участках их разгона. Эффект использования инерционных
сил при этом выше в случае пневматической классификации,
поскольку здесь больше протяженность участка разгона, неже
ли в случае ги дравлической.
Строго говоря, и при разделении по скоростям витания
инерционные силы играют определенную роль, так как
вследствие ударов о сте нки канала, аппарата частицы тормо
зятся, и их скорость относительно потока среды не совпадает
со скоростью витания (после удара частица разгоняется) . Но
эти эффекты в рассмотренных ранее аппаратах играют п одчи
ненную роль, а речь идет о том, чтобы различие в инерционных
свойствах частиц сделать базой разделения. В известной мере
это реализуется в случае сепарации методом отвеивания (см .
ниже) - при подаче разделяемой смеси навстречу потоку.
Устройство и работа инерционн ых воздушных сепар аторов
Цилиндрический полый инерционный воздушный сепаратор.
Схема сепаратора представлена на рис. 23 . 14, а.

В аппарат / наклонным питателем 2 подается смесь / твердых зерен (частиц)
пусть, например, мелких (светлые кружки) и крупных (темные) - навстречу
восходящему воздушному потоку Il. Скорость потока w вьШi е скорости уноса w '
мелких частиц, но ниже скорости уноса w " крупных. Поток, преодолев инерцию
мелких частиц, подхватывает их и уносит (l//); далее воздух отделяется от них в циклонах, в рукавных фильтрах и тому подобных устройствах. Разумеется, для
преодоления инерции мелких частиц (изменения их движения с нисходящего на
восходящее - вместе с потоком) необходима определенная протяженность учас-

-

1 67 9

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

otl//
о

1

о

tп

о

о

о

у

1

•

•

•

•

�

• /V
а

/l

б

в

г

Рис. 23. 14. Инерционные пневм атические сепараторы:
а - nоЛЬIЙ цилиндрический, б - типа "'зиrзаr", s,

г - с наJСЛоЮIЬIМИ полхами
(усrройство и схема потоков rазовз11еси);
1 - корпус сепаратора, 2 - шrrатель, 3 - элементы сепаратора типа "зиrзаr", 4 - на
к.лоЮ1Ь1с потси ;
/ - исхоJU1ая смесь твердых часrиц, // - воздух, /// - rазовзвесь мслхих частиц, JV крупные часпщы

сепаратора под сечением подачи исходной смеси - см. на рисунке пуrь
движения мелкой частицы. Крупные зерна, для которых w < w ·, да еще велики
инерционные свойства, движуrся против воздушного потока и отводятся внизу
(/JI) и выходят из сепаратора.

тка

Достоинство рассмотренного аппарата - в его простоте .
Основной недостаток - однократное использование сил инер
ции (вблизи сечения ввода исходной смеси).
Воздушные сепараторы с многократным использованием инер
ционных сил. Схемы таких аппаратов - типа "зиrзаr" и с на
клонными полками - показаны на рис . 23. 14, 6-г.
Каждое изменение напраВJJ е ния потока rазовзвеси в окрестности полки (см.
рис. 23. 14, в) сопровождается торможением и поворотом движущихся твердых
частиц и потому возникновением (возобно ВJJе нием) сил инерции, что суще
ственно повышает эффективность (четкость) разделения. Увеличение числа
мементов 3 (вид б) в аппарате типа "зигзаг" и наклонных полок 4 (вид в) до
разумного их количества (порядка 1 0) сопровождается повышением эффектив
ности разделения; дальнейшее увеличение числа мементов или полок на эффек
тивности разделения сказывается незначительно.

Сравнение работы этих двух аппаратов показывает, что се
паратор с наклонными полками в общем эффективнее, чем ти1 680

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 23. 15. Простой воздушный сепаратор:

1 - веtПИЛЯТор, 2 - :щцвюкк а , J - бункер исходной смеси, 4 - питатель, 5 - рабочий

канал, 6 - сборI01К промежуточноrо класса, 7 - сборЮIК КТЧ;

/ - исходная смесь ТМ, // - воздух, ///- V - продухты разделения

па "зигзаг", но обладает более высоким гидравлическим сопро
тивлением. В свете аналогии в переносе массы и количества
движения это закономерно .
Сепараторы с наклонными полками дают наибольший эффе кт при наклоне
полок, близком к 45° , и когда полки перекрывают примерно половину сечения
сепаратора.

Классификаторы на основе отвеивания. Принцип классифи
кации способом "отвеивания" состоит в воздействии попереч
ного потока газа или жидкости на падающие зерна разного
размера и (или) плотности (в общем случае - и формы). Зерна
с различными свойствами падают с раз ной скоростью и, кроме
того, по-раз ному сносятся поперечным (горизонтальным, в
более общем варианте - наклонным) потоком среды.
Люди издавна использовали отвеивание для отделения на
ветру мякины от зерна после его обмолачивания.
В качестве примера реализ ации принципа отвеивания рас
смотрим работу простого воздушного сепаратора (рис . 23 . 1 5) .
Схема и принцип работы классификатора ясны из рисунка:
поток выхватывает из смеси МЛЧ , тогда как КТЧ в малой мере
(частицы промежуточных размеров и плотности - в несколько
большей) смещаются потоком .

На рисунке исходная смесь ([), попадающая в рабочий канал 5 из бункера З
с помощью питателя 4, под воздействием потока воздуха 11 (от вентилятора J)
разделяется на три класса: наиболее крупн ые (или тяжелые) частицы попадают в
первый по ходу потока конус (сборник) 7 и затем выводятся из неrо (111); про
межуточный класс относится потоком в большей мере, попадает в конус 6 и
затем выводится из неrо (/V); самые мелкие и легкие частицы уносятся воздуш
ным потоком и выводятся с ним из канала ( /1) в вще rазовзвеси, далее они
отделяются от воздуха (в циклонах, на фильтрах и т.п.)
Реrулирование rраничны:х размеров и плотностей классов возможно за счет
изменения скорости воздуха зад вижкой 2.
'/:26 - За к .

(i� I .

к11.

2

1 68 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

В ходе процесса отвеивания желательно иметь возможн ость
регулировать расстояние l для частиц данного сорта (класса)
или характеристики зерен (крупность, плотность и т.п.), осе
дающих на данном расстоянии /. Параметры, воздействующие
на процесс , - скорость потока w, угол наклона направляющей
плоскости и начальная скорость зерен .
Досто инст во классификации отвеиванием - в простоте спо
соба и его аппаратурного оформления. Недостаток - в невы
сокой четкости разделен ия вследствие не учтенного в предше
ствующем анализе взаимодействия зерен различной крупности
(плотности и т.п.), движущихся с разными скоростями; в ре
зультате - отбираемые (в сборники) на определенных расстоя
ниях l фракции содержат частицы не только целевого класса, но
и заметные количества примесей зерен других сортов. На прак
тике такие сепараторы используют для предварительного обо
гащения, а сам принцип - также в схемах с жидкостными по
токами ("отсадка").
Проходной воздушный сепаратор . Значительного улучшения
четкости разделения удается достигнуть в результате неодно
кратного повторения акrов разделения, однако платить за по
вышение эффективности приходится существенным усложне
нием конструкции . В этом классификаторе совмещено воздей
ствие на частицы силы тяжести и других массовых сил
(центробежной, инерции).
Аппарат (рис. 23. 16, а ) состоит из двух конусов - наружного 1 и внутренне
го 2, соединенных сверху через танrен циальные вставки З ("завихрители") и
снизу через просвет внутреннего конуса и направляющей вставки 7. Исходную
смесь 1 через патрубок 6 вводят в классификатор снизу в виде rазовзвеси, кото
рая движется в аппарате вверх по расширяющемуся кольцевому каналу между
конусами. При этом происходит понижение скорости воздуха (сечение кольце
вого зазора растет снизу вверх ) . Конструктивные размеры в сочетании с расхо
дом воздуха выбираются так, чтобы из поднимающеюся потока воздуха выпада
ли исключительно КТЧ (пусть - не полностью ) , а МЛЧ (пусть с примесью
КТЧ) дОЛJКНЫ подхватываться потоком и через завихрИ1'еЛИ танrенциально по
ступать в полость внутреннего конуса. Последний работает как циклон; его
параметры подбираются так, чтобы с потоком уносИJП1сь через патрубок 4 толь
ко МЛЧ ( //) , а попавшие сюда КТЧ (с примесью МЛЧ) под действием центро
бежной силы выпадали на стенки внутреннею конуса и затем сползали вниз.
Через просвет между устьем конуса и вставкой 7 смесь КТЧ и МЛЧ провали
вается вниз и попадает в нижние зоны наружною конуса, т.е. в область восхо
дящею воздушного потока. Он выхватывает из падающей смеси МЛЧ и уносит
их, а КТЧ присоединяются к т�м КТЧ, что выпали из потока ранее, и они вмес
те сползают к устью наружноrп конуса, оттуда выводятся из аппарата (///) через
патрубок 5.

Рассматриваемый классификатор позволяет достаточно чет
ко делить исходную смесь на классы с заданными размерами
(плотностями) частиц. Регулирование rраничных параметров
разделения (скорости витания; при одинаковой плотности 1 682

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ll

б

а
Рис. 23. 16. Проходной воздушный сепаратор:

а - схема сепаратора, б - фраrмеш внуrреЮ1еrо конуса с танrе1ЩНально располо
женными завихрителями;
1 - наружный конус (корпус) , 2 - внуrреюmй конус, З - таше1ЩНальные вставки
("завихрители"), 4 - патрубок вывода МЛЧ П, 5 - патрубок ВЬ1вода КТЧ 111, 6 - патрубок
ввода исходной смеси 1, 7 - направляющая вставка

размера частиц; при одинаковых раз мерах - плотности частиц)
ведется двумя способами:
- из менением скорости воздушного потока, транспорти
рующего смесь твердых частиц;
- варьированием угла поворота лопаток завихрителей : они
мoryr бьпь расположен ы не только танrенциально (см . рис .
23 . 1 6, б), но и под углом к радиусу, отличающимся от 90°.
Основ ы технологического расчета

Однонаправленное неустановившееся движение в поле сил тя
жести. В основе анализ а движения частицы массой т и пло
щадью м:иделева сечени я F в среде плотностью р (ее скорость
w) лежит уравнение (см . разд. 2.7.4):

du
тd't

=

-

тg

где и - перемен н ая скорость частицы.

+

)::
..,

(и

-

w) 2

2

.г р ,
�

(в)

И з (в) методом масштабных преобраз ований получаются
критерии, харакrеризующие движение частиц с r аз ными
и го
свойствами , а з начит . и их сепаР.ации: Ф руда Fr = gd/Wl
мохронности Но = Wt/l или u't/l, где / - определяющий ли
нейный раз мер (например, расстояние между полками) .
•
'/, 2 6

1 683

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

х

х

у

у

Рис. 23. 1 7. К
а

-

у

6

а

х

\V
-

в

расчету процесса отвеивания:

иде альны е траектории зерен,

зование сил инерции ;
1 - зерна, 2 - траектории зе ре н,
кость

б

-

траектория зерна с участком разrона, в

З - rраница участка разrона, 4

-

-

исполь

направляющая плос

В настоящее время проблему технологического расчета
инерционных сепараторов нельзя считать решенной, т.е. дове
денной до надежных инженерных м етодов. Пока что расчет сепа
раторов - полых, типа "зигзаг" и с наклонными полками - в
значительной мере базируется на эмпирическом материале · .
Процесс отвеивания . Найдем траекторию движения зерна i
го сорта, положив для простоты , что зерно - сферическое ,
падение его происходит в поле сил тяжести, начальная ско
рость зерна равна нул ю , а поперечный поток - горизонтален .
В системе координат х - у (рис . 23 . 1 7) направим вертикальную
ось у вниз , это позволит оперировать положительными отрез
ками и скоростями. Обозначим скорость поперечного потока
среды w, вертикальную составляющую скорости зерна и, гори
зонтальную - v.
Пренебрежем участком разгона зерна, т.е . примем его дви
жение установившимся; для жидких сред и потоков это допу
щение выполняется обычно достаточно точно, для газовых приближенно, иногда - весьма приближенно. С этим упроще
нием горизонтальная составляющая скорости зерна v = w, так
как силой инерции мы пренебрегли, допустив отсутствие
участка разгона, а другие силы , препятствующие движению
зерна в потоке , - отсутствуют. Вертикальная составляющая и
равна скорости витания зерна в среде (в общем случае - стес
ненного Wc, в приближенных оценках или при очень низких
кон центрациях твердых зерен в среде - свободного w8) .
отсчи
Текущие координаты зерна - в момент времен и 't
тываем от начала его движения :
-

Х = Vt = W't ;

• См" например, (2) .

1 684

у = U 't = Wc't .

(г)

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Траектория зерна, заданная уравнениями
(r) в параметри
=
ческой форме, запишется в виде у f{x) при исключении 't:
у=

�х
v

=

wc

х.

w

(д)

При выбранной высоте падения зерна h в горизонтальном
направлении
оно
будет
отнесено
на
расстояние
l
(эксплуатационный подход); для обеспечения определенного
расстояния l потребуется рассчитываемая высота h (проектный
подход).
Если в исходной смеси содержатся зерна различных сортов
(свойств), то при одинаковой высоте h они будут отнесены на
разные (рис. 2 3 . 1 7 , а) расстояния l - в этом и состоит клас
сификация способом отвеивания .
Траектории зерен (д) - прямолинейны. При учете инерци
онных свойств зерен на участках разгона они бы несколько
искри влял ись (рис. 23 . 1 7 , б).
На практике действие инерционных сил чаще всего способ
ствует повышению четкости разделения зерен разного сорта.
В этом случае целесообразно усилить воздействие этих сил,
придав зернам какую-то начальную скорость и направив их под
тупым углом ("навстречу") к разделяющему потоку среды (рис .
23 . 1 7, в) .
Заметим: при включении сил инерции, в особенности - при использовани и
газовых потоков, иmорирование участков разгона может привести к существен
ной погрешности в расчетах. Здесь в исходные уравнения движения типа (ж), (з)
в разд. 2.7.4 и граничные условия к ним должны быть включены следующие
параметры:
- начальные скорости зере н (их составляющие по осям х и у);
dv
du
.
- слагаемые т; - , т; -- JVIЯ 1-ro сорта зерен (т - масса зерна) .
dt
dt

23.4.4. Классификация псевдоожижаемых твердых частиц

Классификация мелкозернистых твердых материалов воз
можна в псевдоожиж ен ном состоянии. Процесс разделения в
этом случае строится исходя из аналогии (разд. 2.7.4) в поведе
нии капельной жидкости и псевдоожиженного слоя (ПС), или
шире - спло шных сред и дисперсных систем * . Причина анало
гии заключается в статистической общности этих систем: неко
торые свойства множеств (коллективов) молекул либо твердых
частиц оказываются качественно сходными, а зачастую и коли
чественно описываются одинаковыми закономерностями. При
этом роль температуры, управляющей основными свойствами
сплошных сред (в частности - жидкостей), и.грают силы внеш• Подробно об аналогии см . ( 1 , 4, 5 J .

1 6 85

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

нею воздействия на дисперсную систему, в большинстве слу
чаев связанные со скоростью w газа (или жидкости), проходя
щею через эту систему.
Гидродииам ическая дист илл.яц ия
и гидродииам ическая ректиф икац ия
Если П С составлен из частиц различных размеров (или
плотностей) и псевдоожижение ведется с выносом части твер
дьIХ частиц из слоя, то унос в сравнении со слоем обогащен
мелкими (или легкими) частицами - в полном соответствии с
1 законом Коновалова (см. разд. 12.2.3). При этом только очень
приближенно можно считать, что уноситься будуг лишь те час
тицы (достаточно мелкие или легкие
их именуют
"мелочью"), скорость витания которьIХ ниже рабочей скорости
ожижающею агента (газа или жидкости) . На самом деле в уно
се оказываются и более крупные (тяжелые) частицы - их увле
кает уносимая мелочь; в то же время, крупные частицы удер
живают в ПС определен ное количество мелочи, хотя по зако
нам витания она должна быть вынесена из слоя. По существу,
между ПС и уносом устанавливается равновесие в составах,
подобное рассматриваемому в процессах переюнки равнове
сию типа жидкость-пар (см. разд . 1 2.2): ПС - аналог жид
кости, унос - аналог пара.
Если ПС состоит из частиц двух сортов, то равновесие мо
жет быть представлено в диаграмме у-х (рис . 23. 1 8), где у и х
- концентрации мелочи (аналога низкокипящею компонента)
в уносе и в слое соответственно. Конфигурация и положение
равновесных кривых определяются свойствами частиц, принад
лежащих к разным сортам ,- эти свойства во многом аккуму
лированы в скоростях н ачала псевдоожижения wo для частиц
разнь�х сортов. Иногда кривые равновесия представляют собой
равнобочные гиперболы и следуют закону Рауля (кривая 5) .
Чем больше для этих сортов частиц различие в скоростях нача
ла псевдоожижения w0 ' и w0" , тем дальше кривые равновесия от
диаюнали (тем выше коэффициент разделения а4 > аз > а2 ) ,
т.е. тем легче разделение: унос в большей мере обогащен мело
чью.
Вынос мелочи из П С в качестве технологическою процесса
с целью ее отделения от крупных (тяжелых) частиц слоя анало
гичен процессу дистилляции (см. разд. 12.3) - будем называть
такой процесс mдродинамической дистилляцией. Принципиаль
ная схема процесса ясна из рис . 23. 1 9. Как и процесс дистил
ляции жидких смесей, гидродинамическая дистилля ция эффек
тивна, прежде всею, в д вух случаях:
- большое различие в свойствах (значениях wo ) мелких и
крупнь�х частиц (кривые равновесия далеки от диаюнали);
1 686

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

[

•

yt

•
.

.

у

.

.

••• • •• •
: . • ПС • • ·
•
·..:: ..=.. •
•

о

х

1

. . .

2

1

Рис. 23. 18. Кривые равновесия типа "Псевдоожи:жеиный слой - Унос" в бинар
ных дисперсных системах:
1 - а - 1, 2-4 - эволюция крИВЬIХ равновесия при возрастаIО\И а, 5 - кривая равно
весия идеальной смеси
Рис. 23. 19. Принципиальная схе ма гидродинамической диСТИJVIЯuии:
1 - аппарат с ПС, 2 - rазорас11редСJDПе.льная решетка;
1 - ОJКЮIСАЮЩИЙ аrе1П, II - унос твердоrо материала;
ПС - зона псевдооJIСЮIСенноrо слоя, У - зона уноса

- производство не нуждается в высокой четкости разделе
ния (в отличие, например, от очистки ПС от следов мелочи),
допустимо наличие примесей: крупных частиц - в уносе, ме
лочи - в слое.
Нередко производству, наоборот, необходимо разделение
исходной смеси зернистых материалов, весьма близких по гид
родинамическим свойствам (скоростям w), на достаточно чис
тые классы. Тогда следует организовать противоточный про
цесс, аналогичный ректификации (разд. 12.4 и след.) - такой
процесс будем именовать rидродинамической ректификацией.
Схема осуществления непрерывной гидродинамической рек
тификации показана на рис . 23 .20.
Колонна 1 выполнена слегка расширяющейся кверху, 'Побы обеспечить по
степенное понижение снизу вверх скорости газа - подобно тому, как в ректи 
фикационной колонне снизу вверх уме н ьшается рабочая температура. Внутри
колонны расположе ны прованьные перфорированные тарелки 2 с размерами
отверстий, на 1 ,0 - 1 , 5 порядка превышающими размер псевдоожижаемых твер
дых частиц. Во избежание н еравномерности газораспределения (для предотвра
щения образования застойных зон) живое сечение перфорированных тарелок н е
должно бьпъ больше .... 3%.
Снизу в колонну подается поток / ожижающего агента (газа), поддержи
вающего ТМ на тарелках в псевдоожиженном состоянии. В промежуточное
сечение питания А подается поток /1 исходной смеси зернистого материала,
подлежащей раздел е нию на две фракции. На каждой тарелке сушествует псевдо
ожиженный слой, а над ним - сепарационное пространство с уносимыми твер
дыми частицами . Отводимая сверху колонны газовзвесь 111 попадает в циклон 3

1 68 7

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

[
3

Рис. 23.20. Коло н н а гидродинамической ректифи
кации:
1 - колонна, 2 - перфорированные тарелки, З циклон;
/ - 0J1О1жающий аrеш (rаз), // - исходная смесь, ///
- rазовэвесь мелких частиц, JV - флегма (возврат ТМ
на орошеЮ1 е) , V - верхний продукт, V/ - Ю1J1СНИЙ

- псевдооJКЮКенный слой, СП - сепарациоЮ1ая

п родукт;
ПС

зона
пс

(аналог конденсатора), где ТМ отделяется от газа.
Далее поток ТМ разделяется на два: верхний
продукr V с высоким содержанием мелких и
(или) легких частиц (аналог диС'ПIЛЛJПа) и воз
вращаемый на орошение /V (аналог фпе1111W ) .
Снизу колонны отводиrся нижний продукr Vl с
высоким содержа н ием крупных и (или) тяжелых
частиц (ан алог кубового остатка) .

Как и в случае ректификации жид
смесей, увеличение числа ступеней
(тарелок) и доли возвращаемого в ко
лонну верхнего продукта (т.е. флеrмо
вого числа) приводит к получению
более чистых продуктов. Смещение
точки подачи исходной смеси из сечения А в сечение В сопровождается
закономерным повышением чистоты
'-VJ
верхнего продукта (поскольку возрастает число ступеней разделения
выше точки питания ) и понижением
чистоты н ижнего продукта.
Техволоmческий расчет процессов гидродинамической ди
стилляции и реIСГификации ведется по той же методике, что и
соответствующих процессов разделения жидких смесей. В
частности, для разделен ия смесей на две фракции необходимо
располагать диаграммами равновесия типа показанных на рис .
23 . 1 8 ; равновесные дан ные получаются экспериментально. Да
лее последовательность расчета зависит от выбранной схемы
разделения и постановки задачи (см. разд. 12.3.2 и разд. 12.7).
Например, при проектном расчете гидродинамической ректи
фикации бинарной смеси надо построить рабочую линию про
цесса и найти число ступеней.
В колон нах гидродин амической ректификации соотношение
верхнего и н ижнего сечений выбирается обратно пропорцио
нальным отношению скоростей начала псевдоож:ижения мел
кой (легкой) и крупной (тяжелой) фракций. В этом случае
удается обеспечить примерно одинаковую интенсивность псев
доожижения в верхней и нижней зонах колонны.
Производительность аппаратов гидродинамической реIСГи
фикации значительно больше, чем грохотов, хотя и уступает в
ких

1 688

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

этом показателе пневмотранс портным сепараторам . Чистота
получаемых продукrов намного выше, нежели при грохочении
- периодическом, а тем более непрерывном. Она заметно пре
вышает и достигаемую в пневмотранспортных сепараторах;
кроме того, при "ректификации" на порядок ниже расходы
газа. Существенный недостаток аппаратов rидродинамической
ректификации состоит в высоЮ1х rидравлических сопротивле
ниях, измеряемых сотнями кПа на 1 м высоты колонны.
Сепарация на основе сегрегации в псевдоожиженном слое
В ряде предшествующих разделов (см. главы 2, 5-8, 1 0, 14,
1 5) говорилось о том , что поведение ТМ в псевдоожиженном
слое близко к модели идеального перемешивания. Это приво
дит к в ыравниванию коицентраций частиц различных сортов в
разных точках объема ПС и тем самым препятствует разделе
нию. Такая ситуация характерна для подавляющего боль
шинства технологичесЮIХ процессов, использующих технику
псевдоожижения.
Однако существуют режимы, в которых начинаюг играть
роль не которые эффекты, обычно не проявляющиеся в про
мышленных псевдоожиженных системах.
Реально в ПС вообще конкурируют два эффекта: перемеши
вание частиц по высоте слоя и их сегрегация, т.е. преимуще
ственное накопление мелких (или ле гких) частиц в верхних
зонах слоя и крупных (или тяжелых) - в нижних. Явление
сегрегации может послужить баз ой для классификации
(сепарации) твердых частиц. Но для этого необходимы усло
вия, при которых сегрегац ия твердых частиц в ПС не подавлена
их перемеш иванием. Эти условия реализуюгся вблизи начала
псевдоожи жения . В случае использования газа в качестве ожи
жающего агента речь идет о непосредственной близости рабо
чей скорости w к скорости начала псевдоожижен ия w0: надо не
допустить появления газовых пузырей, способствующих интен
сивному перемешиванию ТМ. Вести процесс следует в области
"спокойного" псевдоожижения, т.е. при w < ( 1 ,2 7- 1 , З)w0. В
случае жидкостного (однородного) псевдоожижения сегрегация
весьма четко проявляется и при более высоЮIХ рабочих скоро
стях w.
Зам ети м : вблизи начала п сс вдоожижен и я возможны н ежел ател ь н ые эффекты
типа неравномер н ости газор аспределе ни я и появления застойных зон. Таки е
эффекты наруш ают нормальн о е течени е сепарации. Для их предотвращения
повьШi ают ПfДравлическое сопротивлени е rазораспределителя и.ли механически
воздействуют на классификатор (вибрация и т.п.).

Первая технологическая проблема сегрегации заключается в
определении, какого именно сорта части цы накапливаются в
верхних или нижних зо н ах ПС. Проблема легко разрешается в
1 6 89

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

случае частиц одинаковой плотности (тогда наверху - мелкие
частицы) или, что на практике встречается редко, в случае час
тиц одинакового размера (наверху - легкие частицы). Труд
ности возникают, когда мелкие частицы имеют оольшую плот
ность, нежели крупные. Для ответа на поставленный вопрос
полагают, что сеrреrирующий псевдоожиженный слой состоит
из нескольких (минимум - двух) псевдожидкостей; надо уста
новить, какая из них - i-я или j-я - будет преимущественно
накапливаться в верхних зонах слоя . Решение получают, срав
нивая плотности рассматриваемых псевдожидкостей при рабо
чей скорости ожижающего агента w:

Pt = Prt (l - Et) + PEt

И

Pj = Prj ( l - Ej) + PEj,

причем р
плотность ожижающего агента, а порозности от
дельных псевдожидкостей Et и s1 при скорости w зависят от
плотностей твердых частиц Pri, Prj и от их размеров d1, "1·
Значение разности Лр = р1 - PJ определяет направление сеrре
rации и процесса сепарации: более легкая псевдожидкость на
капливается в верхних зонах ПС. Четкость разделения смеси
при прочих равных условиях возрастает при увеличении упо
мянутой разности. По существу, эту разность можно положить
в основу формирования движущей силы сепарационного про
цесса.
На рис. 23 .2 1 , а показана схема rоризонтальноrо сепаратора,
разделяющего смесь зернистых материалов на два продукта.
-

Слой поддерживается в псевдоожиженном состоянии газовым потоком /.
Исходная смесь //, подаваеман в левое сечение, перемещается вправо - вдоль
оси х; при этом в верхних зонах постепенно накапливаются частицы одного
сорта, а в нижних - другого (на рисунке - мелкие и крупные, соответственно).
Распределение (профиль) концентраций мелких частиц по высоте слоя посте
пенно изменяется (рис. 23.2 1 , б) по мере перемещения псевдоожюкаемого ТМ к
сечению выхода - от равномерного при х = О до наиболее сеrреmрованного
при х =
Сrепень сегрегации вблизи в ыходно го сечения х = может оказаться достаточной
д11Я ра:щельноrо вывода часrиц разных сортов (на рис. 23.2 1 , а - через "'слоезатвор"' J,
работающий по принципу фпоре нтинско rо сосуда
см. ра:щ. 1 3.2.3).

L.

L

-

Технолоrический расчет процесса сепарации предусматри
вает:
- определение равновесного профиля концентраций;
- установление закономерностей изменения этого профиля
до конечного , приближающегося к равновесному и позволяю
щего осуществить процесс разделения.
Равновесн ый профиль концентраций определяется из экс
перимента. Связь основных размеров аппарата (в том числе
необходимой его длин ы L) с производительностью и кинетиче
скими характеристиками строится на основе модельных пред
ставлений . Они включают понятия о скоростях вертикального
1 690

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

//

�
3

о

1

х,

1
Х2

а

1

L

2

"

х

б

Рис. 23. 21. Сепарация на основе сеrрегации в псевдоожиженном слое:
а - схема rориэошальиоrо сепаратора, 6 - профили х:о1Щешраций;
1 - аJПiарат, 2 - rаэораспределительная решетха, З - переrороДJСа
"слоезатвора";
/ - OJIOOIC.alOщий аrеш (rаэ), Jl - исходная смесь, /Jl - вepXJDIЙ продухт, /V - нижний

продухт

перемещения частиц разных сортов (явление сеrреrации) и о
коэффициенте эффективной диффузии частиц (явление переме 
шивания). Модели приводят к профилям концентраций, подоб
ным тем, что показаны на рис. 2 3 .2 1 , б, в том числе (при бес
конечной продолжительности процесса) - к равновесному
профилю. Модели достаточно сложны, их рассмотрение выхо
дит за рамки учебника • .
Сепарация на основе сеrрегации возможна также в верти
кальном аппарате - с подачей исходной смеси в некоторое его
промежуrочное сечение и отводом продуктов из аппарата свер
ху и снизу.
Оrличительная особенность рассмотренных процессов со
стоит в низких расходах ож:ижающеrо агента - на уровне не
обходимых для начала псевдоожижения . Осложняющим мо
ментом являются трудности в равномерности распределения
потока ожиж ающего агента, особенно в случае газового псев
доож:иж:ения .
23.5. О НЕКОТОРЫХ ДРУГИХ ВОЗМОЖНОСТЯХ
КЛАССИ Ф И КАЦИИ ТВЕРДЫХ МАТЕРИАЛОВ

Ниже, в дополнение к представленным ранее, кратко рас
смотрены некоторые используемые в химической и смежных
отраслях промышленности методы классификации твердых
материалов по различным признакам. Подробный анализ рабо
ты и технологический расчет этих классификаторов, а также
• См., наприм ер ,

( 1 ).

1 69 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

сведения о некоторых других возможностях классификации ТМ
и аппаратах для их осуществления приводятся в учебной и
специальной литературе · .
Фр икционн ые сепараторы
Фрикционные сепараторы, разделяющее действие которых
основано на использовании сил трения, бывают плоскими и
барабанными .
Рабочий ор rа н плоскоrо се11аратора (рис . 23.22, а) - наклонная плоскость J.
По ней двюкуrся подлежащие разделению зерна (куски) твердоrо материала.
Признак, по которому происходит разделение, - различие в силах трения у зерен
разных формы и размера. Дело в том, 'ПО форма зерна определяет значение
коэффициента ero внешнеrо трения о поверхность: округлые куски (с примерно
равными размерами по разным направл ениям) стремятся к перемещению каче
нием , а сущ е ст венно асимметричные (пластинчатые, иrольчатые и т. п.) - к
п еремещению скол�.женнем. Коэффициент трения в первом случае з начительно
меньше, чем во втором; поэтому округлые куски движутся по наклонной плос
кости с заметно большей скоростью и при сходе с плоскости падают дальше от
точки А.
Кроме тоrо, куски при мерно одинаковой округлой формы разделяются на
наклонной плоскости еще и по pawepy, поскольку коэффициент трения качения
обрати � пропорционален размеру куска. Поэтому более крупные куски наби
рают большую скорость и тоже дальше отбрасываются от точки схода с наклон
ной плоскости.
Зерна разной форм ы (или размеров) собираются в отдельные приемники 2.

Угол наклона а плоскости к горизонту должен быть выбран
ненамно го больше наименьшего из углов внешнего трения
разделяемых материалов. Это, во-первых, гарантирует движе
ние по наклонной плоскости всех разделяемых зерен , а во
вторых - наибольшую разницу в скоростях разделяемых ку
сков, т.е. повышенную эффективность разделения. При уста
новке ряда наклонных плоскостей последовательно возможно
выделение нескольких классов, отличающихся, например, по
крупности (рис . 23 .22, б) .
Рабочий орГ'd Н барабанноrо сепаратора (рис. 23 .22, в) - вращающийся ци
линдр . На сходящий с питающей пластины 3 кусок одновременно действуют
силы - трения Рт и скаты ваю щая Рек· В зависимости от их соотношения кусок
либо будет подхвачен поверхностью барабана и попадет в левый приемник 2
(асимметричные куски с высокими коэффициентами трения), либо скатится по
поверхности барабана и попадет в правый приемник 2 (округлые куски). В
случае округлых зерен (кусков) разноrо размера в правом приемнике будут со
бирать ся преимущественно крупные зер на (низкий коэффициент трения), а в
левом - мелкие зерна (бол е е высокий коэффициент трения) . Разумеется, как и
в случае сепараторов с наклонными плос костями, возможна установка каскада
барабанных сепараторов с разделением исходной смеси ТМ на несколько клас
сов.

• См.

1 69 2

(6, 7, 1 0 , l l J .

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

)�
·1

. /,',

,.// #

�2
а

� {:з
1�1 а�
1

1.Р..!2

,,,�

1
1

.
�
�2 l..!f2�

б

в

Рис. 23. 22. Фрикционные классификаторы:
а - сепаратор с наклонной плоскосrью, б - каскад плоских сепараторов,
ный сепаратор;
1 - рабочий орrан, 1 - приемш1к продукта, З
питатель

г

-

барабан

-

Флотац ия

Флотация заключаетс я в барботаже воздуха через суспен зию,
содержащую жид кость и подлежащи е разделению твердые час
тицы (тяжелее жидкости) с раз ными физ ико-химическим и
свойствами. Разделение происходит здесь по приз наку избира
тельного з акрепления пузырьков воздуха на частицах опреде
ленного типа . То гда конгломерат "ч астица-воздушны й пуз ы
рек" становится ле гч е жидкости и поднимается в ней (часто
собираясь наверху в сл ое образующе йся пены), а остальные
частицы оседа ют в жид кости. Частицы разных типов раздельно
выводятся из флотацион ной машины - чаще всего с помощью
механических устройств .
Для повышен ия эффективности разделения к суспен з ии до
бавляют флотореаrенты, способствующие прилипанию воздуш
ных пуз ырьков к частицам одного типа и в то же время - по
вышению смачиваемости , а значит, - отталкиванию пузырьков
от части ц другого типа.

Флотацию часто применяют Д11Я концентрирования рудных материалов перед
дальнейшей их переработкой, т.е. Д11Я отделения руды от значительной части
пустой породы. Флотации предшествует измельчение исходной смеси ТМ (до
размеров в десятые и сотые доли милл и метра, чтобы разбить сростки исходной
смеси на отдельные инrредиеlПЪI) и приготоаление суспензии. Пример : кон
центрирование сернистых медных и цинковых руд перед их обжигом в псевдо
ожиженном слое в производстве серной кислоты. После флотации доля целевого
компонента в продукте возрастает с 1 -2% до 35-40% . Это позволяет получать
обжиговые rазы с повышенным содержанием диоксида серы.
Схема работы простейшего флотационного аппарата предстаалена на рис.
23.23. Исходная смесь / в виде суспензии (пульпа) поступает в аппарат J. Снизу
в него подается поток воздуха JJ, который дисперrируется и в виде мелких пу
зырьков барботирует через слой суспензии. Процесс разделения происходит в
рабочей зоне А. Плохо смачиваемые частицы захватывают воздушные пузырьки
и с ними поднимаются вверх, где собираются в пенном слое ///. Затем пена
выводится из флотационного аппарата и напрааляется на отделение ТМ от влаги
- в отстойник, фильтр или аюuюrичное устройство. Хорошо смачиваемые час-

1 6 93

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 23. 23. Схема флотационноrо аппарата:

1 - флотационный аппарат, 2 - разделительная переrороДJСа, J - ЛИЮfЯ подачи возду
ха, 4 - усrройсrво для дисперrирования воздуха;
1 - исходная смесь, II - воздух, III - пена, /V - флотационные хвосты, V - JICИДJ(ocrь

тицы (на рисунке зачернены) остаются в нижней части аппарата. Они постепен
но перемещаются к выходному отверстию и снизу выводятся из аппарата (поток
/V - остатки, "флотационные хвосты"). Жидкость из аппарата отводится отдель
но от пены - поток V. Рабочая зона А отделена от зон подачи пульпы и отвода
жидкости разделительными переrородками 2.

В современных флотационных машинах аэрирование сус
пензии производится с помощью импеллера - вращающегося
диска с лопастями на нем . Импеллер засасывает пульпу и воз
дух и дисперrирует последний; пульповоздушная смесь выбра
сывается в рабочее пространство машины, где и происходит
флотационное разделение.
Электромагнитные методы классификации
Магнитная сепарация. Здесь используется различная магн ит
ная проницаемость разных ТМ: обладающие ею (ферро- и па
рамагнитные материалы) притягиваются магнитом, не обла
дающие (диамагнитные материалы) - не притягиваются.
Магнитные сепараторы бывают: ленточные и барабанные;
прямо- и противоточные; с постоянными магнитами и электро
магнитами; сухие и мокрые. На рис. 23 .24 показан сухой прямо
точный бараб а нный сепаратор для обогащения сырья .
На валу 1 укремен барабан 2, заЮiюченный в цитtндрический корпус J.
Подлежащая разделению смесь / кусков, зерен, частиц, обладающих разными
маmитными свойствами, поступает из бункера 4 в пространство межцу бараба
ном и корпусом и движется в напраалении вращения барабана. При этом она
попадает в маrnитное поле постоянных неподвижных маrнитов с чередую
щимися полюсами : N - S - N - S и т.д. Такое чередование позволяет повы
сить четкость разделения: частицы, притянутые к стенке барабана одним полю
сом маmита, сбрасываются при прохождении мимо противоположно направ
ленноrо полюса; при этом нем аrнитные частицы, притянутые к барабану заодно
с маrнитными, освобождаются от контакта со стенкой барабана.

1 694

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 23. 24. Сухой маn11rm ы й се11аратор с чередующимися полюсами маmитов:
1 - вал, 1 - барабан, J - корпус, 4 - бункер исходной смеси, 5 - посrо.янные маrни
ты, 6 - приеиюпси продуктов;
/ - исходная смесь, 11 - немаrниnlЬlе хвосrы, /// - промежуто'IНЫЙ продукт, IV ко1Щешрат
Рис. 23.25. ИJU[}'кционный электростатический сепаратор:
1 - заземленный баоабан. 2 - бvюс:ео исходной смеси, J - оrрJЩательный электрод,
4 - приеl\IНИКИ продуктов, 5 - разделительная переrородКа ;
/ - исходная смесь, // - электропроводящие зерна, JJJ - зерна-диэлектрики
·

В результате магнитной классификации получаются "хвосты"
II немагнитных частиц, промежуrочный продукт III (обла
гороженная смесь магн итных и немагнитных частиц) и кон 
центрат JV с высоким содержанием магнитных частиц.
Электростатическая сепарация . В этом случае производится
разделение разноименно заряженных зерен либо зерен провод
ника и диэлектрика (в последнем случае используется различие
в электрической проводимости разных ТМ) . Электростати
ческую сепарацию делят на три основные группы: контактную
("элекгрическим трением" - возн икновение зарядов при на
рушении контакта тел) ; индукционную; с ионной бомбардировкой
(использование коронного электрода, подобно применяемому в
электрофильтрах - см. разд. 5. 1 .4). В качестве примера н иже
рассматривается принцип индукционной сепарации.
Если электропроводное зерно входит в контакт с заря
женной (или заземленной) поверхностью большой электри
ческой емкости, то оно практически мгновенно принимает
заряд этой поверхности. Если же в такой контакr входит зерно
диэлекrрика, то происходит поляризация зерна (оно становится
диполем) , но в целом зерно остается электрически нейтральным.
1 6 95

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

На этом различии и построена и ндукционная электростатиче
ская сепарация зерен проводников и диэлектриков, схема которо й
показана на рис. 23.25.

Основные рабочие орrаны - барабан 1 (положительно заряженный, а ча
ще - просто заземленный) и отрицательный элекrрод З. Из бункера 2 смесь
зерен проводника и диэлекrрика ! пос1)'пает на поверхность вращающегося бара
бана. Зерна проводника получают положительный заряд и опалкиваются от
одноименно заряженной поверхности барабана (этому еще способствует притя
жение к противоположно заряженному элекrроду). В результате они собираются
(!!) в правом приемнике 4. А в зернах диэлекrрика при кокrакте с положитель
но заряженной поверхностью барабана наводится диполь, обращенный отрица
тельным полюсом к поверхности; поэтому зерна диэлекrрика притягиваются к
барабану. Далее они под действием собственного веса срьmаются с вра
щающегося барабана и собираются (!!!) в левом приемнике 4.

Л ИТЕРАТУРА

к

главе

23

Айнштейн В. Г., Гордонов Б. С. Псевдоожиже'-ие, rл.4 "Сеrреrация зернис
материалов в псевдоожиженном слое' Под ред. В.Г. Айнштейна,
А.П . Баскакова. М . : Химия, 199 1 . 400 с.
2. Барский М.Д., Ревнивцев В.И., Соколкин Ю.В. Гравитационная классифи
кация зернисть�х материалов. М . : Недра, 1974. 232 с.
3. Гельперин Н. И. Основные процессы и аппараты химической технологи и .
М . : Химия, 198 1 . 812 с .
4. Гельперин Н. И., Айнштейн В. Г., Кваша В.Б. Основы техники псевдоожи
жения. М . : Химия, 1967. 664 с.
5. Гельперин Н. И., Айнштейн В.Г. Псевдоожижен)!е, rл.XI "Аналогия между
псевдоожиженным слоем и капельной жидкостью' Под ред. И.Ф. Дэвидсона,
Д. Харрисона: Пер. с анrл. Под ред. Н . И . Гельперина. М . : Химия, 1974. 760 с.
6. Глембоцкий В.А., Классен В.И. Флотация. М . : Недра, 1973. 384 с.
7. Левенсон Л. Б. Машины для обоrащения полезнь�х ископасмЬIХ. М . -Л . :
Госмашметиздат, 1933. 803 с .
8. Левенсон Л. Б., Прейгерзон Г. И. Дробление и rрохочение полезнЬIХ иско
паемых. М . : Гостоптехиздат, 1940. 772 с.
9. Левенсон Л. Б., Цигельный П.М. Дробильно- сортировочные машины и
установки для переработки каменных материалов. М . : Стройиздат, 195) . 428 с.
10. Перри Дж. Справочник инженера-химика: Пер. с англ Под ред.
Н . М . Жаворонкова. Л . : Химия, 1969. 1 144 с.
1 1. Сиденко П. М. Измельчение в химической промышленности . М.: Химия,
1977. 368 с.
тых

1.

/

/

/

/

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Глава 24
СОПРЯЖЕННЫЕ И С ОВ МЕЩЕННЫЕ
ПРО ЦЕСС Ы

Практически каждый из используемых в настоящее время в
химической и родственных ей отраслях промышленности гид 
ромеханических, тепловых, массообменных и реакцщ>нных
процессов имеет ограниченные области технически возможного
или экономически целесообразного применения . Большая
часть этих ограничений связана со специфическими свойства
ми перерабатываемых веществ (реагентов, сред, материалов,
продуктов и т.п.). Например, для массообменных процессов
такие ограничения часто связаны с наличием на диаграммах
фазового равновесия особых точек (азеотропных, эвтектиче
ских, перитектических и др.), а также особых областей
(ограниченной растворимости, термической устойчивости, хи
мического взаимодействия компонентов смеси и т.д.).
Возможности успешного решения возникающих задач в
производстве тех или иных продуктов существенно расширя
ются при комбинировании нескольких технологических процессов.
Так, границы возможного разделения ряда трудноразделяемых
смесей моrуг быть значительно расширены путем сочетания
(комбинации) двух или нескольких однородных либо разно
родных массообменных процессов . При этом такое сочетание
нередко позволяет одновременно добиться снижения энергети
ческих и других затрат, а в ряде случаев - еще и упростить
аппаратурно-технолоrическое оформление производства.
Комбинированные процессы уже сейчас широко используются
в технологии производства различных продуктов. С повышени
ем требований к выходу и качеству целевых продуктов, услож
нением технологии, непрерывным увеличением ассортимента
выпускаемой химической продукции, а также с необходи
мостью решения экологических задач роль комбинированн ых
процессов несомненно будет возрастать и такие процессы бу
дут получать все большее распространение.
Ранее при разработке комбинированных процессов техноло
ги чаще всего действовали на основе прямых функциональных
связей. Если, скажем, при разделении реакционной смеси ме
тодом ректификации сразу не удавалось получить целевое ве
щество заданной чистоты, то продукты перегонки очищали с
1 697

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

использованием других массообменных процессов (той же рек
тификации, кристалл и зации, экстракции, адсорбции и т.д . ) .
Принимаемые таким образом технологические решения зача
стую носят субъективный характер и часто далеки от опти
мальных.
Сочетание двух или нескольких технологических процессов
в единой схеме пороЖдает, как правило, несколько возможных
вариантов решения поставленной задачи . А поскольку многие
технологические процессы мoryr осуществляться несколькими
различными способами, то число возможных вариантов ком
бинированных процессов может быть весьма значительным.
При разделении сложных многокомпонентных смесей число
вариантов решения поставленных задач существенно увеличи
вается и появляется воз можность использования в единой тех
нологической схеме целого ряда массообменных и других про
цессов, тесно связанных прямыми и обратными потоками. В
этих условиях выбор оптимального варианта комбинированно
го процесса представляет собой весьма сложную проблему,
разрешить которую на основании одной интуиции разработчи
ков нельзя .
В химической промышленности чаще всего каЖдую техно
логическую операцию (стадию, процесс) осуществляют в от
дельных аппаратах. Однако это не всегда целесообразно. В це
лом ряде случаев выгоднее проводить несколько процессов в
одном аппарате. Такое совмещение процессов обычно позволя
ет более полно использовать исходное сырье (реагенты, рас
творители и т.д.), увеличить выход целевых продуктов, снизить
энергетические, капитальные и другие виды затрат.

24. 1. ОСНОВНЫЕ ТИП Ы И ОСОБЕННОСТ И
КОМБИНИРОВАНН ЫХ ПРОЦЕССОВ

Условно все комбин ированные процессы можно разделить
на три группы: последовательные, сопряженные и совмещен
ные процессы.
Последовательные процессы состоят из последовательно
(возможно, с ответвлениями) осуществляемых стадий, которые
связаны в основном прямыми потоками. Например, после ста
дии фракционной кристалл изации полученную суспензию пе
редают на стадию фильтрации, а влажную кристаллическую
фазу направляют на стадию сушки. Такого рода комбиниро
ванные процессы в настоящее время наиболее широко исполь
зуются в химической технологии, хотя они не всегда обладают
высокой эффективностью. При разработке таких процессов
технологические режимы последующих стадий обычно прихо-

1698

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

дится устанавливать исходя из физико-химических свойств и
расходов потоков на предшествующих стадиях. Общий анализ
сетей аппаратов для реализации некоторых однородных массо
обменных процессов приведен в разд. 1 0 . 1 1 - 1 0 . 1 3 .
К сопряженным относят комбинированные процессы, со
стоящие из отдельных стадий, связанных между собой как пря
мыми, так и обратными потоками. При этом отдельные стадии
процесса моrуг осуществляться одновременно в различных
аппаратах (как правило, в случае непрерывных процессов) или
же последовательно в одном аппарате (периодические процес
сы). В сопряженных процессах технологические режимы пред
шествующих стадий моrуг зависеть от режимов проведения
последующих стадий. Это объясняется влиянием характеристик
обратных потоков (расхода, концентраций, дисперсного соста
ва, температуры и т.д.) на ход предшествующих стадий.
В совмещенных процессах две или несколько стадий осу
ществляюrся одновременно в одном аппарате. Например, при
вакуумно-вьmарной кристаллизации в кристаллизаторе одновре
менно происходят процессы вьшар ивания леrколетучего компо
нента и кристаллизации растворенного вещества . Иногда в со
вмещенных процессах различные стадии проводятся в отдельных
сеющях одного и того же аппарата. Например, в совмещенном
реакционно-ректификационном процессе стадия химического
превращения может проходить лишь на одной из промежуточных
тарелок ректификационной колонны. На остальных же тарелках
имеет место обычный процесс ректификации .
Как уже указывалось выше, комбинированные процессы ,
как правило, отличаются много ч исленностью возможных вари
антов их проведения . Особенно большое число вариантов ха
рактерно для сопряженных массообменных процессов. Это объ
ясняется, с одной стороны, большим разнообраз ием диаrрамм
равновесия фаз, а с другой стороны, тем, что даже для одной и
той же смеси с использованием только двух сопряженных про
цессов возможен целый ряд вариантов разделения.
При разработке сопряженных и совмещенных процессов
возникает рЯд характерн ых задач:
- выявление возможных вариантов проведения процессов;
- анализ влияния внешних и внутренних параметров на
эффективность выявления вариантов;
- оmимизация параметров процесса;
- выбор оптимального варианта проведения процесса;
- подбор необходимого оборудования.
Наличие большого ч исла возможных вариантов осуществле
ния комбинированного процесса ставит вопрос о методике
выбора оптимального варианта и установления оптимальных
технологических параметров его проведения.
1 699

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рассмотрим в общем IUiaнe такую методику применительно
к процессам разделения веществ. Очевидно, выбор варианта сле
дует производить, исходя из конкретных условий разделения.
Определяющими факторами здесь являются: состав исходной
смеси и ее физико-химичесЮfе свойства, требуемая степень
чистоты продуктов разделения, производительность установЮf,
характер диаграмм равновесия фаз, наличие необходимого обо
рудования, а также энергетичесЮfе , капитальные и другие виды
затрат на процесс разделения.
Представляется целесообразной следующая последователь
ность выбора опrимальноrо вариаwrа разделения и его технологи
ческих (режимных) параметров:
- на основе анализа диаграмм равновесия фаз, данных об
исходном составе смеси, а также данных о требуемых составах
продуктов разделения устанавливаются возможные варианты
сочетания различных процессов разделения данной смеси;
- выясняют факторы, ограничивающие (или делающие во
обще невозможным) использование тех или иных вариантов
разделения;
- выбирают критерий (или критерии), на основании кото
рого будут сравниваться рассматриваемые варианты процесса
разделения и производиться их оптимизация;
- устанавливаюr для всех рассматриваемых вариантов функ 
циопальные зависимости межцу внугренними и промежуточн ыми
параметрами процесса и выбранным крпrерием опrимизации ;
- на основании анализа полученных функциональных зави
симостей находят оптимальные значения критерия для всех рас
сматриваемых вариантов;
- сравнивают между собой оптимальные значения критерия
и выбирают оптимальный вариант процесса разделения и его
параметры.
Для осуществления такого анализа, естественно, необходимо
выбрать критерии оценки рассматриваемых вариантов. В ка
честве последних мoryr выступать:
- приведенные затраты на еди ницу продукции;
- удельные затраты энергии;
- коэффициенты извлечения целевых компонентов;
- предельные концентрации продуктов разделения (степень
ИХ ОЧИСТЮf) ;
- эксергетичесЮfе, э нтропийные и другие критерии оценЮf
эффективности.
К сожалению, все эти критерии не являются универсальны
ми. Каждый из н их обладает теми или иными недостатками .
Например , степень извлечения не позволяет судить об эко
номической эффективности процессов и качестве (степени)
очисТЮf конечных продуктов. Сте пень очиСТЮf (концентрации)

1 700

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

продукrов разделения ничеrо не rовориr о том, какой ценой это
достигается. Эксерrетич еские кригерии позволяюг судкrь лишь об
использовании движущей силы процесса, но не затрагиваюr дру
гих важн ых acпeJcrOB данной проблемы. К тому же значимость
различных кригериев может изменяться с течением времени.
Из всех упомянуrых выше критериев наиболее универсаль
ными являются приведенные затраты, или удельные энергетиче
ские затраты. В настоящее время именно они чаще всеrо ис
пользуются для анализа эффе�сrивности процессов разделения .
Известно, что технолоmческие параметры процессов разде
ления (давление, температура, исходный состав, составы про
межуточных фракций, соотношение потоков и др .) сильно
влияют на их общую эффе�сrивность. Поэтому при решении
технолоmческой задачи необходимо представление о диапазо
нах возможного изменения (варьирован ия) этих параметров.
Такие диапазоны зависят, с одной стороны, от физико
химических свойств разделяемой смеси, а с другой - от техни
ческих возможностей реализации тех или иных процессов в
конкретных рассматриваемых условиях.
Условно все технолоmческие параметры можно разделить
на две группы: внуrренние и переходные (промежуточные, пере
даточные). Внутренние параметры хара�сrерны для отдельных ста
дий комбинированноrо процесса; они определяюг ход процесса
на рассматриваемой стадии и ero показатели. К переходным отно
сят параметры потоков, рециркулирующих ме:>tЩу аппаратами
(стадиями ). В качестве последних часто выступаюr промежуточ
ные концентрации , температуры потоков и их расходы.
Заметим, что эффективность комбинированных процессов
разделения может быть существенно увеличена при правиль
ной организации рекуперации теплоть1 между потоками. Расче
ты показывают, что указанная рекуперация в ряде случаев по
зволяет снизить затраты энерmи на 20-30% и более .
При разработке сопряженных и совмещенных процессов обычно приходится
вьmоJmЯТЬ боmшие объемы повторяющихся расчетных операций; поэтому раз
работку (синrез) возможных вариакrов разделения, их анализ и оптимизацию
рационатно проводить на ЭВМ с использованием соответствующих проrрамм.

24.2. СОПРЯЖЕННЫ Е ПРОЦЕССЫ

Осуществление сопряженных процессов чаще связано либо
с преодолением физ ико-химических (термодинамических)
ограничений, либо с рекуперацией переносимой субстанции импульса, теплоты, вещества. При рекуперации последнего
технолоmческие схемы условно замкнуrы по этому (обычно вспомогательному) веществу - за счет обратных рециркуляци
онньIХ потоков.
1 70 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Некоторые из сопряженных процессов приведены в пре
дыдуших главах, хотя и без акцента на особенности сопряже
ния различных стадий (технологических приемов) . Ниже ряд из
них упомянуг с необходимыми ссьmками на разделы .
Расчет отдельных стадий приводимых ниже сопряженных
процессов рассматривается в соответствующих главах учебника.
Однако при сопряжении стадий требуется согласование проме
жуточных потоков и параметров (обычно - при заданных на
чальных и конечных). Такое согласование, как правило , не яв
ляется однозначным; оно окончательно реализуется на основе
выбранных критериев эффективности сопряженного процесса,
чаще всего - технико-экономических.
24.2. 1 . Процессы с рекуперацией импульса и теплоты

Типичным сопряженным процессом, рекуперирующим меха
ническую энергию, является абсорбционио-десорбционвый. про

цесс, основанный на возрастании растворимости компонентов
газовой смеси с ростом давления (разд. 1 1 .3). Упрощенная схе
•
ма процесса приведена на рис. 24. 1 . Исходный rаз /, содер
жащий поглощаемый компонент, подается в абсорбер 1, рабо
тающий под достаточно высоким давлением. Туда же насосом
4 (центробежным, многоколесным) направляется абсорбент JJ/.
Из абсорбера уходят очищенный rаз II и абсорбент IV, насы
щенный поглощаемым компонентом. Абсорбент, находящийся
после абсорбера под высоким давлением, поступает на турбину
5, где его давление сбрасывается до атмосферного . Из турбины
поток IV направляют в десорбер-сепаратор 2
там происходит
десорбция поглощенного компонента из его смеси с абсорбен
том и их разделение. Поток компонента V выводится к потре
бителю, а регенерированный абсорбент III возвращается насо
сом 4 в абсорбер.
В рассматриваемом аспекте нас интересуют здесь не массо
обменные стадии абсорбции и десорбции, а сопряжение насоса
и турбины: : последняя возвращает заметную долю механи
ческой энергии, затрачиваемой на подачу абсорбента насосом в
абсорбер.
-

Описанный процесс в промЫIШ1енности используется, например, для вьше
ления СО2 из азотоводородной смеси с ним. При этом давление в абсорбере 1 ,6-3,0 МПа, а в десорбере - атмосферное. В комбинации "мотор-насос
турбина" удается возвратить до 40% энергии от затрачиваемой на работу насоса;
остальная энергия восполняется электродвигателем .

Примеры сопряжения процессов сжатия и расширения газов
с рекуперацией механической энергии бьmи приведены при

• Подробнее см .
1 702

(9 ) .

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 24. 1. Принципиальная схема абсорб

ционно-десорбционноrо аrреrзта :
1 - абсорбер, 2 - десорбер-се1 1аратор, З элеnродвиrатель, 4 - насос, 5 - турбина;
1 - HCXO)UIЬIЙ rаз, // - ОЧНЩСllНЫЙ rаз, ///
- абсорбс�п, IV - отработанный абсорбс�п, V
- десорбированный КОМПОНСIП

v
JV

2

/

рассмотрении умеренного (разд.
2 1 .2.3) и глубокого (разд . 2 1 .3 .4,
IIJ
2 1 .3.5) охлаждения с использованием детандеров.
Типичными примерами пе 
риодических сопряженных про- .
цессов с рекуперациеи теплоты моrуг служить процессы с
применением регенеративных теплообменников (см . разд. 7 . 1 ) .
Среди такого рода производств - глубокое охлаждение с ис
пользованием высокотеruюпроводной насадЮI из тонкой ме
таллической гофрированной ленты и с коротЮ1ми тепловыми
циклами; металлургические производства с использованием
крупной керамической насадЮI высокой теплоемкости и с до
статочно длительными тепловыми циклами.
Тепловые процессы часто сопрягаются в непрерывных произ
водствах с рециркулирующими потоками субстанций : нагрев
охлаждение, испарение-конденсация, плавление-отвержде
ние и в других комбинациях. Сопряжение теплообменных про
цессов, как правило, позволяет существенно повысить эконо
мическую эффективность технолоrnческ:их процессов. Сочета
ние тепловых и гидромеханических процессов реализуется в
установках с "тепловыми насосами", а сочетание химических,
массообменных и тепловых процессов - в тепловых аккумуля
торах, например в термоаккумуляторах с гидридными соедине
ниями газов. В будущем таЮ1е сопряженные тепловые процес
сы безусловно получат более широкое распространение.
Наиболее широко в химической технологии представлены
массообменные сопряженные процессы.
�

24.2.2. Ректификация азеотропообразующИХ смесей
в двух колоннах, работающих под разными давлениями
Методический интерес представляет разделение гомогенных
азеотропообразующих смесей в двух ректификационных ко
лоннах, работающих под разными давлениями (рис. 24 .2 , а) . В
основе разделения - смещение азеотропной тоЧЮI в соот
ветствии с правилом Вревского при изменении давления (см .
разд . 1 2.2.4). Это - пример сопряжения двух однородных массо
обменных процессов.

• Подробнее см.

(2-4) .

1 703

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

а

о

1

v

б

Рис. 24.2. Разделение rомоазеотропной смеси в двухколонной реJСТИфикационной
установке:

- схема усrаноахи,
6 - изобрцение на диаrраммах равновесия фаз;
1, 2 - реrrификациоННЬ1е колоННЬJ;
1 - исходная смесь, // и /l/ - первый и второй дисrилляr , IV и V - низкокипящий и
высокоюmящий продукты

а

Пусть смесь компонентов А и В образует азеотропы с ми
нимумом температур кицения, причем при дамении р1 состав
азеотропа равен Xal • а при Р2 < Pl он равен Ха2 (рис.24.2,б).
В первой колонне, работающей при большем дамении р1 ,
смесь состава х1 < Ха ! разделится на сколь угодно чистый высо
коЮ1пящий компонент В (кубовый остаток) и дистиллят, близ
кий по составу к азеотропной смеси с концентрацией ха 1 . Если
подать этот дистиллят во вторую колонну, работающую при
более н изком дамении Р2 (часто - под вакуум ом), то в кубо
вом остатке получим прак:rически чистый низкокипящий ком
понент А и второй дистиллят, близкий по составу к азеотропу с
концентрацией х82. Второй дистиллят присоединяют к потоку
исходной смеси .

Заметим, 'ПО праJСТИЧеское применение двухколонных реJСТИфикационных
установок, зачасrую требующих работы одной из колонн под вакуум ом, встреча
ет большие затруднения при разделении смесей, состоящих из компонентов с
большой летучестью : не исключен подсос в колонну воздуха извне; из-за низкой
температуры ки пе ния таких смесей конденсатор вакуум -ректификационной

1 704

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

колонны нуждается в специа.rtьных хладоаrентах; в весьма жестких условиях
работает вакуум - насос; наблюдаются потери веществ с отсасываемой им парога
зовой смесью . В связи с этим для разделения азеотропообразующих смесей на
пракrике чаще используются и н ые методы (см. разд. 1 2 .9).

Далее рассматриваются разнородные массообменные сопря
женные процессы.
24.2.3. Дистилляция-кристаллизация

Сочетание в единой технологической схеме процессов фрак 
ционной кристаллизации и ifистилл.яции характеризуется доста

точно большим числом возможных вариантов осуmествления
процесса разделения. Дело в том, что каждый из этих массооб
менных процессов может быть проведен несколькими спосо
бами. Как было показано в разд. 1 6.5, фракционную кристалл и 
зацию можно осуmествить в виде однократного, последова
тельного и противоточного процессов, а также методами фрак
ционного плавления , зонной плавки и др. В свою очередь, ди
стилля ция также реализуется несколькими методами (см . разд.
12.3): простая, многократная, с использованием флегмы, в токе
инертного rаза, молекулярная и др . Особенности рассматри
ваемого сочетания сильно зависят от вида диаграмм равнове
сия фаз "жидкость-пар" и "кристаллическая фаза-жидкость".
Рассмотреть (даже кратко) все варианты здесь не представ
ляется возможным . Н иже будут приведены лишь наиболее ха
раперные примеры.
На рис . 24.З показана принципиальная схема одного из ва
риантов разделения бинарной эвтепикообразующей смеси
путем сочетания однократных процессов простой дистилля ц ии
и фракционной кристалл изации . Для упрощения изложения
принято, что на стадиях испарения и кристалл изации достига
ется полное равновесие фаз , а на стадиях сепарации происхо
дит идеальное отделение фаз друг от друrа (с целью упрощения
теплообменники на схеме не показаны).
В данном варианте исходную смесь F с концентрацией хр
легколетучего компонента первоначально подают на стадию
дистилляции Д, rде про цесс проводится при температуре fи. В
результате частичного испарения смеси F образуются пар П с
концентрацией Уп и жидкая фаза (кубовый остаток) Lo с кон 
центрацией xLo . После сепарации С паровую фракцию П на
правляют на стадию кристалл изации Крл, а жидкую фракцию
на стадию кристалл изации Кр 8 , rде они охлаждаются до
Lo
температур tфл и fg,в соответственно . На стадии Крл образуются
кристалл и ческая фаза Кл (практически чистый компонент А) и
маточник Мл. Кристалл и ческая фаза Кл отбирается в качестве
одного из целевых продуктов, а маточник Мл возвращается на
стадию дистилляции . Аналогично на стадии Кр8 получаются
-

1705

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

' "в
lи

а
в

...·'=

t:::

С>
"'-1

t�
А
lд

tв
fф
х

б

Рис. 24.З. Разделение эвтектикообразующей смеси сопряжением однократных
процессов кристалли зации и диСТИJVIЯции (исходная смесь подается на стадию

ДИСТИЛllЯЦИИ):

а - при нципиальная схема разделения , б - изображение процеа:а на диаграммах р ав
новесия фаз

кристалл и ческая фаза К8 , которая представляет собой практи
чески чистый компонент В, и маточник Мв. Последний вместе
с Мл также возвращают на стадию дистилля ц ии.
В рассматриваемом варианте в качестве переходных пара
метров выступаюr концентрации рециркулирующих потоков Уп ,
xLo , хмд и Хм в, а в качестве основн ых внуrренних параметров
- давление на стадии дистилля ции, температуры испарения fи
и фракционирования на стадиях кристалл изации tФА и tФВ·
Кроме описанных выше возможен и ряд других вариантов.
Так, исходную смесь можно первоначально подавать на одну
из стадий кристаллизации: кристаллические фазы - отбирать в
качестве продуктов ра зделения, а маточники - подавать на
стадию дистилл яции, которую в данном случае используют для
перехода через эвтектическую точку. Возможны также вариан
ты, в которых один из конечных продуктов получается на ста
дии кристаллизации, а другой - на стадии дистилля ции .
1 706

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис.24.4. Разделение эвтеlСl'Икообразующей смеси сопряжением процессов кри
сталли зации и последовательной диСТИJVIЯции:
прЮЩJПD1альная схема, б изображеЮ!е процесса на диаrраммах р авновесия ф аз
а
-

-

В качестве критерия оценки эффекrивности сравниваемых
вариантов сопряженного процесса можно использовать удель
ные энергетические затраты, обычно составляющие 80-90 % от
общих затрат на процесс разделения. Обозначим Эд, Экл, Экв,
Эн . Э0хл затраты энергии на стадиях дистилляции, кристал
лизации, нагрева и охлаждения рециркулируемых потоков:
(24. 1 )
Э1: = Эд + Экл + Экв + Эн + Эохл
-

.

Значения отдельных составляющих затрат Э1: зависят ка к от
внутренних, так и от переходных параметров. При выборе оп
тимального варианта, естественно, необходимо установить
функциональные зависимости этих затрат от указанных пара
метров.
Для разделения веществ весьма часто используют процесс
последовател ьной дистил.11.Яции, которая осуществляется в пе
риодическом режиме. Данный процесс также можно сочетать с
фракционной кристалл изацией. Один из вариантов такого со1 707

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

пряженного процесса показан на рис. 24.4. Здесь исходная
смесь F загружается в испаритель (куб) И . Образующиеся пары
П (переменного во времени состава) поступаюr в конденсатор
холодильник КХ, где они конденсируются и охлаждаются до
заданной температуры. Образующаяся при этом жидкая фрак
ция направляется в кристалл изатор Кр . В рассматриваемом
варианте процесс кристалл изации осуществляется в кристалли
зационном поле компонента А при постоянной температуре
фракционирования tФА · Полученную суспензию разделяюr на
фильтре Ф . Кристаллическую фракцию Кл отбираюr в качестве
целевого продукта - в идеале чистого компонента А. Маточ
ник Мл возвращаюr на стадию дистилляции.
Хотя в процессе разделения происходит непрерывное изме
нение составов жидкой фазы в кубе дистиллятора и образую
щихся паров, тем не менее состав получаемой кристалл и ческой
фазы в ходе разделения остается постоянным, так как при кри
сталл и зации выделяется практически чистый компонент А.
По мере отгонки содержание низкокипящего компонента А
в парах ум ен ьшается , соответственно этому снижается выход
кристалл и ческой фазы. Процесс продолжаюr до тех пор, пока
не будет достиrнуrа заданная степень извлечения компонента
А из разделяемой смеси. В конце процесса разделения получа
юr кубовый остаток Lo с концентрацией xLo . Заметим, что в
рассматриваемом варианте предельная степень извлечения
компонента А из кубового остатка зависит от положения точки
эвтектики на диаграмме равновесия "расплав-твердая фаза":
на стадии последовател ьной дистилляции содержание компо
нента А в парах, разумеется, не может стать ниже ХЕ ·
Как известно, при последовательной перегонке получают
целый набор паровых фракций различного состава. Это не
всегда удобно . В данном же случае получается всего два про
дукта: практически чистый компонент А и кубовый остаток Lo,
обогащенный высококипящим компонентом В.
В других вариантах сочетания процессов фракционной кри
сталлизации и последовательной дистилляции исходная смесь
может подаваться на стадию кристаллизации компонента А
либо на стадию кристаллизации компонента В .
24.2.4. Ректификация-кристаллизация

Данное сочетание отличается особенно большим числом
возможных вариантов его осуществления .
На рис. 24. 5 приведен один из вариантов сопряжения не
прерывных процессов ректификации и фракционной кристалл и 
зации примен ительно к разделению бинарной эвтектикообра
зующей смеси, имеющей монотонно выпуклую диаграмму равнове1 708

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

х
-

1

D

РК

а

х

б

Рис.24. 5. Разделение эвтектикообразующей смеси сопряжением процессов рек
тификации и кристаллизации (исходная смесь подается на стадию кристалли за
ции Крд):
а

-

прИJЩИПи ап ьная схема , б - изображение процесса на диаrраммах равновесия фаз

сия "жидкость-пар ". Подобную смесь, как бьuю показано в
разд. 16.5, методами одной лишь фракционной кристаллизации
нельзя разделить на чистые компоненты из-за наличия эвтек
тической точки на диаграмме "расплав-кристаллическая фаза" ;
в лучшем случае можно получить в чистом виде один из ком
понентов смеси и маточник эвтектического состава. Однако
сочетая процессы ректификации и кристаллизации, можно
разделить данную смесь на практически чистые компоненты,
используя одну ректификационную колонну и один или два
кристалл изатора.
Разделение исходной смеси F состава хр > ХЕ проводят сле
дующим образом. Смесь F первоначально направляют на ста
дию кристалл и зации Крл, которую при указанном соотноше
нии концентраций осуществляют в кристаллизационном поле
компонента А. При этом получают кристаллическую фазу Кл
(практически чистый компонент А) и маточник Мл состава хмА,
который направляют на ректификацию РК. Выходящие из ко
лонны РК пары D полностью конденсируюrся в конденсаторе
1 709

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

х
-

х

а

1

х
-

1

х

б

Рис.24.6. Разделение эвтепикообразующей смеси пугем сочетания процессов
ректификации и кристалли зации с подачей исходной смеси на стадию кристал
лизации (а) и на стадию ре ктификации (б)

КО. Часть конденсата L возвращают в колонну в виде флегмы,
а друтую часть П состава х2 > ХЕ направляют в кристаллизатор
Крл. Кубовый остаток Lo состава xio < ХЕ пропускают через
теплообменник Т и подают на стадию кристаллизации Кр8, где
процесс протекает в кристаллизационном поле компонента В .
Н а стадии Крв получают кристаллический продУКJ' Кв
(практически чистый компонент В) и маточник Мв, который
так же, как и Мл, возвращают в ректификационную колонну.
Помимо описанного возможно еще более десятка различн ых
вариантов разделения рассматриваемой смеси: с подачей ис
ходной смеси либо на одну из стадий кристалл и зации Крл или
Крв, либо на стадию ректификации . Возможны варианты, ког
да один из компонентов смеси получают ректификацией, а
другой - кристаллизацией (рис. 24.6). Заметим, что при со
пряжении процессов ректификации и кристалл и зации стадию
ректификации можно осуществлять без специального конден
сатора, используя в качестве флегмы маточник одной из стадий
кристаллизации.
1710

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

х
-

1

х
-

1

о

о
1

в

а

х

б

А

Рис. 24. 7. Разделение бинарных смесей сопряжением процессов ректификации и
кристалли зации:
а - смесь обладает оrраиичею1ой расrворимосrью комnоиенrов в твердом состоЯЮfИ, б
- смесь образует молекуЛJ1Рное соединение в твердом состоянии

Смеси, обладающие ограниченной взаимной растворимостью
компонентов в твердом состоянии, можно разделить, сочетая
процессы ректификации и противоточной кристаллизации. Один
из вариантов такого разделения показан на рис . 24.7,а. Про
цесс проводится с использованием двух противоточных кри 
сталлизаторов, с помощью которых получают конечные про
дукты Кл и К8 . Низкоплавкие фракции со стадий кристалл и за
ции в виде потоков Lл и Lв направляют на стадию ректифика
ции, которая позволяет осуществить переход через эвтекти
ческую точку.
Сопряжением фракционной кристаллизации и ректифика
ции можно разделить смеси, образующие в твердом состоянии
молекулярные соединения. В варианте, показанном на рис . 24.7,б,
исходную смесь подают в ректификационную колонну, и ко
нечные продукты разделения получают на стадиях кристалли171 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

1

х
-

о

�

Li..
tл
/ф

tв
в

-

х

А

Рис. 24. 8. Разделение бинарной азеотропообразующей смеси, образующей непре
рывный ряд твердых растворо в, пуrем сопряжения процессов рекrификации и
кристалл и зации

зации компонентов А и В. Здесь ректификацию используют
для перехода через две эвтектические точки - Е 1 и Е2 (с кон 
центрациями ХЕ1 и ХЕ2) .
Особый интерес представляет сочетание процессов ректи
фикации и кристалл и зации для разделения азеотропообразующих
смесей. Разделить такие смеси с помощью одной лишь ректи
фикации на практичесю1 чистые компоненты (без специальных
приемов) невозможно (t;M. разд . 1 2 .9). При сочетании же рек
тификации и кристалл и зации процесс разделения таких смесей
почти всегда осуществим .
На рис . 24 . 8 представлен один из вариантов разделен ия би
нарной азеотропообразующей смеси с минимальной темпера
турой кипен ия , образующей при кристалл и зации непрерывный
ряд твердых растворов. Здесь однократную кристаллизацию ис
пользуют в основном для перехода через азеотропную точку,
окончательно же смесь разделяют методом ректификации с по
мощью двух колонн .
Сочетан ие рассматриваемых процессов может быть успешно
использовано и для разделения гетероазеотропных смесей, а
также смесе й , имеющих области расслаивания жидких фаз при
температуре 1vc кристалл изации.

1712

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

При анализе эффективности разделения пуrем сопряжения
процессов ректификации и кристаллизации, а также при выбо
ре оптимальн ых параметров такого процесса общие затраты Э r
можно представить в виде суммы затрат на обогрев куба ко 
лонны Экуб, охлаждение дефлегматора Эд, кр и сталл иза ци ю
Экд и Э кв ком п о н е нто в А и В , нагрев Эн и охлаждение Э 0хл
п р о межуrо ч н ых и конеч н ых п родукто в:
Эr = Экуб + Эд + Э кА + Э кв + Эн + Э0хл .
(24 . 2)

Заметим , •по как об щие , так и отдельные составляющие за
траты обычно существен но зависят от внуrренних и про межу
точных (переходящих) параметров. П оэтом у без соответствую
щего технико-экономического анализа всех возможных вари
антов произвести выбор того или иного вар и а нта процесса раз
деления практически невозможно.
24.2.5. Э кстракцня-кристалл и1ация
Сопряжение процессов жидкостной экстракции и кристалл и 
зации в литературе чаfТО выступает под термином экстрак
тивная к.р исталл изация . Оно используется для полного разде
ления эвтектикообразующих смесей, а также смесей, образую
щих п р и кристалл и зации различные х и мичес кие соединения, и
смесей , имеющих коэффициенты распределения целевых (или
примесн ых) компонентов, близЮ1е к единице. Сущность про
цесса состоит в добавлени и на определ е н н ой стадии к разде
ляемой смеси жидко го вспомогательного компонента (э кстра 
гента), изменяющего о п редел ен ным образом равновесие ком:

понентов разделяемой смеси.
Э кстрактивную кристалл и зацию можно проводить двумя
основн ыми способами . В первом из них к разделяемой смеси
добавляют ком п о н е нт образующий с исходной смесью гомоген
иый раствор. Во втором способе добавление вспомоrательноrо
компонента приводит к во з ни кн о вен ию гетерогенной системы.
Э кстракти вная крi1сталл и зация с образованием rомоrенных
растворов сходна с обьl'tной кристаллизацией из раствора (см .
разд 1 6 .5 . 1 ) . Рассмотри м один из вариантов такого процесса
примен ительно к полному разделению бинарной эвтектикооб
раз ую щей смеси (рис. 24 .9).
Исходную жидкую смесь F с концентрацией XF > XEf (где XEf
концентрация эвтектиЮ1) подают на стади ю кристаллизации
Крд, проводимую при температуре, близкой к температуре
кристалл и заuии эвтектиЮI 1Е1 . В результате получается кристал
ли•1еский продукт Кл, п р едста вл я ю щи й собой практически чис
тый ком поне нт А, и маточник Мл, по составу близкий к э вте к
,

.

-

-

•

Подробнее

см.

\6J.
1713

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

F

с

б

Рис. 24.9. Разделение эвтекrикообразующей смеси методом эхстракrивной кри
сталлизации с образованием го моrенной системы:
иэображеЮ1 е проце сса на диаrраммах равновеси я фаз
а
прИ1ЩИПи алъная схе ма, б
-

-

тике ХЕ• Маточник Мл направляют на стадию смешения N , где
его смешивают с экстрагентом С. Последний подбираюг с таким
расчетом, чтобы он образовывал с исходной смесью тройную эв
текгикообразующую систему с тройной эвrекrической точкой Е4,
в которой соотношение компонентов А и В отличалось бы от их
соотн ошения в бинарной эвrекгике Е1 . При этом масса вводимого
раствориrеля должна обеспечивать попадание полученной трой
ной смеси - раствора Р в кристаллизационное поле компонен
та В (в область ВЕ1 Е4Е2). Полученный раствор Р направляют на
стадию кристdJVlизации Крв, в результате которой получают кри
сталличес кий продукт Кв и маточник Мв. Последний направляюr
на стадию отгон ки раст1юриrеля О. После отгон ки регенериро
ванный раствориrель С возвращают на стадию смешения N, а
кубовый остаток Lo, состоящий из компонентов А и В, подаюr на
стадию кристаллизации Крл.
О писанный выше процесс экстрактивной крИL"Галлизации используют для
-

разделения органических смесей, например изомеров ксилола или крезола. При
этом в первом случае в качестве растворителя применяется н- rептан, а во втором
- уксусная кислота.

Один из вариантов разделения бинарной эвтектикообра
зующей смеси с образованием жидкой rеrероrеииой системы
показан на рис . 24 . 1 0 . Здесь процесс экстракции тоже исполь
зуют для перехода через эвтектическую точку.
1714

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

с

б

Рис. 24. 10. Разделение эвтектикоо бразующей смеси методом эксrрактивной кри
сталли зации с образованием rеrероrенной системы:
о - nрИИW1nимьная схема, 6 - иэображеЮtе процесса на диаrраммах равновес:ц фаз

Исходная смесь F п е р вон ачал ьно поступает н а стадию кри
сталл и зации Крл, в результате чего получают кристалл ический
продукт Кл ( п ра ктич ес ю 1 чистый компонент А) и маточник Мл.
П осл ед н ий подают на стадию экстракции Э, rде ero смешивают
с экстраrенто м С. В результате экстракции получаюr экстракr Е и
рафи н ат R, которые н ап раRЛЯЮf на стадии переrонки Р1 и Р2 с
целью регенерации экстрагента С. Оrоmанные фракции экс
трагента С1 и С2 возвращают на стдцию экстракции. Кубовый
остаток L 1 со стадии п ере rон ю1 экстракrа Р 1 подают на стад ию
кр исталлизации Крл, а кубовый остаток �. обогащенный компо
нентом В, направляют на стадию кристаллизации Крв, проводи
мую в кристалл изацион н ом · поле компонента В. П р и кристалли 
зации Крв получают кр исталличес кий продукт Кв (практически
чистый компонент В) и м аточн ик М8, который вместе с маточни
ком Мл поступает н а стми ю э кст г ю.tии.
Возможны и друn1е варианты расс матр иваемоrо р аздел е н ия .
Н ап ример , исходная смесь может первоначально подаваться на
стадию экстракции. Процесс может также осуществляться с
использованием одной стадии кристаллизации; в этом случае
один из продуктов р;�здсления будет получаться на стадии э кс
тракции, а другой - на стадии кристалл изации.
С о п ряже н ие п р оцессов экстракции из твердых тел и кри 
сталл иза14ии весьма ч;�с10 ис пол ьз Уют при переработке различ
ного раст ител ьного и минерального сырья.
На рис.24. 1 1 показан один из вариантов разделения бинар
ной смеси F, со стоя щей из растворяемого А и твердого инерт1715

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

а

т

б

Рис. 24. 11. Разделение бинарной смеси путем сопряжения процессов выщелачи
вания и кристалл изации:
а
принципи альная схема , б изображение процесса на диаrраммах равновесия фаз
-

-

ного Т компонентов. В качестве экстрагента здесь выступает
вспомогательный компонент В. На стадии вьпцелачивания
(фракционного растворения) ФР исходное вещество F при темпе
ратуре fэ смешиваюr с растворителем Н В результате вьпцелачи
вания получаюг экстракт Е и рафинат R, лежащий на JШНИИ ниж
него продукта НП. После 01Т0НКИ О экстрагента (дистилляrа D)
от рафината в идеале получается продукт V, обогащенный инерт
НЬIМ компонентом Т. Эк"'Тракт Е направляюг на стадию кристал
лизации Крл, где получаюr кристаллическую фракцию Кл
(практически чистый компонент А) и маточник Мл. Последний
смешиваюr с дисТИJUIЯТОм D и полученный раствор Н возвращаюr
на стадию выщелачивания в качестве экстраrента.
Если при однократном выщелачивании не удается достичь
заданной степени извлечения компонента А из исходной смеси
F, то кристалл и зацию можно сочетать с двухстадийным выще
лачиванием . Если же при разделении необходимо получить
вещество А высокой чистоты, то одной стадии кристалл и зации
может оказаться недостаточно. Тогда процесс выщелачивания
сочетают с многостадий н ой кристалл изацией.
24.2.6. Адсорбция-десорбция
При разделении газовых смесей, а также для очистки газов
от примесей доволь н о широко используется сопряжение про
цессов адсорбции и десорбции с регенерацией адсорбента. Как уже

1716

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

указывалось в разд . 14.2.2, поглотительная способность адсор
бентов обычно существенно зависит от температуры и давле
ния. Изменяя эти параметры, можно смещать точку равнове
сия в ту или иную сторону. Это позволяет весьма просто орга
низовать сопряженный процесс разделения с использованием
одного или несколью1х аппаратов. Схема адсорбционно
десорбционноrо агрегата, работающего на такой основе, пред
ставлена в разд. 14.3 . 1 .
Приведем также пример короткоциклового сопряженного
адсорбционно-десорбционноrо процесса разделения газов. Его
обычно осуществляют с использованием двух адсорбционных
аппаратов, в которых в циклическом режиме поочередно про
водят стадии адсорбции и десорбции при периодическом изме
нении давления. На стадии адсорбции через аппарат в течение
нескольких минут пропускают газовую смесь при повышенном
давлении. На этой стадии из газовой смеси сорбентом пре
имущественно поглощается один из компонентов смеси (или
несколько компонентов) . На стадии десорбции подачу смеси
прекращают и аппарат вакуум ируют. При этом происходит
десорбция поглощенного компонента и его удаление из аппа
рата. Такой процесс применяют, например, для обогащения
воздуха кислородом, используя цеолиты в качестве сорбента
последнего.
24.2. 7. Некоторые другие сопряженные процессы

Описанные выше примеры далеко не исчерпывают возмож
ные комбинации различных массообменных процессов, они
лишь демонстрируют принципы организации таких процессов
разделения. Заметим, что в приведенных сопряженных процес
сах для простоты рассматривалось разделение в основном би
нарных смесей.
Ниже кратко рассмотрены некоторые другие сопряженные
процессы, успешно используемые в химической и смежных с
ней отраслях промышленности .
Для разделения газовых смесей широко используется со
•
пряженный абсорбционно-десорбционный процесс с рециркуля
цией абсорбента (см . разд. 1 1 .2). При этом регенерацию абсор
бента на стадии десорбции проводят путем изменения давле
н ия или температуры.
Для разделения смесей можно использовать сопряжение
процессов жидкостной экстракции и адсорбции (в частности,
ионообменной сорбции) . Здесь сорбционный процесс позволя
ет извлекать из рециркулирующего экстрагента один из раство
ренных компонентов, что приводит к смещению точки равно-

• Подробнее см. (9).
1717

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

весия в жидкой гетерогенной системе и соответствующему повышению эффективности разделения .
"
В разд . 1 6 . 5 .4 отмечалось, что кристаллизацию из растворов
часто сочетают с выпариванием. Помимо этих процессов при
очистке веществ иногда в единой схеме используют также ста
дию адсорбционной очистки исходного раствора или промежу
точных маточников. Сопряжение процессов кристаллизации,
выпаривания и адсорбции обычно позволяет существенно увели
чить выход целевых продуктов или же повысить их качество .
Н апример , такое сочетание используется при получении высо
кочистой медицинской аскорбиновой кислоты .
Процесс выщелачивания обычно сопрягают с дистилляцией
(отгонкой) . При этом отгонку применяют для извлечения экс
трагента из рафината или экстракта. Если летучести экстраги
руемого компонента и экстрагента близки, то выщелачивание
следует сочетать с процессом ректификации. При разделении
солевых смесей в качестве экстрагента обычно используют во
ду. Так как в этом случае летучести извлекаемых компонентов
и экстрагента сильно различаются, то выщелачивание сочетают
с выпариванием и сушкой.
При переработке веществ, обладающих высоким давлением
паров н ад твердой фазой , часто используют процессы сублима
ции и десублимации. Сопряжение этих массообменн ых процес
сов существенно повышает эффективность разделения и от
крывает новые подходы к аппаратурному оформлению. Здесь
на стадиях сублимации и десублимации можно изменять как
температуру, так и давление , а при использовании инертного
газа-носителя - еще и парциальное давление компонентов в
разделяемой смеси.
При разделении многих веществ процессы сублимации и де
сублимации можно сочетать с ректификацией, адсорбцией, экс
тракцией и друтими массообменными процессами .
Процесс жидкостной экстракции, как правило, сопрягают с
процессами дистилляции и ректификации
с целью регенера
ции экстрагента.
К сопряженным процессам следует отнести и процесс сушки
с рециркуляцией инертного газа (см . разд . 1 5 .6). В сушильной
камере инертн ый газ насыщается парами влаги (происходит ее
десорбция и з высушиваемого материала), а в конденсаторе
сепараторе происходит выделение влаги из сушильного агента
(последний нагревают и возвращают на стадию сушки).
Мембранные процессы разделен ия могуr сочетаться с дистил
ляцией, экстракцией, сорбцией, кристаллизацией. Такие сопря
жен н ые процессы обычно позволяют существенно снизить
-

' П одробнее см ., н а примеr , ( 6 ) .

1718

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

затраты энергии и расширить диапазоны возможного разделе
ния.
Выше было рассмотрено в основном сопряжение различных
массообменных процессов. Однако в химической и ряде других
отраслей промышленности часто используется также сочетание
в единой технологической схеме химических, тепловых, гидро
механических и механических процессов.
Характерным примером сопряженных механических процес
сов является сочетание 11 единой схеме процессов измельчения и
классификации измельченных материалов, объединенных ретур
ными (возвратными) потоками (см. разд. 22. 1 .3). Такое сопря
жен ие позволяет, с одной стороны, получать конечный про
дукт с заданным гранулометрическим составом, а с другой снизить удельные затраты энергии на процесс дробления. Для
получения твердых продуктов с заданным дисперсным соста
вом используется также сопряжение процессов гранулирования
и классиф'1.кации - тоже с ретурными потоками гранулируемого
материала .
24.3. СОВМ ЕЩЕННЫЕ П РОЦЕССЫ

Известные в настоящее время совмещенные процессы можно разделить на три основные группы:
- реакционно-массообменные;
- массообменно-массообменные;
- совмещенные гидромеханические и механические процессы.
Естественно, что такая градация носит в известной мере
условный характер, так как возможны и другие комбинации
различных процессов. Например, реакционные и массообмен 
ные процессы мoryr совмещаться с тепловыми, гидромехани
ческими и механическими процессами.
В ряде случаев в одном аппарате одновременно может про••
П
исходить несколько хим ических реакции . ри этом осо бенно
выгодно совмещать две реакции, одна из которых является
экзотермической, а другая - эндотермической. В этом случае
режим процесса в целом может приближаться к адиабати
ческому, в результате чего не только сокращаются энергетиче
ские затраты , но и повышается конверсия реагентов. Приме
ром такого совмещения реакций может служить окислительное
дегидрирование углеводородов при получении бутадиена- 1 , 3 ,
стирола и а-метилстирола.
v

• Подробнее см. ( 8 ) .
•• Подробнее о совмещени и химических процессов с м .

(10, 11 ).

1719

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

24.3. 1 . Реакционно-массообменные процессы

Среди совмещенных процессов наибольшее значение, без
условно, имеют реакционно-массообменные процессы, кото
рые в случае обратимых реакций позволяют достигать практи
чески полной *конверсии реагентов при высокой избирательности
превращений . При этом сокращаются энергетические затраты,
так как исключаются дополнительные энергоемкие операции,
обусловленные необходимостью выделения продуктов из реак
ционной смеси . Реализация реакционно-массообменных про
цессов часто позволяет повышать эффективность не только
химических превращений, но и массообмена. Все это обуслов
ливает благоприятную перспективу для более широкою приме
нения таких процессов в химической, нефтехимической и
других отраслях промышленности.
Совмещенные реакционно-массообменные процессы по
сравнению с традиционными вариантами организации процес
сов (хим ических превращений с последующим разделением
продуктов реакции) предоставляют дополнительные возмож
ности:
- увеличить выход целевых продуктов;
- повысить селективность процессов;
- обеспечить более высокую движущую силу процессов;
- снизить энергетические затраты;
- упростить организацию непрерывных процессов;
- сделать более компактными технологические схемы и т.д.
Совмещенные реакционно-массообменные процессы весьма
разнообразны, что связано с мноrообразием химических реак
ций и разделительных массообменных процессов.
Реакционные процессы мoryr совмещаться
практически со
••
всеми массоо бменными процессами - дистилляциеи, ректификацией, абсорбцией, адсорбцией, десорбцией, кристалл и за
цией, сублимацией, хроматографией , мембранными процесса
ми и др.
Совмещенные реакционно-массообменные процессы можно
классифицировать по типу реакций или реакционных процессов.
Кроме этоrо, реакционно-массообменные процессы можно
разделить на самопроизвольно-совмещенные и направленво
совмещенные процессы. В совмещенных процессах первого типа
реакционный процесс самопроизвольно сопровождается тем
или иным массообменным процессом . Например, за счет теп
лоты реакции происходит частичное или полное испарение
продуктов реакции или в результате реакции образуются проu

• Более подр обные сведения о совм ещенных реакционно-массообменных
процессах содержатся в специаr�ьной литераrуре
см" например, ( 1 0, 1 1 ) .
•• Подроб нее см . (6, 1 0 , 1 1 ) .
-

1 720

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

дукгы, обладающие малой растворимостью в реакционной сме
си, и они выпадают в виде твердого остатка. В совмещенных
процессах второго типа для проведения стадий разделения
требуется специальная организация процесса (обеспечение
противотока фаз, наложение градиентов температуры, создание
в аппарате специальных зон нагрева, охлаждения, смешения,
расслаивания и т.п.).
Ниже будут кратко рассмотрены лишь отдельные из су
ществующих в настоящее время совмещенных реакционно
массообменных процессов.
Реакционно-ректификационные процессы
Данный совмещенный процесс изучен наиболее полно и в
настоящее время весьма часто используется для получения раз
личных продукгов органического и нефтехимического синтеза.
В совмещенном реакционно-ректификационном процессе
(СРРП) обратимая химическая реаки,и.я проводится совместно (в
одном аппарате) с частичным или практически полным разде
лением образующейся смеси посредством ее ректификаи,ии.
Такая организация процессов по сравнению с раздельным про
ведением химических реакций и процессов последующего раз
деления продукгов реакций в полной мере позволяет реализо
вать отмеченные выше преимущества совмещенных процессов.
Особенности организации реакционно-ректификационного
процесса определяются типом реакций, условиями их протека
ния, структурой диаграммы фазового равновесия "жидкость
пар" для смеси, получаемой в результате реакции, типом юiта
лизатора, составом исходных реагентов, требованиями к соста
вам конечных продукгов и рядом других факторов. Поэтому
использование типовых схем для производства широкой гаммы
продуктов здесь, как правило, не представляется возможным.
Разработка СРРП (как и других совмещенных процессов) в
значительной мере базируется на анализе их статики . В резуль
тате анализа устанавливают принципиальную возможность
осуществления процесса, выявляют предельные конверсии
реагентов для различн ых вариантов ero реализации, определяют
составы и выход конечных продуктов (или фракций), а �е син
тезируют принципиальные схемы совмещенного процесса .
Для получения одних и тех же продуктов с использованием
СРРП обычно возможен целый ряд вариантов их организации.
Например, для осуществления реакции А + В р С при усло
вии , что компоненты В и С образуют азеотроп с минимальной
• Более подробные сведения о рассматриваемом процессе, а также о методи·
ке ero анализа и выборе оптималъноrо варианта приведены в специальной лите 
ратуре - см " например, ( 1 0, 1 1 ).

1 72 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

А

а

Рис. 24. 12. Возможные

А+В� С

6

в

г

вариакrы схем СРРП с химической реакцией типа

температурой кипения tвс и что последовательности темпера
тур кипения компонентов tвс < tc < t8 < tл, возможны по
крайней мере четыре принципиальные схемы организации со
вмещенного процесса (рис. 24. 12) . В случае избытка в исходной
смеси реагента В исполъзуюг варианты, представленные на
рис . 24. 12,а, б, а при избытке реагента А - варианты, пред
ставленные на рис. 24. 1 2, в, г.
Реакционную зову располагают в колонне так, чтобы в ней в
стационарных условиях проведения процесса интенсивно про
текали целевые реакции. Противоток фаз (реагентов) в реакци
онной зоне обеспечивает наиболее высокую движущую силу
химического взаимодействия. При этом для реализации проти
вотока реагентов более летучий компонент подают в нижнюю
часть реакционной зоны, а менее летучий - в верхнюю (для
реакции вида А + В < ) С это показано на рис. 24. 12) .
Уровень подачи реагентов определяется концентрационным
профилем компонентов по высоте колонны, который , в свою
очередь, зависит от структуры диаграммы фазового равновесия
"жидкость-пар" реакционной смеси. При выборе уровня пода
чи реагентов необходимо учитывать влияние их концентраций
на относительную летучесть продуктов реакции . Количествен
ная оценка этого влияния может быть сделана на основе ана
лиза фазового равновесия "жидкость-пар".
Реальная протяженность реакционной зоны в основном опре
деляется соотношением скоростей реакции и массопереноса в
этой зоне . Естественно, чем выше скорость реакции, тем
меньше протяженность реакционной зоны.
Для достижения полной конверсии реагентов большое зна
чение имеют уровень отбора продуктов из колонны, а также
1 722

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

особенности организации внуrренних и внешних (промежу
точных) потоков.
В случае сочетания реакции с простой ректификацией чаще
всего отбирают два продукта - дистиллят и кубовый остаток.
При этом реакционная зона имеет определенную протяжен
ность в направлении обоих отбираемых продуктов и располага
ется в средней части колонны. Однако возможны случаи, когда
реакция протекает сравнительно медленно и протяженность
реакционной зоны в направлении какого-либо из отбираемых
продуктов трудно определима* . Тогда целесообразно один из
продуктов реакции не отбирать, а проводить процесс в одноот
борном режиме, располагая реакционную зону на одном из
концов колонны (рис. 24. 12,б, г).
При организации С РРП важно правильно разместить ката
лизатор в колонне, т.е. определить расположение реакционной
зоны. Расположение данной зоны тесно связано с концентра
ционным профилем компонентов в колонне и схемой отбора
продуктов из колонны.
С целью создания профиля концентраций в колонне, необ
ходимого для достижения максимальной конверсии реагентов,
можно воздействовать на структуру диаграммы фазового рав
новесия "жидкость-пар": за счет введения новых компонентов
(вспомогательных вешеств, экстрагентов, растворителей), пу
тем изменения давления и другими способами. В этих случаях
реакционный процесс по сушеству совмещается со специальны.ми
методами разделения - азеотропной или экстрактивной ректи
фикацией и т.п.
При низких скоростях реакции в колонну иногда вводят
вспомогательное вещество (среднекипящий компонент), кото
рый при стационарной работе может длительно задерживаться
в аппарате. Это вещество позволяет увеличить скорость хими
ческих превращений в результате снижения концентрации
продуктов реакции в реакционной зоне, изменения в ней от
носительной летучести компонентов или за счет снижения вяз
кости жидкой фазы, способствующего интенсификации диффу
зионного переноса.
Совмешенные реакционно-ректификационные процессы
используются для осушествления весьма широкого круга хими
ческих реакци:й • • : этерификации, гидролиза, омьmения, конден 
сации, гидратации, окисления, алкилирования и многих дру
гих. Ниже приведены некоторые примеры практического ис
пользования СРРП.
• Подробный анализ различных схем организации СРРП приведен в ( 1 0, 1 1 ) .
•• Подробнее об использовании СРРП в различных производствах см. ( 1 0,

l l ).

1 723

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

в
2

3

в
Рис. 24. 13. Принципиальная схема получения буrилацетата:
1
реакционно-ректифИJСационная колонна; 2, 3
ректификациоЮ1ЬJс колоЮ1ЬJ; 4
коnдснсатор, 5 декантатор, 6 IJ испарители;
Б
бутанол, УК ухсусная киСJiота, В вода, БА бутилацетат
-

-

-

-

-

-

-

-

-

-

Так, совмещенный реакционно-ректификационный процесс успешно ис
пользуют для производства бутилацетата путем этерификации уксусной кис.лоты
бутанолом- ! . Одна из принципиальных схем такого производства показана на
рис. 24. 1 3 . Установка включает реакционно-ректификационный аппарат 1 и
ректификационные колонны 2, 3. Синтез буrилацетата производят в колонне 1,
которая работает в совмещенном одноотборном режиме. В реакционной зоне
этой колонны размещен катализатор, отформованный в виде насадки типа колец
Рашиrа. Реакционная зона расположена в нижней части колонны. Бутанол- 1
подают в нижнее сечение этой зоны, а уксусную кислоту - в верхнее. В колон
н у 1 подают также некоторое количество воды для образования rетероазеотропа
бутанол-вода. Выходящие из колонны 1 пары азеотропа конденсируются в
конденсаторе 4 и поС'I)'Пают на декантацию в сепаратор 5. Водный (нижний)
слой направляют в колонну 2, а орrанический (верхний) - в колонну 3. Из куба
колонны 2 оrоирают воду, а из куба колонны 3 - буrилацетат. Пары из колонн
2 и 3 возвращают в общий конденсатор 4. Орошение колонны 1 производят
rетероrенной смесью, поступающей из сепаратора 5, орошение колонн 2 и З соответственно водным и орrаническими слоями.
Буrилацетат может бьпь также получен с использованием СРРП из метила
цетата и бутанола- 1 . Совмещенные реакционно-ректификационные процессы в
настоящее время используют и при получении целого ряда друrих веществ
(метилбората, некоторых кремнийорrанических соединений, бромэтилбензола,
ангидридов высших кислот и т.д.).

Реакционн о - крист алл изационные процессы

Такие процессы часто также выступают под названиями хи
мическое осажден ие и аддуктивная кристалл иза ция.
При осуществлении данного совмещенного процесса в ап
парате (реакторе - кристаллизаторе) протекают одновременно
1 724

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис. 24. 14. Принципиальная
кристалли зации

схема

адду ктивной

химическое взаимодейдва процесса:
ствие компон ентов
и кpиcmtl.NlизaцUR
образующегося химического соединения.
Такой процесс обычно имеет место, ког
да образующееся химическое соединение
обладает относительно малой раствори
мостью в маточной (реагирующей) среде.

в

Совмещенный реакционно-кристаллизационный
процесс используют Д11Я получения це.лоrо ряда хи мических соединений. На
пример, при барботировании аммиака через водный раствор соляной кислоты
образуется хлорид аммония, вьшадающий в виде криСТЗ1V1ИЧескоrо осадка. При
добавлении серной кислоты к водному раствору стрептомицина образуется
сульфат стрептомицина, который малорастворим в маточном растворе и вьmа
дает в осадок. При добавлении к диолину гидроксида натрия образуется натрие 
вая соль диолина, также выпадающая в осадок в виде кристалло в.
Рассматриваемый совмещенный процесс очень часто используют также при
качественном анализе различных продуктов и сред: к анализируемой среде до
бавляется тот или иной peareJП, который с одним из компонекrов среды вступа
ет в химическое взаимодействие, сопровождающееся вьшадением в осадок обра
зующеrося соединения.

Скорость совмещен н ого реакционно-кристалли зационного
процесса в данном случае зависит не только от кинетик.и обра
зования к.ристалл ическ.ой фазы (скоростей зарождения и роста
кристалло в), но и от кинетики реакционного процесса; в част
ности, от нее зависит величина создаваемого пересыщения .
Исходные реагенты мoryr подаваться в реактор-кристаллизатор
как в жидком, так и в газообразном состоянии.
Для разделения веществ часто используют совмещенный ре
акционно-кристаллизационный процесс, сопровождающийся
образованием химического соединения, устойчивого лишь в
твердом состоянии, или же комплексного соединения. Такой
процесс называют аддуктивной кристалл изацией, его принципи
альная схема приведена на рис . 24. 14. Процесс разделения со
стоит из двух основных стадий : кристаллизации с химическим
взаимодействием ХК и регенерации Р промежуточного реаген
та. На стадии кристалл и зации к исходной (для простоты бинарной) смеси компонентов А и В добавляется реагент С. В
результате реакции образуется комплексное соединение (ад
дукт) с одним из компонентов смеси (например, с компонен
том А), которое обладает малой растворимостью в маточной
среде и выпадает в кристаллическом виде АС. При этом отво
димый маточник обогащается компонентом В . После отделе
ния кристалл о в АС от маточника их направляют на стадию
регенерации Р, где при нагреве выше точки плавления соеди
нение АС разлагается на компоненты А и С. Далее реагент С
1 725

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

отгоняют от А и возвращают на стадию кристаллизации ХК.
Подчеркнем , что в данной схеме (как и в ряде других техноло
гических процессов) налицо сочетание совмещенно rо (ХК) и
сопряженного (ХК и Р) процессов.
Аддукrивная кристалли зация широко используется для разделения уI11еводо
родных смесей · , например для вьщеления парафинов нормального строения из
нефrяных масел. В этом случае в качестве аддукrообразующего aretпa применя
ют карбамид. Для вьщелени я n- ксилола из ксилольных фракций в качестве pea
retпa используют тетрахлорид углерода.
Аддукrивиую кристаллизацию можно использовать таюке для опреснения
морской воды. Процесс основан на способности воды образовывать с рядом
веществ (пропаном, фреонами, метилхлоридом и др.) термически неустойчивые
комплексные соединения, которые часто назьшают "111Дратами" газов или жид 
костей. В результате термического разложения этих соединений получают обес
соленную воду и pearetп, возвращаемый на стадию аддукrив ной кристаллизации.

Реакционно-десубли.мационные процессы

Хими ческое взаимодействие веществ может быть совмещено
с процессами сублимации и десублимации. Такие совмещенные
процессы используют для получения различных соединений,
нанесения покрытий на поверхности твердых тел, для разделе
ния и очистки веществ от примесей.
При химическом взаимодействии rазообразн ых реагентов
возможно образование соединений, обладающих низкой лету
честью, и они выпадают (десублимируются) из rазообразной
реакционной смеси в виде твердых продуктов (образований)
кристалл ич еского или аморфного строения . Например, при
взаимодействии rазообразного аммиака с парами HCI в кон
такrных башнях образуются снегоподобные кристаллы хлорида
аммония.
При контакте реакционной смеси с холодными поверхно
стями образующиеся соединения моrут десублимироватъся на
этих поверхностях, образуя пористые или плотные покрытия.
При разделении и очистке веществ от примесей используют
так называемые газотранспортные реакции ". Разделение про
изводят с применением вспомоrательного rазообразного реа
гента, вступающего при определенной температуре в химиче
ское взаимодействие с одним из компонентов разделяемой
смеси с образованием леrколетучеrо соединения . Установки
для проведе ния rазотранспортного разделен ия обычно состоят
из двух секций, в которых поддерживаются разные температу
ры (или разные давлен ия). В секции сублимации при более
низкой температуре идет образование летучего химического
соединения (прямая реакция) . В секции десублимации при

•

Более подробные сведения об аддукrивной кристаллизации см. (6 ) .
•• Подробнее см . (7 ) .

1 726

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

более высокой температуре происходит его разложение (обрат
ная реакция). При этом очищенный компонент десублимиру
ется, а вспомоrательный rазообразный агент возвращают в
секцию химической сублимации.
Такой процесс используется, например, для очистки никеля. В секции суб
лимации никель при температуре 45-50 • с ВС1)'пает в химическое взаимодей
ствие с оксидом углерода, образуя летучий тетракарбонил никеля . В секции
десублимации газообразный тетракарбонил никеля при температуре 1 80-200 • с
разлаrается с образованием чистого металлического никеля. Вьщеляющийся при
этом оксид углерода возвращают на стадию сублимации .

К числу совмещенных реакционно-массообменных процес
сов следует отнести также хемосорбцию и химическую адсорбцию.
При проведении хемосорбции происходит поглощение одного
или нескольких компонентов газовой смеси в результате их
химического взаимодействия с реагентом - жидким абсорбен
том (см. разд . 1 1 .3 .2), а при осуществлении химической адсорб
ции
поглощение компонентов из rазовой или жидкой смеси
при химическом взаимодействии с твердым сорбентом (см .
разд . 14.2). Иными словами, проведение упомянугых процессов
характерно совмещением сорбции и химических превращений.
При этом результирующая скорость таких процессов в общем
случае зависит как от интенсивности массопереноса в rазооб
разной и жидкой фазах, так и от скорости протекания химиче
ских реакций .
-

Примерами реакциоюш-абсорбционногv процесса• м шуr служиn, : вьщеление
диоксида yrnepoдa из rnзовых смесей с испалъзованием в качестве pearemoв водных
расrворов щелочей или карбоната юnрия, а также очистка rnзовых смесей от серово
дород11 водными расrворами салей юnрия и калия. Данный совмещенный процесс
используется также в технологии орmническоrо синтеза для вьщеления разтmчных
компонетов из органических смесей; например, буrадиен- 1,3 вьщеляют из его смеси
с бупmенами с помощью расrворов салей аммония, а эrилен извлекают из эmн
эrиленовых фракций с испальзованием серной кислоты.

При переработке многих продуктов (особенно минерального
**
сырья) часто используют процесс химического растворения
(выщелачивания). Здесь исходное сырье обрабатывают различ
ными реагентами (например, минеральными кислотами или
щелочами). В результате образуется химическое соединение (с
одним из компонентов разделяемой смеси), которое растворя
ется в жидком реагенте . В дальнейшем при разложении этого
соединения можно получить в достаточно чистом виде извле
каемый компонент.
JШмические и биохимические процессы могуг совмещаться с
обратным осмосом, ультрафильтрацией, диализом, электродиали Более детальную информацию о пракrическом использовании данного со
вмещенного процесса см., напри.мер, (9- 1 1 / .
•• Подробнее см. ( 1 ).
•

1 727

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

пр оцессами. П р и этом продукты
химическоrо взаимодействия или би охимическоrо синтеза вы 
водят из р еакционно й зон ы че рез полупрон ицаемые пере rо
родЮI (мембр аны) . Как правило , таЮ1е процессы отличаются
высоко й селективностью. Заметим : о н и являются осново й жиз
недеятельн о сти о р га н и з м ов .
В биореакторах (ферментаторах) биохимические процессы
не редко совмещаются с абсорбцией , экстракцией , испарением,
адсорбцие й и другим и массообменными процессами.

зом и другими мембранными

24.3.2. Массообмевво-массообмеввые процессы
ТаЮ1е сов м ещенные процессы весьма часто используются в
химической техн ологии для р азделения различных смесей и
при переработке различ н ых п р одукто в. В данном случае в од
ном аппар ате одн о вре ме н но проводят несколько массооб м ен 
ных процессо в. Совмеще н ие массообменных процессов, как
правило, п озволяет существен н о п овысить эффеJсrИ вность раз
деления, а также сн и з ить э н ергетичесЮ1е и други е затраты
про изводства.

Экстракционно-кристаллизационные процессы
Данн ый совмещенный процесс часто называют также экс
Сущн ость ero закл ючается в до
бавл ении к разделя е м ой смес и вспомогательн ою вещества ,
кото рое образует с р азделяемой смесью жид кую гетеро генную
систему.
В данн ом случае вспо могательное вещество
(э кстрагент) по возможн ости долже н удовлетвор ять следующи м
основн ы м тр е бованиям :
- очищаемое вещество (ко мпонент) и экстрагент должны
обладать п олно й взаи мн ой н ераство р им о стью в жидком со
стоянии;
- растворимость при месе й в экстрагенте должна быть вы
ш е , че м в о ч и щаемо м веществе ;
- те м ператур а кр исталл и зации э кстраге нта должна быть
н иже температур ы охлаждения на стад и и кристалли зации .
Экстракти в ную кристалл изацию можно осуществлять в
несколь Ю1х вар и антах .
Наиболее ч асто экстракцию совмещают с массовой кристал
лизацией. Пр и это м э кстр агент д и сперги руют в исход н о й с м еси
пер ед ее охлажде н ием и ли в процессе охлажд ени я . В лю бо м из
этих случаев пр и кр исталлизации образуется тр ехфазная систе
ма, состоя щая из кр исталлической фазы , маточника и экстрак
та: Так как раствори м ость при м еси в экстр аге нте вы ш е , чем в
маточн ике , то в процессе кр исталл изации о н а переходит из
маточ ника в экстрагент, так что ее содержание в мато чн ике

трактивной кристаллизацией.

1 728

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

падает. Это влечет за собой снижение содержания п римеси в
кри сталл ической фазе , а значит, пов ы шен ие э ффекrивности
р азделения . Можно сказать , что экстрагент в данном случае
выполняет р оль своео бразного буфера для стока примесей.
По окончан ии кристалл изации маточник и экстракт отделя
ют от кристаллической фазы . Далее жид кую гетерогенную
смесь, состо ящую из маточника и экстракта, декантируют. Оr
делен ный экстракт нап равляют на ре генераци ю экстрагента.
Экстракrивную кристалли зш.(Ию можно проводить в колонных аппаратах при
конта1СП1ом способе охлаждения разделяемой смеси (см. разд. 16.5.3). При этом
в качестве жидкого хладоагента может выступать предварительно охлажденный
экстрагент.
ECJDt пло111 ость экстрагента меньше, чем пло111 ость разделяемой смеси, то
его подают через со пла или перфорированный коллектор в нюкнюю часть ко
лонны, в которой хладоагент (экстрагент) и разделяемая смесь движутся проти
вотоком. При такой орrанизации процесса разделения происходит трехфазный
тепломассообмен . Огработанный хладоагент (экстракт) отстаивается в верхней
зоне кристалли затора, откуда он непрерывно выводится на регенерацию. Обра
зующуюся суспензию выводят из нижней части колонны.
ECJDt же плотность экстрагента выше плотности разделяемой смеси, то его
подают сверху, а разделяемую смесь - снизу колонны.

Совмеще н н ый экстракционно-крис талл изацио н ный
про
цесс находит примене н и е та�е при очистке вещест� от пр 11.
u м
месеи
етодам и направленнои кристаллизаи,ии и зоннои плавки .
При таком разделе н ии с и сте ма состоит из двух несме ши
ваю щихся слоев, один из котор ых представляет собой очищае
мое вещество, а другой - раствор удаляемых примесей в экс
тр агенте (экстракт) . В п роцессе разделения п римесь переходит
из расплава в экстрагент, в результате чего равновесные кон 
центрации в с истеме " р асплав-кр исталл ическая фаза" сме 
щаются в бо л ее благоприятную для р азделения сторону.

Сушильно-грануляционные процессы

В разд . 19.З отм ечалось, что гранулирование часто совмещает
ся с сушкой и кристалл11заи,ией. Так, при гранулировании мел
кодис персн ых поро ш ков методо м окатывания п р оизводят
предварительное увлажнен ие исходного дисперсного материа
ла. В грануляторе мелкие частицы постепе нно налипают на
поверхность гранул, за счет чего и ос ушествляется рост гранул .
Одновремен н о происходит их в ысуш ивание, т .е . удаление
влаги из гранул .
.
При гр анулирован и и раствор ов о ни обычно распыляются в
псевдоожиже н ном слое растуших гранул . Мельчай ш ие капл и
раствора п опадают на поверхность гр анул, с которой раствори 
тел ь испаряется за с чет п одвода теплоты с ожижающим аген • Подробнее см. (6 ) .

1 729

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

том. В результате р аство р достигает пересыщен ного состояния ,
и начинаетс я процесс кристалл и зации , сопровождающийся
ростом гранул .
Типичн ы м примером совмеще н н ых массообменных процес
сов я вля ется вакуумная крист алл изация веществ из растворов
(см . разд . 1 6 . 5 .4) . В дан ном случае в ап парате одновременно
происходят два массоо бм енных процесса : вЬ1.паривание легколе
тучего компонента и кристаллизация р астворенного вещества .
При этом перес ы щение раствора дости гается частично вследст
вие удаления раствор ителя (увел иче ние концентрации раство
ренного вещества) , а ч астично - из -за понижения те мперату
р ы раствора за сч ет ум е н ьшения внутренней энергии систем ы ,
затрачиваемой на образование пара при его испарен ии в ре
зультате вакуумирован ия .
При раздел ен ии м н огих продукrов органического и не фте
химического с интеза ис пользуют экстрактивную, автоэкстрак
тивную и азеотропно-экстрактивную ректификацию. Эти про
цесс ы также можно отнести к совмещен н ы м .
Например , при разделении азеотропных и зеотроп ных сме
сей, содержащих компоненты с относительными летучестями ,
близкими к единице , примен я ют экстра1сrивную или автоэкс
тра1сrивную р е1сrиф икацию без подачи флегмы , но при п редва
•
р ительном захол аживании экстрагирующего агента . В верхней
части колон ны (выш е уровня ввода и сходной смеси) протекают
процессы парциальной конденсации и экстраки,ии, а в нижней
части коло н н ы наряду с этими процессами - еще и ректифи
uцuя. Таким образом, в одной коло нне совмещаются несколь
ко массообменных процессов , что позволяет значительн о со
кратить расход энергии на процесс разделен ия .
К совмещен н ым массообмен н ым процессам можно также
отне сти не ко торые мембранные процессы, на пр имер р азделен ие
жид ких смесей путем испарения через мембрану.

24.3.3. Процессы, включающие механические
или гидромеханические операции
Массообменные процессы часто совмещают с механическими
и гидромеханическими. Например , полное или частичное фр ак
ционное растворение твердых продуктов совмещают с дроблени
ем . Такое сов мещение существе н н о ус коряет процесс раство
рения , а при фракц ионном растворении оно позволяет заметно
увеличить степень извл ечения целевых компонентов из исход
ного сырья .
В одном аппарате мoryr одновремен н о происходить два раз
Н ЬIХ механических или гидромеханических процесса. Так, в не• Подробнее см. ( 10, 1 1 ) .

1730

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рис.24. 15. Схема установЮ!. для одновременной грануляции порошка и класси
фикации гранул в псевдоо:жиж�:нном слое:
1
rранулятор, 2 калорифе11ьr, З увлажнитель, 4 воздуходувка, 5 сепарацион
ная зона;
1
порошок, III rранулы
воздух, II
-

-

-

-

-

-

-

-

которых раз м ольных машинах проводят одновременно процес
сы измель11ения и классификации (сортировки) измельченных
дисперсных м ате ри алов (см . разд . 22 . 4. 1 ) .
В качестве конкретн ого примера рас� мотри м совм ещение
пр о цессов гранулирования и классификации , п озволяющее п олу
чать гранул ируемый продукт с ч астицами заданного размера
(см . разд . 23 .4 . 4) .
Гранулято р -классифи катор (рис . 24 . 1 5) представляет со бой
аппарат, составленный из нескольких п о следовательн о распо
ложенных конических рабочих се кци й и верхне й сепарацион 
ной се кции, снабженной улавливающими устрой ствами (на
р исунке не показ аны) . Рабочие се кции имеют разные сечен ия в
устье конусов, нарастающие снизу вверх .
Тонкоизм ельченный порошок 11 сухого И1Пf предвариrелъно
увлажненного препарат-а, иногда с добавкой клеящею ингредиен
та, дозируется mпателем сверху или в одну из промежуrочных
секций мноrоконусноrо аппарата . Воздух 1 подается rазодувкой 4
через калорифер 2 в нижнюю часть колонны и через увлажниrелъ
З в одну из про межуrочных секций, отделяется от взвеси в сепа
рационной зон е 5 и выбрасывается в атмосферу. При псевдоожи
жении порошка в секциях происходит его гранулирование .

•

Подробнее

см.

(5).

1 73 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

С кор о сть воздуха в ы б ирается с таким расчето м , что бы ис 
ходны й то нкоиз мельчен н ы й порошок не мо г по пасть в н ижеле
жащие се кци и : п ор ош о к п оддержи вается воздуш н ым п ото ко м
во взвешенн о м с остоя н ии в устьях верхн их се кци й . В то же
вре мя эта скорость нед о статочна для п одд ержания в о взве ш ен 
н ом с о стоя н ии о бр аз о ва вш ихся гранул, кото рые в ыделя ются из
м асс ы псевдо ожиженно го по рош ка и пр оваливаютс я в ниже 
р асположен н ые секци и . В устьях по следн их скор о сть в ыше (их
сече н ие ме н ьш е ) , п о это му гр ан улы здесь п оддержи ваются во
взвешенн о м с остоя нии , п о ка их размер вследствие п р одол
жающегося гр анули р о вани я не дости гн ет величины , до стато ч
н о й для пре одоления со пр оти вл ен ия воздуш н о го п ото ка в
устье дан н о й с е кци и . У крупненн ы е частицы пр овал и ваютс я в
следующую с е кц ию и т.д . В резул ьтате , в каждо й се кции ко н 
це нтрируются частицы более или менее узко й ф р акц ии , при 
чем р аз мер гранул нар астает от верхне й се кции к нижн е й . Из
р азл ичных се кц ий м ожет о существляться од н ов рем енн ы й отбор
отдельн ых узких фракци й гр анул /JJ.
В нижних се кц иях пр о исход ит п одсуш ка п олученн ых гра 
н ул , в резул ьтате умень шается их с кло нн о сть к сл ипан ию ,
улучш аются сыпучие сво йства гр анул ир о ванн о го м атери ала .
Гран улы, п олученн ы е в тако м аппар ате, я вля ются более од
н ор одны м и по размера м в ср ав нении с пр одукто м , п олучаемым
в пер иодическо м и одн осе кци он н о м гр ан уляторах. Дело в то м ,
что в этих аппаратах в ходе гранул ир о ван ия о браз овав ш иеся
гранул ы тр е буем о го раз м е ра своевременно не выводят ся из гра 
нулятора и пр одолжают увелич и ватьс я в размере ( одн о вре 
м енно с о бр аз ованием м ел ких гр ан ул ) .

Л ИТЕРАТУРА

к главе

24

1 . Аксельруд Г.А., Молчанов А.Д. Растворение твердых веществ. М . : Химия,
1 977. 272 с.
2 . Вольфкович С. И., Егоров А . П., Роговин З.А. и др. Общая химическая техно
логия. т. 1 . М . -Л . : Госхимиздат, 1952. 632 с.
3 . Вольфкович С. И. Роговин 3.А., Руденко Ю.П. и др. Общая химическая тех
нология. т. 1 1 . М . : Госхимиздат, 1959. 848 с.
4. Гельперин Н.И. Основные процессы и аппараты химической технологии.
М.: Химия, 1 98 1 . 812 с.
5 . Гельперин Н.И., Айнштейн В.Г., Кваша В. Б. Основы техники псевдоожиже
ния. М . : Химия , 1967. 664 с.
6. Гельперин Н. И., Носов Г.А. Основы техники фракционной кристаллИзации.
М . : Химия, 1986. 304 с.
7. Горелик А.Г., Амитин А . В. Десублимация в химической промышленности.
М . : Химия, 1986. 272 с.
8. К1ж!rrrк.ов В.Н. Гранулирование минеральных удобрений. М.: Химия, 1976. 224 с.
9. Ромм В.Н. Абсорбция rазов. М . : Химия, 1976. 656 с.
10. Серафимов Л.А., Тhмофеев В. С., Писаренко Ю.А., Сш�охин А.В. Технолоrnя
основною орrаническоrо сииrеза. Совмещенные процессы . М.: Химия, 1993. 420 с.
1 1 . Тимофеев В. С., Серафимов Л.А. Принuипы технологии основного орrани
ческоrо и нефrехимическоrо синтеза. М . : Химия, 1992. 4 3 1 с.

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ПЕРЕЧ Е Н Ь УЧ Е Б Н И КО В ПО ОБЩЕМУ КУРСУ ПАХТ
НА РУСС КО М Я З Ы КЕ
Ниже представлен перечень издаННЪIХ на русском языке

вузовСЮIХ

jl'leбlfыx "YJICOВ по Процессам и аппаратам химической технолоmи

и

ближайпшм отраслям науки и производства, использующим методы
этой технолоmи (независимо от ссылок на них в настоящем учебни 

ке) .

В

В
всего

ПАХТ,

перечне также содержатся издания, формально не относящиеся

к курсу

но фактически излагающие основные его проблемы.

ПАХТ.

отдельны.м

перечень включены только учебники, претендующие на охват
курса

процессам

Некоторые учебники, относящиеся к

(технолоmческим · приемам) ,

приведены в списках литературы

к

входящим

в

данный

курс ,

конкретным главам.

Учебники приводятся в алфавитном порядке - по фамил иям пер 
вых авторов. При наличии нескольких изданий какого -либо учебника
приводится одно из них .

Авербух Я.Д., Заостровский П. Ф., Матусевич Л.Н. Процессы и аппараты хи
мической технолоmи. Курс лекций. Ч. 1/Под ред. К.Н. Шабалина. Свердловск:
Уральский потпехнический институr и м . С.М. Кирова, 1969. 306 с.
Авербух Я.Д., Заостровский П. Ф., Матусевич Л. Н. Процессы и аппараты хи
мической технолоmи. Курс лекций. Ч . 1 1/Под ред. К.Н. Шабалина. Свердловск:
Уральский потпехнический институr и м . С.М. Кирова, 1973. 427 с.
Батунер Л.М. Процессы и аппараты орrанического синтеза и биохимической
технолоmи. М.-Л.: Химия, 1966. 520 с.
Бенедек П., Ласло А. Научные основы химической технолоmи: Пер. с венг.
/Под ред. П . Г. Романкова, М . И . Курочкиной. Л . : Химия, 1 970. 376 с.
Беннет К. О., Майере Дж. Гидродинамика, теплообмен и массообмен: Пер. с
англ./ Под ред. Н . И . Гельперина, И .А. Чарного. М . : Недра, 1966. 726 с.
Берд Р., Стюарт В., Лайфут Е. Я1111е ния переноса: Пер . с англ. /Под ред.
Н . М . Жаворонкова, В.А Маmосова. М . : Химия, 1 974. 688 с.
Бэджер В., Мак-Кэб В. Основные нроцессы и аппараты химических произ
водств. М.-Л.: О НТИ- Госхимиздат, 1 9 3 3 . 476 с.
Гельперин Н.И. Основные процессы и аппараты химической технолоmи. М . :
Химия, 198 1 . В двух томах. 8 1 2 с.
Дытнерский Ю. И. Процессы и аппараты химической технологии. М . : Химия,
1995. 768 с. (ч. 1, 400 с. ; ч. 2, 368 с.)
Касаткин А.Г., Плановскиli А.Н. Процессы и аппараты промышленности ор
ганического синтеза. Ч. 1. М.-Л.: ГОНТИ-Ред. хим. лит . , 1 939. 492 с.
·

1 733

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Касаткин А.Г. Основные процессы и аппараты химической технологии. М . :
Госхимиздат, 1 9 5 5 . 7 5 6 с.
Касаткин А.Г. Основные процессы и аппараты химической технологии . М . :
Химия, 1 97 1 . 784 с .
Коган В. Б. Теоретические основы типовых процессов химической техноло
гии. Л . : Химия, 1 977. 592 с.
Кривошеев Н.П. Основы производств химической технологии . Минск:
ВЬШJэйшая школа, 1972. 304 с.
Макарьин К. И. Краткий курс процессов и аппаратов химической технологии .
Т . 1 . М . : Московский инженерно- экономический институr и м . С . Орджоникид
зе, 1959. 228 с.
Макарьин К. И. Краткий курс процессов и аппаратов химической технологии.
Т. l l . М . : Московский инженерно-экономический институr им. С. Орджоникид
зе, 1960. 346 с.
Jlлановский А. Н., Николаев П. И. Процессы и аппараты химической и нефrе
химической технологии. М . : Химия, 1 9 72 . 494 с.
Скобло А.И., Трегубова И.А., Егоров Н.Н. П р оцессы и аппараты нефrеперера
батьmающей и нефrехимической промьШIЛенности. М . : Химия, 1962. 652 с.
Скобло А.И., Трегубова И.А., Молоканов Ю.К. Процессы и аппараты нефrепе
рерабатывающей и нефrехимической промьllWlенности. М.: Хим ия, 1982 . 584 с.
Фокин Л. Ф. Методы и орудия химической технологии . Ч: 1. П . - М . : Госиздат,
1923. 295 с.
Фокин Л. Ф. Методы и орудия химической технологии. Ч . 1 1 . П .- М . : Госиз
дат, 1925. 540 с.
Циборовский Я. Процессы химической технологии: Пер. с польск./Под ред.
П . Г. Романкова. Л . : Госхимиздат, 1958. 9 32 с.
Циборовский Я. Основы процессов химической технологии: Пер. с
польск./Под ред. П . Г. Романкова. Л.: Госхимиздат, 1 967. 720 с.

Издания последних лет
Скобло А.И., Молоканов Ю.К., Владимиров А.И. и др. Процессы и аппараты нефтегазопереработки и нефтехимии. М.: РГУ нефти и газа имени И.М. Губкина, 2012, 725 с.
Касаткин А.Г. Основные процессы и аппараты химической технологии. М.:
ЁЁ Медиа, 2012, 752 с. Репринт издания 1973 г.
Комиссаров Ю.А., Гордеев Л.С., Вент Д.П. Процессы и аппараты химической технологии. М.: Химия, 2011, 1230 с.
Фролов В.Ф. Лекции по курсу «Процессы и аппараты химической технологии».
СПб.: Химиздат, 2008, 608 с.

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

П РЕДМ ЕТ Н Ы Й УКАЗАТЕЛ Ь

О

Абсолютно белое тело 5 1
Абсолютно черное тело 5 1 0 ел .
Абсорбент(ы) 907
относительная теплоемкость 939
регенерированный 91
требования к ним 909
Абсорбер(ы)
барботажные 9 1 7 , 9 1 8
Вентури 92 1
высота 932 - 3 5
гидравлическое сопротивление
964 -67
каскадный 9 1 3
классификация 9 1 2
конструкции 9 1 1 - 2 1
насадочные 9 1 2, 9 1 4 - 1 7 , 933, 966
пленочные 9 1 2 - 1 4, 933, 966
полочный 9 1 2 , 9 1 3
распылительные 920 - 2 1
расчет 928,37
с о ступенчатым контактом фаз
935, 964 -66
трубчатые 9 1 3 , 966
форсуночные 920
эмульгаuионный 920
Абсорбционно-десорбционная уста
новка 9 1 0
Абсорбция 907 -68
коэффициент ускорения 947
летучим поглотителем 95 1 - 5 8
многокомпонентной смеси 93444
неизотермическая 938-43
с рециркуляцией рабочих потоков
935 - 3 8
теплота 939
фазовое равновесие 922 -27

О

Абсорбция
физическая 907, 922 -25
с химической реакцией см. Хемо
сорбция
Адд и тивность 5 1
Адиабата 326
Адсорбат 1 1 57
Адсорбенты 1 1 57 - 1 1 60
гранулированные см. Иониты
регенерация 1 1 58
требования к н и м 1 1 58
Адсорбер(ы) (десорберы, активаторы)
1 1 67-75
с движущимся слоем сорбента
1 1 27 - 7 3
с неподвижным слоем сорбента
1 1 74
непрерывного действия 1 1 67 - 7 3
полунепрерывного действия 1 1 74
с псевдоожиженным слоем 1 1 67-7 1
расчет 1 1 77 - 8 7
ступенчато-противоточный 1 1 84-8 7
Адсорбтив 1 1 57
Адсорбция 1 1 57 - 1 2 1 2
в движущемся слое сорбента
1 1 87 -90
идеальная 1 1 92 - 1 1 94, 1 1 99- 1 20 1
механизм 1 1 6 1 -63
в неподвижном слое сорбента
1 19 1 - 1 212
непрерывная 1 1 76 -90
периодическая 1 1 74
полунепрерывная 1 1 9 1 - 1 2 1 2
противоточная 1 1 87 -90
в псевдоожиженном слое 1 1 76 - 8 6
равновесие 1 1 63 -67
реальная 1 1 95 -99, 1 20 1

1 73 5

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Аnсорбци• 1 1 5 7 - 1 2 1 2
техно.11 огический расчет 1 1 75
физическая 1 1 6 1 -62, 1 1 65
химическая 1 727

Азео'q)опные

смеси

982

разделение 1 704, 1 7 1 2
Азеотропообразующне с:мес:и 982, 1 066
Активные (активированные) уr.11 и 1 1 59
Алюмогели 1 1 59
Амортизационные затраты 1 73
Аморфные вещества 1 308
Анизотропная среда 49, 95
Ансамбль частиц 1 5 1
Антагонизм свойств 5 1 , 52
Аппараты ХТ 38
барботажные 746 -47
воздушного охлаждения (АВО)

1 583

выпарные см. В ыпарные аппараты
высота 8 1 6
диспергирующие 746-47
насадочные 745
перекрестное соединениt 851-62
пленочные 745 -46
полочные 745 -46
поперечное сечение 8 15
пропускная способ1tость 825 -27
размеры 8 1 4- 1 7
со ступенчатым противотоком 834
с:л. цепи (сети ) 830 с:л .
Атсрмичные тела 5 1 0
Аэрос:ус:пензия 1 668
Байпас 80 1 , 803
Балансы (материальный, тепловой,
энергетический и др. ) 55-60, 547
временной интервал 56, 5 7
пространственный контур 56, 57
с:остаВ.11 е ние 56 - 5 8 , 547
состаВ.11я юшие ( Приход, Уход, Ис:
точннк, Сток, Нако.11 е ние) 56
уравнения 55 сл.
Барботаж 44 1 -43 , 9 1 2
Бародиффузия 773
Безразмерные
величины 44
комплексы 1 00 - 0 1
числа 1 05
Биения 402
Бинода 1 1 39
Бинодаль 1 1 39
Брызrоуловитепи 67 1 , 732
Бураты 1 660

1 736

Вакуум и рование 368 -75
время 374-75
глубокое 373
Вакуум - кристаллизаторы 1336 -67
Вакуумм етр 1 23
Вакуум -насосы (ВН ) 324, 356-59 • 36874
водокольцевые 358
глубокого вакуум а 372-74
диффузионные 373
индикаторная диаграмма 370
поршневые 369 -· 72
специальные 372- 73
Вакуум - сушильный шкаф 1 225-2 6
Вакуум -фильтр барабанный 4 1 7- 1 8 ,
426 - 2 7
Валковый пресс 1485, 1 505
Величнна(ы)
безразмерные 44
интенсивные 50, 5 1
распределенная 50
сосредоточенная 49
удельные 5 1
экстенсивные 50
Вентиль
дроссельный 1 556-57
- игольчатый 1 584
Вентиляторы центробежные 324, 359,

366-67
Вентиляционные потери 403
Вентури абсорберы 92 1
Виброаэросушилка 1222
Виброrранулятор 1 484
Влага
адиабатное испарение 1 24 1 -42
конuентраuия в воздухе 1 230 - 3 3
свободная 1286
связанная 1 286
Влаrоотде.11 ители (сепараторы) 344
Влаrосодержание 1 232
Влажность
абсолютная 1230 - 3 1
относительная 1 23 1
Воэrонка твердой фазы с:м. Сублимация
Воздух 1.11 ажн ый
диаграммы 1237 -39
относительная энтальпия 1 23 5
относитепьный удельный объем 1 234
свойства 1 230-39
Воздух JIСИДКИЙ, разделение на N1 и 02,
агрегат 1 6 1 2 - 1 7
Воздушные колпаки 2 8 5 - 8 8
Волна концентрационная 1 1 94

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Вращение вокруг оси
вертикальной 1 26 - 2 8
горизонтальной 1 28 - 29
Вредное пространство 3 3 8 , 355
Время
защитного действия 1 1 92, 1 1 98
потерянное 1 202, 1 208 - 1 О
пребывания 609, 6 1 8 , 62 1 , 624 - 2 6 ,
629, 6 33 , 638
проскока 1 1 92
среднее 62 1 - 2 2 , 647
Выпаривание 667 -735
дифферен циал ьное 690
непреры ваное 693 - 7 0 3
периодическое 686 -93
полунепрерывное 690
физико-химические основы 675-8 3
Выпарные аппараты 675
вакуумные 696 - 702
с вынесенной зоной кипения 673
емкостные 675
классификаuия 669- 70
конструкции 67 1 -7 5
контактного типа 675
многокорпусные 703 - 1 6
непрерывного действия 693 - 703
периодического действия 6 8 5 - 9 3
пленочные 672, 6 7 4 , 727 - 3 0
с погружной горелкой 675
сепарационное пространство 7 3 0 32
схема расчетная 683 - 8 4
с тепловым насосом 7 1 6 - 2 7
с uиркуляuией раствора 67 1 - 7 4
- принудительной 6 7 3 - 7 4
чистка 6 7 3
Высота см. Напор
Выщелачивание (частичное растворе
ние) 1 393
аппаратура 1 398 - 1 402
с и нертным компонентом 1 4 1 9-26
м ногоступенчатое (перекрестное)
1 42 2 - 2 3
с непрерывным контактом фаз
1 426, 1 43 2 - 34
перекрестное 1 422 - 2 3
в потоке растворителя 1 43 0 - 3 2
проти воточное 1 4 2 3 , 1 43 2 - 34
равновесие 1 420
вэтс 8 5 1
Вязкость 8 3
динамическая 62

кажущаяся (неньютоновских
жидкостей) 1 9 1
Вязкость 8 3
кинематическая 62
турбулентная 1 54
Газ(ы)
барботаж 44 1 -43
идеальные 49
коэффициент сжимаемости 329
неконденсирующиеся 697
обеспыливание см. Обеспылива
ние газов
ожижение дросселированием
1 596 - 1 60 1
осушка 1 1 70
сжатие 323 ел .
степень черноты 5 1 7
Газгольдеры 1 6 1 6
Газлифт (эрлифт) 262, 265, 3 1 4- 1 5 ,
3 1 7 , 320 - 2 1 , 1 397
Газ-носитель 907
Газовзвесь 404
Газовые пузыри, образование и движение 24 1 -46
Газодувка 324, 359
Газопровод. расчет 1 79 - 8 2
Газосодержание 2 4 7 , 3 1 4
Гетероазеотроп 1 066
Гигроскопичность 1 470
Гидравлика 1 1 9 - 260
дисперсных систем 2 1 3 -5 5
сплошных сред 1 1 9 - 2 1 3
Гидравлические потери 1 38
Гидравлический
радиус живого сечения 1 39 - 40
удар 1 82 - 8 5
Гидравлическое сопротивление
движущегося слоя 223
двухфазных систем 256
коэффициент 1 4 1 , 1 59 - 6 2 , 490
местное 1 63 -6 5
неподвижного слоя 2 1 7
пневмотранспорта 250 - 5 5
псевдоожиженного слоя 228 - 3 0
суммарное 1 69
эквивалентная длина 1 64
Гидродинамика 1 32 - 2 5 7
внешняя задача 1 33 , 2 1 9 -20
внутрен няя задача 1 33 , 220
смешанная задача 246
уравнение дифференциальное 8 3

1 737

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Гидростатика 1 1 9 - 1 32
уравнения 1 О, 1 2 1 , 1 64
Гидроциклон ы 4 1 2
Гиперсорбция 1 1 7 1
Гомоазеотроп 1 066
Граничные условия ( ГУ) 98, 99, 575-76
классифи кация 98, 99
Стефана 1 334
Гранулирование 1 469 - 1 5 1 8
агломерацией порошков 1 476,
1 479, 1 496
аппаратура 1 47 8 -90
безретурное 1 500-02
десублимацией 1 477
классификация 1 474-77
кристалл изацией капель расплава
1 475, 1 48 6 - 8 9 , 1 5 1 0 - 1 5
материальные и тепловые балансы
1 49 1 - 9 3 , 1 50 8 - 1 0
окатыванием 1 479, 1 496
из паровой фазы 1 5 1 5
порошков 1 477, 1 490 - 1 507
в потоке хладоагента 1 475, 1 486
прессован ием 1 476, 1 48 5 , 1 504-07
расплавов 1 477, 1 48 6 - 8 9 , 1 508 - 1 5
из растворов 1 47 7 , 1 5 1 5
с ретуром 1 502
с теплоносителем 1 477
технологическая схема 1 478
формованием 1 476, 1 48 5 , 1 507
Гранулометрический анализ 1 658
Гранулирование, кинетика 1 496- 1 5 0 3
Гранулы 1 469
капсулирование 1 5 1 6 - 1 8
механизмы взаимодействия час
тиц в них 1 47 2 - 74
свойства 1 469 - 70
- роста 1 497
слеживаемость 1 470
стадии 1 470 - 7 1
структурирование 1 47 1
формован ие 1 470- 7 1
Гранулятор(ы)
барабанные 1 480
емкостные: 1 48 8
колонные 1 488
ленточный 1 48 1
с псс:вдоожиженым слоем 1 482-8 3
ротационные статистические 1 487
скоростной 1 484
тарельчатый 1 48 1
с фонтанирующим слоем 1 483

1 73 8

Грануляционная башня 1 489
Грохот(ы) 1 657 -63
барабанный 1 660 - 6 1
вибрацион ный 1 66 2 - 6 3
Грохот(ы)
гирационный 1 662 - 6 3
горизонтальные 1 66 3 - 64
многогранные (бураты) 1 660
качающиеся 1 66 1 -62
наклонный 1 66 1
неподвижный 1 66 1
устройство 1 660 -63
Грохочен ие 1 657 -67
расчет 1 66 3 - 6 6
способы 1 659-60
Давление 54
атмосферное 1 23
на боковые стенки сосуда 1 30 - 3 1
внешнее: 1 22
гидростатическое 1 22 , 1 3 1
н а дно сосуда 1 30
закон распределения 1 2 1
избыточное 1 23
критическое 522
локал ьное 54
осмотическое 1 527
при относительном покое 1 24-29
в покоящемся сосуде 1 22 - 2 3
полное 1 2 2
силы 79
среднее 54
ударное 1 8 2 ел.
центр 1 3 1
Движущая сила
гидродинамическая см. Напор
массообмена средняя 805 - 1 7
- при идеальном перемешивании
807
- при противотоке фаз 8 1 1
- при прямотоке фаз 809
тс:плообмс:на 545 с м . также Тем
пературный напор
Движущийся слой (ДС) 2 1 4, 222 - 24
Двухфазные потоки 246 - 5 5 см. также
Массообмен
Дельта-функция Дирака 625
Депрессия
гидравлическая 699
температурная 677
Десорбирующий агент 959
расход 960

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Десорбция 907 , 959-67 см. также
Сушка твердых материалов
методы 960 - 6 1
расчет 96 1 -64
Десубл имат 1 442 -43
плавление 1 468
Десублиматор(ы) (твердофазные кон 
денсаторы) 1 450
емкостные 1 450
объемные 1 45 0 - 5 2
поверхностные 1 450, 1 452, 1 45455
скребковый 1 4 5 3
Десублимация 1 435 ел .
аппаратура 1 44 8 - 5 7
вакуум н ая 1 449 - 5 0
с и нертным газом-носителем
1 444 -45
кинетика 1 44 1
методы 1 444-47
механизм 1 442
объемная 1 444 -47
на охлаждаемых поверхностях
1 443
поверхностная 1 443
применение 1 435
равновесия диаграммы 1 439
расчет 1 46 3 - 6 8
физико-химические основы 1 43 6 40
фракционная 1 446
Детандер(ы) 1 556, 1 584
адиабатический К ПД 1 588
поршневые 1 584, 1 58 , 1 60 2 - 0 5 ,
161 1
центробежные (турбо- ) см. Турбо
детандеры
Дефлегматор 1 О 1 5
Дефлегмация 1 0 1 5
Джоуль 42
Диализ 1 526
Динамический свод 22
Диатермичное тело 5 1 О
Дискретная фаза 2 1 3
Диспергаторы 1 48 6 - 8 7
Диспергирование жидкостей и газов
46 1 -67
при истечен ии из отверстий 46567
механическое 462 - 64
режи мы 465 -66

Дисперсион ная (сплошная) среда 2 1 3 ,
1 1 03
Дисперсия 438
Дисперсная (диспегируемая) фаза 2 1 3 ,
1 1 03
задержка 247 , 25
размер частиц 24 1 -44
скорость движения в сплошной
среде 244-46
Дисперсные материалы, свойства 1 490
Дисперсные системы с твердой фазой
2 14- 1 6
Диссипация энергии 462
Дистиллят 990 , 1 О 1 3
Дистилляционный куб 989
Дистилляция 969 - 7 0 , 988- 1 0 1 0
взаимно нераствори м ых компо
нентов 1 007 -08
гидродинамическая 1 6 86
с дефлегмацией 1 006
многократная 1 008
молекулярная 1 00 2 - 05
однократная 996 -99
полунепрерывная 1 00 5 - 06
постепенная 990 -95, 1 006
простая 990
расчет 990 -96
в токе инертного газа 999 - 1 002
фракционированн ая 996
Диффузия 89, 770
внешняя 87 1
внутренняя 87 1
облегченная 1 529
Диффузор 720 - 2 1 , 723 - 24
Допустимая погрешность 44
Дробилка( и )
валковые ( ВД) 1 634-39
гладковалковая 1 63 5 , 1 637
щековые 1 626 - 3 3
Дросселирование 1 557, 1 58 5 - 8 8
Друк-фильтр 4 1 5 - 1 6
Единицы измерения 4 1 -43
Живое сечение потока 1 39 , 1 40
Жидкость( и)
абсол ютно несжи маемая 48
бингамовские 1 93 , 1 95 -98
вя зкоупругие 1 95
вязкоэластичные 1 95
дилатантные 1 94, 1 99 -202
диспергирование 46 1 -67

1 739

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

идеальная 48
истечение см. Истечение жидко
сти
кипение 502 -06
коэффициент сжимаемости 1 84
неньютоновские 1 90 -202
ньютоновские 1 46 ел" 1 93 , 1 9 5
орошающая 9 1 5
осветленные 378
псевдопластичные 1 94, 1 99 - 202
реальные 48
режимы течения см. Режимы те
чения
реопектантные 1 95
реопектические 1 95
Жидкость( и )
средства перемещения 26 1 ел. , см .
также Н асосы
тиксотропные 1 95
Жидкофазные мостики 1 47 3
Задача(и) переноса
балансовая 57 1 - 72
внешняя 576
внутренняя 576
диффузионная 947
кинетическая 946
обратные 1 70
поверхностная 569, 57 1 ел .
потоковые 570 ел " 5 8 6
прямые 1 7 0
смешанные 57 1 ел " 5 8 5 , 5 8 6 , 947
Задачи
проектирования 4 1 , 1 67
эксплуатационные 4 1 , 1 67
Закон " 1 /7 " 1 59
Закон (ы)
Архимеда 55
Генри 924, 973
Гука 1 8 3
Дарси 66
Коновалова 9 7 5 , 9 8 3
Ньютона 66, 4 8 8
О ма 66
П аскаля 1 2 3
природы 45
пропорциональности 3 0 8 - 0 9
Паузейля 66
Рауля 973, 975, 979 ел .
сообщающихся сосудов 1 24
стенки 1 57
Стефана- Больцмана 477, 5 1 0

1 740

термодинамики 326
турбулентного течения 1 5 1 - 6 2
Фика 6 3 , 66, 488 , 770
Фурье 6 3 , 66, 477, 488
Зародышеобразование 1 32 5 - 29
Затравка 1 500
Затраты 1 7 3
Захлебывание 745 , 9 3 1 , 966
Зеркал ьное тело 5 1 О
Зона(ы)
буферная 1 57
водоворотная 1 63
застойные 64 1 -42
Зонная плавка 1 3 8 4 - 8 5
Идеал ьное вытеснение 49, 6 0 9 , 6 1 1 ,
638

влияние на химическую реакцию
615

Идеальное вытеснение
время пребывания 247 , 6 1 8 - 2 1
коэффициент массопередачи 82 1 24

кривые отклика 620, 627
расчет массообмена 808 - 1 3
результирующий эффект 62 1
Идеальное перемешивание 49 - 5 0 , 6 3 8
влияние на химическую реакцию
615

время пребывания 247, 62 1 - 2 8
коэффициент массопередачи 8 1 8
ел .
кривые отклика 6 2 3 , 627, 629
расчет массообмена 806 ел.
результирующий эффект 624-26
Излучение тепловое 509 - 1 6
абсолютно черного тела 477
газов 5 1 6
поверхностей 5 1 1 - 1 4
поток 5 1 0 - 1 2
экранирование 5 1 5 - 1 6
эффективное 5 1 2
Измельчение твердых материалов
1 6 1 9 - 54

затраты энергии 1 62 1 - 2 3
крупное 1 62 5 ел.
мелкое 1 639 ел.
способы 1 6:20
Изобара 976
Изолиния 60
Изоля ция тепловая 54 1 - 43
толщина 542 -43

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Изоповерхность 60
Изотерма 326, 975
абсорбции 923
растворимости 1 1 39
сорбции 1 1 64
Изотропная среда 49
И нвариантность системы 763
И ндикатор 6 1 8
И нерт 766, 907
И нерционные потери 290 -93
И нжекторы 266, 3 1 6 , 7 1 9 , 72 1
кпд 722 -24
И нкрустация поверхности теплообмена 673
И нтеграл ошибок 1 334
И он иты 1 1 60, 1 470
Испарение
влаги адиабатное 1 24 1 -43
твердой фазы см. Сублимация
Испарител и
адиабатные 727
барабанные 1 58 3
вертикальнотрубные 1 583
кожухотрубные 1 584
многоступенчатые 727
пленочные 672, 674 - 7 5
роторные 6 7 2 , 674 - 7 5
И стечение 202
газа 202 - 1 3
ЖИДКОСТИ 202 - 09
И стирание 1 620 - 2 1
Кавитация 27 1 , 3 1 3
Калорифер 1 245
Камера пылеосадительная 39 1
Капитальные затраты 1 73
Капли 2 4 1 - 46
диаметр отрывной 242 -43
- при диспергировании 464
размеры 24 1 -44
частота отрыва 244
шейка 242
Капсулирован ие 1 5 1 6 - 1 8
Квазистационарность 40
Кипение жидкости 502 -06
Кипятильни ки 990, 1 0 1 4, 1 0 1 8
Кипящий слой 2 2 5 - 2 6 см. так.же
Псевдоожиженный слой
Кирпичева гипотеза 1 6 2 1
Классификатор(ы) (сепараторы)
барабанные 1 692
воздушный 1 676, 1 680 - 8 3

гидравлический 1 677
горизонтальный 1 69 1
инерционные 1 67 9 - 8 0
магнитные 1 694-95
м и тхт 1 676-77
непрерывного действия 1 67 5
с отвеиванием 1 6 8 1
пневматические 1 67 5 - 7 6 , 1 679- 8 0
расчет 1 68 3
фрикционные 1 68 3
Классификация (сепарация) зерни 
стых материалов 1 65 5 - 9 6
грохочением 1 656 - 6 7
гидравлическая 1 656, 1 67 3 -7 9
назначение 1 655
пневматическая 1 656, 1 67 3 - 7 9
в поле инерционных с и л 1 67 9 - 8 3
- с и л тяжести 1 67 5 - 7 9 , 1 684
в псевдоожиженном слое 1 685 - 9 1
резинотканевых смесей 1 676
в тяжелых средах 1 667 - 7 3
электромагнитная 1 694-96
КФ-Классификаuия 739, 740
Колонна(ы) ректификационная(ые)
барботажные 1 О 1 6
насадочные 1 0 1 7
отгон ная часть 1 02 2 , 1 02 8 - 3 0 ,
1 0 5 1 - 5 4 , 1 089 -92, 1 098 - 1 1 00
пленочные 1 0 1 7
полная 1 092, 1 093
укрепляющая часть 1 022 - 2 8 ,
1 046 -5 1 , 1 085 - 89 , 1 095 -98
Колонны экстракционные 1 1 0 8 ел . см
также Экстракторы
с в ибрирующими перфорирован
ными тарелками 1 1 1 1 - 1 2
с вращающимися мешалками 1 1 09
насадочные 1 1 08 - 09
без подвода внешней энергии
1 00 8 - 09
с подводом внешней энергии
1 1 09 - 1 3
пульсационные 1 1 1 0
распылительные 1 1 0 8 -09
секцион ированные 1 1 1 4
ситчатые 1 1 1 0, 1 1 1 4
со ступенчатым контактом фаз
1 1 13-14
Колосники 1 657
Компрессор(ы) 323 ел .
водокольцевые 3 5 8
с водосборником 359

1 74 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

воздушный 1 592
двухроторны й 367 - 6 8
динам ические 3 2 5 , 3 2 8 , 3 5 9 , 3676 7 см. также Турбокомпрессоры
классификация 324 - 2 5
коловратн ые 1 583
КПД 329 - 30

линзовые 524
объем ного действия 325, 328, 3 3 7 ,

сопряженные 793, 1 055
Концепция прилипания 98
Координаты
декартовые 76, 77
сферические 94
цили ндрические 76, 7 7 , 92
Коэффициент(ы)
внутреннего трения 1 4 1 , 1 490
гидравлического сопротивления

356 - 5 9

1 4 1 , 1 59 - 6 2 , 490

осевые 3 2 5
пластин чатые 365 - 5 7
поршневые 3 24 - 2 5 , 330 - 3 1 , 1 58 3 ,

динамической вязкости 62
диффузи и 6 3 , 770, 772
захвата м аточника 1 348
защитного действия слоя сорбента

161 1

11рименен ие 368
ротацион ные 325, 3 56 - 5 7
- мокрые 3 5 8
специалы1ыс 324
степень сжатия , оптим изация
324 - 5 1

струйные 325
термохим ические 1 576
центробежные см. Турбокомпрес
соры
Конвекция 475
вынуЖденная 88, 475, 490 -9 1 , 508
естествен ная 475, 49 1 -94, 508
Конденсат 990
Конденсатоотвод•1 и к 502

Конденсаторы 1 0 1 4, 1 0 1 8
поверхностные 697
смешения 697 - 702
Конденсация 496
капиллярная 1 1 62 , 1 1 6
парциальная 9 8 8 - 9 0 , 999, 1 006-0 9
пленочная 496 - 502
твердофазная см. Десубл имация
- частичная см. Десубли маuия
фракционная
Кондукция см. Твердопроводность
Конода 763, 1 1 39
Концентрационная волна 1 1 94, 1 1 9 6 97

Концентрация(и) 750 - 59
абсол ютные 7 1 , 970
исти нная 25 1 - 5 2
массовые 6 7 5 , 752 - 5 3
номинальная твердой фазы 25 1
объе м н ы е 754
относ ител ьные 7 5 2 - 5 5

пересчет 7 5 2 - 5 5
проскоковая 1 1 92

1 742

1 20 1 , 1 203 сл .

'

избытка воздуха 1 28 1
извилистости 2 1 8
и нжекции 3 1 6, 7 1 9-24
использования насадки 597 -98
истечения из отверстия 466
лобового сопротивления 234, 453
массоотдачи 65, 490, 775, 778, 874
массопередачи 7 8 5 - 8 7
массопроводности 770
местного сопротивления 1 63
незнания 3 3 , 72, 829 - 3 0
объем ного сопротивления 493
отражения 5 1 0
пластической вязкости 1 93
поверхностного н апряжения 54
поглощения 5 1 0
подачи (насосов) 2 7 3 , 28 1
полезного действия см. КПД
продольного перемеши вания 634
ел .
проницаемости 1 522
п ропускания 5 1 0
разделения 978, 1 003
распределения 767
расхода (при истечении жидкости)
204

рециркуляции 802, 1 502
рядности (для пучков труб) 50 1 ,
519

сжатия (сужения) струи 204 - 0 5
сжимаемости 1 84, 329
теплоотдачи 43, 65, 486, 505, 508 09

- излучением 5 1 4
теплопередачи 528 - 3 5
- при параллельном переносе
534 - 3 5

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

- при последовательном переносе
529 -34
теплопроводности 43, 63
ускорения абсорбции 947
холодильный 1 555
- воздушного цикла 1 564
- при веде н н ый 1 577
эффективности разделения 1 348
КПД (коэффициент полезного дейст
вия )
аднабатический 329
г11дравлический 274, 300
изотермический 329
механический 274
объемный (компрессоров) 339 -40
передачи 274
Кривые
гранулометрического состава 38 1 82
отклика см. Отклик
охлаждения расплавов 1 3 1 1
псевдоожижения 227, 228
равновесия 922
растворимости 1 3 1 7 , 1 404-05
сушки 1 28 5 - 8 6
Криогенные установки 1 456
Кристаллизатор ( ы) 1 342
барабан ные 1 343, 1 370, 1 373
с внеш н и м охлаждением 1 352 ел .
с выносной греющей камерой
1 366
выпарной 1 365-66
дисковые 1 344, 1 354
ем костные 1 35 2 - 5 3 , 1 356, 1 362
колонные 1 362, 1 363
поршневой 1 373
пульсационный 1 37 3
распылительн ы й 1 363
ступенчатые 1 372 ел.
трубчатые 1 353, 1 370
циркуляционные 1 355, 1 366
шнековы й 1 372, 1 373
Кристаллизация 1 307 см. также
Фракционная кристаллизация
аддуктивная 1 725
бинарных смесей 1 3 1 3 - 1 7 , 1 33738
вакуум ная 1 365, 1 368
выпарная 1 365, 1 368
кинетика 1 324- 38
контактная 1 360 -62
массовая 1 338, 1 352-64

многокомпонентных смесей
1 337 -38
многоступенчатая 1 372 ел
напрааленная 1 338, 1 347 , 1 382-83
с образованием химических со
единений 1 3 1 4, 1 3 1 6 , 1 3 1 7
однокомпонентных веществ
131 1 -13
особенности 1 308 - 1 1
на охлаждаемых поверхностях
1 369-7 1
из паровой фаэы 1 307 см. также
Десубл имация
применение 1 307
п ротивоточная 1 372-77
расплавов 1 332-37
из растворов 1 3 1 7 , 1 324
скорость 1 335
тройных систем 1 3 1 7 -24
фазовое равновесие 1 3 1 1 -24
фракционная см. Фракционная
кристаллизация
фронт 1 329, 1 332
с частичной отгонкой растворите
ля 1 36 5 - 69
экстрактивная 1 7 1 3 - 1 6
Кристаллы (кристаллические вещест
ва) 1 308
жидкие 1 308
зарождение 1 325 -29
прессование 1 346
рост 1 329 -32
форма 1 338 -40
Критерии см. также Ч исла
Архимеда 23 1 , 38 1 , 492
Био 1 1 3 - 1 4, 576
Вебера 245 , 462
вырождение 1 09
гомохронности 1 04
Грасгофа 493 -94
Льюиса 777
Н уссельта 1 1 3 - 1 4, 487, 49 1 , 494
оценки 1 700
Пекле, диффузионный 1 1 1
- продольного перемешивания
636
. - тепловой 1 1 1
- эффективный 636
подобия 1 05 ел.
П рандтля 1 1 2, 49 1 , 494
разделения 886-87

1 743

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Рейнольдса 1 0 8 - 09 , 1 1 2, 23 1 , 234,
49 1 , 547
Стантона 489 - 9 1
Фика 1 1 1 , 879, 1 298
Фруда 1 08 , 457
Фурье 1 1 0 , 1 1 2 , 879, 1 29 8
Ul ервуда 1 1 3 , 490 , 496, 7 7 5
lll мидта 1 1 2, 490
Эйлера 1 07 , 1 1 2 , 457
Кубовой остаток 990, 1 0 1 3
Ламинарное течение, законы 1 46 - 5 1 ,
1 86
Лапласиан 9 1 , 92
Летучесть относительная 978, 980, 1 003
Лимитирующая стадии 567 - 74
при массопереносе 828
при параллельном теплопереносе
573-74
при последовательном теплопере
носе 567 ел.
Линеаризация 46
Линии
ликвидуса 1 3 1 5
равновесия 764, 922, 926
рафинатов 1 1 40
результирующего разделения 1 1 53
солидуса 1 3 1 5
тарелки питания 1 04 1
тока 1 32 - 3 3
экстрактов 1 1 40
Лопасти
мешалок 456 -59
роторных смесителей 460
М акрокапсул ирование 1 5 1 7
Макропоры 1 1 59
Манометр 1 2 3
Масса 52
Массообмен (массообменные процес
сы) 39, 7 3 5 , 769
движущая сила см. Движущая сила
массообмена
классифи кация 736 -42
между жидкостью (газом) и твер
дыми телами см Выщелачивание
(Адсорбция)
- твердыми телами 87 1
с нелинейными балансами 868-7 0
нестационарный 769 -70, 877
поверхность 737
в псевдоожиженном слое 875 -77

1 744

рабочая область 765
сопряженный 1 705 - 1 9
стационарный 769 - 70
Массообменные устройства 744-4 8
материальный баланс 7 8 8 - 9 0
Массооотдача 7 6 9 , 77 1 , 7 7 3
уравнение 6 6
Массопередача 769
время 1 1 97, 1 20 5 - 0 8
контактная 780 - 8 7
уравнение 78 1
Массоперенос 735 ел. , 768
ВИДЫ 770 - 7 1
внешняя задача 873 -77
внутренняя задача 877 - 8 0
в движущейся жидкости 8 6 - 8 9
диффузионный 7 6 9 , 772-73
кинетика 768 - 7 8
конвективный 77 1 , 7 7 3 - 78
контактный 768 ел .
периодический 862 -65
полунепрерывный 862, 865 -67
потоковая задача 880 - 8 1
смешанные задачи 880 - 8 1
составляющая описания 742 -44
уравнение 86 - 89
элементы 768
Массопроводность 770 см. также
Диффузия
Масштабные преобразования 1 02 -04
Маточ н и к 1 1 03
Межтрубное простанство 524
М ел ьницы
барабанные (БМ) 1 63 9 - 5 2
классификация 1 640 - 4 1
коллоидные 1 65 3 - 54
мокрого помола 1 653
насадки 1 640, 1 642 - 45
шаровые 1 640
Мембранное разделение 1 5 1 9 -50
расчет 1 53 3 -42
с химическим взаимодействием с
мембраной 1 529 - 3 0
без химического взаимодействия
1 526-29
Мембранные ячейки
с идеальным вытеснением потока
1 53 7 - 4 1
- перемешиванием потоков 1 53 3 37
каскадные схемы 1 54 3 - 5 0
конструкции 1 53 0 - 3 3

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

из полых полимерных волокон
1 532 - 3 3
применение 1 520 - 2 1
рулонноrо типа 1 53 1 -32
схема 1 520
Мембраны 1 5 1 9
армированные 1 53 1
классификаuия 1 520
непористные 1 520-24
пористые 1 520 - 2 1 , 1 524 -26
Местное сопротивление см. Гидравли
ческое сопротивление
Метод
вэтс 8 5 1
моментов 650 - 5 5
обобщен ных переменных 7 1
подмены задачи 7 2
полуэм пирический 1 00
Мешалки
вязкостные диапазоны примене
н ия 446
лопастн ые 445 ел .
- М О ЩllОСТЬ 454 -60
типы 446
М идилево сечение, площадь 453
Микрокапсулирован ие 1 5 1 6
М и кропоры 1 1 59
Множители подобия 1 02 ел.
Модель(и) течения жидкости (структу
ры потоков) 6 1 8 -650
беспараметрическая 653
д11ухпараметрическзя 643
диффузионная 634-39
идеальноrо вытеснения см. Иде
альное вытеснение
- перемешивания см. Идеальное
перемеши вание
каскадна11 629 - 34
комбинированная 643
однопараметрическая 639, 653
определение параметров 650 - 5 5
пленочная 1 85 -90
продольноrо перемеш ивания 628 44
ступенчатая 629 -34
ячеечная 629 -34, 639
Модуль сита 1 658
Молекулярное течение 257 -60
Момент(ы)
безразмерные 65 1 - 53
инерuии 1 3 1
начальные 650

нормировка 65 1
центральные 6 5 1
Монтежю 26 1 -62, 320 - 2 1
Мультициклоны 406 -07
Напор (высота)
rеометрическиА (нивелирный) 1 36
динамический 1 36
кинетический (скоростной) 1 36
нивелирный 1 36
падение по длине трубопровода
1 66
полезный 30 1
полный 1 36
потери на участке стабилизации
1s1
потерянный 1 38
пьезометрический 1 23, 1 36
располагаемый 1 69
скоростной 1 36
теоретический 30 1
Напряжение
тепловое 477
трения 54, 62
- критическое 1 92
Насадка(и) массообменные 746, 9 1 5
блочные 9 1 6 - 1 7
rидравлическое сопротивление
967
нереrулярная 1 О 1 7
поверхность удельная 9 1 5
порозность 9 1 5
псевдоожИJКенная 747, 9 1 9
регулярные 9 1 6, 1 0 1 7
сетчатая 9 1 7
"Спрейпак" 9 1 5
требования к ним 9 1 5
хордовая 746, 9 1 6
Насадки теплообменные 595 -98
Насос(ы)
винтовой 265, 3 1 8
вихревые 262, 265
всасывающая способность 272
высота всасывания, rеометриче
ская 266
- - предельная 27 1 -72, 293, 3 1 3
- - реальная 293
- наrнетания, rеометрическая 266
движение поршн11 28 1 -82
диаrональные 265
достоинства и недостатки 3 1 7
классификаuия 262 -66

1 745

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

коэффициент подач и 273, 28 1
- полезного действия 274
лопастн ые 262, 264 - 6 5 , 295 ел .
метаболический 1 530
механические 26 1 -65
мощность 270, 2 7 3 - 7 4
напор 2 6 7 - 6 9
немеханические 2 6 1 - 6 2 , 2 6 5 - 6 6 ,
3 14-22
объемные 262 -65, 3 1 7ё32 1
осевые 297 , 3 1 7 , 3 1 9
пластинчатый 263, 3 1 8
поршневые см. П оршневые насо
сы
производительность 267, 273, 280
- локальная 283
- мгновенная 283
- регулирование 294
пропеллерный 265, 697
рабочая точка 289, 306, 307, 404
реверсивный 264
ротационный 263 , 264
струйные 262, 266, 3 1 6 - 1 7, 3 1 9,
321
тепловой 7 0 3 , 1 553
характеристики 269, 289, 304- 1 0
центробежные см. Центробежные
насосы
шестеренчатый 263 , 3 1 8
шланговый 265
Начальны е условия ( Н У) 97
Недорекуп ерация 1 595
Неизотропная среда 49
Неподвижный слой ( Н С )
гидродинамика 2 1 4, 2 1 7 - 2 2
идеальный 2 1 7
предел устойчивости 222
фиктивны й 2 1 7
Нода 763, 1 1 39
Нутч-фильтр 4 1 5 , 4 1 6
Ньютон 42
Ньютоновские жидкости 1 46 ел " 1 93 ,
1 95
Обеспыливание газов
в отстойных газоходах 39 1
в фил ьтрах 4 1 5
в циклонах 404 - 1 2
Обобщенные переменные 1 00 ел .
для пограничного слоя 1 1 3
в уравнениях переноса 1 06 - 1 2
Обогащение 1 667

1 746

Обратное перемешивание 6 1 1
Ожижающий агент ( ОА) 225
Ожижител ь (О) 1 606
Онзагера соотношения 66, 67
Осадок, промывка 435 - 3 6
Осаждение твердых частиц 378-4 1 3
естественное 3 8 3 - 9 2 , 396
производительность 379
скорость 380 - 8 1 , 396
схема 380
центробежное 392 -4 1 2
- время 395, 398 ел.
- в газах 404 - 4 1 2
- в жидкостях 392 -404
Осмос 1 527
аномальный 1 528
обратный 1 528
Отвеивание 1 68 1 , 1 684
Отверждение расплавов
в тонком слое 1 343 -44
в формах 1 34 1 - 42
Отклик (кривые откли ка) 620, 623, 627,
629
в разных координатах 645
связь с функцией распределения
645
Относительная погрешность 44
Отсев 1 659
Отстойник( и )
классификатор 1 6 7 5 - 7 6
- гидравлический 1 67 7 - 7 8
многополочные 390, 39 1
непрерывного действия 379, 38 1
- вертикальный 384, 387 - 8 8 ,
390
- - горизонтальный 384 - 8 5 , 388 89
очистка от осадка 390
периодического действия 384 - 8 7
- вертикальный 384 - 8 7
площадь 1 659
Отход 1 659
Охладители гранул см. Хладогент(ы)
Охлаждаемая среда 1 580, 1 582
Охлаждающая среда см Хладогент(ы)
Охлаждение
глубокое 1 55 1 , ел .
- аппаратура 1 6 1 0 - 1 2
- классификация 1 58 4 - 8 5
- цикл ы 1 590 ел.
пути 1 585
умеренное 1 55 3 - 84
-

-

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

- аппаратура 1 58 2 - 8 4
Очистка веществ суби мацией -десуб
лимацией 1 457
Палля кольца 9 1 6

Пар

вторичный 667 , 680 - 8 2
перегретый 999 , 1 002
Паскаль 42
Перегонка 969
сублимационнодесублимационная 1 457
физико-химические основы 97087
Перекрестны й ток 546
Перекристаллизация 1 386-9 1
многократная 1 390
однократная 1 389
сублимационно
десублимационная 1 446
Перемешивание 436-60
влияние на растворение 437
время 438
затраты энергии 440, 453
идеальное см. Идеальное переме
шивание
кинетика 438-40
механическое 44 1 , 445 -60
обратное 6 1 1
паст 460
пневматическое жидкостей 44 1 43
поперечное 6 1 0
продольное см. Продольное пере
мешивание
сыпучих материалов 460
циркуляционное 44 1 , 443 -45 , 6 1 2
эффективность 437
Перенос вещества 39 см. также М ас 
соперенос, Перенос субстанции
в движущейся ЖИДКОСТИ 86-89
дифференциальное уравнение 88
через мембраны 1 52 1 -26
Перенос и мпульса 39, 79, 377 ел .
Перенос субстанции 607 ел . см. также
Потоки
активный 1 530
безградиентный 99
движущая сила 60
законы (л инеаризованные) 66
интенсивность 60 ел .
поперечный 607 -08

продольный 607
составление балансов 5 6 - 5 8
уравнение 7 3 ел. , 8 5 ел .
Перенос теплоты см. Теплоперенос
Переохлаждение при кристаллизации
1 328, 1 3 3 1 - 0 2 , 1 340
Пермеат 1 530
Плавление
однократное 1 37 8
последовательное 1 379 - 8 0 , 1 3 8 1
фракционное 1 37 7 - 8 2
Пластичность 1 93
Пленка (слой)
пограничная 470
тепловая 486
Пленочные устрой ства 745
Плотность 52
насыпная 2 1 5
орошения 1 88 , 9 1 5 , 966
распределения 6 24 - 2 5 , 6 3 3 , 638
Пневможелоб 526
П невмотранспортные систем ы 2 5 0 - 5 5
Поверхностное натяжение 5 4
межфазное 4 6 2 , 463
Поверхность( и)
межфазного контракта 874
жидкости свободная 1 22 , 1 27 , 1 29
уровня 1 2 1
Пограничный слой 64
диффузионн ы й 65, 774
П огреш ности расчетов 44
Подмена задачи 72
Подобие
гидродинамическое 1 06 - 1 О
диффузионное 1 1 1
в переносе разных субстанций 1 1 2
тепловое 1 1 0, 1 1 1
физическое 99- 1 0 1
Полиморфизм 1 309
Политропа 326
показатель 327
Полюс диаграммы 954 - 5 5 , 1 0 1 9 , 1 054,
1 08 7 , 1 1 5 1
Помпаж 308
Пористость 2 1 5 , 1 470
Порозность 2 1 5 , 378
критическое значение 1 673
при псевдоожижении 237 -40
Порошки , свойства 1 490 - 9 1
Поршневые компрессоры 3 3 0 - 5 5
влияние влаги 344
вредное пространство 338

1 747

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

двойного действия 3 3 1 - 3 2
затраты энергии 332 - 37 , 352-53
КПД, объемный 339
многоступенчатые 343 - 5 1 , 353
мощность 353
с обводной линией 354
охлаждение 35 1 - 5 2
производительность 337 -42
- регул ирован ие 354 - 5 5
простого действия 3 3 1
с ресивером 332
степень сжатия 342 -43
требования к смазке 343
цикл 3 3 1
Поршневые насосы 263 - 64 , 274-9 4 ,
318
с воздушными колпаками 286
высота всасывания 290 -93
двойного действия 279, 284
диаграммы подачи 2 8 3 - 8 5
достоинства и недостатки 3 1 8
классификация 276
коэффициент подачи 2 8 1
мощность 273 -7 4 , 293
однократного действия 278
плунжерные 2 7 7 - 7 8
производительность 280, 2 8 3
простого действия 278
прямодействующие 277
скальчатые 277
схема 275
тройного действия 279, 2 84 - 8 5
характеристика 289
четверного действия 279, 284
электропроводн ые 277
П отенциал(ы) 60 ел .
градиент 6 1 , 62
П оток(и) вещества 60, 6 1
двухфазные 246 - 5 5
живое сечен ие 1 39 -40
при идеальном вытеснен ии 8 2 1 24
- - перемешивании 8 1 9
с обратным перемешиванием 6 1 1
плотность 6 1 , 770
ПОЛНЫЙ 770
поперечная неравномерность 6 1 1
поршневой 609
при противотоке фаз 8 2 3 - 2 4
проходящий 1 5 1 9 -20
в процессах массопереноса 8 1 7-2 4
при прямотоке фаз 82 1 - 22

1 748

стабилизация гидродинамики 1 50 ,
1 62
стержневой 609
структура 607 -66
- модели 629 -44 см. также Мо
дели течения жидкости
- в модельных системах 6 1 8 - 28
- в реальных системах 628 - 3 8
- учет в расчетах 656 - 66
циркуляционный направленный
612
Поток импульса 62
Поток тепловой см. Тепловой поток
Поток энтальпии 546 - 50
П равила см. также Законы
Бабо 679
Вревского 983
рычага 759-62
смешения 759
фаз 762, 972
П редел текучести 1 92
П ресс валковый 1 48 5 , 1 505
Проводи мость кондуктивная 480
П родольное перемешивание 6 1 0 , 628
ел .
влияние на эффективность ХТП
612-17
в двухфазных системах 6 1 0 - 1 1
коэффициент 634 ел.
кривые отклика 629
модели 628 -44
причины 6 1 1 - 1 2
учет в расчетах 656-66
экспериментальное изучение 644 55
П ропускная способность 68, 1 1 5
массопереноса 79 1 -92
- диффузионного 772
теплопереноса конвективного 1 1 6
- кондуктивного 1 1 6, 480
- нестационарного 574
- п родольного
Просыпь 1 507
П ротивоток 247, 546
П роцессы переноса
в анизотропных средах 95-97
гидромеханические 39, 377 -467
диффузионные 39
интенсивность 60 ел .
классификация 39 -4 1
массоообменные см. Массообмен
механические 39

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

м ногоком понентные 4 1
непрерывные 40
нестационарные 40 , 59, 97
периодические 40
полунепрерывные 40
стационарные 40 , 58 , 98
тепловые 39 см. также Теплопе
ренос
установившиеся 40
химические 39
П роцесс(ы) термодинамические
адиабатические 3 2 6 - 2 7 , 330
изобарн ый 326
изотермический 326
изоэнтальпический 326
политропные 327 - 2 8
П роцессы ХТ
комбинированные 1 697 - 1 70 1
периодические 1 699
последовательные 1 698
совмещенные см. Совмещенные
процессы
сопряженные см. Сопряженные
процессы
холодильные 1 55 1 - 8 4
П рочность пластическая 1 49 1
П рочность статическая 1 470
Прямоток 247, 546
Псевдоожижение
кривые 227 - 2 8
неоднородное 2 2 6 , 239
однородное 225, 2 3 7 - 3 9
в поле с и л тяжести 229
скорость витания единичной час
тицы 2 3 3
- начала 2 2 2 , 225, 2 3 0 - 3 2
- уноса частиц 2 3 2 - 3 6
Псевдоожиженное состояние, скоро
стной диапазон 236
П севдоожиженный слой ( П С ) 2 1 4,
224, 508
виброкипяший 226
высокий 586
высота активного участка 586
гидродинамика 224 - 4 1
гидравлическое сопротивление
228 - 3 0
достоинства и недостатки 225
заторможенный 227
с каналообразованием 226
кипящий 2 2 5 - 2 6
классификация 2 2 5

межфазный теплообмен в нем
583 - 8 8 , 603
поршневой 226
предел устойчивости 225
расширение 238
тонки й 5 8 5 - 8 6
фонтанирующий 2 4 1
Псевдосублимация 1 447
П ульсации 1 52
П ьезодиализ 1 527
П ьезометр 1 2 3
П ьезометрическая высота 1 23 , 1 36
Работа
сжатия 328
- рабочего тела 1 84
удельная 1 590, 1 592, 1 595
Рабочая линия процесса (массообме
на) 793 - 805
построение 797 - 8 0 1
ректификация 1 024
уравнения 794-96
для цепи из двух аппаратов 832
Рабочее тело 4 7 2 -7 4
в холодильных установках 1 5808 1 , 1 588
Равновесие
бинарных смесей 979 - 8 5
динамическое 762
идеальных смесей 973-79
концентрированное 762 -68
многокомпонентных систем 98688
фазовое, газ - жидкость 922 -27
газ - твердое 1 1 6 3 - 6 7 , 1 436-40
- жидкость - жидкость 1 1 37 -4 1
- жидкость - твердое 1 3 1 1 - 1 7 ,
1 402 - 1 0
- пар - жидкость 972 - 79
- твердое - твердое 1 496 - 1 500
Разбавитель 1 1 03
Раздавливание 1 620 - 2 1
Разделяющий агент 1 063 ел .
Разламывание (изгиб) 1 620
Размерность 42
Размольные машины 1 6 1 9 ел .
классификация 1 6 1 9 - 2 1
схемы типовые 1 62 3 - 2 4
требования к ним 1 623
Раскалывание 1 620
Расплавы
кристаллизаторы 1 33 2 - 37
-

1 749

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

отверждение 1 34 1 -44
Рассолы как хладоагенты 1 582
Раствор(ы)
кон центрирование выпариван ием
667 ел .
массовая кон центрация 675
свежий 667
температура кипения 676
теплоемкость 676
упаренный 667
Растворение 1 393 - 428
бинарной смеси в чистом раство
рителе 1 40 5 - 0 7
с инертным компонентом 1 40809, 1 4 1 9 - 26
кин етика 1 4 1 0 - 1 3
однокомпонентного вещества в
бинарном растворителе 1 407 -08
- - в чистом растворителе 1 40304
непрерывное 1 398
полное 1 39 3 - 9 5 , 1 4 1 6 - 1 9
равновесия 1 40 3 , 1 406, 1 408
расчет 1 4 1 6 - 3 4
способы 1 4 1 3 - 1 6
сферического зерна в неподвиж
ной жидкости 1 42 8 - 3 0
схемы потоков 1 4 1 5 , 1 420
теплота 1 409
физико-химические основы 1 40 2 10
фракционное 1 408, 1 4 1 0 , 1 426 -28
химическое 1 393, 1 4 1 0
частичное 1 393, 1 395, 1 408, 1 4 1 9 2 6 см. также В ыщелач ивание
Растворимость твердых тел
кривые 1 3 1 7 , 1 404- 0 5
критическая точка 1 1 40
Растворители (аппараты) 1 396- 1 402
Растворитель 907 , 1 394
регенерация 1 395
Растворяемое вещество 1 39 3 - 94
Расход
массовый 78
объемный 78
путевой 1 76
транзитный 1 77
Рафинад (маточный раствор) 1 1 03
Раши га кольца 746, 9 1 6
Регенератор(ы) 5 2 5 - 2 6
идеал ьный 596

1 75 0

коэффициент использования на
садки 597-98
расчет 594- 600
температурные кривые 595
Режим(ы) течения жидкостей (тонких
пленок) 1 42 - 45
автомодельный 1 44, 1 48
- верхний 1 6 1
- н ижний 1 88
идеального вытеснения см. Иде
альное вытеснение
- перемешивания см. Идеальное
перемешивание
ламинарный 1 43
переходный 1 44
промежуточный 1 44
турбулентный 1 43
Рейнольдса
установка 1 42 , 1 43
число см. Ч исло Рейнольдса
Ректификационные колонны 1 0 1 4
барботажные 1 0 1 6
высота 1 03 2 - 3 3
диаметр 1 03 3 - 34
с непрерывным контактом фаз
1017
последовательный расчет 1 0 3 0 - 3 1
потоки в н их 1 0 1 8 - 2 1
роторно-пленочные 1 0 1 7
с о ступенчатым контактом фаз
1016
тарельчатые 1 0 1 6
тепловой расчет 1 03 5 - 3 6 , 1 045-6 2
эффективность 1 03 7 -39
Ректификация 969, 970, 1 0 1 0 - 1 1 00
азеотропная 1 066, 1 067 -7 0
азеотрообразующей смеси в двух
колоннах 1 70 3 - 0 5
бинарных смесей 1 02 1 -8 1
влияние агрегатного состояния
исходной смеси 1 039 - 44
гидродинамическая 1 68 7 - 8 8
многокомпонентных смесей
1 093 - 1 1 00
непрерываная 1 02 1 -44, 1 060 - 6 3 ,
1 082, 1 084 ел .
периодическая 1 07 1 - 8 2
с разделяющим агентом 1 063 - 7 1
солевая 1 07 0 - 7 1
статика процесса 1 02 1 - 3 1
со ступенчатым контактом фаз
1 046 ел .

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

термическая 1 О 1 7
типовая схема 1 0 1 4
траектория 1 088
тройных смесей 1 08 3 -93
четырехкомпонентных смесей
1 08 3 - 8 4

экстрактивная 1 063-66
Рекуператоры 523, 524
Рекуперация 1 265
Реолоrия 1 9 2
Ресиверы к компрессорам 34 1 -42
Ретур 149 1
Рецикл 80 1 -02
Решета 1 65 8
Решетхи 9 1 2 - 1 6
Риттинzера rипотеза 1 6 2 1
Самоиспарение
жидкости 682
конденсата rpeюwero пара 725
Самотек 26 1
Свяэуюwее 1 470 ел .
Сеrреrация 439, 1 689
Сепаратор(ы) 344 см. также Класси
фикаторы
маrнитные 1 694-95
фрикционные 1 692-93
электростатические 1 695
Сепарация 1 395 см. также Классифи
кация
Сети (цепи) аппаратов 830-3 1 ел .
Сжатие rазов
адиабатическое 335
изотермическое 335
полМТропическое 335-37
степень 342 -43
"сухое" 1 55 8
Сила(ы) 5 3
архимедова 5 5
Ван-дер-Ваальса 1 474
внутреннеrо трения 80, 83
дисперсионные 1 1 6 1
инерции 5 3 , 8 1 , 83
линейные 54
массовые 53, 8 1 , 83
межчастичноrо сцепления 1 47274

поверхностноrо натяжения 54
поверхностные 53, 55, 79, 80
сдвиrа 54, 80
трения 54
Силикаrели 1 1 59

Симплекс 105
Синерrиэм свойсn 51, 52
Система(ы)
rидротранспортные 250
единиц 41 ел.
- международная (СИ) 42
коНденсированные 1 3 1 3
пневмотранспортные 250-55
транспортные см. Транспортные
системы
Сита 1 658
Скорость 52
абсолютная 247
витания частиц 233, 28 1 , 1 674
- стес:ненноrо 239
динамическu 1 4 1 , 1 55
эавис:анu 224
истинная 2 1 6, 2 1 9
критическая 222
в ламинарном потоке 1 50 - 5 1
локальная 52, 1 52
максимальная 1 48
окружная 45 1 , 454
скольжения 223, 239, 247
средняя по-времени 52, 78
- - сечению 53, 148
стесненноrо 0Са.J1t11е ния 239, 39596

в турбулентном потоке 1 52
уноса частиц 225, 232-36
циркумция 673
Слой
вибропс:евдооЖЮ1Сенный 226
движущийся 222 - 24
JСИЛJIЩИЙ 225-26
неподвижный см. Неподвижный
СЛОЙ
псевдооJ1СЮ1Сенный см. Пс:еuо
ожюкенный слой
фонтанирующий 241
Смазочные масла для компрессоров
343
Смачиваемость 1490
Смачивание 1490
Смеси см. mfl/OIU Системы
азеотропные 982
аэеотропообразующие 982
бинарные 972-78, 989 ел. , 1 3 1 3- 1 7
взаимно растворимых компонен
тов973-83
rетероаэеотропные 985
эеотропные 979, 988

1 75 1

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

идеальные 973, 987
исходные 1 0 1 3
монодисперсные 2 1 5
неидеальные (реальные) 9 79 - 8 5
с неограниченной растворимо
стью компонентов в твердом со
стоянии 1 3 1 5
с оrраниченной растворимостью
компонентов в твердом состоянии
1316

однокомпонентные 1 3 1 1 - 1 3
перитектические 1 3 r6
полидисперсные 2 1 5
термолабильные 1 002
тройные 972, 986 - 8 7 , 1 3 1 7-24
эвтектикообразующие, разделение
1 706-07, 1 709 - 1 0, 1 7 1 4- 1 5

эвтектические 1 3 1 6
Смеситель роторный, лопасти 460
Смоченный периметр 1 39
Совмещенные процессы
массообменно-массообменные
1 72 8 - 3 2

с механическими операциям и
1 73 0 - 3 2

реакuионно-десублимационные
1 72 6 - 2 8

- кристализационные 1 724-26
- массообменные 1 720-27
- ректификационные 1 7 2 1 -27
сушильно-грануляционные 1 72930

экстракuионно
кристалл изационные 1 72 8 - 29
Сообщающиеся сосуды 1 24
Соотношения взаимности 66, 67
Сопротивление( я)
nшравлическое см. Гидравличе
ское сопротиаление
местные 1 6 3 -65
переносу массы, диффузионное

дистилля ция - кристалл изация
1 705

ректификация - кристаллизация
1 708
с рекуперацией механической
энерrии 1 702
- - теплоты 1 703
экстракция - кристалл изация
1713-16

Сорбент 1 1 57
емкость 1 1 98 -99, 1 2 1 0
Сортировка твердых материалов 1 655
Сплошная среда 48, 2 1 3
Ста�икога таблица 679
Стенка теплопередающая 470
Степень
влажности 1 572
извлечения 1 1 24
измельчения 1 6 1 9 , 1 620
ожижения 1 59 1
- реальная 1 595, 1 599, 1 605
- теоретическая 1 594, 1 599, 1 604
рециркуляционная 1 266
сухости пара 1 572
черноты rазообразной среды 5 1 7
- ceporo тела 5 1 1 , 5 1 4
шероховатости 1 6 1
Стесненное движение 1 33
Стесненное обтекание 1 3 3
Структурно-коифиrурационный комплекс (СКК) 74 1
Ступень см. Теоретическая ступень
Сублиматор(ы) 1 448 - 57
фракционирующий 1 457
Сублимационная сушка 1 444 , 1 45 8 -63
непрерывная 1 462
периодическая 1 46 1
Сублимация 1435 ел .
аппаратура 1 448 - 5 7
вакуум ная 1 448
с инертным rазом 1 444 - 45, 1 449,
·

827

1 465-66

- субстанции 67
- тепла (термическое) 480, 528,

кинетика 1 44 1
механизмы 1 442
мноrокомпонентных смесей 1 444
полнц 1 444
с псевдоожиженным слоем 1 449
равновесие 1 439
расчет 1 463 -68
физико-химические основы 143 6 -

530

термическое 480, 528, 530
Сопряженные процессы 1 699, 1 70 1 - 1 9
адсорбция - десорбция 1 702
- - с реrенерацией сорбента
1 7 1 6- 1 7

выщелачивание - кристалл и зация
1716

1 752

40

фракционная 1 444

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

частичная 1 444
СубстаЮJиональная проиэводная 82
Суммарные эатраты 1 73
Суспенэии 378 -430
осаждение 1 345
разделение 1 346
Сушилки
аэрофонтанная 1 222-23
барабанные 1 2 1 8 - 1 9
идеальные 1 249-5 1 , 1 260-6 1 ,

1 269-7 1
камерные 1 2 1 7
конвейерные 1 2 1 7
конвективные 1 2 1 6 -25
контактные 1 225 -26
ленточные 1 2 1 7 - 1 8
многоэональные 1 258 -64
пневмотранспортные 1 224
полочные 1 2 1 7 , 1 225-26
простые 1 245 -58
с псевдоожиженным слоем 1 2 1 9-

2 1 , 1 288, 1 290, 1 295, 1 302
распылительные 1 224-25
реальные 1 2 5 1 -58, 1 26 1 -64, 1 27 1 -

73
с рециркуляцией сушильного
агента 1 266, 1 269 -73
специальные 1 225-28
сублимационные 1 227-28
терморадиационные 1 227
туннельные 1 2 1 6 - 1 7
с частичным возвратом отрабо
танного воздуха 1 265-73
шахтные 1 2 1 8
Сушильный аrент (СА) 1 2 1 4, 1 244
Сушка твердых материалов 1 2 1 3 - 1 305
инертным газом 1 273-75
кинетика 1 284-95
конвективная 1 2 1 4
простая, потоки 1 246-48
равновесие 1 243 -44
специальная 1 2 1 4
сублимационная см . Сублимаци
онная сушка
токами высокой частоты 1 227-28
топочными газами 1 275-84
условие 1 229
в условиях внешней 31дачи 1 289-

93
- - внутренней Задачи 1 295 - 1 305
- - потоковой задачи 1 293-95

Таблетирование 1 476
Таблетирующие машины 1 486
Тарелка( и)
колпачково-ситчатая 9 1 8 - 1 9
непровальные 965, 1 0 1 6
питанИJ1 1 0 1 4, 1 042
провальные 966, 1 0 1 6
распределительная 9 1 6
реальные 835, 846
теоретические см. Теоретическая
ступень
Твердофазные мостики 1 473
Тейлора ряд 46
Темера розетки 9 1 7
Температура 47 1
вдоль поверхности теплообмена

550-5 1 , 565-61
кипения жидких смесей 97 1
растворов 676
кристалл изации 1 309- 1 0
ликвидуса 1 3 1 3
мокрого термометра 1 24 1 -42
насыщения 1 24 1
плавления 1 309
предельно-допустимая 1 258
солидуса 1 3 1 3
Температурная депрессия 677
-

Температурные
источники 1 553
поля 47 1
- в катализаторной зоне 535-38
профили при теплообмене 550-5 1
Температурный напор 47 1 -72
при противотоке теплоносителей

553-54
при прямотоке теплоносителей

55 1 -52
средний 545, 550 -58
Температуропроводность 63
Теоретическая ступень (тарелка) 796,

836-37

высота 8 5 1
Тепловой баланс 547-50
Тепловой поток 477, 559-64
при идеальном вытеснении 56 1 ,

562
- - при перемешивании 559-6 1
при противотоке 562
при прямотоке 56 1
Теплоемкость 54, 472
относительная 1241
удельная 54

1 753

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Теплоносители 544
схема .в.вюкени11 546

температурные 551
Теплообмен 47 1 , 544-50
безrра.в.иентный 576-77
.в.вижущая СИ.1\а см. такжtТемпе
ратурный напор
при интенсивном перемешивании
603- 04
конвективный 485-96, 66 1 -66
Jr)'Ч И СТЫЙ 5 1 2
межфазный псев.в.оожюкенном
слое 5 8 3 - 8 8
н а наружной поверхности тр уб 500
нестационарный 549, 574-82,
588-92
поверхность 523
при противотоке 554 ел .
при прямотоке 551
реrулярный 5 8 8 -92
при с ме ш ан н ом токе 557
стационарный 536 ел.
твер.в.оrо тела со сплошной средой
588-92
с твер.в.ыми телами 574- 82
Теплоо бмен н и ки
выбор перспективный 558
классификация 523-27
кожухотрубные 524, 1 583
контактные 526 -27
оросительные 1 583
с псев.в.оожиженным слоем 527
регенеративные 525-26
рекуперативные 523-24
смесительные 526-27
элементные 1 58 3
Теплоотдача 470 см. также Теплопе
ренос
при кипении ЖИ.D.Хости 503, 509,
522
конвективная к шару 495 - 96
при коН.D.енсации пара 497, 509

коэффициент 508 -09
- локальный 499
- сре.в.ни й 499
от поверхности в псевдоожижен 

ном слое 506-08
Теплопере.в.ача 47 1 , 5 2 7 -43
в каталиэаторной эоне 535-38
контактная 7 8 2
коэффициент 528-35
пропускная способность 5 2 8

1 754

ел .

схемы 528
уравнение 528
через стержень бесконечной м и
ны 539-40
Теплоперенос 469, 470-5 1 8 см. также
Теплоотдача
безrра.в.иенткый 474
ВИ.D.Ы 475-76
граничные условия 98, 99
ИЭJr)'ЧеНИеМ 476, 509 - 1 8
- мeJICJly двумя телами 5 1 2 - 1 4
при кипении жидкости 502-06
при конвекции 485-96
- - вынуж.в.енной 490-9 1
- - естественной 49 1 -94
- - пропускная способность 48 7
при КОН.D.енсации пара 496 -502
кондуктивный 475, 478 - 8 5
- через стенки 479- 8 3
лимитирующие стадии 567 -7 4
нестационарный 474
параJVJСЛЬНЫЙ 573
сложный 476
стационарный 474, 478 ел.
- в режиме ИВ 570

- - - ИП 568 ел.
уравнение 85
цели 469
экранирование 5 1 5 - 1 6

Теплопроводность ( кондукция)
475

63,

84,

Теплота
абсорбции 939
.в.еrи.в.ратации веществ 734
коН.D.енсации, удельная 473
плавленИJ1, у.в.ельная 473
растворенИll 1 409
сублимацИJ1 473
Тер модиффуэИJ1 773

Термолабильные вещества 696
Термосифоны 592-94
Технико-экономический расчет (ТЭР)
798
Технологические параметры 1 7 0 1
приемы 3 1 , 32
Течение(я)
газа кнудсеновское 259
- молеку1U1рное 257 -60

- свободномолекулярное 257
двухфазные 246-57
- жидкость - 1'83 255 - 5 7

- ЖИДКОСТЬ - ЖИ.D.КОСТЬ 2'55-57

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

- с твердой фазой 246 -55
жидкостей, ламинарное 1 46-5 1 ,
1 86
- неньютоноаских 1 90 -202
- пластичное 1 93-202
- режимы см. Режимы течения
жидкостей
- турбулентное см. Турбулентное
течение
- эпюра (распределение) скоро
стей 1 96
тонких пленок, гравитационное
1 85-90, 658 -6 1
- - волновое 1 89
- - ламинарное 1 86
- - переходное 1 89
- - пластичное 1 95 -202
- - плоское 1 89
- - псевдоламинарное 1 89
Тонкие пленки 1 85 ел .
Точка (температура)
азеотропная 982 1 7 1 2
росы 1 238
тройная 1 3 1 2
эвтектическая 1 3 1 5
Точность расчетов 44
Транспортные системы 2 1 4
жидхость - rаэ 255 -57
ЖИДКОСТЬ - ЖИДКОСТЬ 255 -57
с твердой фазой 250-55
Тр ассер 6 1 8
ИМnуЛЬСНЫЙ ВВОД 6 1 9
ступенчатый ввод 6 1 9
Труба(ы)
вихревые 1 579
вскипания 673
оребренные 525
тепловые 593-94
Трубка( и)
напорные 1 36
тока 1 33
Трубное пространство 524
Трубопроводы 1 67 ел.
диаметр оптимальный 1 72
простые 1 67- 1 7 1
с путевым и транзитным расхода
ми 1 76-79
разветвленные 1 73 -76
сложные 1 67, 1 76
транспортные 252
характеристика 26 9 , 307
Трубчатые охладители 1 34 1 -42
,

Трубы-с:уwилки 1 223
Typбor&ЭOJG'llКИ 359
Турбодетандеры (детандер.,. 1 589
Турбокомпрессоры (центробежные
компрессоры) 324-25, 359-67,
717, 1 583
кnассификация 359
Кпд nшраалический 361
мноrоколесный 360
напор 36 1 -64
ПроИЭIОдительнОСТЬ 360-61
- реrупирование 365 - 6'.
степен• сжаТИJ1 360, 363 -64
харахтеристики 364-65
Турбулентное течение
коэффициент rидраалическоrо
сопротивления 1 59-6 2
показатель интенсивности 1 52
распределение скоростей 1 55 -59
Тяжелая среда 1 667
Угол
внешнего трения 1 66 1
внутреннего трения 8 3
встречи 1 664
захвата 1 628-30, 1 635-36
конструктивный 298
отрыва в барабанных мельницах
1650
технологический 298
Удар 1 620
Удельный объем 52
Удерживающая способность (задержка) 247
Ультрафильтрация 1 529
Ум формер 68 1
Ураанение(я) (Формулы) см. такж�
Законы
баланса 55-60
Бернулли 1 33 - 39
- дJIJI к.аеальной жидкости 1 34-3 6
- мя реапьной жидкости 1 37
Бпаэнуса 1 60
Гаrена-Пауэейл11 1 49
Дарси-ВеАсбаха 1 4 1 , 2 1 9
движения несжимаемой жидкости
79-83
Женеро 1 60
Клайперона-Менделееаа 326
Колмогорова-�раами 1 50 1
критериальные 1 44, 1 1 5
Ленгмюра 1 1 65

1 755

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Навье- Стокса 8 3 , 1 06 , 1 46
неразрывности потока 74- 7 7
Никурадзе 1 60
Н ьютона 62, 1 90 , 236, 477
переноса 79-97
плоской поверхности 1 25
поверхн ости уровня 1 2 1
равномерного движения 1 4 1
расхода 5 3 , 7 7 , 7 8
сдви га 1 90 , 1 92 -94
сплошности 75
Стокса 235
теплопереноса 85
Тодеса для скорости витан ия 235
- - - начала псевдоожижения 232
Фика 8 8 , 77 1
Фрейндлиха 1 1 65
Фурье-Кирхгофа 85, 89 ел . , 1 1 0 ,
478, 575
Ш илова 1 202 - 1 0
Эргана 222, 4 1 9
Условие(я)
граничные 98
- классификация 98, 99
начальное 97
однозначности 97 -99
Утяжелитель 1 668
Фазовое равновесие 1 3 1 1 - 24
бинарных систем 1 3 1 3 - 1 7
однокомпонентных систем 1 3 1 1 13
тройных систем 1 3 1 7 -24
Фактор
массопереноса 838
сопротивления осадка 420
- перегородки 420
экстракции 1 1 24
Фильтр(ы) 4 1 5 - 1 8
дисковые 4 1 8
классифи кация 4 1 5
непрерывного действия 4 1 7 - 1 8
периодического действия 4 1 5 - 1 7
поверхность 423
простой 4 1 5
схемы 4 1 6 - 1 8
Фильтрат 4 1 4, 422
кривые вымывания из осадка 436
Фильтрование 4 1 3 - 3 5
движушая сила 4 1 9
непрерывное н а барабанном ваку
ум-фильтре 426 - 2 8

1 75 6

оп ределение параметров 428 - 3 0
периодическое, режимы 422 - 2 5
п р и постоянной движушей силе
422 -23
- - с корости 424
продолжительность 422
скорость 4 1 8 - 1 9
схема 4 1 4
уравнение 42 1 , 434
центробежное 430 - 3 5
Фильтр-пресс рамный 4 1 6 - 1 7
Фильтрующая перегородка 4 1 4, 432
Флегма 1 006
Флегмовое число 1 02 3 , 1 02 6 - 2 7
Флорентийский сосуд 1 1 1 7
Флотационный аппарат 1 694
Флотореагенты 1 693
Форвакуум н ый насос 3 7 3 - 74
Формулы см. Уравнения
Фракции , узкие и широкие 2 1 5- 1 6
Фракционная кристаллизация 1 344 - 8 5
п р и контакте с хладоагентом
1 360-64
однократная бинарных смесей
1 348 - 49
с отводом теплоты через охлаж
дающую поверхность 1 352-60
периодическая 1 35 6 - 59, 1 36 1
последовательная ( И В) 1 359-60
- ( И П ) 1 3 56 - 5 8
со стекающей плен кой 1 37 1
Фракцион н ы й состав 1 658
Фреоны 1 5 8 1
Фронт сорбции 1 1 94
время формирован ия 1 1 96
скорость движения 1 203
Хемосорбция 907 , 926, 945 - 5 0 , 1 1 6 1 ,
1 1 66
Хладоагент(ы) (охлаждающая среда)
1 580
газообразный 1 364
жидкий 1 363
испаряющийся 1 36 3 - 64
для контактной кристаллизации
1 36 1 ел.
промежуточные 1 582
свойства 1 58 1
Холодильники-конденсаторы 1 0 1 8 ,
1 58 3
Холодильные машины
абсорбционная 1 574- 7 7

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

идеальная 1 55 3 - 56
компрессионно-воздушная 1 56 3 65

- каскадная 1 578
- п аровая 1 55 6 - 6 3
- - двухступен чатая 1 566-74
пароэжекторная 1 579
термоэлектрические 1 579
Холодообме н н и ки 1 592, 1 6 1 1
Холодопроизводительность 1 56 1
удел ьная 1 594, 1 604
Центр
давления 1 3 1
масс 1 3 1
тяжести 1 3 1
Uентриклоны 4 1 2
Центрифуги 392
вертикал ь11ыс 392, 393 - 94
горизонтал ьные 393
затраты энергии н а работу 399 404

мощность 403 - 04
осадител ьные 393 - 9 5
фильтрующие 4 3 0 , 43 1 ел .
Центрифугирование см. Осаждение
центробежное
Центробежные насосы 265, 295, 296 3 1 4, 3 1 7 , 3 1 9

высота всасы ван ия 3 1 3
с двухсторон н и м всасы ванием 296
достоинства и недостатки 3 1 9 -2 1
К ПД гидравл ический 300
многоступенчатые 297
напор 298 - 302
с односторонним всасыванием 296
одноступенчатые 297
основное уравнение 299
параллельная и последовательная
работа 3 1 1 - 1 3
п роизводительность 303 -04
рабочая точка 3 06 0 7 3 1 1
характеристики 304 - 1 О
- уни версал ьная 304, 309 - 1 О
- частная 304 - 0 6
Цеол иты 1 1 60
Цикл
Гейландта 1 60 2 - 0 5
Капицы 1 606 - 1 О
Карно 1 55 3
Клода 1 602
Л и нде 1 59 3 , 1 596 - 1 602
-

,

охлаждения с детандерами 1 6 0210
- регенеративный 1 592 - 1 602
- эталонный обратный 1 590
Циклон ы
гидравлическое сопротивление
41 1
предельный размер улавливаемых
частиц 409 - 1 О
производительность 408 -09
рабочий объем 405
характеристики 406
Циркуляция жидкости
внешняя 443
внутренняя 443
естественная 670 :... 72
направленная 6 1 2
принудительная 670-74
Число(а) см. также Критерии
безразмерные 1 05
единиц переноса (ЧЕП) массы
8 1 0, 1 022
- - теплоты 556
Жуковского 1 1 1 , 1 5 1
Кltудсена 257
Лященко 239
теоретических тарелок 1 1 54
флегмовое 1 023, 1 1 26 - 2 7
Эжекторы 266, 3 1 6, 1 579
Эквивалентная длина 1 64
Эквивалентны й диаметр
канала 1 40
частиц 2 1 6
Эксплуатационные затраты 1 7 3
Экстенсивные свойства 50, 5 1
Экстрагирующи й агент (экстрагент)
1 1 03 ел.
выбор 1 1 2 1
рабочих расход 1 1 55
регенерация 1 1 46

требован и я к нему 1 064
Экстракт 1 1 03
Экстрактор-отстойни к для выщелачи
вания 1 398
Экстракторы жидкостные см. также
Колонны экстракционные
вибрацион ные 1 1 1 1 - 1 2
в ывод фаз 1 1 1 6 - 1 8
дифферен циально-контактные
1 1 07

1 757

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

насосно-отстойные 1 1 1 5
с непрерывным контактом фаз
1 1 07- 1 3 , 1 1 55
роторно-дисковые ( РДЭ) 1 1 09 - 1 0
ступенчатые смесительно
отстойные (СОЭ) 1 1 1 4 - 1 6
центробежные 1 1 09, 1 1 1 2 - 1 3
ящичные 1 1 1 6
Экстракционные аппараты 1 1 06- 1 6
см . также Экстракторы
высота рабочей зоны 1 1 33
гравитационные 1 1 07
интенсифицированные 1 07
классифи кация 1 1 06
колонные см. Колонны экстрак
ционные
Экстракция
газовая 1 444
жидкостная 1 1 03 - 5 6
однократная 1 1 1 9 , 1 1 23 - 24 , 1 1 43 45
при полной нерастворимости экс
трагента и разбавителя 1 1 27 - 37
порцион ная 1 1 1 9 , 1 1 24 - 2 7 , 1 1 45 47
противоточная непрерывная 1 1 20,
1 1 27 - 3 7 , 1 1 47 - 5 6

- с непрерывным контактом фаз
1 1 32 - 3 7 , 1 1 48
- ступенчатая 1 1 27 - 32 , 1 1 48
ступень 1 1 24
из твердых тел см. Выщелачивание
фактор 1 1 24
при частичной растворимости
реагента и разбавителя 1 1 37 -56
Экструдеры 1485-86, 1 50 7 - 0 8
Экструзия 1 507
Электродиализ 1 527
Электроосмос 1 529
Электрофильтры 4 1 2 - 1 3
Энтальпия 473
насыщеноrо пара 1 046
относительная 1 2 3 5
потоки 546 -48
Эрлифт см. Газлифт
Эффект(ы)
адиабатный 1 588
дроссельный 1 58 5 - 86
Дюфо 67
Онзагера 66-67
Соре 67
·

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Учебное электронное издание

Айнштейн Виктор Герцевич, Захаров Михаил Константинович,
Носов Геннадий Алексеевич, Захаренко Василий Валериевич,
Зиновкина Татьяна Вальтеровна, Таран Александр Леонидович,
Костанян Артак Ераносович

ПРОЦЕССЫ И АППАРАТЫ ХИМИЧЕСКОЙ ТЕХНОЛОГИИ.
ОБЩИЙ КУРС
Ведущий редактор канд. хим. н. Т. И. Почкаева
Редакторы М. В. Миникс, Л. И. Галицкая
Технический редактор А. Л. Шелудченко
Корректоры М. В. Черниховская, Э. В. Назидзе
Подписано 25.10.2013. Формат 84×108/32
Гарнитура Таймс. Усл. печ л. 92,35
Издательство «БИНОМ. Лаборатория знаний»
125167, Москва, проезд Аэропорта, д. 3
Телефон: (499) 157-5272, e-mail: binom@Lbz.ru, http://www.Lbz.ru
Минимальные системные требования определяются соответствующими
требованиями программы Adobe Reader версии не ниже 10-й для платформ
Windows, Mac OS, Android, iOS, Windows Phone и BlackBerry.