Author: Гейзенберг В.
Tags: физика квантовая механика квантовая физика теоритическая физика гтти
Year: 1932
Text
В. rЕЙЗЕНБЕРf
профессор теоретической физики
университета в ЛеАПl1иrе
ФИЗИЧЕСКИЕ ПРИНЦИПЫ
КВАНТОВОЙ ТЕОРИИ
Перевод с иемецкоrо
А. Н. АРСЕНЬЕВОЙ
ПОД редакцией
д. Д. и в А fI Е Н К а
1 9 3 2
rосударственное
технико"теоретическое из). атеЛЬСТ80 11 Лени
Москва.
w. HEISENBERO
DIE PHYSIKALISCHEN PRINZIPIEN
DER QUANTENTH EORIE
ПРЕДИСЛОВИЕ
"Природа писал пятьдесят с лишним лет тому наЗЗ11 ЭН-
rельс' есть пробный камень диалектики", и именно ЭТИМ MHoro-
значительным обстоятельством объясняется тот факт, что величай-
шие идеолоrи рабочеrо класса........... Маркс, Энrелье и Ленин.......... не-
однократно обсуждали историю и результаты COBpeMeHHoro ИМ
естествознания, черпая из последнеrо материал для дальнейшеrо
развития маТериалистической диалектики.
Но естествознание......... которое отражает природу и КОТОрО,е
должно давать ее диалектику творится людьми, принадлежащими
к определенной исторической эпохе и потому разделяющими orpa-
ничеиность ее интересов и средств их осуществления. Естество-
знание, поэтому, никоrда не является лбсолютной, вавершенной
истиной. Но люди, Т60рящие и развивающие естествознание, при-
надлежат не только к некоторой исторической эпохе.......... они при-
надлежат также, сознательно иди бессознательно к тому или иному
определенному классу этой эпохи. Этот фундаментальный факт имеет
своим следствием то явление, что характер зависимости от оrрани-
ченности эпохи и характер отношения к этой исторической orpa-
ниченности неизбежно различны для людей, примыкающих к раз-
личным классовым' позициям и выражающим последние. Консер-
вативные классы каждой данной эпохи возводят ее в свою соб-
ственную орrаниченность в непререкаемый инепереходящий прин-
цип, ....... тоrда как классы проrрессивные свою принадлежность к
данной оrраниченной эпохе выражают лишь тем, что пытаются
переделать ее, выйти за ее пределы.
Этим определяется характер тех лоrических методов и фило-
софских предпосылок, на идейной основе которых, и зачастую
стихийно, осуществляется истолкование TorQ или иноrо явления.
В самом деле: rосподствующий класс COBpeMeHHoro заrниваЮПI.еrо
капитализма, пытающийся сохранить последний, тем самым противо-
поставляется диалектической идее развития с одной стороны и отри-
цает возможность предвидения каких либо новых явлений С друrой
стороны. Эта бессознательно-складывающаяся установка, прелом-
ляясь на специфическом содержании науки, проникает также и в
*
3
физику, не давая адэкватной трактовки новых явлений действитель--
ности, обнаруженных эк :периментом, инеправильно аrНОСТffчески
оценивая роль caMoro эксперимента . развитии физическоrо по-
знания.
ЧТО эти лоrические предпосылки.......... несоответствующие как ДИ&-
лектическому материализму, так и задачам развития самой физики
действительно имеют нередко место в квантовой механике,........... бле..
стящему изложению которой посв,ящена данная работа rейзен--
берrа, може r быть доказано двумя ссылками весьма общеrо ха...
рактера. Именно, Дирак, являющийся одним из больших знато-
'КQвсоIфеМ6ННОЙ теоретической физики, в своей книrе о принципах
ван1'ОВОЙ ме аники утверждает, ЧТО "единственной целью теорети-
ческо,й фивtfки является расчет рез у л ь т а т о B по возможности
ближе отвечающий опыту, и является по меньшей мере бесполеаным
какое-либо удовлетворительное описание Bcero х о д а явлений".
Разделить ,,'результат" от "хода" t иrнорировать тему о про и с х 0-
ж Д е н и и некоторых результатов это и есть то, что, оrраничивая
задачи и возможности науки, называется метафизикой.
Близкая к этой тенденция проводится таkже и в изложении
rейзенберrа. .......... BrпaBe IV предлаrаемой книrи он указывает, 'что
"статистический характер зависимости основан на том, что влияние
измерительных инструментов на измеряемую систему рассматри-
вается иначе, нежели влияние отдельных частей системы друr на
ДI'уrа, ибо и это последнее влияние также обуславливает изменение
,НJаnраuления в rильбертовском пространстве, но эти изменения
В'ПОЛ i l1е определенны. Если бы измерительные приборы были при-
чиалеFiЪ1 к системе, при чем было бы значительно расширено rипь..
'беРТОБское пространство, то изменения BekTopa системы, рассмо-
тренные выше в качестве неопределенных, были бы теперь опреде..
лены'«, и после этоrо: "разделение мира на набл дательную и
наблюдаемую системы препятствует, таким образом, точной форму...
лировке закона причинности" .
Эта предпосылка должна быть решительно оспорена. Ибо по
существу вопрос здесь ставится так, что эксперимент, который
справедливо рассматривается всеrда в качестве средства развития
познания в обсуждаемой области явлений, становится препятствием
для проrресса теории, обуславливая некоторый непереходимыйпре-
дел точности познания. На самом деле соотношение неопределен-
насти rейзенберrа (указания на это имеются у caMoro автора, во
11 и 111 rnaBe) должно было бы быть понято не в этом аrности"
ческам смысле, а «ак показатеJIЬ недостаточности прежде обра..,\
зовзнных понятий классической мехаНИКl1 причинности, волны В
области явлений, обсуждаемых квантовой механикой. Подобно
тому как ма J11табы динамики материальной точки с'овершенно не...
4
в области определений динамики системыI точек (наIlР..,
энсрrии враl1\ения, не моrущий даже бь;ть ПОДНЯТЫМ J3
точки) И потому спосоБныI создать некоторую неопреде...
определений величин, однако преОДОЛИМУIО разработкоЙ
для этоttновой области явлений понятий, так н
nринuип rейзенберrа .должен быть ПОНЯТ как точная форму ,
требования создания новых специфических понятиЯ, кото-
нет еще, для аДЭl{ватноrо выражения принципиально...определи-
соотношений квантово-механических явлений. В отношении
причинности это соображение дает дирекrиву не отказа
принципов материалистическоrо детерминизма, но иной формr I
поспеднеrо, .......... такой, которая соответствовала бы I:пецифичности
изучаемых явлений"
Следовательно I<pyr новых проблем теоретико--познаватепьноrо
xapaiKTepa.......... соотношение средств и объекта эксперимента, стати-
стика и причинность, соотношение волн и частиц и Т. долж€н
быть понят, как указание диалектики новой, недостn--
точно исследованной области явлений, неоБХОДИl\IОСТЬ ревизии
ИЛИ, по крайней мере, оrраничения. и способов на...
lпеrо понимания природы, не в идеолоrическом
СМbIсле, что природа в своих элементарных актах произволь",
ный выбор, который нами не и кот О""
рый заставляет поэтому нас оrраничиться ПОДС1Iетом rОЛI IХ
реэультаТQВ.
Это обстоятельство, при всех всемирно признанных
данной книrи rейзен pra, заставляет нас иметь в виду
ную необходимость C1'pororo и критическоrо к излаrаемыM
идеям. Критика и' самокритика основных физических соста-
вляет для физики одно из, актуальнейших условий ее продвиже-
ния вперед: Во всяком случае следует твердо ПОМНИ1Ь важное
замечание rельмrольца о том, что "критикой методов можно пре-
небреrать лишь. до тех пор, пока возможно оrраничивать\ я приме-
нением методов, уже на деле доказавших свою правильность. 110
ко:rда иссле,nование доходит до той rpани, rде становится сомни-
тельным, следует J1И приписать встречающиеся трудности самому
предмету или :неудовлетворительности метода, критин:а
должна вступить в СВОИ "
п. Шеllн
[JРЕДИСЛОВИЕ К
в ряду всех книr по квантовой механике (1<.ниrи ]{ирака,
Бройля, 30ммерфельда, Борна.wИорда»а, Вейля, Френкеля,
КонДона..Морае, Бертуистля, Ланде и друrих) предлаrаемое'
{)
пию читателей изложение rейзенберrа стоит совершенно особняком..
Здесь нет широкоrо развития математическоrо аппарата, и прочи...
тавши книrу никто не научится "реПlать« квантовые 3ато
ни ОДИН вдумчивый читатель не без убеждения, что но...
вая теория квант принесла с собой существеннейшие изменения
в основных физических ПОНЯ1'ИЯХ: причинная опи...
сание в и времени и Т.. Можно Не соrлашаться
с автором книrи (который является вместе с де Бройлем, Шредин",
repOM, Борном, и Дираком автором современной кван"
товой механики, больше Toro, автором первой работы в этой об..
ласти), можно и дол}кно продискутировать ero rлубокие револю '
ционные выводы, но нельзя ни одному физику, естествоиспытателю,
философу пройти спокойно МИМО.
Книrа rейэенберrа в основном содержит описание"толкование
ОСНОВНЫХ 10, важнейших экспериментов физики
с точки зрения механики. Во всех книrи
фундаментальную роль знаменитый принцип неопределен"
насти, установленный в 1927 rоду (и в развитии
KOToporo 8начен ; подчерки..
вание же невозможности на-
пример скорость и координату, еще раныпе у Дирака)..
rейзенберrу удалось таким подвести принципиально осно-
вание под теории, которая ныне мо}кет считаться практи-
чески законqенной (после работ и Иордана по теории ире...
образований), что, конечно, отнюдь не означает, что приложения
теории даже и rлавнейшие исчерпаны.. rейзенберr касается в книrе
"
отчасти и дальнейшеrо развития теории.......... обобщения ее на случаи,
rде необходимо учесть теорию относительности (случай больших
скоростей ).
Русский перевод, сделанный всяких изменений с 1...ro не..
MeL(Koro издания,сверялся частью с анrлийским, ПРОСМQтренным
aBl"opOM. Ссылки, отмеченные напр.. 18, вставлены нами.
Мы решили не ждать время изменений rеf1зен
берrа, которые он собирается ко 2 MY из..
данию и которые будут флюктуаций и отчасти теории
излучения.. Изложение i измененное соrласно
автора в духе новой math. I{lasse
der Sachsischen A demie Sitzung
vom 19.. Januar 1931) и методике
трактовки излучения даны книrи
внесен ряд дополнений {{ни!"'и. Два
дополнения иллюстрируют и развивают изложение ['ейэенберrа, не
выходя значительно И3 рамок теории (пример с маrнитным мо"
ментом и различные BЬJBOДЫ соотношений неопределенности).
б
обширное дополнение сделано имеЮlцемся раСIlIи....
принципа неопределенности на случай релнтивистской KBaH
механики. rIри всей необходимой осторожности рассу}н:дений
области, указанное обабщение, полученное раз..
авторами, представляется нам заслуживающим сзмоrо
внимания и имеющим тот же суrубо принципиальный
как и выводы книrи. Наконец} мы изложили современное
вопроса о неопределеннос rях для электромаrнитноrо
Отметим еще, что отдельные паРЗI'рафы книrи fейэенберrа
(в переводе) вместе с часто цитируемыми статьями
Бора и р.ядом печаrЗIОТСЯ в сборнике »rIричинность" , под..
rотовляемом в при участии общества физиков-материали-
СТОВ. сборник И настоящая книrа дадут, наконец, советским
читателям авторитетную для дискуссий, ведши).{ся до сих пор
большею частью на популярных статей и "друrоrо сом...
нительноrо материала из вторых рук.
КJ1ючение мы рады принести бпаrодарность автору книrи
за ряд указаний и предоста.вление оттиска работы, напечатанной
в журнале, который не получается ни в ОДНОЙ из библиотек, а
T3I<1I<e В. А. Фоку и В А. Амбарu}миану за участие в обсуждении
nримечаний
ЛеНI-нп'рад, ко- д. ИванеН1СQ
технический инсти'сут
Янuарь 1932 r.
ПРЕДl1СЛОВffЕ
Лекции, про( итанные МИОIО весною 1929 r.. в Университе:rе
в t-Iи\<аrо, дали мне повод еп е раз полностью рассмотреть прин..
нилы l{BaH I{)ВОЙ теории. Со времени ЗIКлю t lИ тельных исследованиЙ
Бора в 1927 f. эти ПРИНЦНЛf.d не испытапи существенных изменений,
а некоторые новые эксперименты подт ердили важнейшие поло..
женин теории (PaMaH " фект). Несмотря на это, MHOl-ие физики
до сих пор еlде им CBoero рода веру в правильность
новых принципов, чем ясное их ПОВИМаНИ поэтому мне }{азалось
прочита вые в I<aro леI(ЦИИ в форме
неболыпой I<ниrи.
Так как KBa OBoA теории
уже доступен неСКОЛl,КИМ прекрасным И3J10жениям,
и el-O rораздо чем знание принци..
ПИЗJlЬНЫХ ТО Я ОI'рЗНИЧИЛСЯ предстаВИII ero в виде
собрания формул в }{онце, книrи.. В тек,,::те же я сr'арался оБОЙТИСJJ
простеЙПIИМИ формулами и вычислениями, ЛОСКОЛЬ)<У 8ТО ТОЛЬКО
лось возможным"
'1
в излож нии придано особенное значение
пускулярноrо и волновоrо представлений, что теперь также
жается и в формализме теории. Эта даJIекб идущая
в отношении слов "корпускула" и "волна", должна,
показать, что в вопросе, скажем, о приrодности закона
насти или друrих принципиальных вопросах ничеrо не
вается, если перейти от одноrо способа представления к
Далее я попытался возможно яснее подчеркнуть разницу
пространственно-временными волновыми теориями с ОДНОЙ стороны
и шрединrеровскими волнами в конфиrурационном прqстранстве
с друrой.
В общем, однако, 9та книrа не заключает в себе ничеrо, чеrо
нельзя было бы уже наЙти в прежних наложениях и в особенности
в известных исследованиях Бора. Цель книrи покажется мне дости!"..
НУТОЙ,если ала несколько будет способствовать распространению
Toro "KoneHrareHCKOI'O духа квантовой теории" (если я так
выразиться), который дал направление.. всему аТоМ....
ной физики.
Мою блаrадарность в первую очередь я при
К. Экарту и д-ру Ф. Хойту, которые не TOJIbKO взяли ыа
желый труд анrлийскоrо перевода, НО также существенно ПОМОI'ЛИ
улучшению книrи разработкой некоторых rJIaB и своими советами.
Я хотел бы также выразить блаrодарность д..ру r. Беку за про
смотр корректуры и ценную помощь при составлении манускрипта.
[3. Fеuзенберz
JlеЙПl1иr, 3 марта 1930 r.
1. Введение.
и ЭКСПЕРИМЕНТ
Подобно веПJ.ам повседневной )кизни физические опыты и их
MorYT быть описаныI с помощью наrлядных понятиЯ
пространстве и времени на обыкновенном языке,КОТОрЫЙ СООТ..
окружающему миру. Если бы физика моrла удовлетво",
опыта описанием, скажем," положе..
или друrих ана оrичных
от всех tJ теорий", то, конечно, всякая теоретика...
бы излишней. Но мы собираем раз-
личные опыты в rруппы, с:вязываем события как "причину" и "след..
ствие" и создаем или развитые, смотря по степени
Тот iKe процесс происходит не только с фи..
и с примитивными опытами повседнев",
образования понятий.
понятий довольно часто по..
. бессознательно делаются необос-
наконец, не возникают противоречия.
основание для фИ:!Jических
потребовать, чтобы дли описания
явлений целиком основанные на опыте понятия.
Это требование, однаI<О, совершенно невозможно провести, так как
тоrда подверI'НУТЬСЯ пересмотру повседневные
понятия и трудно что после этоrо осталось бы от нашеrо
языка. rенеральный пересмотр представляется поэтому
связанным с непреодолимыми трудностями. При таком положении
вещей кажется цеJIесообразным ввести сперва в физическую
теорию значительное количество nонятий, не 11ринимая во внимание
строrую обоснованность на опыте, и предоставить природе в от-
дельном теории решать, требуется ли и в каких
лонятий.
и относительности была характерной
понятий, как' масштаб, часы и Т. Д.. Эта критика
что в наших обычных понятиях сеrда содер--
допущеНYIе О 603МОЖIiОСТИ , принципиальной по
НОй жизни
При
крайней
скоростью.. После Toro как
что в природе не CYluecTByeT
CBeTa j и
РОДЫ, приступили к
проблеме; это
опытов, что
с классическими поннтиями
в конце кониов допустила
CTpaHCTBeHHO BpeMeHHoro совпадения.. По ЭТой
язык к описанию
тационная постоянная и величина обратная
быть рассматриваемы как очень малые
Таким образом, несМОТрЯ на что теория относительности
преДЪЯВЛllет большие требования к к у
физиков, она все же достаточно идет навстречу вы-
текающим из научной традиции, поскольку в допу-
скается CTporoe разделение мира )на и и точная
формулировка Но именно в этом"то пункте и
возникают трудности квантовой В то как в атомной
физике подробная критика понятий "маСIптаба", и If.
представляется излишнеR (ПОСI<ОЛЬКУ не рассматривается ре-
лятивистская механика),
I
BpeMeHHoro совпадения и понятие "наблюдения"
основательно пересмотрены. При обсуждении
особенно дол)кно приниматься во внимание взаимодействие меЖJlУ
объектом и наблюдателем, которое непременно связзно с J<аждым
наблюдением. В классической теории принимапосъ, что ЭТИМ вза
имодействием, как ничтожно малым, можно пренебречь или что
влияние поддается контролю и может быть исключено с помошыо
вычислениЙ.
В атомной физике, ОДНЗl<О, нельзя сделать это так
'как, вследствие прерывности в атомных проиессах, ИМQ-
деfiствЙе может вызвать частью не учитываемые, относительно боль-
шие
Следствием этоrо является ТО, что
опыты, определ IОlцие какую-нибудь физичеСI(УЮ
в ТО же время неllеАствительным ранее добытое
ве.7IИЧИН, так как они влияют
ряемую и
Исследуя это
чаях для одновременноrо
конечный ПРEfдеn точности,
относительности ИСХОДНОЙ точкой
обыденныЙ
rрави
скорости MorYT
критики понятий был посту-
1
что никакоЯ сиrнал не может распространяться СО скоростью,
скорость света.. Таким же образом можно постули...
названные нижние пределы точности для одновременноrо
разных переменных так называемые "соотношения не...
определенности", как закон природы, и сделать их ИСХОДНОЙ
ДЛЯ критики поинтий квантовой теории. Эти "соотнош,ения
IIсопределенности" и дают как раз ту степеиь нарушения классн..
поиятий, которая необходима для непротивиречивоrо о иса-
атомных процессов..
Проrрамма последующих рассуждений, таким образом, должна
следующей" сначала рассмотреть все понятия, введение кота...
непосредственно диктуется опытами, затем установить области
применения для различных понятий и показать, что оrраниqенные
таким путем понятия, вместе с математическим формализмом кван-
товой теории, образуют систему, свободную' от противоречий"
u
2. ОСНОВНЫЕ ПОНЯТИЯ КВАНТОВОИ ТЕОРИИ..
Предварительный обзор важнейших понятий атомной физики
дают следующие опытные факты, характеризуемые известными фо-
тоrрафиями (рис.. 1 4).
а) Фоrпоzрафuu Вильсона. 1 Материальные лучи, исr;ущенные
радиоактивными элементами, ПРОХОДЯ СКВОЗЬ камеру, содержащую
пересыщенный во яной пар, образуют (предполаrая, что лучи об....
падают достаточной энерrией) штрихообразные следы конденсиро-
B8HHoro пара (рис. 1).
Этот опыт доказывает дискретный характер матер.цальных лучей
и показы что вполне целесообразно представпять себе эти
лучи в виде маленьких, быстро летящих частичек.. Каждый след,
образованный водяными каплями в вильсоновекай камере,непосред-
ственно представляет одной частицы. Под частицей или кор-
пускулой понимают при этом всеrда образование, движущееся по-
добно материальной точке в классической механике, т.' е. точечную
систему, на состояние движения которой влияют только фи-
зические поля в непосредственной ее БЛИЗ0СТИ. Обраэование
следа нужно представлять себе так: частица сталкивается в камере
с атомами rаза и их ионизирует.. Полученные ионы вызывают
конденсаЦИIО водяных паров BOKpyr себя и ввиду этоrо дают
центры для образования маленьких ВОДЯНЫХ I<:апель. Таким обра-
зом ВДОЛЬ пути частицы создаются водяны(? капельки,
непосредственно доступные наблюдению.
I!.
Цифры ,,1" И
ОТНQСИТСЯ К Jfитературному указате,ц!о ца Ctp. 115
!1
Известно, что ИЗ опытов с отклонением в
rнитном поле можно определить скорость и массу
возможно ДЗJlее измерить также заряд отдельной частицы.
Ь) Дuффра1(:ция .материальных лучей. 2 (Д Э в И С С О Н.... Ж е р-
м е р, Д Ж. П. т о м с о н, Р у n п.) Если материальныЙ проходит
сквозь решетку (пространственн8.Я реш тка, решетка штрихован), то
имеют место те же явления, которые известны из опти,ки ВИДИМЫХ
И peHTreHOBbIX лучей. (Рис. 2 представлнет собой сделанный' ТОМ-
соном дебай шерреровский снимок с материальными лучами.) По-
добные же явления получаются, ионечно, и при отражении луча
матери!и от решетки. Полезно поэтому лучи материи толковать
наrляДНО как волновые процессы.
Измерение диффракционных максимумов различных ПОряДКОВ
позволяет, как и в оптике, определить длину волны материальных
лучей. Длина еолны находится в ЭМПИl>ической зависимости от
механическоrо импульса р отдельных корпускул, который должен
быть приписан материальным лучам в описанных в параrрафе а)
явлениях.
110 де Бройлю для длины волны имеет место СООТНОUlение:
и ма-
и что
л== h
Р
(h ......... постоянная Планка).
с) Дuффраицuя элеlCпZРОJ4;аzнuтНblХ лучей. Если видимыIe или
реНТI'еиовы лучи проходят сквозь решетку или отражаются от нее,
'то имеют место известные явления интерференции, которые явля-
ются основанием для волновой теории иалучения и MorYT быть
использованы известным способом для измерения длины волны со...
отвеТСfВУЮIll.еrо ивлучения. Рис. rз показы1аетT дебаЙ-Illерреровский
снимок с рентrеновыми лучами. Принцип этоrо снимка заклю-
чается в то:м, что ПУЧОК реитrеновых лучей падает на кристаJIЛИ...,
ческий пороток; отдельные беспорядочно лежащие кристаллики
дают п6мимо прошедшеrо прямо луча еще диффракционные изо....
бражения, что и дает в сумме картину рис. 3..
d) Oпbtпz Кодnтона..Си.м.она. 3 Рентrеновский луч, проходя
через вильсоновскую K1aMepy (срави. а), отрывает электрон при
рассеивании на встречной молекуле rаза (электрон отдачи). Этот
электрон, как описано в а), может быть замечен своему
туманному следу.
Описанное явление можно И СТОЛКО,вать следующим образом
электромаrнитное излучение (в данном случае рентrеновский ЛУЧ)
состоит из отдельных частичек, которые сталкиваются с элеl<:ТрО
нами ra30BbIx молекул (эЙнштейновская rипотеэа световых квантов).
Каждому CQeTOBOMY кванту при этом следует приписатъ энерrию (Е)
12
импульс (р), которые связаны с измеренной в с) частотой V
соответственяоrо излучения следующим обрааом:
h
Е == hv; р -:;;:;::. Т'
Примеыение механических законов столкновения материальны1x
к вэаимодейс1'ВИЮ: световой KBaHT ' элек1'РОН, дает простым
способом зависимость между направлением вылетевщеrо электрона
направлением, в' котором двиrается дальше рассеянный с,ветовой
Опыт Комптона Симона позволяет непосредственно испытать
СJIедствия чисто корпускулярной теории рассеивания peHTreHoBbIX
лучей. Направление BbIpBaHHoro электрона может быть ведь изме...
рено в вильсоновской камере по образованному следу тумана.
Иноrда TaK e возмо/кно наБJlюдать направление рассеянноrо свето...
Boro кванта; а именно, последний может, проходя сквозь вильсо-
новскую камеру, снова вырвать со своей стороны у встречноrо
атома электрон, который становится заметным вследстви образо...
вания .тумана. Наблюдения в вильсоновской камере позволяют
поэтому определить места обоих процессов, вызванных световым
квантом, и вместе с тем, конечно, направление соединяющей их
линии, которое представляет путь CBeToBoro луча. (Нижняя часть
рис. 4 дает снимок TaKoro столкновения, верхняя часть дает тот же
снимок, НО только эдесь пути частицы обозначены стрелками.)
Снимки Комптона...Симона моrли действительно показать, что aKOHЫ
упруrоrо удз,ра выполнены, и тем самым становится очевидной
корпускулярная природа электромаrнитноrо излучения.
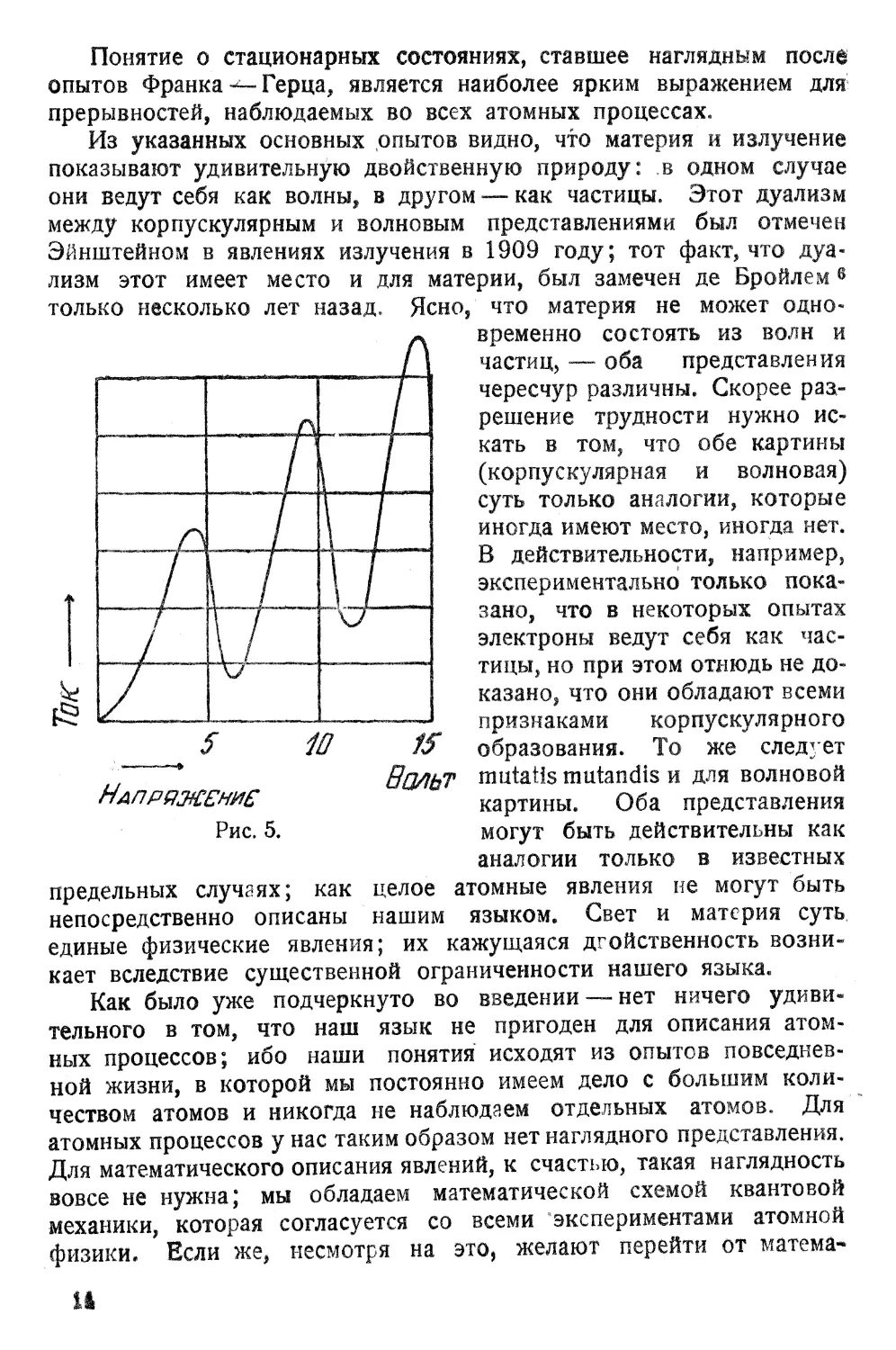
е) Опыты ФраН1Са-rерца со столкновениями. б Если 'пучок
медленных электронов Qдинаковой скорости пропускать через rаз,
то электронный ток при изменении скорости при некоторых дис...
KpeTHНfx значениях скорости (энерrии) меняется скачком. Точный
анализ этих опытов ведет к сл дуюutему объяснению: сами атомы
rаза MorYT иметь лишь известные дискретные значения, эн рrии
(основноИ постулат БGра). ЕСJ1И значецие энерrии известно, ТО по
Бору rоворят о "стационарном состоянии" атома.
Если 9нерI'ИЯ 9л трона недостаточна, чтобы перевести атом И3
первоначальноrо состояния в ближайшее энерrетически высщее
сосrояние, то он, испытывает только упруrие столкновения сато...
мами rаза, не изменяя при этом значения с,корости Если
теперь увеЛИ L Iивать энерrию 9лектронноrо до значения, коrда
кинетическая энерrия каждоrо эле,ктрона достаТОЧН8, чт0;БыI пере..
бросить атом в ближаЙшее высшее энерrетическое СQстояние, тоrда
часть электронов, проходя через rаз, сво,ю энерrию атомам
rаза; электронныМ ток вследствие 9Toro изменяется в критических
точках очень быстро.
18
Понятие о стационарных состояниях, ставшее наrлядным после
опытов Франка....:...... rерцз, является наиболее ярким выражением для
прерывностей, наблюдаемых во всех атомных процессах
Из указанных основных ,Опытов видно, что материя излучение
показывают удивительную двойственную природу .. случае
они ведут себя как волны, в друrоМ.......... как частицы. Этот дуализм
между корпускулярным и волновым лредставлениями был
ЭЙНПIтейном в явлениях излучения в 1909 rоду; тот факт,
лизм этот имеет место и для материи, был замечен де Бройлем 6
только несколько лет назад. Ясно,' что материя не мо}кет ОДНО..
временно состоять из волн и
частиц, оба представления
чересчур различны. Скорее раз...
решение трудности нужно ис-
кать в том, что обе картины
(корпускулярная и волновая)
суть только аналоrии, которые
иноrда имеют нет..
В действительности, например,
экспериментально только пока..
зано, что в некоторых опытах
электроны ведут себя как час-
ТИЦЫ, но при этом ОТНЮДЬ не до-
казано, что они обладают всеми
4r признаками корпускулярноrо
,('" образования.. же следует
BO/Ib1' mutatis mutandis и для волновой
картины. Оба представления
MorYT быть действительны как
аналоrии только в известных
предельных случаях; как целое атомные явления не MorYT быть
непосредственно описаны нашим языком. Свет и материя суть,
единые физические явления; их кажущаяся дrойственность возни-
кает вследствие существенной оrраниченности нашеrо языка..
Как было Уil<е подчеркнуто во введении........... нет ничеrо УДИВИ-
тельноrо в том, что наш язык не приrоден для описания атом-
ных процессов; ибо наши понятия исходят ИЗ опытов повседнев-
ной жизни, В которой МЬ) постоянно имеем дело с большим коли...
чеством атомов и никоrда не наблюдаем отдельных атомов. Для
атомных процессов у нас таким образом нет наr.пядноrо представления.
Для математическоrо описания явлений, к счастью, такая наrлядность
вовсе не нужна; мы обладаем математической схемой квантовой
механики, которая соrласуется со всеми экспериментами атомной
ФИ3ИI<И.. Если же, несмотря на это, желают перейти от матема-
I
j
10
"
НАПРй:Jl(l'НИС
Рис. 5.
1&
.к наrлядному описанию явлениИ, ТО ПРИХОДИТСЯ ДОВО/IЬСТВО'"
неполными аналоrиями, которые нам дают волновая и кор-
скулярная картины.
показал Бор, этот наrлядных представлений также
естественную исходную дЛЯ I<РИТИКИ введенных в
образов и Ибо очевидно.. что, ".ринятое без
одновременное применение волновой и корпускулярной
к нротивореqия . Из одновре..,
существования картин МОЖНО сразу же заключить,
для применения каждой из этих картин природой установлены
является применимой
например, получены из волно-
Бор, 7 этим путем может быть получен
неопределенности между импульсом и
МОЖНО из корпускулярноrо пред..
rраницах, поставленных природой
понятий, нужно ука...
квантовой механики
пониманию атомной физики. Чтобы
понимания СООТНОlцений, формализм
ОН необходим для общих рассуждений,
как М). На Hero мы должны;
примерах, так как без математики
проблем.
, J. Критика физических понятuй
411
к.ОРltускулярнои «apтUHbl.
1. СООТНОШЕliИЯ НЕОПРЕДЕЛЕННОСТИ. 8
Понятия: положение, скорость, энерrия получены из простых
опытов повседневной iКИ3НИ, в которых посредством этих слов
описывается механическое поведение макроскопических образований.
l'И понятия были перенесены ПОТОМ на как элек..
в некоторых основных экспериментах вели в смысле
по.цобно Но так как
u
знаем, что это имеет лишь в оrраниченнои
ТО и область корпус..
картины должна оrраничению
притти по Бору 7 простейшим вспоминая, что все
моrущие быть в пространстве и вре...
атомной физики QПИСЗНЫ Т а к ж е и с по-
картины., одинаково
1
справедливы для J<Зiкдоfl: из трех пространсrвенных координат
трона и будут поэтому проведены только для ОДНОЙ. факт,
что положение электрона' определяется с известной точностыо д'q,
описывается, очеВИДНО'1 в волновой теории посредством
функции, амплитуда котороП заметно отличается от
в очень, маJIQЙ области, приблизительно f.1q.
таким образом волновая функция может
СОСТОЯlдей ИЗ H6KOToporo числа
интерферируют меil{ДУ собой, в
они друr друrа взаимно усиливают, а вне ero
уничтожаются. Такое образование нззывают в о л н о в ы м п а к
т о м. Общая матемаТfIческая теорема rласит, что всеrда воз..
можно, посредством COOTBeTCTBeHHof'O подбора отдельных составVIЯЮ"
щих волн, построить волновой пакет любой формы., С теч.ением
времени такой волновой пакет СБОЮ величину и
форму и, наконец, исключая некоторые случаи,
сеивается по всему пространству., Скорости па кета co
ответствует скорость электрона. однако,
определить посредством он, как
было уже сказано, помимо
во все стороны, рассеивается. Это
определенность, скажем, величины p в
(масса на скорость). Из простейших законов оптики
уравнениями М (203), (204) математическоrо
быть выведено, что:
толы<о
с
может
I1q /1р h.,
1)
Пр дставим себе ВОJIНОВОЙ пакет состоящим из плоских
длины волн которых должны леiкать вблизи значения л == /...0.
Таким образом, в области внутри пакета имеется в общем, примерно,
6aq === п волновых пучностей 'и узлов; вне пакета плоские
o
l{омпенсируются блаrодаря интерференции., Это возможно и
rолько тоrда, если в совокупности применяемых плоских
имеются таК'же и такие, для которых по меньшей п 1 по..
падают в критическую область. l\1.ы имеем,
п 1,
(2)
rде Д-Л дает, примерно, область длин
вования пакета., Таким образом.
Дq
· !J.}, 1 .,
Лn
обра-
16
с друrой стороны, rрупповая скорость волн [СМ. М (204), rде
масса электрона]
h
V g == ,
л о ""
и рассеяние пакетз, соответствующее области I!1л, характеризуется
h
д'V g === ! 2 ДЛ.
ЛО }1
(4)
определению p == Vg, и поэтому соrласно (3) получим:
Ар .1lq ?; h.
(5)
Это соотношение может быть применено дли каil<ДОЙ степени
свободы в отдельности:
А х 1lр х h; llуАру?; h; AzApz?; h.
(6)
Соотношения неопределенности соответствуют прежнему обыч..
ному деJIению фаэовоrо пространства на клетки величиною h и
уточняют физический смысл этоrо деления. Соотношения неопре..
деленности представляются более естественными, чем прежнее де..
ление, потому что таким образом отпадают произвольно YCTaHOB
ленные стенки между отдельными клетками. СООТНОlпения (6) дают
rраницы, до которых MorYT быть применимы понятия корпускуляр
ной теории. Выходящее за пределы (6), более точное употреб
ление слов "положение" , "скорость« также бессодержательно,
как применение слов, смысл которых не определен. 1)
Соотношения неопределенности MOrYT быть также выведены без
непосредственноrо обращения к волновой картине с помощью мате-
матической схемы (М 2) квантовой теории и ее физической
интерпретации. 9
Какое либо знание координаты q электрона может быть выра.,
жено амплитудой вероятности S(q') в том смысле, что выражение
1) Здесь нужно вспомнить, что человеческий язык допускает, вообще.,
образование предложений, из которых нельзя Dывести никаких следствий
и которые поэтому, в' сущности, совершенно бессодержательны, хотя и
дают cBoero рода наrлядное представление. Так, например, утверждение,
что на риду с нашим миром существует еще второй, с которым, однако,
невозможна при н Ц и п и а л ь н о никакая связь, не при водит ни К ка...
кому следствию; несмотря на это, в нашей фантазии возникает при таком
некоторая картина. Вполне понятно, что такое утверждение
не может быть ни доказано, ни onpOBeprHYTO. Особенно осторожно нужно
употреблять выражен е »В « так как ОНО леrко ПрИБQДИТ
тзкоrо рода утверждениям.
2 в. rейае.нберr.
l'
JS(q')I 2 dq' дает вероятность найти 5лектрон
Пусть
+dq'
q === J q'lS(q' )1 2 dq'
(7)
есть среднее значение q, тоrда
2
)i 2d q' ,
(8)
МО}КНО будет
трона.
как неточность в знании
ЭJlек-
I 12
электрона между р' и р'
Мы полаrаемснова
и
р J р'l (р') 1 2d p'
(Llp)2 == 2 J (р' р)2\ (p')12 dp'
(9)
(10)
и обозначаем !1р как неточность в анании импульса электрона.
Между S(p') и S(q') имеет М (188), СООТНО'"
lпение
S (р') == J S q') S (q') dq', (11)
rде S(p'q') обозначает функцию преобразования, которая пере водит
И3 ОДНОЙ координатной системы (в rильберТОВСКQМ пространстве),
в которой q было в друrую, в которой
циаrональной матрицей является р.
Из
тоеда, СОI'ласно
h
S l Р (р) == p(q)
м (169),
d
S (р' ) == р' (р' (j');
(1
s==
е
(13)
Нормируя,
21ti
1 p'qi
(p'q') == Уь е h ·
(14)
Значения !1q и Ар, таким образом, связаны
посредством (11) и (14) и можно спросить, какая
приводит к минимуму произведение
!1q ==
математически
S(q')
(15)
18
Чтобы упростить дальнейшие выIисления,, введем следующие
сокращения:
р; )
I
) [
J
(1
в(х) ==S(q') е
t == S (р') е
ТОI'да
(8) и (10) следует
==:2.[ 18 12 }
(др)2==2J y2It(y)12dy
(1
а из(14) получаем
t (у) ;h f 8(Х) e 21ti ху dx.
(1 (18) ВЫВОДИМ.
(18)
(
,f8
21ti
ху
I
е
(х)
! j t* ху } 17а)
е
( h ,f8* I
h 2 '.1
.
J
Но из очевидноrо СООТНОПlения
s \2 О (19)
венство
12 1 \ \2 ( )
j \
I
(lll] )2\ I
I
* 19
и после инrеrрирования, в виду (11а):
1 1 h 2 1
2 (!:ljJ) 2 2 47t: 2 I:lq2 '
т. е. 1)
p llq
h
21t'
(20)
Минимум может быть достиrнут только для тех функций s(x),
в (19) имеет место знак равенства.
дол)!{но быть
х 2
х
дх (1:l ; N s (х) или s (х) == const. е
(qf q)2 21ti ,
2 (Aq) 2 pq
S (q') == сопst. е
COrJlaCHO (14),
S(p') const. е
(р' p)'J
2 (Ар)2
21ti
q (р р)
411
ССОБское распределение для вероятностей измерения р и q
, следовательно, минимальное значение для Ар. Aq; для всех
б h
друrих распределений произведение неточностей ольше чем 21t .
liужно еще отметить, что 9ТОТ вывод по своему математи
ческому содержанию нисколько не отличается" от вывода COOTHO
Iпениii неопределенности И3 дуализма корпускулярной и волновой
картин; только доказательство формулы (20) здесь произведено точно.
Физически (20) ка>кется сперва более общей, чем (6), так как (6)
относится специально к положению и импульсу свободных электро-
нов, в то как (20) справедлива для каI{ИХ уrодно кано..
нически СОПРЯ}I{енных переменных и применимо также к связан
iНЫM электронам.
()днако, это преимущество (20) по сравнению с (6), как под
черкнул Бор, менее значительно, чем это кажется на первый взrляд,
так как, например, измерение положения или импульса связанноrо
электрона мо}кет быть произведено только в тех экспериментах, в КОТО-
может быть пракrически рассматриваем как свободный.
Нужно заметить, что иноrдз вместо опредеJIенных эдесь величин д.
gHecb стоит дЛЯ рили q) применяеlСЯ "средняя неточность" Ll' ', которая
с нашими величинами связана соотношением a"fJ == 112 6:1)'. Тоrда вмес то (20)
1 h
будет иметь место !J.p' llq' Сравни,' например, Weyl, "Gruppen
11
, стр. 67. Leipzig, 1928.
: O
2. ИЛЛЮСТРАЦИЯ СООТНОШЕНИИ НЕОПРЕДЕЛЕННОС'fИ НА
РАЗЛИЧНЫХ ИЗМЕРИТЕЛЬНЫХ ПРИБОРАХ.
а) Измереuuе положения свободных эле!! тронов.. Сооти ошения
неопределенности относятся к степени точности нашеrо (O)(HOBpe
MeHHoro) знания в настоящий момент различных величин, ветре..
чающихся в квантовоЙ теории. Так как эти соотношения H orpa..
ничивают, например, измерения только положения или измерения
скорости в отдельности, то их действие выражается только в
что каждый эксперимент, позволяющий произвести измерение,
ская{ем, положения, необходимо до некоторой степени нарушает
знание скорости. Если примем, элек-
трона точно известна, а положение напротив вовсе неизвеС'tllО, то
тоrда каждое следующее наблюдение положения ДОЛiКНО ив:менять '
импульс электрона; причем это изменение неопределенно, и эта
неопределенность должна быть такова, чтобы после пропедения
эксперимента наши знания о ДВИ)J{ении электронов были оrрани-
чены соотношениями неопределенности. В последующем это \5удет
доказано на некоторых экспериментах в виде примеров. 3анетим
однако сейчас уЖе, что соотношения ,неопределенности очеВI дао не
относятся к прошлому, так как если сначала известна скорость
электрона, а затем будет точно измерено ПОJIожение, ТО воаможно
и для времени перед измерением ПОllожения точно ВЫЧИСЛИТl. ноло-
жения электрона. Для этоrо прошедшеrо времени произведени ,iq p
меньше, чем обычная rраница. Однако это знание прошлоrо нмеет
чисто умозрительный характер, так как оно (вследствие из!v,енения'
импульса при измерении положения) никаким образом не в:содит
как начальное условие в какое либо вычисление будущей судьбы
электрона и вообще не иrрает ропи ни в каком физическом sкспе...
рименте. Стоит ли названному вычислению прошлоrо ЭЛfК rронз
приписывать какую либо физическую , являетси f:ОЭТОМУ
)
только делом вкуса.
В качестве первоrо примера нарушения знания импульса прибо...
ром для измерения положения MbI :выберем измерение
микроскопом (БОРJ указанная статья). Пусть ЭJIектрон
таком расстоянии от объектива микроскопа, что
исходящим от электрона рассеянным пучком
длина волны и частота падающеrо на света будут C() ,TBeT-
ственно ).. и "У. Точность измерения положения в оси х
будет соrласно законам оптики
Ах
(21)
Для иiзмерения ПQложеиия нужно, чтобы по меНI;шей мере ОДИИ
световой квант был рассеян от электрона и через микроскоп по..
пал :в rлзз наблюдателя.. Этот световой квант вызывает КОМПТОНОВ
скнИ отброс элен:трона порядка . Отброс
с
так как неизвестно направление CBeTOBoro кванта
, лучей (уrол зрения е); так
f для неопределенности отброса
I
: влении х имеем.
ТОЧНО,
пучка
образом
в напра...
А hv.
IdPX "Slne,
с
(22)
и для движения электрона после опыта
следует:
pxel1x h..
(23)
Против сперва MorYT
лриведены возражения.. Не..
обусловлена ведь
какой прохо-
лучей.
бы попробовать устано...
путь таким способом: еде.
подвижным и иамерять
микроскопом от
Однако это не по-
uеопре-
сейчас же возникает
вопрос о положении микроскопа, а и импульса Bcero
,микр?скопа имеем снова соотношения Конечно мо)кно избежать
измерения положения микроскопа, например одновременно
наблюдать электрон и ДВИЖУЩИЙСЯ
микроскоп. Но одно...
временно через микроскоп к rnазу по крайней мере
два световых кванта (ОДИН ОТ шкалы, друrой ОТ электрона), и тоrда
ОДНО ТОЛЬКО иамерение отброса микроскопа уже не поможет полу-
чить сведения об идущем от электрона световом кванте и Т. Д.
Можно было бы также думать о СУIцественном повышении точ
ности измерения положения путем точноrо измерения
диффракционной создаваемой микроскопом. нужно
однако что ЭТО возможно только тоrда, диффрак-
ционная · (на фотоrрафической ,плаСТИliке в rлазу)
создана квантами" Элементарный пока...
зывает, что максимум ширины Ах диффрвкционной картины, соз...
данной "1. световыми квантами, может быть с точностью
i
)
''1'
Можно
вить
х
Рис. 6..
аа
дх
Таким образом получается действительно повышение
пl
точности
каждый И3 т с
h'J
импульса д.Рх ==
с
ния независимых ошибок) будет:
положения в V т раз. С друrой CTOPOHbI t
квантов дает неточность в определении
е, и общая неточность (по теореме слоя<е..
Ар' х ==
== v n1, !J.px,
т. е. снова имеет
Ар'х
Для
менное применение
няем по существу,
этот в
9Toro эксперимента характерно одновре...
картин" Мы приме
Друrое опре...
деление может
быть произведено следую..
IЦИМ образом"
Пусть ВПОЛ
не известна скорость
ных
(рис. 7)
Если электрон проходит сквозь
ние в направлении параллельном
Если же летящий
де Бройля, то тотчас же видно, что с
связано также и ВыходящиЙ
расхождения а, который на основании
определяется следующим
возмож"
щели в экране шириною d
с
щель, то очевидно ero положе...
определено с точностыо d.
как плоскую волну
шириною d
имеет конечный уrол
законов оптики
(л == длине волн де Бройля).. Таким образом, импульс электрона
параллельно экрану после прохожденин электрона сквозь lцель ста.,
новится неопределенным на величину
Др
JI .
· s 1 n CI.
)" '
(25)
h
так как '"\ есть импульс электрона в направлении луча. Из
А
что dq -=: d, следует: д'р д'q h. В этом выводе нет речи о ДУЗJIизме
"волна - частица" в теории излучения, но зато он применен эдесь
в теории материи.
Как последний эксперимент для измерения положения рассмотрим
обычные способы: наблюдения СЦИНЦИJIЛЯЦИЙ и вильсоновские
снимки.
Для этих способов характерно, что укаJателем ПРИСУТСТВИЯ
частицы! служит обусловленная ею ионизация атома.. Очевидно
нижний предел точности при таком измерении положения дается
величиной ионизуемоrо атома д'q. При ионизации изменяется им--
пульс ударяющей частицы. Так как импульс BbJpBaHHoro из атома
электрона может быть измерен, то неопределенность в изменении
импульса ударяющей частицы равна неточности импульса Ар
электрона, пока он eи e связан в атоме. Эта неточность импульса
связана с величиной атома опять-таки известным соотношением:
Ар D.q h.
(Как должно быть рассмотрено позже, здесь обыкновенно имеет
место Ар д'q nh, rде п обозначает квантовое число со ответ...
ствующеrо стационарноrо состояния.) Следовательно также и для
3Toro типа измерения положения справедливо соотношение неопре
деленности. Дуализм волны частицы не выступает в этом выводе
непосредственно; соотношения неопределенности являются след-
ствием квантовых условий для стапионарных состояний, но конечно
дуализм все же заключен неявио в квантовых условиях..
Ь) ИЗJtеренuе сuороспхи или импульса свободных эле п'lрОflО8.
Прос rейшее определение скорости, непосредственно соответствующее
первоначальному определению слова скорость, совершается путем
измерения положения в различные моменты времени. взять
очень большие промежутки времени между такими измерениями
положения, то можно с любой точностыо определить ча-
стицы п е ре д последним измерением положения. п о с л е
определения положения, которая только и представля зический
интерес, будет, разумеется, известна не так точно; свя-
занное с последним измерением положения изменение импульса
21
снова обусловливает справедливость соотношений неопределенности,
как было показано в предыдущем параrрафе..
Друrой, часто употребляемый метод мзме ,ения скорости заря-
женных частиц основан на эффекте Допплера (Бор, 1.. с.).
Возьмем наприм такую установку..
импульс элеI<трона параллельно падающему свету
[направление х] точно известен) т. е. el'O положение в направле-
нии х неизвестно' напротив, пусть положение в направле...
нии у очень точно известно импульс же вовсе неизвестен.. Речь
следовательно идет об определении скорости в направлении у
и нужно 9Toro определения знание поло..
жения в направлении у теряет СБОЮ точность настолько, что после
опыта снова справедливы СООТНQlпения неопределенности.
Пусть свет на...
блюдается в направлении у
(нужно заметить, что эффект
Допплера установке
исчезает коrда == Ру,
т.. е.. коrда
параллельно прямой х =--= О) , ..... 1)
Для теории ДОППJlер... эффекта
(который здесь по существу
тождественен с эффектом Комп"
тона) нужны только законы
сохранения энерrии и импульса,
примененные к столкновению
электрона со световым квантом.
Величины без lllТрИХОВ 060зна--
чают значения до удара, со штри"
Х:1МИ значения поспе удара.
1
\j
t
"f\
............
- х
1
у
Рис. 8.
hv Е == Ьоу' + Е' )
hv + I I
РХ Р х
С }
hv' I
Р Р '
у:'=с YJ
(26)
Е === [ 2' )
h ('; -у') == Е' p ' Р; p ]
2т РХ
[!р'х Рх) Рх (р'у Ру) Ру] } (27)
т I
1 i 1
Ь/ hv
f1l t c cPv Cfп(PX Py), I
,
25
Так как Рх и 'V приняты известными, то
' связана непосредственно с точностыо измерения
v
- Ару.
те
определения
(28)
Для измерения с точностью поток волн опреде-
ленной длины. Время для испускания TaKoro потока ВОЛН по про...
стеtlшим ззконам оптики равно
Т==
Так как мы не знаем, испущен ли световой квант в начале или
конце этоrо промежутка времени, то неизвестно, движется ли элек
1
трон в npOMe>I(YTKe времени в направлении у со скоростью ру
"Х
1
у" Вызванная вследствие
недоето-
или СО скоросты{)
m
верность в положепи
будет:
в конце про Me}l{YTKa времени
Ау
1
lп (Ру
h'/
р'у) т === Т.
те
(30)
Из (28), (23) и (30)
h.
Третий метод на отклонении заря...
женных частиц н маrнитном Возьмем следующую установку'
щель шириною d выделяет материальный луч; луч вступаеr эат,ем
в однородное маrнитное поле, перпендикулярное плоскости чер..
I
тежз, проходит в нем отрезок отклоняется в поле вниз и выхо"
дит из :маrнитноrо поля под а к напра...
влению.. Далее, пройдя отрезок [, луч проходит через щель;
положением этой щели может быть определен уrол а.. Скорость
частицы 1J === L в направлении луча определяется из уравнения:
m
а 'v
..H..e
v с
(.( === .. ...............
тcv
(31 )
И' для соответствующих неточностей имеем
6.(.( == аНе д.v ..
те v я
(32)
Пусть далее в начале опыта положение частицы в н а пр а..
п л е н и и л у ч а известно с большой точностью; это достиrается,
скажем, путем быстроrо открывания и закрывания щели. Нужно
токазать, что такое знание положения во время опыта теряет свою
вочност:ь в такой мере, что после опыта справедливо Ilpf1q Z h..
Точность, которую можно достиrнуть в измерении <1, очевиДНО
, d
есть Аа. l + а (d == ширине обеих щелей).
,
J
.
.
.
,
.
$
I
.
Н ·
.
...... .. ...... ........ Т.... ...........
.
,
I
I
v
f
.
.
I
.
.
,
............
а
Рис. 9.
Но и эта точность может быть достиrнута только тоrда, коrда
d
естественное (де бройлевское) рассеяние лучей меньше, чем 1 а '
в противном случае неточвость измерения а дается этим рассея-
Л
ннем: Il<% d " Это значит, что имеют место оба VDавнения,,:
d
a, > 1
,.....""" а
л-
и Ila Z d
отсюда:
А
(L\a) 2 Z 1
а
(33)
Далее имеет место:
тcv 2
1J === .Да.
аНе
(34)
Неточность в знании положения после ОПЫТ 'Равна времени,
необходимому для прохождения пути между обеими utелями, YMHO
женному на неопределеццость скорости:
!1q 1 а Av
(35)
v
и, соrласно (34) и (35),
AvAq' 1 л 1 1 h
.. ==- лv
v (12 (;(2 т'
т. е.
Ap q h 2 > h,
(1
так как весь вывод справедлив только для малых CI.. Для больших
значений а нужно в особенности отметить, что посредством о ыта
нельзя ведь различить ме}кду (1::::::::: О И а == 21С, ежели вообще
значение а::=.:: 2'1t И возможно, если только не ввести в установку
И8менений, требующих HOBoro обсуждения Bcero опыта в целом.
с) Свлза-н,flые эле!Стро-н,bl.. Если rоворить о неточности в зна..
нии положения и импульса связанных электронов, то нужно ясно
различать две проблемы: Ба первых, можно рассматривать энерrию,
т. е. стационарное состояние системы, как величину известную и
спросить, какая степень точности в анании положенt-iЯ и импульса
следует из этоrо анания энерrии ил , во всяком случае) с ним
совместима. Во вторых, пренебреrая ананием стационарноrо состоя..
ния, можно поставить вопрос о высшей точности для названных
величин, осуществимой экспериментально, т о е. не считаясь с тем,
что необходимые для этоrо измерения моrли бы сделать HeB03
можным знание энерrии или стационарноrо состояния.
Мы займемся сначала пер в о й проблемой и рассмотрим опре-
деленное стационарное состояние. При этом, соrласно с Бором, из
классической теории КОРПУСI<УЛЯРНОЙ картины можно заключить,
что неопределенность в знании положения и импульса вооБI.це
больше, чем ApAq h. Очевидно речь идет просто об определении
области изменения !{оординат и скоростей электрона в атоме. Из
соотношения, справедливоrо для п..oro KBaHTOBoro состояния
fp dq пh,
(36)
следует
flps дqs ) nh.
(37)
Леrче BCero можно усмотреть Э о, начертив замкнутые траекто"
рин классической механики в фазовом пространстве (рис. 1 О),
28
!pdq даеТ пЛоЩАДЬ, оrраниченную траекторией, а 6.ps q9 будет ( Цe
ВИДНО Toro же порядка величины. Мы отличаем эдесь неопреД€J:t:Н
ности 6.р, tJ.q индексом s, чтобы напомнить о том, что речь идет
не о высшей достиrаемой точности в определении J) и q, но оспе..
циальной неопределенности в внании р и q, которая появляется,
если стационарное состояние, Т. е. энерrия атома точно И38естна.
Эта неопределенность встречается например в обсуждении наблю..
дений сцинцилляций (11, 2а). Для классической теории БЫIIО бы
чуждо интерпретировать область изме1iения координат Ilqs как
неопределенность положения. В квантовой теории нужно однако
помнить о том, что и знание энерrии также представляет "случай
чистоrо собрания((, Т. е. случай, который в математической схеме
будет представлен посредством вполне определенноrо волновоrо
пакета (именно шредин...
rеровойфункцией соответ-
ствующеrо стационаРllоrо
состояния). Есл проиа-
вести вычисления (П, 1)
для 9Toro ВОЛНОВОI'О па...
кета, то значения !J.ps
fJ.q s будут тем больше,
ч.ем больше нулевых то-
чек имеет в aTo e со от:"
ветственная собственная
функция, т. е. чем чаще
колеблется собственная
функция в области атома.
Если например мы paCCMO
трим собственную функцию (проблема одной степени свободы),
которая имеет ровно п нулевых точек (узлов), то тоrда вычисле-
ние показывает, что в правой части (37) появляется множитель n.
Теперь мы рассмотрим в т о ру ю из вышеназванных проблем..
Очевидно наивысшая достиrаемая точность в знании р и q будет
дана через IIp tJ.q r-...... h, если пренебречь знанием стационарноrо
состояния, так как всеrда измерения положения и импульса MorYT
быть произведены с такими МОIЦНЫМИ средствами, что электрон при
этом практически может быть рассматриваем как свободный. Им-
пульс электрона, находящеrося в атоме, можно, например, измерить
простеЙIIIИМ образом, выключив в некоторый определенный момент
времени взаимодействие электрона с ядром и остальными электро-
нами. Электрон тоrда ДВИjнется по инерции и ero импульс может
быть измерен известныIM способом. Необходимое для измерения
воздействи& в этом случае очевидно 1'oro же порядка, что и ':ВЯ3Ь,
У держиваюu ая электрон в ЗТQме..
р:
..q
Рис, 1 О,
29
Соотношение (37), как подчеркивает Бор, ., важно для перехода
от квантовой механики к классической в предельном случае боль-
ших квантовых чисел" Мы ставим вопрос о возможности понятия
траектории в квантовой механике.. Так как наилучшее возможное
знание положения и импульса удовлетворяет соотношению !lp Ilq h,
то ero можно представить волновым пакетом (/S(p *'S(q')j2)
(СМ. М Э 2) площадью h в пространстве р, q. Такой пакет
может описывать в фазовом почти замкнутые траек-
тории, которые хорошо опредеJIены тоrдз, коrда площадь, orpa:-
ниченная траекторией, 8начитеJIЬНО БОJIыпе чем площадь h l1акета,
т. е. соrласно (36) и (31) в предельном случае высоких квантовых
чисел п.. Для малых квантовых чисел однако понятие траектории
должно терять свой смысл как в фазовом, так и в оБЫКliовенном
пространстве. Поэтому реIllающим для возможности понятия траек-
тории в пределе высоких квантовых чисел является наличие в пра
вой части (36) и (37) мно}кителя n..
Невозможность существования понятия траектории в области
малых квантовых чисел можно уяснить себе непосредственно физи-
чески следующим образом: под траекторией мы понимаем времен-
ную последовательность точек пространства, в которых будет аа...
стиrнут электрон 80 время CBoero движения.. Так как размеры
атома в ни}кнем квантовом состоянии порядка 10 8 СМ, то Д1IЯ
определения траектории электрона нужны измерения поло...
жения с точностью по меньшей мере 10 9 т.. е. атом должен
быть например освещен светом ДJIИНЫ ВОЛНЫ А 1 o 9 см. Но уже
одноrо кванта тзкоrо света достаточно, чтобы вследствие эффекта
Комптона удалить электрон из атома: следовательно изо всей тра-
ектории будет наБЛIодаема только одна единственная точка. Однако
эти иамерения положения можно повторить на мноrих атомах, и
тоrда получается некоторое вероятное распределение электронов
в ат'оме, которое дается по Борну 14 через ф* Ф (и, если в атоме
.
находится MHoro электронов, через среднее по координатам осталь-
ных электронов значение ф*ф; Ф означает шрединrеровскую функ..
ЦИЮ, СМ. М 170). В этом заключается физический смысл утвер-
ждения, что ф*ф дает вероятность найти электрон в определенном
месте. Но этот результат более удивителен, чем на
вый взrляд.. Как известно, ф*ф убывает по показательному закону
с возрастанием расстояния от зrомноrо ядра, значит всяком
случае СУlцесrrвует еще конечная вероятность Toro, что электрон
можно найти на очень далеком расстоянии от ядра.. Потенциальная
энерrия электрона там хотя и отрицательна, но очень кине...
тическая энерrия всеrда положительна и вычисленная путем ело...
, (j
женин общая Эllсрrия очевидно б о л ь ш е, чем всеrда некоторая
80
" статистичеСI{оrо
зательноrо
можно иноrда
от ядра.
бы
для
отброса, и
конечная отрицательная общая энерrия стаЦИQнарноrо СОСТОЯНИI.
Этот парадокс разрешается следующим рассуждением. Сначала все
выrлядить так, как будто бы здесь имеется нарушение закона со...
Iio только кажущееся, так как
так)ке во применен..
квант и от Hero
значительно больше,
справедливостьзако-
Комптон..эффекта
служить поучительным
применения
" Вследствие пока..
как было сказано,
также и на далеких расстояниях
что их обнаружения было
положения с к р а с н ы м светом;
заметноrо комптоновскоrо
остался бы ВО
свет н и к а к
электронов;
свет по фОРМУJIам обык"
представляется вполне
(по классической корпуску
несколько обращений во
образом статистические
в связи с ЭI<спе-
наблюдать явления,
лярной
время одноrо
положения
риментами, которые
рассматриваемые в
Понятие мысл только ДЛЯ высших Бозбу;..
тденных состояний aTOl\'Ia. и здесь положения
должно сделано с такой точностью, чтобы средняя ошибка
была мала в сравнении с размерами атома. Но отсюда не следует,
что электрон будет выБРОlпен из атома блаrодаря комптоновскому
отбросу. Напротив, в силу (37) дЛЯ БОЛЫIIИХ п отброс может быть
Меtlьше, чем знаqения импульса электрона в стационарном состоя-
нии. Мы проделаем вычисления.
Должно иметь меСТОе
л « I:lQs;
е. соrласно
п
Переданнан при
порядка
будет таким
81
(Е..........энерrия aTOМ , fJ. масса элек,трона); поэтому эта переданная ЭНер-
rИlI можеt быть мала по сравнению с jEj ДJIЯ больших п, Сдруrой
стороны она Bcerna велика по сравнению с энерrетическим
Впрочем,
соседних уровней, которое вообще rоворя
h p 'Е!
и:а » также тотчас же следует, что }l'J тф что
л п п
частота примененноrо для измерения положения света чем
частота вращения электрона в атоме.
КомптоновскиП отброс приведет все таки к тому, что атом будет
переброшен из стационарноrо состояния, в котором, скажем, п== 1000,
в какое-нибудь состояние между п == 950 и п == 1050, при
этом в силу показанной в (11, 1) неопределенности отброса CTa
ционарное состояние, в которое переходит атом, принци
пиально неизвестным в некоторых rраницах.. образом резуль..
тат измерения положения в математической схеме квантовой меха-
ники может быть представлен в конфиrурационном пространстве
пакетом вероятности, который в сушественной части состоит И3
собственных функций стационарных между п == 950 и
п == 1050, и величина KOToporo ия поло..
жения" Этот лакет описывает траеКТОрИfО, подобную частицы
в классической теории, и одновременно распространяется во все сто..
роны. Результат последующеrо положения может быть,
следовательно, предсказан вообще только С каждым
новым измерением математическое ческоrо про..
цесса изменяется прерывно; из множества
возможностей одну определенную, и, вместо
расползшеrося пакета вероятностей, появляется снова м па...
'кет, представляющий результат наблюдения. как с каждым
наблюдением HaIlle знание системы изменяетсн
CT eHHЫM образом, и ero математическое представление изменяется
прерывно, как и в КJIассической статистике. положение вещей
можно также выразить посредством что ина
электрона зависит от опыта, примененноrо для измерения поло-
жения. Движение и расползание пакеТQВ вероятности MHoro
раз подробно изучено в литературе 10 и не будут
излаI'аться математические выводы. Мы приведем только стое
рассуждение Эренфеста. 11 ИССJfедуем движение одноrо
в силовом по.пе, потенциал KOToporo V(q).
Шрединrеровское уравнение ДЛЯ этой задачи rласит:
h 2
Llff
81t2
е Vff ===
82
Среднее значение для q дается через q ==: J q * dv (d't 1 dxdj'dz),
q представляет какую нибу дь прямоуrОJlЬНУЮ координа! у элек..
Дифференцирование по времени дает:
== IL J q C !: ) dv,
инtеrрируя по частям, имеем.
f
I 4тс
д( * )
} ! dv.
aq дС!
дифференцирования по
)ке
после
ef
на
размеры KOTOpOI'O
V
малы с
ТО MO)I\ilO написать'
дV(q)
.
aq
I
ПЗI<ет веРОfIТНОСТИ описывает
мы замечание О скорости расползания волно-
ных пакетов. Если классическое д.. ижение системы прОисходит Ре..
риодически, то мо)кет случиться) что и величина волновоrо пакета
иаменяется сначала только периодически. О максимальном числе
мо}кет сделать пакет до полноrо рассеяния
атома, МО}КНО получить качественное представление
образом. Если бы пакет не испытывал никаК{)I О рас...
сеивания, ТО бы ВО3МО}JПIО такое рззло}кение в ряд Фурье
распределения зарядов, в котором имеIОТСЯ только
основной частсты. В действительности же в 1{ BaH
ТОВОЙ теории обертоны не соотвеТСТИУIОТ точно кра'l ным
OCHOBHoro колебания. Время, в течение частота
полностью по
качественно
волновоrо па
систем
ПQЛНОI'О расползания
числеННаЯ переменная
ТО
1
11
и число обраutений до расползания
'J
N
h дv
д]
(38)
в частном rармоническоrо осциллятора N
велико, т. е. волновой пакет сохраняется неопределенно В
обlцем случае, однако, N соrласно (38) будет порядка I{взнтовоrо
числа n. Для больших значений п понятие орбиты имеет,
образом, оправдание и в квантовой теории.
В. связи с этими рассуждениями здесь должно быть указано
на мысленный эксперимент, предложенный Эйнштейном. Вообразим
один световой квант, который представлен посредством волновоrо
пакета, построенноrо из максвеллевских волн 1) и которому, таким
образом, приписана известная область пространства и, в смысле
соотношений неопределенности, также определенная область частот.
Il0средством отражения от полупрозрачной пластинки мы можем
очевидно леrко разложить этот на части.
отраженную и прошедшую. Тоrда определенная вероят
насть найти световой KBaHt и л и в ОДНОЙ, и л и в друrой части
волновоrо пакета. Через достаточно долrое время обе части будут
сколько уrодно далеко удалены друr от друrа. Если теперь посред
СТВОМ опыта будет установлено, что световой квант находится,
положим, в отраженной час I'И волновоrо пакета, то Э1'О OДHOBpe
менно даст, что вероятность нахождения CBeTOBoro кванта в друrоt1
части равна нулю. Опыт на месте отра}кенной половины пакета
производит тем самым HeKOTOpo действие (сведение волновоrо
naKeTaI) на сколь уrодно удаленном расстоянии, rде находится дру-
rая половинз, и леrко видеть, что это действие распространяется
со сверхсветовой скоростью.. Одновременно, конечно, также видно,
что подобltое распространение действия никоrда не может быть
использовано для Toro, например, чтобы посылать сиrналы со сверх..
св товой скоростью, так что изложенное здесь поведение BOJIHOBOI'O
пакета никаким обраЗ0М не противоречит основным постулатам
теории относительности. ,
d) Измерение энерzuu. Определение энерrии свободных элек--
тронов тождественно с измерением, скорости частиц и поэтому
новое обсуждение различных уже изложенных методов является
излишним..
1) JL,J1S1 CBeTOBoro кванта простраНС'i'ВQ
только три измерения, и таким образом максвеллевские
быть рассматриваемы как шрединrерОБское
801'0 кванта.
с:нова
CBeTO
34
Друrой еще неизложенный метод измерения энерrии свободных
электронов состоит в том, что электроныI заставляют проходить
через некоторый известный пороr потенциальной энерrии. Если
электроны перейдут этот пороr, то тоrда по классической теории
обыкновенно принимают, что их энерrия была больше, чем энерrия,
соответствующая высшей точке потенциальноrо nopora, если же
они будут отражены, то принимают, что их энерrия была меньше,
чем это критическое значение" Такое заключение несомненно не...
правильно в квантовой теории, поэтому мы здесь коротко остано-
вимся на рассмотрении этоrо пункта.
Если энерrия электронов меньше, чем критическое значение
потенциала, то все же всеrда некоторое количество электронов
может еще перейти потенциальный
пороr, еСJIИ ero Iпирина не велика
в сравнении с длиной, соответствую...
щей электрону де бройлевской
волны. Число проходящих электро"
нов убывает показательно с воз..
растанием П1ИРИНЫ и высоты по""
pora. 1)
И обратно: если бы энерrия
электронов и была достаточна дли
перехода через пороr, все же
всеrда'еrце значительная часть элек-
тронов отразится от пороrа в том
случае, если возрастание потенциала
происходит на отрезке, который не мноrим больше чем длина
де бройлевской волны электрона. Для практически ВЫПtJЛНИМЫХ
экспериментов изменения потенциала всеrда, конечно, происходят
на отрезках, которые велики в сравнении с длиной волны электро-
нов, таким образом, можно практически в большинстве случаев
вычислять по классической теории.
Как пример для математической трактовки только что изло...
женноrо положения вещей, рассмотрим отражение электронов
резко возрастающей потенциальной стены.
Мы пользуемся уравнением I.Ilрединrера
трона (М ' 2 и 3). Для падающей Ф волны
сти 1 :
1
1{
с
р.
v
PJJ;
I
!
\
Рис. 11.
одноrо элеI(
место в обла-
1) Этот факт вполне аналоrичен известному из ОПТИКИ и эксперимен-
тально установленному явлению, что при полном отражении CBerOBoro
луча ОТ металлической фольrи очень малая ДОЛЯ света проходит через
фольrу. Эта доля будет заметна только тоrда, коrда ТОЛIцина' фольrи
Toro же порядка, что и длина волны ПРОХО,l1ЯIдеrо света,
.
'! 1 О
ер ==-- ае , 2tJ-
Для проходящей волны в области II имеем:
1
, 2t-t
ДrJЯ отраженной волныl в СТИ 1
r1 а " е Р,
I CI>
о
Если р' х МНИМО, то имеет место полное отражение и
принять р' х полотитеJlыIo мнимым. На ПJIОСКОСТИ
х О и оставаться непрерывными,
ОТСlода
а [
I
(а
1 РХ
I
а РХ
х
Число электронов, ПрОХОДЯIЦИХ в единицу
деленное сечение, дается (вплоть до мно'Н{ителя
ности) произведением И3 квадрата аб олютноrо
на импульс, т" е. для падающеrо, проходsпцеrо и OTpa}l{eHHOrO
(ДJIЯ ве'iцественных р' х) имеет место:
J==l a I 2 px; J' lal 2 1 2рх I J2p'x;}"
11) х Р х \
Для мнимых значений Рх' J' о и
веЧlIО, всеrда:
вероятность отра}кения или 11
COfJlaCHO (42):
\2
\
2, /
V ' VE V
1
р'
2
а f
р \'
1.+
J == J'
9лек')
W'
а'
}
а
\
I
1 )
а
х
J
I I ! Px p'x
a l !
J" .
)
51
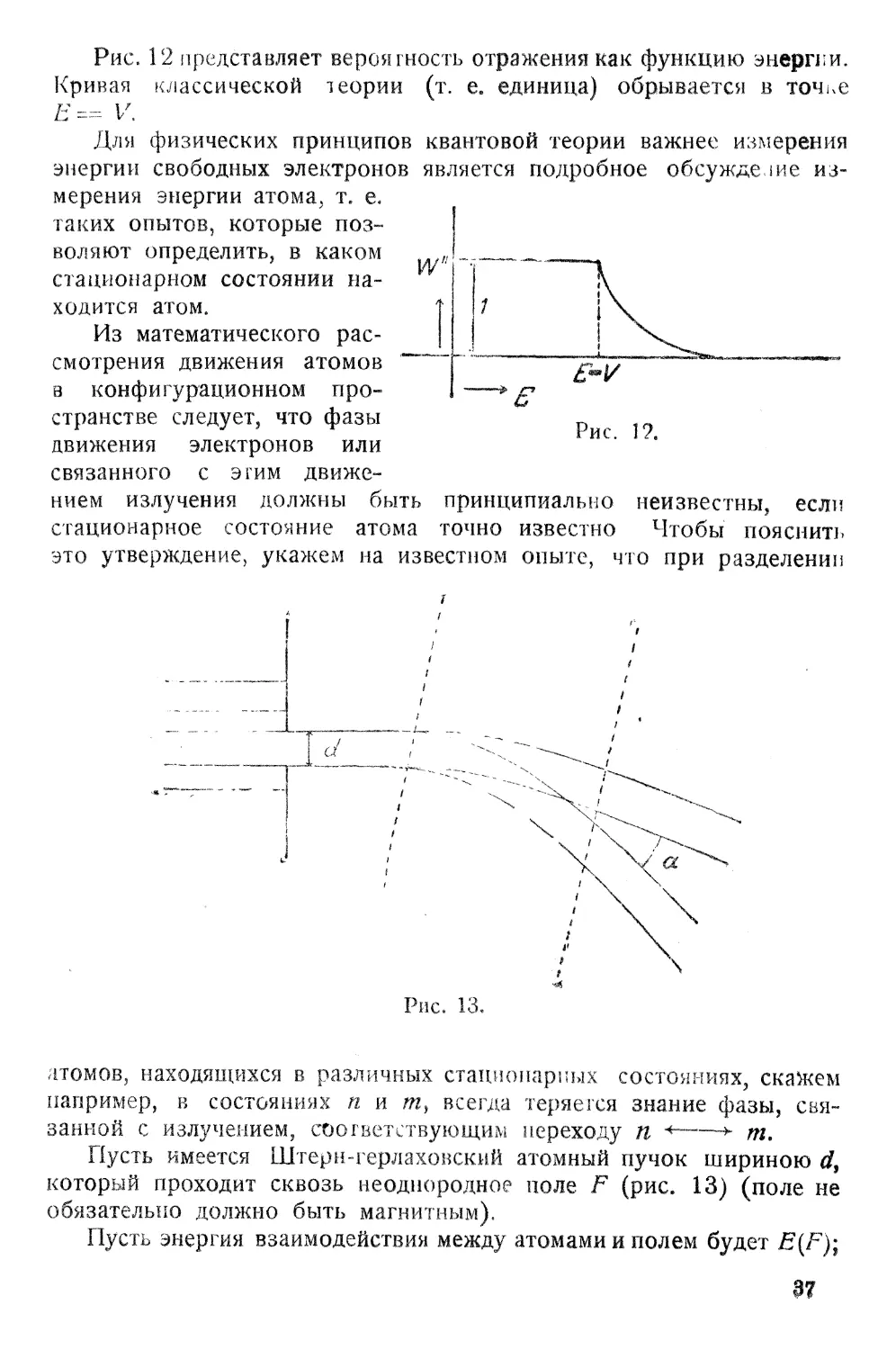
12 п [НОСТЬ отражения как ФУНКЦИЮ энерrl! И.
Кривая классической 1 еории (т. е.. единица) обрываетсSl в ТОЧI,е
== '.
l лн l1Jизических принципов квантовой теории важнее иэмерения
свободных электронов является подробное обсужде,IИ И3
мерения энерrии атома, Те е.
таких опытов, которые поз...
воляют определить, в каком
стационарном состоянии Ha
ходится атом.
Из математичеСI<оrо pac
смотрения движения атомов
в конфиrурационном про....
странстве следует, что фазы
движения электронов или
связзнноrо с э l'ИМ дви}кс
нием излучения ДОЛ)l{НЫ быть принципиально неизнестны, если
стационарное состояние атома точно известно Чтобы пояснит})
это утверждение, укажем на известном опыте, что при разделении
wJ.c
...............Е:
1
I
t
I
I
f
в ичных
В состояниях п и nz,
с И3JIучением
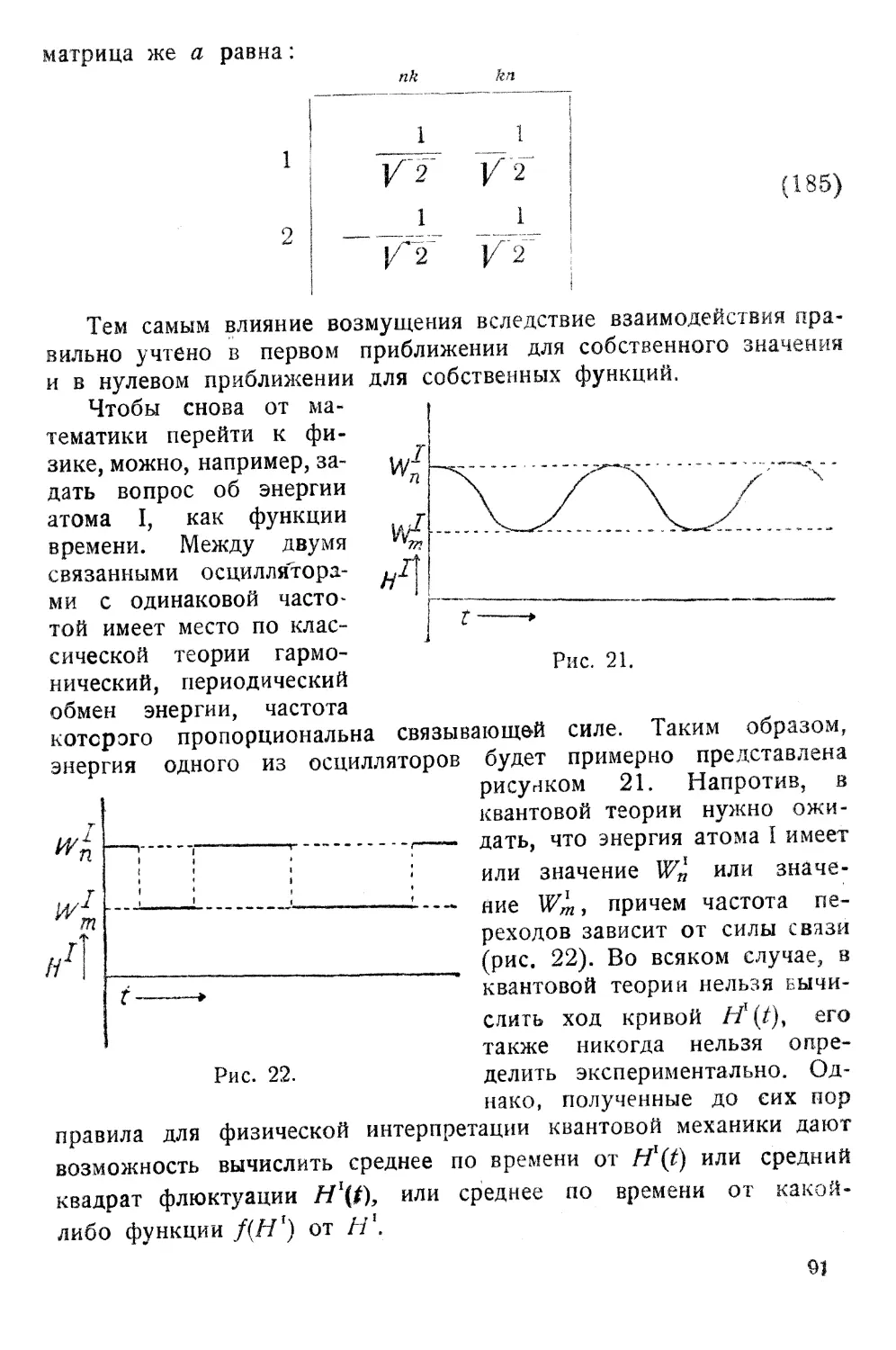
[fYCTb имеется
который проходит сквозь
ДОЛ)l{НО быть
энерrия взаимодействии между атомами и полем будет E(F);
,'"
I
I
I
I
t
I
I
j
Рис.
Рис. 17.
I
I
(
I
I
I
I
I
1
АI
,
,
'OIt!:
01
скажем
знание фазы, сня'"
п т..
атомный пучок шириною d J
поле F (рис. 13 ) (поле не
i17
им <,)ТКJIоняющая сида поля в направлении х при--
в нерпендикулярным к направлению луча) есть
дЕ(Р) dE' д?
дх == dF
Если Т время, в течение KOToporo атомы двиrаются в поле
а составляющая импульса атомов в направлении то от-
клонение атомов ll ro состояния будет 6
д !1/!). т
ду;
Р
(45)
И,следовательно, для
и m I'O состояний имеем:
уrлов отклонения (а) JJучей атомов п I'O
дх
(J. ==
(46)
р
а и быть больше, чем естественное рассеяние
aTOMHoro луча, чтобы было возможно разделение атомов различных
сортов, Т. е.
а
А h
d dp ·
(47)
Шрединrеровская ФУНКЦИЯ состояния п содержит периодический
2тci Е
множитель е 11: n t . Е в поле изменяется и вместе с тем изменяетя
частота и фаза BOJIHbl. Это изменение до известной степени не..
определенно, так как остается принципиально не наблюдаемым, rде
движется атом внутри aToMHoro луча.
Общая неопределенность изменения фазы Ll<? излучения, соот-
21С!
(Е п Вт)!
ветствующеrо комбинаuионному J<олебанию е n ,
поэтому
d(cJEb ) . д E ; ))
cp .". ..
h
11 И3 (46) и (47) следует сейчас }I{e
)
;
а это 0зва (IaCT
неопределенность
Это вычисление белее наrлядным, еСJIИ оrраничиться слу
чаем неоднородноrо маrнитноrо поля и применить теорему Лармора.
Если пренебречь спином электрона (собственным маrнитным м о...:
ментом эпекrрона), то, как известно, весь атом прецессирует во...
l(pyr направления маrнитноrо ПОЛЯ с уrловой скоростью
е .Н.
2 c
ill
скорость прецессии различна для различных атомов внутри
луча в виду ero конечной ширины.. Вследствие этоrо фазовые со..
ОТНОlпения между шаровыми волнами, посланными атомами, будут
НЗРУIllены" Неопределенность лаРМОРОВСI{ОЙ прецессии будет:
ф е дН d'
2 С дх '
fJ'
разность отклонения атомных лучеЯ для состояниА с маrпит"
выми квантовыми числами т и-ln 1 равна:
е a/i h
2 c
а==
р
Из Toro, что (1.
А
d
h
dp'
L\ф «1 Т> 27t.
...........,
Таким образом, все фазовые соотноrпения между атомами будут
полностью HapYlueHbl"
Бором 7 обсуждался следующий мысленный эксперимент. Атомы
Штерн-rерлаховскоrо луча, которые первоначально находятся,
ска)кем , в нормальном состоянии, прежде чем они попадут в Не....
однородное маrнитное поле, ДОЛЖНЫ быть возбуждены по сред..,
СТВОМ освещения светом резонансной частоты к излучению света
ФЛlооресценции.. Они излучают тоrда коrерентный резонансный
свет. Свойства коrерентности этоrо света MorYT описаны reo-
метрически посредством шаровых волн малой амплитуды, I(OTOpbIe
испускаются к а ж Д ы м атомом с (для каждоrо атома
одинаковой) разностью относительно падающеrо света..
чевидно, при этом неопределенным, ко..
леблется ли данный атом в нижнем ИЛИ в верхнем состоянии. Если
}ке атомы ПРОХОДЯТ через маrнитное поле, ОНИ вы..
нуждаются 1< обнаружению их стационарноrо состояния. ]:ак
J<aK по иа лоля относительно неQольшая
часть атомов излучает в BbICllIeM состоянии, то излучение, OTHOCJ '"
тедьно ero свойств коrереtп ности, может быть предстаВJlено как
сумма незначительноrо числа шаровых волн с большой амплитудоЙ,
т. е. во всяком случае оно ведет себя практически как
вполне независимых центров, ме}!{ду которыми не
каких фазовых соотношений. Следовательно, если
поле не оказало влияния на фазы излученных атомов
тоrда возн п{ло бы противоречие. Однако, уравнение
вает, что нарушение фазовых соотношений является
следствием измерения энерrии. Уравнение (48) снова, таким
разом, дает пример Toro, что измерение одной квантовой величины
(в данном случае энерrии) необходимо НЗРУПJает знание друrих
величин.. Из обсуждения мысленноrо эксперимента Бора
далее, что наличие ЭТОI'О нарушения непротиворе..
чивоrо проведения теории..
НИ
маrнитное
то
показы...
///. Критика
..,
80Л1l080и «артины.
в предыдуutf..'Й rлаве простеЙllIие эксперимеНТЗ1IЬНО
обоснованные основные факты волновой
предположены "правильными " Они были
пункт для критики корпускулярноrо
что это последнее может быть применимо только
",.,
rраниц и эти rраницы оыли
корпускулярная картина должна СЛУ}КИТЬ
критики волновоrо представления. И волновая картина применима
тоже только в известных rраницах, которые установить.
vIсторически, так же, как и в случае
были сперва построены т р е х м е р н ы е
(максвеллевские и де бройлевские ВОЛНЫ)
rраниц. Эти теории мы будем обозначать как КJIзссические вол
новые теории". Они находятся в таком же ОТНОПlении к
теории волн, как классическая механика к
J атематическая схема классической и
н М. (Читатель дол}кен быть же
классической волновой теории
ВОЛIi в фазовом пространстве.)
КОРПУСКУЛЯРНОЙ картины проведена также
волновоrо представления, ТО все противоречия
тинами исчезают, всеrда будут внимание
rраницы справедливости обеих
40
Е,
В волн ОН
и Mar..
первоначально ИСХОДЯТ из
например, при наблю
Эти понятия
как мы теперь
нам одновременно И3-
тоже применимы для
волновоЙ
MHoro
ВУ-"Iведены из
сначала теорией
скажем, значения и S) для напряжения поля (усредненные по av),
Если бы эти значения и были т о ч н о . известны, то это вы
звало бы противоре.чие с корпускулярной картиной.. Именно: так
как энерrия и импульс небольшоrо объема av даютсSI вы...
ра)кения
Е
1
бv 87t ( 2 I 2), @ ==
1
[ &],
(49)
то правые части обоих равенств при достаточно малых av
были бы сами достаточно малы, в то время как нам И3 корпуску"
лярной картины известно, что энерrия и импульс небольшоrо объема
всеrда состоят И3 отдельных конечных ПОРЦИЙ h и соответственно
hv
.. И так как для наивысшей частоты, которая еще может быть
с
hc
обнаружена, имеет место: hv '01 ('А. (0/), то правые части (49)
ДОЛЖНЫ быть н е о п р е д е л е н н Ы, как раз до значения порядка
этих световых квантов (hv и соответственно v ), чтобы не всту-
пить в противоречие с корпускулярной картиной. Между компо-
нентами и должны поэтому существовать соотношения неопре
деленности, которые и дают для вычисленноrо И3 (49) значеl.tИЯ
hc
неопределенность порядка 8/ и для Ф неопределенность порядка
h
01 " Если Ll и Ll суть неопределенности для @ и , то неопре
деленности для Е и & будут:
D.E == : {21 D. I + 21& D.&I (M )2 + (М))2)
А@х=== 4 8v {I [ D.&]x/ I [ ilS)]xl + I [il!& LlS)J J
7tC
и далее циклически для у и z..
Так как вероятнейшие значения для и
то члены в правых сторонах, содеРЖ,ащие только д@ и
быть сами по себе достаточны, чтобы дать нужную неопределенность
для и Ф.. Этоrо мы достиrнем, полаrая
., hc hc
Q;x.. Д y av о[ === o14
(и далее в
42
Эти соотношения неточности относятся к одновременному зна...
чению x И Sjy В О Д Н О Й и т о й же части пространства. Однако
в разных частях пространства x и SJy Moryr быть свободно И3...
вестны с любой точностью.
Соотношения (50) MorYT быть выведены точно так же, как и в
случае корпускулярной картины, непосредственно из перестано .
вочных соотношений для и (М 9). Именно, если разделить
пространство на конечные клетки величиной OV, то в лаrранжевой
функции L СМ. М (215), на месте интеrрала по dv появляется сумма
по всем клеткам OV пространства. Как канонически сопряженный
импульс к Ya.(r) в клетке r появляется тоrда [ер. М, уравнение (224)],
величина:
aL
8v дф (r) =-= avll,,(r)
и вместо М (231) следует:
h 1
П tt (У) ф@ (s) .......... ff (s) Па (У) == OO: Ors 2rr:i av'
(51)
(52)
3rs обозначает теперь обыкновенную Q функцию
( ors == { Д:Я Ф : }) .
в пределе av o (52) переходит в М (231).
В применении к электрическим и маrНИТНЬJМ НОJIЯМ из (52) и
М (259) имеем:
Q;i (r) Фа (8) Фа (8) Q;j (r) == 2hcia rs d al . (53)
ov
Если еще принять во внимание, что неопределенность Фh обу-
словливает для создаваемой Фh силы поля неопределенность но-
Фh
[151дка 01 ' то видно, что (53) приводит непосредственно к СООТ-
ношениям неопределенности (50).
Совершенно аналоrичные рассуждения можно было бы применить
также и к волнам материи, но нужно заметить, что вообще не
существует экспериментов, позволяющих непосредственное измерение
амплитуд , что можно заКЛ!QЧИТЬ уже из TOl O, что де бройлевские
волны представляют собой комплексные величины. Если бы И3
перестановочных СООТНОIllений для и * было сделано фор...
мально заключение о соотношениях неопределенности для вол...
новых амплитуд, то, при применении статистики Базе, это дало бы
физически разумный результат; при при.менении же действи-
тельно наБJнодаемой q)ерми дираковской статистики, напротив, по-
I
лучается лишенное смысла следствие, что Ф и * не MorYT быть
одновременно ТОЧНО измерены даже в совершенно различных точках
пространства, так как перестановочные соотношения 249) со...
дер)J{ат положительный знак. Удовлетворительно что
вообщ,е не существует опытов, позволяющих измерить значение (}
в определенной точке, в определенный момент времени. Матема-
тически это находит основание в том, что также и в выражении
взаимодействия излучения и материи часть, относящаяся к последней,
содержит ТОЛЬКО члены BToporo порядка относительно Ф (в виде
( f}*). Из вышеизложенноrо рассуждения МО}КНО также заключить,
что статистика Бозе для световых квантов является физической
необходимостью, поскольку будет сделано ка}l{ущееся вполне есте..
ственным предположение, что измерения напряжений электрическоrо
и маrнитноrо поля в разных точках пространства должны быть
между собою неззвисимы.
u
2. ИЛЛЮС 1 РАЦИЯ СООТНОШЕНИИ НЕОПРЕДЕЛЕННОСТИ НА
НЕКОТОРОМ ОПЫТЕ.
110добно тому, как при обсуждении корпускулярноЙ карти
жно быть ВОЗМО)I{llО И теперь непосредственно на опытах пока что
измерения @; и S) точнее, чем это да-
ется (150), неОL:уществимы. Простейш
метод измерения элеl{ТРИ ческих и м аrнит"
ных основан на отклонении
женных 13 этих полях
Одновременное и
IцеСТВJlяется посредством двух лучеЙ,
иаущих один в поло)китеЛЬНОМ t
в отрицательном направлении оси У,
ДЛЯ которых определяется отклонение
в направлении внутри луча
поле заметные неоднородности,
ТО становится и Tor да
простое измерение сил поля ПО от...
КЛОJiению становится невозможным. Мы примем, что
сечение Jlуча есть прямоуrольник;' в направлении
быть 81 [т. е. вся ширина ве"ТIИЧИНЫ
правлении Х мы предположим меньшую UIИрИНУ
возможно было независимо расположить оба
один над друrим (СМ. рис. 14).
Если расстояние между обоими лучами в оси Х
будет порядка '01, то и здесь возможные неоднородности в среднем
14.
уничт()жаIОТСЯ; иноrда расстояние между лучами возможНО и взрьи...
ДЛЯ этой це.пи. Набросанная здесь установка позволяет
изм'ерение @х и SJz, если поля внутри ( 1)3 достаточно однородны;
если же имеlОТСЯ значительные неОl(НОРОДНОСТИ, ТО измерение не
никакоrо определенноrо результата.
по r:
е
)
Вследствие eCTeCTBeHHOI'O
и
лучей мз
ИИ ТОЧНОСТЬ из
<&x
и
}1С
(55)
o/'r
Но СУIцестненпый пункт: наХОДЯlциеся в луче
электроны изменя.lОТ со своей стороны электрическое поле в
и В:\1есте с тем и путь I JtPYl'OI'O луча материи (отклонение обоих
дол)кно быть измерено одновременно). изменение не...
01 до некотороЙ степени, так как неизвестно в какой
JIуча находитсн ДВИ)КУIЦИЙСЯ электрон. (Такая неопределен'"
ность не имела если возмо)кно использовать
волн неопределен
и
р
(56)
1/1
и
б)
д
Izc
(al)4 ·
(57)
3'1'01"0
СООТНОIuениЙ
l(ОРПУСКУ ЛЯ рвоН и
J
теории.
1. МЛТFМ
Р.
11
случаях идет речь о применении линейной алrебры; можно, таким
образом, сравнить матрицы квантовой теории с симметричными
тензорами специальной теории отн6сительности. Как на существенные
различия должно быть указано на то, что пространство, к которому
относятся тензора квантовой теории, имеет бесконечно боль[пое
число измерений, и что это пространство не вещественно; место
ортоrональных преобразований заступают так называемые унитарные
преобраЗ0вания. . Если мы, ради Toro, чтобы получить наrлядную
картину, пренебрежем этими важными различиями, то каждую вели..
чину квантовой Теории можно представить посредством HeKOToporo
тензора, rлавные направления осей KOToporo MorYT быть нарисованы
в пространстве; чтобы иметь ясную картину, вспомнить о тензоре
моментов инерц и твердоrо тела. Направления rлавных осей для
каждой величины квантовой теории вообще различны и только
переместимые матрицы дают одинаковые направления. Точное зна..
нне какой..либо квантово теоретическоА
величины соответствует установлению в
пространстве HeKoToporo, вполне опреде-
ленноrо направления (луч в унитарном
пространстве) Точно так же, например,
посредством точноrо знания момента инер-
ции твердоrо тела определяется соответ...
ственная rпавная ось, к которой принадле
жит момент инерции (нужно принять при
этом, что не существует никаких выро",
ждений). Ha3B HHoe направление парап..
леJIЬНО, следовательно, той rлавной оси k тензора Т, которой
соответствует компонента Tkk 9Toro тензора, имеющая как раз
измеренное значение. Точное знание направления (с точностью
ДО HeKOToporo фазовоrо множителя) в унитарном пространстве есть
максимальное знание квантово",теоретических величин, которое мо-
жет быть достиrнуто.. Вейль 12 поэтому обозначил эту степень
знания, как "случай чистоrо собрания"" Атом в некотором (не...
вырожденном) стационарном состоянии представляет, например,
такой "случай чистоты". Характеризующее ero направление со....
ответствует той rлавной оси k тензора Е, которая относится к зна..
чению энерrии Ekk соответствующеrо стационарноrо состояния.
Очевидно не имеет никакоrо смысла 'rоворить о значении например
переменной рили q в названном (определяемом одной из rлавных
осей Е) направлении. Как известно, для механическоrо рассмотрения
какоrо-нибудь частноrо случая движения твердоrо тела столь же мало
достаточно задания момента инерции BOKpyr некоторой оси, отличной
от rлавной. Только тензора, направления rлавных осей которых совла..
nают с таковыми дЛЯ Е, имеют определенное значение в данном направ-
j{
Рис. 1
Аа
nении. В унитар:ном пространстве, например" общий момент коли....
чества движения атома может быть определен одновременно с энер"
rией. Если должно быть произведено измерение значения q, то
сначала вместо точноrо знания направления должно выступить не-
точное, которое может быть представлено, как снабженная коэф-
фициентом вероятности )) смесь t4 направлений, соответствующих
rлавным осям Е. Например при измерении положения посредством
микроскопа, неопределимая часть комптоновскоrо отброса пере..
водит "случай чистоты" Ekk в такую ,'"смесь" (ер. 11, 2а). Эта
смесь должна быть TaKoro рода, чтобы ее также можно было при..
нять за снабженную соответственными коэффициентами вероятности
смесь направлений, соответствующих rлавным осям q. Из полу..
ченной смеси измерение выбирает определенное значение q', как
действительный результат. Из Bcero процесса следует, что значение
q не может быть однозначно предсказано из опыта, позволяв' ero
определить Е, так как между двумя опытами имело место до из...
вестной степени не подлежащее контролю возмущение системы.
1-1:0 это возмущение определимо качественно, если знают, что в ре.
зультате должно быть известно т о ч н о е значение q. В этом случае
вероятность нахождения q, после Toro, н:ак Е было измерено, дается
квадратом косинуса уrла между пер во начальным направлейием »Е"
и направлением "q", или, правильнее, соответствующим этому
квадрату косинуса выражением в унитарном пространстве [S (Е, q)]2.
Это положение образует один из фундаментальных постулатов
квантовой теории и не может быть более непосредственно обосно-
вано. Из этой аксиомы следует: значения двух квантовотеоретиче-
ских величин связаны причинно друr с друrом тоrда и только тоrда,
коrда соответствующие обеим величинам тензора имеют параллель...
ные rлавные оси" Во всех друrих случаях не существует никакой
причинной связи. Решающим для статистической связи посредством
некоторых коэффициентов вероятности является вызванное измери...
тельными приборами' возмущение системы. Без наличия этоrо воз..
мущения не имеет никакоrо смысла rоворить о значении или о
вероятном значении переменной в некотором направлении в уни
тарном пространстве, если это направление не параллельно с на..
правлением одной из rлавных осей соответствующеrо этой п::,ре
мен ной тензора. Например приходится запутываться в пратино...
речиях, rоворя о вероятности положения электрона и не принимая
в рассмотрение примененный для измерения положения эксперимент
(отрицательная кинетическая энерrия, сравни стр. 35). Нужно также
подчеркнуть, что статистический характер зависимости основан
па том, чтр влияние измерительных приборов на измеряемую си-
стему трактуется иначе, чем влияние отдельных частей системы Dpyr
на друrа, ибо и это последнее влияние также обусловливает изме..
"?
произвести
ТО 1\10}КНО
r дев
тоноЙ механик'"
ности В
известные
пения направления вектора
:но эти изменения вполне
инструменты были ичислены к
ственно
выше, как
теперь
толькр
было
блюдений
были скажем,
избежать
счете проследить
БЫJlО только,
исчезла и осталась
JIение на
таким образом
системой не
наБЛlодатель, вмес ro
п фото
КОНЫ
И В кнан 1'0
моменты
l'лаННhIе оси
только атомы, находяп{иеся в стационарном состоянии п, проходит
через поле Рl' сильно неоднорОДtlое в направлении пучка и вызы-
ваlощее п реходы в виду резкой неоднородности.. Относящаяся к
Р 1 ФУННЦИЯ прсобраЗОf.{ания пусть будет "S ; вероятность найти
атом позади Р 1 в состоянии l1Z равна, спедова, ельно, Is ;l12 IIJ Поел
HeKOT ) 'Oro отрезка пути атомы проходят через второе поле Р 2
подобное пе, 'ВО ОтнОСЯllхаяся к нему функция преобраЗ0вания
пусть будет S }. Позади Р 2 и
будет опр',"дслят,.ся о ар....
пае состояние атома..
Для ато которые по-
за Рl были В состоянии т,
)
вероятность перехода состоя-
ние 1 при ПРОХОII<дении через
дается ажением I 112.
Соrласно ЭТОЙ apr ментации
о число атомов, которые после ПрОХОЖ1ения Р 2 находятся
в СОСТОЯН1И l, должно быть : H выражение\l
r:
V
f
v
Рис, 16.
I
т '
I
12 I 2
(1) I S ( .;)
! ml..
(58)
с ('ароны функция ! реобраЗОВ:1НИЯ, ОТНОСЯlцаяся к по
ля и Р2, R целом, есть
(12) (1) (2)
Sпl == ....)пт Sml,
т
1. число атомов в СQ\.:ТОЯНИИ 1 позади Р 2 ДОЛЖНО быть par НО.
2
) S (l)
.... п т
т
2
(2)
Sтl ,
(59)
S (12)
п!
ЧI(j про иворечит (58)..
Но НрОlиворечие исчезает, СJIИ ПРИНЯfЬ ВО внимание, что фор...
мулы (58) и (59) в деЙСТВИТ )J1ЬНОСiИ ОТНОСЯl'СЯ к двум раЗЛИЧНЫ:VI
о ытам. ВЫВОД (58) илен T0J11,KO тоrда, коrда ме}кду Р 1 и Р 2
имел сто ЭКСlIеримент, ПОЗВОЛЯlОЩИй определить стационарное
состояние аlома. Такой ЭКСllерим нт пео"бходимо изменя:,т фа 'у
относящейся к 11Х-НОМУ СОСТ'JЯНИЮ ПlрединrерО8СКО волны на Не....
извеСТНУIО величину порядка те, как это было вычислено в 11, 2 d.
При ПРИ1\:енении ырз)к ния (59) к этому эксперименту нужно
умножить ПОД 3 ,аком суммы й член (1) S на некотоrую
фазу e icpm и, наконе образовать среднее по фазе от
В.
49
правой части (59). Как nerKO ВЫЧИСЛИТЬ, ЭТС> среднее по фазе
совпадает с (58). Если же межr!у Р 1 и F 2 не имел места никакой
лромежуточный опыт, по валяющий определение состояния, то ко..
He4Hы 1 результат опыта ; ается формулой (59); ВЫВОД тоrда
неправилен, так как т о r Д а в о в с е н е л ь 3 Я О О Р О Т О
что между Р 1 и Р 2 атом наход а ом т пр е...
деленном состоянии.
ОХdрактеризуем еще раз все три
различать между собой.
1 э к с пер и м е н т. lVlе>нду и атомы не Б03-
мущения. ВерОЯIНОСТЬ для СОСl0ЯНИЯ 1
S
т
2
11 9!{ С пер и м ( н М 2}КДУ И F 2 имеет 1\1 есто некоторое
воздействие на атомы, П о 3 В О Л Я 10 Щ е их стационарное
состояние; однако результат нзмерения не
викает )7 смесь".) Вероятность состояния
2
т
111 9 К С пер и м е н т.
l.оздей-.': вне на атомы,
состояние; это измерение дает
состояния 1 позади Р 2 (СТЬ
имеет место некоторое
их е
I s i 12 .
Различие ме)кду случаями П и ПI привычно уж И3
теории. Принципиальное рзэличие 1 и Il, однако! образует» будучи
соответственно обобп{ено, центральный пункт квантовой 'Iеории.
Здесь Так}ке видна связь с преДЫДУIцеrо параrрафа.
И мерение н \ величины 11 состоит, вообще
I'ОВОрЯ, в ТОМ, Чl'О мы наблюдаемую систему, которой величина 11
перед измерением сопоставлена с неточыостью Ll 1 '1l, изменяем тан:,
что после измерения эта величина 'может быть ей соr:оставлена
С меньшей неточностью Ll 2 11 Ll 1 11. Этот процесс измерения, со...
rласно сказанному, должен быть разделен на два CTporo раэличае-
1\1ые a (Ta. Первый шаr измерения состоит в том, что под..
верrается внешнему, физически реальному, измеНЯЮlцему собы-
ТИй воздеЙСТВИIО, например: освещение светом или пuля.
Это воздействие приводит к тому, что наблюдаемая
ходит B "смесь" со вообще rоворя мноrих, НО
60
ЛЯ которых остается общим то, что величина 1J может быть им со-
поставлена снеточностью il 2 '1).
Второй акт измерения выбирает из бесконечно БОЛЫllоrо числа
СОСТОЯНИЙ смеси некоторое вполне определенное,как действительно
реализованное. Этот второй шаr представляет собой qроцесс, ко..
торый сам не воздействует на ход событий, но который только
изменяет наше знание реальных соотношений.
3. БОРОВСКОЕ ПОНЯТИЕ ДОПОЛНИТЕЛЬНОСТИ.
Мир понятиА, возникших из повседневных опытов, был впервые
оставлен в эйнштеЯновскоR теории относительности. \ Там выясни..
лось, что обыкновенные понятия можно применять только к про-
пессам, в которых скорость распространения света может быть
практически рассматриваема как бесконечно большая. Уточненный
опытный материал современной экспериментальной физики прину..
дил, таким образом, к пересмотру старых и к образованию новых
понятий. Но наше мышление моrло только постепенно свыкнуться
с расширенноА: областью фактов и ее миром понятий И поэтому
-теория относительности казалась сначала ЧУЖДОЙ и абстраJtтной.
Как следует И3 скаэанноrо ДО оих пор, опыты И3 мира атомов при-
нуждают к еще более далеко идущему отказу от привычных ДО
сих пор понятиА. Наше обычное описание природы и в особен-
ности мысль о строrой закономерности в процессах ПрИрОД I осно-
ваны, в действительности, на предположении, что явления возможно
наблюдать, не оказывая на них З8метноrо влияния. Относить неко"
торое определенное следствие к определенной причине имеет СМЫСЛ
только тоrда, коrда мы можем наблюдать следствие и причину, не
производя одновременно в пропессе нарушающеrо воздействия.
Таким образом, закон. причинности в ero классической форме мо-
жет быть определен, соrласно ero сути, только для замкнутых
систем. В атомной же физике вообще с каждым наблюдением С Я...
зано конечное, до известной степени не подлежащее контролю, воз...
мущение, как это можно было заранее ожидать ,в физике принци-
пиально наименьших величин. Но так как с друrой стороны каждое
пространственно-временное описание физическоrо процесса обус...
ловлено 11аблюдение.м этоrо процесса, то отсюда следует, что про..
странственно-временное описание процессов с одной стороны и
классический закон причинности с друrой представляют дополни-
тельные, исключающие друr друrа черты физических ПрОII.ессов.
Этому положению вещей в формализме теории соответствует то, что
хотя и cyrцecTByeT математическая схема квантовой теории, но эта
схема не может быть истолкована как простая связь в пространстве
и времени.
.
61
Блаrодаря этой ДOn61tнительности I1pOCTpaHcTtJeHHO"'BpeMeHHoro
описания с ОДНОЙ стороны и причинной связи С ДРУI ОЙ, высту'"
пает далее некоторац своеобразная неопределенность понятия "Ha
блюдение" , состоящая в том, что всеrда остается произвольным,
какие предметы нужно причислить к наБЛlодаемоtt системе и какие
рассматривать как средства наблюдения. В формаJJизме теории этот
произвол приводит К тому, ЧТО для ТОЛf<ования I<aKoro либо физи
QeCKOrO эксперимента часто MorYT быть использованы весьма раз..
личные методы, чему позднее будет приведено несколько примеров.
Но даже если и примириться С названным произволом, понитие
» ваблюдения «, CTporo rоворя, принадлежит к миру идей, взятых из
Ha111erO пО'вседневноrо опыта; оно может быть перенесеНQ на атом..
ные явления толы{о тоrда, коrда принято во внимание данное в соот",
НОLuениях неопределенности оrраничение всех нространственно вре...
менных картин. Так как каждое наблюдение 'по определению СВЯ-
ззно с пространствим и временем, то это понятие и имеет смысл
только внутри I'раниц, которые даются соотношениями неточноети.
Было УПОМЯНУТО уже раньше, что СУUJ,ествуют спеЦиальные случаи,
в которых требования классическоrо закона причинности в извест-
ном приближении MorYT быть соrласованы с пространственно-вре:
менным описанием. В общем случае, однако, положение вещей можно
охарактерИ80вать примерно слеДУЮlцей схемой (Бор, цитир. статьи):
......... Классическая I
теория
..........
Квантовая теоl'ИЯ
или ИЛ
I 'описание в простран-
стве и времени
.:
I Причинность
Описание в простран
стве и времени.
I
I ::::
(j) u
::1'::S:::s::
ca....
(.) C'Q U
CI')C
(l)
<:О:=:
Е--о
U u
Математическая cxc
ма вне простран-
ства и времени.
Причинность.
Соотношения нео-
пределенности.
Только после Toro, как при образовании лонятий будут сде-
паны попыIкии I1РИСrf'особиться к этой основной дополнительности
описания в пространстве времени и причинности, мо»<но будет cy
дить О свободе от противоречий методов квантовой теории (в осо-
беннос.ти интерпретации теории преобразований). Приспособление
нашеrо мышлеН'ПI и нашеrо языка к опытам атомной физики ВО
всяком случае, как и в теории относительности, связано с боль-
IIlИМИ трудностями. В теории относительности этому приспособле
иию очень помоrли философские дискуссии прежнеrо времени, ОТНО",
СИВlпиеСR к проблеме пространства и времени. r Iодобным образом
62
,можно и' в атомной физике иавлечь пользу Н8 ОСНОВНЫХ для всех
теорий познания рассуждений О трудностях, которые связаны с раз--
деле»ием мира на субъект и объект. Обсуждение некоторых аб-
стракций, характерных для современноf:iтеоретическоЯ физики, можно
найти уже в философии прошлоrо столетия. В то время, как эти
абстракции моrли быть тоrда, как иrра мыслей, отброшены основы...
вающимися только на действительности учеными, утонченное экспе-
риментальное искусство современной физики заставляет нас теперь
подробно продискутировать эти абстракции.
v. Обсу:нсдение ва:нснейших экспериментов.
в предыдущих параrрафах были подробно рассмотрены прин...
НИНЫ квантовой теории.. Действительное их понимание однако обу
словлено ПРИСПDсоблением нашеrо МЬПllления к положению вещей
созданному экспериментами, и особенно к только что обсуждав-
Iпейся взаимности закона причинности и описания в пространстве-
времени. IIo3TOMY обсуждение основных экспериментов OKa eT боль..
IlIУЮ пользу для понимания теории.
1. ФотоrРАФИИ ВИЛЬСОНА.
а) Существеннейшие черты ВИ,llЬСОНОНСКИХ фотоrрафиЯ MQI"YT
быть прежде Bcero истолкованы с помощью лассической теории
корпускулярноrо представления. Это толкование совершенно спра
ведливо также и с точки зрения квантовой теории, так каl{ при
измерении положения частицы в ВИЛЬСОНОВСI<ОЙ камере соотноше-
ния неточности (как это ясно подчЙспено в П) хотя тривиальным
образом и имеют место, но они несущественны для толкования
важнейших результатов вильсоновских фотоrрафий (наrlрИМер пря-
молинеtlности путей а.. лучей). Для заключений TaKol O рода клас-
сическая теория может быть всеrда по праву применима так же как
и для макроскопических процессов, так как квантовая теория су--
щественна только для более тонких сторон явления, так сказать,
внутри соотношений неопределенности.
) Несмотря на это, все же полезно обсудить ближе также и
квантовую теорию ВИЛЬСОНОБСКИХ снимков. Здесь сейчас же высту...
пает вышеописанный произвол понятия наблюдения, так как является
простым вопросом целесообразности: нужно ли ионизуемые моле-
кулы воды причислить К одной системе с а.... частицей или к на-
блюдающему прибору? Мы станем сначала на последнюю точку
зрения. Наблюдаемая система состоит тоrда И3 одной а.. частицы
и реэультат измерения положения посредством ионизации булет
представлен в математической схеме теории посредством пакета не..
ё
роятности JS(q')!2 В пространстве координат х, у, z, а.. частицы.
Последующие вычисления, удобства ради, будут проделаны только
для ОДНОЙ степени свободы частицы, скажем, для координаты q, 8. 9
Если положение частицы известно уже в преДIllествующие моменты
времени, то названное выше измерение положения дает, хотя и соот-
ветственно неточное, знание скорости (ер. 11, 2 Ь), которое позво-
ляет точное определение s( ч) п уравнению (11). Мы обозначим та..
ким образом снова через q, р средние значения q и р в мо-
мент времени t == о; через Aq, IIp средние ошибки. Значок О в Qo'
напоминает, что это значение OTHor ':СЯ ко времени t == о. Тоrда
для t == О имеет место, например со\ дасно 11 1:
(qo ({)2 21С; ( , )
. p q q
S(qo') == const. е (L1q}2 h lJ (60)
Для свободноrо движения, без действия каких либо сил, спраsсд....
ливы уравнения:
Р == onst == Ро 1
q == р, т. е. j
'; .
q -== p.t qo
}.t
Чтобы найти распределение вероятности в момент времени t, мы
Выч iслим по уравнению М (169) функцию преобраэования S(qo', q') :
( i 2 h . д д I + qo' ) S(qo' q') == q' )(qo' q'). (62)
fJ- 'P:l q О
Решением (62) будет:
21С/р' ( , , 1 fЙ )
q qo qo
S(Qo'q') ==const.e ht 2 о (63)
(61)
и МЫ НClХОДИМ для распределения в момент времени t СОI"ласно
JV\ (188):
S(q') == J S(qo')S(qo' q')dqo',
(64)
т. е.
S (q') == const. е
[q+) (q' Р)]'
i
1+
(65)
rде положено
h t 1 t 1
=:: . == IIp ·
21t ( q)2 дq'
04
далее следует:
I ,<)( q') 12 const.
((1 q)2
(Aq'f + (v: ь. р }J
(66)
t
Среднее значение , таким образом, равно р q, как это
1J.
и нужно было ожидать по классической теории, и средний квадрат
ошибки для q' равен Aq2 ( ; .Ар У , т. е. складывается из двух
частей, непосредственно соответствующих неточностям Qo' и Ро'
в момент времени t == О..
Если примен ть (66) к трем степеням свободы х, у, z а... ча...
СТИЦЫ, ТО видно, что путь пакета вероятности представляет прямую
линию, если отвлечься от расползания пакета. Но нужно заметить,
что уравнение (66) только тоrда имеет место, если а... частица
ДВИ)I<ется беспрепятственно.. Каждая последующая иониззцця моле..
кулы превращает пакет (66) в "смесь" таких пакетов (переход
от случая 1 к случаю 11 в схеме IV, 2). Если ионизация связана
с измеgением положения, то из ЭТОЙ »смеси" будет снова выделен
неболыпой пакет веР::1ЯТНОСТИ вида (60), как результат измерения;
он и образует исходный пункт для дальнейшеrо вычисления траекто-
рий (слуifaЙ III в схеме IV" 2) и То Д.
ОТСТУПJIения ОТ прямолинейности сзязаны с величиной изМеНе....
ния импульса при ионизации в отношении к импульсу частицы.
Отсюда сразу становится панятным различие между путями сх - ча-
стиц и .. частиц. Неопределенность изменения импульса связана
соrласно 11, 2 с веЛИЧИНОIО области значений импульсов выбро..
шенноrо И3 молекулы электрона перед столкновением, и таким об
разом косвенно с величиной молекулы.
Что касается формальной
числений, то НУ/ИНО отметить,
может быть сделано также кружным путем при
rl1И; соrласно М (188) вообll 'е имеет место
вы..
е от q о' к q'
энер"
S(qo'q') == f S(Qo' E)S(Eq')dE
(67)
а IIОЭТОМУ
f
, (Qo') (qo · S(Eq').
(68)
Функции S (Qo' Е) представляют обыкновенные шредин
l epOBCKIIe волны в фазовом пространстве. Функция S (q) может
быть ПОJlучена, таким образом, путем наложения таких шрединrеров
55
ских функций. Этим методом Дарвин 10 исследовал па
кетов вероятности.
1) Наконец, мы проведем еще математическую трактовку ВИЛЬ
СоиОвских фотоrрафий при предположении, что ионизуемые моле
купы ВОДЫ ПРИЧИСJlены к наблюдаемой системе. Это хотя и слож..
нее, чем предыдущие методы, но зато позволяет представить
менее странным чуждый HallleMY обычному представлению элемент
квантовой теории, который в преДЫДУП.I.ем вычислении сказался
в сведении (редукции) волновоrо пакета при наблюдении
не слишком затруднять вычисления, примем, что наша система кроме
а частицы содержит только две молекулы воды. Пусть далее
вектор импульса (РХ» Ру, pz) а.. частицы перед ионизацией точно
известен, следовательно, положение r (х, у, z) совеРПlенно неиз
вестно. Мы ИIl(ем вероятность Toro, что обе молекулы будут иони"
зованы, и покажем, что эта вероятность т о л ь к о т о r Д а при н и
м а е т з а м е т н о е 3 н а ч е н и е, l{ о r Д а л и н и с в я 3 Ы В а ю...
IЦ а я II е н т р ы о б е и х м о л е к у Л, пар а л л е J1 ь Н а н а п р а в л е..
н и ю с к о р о с т и а... ч а с т и Ц Ы. МЫ обозначим координатыI цeHT
рОБ тяжести обеих молекул, принятых за неподвижные, через
и Хн, )'п, Zп, а внутренние координаты молекул и {/Н.
liaIIIe конфиrурационное пространство заключает в общем коорди
наты (х, у, z; qI; qп). Мы пренебрежем далее взаимодействием
между молекулами; взаимодействие же между а-частицей и моле....
кулами рассмотрим как ВО3МУI.цение; соответственные
тоновой функции пусть будут НР)(х, QI,) и НП)
нР) и HiP рассматриваются как операторы, деttСТВУЮI.цие на вол.
новую функцию (х, У, z; QJ, Qп) шр..:динrеровской теори
Таким образом, шрединrеровское волновое уравнение
окончательно rласить 1)
( 8::' ( :: '
\
д 2
H O) (qI)
"v"
а-частица
(нР) HfP)
....... """"......... ........
Взаимодействие
MOJ1e MOJle
купа 1 купа II
'Х д )
2тci ' д! Ф =:: о.
(69)
). есть малый параметр возмущения, по которому
1) fl0СЛСДУЮIцее вычисление взято в существенном из работы Борна. 14
В дальнейшем мы пренебреrаем взаимодействием а: частиц С атомнымц
я Д р а м и в молекулах.
56
полаI'2С'М Ф (}О f
и получаем из (69)
01
}(70)
. t П) 1) И Т
(70)
на..
в
)
t
(71 )
и
ожеНbl по
ql И Чн должны
СРпl (qI) СРпп ( II),
ыть
" "'V(l)
. пт,
nп
(72)
мы разуем матричные элементы 9нерI'ИИ ВОЗМУllН НИЯ:
9п! (ц!) Il ) т! (х, z) СРтl ) !
тI (73)
1) (1) .
П <рпп (qп) == h пп mп (х, (qп) I
тв J
Нсвозмущенное состояние в момент t == О, И3 KOToporo
мы исходим, дается через
О. /1 О \, \ ( () [ О ) Е В ,(о)
п, == пI' п:::::: nн; 1" == 1"0 p .......... == ру; pg == pz J О
Подставляя (72) и (73) в (70), мы получаем:
( д2 д 2 )
Д == дх 2 + ду2 az 2 ;
( Ь2 ,,(O) (О) + fl д ) (1)
sit J }1 + Еn, Е1I1 2 1ti at 'V 1I ,1I11 (х, у, z, t)
( \ 1) + (1 ) ) ) 2 ( O 1; ') . (7 4)
b о (х, у, Z)e Q О h () (х,у, z о о е
п I пl n п n п n ll П ll nl nl
Если положить здесь
(1) (
v пI nll Х, )', z, t) == е
21ft ( О )
E t
h о (1) ( )
· W пI nп Х, У, z ,
ТО В силу
Е (й) Е (о) + Е (о) + ( (0)2
О .. о J () 2 РХ
пI II V#
(0)2 + (0)2 )
ру f}z
най дем:
{
h 2
A
81t 2 f1
[ If:/
Е(О) + E«(
"1 п II
(О) I 1 ( (О» ) 2 ]} (1)
Е п r 2 i' w пI nп ("t', у,
II fL
21ti ( O t)
h
а о ) е
п 1 "1
(75)
(h (t) ( ) '" +h (l) (
== о х,у, z r, о о Х,
n I n п 1'l п nп n п n п
I w ) nп (х, у, z) 12 дает соrласно IV, 1 в первом приБЛИЖLНИИ ве-
роятность Toro, что молекулы перешли, соответственно, в состоя-
ния nI и nп и а-частица находится в точке х, у, Z. ИЗ (75) мы
зан:лючаем, что в первом приближении :может быть возбу}кдсна
только о д н а молекула, так как иначе по (75), w пI nп исчезает, если
о
и пI и вместе с тем nп отличны от начальных значений пI И, COOT
ветственне, п I' Прежде чем перейти ко второму прибли)кению, рас-
смотрим поведение W(l) (х, у, z) в пространстве (х, у, z). Левая
часть (75) соответствует обыкновенному волновому уравнению
h
tJ.и + k 2 и == О, причем длина волны л === w вычисляется из
р
1 ( (1» ) о + ЕО Е + 1 ( \1(0) ) 2
2fi: \) Е", Еn, nll 1111 2}1 t'
(76)
в правой части (75) стоят ИСТОЧНИI<И этих волн. Таким образом..
выражение 'Ш(1) (х, у, z) может быть получено из принципа rюй...
58
I'eHca, путем напо)кения шаровых вопн описанноrо вида, соrласно
функции распределения:
21tt ( 110 )
(1) О) h 1" t
....... (hпo I п I (х, у, z) апо п n п + h n о н n lI (х, У, z) 3 п О I n r ) е . (71)
Если i!1 (р(О»)11 велико в сравнении с разностями энерrий в моле-
кулах, то леrко видеть, что w l!пJJf) (х, у, z) практически ОТЛИIffiО
ОТ нуля только в полосе позади молекулы 1, в направлении (O).
Поперечное сечение этой полосы (вблизи молекулы 1), соответствует
примерно размерам молекулы. Полоса имеет конечное расширение,
р /О)
.. n =
l :
...................
) W 11 l'
1 iJ. '
Л CE :: . -=
.
...........
о ,
111 11 л
Рис. 17.
СООТRеТСТВУЮIl ее относительно ничтожным изменениям импульса а..
частицы при возбуждении. То же самое справедливо mutatis mutan-
dis для w ; n ll (х, у, z) (СМ. рис. 17).
После ЭТОЙ подсоrовки мы перейдем ко второму приближению.
Из уравнения (70) для W 2!пll (х, у, z) следует:
{ h д r Е п . .. Е п + ЕnО Е п . +
8п 2fL I 1 I П Il
+ 1 ( (о) ) 2 ] } (2)
J;> W ЛI Л Н (х, у, z) ===
х' (1) [ (1) "
W тl т ll (х, у, z) h тI n f (х, у, z) Отпп п +
т I m п (18)
+ }l} ;l n ll (х, У, z) '3т! п I ] ==
::::= ]W ;пlI (х, у, z) h пI (х) У, z)
т I
(1) пО) ( )
Wпl т н mцll п Х, у, Z ·
т!1
IQ
Мы ящем условия, при которых w ) n п (п п 1 0, fl п ll н О ) мо-
жет быть заметно отлично от Н у ля. J!ля этих членов W ;)l1 в C Y M
1 п
мах в правой части (78) остается TOJIbKO по одномуслаrаемому т I ==
п I O И, соответственно, тв === n п о ; Т. е. w ) n только тоrда за...
1 п
метно отлично от Н у ля, коrда и л и W;l n И h ) n отличны ОТ нуля
1 П I 1
В одинаковых областях пространства х, \ у, Z, и л и w ? пОП И h IпII
ОТЛИЧНЫ ОТ нуля в одинаковых областях пространства (х, у, z).
Э т О в о 3 М О Ж Н О Т О Л Ь I{ О Т О r Д а, к о r Д а и л и м о л е к у л а 1
л е ж и т в п о л о с е w : п п И iI и м о л е к у л а 1 1 R П О Л О С е w ; ПОп.
Если обобu ить эти рассуждения па случай любоrо числа моле..
KYJI при этом не появится ничеrо H080ro...... то тем самым прямо-
линейность путей а...часrиц будет доказана. То, что неопредеnенность
изменения импульса при ионизации связана с точностью иамерения
положения........... именно с величиной молекул, сказывается в этом вы..
ЧИСJIСНИИ при применении принципа rЮЙI'енса. l..IeM менее область
источников h(l) (х, у, z) рассеянных волн, тем БОЛЬUlе телесный
уrол "ПОJIОС' 1v(1). Прерывное изменение 11акетов вероятности
стало бы здесь иrрать роль, однако, только TorAa, коrда мы 3 а....
дали бы вопрос о "возможностях наблюдения ионизации молекул.
2. ДИФФРАКЦИОННЫЕ опыты.
т
УI
а) J иффракция лучей света и материи от peIllerOK (д ВиссоН..........
lLжермер, Томсон, Рупп, Кикучи) может быть простейшим образом
объяснена с помощыо классиче..
ской волновой теории света й Ma
терии. Применение пространствен..
но-временной волновой теории к
этим опытам вполне оправдывается
также и с точ и зрения квантовой
теории, потому что для rеометрии
волн соотношения неопределен..
насти между волновыми амплиту"
дами не иrрают никакой роли.
Квантовая теория будет сущеет..
венна только для вопросов об энер"
импульсе волн и Т. П.
) Квантовая теория\ волн во всех существенных пунктах явле..
ний диффракции совпадает с классической волновой теорией,
поэтому представляется излишним приводитъ математическую схему
этих вычислений. С друrой стороны ПО Дьюэну 15 можно получить
..
х
Рис. 18.
tЮ
интереСНЬtА вывод диффран:ционных явлений И3 кванто ой теории кор-
пускулирноrо представления. Мы представим себе ПРОСТQТЫ ради
отражение корпускул ОТ плоской штриховой решетки (постояннан
реlпетки d). (Штрихи параллельиы оси z перпендикулярной к чер-
тежу рис. 18,,) Если представить, что решетка сама подвижна, то ее
перемещение в направлении х может быть рассматриваемо как
пеРИОДl'Iческое движение с периодом d, посн:ольку в расчет при...
нята будет только взаимодействие падаЮIЦИХ частиц с реIuеткой,
так как при смещении всей решетки на отрезок d это взаимодей-
ствие осrается неизменным. ОТСlода можно заключить, что Движе...
нне реlнетки в направлении Х "проквантовано " импульс Рх мо"
h
ЖСl' изменяться только на целое кратное знач ния d (ер. в преж-
нем представлении квантовой теории: f pdq === nh).
Так как при отражении частицы от реlпетки импульс всей
системы сохраняется, то х",овая составляюu{ая импульса частицы
h
изменяется TaK}l{e только на целое {{ратное d- Отсюда следует:
,
Рх === Рх
h
m(j"
(79)
Кроме Toro, решетка в СИ 11У ее большой массы не мо)кет ПQПУ-
ЧИТh заметной энерrии, таким образом:
Р '2 +J) '2 p 2 Р 2 p 2
х y х y '
(80)
{} УI'ОЛ падения, а' УI'ОЛ отражения луча, то имеет место
cos f} === РУ ; sin.f} === рх
р р
sin {}' sin f} == т d ·
(81)
Из формулы М (203) для ДЛИНЫ волн, сооrвеТСТВУIОЩИХ кор...
пускулам, елепует:
(sin {}'
sin О) d =:::: !nА,
(8 )
R соrласии с волновой теорией.
"() То обстоя ельс'fВО, что материя и световое излучение имеют
как корпускулярнь е, тан: и BOJIHOBbIe св!)йства, до об'ьясненин
l{l3антово теоретических принципов давало часто повод к эатруд....
нениям. В особенности часто оБСУiкдался следуюu ий парадокс:
силы взаимодействия между отраж нными от решетки электронами
и материей UIТРИХОВ реПlетки быстро :)lвают С расстоянием;
61
таким образом, для направления отражения Moryr иметь значение
только непосредственно бливкие к частице штрихи р\:шетки.
Несмо1рЯ на это и удаленные штрихи имеют влияние на 01ражеfiие,
так как вся решетка в целом определяет остроту максимумов в иф-
фракции. Основанием этоrо противоречия являе ся смешени;:: двух
, ,
различных опытов (ер. 9ксперимеАТ 1 и iI в IV, 2) Если н е и м е е т
места опыт, ПО3ВUЛЯЮЩИЙ установить положение электрона перед
отражением, то нет никакоrо смысла rоворить о положении элект-
рона и поэтому вполне понятно, что вся решетка имеет значение
для процесса. Если же такой опыт для измерения положения
электрона (с точностью fJ.q) имеет место, то он изменяет импульс,
а вместе с тем и длину волны электрона на частью неизвестную
величину
( Ар )
qJ
Отражение происходит тоrда в неточно известном lfаправл нии,
. А )
,<ак это и нужно ожидать при отражении от немноrих ( ; штри-
ХОВ решетки. Если I:1q будет меньше d, то диффракционные мак-
( 1, \
симумы стаНОВЯl св совсем размытыми Ар > ([)' Однако в том
случае, если измерение положения действительно производится,
можно все же сделать более точные заключения о пути соответ...
cTReHHoro ЭJIектрона (различие между П и III в IV, 2); например
решить, попадет ли элекrрон на штрих решетки или нет и т. д.
3. ОПЫТ ЭЙНШТЕЙНА И РУППА. 16
ОДНО из нротиворечий между теорией световых квантов и вол...
новой теорией казалось можно было установить на слеДУlощем
опыте: в каналовом луче светящийся атом летит параллельно экрану
мимо щели S шириною d (см рис. 19). Испускаемый атомом
и ПРОХОДЯЩИЙ через щель свет наблюдается в точке Р в спектро...
скоп. Пусть скорость атома в луче будет V, частота испускаемоrо
им монохроматическоrо света v. Так как свет от атома может
достичь Р только за короткий промежуток времени t, в который
атом ПРОJIетает как раз МИМО щели, то наблюдаемый в Р поток
ВОЛН имеет конечную длину и ero частота мо)кет быть поэтому по
законам оптики определена только неточно. В Р будет наблю-
даться, следовательно, расширение линии v порядка.
1 v
fj, \j
у t d'
(83)
02
Напрот в, по квантовой теории света расширение JlИНИИ ка-
жется невозможным, так как атом испускает монохроматический
свет, а экран не может изменить энерrии CBeTOBoro кванта, так как
экран хотя и получает импульс, но, в силу своей большой массы,
не может получить энерrии. Ошибка этоrо рассу}кдения, соrласно
Бору, ваключае'l СЯ в пренебрежении эффектом Допплера и рассеянием
света Hr\ щели. Световые кванты, попадаЮlцие ив атома в Р, не все
испускаются перпендикупярно направлению луча; также и те све-
товые кванты, KOTopr.Je бу.LLУТ испуu ены под уrлом а к направле-
нию (атом Р), порядка
. :l
Sln а r-.J
d'
(84)
: .
1/:... .' а
IV!IIМO&JИ.llуq:. Z
_ '\J
S : ri '
I t
t .
I ,
: I
t
,
t
MorYT попасть в Р вследствие рас...
А.
сеяния порядка d ня IЦ ЛИ. До! В-
лер..эффект ИСПУlItенноrо ЭТОМ на...
правлении имеет величину
л . v
LJ.V Sln а 'У,
с
р
(85)
'IiI
Рис. 19.
т. е.
л. v v
..., r-.J .. V,.....,..,J
d С d
(86)
в соrласии с (83).
Также и в рассмотренном эдесь опыте еТрОI'ая справедливость
закона сохранения энерrии д.пя ча'СТЯЦ соединима с требованиями
классической волновой оптики.
4.. ИСПУСКАНИЕ, поrЛОIЦЕНИЕ и ДИСПЕРСИЯ ИЗЛУЧЕНИЯ.
а) Прu.мен,ение заICОflО8 сохранения. I{ачественное толкование
поведения атомов в процессах излучения возмо}кно уже на ОСНО"
вании постулата о СУlltеСТВОllании дискретных стационаРtlых со...
стояний И теории, световых квантов. Действительно, это толкuвание
и было первым решающим успехом боровской теории. мыI ПОВl о-
рим вкратце важнейшие качественные результаты этой теории.
Пусть стационарные состояния атома, начиная с нормальноrо, пере-
нумерованы через 1, 2, 3.. . (ер. схему урuвней рис. 20).
Атом в (остоянии 3, например, может из этоrо состояния,
посредством испускания CBeTOBoro кванта hVЗ2! нерейти в состояние 2;
ТЗl{же атом из состояния 1, например, может, поrлощая световой
68
н:взнт hv] 3, перейти в состояние 3. Нужно особенно подчеркнуть,
ЧТО только что высказанные положения следует принимать
буквальнр, и что они ни коим образом не имеют только "СИМВО
лический характер", так как можно, например, посредством опытов
Il1терна..rерлаха экспериментально установить, в каком стационар..
НОМ состоянии находится атом. ОТСIОЛЗ, специально, следует, что
интенсивно,:ть какой нибудь линии испускания циональна
числу атомов в верхнем (ОТНОСЯlцемся к этой линии испускания)
состоянии; точно также интенсивность какой..либо линии п ['ЛОIце...
ния пропорциональна числу атомов в НИ}l{нем, ОТНОСяtцемсн к соответ-
ствующей линии поrлощения,'СОСТОЯНИИ. Эти результаты, достаточно
часто подтвержденныIe опытом, характерны для квантовой теории.
Они не MorYT быть выведены из классичской теории ни волновой
НИ корпускулярной картин, так как уже существование дискретных
значений энерI'ИИ не может быть объяснено классической теорией.
Совершенно :ш:е co
отношения имеются в теории ДИС"
персии, в особенности
Horo рассеянноrо
кали. 17
Если атом в состоян 1 будет
воэБУЖ:lен световым квантом h'l, то
он не изменя состояния,
же световой квант
масса aToMHoro ядра принита
может также
перейТИ в состояние 2 и при этом и смещенный в сто...
рану длинных волн световой квант /xv'. Интенс IBHQCTb обоих ВИ"
*"
дав рассеянноrо света пропорциональна числу атомов в состоянии
1. Если атом в состоянии 2 будет освещен светом час оты '1, то
ОН может при переходе в состояние 1 испускать, как иекоrерент",
ный рассеянный свет, также световые кванты к )РОI КОЙ
длины волны hv'. интенсивность 9Toro сорта рассеЯННОI'О
света (антистоксовский рассеянный свет) пропорциональна числу
атомов в сосrОЯJ1ИИ 2. Это было подтверждено
опытами Рамана. 18
Ь) Полная тра/(mО8/(а. Однако эти качественные заключения
о законах сохранения не Д1ЮТ по существу никаких сведений
относительно интерфереНЦИОННflIХ СВОЙСТВ испускаемоrо атомом
света или о значениях вероятностей переходов. Для нения
интерференционныIK свойств света достаточна, ,<ак наприме;->
В, опыте Дэвиссона..Джермера, клаССИЧЕ:СКЗ,1 теория.
теория ничеrо не изменяет В rеометрии
Однако q вероятн стей
4
э
2
1032
13
IUJ
1 .
64
менение квантовой теории, хотя и можно, как показал Кдейн,
посредством умелой комбинацйи aprYMeHTOB принципа соответствия
и квантовой теории материи избежать применения квантовой теории
излучения. Но такая формулировка проблемы излучения пред-
ставляется не вполне удовлетворительной и может привести при
поверхностном применении к неправильным заКЛlочениям.. Во вся...
ком случае приложение Э1'оrо метода соответствия требует боль....
шой осторожности при учете различных требований квантовой
теории.
Последовательное рассмотрение явлений излучении получается
при применени r : квантовой теории к излучению и материи, при
этом, конечно, безразлично, исходить л ,'1 И3 корпускулярной или
И3 волновой картины. Дирак в своей теории излучения 19 употребляет
язык корпускулярной картины, но при выводе rамильтоновой
функции использует частью следствия волновой теории излучения.
Здесь будут вкратце приведены только основные черты этой теории.
Атом предстаВJlен электроном, движуrцимся в электростатическом
силовом поле 4)0' По Дираку 20 релятивистски инвариантное ура вне...
иие для зада и одноrо электрона rласит:
РО + ; Ф О + О:, (Р' + ; Ф i ) + <X 4 fLC === О (87)
или
н == еФ о <Xi C Vi+ Фi) Ч.tс 2 ,
фо скалярный потенциал, Ф, (i == 1, 2, 3) электромаrнитные потен
циапы; по одинаковым значкам всеrла суммируется (i == 1, 2, 3).
Здесь, как и раньше, Pi обозначаIОТ канонически сопряженные qi
моменты, ai операторы, УДОВЛ ТВОРЯЮIЦi е уравнениям:
[ 1 для i == k
СЧ(Хk + (ХkGЧ == 20 ik ; C%iCX4 + cx4Gti== о; 0:42 === 1; Oik == О в друrих (89)
случаях..
(88)
Из уравнений движения следует,
дН. дН
Pi=== aqi ; qi== дjJi:='
а; тожд ственны, следовательно, с матрицами скорости вплоть до
множитеJIЯ .......... С. ИЗ (88) следует, что энерrия взаимодеЙствия между
атомом и полем излучения может быть написана в виде:
а,.с
(90)
.......... с:че q) i === q i Ф i ,
С
(9])
5 В. l'ейве:нберr"
если положить
ИУJJIО.
fамильтонова
излучения, имеет
скалярный потенциал поля излучения равным
функция всей системы, заключающей атом и поле
таким образом следующий вид:
е .
Н всей системы == Натома + qi Ф ' + Н поля излучеНJIЯ. (92)
С
Чтобы привести задачу к простой матемаТ.1ческой форме, рас-
сматриваЮI' поле излучения в сосуде; таким образом, решение
маI<свеллевских уравнений для сосуда дает систему ортоrональных
функций, по которой MorYT быть разло}кены Фi. Соrласно М (246),
как коэфициенты системы opTOrOHaJIbHblX ФУНI{ЦИЙ появляются
величины
2тr.! в r
h N 2
а , == е r ,
N r означает число световых квантов собственноrо колеба..
ния 1':. Обu ая энерI'ИЯ поля излучения (без взаимодействия) просто
выражается в этих переменных
Н поля И3Лj чения == N,llV r .
r
(93)
При разложении Фi "по Оt"тоrона,IЬНОЙ системе, отдельные члены
раЗЛО}I<ения зависят еще от положения атома в сосуде. Но так как
эта зависимость в KOHe'IHOM результате исчезает при усреднении,
ссли сосуд принят достаточно БОЛЫI1ИМ, то целесообразно в отдель-
ный член раЗ{lожения ввести "среднюю ({ амплитуду таким спосо-
бом, чтобы квадрат этой средней амплитуды овпал со средним
зна чением l<вадрата пеРВQна чальной амплитуды; здесь" полразуме..
вается среднее значение по всем возможным положениям атома
в сосуде. Т'аким образом для Фi получается:
1 1 1 21\:[ 2ni 1
Фj == ( 2 CY cos GЧ{ : ) 2" [ N r 2 e h °r + e 7! 6 r Nr2j; (94)
r
('J.ir означает здесь уrол между электрическим Bel<TopOM собствен...
Horo колебания r и осью qi; О, есть число собственных колебаний
в интервале частот Il'/r и в телесном уrле Фr, разделенное на
66
1:1'J1".6.<Or, Итак для rам,илътонои-ОЙ ФУНКЦИИ всей системы мы полу--
чаем:
1 1
Н -== Натом + -.., Nrh r + ( 2 h ) q'r ( 'Jr ) 2
С ТСС I О/
r r
1 11'a 2ТСl 1
r hf), ...... тв !' Т ]
N r е + е N r ,
(95)
rде qr означает компоненту вектора q в направлении 9лектрическоrо
вектора собственноrо колебания r.
Из (95)' MOl'YT быть непосредственно выведены все результаты,
которые выше ,были получены путем применения законов сохране-
ния, так как постоянство Н следует, вообще, из уравнений кван-
товой механики. Из (93) вытекает далее, что для испускания или
поrлощения CBeTOBoro кванта hV r важен тот матричный эле..
.
мент Qr, который относится к соотвеТСТВУЮl1l,ему переходу атома.
Вплоть ДО множителей, которые здесь не будут ВЫЧИСЛЯIЪСЯ, Be
РОЯТНОСТЬ перехода непосредственно дается квадратом этоrо матрич"
Horo элемента. Если ПРОкJзвести вычисление для случая возмущения
(члены взаимодействия рассматриваются как небольшое возмущение),
то в первом приближении получаются только процессы испускания
и поrЛОlцения, а ВО втором так}ке и дисперсии. Мы опускаем здесь
ВЫ'-Iисления. 1)
Недостаток формулиров;,(и (95) rа\1ИЛЬТОНОВОЙ функции для
излуче ия ааключаеl'СЯ в ТОМ, что ,она как будто не содержит ука..
ваний относительно свойсrв интерференции и коrерентности И3ЛУ-
чения. Но это верно только тоrда, коrда в (94) вводится, как это
было сделано выше, средняя амплитуда. Если же оставить действи-
тельные амплитуды, которые следуют из разложения Фi по системе
орrоrональных функций, то последние, будучи составлены из реше..
ний максвеллевских уравнений, rарантируют нам, что интерферен",
ция и свойства коrерентности излучения соответствуют макьвеллев",
СКИМ уравнениям. Например, МНО}l{ителями у величин a r см.. М
(246) появляются реlпения максвеллевских уравнений; эти МНОЖИ'"
.тели исчезают в области rде находится атом, если максвеллевские
вектор"потенциады исчезают там, скажем, вслсдствие интерферен-
1) ,Иирак (вьппе пр'Иведен. статья) вместо rамильтоновой функции (88)
употребляет прежнюю шрединrеровскую форму. Однако, при примене..
вии (88) все выIисленияя упрощаются, так как в знерrии взаимодействия
выпадают члены квадратичные относительно Ф i; результаты при этом те же,
что и у Дираr<:а.
*
67
ции. Поrлощение света не имеет места также в тех областях, 'в
которых по классической теории интерференции поrлощение
было бы невозможно.. Из этих рассуждений непосредственно еле..
дует, что классическая волновая теория достаточна для обсуждения
всех вопросов коrерентности и интерференции.
5. ИНТЕРФЕРЕНЦИЯ И ЗАКОНЫ СОХРАНЕНИЯ..
Для нас всеrда является большой трудностью наrлядно предста-
ВИТЬ, что квантовая теория света He противоречит требованиям
максвеллевских уравнений. Потому раньше еще, до понимания кван"
товоЙ теории, нытались построить реПJенияуравнениtl Максвелля
в випе иrольчатоrо излучения. Такие решения имеют смысл также
и в квантовой теории, так как если какой' либо опыт дает воз..
можность сделать заключение о направлении, в котором испускается
СЕетовой квант, то этот опыт автоматически строит решение макс-
веллевских уравнений названноrо типа (ер.. редукция волновых
пакетов в Э 11, 2 с).
Как пример мы рассмотрим связанный с испусканием cBeTOBoro
кванта отброс. 21 Атом должен перейти при испусканци CBeTOBoro
кванта из состояния 2 в состояние 1, при этом ero общий импульс
испытывает соответствующее изменение. Так как в данный момент
мы интересуемся только свойствами коrереНТНQСТИ излучения, то мы
воспользуемся упомянутым в 4 Ь методом принципа соответствия,
который применяет для излучения классическую теорию. Как источ...
ник излучения служит распре.:еление зарядов, соответствующее BЫ
ражениям М (205) КJlассической волновой теории материи. Атом
представляется посредством электрона [масса 11, заряд е, коорди-
наты t е(е, "1" С)], враlцающеrося BOKpyr ядра [масса М, заряд е, KOOp
динаты ik(X, у, z)].. Шрединrеровская функция для стационарноrо
состояния n, в котором атом как целое имеет трансляционный
импульс (Р Х) Ру, Pz), имеет вид:
2 i 2 ;
h rS тЕп,р t
е. tf n (te tk) · е
,
(96)
t-11 e Mrk
rде t s == 11 М представляет координаты центра тяжести.
Если обраЗ0ватъ относящиtiся к пеl еходу ' матричный
элемент "лат насти вероятности, то мы получаем:
2'lti ( т ' ) 21i.i
h 1" 1-' 1:8 h( EпtP Eт,p )t
е tk)Фт *(t e t k ) е . (97)
Усредняя это выражение соответственно по координатам ядра и
электрона и складывая, мы получаем ПJIОТНОСТЬ заряда, которая бу-
68
дучи принята за виртуальный источник 'излучения, и дает нам еве'"
деиия относительно коrерентности испускаемых лучей.
Для обеих частей получается (множитель е при общем заряде
выпущен, t == re tk есть переменная интеrрации; соответствую...
щиП элемент объема dv):
2тс' ( ')te J 2т t( ') 21ti (E E ,)t
Pe==e h е h +M Фп(r)Фт*(r)dv.е h (98)
2rci ( ')tk J. rci t( ') 2rci (E E')t
'Pk== е h е h !J.+ M jn(r)Фт*(t)dvе h ,
т. е. общая плотность заряда будет:
2тс! [( Ч5')t ....... (Е E')t]
h
Р == с onst · е ,
(99),
rде значение постоянной неинтересно для последующих рассужде,
ний. Совершенно аналоrично построенные выражения получаются и
для плотностеП тока. Испущенное этим распределением зарядов
излучение опредеJlИТСЯ через запаздывающие потенциалы:
f (t ; )
Фо(Р) == R dvp,;
рр'
(100)
соответственные выражения имеют место и для Фt. R обозначает
расстояние между переменной точкой Р', по которой интеrрируется
и точкой Р (смешение с аБСОЛЮ1НЫМ значением общеrо импульса Р,
конечно, не представляет опасности), в которой должно быть Вычи....
елена ИЗJlучение.
Таким образом, находим:
f [< I)rp, (E E') (t R p' )J
ФоС Р ) == const dvp' е (101)
(и соответственно для Фi).
Если принять теперь, что положение атома каким"нибудь апы...
том определено с известной точносrью (тоrда импульс может
быть известен только соответственно неТQЧI10), ТО это 03Н34зет,
что распределение заряда плотности р имеется только в конечной
области пространства, ПQЛО)J{ИМ ,6,v. Если при этом излучение нссле..
дуется на ДЗJlеких раССТQЯНИЯХ от д.<'V J ТО Rpp' МQжет быть разложено в
оэ
ряд. Если, например, начало координат ле>кит в 6v, ТО прибли..
женио мо}кно положи ть:
Х р
Rppl== Rp · Хр/
Rp
У р Zp
YP' Zpl
Rp яр
(102)
Тоrда из (101) имеем:
2 i (E .E') (t ; ) f v .e 2 i ( ' v : )rp' ( 10ij )
Фо(Р) == const. е Rpp'
!:,:о
Здесь положено Е............. Е' == hv.
Потенциалы заметно отличны ОТ нуля только там, rде мНОжи....
тель при tp' в показателе меньше, чем обратные линейные размеры
(д!) l объема V; во всех друrих местах излучение изчезае1 вслед..
ствие интерференции и мы получаем:
\13 \15' == hv p
с Rp
h
/ll
(104 )
11'/
Таким образом, атом испытывает отброс велич.ны ( С 1'01.1
С
ностью ДО естественной неопределенности :z ). Если направление
отброса экспериментально установлено (поскольку ЭТО позволяют
соотношения неопределенности), то излучение ведет себя вотно"
шении свойств !<оrерентности как иrольч'атое излучение, потен...
циалы KOToporo представлены формулой (103). НО ЭТО иrольчатое
излучение есть ТОЛЬКО возможный частный случай, КОТОрЫЙ экспе...
риментально ОСУlllествим TorJla, !(оrда qs и ' известны достаточно
точно, а координаты центра тяжести неrочно. Друrой частный
случай имеет место тоrД8, коrда экспериментально место центра
h с
тяжести атома устанавливается точнее, чем 'l == v == А, т. е.
точнее, чем длина волны испускаемоrо света. Уравнение (103) даеr
тоrда правильную IllЗРОВУЮ волну, а об отбросе ничеr'о нельзя
h
сказать, так как неопределенность отброса Дl больше чем ero
hv
вероятное значение .
с
На этом примере весьма ясно видно, как в квантовой теории
и световые волны также теряют первоначалвную реальность) кота...
70
PYIO они имели в классической теории, поскольку COOTBeTCTBYIOU{e
аТОМНОМУ излучению решение максвеллевских уравнений зависит
от нашеrо знания координат центра тяжести атома.
6. ЭФФЕКТ КОМПТО,НА и' ОПЫТ КОМПТОНА-СИМОНА. 3
Совершенно аналоrичные соотношения мы находим и в теории
эффекта Комптона, и, :хотя вычисления вполне сходны с выкладками
предыдущеrо параrрафа, мы все же приведем снова важнейшие
результаты. Иытереснее при этом исходить из рассмотрения не ева..
бодных, а связанных электронов, потому что Torlla (если принять
положение aToMHoro ядра заданным) уже наперед имеется некоторое
знание относительно положения рассеивающеrо электрона. Законы
сохранения дают:
h'J + Е == hv' + Е'
Il'J А h'J', + '
.e /. .:.1 == e р.
с с
(105)
Здесь буквы без штрихов относятся к переменным до столкно
вения, со штрихами после столкновения; обозначает импульс тран-
сляционноrо дви/кения электронов, е и, соответственно, е' еди-
ничные вектора в направлении движения CBeToBoro кванта, p обо..
значает область изменения импульса электрона в атоме. Если
, h'J
мало в сравнении с р и , то (105) дает соответственно точные
с
сведения о связи на равлений е' и. '; если ' будет, например,
измерено в вильсоновской камере, то ожидаемое излучение имее1
все СБойства иrольчатоrо излучения; так как установлено напра..
в..i.ение, в, котором будет ИСПУI.цен световой квант. Если ' ,
то собственную функцию трансляционноrо дви)кения можно при-
ближенно рассматривать как плоскую ВОJlНУ (t вектор координаl
элеI(трона):
:1tJ(V't E '/)
е h ..
Пусть собственная функция исходноrо состояния Е, принятоrо
211:[ Е!
за нормаЛlн)е, будет E(r)e h , rде Ф соrласно (37) отлично от нуля
в области, линеt1ный размер которой f11[ 111.l 1 '"'-' п].. Падающая
волна с частотой 'J возмущает эти волновые функции, причем
функция В03МУIцения представляет собой периодическую функцию
с
пространственных координат длины волны А == , так что в кон( ч-
'J
71
НОМ счете, как возмущение распределения заряда, появляется выра...
}i{ение вида:
2п! . ( re ) 21ti ] J
т Е! 211:l r .......vt. h [p'r Е'!
р const -f(t)e · е · е == ( 106 )
21ti [( h'l h 1 ) ( Е " I ]
е.........,.. t........ E +hv)t
== const .f( х)е h с ,
rде снова ftt) отлично от нуля в области линейноrо размера,......" Al.
Если опять образовать, как в (103), запаздываЮIp.ие потенциалы на
далеком расстоянии от атома, то получим (обозначения те же, что
э1
и в (103); R: == е'):
21ti (Е....... Е' hv) (t ).
Фо(Р)==сопst.е h с
2 тr.i ( h'l 1 hv', ) ( 1 07)
J dV J .....L """'.fJ ......... e r ,
о f(tp') е h с еР;
Rpp'
область ато ма
при этом положено hy' == Е........... Е' + hv.
Множитель в (107), ззвисящий от времени, показывает,ЧТО
частота рассеянноrо излучения есть v' и СОО1ветствует уравнению
(105). Далее, вследствие интерференции интеrрал в правой части (107)
исчезает, если мно}китель при 'Ср' значительно больше, чем обрат-
ное значение линейноrо размера атома, Отсюда следует, в силу
Toro, что дlJд 1 "'--' h :
h V }l V '
е == е' 1.>' =t: 1L.\vl (108)
с с
в соrласии со вторым -уравнением (105), Таким образом, рассеянное
излучение ведет себя в отношении l<оrерентности, как иrоль-
чатое излучение. Впрочем, направление CBeToBoro кванта не
предписано вполне точно, что можно рассматривать, как следствие
неопр деленности импульса в исходном стационарном состоянии.
Эта неопределенность импульса может быть уменьшена, если опыт
производить на слабо связанных электронах. При этом, конечнu,
соответственно увеличивается поперечное сечение атома. Если про-
извести рассуждение для возбуждеНfIоrо атома, то вм\есто Ll Ll,,1 h
появляется СООТНОllJение (37) lIA 1 r--w nh и при оценке эапаздыва..
ЮIЦИХ по rенциалов нужно принять во внимание число узловых по...
верхностей в ф(r); так как в этом случае возникают только не
имеющие значеция УСJlожнения, то мы оrраничились рассмотрением
нормальноrо состояния.
Если МЫ хотим объяснить опыт rейrера...Боте 22 об одновремен...
tlОСТИ появления ЭJIекrроно 9т6роса и рассеянноrо CBeTOBoro
.,
кванта, то нужно, если при этом оrраничиваются изложенным здесь
методом принципа соответствия, ввести плотности зарядов, излуча...
ющих только в некоторый определенный интервал времени. Исход-
ное состояние электрона можно представить, скажем, как покоя...
щийся, конечное состояние, как движущийся волновой пакет.
Тоrда плотность заряда, получающаяся из произведения обоих паке.
тов, может быть отлична от нуля только OqeHb KupoTKoe время.
Возникающее излучение состоит поэтому из оzраfluчеflliОZО потока
волн, распространяющеrося со CKOpOCTblO света. Более' последова-
тельное, хотя во всех существенных чер rax и эквивалентное объяс-
нение опыта rейrера Боте можно ПОЛУЧИТI') из квантовой теории
излучения. В последней справедливы, впрочем, как было показано
раньше, законы сохранения, примененные к световым квантам и
электронам, так что безо всяких сомнений можно употреблять
обыкновенную корпускулярную теорию вышеназванIJыIx опытов.
u
7. ЯВЛЕНИЕ ФЛЮКТУ АКЦИИ ИЗЛУЧЕНИЯ.
Доказательство Toro, что БОЛЫIIие средние значения квадратов
флюктуаций, получающиеся из корпускулярной теории, действи-
тельно заключаются в математической схеме квантовой теории,
будет проведено во второй части лекций (М 5). Но особенно
поучительно проследить отношения между различными физическими
картинами, с которыми оперирует квантовая теория, на флюктуациях
HeKoToporo поля излучения. flYCTb нам дан сосуд QБЪf;ма V с нэлу--
чением, находящимся в температурном равновесии. Тоrда средняя
энерrия Е небольшой части объема il V в интервале частот между 'V
и v+ь.v по планковской формуле будет:
Е == 8 1tV 2 Ii 'V hv ( 1 09) ,
с з ( е :; 1 )
(k ....... больцманновская ? стоянная, Т температура).. Для среднеrо
квадрата флюктуаций f1E2 энерrии Е соrласно общим законам, тер...
модинамики имеет место:
АЕ2 == kT2 dE
dT J
Т. е. в данном случае, как показал ЭЙНIlIтейн: 23
Квантовая теория. Волны частицы
,...
........ .....л....
f1E2 == hv. E +
l'
I
классическая
теория vастJЩ
с 3
Е2
8 1ty 2LlvLl V
t
классическая
еорВ. BOJl
(11 О)
78
Это значение среднеrо квапрата флюк' уации получается из
классической теории только частично. КОРПУСКУЛЯРНQе предста ле.
вие Д1lет сцачала:
Е == hv .. п, ( 111 )
rде п обознач\ает среднее- число световых квантов в объеме V с
частотой между 'J и 'J + v; отсюда, соrласно законам теории веро-
ятности, следует:
...............
iln 2 == п; т.. е..
АЕ2 == (h'i)2. п == hv E.
(112)
Таким образом, классическая теория корпускулярной картины
дает тол.ко пеР6УЮ часть форм}{лы (110)со Напротив, классическая
волновая теория излучения приводит точно ко второй части (110).
Относя\щwес'я сюда вычисления будут даны ниже в связи с кван-,
товой теорией. Для вывода (110), как ВИДНО, 1iеобходима квантовая
теория, причем, конечно, безразл.IЧНО, I:IСХОДИТЬ ли из волновоrо
или корпускулярноrо представления. Если ДТ1Я рассмотрения про...
блемы используют конфиrурационное пространство частиц для
световых квантов, что, правда, не было последовательно 1) про-
ведено до сих ПОР1 23 то нужно принять во внимание, что цся
система термов этой проблемы может, быть разделена на не-
комбинирующие частные системы, из которых одна определенная
может быrь выбрана как решение (М 7). В силу ..лерестановоч-
ны,х сеОТНОШ,ений М (260), получаl0ПJ.ИХСЯ через соответствующие
соотношения неопределеННОС11И, нужно BhI5paTb такую систему Tep
мов, собственные функции I<ОТОРОЙ симметричны в координатах
световых квантов. Этот выбор приводит к статистике Бозе для CBe
ТОВЫХ кванто-в и, как пок зал Бпзе, к уравнениям (109) и (11 О).
Если исходить из волновоrо представления, то мы от амплитуд
собственных колебаний, как и в М (246), придем к числу свето-
вых квантов, связанных с соответствующими колебаниями и, вместе
с тем, к той же математической схеме. 24 Чтобы не слишком услож
нять вычисления, рассмотрим вместо излучения в сосуде колеблю-
I ЦУЮСЯ струну длиною 1. Пусть qJ(X, t) ее боковое отклонение, а c
скорость распространения звука в струне. Функция Лаrранжа для
9TOfO случая будет:
L == ! [ ( aqJ ) 2 ( д ) .2 ]
2 с 2 д! дх
( 113)
1) Прим ред. Недавно JIандау и Пайерпс (СМ. литературн. указатель 23)
пострuили теорию фОТОНОВ в конфпrурационном пространстве. Их схема
эквивалентна теории квантовой электродинамики rеИзенберrа Паупи и со-
держит те же трудности.
. 74
,'. с.
11 1 д
с 2 д!
(114)
и
"
н J{ с 2 А
о
1
( _ '-Р ) 2 } dХ == [ ( 1 ( t,p ) 2 + ( q:» 2 ) dx (115 )
дх 2 \ с 3 at at .
Далее справедлины перестановочные СООТНОI11ения
П(х)<р(х') <р(х') п(х) == (x х') 2 i. (116)
При подстановке
со
/ 2 7t
<р(х, t) == 1 t qk(t) sin k l х
k==!
н п рехолит В
ff 1}J i qk 2 + (k Yqk2}
(117)
ДаJlее
положить
1 ·
Pk с 2 Qk,
Iz
/Jkql qlPlC == °hZ 2 .- .
7tl
(118)
н (ер. М 246):
../ k тr ./ h f 1 6k B" }
Pk V сl V tNk е +е N k
(lk==V IС tI -t {Nk}е21tiОk е 2 ' BkNk;H
Собственные частоты струны будут
с
'Vk === k "
( 119)
( 120)
113} (11 7) имеем таким образом.
00
---,
· (N k
- )
2"
(121 )
k l
76
Однако, для энерrии в неБОЛЫlIОМ отрезке струны (о, а) получаем:
('II"'Y)
1 1.. 1t 1t I
E==yJ lC2qjqk sin jyX sin k7 x + (122)
о j, ",.=1
+ qjq/tjk ( У cos j cos k : х} Ifx. J
Если ИЗ этой суммы специально выбрать ЧJJены j === k, то, при
непременном предположении, что входящие в рассмотрение длины
а
волн все меньше а, получим значение т Н =::: Е.
Таким образом, флюктуация IiE == Е Е получается, если иа
(122) вычеркнуть члены j == k.
Интеrрирование дает:
100 . { l. ( 1t ) 2 }
E== 2[ . CfQjQk!Vk+jkqjqk Т K'jk I
j,k 1
j =/-= k
(123)
rде
sin ('/} V k) !!:. sin ('/} + '/ k) I
с с
Kik == С С
'Jk)
I (124)
sin (Vj Vk) ; sin (Vj+ Vk) ; .
K'jk== С +с
('Jj 'Jk) (Vj+Vk)
Поэтому для среднеаО квадрата фЛIоктуации получаем:
1 { 1 '7""'"7"""'" ( 7t ) 4 ')
E2 == 2[2 .': CiQ/qk 2 l(2jk+ j2k 2 Т Q!Qk 2 K'jk +
},k == 1
k
+( )2 :2 jk ( Qj{zjQkqk + qЛiqkqk) !VkКl ik }. (125)
Сумму по j и k целесообразно затем заменить через интеrрал
ПО частотам '/j и '/k при предположении, что струна 1 очень длинна,
так что ее собственные колебания лежат плотно друr к ДРУIу. На-
конец, примем еще, что а велико и используем соотношение
+V
1 J sin2 va
Вт 2 j(v)dv;=: тr.f(O) для 'Jl' '12 > о;
а V
0."":'00
У;
(126)
7'
1'оrла двойной интеrраn переходит в простой и мы находим:
AE2 ; !dV{ :4 ( qv 2 )2 + [( 2;V )2 qv 2 ]2 +
( 21t'Y ) 1 2 2 }
+ с 2 C2[(Qv Q v) + (qvqv)] .
( 127)
в силу перестановочных соотношений (118) имеем:
h
qvQv == Qvqv == с 2 .. 4п}
(128)
и ДЗJlее
. а J { 1 ( 21t'Y ) 2 }
Е == c dv с 2 Q'J2 t c q,/2 ==
== ; J dv.z,hv (Nv+ ).
(129)
Здесь Zvdv обозначает число собственных колебаний в интервале
21
частот dv, т. е. в этом случае Zv == .
с
Если распространить интеrралы по интервалу частот Av, то по...
лучим, следовательно
а ( 1 )
E==T'Zv..!lv.h'Y N"+T о
(130)
АЕ === ; Avl+( ::v Y (hVY]. (131)
Затем делят Е на среднюю тепловую энерrИIО Е* и на энерrию
при абсолютном нуле
а hv...... а
Е== Е* + TZv 'Y2 Е* + e f1'Y..h'J (132)
и находят
l ( /:;""* ) 2
== 2: Av aA
2 Е* с . hv 1
af1 'J 1
h'J ·
(133)
А'У ..
а
1
Это значение ТОЧНО соответствует формуле (110). Уравнение
классической волновой теории получается, если в (133) перейти
77
к пределу h О.kлассическая теория, таким образом, ПрИВQДИТ
только К первому члену уравнения (133). Квантовая же теория,
которую по желанию можно интерпретировать и как корпускуляр
НУЮ И как волновую теорию, приводит к полной формуле для
флюктуаций.
. u
8. РЕЛЯТИВИСТСКАЯ ФОРМУЛИРОВКА КВАНТОВОИ ТЕОРИИ..
В большинстве проведенных в этой книrе обсуждений требова..
dИЯ теории относительности БЫJIИ оставлены без внимания. Выве..
денные результаты поэтому справедливы вообще только для тех
опытов, в которых скорость света может быть рассматриваема прак"
тически бесконечной. rраницы справедливости ДОПУПJ,енных до сих
пор формулировок можно, по}калуй, принять несколько более ши...
рокйМИ В теории излучения, но вообll(е в наСТОЯlцее время постоян-
ная с отмечает поrраничную .ЛИНИЮ между неисследованной и иееле..
дованной областями в квантовой теории. В вопросах о принци-
пиальных основах мы оrраничились поэтому вполне до rоверными
данными теории. Ниже мы обсудим вкратце попытки релятивист...
екай ФОРМУЛИРОВI{И теории и связанные с ней затруднения. Дирак
установил релятивистски инвариантное волновое уравнение для за..
дачи одноrо электрона (ср. V, 4 Ь), которое удовлетворяет тре..
бованиям как квантовой теории, так и теории относительности.
Существенные трудности для тзкоrо уравнения лежат однако в на-
личии соотношения
Е2 == u. 2 C 2 +p p2 + tJ 2 1 p 2
с 2 I х 1 У"I z
(134)
для свободноrо движения электрона, соrласно которому для данных
импульсов всеrда возможны два значения энерrии, отличающиеся
друr от друrа только знаком. Это обстоятельство приводит к тому,
что в каждой атомной задаче на ряду с обычными значениями
энерrии существует бесконечно MHoro отрицательных собственных
значений, не соответствующих д йствительности. Вероятности
перехода из состояний с положительной в состояния с отрицатель-
ной энерrией также никоим образом не Moryr быть рассматриваемы
как малые, так что, собственно rоворя, весьма удивительно, что
для положительных энерrий, по крайней мере в одно электронной
задаче, можно получить значения, соответствующие действитель
ности. В особенности разительно выражается, как отметил Клейн,
названная трудность в том, что соrласно какому..либо волновому
уравнению, которое использует непосредственно выражение (134),
9лектро.rlЫ MorYT беспрепятственно проходить через потенциальные
пороrи высотою 2 c2. Если рассматривать, например, только
'18
ДВИЖение в направлении осих (Ру == pz == О) и произвести вычи--
сления II$ 2 d COrJ1aCHO с (134), то получается:
Е2
С2==11 2 с 2 +рх 2 (135)
СЕ ) == !1 2с2 + Р
с 2
Т. е"
, 2 2 + (Е vy Е2 .
Р х Рх I
flаправо от потенцнаJIьt10rо... пороrа волновая функция имеет вид:
2ni ( , E 'J. )
pxx t
е h ( 1 3,6)
Для очень малых значений V р'х веlцественно, т. е. получаются
проходящие волны, как и в II, 2 d. Для больших V р'х мнимо и
волна испытывает полное отражение на пороrе. Попадающая в
Qбласть П (ер. рис. 11) часть волн материи убывает по показа-
'тельному закону. Однако, для очень больших значениЙ V р' х снова
становится вещественным, Т. е. электроны MorYT с известной веро-
ятностью беспрепятственно проходить через очень высокие потен....
циальные пороrи. Более точное вычисление показывает, что эта
вероятность не равна нулю. Друrая, несколько иная трудность
возникает в релятивистской квантовой теории в связи с вопросом
об энертии созданноrо электроном поли. J(ля точечноrо электрона
t
электромаrнитная энерrия эrоrо поля будет, как известно уже из
классической теории, бесконечно большой. Поэтому классическая
теория, чтобы избежать этой трудности, прину,кдена ввести неко-
торую универсальную длину, имеrfНО диаметр электрона.. 3амеча-
-'
тельно, что в нерелятивистской квантовой теории, соrласно Иор-
дану и КлеЙну, 38 возможно через соответственный выбор порядка
непереместимых множителей в rамильтоновой функции совершенно
избежать появления этой бесконечной собственной энерrии элек-
трона. В релятивистской теории поля до сих пор еIпе не найдено
подобноrо выхода.
Часто высказывается надежда, что квантовая теория после раз-
реluения только что названных проблем, может быть, снова будет
в значительной степени сведена к классическим понятиям. Но даже
поверхностный взrлнд на развитие физики за последние тридцать
лет показывает нам, что скорес, наоборот, можно ожидать еще
более широких оrраничений классическоrо мира понитиИ. В доба-
вление к изменениим нашеrо обыкновенноrо пространственно..вре..
19
MeHHoro мира, которые были потребованы теорией относительности
и для которых характерна постоянная с и к соотношениям неопре-
деленности квантовой теории, символом которых может служить
планковская постоянная h, появятся еще друrие оrраничения, стоя-
щие в связи с универсальными постоянными е, f1, М (масса протона).
Каковы будут эти дальнейшие оrраничения, пока еще нельзя пред..
видеть.
Математический аппарат квант,овой теории.
Для вывода математической схемы квантовой теории (это ОТНО""
сится как к корпускулярному, так и к волновому представлению)
мы имеем в распоряжении два источника: эмпирические факты и
принцип соответствия. Боровский принцип соответствия в своей
наиболее общей формулировке rласит, что между квантовой теорией
и соответствующей данной примененной картине классической тео-
рией существует качественная аналоrия, которая может быть про..
ведена до деталей. Эта аналоrия не только дает указания для на..
хождения формальных законов, ее особенное значение заключается
rлавным образом в том, что она одновременно дает и физическую
интерпретацию найденных законов.
1. КОРПУСКУЛЯРНОЕ ПРЕДСТАВЛЕНИЕ (МАТЕРИЯ).
Если исходить из корпускулярноrо представления, то тоrда,
соrласно ПРИНЦИllУ соответствия, между классической и квантовой
механиками существует внутреннее родство. Основные уравнения
классической механики заключены в следующей схеме:
. дН. дН
Pk== ; qk== д ; H(p,q) w== О
oqk 'Pk
(137)
q ........ q . 2rci ( 1't1 + 'I2't r . . . . vr'tr)t
k ............. k, 't 11:2' . . . 't r е
1:1't . . . . т,
(138)
Wk == 'Jk t + k; J k канонически СОПРЯ}l{ено с Wk
. дН . дН
J k === ......... :;:= о; Wk == 'Jk ==
aWk д
( 139)
в этой схеме Н обозначает rам.ильтонову функцию канониче-
ски сопряженных переменных Pk и qk; 'Уl, '12 .... основные ча-
стоты ДПИiкения, принятоrо за кратнопериодическое ; Wk COOTBeT'"
80
ствующие уrловые переменные, Jk.......... сопряженные переменные дей-
ствия.. W есть общая энерrия системы, t время.
К этой схеме классической механики должен быть найден подоб-
ный ей формализм, позволяющий у:честь следующие эмпирические
факты: между характеристическими частотами излучения атома су-
[цеСТВУIОТ соотношения вида:
'Yik + 'YkZ == 'Уа
(14
(комбинационный принцип Ридберrа-Ритца).
Энерrия атома может принимать только определенные дискрет",
ные значения W i - Между этими значениями и собстнеННЫl\/IИ ча-
стотами атома существуют СООlНОlпения
1
'У ik === ( W i W k )
Il
(141)
(реновной барОБСКИЙ постулат квантовой теории)..
Уравнение (141) следует, очевидно, рассматриваrь как зналоr (139)
Ч:тобы провести аналоrи ю дальше, q в }{вантовой теории, соотнет",
ственно уравнеНИIО (138), представляют совокупностью "членов
ряда Фурье":
I 21ti'J ' k t I
q qik e 1 ·
(142)
Эту квадраТНУIО таблицу обозначают как матриuу; так как q
должно быть вещественно, то клаtсически следует q-r === q* -r, И ПО..
этому по квантовой теории Qik == q*ki (* означает "КОМПJlексно со-
пряженное"); такие матрицы называются "эрмитовыми". Далее можно
и р представить как матрицу, а также функции от q и р.
Умножение двух рядов Фурье в классической механике
ВОДИТСЯ ПJ схеме:
(pq)-r == . р 1: J q -r 1:'
(14
-с'
110 принципу соответствия аналоrом ЭТО
механике будет:
в ква
(pq)и
k
( 4
(формула для перемножения матриц).
нения (144) является особенно ясным
формуле (140).
утве\/'мдение ypaB
эмпиричес
{) В. l'еЙзенберr,
81
Для матриц справедливы обычные законы алrебры за исключе
ннем коммутативноrо закона умножения:
х+у===у+х
х(у + z) == ху + xz
(х у) z === х+ (y+z)
x(yz) === (xy)z
(145)
Однако, вообще,
ху ух.
(146 )
выIаженияя ху ух образуют, как ПОf<аззл Дирак, 28 с точ"
21ti
"остью до множителя Т' аналоrи пуассоновским скобкам класси
ческоЙ механики в духе принципа соответствия.
[ху]=== ( дX ду дх ду \
aPk aqk aqk apk)
k
Соответственно этой анаJIоrии для канонически сопряженных
переменных Pk и qk принимаются следующие перестановочные СООТ-
НОПlения:
Qz Q/Pk === a fll ( Okl :::::::: 1
21tl О
PkPl""-"" P1Pk === О
qkql qlqk===O
для
k == 1 )
k 1
"
(147)
Далее для !7k И qk должны быть опять справедливы каНОНИ4С
ские уравнения
дН дН
Pk === д qk ; qk === apk .
J;Трзвнения (147) и (148) не неззвисимы друr ОТ друrа.
Уравнения (147), собственно, MorYT быть приняты ТОЛЬКО. ДJIЯ
HeKoToporo определенноrо момента времени t, тоrда, соrласно (148),
перестановочные СООТНОlпения определены для Bcero последующеrо
времени. Проведение 91'oro вычисления показывает, однако, что
уравнения (147) и (148) не противоречат друr друrу"
Из (147) и (148) MorYT быть выведены закон сохранения энер"
rии и баровское соотношение для частот. Сначала конструируется
матрица W, удовлеТВОРЯЮlцан уравнеНИIО (141) при ПОМОIДИ системы
вначений W i ; при ЭТОМ eиte не принимается, что U?i связаны }<ЗК
148)
82
либо со значениями энерrии системы. Матрица W дол)кна быть
диаrональной матрицей, члены которой УДОВ.1Jетворнют уравнению:
W ik === 3ik W i .
(149)
Соответствующий этой матрице аналоr по принципу соответствия
есть, таким образом, величина, не заВhСЯШ,ая от времени. Тоrда
соrласно (141) имеет место:
( ' ) . 2rr:i (W W )
q ik 2ТCl'Jikqik == ii i k qik
( 150)
. 2 ! tVl
q===h- (Wq qw).
Далее, для какой-либо функции
имеет место:
ОТ Р и q СОI'ласно ( 147)
h д! ,
fp== 2;'i aq fq
}Е
2тci др.
(151 )
[Iодставляя 13 (148), имеем:
1Vq qW==Hq qH; Wp pW===Hp pH,
(152)
W H, таким образом, переместимо с р и q и поэтому с каждой
ФУНI<цией от р и q, значит также и с f/. ОТСlода следуеr
WJH
о.
,
::=:: О.
(153)
Далее,
не зависит от р и q, значп r
{х' t
(154)
и, следовательно, W (с точностью до неКQТОРОЙ ПРОИ3ВОJlЬНОЙ по..
стоянной) тождественно с энерrиеЙ системы. Матрица Н есть диаrо'"
нальная матрица.
Этим установлен математический аппарат, относящийся к кор..
ПУСКУЛЯРНОМУ представлени 10.
Для физической интерпретации из веденноrо в духе
принципа соответствия, вывода этой математическоЙ схемы полу..
чаем следующие правила:
1. Среднее по времени значение некоторой переменной в каком..
нибудь стационарном состоянии соответстнующим
этому СОСТОЯНИIО диаl'ОН3ЛЬНЫМ членом матрицы, I{оторая представ"
ляет перемеННУI0.
*
83
2. Если обозначим электрический ДИПОЛЬНЫЙ момент атома
через er, rде [r === (х, у, z)]
х== ]q ; у== q{;
"5 :....
'7 ?
IV ,
(qz, q{, q прямоуrо.пьные координатыI электронов), то выражение
1 2 е 2
(2ТC'lik)4 I
hVik 3 С З
\2.2
( 155)
дает вероятность для спонтанноrо испускания одноrо CBeToBoro
кванта при переходе атома из энерrетически более BbIcoKoro со-
стояния i в состояние k с меньшей энерrией. атричные элементы
должны, таким образом, стоять в таком же отношении к излучению
атома, как коэффициенты ряда Фурье классической модели к ее излу-
чению. Сперва MorYT возникнуть сомнения в справедливости (155),
так как ведь и максвеллевская теория подлежит еще KBaHTOBO Teope.-
тическому перетолкованию. В выводе (155), пднако, иrрают роль
(так как здесь идет речь о средних по времени значенияхизлучае-
мой энерrии) только те стороны максвелл.евской теории, которые
не изменяются квантовой теорией; это будет доказано при
обсуждении волновой картины.
2. ТЕОРИЯ ПРЕОБРА30ВАНИЙ.
Если имеют место уравнения
q==
1
QoS,
(1
ТО для всякой функции от р и q справедливо
f (p,q) ==
(15 l)
Если матрицы рассматривать как тензора в MHorOMepHOM про...
странстве (координаты , 1 , /2... . .. , то уравнение
р == S ll}oS
соответствует унитарному преобразоваНИIО координатной системы,
причем Ро 0значает тензор в координатной системе Ко, р тот же
теНЗ0Р в системе 1(. Между координатными системами Ko(io 1./02. .
и K(t 1 , ' 2 ....) имеют место соотношения
t o === 5! или , Ё о ==
k
( 158)
84
Примем далее:
Sik 5 * il ==
i
{ 1 для l == k
о " lфk
(159)
Это значит, что S 1 == S* ( обозначает перестановку знач'"
ков).
Вообще, целесообразнее различные координатные системы от..
личать не посредством нов:ых значков у теНЗ0РОВ, а ввести ДJIЯ
различных систем различные буквы при перечислении координат.
Мы будем в дальнейшем КЗ)J{ДУЮ координатную систему обозначать
своей буквой, а различные численные значения этой буквы отли-
чать друr от друrа штрихами, так что, например, (156) напишется
в виде:
Раа ==] ( S ...:,. 1 alPU' SZ'a' .
l l'
(160)
Оба значка матрицы нреобраЗQВ3НИЯ S относятся, конечно
к разным !{оординатным системам.
Если перестановочные соотношения справедливы для р и q
в какой-нибудь координатной системе, то, соrласно (157), они
справедливы 1 акже и во всякой друrой координатной системе, так
как единичная матрица при преобразовании переходит в епиничную.
Примем, что в некоторой координатной системе найдены матрицы
jJ и q, удовлеТВОРЯlощие перестановочным соотношениям; тоrда
rамильтонова функция Н (pq) таJ{же может быть представлена как
матрица в этой координатной системе. Однако, Н, вообще, не будет
при этом диаrональной матрицей, так как р и q, вообще, не будут
решениями уравнений движения. Решение квантово-механической
проблемы (148) сводится к задаче преобразования матрицы Н в диаrо-
нальную, т. е. нахождения такой матрицы преобраэования /::;, которая
из данной координатной системы переводит в новую, координатные
оси I(ОТОРОЙ совпадают с rлавными осями тензора Н. Уравнениями
для S будут по (157) следующие:
W'aa' == ' ( 1 Но'
аа
[ ['
или
Sla \V aa == О (161)
а
а !f
,
(161) представляет систему бесконечноrо числа однородных линей..
ных уравнений с бесконечным числом неизвестных Sla. Система
85
разреIJIима только для определенных значений W aa "собственных
'значений" матрицы W. Эти собственные значения MorYT быть
дискретны илч: непрерывны. До сих пор мы все ВРС\1'Я молчаливо
пр.инимали, что значки у матриц пробеrают дискретные значения, и
брали наши результаты из теории конечных матриц. Это может быть
математически оправдано только при известных оrраничениях. Прежде
Bcero, матричные соотношения должны быть распространеныI на
,
случай непрерывно изменяющихся значков. Мы следуем здесь ме-
тодам Дирака. 29 Эти методы весьма ясны, но должны быть приме
нимы, правда, только с известной математической осторо}кностью;
но так как они MorYT быть CTporo оправданы во всех практически
встречающихся случаях, то относительно их применения здесь не
возникает сомнения. Прежде Bcero вместо суммы по некоторому
значку появляется интеrрал по соответствуюu ей области значений
(Sp )dl === f dl' Sal' Pl'l .
(162)
ЕД!lничная матрица является здесь несобственной. Чтобы пред-
ставить ее, Дирак ВВОДИТ некоторую ФУН({ЦИЮ В(х), обпадаIОЩУЮ
следующими свойствами
о (х) =---= О для х
ь
О и .! а (х) dx == 1,
а
если значение лежит в интервале между а и Ь. Единичная мат..
рица для непрерывноrо значка будет тоrла
(1 )l'l" == О (1' /f!).
( 16 )
в квантовой теории имеют значение те координатные системы,
в которых определенные матрицы являются диаrональными. Значки
в координатной системе, в которой матрицы Хl, Х2 .. ... диаrональны,
мы будем в дальнейшем постоянно обозначать через х' 1, x"t....
Х2', Х2""." и т. д.; т.. е. мы нумеруем координаты по .:обствен-
ным значениям Хl, Х2'" Сами матрицы х в принадлежащей
им координатной системе, в случае непрерывно изменяющихся
значков имеют след\ ЮillИЙ вид
(Xi) х" Xi o(xt' Х/') о(х 2 ' х 2 ")
(16.4)
Матрицы Xt, х2'.... MorYT быть тоrда и ТОЛЬКО тоrда ОДН()-
временно приве.lеilЫ к диаrональному виду, если они переместимы
меящу собой.
86
З. ДIIФФЕРЕНЦИАJIЬНОЕ УРАВНЕНИЕ ШРЕдинrЕРА. 3()
Пространственные координаты электронов qt, q2 ... qj MorYT
быть в частности одновременно приведены к диаrональному виду:
(qk)q'qll == Q'k o(q' 1 q/') o(q'2.......... qfl 2 ). .. a(q'f q"j). (165)
В этой координатной системе возможное представление для
импульсов Pk, удовлетворяющее перестаНОВОЧНЫl\f соотношениям,
будет:
(Pk)q'q" ==
( а' (х) == д )
h , ( , fI ) ( ' " ) ( , (1 )
2 · u q k q k () q 1 - q 1 ." <;. q k 1 q k 1
'1tl
(3 (q'k+l.........q"k+l). . o{r/I q"f). (166)
Дока зательство для одно tt степени свободы:
(pq qp) q'q" === 2:i J dq'" [а' (q' q"') qfffo (q'" q")
q'o (q' q"') о' (q'" q")] == J d Q '" [o'(q' q"')
27tl
qlf! Q (qf!/ q")+ а (q' ......,...q'//) о (q'f' qfl) q' о' (q' qf")
" ( П! " )] h ( ' " ) h (1)
о q q . ==............... а q Q == · q' q" .
2п-l 21tl
(167)
Чтс;>бы некоторую заданную функцию F переменных р и q при-
вести к диаrональному виду, нужно решить, анзлоrично (161),
уравнение
f [F(pq)]qlqll dq" Sq"F' Sq1r' == О ·
( 168)
Так как р и q, входящие в F, даны как матрицы вида (165) и
(167), то интеr'рация в левой части (168) может быть выполнена
и мы получаем
P ( ql ) S q F S 'Р', F о; ( 169 )
21tl aQ' , q
h д
Pk В F должно быть заменено оператором 2 . д ·
ТCl qk
Если, В частности, rамидьтонова функция Н для решения
уравнений движения квантовой механики будет IIриведена к диаrо-
81
нальному виду, то (169) переходит тоrда в уравнение UUрединrер
(МЫ пишем ' w(q') вместо Sq'li') q вместо q' и W вместо Н'):
н ( q) '1 ........... "1 w=== о.
2 . д , I W 'fw
те! q
(170)
в специальной коордиllатной системе, которая была исходным
ПУНКТОМ теории и в которой Н имеет диаrональный БИД, матрицы
для р и q будут следующие:
'-
J " 11 д,
р w"w '{ == ар fJ('!fю 2тci дq f r w'
Qw'w" == f dq Фt,1JФw,"
(171)
этих ура'виениях использовано СООТНОUlение S 1 == S*.
равнения (1 7 О) и (1 71 ) представляют собой наиболее мощные
математические методы ДJIЯ разработки квантово-теоретических
проблем. Для физическоrо толкования, однако, эти методы пока
что не дают нам ничеrо HOBoro. Потребовалось особое исследование,
чтобы выяснить физический смысл матриц преобразования s.
о
4. ТЕОРИЯ ВОЗМУЩЕНИИ. 24
Для введения должны быть сначала описаны основные поло-
жения теории возмущений в квантовой механике. Пусть rамильто..
нова функция MOiKeT быть разложена по некоторому малому пара..
метру ),,:
н == Но +. А Н 1 + ).2 Н 2 + ...
( 172)
Далее, пусть при надлежащая Но задача движения решена; это
значит, что известны матрицы для р и q и любой функции от р
и q в такоtl координатной системе, в которой Но == W o имеет
диаrональный вид. В дальнейшем мы будем употреблять букву Н
для обозначения матрицы 9нерrии в только что названной системе,
а букву W для матрицы 9нерrии в системе, в которой она ЯВ-
ляется диаrональной матрицей" Пусть \\7' == W o + А W 1 + 12 W 2 +
. .. и, ДЗJJее, для матрицы преобразования, служащей для
перехода из первой вышеупомянутой системы во вторую, имеет)
место:
S==Sо(1'1 )'S]+л2S2+ ...)
s 1 == (1 }\о S 1 + ) 2 (S 1 2 . 52) . . .'") s о 1 .
(173)
88
Из уравнения S 1 HS === W через сравнение коэффициентов при
одинаковых степенях :л., получаем следующую систему уравнений:
So 1 HoSo== W o
80 ......1 (но 51 S1 Но + Н 1 ) So =:: W 1 (174)
So 1 (HOS2 S2Ho+S12Ho+HlS1 SlHl +H 2 )Sl== W 2
............ ............ .............. ............. .............. ......... ............ """"'"""'" ............ .............. ............... .......... ............. .............. ............ "'........ .......... .......... ........... ........,., ............ ....... ........ ............... ........... ............. ............... .. .
50 1 r 110 ')r......... Sr Но + Fr (1-/0 . .. Нт, 51.... Sr 1)] So == 1f7 r
К этому еIl е имеем:
58*==1.
( 175),
Если невозмущенная система не вырождена, то И3 пеРВОf()'
уравнения (174) и И3 (175) следует:
ISol == 1.
1"'оrда возможно из каждоrо следующеrо уравнения, образуя диаrо.,
нальный элемент, получить соответствующий член для собствен..
Horo значения:
(Fr)пп=== (wr)п,
(176),
\
а из остальных членов искомую матрицу Sr
S r тn == h Frпт . ( 1 .......... O'tт ) . (1 )
'J пт
В случае выро}кдения, однако, из Hoso:.--- WoS o еще Не C.пe...
дует, что 150\ ==:. 1. Если, скажем, WO Il + 1 == WO п + 2 == . .. WO n '
ТО SO может содержать все же и матричные элементы, которые
соответствуют каким либо переходам между состояниями п + 1
. . . . . . . ..п + Т.
Второе уравнение (174) дает в таком случае систему линейных
уравнениий для определения So и W 1 . Если сначала образовать.
среднее по времени значение для неВОЗМУlпенноrо движения (это!
значит, что выбирают строки и колонны таким образом, что от...
носящиеся сюда 'У пт исчезаIОТ), то тоrда следует:
f--J 1 So == ...."0 W 1
(178}
(111 означает среднее по времени or Н 1 по не возмущенному
дви)кению). Уравнение (178) можно рассматривать, как уравнение-
, вековых возмущений (( . Относящийся К нему определитель имеет вид
Н 1п + 1, п + 1 W 1 f--J 1n .+ 1, п +2 · · Н 1п 1, п +r
Н 1 п + 2, п 1 Н 1п + 2, п +2 W 1 . · Н]п + 2, п
. .
(179}
н
11] .+ r, 11
· · Н 111
r, 11
wr
l' 1 j
89
ДальнеЙllIие вычисления подобны вычислениям для невырожден..
ных систем.
5. РЕЗОНАНС МЕЖДУ ДВУМЯ АТОМАМИ; 31 ФИЗИЧЕСКОЕ 3HA
ЧЕНИЕ МАТРИЦ ПРЕОБРА30ВАНИЯ.
Пусть два атома со спектрами собственных значений W , W
имеют одну общую собственную частоту, это значит, например,
1 п
что " пm === 'Vik,
или
W!
W i
lV .
( 180)
в таком случае ме}l{ДУ обоими атомами, даже при очень слабой
связи, мо}кет иметь M CTO обмен энерrиями таким образом, что
атом 1 переходит из состояния п в с.остояние т и при этом ОТ-
дает энерrию hv пm , а атом 11 посредством перехода из 1t-ТОrО со-
,СТОЯНИЯ в Ё-тое получает эту энерI'ИЮ hV пm == hVik (и обратно). Если
назвать энерrию взаимодействия обоих атомов чеrез Hl, И рас-
-сматривать систему как "невозмущенную", коrда оба атома разде-
,лены, а взаимодействие ПРИРЯТЬ за возмущение, то тоrда невоз..
1Vlущенная система вырождена:
1vr I j W 11 W 1 + W .I1
WnI k ,п l е
(18])
Соответствующий взаимодействию определитель BeKoBoro урав-
ения соrласно (179) будет:
Hl пk . nk Vl
,
Н l . k
тt; n
J п! , т!.
1 1j.тl; mi W 1
== о.
(182)
Пусть оба ero решения обозначены через W и WJ, а соот-
ветствующие нормированные решения линейных уравнений (182)
будут:
для
П rJ 1 1 е . S il] 1
l-V nk, 1 == ank l 1 е ;
S if'J..
mi,l == а mi, 1 е 1
( 183)
для
W 1 S lf'JJ
1 : nk l 2 == апТс) /}, е ;
S 'а)
тi,2 == a т i)2 е .
Величины 0:1 И IZ 2 произвольные фЗЗОВJ.Iе КОЭффИIlиенты.
В частном случае, коrдз оба атома 1 и 11 о д и н а к о в ы (Т. е.
,tп == k и i === nL Hl пk ; kn == Hl kп ; llТс (и поэтому вещественно);
далее Н 1 nk; nk ::::= Нl kn; 1m И
\r 11,2 == f/llk; uk ---+--- H пk ; ku
(184)
00
матрица }ке а равна:
nk kn
1 1
V 2 V 2 (185)
1 1
............... ........
V 2 Y 2
Тем самым влияние ВО3МУll ения вследствие взаимодействия пра-
вильно учтено в первом прибли}кении для собственноrо значения
и в нулевом приБЛИjкении для собственных функций.
Чтобы снова от ма..
тематики перейти к фи-
зике, МОЖНО, например,з
дать вопрос об энерrии
атома 1, как функции
времени. Между двумя
связанными осцилляторэ.
ми с одинаковой часто
той имеет место по клас
сической теории rapMo
ническиЯ, периодический
обмен энерrии, частота
KOToporo пропорциональна СВЯ3ЫВ3Iоще-й силе. Таким образом,
энерrия одноrо из осцилляторов будет примерно представлена
РИСуrIКОМ 21. Напротив, в
квантовой теория ну}кно ожи..
\ .. ...... _..,...........-- дать, что энерrия атома 1 имеет
или значение W или значе-
ние W , причем частота "е...
реходов зависит ОТ силы СВЯЗИ
(рис. 22). Во всяком случае, в
квантовой теории нельзя БЫ4И
слить ход кривой н I (/), ero
также никоrда нельзя опре
делить экспериментально. Од..
нако, полученные до сих нор
правила для физической интерпретации квантовой механики ДЗIОТ
возможность вычислить среднее по времени от HI(t) или средний
квадрат флюктуации HI(j), или среднее по времени от какой...
либо функции f(HI) ОТ H 1 .
1
2
т
W L
п
- " ""I
I
,
,
I
I
I
I
.
!
...... .. .}
w 1
т
Hlj
t
..
Рис. 22.
t
W I
п
, . .. . \ . . . ..,/,
w!. .Pp р.'.' .. .. .
7/'!
HIJ
r t
,.
Рис. 21.
91
Для состояния 1, скажем, следует:
/(H I ) == [f(HI) ]11 == S*пk , lf'l1k; п S nk} 1 t-
S*тi, 1 fтi 1 т! Smi, 1 == I Sпk,l !2. f(W ) + I Sтi, 112 f( W ). (186)
Это уравнение эквивалентно с зависимостью между н 1 иt
типа, изображенноrо на рис. 22, если ISпk,112 И, соответственно,
15 mi ,11 2 рассматривать как вероятности найти всю систему в кон..
фиrурации nk или, соответственно, тЁ. ПредСl1lавляется 80З.МОЖ
ны,м, обобщить эпtу фuзuчесltУЮ UНlnерпреmацuю матриц преобра...
зованuя u pacc;ual1zpunafпb
ISal b l 1 2
(187)
/(alC вероятность тО20, чпzо 6удеп?' найдено значение а' величины а,
еслu извеСnlНО, Чl1Z0 величина Ь приняла в системе значение Ь'..
К этому физическому ТОJIковаНИIО, однако, нужно добавить суще-
ственное условие, что рассматриваемый опыт действительно ПО3ВО
ляет определить значения для а. Это условие, кажущееся сначала
тривиальным, существенно, однако, так как какое-либо приме..
нение толкования (187) без учета опытов, ведущих к измере
пию а', дает тотчас же повод к лоrическим противоречиям.
ЕСJIИ произвести одно за друrим сначала преобразование от а
Ь и затем от Ь к С, то соrласно умножению матриц будет иметь
место
"'v
Sa'c' == "')а' Ь' 5;:/ с' ,
Ь'
(188)
е. совершенно неззвисимо от с " амплитуда вероятности" S а'с l
всеrда может быть представлена как линейная ФУНI<ЦИЯ от Sa'b"
Следовательно, амплитуда вероятности Sa' для наХО>l<дения значе-
ния а' даже 'в самом общем случае является всеrда линеt:1ной
фу кцией от матриц преобрззования Sa'b'; В частности, можно, на..
пример, положить
Sa' == Sa'\v' C\V"
w'
(1 89)
[де Sa'wl обозначает матрицу преобраЗОВ2НИЯ для энерrии "?', а
c w / какую либо постоянную.
В то время, как вероятности I S a'w,j2 всеrда неа3ВИСИМLI ОТ Bpe
мени, потому что ОНИ относятся к стаuионарному состоянию U'l',
ЭТО не является, вообwе, необходимым для !Sa'12. Зависимость от
времени Sa' MO)J{eT быть найлена путем слеДУlощеrо рассуждения.
92
Соrласно (142) матричный элемент fik имеет зависящий от вре--
2тci ( W W t
мени мно>китель e 21ti 'Jik i === е h i k)
Далее, имеет место
fik === Sh'ifa'a" )a'lk .
а'а"
(1
Таким образом, мы получим правильную зависимость от времеНИ t
21ti W.t
если введем в Sa'i множитель е h l. Так как до сих пор в
постоянно входил один произвольныЙ фазовый множитель абсо...
Л!ОТНОI О значения 1, то в будущем мы будем понимать под Sa'i ма-
трицу преобразования, ВКЛlочающую также зависящий от времени
l\Iножитель. Амплитуда вероятности caMoro общеrо вида Sa f удо..
влетворяет тоrда соrласно (161) уравнению:
h дS а ,
Ha'aflL)a" + . == о.
27Cl at
а"
(191)
Если выберем специально а === q, то получим:
( 'l ) , д(t
н 2тсЁ дq' q q; I 2тci at О,
( 192\
т. е. волновое уравнение Шрединrера.
Чтобы д.ать иллюстраЦ lIО (191), мы снова рассмотрим пример
двух связанных атомов. Пусть при измерении в момент BpeMeHh
t === О атом 1 находится в состоянии n, а атом II в k. Для
t === О таким образом ISпk 1=== 1 и ISтij === О. Эти начальные усло-
ния МЫ ВВОДИМ В уравнение (191) и наХQДИМ ПО (183) (aп,k,l и Т..
не зависят от времени, аl' а'2 ДОЛ)КНЫ зависеть ОТ времени):
ank, 1
I а т i, 2
2 a;r:l, 1 a п k,2 \
21ti
t
Sпk ==
Sтi =-:=
2 Gтi, 1
I
r 1
1
1 а nk} 2 е
2 tlтi, 1
Для частноrо случая одинаковых атомов, принимая во внимание
(185), }1меем:
2 ,.,..t
I. \f/lt
+e 2 I W2t)
t 21ti W
2 t
е
е
e
(1
ОТСJода для вероятностей:
! 2 1 [ 2тс 1 ]
ISпk :== 2.1 + cos 7l(W 1 W2)t
2 1 [ 2 J
Skп == 2 1 cos 71(1:171 W 2 )t
(195)
Эти формулы дают вероятности найти "пk" или "kfl" как ФУНК
цИИ времени. Так как разности W 1 W 2 малы, порядка энерrии
,взаимодействия между атомами, то вероятность изменяется только
медленно. Спустя короткое время после первоrо измерения (Т. е.
для очень малых значений t) весьма вероятно вновь найти конфи-
rурацию nk. Если же между первым и вторым измерением прохо-
1 h
точно время Т == 2 w W ' то с определенностыо будет наЙ..
1 2
дена конфиrурация kn. Все эти рассуждения справедливы только
тоrда, коrда за время между двумя измерениями система действи-
тельно остается невозмущенной, т. е. действительно подчиняется
уравнению (191). Несмотря на то, что это условие опять--таки три...
виально, оно все же здесь особенно подчеркнуто, как имеющее
рещаЮIцее 31:1ачение для свободноrо от противоречиЙ построения
теории.
Только что данное толкование матриц преобразования, как
функций вероятностей, дает полную схему для применеНI1Я матема-
тически" методов квантовой механики ко всем физическим проб,1е-
мам.
КОРПУСКУЛЯРНАЯ KAPTl1HA ИЗЛУЧЕНИЯ.
эtiнштеtlновской теории световых квантов МО)l{ИО
представить световое излучение, как де ствие быстро-леТЯIЦИХ частиц.
Скорость их всеrда равна с. Между энерr'ией Е и импульсом
световых квантов CYll ecTByeJ соотношение
Е === с · ре
(1
Э4
Цвет света определяется энерrией Е.
Световые кванты Moryr возникать и исчезать, следовательно их
число, в противоположность представлениям корпускулярной теории
материи, переменно. Ме:и<пу отдельными световыми квантами (по
скольку не принято во внимание тяrотение) нет никакоrо взаимо
действия, НО взаимодействие между световыми квантами и материеЙ,
существенно для явлений поrлощения) испускания и дисперсии нзлу'"
чения. Так как это взаимодействие сформулировано в классической
теории только при применении волновоrо представления об элеl<""
тромаrнитном излучении, то представляется целесообразным перейти к
квантовой теории излучения ИСХОДБ из волновой картины.
7. I\ВАНТОВАЯ СТАТИСТИКА.
Мы рассмотрим систему п совершенно одинаковых, друr от
llpyra неотличимых частиц (электронов, световых квантов). Ради,.
ПрОСТDТЫ мы предположим, что система обладает ТОЛЬКО' одним.
дискретным спектром собственных значений, затем отвлечемся ПОI<З
от взаимодействия частиц ме}I<ДУ собой. Задача тоrда МО)l{ет быть.
рассмотрена таким образом, что сначала, определяются состояния
соотвеТСТВУЮll ие им собственные СРУНКЦИИ Фа(r) отде..'ЬНОЙ частицы
и затем уже спрашивают о распределении 11. частиц по этим состоя
ниям. Чтобы высказать утверждения о статистическом распределеНИИl
частиц по различным состояниям, нужно установить сначала апри
орные вероятности этих состояний или установить, лучше, каковы.
MorYT быть возмо}кные состояния всей системы.
В классической статистике (больцманновская статистика) можно'
было распределить п части Ц по 11. различным состояниям п! раз-
личными способами. Этот факт имеет то следствие, что в кванта..,
вой теории I<аждому распределению п частиц по п различны
состояниям соответствует п! раз выро)кденный терм всей системы..
ОТНОСЯI.циеся сюда п! линейно"независимых собственных функпий,
получим, производя В выражении:
1 (Y(3J O:2 (r ;) · .. . . ( aп (J"i п)
(1
1l! перестановок Y x при неизменных ai-
Вместо q)ункций (197) можно, как известно, для описания
нашей задачи п тел применить также каКУЮ"JIибо систему п! ДИ..,
нейно"н€ззвисимых линейных комбинаций (197).
К подобной системе собственных функций мы придем, напри-
мер, если, соrл сно 4, попробуем взаимодействие
,..,
ме)кду частицами как возмуu ение. всех таким ооразом полу...
95
чающихся п! линейных комбинаций приведем здесь две особенно
просто построенные:
Yal (rl) 1X2(r2) . · · aп(rn)
П всем перестаНО8К&М
( 198)
определитель
I Уа i ( УХ) \ i, Х == 1) 2 . . . п ·
( 199)
Выражение (198) остается неизменным при какой-либо пере-
становке двух частиц и обозначается как с и м м е т р и ч н а я соб...
ственная функция системы; выражение (199) изменяет при пере...
становке двух частиц только свой знак и называется а н т и с и м-
м е т р и ч н о й собс'rвенной функцией. 32 Если мы предположим,
'ЧТО a нормированы, и потребуем, чтобы и собственные ФУJ;;Jl{ЦИИ
системы были также нормированы на 1, то леrко ПОRёtзать,
что (198) и, соответственно, (199) нужно умножить на" / 1,
V п.
Мы поясним сказанное на простейшем примере п == 2. Тоrда
состоянию, при котором одна частица находится в состоянии Cf.l,
а друrая в состоянии а2, принадлежит дважды вырожденный терм
две собственные функции.
'Ys( 1,2) === 2 { al (rд7а,,(r 2) + a! (r2) (L,(rl) I
1
Уа( 1,2) == 2 {Y(/1({1) a2(r2) Yal(r2) a1(rl)} .
Сначала можно леrко показать, что термы с симметричными
l4 термы с антисимметричными собственными функциями не ком..
бинируют между собой. Именно, вероятность для таких переходов
дается всеrда матричным элементом вида:
Jf(1,2) Ys(1,2) (.«(1,2) d'tl di.2'
(200)
'причем f (1,2) есть функция, которая не должна изменяться при
перестановке обеих частиц, так как последние не ДО.ПЖНЫ разли-
'чаться между собой. Если мы переставляем в (200) оба электрона,
то, очевидно, значение интеrрала не должно измениться, так как
в нем будут изменены только обозначения переменных интеrриро-
'вания; с друrой стороны, при этом нзменяется знак у a( 1,2), в то
,время как все друrие величины под знаком интеrрала остаются
иеизменными. Таким образом (200) дол»\но исчезнуть.
Подробное математическое исследование на основании теории
е6
представлений 36 показывает, что наш частный результат может
быть обобщен слеДУЮЩИl\1, путем.
Термы системы, состоящей И3 п частиц, можно всеrда разло
жить на отдельные системы, таким образом, что только термы каж
дай отдельной системы. комбинируют между собою. В частности,
получаются всеrда две такие системы термов, собственные функции
которых при перестаНО8ке каких..либо двух частиц ведут себя сим..
метрично или антисимметрично.
Этот результат сохраняет силу при любом взаимодействии чао.
стиц, ero вывод предполаrает тодько, что ЭТО взаимодействие есть
симметричная функция от координат электронов.
Факт неВО3МОЖНQСТИ комбинаций двух разли ных систем термов
между собою дает возмо}кность Toro, что одна отдельная система
термов сама по себе может быть физически реализована.
Рассмотрим, например, отдельно симмеТРИЧНУIО систему тер..
мон. Каждому опредеJlенному распределению частиц по отдельным
состояниям одной частицы.......... если мы снова пренебреrаем взаимо...
дей ствием ......... соответствует в этой системе термов только одна
единственная собственная функция. Представленные в симметрич-
ной системе термов возможности соответствуют состояниям, разли-
чимым в Бозе-эйнштейновской 83 статистике.
В системе термов, относящейся к антисимметри4.НЫМ собствен--
ным ФУНКЦИЯМ, последние исчезают всеrда, коrда две частицы на..
ходятся в одном И том же состоянии. Это есть квантовомеханиче",
ское выражение запрета Паули 84 для эквивалентных орбит элек-
тронов н протонов. Отбор термов в антисимметричной системе
соответствует статистике Ферми...Дирака. 35
Квантовая статистика выбирает поэтому из возможноrо мно-
жества термов некоторую систему термов с симметричными или
антисимметричными собственными ФУНКЦИЯМИ, как единственно
осуществлеННУIО, и предписывает каждому терму так выбранной
системы одинаковую априорную вероятностъ. Первый случай соот-
ветствует статистике Боэе"ЭЙНlllтейна, справедливоtl для световых
квантов, последний статистике Паули-Ферми Дирака. Особенно
следует подчеркнуть, что такая формулировка
вой при любом взаимодействии частиц.
При применении принципа Паули к электронам или протонам
нужно обратить внимание на то, что в фа (rX) помимо
трех пространственных координат Х-ТОЙ частицыI представляет таI{же
и четвертую переменную, описываюшую спин и м принимать
1 1
только значения + 2 или ......... '2-
о формулировке квантовой статиСтики в квантовой механике
волновой картины речь будет итти ниже.
'1 в r ей. ев 6.,1'.
.,
ВОЛНОВОЕ ПРЕДСТАВЛЕНИЕ МАТЕРИИ И ИЗЛУЧЕНИЯ; HJIAC..
ТЕОРИЯ.
в этом параI'рафе будет итти речь о световых волнах и тех
волнах материи, которые MOI'YT при писаны отриuательным
электронам. приписываемые протонам, MorYT рассмо"
трены затем подобным же мы не будем
ВО внимание относительности и построим, т. . по примеру
Шрединrера, теОРИIО. В этой теории
будем тоrда во внимание в первом при
ближении только электростатические пренебреrая маI НИТ"
ными эффектами и запаздыванием.
Волновое уравнение для волн получается
сто из шрединrеровскоrо дифференuиальноrо уравнения (192)
в конфиrурапионном пространстве. Именно, С. 'IУ4ая одноrо един-
CTBeHHoro это (192) переходит в трехмерное
уравнение" Кажется поэтому сперва
в виде пробы рассматривать ero, KaI( классическое, т. е. простран..
ственно"временное уравнение материи. элек
трона в корпускулярном представлении состоит из !{инети""
ческой.
и потенциальной ·
=== e
[де V электростатический потенuиал. В нерелятивистской тео...
ПОСJIедовательно пренебреrаем маl НИТНЫМИ СИJlами и их потен
циалами. Таким образом, искомое волновое (169)
будет:
е
01а)
и комнлексно
к
е
о
1Ь)
[ А
масса электрона, е ero заряд).
Схема, характеризуемая этими уравнениями, при СУlцественном
изменении сих пор изи ческой мо>н:ет
98
быть рассматриваема как "классическая" волновая теория. Этой
схеме может быть сопоставлена (так как она содеР)l(ИТ только функ-
иии от х, У, z и t), как и максвеллевским уравнениям, наrлядная
пространственно-временная картина. Об электронах тоrда в этой
теории нет болыпе речи, е и }L суть только универсаЛЬНI>lе постоян-
ные волновоrо уравнения. Несмотря на то, что уравнения (201 а
и Ь) получены из теории одноэлектронной проблемы в корпуску-
лярном представлении, они никоим образом в дальнеЙIнем не должны
иметь место скажем "для одноrо. электрона", это было бы ведь
лишено смысла в волновом представлении, но должны явиться УНИ
версальными для "волн отрицательноrо заряда". ОТСIода непосред
ственно следует, что в этой теории (в противоположность кванто"
вой теории проблемы одноrо электрона) потенциал V не предста
вляет собой только потенциал внешних сил, но включает также
теперь и часть, зависящую от самих волн материи, т. е. обратное
действие волн отрицательноrо заряда на самих себя. Эта теория,
конечно, так же мало, как и максвеJIлевская, будет соrласована с
экспериментами в пределах атома, но она имеет без сомнения боль
шое эврисrическое значение, как аналоr в духе принципа соответ-
ствия квантовой теории волн.
Рассмотрим сначала частный случай малых волновых амплитуд,
т. е. очень незначительной плотности материи и отсутствия внеlП
них сил. В этом случае V исчезает в достаточном приближении и
уравение (201) rласит.
h 2 h дФ
81t2!L 'f 21ti at === О.
EI'O решением будут какие-либо плоские волны вида:
2тr.i
h (PxX РуУ pzz Et)
1 == е
т ,
(202)
eCJ! и ме:н{ду
и ]7х, ру) р!! имеет место СООТНQlllение:
1 1
(j7x2 Ру2 t-l}z2) == 172
2!", 2
Направление нормали волны дается ОТНОIlIеllИЯМИ
длина волны равна:
h
)", == , а частота 'J
р
, ,
J} Р
Iz
(203 )
фазовая скорость волн равна:
V(F
р
р 21-L
..
gg
и наконец, rрупповая скорость V g , corJ1aCHO элементарным законам
оптики, будет
dE Р h
V g === dp === !J. === л.!J. . (204)
Уравнения (202) и (203) соrласно де Бройлю объясняют явле..
ния интерференции и диффракции волн материи очень малой плот
насти. Особенно зависимость (204) между rрупповой скоростью и
длиной волны позволяет ДВИЖУЩИМСЯ комплексам отрицательноrо
заряда сопоставить ДЛИНЫ волн без обхода через корпускулярное
представление. Эта теория де Бройля учитывает поэтому качественно
простым путем основные опыты Дэвиссона..Джермера, Томсона,
Руппа и друrих. Аналоrично этому, как известно, уже классическая
механика дает удовлетворительное объяснение вильсоновским фо-
тоrрафиям, опытам с отклонением и проч. Несмотря на это, подоб.
ные объяснения атомных явлений посредством классичеСКАХ теорий
нужно толковать только как указание на сходство в смысле прин-
ципа соответствия между КJЮ.сснческой и квантовой теориями; во
всех количественных вопросах следует прибеrать к помощи KBaH
ТОБОЙ теории"
Однако, сначала рассмотрим еще несколько подробнее классиче..
СКУЮ волновую картину. ДJIЯ этой цели мы сделаем слеДУЮlпие
предположения:
Плотность заряда р:::::::: е t}*ф
h
Плотность тока == е 47ti ( * grad Ф .......... Ф grad *) (205)
h 2
Плотнос ть энерrии u 8 2 " grad ф* grad ф.
1ttJ-
Оправдание этих предполо)кений может быть найдено только
позже, в квантовой теории волн. Все же для их пояснения MorYT
быть выведены из (201) следующие законы сохранения:
а) сохранение заряда:
d !P dV:::=: о
dt '
Ь) сохранение импульса:
! Mv === е f grad Vф*фdv
с) сохранение энерrии:
! иdv=== Iе V ( *Ф)dV;
dv здесь означает элемент объема; интеrралы должны быть рас..
пространены по всему пространству. При ЭТОМ flриняrо, что в бес-
(206)
100
конечности волновые функции достаточно быстро исчеЗllЮТ, так
что при интеrрировании по частям поверхностные интеrралы
отпадают. Для вывода (206а) нужно умножить уравнение (201а)
на ф* а уравнение (201 Ь) на ф, вычесть одноrо из друrоrо и про....
интеrрировать по всему пр о странству. Для доказательства
дф*
(206 Ь) умножаIОТ (201а) на дх ' продифференцировав (201Ь) по х,
умножив на ф, затем ОДНО уравнение опять вычитают из
друrоrо и интеrрируют по всему пространству. Наконец для вы..
, д * дф
пода (206с) умножают (201а) на at ' (20th) на дt ' складывают и
снова интеrрируют по всему пространству.
Помимо волн отрицательноrо заряда; в пространстве MorYT
находиться еще и друrие электрические заряды, например, атомные
ядра, заРЯ)I<енные конденсаторы и Т. Д. Назовем соотнетствующую
им плотность заряда Ро, тоrда электрический потенциал V опреде...
литея из известноrо электростатическоrо уравнения:
div == 4'lt(p + Ро) или !1 V === ......... 4тс(р + Ро)
(207)
.Уравнения (201а,Ь) и (207) MorYT быть вместе выведены И3 ва"
риационноrо принципа. Мы полаrаем:
L==
h 2 h ( д д * )
grad ф* grad ......... . у* ф
8тc2 47tt,- dt дt
1
+ е vф * (10 V + Q,.u (grad У)2
u ;1.
} (208)
f L dvdt === экстремум
Вариация * и, соответственно, дает (201а) и, соот'ветственно,
(201 Ь), вариация V дает уравнение (207).
Общая энерrия системы складывается из энерrии волн :материи
и энерrии элеКТРОС'Iатическоrо ПОЛЯ. Таким образом, для плотности
общей энерrии & получается:
h 2 1
$) == . grad ф* g'rad (grad V)2.
8 7t2 87t
(209 )
всей системы справедлив тоrда
сохранения энерrии:
H !
......... с о n s t )
(21 О)
если ро не заВИGИТ ОТ Bpe eHЦ
}/Iз ( {)9), (207) и (206) следует именно:
d H == f dV l дu V !::. V J ==
dt l дt 41t д!
f dv l v ( e * 7 ) j О. (211 )
Эта замкнутая в себе, нодобно классическим теориям простран..
CTBeHHO временная теория поля до сих пор не содеР}I{И l' в себе
ни одноrо ,элемента квантовой теории. Это особенно видно из Toro,
что обlllИЙ зз ряд системы
J pdv == е J * <{;dv
(212)
может принимать Лlобые значения, а это ведь наверно противоре.чит
опыту. (В действительности, об[ций заряд всеrда представляет целое
кратное от . е.) Также значения энерrии системы и собственные
частоты в этой теории изменяются непрерывно. (В силу нелиней..
ности дифференциаЛЬНОl О уравнения собственные частоты зависят
от амплитуд .) f-Iесмотря на это, можно с пользой применять и
эту классическую теорию поля, точно так же как классическую меха...
нику для модели атома в корпускулярной картине. Совершенно
так же, как Бору и 30ммерфельду добавлением к классической
механике квантовых условий вида fPk dqf(,:::::: пkh удалось получить
ка чественное объяснение атомных спектров, Хартри 37 удалось
произнести качественное вычисление атомных спектров посредством
прнбавки квантовых условий к только что приведенной теории
поля. 1) Квантовые условия Хартри rласяr: f'f k * kdv == пk, rде
пk целое число, а индекс /\ относится к собственным колебани ям
волновой системы. rlоследовательное применение отдельных квантовых
условий возможно и здесь только ТОI да, коrда пренебреrают перио-
дическими во времени колебаниями V; ЭТО стоит в точной аналоrии
СР соответственными трудностями в корпускулярноЙ картине. Харак-
терно, что описанная теория поля, в силу нелинейности дифферен-
циальных уравнений, с математической точки зрения трактуется с
таким }ке трудом, как классическая механика; БО всяком случае
MHoro труднее чем квантовая теория поля или l(ванrовая теория
корпускулярной картины.
О классической теории излучения мне, пожалуй, сказать
нечеI О, это есть хорошо известная теория Максвелла. Она не
содержит никаких элементов квантовой теории; как указание на это
1) Как показал Хартри, достаточно хорошее приБJIи}кение к законам
квантовой теории ПО..'Iучается, правда, только тоrда коrда из уравнени
исклюqаlОТ деЙСТ{Jие электрона на CaMQfO себя.
102
МОЖНО рас....матривать ТОТ
РЫБНО. Мо:н{но снова попыIатъся.. ЭТО ПОJIо}кение
СТБОМ квантовых типа Хартри, смол{ет изме..
няться ТОЛЬКО на величину hv, НО ЭТИМ мы еlце не
К квантовой теории
9. КВАНТОВАЯ
()
ВОЛНОВЫХ ПОЛЕН 38
Вспомоrательные математические
полей быть в
НИI{ОЙ, если
форму аналоrичную
что рассматриваемая классическая
выведена из
функция этой
a [ « == C(
их первые производные по пространственным координатам
квантовой и
аналоrии с квантовой Mexa
волновой теории придать
механике.. Примем,
волновая теория может
лзr'ранжева
волновые функции
t); а =:.: 1,2 .... fJ,
у,
== 1, 2, 3)
и их первые
по времени
е.
име rb место:
f L (ф., ,. ) dvdt==- экстремум.
Известно, что механическая система может быть
посредством принципа rамильтона
(21
L
qk)
LIтобы получить формальное XOДCTBO между
ПОJlаrаем :
13) и
14)
14 ), м ыI
( .
1 ( , д a
J 1Ja,
Тоrда должно иметь место
L ( a,
)
16)
то время, как Е
и их про-
Н3ВОДНЫХ ПО
значениями
и
L (q", qk) и l ( "' !: ' a)' нужно, таким образом, рассматривать
ТОЧКУ пространства Р как индекс у волновой ФУНКЦИИ; тоrда
последняя имеет два рода значков, ОДИН прерывно изменяющиАся
значок С( И друrой непрерывно изменяющийся значок Р (или пра--
вильнее три таких значка, именно х, у, z). Далее, по аналоrии
с формулой
дL (qi qд 1 . L (qi + Qik q, q') L (qlq;)
== 1т · (217)
дС]k Aq О llq
мы определяем:
( (Р') \
(Р') дy . (Р')
uL ф, , p
дх; J == 1im { L ( r) + ()<x 8 (P P') ; ( 218 )
O ) Аф О {
д r ,,/PI>, + о о ( Р Р' ) f'l ] . ,tj(Pf» L ( "I(pr). дф · "} )}
дх, '1"' a r а '( '( , дХi' "( ..
Здес!:) о (Р Р') определено подобно дираковской о - функции
(ер. М Э 2) формудами :
а (Р Р') == о для Р Ф р' ;
J8(P P')dvp== 1 или О,
(219)
смотря ПО тому) содеР}I{ИТ ли объем, по которому интеrрируют,
точку р' или нет, Соrла СНО (215) имеет место
o L д 1., д дL
3 ' д } дх. . д 1; J
, '! '1. I се i l д
дх!
(220)
oL
оБО3rt:I чает таким образом, вариационную производную от L.
Из (216) путем вариации получаются волновые уравнения
дL д дld д дL
. о
a( tX a l df дt дфа ·
l (I
д О#-С i
(221 )
виду наличия тривиальноrо соотношения
oL aL
== ,
a д(1'
t& .
(222)
104
(221) переходит в
oL д oL ........ О
............... ----- --- ---:----.......... ,
фа дt фtL
(223 )
в полной аналоrии с лаrранжевыми уравнениями классической меха-
ники. Мы определяем поэтому канонически сопряженную к вол-
новой функции ф« функцию Па (момент) соrласно уравнению
П.== O == д
(1фа дфа
(224)
и ВВОДИМ обычным способом rамильтонову функцию
н == f dv п..ф.. L, (225)
или
н == п"Ф" L; Н == f Hdv.
(2 6)
«
Тоrда справедливы, как и в классической механике, СООТНО'"
lпения:
. о Н о оН
0/" === оП" ; П" == a, " · (227)
Отсюда ВЫВОДИТСЯ закон сохранения энерrии:
dH
dt == о.
(228)
Далее, справедливы законы сохранения:
:t f п" : ; dv О (i == 1, 2, 3) j
именно из (227) следует:
d J ,-, д( a: f r д аЕ!
dt dv +П" aXi == dv п. JXi дl i.
== ( dV [ П,, ,ан + alj1" ан _ / == j " дН О. (230)
i)xi oIl« дХj a
., 11 ..
(229)
д a а ff
Уравнения (229) выражаlОТ импульса. [Iри выводе
(228) и (229) предположено, что Н не содержит никаких друrих
функций пространственных координат или времени кроме функций
п. !1 t«-
105
Переход от классической теории к квантовой соверluается
теперь без дальнейших трудностеЙ по аналоrии с М 1. Вол-
новые функции рассматриваются как некоммутативные (неперемести..
мые) переменные, которые MorYT быть представлены как матрицы
(в соответственно выбранной координатной системе в I'ильбеР10В"
ском пространстве).
К дифференциальным уравнениям (227) добаВJIЯЮТ (ер. фор
мулу 147) перестановочные СООТНОПlения:
ПС( (Р) y (Р') ф (Р') lla (Р) == Or.l. О (Р Р') 2 '
ТCl
Па (Р) rl (Р') П (Р') Па (Р) == о (231)
фа (Р) q; (Р') ф (Р') фа (Р) == о.
в этой квантовой теории волновых полей координат лростран
ства времени х, у, z, t суть параметры, Т" е. числа в обыкно"
венном смысле и поэтому онп переместимы со всякой друrой
величиной.
Снова справедливы, как это без труда получается при ПОМОII И
перестановочных соотношений, законы сохранения
J - д'
Н == const; Па д dv == const.
(232)
Простейший путь ДJIЯ математической трактовки определенной
посредством (227) и (231) квантово механической волновой за
дачи это разложение волн по соответственно выбранной 0pToro
нальной системе функций:
(f == a r (t) a (Р); П а :== ы' (t) · a (Р)
r r
(233)
и (Р) представляют ПРОИ3ВОЛЬНО избираемую ортоrОНЗJ1ЬНУfО си
стему функций, следовательно, a (Р) суть обыкновенные функпии
(с числа, classical) пространственных координат; a r , напротив, веном..
мутативные, заВИСЯIцие ОТ времени, переменные (q числа, quantom).
Если подставить (233) в переСТJновочные COOTHOllIe НИI (231),
умно)кить обе части уравнений на a (/J) и (Р'), проинтеrрировать
по Р и l)l И просумм ировать по а и , то тоrда ПОЛУ4аIотея перестано...
вочные соотношения для а и Ь
h
Ь sat а,Ь.с; == 2 ;: · Ost.
та
asat atas == О
bsb t btb == О.
4)
106
При ЭТОМ применены УСJIОВИЯ ортоrонаJIЬНОСТИ для и:
j.dVP и (p) U (p)==a,.S'
(235)
Уравнения (234) вполне эквивалентны перестановочным соотно-
lпениям (231). Также и rамильтонова функция Н может быть выпи...
сана как функция от a r и b r . Единственное формальное различие
ме)l{ДУ квантовой теорией волновых полей и квантовой механикой
состоит в том, ЧТО число переменных в волновой теории беско-
нечно, а в корпускулярной конечно.
10. ПРИМЕНЕНИЕ К ВОЛНАМ ОТРИЦАТЕльноrо ЗАРЯДА.
Классическая лаrранжева функция для волн отрииатеЛЬНОl"О
заряда соrласно (208) будет:
h 1
k == grad (1* grad (grad V)2 +
8тr: 2 f-L I 87t'
* h ( дФ д * )
eVtL t'j V P ('1* ,Уl
т r о 47ti дt I д! 'f ·
(236)
ЕСJlИ разложить V на части V o и V соrласно соотношениям
Д V o == 4тr:po; д V 1 == 4тr:еф* , (237)
то можно, прибавляя полные пространственные или временные диф...
ференциалы, преобразовать L и привести ее к следующему виду:
h 2 h д
L == grad f: grad Ф . (}* +
8тr:2 2 l д'
1
8 (g1'Cld V 1 )2 + е ( V () V 1 ) * .
(238)
BblopOlueHbI аддитивные постоянные, зависящие от Bpe
мени, которые содер}кат только РО; поэтому в величине L из (238)
ДОЛ}I{НЫ варьироваться еще только , 'f* и V 1 .
llроизводная по времени от V 1 не входит в (238), так что V 1
невозмо}кно рассматривать, как самостоятельную волновую функцию
в смысле предыдущеl'О п в противном случае, исчезла
бы функция, канонически соприженнаи с V 1 (момент) и было бы невоз"
МО)КНО введение перестаllОВОЧВЫХ СООТНОIllСНИЙ соrласно (231).
ПростеЙПIИЙ выход из этоrо следуюпI,ИЙ: полученное
чосредством вариации V ВОЛНОВQе уравнение нужно рассматривать
I<al{ дополнительное услоние и при ero помощи выразить V 1 как
функцию от * и 1-
Из
А 1/'1 == 4тсе ф* Ф
следует:
V 1 (Р) == е f G (РР') 7* (Р') Ф (Р/) dvp',
(239)
Здесь G (РР') обозначает функцию rрина области пространства,
в . которой происходит волновой процесс; следовательно, вообще,
1
просто функцию .
'рр'
Тоrда из (238) опять через преобраЗ0вание посредством при..
бавления полных дифференциалов следует:
h 2 h дф
L === ........ g'rad ф* grad Ф .......... ф* +
81t2 21tl at
+ eV o , * Ф e f dvр/ф* (Р) 7(Р) ф* (Р') 7 (Р') G (РР'). (240)
Для канонически сопряженноrо к Ф момента мы находим:
11 iJL h ,'.*
дф ......... 21ti 'f ..
rамильтонова ФУНКUИЯ имеет следующий вид:
h дф
Н ==........ 21ti ф* ai L
и
н == J dv [ h grad 7* grad Ф е V o * Ф ]
8 тr 2 f-1 .
+ e J J dvpdvp,G(PP') 7* (Р) НР)7* (Р')7(Р'). (241)
fIереход к квантовой теории совершается посредством введения
l1ерестановочных соотношений между П и ф:
Ф (Р) ф* (Р') (f* (Р') Ф (Р) == а (p. Р').
Ф (Р) (Р') ф (Р')ф (Р) == О. (242)
ф* (Р) ф* (Р') * (Р') ф* (Р) == о.
rамилътонову ФУНКЦИIО можно снова взять непосредственно из
классической теории (241), однако классическая теория н е YCTa
навливает последовательности мцожит лей, которая теперь важна
HJi
Таким образом, правильный вид rамильтоновой функции, поскольку
это касается последовательности множителей, можно получить только
из опыта.
u
Иордан и Клейн нашли, что правильная rамильтонова функция
для волн материи rласит:
Н J dv [ 8 :1'- grad * grad eV o * Ф] +
+ J f dvp dvp' а (РР') * (Р) * (Р') Ф (Р) Ф (Р').
(243)
Нуя{но еще sамстить, что утверждение: * должно быть КОМ....
плексно сопряжено с ф, требует некоторой осторожности. Если,
например, дано как функция от эрмитовых матриц, то переход
от Ф и * совершается не только посредством замены i на ........... i,
но в силу ЭРМИТQБоrо характера матриц должна быть изменена и
последовательность множителей [имеет место: (pq)* == q*.. р*].
Также и в квантовой теории волн материи полный заряд мате-
рии е f dv * не зависит от времени; это доказывается наииро...
стейшим образом тем, что он переместим с Н. Покажем теперь,
что собственные значения матрицы f dv ф* Ф будут положительные
целые числа, как это требует опыт. Соrласно с (233) полаrаем:
Ф == ] а , U r (Р); ф* == a r * а,* (Р); J а , а в * dv == Ors ; (244)
тоrда иа (242) следует:
* * J
а , а в а в G r == и в,
а , а в а в а , == О
'* * * * О
а , а в а в a r === .
(245)
Эти уравнения удовлетворяются посредством подстзновок
....... 21tl 6 1
а е h r N 2. а * N
'............ r , r r
(246)
rде N r и: О, эрмитовы операторы, УДОВJIеТВОРSlIоrцие слеДУIОЩИМ пе...
рестановочным соотношениям.
21ti
е 8]" f(N r )
1)
8,
(247)
Собственные значения пы
числа. Далее, И3 (246)
J dv * :==: f dv a,* а в
'8
положительные целые
и s == ]a r * a r :==: Nr'
(248)
109
Таким образом квантовая теория ВОЛН материи без труда объ
ясняет тот факт, что заряд всеrда есть целое кратное основной
единицы. Правда, она не смоrла выяснить, почему существует
только одна такая основная единица вполне определенной вели..
чины. Квантовые условия Хартри являются аналоrом перестано
вочных соотношений (242) в духе принципа соответствия. Так
как Nr есть постоянная интеrрации уравнения (227), то можно
рассм триваrь специально те стационарные состояния системы, для
которых эта сумма имеет значение N.
Впрочем Nr остается постоянной даже тоrда, коrда V o за
висит от времени. Иордан и Клейн доказали, что решения (243)
для случая Nr === N математически и физически эквивалентны ре...
шениям проблемы N электронов в корпускулярной теории, полу-
ченным в М 2, но, правда, не все.м решениям этой проблемы;
напротив, из возможных решений должны быть выбраны только те,
в которых функция преобразования Ф симметрична относительно
координат электронов. Эти решения образуют замкнутую систему
термов, а именно такую, которая соответствует статистике Бозе..
Эйнштейна. Из квантовой теории волн :материи, т. е. из переста
новочных соотношений (242) следует, таким образом, Бозе-эйн"
штейновская статистика для соответственной корпускулярной кар-
тины. НО перестановочные соотношения (242) представляют только
одну частную возможность для квантовой теории волновых полей.
Друrая равноправная возможность получается, если во всех пере...
становочных соотношениях отрицательныЙ знак заl\lенить положи...
тельным
ф(Р) {f*(P') + *(Pf) (P) == о(Р Р') )
ф(Р) ф(Р') + (P') (P) == о
(f*(P) ф*(Р') + (f*(P') *(P) == о J
Соrласно Иордану и Виrнеру полученной таким способом кван...
ТОБОЙ теории волн материи соответствуют те решения I1Iрединrе...
pOBcKoro уравнения 8 корпускулярной теории, функция преобразо-
вания которых антисимметрична относительно координат электронов.
Это значит, что перестановочные соотношения (249) приводят
к принципу Паули и соответственно к Ферми...дираковской стати..
стике для корпускулярной картины.
(249)
11. ДОКАЗАТЕЛЬСТВО МАТЕМАТИЧЕСКОЙ ЭКВИВАЛЕНТНОСТИ
КВАНТОВЫХ ТЕОРИЙ КОрПуСf{у ЛЯРНОЙ И ВОЛНОВой "АРТИН.
ЦентральноЙ проблемой квантовой теории является факт, что
корпускулярная и волновая кар1'ИНЫ предстаВЛЯI0Т две различные
110
ормы явлений ОДНОЙ и той же физической реальности. Удовле...
ОРИl'ельно, что и в матемаI'ичеСКQМ аппарате теории имеется
полная анаЛОI'ИЯ с только что рассмотренной двойственностью при
роды атомных явлений. Аналоrия заключается в том, что одна и
та }ке математическая схема может быть интерпретирована или как
квантовая теория корпускулярной картины, или как квантовая
теория волновой картины.
Мы проведем доказательство в оБIцем виде, не оrраничиваясь
случаем некоторой определенной rамильтоновой функции. Шре..
динr ровское уравнение корпускулнрной теории должно иметь сле
ДУЮЩИЙ вид:
{ }: оп + опт+. . . + 2 i · :t } cp(rl, Т2,.. Т п ) === о (250)
п п т
Здесь оп предстапляет собой оператор, который действует на
пространственные координаты одной частицы (п той), опт на про
странственные координаты двух частиц (п-той и т-той) и т. Д.
Пусть далее задана система ортоrональных функций ur(r) , ПО
которым может быть разложена ка)кдая, имеющая физический
смысл функция координат TpeXMepHoro пространства, удовлетворя-
IОlцая rраничным условиям. Тоrда ер (Т1 . .. . tN) может быть разло..
жена по произ едениям этих ортоrональных функций:
<р (1"1 . · . r N) === b(r 1 r 2 . · · r N · t) u r 1 ( r 1 )а r/ Т'}.) · . .. U r N( t N ) (251 )
!....rN
Величина I Ь 2 \ может быть рассматриваема, как вероятность
найти электрон (1) в состоянии '1, электрон (2) в состоянии '2
И Т. дО
Подставим это значение (251) для ер в (250), умножим левую
уравнения (250) на U S1 (rl) U S ;z(t 2 ) . " . USN(rN) и проинтеrрируем по
rt, .. tN, тоrда, в силу условий ортоrональности, получим:
О 2:i :t b(Sl S 2 · · · SN) + O:п, У n b(Sl .. · · . SN)
n, Т п
,-, O;т s . r r Ь (S1 . · " ' п .. .. SN) (252)
. т' п т
п>m Т п , r m
3 О п О пт
десь s,. и, соответственно, s означают мат р ичные
11.' п Il'
элементы СОО"i'ветствующих операторов в координатной системе, ха-
рактеризуемой ортоrональными функциями В силу симметрии
rамильтоновой функции относительно частиц, численные значения
соотвеrствеиuых матричных элеменrов зависят только ОТ букв S,
111
Но не от tt или 1n. Так как величины b(Sl." SN) в случае Бозе...'
эйнштейновской с r8ТИСТИКИ симметричныI относительно квантовых
чисел частиц, то можно как арrумеиты применить также числа N r
частиц в состоянии r. Так как априорная вероятность найти N 1 ча..
СТИЦ в состоянии 1, N 2 частиц в состоянии 2 и т. д. дается через
N!
N , N , "..., то удобно ввести:
1" 2'
( N! )
b(N]N 2 ..) == -- л i Т- N '' · b(r]1 }'2' ..)
1 . .
(252а)
2rci
- ОТ
Введем далее, СОI'ласно (247), оператор е h , который пере d
водит N r в N r + 1.
Тоrда из (252) следует, после суммирования по n и I1t,
21ti
{ h д h (е s в, )
о === 2тr.i д! + NsOs, , е +
s. r
1 2r:.i" fj п" }
+ " fi- (IJ S + V s ' и, 0,/) + .
2 N s (N s ' ss/) Oss',rr,e · · ·
ss', тт'
.( N1 1 . ..} b(N 1 ...) (253)
Умно)кая на
( N' )
, .. 2 С левоЙ стороны и перемеlцая оле...
N 1 .. "..
211Ё 6
раторы е h направо, получим окончательно:
{ h д 1 1 21П'
0== + Ns2.(Nr 3rs + 1)2.0sr. e h (6s er) +
21Cl at s, r
+ Ns+ (Ns' 3ss,)+(N r +l 3rs 3 rs ')+'
S8', тт'
1 2rci
2 h (6$ + e s ' 8, 61")
· (Nri + 1 + 0r,r 0Т'$ ОТ'8') .. е +
+ . .. ..} Ь( N 1 . .. .) (254)
с друrой стороны rамильтонова фУН-КЦИЯ волновой теории,
I1р.инадлежащая к уравнению ('250) ,корпускулярной теории, есть
........... f * 1 11 * * ,
Н== dvрфрОР Р+2 dVрdVр'фр'фр ОРР р'фр... (255)
112
Отсюда, corпaCHO уравнению (244) получается:
* + 1 ** 0 1
Н== asa1'Osr 2 ,asas,ara1" ss'rr'T......
sr ss',1'1'
Подставляя (246) в уравнение
h д
HS + 21ti .. дi S == О,
получаем:
{ h д ......,..!.... 21ti( б s 6 ) 1
0=== 2тci дt + N$2 Osre h r N 1'
s,.
1 2ni б s 1 2пl 8s' 2rr.i в ,. 1
2 Ns2 е h N s ' е h Oss',rr' е h N,.
S$' , 1''''
2ni 1 }
От'
е h . N 1' ,2 +... s(N 1 N;!......)
21ti в
Если снова сместить все операторы е h направо, то получа..
ется:
{ ! 1 21ti
h д т . (ea 6T)
0== 2тci " дi+ N s (Nr 3$1'+ 1) 2 Оа1' е h +
1 1 1
+ N s 2 (N s ' 8 8S ') 2(N r + 1 8 rs ' 8rs)"'2 (N r , + 1 +
$$' , Т1"
-} 1ti (0$+ 8 а , 8r...... 8у') }
+ 01'1" ........ 8,.'$........ 8 "'8') е +. ... s (256)
Это уравнение тождественно с (254), чем и доказана математи..
ческая эквивалентность корпускулярной и волновой картин. В слу-
чае справедливости принципа Паули и перестановочных COOTHOIIIe..
ний (249) доказательство проводится подобным же способом.
Несмотря на то, что классические теории корпускулярной и вол...
новой картин абсолютно различны как математически, так и физи...
чески, квантовые теории обоих представлений математически и фи-
зически тождественны..
12. .ПРИМЕНЕНИЕ К ТЕОРИИ ИЗЛУЧЕНИЯ.
Максвеллевские уравнения получаются посредством вариации
потенциалов из следующей лаrранжевой функции'
1
L == 8тс ( 2 2) + Ф SrJ." (257)
8 В. I'ейвев:берr.. 113
Эдесь 8(1. (а == 1, 2, 3, 4) dбозна чают плотности токов, Фа ..........
максвеллевские пqтенциалы; Ф4== iФо; Х4 == ict; поэтому L будет явно
написана в функции потенциалов так:
1 [ ( 1 дФi дФо ) 2 ( дФi дФk ) 2 ]
L == 811: С дх + дх; дХk дх; + ФflSfl (258)
(Латинские значки здесь и впослеДУlощем постоянно беrут от 1
до 3, rреческие от 1 до 4.) Канонически сопряженные с Фi функ...
дии (моменты) по (244) будут:
П; == дL == ( дФi + дФо ) == @t.
дФi 411: С С д! дх; 411:С (259)
Так как для световых квантов справедлива статистика Бозе'""Эtlн..
Iuтейна, то отсюда вытекают следующие перестаНОВОЧНЬJе соотно-
шения:
i(P) ФС(Р') ......... Фсх(Р') i(P) ==........ 2hciB(P Р') а/а,
откуда после дифференцирования:
i(P) k(P')........ k(PI) i(P) == О
SJi(P) Sjk(P') k(P') &i(P) == О
@l(P) 2(PI) 2(P') @l(Р) == 2hci дО<:Х f')
(260)
и далее в KpyroBoM порядке.
Некоторую трудность представляет то обстоя-тельство, что ФО
не встречается в лаrранжевой функции. Но эта ТРУДНОС1Ъ суще-
ственна только для перестановочных соотношений потенциалов
с составляющими напряжения поля и не касается перестаНОВQЧНЫХ
соотношений (260).
Если Фа разложить по соответственно выбранной системе орта-
rональных функций (например, стоячие колебания в некотором со-
суде), ТО ЭНерrия, оrносящаяся к собственному колебанию частоты 'У,
выразится, как целое кратное hv; тоrда можно числа световых кван-
тов в каждом состоянии собственноrо колебания рассматривать как
переменные системы, как это сделал Дирак в своей теории излу-
чения, и таким образом развивать далее КОРПУСКУЛЯРНУIО теорию.
114
Дополнения " Pycc"o.lJtY изданию.
1. К выводу соотношений неопределеиности (11, 1).
1. Всякое волновое поле классическая ОПТИI{а рассматривает
состоящим из некоторых элементарных образований элементарных
пучков лучей. Число элементарных пучков лучей равно числу CTe
леней свободы данноrо волновоrо образования или, математически,
числу неззвисимых членов при rармоничеСКQМ анализе, т. е. при
разложении поля в ряд Фурье на плоские монохроматические волны.
Это число совпахает также с числом собственных независимых KO
лебаниИ данноrо волновоrо поля.
Элементарный пучок, изучавшийся в частности Дебаем и Лауе 1),
являеrrся некотороА индивидуальностью, CBoero рода атомом, в том
смысле, что он означает нижнюю rраницу различимости свойств
волновоrо образования.
Число С1'епеней свободы поля стоит в тесной связи с возможностью
различить составные части волновоrо образования или пакета, т. е.
с понятием раэрешаlощей силы в оптике. Действительно, две точки
различимы только тоrда, коrда расстояние между ними e будет
порядка длины волны Л, деленной на уrол пучка лучей, сведенных
линзой или микроскопом; Т. е. (см. формулу текста (21)]
л
e L\a 2) (1)
(в знаменателе в сущности должно стоять хорошо известное в
оп rике выражение п sin L\a; эдесь же у нас п == 1, а sin L\a '""" L\a).
Наименьшая площадка I1f, которая может быть изображена не как
точка, будет порядка:
А2 2 А 2
L\f АЕ2 L\a 2 Q Q coSf ' (2)
1) М. У. La1te, Апп. d. Phys. 44, 1197, 1914; см. А. Lande, статья в
Handbuch d. Phys.
2) Анализ этоrо оптическоrо соотношения в связи с определением по
,;rJожепия электрона СМ. К. Р. У. Weizsacker, ZS f. Phys. 70, 114, 1931.
.
115
rде ЬQ телесный уrол, и последнее приближенное равенство имеет
место в том случае, если нормаль к д.! образует с направлением
лучей уrол 6 О. Таким образом всякая поверхность f соста-
влена И3 Z == {! независимых элементарных, моrущих быть изо-
браженными в конечном виде (не как точки) площадок.. Это по-
следнее число, суп ественное очевидно для разрешающей силы, равно
числу степеней свободы пучка лучей, выходящеrо ОТ f. Действи-
тельно, суммируя по всем уrлам и по всем площадкам, т.. е. но
всей поверхности сосуда, в котором находится волновое поле или
излучение, имеем:
Z == z == . ! == Еjд.Q cos 6 'J2! l\Q cos 6у2
4 Ц ·
(3)
с f друrой стороны, если длина волновоrо пакета (или СОСУД2,
в котором заключено волновое поле) конечна и равна 1, то пакет
должен быть составлен И3 ВОЛН HeKOToporo участка частот или
1
длин вопн д.v == СЬ. Если длина пакета 1, то в пакет войдут
волны с длиной волны A.k == , rде k целые Чlfсла; в интервале
А., л+ Ал поместится k волн, rде k определится И3 неравенств:
1 1 1
k А. + A. или Т > k А. + A. '
л.
т. е.
( 1 1 ) 1 1
k ==.1 А+ л. T ==1 T==cA". (4)
Элементарное же lсолебанuе определяется одной волной, т. е. для
Hero будет соблюдено условие:
1
v == 1. (4.1)
с
Перемножая Z и k, пол.учим общее число степеней свободы Р:
v 2 д.v "" 'Y2 oy
F==Zk-== сзl !llQ cos O==7.4 VJ (5)
ибо g == 4'1t, а 1 ! cos (1 дает общий объем V. Как известно,
этот результат не зависит от формы объема УЧТЯ поляризацию,
т" е. МН9житеJIЬ 2 для излучения, получим классическую формулу
Рэлея... Джинса ..
р' ::.= 2f" == 81tV2 V . . V
с 3 ·
(6)
118
Формулы (5) и (6) в случае волн материи или излучения (на-
бора фотонов) дают объем фазовоrо пространства, соответствующий
интервалу частот :y (если ОТ "i перейти к переменной импульса
hv
р == ). Число же клеток фазовоrо пространства получим, раз-
е
делив общий объем (5) или (6) на объем каждой клетки, т. е. на h 3 .
С друrой стороны, принцип неопределенности вводит НИ)J{ffЮIО
rраницу для Пl)оизведения p x h, что соответствует оптически
соотношению:
дv
Llx 1
с
1
или т x 1. (7)
вида (7) для х, у, z соответствует
Произведение трех членов
одной фазовой KJleTKe.
Каждая клетка фаЗ0воrо пространства соответствует о.дной
степени свободы и в статистическом смысле дает НИЖНЮIО
rраницу различимости. Мы видим, что 1" фОР'м'улам Неопреде....
ленностu (7) .можно пoaouпzu или из статистики или со сто-
роны подсчета числа степеней свободы, IlZ. е. числа эле.мен-
mарны,х пучков. Важно усmаНО8ипхь нижнюю zран-ицу разлuчи..
MOCfnU 8 оптическо.,М" статистuчесftо.м, и т. д. с-мысле. В случае,
1
если импульс меняется по величине, то имеем формулу !.l 6.х 1,
I:1rz
если же импульс меняется по направлению, то т e 1, rде а уrол,
характеризующий направление. Таким образом, формулы принципа
неопределенности непосредственно примыкают к оптйческим: для
CBera они являются простой их перепиской при ПОМОIЦИ соотноше..
hv
ния Эйнштейна р == , для волн ,1\! атерии же нужно учесть
с
h
соотношение де Бройля р == т и Т. Д.
Строя волновой пакет длины Llx, мы находим И3 анализа пакета
по Фурье, что НУ}КНО В3ЯТЬ волны И3 интервала волновых чисел
1 1
t.k == Ll 'л. paBHoro дх ; обратно, построив пакст И3 ноли интер
1
вала !.l л ' ВИДИМ, что ero длина будет r:орядка x
вне 9Toro участка интенсивность волн весьма
1
, т. е
л
мала. 1) Это рас..
J) Напр. J. Р'rепkеI, Еiпfi1hruнg 1п die \Vcllenmechanik; L. de BrogHe
Введение в волновую механику (печатается русский перевод).
117
сужление (сравни текст стр. 16 И формулу (4 I), которое тоже
дает ни}кнюю rраницу различимости), конечно, весьма примьи<ает
к предыдущим. Оно также ценно потому, ЧТ берет самые общие
волновые соотношения и сразу после применения формулы де Бройля
дает формулы неопределенности. Действительно, пусть неКОIорая
функция I имеет вид:
f::=: aeiko'X,
['де а отлично ОТ нуля и равно единице только в промежутке
l1х Llx
2 -< х :s;;; 2. Имеем:
l f ikX
j== ]/2; Ье dx;
Ь==
Ах
2
.!
....... Ах
2
i (ko
е
k)X d
X=:z
2 Sin(ko k)il;
......
V 2тc (ko k)
(8)
Ах
V2
sin (ko k)
(kO !k) '2"
Выражения для I ь 12, пропорциональные инrенсивностям пар
циальных волн, заметно отличны ОТ нуля только в области меЖilУ
двумя нулями синуса, ТО е. в участке
Ilk!::.x 1, (9)
1
если k ko обозначим через dk; отсюда, полаrая tJ.k ==!J. Т ==
== il .. ' и получаем формулу неопределенности, как было отме-
чено выше.
Кроме формул для ошибок импульса и координаты, аналоrично,
оптическим путем или построением волновых пакетов и иханаЛИЗ0М
по Фурье можно получить еще и формулу, связываюшую время
прохо}кдения волновоrо пакета и спектральную область частот, из
которых пакет составлен. Например, непосредственно формулу (4)
перепишt?l\( та 1<: :
1
'; == Atllv,
с
(10)
118
rде tл! время лрохождения пакета через HeKOTOPYIO rочку; СТОЛЬКО
ЧJIенов ряда Фурье, Т. е. отдельны: волн, нужно для опи'сания па-
I 1
кета длины 1 или BpeMeHHoro протяжения . Если это число
с
приравнять единице, ТО мы получим соотношение ме}кду временем
и частотой, выполненно для элементарноrо волновоrо пучка, т. е.
получим нижнюю rранацу или условие различимости для частоты
и времени:
А. v I1t,....., 1.
(11)
Формула (11), как и (1), определяет элементарный пучок лучей.
Смысл 3Toro СQОТНОПlения совершенно подобен содержанию
формулы pl1x: если мы имеем волновой пакет, составленный из
частот области !.1v, то ero времеНН1Я ДJхина (или время прохождения
1
через некоторую точку) будет порядка Iit "'-' 'J ' Например, еслИ
мы анализируем пакет некоторое вре я 8.t, т. е. после f1t секунд
от начала опыта обрезаем хвост Болновоrо потока, ТО мы не смо)кем
1
отличить разности частот меньше 11 At . Соотношение (11) име..
лось уже, соrласно принципу соответс 1 вия, в старой теории Бора,
rде частоты, соотвеТСТВУI{)щие стационарным состояниям, не моrли
быть определены точнее, чем дО A'J, так как стационарные состояния
существовали не \ ,бесконечное время, но имели конечное время
}КИ3НИ Iit. Время измерений очезидно должно быть равно или
больше врем,ени н{иэни, т. е. будем иметь l1'iAt> 1.
Попрежнему для фотонов из формулы (11) следует после под-
е
становки 'J ==: Ь' rде е энерrия фотона
А; М,,-, 1.
(12)
Так же точно, ПО rJставляя вместо по де Бройлю частоту, СООТ...
8
ветствующую энерrии частицы == h ' будем иметь ту же формулу
(12) для точносrи определения энерrии атома, электрона и т. д.
Е1
Если }ке v означает частоту перехода у::= ТО вместо
(12) получим
А ( s 1 .......... $2) t h.
(13)
[10 Бору переход между двумя состояниями имеет такой )1 е
119
индивидуальный характер, как и самое состояние 1). Ландау и
Пайерлс (25. f. Phys. 69, 56, 1931) применили формулу (13) для
определения точности в импульсе. Для свободноrо электрона имеем:
Lls 1 == 711 A Pl
S2 == 71 2 AP2,
(14)
rде значок 1 означает состояние до переходз, а 2 окончательное
состояние. В виду закона сохранения импульса: АР1 == !lp2 И из
(15) и (14) имеем
(711 7(2)Ap!lt h.
(15)
в релятивистском случае 711............ V2 не может быть Болыlеe с и
из (15) мы получим
h
ApAt"'""
с
(16)
формула (16) показывает, что импульс в данном случае нельзя
ИЭ;\1ерить MrHOBeHHO. В нерелятивистской же области разность ско-
ростей может принципиально быть сколько уrодно большой, так
что и Ар О при At.......... О (хотя как раз для больших скоростей
нерелятивистская механика и неприrодна).
Заметим, что соотношения неопределенности, в которые входит
время, трактуются различными авторами различно. Трудность лежит
по CYLЦecTBY в том, что время в нерелятивистской теории является
просто (классическим) числом (е ...number), а не оператором
(q - number) (квантовым числом).. Для чисел никаких соотношений
неопределенности нет, поэтому, вводя все же таковые для времени,
мы пытаемся трактовать ero как оператор, т. е. заходим в не по-
строенную еще область.
2. Шрединrер (Ber1. Ber., 296, 1930) дал очень простой и
общий вывод формулы для произведения ошибок двух квантово-
механических величин. За исходный пункт возьмем неравенство
Шварца:
(a1 a i +a2a +... aпa:z) (Ь 1 ЬТ+... bпb ) >1 аl Ь 1 +а2 Ь 2+'.' п п ь п l 2 , (13)
rде звездочка обозначает сопряженную величину. Наrлядный смысл
этой формулы станет весьма ясен, если взять, например, п == 1, 2, 3 и
положить все а и Ь вещественными, или же положить а1 == (;(1 i l'
все а2." ал == О и все Ь равными 1.
1) N. Bol1r. Сборник статей, цитированных на стр. 142, ИЛИ по русски
В сборнике "Причинпость". Е. Sсhrбdillgеr, BerI. Ber. 1931 (, Speziellc
Relativltatsthcol'ie ul1d Quantenmechanik ").
120
в случае непреРЫВlJО меняющихся значков суммы заменяются
интеrралами:
fffdx f ggdx>IJfgdxl l . (14)
*
Положив здесь f == B , g == A , rде А, В любые два эрмитовы
оператора, а Ф любая волновая функция, получим:
J фВ2фdх J $А2фdх >-- I J фА8фdх 12 (15)
или 82 А2 :> 1 АВ 12, rде черточка означает среднее.
Вместо правой части f АВ 12 можно написать:
I АВ 1 2== ( АВtвл у'+ АВ 2 ВА 2
(разлаrая на эрмитову симметричную и антисимметричную части и
АВ БА
имея в виду, что среднее антисимметрической части 2
4И...
сто мнимо).
Чтобы волучить еще более общее выражениэ, заменим А и В
на А АI и В 81, rде 1 означает единичную матрицу. Оконча-
тельно имеем для ошибок i1A и f1B
(ДА)2 (дВ)2:> ( AВt ВA A ВУ + AВ ВA 2, (16)
dA==V(A A) 2== V A2 (A )2.
Если отбросить первый ЧJlен суммы справа, то неравенство
будет только усилено; если к тому iKe взять за А и В и канонически
Jl
сопряженные величины, для которых АВ........... ВА == 2ТC' ё ' тоrда получим
формулу rейзенберrа (20), если под А и В иметь в виду ИМПУЛЬС
и координату электрона:
h
llА · 118 > 4ТС' 1»
(11)
Отметим здесь важное применение формулы (17). Ваяв за А
и В канонически сопряженные величины энерrию и время, получим:
l1E t h. (18)
Таким образом, при измерении, длящеМСfl время дt, нельзя
h
измерить энерrию точнее, чем до величины АЕ r-...; At .
1.21
Если речь идет об энерI ИИ перехода (Е1.......... Е 2 ), то будет иметь
место формула:
А (Е 1 .... Е 2 ) ' h.
(19)
Эти соотношения MorYT быть получены и друrими методами) СМ.
стр. 119, формулы (12) и (13).
2. Маrнитный момент лектрона.
Бор указал следующее применение СОQтношеНIiЙ неоиределен"
ности при рассмотрении собственноrо маrнитноrо момента электрона
(спина). KorAa электрон находится в атоме, ero маrнитныЙ момент
входит как часть в маrнитный момент aTQMa и поэтому непосред",
ственно неиаБJlюдаем. СпраШИJ3аеrся, мржно ли с помощью маrни..
тометра наблюдать маrнитный, момент свободноrо электрона? Пусть
ЭJlектрон находится на ра<:стоянии 1 от маrНИТQмеrра и создает
следовательн,о маrнитное поле
tJ.
*73'
(1)
eh
r де O маrнитный момент электрона, равный БОрОБСКОМУ Mar.
lпс
нетону (МЫ рассматриваем только порядок величин и отвлекаемся
от учета направления). Но мы никоrда не можем быть уверены,
что электрон, положение KOToporo известно с точностью 1:11, не
двиrается со скоростью !!.!V (так чтобы Alllv > ) .
Дни}{(ущийся }ке электрон создает маl'нитное поле величины
e/1v
2.
(2)
ДЛЯ ТО1'0 чтобы
чтобы поле (1) было
eJz
тcl.)
действие спина было наблюдаемо,
болыпе, чем поле (2), Т. е.
eLlv eh еЬ
cl 2 [ 2 > . l2 1 ; или l > 1,
те те 1,
нужно,
(3)
Т. е, условие непосредственной наблюдаемости маrнитноrо поля
спина невыполнимо, так как неопределенность поля (1)' будет
БОilыпе, чем самое поле (ибо неопределенность в расстоянии элек...
трона от прибора должна была БОJIыuе ero расстояния 1). Это не
значит, что спин свободных электронов вообще ненаблюдаем, но то, что
ero нельзя толковать наrлядно с помощью классическоЙ механики,
понятия траектории и пр.
122
Бор подчеркнул также,' что невозможно наблюдать спин элек-
трона методом Штерна..rерлаха. B03bM J eM пучок электронов, дви...
rающихся параllлельно оси у в неоднородном маf'НИТНОИ поле
Н, расположенном в плоскости XZ; пусть, кроме TOf'O, ДJIЯ Х == О
Нх == о. ОДН8 i КО вообще, вне плоскости yz имееМ: 1
дН х А дН z
Нх==' дх '-lx== дz X,
( · дН х + дНу + aHz Н О
в силу условия dlV Н == дх дУ дz == О, Т. е. при у ==
д Н х .......... д Н Z )
...............""""""" .
дх az
(4)
aH z (
На электрон действуют две СИJIЫ: 1) сила tto в виду на-
дz
лоренцова сила в направ-
личия спина) по направлению z и 2)
е
лении х: vyHz, вне плоскости Hz.
с
Лоренцова сипа на
расстоянии X ОТ оси равна
е дН z
c V y дz f:,.x.
(5)
Для успеха опыта Штерна-rерлаха нужно, чтобы
е дН z eh дН z h
Vy X , т. е. Х Л
с az 111C дz lпv y '
т. е. мы находимся вне области приrодности классических механи-
ческих понятнА. Случай движения электронов параллельно оси х
ведет к тому )ке результату.
Интересна, наконец, критика Бором
ЛIОЭНОМ ДЛЯ обнаружения маrнитноrо
троны двиrаются параллельно оси z в
(6)
опыта, предложенноrо Брил..
момента спина. Пусть элек..
неоднородном поле, напра..
дН
вленном в сторону обрат!ную их движения. Пусть z
О, тоrда
дН
э.пектроны со спином, подвеРI'аясь действию силы (так же,
как и тело, брошенное вверх), направленной в сторону z, через
некоторое время остановятся и затем повернут обратно. Из
dv z дН z
т ==........... t-to для времени t получаем
dt дz
t==
1пVo
110 az
(7)
128
Таким образом, число электронов, которые мы встретим дальше
отрезка vzt, будет вдвое меньше, чем в случае отсутствия спина.
Но, как и в предыдущем при мере, нельзя осуществить попе, везде
CTporo параллельное оси z.
Если для х == О и Hz 11 z, то НХ дается формулой (4) для рас..
стояния x от оси х. Но электроны под действием силы Нх будут
1
описывать круrи С периодом 1: == , I'де ш уrловая скорость, рав-
о)
еНх
ная , т. е,
тос
тос
1: == дН .,
е !lx
дz
Чтобы поворот скорости произошел от действия спина, а не
под влиянием силы Лоренца, нужно, чтобы t 1:, Т. е..
(8)
те mv z
eh дНz
дz
nzc
дfj x '
е дz
(9)
следовательно mv z 6.x h или 6.х Л,
Т. е. опять мы находимся вне сферы действия rеометрической оп
eh
ТИ1<И. Если бы вместо O "-1 мы I1мели бы какой..то маrнитный
nzc
момент fl, то, как леrко видеть при f1 » t1o, в последнем примере, как
и в друrих, опыты позволили бы обнаружить наличие момента.
В докладе Паули указаны и друrие иллюстрации тезиса Бора о
невозможностИ наблюдать спин в смысле применения классических
механических применений о движении.
Л и т е р а т у р а: N. Р. Mott, Proc. Roy. Soc. А, 124, 425, 1929.
W. РаиН, Rapports de Congres Solvay, 1930.
3. К подсчету флюктуаций (V, 7).
(СМ. W. Heisenberg, Berichte d. Sachs. Akad. Leipzig, 83, 19/1, 1931),
Оказывается, что прежние подсчеты Борна, Йордана и автора
книrи на основании квантовой механики были основаны на
ОIпибке. Выражение для среднеrо квадрата флюктуации энерrии
давалось интеrралом по частотам, а подинтеrральное выражение co
держало члены q пропорциональные частотам hVj, в результате"
чеrо интеrрал оказывался расходящимся. Так как речь идст о флюк-
туациях лучистой энерrии, то можно было бы думать, что обра..
щение УПОМЯНУТQI'О интеrрала в бесконечность связано с наличием
124
в энерrии 9лектромаrнитноrо поля бесконечно большой, так 8аЗВ1--
ваемой нулевой энерrии (Nullpunktsenergie). Однако это не так,
и трудность лежит в самом определении флюктуаций.. Чтобы по-
казать это, исследуем более простую модель, заведомо не имеющую
бесконечной нул вой энерrии возьмем, именно, движение ма-
териальной точки массы t вдоль отрезка длины 1, оrраниченноrо
непроницаемыми стенками.
Энерrия частицы дается выражением
B == J J2 rде P h d
2 ' 2 . d
т rcl Х
(1)
Собственные значения 9нерrии и собственные ФУНКЦИИ найдутся
ИЗ уравнения UUрединrера
h 2 d 2 ф
81t 2 m dx 2 + Еф == О
(2)
с поrраничными условиями: Ф == о при { Х == О
x==l
Отсюда, принимая во внимание условие нормировки, получаем"
== v ak sin 1t k.
1 ( h ) 2
Ek == 2 "х 2 1 k ,
(3)
rде k целые числа'.
Интересно HaIlI результат получить прежде Bcero с помощью
представления о квантованных колебаниях в обычном, в данном
случае одномерном пространстве.
Для этоrо нужно амплитуды функции считать неперемеСТИМbJМИ
операторами. Иа (3) имеем:
/ 00
ф == v ak sin 1t ; k.
(4)
rде
akal* ........ al*ak == 3kl..
ПослеДНЮIО формулу мы написали в предположении, что у нас
имеется на всем участке совокупность одинаковых частиц, УДОВJlетво-
125
РЯЮЩИХ етатистике Бове"ЭМншtейна. Соrласно М (246) можно по...
ПОЖИТЬ:
1 1
A + N 2 * 1\ 12 ,, 1
ak:= k.. -;, ak :::::: 1'1 k k )
(5)
rде N k означает число частиц в СОСТОЯНИИ k.
Для энерrии небольшоrо участка от Хо до Хl J СОl'ласно опре-
делеНИlО плотности энерrии М (209), имеем:
Jt 1
Е === f dX h2 ?о/* Ф ==
81tm дх dx
)
ХО
h 2 2 f X' * х х ( 7t ) 2
=== dx a/r, 'а я cos 1t k cos те п пl ==
8 1t 2 ,п 1 kn 1 1 l
Ха
} (6)
h 2 * f
== 8 2пl ak а п kll,
kn
rде
'It JSi!1 (k+п)Xl Sin ; (k+п)x o
fkn === [2 ku I k п +
sin ; (k п) хl sin ; (k п) Ха f
т ·
п
Среднее по времени значение 9нерrии дается диаrональным членом,
т. е.
h 2
Е == 8 'lt2m ak*akfkk"
(7)
Таким образом для флюктуации имеем:
h 2 ,,
/j"E== 8 2 а;; a п !k1J,
1tт k
п
'Тп
(8)
126
и для среднеl'О квадрата
t::..E2 (
(
== (8 7t 2 ni)2 ;
k::j:::.n
1
J
Отсюда ВИДНО, что llE равно бесконечности, так как сумма В (9)
расходится даже в случае одной только частицы. Именно для
Nk==l,N п ==Оип k t::..Е2 ==( 8 ::т У ; лn, (10)
k '::t:. п
причем число членов бесконечно, а !kп не уменыпается для балf:....
ших n.
Перейдем теперь к обычному способу конфиrурационноrо про-
странства. Допустим, что энерrия внутри HeKOToporo промея{утка
Ха <: х -< Хl задается оператором
1
2m pD (x)p,
(11 )
rJLe D (х) внутри промежутка ХО Х 1 равно 1, а вне ero равно
нулю. С помощыо собственных ФУНКЦИй (3) найдем cpeДH e значе
иие 9нерrии в состоянии k
1
h 2 2 J ( 7tk ) 2 7t
== 8 2m 7 ' T cos 1 xkD (х) dx
о
1
1t
11 '1 x/(dx ==
} (12)
J( 2 . 7t 1 h д h д .. ( 2
Slп хk -- D(х)
1 1 2 f1Z 2 rci дх 2 1
о
1
121
Для среднеrо квадрата энерrии получаем:
J / /2 те ( 1 ) 2 /2 те 1
Е2 === V т sin 1 xk 2 т pD (х) p2D (х) р V т sin [xkdx==
о
l
== 8 :2 2 т ( ) J cos ; xkD (х) ::2 D(x)cos 7 xk ( k У dx ==
о
h 2 ' \ 2 J / те ( k ) 4
== 8 1t211t T cos 2 Т xkD2 (х) --т dx +
о
1
f cos . xkD (х) 2 D' (х) sin xk ( ::lk У dx
о
/cos 2 xkD (;:)D" (х) ( те: у dX!;
(13)
или
E 2== (8 :т )21. ! sin 2 xkD2(X) (тс: у dx
i oflCOS 2 ; xkD(x)D".(x) ( '/f;r' y dX! (14)
}...{ctле-е по определению
dE2 == Е2 """'"'""" Е 2 .
(15)
Первый интеrрал в правой части (13) дает среднее значение квад-
рата энерrии, ибо Н3 (3) следует
1 %1
8 :т J sin 2 тe kD2 (х) (тe,kY dx === W} f sin 2 тe kdx, (16)
о
%..
rде i J sin 2 те kdx обозначает вероятность найТИ 'IaСТИЦУ
Х 1
между ХО и Хl-
128
Но второй интеrрал в формуле (14) обращается в бесконеч.
насть, так как содержит в подиптеrральном выра)кении BTOPYIO
ПРОИЗВОДНУIО от D{x) (очевидно 'бесконечную). Таким образом,
результате' и средний квадра'Р флюктуации эн.ерrии оказываетсн
бесконечным. Дело лежит, очевидно, в СЛИIПКОМ резком выделении
отрезка Хо.......... 'х ! введением "H xopOllIett ФУНКЦИИ" [) (х).Если на
место такой резкой ФУНН:ЦИИ ввести .функцию сrлажеННУIО, то ВТО"
рой интеrралв' (14) .вообще, сходиться и даст ЛИIПЬ весьма
небольшой при весок к значению Е2.
Взяв, например,
х
D(x)== d ; .r( е
о
dx,
( 17)
I'MeeM для большей части BToporo интеrрала в (14), получ:енной
росле интеrрации по частям, т. е. для
1
( 8 : пl Y fcos 2 Т xk ( ;k )2 D
о
(18)
'Jырз)кение.
( h2 ) 2 1 ( 1Ck ) 2 1 r d2 2 ( 21t 4)27t )]
Q . 2 4 е COS2 X k+COS" Xlk . .
81i. пt 1 1 d V 2тс 1 о 1
I
(19)
Еели d велико по сравнению с длиной волны состояния k, ТО
вторым интеI'ралом можно пренебречь по сравнению с первым в
формуле (14).
Физически следует иметь в виду, ЧТО энтропии двух связанных
систем можно считать аддитивными с точностью до величины вззи
модеЙствия уиетем (СМ. w. Heis nberg, ZS. f. Phys. 40, 501, 1926):
Измерение энерrии в резко оrраниченном участке (Хl Ха) воз...
МОЖНО только при действительной полноЙ изоляции 9Toro участка
и полноrо разрыза ero взаимодействия с дру['ими участками (по
классической теории изоляция не обязательна); такая изоляции
требует "бесконечно большоrо" вмешательства и поэтому физически
неосуществима. Практически BcerJla rраницi>! участка будут не..
колько размыты, т. е. останется Н2которое взаимодействие изме..
ряемоrо участка с соседним. Из сказанноrо следует, что как раз
в виду неаддитив.ности энтропии, что было СУIl ествеIIНОЙ rипотеаоЙ
при прежнем выводе, квантовая механика не даеl' формулы Эйнштейна.
9 13.
129
4. Примечание к теории излучения (V, 4).
Автору книrи удалось найти более простой метод полученип
результатов теории излучения (W. Heisenberg, Ann. 'd. Pbys. 9,
338, 1931). Рассуждения эти весьма близко примыкают к методу
принципа соответствия (см. О. Klein, ZS. f. Phys. 41) 407, 1927, также
L. Rosenfeld, там же, 65, 589, 1930).
Расчет ведется обычным в квантовой механике путем: на атом..
чую систему, описываемую уравне"ием Дирака, посылаются света...
вые волны и ищется изменение числа элеКТРОнt)В внекотором
состоянии. Но, в отличие от теории дисперсии ШреДRНrера (Ann.d.
Phys. 81, 109, 1926), амплитуды а n функций Ф и амплитуды Ь п
падающей 'возмущаЮlлей волны принимаются теперь операторами.
2тti8 п
Как в М (245 и дальше) полаrается: ал == е Nпl/'J ==A N 1 /s,
rде А:-п превращает N n в 1........... N n (статистика Ферми); Ь п == + м 1/\
rде .6,+ превращает М в М + 1 (статистика Бозе"Эйнштейна).
Операторный характер мплитуд не портит наrлядности расчета
и сказывается .олько в окончательных формулах. Весьма просто
получаются коэфициенты А и В Эйнштейна, исследование рассеяния
света и проч. Розенфельд (28. f. Phys. 71, 273, 1931) получил этим
методом коэфициент затухания (и вместе естественную ширину ли..
ний) rораздо проще, чем прежде. Комбинация рассуждений прин..
ципа соответствия с формализмом операторных амплитуд дает таким
образом все результаты дираковской теории излучения. Правда, это
касается только первоrо приближения теории, но как раз высшие
приближения даIQТ ряд парадоксальных следствий (бесконечности
разноrо рода).
5. К релятивистской квантовой механике (V, 8).
Соотношения неоuредеJ1енности, выведенные в книrе, не учнты'"
вали требований теории относительности.. Типичным моментом их
вывода было оrраничение корпускулярных представлений волно-
выми и наоборот. Релятивизм, т,ак же как и корпускулярно"
волновой дуализм, накладывает характерные новые оrраничения на
понятия координаты, времени и т. д.
Хотя В настоя[Цее врамя нет разработанной теории релятивист-
ской квантовой механики, но весьма вероятно, что в известном
приближении останутся в силе соображения инвариантности, пре ,
образования Лоренца и проч. Скорее следует думать, что измене...
ние и оrраничение понятнй В" будущей теории окажется еlце более
rлубоким, чем то, которое мы получим путем предварительных
130
рассуждений. rоворя об отсутствии теории в данной dБJlасти мьУ
имеем в виду два обстоятельства.. Во...первых, существующие кван",
товые схемы, формально удовлетворя'ющие требованиям релятивист-
ской инвариантности, заключают в себе ряд неверных утверждений.
Во-вторых, оказывается необходимым положить в основу отнюдь
не обычные понятия координаты, времени и проч., но существенно
видоизмененные. Конечно, оба обстоятельства по существу связаны
ftpyr с друrом.
Отметим прежде Bcero существенные затруднения в квантовой
электродинамике, развитой Йорданом? Паули и I'ейзенберrом (см.
стр. 103). Теория приводит, каК и классическая электродинамика,
к разложению поля на совокупность бесконечно большоrо числа
,осцилляторов. Энерrи:я осuиллятора в п"ом квантовом состоянии по
квантовой механике равна (n + ) h'/, Т. е. в нулевом состоянии
1
тоже имеется энерrия 2 h"/ (Nullpunktsenergie).
С одной стороны введение нулевой энерrии означало большой
успех квантовой механики, так как целый ряд экспериментальных
фактов, в частности И3 области рассеяния peHTI'eHOBbIX лучей
(СМ., например, James, Wal1er, Hartree,Proc. Roy. Soc. 118, 334, 1928),
16пределенно rоворил за реальность члена hv.
С друrой стороны, для излучения сумма нулевых энерrий бес-
конечноrо собрания осцилляторов равна 6есконечности.
Эта довольно формальная трудность квантовой электродинамики
связана с видом rамильтоновой функции электромаrнитноrо поля;
во всяком случае, путем изменения вида этой функции, удается
избежать бесконечной нулевой энерrии (см., например, L. R,osen...
feld et J. Solomon, Journ. d. phys. 2, 139, 1931).
Вторая или, ЛУЧIllе сказать, первая существенная трудность
электродинамики обязана виду OCHoBHoro закона взаимодействия,
который дается теорией.. В сущности речь идет о трудНо....
сти, имевшеfiiся и в классической теории: энерrия вваимодей...
ствия точечноrо электрона с самим соБОIО равна бесконечности,
е 2
что вытекает И3 обращения в 00 при r о. Введение электрона
r
шарика с конечным радиусом спасает дело в классической теории
и дает конечную энерrию или массу электрона.. До сих пор кван-
товая механика имела дело с электроном:точкой, введение rрубой
модели шарика не представляется возможным (уже и в классической
теории такая модель не была свободной от затруднений, см. Frenkel,
Lehrbuch der ElektrodYllatnik).
.
181
Не только 9лектромаrниtное, но и rравитаЦИОI1ное взаимодей->
ствие электрона с самим собою оказывается бесконечно большим
(СМ. L. Rosenfeld, ZS. f. Phys. 65, 589, 1931), причем это имеет
место и по устранении трудности бесконечной нулевой энерrии
(J. Solomon, ZS. f. Phys. 71, 162, 1931).
Ряд друrих трудностей теории излучения} имеющихся даже
в более простой форме теории, данной первоначально Дираком,
указан Валлером и Розенфельдом (СМ. L. Rosenfeld ZS. f. Phys. 71,
162, 1931 и ero JIекции в Institut Henri Poincare, 1931).
Не только существующая схема квантовой электродинамики
I лубоко неудовлетворительна, но и теория электрона Дирака пора....
}кена отмеченной самим Дираком, так называемой плюс-минус труд....
ностью (см. стр. 79). Как и следовало ожидать, факт наличия
отрицательных значений энерrии в спектре любой системы затра-
rивает не только энерrию, но и друrие величины.
Оказывается, что все, вообще rоворя, операторы, сопоставлен
ные координате, скорости, спину и Т. д. электрона, содержат
в себе части, соответствующие переходам на отрицательные со..
стояния. В виду этоrо операторы теории Дирака иноrда имеют
трудно объяснимый физический смысл. Например, скорость всякоrо
электрона или протона оказывается всеrда равной скорости света.
Действительно, из ур-ия (87) имеем по определению скорости:
. l) 2
Х == ............... == са х и так как (J.k == 1, то собствеННl>Iе значения опера..
l)px
тора '(J.k, т. е. ero наблюдаемыe значения, по обычному толко анию
квантовой механики равны уl == ---+ 1 и возможные значения ско-
рости
.
х == с.
Шрединrер (Berl. Ber. 24, 418, 1931) указал, каким образом
можно каждыЙ данный оператор разбить на две части: обычную
"четную" и "нечетную" , соотвеТСТВУЮЩУIО переходам на отрица-
тельные состояния. Нечетная часть всеrда представляет собой член
быстропеременный во времени. Таl<ИМ образом всякий оператор Q
имеет :вообще слеДУIОЩИЙ вид (но бывают и чисто четные или нечет...
ные операторы):
n ()' n e i'/t
== i::Jfj о i::JQ 1 ,
(1)
I'де !;d o четная часть, а v частота переходов на отрицательные
состояния (частота "ДРО}l{ания" свободноrо электрона Zitterbe..
wegang).
В частности) координата и скорость свободно! электрона
182
даIОТСЯ в?ыраже'ниями
с 2 pt ch
f! 41ti/1 "fje
ФrсiНt
Iz
(2)
41tiHt
н + С'У1 е
(а)
,'де /1 I'UМИЛЬТОНОR оператор, р импульс электрона, а 1] ане...
paTOp модуль I{OTOPOI O равен единице.
МЫ ВИДИМ, что четная часть оператора скорости, т. е. i:, дает
обычные (любые) значения.
Как временный выход И3 затруднений, связанных с наличием
труднqсти теории Дирака, напрашивается слеДУЮIЦИЙ: за наблю..
даемые величины нужно брать не собственные значения операторов,
но собственные значения операторов, усредненных по ("дрожанию.')
колебательному движению Шрединrера, или иначе: у всех операторов
отбросить не,четные части (Е.. Sсhrбdiпgеr, Berl. Ber. 63, 1931)..
(D. Iwапепkо, ZS f. Phys. 72, 621, 1931). Таким путем мы изба...
вляемся от переходов на отрицательные состояния, но в опре-
делении всех величин, у которых ранее были нечетные части у опе..
раторов, совершаем некоторую "индивидуальную tt ошибку (в про
ТИВОllОЛОЖНОСТЬ парной ошибке, например в rейзенберrовском
СООТНОluении I1р д.q). Величина индивидуальной ошибки равна, оче-
видно, абсолютному значению амплитуды дрожания
Q==IQI.
(4)
Индивидуальная ОllIибка в координате будет, например,
D.q == hc
Е
Iz
==l"
те '
(5)
последнее при малых скоростях.
Усреднение по времени операторов и наличие индивидуальных
ошибок представляется странным с точки зрения обычной нереля
тивистскоtl квантовой механики. В теорию Дирака усреднение тоже
привнесено извне. Оказывается) однако, что и усреднение и факт
существования индивидуальных ошибок выводятся и безо всяк:ой
связи С теорией Дирака (сомнительной именно в этих опасных
пунктах).. Оказывается, что и пространственные координаты и время
MorYT быть измерены не абсолютно точно, но имеют некоторую
нижнюю rраиицу, l1ричем для координаты, например, эта rраница
1ЗЗ
как раз равна индивидуальной ошибке) полученной выlеe путем
усреднения из теории Дирака.
Действительно, измеряя координату с помощью освещения
светом ДnИНЫ волны А., МЫ должны учесть, кроме ошибки А. (упо-
минавшейся выllеe на стр. 22), еще поправку на сокращение
h
Лоренца. Импульс, переданный светом f1p l' вызовет движение
измеряемоrо маСIlIтаба со скоростью порядка 1.1, rде 1.1 определится
И3 равенства:
h mv
Y y .
1...........;
с 2
(6)
Это, движение поведет аа собой сокраlцение изм ряеМОI'О мае...
штаба, характеризуемое лоренцовым множителем y; V
== V l 2 . Чтобы учесть сокраlцение, мы измеряемую длину 1
разделим на V 1 .......... 2 ; таким образом эта часть ОШИОки окажется
равной 1 ( 1 ) .
1 .......... 2
Окончательно,
Aq == ),. + 1 ( /' 1 1 ) ..
1 2
(7)
Казалось бы, что для более точноrо измерения нужно брать
все меньшJ.fе ДЛИНЫ волн А., т. е. уменьшать пеРВУIО часть ошибки,
но тоrда будет возрастать вторая часть. При некоторой, длине волны
ошибка будет минимальной. Мы .видим, что характерное оrраниче..
ние, привносимое релятивизмом (сокращение Лоренца), весьма по-
хоже на оrраничения, обязанные корпускулярно-волновому дуализму.
Для нахождения минимальной ошибки найдем производную
от lq по л и .приравняем ее нулю. Мы оrраничимся здесь дия
простоты случаем больших длин 1, коrда можно брать сравнительно
большие л и, следовательно, добавочная скорость, получ енная те...
лом, будет мала (так что можно будет положить Vl 2 ==
== 1 2). В этом случае ошибка будет равна
1
Aq == А 2 2.
(8)
1"
С той же степенью точносrи из (6) имеем:
h
== ,
lпс)...
(9)
т. е.
А q :::::: А.
l ( ) 2 И Aq' == 1 ( l: ) 2 .
2 l1lC )...2 }...Н пzc
(10)
Таким образом наименьшая ошибка ПОJIуqится при
1 == [[ ( c Y Т/а
11 бу ltCT равна:
[ ( h ) 2 j 11з
Aqmin == 1 тc
h
те
/1 '3 ( h ) 2/. == 3 ['/'
2 П1С 2
При 1
h
А q mill >
r'V те'
(11)
h
т. е. НИ)I{ней rранице точности измерения оказывается величина ..
. те
h
Более точный подсчет показывает, что и для случая 1 все
Inc
h
равно остается rраницей точности измерения координаты длины..
те
ОТСЮ,1J.а следует, что в релятивистски"квантовых рассуждениях дли н
h
менее ,.-......., не имеют смысла.
пte
Точно так же оказывается, что и для времени имеется индиви-
h
дуальная ошибка At == 2 И что премежутки времени менее ЭТОЙ
те
величины лишены смысла (СМ. V. Ambarzumian und D. Iwanenko.
ZS. f. Phys. 64, 563, 1930 и Е. Schrodinger, Ber1. Ber. ХН, 1931).
Как мы видим, наличие индивидуальных ошибок можно считать
существенной чертоЙ релятивистской квантовой теории в проти-
воположность нерелятивистской квантовой механике с ее основным
принципоМ неопределенности rейзенберrа и l1ЗРНЫМИ ошибками
у канонически сопряженных величин. fIОВИ2НМQМУ, в квантовой
элеl{тродивамик тоже будут введены индивидуаЛl;ные ошибки (см.
!35
наСТОSlIцие Ilримечания стр. 137). Индивидуальная ошибка указанной;
величины в измерении координаты была введена также Ландау
и Пайерлсом совершенно друrим путем (ZS. f. Phys. 69, 56, 1931).
Та/(им образом u /(oopaUHal1ZY u время нельзя измерить СI'ОЛЬ
j J 20aHO l1Z0ЧflО, !n. е.. и /(oopaufla111a u время пlеряюпz свой обычный
СМЫСЛ 8 реЛЯlllU8uспzс/(ой кванпZО80Й lnеориu. Раз не существует
l\1rновеиных измерений ( ! == О), то очевидно все измерения дают
среднее по некоторому промежутку времени, С этой точки зрения
Dправдывается постулат усреднения, который мы ввели в теОрИIО
Дирака для устранения переходов на отрицательные состояния.
Изложенный Kpyr идей представляется единственным рядом сообра
)кений, ДЗIОЩИХ нечто положительное в направлении построения
будущей релятивистской квантовой теории.
Упомянем еще о попытке rеометризации идеи индивидуальных
ОIlIибок (w. Heisenberg, Z8. f. Phys. 65, 4, 1930) (V. Ambarzumian
ппd о. Iwanenko, ZS. f. Phys. 64, 563, 1930) СМ. 'Born und Rumer,
ZS. f. Phys\ 69, 141, 1931). Наличие инимальной длиflы иминималь..
IIOI'O времени можно толковать как отсутствие непрерывной структуры
у пространства. времени, которое распадается на отрезки Дq и дt.
1=3 таком прерывном ("квантованном") пространстве"времени обычные
дифференциальные уравнения следует заменить уравнениями в ко-
нечных разностях. Интересно, что вместо обычной rриновской функ..
1
нии rO.J В прерывном пространстве получается выражение, кото-
r
рое при r == О остается конечным и р,авным по порядку вели-
1
чины rO.J ilq .
Таким образом было бы возможно избежать трудностей, свя-
занных с точечным электроном и бесконечной ero массой (см. выlеe
стр. ,131). Квантованное пространство вместе с минимальным ilt вво-
дит и понятие максимальной возможной частоты ОУШа:Х И приводит
Мпротона hc
К соотношению: 2 ' Как правильно указал rей..
электрона е
зенберr, теория точечноrо пространства является слишком простым
и rрубым приближением. "Die Theorie HIUSS nicht so einfach
seinU. теория не должна быть столь простой, как сказал Бор!
Новейший подход к этому вопросу (А. Markoff, Phys. ZS. d.
Sоwjеtuпiоп, 1, 387, 1932) использует tополоrическое понятие
"ДО после". Возмо}{{но, что" вводя явную асимметрию в смысле
времени, мы сумеем избавиться и от ПЛIОС"'МИНУС трудности.
Можно все же надеяться, что самый путь rеометриззции новых
представлений, заключавшийся в попытке построения квантован-
Horo пространства, имеет В себе некоторое зерно истины. Не забу..
136
дем, что релятивистское обобщение квантовой мехаНИI<И должно,
по всей видимости, дать основу для теории ядра, а это цель,
для достижения которой поистине необходимо испробовать все
имеЮI.циеся средства.
Необходимость самых радикальных изменений в существующих
представлениях при трактовке ядра видна из факта потери ядерными
электронами целоrо ряда своих нормальных своЙств, как например
спина и маrнитноrо момента. Повидимому вооБIце нельзя более
I'ОВОрИТЬ об ядерных электронах Kal( индивидуальных частицах
и распад подобен испусканию фотонов, которые прежде не су-
ll\ествовали как отдельные частицы (V. Ambarzumian und D. Iwa-
nenko, Доклады Ак. Наук, ,Лнr., 1930. D. Iwanenko, Phys. ZS.
d. Sowjetunion, N2 6, 1932. W. Heisenberg, ZS. f. Phys. в печати).
Мы видим, что в области ядра, в области будущей релятивист-
ской квантовой механики даже обычный атомизм материи должен
подверrнуться пересмотру (СМ. фарадеевскую лекцию N.' BJhr,
Journ. СЬет. Soc.. февраль 1932 r.).
6. О соотношениях неопределенности для электромаrнит&
НОI'О поля (1{ rлаве 111).
Соотношения неопределенности для электромаrнитноrо поля (50)
получены без введения материальных частиц. Этот путь подобен
выводу формулы (25) для материи, rде корпускулярное представ-
ление критикуется волновым. Формула (50) еще раз выведена
(СМ. 57) с помощью измерения поля двумя электронами, Т. е. анало..
rично выводу соотношения (23).
Иордан и Фок (Z5. f. Phys. 66, 706, 1930) обратили внима
ине на то, что, взяв в качестве измеряющеrо "пробноrо" тела
ОДИН электрон, мы получим неточности отдельно для электриче..
CKoro и маrнитноrо поля, "индивидуальные", так Сl<азать, поrреш..
насти, в прбтивоположность парным ошибкам для сопряженных
величин в соотношениях rейзенберrа. Формулы Йордана..Фока
имеются неявно и у rейзенберrа, но ясное введение индивидуаль-
ных ошибок является важным принципиальным luarOM вперед.
Электрическое поле Е мы хотим измерить по величине уско-
рения, попученноrо электроном. В среднем за НСI<ОТОрЫЙ проме....
жуток времени для х"овых состаВЛЯЮIЦИХ будем иметь'
Е . 1 dpx
х .......... е d t '
rде dpx увеличение импульса, обязанное полю..
Но поrрешность Арх величины по формуле rейаенберrа
связана с участком X, на котором получено ускорение:
Ap x l1x h,
(1)
187
Отсюда ДJIЯ неопределеННОСТJ1 поля получим:
h 1
AEx>
е xAt
(2)
и также
!1E y tJ. y !
h
e '
Ez zAt
h
.
е
По существу формулы Йордана Фока утверждают, что
f J hc
ФlJ-dХ(J- == F(J-vd S v > e'
(3)
!'де Фр............ компонента четырехмерноrо потенциала, FfJoV............ теНЗ0Р элек...
тромаrнитноrо ПОJlЯ, а dS.,..., двумерный элемент fиперповерхности.
Отсюда, или также путем npoeToro мысленноrо эксперимента, для
индивидуальной ошиб и в маrнитном поле Н, получаем:
hc 1
Hz >--
е Ь.хАу
(4)
и для Н Х1 , Ну В циклическом порядке.
Эти формулы получаются И3 формулы (55) rейэенберrа, если
положить там : == I:J.t и d == I:J.x. Интересен рмятивистски инва.
риантный вид этих соотношений и ТО, что усреднение Е и Н произ-
водится вообще и по времени, и по проеrранству. С друrой стороны
эдесь не удовлетворяется требование rейзенберrа о том, чтобы ошибка
с
в энерrии должна быть hv :::::: h ).. ' rде л порядка линейных раз-
меров сосуда. Против соотношений Йордана-Фока было выдвинуто
возражение (СМ. напр. J.. Solomon, Theses, Paris, 1931) что наличие
заряда в знаменателе позволяет будто бы........... сдеJlав этот заряд сколь
УI'ОДНО большим измерить поле сколь уrодно точно. Несомненно
это так, но не нужно забывать, что большие заряды реализованы
в природе в образованиях, занимающих большой объем, и, выиrрывая
в точности измерения поля, мы проиrрываем, усредняя это поле по
большим областям. Если бы можно было сосредоточить иеоrра..
ниченно большой заряд на неБОЛЬШQМ пространстве, тоrда только
удалось бы по формулам (2) и (4) измерить поле с любой точ"
ностью.. Таким образом здесь мы неожиданно сталкиваемся с ВОПРОСО.I
1
О возможности существования максимальной электрической плотности..
Бор, Ландау и Пайерлс (ZS. f. P,hys. 69, 56, 1930) устана-
вливаl{)Т новую rраницу для точности измерения электрическоrо п
138
маrнитноrо ПОJIЯ, учитывая наличие излучении энерrии частицей
служащей пробным телом при измерении. Так же как у Йордана
Фока, здесь нет речи о квантовой электродинамике; за основу
берется уравнение движения, из KOToporo получается, как и выше:
e/1E x /j,t > !:J.px' (5)
ЭнеРI'ИЯ, излученная за время dt, равна:
е 2 " ! .
АЕ == с 3 1) 2 dt.
Здесь взят нерелятивистский случай, как более выrодный, ибо
при v с Ь.Е будет больше. Также берем наИВЬJrоднеАшиR случай
paBHoYCKopeHHoro движения, при котором
v==
,
v v
!J.t
..
Отсюда для неонределенности в энерI ИИ:
е 2 (v' v)
j),E == & At ·
Эта энерrия связана с изменением импульса t!P2 формулоЙ (см.
стр. 123):
АВ == (v' ......... v) АР2,
(Q)
откуда для ошибки в импульсе, происшедшей от излучения, по-
лучим:
е 2
6.p 2 f:.t .........., C3 (v' v) ·
(7)
Прежде (стр. 123) мы имели, в виду неопределенности энерI ии
h h
ы ' ошибку в импульсе !!,.Рl""" (v' v) t ·
Комбинируя обе неэависимые ошибки, получаем для всей ошибки
в р:
6.р2 == Ap12 + АР2 2 == ( Pl АР2)2 + 2АРl6.Р2, . е. 1lp2 > 2IlРI Д j J 'l.
11
'11 / .. / h I / е 2
!!"р > v 2 v !!,.P 1 l:1P2 ,...., сМ V hc ·
Окончательно из (5) и (8) для неопредеJlенности
СКОМ поле имеем :
(8)
в электриче..
V' hc
АЕх r-..J
(c!:1t)2
.
(9)
Ландау и rlайеРJlС замечают, что рассмотрение движения мзr...
нитиой стреJIКИ ведет дли неопределенности маrНИТНОI'О поля к точно
такой же: формуле:
'V hc
.н х,..., (сМ)!!
И то же для всех компонент.
Здесь мы имеем неззвисимые индивидуальные ошибки, как и у
Йордана..Фока. Формулы (9) и (1 О) удовлетворяют требоваНИIО
['ейзенберrа о неопределенности в энерrии hv, после подстановки
е 2
cf1t f11. Так как для электрона. hc < 1, o фОрМУJIа (7) ДЛИ
Ар дает более низкую rраниuу, чем (16, стр. 123) и не иrрает
поэтому роли в этом случае.
Как и следовало ожидать, излучение следует УtIитывать для
частиц большоrо заряда.
IIроизведение независимых Оlllибок для электрическоrо и МЗl".
нитноrо полей будет
(10)
дЕЬ.Н,..., hc (1'1)
(Cdt)4 ·
С ДРУI'ОЯ стороны, как видно из вывода rейзенберrа, при одно...
временном измерении электрическоrо и маrнитноrо полей НУЖ,iО
учесть, что добавочное маrнитное поле, вызванное движением заря-
женноrо пробноrо тела, равно:
,
ДH е (12)
(:l1)2 с '
('де dl расстояние от тела до места, rде измеряетси поле Н.
Перемножая (9) и (12), ПОJIУЧИМ дЛЯ одновременных ошибок
(v::=O)
hc 1
ДEдH (сМ)2 (Ы)2 ·
Но на далеких расстояниях, больших длины волны, rде Al» l)
т. е. в волновой зоне, нужно однако все равно брать формулу для
независимых ошибок dE и дН, ибо (13) дает более rрубую rраницу
(положим, например 1l1 103 л И заметим, что cdt Л, т. е. л<.сАt).
Если же закрепить не расстояние, а время опыта At, то сдt 1"'-' Лmiп
(rде А. минимальная длина, моrущая быть обнаруженной) и нельзя
брать Дl < л < cdt, Т. е. опять !аки имеет место формула для не..
зависимых ошибок. Таким образом, поскольку эле трическое и
маrнитное поля вообще измеримы, они MorYT быть измерены одно.
временно. Из формул видно, что при Д' == 00 3 Т, e в статиqе ком
(13)
140
измерить с олько уrодно точно. Это заклю-
выводам rеfiзенберrа, в которые всвсе не
ввести ero через ctJ.t 6.1). С
допускают возможность определения
и у ["ейзенберrа и у Йордана...Фока,
пространственное усреднение. В виду
ОIпибки В координате, действительно не
eTC 1 возможным rОВОрИl'Ь об измерениях в 'точке.
МЫ Вl1ДИМ, что, несмотря на ряд интересных
ленных экспериментов, нелlт3Я считать окончательно
соотношения неопределенности для электромаrНИТIIОl'О
соответствует отсутстви.JО разработанной непроти
ТОБОЙ электродинамики.
ЛИТЕРАТУРНЫЙ УКАЗАТЕЛЬ.
1) с. Т. R. Wilson, Ртос. Roy. Soc. А. 85,285, 1911; сравни Jahr...
bl1cll d. Radtoakt. 10, 34; 1913.
2} D а v i s s о n и G е r m е r, Phys. Rev. 30, 705, 1927; Ptoc. Na.t. Acad t
14, 317; 1928. О. Р. '( h о m s оп, Proc. Roy. Soc. А. 117, 600, 1928' А. t 19,
651; 1928. I( i k u с h i, Jap. Journ. Phys. 5, 83; 1928, Rupp. Апп. d.
Phys. 85, 981; 1928. '
3) А. Н. С о m р t о n и A..S i m о п. Phys. Rev. 25, 306; 1925.
4) А. Е i n s t е i п, Апп. d. Phys. 17, 145; 1905.
5) J. F r а n с k и О. Н е r t z, Verh. d. Deutsch. Pltys. Ges. 15, 613;
1913.
6) L. de В r о g 1 i е, Апп. d. Phys. Ser. 10, 2; 1925.
7) N. В о h т, Naturwissenschaften 16, 245, 1928. Срав. также N. В о h r,
Н. А. I< r а ш е r 8, J. С. S 1 а t е т, ZS. {. Phys. 24, 69; 1924.
8) W. н е i s е n Ь е f g, ZS. '. РЬуз. 4Э, 172; 1927.
9) Срав.8 и I( е n 11 а r d, ZS. f. РЬув. 44, 326; 1921.
10) Срав. К е n n а r d 9 И с. D а r w i п, Proc. Roy. Soc. А. 111, 258;
1927.
11) Р. Е h r е n f е s t, ZS. '. Phys. 45, 455; 1927.
12) Н. W е у 1, ZS. '. Phys. 46, 1; 1927.
13) N. В о h r '1 и Naturwiss. 17, 483, 1929 и 18, 73, 1930; J(злее Atom-
teori og Naturbeskrivelse, Юqилейный сборни к Копенrаrе4lскоrо универ
ситеТ8 1929. Atomtlleorie und Naturbeschreibung, 1931. .
14) М. В о r n, ZS. f. РЬуз. 38, 803; 1926. Срав. также N. Р. М о t t,
Pr0c.Roy. Soc. А. 126, 79; 1930.
15) D u а n е, Proc. Nat. Acad. 9, 158; 1923.
16) А. Е i n s t е i л, Sitzungsber. d. preuss. Akad. 334; 1926. А. R u р р.
Sitzungsber. d. preuss. Akad. 341; 1926.
17) А. Smekal, Naturwiss.l1,873; 1923; H.Kramers и'W.Неisеп
Ь er g, ZS. f. Phys. 31, 681; 1925.
18) С. R а m з п, Nature 121, 501; 122, 12; 1928.
18') О. L а n d s Ь е r g и L. М а n d е 1 s t а т, Naturwiss. 16, 558, 1928.
19) Р. А. М. Dirac, Рсос. Roy. Soc. А. 114.243,710; 1927.
20) Р. А. М. Dirac, Proc. Roy. Soc. А.117, 610; 1928; А. 118,351; 1928.
21) О. В r е i t, Journal of the Optical Society Ат. 14, 374; 1927.
22) W. В о t h е и Н. G е i g е r, ZS. f. Phys. 32, 639; 1925.
23') L. L а n d а u и . Ре i е r 1 s, ZS. f. Phys. 62, 188; 1930.
23) А. Е i n s t е i п, Phys. ZS. 10, 185; 1909.
24) М. В о r п, W. н е i s е n Ь е r g, Р. J о r d а п, ZS. f. Phys. 35, 557;
1926. .
25) о. К 1 е i n, ZS. f. Phys. 53, 157; 1929.
26) N. В о h r, lS. f. Phys. 13, 117; 1923.
27) w. Н е i s е n Ь е r g, ZS. f. Phys. 33, 879, 1925; М. В о r пиР. J о {...
d а n, ZS. {. Phys. 34, 858; 1925 и 24; СМ. также W. Н е i s е n Ь е r g, Ма..
tllem. Ann. 25, 683, 1926.
142
А. 100,
А. 113,
d. РЬуз. 79, 361,
f. Phys. 40, 501; 1926.
D i r а с, Рсос. Roy. Soc. А. 112,
f. PI1YS. 26, 178; 1924. А. Е i n s t е i
Ь 1, 1924. PJ
f. Phys. 31, 765; 1925.
f. Phys. 36, 902; 1926 и 82.
11 f. Phys. 40, 883; 1927. ,
r t r ее. Proc. Cambr. Phil, Soc. '24; 89; 1928.
о к, Труды roc. оптическоrо института, 1931.
38) Срав. O и Р. J о r d а n и w. :р а u 1 i, ZS. f. Phys. 45,
Р. Jordan и о. Klein, ZS. {. Phys. 45, 751; 1927. J
Е. W i g n е r, ZS. f. РЬуз. 47, 631; 1928. о. М i е, Ann. d.
1928. W. н е i s е n Ь е r g и w. р а u 1 i, ZS. f. Phys.
168; 1930. Е. F е r m i, R.endiconti д. R. Асс. d.L'ncet (6)
Jo
ИМЕННОЙ И ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ.
еж - лучи. 11. 53
Амбарцумьян (доп.) 135. 137.
Бор (Bohr). 13. 15. 21. 25. 28. 39.
51. 63. 80. 122. 125. 138.
Борн (Born). 30. 45. 56. 74.
Боте (Bothe). 12.
Брейт (Breit). 68.
Бройль (де) волны де Бройля (de
Broglle). 12. 23. 40. 98.
Вейль (Wey1). 46.
Вероятности пакет.16.29.32.34.54.
Виrнер (Wigner). 110.
Вильсов (Wilson). 11.
Вильсоновские фотоrрафии 11. 24.
53.
Возмущений теория 88.
Волновой пакет. 16. 29. 32. 34. 54.
rейrер (Geiger). 72.
"'ейrера-Боте опыт. 72.
rерц (Hertz). 13.
Дарвин (Darwin)" 56.
Джермер (Оесmес). 12. 60. 64.
Дирак (Dirac). 45. 65. 82. 86. 114.
Диффракция лучей материй. 12.
23. 60.
Диффракция света. 12.
Допппер-эффект.
Дьюэн (Duall0). 60.
ДЭВИССОН 12. 60. 64.
Запрет (принцип) ПаУJrи.97.
30ммерфельд (Sommerfeld). 102.
ИrОJlьчатое излучение. 68.
Излучения т ория., 63.
Измерение импульса. 24.
,. положениSl. 17.21.
.. скорости. 24.
" энерrии. 34
Индивидуальные ОIlIибки (лоп.) 133.
48.
137.
(д оп)
1
1 ,
JН1ндау-llайерлс (Peierls) (дон.) 74.
136, 138.
Лауэ пучок (доп.) 115.
Маrнитное ОТКЛОllение лучей Ma
repJi и. 26. 37. -14.
Маrнитный момент электрона (доп.)
122.
Матрицы. 81.
Микроскоп. 21.
Наблюдение. 46.
Наложение (Superposition). 49. 55.
НеОflред леННО 1И соотношения в
КОРПУСКУЛЯРНОЙ картине. 15. 115.
Неопределенность в волновой Kap
тине. 41. 137.
Отброс приизлучении. 68.
Оrносительности теория. 51. 65. 78.
Паули (РаиН). 97. 110. 113.
Перестановочные соотношения. 82.
106.
Плюс-минус трудность 78. 132.
Потенциальный nopor. 35.
П рео6разовзний теория. 46. 84.
П риицип соответствия. 65. 80.
Причинности закон. 46. 52.
Раман (Rаmаi1) эффект 64.
Расползание(волновых пакетов). 33.
Резонанс. 90.
Релятивистские соотношени я He
определенности. (доп.) 135..
Релятивистское волновое урав-
неНйе. 65.
Розенфельд (Rosenfeld). (доп.) 132.
Рупп (RLlpp). 12. 60. 62.
Световые кванты. 12. 14. 21 :jO. 34.
62. 65. 74. 94.
Связанные электроны. 28.
Симон (Simon). 12. 71. .
Случай чистоrо собрания (Reiner
РаН).. 47.
Смекаль (Smekal). 64.
Смесь (Gemenge). 47, 50.
Сохранения законы. 48. 63. 68. 100.
Статистика. 95.
" Бозе (Воsе)-Эйншrейна.
43. 74. 97. 110. 114.
Статистика Ферми Дирака. 44. 97.
Статистическое толкование KBaH
ТОБОЙ теории. 45.
Сцинцилляции. 24.
Томсон (Thomson). 12. 60.
Траектории (орбиты) понятие. 30.
Ферми. 44. 97.
Флюктуации. 73. 91. 124.
Ф.rIюоресценция резонансная. 39.
(Рок (доп.) 137.
Франк (Franc]{). 13.
Хартри 102.
Шрединrер (Schrodinger). 30. 56.
93. 98. 132.
l1Jрединrеровская волновая ФУНК-
ЦИЯ. 32. 35. 81.
UJTepHa (Stеrл). r .рлаха (Gerlach)
ОПЫТ. 37. 48. 64.
Эйнштейн (Einstein).14. 34. 62. 73.
129.
Электронный удар. 13.
Эренфест (E1Henfest). 32.
СОДЕРЖАfJИЕ
Предисловие от издате.ТIьства . .. .. .. . . з
Предисловие к русскому изданию. . . . 5
Предисловие .. . .. . . . . . . .. . 7
1. Введение.
1. Теория и э к с пер и м е н r . . . . . . . . . .. . . 9
2. Основные понятия квантовой теории . .. . .. . . . . 11
а) Фотоrрафии Вильсона.. ....
Ь) Диффракция материальных дучей (Лэвиссон .. Джермер,
Томсон, Рупп). . . . . . . . . . . . . . . 12
с) Диффракция Э.,1Jектромаrнитноrо излучения .. . .. . . .
d) Опыт Комптона Симона . . . . . . . . . .. . .. .. . .
е) Опыты Франка и repua со столкновениями . .. . .. . .. 13
1/. Критика физических nоН,ятuй корпускулярной картины
1. Соотношения неопределенности.. . . .. . . . .. . . . . . 15
2. Иллюстрация соотношений неопределенности на различных
измерит льных приборах .. . . " . . . .. .. . .. . . . .. 21
а) Измерение положения свободных электронов . . . . . .
Ь) Измерение скорости ипи импульса свободных электронов 24
с) Связанные электроны . . .. . . . .. . .. .. . . >4 28
d) Измерение энерrии . . . . .. , . .. . .. . . . .. . .. . ... 34
;//. Критика физических nоняtпиu волновой картины
1. Соотношения неопределенности в волновой картине. " . ... 41
2. ИЛЛЮСl'рация соотношений неопределенности на не котором
опыте .. .. . . . . . . . . .. .. е .. .. . .. . . .. . . .. '" 44
/v. Статистическое толкование квантовой теории
1. Математические рассуждения. . . . .. . . . .. . ..
2. Интерференция вероятностей . . . .
3. Баронское понятие дополнительности .
45
48
51
У. ОБСУJlCденuе ва:НСl-tейшuх опытов
1. ФОТОI рафии Вил ьсона . . . .
2. Диффраl\ционные опыты . .. . . .
3. Опыт Эйнштейна и Руппа . . ., .
4. Испускание, поr.ТIощение и дисперсия излучения
а) Применение законов сохранения. . . .. '..
Ь) Полная TpaKTOBI<a. " " .." . . . . . " . . . .
5. Интерференuия и законы сохранения .. . . ., .. . . .. . . . .
6. Эффект Комптона и опыт Комптона-Симона. . .. " . ..
7. Явление флюктуаций излучения. . . .. . . .
8. Релятивистская формулировка квантовой теории
111 О . .
53
60
62
63
64
68
71
73
78
,.. . . . .
1j810 В. Тейаенберr.
145
У/. Математический аппарат квантовой теории
1. Корпускулярное представление (материи) 80
2. Теория преобраЗОВ(lНИЙ . . . . . . . . ' · ., · · · · . 84
3. Дифференциальное уравнение Шрединrера ., . . · <1 8.7
4. Теория во мущений., . . . . . . . . " · .. 88
5. Резонанс между двумя атомами. Физическое значение матриц
преобразования. . . .. .."..". · 90
6. Корпускулярная картина излучения . . . . . . . .. . · .. 94
7. Квантовая статистика " . . . . . . . . . . . . ., .. · · .. 95
8. Волновое представление материи и излучения; классическая
теория . . . . . . . . . . . . . . . . . . . 98
9. Квантовая теория волновых полей. . . . . . . . . . . .. 103
10. Применение к Болна\1. отрицательноrо заряда. . . . . ., .. 107
11. Доказательс.тво математической экви.валентности квантовь:х
теорий корпускулярной и волновой картин . . . .., 110
12. Применение к теории излучения" . . . . . . . . . ., . .. 113
;!ополненuя к русскому изданию
1. К выводу соотношений неопред леНfIОСl и
2. Маrнитный момент электрона . . .
3. К подсчету флюктуаций. . . . · . · · · · .. .. ·
4. Примечание к теории излучения. . . ....... · · .. ·
5. К релятивистской квантовой механике.. .. .. ·
6. О соотношениях НtОllределенности ДЛЯ электромаrнитноrо
ПОЛЯ . . . . . . . . . 11 . . \1i . 11 .
115
122
124
130
Литературный указатель . .. . · . .
Им нной И предметный указатели
. . .
. . ..
137
142
143.
OrB. рецактор С. М. В е ч е с JI О В. Тех". редактор 1\1. Ф и ш м а и.
ОНТИ N 65. Индекс Т-Т.] 2-5 2. Сдано в ",.60Р 15 111 1932 с. ПОJl.n сано в печать 8/УНI 32 r
Т.раж 5000. Формат бумаrи 82 Х 11' 11 чаНt 4 1 'Е! ЛЛ. f{олич. бумаЖНblХ листов 45/.
КОJlИЧ. печатных ЗН. на бумажном Листе 17h I) O. ::"аказ Nl 358. Лt:нrорлит М 48465. BblXOJ
8 CfH l 8"'''"YI.''T 1932 r.
З-я типоrрафия онти им h)''Аtll.рина. Лениrrrрад, ул. Моисеенко, 10.
Рис.. 1.
Рис. 2.
В. fеЙ_6аоерl'..
Рис. З.
Рис. 4.