йзгетз ГГГ
чт> Г."
Ж
я-
■' '■ • “ .* . - - ' *• ' - : • ‘
шт. ■ т - кш;
viiJ

Roger Penrose
The Road to
Reality
A Complete Guide to the Laws
of the Universe
JONATHAN CAPE
LONDON

Роджер ПЕНРОУЗ
ПУТЬ К РЕАЛЬНОСТИ,
или
ЗАКОНЫ, УПРАВЛЯЮЩИЕ
ВСЕЛЕННОЙ
Полный путеводитель
Перевод с английского
А. Р. Логунова и Э. М. Эпштейна
R&C
Т>циемис&
Москва + Ижевск
2007

г
*
УДК 530.1
Интернет-магазин
http://shop.rcd.ru
•	физика
•	математика
•	биология
•	нефтегазовые
технологии
Издание осуществлено при финансовой поддержке Российского фонда
фундаментальных исследований по проекту №06-02-30045.
I
Пенроуз Р.
Путь к реальности, или законы, управляющие Вселенной. Полный путеводитель. — М-
Ижевск: Институт компьютерных исследований, НИЦ «Регулярная и хаотическая динами*
ка», 2007.-912 с.
Целью монографии известного физика и математика Роджера Пенроуза является поиск фундамен¬
тальных принципов, положенных в основу нашего мироздания и управляющих протекающими в нем
процессами. Можно сказать, что книга эта, в сущности, посвящена отношениям между математикой
и физикой, тому взаимодействию между двумя дисциплинами, которое играет далеко не последнюю
роль в стремлении двигаться дальше в поисках лучшей теории для описания Вселенной. Специа¬
лист из любой области найдет в этой фундаментальной монографии что-нибудь для себя полезное;
возможно, точка зрения автора на некоторые предметы отличается (а порой и весьма радикально) от
общепринятой, но именно это позволит посмотреть на актуальные проблемы современной науки с раз¬
ных сторон и приблизиться к истине. Несомненный интерес представляет его мнение относительно
ряда современных теоретических построений, таких, например, как теория суперсимметрии, космо¬
логия расширяющейся Вселенной, гипотезы о природе Большого взрыва и черных дыр, теория струн
или М-теория, переменные цикла в квантовой гравитации, теория твисторов, да и собственно фун¬
даментальные принципы квантовой теории. Книга вызовет несомненный интерес как у специалистов
естественно-научных дисциплин, так и у широкого круга читателей.
ISBN 978-5-93972-618-4
Публикуется с разрешения автора и его литературных агентов MBA Literary Agents, Ltd (Великобри¬
тания) и Агентства Ал. Корженевского (Россия).
© Р. Пенроуз, 2004
© Перевод на русский язык:
НИЦ «Регулярная и хаотическая динамика», 2007
http://shop.rcd.ru
http://ics.org.ru

Оглавление
Предисловие	 15
Благодарности	 21
Об условных обозначениях	 23
Пролог	 26
Глава 1.	Истоки науки	  30
1.1.	Силы, движущие миром	 30
1.2.	Математическая истина 	 32
1.3.	«Реален» ли математический мир Платона?	 34
1.4.	Три мира и три великие загадки	 39
1.5.	Истина, Добро и Красота 	   42
Глава 2.	Древняя теорема и современный	вопрос	 45
2.1.	Теорема Пифагора . . .  	 45
2.2.	Постулаты Евклида	 47
2.3.	Другое доказательство теоремы Пифагора	 49
2.4.	Гиперболическая геометрия: конформное представление	 51
2.5.	Другие представления гиперболической геометрии  	 55
2.6.	Гиперболическая геометрия в исторической перспективе 	 59
2.7.	Гиперболическая геометрия и физическое пространство	 62
Глава 3.	Виды чисел в физическом мире	    67
3.1.	Катастрофа пифагорейцев? 	 67
3.2.	Система вещественных чисел	   69
3.3.	Вещественные числа в физическом мире	  73
3.4.	Нуждаются ли натуральные числа в наличии физического мира?	 76
3.5.	Дискретные числа в физическом мире	   77
Глава 4.	Магические комплексные числа	 82
4.1.	Магическое число г	 82
4.2.	Решение уравнений с комплексными числами	 84
4.3.	Сходимость степенных рядов	 86
4.4.	Комплексная плоскость Каспара Весе едя 	 89
4.5.	Как построить множество Мандельброта 	 92
Глава 5.	Геометрия логарифмов, степеней	и	корней	   94
5.1.	Геометрия комплексной алгебры 	   94
5.2.	Идея комплексного логарифма 	 97
5.3.	Многозначность, натуральные логарифмы	 99
5.4.	Комплексные степени 	 102
5.5.	Связь с физикой элементарных частиц	 104

6
Оглавление
Глава 6. Исчисление вещественных чисел	 107
6.1. Что создает настоящую функцию?	107
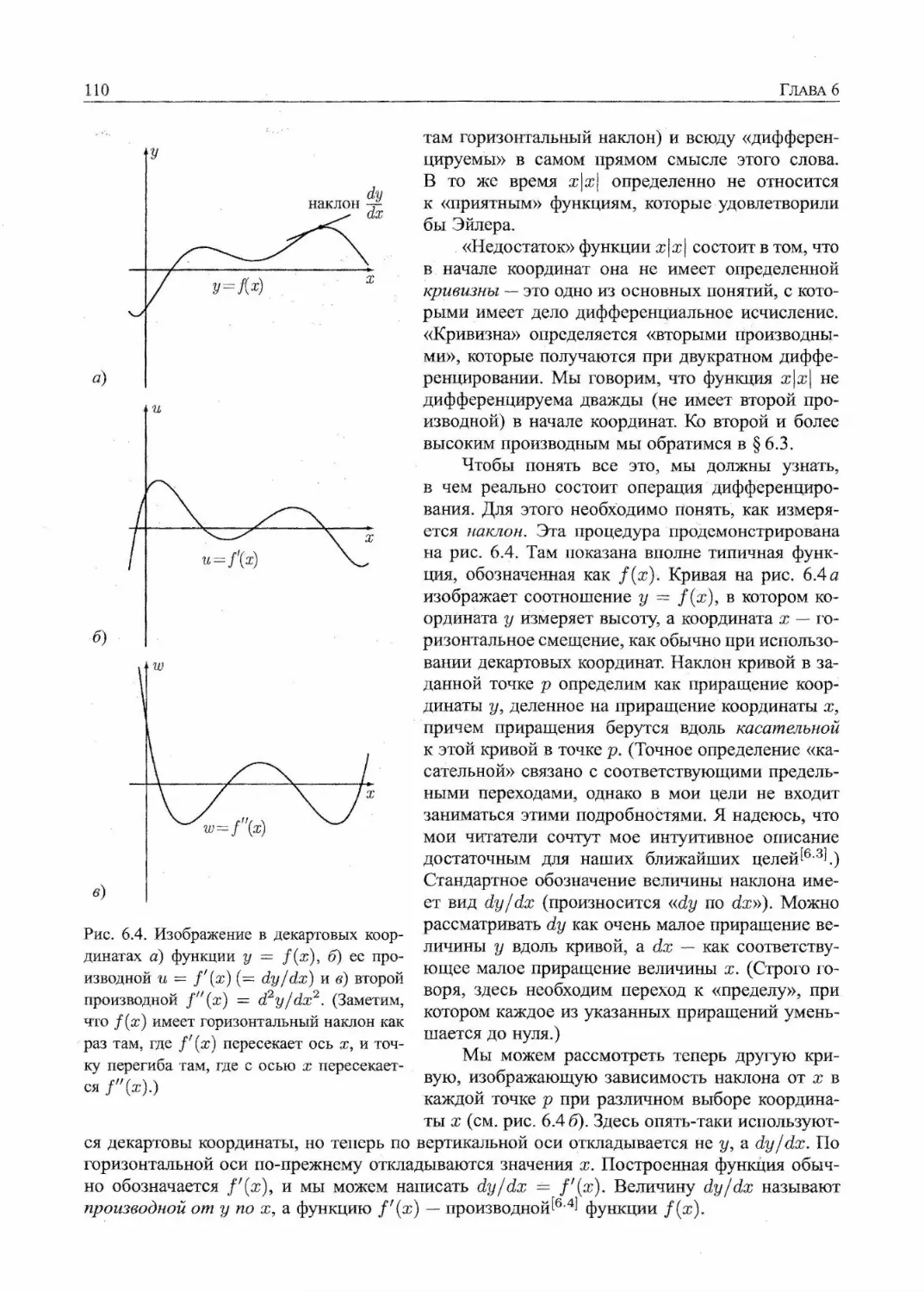
6.2. Наклон функции 	109
6.3. Высшие производные, С°°-гладкие функции  	111
6.4. Каково «эйлерово» понимание функции? 	 113
6.5. Правила дифференцирования	 115
6.6. Интегрирование	117
Глава 7. Исчисление комплексных чисел  	122
7.1. Комплексная гладкость, голоморфные функции	  122
7.2. Контурное интегрирование 	  123
7.3. Степенные ряды, получаемые из комплексной гладкости	  126
7.4. Аналитическое продолжение . . . .	  127
Глава 8. Римановы поверхности и комплексные отображения	133
8.1. Идея римановой поверхности	  133
8.2. Конформные отображения	   136
8.3. Сфера Римана	139
8.4. Род компактной римановой поверхности	  141
8.5. Теорема о римановом отображении  	144
Глава 9. Разложение Фурье и гиперфункции	    148
9.1. Ряды Фурье	  148
9.2. Функции на окружности  	  151
9.3. Расщепление частот на сфере Римана	  154
9.4. Преобразование Фурье	  156
9.5. Расщепление частот, получаемое из преобразования Фурье	  158
9.6. Какие функции приемлемы?  	  160
9.7. Гиперфункции	  163
Глава 10. Поверхности				 169
10.1. Комплексные и вещественные размерности	  169
10.2. Гладкость, частные производные	  .	    170
10.3. Векторные поля и 1-формы  	   174
10.4. Компоненты, скалярные произведения	   178
10.5. Условия Коши-Римана	   180
Глава 11. Гиперкомплексные функции	.	.	184
11.1. Алгебра кватернионов	184
11.2. Какова роль кватернионов в физике?	186
11.3. Геометрия кватернионов	  188
11.4. Как складывать вращения	  190
11.5. Алгебры Клиффорда	    191
11.6. Алгебры Грассмана	194
Глава 12. n-мерные многообразия 	     198
12.1. Зачем изучать многомерные многообразия?	198
12.2. Многообразия и координатные лоскуты . '	201
12.3. Скаляры, векторы и ковекторы	203
12.4. Грассмановы произведения	 206
12.5. Интегрирование форм  	  208
12.6. Внешняя производная  	    210
12.7. Элемент объема, правило суммирования  	    213

Оглавление
7
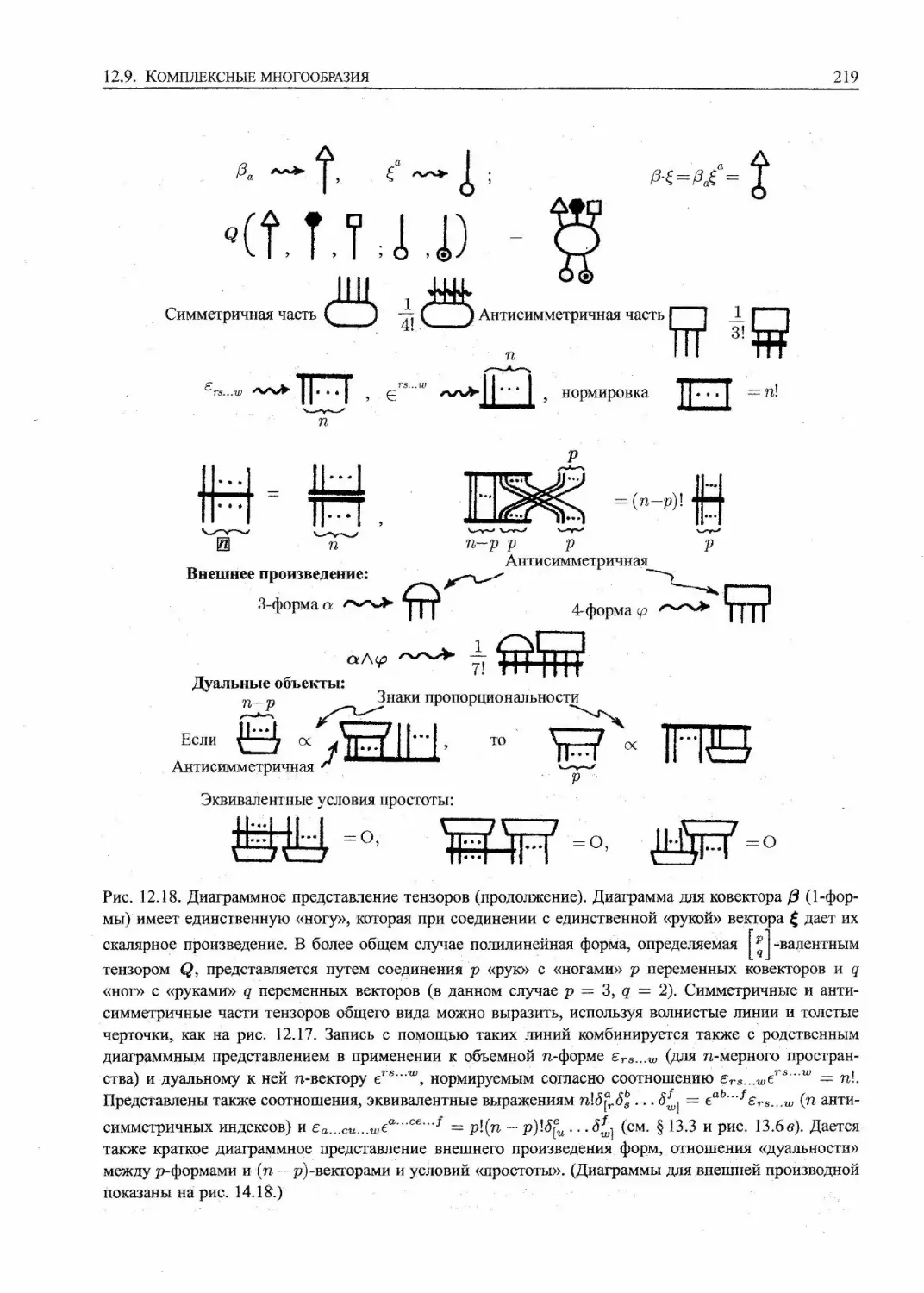
12.8.	Тензоры. Абстрактные индексы и диаграммное представление	216
12.9.	Комплексные многообразия	217
Глава 13.	Группы симметрии	223
13.1. Группы преобразований	  .	223
13.2.	Подгруппы и простые группы	  225
13.3.	Линейные преобразования и матрицы	229
13.4.	Определители и следы	  233
13.5.	Собственные значения и собственные векторы	235
13.6.	Теория представлений и алгебры Ли	238
13.7.	Тензорные пространства представлений. Приводимость	241
13.8.	Ортогональные группы	245
13.9.	Унитарные группы	250
13.10. Симплектические группы	254
Глава 14.	Математический анализ на	многообразиях	259
14.1.	Дифференцирование на многообразии? 	259
14.2.	Параллельный перенос	260
14.3.	Ковариантная производная	264
14.4.	Кривизна и кручение	267
14.5.	Геодезические, параллелограммы и кривизна	268
14.6.	Производная Ли	274
14.7.	Что может дать нам метрика	279
14.8.	Симплектические многообразия	283
Глава 15.	Расслоенные пространства	и калибровочные связности	286
15.1.	Физическая мотивация расслоенных пространств	286
15.2.	Математическая идея расслоения	288
15.3.	Сечения расслоений	291
15.4.	Расслоение Клиффорда-Хопфа	293
15.5.	Комплексные векторные расслоения, (ко)касательные расслоения 	296
15.6.	Проективные пространства	298
15.7.	Нетривиальность в связности расслоения	303
15.8.	Кривизна расслоения	306
Глава 16.	Лестница бесконечности	311
16.1.	Конечные поля 	311
16.2.	Конечная или бесконечная геометрия нужна физике?	312
16.3.	Бесконечности разного размера	   316
16.4.	Диагональная косая черта Кантора	319
16.5.	Загадки оснований математики	322
16.6.	Машины Тьюринга и теорема Гёделя	324
16.7.	Размеры бесконечности в физике	327
Глава 17.	Пространство-время	331
17.1.	Пространство-время физики Аристотеля	331
17.2.	Пространство-время галилеевой относительности 	333
17.3.	Ньютоновская динамика на языке пространства-времени 	334
17.4.	Принцип эквивалентности	337
17.5.	«Ньютоновское пространство-время» в представлении Картана	340
17.6.	Фиксированная конечная скорость света	344
17.7. Световые конусы	  .	.	  345
17.8.	Отказ от абсолютного времени	348

8
Оглавление
,	17.9. Пространство-время общей теории относительности Эйнштейна	. . 351
Глава 18.	Геометрия Минковского	355
18.1.	4-пространство Евклида и Минковского	   355
18.2.	Группы симметрии пространства Минковского	  357
18.3.	Лоренцева ортогональность. «Парадокс часов»	359
18.4.	Гиперболическая геометрия в пространстве Минковского	362
18.5.	Небесная сфера как сфера Римана	  369
18.6.	Ньютоновская энергия, импульс и момент импульса	 371
18.7.	Релятивистская энергия, импульс и момент импульса . .  	  373
Глава 19.	Классические поля Максвелла и Эйнштейна 	   378
19.1.	Эволюция ньютоновской динамики	   378
19.2.	Максвелловская теория электромагнетизма	379
19.3.	Законы сохранения и потоки в теории Максвелла	 383
19.4.	Максвелловское поле как калибровочная кривизна	 385
19.5.	Тензор энергии-импульса	  390
19.6.	Эйнштейновское уравнение поля	  392
. 19.7.	Дальнейшее развитие. Космологическая постоянная, тензор Вейля 	395
19.8.	Энергия гравитационного поля	397
V"
Глава 20.	Лагранжианы и гамильтонианы  	 403
20.1.	Магический лагранжев формализм . .  	    403
20.2.	Более симметричная гамильтонова картина	406
20.3.	Малые колебания	  409
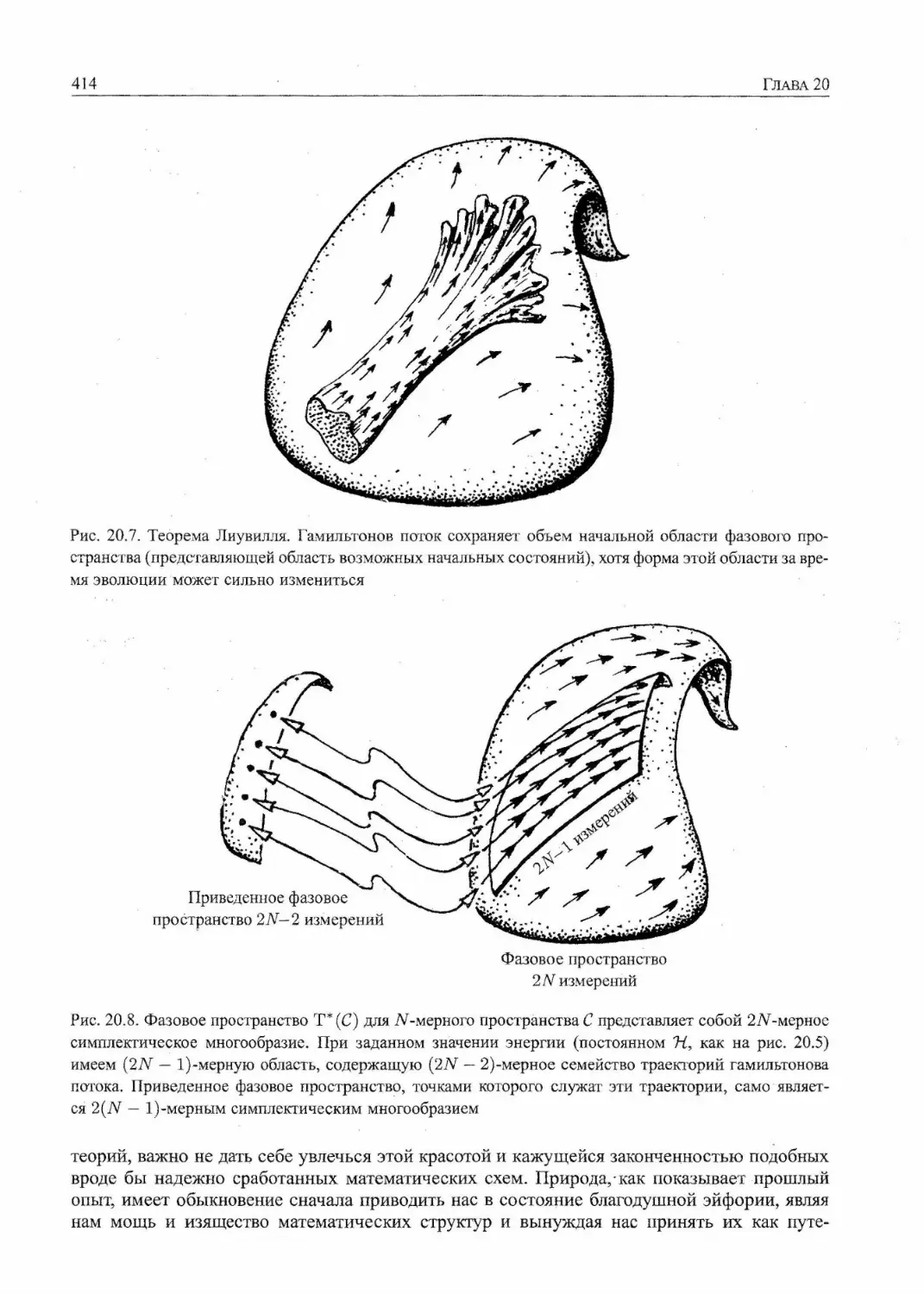
20.4.	Гамильтонова динамика как симплектическая геометрия  	  413
20.5.	Лагранжева трактовка полей  	    415
20.6.	Как лагранжианы двигают современную теорию	416
Глава 21.	Квантовая частица	421
21.1.	Некоммутирующие переменные			 421
21.2.	Квантовые гамильтонианы	  423
21.3. Уравнение Шредингера	  .	425
21.4.	Экспериментальные основания квантовой теории	  426
21.5.	Обсуждение дуализма волна-частица			 .	430
21.6.	Что есть квантовая «реальность»?	     .	432
21.7.	«Целостная» природа волновой функции  	 436
21.8.	Таинственные «квантовые скачки»	 439
21.9.	Распределение вероятностей в волновой функции 	  440
21.10. Координатные состояния	  442
21.11. Описание в импульсном пространстве  	   443
Глава 22. Квантовая алгебра, геометрия и спин . . .  	  .	.	. * . 448
22.1.	Квантовые процедуры U и R	448
22.2.	Линейность U и возникающие в связи с этим проблемы для R	450
22.3.	Унитарная структура, гильбертово пространство и	обозначения	Дирака	...	452
22.4.	Унитарная эволюция. Представления Шредингера	и Гейзенберга	.......	454
V
22.5. Квантовые «наблюдаемые» 	. .	  457
22.6.	Измерения ДАЛ4ЕТ. Проекторы  	  460
22.7.	Нулевые измерения. Спиральность	461
22.8.	Спин и спиноры	  466
22.9.	Сфера Римана для систем с двумя состояниями				 .	469
22.10. Высокие значения спина. Представление Майораны  	474

Оглавление	9
22.11. Сферические гармоники	  .	  476
22.12. Релятивистский квантовый момент импульса  	  480
22.13. Общий случай изолированного квантового объекта	  483
ГЛАВА 23. Перепутанный квантовый мир  	  490
23.1. Квантовая механика систем многих частиц	  490
23.2. Гигантский объем пространства многочастичных состояний  	491
23.3. Квантовое перепутывание. Неравенства Белла . .  	493
23.4.	ЭПР-эксперименты по Бому	   495
23.5.	ЭПР-эксперимент по Харди — почти без вероятностей	  499
23.6. Две загадки квантового перепутывания 	500
23.7. Бозоны и фермионы	  502
23.8. Квантовые состояния бозонов и фермионов	  504
23.9. Квантовая телепортация	 506
23.10. Кванглеменция	  509
Глава 24. Электрон Дирака и античастицы  	 515
24.1. Конфликт между квантовой теорией и теорией относительности	515
24.2. Почему античастицы приводят к квантовым полям?	516
24.3.	Положительность энергии в квантовой	механике	517
24.4.	Проблемы с релятивистской формулой	для энергии 	519
24.5. Неинвариантность оператора d/dt	 520
24.6. Квадратный корень из волнового оператора по Клиффорду-Дираку ..... 522
24.7.	Уравнение Дирака 	 523
24.8.	Как Дирак пришел к позитрону  	 525
Глава 25. Физика элементарных частиц: стандартная модель	530
25.1. Истоки современной физики элементарных частиц	530
25.2. Зигзаг-представление электрона	 531
25.3. Электрослабое взаимодействие. Симметрия относительно отражения .... 534
25.4. Зарядовое сопряжение, четность и обращение времени	539
25.5. Электрослабая группа симметрии	  540
25.6. Сильно взаимодействующие частицы . . . .  	 544
25.7.	«Цветные кварки»  	    546
25.8. За пределами стандартной модели	548
Глава 26. Квантовая теория поля	552
26.1. Фундаментальный статус квантовой теории поля в современной теоретиче¬
ской физике	  552
26.2. Операторы рождения и уничтожения	 553
26.3. Бесконечномерные алгебры	  556
26.4. Античастицы в КТП	    557
26.5. Альтернативные вакуумы . .  	.	.	558
26.6. Взаимодействия: лагранжианы и интегралы по траекториям	560
26.7. Расходящиеся интегралы по траекториям: ответ Фейнмана	563
26.8. Построение фейнмановских диаграмм. S-матрица	  565
26.9. Перенормировка 	  568
26.10. Фейнмановские диаграммы из лагранжианов .  	571
26.11. Фейнмановские диаграммы и выбор вакуума  	   572

10
Оглавление
Глава 27.	Большой взрыв и его термодинамическое наследие	  577
27.1. Временная симметрия в динамической эволюции	  577
27.2. Субмикроскопические составные части  	  578
27.3. Энтропия 	   580
27.4. Прочность концепции энтропии . . . .  	 582
27.5. Вывод Второго закона... или нет?	    585
27.6. Является ли Вселенная в целом «изолированной системой»?  	587
27.7. Роль Большого взрыва	589
27.8. Черные дыры . . .  	   594
27.9. Горизонты событий и пространственно-временные сингулярности ...... 597
27.10. Энтропия черной дыры	599
27.11. Космология	 601
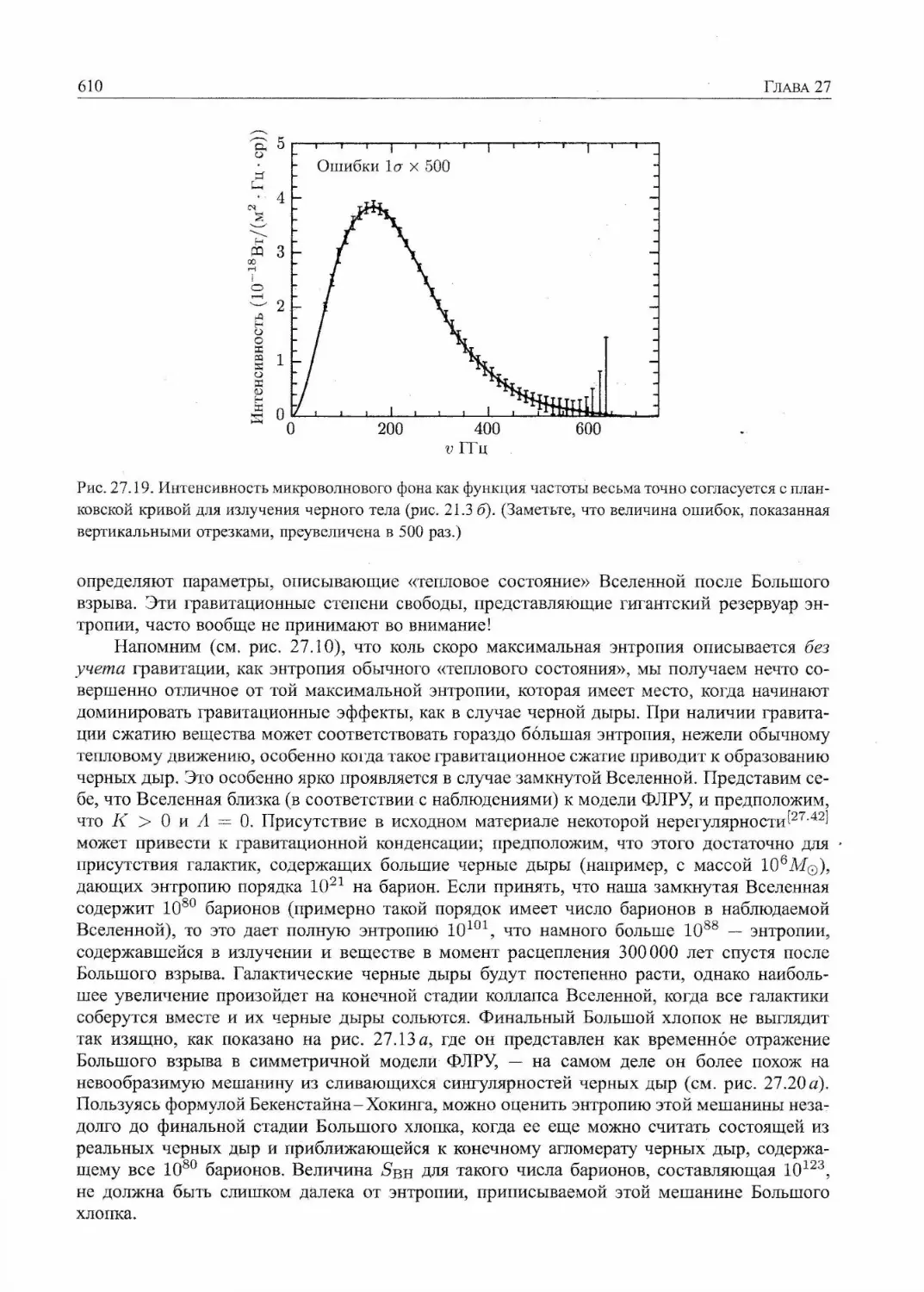
27.12. Конформные диаграммы	  606
27.13. Наш собственный особенный Большой взрыв	609
Глава 28.	Умозрительные теории ранней Вселенной  	617
28.1. Спонтанное нарушение симметрии в ранней Вселенной . .  	617
28.2. Космические топологические дефекты	    620
28.3. Проблемы с нарушением симметрии в ранней Вселенной	623
28.4. Инфляционная космология 	626
28.5. Справедливы ли предпосылки инфляционной модели?	  631
28.6. Антропный принцип	  634
28.7. Особая природа Большого взрыва: антропный ключ?	638
28.8. Гипотеза кривизны Вейля	 640
28.9. Гипотеза отсутствия границ Хартла - Хокинга	644
28.10. Космологические параметры: согласие с результатами наблюдений	646
Глава 29.	Парадокс измерения 	 654
29.1. Традиционные онтологии квантовой теории	654
29.2. Нетрадиционные онтологии квантовой теории 	  656
29.3. Матрица плотности	661
29.4. Матрицы плотности для спина Сфера Блоха .  	663
29.5. Матрица плотности в условиях ЭПР-эксперимента	666
29.6. Практическая философия декогеренции, создаваемой окружением ...... 670
29.7. Кошка Шредингера в «копенгагенской» онтологии  	  .	671
29.8. Способны ли разрешить «кошачий» парадокс другие традиционные онтологии?673
29.9. Чем могут помочь нетрадиционные онтологии?	 676
Глава 30.	Роль гравитации в редукции квантового состояния	  681
30.1. Окончательна ли современная квантовая теория?	  681
30.2. Подсказки со стороны космологической временной асимметрии	.  	682
30.3. Роль временной асимметрии в редукции квантового состояния	683
30.4. Хокингова температура черной дыры	  .	.	.	    686
30.5. Температура черной дыры и комплексная периодичность			690
30.6. Векторы Киллинга, поток энергии и.. . путешествие во времени!	.  	694
30.7. Орбиты с отрицательной энергией и уход энергии с них  	697
30.8. Взрывы Хокинга  	  699
30.9. Более радикальный взгляд  	  .	.	.	.	.	.	.	702
30.10. Шредингеров объект	   705
30.11. Фундаментальный конфликт с принципами теории Эйнштейна	  708
30.12. Предпочтительные состояния Шредингера-Ньютона ......	.  	711

Оглавление
11
30.13. Эксперимент FELIX и другие аналогичные предложения	  .	713
30.14. Природа флуктуаций в ранней Вселенной	717
Глава 31.	Суперсимметрия, надразмерность и струны	724
31.1. Необъяснимые параметры	724
31.2. Суперсимметрия	727
31.3. Алгебра и геометрия суперсимметрии	•	.	.	.	729
31.4. Пространство-время с увеличенным числом измерений	732
31.5. Первоначальная адронная теория струн .  	735
31.6. На пути к струнной теории мира	738
9
31.7. Побудительные мотивы введения лишних измерений пространства-времени
в теории струн 	740
31.8. Теория струн как квантовая гравитация?	741
31.9. Динамика струн	743
31.10. Почему мы не видим дополнительных пространственных измерений? .... 745
31.11. Следует ли принимать аргументацию с точки зрения квантовой стабильности? 749
31.12. Классическая нестабильность дополнительных измерений	 751
31.13. Конечна ли струнная квантовая теория поля?	753
31.14. Магические пространства Калаби-Яу; М-теория	755
31.15. Струны и энтропия черных дыр	760
31.16. «Голографический принцип» 	763
31.17. D-браны	765
31.18. Физический статус теории струн	767
Глава 32.	Узкая тропа Эйнштейна. Петлевые переменные	775
32.1. Каноническая квантовая гравитация	775
32.2. Киральность и переменные Аштекара	776
32.3. Вид переменных Аштекара	778
32.4. Петлевые переменные	780
32.5. Математика узлов и связей 	782
32.6. Спиновые сети	784
32.7. Статус квантовой гравитации с петлевыми переменными	789
Глава 33.	Более радикальный взгляд. Теория твисторов	794
33.1. Геометрия с дискретными элементами	794
33.2. Твисторы как световые лучи . .  	797
33.3. Конформная группа. Компактифицированное пространство Минковского . . 802
33.4. Твисторы как многомерные спиноры	  805
33.5. Элементарная твисторная геометрия и система координат	807
33.6. Геометрия твисторов как вращающихся безмассовых частиц	810
33.7. Квантовая теория твисторов	814
33.8. Твисторное описание безмассовых полей	  816
33.9. Твисторная когомология пучков	818
33.10. Твисторы и расщепление на положительные и отрицательные частоты .... 822
33.11. Нелинейный гравитон	824
33.12. Твисторы и общая теория относительности	828
33.13. На пути к твисторной теории элементарных частиц 	830
33.14. Каково будущее теории твисторов?	831

12
Оглавление
Глава 34. Где лежит путь к реальности?	 837
34.1.	Великие физические теории XX века — что дальше?	837
34.2.	Фундаментальная физика, движимая математикой  	840
34.3.	Роль моды в физической теории	842
34.4.	Можно ли экспериментально опровергнуть неверную теорию?	  844
34.5.	Откуда ожидать следующую физическую революцию?	848
34.6.	Что есть реальность?	   850
34.7.	Роль ментальности в физической теории	852
34.8.	Наш долгий путь к реальности	854
34.9.	Красота и чудеса	 857
34.10. Многое понято, еще больше понять предстоит .  	861
Эпилог	 865
Литература	867
Предметный указатель	904

Эту книгу я посвящаю
ДЕННИСУ СКЬЯМЕ,
открывшему мне глаза на то, какой увлекательной может быть физика.

Предисловие
В этой книге читателя ждет рассказ о путешествии, полном открытий, о путешествии,
которое представляется мне едва ли не самым важным и увлекательным из всех путеше¬
ствий, в какие на протяжении своей истории пускалось человечество. Целью этого путе¬
шествия является поиск фундаментальных принципов, положенных в основу нашего миро¬
здания и управляющих протекающими в нем процессами. В пути мы находимся вот уже
более двух с половиной тысячелетий, поэтому не следует удивляться, что наш поиск при¬
вел наконец к некоторым существенным результатам. Впрочем, путь, которым мы шли, не
был (да и не мог быть) легок — истинное понимание приходило не сразу, зачастую скры¬
ваясь за поворотами дороги и манящими миражами. Таково неотъемлемое свойство этого
пути, и многие из нас, отчаявшись, отставали, а иные сворачивали с дороги, устремившись
в неверном направлении, — на их примере оставшиеся учились осторожности. Но вот насту¬
пил двадцатый век, век выдающихся открытий и откровений — порой настолько поразитель¬
ных, что многие ученые не стеснялись во всеуслышание заявлять о том, что человечество
наконец-то вплотную приблизилось к ясному пониманию природы всех фундаментальных
физических процессов. Поскольку я предпринимаю свое описание современного состояния
фундаментальных теорий в момент, когда двадцатый век уже благополучно завершился,
я постараюсь придерживаться более трезвого взгляда на вещи. Не все мои высказывания
будут благосклонно приняты вышеупомянутыми «оптимистами», однако я ожидаю в бли¬
жайшем будущем еще более радикальных перемен в «направлении движения», нежели те,
что произошли в прошедшем столетии.
Читатель очень скоро обнаружит, что в этой книге я решительно изменяю своей обычной
практике избегания математических формул, несмотря на неоднократные зловещие преду¬
преждения издателей о том, что такой мой шаг повлечет за собой значительное сокращение
читательской аудитории. Я очень серьезно обдумал этот вопрос и пришел к выводу, что без
привлечения языка математики и рассмотрения некоторых чисто математических концепций
сказать то, что я намерен сказать, просто невозможно. Наше понимание тех принципов, что
в действительности управляют поведением окружающих нас физических объектов, в зна¬
чительной мере опирается на соответствующий математический аппарат. Возможно, это
обстоятельство повергнет в отчаяние тех, кто почему-либо убежден, что напрочь лишен
способностей к математике, какой бы элементарной она ни была. Как можно, скажут они,
понять смысл исследований, ведущихся на переднем крае теоретической физики, если мы
не можем совладать даже с обыкновенными дробями? Что ж, согласен, это будет нелегко.
И все же, когда дело доходит до объяснения вещей, в принципе доступных понима¬
нию, я склонен считать себя оптимистом. Можно даже сказать, неисправимым оптимистом.
Мне кажется, что читатели, не способные оперировать дробями (точнее, те, кто утверждает,
что не способен оперировать дробями), слегка себя обманывают — в большинстве своем
эти люди обладают потенциальной способностью к такого рода деятельности, но по разным
причинам предпочитают об этом «не знать». Без сомнения, есть среди них и такие, кто, глядя
на строку математических символов, даже самых простых, видит перед собой лишь строгие
лица родителей и учителей, пытавшихся вдолбить в них «знания» и требующих взамен по¬
пугайского повторения, видимости понимания, не нуждающейся в понимании истинном, —
ты должен выучить от сих до сих, иначе будет плохо, — до волшебства же и красоты изуча¬
емого предмета при таком «обучении», скорее всего, никому нет дела. Возможно, до кого-то

16
Предисловие
я уже не достучусь — слишком поздно, — однако, как я уже сказал, я неисправимый опти¬
мист и верю, что многие мои читатели, даже те, кто так до сих пор и не освоил операции
с дробями, смогут хотя бы краем глаза увидеть тот удивительный мир, который, я убежден,
откроется перед ними во всей своей красе, стоит им только захотеть.
Одна из ближайших подруг моей матери, довольно известная балерина, в бытность
свою школьницей тоже никак не могла освоить действия с дробями. Много лет спустя, уже
после успешного завершения своей балетной карьеры, она как-то упомянула об этом факте
в моем присутствии. Я тогда был еще молод, еще не посвятил себя целиком математической
деятельности, но о моем увлечении математикой многие уже знали. «Все неприятности на¬
чались с сокращения дробей, — сказала она мне. — Я просто не понимала, как это делается.
Так с тех пор и не научилась». Она была настоящей леди, изысканной и остроумной, и я ни¬
чуть не сомневался, что ментальных качеств, необходимых для восприятия и исполнения
сложных хореографических композиций, без которых не обходится ни один балет, должно
с лихвой хватить и на решение столь пустячной математической задачи. И вот, изрядно пе¬
реоценив свои преподавательские способности, я попытался превзойти своих незадачливых
предшественников и донести наконец до этой замечательной женщины простоту и логич¬
ность процедуры «сокращения».
Насколько я могу судить, моя попытка оказалась столь же безуспешной, что и по¬
пытки прежних «учителей». (Отец ее, кстати сказать, был выдающимся ученым, членом
Королевского общества, так что можно предположить, что научные материи не были ей
в диковинку. Может быть, здесь сыграл свою роль фактор «строгого лица», не знаю.) С тех
пор я много размышлял об этом и теперь мне кажется, что у нее, как и у многих других
людей такого склада, отсутствует необходимый рационализирующий «пунктик», а я, будучи
«зациклен» на математике, просто не обратил на это обстоятельство должного внимания.
В самом деле, и в математике, и в математической физике мы то и дело сталкиваемся с одной
фундаментальной проблемой, причем впервые это происходит как раз в таких на первый
взгляд невинных операциях, как сокращение числителя и знаменателя самой обыкновенной
арифметической дроби на некий общий множитель.
Те, для кого сокращение дробей успело стать — в результате бесчисленных повторений —
действием столь же привычным и естественным, как дыхание, скорее всего, и представить
себе не смогут всю ту сложность, которая в действительности кроется в такой, казалось
бы, простой процедуре. Возможно, многие из тех, кто находит сокращение дробей непо¬
стижимым и таинственным, способны увидеть упомянутую фундаментальную сложность
более ясно, нежели мы, склонные, по-видимому, полностью игнорировать ее, решая задачи
методом лихого кавалерийского наскока. Что же это за сложность такая? Скажем пока так:
она непосредственно связана с тем, как именно математики вызывают из небытия математи¬
ческие объекты, причем степень ее зависит от соотносимости таких объектов с физической
реальностью.
Я припоминаю один случай из своего детства — мне было тогда лет одиннадцать, и я еще
учился в школе. На одном из уроков математики учитель задал классу немало поразивший
меня вопрос: что в действительности представляет собой обыкновенная арифметическая
О
дробь (такая, например, как |)? Со всех сторон тут же посыпались предположения, сводив¬
шиеся в основном к разделению на части пирога и прочих продуктов, однако учитель их
сходу отверг на том (здравом, надо сказать) основании, что эти ответы всего лишь описывают
некие не поддающиеся точному определению физические ситуации, к каким следует приме¬
нять точную математическую концепцию дроби, — четкого математического понятия дроби
О
они отнюдь не содержат. На что кто-то из учеников заметил, что в таком случае дробь ~ — это
О
«такая штуковина с тройкой вверху, восьмеркой внизу и чертой посередине». Представьте
себе мое изумление, когда я обнаружил, что учитель, похоже, воспринял это «определение»

Предисловие
17
вполне серьезно! Я сейчас не помню в точности, к какому ответу мы тогда пришли, одна¬
ко, оглядываясь назад с высоты приобретенного позднее, в университете, математического
опыта, могу предположить, что наш учитель предпринял на том уроке отважную попытку
дать нам определение дроби в терминах такого универсального математического понятия,
как класс эквивалентности.
Что же это такое — класс эквивалентности? Как это понятие может объяснить нам, что
в действительности представляет собой дробь? Начнем с предложенного моим одноклассни-
ком определения «с тройкой вверху и восьмеркой внизу». В сущности, оно предполагает, что
дробь задается упорядоченной парой целых чисел — в нашем случае это числа 3 и 8. Однако
очевидно, что отождествлять дробь с такой упорядоченной парой чисел нельзя, поскольку
дробь, например, описывает то же число, что и дробь §, а пара чисел (6, 16) безусловно
10	о
отлична от пары (3, 8). Здесь нам и поможет сокращение — мы можем записать дробь ™
о о	о
в виде и «убрать» двойку из верхней и нижней части, получив при этом дробь §.
Что же позволяет нам произвести такой финт и тем самым в некотором роде «приравнять»
пару (6, 16) к паре (3, 8)? У математика есть на это простой ответ (который со стороны,
если честно, выглядит просто жалкой отговоркой): в определение дроби изначально встро¬
ено правило сокращения, согласно которому считается, что пара целых чисел (а • n, Ь * п),
где п — любое целое число, отличное от нуля (6 здесь также должно быть отлично от нуля),
представляет ту же самую дробь, что и пара (а, 6).
Впрочем, легче нам от всего этого не стало. Мы по-прежнему не знаем, что такое дробь;
мы лишь узнали кое-что о способе представления дробей. Так что же такое дробь? Призвав
на помощь понятие «класс эквивалентности», математик ответит нам, что дробь, напри-
О
мер, ™ представляет собой всего-навсего бесконечный набор, составленный из следующих
О
пар чисел:
(3, 8), (-3, -8), (б, 16), (-6, -16), (9, 24), (-9, -24), (12, 32), ...,
где каждая пара может быть получена из любой другой пары набора посредством примене¬
ния (однократного или многократного) вышеописанного правила сокращения*. Сюда необ¬
ходимо еще добавить правила (не конфликтующие с обычными алгебраическими правила¬
ми), в соответствии с которыми мы сможем выполнять над такими бесконечными наборами
целых чисел арифметические действия (сложение, вычитание, умножение) и идентифици¬
ровать собственно целые числа как дроби особого типа.
Такое определение включает в себя все, что нам необходимо, с математической точки
зрения, знать о дробях (например, то, что число ^ при сложении с самим собой дает еди¬
ницу, и т.д.), причем операция сокращения, как мы убедились, и в самом деле встроена
в определение изначально. И все же как-то все это чересчур формализовано, поневоле начи¬
наешь сомневаться, действительно ли такое определение адекватно описывает имеющееся
у нас интуитивное понятие о дроби. Хотя повсеместно применяемая в чистой математике
процедура построения класса эквивалентности (представленное выше определение — лишь
один из множества примеров ее применения) является очень мощным математическим ин¬
струментом для доказательства непротиворечивости и установления математического суще¬
ствования, результатом ее зачастую являются чрезвычайно громоздкие конструкции. Едва
ли такая процедура способна дать кому бы то ни было интуитивно ясное представление о,
* Класс эквивалентности называется так потому, что он, по сути, представляет собой класс объектов (в дан¬
ном конкретном случае такими объектами являются пары целых чисел), в котором каждый элемент считается в
определенном смысле эквивалентным любому другому элементу.

18
Предисловие
о
скажем, дроби -. Неудивительно, что подруга моей матери никак не могла взять в толк, чего
О
от нее хотят.
В дальнейшем при описании математических понятий я постараюсь по мере возмож¬
ности избегать той математической педантичности, что предписывает нам определять дробь
как «бесконечный класс пар целых чисел», хотя с точки зрения математической строгости
и точности такой подход, безусловно, имеет множество преимуществ. Я постараюсь сосре¬
доточиться на передаче идей, лежащих в основе тех или иных важнейших математических
концепций, не упуская при этом из виду присущие этим концепциям красоту и чуть ли не
,	О
волшебную силу. Идея, скажем, дроби f как математического объекта очень проста: сложив
О
вместе 8 таких объектов, мы получим в сумме число 3. Сила же состоит в том, что идея
дроби действительно работает, невзирая на то обстоятельство, что в реальном физическом
мире мы не имеем дела с объектами, которые можно было бы точно описать дробями —
куски пирога не в счет, поскольку здесь речь может идти лишь о приближениях разной
степени точности. (Этим дроби отличаются от натуральных чисел — 1,2,3 и т.д., — кото¬
рые вполне точно описывают всевозможные объекты, встречающиеся нам в повседневной
жизни.) Один из способов наделить понятие дроби непротиворечивым смыслом как раз
и заключается в том, чтобы дать этому понятию математическое «определение», описав
его (как мы сделали выше) как бесконечный набор пар целых чисел. Однако это вовсе не
О
означает, что дробь ~ и в самом деле представляет собой такой набор. Правильнее будет
О
рассматривать дробь как объект, обладающий некоей собственной реальностью (в платонов¬
ском смысле), а бесконечный набор пар чисел — просто как один из способов, посредством
которого мы можем объект такого типа непротиворечиво описать. По мере «привыкания»
к дробям мы все чаще ловим себя на мысли, что нам совсем не сложно воспринимать дробь,
О
например, ~ как реальный, существующий независимо от нас объект, а описание ее в виде
О
«бесконечного набора пар чисел» представляется нам всего-навсего подпоркой для педан¬
тов — подпоркой, надобность в которой отпадает как только мы осознаем ее смысл. Большая
часть математики именно так и устроена.
Для математиков (по крайней мере, для большинства математиков, насколько мне из¬
вестно) математика является не просто родом общественно полезной деятельности, который
мы сами для себя и придумали, — она существует сама по себе, отдельно от нас, находясь
при этом в поразительной гармонии с физической Вселенной. Невозможно достичь сколько-
нибудь глубокого понимания законов, управляющих физическим миром, не погрузившись
с головой в мир математики. В частности, упомянутое выше понятие класса эквивалент¬
ности оказывается полезным для понимания не только множества важнейших (и крайне
запутанных) математических концепций, но и немалого количества не менее важных (и
зачастую еще более запутанных) концепций физических — таких, например, как общая те¬
ория относительности Эйнштейна или принципы «калибровочной теории», описывающие
действующие в природе силы с точки зрения современной физики элементарных частиц.
Ни один физик сегодня не может считать себя свободным от необходимости разбираться
в тонкостях математики, причем математики весьма мудреной. Именно по этой причине
я отвел первые шестнадцать глав книги исключительно на описание математических идей.
Тем читателям, кто слабо представляет себе, что им теперь со всей этой математикой де¬
лать, я скажу лишь одно: погодите отчаиваться. Эту книгу можно читать четырьмя разными
способами — в зависимости от желаемого уровня сложности. Допустим, вы принадлежите
к первой группе читателей (наименьший, по нашей шкале, уровень сложности), то есть
к тем, кто, завидев какую угодно математическую формулу, просто отключается (многие
из этой группы, скорее всего, испытывают непреодолимые трудности и при столкновениях
с дробями). Даже в этом случае, я уверен, вы сможете многое извлечь из книги, просто

Предисловие
19
пропуская все формулы и читая только текст. Мне кажется, это не многим отличается от
того, как я сам, будучи подростком, просматривал время от времени шахматные журналы,
повсюду разбросанные в нашем доме. В жизни моих братьев и родителей шахматы занимали
весьма важное место, я же шахматами почти не интересовался, хотя мне нравилось читать
о достижениях тех незаурядных и зачастую весьма странных людей, что посвятили себя
этой игре. Читая о сыгранных ими партиях и блестящих ходах, я узнавал для себя что-то
новое, пусть не совсем понимая, что именно вызывает такое восхищение у знатоков, и даже
не пытаясь разобраться в обозначениях, описывающих те или иные позиции. Несмотря на
недопонимание, я все же находил это занятие интересным и в чем-то даже поучительным;
во всяком случае оно надолго удерживало мое внимание. Надеюсь, что в представленных
далее математических рассуждениях также найдется что-нибудь, способное заинтересовать
даже самого далекого от математики читателя, буде он — преисполнившись отваги или же
из простого любопытства — решит составить мне компанию в экспедиции по исследова¬
нию математических и физических идей, призванных объяснить, как устроена и работает
физическая Вселенная. Не бойтесь пропускать уравнения (я и сам часто так делаю), куски
глав, если хотите, или даже целые главы, где, на ваш взгляд, я хватил через край. Представ¬
ленный в книге материал очень разнообразен по сложности и, если можно так выразиться,
«специальности», так что, пропустив одно, вы непременно найдете что-то другое, что при¬
дется вам больше по душе. Можно и просто заглядывать в любое место и просматривать
страницу-другую. Надеюсь также, что обширная система перекрестных ссылок поможет
в достаточной степени прояснить любое незнакомое понятие и позволит быстро найти все,
что необходимо, в пропущенных но какой-либо причине главах.
Ко второй группе я отношу читателей, обладающих достаточной подготовкой для чтения
и понимания возникающих по ходу рассуждения математических формул, но, возможно, не
расположенных (в силу отсутствия свободного времени или по каким-то другим причинам)
лично проверять истинность моих утверждений. На тот случай, если такое желание все же
возникнет, рекомендую обратить внимание на упражнения, которыми я сопроводил многие
математические утверждения в книге. Эти упражнения делятся по сложности на три группы:
очень просто
требуется немного подумать,
придется серьезно потрудиться.
Разумеется, необходимости в проверке нет; если хотите, можете совершенно спокойно при¬
нять все мои утверждения на веру, целостность восприятия при этом ничуть не пострадает.
Надеюсь, впрочем, что предложенные упражнения будут полезны тем читателям, кто
хотел бы разобраться во встречающихся на этих страницах разнообразных (и порой весьма
важных) математических концепциях, но не знаком в достаточной мере с тем или иным пред¬
метом обсуждения. Общеизвестно, что навык приобретается при упражнении, и математика
в этом смысле не исключение — небольшой практический опыт самостоятельного размыш¬
ления над какой-либо задачей может дать гораздо более глубокое понимание предмета, чем
простое прочтение десятка описаний. (Решения всех задач можно при необходимости найти
на веб-сайте www. roadsolutions . ox. ас. uk.)
И наконец, читатели-специалисты. В этом случае сложностей с математикой (не так
уж она, вообще говоря, и запредельна), разумеется, не возникнет вовсе и тратить время на
выполнение упражнений, скорее всего, необходимости нет. Однако и специалист, возмож¬
но, найдет что-нибудь для себя полезное в моей точке зрения на различные предметы, как
правило, отличной (а порой и весьма радикально) от общепринятой. Не исключено, что

20
Предисловие
специалисту любопытно будет ознакомиться с моим мнением относительно ряда современ¬
ных теоретических построений (таких, например, как теория суперсимметрии, космология
расширяющейся Вселенной, гипотезы о природе Большого взрыва и черных дыр, теория
струн или М-теория, петлевые переменные в квантовой гравитации, теория твисторов, да
и собственно фундаментальные принципы квантовой теории). Не сомневаюсь, со многим
из изложенного в книге специалист нипочем не согласится, однако я убежден также, что
в споре рождается истина и полемика играет в развитии науки исключительно важную
роль, — поэтому без колебаний представляю на суд читателя свои выводы, которые, вполне
возможно, в чем-то противоречат некоторым из общеизвестных достижений современной
теоретической физики.
Можно сказать, что книга эта, в сущности, посвящена отношениям между математи¬
кой и физикой, тому взаимодействию между двумя дисциплинами, которое играет далеко
не последнюю роль в нашем стремлении двигаться дальше в поисках лучшей теории для
описания Вселенной. Во многих современных исследованиях такое стремление изначально
в значительной степени обусловлено соображениями математической красоты, глубины и
изящества. Очевидно, что подобные математические факторы могут оказаться чрезвычайно
продуктивными — и не раз оказывались, достаточно вспомнить кое-какие из наиболее впе¬
чатляющих достижений физики XX века: уравнение Дирака для электрона, общие основы
квантовой механики и общую теорию относительности Эйнштейна. Однако решающими
критериями принятия тех или иных теоретических предположений во всех этих случаях
были все-таки соображения физические — главным образом результаты наблюдений. Имен¬
но адекватного физического подтверждения — т. е. экспериментальных данных или хотя бы
возможности экспериментального исследования — и недостает многим современным иде¬
ям, призванным вывести наше понимание законов Вселенной на новый фундаментальный
уровень. Закономерный вопрос: можно ли исходя из доступного нам математического желае¬
мого оценить шансы этих идей на успешное соответствие действительному? Вопрос весьма
деликатный, и я намерен рассмотреть его с тех сторон, которые, как мне представляется, не
получили достаточного освещения в литературе.
Что касается тех из моих воззрений, которые могут показаться спорными, то я особо
постарался недвусмысленно отметить для читателя все те места, где я позволяю себе подоб¬
ные вольности. Таким образом, перед вами самый настоящий путеводитель — путеводитель
по достопримечательным идеям (и чудесам) современной физики. Подойдет эта книга и на
роль учебного пособия — введения в современную физику, какой она представляется нам
в первые годы третьего тысячелетия.

Благодарности
В работе над книгой мне помогали очень многие люди — что, при таком объеме этой
самой книги (и почти восьми годах, потребовавшихся на ее написание), совсем неудиви¬
тельно. Почти так же неудивительно и то, что ценный вклад некоторых из этих людей так
и не будет нигде упомянут из-за свойственной мне неорганизованности и забывчивости.
Поэтому позвольте прежде всего выразить особую признательность — а также принести
искренние извинения — именно им: великодушно помогавшим мне людям, имен которых
я, к сожалению, не могу здесь перечислить. Другим повезло больше, и я спешу побла¬
годарить за самые разнообразные сведения и другую помощь следующих людей: Майкла
Атья, Джона Баэза, Майкла Берри, Роберта Брайанта, Дордже Броди, Райнера Вайсса, Дже¬
ральда Вестхаймера, Джеймса Викерса, Ника Вудхауса, Маргарет Глисон, Джереми Грея,
Эндрю Даггинса, Фримена Дайсона, Теда Джейкобсона, Мацея Дунайски, Криса Ишема,
Бернарда Кея, Джой Кристиан, Уильяма Маршалла, Лайонела Мейсона, Чарлза Миснера,
Стелиоса Негрепонтиса, Сару Джонс Нельсон, Тристана Нидема, Эзру (Теда) Ньюмена,
Дэниела Оя, Роберта Оссермана, Чарлза Оукли, Дона Пейджа, Оливера Пенроуза, Алана
Рендалла, Вольфганга Риндлера, Джозефа Силка, Кристофа Симона, Джорджа Спарлинга,
Генри Стаппа, Джона Стейчела, Пола Тода, Ричарда Томаса, Герарда ’т Хоофта, Джона Уиле¬
ра, Роберта Уолда, Ронни Уэллса, Дэвида Фаулера, Стюарта Хамероффа, Кита Ханнабасса,
Люсьен Харди, Джима Хартла, Джима Хауи, Найджела Хитчина, Эндрю Ходжеса, Тома Хо¬
кинса, Дипанкара Хоума, Антона Цайлингера, Хунмо Чаня, Бернарда Шутца, Энгельберта
Шюкинга и Артура Экерта. Отдельную благодарность я хочу выразить Ли Смолину, Келли
Стеллу и Лейну Хьюстону — за то, что они всегда были готовы помочь мне всем, чем мог¬
ли. В огромном долгу я перед Флоренс Цоу (Шэн Цунь) за обширную помощь в вопросах
физики элементарных частиц, перед Фей Даукер за помощь и здравый смысл в отношении
самых разных вопросов (по большей части, тех, что возникли у меня при представлении
некоторых квантовомеханических идей), перед Субиром Саркаром за ценную информацию
о космологических экспериментальных данных и их интерпретации, перед Вахе Гурзадяном
за аналогичную информацию и за некоторые предварительные сведения о его космологиче¬
ских находках, проливающих свет на общую геометрию Вселенной, и в особенности перед
Абхаем Аштекаром за исчерпывающую информацию о теории циклических переменных
и о некоторых тонких вопросах теории струн.
Я благодарен Национальному научному фонду за поддержку в виде грантов PHY 93-
96246 и 00-90091, а также Фонду Леверхульме за двухгодичную почетную стипендию
(2000-2002). Написанию этой книги в немалой степени способствовала моя работа в лон¬
донском Грешем-колледже (1998-2001) и в Центре гравитационной физики и геометрии
при Университете штата Пенсильвания (США); чрезвычайно полезной оказалась и помощь
секретаря (в особенности я благодарен Рут Престон) вкупе с местом для работы в Матема¬
тическом институте Оксфордского университета.
Поистине бесценную поддержку я получил со стороны редакторов — особенно если
учесть жесткие временные рамки контракта и безалаберную манеру работы автора. На ран¬
нем этапе мне очень помог Эдди Мицци — без него я, пожалуй, так и не решился бы запу¬
стить процесс превращения моих беспорядочных записок в настоящую книгу; далее эстафе¬
ту принял Ричард Лоуренс — его знание дела, опыт и терпеливая мягкая настойчивость стали
ключевым фактором в доведении проекта до успешного завершения. Джон Холмс, несмотря

22
Благодарности
на все препятствия, превосходно проделал непростую работу по составлению безукоризнен¬
ного предметного указателя, за что я ему очень признателен. Отдельно я хочу поблагодарить
Уильяма Шоу за помощь в создании замечательной компьютерной графики, использованной
для представления множества Мандельброта и гиперболической плоскости (рис. 1.2 и 2.19),
а также при построении преобразований, легших в основу рис. 2.16 и 2.19. Сколько бы я ни
старался, мне никогда не удастся отблагодарить по справедливости Джейкоба Фостера за
его титанический труд по отысканию и сортировке ссылок, за тщательную проверку всей
рукописи в предельно сжатые сроки и затыкание бесчисленных дыр, оставленных автором.
Примечания в конце глав также являются, по большей части, заслугой Фостера и несут на
себе яркий отпечаток его неординарной личности. Разумеется, никто из упомянутых людей
не имеет никакого отношения к тем ошибкам и упущениям, которые читатель, возможно,
обнаружит в книге, -—все эти недостатки целиком и полностью на совести автора.
Особую благодарность я хочу выразить компании «The М. С. Escher Company» (Голлан¬
дия) за любезное разрешение воспроизвести в книге работы М. Эшера (рис. 2.11, 2.12, 2.16
и 2.22) и отдельно за разрешение опубликовать рис. 2.11 в несколько модифицированном
виде (рис. 2.12 и 2.16; последний рисунок представляет собой результат явного математи¬
ческого преобразования). Права на все использованные в книге работы Эшера принадлежат
компании «The М. С. Escher Company» (© 2004). Также я признателен администрации Ин¬
ститута теоретической физики при Гейдельбергском университете и Чарлзу Х.Лайнуиверу
за любезное разрешение на публикацию графиков, представленных на рис. 27.19 и 28.19
соответственно.
И самое главное; я бесконечно благодарен своей горячо любимой жене Ванессе —
причем отнюдь не только за предоставление по первому же моему требованию замечатель¬
ных компьютерных иллюстраций (рис. 4.1, 4.2, 5.7, 6.2-6.8, 8.15, 9.1, 9.2, 9.8, 9.12, 21.36,
21.10,	27.5, 27.14, 27.15, а также многогранники на рис. 1.1), но и за неизменную любовь
и заботу, за глубокое понимание и чуткость, несмотря на долгие годы жизни с человеком,
который постоянно наполовину отсутствует, погруженный в какие-то свои мысли. Огромное
спасибо я хочу сказать и Максу, вынужденному всю свою жизнь наблюдать меня как раз
в таком отвлеченном состоянии, — спасибо не только за замедление работы над этой книгой
(что в итоге поспособствовало увеличению срока ее жизни, поскольку в результате в нее
вошли по крайней мере две важные вещи, о которых иначе я не упомянул бы), но и за
постоянно хорошее настроение, за излучаемые им бодрость и оптимизм, которые, в свою
очередь, не дают унывать и мне. В конце концов, именно благодаря обновлению жизни
(живым символом которого он является) возникают новые источники идей и интуитивных
озарений, необходимые для подлинного движения в будущее, движения к пониманию тех
самых фундаментальных законов, которые в действительности управляют окружающей нас
Вселенной.

Об условных обозначениях
(Читать только в том случае, если вы знакомы с общими концепциями, но не совсем
понимаете, какие буквы что обозначают у меня.)
Используя в книге различные шрифты, я старался быть по возможности последователь¬
ным, однако, поскольку не все мои обозначения совпадают со стандартными, думаю, будет
нелишним подробно разъяснить принятую в дальнейшем систему.
Латинские или греческие буквы в светлом курсивном начертании — например, гг2, рп,
lg z, cos в, егв или ех — обозначают, как общепринято, математические переменные с числен¬
ным (или скалярным) значением (обратите внимание, что для обозначения функций — таких
как sin, cos или lg — используется прямой шрифт). Курсив применяется и для стандартных
численных и физических констант: г, е, гг; с, G, /г, ft, д или к.
Векторные или тензорные величины в их целостном (абстрактном) представлении обо¬
значаются полужирным курсивным шрифтом — например, риманов тензор кривизны R, —
тогда как для записи их компонент (как главного символа, так и соответствующих индек¬
сов) используется светлый курсив: Rabcd• В абстрактно-индексном представлении тензоров
(см. § 12.8) запись Rabcd может также обозначать и весь тензор R (в тех случаях, когда такая
интерпретация уместна), однако из контекста, как правило, очевидно, что именно имеется
в виду. Абстрактные линейные преобразования также являются в некотором роде тензо¬
рами, поэтому здесь я тоже использую полужирный курсив — например, Т. Допускают
абстрактные линейные преобразования (в определенных случаях) и запись в абстрактно-
индексной форме: Таь (необычное расположение индексов здесь указывает на очередность
матричного умножения). Таким образом, (абстрактно-)индексная запись SabTbc соответству¬
ет произведению ST линейных преобразований. Как и в случае с тензорами, Заь или Тьс
может (в зависимости от контекста или согласно явному указанию в тексте) обозначать
и упорядоченный массив компонент — т. е. матрицу; матрицы у меня обозначаются также
полужирными прямыми буквами (в данном случае S или Т). Таким образом, ST обозначает
произведение соответствующих матриц. «Двойственная» интерпретация таких обозначений,
как Rabcd или Заь (массив компонент или уже собственно абстрактный тензор), не должна
стать причиной путаницы, так как и в той, и в другой интерпретации алгебраические (или
дифференциальные) соотношения, в которых эти обозначения участвуют, абсолютно иден¬
тичны. Иногда для таких величин используется и третий способ записи — схематический,
или диаграммный (см., например, рис. 12.17, 12.18, 14.6, 14.7, 14.21 и 19.1).
Кое-где в книге мне необходимо было провести различие между величинами четырех¬
мерного пространства-времени теории относительности и соответствующими трехмерными,
чисто пространственными величинами. В этих случаях я использовал для четырехмерных
величин полужирный курсивный шрифт (например, четырехмерные импульс р или коорди¬
ната ж), а для соответствующих трехмерных — полужирный прямой шрифт (т. е. р или х).
По аналогии с предложенной выше оппозицией Т (матрица) и Т (абстрактное линейное
преобразование) обозначение р или х мы будем рассматривать как «символ» набора из трех
пространственных компонент, тогда как р или х вполне можно интерпретировать более
абстрактным, бескомпонентным образом (впрочем, я не собираюсь придерживаться такой
интерпретации слишком строго). Евклидову «длину» трехмерной векторной величины а =
= (aiy <22, аз) мы можем обозначить буквой а, где а2 — а\ Л-а^ 4- а2, а скалярное произведе¬
ние векторов а и b = ({ц, 62, &з) — записать как а • b = а\Ь\ +	Такое	«точечное»

24
Об условных обозначениях
обозначение скалярного произведения пригодится нам и в более общем, n-мерном, контек¬
сте — например, для записи скалярного (или внутреннего) произведения с* • £ абстрактного
ковектора а и вектора £,
Некоторая дополнительная сложность возникает с квантовой механикой, поскольку фи¬
зические величины здесь чаще всего представляются в виде линейных операторов. Более или
менее стандартной практикой является обозначение квантово-операторных вариантов при¬
вычных классических величин посредством добавления к соответствующим буквам «кры¬
шечки» (циркумфлекса). Однако меня такой подход не совсем устраивает, так как это, на мой
взгляд, ведет к совершенно ненужной перегруженности формул. (Мне больше по душе точ¬
ка зрения философского характера, согласно которой классические и квантовые величины
представляют собой, в сущности, «одно и то же», — а посему будет только справедливо,
если мы оставим для их обозначения одинаковые символы, — отличие лишь в том, что
в классическом случае мы обоснованно пренебрегаем величинами порядка Н; иначе гово¬
ря, классический коммутативный закон аЪ — Ьа справедлив всегда, тогда как в квантовой
механике аЬ вполне может отличаться от Ьа на некоторую величину порядка Н.) Вообще
говоря, логичности ради, для обозначения таких линейных операторов следовало бы тоже
воспользоваться полужирным курсивным шрифтом (например, Т), однако это свело бы на
нет все преимущества философского подхода и разрушило бы границы, намеченные в пре¬
дыдущем абзаце. Соответственно, когда речь пойдет о конкретных квантовомеханических
величинах — таких как импульс р или р либо координата х или ж, — я буду использовать
те же обозначения, что и в классическом случае. Что же касается квантовых операторов,
так сказать, более общего назначения, то здесь полужирный курсив будет вполне уместен
(например, Q).
В математике уже стало привычным использовать ажурные буквы N, Z, М, С и Fg для
обозначения соответственно множества натуральных (т. е. неотрицательных целых) чисел,
множества целых чисел, множества вещественных чисел, множества комплексных чисед
и конечного поля, содержащего q элементов (где q — некоторая степень простого числа,
см. § 16.1), a Nn, Zn, Сп и — для обозначения систем упорядоченных наборов из п
таких чисел. Все это — стандартные обозначения канонических математических объектов.
В настоящей книге я решил несколько расширить (что в общем-то не так уж и необычно)
употребление таких символов, добавив к вышеупомянутым некоторые другие стандартные
математические структуры — например, евклидово пространство Е (трехмерное) или, в об¬
щем случае, Еп (n-мерное). Часто упоминается в книге стандартное плоское четырехмерное
пространство-время Минковского, являющееся, по сути, некоей разновидностью этакого
«псевдоевклидова» пространства — для обозначения этого пространства я предлагаю «пу¬
стотелую» букву М (Мп здесь обозначает n-мерный вариант пространства Минковского —
лоренцево пространство-время с одним временным и (п — 1) пространственными измере¬
ниями). Иногда я использую С в качестве прилагательного (со значением «комплексифи-
цированный») — например, комплексное четырехмерное евклидово пространство получает
в такой нотации обозначение СЕ4. Ажурную букву Р также можно использовать и как при¬
лагательное (со значением «проективный», см. § 15.6), и как существительное; в последнем
случае Рп обозначает проективное n-мерное пространство (иногда я пишу РРП или СРП,
если необходимо подчеркнуть, что нас интересует именно вещественное или соответственно
комплексное проективное п-пространство). В теории твисторов (глава 33) существует такое
понятие, как комплексное четырехмерное пространство Т, канонически связанное с про¬
странством М (или его комплекеификацией СМ), и его проективный вариант РТ. В той же
теории определяют пространство N нулевых твисторов («двойное» употребление этой буквы
в данном случае конфликта не вызывает) и его проективный вариант PN.
Не следует путать С, употребленное в качестве прилагательного, со светлым рубле¬
ным С, которым я обозначаю «комплексное сопряжение» (см., например, §§ 13.1, 13.2).

Об условных обозначениях
25
Такое употребление, по сути, аналогично употреблению буквы С в физике элементарных
частиц, где этот символ используется для обозначения операции зарядового сопряжения
(иначе говоря, замены каждой частицы ее античастицей; см. главы 25 и 30). Эту операцию
обычно рассматривают вместе с двумя другими фундаментальными операциями физики
частиц, а именно: операции зеркального отражения (или четности) Р и операции обраще¬
ния времени Т. Полужирный рубленый шрифт служит в этой книге несколько иной цели,
обозначая векторные пространства (чаще всего используются буквы V, W и Н). Буква Н
закреплена за гильбертовыми пространствами квантовой механики, а Нп обозначает гиль¬
бертово пространство с n-комплексными измерениями. Векторные пространства являются,
в очевидном смысле, плоскими. Пространства же искривленные (либо допускающие ис¬
кривление) обозначаются буквами каллиграфического начертания — например, А4, S или Т
(особое применение найдено другому варианту каллиграфического шрифта: буквой У я обо¬
значаю нуль-бесконечность). Кроме того, следуя вполне уже сложившейся традиции (ввиду
особого статуса этих объектов в -физической теории), я использую каллиграфические буквы
для обозначения лагранжианов (С) и гамильтонианов (Н).

Пролог
Стояла глубокая ночь. Ам-теп, главный царский мастер, искусный ремесленник и насто-
ящии художник своего дела, спал на скамье в мастерской, утомленный вечерними трудами.
Однако сон его был беспокоен — возможно, из-за какого-то неуловимого напряжения, раз¬
литого в воздухе. Впоследствии Ам-теп не мог ясно вспомнить, действительно ли он спал,
когда все это случилось. Вдруг стало светло — словно пришло утро, — хотя старые кости
мастера и уверяли его, что этого не может быть, что ночь не могла кончиться так скоро.
Ам-теп резко встал со скамьи. Что-то не так. Не может заря разгораться на севере,
О
однако тревожный красный свет проникал именно через северное окно мастерской, выхо¬
дящее на море. Мастер подошел к окну и в недоверчивом изумлении уставился наружу.
Не восходит солнце на севере — и все тут! Он был настолько изумлен, что лишь через
несколько мгновений сообразил, что в открывшейся его глазам картине никакого солнца нет
и в помине..., а есть лишь далекий пламенеющий столб багрового света, бьющего отвесно
вверх, из моря в небеса.
Пока мастер стоял у окна, верхушка столба окуталась шапкой плотного дыма, словно
кто-то развернул над морем огромный черный зонт с объятой зловещим пламенем ручкой.
Дымовая туча принялась расползаться вширь, становясь при этом все чернее — несомненно,
в мир явился демон из преисподней. С ясного ночного неба одна за другой пропадали звезды,
затмеваемые чудовищной громадой.
Охваченный вполне понятным ужасом, Ам-теп тем не менее не пытался бежать, на¬
столько его заворожили совершенная симметричность и сверхъестественная красота разво¬
рачивающего перед ним действа. Мало-помалу страшная туча начала едва заметно двигаться
к западу, увлекаемая постоянно дующими над морем ветрами, — увидев это, мастер облег¬
ченно перевел дыхание, и сковавшие его чары рассеялись. Однако мрачное предчувствие
тут же вернулось — земля под ногами задрожала, а мгновением позже до ушей донесся ни¬
когда не слыханный мастером прежде зловещий рокот. «Что же могло вызвать такую ярость
природы», — недоуменно спросил себя Ам-теп. Никогда еще на памяти мастера Бог не являл
людям столь гневного лика.
Первым делом мастер вспомнил о священной чаше, которую он только этим вечером
закончил, — с этой чашей с самого начала все шло как-то наперекосяк. Быть может, он изоб¬
разил Быкоглавого недостаточно устрашающим? И Бога это разгневало? Впрочем, вскоре
мастер осознал всю нелепость таких мыслей. Не мог столь пустячный проступок вызвать
ярость, подобную той, что он только что наблюдал; к тому же, ярость эта вовсе не была
направлена на него лично. Вот в Великом Дворце сейчас, наверняка, настоящий переполох.
Царь-жрец, без сомнения, понимает, что медлить нельзя; должно быть, он уже сейчас пы¬
тается умилостивить этого могучего Бога всех демонов. А это означает жертвоприношения.
Обычных жертв — вроде плодов или даже животных — недостаточно, чтобы укротить гнев
такой силы. То есть жертвоприношения будут человеческими.
Вдруг, к вящему своему изумлению, Ам-теп оказался отброшен вглубь комнаты мощ-
ным ударом словно сгустившегося в каменный кулак воздуха; следом в окно ворвался
бешеный ветер. Все это сопровождалось настолько оглушительным грохотом, что мастер
на какое-то время лишился слуха. Почти все его горшки, украшенные затейливыми узора¬
ми, смело с полок и разбило о стену. Придя в себя, Ам-теп обнаружил, что лежит на полу
в углу, куда его зашвырнул порыв чудовищного ветра, а в комнате царит полный разгром.

Пролог
27
С болью взирал мастер на разбитую в мелкие черепки большую урну, которой он особенно
гордился, на обращенные в прах тонкие орнаменты, потребовавшие многих часов и дней
кропотливого труда.
Ам-теп неуверенно поднялся на ноги и, помедлив, снова приблизился к окну, на сей
раз с гораздо большим трепетом, и опять устремил взгляд на жуткое зрелище за морем.
Ему показалось, что в освещенном далекой пылающей печью море что-то движется, причем
движется, похоже, в его сторону. Некоторое время спустя он уже ясно мог различить, что на
поверхности моря образовалось некое подобие длинного и широкого рва, который с боль¬
шой скоростью перемещается по направлению к берегу, а за ним следует крутая, точно стена
береговых утесов, волна. Мастер снова замер на месте, завороженно следя, как приближа¬
ющаяся волна растет, вздымаясь в самое небо. Наконец край водяного рва достиг берега,
и тут же море отступило прочь, обнажив дно, усеянное беспомощными кораблями. Отвесная
стена огромной волны не заставила себя ждать — она ударила в берег с чудовищной силой,
мгновенно разбив в щепки все без исключения корабли и многие из близлежащих домов.
Впрочем, дом Ам-тепа уцелел, хотя вода и поднялась на невероятную высоту — мастер жил
на холме и довольно далеко от моря.
Великий Дворец также уцелел, однако Ам-теп подозревал, что худшее еще впереди,
и он оказался прав, хотя и не знал в тот момент, насколько прав. Одно он знал твердо:
принесением в жертву простого раба теперь не обойтись. Для укрощения буйного гнева
ужасного Бога понадобится нечто большее. Он обратился мыслью к своим сыновьям и до¬
черям, к новорожденному внуку. Даже они теперь не в безопасности.
Относительно новых человеческих жертвоприношений Ам-теп тоже оказался прав.
Вскоре жрецы схватили девушку и юношу хорошего рода и доставили в ближайший храм,
расположенный высоко на склоне горы. Последующий ритуал был уже близок к завер¬
шению, когда ударила новая опустошительная катастрофа. Земля содрогнулась с небыва¬
лой силой, и крыша храма обрушилась, погребя под обломками всех до единого жрецов
и обе предполагаемые жертвы. Ритуал был прерван, причем случилось так, что тела его
участников пролежали непотревоженными под развалинами храма три с половиной тыся¬
чи лет.
Разрушения потрясали воображение, однако конец света не наступил. Многие обитатели
острова, на котором жил Ам-теп, пережили ужасающее землетрясение, хотя сам Великий
Дворец оказался разрушен почти до основания. За последующие годы большинство домов
отстроили заново. Даже Дворец, возведенный на руинах прежнего, казалось, вернул себе
т т тш
немалую долю былого великолепия. И все же Ам-теп дал обет покинуть остров. Мир стал
другим, и прошлого не вернуть.
Тот мир, который знал Ам-теп, тысячу лет не знал войн, благословленный просвещен¬
ным владычеством Богини Земли. Пышным цветом расцветали изящные искусства, купцы
беспрепятственно торговали с соседними землями. Величественный Дворец представлял
собой огромных размеров лабиринт, потрясающий роскошью убранства, целый город, укра¬
шенный превосходными фресками с изображениями животных и цветов. Помимо красот во
Дворце имелись проточная вода и тщательно продуманная сеть сточных труб. Война в этом
мире была почти неизвестна, а потому необходимости в защитных сооружениях никто не
видел. Теперь же, как понял Ам-теп, престол Богини Земли занял Бог, обладающий совсем
иными представлениями о том, что важно, а что нет.
Впрочем, уехать с острова Ам-теп вместе с остатками семьи смог лишь через несколько
лет — на корабле, восстановленном его младшим сыном, искусным плотником и моряком.
Внук Ам-тепа к тому времени вырос в бойкого мальчугана, живо интересующегося всем
на свете. Путешествие заняло несколько дней, и все эти дни стояла на удивление хорошая
погода. Однажды ясным вечером, когда Ам-теп рассказывал внуку об узорах, образуемых
звездами в небесах, его посетила странная мысль: «А ведь рисунки созвездий не изменились

28
Пролог
ни на йоту — какими они были до Катастрофы, сопровождавшей явление ужасного демона,
такими остаются и сейчас».
Рисунки созвездий Ам-теп знал очень хорошо — как всякий настоящий художник, он об¬
ладал цепким взглядом и отличной памятью. Почему же эти крохотные огоньки не смести¬
лись даже на малое расстояние? Почему яростный ветер той ночи не унес их прочь, не
разметал по небу, как разметал он горшки в доме Ам-тепа и разбил вдребезги драгоценную
урну? Все так же светила с небес Луна, и насколько мог судить Ам-теп, путь ее среди звезд
тоже ничуть не изменился. Несколько месяцев после Катастрофы небо выглядело иначе, чем
обычно, — полутьма даже днем, низко нависшие мрачные тучи, Солнце и Луна какого-то
странного цвета, — но потом все это прошло, движение же светил, похоже, не менялось
и тогда. Звезды тоже остались на прежних местах.
«Если небеса, куда как более могущественные, нежели любой даже самый жуткий
демон, обратили на Катастрофу столь мало внимания, —- рассуждал Ам-теп, — то почему
тех, кто послал этого демона, должно хоть как-то волновать, что делают маленькие люди,
живущие на маленьком острове и развлекающиеся глупыми ритуалами и человеческими
жертвоприношениями?» Он вдруг устыдился, вспомнив свои собственные глупые мысли
в тот момент: будто бы демону есть дело до узоров на его горшках.
«Так почему же? — все спрашивал себя Ам-теп. — Какие могучие силы управляют
миром и почему они порой проявляют себя столь бурным и непостижимым образом?»
Мастер поделился своими сомнениями с внуком, однако вопросы так и остались без ответа.
t <	♦
Прошел век, миновало тысячелетие, а ответа все не было.
+ # •
Всю свою жизнь мастер Амфос прожил в том же маленьком городке, в каком жили его
отец, дед и прадед. Он зарабатывал на жизнь изготовлением затейливо украшенных золотых
браслетов, серег, церемониальных чаш и прочих изящных изделий, которые по праву можно
было счесть настоящими произведениями искусства. Ремесло это передавалось в семье от
отца к сыну вот уже сорок поколений — с тех самых пор, как одиннадцать веков назад в этой
земле обосновался старый Ам-теп.
Впрочем, от отца к сыну переходили не только умения и мастерство. Вопросы, которые
задавал себе Ам-теп, не давали покоя и Амфосу. Из поколения в поколение передавался
и рассказ о Великой катастрофе, уничтожившей процветающую древнюю цивилизацию,
и размышления Ам-тепа о природе этой катастрофы. Как и далекий предок, Амфос понимал,
что небеса высоки и безбрежны, им нет дела до земных катастроф. Тем не менее, те же
катастрофы способны с легкостью уничтожить маленьких людей вместе с их хрупкими
городами, человеческими жертвоприношениями и бессмысленными ритуалами. Вряд ли
столь чудовищные силы снизойдут до того, чтобы обратить на ничтожные действия людей
хоть какое-то внимание. Между тем, о природе этих сил люди во времена Амфоса знали
ничуть не больше, чем знал Ам-теп.
Амфос тщательно изучил строение растений, насекомых и прочих мелких живых су¬
ществ, а также кристаллов. Острый взгляд и наблюдательность помогли ему создать немало
новых декоративных орнаментов. Интересовался он и земледелием, зачарованный тайной
превращения маленького зернышка пшеницы в целый колос. Однако ничто из того, что он
видел, не приближало его к ответу на главный вопрос — почему? — и Амфосом постепенно
овладевало разочарование. Он верил, что все в природе должно иметь свои причины, но
обнаружить эти причины не мог.
Однажды ясной ночью Амфос смотрел в небо, пытаясь разглядеть в расположении звезд
фигуры героев и героинь, обретших бессмертие в виде созвездий. На его взгляд скромного

Пролог
     - —*
29
художника, сходство было весьма отдаленным. Даже он справился бы с размещением звезд
лучше — во всяком случае, сходства добился бы большего. Амфос задумался, почему же Боги
не потрудились расположить звезды более упорядоченно. Больше похоже на зерна пшеницы,
разбросанные торопливым сеятелем наугад по черному полю неба, нежели на воплощение
божественного замысла. Вдруг ему в голову пришла странная мысль: «Не ищи причин
в расположении звезд или других рассыпанных предметов; ищи скрытый всеобщий порядок
в поведении вещей».
«В самом деле, — размышлял Амфос, — порядок мы находим вовсе не в рисунке, какой
образуют брошенные на землю зерна, но в том чудесном превращении, в результате которого
каждое из этих зерен становится живым растением со сложным строением, повторяющим
в мельчайших подробностях строение остальных растений того же вида. Смысл следует
искать не во взаимном расположении зерен на том или ином участке поля, но в незримом
таинстве внутренних сил, направляющих рост каждого отдельного зерна по одному и тому
же удивительному пути. Для того, чтобы это было возможно, законы природы и в самом
деле должны действовать в чрезвычайно точном согласии».
Амфос пришел к убеждению, что без точных фундаментальных законов в мире не могло
бы существовать никакого порядка; между тем, поведение самых различных объектов сви¬
детельствует, что порядок присутствует во всем. Более того, порядок должен быть и в наших
размышлениях относительно этих материй, иначе мы рискуем впасть в серьезное заблужде¬
ние.
Случилось так, что ушей Амфоса достигли слухи о некоем живущем за морем мудреце,
убеждения которого во многом совпадали с выводами Амфоса. Мудрец этот считал, что
нельзя слепо полагаться на традиции и учения прошлых веков. Необходимо формировать
собственные убеждения, в истинности которых может убедиться любой, а для этого следует
научиться получать точные умозаключения с помощью безупречных рассуждений, которые
невозможно оспорить. Упомянутой точности можно достичь лишь математическим путем,
то есть в основе всех рассуждений должно лежать понятие числа и его применения к гео¬
метрическим формам. Соответственно, и весь мир должен в конечном счете управляться
не мифами и суевериями, но числом и геометрией.
Как и Ам-теп одиннадцать веков назад, Амфос пустился в плавание. Он добрался до го¬
рода под названием Кротон, в котором трудились в поисках истины мудрец и возглавляемое
им братство, состоявшее из 571 мужчины и 28 женщин. Некоторое время спустя Амфос был
принят в это братство. Мудреца же звали Пифагор.

Глава 1
Истоки науки
1.1.	Силы, движущие миром
Какие законы правят Вселенной? Способны ли мы их познать? И если да, то как это
знание может помочь нам понять устройство мира и обратить тем самым происходящие
в нем процессы себе на пользу?
Вопросами такого рода человечество задается с древнейших времен. Сначала люди
пытались осмыслить силы, оказывающие реальное воздействие на окружающий мир, в рам¬
ках собственного повседневного опыта. Они представляли себе, что тот некто (или нечто),
что управляет всем вокруг, руководствуется в своей деятельности теми же соображениями,
какими руководствуются они сами в стремлении перестроить окружающее пространство
под свои нужды: люди полагали, что их жизни и судьбы находятся во власти неких могу¬
щественных существ, поступки которых определяются разнообразными, но все же вполне
привычными человеческими страстями и побуждениями. Такими, как гордость, тщеславие,
любовь, ревность, гнев, страх, преданность, жажда возмездия или, к примеру, тяга к пре¬
красному. Соответственно явления природы и прочие естественные события — свет Солнца,
дожди, бури, голод, болезни и т. д. — следовало воспринимать как прихоти богов и богинь,
действующих под влиянием понятных человеческих порывов. Повлиять же на происходящие
события можно в такой ситуации одним-единственным образом — попытаться как-нибудь
умилостивить соответствующего божественного персонажа.
Однако со временем люди начали отмечать в природных явлениях вполне определенные
и надежные закономерности. Наиболее очевидный пример такой закономерности: размерен¬
ное движение Солнца по небосводу и явная связь этого движения со сменой дня и ночи.
Не могло остаться незамеченным и то, что положение Солнца относительно сферы непо¬
движных звезд тесно связано с временами года, сменяющими друг друга с неумолимой
регулярностью, что сопровождается ярко выраженными изменениями погодных условий и,
как следствие, самым радикальным образом влияет на поведение животных и растений.
Движение Луны, по всей видимости, также подчинено жесткому графику, а фазы ее опре¬
деляются положением, которое она занимает но отношению к Солнцу. Люди, населявшие
те области суши, что имели выход к открытому морю, обратили внимание на регулярность
приливов и отливов и явную связь этих явлений с положением (и фазой) Луны. В конечном
итоге перед пытливым разумом сдались и куда более сложные видимые траектории движе¬
ния планет, открыв невиданные прежде точность и регулярность. Если небесами и впрямь
правит прихоть богов, то прихоть эта по какой-то причине заключается в беспрекословном
подчинении точным математическим законам.
Ту же математическую регулярность, что направляла руку богов в небесах, демонстри¬
руют и законы, управляющие феноменами вполне земными (например, суточными и годо¬
выми изменениями температуры, приливами и отливами на море, ростом растений), но в той
или иной степени подверженными — как не без оснований полагали наши предки — небес¬
ному влиянию. Впрочем, степень влияния небесных тел на земные дела люди зачастую
преувеличивали, а природу его представляли себе превратно, склоняясь к оккультным и ми¬
стическим объяснениям астрологического толка. Прошло немало веков, прежде чем строгий

1.1. Силы, ДВИЖУЩИЕ МИРОМ
31
научный подход позволил выделить истинную картину влияния небесных тел из вороха все¬
возможных мистических гипотез. Как бы то ни было, уже в древние времена люди ясно
понимали, что такое влияние существует, а математические законы, управляющие небеса¬
ми, актуальны и на Земле.
В поведении земных объектов наблюдались и другие закономерности, не имеющие на
первый взгляд отношения к уже упомянутым. Например, демонстрируемое всеми окружаю¬
щими предметами стремление двигаться в одном и том же направлении — в нашем случае
вниз — под действием силы, называемой силой тяжести или гравитационным притяже¬
нием. Многие видели, как материя в определенных условиях преобразуется из одной формы
в другую — например, при таянии льда или растворении соли в воде, — однако общее
количество материи при таких преобразованиях, похоже, остается неизменным, в полном
согласии с так называемым законом сохранения массы. Вдобавок некогда было замечено,
что многие материальные объекты способны сохранять свою форму; из этого наблюдения
выросла концепция пространственного движения твердых тел, а мы научились представлять
пространственные отношения тел в терминах точной формальной геометрии — той самой
геометрии трехмерного пространства, которую мы сегодня называем евклидовой. Более того,
как оказалось, «прямая» в геометрии Евклида и «прямая», по которой распространяется луч
света, полностью идентичны. Всем этим идеям присущи замечательная точность и красо¬
та, обладавшие неотразимой притягательностью в глазах наших предков и не утратившие
своего очарования и по сеи день.
Вместе с тем применительно к обыденной, повседневной жизни математическая точ¬
ность мирового порядка выглядела зачастую сухой, непривлекательной и какой-то ограни¬
ченной, несмотря на всю, казалось бы, фундаментальную истинность математики самой
по себе. Соответственно многие в те давние времена позволяли себе, завороженные красо¬
той изучаемого предмета, унестись на крыльях воображения далеко за пределы разумного.
В астрологии, например, геометрическим фигурам часто приписывали еще и мистические
и оккультные свойства — взять хотя бы пентаграммы и гептаграммы, которые, как предпо-
Рис. 1.1. Плод богатого воображения древних греков — представление о связи пяти Платоновых тел
с четырьмя «стихиями» (огнем, воздухом, водой и землей) и небесным сводом (представлен додекаэд¬
ром)
л

32
Глава 1
лагалось, обладали магической силой. Предпринимались попытки и усмотреть связь между
Платоновыми телами и элементарными состояниями материи (см. рис. 1.1). Лишь спустя
много веков смогло человечество нащупать тот путь, что привел его сегодня к более глубоко¬
му пониманию действительных связей между массой, гравитацией, геометрией, движением
планет и поведением света.
1.2.	Математическая истина
Прежде чем предпринять первые шаги к постижению тех реальных сил, что управляют
Вселенной, требовалось научиться как-то отделять истину от нагромождений умозритель¬
ных предположений. Однако для того чтобы такое отделение было хоть сколько-нибудь
достоверным, древним предстояло сделать кое-что еще. Необходимо было отыскать способ,
который позволил бы отделять истину от предположений в математике, — некую фор¬
мальную процедуру, применив которую можно было бы с уверенностью сказать, является
данное математическое утверждение истинным или нет. Пока эта задача должным образом
не разрешена, вряд ли можно всерьез надеяться на успех в решении других, значительно
более сложных, задач — тех, что касаются природы движущих миром сил, какие бы взаи¬
моотношения эти самые силы с математической истиной ни связывали. Осознание того, что
ключом к пониманию Вселенной является неопровержимая математика, является, пожалуй,
первым из важнейших прорывов в науке вообще.
О математических истинах самого разного рода догадывались еще древние египтяне
и вавилоняне, однако первый камень в фундамент математического понимания (а стало
быть, и науки в целом) был заложен лишь с появлением — благодаря трудам великих гре¬
ческих философов Фалеса Милетского (ок. 625-547 г. до н.э.) и Пифагорам-4* Самосского
(ок. 572-497 г. до н. э.) — концепции математического доказательства. Первым формаль¬
ную процедуру доказательства предложил, судя по всему, Фалес; Пифагор же и его ученики
первыми начали активно использовать эту процедуру для установления фактов, иначе не
очевидных. Пифагор, кроме того, похоже, истово верил в то, что физическим миром правят
арифметические идеи вообще и числа в частности. Едва ли не решающим доводом в под¬
держку этой веры стало, как говорят, обнаружение Пифагором удивительной закономер¬
ности: наиболее гармонично звучат те лиры, отношения длин струн которых представляют
собой простейшие дроби (то же верно и для свирелей, только здесь значимы отношения длин
стволов). Судя по всему, именно Пифагор предложил так называемый «пифагоров строй»:
ряд численных отношений частот (в современной терминологии), определяющий главные
частотные интервалы, на которых, в сущности, основывается вся западная музыка^12!. И все
же наиболее, пожалуй, убедительно демонстрирует наличие точно определяемой связи меж¬
ду арифметикой чисел и геометрией физического пространства знаменитая теорема Пифа¬
гора — квадрат гипотенузы прямоугольного треугольника равен сумме квадратов его катетов
(см. главу 2).
У Пифагора было немало последователей — так называемых пифагорейцев, — прожи¬
вавших в городе Кротон (что на юге современной Италии), однако распространению его
идей это отнюдь не способствовало, поскольку все члены Пифагорейского братства давали
строгий обет хранить свои изыскания в тайне. В результате почти все их труды канули в Ле¬
ту вместе с ними. Кое-что, впрочем, просачивалось время от времени наружу, несмотря на
угрозу сурового наказания (достоверно известно, что одного из ослушников за разглашение
тайны утопили в море).
И все же в конечном счете вклад пифагорейцев в прогресс человеческой мысли оказал¬
ся чрезвычайно велик. Вместе с формальной процедурой математического доказательства у
Примечания, ссылки на которые даны в тексте в квадратных скобках, см. в конце глав (в данном случае на
с. 43).

1.2. Математическая истина
33
людей впервые появилась возможность формулировать достоверные и заведомо неопровер¬
жимые утверждения — утверждения, истинность которых не вызывает сомнений и сегодня,
несмотря на то что наука с тех времен шагнула далеко вперед. Людям впервые приоткрылась
поистине вневременная природа математики.
Что же это такое — математическое доказательство? В математике доказательством
называют безупречное рассуждение, использующее лишь приемы чистой логики и поз¬
воляющее сделать однозначный вывод о справедливости того или иного математического
утверждения на основании справедливости каких-либо других математических утвержде¬
ний, либо заранее установленной аналогичным образом, либо не требующей доказатель¬
ства вовсе (особые элементарные утверждения, истинность которых, по общему мнению,
самоочевидна, называются аксиомами). Доказанное математическое утверждение принято
называть теоремой.
Среди дошедших до нас пифагорейских теорем имеются как утверждения геометриче¬
ского характера, так и утверждения «о числах». Утверждения, касающиеся только чисел,
и сегодня остаются такими же абсолютно и бесспорно справедливыми, какими они были
во времена Пифагора. Что до геольетрических теорем, полученных пифагорейцами с помо¬
щью процедуры математического доказательства, то, хотя справедливость этих утверждений
по-прежнему не вызывает сомнений, сегодня здесь приходится делать оговорку, необходи¬
мость в которой, очевидную с точки зрения современной науки, пифагорейцы предвидеть
по понятным причинам не могли. У древних была одна-единственная геометрия — та са¬
мая, что теперь называется евклидовой, — нам же известны и другие. Таким образом, при
рассмотрении геометрических теорем древних греков необходимо всегда помнить о том,
что справедливы эти теоремы только в евклидовой геометрии. (Подробнее эти вопросы мы
обсудим в § 2.4 на примере одной из известнейших неевклидовых геометрий.)
Евклидова геометрия — это вполне определенная математическая структура, основанная
на собственном наборе вполне определенных аксиом (куда входят и несколько менее оче¬
видных утверждений, называемых постулатами) и дающая превосходное приближение при
описании вполне определенного аспекта реального физического мира. Того самого аспекта,
с которым были прекрасно знакомы древние греки и где действуют законы, управляющие
геометрией твердых тел и их относительным положением относительно других твердых тел
при движении в трехмерном пространстве. Некоторые геометрические свойства тел казались
настолько привычными и самодостаточными, что как-то сами собой перешли в разряд «са¬
моочевидных» математических истин и были приняты в качестве аксиом (или постулатов).
Однако, как мы увидим далее (см. главы 17-19, а также §§ 27.8, 27.11), специальная (с про¬
странством-временем Минковского) и общая теории относительности Эйнштейна предлага¬
ют для описания физической Вселенной иные геометрии, не только отличные от евклидовой
геометрии древних греков, но и существенно более точные — хотя и точность евклидовой
геометрии, надо признать, чрезвычайно высока. Таким образом, при рассмотрении геометри-
KJ
ческих утверждении следует проявлять осторожность — далеко не всем «аксиомам» можно
доверять как подлинно истинным, в любом смысле этого слова.
Что же в таком контексте следует понимать под «истиной»? Вопрос непростой, и слож¬
ность его хорошо понимал великий древнегреческий философ Платон, живший в Афинах
с 429 по 347 г. до н. э., приблизительно через полтора столетия после Пифагора. Платон
был убежден, что математические высказывания — т. е. предположения, истинность которых
может быть установлена неопровержимо, — описывают в действительности не реальные
физические объекты (такие, например, как приближенные изображения на песке квадратов,
треугольников, окружностей, сфер или кубов или их же модели, выполненные из дерева или
камня), но некие идеальные сущности. Он полагал, что такие идеальные сущности образуют
в совокупности собственный мир, отдельный и отличный от мира физического. Сегодня мы
называем этот мир платоновским миром математических форм. Физические структуры —
квадраты, круги или треугольники, вырезанные из папируса или нанесенные каким-либо

34
Глава 1
инструментом на плоской поверхности, равно как и кубы, тетраэдры или шары, вырезан¬
ные из мрамора, — могут очень близко подойти к этим идеалам, но никогда не совпадут
абсолютно. Настоящие математические квадраты, кубы, окружности, сферы, треугольники
< '
и т, д. не принадлежат физическому миру, но существуют в платоновском идеальном мире
математических форм.
1.3.	«Реален» ли математический мир Платона?
• * #
Для своего времени идея была просто исключительной и, как выяснилось впоследствии,
очень и очень продуктивной. Но можно ли сказать, что платоновский математический мир
действительно существует (в каком бы то ни было постижимом смысле этого слова)? Мно-
гие, в том числе и философы, сочтут такой «мир» чистым вымыслом — порождением исклю¬
чительно необузданного воображения. И все же точка зрения Платона обладает огромной
научной ценностью. Прежде всего потому, что проводит четкое разделение между точными
математическими объектами и теми приближениями, что мы наблюдаем в физическом мире
вокруг нас. Кроме того, она снабдила нас шаблоном, которому с тех самых пор и по сего¬
дняшний день следует наука вообще. Ученые предлагают те или иные модели мира — или,
чаще, отдельных аспектов мира, — которые затем проверяются на соответствие результатам
предшествующих наблюдений или тщательно спланированных экспериментов. Если модель
выдерживает все строгие испытания (и если она к тому же внутренне непротиворечива),
то ее признают адекватной и делают соответствующие выводы. Обратите особое внима¬
ние модели эти в большинстве своем являются чисто абстрактными математическими
построениями. Одна лишь постановка вопроса о внутренней непротиворечивости научной
модели предполагает, в частности, что модель должна быть описана каким-либо точным
образом. Необходимая степень точности достижима лишь при условии, что модель являет¬
ся математической, в противном случае мы не можем гарантировать, что на поставленные
вопросы существуют вполне определенные ответы.
Если вообще можно говорить о какой-либо форме существования применительно к ма¬
тематической модели, то самым подходящим местом для такого существования является
платоновский мир математических форм. Можно, разумеется, принять и противоположную
точку зрения: модели существуют исключительно в наших многочисленных разумах, и для
их благополучного существования вовсе не требуется наделять платоновский мир какой бы
то ни было абсолютностью или «реальностью». Однако полностью отрицая собственную
реальность математических структур, мы рискуем, как мне представляется, упустить нечто
важное. Всем известно, как вопиюще неточны, ненадежны и противоречивы в суждениях
наши индивидуальные разумы. От научных же теорий мы, напротив, ожидаем точности,
достоверности и непротиворечивости, то есть чего-то такого, чего не найти ни в одном
из наших индивидуальных (не заслуживающих, вообще говоря, никакого доверия) разу¬
мов. В математике неизмеримо больше здравого смысла, нежели можно обнаружить в лю-
бом отдельно взятом разуме. Не является ли это прямым указанием на то, что математика
существует вне нас, что она обладает собственной реальностью, недоступной ни одному
отдельному индивидууму?
Впрочем, здесь возможно иное объяснение: математический мир не обладает независи¬
мым существованием, это всего лишь совокупность неких идей, выкристаллизовавшихся из
многочисленных индивидуальных разумов, идей, которые, по всеобщему согласию, заслужи¬
вают полного доверия и принимаются как абсолютные истины. Однако и это объяснение —
при всей своей привлекательности — ничего, похоже, не объясняет. Следует ли нам под
«всеобщим согласием» понимать действительно «всеобщее согласие», или все же «согла¬
сие всех тех, кто в здравом уме», или, еще лучше, «согласие всех математиков, имеющих
ученую степень не ниже доктора» (хотя ко временам Платона это, пожалуй, не подходит)?

1.3. «Реален» ли математический мир Платона?
35
И кто обладает правом на выдвижение «официального» мнения в случае чего? Возникает
опасность «зацикливания» — для того чтобы решить, в «здравом» ли, например, уме тот
или иной соглашающийся, необходимо наличие некоего внешнего стандарта. Требует на¬
личия стандарта и критерий «официальности мнения», разве что мы примем за таковой
какой-либо из стандартов ненаучного характера — например, «мнение большинства» (наде¬
юсь, читатель четко представляет себе, что мнение большинства, при всей своей важности
для демократически настроенного правительства, ни в коем случае не может использо¬
ваться в качестве критерия научной приемлемости). Математика же сама по себе обладает
такой «здравостью», какая и не снилась ни одному отдельно взятому математику. У тех,
кто занимается математикой профессионально (неважно, принимают ли они сами активное
участие в математических исследованиях или просто используют результаты, полученные
другими), рано или поздно возникает, как правило, ощущение, что они — всего лишь пу¬
тешественники в огромном мире, живущем собственной жизнью, в мире, который наделен
объективной реальностью, независимой от каких бы то ни было частных мнений, будь
это их собственные мнения или предположения других математиков, пусть даже и всеми
признанных экспертов.
Возможно, мне стоит, для большей убедительности, облечь свои аргументы в пользу
действительного существования платоновского мира в несколько иной форме. Когда я го¬
ворю о «существовании» платоновского мира, я имею в виду всего-навсего объективность
математической истины. Существование платоновского мира, как я себе представляю, рав¬
носильно существованию некоего объективного внешнего стандарта, который не зависит
ни от наших индивидуальных мнений, ни от особенностей нашей культуры. Таким «суще¬
ствованием» могут обладать и другие абстракции, порой весьма далекие от математики,
например, мораль или эстетика (см. § 1.5), однако я в данном случае предпочитаю ограни¬
читься проблемой математической объективности, существенно менее запутанной, на мой
взгляд.
В качестве иллюстрации рассмотрим один знаменитый пример математической исти¬
ны, причем особое внимание уделим вопросу ее «объективности». В 1637 году Пьер де
Ферма сформулировал свое знаменитое утверждение, ныне известное как «последняя тео¬
рема Ферма» (никакая пара возведенных в степень п положительных целых чисел [1,31 не
может дать в сумме третье число в той же степени гг, если п — целое число, больше двух),
записав его на полях своего экземпляра «Арифметики», книги, написанной греческим мате¬
матиком III века Диофантом. Ниже Ферма добавил: «Я также нашел воистину удивительное
этому доказательство, однако оно здесь не поместится — поля слишком узки». Более 350 лет
последняя теорема Ферма оставалась недоказанной, несмотря на последовательные усилия
многих выдающихся математиков. Наконец, в 1995 году, Эндрю Уайлз (опиравшийся на
труды нескольких предшественников) опубликовал доказательство, которое на сегодняшний
день принято математическим сообществом как обоснованное.
Итак, принимаем ли мы точку зрения, согласно которой утверждение Ферма было ис¬
тинным всегда, в том числе и задолго до того момента, как Ферма его высказал? Или же
справедливость этого утверждения есть феномен исключительно культурный, зависящий
от субъективных стандартов сообщества математиков-людей, какими бы эти стандарты ни
были? Попробуем для начала допустить, что справедливость утверждения Ферма и в самом
деле субъективна. В этом случае ничто не помешало бы какому-либо другому математику,
назовем его X, найти некий реальный и конкретный контрпример, опровергающий утвержде¬
ние Ферма, — при условии, разумеется, что X сделает это до 1995 года^1'4^. Математическому
сообществу не останется ничего иного, как принять правильность доказательства X. После
этого любые попытки Уайлза доказать утверждение Ферма обречены на провал — по той
простой причине, что X представил свой контрпример первым, и, стало быть, утвержде¬
ние Ферма ложно! Зададим себе еще один вопрос: следует ли из справедливости гряду¬

36
Глава 1
щего контрутверждения X, что сам Ферма непременно ошибался, полагая обоснованным
свое не поместившееся на полях, но «воистину удивительное» доказательство? При субъ¬
ективной трактовке математической истины дело вполне может обернуться так, что Ферма
в свое время нашел обоснованное доказательство (которое было бы принято как таковое
собратьями-математиками, потрудись Ферма его обнародовать), однако скрытность ученого
привела к тому, что впоследствии X смог получить доказательство противоположного. Я убе¬
жден, что практически все математики, независимо от демонстрируемого ими отношения к
«платонизму», сочтут возможность такого развития событий откровенно абсурдной.
Разумеется, нельзя исключить, что в рассуждения Уайлза действительно вкралась ошиб¬
ка и, следовательно, утверждение Ферма все-таки ложно. Не исключено также и то, что
рассуждения Уайлза фундаментально ошибочны, однако утверждение Ферма тем не ме¬
нее истинно. А может оказаться, что доказательство Уайлза по сути верно, но содержит
«нестрогие элементы», что абсолютно недопустимо по стандартным правилам математиче¬
ской приемлемости, разработанным математиками отдаленного будущего. Однако все эти
возможности не имеют никакого отношения к тому, о чем я здесь говорю. Речь идет об
объективности самого утверждения Ферма, а вовсе не о том, покажется ли убедительной
математикам той или иной конкретной эпохи чья-либо демонстрация истинности (или лож¬
ности) этого утверждения.
Следует, пожалуй, упомянуть и о том, что с точки зрения математической логики
утверждение Ферма представляет собой чрезвычайно простое математическое высказыва¬
ние [1-5] — из тех, объективность которых видна невооруженным глазом. Очень немногие
математикиt1*6! склонны полагать, что истинность таких высказываний может быть хоть
сколько-нибудь «субъективной» — до некоторой степени субъективно здесь можно подойти
разве что к оценке убедительности того или иного доказательства. Однако в математи¬
ческих утверждениях других классов истинность вполне может оказаться «зависимой от
мнения». Самым, наверное, известным из таких утверждений является так называемая ак¬
сиома выбора. В сущность аксиомы выбора нам пока вникать не обязательно (я расскажу о
ней подробнее в § 16.3). Я упомянул о ней здесь просто в качестве примера. Большинство
математиков, вероятно, сочтут аксиому выбора «очевидно истинной», другие, напротив,
укажут, что утверждение это выглядит несколько сомнительно и вполне может оказаться
ложным (я, собственно, и сам до некоторой степени склоняюсь к такой точке зрения). Тре¬
тьи отнесут аксиому выбора к утверждениям, «истинность» которых зависит от мнения,
или, скорее, к утверждениям, которые можно рассматривать и так и эдак — в зависимости
от того, какую систему аксиом и правил действия (так называемую «формальную систе¬
му», см. § 16.6) вы для себя выберете. Математиков, придерживающихся последней точки
зрения (но признающих при этом объективность истинности простых и ясных математи¬
ческих утверждений — таких, например, как рассмотренное выше утверждение Ферма),
тоже можно назвать платонистами, только более мягкого толка. Те же, кто упорно отстаи¬
вает объективность истинности даже аксиомы выбора, принадлежат к лагерю платонистов
ортодоксальных.
К аксиоме выбора я еще вернусь в § 16.3, так как она имеет некоторое отношение
к математике, описывающей поведение физического мира на фундаментальном уровне, —
несмотря на то обстоятельство, что физики-теоретики по какой-то причине почти не обра¬
щают на эту аксиому внимания. До той поры чрезмерно погружаться в детали необходи¬
мости нет. Если истинность аксиомы выбора можно так или иначе установить посредством
какого-либо неопровержимого математического рассуждения ^'7\ то эта истинность целиком
и полностью объективна, в каковом случае либо сама аксиома, либо ее отрицание непре¬
менно принадлежит платоновскому миру идей — в том смысле, в каком я понимаю термин
«платоновский мир». Если же истинность аксиомы выбора зависит от точки зрения или
каких-либо произвольных предпочтений с нашей стороны, то тогда в платоновском мире аб¬

1.3. «Реален» ли математический мир Платона?
37
солютных математических форм вы не найдете ни аксиомы выбора, ни ее отрицания (хотя
не исключено, что вам встретятся утверждения вида «то-то и то-то следует из аксиомы вы¬
бора» или «аксиома выбора является теоремой согласно правилам такой-то математической
системы»).
Платоновскому миру могут принадлежать только те математические утверждения, ис¬
тинность которых объективна. Я бы даже сказал, что именно в математической объектив¬
ности и заключается главный смысл всей концепции математического платонизма. Фраза
«такое-то математическое утверждение обладает независимым платоновским существова¬
нием» означает всего-навсего, что утверждение это истинно в объективном смысле. То же
применимо и к математическим понятиям (таким, как понятие числа, например, 7, или
правило умножения целых чисел, или понятие множества, содержащего бесконечное коли¬
чество элементов) — все они существуют в платоновском мире, поскольку объективны. По
моему мнению, платоновское существование есть не что иное, как существование объек¬
тивное, и поэтому в нем, конечно же, нет ничего «мистического» или «ненаучного», пусть
даже кому-то и удобнее эту мистику и ненаучность в нем видеть.
Впрочем, как и в случае с аксиомой выбора, признание «права» на объективное су¬
ществование того или иного предлагаемого математического объекта (либо отказ в таком
признании) может быть сопряжено с решением весьма деликатных и порой исключительно
формальных вопросов. Тем не менее, для того чтобы оценить общую «здравость» многих
математических концепций, нам совершенно необязательно быть математиками. На рис. 1.2
представлен знаменитый математический объект, называемый множеством Мандельброта,
и три увеличенных его участка. Множество Мандельброта чрезвычайно сложно и замыслова¬
то устроено, причем «устроено» не человеком. Самое замечательное здесь то, что структура
множества целиком и полностью определяется математическим правилом исключительной
простоты. Дабы не отвлекаться от наших насущных целей, я не буду подробно описывать
это правило здесь — в свое время (§ 4.5) мы до него доберемся.
Однако вот на что я хочу обратить ваше внимание: когда Бенуа Мандельброт обна¬
ружил невероятную сложность тонкой структуры полученного множества, никто — и сам
Бенуа Мандельброт в том числе — не имел реального представления о том, какие богат¬
ства это множество в себе содержит. Множество Мандельброта совершенно определенно не
является изобретением человеческого разума. Оно просто объективно существует в самой
математике. Если вообще имеет смысл говорить о существовании множества Мандельброта,
то существует оно отнюдь не в наших с вами разумах, ибо ни один человек не в состоя¬
нии в полной мере постичь бесконечное разнообразие и безграничную сложность этого
математического объекта. Равным образом не может оно существовать и в многочисленных
компьютерных распечатках, которые пока только начинают охватывать некую малую толику
его невообразимо сложно детализированной структуры, — на этих распечатках мы видим не
само множество Мандельброта и даже не приближение к нему, но лишь бледную тень очень
грубого приближения. И все же множество Мандельброта существует и существует вполне
устойчиво: кто бы ни ставил перед компьютером задачу построения множества, каким бы ни
был этот самый компьютер, структура в результате получается всегда одинаковая — и чем
«глубже» мы считаем, тем более точной и детальной будет картинка. Следовательно, су¬
ществовать множество Мандельброта может только в платоновском мире математических
форм, больше нигде.
Я понимаю, что многим читателям и после такого предисловия сложно будет предста¬
вить себе математические структуры, наделенные каким-то действительным, независимым
существованием. К таким читателям я хочу обратиться с одной простой просьбой: попро¬
буйте слегка расширить рамки привычного значения слова «существование». Разумеется,
математические формы в платоновском мире существуют не совсем так, как существуют
обычные физические объекты — скажем, столы и стулья — в мире нашем. Они не имеют

38
Глава 1
*
а)
.sV *
- .*
л / - •.
* •	'	г
v^\>, .
• -X
'•<: •/>'
б)
• ■’	Г*.*’	-.	7	.-f	,	*>“¥	.у
л,,/,!;<	‘	■■■''?:!'; v • л> ‘
*»; '	./s	/	л*л	>
У • *-в
'^W
■ 4 'Л
/ ъ.
• >
% •	-	*■	.-S
:.;• v- -л
* ' 1-
-.40.
л *У
>*,. <*•
"7
•А-
ЬУ. ".
■К
Ч
:-А/' ■	fC	УАЯЬСЛ-	ъ
- • ай~*< * ..<	^ - ушк&-
* Г-*- •	• -А ■•'
Л '<	V *'•..	.>	•	•/	у	/Чу,’	/у,
л- •	:	/ • ,v^. Jv/*/#.	/4.	■•	\	•	С
>-«ГА :;Шч^ V. з
ч	'	*1*И|
.• ‘/ПЯК / .
Г •	•.	,'	//TJWW	'	.’л	v.‘ АГ л, /,/«»4 .i4	.УУ/У	•
:--V. .л> Vf^vV- .!;. r-V’	*i *4%
г :/ К -	*4в*	“ЗЗШ-
-	N1	.	/	v>/	•’	А*ЯЁй£.'
/г: ?'У**$л ,	%%*>
\	•••.».	/iv^vW'V/.	.	./у	.
о\	*	.''хмив	>'	&	W+
*	..	4/3W^/#f‘.	.v^>	‘^/. у. . лЛ. >. А У ‘ • V
"г
'Ai.
~''Л 2
•<ч /2
-.-	.	л/	>У>
Рис. 1.2. а) Множество Мандельброта, б), в) и г) Увеличенные (в 11,6; 168,9 и 1042 раза) изображения
некоторых участков, позволяющие увидеть чрезвычайно сложную структуру множества. Количество
шагов итерации: 300 а), 300 б), 200 в), 200 г); см. примечание 4.10
пространственного местоположения, не существуют они и во времени. Объективные ма¬
тематические понятия следует представлять как вневременные объекты; не нужно думать,
будто их существование начинается в тот момент, как только они в том или ином виде
возникают в человеческом воображении. Замысловатые завитки множества Мандельброта,
изображенные на рис. 1.2 в и 1.2 г, не были вызваны из небытия в то мгновение, когда кто-то
увидел их на экране компьютера или на распечатке. Не возникли они и тогда, когда впер¬
вые была выдвинута человеком лежащая в основе множества Мандельброта общая идея —
причем не обязательно самим Мандельбротом (действительно первым в этом смысле), но,
скажем, Р, Бруксом и Дж. П. Мате леки в 1981 году или, может быть, кем-то другим и еще
раньше. Потому что ни Брукс, ни Мателски, ни даже Мандельброт в начале своих экспери¬
ментов не имели сколько-нибудь реального представления о тех изящных тонких узорах, что
воспроизведены на рис. 1.2 в и 1.2 г. Эти узоры «существовали» и прежде, они существуют с
незапамятных времен и будут существовать всегда — в потенциально вневременном смысле,
предполагающем, что в какое бы время, в каком бы месте, какое бы обладающее сознанием
существо ни решило исследовать их структуру, оно всякий раз увидит в точности то же
! /
самое, что видим сегодня мы с вами.

1.4. ТРИ МИРА И ТРИ ВЕЛИКИЕ ЗАГАДКИ
39
1.4.	Три мира и три великие загадки
Таким образом, математическое существование отличается не только от существования
физического, но и от того существования, которым способно наделить объект наше созна¬
тельное восприятие. Тем не менее оно явно связано с двумя последними формами суще¬
ствования — т. е. с физическим и ментальным существованием, — причем соответствующие
связи настолько же фундаментальны, насколько и загадочны. На рис. 1.3 я схематически
изобразил все эти три формы существования — физическую, ментальную и платоновскую
математическую — в виде сфер, представляющих собой объекты, принадлежащие трем раз¬
личным мирам. Здесь же показаны и загадочные связи между мирами, причем, нарисовав
их таким образом, я тем самым некоторым образом навязываю читателю кое-какие свои
представления (или предубеждения) относительно природы этих загадок.
Рис. 1.3. Три «мира» — платоновский математический, физический и ментальный — и три связывающие
их фундаментальные загадки
Что касается загадки номер один — той, что связывает платоновский математический
мир с миром физическим, — из рисунка видно, что непосредственное отношение к процессам
физического мира имеет лишь некая малая часть мира математики. В самом деле, подав¬
ляющее большинство исследований в современной чистой математике не связаны сколько-
нибудь очевидным образом ни с физикой, ни с иными науками (см. § 34.9), хотя математика
и не устает удивлять нас своими неожиданными и важными практическими применения¬
ми. Аналогичное заключение можно сделать и относительно второй загадки: каким образом
в определенных физических структурах (если точнее, то в здоровых и бодрствующих челове¬
ческих мозгах) возникает феномен мыслительной деятельности — я отнюдь не настаиваю на
том, что структуры, способные на ментальные процессы, должны непременно преобладать
в физическом мире. Возможно, мозг кошки и впрямь способен развить в себе ментальные
качества, однако от, скажем, камня того же ожидать, наверное, не стоит. И наконец, третья
загадка — здесь, полагаю, и без пояснений очевидно, что размышления об абсолютных ма¬
тематических истинах составляют весьма малую долю от нашей совокупной мыслительной
деятельности. (По большей части, деятельность эта посвящена разнообразным заботам, ра¬
достям, огорчениям, волнениям, удовольствиям и тому подобным вещам, наполняющим на¬
шу повседневную жизнь.) В соответствии с указанным обстоятельством, основания «лучей»,
платоновский
физический
мир

40
Глава 1
связывающих каждый мир со следующим, захватывают очень небольшие части исходных
миров (миры рассматриваются в направлении движения часовой стрелки). В то же время
именно в таком построении и проявляется то предвзятое отношение, о котором я упоминал
выше: получается, что весь следующий мир в некотором роде содержится в малой области
мира предыдущего.
Итак, согласно изображенной на рис. 1.3 схеме, весь физический мир управляется ма¬
тематическими законами. В последующих главах книги мы увидим, что имеются веские
(хоть и неполные) свидетельства в поддержку такой точки зрения. Если верить этим свиде¬
тельствам, то приходится признать, что все, существующее в физической Вселенной, вплоть
до самых мельчайших мелочей, и в самом деле управляется точными математическими
принципами — может быть, уравнениями (с некоторыми из таких уравнений мы очень скоро
познакомимся), а может, какими-то другими, неизвестными пока математическими струк¬
турами, фундаментально отличными от тех, что мы сегодня обозначаем термином «уравне¬
ние». Если это так, то и наши с вами физические действия целиком и полностью подчинены
такому всеобщему математическому контролю, хотя «контроль» этот все же допускает опре¬
деленную случайность в поведении, управляемую строгими вероятностными принципами.
Многие люди от таких предположений начинают чувствовать себя очень неуютно; у ме¬
ня и у самого, признаться, эти мысли вызывают некоторое беспокойство. Тем не менее даже
мои собственные предрассудки, похоже, свидетельствуют, в общем и целом, в пользу опи¬
санной точки зрения, поскольку совершенно невозможно определить, где же следует прове¬
сти границу между физическими действиями, подчиненными математическому контролю,
и действиями, такому контролю неподвластными. Мне кажется, что наше общее беспокой¬
ство возникает отчасти из-за крайне ограниченного представления об истинной сути этого
пресловутого «математического контроля». Эта книга как раз и написана, помимо проче¬
го, для того, чтобы показать читателю хотя бы малую часть того невероятного богатства,
мощи и красоты, которые могут открыться нам, как только мы сумеем отыскать нужные
математические понятия.
Одно только множество Мандельброта (см. рис. 1.2) может дать некоторое первоначаль¬
ное понимание как возможностей, которые открывают перед нами такие объекты, так и при¬
сущей им красоты. А ведь множество Мандельброта и подобные ему структуры занимают
лишь крохотный островок в бескрайнем море математики — ту область, где поведение объ¬
ектов регулируется строгим вычислительным контролем. За пределами же этой области нас
ждут несметные, неведомые еще богатства. Какие же в самом деле чувства вызывает у меня
возможность того, что все мои действия и все поступки моих друзей управляются в конеч¬
ном итоге такого рода математическими принципами? Думаю, я смогу это вынести. Думаю
даже, что для меня предпочтительнее считать, что всеми этими действиями управляет нечто,
существующее в некотором объективном смысле в идеальном математическом мире Пла¬
тона, нежели позволить убедить себя в том, что поведение человека целиком и полностью
определяется упрощенно-низменными мотивами вроде жадности, агрессивной жестокости
или стремления к удовольствиям, каковое мировоззрение, как уверяют многие, и должно
стать единственным результатом применения строго научного подхода.
Впрочем, я вполне могу себе представить, что немалая часть читателей все равно не смо¬
жет с легкостью принять идею тотального владычества математических законов во Вселен¬
ной. Равным образом, многие, несомненно, найдут что возразить и на другие два предубе¬
ждения, отразившиеся на нарисованной мною схеме (рис. 1.3). Возможно, им покажется,
что, изобразив на схеме, будто вся и всяческая ментальность уходит корнями в физический
мир, я продемонстрировал слишком уж «твердолобонаучный» взгляд на вещи. Я готов при¬
знать, что это и в самом деле всего лишь предубежденность — хоть мы и не располагаем
никакими рациональными научными свидетельствами в пользу существования «разумов»,
не нуждающихся в физическом «носителе», полной уверенности в невозможности такого

1.4. Три мира и три великие загадки
41
феномена у нас нет. Кроме того, не следует сбрасывать со счетов и крайне настойчивую
аргументацию всевозможных религиозных деятелей, которые не только утверждают, что
независимый от физического тела разум возможен, но и приводят неопровержимые (по их
мнению) доказательства этого утверждения — правда, доказательства эти несколько иного
рода, нежели те, что «добывает» обычная наука.
И наконец, последнее мое предубеждение проявляется в том, что платоновский мир
на схеме, похоже, целиком и полностью происходит из мира ментального. Этим я всего
лишь хотел показать, что не бывает математических теорий, непостижимых разумом, —
по крайней мере, в принципе. Существуют, разумеется, математические утверждения (даже
среди, казалось бы, самых обычных арифметических задач на сложение), настолько безмерно
сложные, что никто пока не нашел в себе достаточно интеллектуальных сил, чтобы с ними
справиться. Однако даже такие задачи потенциально не выходят за пределы ментальных
возможностей человека и вполне вписываются в схему на рис. 1.3 в том смысле, какой
я в нее вкладывал. Тем не менее мне следовало бы учесть, что возможны математические
утверждения, не постижимые разумом даже потенциально, — таким утверждениям места на
первоначальной схеме не нашлось. (Подробнее об этой проблеме мы поговорим в § 16.6;
там же попробуем разобраться, какое отношение имеет к ней знаменитая теорема Гёделя
о неполноте.)t1*8!
Поскольку читатель вовсе не обязан разделять все мои личные предубеждения, я решил
пойти на уступки и перерисовать связи между тремя мирами таким образом, чтобы снять
все возможные противоречия (результат представлен на рис. 1.4). На новой схеме учте¬
на возможность физического действия, неподвластного математическому контролю; преду¬
смотрено место для ментальной деятельности, свободной от физических структур, и для
истинных математических утверждений, установление истинности которых принципиально
недоступно ни разуму, ни интуиции.
Такая «расширенная» схема непременно задаст нам другие загадки, еще более голово¬
ломные, чем те, с которыми я смирился в своей первоначальной картине мира (рис. 1.3).
На мой взгляд, и в прежней, более компактно организованной и строго научной схеме, за¬
гадок было вполне достаточно. Причем переход к менее строгой схеме (рис. 1.4) старые
загадки отнюдь не разрешил. Я по-прежнему недоумеваю, почему математические законы
Рис. 1.4. Модификация схемы с рис. 1.3 с учетом феноменов, противоречащих предубеждениям автора
платоновский
математический
физический
мир

42
Глава 1
непременно должны описывать физический мир с такой феноменальной точностью. (Неко¬
торое представление об исключительной точности фундаментальных физических теорий мы
получим в §§ 19.8, 26.7, 27.13.) И если бы дело было только в точности! Но нет — ничуть
не менее загадочны утонченная сложность и математическая красота успешных теорий. По-
прежнему абсолютно непонятно, как в определенным образом организованной физической
материи — здесь я имею в виду живой человеческий (или животный) мозг — вдруг ни с того
ни с сего возникает ментальное качество осмысленного осознания. И наконец, все так же
неясно, каким таким хитроумным способом человек оценивает истинность математического
утверждения. Это ментальное качество невозможно объяснить только тем, что наш мозг
якобы запрограммирован на корректное выполнение тех или иных «вычислений». Должно
быть что-то еще помимо вычислений, что-то такое, что позволяет даже самому никудыш-
U	о
ному математику интуитивно схватывать действительный смысл таких, например, понятии,
как «нуль», «один», «два», «три», «четыре» и т. дД1*9!
Некоторые из вопросов, возникающих в связи с третьей загадкой, мы рассмотрим в
следующей главе (а также более подробно в §§ 16.5, 16.6) применительно к формальной
процедуре математического доказательства. Однако главной темой книги является все
же первая из перечисленных загадок, т. е. говорить мы будем в основном о том, что имеет
отношение к замечательной взаимосвязи математики и действительного поведения физиче¬
ского мира. Невозможно составить сколько-нибудь адекватное представление о необычайной
мощи современной науки без хотя бы поверхностного знакомства с наиболее выдающими¬
ся математическими идеями. Не сомневаюсь, найдется немало читателей, которые сочтут
необходимость разбираться со всей этой математикой слишком высокой ценой за упомя¬
нутое адекватное представление. Давайте не будем спешить — может быть, черт вовсе не
так страшен, как вам показалось. Кроме того, я все еще надеюсь, что мне удастся убедить
большинство из вас (несмотря на тот, возможно, негативный опыт, что вы успели накопить):
математика-таки может быть увлекательным занятием!
Что касается второй из великих загадок, схематически представленных на рис. 1.3
и 1.4, — т. е. тайны возникновения ментальности и в особенности осмысленного осознания
— то особо оетанавливать-
в
ся на ней мы здесь не будем (за исключением § 34.7, где я вкратце затрону этот непростой
вопрос). Ограничимся исследованием физической Вселенной и неразрывно связанных с ней
математических законов — эта тема достаточно обширна, чтобы надолго занять даже самый
пытливый ум. Вдобавок ко всему, вопросы, связанные с мышлением, как правило, крайне
неоднозначны, и я боюсь, что обсуждение всех спорных моментов отвлечет наше внимание
от главной цели книги. Хотя одно краткое замечание будет здесь, пожалуй, уместным: при
нынешнем уровне знании о фундаментальной структуре физическом реальности у нас очень
мало шансов достичь сколько-нибудь глубокого понимания природы разума. Как станет ясно
из рассуждений, представленных в последующих главах, я убежден, что наше понимание
окружающего физического мира давно уже нуждается в радикальных революционных пе¬
ременах. До тех пор пока такие перемены не настали, любое заявление о возможности
реального прогресса в понимании истинной природы мыслительных процессов Представля¬
ема 14*
ется мне проявлением оезудержного оптимизма
10]
1.5.	Истина, Добро и Красота
Схемы на рис. 1.3 и 1.4 поднимают вопросы и иного рода. До сих пор я рассматривал
платоновский «мир идеальных форм» лишь в ограниченном смысле математических форм.
Ключевым для математики является идеал Истины. Сам же Платон учил, что помимо истины
существуют еще два фундаментальных абсолютных идеала, а именно: Добро и Красота.
Я вполне готов признать существование таких идеалов и расширить понятие платоновского
мира, с тем чтобы включить туда и их тоже.

1.5. Истина, Добро и Красота
43
В самом деле, еще до конца книги нам встретится несколько совершенно замечатель¬
ных примеров соотношений между истиной и красотой, проливающих свет (в котором лишь
яснее видно, насколько здесь все запутано) на некоторые темные моменты, связанные с от¬
крытием и последующим принятием физических теорий (см., в частности, §§ 34.2,34.5,34.9;
см. также рис. 34.1). Более того, даже если не говорить о несомненно важной (хотя зачастую
и неоднозначной) роли красоты в математике, описывающей фундаментальное устройство
физического мира, именно эстетические критерии выходят на первый план при разработ¬
ке математических идей самих по себе, именно эстетические критерии дают стимул для
движения к открытию и в большинстве случаев указывают, куда, собственно, нужно дви¬
гаться. Я бы даже предположил, что распространенная среди математиков убежденность
в существовании где-то вовне реального, независимого от человека платоновского мира
основывается не в последнюю очередь на исключительной и неожиданной, скрытой прежде
красоте, которая часто обнаруживается в самих идеях.
Не столь очевидно связан с обсуждаемыми в этой книге темами (хотя и несомненно
важен в более широком контексте) вопрос об абсолютном идеале этики: что такое хорошо
и что такое плохо, и как эти абсолютные ценности воспринимаются нашим разумом? Этика
составляет неотъемлемую часть ментального мира, поскольку обусловлена ценностями, фор¬
мируемыми разумными существами, и, что более значимо, самим фактом наличия сознания.
Вряд ли можно говорить о какой бы то ни было этике в отсутствие существ, обладающих
разумом. Понимание физических основ ментальности приобретает по мере развития науки
и техники все большую значимость. Думаю, что в условиях современной технологической
культуры как никогда важно не забывать при решении научных проблем и об этической
стороне дела. Впрочем, рассмотрение этих вопросов сейчас может увести нас весьма далеко
в сторону от непосредственной цели книги. Прежде чем приступать к разделению добра
и зла, необходимо научиться адекватно отделять истинное от ложного.
И наконец, еще об одной загадке рис. 1.3. Я сознательно нарисовал схему таким образом,
чтобы возник парадокс. Если верить рисунку, то получается, что каждый мир (согласно моим
предубеждениям) заключает в себе весь следующий мир целиком. Как же такое возможно?
Я не считаю это обстоятельство достаточно веской причиной для того, чтобы расстаться
с упомянутыми предубеждениями, я лишь хочу продемонстрировать наличие еще более
головоломной загадки, превосходящей все те, на которые я указывал выше. Возможно,
в некотором смысле три мира вовсе не являются отдельными сущностями, но лишь отражают
различные аспекты некоей более фундаментальной истины, описывающей мир, как целое, —
истины, о которой в настоящее время мы не имеем ни малейшего понятия. Прежде чем мы
сможем должным образом объяснить все эти материи, нам еще очень во многом предстоит
разобраться.
На этом предлагаю лирическое отступление (которое, боюсь, и так уже чересчур затя¬
нулось) завершить. Главная его цель заключалась в том, чтобы подчеркнуть, что с глубокой
древности и до наших дней математика занимает в науке центральное место. Теперь давайте
попробуем краем глаза заглянуть в платоновский мир — по крайней мере в ту относитель¬
но небольшую, но чрезвычайно важную его часть, которая имеет самое непосредственное
отношение к природе физической реальности.
Примечания
§1.2.
1.1.	К сожалению, достоверными сведениями о Пифагоре, его жизни, его последователях и их науч¬
ной деятельности мы почти не располагаем — с уверенностью можно говорить лишь, что люди
эти действительно существовали и что сам Пифагор отводил простым отношениям частот ре¬
шающую роль в музыкальной гармонии (см. [115]). С другой стороны, фундаментальный вклад

44
Глава 1
пифагорейцев в науку общепризнан. Соответственно я буду употреблять слова «пифагорейцы»
и «пифагорейский» просто как удобные ярлыки, никоим образом не претендуя на историческую
точность.
1.2. Пифагоров строй представляет собой чисто «диатоническую гамму», в которой частоты (обрат¬
но пропорциональные длинам звучащих элементов) связаны отношениями 24 : 27 : 30 : 32 :
36 : 40 : 45 : 48 — такой ряд дает множество простых отношений, порождающих приятные
для слуха гармонии. «Белые клавиши» современных фортепьяно настраиваются (с неизбеж¬
ными поисками компромисса между пифагоровой чистотой гармонии и возможностями на¬
строечного ключа) в приблизительном соответствии с этими пифагоровыми отношениями —
точнее, в соответствии с равномерно-темперированным строем, частоты в котором соотносят¬
ся как 1 : о? : а4 : а5, : а? : а9 : а11 : <д12, где а = 1у/2 — 1,05946... (Примечание: запись а5
означает «число а, возведенное в пятую степень», т. е. а х а х а х а х а. Величина 1у/2
представляет собой корень двенадцатой степени из двух, т. е. 21/12; таким образом, а12 — 2.
См. также примечание 1.3 и §5.2.)
§1.3.
1.3. Напомню (см. примечание 1.2), что под возведением числа в степень п понимается умножение
этого числа на самое себя п раз. То есть 5 в степени 3 равно 125 (записывается как 53 — 125), 3
в 4-й степени равно 81 (З4 = 81) и т.д.
1.4. Собственно, пока Уайлз пытался залатать «дырку» в своем доказательстве последней теоре¬
мы Ферма (обнаруженную уже после первого представления им доказательства в Кембридже
в 1993 году), среди математиков распространился слух, будто Ноам Элькис наплел контрпри¬
мер, опровергающий утверждение Ферма. Ранее, в 1988 году, именно Элькис отыскал пример,
противоречащий предположению Эйлера (уравнение х4 4- у4 + z4 — w4 не имеет решения в по¬
ложительных целых числах), доказав тем самым его ложность. Почему бы, в самом деле, ему
же и не доказать ложность утверждения Ферма? Впрочем, как вскоре выяснилось, электрон¬
ное почтовое сообщение, послужившее источником слухов, было датировано первым апреля
и оказалось розыгрышем, устроенным Анри Дармоном (см. [726], с. 293).
1.5. Формально утверждение Ферма является Пт-высказыванием (см. § 16.6).
1.6. Я понимаю, что, делая такое заявление, я в некотором смысле попадаю в собственноручно
расставленную ловушку. Дело здесь, вообще говоря, вовсе не в том, составляют ли в дей¬
ствительности меньшинство те математики, что придерживаются столь крайних субъективных
взглядов (о чем я, разумеется, не могу судить, так как не проводил среди математиков социоло¬
гического опроса на этот счет), а в том, следует ли такую экстремистскую позицию принимать
всерьез. Думаю, ответ на этот вопрос читатель знает и без меня.
1.7. Кое-кто из читателей, возможно, знаком с результатами Гёделя и Коэна, согласно которым ак¬
сиома выбора независима от более базисных стандартных аксиом теории множеств (системы
аксиом Цермело - Френкеля). Необходимо пояснить, что из самой по себе аргументации Гёделя -
Коэна вовсе не следует, что истинность аксиомы выбора никогда не будет так или иначе установ¬
лена. Это особо подчеркивается, например, в последнем параграфе книги Пола Коэна «Теория
множеств и континуум-гипотеза» ([153], гл. 14, § 13) — хотя там, надо признать, Коэн более
пристальное внимание уделяет все же континуум-гипотезе, а не аксиоме выбора (см. § 16.5).
§1.4..
1.8. Существует некая ирония в том, что вполне законченному антиплатонисту, искренне убежден¬
ному в том, что вся математика содержится «внутри разума» и больше нигде, приходится, по
всей видимости, верить и в невозможность истинных математических утверждений, принципи¬
ально разумом непостижимых. Например, если бы последняя теорема Ферма была недоступна
(в принципе) разуму, то наш антиплатонист не смог бы прийти к обоснованному заключению
ни относительно ее истинности, ни относительно ее ложности, поскольку такое обоснованное
заключение можно получить лишь через посредство ментального акта восприятия соответству¬
ющего доказательства или опровержения.
1.9. См., например, [616].
1.10. Свои представления о возможном характере перемен в нашем физическом мировоззрении, необ¬
ходимых для объяснения феномена сознательного мышления, я изложил в [610, 613, 615, 616].

Глава 2
Древняя теорема и современный вопрос
2.1.	Теорема Пифагора
Начнем с геометрии. Что это за «другие геомет¬
рии», о которых мимоходом упоминалось в предыду¬
щей главе? Для того чтобы ответить на этот вопрос,
вернемся к Пифагору и рассмотрим знаменитую те¬
орему, носящую его имя^2л1; в любом прямоуголь¬
ном треугольнике квадрат длины гипотенузы (сто¬
роны, противоположной прямому углу) равен сумме
квадратов длин катетов (остальных двух сторон) (см.
рис. 2.1). Почему мы должны верить, что это утвер¬
ждение истинно? Как, в самом деле, «доказать» те¬
орему Пифагора? Из всех известных способов дока¬
зательства (а их немало) я выбрал для рассмотрения
два — оба исключительно прозрачны, но используют
несколько различные подходы.
Для доказательства первым способом нам по¬
требуется построение, изображенное на рис. 2.2. Оно
состоит исключительно из квадратов двух разных размеров. Можно полагать «очевидным»,
что такое построение, будучи бесконечно продолжено во все стороны, позволяет запол¬
нить квадратами всю плоскость без разрывов и перекрытий, регулярным и периодическим
образом. Для того чтобы убедиться в периодичности этого заполнения, соединим центры
примыкающих друг к другу больших квадратов прямыми линиями; в результате мы полу¬
чим решетку из квадратов несколько большего размера, слегка наклоненную относительно
исходного построения (см. рис. 2.3), но точно так же заполняющую всю плоскость. «Узоры»
Рис. 2.2. Заполнение плоскости квадратами двух Рис. 2.3. Центры больших квадратов совпадают
разных размеров	с узлами решетки, составленной из еще больших
квадратов, наклоненных относительно исходных
2 . , 2 2
а + о = с
Рис. 2. i. Теорема Пифагора: в любом пря¬
моугольном треугольнике квадрат длины
гипотенузы с равен сумме квадратов длин
катетов а и b

46
Глава 2
внутри каждого наклонного квадрата совершенно одинаковы и образуют в совокупности
исходное «двухквадратное» построение. То же самое получится, если вместо центра мы вы¬
берем в каждом большом квадрате исходного построения любую другую точку (одну и ту же,
разумеется, во всех квадратах). Новая наклонная квадратная решетка окажется точно такой
же, как и в предыдущем случае, только сместится в какую-либо сторону с сохранением угла
наклона — такое смещение называется параллельным переносом. Простоты ради выберем
новую начальную точку в одной из вершин исходного построения (см. рис. 2.4).
Очевидно, что площадь наклонного квадрата должна быть равна сумме площадей двух
меньших квадратов — в самом деле, если разбить этот наклонный квадрат по оказавшимся
внутри него линиям исходного построения (вне зависимости от выбора начальной точки), то
из полученных кусков (перемещая их без поворотов друг относительно друга) можно соста¬
вить два меньших квадрата (см., например, рис. 2.5). Более того, как ясно видно на рис. 2.4,
сторона большого квадрата представляет собой гипотенузу прямоугольного треугольника,
длины катетов которого равны длинам сторон соответствующих исходных квадратов. Таким
образом, теорему Пифагора можно считать доказанной: квадрат гипотенузы действительно
равен сумме квадратов катетов.
Рис. 2.4. Наклонная квадратная решетка смещена Рис. 2.5. При любой начальной точке наклонный
таким образом, что ее узлы совпадают с верши- квадрат делится на части, из которых можно со-
нами исходного двухквадратного построения — ставить два меньших исходных квадрата
при этом сторона наклонного квадрата оказыва¬
ется гипотенузой прямоугольного треугольника
(затушеванного), длины катетов которого равны
длинам сторон соответствующих исходных квад¬
ратов
Вышеприведенное рассуждение и в самом деле содержит в себе все, что требуется для
Л	ш
простого доказательства теоремы Пифагора, и даже дает нам некоторые «разумные осно¬
вания» поверить в ее истинность, — каковых оснований мы вполне могли бы не получить,
ограничься я каким-либо более формальным рассуждением, т. е. последовательностью логи¬
ческих шагов без наглядного объяснения их необходимости. Однако следует отметить, что
в нашем «доказательстве» мы сделали несколько неявных допущений, из которых далеко
не последним является допущение о том, что очевидное на первый взгляд периодическое
построение из квадратов, изображенное на рис. 2.2 (да и на рис. 2.6, если уж на то пошло),
действительно возможно геометрически — не говоря уже о том, что мы почему-то решили,
что геометрически возможна такая фигура, как квадрат. Что, вообще говоря, мы подразу-
ф	%
меваем под словом «квадрат»? Обычно квадратом называют плоскую фигуру, все стороны
которой равны, а все углы являются прямыми. А что такое прямой угол? Вообразим себе

2.2. Постулаты Евклида
47
*
4—
в
ID
\Е
С
Рис. 2.6. Самая обыкновенная решетка, состоя-
щая из одинаковых квадратов. Откуда нам извест¬
но, что такая решетка геометрически возможна?
Рис. 2.7. Строим квадрат. Отрезки АВ, ВС и CD
равны по длине, а углы ABC и BCD — прямые.
Следует ли из этого, что отрезок DA равен трем
предыдущим, а углы DAB и CDA также являются
прямыми?
две прямые, пересекающиеся в некоторой точке таким образом, что все четыре угла при
этой точке оказываются равными. Каждый из этих равных углов и будет прямым.
Попробуем теперь построить квадрат. Возьмем три одинаковых отрезка прямой (АВ, ВС
и CD) и расположим их так, чтобы углы ABC и BCD были прямыми, а точки D и А рас¬
полагались бы по одну сторону от отрезка ВС (как показано на рис. 2.7). Вопрос: равен ли
отрезок AD по длине трем первоначальным отрезкам? И еще: являются ли углы DAB и CDA
также прямыми? Эти углы должны быть равны между собой, поскольку получившаяся фи¬
гура симметрична, но являются ли они на самом деле прямыми? Ответы на эти вопросы
кажутся нам очевидными потому, что с идеей квадрата мы давно и хорошо знакомы — воз¬
можно, мы помним, как нам рассказывали в школе о каком-то Евклидовом «постулате»,
по которому выходит, что стороны В А и CD должны быть «параллельны» одна другой,
и еще о том, что если через пару параллельных прямых провести «секущую», то «соот¬
ветственные» углы между этой секущей и параллельными непременно будут одинаковыми.
Отсюда следует, что угол DAB должен быть равен углу, дополнительному к углу ADC
(т. е. углу EDC на рис. 2.7, поскольку угол ADE здесь является развернутым), а также (как
отмечено выше) и самому углу ADC. Угол (ADC) может быть равен своему дополнитель¬
ному углу (EDC) только в том случае, если он является прямым. Нужно еще доказать, что
длина стороны AD равна длине стороны ВС, но это следует все из тех же свойств секущих
к параллельным прямым (например, В А и CD). Таким образом, с помощью этого евклидова
рассуждения мы и в самом деле можем доказать, что квадраты действительно существу¬
ют, а все углы в них действительно являются прямыми. Впрочем, и тут не обошлось без
подводных камней.
2.2.	Постулаты Евклида
* • • ( «
При создании своей геометрии Евклид самое пристальное внимание уделял тем до¬
пущениям, на основании которых он выстраивал свои доказательства^2'2^ В частности, он
проводил четкую границу между аксиомами (т. е. утверждениями, принимаемыми без дока¬
зательства, самоочевидно истинными; сюда в основном входят определения основных по¬
нятий — точки, прямой и т. д.) и пятью постулатами (допущениями, истинность которых не
столь очевидна, но которые тем не менее достаточно правдоподобно описывают геометрию
нашего мира). Последнее из этих допущений — так называемый пятый постулат Евклида —
считалось менее очевидным, нежели остальные, и на протяжении многих веков математи¬
ки полагали, что должен существовать способ доказать его, исходя из этих самых четырех

48
Глава 2
постулатов. Пятый постулат Евклида называют также постулатом о параллельности, и в
дальнейшем я буду придерживаться именно этого термина.
Прежде чем перейти к постулату о параллельности, давайте выясним, что же представ¬
ляют собой первые четыре постулата Евклида. Постулаты эти описывают геометрию плос¬
кости (евклидовой), хотя в более поздних трудах Евклид рассматривал и трехмерное про¬
странство. Основными элементами плоской евклидовой геометрии являются точки, прямые
и окружности. В дальнейшем под «прямой линией» (или просто «прямой») я буду понимать
линию, бесконечно протяженную в обе стороны; в противном случае я буду говорить об «от¬
резке прямой». Согласно первому постулату Евклида, любые две точки можно соединить од¬
ним и только одним отрезком прямой. Второй постулат утверждает, что любой отрезок пря¬
мой можно бесконечно (непрерывно) продолжать в обе стороны. Третий постулат говорит
о возможности построения окружности с центром в любой точке и радиусом любой длины.
И наконец, четвертым постулатом устанавливается равенство всех прямых углов J2-3!
С современной точки зрения некоторые из этих постулатов могут показаться несколько
странными (в особенности четвертый) — впрочем, от этой странности не останется и следа,
если вспомнить о происхождении идеи, легших в основу евклидовой геометрии. В сущности,
Евклид исследовал движение идеальных твердых тел, а также феномен конгруэнтности, ко¬
торый имел место, когда одно такое идеальное твердое тело совмещалось в своем движении
с другим идеальным твердым телом. Если прямые углы в двух телах равны, то эти тела мож¬
но совместить таким образом, что прямые, образующие прямой угол в одном теле, совпадут
с соответствующими прямыми другого тела. По сути, четвертый постулат устанавливает
изотропность и однородность пространства — в таком пространстве две геометрические фи¬
гуры могут быть одинаковыми по форме (т. е. конгруэнтными), где бы они ни находились
друг относительно друга. Второй и третий постулаты выражают идею неограниченной про¬
тяженности пространства и отсутствия в нем «дыр», первый же описывает элементарную
природу отрезка прямой. Хотя взгляды Евклида на геометрию весьма отличны от сегодняш¬
них, его первые четыре постулата в общем и целом охватывают современное представление
о метрическом пространстве (двумерном), бесконечно протяженном и обладающем абсолют¬
ной однородностью и изотропностью. Более того, похоже, что такая картина довольно точно
соответствует, по данным современной космологии (см. §§27.11, 28.10), макроскопической
пространственной природе реально существующей Вселенной.
В чем же заключается пятый постулат Евклида, постулат о параллельности? В первона¬
чальной формулировке Евклида он, в сущности, сводится к следующему: если две прямые а
и 6, расположенные в одной плоскости, пересекают третью прямую с (такая прямая с на¬
зывается секущей по отношению к прямым а и Ь) таким образом, что сумма внутренних
углов по одну сторону прямой с оказывается меньше двух прямых углов, то прямые а и 6,
будучи продолженными в ту же сторону достаточно далеко, в некоторой точке пересекутся
(см. рис. 2.8 а). В другой, эквивалентной, формулировке (называемой иногда аксиомой Плей¬
фера) этот постулат выглядит так: если взять любую прямую и любую точку, не лежащую на
этой прямой, то через эту точку можно провести лишь одну прямую, параллельную данной
прямой (см. рис. 2.8 б). «Параллельными» здесь называются прямые, лежащие в одной плос¬
кости и нигде не пересекающиеся (вспомним также, что под «прямыми» я подразумеваю не
«отрезки прямых», как Евклид, но настоящие прямые, продолжающиеся бесконечно в обе
стороны) .
Теперь, когда у нас есть постулат о параллельности, мы можем доказать свойство,
• • • % •
необходимое для обоснования существования квадрата. Если секущая пересекает две пря¬
мые таким образом, что сумма внутренних углов по одну сторону от секущей составляет
Покажите, что вывод Плейфера о том, что через точку вне прямой проходит одна-единственная пря¬
мая, параллельная данной, является следствием из евклидовой формулировки (при условии, что она справедлива)
постулата о параллельности.

2.3.	Другое доказательство теоремы Пифагора
>1
49
с
\	а
Если сумма этих
углов меньше двух
прямых углов,
то прямые а и b
пересекаются
Через точку Р проходит	6)
одна-единственная
прямая, параллельная а
»
Рис. 2.8. а) Евклидов постулат о параллельности. Прямая с является секущей по отношению к прямым а
и Ь, при этом внутренние углы при точках пересечения прямых а и b с прямой с оказываются в сумме
меньше двух прямых углов. Если теперь прямые а и b бесконечно продолжить, то они обязательно
где-нибудь пересекутся. 6) Аксиома Плейфера (эквивалентная постулату о параллельности): через
точку Р, не лежащую на прямой а, можно провести одну и только одну прямую, параллельную а
два прямых угла, то можно доказать, что эти прямые действительно параллельны. Более
того, отсюда непосредственно следует, что любая другая секущая по отношению к такой
паре прямых обладает тем же свойством. Собственно, для того чтобы построить квадрат,
нам больше ничего и не нужно. В самом деле, используя один лишь постулат о параллель¬
ности, мы можем показать, что в результате нашего построения действительно получается
квадрат, т. е. фигура, все стороны которой равны, а все углы являются прямыми. Без по¬
стулата о параллельности возможность существования квадратов (в общепринятом смысле
этого термина, предполагающем, что все четыре угла квадрата — прямые) доказать невоз¬
можно.
Вероятно, кому-то покажется, что столь преувеличенное беспокойство о том, какие
именно допущения необходимо сделать для того, чтобы выстроить «строгое доказатель¬
ство» существования такой очевидной вещи, как простой квадрат, является не чем иным,
как проявлением чрезмерного математического педантизма. К чему все эти тонкости, когда
речь идет всего лишь о «квадрате» — самой обыкновенной фигуре, которая всем нам хорошо
знакома? Что ж, как мы вскоре увидим, Евклид, уделяя пристальное внимание упомянутым
тонкостям, проявил, вообще говоря, чрезвычайную проницательность. Благодаря своей пе¬
дантичности, Евклид ухитрился заглянуть в глубинную суть вещей и сделать во многих
отношениях верные выводы о действительной геометрии Вселенной. В частности, вовсе
не очевидно, что в космологическом масштабе реальной Вселенной физические «квадраты»
в самом деле существуют. Для подтверждения их существования необходимы наблюдения,
результаты же таких наблюдений на данный момент представляются весьма противоречи¬
выми (см. §§ 2.7, 28.10).
2.3.	Доказательство теоремы Пифагора, основанное на подобии
треугольников
К математической значимости отказа принимать постулат о параллельности на веру мы
вернемся в следующем параграфе. Соответствующие физические вопросы будут подробно
а)

50
Глава 2
рассмотрены в §§ 18.4, 27.11, 28.10, 34.4. Однако прежде чем мы перейдем к обсуждению
этих вопросов, думаю, будет небесполезно ознакомиться с обещанным мною выше другим
доказательством теоремы Пифагора.
Один из простейших способов убедиться в том, что в евклидовой геометрии утвержде¬
ние Пифагора действительно истинно, заключается в следующем: разделим данный прямо¬
угольный треугольник на два меньших треугольника, опустив из прямого угла перпендику¬
ляр на гипотенузу (рис. 2.9). Теперь на рисунке изображены три треугольника: исходный
и два меньших, полученных в результате разделения. Очевидно, что площадь исходного
треугольника равна сумме площадей двух меньших треугольников.
Рис. 2.9. Доказательство теоремы Пифагора с помощью подобных треугольников. Возьмем прямо¬
угольный треугольник и опустим перпендикуляр из прямого угла на гипотенузу. Площади полученных
таким разделением меньших треугольников составляют в сумме площадь исходного треугольника.
Все три треугольника подобны, а это значит, что их площади пропорциональны квадратам их гипоте¬
нуз. Теорема Пифагора доказана
Нетрудно убедиться, что все три треугольника подобны друг другу. Это означает, что
они одинаковы по форме (хотя и различаются размерами), т. е. один такой треугольник мож¬
но получить из другого посредством равномерного расширения или сжатия и перемещения
(с сохранением формы). Подобие этих треугольников следует из того факта, что каждый из
углов одного треугольника в точности равен соответствующему углу другого треугольника.
Один из углов каждого меньшего треугольника совпадает с одним из углов большого тре¬
угольника, и, кроме того, один из углов в каждом из трех треугольников прямой. Третьи
углы также должны быть равными, поскольку сумма углов любого треугольника одинакова.
А среди общих свойств подобных плоских фигур имеется следующее: их площади пропор¬
циональны квадратам их линейных размеров. За такой линейный размер мы можем принять
длину самой длинной стороны каждого треугольника, т. е. длину гипотенузы. Отметим, что
гипотенуза каждого из меньших треугольников есть не что иное, как один из катетов исход¬
ного треугольника. Поскольку площадь исходного треугольника равна сумме площадей двух
меньших треугольников, отсюда непосредственно следует, что квадрат гипотенузы исходно¬
го треугольника действительно равен сумме квадратов его катетов: именно это и утверждает
теорема Пифагора\
Впрочем, и в этом рассуждении мы не обошлись без некоторых допущений, требующих
дополнительного рассмотрения. Одной из важных составляющих нашего рассуждения явля-
* -•*** * *
ется утверждение о том, что сумма углов любого треугольника всегда одинакова. (Равна эта
сумма, разумеется, 180°, однако Евклид предпочитал говорить о «двух прямых углах». В бо¬
лее современной «естественной» математической терминологии говорят, что сумма углов
треугольника в евклидовой геометрии равна 7г. При этом в качестве абсолютной меры угла
используется единица, называемая радианом —• 1 градус (°) равен 7г/180 радиан, т. е. 180° =
= 7Г.) Общепринятое доказательство этого утверждения проиллюстрировано на рис. 2.10.
Продолжим отрезок СА до точки Е и проведем через точку А прямую AD, параллель¬
ную СВ. Углы EAD и АСВ равны (что следует из постулата о параллельности), также равны
углы DAB и СВА. Поскольку углы EAD, DAB и ВАС составляют в сумме 7г радиан (или 180°,

2.4. Гиперболическая геометрия: конформное представление
51
В
Я/х
Е
Рис. 2.10. Докажем, что сумма углов треугольника равна 7Г радиан (или 180°, или двум прямым углам).
Продолжим СА до точки Е и построим отрезок AD, параллельный СВ. Из постулата о параллельности
следует, что углы EAD и АСВ равны, также равны углы DAB и СВА. Поскольку углы EAD, DAB
и ВАС составляют в сумме д, сумма углов АСВ, СВА и ВАС также должна быть равна 7г
или два прямых угла), этой же величине должна быть равна и сумма углов АСВ, СВА и ВАС
исходного треугольника — что и требовалось доказать. Отметим, впрочем, что для доказа¬
тельства нам пришлось воспользоваться постулатом о параллельности.
В приведенном доказательстве теоремы Пифагора мы также воспользовались утвержде¬
нием о том, что площади подобных фигур пропорциональны какому-либо из их линейных
размеров (в качестве такого линейного размера мы выбрали длину гипотенузы каждого
треугольника). Это утверждение опирается не только на саму возможность существования
подобных фигур, различных по величине (каковую возможность в случае треугольников на
рис. 2.9 мы установили с помощью постулата о параллельности), но и на некоторые суще¬
ственно более сложные соображения, связанные с тем, как мы, вообще говоря, определяем
«площади» непрямоугольных областей. При рассмотрении общих вопросов такого рода не
обойтись без обращения к методам перехода к пределу, углубляться же в обсуждение этих
материй представляется мне пока несколько преждевременным, поскольку оно неизбежно
повлечет за собой другие, еще более общие, вопросы, связанные с используемыми в геомет¬
рии типами чисел (о типах чисел мы поговорим в §§ 3.1-3.3).
В предыдущих параграфах содержится, помимо прочего, одна наиважнейшая идея:
доказуемость теоремы Пифагора, по всей видимости, целиком и полностью зависит от ис¬
тинности постулата о параллельности. Так ли это на самом деле? А что если постулат
о параллельности ложен? Означает ли это, что и сама теорема Пифагора также может не со¬
ответствовать истине? Имеет ли такое предположение хоть какой-нибудь смысл? Попробуем
разобраться, что же получится, если предположить, что постулат о параллельности может
быть ложным. Хочу сразу предупредить читателя: мы входим в таинственный воображаемый
мир, где геометрия, которой нас учили в школе, буквально вывернута наизнанку. Впрочем,
путешествие это мы предпринимаем не только забавы ради — как мы вскоре увидим, есть
и более серьезная причина.
2.4.	Гиперболическая геометрия: конформное представление
Взгляните на репродукцию гравюры М. К. Эшера «Предел круга I», помещенную на
рис. 2.11. Наряду с прочими своими достоинствами, эта гравюра замечательна еще и тем,
что дает очень точное представление о так называемой гиперболической геометрии (или
геометрии Лобачевского) — той самой геометрии, в которой постулат о параллельности
ложен, теорема Пифагора не выполняется, а сумма углов треугольника не равна 7г. Более
того, для фигуры данного размера здесь, в общем случае, не существует подобной фигуры
большего размера.
Эшер воспользовался в своей гравюре таким представлением гиперболической геомет¬
рии, где вся «Вселенная» гиперболической плоскости «втиснута» во внутреннюю область

52
Глава 2
.0*'
•i "A
л О
#°
тт
(ЕЛ
о о
■'с1 о'
к
iM
.5с
f
***
Рис. 2.11. М. К. Эшер, «Предел круга I». Гравюра на дереве, очень точно иллюстрирующая конформное
представление гиперболической плоскости
самой обычной евклидовой плоской окружности. Для этой гиперболической Вселенной
ограничивающая ее окружность является «бесконечностью». Чем ближе к ограничивающей
окружности, тем теснее «сбиваются» рыбы на рисунке Эшера. Однако это не более чем ил¬
люзия. Представьте себя на месте одной из этих рыб. Неважно, где вам случилось оказаться,
на краю рисунка или же неподалеку от центра — в обоих случаях прочая (гиперболическая)
Вселенная будет выглядеть для вас совершенно одинаково. Понятие «расстояния» в гипер¬
болической геометрии не совпадает с таковым на евклидовой плоскости (на которой его,
собственно, и приходится изображать). Глядя на рисунок Эшера с точки зрения евклидовой
геометрии, мы видим, что рыбы по мере приближения к краю становятся все меньше и
меньше. С «гиперболической» же точки зрения самих рыб (как белых, так и черных), их
размеры и форма ничуть не отличаются от размеров и формы рыб, находящихся в центре.
Внешнему евклидову наблюдателю также представляется, что рыбы подбираются к ограни¬
чивающей окружности все ближе и ближе, однако для гиперболических рыб эта граница
всегда остается бесконечно далекой. С точки зрения рыб, ни сама окружность, ни какое бы
то ни было «евклидово» пространство за ней просто-напросто не существуют. На наш же
взгляд, вся их бесконечная Вселенная умещается исключительно в области, ограниченной
окружностью.
Как описать такую гиперболическую Вселенную в более строгих математических тер-
минах? Представьте себе окружность в евклидовой плоскости. Множество точек, лежащих
внутри этой окружности, соответствует множеству точек во всей гиперболической плоско¬
сти. Прямые в гиперболической геометрии представляются дугами евклидовых окружно¬
стей, пересекающих ограничивающую окружность ортогонально — т. е. под прямым углом.
Как оказалось, гиперболическое понятие угла между двумя пересекающимися кривыми
в точности совпадает с понятием угла при точке пересечения двух евклидовых кривых.
Представления такого рода принято называть конформными. Поэтому представление гипер¬

2.4. Гиперболическая геометрия: конформное представление
53
болической геометрии, которым воспользовался в своей гравюре Эшер, называют иногда
конформной моделью гиперболической плоскости. (Другое распространенное название этой
модели — диск Пуанкаре, хотя с точки зрения исторической справедливости термин этот
весьма сомнителен, см. § 2.6.)
Теперь у нас есть все необходимое для того, чтобы наконец выяснить, равна ли двум пря¬
мым углам сумма углов треугольника в гиперболической геометрии. Бросив беглый взгляд
на рис. 2.12, можно заподозрить, что не равна и что, скорее всего, она окажется меньше.
Так, вообще говоря, и есть: сумма углов треугольника в гиперболической геометрии всегда
меньше тт. Может показаться, что в этом отношении гиперболическая геометрия несколько
неудобна — во всяком случае на вопрос о сумме углов треугольника «однозначного» отве¬
та здесь, похоже, нет. Впрочем, в действительности все не так уж плохо. Сложение углов
гиперболического треугольника дает поразительный и весьма изящный результат; «недоста¬
ча» в сумме углов всегда пропорциональна площади треугольника. Иными словами, если
обозначить углы треугольника буквами а, (3 и 7, то справедливо следующее равенство (об¬
наруженное Иоганном Генрихом Ламбертом, 1728-1777):
7г — (а + (3 + 7) = СД,
где Д
- площадь треугольника, а С — некоторая постоянная. Величина этой постоянной за¬
висит от «единиц», выбранных для измерения длин и площадей. Мы всегда можем выбрать
масштаб таким образом, чтобы постоянная С была равна единице. Возможность выразить
площадь треугольника таким простым образом является весьма примечательной особенно¬
стью гиперболической геометрии. В евклидовой геометрии выразить площадь треугольника
Рис. 2.12. Та же гравюра Эшера, что и на рис. 2.11, только теперь на ней выделены гиперболиче¬
ские прямые (евклидовы прямые или дуги евклидовых окружностей, пересекающие ограничивающую
окружность под прямым углом) и гиперболический треугольник. Гиперболические углы совпада¬
ют с евклидовыми углами. Постулат о параллельности (в формулировке, проиллюстрированной на
рис. 2.8 б) явно нарушается, а углы треугольника дают в сумме величину, меньшую 7Г

54
Глава 2
только через его углы невозможно, определение же площади треугольника через длины его
сторон значительно сложнее.
Однако на этом описание гиперболической геометрии в ее конформном представле¬
нии не заканчивается, поскольку я еще не рассказал, как определяется гиперболическое
расстояние между двумя точками (кроме того, мы должны знать, что такое «расстояние»,
прежде чем сможем всерьез говорить о площадях). Позволю себе привести выражение для
определения гиперболического расстояния между точками А и В, расположенными внутри
ограничивающей окружности:
log
QA-PB
QB РА’
Рис. 2.13. В конформном представлении
гиперболическое расстояние между точ¬
ками А и В равно log(QA * PB/QB • РА),
где QA и т. д. — евклидовы расстояния,
а Р и Q — точки, в которых евклидова
окружность (гиперболическая прямая),
проходящая через точки А и В и ортого¬
нальная к ограничивающей окружности,
пересекает эту окружность
где Р и Q — точки пересечения евклидовой окруж¬
ности (т. е. гиперболической прямой), проходящей
через точки А и В и ортогональной к ограничива¬
ющей окружности, с этой самой ограничивающей
окружностью; QA и т. д. — евклидовы расстояния (ем.
рис. 2.13). Если хотите включить сюда постоянную С
из формулы Ламберта для площади гиперболическо¬
го треугольника (в случае С ф 1), то нужно просто
умножить записанное выше выражение на С"1/2 (т. е.
на величину, обратную квадратному корню из С) ^ .*
По причинам, которые, надеюсь, вскоре станут понят¬
ными, величину С ~1 ‘ 2 я буду называть псевдорадиу¬
сом данной геометрии.
Если вас уже пугают математические выраже¬
ния — вроде вышеприведенной формулы с логариф¬
мом (log), — прошу вас, не беспокойтесь. Я приво¬
жу их исключительно для тех, кому интересны по¬
дробности. Как бы то ни было, объяснять, почему
это выражение «работает» (т. е. почему определенное
таким образом кратчайшее гиперболическое расстоя¬
ние между двумя точками и в самом деле измеряется
вдоль гиперболической прямой или почему расстоя¬
ния, отложенные на гиперболической прямой, «скла¬
дываются» так же, как и обыкновенные евклидовы
расстояния) , я не стану. В общем, я прошу проще¬
ния за логарифм, но без него тут не обойтись — такова природа вещей (хотя если быть
совсем точным, то здесь должен стоять так называемый натуральный логарифм или, иначе
говоря, «логарифм по основанию е»). Об этом и других логарифмах я подробно расскажу
в §§ 5.2, 5.3. Мы увидим, что математические объекты, называемые логарифмами, не только
чрезвычайно красивы и загадочны (как, собственно, и число е), но и во многих случаях
совершенно незаменимы.
Обзаведясь определением расстояния, гиперболическая геометрия получает все свой-
ства евклидовой геометрии, за исключением тех, что нуждаются в постулате о параллель¬
ности. Мы можем строить треугольники и прочие плоские фигуры различных форм и раз¬
Можете ли вы указать простую причину необходимости такого преобразования?
Попробуйте доказать, что если А, В и С — три последовательные точки на гиперболической прямой,
то определенные по вышеприведенной формуле гиперболические расстояния (обозначим их 'АВ’ и т.д.) удо¬
влетворяют равенству ’АВ’ + ’ВС’ = ’АС’. Можно допустить, что логарифмы обладают следующим общим
свойством: log(a6) = log а 4- log6 (см. §§ 5.2, 5.3).

2.5. Другие представления гиперболической геометрии
55
меров, мы можем «жестко» (т. е. сохраняя гиперболические форму и размер) перемещать их
по гиперболической плоскости, причем так же свободно, как мы могли перемещать фигуры
в евклидовой геометрии — естественным образом возникает понятие «конгруэнтности» двух
фигур, совпадающее с аналогичным понятием евклидовой геометрии, где конгруэнтными
называются фигуры, которые можно точно совместить друг с другом посредством тех или
иных «жестких» перемещений. С точки зрения гиперболической геометрии, все белые —
равно как и черные — рыбы на гравюре Эшера конгруэнтны.
2.5.	Другие представления гиперболической геометрии
Разумеется, белые рыбы отнюдь не выглядят одинаковыми по форме и размерам, но
это только потому, что мы смотрим на них не в гиперболическом, а в евклидовом «ра¬
курсе». Эшер в своем рисунке всего лишь воспользовался одним из частных евклидовых
представлений гиперболической геометрии. Сама по себе гиперболическая геометрия — чи¬
стая абстракция, и никакое евклидово представление не описывает ее в полной мере. Тем
не менее такие представления могут оказаться очень полезными, поскольку позволяют ви¬
зуализировать гиперболическую геометрию путем соотнесения ее с вещами, более, на наш
взгляд, привычными и «конкретными» — в данном случае с евклидовой геометрией. Кроме
того, эти представления ясно и недвусмысленно показывают, что гиперболическая геомет¬
рия является непротиворечивой структурой и, следовательно, постулат о параллельности
невозможно доказать, опираясь на прочие законы евклидовой геометрии.
Существуют и другие представления гиперболической геометрии средствами геометрии
евклидовой, отличные от конформного представления, использованного в рисунке Эшера.
Одним из таких представлений является так называемая проективная модель. Согласно
этой модели, гиперболическая плоскость так же умещается целиком внутри окружности на
евклидовой плоскости, однако гиперболические прямые представлены здесь не в виде дуг
окружности, но в виде самых обычных евклидовых прямых. За это очевидное упрощение,
впрочем, приходится платить (причем многие находят плату чересчур высокой): гипербо¬
лические углы в проективном представлении не равны евклидовым углам. Формула для
определения гиперболического расстояния между точками А и В выглядит в данном случае
следующим образом (см. рис. 2.14):	*
1т RA ♦ SB
2 RB•SA ’
где R и S — точки пересечения прямой, проведенной через точки А и В, с ограничивающей
окружностью (отметим, что при <7=1 это выражение почти совпадает с выражением для
определения расстояния в конформном представлении). Проективное представление гипер¬
болической геометрии можно получить из конформного представления путем так называе¬
мого радиального расширения (т. е. смещения всех точек внутри окружности в направлении
от центра) на величину
2Д2
Д2 + г2’
где R — радиус ограничивающей окружности, а гс — евклидово расстояние от точки в кон¬
формном представлении до ограничивающей окружности, измеренное вдоль радиуса, прове-
денного через эту точку (см. рис. 2.15) . На рис. 2.16 представлен результат преобразования
рисунка Эшера (рис. 2.11) из конформного вида к проективному с помощью этой формулы.
(Несмотря на то что многие мелкие детали стали вовсе неразличимыми, безукоризненная
точность кисти Эшера очевидна и здесь.)
* ЛИ Покажите, что это действительно так. (Подсказка: если хотите, можете воспользоваться геометрическим
представлением Бельтрами; см. рис. 2.17.)

56
Глава 2
Рис. 2Л4. В проективном представлении форму¬
ла для определения гиперболического расстоя-
1
ния имеет вид - log(RA • SB/RB • SA), где R
и S — точки пересечения евклидовой (гипербо¬
лической) прямой АВ с ограничивающей окруж¬
ностью
Рис. 2.15, Для того чтобы перейти от конформ¬
ного представления к проективному, сместим все
расположенные внутри окружности точки в на¬
правлении от центра на величину 2R2/(R2 4-
+ г с), где R — радиус ограничивающей окруж¬
ности, а г с — евклидово расстояние от точки в
конформном представлении до ограничивающей
окружно сти
Рис. 2.16. Гравюра Эшера (рис. 2.11) в проективном представлении
Между конформным и проективным представлениями существует и более наглядная
геометрическая связь — через посредство еще одного хитроумного представления все той
же геометрии. Всеми этими тремя представлениями мы обязаны гению итальянского геомет¬
ра Эудженио Бельтрами (1835-1900). Вообразим себе сферу 5, экватор которой совпадает

2.5. Другие представления гиперболической геометрии
у
57
с ограничивающей окружностью описанного выше проективного представления
ческой геометрии (см. рис. 2.17). Теперь попробуем построить представление гиперболиче¬
ской геометрии на северной полусфере S+ сферы S (это представление я буду называть полу¬
сферическим). Для того чтобы перейти от проективного представления в плоскости (в нашем
случае горизонтальной) к новому представлению на сфере, мы просто-напросто проецируем
все точки внутри окружности вертикально вверх (рис. 2.17 а). Прямые в плоскости, явля¬
ющиеся представлениями гиперболических прямых, на полусфере S+ предстанут в виде
полуокружностей, ортогональных к экватору. Для того чтобы теперь получить из представ¬
ления на S+ конформное представление на плоскости, нам потребуется другая проекция,
а именно: центральная проекция с центром в южном полюсе сферы (рис. 2.176). Такая про-
екция называется стереографической, и мы еще не раз встретимся с ней на страницах этой
книги (например, в §§ 8.3,18.4,22.9,33.6). Отметим два важных свойства стереографической
проекции (подробнее см. § 8.3): 1) она конформна, т.е. сохраняет углы, и 2) окружности на
сфере проецируются в окружности (или, в особых случаях, в прямые) на плоскости
* **
Рис. 2.17. Геометрическое представление Бельтрами, связывающее три представления гиперболиче¬
ской геометрии, а) Вертикальная проекция полусферического представления (конформного на север¬
ной полусфере 5+) на экваториальный диск дает проективное представление, б) Стереографическая
проекция (с центром в южном полюсе сферы) того же полусферического представления дает на эква¬
ториальном диске конформное представление
Пользуясь этими свойствами стереографической проекции и описанием конформного представления
гиперболической геометрии, данным в §2.4, покажите, что полусферическое представление Бельтрами, где «ги¬
перболические прямые» имеют вид вертикальных полуокружностей, конформно.
Попробуйте доказать эти свойства. (Подсказка: покажите, что в случае окружностей конус проекции
пересекают две плоскости с противоположным наклоном.)

58
Глава 2
Такое изобилие различных представлений гиперболической геометрии средствами ев¬
клидова пространства лишний раз подчеркивает, что все эти представления являются все¬
го лишь евклидовыми моделями — о том, что в действительности представляет собой
гиперболическая геометрия, вы из них не узнаете. Гиперболическая геометрия обладает
собственным «существованием в платоновском смысле» — точно так же, как и евклидова
геометрия (см. § 1.3 и предисловие). Ни об одной из моделей нельзя сказать, что она описы¬
вает гиперболическую геометрию более «корректно», нежели прочие. Рассмотренные пред¬
ставления в значительной степени облегчают нам понимание исходного математического
объекта, однако лишь потому, что евклидов взгляд на мир нам более привычен. Разумному
существу, всю жизнь прожившему в условиях непосредственного восприятия гиперболи¬
ческой (а не евклидовой) геометрии, показалось бы куда более естественным попытаться
представить евклидову геометрию гиперболическими средствами. В § 18.4 мы рассмотрим
еще одну модель гиперболической геометрии, на этот раз воспользовавшись геометрией
четырехмерного пространства Минковского.
В
С
D
Рис. 2.18. Вершины гиперболического «квадрата» ABCD располагаются в точках пересечения двух
прямых, пересекающихся под прямым углом в точке О, с какой-либо окружностью с центром в этой
же точке О. Благодаря симметрии, все четыре стороны квадрата равны; равны и все четыре его угла.
Эти углы не являются прямыми, но могут составлять любую положительную величину, меньшую ^7г
В завершение параграфа вернемся к вопросу о существовании в гиперболической гео¬
метрии таких объектов, как квадраты. Привычных квадратов с прямыми углами здесь, разу¬
меется, нет, но зато имеются «квадраты» более общего вида — если такой термин применим
к фигуре, все углы которой являются острыми. Для построения гиперболического квадра¬
та проведем две прямые, пересекающиеся под прямым углом в точке О. Четырехугольник
с вершинами в точках пересечения этих прямых (обозначим эти точки буквами А, В, С и D;
см. рис. 2.18) с некоторой окружностью с центром в точке О и будет искомым «квадра¬
том». Поскольку фигура симметрична, все четыре стороны четырехугольника ABCD равны;
равными должны быть и все четыре угла. Однако являются ли эти углы прямыми? В гипер¬
болической геометрии — определенно нет. Углы квадрата здесь могут иметь любую величину
в интервале между 0 и 90° . Чем больше квадрат (гиперболический) — иначе говоря, чем боль¬
ше окружность в описанном построении, — тем меньшими будут его углы. На рис. 2.19 а)
я изобразил решетку гиперболических квадратов в конформном представлении; в каждой

2.6. Гиперболическая геометрия в исторической перспективе
59
ч
вершине сходятся пять квадратов (вместо четырех в евклидовой плоскости), а значит, каж-
2
дый угол такого квадрата равен	или 72°. На рис. 2.19 б) показана та же решетка, но уже в
О
проективном представлении. Нетрудно видеть, что двухквадратную решетку вроде той, что
изображена на рис. 2.2, из этих квадратов построить нельзя*.
Рис. 2.19. Решетка из квадратов в гиперболической плоскости; в каждой вершине сходятся пять квад
2	о
ратов, вследствие чего каждый угол квадрата равен -тг или 72°. а) Конформное представление. 6) Про
ективное представление
5
2.6.	Гиперболическая геометрия в исторической перспективе
Обратимся к истории открытия гиперболической геометрии. В течение многих столе¬
тий после того, как Евклид (приблизительно в 300 г. до н.э.) обнародовал свои знаменитые
«Начала», многие математики предпринимали попытки доказать пятый постулат, опираясь
на другие аксиомы и постулаты. Своей кульминации эти героические усилия достигли в мо¬
нументальном трактате иезуита Джироламо Саккери, опубликованном в 1733 году. Сам Сак-
кери, похоже, пришел в конце концов к выводу, что труд всей его жизни представляет собой
одно сплошное недоразумение, поскольку сводится единственно к неудавшейся попытке
доказать постулат о параллельности посредством демонстрации противоречивости предпо¬
ложения, что сумма углов треугольника может быть меньше двух прямых углов. Осознав,
что логического доказательства, несмотря на все старания, ему получить не удастся, Саккери
неубедительно заключает:
С.
Гипотеза об остром угле, безусловно, не имеет ничего общего с истиной, ибо
противна самой природе прямой линии.
Упомянутая гипотеза об «остром угле» допускает, что прямые а и b иногда не пересекают¬
ся. Гипотеза эта, вообще говоря, вполне жизнеспособна, и логическим следствием из нее
является не что иное, как гиперболическая геометрия!
Как же так получилось, что Саккери, по сути дела, открыл нечто, по его искреннему
убеждению, невозможное, причем к открытию привела как раз попытка эту самую невоз¬
можность доказать? Для доказательства пятого постулата Евклида Саккери выбрал простой
способ: сначала допустить, что пятый постулат ложен, а затем показать, что такое допуще¬
ние приводит к противоречию. Иначе говоря, он решил воспользоваться одним из самых
Попробуйте построить нечто подобное из гиперболических правильных пятиугольников и квадратов.

60
Глава 2
древних и плодотворных принципов математического доказательства — принцип этот, впер¬
вые предложенный, по всей видимости, еще пифагорейцами, называется доказательство от
противного (или reductio ad absurdum*, если на латыни). В соответствии с этой процедурой,
для доказательства истинности какого-либо утверждения необходимо сначала предположить,
что утверждение это ложно, а затем путем логических рассуждений показать, что в этом
случае возникает то или иное противоречие. Обнаружив такое противоречие, математик
делает вывод, что исходное утверждение является-таки истиннымJ2*6^ Доказательство от
противного представляет собой очень мощный метод математического рассуждения и ши¬
роко применяется по сей день. Думаю, здесь будет уместно привести слова выдающегося
математика Г. X. Харди:
Столь любимое Евклидом reductio ad absurdum предоставляет математику один из
самых эффективных инструментов. Оно намного превосходит по изяществу любой
шахматный гамбит: шахматист может пожертвовать пешкой или даже фигурой,
математик же с легкостью жертвует всей игрой сразу. I2,7!
У нас еще будет возможность увидеть этот замечательный принцип в действии (см. §§3.1,
16.4,	16.6).
Саккери, впрочем, отыскать противоречие не удалось. Следовательно, доказать пятый
постулат он так и не смог. Однако его настойчивые попытки привели, в сущности, к тому, что
он обнаружил нечто неизмеримо большее: новую геометрию, отличную от геометрии Евкли¬
да, геометрию, которую мы сегодня называем гиперболической (подробнее см. в §§ 2.4, 2.5).
Из допущения ложности пятого постулата Евклида Саккери вместо ожидаемого противоре¬
чия вывел целый сонм странных на вид, почти невероятных, но чрезвычайно интересных
теорем. Причем какими бы странными ни казались на первый взгляд полученные им резуль¬
таты, ни один нельзя было с чистой совестью счесть противоречием в истинном смысле этого
слова. Как мы сегодня знаем, шансов найти таким образом подлинное противоречие у Сак¬
кери не было, — по той простой причине, что гиперболическая геометрия действительно
существует, т. е. существует в математическом смысле в виде целостной непротиворечивой
структуры. В терминах, предложенных в § 1.3, можно сказать, что гиперболическая геомет¬
рия пребывает в платоновском мире идеальных математических форм. (Вопрос о физической
реальности гиперболической геометрии мы вкратце рассмотрим в §§ 2.7, 28.10.)
Вскоре после Саккери попытку доказать пятый постулат Евклида от противного
предпринял удивительно проницательный немецкий математик Иоганн Генрих Ламберт
(1728-1777) — он также получил множество завораживающих геометрических результатов,
включая и то изящное выражение (упомянутое в § 2.4), что позволяет вычислить площадь
гиперболического треугольника, если известна сумма его углов. Можно предположить, что
у Ламберта вполне могло в тот или иной момент сформироваться убеждение в том, что после¬
довательное отрицание пятого постулата Евклида может привести к открытию новой непро¬
тиворечивой геометрии. По всей видимости, в качестве пробной попытки Ламберт решил
исследовать теоретическую возможность геометрии на «сфере мнимого радиуса», т. е. такого
радиуса, который при возведении в квадрат даст отрицательное число. Согласно Ламберту,
площадь Л гиперболического треугольника вычисляется по формуле 7Г— (а + /3 + 7) =
— С А, где а, /3 и 7 — углы этого треугольника, а С — некая постоянная (величина —С
в современной терминологии называется гауссовой кривизной гиперболической плоскости).
Эта формула, в сущности, идентична предложенной еще в 1603 году Томасом Хэриотом
(1560-1621) формуле, Л = R2(a -f /? + 7 — 7г), для вычисления площади Л сферическо¬
го треугольника, образуемого дугами окружности большого круга^2 81 на сфере радиуса R
(см. рис. 2.20) . Для того чтобы получить из этого выражения формулу Ламберта, следует
’Доведение до нелепости (лат.). — Прим. перев.
Попробуйте доказать справедливость формулы площади сферического треугольника, используя лишь
соображения симметрии и тот факт, что общая площадь поверхности сферы равна 47ГЙ2. (Подсказка: начните

2.6. Гиперболическая геометрия в исторической перспективе
61
всего лишь положить
Однако если мы хотим добиться положительного значения С (требуемого для гиперболиче¬
ской геометрии), радиус сферы должен быть «мнимым» (иначе говоря, представлять собой
квадратный корень из отрицательного числа). Отметим, что радиус R выражается мнимой
величиной (—С)”1/2. Отсюда термин «псевдорадиус», который мы ввели в § 2.4 для обозна¬
чения вещественной величины С-1/2. В современной науке построения Ламберта находят
блестящее подтверждение (см. главу 4 и § 18.4, рис. 18.9), что говорит о его математическом
таланте и силе предвидения.
Рис. 2.20. Формула Хэриота для вычисления площади сферического треугольника имеет вид: Д =
= R2{a + (3 Н- 7 — 7г), где a, j3 и 7 — углы треугольника, a R — радиус сферы, на поверхности которой
этот треугольник построен. Постоянная С в формуле Ламберта для гиперболического треугольника
равна С = — 1/R2
Впрочем, традиционно (и несколько несправедливо, на мой взгляд) принято считать, что
Ламберт тут вовсе не при чем, а честь построения первой неевклидовой геометрии принад¬
лежит великому немецкому математику Карлу Фридриху Гауссу — именно он якобы первым
(на полстолетия позже Ламберта) пришел к ясному пониманию возможности существова¬
ния полностью непротиворечивой геометрии, отличной от геометрии Евклида, геометрии,
в которой постулат о параллельности ложен. Будучи человеком крайне осторожным и устра¬
шившись бурной реакции, которую могло вызвать обнародование этого открытия, Гаусс
решил сохранить свои находки в тайне и отказался от их публикации. 12*9^ Приблизительно
через тридцать лет после того, как Гаусс начал исследования в этом направлении, гипербо¬
лическая геометрия была открыта вновь. На этот раз «открывателей» оказалось несколько,
причем каждый работал совершенно самостоятельно, — среди прочих отметим венгерского
математика Яноша Больяи (1829) и, особо, русского геометра Николая Ивановича Лоба¬
чевского (1826), в честь которого гиперболическую геометрию часто называют геометрией
Лобачевского.
Вышеописанные проективная и конформная реализации гиперболической геометрии
(а также некоторые другие изящные представления, включая и упомянутое в § 2.5 полусфе¬
рическое представление) были предложены Эудженио Бельтрами в 1868 году. Конформное
с отыскания площади поверхности сегмента сферы, ограниченного двумя дугами окружности большого крута,
соединяющими две диаметрально противоположные точки на сфере; далее рассуждайте по аналогии, не забывая
о симметрии. Пользуйтесь рис. 2.20.)

62
Глава 2
представление, однако, более известно под названием «модель Пуанкаре», поскольку повтор¬
ное открытие этого представления Пуанкаре в 1882 году наделало гораздо больше шума,
нежели оригинальная работа Бельтрами (в основном благодаря интересному применению,
найденному Пуанкаре для этой модели).12Л°] С проективным представлением всеми позабы¬
того старика Бельтрами произошла аналогичная история — его чаще называют «представле¬
нием Клейна». Случаи, когда с математической концепцией ассоциируется в конечном счете
имя, не имеющее ничего общего с именем первооткрывателя, в математике не редкость.
По крайней мере, здесь Пуанкаре действительно повторно открыл конформное представле¬
ние (а Клейн — проективное в 1871 году). А то бывало и так, что математики, чьи имена
«прицепили» к тому или иному результату, о существовании этого самого результата даже
В том же 1868 году Бельтрами предложил еще одно представление гиперболической
геометрии, которое и принесло ему заслуженную известность. Речь идет о представлении
геометрии на поверхности, которая называется псевдосферой (см. рис. 2.21). Псевдосфера
получается путем вращения так называемой трактрисы (впервые исследованной Исааком
mw
Ньютоном в 1676 году) вокруг ее асимптоты. Асимптотой кривой называют прямую, к ко¬
торой эта кривая в бесконечности приближается сколько угодно близко, но никогда не каса¬
ется. В данном случае представим, что такая асимптота проходит по некоторой шероховатой
горизонтальной плоскости; представим также, что по этой плоскости скользит легкий, пря¬
мой, жесткий стержень, к одному концу (Р) которого прикреплен тяжелый точечный груз,
а другой конец (R) свободно движется вдоль асимптоты. При движении такого стержня
точка Р будет описывать трактрису. В 1839 году Фердинанд Миндинг установил, что псев¬
досфера имеет постоянную отрицательную внутреннюю геометрию; опираясь на этот факт,
Бельтрами и построил впоследствии первую модель гиперболической геометрии. Похоже,
именно пс евд о сферическая модель Бельтрами убедила-таки математиков в непротиворечи¬
вости плоской гиперболической геометрии, поскольку на такой поверхности мера гипербо¬
лического расстояния вполне соответствует мере расстояния евклидова. Впрочем, модель
эта не совсем удобна, поскольку представляет гиперболическую геометрию лишь локально,
а не описывает ее целиком, как другие модели Бельтрами.	4
2.7.	Гиперболическая геометрия и физическое пространство
Двумя измерениями гиперболическая геометрия отнюдь не ограничивается. Имеют¬
ся версии как конформного, так и проективного представлений для большего количества
измерений. Например, в случае трехмерной гиперболической геометрии место ограничи¬
вающей окружности занимает ограничивающая сфера. Внутри этой конечной евклидовой
Рис. 2.21. Псевдосфера а) получается путем вращения трактрисы б) вокруг ее асимптоты. Для того
чтобы построить трактрису, вообразим горизонтальную шероховатую плоскость, по которой скользит
легкий, прямой, жесткий стержень. К одному концу стержня прикреплен тяжелый точечный груз Р,
другой конец R свободно (без трения) движется вдоль (прямолинейной) асимптоты
не подозревали! ^211^
R асимптота
б)

2.7. Гиперболическая геометрия и физическое пространство
63
сферы умещается вся бесконечная трехмерная гиперболическая геометрия. В остальном та¬
кие трехмерные модели, по сути, ничем не отличаются от тех, что мы рассмотрели выше.
•'	•	• *
В конформном представлении гиперболические прямые имеют вид дуг евклидовых окруж¬
ностей, упирающихся в ограничивающую сферу под прямым углом, углы соответствуют по
величине евклидовым углам, а расстояния задаются той же формулой, что и в двухмерном
случае. В проективном представлении гиперболические прямые выглядят как евклидовы
прямые, а расстояния вычисляются по той же формуле, какая применялась в двухмерной
модели.	'	.L;'	/
* •	.	'•	я*	'
•< 4	%	v
А что же наша реальная Вселенная в космологическом масштабе? Следует ли пола-
•	*	V	•	•
гать, что ее пространственная геометрия все-таки евклидова, или не исключено, что более
••	I	Aj	•	.
точное описание Вселенной дает какая-либо другая геометрия — например, вот эта замеча-
• •
тельная гиперболическая геометрия, которой мы посвятили §§ 2.4-2.6 (в трехмерном, разу¬
меется, своем варианте). Вопрос серьезный и непростой. Из общей теории относительности
Эйнштейна (см. §§ 17.9, 19.6) нам известко, что евклидова геометрия представляет собой
всего лишь приближение (пусть и чрезвычайно точное) к реальной геометрии физического
пространства. Эта реальная физическая геометрия даже не является вполне равномерной:
в присутствии плотной материи пространство искажается «рябью» нерегулярности. Самое
поразительное здесь, впрочем, то, что, согласно результатам наолюдении, выполненных с по¬
мощью точнейших из имеющихся в распоряжении ученых-космологов приборов, рябь эта
в космологических масштабах некоторым образом «сглаживается» (причем сглаживается
практически идеально; см. §§27.13, 28.4-28.10) и пространственная геометрия реальной
Вселенной приходит в замечательно точное соответствие геометрии равномерной (одно¬
родной и изотропной; см. §27.11). Во всяком случае первые четыре евклидовых посгулата
испытание временем, похоже, выдержали с честью и сдаваться пока не намерены.
Здесь необходимо некоторое пояснение. В сущности, из известных нам геометрий усло¬
виям однородности (все точки пространства одинаковы и равнозначны) и изотропности
(одинаковы и равнозначны все направления в пространстве) удовлетворяют три: евклидова
геометрия, гиперболическая и эллиптическая. С евклидовой геометрией мы знакомы дав¬
но (что-то около двадцати трех столетий) и очень хорошо. О гиперболической геометрии
достаточно полное представление дает настоящая глава. А что же такое эллиптическая гео¬
метрия? Если коротко, то эллиптическая плоская геометрия — это геометрия фигур, начер¬
ченных на поверхности сферы. Мы уже упоминали мельком о таком представлении в § 2.6,
когда обсуждали подход Ламберта к гиперболической геометрии. На рис. 2.22 показано эше-
ровское воплощение эллиптической, евклидовой и гиперболической геометрий на примере
одинаковой во всех трех случаях мозаики из ангелов и дьяволов, причем последний пред¬
ставляет собой интересную альтернативу мозаике на рис. 2.11. (Существует и трехмерная
версия эллиптической геометрии, а также версии, в которых диаметрально противоположные
точки сферы рассматриваются, как одна и та же точка. Несколько более подробно об этих
моделях я расскажу в §27.11.) Со всей уверенностью можно сказать, что в эллиптической
геометрии нарушаются второй и третий постулаты Евклида (как, собственно, и первый) —
эта геометрия конечна (а через пару точек здесь можно провести несколько прямых).
Так что же можно сказать, исходя из результатов наших наблюдений, о пространствен¬
ной геометрии Вселенной в космологическом масштабе? Если честно, то мы пока ничего
о ней не знаем, хотя в последнее время большой популярностью пользуются заявления
о том, что Евклид-таки с самого начала был абсолютно прав, его пятый постулат повсю¬
ду справедлив, а посему пространственную геометрию Вселенной можно в целом считать
вполне евклидовой!2 Л2^. С другой стороны, имеются свидетельства (некоторые из них полу¬
чены во время тех же самых экспериментов), решительно и недвусмысленно указывающие
на в общем и целом гиперболическую природу пространственной геометрии Вселенной !2Л31.
Более того, отдельные теоретики последовательно отстаивают эллиптическую точку зрения,

64
Глава 2
а)
б)
в)
Рис. 2.22. Три основные разновидности плоской равномерной геометрии, проиллюстрированные Эше¬
ром на примере мозаики, составленной из ангелов и дьяволов, а) Эллиптическая геометрия (положи¬
тельная кривизна), б) евклидова геометрия (нулевая кривизна) и в) гиперболическая геометрия (отри¬
цательная кривизна) в конформном представлении (гравюра «Предел круга IV», сравните с гравюрой
на рис. 2.11)
причем, находят ей подтверждение все в тех же данных, которые сторонники евклидовой
геометрии Вселенной интерпретируют в свою пользу (см. заключительные абзацы § 34.4).
Как читатель вскоре сможет убедиться самостоятельно, вопрос этот полон противоречий,
что, как можно ожидать, часто приводит к весьма горячим спорам. В последних главах книги
я попытаюсь изложить все основные взгляды на эту животрепещущую проблему (сохраняя

2.7. Гиперболическая геометрия и физическое пространство
65
по возможности беспристрастность, но в то же время отнюдь не скрывая, что сам я отдаю
предпочтение гиперболической точке зрения).	г	.	:
К счастью для всех тех, кто, подобно мне, очарован как красотами гиперболической гео¬
метрии, так и великолепием современной физики, эта замечательная геометрия находит еще
одно применение, бесспорно, играющее самую что ни на есть фундаментальную роль в сего¬
дняшнем понимании физической Вселенной. В самом деле, пространство скоростей в тео¬
рии относительности Эйнштейна есть не что иное, как трехмерная гиперболическая геомет¬
рия (см. § 18.4) — в отличие от евклидова пространства скоростей, которым оперирует клас¬
сическая теория Ньютона. Такой подход позволяет объяснить некоторые загадки относитель¬
ности. Представим себе, например, некое транспортное средство, движущееся мимо некоего
здания со скоростью, близкой к скорости света; представим также, что это транспортное
• •
средство выпускает в направлении своего движения снаряд, разгоняя его, в свою очередь,
до околосветовой скорости. Однако скорость снаряда относительно здания никак не может
превышать скорость света. Несмотря на кажущуюся парадоксальность, в терминах гипербо¬
лической геометрии ситуация получает простое и логичное объяснение (см. § 18.4). Впрочем,
у нас еще будет возможность обсудить эти захватывающие темы несколько позднее.
Вернемся к теореме Пифагора. Поскольку для гиперболической геометрии она, как мы
видели, не годится, не означает ли это, что нам следует вовсе отказаться от этого величай¬
шего дара пифагорейцев последующим поколениям? Ни в коем случае! Гиперболическая
геометрия — как, собственно, и все «римановы» геометрии, обобщающие гиперболическую
геометрию на пространства нерегулярной кривизны (и составляющие необходимый элемент
общей теории относительности Эйнштейна; см. §§ 13.8, 14.7, 18.1, 19.6), — в значитель¬
ной степени опирается на тот факт, что в пределе малых расстояний теорема Пифагора
истинна и здесь. Кроме того, без теоремы Пифагора не обходится, по всей видимости, ни
одна сколько-нибудь заметная область математики и физики (взять хотя бы «унитарную»
метрическую структуру квантовой механики, см. §22.3). Несмотря на то что для случая
«больших» расстояний эта теорема часто оказывается в некотором смысле «неактуальной»,
она сохраняет свою центральную роль в геометрических структурах малых масштабов, нахо¬
дя при этом удивительно разнообразные применения, далеко превосходящие самые смелые
предположения ее первооткрывателей.
Примечания
§2.1.
2.1. Вообще говоря, у нас нет исторически достоверных сведений о том, кто на самом деле пер¬
вым доказал теорему, которую мы сегодня называем теоремой Пифагора (см. примечание 1.1).
Известны многие случаи применения этой теоремы древними египтянами и вавилонянами.
Об истинной роли Пифагора или его последователей в доказательстве теоремы можно лишь
догадываться.
§2.2.
2.2. Несмотря на всю его тщательность, многие допущения в трудах Евклида так и остались
«неучтенными» — в основном те, что связаны со всевозможными «топологическими» (в совре¬
менной терминологии) вопросами, представлявшимися Евклиду и его современникам «интуи¬
тивно очевидными». Лишь многие века спустя ученые обратили внимание на эти неупомянутые
допущения (в частности, Гильберт в конце XIX века). В нашем дальнейшем рассуждении эти
допущения никакой роли не играют, поэтому я также не стану о них упоминать.
2.3. См., напр., [775]. Сравните с [704], где дано изящное аксиоматическое описание четырехмерной
пространственно-временной геометрии Минковского (§§ 17.8, 18.1).
§2.4.
2.4. «Степенная» запись вида С~1^2 используется в этой книге весьма часто. Как я уже пояснял
в примечании 1.2, запись а5 означает ах ах ах ах а\ соответственно произведение числа а на

66
Глава 2
себя в общей сложности п раз (где п — любое положительное целое число) записывается как ап.
Вышесказанное распространяется и на отрицательные показатели степени: так, аГ1 есть число,
обратное а, или 1/а, а а~п — число, обратное ап, или 1/ап, или, что то же самое, (а_1)п.
Согласно более общему представлению (см. § 5.2), запись а1^п (где а — любое положительное
число) означает «корень п-й степени из а», т. е. число (положительное), удовлетворяющее ра¬
венству {а1/п)п = а (см. примечание 1.2). Отметим также, что число агп^п равно числу а1//п,
возведенному в m-ю степень.
§2.6.
2.5. См. [681], XXXIII.
2.6. Существует точка зрения (так называемый интуиционизм), разделяемая некоторым (весьма
небольшим) количеством математиков, в рамках которой принцип «доказательства от против¬
ного» считается неприемлемым. Основная причина такой непримиримости заключается в том,
•	.	•	с
что этот принцип не всегда конструктивен, т. е. его применение может привести к утверждению
о существовании математического объекта, который невозможно конструктивно определить ни¬
какими имеющимися средствами. Некоторое отношение к этой точке зрения имеют вопросы,
обсуждаемые в § 16.6. См. также [382].
2.7. См. [353], с. 34.
2.8. Дуги окружности большого круга образуют «кратчайшие» пути (так называемые геодезические
кривые) на поверхности сферы; эти дуги лежат в плоскостях, проходящих через центр сферы.
2.9. Историки пока не пришли к единому мнению относительно истинной цели этих его изысканий:
не исключено, что Гаусс, профессионально занимавшийся геодезическими проблемами, пытал¬
ся таким образом обнаружить в физическом пространстве измеримые отклонения от евклидовой
геометрии. Принимая во внимание известную скрытность Гаусса во всем, что касалось неев¬
клидовой геометрии, представляется маловероятным, что он стал бы об этом распространяться,
будь оно действительно так — тем более что такой поиск (как нам теперь известно) был бы
изначально обречен на провал ввиду малости эффекта (согласно современным теоретическим
оценкам). До поры решено считать, что Гаусс «просто занимался геодезией» и интересовала его
кривизна не пространства, а всего лишь поверхности Земли. Однако мне как-то не верится, что
при этом он совершенно отказался от идеи отыскать какое-нибудь существенное расхождение
с евклидовой геометрией; см, [254, 315].
2.10. Представлением в виде так называемой «полуплоскости Пуанкаре» (с метрической фор¬
мой (dx2 + dy2)/y2; см. §14.7) мы также обязаны Бельтрами; см. [71]. Постоянная отрица¬
тельная кривизна «метрики Пуанкаре» 4(dx2 -f dy2)/{ 1 — х2 — у2)2 (см. рис. 2.11-2.13) была
в действительности обнаружена Риманом в 1854 году.
2.11. Не избежал этого и сам великий Гаусс (который, впрочем, очень часто предвидел результаты
других математиков). В топологии известна «теорема Гаусса-Бонне», которая изящно дока¬
зывается с помощью так называемого «отображения Гаусса», — при том что саму теорему
сформулировал в действительности Блашке, а упомянутое изящное доказательство представил
Олинде Родригес. Ни Гаусс, ни Бонне не имели, по всей видимости, ни малейшего отноше¬
ния ни к теореме, ни к ее доказательству. Существует и более элементарная «теорема Гаусса-
Бонне» (см., напр., [838] или [666]).
§2.7.
2.12. Основным источником сведений об общей структуре Вселенной, как единого целого, являет¬
ся детальный анализ космического микроволнового фонового излучения (***КМФ ); подробнее
см. §§ 27.7, 27.10, 27.11, 27.13, 28.5, 28.10, 30.14. Из литературы порекомендую в качестве крат¬
кого введения статью [180]; более новые и точные данные можно найти в работе [547] (проект
BOOMERANG). См. также [346] (о проекте MAXIMA), [338] (о проекте DASI) и [72] (о проекте
WMAP).
2.13. Теоретические обоснования изложены в работах [334] и [333], а анализ реальных данных по
КМФ можно найти в статьях [332] (данные, полученные со спутника СОВЕ), [329, 330] (данные
проекта BOOMERANG) и [331] (данные проекта WMAP).
****Английская аббревиатура — СМВ, т.е. cosmic microwave background (radiation). — Прим. перев.

Глава 3
Виды чисел в физическом мире
1
3.1.	Катастрофа пифагорейцев?
Вернемся теперь к принципу доказательства от противного — тому самому принципу,
с помощью которого Саккери пытался доказать пятый постулат Евклида. В классической
математике есть много примеров, когда этот принцип успешно работал. Один из наиболее
известных восходит к пифагорейцам, которые с помощью этого принципа пришли к мате-
матическому результату, глубоко взволновавшему их. Вопрос состоял в следующем: можно
ли найти рациональное число (т. е. дробь), квадрат которого был бы точно равен 2? Ответ
оказался отрицательным, и математическое утверждение, которое я сейчас вкратце изложу,
состоит в том, что такого рационального числа не существует.
Чем же так взволновало пифагорейцев это открытие?
Напомним, что дробь (т. е. рациональное число) можно
представить в виде отношения а/Ь двух целых чисел а
и 6, где число b отлично от нуля (см. обсуждение опреде¬
ления дроби в предисловии). Пифагорейцы вначале надея¬
лись, что вся их геометрия может быть изложена в терминах
длин, измеряемых рациональными числами. Рациональные
числа — довольно простые величины, которые можно опи¬
сать и понять, оставаясь в рамках простых конечных тер¬
минов. Пользуясь ими, можно определять расстояния как
сколь угодно малые, так и сколь угодно большие. Если бы
всю геометрию можно было построить, пользуясь одними
лишь рациональными числами, это сделало бы ее относи-
тельно простой и легко понимаемой. В то же время запись
иррационального числа есть бесконечный процесс, что, по
понятным причинам, представляло для древних значитель¬
ную трудность. Что же такого трудного для понимания
в том, что никакое рациональное число, будучи возведенным в квадрат, не дает 2? Труд¬
ность вытекает из самой теоремы Пифагора. Если взять (в евклидовой геометрии) квадрат,
длина стороны которого равна 1, то длина его диагонали равна числу, квадрат которого ра¬
вен I2 -{-12 = 2 (см. рис. 3.1). Если никакое реальное число не может служить мерой длины
диагонали квадрата, то для геометрии это действительно катастрофа. Поначалу пифаго¬
рейцы пытались описывать ситуацию с помощью «реальных чисел», представимых в виде
отношений целых чисел. Посмотрим, почему такой подход не работает.
Требуется понять, почему уравнение
Рис. 3.1. Согласно теореме Пифа¬
гора, квадрат с длиной стороны 1
имеет диагональ длиной л/2
2
с положительными целыми числами а и b не имеет решения. Мы воспользуемся методом
доказательства от противного, чтобы показать, что таких чисел анЬ не существует. Для этого

68
Глава 3
мы попробуем предположить, что такие а и Ь, напротив, существуют. Умножив обе части
нашего уравнения на 62, получим его в виде
а2 — 2 Ъ2,
откуда ясно видно что о2 > Ъ2 > 0; Правая часть последнего уравнения 2Ъ2 четна,
откуда следует, что число а также должно быть четным (оно не может быть нечетным,
поскольку квадрат любого нечетного числа есть нечетное число). Следовательно, а = 2с,
где с — некоторое положительное целое число. Подставив в последнее уравнение 2с вместо а
и выполнив операцию возведения в квадрат, получим
4с2 — 2 Ъ2,
или, разделив обе стороны на 2,
Ъ2 = 2с2,
откуда следует Ь2 > с2 > 0. То есть мы получили то же самое уравнение, что и выше,
но с заменой а на Ъ и b на с. Заметим, что соответствующие целые числа теперь стали меньше,
чем прежде. Мы можем повторять эти рассуждения снова и снова, получая бесконечную
последовательность уравнений
а2 = 2Ь2, Ъ2 = 2с2, с2 = 2d2, d2 = 2е2,...,
где
а2 > Ь2 > с2 > d2 > е2 > ...,	•
причем все целые числа положительны. Но любая убывающая последовательность положи¬
тельных целых чисел должна иметь конец в противоречии с тем фактом, что наша после¬
довательность бесконечна. Мы пришли к противоречию с тем, что предполагалось вначале,
именно что существует рациональное число, квадрат которого равен 2. Следовательно, та¬
кого рационального числа не существует, — что и требовалось доказать t3*2!.
По некоторым пунктам приведенного рассуждения следует сделать ряд замечаний.
Прежде всего, в соответствии с нормальной процедурой математического доказательства
некоторые свойства чисел в этом рассуждении предполагались либо «очевидными», либо
установленными ранее. Например, мы использовали тот факт, что квадрат нечетного числа
всегда является нечетным числом и, кроме того, что если целое число не нечетно, то оно
четно. Мы также использовали тот фундаментальный факт, что всякая строго убывающая
последовательность положительных целых чисел должна быть конечной.
Одна из причин, по которой важно уточнить допущенйя, сделанные в ходе доказатель¬
ства (несмотря на то что некоторые из них могут быть действительно совершенно «очевид¬
ными»), состоит в том, что математиков зачастую начинают интересовать иные сущности,
нежели те, к которым первоначально относилось доказательство. И если эти другие сущно¬
сти удовлетворяют тем же самым допущениям, то доказательство будет применимо и к ним,
и окажется, что доказанное утверждение обладает большей общностью, чем предполагалось
заранее, поскольку оно применимо также и к другим сущностям. И наоборот, если некото¬
рые из необходимых предположений для этих альтернативных сущностей не выполняются,
то рассматриваемое утверждение в отношении них является ложным. (Например, важно от¬
метить, что постулат о параллельных, использованный в § 2.2 при доказательстве теоремы
Пифагора, определенно ложен в гиперболической геометрии.)
В вышеприведенных рассуждениях исходными сущностями были целые числа, а ин¬
тересовались мы другими — рациональными — числами, которые строились как частные
от деления целых чисел. Для таких чисел действительно утверждение, что никакое из них,

3.2. Система вещественных чисел
69
будучи возведенным в квадрат, не дает 2. Однако существуют и другие виды чисел, от¬
личных от целых и рациональных. Надобность в квадратном корне из 2 заставила древних
греков, в те времена во многом помимо их воли, выйти за рамки целых и рациональных
чисел — тех единственных видов чисел, которые до тех пор считались возможными. Тот вид
чисел, к которому они оказались вынуждены приити, мы ныне называем «вещественными
числами» и представляем в виде разложений в бесконечные десятичные дроби (хотя такое
представление было недоступно древним грекам). На самом деле квадратный корень из 2
существует в виде вещественного числа, а именно (в нашей современной записи)
у/2 = 1,41421356237309504880168872...
Физический статус таких «вещественных» чисел будет подробнее рассмотрен в следующем
разделе.
Из любопытства можно задать вопрос: а почему приведенное выше доказательство
несуществования квадратного корня из 2 нельзя отнести и к вещественным числам (или к от¬
ношениям таких чисел, что, в сущности, то же самое)? Что будет, если во всем рассуждении
мы заменим слова «целое число» на «вещественное число»? Основное отличие состоит
в том, что становится неверным утверждение, будто любая строго убывающая последова¬
тельность положительных вещественных чисел должна быть конечной, — именно в этом
пункте разрывается цепочка рассуждений f3*3l (Примером может служить бесконечная по-
1111 1
следовательность 1,	—,...)	Может	возникнуть сомнение, возможно ли исполь¬
зование в этом контексте «нечетных» и «четных» вещественных чисел. На самом деле здесь
не возникает трудностей, поскольку все вещественные числа можно считать четными, так
как для любого вещественного числа а всегда найдется вещественное число с такое, что а ~
= 2с, т. е. деление вещественных чисел на 2 всегда возможно.
3.2.	Система вещественных чисел
Итак, древние греки вынуждены были прийти к выводу, что рациональные числа недо¬
статочны для успешного развития идей евклидовой геометрии. Сегодня нас уже не будет
слишком волновать тот факт, что какую-то геометрическую величину нельзя измерить с ис¬
пользованием одних лишь рациональных чисел, поскольку понятие вещественного числа
стало для нас вполне привычным. Хотя наши карманные калькуляторы дают лишь числа
с конечным числом цифр, мы хорошо понимаем, что это всего лишь приближение, связанное
с тем фактом, что калькулятор есть конечный объект. Мы готовы принять, что изображение
идеального (Платонова) математического числа может потребовать бесконечно продолжа¬
ющегося десятичного разложения. Это относится, конечно, к десятичному представлению
большинства дробей, напрймер
1
3
29
12
0
2,
Я •	«
| = 1,285714285714285...,
237
148
1,60135135135...
Для простых дробей десятичное разложение всегда периодично, т. е., начиная с некото
рого места, бесконечная последовательность цифр состоит из некоторой бесконечно повторя

70
Глава 3
ющейся конечной последовательности. В приведенных примерах такими повторяющимися
последовательностями будут соответственно 3, 6, 285714 и 135.
Древние греки не знали десятичных разложений, но у них были собственные способы
представления иррациональных чисел. Фактически они использовали систему представле¬
ния чисел, которую нынче называют непрерывными дробями. Здесь нет необходимости вхо¬
дить во все детали, однако уместны некоторые краткие пояснения. Непрерывная дробь 1341
есть конечное или бесконечное выражение а + (Ь4- (с-Ь (d4 где а, Ь, с, d... —
положительные целые числа:
а 4-
b 4-   -
с 4-	1
d 4-
• *
Всякое рациональное число, большее 1, можно записать в виде такого выражения, име¬
ющего конечную длину (во избежание неоднозначности обычно требуют, чтобы последнее
целое число было больше 1), например, 52/9 = 5 4- (1 4- (3 4- (2)”1)“1)“1:
52	5	+	1
3+г
Чтобы представить положительное рациональное число, меньшее 1, мы просто положим
/
первое целое число в этом выражении равным нулю. Для представления вещественного
числа, которое не является рациональным, мы должны позволить непрерывной дроби про¬
должаться бесконечно*. Вот некоторые примеры^3*5!;
у/2 = 1 + (2 + (2 + (2 + (2 + • • • Г1)-1)-1)-1.
7 - V3 = 5 + (3 + (1 + (2 + (1 + (2 + (1 +
+(2 + .. .Г1)-1)-1)-1)-1)"1)-1,
7г = 3 + (7+ (15 + (1 + (292 +
+(1 + (1 + (1 + (2 + ...)-1)-1Г1Г1)-1Г1Г1Г1.
В двух первых примерах последовательности натуральных чисел — 1, 2, 2, 2, 2,...
в первом случае и 5, 3, 1, 2, 1, 2,... во втором — обладают свойством периодичности (в пер-
вом случае бесконечно повторяется число 2, во втором — последовательность 1,2) . Как уже
упоминалось, в обычной десятичной записи рациональным числам соответствуют конечные
или бесконечные периодические разложения. В пользу древнегреческого представления чи¬
сел в виде непрерывных дробей можно записать то обстоятельство; что рациональные числа
при этом всегда допускают конечное описание. В этой связи естественно спросить: какие
числа дают бесконечное периодическое разложение в представлении непрерывных дробей?
Ответ дает замечательная теорема, впервые доказанная, насколько мне известно, великим
Поэкспериментируйте с вашим калькулятором (если на нем есть кнопки у/ и х *), чтобы получить эти
разложения с достаточной точностью. Возьмите 7г = 3.141592653589793 ... (Подсказка: запишите целую часть
числа, вычтите ее из исходного числа и найдите обратную величину полученного результата, с которой продолжайте
ту же последовательность операций.)
В предположении такой периодичности покажите, что число, представляемое каждой из этих' двух непре¬
рывных дробей, равно величине в левой части равенства. (.Подсказка: найдите квадратное уравнение, которому
удовлетворяет эта величина, и используйте примечание 3.6.)

w
3.2. Система вещественных чисел
71
математиком XVIII века Жозефом Лагранжем (с его другими важнейшими идеями мы столк¬
немся позже, в частности, в главе 20). Согласно этой теореме, бесконечное периодическое
разложение в непрерывную дробь дают так называемые квадратичные иррациональные чис~
ла^6К
Что же это за числа и почему они так важны для геометрии древних греков? Это такие
числа, которые можно записать в виде
а + л/b,
где а и b — дроби, причем Ъ не является полным квадратом. Такие числа играют важную
роль в евклидовой геометрии, поскольку они часто встречаются в задачах на построение
при помощи циркуля и линейки. (Напомним, что теорема Пифагора привела нас в §3.1
к проблеме л/2; другие простые построения евклидовых отрезков непосредственно приводят
нас к другим числам указанного вида.)
Частным случаем квадратичных иррациональных чисел являются такие числа, у кото¬
рых а = 0, а b есть натуральное число (не являющееся полным квадратом) или рациональное
число, большее 1:
у/2, л/3, л/5, л/6, л/7, л/8, vTo, у/П,...
Представление, таких чисел в виде непрерывных дробей выглядит весьма впечатля¬
юще. Последовательность натуральных чисел, определяющих разложение в непрерывную
дробь, обладает любопытным свойством. Она начинается с некоторого числа А, затем сразу
следует «палиндромная» последовательность (т. е. такая, которая одинаково читается слева
направо и справа налево) В, С,	С,	В, далее следует 2А, после чего последо¬
вательность В, С, D,... , D, С, В, 2А бесконечно повторяется. Например, для числа л/14
такая последовательность имеет вид
3, 1, 2, 1, б, 1, 2, 1, 6, 1, 2, 1, б, 1, 2, 1, 6,,..
Здесь А — 3, а палиндромная последовательность В, С, Л,..., D, С, В сводится к после¬
довательности из трех членов: 1, 2, 1.
Что из всего этого было известно древним грекам? Весьма вероятно, что они знали
очень много, вполне возможно, всё, что было изложено выше (включая теорему Лагранжа),
хотя строгих доказательств всего этого у них, скорее всего, не было. Современник Платона
Теэтет установил, по-видимому, большинство указанных фактов. Имеется даже некоторое
подтверждение такого знания (включая упомянутые повторяющиеся палиндромные после¬
довательности) в диалектике ПлатонаI3,7J.
Хотя введение квадратичных иррациональных чисел несколько приблизило нас к чис¬
лам, появляющимся в евклидовой геометрии, всё же это еще не всё, что нужно. В десятой
(и наиболее трудной) книге Евклида рассматриваются числа типа л/a -f \fb (где cl m b —
положительные рациональные числа). Такие числа в общем случае не являются квадратич¬
ными иррациональными числами, тем не менее они встречаются в задачах на построение
при помощи циркуля и линейки. Числа, достаточные для проведения таких геометрических
построений, могут быть получены из натуральных чисел последовательным применени¬
ем операций сложения, вычитания, умножения, деления и извлечения квадратного корня.
Однако операции исключительно с такими числами весьма сложны, и эти числа редко ис¬
пользуются в задачах евклидовой геометрии, выходящих за рамки построений циркулем
и линейкой. Гораздо лучше сделать смелый шаг (насколько он смелый, будет объяснено
в §§ 16.3-16.5) и рассматривать бесконечные разложения в непрерывные дроби самого обще¬
го вида. Это позволило древним грекам описывать числа, которые оказываются адекватными
евклидовой геометрии.

72
Глава 3
Именно такими числами, по современной терминологии, являются вещественные числа.
Хотя полностью удовлетворительное описание таких чисел было достигнуто лишь в XIX ве¬
ке (в работах Дедекинда, Кантора и других авторов), великий древнегреческий математик
и астроном Евдокс, который был одним из учеников Платона, выдвинул важные идеи уже
в IV веке до нашей эры. Здесь уместно сказать несколько слов об идеях Евдокса. Прежде все¬
го заметим, что числа в евклидовой геометрии могут быть представлены в виде отношений
длин отрезков, а не самих длин. В таком случае не требуются специальные единицы длины
(такие, например, как «дюйм» или, если по-гречески, «дактилос»). Кроме того, при работе
с отношениями длин нет ограничений в числе таких сомножителей при их перемножении
(тем самым отпадает необходимость в многомерных «гиперобъемах», когда перемножаются
более трех длин). Первым шагом в теории Евдокса было получение критерия, позволяющего
установить, что отношение длин а : Ь будет больше другого аналогичного отношения с : d.
Такой критерий состоит в том, что существуют некоторые положительные целые числа М
и N такие, что длина а, сложенная сама с собой М раз, превышает длину Ь, сложенную сама
с собой N раз, тогда как длина d, сложенная сама с собой N раз, больше длины с, сложенной
с самой собой М раз*. Существует аналогичный критерий, позволяющий установить, что
отношение длин а : b меньше отношения с : d. Условие равенства этих отношений долж¬
но состоять в том, что не выполняется ни один из этих критериев. При такой остроумной
формулировке условия равенства отношений Евдокс пришел, в сущности, к абстрактно¬
му понятию вещественного числа, выраженному в терминах отношений длин. Он также
получил правила сложения и умножения для таких вещественных чисел .
Существует, однако, фундаментальная разница между понятием вещественного числа
у древних греков и современным понятием, поскольку греки рассматривали систему чисел
как «данную» нам в виде расстояний в физическом пространстве, так что проблема состояла
в том, чтобы выяснить, как ведут себя эти меры расстояний. «Пространство» могло быть
воплощением платоновского абсолюта, даже несмотря на то, что реальные физические объ¬
екты, существующие в этом пространстве, неизбежно далеки от платоновского идеала t3*8].
(В §§ 17.9, 19.6, 19.8 мы увидим, как общая теория относительности Эйнштейна коренным
образом изменила такой взгляд на пространство и материю.)
Физические объекты, такие как квадрат, нарисованный на песке, или куб, высеченный
из мрамора, рассматривались древними греками как разумное, а иногда и отличное прибли¬
жение к платоновскому геометрическому идеалу. В то же время любой такой объект был
лишь приближением. За рамками такого приближения к платоновским формам могло быть
лишь само пространство; такая абстракция рассматривалась как непосредственное воплоще¬
ние платоновской реальности. Мерой расстояния в такой идеальной геометрии было нечто,
подлежащее определению. В соответствии с этим было естественно пытаться извлечь по¬
нятие вещественного числа из геометрии евклидова пространства, которая предполагалась
заданной. Именно это фактически и удалось сделать Евдоксу.
Однако в XIX и XX веках появилась такая точка зрения, что математическое понятие
числа должно быть отделено от природы физического пространства. Поскольку было пока¬
зано, что существуют математически последовательные геометрии, отличные от евклидовой,
оказалось не вполне уместным настаивать на том, чтобы математическое понятие «геомет¬
рии» непременно выводилось из предполагаемой природы «реального» физического про¬
странства. Более того, оказалось очень трудным (если вообще возможным) делом объяснять
природу такой «платоновской физической геометрии» в терминах поведения несовершен¬
ных физических объектов. Чтобы познать природу чисел, используемых для определения
«геометрического расстояния», необходимо знать, например, что происходит на бесконеч¬
но малых и бесконечно больших расстояниях. Даже сегодня на эти вопросы нет четкого
•
* Понятно ли, почему это так?
Можете ли вы сформулировать их?

3.3. Вещественные числа в физическом мире
73
ответа (и я обращусь к ним снова в последующих главах). Поэтому было гораздо более
приемлемо изучать природу чисел способом, не связанным непосредственно с физически¬
ми мерами. В соответствии с этим Рихард Дедекинд и Георг Кантор развивали свои идеи
о природе вещественных чисел, используя понятия, не имеющие непосредственной связи
с геометрией.
Дедекиндово определение вещественного числа использует бесконечные ряды рацио¬
нальных чисел. Мы считаем, что рациональные числа, как положительные, так и отрица¬
тельные (а также нуль), можно расположить по их величине. Можно представить, что такое
упорядочение направлено слева направо, так что отрицательные рациональные числа уходят
в бесконечность влево, 0 находится в середине, а положительные рациональные числа ухо¬
дят в бесконечность вправо. (Мы делаем это лишь для наглядности; процедура Дедекинда
фактически полностью абстрактна.) Дедекинд рассматривает «сечение», которое делит эту
картину на две части таким образом, что все числа слева от сечения меньше любого числа
справа от него. Если «лезвие ножа» такого сечения «не попадает» на одно из рациональ¬
ных чисел, а оказывается между ними, мы говорим, что сечение определяет иррациональное
вещественное число. Точнее говоря, так получается, когда слева нет наибольшего числа,
а справа нет наименьшего числа. Если систему иррациональных чисел, определяемую се¬
чением, добавить к имеющейся у нас системе рациональных чисел, то получится полное
семейство вещественных чисел.
При использовании простых определений процедура Дедекинда непосредственно при¬
водит к законам сложения, вычитания, умножения и деления вещественных чисел. Более
того, она позволяет двинуться дальше и определить понятие предела, посредством которого
в категорию вещественных чисел включаются, например, уже известная нам бесконечная
%
непрерывная дробь
1 + (2 + (2 + (2 + (2 • • • )-1)-1)-1)-1
или бесконечная сумма
1 _1 , 1_1 + 1
1	3	5	7	9
выражений дает нам иррациональное число у/2, второе — ~7г. Переход
серен для многих математических понятий, и это придает особую силу ве-
лам!3*9!. (Напомним читателю, что необходимость «предельных процедур»
возникла
3.3.	Вещественные числа в физическом мире
Существует глубокий вопрос, которого мы сейчас коснемся. При развитии математи¬
ческих идей важной движущей силой вначале всегда было стремление найти математиче¬
ские структуры, которые отражали бы поведение физического мира. Однако обычно бывает
невозможно познать физический мир настолько детально, чтобы непосредственно из него
извлекать четкие математические понятия. На самом деле прогресс возможен потому, что
математические понятия обладают своим собственным «импульсом развития», причем со¬
здается впечатление, что этот импульс по большей части возникает внутри самой математи¬
ки. Математические идеи развиваются, и различные задачи возникают как бы естественным
образом. Некоторые из них (как было в случае задачи о нахождении длины диагонали
квадрата) могут привести к существенному расширению первоначальных математических
понятий, использовавшихся при формулировке задачи. Некоторые обобщения могут казать¬
ся вынужденными, другие могут оправдываться соображениями удобства, согласованности
или математического изящества. При этом развитие математики может отклоняться от пер¬

74
Глава 3
воначального стремления описать физическую реальность. Есть, однако, много примеров,
когда стремление к математической согласованности и изяществу приводило к математиче¬
ским структурам и понятиям, отражающим физический мир более глубоко и широко, нежели
исходные структуры. Создается такое впечатление, что сама природа руководствуется теми
же критериями согласованности и изящества, что и человеческая математическая мысль.
Возьмем для примера все те же вещественные числа. В природе мы не находим прямых
указаний на существование физического понятия «расстояния», распространяющегося на
сколь угодно большие масштабы. Еще меньше свидетельств того, что такое понятие мо¬
жет распространяться на бесконечно малые масштабы. В самом деле, нет подтверждений
того, что «точки в пространстве» действительно существуют в соответствии с геометрией,
оперирующей с расстояниями, описываемыми вещественными числами. Во времена Евкли¬
да не было даже предмета спора о том, могут ли евклидовы «расстояния» простираться
более чем, скажем, на 1012 метров или быть меньше, чем 10“5 метров. Тем не менее,
имея систему вещественных чисел, построенную в соответствии с требованиями математи¬
ческой согласованности и изящества, мы во всех без исключения успешных современных
•* •
физических теориях остаемся верными древнему понятию «реального числа». Может по¬
казаться, что опираться на представления времен Евклида не вполне оправданно, однако
наша вера в систему вещественных чисел оказалась вознагражденной. Вполне успешные
современные космологические теории позволяют нам расширить область расстояний, изме¬
ряемых вещественными числами, до 1026 метров и более, тогда как точность современных
теорий физики элементарных частиц позволяет распространить эту область на расстояния,
меньшие 10“17 метров. (Единственный масштаб, на котором можно ожидать серьезных
изменений, меньше указанного на 18 порядков, т. е. 10~35 метров, — это так называемая
«планковская длина» в квантовой теории гравитации, которая будет фигурировать в наших
последующих обсуждениях; см. §§31.1, 31.6-31.12, 31.14, 32.7.) Оправданием использо¬
вания математических идеализаций может служить тот факт, что область применимости
системы вещественных чисел, от наименьшего до наибольшего, охватывающая во времена
Евклида 17 порядков, в наших современных теориях расширена до 43 порядков, то есть
в 1026 раз.
Существуют еще более весомые подтверждения физической применимости системы
вещественных чисел, нежели приведенные выше. Прежде всего мы должны заметить, что
площади и объемы также являются величинами, для измерения которых вещественные чис¬
ла вполне пригодны. Мерой объема служит куб меры длины (а мерой площади — квадрат
длины). Поэтому, рассматривая объемы, мы должны считать, что куб упомянутой обла¬
сти также должен быть доступен для описания. Во времена Евклида это давало область
порядка (1017)3 = 1051, в современных теориях— по крайней мере (1043)3 — 10129. Бо¬
лее того, в соответствии с современными теориями, существуют другие физические меры,
для описания которых требуются вещественные числа. Наибольшего внимания из таких
мер заслуживает время. Согласно теории относительности, оно должно быть объединено
с пространством в единое пространство-время (это будет предметом нашего обсуждения
в главе 17). Объемы в пространстве-времени четырехмерны, поэтому временная область
(которая, согласно хорошо проверенным теориям, порядка 1043 или больше) должна быть
объединена с пространственной; это дает по меньшей мере 10172. При последующем обсу¬
ждении (см. §§ 27.13, 28.7) мы встретимся с еще большими вещественными числами, хотя в
> • / • ч*
некоторых случаях и не вполне ясно, существенно ли использование именно вещественных
чисел (а не, скажем, целых чисел).
Для физической теории от Архимеда, Галилея, Ньютона до Максвелла, Эйнштейна,
Шредингера, Дирака и остальных более важной была та критическая роль, которую система
вещественных чисел играет в создании необходимой основы для стандартной формулировки
математического анализа (см. главу 6). Все известные динамические теории формулиру¬

3.3. Вещественные числа в физическом мире
75
ются с использованием понятий математического анализа. Общепринятый подход к анализу
требует существования бесконечно малых величин. Другими словами, на малых масштабах
должна существовать область всех вещественных чисел, которые в принципе могут пона¬
добиться. Идеи математического анализа лежат в основе таких физических понятий, как
скорость, импульс и энергия. Таким образом, система вещественных чисел фундаменталь¬
ным образом входит в физические теории также при описании всех этих величин. Здесь, так
же как при определении площади (см. §§2.3, 3.2), становится востребованным бесконечно
малый предел мелкомасштабной структуры системы вещественных чисел.
Впрочем, это еще не гарантирует, что система вещественных чисел пригодна для описа¬
ния физической реальности на ее самых глубоких уровнях. Когда в начале XX века возникли
идеи квантовой механики, появилось ощущение, что природа физического мира на его наи¬
меньших масштабах может оказаться дискретной (зернистой)!3 Л1!. Энергия, как оказалось,
существует лишь в виде дискретных сгустков — «квантов», а такие физические величины,
как действие и спин, могут быть лишь кратными значениями некоторой фундаментальной
единицы (классическое определение действия см. в §§20.1, 20.5, его квантовый аналог —
в §26.6; определение спина см. в §§22.8-22.12). В связи с этим некоторые физики попыта¬
лись построить альтернативную картину мира, в которой все действия на наиболее малых
масштабах определяются дискретными процессами.
Однако, насколько мы сейчас понимаем квантовую механику, эта теория не приводит нас
к той точке зрения (и тем более не вынуждает ее принять), что пространство, время и энергия
на низших уровнях имеют дискретную (зернистую) природу (см. главы 21 и 22, особенно
последнее предложение в § 22.13). Тем не менее осталась идея, что природа в конечном счете
может обладать фундаментальной дискретностью, несмотря на то что квантовая механика
в своей стандартной формулировке, конечно же, этого не предполагает. Например, великий
физик Эрвин Шредингер одним из первых предположил, что может оказаться необходимым
переход к некоторой форме фундаментальной пространственной дискретности !ЗЛ2Ь
Идея непрерывной области, столь обычная сегодня для математиков, есть нечто
совершенно чрезмерное, далеко идущая экстраполяция того, что доступно для нас.
Он связал свое предположение с некоторыми мыслями древних греков относительно дис-
•	«	.	I
кретности Природы. Эйнштейн в одной из последних работ также предполагал, что дискрет¬
ная («алгебраическая») теория могла бы стать направлением движения будущей физики !злз1:
Можно привести серьезные доводы в пользу того, что реальность не может быть
представлена как непрерывное поле Квантовые явления... должны привести
к попытке найти чисто алгебраическую теорию для описания реальности. Однако
никто не знает, как получить основу для такой теории!314!.
Подобные идеи выдвигались и другими!315! (см. §33.1). В конце 1950-х годов я сам
сделал такую попытку, предложив схему, которую я назвал теорией «спиновых сетей». Дис¬
кретная природа квантово-механического спина рассматривалась в качестве основного стро¬
ительного блока комбинаторного (т. е. дискретного, а не основанного на вещественных
числах) подхода к физике. (Эта схема будет кратко изложена в § 32.6.) Мои идеи не при¬
вели к созданию стройной теории (хотя и трансформировались впоследствии в «теорию
твисторов», см. § 33.2), однако теория спиновых сетей ныне используется другими авторами
в одной из главных программ наступления на фундаментальную проблему квантовой гра¬
витации(t3 161. Краткое изложение различных идей этого рода будет дано в главе 32. Тем не
менее в общепринятых современных теориях, как и в прошедшие двадцать четыре столетия,
вещественные числа составляют фундаментальную часть нашего понимания физического
мира.

76
Глава 3
3.4.	Нуждаются ли натуральные числа в наличии физического мира?
При изложении подхода Дедекинда к системе вещественных чисел в § 3.2 я предполагал,
что рациональные числа нам уже «понятны». Переход от целых чисел к рациональным
несложен: рациональные числа суть просто отношения целых чисел (см. предисловие).
Что тогда можно сказать о самих целых числах? Лежат ли они в основе физических идей?
Дискретный подход к физике, о котором шла речь в конце предыдущего раздела, определенно
опирается на понятие натурального числа (т. е. чисел, употребляемых при счете) и его
обобщения на целые числа путем включения отрицательных чисел. Отрицательные числа
не рассматривались древними греками как «настоящие» числа, поэтому продолжим наше
обсуждение, задавшись сначала вопросом о физическом статусе самих натуральных чисел.
Натуральные числа — это величины, которые мы обозначаем как 0, 1, 2, 3, 4 и т.д.,
то есть это неотрицательные целые числа. (Современная процедура включает в этот список
О, что вполне естественно с математической точки зрения, хотя древние греки не признавали
нуль в качестве «настоящего» числа. Для этого пришлось ждать индийских математиков, на¬
чиная от Брамагупты в VII веке до Махавиры и Бхаскары соответственно в IX и XII веках.)
Роль натуральных чисел ясна и недвусмысленна. Это действительно наиболее элементар¬
ные «единицы счета», каковы бы ни были законы геометрии или физики. Натуральные
числа подвергаются определенным известным операциям, наиболее знакомыми из которых
являются действия сложения (например, 37 + 79 = 116) к умножения (например, 37 х 79 —
= 2923), при которых пары натуральных чисел комбинируются, давая новые натуральные
числа. Такие операции не зависят от природы геометрии реального мира.
Можно, однако, задать вопрос: действительно ли натуральные числа имеют смысл сами
по себе и действительно ли они существуют независимо от реальной природы физического
мира? Возможно, что наше понятие натуральных чисел связано с существованием в нашей
Вселенной достаточно хорошо определенных дискретных объектов, сохраняющихся во вре¬
мени. В конце концов, натуральные числа возникли, когда появилось желание сосчитать
какие-то предметы. Но это, по-видимому, зависит от того, действительно ли существуют во
Вселенной сохраняющиеся различимые «предметы», пригодные для того, чтобы их считать.
Допустим, что наша Вселенная такова, что ряд объектов имеет тенденцию непрерывно ме¬
няться. Могут ли натуральные числа быть естественным («натуральным») понятием в такой
Вселенной? Более того, возможно, что Вселенная содержит лишь конечное число таких
«предметов», так что ряд натуральных чисел может сам собой приходить к концу в некото¬
ром месте! Можно даже представить себе Вселенную, которая состоит лишь из аморфной
бесформенной субстанции, в отношении которой само понятие численной квантификации
неприемлемо по самой ее природе. Будет ли понятие натурального числа пригодным для опи¬
сания Вселенной такого рода?
Даже если обитатели такой Вселенной решат, что нашему математическому понятию
натурального числа нелегко найти применение, трудно представить, чтобы столь фундамен¬
тальное понятие не играло важной роли. Имеются разные пути, которыми можно ввести
натуральные числа в чистую математику, и они представляются не зависящими от реальной
природы физической Вселенной. Существует понятие множества, которое является абстрак¬
цией, не связанной с конкретной структурой физической Вселенной. Фактически в этом
вопросе имеются некоторые тонкости, и я вернусь к ним позже (в § 16.5). Пока удобнее
игнорировать эти тонкости.
Рассмотрим один из способов (развитый Кантором из идей Джузеппе Пеано и усовер¬
шенствованный выдающимся математиком Джоном фон Нейманом) введения натуральных
чисел, просто используя абстрактное понятие множества. Он приводит также к понятию
«порядковых чисел». Простейшим из всех является так называемое «нулевое множество»,
или «пустое множество», определяемое тем фактом, что оно вообще не содержит элементов.

3.5. Дискретные числа в физическом мире
77
Пустое множество обычно обозначается символом 0, и мы можем записать определение
0 = п,
«•
в котором фигурные скобки означают множество; внутри скобок указываются элементы
множества. В данном случае внутри скобок ничего нет, так что это множество действительно
является пустым. Сопоставим множеству 0 натуральное число 0. Можно двинуться дальше
и определить множество, единственным элементом которого является 0, т. е. множество {0}.
Важно отметить, что {0} — не то же самое, что пустое множество 0. Множество {0} со-
*
держит один элемент (а именно 0), тогда как 0 не содержит ни одного. Множеству {0}
сопоставим натуральное число 1. Далее определим множество, двумя элементами которо¬
го являются два только что рассмотренных множества, 0 и {0}, так что это множество
имеет вид {0, {0}}; мы сопоставим ему натуральное число 2. Затем мы сопоставим число
3 коллекции из трех множеств, с которыми мы только что имели дело, а именно множе¬
ству {0, {0}, {0, {0}}}, а число 4 — множеству {0, {0}, {0, {0}}, {0, {0}, {0, {0}}}},
элементами которого опять-таки являются множества, рассмотренные раньше, и так далее.
Это, возможно, не совпадает с нашим привычным представлением о натуральных числах, но
это один из путей, которым математики могут прийти к этому понятию. (Сравните это с об¬
суждением в предисловии.) Кроме того, отсюда видно, по крайней мере, что такие понятия,
как натуральные числа^3 171, могут появиться буквально из ничего, просто из абстрактного
понятия «множества». Мы получаем бесконечную последовательность абстрактных (плато¬
новских) математических сущностей — множества, содержащие нуль, один, два, три и т.д.
элементов, по одному множеству для каждого из натуральных чисел, совершенно незави¬
симо от реальной физической природы Вселенной. На рис. 1.3 мы уже встречались с при¬
мером независимого «существования» платоновских математических объектов (в данном
случае самих натуральных чисел), и это «существование» может показаться (и определен¬
но является) просто упражнением нашего воображения вне какой-либо связи с детальной
природой физической Вселенной. Более того, построение Дедекинда показывает, каким об¬
разом такая чисто умозрительная процедура может быть распространена дальше, и позволит
нам построить всю систему вещественных чисел^318!, — опять-таки без какого-либо обра¬
щения к реальной физической природе нашего мира. Тем не менее, как отмечено выше,
вещественные числа представляются имеющими прямое отношение к реальной структуре
мира, что свидетельствует о весьма загадочной природе «первой тайны», отображенной на
рис. 1.3.
3.5. Дискретные числа в физическом мире
Однако я несколько забежал вперед. Напомню, что в построении Дедекинда могут
использоваться множества не натуральных, а рациональных чисел. Как отмечено выше,
нетрудно «определить», что мы понимаем под рациональным числом, коль скоро у нас
есть понятие натурального числа. В качестве промежуточной стадии имеет смысл ввести
понятие целого числа, которое может быть натуральным числом либо отрицательным по
отношению к натуральному (при этом нуль является отрицательным относительно самого
себя). В формальном смысле математическое определение отрицательного числа не связано
с какими-либо трудностями: грубо говоря, мы просто добавляем некоторый «знак», обо¬
значаемый как «—», к каждому из натуральных чисел (за исключением 0) и определяем
все обычные арифметические правила сложения, вычитания, умножения и деления (кроме
деления на 0). Это, однако, не дает ответа на вопрос о «физическом смысле» отрицатель¬
ных чисел. Что могло бы означать, например, утверждение, что на лугу пасутся минус три
• * * *
коровы?

78
Глава 3
Должно быть ясно, я полагаю, что, в отличие от натуральных чисел, понятие отри¬
цательного числа физических объектов не имеет очевидного физического содержания. От¬
рицательные числа определенно играют крайне важную организующую роль в банковских
балансах и других финансовых операциях. Но имеют ли они непосредственное отношение
к физическому миру? Когда я говорю «непосредственное отношение», я не имею в ви¬
ду случаи, когда они возникают как отрицательные вещественные числа, служащие мерой
чего-либо; например, расстояние, измеренное в одном направлении, считается положитель¬
ным, а измеренное в противоположном направлении, — отрицательным (то же относится
и ко времени — время, отсчитываемое в прошлое, можно назвать отрицательным). Я имею
в виду числа, которые являются скалярными величинами в том смысле, что они не имеют
направленного (или временного) характера. Именно в этом случае система целых чисел,
положительных и отрицательных, будет иметь непосредственный физический смысл.
Примечательно, что лишь в последнюю сотню лет стало ясно, что система целых чисел
действительно имеет непосредственное физическое содержание. Первым примером физи¬
ческой величины, для измерения которой требуются целые числа, является электрический
заряд1ЗЛ91. Насколько известно (хотя этот факт пока не имеет полного теоретического обос¬
нования), электрический заряд любого отдельного изолированного тела выражается в виде
целого числа (положительного, отрицательного или нуля), умноженного на некоторую ве¬
личину, — заряд протона (или электрона, который несет тот же заряд, но противоположного
знака)[3-2°] 3 настоящее время считается, что протоны являются сложными объектами,
состоящими из более мелких сущностей, именуемых кварками (и дополнительных незаря¬
женных сущностей, называемых глюонами). Каждый протон содержит три кварка с заряда-
2 2 1
ми	Сложение	этих	зарядов дает полный заряд протона, равный 1. Если кварки
являются наиболее фундаментальными сущностями, то основная единица заряда должна
быть третьей частью того, что считалось ранее. Тем не менее и в этом случае электриче¬
ский заряд будет измеряться целыми числами, умноженными на одну треть заряда протона.
(Роль кварков и глюонов в современной физике элементарных частиц будет обсуждаться
в §§25.3-25.7.)
Электрический заряд может служить примером того, что называется аддитивным кван-
г	»
товым числом. Квантовыми числами называются величины, которые служат характеристи¬
ками частиц Природы. Такое квантовое число, рассматриваемое как вещественное число
некоторого рода, является «аддитивным», если его значение для составной системы получа¬
ется просто сложением соответствующих значений для составляющих ее частиц — с учетом,
конечно, их знака, как в упомянутом случае протона и составляющих его кварков. Весьма за¬
мечателен тот факт, что, в соответствии с современным состоянием наших знаний в области
физики, все известные аддитивные квантовые числа I3*2^ описываются системой целых чи¬
сел, а не вещественных и не просто натуральных чисел, так что возможны и отрицательные
значения.
Физика XX века показала, что имеет смысл приписывать отрицательные значения фи¬
зическим величинам. Великий физик Поль Дирак выдвинул в 1929-31 годах теорию анти-
частиц, согласно которой (как было понято позже) для частиц каждого типа существуют
соответствующие античастицы, для которых каждое из аддитивных квантовых чисел от¬
личается знаком от аналогичного квантового числа исходной частицы (см. §§24.2, 24.8).
Таким образом, система целых чисел (включая отрицательные) имеет прямое отношение
к описанию физической Вселенной, причем это стало ясно лишь в XX веке, несмотря на то
что в течение многих прошлых веков целые числа играли огромную роль в математике,
коммерции и многих других областях человеческой деятельности.
Здесь, однако, следует дать немаловажное пояснение. Хотя антипротон, в некотором
смысле, действительно можно рассматривать как отрицательный протон, на самом деле он
не представляет собой просто «минус один протон». Причина состоит в том, что изменение

3.5. Дискретные числа в физическом мире
79
5
знака претерпевают только аддитивные квантовые числа, тогда как понятие массы в совре¬
менной физической теории не аддитивно. Этот вопрос будет объяснен подробнее в § 18.7.
«Минус один протон» должен быть антипротоном, масса которого отрицательна по отноше¬
нию к массе обычного протона. Однако масса реальной физической частицы не может быть
отрицательной. Антипротон имеет такую же (положительную) массу, что и обычный протон.
Далее мы увидим, что, согласно идеям квантовой теории поля, существуют так называемые
«виртуальные» частицы, масса (или, точнее, энергия) которых может быть отрицательной.
«Минус один протон» мог бы быть виртуальным антипротоном. Однако виртуальные части¬
цы не имеют независимого существования в качестве «реальных частиц».
Зададим теперь аналогичный вопрос в отношении рациональных чисел. Имеет ли эта
система чисел непосредственное отношение к физической Вселенной? Насколько извест¬
но, это не так, по крайней мере в современной теории. Известно несколько физических
курьезов t3*22^, когда семейство рациональных чисел действительно играет роль, но было бы
трудно утверждать, что это свидетельствует о сколько-нибудь фундаментальной физической
роли рациональных чисел. С другой стороны, рациональные числа могут играть некоторую
роль в отношении фундаментальных квантово-механических вероятностей (вероятность,
выражаемая рациональным числом, может соответствовать выбору между альтернативами,
каждая из которых включает лишь конечное число возможных вариантов). Такое имеет место
в теории спиновых сетей, о чем будет кратко сказано в § 32.6. В настоящее время истинный
статус этих идей не вполне ясен.
Существуют и другие виды чисел, которые, согласно общепринятой теории, играют
фундаментальную роль в описании Вселенной. Наиболее важными и поразительными яв¬
ляются комплексные числа, в которых фигурирует кажущаяся мистической величина л/~1,
обычно изображаемая буквой г, объединяемая с системой вещественных чисел. Впервые
с ними столкнулись в XVI веке, но в течение сотен лет относились к ним с недоверием.
Понимание математической полезности комплексных чисел постепенно овладевало матема¬
тическим сообществом все в большей и большей степени, пока они не стали непременным,
даже магическим, элементом нашего математического мышления. Было обнаружено, что
они являются фундаментальными не только в математике: эти странные числа играют также
чрезвычайно важную роль в описании физической Вселенной в ее самых малых масшта¬
бах. Это должно вызывать удивление как еще более поразительный пример связи между
математическими идеями и глубинными свойствами физической Вселенной по сравнению
со случаем вещественных чисел, рассмотренных в этом разделе. Далее мы перейдем к этим
замечательным числам.
Примечания
§3.1.
3.1. В этой книге часто используются обозначения >, <,	означающие	соответственно	«боль¬
ше», «меньше», «больше или равно» и «меньше или равно».
3.2. Некоторым читателям может быть известно более короткое рассуждение, начинающееся с тре¬
бования, чтобы число а/b «содержало наименьшие члены» (т. е. чтобы числа а и 6 не имели
общих множителей). Однако это предполагает, что такие выражения с наименьшими членами
всегда существуют; это, хотя и совершенно верно, требует доказательства. Нахождение такого
выражения для данной дроби А/В (неявное или явное, — например, с использованием процеду¬
ры, известной под названием алгоритма Евклида; см., например, [355, 174, 491, 610]) содержит
рассуждения, подобные приведенным в тексте, но более сложные.
3.3. Можно возразить, что несколько странно использовать в вышеприведенном доказательстве ве¬
щественные числа, поскольку «вещественные рациональные числа» (т. е. частные от деления
одного вещественного числа на другое) будут опять-таки вещественными числами. Это, однако,
не опровергает только что сказанного. Можно заметить, что в исходном рассуждении числа а

80
Глава 3
и b можно считать целыми числами. Поэтому если а и Ъ — рациональные числа, то рассужде¬
ния с «убывающей последовательностью» не проходят, хотя результат сам по себе остается
правильным.
§3.2.
3.4. На первый взгляд выражения типа а + (6 4- (с + (d + • • ♦ )-1)~1)-1 могут выглядеть довольно
необычно. Однако они вполне естественны для мышления древних греков (хотя они и не пользо¬
вались такой записью). В примечании 3.2 был упомянут алгоритм Евклида в связи с проблемой
нахождения наиболее краткой формы дроби. Применение алгоритма Евклида приводит как раз
к подобной непрерывной дроби. Грекам следовало применить аналогичную процедуру к отно¬
шению двух геометрических длин. В наиболее общем случае результатом была бы бесконечная
непрерывная дробь вроде той, что была рассмотрена выше.
3.5. Более подробную информацию о непрерывных функциях (с доказательствами) можно найти
в главе 4 книги Давенпорта [174]. Можно отметить, что представление вещественных чисел
непрерывными дробями в некоторых отношениях глубже и интереснее обычного разложения
в десятичную дробь, поскольку находит применение во многих разделах современной матема¬
тики, включая гиперболическую геометрию, обсуждавшуюся в §§ 2.4, 2.5. Однако непрерывные
дроби не всегда пригодны для большинства практических расчетов, поскольку обычное деся¬
тичное представление намного проще в использовании.
3.6. Квадратичные иррациональные числа называются так потому, что они возникают при решении
квадратного уравнения общего вида
Ах2 + Вх -f С — 0,
нуля,
_д + , в „ _
2A V V 2А У А	2А
чтобы оставаться в мире вещественных чисел, мы должны принять, что В2 больше 4АС. Если
коэффициенты А, В и С — целые или рациональные числа и уравнение не имеет рациональных
решений, то решения будут квадратичными иррациональными числами.
3.7. Профессор Стелиос Негрепонтис сообщил мне, что такое утверждение можно найти в платонов¬
ских диалогах «Политик» — третьей книге трилогии «Теэтет»-«Софист»-«Политик» (см. [545]).
3.8. Относительно взглядов древних греков на природу пространства см. [736, 737].
3.9. См. [352, 161, 116].
■*
§3.3
1 о
3.10. «Научная» запись 10 , обозначающая «миллион миллионов», использует показатели, как опи¬
сано в примечаниях 1.2 и 2.4. В этой книге я буду стремиться избегать словесных терминов,
таких как «миллион» и особенно «биллион», предпочитая более четкое научное обозначение.
Слово «биллион» особенно часто приводит к недоразумениям, поскольку в Америке (а теперь
и в Великобритании) «биллион» означает 109, тогда как более старое (и более логичное) ан¬
глийское определение, как и в большинстве других европейских языков, относится к 1012.
Отрицательные показатели, например в 10“6 (что означает «одна миллионная»), также будут
использоваться здесь в соответствии с обычными научными обозначениями.
Расстояние 1012 метров приблизительно в 7 раз больше расстояния от Земли до Солнца. Это при¬
близительно равно расстоянию от Солнца до Юпитера, хотя во времена Евклида это расстояние
не было известно и предполагалось довольно малым.
3.11. См., например, [678], гл. 4.
3.12. См. [699].
3.13. См. [741].
3.14. См. [243].
3.15. См., например, [735, 693, 13].

3.5. Дискретные числа в физическом мире
81
3.16. См. [30, 36, 730, 731, 673, 674].
§3.4
3.17. Понятие «порядкового числа», которое здесь используется в отношении конечных чисел, обоб¬
щается также на бесконечные порядковые числа, наименьшим из них является канторово чис¬
ло которое представляет собой упорядоченное множество всех конечных порядковых чисел.
3.18. Слово «построить» не следует понимать буквально. В § 16.6 мы увидим, что существуют неко¬
торые вещественные числа (фактически большинство из них), которые не допускают какой-либо
вычислительной процедуры.
§3.5.
3.19. Элементарный электрический заряд впервые приближенно оценил ирландский физик Джордж
Джонстон Стони в 1874 году; в 1891 году он предложил для этой фундаментальной величи¬
ны термин «электрон». В 1909 году американский физик Роберт Эндрю Милликен поставил
свой знаменитый эксперимент с масляными каплями, который точно показал, что заряд элек¬
трически заряженных тел (в данном эксперименте — капель масла) выражается целым числом,
умноженным на определенную величину — заряд электрона.
3.20. В 1959 году Р. А. Литлтон и Г. Бонди (см. [501]) предположили, что небольшая разность в заря¬
дах протона и электрона (с обратным знаком) порядка 10~18 могла бы объяснить расширение
Вселенной (см. §§27.11, 27.13 и гл. 28). К сожалению (для этой теории), эксперименты вскоре
опровергли наличие такой разности. Тем не менее эта идея может служить отличным примером
творческого мышления.
3.21. Я делаю здесь различие между «аддитивными» квантовыми числами и числами, которые физики
называют «мультипликативными» (см. § 5.5).
3.22. Примером явления, в котором рациональные числа играют ключевую роль, может служить
так называемый дробный квантовый эффект Холла (см., например, [274]).

Глава 4
Магические комплексные числа
4.1.	Магическое число i
Как может существовать квадратный корень из —1? Квадрат положительного числа
всегда положителен, а квадрат отрицательного числа опять-таки положителен (а квадрат
нуля есть нуль, что сейчас для нас несущественно). Поэтому представляется невозможным
найти число, квадрат которого отрицателен. С такой ситуацией мы уже сталкивались, когда
обнаружили, что квадратный корень из 2 не существует в системе рациональных чисел.
В том случае проблема была разрешена путем расширения нашей системы рациональных
чисел до более обширной системы вещественных чисел. Возможно, такой прием сработает
и здесь.
И это действительно так. Фактически то, что нам предстоит сделать, намного проще
перехода от рациональных к вещественным числам. (Рафаэль Бомбелли проделал такую
процедуру в 1572 году в своей работе L’Algebra вслед за Джироламо Кардано, который
столкнулся с комплексными числами в 1545 году в работе Ars Magna.) Все, что нам нужно
сделать, — это ввести единственную величину, обозначаемую г, квадрат которой равен — 1,
и, присоединив ее к системе вещественных чисел, получить комбинации г с вещественными
числами в виде выражений типа
а 4- гб,
где а и b — произвольные вещественные числа. Всякая такая комбинация называется ком¬
плексным числом. Легко понять, как складывать комплексные числа:
(а + ib}4- (с 4- id) — (а + с) + i(b + d).
Полученное выражение имеет тот же вид, что и выше, только вместо а и b стоят веще¬
ственные числа а + с и Ъ + d. А как насчет умножения? Это почти так же просто. Найдем
произведение чисел а 4- ib и с + id. Просто перемножим эти сомножители, расписывая
полученное выражение по обычным правилам алгебры f41b
(а + ib)(c 4- id) — ас 4- ibc 4- aid 4- ibid = ас -f i(bc 4- ad) + i2bd.
Ho i2 — —1, поэтому можно переписать это в виде
(а 4- ib)(c 4- id) = (ас — bd) + i(bc -f- ad),
что опять-таки имеет первоначальную форму а 4- ib с заменой а на ас — bd, а b — на be 4- ad.
Достаточно легко найти разность двух комплексных чисел, но как быть с делением?
Напомним, что в обычной арифметике разрешается делить на любое вещественное число,
отличное от нуля. Попробуем разделить комплексное число а 4- ib на комплексное чис¬
ло с + id. Мы должны считать последнее отличным от нудя, это означает, что вещественные
числа с и d не могут одновременно быть равны нулю. Следовательно, с2 + d2 > 0, а зна¬
чит, с2 -f d2 ф 0, так что мы можем делить на с2 -yd2. Легко проверить* (умножая обе части
*$11 Сделайте это. (А можно ли это проверить другим способом, умножив обе части равенства на (с — id)1?)

4.1. Магическое число %
83
приведенного ниже выражения на с 4- id), что
(a + ib)
- ас ^ bd .Ъс — ad
(с 4- id) с2 -h d2 с2 4- с?2
Это выражение имеет тот же общий вид, что и выше, то есть это опять-таки комплексное
число.
Когда мы имеем дело с этими комплексными числами, мы рассматриваем числа а 4- ib
не как пары двух вещественных чисел а и 6, но как некий единый объект сам по себе,
который можно обозначить одной буквой z, т. е. z — а 4- ib. Можно проверить, что все обыч¬
ные правила алгебры выполняются для комплексных чисел.* Фактически всё это гораздо
проще, чем аналогичная проверка для вещественных чисел. (Для такой проверки мы долж¬
ны сначала убедиться, что правила алгебры выполняются для дробей, а затем использовать
«сечения» Дедекинда, чтобы показать, что правила выполняются также для вещественных
чисел.) С такой точки зрения представляется довольно странным то, что к комплексным
числам так долго относились с подозрением, тогда как гораздо более сложный переход от
рациональных чисел к вещественным со времен древних греков обычно принимался без
особых возражений.
Такие подозрения, возможно, были связаны с тем, что комплексные числа не прояв¬
ляются каким-либо видимым образом в физическом мире. В случае вещественных чисел
представлялось, что такие числа нужны для измерения расстояний, времени и других физи¬
ческих величин, тогда как комплексные числа казались просто плодом воображения матема¬
тиков, которым потребовались числа более общего характера, нежели те, которые они знали
раньше. Однако следует напомнить (см. § 3.3), что связь математических вещественных чи¬
сел с физическими понятиями расстояния и времени тоже не столь ясна, как казалось. Мы
не может непосредственно увидеть тонкие детали дедекиндова сечения; неясно также, дей¬
ствительно ли существуют в природе произвольно большие или произвольно малые времена
и расстояния. Можно сказать, что так называемые «вещественные числа» в такой же мере
являются плодом воображения математиков, что и комплексные числа. Вскоре мы увидим,
что комплексные числа, как и вещественные, а может быть, и в еще большей степени, об¬
наруживают поистине замечательное единство с природой. Это выглядит так, как если бы
сама природа была, как и мы, под впечатлением от общего и последовательного характера
системы комплексных чисел и поручила им описывать тонкие процессы в самых малых
масштабах. В главах 21-23 мы увидим подробнее, как это происходит.
Более того, указание на общность и согласованность системы комплексных чисел еще
не воздает ей должное в полной мере. На мой взгляд, в ней есть нечто большее, что можно
охарактеризовать как «магическое». В остальной части этой главы, а также в следующей
я постараюсь донести до читателя аромат этой магии. Далее, в главах 21-23, мы опять
станем свидетелями этой магии в ее наиболее впечатляющих и неожиданных проявлениях.
В течение тех четырех веков, когда были известны комплексные числа, их магические
свойства проявлялись постепенно. Сначала они ощущались лишь внутри самой математики,
создавая единство и глубину математического понимания, недостижимую при использова¬
нии одних лишь вещественных чисел. Не было никаких оснований ожидать, что физический
мир должен иметь к ним какое-то отношение. И в течение приблизительно 350 лет с тех
пор, как эти числа были введены работами Кардано и Бомбелли, магия комплексных чисел
проявлялась лишь в их чисто математической роли. Для всех тех, кто высказывал недоверие
в отношении комплексных чисел, несомненно, оказалось большим сюрпризом, что, соглас¬
но физике последних трех четвертей XX века, законы, управляющие миром в его наиболее
малых масштабах, определенно описываются системой комплексных чисел.
Проверьте это в отношении правил w 4 z = 2 + w, w 4 (и 4- z) = (w + и) + z, wz = zw, w(uz) =
= (wu)z, w(u + z) — wu + wz, w 4* 0 = w, w • 1 ~ w.

84
Глава 4
Эта тема станет центральной для нескольких последующих глав этой книги (в част¬
ности, глав 21-23, 26 и 31-33). Пока же мы сосредоточимся на математической магии
комплексных чисел, отложив их физическую магию на будущее. Напомним, что всё, что мы
сделали, — это потребовали, чтобы существовал квадратный корень из — 1 и чтобы сохраня¬
лись обычные правила арифметики. Мы убедились, что эти требования могут быть успешно
выполнены. Сделать это оказалось совсем просто. А теперь займемся магией!
4.2.	Решение уравнений с комплексными числами
Далее мне придется несколько чаще, чем прежде, прибегать к математическим выра¬
жениям. За это я заранее приношу извинения. Однако вряд ли можно изложить серьезные
математические идеи, не пользуясь математическими формулами. Я сознаю, что многим чи¬
тателям это не понравится. Мой совет таким читателям состоит в том, чтобы читать только
текст и не слишком огорчаться результатами попыток понять уравнения. Или, по крайней
мере, бегло просматривать формулы и читать дальше. В этой книге встречается ряд се¬
рьезных математических выражений, особенно в более поздних главах. По моему мнению,
некоторый уровень понимания в конце концов появится, даже если вы не будете пытаться
понять во всех подробностях, что же все эти выражения означают на самом деле. Поэтому
я надеюсь, в частности, что магия комплексных чисел будет оценена по достоинству. Ес¬
ли к тому же вы сумеете справиться с математическими обозначениями, будет, конечно, еще
лучше.
Прежде всего зададимся вопросом, существует ли квадратный корень из других чисел.
Например, что такое корень из —2? Это просто. Комплексное число i у/2, будучи возведенным
в квадрат, дает —2; то же относится и к —гл/2. Более того, для любого положительного
числа а комплексное число гл/а в квадрате дает —а, и то же относится к — г л/а. Здесь пока
никакой магии нет. Но как быть с комплексным числом общего вида а + ib (где а и b —
вещественные числа)? Оказывается, что комплексное число
; v \ (—а	л/а2 -h b2^j,
будучи возведенным в квадрат, дает а 4- ib (то же дает и число, имеющее обратный
знак)/ Таким образом, мы видим, что хотя мы добавили квадратный корень лишь для
одной величины (а именно —1), оказывается, что любое число получающейся при этом
системы теперь автоматически имеет квадратный корень! Это совершенно отлично от то¬
го, что мы видели при переходе от рациональных чисел к вещественным. Там введение
одной лишь величины л/2 в систему рациональных чисел почти ни к чему бы не при¬
вело.
Но это лишь самое начало. Мы можем задать вопрос относительно кубического корня,
корня пятой степени, корня 999-й степени и даже корня г-й степени. Мы найдем, что какое
бы комплексное число мы ни взяли и корень какой комплексной степени (за исключением 0)
из него ни извлекли, мы удивительным образом всегда получим в ответе комплексное число.
(Как мы вскоре увидим, такая задача обычно имеет несколько различных решений. Выше
мы отмечали, что при извлечении квадратного корня получаются два решения, поскольку
величина, отрицательная по отношению к квадратному корню из комплексного числа г,
также является квадратным корнем из z. У корней более высокой степени имеется больше
решений; см. §5.4.)
Пока что мы лишь царапали поверхность магии комплексных чисел. Всё, что утвержда¬
лось выше, действительно легко показать (пока мы не столкнемся с понятием логарифма
Проверьте это.

4.2. Решение уравнений с комплексными числами
85
комплексного числа, см. главу 5). Несколько более примечательна так называемая «основная
теорема алгебры», которая утверждает, что любое полиномиальное уравнение, такое как
1 — z.+	=	О
или
7Г + iz- V417z3 + г999 = 0,
% > *
!•
должно иметь решения в виде комплексных чисел. Более точно, всегда должно существовать
решение (обычно несколько различных решений) любого уравнения вида
а0 + a\Z + a^z2 + a^z3 4 h anzn = 0,
где ао, ai, аз, • • • , an — заданные комплексные числа, причем ап берется не равным
нулю^. (Здесь п может быть любым положительным целым числом, сколь угодно боль-
шим.) Для сравнения можно напомнить, что число г было введено, по существу, просто
для того, чтобы получить решение одного частного уравнения:
1 + 22-0.
Всё остальное мы получаем бесплатно!
Прежде чем идти дальше, следует упомянуть о проблеме, которой занимался Кар¬
дано с 1539 года, когда он впервые столкнулся с комплексными числами и обнаружил
намек на другой аспект присущих им магических свойств. Проблема, по существу, состоя¬
ла в том, чтобы найти общее решение (вещественного) кубического уравнения (с высшей
степенью п — 3). Кардано обнаружил, что простым преобразованием общее кубическое
уравнение можно привести к виду
х3 = 3рх + 2 q.
Здесь р и q — вещественные числа, и я возвращаюсь к использованию в этом уравнении х
вместо г, чтобы показать, что сейчас мы имеем дело с вещественными, а не с комплексными
решениями. Полное решение Кардано, опубликованное в 1545 году в его книге Ars Magna,
по-видимому, является развитием частного решения, которое он в 1539 году узнал от Никко¬
ло Фонтанны (Тартальи), хотя это частное решение было найдено еще раньше (до 1526 года)
Сципионом дель Ферро Решение (дель Ферро - )Кардано, записанное в современных
обозначениях, имеет следующий вид:
*
1 1
х — (я + w)3 4- (q — w)3,
где
i
w = (q2 — p3)2.
Заметим, что это уравнение не приводит к фундаментальной проблеме в рамках системы
вещественных чисел, если
q2 ^ р3.
В этом случае уравнение имеет одно вещественное решение относительно х, правильно
описываемое данной выше формулой (дель Ферро - )Кардано. Однако в так называемом
неприводимом случае хотя и существуют три вещественных решения, тем не менее форму¬
ла содержит квадратный корень из отрицательного числа q2 —р3? и поэтому нельзя обойтись
без связи с комплексными числами. Как показал позже Бомбелли (во второй главе своей кни¬
ги L ’Algebra, 1572), если позволить себе принять комплексные числа, то указанная формула

86
Глава 4
правильно описывает все три вещественных решения I4*4!. (Это имеет смысл, поскольку ука¬
занное выражение содержит сумму двух комплексных чисел, при этом части, содержащие г,
в этой сумме взаимно сокращаются, давая в ответе вещественное число.) t4*5! Загадочно
здесь вот что: несмотря на то что задача выглядит не имеющей отношения к комплексным
числам — уравнение имеет вещественные коэффициенты и все его решения вещественны
(в «неприводимом случае»), — приходится совершать путешествие через чужую территорию
мира комплексных чисел, чтобы наша формула позволила нам вернуться, имея чисто веще¬
ственные решения. Если бы мы ограничились прямой и узкой тропой вещественных чисел,
нам пришлось бы вернуться с пустыми руками. (По иронии судьбы, комплексные решения
исходного уравнения могут возникать лишь в тех случаях, когда формула не предполагает
такого проникновения в комплексную область.)
4.3.	Сходимость степенных рядов
Несмотря на столь замечательные результаты, мы пока це слишком углубились в магию
комплексных чисел. Пройти предстоит гораздо больше! Например, одна из областей, где
комплексные числа играют неоценимую роль, — это понимание поведения так называемых
степенных рядов. Степенной ряд — это бесконечная сумма вида
ао + а>\х + а2Х2 + а^х3 +
Поскольку сумма содержит бесконечное число членов, ряд может расходиться.
Это означает, что при добавлении всё новых членов сумма не стремится к какому-нибудь
конечному значению. Например, рассмотрим ряд
1 + х2 + х4 + х6 + Xs + • • •
(в котором	я	положил ао = 1, а\ =	0, ач = 1, аз = 0,	=	1,	а$ = 0, аб = 1,...).
Если взять	х	=	1, то, последовательно	добавляя члены, будем иметь
1,	1 + 1 = 2,	1 + 1 + 1 ==3,
1 + 1 + 1 + 1 =	4,	1	+ 1 + 1 + 1 + 1	=	5	и т.д.,
и мы видим, что у этого ряда нет шансов свестись к какому-либо конечному значению,
то есть он расходится. Еще хуже будет, если взять, например, х = 2, так как теперь от¬
дельные члены будут становиться еще больше, и последовательное добавление слагаемых
дает
1,	1	+	4	=	5,	1+4	+	16	=	21,	1	+	4+ 16 + 64 = 85 ит.д,
Л
что означает очевидную расходимость. С другой стороны, если положить, например, х =
будем иметь
1	1	I	1	—	5	i.l.	1	_	21	1,1,	1,1	w	„
4 ~ 4’	4	16	—	16’	41б	64	—	64	ИТ‘Д-
Эти числа оказываются всё ближе и ближе к предельному значению §, так что ряд теперь
сходится.
,	s
Имея эти ряды, нетрудно ощутить глубинную, в некотором смысле, причину того, что
ряд не может помочь в вычислениях и расходится при х = 1 и х = 2, но сходится при х =
4W

4.3. Сходимость СТЕПЕННЫХ РЯДОВ
87
4
3
выпишем
.8
(1
,2)
-1
О 1, то есть «бесконечность»f4-6^,
При подстановке х = 1 мы получаем в ответе (l — 12)
и это позволяет понять, почему ряд должен расходиться при этом значении х. Если же под-
-1
ставить х — i то ответом будет
. Z
1-1
4
4
даваемый явной формулой, (1 — 4.)
-, и ряд действительно сходится к указанному
О
определенному значению, как и было установлено выше.
Всё это выглядит вполне разумно. Но как быть с х = 2? Хотя существует «ответ»,
-11
трудно представить, как можно его получить,
О
просто складывая члены ряда. Мы едва ли могли получить такой ответ, поскольку склады-
1
вали положительные числа, тогда как число — ~ отрицательно. Причина, по которой ряд
О
расходится, состоит в том, что при х = 2 каждый член существенно больше соответствую¬
щего члена при х — 1, так что расходимость при х = 2 логически следует из расходимости
при х = 1. В случае х — 2 расходимость проявляется не в том, что «ответ» получается
бесконечным, а в том, что мы не можем получить его, пытаясь непосредственно просумми¬
ровать ряд. На рис. 4.1 показаны частичные суммы ряда (т. е. суммы некоторого конечного
числа членов), вплоть до четырех членов вместе с «ответом» (l — х2)	. Если х лежит
строго между —1 и	то	кривые, изображающие соответствующие частичные суммы,
действительно сходятся к этому ответу, а именно (1 — х2)	, как мы и ожидали. Однако вне
этой области ряд просто расходится и вообще не достигает какого-либо конечного значения.
Область,
не описываемая
рядом
Рис. 4.1. Частичные суммы 1,1 + x'zy 1 -f х2 + ж4,1 4- хг -f а;4 + х6 (показаны пунктирными линиями)
ряда для (1 — х2) 1. Видна сходимость ряда к (1 — X2) при |сс| < 1 и расходимость при jx| > 1
Сделаем небольшое отступление, которое окажется нам полезным в дальнейшем. Зада
димся следующим вопросом: имеет ли какой-нибудь смысл то равенство, которое мы полу¬
чаем, полагая в вышеприведенном выражении х = 2, а именно:
1 + 2Z + 2“ + 26 + 2° +
,8
(1 - 22) 1
1?
3'
Попробуйте проверить это выражение формальным алгебраическим способом.

88
Глава 4
Великий математик XVIII века Леонард Эйлер часто писал выражения, подобные этому,
и стало модным подшучивать над ним за склонность к подобному абсурду, однако его
можно извинить на том основании, что в его время еще не было должного представления
о сходимости рядов и тому подобном. Строгая математическая трактовка рядов появилась
не ранее конца XVIII-начала XIX века в работах Огюста Коши и других авторов. Согласно
этой строгой трактовке, подобные выражения должны быть классифицированы как «бес¬
смысленные». Однако, я полагаю, следует отметить, что в определенном смысле Эйлер
в действительности знал, что делал, выписывая кажущиеся абсурдными выражения тако¬
го рода, и что существует смысл, в котором такие выражения можно рассматривать как
«правильные».
Математика требует абсолютной ясности, при которой соотношения имеют строгий
и точный смысл. Однако не менее важно, чтобы она была достаточно восприимчива к «про¬
исходящему за сценой», поскольку это в конечном счете может привести к более глубокому
пониманию. Многое можно потерять из виду, если слишком жестко следовать лишь тому,
что представляется строго логическим, например, тому факту, что 1 + 4 + 16 + 64 + 256 +
1
+ • • • не может быть равно — -г. В качестве подходящего примера напомним о логической
О
абсурдности поисков вещественного решения уравнения х2 +1 == 0. Такого решения нет, од¬
нако если бы мы оставили поиски, то потеряли бы то глубокое понимание, которое пришло
благодаря введению комплексных чисел. Подобное замечание относится и к абсурдности
рационального решения уравнения х2 — 2. Фактически вполне возможно придать математи¬
ческий смысл ответу — | в рассмотренном случае бесконечных рядов, но нужно внимательно
относиться к тому, что разрешают и что запрещают правила. В мои цели не входит подроб¬
но обсуждать здесь такие вопросы^, однако можно отметить, что в современной физике,
особенно в области квантовой теории поля, расходящиеся ряды такой природы часто встре¬
чаются (см., например, §§ 26.7,26.9,31.13). Это очень деликатная проблема — решить, имеют
ли смысл получаемые таким путем «ответы», и тем более правильны ли они. Иногда весьма
►
точные результаты действительно получаются путем манипуляций с подобными расходящи¬
мися выражениями и иногда они поразительным образом подтверждаются при сравнении
с реальным экспериментом. С другой стороны, так везет не всегда. Эта деликатная тема иг¬
рает важную роль в современных физических теориях и имеет прямое отношение к нашим
попыткам проникнуть в них. В данный момент непосредственный интерес представляет
тот факт, что «смысл», который можно приписать внешне бессмысленным выражениям,
зачастую существенным образом зависит от свойств комплексных чисел.
Вернемся теперь к рассуждениям о сходимости рядов и попытаемся понять, как укла¬
дываются в эту картину комплексные числа. Для этого рассмотрим функцию, мало отлича¬
ющуюся от (1 — х2)	,	а именно (1 + х2)	, и посмотрим, имеет ли смысл ее разложение
в степенной ряд. Видно, что теперь шансы на полную сходимость выше, поскольку функ¬
ция (l + х2) 1 остается гладкой и конечной во всей области вещественных чисел. Дей¬
ствительно, для (1 + х2) 1 мы имеем простой степенной ряд, лишь немного отличающийся
от предыдущего:
1 — х2 + ж4 — х6 + х8 — * — = (1 + гс2) 1;
разница лишь в изменении знака при чередовании членов ряда.* На рис. 4.2 я аналогич¬
но прежнему изобразил частичные суммы этого ряда, вплоть до 5 членов, вместе с отве¬
том (1 + х2) 1, Что здесь кажется удивительным, так это тот факт, что частичные суммы
по-прежнему сходятся к ответу лишь в области между —1 и +1 (без концов). Вне этой
области мы имеем расходимость, хотя ответ, в отличие от нашего предыдущего случая,
* йЭ Укажите элементарную причину такого простого соотношения между двумя рядами.

4.4. Комплексная плоскость Каспара Весселя
89
Рис. 4.2. Частичные суммы 1,1 — х2,1 — х2 + х4,1 — х2 + х4 — х6,1 — xz 4- х
для (1 Н- ж2) показаны пунктиром. Здесь опять-таки имеет место сходимость при
- х6 + х8 ряда
х\ < 1 и расхо-
каких-либо особенностей пои х = ±1
вовсе не стремится к бесконечности. Мы можем проверить это явно, взяв те же три значе¬
ния х ~ 1, х = 2, х = Мы увидим, что, как и прежде, сходимость имеет место только
2
1
в случае х — где ответ для суммы всего ряда стремится к правильному предельному
значению
4.
5'
х
X
1 :	1,	0, 1, 0, 1, 0, 1 и т.д.
2 :	1,	—3, 13, -51, 205, -819 ит.д
= ! • 1 3 13 51 205 _819_
2 ‘	4’	16’	64’	256’	1024
и т.д..
Отметим, что в первом случае «расходимость» выражается в том, что частичные суммы
ряда не сходятся к какому-либо определенному пределу, хотя и не стремятся к бесконеч¬
ности.
Таким образом, в рамках одних лишь вещественных чисел остается загадочным несоот¬
ветствие между результатами непосредственного суммирования ряда и прямым переходом
к «ответу», который, как предполагается, представляет сумму бесконечного ряда. Частич¬
ные суммы просто «отрываются» от него вверх и вниз, причем на том же самом месте
(а именно при х — ±1), на котором возникали проблемы в предыдущем случае, хотя теперь
предполагаемый результат для бесконечной суммы (1 + ж2) вовсе не содержит на этом
месте сколько-нибудь заметных особенностей. Разгадка этой тайны будет найдена, если
мы не ограничимся вещественными значениями этой функции, а рассмотрим ее комплекс¬
ные значения.
4.4.	Комплексная плоскость Каспара Весселя
Чтобы понять, в чем тут дело, следует воспользоваться нестандартным геометрическим
представлением комплексных чисел на евклидовой плоскости. Каспар Вессель в 1797 году,
Жан Робер Арган в 1806 году, Джон Уоррен в 1828 году и Карл Фридрих Гаусс во всяком
случае раньше 1831 года независимо пришли к идее комплексной плоскости (см. рис. 4.3),
с помощью которой они дали ясную геометрическую интерпретацию действий сложения
и умножения комплексных чисел. На рис. 4.3 я пользуюсь стандартными декартовыми ося¬
ми, при этом ось х направлена по горизонтали вправо, а ось у — по вертикали вверх.

90
Глава 4
-2
-1+2 г
-1+2
1
1 ~г
Мнимая ось
А
Зг
2г
У
1+22
1+г
0
—г
1
1-2
z~x+ iy
2+2
2
2-2
3+2
X
3
3-2
Вещественная
ось
Рис. 4.3. Комплексная плоскость £ = х + iy. В декартовых координатах (х, у) ось х, направленная
по горизонтали вправо, представляет вещественную ось; ось у, направленная по вертикали вверх, —
мнимую ось
Комплексное число
z — х iy
изображается на этой плоскости точкой с декартовыми координатами (я, у).
Будем теперь рассматривать вещественное число х как частный случай комплексного
числа 2 — х + iy, у которого у = 0. Тогда мы можем считать, что ось х на нашей диаграмме
представляет собой вещественную прямую (т. е. множество вещественных чисел, линейно
упорядоченное вдоль прямой линии). Таким образом, комплексная плоскость дает нам на¬
глядное представление о том, как система вещественных чисел расширяется вовне и дает
полную систему комплексных чисел. Вещественную прямую часто называют «веществен¬
ной осью» на комплексной плоскости. Соответственно ось у называют «мнимой осью». Она
состоит из всех вещественных чисел, умноженных на г.
Теперь вернемся к нашим двум функциям, которые мы пытались представить в виде
степенных рядов. Тогда мы считали их функциями вещественной переменной я, а имен¬
но
(1
х
)
-1
и (1 + х2)	.	Теперь	мы	расширим	эти	функции,	применив	их	к	комплексной
переменной Здесь нет никакой проблемы: мы просто запишем наши расширенные функ¬
ции в виде соответственно (1
-1
)
и (1 + 22) \ В случае первой вещественной функ¬
ции, (1 — х2) \ было легко узнать, где начнутся проблемы с «расходимостью», посколь¬
ку эта функция сингулярна (то есть обращается в бесконечность) в двух местах, х = — 1
и х — +1. Но в случае функции (1 + х2) мы не видим в этих местах сингулярности,
и никаких вещественных сингулярностей нет вовсе. Однако в отношении комплексной пе¬
ременной z эти две функции гораздо более равноправны. Отметим сингулярности функ¬
ции (1
2\-i
)
в двух точках 2 = ±1, на единичном расстоянии от начала координат вдоль
вещественной оси. Но теперь мы видим, что (1 + z2) 1
местах 2 = ±г (поскольку тогда 1 + z2 =
от начала координат на мнимой оси.
также имеет сингулярности в двух
0), — это будут две точки на единичном расстоянии

4.4. Комплексная плоскость Каспара Весселя
91
Но какое отношение имеют эти комплексные сингулярности к вопросу о сходимости
или расходимости соответствующих степенных рядов? Ответ на этот вопрос будет пора¬
зительным. Сейчас мы рассматриваем наши степенные ряды как функции комплексной
переменной z (а не вещественной переменной х) и можем поставить вопрос о тех местах
на комплексной плоскости, где ряд сходится, и тех, где он расходится. Существует замеча¬
тельный общий ответ для всякого степенного ряда вида
ао + oi £ + a2z2 + азг3 +
# # ♦
существует некоторый круг в комплексной плоскости с центром в начале координат, на¬
зываемый кругом сходимости, который обладает следующим свойством: если комплексное
число z лежит строго внутри круга, то при таких значениях z ряд сходится, если же z лежит
строго вне круга, то ряд расходится. (Сходится или расходится ряд, когда 2 лежит точно
на окружности, — это довольно тонкий вопрос, которого мы здесь не будем касаться, хотя
он и имеет отношение к теме §§ 9.6, 9.7.) В это утверждение я включаю два предельных слу¬
чая: когда ряд расходится при всех отличных от нуля значениях з, то есть круг сходимости
сжимается до нулевого радиуса, и когда он сходится при всех z9 то есть круг расширяется до
бесконечного радиуса. Чтобы выяснить, каков на самом деле круг сходимости для данной
функции, мы должны узнать, как расположены сингулярности данной функции в комплекс¬
ной плоскости, и нарисовать наибольший круг с центром в начале координат z — 0, который
не содержал бы внутри себя сингулярностей (т. е. мы должны провести окружность через
сингулярность, ближайшую к началу координат).
В только что рассмотренных частных случаях (1 — z2) 1 и (l + z2) 1 мы имеем син¬
гулярности простого типа, называемые полюсами (они возникают, когда обратная величина
от некоторого многочлена обращается в нуль). Здесь все полюсы лежат на единичном рас¬
стоянии от начала координат, и мы видим, что кругом сходимости в обоих случаях является
-1
jdr а	»
/. Полюсы.
для
.	.	(Л 2ч-1
(1-Z )
-1
>
\
1
для - :J
: (1+zy.v
—г
Рис. 4.4. В комплексной плоскости функции (l — z2) 1 и (l + z2) 1 имеют один и тот же круг
сходимости. В первом случае полюсы расположены при z — ±1, во втором — при z = все они
находятся на одном и том же (единичном) расстоянии от начала координат

92
Глава 4
как раз круг единичного радиуса вокруг начала координат. Места, где ограничивающая его
окружность встречается с вещественной осью, в обоих случаях одни и те же, а именно две
точки z = =Ы (см. рис. 4.4). Это объясняет, почему эти две функции сходятся и расходятся
в одних и тех же областях, — факт, который не следует непосредственно из их свойств как
функций вещественной переменной. Таким образом, комплексные числа дают нам глубо¬
кое понимание поведения степенных рядов, недоступное, если рассматривать их структуру
при вещественных значениях переменной.
4.5.	Как построить множество Мандельброта
В заключение этой главы рассмотрим другой тип сходимости/расходимости. Он лежит
в основе построения необычной конфигурации, описанной в § 1.3, изображенной на рис. 1.2
и известной под названием множества Мандельброта. Фактически это есть подмноже¬
ство комплексной плоскости Весселя, которое можно определить способом, удивительно
простым, если учесть крайнюю сложность этого множества. Всё, что нам нужно, — это рас¬
смотреть последовательное применение замены
Z Z2 + с,
где с — некоторое заданное комплексное число. Мы будем рассматривать с как точку на ком¬
плексной плоскости и начнем с z = 0. Затем мы будем итерировать это преобразование
(т. е. последовательно проводить его снова и снова) и следить за поведением точки z на плос¬
кости. Если она уходит на бесконечность, мы окрашиваем соответствующую точку с в белый
цвет, если же она блуждает в некоторой ограниченной области, не уходя на бесконечность,
окрасим точку с в черный цвет. Черная область и дает нам множество Мандельброта.
Опишем эту процедуру чуть более подробно. Как проводятся итерации? Сначала мы
фиксируем с. Затем мы берем некоторую точку z и применяем к ней преобразование, так
что с превращается в z2 + с. Затем, применяя его снова, заменяем 0 в z2 + с на г2 + с
и получаем {г2 -}-с)2 ■+ с. Далее заменяем г в z2 -f с на (z2 + с)^ + с, так что наше вы¬
ражение принимает вид ^(z2 + cf + cj + с. Заменяя г в z2 + с на 4* с)2 -f cj + с,
2
2
получаем [z* + с) + сJ + сJ + с и так далее.
Посмотрим, что получится, если мы стартуем из точки z = 0 и проводим итерации
указанным путем. (Для этого достаточно просто положить в полученных выражениях г = 0.)
Мы получаем последовательность
0, с, с2 + с, (с2'+ с)2 + с, ((с2 + с)2 + с) -he,...,
Она задает нам ряд точек на комплексной плоскости. (С помощью компьютера можно про¬
делать эту работу в численном виде для каждого отдельного выбора точки с, не прибегая
к приведенным алгебраическим выражениям. В вычислительном отношении гораздо «деше¬
вле» каждый раз проводить расчет заново.) При любом заданном значении с возможно одно
из двух: 1) либо точки последовательности постепенно уходят всё дальше и дальше от нача¬
ла координат, то есть последовательность является неограниченной, 2) либо каждая из точек
лежит в пределах некоторого фиксированного расстояния от начала координат (т. е. внутри
некоторого круга на комплексной плоскости с центром в начале координат), в этом случае
мы имеем ограниченную последовательность. Белые области на рис. 1.2,а соответствуют
тем значениям с, которые дают неограниченную последовательность (1), а черные — по¬
ложения точек с, соответствующих ограниченной последовательности (2); само множество
Мандельброта включает всю черную область 14101.

4.5. Как построить множество Мандельброта
93
Сложность множества Мандельброта обусловлена тем фактом, что существует мно¬
го различных, и зачастую весьма запутанных, вариантов, при которых итерированная по¬
следовательность может оставаться ограниченной. Можно придумать комбинации циклов
и «почти циклов» разного рода, заполняющих плоскость различными запутанными спосо¬
бами, но нас завело бы слишком далеко, если бы мы попытались понять во всех подроб¬
ностях, как возникает необычная сложность этого множества, включая сложные вопросы
комплексного анализа и теории чисел. Интересующийся читатель может обратиться к кни¬
гам [578, 579] за дальнейшей информацией и к работе [217], которая содержит рисунки.
Примечания
§4.1.
4.1. По поводу этих правил см. упражнение 4.2.
§4.2.
4.2. Это есть непосредственное следствие того, что комплексный многочлен от одной переменной £
ч.
разлагается на линейные множители
ао + a±z + a2Z2 Н Ь anzn = an(z - bi)(z - 62) * • • (z - bn);
именно это утверждение обычно называют «основной теоремой алгебры».
4.3. Как говорят, Тарталья познакомил Кардано со своим частным решением только после того, как
Кардано поклялся сохранить его в тайне. Поэтому Кардано не мог опубликовать свое более
общее решение, не нарушая данного обещания. Однако во время своей последующей поездки
в Болонью в 1543 году Кардано узнал о посмертных работах дель Ферро и признал его при¬
оритет. Он решил, что это освобождает его, и опубликовал все свои результаты в Ars Magna
в 1545 году. Тарталья с этим не согласился, и их полемика имела весьма неприятные последствия
(см. [855]).
4.4. Более подробную информацию можно найти в книге Ван-дер-Вардена [799].
4.5. Причина состоит в том, что мы складываем два числа, которые являются комплексно¬
сопряженными по отношению друг к другу (см. § 10.1), и такая сумма всегда является ве¬
щественным числом.
§4.3.
4.6. Напомним, что, согласно примечанию 2.4, О”1 означает т. е. это есть «единица, деленная на
нуль». Это удобное краткое представление «результата» недозволенной операции «0 1 = оо».
4.7. «Строго» означает, что значения на концах области не включаются в нее.
4.8. Более подробную информацию можно найти в книге Харди [354].
§4.4.
4.9. См., например, [648], стр. 71 (там говорится о «радиусе сходимости») и [544], стр. 67, 264.
§4.5.
4.10.	При построении картин множества Мандельброта (подобных рис. 1.2) с помощью компьютера
невозможно, конечно, вычислять бесконечно, чтобы убедиться, что последовательность, кажу¬
щаяся ограниченной, действительно является таковой. Обычно «обрывают» итерацию на неко¬
тором достаточно большом числе шагов. Простое увеличение числа шагов, однако, не всегда
улучшает точность картины, поскольку нити могут сливаться и теряться.
Покажите это. (Подсказка: Покажите, что при делении этого многочлена на. z — b не получается остатка
всякий раз, когда z ~ Ь является решением этого уравнения.)

Глава 5
Геометрия логарифмов, степеней и корней
5.1.	Геометрия комплексной алгебры
/
Аспекты магии комплексных чисел, изложенные в конце предыдущей главы, содер¬
жат много тонкостей, поэтому вернемся немного назад и взглянем на некоторые более
элементарные, хотя и столь же загадочные и важные, стороны этой магии. Прежде всего
посмотрим, как представить геометрически на комплексной плоскости те правила сложения
и умножения, с которыми мы столкнулись в §4.1. Можно сформулировать их соответствен¬
но как правило параллелограмма и правило подобных треугольников, иллюстрированные на
рис. 5.1 а, б. Для двух произвольных комплексных чисел w и z точки, представляющие w + z
и wz, определяются следующим образом:
точки 0, w, w + z, z являются вершинами параллелограмма
и
/
треугольники с вершинами 0, 1, w и 0, z, wz подобны.
Рис. 5.1. Геометрическое представление основных правил алгебры комплексных чисел, а) Правило
параллелограмма для сложения: точки 0, w9 w -f zt z служат вершинами параллелограмма, б) Правило
подобных треугольников для умножения: треугольники с вершинами 0, 1, w и 0, z, wz подобны
(Здесь приняты обычные соглашения относительно порядка и ориентации. Так, пред¬
полагается, что мы обходим параллелограмм циклически, так что отрезок прямой от w
до w + z параллелен отрезку от 0 до z и т. д., а также что подобие двух треугольников
не предполагает какого-либо «отражения». Существуют особые случаи, когда треугольники
или параллелограмм вырождаются тем или иным способом*.) Заинтересовавшийся читатель
может проверить эти правила с помощью тригонометрии и путем непосредственного вы-
jjt
числения . Существует, однако, другой способ, который не требует подробного расчета
и дает лучшее понимание.
* Рассмотрите различные возможные случаи.
** ЛЭ Проделайте это.

5.1. Геометрия комплексной алгебры
95
Будем рассматривать сложение и умножение как некоторые отображения (или преоб¬
разования), которые переводят всю комплексную плоскость в самое себя. Любое заданное
комплексное число w определяет «отображение сложения» и «отображение умножения»
как такие операции, которые, будучи применены к произвольному комплексному числу z9
соответственно прибавляют w к z и дают произведение w на z9 то есть
WZ.
Легко видеть, что отображение сложения просто сдвигает комплексную плоскость без вра¬
щения или изменения размера либо формы — это пример трансляции (см. §2.1), — смещая
начало координат 0 в точку w (см. рис. 5.2 а). Правило параллелограмма есть лишь дру¬
гая формулировка этого факта. А как насчет отображения умножения? Оно представляет
преобразование, которое оставляет начало координат фиксированным и сохраняет форму,
сдвигая 1 в точку w. В общем случае оно является комбинацией поворота (без отражения)
и однородного растяжения (или сжатия) (см. рис. 5.2 б). Правило подобных треугольников
выражает именно это. Это отображение будет иметь для нас особое значение в § 8.2.
А
z+w
WZ
1
W
1
(б)	*
Рис. 5.2. а) Отображение сложения «-Ии» производит трансляцию комплексной плоскости, сдвигая О
в точку w, 6) Отображение умножения «хю» производит поворот комплексной плоскости вокруг О
с растяжением (или сжатием), переводя 1 в w
В частном случае w = г отображение умножения представляет собой просто правый
7Г
. Если повторить эту опера-
(т. е, против часовой стрелки) поворот на прямой угол .
цию дважды, получится поворот на 7г, что есть просто отражение в начале координат;
другими словами, именно отображение умножения превращает каждое комплексное число
в противоположное ему по знаку. Это дает нам графическую иллюстрацию «загадочного»
соотношения г2 = — 1 (рис. 5.3). Операция умножения на г реализуется как геометрическое
преобразование в виде поворота на прямой угол. При таком подходе уже не кажется таким
загадочным то, что «квадрат» этой операции (т. е. операция, повторенная дважды) приводит
к тому же результату, что и изменение знака на противоположный. Это, конечно, не раз¬
рушает магии и загадки: почему комплексная алгебра работает так хорошо? Как ничего не
говорит нам о физической роли этих чисел. Можно, например, спросить: почему поворот
происходит только в одной плоскости, как насчет трех измерений? Я обращусь к различ¬
ным сторонам этих вопросов позже, в частности, в §§ 11.2, 11.3, 18.5, 21.6, 21.9, 22.2, 22.3,
22.8-22.10,33.2,34.8.
В нашем описании комплексной плоскости мы пользовались стандартными декарто¬
выми координатами точки на плоскости (х9у)9 но можно использовать и полярные коорди¬
наты [г, 9]. В этом случае положительное вещественное число г определяет расстояние от
Попробуйте показать это без подробных вычислений и без тригонометрии. (Подсказка: это есть следствие
«закона дистрибутивности» w(z± -j- Z2) = wz\ + WZ2, который показывает, что сохраняется «линейная» структура
комплексной плоскости, и равенства w(iz) — i(wz), которое показывает, что сохраняются прямые углы.)

96
Глава 5
-1
Рис. 5.3. Операция умножения на г реализуется в комплексной плоскости как геометрическое преоб¬
разование поворота на прямой угол. Это делает наглядным «загадочное» соотношение г2 = — 1
начала координат, а угол в — угол, образуемый прямой, проведенной из начала координат
в точку г, с вещественной осью, отсчитываемой против часовой стрелки (см. рис. 5.4а).
Величина г называется модулем комплексного числа г, что иногда записывается так:
г
а в — его аргументом (в квантовой теории в иногда называют фазой). При z — 0 нам
не нужно думать об аргументе 0, но мы по-прежнему определяем г как расстояние от начала
координат, что в данном случае дает просто г = 0.
а)
б)
Рис. 5.4. а) Переход от декартовых координат (х, у) к полярным [г, 0], где модуль г — \z\ есть рас-
стояние от начала координат, а аргумент 9 — угол, который прямая, проведенная из начала координат
в точку z, образует с вещественной осью (отсчитывается против часовой стрелки), б) Если мы не
настаиваем на условии — п < в ^ тг, мы можем позволить точке z много раз обходить вокруг начала
координат, добавляя к 9 произвольный угол, кратный 2д-
Для определенности мы можем предположить, что в меняется в ограниченной области,
например, — ж < в < 7г (это обычное соглашение). Вместо этого можно рассматривать
неоднозначный аргумент, к которому можно добавлять ни на что не влияющие слагаемые,
кратные 27г. Это позволяет нам при измерении угла обходить вокруг начала координат
любое число раз в любом направлении (см. рис. 5.46). (Вторая точка зрения является более

5.2. Идея комплексного логарифма
97
дальновидной, в чем мы скоро убедимся.) Из рис. 5.5
и элементарной тригонометрии следует
х = г cos в, у = г sin #
и, наоборот,
?/—rsin#
/	^7
г = уж2 + I/2? # = arctg # >
где 0 — arctg (у/ж) означает некоторое частное значе¬
ние многозначной функции arctg. (Для тех читателей,
которые успели забыть всю тригонометрию: первые
две формулы как раз являются определением синуса и
x—rcosO
Рис. 5.5. Связь между декартовой и
полярной формами комплексного чис¬
ла: х = г cos 0 и у — г sin в и наобо-
косинуса угла в прямоугольном треугольнике, а имен- рот: г	+	у2 ~ arctg(у/х)
но: «косинус угла равен отношению прилежащего ка¬
тета к гипотенузе» и «синус угла равен отношению
противолежащего катета к гипотенузе», гипотенуза здесь равна г; две следующие формулы
выражают теорему Пифагора и в обращенной форме определение: «тангенс утла равен отно¬
шению противолежащего катета к прилежащему». Отметим также, что arctg есть обратная
функция по отношению к tg, так что вышеприведенное соотношение 0 = arctg (у/х) озна¬
чает tg9 = у/х. Функция arctg неоднозначна, так что при добавлении к в любого угла,
кратного 27г, это соотношение по-прежнему выполняется.^51!
5.2.	Идея комплексного логарифма
«Правило подобных треугольников» для перемножения двух комплексных чисел, изоб¬
раженное на рис. 5.1 б, можно переформулировать с учетом того факта, что при перемноже¬
нии двух комплексных чисел их аргументы складываются, а модули перемножаются*. Отме¬
тим здесь замечательное следствие правила для аргументов: умножение превращается в ело-
• %
жение. Этот факт лежит в основе использования логарифмов (логарифм произведения двух
чисел равен сумме их логарифмов, log ab = log а 4- log 6), иллюстрацией чего может служить
логарифмическая счетная линейка (рис. 5.6); это свойство имело фундаментальное значение
для вычислительной практики в прежние времена^5*2!. Сейчас для умножения мы используем
/ . •
электронные калькуляторы. Хотя это намного быстрее и гораздо точнее, чем при использо¬
вании логарифмической линейки или таблиц логарифмов, мы теряем при этом нечто очень
существенное для нашего понимания, поскольку не имеем непосредственного опыта в обра¬
щении с логарифмами. Мы увидим, что логарифмы играют огромную роль именно в связи с
комплексными числами. Действительно, аргумент комплексного числа является логарифмом
во вполне определенном смысле. Мы постараемся понять, как это получается.
Напомним сделанное в § 4.2 утверждение, что извлечение корня из комплексных чисел
закладывает основу для понимания комплексных логарифмов. Мы увидим, что существуют
замечательные соотношения между комплексными логарифмами и тригонометрией. Попы¬
таемся увидеть, как всё это работает вместе.
Сначала напомним кое-что об обычных логарифмах. Логарифм — это действие, обрат¬
ное возведению числа в степень. «Возведение в степень» есть операция, преобразующая
сложение в умножение. Почему это так? Возьмем некоторое число Ь (отличное от нуля).
Теперь напишем формулу (превращающую сложение в умножение)
Ьш+п = ЬтхЬ
п
Проверьте это.

98
Глава 5
1	2	3	456789	10
Рис. 5.6. На логарифмической линейке числа сдвигаются на логарифмической шкале, что позволяет
заменять умножение сложением расстояний в соответствии с формулой logb(p х q) '= log6 р + logb q.
(Иллюстрируется умножение на 2.)
которая очевидна, если тип — положительные целые числа, поскольку обе стороны ее
содержат т + п множителей 6. Нам нужно найти способ обобщить эту формулу так, что¬
бы числа шипне были обязаны быть целыми положительными, а могли быть любыми
комплексными числами. Для этого мы должны найти правильное определение для опера-
ции возведения числа 6 в комплексную степень z9 причем так, чтобы сохранялась прежняя
формула, то есть bw+z = bw х bz, где показатели w и z — комплексные числа.
Такая процедура фактически отражает в некотором отношении всю историю обобще¬
ния, шаг за шагом, понятия числа от положительных целых чисел до комплексных чисел,
которое было проведено, начиная с Пифагора и работ Евдокса и Брамагупты до Кардано
и Бомбелли и далее (см. §§3.4, 4.1). Вначале запись bz (где z есть целое положительное
число) понималась просто как b х Ъ х • • • х 6, где число сомножителей b равно z\ в частно¬
сти, Ъ1 = Ь. Затем, следуя указаниям Брамагупты, мы позволяем числу z принимать нулевое
значение, понимая, что для сохранения формулы bw+z = bw х bz мы должны ввести опре¬
деление 6° = 1. Далее мы позволяем числу z становиться отрицательным, учитывая, по той
же причине, что для случая z = — 1 мы должны определить Ь~1 как величину, обратную Ь
(т. е. 1/6), и что величина 6“п при натуральном п должна быть n-й степенью числа 6-1. За¬
тем мы попробуем обобщить все это на случай дробного числа z9 начиная со случая z — 1 /п,
где п — положительное целое число. Повторное использование формулы bw х bz = bw+z
приводит нас к выводу, что (bz)n — bzn. Полагая z = 1/п, обнаруживаем, что Ъг^п есть
корень n-й степени из 6.
Всё это можно проделывать, оставаясь в мире вещественных чисел, если считать чис¬
ло 6 положительным. Мы можем считать 6единственным положительным корнем п-й
степени из 6 (где п — положительное целое число) и, продолжая, однозначно определить bz
для любого рационального числа z — т/п как m-ю степень корня n-й степени из 6, а затем
(используя предельный процесс) для любого вещественного числа г. Однако если позво-
*
лить числу 6 быть отрицательным, то при 0 = ~ мы натыкаемся на препятствие, поскольку
тогда у/b требует введения г, и мы скатываемся в область комплексных чисел. Там мы обна¬
руживаем наш магический комплексный мир, поэтому приободримся и пройдем весь путь
до конца.
Нам требуется определить Ьр таким образом, чтобы для всех комплексных чисел р9 q
и 6 (6 ф 0) мы имели
\?+q = ff xbq.
- * ,
Тогда мы можем надеяться определить логарифм по основанию b (эта операция обозначается
так: «logb») как обратную функцию по отношению к f(z) = bz9 то есть
z — log6 гг, если w = bz

5.3. Многозначность, натуральные логарифмы
99
Тогда можно ожидать, что
log ь(рх я) = log Р + logb я,
так что понятие логарифма действительно позволяет преобразовать умножение в сложение
5.3.	Многозначность, натуральные логарифмы
Хотя всё это в основном верно, при работе с этим возникают некоторые технические
трудности (сейчас мы вкратце разберем, как обращаться с ними). Прежде всего, функция bz
многозначна. Это означает, что в общем случае имеется много различных ответов на вопрос,
что такое bz. Аддитивная многозначность имеет место также в отношении log6 w. Мы уже
1
сталкивались с многозначностью bz в случае дробных значений г. Например, если z —
то bz следует понимать как «некоторую величину £, квадрат которой равен 6», поскольку
1 1 11
мы требуем, чтобы выполнялись равенства t2 = t х t — b2 X b2 = b2 2 — bl — 6. Если
некоторое число t удовлетворяет этому требованию, то число —Ь также будет удовлетворять
ему (поскольку (—t) х (—t) — t2 — b). Предполагая b ф 0, мы получаем два разных ответа
I
(записываемых обычно в виде ±Vo). В более общем случае для Ьп, где п есть положительное
целое число: 1, 2, 3, 4, 5,..., мы имеем п различных комплексных ответов. Фактически мы
получаем некоторое конечное число ответов всякий раз, когда п есть рациональное число
(отличное от нуля). Если п — иррациональное число, то, как мы вскоре увидим, получается
бесконечное число ответов.
Попытаемся понять, как можно справиться с такой неоднозначностью. Начнем с того,
что выберем для Ъ некоторое определенное значение, а именно фундаментальное число е,
называемое основанием натуральных логарифмов. В качестве его определения возьмем со¬
отношение
е = 1 + “ + — +	+	— 2,7182818285...,
где восклицательные знаки означают факториалы, т. е.
п! = 1х2хЗх4х-**хп,
так что 1! = 1, 2! = 2, 3! = 6, и т.д. Функция f(z) = ez называется экспоненциальной
функцией и иногда записывается в виде ехр, так что exp(z) означает «е в степени z»9
эта «степень» определяется следующей модификацией вышеприведенного ряда для е:
9	Ъ	4
'У'"	'У	У
е* = 1 + П + 2! + 3! + 4! " ' •
Этот важный степенной ряд сходится при всех значениях z (то есть он имеет бесконечный
круг сходимости, см. § 4.4). Эта бесконечная сумма делает определенный выбор в условиях
1
неоднозначности величины bz при Ь = е. Например, при z = - этот ряд определяет по-
1
ложительную величину +д/е, а не —л/ё. То, что при z = ~ получается число е2, квадрат
которого равен е, следует из того факта, что функция ezy определенная этим рядом , всегда
обладает требуемым свойством «перевода сложения в умножение»:
еа+6 = еаеЪ^
1 11 11
так что (е2)2 == е2е2 ~ е2 2 — е1 = е.
*т Проверьте это непосредственно с помощью ряда. (Подсказка: «Биномиальная теорема» для целых пока¬
зателей утверждает, что коэффициент при apbq в разложении бинома (а + Ь)п имеет вид n\/p\q\.)

100
Глава 5
Попробуем применить это определение ez, чтобы получить однозначное определение
логарифма как обратной функции по отношению к экспоненциальной функции:
z — logit;, если w = ez.
Это называется натуральным логарифмом (я буду записывать эту функцию просто «log»
без указания основания логарифма) ^5,31. Из указанного «перевода сложения в умножение»
следует правило «перехода от умножения к сложению»:
log ab = log a -f log Ъ.
Сразу не вполне очевидно, что такая функция, обратная по отношению к е2, непременно
должна существовать. Оказывается, однако, что для любого комплексного числа гг, отлич¬
ного от нуля, существует такое z, что w — ez, так что можно определить log гг — z. Здесь,
однако, возникает препятствие: имеется более одного ответа.
Как представить эти ответы? Если [г, 9} есть представление числа гг в полярных ко¬
ординатах, то его логарифм z в обычной декартовой форме (z = х + гу) можно записать
так:
Z = log V + 20,
где log г — обычный натуральный логарифм положительного вещественного числа — обрат¬
ная функция от вещественной экспоненциальной функции. Почему? Из рис. 5.7 интуитивно
ясно, что такой вещественный логарифм существует. На рис. 5.7а показан график функ¬
ции г = ех. Чтобы получить график обратной функции достаточно поменять местами оси
(см. рис. 5.7 б). Неудивительно, что вещественная часть z ~ log гг действительно есть обыч¬
ный вещественный логарифм. Более интересно^, что мнимой частью z является угол в —
аргумент комплексного числа гг. Этот факт делает ясным сделанное ранее утверждение, что
аргумент комплексного числа действительно есть некоторая форма логарифма.
Рис. 5.7. Чтобы получить логарифм положительного вещественного числа г, рассмотрите график функ¬
ции г = ех «). Переменная г пробегает все положительные значения, поэтому, перевернув рисунок,
мы получаем график обратной функции х = log г для положительных значений г б)
Напомним, что в определении аргумента комплексного числа имеется некоторая неод¬
нозначность. Мы можем прибавить к в любое целое число, умноженное на 2гг, и это ничего
не изменит (вспомним рис. 5.46). В соответствии с этим, имеется множество различных
решений z при данном выборе гг в соотношении гг — ez. Если взять одно из таких реше¬
ний z, то z ~Ь 27гт, где п — любое целое число, также будет возможным решением. Таким

5.3. Многозначность, натуральные логарифмы
101
образом, логарифм числа w определяется с точностью до слагаемого в виде любого цело¬
го числа, умноженного на 2iri. Необходимо помнить об этом при работе с выражениями
типа log ab — log а 4- log b, чтобы быть уверенным в правильном выборе логарифма.
Эта особенность комплексного логарифма на данной стадии должна, по-видимому, вы¬
зывать некоторое раздражение. Однако, как мы увидим в § 7.2, это лежит в основе некоторых
наиболее сильных, полезных и магических качеств комплексных чисел. От них критическим
образом зависит комплексный анализ. Попробуем кратко обсудить природу неоднозначно¬
сти.
Одну из возможностей понять неоднозначность log w дает замечательная формула
е2™ = 1,
откуда ег+2,гг е~ — w и т. д. Это показывает, что число г + 2;п столь же хорошо подходит
на роль логарифма от w9 как и г (и мы можем повторить эту процедуру любое число раз).
Предыдущее соотношение тесно связано с известной формулой Эйлера
+ 1 = 0
(которая связывает пять фундаментальных чисел 0,1, г, 7Г и е в единое почти мистическое
выражение)*.
Мы сможем лучше понять эти свойства, если возьмем экспоненциальную функцию
от выражения z ~ log г + i0:
w = ez = elog r+ie = eiogrei8 = reie
Видно, что полярную форму любого комплексного числа w9 которое мы раньше обозначали
как [г, в], можно записать в более наглядной форме:
w — ге.
При такой записи очевидно, что если мы перемножим два комплексных числа, то получим
произведение их модулей и сумму их аргументов, гегвse1^ = rse^e+<^\ так что г и s пере-'
множаются, а в и ф складываются (помните, что вычитание 27т из #+ф не меняет результата),
что неявно заложено в правиле подобных треугольников (рис. 5.1 б). Далее мы будем поль¬
зоваться вышеприведенным выражением вместо прежнего обозначения [г, в]. Заметим, что
при г = 1 и в = 7г мы получаем —1 и переоткрываем известное эйлеровское ет + 1 = 0,
используя геометрию рис. 5.4 а; если г = 1 и в = 27г, мы получаем +1 и переоткрываем
равенство e27Tl = 1. Окружность г — 1 называется единичной окружностью' (см. рис. 5.8).
В соответствии с вышеприведенным выражением, она определяется уравнением w = егв
с вещественным значением в. Сравнение с данными выше соотношениями х — г cos в
и х — г sin 0 для вещественной и мнимой частей величины w = х + iy дает плодотворную
формулу (Котеса-)Эйлера‘ 51
е10 = cos# + i sinO,
которая, по существу, заключает в себе всю тригонометрию и сводит ее к гораздо
простым свойствам комплексной экспоненциальной функции.
Посмотрим, как это работает в простых случаях. Основное соотношение еа^ь =
будучи разложенным на вещественную и мнимую части, немедленно дает гораздо более
сложные на вид соотношения (несомненно, знакомые до боли некоторым читателям)
еаеЬ
*
**
Выведите отсюда, что z + 7гг есть логарифм числа —w.
Проверьте это.

102
Глава 5
Единичная
окружность
Рис. 5.8. Единичная окружность, содержащая комплексные числа с модулем, равным 1. По формуле
• /}
Котеса-Эйлера такие числа имеют вид е = cos в + г sin 0 с вещественным значением в
cos(a -f Ъ) = cos a cos b — sin a sin 6,
sin(a -f b) — sin a cos b + cos a sin b.
Аналогично, разлагая, например, e
Згв
(ег0)3, немедленно получаем^5*6!
cos 30 — cos3 0 — 3 cos 0 sin2 в,
sin 30 = 3 sin 9 cos2 0 — sin3 0.
Действительно есть какая-то магия в том, как из простых выражений с комплексными чис
лами получаются довольно сложные формулы.
5.4.	Комплексные степени
Вернемся теперь к вопросу об определении wz (или bz в прежнем обозначении). Мы мо¬
жем сделать это, написав
гг
,z log W
• • • ,
(поскольку мы ожидаем, что ezlogw — (elogw)z и elogw = w). Отметим, однако, что из-за
неоднозначности log гг можно добавить к log гг любое целое число, умноженное на 2ггг,
и получить другой допустимый ответ. Это означает, что всякое частное значение wz можно
умножить или разделить на ez'27Гг любое число раз и снова получить при этом допустимое
значение wz. Интересно посмотреть, каково соответствующее расположение точек на ком¬
плексной плоскости в общем случае. Это показано на рис. 5.9. Точки лежат на пересечении
двух равноугольных спиралей. (Равноугольная — или логарифмическая — спираль есть плос¬
кая кривая, образующая постоянный угол с прямыми линиями, исходящими из некоторой
Неоднозначность может создать проблемы разного рода, если не подойти к ней со
всей серьезностью . Лучший способ устранить такие проблемы — это принять правило,
согласно которому обозначение wz используется только при определенном выборе значе¬
ния log гг. (В частном случае функции ez всегда принимается молчаливое соглашение, по
которому loge = 1. При этом стандартная запись ez согласуется с нашим более общим вы¬
ражением wz.) Коль скоро сделан такой выбор в отношении log гг, функция wz становится
однозначно определенной для всех значений г.
**
***
Проделайте это.
т •
Покажите это. Сколькими способами можно это сделать? Найдите все частные случаи.
Разрешите такой парадокс: е = е1+27гг, так что е = (е1+2‘лч)1+27Гг = е1+4?гг~47г2 = е1_47г2

5.4. Комплексные степени
103
Рис. 5.9. Различные значения функции гг*(= ezlosw).
К log w можно прибавить любое целое число, умноженное
на 2т, при этом wz целое число раз умножается или делится
на ег-27Г\ В общем случае эти значения представляются на
комплексной плоскости точками пересечения двух логариф¬
мических спиралей (каждая из которых образует постоянный
угол с прямыми линиями, проведенными из начала коорди¬
нат)
Здесь можно заметить, что для определения упомянутого в начале этого раздела «ло¬
гарифма по основанию Ь» (обозначаемого как logb) нам нужно уточнить понятие log 6, по¬
скольку для определения z = logb w должно иметь однозначный смысл выражение w ~bz.
Функция log6 w будет, конечно, многозначной (как и log гг), поскольку к logъ гг можно доба¬
вить любое целое число, умноженное на 2т/ log b. *
В прошлом математиков сильно интриговал такой курьез, как г\ Эта величина пред¬
ставляется «настолько мнимой насколько это возможно». Однако ответ оказывается веще¬
ственным:
. 1 .
е = е*log * = е*'2 ™ = е~1Г/2 = 0,207879576
здесь сделан выбор log г = -7гг. Существует и множество других ответов при другом
выборе log i. Они получаются умножением вышеприведенного результата на е2™, где п —
любое целое число (или, что то же самое, возведением его в степень вида 4n + 1, где п —
положительное или отрицательное целое число).*** Замечательно, что все значения г1 —
вещественные числа.
Выясним, каково значение функции wz при z = А. Ожидается, что две величины ±^/w
можно представить как гг1/2. Мы получаем эти две величины, просто выбирая сначала одно
значение для log гг, а затем другое, которое получается из первого добавлением 2т. Такое
добавление приводит к изменению знака у гг1/2 (поскольку по формуле Эйлера е7™ = — 1).
Аналогично можно получить все п решений уравнения zn = гг при п — 3, 4, 5,... в виде
величины гг1/72, придавая величине log гг различные значения****. В более общем случае
можно вернуться к вопросу, поставленному в § 4.2, о корне z-й степени из гг, где w и z —
любые комплексные числа, отличные от нуля. Такой корень z-й степени можно представить
как гг1/2 и получить в общем случае бесконечное множество возможных решений в зави¬
симости от выбора, сделанного для log гг. При правильно сделанном выборе для log гг1/*,
который дается выражением (log гг)/г, мы действительно получаем (гг1/*)* = гг. В более
общем случае имеем
(гга)6 = гг°6.
Коль скоро мы сделали выбор в отношении log w (в правой части равенства), мы должны
1	ГЗ	/	i>	\
- *****
выбрать logtra (в левой части равенства) в виде a log гг.
* Й© Покажите это.
** $© Почему допустим такой выбор?
***f@ Объясните, почему это так.
****Й© Проверьте это.
***** Покажите это. •_

104
Глава 5
Рис. 5.10. Корни п-й степени из единицы Рис. 5.11. Равносторонний треугольник, пред-
е2тгтг/п	2,..., п), равномерно располо-	ставляющий кубические корни из единицы 1, со
женные вдоль единичной окружности, образуют	и со2. При умножении на со он поворачивается
вершины правильного n-угольника. В данном	на 120° против часовой стрелки, при умножении
случае п = 5	на о;2 — по часовой стрелке
%
Если z ~ п есть положительное целое число, положение существенно упрощается,
и мы имеем ровно п корней. Здесь особый интерес представляет случай w = 1. Последова¬
тельно выбирая возможные значения величины log 1, а именно 0, 27гг, 4тгг, бтгг,..мы полу¬
чаем 1, е°, е27Гг/п, е47Гг/п, еб7Гг/п,... в качестве возможных значений величины 11/п. Можно
записать их в виде 1, е, е2, е3,..., где е = е27г\ На комплексной плоскости им соответству¬
ют п точек, равномерно расположенных на единичной окружности и называемых корня¬
ми п-й степени из единицы. Эти точки образуют вершины правильного n-угольника (см.
рис. 5.10). (Заметим, что если выбрать в качестве logl значения — 27гг, -47гг, —б7гг и т.д.,
мы получим те же самые п корней, но взятые в обратном порядке.)
Интересно отметить, что при заданном п корни n-й степени из единицы образуют так
называемую конечную мультипликативную группу или, более точно, циклическую группу Ъп
(см. §13.1). Мы имеем п величин, обладающих тем свойством, что при перемножении любых
двух из них получается величина, принадлежащая той же группе. Можно также разделить
одну из них на другую и получить третью величину. В качестве примера рассмотрим слу¬
чай п = 3. Мы получаем три элемента: 1, о; и о;2, где со = е27™/3 (так что со3 — 1 и о;”1 — си2).
Для этих чисел мы имеем следующие простые таблицы умножения и деления:
X
1
СО
о;2
♦
♦
1
со
со2
1
1
си
о;2
1
1
	9
со
со
со
СО
и2
1
со
со
1
и2
СО2
си2
1
и
о;2
со2
со
1
На комплексной плоскости этим частным значениям соответствуют вершины равно-
о
стороннего треугольника. При умножении на си треугольник поворачивается на угол ~тс
О
(т. е. 120°) против часовой стрелки; при делении поворот происходит в обратную сторону
(см. рис. 5.11).
**4
5.5.	Связь с физикой элементарных частиц
Рассматриваемые числа представляют интерес для физики элементарных частиц, по¬
скольку могут использоваться в качестве мультипликативных квантовых чисел. В § 3.5 об¬

5.5. Связь С ФИЗИКОЙ ЭЛЕМЕНТАРНЫХ ЧАСТИЦ
105
суждался тот факт, что аддитивные (скалярные) квантовые числа в физике элементарных
частиц, насколько нам известно, неизменно выражаются целыми числами. Имеются также
примеры мультипликативных квантовых чисел, которые можно выразить через корни п~й
степени из единицы. Мне известно лишь несколько примеров из общепринятой физики
элементарных частиц, и большинство из них относится к сравнительно малоинтересному
случаю п = 2. Есть еще один несомненный случай с п ~ 3 и, возможно, один случай сп =
= 4. К сожалению, в большинстве случаев такое квантовое число не универсально, то есть
его нельзя применить ко всем элементарным частицам. В такой ситуации можно говорить
лишь о приближенном квантовом числе.
Примером (приближенного) мультипликативного квантового числа с п — 2 может слу¬
жить величина, называемая четностью. (Существуют и другие приближенные величины,
для которых п — 2 и которые во многих отношениях подобны четности, например, g-
четность. Я не буду их здесь обсуждать.) Понятие четности составной системы опре¬
деляется как произведение четностей составляющих частиц. Четность составной частицы
положительна, если зеркальное отражение частицы тождественно, в определенном смысле,
самой частице, и отрицательна, если зеркальное отражение представляет собой соответ¬
ствующую античастицу* (см. §§ 3.5, 24.1-24.3, 24.8, 26.4). Поскольку операции зеркального
отражения или перехода от частицы к античастице, будучи «возведенными в квадрат», дают
единицу (т. е. двукратное применение этих операций приводит нас к тому, с чего мы начали),
соответствующее квантовое число (обозначим его е) должно обладать свойством е2 = 1, так
что оно должно быть «корнем n-й степени из единицы» при п — 2 (т. е. е = 4-1 или е = —1).
Это понятие лишь приближенное, поскольку четность не сохраняется в так называемых
слабых взаимодействиях и вследствие этого некоторые частицы не обладают определенной
четностью (см. §§25.3,25.4).
При стандартном описании понятие четности применяется только к семейству частиц,
называемых бозонами. Остальные частицы принадлежат к другому семейству и называются
фермионами. Различие между бозонами и фермионами играет очень важную роль, но имеет
довольно сложный характер, и мы отложим его до §§23.7, 23.8. (Это различие проявляется,
в частности, если мы поворачиваем частицу непрерывным образом на полный угол 2ir (т. е.
на 360°). При таком повороте только бозоны полностью восстанавливают свои исходные
состояния. У фермионов это происходит лишь при двукратном повторении такого поворота,
см. §§ 11.3, 22.8.) В некотором смысле «два фермиона образуют бозон» и «два бозона так¬
же образуют бозон», тогда как «бозон и фермион образуют фермион». Таким образом, для
описания природы частиц как фермионов или бозонов можно приписать мультипликативное
квантовое число —1 фермиону и -hi — бозону, и здесь мы имеем другое мультипликативное
квантовое число с п = 2. Насколько известно, эта величина является точным мультиплика¬
тивным квантовым числом.
Мне представляется, что можно ввести понятие четности, применимое к фермионам,
хотя это и не совпадает с общепринятой терминологией. Для этого надо скомбинировать
четность с фермион-бозонным квантовым числом и получить комбинированное мультипли¬
кативное квантовое число с п = 4. Для фермиона четность должна принимать значения -hi
или —г, тогда двукратное зеркальное отражение будет эквивалентно повороту на 2тг. Для бо¬
зона, как и прежде, четность будет принимать значения ± 1.
Я должен также упомянуть мультипликативное квантовое число с п = 3, которое я на¬
зову кваркностью. (Этот термин отнюдь не стандартный, и эта величина обычно вообще
не используется в качестве квантового числа, однако она заключает в себе важный ас¬
пект современного понимания физики элементарных частиц.) В § 3.5 я упомянул о совре¬
менной точке зрения, согласно которой «сильно взаимодействующие» частицы, известные
* Согласно оригиналу, четность (parity) может быть четной (even) и нечетной (odd). Во избежание тавтоло¬
гии («четная четность») при переводе эти характеристики были заменены соответственно на «положительную»
и «отрицательную» четность. — Прим. перев.

106
Глава 5
под названием адронов (протоны, нейтроны, 7г-мезоны и др.), считаются состоящими из
кварков (см. §25.6). Кварки имеют электрический заряд, равный не целому числу заря¬
дов электрона, а целому числу, умноженному на одну треть этого заряда. Однако кварки
не могут существовать как отдельные самостоятельные частицы, а построенные из них
составные частицы могут самостоятельно существовать, только если их результирующий
заряд дополняется до целого числа зарядов электрона. Пусть q есть величина электриче¬
ского заряда, измеряемого в зарядах электрона с обратным знаком (так что для самого
электрона имеем q ~ — 1, обычно заряд электрона считают отрицательным). Для кварков
2	1	12
мы имеем q = ^ или — ± а для антикварков — q — ~ или — Если взять в качестве
О	О	О	О
кваркности мультипликативное квантовое число e~2qni, мы найдем, что она принимает зна¬
чения 1, со и а;2. Для кварка кваркность равна со, для антикварка — со2. Частица может
существовать сама по себе, только если ее кваркность равна 1. В соответствии с §5.4,
степени кваркности образуют циклическую группу Z3. (В § 16.1 мы увидим, как, добав¬
ляя элемент «0» и вводя понятие сложения, можно расширить эту группу до конечного
поля F4.)
В этом и предыдущем разделах я представил некоторые математические аспекты магии
комплексных чисел и намекнул лишь на несколько возможностей их применения. Но я еще
не упоминал о тех особенностях комплексных чисел (о них пойдет речь в главе 7), которые
я сам воспринял как наиболее магические из всех, когда изучал математику в студенческие
годы. Позже я нашел еще более поразительные стороны этой магии, и одна из них (описы¬
ваемая в конце главы 9) странным образом дополняет ту, которая произвела на меня наи¬
большее впечатление при первом изучении. Эти вопросы, однако, опираются на некоторые
основополагающие понятия математического анализа, поэтому, чтобы донести что-нибудь
из этой магии до читателя, будет необходимо сначала сказать кое-что об этих понятиях.
Для этого, конечно, есть и другая причина — математический анализ абсолютно необходим
для настоящего понимания физики!
Примечания
§5.1.
5.1. Следует еще упомянуть тригонометрические функции ctg# = cos#/sin# = (tg#) 1, sec# =
= (cos#)""1 и cosec# = (sin#)-1, а также «гиперболические» аналоги тригонометрических
функций: sht = i(e* — e-t), eht — ~(e1 + e“*), tht = sht/cht и т.д.
§5.2.
5.2. Логарифмы были впервые введены Джоном Непером в 1614 году и доведены до практического
использования Генри Бриггсом в 1624 году.
§5.3.
5.3. Натуральный логарифм также обозначается как «1п».
5.4. Из того, что мы установили до сих пор, мы не можем заключить, что вместо г# в формуле £ —
= log г-\-i$ не может стоять вещественное число, умноженное на г#. Такое заключение требует
анализа.
5.5. Роджер Котес (1714) получил эквивалентную формулу log(cos# -f- г sin#) = г#. Эйлеровская
формула егв = cos # + г sin # появилась, по-видимому, на 30 лет позже (см. [252]).
5.6. Я использую здесь удобную (хотя и несколько нелогичную) запись cos3 # вместо (cos #)3 и т. п.
Следует отметить несогласованность с более логичным обозначением cos”1 #, которое в англий¬
ской литературе часто понимается как arccos#. Формулу cosn# + г sin пв = (cos# + г sin#)71
иногда называют теоремой Муавра. Абрахам де Муавр, современник Роджера Котеса (см. преды¬
дущее примечание), также, по-видимому, был в числе открывших формулу егв = cos # + г sin #.
Более подробную информацию о комплексных числах и их истории можно найти в [539].

Глава 6
Исчисление вещественных чисел
6.1.	Что создает настоящую функцию?
Исчисление, или математический анализ, состоит из двух основных частей — диффе¬
ренциального исчисления и интегрального исчисления. Дифференциальное исчисление име¬
ет дело со скоростями, ускорениями, наклоном и кривизной кривых и поверхностей и тому
подобным. Всё это скорости, с которыми происходит изменение чего-то, и они являются
величинами, определяемыми локально, через структуру или поведение точек, находящихся
т	•	•
в ближайшем соседстве с выбранной точкой. Интегральное исчисление имеет дело с пло¬
щадями и объемами, с центрами тяжести и многими другими понятиями того же характера.
Эти понятия включают в себя меру совокупности того или иного рода, и они не определяют¬
ся лишь тем, что происходит в ближайшем соседстве с отдельными точками. Замечательный
факт, называемый основной теоремой анализа, состоит в том, что каждый из двух указанных
ингредиентов, по существу, является обратным по отношению к другому. Именно этот факт
позволяет объединить эти две важные области математического знания и получить мощный
инструмент для понимания и математического исследования.
Математический анализ, созданный в XVII веке Ферма, Ньютоном и Лейбницем с ис¬
пользованием идей, восходящих к Архимеду (III век до нашей эры), называют «исчисле¬
нием», поскольку он действительно дает инструмент для вычислений, причем те задачи,
за которые в ином случае трудно было бы взяться, здесь зачастую можно решать «авто¬
матически», просто следуя некоторым сравнительно простым правилам, и это не требует
особой проницательности. В этом исчислении имеется резкий контраст между операция¬
ми дифференцирования и интегрирования в отношении того, какая из них «легкая», а какая
«трудная». В случае когда эти операции применяются к явным формулам с известными функ¬
циями, дифференцирование следует считать «легким», а интегрирование — «трудным», и во
многих случаях интегрирование вообще не может быть выполнено в явном виде. С другой
стороны, когда функции не заданы в виде формул, а имеют вид таблицы численных дан¬
ных, интегрирование становится «легким», а дифференцирование — «трудным», поскольку
последнее, строго говоря, не выполняется обычным путем. Численные методы обычно име¬
ют дело с приближениями, но здесь тоже наблюдается близкая аналогия с точной теорией,
и опять-таки интегрирование можно провести в таких случаях, когда дифференцирование
невозможно. Попробуем понять кое-что из этого. Для этого необходимо познакомиться с по¬
нятием функции.
Для Эйлера и других математиков XVII и XVIII веков «функция» означала нечто такое,
что можно записать в виде явной формулы вроде ж2, или sin ж, или log(3 — х + ех), или,
возможно, что-то, определяемое интегралом или задаваемое степенным рядом. В наши дни
предпочитают говорить об «отображении», посредством которого некоторый набор чисел
(или сущностей более общего характера) А, называемый областью определения функции,
«отображается» на некоторую другую область В, называемую областью значений функции
(см. рис. 6.1). Существенно здесь то, что функция сопоставляет каждому члену области
определения А некоторый член области значений В. (Представьте себе, что функция «рас¬
сматривает» числа, принадлежащие области А, и, в зависимости от того, какое взято число,

108
Глава 6
Область	Область
определения	значений
Рис. 6.1. Функция как «отображение», посредством которого ее область определения (некоторый
набор А чисел или иных сущностей) «отображается» на ее область значений (некоторый другой
набор В). Каждому из элементов множества А сопоставляется некоторый определенный элемент
из множества В, при этом нескольким различным элементам из А может сопоставляться одно и то же
значение из В, а некоторые значения из В могут ничему не сопоставляться
она производит определенное число, принадлежащее области В.) Функцией такого рода мо¬
жет быть просто справочная таблица. При этом не обязательно, чтобы существовала какая-то
разумно выглядящая «формула», определяющая действие функции явным образом.
Рассмотрим несколько примеров. На рис. 6.2 показаны графики трех простых
функций^6л1, а именно х2,
х| и в(х). Во всех трех случаях областью определения и об¬
ластью значений является множество вещественных чисел, это множество обычно обозна¬
чают символом Е. Функция, обозначаемая как х2, дает просто квадрат вещественного числа.
Функция, обозначаемая как |х| (ее называют абсолютным значением числа), дает х, если х —
неотрицательное число, и —х, если х — отрицательное число; таким образом, функция |х
никогда не принимает отрицательных значений. Функция в(х) равна 0 при отрицательных х
и 1 при положительных х; обьгчно принимается 0(0) = ~. (Эта функция называется сту¬
пенчатой функцией Хевисайда; в §21.1 можно прочитать о другом важном вкладе Оливера
Хевисайда в математику. Более всего он, вероятно, известен тем, что постулировал существо¬
вание в атмосфере Земли «слоя Хевисайда», играющего важную роль в распространении
радиоволн.) Каждая из трех функций вполне хороша в современном смысле этого слова,
однако Эйлер ^6*2^ вряд ли согласился бы считать
X
или 0(х) функциями в его смысле этого
термина.
Почему так могло быть? Возможно, неприятие |х| и в(х) обусловлено тем, что эти
функции не изображаются «приятными» формулами и здесь мы, скорее, имеем дело с ин¬
струкциями такого рода: «при таких-то значениях х делаем то-то, при таких-то х...». Здесь,
б)
Z2
у=в{х)
X
X
в)
Рис. 6.2. Графики функций а) \х\, б) х2 ив) 0{х). Во всех случаях областью определения и областью
значений является система вещественных чисел

6.2. Наклон функции
yt
109
однако, много неясного; во всяком случае нежелание считать \х\ формулой может вызывать
удивление. Более того, коль скоро мы приняли \х\, для 9(х) можно написать формулу*:
в(х)
х
+ х
2х
(хотя можно усомниться в том, дает ли она правильное значение для 0(0), поскольку полу¬
чается отношение 0/0). Ближе к истине предположение, что функцию |ж| отвергали, потому
, ^ ,
что она «негладкая», а не из-за ее «неприятного» явного вида. Это проявляется в наличии
«угла» в середине рис. 6.2 а. Из-за этого угла функция |ж| не имеет определенного наклона
при х = 0. Познакомимся теперь с этим понятием.
. Заметим, что 9(х)
6.2.	Наклон функции
Как уже отмечалось, одна из задач, с которой имеет дело дифференциальное исчисле¬
ние, — это определение наклона. График функции \х\ на рис. 6.2 а ясно указывает на от¬
сутствие однозначно определенного наклона в начале координат (при х = 0), где находится
наш злополучный угол. Всюду, кроме начала координат, наклон хорошо определен, а в на¬
чале — нет. Из-за этой неприятности мы говорим, что функция \х\ не дифференцируема
в начале координат или, что то же самое, она там негладкая. Функция ж2, как показывает
рис. 6.26, наоборот, всюду имеет однозначно определенный наклон, то есть функция х2
всюду дифференцируема.
Как видно из рис. 6.2 в, ситуация с функцией 9(х) еще хуже, чем с \х
содержит неприятный «скачок» в начале координат (при х = 0). Мы говорим, что функ¬
ция 9(х) претерпевает разрыв в начале координат. В отличие от нее, функции х2 к \х\ всюду
непрерывны. Недостатком функции \х\ является утрата не непрерывности, а дифференци¬
руемости в начале координат. (Хотя потеря непрерывности и гладкости — понятия разные,
они все же взаимосвязаны, в чем мы скоро убедимся.)
Оба указанных недостатка, скорее всего, не понравились бы Эйлеру, и это, по-видимому,
та причина, по которой \х\ и 9{х) не признавались «подходящими» функциями. Рассмот¬
рим, однако, две функции, показанные на рис. 6.3. Первая из них, ж3, приемлема по всем
критериям, а как обстоит дело со второй, х\х\, которая выглядит как ,т2 при неотрицатель¬
ных х и как —х2 при отрицательных х2 На первый взгляд два графика довольно похожи
между собой и определенно имеют «гладкий» вид. Действительно, они имеют вполне опре¬
деленный, а именно нулевой, наклон в начале координат (это означает, что кривые имеют
X
Рис. 6.3. Графики функций а) х3 и б) х\х\ (т. е. х2 при ж^Ои ~х2 при х < 0)
Покажите это (опуская случай х = 0).

110
Глава 6
-	.	'	I
Рис. 6.4. Изображение в декартовых коор¬
динатах а) функции у = f(x)9 б) ее про¬
изводной и = f'{x) (= dy/dx) и в) второй
производной f"(x) = d2y/dx2. (Заметим,
что f{x) имеет горизонтальный наклон как
раз там, где f'(x) пересекает ось х, и точ-
там горизонтальный наклон) и всюду «дифферен¬
цируемы» в самом прямом смысле этого слова.
В то же время х\х\ определенно не относится
к «приятным» функциям, которые удовлетворили
бы Эйлера.
«Недостаток» функции х\х\ состоит в том, что
в начале координат она не имеет определенной
кривизны — это одно из основных понятий, с кото¬
рыми имеет дело дифференциальное исчисление.
«Кривизна» определяется «вторыми производны¬
ми», которые получаются при двукратном диффе¬
ренцировании. Мы говорим, что функция х\х\ не
дифференцируема дважды (не имеет второй про¬
изводной) в начале координат. Ко второй и более
высоким производным мы обратимся в § 6.3.
Чтобы понять все это, мы должны узнать,
в чем реально состоит операция дифференциро¬
вания. Для этого необходимо понять, как измеря¬
ется наклон. Эта процедура продемонстрирована
на рис. 6.4. Там показана вполне типичная функ¬
ция, обозначенная как f(x). Кривая на рис. 6.4 а
изображает соотношение у — /(.г), в котором ко¬
ордината у измеряет высоту, а координата х — го¬
ризонтальное смещение, как обычно при использо¬
вании декартовых координат. Наклон кривой в за-
данной точке р определим как приращение коор¬
динаты у, деленное на приращение координаты х,
причем приращения берутся вдоль касательной
к этой кривой в точке р. (Точное определение «ка¬
сательной» связано с соответствующими предель¬
ными переходами, однако в мои цели не входит
заниматься этими подробностями. Я надеюсь, что
мои читатели сочтут мое интуитивное описание
достаточным для наших ближайших целей I6,3!.)
Стандартное обозначение величины наклона име¬
ет вид dy/dx (произносится «dy по dx»). Можно
рассматривать dy как очень малое приращение ве¬
личины у вдоль кривой, a dx — как соответству¬
ющее малое приращение величины х. (Строго го¬
воря, здесь необходим переход к «пределу», при
ку перегиба там, где с осью х пересекает-
ся
котором каждое из указанных приращении умень-
шается до нуля.)
Мы можем рассмотреть теперь другую кри¬
вую, изображающую зависимость наклона от х в
каждой точке р при различном выборе координа¬
ты х (см. рис. 6.4 б). Здесь опять-таки используют¬
ся декартовы координаты, но теперь по вертикальной оси откладывается не у, a dy/dx. По
горизонтальной оси по-прежнему откладываются значения х. Построенная функция обыч¬
но обозначается f'(x), и мы можем написать dy/dx = f'(x). Величину dy/dx называют
производной от у по х, а функцию f'(x) — производной^ функции f(x).

6.3. Высшие производные, С00-гладкие функции
111
6.3.	Высшие производные, С°°-гладкие функции
■ч.
Посмотрим теперь, что получается, когда мы берем вторую производную. Это озна¬
чает, что в качестве исходной мы теперь рассматриваем кривую и = f'{x) на рис. 6.46
(буква и обозначает dy/dx). На рис. 6.4 в я изобразил функцию «наклона второго порядка»,
представляющую собой зависимость du/dx от х9 подобно тому, как это было сделано рань¬
ше для dy/dx, так что величина du/dx дает нам теперь наклон другой кривой, и = f'(x).
Именно эта величина называется второй производной исходной функции f(x) и обознача¬
ется обычно ff/{x). Подставляя dy/dx вместо и в выражение du/dx, мы получаем вторую
производную от у по х9 обозначаемую (несколько нелогично) как d2y/dx2 (произносится «d
два у по dx квадрат»).
Заметим, что значения х9 при которых исходная функция f(x) имеет горизонтальный на¬
клон, — это как раз те значения, при которых функция f'(x) пересекает ось х (так что dy/dx
обращается в нуль при этих значениях х). В этих точках функция f(x) достигает (локаль¬
ного) максимума или минимума; это важно, если мы хотим найти (локальные) наибольшие
и наименьшие значения некоторой функции. Что можно сказать о тех точках, где ось х
пересекает вторая производная f"{x)? Это происходит там, где обращается в нуль кривизна
функции fix). В общем случае это те точки, где направление, в котором «изогнута» кри¬
вая у — f(x)9 меняется от одной стороны кривой к другой; такие точки называются «точками
перегиба». (На самом деле было бы неправильно сказать, что f"(x) в общем случае действи¬
тельно равна кривизне кривой, определяемой функцией f{x). В действительности кривизна
определяется более сложным выражением !6*5V чем f"(x)9 но это выражение содержит f,f(x)9
и кривизна обращается в нуль вместе с f''(x).)
Рассмотрим теперь в общих чертах наши две похожие одна на другую функции хг
и х\х\. На рис. 6.5 а,6, в показана функция х3 и ее первая и вторая производные, как это
было сделано для функции f{x) на рис. 6.4; на рис. 6.5 г, д, е то же сделано для функции х\х
В случае х3 мы видим, что не возникает никаких проблем с непрерывностью или гладко¬
стью первой и второй производных. Первая производная равна Зх2, вторая 6х, и ни одна из
них ни на минуту не заставила бы усомниться Эйлера. (Скоро мы увидим, как найти эти
явные выражения производных.) Однако в случае х\х\ мы обнаруживаем что-то подобное
«углу» на рис. 6.2 а в случае первой производной и поведение, подобное «ступенчатой функ¬
ции» на рис. 6.2 в, в случае второй производной. Мы имеем нарушение гладкости у первой
производной и нарушение непрерывности у второй производной. Эйлер вообще не стал бы
иметь с ними дела. Первая производная здесь равна 2|аг|, вторая —2 4- 49(х). (Наиболее
педантичные из моих читателей могли бы сказать, что мне не следует так лихо выписывать
«производную» для функции 2\х\, которая в действительности не дифференцируема в на¬
чале координат. Всё так, но это лишь временная уловка, полное обоснование будет дано
на основе понятий, вводимых в конце главы 9.)
Легко представить себе функции, для которых подобное нарушение гладкости или
непрерывности не будет проявляться, пока мы не начнем вычислять производные доста¬
точно высокого порядка. Действительно, такое будет происходить с функциями вида хп х
где п — положительное целое число, которое можно взять сколь угодно большим. По терми¬
нологии математиков, функция f{x) называется Сп-гладкой, если ее можно продифференци¬
ровать п раз (в каждой точке ее области определения) и ее n-я производная непрерывна!6*6!.
Функция хп\х\ является Сп-гаадкой, но Cn+1-негладкой в начале координат.
Насколько велико должно быть число п9 чтобы удовлетворить Эйлера? Очевидно, что
он не согласился бы довольствоваться никаким частным значением п. Эйлер одобрил бы
лишь те функции, которые можно дифференцировать сколь угодно большое число раз. Что¬
бы охватить такой случай, математики называют функцию С00-гладкой, если ее можно счи¬
тать Сп-гладкой при всех положительных целых значениях п. Другими словами, С00-гладкая
функция должна быть дифференцируема сколь угодно большое число раз.

112
Глава 6
•> *
х
д)
Рис. 6.5. Графики а) функции ж3, 6) ее первой производной Зх2, в) ее второй производной 6х, г) функ-
х|, д) ее первой производной 2|х| и (е) ее второй производной у = — 2 -f 4#(х)
ЦИИ X
1
X
X
В эйлеровом понимании, от функции требовалось,
мы полагаем, что-то вроде С°°-гладкости. По крайней
мере, можно представить, что он ожидал от своих функ¬
ций С00-гладкости в большей части области опреде¬
ления. Но как быть с функцией 1/х? (См. рис. 6.6.)
Она определенно не обладает С00-гладкостью в нача¬
ле координат. Она даже не определена там (в совре¬
менном понимании функции). Однако наш Эйлер несо¬
мненно принял бы ее как вполне приличную «функ¬
цию», несмотря на эту проблему. Для нее, в конце кон¬
цов, имеется простая, естественно выглядящая форму¬
ла. Можно предположить, что Эйлер не так уж забо¬
тился о том, чтобы его функции были С°°-гладкими
в каждой точке их области определения (если при¬
нять, что его вообще заботили эти «области опреде¬
ления»). Возможно, что аномалии в одной или несколь¬
ких особых точках не имели значения. Но функции \х
и в(х) содержат аномалии в той же самой «особой точке», что и 1/х. Представляется,
что, несмотря на все наши усилия, мы пока не смогли «ухватить» эйлерово определение
функции.
Возьмем другой пример. Рассмотрим функцию h(x)9 определяемую следующим обра¬
зом:
Рис. 6.6. График функции ^
h(x)
О при х < О,
- — 1 /г 	 г\
= Ъх1

6.4. Каково «эйлерово» понимание функции?
113
График этой функции показан на рис. 6.7. Она определенно выглядит как гладкая функция.
Более того, как очень гладкая функция. Она обладает С00-гладкостью во всей области веще¬
ственных чисел. (Доказательство этого факта входит в университетский курс математики.
Я помню, как сам занимался этим, будучи студентом*.) Несмотря на замечательную глад¬
кость этой функции, можно представить, как воротил бы нос Эйлер от функции, заданной
подобным образом. В смысле Эйлера, это определенно «не одна функция». Это «две функ¬
ции, склеенные вместе», независимо от того, насколько точно произведена склейка в начале
координат. Функция по Эйлеру, — это, наоборот, одна функция, несмотря на то, что она
разделена на два куска неприятным «выбросом» в начале координат, где нарушается даже
непрерывность, не говоря о гладкости (см. рис. 6.6). Для Эйлера, как мы его себе представ¬
ляем, функция h(x) ничем не лучше |х| или в(х). В последних случаях мы действительно
имеем «две функции, склеенные вместе», хотя и гораздо более грубо (что касается в(х)9
то кажется, что склеенные куски вообще не образуют единого целого).
6.4.	Каково «эйлерово» понимание функции?
Как нам представить себе эйлеров критерий, позволяющий отличить одну единую функ¬
цию от мешанины из нескольких отдельных функций? Пример функции h (х) ясно показы¬
вает, что С00-гладкости для этого недостаточно. Оказывается, что существуют два подхода
к этой проблеме, выглядящих совершенно по-разному. Один из них использует комплекс¬
ные числа и обманчиво прост по постановке, хотя имеет важные применения. Мы просто
требуем, чтобы нашу функцию f(x) можно было расширить до функции f(z) комплексной
переменной г таким образом, чтобы функция f(z) была гладкой в простейшем смысле — од¬
нократно дифференцируемой по комплексной переменной г. (Таким образом, f(z) обладает
чем-то вроде С1-гладкости в комплексной области.) Это необычное проявление подлинной
магии, и кроме нее нам уже ничего не требуется. Если функцию f(z) можно продиффе¬
ренцировать один раз по комплексному параметру z, то ее можно дифференцировать любое
число раз!
Я вернусь к комплексному анализу в следующей главе. Существует, однако, другой
подход к решению проблемы под названием «Эйлерово понятие функции», использующий
только вещественные числа и понятие степенного ряда, с которым мы уже сталкивались
в § 2.5. (В чем Эйлер был подлинным мастером, так это в обращении со степенными ряда-
Попробуйте доказать это, если обладаете достаточной подготовкой.

114
Глава 6
ми.) Будет полезно рассмотреть вопрос о степенных рядах в этом разделе, до возвращения
к проблеме дифференцирования в комплексной области. Тот факт, что локальная дифферен¬
цируемость в комплексной области оказывается эквивалентной возможности разложения
в степенной ряд, — это поистине одна из главных сторон магии комплексных чисел.
Ко всему этому я вернусь в свое время, а пока на минуту задержимся на функциях
вещественной переменной. Предположим, что некоторую функцию f(x) можно представить
в виде степенного ряда:
f(x) = ао -Ь а\х + а^х1 + азх3 4- а^х4 Н .
Существуют методы определения коэффициентов ао, ai, а2?	... для заданной функ¬
ции f(x). Для того чтобы существовало подобное разложение, необходимо (хотя и не до¬
статочно, как мы вскоре увидим), чтобы функция f(x) была С00-гладкой, то есть чтобы
существовали новые функции f'(x), f"(x), f'”{x), f""(x) и т.д., которые представляют со¬
ответственно первую, вторую, третью, четвертую и т. д. производные функции f(x). Реально
нас будут интересовать значения этих функций только в начале координат (при х = 0), так
что нам нужна С00-гладкость функции f(x) лишь в этой точке. Результат (называемый
иногда рядом Маклорена^1^) состоит в следующем: если функцию f(x) можно разложить
в степенной ряд, то*
. _	.	__ /'(о)	_	_ /"(о)	„	_ /'"(о)	_	/""(о)
«о /(Б),	а±	И 7	^	2!	?	^	3!	,	4!	>	•	*	• •
(Напомним (см. § 5.3), что п\ — 1 х 2 х ... х п.) Но что будет происходить поблизости?
Если коэффициенты а задаются указанным образом, то следует ли из этого, что сумма
ряда действительно дает нам функцию f(x) в некотором интервале, окружающем начало
координат?
Вернемся к нашей внешне гладкой функции h(x). Возможно, мы сможем обнару¬
жить изъян в месте склейки (х = 0), используя идею разложения в ряд. Попробуем
понять, действительно ли существует разложение функции h(х) в степенной ряд. Поло¬
жив в вышеприведенных выражениях f(x) = h(x), рассмотрим различные коэффициен¬
ты ао, ai, а2, аз,	помня, что все они должны обращаться в нуль, поскольку ряд
должен согласоваться со значением h(x) =0 при всех х слева от начала координат. Более
того, мы обнаруживаем, что они все должны обращаться в нуль также для е
-1/х_ в
этом
состоит причина С00-гладкости функции h(x) в начале координат, при которой согласуются
все производные, взятые по обе стороны от начала координат. Но это означает, что степенной
ряд никоим образом не описывает нашу функцию, поскольку все члены ряда равны нулю
(см. упражнение 6.2), так что его сумма не равна е~1?х. Таким образом, изъян в месте склей¬
ки х — 0 действительно имеется: функция h{x) не может быть представлена в виде степенно¬
го ряда. В таком случае говорят, что функция h(x) не является аналитической в точке х = 0.
В приведенном рассуждении мы рассматривали разложение в степенной ряд вблизи
начала координат. Подобное обсуждение можно провести и для любой другой точки в ве¬
щественной области определения функции. Но тогда мы должны будем «сдвинуть начало
координат» в некоторую другую точку, определяемую вещественным числом р в этой об¬
ласти, что означает замену х на х — р в вышеприведенном разложении в степенной ряд.
МЫ ПОЛуЧИМ	2	4
f (х) = а0 + ai(x - р) + а2(х - рУ + а3(х - ру-\	,
где теперь
«о = f(p), ai =
Это называется разложением в степенной ряд вблизи точки р. Функция f(x)* называет¬
ся аналитической в точке р, если ее можно представить в виде такого степенного ряда
Покажите это, используя правила, данные в конце § 6.5.
Чр)
1!
ai
Г(р)
2!
а з
ГЧр)
3!

6.5. Правила дифференцирования
115
в некотором интервале, окружающем точку р. Если функция f(x) аналитична во всех точ¬
ках ее области определения, ее называют аналитической функцией или, что эквивалент¬
но, -гладкой функцией. Аналитические функции в некотором смысле еще более гладки,
чем С°°-гладкие функции. Вдобавок они обладают свойством, которого нельзя добиться,
склеивая вместе две «разные» аналитические функции на манер рассмотренных выше функ¬
ций в(х)9 \х\9 х\х\9 хп\х\ или h(x). Эйлеру аналитические функции, несомненно, понравились
бы. Это действительно «настоящие» функции!
Однако иметь дело со всеми этими степенными рядами довольно неприятно, даже
в воображении. «Комплексный» способ рассмотрения намного экономичнее. Более того, он
1
дает более глубокое понимание. Например, функция ~ не аналитична при х = 0, хотя это
эк ц
«одна функция» . «Философия степенных рядов» нам прямо об этом не говорит. Но с точки
зрения комплексных чисел, как мы увидим, — несомненно одш
функция
6.5.	Правила дифференцирования
Прежде чем обсуждать подобные материи, полезно сказать немного об удивительных
правилах, которые предоставляет нам дифференциальное исчисление и которые позволяют
дифференцировать функции, почти не задумываясь (но, конечно, после нескольких месяцев
практики!). Эти правила дают возможность сразу выписывать производные многих функций,
особенно когда их можно представить в виде степенных рядов. Ранее я уже мимоходом
отметил, что производной от х3 является Зх2. Это частный случай простой, но важной
формулы: производной от хп является пхп~19 что можно записать так:
d(xn)	г
—V - = пхп \
ах
(Нас сильно отвлекло бы, если бы я стал объяснять, почему выполняется это соотношение.
На самом деле это нетрудно показать, и заинтересованный читатель сам может найти все
необходимое в любом элементарном учебнике математического анализа ^6*8^. Между про¬
чим, число п здесь не обязано быть целым.) Можно также представить^6*9^ это выражение
(«умножив его на dx») в более удобном виде
d(xn) = пхп 1 dx.
Сверх этого знать о дифференцировании степенных функций нужно не так уж много. Важ¬
ными являются следующие две вещи. Во-первых, производная суммы функций равна сумме
производных этих функций:
d[f(x) + д(х)] =	)	+	dg{x).
Суммирование здесь можно распространить на любое конечное число функций l610'. Во-
вторых, производная от функции, умноженной на постоянную величину, равна производной
от этой функции, умноженной на эту постоянную:
d{a f (х)} — a df (х).
Под «постоянной» я понимаю здесь число, которое не меняется при изменении х. Ко¬
эффициенты степенного ряда ао, аъ а2, аз,... являются постоянными. Пользуясь этими
правилами, можно продифференцировать любой степенной ряд .
Рассмотрите «одну функцию» е~1^х . Покажите, что она обладает С00-гладкостью, но не аналитична
в начале координат.
С помощью степенного ряда для функции ех (см. § 5.3) покажите, что dex = ех dx.

116
Глава 6
Тот факт, что а — постоянная величина, можно выразить другим способом:
da — 0.
Имея это в виду, находим, что предпоследнее правило в действительности является частным
случаем (при д(х) = а) «формулы Лейбница»
d{f{x)g{x)} = f(x) dg(x) + g(x)df(x)
(формулу d(xn)/dx = nxn~x при любом натуральном n также можно вывести из формулы
Лейбница*). Еще одно полезное правило:
= f(g(x))g'(x)dx.
Подставляя в формулу Лейбница /(ж)[<?(ж)]_1> из первого и двух последних соотношений
**
можно вывести
р(ж) d£{x)- /(ж)
Вооружившись этими правилами (а также упорно тренируясь), можно стать «специалистом
по дифференцированию» даже без реального понимания того, почему эти правила работа-
ют! В этом сила хорошего исчисления . Еще более крупным специалистом можно стать,
зная правила дифференцирования всего нескольких частных функций****. Для того чтобы
неподготовленный читатель мог стать «действительным членом» клуба специалистов по
дифференцированию, я приведу главные правила^6Л1^
d(ex) = ех dx,
dx
*****
d( log®)= x,
d(sin x) — cos x dx,
d( cos x) = — sin x dx,
d(tgx)
dx
d(arcsin x)
d(arccos x)
2 ’
COS X
dx
\/l — x2 ’
— dx
У
d( arctg x)
л/l — x2
dx
1 -f x
2 *
т
Это подтверждает точку зрения, высказанную в начале данного раздела: если у нас есть
явные формулы, то операция дифференцирования становится «легкой». Конечно, я не имею
* »
в виду, что вы сможете делать это даже спросонок. Отнюдь нет, в некоторых случаях мо¬
гут получаться очень сложные выражения. Когда называю эту операцию «легкой», я имею
J3 Покажите это.
**
Выведите это.
Вычислите dy/dx для у = (1 — х2)А и у = (1 + ж)/(1 — ж).
****Ж Вычислите d(loga х), ^(log^ a), d(xx), где a — постоянная величина.
*****£§_ Относительно первого из этих правил см. упражнение 6.5; второе выведите исходя из й(е1о&ж); третье и
четвертое — из detx, предполагая, что с комплексными числами можно обращаться так же, как и с вещественными;
остальные выведите из предыдущих, используя d(sin(arcsine)) и т.д., а также учитывая, что cos2 х + sin2 х = 1.
)

6.6. Интегрирование
117
в виду лишь то, что для проведения дифференцирования существует некоторая явная вычис¬
лительная процедура. Если мы знаем, как дифференцировать каждую из составных частей
какого-либо выражения, данные выше правила говорят нам, как подойти к дифференциро¬
ванию всего выражения в целом. «Легкое» здесь означает нечто такое, что можно поручить
компьютеру. Однако всё меняется, если мы попытаемся двинуться в обратном направлении.
6.6.	Интегрирование
Как было упомянуто в начале этой главы, интегрирование есть действие, обратное диф¬
ференцированию. Оно состоит в попытке найти функцию д(х), для которой д'{ х) = f{x),
т. е. найти решение у — д(х) уравнения dy/dx = f(x). Другими словами, вместо того чтобы
двигаться сверху вниз на рис. 6.4 (или рис. 6.5), мы попробуем двинуться снизу вверх. Пре¬
лесть «основной теоремы анализа» в том, что эта процедура позволяет нам найти площадь
под каждой кривой. Посмотрите на рис. 6.8. Напомним, что нижнюю кривую и — f(x)
можно получить из верхней кривой у = д(х)9 поскольку она описывает наклон последней в
каждой точке, т. е. f(x) есть производная функции д(х). Это мы уже имели раньше. А теперь
начнем с нижней кривой. Мы обнаруживаем, что верхняя кривая просто отображает пло¬
щадь, расположенную под нижней кривой. Немного точнее: если взять на нижнем рисунке
две вертикальные прямые, определяемые уравнениями х — а и х = Ь, то площадь, ограни¬
ченная этими прямыми, осью х и самой кривой, будет равна разности высот верхней кривой
в тех же самых точках х. Конечно, в подобных случаях необходимо помнить о знаках. В
тех местах, где нижняя кривая проваливается под ось х9 площадь считается отрицательной.
Кроме того, на рисунке я взял а < b и «разность высот» верхней кривой в виде д{Ъ) — д(а).
Если же а > Ь, знак должен измениться на противоположный.
На рис. 6.9 я попытался сделать это обратное соотношение между наклонами и площа¬
дями интуитивно правдоподобным. Пусть b будет больше а на очень малую величину. Тогда
рассматриваемая площадь на нижнем рисунке будет иметь вид очень узкой полоски, ограни¬
ченной соседними прямыми х = а и х — Ъ. Мерой этой площади будет произведение малой
ширины этой полоски (т. е. Ь — а) на ее высоту (от оси х до кривой). Но высота полоски,
как предполагалось, есть мера наклона верхней кривой в той же точке. Следовательно, пло¬
щадь полоски равна этому наклону, умноженному на ширину полоски. Но наклон верхней
кривой, будучи умноженным на ширину полоски, дает величину, на которую верхняя кривая
возрастает на отрезке от а до Ь, то есть разность д(а) — д{Ь). Таким образом, для очень узких
полосок площадь действительно измеряется указанной разностью. Широкие полосы можно
представить состоящими из большого числа узких полос, поэтому мы находим, что полная
площадь измеряется повышением верхней кривой на всем интервале.
Здесь необходимо прояснить существенный пункт. При переходе от нижней кривой
к верхней имеется неоднозначность в том, как высоко должна быть расположена вся верх¬
няя кривая. Мы имеем дело лишь с разностью высот на верхней кривой, поэтому сдвиг
всей кривой на некоторую постоянную величину вверх или вниз ничего не изменит. Это яс¬
но также из интерпретации «наклона», поскольку наклон в различных точках на верхней
кривой при ее сдвиге вверх или вниз остается прежним. В наших вычислениях это озна¬
чает, что при добавлении постоянной С к д(х) производная полученной функции будет
по-прежнему равна f(x):
d(g(x) + С) ~ dg{x) + dC = f(x) dx -f 0 = f(x) dx.
Такая функция g(x) или, что эквивалентно, д(х)+С с некоторой произвольной постоянной С
называется неопределенным интегралом от функции f(x); это записывается так:
J f(x) dx — g(x) + const.

118
Глава 6
Рис. 6.8. Основная теорема анализа: другая интерпретация рис. 6.4 а, б с переходом не от верхнего
рисунка к нижнему, а наоборот. Верхняя кривая а) дает площадь под нижней кривой б). Площадь,
ограниченная двумя вертикальными прямыми х = а и х = 6, осью х и нижней кривой, равна разности
высот верхней кривой в тех же двух точках х, д(Ь) — д(а) (с учетом знаков)
Это лишь другой способ представления соотношения d[g(x) + const] = f(x)dx, так что
можно рассматривать знак f как операцию, обратную по отношению к символу d. Если нас
интересует площадь между х = а и х — Ь, то нам нужен так называемый определенный
интеграл, который записывается так:
ъ
J / (х)da; — g(b) — g(
а
• •
Если нам известна функция f(x) и мы хотим получить ее интеграл д(х), то необходимо
иметь в виду, что здесь нет таких четких правил, как в случае дифференцирования. Име¬

6.6. Интегрирование
119
g(b)-g{a)
= площадь
затененной полоски
Рис. 6.9. Пусть b будет больше а на очень малую величину. На нижнем рисунке площадь очень узкой
полоски между соседними прямыми х = а и х — Ъ равна произведению ширины полоски b — а на ее
высоту (от оси х до кривой). Эта высота равна наклону верхней кривой в той же точке. Отсюда следует,
что площадь полоски равна этому наклону, умноженному на ширину полоски, а это есть величина,
на которую верхняя кривая возрастает на отрезке от а до b, то есть д(а) — д(Ь). Складывая много
узких полосок, находим, что площадь широкой полосы под нижней кривой равна соответствующей
величине, на которую возрастает верхняя кривая
ется множество различных приемов, часть которых можно найти в стандартных учебниках
и компьютерных программах, но они не охватывают всех возможных случаев. Часто оказыва-
*	*	I
ется, что при расширении семейства ранее использовавшихся явных стандартных функций
приходится «изобретать» новые функции для представления результатов интегрирования.
Мы уже видели это на нескольких частных примерах. Предположим, что мы знакомы только
с функциями, построенными из комбинаций степеней х. Интеграл от степенной функции хп
дает хп+1/(п + 1). (Это получается из формулы в § 6.5, если заменить в ней пнап + 1:
d(xn+1)/dx = (n-f 1)о:п.) Всё будет хорошо, пока мы не зададимся вопросом, что будет
в случае п — — 1. Если взять выражение хп+1/(п -f 1), то оно не работает, так как дает
нуль в знаменателе. Как же тогда интегрировать х~1с! По счастливой случайности, в нашем
списке в § 6.5 имеется формула d(log х) = х~г dx. Поэтому ответ имеет вид log я + const.
Пока всё прекрасно! Так получилось, что по разным причинам мы уже знаем о лога¬
рифмической функции и ее свойствах. Но в других случаях может оказаться, что у нас нет
никакой ранее известной функции, через которую можно выразить ответ. И действительно,
интегралы часто используются для определения новых функций. Именно в этом смысле
интегрирование явно заданных функций оказывается «трудным».
Если же нас интересуют не явные выражения, а вопрос о существовании функций, слу¬
жащих производными или интегралами данных функций, то всё обстоит как раз наоборот.
Теперь интегрирование протекает гладко, а дифференцирование может порождать пробле¬
мы. То же относится и к применению указанных операций к численным данным. Проблемы
при дифференцировании связаны в основном с тем, что дифференцирование существенно

120
Глава 6
зависит от тонких деталей дифференцируемой функции. Это может представить пробле¬
му, если у нас нет явного выражения для функции, которую нужно продифференцировать.
С другой стороны, интегрирование сравнительно нечувствительно к подобным материям
в широком классе интегрируемых функций. Фактически можно проинтегрировать любую
непрерывную функцию (С0-функцию), область определения которой представляет «замкну¬
тый» интервал а ^ х ^ fr^612! результатом будет Сх-функция (т. е. С1-гладкая функция).
Ее можно проинтегрировать снова, получив С2, затем опять, что даст С3-гладкую функцию,
и т.д. Интегрирование делает функции все более и более гладкими, и его можно прово¬
дить бесконечно. Дифференцирование, наоборот, ухудшает положение, и мы можем в конце
концов прийти к тому, что функция станет «недифференцируемой».
В этом вопросе существуют подходы, которые позволяют продолжить процесс диффе¬
ренцирования до бесконечности. Я уже упомянул об этом, когда позволил себе дифференци¬
ровать функцию |ж|, чтобы получить 0(х), хотя функция \х\ «недифференцируема». Можно
попытаться пойти дальше и продифференцировать также 0(х), несмотря на то что она име¬
ет бесконечный наклон в начале координат. «Результатом» будет так называемая дельта-
функция Диракаf613^ — весьма важное понятие в математическом аппарате квантовой ме¬
ханики. Дельта-функция в действительности совсем не функция в обычном (современном)
понимании «функции» как отображения области определения на пространство значений.
У дельта-функции не существует значения в начале координат (она там бесконечна), а всю¬
ду вне его она равна нулю. Тем не менее дельта-функция получает ясное математическое
определение в широком классе математических объектов, известных под названием распре¬
делений.
Для этого мы должны обобщить наше понятие Сп-функций на случай отрицательных
целых значений п. Тогда в(х) будет С-1-функцией, а дельта-функция — С ~2-функцией. Каж¬
дый раз, когда мы дифференцируем, мы понижаем класс дифференцируемости на единицу
(т. е. класс дифференцируемости становится более отрицательным на одну единицу). Чув¬
ствуется, что при этом мы всё дальше уходим от эйлерова понятия «правильной функции»
и что Эйлер посоветовал бы нам не заниматься подобными ухищрениями, даже несмотря
на то, что они кажутся полезными. В свое время мы увидим, что именно здесь комплекс¬
ные числа поражают нас своей утонченной магией. Чтобы убедиться в этом, мы должны
подождать до конца главы 9, поскольку пока я не могу описать это должным образом. По¬
ка читателю придется потерпеть, так как необходимо сначала подготовить почву, которая
также будет устлана другими проявлениями магии.
Примечания
§6.1.
6.1. Я допустил здесь некоторое смешение понятий, так как, например, х2 представляет значение
функции, а не саму функцию. Сама функция отображает а: на т2 и должна бы обозначать¬
ся х ь-> х2 или, согласно ламбда-исчислению Алонсо Чёрча [147], Хх[х2} (см. также [610]).
6.2. В этом разделе я буду часто ссылаться на мнение Эйлера в отношении понятия функции.
Здесь, однако, я должен пояснить, что «Эйлер», на которого я ссылаюсь, в действительности
есть лишь гипотетический или идеализированный персонаж. У меня нет непосредственной
информации о мнениях реального Леонарда Эйлера в том или ином конкретном случае. Однако
те взгляды, которые я приписываю моему «Эйлеру», представляются не слишком отличными
от тех, которые мог бы высказывать реальный Эйлер. Более подробные сведения об Эйлере
можно найти в книгах [99, 768, 226].
§6.2.
6.3. Более подробно см. [116].
6.4. Точнее, именно функция f в целом является производной функции /; мы не можем определить
значение /' в точке х просто по значению / в этой точке. См. примечание 6.1.

6.6. Интегрирование
121
§6.3.
6.5. А именно f"(x)/[ 1 4- f'(x)2]3/2.
6.6. Фактически это подразумевает, что непрерывными должны быть все производные до п-й вклю¬
чительно, поскольку определение дифференцируемости предполагает непрерывность.
§6.4.
6.7. Такое разложение в степенной ряд вблизи нуля традиционно (хотя исторически и неоправдан¬
но) называют рядом Маклорена, более общий результат для разложения вблизи произвольной
точки р приписывают Бруку Тейлору (1685-1731).
§6.5.
6.8. См. [234].
6.9. Пока вы можете воспринимать следующие выражения формально или, если угодно, мысленно
«обратно делить на dx». Используемая здесь запись согласуется с принятой в теории диффе¬
ренциальных форм, обсуждаемой в §§ 12.3-12.6.
6.10. Имеются, однако, тонкости в применении этого правила к сумме бесконечного числа членов,
как в случае степенного ряда. Эти тонкости можно игнорировать, если значения х находятся
строго внутри круга сходимости (см. §4.4). См. [648].
6.11. Напомним (см. §5.1), что arcsin, arccos и arctg суть обратные функции соответственно
от sin, cos и tg. Таким образом, sin (arcsin х) -жит.д. Следует иметь в виду, что эти обратные
srr	srr
функции «многозначны», однако обычно выбирают значения, при которых — — ^ arcsin х ^ —,
0 ^ arccos х ^ 7г и — ^ < arctg х < ~.
§6.6.
6.12. Существенное требование, предъявляемое к области определения, — это чтобы она была ком¬
пактной (см. § 12.6). Конечные интервалы на вещественной оси, включающие концевые точки,
являются компактными.
6.13. Оливер Хевисайд, по-видимому, предложил дельта-функцию задолго до Дирака.

Глава 7
Исчисление комплексных чисел
7.1.	Комплексная гладкость, голоморфные функции
Как следует понимать операцию дифференцирования в применении к комплексной
функции f(z)l Рассмотреть этот вопрос во всех деталях я в этой книге определенно не
смогуЯ не смог должным образом обсудить его в § 6.2 даже в отношении функций ве¬
щественной переменной. Но я по крайней мере попытался сформулировать суть проблемы.
Нижеследующее представляет собой очень беглый обзор основных положений, касающих¬
ся дифференцируемости функций комплексной переменной. После чего я коснусь немного
подробнее наиболее удивительных деталей.
Для комплексного дифференцирования прежде всего необходимо сформулировать поня¬
тие «наклона» комплексной кривой w = f(z) в любой точке z области определения функции.
(Функция f(z) и переменная 0 теперь могут принимать комплексные значения.) Чтобы такое
понятие «наклона» имело согласованный смысл при небольшом смещении точки z в любом
направлении на комплексной плоскости, необходимо, чтобы функция z удовлетворяла неко¬
торой паре уравнений, называемых условиями Коши -Римана^7'2\которые содержат произ¬
водные от вещественной и мнимой частей функции f(z) по вещественной и мнимой частям
переменной z; см. § 10.5). Эти уравнения открывают нам нечто значительное относительно
комплексного интегрирования, позволяющее определить новое понятие — контурное ин¬
тегрирование. Контурное интегрирование позволит нам далее написать красивую формулу
для n-й производной функции f(z). Таким образом, если мы знаем первую производную,
мы легко можем получить все высшие производные.
Далее мы применим эту формулу, чтобы получить коэффициенты предполагаемого ряда
Тейлора, который, как мы должны показать, действительно сходится к функции f(z). Проде¬
лав это, мы получим разложение функции f(z) в ряд Тейлора, справедливое внутри любого
круга на комплексной ^-плоскости, где функция f(z) определена и дифференцируема. Та¬
ким образом, налицо магический факт: любая комплексно-гладкая комплексная функция по
необходимости является аналитической!
В соответствии с этим в комплексном анализе не возникает проблем при выяснении
ограничений на «склеивание» некоторых С00-функций, например h(x), в предыдущей главе.
Понятие комплексной гладкости, несомненно, доставило бы удовольствие Эйлеру. (К сожа¬
лению для реального Леонарда Эйлера, поразительная мощь комплексной гладкости про¬
явилась слишком поздно для него, в 1821 году в трудах Огюста Коши, спустя 38 лет после
смерти Эйлера.) Мы увидим, что комплексная гладкость предоставляет гораздо более эко¬
номный способ для выражения того, что требует «эйлерово» понимание функции, обеспечи¬
вающее существование разложения в степенной ряд. Имеется и другое преимущество при
рассмотрении таких функций с комплексной точки зрения. Напомним о наших затруднениях
с функцией 1/х, которая кажется «одной функцией», несмотря на тот факт, что реальная
кривая у = 1/х состоит из двух отдельных кусков, которые не соединяются «аналитически»
одна с другой через вещественные значения х. С комплексной точки зрения, ясно видно,
&
что l/z~~ действительно единая функция. Единственное место, где эта функция «неправиль¬
но ведет себя» в комплексной плоскости, — это начало координат. Если мы удалим эту одну

7.2. Контурное интегрирование
123
точку из комплексной плоскости, мы получим всё еще связную область. Часть веществен¬
ной оси, для которой х < 0, соединяется с частью, для которой х > 0, через комплексную
плоскость. Таким образом, 1 /z — действительно одна связная комплексная функция, что
в корне отлично от ситуации с вещественными числами.
которые в этом смысле являются комплексно-гладкими (комплексно-
аналитическими), называются голоморфными. Голоморфные функции будут играть важней¬
шую роль во многих наших последующих обсуждениях. Мы поймем их значение в связи
с конформными отображениями и римановыми поверхностями в главе 8 и с рядами Фу¬
рье (незаменимыми в теории колебаний) в главе 9. Как мы увидим в §§24.3, 26.3, эти
функции играют важную роль в квантовой механике и квантовой теории поля. Они служат
также фундаментом для развития новых физический теорий (в частности, теории твисторов
(см. главу 33) и играют существенную роль в теории струн (см. §§31.5, 31.13, 31.14)).
7.2* Контурное интегрирование
Хотя здесь не место проверять все детали математических рассуждении, приведен¬
ных в §7.1, тем не менее необходимо несколько развить изложенное выше. В частности,
будет полезно объяснить понятие контурного интегрирования, что позволит читателю по¬
нять, каким образом можно использовать такое интегрирование для установления требова¬
ний, введенных в § 7.1. Сначала напомним ту запись для определенного интеграла, которая
в предыдущей главе применялась к вещественной переменной х> а теперь — к комплексной
переменной z:
f(z) dz = g{b) - g(a)
a
где g'(z) = f(z). В случае вещественных чисел ин¬
теграл оерется от одной точки а на вещественной
оси до другой точки 6 на той же оси. Имеется только
один способ пройти от а до b вдоль вещественной
оси. Теперь взглянем на эту формулу как на ком¬
плексную. Здесь а и 6 — две точки на комплексной
плоскости. Теперь уже нет одного-единственного
пути от а до 6, вместо этого можно нарисовать мно¬
жество различных траектории, соединяющих точ¬
ки а и Ъ. Условия Коши - Римана утверждают, что
если провести интегрирование вдоль одного из та¬
ких путей Г7*3!, то мы получим тот же результат, что
и при интегрировании вдоль другого такого пути,
который получается из первого путем непрерыв¬
ной деформации внутри области определения функ¬
ции. (См. рис. 7.1. Это свойство является следстви¬
ем простого частного случая «основной теоремы
внешнего анализа», изложенной в § 12.6.) У некото¬
рых функций, например 1/z, область определения
содержит «прокол» (в случае функции 1 jz прокол
находится в точке z = 0), так что имеется несколько
существенно различных путей перехода от а до Ъ.
Термин «существенно различные пути» означает,
что один из путей не может быть деформирован
Рис. 7.1. Различные пути от а до 5. Инте¬
грирование голоморфной функции / вдоль
одного из путей дает тот же результат, что
и вдоль любого другого пути, получаемо¬
го из первого непрерывной деформацией
внутри области определения /. Для неко¬
торых функций область определения со¬
держит «прокол» (например, z. = 0 в слу¬
чае функции 1/z), препятствующий осу¬
ществлению некоторых деформаций, так
что могут получаться различные ответы

124
Глава 7
в другой непрерывным образом, оставаясь в области определения функции. В таких случаях
интеграл от а до Ь имеет разное значение для различных путей.
Здесь необходимо сделать разъяснение (или, скорее, внести поправку). Когда я говорю,
что один путь непрерывно деформируется в другой, я имею в виду то, что математики назы¬
вают гомологическими деформациями, в отличие от гомотопических деформаций. В случае
гомологической деформации принимается, что части траекторий, проходимые в противо¬
положных направлениях, уничтожают одна другую. На рис. 7.2 приведен пример такой
допустимой деформации. Про две траектории, деформируемые одна в другую подобным
образом, говорят, что они принадлежат к одному и тому же классу гомологий. Гомотопиче¬
ские деформации, в отличие от гомологических, не допускает такого взаимного уничтоже¬
ния. Траектории, деформируемые одна в другую при запрещении взаимного уничтожения,
принадлежат к одному и тому же гомотопическому классу. Гомотопические кривые всегда
являются гомологическими, обратное утверждение справедливо не всегда. Для непрерывных
движений гомотопия и гомология эквивалентны, и они составляют часть предмета тополо¬
гии. Далее мы увидим, что различные аспекты топологии играют важную роль и в других
областях.
Рис. 7.2. При гомологической деформации части траектории, проходимые в противоположных направ¬
лениях, уничтожают одна другую. Это иногда приводит к возникновению отдельных петель
Функция f(z) = 1/z представляет пример функции, для которой получаются различные
ответы, когда траектории не гомологичны. Можно понять, почему этот так, на основании
того, что мы уже знаем о логарифмах. В конце предыдущей главы было сказано, что log z
есть неопределенный интеграл от 1/z. (Там это было установлено лишь для вещественной
переменной х9 но те самые рассуждения дают аналогичный результат для комплексных
величин. Это общий принцип, применимый и к другим явным формулам.) Таким образом,
мы имеем
ь
J Ц- = log Ъ - log а.
а
Напомним, что, согласно §5.3, для комплексного логарифма существуют различные воз¬
можные «ответы». Существенно, что мы можем непрерывным образом перейти от одного
ответа к другому. Чтобы показать это, зафиксируем а и будем изменять Ъ. Позволим точке Ь
совершить непрерывным образом полный оборот вокруг начала координат в положительном
направлении (т. е. против часовой стрелки, см. рис. 7.3 а) и вернуться в исходное.положение.
Напомним (см. §5.3), что мнимая часть logb есть просто аргумент числа Ъ (т.е. отсчиты¬
ваемый в положительном направлении угол, образуемый отрезком, соединяющим точку Ь
с началом координат, с положительной вещественной осью; см. рис. 5.4 б). При указанном

7.2. Контурное интегрирование
125
движении этот аргумент увеличивается точно на 2л, так что log Ъ увеличивается на 2лг
(см. рис. 7.3 б). Таким образом, значение нашего интеграла увеличивается на 27гг, когда
траектория, по которой берется интеграл, делает еще один оборот вокруг начала координат
в положительном направлении.
б)
«)
а
г)
Рис. 7.3. а) Интегрирование z~x от а до 6 дает log b — log а. б) Если зафиксировать а и позволить
точке b сделать полный оборот вокруг начала координат против часовой стрелки, то log b увеличится
на 2iri. в) Вернемся затем в точку а по прежнему пути, г) Если часть пути из а уничтожается, остается
контурный интеграл по замкнутому контуру, взятый против часовой стрелки, j> z~1dz — 2л г
Этот результат можно переформулировать в терминах замкнутых контуров, существо¬
вание которых является характерной важной особенностью комплексного анализа. Рассмот¬
рим разность между второй и первой из наших двух траекторий, то есть пройдем сна¬
чала вдоль второй траектории, а затем вдоль первой в обратном направлении (рис. 7.3 в).
Мы рассматриваем эту разность в гомологическом смысле, так что части, проходимые туда
и обратно, взаимно компенсируются, а остальная часть распрямляется непрерывным обра¬
зом. В результате получается замкнутая траектория, или контур, однократно охватывающий
начало координат (см. рис. 7.3 г) и не зависящий от расположения точек а и 6. Это дает
пример интеграла по (замкнутому) контуру, обозначаемого обычно символом j>; в данном
случае*
= 2лг.
Пользуясь этим символом, мы должны, конечно, ясно представлять себе, по какому контуру
• ■ 9 ■ •
проводится интегрирование, или, вернее, каков класс гомологий используемого контура.
Если наш контур обходится дважды (в положительном направлении), мы получим ответ 4лг\
Если же контур проходится один раз в противоположном направлении (по часовой стрелке),
то ответом будет —2лг.
Интересно, что получение нетривиального ответа для такого замкнутого контура кри¬
тическим образом зависит от многозначности комплексного логарифма, которая может по¬
казаться следствием неадекватного определения логарифма. Сейчас мы увидим, что это
не просто курьез. На этом фактически зиждется мощь комплексного анализа. В следую-
Объясните, почему § zn dz = 0, когда п — целое число, отличное от — 1.

126
ГЛАВА 7
представлю некоторые приложения фактов такого р
як сможет кое-что усвоить из нашего обсуждения, и
ное, что заключено в математических рассуждениях
7.3.	Степенные ряды, получаемые из комплексной гладкости
Приведенное выше выражение представляет частный случай (для постоянной функ¬
ции f(z) = 2тгг) известной формулы Коши, которая связывает значение голоморфной функ¬
ции в начале координат с интегралом по контуру, окружающему эту точку
/(0).
Здесь f(z) — функция, голоморфная в начале координат (т. е. комплексно-гладкая в неко¬
торой области, окружающей эту точку), а контур представляет собой некоторую петлю,
окружающую начало координат (или он может быть любой другой петлей, гомологичной
с указанной), в области определения функции, из которой исключено начало координат.
Таким образом, мы имеем замечательный факт: поведение функции в начале координат
полностью определяется тем, что происходит во множестве точек, окружающих начало
координат. (Формула Коши вытекает из условий Коши-Римана и вышеприведенного выра¬
жения § —■ = 2тгг, взятого в пределе малой петли, но здесь не место входить во все детали.)
Если в формуле Коши вместо l/z взять l/zn+1, где п — некоторое положительное целое
число, то мы получим вариант формулы Коши «более высокого порядка», описывающий
поведение n-й производной f^n\z) от f(z):
(Определение п! см. в § 5.3.) Можно убедиться, что эта формула «должна быть правильным
ответом», рассмотрев степенной ряд для функции f{z)* однако при этом возникает вопрос
об использовании этого факта, поскольку мы пока не знаем, существует ли разложение в сте¬
пенной ряд и даже существует ли n-я производная функции /(#). На этой стадии мы знаем
лишь, что функция f(x) — комплексно-гладкая, и не знаем, можно ли ее дифференцировать
более чем один раз. Однако мы просто будем использовать эту формулу как определение п-й
производной в начале координат. Можно затем подставить это «определение» в формулу
Маклорена ап = f^(0)/n\ (см. § 6.4) для коэффициентов степенного ряда
ао 4- a\z 4- a2Z2 4- a3z3 4- a^z4 -I
и после небольшой работы убедиться, что сумма этого ряда действительно равна f(z) в неко¬
торой области, окружающей начало координат. Следовательно, функция имеет га-ю про-
изводную, определяемую указанной формулой . Здесь заключена сущность рассуждении,
показывающая, что комплексная гладкость в области, окружающей начало координат, дей¬
ствительно означает (комплексную) аналитичность функции в начале координат (т. е. ее го¬
ломорфность).
Во всех этих рассуждениях начало координат, разумеется, ничем не выделено. С рав¬
ным правом можно говорить о разложении в степенной ряд вблизи любой другой точки р
Покажите это, просто подставив в этот интеграл ряд Маклорена для функции f(z).
Покажите это хотя бы на уровне формальных выкладок, не заботясь о строгом обосновании. (iПодсказка:
рассмотрите формулу Коши со сдвинутым началом координат.)

7.4. Аналитическое продолжение
            ■ " 1 « —■■■ ' ■ ■■■■■■—■»
127
комплексной плоскости и использовать ряд Тейлора, как это было сделано в § 6.4. Для это¬
го просто сместим начало координат в точку р и получим формулу Коши «со сдвинутым
началом координат»
= /(И,
а также формулу для n-й производной:
% * л
<*> •
в которых контур интегрирования окужает точку р комплексной плоскости. Таким образом,
комплексная гладкость влечет за собой аналитичность (гомоморфность) в каждой точке
области определения.
Я предпочел продемонстрировать основы доказательства того, что локальная комплекс¬
ная гладкость означает аналитичность, нежели предложить читателю принять этот результат
на веру, потому что это — удивительный пример того, как математики порой могут полу¬
чать свои результаты. Ни посылка (f(z) есть комплексно-гладкая функция), ни заключение
(функция f(z) аналитична) не содержат какого-либо намека на понятие контурного инте¬
грирования или многозначность комплексного логарифма. Тем не менее эти ингредиенты
указывают правильный путь к нахождению ответа. Трудно представить себе какое-то «пря¬
мое» рассуждение (каким бы оно ни было), которое могло бы привести к нему. К цели
ведет математическая любознательность. Увлекательная природа комплексного логарифма
сама по себе побуждает к изучению его свойств. Эта внутренняя привлекательность, по-
видимому, не зависит от каких-либо применений, которые мог бы найти логарифм в других
областях. То же самое, в еще большей степени, относится и к контурному интегрирова¬
нию. Есть особое изящество в основной концепции, сочетающей топологическую свободу
с явными соотношениями*. Но здесь не просто изящество — контурное интегрирование
дает также очень мощный, полезный математический метод, работающий во многих обла¬
стях и содержащий многие стороны магии комплексных чисел. В частности, оно приводит
к удивительному способу вычисления определенных интегралов и суммирования различ-
•J» ^ ^
ных бесконечных рядов »	. Оно находит также множество других применений в физике
и технике, а также в других областях математики. Эйлер наслаждался бы им!
7.4.	Аналитическое продолжение
Теперь мы имеем замечательный результат: комплексная гладкость в некоторой об¬
ласти эквивалентна существованию разложения в степенной ряд вблизи некоторой точки
Функция f(z) голоморфна на замкнутом контуре Г, а также внутри Г за исключением конечного
множества точек, в которых / имеет полюсы. Напомним (§ 4.4), что полюс порядка п в точке z = а возника¬
ет, когда f(z) имеет вид h(z)/(z — а)п, где функция h(z) регулярна в точке а. Покажите, что § f(z)dz =
= 2т х {сумма вычетов в этих полюсах}, где вычет в полюсе а есть	(а)/(п — 1)1	»- - •
^	ОО
** пт Покажите, что f х~} sin х dx = —, путем интегрирования z~1etz по замкнутому контуру Г, состоящему
о	^	":"
из двух отрезков вещественной оси — от —Л до — е и от € до Л (где Л > е > 0) и двух соединяющих их
полуокружностей в верхней полуплоскости с соответствующими радиусами 6 и Л. Затем перейдите к пределам и —»
0 и R —* оо.
ill	2
Покажите, что 1 4—- 4—- 4—4- * * • — -тг, интегрируя f(z) = z~2 ctgirz (см. примечание 5.1) по
2 З2 4	6
большому контуру, например, квадрату со стороной 2N 4- 1 и центром в начале координат (N — большое целое
число), затем перейдите к пределу N	оо. (Подсказка: используя упражнение 7.4, найдите полюсы функции f(z)
и вычеты в них. Попробуйте объяснить, почему интеграл от f(z) по контуру Г стремится к предельному значению 0,
когда N —► оо.)

128
Глава 7
в этой области. Однако мне хотелось бы пояснить,
что здесь понимается под «областью». Я имею в ви¬
ду то, что математики называют открытой областью.
Ее можно определить следующим образом: если точ¬
ка а находится в данной области, то существует неко-
с#
Рис. 7.4. Открытый единичный диск
х <1. Любую точку, лежащую стро¬
го внутри него (независимо от того, на-
сколько она близка к окружности), мож¬
но окружить гораздо меньшей окружно¬
стью, внутренняя область которой лежит
строго внутри единичного круга. В слу¬
чае закрытого диска \х\ ^ 1 точки на
границе этим свойством не обладают
торыи круг с центром в точке а, внутренняя часть
которого также содержится в данной области. Та¬
кое определение не очень наглядно, поэтому приведу
некоторые примеры. Одна точка не образует ни от¬
крытой области, ни обычной кривой. Однако вну¬
тренняя область единичного круга на комплексной
плоскости, то есть множество точек, расстояние ко¬
торых от начала координат строго меньше единицы,
есть открытая область. Так обстоит дело потому, что
любая точка, лежащая строго внутри крута, независи¬
мо от того, насколько она близка к ограничивающей
окружности, может быть окружена гораздо меньшей
окружностью, так что внутренняя область соответ¬
ствующего круга будет лежать строго внутри еди¬
ничного круга (см. рис. 7.4). Наоборот, замкнутый
диск, состоящий из точек, расстояние которых от на¬
чала координат меньше или равно единице, не явля¬
ется открытой областью, поскольку теперь включает
окружность, каждая точка которой не ооладают тем свойством, что существует круг с цен¬
тром в этой точке, внутренняя часть которого содержится внутри этой области.
Рассмотрим область определения^7D некоторой голоморфной функции f(z), при¬
чем D — открытая область. В каждой точке области D функция f(z) обладает комплексной
гладкостью. Если, в соответствии с вышесказанным, выбрать некоторую точку р в этой
области, то мы будем иметь сходящийся степенной ряд вблизи этой точки, который пред¬
ставляет функцию f(z) в некоторой области, содержащей точку р. Но насколько велика эта
«некоторая область»? Может оказаться, что при заданном р степенной ряд не будет схо¬
диться во всей области £>. Напомним о круге сходимости, введенном в § 4.4. Это есть круг
с центром в точке р (возможен и бесконечный радиус), обладающий тем свойством, что
степенной ряд сходится для всех точек, лежащих строго внутри этого круга, и расходится
для точек z, лежащих строго вне этого круга. Предположим, что функция f(z) содержит
сингулярность в некоторой точке q> где эта функция не может быть разложена в ряд, хо¬
тя и остается комплексно-гладкой. (Например, функция f (z) = 1/z сингулярна в начале
*
координат q — 0; см. §7.1. Сингулярность иногда называется сингулярной точкой данной
функции. Регулярной называется точка, в которой функция несингулярна и, следователь¬
но, голоморфна.) Тогда круг сходимости не может быть настолько велик, чтобы содержать
внутри себя точку q. Следовательно, мы будем иметь нагромождение кругов сходимости
(обычно бесконечное число их), которые покрывают всю область D, тогда как ни один от¬
дельный круг, в общем случае, ее не покрывает. Случай f(z) — 1/z иллюстрирует такую
ситуацию (см. рис 7.5). Здесь областью D служит вся комплексная плоскость с удаленным
из нее началом координат. Если взять в области D некоторую точку р, то кругом сходимо-
сти будет круг с центром в точке р, граница которого проходит через начало координат .
*	s
Для того чтобы покрыть всю область 17, потребуется бесконечное число таких кругов.
Это приводит нас к важному понятию аналитического продолжения. Пусть задана
некоторая функция f(z), голоморфная в некоторой области D, и мы задаемся вопросом:
Какой вид имеет степенной ряд для функции f(z) = 1/z вблизи точки р?

7.4. Аналитическое продолжение
129
Рис. 7.5. Для функции f(z) = 1/z областью определения D служит комплексная плоскость с уда¬
ленным из нее началом координат. Круг сходимости вокруг произвольной точки р в этой области
ограничен окружностью с центром в точке р, проходящей через начало координат. Чтобы покрыть всю
область D, требуется бесконечное множество таких кругов
можно ли расширить область D до некоторой области большего размера D\ так чтобы
функция f (z) осталась голоморфной во всей области £)'? Например, функция f(z) может
быть задана в виде степенного ряда, сходящегося внутри своего круга сходимости, и мы
хотим расширить f(z) за пределы этого круга. Часто это оказывается возможным. В § 4.4
мы рассматривали ряд 1 ~~ z2 + z4 — z6 -I , для которого кругом сходимости служит круг
единичного радиуса. Естественным расширением его будет функция (1+22)-1, голоморфная
во всей комплексной плоскости, из которой удалены лишь две точки, -И и — г. Таким образом,
функция в этом случае может быть расширена аналитическим образом далеко за пределы
области, в которой она была первоначально задана.
В данном случае можно написать для нашей функции явную формулу, но в других
случаях это может оказаться не так просто. Тем не менее существует некоторая общая
/ *
процедура, с помощью которой часто бывает можно провести аналитическое продолжение.
Мы можем исходить из некоторой малой области, где известно локально справедливое пред-
4
ставление голоморфной функции/(z) в виде степенного ряда. Затем можно двигаться вдоль
некоторого пути, продолжая эту функцию вдоль пути следования и проводя там разложение
в ряд около различных точек. Для этого мы должны взять последовательность точек вдоль
пути и проводить разложение в ряд поочередно вокруг каждой из этих точек. Получается
конфигурация, определяемая условием, что внутренние области соседних кругов сходимо¬
сти могут перекрываться (см. рис. 7.6). Если эту процедуру можно провести согласованным
образом, результирующая функция однозначно определяется значениями функции во вну¬
тренней области и на пути, вдоль которого проводится ее продолжение.
Таким образом, существует замечательная «жесткость» в отношении голоморфных
функций, проявляющаяся в этом процессе аналитического продолжения. В случае веще¬
ственных С00-функций можно было «изменить намерения» в отношении того, как должна
вести себя функция (так, в § 6.3 гладко сшитая функция h(x) резко «взмывала вверх» после
того, как она была равна нулю при всех отрицательных значениях х; см. рис. 6.7). С го¬
ломорфными функциями такого произойти не может. Коль скоро задана функция в ее на¬
чальной области и путь, вдоль которого ведется ее продолжение, уже не остается выбора
относительно того, как эта функция должна быть продолжена. Фактически то же самое спра¬
ведливо и в отношении вещественных аналитических функций вещественной переменной.
Они также обладают подобной «жесткостью», но теперь не так уж много возможностей
при выборе пути. Можно выбирать лишь между тем или иным направлением вдоль ве-

130
Глава 7
последовательности точек. Результат получается однозначным при условии, что последовательные
. \
круги перекрываются
щественной оси. Аналитическое продолжение комплексных функций может быть намного
интереснее, поскольку имеется свобода выбора пути на двумерной плоскости.
Чтобы проиллюстрировать это, обратимся к нашему старому другу log z. Он определен¬
но не может быть разложен в степенной ряд вблизи начала координат, поскольку имеет там
сингулярность. Однако если нам хочется, можно разложить его, скажем, около точки р = 1
и получить ряд*
logz = (z - 1) - |(z - l)2 + |(г - l)3 - |(г - l)4 + • • • .
Кругом сходимости этого ряда служит круг единичного радиуса с центром в точке z = 1.
Представим себе аналитическое продолжение вдоль пути, который обходит начало коорди¬
нат в направлении против часовой стрелки. Мы можем, если хотим, взять степенной ряд
последовательно в точках 1, и;, и;2 и затем снова 1, вернувшись, таким образом, в исходную
точку после одного полного обхода начала координат (рис. 7.7). Здесь я использовал три
кубических корня из единицы, равномерно расположенных вдоль единичной окружности,
а именно 1, си ~ е2пг13 и си2 —	ш	обсуждалось в конце § 5.4; путь обхода вокруг
начала координат можно выбрать в виде равностороннего треугольника. Вместо этого мож¬
но было выбрать путь 1, г, —1, —г, 1, что несколько менее экономично. В любом случае
нет надобности проводить разложение в степенной ряд, поскольку мы уже знаем явный вид
самой функции, а именно log z. Существует, конечно, проблема: если мы обходим один раз
вокруг начала координат, однозначно следуя поведению функции, то обнаружим, что одно¬
значно продолжили ее до значения, отличного от того, с которого начинали. После обхода
к нашей функции добавляется 2т. Если бы мы обошли вокруг начала координат в проти¬
воположном направлении, то нашли бы, что 2т вычитается из исходной функции. Так что
однозначность аналитического продолжения может быть весьма тонкой штукой, и оно опре¬
деленно может зависеть от выбранного пути. Для «многозначных» функций, более сложных,
чем log z9 мы можем получить что-нибудь гораздо более изощренное, чем просто добавление
к функции некоторой постоянной (вроде 2ти).
Попутно стоит заметить, что понятие аналитического продолжения можно ввести, не об¬
ращаясь к степенным рядам, несмотря на то что сам я счел полезным использовать их в сво-
* Получите этот ряд.

7.4. Аналитическое продолжение
131
••
Рис. 7.7. Начиная с z = 1, проводится аналитическое продолжение функции f(z) — log г вдоль пути,
обходящего начало координат против часовой стрелки (с разложением в ряд последовательно около
точек 1, из, и2, 1; из = е27Гг^3). В результате к функции / прибавляется 2дг
ем изложении. Например, существует другой класс рядов, играющих важную роль в теории
чисел, так называемых рядов Дирихле. Наибольшее значение из них имеет дзета-функция
(Эйлера~)Римана\7,6£ определяемая бесконечной суммой'7-7^
£(*) = l~z + 2~z + 3~z -h	H	,
которая сходится к голоморфной функции, обозначаемой £(z)9 когда вещественная часть
переменной г больше 1. Аналитическое продолжение этой функции определяет ее един¬
ственным образом («однозначно») на всей комплексной плоскости, но с удаленной из нее
точкой z ~ 1. Возможно, наиболее важной из нерешенных математических проблем сегодня
является гипотеза Римана, имеющая дело с нулями аналитически продолженной дзета-
функции, то есть с решениями уравнения ф) = 0. Сравнительно легко показать, что £(2:)
обращается в нуль при £ — —2, —4, —6,...; это вещественные нули дзета-функции. Гипо-
теза Римана утверждает, что все остальные нули лежат на прямой Re(z) = то есть ф)
обращается в нуль (если 2 не является отрицательным четным числом), только если веще¬
ственная часть z равна -. Все проведенные до сего дня численные проверки подтверждают
эту гипотезу, однако ее истинность пока не доказана. Эта гипотеза имеет фундаментальное
значение для теории простых чисел^7*8!.
Примечания
§7.1.
7.1. Читателю, желающему изучить эти увлекательные материи с геометрическими подробностями,
я настоятельно рекомендую книгу Нидхема [544].
7.2. Я изложу их в § 10.5 после введению понятия частной производной.
§7.2.
7.3. Более точно, интеграл от функции / «вдоль» пути, задаваемого уравнением z — p(t) (где р есть
гладкая комплекснозначная функция от вещественного параметра t), можно представить в виде
v	b
определенного интеграла f /(p(t))p'(t) dt = f f(z)dz, где p(u) есть начальная точка пути а,
и	а
a p(v) — его конечная точка Ь.

132
Глава 7
§7.3.
7.4. «Причина», по которой формула Коши должна быть справедлива, состоит в том, что для малой
петли вокруг начала координат функцию f(z) можно рассматривать как постоянную величи¬
ну /(0), и тогда ситуация сводится к рассмотренной в § 7.2.
7.5. Одним из недостатков терминологии данного предмета является то, что термин «область» имеет
два различных значения. Одно из них {не использованное здесь) — это просто «связная открытая
область в комплексной плоскости». Здесь же, как и раньше (см. §6.1), я имею в виду область,
в которой определена функция / и которая в общем случае не должна обязательно быть ни
открытой, ни связной (хотя здесь она предполагается открытой).
7.6. Дзета-функция впервые рассматривалась Эйлером, но обычно носит имя Римана в честь его
фундаментальной работы, в которой исследовалось продолжение этой функции в комплексную
плоскость.
7.7. Отметим в качестве курьеза «взаимно перевернутое» соотношение между этим рядом и обыч¬
ным степенным рядом {—z) + (—z)2 4- (—z)3 + • • • = —z( 1 -f z)-1.
7.8. Дальнейшую информацию о С-функции и гипотезе Римана можно найти в книгах Апостола [25]
и Пристли [648]. Более популярное изложение имеется в книгах [182, 189, 190, 225, 680].
/
••
*

Глава 8
■
Римановы поверхности и комплексные
отображения
8.1.	Идея римановой поверхности
Существует способ описания того, что происходит
при аналитическом продолжении логарифмической функ¬
ции (или любой другой «многозначной функции»), на осно¬
ве так называемых риманоеых поверхностей. Идея Римана
состояла в том, чтобы считать такие функции определен¬
ными в области, которая представляет собой не просто под¬
множество комплексной плоскости, а некоторую многолист¬
ную область. В случае log z мы можем представить ее как
некоторый спиральный подъем, вертикально возносящий¬
ся над комплексной плоскостью. Я попытался изобразить
это на рис. 8.1. На этом закрученном многолистном вари¬
анте комплексной плоскости логарифмическая функция од¬
нозначна, поскольку всякий раз, когда мы обходим вокруг
начала координат и должны добавить к значению логариф¬
ма 27гг, мы оказываемся на другом листе нашей области. Те¬
перь уже не возникает конфликта между различными значе¬
ниями логарифма, потому что его областью определения те¬
перь служит это расширенное закрученное пространство —
пример римановой поверхности,— имеющее тонкие отличия
от самой комплексной плоскости.
Бернхард Риман, предложивший эту идею, был одним из величайших математиков,
и за свою недолгую жизнь (1826-1866) он выдвинул множество математических идей, ко¬
ренным образом изменивших ход математической мысли на нашей планете. В этой книге
мы еще столкнемся с некоторыми из них, в частности, с той, которая легла в основу общей
теории относительности Эйнштейна (другой очень важный вклад Римана уже упоминался
в конце главы 7). До того как Риман ввел понятие того, что ныне именуется «римановой
поверхностью», среди математиков были разногласия относительно того, как трактовать так
называемые «многозначные функции», одним из простейших примеров которых может слу¬
жить логарифм. Если быть строгим, то необходимо сказать, что многие считали нужным
рассматривать эти функции способом, который я лично счел бы безвкусным. (При том что
именно этот способ я сам намеревался применить в годы моей учебы в университете, несмот¬
ря на то что это происходило почти век спустя после появления эпохальной работы Римана
по этому предмету.) В частности, предлагалось произвольным образом «разрезать» область
определения логарифмической функции по прямой, проведенной из начала координат в бес¬
конечность. На мой взгляд, это грубо калечит величественную математическую структуру.
Риман учит нас действовать по-другому. Голоморфные функции становятся неудобными при
нашем обычном понимании «функции», которая отображает заданную область определения
Рис. 8.1. Риманова поверхность
для log z9 имеющая вид верти¬
кально восходящего спирального
подъема

134
Глава 8
на определенное пространство значений. Как мы видели, при аналитическом продолжении
голоморфная функция «имеет собственное мнение» и сама решает, какова должна быть ее
область определения, независимо от того, какую область комплексной плоскости мы ей
изначально назначили. Если же считать, что область определения функции представлена
соответствующей римановой поверхностью, то эта область не задается раньше времени;
вместо этого явный вид самой функции говорит нам, какая риманова поверхность действи¬
тельно служит областью определения.
Вскоре мы встретимся с различными другими видами римановых поверхностей.
Эта красивая концепция играет важную роль в некоторых современных попытках найти но¬
вую основу для математической физики, — наиболее заметных в теории струн (§§31.5,31.13),
но также и в теории твисторов (§§33.2, 33.10). Риманова поверхность для logz — одна из
простейших таких поверхностей. Она лишь дает намек на то, что нас ожидает. Функция za
в том, что касается ее римановой поверхности, более интересна, чем log 'z, но только когда
комплексное число а рационально. Если число а иррационально, то риманова поверхность
для имеет такую же структуру, как и для log г, однако для рациональных значений а
низший член разложения имеет порядок а = т/п и листы, закрученные в спираль, снова
соединяются между собой после п оборотов*. Начало координат z = 0 во всех этих приме¬
рах называется точкой ветвления. Если листы соединяются вместе после конечного числа
оборотов п (как в случае функции zm/n, где т и п не имеют общих множителей), то гово¬
рят, что точка ветвления имеет конечный порядок или что это точка ветвления п-го порядка.
Если же листы не соединяются вместе после любого числа оборотов (как в случае log z),
то говорят, что точка ветвления имеет бесконечный порядок.
Выражения типа (1 — г3)1/2 дают нам больше пищи для размышлений. Эта функция
имеет три точки ветвления, z — z = ojviz = ui2 (где и; = е27Г*/3, см. §§5.4, 7.4), поэто¬
му 1 — z3 = 0, и еще имеется «точка ветвления на бесконечности». Если совершить один
полный оборот вокруг каждой из точек ветвления, оставаясь в непосредственной близости
от нее (в том числе и вокруг точки на бесконечности; это означает обход по очень большой
окружности), мы обнаружим, что функция меняет знак; при следующем обходе функция
вернется к начальному значению. Таким образом, мы видим, что все точки ветвления имеют
порядок 2. Риманова поверхность содержит два листа, сшитые вместе так, как я попытал¬
ся показать на рис. 8.2 а. На рис. 8.2 б с помощью топологических деформаций показано,
что риманова поверхность имеет топологию тора (бублика), но с четырьмя маленькими
отверстиями в нем, соответствующими самим точкам ветвления. Эти отверстия можно за¬
крыть четырьмя отдельными точками, и тогда получится риманова поверхность с точной
топологией тора .
Римановы поверхности представляют первые примеры общего понятия многообра¬
зия — пространства, которое можно «искривлять» различным образом, но которое локально
(т. е. в достаточно малой окрестности любой из его точек) выглядит как обычное евклидово
пространство. В главах 10 и 12 мы столкнемся с многообразиями более серьезно. Поня¬
тие многообразия играет важнейшую роль во многих областях современной физики. Более
конкретно, оно образует существенную часть общей теории относительности Эйнштейна.
Многообразия можно считать склеенными из различных кусков («лоскутов»), причем без
швов, в отличие от ситуации с функцией h(x) в конце § 6.3. Отсутствие швов определя¬
ется тем, что всегда существует соответствующая (открытая) область перекрытия между
соседними сшиваемыми кусками (см. рис. 8.2 в, а также рис. 12.5 в § 12.2).
В случае римановых поверхностей многообразие (т. е. сама риманова поверхность) скле¬
ивается из различных кусков комплексной плоскости, соответствующих различным «ли¬
стам», из которых состоит поверхность в целом. Мы можем разделаться с несколькими
**
Объясните, почему это так.
S3 Теперь попробуйте проделать то же самое с функцией (1 — z4)1/2.

8.1. Идея римановой поверхности
135
Открытая
область
я)
б)
в)
Рис. 8.2. а) Построение римановой поверхности для функции (1 — z3)1'/2 из двух листов с точка¬
ми ветвления второго порядка 1, ш и о;2 (а также оо). 6) Чтобы увидеть, что риманова поверхность
для (1 — z3)х^2 имеет топологию тора, представьте плоскости на рис. а как две римановы сферы
со щелями, прорезанными от w до w2 и от 1 до оо, как показано стрелками. Получаются два топо¬
логических цилиндра, при соответствующем склеивании которых получится тор. в) Чтобы получить
риманову поверхность (или, в более общем случае, многообразие), можно склеить куски коорди¬
натного пространства — в данном случае открытые участки комплексной плоскости. Между этими
участками должны существовать открытые области перекрытия (и при их соединении не должно быть
«не-хаусдорфова разветвления», как в последнем вышеприведенном случае; см. рис. 12.5 6 в § 12.2)
«дырками» в виде удаленных из нее отдельных точек, соответствующих точкам ветвления
конечного порядка. Эти удаленные точки всегда можно восстановить однозначным обра¬
зом, как указано выше. Однако в случае точек ветвления бесконечного порядка ситуация
становится более сложной, и подобные общие утверждения делать уже нельзя.
В качестве примера рассмотрим риманову поверхность в виде «спирального подъема»
для логарифмической функции. Один из способов соединить ее в целое (например, в виде
бумажной модели) — это последовательно брать чередующиеся копии (а) комплексной плос¬
кости с удаленными из нее неотрицательными вещественными числами и (б) комплексной
плоскости с удаленными неположительными вещественными числами. Верхняя половина
каждого такого куска типа (а) должна склеиваться с верхней половиной следующего куска
типа (б), а нижняя половина каждого куска типа (б) — с нижней половиной следующего
куска типа (а) (см. рис. 8.3). Здесь имеется точка ветвления бесконечного порядка в начале
координат, а также на бесконечности. Как ни странно, оказывается, что весь спиральный
подъем эквивалентен просто сфере с одной удаленной из нее точкой, которая может быть
восстановлена однозначным образом, так что получается просто сфера .
* Л Понятно ли, как это происходит? (Подсказка: рассмотрите риманову сферу переменной w{= log z);
см. § 8.3.)

136
Глава 8
а)
6) .
Рис. 8.3. Можно построить риманову поверхность для функции log г, беря поочередно куски а) ком¬
плексной плоскости с удаленной из нее неотрицательной вещественной полуосью и б) комплексной
плоскости с удаленной неположительной вещественной полуосью. Верхняя половина каждого куска
типа а) склеивается с верхней половиной следующего куска типа б), а нижняя половина каждого куска
типа б) — с нижней половиной следующего куска типа а)
8.2.	Конформные отображения
При соединении кусков отображения мы должны следить за тем, какая локальная струк¬
тура должна сохраняться при переходе от одного куска к другому. Обычно имеют дело
с вещественными многообразиями, так что различные куски являются частями евклидова
пространства (некоторой заданной размерности), которые склеиваются вместе по различным
(открытым) перекрывающимся областям. Локальная структура, которую следует согласовы¬
вать при переходе от одной части к следующей, обычно должна удовлетворять требованиям
непрерывности или гладкости. Эта сторона дела будет обсуждена в § 10.2. В случае же ри-
мановых поверхностей мы имеем дело с комплексной гладкостью, которая, напомним § 7.1,
имеет более тонкий характер, связанный с условиями Коши-Римана. Хотя мы пока и не ви¬
дели их явно (это произойдет в § 10.5), здесь будет уместно понять геометрический смысл
структуры, заложенной в этих условиях. Эта структура обладает замечательным изяще¬
ством, гибкостью и мощью, приводя к математическим концепциям с широким спектром
применения.
Одной из таких концепций является конформная геометрия. Грубо говоря, в конформ¬
ной геометрии мы интересуемся формой и не интересуемся размером, сводя, таким образом,
форму на уровень бесконечно малых масштабов. При конформном отображении одной (от¬
крытой) области плоскости на другую форма конечных участков в общем случае искажается,
однако форма бесконечно малых участков сохраняется. Можно понять это, рассматривая ма¬
лые (бесконечно малые) круги, нарисованные на плоскости. При конформном отображении
эти маленькие круги могут расширяться или сжиматься, но они не могут деформироваться
в маленькие эллипсы (см. рис. 8.4).
Чтобы получить представление о том, на что может быть похоже конформное отображе¬
ние, взглянем на рисунок Морица Эшера (рис. 2.11), где дается конформное представление
гиперболической плоскости в евклидовом пространстве, описанное в § 2.4 («диск Пуанка¬
ре», построенный Бельтрами). Гиперболическая плоскость обладает высокой симметрией.
В частности, существуют преобразования, которые превращают фигуры в центральной об¬
ласти рисунка Эшера в соответствующие очень мелкие фигуры, лежащие внутри ограни-

8.2. Конформные отображения
137
Рис. 8.4. При конформном отображении маленькие (бесконечно малые) круги могут расширяться или
сжиматься, но не могут деформироваться в маленькие эллипсы
чивающей окружности. Такое преобразование можно представить как конформный перенос
евклидовой плоскости, отображающий внутренность ограничивающей окружности на саму
окружность. Ясно, что такое преобразование в общем случае не будет сохранять размер
отдельных фигур (поскольку фигуры в средней части рисунка гораздо больше фигур по
краям), однако форма приближенно сохраняется. Сохранение формы становится тем более
точным, чем мельче рассматриваемые детали фигуры, так что бесконечно малые формы бу¬
дут оставаться совершенно неизмененными. Возможно, читатель сочтет более приемлемой
слегка измененную формулировку: конформное отображение сохраняет неизменными углы
между кривыми. Это условие характеризует конформную природу преобразования.
Как влияет это свойство конформного отображения на комплексную гладкость (го¬
ломорфность) некоторой функции f{z)l Попробуем получить интуитивное представление
о геометрическом содержании комплексной гладкости. Вернемся к точке зрения на функ¬
цию / как на отображение и будем рассматривать соотношение w — f(z) как отображение
некоторой области комплексной z-roioскости (области определения функции /) на комплекс¬
ную л;-плоскость (область значений); см. рис. 8.5. Зададимся вопросом: какое локальное
геометрическое свойство определяет голоморфный характер этого отображения? Ответ ока¬
зывается поразительным. Голоморфность функции / эквивалентна отображению, которое
является конформным и нерефлективным (нерефлективное, или сохраняющее ориентацию,
означает, что форма малых областей, сохраняющаяся при отображении, не претерпевает
отражения, т. е. «не переворачивается»; см. конец § 12.6).
Рис. 8.5. Отображение w = f(z) имеет открытую область определения в комплексной z-плоскости
и открытую область значений в комплексной ш-плоскости. Голоморфность функции / эквивалентна
конформности и нерефлективности
z-плоскость
ш-плоскость
Понятие «гладкости» нашего преобразования w — f(z) относится к тому, как оно
действует при предельном переходе к бесконечно малым величинам; Сначала рассмотрим

138
Глава 8
вещественную функцию у — f(x) из § 6.2, график которой показан на рис. 6.4. Функция /
является гладкой в некоторой точке, если в этой точке графика существует хорошо опре¬
деленная касательная. Можно изобразить касательную, представив, что мы рассматриваем
кривую в данной точке со всё большим увеличением. Если кривая гладкая, то по мере повы¬
шения степени увеличения она выглядит всё более похожей на прямую линию, проходящую
через эту точку, и в пределе бесконечного увеличения совпадает с касательной. Ситуация с
комплексной гладкостью аналогична, но теперь мы применим эту идею к отображению z-
плоскости на гг-плоскость. Чтобы исследовать природу отображения в бесконечно малом,
попробуем изобразить непосредственную окрестность точки г одной плоскости, отображая
ее на непосредственную окрестность точки w другой плоскости. Чтобы рассмотреть непо¬
средственную окрестность точки, представим себе, что мы сильно увеличиваем окрестность
точки z и во столько же раз увеличиваем окрестность точки w. В пределе бесконечно боль¬
шого увеличения отображение увеличенной окрестности z на увеличенную окрестность w
будет просто линейным преобразованием плоскости, однако если функция голоморфна,
это будет одним из преобразований, рассмотренных в §5.1. Отсюда, по некотором раз¬
мышлении, следует, что в общем случае преобразование от окрестности z к окрестности w
является комбинацией поворота и однородного растяжения (или сжатия); см. рис. 5.2 б). Так
что формы малых фигур (или углы) сохраняются без отражения, показывая тем самым, что
отображение действительно является конформным и нерефлективным.
Рассмотрим несколько простых примеров. Упоминавшиеся в § 5.1 (см. рис. 5.2) частные
случаи отображений, получаемых прибавлением к z некоторой постоянной b или умноже¬
нием z на постоянную а, очевидным образом голоморфны (функции z + Ъ и az несомненно
дифференцируемы) и столь же очевидно конформны. Это частные примеры общего случая
комбинированного (неоднородно-линейного) преобразования
w — az -f b.
Такие преобразования реализуют евклидовы перемещения плоскости (без отражения) в со¬
четании с однородным растяжением (или сжатием). Они представляют собой единствен¬
ный тип конформного отображения всей комплексной z-плоскости на всю комплексную w-
плоскость. Они обладают также очень специфическим свойством отображать реальные (а не
бесконечно малые) окружности на реальные окружности и прямые линии на прямые линии.
Другой
W — Z
которая отображает комплексную плоскость с удаленным из нее началом координат на дру¬
гую комплексную плоскость тоже с удаленным началом координат. Замечательно, что это
преобразование также отображает реальные окружности на реальные окружности (мы рас¬
сматриваем прямую линию как частный случай окружности, имеющей бесконечный радиус).
Это преобразование в сочетании с отражением относительно вещественной оси называется
инверсией. Комбинируя это с только что рассмотренным неоднородно-линейным преобразо-
ванием, получаем более общее преобразование
az + Ь
w —
cz + d
называемое билинейным преобразованием или преобразованием Мёбиуса. Из вышесказан¬
ного следует, что это преобразование также отображает окружности на окружности (пря¬
мые линии опять-таки рассматриваются как частный случай окружностей). Преобразование
Покажите это.
**$0? Проверьте, что последовательность преобразований z *—>• Az 4- В, г t—> z~1, ги Cz + D действительно
приводит к билинейному отображению.

8.3. Сфера Римана
139
Мёбиуса отображает комплексную плоскость с удаленной из нее точкой —djс на комплекс¬
ную плоскость с удаленной точкой а/с. Чтобы преобразование осуществляло нетривиальное
отображение, необходимо выполнение условия ad Ф Ъс (так чтобы числитель не был кратен
знаменателю).
Заметим, что точка z — — d/c, удаленная из г-плоскости, — это значение, соответ¬
ствующее w = оо, а точка w = . а/с, удаленная из гт-плоскости, соответствует z ~ оо.
Всё преобразование в целом обрело бы более глобальный смысл, если бы мы включили
значение «сю» в область определения и область значений. В этом состоит один из способов
рассмотреть простейшую из всех (компактных) римановых поверхностей — сферу Римана.
•*
8.3.	Сфера Римана
Простое добавление к комплексной плоскости лишней точки «сю» не дает уверен¬
ности в том, что в окрестности сю имеет место требуемая гладкая структура такая же,
как и в остальных местах. Мы можем подойти к этому вопросу, рассматривая сферу, постро¬
енную из двух «координатных лоскутов», одним из которых служит ^-плоскость, а другим —
л1-плоскость. Все точки сферы, кроме двух, имеют как г-, так и щ-координату (связанные
приведенным выше преобразованием Мёбиуса). Но одна точка имеет только z-координату
(в этой точке w обращается в бесконечность), а другая — только гг-координату (в этой точке
в бесконечность обращается z). Мы воспользуемся одной из точек z или w или ими обеими
для определения требуемой конформной структуры, и когда мы используем обе точки, по¬
лучается такая же структура, как и при использовании одной из них, поскольку связь между
двумя координатами голоморфна.
Нам фактически не понадобится столь сложное преобразование, связывающее z и гг,
как преобразование Мёбиуса общего вида. Достаточно рассмотреть более простой частный
случай этого преобразования, определяемый соотношениями
1 1
w = z*- z=w'
в которых значения z = 0 и w = 0 соответствуют бесконечному значению другой коор¬
динаты. На рис. 8.6 показано, как это преобразование отображает координатные линии,
параллельные вещественной и мнимой осям на z-плоскости.
Всё сказанное определяет сферу Римана довольно абстрактным образом. Причина,
по которой сфера Римана именуется именно «сферой», станет понятнее, если воспользовать¬
ся конфигурацией, показанной на рис. 8.7а. z-плоскость представляет там экваториальную
плоскость геометрической сферы. Точки сферы отображаются в точки плоскости с помо¬
щью так называемой стереографической проекции из южного полюса. Это означает, что мы
проводим прямую линию в трехмерном евклидовом пространстве (в котором мы представ¬
ляем всё происходящее) из южного полюса сферы через точку z плоскости. Там, где эта
прямая снова встречается с поверхностью сферы, находится точка сферы, представляющая
комплексное число z. На сфере имеется одна дополнительная точка, а именно сам южный
полюс, представляющая z — сю. Чтобы увидеть, каким образом в эту картину вписывает¬
ся гг, представим соответствующую комплексную плоскость перевернутой «вверх дном»
(w = 1, % —1, —г отвечает соответственно значениям z ~ 1, —г, —1, г) и построим стерео-
графическую проекцию из северного полюса (рис. 8.7 5) . Важное и красивое свойство сте¬
реографической проекции состоит в том, что она отображает окружности на сфере в окруж¬
ности (или прямые линии) на плоскости^81!. Таким образом, билинейные преобразования
(преобразования Мёбиуса) отображают окружности в окружности на сфере Римана. Этот за-
* Проверьте, что две эти стереографические проекции связаны соотношением w = z ~1.

140
Глава 8
А
-1
о
1
— г
z-плоскость	w-плоскость
Рис. 8.6. Построение сферы Римана из комплексных z- и w-плоскостей с помощью соотношений w =
= 1/z п z = 1/w. (Здесь линии координатной сетки на z-плоскости показаны также на гоплоскости.)
Области перекрытия включают только начала координат z = 0 и w = 0, которым соответствует оо на
другой плоскости
• • '
• • • # • ;
а
:*.•#-
-	-J, .	.	•
мечательный факт играет значительную роль в теории относительности, как будет показано
в § 18.5, и имеет глубокую связь с теорией спиноров и твисторов (см. §§ 22.8,24.7,33.2,33.4).
Ф	а	*
Сфера Римана для z — сфера Римана для w — ~
At
Вещественная
окружность
2-ПЛОСКОСТЬ
а)
б)
w-плоскость
«вверх дном»
«)
Рис. 8.7. а) Сфера Римана в виде сферы единичного радиуса, экватор которой совпадает с единичной
окружностью в (горизонтальной) комплексной z-плоскости. Сфера стереографически проектируется
на z-плоскость прямыми линиями, проведенными через ее южный полюс, который соответствует
••
значению z — оо. б) Переинтерпретация экваториальной плоскости как гн-плоскости, изображенной
«вверх дном», но с той же вещественной осью; стереографическая проекция теперь производится из
северного полюса (гн = оо), w — 1/z. в) Вещественная ось представляет большую окружность на этой
сфере Римана, подобную единичной окружности, но нарисованную не горизонтально, а вертикально
Заметим, что с точки зрения сферы Римана вещественная ось есть лишь «другая окруж¬
ность», не отличающаяся существенно от единичной окружности, но нарисованная не го¬
ризонтально, а вертикально (рис. 8.7 в). Одна из этих окружностей получается из другой
• • • • {
путем поворота. Этот поворот определенно является конформным преобразованием, поэто¬
му он получается голоморфным отображением сферы на самое себя. Фактически каждое
(нерефлективное) конформное отображение, преобразующее всю сферу Римана в самое се¬
бя, можно получить билинейным (мёбиусовским) преобразованием. Упомянутый частный
случай поворота можно рассматривать как связь между сферами Римана для комплексных

8.4. Род КОМПАКТНОЙ РИМАНОВОЙ ПОВЕРХНОСТИ
141
параметров z и £, определяемую билинейным соответствием
г
,  z — 1	^
• I • >	^	«I* *
гг -f г	t	+	г
На рис. 8.8 это соответствие представлено в виде комплексных t- и г-плоскостей, при этом
показано, как верхняя i-полуплоскость, ограниченная вещественной осью, отображается на
единичный диск в г-плоскости, ограниченный единичной окружностью. Это преобразование
будет играть важную роль в следующей главе.
^-плоскость	z-плоскость
. И
Рис. 8.8. Соответствие t = (z — 1)/(гг + i), г — (—t -f i)/(t + г), представленное на комплекс-
• ^	• • • • •
ных t- и г-плоскостях. Верхняя ^-полуплоскость, ограниченная вещественной осью, отображается на
единичный диск в г-плоскости, ограниченный единичной окружностью
Сфера Римана представляет собой простейший случай компактной (или «замкнутой»)
римановой поверхности^8*2^. Понятие компактной поверхности объясняется в § 12.6. В отли¬
чие от такой поверхности, описанная ранее риманова поверхность логарифмической функ¬
ции в виде спирального подъема некомпактна. В случае римановой поверхности функ¬
ции (1 — г3)1//2 нам необходимо закрыть четыре отверстия, возникшие из-за наличия точек
ветвления, чтобы сделать ее компактной (если не сделать это, она остается некомпактной).
Такая «компакгификация» является обычной процедурой. Как уже отмечалось, такое «запол¬
нение отверстий» всегда возможно в случае точек ветвления конечного порядка. Как было
показано в конце §8.1, в случае логарифма мы можем заполнить точки ветвления в на¬
чале координат и на бесконечности одной-единственной точкой и получить сферу Римана
как результат компактификации. Существует полная классификация римановых поверхно¬
стей (проведенная еще самим Риманом), используемая во многих областях (включая теорию
струн). Далее я кратко изложу эту схему.
• , • • \
I
8.4.	Род компактной римановой поверхности
• • •
, • ' •
На первой стадии поверхности классифицируются по их топологии, в соответствии
со свойствами, сохраняющимися при непрерывных преобразованиях. Топологическая клас¬
сификация компактных двумерных ориентируемых (см. конец § 12.6) поверхностей в дей¬
ствительности очень проста. Для этого используется единственное натуральное число —
род поверхности. Грубо говоря, всё, что необходимо сделать, — это подсчитать количество
* Покажите это.

142
Глава 8
д= 0:
9=1:
д= 2:
3:
Рис. 8.9. Род римановой поверхности определяется числом имеющихся у нее «ручек». Род сферы
равен 0, род тора или чайной чашки равен 1. Поверхность кренделя имеет род 3
«ручек», имеющихся у данной поверхности. В случае сферы род равен 0, у тора он равен 1.
Поверхность обычной чайной чашки также имеет род 1 (одна ручка!), так что топологически
она эквивалентна тору. Поверхность кренделя имеет род 3. Несколько примеров показано
на рис. 8.9.
Род сам по себе не определяет римановой поверхности,
за исключением случая, когда он равен 0. Необходимо знать еще
некоторые комплексные параметры — модули. Проиллюстрируем
это понятие на примере тора (род равен 1). Простейший способ
построить риманову поверхность рода 1 — это взять на ком¬
плексной плоскости область, ограниченную параллелограммом,
например, с вершинами 0, 1, 1 -Ьр, р (перечисленными в цикли¬
ческом порядке); см. рис. 8.10. Теперь представим себе, что мы
Рис. 8.10. Чтобы построить
риманову поверхность ро¬
да 1, возьмите область ком¬
плексной плоскости, огра¬
ниченную параллелограм¬
мом с вершинами 0, 1, 1 +
+ р, р (в циклическом по¬
рядке) и соедините проти-
/
воположные стороны. Вели¬
чина р дает модуль полу¬
ченной римановой поверх¬
ности
склеиваем вместе противоположные стороны параллелограмма,
то есть сторона от 0 до 1 склеивается со стороной от р до 1 -Ь р, а
сторона от 0 до р — со стороной от 1 до 1+ р. (При желании мы
всегда можем найти другие куски, чтобы закрыть места склейки.)
Полученная риманова поверхность топологически эквивалентна
тору. Оказывается, однако, что поверхности, соответствующие
различным значениям р, в общем случае не эквивалентны меж¬
ду собой, то есть одну из них нельзя превратить в другую с по¬
мощью голоморфного отображения. (Существует тем не менее
некоторая дискретная эквивалентность при замене р на 1 4- р, — р
или 1/р.*) Тот факт, что не все римановы поверхности одина¬
ковой топологии могут быть эквивалентны между собой, можно
сделать интуитивно правдоподобным, рассматривая два случая,
показанные на рис. 8.11. В одном случае выбрано очень малое значение р, и тор получился
очень тонким, в другом параметр р взят близким к г, и тор оказался толстым. Интуитивно ка¬
жется вполне ясным, что между двумя торами не может быть конформной эквивалентности,
и ее действительно нет.
Покажите, что такие замены дают голоморфно-эквивалентные пространства. Найдите все частные значе¬
ния р, при которых эта эквивалентность приводит к дополнительной дискретной симметрии римановой поверхно¬
сти.

8.4. Род КОМПАКТНОЙ РИМАНОВОЙ ПОВЕРХНОСТИ
143
Рис. 8.11. Две неэквивалентные римановы поверхности с топологией тора
В случае поверхностей рода 1 существует лишь
один комплексный модуль р, но у поверхностей рода 2
таких модулей уже три. Чтобы построить риманову по¬
верхность рода 2 путем склеивания какой-либо фигуры
(вроде параллелограмма, использованного выше), мож¬
но выкроить фигуру из куска гиперболической плос¬
кости (см. рис. 8.12). То же остается справедливым и
для поверхностей более высокого рода. Число га ком¬
плексных модулей для поверхности рода д при д > 2
равно га = Зд ~ 3.
Можно счесть некоторой странностью тот факт,
что формула Зд — 3 для числа модулей справедлива
при всех значениях д — 2, 3, 4, 5,..., но перестает
работать при д = 0 или 1. На это есть «причина»,
связанная с числом 5 комплексных параметров, необ- Рис. 8.12. Восьмиугольная область ги~
ходимых для задания различных непрерывных (голо- перболической плоскости в конформ¬
ном представлении рис. 2.12 с указа¬
нием мест склеики, дающая риманову
поверхность рода 2 *
морфных) самопреобразований римановой поверхно¬
сти. При д ^ 2 таких непрерывных самопреобразова¬
ний нет (хотя могут существовать дискретные само-
преобразования), поэтому s = 0. Однако при д = 1
комплексную плоскость параллелограмма на рис. 8.10 можно переместить (поступатель¬
но, без вращения) в любом направлении вдоль плоскости. Величину (и направление) этого
смещения (трансляции) можно задать одним комплексным параметром а, определяющим
отображение z г -f а, так что s — 1 при д ~ 1. В случае сферы (поверхности ро¬
да 0) самопреобразования реализуются описанными выше билинейными преобразования¬
ми 2 i-> (az + b)(cz + d). Степень свободы преобразования определяется тремяt8*3^ неза¬
висимыми отношениями а : Ъ : с : d. Таким образом, в случае д = 0 имеем s — 3.
Следовательно, во всех случаях разность га — s между числом комплексных модулей и чис¬
лом комплексных параметров, необходимых для задания самопреобразования, удовлетворяет
условию
т — s — Зд — 3.
(Эта формула связана с более глубокими материями, выходящими за рамки этой
книги^М.)
Ясно, что внутри семейства конформных (голоморфных) преобразований имеется зна¬
чительная свобода в отношении видимой «формы» римановой поверхности при сохранении
ее структуры как римановой поверхности. Например, в случае сферической топологии воз¬
можны многие различные метрические конфигурации (как показано на рис. 8.13), тем не
менее все они конформно идентичны стандартной («круглой») единичной сфере. (Более
подробно о понятии «метрики» будет сказано в § 14.7.) Более того, для римановых поверх¬
ностей более высокого рода кажущаяся большая степень свободы в выборе «формы» поверх¬
ности может быть сведена к конечному числу комплексных модулей, определяемому выше-
•	у	%	•
приведенными формулами. Остается, однако, некоторая общая информация относительно
формы поверхности, не устраняемая в результате использования этой конформной свободы,

144
Глава 8
а именно та, которая определяется самими модулями. Точное представление о том, что может
дать глобальное использование такой свободы, представляет собой весьма тонкую материю.
Рис. 8.13. Всякая метрическая конфигурация с д = 0 конформно идентична стандартной («круглой»)
сфере
8.5.	Теорема о римановом отображении
л
Некоторое представление о значительной свободе, допускаемой голоморфными преоб¬
разованиями, можно получить, используя знаменитую теорему о римановом отображении.
Она гласит, что если мы имеем некоторую замкнутую область на комплексной плоскости
(см. примечание 8.2), ограниченную замкнутой петлей без самопересечений, то существу¬
ет голоморфное отображение, преобразующее эту область в замкнутый единичный диск
(см. рис. 8.14). (Имеются некоторые нежесткие ограничения на «податливость» этой петли,
однако они не мешают петле содержать углы и другие особенности, в которых петля может
быть недифференцируемой, как показывает частный пример на рис. 8.14.) Можно пойти
дальше: выбрать на петле совершенно произвольным образом три различные точки а, 6, с
и потребовать, чтобы они отображались в три определенные точки а', У, с' на единичной
окружности (например, а1 = 1, У — и, с' — со2), с единственным ограничением, чтобы
циклический порядок точек а, 6, с на петле совпадал с порядком точек а\ Ъс' на единич¬
ной окружности. Более того, отображение тогда определяется однозначно. Другой способ
однозначного определения отображения состоит в том, чтобы выбрать лишь одну точку а
на петле и одну дополнительную точку j внутри нее, а затем потребовать, чтобы точка а
отображалась на определенную точку af единичной окружности (скажем, а' = 1), а точка j
на определенную точку f внутри этой окружности (например, j' ~ 0).
Рис. 8.14. Теорема о римановом отображении утверждает, что любую открытую область в комплексной
плоскости, ограниченную простой (не обязательно гладкой) петлей, можно голоморфно отобразить на
внутренность единичного круга, при этом границы также отображаются соответственно

8.5. Теорема о римановом отображении
145
Теперь представим себе, что мы применяем теорему о римановом отображении не на
комплексной плоскости, а на сфере Римана. С точки зрения сферы Римана, «внутреннюю»
область замкнутой петли можно рассматривать на равных правах с ее «внешней» областью
(последняя соответствует взгляду на сферу с другой стороны), поэтому теорему можно
применять как к внутренней, так и к внешней области петли. Таким образом, теорема
о римановом отображении имеет «инвертированный» вариант, согласно которому внешняя
область петли на комплексной плоскости может быть отображена на внешнюю область
единичной окружности. Однозначность здесь обеспечивается простым требованием, чтобы
одна определенная точка а на петле отображалась на одну определенную точку а1 единичной
окружности (скажем, а' = 1), а оо принимает на себя ту роль, которую играли j и j'
в описании, приведенном в конце предыдущего абзаца
Требуемые отображения часто можно получить в явном виде, и одна из причин того,
что такие отображения действительно требуются, состоит в том, что они могут помочь
в решении интересных физических проблем, например, в определении воздушного потока
за обтекаемым телом (в идеализированном случае невязкой, несжимаемой и безвихревой
среды). Я помню то сильное впечатление, которое произвели на меня, студента-математика,
подобные факты, особенно так называемое преобразование Жуковского (рис. 8.15), которое
можно представить как действие преобразования
w
на подходящую окружность, проходящую через точку z — —1. Полученная форма дей¬
ствительно сильно напоминает поперечное сечение крыла самолета 1930-х годов, так что
(идеализированный) воздушный поток вокруг него можно сразу получить, зная поток вокруг
«крыла» кругового сечения, который в свою очередь получается с помощью другого такого
голоморфного преобразования. (Я уже однажды сказал, что причина, по которой крылья
самолетов обычно имеют такую форму, состоит просто в том, что тогда ее можно изучать
математически, используя преобразование Жуковского. Хочу надеяться, что это не так!)
В основе приложений, подобных этому, конечно, лежат определенные допущения
и упрощения. Это не только обычные предположения о нулевой вязкости и несжимае¬
мом, безвихревом течении, но и весьма радикальное упрощение, согласно которому поток
Рис. 8.15. Преобразование Жуковского га
проходящей через точку 'z = —1, на обте
потока вокруг него
z
внешнюю
позволяя

146
Глава 8
можно считать однородным по всей длине крыла, так что трехмерная, по сути, задача мо¬
жет быть сведена к двумерной. Очевидно, что действительно реалистический расчет потока
воздуха вокруг крыла самолета требует гораздо более трудоемкой математической работы.
Нет оснований ожидать, что в результате такой работы мы сможем получить что-либо подоб¬
ное прямому и изящному применению голоморфных функций, как в случае преобразования
Жуковского. Следует признать, что требуется значительный элемент везения для того, чтобы
найти столь впечатляющее применение комплексных чисел к проблеме, имеющей особую
важность для реальной жизни. Воздух, как известно, состоит из огромного числа отдельных
частиц (порядка Ю20 в одном кубическом сантиметре), поэтому макроскопическое описание
воздушного потока предполагает усреднение и упрощение реальной ситуации. Нет никаких
оснований ожидать, что уравнения аэродинамики будут отражать значительную часть той
математики, которая глубоко проникает в физические законы, управляющие этими отдель¬
ными частицами.
В §4.1 я упомянул об «особой и очень важной роли», которую комплексные числа иг¬
рают на самых малых масштабах физического мира, и действительно, поведением частиц
управляет голоморфное уравнение (см. §21.2). Однако в макроскопических системах эта
«комплексная структура» обычно оказывается полностью скрытой, и получается, что только
в исключительных ситуациях (как, например, в рассмотренной выше проблеме воздушного
потока) комплексные числа и голоморфная геометрия находят естественное применение.
Всё же существуют ситуации, когда фундаментальная внутренняя комплексная структура
проявляется даже на макроскопическом уровне. Это можно видеть на примере теории макс¬
велловской теории электромагнитного поля и других волновых явлений. Особенно замеча¬
тельным примером является теория относительности (см. § 18.5). В следующей главе мы
увидим, каким замечательным образом комплексные числа и голоморфные функции могут
проявлять свои магические свойства, находясь за сценой.
Примечания
§8.3.
8.1. См. упражнение 2.5.
8.2. Существует опасность терминологических недоразумений при использовании слова «замкну¬
тый» в отношении поверхностей или отображений более общего вида (n-поверхностей), которые
будут рассмотрены в главе 12. Для такого отображения «замкнутое» означает «компактное без
границ», а не просто «замкнутое» в топологическом смысле; последнее есть понятие, дополни¬
тельное к понятию «открытое», введенному в § 7.4. (В топологии замкнутое множество — это
множество, содержащее все свои предельные точки.Дополнением замкнутого множества служит
открытое множество и наоборот; здесь под дополнением множества S в некотором окружаю¬
щем его топологическом пространстве V понимается множество элементов пространства V,
отсутствующих в <S.) Возможно еще недоразумение в связи с термином «граница», фигуриру¬
ющим в понятии «множество с границей», которое не обсуждается в этой книге. Для обычных
отображений, рассматриваемых в главе 12 (т. е. отображений без границы), понятие «замкнуто¬
го» отображения (в противоположность топологическому отображению) эквивалентно понятию
«компактного» отображения. Во избежание недоразумений я в этой книге обычно пользуюсь
термином «компактное», а не «замкнутое». Исключение составляют термины «замкнутая кри¬
вая» для вещественного одномерного отображения, топологически эквивалентного окружно¬
сти S1, и «замкнутая Вселенная» для пространственно компактной модели Вселенной, то есть
модели, содержащей компактную пространственноподобную гиперповерхность (см. примеча¬
ние 27.36).
у
У
§8.4.	. *
8.3.	Преобразование не меняет вида, если умножить каждое из чисел а, 6, с, d на одно и то же
комплексное число, отличное от нуля (то есть изменить масштаб), однако оно меняется при

8.5. Теорема о римановом отображении
147
изменении какого-то одного из них. Такая свобода в выборе масштаба уменьшает на единицу
число независимых параметров, определяющих преобразование, — с четырех до трех.
8.4. Эту формулу можно рассматривать как начало длинной истории, развязкой которой служит
очень общая и сильная теорема Атья- Сингера [43].
§8.5.
8.5. Следует отметить, что полная гладкая сфера Римана получается из обоих вариантов теоремы
о римановом отображении, только если петля представляет собой точную окружность.

Глава 9
Разложение Фурье и гиперфункции
9.1.	Ряды Фурье
Вернемся к вопросу, возникшему в §6.1: что Эйлер и его современники могли бы
рассматривать в качестве приемлемого понятия «настоящей функции»? В §7.1 мы догово¬
рились, что голоморфная (комплексно-аналитическая) функция наилучшим образом удовле¬
творяет тому образцу, который мог иметь в виду Эйлер. Сегодня большинство математиков
сочло бы такое понятие «функции» излишне ограниченным. Кто из них прав? В конце
этой главы мы придем к совершенно замечательному ответу на этот вопрос. Но сначала
постараемся понять, в чем суть разногласий.
В процессе применения математики к проблемам физического мира часто выдвигается
требование гибкости, которой не обладают ни голоморфные функции, ни их вещественные
аналоги — аналитические (т. е. Сw-гладкие) функции. Вследствие однозначности аналити¬
ческого продолжения, описанного в §7.4, глобальное поведение голоморфной функции,
определенной в некоторой связной открытой области V комплексной плоскости, полно¬
стью задано, коль скоро оно известно в некоторой малой открытой подобласти области V.
Аналогично аналитическая функция вещественной переменной, определенная на некотором
связном отрезке 1Z вещественной прямой R, также полностью задана, если известно поведе¬
ние этой функции на некоторой малой открытой подобласти отрезка 7Z. Подобная жесткость
представляется неприемлемой для реалистического моделирования физических систем.
Это особенно опасно, когда рассматривается распространение волн. Это явление ис¬
пользуется для посылки сигналов, наложенных на электромагнитные колебания радиоволн
или света, и наиболее полезно тем, что таким путем можно передавать информацию. Каж¬
дое значение сигнала в конечном счете может нести сообщение, которое может оказаться
неожиданным для получателя. Если форма сигнала описывается аналитической функцией, то
отсутствует возможность «изменить намерения» в середине сообщения. Любая малая часть
сигнала будет полностью определять его значение в любой момент времени. И действитель¬
но, распространение волн часто изучается в рамках вопроса, как будут распространяться
разрывы или другие отклонения от аналитичности.
Будем рассматривать волны и зададимся вопросом, как математически описывать подоб¬
ные явления. Один из наиболее эффективных способов изучения формы волн предоставляет
процедура, известная под названием фуръе-анализа. Французский математик Жозеф Фурье,
живший с 1768 по 1830 годы, поставил вопрос о разложении периодических колебаний
на компоненты в виде синусоидальных волн. В музыке с этим сталкиваются при разло¬
жении музыкальных звуков на составляющие их «чистые тона». Термин «периодический»
означает, что картина (например, физическое смещение колеблющегося объекта) в точности
повторяется через некоторый период времени, или же этот термин может относиться к пери¬
одичности в пространстве, например, к периодическим картинам в кристалле или на обоях
либо к волнам в открытом море. Математически это означает, что функция / (например, от
вещественной переменной х) является периодической, если при всех х она удовлетворяет
условию
Дх + 0 = fix),

9.1. Ряды Фурье
149
где I — некоторое заданное число, называемое периодом. Таким образом, если «сдвинуть»
график функции у — f(x) вдоль оси х на величину I, то он будет выглядеть точно так же,
как и до сдвига (см. рис. 9.1 а). (Метод, примененный Фурье к непериодическим функциям,
с использованием так называемого преобразования Фурье будет описан в § 9.4.)	=
«Чистыми тонами» служат функции вида sin х или cos х (Рис- 9.16). Они имеют пери¬
од 2тг, поскольку
sin(x -f 2тг) = sin х,	co:s(x + 2тг) = cos х*
Эти соотношения возникают как проявление периодичности одной-единственной комплекс¬
ной величины е%х — cos х + i sin х,
еДх4*2тг) = е<Х	'
б)
Рис. 9.1. Периодические фикции, а) Функция /(х) имеет период I, если /(х) = /(х + 0 для всех х-
Это означает, что, если мы сдвинем график функции у — f (x) на I вдоль оси х> он будет выглядеть так
же, как и до сдвига, б) Основные «чистые тона» sin х или cos X (последний показан пунктиром) имеют
период I = 2тх. в) «Чистые тона» высших гармоник совершают несколько колебаний за период I; они
по-прежнему имеют период Z, а также более короткий период (показана функция sin 3x, имеющая
период I = 27г, а также более короткий период 27г/3)]

150
Глава 9
с которой мы уже сталкивались в §5.3. Если мы хотим, чтобы период был не 27г, а I,
то мы можем «перенормировать» фигурирующую в этой функции величину х и взять ег2'кх'1
л
вместо егх. Вещественная и мнимая части, соответственно cos(2ttx/0 и sin(27rx/0> также
имеют период I. Но это не единственная возможность. Вместо того чтобы совершать за пе¬
риод I лишь одно колебание, функция может совершать два, три или даже п колебаний,
где п — любое положительное целое число (см. рис. 9.1 в), так что каждая из функций
state*), cos(^)
имеет период I (в дополнение к меньшему периоду 1/п). В музыке эти выражения сп =
= 2, 3, 4,... называются высшими гармониками.
Задача, которую поставил (и решил) Фурье, состояла в том, чтобы представить произ¬
вольную периодическую функцию /(х) с периодом I в виде суммы чистых тонов. Вклад
в эту сумму чистых тонов с разными значениями п в общем случае будет различным, за¬
висящим от формы волны (т. е. от вида графика у — /(х))- Несколько простых примеров
показано на рис. 9.2; однако необходимо иметь в виду, что число различных чистых тонов,
вносящих вклад в /(х), обычно бывает бесконечным. Более точно: то, что требовалось Фу¬
рье, — это набор коэффициентов с, a'i, £>ь а2, &2> &з?	• • • в разложении функции /(х)
на составляющие чистые тона, которое определяется выражением
fix) = с + ai cos иХ + h sin + а2 cos ^Х + fa sin 2и;\ +
.	|	«	л
-Газ cos 3u;x + 63 sin 3u;x +
Для упрощения этого выражения я ввел здесь угловую частоту а;, определяемую как и> =
= 27х/1 (она не имеет ничего общего с и в §§ 5.4, 5.5, 8.1).
Некоторые читатели могут счесть это представление функции /(х) чересчур сложным,
и они, несомненно, будут правы. Формула будет выглядеть гораздо приятнее, если мы объ¬
единим члены с косинусами и синусами и выразим их через комплексные экспоненты. Тогда
f(x) = .... + a_2e“2^ + a-ie~iuJX -f a0 +	+	a2e2^* + a3e3ia;* + • • • ,
где*’Г9,21
ci>n — a1'i T- ol—71,,	t)fi — 'iotji	с	—	ао
при п — 1, 2, 3, 4,... Наша формула станет еще красивее, если положить 0 — ег^х и опре¬
делить функцию F(z) как ту же самую величину /(х), но выраженную теперь через новую
комплексную переменную г. Тогда мы получим
Fi^z} — ’ * * Т о:_2^ ^ Т ol-\z ^ ”Ь aQZ9 -}- ol\z}~ Т a^z^ Qf323 -Г • • • ,
где
F(z) =	F(eiwx) =	f(x).
Можно сделать эту формулу еще более компактной, воспользовавшись знаком суммирова¬
ния 53, который здесь означает «сложить все члены для всех целых значений г»:
F(z) = У, arz
Г
Это выглядит как степенной ряд (см. §4.3), за исключением того, что здесь наряду с по¬
ложительными степенями присутствуют и отрицательные. Такие ряды называются рядами
Лорана. Мы узнаем об их важной роли в следующем разделе .
Покажите это.
Покажите, что для функции F, аналитической на единичной окружности, коэффициенты ап и, следова¬
тельно, ап,Ъп и с можно получить, пользуясь формулой ап = (27гг)-1 <f z~n~1F(z) dz.

9.2. Функции на окружности
151
Рис. 9.2. Примеры разложения периодических функций в ряд Фурье. Форма волны (вид графика)
определяется коэффициентами Фурье. Ниже приводятся функции и их отдельные компоненты Фурье.
«)/(х) = |+2sinx+|cos2x+isin2x+|sin3x. б) fix) - |+sin х~| cos 2у-1 sin 2х~ | sin3x
9.2.	Функции на окружности
Ряд Лорана, несомненно, дает весьма экономичный способ представления рядов Фу¬
рье. Но это выражение открывает также интересный альтернативный взгляд на разложение
Фурье. Поскольку периодическая функция просто бесконечно повторяется, мы можем рас¬
сматривать такую функцию (вещественной переменной х) как заданную на окружности
(рис. 9.3), при этом период функции I равен длине окружности, а х измеряет расстояние,
отсчитываемое вдоль окружности. В отличие от расстояний, просто убегающих вдаль по
прямой линии, здесь расстояния «накручиваются» на окружность, так что периодичность
учитывается автоматически.

152
Глава 9
Рис. 9.3. Периодическую функцию вещественной переменной х можно считать заданной на окруж¬
ности длины I, «закрутив» вещественную ось % в окружность. При I = 2тг можно рассматривать эту
окружность как единичную в комплексной плоскости
Для удобства я (по крайней мере, временно) в качестве этой окружности буду исполь¬
зовать окружность единичного радиуса на комплексной плоскости с длиной окружности 2тг,
так что период I будет равен 27г. Соответственно
ш
1, так что z
гх
(При любом другом значении периода достаточно переопределить величину со путем соот-
• *
ветствующей перенормировки переменной %•) Различные члены с косинусами и синусами,
представляющие разные «чистые тона» в разложении Фурье, теперь выражаются просто по¬
ложительными или отрицательными степенями z, а именно z±n для n-й гармоники. На еди¬
ничной окружности эти степени дают требуемые осциллирующие члены с косинусами и
синусами (см. рис. 9.4).
{* \
I
а. аЛг * Л # ]
И 1 ЛГ
tvA
Ж
I
■гИЁ
i
Jl /
■ А —■ * *
1
j \ ГТм
f
ш
1 9 \ 9 *1 fllVj
I i * 1 ' - «'•/
\ -V kf
\ * • 4r
• 9
Щ Я
\ \ I
/
m
I
л
/4
Рис. 9.4. На единичной окружности вещественная и мнимая части функции zn проявляются как п-е
гармоники косинусоидальных и синусоидальных волн (соответственно вещественные и мнимые части
величины егпх, где z = егх). Здесь для случая п = 5 показана вещественная часть величины z5
Теперь у нас имеется очень изящный способ представления разложения Фурье неко¬
торой периодической функции f(x)- Мы считаем функцию f(x) = F(z) заданной на еди¬
ничной окружности в ^-плоскости, где z = егх. Тогда разложение Фурье совпадает с описа¬
нием этой функции с помощью ряда Лорана по комплексной переменной z, Но изящество
описания здесь не единственное преимущество. Такое представление дает более глубокое
понимание природы рядов Фурье и характера описываемых ими функций. Для конечной
цели этой книги более существенно то, что оно имеет важную связь с квантовой механикой
и, следовательно, позволяет глубже понять Природу. Это связано с магией комплексных чи¬
сел, благодаря которой мы можем пользоваться рядами Лорана, даже когда число г лежит

9.2. Функции на окружности
153
вне единичной окружности. Оказывается, что этот ряд сообщает нам нечто важное о функ¬
ции F(z), где z лежит на единичной окружности, выражая это в виде ряда для случая,
когда z находится вне единичной окружности.
Напомним теперь (см. § 4.4) о понятии круга сходимости, внутри которого степенной
ряд сходится, а вне которого расходится. В случае ряда Лорана имеется близкая аналогия
в виде кольца сходимости. Это есть область, лежащая строго между двумя окружностями
в комплексной плоскости, центры которых находятся в начале координат (см. рис. 9.5 а).
Это легко понять исходя из понятия круга сходимости обычного степенного ряда. Часть
ряда Лорана с положительными степенями t9*3!
F~ — ад z1 4- 02z2 4 азz3 Н
будет иметь обычный круг сходимости радиуса, скажем, А, так что эта часть ряда сходится
при всех значениях z с модулем, меньшим А. Что касается части ряда с отрицательными
степенями
  b а_з2-3 4 a-2Z~2 4
то ее можно рассматривать как обычный степенной ряд по степеням обратной перемен¬
ной w = 1/z. В w-плоскости будет существовать круг сходимости радиуса, скажем, 1/В,
и эта часть ряда будет сходиться при значениях числа w с модулем, меньшим 1 /В. (Мы здесь
фактически говорим о сфере Римана, описанной в главе 8 (см. рис. 8.7), с ^-координатой,
отнесенной к одной полусфере, и w-координатой, отнесенной к другой полусфере (см.
рис. 9.5 б). Мы обсудим этот аспект сферы Римана в следующем разделе.) Следователь¬
но, при значениях z с модулем, большим В, часть ряда с отрицательными степенями будет
сходиться. При условии В < А две области сходимости будут перекрываться, и мы полу¬
чаем кольцо сходимости для всего ряда Лорана в целом. Заметим, что полный ряд Фурье
или Лорана для функции f(x) — F{elx) ~ F(z) имеет вид
F(z)^F+ Ч-ao + F";
здесь необходимо включить постоянный член <эо>
Используется z
S ^-плоскость
Используется w
а)	,	6)
• .»
л
I	ч	*
Рис. 9.5. а) Кольцо сходимости для ряда Лорана F(z) =	4- ao + F~, где F+ = * • • 4 oc-2z~2 4
4 a~iz~1, F~ = aiz1 4 a^2 4 •••. б) To же на сфере Римана (см. рис. 8.7), где z относится
к расширенной северной полусфере, а w(= z~l) — к расширенной южной полусфере
■	Л
В данной ситуации зададимся вопросом о сходимости на самой единичной окружно¬
сти, поскольку там мы имеем г — егх для вещественных значений х и вопрос о сходимости

154
Глава 9
•. ‘ ,
нашего ряда Фурье для f(x) в точности совпадает с вопросом о сходимости ряда Лорана
для F(z), когда 2 лежит на единичной окружности. Таким образом, представляется необхо¬
димым выполнение условия В < 1 < А, при котором единичная окружность лежит внутри
кольца сходимости. Означает ли это, что для сходимости ряда Фурье необходимо потребо¬
вать, чтобы единичная окружность лежала внутри кольца сходимости?
Так действительно было бы в том случае, если бы функция /(%) была аналитической
(т.е. -гладкой), потому что тогда функцию /(%) можно отобразить на функцию F(z),
голоморфную в некоторой открытой области, содержащей единичную окружность Ес¬
ли же функция f(x) не аналитична, возникает интересный вопрос. В этом случае кольцо
сходимости либо стягивается и становится единичной окружностью (что, строго говоря, не
допустимо для истинного кольца сходимости, поскольку оно обязано быть открытой обла¬
стью, каковой единичная окружность не является), либо единичная окружность становится
внешней или внутренней границей кольца сходимости. Эти вопросы окажутся важными для
нас в § 9.6.
Пока мы не будем беспокоиться о том, что случится, если функция f(x) не анали¬
тична, и рассмотрим более простую ситуацию, когда она аналитична. Тогда единичная
окружность в 2-плоскости будет находиться строго внутри истинного кольца сходимости
функции F(2), ограниченного окружностями с радиусами А и В и центром в начале коор¬
динат, причем В < 1 < А. Часть ряда Лорана с положительными степенями F~ сходится
в точках z-плоскости с модулем, меньшим А, а часть с отрицательными степенями F+ схо¬
дится в точках с модулем, большим В, поэтому внутри самого кольца сходятся обе части
(и, во вполне тривиальном смысле, постоянный член ао, очевидно, «сходится» при всех z).
Это позволяет «расщепить» функцию F(z) на две части, одна из которых голоморфна вну-
три внешней окружности, а другая — вне внутренней окружности; эти части определяются
соответственно разложениями в ряд функций F~ и F+.
Имеется некоторая неопределенность в том, куда при таком расщеплении включать по¬
стоянный член ао — в F~ или в F+. По-видимому, лучше продолжать оставаться с этой
неопределенностью, поскольку между F~ и F+ существует симметрия, которая станет яс¬
нее, если мы воспользуемся вышеупомянутым представлением сферы Римана (см. рис. 9.5 б).
Это дает более полную картину ситуации, поэтому в дальнейшем мы будем пользоваться
указанным представлением.
9.3.	Расщепление частот на сфере Римана
Координаты 2 и w(= 1/z) определяют две части покрытия сферы Римана. Единичная
окружность становится экватором сферы, а кольцо сходимости — «поясом» вокруг экватора.
Мы рассматриваем наше расщепление функции F(z) как представление ее в виде суммы
двух частей, одна из которых голоморфно продолжена на южную полусферу (назовем ее
положительно-частотной частью функции F(z)) и содержит произвольно выбранную часть
постоянного члена, а другая голоморфно продолжена на северную полусферу (назовем ее
отрицательно-частотной частью функции F(z)) и содержит остальную часть постоянного
члена. Если не учитывать постоянный член, то такое расщепление однозначно определяется
требованием голоморфности продолжения на ту или иную полусферу .
Будет удобно иногда определять «внутреннюю» и «внешнюю» части окружности
(или другой замкнутой петли), нарисованной на сфере Римана, указывая ориентацию, кото¬
рая должна быть приписана этой окружности. Стандартная ориентация единичной окруж¬
ности на 2-плоскости соответствует направлению увеличения стандартной координаты 0,
т. е. направлению против часовой стрелки. Если изменить знак ориентации (т. е. заменить в
на —0), то положительно- и отрицательно-частотные части меняются местами. Это совпада-
Понятно ли, отчего это так?

9.3. Расщепление частот на сфере Римана
155
ет с нашим соглашением относительно замкнутой петли об¬
щего вида. Ориентация «против часовой стрелки» соответ¬
ствует положению «циферблата часов» внутри петли, ориен¬
тация «по часовой стрелке» — положению «циферблата» вне
петли. Это соглашение используется для определения «вну¬
тренней» и «внешней» частей ориентированной замкнутой
петли. Рис. 9.6 поясняет ситуацию.
Расщепление функции на положительно- и отрицатель-
Рис. 9.6. Ориентация, припи¬
сываемая замкнутой петле на
сфере Римана, определяет ее
«внутренюю» и «внешнюю» ча¬
сти. Ориентация против часо¬
вой стрелки соответствует «ци¬
ферблату часов» внутри петли,
а ориентация по часовой стрел¬
ке — «циферблату» вне петли
но-частотные части представляет важный компонент кванто¬
вой механики и особенно квантовой теории поля, как мы уви¬
дим в §§ 24.3, 26.2-26.4. Данная здесь формулировка — не
совсем обычный способ представления расщепления, однако
он имеет значительные преимущества в ряде случаев (напри¬
мер, в теории твисторов, см. § 33.10). Обычная формулиров¬
ка связывается не с голоморфными продолжениями, а непо¬
средственно с разложением Фурье. Положительно-частотные
компоненты определяются как кратные е~гпх (п — положи¬
тельное целое число), а отрицательно-частотные — как крат¬
ные егпх. Положительно-частотная функция содержит только
положительно-частотные компоненты.
Однако такое описание не обеспечивает полной общно¬
сти определения расщепления. Существует много голоморф¬
ных отображений сферы Римана на самое себя, которые преобразуют в себя каждую из по¬
лусфер, но не сохраняют северный или южный полюсы (т.е. точки z = 0 или z — оо)*.
При этом сохраняется расщепление на положительно- и отрицательно-частотные части, но
не сохраняются отдельные компоненты Фурье е~гпх или егпх. Таким образом, понятие рас¬
щепления на положительные и отрицательные частоты (играющего важную роль в квантовой
теории) имеет более общий характер, чем выделение отдельных фурье-компонент.
При стандартном изложении квантовой механики расщепление на положительные и от¬
рицательные частоты относится к функциям времени t, а время мы обычно не считаем
движущимся по кругу. Можно, однако, применить простое преобразование, чтобы получить
всю область изменения переменной t от «бесконечного прошлого» t = —ос до «бесконечного
будущего» t = ос, когда переменная х один раз обегает окружность. Здесь предполагается,
что х меняется от х = ~7Г Д° X — к (так чт0 ^ — егх обегает единичную окружность
в комплексной плоскости против часовой стрелки от точки z = — 1 и снова возвращается
в ту же точку (см. рис. 9.7)). Такое преобразование имеет вид
t
График этой формулы показан на рис. 9.8, а простое геометрическое описание приводится
на рис. 9.9.
Преимущество такого преобразования в том, что оно допускает голоморфное продол¬
жение на всю сферу Римана, будучи преобразованием, уже рассмотренным в §8.3 (см.
рис. 8.8), которое отображает единичную окружность (в г-плоскости) на вещественную ось
(в t-плоскости)**:
t
Z
1
t 4* i
ф \	*	5
iz +1
t T i
**
J53 Каков явный вид таких отображений?
! Покажите, что это дает ту же величину t, что и выше.

156
Глава 9
-1
О
Рис. 9.7. В квантовой механике расщепление на положительные и отрицательные частоты применяют
к функциям от времени t, которое не предполагается периодическим. Тем не мейее расщепление,
приведенное на рис. 9.5, можно применять к полной области изменения t (от —оо до +оо), если вос¬
пользоваться преобразованием, связывающим t с z(?= е%х), при котором мы обходим вокруг единичной
окружности против часовой стрелки от точки 2 = ~1 и снова возвращаемся в ту же точку, так что х
пробегает от — 7г до 7г
Внутренняя часть единичного круга в z-плоскости соответствует верхней t-полуплоскости,
а внешняя часть единичного z-круга — нижней t-полупло скости. Следовательно, положи¬
тельно-частотные функции от t — это те функции, которые голоморфно продолжаются
на нижнюю t-полуплоскость, а отрицательно-частотные функции — на верхнюю полуплос¬
кость. (Имеется, однако, значительная дополнительная техническая трудность, состоящая
в том, что мы должны быть внимательны в обращении с точкой «оо» в t-плоскости, для
этого лучше всегда рассматривать сферу Римана, а не просто комплексную t-плоскость.)
Однако при стандартном представлении понятие положительной частоты, выраженное
через временную координату t, устанавливается обычно не тем способом, который изложен
здесь, а с использованием так называемого преобразования Фурье функции /(х)- Результат
обычно получается тот же самый^9,5!, что и приведенный здесь, однако в связи с тем что
преобразования Фурье играют решающую роль в квантовой механике (а также во многих
других областях), необходимо объяснить здесь, что представляет собой это преобразование.
Х = 7Г
9.4.	Преобразование Фурье
Преобразование Фурье, по существу, есть предельный случай ряда Фурье, получающий¬
ся, когда период I нашей периодической функции /(%) становится всё больше и больше,

9.4. Преобразование Фурье
157
Рис. 9.9. Геометрическое описание зависимости t = tg
пока не станет бесконечным. В этом пределе бесконечного периода требование периодично¬
сти функции f(x) вообще отсутствует, то есть это может быть любая обычная функция Г96!.
Это дает значительные преимущества, когда мы изучаем распространение волн и возмож¬
ность отправлять «неожиданные» сигналы. Потому что тогда мы не хотим требовать, чтобы
сигнал имел периодическую форму. Преобразование Фурье позволяет рассматривать по¬
добные сигналы, продолжая анализировать их с использованием периодических «чистых
тонов». Для этого будем считать, что наша функция /(%) имеет период I —* со. По мере
увеличения периода I частоты гармоник чистых тонов с периодом 1/п при некотором по¬
ложительном целом числе п будут приближаться к любому выбранному положительному
вещественному числу. (Напомним, что любое вещественное число можно с произвольной
точностью аппроксимировать рациональными числами.) Это означает, что любой чистый тон
любой частоты может служить фурье-компонентой. Вместо того чтобы представлять функ¬
цию f(x) дискретной суммой фурье-компонент, теперь мы выражаем /(х) в виДе непрерыв¬
ной суммы по всем частотам; это означает, что /(х) представляется интегралом (см. § 6.6)
по частоте.
Посмотрим в общих чертах, как это выглядит. Сначала напомним о нашем «изящном»
представлении разложения в ряд Фурье периодической функции /(х) с периодом I:
F(z) = arzr, где z — е
ги>х
(угловая частота и определяется соотношением и = 2п/1). Возьмем сначала период рав¬
ным 2тг, так что и = 1. Теперь мы попробуем увеличить период, умножив его на некоторое
большое целое число N (так что I = 2ttN)7 при этом частота уменьшится во столько же раз
(т. е. ш = iV"*1). Осциллирующая волна, которая использовалась в качестве основного тона,
теперь становится N-й гармоникой по отношению к этой новой более низкой частоте. Чи¬
стый тон, соответствовавший n-й гармонике, теперь будет (пАГ)-й гармоникой. Если перейти
к пределу при JV, стремящемся к бесконечности, становится нецелесообразным пытаться
сохранить следы отдельных осциллирующих компонент, приписывая им «номера гармоник»
(т. е. номера п), поскольку эти числа при переходе к пределу непрерывно меняются. Не стоит
нумеровать эти компоненты целыми числами г в вышеприведенной сумме, поскольку фик¬
сированное значение г относится к определенной гармонике (г = ±п для n-й гармоники),

158
Глава 9
а не следит за определенной частотой тона. Вместо этого за частотой следит r/N, и для
нумерации необходима новая переменная. Имея в виду ту важную роль, которую будут иг¬
рать преобразования Фурье в последующих главах (см., в частности, § 21.11), я обозначаю
эту переменную буквой р, поскольку в пределе, когда N стремится к бесконечности, она
соответствует импульсу^9^ некоторой квантово-механической частицы, положение которой
измеряется переменной х* В этом пределе можно также при желании вернуться к обычному
использованию х вместо %. Ниже мы убедимся, что в указанном пределе х действительно
становится вещественной частью комплексной переменной z.
При конечном значении N имеем
г
P=N-
В пределе N оо параметр р становится непрерывной переменной. Поскольку коэффи¬
циенты аг в нашей сумме будут тогда зависеть от непрерывного вещественного парамет¬
ра р (а не от дискретного целочисленного параметра г), лучше обозначать зависимость
коэффициентов аг от г с помощью стандартной функциональной записи, например, д(р),
а не посредством индекса (например, др), как в случае аг. Мы сделаем замену
*-* д(р)
виду,
ло членов, попадающих в малую область значении р (приблизительно пропорционально N,
поскольку нас интересуют дроби n/N9 находящиеся в этой области). Соответственно величи-
на д(р) является мерой плотности и должна сопровождаться дифференциалом dp в предель¬
ном переходе, при котором сумма превращается в интеграл /. В заключение рассмотрим
член zr в нашей сумме ^arzr. Мы имеем z = eZCJX, где to = N~1, так что z — ezx^N. Таким
образом, гг = errXj/N — е1ХР. С учетом всего этого в пределе N —> оо получаем выражение
Е
otrzr —> / д(р)егхр dp,
— ОС
представляющее нашу функцию /(%). В интеграл обычно включают нормирующий множи¬
тель (27г)-1/2, потому что тогда возникает замечательная симметрия: обратное соотноше¬
ние, выражающее д(р) через /(х)? имеет точно такой же вид (за исключением знака «минус»
в показателе экспоненты), что и соотношение, выражающее f(x) через д(р):
/
/
оо	оо
fix) = (2тг) 1/2 J д(р)егхр dp, д{р) — (2ж) 1/2 , f(x)e %хр d\
— ОО	—ОО
Функции /(х) и д(р) называются фуръе-преобразованиями друг друга*.
9.5,	Расщепление частот, получаемое из преобразования Фурье
Комплексная функция /(х)? определенная на всей вещественной оси, называется
положительно-частотной, если ее преобразование Фурье д(р) обращается в нуль при р ^ 0.
При этом функция f(x) состоит только из компонент вида егхр с р < 0. Эйлеру опре-
Покажите (в общих чертах), как выразить д(р) через f{x), используя предельную форму выражения
с контурным интегралом ап — (2тгг)-1 § z~n~1 F(z) dz из упражнения 9.2.

9,5. Расщепление частот, получаемое из преобразования Фурье
159
деленно не понравилась бы (см. § 6.1) такая функция д(р)9 которая кажется результатом
«склеивания» ненулевой функции при р < 0 и просто нуля при р > 0. Тем не менее
указанное определение выражает вполне «голоморфное» свойство функции /(х). Другой
способ выразить это условие положительности частот основан на возможности голоморф¬
ного продолжения функции /(х)> как это было сделано раньше для ряда Фурье. Теперь
мы используем переменную % для обозначения точек на вещественной оси (так что на
этой оси можно положить х = х); на сфере Римана эта «вещественная ось» (включая точ¬
ку х = оо) превращается в «вещественную окружность» (см. рис. 8.7 в). Эта окружность
делит сферу на две полусферы, из которых «внешняя» соответствует нижней полуплоскости
в стандартной картине комплексной плоскости. Условие того, что функция /(х) является
положительно-частотной, означает теперь возможность ее голоморфного продолжения на эту
внешнюю полусферу.
Существует, однако, одна тонкость, требующая внимательного отношения при сравне¬
нии двух определений «положительной частоты». Она связана с точкой z = оо, поскольку
функция /(х) в общем случае имеет в этой точке сингулярность некоторого вида. С неко¬
торой «гиперфункциональной» точки зрения, которая будет описана ниже (в § 9.7), эта син¬
гулярность при г = оо не приводит к существенным трудностям. При надлежащем взгляде
на «/(оо)» оказывается, что два определения положительной частоты, данные в предыдущем
абзаце, в основном согласуются друг с другомt9,8l.
Для интересующегося читателя может оказаться полезным рассмотреть с точки зре¬
ния сферы Римана некоторые геометрические конструкции, относящиеся к переходу от ря¬
да Фурье к преобразованию Фурье (§ 9.4). Вернемся к ранее рассмотренному описанию
на z-плоскости функции /(х) с периодом 27т, при котором х служит мерой длины дуги, от¬
считываемой вдоль окружности единичного радиуса. Допустим, мы хотим изменить период,
сделав его больше 2тг, посредством последовательно увеличивающихся шагов, сохраняя при
этом интерпретацию величины х как расстояния вдоль окружности. Это можно сделать,
рассматривая последовательность всё больших окружностей, но для того чтобы придать
предельной процедуре геометрический смысл, предположим, что все окружности соприка¬
саются в исходной точке х = 0 (см. рис. 9.10 а). Для простоты изложения мы возьмем эту
точку за начало координат z = 0 (а не z = 1), так что все окружности будут лежать в нижней
полуплоскости. Тогда центром нашей исходной единичной окружности для периода I = 2тг
будет точка z = —г, а не начало координат. Для периода I > 2тс центром окружности бу¬
дет точка С — —И/2тг на комплексной плоскости, и в пределе I —> оо мы получаем саму
• *
вещественную ось (так что х = при этом «центр» сдвигается в бесконечность вдоль
отрицательной мнимой оси. Во всех случаях величина х служит мерой длины дуги вдоль
окружности, отсчитываемой по часовой стрелке (или, в предельном случае, положительного
расстояния вдоль вещественной оси), с х = 0 в начале координат. Поскольку наши окружно¬
сти теперь имеют нестандартную ориентацию (по часовой стрелке), их «внешняя часть» —
это в действительности их внутренняя часть (см. §9.3, рис. 9.6), так что наше условие
положительной частоты относится к этой внутренней части. Теперь мы имеем соотношение
между х И z в виде*
1).
При конечном значении I можно представить /(х) в виде ряда Фурье, используя ряд Лорана
вокруг точки С = —И/2тг. Перейдя к пределу I —> оо, получаем преобразование Фурье.
При конечном I условие положительных частот можно представить как условие возмож¬
ности голоморфного продолжения функции /(х) на внутреннюю часть соответствующего
круга; в пределе I —> оо это означает возможность голоморфного продолжения на нижнюю
полуплоскость в соответствии со сказанным выше.
* Л! Выведите это соотношение

160
Глава 9
• Г
+ л
Вещественная
ось
I
С
и
2тг
\
\
/
Смещенная
единичная |
окружность j
/
/
а)
б)
Смещенная
единичная
окружность
Рис. 9.10. Условие положительных частот при I —> ос, где I — период функции /(х)- я) Начинаем
с I — 27Г, при этом функция / определена на единичной окружности, смещенной таким образом,
что ее центр находится в точке z — —i. При увеличении I окружность имеет радиус I и центр
в точке С = —il/2n. Во всех случаях величина х служит мерой длины дуги, отсчитываемой по часовой
стрелке. Положительная частота соответствует возможности голоморфного продолжения функции /
на внутреннюю часть круга, а в пределе I — ос — на нижнюю полуплоскость, б) То же на сфере
Римана. При конечном I ряд Фурье получается из ряда Лорана вблизи точки 2 = — il/2n, однако на
сфере эта точка не является центром окружности и становится точкой оо (лежащей на окружности)
в пределе I = оо, когда ряд Фурье превращается в преобразование Фурье
Что происходит с рядом Лорана в пределе I —> оо? Чтобы понять это, взглянем на сфе¬
ру Римана. Для каждого конечного значения I точка С(= — И/2тт) служит центром х_
окружности, однако на сфере Римана точка С совсем не похожа на центр окружности.
С ростом I точка С(= —И/2тг) перемещается вдоль окружности на сфере Римана, представ¬
ляющей мнимую ось (см. рис. 9.106), и становится всё менее похожа на центр окружности.
Наконец, по достижении предела I — оо точка С становится точкой z = оо на сфере Римана.
Но при С — оо мы обнаруживаем, что эта точка лежит на окружности, центром которой она,
по предположению, должна быть! (Эта окружность теперь, конечно, является вещественной
осью.) Таким образом, имеется некоторая странность в поведении степенного ряда вблизи
этой точки, которую, конечно, и следовало ожидать, поскольку теперь мы имеем не сумму
отдельных членов, а непрерывный интеграл.
9.6,	Какие функции приемлемы?
Вернемся к вопросу, поставленному в начале этой главы, о том, какого типа функции
целесообразно использовать. Зададим вопрос: какие функции можно представлять в виде
преобразования Фурье? Кажется нецелесообразным ограничиваться только аналитическими
(т.е. -гладкими) функциями, поскольку, как сказано выше, фурье-преобразование д(р)
положительно-частотной функции /(х) (которая, несомненно, может быть аналитической)
является определенно не аналитической функцией, полученной путем «склеивания» ненуле¬
вой функции с нулевой. Связь между функцией и ее фурье-преобразованием симметрична,
поэтому кажется неразумным применять к ним разные стандарты. Выше отмечалось, что
поведение функции /(х) в точке х — 00 имеет отношение к понятию расщепления поло¬
жительных и отрицательных частот, но лишь в некоторых особых случаях функция /(х)
действительно будет аналитической (С^-гладкой) при х — оо (поскольку для этого требу¬

9.6. Какие функции приемлемы?
161
ется точное согласование в поведении /(х) при х 4-ос и X ~> ~ос). В дополнение ко
всему этому существует наша изначальная физическая мотивация к изучению преобразо¬
ваний Фурье, а именно возможность применения их к обработке сигналов, которые могут
переносить «неожиданные» (неаналитические) сообщения. Поэтому мы должны вернуться
к вопросу, с которым столкнулись в начале этой главы: функции какого вида можно признать
«правильными»?
Напомним, что, с одной стороны, Эйлер и его современники могли бы, вероятно, дого-
%
, •
вориться считать голоморфную (или аналитическую) функцию именно тем, что они понима¬
ли под «настоящей» функцией, но, с другой стороны, использование только таких функций
представляется неоправданным ограничением при решении многих математических и физи¬
ческих проблем, в частности, связанных с распространением волн, поэтому требуется более
общее понятие. Является ли одна из этих точек зрения «более правильной», чем другая?
Преобладает, вероятно, мнение, что первая точка зрения «старомодна» и что современные
концепции тяготеют ко второй, так что голоморфные или аналитические функции — это всего
лишь очень частные случаи общего понятия «функции». Но так ли необходимо принять эту
позицию в качестве «правильной»? Попробуем представить себе образ мыслей XVIII века.
Посетим Жозефа Фурье в начале XIX века. Те, кто принадлежал к «аналитической» («эй¬
леровой») школе, должны были пережить тяжелый удар, когда Фурье показал, что некото¬
рые периодические функции, такие как прямоугольная или пилообразная волны, показанные
на рис. 9.11, имеют вполне разумно выглядящие фурье-представления! Фурье столкнулся
с сильным сопротивлением математического сообщества того времени. Многие отказыва¬
лись принять его выводы. Какой, например, должна быть «формула» для прямоугольной
волны? Однако, как показал Фурье, суммой ряда
s(x)
111
sin х -f - sin Зх -f - sin 5x 4- ^ sin +
1
является именно прямоугольная волна, осциллирующая между постоянными значениями ~тх
4
и
1
4
7г каждый полупериод 7г (см. рис. 9.12).
а)
Y
Рис. 9.11. Разрывные периодические функции (со вполне разумно выглядящими фурье-представлени-
ями). а) Прямоугольная волна. 6) Пилообразная волна
Опишем это с помощью ряда Лорана, как показано выше. Мы имеем довольно изящно
выглядящее выражение*
• • ♦
i*-*-
5
lz- з
3"
z~* + z + \zb + \гъ +
3	5
Покажите это.

162
Глава 9
X
1	11	1
Рис. 9.12. Частичные суммы ряда Фурье s(x)	= sin \ + о s*n ^Х + г s*n ^Х + 7 ?Х + о s^n +
, О	0.1	У
сходящиеся к	прямоугольной волне,	подобной показанной на	рис. 9.11 а
41	»
где z — егх. Это пример того, как кольцо сходимости сжимается до единичного круга без от-
верстия в середине. Однако можно выразить суть на языке голоморфных функций, разделив
ряд Лорана на две половины, одна из которых содержит положительные степени и представ¬
ляет собой обычный степенной ряд по г, другая, с отрицательными степенями, — степенной
ряд по z 1. Фактически это хорошо известные ряды, допускающие точное суммирование":
S~ = Z + h3 + \zb + • • • = i log ^ + *
3	5	2	\	1	—	z
И
5+='"-К5-к3-^=-1‘»ЧШ^г
что дает 2is(x) = S~ -f-	Небольшие преобразования этих выражений приводят к выводу,
что S~ и отличаются лишь на ± |г7г, так что s(x) = =Ь^-7г.** Нам следует посмотреть вни¬
мательнее, почему у нас действительно получается прямоугольная волна, осциллирующая
между двумя указанными чередующимися значениями.
Несколько легче понять, в чем дело, если воспользоваться приведенным в § 8.3 преобра¬
зованием t = (z — 1 )/(iz + г), которое отображает внутреннюю часть единичного круга на z-
плоскости на верхнюю t-полуплоскость (как показано на рис. 8.8). На языке переменной t
величина S*~ теперь относится к верхней полуплоскости, а5+-к нижней, и мы получаем
(с возможной неопределенностью значения логарифмов 2т)
S~	= — i logt + I logz, = I log + I logi.
Проследив за логарифмами, начиная с исходных точек t = i (где S~ = 0) и t = — i (где S+ =
= 0), мы найдем, что на положительной вещественной t-оси мы имеем S~ + S+ =
а на отрицательной вещественной t-оси — S~ +	Отсюда мы делаем вывод,
что на верхней половине единичной окружности в z-плоскости $(х) = + ^тг, а на нижней
**
***
Проделайте это, воспользовавшись разложением для log z вблизи z = 1, приведенным в конце § 7.4.
Покажите это (предполагая, что |s(x)| < 37г/2).
Покажите это.

г
9.7. Гиперфункции
163
•j
половине s(x) = — ^-тг. Это означает, что суммирование ряда Фурье действительно дает
прямоугольную волну, как и утверждал Фурье.
Какую мораль можно вывести из этого примера? Мы видели, что некоторая периоди¬
ческая функция, даже не непрерывная, не говоря о дифференцируемости (будучи в данном
случае С “1-функцией), может быть представлена в виде вполне разумно выглядящего ряда
Фурье. Аналогично функцию, определенную на единичной окружности, можно представить
в виде столь же разумно выглядящего ряда Лорана, хотя и такого, для которого кольцо схо¬
димости сжимается до единичного круга, положительная и отрицательная половины этого
ряда Лорана в результате суммирования дают вполне хорошие голоморфные функции на по¬
ловине сферы Римана. Одна из них определена на одной стороне единичной окружности,
другая — на другой стороне. Мождо считать^ что «сумма» этих двух функций дает требуемую
* , у. ^
прямоугольную волну на самой единичной окружности. Из-за существования сингулярно¬
стей ветвления в двух точках z = ±1 на единичной окружности эта сумма может «скакать»
с одной стороны на другую, в результате чего она описывает прямоугольную волну. Син¬
гулярности ветвления препятствуют также сходимости степенных рядов на двух сторонах
окружности за пределами круга сходимости.
9.7.	Гиперфункции
Рассмотренный пример есть лишь очень частный случай, однако он показывает, что мы
должны делать в общем случае. Зададимся вопросом: каков общий тип функций, которые
можно определить на единичной окружности (на сфере гимана) и представить в виде «сум¬
мы» некоторой голоморфной функции F+ в открытой области на одной стороне окружности
и другой голоморфной функции Г" в открытой области на другой стороне, как в только что
рассмотренном примере. Мы обнаружим, что ответ на этот вопрос приводит нас непосред¬
ственно к экзотическому, но важному понятию
Более нахлядно рассматривать функцию / как разность функций F~ и — F+. Причина
в том, что в большинстве случаев общего характера функция F" или F+ может не иметь
аналитического продолжения на единичную окружность, поэтому не очевидно, какой смысл
будет иметь такая «сумма» на самой окружности. В то же время можно рассматривать
разность функций F~ и ~~F+ как «скачок» между этими двумя функциями, когда их области
определения соприкасаются на единичной окружности.
Идея «скачка» между голоморфной функцией на одной стороне кривой в комплексной
плоскости и другой голоморфной функцией на другой стороне, причем ни одна из голо¬
морфных функций не нуждается в голоморфном продолжении на саму кривую, приводит
нас к новой концепции «функции», определенной на кривой. Это есть фактически определе¬
ние гиперфункции на (аналитической) кривой. Это удивительное понятие было предложено
японским математиком Микио Сато в 1958 году^9’9^, хотя, как мы вскоре увидим, определе¬
ние, данное Сато, гораздо изящнее приведенного здесь 19Л01
Чтобы определить гиперфункцию, необязательно рассматривать замкнутую кривую вро-
v>
де целой единичной окружности, достаточно взять лишь некоторую часть кривой,
считать гиперфункции определенными на некотором отрезке 7 вещественной оси. Пусть 7
есть отрезок вещественной оси между вещественными числами а и 6, причем а < Ь. Тогда
гиперфункция, определенная на 7, представляет собой скачок через 7 от голоморфной функ¬
ции / на открытом множестве 1Z~~ (у которого 7 служит верхней границей) к голоморфной
функции д на открытом множестве 7Z+ (с 7 в качестве нижней границы); см. рис. 9.13.
Простое введение «скачка» указанным образом не дает конструктивных идей, как посту¬
пать в подобных случаях, к тому же оно недостаточно точно в математическом отношении.
Сато нашел изящное решение проблемы необычайно простым
способом. Скачок представляется просто как пара голоморфных функций (/, д)-9 которая ечи-

164
Глава 9
<
Комплексная
плоскость
*
.... |
4	•	•	.	‘
Рис. 9.13. Гиперфункция на отрезке вещественной оси 7 описывает «скачок» от голоморфной функции
с одной стороны 7 к голоморфной функции на другой стороне
• » •
тается эквивалентной другой подобной паре (/о, до), если последняя получается из первой
добавлением к / и д одной и той же голоморфной функции /г, определенной в комбини¬
рованной (открытой) области 1Z, которая состоит из областей 7Z~~ и 1Z+, соприкасающихся
вдоль отрезка кривой 7 (см. рис. 9.14). Можно сказать, что
пара (/, д) эквивалентна паре (/ + h, д -f h)\
здесь голоморфные функции д и / определены соответственно на и a h — произ¬
вольная голоморфная функция в комбинированной области 1Z. Любое из вышеприведенных
выражений можно использовать для представления одной и той же гиперфункции. Сама ги-
перфункция математически определяется как класс эквивалентности таких пар; «модулем
приведения»!911! служат голоморфные функции /г, определенные на 1Z. Читатель может
вспомнить понятие «класса эквивалентности», введенное в предисловии в связи с опреде¬
лением дроби. Здесь та же самая идея (и не меньше путаницы). Существенный пункт здесь
состоит в том, что добавление h не влияет на «скачок» между / и д, однако h может ме¬
нять /яд таким образом, что это не сказывается на величине скачка. (Например, может
изменять поведение этих функций при продолжении от 7 в открытые области 1Z~~ и 1Z+.)
Таким образом, скачок сам четко определяется классом эквивалентности.
Читатель может быть искренне возмущен тем, что это хитрое определение выглядит
сильно зависящим от произвольного выбора открытых областей *Rr и 7£+, ограниченного
лишь тем, что области соприкасаются вдоль их общей границы 7. Замечательно, однако, что
определение гиперфункции не зависит от этого выбора. Согласно удивительной теореме,
известной под названием теорема вырезания, такое понятие гиперфункции действительно
совершенно не зависит от выбора 7^~ и 1Z+; см. верхние три примера на рис. 9.15.
Фактически теорема вырезания дает нам еще больше. Мы не требуем, чтобы наша
открытая область 1Z оказалась разделенной на две части (1Z~ и 1Z+) в результате удале¬
ния 7. Требуется лишь, чтобы открытая область 1Z в комплексной плоскости содержала

Рис. 9.14. Гиперфункция на отрезке 7 вещественной оси, определяемая парой голоморфных функ¬
ций (/, д), причем функция / определена на некоторой открытой области Л~, простирающейся вниз
от 7, а д — на открытой области Л+, расположенной вверх от 7. Реально гиперфункция на 7 есть
пара (/, #), равная (/ + h, д + К) по модулю h, где /1 — голоморфная функция на объединении Л
множеств Л~, 7 и Л+
а)
\
б)
Рис. 9.15. Теорема вырезания утверждает, что понятие гиперфункции не зависит от выбора открытой
области Л, коль скоро Л содержит заданную кривую 7. а) Область Л — j может состоять из двух
отдельных кусков (так что мы получаем две различных голоморфных функции fug, как на рис. 9.14).
б)	Область Л — 7 может быть одним связным куском; в этом случае jug — просто две части одной
и той же голоморфной функции
открытый^9*12! отрезок 7. Может оказаться, что область Л — 7 (т. е. то, что останется от об¬
ласти Л после удаления из нее 7)19Л31 состоит из двух отдельных кусков, как мы считали до
сих пор, однако в более общем случае удаление 7 из Л может оставить нам одну связную
область, как показывают три нижних примера на рис. 9.15. В этих случаях мы должны так¬
же удалить любую из внутренних концевых точек отрезка 7 (а или Ь), так чтобы осталось
открытое множество, которое я обозначаю как Л — 7. В этом более общем случае наши
гиперфункции определяются как «голоморфные функции на Л — 7, приведенные по. модулю
к голоморфным функциям на Л». Замечательно, что столь либеральный выбор Л не делает
различия между классами «гиперфункций», определенными таким образом*. Случай, когда
обе точки а и b лежат внутри Л, благоприятен для вычисления интегралов от гиперфункций,
поскольку тогда можно использовать замкнутый контур в области Л — 7.
Всё сказанное относится также к нашему предыдущему случаю окружности на сфере
Римана. Здесь имеется некоторое преимущество из-за того, что в качестве области Л бе¬
рется вся сфера Римана, поскольку тогда те функции, с которыми мы должны иметь дело,
голоморфны на всей сфере Римана, и существует теорема, утверждающая, что эти функ¬
* blO Почему определение «голоморфные функции на 7Z, приведенные по модулю к голоморфным функциям
на Л — 7», переходит в определение гиперфункции, данное раньше, когда Л расщепляется на Л~ и ЛЛ?

166
Глава 9
ции суть просто постоянные. (Это «постоянные» ао, которыми мы в §9.2 договорились
не заниматься.) Таким образом, с точностью до постоянных, гиперфункция, определенная
на окружности, принадлежащей сфере Римана, задается просто одной голоморфной функ¬
цией во всей области на одной стороне окружности и другой функцией на другой стороне.
Это обеспечивает однозначное (с точностью до постоянных) расщепление произвольной
гиперфункции на окружности на положительно- и отрицательно-частотные части.
В заключение рассмотрим некоторые основные свойства гиперфункций. Я пользуюсь
записью ([/, д\) для обозначения гиперфункции, заданной парой функций / и д, голоморфно
определенных соответственно на 1Z~ и 7£+ (мы возвращаемся к случаю, когда 7 делит 7Z
на 1Z~ и 7£+). Таким образом, если мы имеем два различных представления (\f,g\) и (|/о> #о|)
одной и той же гиперфункции (то есть (\f,g\) = (|/о, £о|)Х то / — /о и д — д$ будут одной и
той же голоморфной функцией h, определенной на 7Z, но относящейся соответственно к
и 1Z+. Тогда естественно определить сумму двух гиперфункций, производную гиперфункции
и произведение гиперфункции на аналитическую функцию q, определенную на 7:
(I/, #|) + (|/ь 5il) = (I/ + /1, 9 + 9i\),
d{\f, gI) _ f
df
dg
dz \
dz’
dz
?(1/, si) = (Is/, ssl);
в последнем выражении аналитическая функция q голоморфно продолжена в окрест¬
ность^914^ отрезка 7.* Мы можем представить саму функцию q как гиперфункцию: q =
= (\q, 0|) = (|0, —<?|), однако общего определения произведения двух гиперфункций не
существует. Отсутствие такого определения не является недостатком именно гиперфунк-
ционального подхода к обобщенным функциям. Это отличает все подходы^915!. Например,
тот факт, что дельта-функцию Дирака (определенную в § 6.6, также см. ниже) нельзя возве¬
сти в квадрат, причиняет массу неприятностей многим специалистам в области квантовой
теории поля.
Простыми примерами гиперфункционального представления в случае, когда 7 — R,
a 1Z~ и 7— верхняя и нижняя открытые комплексные полуплоскости, могут служить
ступенчатая функция Хевисайда в(х) и дельта-функция Дирака(~Хевисайда) 5(х)(= dO/dx)
(см. §§ 6.1, 6.6):
в(х)
1
7 lOg Z
1
8(х)
2тг %
1
27гг*’ 2т
2т
г log Z 1
1
У
здесь берется та ветвь логарифма, на которой log 1 = 0. Интеграл от гиперфункции (|/, д\)
по всей вещественной оси можно представить как интеграл от / по контуру, расположенному
непосредственно под вещественной осью, минус интеграл от д по контуру, расположенному
непосредственно над вещественной осью (предполагается, что интегралы сходятся); контур
ф А
в обоих случаях проходится слева направо . Заметим, что гиперфункция может быть нетри¬
виальной, даже когда fug представляют собой аналитические продолжения одной и той
же функции.
Насколько общий характер имеют гиперфункции? Они определенно включают в себя
все аналитические функции. Они включают также разрывные функции вроде в(х) и прямо¬
угольной волны (как показали вышеприведенные обсуждения), а также другие С"1-функции,
• • /
Здесь имеется небольшая тонкость. Охарактеризуйте ее. (Подсказка: обратите внимание на область опре-
Проверьте стандартное свойство дельта-функции: f q(x)S(x) dx — q(0), когда функция q(x) аналитична.
деления.)

9.7. Гиперфункции
167
получающиеся при сложении подобных функций. Фактически все С-1-функции могут слу¬
жить примером гиперфункций. Далее, поскольку мы можем дифференцировать гиперфунк¬
ции и получать при этом другие гиперфункции, любую С ~2-функцию можно получить как
производную некоторой С“1-функции, отсюда следует, что все С ~2-функции также являют¬
ся гиперфункциями. Мы видели, что к таким функциям относится и дельта-функция Дирака.
Можно дифференцировать снова и снова, поэтому любая С~п-функция при любом целочис¬
ленном п будет гиперфункцией. Как же обстоит дело с С-00-функциями, которые были
названы распределениями (см. § 6.6)? Правильно, все они тоже являются гиперфункциями.
Распределение^9-15! обычно определяется как элемент так называемого дуального про¬
странства С°°-гладких функций. Понятие дуального пространства обсуждается в § 12.3
(см. также § 13.6). Пространством, в некотором смысле дуальным по отношению к про¬
странству Сп-функций, является пространство С_2_п-функций, где п — произвольное целое
число; это относится также и к случаю п — оо, если принять —2 — оо = — оси—2 + оо — оо.
Соответственно С~°°-функции дуальны С°°-функциям. Как обстоит дело с С-функциями,
дуальными Cw-функциям? При надлежащем определении «дуальности» эти С-функции,
несомненно, будут гиперфункциями.
Мы описали полный крут в своих рассуждениях. Пытаясь обобщить понятие функции,
чтобы как можно дальше уйти от весьма ограниченного понятия аналитической или голо¬
морфной функции (того типа функции, который привел бы в восторг Эйлера), мы пришли
к крайне общему и гибкому понятию гиперфункции. Но гиперфункции сами определяются
очень простым образом, через те же самые «эйлеровы» голоморфные функции, от кото¬
рых мы вынужденно собирались отказаться. На мой взгляд, это одно из наиболее ярких
проявлений магии комплексных чисел (9Л6!. Если бы Эйлер был жив, чтобы оценить этот
удивительный факт!
Примечания
§9.1.
9.1. Я использую здесь греческую букву х («хи») вместо обычной х, которая выглядела бы бо¬
лее естественно, только для того, чтобы отличить эту переменную от вещественной части х
комплексного числа z> которая будет играть важную роль в последующем изложении.
9.2. Здесь не требуется, чтобы функция /(х) была вещественной при вещественных значениях х,
то есть чтобы ап, Ъп и с были вещественными числами. Вполне возможно рассматривать ком¬
плексные функции от вещественных переменных. Условие вещественности функции /(х) озна¬
чает, что величина а_п является комплексно-сопряженной величине ап. Понятие комплексного
сопряжения обсуждается в § 10.1.
§9.2.'
9.3. Несколько странно выглядящие обозначения F~ для части ряда с положительными степе¬
нями и F+ для части с отрицательными степенями связаны с тем, возможно, неудачным,
выбором знаков, который стал почти универсальным в литературе по квантовой механике
(см. §§ 21.2, 21.3, 24.3). Я приношу извинения, но ничего не могу с этим поделать!
9.4. Существует общий принцип, согласно которому для любой С_а?-функции /, определенной на
вещественной области 7Z, можно подобрать несколько расширенную комплексную область CJZ,
именуемую «комплексным утолщением» области 1Z и содержащую 7Z внутри себя, такую, что /
однозначно продолжается на голоморфную функцию, определенную на CFL.
9.5. См., например, [51].
§9.4.
9.6. С другой стороны, на функцию /(х) налагается требование «разумного» поведения, когда х
стремится к положительной или отрицательной бесконечности. Здесь это не имеет для нас
особого значения, и в любом случае при используемом здесь подходе обычные требования
будут чрезмерно ограничительными.

168
Глава 9
9.7. В квантовой механике имеется еще постоянная величина h, вводимая для задания масштаба, со¬
ответствующего координате а; (см. §§ 21.2,21.11), но для упрощения я временно полагаю h— 1.
На самом деле h есть дираковский вариант постоянной Планка (т. е. h/27т, где h — первоначаль¬
ный «квант действия», введенный Планком). Выбор h — 1 всегда возможен при надлежащем
выборе основных единиц измерения; см. §27.10.
§9.5.
9.8. См. [51].
§9.7.
9.9. См. [690,691,692].
9.10. См. также [105], хотя термин «гиперфункция» в этой работе явно не используется.
9.11. Другой аспект понятия «приведения по модулю» обсуждается в §16.1 (см. также примечание
3.17).
9.12. Термин «открытый отрезок» означает здесь, что концевые точки а и Ь не включены в 7, так что
множество 7Z, содержащее 7, не содержит а и Ь.
9.13. «Разность» множеств 1Z и 7 обычно обозначается так:
9.14. «Окрестность чего-либо» на более строгом математическом языке означает «открытое множе¬
ство, содержащее это что-либо».
9.15. Более стандартный подход к «обобщенным функциям» как к «распределениям» содержится
в книгах [705, 271, 280, 793]. Альтернативный вариант, полезный в «нелинейном» контек¬
сте, который сводит «проблему несуществования произведения» к проблеме неоднозначности,
см. в [155, 156, 324].
9.16. Существуют также важные связи между гиперфункциями и когомологией голоморфных пучков,
которые будут обсуждены в § 33.9. Подобные идеи играют важную роль в теории гиперфункций
на поверхностях высокой размерности (см. [691, 692, 361]).

Глава 10
Поверхности
10.1.	Комплексные и вещественные размерности
Одним из наиболее впечатляющих достижений в математике двух последних столе¬
тий стала разработка замечательных методов, позволяющих работать с неплоскими про¬
странствами различной размерности. Представляется важным для наших целей сообщить
читателю кое-что из этих идей, жизненно важных для современной физики.
До сих пор мы рассматривали только одномерные пространства. Читателя, возмож¬
но, удивит это заявление, поскольку в нескольких предыдущих главах мы рассматривали
комплексную плоскость, сферу Римана, различные другие римановы поверхности. Однако
в контексте голоморфных функций эти поверхности в действительности следовало бы счи¬
тать существующими всего лишь в одном измерении; это было комплексное измерение, о чем
уже упоминалось в § 8.2. Точки такого пространства отличаются о/дна от другой (локально)
единственным параметром, хотя этот параметр и оказывается комплексным числом. Таким
образом, эти «поверхности» в действительности следует понимать как «кривые», а именно
комплексные кривые. Можно, конечно, разбить комплексное число на вещественную и мни¬
мую части (а?, у), так что z = x-riy, и рассматривать х и у как два независимых веществен¬
ных параметра. Однако процесс такого разбиения комплексного числа не относится к разряду
голоморфных операций. До сих пор мы имели дело только с голоморфными структурами,
и поскольку теперь мы рассматриваем комплексные пространства, следует рассматривать
один комплексный параметр как определяющий одно измерение. Таков, по крайней мере,
тот способ мышления, который я рекомендовал бы принять.
С другой стороны, можно занять противоположную позицию, а именно что голоморф¬
ные операции представляют собой лишь частный пример операций более общего характера,
при использовании которых можно, при желании, рассматривать х и у как отдельные неза¬
висимые параметры. Возможным путем к этому может служить понятие комплексного со¬
пряжения, которое является неголоморфной операцией. Комплексно-сопряженным по отно¬
шению к комплексному числу х 4- гу, где х и у — вещественные числа, является комплексное
число z9 определяемое следующим образом:
= х — гу.
На комплексной плоскости операция сопряжения комплексного числа соответствует от¬
ражению этой плоскости в вещественной оси (см, рис. 10.1). Напомним (см. §8.2), что
голоморфные операции всегда сохраняют ориентацию комплексной плоскости. Если мы
хотим рассмотреть конформное отображение комплексной плоскости (или ее части), сохра¬
няющее ориентацию (например, поворот комплексной плоскости вокруг самой себя), мы
ш	.	•	•	•	•	и	ш	в
должны включить сюда и операцию комплексного сопряжения. Однако при включении сов¬
местно с другими стандартными операциями (сложением, умножением, переходом к пре¬
делу) комплексное сопряжение также позволяет нам обобщить наши отображения таким
образом, что они уже не обязательно будут конформными. Фактически всякое отображение
одной части комплексной плоскости на другую (например, посредством непрерывного пре-

170
-
Глава 10
А
м
х+ гу
Вещественная ось
£= х— гу
Рис. 10.1. Комплексно-сопряженным
числом по отношению к z —
(х, у -
ЧИСЛО Z
= х + гу
вещественные числа) является
образования) можно получить, применяя комплексное
сопряжение в сочетании с другими операциями.
Позвольте мне развить это замечание. Можно счи¬
тать, что голоморфные функции строятся путем при¬
менения к комплексным числам операций сложения
и умножения, а также процедуры предельного перехо¬
да (поскольку эти операции достаточны для построе¬
ния степенного ряда — бесконечной суммы, являющей¬
ся пределом последовательности частичных сумм*).
Если добавить сюда операцию комплексного сопряже¬
ния, то мы сможем создавать (непрерывные) функции
общего вида от х и у, поскольку можно выразить х и у
по отдельности с помощью формул
X
- гу, получающееся при
отражении ^-плоскости в веществен¬
ной оси
х
z + z
2
У —
z
2 %
(Любую непрерывную функцию от х и у можно по¬
строить из сумм, произведений и пределов веществен¬
ных чисел.) При рассмотрении неголоморфных функций от z я буду стараться пользоваться
записью F{z,z), явно упоминая z. Это будет подчеркивать тот факт, что, пока мы оста¬
емся в голоморфном мире, следует считать наши функции определенными в двумерном
вещественном пространстве, а не в пространстве одного комплексного измерения. Нашу
функцию F(z, z) с тем же правом можно считать функцией вещественной и мнимой ча¬
стей, х и у, комплексного числа г и записывать ее в виде, например, /(ж, у). Тогда мы
имеем f(x, у) = F(z, z)9 хотя, конечно, явный математический вид функции / будет в об¬
щем случае совершенно отличен от вида функции F. Например, если F(z, z) = z2 -Г z2,
то /(ж, у) ~ 2х2 - 2у2. В качестве другого примера можно рассмотреть F(z, z) — zz\ тогда
/(ж, у) = х2 + у2, что является квадратом модуля \z\ комплексного числа г, то есть**
10.2.	Гладкость, частные производные
Поскольку, приступая к изучению функций от более чем одной переменной, мы начи¬
наем осваивать пространства с большим числом измерений, необходимо сделать некоторые
замечания относительно «исчисления» в таких пространствах. Как будет показано в главе 12,
пространство, называемое также многообразием, может иметь любое число измерений п,
где п — положительное целое число, (n-мерное многообразие часто называют просто п-мно¬
гообразием.) Общая теория относительности Эйнштейна для описания пространства-време¬
ни использует 4-многообразие, многие современные теории оперируют с многообразиями
еще большей размерности. В главе 12 мы будем иметь дело с n-многообразиями общего
вида, но в этой главе мы для простоты рассмотрим случай вещественного 2-многообразия
(т. е. поверхности) S. Тогда для обозначения различных точек поверхности S (в некоторой
локальной области S) можно использовать локальные (вещественные) координаты х и у.
Фактически обсуждение будет во многом применимо и к общему n-мерному случаю.
Двумерная поверхность может, например, быть обычной плоскостью или обычной сфе¬
рой. Но поверхность нельзя понимать как «комплексную плоскость» или «сферу Римана»,
**
Объясните, как перейти отсюда к вычитанию и делению.
Проверьте оба эти примера.

10.2. Гладкость, частные производные
171
^ L- 1 ^ * * |—ш      ’
поскольку мы не будем приписывать ей структуру комплексного пространства (с сопутству¬
ющим понятием «голоморфной функции», определенной на этой поверхности). Ей предпи¬
сывается лишь структура гладкого многообразия. Геометрически это означает, что нам не
надо следить за чем-то вроде локальной конформной структуры, как мы делали это в отно¬
шении наших римановых поверхностей в § 8.2, однако мы должны быть в состоянии понять,
когда можно считать «гладкой» функцию, определенную на этом пространстве (т. е. функ¬
цию, областью определения которой служит это пространство).
Для интуитивного понимания того, что есть «гладкое» многообразие, взглянем на сфе¬
ру как противоположность кубу (в обоих случаях, конечно, имеется в виду поверхность без
внутренней части). Примером гладкой функции на сфере может служить «высота», т. е. рас¬
стояние от экваториальной плоскости (при этом сфера изображается помещенной в обычное
евклидово 3-пространство, расстояния, отсчитываемые вниз от экваториальной плоскости,
считаются отрицательными; см. рис. 10.2 а). С другой стороны, если наша функция является
модулем высоты (см. § 6.1 и рис. 10.2 б), так что расстояния под экватором также считаются
положительными, то функция будет негладкой вдоль экватора. Если же мы рассматриваем
квадрат высоты, то функция будет гладкой на всей сфере (рис. 10.2 в). Поучительно, что
во всех этих случаях функция сохраняет гладкость на северном и южном полюсах, несмотря
на «особый» вид контурных линий постоянной высоты на полюсах сферы. Единственный
случай нарушения гладкости (на экваторе) имеет место во втором примере.
а)
б)
в)
Рис. 10.2. Функции на сфере S, расположенной в евклидовом 3-пространстве; величина h служит мерой
расстояния, отсчитываемого от экваториальной плоскости, a) h — гладкая функция на $ (отрицательные
значения показаны прерывистой линией), б) Модуль \h\ (см. рис. 6.2 а теряет гладкость на экваторе.
в)	Квадрат h2 сохраняет гладкость на всей сфере S
\
Чтобы яснее понять всё это, введем «систему ко¬
ординат» на нашей поверхности S. Эти координаты
следует применять лишь локально, и мы можем пред¬
ставить себе поверхность S как «склеенную» из от¬
дельных локальных кусков — координатных лоскутов,
подобно тому как это делалось в отношении римановых
поверхностей в § 8.1. (Для сферы, например, не потре¬
буется более одного лоскута.) В пределах одного ло¬
скута гладкие координаты нумеруют различные точки
(см. рис. 10.3). Наши координаты должны выражаться
вещественными числами, назовем их х и у (без какого-
либо намека на то, что они могли бы быть объединены
в виде комплексного числа). Предположим теперь, что
мы имеем некоторую гладкую функцию Ф9 определен¬
ную на S. По современной математической термино¬
логии, Ф есть гладкое отображение поверхности S на
пространство вещественных чисел R (или комплекс¬
ных чисел С в случае, когда Ф есть комплекснозначная
Рис. 10.3. В пределах одного локаль¬
ного координатного лоскута точки ну¬
меруются гладкими (вещественными)
координатами

172
Глава 10
функция на S), поскольку Ф приписывает каждой точке поверхности S некоторое веществен¬
ное (или комплексное) число, х е. Ф отображает S на вещественные (или комплексные)
числа. Такую функцию иногда называют скалярным полем на 5. На отдельном координатном
лоскуте величину Ф можно представить как функцию от двух координат:
ф = /(*, у),
при этом гладкость величины Ф проявляется как дифференцируемость функции /(х, у).
Я пока не объяснил, как понимать дифференцируемость функции более чем одной
переменной. Хотя это интуитивно ясно, дать прямо здесь строгое определение несколько
затруднительно^101^. Тем не менее здесь уместны некоторые поясняющие замечания.
Прежде всего, чтобы функция f была дифференцируемой как функция от пары пе¬
ременных (х, у), определенно необходимо, чтобы при рассмотрении /(х, у) как функции
лишь одной переменной х при некотором постоянном значении у эта функция была гладкой
(по крайней мере, С1) по х в том же смысле, в каком это понятие применялось к функциям
одной переменной (см. § 6.3). Далее, если мы рассматриваем /(х, у) как функцию одной пе¬
ременной у, сохраняя постоянной величиной теперь уже х, то она должна быть гладкой (С1)
как функция от у. Однако этого далеко не достаточно. Существует много функций f(x1 у),
гладких в отдельности по х и по у, которые было бы крайне неразумно назвать гладкими
по паре переменных (х, у)* Дополнительное достаточное условие гладкости состоит в том,
что каждая из производных по х и у в отдельности должна быть непрерывной функцией
пары (х, у). Аналогичное утверждение остается в силе, если мы рассматриваем функцию
более чем двух переменных. Для обозначения дифференцирования по одной переменной при
сохранении других постоянными используется символ «частной производной» д. Частные
производные функции /(х, у) по х и у записываются соответственно как
df df
дх и ду *
(В качестве примера: если /(х, у) = х2 +ху2Н-у3, то df /дх — 2х+у2, df /ду = 2ху + 3у2.)
Если эти величины существуют и непрерывны, то говорят, что Ф есть (С1-)гладкая функция
на поверхности <S.
Можно также рассмотреть производные более высокого порядка, обозначив вторую
частную производную функции / по х и у соответственно как
дх2 ' ду2
(Теперь, конечно, необходима С2-гладкость.) Существует также «смешанная» вторая про¬
изводная д2 f jdxdy, которая означает d(df /ду)/дх, а именно частную производную по х
* шт	1
Рассмотрите вещественную функцию /(ж, у) = ху{х2 + y2)~N при N = 1, 2и Покажите, что во
всех случаях эта функция дифференцируема (Cw) по х при любом фиксированном значении у (то же имеет место
при обмене местами х и у). Тем не менее отсутствует гладкость / как функции пары (ж, у). Покажите это для слу¬
чая N = 2, продемонстрировав, что эта функция даже не ограничена в окрестности начала координат (0, 0) (т. е.
она принимает там произвольно большие значения), для случая N = 1, продемонстрировав, что эта функция, хотя
1
и будучи ограниченной, не является непрерывной как функция пары (ж, у), а также для случая N = —, показав,
что эта функция, хотя и непрерывна, не является гладкой вдоль прямой ж = у. (Подсказка: рассмотрите значения
каждой функции вдоль прямых линий, проходящих через начало координат в плоскости (ж, у).) Некоторые чита¬
тели могут проиллюстрировать это, воспользовавшись, если есть такая возможность, компьютером с трехмерным
графопостроителем, — однако это ни в коем случае не обязательно.

10.2. Гладкость, частные производные
173
от частной производной функции / по у. Можно взять эту смешанную производную в обрат¬
ном порядке и получить величину d2f/дудх. Из условия (второй) дифференцируемости
функции / следует равенство этих двух величин*:
d2f
а2/
дхду	дудх *
(Этого требует полное определение С2-гладкости для
**
соответствующие выражения
дх3
а3/
а3/
а3/
дх2ду дхдудх дудх
и т.д.
Важная причина того, что я так различал здесь f и Ф,
используя для них разные буквы (далее я буду обра¬
щать на это меньше внимания), состоит в том, что нам
может понадобиться рассмотреть величину Ф, опреде¬
ленную на поверхности, но описываемую в различ¬
ных координатных системах. Математическое выраже¬
ние для функции /(ж, у) может меняться от одного ло¬
скута к другому, хотя значение величины Ф в некоторой
определенной точке поверхности, «покрываемой» эти¬
ми лоскутами, не меняется. Точнее, это может происхо¬
дить в области перекрытия между различными коорди¬
натными лоскутами (см. рис. 10.4). Если другой набор
координат обозначить через (X, У), получится новое
выражение
Ф = F{X, У)
для значений Ф на новом координатном лоскуте. Сле¬
довательно, в области перекрытия между двумя лоску-
• •
тами мы будем иметь
, , *• ,
F(X, Y) = у),
Рис. 10.4. Чтобы покрыть всю по¬
верхность S, может оказаться необ¬
ходимым «склеить» несколько коорди¬
натных лоскутов. Гладкая функция Ф
на $ имеет координатное представле¬
ние Ф — /(ж, у) на одном лоскуте
и Ф — F(X, У) на другом (с соот¬
ветствующими локальными координа¬
тами (х, у), (X, У)). В области пе¬
рекрытия /(ж, у) = F(X, У), где X
и У — гладкие функции от ж и у
хотя, как указано выше, явный вид выражения, пред¬
ставляемого функцией F в переменных X и У, в общем
случае совершенно отличен от выражения, представля¬
емого функцией / в переменных х и у. Действитель¬
но, X может быть некоторой сложной функцией от ж и у, так же может обстоять дело и с У,
и эти зависимости должны учитываться при переходе от / к F. Подобные функции,
выражающие координаты одной системы через координаты другой,
Х = Х(х,у)
И
T = Y(x, )
Докажите, что смешанные вторые производные д2 f /дудх и д2 f /дхду всегда равны между собой,
если /(ж, у) — многочлен. (Многочленом по ж и у называется выражение, построенное из ж, у и постоянных
с использованием только сложения и умножения.)
Покажите, что смешанные вторые производные от функции / = ху(х2 — у2)/(х2 + у2) не равны между
собой в начале координат. Проверьте непосредственно нарушение непрерывности вторых частных производных
в начале координат.
Найдите явный вид функции F(X, Y), если /(ж, у) — ж3 — у3, X ~ х — у> Y = ж у. (.Подсказка:
♦ **
как выглядит ж2 + ху -\- у2 в переменных X и У? Какое отношение это имеет к /?)

174
Глава 10
и наоборот
x = x(X,Y) и у = у(Х, Y),
называются функциями перехода и описывают изменение координат от одного лоскута к дру¬
гому. Эти функции перехода должны быть гладкими (для простоты пусть они будут С 00-глад¬
кими), откуда следует, что понятие «гладкости» функции Ф не зависит от выбора координат,
используемых в области перекрытия лоскутов.
10.3.	Векторные поля и 1-формы
Существует понятие «производной» от функции, не зависящее от выбора координат.
В применении к функции Ф, определенной на S, стандартное обозначение выглядит следу¬
ющим образом:
df	df
дФ — — dx + тг— dy.
ox	ay
Здесь мы начинаем сталкиваться с некоторой путаницей в понятиях, и к этому нужно при¬
выкнуть. Прежде всего, такие величины, как dФ и dx, сразу воспринимаются как «бесконечно
малые», возникающие при использовании предельной процедуры, применяемой в матема¬
тическом анализе при определении производной dyjdx (см. § 6.2). В § 6.5 также использова¬
лись выражения вроде d(\og х) = dx/x. На той стадии эти выражения рассматривались чисто
формально[10>21, в частности, последнее выражение понималось просто как удобный способ
(«умножение на dx») представления «более правильного» выражения d(logx)/dx = 1/х.
Когда же я пишу dФ в вышеприведенной формуле, я имею в виду некоторую геометри¬
ческую сущность, которая называется 1-формой (хотя это не самый общий вид 1-формы,
см. §§10.4, 12.6) и сохраняет смысл также для выражений типа d(log ж) =dx/x. 1-форма не
является «бесконечно малой величиной», а имеет несколько иную интерпретацию, которая
с годами становится все более важной и к которой я вскоре вернусь. Замечательно, одна¬
ко, что, несмотря на такое значительное изменение интерпретации символа d, формальные
математические выражения (вроде тех, что рассматривались в § 6.5) совсем не изменились
(при условии, что мы не будем пытаться делить на dx),
В вышеприведенной формуле имеется еще один возможный источник недоразумения,
связанный с тем, что в левой части используется Ф, а в правой /. Я поступил так в основном
из-за сделанных выше предупреждений относительно разницы между Фи/. Величина Ф
есть функция, областью определения которой служит многообразие S, тогда как областью
определения функции / является некоторая (открытая) область на плоскости (х, у), пред¬
ставляющая собой один из координатных лоскутов. Если я пользуюсь понятием «частная
производная по х», я должен знать, что это означает «сохраняя другую переменную у посто¬
янной». Именно по этой причине справа стоит /, а не Ф, поскольку / «знает» о координатах х
и у, а Ф — нет. Помимо этого, налицо путаница, связанная с тем, что в формуле не указаны
аргументы функций. Функция Ф слева действует на выбранную точку р 2-многообразия S,
тогда как / действует на значения координат (х, у), которые координатная система приписы¬
вает точке р. Строго говоря, этот факт следует сделать явным, для того чтобы обсуждаемое
выражение имело смысл. Однако чтобы не говорить об этом всякий раз, гораздо удобнее
записывать его в виде
дх ду
или в «обобщенной» операторной форме
d = dx-^~ + dy
дх ду'

10.3. Векторные поля и 1-формы
175
Здесь я пытаюсь разъяснить смысл таких понятий. Эти формулы представляют собой при¬
меры так называемого цепного правила. Необходимо выяснить смысл, приписываемый обо¬
значениям вроде дФ/дх9 где Ф — некоторая функция, определенная на S.
Как мы должны понимать оператор вроде д/дх — как нечто, действующее на функ¬
цию типа Ф, определенную на многообразии S, или же на функцию от переменных х и у!
Посмотрим сначала, что означает операция д/дх по отношению к некоторой другой коорди¬
натной системе (X, У). Соответствующая формула, выражающая «цепное правило», теперь
принимает вид
д дХ д ,дУ д
\
дх дх дХ дх дУ
•	s
Таким образом, в переменных системы (X, У) мы имеем выражение более сложного ви¬
да (дХ/дх)д/дХ 4- (дУ/дх)д/дУ для представления той же самой операции, что и более
простое выражение д/дх в системе (х> у). Это более сложное выражение можно рассмат¬
ривать как величину £ вида
£ = А^- + В д
дХ дУ'
где А и В — (С00-) гладкие функции от X и У. В только что рассмотренном конкретном
случае, где £ представляет д/дх, мы имеем А == дХ/дх и В — дУ/дх. Но можно рас¬
смотреть подобные величины £ более общего характера, в которых Л и В не имеют такого
частного вида. Такая величина £ носит название векторного поля на S (на координатном
лоскуте (X. У)). Можно переписать £ в первоначальной системе (ж, у), тогда оказывается,
что £ имеет ту же самую общую форму, что и в системе (X, У):
t=aTx+biv
(хотя функции а и b в общем случае совершенно отличны ох А я В) . Это позволяет нам
продолжить векторное поле с лоскута (X, У) на перекрывающийся с ним лоскут (ж, у).
Таким путем, взяв столько лоскутов, сколько потребуется, мы можем продолжить векторное
поле на все многообразие S.
Всё это может привести читателя в некоторое замешательство. Однако моей целью было
не запутать его, а найти правильную аналитическую форму для очень важного геометриче¬
ского понятия. Дифференциальный оператор £, который мы назвали векторным полем, с его
весьма специфическим способом преобразования при последовательном переходе от одного
лоскута к другому имеет ясную геометрическую интерпретацию, проиллюстрированную на
• •	• * • ,
рис. 10.5. Величина £ изображается там как «поле маленьких стрелою) на поверхности S,
хотя на некоторых участках этой поверхности стрелки могут сжиматься вблизи некоторых
точек, в которых £ принимает нулевое значение. (Чтобы представить себе хорошую картину
векторного поля, вспомните карту ветров в телевизионных сводках погоды.) Стрелки ука¬
зывают направления, в которых должна быть взята производная от функции, на которую
действует £. Если в качестве такой функции выбрать Ф, то действие £ на Ф, а именно £(Ф). =
= адФ/дх -Ь ЪдФ/ду9 может служить мерой скорости увеличения Ф в направлении стрелок
(см. рис. 10.6). Величина («длина») стрелки также имеет значение, определяя «масштаб»,
в котором должно измеряться это увеличение. Более длинная стрелка соответствует большей
скорости увеличения. Более точно: все стрелки следует представлять себе бесконечно ма¬
лыми; каждая из них соединяет точку р на S («хвост» стрелки) с «соседней» точкой р( на S
(«острие» стрелки). Чтобы сделать это несколько более наглядным, выберем в качестве меры
Выразите А и В через а и 6; по аналогии выразите а и 6 через А и В.

176
Глава 10
Рис. 10.5. Геометрическая интерпретация векторного поля £ как «поля стрелок», нарисованных на по¬
верхности S
/
Увеличе¬
ние с-1 раз
Рис. 10.6. Действие £ на скалярное поле Ф определяет скорость роста Ф в направлении стрелок £.
Стрелки следует представлять себе бесконечно малыми, каждая из них соединяет точку р на S («хвост»
стрелки) с «соседней» точкой р' на S («острие» стрелки). Показана картина с большим увеличением
(вбч раз, где е — малая величина). Разность Ф(р') — Ф(р), деленная на е, дает (в пределе е —> 0)
градиент £ (Ф) функции Ф вдоль £
расстояния между двумя точками р и рг в направлении £ некоторое малое положительное
число б, Тогда разность Ф(р') — Ф(р), деленная на е, дает приближенное значение величи¬
ны £(Ф). Чем меньшее значение б выбрано, тем более точное приближение мы получим.
В предельном случае, когда pf стремится к р (так что е —► 0), мы получаем величину £(Ф),
иногда называемую градиентом (или наклоном) функции Ф в направлении £.
В частном случае векторного поля д/дх все стрелки указывают вдоль координатных
линий постоянного значения у. Это является источником часто возникающих недоразумений
при использовании стандартного математического обозначения частной производной д/дх.

10.3. Векторные поля и 1-формы
177
Можно было бы подумать, что выражение д/дх полностью относится к величине х. Однако
на самом деле оно в большей степени относится к переменной (переменным), которая здесь
явно не упоминается (в данном случае у), а не к х. Такая запись особенно поучительна, когда
рассматривается изменение координатных переменных, скажем, переход от (ж, у) к (.X, Y),
при котором одна из координат
изменение координат:
X = х, Y — у + х.
случае
д
д
д
д
д
дХ дх ду' дУ ду
Таким образом, мы видим, что
д
дХ
самое, что и х, тогда как
д
д	лг
отличается от несмотря на то, что X есть то же
8
^ — то же самое, что и хотя Y отличается от у. Это пример
того, что мой коллега Нир Вудхауз называет «вторым фундаментальным недоразумением
анализа»! ^10*31 Однако с геометрической точки зрения ясно, почему -™- ф \ соответству-
оХ ох
ющие «стрелки» направлены вдоль разных координатных линий (рис. 10.7).
У i
1
у = const
ц
LJ
у — const
д
дх
у — const
X
+=>
со
с
О
П . , -п
СО
й
о
СО
Й
О
н
II
;
Л * /5
Рис. 10.7. Иллюстрация к «второму фундаментальному недоразумению анализа»: —— ф —, несмотря
на то, что X — х и
д
д
дХ ' дх
, хотя Уфу, при замене координат X = ж, Y ~ у + х. Интерпретация
дУ ду
операторов частного дифференцирования как «стрелок», указывающих вдоль координатных линий,
разъясняет геометрию (х — const согласуется с X ~ const, но у — const не согласуется с Y = const)
Теперь можно интерпретировать величину (1Ф. Она называется градиентом (или внеш¬
ней производной) функции Ф и содержит информацию о том, как изменяется Ф во всех
возможных направлениях вдоль поверхности S. Для геометрического представления
удобно воспользоваться системой контурных линий на S (см. рис. 10.8 а). Можно предста¬
вить себе S как обычную географическую карту, которая может иметь вид сферического
глобуса, если мы хотим учесть возможность искривленного многообразия S. Функция Ф
может представлять высоту земной поверхности над уровнем моря. Тогда (1Ф имеет смысл
наклона поверхности к горизонту. Контурные линии (горизонтали) соединяют местах оди-
Выведите это в явном виде. (Подсказка: Вы можете воспользоваться «цепным правилом» для д/дХ
и д/дУ в полной аналогии с приведенным выше выражением для д/дх.)

178
Глава 10
• %
\
Поверхность
5
я)
d<P
дает направление
контуров
Ось
наклона
^-направление,
в котором
€(*)=о
Поверхность
5
б)
Рис. 10.8. Мы можем геометрически изобразить полный градиент (внешнюю производную) 6Ф скаля¬
ра Ф в виде системы контурных линий на S. а) Значение Ф откладывается вертикально вверх над S,
> .
так что контурные линии на S (линии постоянных значений Ф) соответствуют постоянной высоте. 6)
В каждой точке р поверхности S направление контурной линии указывает то направление, в котором
градиент обращается в нуль («ось отсчета» наклона холма), то есть направление стрелок £ в точке р,
для которого £(Ф) = 0. При пересечении контурных линий происходит увеличение либо уменьшение
в
величины Ф, и £(Ф) является мерой плотности числа линий в направлении £
наковой высотой над уровнем моря. В каждой точке р поверхности S направление контурной
линии указывает направление, в котором градиент обращается в нуль («ось отсчета» наклона
поверхности), т. е. то направление стрелки £ в точке р, в котором £(Ф) == 0. Двигаясь вдоль
контурной линии, мы ни поднимаемся, ни опускаемся. Если же мы пересекаем контурные
линии, то Ф будет увеличиваться либо уменьшаться, и скорость, с которой это происходит,
а именно £(Ф), будет измеряться плотностью числа контурных линий в том направлении,
в котором мы ее пересекаем (см. рис. 10.86).
л	%	в	•>	*	в	•	•	9
10.4.	Компоненты, скалярные произведения
В соответствии с выражением
€
а-£-+ Ь д
дх
ду'

10.4. Компоненты, скалярные произведения
179
векторное поле £ можно считать состоящим из двух частей, одна из которых пропорцио-
А
нальна и содержит точки, лежащие на линиях постоянного значения у, а другая про-
Л
порциональна — и содержит точки, лежащие на линиях постоянного значения х. Таким
ду
образом, в (ж, у)-координатной системе для описания £ можно использовать пару соответ¬
ствующих весовых множителей (а, 6). Числа а и Ъ называются компонентами векторного
поля £ в этой координатной системе (см. рис. 10.9). (Строго говоря, двумя «компонента¬
ми» величины £ следовало бы считать два векторных поля ад/дх и Ьд/ду, из которых
строится векторное поле £, как показано на рис. 10.9; аналогичное замечание относится
и к компонентам величины (1Ф (см. ниже). Однако термин «компонента» в настоящее время
приобрел смысл «координатного указателя» в большей части математической литературы,
в частности, в тензорном исчислении (см. § 12.8).)
Рис. 10.9. Вектор £ = ад/дх + Ьд/ду можно считать состоящим из двух частей, одна из которых, про¬
порциональная д/дх, направлена вдоль у = const, другая, пропорциональная д/ду, направлена вдоль
х = const. Пара соответствующих весовых множителей (а, Ь) называется компонентами векторного
поля £ в координатной системе (#, у)
Аналогично величина дФ («1-форма») строится из двух частей, dx и dy, в соответствии
с выражением
d<P = udx -b v dy,
и потому для описания dФ можно использовать пару (и, v)9 так что числа и и v являются
компонентами дФ в той же координатной системе. (Фактически мы имеем здесь и = дФ/дх
и v = дФ/ду.) Связь между компонентами (и, v) 1-формы dФ и компонентами (а, Ъ) век¬
торного поля £ осуществляется через величину £(Ф), которая, как мы видели, служит мерой
скорости увеличения Ф в направлении £. Получается*, что значение £(Ф) определяется со¬
отношением
т = аи + bv.
Величина аи + bv называется скалярным (или внутренним) произведением величины £, опре¬
деляемой компонентами (а, b), и величины дФ9 определяемой компонентами (гц г»). Это ска¬
лярное произведение мы иногда будем записывать в виде дФ • £, если захотим представить
Покажите это в явном виде, используя «цепное правило».

180
Глава 10
его в абстрактной форме без указания какой-либо конкретной координатной системы. Тогда
мы будем иметь
Причина, по которой здесь используются два разных обозначения для одной и той же вели¬
чины, состоит в том, что представление с1Ф-£ применяется также в отношении 1-форм более
общего вида, нежели те, которые можно представить в виде дФ (см. § 12.3). Если rj являет¬
ся одной из таких 1-форм, то существует ее скалярное произведение с любым векторным
полем £, которое записывается в виде rj • £.
Определение 1-формы, в сущности, состоит в том, что эта величина в комбинации
с некоторым векторным полем дает «скалярное произведение». Именно тот факт, что ве¬
личина с1Ф естественным образом образует скалярное произведение с векторными полями,
характеризует ее как 1-форму. (В зависимости от контекста, 1-форму иногда называют ко-
вектором.) В этом смысле говорится, что 1-формы (ковекторы) дуальны векторным полям.
Понятие «дуального» объекта более подробно обсуждается в § 12.3, где будет показано, что
идеи такого рода применимы к общему случаю «поверхности» любого числа изменений (т. е.
к п-многообразию). Геометрический смысл 1-формы также будет расширен в §§ 12.3-12.5
применительно к большему числу измерений. В данный момент мы пользуемся семей¬
ством контурных линий, которые представляют те направления, в которых должны указывать
стрелки £, когда дФ • £ = 0 (т. е. при £(Ф) = 0).
ч
10.5.	Условия Коши-Римана
• а
Прежде чем совершить скачок ко многим измерениям (мы планируем сделать это в сле¬
дующей главе), вернемся к тому, с чего мы начали в этой главе, — к свойству двумерной
поверхности, позволяющему интерпретировать ее как комплексное 1-многообразие. Всё, что
здесь требуется, — это иметь способ описания тех комплекснозначных функций Ф, которые
являются голоморфными. Условие голоморфности имеет локальный характер, так что мы
можем получить его для каждого координатного лоскута, а затем для областей перекры¬
тия между лоскутами. На (ж, у)-лоскуте требуется, чтобы функция Ф была голоморфной
функцией комплексного числа z = х + гу, а в области перекрытия с (X, У)-лоскутом —
голоморфной функцией от Z = X 4- гУ. Совместимость этих условий обеспечивается тре¬
бованием, чтобы в области перекрытия величина Z была голоморфной функцией от г и нао¬
борот. (Если Ф — голоморфная функция от z9 a z — голоморфная функция от Z, то величина Ф
должна быть голоморфной функцией от Z, поскольку голоморфная функция от голоморфной
функции есть опять-таки голоморфная функция.*)
Как нам выразить условие голоморфности Ф как функции от z через вещественную
и мнимую части величин Ф и z7 Эту роль выполняют знаменитые условия Коили-Римана,
упомянутые в §7.1. Каков явный вид этих условий? Можно представить Ф как функцию
от z и z (поскольку, как мы видели в начале этой главы, вещественную и мнимую части
числа 0, т. е. х и у, можно выразить через z и zy пользуясь соотношениями х = (z + z)/2
и у — (z ~z)/2i). Нам, в сущности, нужно найти условие того, что Ф зависит только от г
(т. е. не зависит от z).
Что это означает? Представим себе, что вместо пары комплексно-сопряженных пере¬
менных z и z мы имеем пару независимых вещественных переменных, скажем, и иг;,
и хотим выразить тот факт, что некоторая функция Ф от и и v в действительности не зависит
•	•	т
* J© Объясните это с трех различных точек зрения: а) интуитивной, из общих принципов (откуда могло бы
появиться число z?), б) используя геометрию голоморфных отображений, описанную в § 8.2, и в) в явном виде,
используя цепное правило и условия Коши - Римана, к которым мы сейчас перейдем.

10.5. Условия Коши-Римана
181
от v. Этот факт независимости можно представить в виде
gUo
OV
(поскольку это уравнение сообщает нам, что для каждого значения и величина Ф как функция
от v является постоянной, так что Ф зависит только от w)f10,4j\ Соответственно независи¬
мость Ф от z выражается в виде
дФ
dz
0,
и это действительно представляет условие голоморфности Ф (хотя «аргументация по ана¬
логии», к которой я только что прибегнул, не должна служить доказательством этого
факта)^10*5!. Используя цепное правило, можно выразить это условие1" через частные произ¬
водные в системе (я, у):
9Ф + 1дФ = о
С\	1	^ г\	^	•
ох ду
Выразив величину Ф через ее вещественную и мнимую части
Ф = а + i/З,
где а я (3 — вещественные величины, получаем условия Коши-Римана* Л10-6!
да _	да	__	9(3
дх	ду5	ду	дх
Как уже отмечалось, в области перекрытия координатных лоскутов (#, у) и (X, Y) мы тре¬
буем, чтобы величина Z = X + iY была голоморфной функцией от z = х + гу, поэтому
мы получаем, что условия Коши-Римана выполняются также между (яг, у) и (X, У):
дХ =	дУ_	дХ	=	д¥
дх	ду1	ду	дх'
Если это условие выполняется для любой пары координатных лоскутов, то мы можем по¬
строить риманову поверхность <S. (Это те требуемые аналитические условия, которые были
вскользь упомянуты в §7.1.) Напомним, что такую поверхность можно рассматривать как
комплексное 1-многообразие. Однако согласно нашей нынешней «коши-римановой» точке
зрения, S представляет вещественное 2-многообразие со структурой частного вида, опреде¬
ляемой условиями Коши-Римана.
Имеется некоторая «наивность» в попытке ограничиться голоморфными операциями
(такая перспектива станет важной для нас позже, в главе 33 и в § 34.8) и рассматривать S
как «кривую». Альтернативная «коши-риманова» точка зрения оказывается плодотворной
в ряде других контекстов. Например, она позволяет получать результаты с помощью мно¬
гих полезных методов в теории существования дифференциальных уравнений в частных
производных. Я попытаюсь дать почувствовать это лишь на одном (но важном) примере.
т~1	ту г» да д(3 да д(3
Если выполняются условия Коши-Римана	я	—	=	——, то оказывается,
ох ду ду	дх
что каждая из величин а и (3 удовлетворяет некоторому уравнению (уравнению Лапласа).
Мы имеем
V2a = 0,	V2/3	=	0,
***
**
Проделайте это.
Дайте более прямой вывод условий Коши - Римана исходя из определения производной.
Покажите это.

182
Глава 10
где используется дифференциальный оператор второго порядка V2, называемый (двумер¬
ным) лапласианом и определяемый следующим образом:
г?2 _ д2 , д2
Лапласиан играет важную роль во многих физических ситуациях (см. §§ 21.2,22.11,24.3-24.6).
Например, если мыльная пленка на проволочной петле очень слабо отклоняется вверх и вниз
от горизонтальной плоскости, то высота пленки над этой плоскостью будет описываться ре¬
шением уравнения Лапласа (с тем лучшим приближением, чем меньше это вертикальное
отклонение) [10-7J (см. рис. 10.10). Уравнение Лапласа (в трех измерениях) играет фунда¬
ментальную роль также в ньютоновской теории гравитации (а также в электростатике, см.
главы 17 и 19), поскольку этому уравнению удовлетворяет потенциальная функция, опреде¬
ляющая гравитационное (или статическое электрическое) поле в свободном пространстве.
Рис. 10.10. Мыльная пленка на проволочной петле слабо отклоняется вверх и вниз от горизонтальной
плоскости. Высота пленки над этой плоскостью дается решением уравнения Лапласа (с тем лучшим
приближением, чем меньше вертикальное отклонение)
Решение уравнений Коши-Римана можно довольно прямым образом получить из ре¬
шений двумерного уравнения Лапласа. Если некоторая величина а удовлетворяет уравне¬
нию V2a — 0, то можно построить величину /? = /(да/дх) dy и убедиться, что оба условия
Коши-Римана выполняются*. Этот факт можно использовать для иллюстрации некоторых
утверждений, сделанных в конце предыдущей главы.
В частности, рассмотрим замечательный факт, отмеченный в конце § 9.7, а именно что
любую непрерывную функцию /, определенную на единичной окружности в комплексной
плоскости, можно представить в виде гиперфункции. Это утверждение означает, что любая
непрерывная функция / является суммой двух частей, одна из которых голоморфно про¬
должается на внутреннюю часть единичного круга, а другая — на его внешнюю часть, при
этом комплексная плоскость дополняется до сферы Римана. Согласно обсуждению в § 9,2,
это утверждение фактически эквивалентно существованию фурье-представления функции /,
которая предполагается периодической функцией вещественной переменной. Для простоты
предположим, что функция / принимает вещественные значения. (Комплексную функцию
можно разбить на вещественную и мнимую части.) Существуют теоремы, утверждающие,
что функцию / можно продолжить непрерывным образом на внутреннюю часть круга, ес¬
ли / удовлетворяет уравнению V2/ = 0 внутри круга. (Этот факт представляется вполне
% ■ •
* Л Покажите это.

10.5. Условия Коши-Римана
183
правдоподобным в соответствии с приведенными выше рассуждениями относительно мыль¬
ной пленки; см. рис. 10.10. Проведя масштабное преобразование функции / к новой функ¬
ции б/ с некоторым фиксированным малым в, можно представить себе, что наша проволоч¬
ная петля лежит на единичной окружности в комплексной плоскости, слегка отклоняясь t10*8}
от нее вверх и вниз в вертикальном направлении на величину б/, определенную на единич¬
ной окружности. Высота мыльной пленки определяет значения б/ и, следовательно, / внутри
окружности.) В соответствии со сделанным предположением (д = f (df /дх) dy), мы можем
добавить к / мнимую часть g, так что функция f + ig голоморфна внутри единичного круга.
Эта процедура дает также мнимую часть g к функции / на самой единичной окружности
(в общем случае в виде гиперфункции), так что / 4- гд — отрицательно-частотная функция.
Подобную процедуру можно повторить в отношении внешней части единичной окружно¬
сти (считая ее лежащей на сфере Римана) и найти, что туда продолжается положительно-
1 1
частотная функция f -гд. Разбиение f — ^(/■+ гд) + -(/ — гд) решает поставленную задачу.
Примечания
§10.2.
10.1. Подробное обсуждение дифференцируемости функций нескольких переменных можно найти
в книге [517].
§10.3.
10.2. Обозначение dx, впервые введенное Лейбницем в конце XVII века, обладает большой гибко¬
стью, позволяя рассматривать величины типа dx на равных правах с другими алгебраическими
объектами. Это, однако, не распространяется на обозначение d2x для вторых производных.
Если воспользоваться измененным обозначением второй производной у по х в виде (d2y —
— d2x dy/dx)/dx2, то величина d2x будет вести себя как обычный алгебраический объект (при
этом d2x будет означать dxdx и т. д). Не ясно, однако, как воспользоваться этим практически,
учитывая сложный вид приведенного выражения.
10.3. «Первым фундаментальным недоразумением» следует считать путаницу в использовании /
и Ф, с которой мы столкнулись в § 10.2, особенно в связи с определением вторых производных.
См. [852].
§10.5.
10.4. Это условие следует понимать лишь в локальном смысле. Например, можно взять гладкую
функцию Ф(и, v), определенную в некоторой овальной области плоскости (и, v), внутри кото¬
рой ЭФ/dv = 0, однако Ф не является функцией только от и*
10.5. Не будучи наиболее строгим подходом к условиям Коши-Римана, эти рассуждения дают объ¬
яснение вида этих условий.
10.6. На самом деле Жан Лерон Даламбер получил эти условия в 1752 году, задолго до Коши
или Римана (см. [751]).
10.7. Оказывается, что точное уравнение мыльной пленки (по отношению к которому уравнение
Лапласа является приближением) имеет замечательное общее решение через голоморфные
функции, найденное Вейерштрассом в 1866 году.
10.8. Поскольку функция f непрерывна на окружности, она должна быть ограниченной (т.е. ее зна¬
чения должны лежать между фиксированным нижним значением и фиксированным верхним
значением). Из стандартных теорем следует, что окружность является компактным простран¬
ством. (Определение компактности см. в § 12.6, а также в [428, 269].) Можно перенормировать
функцию / (умножив ее на малую постоянную б), так что верхняя и нижняя границы будут
весьма малыми. Аналогия с мыльной пленкой дает правдоподобные аргументы в пользу суще¬
ствования продолженной внутрь окружности функции б/, которая удовлетворяет уравнению
Лапласа. Это, конечно, не может служить доказательством; более строгое решение этой так
называемой «задачи Дирихле для диска» см. в книгах [748, 109].
• • т \
Проверьте это для функции Ф(и, v) = 0(v)h(u), где функции в и h определены в §§ 6.1, 6.3. Овальная
область должна исключать неотрицательную полуось и.

кТЛ
с'**-*'* |
Глава 11
Гиперкомплексные функции
11.1.	Алгебра кватернионов
Как обобщить все это на случай большего числа измерений? Стандартный (современ¬
ный) подход к изучению n-многообразий я изложу в следующей главе, однако было бы
полезно, по ряду причин, если бы я сначала познакомил читателя с некоторыми более ран¬
ними идеями, предложенными для изучения многих измерений. Эти ранние идеи оказались
непосредственно связанными с некоторыми современными течениями в теоретической фи¬
зике.
и мощь комплексного анализа, в частости, вышеупомянутое свойство, поз¬
воляющее простым образом выразить решения двумерного уравнения Лапласа, играющего
важную роль в физике, через голоморфные функции, побудили математиков XIX века ис¬
кать «обобщенные комплексные числа», которые можно было бы естественным образом
Фименить к трехмерному пространству. Знаменитый ирландский математик Уильям Роуан
Гамильтон. (1805-1865) был одним из тех, кто долго и глубоко размышляя над этой про¬
блемой. И в конце концов 16 октября 1843 года, когда он с женой прогуливался по берегу
Королевского канала в Дублине, к нему неожиданно пришло решение. Открытие привело
его в такой восторг, что он тут же высек на камне дублинского Брукхэмского моста свои
Фу
I
>я;
i2 = j2 = k2
• Л -я	^
1JK = --1.
Каждая из трех величин i, j и к представляет собой независимый «квадратный корень
из — 1» (подобно одной такой величине г в комплексных числах), а их комбинация общего
вида
q = t -h ш -h vj +
где tyu, v и w —т вещественные числа, определяет кватернион. Такие величины подчиняются
всем обычным правилам алгебры, кроме одного. Исключение (в котором и содержится
подлинная новизна^111! величин, введенных Гамильтоном) составляет нарушение закона
коммутативности умножения. Гамильтон показал, что*
• *
ц
ji, jk
kj, ki
ik;
это является грубым нарушением стандартного закона коммутативности аЪ =. Ьа.
Кватернионы удовлетворяют законам коммутативности и ассоциативности сложения,
закону ассоциативности умножения и закону дистрибутивности умножения относительно
Покажите это непосредственно из гамильтоновых «уравнений Брукхэмского моста», предполагая лишь
выполнение закона ассоциативности а(Ъс) = (аЪ)с.

11.1. Алгебра кватернионов
185
сложения
а -Ь 6 — Ъ сь,
а + (6 + с) = (а + 6) + с,
а(6с) = (аб)с,
а(Ь + с) — ab + ас,
(а + 6)с = ас + 6с.
Сюда следует добавить существование аддитивного и мультипликативного «тождественных
элементов» 0 и 1, так что
а + 0=а, 1а “ а1 = а.
Эти соотношения, за исключением последнего, определяют то, что алгебраисты называ¬
ют кольцом. (На мой взгляд, термин «кольцо», как и большинство терминов абстрактной
алгебры, совершенно не согласуется с интуицией, и я не имею представления о его про¬
исхождении.) Если включить и последнее соотношение, мы получим «кольцо с единичным
элементом».
Кватернионы представляют также пример «векторного пространства» на множе¬
стве вещественных чисел. В векторном пространстве можно складывать два элемента
(вектора^11,21) £ и р, образуя сумму £ + р, обладающую свойствами коммутативности и ас¬
социативности:
(£ + п) + С = £ + (ч + О-
Векторы можно умножать на «скаляры» (в данном случае вещественные числа / и д),
при этом выполняются следующие свойства дистрибутивности и ассоциативности:
(/ + <?)£ = /£ + 9%у
/(£ + »?) = /£ • fv*
f(g£) = ifg)€>
Ч = t
Кватернионы образуют четырехмерное векторное пространство на множестве веще¬
ственных чисел, поскольку существуют ровно четыре независимые «базисные» величи¬
ны 1, i, j, к, охватывающие все пространство кватернионов. Так что любой кватернион
можно однозначным образом представить в виде суммы произведений вещественных чисел
на эти базисные элементы. В дальнейшем мы встретимся со многими другими примерами
векторного пространства.
Кватернионы представляют также пример алгебры на множестве вещественных чисел,
поскольку существует описанный выше закон умножения. Но что замечательно в гамильто¬
новых кватернионах — так это существование, кроме того, операции деления, что равносиль¬
но существованию (мультипликативной) обратной величины q"1 для каждого ненулевого
кватерниона q. Эта обратная величина удовлетворяет соотношениям
q~1q = qq~1 = l,
*{£§ Представьте сумму и произведение двух кватернионов общего вида таким образом, чтобы все эти соот¬
ношения выполнялись.

186
Глава 11
что придает кватернионам структуру кольца с делением. Обратную величину можно пред¬
ставить в явном виде:
q~x = я(яч)~г,
где кватернион q, сопряженный относительно кватерниона q = t+ui+vj+wk, определяется
следующим образом:
q = t — ui — V} — wk.
Мы находим, что
qq — t2 + и2 + v2 + w2,
так что вещественное число qq не может обратиться в нуль, за исключением случая q = О
(т. е. t — и = v = w = 0). Следовательно, величина (<z<z)_1 существует, откуда следует, что
величина q~г определена при условии q ф 0.*
11.2.	Какова роль кватернионов в физике?
Всё это дает нам очень красивую алгебраическую структуру и, казалось бы, возмож¬
ное удивительное исчисление, хорошо подходящее для исследования физики и геометрии
нашего 3-мерного физического пространства. И действительно, сам Гамильтон посвятил
оставшиеся 22 года своей жизни попыткам создать такое исчисление. Однако, окидывая
взглядом XIX и XX века с нашей нынешней позиции, мы должны оценить эти героические
усилия как относительную неудачу. Это не означает, что кватернионы не оказали никакого
влияния на математику (и даже на физику). Они сыграли определенную роль и, в несколько
косвенном смысле, оказали весьма большое влияние благодаря обобщениям разного рода.
Однако изначальные «чистые кватернионы» пока не оправдали тех больших надежд, которые
на них когда-то возлагали.
Почему так произошло? Не должно ли это служить для нас уроком при оценке совре¬
менных попыток найти «правильную» математику для описания физического мира? Сразу
имеется очевидный ответ. Если мы рассматриваем кватернионы как многомерный аналог
комплексных чисел, то должны иметь в виду, что переход от комплексных чисел к кватернио¬
нам означает переход от двух измерений не к трем, а к четырем измерениям. В обоих случаях
одним из измерений служит «вещественная ось», соответствующая t-компоненте указанного
представления q через i, j, к. Было сильное искушение приписать t смысл времени^11 что¬
бы кватернионы описывали не просто пространство, а четырехмерное пространство-время.
Это могло показаться очень привлекательным с позиций XX века, поскольку четырехмерное
пространство-время, как мы увидим в главе 17, занимает центральное место в современной
теории относительности. Оказывается, однако, что кватернионы не подходят для описания
пространства-времени, так как «естественная» для кватернионов квадратичная форма qq =
= t2+и2+v2+w2, с точки зрения теории относительности, имеет «неправильную сигнатуру»
(к этому понятию мы придем позже, см. §§ 13.8,18.1). Конечно, Гамильтон ничего не знал об
относительности, поскольку жил в другом веке. Во всяком случае это довольно запутанный
вопрос, и здесь я не хочу больше на нем останавливаться. Немного позже я к нему вернусь
(см. §§ 13.8, 18.1-18.4, конец §22.11, §§28.9, 31.13, 32.2).
Имеется и другая, возможно, более фундаментальная причина, по которой кватернио¬
ны не оказались такими математически полезными, как казалось с первого взгляда. В них
относительно мало «магии», и они определенно не могут конкурировать в этом отношении
с комплектными числами. Причина состоит в отсутствии удовлетворительного^11^ кватер-
нионного аналога понятия голоморфной функции. Основная причина этого проста. Мы
* Й0 Проверьте, что такое определение величины q 1 действительно работает.

11.2. Какова роль кватернионов в физике?
187
видели в предыдущей главе, что голоморфная функция комплексной переменной z. харак¬
теризуется как «голоморфно-независимая» от комплексно-сопряженной величины z. Что же
касается кватернионов, то кватернион д, сопряженный кватерниону д, можно с помощью
алгебраических действий выразить через g и постоянные величины i, j, k:*
Я = ~\{я + rn + № + kgk).
Если «кватернионная голоморфность» означает возможность построения из кватернионов
с использованием сложения, умножения и предельного перехода, то g следует считать
кватернионно-голоморфной функцией от д, что изрядно портит всю идею.
Нельзя ли найти такую модификацию кватернионов, которая имела бы более прямое от¬
ношение к физическому миру? Мы увидим, что это вполне возможно, но для этого придется
пожертвовать упомянутым выше ключевым свойством кватернионов, а именно возможно¬
стью делить на них (если кватернион отличен от нуля). А как быть с обобщением на большее
число измерений? Вскоре мы увидим, как достиг этого Клиффорд и как обобщение такого
рода оказалось полезным для физики. Но все эти обобщения приводят к отказу от алгебры
с делением.
Существуют ли обобщения кватернионов, сохраняющие возможность деления? Да, су¬
ществуют, но существуют и теоремы, утверждающие, что это невозможно, пока мы не смяг¬
чим правила алгебры в еще большей степени, чем наш отказ от коммутативности умножения.
В 1843 году, через пару месяцев после получения от Гамильтона письма, извещавшего об от¬
крытии кватернионов, Джон Грейвс обнаружил, что существует в некотором роде «двойной
кватернион» — объект, ныне именуемый октонионом. Октонионы были переоткрыты в 1845
голу Артуром Кэли. Октонионы не подчиняются ассоциативному закону умножения а(Ьс) =
— (ab)c (хотя остатки этого закона проявляются в виде тождеств более частного характе¬
ра а(аЪ) = а2Ъ и (аЪ)Ъ = ab2). Красота этой структуры состоит в том, что она продолжает
быть алгеброй с делением, хотя и неассоциативной. Октонионы образуют восьмимерную
неассоциативную алгебру с делением. Они содержат семь аналогов величин i, j, к алгебры
кватернионов, которые вместе с 1 охватывают восемь измерений алгебры октонионов. От¬
дельные законы умножения для этих элементов (аналоги ij = к — — ji и т.д.) усложняются
мало, и лучше отложить это до § 16.2, где будет предложено изящное описание, иллюстриро¬
ванное рис. 16.3. К сожалению, не существует полностью удовлетворительного обобщения
октонионов на большее число измерений, если сохранять возможность деления. Это следует
из алгебраического результата Гурвица (1898), который показал, что кватернионное (и ок-
тонионное) тождество «дд = сумма квадратов» не выполняется при размерности, отличной
от 1, 2, 4, 8. Более того, помимо этих частных значений размерности, вообще не может
быть алгебры, в которой всегда возможно деление (кроме деления на нуль). Это следует
из замечательной теоремы топологии^115!, с которой мы встретимся в § 15.4. Так что един¬
ственные алгебры с делением — это вещественные числа, комплексные числа, кватернионы
и октонионы.
Если мы подготовлены к тому, чтобы отказаться от операции деления, то оказыва¬
ется возможным важное обобщение понятия кватернионов на большее число измерений,
и такое обобщение действительно имеет интересные применения в современной физике.
Таким является понятие клиффордовой алгебры, предложенной английским математиком
Уильямом Кингдоном Клиффордом, прожившим короткую, но яркую жизнь (1845-1879).
Алгебру Клиффорда можно считать выросшей из двух источников, каждый из которых свя¬
зан с попыткой выйти за рамки пространства двух измерений, описываемого комплексными
числами. Одним из таких источников была рассмотренная здесь алгебра гамильтоновых
кватернионов, другим были важные открытия, сделанные в 1844 и 1862 годах малоизвест¬
ным немецким школьным учителем Германом Грассманом (1809-1877). Алгебры Грассмана
•	•	•	V
Проверьте это.

188
Глава 11
сыграли непосредственную роль и в современной теоретической физике. (В частности, на
них опирается современное понятие суперсимметрии (см. §31.3), которое неизменно при¬
сутствует в нынешних попытках расширить фундамент физики за рамки его стандартной
модели.) Для нас будет необходимо познакомиться здесь с алгебрами Грассмана и Клиффор¬
да, и мы сделаем это соответственно в §§ 11.6, 11.5.
Алгебры Клиффорда и Грассмана содержат новый ингредиент, обусловленный высокой
размерностью рассматриваемого пространства. Прежде чем мы сумеем должным образом
усвоить его, лучше будет взглянуть на кватернионы еще раз, но в несколько иной — гео¬
метрической — перспективе. Это приведет нас также к некоторым другим соображениям,
играющим фундаментальную роль в современной физике:
ф • • " •
11.3.	Геометрия кватернионов
Будем рассматривать базисные кватернионные величины i, j, к как три взаимно-пер¬
пендикулярные оси, образующие правую тройку, в обычном евклидовом 3-пространстве
(см. рис. 11.1). В §5.1 отмечалось, что величину г в теории обычных комплексных чисел
можно интерпретировать как операцию умножения на г, которая в отношении комплексной
плоскости означает поворот на прямой угол вокруг начала координат в положительном на¬
правлении. Можно предположить, что кватернион i можно интерпретировать в том же духе,
но теперь как поворот в трехмерном пространстве в положительном направлении (в соответ¬
ствии с правой тройкой осей) вокруг оси i (так что плоскость (j, к) играет роль комплексной
плоскости). Соответственно можно трактовать j как поворот (в положительном направле¬
нии) вокруг оси j, а к — как поворот вокруг оси к. Но если эти повороты производятся на
прямой угол, как в случае комплексных чисел, то не выполняются формулы для произведе¬
ний, поскольку поворот вокруг j после поворота вокруг i не эквивалентен (даже с точностью
до множителя) повороту вокруг к.
В этом совсем легко убедиться, взяв какой-нибудь обычный объект и физически повер¬
нув его. Возьмем, например, книгу. Положите ее перед собой плашмя на горизонтальную
поверхность стола в закрытом виде, как если бы вы собирались раскрыть и читать ее. Пред¬
ставьте, что ось к направлена вверх и проходит через центр книги, ось i направлена вправо,
а ось j — непосредственно от вас, эти оси также проходят через центр. Если повернуть книгу
на прямой угол вокруг i (в положительном направлении), а затем вокруг j, то книга окажется
в положении корешком вверх, из которого ее нельзя вернуть в первоначальное состояние
никаким простым поворотом вокруг к (см. рис. 11.2).
Рис. 11.1. Базисные кватернионы i, j, к от-	Рис. 11.2. Кватернионные операторы i, j, k
носятся к трем взаимно-перпендикулярным	можно рассматривать как повороты некоторо-
осям, образующим правую тройку, в обычном	го объекта (книги) на 180°, т. е. 7г
евклидовом 3-пространстве
1к

11.3. Геометрия кватернионов
189
Чтобы добиться этого, мы должны были поворачивать книгу на два прямых угла
(т. е. на 180°, или л). Это выглядит несколько странно, поскольку это никак не может слу¬
жить прямым аналогом того, как мы трактовали действие комплексного числа г. Более всего
вызывает беспокойство тот факт, что если мы проведем такую операцию дважды вокруг од¬
ной и той же оси, то получим поворот на 360° (или 2л), который возвращает объект (скажем,
нашу книгу) в ее исходное положение, так что мы получаем i2 = 1 вместо i2 = —1. Но здесь
возникает новая удивительная идея, имеющая фундаментальное значение для квантовой фи¬
зики элементарных частиц — электронов, протонов и нейтронов. Как мы увидим в §23.7,
следствием этой идеи является возможность существования обычного твердого вещества.
Эта идея заложена в математическом понятии спинора\11Я\
Что такое спинор? По существу, это объект, который превращается в свою противопо¬
ложность при полном обороте на 2л. Это может показаться абсурдным, поскольку любой
классический объект из повседневного обихода при таком повороте всегда возвращается
в исходное положение, а не в какое-нибудь иное. Чтобы понять это удивительное свойство
спиноров (или спинорных объектов), вернемся к нашей книге, лежащей на столе перед
нами. Нам нужно иметь некоторый способ проследить за тем, как выполняются повороты.
Для этого можно прочно зажать один конец длинного ремня между страницами нашей книги,
а пряжку ремня жестко соединить с какой-нибудь фиксированной структурой, например, со
стопкой других книг (см. рис. 11.3 а). Поворот книги на 2л закручивает ремень, так что его
нельзя раскрутить, не поворачивая книгу (рис. 11.3 6). Но если мы еще раз повернем книгу
на угол 2л, что означает полный поворот на 4л, то обнаружим, с некоторым удивлением,
что закрутку ремня можно полностью устранить, просто обведя его над книгой, сохраняя
при этом неизменным положение самой книги в течение такого маневра (рис. 11.3 в). Таким
образом, ремень отслеживает четность числа совершаемых книгой поворотов на 2л, а не
полное их число. Так что если мы повернем книгу на 2л четное число раз, закрутку ремня
можно будет полностью ликвидировать, если же число таких поворотов было нечетным, то
ремень неизбежно останется закрученным. Так будет при повороте вокруг любой оси и при
последовательности поворотов вокруг различных осей.
Таким образом, спинорный объект можно наглядно представить себе в виде обычного
объекта в пространстве, имеющего воображаемую гибкую связь с некоторой фиксированной
внешней структурой; в рассматриваемом случае такая воображаемая связь осуществлялась
а)
б)
*)
Рис. 11.3. Спинорный объект, представленный книгой с рис. 11.2. Четное число поворотов книги на 2л
эквивалентно отсутствию поворотов, в случае нечетного числа поворотов это не так. а) Мы следим за
четностью числа поворотов книги на 2л, соединив ее длинным ремнем с некоторым фиксированным
9
объектом (в данном случае со стопкой книг), б) Поворот нашей книги на 2л закручивает ремень, так
что его нельзя раскрутить, не поворачивая книгу, в) Поворот книги на 4л создает закрутку, которую
можно полностью устранить, обведя ремень над книгой

190
Глава 11
с помощью ремня. Связь может перемещаться любым непрерывным образом, но ее концы
должны быть фиксированы — один на самом объекте, другой на фиксированной внешней
структуре. Конфигурация нашей «спинорной книги» должна содержать воображаемую связь
с некоторой фиксированной внешней структурой; две конфигурации должны считаться эк¬
вивалентными, только если связь одной из них можно непрерывным образом деформировать
в связь другой из них. Каждой конфигурации обычной книги соответствуют в точности две
неэквивалентные конфигурации спинорной книги, и мы рассматриваем одну из них как про¬
тивоположность другой. Посмотрим теперь, приводит ли это к верному правилу умножения
для кватернионов. Как и прежде, положим книгу на стол перед собой, но теперь ремень
пусть жестко удерживается между ее страницами. Повернем книгу на 7г вокруг i, затем на 7г
вокруг j. Мы получим конфигурацию, эквивалентную повороту на 7Г вокруг к, как и должно
быть согласно гамильтоновскому правилу ij = к.
Так ли это? Имеется лишь один небольшой камень преткновения. Если внимательно
проследить за тем, чтобы все повороты происходили в положительном направлении, то,
проследив за кручением ремня, мы придем к выводу, что ij = —к. Это, однако, не так уж
важно и может быть исправлено разными способами. Либо мы можем представить себе,
,	*	I	'	*	•”	ч,#	«	•
что повороты наших кватернионов на 7г происходят не в положительном, а в отрицательном
направлении (в этом случае восстанавливается равенство ij — к), либо взять не правую,
а левую тройку осей i, j, к. Или, еще лучше, можно условиться о порядке умножения опе¬
раторов, вполне обычном в математике, а именно что произведение pq означает оператор q,
за которым следует р, а не наоборот,
Для такого странного соглашения есть основания. Так обстоит дело е операторами
(например, д/дх\ которые считаются действующими на объекты, стоящие справа от них.
Так, оператор Р, действующий на Ф, записывается в виде Р(Ф) или просто РФ. Соответ¬
ственно, если на Ф сначала действует оператор Р, а затем Q, то мы получаем ф(Р(Ф))
или просто С}РФ, что означает оператор QP, действующий на Ф.
Мой собственный способ преодоления этой трудности со знаками для кватернионов
состоит в том, чтобы рассматривать всё в стандартной правой системе координат и принять
«обычное» в математике соглашение об обратном порядке операторов. Читатель может про¬
верить, что все гамильтоновские «уравнения Брукхэмского моста» i2 — j2 = k2 = ijk — — 1
выполняются для нашей «спинорной книги». Мы имеем в виду, конечно, что произведе¬
ние ijk теперь означает, что сначала действует оператор к, затем j, затем ij11*9!
11.4.	Как складывать вращения
»
ч	•	я
• * , « •
Любопытное свойство удвоения углов поворота по сравнению с тем, что ожидается
из геометрических соображений, можно продемонстрировать другим способом. В трех из¬
мерениях повороты (собственно повороты, без отражения) обладают тем свойством, что
комбинация любого числа поворотов всегда дает поворот вокруг некоторой оси. Как найти
эту ось простым геометрическим построением и какова величина угла поворота? Изящный
ответ на этот вопрос был получен Гамильтоном[идо] Посмотрим, как это можно сделать.
Мое изложение здесь немного отличается от первоначально предложенного Гамильтоном.
Напомню, что при сложении двух различных перемещений, являющихся простыми пе¬
реносами (iтрансляциями), для получения ответа можно воспользоваться стандартным пра¬
вилом треугольника (эквивалентным правилу параллелограмма, показанному на рис. 5.1 а).
Мы можем представить первую трансляцию вектором (под которым я понимаю ориентиро¬
ванный отрезок прямой, направление ориентации которого указывается стрелкой на конце
отрезка), а вторую трансляцию — другим аналогичным вектором, хвост которого совпадает
с острием первого вектора. Вектор, протянутый от хвоста первого вектора к острию второго,
представляет сумму двух векторов трансляции (см. рис. 11.4 а).

11.5. Алгебры Клиффорда
191
Можно ли проделать что-то подобное с поворотами? Примечательно, что, как оказыва¬
ется, можно. Представьте себе «векторы» в виде ориентированных дуг большой окружности,
нарисованных на сфере и снабженных стрелками, указывающими направление ориентации.
(Большой окружностью на сфере называется линия пересечения сферы плоскостью, про¬
ходящей через ее центр.) Можно представить себе, что такая «векторная дуга» использу¬
ется для обозначения поворота в направлении стрелки. Поворот происходит вокруг оси,
проходящей через центр сферы перпендикулярно плоскости большой окружности, которой
принадлежит дуга со стрелкой.
Можно ли получить композицию из двух поворотов, представленных таким образом,
пользуясь «правилом треугольника», подобно тому, как это было в случае обычных транс¬
ляций? Оказывается, можно, но есть одна хитрость. Угол поворота, представляемого нашей
«векторной дугой», должен быть ровно вдвое больше угла, определяемого длиной дуги.
(Для удобства можно взять сферу единичного радиуса. Тогда угол, определяемый дугой,
есть просто расстояние, измеряемое вдоль дуги. Чтобы выполнялось «правило треугольни¬
ка», угол поворота должен быть вдвое больше этой длины дуги.) Причина выполнения «пра¬
вила треугольника» поясняется на рис. 11.4 б). Криволинейный (сферический) треугольник
в центре иллюстрирует «правило треугольника», а три внешних треугольника представляют
отражения в трех его вершинах. Два исходных поворота переводят один из этих внешних
треугольников во второй, а затем второй — в третий, так что композиция из двух поворо¬
тов переводит первый треугольник в третий. Можно заметить, что каждый из поворотов
происходит на угол, ровно вдвое больший соответствующей длины дуги исходного криво-
линейного треугольника . С вариантом этого построения мы встретимся в релятивистской
физике (см. § 18.4, рис. 18.13).
Можно проверить все это на рассмотренном выше частном примере и попытаться про¬
иллюстрировать соотношение для кватернионов ij ~ к. Каждый из поворотов, описываемый
величинами i, j и к, происходит на угол тг. Чтобы получить «правило треугольника», мы бе-
1
рем длины дуг, вдвое меньшие этого угла, т. е. ~тг. Это показано на рис. 11.4 в) (для ясности
в виде i(—j) = —к). Можно также заметить, что соотношением2 — — 1 иллюстрируется
тем фактом, что дуга большой окружности длины тг протягивается от точки на сфере к ан¬
типодной точке (соответствующей —1). Это в корне отлично от дуги нулевой длины или
длины 2тт, несмотря на то обстоятельство, что каждая из них представляет поворот сфе¬
ры, восстанавливающий ее исходное положение. Описание с помощью «векторных дуг»
правильно воспроизводит повороты «спинорного объекта».
v	•
/ '
11.5.	Алгебры Клиффорда
* •
Чтобы перейти к многомерному пространству и к идее алгебры Клиффорда, мы должны
выяснить, что в этом случае будет аналогом операции «поворот вокруг оси». В простран¬
стве п-измерений «осью» будет служить не одномерная прямая линия, с которой мы имели
дело при обычных трехмерных поворотах, а (п — 2)-мерное пространство. Тем не менее
поворот вокруг (п — 2)-мерной оси подобен знакомому нам случаю обычного трехмерного
поворота вокруг одномерной оси в том отношении, что этот поворот полностью определя¬
ется направлением оси и величиной угла поворота. Здесь мы опять-таки имеем спинорные
объекты, обладающие тем свойством, что при непрерывном повороте объекта на угол 2тг
он возвращается не в исходное состояние, а в состояние, которое мы считаем «отрицатель-
В оригинальном варианте Гамильтона используется «дуальный» сферический треугольник, вершины
которого находятся в точках пересечения сферы с тремя осями поворота, рассматриваемыми в данной проблеме.
Продемонстрируйте (возможно, путем «дуализации» рассуждений, приведенных в тексте), что углы поворота вдвое
больше углов этого дуального треугольника.

192
Глава 11
а)	6)	в)
*	*	»	^	•	а	•
. * # * * ,
• ••	а
Рис. 11.4. а) Трансляции в евклидовой плоскости представляются ориентированными отрезками пря¬
мых. Отрезок с двойной стрелкой, согласно правилу треугольника, представляет композицию (сложе-
**• • * . %•
ние) двух других, б) В случае поворотов в евклидовом 3-пространстве отрезками служат дуги боль¬
шой окружности, нарисованные на единичной сфере; каждая из них представляет поворот на угол,
9	,	•	•	••
вдвое больший угла, измеряемого этой дугой (описываемой вокруг оси, перпендикулярной плоскости
• / % *
соответствующей большой окружности). Чтобы увидеть, как это получается, отразим треугольник,
образуемый дугами, по очереди в каждой из его вершин. Первый поворот переводит треугольник 1
в треугольник 2, второй поворот переводит треугольник 2 в треугольник 3, их композиция перево¬
дит треугольник 1 в треугольник 3. в) Соотношение для кватернионов ij — к (в виде i(—j) = —к)
как частный случай. Каждый из поворотов происходит на угол тг, но представляется половинным
7Г
углом —
•	9	•
ным» по отношению к исходному. Поворот на 47т всегда возвращает объект в первоначальное
состояние.
Имеется; однако, «новый ингредиент», упоминавшийся выше: при числе измерений,
большем 3, композиция базисных поворотов вокруг (п ~ 2)-мерных осей не обязательно
будет поворотом вокруг (п — 2)-мерной оси. В многомерном случае композиция поворо¬
тов общего вида не может быть описана простым образом. Такой (обобщенный) поворот
• .»
может иметь «ось», т. е. пространство, которое остается неизменным при вращательном
движении; размерность этого пространства может принимать различные значения. Таким
образом, для алгебры Клиффорда в п измерениях требуется иерархия операций для описа¬
ния поворотов разного рода. Лучше начать с операции, более элементарной, чем поворот
на 7г, а именно отражения в (п — 1)-мерной (гипер)плоскости. Композиция из двух таких
отражений (по отношению к двум таким взаимно-перпендикулярным плоскостям) дает по¬
ворот на 7г, так что прежние базисные 7г-повороты становятся «вторичными», а первичными
оказываются отражения*.
Обозначим такие базисные отражения через 7Х, 72, 7з> •	гДе 'Уг отражает г-ю
координатную ось, не затрагивая все другие оси. Для подходящего типа «спинорного объ¬
екта» двукратное отражение в одном и том же направлении дает тот же объект р обратным
знаком, так что мы имеем п соотношений кватернионного типа
' ~l\ = -1, 72 =-1> 7з = -1>	•••>	7п = -1,
которым удовлетворяютпервичные отражения. Вторичные операции, представляющие наши
прежние 7г-повороты, представляют собой произведения пар различных отражений 7, и эти
произведения, как и кватернионы, обладают антикоммутационными свойствами:
ЪЪ =	(р	±	<?)•
Рассмотрите геометрическую природу преобразования в евклидовом 3-пространстве, представляющего
композицию двух отражений в плоскостях, взаимно не перпендикулярных.

11.5. Алгебры Клиффорда
193
В частном случае трех измерений (п = 3) можно определить три различные величины
«второго порядка»
1 = 727з> J = 7з7г» k = 7i72-
Легко проверить, что эти три величины i, j и к подчиняются правилам алгебры кватернионов
(гамильтоновым «уравнениям Брукхэмского моста»)*.
Общим элементом алгебры Клиффорда для n-мерного пространства является сумма
произведений на вещественные числа (т. е. линейная комбинация) набора различных опе¬
раций 7. Операциями первого порядка («первичными операциями») будут п различных
отдельных операций Операциями второго порядка («вторичными операциями») слу-
1 1
жат -п(п — 1) независимых произведений 7р7д (ПРИ этом р < q). Существуют |п(п —
\ *
- 1 )(п — 2) независимых операций третьего порядка 7p7g7r> ^n(n “ l)(n ~ ^)(n ~ 3)
независимых операций четвертого порядка и т. д., и, наконец, единственная операция п-го
порядка 7]727з * * * 7п* Собирая всё это вместе с единственной операцией нулевого поряд¬
ка 1, получаем, что всего имеется
1 + п + ^п(п — 1) + ^n(n — 1 )(п — 2) Н + 1 = 2п
операций , и общим элементом алгебры Клиффорда является линейная комбинация, со¬
ставленная из них всех. Таким образом, элементы алгебры Клиффорда образуют 2п-мерную
алгебру в смысле, описанном в §11.1. Они образуют кольцо с единичным элементом, но,
в отличие от кватернионов, не ооразуют кольца с делением.
Одной из причин интереса к алгебрам Клиффорда является та роль, которую они играют
в определении спиноров. В физике спиноры появились в знаменитом уравнении Дирака для
электрона [200], где состояние электрона описывается спинорной величиной (см. главу 24).
Спинор можно рассматривать как объект, на который элементы алгебры Клиффорда дей¬
ствуют как операторы — базисные отражения и повороты рассмотренного нами «спинорного
объекта». Само понятие «спинорного объекта» несколько неопределенно и неинтуитивно,
и некоторые предпочитают чисто алгебраический^11*11^ (клиффордов) подход к изучению та¬
ких объектов. Подобный подход имеет свои преимущества, особенно при общем и строгом
n-мерном обсуждении, однако мне кажется важным не утратить и геометрического зрения,
и я старался подчеркивать здесь именно этот аспект.
В случае п измерений!11125 полное пространство спиноров (называемое иногда «спи¬
новым пространством») является 2П//2-мерным при четном п и 2^г_1^2-мерным при нечет¬
ном п. При четном п пространство спиноров расщепляется на два независимых простран¬
ства (иногда называемые пространствами «приведенных спиноров» или «полуспиноров»),
каждое из которых имеет 2^п~2^2 измерений, то есть каждый элемент полного простран¬
ства является суммой двух элементов — по одному из каждого приведенного пространства.
Отражение от n-мерного пространства (при четном п) превращает одно из этих приве¬
денных спиновых пространств в другое. Элементы одного из приведенных спиновых про¬
странств имеют определенную «киральность», или «спиральность», а элементы другого —
противоположную киральность. Это играет огромную роль в физике; я здесь имею в виду
спиноры в обычном 4-мерном пространстве-времени. Каждое из двух приведенных спи¬
новых пространств имеет два измерения, одному из них приписывают правую спираль¬
ность, другому — левую. Представляется, что природа приписывает различную роль каж¬
дому из этих двух приведенных спиновых пространств, поскольку возможны физические
Покажите это.
** Объясните, как проводится весь этот подсчет. (.Подсказка: рассмотрите (1 4- 1)п.)

194
Глава 11
процессы, не инвариантные относительно отражения. И действительно, одним из наиболее
удивительных (можно сказать, «шокирующих») открытий XX века, теоретически предска¬
занных Янг Чжень-нином и Ли Цзун-дао и экспериментально подтвержденных By Чень-
шинь и ее группой в 1957 году, было обнаружение того факта, что в природе существуют
фундаментальные процессы, которые никогда не происходят в зеркально отраженной фор¬
ме. К этим фундаментальным понятиям я вернусь позднее (§§25.3, 25.4, 32.2, 33.4, 33.7,
33.11,33.14).
Спиноры играют также важную роль и при решении других теоретических проблем Е11 • 131
(см. §§22.8- 22.11, 23.4, 23.5, 24.6, 24.7, 32.3, 32.4, 33.4, 33.6, 33.8, 33.11); при некоторых
расчетах они могут иметь и практическое значение. Благодаря «экспоненциальной» связи
между размерностью спинового пространства (2п^ и т.д.) и размерностью п исходного
пространства, неудивительно, что спиноры оказываются более выгодными с практической
точки зрения, когда число п достаточно мало. Например, для обычного 4-мерного про¬
странства-времени каждое из приведенных спиновых пространств имеет размерность всего
лишь 2, тогда как для 11-мерной современной «М-теории» (см. § 31.14) спиновое простран¬
ство имеет 32 измерения.
11.6.	Алгебры Грассмана
Вернемся, наконец, к алгебре Грассмана. С точки зрения проведенного обсужде¬
ния, алгебру Грассмана можно рассматривать как некоторый вырожденный случай алге¬
бры Клиффорда. Здесь мы имеем антикоммутирующие базисные генерирующие элемен¬
ты Т71? 772, г/з,..., г)п, аналогичные элементам 7Х, 72, 73,,.., 7П алгебры Клиффорда, но
квадрат каждой из величин rjs равен не — 1, как в алгебре Клиффорда, а нулю:
Vl = О, T)2 = °>	■■■>	Vn =
Правило антикоммутации
VpVq = -'Пд'Пр,
как и прежде, выполняется, за исключением того, что алгебра Грассмана более «система¬
тична», чем алгебра Клиффорда, поскольку в последнем равенстве не требуется выполнение
условия рф q. Случай г]pr}p = —r]prip просто принимает вид т]р = 0.
Действительно, алгебры Грассмана более просты и универсальны, чем алгебры Клиф¬
форда, поскольку они лишь в минимальной степени зависят от локальной структуры. Дело
в том, что алгебра Клиффорда должна «знать», что означает «перпендикулярность», так
что обычные повороты можно строить из отражений, тогда как в алгебре Грассмана понятие
поворота не входит в число описываемых понятий. Чтобы принять этот другой способ описа¬
ния, обычные понятия алгебры Клиффорда и спинора требуют наличия метрики простран¬
ства, тогда как для алгебры Грассмана это не обязательно. (Понятие метрики обсуждается
в §§ 13.8, 14.7.)
Основной идеей алгебры Грассмана является «элемент плоскости» для различного числа
измерений. Будем считать, что каждая из базисных величин г] 1? rj2l rj3,..., г}п определяет
«линейный элемент», или «вектор» (а не гиперплоскость отражения), в начале координат
некоторого n-мерного пространства, при этом каждая величина г] связана с одной из п ко¬
ординатных осей. (Это может быть и «наклонная» ось, поскольку в алгебре Грассмана нет
понятия ортогональности, см. рис. 11.5.) Вектор общего вида в начале координат представ¬
ляется комбинацией
Q> ~ alVl + а2??2 + “ ' + апгПп->

11.6. Алгебр# Грассмана
195
где ai, аз,..., ап — вещественные числа. (В случае
комплексного пространства числа а* могут быть и ком¬
плексными, однако в обоих случаях имеет место сход¬
ная алгебраическая структура.) Для описания двумер¬
ного элемента плоскости, определяемого двумя векто¬
рами а и Ь, где
ь = biT]1 + b2V2
т
построим грассманово произведение векторов а и Ь.
Во избежание недоразумений с другими видами про¬
изведения, для этого произведения здесь использует¬
ся (стандартное) обозначение а А Ъ (называемое V-
произведением) вместо того, чтобы просто записывать
символы рядом. Соответственно то, что раньше запи¬
сывалось в виде r]prjq, теперь будем обозначать г)рАг)г
Правило антикоммутации для величин г] теперь при¬
нимает вид
VP А г?
Va Л v
р*
Если принять правило дистрибутивности (см. §11.1)
для произведения а Л Ь, то получится более общее
правило антикоммутации*
а А b
b А а
Рис. 11.5. Каждый базисный эле¬
мент т}г, щ, *73,..., rin алгебры Грас¬
смана определяет вектор в некото¬
рой точке О n-мерного пространства.
Эти векторы можно направить вдоль
различных координатных осей (кото¬
рые могут быть «наклонными», так
как в алгебре Грассмана нет понятия
ортогональности). Вектор общего ви¬
да О представляет линейную комбина¬
цию а =	+	а2т/2 Н Ь ап»7п
✓
для произвольных векторов а и Ъ. Величина а АЪ да¬
ет алгебраическое представление элемента плоскости,
определяемого векторами а и 6 (рис. 11.6 а). Заметим,
что эта величина содержит информацию не только об
ориентации элемента плоскости (поскольку знак про¬
изведения а А b зависит от того, какой из векторов
стоит первым — а или 6), но и о «величине», припи¬
сываемой элементу плоскости.
Можно задаться вопросом, как представить величину вида а А b в виде набора ком¬
понент, соответствующих тому, что а можно представить как (ai, »2,•.•, ап)9 а b —
как (Ьг, 62,..., Ьп); эти наборы коэффициентов получаются, если представить а и b в ви¬
де линейных комбинаций векторов 77Т72,.. *, ??п. Величину а А Ь соответственно можно
представить как линейную комбинацию векторов г)± А щ, г)г A rj3 и т.д., и тогда нам по¬
требуются появляющиеся при этом коэффициенты. Здесь имеется определенный элемент
соглашения, поскольку, например, векторы rf1 А г)2 и г]2 А г)± не являются независимыми
(один от другого отличается знаком), поэтому можно было бы выбрать тот или иной поря¬
док расположения. Более систематический подход состоит в том, чтобы сохранить оба члена
и разделить соответствующий коэффициент поровну между ними. Тогда мы найдем , что
коэффициентами (то есть компонентами) вектора а А Ь будут различные величины d[pbq],
где квадратные скобки вокруг индексов означают антисимметризацию, определяемую сле¬
дующим образом:
А
\ря\
2 (А*?
Aqp)'
**
Покажите это.
йИ Выпишите полностью а Л 6 для случая п = 2 и посмотрите, как это получается.

196
Глава 11
а)	б)
Рис. 11.6. а) Величина аЛЬ представляет (ориентированный и масштабированный) элемент плоскости,
определяемый векторами а и Ь. б) Тройное грассманово произведение аЛЬЛс представляет 3-элемент,
определяемый векторами а, b и с
Отсюда
®[рЬд] — 2 (apbq ttqbp)'
А как обстоит дело с трехмерным «элементом плоскости»? Для представления этого
3-элемента (опять-таки с указанием ориентации и величины) возьмем три независимых
вектора а, 6, с и построим тройное грассманово произведение а А Ъ А с. Оно обладает
антикоммутационными свойствами
аЛЬЛс — Ъ А с А а —с Л а Л b = ~Ь Л а Л с = —а, Л с Л b = —с Л b Л а
(см. рис. 11.6 б). В соответствии с изложенным, компоненты вектора а А б А с берутся в виде
1
— g-~I- QjqbrCp T- O-pbpCq CLqbpCf Opb^Cq * Q/'pbqCp^^
квадратные скобки по-прежнему обозначают антисимметризацию, как показано в правой
части этого соотношения.
Подобные выражения определяют общие r-элементы, где г пробегает значения вплоть
до размерности п всего пространства. Компоненты V-произведения r-го порядка получа-
ются, если взять антисимметризованное произведение компонент отдельных векторов * .
Таким образом, алгебра Грассмана дает мощный метод описания базисных геометрических
линейных элементов произвольной (но конечной) размерности.
Алгебра Грассмана является градуированной алгеброй в том смысле, что она содержит
элементы r-го порядка (где г есть число «V-перемножаемых» векторов rj). Число г (где г =
= 0, 1, 2, 3, ..., п) называется рангом элемента алгебры Грассмана. Следует отметить, од¬
нако, что общим элементом алгебры ранга г не обязательно будет просто V-произведение
(например, а А Ъ А с в случае г = 3), а может быть сумма таких выражений. Соответствен¬
но имеется много элементов алгебры Грассмана, которые не описывают непосредственно
геометрические r-элементы. Роль таких «негеометрических» грассмановых элементов про¬
явится позже (§ 12.7).	. ■ м ■ .
Вообще, если Р есть элемент ранга р, a Q — элемент ранга q, то можно определить
их V-произведение Р A Q ранга р + q с компонентами P[a...cQd.../]> гДе ра...с и Qd...f суть
Выпишите это выражение в явном виде для случая V-произведения четырех векторов.
** Покажите, что V-произведение остается неизменным при добавлении к вектору а любого из других
векторов, участвующих в этом произведении, умноженного на произвольное целое число.

11.6. Алгебры Грассмана
197
компоненты соответственно векторов Р и Q, Тогда мы полупим
Р A Q
+ Q А Р, если число р9 или q, или с
— Q А Р, если числа р и q нечетны.
ранга г опять-таки будет элементом ранга г. Можно также
дывать элементы различного ранга, при этом получается «смешанная» величина, не имею¬
щая определенного ранга. Такие элементы алгебры Грассмана не имеют, однако, наглядной
интерпретации.
Примечания
§11.1.
11.1. Согласно Эдуарду и Клейну, Карл Фридрих Гаусс, по-видимому, сформулировал правило умно¬
жения кватернионов уже в 1820 году, но не опубликовал его [279]. Это, однако, оспаривалось
Тейтом [765] и Ноттом [451]. Дальнейшая интформация содержится в книге [170].
11.2. Термин «вектор» имеет целый спектр значений. Здесь не предполагается какой-либо связи
с понятием дифференцирования «векторного поля», описанным в § 10.3.
§11.2.
11.3. Мне не вполне ясно, в какой мере был подвержен этому искушению сам Гамильтон. Еще до
изобретения кватернионов он интересовался алгебраической трактовкой «течения времени»,
и это могло оказать некоторое влияние на его готовность ввести четвертое изменение в
кватернионов. См. [170].
11.4. Тем не менее значительное число работ было посвящено поиску кватернионного аналога по¬
нятия голоморфности и его роли в физической теории (см. [327, 5]). Можно было бы рас¬
сматривать формулы теории твисторов (§§33.8, 33.9) для решения уравнений безмассового
свободного поля как четырехмерный аналог метода решения уравнения Лапласа с использо¬
ванием голоморфных функций. Там, однако, используется не кватернионный, а комплексный
анализ. Общий обзор кватернионов и октонионов содержится в книге [164].
11.5. См. [4].
11.6. См. [151]. Современное состояние проблемы изложено в книгах [381, 496].
11.7. См. [313, 314, 799, 170].
§11.3.
11.8. Это слово произносится так, как если бы оно писалось «spinnor» (а не «spynor»); см. примечание
24.12.
11.9. Я не знаю, кто впервые предложил такой способ демонстрации умножения кватернинов. Конвей
использовал его в частной беседе на Международном конгрессе математиков в Хельсинки
(1978); см. также [554, 626].
§11.4.
11.10. См. [575].
§11.5.
11.11. В книге [474] излагается подход ко многим физическим проблемам с использованием алгебры
Клиффорда; имеются также соответствующие ссылки.
11.12. См. [126, 103, 627, 362, ИЗ].
11.13. См. несколько примеров в [496, 126, 171, 142, 430].
 Покажите это.
Докажите, что Р А Р = 0 при нечетных значениях ранга р,

Глава 12
*
n-мерные многообразия
Ч
■
12.1.	Зачем изучать многомерные многообразия?
* •
Перейдем теперь к общей процедуре построения многомерных многообразий, у кото¬
рых размерность п может принимать любое положительное целое значение (и даже нуле¬
вое, если мы позволим себе считать, что одна отдельная точка образует 0-многообразие).
Понятие многообразия весьма существенно почти для всех современных теорий фундамен¬
тальной физики. Читатель может удивиться: какой интерес рассматривать п-многообразия
с размерностью п, большей 4, если обычное пространство-время имеет всего четыре измере¬
ния? Однако многие современные теории, например теория струн, оперируют с «простран¬
ством-временем», размерность которого гораздо больше четырех. Мы перейдем к материям
такого рода позднее, в §§ 15.1, 31.4» 31.10-31.12,31.14-31.17, где будет обсуждаться степень
физического правдоподобия общей идеи. Однако совершенно безотносительно к вопросу о
том, действительно ли реальное «пространство-время» может адекватно описываться как п-
многообразие, существуют и совсем иные, весьма веские, причины для изучения п-много-
образий в применении к физике в целом.
Например, конфигурационное пространство обычного твердого тела в евклидовом
3-пространстве (под которым я понимаю пространство С, разным точкам которого соот¬
ветствуют физически различные положения тела) представляет собой неевклидово 6-много¬
образие (см. рис. 12.1). Откуда берутся шесть измерений? Имеются три измерения (степени
свободы), соответствующие положению центра тяжести, и еще три, соответствующие вра¬
щательным степеням свободы*. Почему многообразие неевклидово? Тому имеется много
причин, но наиболее удивительна та, что даже топология этого многообразия отлична от то-
I
Рис. 12.1. Конфигурационное пространство С, каждая точка которого представляет одно из возможных
положений данного твердого тела в евклидовом 3-пространстве Е3. Пространство С есть неевклидово
6-многообразие
Объясните более подробно, как получается такая размерность.

12.1. Зачем изучать многомерные многообразия?
199
пологии евклидова 6-пространства. Такая «топологическая нетривиальность» С проявляется
уже в трехмерном характере пространства, относящегося к вращательной ориентации тела.
Назовем это 3-пространство пространством. Каждая точка 1Z представляет некоторую
определенную ориентацию твердого тела. Вспомним, как мы рассматривали повороты книги
в предыдущей главе. Будем считать, что наше твердое тело — эта та самая книга (которая,
конечно, должна оставаться закрытой, в противном случае конфигурационное пространство
будет иметь гораздо больше измерений, соответствующих движению страниц).
Как понять «топологическую нетривиально сть»? Может показаться, что в случае 3- или
6-многообразия это не так легко. Существует, однако, несколько математических процедур,
позволяющих понять подобные вещи. Вспомним, что при объяснении римановых поверх¬
ностей в §8.4 (см. рис. 8.9) мы рассматривали различные топологически нетривиальные
2-поверхности. Если не считать сферы (сферы Римана), простейшей такой поверхностью
является тор (поверхность рода 1). Как отличить тор от сферы? Один из способов состоит
в том, чтобы рассматривать замкнутые петли на поверхности. Интуитивно ясно, что на торе
можно нарисовать такие петли, которые не удастся путем непрерывной деформации стянуть
в точку. В то же время на сфере любую замкнутую петлю таким путем можно сделать сколь
угодно малой (см. рис. 12.2). Петли на евклидовой плоскости также можно стянуть в точку.
Можно сказать, что в силу такого свойства «сжимаемости» сфера и плоскость являются од¬
носвязными областями. Тор (и поверхности более высокого рода) являются много связными,
поскольку на них существуют несжимающиеся петли!12Это дает нам простой способ,
находясь внутри самой поверхности, отличать тор (и поверхности более высокого рода) от
сферы и плоскости.
Рис. 12.2. Некоторые петли на торе не могут бесконечно стягиваться (вплоть до одной точки), про¬
должая оставаться на поверхности. В то же время на плоскости или сфере такое возможно для любой
замкнутой петли. В соответствии с этим плоскость и сфера являются односвязными областями, а тор
(и поверхности более высокого рода) — многосвязными
Ту же самую идею можно применить, чтобы отличить топологию 3-многообразия 7Z
«тривиальной»
а «книге», которую
структурой при noiv
воображаемого ремня. Каждая отдельная вращательная ориентация книга представляется
соответствующей точкой многообразия 1Z. Если непрерывным образом повернуть книгу на
угол 2л, так что она вернется к своей первоначальной вращательной ориентации, то та¬
кое движение будет представлено в 1Z некоторой замкнутой петлей (см. рис. 12.3). Можно
ли деформировать непрерывным образом эту замкнутую петлю так, чтобы она стянулась
в точку? Такая деформация петли будет соответствовать постепенному изменению вра¬
щения нашей книги, пока движение не прекратится вовсе. Вспомним, однако, о нашем
воображаемом ремне (который может быть вполне реальным). Поворот на 2тг оставляет ре¬
мень закрученным, и это состояние нельзя устранить, двигая непрерывным образом ремень
при неподвижной книге. Такая 27Г-закрутка должна сохраняться (или трансформироваться

200	Глава	12
Петля, соответствующая
Рис. 12.3. Понятие многосвязности, иллюстрируемое на рис. 12,2, позволяет отличить топологию
3-многообразия 1Z (пространства вращений) или 6-мношобразия С (конфигурационного пространства)
от «тривиальной» топологии евклидова 3- или 6-пространства. В 1Z или С петлю, представляющую
непрерывный поворот на угол 2л, нельзя стянуть в точку, то есть многообразия 1Z и С многосвязны.
В то же время петлю, пройденную дважды (представляющую поворот на 4л), можно стянуть в точку
(топологическое кручение); см. рис. 11.3. (N.B. Изображенное здесь 2-многообразие, будучи лишь
схематическим, не отражает этого свойства.)
в закрутку на угол, равный нечетному целому числу, умноженному на 2л) при постепен¬
ной деформации вращения книги. Поэтому мы должны заключить, что 2тг-поворот нельзя
деформировать непрерывным образом к полному отсутствию вращения. Соответственно
невозможно стянуть в точку нашу выбранную замкнутую петлю на 1Z путем непрерыв-
• <
ной деформации. В соответствии с этим 3-многобразие 1Z (и аналогично 6-многообразие С)
должно быть многосвязным и, следовательно, топологически отличным от односвязного
евклидова 3-пространства (или 6-пространства)^12,21
Следует отметить, что многосвязность пространств 1Z и С имеет более интересную при¬
роду, чем та, с которой мы сталкиваемся в случае тора. Наша петля, представляющая 2л-по-
воррт, обладает любопытным свойством: если обойти ее дважды (4л-поворот), получается
петля, которая теперь уже может быть стянута в точку путем непрерывной деформации .
*
(В случае тора такого определенно быть не может.) Эта любопытная особенность петель
вТгиС представляет пример так называемого топологического кручения.
Из всего этого следует, что пространства, подобные 6-многообразию С, представляют
интерес для физики, поскольку они не только имеют размерность, большую чем у обычного
пространства-времени, но и могут обладать нетривиальной топологией. Более того, такие
пространства, используемые в физике, могут иметь размерность, неизмеримо большую 6.
Пространствами очень большого числа измерений могут быть конфигурационные простран¬
ства, а также так называемые фазовые пространства для систем, содержащих большое
число отдельных частиц. Конфигурационное пространство К газа, частицы которого описы¬
ваются как отдельные точки в 3-мерном пространстве, имеет 3N измерений, где N — число
частиц газа. Каждая точка пространства К представляет конфигурацию газа, в которой опре¬
делено положение каждой из частиц (рис. 12.4а). В случае фазового пространства газа V
мы должны следить также за импульсом каждой частицы (импульс — это произведение скоро¬
сти частицы на ее массу), который является векторной величиной (с тремя компонентами для
*
*Ш Покажите, как это можно сделать, например, воспользовавшись представлением 1Z, данным в упражне¬
нии 12.17.

12.2. Многообразия и координатные лоскуты
201
Положения п
частиц
Конфигурационное
пространство
о)
Положения
и импульсы
п частиц
Фазовое
пространство
6)
Рис. 12.4. а) Конфигурационное пространство JC для системы из п точечных частиц в некоторой
области 3-пространства имеет Зп измерений, при этом каждая отдельная точка пространства К пред-
. * \ •
ставляет положение всех п частиц, в) Фазовое пространство V имеет 6п измерений, каждая точка
этого пространства представляет положения и импульсы всех и частиц. (N.B. Импульс = скорость х
масса.)
каждой частицы), так что полное число измерений равно 6JV. Таким образом, каждая точка
пространства V представляет не только положение всех частиц газа, но и движение каждой
[1-2.3]
из частиц (рис. 12.4 б). Наперсток с обычным воздухом содержит порядка 10 молекул
так что пространство V имеет что-то вроде 60000000000000000000 измерений! Фазовые
пространства особенно полезны при изучении поведения (классических) физических систем
многих частиц, поэтому пространства столь большого числа измерений могут иметь вполне
четкий физический смысл.
12.2.	Многообразия и координатные лоскуты
Посмотрим теперь, как можно математически описать структуру п-многообразия.
п-многообразие КА можно построить точно так же, как как мы строили поверхность S
из нескольких координатных лоскутов в главах 8 и 10 (см. § 10.2). Но теперь для каждо¬
го лоскута потребуется больше координат, нежели просто пара чисел (ж, у) или (X, У).
Для каждого из лоскутов понадобится п координат, где п — заданное число {размерность
многообразия КА), которое может быть любым положительным числом. Поэтому удобнее не
пользоваться отдельной буквой для каждой координаты, а нумеровать различные координаты
ггА"	/у.Ч'
\kj	у	kKj	у	kXj	у	+	+	•	у	1Ли/
(верхним) численным индексом. Во избежание недоразумений подчеркнем, что здесь выпи¬
саны различные независимые вещественные числа, а вовсе не разные степени одной и той
же величины х. Читателю может показаться странным, что я сознательно даю повод к недо¬
разумению, используя верхние индексы вместо нижних (например, x\i, Ж2,	* • • ? хп), хотя
из-за этого легко спутать, например, координату х>3 с кубом некоторой величины х. Недо¬
вольный читатель будет прав в своем недовольстве. Я и сам нахожу всё это не только
сбивающим с толку, но временами и раздражающим. Однако по некоторым историческим
причинам такими оказались стандартные обозначения тензорного анализа, к которому, на
более серьезном уровне, мы придем далее в этой главе. Правила тензорного анализа строго
определяют верхнее либо нижнее положение индексов, и согласно им у самих координат
индекс должен быть в верхнем положении. (На практике эти правила вполне хорошо рабо-

202
-
Глава 12
тают, однако вызывает сожаление, что в свое время не был сделан противоположный выбор.
Тем не менее с этим приходится жить.)
Как можно изобразить наше многообразие А4? Мы можем представить его «склеен¬
ным» из нескольких координатных лоскутов, каждый из которых является открытой обла¬
стью пространства Rn. Здесь Мп означает «координатное пространство», точками которого
служат просто наборы из п вещественных чисел (ж1, ж2, ж3,..., жп); напомним, что, соглас¬
но § 6.1, К. обозначает систему вещественных чисел. В нашей процедуре склеивания будут
фигурировать функции перехода, которые выражают координаты на одном лоскуте через
координаты на другом всякий раз, когда один координатный лоскут многообразия М пе-
• • 1
рекрывается с другим. Эти функции перехода должны удовлетворять некоторым условиям,
обеспечивающим согласованный характер всей процедуры в целом. Эта процедура иллю¬
стрируется на рис. 12.5 а). Однако следует быть внимательным, чтобы получить многообра¬
зие стандартного вида^12*4!, которым является хаусдорфово пространство. (Не-хаусдорфово
многообразие может «разветвляться» подобно тому, как показано на рис. 12.5 б и 8.2 в.) Хаус¬
дорфово пространство обладает определяющим его свойством: для каждых двух точек этого
пространства существуют непересекающиеся открытые множества, содержащие по одной
из этих точек (рис. 12.5 в).
Производится *
склеивание
Не-хаусдорфово
пространство
Требуется
согласованность
при тройном
перекрытии
Условие
хаусдорфовости
я)
б)
в)
Рис. 12.5. а) Функции перехода, связывающие координаты перекрывающихся лоскутов, должны удо¬
влетворять условию согласования в области тройного перекрытия, б) (Открытые) области перекрытия
пар лоскутов должны быть согласованы, в противном случае может возникнуть «разветвление», харак¬
терное для не-хаусдорфова пространства, в) Хаусдорфово пространство обладает тем свойством, что
у любых двух отдельных точек имеются неперекрывающиеся окрестности. (Для того чтобы «склеен¬
ная» часть на рисунке б была открытым множеством, ее «край», на котором происходит разветвление,
должен оставаться отделенным; видно, что условие хаусдорфовости нарушается.)
Не следует думать, однако, будто многообразие М «знает», где находятся отдельные
лоскуты или каковы значения координат данной точки. Разумнее считать, что это многообра¬
зие можно построить, собирая вместе ряд координатных лоскутов и выбирая определенный
порядок, в котором берутся лоскуты. Отображение представляет собой вполне определен¬
ную математическую структуру, и координаты при желании вводятся как вспомогательные
величины лишь для удобства. Однако точное математическое описание отображения (для ко¬
торого существует несколько альтернатив) увело бы нас слишком далеко.

12.3. Скаляры, векторы и ковекторы
203
12.3,	Скаляры, векторы и ковекторы
Как и в § 10.2, введем понятие гладкой функции Ф, определенной на М, (иногда имену¬
емой скалярным полем на М). Функция Ф определяется на любом локальном координатном
лоскуте как гладкая функция от п координат на этом лоскуте. «Гладкость» функции здесь
всегда будет пониматься в смысле «С°°-гладкости»(см. § 6.3), поскольку это приводит к бо¬
лее удобной теории. В каждой области перекрытия двух лоскутов координаты на каждом
лоскуте являются гладкими функциями от координат на другом лоскуте, так что гладкость Ф
как функции одного набора координат в области перекрытия предполагает ее гладкость как
функции другого набора координат. При этом локальное («лоскутное») определение гладко¬
сти скалярной функции Ф распространяется на все многообразие М, так что можно говорить
просто о гладкости Ф на Л4.
Далее введем понятие векторного поля £ на Л4, геометрической интерпретацией кото¬
рого служит семейство «стрелок» на М (рис. 10.5), где £, действуя на любое (гладкое) ска¬
лярное поле Ф, создает другое скалярное поле £(Ф) подобно оператору дифференцирования.
Поле £(Ф) должно интерпретироваться как «скорость возрастания» функции Ф в направ¬
лении, указываемом стрелками, представляющими £, подобно тому как это делалось для
2-поверхностей в § 10.3. Будучи «оператором дифференцирования», £ удовлетворяет неко¬
торым характеристическим алгебраическим соотношениям (по существу, тем, с которыми
мы встречались раньше в § 6.5, а именно d(f 4- g) — df -1- dg, d(fg) = f dg + g df, da = 0,
если a — постоянная величина):
m+^) = m+m,
£(<№) = Ф£{Ф)+Ф£(Ф),
£(&) — 0, если к — постоянная величина.
Существует теорема, которая гласит, что эти алгебраические свойства достаточны, чтобы
характеризовать £ как векторное поле^12,6^
Можно также воспользоваться подобными чисто алгебраическими средствами, чтобы
определить 1-форму, или, что то же самое, ковекторное поле. (Геометрический смысл ко-
вектора мы вскоре обсудим.) Ковекторное поле а можно рассматривать как отображение
векторных полей на скалярные поля. Действие ос на £ записывается как а • £ (скалярное
произведение ос на £, см. § 10.4). Для любых векторных нолей £ и 77 и скалярного поля Ф
выполняются условия линейности:
ос ♦ (£ + 77) — ос • £ 4- ос • 77,
а • (Ф£) = Ф(а-£).
Эти соотношения определяют ковекторы как дуальные объекты по отношению к векторам
(что и означает приставка «ко»). Связь между векторами и ковекгорами оказывается сим¬
метричной, так что имеют место соответствующие соотношения
(ос 4- /3) * £ = ос • £ 4- /3 • £,
(Фсх) • £ = Ф(ос • £),
что приводит к определению суммы двух ковекторов и произведения ковектора на скаляр.
Если взять пространство, дуальное к пространству ковекторов, то мы получим обычное
пространство векторов. (Другими словами, «ко-ковектор» должен быть вектором.)
Эти соотношения могут относиться как к полю в целом, так к величинам, определен¬
ным в одной точке многообразия М. Векторы, взятые в некоторой фиксированной точке о,
образуют векторное пространство. (Как сказано в § 11.1, в векторном пространстве можно

204	     Глава	12
складывать элементы £ и г), образуя сумму £ + rj, при этом £ + »7=Т7 + £ и (£ + С =
— £ + (г) -f С)? а также умножать их на скаляры — в данном случае вещественные числа /
и д, - при этом (/ + #)£ = /£ 4- Я, /(£+ Ч) = /£ + /*7> /(Я) = (/£)£> 1C = СО Можно
считать, что это (плоское) векторное пространство задает структуру многообразия в непо¬
средственной близости от точки о (см. рис. 12.6). Это векторное пространство можно назвать
касательным пространством Т0 к М. в точке о. Касательное пространство Т0 можно нагляд¬
но представить себе как предельное пространство, которое получается, когда всё меньшая
окрестность точки о в Л4 рассматривается с соответственно всё большим увеличением.
При таком рассмотрении непосредственная окрестность точки о в Л4 оказывается беско¬
нечно «растянутой». В предельном случае любая «кривизна» М «разглаживается» в плос¬
кую структуру Т0. Векторное пространство Т0 имеет (конечную) размерность п, поскольку
в точке о можно выбрать набор из п базисных элементов в виде величин д/дх1, ..., д/дхп,
направленных вдоль координатных осей, через которые любой элемент пространства Т0
можно однозначно выразить в виде линейной комбинации (см. также § 13.5).
Касательная
п-плоскость Т,
можно наглядно
как предельное пространство, когда все меньшая окрестность точки о рассматривается со все оольшим
увеличением. (Ср. рис. 10.6.) В результате Т0 оказывается плоским n-мерным векторным простран¬
ством
Можно, как описано выше, построить дуальное векторное пространство к простран¬
ству Т0 (пространство ковекторов в точке о), которое называется кокасателъным про¬
странством Т* к ЛЛ в точке о. Частным случаем ковекгорного поля является гради¬
ент (или внешняя производная) йФ скалярного поля Ф. (Мы уже сталкивались с такой
записью применительно к двумерному случаю, ем. § 10.3.) Ковектор йФ (с компонента¬
ми дФ/дх..., дФ/дхп) обладает определяющим свойством
■■<*Ф.£ = £(Ф)
4	•	•
• 0 • *
(см. также § 10.4)*. Хотя не все ковекторы имеют форму дФ с некоторой функцией Ф, все
они могут быть представлены таким образом в любой отдельной точке. Вскоре мы увидим,
почему это не может быть распространено на ковекторные поля.
В чем состоит геометрическая разница между ковектором и вектором? В каждой точ¬
ке многообразия М (ненулевой) ковектор а определяет элемент (п — 1)-мерной плоско¬
сти. Направления в этом элементе (п — 1)-плоскости определяются векторами £, для кото¬
рых а * £ = 0; см. рис. 12.7. В частном случае а = йФ эти элементы (п — 1)-гоюскости
являются касательными к семейству (п — 1)-мерных поверхностей** с постоянным значени-
Покажите, что величина d<P, определенная таким образом, действительно удовлетворяет упомянутому
условию линейности ковекторов.
т Почему?
**

12.3. Скаляры, векторы и ковекторы
205
ем Ф (которые обобщают понятие «контурных линии», показанных на рис. 10.8 а). Однако
в общем случае элементы (га — 1)-плоскости, определяемые ковектором а, будут закручи¬
ваться, что препятствует им касаться какого-либо подобного семейства (n — 1)-поверхностей
(см. рис. 12.8)J12;!7!.
Ковектор ос определяет
элемент (га— 1)-мерной
плоскости
Рис. 12.7. (Ненулевой) ковектор а в точке мно¬
гообразия Л4 определяет здесь элемент (п — 1)-
мерной плоскости. Векторы £, удовлетворяю¬
щие условию а•£ = 0, определяют направления
внутри нее
Рис. 12.8. Элементы (п — 1)-плоскости, опреде¬
ляемые ковекторным полем а, в общем случае
закручиваются, что мешает им касаться семей¬
ства (га — 1)-поверхностей, хотя в частном слу¬
чае а — скФ (где Ф — скалярное поле) они могут
касаться поверхностей Ф — const (обобщаю¬
щих «контурные линии» на рис. 10.8)
Для любого координатного лоскута с координатами ж1, ..., хп можно представить век¬
тор (векторное поле) £ набором компонент (£х, £2, ..., £п), в качестве которых служат
коэффициенты в формуле, выражающей вектор £ через операторы частного дифференциро¬
вания на этом лоскуте (см. § 10.4):
д
дх
1 + £
д
дх2
+ * * * + £
П
д
дх
п
Для вектора в данной точке коэффициенты £ , £ , ..., £п — это п вещественных чисел; для
векторного поля на некотором координатном лоскуте коэффициентами будут п (гладких)
функций координат 00 у 00 у • • • у 00 (напомним читателю, что £п не означает га-ю степень
числа £ и т. д.). Каждый из операторов д/дхг определяет скорость изменения в направле¬
нии r-й (локальной) координатной оси. Приведенное выше выражение для £ просто пред¬
ставляет этот вектор (который, напомним, будучи оператором, определяет скорость измене¬
ния в направлении £) в виде линейной комбинации векторов, направленных вдоль каждой
из координатных осей (см. рис. 12.9 а).
Аналогичным образом ковектор (ковекторное поле) представляется на координатном
лоскуте набором компонент (ац, а.ъ, • • •, otn). Здесь используется представление ковекто-
ра ol в виде линейной комбинации
а
ад dx1 -f а2 dx2 Н -f ап dxn,
базисных 1-форм (ковекторов)^2*8! dx1, dx2, ...,dxn. Геометрически каждая из вели¬
чин dxr представляет элемент (п—1)-плоскости, определяемый всеми координатными осями
за исключением оси хТ (см. рис. 12.9 6) . Скалярное произведение ос • £ определяется выра-
В качестве примера покажите, что dx2 имеет компоненты (0, 1, 0, ..., 0) и представляет элементы
касательной гиперплоскости к поверхности х2 = const.

206
Глава 12
а)
б)
Рис. 12.9. Компоненты на координатном лоскуте (ж1, ..., хп) (здесь п = 3). а) Для вектора (векторно¬
го поля) £ компонентами служат коэффициенты (£х, £2, ... хп) разложения £ = £}д/дх1 + ^2д/дх2 +
£пд/дхп, где д/дхг определяет скорость изменения вдоль r-й (локальной) координатной оси
(см. также рис. 10.9). 6) Для ковектора (ковекторного поля) а. компонентами служат коэффициен¬
ты (ад, «2, • • •, OLn) в разложении а = ад cte1 -Г а-2 cfo:2 + • • ♦ -f ап dxn, где dxr означает градиент
от хт и относится к элементу (п — 1)-плоскости, определяемому всеми (локальными) координатными
осями за исключением (локальной) оси хт
жением
* •
71
12.4.	Грассмановы произведения
Рассмотрим теперь представление элементов плоскости различной размерности, ис¬
пользуя идею грассманова произведения, определенного в § 11.6. Элемент 2-плоскости в точ¬
ке многообразия М (или поле элементов 2-плоскости над М) представляется величиной
£ А г/,
где £ и г] — два независимых вектора (или векторных поля), на которых построена 2-плос-
кость (плоскости) (см. рис. 11.6а и 12.10 а). Величину £ А 77 иногда называют (простым)
бивектором. Ее компоненты в соответствии с изложенным в конце предыдущей главы вы¬
ражаются через компоненты векторов £ и г) следующим образом:
/
Сумма простых бивекторов £ А г] также называется бивектором, ее компоненты обладают
свойством антисимметрии по г и s, т. е. грг$ = —ф37'.
Аналогично элемент 3-плоскости (или поле таких элементов) можно представить про¬
стым тривектором
£ л *? л С>
*	Используя цепное правило (см. § 10.3), покажите, что формула для а согласуется с равенством d<P*£ =
= £(Ф) в частном случае а = d<P.

12.4, Грассмановы произведения
207
«)
г)
Рис. 12.10. а) Элемент 2-плоскости в точке многообразия Л4, определяемый независимыми векто¬
рами £, т}, описывается бивектором £ Л 7]. 6) Аналогично элемент 3-плоскости, определяемый век¬
торами г?, £, описывается произведением £ Л 77 Л £. в) Элемент (п — 2)-плоскости, являющийся
пересечением двух элементов (п — 1)-плоскости, определяемых 1-формами а, /3, записывается в ви¬
де а Л/3. г) Элемент (п — 3)-плоскости, являющийся пересечением трех элементов (п — 1)-плоскости,
определяемых 1-формами с*, /3, % описывается произведением а Л /9 Л 7
где векторы
имеют вид
£, 77, £ определяют 3-плоскость (рис. 11.66 и 12.106. Компоненты тривектора
£[vct] = lie ns С+cvcr+eve
rvcs - ? »?8cr - evrc)•
/Г
Тривектор общего вида г имеет полностью антисимметричные компоненты rrst и всегда
должен быть суммой таких простых тривекторов. Аналогично можно перейти к определе¬
нию элементов 4-плоскости, представляемых простыми 4-векгорами, и так далее. Общий п-
вектор имеет набор полностью антисимметричных компонент. Его всегда можно представить
как сумму простых п-векторов.
Здесь имеет место одно обстоятельство, которое может показаться загадочным. Ока¬
зывается, что теперь у нас имеется два различных способа представления элемента
(п— 1)-гоюскости — либо как 1-формы (ковектора), либо как (п — 1)-векторной величи¬
ны, получаемой в результате «V-перемножения» п — 1 независимых векторов, определяю¬
щих (п ~~ 1)-плоскость. Между величинами, описываемыми этими двумя разными способа¬
ми, имеется геометрическое различие, однако оно довольно тонкое. Разница состоит в том,
что 1-форму следует понимать как некоторую «плотность», тогда как (п — 1)-вектор таковой
не является. Чтобы пояснить это, будет полезно ввести сначала общее понятие р-формы.
По существу, мы будем иметь дело с такими же мультивекторами, что и выше, но исходя
не из векторов, а из 1-форм. Взяв р (независимых) 1-форм а, /3, ..., 6, можно построить
из них V-произведение
а А /3 А • • • А <5,
которое имеет компоненты
^■[rPs * * *
# e '
на некотором координатном лоскуте (здесь используется общий вид записи в виде квадрат¬
ных скобок вокруг индексов, см. § 11.6). Такая величина определяет элемент (п ~ ^-плос¬
кости (или поле таких элементов), этот элемент является пересечением элементов различ¬
ных (n — 1)-плоскостей, определяемых в отдельности векторами а, /3, ..., S (рис. 12.10в, г).

208
Глава 12
Эта величина называется простой р-формой. Как и в случае р-векторов, наиболее общая
р-форма не выражается непосредственно в виде V-произведения ковекторов, однако (за ис¬
ключением частных случаев р — 0? 1, п—1, п) может быть представлена в виде суммы таких
произведений. Общая р-форма р на любом координатном лоскуте может быть представлена
набором величин
PrS.'.U)
антисимметричным по его индексам г, s, ..., и; каждый из р индексов г, s, ..., и про¬
бегает значения от 1 до п. Как и раньше, антисимметрия означает, что при перестановке
любой пары индексов мы получаем ту же величину с противоположным знаком. В нашей
записи с использованием квадратных скобок (§11.6) свойство антисимметрии выражается
следующим образом :
(firs...и] — PrS...U'
Можно также отметить, что (р + q)-форма р А х> представляющая собой V-произведение
р-формы р и g-формы х? имеет компоненты
(P[rs...uXjk...m] 5
антисимметризация проводится по всем индексам (Xjk...m — компоненты вектора х) • Ана¬
логичная запись используется для V-произведения р-вектора и д-векгора.
12.5.	Интегрирование форм
Вернемся теперь к р-форме как некоторой «плотности». Напомним, что в обычной фи¬
зике под плотностью некоторого объекта понимается его масса, приходящаяся на единицу
объема. Плотность есть свойство материала, из которого сделано данное тело. Мы пользуем¬
ся понятием плотности, когда хотим оценить полную массу объекта, зная его полный объем
и природу материала, из которого он изготовлен. В математическом отношении для этого
нужно проинтегрировать плотность объекта по занимаемому им объему. Для нас важен тот
факт, что плотность есть такая величина, которую мы можем проинтегрировать по неко¬
торой области, то есть поместить под знак интеграла. Мы должны различать интегралы
по пространствам различной размерности. (Например, «масса на единицу площади» — это
иная величина, нежели «масса на единицу объема».) Мы сейчас убедимся, что р-форма есть
подходящая величина для интегрирования по р-мерному пространству.
Начнем с простейшего случая 1-формы. Здесь мы имеем дело с интегралом от некото¬
рой величины по 1-мерному многообразию, то есть вдоль некоторой кривой 7. Напомним
(см. § 6.6), что обычные (одномерные) интегралы записываются в виде
J f(x)dx,
где х — некоторая вещественная величина, которую можно считать параметром, меняю-
щимся вдоль кривой 7. При этом мы должны считать, что величина f(x) dx обозначает
1-форму. Такое обозначение для 1-формы выбрано, чтобы имело место согласие с обозна¬
чением обычных интегралов. Здесь анализ XX века (называемый также внешним анализом),
предложенный выдающимся французским математиком Эли Картаном (1869-1951) (с ним
* • •
мы еще встретимся в главах 13, 14 и 17), прекрасно согласуется с символом dx, введенным
Объясните, почему это так.
Подтвердите тот факт, что А х — & л * • • А 7 Л А Л • • • Л v, где <р — а Л • • • Л 7, х = л Л • • * Л и.

12.5. Интегрирование форм
209
в XVII веке Готфридом Вильгельмом Лейбницем (1646-1716). В схеме Картана dx рас¬
сматривается уже не как бесконечно малая величина, а как элемент плотности (1-формы),
которую можно интегрировать вдоль кривой.
Одно из преимуществ такого обозначения состоит в том, что оно автоматически учиты¬
вает все изменения выбранной переменной. Если, например, заменить параметр х на другой
параметр X, то можно считать, что 1-форма а = f(x) dx остается прежней, в том смысле,
что не изменяется интеграл J а, несмотря на то, что изменяется явный вид функциональ¬
ной зависимости от выбранной переменной (х или X)*. Можно также считать 1-форму а.
определенной в некотором пространстве оольшеи размерности, в котором находится наша
кривая. В качестве параметра х (или X) можно взять одну из координат координатного
лоскута в этом пространстве, при этом, можно легко переходить к другой координате при
переходе на другой координатный лоскут. Всё получается автоматически. Можно просто
записать этот интеграл в виде
а или / а.
где X обозначает некоторую часть заданной кривой у, по которой берется интеграл.
Как обстоит дело с интегралами по областям большей размерности? В случае двумер¬
ной области под знаком интеграла должна стоять 2-формаf12,9l Это может быть некоторая
величина /(ж, у) dx A dy (или сумма подобных величин), так что можно написать
/(ж, у) dx A dy = а,
(или изобразить сумму таких величин); X теперь есть двумерная область, по которой должно
проводиться интегрирование, лежащая внутри заданной 2-поверхности. Параметры х и у,
являющиеся локальными координатами поверхности, опять-таки можно без труда заменить
любой другой аналогичной парой. Это применимо, если 2-форма определена в некотором
пространстве более высокой размерности, в котором находится 2-область X. Всё это спра¬
ведливо также для 3-форм, интегрируемых по трехмерным областям, для 4-форм, инте¬
грируемых по четырехмерным областям, и т.д. Запись V-произведения в виде картановых
дифференциальных форм (вместе с внешней производной, см. § 12.6) сама следит за всем
при изменении координат. (Это исключает упоминание о таких неприятных вещах, как «яко-
бианы», которые пришлось бы вводить в противном случае.)
Напомним (см. § 6.6) основную теорему анализа, которая утверждает, для одномерных
интегралов, что интегрирование есть операция, обратная дифференцированию, или, другими
словами,
/ dx = ^ ~
а
Существует ли многомерный аналог этого? Такие аналоги для различного числа измерений
действительно существуют под разными именами (Остроградского, Гаусса, Грина, Кельвина,
Стокса и др.), но общий результат, как часть картанова внешнего анализа дифференциальных
форм, здесь будет именоваться «основной теоремой внешнего анализа» 112Л°]. Это связано
с общим понятием внешней производной Картана, к изучению которой мы сейчас переходим.
ь
Покажите это в явном виде и объясните, как обстоит дело с пределами определенного интеграла J ot.
а
ос	2	2	2
Пусть G — / е~х dx. Объясните, почему G2 — f е~(х +у 1 dx A dy, и вычислите эту величину,
— ос	1R 2
перейдя к полярным координатам (г, в) (см. § 5.1). Покажите, что в результате получается G = л/тг.

210
Глава 12
12.6.	Внешняя производная
«Координатно-независимый» подход к определению этого важного понятия состоит
в том, чтобы ввести внешнюю производную аксиоматически, как некоторый единый опе¬
ратор «с?», переводящий р-формы в (р -f 1)-формы (р = 0, 1, ..., п - 1), который обладает
следующими свойствами:
d(a -Ь /3) — doc -j- d/3,
d(cx A 7) — da A 7 + (—l)pa A d7,
d(da) = 0,
где a есть р-форма. Величина d<& имеет тот же смысл («градиент Ф») для 0-формы (т. е. для
скаляра), что и в нашем предыдущем обсуждении (она определяется соотношением dФ • £ =
= £(Ф), при этом символ d в dx также имеет прежний смысл). Последнее уравнение в вы¬
шеприведенном списке часто записывается просто как
d2 — 0,
что является ключевым свойством оператора внешней производной d. (Причина появления
неизящно выглядящего множителя (—1)р во втором из указанных уравнений состоит в том,
что следующий за ним оператор d занимает «неправильное» положение, «протолкнувшись»
через ковектор а с его р антисимметричными индексами. Это проявляется яснее в приве¬
денной ниже индексной записи.)
1 -форма а, будучи градиентом а = d<P, согласно вышеизложенному, должна удовле¬
творять условию da = 0.** Однако этому условию удовлетворяют не все 1-формы. На са¬
мом деле, если 1-форма а удовлетворяет условию da = 0, то отсюда следует, что она
локально (т. е. на достаточно малом открытом множестве, содержащем данную точку) имеет
вид a = дФ для некоторого Ф. Это есть пример важной леммы Пуанкаре^12Л1Ь***? которая
утверждает, что если р-форма /3 удовлетворяет условию d/З — 0, то она локально имеет
вид /3 = d7, где 7 есть некоторая (р — 1)-форма.
Внешняя производная станет более понятной, если перейти к компонентам. Рассмот¬
рим р-форму а. На координатном лоскуте с координатами х1, ..., хп величина а представ¬
ляется антисимметричным набором компонент (=	где	число индексов г, ..., t
равно р; см. § 11.6). Такое представление можно записать в виде
a — ^ ar...t dxr A • • • A dxb,
где суммирование (обозначаемое символом ^Р) проводится по всем наборам из р чи¬
сел г,	каждое из которых принимает значения 1, ..., п. (Некоторые предпочитают не
иметь дела с этим выражением, громоздким из-за того, что антисимметрия V-произведения
приводит к повторению р! раз каждого члена, отличного от нуля. Однако такая запись, если
привыкнуть к ней, работает гораздо лучше, и я предпочитаю именно ее.) Внешняя произ¬
водная от р-формы а представляет собой (р ~f 1)-форму, которая записывается в виде da
и имеет компоненты
(da)qr...t = yyar-t}-
*	Используя вышеприведенные соотношения, покажите, что d{A dx + В dy) = (дВ/дх — дА/ду) dx A dy.
Почему?
Используя результат упражнения 12.11, докажите лемму Пуанкаре для р — 1.

12.6. Внешняя производная
И!
211
(Запись выглядит довольно неуклюже. Антисимметризация, которая является основной осо¬
бенностью этого выражения, проводится по всемр-1-1 индексам, включая тот, что находится
над знаком производной.) »
Теперь мы можем сформулировать основную теорему внешнего анализа. Она выража¬
ется следующей очень изящной (и мощной) формулой для р-формы <р (см. рис. 12.11):
дп
Здесь 7Z есть некоторая компактная (р + 1)-мерная (ориентированная) область, р-мерная
(ориентированная) граница которой (также, естественно, компактная) обозначается 31Z.
а)
б)
Рис. 12.11. Основная теорема внешнего анализа f dip = Sv- а) Классический случай (XVII век):
к	дп
ь
/ /' (ж) dx =. f(b) — /(а); здесь <р = f(x), a 1Z — отрезок кривой 7 от а до 6, параметризованный
а
переменной х, так что ду состоит из концевых точек отрезка у, х — а (берется со знаком минус)
я х = b (берется с плюсом), б) Общий случай для р-формы ip; здесь 1Z есть компактная ориентиро¬
ванная (р + 1) -мерная область с р-мерной границей dlZ
Здесь были использованы некоторые термины, пока не получившие объяснения. Тер¬
мин «компактный», в соответствии с интуитивным представлением, для наших целей озна¬
чает, что область 7Z не простирается до бесконечности и не содержит дыр и удаленных
частей границы. Более точно для наших целей можно определить компактную область 1Z
как область, обладающую тем свойством, что любая бесконечная последовательность точек,
принадлежащих 7Z, должна накапливаться около некоторой точки внутри 1Z (рис. 12.12 а).
Точка накопления у на рисунке обладает тем свойством, что любое открытое множество
в 1Z (см. § 7.4), содержащее эту точку, должно содержать также члены бесконечной после¬
довательности (так что точки этой бесконечной последовательности становятся все ближе
и ближе к точке у). Бесконечная евклидова плоскость некомпактна, тогда как поверхность
сферы компактна; то же относится и к тору. Так же обстоит дело и со множеством точек,
♦
Покажите непосредственным вычислением, что все «аксиомы» для внешней производной выполняются
при таком координатном определении.
Покажите, что это координатное определение дает одну и ту же величину dot независимо от выбора
координат, если преобразование компонент данной формы аг..л определяется требованием, чтобы сама форма ot
не менялась при изменении координат. (Подсказка: покажите, что это преобразование эквивалентно пассивному
преобразованию компонент ^ j -валентного тензора (см. § 13.8).)

212
Глава 12
' '• .
а)
б)
Рис* 12.12. Компактность, а) Компактное пространство 7Z обладает тем свойством, что любая беско¬
нечная последовательность точек pi, р2, Рз, • ♦ • в 'П должна в конечном счете накапливаться около
некоторой точки у в 7Z, так что любое открытое множество J\f в 7£, содержащее точку у, должно также
содержать бесконечно много членов указанной последовательности, б) У некомпактного множества
это свойство отсутствует
лежащих внутри единичной окружности или на ней в комплексной плоскости, образуя зам¬
кнутый единичный диск. Если же удалить из этого множества саму окружность или хотя бы
ее центр, то полученное множество окажется некомпактным (см. рис. 12.13).
/
/\ •
V V'
ч ‘
\
*/
• */
л*
а)
б)
Рис. 12.13. а) Некоторые некомпактные пространства: бесконечная евклидова плоскость, открытый
единичный диск, замкнутый диск с удаленным центром, б) Некоторые компактные пространства:
сфера, тор, замкнутый единичный диск. (Сплошные граничные линии являются частью множества,
прерывистые граничные линии в множество не входят.)
Термин «ориентированный» означает, что каждой точке в 7Z приписывается некоторая
• •**»• - ••
ориентация (рис. 12.15). Для 0-многообразия, или набора дискретных точек, ориентация
просто приписывает каждой точке «положительное» (+) или «отрицательное» (—) зна-

12.7. Элемент объема, правило суммирования
213
•+
•+
а)
б)
*)
г)
Рис. 12.15. Ориентация, а) (Многокомпонентное) 0-многообразие представляет собой набор дискрет¬
ных точек; ориентация просто приписывает каждой из них «положительное» (+) или «отрицательное»
(—) значение, б) В случае 1-многообразия, или кривой, ориентация означает указание «направления»
вдоль этой кривой, на диаграмме оно изображается стрелкой, в) Для 2-многообразия ориентация
изображается маленькой дугой окружности со стрелкой на ней, указывающей «положительное» на¬
правление вращения касательного вектора, г) В случае 3-многообразия ориентация определяет, какие
тройки независимых векторов в данной точке следует считать «правыми» (ср. рис. 11.1)
чение (рис. 12.15 а). В случае 1-многообразия, или кривой,
ориентация означает указание «направления» вдоль кривой.
Это можно представить в виде диаграммы, снабдив кривую
«стрелкой», указывающей такое направление (рис. 12.15 6).
Для 2-многообразия ориентацию можно изобразить в виде
маленькой окружности либо дуги окружности со стрелкой на
ней (рис. 12.15 в), указывающей, какое направление вращения
Рис. 12.14. Лента Мёбиуса как
пример неориентируемого про¬
странства
касательного вектора в данной точке поверхности рассматри¬
вается в качестве положительного. В случае 3-многообразия
i
ориентация определяет, какую тройку независимых векторов
в данной точке следует считать «правой», а какую — «левой»
(напомним § 11.3 и рис. 11.1); см. рис. 12.15г. Приписать
ориентацию не удается лишь довольно необычным простран¬
ствам. Примером такого «неориентируемого» пространства
служит лента Мёбиуса, показанная на рис. 12.14.
Граница 87Z (компактной ориентированной) (р + 1)-мерной области состоит из точек
многообразия 1Z, не лежащих в его внутренней области. Если многообразие 71 не отно¬
сится к разряду «патологических», то 871 будет (компактной ориентированной) р-мерной
областью, хотя, возможно, и пустой. Ее граница 8871 является пустым множеством. Таким
образом, д2 — 0, что дополняет ранее полученное соотношение d2 = 0.
Границей замкнутого единичного диска в комплексной плоскости служит единичная
окружность, граница единичной сферы — пустое множество, граница конечного цилиндра
(цилиндрической 2-поверхности) состоит из двух окружностей на каждом из торцов, имею¬
щих противоположную ориентацию; граница конечного отрезка кривой состоит из двух его
концевых точек, одна из которых считается положительной, а другая — отрицательной (см.
рис. 12.16). Обычный одномерный вариант основной теоремы анализа оказывается, как ука¬
зано выше, частным случаем основной теоремы внешнего анализа, когда многообразием 7Z
служит такой отрезок кривой.	’
• ■ . 1 •
12.7.	Элемент объема, правило суммирования
Вернемся теперь к разнице между р-формой и (п ~ р)-вектором (а также к связи между
ними) на n-многообразии Л4. Чтобы понять, каково соотношение между ними, лучше начать

214
Глава 12
д
д
0
я)
б)
•+
в)
г)
Рис. 12.16. Границей &R непатологической компактной ориентированной (р + 1)-мерной области Л
является (компактная ориентированная) р-мерная область (она может быть и пустой), состоящая из
тех точек области Л, которые не лежат во внутренней (р+1)-мерной области, а) Границей замкнутого
единичного диска (определяемого неравенством \z\ ^ 1 в комплексной области Q служит единичная
окружность, б) Граница единичной сферы представляет собой пустое множество (обозначаемое 0,
см. §3.4). в) Граница цилиндрической поверхности конечной длины состоит из двух окружностей на
торцах, имеющих противоположную ориентацию, г) Граница конечного отрезка кривой состоит из
двух концевых точек, одна из которых считается положительной, а другая —отрицательной
с крайнего случая р = п, по этому рассмотрим соотношение между /г-форм ой и скалярным
полем на М. В случае п-формы е соответствующим элементом n-поверхности в точке о мно¬
гообразия М служит вся касательная п-плоскость в точке о. Мерой для е служит просто п-
плотность, не имеющая какого-либо направления. Такую п-плотноеть (предполагаемую не
всюду равной нулю) иногда называют элементом объема п-многообразия М. Используя эле¬
мент объема, можно перейти от (п — р)-векторов к р-формам и наоборот. (Иногда элемент
объема приписывается многообразию как часть его «структуры», в этом случае исчезает
существенное различие между р-формой и (п — р)-вектором.)
Как, используя элемент объема, преобразовать (п — р)-вектор в р-форму? На каждом ко¬
ординатном лоскуте п-форму в можно выразить через компоненты с п антисимметричными
нижними индексами
£
V...W •
(Некоторые предпочтут ввести сюда множитель (п!)	; относительно смысла знака «!»
%
см. §5.3. Я, однако, не стану связываться с возникающими здесь факториалами, чтобы
не отвлекаться от главных идей.) Можно использовать величину £r...w> чтобы преобразовать
семейство компонент 'ф7'*"™ (п — р)-вектора ф в семейство компонент р-формы а.
Мы проделаем это, воспользовавшись преимуществами операций тензорной алгебры, к бо¬
лее полному изложению которой мы перейдем в следующем разделе. Эта алгебра позволяет
«склеить» n^-р верхних индексов величины 'фг"'и) с п—р нижними величины £r,,.w, оставляя
нетронутыми р нижних индексов, которые нужны нам для ar_t. Операция такого «склеи¬
вания» носит название «свертки» (или «трансвекции») тензоров. Она позволяет провести
суммирование по парам, составленным из верхнего и соответствующего нижнего индексов,
так что оба набора индексов исключаются из конечного выражения.
Типичным примером может служить скалярное произведение (см. § 12.3), которое ком¬
бинирует компоненты (Зг ковектора /3 с компонентами £г вектора £ путем перемножения
•	*	ж»	•
соответствующих элементов двух наборов компонент и суммирования по повторяющимся
индексам. В результате получается

12.7. Элемент объема, правило суммирования
215
где суммирование проводится по повторяющемуся индексу г (одному сверху и одному
снизу). Процедура суммирования применяется также к величинам со многими индекса¬
ми. Физики сочли чрезвычайно удобным принять правило суммирования, предложенное
Эйнштейном. Правило состоит в том, что знак суммы опускается и предполагается,
что суммирование проводится по паре одноименных индексов, один из которых находится
сверху, другой — снизу, при этом индекс пробегает значения 1, . ,., п. В соответствии с этим
скалярное произведение можно записать в более простом виде
Используя такое соглашение, можно применить вышеуказанную процедуру, чтобы выра¬
зить р-форму через соответствующий (п — р)-вектор, а элемент объема представить в виде
&Г..Л' ОС £г..Ли...и)'Ф
U...W
со сверткой по п — р индексам и, ... w. Символ ос означает здесь пропорциональность двух
величин, то есть каждая из них равна другой, умноженной на некоторый множитель, отлич¬
ный от нуля. Он используется здесь для того, чтобы можно было не связываться с фактори¬
алами, усложняющими вид выражения. При выполнении указанного соотношения (в виде
пропорциональности двух величин) иногда говорят, что (п — р)-вектор ф и р-форма взаим¬
но сх дуальны[12Л41; в этом случае имеет место также соответствующая обратная формула
„LU...W ^ _	jr..Ли.'.иУ
V ос аг„ле
для некоторого обратного объема (п-вектора) €, который часто «нормируется» относитель¬
но е в соответствии с соотношением
е • € = £r...w£r'"w = п\
(хотя вопрос нормировки не входит здесь в число основных).
Эти формулы составляют часть классической тензорной алгебры (см. § 12.8). Они обес¬
печивают мощный вычислительный формализм (получающий обобщение в тензорном ана¬
лизе, с которым мы подробнее познакомимся в главе 14), основанный на использовании
индексной записи в сочетании с правилом суммирования Эйнштейна. Обозначение антисим¬
метризации с помощью квадратных скобок (см. § 11.6) также играет заметную роль в этой
алгебре. Это относится также к дополнительной операции симметризации, обозначаемой
круглыми скобками:
= \ {Фаь+Фьа),
£
ф(а Ьс) = 1(ф*Ьс + фасЬ +	ф + фЬас + фсаЬ + )
и т. д.; все минусы выражения с квадратными скобками заменяются здесь плюсами.
В качестве следующего примера использования скобок посмотрим, как можно записать
условие того, что р-форм а сх или g-вектор ф являются простыми, то есть V-произведением р
отдельных 1-форм или q обычных векторов. В компонентах это условие принимает вид
a[r...t«u]o...w = О или ф\г-1ф*\ч-™ = о,
где все индексы первого сомножителя «переставляются» лишь с одним индексом второго
сомножителя^1215^. Если схпф взаимно дуальны, то можно записать любое из этих условий
в виде

216
Глава 12
где один индекс величины тр свертывается с одним индексом величины а. Симметрия этого
выражения показывает, что дуальным к простой р-форме является простой (п — р)«вектор
и наоборот*.
12.8.	Тензоры. Абстрактные индексы и диаграммное представление
Здесь появляются величины, при обозначении которых иногда возникает конфликт меж¬
ду физиками и математиками. Два возможных вида обозначений представляются двумя ча¬
стями приведенного выше равенства /3 • £ = j3r£r. Обозначение, используемое математиками,
очевидным образом не зависит от координат; видно, что выражение (3 • £ (в математической
литературе используются также обозначения (/3, £) и (/3, £)) не связано с какой-либо си¬
стемой координат, то есть операция скалярного умножения описывается в геометрических
и алгебраических терминах. В то же время обозначение /Зг£г, используемое физиками, яв¬
ным образом связано с компонентами в некоторой системе координат. Эти компоненты будут
меняться при переходе с одного координатного лоскута на другой, кроме того, такая запись
использует соглашение о суммировании, которое может вызвать возражения и не согласуется
с привычными математическими стандартами. Тем не менее обозначение физиков обладает
значительной гибкостью, проявляющейся, в частности, в той легкости, с которой оно мо¬
жет быть использовано для конструирования новых операций, что не так просто сделать
в рамках привычных операций математиков. Несколько более сложные вычисления (подоб¬
ные выписанной выше паре соотношений) часто оказываются почти невыполнимыми, если
пользоваться лишь безындексными выражениями. «Чистые» математики часто вынуждены
прибегать, хотя и с некоторым смущением, к «координатным» вычислениям, когда требу¬
ется подкреплять рассуждения вычислениями, при этом они изредка следуют соглашению
о суммировании.
По моему мнению, этот конфликт носит во многом искусственный характер, и его
можно преодолеть, несколько изменив точку зрения. Когда физик использует величину £а,
он обычно имеет в виду полную векторную величину £, а вовсе не набор ее компонент
в некоторой произвольно выбранной системе координат. То же относится и к величине аа,
которую следует понимать как полную 1-форму. Такое понимание можно сделать вполне
строгим в рамках так называемых абстрактных индексных обозначений^12В этой схеме
индексы обозначают не одно из значений 1, 2, ..., п, относящихся к некоторой системе
координат, а некоторые абстрактные метки, в терминах которых формулируется алгебра.
Это позволяет сохранить практические преимущества индексной системы записи без ее
концептуальных недостатков, связанных с необходимостью явного или неявного обращения
к некоторой системе координат. Более того, абстрактные векторные обозначения обладают
многими дополнительными практическими преимуществами, особенно в связи со спинор-
ным формализмом^12-17!.
Тем не менее схема абстрактных индексных обозначений сталкивается с очевидной
проблемой, состоящей в том, что в формуле нелегко представить все важные подробности,
поскольку мы стараемся сделать индексы поменьше и бывает трудно установить их точ¬
ное расположение. Эту трудность можно частично устранить, если ввести другую запись
тензорной алгебры, которую я сейчас вкратце опишу. Речь пойдет о диаграммном представ¬
лении.
Прежде всего следует узнать, что такое тензор. В индексных обозначениях тензор
обозначается как величина вида
*• *
Подтвердите эквивалентность всех этих условий; для простоты докажите достаточность усло¬
вия &[rsau}v = 0 в случае р = 2. (.Подсказка: сверните это выражение с двумя векторами.)

12.9. Комплексные многообразия
ч
217
которая может иметь q нижних и р верхних индексов с любыми р, q > 0, не обладающих
какой-либо особой симметрией. Эту величину называют тензором валентности i12 181
р
я
(или
р
я
-валентным тензором, или просто
-тензором). В алгебраическом смысле тензор
р
я
представляет собой некоторую величину Q, которую можно рассматривать как функцию
(так называемую полилинейную функцию) от q векторов А, ..., Сир ковекторов F, ..., Н
вида
Q(A,	...,С;	F, ..., Н) =	Аа ...CcQfa;;hcFf
В диаграммном представлении тензор Q обозначается как некоторый символ (например,
прямоугольник, или треугольник, или овал — как удобнее), к которому присоединены q
линий, идущих вниз («ноги»), и р линий, идущих вверх («руки»). В каждом члене тензор¬
ного выражения различные перемножаемые элементы сопоставляются друг другу, однако
они не обязаны быть линейно упорядоченными в направлении поперек страницы. Если
какие-нибудь два индекса свертываются между собой, то соответствующие линии должны
•• • •
быть соединены, верхняя с нижней. На рис. 12.17 и 12.18 показано несколько примеров,
иллюстрирующих некоторые формулы, с которыми мы только что сталкивались. В дан¬
ных обозначениях черта, нарисованная поперек линий, изображающих индексы, означает
антисимметризацию, что соответствует квадратной скобке в индексной записи (хотя оказа¬
лось удобнее принять иное соглашение в отношении множителей-факториалов). Извилистая
черта означает симметризацию. Хотя диаграммное представление обычно трудно воспроиз¬
водить при печати, оно может оказаться необычайно удобным при вычислениях вручную.
Я сам пользуюсь им уже более 50 лет! t12-20!
12.9* Комплексные многообразия
Вернемся, наконец, к понятию комплексного многообразия, упомянутого в главе 10.
Считая риманову поверхность одномерной, мы рассуждали в терминах голоморфных опе¬
раций над комплексными числами. С тех же позиций можно подойти к многомерным
многообразиям, рассматривая теперь наши координаты ж1, ..., хп как комплексные чис¬
ла z1, ..., zn> а наши функции от них — как голоморфные функции. Наше многообразие
по-прежнему предполагается «склеенным» из нескольких координатных лоскутов, каждый
из которых теперь является открытой областью координатного пространства Сп, точками
которого служат наборы из п комплексных чисел (z1, z2, ..., zn) (напомним, что, соглас¬
но § 10.2, С означает множество комплексных чисел). Функции перехода, определяющие
преобразования координат при переходе с одного координатного лоскута на другой, теперь
задаются исключительно в виде голоморфных функций. Можно определить голоморфные
векторные поля, ковекторы, р-формы, тензоры и т. д. точно так же, как это делалось раньше
в случае вещественного п-многообразия.
Оказывается, однако, возможной альтернативная точка зрения, согласно которой мы мо¬
жем выразить все наши комплексные координаты через их вещественные и мнимые ча-
» ♦ •
сти z3 = х3 + гу3 (или, что эквивалентно, включить комплексное сопряжение в категорию
приемлемых функций, так что операции уже не должны быть непременно голоморфными,
см. § 10.1). Тогда наше «комплексное n-многообразие» будет рассматриваться уже не как
n-мерное пространство, а как вещественное 2п-многообразие. Разумеется, это 2п-многооб-
разие имеет локальную структуру весьма частного вида, называемую комплексной структу¬
рой.
Существуют разные способы формулировки этого понятия. По существу, всё, что тре¬
буется, — это многомерный вариант условий Коши-Римана (см. § 10.5), однако обычно

218
Глава 12
а Ь с
^ абс . гЧ abc	I	а
% ~+ О, % “2 Qot
,«.(<* пф
? ЛаЬ[с^М
с а
i
а
+ \Л + Д/+	+	-I-
. W-III+XWK-ХНХ
+X, "t+f=
, at т+ш-жъ-х
«v—~tr ~*1
Рис. 12.17. Диаграммное представление тензоров. [ ^ ] -валентный тензор Q изображается овалом с тре¬
мя «руками» и двумя «ногами», тогда как изображение j^J-валентного тензора общего вида должно
содержать р «рук» и q «ног». В диаграммном представлении выражения вида Qfbgc — 2QbgCfa концы
«рук» и «ног» располагаются таким образом, чтобы можно было проследить за положением каждого
индекса, вместо того чтобы обозначать индексы буквами. Свертка тензорных индексов представля¬
ется соединением «руки» и «ноги», как показано на диаграмме для £aA^c.D^j. На этой диаграмме
показана также толстая черта поперек индексных линий, обозначающая антисимметризацию, и извили-
: 1
стая черта, означающая симметризацию. Множитель — на диаграмме, используемый для облегчения
вычислений, связан с тем обстоятельством, что в диаграммном представлении опускаются обыч¬
ные знаменатели с факториалами, возникающими при симметризации и антисимметризации (поэтому
111
в данном случае мы имеем — х — = —). В нижней части рисунка антисимметризация и симметри-
21 о! I*
зация показаны «в разобранном виде» с использованием диаграммного представления дельта-символа
Кронекера , который будет введен в § 13.3 (см. рис. 13.6 в). Затем это используется для представления
(мультивекторных) V-произведений £ А1] и £ А г) А £
используются несколько иные выражения. Посмотрим, в каком соотношении находятся ком¬
плексные и вещественные векторные поля на многообразии. Комплексное векторное поле £
можно представить в виде
С £ + щ,
где £ и г} — обычные вещественные векторные поля на 2п-многообразии. «Комплексная
структура» определяет связь этих вещественных векторных полей между собой и те диф¬
ференциальные уравнения, которым они должны удовлетворять, чтобы функция £ была
«голоморфной». Рассмотрим новое комплексное векторное поле, получающееся при умно¬
жении £ на мнимую единицу г. Для выполнения условия согласованности должно быть г£ =
= — г) 4- г£, так что вещественное векторное поле £ теперь заменяется на —гj, а г] — на £.

12.9. Комплексные многообразия
219
А
а
£
Q
ct.r
,п)
Симметричная часть
ж
о
Н=РЛ
а
о
Антисимметричная часть
п
s?*s
5 нормировка
п\
п
(п-р)\
Внешнее произведение:
3-форма а
п р р р
Антисимметричная
4-форма (р
cx/\ip
1
71
Дуальные объекты:
п^_р	_	Знаки	пропорциональности
Если
Антисимметричная
то
Эквивалентные условия простоты:
О,
О,
О
Рис. 12.18. Диаграммное представление тензоров (продолжение). Диаграмма для ковектора 0 (1-фор¬
мы) имеет единственную «ногу», которая при соединении с единственной «рукой» вектора £ дает их
скалярное произведение. В более общем случае полилинейная форма, определяемая
валентным
тензором Q, представляется путем соединения р «рук» с «ногами» р переменных ковекторов и q
«ног» с «руками» q переменных векторов (в данном случае р = 3, q = 2). Симметричные и анти¬
симметричные части тензоров общего вида можно выразить, используя волнистые линии и толстые
черточки* как на рис. 12.17. Запись с помощью таких линий комбинируется также с родственным
диаграммным представлением в применении к объемной n-форме £rs...w (для n-мерного простран¬
ства) и дуальному к ней n-вектору ers"'w7 нормируемым согласно соотношению
Представлены также соотношения, эквивалентные выражениям п!<5[^ ... <5^ = eab"'fers...w (п анти¬
симметричных индексов) и ea...cu...w£a'"ce"= рКп ~ р)Щи • • • (см- § *3.3 и Рис* *3.6 в). Дается
также краткое диаграммное представление внешнего произведения форм, отношения «дуальности»
между р-формами и (п — р) -векторами и условий «простоты». (Диаграммы для внешней производной
показаны на рис. 14.18.)

220
Глава 12
Операция J, осуществляющая такую замену (т. е. J(£) = —rj и J(rj) = £), и есть то, что
обычно называют «комплексной структурой».
Будучи примененной дважды, операция J меняет знак того, на что она действует (по¬
скольку г2 — —1), так что можно написать
J2 = -1.
Это условие само по себе определяет так называемую почти комплексную структуру. Чтобы
применить это к настоящей комплексной структуре и получить согласованное понятие «го-
+ •
ломорфного» многообразия, величина J должна удовлетворять некоторому дифференциаль¬
ному уравнению^12 21]. Существует замечательная теорема Ньюлендера-Ниренберга^12*22^
%
которая гласит, что этого достаточно (а не только необходимо) для того, чтобы 2п-мерное
вещественное многообразие с такой J-структурой можно было интерпретировать как ком¬
плексное n-многообразие. Эта теорема позволяет нам свободно выбирать между двумя точ¬
ками зрения на комплексные многообразия.
Примечания
§12.1.
12.1. Такая «сжимаемость» понимается в смысле гомотопии (см. § 7.2, рис. 7.2), так что не допускает¬
ся «взаимная компенсация» противоположно ориентированных участков петли; таким образом,
понятие многосвязности является неотъемлемой частью теории гомотопий. См. [404, 757].
12.2. Строго говоря, это рассуждение неполно, поскольку не представлены убедительные причины
того, что закрутка ремня на 2к не может быть устранена непрерывным образом, если концы
ремня зафиксированы . См. [626], стр. 41-44.
12.3. Мы рассматриваем здесь молекулы как точечные частицы. Для молекул, имеющих внутренние
или вращательные степени свободы, размерность пространства V будет значительно больше.
§12.2.
12.4. Обычное понятие «многообразия» предполагает, что наше пространство М является прежде
всего топологическим пространством. Приписать пространству Л4 топологию — означает точ¬
но определить, какое множество его точек должно называться «открытым» (ср. § 7.4). Открытые
множества должны обладать тем свойством, что пересечение любых двух из них и объединение
любого (конечного или бесконечного) числа таких множеств является открытым множеством.
В дополнение к упомянутому выше условию Хаусдорфа обычно требуют, чтобы топология М.
была ограничена некоторыми другими условиями, чаще всего это условие «паракомпактности».
Для понимания этого и других родственных терминов интересующийся читатель отсылается
к книгам [441, 251] и другим стандартным учебникам по общей топологии. Для наших нынеш¬
них целей достаточно просто принять, что многообразие М построено из локально конечных
лоскутов открытых областей множества Мп; «локально конечными» называют лоскуты, каждый
из которых пересекается лишь с конечным числом других лоскутов.
Последнее требование, которое иногда выдвигается при определении многообразия, состо¬
ит в том, что оно должно быть связным. Это означает, что многообразие должно состоять
лишь из «одного куска», то есть не быть несвязным объединением двух непустых открытых
множеств. Я не буду здесь настаивать на этом; если требуется связность, то это будет фор¬
мулироваться в явном виде (однако несвязность в любом случае будет допускаться только
для конечного числа отдельных кусков).
Представляя поворот в обычном 3-пространстве вектором, направленным вдоль оси поворота и имеющим
длину, равную углу поворота, покажите, что топологию множества 1Z можно описать как топологию твердого шара
(радиуса 7г), ограниченного обычной сферической поверхностью, каждая точка которой идентична ее антиподной
точке. Объясните, почему замкнутая петля, представляющая поворот на 27т, не может быть деформирована в точку
непрерывным образом.

12.9. Комплексные многообразия
221
12.5. См., например, [452, 384, 470, 370]. Возможная интересная процедура определения многооб¬
разия М. состоит в том, чтобы построить само многообразие Л4 исходя из коммутативной
алгебры скалярных полей, определенных на Л4, см. [141, 562, 626]. Идея такого рода обоб¬
щается на некоммутиативные алгебры и приводит к понятию «некоммутативной геометрии»
Алана Конса [158], который предложил современный подход к «квантовой геометрии простран¬
ства-времени» (см. §33.1).
§12.3.
12.6. См., например, [379, 269].
12.7. Общим условием того, что семейство элементов (га — 1)-плоскости, определенное 1-формой а,
касается однопараметрического семейства (п — 1)-поверхностей (так что а = ХбФ для неко¬
торых скалярных полей Л, Ф), служит условие Фробениуса а Л da. = 0; см. [266].
12.8. Легко возникает противоречие между «классической» идеей, согласно которой dxr должно
означать бесконечно малое смещение (вектор), и тем, что здесь мы рассматриваем его как
ковектор. На самом деле здесь все согласуется, но, чтобы увидеть это, нужна ясная голова!
Величина dxr кажется векторной из-за ее верхнего индекса г, и это действительно так, ес¬
ли рассматривать г как абстрактный индекс в соответствии с § 12.8. С другой стороны, если
считать г численным индексом, например г = 2, то мы получаем ковектор dx2, который есть
градиент скалярной величины у = х2 (здесь это «икс-два», а не «икс-квадрат»). Но это зави¬
сит от интерпретации символа «d>\ означающего градиент, а не бесконечно малую величину,
как было бы согласно классической традиции. Фактически если рассматривать г как абстракт¬
ный индекс, a d как градиент, то «dxr» будет означать просто (абстрактный) дельта-символ
Кронекера!
§12.5.
12.9. Это означает отказ от понимания величин типа «dx» как бесконечно малых. Здесь антикомму-
тационные свойства величины dx Л dy указывают на то, что мы работаем с плотностями по
отношению к мерам ориентированных площадей.
12.10. Это название предложил мне Н. М. Дж. Вудхауз. Иногда эту теорему называют просто теоремой
Стокса. Однако это кажется мне не совсем правильным, поскольку весь вклад Стокса состоял
в том вопросе, который он поставил на Кембриджском экзамене перед Уильямом Томсоном
(будущим лордом Кельвином).
§ 12.6.
12.11. См. [266]. (В этой книге утверждение, которое я называю «леммой Пуанкаре», считается обрат¬
ным по отношению к этой лемме.)
12.12. Существует более широко применимое определение компактности топологического простран¬
ства, которое, однако, не столь наглядно, как приведенное в тексте. Пространство 1Z компактно,
если при любом способе представления его в виде объединения открытых множеств существует
конечный набор таких множеств, объединением которых является все еще 1Z.
12.13. Более полную информацию по этому вопросу можно найти в книге [838].
§ 12- 7.
12.14. Такое понятие «дуальности» заметно отличается от «дуальности» ковектора вектору, описан¬
ной в § 12.3. Оно, однако, тесно связано с другой концепцией дуальности — дуальностью
Ходжа. Последняя играет определенную роль в электромагнетизме (см. § 19.2), а ее вариан¬
ты — в различных подходах к квантовой гравитации (см. §§31.5, 31.14, 32.2, 33.11, 33.12)
и в физике элементарных частиц (см. § 25.8). К сожалению, это лишь одно из многих мест,
где ограничения математической терминологии могут привести к недоразумениям.
12.15. См. [626].
§12.8.
12.16. См. [590, 626, 595].
12.17. См. [590, 626, 627, 595, 564].

222
Глава 12
12.18. Для величины р -f q иногда используется термин ранг, но это приводит к недоразумениям,
поскольку «ранг» имеет другой смысл в теории матриц; см. примечание 13.10 в § 13.8.
12.19. Полилинейность означает линейность по каждой из величин А, ..., С, F. ... Н в отдельно¬
сти, см. §§ 13.7-13.9.
12.20. См. [626] (приложение), [595, 172].
U 2.9.
\J
12.21. Это есть условие обращения в нуль некоторого выражения, называемого «тензором Нойенхейса,
построенным из J», которое можно представить в виде JdadJ^/dxd + J%dJda/dxb^ ~ 0.
12.22. См. [548].

Глава 13
Группы симметрии
1
*
13Л. Группы преобразований
Симметричным пространствам придается большое значение в современной физике.
Почему? Можно думать, что совершенно точная симметрия встречается лишь в исключи¬
тельных случаях либо, возможно, является лишь некоторым удобным приближением. Хотя
симметричные объекты, например квадрат или сфера, несомненно, существуют как идеа¬
лизированные («платоновские»; см. § 1.3) математические структуры, всякую физическую
реализацию таких объектов следует обычно рассматривать просто как некоторое прибли¬
женное воплощение платоновского идеала, поэтому реальную их симметрию нельзя считать
точной. Примечательно тем не менее, что, согласно наиболее успешным физическим те¬
ориям XX века, все виды физического взаимодействия (включая гравитацию) действуют
в соответствии с идеей, которая, строго говоря, решающим образом зависит от некоторых
физических структур, обладающих симметрией, которая на фундаментальном уровне опи¬
сания должна быть совершенно точной!
Что это за идея? Это концепция, получившая название «калибровочная связность».
Название само по себе мало что объясняет. Но эта важная идея позволяет ввести тонкое
(«закрученное») понятие дифференцирования, применяемое к различным объектам на мно¬
гообразии, имеющим более общий характер, нежели р-формы, к которым применялась опе-
ращш внешнего дифференцирования, описанная в главе 12. Эти материи составят предмет
двух следующих глав, а пока нам необходимо познакомиться с фундаментальным поня¬
тием группы симметрии. Оно имеет много других важных применений в физике, химии
и кристаллографии, а также во многих других областях самой математики.
Разберем простой пример. Какова симметрия квадрата? На этот вопрос можно дать два
разных ответа в зависимости от того, допустимы ли преобразования симметрии, меняющие
ориентацию квадрата (т. е. такие, при которых квадрат переворачивается). Сначала рассмот¬
рим случай, когда такие преобразования, меняющие ориентацию, запрещены. Тогда симмет¬
рия квадрата порождается поворотом на прямой угол в плоскости квадрата, повторенным
различное число раз. Для удобства можно описывать эти движения с помощью комплексных
чисел, как это делалось в главе 5. Можно, при желании, сопоставить вершинам квадрата
точки комплексной плоскости 1, % — 1, —г (рис. 13.1 а), тогда основному повороту на прямой
угол будет соответствовать умножение на г (т. е. операция «гх»). Различные степени числа г
представляют все наши повороты, всего таких будет четыре:
•О -|	*1	*	*2 I *3	*
г = 1, г = г, г = —1, г = —г
(см. рис. 13.1 б). Четвертая степень i4 = 1 возвращает нас к началу, то есть не добавляет
новых элементов. Произведение любых двух из этих четырех элементов снова равно одному
из них.
Эти четыре элемента могут служить простейшим примером группы. Группу определяет
набор ее элементов и правило попарного их «умножения» (умножение обозначается просто
размещением двух элементов рядом), для которого выполняется закон ассоциативности
ч
а(Ъс) = (ab)c.

224
Глава 13
а)
1
* *
^ 4
С
Сг
-1
С
-Сг
б)
«)
Рис. 13.1. Симметрия квадрата, а) Вершины квадрата можно представить точками 1, г, — 1, —г в ком¬
плексной плоскости С б) Группа симметрии без отражения представляется в плоскости С умножением
соответственно на 1 = г°, г = г1, —1 = г2, — г == г3, в) Симметрии с отражением в плоскости С опи¬
сываются операциями С (комплексное сопряжение), Сг, —Си —Сг
В группе существует единичный элемент 1, обладающий свойством
1а = а\
а
•>
и каждому элементу группы а соответствует обратный элемент а 1 такой, что
а 1а = аа 1
1.
Операции симметрии, посредством которых объект (не обязательно квадрат) переводится
в самого себя, всегда удовлетворяют этим законам, называемым групповыми аксиомами.
Напомним о соглашении, принятом в главе 11, согласно которому мы считаем, что в про¬
изведении аЬ сначала действует Ъ, а затем а. Мы можем рассматривать эти элементы как
операции, производимые над некоторым объектом, стоящим справа. Таким образом, можно
рассматривать движение 6, выражающее симметрию некоторого объекта #, как Ф Ъ(Ф),
а следующее за ним другое подобное движение а — как Ь(Ф) ь-> а(Ь(Ф)). Результатом будет
комбинированное действие Ф а(Ь(Ф)), что мы записываем просто в виде Ф \—> аЬ(Ф),
соответствующем движению ab. Единичный элемент оставляет объект в первоначальном со¬
стоянии (которое, очевидно, всегда симметрично самому себе), а обратный элемент соответ¬
ствует обратной операции данного преобразования симметрии и переводит объект обратно
в исходное состояние.
В нашем частном примере поворотов квадрата без отражения мы получаем дополни-
v>
тельное свойство коммутативности
ab — Ьа.
Группы, коммутативные в этом смысле, называются абелевыми в честь трагически рано
ушедшего из жизни норвежского математика Нильса Хенрика Абеля l13-1!. Очевидно, что
любая группа, которую можно представить просто путем перемножения комплексных чи¬
сел, должна быть абелевой (поскольку умножение отдельных комплексных чисел всегда
коммутативно). Мы встречались с другими подобными примерами в конце главы 5, где
был рассмотрен общий случай конечной циклической группы Zn, порождаемой корнем п-й
степени из единицы
т Покажите, что если для всех элементов а положить 1а
а и а
= 1, а также принять закон ас¬
социативности а(Ьс) — (аЪ)с, то свойства al = а и аа"1 — 1 можно вывести. (Подсказка: разумеется, а —
не единственный элемент, для которого имеется обратный элемент.) Объясните, почему, с другой стороны, усло¬
вий al = a, a~la = 1 и a(bc) = (аб)с не достаточно для определения группы.
Объясните, почему любое векторное пространство есть абелева группа -
называемая аддитивной абеле¬
вой группой, — у которой групповой операцией «умножения» служит операция сложения в векторном пространстве.

13.2. Подгруппы и простые группы
225
Сделаем теперь возможными отражения, изменяющие ориентацию нашего квадрата.
При этом все еще можно пользоваться прежним представлением, использующим комплекс¬
ные числа, однако необходимо ввести новую операцию — комплексное сопряжение, — обо¬
значаемую как С. (Эта операция переворачивает квадрат вокруг горизонтальной прямой,
см. § 10.1, рис. 10.1.) Теперь мы получаем (см. рис. 13.1 в) следующие «правила умноже¬
ния»* :
Сг = (-г)С,	С(—1) = (-1)С,	С(-г) = гС, СС - 1
(впредь я буду вместо (—г)С писать просто —гС и т. n.)f13*2l. Мы можем получить правила
умножения для всей группы из следующих основных соотношений :
• *
%
• %
*
а •
г4 — 1, С2 = 1, Сг — г3С;
данная группа неабелева, что проявляется в последнем из этих соотношений. Полное чис¬
ло различных элементов в группе называется ее порядком. Порядок данной группы ра¬
вен 8.
Рассмотрим теперь другой простой пример — группу вращательной симметрии обычной
сферы. Как и прежде, сначала можно взять случай, когда отражения исключены. Тогда наша
группа симметрии будет иметь бесконечное число элементов, поскольку можно поворачи¬
вать сферу на любой угол вокруг оси любого направления в 3-пространстве. То есть группа
симметрии образует трехмерное пространство — 3-многообразие, обозначенное как Л в гла-
ве 12. Теперь дадим этой группе (3-многообразию) ее официальное наименование. Это так
называемая группа SO(3) — ортогональная группа без отражений в трех измерениях^13*35.
Если теперь включить отражения, то получится целое новое множество симметрий — другое
3-многообразие, не связанное с первым. Это множество содержит обращение ориентации
сферы. Полное семейство групповых элементов опять-таки образует 3-многообразие, состо¬
ящее из двух отдельных связных частей (см. рис. 13.2). Пространство полной группы носит
название 0(3).
Приведенные два примера иллюстрируют две из наиболее важных категорий групп —
конечные группы и непрерывные группы (или группы Ли, см. § 13.6)t13,4l. Хотя между груп¬
пами этих двух типов существует большое различие, тем не менее многие важные свойства
групп являются для них общими.
13.2.	Подгруппы и простые группы
Особенно важным является понятие подгруппы данной группы. Чтобы получить под¬
группу, мы выделяем внутри группы некоторый набор элементов, который сам по себе
образует группу с теми же операциями умножения и инверсии, что и у всей целой группы.
Подгруппы играют важную роль во многих современных теориях физики элементарных
частиц. Принято считать, что существует некоторая фундаментальная симметрия Природы,
которая связывает между собой различные виды частиц и различные типы взаимодействия
между ними. Пока еще не понятно в полной мере, как действует эта полная группа симмет¬
рии, однако видно, что эта симметрия «нарушается», понижаясь до некоторой подгруппы
исходной группы, и именно эта подгруппа играет главную роль и определяет симметрию.
Поэтому важно знать, какие именно возможные подгруппы предполагаемой «фундаменталь¬
ной» группы симметрии действительно существуют, для того чтобы те симметрии, которые
* ЙИ Проверьте эти соотношения (имея в виду, что Сг означает операцию г х, за которой следует операция С
и т. п.) (Подсказка: эти соотношения можно доказать, просто проверив, как они действуют на 1 и г. Почему?)
** Покажите это.

226
Глава 13
Подгруппа
симметрий
без отражения
Сфера
с отражением
0(3)
Рис. 13.2. Вращательная симметрия сферы. Полная группа симметрии 0(3) представляет несвязное
3-многообразие, состоящее из двух кусков. Компонентой, содержащей единичный элемент 1, явля¬
ется (нормальная) подгруппа S0(3) симметрии сферы без отражений. Другой компонентой служит
3-многообразие симметрий с отражением
реально проявляются в природе, можно было рассматривать как подгруппы этой предпола¬
гаемой группы. Я вернусь к этому вопросу в §§ 25.5-25.8, 26.11, 28.1.
Обратимся к некоторым частным случаям подгрупп, используя рассмотренные при¬
меры. Симметрия квадрата, не содержащая отражений, образует 4-элементную подгруп¬
пу {1, г, — 1, —г} полной 8-элементной группы симметрии квадрата. Аналогично группа
вращений без отражения SO(3) образует подгруппу полной группы 0(3). Другая подгруппа
симметрии квадрата состоит из четырех элементов {1, — 1, С, —С}; еще одна содержит все¬
го два элемента {1, —1}.* Кроме того, всегда имеется «тривиальная» подгруппа, состоящая
всего из одного единичного элемента {1} (и сама полная группа, столь же тривиальным
образом, всегда является подгруппой самой себя).	>
Все только что описанные подгруппы обладают важным особым свойством — они явля¬
ются примером так называемых нормальных подгрупп. Важная роль нормальных подгрупп
определяется тем, что действие каждого элемента полной группы не меняет состава нор¬
мальной подгруппы, или, более формально, каждый элемент полной группы коммутирует
с нормальной подгруппой. Поясню подробнее. Возьмем полную группу Q и ее подгруп¬
пу S. Если выбрать из группы Q какой-нибудь элемент д, то через Sg можно обозначить
множество, состоящее из всех элементов множества S, каждый из которых в отдельности
умножен справа на д (это называется послеумножением на д). Таким образом, если в случае
частной подгруппы группы симметрии квадрата S = {1, —1, С, —С} выбрать д — г, то по¬
лучится Si — {г, —г, Сг, —Сг}. Аналогично запись gS будет означать множество, состоящее
из всех элементов множества 5, каждый из которых в отдельности умножен на д слева
{предумножение на д). В нашем случае мы теперь будем иметь iS — {г, —г, гС, —гС}. Что¬
бы множество S было нормальной подгруппой группы Q, два вышеуказанных множества
должны совпадать, т. е.
•
Sg — gS для всех д в Q.
*£§1 Проверьте, что все множества, перечисленные в этом абзаце, действительно являются подгруппами
(учтите упражнение 13.2).	^

13.2, Подгруппы и простые группы
227
В нашем частном случае это действительно имеет место (поскольку С г — — гС и —С г ~ гС),
при этом нужно иметь в виду, что набор элементов в фигурных скобках следует рассмат¬
ривать как неупорядоченное множество (так что не имеет значения тот обратный порядок,
в котором стоят элементы —гС и гС в явных выражениях для St и iS).
В качестве примера ненормальной подгруппы группы симметрии квадрата можно взять
подгруппу их двух элементов {1, С}. Она не является нормальной, поскольку {1, С}г =
= {г, Сг}, тогда как г{1, С} — {г, —Сг}. Заметим, что эта подгруппа возникает как но¬
вая (приведенная) группа симметрии, если снабдить наш квадрат горизонтальной стрел¬
кой, направленной вправо (см. рис. 13.3 а). Можно получить и другую ненормальную под¬
группу, {1, Сг}, если пометить квадрат стрелкой, направленной по диагонали вправо вниз
(рис. 13.3 б) . В случае группы 0(3) оказывается, что существует всего одна нетривиальная
нормальная подгруппа**, а именно S0(3), однако имеется много ненормальных подгрупп.
Примеры ненормальных подгрупп можно получить, выбрав на сфере некоторое конечное
множество точек и задавшись вопросом о симметрии сферы, на которой отмечены эти точ¬
ки. Если отметить всего одну точку, то подгруппа состоит из вращений сферы вокруг оси,
соединяющей начало координат с этой точкой (рис. 13.3 в). Вместо этого можно, напри¬
мер, отметить на сфере точки, являющиеся вершинами правильного многогранника. Тогда
подгруппа будет конечной и будет состоять из группы симметрии этого многогранника
(см. рис. 13.3 г).
о)	б)	в)	г)
Рис. 13.3. а) Если на квадрат с рис. 13.1 нанести стрелку, направленную вправо, то его группа сим¬
метрии понизится до ненормальной подгруппы {1, С}, б) Стрелка, направленная по диагонали вправо
вниз, дает другую ненормальную подгруппу, {1, Сг}. в) Если отметить одну точку на сфере с рис. 13.2,
то симметрия сферы понизится до (ненормальной) подгруппы 0(2) группы 0(3) — группы враще¬
ний вокруг оси, соединяющей начало координат с этой точкой, (г) Если отметить на сфере вершины
правильного многогранника (в данном случае додекаэдра), то ее группой симметрии станет конечная
(ненормальная) подгруппа группы 0(3)
Одна из причин* по которой так важны нормальные подгруппы, состоит в следующем.
Если группа Q обладает нетривиальной нормальной подгруппой, то группу Q можно разбить
на меньшие группы. Пусть S есть нормальная подгруппа группы Q. Тогда оказывается, что
различные множества Sg (где g может быть любым элементом группы Q) сами образуют
группу. Заметим, что при заданном множестве Sg выбор элемента д, вообще говоря, неод¬
нозначен, так как может выполняться равенство Sg\ = Sg% для различных элементов д±, g<i
группы Q. Множества вида Sg, где S — любая подгруппа, называются смежными классами
группы Q\ если подгруппа S нормальна, то смежные классы образуют группу. Причина со¬
стоит в том, что для двух таких смежных классов Sg и Sh (где д и h — элементы группы Q)
можно определить «произведение» Sg и Sh:
	 (Sg)	(Sh)	=	S(gh)
* Ш Проверьте эти утверждения, найдите еще две ненормальные подгруппы и покажите, что кроме них таких
подгрупп нет.
Покажите это. СПодсказка: какие множества вращений могут быть вращательно-инвариантными?)

228
Глава 13
и убедиться, что если подгруппа S нормальна, то все групповые аксиомы выполняются,
поскольку правая часть этого равенства хорошо определена независимо от того, какие эле¬
менты д и h выбраны для образования смежных классов в левой части равенства*. Группа,
полученная таким образом, называется фактор-группой группы Q по нормальной подгруп¬
пе S. Фактор-группа группы Q по подгруппе <S обозначается Q/S. Обозначение Q/S можно
использовать также для фактор-пространства (не группы!) различных смежных классов Sg,
даже когда подгруппа S не является нормальной .
Группы, не содержащие нетривиальных нормальных подгрупп, называются просты¬
ми группами. Примером простой группы является группа SO(3). Простые группы служат,
в некотором смысле, основными строительными блоками теории групп. Важным успехом
математики XIX и XX веков можно считать то, что ныне известны все конечные и непрерыв¬
ные простые группы. Что касается непрерывных групп (групп Ли), то для них в математике
существует поворотный момент, начатый выдающимся немецким математиком Вильгель¬
мом Киллингом (1847-1923), основные работы которого появились в 1888-1890 годах, и, по
существу, завершенный в 1894 году одной из наиболее важных написанных когда-либо мате¬
матических работ'13,принадлежащей великолепному геометру и алгебраисту Эли Картану
(с которым мы уже встречались в главе 12 и еще встретимся в главе 17). Классификация
групп продолжает играть фундаментальную роль во многих областях математики и физики
I
вплоть до сегодняшнего дня. Оказывается, что существуют четыре семейства классических
групп (см. конец § 13.10), обозначаемых Aw, Вт, Cm, Dm (m = 1, 2, 3, ...), с размерно¬
стью соответственно m(m + 2), га(2m + 1), га(2га +1), га(2m — 1) и пять исключительных
групп Eq, JE?7, Eg, F4, С?2 е размерностью соответственно 78, 133, 248, 52, 14.
Более недавняя (и даже более трудная) работа по классификации конечных простых
групп проводилась большим числом математиков в течение многих лет XX века (в последнее
время с помощью компьютеров) и завершилась лишь в 1982 году^13*6^. Здесь опять-таки
имеется несколько систематических семейств и конечный набор исключительных конечных
простых групп. Наибольшая из этих исключительных групп получила название монстр, ее
порядок равен
808 017 424 794 512 875 886 459 904 961 710 757 005 754 368 000 000 000 =
= 246 х З20 х Б9 х 76х II2 х 133 х 17 х 19 х 23 х 29 х 31 х 41 х 47х
х 59 х 71.
Исключительные группы оказались весьма привлекательными для многих современных
физиков-теоретиков. Группа Eg играет важную роль в теории струн (§ 31.14), при этом
разные люди выражали надежду, что и гигантский, но конечный монстр может найти свое
место в некоторой будущей теории^13*7^.
Классификацию простых групп можно рассматривать как важный шаг на пути к клас¬
сификации групп вообще, поскольку, как сказано выше, группу общего вида можно считать
построенной из простых групп (включая абелевы группы). История здесь не кончается, так
как имеется дополнительная информация о том, как одну простую группу можно построить
на основе другой. Я не намерен входить здесь в подробности, следует лишь упомянуть один
простой способ сделать это. Пусть Q и И — две какие-либо группы, тогда из них можно со¬
ставить так называемое групповое произведение Q х Н, элементами которого служат просто
пары (д, /г), где д принадлежит группе Q, а /г — группе Н. Правило группового умножения
для элементов {gi, hi) и (д<2, /12) группового произведения Q х Н определяется следующим
образом:
(Si, hi)(g2, h2) = (0102, hih2);
. *
**
Проверьте это и покажите, что аксиомы не выполняются, если S не является нормальной подгруппой.
Объясните, почему число элементов в Q/S для любой конечной подгруппы S конечной группы Q равно
порядку группы Q, деленному на порядок подгруппы S.

4
13.3. Линейные преобразования и матрицы	229
легко проверить, что оно удовлетворяет групповым аксиомам. Многие группы, используемые
в физике элементарных частиц, являются фактически групповыми произведениями простых
групп (или их несложной модификацией)*.
t
• • •
13.3. Линейные преобразования и матрицы
• * , • .
При изучений групп выделяется некоторый класс групп симметрии, которые, как оказа¬
лось, играют центральную роль. Это группы симметрии векторных пространств. Симметрия
векторного пространства определяется линейными преобразованиями, сохраняющими струк¬
туру векторного пространства.
Напомним (см. §§11.1, 12.3), что структура век¬
торного пространства V определяется путем введения
операций сложения векторов и умножения вектора на
число. Отметим тот факт, что геометрическая картина
сложения получается при использовании правила па¬
раллелограмма, а умножение на число иллюстрируется
как увеличение (или уменьшение) длины вектора в со¬
ответствующее число раз (рис. 13.4). Здесь мы изоб¬
разили векторы как вещественные величины, однако
возможны и комплексные векторные пространства (ко¬
торые во многих случаях оказываются весьма важными
всё из-за той же комплексной магии!), хотя их и нелег¬
ко изобразить на диаграмме. Линейное преобразование
векторного пространства V — это такое преобразование,
которое переводит пространство V в само себя, сохра¬
няя его структуру, определяемую указанными основны¬
ми операциями. При более общем подходе можно также
рассматривать линейные преобразования, переводящие
одно векторное пространство в другое.
Линейное преобразование можно описать в явном
виде с помощью таблицы чисел, именуемой матрицей.
Матрицы играют важную роль во многих математиче¬
ских контекстах. В этом разделе (а также в §§ 13.4,13.5)
мы рассмотрим эти крайне интересные объекты и изящ¬
ные алгебраические правила, которым они подчиняют¬
ся. Фактически можно рассматривать §§ 13.3-13.7 как
краткий курс теории матриц с приложениями к теории непрерывных групп. Описанные здесь
понятия необходимы для должного понимания квантовой теории, однако читатели, уже зна¬
комые с этим материалом (а также те, кто предпочтет менее детальное изучение квантовой
теории, когда мы к ней перейдем), могут пропустить, по крайней мере на время, эти разделы.
Чтобы понять, как выглядит линейное преобразование, рассмотрим сначала случай
трехмерного векторного пространства и его связь с обсуждавшимися в § 13.1 группами вра¬
щений 0(3) (или S0(3)), которые описывают симметрию сферы. Можно принять, что эта
сфера погружена в евклидово трехмерное пространство Е3 (это пространство рассматрива¬
ется как векторное пространство с началом координат О в центре сферы 113*81) и является
геометрическим местом точек, удовлетворяющих уравнению
• 1
2,2.2	i
X +у + Z — 1
*$$$} Проверьте, что для любых двух групп Q и Ti их групповое произведение Q х 7i является группой и что
фактор-группа (Q х 7i) IQ совпадает с Н.
Рис. 13.4. Линейное преобразование
сохраняет структуру пространства, на
которое оно действует. Эта структура
определяется операцией сложения (ко¬
торая иллюстрируется правилом па¬
раллелограмма) и операцией умноже¬
ния на скаляр А, который может быть
как вещественным числом, так и ком¬
плексным (в случае комплексного век¬
торного пространства). Такое преоб¬
разование сохраняет «прямизну» пря¬
мых линий и свойство параллельно¬
сти прямых при фиксированном нача¬
ле координат О

230
Глава 13
ф
в обычных декартовых координатах '(х, у) z). Вращения сферы выражаются теперь как ли¬
нейные преобразования пространства Е3, но очень частного вида, а именно ортогональные
преобразования, к которым мы перейдем в § 13.8 (см. также § 13.1).
Линейные преобразования общего вида будут, однако, сплющивать или растягивать
сферу, превращая ее в эллипсоид, как показано на рис. 13.5. С геометрической точки зрения,
линейное преобразование — это преобразование, сохраняющее «прямизну» прямых линий
и понятие «параллельных» прямых при фиксированном начале координат О. Однако оно
не обязано сохранять прямые или какие-нибудь другие углы, поэтому формы могут сжи¬
маться или растягиваться однородным, но анизотропным образом.
Рис. 13.5. Линейное преобразование, действующее на пространство Е3 (выраженное в декартовых
координатах ж, у, z), в общем случае будет сжимать или растягивать единичную сферу х2 + у2 + z2 ==
= 1, превращая ее в эллипсоид. Ортогональная группа 0(3) состоит из линейных преобразований
пространства Е3, сохраняющих единичную сферу
Как выражаются линейные преобразования в координатах х, у, zl Ответ таков: каждую
новую координату нужно представить как (однородную) линейную комбинацию из прежних
координат, т. е. в виде ax+py+'yz, где а, /3 и 7 — постоянные числа . При этом мы получим
3 таких комбинации, по одной для каждой новой координаты. Чтобы записать всё это в ком¬
пактном виде, полезно воспользоваться индексными обозначениями, введенными в главе 12.
Для этого введем координаты (х1, х2, х3), где
X
X, X
у, X
Z
имея, как и прежде, в виду, что верхние индексы не означают здесь показателей степени
*	^	•	•	•	т
(см. § 12.2). Точка общего положения в нашем евклидовом трехмерном пространстве имеет
координаты ха, где а — 1, 2, 3. Преимуществом индексных обозначений является возмож-
г	•'	'
ность применения их к любому числу измерений, так что индекс а (или любой другой
буквенный индекс) можно считать пробегающим значения 1,' 2, ..., гг, где п — некоторое
фиксированное положительное целое число. В только что рассмотренном случае п = 3.
В индексных обозначениях с учетом правила суммирования Эйнштейна (§12.7) линей¬
ное преобразование общего вида выглядит как*** » !13,91
ха Таьхъ.
Обозначая это линейное преобразование как Т, мы видим, что Т определяется набором
компонент Таъ. Такой набор компонент называют матрицей пхп и располагают обычно
Покажите, что это уравнение, определяющее точки, находящиеся на единичном расстоянии от точки О,
следует из теоремы Пифагора (§2.1).
J0 Попробуйте объяснить, почему это так. Рассмотрите, для простоты, двумерный случай.
Покажите это в явном виде для трехмерного случая.
**
***

13.3- Линейные преобразования и матрицы
231
в виде квадратной или, в другом контексте (см. ниже), прямоугольной (ш х п) таблицы
чисел. Вышеприведенное соотношение в трехмерном случае можно записать в виде
т\ Т\ Т1 з
| Т\ Т22 Т23
Г3 г Т32 Т3з
Здесь написаны три соотношения, начиная с^и Т1!®1 + Т12Х2 + Т1 з®3.*
Можно написать это и без индексов и явных координат в виде х Тх. При желании
можно принять абстрактные индексные обозначения (§ 12.8), в которых запись ха ь-> Таъхь
обозначает не компоненты, а абстрактное преобразование х Тж. (В тех случаях, ко¬
гда важно понимать, означает ли формула с индексами абстрактное преобразование или
же компоненты, будут даваться словесные пояснения.) Вместо этого можно воспользовать¬
ся диаграммным представлением, показанным на рис. 13.6 а.) В моем изложении матрица
чисел (Таь) и абстрактное линейное преобразование Т будут использоваться взаимозаменя¬
емым образом, пока несущественны технические различия между этими двумя понятиями
(первое из них зависит от выбора определенных координат нашего векторного простран-
*• 1 • /
ства V, последнеене зависит).
j
X
а
*
Т\хь 'и *—С? STU
S f^J>S	v	)	I	I
ST
с &
т. е. хл—► Тх
а)	б)	в)
Рис. 13.6. а) Линейное преобразование ха Таъхъ9 записанное без индексов в виде ж ь-» Тх (или чи¬
таемое с индексами как абстрактное обозначение, см. § 12.8), в диаграммной форме, б) Диаграммы
для линейных преобразований S, Т, U и их произведений ST и STU. При перемножении несколь¬
ких сомножителей они располагаются сверху вниз, в) Дельта-символ Кронекера , или тождественное
преобразование I, изображается «бесформенной» линией, так что соотношения Таъбь — Тас = S^Tbc
в такой записи выполняются автоматически (см. также рис. 12.17)
Рассмотрим второе линейное преобразование 5, действующее вслед за Т. Произведе¬
ние R этих двух преобразований, записываемое как R — ST, будет иметь компонентное
(или абстрактно-индексное) обозначение
ра   о а пп
К с= D Ъ±
Ъ
с
(помните о соглашении относительно суммирования по повторяющимся индексам ком¬
понент!)**. Диаграммная форма произведения ST показана на рис. 13.66. Заметим,
что при диаграммном представлении произведения нескольких линейных преобразований
мы располагаем их в ряд сверху вниз. Такая запись оказывается удобной, при этом с одинако¬
вым успехом можно пользоваться различными соглашениями относительно горизонтально
нарисованных соединяющих «индексных линий». (Это устанавливает тесное соответствие
между алгебраическими и диаграммными обозначениями.)
Выпишите все эти соотношения полностью, объяснив, как они выражают соотношение ха н-»■
Какой вид будет иметь это соотношение между R, S и Т, если выразить его в явном виде через элементы
квадратной таблицы 3x3, составленной из компонент? Вы можете узнать здесь обычное правило «умножения
матриц», если вы с ним знакомы.

232
Глава 13
Тождественное линейное преобразование I имеет компоненты, записываемые обычно
в виде символа Кронекера 5% (здесь индексы обычно не записываются ступенькой), у кото¬
рого
если а = 6,
если афЪ,
так что мы имеем*
Таь6ьс = Тас = 5%ТЪС,
что совпадает с алгебраическими соотношениями Т1' = Т — IT. Квадратная матрица,
составленная из компонент <5£, содержит единицы на так называемой главной диагонали,
проведенной из верхнего левого угла в нижний правый угол. При п — 3 такая матрица
имеет вид
1
0
0
1
0 ,
0
0
1/
В диаграммном представлении мы просто изображаем символ Кронекера «бесформенной»
линией, при этом вышеприведенные алгебраические соотношения в такой записи выполня¬
ются автоматически (см. рис. 13.6в).
Линейные преобразования, отображающие все пространство в целом на область мень¬
шей размерности (подпространство) в этом пространстве, яазывгются^сингулярнымиt13-10).
Эквивалентным условием сингулярности преобразования Т является существование неко-
торого ненулевого вектора v, для которого
- Tv = 0.
Если преобразование несингулярно, то существует обратное преобразование , обозначае¬
мое Т”1, для которого выполняется равенство
ТТ~1 = 1= Т_1Т,
как и должно быть для обратной величины. В диаграммном представлении для этого обрат¬
ного преобразования можно получить явное выражение; см. рис. 13.7, где представле¬
ны полезные диаграммы для антисимметричных величин (так называемого тензора Леви-
Чивита) еа...с и еа "с (с нормировкой еа...с£а'"с = п\)9 которые уже применялись в § 12.7
(см. рис. 12.18)
Матричная алгебра (основы которой были заложены английским математиком и юри¬
стом Артуром Кэли в 1858 году)^13Л11 нашла широкое применение (например, в статистике,
инженерном деле, кристаллографии, психологии, вычислительной технике, не говоря уже
о квантовой механике). Она является обобщением алгебры кватернионов и алгебр Клиффор¬
да и Грассмана, изучаемых в §§ 11.3, 11.5, 11.6. Я буду использовать жирные прямые буквы
(А, В, С, ...) для обозначения таблиц, составленных из компонент, которые и образуют
матрицы (в отличие от абстрактных линейных преобразований, для которых используются
жирные курсивные буквы).
**
Проверьте.
Почему? Покажите, что так, в частности, обстоит дело, если таблица, составленная из компонент, содер¬
жит столбец, сплошь состоящий из нулей, или два одинаковых столбца. Почему это имеет место также в случае
двух одинаковых строк? {Подсказка: относительно этого последнего пункта см. изложенные ниже свойства опре¬
делителей.)	*
Покажите это, не используя явных выражений.
JSg Используя диаграммные соотношения, показанные на рис. 12.18, проверьте, что из этого определения
следует ГТ”1 = I = Т~гТ. {Подсказка: см. рис. 13.8.)

13.4. Определители и следы
233
Нв
Рис. 13.7. Матрица Т”1, обратная по отношению к несингулярной (п х п)-матрице Т, представлена
явно в диаграммной форме. Используется диаграммное представление антисимметричных величин
t»
Леви-Чивита £а...с и еа'"с (с нормировкой £а...сеа“‘с — п\), введенных в § 12.7 и изображенных
на рис. 12.18
Если ограничиться матрицами п х п с заданным значением п, мы получаем систему
записи операций сложения и умножения, в которой выполняются обычные алгебраические
правила:
•	.	S	•
.	А + В = В + А, А + (В + С) = (А + В) + С,	А(ВС) = (АВ)С,
А(В + С) = АВ 4- АС, (А + В)С = АС + ВС.
(Каждый элемент матрицы А Н- В есть просто сумма соответствующих элементов матриц А
и В.) Однако правило коммутативности умножения обычно не выполняется, так что в общем
случае АВ ф ВА. Кроме того, как мы видели, для ненулевой матрицы п х п не всегда
существует обратная ей матрица.
Следует отметить, что алгебраические правила распространяются также на прямоуголь¬
ные матрицы m х п, где га не обязательно равно п. Однако сложение матриц пп х п и р х q
определено лишь при га = р и п = q, а умножение — лишь при п — р; в результате умноже¬
ния получается матрица mxq. Такие обобщенные правила относятся также к рассмотренным
выше произведениям вида Тх, где «вектор-столбец» х понимается как матрица п х 1.
Общая линейная группа GL(n) есть группа симметрии n-мерного векторного простран¬
ства, она реализуется в явном виде как мультипликативная группа несингулярных мат¬
риц п х п. Если мы хотим подчеркнуть, что наше векторное пространство вещественно
и в наших матрицах фигурируют соответственно вещественные числа, то эта полная ли¬
нейная группа обозначается как GL(n, R). Можно рассматривать и комплексные простран¬
ства, тогда получается комплексная полная линейная группа GL(n, С). Каждая из таких
групп имеет нормальную подгруппу, обозначаемую соответственно SL(n, М) и SL(n, S)
или короче, если соответствующее поле (см. §16.1) R или С подразумевается, — SL(n);
это называется специальной линейной группой. Такие группы получаются, если ограни¬
читься матрицами, определитель которых равен нулю. К понятию определителя мы сейчас
переходим.
13.4.	Определители и следы
V*
Что такое определитель матрицы п х п? Это есть просто число, определяемое эле¬
ментами матрицы, которое обращается в нуль тогда и только тогда, когда матрица син¬
гулярна. В диаграммном представлении определитель удобно записывается в явном виде,
см. рис. 13.8 а. В индексной записи он равен
^eab-dTeaTfb...Thdeef...h,
♦
Объясните это и сформулируйте полные алгебраические правила для прямоугольных матриц.

234
Глава .13
d)
det
б)
1
л!
1
ft!
1
п!
Рис. 13.8. а) Диаграммное представление определителя det(Tab) — det T — |T|. б) Диаграмм¬
ное доказательство формулы det(ST) = det 5 det Т. Антисимметризующую черту можно ввести
в средний член, поскольку антисимметрия уже содержится в пересекаемых ею индексных линиях.
См. рис. 12.17, 12.18
где величины еа‘"d и ее...л
ровкой
антисимметричные тензоры (тензоры Леви-Чивита) с норми-
€а * « • d л
п\
1x2x3 х • * • х п); число индексов
для n-мерного пространства (напомним, что п! =
в каждом из наборов а... d и е... h равно п.
Определитель обозначается как det(Ta&) или det Т (или иногда | Т|, или так же, как
таблица, изображающая матрицу, но с вертикальными чертами вместо круглых скобок).
В частных случаях матриц 2 х 2 и 3 х 3 определитель вычисляется по следующим формулам :
det
а b
с d
ad — be,
a b e
det I d e. f
9 h
aej — afh 4- bfg — bdj 4 cdh — eeg
важным и довольно замечательным свойством
det(AB) — det A det В
*
справедливость которого видна из диаграммного представления (рис. 13.8 б). Основную роль
здесь играют формулы, иллюстрируемые рис. 12.18, которые в индексных обозначениях
принимают вид
(относительно обозначений со скобками и индексами см. § 11.6) и
Существует также понятие следа матрицы (или линейного преобразования) Tr Т,
ТгТ = Таа
Т\ -j-	2	4*	*	*	*	4"	Т
п
**
Выведите эти формулы из соотношений на рис. 13.8 а.
Объясните, почему это так.

&
13.5. Собственные значения и собственные векторы	235
т. е. суммы элементов, стоящих на ее главной диагонали
(см. § 13.3); в диаграммном представлении это показано на
рис. 13.9. В отличие от ситуации с определителями, не суще¬
ствует соотношения, связывающего след произведения двух
матриц АВ со следами матриц-сомножителей А и В. Вместо
этого имеет место соотношение*
I
Тг
Рис. 13.9. Диаграммное пред¬
ставление для ТгТ(— Таа)
Tr(A -f В) = Тг А 4 ТгВ.
;
Существует интересная связь между определителем и следом, относящаяся к опре¬
делителю «бесконечно малого» линейного преобразования, задаваемого матрицей пхп
вида I 4 еА, где число г рассматривается как бесконечно малая величина, так что можно
пренебречь ее квадратом е2 (а также более высокими степенями е3, с4 и т.д.). В этом случае
мы имеем
det(I + еА) = 1 4 е Тг А
(в пренебрежении е2 и т. д.). В частности, бесконечно малые элементы группы SL(n), т. е. эле¬
менты этой группы, представляющие бесконечно малые повороты, имея определитель, рав¬
ный 1 (в отличие от определителя элементов группы GL(n)), характеризуются тем, что
след матрицы А в выражении I 4 еА равен нулю. Важная роль этого факта будет показана
в §13.10. Вышеуказанное соотношение можно обобщить на случай конечных (то есть не
бесконечно малых) линейных преобразований в виде
***
А „Тг А
det е — е
где выражение еА для матриц определяется так же, как и для обычных чисел (см. § 5.3), т. е.
еА = I + А + | А2 + ±А3 + ^А4 +
Мы еще вернемся к этим понятиям в §§13.6, 14.6.
13.5.	Собственные значения и собственные векторы
К наиболее важным понятиям, связанным с линейными преобразованиями, относятся
так называемые «собственные значения» и «собственные векторы». Они играют жизненно
важную роль в квантовой механике (см. §§21.5, 22.1, 22.5), а также во многих областях
математики и ее приложений. Собственным вектором линейного преобразования Т на¬
зывается ненулевой комплексный вектор v, действие преобразования на который сводится
к умножению этого вектора на некоторое число. Другими словами, существует некоторое
комплексное число Л, называемое собственным значением, для которого
Tv = Xv, т.е. Tabvb = \va.
Это уравнение можно также записать в виде (Т — XI) v =0, так что, если Л есть собственное
значение преобразования Т, величина Т — XI должна быть сингулярной. И наоборот, если
величина Т — XI сингулярна, то Л есть собственное значение преобразования Т. Заметим,
 Покажите это.
**	Покажите это.
Докажите это соотношение.	(Подсказка:	Воспользуйтесь	«канонической	формой» матрицы,	выраженной
через ее собственные значения	(как	описано	в	§	13.5)	,	предполагая	вначале,	что	эти собственные	значения	не
равны между собой; используйте также результаты упражнения 13.27. Затем выведите из общих соображений, что
равенство между собой некоторых собственных значений не может нарушить тождества такого рода.)

236
Глава 13
что если v есть собственный вектор, то таковым же будет результат его умножения на любое
ненулевое комплексное число. Комплексное одномерное пространство таких множителей не
меняется под действием преобразования Т, это свойство характеризует v как собственный
вектор (рис. 13.10).
Рис. 13.10. Действие линейного преобразования Т. Его собственные векторы всегда образуют линей¬
ные пространства, проходящие через начало координат (в данном случае это три прямые). Эти про¬
странства не меняются под действием Т. (В данном примере имеются два (не равных между собой)
положительных собственных значения (стрелки направлены наружу) и одно отрицательное (стрелка
направлена внутрь))
• ^
Из вышеизложенного вытекает следующее условие того, что Л есть собственное значе¬
ние преобразования Т:
det(T — XI) — 0.
Раскрывая это выражение, мы получаем полиномиальное уравнение п-й степени относитель-
но Л. Согласно «основной теореме алгебры» (§4.2), полином det(T — XI) по степеням Л
можно разложить на линейные множители. Это приводит к уравнению
(Ai — А)(А2 — А)(Аз — А)... (Ап — А) — 0,
в котором комплексные числа Ai, А2, A3, ..., Ап представляют собой различные собствен¬
ные значения преобразования Т. В частных случаях некоторые из множителей могут совпа¬
дать между собой, тогда мы имеем кратное собственное значение. Кратность т собственно¬
го значения Аг — это число раз, которое множитель Аг — А встречается в вышеприведенном
произведении. Полное число собственных значений преобразования Т, подсчитанное с уче-
* *
том кратности, для матрицы п х п всегда равно п.
Для данного собственного значения А кратности г пространство соответствующих соб¬
ственных векторов образует линейное пространство размерности d, причем 1 < d ^ г.
Для некоторых типов матриц, включая унитарные, эрмитовы и нормальные матрицы, пред¬
ставляющие наибольший интерес для квантовой механики (см. §§ 13.9, 22.4, 22.6), это про¬
странство всегда имеет максимальную размерность d = г (несмотря на то что d— 1 является
наиболее «общим» случаем при заданном г). И это хорошо, потому что более общие слу¬
чаи, когда d < г, трудны для рассмотрения. В квантовой механике кратность собственных
значений называется вырождением (ср. §§22.6, 22.7).
Можете ли вы получить коэффициенты этого полинома в диаграммной форме? Сделайте это для случа-
ев п — 2 и п — 3.	.
Покажите, что det Т = Ai А2 • • • Ап и Тг Т = Ai + А2 Ч h Ап.

13.5. Собственные значения и собственные векторы
237
Базисом n-мерного векторного пространства V называется упорядоченное множе¬
ство е = (ei, ..., состоящее из п векторов ei, . -., еп, которые линейно независимы
в том смысле, что не существует соотношения вида aieH 1- апеп ~ 0, в котором не все
коэффициенты ai, ..., ап равны нулю. Тогда каждый элемент пространства V можно од¬
нозначным образом представить в виде линейной комбинации таких базисных элементов *.
Фактически это свойство определяет базис в более общем случае, когда пространство V
бесконечномерно, и условие линейной независимости само по себе не достаточно.
Таким образом, при заданном базисе е = (е*, ..., вп) любой элемент х пространства V
можно однозначным образом представить в виде
X
х1е1 +х2е2  Ь хп еп
X3 ej
(индексы j здесь не являются абстрактными), где (х1, х2, ..., хп) есть упорядоченное мно¬
жество компонент вектора х относительно базиса е (ср. § 12.3). Несингулярное линейное
преобразование Т всегда переводит один базис в другой; более того, если ей/— два задан¬
ных базиса, то существует единственное преобразование Т, переводящее каждый вектор е3
в соответствующий ему вектор f3:
r^ej = fj* '
Будучи выраженными через компоненты векторов е3 в базисе е, сами базисные эле¬
менты ei, е2, ..., вп принимают вид соответственно (1, 0, 0, ... , 0), (0, 1, 0, ..., 0), ...,
(0, 0, 0, ..., 1). Другими словами, компонентами вектора е3 служат символы Кронеке-
ра (5), 62у 6j, ..., 6™)** Если все компоненты берутся по отношению к базису е, то пре¬
образование Т представляется матрицей (Т% ) и компонентами вектора /? в базисе е будут
служить
(rpl гр2 . грЗ .	грп \
Напомним, что концептуальное различие между линейным преобразованием и матрицей
состоит в том, что последняя представляется в виде, зависящем от выбранного базиса, тогда
как линейное преобразование является абстрактным, не зависящим от базиса.
Если предположить, что каждое кратное собственное значение (если таковые имеют¬
ся) удовлетворяет условию d = г (т. е. размерность соответствующего пространства соб¬
ственных векторов равна кратности), то для векторного пространства V можно найти ба¬
зис (ei, ег, ..., еп), каждый элемент которого является собственным вектором преобразо-
*ф>	^	^
вания Т. Пусть соответствующими собственными значениями будут Ai, А2, ..., Ап:
Те 1	А^ е\,	Те2	А262) • • • >	Апвп*
Если, как и выше, Т преобразует базис е в базис /, то элементами базиса / будут f± —
= Aiei, /2 = А2в2, ..., fn — Ап&п- Следовательно, преобразование Т, отнесенное к бази-
су е, принимает вид диагональной матрицы
/Ai 0 ... 0 \
0 А2 ... 0
\ 0	0	...	Ап	/
Покажите это.
Объясните эту запись.
Почему? Какими будут компоненты вектора е* в базисе /?
Д85 Попробуйте доказать это. (Подсказка: для каждого собственного значения кратности г выберите г линейно
независимых собственных векторов. Покажите, что линейное соотношение между векторами всего набора приводит
к противоречию, если предварительно умножить это соотношение на Т.)
**
***

238
Глава 13
то есть Т1! = Ai, Т22 = А2, ..., Тпп — Хп, а остальные компоненты равны нулю. Такая
каноническая форма линейного преобразования оказывается весьма полезной как в концеп¬
туальном, так и в вычислительном отношении f13,12l.
• •'	• 1 /
13.6.	Теория представлений и алгебры Ли
Существует важная область идей (имеющая особое значение для квантовой теории)
под названием теории представлений групп. С очень простым примером представления
группы мы столкнулись в § 13.1, где было показано, что операции симметрии квадрата, не
содержащие отражений, можно представить комплексными числами, при этом группово¬
му умножению в точности соответствует обычное умножение комплексных чисел. Однако
в случае не абелевых групп не всё так просто, поскольку умножение комплексных чисел
коммутативно. В то же время линейные преобразования (или матрицы) обычно не коммути¬
руют, поэтому разумно попробовать использовать их для представления неабелевых групп.
И мы действительно уже сталкивались с подобным в начале § 13.3, где группа вращений 0(3)
представлялась линейными преобразованиями в трех измерениях.
Как мы увидим в главе 22, квантовая механика постоянно имеет дело с линейными пре¬
образованиями. Более того, в современной физике элементарных частиц имеют решающее
значение различные группы симметрии, в частности, группа вращений 0(3), группы сим¬
метрии теории относительности (глава 18) и группы симметрии, лежащей в основе разного
рода взаимодействия между частицами (глава 25). Поэтому неудивительно, что представле¬
ния этих групп, в частности, использующие линейные преобразования, играют фундамен¬
тальную роль в квантовой теории.
••
Оказывается, что квантовая теория (в частности, квантовая теория поля, излагаемая
в главе 26) часто имеет дело с линейными преобразованиями бесконечномерных пространств.
Здесь, однако, я для простоты буду говорить о представлениях линейными преобразованиями
в случае конечной размерности. Большинство идей, с которыми мы столкнемся, применимо
также и к бесконечномерным представлениям, хотя в некоторых случаях разница может
быть существенна.
Что же такое представление группы? Рассмотрим группу Q. Теория представлений за¬
нимается отысканием некоторой подгруппы группы GL(n) (т. е. мультипликативной группы
матриц п х п)9 обладающей тем свойством, что для каждого элемента g группы Q существует
соответствующее линейное преобразование Т(д) (принадлежащее группе GL(n)) такое, что
закон умножения в группе Q сохраняется в операциях группы GL(n), т. е. для любых двух
элементов д и h группы Q мы имеем
T(g)T(h) = T{gh)
Представление называется точным, если преобразование Т(д) отлично от T(h) всякий раз,
когда элемент д отличен от h. В таком случае мы имеем тождественную копию группы Q
в качестве подгруппы группы GL(n).
Фактически каждая конечная группа имеет точное представление в GL(n, R), где п —
порядок группы Q\ часто имеется также много неточных представлений. В то же время
отнюдь не обязательно, чтобы каждая (конечномерная) непрерывная группа имела точное
представление в некоторой группе GL(n). Однако если не заботиться о глобальных аспектах
данной группы, то локально представление всегда возможно^13 131
* Покажите это. (Подсказка: пометьте каждый столбец представляющей матрицы отдельным элементом
конечной группы Q, а также пометьте каждую строку соответствующим элементом. Поместите 1 в любое положение
в этой матрице, для которого выполняется некоторое соотношение (найдите его!) между элементом группы Q,
нумерующим строку, элементом, нумерующим столбец, и элементом группы Q, представляемым этой матрицей.
Если для данного положения в матрице это соотношение не выполняется, поместите туда 0.)

13.6. Теория представлений и алгебры Ли
239
Существует красивая теория, созданная глубоко оригинальным норвежским математи¬
ком Софусом Ли (1842-1899), которая дает полную трактовку локальной теории непрерыв¬
ных групп. (Поэтому непрерывные группы обычно называют «группами Ли», см. § 13.1.)
Эта теория основана на изучении бесконечно малых элементов групп [13Л41. Такие беско¬
нечно малые элементы определяют некоторый вид алгебры — так называемую алгебру Ли,
которая дает полную информацию относительно локальной структуры группы. Хотя алгебра
Ли, возможно, и не дает сведений о глобальной структуре группы, это обычно считается не
столь важным.
Что такое алгебра Ли? Пусть матрица (или линейное преобразование) I 4- еА пред¬
ставляет «бесконечно малый» элемент а некоторой непрерывной группы Q, где е считается
«малой» величиной (сравните со сказанным в конце § 13.4). Если построить произведение
матриц I 4- в А и I 4- еВ, представляющее произведение ab двух таких элементов а и 6,
мы получим
(I + eA)(I 4- еВ) — Г + е(А + В) + е2АВ
= 1 + е(А + В)
при условии, что величиной е2 можно пренебречь как «слишком малой». В соответствии
с этим сумма матриц A f В представляет групповое произведение ab двух бесконечно малых
элементов а и Ъ.
Операция суммирования представляет часть алгебры Ли для величин А, В, Но сум¬
ма коммутативна, тогда как группа Q может быть неабелевой, поэтому мы не сможем ухва¬
тить многое из структуры группы, если будем рассматривать только суммы (фактически они
говорят лишь о размерности группы Q). Неабелева природа группы Q проявляется в группо¬
вых коммутаторах*
аЪа~1Ь~~1.
Выразим это через 14- еА и т. д., используя разложение в степенной ряд (J 4- еА) “1 = I —
— еА 4- е2А2 — е3А3 + • * • (это разложение легко проверить, умножив обе части равенства
на I 4- еА). Теперь отбросим как «слишком малую величину» г3, сохранив, однако, е2
Тогда
(1 + еА)(1 + еВ)(1 + £А)-1(1 + еВ)-1 =
- (J + sA)(I + еВ){1 -еА + e2A2)(I -el3 + е2В2) =
= I + е2{АВ - ВА).
Отсюда видно, что, если мы хотим проследить, каким именно образом группа Q становится
неабелевой, мы должны рассмотреть «коммутаторы», или скобки Ли
[А, В] = АВ — ВА.
Алгебра
также умножение
(которые могут быть как вещественными, так и комплексными). «Дополнительны?
том алгебры является обычная структура векторного пространства (как и в случа
нионов, см. § 11.1). Кроме того, скобки Ли обладают свойством дистрибутивности
[А 4- В, С] - [А, С) + [.В, С], [ХА, В} - А [А, В],
свойством антисимметрии
[А, В -[В, А]
**
Почему это выражение становится единичным элементом группы, когда а и b коммутируют?
Проверьте этот расчет «во втором порядке по е».

240
Глава 13
(откуда следует также [А, С + D] — [А, С] + [А, D], [А, АВ] = А[А,-В]), а также удовле¬
творяют изящному соотношению, известному под названием тождества Якоби":
& ^	•
• • • •
[Д, [В, С]] + [В, [С, А}} + [С, [А, В}} = 0
(с более общей формой которого мы встретимся в § 14.6).
Для векторного пространства наших матриц А, В, С,... можно выбрать базис (JEq,
Да, ... JSjv) (где Аг есть размерность группы если представление точное). Формируя
из элементов базиса различные коммутаторы [Е&, Ер] и выражая их через базисные эле-
менты, получаем (с учетом соглашения о суммировании по повторяющимся индексам)
[Д*, Ер] = уархЕх.
N3-компонентные величины 7ар х называются структурными константами группы Q.
Они не являются взаимно независимыми, поскольку удовлетворяют соотношениям (по по¬
воду скобочных обозначений см. § 11.6)
7осЦ Х = -7/За Х, 7[а/3 7*]£ С = 0
в силу условия антисимметрии и тождества Якоби . На рис. 13.11 эти соотношения пред¬
ставлены в диаграммной форме.
7а/?Х
6) JL \	=0,	т.	е.
Рис. 13.11. а) Структурные константы 7арх в диаграммной форме, отображающей антисимметрию
по а, /3 и б) тождество Якоби
Замечательным фактом является то, что знания структуры алгебры Ли для точного
представления (то есть, по существу, структурных констант 7ар х) оказывается достаточно
для определения точной локальной природы группы Q. «Локальная» означает здесь, что
рассматривается (достаточно малая) iV-мерная открытая область N, окружающая единич¬
ный элемент I в «групповом многообразии» Q, точки которого представляют различные
элементы группы Q (см. рис. 13.12). Более того, исходя из некоторого элемента А груп¬
пы Ли можно построить соответствующий конечный (т. е. не бесконечно малый) групповой
элемент с помощью операции «потенцирования» еА, определенной в конце § 13.4. (Несколь¬
ко подробнее это будет рассмотрено в § 14.6.) Таким образом, теория представлений групп
линейными преобразованиями (или матрицами) может быть в значительной степени перене¬
сена на теорию представлений алгебр Ли такими преобразованиями, — в физике это обычная
процедура.
**
Докажите всё это.
Покажите это.

13.7. Тензорные пространства представлений. Приводимость
241
Это особенно важно в квантовой механике, где
часто сами элементы алгебры Ли замечательным об¬
разом интерпретируются непосредственно как физи¬
ческие величины (например, угловой момент, когда б
есть группа вращений; это будет показано в § 22.8).
Матрицы алгебры Ли обычно имеют гораздо бо¬
лее простую структуру, чем соответствующие матрицы
группы Ли, поскольку подчиняются не нелинейным,
а линейным ограничениям (для случая классических
групп это рассмотрено в § 13.10). Физики очень любят
пользоваться ими!
Рис. 13.12. Алгебра Ли для (точно¬
го) представления группы Ли Q (по
существу, знание структурных кон-
Ч
стант 7арх) определяет локальную
структуру группы Q, т. е. фиксирует
структуру группы б в некоторой (до¬
статочно малой) открытой области Л/*,
окружающей единичный элемент I, но
ничего не говорит о глобальной приро¬
де группы Q
13.7.	Тензорные пространства
представлений. Приводимость
Существуют способы построения более сложных
представлений группы б исходя из некоторого част¬
ного представления. Как это сделать? Пусть группа б
представляется некоторым семейством линейных пре¬
образований Т, действующих на n-мерное векторное
пространство V. Пространство V называют простран¬
ством представлений группы б- Любой элемент t группы б теперь представляется соот¬
ветствующим линейным преобразованием Т из семейства Т, которое производит отобра¬
жение х 1—> Тх для каждого вектора ж, принадлежащего пространству V. В (абстрактной)
индексной записи (см. § 12.7) это имеет вид ха н-> Таьхь, как в § 13.3, или в диаграммной
форме, как на рис. 13.6а. Посмотрим, как можно найти другие пространства представлений
для б исходя из данного пространства V.
В качестве первого примера напомним (см. § 12.3) определение дуального простран¬
ства V* по отношению к V. Элементы пространства V* определяются как линейные отобра¬
жения элементов пространства V на скаляры. Действие элемента у из V* на элемент ж из V
в индексных обозначениях (§ 12.7) можно записать в виде уа%а* Ранее (§ 12.3) использова¬
лась также запись у * х (у • х..= уаха), но теперь мы можем также пользоваться матричной
записью
Ух
УаХа,
где у рассматривается как вектор-строка (т. е. матрица 1 х п), а х - как векюр-столбец
(матрица п х 1). В соответствии с нашим преобразованием х Тх, понимаемым теперь
как преобразование матриц, дуальное пространство V* подвергается линейному
зованию
У yS, т. е. Уа ^ VbSba,
где S есть преобразование, обратное преобразованию Т:
S=T
так что SabT
Sac
(поскольку если х »—> Тх, то необходимо у s—> уТ”1, чтобы обеспечить сохранение произ¬
ведения ух при отображении н-»).
Использование выше вектора-строки у приводит нас к нестандартному порядку умно¬
жения. Более привычный порядок записи получается при использовании матрицы Ат,
транспонированной по отношению к А. Матрица Ат содержит те же элементы, что и А,
но строки и столбцы в ней меняются ролями. Если матрица А квадратная (пх п), то такой

242
Глава 13
же будет и матрица Ат; она получается из А путем отражения всех элементов в главной
диагонали (см. § 13.3). Если матрица А прямоугольная (га х п), то матрица Ат, отраженная
соответствующим образом, будет иметь вид п х га. Тогда уТ есть обычный вектор-столбец,
и мы можем записать вышеприведенное соотношение у ь-* yS в виде
УТ *-* STyT,
поскольку операция транспонирования 1 меняет порядок умножения на обратный: (АВ)
— ВТАТ. Таким образом, мы видим, что дуальное пространство V* любого простран¬
ства представлений V само является пространством представлений группы Q. Заметим, что
операция перехода к обратной матрице -1 также меняет порядок умножения, (АВ)-1 =
== В“1А“1,* благодаря чему восстанавливается необходимый для представления порядок
умножения.
Соображения такого же рода применимы и к различным векторным пространствам
тензоров, построенных на основе векторного пространства V (см. § 12.8). Напомним, что
тензор Q валентности [р] (на векторном пространстве V) в индексной записи имеет вид
af
т
Qt:
h
с
**
с q нижними и р верхними индексами. Тензоры можно складывать с другими тензорами
той же валентности, а также умножать их на скаляры; тензоры заданной валентности [v]
образуют векторное пространство размерности пр+9, равной полному числу компонент
В абстрактном смысле, можно считать, что Q принадлежит некоторому векторному про¬
странству, которое мы представим в виде тензорного произведения
V* <g> V* 0 ... О V* 0 V О V О ... 0 V,
составленного из q копий дуального пространства V* и р копий пространства V (р, q > 0).
(Мы рассмотрим понятие «тензорного произведения» подробнее в § 23.3.) Напомним данное
в § 12.8 абстрактное определение тензора как полилинейной функции (для наших нынешних
целей этого будет достаточно, хотя имеются некоторые тонкости в случае бесконечномер¬
ного пространства V в связи с применением к многочастичным квантовым состояниям
в §23.8)113-15'.
Применение линейного преобразования ха Таьхь к пространству V приводит к со-
ответствующему линейному преобразованию упомянутого пространства тензорного произ-
ведения, явный вид которого дается следующим выражением :
• •	.
Qt.c -> 5й'а • • • Sc'cTff,... Thh,Qp;;hP
t
Все эти индексы требуют хорошего зрения и внимательного отношения, чтобы четко пони¬
мать, что с чем суммируется; поэтому я рекомендую пользоваться более ясным диаграммным
представлением, показанным на рис. 13.13. Видно, что каждый нижний индекс у Q;; пре¬
образуется обратной матрицей S = Т-1 (или, что то же самое, ST) как связанный с уа,
а каждый верхний индекс — матрицей Т как связанный с ха. Соответственно простран¬
ство [р ]-валентных тензоров на пространстве V также является пространством представле-
* *
ний группы Q размерности пр+я.
***
Почему?
Откуда берется это число?
Покажите это.

13.7. Тензорные пространства представлений. Приводимость
243
Рис. 13.13. Линейное преобразование ха ^ Таъхъ, действующее на вектор х в векторном простран-
стве V (преобразование Т изображено в виде светлого треугольника), распространяется на дуальное
пространство V* с помощью обратного преобразования S = Т-1 (показано в виде темного тре¬
угольника) и далее на пространства V* 0 ... 0 V* 0 V 0... 0 V [р ]-валентных тензоров Q. Показан
ж
случай р = 3, q — 2. Тензор Q, изображенный в виде овала с тремя «руками» и двумя «ногами»,
подвергается преобразованию Qabcde	Sa'aSb'ьТ°c>TddtTee/.Qa*v c d e
Такие пространства представлений чаще всего являются так называемыми приводимы
ми пространствами. Чтобы проиллюстрировать ситуацию, рассмотрим [^-валентный тен
зор Qab. Любой такой тензор можно разбить на симметричную часть Q(ab^ и антисиммет
ричную часть Qla4 (см. §§ 12.7, 11.6):
♦
Qab = Q(ab) + д[«Ч
где
Q(a,b) = I (Qab + Qba^ Q[ab} = 1 (Qab _ Qbay
1
Размерность симлштричного пространства V+ равна ~п{п 4* 1), размерность антисим¬
метричного пространства V_ равна ~п(п — 1).* Нетрудно видеть, что при преобразова¬
нии ха Таъхъ, когда Qab н-» TacTbdQcd, симметричная и антисимметричная части пре-
«fc ijc
образуются в тензоры, опять-таки соответственно симметричный и антисимметричный
В соответствии с этим пространства V+ и V_ будут, каждое в отдельности, пространствами
1
представлений группы Q. Выбирая для пространства V базис, в котором первые -n(n + 1)
элементов берутся из V+, а остальные ~п(п — 1) — из V_, мы получаем представление,
в котором все матрицы имеют «блочно-диагональную» форму п2 х п2:
А О
О В
где А есть матрица |n(n + 1) х ~п(п -f 1), В — матрица ^п(п — 1) х -n(n — 1), а две
матрицы О обозначают подходящие по размеру прямоугольные блоки, состоящие из нулей.
Представление такого вида называют прямой суммой представления, задаваемого
матрицами А, и представления, задаваемого матрицами В. В этом смысле представле-
**
Покажите это.
Объясните это.

244
Глава 13
ние, задаваемое [^-валентными тензорами, является приводимым*. Понятие «прямой сум¬
мы» применимо также к любому (возможно, и бесконечному) числу меньших представ¬
лений.
Термин «приводимое представление» фактически имеет более общий смысл, а имен¬
но приводимость означает возможность такого выбора базиса, при котором все матрицы
представления можно представить в несколько более сложном виде
где А есть матрица р х р, В — матрица q х q и С — матрица р х q, при этом р, q ^ 1 (числа р
и q заданы). Если все матрицы представления имеют такой вид, то матрицы А и В, каждая
в отдельности, образуют (меньшее) представление группы Q** Если все матрицы С равны
нулю, то мы получаем предыдущий случай, когда представление является прямой суммой
двух меньших представлений. Представление называется неприводимым, если его нельзя
привести к указанному виду (с матрицей С или без нее). Представление называется вполне
приводимым, если такая ситуация невозможна (при ненулевой матрице С) и оно является
U	V/	о
прямой суммой неприводимых представлении.
Существует важный класс непрерывных групп, именуемых полупростыми группами.
Этот интенсивно изучаемый класс включает простые группы, упомянутые в § 13.2. Компакт¬
ные полупростые группы обладают тем привлекательным свойством, что все их представ¬
ления вполне приводимы. (Относительно определения компакта эсти см. § 12.6, рис. 12.12.)
Поэтому достаточно изучить неприводимые представления такой группы, при этом каждое
представление будет просто прямой суммой этих неприводимых представлений. Каждое
неприводимое представление такой группы будет иметь конечную размерность (не так об¬
стоит дело в случае некомпактной полу про стой группы, когда могут появиться не вполне
приводимые представления).
Что такое полупростая группа? Напомним о «структурных константах» уар х (§ 13.6),
которые входят в определение скобок Ли и определяют локальную структуру группы Q. Су¬
ществует важная величина^1316!, называемая формой Киплинга к, которую можно построить
*4,	***
из 7^*:
Ка/3 = 'УаС, ** = К/За*
Диаграммное представление этого выражения показано на
рис. 13.14. Условие того, что группа Q является полупростой,
Форма	/ К	состоит в несингулярности матрицы кар.
Киллинга: I I /	\	Следует	сделать	некоторые	замечания	относительно
условия компактности полупростой группы. При заданном
наборе структурных констант х и предположении, что
Рис. 13.14. «Форма Киллин-	в качестве таковых можно взять вещественные числа, мы
га» кар, связанная со структур-	можем рассматривать как вещественную, так и комплексную
ными константами 7«/зх соот-	^aireQpy ди? получаемую из них. В случае комплексной ал-
ношением — 7аС 7/?£	гебры мы не получаем компактную группу Q, но в случае
вещественной алгебры получить компактную группу мож¬
но. Реально компактность в последнем случае получается, когда величина — кра положи¬
тельно определена (смысл этого термина будет разъяснен в § 13.8). При заданных гуссрх
Покажите, что пространство представлений [ * j -валентных тензоров также приводимо. (Подсказка: раз¬
бейте каждый такой тензор на части с нулевым и ненулевым следом.)
Подтвердите это.
т Почему = крср
**
***

13.8. Ортогональные группы
245
в случае вещественной группы Q мы всегда можем построить (по крайней мере, локально)
комплексификацию СQ группы Q, которая получается путем использования тех же самых
констант 7х, но с комплексными коэффициентами данной алгебры Ли. Однако различ¬
ные вещественные группы Q могут иногда приводить к одной и той же группе C(/J13,171
Такие различные вещественные группы называют различными вещественными формами
комплексной группы. Важные примеры этого мы найдем в последующих главах, в частно-
*	*	•"	*	•	•	.	•	.	•	,	а	I	•	...
сти, в § 18.2, где сравниваются евклидовы движения в четырех измерениях и симметрии
Лоренца - Пуанкаре в специальной теории относительности. Замечательным свойством лю¬
бой комплексной полупростой группы Ли является то, что она имеет ровно одну компактную
вещественную форму Q.
13.8.	Ортогональные группы
Вернемся теперь к понятию ортогональной группы. В начале § 13.3 мы уже видели,
как построить точное представление группы 0(3) или S0(3) линейными преобразованиями
трехмерного вещественного векторного пространства с обычными декартовыми координа¬
тами (х, у, z), оставляющими неизменной сферу
х2 + у2 + z2 = 1
(верхний индекс 2 в данном случае
уравнение в индексных обозначени
Уравнение нашей сферы примет вщ
9аЪХаХЪ
1,
что означает (ж1)2 Н	Ь (хп)2	= 1; компоненты даъ определяются следующим образом:
.п\2
9аЪ
при а = Ь,
при а^Ъ.
В диаграммной записи я рекомендую изобра¬
жать даь в виде арки, как показано на рис. 13.15а.
Я буду использовать также обозначение даЬ (с тем
же явным видом компонент, что и у даъ) для обрат¬
ной величины («опрокинутой арки» на рис. 13.15а):
9ab9
Ъс
а
gCb9ba
Недоумевающий читатель может задать вполне
резонный вопрос: почему я использую две новые
величины, даь и даЪ, для совершенно одинаковых
компонент матрицы, обозначенных <5% в § 13.3? Это
связано с необходимостью согласованной записи
и с тем, что получается, когда линейное преобра¬
зование применяется к координатам, приводя к за¬
мене
ха tabXb.
а) 9аь
п,
б)
аЪ
9
Рис. 13.15. а) Метрический тензор даъ
и обратный ему даЬ в диаграммной запи¬
си с «арками», б) Соотношения даъ = 9ьа
(т.е. д
т
д\ 9
ab
9Ьа и даЬдЬс
5
а
в диаграммной записи
•V

246
Глава 13
Если tab
улярная
t\s
Sa
С
sabt'
Формально это тот же самый вид линейного преобразования, который мы рассматривали
в §§ 13.3,13.7, однако теперь мы понимаем его совсем по-иному. В тех разделах наше линей¬
ное преобразование считалось активным, так что векторное пространство V рассматрива¬
лось как движущееся^нутри самого себя). Здесь же мы считаем преобразование пассивным
в том смысле, что рассматриваемые объекты (и, конечно, само векторное пространство V)
остаются поточечно фиксированными, а меняется их координатное представление. Другими
словами, тот базис (ei, ..., еп), который использовался раньше (для выражения векторных
и тензорных величин через их компоненты^13 181), теперь должен быть заменен некоторым
другим базисом (см. рис. 13.16).
Рис. 13.16. Пассивное преобразование в векторном пространстве V оставляет это пространство пото¬
чечно фиксированным, но изменяет его координатное описание, т. е. базис ei, в2, ..., Сп заменяется
некоторым другим базисом (рассматривается случай п = 3)
В точном соответствии с тем, что говорилось в § 13.7 относительно активного преобра¬
зования тензора, мы находим, что соответствующее пассивное изменение компонент
тензора Q описывается соотношением
QpZr *V • • tcfQ p ...
Применив это преобразование к тензору мы увидим, что его компоненты остаются неиз-
менными , тогда как в случае даь дело обстоит иначе. Более того, в результате такого
изменения координат компоненты матрицы даЬ в общем случае будут совершенно отличны
от компонент обратной матрицы даь• Таким образом, причина использования двух симво¬
лов даЬ и даь состоит просто в том, что они, как и <5^, могут представлять одну и ту же
матрицу компонент лишь в определенной координатной системе (в декартовых координа¬
тах), а в общем случае компоненты будут совершенно различны. Это обстоятельство имеет
особо важное значение в общей теории относительности, где система координат обычно
не может быть приведена к такой специальной (декартовой) форме.
В общем случае изменение координат может придать матрице компонент даь более
сложную форму, хотя и не самого общего вида. Она сохраняет симметрию между индекса¬
ми а и 6, оставаясь симметричной матрицей. Термин «симметричная» означает, что квад¬
ратная таблица, составленная из компонент, обладает симметрией относительно ее главной
Чтобы доказать это, воспользуйтесь примечанием 13.18.
Почему?

13.8* Ортогональные группы
247
диагонали, т.е. gT — g (используется обозначение транспонированной матрицы из § 13.7).
В индексной записи такая симметрия выражается в одной из двух эквивалентных* форм:
'•	_	  ~	„аЬ	_ .Ъа
9ab — 9bay 9	— 9
•	*	•	**	.	•	I	(	*	*
Диаграммная форма этих соотношений показана на рис. 13.15 б.
Как обстоит дело с обратным утверждением? Можно ли любую несингулярную веще¬
ственную симметричную матрицу пхп свести к компонентной форме дельта-символа Кро-
некера? Оказывается, нет — с помощью вещественного линейного преобразования координат
это можно сделать не всегда. Можно лишь привести матрицу к такому виду, что на главной
диагонали будет стоять некоторое число элементов 1 и некоторое число элементов —1. Число
р элементов, равных 1, и число q элементов, равных —1, являются инвариантами, то есть мы
не сможем получить какое-то другое число, взяв некоторое другое вещественное линейное
преобразование. Этот инвариант (р, q) называется сигнатурой матрицы g. (Иногда сигнату¬
рой называют разностьp—q, иногда просто пишут +.. .4— ... — с соответствующим числом
плюсов и минусов.) Фактически это применимо также к сингулярной матрице g, но тогда
на главной диагонали появляются также нули, и число нулей становится частью сигнатуры
наряду с числом элементов 1 и —1. Если на главной диагонали находятся только элемен¬
ты 1, так что матрица g несингулярна и q — 0, то говорят, что эта матрица положительно
определена. Несингулярная матрица g, у которой р — 1 и q ф 0 (или q = 1 и р ф 0), назы¬
вается лоренцевой в честь голландского физика Г. А. Лоренца (1853-1928), работы которого
заложили один из краеугольных камней теории относительности; см. §§ 17.6-17.9,18.1-18.3.
Альтернативное определение положительно определенной матрицы А, играющее важ-
ную роль в некоторых других контекстах (см. §§20.3, 24.3, 29.3), состоит в том, что веще¬
ственная симметричная матрица А должна удовлетворять условию
хтАх >0
для всех х ф 0. В индексной записи это означает, что Ааъхахь > 0, если вектор ха не равен
нулю . Матрица А называется неотрицательно определенной (или положительно полу-
определенной), если в предыдущем определении заменить > на > (так что теперь возмож¬
но хт Ах — 0 для некоторых ненулевых х).
В подходящих обстоятельствах симметричный несингулярный [ 2 ] -тензор даь называют
метрическим (или иногда псевдометрическим, если матрица g не является положительно
определенной). Такая терминология применяется, если нам приходится использовать ве¬
личину ds, определенную своим квадратом ds2 = gabdxadxb, которая позволяет ввести
понятие «длины», отсчитываемой вдоль некоторой кривой. В § 14.7 мы увидим, как при¬
меняется это понятие к искривленным многообразиям (см. §§ 10.2, 12.1, 12.2), а в § 17.8 —
как в лоренцевом случае оно дает меру «расстояния», которое в действительности есть время
теории относительности. Иногда мы будем называть величину
I
«| =	(9abVaVb)2
длиной вектора v9 имеющего индексную форму va.
Вернемся к определению ортогональной группы О(п). Это есть просто группа ли¬
нейных преобразований в п измерениях (называемых ортогональными преобразованиями),
которые сохраняют данную положительно определенную матрицу g. «Сохранение» g озна¬
чает, что ортогональное преобразование Т должно удовлетворять соотношению
9abTacTbd — gcd.
Почему эквивалентных?
** л Попробуйте обосновать это определение.

248
Глава 13
Это есть пример применения к даъ правила (активного) преобразования тензоров, описан-
• 4 • •
ного в § 13.7 (см. также диаграммную запись этого соотношения на рис. 13.17). Другая
формулировка состоит в том, что метрическая форма ds2 из предыдущего абзаца остает¬
ся неизменной при ортогональном преобразовании. Мы можем, при желании, считать, что
компонентами даъ служит дельта-символ Кронекера (это в конечном счете приводит к опре¬
делению группы О(п), данному в §§ 13.1, 13.3), но группа оказывается одной и той же!13*19!
независимо от того, какая положительно определенная матрица пх п выбрана нами в каче¬
стве Qab-
ортогонально, ^
если
***
Рис. 13.17. Т есть ортогональное преобразование, если даъТасТъа = gcd
При выборе в качестве компонент даъ символа Кронекера матрицы, описывающие наши
ортогональные преобразования, должны удовлетворять условию
т-1 = Тт;
они называются ортогональными матрицами. Вещественные ортогональные матрицы пх п
обеспечивают конкретную реализацию группы О(п). Чтобы перейти к группе SO(n) без от¬
ражений, потребуем, чтобы определитель был равен единице
• •*	•
det Т — 1.
Можно также рассмотреть соответствующие псевдоортогоналыше группы О (p. q)
и SO(р, д), которые получаются, когда матрица g хотя и несингулярна, но не обязатель¬
но положительно определена и имеет более общую сигнатуру (р, д). Случай, когда р = 1
и q = 3 (или, что эквивалентно, р — 3 и q ~ 1), называется группой Лоренца и играет
фундаментальную роль в теории относительности, как уже отмечалось выше. Можно также
показать, что (если игнорировать временные отражения) группа Лоренца есть то же самое,
что и группа симметрии гиперболического 3-пространства, описанного в § 2.7, а также (если
игнорировать пространственные отражения) группа симметрии сферы Римана, получаемой
в результате билинейных преобразований (преобразований Мёбиуса), рассмотренных в § 8.2.
Лучше будет отложить объяснение этих замечательных фактов до исследования геометрии
пространства-времени Минковского в специальной теории относительности (§§ 18.4, 18.5).
В § 33.2 мы увидим также, что эти факты имеют решающее значение для теории твисторов.
Насколько «различны» разные группы О(p,q) при заданном значении числа n—р+д?
(На рис. 13.18 противопоставляются случаи положительно определенной и лоренцевой мат¬
риц для п = 2 и п = 3.) Они тесно связаны, поскольку все имеют одинаковую размер¬
ность ~п(п — 1) и являются вещественными формами одной и той же комплексной груп-
пы О(п, С), которая является комплексификацией группы О(п). Эта комплексная группа
определяется так же, как и О(п) О(n, М)), но линейное преобразование может быть
и комплексным. Хотя в этой главе я излагал свои соображения в терминах вещественных ли¬
нейных преобразований, возможно параллельное обсуждение, в котором слово «веществен¬
ная» заменяется словом «комплексная» (так что координаты ха становятся комплексными,
* Jll Объясните почему.
** ЛШ Объясните это. Чему равна матрица Т~1 для псевдоортогональной матрицы Т (определенной в следу¬
ющем абзаце)?
» Объясните, почему это эквивалентно сохранению формы объема, определяемой величиной £а...с,
т. е. €а...сТар ... Т°г = £р...г? Почему достаточно сохранения ее знака?
***

13.8. Ортогональные группы
249
/Ж
S?; * •
’л/
•аь\
л)
б)
W-
Рис. 13.18. а) Противопоставляются группы 0(2, 0) и 0(1, 1). б) Аналогичное противопоставле¬
ние групп 0(3, 0) и 0(1, 2); в обоих случаях показана «единичная сфера». Для группы 0(1, 2)
(см. §§2.4, 2.5, 18.4) такой «сферой» служит гиперболическая плоскость (или две ее копии)
и то же относится к компонентам матриц). Единственная существенная разница, как мы ви¬
дели, связана с понятием сигнатуры. Существуют комплексные линейные преобразования
координат, которые могут преобразовать —1 в диагональной реализации матрицы даъ в +1
и наоборот*, поэтому теперь у нас нет осмысленного понятия сигнатуры. В комплексном
случае единственным инвариантом I13*20! матрицы g является так называемый ранг — коли¬
чество отличных от нуля членов в ее диагональной реализации. У несингулярной матрицы g
ранг должен быть максимальным, т. е. равным п.
Когда различие между такими разными вещественными формами оказывается суще¬
ственным? Это может оказаться тонким вопросом, однако физики зачастую игнорируют
подобное различие, хотя оно и может оказаться важным. Положительно определенные мат¬
рицы имеют то преимущество, что им соответствуют компактные группы и их матема¬
тическое описание проще (см. § 13.7). Некоторые непринужденно переносят результаты,
полученные для компактных групп, на некомпактные группы (р ф О Ф q), но это часто ока¬
зывается неоправданным. (Например, в случае компактных групп необходимо иметь дело
только с конечномерными представлениями, тогда как в случае некомпактных групп воз¬
никают дополнительные бесконечномерные представления.) С другой стороны, существуют
и другие ситуации, когда можно достигнуть значительного продвижения, игнорируя указан¬
ные различия. (Можно сравнить это с выводом формулы Ламберта, выражающей площадь
гиперболического треугольника через его углы, в § 2.4. Эта формула была получена в пред¬
положении, что сфера может иметь мнимый радиус. В § 18.4 (см. рис. 18.9) я постараюсь
показать, что применение подхода Ламберта к неевклидовой геометрии вполне оправданно.)
Различные возможные вещественные формы группы 0(п, С) характеризуются с помо¬
щью некоторых систем неравенств, которым должны удовлетворять матричные элементы
Почему?

250
Глава 13
(например, det Т > 0), Отличительной чертой квантовой теории является то, что такие
неравенства часто нарушаются в физических процессах. Например, мнимые величины мо¬
гут, в некотором смысле, иметь физически реальный смысл в квантовой механике, так что
,% *
разница между различными сигнатурами становится несколько размытой. С другой сто¬
роны, по моим впечатлениям, физики зачастую относятся к подобным проблемам менее
внимательно, чем следовало бы. В действительности этот вопрос окажется для нас весьма
существенным при изложении ряда современных теорий (§§28.9, 31.13, 32.3). Но об этом
позже. Это тот самый запутанный вопрос, о котором я уже упоминал (§ 11.2)!
13.9.	Унитарные группы
Группа О (гг, ^) дает нам один из способов обобщения понятия «группы вращений»
с вещественных чисел на комплексные. Но есть и другой способ, который в некоторых
случаях имеет еще большее значение. Этот способ связан с понятием унитарной группы.
Что означает «унитарная»? Ортогональная группа связана с сохранением квадратич¬
ной формы, которая записывается в виде даьхахь или, что эквивалентно, xTgx. В случае
унитарной группы используются комплексные линейные преобразования, которые теперь
сохраняют эрмитову форму (названную в честь видного французского математика XIX века
Шарля Эрмита (1822-1901)).
Что такое эрмитова форма? Вернемся к случаю ортогональных групп. Вместо квадра¬
тичной формы (от х) мы с тем же успехом можем взять симметричную билинейную форму
•т.	•
(от £ и у)
д(х, у) = 9аьхауь = X^gy.
Она получается как частный пример данного в § 12.8 определения тензора через «поли¬
линейную функцию», примененного к -тензору д (полагая у = ж, мы возвращаемся
к вышеупомянутой квадратичной форме). Симметрия тензора д выражается в виде
9(х,у) = д(у,х),
а линейность по второй переменной у — в виде
д(х, у + w) =	д(х, у) +	д(х,го),
В случае билинейности требуется также линейность по первой переменной ж, но теперь
это следует из условия симметрии.
Эрмитова форма /г(ж, у) удовлетворяет вместо этого условию эрмитовой симметрии
h(x, у) = Ыу, х)
и условию линеиности по второй переменной у
/г(ж, у + w) — h(x, у) + h(x, w), h(x, Ху) — А/г(ж, у).
Эрмитова симметрия предполагает теперь так называемую антилинейностъ по первой пе-
О
ременной:	_
h(x +	w, у) = h(x, у) +	h(w, у),
В то время как ортогональная группа сохраняет (несингулярную) симметричную билиней¬
ную форму, комплексные линейные преобразования, сохраняющие несингулярную эрмитову
форму, дают нам унитарную группу.
А что дают нам такие формы? Несингулярная (не обязательно симметричная) били¬
нейная форма д дает нам средство для определения векторного пространства V, которому

13.9. Унитарные группы
251
принадлежат векторы ж и у, а также дуального пространства V*. Таким образом, если v
принадлежит V, то #(г;, ) дает линейное отображение на V, отображая элемент ж из V
на число g(v, ж). Другими словами, g(v, ) есть элемент пространства V* (см. § 12.3). В ин¬
дексной форме такой элемент имеет вид ковектора Vagab, который обычно изображается
той же буквой г;, но с индексом (см. также § 14.7), опущенным с помощью gab:
• *	\ •
4 = vagab.
Операция, обратная этой, получается путем поднятия индекса у с помощью обратного
метрического [jj] -тензора даЬ:
va = gabvb.
* : ,• ' , ••
Далее нам понадобится аналог этих соотношений для эрмитовых форм. Как и прежде,
каждый выбор элемента v векторного пространства V дает нам элемент h(v, ) дуального
пространства V*. Различие, однако, состоит в том, что теперь h(v, ) зависит от v не линейно,
а антилинейно, так что h(\v, ) = \h(v, ).
Можно также сказать, что величина h(v, ) линейна по гГ, где векторная величина v
является комплексно-сопряженной по отношению к v. Мы примем, что такие комплекс¬
но-сопряженные векторы образуют отдельное векторное пространство V. Такая точка зрения
особенно полезна при использовании (абстрактной) векторной записи с особым «алфави¬
том» индексов, например а', 6', с', ..., для комплексно-сопряженных элементов, причем
свертка (суммирование) по штрихованным и нештрихованным индексам не допускается.
Операция комплексного сопряжения меняет местами штрихованные и нештрихованные ин¬
дексы. В индексной записи наша эрмитова форма представляется таблицей, составленной
из величин hafb9 имеющих по одному (нижнему) индексу каждого типа, так что
у) = hafbo^'yb
(ха' обозначает элемент, комплексно-сопряженный элементу ха), причем «эрмитовость»
выражается соотношением
^а'Ъ — ^Wa,*
Таблица, составленная из величин На/ь позволяет опускать и поднимать индексы, но те¬
перь она также меняет штрихованные индексы на нештрихованные и наоборот; поэтому она
приводит нас к пространству, дуальному относительно комплексно-сопряженного простран¬
ства:
ha'by Va' = ha'bVb.
Для получения обратных операций (когда эрмитова форма предполагается несингулярной,
т. е. несингулярна матрица, составленная из компонент hab ) необходимо найти матрицу hab ,
обратную по отношению к На'ъ> которая удовлетворяет соотношениям
hab' hb'с ~	ha'bh**'	=	$,
откуда следует*
уа = щкЬа , va = habVb'.
Заметим, что все штрихованные индексы можно исключить, используя hafb (а также соответ¬
ствующие компоненты обратной матрицы hab ) и вышеприведенные соотношения, которые
можно применять поиндексно к любой тензорной величине. Таким образом, комплексно-со¬
пряженное пространство «отождествляется» с дуальным пространством вместо того, чтобы
рассматриваться как совершенно отдельное пространство.
Проверьте эти соотношения, объяснив согласованность записи для hab .

252
Глава 13
Операция «комплексного сопряжения» (обычно называемая эрмитовым сопряжением),
которая включает такое отождествление с дуальным пространством в само понятие ком¬
плексного сопряжения (хотя и не записывается в индексных обозначениях), играет важней¬
шую роль в квантовой механике, а также во многих других областях математики и физики
(например, в теории твисторов, см. § 33.5). В литературе по квантовой механике эта операция
часто обозначается крестиком (f), но иногда и звездочкой (*).
Сам я предпочитаю звездочку, которая более привычна в математической литературе,
так что я буду использовать здесь именно ее. Звездочка здесь уместна, потому что она
меняет ролями векторное пространство V и дуальное ему пространство V*. Комплексный
тензор валентности [р] (все штрихованные индексы, как и прежде, опущены) операцией *
X
отображается на тензор валентности Ц ]. Таким образом, под действием операции * верхние
Jr
индексы становятся нижними, а нижние — верхними. Применительно к скалярам * сводится
к обычной операции комплексного сопряжения. Операция * эквивалентна понятию самой
эрмитовой формы h.
Наиболее известная операция эрмитова сопряжения (которая получается, когда в каче¬
стве компонент Ьа*ь берется символ Кронекера) состоит в комплексном сопряжении каждой
компоненты, преобразующем компоненты таким образом, что верхние индексы становят¬
ся нижними, а нижние — верхними. Соответственно матрица, составленная из компонент
линейного преооразования, используется для транспонирования комплексно-сопряженной
матрицы (эту операцию иногда называют сопряженным транспонированием матрицы), так
что в случае 2x2 мы имеем
ьч*
Эрмитовой называется матрица, равная своей эрмитово-сопряженной в указанном смысле.
Это понятие и более общее понятие абстрактного эрмитова оператора играют важную роль
в квантовой теории.
Заметим, что операция * антилинейна в следующем смысле:
(Т + иу = Г* + и
*
(zT)* = zT*
где Т и U — тензоры одинаковой валентности, a z — произвольное комплексное число.
Операция * должна также сохранять произведение тензоров, однако, меняя порядок рас¬
положения индексов, она меняет порядок, в котором производится свертка. В частности,
применение ее к линейным преобразованиям (рассматриваемым как тензоры с одним верх¬
ним и одним нижним индексом) меняет порядок умножения:
(LM)* = M*L*
ч
В диаграммной записи удобно изобразить операцию сопряжения в виде отражения в го¬
ризонтальной плоскости. При этом, как и требуется, верхние и нижние индексы меняются
местами (см. рис. 13.19).
Операция * позволяет определить эрмитово скалярное произведение двух элемен¬
тов V-пространства v и w как скалярное произведение ковектора v * на вектор w (в разном
контексте используются различные обозначения):
(v\w) = v* ' w = h(v. w)
(см. также рис. 13.19), так что

13.9. Унитарные группы
253
<D
к
cd
d>
£
с
о
о
о
PQ
О
н
А
T.t
зеркало	зеркало
It s. -Л г*—A <!?.
1
ГА*
ii
«. t) * J
Рис. 13.19. Операцию эрмитова сопряжения (*) удобно представить в виде отражения в горизонтальной
плотности. Это производит взаимную замену «рук» и «ног» и меняет порядок умножения: (ST)* =
_ j»*£* Приводится диаграммная запись эрмитова скалярного произведения (v\w) = v* * w (опе¬
рация комплексного сопряжения переворачивает диаграмму в правой части рисунка «вверх ногами»)
В частном случае w = v мы получаем норму вектора v по отношению к операции *:
г? || — (^|г?).
В пространстве V можно выбрать базис (ei, в2, ..., еп), тогда компонентами Ка>ъ в этом
базисе будут просто п2 комплексных чисел
ha'b ~ еь) —
образующих элементы эрмитовой матрицы. Базис (ei, ..., е**) называется псевдоортонор-
мированным относительно операции *, если
±1 при г = j,
О	при	i ± j;
в случае, если вместо ± стоит +, т. е. 1 вместо ±1, базис называется ортонормированным.
Псевдоортонормированный базис можно найти всегда, причем существует множество
вариантов выбора. По отношению к любому такому базису матрица hafb диагональна,
и вдоль диагонали стоят числа 1 и —1. Для заданной операции * число р элементов +1
всегда остается одним и тем же независимо от выбранного базиса; то же относится к числу q
элементов —1. Это позволяет ввести инвариайтное понятие сигнатуры (р, q) операции *.
Если q — 0, то мы говорим, что операция * положительно определена. В этом
случае^13■2^ норма всякого ненулевого вектора всегда положительна"':
v ф 0 означает, что ||г;|| > 0.
Заметим, что понятие положительной определенности обобщает аналогичное понятие, вве¬
денное в § 13.8, на случай комплексных величин. Линейное преобразование Т, обратным
которому служит Т*, так что
Г-1- = Т*, т.е. ТТ* = I = Т*Т,
называется унитарным, если операция * положительно определена, и псевдоунитарным
в остальных случаях . Термин «унитарная матрица» относится к матрице Т, удовлетворяю¬
щей предыдущему соотношению, в котором операция * означает обычное транспонирование
с комплексным сопряжением, так что Т~г = Т.
Покажите это.
** £3 Покажите, что такие преобразования сохраняют эрмитово соответствие между векторами v и ковектора-
ми v*, а также сохраняют компоненты ha(^.

254
Глава 13
Группа унитарных преобразований в п измерениях, или унитарных матриц (п х га),
называется унитарной группой U (п). В более общем случае, когда операция * имеет сигна-
туру (p. q), мы получаем псевдоунитарную группу U(p, g).!13*22) Если определитель преоб¬
разования равен 1, получаем соответственно SU (п) и SU(p, q). Унитарные преобразования
играют важную роль в квантовой механике (а также во многих областях чистой математики).
►
13.10.	Симплектические группы
I
В двух предыдущих разделах мы рассматривали ортогональные и унитарные группы.
Это примеры так называемых классических групп, а именно простых групп Ли, отличных
от исключительных групп (см. § 13.2). Список классических групп завершается семейством
симплектических групп. Симплектические группы играют важную роль в классической фи¬
зике, как будет показано, в частности, в § 20.4, а также в квантовой физике, особенно в бес¬
конечномерном случае (§ 26.3).
Что такое симплектическая группа? Вернемся снова к понятию билинейной формы,
но вместо симметрии (д(х, у) = д(у, ж)), требуемой определением ортогональной группы,
наложим требования антисимметрии
з(х,у) = , ж)
и линейности
s(x,	у +	w) =	s(X,у) + s(x, w), Ay) - As(x, y),
при этом линейность по первой переменной х теперь следует из антисимметрии. Нашу
антисимметричную форму можно также записать в виде
а(х, у) = xasabyb = xTSy,
таком же, как и в симметричном случае, но компоненты sab теперь антисимметричны:
$Ъа ~ $abi Т. е. S ~ S,
где S есть матриц^ с компонентами sab. Потребуем, чтобы преобразование S было несингу¬
лярным. Тогда матрица sab имеет обратную матрицу sab, удовлетворяющую условию!13,23)
SabSbc = 5Са = ScbSbai
где sab — —sba.
Заметим, что, по аналогии с симметричной матрицей, антисимметричная матрица S
равна транспонированной ей с обратным знаком. Важно отметить, что антисимметрич¬
ная (п х п)-матрица S может быть несингулярной, только если число п четно*. Здесь п есть
размерность пространства V, которому принадлежат векторы х и у, и мы будем считать
число п четным.
Элементы Т группы GL(n), сохраняющие несингулярную антисимметричную матри¬
цу sab (или, что то же самое, билинейную форму s) в том смысле, что
SabTacTbd = Scd, т. е. TtST = S,
называются симплектическими, а группа таких элементов — симплектической группой
(как мы увидим в § 20.4, такие группы играют очень важную роль в классической механике).
В литературе, однако, имеется некоторая путаница с терминологией. В математическом отно¬
шении правильнее определить (вещественную) симплектичекую группу как вещественную
		 »»	II	■	III	HiHBUHa	^» i	i	#
* Проверьте это.

13.10. СИМПЛЕКТИЧЕСКИЕ ГРУППЫ
255
t-
форму комплексной симплектической группы Sp(~n, С), которая представляет собой группу
%     * •
комплексных элементов Таь (или Т), удовлетворяющих вышеприведенному соотношению.
Определенная таким образом вещественная форма некомпактна, однако в соответствии с за-
1 \
мечаниями в конце § 13.7, поскольку группа Sp(^, С) полупростая, существует еще одна
вещественная форма этой комплексной группы, которая является компактной, и ее-то обыч-
/1
но считают (вещественной) симплектической группой Sp(^n).
Как найти эти различные вещественные формы? Как и в случае ортогональных групп,
здесь имеется понятие сигнатуры, которое не столь известно, как в случае ортогональных
и унитарных групп. Симплектическая группа вещественных преобразований, сохраняющих
11ч
величины sab, имеет «расщепленную» сигнатуру (~п, ^п). Компактная симплектическая
группа имеет сигнатуру (п, 0) или (0, п).
Как определяется такая сигнатура? Для каждой пары натуральных чисел р и q таких,
что р 4- q = п, можно определить соответственную «вещественную форму» комплексной
группы Sp(in, С), взяв только те элементы, которые являются также псевдоунитарными
для сигнатуры (р, q), т. е. принадлежат группе U(р, q) (см. § 13.9). Это дает нам^13*24^ (псев-
до)симплектическую группу Sp(p, q). (Другими словами, Sp(p, q) есть пересечение мно-
1
жеств Sp(-гг, С) и U(р, д).) В индексной записи можно определить Sp(p, g) как группу
комплексных линейных преобразований Таь, сохраняющих, как и раньше, антисимметрич¬
ные величины sab, ^ также эрмитову матрицу Н с компонентами На>ъ в том смысле, что
Та b>Tabha'a = hb>by
Здесь Н имеет сигнатуру (р, q), так что можно найти псевдоортонормированный базис,
в котором матрица Н диагональна с р элементами 1 и q элементами — 1 на главной диагонали
(см. § 13.9)[13*25]. Компактная классическая симплектическая группа Sp( ~п) — это есть наша
группа Sp(n, 0) (или Sp(0, п)), однако формой, наиболее важной для классической физики,
является Sp(~п, 2п)*	-
Что касается ортогональных и унитарных групп, то мы можем выбрать базис, в ко¬
тором компоненты sab имеют наиболее простой вид. Мы не можем, однако, сделать эту
форму диагональной, поскольку единственной антисимметричной диагональной матрицей
является нулевая матрица! Вместо этого можно взять матрицу из компонент sab9 состоящую
из блоков 2x2 вида
' 0 1
-1
расположенных вдоль главной диагонали. В обычном случае расщепленной сигнату-
1 1
ры Sp(^n, ±п) можно взять вещественные линейные преобразования, сохраняющие такую
форму. Общий случай Sp(p, q) получается, если вместо вещественных преобразований взять
псевдоукитарные с сигнатурой (р, q).
При различных (малых) значениях р и q некоторые ортогональные, унитарные и сим-
плектические группы одинаковы («изоморфны») или, по крайней мере, одинаковы локаль¬
но («локально изоморфны») в том смысле, что они имеют одни и те же алгебры Ли
Ж Используя вышеуказанную процедуру, найдите описание групп Sp(l) и Sp(l, 1) в явном виде. Понятно
ли, почему группы Sp(n, 0) компактны?
**
ш Объясните, почему два различных описания эквивалентны в случае р — q ~ ~п.

2:56
Глава 13
(см. § 13.6)f13 26l Наиболее простой пример дает группа симметрии круга без отраже¬
ний SO (2), совпадающая с унитарной группой U(l) — мультипликативной группой ком¬
плексных чисел с единичным модулем егв {в — вещественное число)*. Особо важные для
физики группы SU(2) и Sp(l) совпадают между собой и локально совпадают с SO(3) (буду-
U
чи двукратным покрытием этой последней группы, в соответствии с двукратной природой
кватернионного представления вращений в 3-пространстве, описанной в § 11.3). Эти группы
имеют особенно большое значение для квантовой физики спина (§ 22.8). Для теории отно¬
сительности важен тот факт, что группа SL(2, С), будучи тем же, что и Sp(l, С), локально
совпадает с неотражательной частью группы Лоренца 0(1, 3) (опять-таки будучи ее дву¬
кратным покрытием). Мы видим также, что совпадают группы SU(1, 1), Sp(l, 1) и S0(2, 1);
имеются и другие примеры. Для теории твисторов представляет особый интерес локальное
тождество группы SU(2, 2) и неотражательной части группы 0(2, 4) (см. § 33.3).
Алгебра Ли симплектической группы получается, если найти решения X матричного
уравнения
XTS + SX = 0, т.е. SX = (SX)T,
так что бесконечно малое преобразование (элемент алгебры Ли) X есть просто матрица S-1,
умноженная на симметричную матрицу п х п. Это позволяет сразу определить размер¬
ность симплектической группы, равную ~п(п -f 1). Заметим, что матрица X не имеет следа
(т. е. Tr X = 0; см. § 13.4).** Алгебры Ли для ортогональных и унитарных групп также легко
выразить соответственно через антисимметричные матрицы и эрмитовы матрицы, умножен-
ные на чисто мнимый множитель, соответствующие размерности равны п(п — 1)/2 и п .
Как показано в § 13.4, у преобразований с определителем, равным 1, след бесконечно
малого элемента X должен обращаться в нуль. Для элементов симплектической группы
это выполняется автоматически (см. выше), а в случае ортогональных групп все бесконеч-
«к эк эк эк
но малые элементы имеют определитель, равный единице . В случае унитарной группы,
ограничиваясь группой SU(ra), имеем дополнительное условие ТгХ = 0, так что размер¬
ность группы понижается до п2 — 1.
Классические группы, рассмотренные в § 13.2, которые иногда обозначают Ат, Вт,
Ст, Dm (т — 1, 2, 3, ....), — это просто соответствующие группы SU(m + 1), SO(2m 4- 1),
Sp(m) и SO(2m), которые мы ввели в §§ 13.8-13.10, и из вышеизложенного следует, что
они имеют размерность соответственно т(т 4- 2), т(2т + 1), т(2т 4- 1) и т(2т - 1),
как утверждалось в § 13.2. Таким образом, читатель получил возможность познакомиться со
всеми классическими простыми группами. Как мы видели, такие группы, а также некоторые
другие «вещественные формы» (и их комплексификации) играют важную роль в физике. Мы
продолжим это знакомство в следующей главе. Как упоминалось в начале этой главы, в со¬
временной физике все виды физического взаимодействия определяются «калибровочными
связностями», которые сильно зависят от пространств с точной симметрией. Однако нам
необходимо еще узнать, что такое калибровочная теория. Этим мы займемся в главе 15.
Примечания
§13,1.
13.1.	Абель родился в 1802 году и умер от чахотки (туберкулеза) в 1829 году в возрасте 26 лет.
Теория более общих неабелевых групп (ab ф Ъа) была основана французским математиком
*
#*
***
****
Почему эти группы одинаковы?
Объясните, откуда взялось уравнение XTS 4- SX = 0 и почему SX — (SX)T. Почему ТгХ — 0?
алгебру Ли в явном виде. Почему она имеет указанную выше размерность?
Опишите эти алгебры Ли и определите их размерность.
Почему? Что это означает геометрически?

13.10. СИМПЛЕКТИЧЕСКИЕ ГРУППЫ
%
257
с еще более трагической судьбой — Эваристом Галуа (1811-1832), который, не достигнув 21
года, был убит на дуэли. В ночь накануне дуэли он лихорадочно излагал свои революционные
идеи, касающиеся применения таких групп для решения алгебраических уравнений; ныне это
называется теорией Галуа.
13.2. Следует также отметить, что —С означает комплексное сопряжение и последующее умножение
на —1, т. е. —С — (—1)С.
13.3. Буква S означает «специальная» (имеется в виду определитель, равный 1), что в данном контек¬
сте просто сообщает об исключении движений, меняющих ориентацию на противоположную.
Буква О означает «ортогональная» и отражает тот факт, что представляемые группой движе¬
ния сохраняют «ортогональность» (т. е. прямоугольный характер) системы координатных осей.
Число 3 указывает на то, что рассматриваются вращения в трех измерениях.
13.4. Существует замечательная теорема, которая гласит, что каждая непрерывная группа является
не только гладкой (в обозначениях §§ 6.3, 6.6 это означает, что из С0 следует С1 и даже С°°), но
и аналитической (так что из С0 следует Сы). Этот замечательный результат, представляющий
решение задачи, известной под названием пятой проблемы Гильберта, был получен в 1953
году Эндрю Глисоном, Дином Монтгомери, Лео Зиппином и Хидехико Ямабе (см. [531]).
Он оправдывает использование степенных рядов в § 13.6.
§13.2.
13.5. См. [799], стр. 166-174.
13.6. См. [189].
13.7. См. [163, 214].
§13.3.
13.8. В § 14.1 мы увидим, что евклидово пространство представляет собой пример аффинного про¬
странства. Если выбрать в нем некоторую фиксированную точку (начало координат) О, оно
становится векторным пространством.
13.9. Во многих местах этой книги удобно (иногда существенно удобнее) располагать ступенькой
индексы у символов тензорного типа. В случае линейного преобразования это необходимо,
чтобы указать порядок, в котором производится умножение матриц.
13.10. Эта область является векторным пространством размерности г (причем г < п). Мы называ¬
ем г рангом матрицы или линейного преобразования Т. Несингулярная матрица п х п имеет
ранг, равный п. (Понятие ранга применяется также к прямоугольным матрицам.) Сравните
с примечанием 12.12.
13.11. История теории матриц изложена в [502].
§13.5.
13.12. В вырожденных случаях, когда собственные векторы не охватывают всего пространства
(т. е. некоторые значения d меньше соответствующих значений г), мы все же можем най¬
ти каноническую форму, но теперь единицы могут появляться непосредственно над главной
диагональю, находясь внутри квадратных блоков, диагональными элементами которых слу¬
жат одинаковые собственные значения (это так называемая жорданова нормальная форма;
см. [24]). Фактически такую нормальную форму, по-видимому, впервые нашел Вейерштрасс
двумя годами раньше Жордана (см. [375]).
§13.6.
13.13. Чтобы проиллюстрировать эту точку зрения, рассмотрим группу SL(n, R) (т. е. элементы самой
группы GL(n, М) с определителем, равным 1). Эта группа имеет «двойное покрытие» SL(n, R)
(при условии, что п ^ 3), которое получается из SL(n, М) в основном тем же путем, каким
мы получили двойное покрытие SO(3) группы SO(3), когда рассматривали повороты книги,
соединенной с ремнем, в § 11.3. Таким образом, 80(3) есть группа вращений (без отражений)
спинорного объекта в обычном 3-пространстве. Аналогично можно рассматривать «спинорные

258	Глава	13
" '  		 		■■»■»■■»■       ■ »■■■■■  i—m — ■ ■ I "    ■ .и	       *'	1	■'	р—	      ■.«.	.	 ■■■■■	 и
объекты» при линейных преобразованиях более общего вида, допускающих «сжатие» или «рас¬
тяжение», которые обсуждались в § 13.3. Следуя этому пути, мы приходим к группе SL(n, R),
которая локально есть то же, что и SL(n, М), но не может быть точно представленной в любой
группе GL(n). См. примечание 15.9.
13.14. Это хорошо определенное понятие — см. примечание 4 к этой главе.
§13.7.
13.15. См. [774].
9 • •• “ ’ . . .
13.16. Здесь мы снова сталкиваемся с примером нелогичности в наименовании математических поня¬
тий. В то время как многие важные понятия в данной области, связываемые обычно с именем
Картана (например, «субалгебра Картана», «картаново целое число»), были впервые введены
Киплингом (см. §13.2), тем, что мы называем «формой Киплинга», мы в действительности
• • /■
обязаны Картану (и Герману Вейлю); см. [376], раздел 6.2. Однако «вектор Киплинга», с кото¬
рым мы столкнемся в § 30.6, был действительно введен Киллингом ([376], примечание 20 на
стр. 128).
13.17. Я допускаю (умышленно) некоторую небрежность, с математической точки зрения, в исполь¬
зовании слов «такой же», «тот же самый». Строгий математический термин — «изоморфный».
§13.8.
13.18. Я пока не описывал эту процедуру в достаточно явном виде. Базис е = (ei, ..., еп) для про¬
странства V связан с дуальным базисом е* = (е1, ..., еп) для пространства V* соотношени-
* *
ем ег • ej = 6). Компоненты [^-валентного тензора Q получаются действием полилинейной
У
функции из §12.8 на различные наборы, состоящие из р элементов дуального базиса и q
элементов исходного базиса: Q'£;;;£ =	*	- *, е/г; еа, ..., ес).
13.19. См: примечание 13.3.
13.20. См. примечание 13.10. Читатель, возможно, недоумевает: почему тензор Таъ в § 13.5 может
иметь много инвариантов (а именно все его собственные значения Ai, А2, A3, ..., Ап), тогда
как даь их не имеет. Причина состоит просто в разном поведении при преобразованиях, неявно
заложенном в различном расположении индексов.
§13.9
а
13.21. Заметим, что в положительно определенном случае (е£, е|, ..., е£) есть дуальный базис по от¬
ношению к (ei, €2, »•., е?г) в смысле, указанном в примечании 13.18.
13.22. Группы U(p, q) с заданным значением р + q — п имеют ту же комплексификацию, что
и GL(n, R), а именно GL(n, С), и все они могут рассматриваться как различные вещественные
формы этой комплексной группы.
§13.10
.13.23, Можно использовать sab и sab для поднятия и опускания индексов тензоров так же, как и с по¬
мощью даь и даЬ, при этом va — sabVb, va = sabsb (см. § 13.8); однако из-за антисимметрии
необходимо более внимательно подходить к упорядочению индексов. Читатели, знакомые с ис¬
числением 2-спиноров (см. [626]), возможно, отметят некоторое несоответствие между нашим
обозначением sab и sab в указанном исчислении.
13.24. Я не знаком со стандартной терминологией и обозначениями различных вещественных форм,
поэтому для наших нынешних целей было придумано обозначение Sp(p, q).
I
13.25. На самом деле каждый элемент группы Sp(-n, С) имеет определитель, равный 1, поэтому нам
1
не требуется вводить «SSp(-п)» по аналогии с SO(n) и SU(ra). Причина состоит в том, что су¬
ществует выражение («пфаффиан») для тензоров Леви-Чивита s... в терминах величин заъ,
которые должны сохраняться всякий раз, когда сохраняется sab*
13.26. См. примечание 13.17.

Глава 14
Математический анализ на многообразиях
14.1.	Дифференцирование на многообразии?
В предыдущей главе (в §§13.3, 13.6-13.10) мы говорили о действии групп симметрии
на векторные пространства, описываемом как линейные преобразования этих пространств.
Для некоторой заданной группы можно рассматривать векторное пространство как обла¬
дающее некоторой определенной структурой, сохраняющейся при преобразованиях. Такое
понятие «структуры» оказывается очень важным. Например, это может быть метрическая
структура в случае ортогональной группы (§13.8) или эрмитова структура, сохраняюща¬
яся при действии унитарной группы (§ 13.9). Как уже отмечалось, представление теории
групп в терминах действия на векторные пространства играет важную роль во многих обла¬
стях математики и физики, особенно в квантовой теории, где, как мы увидим (в частности,
в § 22.3), векторные пространства с эрмитовой структурой (скалярным произведением) со¬
ставляют существенную часть основы теории.
Но векторное пространство само по себе есть лишь весьма частный случай простран¬
ства, и от математики в современной физике требуется нечто гораздо большее. Даже древняя
геометрия Евклида не описывается векторным пространством, поскольку векторное про¬
странство обязано иметь некоторую выделенную точку, а именно начало координат (соответ¬
ствующее нулевому вектору), тогда как в евклидовой геометрии все точки рассматриваются
на равных правах. На самом деле евклидово пространство есть пример так называемого
аффинного пространства. Аффинное пространство подобно векторному, но в этом случае
мы «забываем» о начале координат, так что в этом пространстве существует согласованное
понятие параллелограмма ’ . Коль скоро мы выбираем некоторую точку в качестве начала
координат, мы получаем возможность определить сложение векторов «правилом параллело¬
грамма» (см. § 13.3, рис. 13.4).
Искривленное пространство-время замечательной общей теории относительности Эйн¬
штейна, несомненно, является пространством более общего вида, нежели векторное про¬
странство, — это есть 4-многообразие. Эйнштейновское понятие геометрии простран¬
ства-времени предполагает наличие некоторой (локальной) структуры и гладкого многооб¬
разия (изучавшегося в главе 12). Аналогично конфигурационные пространства или фазовые
пространства физических систем (кратко рассмотренные в § 12.1) также имеют тенденцию
к обладанию локальной структурой. Какие свойства мы приписываем этой требуемой струк¬
туре? Такая локальная структура должна предоставить некоторую меру «расстояния» между
точками (в случае метрической структуры), или «площади» поверхности (как она была
определена для симплектической структуры, сравните § 13.10), или «угла» между кривыми
Пусть запись [а, 6; с, d] означает, что существует параллелограмм abdc (точки а, 6, d, с являются вер¬
шинами параллелограмма и берутся в циклическом порядке, как в §5.1). Примем в качестве аксиом, что: 1) для
любых а, Ъ и с существует такая точка d, что имеет место [а, b; с, d]; 2) если [а, 6; с, d], то [6, a; d, с] и [а, с; 6, d\;
3) если [а, 6; с, d] и [а, 6; е, /], то [с, d; е, /]. Покажите, что если выбрать некоторую точку в качестве начала
координат, то такая алгебраическая структура сводится к структуре «векторного пространства», но без операции
«скалярного умножения», определенной в §11.1, то есть мы получаем правила, соответствующие аддитивной
абелевой группе (см. упражнение 13.2).
Можете ли вы обобщить это на случай неабелевой группы?

260
Глава 14
(как в случае конформной структуры римановой поверхности; см. § 8.2) и т. д. Во всех этих
примерах понятие векторного пространства необходимо, чтобы указать, какова эта локаль¬
ная геометрия. Рассматриваемое векторное пространство является n-мерным касательным
пространством Тр типичной точки р многообразия М. (мы считаем Tv «бесконечно растя¬
нутой» непосредственной окрестностью точки р в М; см. рис. 12.6).
В соответствии с этим различные групповые структуры и тензорные величины, с ко¬
торыми мы имели дело в главе 13, могут быть локально сопоставлены отдельным точкам
многообразия. Мы увидим, что эйнштейновское искривленное пространство-время действи¬
тельно имеет локальную структуру, задаваемую лоренцевой (псевдо)метрикой (§ 13.8) в каж¬
дом касательном пространстве, тогда как фазовые пространства классической механики
(сравните § 12.1) имеют локальную симплектическую структуру (§13.10). Оба эти примера
многообразий со структурой играют важнейшую роль в современной физической теории.
Однако какую форму исчисления можно применять в таких пространствах?
Как уже отмечалось, n-мерные многообразия, изучавшиеся в главе 12, должны все¬
го лишь быть гладкими, никакая локальная структура при этом не задается. В подобном
неструктурированном гладком многообразии М определено сравнительно мало вычисли¬
тельных операций, имеющих смысл. Важнее всего, что мы не имеем пока общего понятия
дифференцирования, применимого всюду в М.
Здесь я должен дать некоторые пояснения. На любом выбранном координатном ло¬
скуте мы могли бы просто дифференцировать различные интересующие нас величины по
каждой из координат этого лоскута ж1, х2, ..., хп, используя операторы (частных) про¬
изводных д/дх1, д/дх2, ..., д/дхп (см. § 10.2). Однако в большинстве случаев результат
будет геометрически бессмысленным, поскольку он зависит от сделанного конкретного (про¬
извольного) выбора координат, так что в общем случае результаты не будут согласоваться
при переходе от одного лоскута к другому (сравните с рис. 10.7).
Мы упоминали, однако, в § 12.6 об одном важном понятии дифференцирования, кото¬
рое применяется к (неструктурированному) гладкому п-многообразию общего вида и дает
согласованные результаты при переходе от одного лоскута к другому, а именно о внешней
производной дифференциальной формы. Пока эта операция имеет несколько ограниченное
применение — только к р-формам, причем она не дает существенной информации о том,
как меняется такая р-форма. Нельзя ли дать законченное понятие «производной» некоторой
величины на гладком многообразии общего вида, например, векторного или тензорного по¬
ля? Такое понятие должно быть определено независимо от какого-либо выбора координат,
которые можно было бы ввести для обозначения точек на некотором координатном лоскуте.
Хорошо было бы иметь некоторое не зависящее от координат исчисление, которое можно
применять к структурам на многообразиях и которое позволяло бы следить, как меняется
векторное или тензорное поле при переходе от одного лоскута к другому. Однако как это
осуществить?
14.2.	Параллельный перенос
Напомним (см. §§ 10.3,12.3), что в случае скалярного поля Ф на гладком п-многообразии
общего вида Л4 мы смогли построить подходящую меру «скорости изменения» поля, а имен¬
но 1-форму дФ, обладающую тем свойством, что равенство дФ = 0 является условием по¬
стоянства Ф на связных областях многообразия М. Однако эта идея не работает в случае
тензорной величины общего вида. Она неприменима даже к векторному полю £. Почему?
Одна из причин связана с тем, что у многообразия общего вида, как мы вскоре увидим, нет
подходящего понятия постоянства вектора тогда как любая самосогласованная операция
дифференцирования («градиент»), применяемая к £, должна обладать тем свойством, что
равенство этой величины нулю сиг нализирует о постоянстве £ (так же, как дФ — 0 означает

14.2. Параллельный перенос
261
постоянство скалярного поля Ф). В более общем случае можно ожидать, что для «непосто¬
янной» величины £ такая производная должна быть мерой отклонения £ от постоянства.
Почему возникает проблема с понятием «постоянства» вектора на n-многообразии М
общего вида? В обычном евклидовом пространстве постоянное векторное поле £ должно
обладать тем свойством, что все «стрелки», используемые при его геометрическом описании,
должны быть параллельны одна другой. Таким образом, некоторое понятие «параллелизма»
должно быть составной частью структуры многообразия М. Это может вызвать некоторое
беспокойство, если вспомнить судьбу пятого постулата Евклида (постулата о параллельных),
обсуждавшегося в главе 2. Например, гиперболическая геометрия не допускает векторных
полей, которые можно было бы однозначным образом признать «параллельными» всюду.
В любом случае понятие «параллелизма» не присуще многообразию М просто в силу того,
что оно является гладким многообразием. На рис. 14,1 эта трудность иллюстрируется для
случая 2-многообразия, получаемого объединением двух лоскутов евклидова пространства.
Обычное евклидово понятие «параллельности» не согласуется с переходом с одного лоскута
на другой.
Несогласованная
параллельность
Рис. 14.1. Евклидово понятие «параллельности» оказывается несогласованным при перекрытии коор¬
динатных лоскутов
Чтобы понять, какого рода параллелизм нам нужен, полезно рассмотреть сначала вну¬
треннюю геометрию обычной двумерной сферы S2. Выберем на S2 некоторую точку р
(например, для определенности, на северном полюсе) и некоторый касательный вектор v
в точке р (направленный, например, вдоль Гринвичского меридиана; см. рис. 14.2а). Какие
другие касательные векторы в других точках сферы S2 мы должны считать «параллельны¬
ми» вектору v? Если воспользоваться евклидовым понятием «параллельности», унаследо¬
ванным от стандартного погружения S2 в евклидово 3-пространство, то мы найдем, что
в большинстве точек q сферы S2 не существует касательных векторов к S2, которые были
бы «параллельны» вектору v в указанном смысле, поскольку касательная плоскость в точ¬
ке q, как правило, не содержит направления v. (Точки, в которых имеются касательные
векторы к S2, могущие быть «параллельными» вектору v в этом смысле, содержит лишь
большая окружность, проходящая через точку р перпендикулярно к Гринвичскому мериди¬
ану.) Подходящее понятие параллелизма на S2 должно относиться только к касательным
векторам, поэтому лучшее, что мы можем сделать, — это переносить направление векто¬
ра г? в тангенциальную плоскость в точке q по мере постепенного удаления точки q от р.
Эта идея прекрасно работает, но теперь возникает новая особенность: вводимое таким обра¬
зом понятие параллелизма зависит от пути, по которому точка q смещается от точки р^ыл^.
Зависимость понятия «параллелизма» от такого пути — это существенная новая черта, раз-
личные варианты которой лежат в основе успешных современных теории взаимодействия
элементарных частиц помимо общей теории относительности Эйнштейна.
Постараемся понять это получше. Рассмотрим кривую у на S2, начинающуюся в точке р
и заканчивающуюся в некоторой другой точке q на S2. Представим себе, что кривая 7 постро¬

262
Глава 14
а)	б)
Рис. 14.2. Параллелизм на сфере S2. Выберем точку р на северном полюсе, касательный вектор v напра¬
вим вдоль Гринвичского меридиана. Какие касательные векторы в других точках сферы S2 мы должны
считать «параллельными» вектору v? а) Непосредственное применение евклидовой «параллельности»,
О	 о
когда сфера S считается погруженной в пространство Е' , не работает (за исключением направления
вдоль меридиана, перпендикулярного Гринвичскому), поскольку векторы, параллельные v, не оста¬
ются касательными к S2. б) Чтобы исправить положение, будем двигать вектор v вдоль заданной
кривой 7, постоянно проектируя его на касательную плоскость к сфере. (Полагаем, что кривая 7 по¬
строена из большого числа мелких отрезков popi, PiP2, Р2рз? * • проектируемых на каждой стадии.
щ
Затем переходим к пределу, в котором отрезки становятся все меньше.) Такое понятие параллельного
переноса показано на рисунке для Гринвичского меридиана, а также для кривой общего вида 7
ена из большого числа N мелких отрезков роРг, Р1Р2, Р2Рз, • * * > Pn-iPn\ здесь р0 = р —
начальная точка, а последний отрезок оканчивается в точке рм = Я- Будем передвигать
вектор v вдоль 7, причем на каждом из отрезков pr_ipr перемещать его параллельно са¬
мому себе (в обычном смысле, с использованием евклидова трехмерного пространства),
а затем проектировать на касательное пространство в точке рг (см. рис. 14.2 б). Эта проце¬
дура заканчивается касательным вектором в точке q. Приближенно можно принять, что этот
вектор скользил вдоль кривой 7 от р к q, оставаясь параллельным самому себе настолько,
насколько это возможно на данной поверхности. На самом деле эта процедура несколько
зависит от того, как именно кривая 7 аппроксимируется последовательностью отрезков.
Можно показать, однако, что в пределе, когда отрезки становятся все меньше, мы получаем
вполне определенный ответ, не зависящий от способа разбиения кривой 7 на отрезки. Такая
процедура называется параллельным переносом вектора v вдоль кривой 7. На рис. 14.3 по¬
казано, как будет выглядеть параллельный перенос вдоль пяти различных кривых (больших
окружностей) с началом в точке р.
Что в таком случае означает отмеченная выше зависимость от траектории переноса?
На рис. 14.4 отмечены точки р и q на S2 и два пути от р к q, один из которых следу¬
ет непосредственно вдоль большой окружности, а другой состоит из пары дуг больших
окружностей, сходящихся в промежуточной точке г. Из картины на рис. 14.3 видно, что па¬
раллельный перенос вдоль этих двух путей (один из них содержит угол, но это не так важно)
приводит к двум совершенно различным конечным результатам, отличающимся, в данном
случае, поворотом на прямой угол. Заметим, что расхождение сводится к изменению направ¬
ления вектора. Существуют общие причины того, что определенное таким образом понятие
параллельного переноса всегда сохраняет длину вектора. (Имеются, однако, и другие типы
«параллельного переноса», при которых дело обстоит иначе. Такие случаи окажутся ин-

14.2. Параллельный перенос
263
Рис. 14.3. Параллельный перенос вектора v вдоль пяти различных кривых (все они являются большими
окружностями)
тересными для нас в последующих разделах (§§ 14.7, 15.7, 15.8, 19.4).) Крайним случаем
углового несоответствия является такой, когда наша траектория у представляет собой зам¬
кнутую петлю (так что р — q) и имеет место несовпадение между начальным и конечным
направлениями параллельно переносимого касательного вектора. Для точной геометриче¬
ской сферы единичного радиуса такое несовпадение сводится к углу поворота, который,
будучи измерен в радианах, в точности равен полной площади петли (при этом площадь
области, обходимой в отрицательном направлении, считается отрицательной)*.
Рис. 14.4. Зависимость параллельного переноса от траектории движения. Показаны два различных
пути от точки р к точке q, один из которых следует прямо по дуге большой окружности, а другой
состоит из пары дуг больших окружностей, пересекающихся в некоторой промежуточной точке г.
Параллельный перенос вдоль этих двух траекторий приводит к двум разным результатам в точке q,
один из которых получается из другого поворотом на прямой угол
* Попробуйте подтвердить справедливость этого утверждения в случае сферического треугольника (тре¬
угольника на S2, образуемого дугами больших окружностей), воспользовавшись формулой Гарио (1603) для пло¬
щади сферического треугольника, приведенной в § 2.6.

264
Глава 14
14.3.	Ковариантная производная
Как можно воспользоваться понятием «параллельного переноса», чтобы ввести под¬
ходящее понятие «дифференцирования» векторных полей (а значит, и тензоров, в общем
случае)? Существенная идея состоит в том, чтобы сравнить поведение векторного (или тен¬
зорного) поля в некотором направлении, исходящем из точки р, с таковым при параллельном
переносе того же вектора из точки р в том же направлении путем вычитания второго из пер¬
вого. Эту идею можно применить к конечному перемещению вдоль некоторой кривой у,
однако для определения (первой) производной векторного поля нам потребуется лишь бес¬
конечно малое смещение от точки р, которое зависит только от пути, по которому эта кривая
«стартует» из точки р, т. е. только от касательного вектора w к кривой 7 в точке р (рис. 14.5).
Для обозначения определенного таким образом дифференцирования обычно используют
символ V («набла»), называемый оператором ковариантной производной или просто связ¬
ностью.
Рис. 14.5. Понятие ковариантной производной можно объяснить на основе параллельного переноса.
Характер изменения векторного поля £ на многообразии Л4 от одной точки к другой (это показано
стрелками с черным острием) определяется отклонением от стандарта, задаваемого параллельным
переносом (показанного стрелками со светлым острием). Сравнение может быть сделано вдоль всей
кривой 7 (начиная с точки р), но для нахождения ковариантной первой производной V в точке р
W
достаточно знать лишь	касательный вектор w к	кривой 7 в точке р, который определяет ковариантную
производную V£ от	£	в	точке р	в	направлении	w
W
Основное требование, которое предъявляется к такому оператору (и которое выполняет¬
ся для понятия, определенного выше в общих чертах для сферы S2), состоит в его линейной
зависимости от вектора w. Если обозначить ковариантную производную, определяемую
смещением (направлением) w, символом V, то для двух таких векторов смещения w и и
W
должно выполняться условие
V	- V + V,
W + 'U	W и
а для скалярного множителя Л — условие
V = AV.
Xw w
Может показаться, что размещение векторного символа под знаком V выглядит не слишком
красиво, — и это действительно так! Существует, однако, несоответствие между обозначени¬
ями математиков и физиков при использовании выражений вида V. Математики обозначают
W

14.3. КОВАРИАНТНАЯ ПРОИЗВОДНАЯ
265
так операцию, которую я здесь обозначил как V, тогда как физики предпочитают считать w
W
не векторным полем, а индексом. В записи физиков можно представить оператор V в виде
W
V = w“Va,
W
а вышеприведенные условия линейности принимают вид
(wa + иа)Va -	+	uaVa и (\wa)Va = \(waVa).
Положение нижнего индекса у V согласуется с дуальным характером этого операто¬
ра по отношению к векторному полю (это проявляется и в вышеприведенных условиях
линейности, см. §12.3), т. е. V есть ковекторный оператор (имеется в виду оператор ва¬
лентности [J]). Таким образом, при действии V на векторное поле £ (валентность [J])
получающаяся величина V£ представляет собой [*]-тензор. Это проявляется в индексной
записи в виде Va£b при компонентном (или абстрактно-индексном) представлении тензо¬
ра V£. Имеется естественный способ расширить рамки действия оператора V от векторов
до тензоров произвольной валентности, при этом действие V на [р] -валентный тензор Т
дает [ Д2]-валентный тензор V Т. Соответствующие правила удобно выразить в индексной
записи, однако обозначения математиков, как мы увидим, оказываются не вполне удобными.
При действии на векторные поля оператор V подчиняется правилам того же рода,
что и дифференциальный оператор d (§ 12.6):
+ *?) —
и правилу Лейбница
V(A£) = AV* + *VA,.
где £ и г] — векторные поля, а А — скалярное поле. Одно из требований, налагаемых
на связность, состоит в том, что действие V на скаляр должно быть идентично действию
на этот скаляр градиента (внешней производной) d:
W - йФ.
Обобщение действия V на случай произвольного тензорного поля однозначно определя¬
ется* следующими двумя естественными требованиями. Первым является аддитивность
(для тензоров Т и U одинаковой валентности):
V(T+ 17) = VT-f-VH.
Второе требование сводится к соответствующей форме правила Лейбница. Это правило
несколько сложно сформулировать, особенно в обозначениях математиков, избегающих ин¬
дексов. Простейшее выражение этого правила имеет следующий вид:
V(T • U) — (VT) • Z7+T-V17,
однако оно требует пояснения. Точка • должна означать некоторую форму произведения
со сверткой, при этом множество верхних и нижних индексов тензора Т свертывается
с множеством нижних и верхних индексов тензора U (допускается, что множества мо¬
гут быть и пустыми, так что произведение становится внешним, не содержащим сверток).
В вышеприведенной формуле свертки в обоих членах правой части точно отражают свертки
в левой части, а индексная буква у V одна и та же во всем выражении.
* Объясните, почему однозначно. (Подсказка: рассмотрите действие V на a * £ и т. п.)

266
Глава 14
При написании в обозначениях математиков формулы, выражающей правило Лейб¬
ница для тензоров, возникает определенная трудность, связанная с отсутствием индексов.
Ситуация несколько облегчается, если вместо V использовать V, поскольку w следит за ин-
W
дексами у V, и мы можем при желании сделать нечто подобное и с другими индексами,
свертывая каждый из них с векторным или ковекторным полем (на которые V не действу¬
ет). По моему собственному мнению, положение упрощается при использовании индексов,
однако в гораздо большей степени это происходит в диаграммной записи, где дифференци¬
рование изображается в виде окружности вокруг дифференцируемой величины. На рис. 14.6
это показано на примере тензорного правила Лейбница.
12V0{£bA
Рис. 14.6. В диаграммной записи ковариантное дифференцирование удобно изображать в виде окруж¬
ности вокруг дифференцируемой величины. Здесь это показано на примере тензорного правила
Лейбница, примененного к Va{£bA^d^gh}} (см* Рис* 12.17). Коэффициенты, учитывающие (ан¬
тисимметрию, дают множитель 12
Всеми указанными свойствами должен обладать также оператор «координатной про¬
изводной» д/дха, используемый вместо Va. Действительно, на любом координатном ло¬
скуте мы можем использовать оператор д/дха, определяющий связность на этом лоску¬
те, которую я буду именовать координатной связностью. Это не слишком интересная
связность, поскольку координаты выбираются произвольным образом. (Она вводит по¬
нятие «параллелизма», при котором координатные линии считаются «параллельными».)
При взаимном перекрытии двух координатных лоскутов связность, определяемая коорди¬
натами одного из них, обычно не согласуются со связностью, определенной на другом
лоскуте (см. рис. 14.1). Хотя координатная связность «неинтересна» (во всяком случае
не представляет физического интереса), ее явное представление часто оказывается по¬
лезным. Причина состоит в том, что если взять разность двух связностей, то действие
этой разности на некоторую тензорную величину Т всегда можно выразить в чисто алге¬
браической форме (т. е. без какого-либо дифференцирования) через Т и некоторую тен¬
зорную величину Г валентности [*].* Это позволяет выразить в явном виде результат
действия V на произвольный тензор Т через координатные производные f14 ^ компонент
тензора	и	некоторые	дополнительные слагаемые, содержащие компоненты тензо-
Ра 1 ъс-
Попробуйте показать это, получив явное выражение. (Подсказки: сначала посмотрите, как действует
разность двух связностей на векторное поле £ и получите ответ в индексной форме £СГ£С. Далее покажите,
что эта разность связностей, действуя на ковектор о, принимает индексную форму —асГ£а. Затем, используя
определение [ *4-валентного тензора Т как полилинейной функции от q векторов и р ковекторов (сравните с § 12.8),
найдите общее индексное выражение для разности двух связностей, действующей на Т.)
В качестве применения этого возьмите две связности в виде V и координатной связности. Найдите
координатное выражение для действия V на произвольный тензор и покажите, как получить в явном виде компо¬
ненты Г£с из соотношений	,	..., Г£п = V^<5£, представив их как результат действия V на каждый
из координатных векторов. (Здесь а есть векторный индекс, который можно считать «абстрактным индексом»
в соответствии с § 12.8, так что 5J и т.п. действительно означают векторы, а не просто набор компонент, а п обо¬
значает размерность пространства. Заметьте, что координатная связность аннулирует каждый из этих координатных
векторов.)

14.4. Кривизна и кручение
267
14.4.	Кривизна и кручение
Координатная связность представляет довольно частный пример связности в том от¬
ношении, что, в отличие от общего случая, она определяет параллелизм, не зависящий
от пути переноса. Это связано с тем фактом (уже отмеченным в § 10.2 в виде д2//дхду =
= д2 f /дудх), что операторы координатной производной коммутируют:
д2	д2
дхадхь дхьдха
Другими словами, величина д2/дхадхъ симметрична по индексам а и Ъ. Вскоре мы увидим,
как это связано с независимостью параллелизма от пути переноса. В случае связности V
общего вида это свойство симметрии не выполняется для оператора Va V&, антисимметрич¬
ная часть которого V[aV^ приводит к появлению двух особых тензоров, один из которых,
с валентностью [*], называется тензором кручения г, а другой, с валентностью [д], — тен¬
зором кривизны R. Кручение присутствует, когда действие оператора V[aV&] на скалярную
величину отлично от нуля. В большинстве физических теорий оператор V берется свобод¬
ным от кручения (г = 0), и это определенно облегчает жизнь. Существуют, однако, теории,
например супергравитация или теории спинового кручения Эйнштейна - Картана - Скьямы-
Киббла, в которых используется ненулевое кручение, играющее важную физическую роль;
см. §31.3 и примечание 19.10. При наличии кручения его индексное представление гаьс,
як
антисимметричное по индексам а, 6, определяется соотношением
(VaV6 - VbVa)<? = таЬсУсФ.
Тензор кривизны R в отсутствие кручения** можно определить^14*3} как***
(VaVb - V6Va)£d =
Как обычно в таких случаях, мы получаем устрашающие выражения с большим чис-
лом мелких индексов, поэтому для этих ключевых соотношении я предлагаю диаграммный
вариант (см., например, рис. 14.7 а, б), В любом случае я также рекомендую там, где мож¬
но, воспринимать индексированные величины как тензоры с абстрактными индексами (как
в § 12.8). (В литературе существует много различных соглашений относительно располо¬
жения индексов, знаков и т. д. Я предлагаю читателю те, которые стремлюсь использовать
сам, — по крайней мере в тех статьях, где я являюсь единственным автором!) Тот факт, что
тензор Rabcd антисимметричен по первой паре индексов а, 6, а именно
г
Rbacd = ~Rabcd
(см. рис. 14.7 в), очевидным образом следует из соответствующего свойства антисиммет¬
рии VaVfr — VbVa = 2 V[aV*,]. Мы вскоре убедимся в важной роли антисимметрии. При от-
зфс эфе эфе эфе
сутствии кручения мы имеем дополнительное условие симметрии (рис. 14.7 г)
R[abc]d — 0) Т. е. R<xbcd т Rbcad + Rcabd ~ 0.
Объясните, почему правая часть должна иметь такую общую форму; выразите компоненты тъса через Г£с.
См. упражнение 14.6.
Покажите, что при наличии кручения в этом выражении должен появиться дополнительный член.
Каково соответствующее выражение для оператора VaVb “ V&Va, действующего на ковектор? Найдите
**
***
выражение для случая общего тензора валентности [ £ ].
•фС ^	А
Во-первых, объясните «т. е.» в этой формуле, во-вторых, получите это соотношение из вышеприведенного
определения тензора Rabcd, раскрыв выражение V[aVb(£dV^]^). (Здесь могут помочь диаграммы.)

268
Глава 14
R
d
abc
О, т.е.
г)
б)
в)
О
О
д)
Рис. 14.7. а) Удобная диаграммная запись для тензора кривизны Rabcd. б) Тождество Риччи (Va Vb
— VbVa)£d = Rabca£°. в) Антисимметрия Rb
d
d
ас
СВОДИТСЯ К соотношению Rabcd + Rbcaa + Rcab
d
d
-Rabcd• г) Симметрия Бьянки R[abc]d
0. б)) Тождество Бьянки S7[aRbc]e — 0
0, которая
Это соотношение иногда называют «первым тождеством Бьянки». Я буду называть это сим¬
метрией Бьянки. Термин тождество Бьянки (рис. 14.7 Э) обычно сохраняют для «второго»
подобного тождества, которое при отсутствии кручения имеет вид*
^ [a Rbc]
0, Т. е. VaRbcde + VbRcade + VcRabd
0.
Как мы увидим в § 19.6, тождество Бьянки является краеугольным камнем эйнштейновской
теории поля.
Кривизна является существенным свойством, выражающим зависимость связности
от пути переноса (по крайней мере, в локальном масштабе). Если рассмотреть перенос
вектора вдоль замкнутой петли в пространстве Л4, используя понятие параллельного пере¬
носа, определяемое оператором V, то мы найдем, что именно тензор R служит мерой того,
насколько изменился вектор при возвращении в исходную точку. Проще всего взять петлю
в виде «бесконечно малого параллелограмма» в пространстве М. (Как мы увидим, такие
параллелограммы определенно «существуют», когда оператор V свободен от кручения.)
Однако прежде необходимо дать пояснения к некоторым понятиям.
14.5.	Геодезические, параллелограммы и кривизна
Прежде чем строить параллелограмм, рассмотрим понятие геодезической (линии), опре¬
деляемой связностью V. Геодезические важны для нас и по другим причинам. Они являются
аналогом прямых линий евклидовой геометрии. В рассмотренном выше примере сферы S2
(рис. 14.2-14.4) геодезическими служат большие окружности на сфере. В более общем слу¬
чае искривленной поверхности в евклидовом пространстве геодезическими будут кривые
минимальной длины (измеряемые, например, нитью, туго натянутой вдоль поверхности).
Позже (в § 17.9) мы увидим, что геодезические играют фундаментальную роль в общей
теории относительности Эйнштейна, представляя те пути в пространстве-времени, которые
описывают свободное падение тел. Что дает нам наша связность V в отношении понятия
геодезической? Прежде всего, геодезическая есть кривая 7, которая продолжается «парал¬
лельно самой себе» в соответствии с параллелизмом, определяемым связностью V. Каково
точное выражение этого требования? Предположим, что вектор t (т. е. ta) направлен по ка¬
сательной к кривой 7. Требование, чтобы его направление оставалось параллельным самому
*J0 Выведите это из приведенного выше соотношения, определяющего Ra.bcd> раскрыв двумя способами
выражение V[aVbVd]£c. (Здесь также могут помочь диаграммы.)

14.5. Геодезические, параллелограммы и кривизна
269
себе вдоль кривой 7, можно выразить в виде^14,41
Vtoct, т.е. TaVatb<xtb
t
(символ ос означает пропорциональность следующей за ним величине, см. § 12.7). При вы¬
полнении этого условия вектор t в процессе переноса вдоль кривой 7 может растягиваться
или сжиматься, но его направление «остается направленным в одну и ту же сторону» в соот¬
ветствии с понятием параллелизма, определяемым оператором V. Если принять, что «рас¬
тяжение или сжатие» не имеет места, так что вектор t остается постоянным вдоль кривой 7,
то получается более жесткое условие, что касательный вектор t претерпевает параллельный
перенос вдоль 7, так что условие
Vt == 0, т. е. taVatb = О
выполняется вдоль всей кривой 7; здесь вектор t (ta в индексной форме) является касатель¬
ным вектором к 7 вдоль всей кривой.
Согласно этому более жесткому условию, сохраняться вдоль кривой 7 будет не только
направление вектора t, но и его «масштаб». Что это значит? Прежде всего следует отметить,
что любая кривая (необязательно геодезическая), параметризованная (достаточно гладкой)
координатой и9 соответствует определенному выбору масштаба для касательного векто¬
ра t вдоль кривой. Так получается потому, что вектор t соответствует дифференцированию
(d/du) по и вдоль кривой. Это условие можно записать в виде
t(u) = 1
либо
Vti = 1, т. е. taVau — 1
t
вдоль кривой*.
В случае геодезической 7 такой более жесткий выбор масштаба вектора £, при кото¬
ром Vt = 0, соответствует определенному типу параметра и9 известному под названием
аффинного параметра (см. рис. 14.8). Если у нас есть подходящее понятие «расстояния»,
отсчитываемого вдоль кривых, то обычно в качестве меры расстояния можно взять наш
аффинный параметр. Однако аффинные параметры имеют более общий смысл. Например,
в теории относительности оказывается, что подобные параметры необходимы для световых
лучей, при этом «мера расстояния» здесь оказывается бесполезной, поскольку она равна
нулю! (См. §§17.8, 18.1.)
Попробуем теперь построить параллелограмм из геодезических. Начнем с некоторой
точки р многообразия Л4 и проведем в М геодезические Л и р из точки р с соответ¬
ствующими касательными векторами L и М в точке р и соответствующими аффинными
параметрами I и т. Выберем некоторое положительное число е и измерим аффинное рас¬
стояние I — е вдоль Л от точки р до точки q и аффинное расстояние т — е вдоль р
от точки р до точки г; см. рис. 14.9 а. (Интуитивно можно представить, что отрезки геоде¬
зических pq и рг имеют «направленные длины» соответственно eL п еМ при некотором
* ill Продемонстрируйте эквивалентность всех этих условий.
** J3? Покажите, что если и иг? — два аффинных параметра на кривой 7 относительно двух различных вариантов
выбора вектора t, то v = Аи Н- В, где А и В остаются постоянными вдоль кривой 7.

:а.
jW
ш?.
270
Глава 14
а
11
я
4
ж
ж
I
*
VV': *
Л
#
• •'У.
Ш'
• •
‘< \
V.,. .
. '■У'-.'
ф.
И' •'
...7л
• Vf:.
&•
Рис. 14.8. Для любого (достаточно гладкого) параметра иу определенного вдоль кривой 7, поле каса¬
тельных векторов t к кривой 7 естественно связывается с и, так что вдоль 7 вектор t соответствует
дифференцированию d/du (что означает t(u) = 1 или taVau = 1). Если 7 — геодезическая кри¬
вая, то и называется аффинным параметром при параллельном переносе вектора t, так что V t = 0
вместо vt а Г Значения аффинного параметра откладываются вдоль 7 через равные промежутки
в соответствии с V
малом е.) Чтобы замкнуть параллелограмм, нам придется двигаться от точки q вдоль новой
геодезической /г' в направлении, «параллельном» вектору М. Чтобы выполнить условие
«параллельности», переместим вектор М из р в q вдоль Л путем параллельного переноса
(это означает, что вектор М должен удовлетворять условию VM = 0 вдоль Л). Теперь по-
L
пробуем поместить последнюю вершину параллелограмма в точку s, отмеренную вдоль /Т
на аффинном расстоянии т = е от точки q. Однако вместо этого мы можем попробовать
позиционировать эту последнюю вершину иным образом, перемещаясь от точки г на аф¬
финное расстояние I — е до конечной точки s' вдоль геодезической А', выходящей из точки г
в направлении вектора М, который был перенесен параллельным образом вдоль // из р в г.
Чтобы получить подлинный параллелограмм, мы должны потребовать, чтобы эти альтерна¬
тивные последние вершины s и s' были одной и той же точкой (s = s')!
Однако за исключением весьма специальных случаев (вроде евклидовой геометрии)
эти две точки не совпадают. (Вспомните наши попытки построить квадрат в § 2.1!) Эти точ¬
ки не могут быть, так сказать, «слишком» различными, если векторы zL и еМ выбраны
достаточно малыми. То, насколько они различны, определяется кручением т. Чтобы как сле¬
дует понять это, нам потребуется несколько больше сведений из математического анализа,
нежели было дано выше. Существенный пункт состоит в том, что мы должны рассматри¬
вать отклонения от евклидовой геометрии проявляющимися в некотором масштабе, который
зависит от выбора нашей малой величины в. Поэтому мы будем иметь дело не с реальной
величиной отклонения от плоского пространства, а с той скоростью, с которой она стремит¬
ся к нулю, когда параметр е неограниченно уменьшается. Так что нас интересует не столько
точное значение этого параметра, сколько то, будет ли величина Q стремиться к нулю,

14.5. Геодезические, параллелограммы и кривизна
271
а)
б)
*)
Рис. 14.9. а) Попробуем построить параллелограмм из геодезических. Возьмем на многообразии М
две геодезические Лид, проходящие через точку р, с соответствующими касательными векторами L
и М в точке р и соответствующими аффинными параметрами I и т. Возьмем точку г на аффинном
расстоянии т — е от точки р вдоль д и точку q на аффинном расстоянии / = е от точки р вдоль Л
(е > 0 — фиксированный малый параметр). Отрезки геодезических pq и рг имеют «направленные
длины» eL и еМ. Чтобы образовать параллелограмм, перенесем вектор М параллельным образом
из р в q вдоль Л (ум
О вдоль Л), что дает геодезическую р!, соседнюю с д, простирающуюся
от q до 5 на аффинное расстояние е вдоль новой «параллельной» стрелки еМ'. Аналогично перенесем
вектор L параллельным образом из р в г вдоль д и протянем от г до s вдоль параллельной стрелки eL*
от точки q на аффинное расстояние т — е вдоль А'. б) В общем случае s Ф s', так что точно
замкнуть параллелограмм не удается, однако получающийся зазор имеет порядок всего лишь 0(е3),
если кручение исчезающе мало, в) При наличии ненулевого кручения появляется зазор порядка 0(е2)
как е, или как е2, или как е3, или, возможно, как какая-нибудь другая функция от е. (Мы уже
видели нечто подобное в § 13.6.) Слова «стремиться к нулю, как» означают здесь, что при ис¬
пользовании некоторой координатной системы абсолютные значения компонент тензора Q
будут меньше некоторой положительной постоянной величины, умноженной соответствен¬
но на е9 или на в2, или на в3, или на некоторую другую функцию от е. (Так что наше «как»
включает в себя и «быстрее, чем»!) В этих случаях мы можем говорить, что величина Q
порядка £, или е2, или е3 и т.д., и записывать это как 0(e), или 0(е2), или 0(е3) и т.д.
Этот факт не зависит от конкретного выбора координат, и по этой причине понятие «порядка
малости» оказывается таким чувствительным и плодотворным. Мое изложение было здесь
слишком кратким, и я отсылаю непосвященного интересующегося читателя к литературе по
этой замечательной и вездесущей теме^14,5!. На интуитивном уровне следует иметь в виду,
что величина 0(е3) предполагается весьма малой по сравнению с величиной 0(с2), которая
в свою очередь мала по сравнению с 0(e), и т. д.
Теперь вернемся к нашей попытке построить параллелограмм. Исходные векторы eL
и£М в точке р оба имеют порядок 0(e), так что стороны pq и рг и, следовательно, qs
и г s' будут того же порядка. Насколько большим будет в таком случае «зазор» ss'l От¬
вет на этот вопрос следующий: если связность не содержит кручения, то он всегда имеет
порядок 0(е3) (см. рис. 14.95). Фактически это свойство полностью определяет условие от¬
сутствия кручения. Если же имеется ненулевое кручение, то это проявляется в (некоторых)
параллелограммах как член 0(е2) (см. рис. 14.9 в)*. Иногда говорят (довольно неточно), что
отсутствие кручения является условием замыкания параллелограмма (что в действительно¬
сти означает замкнутость с точностью до е2).
ж Найдите этот член.

272
Глава 14
Предположим теперь, что кручение отсутствует. Можно ли использовать наш парал¬
лелограмм для интерпретации кривизны? Да, можно. Пусть мы имеем в точке р третий
вектор N, который мы переносим параллельным образом вокруг нашего параллелограмма
от р до s через q, а затем сравниваем результат с переносом от р до sf через г. (При отсут¬
ствии кручения такое сравнение имеет смысл с точностью до е2, поскольку в этом случае
зазор между s и s! имеет порядок 0(е3) и им можно пренебречь. При наличии кручения
необходимо помнить о дополнительном крутильном члене; см. упражнение 14.7.) Разность
между результатами переноса psq и переноса prsf будет иметь вид
г2 La Мь № Rabcd.
Это дает нам наглядную геометрическую интерпретацию тензора кривизны R (см.
рис. 14.10). (Эквивалентный вариант этой интерпретации получается, если представить се¬
бе перенос вектора N вокруг всего параллелограмма с началом и концом в одной и той
же точке р, игнорируя несоответствия порядка 0(г3) в вершинах параллелограмма. Раз¬
ностью между начальным и конечным значениями N будет опять-таки вышеприведенная
величина е2LaМъNсRabCd•)
Разность значений
V
Рис. 14.10. Используйте параллелограмм для интерпретации кривизны при т == 0. Перенесите тре¬
тий вектор N параллельным образом из р в s через q и сравните результат с переносом этого
вектора из р в s' через г. Член 0{е2), являющийся мерой разности, имеет вид е2LaМьNсRabcd>
т.е. £2R{L, М, N), что дает наглядную геометрическую интерпретацию тензора кривизны R
Вспомним об антисимметрии тензора Rabcd по индексам а, 6. Она означает, что вы¬
шеприведенное выражение чувствительно только к антисимметричной части	вели¬
чины LaMb, т.е. к V-произведению L Д М (см. § 11.6). Таким образом, мы имеем дело
с элементом 2-плоскости, построенным на векторах L и М, в точке р. В случае, когда мно¬
гообразие М само является 2-поверхностью, имеется всего одна независимая компонента
тензора кривизны (поскольку элемент 2-плоскости должен быть касательным к М в точке р).
Эта компонента дает нам гауссову кривизну 2-поверхности, упомянутую в § 2.6, которая слу¬
жит для описания локальной геометрии сферы, евклидовой плоскости и гиперболического
пространства. При большем числе измерений ситуация усложняется, поскольку существу¬
ет больше компонент тензора кривизны из-за различных возможностей выбора элемента
2-плоскости LAM.
Существует некоторый особенно важный вариант геометрической интерпретации кри¬
визны. Он получается, если взять в качестве вектора N тот же вектор L. Тогда можно

14.5. Геодезические, параллелограммы и кривизна
273
Рис. 14.11. Отклонение геодезических. Выберем N = L в паралле¬
лограмме на рис. 14.10. Стороны pq и г s' являются отрезками двух
соседних геодезических 7 и у' (здесь используется 7 вместо Л и 7'
вместо Л'), выходящих соответственно из точек р и г, с параллельны¬
ми касательными векторами LylL'; вектор М является связывающим
л
в точке р. Отклонение между геодезическими 7 и 7 измеряется раз¬
ностью между результатами параллельного перемещения вектора L
по путям prs' и pqs, которая равна е2La Мь№Rabcd
рассматривать стороны нашего параллелограмма pq и г s’ как отрезки двух соседних гео¬
дезических, соответственно 7 и 7', а вектор L — как касательную к этим геодезическим.
Вектор еМ в точке р может служить мерой смещения кривой 7 относительно 7' в точ¬
ке р. Вектор М иногда называют связывающим вектором. Геодезические 7 и 7' следуют
параллельно одна другой (если сравнивать их на двух «концах» связывающего вектора,
т. е. на отрезке рг). При параллельном переносе вектора L(= N) в точку sf по другому
пути prsf он остается касательным к геодезической 7' в точке s'. Однако при переносе
вектора L в s по первому пути pqs мы придем к исходному вектору для другой геодези¬
ческой 7", соседней с 7, причем 7" идет параллельно 7 в другой точке q. Разность 0(е2)
между двумя вариантами (вектор L в s и в s'), равная е2LaМьNсRabcd> служит мерой «от¬
носительного ускорения», или «отклонения» геодезической 7' от 7 (см. рис. 14.11). (Это от¬
клонение математически описывается так называемым уравнением Якоби) На рис. 14.12
показано такое отклонение геодезической, когда многообразие М. представляет собой 2-по¬
верхность положительной и отрицательной (гауссовой) кривизны. Если кривизна положи¬
тельна, то соседние геодезические, параллельные в начале пути, изгибаются навстречу одна
другой, если же кривизна отрицательна, они изгибаются в разные стороны. Как мы уви¬
дим в §§ 17.5, 19.6, этот факт имеет большое значение для общей теории относительности
Эйнштейна.
а)	6)
Рис. 14.12. Отклонение геодезических, когда многообразие ЛЛ представляет собой 2-поверхность
а) положительной (гауссовой) кривизны, так что геодезические 7 и у’ изгибаются навстречу одна
другой, и б) отрицательной кривизны, когда они изгибаются в разные стороны

274
Глава 14
14.6.	Производная Ли
Обсуждая зависимость параллелизма от пути переноса при использовании связности V,
я пользовался индексными обозначениями, предпочитаемыми физиками. В обозначениях ма¬
тематиков непосредственная аналогия между различными частными выражениями просле¬
живается не так явно. Вместо этого приходится действовать несколько иначе. (Примечатель¬
но, что разница в ооозначениях может порой повернуть оосуждаемую тему совсем в ином
направлении!) Этот иной способ предполагает другую операцию дифференцирования — так
называемые скобки Ли, — которая представляет собой обобщение одноименной операции,
введенной в § 13.6. Это, свою очередь, есть частный пример важного понятия — производной
Ли. Эти понятия не зависят от какого-либо конкретного выбора связности (и, следователь¬
но, применимы к произвольному неструктурированному гладкому многоооразию), так что
имеет смысл обсудить производную Ли и скобки Ли в общем виде, прежде чем мы вернемся
к их связи с кривизной и кручением в конце этого раздела.
Чтобы определить производную Ли на многообразии М, необходимо задать на М
некоторое векторное поле £. Производная Ли, обозначаемая символом <£, представляет со¬
бой некоторую операцию над векторным полем £. Производная £ Q служит мерой того,
как меняется некоторая величина Q по сравнению с тем, что было бы, если бы ее просто
«перетащили» с помощью векторного поля £ (см. рис. 14.13). Эта операция применяется
к тензорам общего вида (и даже к понятиям, отличным от тензоров, например, к связно¬
стям). Для начала мы просто рассмотрим производную Ли от векторного поля rj(~ Q)
по другому векторному полю £. Мы убедимся, что это та самая операция, которую мы назы¬
вали «скобками Ли» в § 13.6, но в несколько более общем контексте. Затем мы посмотрим,
как обобщить это на тензорное поле Q,
Напомним (см. § 12.3), что само векторное поле можно рассматривать как дифферен¬
циальный оператор, действующий на «скалярные» поля Ф, S', ... и подчиняющийся следу¬
ющим трем правилам: 1) £(Фу-Ф) — £(Ф) + £($% 2) £(ФФ) = Ф£(Ф) +Ф£(Ф) и 3) £(&) ™ О,
если к — постоянная величина. Легко показать*, что оператор и?, определяемый соотноше¬
нием
U)
5
подчиняется тем же трем правилам при условии, что им подчиняются £ и 77; поэтому
величина и) также должна быть векторным полем. Вышеприведенный коммутатор двух
операций £ и г/ часто записывается (как и в § 13.6) в виде скобок Ли:
ш = €т]- »?£ = К, г) ■
Геометрический смысл коммутатора двух векторных полей £ и г/ иллюстрируется
на рис. 14.14. Мы пытаемся построить четырехугольник из «стрелок», которые берутся
по очереди из векторных полей £ и г) (каждая из них имеет порядок О(е)) и обнаружи¬
ваем, что и) служит мерой «зазора» (порядка 0(е2)). Можно убедиться**, что коммутатор
удовлетворяет следующим соотношениям:
К* *}] = - Ь?> €] > К + п, С] = [£, С] + [*7, С].
[£> Ь?> С]] + [v, [С. £]] + [С К, г?]] = о,
как и в случае коммутатора двух бесконечно малых элементов группы Ли (см, § 13.6).
Как связана определенная выше операция коммутации с алгеброй бесконечно малых
элементов группы Ли (§ 13.6)? Чтобы объяснить это, позволю себе небольшое отступление.
 	    *	т*
*
ЯгГо
 Покажите это.
1 Сделайте это.
ад

14.6. Производная Ли
275
t
г.
* J	-гг
// # '	'	.	1	*	1Ш*	*	if	*	*	*
//ТТ^7
( Разность,
[ измеряемая £г/
«Перерви- т
нутый» / Разность,
вектор 77 / измеряемая £Q
а//'
&
%
«Передви-!
нутый»
^тензор Q
* - 1	а
L«l •	^	•	f	^	\
LliS I4A	•-	^
ПК Ш 'I III r* 4fi
V—УI	Тензорное
{ * ) поле Q
* #
*
*
+ *+4
/• вл4
р« Ф:
Рис. 14.13. Производная Ли £, определенная на многообразии общего вида М, берется по отноше¬
нию к некоторому заданному гладкому векторному полю £ на Л4. Величина £ является мерой того,
насколько величина Q (например, векторное поле г} или тензорное поле Q) реально меняется по
сравнению с величиной, «передвинутой» векторным полем £
Мы рассматриваем группу как некоторое многообразие Q
(называемое «групповым многообразием»), точками ко¬
торого служат элементы нашей группы Ли. В более
общем случае мы могли бы рассматривать произволь¬
ное многообразие 77, элементы которого действуют как
некоторые гладкие многообразия (например, сферу S2
в случае группы вращений Q = SO(3); см. рис. 13.2).
Но сейчас мы рассматриваем в первую очередь группо¬
вое многообразие Q, а не более общее 77, поскольку нас
интересует, как связана группа Q в целом со структурой
ее алгебры Ли. Бесконечно малые групповые элементы
следует изображать в виде некоторых векторных полей
на Q (или даже 77). То есть мы рассматриваем беско¬
нечно малое движение вдоль соответствующего вектор¬
ного поля £ на Q, чтобы представить преобразование,
Рис. 14.14. Скобки Ли [£, 7jj (
£f\)
для двух векторных полей £ и г)
служат мерой зазора порядка 0(е2)
в незавершенном четырехугольнике
из чередующихся «стрелок» и ет]
порядка О(с)
соответствующее предварительному умножению каждо¬
го элемента группы на бесконечно малый элемент, пред¬
ставляемый вектором £ (см. рис. 14.15 а).
Выбрав малую положительную величину е, можно рассматривать как движение груп¬
пы Q порядка 0(e) вдоль векторного поля при этом тождественный групповой элемент I
соответствует нулевому движению. Произведение двух таких малых групповых действий
и ет] с точностью О (в) дается суммой е£ + erf, так что «стрелки» е£ и ег] просто склады¬
ваются по правилу параллелограмма (рис. 14.156). Но это дает мало информации относи-

276
Глава 14
а)
б)
Касательное
пространство
»)
Рис. 14.15. Операции алгебры Ли, геометрически интерпретируемые на непрерывном групповом мно¬
гообразии Q. а) Предварительное умножение каждого элемента группы Q на бесконечно малый груп¬
повой элемент £ (элемент алгебры Ли) дает бесконечно малый сдвиг на Q, т. е. векторное поле £
на Q. б) В первом порядке по е произведение двух таких бесконечно малых движений £ и г) дает
просто £ + т7, что отражает структуру касательного пространства (на тождественном групповом эле¬
менте I). в) Во втором порядке появляется локальная групповая структура, е1 [£, г]\, которая дает
зазор О {г2) в «параллелограмме» с чередующимися сторонами е£ и ет) на I
тельно структуры группы (фактически только о ее размерности, поскольку мы обнаружили
аддитивную структуру касательного пространства в тождественном элементе группы I).
Чтобы определить групповую структуру, нам нужно перейти к величинам порядка 0(е2);
как и в § 13.6, это делается путем рассмотрения коммутатора £77 —	=	[£,77]. Величи¬
на е2 [£, 77] соответствует зазору порядка О (в2) в «параллелограмме», исходными сторонами
которого служат t£ и ег) в «начале координат» I. Соответствующее понятие «параллелизма»
вытекает из группового действия, позволяя получить необходимое понятие «параллельного
переноса», которое в действительности определяет связность с кручением, но без кривизны*
(см. рис. 14.15 в).
Как уже отмечалось в § 13.6, алгебра Ли таких векторных полей дает полную (локаль¬
ную) структуру группы. Здесь можно указать процедуру, посредством которой из элемента £
алгебры Ли получается обычный конечный (т. е. не бесконечно малый) групповой элемент х.
Это называется возведением в степень (потенцированием) (сравните с §§5.3, 13.4):
х
&
I + €+Ы2 + l€3 +
* *
2
б
су
Здесь £ означает оператор второй производной с двукратным применением £ и т.п., I
единичный оператор. Это, по существу, вариант теоремы Тейлора, изложенной в § 6.4.
**
Попробуйте объяснить, почему здесь имеется кручение и нет кривизны.
Объясните (на формальном уровне), почему еа djfdy f (у) ~ f{y + а), где а — постоянная.

14.6. Производная Ли
277
Произведение двух конечных групповых элементов х и у дается тогда выражением е^е71.
Оно отличается от е^+г? (сравните с § 5.3) на величину, описываемую формулой алгебры
Ли!14-6!,
в которую входят только ^ и г/.
Можно отметить, что некоторый вариант операции возведения в степень применим
также к векторному полю £ на многообразии общего вида АА (при этом М и £ предпо¬
лагаются аналитическими, т.е. Сы-гладкими, см. §6.4). Напомним (см. § 12.3 и рис. 10.6),
что если выбрать е малым, то е£(Ф) с точностью 0(e) определяет увеличение скаляр¬
ной функции Ф от хвоста к острию «стрелки», изображающей е£. Точнее, величина е^(Ф)
определяет полное значение Ф, которое достигается, когда мы следуем вдоль «£-стрелок»
от исходной точки О к конечной точке, заданной параметром и = £, причем параметр и
нормирован так, чтобы было £(гг) = 1 (сравните с § 14.5 и рис. 14.8). Все производные
(т.е. r-ая производная в случае £Г(Ф)) в степенном ряду для е^(Ф) должны вычисляться
в точке О (при этом предполагается сходимость). Слова «следуем вдоль стрелок» означают,
что мы двигаемся вдоль так называемой «интегральной кривой» вектора £, то есть вдоль
кривой, касательными к которой служат векторы £ (см. рис. 14.16)^14,71
4
Рис. 14.16. Интегральная кривая векторного поля £ на М — это такая кривая 7, которая «следует
вдоль £-стрелок», т.е. касательными векторами к которой служат векторы £, соответствующие па¬
раметру и в том смысле, что £(ад) = 1 (сравните с § 14.5 -и рис. 14.8). Предположим, что Л4, £
и скалярное поле Ф аналитичны (т.е. -гладки) и что кривая 7 протянута от некоторой базисной
точки О (и = 0) до другой точки р(и — £). Тогда (в предположении сходимости) значение Ф в точке р
дается величиной е^(Ф), вычисленной в точке О; здесь ef*
1 + 14+ h2e + h3f +
. £
взятую
Каково в таком случае определение производной Ли? Прежде всего просто перепишем
ки Ли в виде операции £ (зависящей от £), которая действует на векторное поле гр.
£

278
Глава 14
Это соотношение должно служить определением производной Ли £ (по переменной £)
£
от [^]-тензора (т. е. вектора) 77. Выразим это через некоторую заданную связность без кру¬
чения V. Соответствующее выражение (его диаграммное представление см. на рис. 14.17 а)
£rj = V77-VC, т.е (£т})ь = ZaVaVb - T?aVa£6
£	€	v	£
получается сразу, если воспользоваться соотношением £(Ф) — £аУаФ и т.п.*’ ** Чтобы
получить производную Ли для тензора общего вида, воспользуемся тем обстоятельством,
что £ подчиняется тем же правилам, что и связность V (за исключением линейности по £).
Правила эти следующие: £Ф = £(Ф) для скаляра Ф, £(T-\-U) — £T + £U для тензоров Т
и U одинаковой валентности, £(Т • U) — (JST) • U + Т • £U с одинаковым порядком
£ £ £
свертывания в каждом из слагаемых. Отсюда с учетом соотношения £г) — [£, 77] немедленно
С
получаем результат действия операции £ на произвольный тензор^1481 В частности, для
ковектора а (валентность ® ]) имеем
£ot = Va + a • (V£)> т-e- {£ot)a ~ £6V*aa + о?ьУа^ь,
£ £ £
где V не содержит кручения; см. рис. 14.176. Для тензора Q валентности [i] имеем
(см. рис. 14.17 в)
£Qcab = eVuQlb + QlbVaC + QcavS ьС -
l Tt	+
a)	6)	в)
Рис. 14.17. Диаграммы для производной Ли а) от вектора 77: (£г})ь — £aVa?76 ~VaVa£b, б) от ковекто¬
ра а: (£а)а = £bVbCta + аьУа£6, в) от [^-валентного тензора Q: £Qcab —	+	Qub^aC +
+ QauVbC ~ QabV^C
Заметим, что производная Ли, рассматриваемая как функция от £ и величины Q (тензор¬
ного поля), на которую она действует, не зависит от связности, т. е. от выбора оператора Va,
не содержащего кручения. (Так получается, потому что оператор £ однозначно выводится из
оператора градиента d.) В частности, вместо Va можно использовать оператор координатной
производной д/дха (в произвольной локальной системе координат), при этом получается
тот же результат. Даже если мы имеем связность с кручением, мы можем поступить таким же
Выведите эту формулу для £т}.
£
Как изменится формула в упражнении 14.9 при наличии кручения?
*** Jslt Проверив вышеприведенную формулу для ковектора, докажите единственность и получите явное выра¬
жение для производной Ли от тензора общего вида.

14.7. Что МОЖЕТ ДАТЬ НАМ МЕТРИКА
279
образом, выразив ее через другую связность, которая не содержит кручения и однозначно
определяется заданной связностью как результат «вычитания» из нее кручения*.
В отношении свойства независимости от связности производная Ли сходна с внеш¬
ней производной (см. § 12.6), в соответствии с чем для любой р-формы а с индексным
представлением имеем
аь...d	^[а^6...<2]?
где V — произвольная связность без кручения (см,
рис. 14.18). Это то же самое выражение, что и в § 12.6,
за исключением того, что там использовалась коорди¬
натная связность д/дха в явном виде. Легко видеть,
что вышеприведенное выражение действительно не за¬
висит от выбора связности, не содержащей кручения**.
Более того, из этого выражения немедленно следует
ключевое свойство d2a = 0.*** Существуют и некото¬
рые другие выражения, обладающие тем же свойством
независимости от связности в указанном смысле^14,9^.
Вернувшись, наконец, к вопросу о кривизне на на¬
шем многообразии М со связностью V, мы обнару¬
жим, что скобки Ли нужны нам для определения тен¬
зора кривизны в обозначениях математиков:
VV-VV- V ) N - R(L, М. JV),
L М ML [L,M)J
где i?(X, М, N) означает вектор LaМъ№Rabcd•**** Хотя присутствие лишнего коммутато¬
ра может рассматриваться как недостаток этой записи, имеется и компенсирующее преиму¬
щество в том, что теперь кручение учитывается автоматически (в отличие от обозначений
физиков, где для кручения понадобилось дополнительное слагаемое). Вспомним, какой гео¬
метрический смысл имеет коммутатор (рис. 14.14). Он описывает «зазор» порядка 0(е2)
в четырехугольнике порядка 0(e), построенном из векторных полей L и М. Здесь имеется
дополнительное преимущество, состоящее в том, что петлю, вдоль которой мы переносим
вектор N9 необязательно считать «параллелограммом» (с указанной выше точностью), это
может быть и (криволинейный) четырехугольник (см. рис. 14.19). Если [L, М) = 0, то этот
четырехугольник замыкается (с точностью 0(е2)).
d
2?-форма
1
(р -f-1)!
Р+1
Рис. 14.18. Диаграмма для внешней
производной отр-формы: (da)ab...d —
= V[aab...d]
14.7.	Что может дать нам метрика
До сих пор мы считали, что связность V просто приписана к нашему многообразию М.
Это придавало многообразию М структуру определенного вида. Очень выгодно, однако,
рассматривать связность как некоторую вторичную структуру, возникающую из метрики,
определенной на М. Вспомним (см. §13.8), что метрика (или псевдометрика) задается
несингулярным симметричным [9]-валентным тензором g. Потребуем, чтобы величина g
описывала гладкое тензорное поле, которое действует на касательные пространства в раз¬
личных точках многообразия М. Многообразие с приписанной к нему таким образом мет¬
рикой называетсяримановым или, возможно, псевдоримановым^14лоч (Мы уже встречались
Покажите, как можно найти эту вторую связность, учитывая, что величина Г для разности связностей
асимметрична по двум нижним индексам. (См. упражнение 14.5.)
Докажите это и покажите, как изменится это выражение при наличии тензора кручения т.
Покажите это.
Продемонстрируйте эквивалентность (при отсутствии кручения) с соответствующим выражением в обо¬
значениях физиков.
**
***
****

280
Глава 14
Векторная
разность:
е2 R(L,M,N)
eL}
Газ: 0[ег)
Рис. 14.19. Кривизна «в обозначениях математиков»	“	]^У	~	^	})	^ =	0ПРе"
деляемая по величине зазора порядка 0(е2) при параллельном переносе вектора N вокруг (неза¬
мкнутого) «четырехугольника» со сторонами sL, еМ, eL\ еМ'. Вклад скобок Ли г2 [L, М] за¬
полняет зазор порядка 0(е2) с точностью О (г3). (Индексная запись вектора R(L, М, N) имеет
вид LaMbNcRabcd
с великим математиком Бернхардом Риманом в главах 7 и 8. Он ввел понятие n-мерного мно¬
гообразия с метрикой, следуя Гауссу, который ранее изучал «римановы» 2-многообразия.)
Обычно римановыми называют многообразия с положительно определенной метрикой д
(см. § 13.8). В этом случае имеется (положительная) мера расстояния вдоль любой гладкой
кривой, определяемая взятым вдоль кривой интегралом от ds (рис. 14.20), где
ds2 — gabdxa dxb<
Вполне естественно интегрировать вдоль кривой, что¬
бы определить ее длину, которая совпадает с «дли¬
ной» в обычном смысле слова, когда метрика g по¬
ложительно определена. Хотя величина ds не является
1-формой, она обладает свойствами 1-форм в доста¬
точной мере, чтобы признать законным интегрирова¬
ние ее вдоль кривой. Таким образом, длину £ кривой,
соединяющей точку А с точкой В, можно представить
в виде^14*11]
1
ь
£ —	ds,	где ds ~ {даъ dxa dx)2.
Можно отметить, что в случае евклидова про-
Рис. 14.20. Длина гладкой кривой равна	л	Л
„	g _ Га. ь	странства	это	в точности совпадает с обычным опреде-
J s, где s — даь х х	лением	длины	кривой, что проще всего заметно в де¬
картовой системе координат, где компонентами даъ
служат компоненты дельта-символа Кронекера (см. §13.3), т. е. компоненты равны 1
при а = Ь и 0 при а ф Ъ. Как отмечалось в § 13.3 (см. упражнение 13.11), формула для ds
выражает, по существу, теорему Пифагора (§2.1), но действующую на уровне бесконечно
Длина = I ds

14.7. Что МОЖЕТ ДАТЬ НАМ МЕТРИКА
281
малых величин. Однако на римановом многообразии общего вида мера длины кривой, со¬
гласно приведенной формуле, определяет геометрию, отличную от евклидовой. Это проявля¬
ется в неприменимости теоремы Пифагора к конечным интервалам (в отличие от бесконечно
малых). Тем не менее замечательно, что эта древняя теорема продолжает играть фундамен¬
тальную роль — теперь уже на уровне бесконечно малых величин. (Вспомните последний
абзац в § 2.7.)
Как будет видно из § 17.7, случай сигнатуры Н — играет особую роль в теории отно¬
сительности, в которой (псевдо)метрика непосредственно измеряет время, регистрируемое
идеальными часами. Далее, любой вектор v имеет длину |?;|, определяемую соотношением
v
9abVavh;
при положительно определенном тензоре g длина положительна, если только вектор v отли¬
чен от нуля. Однако в теории относительности мы используем лоренцеву метрику (см. § 13.8),
так что величина \ v\2 может иметь любой знак. Позднее (§§ 17.9, 18.3) мы поймем значение
этого факта.
Каким образом несингулярная (псевдо)метрика g однозначно определяет связность V,
не содержащую кручения? Один из способов сформулировать условия, налагаемые на опера¬
тор V, состоит просто в требовании, чтобы параллельный перенос вектора всегда сохранял
его длину (такое свойство параллельного переноса на сфере S2 предполагалось в § 14.2).
Можно также представить это требование в виде
Vg = 0.
Это условие (вместе с условием отсутствия кручения) достаточно для полного определения
связности V. Такую связность называют по-разному — связностью Римана, связностью
Кристоффеля либо связностью Леви-Чивита (в честь Бернхарда Римана (1826-1866), Элвина
Кристоффеля (1829-1900) и Туллио Леви-Чивита (1873-1941), каждый из которых выдвинул
^ pfc
важные идеи, связанные с этим понятием) .
Существует и другой способ понять, каким образом метрика g (в частности, поло¬
жительно определенная) задает связность. Непосредственно из метрики можно получить
понятие геодезической. Кривая на многообразии М между двумя заданными точками, кото¬
рая имеет минимальную длину / ds (эта величина иллюстрируется на рис. 14.20), и будет
геодезической для метрики g. Знать расположение геодезических — это большая часть того,
что требуется для задания связности V. Для полного задания V еще нужна информация
об аффинных параметрах, заданных на геодезических. Таковыми оказываются параметры,
определяющие длину дуг кривых, и постоянные множители при них; все это опять-таки
^
задается тензором д. Если метрика д не является положительно определенной, то рас¬
суждения в основном остаются в силе, но теперь геодезические не минимизируют / ds;
этот интеграл называется «стационарным» для геодезической. (К этому понятию мы еще
вернемся; см. §§ 17.9, 20.1.)
В (псевдо)римановой геометрии метрику даъ или обратную ей величину даЬ (определяе¬
мую соотношением даЬдьс — <££) можно использовать для поднятия или опускания индексов
# Ш	1	.
Выведите явное выражение в компонентной записи Г£с = -7^gad (dgbdjdx0 4- dgC(i/dxb — dgcb/dxd)
для коэффициентов связности (символов Кристоффеля) Г£с- (См. упражнение 14.6.)
**ДД Выведите классическую формулу Rabcd — dTdb/dxa — dTda/dxh + Г^&Г^а — Г£аГ^> выражающую
тензор кривизны через символы Кристоффеля. (Подсказка: воспользуйтесь определением тензора кривизны в § 14.4,
взяв в качестве координатные векторы <5£, ..., <5®. (Как и в упражнении 14.6, величины <5	6$	и т.д. следует
рассматривать как самостоятельные векторы, а верхний индекс а — как абстрактный индекс в соответствии с § 12.8.))
***Д55 Приведите подробности этого рассуждения.

282
Глава 14
у тензора. В частности, векторы могут превращаться в ковекторы, а ковекторы — в векторы
(и обратно), как в § 13.9:
v
а
9аЪV
и а
а
9
Обычно используется один и тот же корневой символ (в данном случае v и а), а положением
индекса задается геометрический характер данной величины. Применяя эту процедуру для
опускания верхнего индекса тензора кривизны, получаем тензор Римана (или Римана-
Кристоффеля)
Rabcd ~ Rabc 9ed?
имеющий валентность . В дополнение к двум рассмотренным ранее свойствам (антисим¬
метрии по индексам а, b и симметрии Бьянки, т. е. обращению в нуль части, антисимметрич¬
ной по индексам а, 6, с) этот тензор обладает замечательными свойствами симметрии * —
антисимметрией по индексам с, d и симметрией относительно перестановки пар индексов аЪ
и cd:
Rabcd
Rabdc — Rcdab•
Диаграммное представление этих соотношений показано на рис. 14.21. В общем слу-
-валентный тензор на п-многообразии имеет п4 компонент, однако у тензора Римана
чае
о
.4J
из-за его симметрии только ~~n2(n2 — 1) из этих компонент являются независимыми*5".
1 jLu
V
а
V
а
abed
1 г~г
гп
n
R
d
abc
; вектор Киллинга
О
Рис. 14.21. Поднятие и опускание индексов в диаграммной записи: va — gabVb = УЬдъа, va
Ъа т~>	г>	е	п	d	in	_.ed	73
? abed —
gabvb
VbQ , Rabcd, — Rabc Qed, Rabc — Rabce9
еСЛИ V(a^b) = 0
Rabdc — Rcdab', на есть вектор Киллинга
Здесь уместно представить вниманию читателя понятие вектора Киллинга на (псев-
до)римановом многообразии Л4. Это есть векторное поле к, обладающее тем свойством,
что взятая по нему производная Ли от метрики обращает ее в нуль:
£д = 0.
К
Это уравнение можно переписать в индексных обозначениях (скобки означают симметриза
цию, как в § 12.7; см. также рис. 14.21):
VeKb + УбКа = 0, т. е. V(aK6) = 0,
Получите эти соотношения, сначала установив антисимметрию по с, d, исходя из равенства V [а^ь] = 0, а
затем используя две антисимметрии и симметрию Бьянки, чтобы получить симметрию относительно перестановки.
Проверьте, что при п = 4 симметрия допускает лишь 20 независимых компонент.

14.8. СИМПЛЕКТИЧЕСКИЕ МНОГООБРАЗИЯ
283
где V — обычная связность Леви-Чивита . Вектор Киллинга на (псевдо)римановом много¬
образии Л4 является генератором непрерывной симметрии этого многообразия (если по¬
следнее некомпактно, то симметрия будет лишь локальной) Г14Л21 Если А4 содержит более
одного независимого вектора Киллинга, то коммутатор двух таких векторов снова будет
вектором Киллинга **. Как мы увидим в §§ 19.5, 30.4, 30.6, 30.7, векторы Киллинга играют
важную роль в теории относительности.
14.8.	Симплектические многообразия
Следует отметить, что имеется не так уж много локальных тензорных структур, од¬
нозначно определяющих связность, поэтому нам повезло в том отношении, что метрика
(или псевдометрика) часто определяется физическими соображениями. Важное семейство
примеров, для которого однозначность не имеет места, получается, когда структура задается
(несингулярным) антисимметричным тензорным полем 5, определяемым своими компо¬
нентами Sab. Такой структурой обладают фазовые пространства классической механики
(§20.1). Об этих замечательных пространствах будет сказано позднее в §§20.2, 20.4, 27.3.
Это примеры так называемых симплектических многообразий. Помимо свойств антисиммет-
jJj jjg ,
рии и несингулярности, симплектическая структура Ь должна удовлетворять условию
dS = 0.
(Это стандартный случай вещественной симплектической формы на 2га-мерном веществен¬
ном многообразии, в котором локальная симметрия задается обычной симплектической
группой «с расщепленной сигнатурой» Sp(m, т) (см. § 13.10). «Симплектические многооб¬
разия» с иной сигнатурой, насколько мне известно, сколько-нибудь широко не изучались.)
Величина Sab, обратная величине Баь (она определяется соотношением SabSbC ~
определяет так называемые скобки Пуассона (названные в честь выдающегося французского
математика Симеона Дени Пуассона (1781-1840)). Они представляют собой комбинацию
двух скалярных полей Ф и Ф, заданных на фазовом пространстве, в результате которой
получается третье поле:
{Ф, Ф} = -isabVa<£Vb^
(множитель — i вводится просто для согласования с обычными координатными обозна-
чениями). Эта величина играет важную роль в классической механике. Далее (в §20.4)
мы увидим, как при ее помощи записываются уравнения Гамильтона, образующие фунда¬
мент для всеобъемлющего описания динамики в классической физике и установления связи
с квантовой механикой. Из антисимметрии тензора S и условия dS = 0 следуют изящные
эк эк эк
соотношения:
{Ф, Ф} =	-{Ф,Ф}, {в,	{Ф,Ф}} + {Ф, в}} + {Ф, {в, ф}} = о.
Это можно сравнить с соответствующими тождествами для коммутаторов (скобок Ли)
в § 14.6. (Вспомните тождество Якоби.) Мы вернемся к замечательно богатой геометрии
симплектических многообразий, когда займемся геометрическим описанием классической
механики в § 20.4.
* Выведите это уравнение.
** Проверьте это «геометрически очевидное» утверждение непосредственным вычислением и объясните,
почему оно «очевидное».
***($& Объясните, почему это можно записать в виде VaSbc + V65ca + VcSab = 0, где V — произвольная
связность без кручения.
Выведите эти соотношения, предварительно установив, что	—	0.

284
Глава 14
Локальная структура симплектического многообразия являет пример того, что можно
назвать «гибкой» структурой. Не существует, например, понятия кривизны симплектиче¬
ского многообразия, которое позволило бы локально отличать одно симплектическое мно¬
гообразие от другого. Если мы имеем два вещественных симплектических многообразия
одинаковой размерности (и одинаковой «сигнатуры», сравните с § 13.10), то они локально
полностью идентичны (в том смысле, что для любой точки р одного многообразия и лю¬
бой точки q другого многообразия существуют открытые множества р и q, совпадающие
между собой)!14*13!. Это полностью противоположно ситуации в случае (псевдо)римановых
многообразий или многообразий, на которых просто задана связность. В последних случа¬
ях тензор кривизны (и, например, его различные ковариантные производные) определяют
некоторую различимую локальную структуру, которая, скорее всего, будет различной для
разных многообразий.
Существуют и другие примеры подобных «гибких» структур. К ним относится ком¬
плексная структура, определенная в § 12.9, позволяющая интерпретировать 2т-мерное ве-
щественное многообразие как га-мерное комплексное многообразие. В этом случае гибкость
v>
очевидна, поскольку ясно, что кроме комплексной размерности т не существует характе¬
ристики, которая локально отличала бы одно многообразие от другого (или от Ст). Такая
структура будет оставаться гибкой и в том случае, если придать ей комплексную (голоморф-
ную) симплектическую структуру (и тогда нам не придется даже заботиться о понятии
«сигнатуры» для комплексной величины Sabl см. § 13.10).
Можно привести множество других примеров гибких структур. Одной из них является
вещественное многообразие с заданным на нем векторным полем, не всюду равным нулю.
В то же время вещественное многообразие с двумя векторными полями общего вида не будет
гибким**. Как мы увидим в § 33.11, понятие гибкости играет определенную роль в теории
твисторов.
Примечания
§14.2.
14.1. В действительности существует топологическая причина, по которой нельзя непрерывным
образом сопоставить вектору v параллельный ему вектор во всех точках сферы S2 (проблема
«причесывания сферической собаки»!) . Однако аналогичное утверждение для S3 неверно,
как показывает построение параллелей Клиффорда, приведенное в § 15.4.
§14.3.
14.2. В большей части физической литературы и в старой литературе по математике координатная
производная д/дха обозначается путем добавления нижнего индекса, которому предшествует
запятая, к правому краю списка индексов дифференцируемой величины. В случае Va вместо
запятой часто используется точка с запятой.
Обозначение Va хорошо работает в индексной записи (§ 12.8), и последующие уравнения
в основном тексте этой книги можно (и нужно) читать именно таким образом. Координатные
выражения в этой записи также легко читаются, однако следует различать индексы двух типов —
компонентные и абстрактные (см. [590, 626]).
§14.4.
14.3. Ступенчатое расположение индексов понадобится, когда будет вводиться метрика (§ 14.7) и по¬
требуется пространство для поднятия и опускания индексов.
Объясните почему.
Дайте объяснение для обоих случаев. (.Подсказка: постройте координатную систему с £ = д/дх1, затем
возьмите повторные производные Ли, чтобы построить базис, и т. д.)
Существует более короткая формулировка: «Нельзя причесать ежа!». — Прим. перев.
***

14.8. СИМПЛЕКТИЧЕСКИЕ МНОГООБРАЗИЯ
285
§14.5.
14.4. Строго говоря, V действует на поля, определенные на многообразии М, а не просто вдоль
кривых, лежащих в М. Однако это уравнение имеет смысл, поскольку данный оператор диф¬
ференцирует только вдоль кривой. При желании можно считать, что область определения
вектора t гладким образом распространяется от кривой 7 по многообразию ЛЛ в произвольном
направлении. Конкретный способ реализации этого несуществен, поскольку нас интересует
лишь то, выполняется ли уравнение для t на кривой 7.
14.5. См., например, [543, 725].
§14 А
14.6. Роль алгебры Ли коммутаторов проявляется в формуле Бейкера-Кемпбелла-Хаусдорфа,
£ п	ч]+т^([С[С*?]]+[{£>ч]>»?])+•••
несколько первых членов которой выглядят так:	= е 2	12	;
здесь многоточие подразумевает продолжение в виде многократных коммутаторов от £ и 77,
т. е. элементов алгебры Ли, порождаемых величинами £ и г}.
14.7. Точнее, мы можем считать координаты я2, т3, ... хп постоянными вдоль этой кривой, аж1 -
= t, тогда вдоль этой кривой С = d/dt. Это есть просто теорема Тейлора (§ 6.4), согласно
которой приведенное выражение дает е^(Ф).
14.8. По аналогии с экспонентой еь* от £, которая дает значение скалярной величины Ф на некотором
конечном расстоянии, существует соответствующее выражение с £ вместо £, описывающее
тензор Q на конечном расстоянии в «сдвинутой» системе отсчета.
14.9. См. [696] и [626], стр. 202.
§14.7
14.10. В некоторых книгах по математике (см. [565]) для случая положительно не определенной
метрики используется термин «полуримановы многообразия», однако мне кажется, что термин
«псевдоримановы многообразия» более уместен.
14.11. Обычный способ придать смысл этому выражению состоит в том, чтобы ввести некоторый
параметр и, меняющийся вдоль кривой, и писать ds = (ds/du)du. Величина ds/du есть
обычная функция от и, выражаемая через dxa jdu.
14.12. «Локальность» здесь можно понимать в следующем смысле. Для каждой точки р многооб¬
разия М существует экспонента (§ 14.6) от некоторой отличной от нуля малой постоянной
величины, умноженной на вектор к, которая переводит некоторое открытое множество, содер¬
жащее р, в некоторое другое открытое множество, содержащееся в М, с такой же метрической
структурой.
§14.8.
14.13. «Совпадающие» означает здесь, что каждое из множеств можно отобразить на другое таким
структуры

Глава 15
Расслоенные пространства и калибровочные
связности
15.1.	Физическая мотивация расслоенных пространств
Математический аппарат, представленный в главах 12 и 14, достаточен для изложения
общей теории относительности Эйнштейна и фазовых пространств классической механи¬
ки. Однако развитие современной теории взаимодействия элементарных частиц во многом
зависит от обобщения понятия «связности» (или ковариантной производной), введенного
в § 14.3; это обобщение носит название калибровочной связности. Наше исходное поня¬
тие ковариантной производной базировалось в основном на параллельном переносе вектора
вдоль некоторой кривой на нашем многообразии М (§ 14.2). Зная, что такое параллельный
перенос вектора, мы можем обобщить это понятие на перенос любой тензорной величины
(§ 14.3). Векторы и тензоры относятся здесь к касательным пространствам в точках многооб¬
разия М (см. §§ 12.3,14.1 и рис. 12.6). В отличие от этого, калибровочная связность относит¬
ся к «параллельному переносу» некоторых величин, представляющих физический интерес,
которые лучше всего представлять себе как относящиеся в некоторому виду «пространства»,
отличного от касательного пространства в точке р многообразия А4, но, в некотором смысле,
«расположенного в точке р».
Чтобы стало немного яснее, что здесь требуется, напомним (см. §§ 12.3, 12.8), что коль
скоро мы имеем некоторое векторное пространство (в данном случае пространство каса¬
тельных векторов в некоторой точке), мы можем построить дуальное ему (пространство
ковекторов), а также все различные пространства
v
я
-валентных тензоров. Таким обра¬
зом, пространства
v
я
-тензоров (включая кокасательные пространства, поскольку ковек-
торы представляют собой [J -тензоры) не являются чем-то новым, коль скоро мы имеем
касательные пространства Тр в точках р. (Почти такое же замечание должно относить¬
ся, — по крайней мере, с моей собственной точки зрения — и к пространствам спиноров
в точке р; см. § 11.3. Другие могут придерживаться иного взгляда на спиноры, но таких
альтернативных воззрений мы здесь не будем касаться.) Пространства, необходимые для
калибровочных теорий взаимодействия частиц (за исключением гравитационного взаимо¬
действия), отличаются от упомянутых пространств (и поэтому они действительно представ¬
ляют собой нечто новое), и их лучше рассматривать как своего рода «пространственное»
измерение, дополнительное к обычному пространству и времени. Подобные лишние «про¬
странственные» изменения часто называют «внутренними» размерностями, поскольку при
движении вдоль такого «внутреннего направления» мы в действительности не уходим от той
пространственно-временной точки, в которой мы находимся.
Чтобы придать этой идее геометрический смысл, нам потребуется понятие «расслоен¬
ного пространства». Это вполне строго определенное математическое понятие, которое мы
рассмотрим подробнее в § 15.2. Оно оказалось полезным в чистой математике 115,11 задолго
до того, как физики обнаружили, что некоторые важные понятия, которыми они пользова¬
лись, можно изложить на языке расслоенных пространств. В последующие годы физики-

15.1. Физическая мотивация расслоенных пространств
287
теоретики овладели необходимыми математическими концепциями и ввели их в свои теории.
Однако в некоторых современных теориях эти понятия представляются в модифицирован¬
ном виде, в связи с чем само пространство-время приобретает дополнительные измерения.
Действительно, во многих, если не в большинстве, современных попытках найти более
глубокое обобщение фундаментальной физики (например, в супергравитации или теории
струн) само понятие «пространства-времени» расширяется до большего числа измерений.
Эти лишние пространственные измерения, рассматриваемые на равных правах с измерени¬
ями обычного пространства и времени, порождают «внутренние измерения». В результа¬
те получается «пространство-время» с числом измерений, большим обычного значения 4.
Идеи такого рода восходят к 1919 году, когда Теодор Калуца и Оскар Клейн предложили
обобщение общей теории относительности Эйнштейна, в котором число пространственно-
временных измерений увеличивалось с четырех до пяти. Это лишнее измерение позволило
распространить «геометрическое описание пространства-времени» на созданную Максвел¬
лом величественную теорию электромагнетизма (см. §§ 19.2, 19.4). Однако это «пятое из¬
мерение» следует считать «скрученным» в петлю малого размера, и потому оно не может
рассматриваться непосредственно как обычное пространственное измерение.
Часто используется аналогия со шлангом (см. рис. 15.1), представляющая модификацию
Калуцы - Клейна применительно к одномерной Вселенной. С большого расстояния шланг
действительно выглядит одномерным, и это измерение — его длина. Однако при более близ¬
ком рассмотрении мы обнаружим, что поверхность шланга в действительности двумерна,
при этом дополнительное измерение свернуто в петлю гораздо меньшего масштаба, нежели
его длина. Это есть непосредственная аналогия того, как следует представлять себе четы¬
рехмерное физическое пространство-время в пятимерном полном «пространстве-времени»
Калу цы - Клейна. Пятимерное пространство Калуцы - Клейна есть прямая аналогия двумер¬
ной поверхности шланга, тогда как четырехмерное пространство мы рассматриваем как
аналог одномерного видимого проявления шланга.
Эта остроумная идея привлекательна во многих отношениях. Сторонники современных
спекулятивных физических теорий (например, супергравитации или теории струн, которые
мы рассмотрим в главе 31) сочли необходимым рассматривать варианты идеи Калуцы -
Рис. 15.1. Аналогия со шлангом. С большого расстояния шланг выглядит как одномерный объект,
однако при более подробном рассмотрении он оказывается двумерной поверхностью. Подобно этому,
согласно идее Калуцы - Клейна, могли бы существовать «малые» дополнительные пространственные
г
измерения, не наблюдаемые в обычном масштабе

288
Глава 15
Клейна с еще большим числом измерений (наиболее популярны варианты с полной раз¬
мерностью 26, 11 и 10). Такие теории позволяют рассматривать другие взаимодействия,
помимо электромагнетизма, используя идею калибровочной связности, с которой мы вскоре
познакомимся.
Следует, однако, подчеркнуть, что идея Калуцы - Клейна пока остается спекулятивной.
«Внутренние измерения», на существование которых рассчитывают современные калиб¬
ровочные теории взаимодействия элементарных частиц, не следует рассматривать на рав¬
ных правах с обычными пространственно-временными измерениями, и они не возникают
непосредственно из схемы типа Калуцы - Клейна. Это интересный вопрос: следует ли рас¬
сматривать внутренние измерения современных калибровочных теорий как возникающие
в конечном счете из такого рода «расширенного пространства-времени» (типа Калуцы-
Клейна)^15‘21? Я вернусь к этому вопросу позже (§31.4).
Вместо того чтобы рассматривать эти внутренние измерения как часть простран¬
ства-времени более высокой размерности, более приемлемо считать, что они создают так
называемые расслоенные пространства (или просто расслоения) над пространством-време¬
нем. Это важное понятие играет центральную роль в современных калибровочных теориях
взаимодействия элементарных частиц. Мы предполагаем, что «над» каждой точкой про¬
странства-времени находится другое пространство, называемое слоем. Согласно изложенной
выше физической картине, слой содержит все внутренние размерности. Однако понятие рас¬
слоения имеет гораздо более широкое применение, поэтому будет лучше, если мы не будем,
по крайней мере временно, связывать его с подобной физической интерпретацией.
15.2.	Математическая идея расслоения
п
Расслоение (или расслоенное пространство) В есть многообразие с некоторой структу¬
рой, определяемое двумя другими многообразиями М и V, где М называется базисным про¬
странством (в большинстве физических приложений это есть само пространство-время),
а V — слоем (в физических приложениях это обычно внутреннее пространство). Само рас¬
слоение В состоит из целого семейства слоев У, так что его можно рассматривать как некое
«имущество» пространства М в виде пространств V (см. рис. 15.2). Простейшим видом рас¬
слоения является так называемое произведение пространств. Это может быть тривиальное
или «незакрученное» расслоение, однако более интересны закрученные расслоения. Вскоре
я приведу некоторые примеры тех и других. Важно отметить, что пространство V обладает
некоторой симметрией, и именно наличие симметрии открывает возможность закручивания,
которое делает понятие расслоения более интересным. Интересующая нас группа симмет¬
рии Q пространства V называется группой расслоения В. Часто говорят, что В есть рас¬
слоение Q над Л4. Во многих случаях в качестве V берется векторное пространство, тогда
расслоение называется векторным. В таком случае группой Q служит линейная группа об¬
щего вида с соответствующим числом измерений или ее подгруппа (см. §§ 13.3, 13.6-13.10).
Не следует считать М частью В (т. е. М не находится внутри В), наоборот, нужно
рассматривать В как пространство, отдельное от А4, которое мы пытаемся представить себе
стоящим, в некотором смысле, над базисным пространством Л4. В расслоении В имеет¬
ся множество копий слоя V, и над каждой точкой пространства М располагается полная
копия пространства V. Все копии слоев не связаны между собой (т. е. никакие две из них
не пересекаются), и все вместе они образуют полное расслоение В. Пространство Л4 по
отношению к В является фактор-пространством расслоения В по семейству слоев V. Дру¬
гими словами, каждая точка пространства М соответствует точно одной отдельной копии
пространства V. Существует непрерывное отображение В на Л4, называемое канонической
проекцией В на Л4, которое стягивает каждый слой V в ту точку пространства М, над
которой он находится (см. рис. 15.2).

15.2. Математическая идея расслоения
289
Рис. 15.2. Расслоение В с базисным пространством АЛ и слоем V можно рассматривать как некое
«имущество» пространства АЛ в виде пространств V. Каноническая проекция В на АЛ приводит
к стягиванию каждого слоя V в одну-единственную точку
Произведение пространств Л4 и V (тривиальное расслоение V над АЛ) записывается
в виде АЛ x .V. Точками такого произведения служат пары элементов (а, Ь), в которых а
принадлежит АЛ, а Ъ принадлежит V; см. рис. 15.3 а. (Мы уже встречались с такой идеей
применительно к группам в § 13.2.115 3^) Более общее «закрученное» расслоение В над АЛ
напоминает АЛ х V локально в том смысле, что часть В, лежащая над какой-либо доста¬
точно малой открытой областью пространства АЛ, имеет такую же структуру, что и часть
произведения АЛ х V, лежащая над той же малой открытой областью пространства АЛ;
см. рис. 15.36. Однако при движении по пространству АЛ слои над ним могут закру-
Ъ
A4xV
i а ^	+
а)
АЛ
б)
Рис. 15.3. а) Частный случай «тривиального» расслоения, которое является произведением АЛ х V
пространств АЛ и V. Точки произведения АЛ х V можно интерпретировать как пары элементов (а, Ъ),
в которых а принадлежит АЛ, а Ъ принадлежит V. б) Более общий случай «закрученного» расслое¬
ния В над АЛ со слоем V напоминает АЛ х V локально, т. е. часть пространства В над некоторой
достаточно малой открытой областью пространства АЛ идентична части АЛ х V над той же областью
S	.Л	,
пространства АЛ. Однако если слои закручиваются, то в глобальном отношении В — не то же самое,
что АЛ х V

290
Глава 15
чиваться, так что расслоение В в целом будет отлично (часто и топологически отлично)
от М, х V. Размерность В всегда равна сумме размерностей Л4 и V, независимо от закру¬
чивания* .
Все это выглядит несколько запутанным, поэтому, чтобы дать почувствовать, на что
похоже расслоение, я приведу пример. Сначала возьмем наше пространство М в виде
окружности S1, а слой V — в виде одномерного векторного пространства (которое можно
топологически изобразить как копию вещественной оси М с отмеченным началом коорди¬
нат 0). Такое расслоение называется (вещественным) линейным расслоением над S1. То¬
гда произведением М х V будет двумерная цилиндрическая поверхность (см. рис. 15.4а).
А как построить над М закрученное расслоение В со слоем над V? Можно взять ленту
Мёбиуса, см. рис. 15.46 (и рис. 12.14). Убедимся, что это есть расслоение, «локально» то
же самое, что и цилиндрическая поверхность. Мы можем создать адекватно «локальную»
область базисного пространства S1, удалив из S1 некоторую точку р. При этом базисная
окружность разрывается и превращается в односвязный f15,4J отрезок^15,5^ S1 — р, а часть
пространства В, лежащая выше этого отрезка, есть то же самое, что и часть цилиндрической
поверхности над отрезком S1 — р. Различие между лентой Мёбиуса В и цилиндрической
поверхностью появляется, только когда мы рассматриваем то, что находится над полной
областью S1. Можно представить себе, что S1 состоит из двух таких лоскутов — S1 — р
и S1 — д, где р и q — две различные точки области S1. Тогда полную область В можно соста¬
вить из двух соответствующих лоскутов, каждый из которых есть тривиальное расслоение
над одним из двух отдельных лоскутов области S1. При таком «склеивании» двух триви¬
альных лоскутов расслоения и появляется «закрученное» расслоение в виде ленты Мёбиуса
(рис. 15.5). Появление ленты Мёбиуса с однократным закручиванием становится особенно
понятным, если уменьшить размер наших лоскутов области S1, как показано на рис. 15.5 б;
такое уменьшение не меняет структуру области В.
нуль
М = S
а)	б)
Рис. 15.4. Чтобы понять, как возникает закручивание, рассматриваем случай, когда областью Л4 служит
окружность S1, а слоем V — одномерное векторное пространство (т. е. пространство, определенное
на множестве М, в котором, однако, задано лишь начало координат 0 и не заданы никакие другие
значения (например, тождественный элемент 1)). а) Тривиальный случай М х V, здесь это просто
двумерная цилиндрическая поверхность, б) В случае с закручиванием мы получаем ленту Мёбиуса
(как на рис. 12.14)
Важно понимать, что возможность такого закручивания есть следствие определенной
симметрии, которой обладает слой V, а именно операции симметрии, меняющей знак эле¬
ментов одномерного векторного пространства V (т. е. v — г; для каждого вектора v в V).
Эта операция сохраняет структуру V как векторного пространства. Следует отметить, что
*
* ЙЭ Объясните, почему размерность Л4 х V равна сумме размерностей Ai и V,
1

15.3. Сечения расслоений
291
Рис. 15.5. Можно получить адекватно «локальную» (односвязную) область базисного пространства S1,
удалив из него некоторую точку р, при этом часть расслоения над областью S1 — р будет указанным
выше произведением. То же относится и к части области В над областью S1 — д, где g — некоторая дру¬
гая точка области S1. Мы получаем цилиндрическую поверхность при непосредственном соединении
двух частей области В и расслоение в виде ленты Мёбиуса, как показано выше, в случае применения к
одной из соединяемых частей операции отражения, меняющей местами верх и низ (операции симмет¬
рии области V). б) Появление ленты Мёбиуса становится несколько более понятным, если уменьшить
две части области S1 так, чтобы получились лишь малые области перекрытия
эта операция не является операцией симметрии системы вещественных чисел R. Сама по
себе система R не обладает какой-либо симметрией. (Например, число 1 определенно от¬
личается от —1, и отображение х ~х не является операцией симметрии множества R,
поскольку не сохраняет мультипликативную структуру этого множества*.) Именно по этой
причине в качестве слоя V берется одномерное вещественное векторное пространство, а не
просто сама вещественная ось М. Иногда говорят, что V моделируется вещественной осью.
Вскоре мы увидим, как другие виды симметрии слоев делают возможными другие варианты
закручивания.
%
15.3.	Сечения расслоений
• я •
Один из возможных способов характеризовать различие между цилиндрической по¬
верхностью и лентой Мёбиуса состоит в использовании так называемых сечений расслое¬
ния. Геометрически сечение расслоения В над М можно представить как непрерывный об¬
раз М в В, который встречается с каждым отдельным слоем в одной точке (см. рис. 15.6а).
* $0 Объясните это.

292
Глава 15
а)	б)
Рис. 15.6. а) Сечение расслоения В есть непрерывный образ М в В, который встречается с каждым
отдельным слоем в одной точке, б) Это является обобщением обычной идеи графика функции
Это можно назвать «подъемом» базисного пространства М в расслоение. Заметим, что если
применить отображение, которое поднимает М до сечения расслоения 23, а затем канони¬
ческую проекцию, мы получим тождественное отображение пространства М. в само себя
(другими словами, каждая точка этого пространства возвращается просто в самое себя).
Для тривиального расслоения М х У сечения можно интерпретировать просто как
непрерывные функции базисного пространства Л4, областью значений которых служит про¬
странство V (т. е. они представляют собой непрерывные отображения Л4 в V). Таким обра¬
зом, сечение расслоения М х V сопоставляет непрерывным образом некоторую точку про¬
странства V каждой точке пространства М. Это похоже на обычную идею графика функции
(см. рис. 15.66). В более общем случае закрученного расслоения В каждое сечение расслое¬
ния определяет понятие «закрученной функции», более общее, чем обычная идея функции.
Вернемся к нашему частному примеру в § 15.2. В случае цилиндрической поверхности
(расслоения произведений М х V) наши сечения можно представить просто как кривые,
обходящие один раз цилиндрическую поверхность и пересекающие при этом каждый слой
ровно один раз (рис. 15.7 а). Поскольку это расслоение является произведением пространств,
можно рассматривать каждый слой просто как копию вещественной оси, так что слоям
можно приписать координаты, задаваемые вещественными числами. Значение координаты О
в каждом слое относится к нулевому сечению «помеченных точек», представляющих нули
векторных пространств V. В общем случае сечение определяет непрерывную вещественную
функцию, заданную на окружности (при этом значением функции в каждой точке окружно¬
сти служит «высота» над нулевым сечением). Ясно, что существует множество сечений, не
пересекающих нулевое сечение (т. е. функций, не обращающихся в нуль на S1). Например,
можно выбрать сечение цилиндрической поверхности, параллельное нулевому сечению и не
совпадающее с ним. Такому выбору соответствует отличная от нуля постоянная функция,
заданная на окружности.
Если же взять расслоение В в виде ленты Мёбиуса, то мы обнаружим совершенно иную
ситуацию. Читателю будет нетрудно согласиться с тем, что теперь каждое сечение рассло-
ения В должно пересекать нулевое сечение (рис. 15.76). (Понятие нулевого сечения здесь
по-прежнему применимо, поскольку V есть векторное пространство с «отмеченным» нулем.)
Качественное отличие от предыдущего случая делает очевидным, что расслоение В должно
быть топологически отлично от Л4 х V. Для большей конкретности можно, как и выше,
приписать вещественные координаты различным слоям V, однако теперь мы вынуждены
договориться, что в некоторой точке окружности знак должен измениться (х i—► — х), так что
сечение расслоения В соответствует вещественной функции, заданной на окружности; эта

15.4. Расслоение Клиффорда-Хопфа
293
а)	б)
/
Рис. 15.7. Сечение линейного расслоения над S1 представляет собой петлю, однократно обходящую
поверхность и пересекающую каждый слой ровно один раз. а) Цилиндрическая поверхность. Имеются
сечения, нигде не пересекающие нулевое сечение. 6) Расслоение в виде ленты Мёбиуса. Каждое
сечение пересекает нулевое сечение
функция должна быть непрерывной за исключением того, что она меняет знак при обходе
окружности. Любое такое сечение где-то должно принимать нулевое значение .
В этом примере характер семейства сечений достаточно ясен для того, что отличить
ленту Мёбиуса от цилиндрической поверхности. Рассмотрение семейства сечений часто ока¬
зывается полезным способом распознать природу различных расслоений над одним и тем же
базисным пространством Л4. Однако различие между расслоением в виде ленты Мёбиуса
и произведением пространств (цилиндрической поверхностью) несколько менее кардиналь¬
но, чем в некоторых других примерах расслоений. Иногда расслоение вообще не имеет
сечений! Далее мы рассмотрим один из наиболее важных и известных примеров такого
рода.
15.4.	Расслоение Клиффорда-Хопфа
Этот пример требует несколько более серьезного внимания. Базисным простран¬
ством М служит двумерная сфера S2, а расслоением Б — трехмерная сфера S3. Слоя¬
ми V служат окружности S1 («1-сферы»). Это обычно называют расслоением Хопфа S3,
поскольку на такое топологическое построение указал Хайнц Хопф в 1931 году. Однако
процедура, предложенная Хопфом, непосредственно основывалась (с должными ссылками)
на более раннем геометрическом построении «клифордовых параллелей», предложенном
уже знакомым нам (по главе 11) Уильямом Клиффордом. Я буду называть поверхность S3,
геометрически расслоенную указанным образом, расслоениемi Клиффорда (или расслоением
Клиффорда -Хопфа).
Наиболее простой способ получить расслоение Клиффорда-Хопфа состоит в том, что¬
бы сначала рассмотреть пространство С2 пар комплексных чисел (гг, z). (Подходящей струк¬
турой для С2 является просто двумерное комплексное векторное пространство, см. § 12.9.)
Наше расслоенное пространство В (= S3) следует понимать как единичную 3-сферу S3,
помещенную в С2 и определяемую уравнением (см. конец § 10.1)
w
2
+ Z2 = l.
Это соответствует вещественному уравнению 3-сферы г/2 -f v2 4- х1 + у2 — 1, где w — и -f iv
и z = х + гу — соответствующие выражения для w и z через их вещественные и мнимые
лоскутов.

294
Глава 15
части. (Это есть непосредственный аналог уравнения обычной 2-сферы х2 4- у2 + z2 = 1
в евклидовом 3-пространстве с вещественными декартовыми координатами ж, у, 2.)
Чтобы получить расслоение, мы должны рассмотреть семейство комплексных прямых
линий, проходящих через начало координат (т. е. комплексные одномерные векторные под¬
пространства пространства С2). Каждая такая линия задается уравнением вида
Aw + Bz = О,
где А я В — комплексные числа (не обращающиеся в нуль одновременно). Будучи ком¬
плексным одномерным векторным пространством, такая линия является копией комплекс¬
ной плоскости, пересекающей сферу S3 по окружности S1, которую можно считать еди¬
ничной окружностью в указанной плоскости (рис. 15.8). Такие окружности будут наши¬
ми слоями V = S1. Различные линии могут пересекаться только в начале координат, так
что никакие две различные окружности S1 не могут иметь общую точку. Таким образом,
семейство окружностей S1 действительно образует слои, задающие S3 как расслоенную
структуру.
Каково здесь базисное пространство МР Очевидно, мы получим ту же самую ли¬
нию Aw Л- Вz ~ 0, если умножим А и В на одно и то же комплексное число, не равное
нулю, поэтому реально одну линию от другой отличает отношение А : В. Числа А и В могут
быть равны нулю в отдельности, но не одновременно. Пространством таких отношений яв¬
ляется сфера Романа, довольно подробно описанная в § 8.3. Поэтому можно отождествить
базисное пространство М нашего расслоения с этой сферой Римана S2. Соответственно
нетрудно заметить, что сферу S3 можно рассматривать как расслоение S1 над S2. (Мы не
должны ожидать, что так же обстоит дело и при другой размерности, если мы требуем, что¬
бы расслоение, базисное пространство и слои были сферами. Однако в действительности
оказывается, что S7 можно рассматривать как расслоение S3 над S4, в чем, при некотором
старании, можно убедиться, заменив в приведенных рассуждениях комплексные числа w и z
Сфера Римана,
соответствующая
отношениям А:В
Рис. 15.8. Расслоение Клиффорда - Хопфа. Возьмем пространство С2 с координатами (ад, z), содержа¬
щее 3-сферу В = S , задаваемую уравнением
w
1. Каждый слой V = S1 представляет собой
единичную окружность на комплексной прямой линии, проходящей через начало координат, Aw +
+ Bz = 0 (комплексное одномерное векторное подпространство пространства С2 ); окружность опре¬
деляется отношением А: В. Сфера Римана S2, образуемая такими отношениями, является базисным
пространством М.

15.4. Расслоение Клиффорда - Хопфа
295
кватернионами ", a Sb можно рассматривать как расслоение S7 над S8 (w и z теперь заме¬
няются октонионами (см. §§ 11.2, 16.2)); в случае любых других сфер высокой размерности
такая ситуация не имеет места!15*6!.)
Особенно интересно семейство окружностей в S3, именуемое клиффордовыми парал¬
лелями. Окружности, являющиеся большими окружностями сферы, закручиваются одна во¬
круг другой, при этом расстояние между ними все время остается неизменным (отсюда
название «параллели»). Любые две из этих окружностей сцеплены между собой, поэтому
они скрещиваются (не лежат на одной сфере). В евклидовом 3-пространстве скрещиваю¬
щиеся (некомпланарные) прямые линии обладают тем свойством, что они расходятся все
дальше одна от другой при удалении в бесконечность. Однако 3-сфера имеет положитель¬
ную кривизну, поэтому клиффордовы окружности, будучи геодезическими на S3, имеют
компенсирующую тенденцию изгибатьсд навстречу одна другой в соответствии с эффектом
отклонения геодезических, рассмотренным в § 14.5 (см. рис. 14.12). В случае клиффордовых
параллелей эти два эффекта в точности компенсируют друг друга (рис. 15.9). Чтобы полу¬
чить картину семейства клиффордовых параллелей, можно стереографически спроектиро¬
вать сферу S3 из ее «южного полюса» на экваториальное евклидово 3-пространство в точной
аналогии с соответствующей стереографической проекцией сферы S2 на евклидову плос¬
кость, как мы это делали при изучении сферы Римана в § 8.3 (см. рис. 8.7). Как и в случае
стереографической проекции сферы S2, окружности на S3 при такой проекции отобража¬
ются на окружности в евклидовом 3-пространстве. Картина семейства спроектированных
клиффордовых окружностей показана на рис. 33.15. Такая конфигурация играет решающую
роль в теории твисторов!15*7!, соответствующая геометрия будет описана в § 33.6.
а)	б)
Рис. 15.9. а) В евклидовом 3-пространстве расстояние между скрещивающимися прямыми растет при
удалении в бесконечность, б) На сфере S3 положительная кривизна создает компенсирующую тенден¬
цию к изгибанию геодезических (больших окружностей) навстречу одна другой (эффект отклонения
геодезических, см. рис. 14.12). В случае клиффордовых параллелей имеет место точная компенсация
Выше утверждалось, что такое расслоение (расслоение Клиффорда - Хопфа) относит¬
ся к тем, которые совсем не имеют сечений. Как это понять? Прежде всего следует от¬
метить, что «закручивание» расслоения Клиффорда обязано своим существованием тому
обстоятельству, что слои-окружности обладают точной симметрией, задаваемой вращени¬
ем окружности (группа 0(2), или, что эквивалентно, U(l), см. упражнение 13.59). Мы не
можем идентифицировать каждый из этих слоев с какой-то заданной окружностью, напри¬
мер, с единичной окружностью на комплексной плоскости С. Если бы это было возможно,
мы могли бы выбрать на окружности некоторую определенную точку (например, точку 1
на единичной окружности в С) и таким путем получить сечение расслоения Клиффорда.
Несуществование сечений связано с тем, что клиффордовы окружности лишь моделируются
на единичной окружности С, но не отождествляются с ней.
Разумеется, это само по себе не объясняет, почему расслоение Клиффорда не имеет
непрерывных сечений. Чтобы понять это, полезно взглянуть на расслоение Клиффорда под
другим углом. Фактически оказывается, что каждую точку нашей сферы S3 можно интер-
Проведите такое рассуждение. Понятно ли вам, как поступить в случае S15?

296
Глава 15
претировать как «спинорный» касательный вектор единичной длины к сфере S2 в одной из
его точек^15,5]. Напомним* (см. § 11.3), что спинорный объект представляет собой величину,
которая меняет знак при полном обороте на угол 27г. Согласно сделанному утверждению,
сечение нашего расслоения В(= S3) должно представлять собой непрерывное поле та¬
ких епинорных единичных векторов на многообразии M(~ S2). Из топологии известно,
что на S3 не существует глобального непрерывного поля обычных единичных касательных
векторов на S2. (Это та самая проблема причесывания «сферической собаки»! Невозможно
непрерывным образом расположить волосы так, чтобы они гладко лежали над сферой.) Если
сделать эти направления «спинорными», это, очевидно, не поможет, поэтому никакое гло¬
бальное непрерывное поле единичных епинорных касательных векторов также существовать
не может. Следовательно, наше расслоение В(= S3) не имеет сечений.
Это заслуживает дополнительного обсуждения, поскольку из данного примера можно
извлечь много полезного. Прежде всего, путем небольшого видоизменения описанного выше
расслоения Клиффорда можно получить расслоение В', состоящее из единичных касатель¬
ных векторов к сфере S2. Поскольку каждый обычный единичный касательный вектор имеет
всего два возможных проявления как спинорный объект (одно из них отличается от другого
знаком), их можно отождествить, если мы хотим перейти от епинорных векторов к обыч¬
ным. На языке расслоения Клиффорда В(= S3) это означает, что нужно отождествить две
точки сферы S3 для того, чтобы получить одну точку!15*8] расслоения В'9 из единичных ка¬
сательных векторов к S2. Пары точек сферы S3, подлежащих отождествлению между собой,
являются антиподными точками этой 3-сферы (см. рис. 15.10). Слоями расслоения В' по-
прежнему служат окружности. Каждый слой расслоения В(= S3) «дважды наматывается» на
каждый слой (окружность) расслоения В'. Каждая точка расслоения В' теперь представляет
точку сферы S2 с единичным касательным вектором в этой точке. Фактически простран¬
ство В1 топологически идентично пространству 1Z, с которым мы познакомились в § 12.1
и которое представляет различные пространственные ориентации объекта (вроде книги,
рассмотренной в §11.3) в евклидовом 3-пространстве. Это становится очевидным, если
в качестве нашего «объекта» взять сферу S2 с помеченной стрелкой (единичным касатель¬
ным вектором) в одной из ее точек. Эта стрелка полностью определяет пространственную
ориентацию сферы.
15.5,	Комплексные векторные расслоения, (ко)касательные расслоения
Небольшое обобщение идеи, стоящей за расслоением Клиффорда (а также В'), да¬
ет хороший пример комплексного векторного расслоения, которое в данном случае имеет
обозначение Вс (и соответственно В/С). Каждая прямая Aw + Bz сама по себе является
комплексным векторным пространством. (Вся линия состоит из семейства, получаемого
умножением одного вектора (w, z) на комплексные числа Л, при этом z) превращается
в (Лгу, Лz).) Комплексное векторное 1-пространство можно взять в качестве нашего слоя V.
Базисным пространством А4, как и прежде, будет сфера Римана S2.
Чтобы получить правильное комплексное векторное расслоение Вс, необходимо, одна¬
ко, сделать кое-что еще. В пространстве С2 различные слои не разъединены, все они имеют
общее начало координат (0, 0). Поэтому для получения Вс необходимо модифицировать С2,
заменив начало координат копией всей сферы Римана СР1 (см. § 15.6). Тогда вместо одно¬
го нуля мы будем иметь все множество нулей сферы Римана, по одному на каждый слой,
дающее нулевое сечение расслоения (см. рис. 15.11). Эта процедура называется раздутием
начала координат пространства С2 (эта идея играет важную роль в алгебраической гео¬
метрии, теории комплексных многообразий, теории струн, теории твисторов и во многих
*5© Покажите это. (.Подсказка: возьмите касательный вектор в виде ud/dv — vd/du + хд/ду — уд/дх.)

15.5. Комплексные векторные расслоения, (ко)касательные расслоения
297
Рис. 15.10. Расслоение В' из единичных касательных векторов к S2 получается в результате неболь¬
шой модификации расслоения Клиффорда, состоящей в отождествлении антиподных точек сферы S3.
Без такого отождествления сфера S3 представляет собой (клиффордово) расслоение В из спинорных
касательных векторов к сфере S2. Слоями расслоения В' по-прежнему служат окружности, но каждый
слой-окружность расслоения В «дважды наматывается» на каждый слой-окружность расслоения В'
других областях). Поскольку теперь в слоях могут быть нули, существуют непрерывные
сечения расслоения В. Оказывается, что такие сечения представляют спинорные поля на S2.
«Спинор» в некоторой точке сферы S2 следует изображать не как «спиноркый единичный
касательный вектор» в точке сферы S2, но как вектор, который теперь может увеличиваться
и уменьшаться с некоторым коэффициентом в виде положительного вещественного числа,
в том числе может обращаться в нуль. Можно показать, что всевозможные такие «спиноры»
в точке сферы S2 образуют двумерное комплексное векторное пространство[15-9Ь *.
Полное расслоение Вс представляет собой комплексную (т. е. голоморфную) структуру,
и его называют комплексным линейным расслоением, поскольку слоями служат одномерные
комплексные прямые. Это есть голоморфный объект, поскольку его построение произво-
дится полностью в терминах голоморфных понятий . В частности, базисное пространство
представляет собой комплексную кривую — сферу Римана (см. § 8.3), а слои — одномерные
комплексные векторные пространства. В соответствии с этим существует другое понятие
сечения, особенно уместное здесь, — голоморфное сечение. Голоморфным называется се¬
чение комплексного расслоения, которое само является комплексным подмногообразием
I
расслоения (это просто означает, что оно локально описывается голоморфными уравне¬
ниями). Иногда, в случае комплексного линейного расслоения, такое сечение называется
закрученной голоморфной функцией, заданной на базисном пространстве. Эти понятия иг¬
рают важную роль во многих областях чистой математики и математической физики С15Л°].
Особое значение они имеют в теории твисторов (см. § 33.8). Голоморфные сечения образуют
плохо управляемое, но важное семейство. В случае Вс оказывается, что не существует (гло¬
бальных) голоморфных сечений, отличных от нулевого сечения (т. е. сечения, состоящего
из одних нулей).
При небольшой модификации этой конструкции (соответствующей переходу от В к В')
вместо спинорных полей получаются векторные поля на S2. Соответствующее расслое¬
ние В/С снова можно интерпретировать как комплексное векторное расслоение — это так
называемый квадрат векторного расслоения Вс. Оно строится так же, как Бс, за ис¬
ключением того, что теперь каждая точка (гг, z) отождествляется с «антиподной» точ-
Почему каждое такое спинорное поле принимает нулевое значение по крайней мере в одной точке
сферы S2?
**
Объясните это подробнее.

298
Глава 15
Рис. 15.11. Взяв всю прямую Aw + Bz = 0 (комплексную плоскость), а не просто единичную окруж¬
ность в ней, мы получаем пример комплексного линейного расслоения Бс} при этом слой V становится
комплексным одномерным векторным пространством. Базисным пространством АЛ по-прежнему слу¬
жит сфера Римана S2 = СР1 (также комплексное многообразие, см. §§ 8.3, 15.6). Однако чтобы разъ¬
единить различные слои, мы должны «раздуть» начало координат (0, 0), заменив его полной сферой
Римана, в результате чего получается множество нулей, принадлежащих сфере Римана
кой (—го, —г), так что умножение (гг?, z) на комплексное число Л дает теперь (Л1/2^, A1у/2з)
(а не (Агщ Аз)).
В заключение этого раздела я должен отметить, что расслоение Б1 легко интерпрети¬
ровать на языке вещественных величин, используя понятие так называемого касательного
расслоения T(S2) сферы S2. Касательным расслоением Т(АЛ) произвольного многообра¬
зия АЛ называется такое пространство, каждая точка которого представляет некоторую точку
многообразия АЛ вместе с касательным вектором к А\Л в этой точке (рис. 15.12а)*. Сечение
расслоения Т(АЛ) представляет собой векторное поле на А4. Возможно, еще более важным
для физики является понятие кокасательного расслоения Т*(Л4) многообразия АЛ, Каждая
точка этого расслоения представляет точку многообразия АЛ вместе с ковектором в этой
точке (рис. 15.126). В главе 20 будет освещена важная роль этих идей. Сечения расслое¬
ния Т*(Л4) представляют ковекторное поле на АЛ, Оказывается, что кокасательные рассло¬
ения всегда являются симплектическими многообразиями (см. §§ 14.8, 20.2, 20.4), этот факт
играет важную роль в классической механике. Соответствующим образом можно опреде¬
лить различные виды тензорных расслоений. Тензорное поле можно интерпретировать как
сечение такого расслоения.
15.6.	Проективные пространства
Другим важным понятием, связанным с векторным пространством общего вида, явля¬
ется понятие проективного пространства. Векторное поле само является «почти расслое-
Покажите, что интерпретируемое как вещественное расслоение над S2, действительно есть то же
самое, что и T(S2). (.Подсказка: вернитесь к упражнению 15.5.)

15.6. Проективные пространства
299
а)
6)
Рис. 15.12. а) Каждая точка касательного расслоения Т(М) произвольного многообразия Л4 пред¬
ставляет некоторую точку этого многообразия с касательным вектором к М.. 6) Кокасательное рассло¬
ение Т*(.М) отличается тем, что вместо векторов фигурируют ковекторы. Кокасательные расслоения
всегда являются симплектическими многообразиями
нием» над проективным пространством. Если из векторного пространства удалить нача¬
ло координат, то мы действительно получим расслоение над проективным пространством,
а слоем будет линия с удаленным началом координат. Вместо этого, как и в приведенном
выше частном случае расслоения Вс (§ 15.5), можно «раздуть» начало координат векторного
пространства. (Скоро я вернусь к этому.) Проективные пространства имеют большое значе¬
ние в математике и играют особую роль в геометрии квантовой механики (см. §§21.9, 22.9),
а также в теории твисторов (§33.5). Поэтому естественно кратко рассмотреть здесь эти
пространства.
Идея проективного пространства первоначально возникла при изучении перспективы
в изобразительном искусстве, то есть в рамках евклидовой геометрии. Напомним, что на
евклидовой плоскости две различные прямые всегда пересекаются, если только они не
параллельны. Но если вы изображаете на вертикальном листе бумаги пару параллельных
прямых, уходящих вдаль по горизонтальной плоскости (например, границы прямой дороги),
то вы обнаружите, что на рисунке эти прямые выглядят пересекающимися в какой-то «ис¬
чезающей точке» на горизонте (см. рис. 15.13). Проективная геометрия воспринимает такие

300
Глава 15
Рис. 15.13. Проективная геометрия добавляет к евклидовой плоскости «точки на бесконечности» и до¬
пускает пересечение там параллельных прямых. На картине, которую художник пишет на вертикаль¬
ном холсте, две уходящие вдаль горизонтальные параллельные прямые (границы прямой горизонталь¬
ной дороги) кажутся пересекающимися в «исчезающей точке» на горизонте
исчезающие точки всерьез, добавляя к евклидовой плоскости «точки на бесконечности»,
что позволяет параллельным прямым пересекаться в этих дополнительных точках.
Существует много теорем относительно прямых в обычном евклидовом 3-простран¬
стве, которые трудновато формулировать из-за исключений для параллельных прямых.
На рис. 15.14 представлены два замечательных примера — теоремы Паппа (сформулирована
в конце III века нашей эры) и Дезарга (1636). В обоих случаях теорема (которую я фор¬
мулирую в «обратной» форме) утверждает, что если все прямые, показанные на диаграмме
(9 прямых для теоремы Паппа и 10 для теоремы Дезарга), пересекаются по три во всех,
кроме одной, точках, отмеченных черными пятнами (так что всего имеется 9 пятен в слу¬
чае теоремы Паппа и 10 в случае теоремы Дезарга), то тройка прямых, которые показаны
а)	6)
•
Рис. 15.14. Конфигурации двух известных теорем проективной геометрии на плоскости: а) теоремы
Паппа с 9 прямыми и 9 помеченными точками и б) теоремы Дезарга с 10 прямыми и 10 помеченными
точками. В обоих случаях утверждается, что если все помеченные точки, кроме одной из них, являются
точками пересечения тройки прямых, то оставшаяся помеченная точка также обладает этим свойством

15.6. Проективные пространства
301
как пересекающиеся в оставшемся черном пятне, действительно имеет общую точку. Одна¬
ко в такой формулировке эти теоремы истинны, только если принять, что тройка взаимно
параллельных прямых имеет общую точку «на бесконечности». При такой интерпретации
теорема остается истинной и для параллельных прямых. Она остается справедливой, да¬
же если одна из линий целиком лежит на бесконечности. Таким образом, теоремы Паппа
и Дезарга больше подходят для проективной геометрии, чем для евклидовой.
Как построить n-мерное проективное пространство Рп? Наиболее прямой путь —
это взять (п + 1)-мерное векторное пространство Vn+1 и рассматривать наше простран¬
ство Рп как пространство одномерных векторных подпространств пространства Vn+1. (Та¬
кими одномерными векторными подпространствами служат прямые, проходящие через на¬
чало координат пространства Уп^д.) Прямая линия в Рп (которая сама является примером
пространства Р1) задается двумерным подпространством пространства Vn+ 1 (плоскостью,
проходящей через начало координат), при этом коллинеарные точки пространства Рп появ¬
ляются в виде прямых, лежащих в такой плоскости (рис. 15.15). Существуют также плоские
подпространства пространства Рп с более высокой размерностью, представляющие собой
проективные пространства Рг, содержащиеся в Рп (г < п). Каждое пространство Рг соот¬
ветствует (г -f 1)-мерному векторному подпространству пространства Vn+ .
Рис. 15.15. Чтобы построить n-мерное проективное пространство Рп, возьмем (п 4 1)-мерное век¬
торное пространство Vn+l и будем рассматривать Рп как пространство одномерных векторных под¬
пространств пространства Vn+1 (прямых, проходящих через начало координат пространства Vn+1).
Прямая линия в Рп задается двумерным подпространством пространства Vn+1 (плоскостью, прохо¬
дящей через начало координат), при этом коллинеарные точки пространства Рп появляются в виде
прямых, лежащих в такой плоскости и проходящих через точку О. Это применимо как к веществен¬
ным пространствам (МРП), так и к комплексным (СРП). Геометрия пространства МР2 формализует
процедуру определения перспективы в графическом представлении. Пусть глаз художника располо¬
жен в начале координат О пространства V3, которое представляет собой евклидово 3-пространство,
окружающее художника. Луч света, проходящий через точку О, воспринимается художником как одна
точка. То, что художник изображает как «прямую линию» (МР1 в МР2) (при некотором заданном по¬
ложении холста художника), на самом деле соответствует плоскости (V2), соединяющей эту прямую
с точкой О. (Например, две нижние граничные прямые в левой части рисунка играют роль границ
дороги на рис. 15.13.)
Такое построение (для случая п = 2) формализует процедуру определения перспективы
в графическом представлении, поскольку мы можем считать, что глаз художника расположен
в начале координат О векторного пространства V3, которое представляет собой евклидово
3-пространство, окружающее художника. Луч света, проходящий через точку О (глаз худож¬
ника), воспринимается художником как одна точка. Тогда «поле зрения» художника, опре¬
деляемое всем множеством таких световых лучей, можно рассматривать как проективную
плоскость Р2 (см. рис. 15.15). Любая воспринимаемая художником прямая линия (не про¬

302
Глава 15
ходящая через точку О) соответствует плоскости, соединяющей эту прямую с точкой О.
в соответствии с данным выше определением «прямой линии» в пространстве Р2.
Представим себе, что художник рисует точную картину воспринимаемой им сцены на
холсте, совпадающем с некоторой плоскостью (не проходящей через точку О). Каждая такая
плоскость содержит лишь часть полного пространства Р2. В частности, она определенно не
пересекает тех световых лучей, которые параллельны ей. Однако несколько таких плоскостей
образуют некоторое адекватное «лоскутное одеяло», покрывающее пространство Р2 целиком
(в действительности достаточно трех плоскостей*Л15-11]). Параллельные прямые на одной
такой плоскости будут изображаться как прямые с общей исчезающей точкой на другой
плоскости.
Можно рассматривать как вещественные проективные пространства (Pn — RPn).
так и комплексные (Рп = СРП). Один пример комплексного проективного пространства
мы уже рассматривали — это сфера Римана, которая представляет собой пространство СР1.
Напомним, что сфера Римана появляется как пространство отношений пар комплексных
чисел (гщ z)9 не равных нулю одновременно, которое является в то же время пространством
комплексных прямых, проходящих через начало координат в пространстве С2 (см. рис. 15.8).
В более общем случае любому проективному пространству можно сопоставить так назы¬
ваемые однородные координаты. Это координаты z°, г1, £2, .zn для (п + 1)-мерного
векторного пространства Vn+1, из которого получается пространство Рп, однако в качестве
«однородных координат» для Рп берутся не сами значения переменных г, а п независимых
отношении
z° : z1 : z2 :	:	zn,
где величины г не обращаются в нуль одновременно . Если все величины zr вещественны,
то эти координаты описывают RPn, и пространство Vn+1 можно отождествить с Rn+1
(это есть пространство п + 1 вещественных чисел, см. § 12.2). Если все эти величины
являются комплексными, то они описывают СРП, и пространство Vn+1 можно отождествить
с Cn+1 (это есть пространство п + 1 комплексных чисел, см. § 12.9).
Поскольку мы исключаем точку О = (0, 0, ..., 0) из числа допустимых однородных ко¬
ординат, начало координат пространства Rn+1 или Cn+1 исключается из рассмотрения I1512;
(так что получается Rn+1 — О или Cn+1 — О), когда мы рассматриваем эти пространства как
расслоение соответственно над RP или СР . Следовательно, из слоя начало координат то¬
же должно быть удалено. В случае вещественных пространств это приводит к расщеплению
слоя на две части (но это не означает, что на две части разделяется расслоение; на самом
деле пространство Rn+1 — О является связным при п > 0). *** В случае комплексных про¬
странств слоем служит пространство С — О (часто записывается в виде С*), которое является
связным. В любом случае мы можем предпочесть восстановить в слое начало координат, при
этом получается векторное расслоение. Но если сделать это, то получится нечто большее,
чем просто возвращение начала координат в Rn+1 или Cn+1. Как и в рассмотренном выше
частном случае пространства С2, мы должны вернуть начало координат в каждый отдель¬
ный слой, поэтому начало координат «раздувается». Расслоенное пространство принимает
вид Rn+1 с заменой О на RPn или Cn+1 с заменой О на СРП.
В случае комплексных пространств можно рассмотреть также единичную (2п-Ь 1)-сфе-
ру S2n+1 в Cn+1 точно так же, как мы делали это в частном случае п — 1 при построении
Объясните, как это можно сделать. (Подсказка: попробуйте взять декартовы координаты (ж, у, z). Вначале
возьмите две координаты, а положение холста описывайте третьей координатой, положив ее равной 1.)
Объясните, почему имеется п независимых отношений. Найдите п + 1 наборов из п обычных координат
(построенных из переменных z) для п -f 1 различных координатных лоскутов, которые вместе покрывают Рп.
Объясните эту конфигурацию, показав, что расслоение Rn+1 — О над ШРП можно рассматривать как
***
композицию из расслоения Мп+1 — О над Sn (слой М+ есть пространство положительных вещественных чисел)
и Sn как двукратного покрытия пространства МРП

15.7. Нетривиальность в связности расслоения	303
-  		 И. «« » » * « ■	...				 II ■■ ■ -	 , *   	 ■	     I	■	     .	*	.	.
расслоения Клиффорда. Каждый слой пересекает сферу S2n+1 по окружности S1, поэтому
теперь мы получаем S2n+1 как расслоение S1 над СРП. Такая структура лежит в основе
геометрии квантовой механики (хотя этот замечательный геометрический факт лишь изред¬
ка оказывает влияние на размышления тех, кто занимается квантовой физикой), в которой,
как мы увидим, пространство физически различных квантовых состояний в системе с п + 1
состояниями имеет вид СРП. Кроме того, имеется такая величина, как фаза, под которой
обычно понимается комплексное число с единичным модулем (ег(9, где в ~~ вещественное
число, см. § 5.3), тогда как в действительности она является закрученным комплексным чис¬
лом с единичным модулем
[15.13]. К
этому вопросу мы еще вернемся в конце этой главы,
а также когда мы всерьез займемся квантовой механикой в главах 21 и 22 (см. §§21.9, 22.9).
15.7. Нетривиальность в связности расслоения
Я увлек читателя в головокружительную экскурсию по расслоенным пространствам
и некоторым связанным с ними важным понятиям! Кое-что из рассмотренной геометрии
и топологии довольно сложно, поэтому читателю не следует смущаться, если все это по-
t
кажется ему слегка запутанным. Позвольте мне теперь вернуться к гораздо более простым
вещам, в том смысле, что они не требуют привлечения многих измерений (по крайней
мере, на первых порах!) для того, чтобы донести основную идею. Хотя мой следующий
пример расслоения действительно очень прост, он выражает важную тонкость в понятии
расслоения, которой мы пока не касались. Во всех рассмотренных примерах расслоений
нетривиальность расслоения проявлялась как некоторое топологическое качество геомет¬
рии, «закрученность» имела топологический характер. Однако вполне возможно, что рас¬
слоение будет нетривиальным в некотором важном смысле, будучи при этом топологически
тривиальным.
Вернемся к нашему первоначальному примеру, когда базисным пространством М слу¬
жила обычная окружность S1, а слоем V было одномерное вещественное векторное про¬
странство. Теперь мы построим наше расслоение В несколько иным способом, отличным от
простого «переворачивания» слоя V при обходе пространства Л4, в результате чего получа¬
лось расслоение в виде ленты Мёбиуса. Вместо этого давайте «растянем» этот слой в два
раза, как изображено на рис. 15.16. Здесь используется симметрия одномерного веществен¬
ного векторного пространства, отличная от симметрии «переворота» v	~~v, приводившего
к ленте Мёбиуса. Преобразование «растяжения» v 2v также сохраняет для V структуру
векторного пространства. Но теперь топология расслоения не является проблемой. В тополо¬
гическом отношении мы просто имеем цилиндрическую поверхность S1 х R, как и в нашем
первом примере на рис. 15.4л, но теперь расслоение претерпевает «деформацию» иного
вида, которую можно описать как действие на него связности некоторого вида.
Наш предыдущий тип связности, рассмотренный в главе 14, основывался на поня¬
тии «параллелизма» для касательных векторов вдоль кривых на многообразии М. Чтобы
представить это в нынешнем контексте, следует рассмотреть касательное расслоение Т(М)
многообразия М. Поскольку точка пространства Т{М) представляет касательный вектор v
к Л4 в некоторой точке а, принадлежащей Л4, перенос вектора v вдоль некоторой кривой 7
в М представляется просто кривой 7*, в Т (Л4) (см. рис. 15.17 а). Знание того, что значит «па¬
раллель» для переноса вектора v, эквивалентно знанию того, что значит «горизонталь» для
кривой 7* в расслоении (поскольку сохранение «горизонтальности» кривой 7* в расслоении
равносильно сохранению «постоянства» v вдоль кривой 7 в базисном пространстве). Идея
здесь состоит в обобщении этого понятия таким образом, чтобы оно стало применимым и
к расслоениям, отличным от касательного (см. рис. 15.176). Начало такого обобщения мы
уже видели в главе 14, когда обобщали понятие связности на объекты, отличные от каса¬
тельных векторов, — ковекторы и вообще [р]-тензоры. Однако, как отмечалось в § 15.1, это

304
Глава 15
В
Попытка
горизонтального
сечения
Нулевое
сечение
базисное
пространство S
Ъ
Рис. 15.16. «Деформированное» линейное расслоение В над М = S1, использующее иную симметрию
слоя V, нежели на рис. 15.4, 15.5 и 15.7 (при этом V по-прежнему остается одномерным веществен¬
ным векторным пространством V1), а именно растяжение с положительным коэффициентом (в данном
случае равным 2). Получается топология цилиндрической поверхности S1 хМ, но здесь имеет ме¬
сто «деформация», которую можно описать как действие на В некоторой связности. Эта связность
определяет локальное понятие «горизонтали» для кривых в В. Однако рассмотрим два пути от а до Ь
в базисном пространстве — прямой (черная стрелка) и непрямой (светлая стрелка). Когда мы достигнем
точки 6, мы обнаружим расхождение (в 2 раза), показывающее, что понятие «горизонтали» зависит
здесь от выбранного пути
весьма ограниченный вид обобщения, поскольку расширение области действия связности
от векторов на указанные иные виды объектов однозначно предписано и не оставляет до¬
полнительной свободы (в сущности, из-за того, что кокасательное расслоение и тензорные
расслоения полностью определяются касательным расслоением). Произвольное расслоение
над М не нуждается ни в какой связи с касательным расслоением, так что способ действия
связности на такое расслоение можно задать независимо от того, каким образом оно действу¬
ет на касательные векторы. В случае расслоения над ЛТ, никак не ассоциированного с Т(Л4),
нецелесообразно вести разговор в терминах «параллелизма», поскольку (локальное) понятие
«параллели» относится к направлениям, которые преимущественно означают направления
касательных векторов. Полезнее оперировать локальным «постоянством» величины, описы¬
ваемой расслоением, а не «параллелизмом», который относится к касательным векторам,
описываемым пространством Т(М). Такое локальное понятие «постоянства» (т. е. «гори¬
зонтальности» в расслоении) приводит к структуре, известной под названием связность
расслоения.
Вернемся теперь к нашему «деформированному» расслоению В над окружностью S1,
показанному на рис. 15.16. Рассмотрим часть расслоения £>, «тривиальную» в том смыс¬
ле, что она находится над некоторой «топологически тривиальной» областью окружно¬
сти S1; пусть это будет часть Вр, находящаяся над односвязным отрезком S1 — р (как на
рис. 15.5), где р есть некоторая точка окружности S1. Можно считать Вр произведением
пространств (S1 — р) xl, тогда наша связность расслоения должна определить понятие
постоянства сечения, которое можно понимать как постоянство в обычном смысле неко¬
торой вещественной функции, заданной на S1 — р. Таким путем мы получаем постоянные
сечения, представленные на рис. 15.18 как настоящие горизонтальные линии в Вр. То же
относится и к другой части Bq (q Ф р), при этом полное расслоение получается склеиванием
двух частей. При склеивании, однако, имеет место относительное растяжение с коэффици¬
ентом 2 между правой и левой частями (на рисунке правая часть показана с двукратным

15.7. Нетривиальность в связности расслоения
305
Горизонталь
а)
6)
Рис. 15.17. Сравнение типов связности на многообразии общего вида Л4. а) Исходное понятие (§ 14.3),
определяющее «параллельность» касательных векторов, переносимых вдоль кривых в Л4, описывается
с помощью касательного расслоения Т{М) многообразия Л4 (рис. 15.12 а). Некоторый касательный
вектор v в точке а многообразия М представлен в Т(М) соответствующей точкой слоя над точкой а.
Выходящая из этой точки «горизонтальная» кривая 7V в Т{М) представляет параллельный перенос
вектора v вдоль кривой 7 в М.. б) Та же самая идея применима к отличному от Т(М) расслоению В
над М, в котором «постоянный перенос» в М определяется исходя из понятия «горизонтали» в В
растяжением). Тогда (ненулевое) сечение, которое остается локально горизонтальным, бу¬
дет претерпевать деформацию с коэффициентом 2 при обходе базисного пространства S1
(рис. 15.16). В соответствии с этим расслоение В не имеет локально горизонтальных сечений
(помимо нулевого сечения), отвечающих выбранной нами связности расслоения.
Можно взглянуть на ситуацию с несколько иной стороны. Представим себе кривую
в базисном пространстве S1, которая начинается в точке а и оканчивается в точке 6, и рас¬
смотрим «постоянный перенос» расслоенной функции на S1 из а в Ъ. Другими словами, рас¬
смотрим некоторую кривую на пространстве В, которая локально является горизонтальным
сечением над указанной кривой (см. рис. 15.16). Теперь на базисном пространстве имеется
Рис. 15.18. Рассмотрим часть Вр расслоения В (с рис. 15.16) над «тривиальной» областью S1 —р
окружности S1 и аналогичную часть Bq подобно рис. 15.5 а. В каждой части возьмем «горизонталь»,
понимаемую в обычном смысле. Однако при склеивании двух частей возникает относительное рас¬
тяжение между частями с коэффициентом 2 (как показано в правой части рисунка). Это определяет
связность, иллюстрированную на рис. 15.16

306
Глава 15
более одной кривой между точками а и Ъ. Если мы пройдем по одному пути, то конечное
9
значение в точке b будет отличаться от того, которое получается при прохождении другого
пути. Определенное нами понятие постоянного переноса зависит от пути, по которому
происходит перенос.
Это не совсем та зависимость от пути, с которой мы встретились при рассмотрении
связности V касательного расслоения в главе 13. Там имела место локальная зависимость
от пути, возникающая даже в случае бесконечно малой петли обхода и проявляющаяся
в кривизне связности. В случае же нашего «деформированного» расслоения В зависимость
от пути имеет глобальный характер. В этом примере, конечно, отсутствует возможность
локальной зависимости, поскольку базисное пространство одномерно. Однако этот пример
попутно указывает на возможность глобальной зависимости от пути, даже при отсутствии
локальной зависимости.
15.8.	Кривизна расслоения
Можно модифицировать наш пример таким образом, чтобы получить расслоение над
двумерным пространством, в котором выбрана некоторая окружность для представления
нашего пространства S1. Для удобства возьмем S1 в виде единичной окружности в ком¬
плексной плоскости, тогда базисное пространство Мс нашего нового расслоения Вс будет
иметь вид Мс = С (см. рис. 15.19). При этом слоями должны по-прежнему служить копии
вещественной оси М. Посмотрим, как можно распространить нашу связность расслоения
на это пространство.
Рис. 15.19. Чтобы получить локальную зависимость
от пути (при наличии кривизны) в нашем расслое¬
нии (теперь это Вс), необходимы по крайней мере
два измерения в базисном пространстве Мс, кото¬
рое теперь выбирается в виде комплексной плоско¬
сти С, так что S1 с рис. 15.16 является единичной
окружностью этой плоскости. Слоями по-прежнему
служат векторные пространства V1 (копии веществен¬
ной оси Е). Используя комплексную координату z
для С = Мс
ности V =
получаем явное выражение для связ-
д/dz — А, где А — гладкая комплексная
функция от z. Если функция А голоморфна, кривиз¬
на расслоения исчезает, если же А = ikz (с подхо¬
дящим к), получается деформированное расслоение
с рис. 15.16 для части, расположенной над единич¬
ной окружностью. Кривизна расслоения проявляет-
ся в незамкнутости горизонтального многоугольника
над параллелограммом малого размера в Мс
Если бы наше новое расслоение Вс не содержало «деформации», мы могли бы пони¬
мать под такой связностью непосредственное дифференцирование по обычным координа¬
там (z, z) в комплексной плоскости Мс. Тогда «постоянство» сечения Ф (которое является
вещественной функцией от z и z) можно рассматривать просто как постоянство в обычном
смысле, а именно дФ/dz = 0 (откуда следует также дФ/dz = 0, поскольку функция Ф

15.8. Кривизна расслоения
307
вещественна). Чтобы ввести «деформацию» в связность расслоения, можно вместо опера¬
тора d/dz взять новый оператор V в виде
\7 = — - Л
dz ’
где величина А представляет собой комплексную (не обязательно голоморфную) гладкую
функцию от z9 которая «действует» просто как операция (скалярного) умножения. Опера¬
тор V действует на величины, подобные Ф. В топологическом отношении наше рассло¬
ение Вс должно быть просто тривиальным расслоением С х 1, поэтому для Вс можно
пользоваться глобальными координатами (z, Ф) с комплексным z и вещественным Ф.
Сечение расслоения 23е определяется величиной Ф, задаваемой в виде функции от г:
Ф(г, z)
(появление £ указывает на отсутствие голоморфности, см. § 10.5). Чтобы сечение было
постоянным (т. е. горизонтальным), мы потребуем выполнения равенства = 0 (откуда
следует также = 0, поскольку функция Ф вещественна), т. е.
In =
OZ
ч
Если функция А голоморфна, решение этого уравнения не составляет проблемы, посколь¬
ку выражение вида Ф = е^в+в\ где В = f Adz, удовлетворяет всем условиям*. Однако
в общем случае неголоморфной функции А мы не стремимся получить ненулевые решения
из-за коммутаторного соотношения
VV - VV = — - —
dz dz’
действующего на Ф. (Правая часть дает число, умножаемое на Ф, которое в общем слу¬
чае не обращается в нуль, хотя левая часть обращает в нуль любое вещественное решение
уравнения дФ/dz.) Этот коммутатор служит для определения кривизны связности V, зада¬
ваемой мнимой частью величины ; эта кривизна служит мерой локальной «деформации»
расслоения.
Выбрав функцию А таким образом, чтобы этот коммутатор принимал постоянное нену¬
левое значение, например, взяв А = ikz с подходящей вещественной постоянной &, можно
найти «коэффициент растяжения» для обхода замкнутого контура в Мс, который просто
пропорционален площади, ограниченной контуром. Это применимо, в частности, к единич¬
ной окружности S1, так что можно воспроизвести наше первоначальное «деформированное»
расслоение В над S1, взяв ту часть расслоения, которая лежит над S1. Выбрав подходящее
значение постоянной к, мы получим требуемое «растяжение в два раза» над единичной
окружностью
Вышеуказанный коммутатор является прямым аналогом рассмотренного в § 14.4 комму¬
татора операторов Va, который порождает кручение и кривизну. Можно положить кручение
равным нулю. (Кручение связано с действием оператора связности на касательные векторы
и не имеет прямого отношения к рассматриваемому здесь расслоению, не связанному с ка-
%
сательным расслоением.) Для n-мерного базисного пространства М мы имеем величины,
**
***
Проверьте это.
Проверьте эту формулу.
Подтвердите это, найдя явное значение постоянной к, которое дает этот требуемый коэффициент 2.

308
Глава 15
подобные Va и V из главы 14, за исключением того, что теперь они действуют на вели-
X
чины, относящиеся к расслоениям [15Л41. При надлежащем построении их коммутаторов мы
найдем кривизну связности расслоения. Если эта кривизна обращается в нуль, мы получа¬
ем много локально постоянных сечений расслоения, в противном случае при определении
таких сечений мы сталкиваемся с препятствиями в виде локальной зависимости связности
от пути. Кривизна описывает эту зависимость на уровне бесконечно малых величин, как
показано на рис. 15.19.
При использовании индексных обозначений связность обычно выражается (в некоторой
системе координат) как оператор, имеющий общий вид
у ~ ...ft . _ а
а дха а’
где величину Аа можно считать имеющей некоторые скрытые «индексы расслоения».
Мы будем обозначать их греческими буквами^15 15^ (предполагается, что мы имеем дело
с векторным расслоением, так что будут применяться тензорные обозначения), тогда вели¬
чина Аа примет вид Аа^\. (Чтобы получить полную индексную запись, два других члена
в приведенном выражении следует умножить на Кривизной расслоения будет величина
Fab^X,
в которой антисимметричная пара индексов аЪ относится к направлениям касательной
2-плоскости в М. точно так же, как в рассмотренном случае тензора кривизны, однако
индексы Л и р теперь относятся к направлениям слоя (в большинстве случаев их явно
не выписывают). Существует прямая аналогия с (вторым) тождеством Бьянки (см. § 14.4).
(В частном случае расслоения Вс комплексные координаты использовались лишь для удоб¬
ства; можно было воспользоваться индексной записью так же, как в n-мерном случае.)
Следует отметить, что во многих случаях расслоенных пространств симметрия, ис¬
пользуемая при построении расслоения, не обязательно полностью совпадает с симметрией
слоя. Например, в случае «деформированного» расслоения В над S1 (или Вс над С) можно
рассматривать одномерный слои как расширенный в двумерное вещественное векторное
пространство, при этом «деформация» слоя представляется как однородное расширение
векторного 2-пространства. Можно также снабдить это вещественное двумерное векторное
пространство дополнительной структурой, образующей одномерное комплексное векторное
пространство, при этом «растяжение» соответствует умножению на некоторое веществен¬
ное число (рис. 15.20). Это приводит к необходимости рассмотреть, что происходит в случае
«комплексного растяжения». Частным случаем может служить умножение на комплексное
число с единичным модулем (хег$ , где в — вещественное число), которое соответствует пово¬
роту, а не реальному растяжению (рис. 15.21); идея такого рода содержится в рассмотренном
выше расслоении Клиффорда-Хопфа. В данном случае используется группа U(l) — мульти¬
пликативная группа унимодулярных комплексных чисел (см. § 13.9). Связности расслоения
с группой симметрии U(l) играют важную роль в физике, поскольку, как мы увидим в § 19.4,
они описывают электромагнитное взаимодействие. Сущность такого расслоения можно
понять, если моделировать слой не на всей комплексной плоскости С, а на единичной
окружности S1. Это в некотором смысле «экономичнее», поскольку остальная часть плос¬
кости просто «переносится» вместе с окружностью, не давая дополнительной информа¬
ции. Тем не менее использование в качестве слоя комплексной плоскости дает некото¬
рые преимущества, поскольку тогда наше расслоение становится (комплексным) векторным
расслоением^15*16^.
В последующих главах мы убедимся в мощи этих идей в.связи с современными теория¬
ми физических сил. Связности расслоения под именем «калибровочные связности» фигури¬
руют там в качестве основного ингредиента, и некоторые физические поля появляются как

15.8. Кривизна расслоения
309
Рис. 15.20. Можно ввести слой в комплекс- Рис. 15.21. Вместо этого можно ввести «ком-
ное одномерное векторное пространство, при
этом «растяжению» соответствует умножение
на некоторое вещественное число
плексное растяжение», соответствующее умно¬
жению на комплексную фазу егв, где в — ве¬
щественное число, так что группой расслоения
теперь будет U(l) — мультипликативная группа
этих комплексных чисел
кривизна этих связностей (примером может служить электромагнетизм Максвелла). Мы ви¬
дели, насколько существен для этих идей тот факт, что слои обладают точной симметрией.
Это поднимает фундаментальные вопросы о природе такой симметрии и о том, какова она
в действительности. Я вернусь к этому важному вопросу позднее, в основном в главах 28, 31
и 34.
Примечания
§15.1.
15.1. См., например, [745]. Одним из первых физиков, оценивших (в 1967 году), что используемое
физиками понятие «калибровочной теории» тесно связано со связностью на расслоении, по-
видимому, был Анджей Траутман [790] (см. также [628], стр. А4).
15.2. Дополнительные пространственно-временные размерности (пространства Калаби-Яу,
см. §31.14) в теории струн не следует понимать непосредственно как «слои» расслоенного
пространства. Такими слоями будут пространства некоторых спинорных полей в простран¬
ствах Калаби-Яу.
W
§15.2.
15.3. Для полного определения произведения пространств требуется дополнительная информация,
чтобы корректно определить понятия топологии и гладкости для АЛ х V. Если приписать
каждому из пространств АЛ и V некоторую меру объема, то объем произведения АЛ х V будет
произведением объемов АЛ и V. Мне трудно входить здесь глубже в эти материи, хотя, строго
говоря, они необходимы. См. соответствующую литературу [441, 481, 537].

310
Глава 15
15.4. Относительно общего смысла «односвязности» см. § 12.1.
15.5. Для упрощения записи я использую не совсем правильное обозначение S1 — р для простран¬
ства S1, из которого удалена точка р. Ревнители чистоты написали бы S1 — {р} или, веро¬
ятнее, Si\{p} (см. примечание 9.13). Такая запись означает «разность» двух множеств, при
этом {р} есть множество, единственным элементом которого служит точка р.
§15.4.
15.6. См. [4].
15.7. См. [605, 627].
15.8. Мы говорим, что В является накрывающим пространством по отношению к Б'. Точнее, В
есть так называемое универсальное накрывающее пространство по отношению к Б'. Последнее,
будучи односвязным, не может быть накрыто дополнительно.
§15.5.
15.9. Такое геометрическое описание 2-спиноров подробнее обсуждается в книге [626], гл. 1.
15.10. Например, в § 9.5 разделение функций (вещественной переменной) на положительно-частотную
и отрицательно-частотную части (играющее важную роль в квантовой теории поля) анализи¬
ровалось в связи с обобщением на голоморфные функции; однако читатель может испыты¬
вать некоторое неудобство в связи с постоянными функциями. Данное понятие станет гораздо
яснее, когда мы применим его к закрученным голоморфным функциям в теории твисторов
в §§33.8, 33.10.
§15.6.
15.11. Было бы разумно считать полем зрения художника не пространство Р, а сферу S2, где поле
зрения художника определяют направленные световые лучи, проходящие через точку О, а не
ненаправленные, которые я (неявно) использовал в тексте. Сфера представляет собой двукрат¬
ное накрытие проективной плоскости, и единственная неприятность при ее использовании
состоит в том, что в порождаемой ею «геометрии» пары «линий» (больших окружностей)
пересекаются в парах точек, а не в отдельных точках. Чтобы накрыть сферу S2, художнику
понадобятся не три, а четыре холста.
15.12. См. примечание 15.5.
15.13. Этот факт имеет отношение к интригующему и важному квантово-механическому понятию,
именуемому «фазой Берри» (см. [76, 77, 724, 8, 716], а также [852], стр. 225-249), которое
учитывает тот факт, что мы не знаем, где находится 1 на единичной окружности, т. е. такое
«число» является элементом 8*-слоя S1-расслоения; в данном случае S2n+1 над ОРп.
§15.8.
15.14. В случае оператора Va необходимо также, чтобы он действовал на (ко)касательные векторы
и мог действовать на величины с пространственно-временными индексами, чтобы имел смысл
коммутатор V[aVb]. В случае оператора V можно пользоваться коммутаторным выражени-
ем VV-VV- V , для которого это не требуется.
L М М L [L, М]
15.15. Индексная запись такого вида для индексов расслоения используется в явном виде в книге [626],
гл. 5.
15.16. С другой стороны в случае, когда слоем служит единичная окружность, наше расслоение ока¬
зывается примером главного расслоения, которое имеет преимущества в других контекстах.
Главным называется расслоение, у которого слой V моделируется на его собственной группе
симметрии Q. Грубо говоря, для главного расслоения Q и V — «одно и то же». Более точно, V
есть группа Q, относительно которой «забыли», какой из ее элементов является тождествен¬
ным. Соответственно V есть аффинное пространство (не обязательно абелево), что согласуется
с § 14.1 и упражнениями 14.1 и 14.2.

Глава 16
Лестница бесконечности
16.1.	Конечные поля
Универсальной особенностью математики, лежащей, как обычно считают, в основе
устройства нашей физической Вселенной, представляется ее фундаментальная зависимость
от понятия бесконечного. Во времена древних греков, еще до того, как они оказались выну¬
ждены рассматривать систему вещественных чисел, уже практически привыкли пользовать¬
ся рациональными числами (см. § 3.1). Система рациональных чисел бесконечна не только
в том смысле, что она допускает сколь угодно большие величины (этим свойством обладает
и система натуральных чисел), но и в том, что она позволяет проводить неограниченное
утончение в бесконечно малом масштабе. Некоторых беспокоят оба эти аспекта бесконечно¬
сти. Они предпочли бы, чтобы Вселенная, с одной стороны, имела конечную протяженность,
а с другой, — была делимой лишь до некоторого конечного предела, так что на самых мелких
масштабах проявлялась бы фундаментальная дискретность.
Хотя подобная точка зрения должна считаться определенно нестандартной, она не яв¬
ляется внутренне противоречивой. Существует идея, что видимая фундаментальная физи¬
ческая роль системы вещественных чисел М на самом деле является некоторым приближе¬
нием к «истинной» физической системе чисел, содержащей лишь конечное число элемен¬
тов. (Вариант такого подхода разрабатывался, в частности, Ахмаваарой [13] и некоторыми
его сотрудниками, см. §33.1.) Как понимать смысл такой конечной системы чисел? Про¬
стейшие примеры можно построить из целых чисел путем «приведения их по модулю р»,
где р — некоторое простое число. (Напомним, что простыми называются натуральные чис¬
ла 2, 3, 5, 7, 11, 13, 17, ..., не имеющие делителей кроме самого себя и 1, при этом 1 не
считается простым числом.) Приведение целых чисел по модулю р состоит в том, два целых
числа считаются эквивалентными, если их разность кратна р, то есть -
a ~b (mod р)
тогда и только тогда, когда
a —b — кр (для некоторого целого к).
Согласно этому определению, целые числа распадаются на р «классов эквивалентности»
(относительно понятия класса эквивалентности см. предисловие), так что числа а и b при¬
надлежат к одному классу эквивалентности всякий раз, когда а = Ь. Эти классы рассмат¬
риваются как элементы конечного поля Fp, таких элементов будет ровно р. (Я использую
здесь термин «поле» в том смысле, который вкладывают в это слово алгебраисты. Не следу¬
ет путать его с «полями» на многообразии, например векторными или тензорными полями,
и с физическим (например, электромагнитным) полем. Поле алгебраистов есть коммутатив¬
ное кольцо с делением, см. § 11.1.) Для элементов поля ¥р справедливы обычные правила
сложения, вычитания, (коммутативного) умножения и деления . Однако здесь имеется до¬
полнительное забавное свойство: если сложить р одинаковых элементов, всегда получится
нуль (и, конечно, само простое число р должно считаться «нулем»).
Покажите, что эти правила выполняются, и объясните, почему число р должно быть простым.

312
Глава
Заметим, что при таком определении множества ¥р его элементы сами определяются каз
«бесконечные множества целых чисел», поскольку сами «классы эквивалентности» пред¬
ставляют собой бесконечные множества, как, например, класс эквивалентности {..., — “
—2, 3, 8, 13, ..определяющий элемент множества Fp, который можно обозначить чис¬
лом 3. Таким образом, мы апеллируем к бесконечности для того, чтобы определить величи¬
ны, образующие нашу конечную систему чисел! Это пример того, как математики зачастую
получают строгое описание математических понятий, определяя их через бесконечные мно¬
жества. Это та самая процедура «классов эквивалентности», включаемая в определение
дробей, о которой я рассказывал в предисловии в связи с «сокращением» дробей, которое
подруга моей матери находила таким запутанным! Я полагаю, что тем, кто убежден в «ре¬
альном» существовании в природе системы чисел Fp (с некоторым подходящим значением
числа р), процедура «классов эквивалентности» нужна лишь для удобства, как способ стро¬
гого описания на (исторически) более привычном языке бесконечных процедур. На самом
деле здесь не требуется привлекать бесконечные множества целых чисел, просто такая про¬
цедура имеет наиболее систематический характер. В любом конкретном случае вместо этого
можно просто перечислить все операции, поскольку их число конечно.
В качестве примера рассмотрим подробнее случай р = 5. Мы можем пронумеровать
элементы множества Fp обычными символами 0, 1, 2, 3, 4 и получить таблицы сложения
и умножения:
+
0
1
2
3
4
X
0
1
2
3
4
0
0
1
2
3
4
0
0
0
0
0
0
1
1
2
3
4
0
1
0
1
2
3
4
2
2
3
4
0
1
2
0
2
4
1
3
3
3
4
0
1
2
3
0
3
1
4
2
4
4
0
1
2
3
4
0
4
3
2
1
Заметим, что каждый элемент, отличный от нуля, имеет мультипликативную обратную
величину:
1-1 = 1,	2-1 = 3,	З-1	= 2,	4-1 = 4
в том смысле, что 2x3 = 1 (mod 5) и т. п. (Далее при работе с элементами конкретной
конечной системы чисел я буду пользоваться знаком «=» вместо «=».)
Существуют и другие конечные поля ¥я, построенные несколько более сложным обра¬
зом, у которых полное число элементов равно некоторой степени простого числа: q — рт.
В качестве простейшего примера возьмем случай q = 4 = 22. Здесь можно обозна¬
чить различные элементы как 0, 1, сщ о;2, где о;3 = 1 и каждый элемент х удовлетворя¬
ет условию х + х ~ 0. Это несколько расширяет мультипликативную группу комплексных
чисел 1, cj, и2, которые являются кубическими корнями из 1 (они описаны в § 5.4 и упоми¬
наются в § 5.5 как описывающие кварковую природу сильно взаимодействующих частиц).
Чтобы получить множество F4, достаточно добавить нуль (0) и определить операцию «ело-
жения» вида х 4- х — 0. В общем случае Fрт мы будем иметь х~\-х-\ Ь £ = 0, где число
слагаемых х равно р.
16.2.	Конечная или бесконечная геометрия нужна физике?
Неясно, действительно ли подобные материи играют значительную роль в физике, од¬
нако эта идея возрождается время от времени. Если бы множество ¥я заняло место системы
Составьте полные таблицы сложения и умножения для F4 и проверьте, что правила алгебры выполняются,
если предположить, что 1 + сц + о?2 — 0.

16.2. Конечная или бесконечная геометрия нужна физике?
313
вещественных чисел, в некотором существенном смысле, то число р должно было бы быть
очень велико (чтобы соотношение х 4- х + • • • + х = 0 не приводило к серьезным проти¬
воречиям с наблюдаемой действительностью). На мой взгляд, физическая теория, которая
фундаментальным образом зависит от некоторого невообразимо огромного простого числа,
должна быть намного более сложной (и неправдоподобной), чем теория, которая может за¬
висеть от простого понятия бесконечности. Тем не менее имеет смысл продолжить эту тему.
Если в качестве координат взять элементы некоторого множества Fg, то большая часть гео¬
метрии сохранится. Идеи анализа требуют большего внимания, тем не менее многие из них
также остаются в силе.
Поучительно (и занимательно) посмотреть, какова будет проективная геометрия, ис¬
пользующая конечное полное число точек и соответственно проективные п-простран¬
ства Pn(Fg) над полем Fg. Мы найдем, что пространство Pn(Fg) содержит ровно 1 +
4- q + q2 4- • • • + qn = (qn+1 — l)/(g — 1) различных точек*. Особенно привлекательны
проективные плоскости P2(Fg), поскольку для них можно построить весьма изящные кон¬
струкции. Их можно описать следующим образом. Возьмем круглый диск, сделанный из
какого-нибудь подходящего материала, например из картона, и с помощью канцелярской
кнопки, протыкающей его в центре, прикрепим его к другому, фиксированному (фоновому),
куску картона так, чтобы диск мог свободно вращаться. На фоновом картоне пометим вдоль
окружности диска 1 + q + q2 равноудаленных точек, пронумеровав их в направлении против
часовой стрелки числами 0,1,2,..., q( 1 + q). На вращающемся диске отметим 1 + q точек,
выбранных особым образом. Положение таких точек выбирается так, чтобы при любом вы¬
боре каких-нибудь двух точек, отмеченных на фоновом картоне, существовало ровно одно
положение диска, при котором две выбранные точки совпадают с двумя особыми точка¬
ми на диске. Другими словами, если ао, ai, ..., aq — последовательные расстояния вдоль
окружности между соседними особыми точками, взятыми в циклическом порядке (при этом
расстояние вдоль окружности между последовательными отмеченными точками на фоновой
окружности принимается за единицу расстояния), то каждое из расстояний 1, 2, 3, ..., q +1
можно однозначным образом представить в виде суммы некоторого набора циклически по¬
следовательных значений величин а. Назовем такой диск магическим диском. На рис. 16.1
изображены магические диски для q = 2, 3, 4 и 5, на которых в качестве значений а0, ..., aq
выбраны числа соответственно 1, 2, 4; 1, 2, 6, 4; 1, 3, 10, 2, 5; 1, 2, 7, 4, 12, 5. ' В случа¬
ях д = 7, 8, 9, 11, 13и16 можно построить магические диски, определяемые соответствен¬
но числами 1, 2, 10, 19, 4. 7, 9, 5; 1, 2, 4, 8, 16, 5, 18, 9, 10; 1, 2, б, 18, 22, 7, 5, 16, 4, 10;
1/2, 13, 7, 5, 14, 34, б, 4, 33, 18, 17, 21, 8;	1, 2, 4, 8, 16, 31, 27, 26, 11, 9, 45, 13, 10, 29,
5, 17, 14, 34, 6, 4, 33, 18, 17, 21, 8; 1, 2, 4, 8, 16, 32, 27, 26, 11, 9, 45, 13, 10, 29, 5, 17, 18.
В математике имеется теорема, согласно которой существуют магические диски для лю¬
бого пространства F2(Fg) (где q — показатель степени, в которую возводится простое
число)!16,1!. Читатель может развлечься, проверяя различные примеры теорем Паппа и Дез-
арга (см. § 15.6, рис. 15.14)!16*2/ (Возьмите q > 2, чтобы число точек было достаточно для
невырожденной конфигурации!) Два примера (теорема Дезарга для q = 3 и теорема Паппа
для q = 5 с использованием дисков с рис. 16.1) показаны на рис. 16.2.
Особый интерес представляет случай q = 2, Такая плоскость с 7 точками, называемая
плоскостью Фано, изображена на рис. 16.3, где окружность рассматривается как «прямая
Покажите это.
**Щ$ Покажите, как построить новые магические диски с q = 3, 5, исходя из какой-либо точки, отмеченной
мною на одном из дисков, и умножая затем каждое из угловых расстояний от других отмеченных точек на некоторое
фиксированное целое число. Почему можно пользоваться этим способом?
Конечное поле Fs содержит элементы 0, 1, е, в2, £3, в4, е5, е6, где е7 — 1 и 1 -j- 1 = 0. Покажите,
что либо 1) выполняется тождество вида еа + еь + £с = 0, коль скоро а, b и с — числа на фоновой окружности
с рис. 16.1«, которые можно сопоставить трем точкам на диске, либо 2) выполняется то же тождество, но с в3
вместо е (т. е. е3а -f езъ + е3с — 0).

314
Глава 1 с
а)
«)
15 16
22 23 24
г)
Рис. 16.1. «Магические диски» для конечных проективных плоскостей P2(Fq) (q — показатель степени,
в которую возводится простое число). 14- q + q2 точек пронумерованы числами 0, 1, 2, ..., q( 1 —
4-<?), расположенными эквидистантно вдоль фоновой окружности. На свободно вращающемся круглом
диске стрелками отмечены 1 + q выбранных точек, это точки на прямой в пространстве Р2{Fg). Дело
обстоит так, что для каждой пары различных чисел существует ровно один диск, расположенный таким
образом, что стрелки указывают на эти числа. Показаны магические диски для a) q = 2, б) q = 3.
в) q — 4 — 22 и г) q = 5
линия». Хотя ее значение в геометрии довольно ограничено, она играет важную роль разного
рода, определяя правило умножения для октонионов (см. §§ 11.2, 15.4). Плоскость Фано со-
,	v
держит 7 точек, и каждая точка связана с одним из генерирующих элементов io, ii, 12, • • •, h
алгебры октонионов. Каждый из них удовлетворяет условию i2 = —1. Чтобы получить про¬
изведение двух различных генерирующих элементов, достаточно найти на плоскости Фано
прямую, соединяющую точки, представляющие эти элементы, тогда оставшаяся точка на
этой прямой представляет искомое произведение (с точностью до знака). Поэтому простая
б)
Рис. 16.2. Аналоги теорем с рис. 15.14 для конечной геометрии: а) теорема Паппа (с q — 5) и б) теорема
Дезарга (с q = 3). Иллюстрация с использованием соответствующих дисков на рис. 16.1 г и 16.1 б

16.2. Конечная или бесконечная геометрия нужна физике?
315
картина плоскости Фано не вполне достаточна,
поскольку неооходимо знать также знак произ¬
ведения. Этот знак можно определить, возвра¬
тившись к описанию с помощью диска, изоб¬
раженного на рис. 16.1а, либо используя (эк¬
вивалентное) расположение стрелок (с учетом
цикличности) на рис. 16.3. Припишем отмечен¬
ным точкам на диске определенный цикличе¬
ский порядок (например, против часовой стрел¬
ки). Будем считать, что = iZ9 если располо¬
жению на диске соответствует порядок ix
= — iz в обратном случае. В частности,
имеем i0ii = i.3 = -Ыо» hh = ie, hk =
4JL
(ьл
ТзТ
а 1
И 1х1 у
Рис. 16.3. Плоскость Фано с 7 точками и 7 пря-
*
I5, I4I2 — и т. п.
Хотя такие геометрические и алгебраиче-
мыми (окружность рассматривается как «пря¬
мая линия»), пронумерованными в соответ-
ские структуры ооладают определенным изя-	ствии с рис. 16.1 а. Это дает таблицу умноже-
ществом, они, по-видимому, имеют мало то-	ния для базисных элементов i0, ii, i2, .ie
чек соприкосновения с физической реально-	алгебры октонионов с делением. Циклическое
стью. Вероятно, это нас не должно удивлять,	упорядочение, показанное стрелками, соответ-
если принять точку зрения, выраженную на	ствУет знаку«+»
рис. 1.3 в § 1.4. Поскольку математика, имею¬
щая сколько-нибудь прямое отношение к физическим законам, управляющим нашей Все¬
ленной, — это всего лишь малая часть платоновского математического мира как целого, по
крайней мере, как мы это сейчас понимаем. Возможно, что в будущем, по мере углубления
наших знаний, выяснится важная роль таких изящных конструкций, как конечная геометрия
или алгебра октонионов. Но в настоящее время, на мой взгляд, все это еще надлежит сделать
более убедительным^16,3!. Представляется, что одного лишь математического изящества для
этого далеко не достаточно (см. также § 34.9). Это побуждает нас проявлять осторожность
при поиске принципов, лежащих в основе законов Вселенной!
От флирта с завлекающими конечными структурами вернемся к внушающему благого¬
вение математическому богатству, которое присуще бесконечности. Прежде всего, следует
отметить, что бесконечные структуры (например, множество натуральных чисел N) могут
быть частью некоторого математического формализма, созданного для описания реальности;
при этом не предполагается, что эти оесконечные структуры допускают непосредственную
физическую интерпретацию как бесконечно большие (или бесконечно малые) физические
сущности. Например, делались попытки построить схему, в которой дискретность (и соот¬
ветственно конечность) появляется на уровне наиболее малых масштабов, тогда как остается
возможность описания неопределенно больших (и даже бесконечно больших) структур. Это
относится, в частности, и к моим собственным ранним идеям построения пространства ко¬
нечным образом с использованием теории спиновых сетей, которые будут кратко описаны
в § 32.6. Эти идеи связаны с тем фактом, что, согласно стандартной квантовой механике,
спин любого объекта равен натуральному числу, умноженному на некоторую вполне опре-
1
деленную величину (~ft). Как я упоминал в § 3.3, на заре квантовой механики была большая
надежда (не реализовавшаяся в результате дальнейших исследований), что квантовая теория
приведет к созданию картины мира, в которой существует дискретность на низших уров¬
нях. В наших сегодняшних успешных теориях пространство-время остается непрерывным
даже с учетом квантовых концепций, так что идеи дискретности пространства-времени на
Покажите, что «ассоциатор» a(bc) — (аЬ)с антисимметричен по а, 6, с, когда это генерирующие элементы,
и покажите, что это (а также следующее отсюда соотношение а(аЬ) = а2Ь) справедливо для всех элементов,
i Подсказка: воспользуйтесь рис. 16.3 и полной симметрией плоскости Фано.)

316
Глава 16
малых масштабах следует рассматривать как «нестандартные» (см. §33.1). Непрерывность
существенным образом проявляется даже в тех теориях, которые пытаются применить идет:
квантовой механики к самой структуре пространства и времени. Это относится, в частности,
к теории петлевых переменных Аштекара-Ровелли-Смолина-Якобсона, в которой ключе*
вую роль играют дискретные (комбинаторные) идеи теории узлов и связей, а спиновые сети
входят в качестве базисной структуры. (Кое-что из этой замечательной схемы будет изложено
в главе 32; в § 33.1 мы вкратце познакомимся с некоторыми другими идеями, относящимися
к «дискретному пространству-времени».)
Оказывается, таким образом, что (по крайней мере, пока) мы должны всерьез отно¬
ситься к бесконечности, особенно к ее роли в математическом описании физической непре¬
рывности. Но какой вид бесконечности здесь требуется? В § 3.2 я кратко описал метод
«сечения Дедекинда» для построения системы вещественных чисел на языке бесконечных
множеств рациональных чисел. Фактически это был гигантский скачок, приводящий к по¬
нятию бесконечности, намного превосходящей ту бесконечность, которая связана с самими
рациональными числами. Для нас будет полезно обратиться здесь к этой теме. Как пока¬
зал в 1874 году великий датско-русско-немецкий математик Георг Кантор (это было частью
теории, которую он продолжал развивать до 1895 года), существует бесконечность разного
размера! Наименьшим оказывается размер бесконечности натуральных чисел, и существу¬
ют различные бесконечности все большего и большего масштаба. Попробуем дать набросок
основополагающих фундаментальных идей Кантора.
16.3.	Бесконечности разного размера
Первой из основных составляющих революции Кантора является идея взаимно-одно¬
значного соответствия^16 ^. Мы говорим, что два множества имеют одинаковую мощность
(на обычном языке это означает, что они содержат «одинаковое число элементов»), если
можно установить взаимно-однозначное соответствие между элементами одного и друго¬
го множества, так что не окажется элементов какого-либо множества, не принимающих
участия в установлении соответствия. Ясно, что такая процедура дает правильный ответ
(«одинаковое число элементов») для конечных множеств (т. е. множеств, содержащих ко¬
нечное число членов 1, 2, 3, 4, ... или даже 0 элементов, в последнем случае должно быть
г
соответствие с пустым множеством). Однако в случае бесконечных множеств имеется неко¬
торая новая особенность (отмечавшаяся еще в 1638 году великим физиком и астрономом
Галилео Галилеем)^6,5Ь бесконечное множество имеет ту же мощность, что и некоторые
из его собственных подмножеств («собственное» означает, что данное подмножество отлич¬
но от полного множества).
Покажем это на примере множества натуральных чисел N:
N = {0, 1, 2, 3, 4, 5, ...}.
Если удалить из этого множества 0j16,6l мы получим новое множество N — 0, которое, оче¬
видно, имеет ту же мощность, что и Н, поскольку можно установить взаимно-однозначное
соответствие, при котором элемент г множества N сопоставляется элементу г + 1 множе¬
ства N — 0. Вместо этого можно взять пример, предложенный Галилеем, и обнаружить, что
множество квадратов чисел {0, 1, 4, 9, 16, 25, ...} также должно иметь ту же мощность, что
*
и N, несмотря на тот факт, что, с точки зрения здравого смысла, квадраты чисел составляют
исчезающе малую долю всех натуральных чисел. Можно также заметить, что ту же мощ¬
ность имеет множество всех целых чисел Z. Это можно показать, рассматривая следующее
упорядочение множества Z:

16.3. Бесконечности разного размера
317
и сопоставляя его элементы элементам {0, 1, 2, 3, 4, 5, 6, 7, 8, ...} множества N. Более
поразителен тот факт, что множество рациональных чисел опять-таки имеет ту же мощность,
что и N. Есть много способов увидеть это непосредственно » , однако вместо того чтобы
подробно демонстрировать это здесь, посмотрим, как укладывается этот частный пример
в общие рамки созданной Кантором удивительной теории бесконечных кардинальных чисел.
Прежде всего, что такое кардинальное число? По существу, это есть «число» элементов
некоторого множества, при условии, что мы считаем два множества имеющими «одинако¬
вое число элементов» тогда и только тогда, когда можно установить взаимно-однозначное
соответствие между ними. Можно попробовать уточнить это, используя идею «классов эк¬
вивалентности» (которая применялась в § 16.1 при определении множества ¥р для простого
числа р\ см. также предисловие) и назвав кардинальным числом а некоторого множества А
класс эквивалентности всех множеств той же мощности, что и А. Фактически именно это
пытался сделать логик Готлиб Фреге в 1884 году, но оказалось, что существуют фунда¬
ментальные трудности, связанные с такими нечетко определенными понятиями, как «все
множества», и приводящие к серьезным противоречиям (как мы увидим в § 16.5). Чтобы
устранить их, представляется необходимым наложить некоторые ограничения на размер
«мира возможных множеств». Я должен сделать несколько замечаний относительно этого
спорного вопроса. Для начала попробуем уклониться от него, найдя прибежище в ситуации,
которую мы уже рассматривали раньше (в предисловии, в связи с определением «класса
эквивалентности» для рациональных чисел). Примем кардинальные числа просто как некие
математические сущности (обитатели платоновского мира!), которые можно отделить от
понятия взаимной эквивалентности множеств. Будем говорить, что множество А «имеет
мощность а» или что оно «содержит а элементов», и считать, что множество В также
«имеет мощность а» или что оно «содержит а элементов», в том и только том случае,
если можно привести множества А и В во взаимно-однозначное соответствие. Заметим,
что в этом смысле все натуральные числа можно рассматривать как кардинальные числа,
и это гораздо ближе к интуитивному пониманию того, что есть натуральное число, нежели
«порядковое» определение (0 = {}, 1 — {0}, 2 = {0, {0}}, 3 = {0, {0}, {0, {0}}}, ...),
данное в §3.4! Фактически натуральные числа являются конечными кардинальными чис¬
лами (в том смысле, что бесконечные кардинальные числа представляют мощность таких
множеств, как N, которые содержат собственные подмножества той же мощности, что и они
сами).
Далее, можно установить соотношения между кардинальными числами. Мы будем го¬
ворить, что кардинальное число а меньше кардинального числа (3 или равно ему, и писать
а ^ /3
(или, что то же самое, (3 ^ о), если элементы множества А мощности а можно привести
во взаимно-однозначное соответствие с элементами некоторого подмножества (не обяза¬
тельно собственного) элементов множества В мощности (3. Ясно, что если а ^ /3 и /3 ^ 7,
то а ^ 7.*** Один из красивых результатов теории кардинальных чисел состоит в том,
что если
а < (3 и (3 ^ а,
то
а = /3;
Можете ли вы предложить явную процедуру такого рода, найдя некоторый систематический способ
упорядочения всех дробей? Здесь может оказаться полезным результат упражнения 16.8.
1
** Щ Покажите, что функция -((а + 6)2 + За + 6) явным образом устанавливает взаимно-однозначное соот¬
ветствие между натуральными числами и парами натуральных чисел (а, 6).
Проверьте это подробнее.
***

318
Глава It
это означает, что имеет место взаимно-однозначное соответствие между А и В.* Можно
задать вопрос, существуют ли пары кардинальных чисел а и /3, для которых не выполняется
ни одно из соотношений а < 0 и 0 < а. Такие кардинальные числа были бы несравнимыми
На самом деле, как следует из предположения, известного под названием аксиомы выборе
(упомянутой в § 1.3), несравнимые кардинальные числа не существуют.
Аксиома выбора гласит, что если мы имеем множество А, все члены которого представ¬
ляют собой непустые множества, то существует некоторое множество В, содержащее ровно
по одному элементу каждого из множеств, принадлежащих множеству А. Вначале может
показаться, что аксиома выбора утверждает нечто абсолютно очевидное! (См. рис. 16.4."*
Однако не вполне бесспорно, что аксиому выбора следует воспринимать как универсально
справедливую. Сам я занимаю в этом отношении осторожную позицию. Беспокойство вызы¬
вает тот факт, что эта аксиома утверждает лишь «существование» без какого-либо указания
на способ определения множества В. К тому же, она приводит к ряду тревожных следствий.
Одним из них является теорема Банаха - Тарского ^16*7^ один из вариантов которой утвержда¬
ет, что обычную единичную сферу в евклидовом 3-пространстве можно разделить на пять
кусков, из которых путем простых евклидовых движений (т.е. трансляций и поворотов*
можно построить две полные единичные сферы! Эти «куски» представляют собой, конеч¬
но, не твердые тела, а сложные наборы точек и определяются весьма неконструктивным
образом, так что утверждается лишь «существование» с использованием аксиомы выбора.
Рис. 16.4. Аксиома выбора гласит, что для любого множества А, все члены которого представляют
собой непустые множества, существует множество В, содержащее ровно по одному элементу каждого
из множеств, принадлежащих множеству А
Перечислим без доказательства несколько наиболее важных свойств кардинальных чи¬
сел. Прежде всего, символ < имеет обычный смысл (см. примечание 1 к главе 3) в приме¬
нении к натуральным числам {конечным кардинальным числам). Далее, любое натуральное
число не больше (^) любого бесконечного кардинального числа, и, конечно, оно строго
• * /
меньше (<) такого кардинального числа и не равно ему. Предположим теперь, что 0 ^ а.
где а бесконечно. Тогда (в резком противоречии с тем, к чему мы привыкли в отношении
конечных чисел) мощность объединения A U В равна просто большей из этих мощностей
(а именно а), а мощность произведения Ах В также равна а. (Мы уже встречались с при¬
мерами произведений в §§ 13.2, 15.2. Множество Ах В состоит из всех пар (а, 6), где а
берется из множества А, а Ъ — из множества В. В случае конечных множеств мощность их
произведения, рассматриваемого как множество, есть обычное арифметическое произведе¬
ние их мощностей, которое для конечных множеств, содержащих более одного члена, всегда
Докажите это. Набросок: имеются взаимно-однозначное отображение 6, переводящее А в некоторое
подмножество ЪА{= 6(A)) множества В, и взаимно-однозначное отображение а, переводящее В в некоторое
подмножество аВ множества А. Рассмотрите отображение А в В, которое использует 6, чтобы отобразить А — аВ
вЪА — ЪаВ, аЪА ~ аЬаВ в bob А — ЪаЪаВ и т. д., и использует а”1, чтобы отобразить аВ — аЪА в В — 6А, аЪаВ —
— аЬаЪА в ЬаВ — баб А и т. д. Решите, что делать с остальной частью множеств А и В.
А

16.4. Диагональная косая черта Кантора
319
больше мощности каждого из этих множеств в отдельности.) Нас, по-видимому, не заведет
слишком далеко, если мы захотим найти бесконечности, большие тех, с которыми мы уже
имели дело. Мы, кажется, слишком «привязались» к а.
В следующем разделе мы увидим, как можно «отвязаться» от этого. А пока мы увидим,
что сказанного выше по крайней мере достаточно для того, чтобы показать, что количество
рациональных чисел равно количеству натуральных чисел. Следуя Кантору, обозначим сим¬
волом Ыо («алеф-нуль») мощность множества натуральных чисел N, которая, как мы видели,
совпадает с мощностью множества целых чисел Z. В действительности бесконечное чис¬
ло Но является наименьшим из всех бесконечных кардинальных чисел. А как обстоит дело
с мощностью р множества рациональных чисел? Любое рациональное число можно предста¬
вить (причем многими способами) в виде а/Ъ, где а и Ъ — целые числа. Выбрав один из этих
способов (например, взяв наименьшие целые числа) для каждого из рациональных чисел, мы
получим взаимно-однозначное соответствие между множеством рациональных чисел и под¬
множеством множества N х N. Следовательно, мощность р не превышает мощности N х N.
Но из вышеизложенного (или непосредственно из упражнения 16.8) следует, что мощность
множества N х N равна мощности Но множества N. Таким образом, р ^ Но. Но целые числа
содержатся в множестве рациональных чисел, поэтому Но ^ р. Следовательно, р — Но-
16.4.	Диагональная косая черта Кантора
Теперь вернемся к раннему удивительному результату Кантора — к демонстрации того,
что действительно существуют бесконечности, строго большие мощности и что мощ¬
ность множества вещественных чисел R является такой бесконечностью. Я приведу здесь
этот результат как частный пример более общего канторовского результата
о< 2а,
где а < (3 означает а < (3 и а ф /3 (и, конечно, можно также записать а < (3 в виде (3 > а).
Замечательное доказательство этого результата Кантором (как и сам результат) представляет
одно из наиболее оригинальных и влиятельных достижений во всей математике. В то же
время оно достаточно просто для того, чтобы привести его здесь во всей полноте.
Сначала я должен объяснить обозначения. Если мы имеем два множества А и 5, то мно¬
жество ВА есть множество всех отображений А в В, Какое разумное объяснение имеет
такое обозначение? Представим себе, что множество А развернуто перед нами и каждый
элемент этого множества представлен в виде некоторой «точки». Чтобы изобразить элемент
множества ВА, поместим в каждую из этих точек один из элементов множества В. Это
есть отображение А в В, поскольку каждому элементу множества А сопоставляется эле¬
мент множества В (см. рис. 16.5). Причина «экспоненциальной записи» ВА состоит в том,
что, когда мы применяем эту процедуру к конечным множествам, например к множеству А
с а элементами и множеству В с b элементами, полное число способов сопоставить эле¬
мент множества В каждому элементу множества А действительно равно Ьа. (Имеется b
способов для первого члена множества А, b способов для второго члена, b способов для
третьего и так далее для всех членов множества А. Следовательно, полное число способов
равно b х Ъ х Ъ х ... х 6; число сомножителей Ъ в этом произведении равно а, так что оно
равно Ьа.) Кантор использовал для мощности множества ВА обозначение
Г,
где /3 и а — соответственно мощности множеств В и А.
Особое значение имеет случай (3 = 2. Можно взять в качестве множества В множество
с двумя элементами, обозначаемыми индексами «in» и «out». Элементы множества ВА по-

320
Глава :
В
X
i_f_
X
£
X
X
ВхА
А
Рис. 16.5. Для произвольных множеств Аи В множество всех отображений А в В обозначается как В*'
(см. также рис. 6.1). Каждому элементу множества Л сопоставляется один элемент множества Б
Это дает пересечение множеств ВхА, рассматриваемое как расслоение над А (как на рис. 15.6 j
за исключением того, что не вводится какого-либо понятия непрерывности
лучаются сопоставлением элемента «in» или «out» каждому элементу множества Л. Такое
сопоставление равнозначно просто выбору некоторого подмножества множества Л (подмно¬
жества элементов «in»). Таким образом, в данном случае ВА есть множество подмножеств
множества А (это множество часто обозначают как 2Л). Соответственно
I
2а есть полное число подмножеств любого множества, содержащего а элементов.
Теперь об удивительном доказательстве Кантора. Оно проводится в соответствии с клас¬
сической традицией древних греков «доказательства от противного» (§§2.6, 3.1). Прежде
всего попробуем предположить, что а — 2а, так что имеет место взаимно-однозначное
соответствие между некоторым множеством Л и множеством его подмножеств 2Л. При та¬
ком соответствии каждому элементу а множества А сопоставляется некоторое подмноже¬
ство S(a) множества Л. Можно ожидать, что хмножество S(a) иногда будет содержать в ка¬
честве своего члена сам элемент а, а иногда — нет. Рассмотрим набор всех элементов а, для
которых S(a) не содержит а. Этот набор будет некоторым подмножеством Q множества Л
(это подмножество может быть как пустым множеством, так и всем множеством Л). В пред¬
положении взаимно-однозначного соответствия мы должны иметь Q — S(q) для некоторого
элемента q в 5. Зададимся вопросом: содержится или нет q в Q? Сначала допустим, что
не содержится. Тогда элемент q должен принадлежать к набору элементов множества Л.
которые мы уже выделили как подмножество Q, так что элемент q в конечном счете должен
содержаться в Q — налицо противоречие. Это оставляет нам альтернативное допущение,
что q содержится в Q. Но q не может принадлежать к набору, который мы назвали Q, так
что q в конечном счете не принадлежит к Q — снова получается противоречие. Мы, следо¬
вательно, приходим к выводу, что предполагаемое нами взаимно-однозначное соответствие
между множествами Л и 2Л не может существовать.
Наконец, мы должны показать, что а ^ 2а, т. е, что имеется взаимно-однозначное
соответствие между множеством А и некоторым подмножеством множества 2Л. Это до¬
стигается просто путем использования взаимно-однозначного соответствия, при котором
каждый элемент а множества А сопоставляется подмножеству этого множества, содержа¬
щему элемент а и никаких других. Таким образом, мы показали, что а < 2а, но а -ф 2°.
следовательно, а < 2а, что и требовалось доказать.

16.4. Диагональная косая черта Кантора
321
Хотя это рассуждение может показаться слегка запутанным (запутавшийся читатель
может перечитать всё это снова), оно крайне «элементарно» в том смысле, что оно не апел¬
лирует к математическим идеям, требующим каких-либо специальных знаний. С этой точки
зрения, совершенно замечательно, что его применение имеет далеко идущие последствия.
Оно не только позволяет нам узнать, что вещественных чисел существенно больше, чем на¬
туральных чисел, но и показывает, что нет конца и края огромному множеству возможных
бесконечных чисел. Более того, это рассуждение в несколько измененной форме показывает,
что не существует способа вычисления, позволяющего решить, дойдет ли когда-нибудь всё
вычисление до конца (Тьюринг); следствием этого является знаменитая теорема о непол¬
ноте Гёделя, утверждающая, что не существует такого набора надежных математических
правил, который заключал бы в себе все процедуры установления математических истин.
В следующем разделе я попытаюсь дать почувствовать, как получаются такие результаты.
Чтобы закончить этот раздел, посмотрим, каким образом вышеприведенный резуль¬
тат действительно приводит к первому замечательному достижению Кантора, касающемуся
бесконечностей, а именно что вещественных чисел намного больше, чем натуральных, и это
несмотря на тот факт, что дробей имеется ровно столько же, сколько натуральных чисел.
(Это достижение означает, что действительно существует нетривиальная теория бесконеч¬
ности!) Такое следствие получается, если мы сможем показать, что мощность множества
вещественных чисел, обычно обозначаемая буквой С, равна 2Ы°:
Тогда, в соответствии с вышеприведенным рассуждением, С > Ко, что и требуется доказать.
Есть много способов показать, что С = 2К°. Чтобы показать, что 2К° < С (а это все, что
нам нужно для доказательства неравенства С > Ко), достаточно убедиться в существовании
взаимно-однозначного соответствия между множеством 2п и некоторым подмножеством
множества R. Каждый элемент множества 2N можно получить, сопоставив каждому на¬
туральному числу 0 или 1 («out» или «in»), т. е. такой элемент можно рассматривать как
бесконечную последовательность, например:
100110001011101...
(Этот конкретный элемент множества 2N сопоставляет 1 натуральному числу 0,0 — натураль¬
ному числу 1,0 — натуральному числу 2,1 — натуральному числу 3, 1 — натуральному числу
4 и т.д., так что наше подмножество имеет вид {0, 3, 4, 8, ...}.) Теперь мы можем попро¬
бовать прочитать всю эту последовательность цифр как двоичное представление некоторого
вещественного числа, у которого десятичная запятая находится далеко слева. К сожалению,
это работает не слишком хорошо из-за неопределенности некоторых таких представлений,
а именно тех, которые оканчиваются бесконечной последовательностью, состоящей только
f*'
из нулей или только из единиц . Эту неприятность можно обойти многими простыми спо¬
собами. Один из них состоит в том, чтобы вставить между двоичными цифрами, например,
цифру 3, получить
0,313030313130303031303131313031...
и прочитать это число как обычное десятичное разложение некоторого вещественного числа.
Таким образом, мы установили взаимно-однозначное соответствие между множеством 2м
и некоторым подмножеством множества R (а именно подмножеством, десятичное разло¬
жение которого имеет такую странную форму с чередующимися цифрами). Следователь¬
но, 2К° ^ С, и мы получаем результат Кантора С > что и требовалось.
Чтобы вывести равенство С = 2К°, мы должны суметь показать, что С ^ 2^°. Каждое
вещественное число, расположенное строго между 0 и 1, имеет двоичное представление
* Объясните это.

322
Глава ! ?
(подобное представленному выше), хотя иногда и избыточное; таким образом, это конкрет¬
ное множество, составленное из вещественных чисел, определенно имеет мощность ^ 2N:
Существует много простых функций, значения которых лежат в этом интервале на всем
множестве М.* Это приводит к неравенству С < 2Н° и, следовательно, к равенству С = 2R:.
которое требуется доказать.
Оригинальный вариант рассуждений Кантора несколько отличается от приведенного
здесь, хотя сущность та же самая. Он также является доказательством от противного, но бо¬
лее прямым. Рассматриваемое гипотетическое взаимно-однозначное соответствие между Г'
и вещественными числами, расположенными строго между 0 и 1, представлялось в виде вер¬
тикального списка всех вещественных чисел, записанных в виде десятичного разложения.
Противоречие с предположением полноты списка было получено путем «диагонального рас¬
суждения», посредством которого новое вещественное число, не представленное в списке,
получается путем движения вниз по главной диагонали таблицы, начиная с верхнего левого
угла, и вычитания числа на п-м месте из n-го вещественного числа в списке. (Существует
много популярных вариантов этого, см., например, вариант, изложенный в третьей главе
моей книги «Новый ум короля». ) Этот общий тип рассуждения (включая тот, который
был использован в начале этого раздела, чтобы показать, что а < 2а) иногда называют
«диагональной косой чертой Кантора».
16.5.	Загадки оснований математики
Как уже отмечалось, мощность континуума (т. е. множества Ж) 2Ы° часто обозначается
буквой С. Кантор предпочитал обозначать ее символом Hi, понимая под ним «следующее
наименьшее кардинальное число» после Но- Он пытался, но не смог доказать, что 2К° = Нь
Это утверждение, известное под названием континуум-гипотезы, было знаменитой нере¬
шенной проблемой в течение многих лет после того, как эта гипотеза была высказана
Кантором. В некотором «абсолютном» смысле она не решена до сих пор. Курт Гёдель
и Пол Коэн сумели показать, что континуум-гипотеза (а также аксиома выбора) неразре¬
шима средствами стандартной теории множеств. Однако вследствие теоремы о неполноте
Гёделя, к изложению которой я вскоре перейду, и связанных с нею предложений это само
по себе не может решить вопрос об истинности континуум-гипотезы. Возможно, что ме¬
тоды доказательства, более мощные, чем методы стандартной теории множеств, могли бы
решить, истинна или нет континуум-гипотеза; с другой стороны, может оказаться, что ее
истинность или ложность зависит от точки зрения, которой придерживается тот или иной
математик^16*8!. Такая возможность упоминалась в § 1.3, но в связи в аксиомой выбора, а не
с континуум-гипотезой.
Как мы видели, неравенство а < 2а означает, что не может быть какой-то наибольшей
бесконечности, поскольку если предположить, что Q есть наибольшее кардинальное число,
то кардинальное число 2Q оказывается еще больше. Этот факт (и рассуждение Кантора,
посредством которого он был установлен) имеет большое значение для оснований матема¬
тики. В частности, философ Бертран Рассел, который первоначально считал, что должно
существовать наибольшее кардинальное число (а именно кардинальное число класса всех
классов), с подозрением отнесся к выводу Кантора, однако после детального его изучения
в 1902 году изменил свое мнение. В дальнейшем он применил рассуждение Кантора к «мно¬
жеству всех множеств», что сразу привело его к известному теперь «парадоксу Рассела».
Этот парадокс состоит в следующем. Рассмотрим множество 1Z, состоящее из «всех
множеств, которые не являются членами самого себя». (Пока не важно, готовы ли вы пове-
Назовите одну из них. (.Подсказка: см., например, рис. 9.8.)
Объясните, почему это рассуждение, по существу такое же, как и приведенное мною для случая а = Ко-
и покажите, что а < 2а.

16.5. Загадки оснований математики
323
т
рить, что множество может быть членом самого себя. Если никакое множество не является
членом самого себя, то 1Z есть множество всех множеств.) Зададимся вопросом: что пред¬
ставляет собой само множество 1Z1 Является ли 71 членом самого себя? Предположим, что
это так. Тогда, поскольку в этом случае оно принадлежит к множеству 7Z всех множеств,
которые не являются членами самого себя, оно в конечном счете не принадлежит самому
себе — налицо противоречие! Альтернативное предположение состоит в том, что оно не
принадлежит самому себе. Но тогда оно должно быть членом целого семейства множеств,
которые не являются членами самого себя, а именно множеством 71. Таким образом, 1Z
принадлежит к 1Z, что противоречит сделанному предположению, согласно которому оно
не принадлежит самому себе. Здесь явное противоречие!
Можно заметить, что все это получается из неравенства Кантора а < 2а, если при¬
менить его к случаю, когда в качестве а берется «множество всех множеств»*. Именно
так Рассел пришел к своему парадоксуНа что действительно указывает это рассу¬
ждение, так это на то, что не существует такого объекта, как «множество всех множеств».
(Фактически это понимал уже Кантор, и о «парадоксе Рассела» он узнал на несколько лет
раньше самого Рассела^1610^.) Может показаться странным, что такое простое понятие, как
«множество всех множеств», оказывается запрещенным. Казалось бы, любое предположе¬
ние относительно какого-то множества должно быть вполне приемлемым, если существует
четкое правило, сообщающее нам, когда нечто принадлежит к этому множеству и когда
оно не принадлежит к нему. В данном случае представляется, что такое правило опреде¬
ленно существует, и согласно ему в это множество входит каждое множество! Ловушка,
по-видимому, состоит в том, что мы приписываем одинаковый статус как этому выдающе¬
муся собранию, так и каждому из его членов, называя то и другое просто «множеством».
Все рассуждение зависит от того, имеется ли у нас ясная идея относительно того, что есть
множество. И коль скоро такая идея у нас есть, возникает вопрос: можно ли считать множе¬
ством собрание всех таких объектов? Кантор и Рассел говорят нам, что ответ на этот вопрос
должен быть отрицательным!
Способ, которым математики вводят термины в этой явно парадоксальной ситуации,
состоит в том, чтобы различать «множества» и «классы». (Можно представлять себе классы
как некие большие буйные группы, не подлежащие объединению в клубы, а множества — как
группы, достаточно респектабельные для такого объединения.) Грубо говоря, любое собра¬
ние множеств, которое можно рассматривать как целое, должно именоваться классом. Неко¬
торые классы достаточно респектабельны для того, чтобы считаться множествами, другие
оказываются «слишком большими» или «слишком неорганизованными» для этого. С другой
стороны, нам не обязательно позволять классам объединяться вместе, образуя объекты боль¬
шего размера. Таким образом, не допускается «множество всех множеств» (как и «класс всех
классов»), но «класс всех множеств» следует считать законным объединением. Кантор обо¬
значал этот «класс» буквой i?, придавая ему почти божественное значение. Не позволяется
формировать классы, большие чем Q. Неприятность с 2^ состоит в том, что это собра¬
ние получается путем объединения всех различных «подклассов» класса J7, большинство
которых не являются множествами, поэтому такое объединение не допускается.
Что-то во всем этом представляется не вполне удовлетворительным. Должен признать¬
ся, что и сам я этим решительно не удовлетворен. Эта процедура была бы разумной, если
оы существовал четкий критерии, позволяющий квалифицировать класс как множество.
Однако при определении «различия» между ними часто получается замкнутый круг. Класс
считается множеством тогда и только тогда, когда он сам может быть членом некоторо¬
го другого класса, — это представляется мне лишь иллюзиеи решения вопроса,
беспокойство то, что нет явного указания, где провести границу между этими понятиями.
Как только такая граница проведена, тут же начинает казаться, что она налагает слишком
Покажите, что это так.

324
Глава
сильные ограничения. Кажется, что нет оснований исключать некоторые достаточно боль¬
шие (или достаточно неорганизованные) классы из «клуба» множеств. Конечно, следует
избегать очевидных противоречий. Оказывается, однако, что чем либеральнее правила член¬
ства в «клубе» множеств, тем мощнее те методы математического доказательства, которым*
устанавливается понятие множества. Но стоит открыть дверь в этот «клуб» слишком ши¬
роко, как происходит катастрофа — возникает ПРОТИВОРЕЧИЕ, и все здание рушится
Проведение подобной границы — одна из наиболее тонких и сложных процедур во всей
математике'I16*11!,
Многие математики предпочли повернуть от такого крайнего либерализма к жесткс
консервативному подходу «конструктивистов», согласно которому множество получает пра¬
во на существование, только если существует такое прямое построение, которое позволяет
установить, когда элемент принадлежит к данному множеству, а когда не принадлежит. Без¬
условно, те «множества», которые определяются просто путем применения аксиомы выбора,
при столь строгих правилах не будут удовлетворять критерию членства! Оказывается, одна¬
ко, что и эти крайние консерваторы застрахованы от «диагональной косой черты Кантора*
не в большей степени, чем крайние либералы. В следующем разделе мы увидим, в чем
кроется источник опасности.
••
16.6.	Машины Тьюринга и теорема Гёделя
Прежде всего необходимо иметь представление, что значит «построить» что-либо в ма¬
тематике. Для нашей цели наиболее простого рассмотрения лучше всего сосредоточить вни¬
мание на подмножествах множества натуральных чисел N. Можно задать вопрос: какие из
таких подмножеств определяются «конструктивно»? К счастью, в нашем распоряжении име¬
ется удивительное понятие, введенное различными логиками ^16 Л21 в первой трети XX века
и поставленное на твердую почву Аланом Тьюрингом в 1936 году. Это понятие вычислимо¬
сти, и, поскольку электронные компьютеры стали для нас теперь вполне привычными, будет,
по-видимому, достаточно ссылаться на действие этих физических устройств, а не на соответ¬
ствующие идеи, выраженные в виде строгих математических формулировок. Грубо говоря.
вычисление (или алгоритм) — это то, что выполняет некоторый идеальный компьютер; сло¬
во «идеальный» означает, что компьютер может работать сколь угодно долго «без износа»,
никогда не делает ошибок и обладает неограниченным запасом памяти. В математическом
отношении такое устройство представляет собой так называемую машину Тьюринга^16,13'1.
Каждая отдельная машина Тьюринга Т соответствует некоторому определенному вы¬
числению, проводимому над натуральными числами. Действие Т на некоторое натуральное
число п обозначается Т(п); это действие обычно дает некоторое (другое) натуральное чис¬
ло та:
Т(п) ~ га.
Машина Тьюринга может иметь свойство «застревать» (или «попадать в петлю»), так что
проводимое вычисление никогда не заканчивается. Мы будем называть машину ошибочной.
если она не может закончить вычисление над некоторым натуральным числом п. Если же
она всегда заканчивает вычисление над любым числом, будем называть ее эффективной.
Примером ошибочной машины Тьюринга Т, не заканчивающей вычисление, может слу¬
жить машина, которая по заданному числу п пытается найти наименьшее натуральное число,
которое не является суммой п квадратов чисел (включая О2 = 0). Мы получаем Т{0) =
= 1, Т(1) = 2, Т(2) = 3, Т(3) = 7 (смысл этих уравнений можно пояснить на примере
последнего из них: «7 есть наименьшее число, которое не является суммой 3 квадратов») .
Дайте приблизительное описание работы нашего алгоритма и объясните, как получаются эти частные
значения.

16.6. Машины Тьюринга и теорема Гёделя
325
Если же применить операцию Т к 4, то машина будет совершать вычисление вечно, пытаясь
найти число, которое не является суммой четырех квадратов. Причиной такого сбоя машины
является знаменитая теорема, принадлежащая великому франко-итальянскому математику
XVIII века Жозефу Луи Лагранжу, которому удалось доказать, что каждое натуральное чис¬
ло можно представить в виде суммы четырех квадратов. (С Лагранжем мы еще встретимся
%
в различных контекстах, в частности, в главах 20 и 26.)
Каждая отдельная машина Тьюринга (как ошибочная, так и эффективная) имеет неко¬
торую «таблицу инструкций», определяющую тот частный алгоритм, который реализует
эта машина. Такая таблица может быть полностью задана некоторым «кодом», который
можно записать в виде некоторой последовательности цифр. Эту последовательность мож¬
но интерпретировать как некоторое натуральное число t. Это число кодирует «программу»,
позволяющую машине реализовать данный алгоритм. Обозначим машину Тьюринга, которая
кодируется таким способом с помощью натурального числа £, символом Tt. Код, возможно,
будет работать не при всех натуральных числах t; если по какой-то причине это так, то мож¬
но считать машину Tt «ошибочной» в дополнение к случаям, подобным рассмотренному,
когда машина не может остановиться при действии на некоторое число п. Эффективными
машинами Тьюринга Tt будут лишь те, которые при действии на любое число п дают ответ
за конечное время.
Одно из фундаментальных достижений Тьюринга состоит в доказательстве возмож¬
ности создания такой одной машины Тьюринга, называемой универсальной машиной Тью¬
ринга U, которая может имитировать любую машину Тьюринга. Все, что требуется от ма¬
шины U, — это подействовать сначала на натуральное число t, задав некоторую машину
Тьюринга Tt, которую предстоит имитировать, после чего действовать на число п, переходя
таким образом к вычислению Tt(n). (Современные многоцелевые компьютеры являются,
по существу, универсальными машинами Тьюринга.) Я буду записывать такое комбиниро¬
ванное действие в виде U(t, п), так что
t/(t, п) = Tt(n).
Следует иметь в виду, что определенные таким образом машины Тьюринга предполагаются
действующими на одно-единственное натуральное число, а не на пару (£, п). Нетрудно,
однако, закодировать пару натуральных чисел одним натуральным числом, как мы видели
раньше (например, в упражнении 16.8). Машина U будет сама определяться некоторым
натуральным числом и, так что мы имеем
ь
U = Ти.
Как узнать, является машина Тьюринга эффективной или ошибочной? Можно ли най¬
ти какой-нибудь алгоритм, позволяющий ответить на этот вопрос? Важным достижением
Тьюринга было доказательство того, что ответ на этот вопрос должен быть отрицательным!
Доказательство основано на «диагональной косой черте Кантора». Рассмотрим, как и преж¬
де, множество N, но, вместо того чтобы рассматривать все подмножества этого множества,
рассмотрим лишь те из них, для которых можно путем вычислений решить, являются ли они
элементами этого множества. (Таковыми не могут быть все подмножества множества N,
поскольку число различных вычислений равно всего лишь Ко, тогда как число всех подмно¬
жеств равно С.) Такие множества, определяемые путем вычислений, называются рекурсив¬
ными. Фактически любое рекурсивное подмножество множества N определяется выходом
некоторой эффективной машины Тьюринга Т частного вида, которая на выходе дает лишь
О или 1. Если Т(п) = 1, то число п является членом рекурсивного множества, определя¬
емого машиной Т («in»), если же Т(п) = 0, то п не является его членом («out»). Теперь
применим рассуждение Кантора, проведя его как и раньше, но в отношении лишь рекурсив¬
ных подмножеств множества N. Из этого рассуждения немедленно следует, что множество

326
Глава к
натуральных чисел t, для которого машина Tt эффективна, не может быть рекурсивным
Не существует алгоритма, применимого к любой заданной машине Тьюринга Т, который
позволил бы узнать, ошибочна машина Т или нет!
Полезно познакомиться с этим рассуждением поближе. Что действительно показывают
рассуждения в духе Тьюринга и Кантора, так это то, что множество чисел £, для которых
машина Tt эффективна, не является даже рекурсивно перечислимым. Что такое рекурсив¬
но перечислимое подмножество множества N? Это есть множество натуральных чисел,
для которого существует эффективная машина Тьюринга Т, которая, будучи примененной
к последовательности 0, 1, 2, 3, 4, ..., в конце концов генерирует (и, возможно, более од¬
ного раза) каждый член этого множества. (То есть ш является членом этого множества
в том и только том случае, если га = Т(п) для некоторого натурального числа п.) Под¬
множество 5 множества И рекурсивно в том и только том случае, если оно рекурсивно
перечислимо и его дополнение N — S также рекурсивно перечислимо*. Предполагаемое
взаимно-однозначное соответствие, при помощи которого рассуждение Тьюринга - Канто¬
ра приводит к противоречию, представляет собой рекурсивное перечисление эффективных
машин Тьюринга. Небольшое обсуждение показывает, что мы узнали лишь то, что не суще¬
ствует какого-нибудь общего алгоритма для решения вопроса о том, когда действие машины
Тьюринга Tt будет продолжаться безостановочно.
В конечном счете всё это означает, что, несмотря на надежду занять позицию «крайнего
О
консерватизма», при которой единственно приемлемыми множествами являются рекурсив¬
ные множества, принадлежность к которым определяется четкими правилами вычисления,
такая точка зрения немедленно приводит нас к необходимости рассматривать нерекурсив¬
ные множества. Эта точка зрения сталкивается даже с фундаментальной трудностью в виде
отсутствия вычислительной процедуры для решения в общем виде, являются ли два ре¬
курсивных множества одним и тем же или разными множествами, если они определяются
двумя различными эффективными машинами Тьюринга Ti и Т3! * * Кроме того, проблема
такого рода возникает снова и снова на различных уровнях, когда мы пытаемся ограничить
наше понятие «множества» слишком консервативной точкой зрения. Мы всегда вынуждены
рассматривать классы, которые не принадлежат к нашему ранее разрешенному семейству
множеств.
Эти результаты тесно связаны со знаменитой теоремой Курта Гёделя. Гёдель занимался
вопросом о методах доказательства, доступных математикам. На рубеже XX века и много лет
спустя математики пытались устранить парадоксы (вроде парадокса Рассела), которые воз¬
никают при либеральном подходе к теории множеств, путем введения идеи математической
формальной системы, согласно которой в основу должен быть положен набор абсолютно
четких правил рассуждения, признаваемых в качестве математического доказательства. Гё¬
дель показал, что эта программа неосуществима. Точнее, он продемонстрировал, что если
мы готовы считать правила некоторой формальной системы F заслуживающими доверия
и дающими нам математически единственно верные выводы, то мы должны также принять
в качестве истинного некоторое четкое математическое утверждение G(F), не доказуемое
методами одной лишь системы F. Тем самым Гёдель показал, как перейти границы любой
системы F, которой мы готовы доверять.
Существует общее заблуждение, согласно которому теорема Гёделя якобы утверждает
существование «недоказуемых математических утверждений» и областей «платоновского
мира» математических истин (см. § 1.4), принципиально не доступных для нас. Это очень
далеко оттого вывода, который мы должны сделать из теоремы Гёделя. В действительности
  Покажите это.
**Ш§ Понятно ли, почему это так? (Подсказка: действие произвольной машины Тьюринга Т на п можно
рассмотреть на примере эффективной машины Тьюринга Q, обладающей тем свойством, что Q{r) = 0, если
машина Т, действуя на п, не останавливается после г шагов вычисления, и Q(r) = 1 в противном случае. Чтобы
получить Ts(n), возьмите сумму Q(n) и Ti{n) по модулю 2.)

16.7. Размеры бесконечности в физике
327
Гёдель утверждает, что какие бы правила доказательства мы ни сформулировали заранее,
предположив их заслуживающими доверия (т. е. не способными привести нас к ложному
заключению) и не слишком ограничительными, мы в результате получим новый способ до¬
ступа к некоторым математическим истинам, которые невозможно вывести в рамках данных
правил.
Результат Гёделя непосредственно следует из результата Тьюринга (хотя исторически
порядок их получения был обратным). Как это получается? Суть рассуждений о формальной
системе состоит в том, что не требуется дополнительного математического обоснования для
того, чтобы решить, правильно ли применяются правила системы F. Мы обнаруживаем,
что для любой системы F множество математических теорем, которые можно доказать,
используя ее правила, обязательно будет рекурсивно перечислимым.
Теперь можно сформулировать некоторые известные математические утверждения в ви¬
де «действие такой-то машины Тьюринга не прекращается». Мы уже встречались с одним
таким примером, а именно теоремой Лагранжа, согласно которой каждое натуральное число
можно представить в виде суммы четырех квадратов. Другим еще более известным при¬
мером может служить «последняя теорема Ферма», доказанная в конце XX века Эндрю
Уайлзом (§ 1.3)^16л41. Еще одной (пока не решенной) проблемой является известная «ги¬
потеза Гольдбаха», согласно которой любое четное число, большее 2, можно представить
в виде суммы двух простых чисел. Утверждения такого рода специалисты по математиче¬
ской логике называют высказываниями. Из вышеприведенного рассуждения Тьюринга
немедленно следует, что семейство истинных Щ-высказываний образует не-рекурсивно пе¬
речислимое множество (т. е. оно не является рекурсивно перечислимым). Таким образом,
существуют истинные Щ -высказывания, которые нельзя получить из правил системы F
(при этом система F предполагается заслуживающей доверия). Такова основная формули¬
ровка теоремы Гёделя. При несколько более детальном рассмотрении можно усовершен¬
ствовать данное рассуждение, чтобы получить вариант, приведенный выше, и некоторое Пх-
высказывание G(jF), которое, при условии, что мы считаем систему F дающей только ис¬
тинные Пх-высказывания, должно избежать сетей, расставленных системой F, несмотря на
тот замечательный факт, что мы должны считать G(F) также истинным Пх -высказываниемГ
16.7.	Размеры бесконечности в физике
В заключение посмотрим, как соотносятся понятия бесконечности и конструктивности
с математикой, изложенной в предыдущих главах, и с нашим современным пониманием
физики. Ввиду тесной связи между математикой и физикой примечательно, что такие важ¬
ные разделы математики, как теория трансфинитных множеств и теория вычислимости,
пока оказывают весьма ограниченное влияние на наше описание физического мира. По мо¬
ему мнению, понятие вычислимости в конце концов окажется имеющим глубокую связь
с будущей физической теорией^16,151, однако пока эти идеи очень слабо используются в ма¬
тематической физике^16,16!.
Что касается размера бесконечности, имеющего определенное значение, то интерес¬
но, что почти никакая физическая теория как будто не нуждается в выходе за преде¬
лы С(= 2^°) — мощности системы вещественных чисел М. Комплексное поле С имеет ту же
мощность, что и R (а именно С), поскольку С есть просто R х R (множество пар веществен¬
ных чисел) с определенными правилами сложения и умножения. Аналогично векторные
пространства и рассмотренные выше многообразия строятся из семейств точек, которым
приписываются координаты из множеств 1хМх ... хМ (или С х С х ... х С) или из ко¬
нечного (либо бесконечного, но счетного, мощности No) множества таких координатных
лоскутов, опять-таки имеют мощность С.
*3St Попробуйте установить этот факт.

328
Глава 16
Что можно сказать о семействах функций на таких пространствах? Если мы рассмот¬
рим, например, семейство всех вещественных функций на некотором пространстве с С точ-
г
ками, то после некоторых размышлений обнаружим, что это семейство содержит С членов
(оно отображает пространство с С элементами на пространство с С элементами). Это число
определенно больше, чем С. Фактически Сс = 2е. (Это следует из того факта, что каждый
элемент множества Мм можно интерпретировать как некоторый элемент множества 2ШхШ.
а именно как сечение (обычно далеко не непрерывное) расслоения R х R, а мощность множе¬
ства IxR равна С.) Однако число непрерывных вещественных (или комплексных) функций
(или тензорных полей, или связностей) на многообразии равно всего лишь С, поскольку
непрерывная функция полностью определена, коль скоро известны ее значения на множе¬
стве точек с рациональными координатами. Число таких значений равно Сн°, так как число
точек с рациональными координатами равно No. Но Сн° — (2К°)К° = 2к°хН° = 2^° = С.*
В §§6.4, 6.6 мы рассмотрели некоторые обобщения непрерывных функций и пришли к та¬
кому значительному обобщению, как гиперфункции (§ 9.7). Однако число их по-прежнему
не превышает С, поскольку они определяются парами голоморфных функций, а число таких
функций равно С.
В § 22.3 мы увидим, что квантовая теория требует использования определенных про¬
странств, известных под названием гильбертовых пространств, которые могут иметь бес¬
конечно много измерений. Однако, хотя эти бесконечномерные пространства значительно
отличаются от пространств конечной размерности, число непрерывных функций на них не
больше, чем в конечномерном случае, и полное их число по-прежнему равно С. Лучший
способ пойти дальше состоит в использовании формулировки квантовой теории в пред¬
ставлении интегралов по траекториям (такая формулировка рассматривается в § 26.6), где
рассматривается пространство диковато выглядящих кривых (или соответственно конфи¬
гураций физических полей) в пространстве-времени. Однако для полного числа их мы по-
прежнему получим значение С, поскольку, несмотря на дикий вид, эти структуры сохраняют
достаточную память о своей непрерывности.
Понятие мощности представляется недостаточно четким для того, чтобы дать ясное
представление о размере пространств, которые встречаются в физике. Почти все такие про¬
странства содержат всего С точек. Тем не менее «размеры» этих пространств значительно
различаются, если под «размером» мы в первую очередь понимаем размерность векторного
пространства или рассматриваемого многообразия М. Размерность многообразия М может
быть натуральным числом (например, 4 в случае обычного пространства-времени или 6 -1019
в случае фазового пространства, рассмотренного в § 12.1) или может быть бесконечным, как
большинство гильбертовых пространств состояний, которые возникают в квантовой механи¬
ке. В математическом отношении простейшим бесконечномерным гильбертовым простран¬
ством является пространство последовательностей комплексных чисел (zi, z<i, 23, ...), для
которых сходится бесконечная сумма \zi\2 4- \z212 4- |^з|2 + • • • В случае бесконечномерно¬
го гильбертова пространства уместнее всего считать, что его размерность равна No- (Здесь
есть разные тонкости, но о них пока лучше не упоминать.) Относительно вещественного п-
мерного пространства будем говорить, что оно содержит ооп точек (это означает, что этот
континуум точек образует n-мерную решетку). В случае бесконечномерного пространства
мы припишем ему оо°° точек.
Нас интересуют также пространства разного рода полей, определенных на М. Обычно
они предполагаются гладкими, но иногда имеют более общий вид (примером могут слу¬
жить распределения), попадая в область действия теории гиперфункций (см. §9.7). Они
могут описываться дифференциальными уравнениями в частных производных, что ограни¬
чивает их свободу. Если бы такого ограничения не было, их следовало бы рассматривать
Объясните, почему (Ав)с можно отождествить с АВхС для множеств А, В, С.

16.7. Размеры бесконечности в физике
329
как «функции от п переменных» (в случае стандартного пространства-времени п — 4).
В каждой точке поле может иметь к независимых компонент. Тогда можно сказать, что
поле имеет ооко°п степеней свободы. Обоснование такой записи!1617! состоит в том, что
поле можно рассматривать (приближенно и локально) как отображение пространства с осп
точками на пространство с оск точками и воспользоваться (формальным) соотношением
(oofc)°°" = oofcoc”.
Если на поле наложено ограничение в виде дифференциальных уравнений в частных
производных, то оно может полностью определяться заданными начальными условиями (см.,
в частности, § 27.1), то есть некоторыми дополнительными значениями поля, определенны¬
ми на некотором пространстве S меньшей размерности, имеющем, например, q измерений.
Если эти значения можно выбрать свободно (это означает отсутствие ограничений, налага¬
емых на вид дифференциальных или алгебраических уравнений, которым должны удовле¬
творять эти значения на S) и если эти значения в каждой точке пространства S имеют г
независимых компонент, то можно сказать, что поле имеет ooTO°q степеней свободы. Во
многих случаях найти г и q бывает нелегко, но важно то, что они являются инвариантными
величинами, не зависящими от того, как можно выразить поле через другие эквивалент¬
ные величины!16Л81 Этот факт будет в дальнейшем иметь для нас существенное значение
(см. §§23.2, 31.10-31.12, 31.15-31.17).
Примечания
§16.2.
16.1. См. [399], стр. 269-271; [385], стр. 098. Магические диски эквивалентны так называемым
совершенным разностным множествам.
16.2. По-видимому, не известно, существуют ли магические диски (не связанные с простран¬
ством P2(Fg)), для которых не выполняется теорема Дезарга (или, что эквивалентно, теорема
Паппа), и существуют ли n-точечные проективные плоскости (на которых эти теоремы не
обязательно нарушаются) с п ф q2 + q + 1, где q — степень простого числа.
16.3. Хотя время от времени возникает обсуждение физической роли октонионов (см., напри¬
мер, [328, 212, 512, 221]), построение общей «октонионной квантовой механики» наталкива¬
ется на фундаментальные трудности [5]. Положение с «кватернионной квантовой механикой»
несколько лучше. Другой системой чисел, претендующей на важную роль в физике, являются
«р-адические числа». Они образуют систему чисел, к которым применимы правила анализа
и которые могут быть представлены подобно десятичному разложению обычных веществен¬
ных чисел с той разницей, что цифрами служат 0, 1, 2, 3, ..., р — 1 (где р — выбранное
простое число) и что они могут быть бесконечными противоположным образом по сравнению
с обычными десятичными дробями (и не нуждаются в знаке «минус»). Например,
 24033200411.3104
представляет частный случай 5-адического числа. Правила сложения и умножения таких чи¬
сел совпадают с соответствующими правилами в «обычной» р-ичной арифметике (в которой
символ 10 означает простое число р и т.д.). См. [508, 312, 104, 806, 642].
U 6.3.
\-т
16.4. Современная математическая терминология называет это изоморфизмом множеств. Имеются
и другие слова, такие как «эндоморфизм», «эпиморфизм», «мономорфизм» (или просто «мор¬
физм»), которыми пользуются математики в общем контексте для обозначения отображений
одного множества (или структуры) на другое. В этой книге я предпочитаю избегать термино¬
логии такого рода, поскольку она потребовала бы для привыкания к ней больших усилий, чем
следовало бы.

330
Глава 16
16.5. О некоторых еще более ранних размышлениях на эту тему см. [532], гл. 3.
16.6. Напомню (см. примечание 15.5), что я готов принять упреки, связанные с использованием
обозначения N — 0 для множества натуральных чисел, отличных от нуля. Здесь заключена
ирония: если принять, казалось бы, «более правильное» обозначение N — {0}, принимая од¬
новременно обозначение {0} — 1 в § 3.4, мы получим для рассматриваемого множества еще
более неприемлемое обозначение N — 1!
16.7. См. [808] и популярный обзор [676].
§16.5.
16.8. Подобные замечания относятся и к обобщенной континуум-гипотезе Кантора 2На — Ка_:
(где а теперь означает «порядковое число», определения которого я здесь не обсуждал), а также
к аксиоме выбора.
%
16.9. См. [677], стр. 362, второе подстрочное примечание (в издании 1937 года).
16.10. См. [800], стр. 114.
16.11. Современный подход к этим вопросам изложен в [853]. Более общими учебниками по основа¬
ниям математики являются [1] и [833].
§15.6.
16.12. Предшественниками Тьюринга были в основном Алонсо Чёрч, Хаскел Кэрри, Стефан Клини.
Курт Гёдель и Эмиль Пост; см. [276].
16.13. Подробное описание машины Тьюринга см., например, в [610], гл. 2 и [175] или, в оригинальном
изложении, в [794].
16.14. См. [726, 834].
§16.7.
16.15. См. [610, 613, 615, 616].
16.16. См. [457] и [288], §34.7.
16.17. Этим полезным обозначением я обязан Джону Арчибальду Уилеру (см. [826], стр. 67).
16.18. См. [125], особенно §§68, 69, стр.75, 76 (в оригинальном издании). Требуется определенное
внимание, чтобы быть уверенным в правильном вычислении величины г в выражении оо
Две системы могут быть эквивалентными, но иметь различные значения г и на первый взгляд
казаться различными. Однако при определении значения q неопределенности быть не может.
Строгая современная трактовка этих вопросов делает их более ясными, она дается в терминах
теории струйных расслоений (см. [110]). Можно упомянуть, что имеется некоторое усовершен-
2 1
ствование обозначения Уилера (см. [623]), например, символом оо200 +3о° +5 обозначается
«поле, зависящее от двух функций двух переменных, трех функций одной переменной и пяти
( ос )
постоянных величин». Таким образом, мы приходим к рассмотрению выражений вида оор ,
где р означает многочлен с неотрицательными целочисленными коэффициентами.
гоод

Глава 17
•
Пространство-время
17.1.	Пространство-время физики Аристотеля
Начиная с этого места книги, наше внимание с преимущественно математических во¬
просов, занимавших нас в предыдущих главах, переключается на картины физического
мира, к которым приводят теория и наблюдения. Для начала постараемся понять ту арену,
на которой разворачиваются все явления физической Вселенной, — пространство-время.
Мы обнаружим, что это понятие играет важнейшую роль в оставшейся части этой книги!
Прежде всего мы должны задать вопрос: почему «пространство-время»? Почему непра¬
вильно рассматривать пространство и время по отдельности, не пытаясь объединить эти два
вроде бы очень разные понятия в одно целое? Несмотря на общее восприятие этой темы
и на совершенно великолепное развитие этой идеи Эйнштейном в рамках его общей теории
относительности, пространство-время не только не было оригинальной идеей Эйнштейна,
но и, как оказывается, эта идея не привела его в восторг, когда он впервые услыхал о ней.
Более того, если без предубеждения оглянуться на более ранние релятивистские воззрения
Галилея и Ньютона, мы обнаружим, что они также могли в принципе принести большую
пользу в понимании пространства-времени.
Чтобы понять это, вернемся далеко назад и попробуем увидеть, какая структура про¬
странства-времени была бы подходящей для динамики Аристотеля и его современников.
В физике Аристотеля существует понятие евклидова 3-пространства Е3, описывающего
физическое пространство, и точки этого пространства сохраняют свою идентичность от од¬
ного момента времени к другому. Это обусловлено тем, что в схеме Аристотеля состояние
покоя динамически предпочтительнее всех других состояний движения. Мы занимаем по¬
зицию, согласно которой некоторая точка пространства, определенная в данный момент
времени, является той же самой точкой пространства в более поздний момент време¬
ни, если частица, помещенная в эту точку, остается в покое между этими моментами.
Наша картина реальности подобна экрану в кинотеатре, где данная точка на экране со¬
храняет свою идентичность независимо от того, какое движение проектируется на экран
(см. рис. 17.1).
Время также представляется как евклидово пространство, но довольно тривиальное,
а именно как одномерное пространство Е1. Таким образом, мы и время рассматриваем как
физическое пространство, как некоторую «евклидову геометрию», а не как копию веще¬
ственной оси М. Причина состоит в том, что R содержит выделенный элемент 0, который
должен представлять «нуль» отсчета времени, тогда как с точки зрения нашей «аристоте¬
левой» динамики никакого выделенного начала отсчета быть не должно. (Здесь я излагаю
идеализированный взгляд на то, что можно было бы назвать «динамикой Аристотеля» или
«физикой Аристотеля», и у меня нет уверенности в том, что мог думать на этот счет ре¬
альный Аристотель !)^17л1 Если бы существовало выделенное «начало времени», то зако¬
ны динамики могли бы изменяться с течением времени, отсчитываемого от этого начала.
При отсутствии выделенного начала отсчета законы должны оставаться неизменными в те¬
чение всего времени, поскольку нет такого временного параметра, от которого могли бы
зависеть эти законы.

332
Глава 1
Рис. 17.1. Подобно ли физическое движение изображаемому на экране кинотеатра? Выбранная точка
на экране (отмеченная крестиком) сохраняет свою идентичность независимо от того, какое движение
проектируется на экран
Аналогично я принимаю точку зрения, согласно которой не должно быть выделенного
пространственного начала координат и пространство неограниченно продолжается во всех
направлениях при полной однородности динамических законов (опять-таки безотносительно
к тому, что думал на этот счет реальный Аристотель!). В евклидовой геометрии, одномерной
или трехмерной, существует понятие расстояния. В случае трехмерного пространства это
обычное евклидово расстояние (измеряемое, например, в метрах или футах), в одномерном
случае таким расстоянием является обычный временной интервал (измеряемый, например,
в секундах).
В физике Аристотеля (а также в более поздних динамических схемах Галилея и Нью¬
тона) существует абсолютное понятие одновременности. Поэтому в таких динамических
схемах имеет абсолютный смысл утверждение, что время здесь, в этот самый момент,
когда я пишу эти строки в моем кабинете дома в Оксфорде, — это «то же самое время», что
и время некоторого события, происходящего в туманности Андромеды (например, взрыва
некоей сверхновой звезды). Возвращаясь к нашей аналогии с экраном кинематографа, мож¬
но задать вопрос: одновременно ли происходят события на двух картинах, проектируемых
на два далеко отстоящие друг от друга куска экрана? Здесь ответ очевиден. События следует
считать одновременными в том и только том случае, если они происходят на одном и том же
куске экрана. Таким образом, мы имеем ясное представление не только о том, происходят
ли два (разделенных во времени) события в одном и том же месте на экране, но и о том,
происходят ли два (пространственно разделенных) события в один и тот же момент време¬
ни. Более того, если события происходят в разных местах, мы ясно представляем, каково
расстояние между ними, независимо от того, происходят они одновременно или нет (это
есть просто расстояние, измеряемое на экране). Аналогично, если два события происходят
в разное время, мы ясно представляем себе временной интервал между ними, независимо
от того, находятся ли они в одном и том же месте.
Все это означает, что в нашей аристотелевой схеме естественно рассматривать про¬
странство-время просто как произведение
Л — Е1 хЕ3,
которое я буду называть пространством-временем Аристотеля. Это есть просто простран¬
ство пар (tг х), где t — элемент пространства Е3 («время»), ах — элемент пространства Е3
(«точка в пространстве») (см. рис. 17.2). Для двух различных точек пространства Е1 х Е3,

17.2. Пространство-время галилеевой относительности
333
Время Пространство
Рис. 17.2. Пространство-время Аристотеля Л — Е1 хЕ3 есть пространство пар (tf х), где t («время»)
меняется в евклидовом 1-пространстве Е1, ах («точка в пространстве») — в евклидовом 3-простран¬
стве Е3
скажем, (£, х) и (t\ х'), т.е. для двух различных событий, мы имеем четко определенное
понятие пространственного расстояния между ними — это есть расстояние между точками х
и х' пространства Е3; аналогично мы имеем четкое понятие о временном интервале между
ними как расстоянии между t и Г в пространстве Е1. В частности, мы знаем, происходят
ли два события в одном и том же месте (при этом пространственное расстояние обраща¬
ется в нуль) и случаются ли они в один и тот же момент времени (равен нулю временной
интервал между ними).
17.2.	Пространство-время галилеевой относительности
Теперь посмотрим, какое понятие пространства-времени соответствует динамической
схеме, предложенной Галилеем в 1638 году. Мы хотим ввести в нашу картину простран¬
ства-времени принцип относительности Галилея. Попробуем напомнить, что утверждает
этот принцип. Вряд ли это можно сделать лучше, чем процитировав самого Галилея (в пере¬
воде Стиллмена Дрейка^17-2!, который я привожу здесь в сокращенном виде; я настоятельно
рекомендую тем, у кого есть такая возможность, познакомиться с полной цитатой):
Уединитесь с каким-нибудь приятелем в просторное помещение под палубой боль¬
шого корабля и пустите туда мух, бабочек и других подобных мелких летающих
насекомых... Подвесьте наверху бутылку, из которой капля за каплей вытекала бы
вода в широкий сосуд, поставленный внизу... Заставьте привести корабль в движе¬
ние с какой угодно скоростью, так чтобы движение было равномерным и без качки
в ту и другую сторону... Капли будут падать... в сосуд, не отклоняясь в сторону
кормы, хотя в то время, как капли находятся в воздухе, корабль проходит некоторое
расстояние... Бабочки и мухи будут продолжать свободно летать во всех направ¬
лениях, не накапливаясь со стороны кормы, как было бы, если бы они устали
следовать за нашим кораблем...
Галилей учит нас, что законы динамики в точности одинаковы в любой равномерно
движущейся системе. (Это существенная часть его искренней приверженности учению Ко¬
перника, согласно которому Земля может двигаться без какого-либо восприятия нами этого
движения, вопреки более раннему учению Аристотеля, по которому Земля в этом случае
должна находиться в неподвижном состоянии.) Никаким образом нельзя отличить физику
состояния покоя от физики равномерного движения. В прежних терминах это означает, что
не существует динамического способа определить, является ли данная точка пространства

334
Глава 1
той же самой точкой в более поздний момент времени. Другими словами, наша аналогия
с экраном кинематографа оказывается несостоятельной! Не существует фонового простран¬
ства («экрана»), которое остается фиксированным с течением времени. Мы не можем уве¬
ренно сказать, является ли данная точка пространства р (например, точка в восклицательном
знаке на клавиатуре моего портативного компьютера) «той же самой» точкой пространства,
что и минуту назад. Для большей убедительности в этом вопросе рассмотрим вращение
Земли. Вследствие этого движения фиксированная точка на земной поверхности (например,
на широте Оксфорда) за указанную минуту сместится приблизительно на 10 миль. Соответ¬
ственно выбранная мною точка р окажется где-то в окрестности соседнего города Уитни.
Но погодите! Я же не принял во внимание движение Земли вокруг Солнца. Если сделать
это, то точка р окажется приблизительно в сто раз дальше, причем в противоположном на¬
правлении (поскольку в данный момент, сразу после полудня, поверхность Земли движется
в направлении, противоположном направлению движения Земли вокруг Солнца), то есть
Земля сдвинется настолько, что точка р попадет за пределы земной атмосферы! Но могу
ли я не учитывать движение Солнца относительно центра нашей Галактики — Млечного
Пути? А как насчет «собственного движения» самой Галактики внутри локальной группы
галактик? Или движения этой локальной группы относительно центра скопления галактик
в созвездии Девы, малой частью которого она является, или движения этого скопления от¬
носительно сверхскопления в созвездии Волосы Вероники, или движения сверхскопления
в направлении «Большого Аттрактора» (§ 27.11)?
Очевидно, что мы должны принимать Галилея всерьез. Не имеет смысла придерживать¬
ся представления, что любая точка пространства, выбранная минуту назад, должна призна¬
ваться той же самой точкой пространства, что и выбранная в данный момент. В галилеевой
динамике мы не можем считать одно евклидово 3-пространство IE3 ареной всего происхо¬
дящего в физическом мире, эволюционирующем во времени. В каждый момент времени
мы имеем другое пространство Е3, и эти разные пространства не идентифицируются одно
с другим.
Может вызвать тревогу то обстоятельство, что само наше понятие физического про¬
странства представляется чем-то таким, что целиком улетучивается, когда проходит данный
момент времени, и появляется в качестве совсем другого пространства, когда наступает сле¬
дующий момент! Но здесь нам на выручку приходит математика из главы 15, поскольку
там изучалась ситуация того же рода. Галилеево пространство-время —- это не простран¬
ство Е1 х Е3, а расслоенное пространство^17*31 с базисным пространством Е1 и слоем Е3!
В расслоенном пространстве отсутствует поточечная идентификация между слоями, тем
не менее слои, собранные вместе, образуют связное целое. Каждому событию в простран¬
стве-времени естественным образом приписывается время как определенный элемент неко¬
торого «пространства часов» Е1, однако отсутствует сопоставление с пространственным
расположением в одном определенном «пространстве положений» Е3. На языке расслое¬
ний (§ 15.2) такое естественное сопоставление некоторого времени достигается с помощью
канонической проекции Q на Е1 (см. рис. 17.3, сравните также с рис. 15.2).
17.3.	Ньютоновская динамика на языке пространства-времени
«Расслоенная» картина пространства-времени всем хороша, но как выразить на этом
языке динамику Галилея - Ньютона? Неудивительно, что Ньютон, формулируя свои законы
динамики, был вынужден прибегнуть к описанию, использующему понятие «абсолютного
пространства». На самом деле Ньютон, по крайней мере вначале, был «галилеевским реля¬
тивистом» не в меньшей мере, чем сам Галилей. Это ясно видно из того факта, что в своей
первоначальной формулировке законов движения он явно провозглашает принцип относи¬
тельности Галилея как фундаментальный закон (согласно этому принципу, физические яв-

17.3. Ньютоновская динамика на языке пространства-времени
335
з
Е -пространство
Е -пространство
4су _3
-пространство
^Е -пространство
Рис. 17.3. Галилеево пространство-время Q представляет собой расслоенное пространство с базисным
пространством Е1 и слоем Е3, так что отсутствует поточечная идентификация между различными сло¬
ями Е? (нет абсолютного пространства), но каждому событию в пространстве-времени приписывается
некоторое время при помощи канонической проекции (абсолютное время). (Сравните с рис. 15.2; здесь
каноническая проекция на базисное пространство изображена горизонтально.) Истории (мировые ли¬
нии) частиц представляют собой сечения расслоения (сравните с рис. 15.6 а), инерциальное движение
частиц изображается «прямыми» мировыми линиями, определяемыми структурой пространства-вре¬
мени Q
ления не замечают перехода от одной равномерно движущейся системы к другой, а понятие
времени абсолютно, как следует из картины галилеевского пространства-времени Q).
Первоначально Ньютон предложил пять (или шесть) законов, четвертым из которых был
принцип Галилеяf17*4-1, но позднее, в своих «Математических началах натуральной филосо¬
фии», он упростил их до трех знакомых нам «законов Ньютона», из которых можно вывести
все остальные. Чтобы установить точные рамки для своих законов, Ньютону пришлось вве¬
сти понятие «абсолютного пространства», относительно которого должны описываться все
движения. Если бы в то время было известно понятие расслоенного пространства (пред¬
положим такую неправдоподобную возможность), то Ньютон мог бы сформулировать свои
законы в полностью «галилеевски-инвариантном» виде. Однако при отсутствии такого по¬
нятия нелегко представить, как бы Ньютон смог обойтись без введения некоторого понятия
«абсолютного пространства», что он действительно и сделал.
Какого рода структуру следует приписать нашему «галилеевскому пространству-време¬
ни» Q1 Определенно было бы слишком щедро снабдить наше расслоенное пространство Q
связностью расслоения (§ 15.7). Вместо этого нам следовало бы снабдить его чем-то таким,
что согласовалось бы с первым законом Ньютона. Этот закон гласит, что движение частицы,
на которую не действуют никакие силы, должно быть равномерным и прямолинейным. Такое
движение называется инерциальным. На языке пространства-времени движение (т. е. «исто¬
рия») любой частицы, независимо от того, является ее движение инерциальным или нет,
представляется некоторой кривой, называемой мировой линией частицы. В нашем галилеев¬
ском пространстве-времени мировые линии фактически всегда должны быть сечениями га¬
лилеевского расслоения** (см. § 15.3 и рис. 17.3). Понятие движения, именуемого в обычных
пространственных терминах равномерным прямолинейным (инерциальным) движением, на
пространственно-временном языке интерпретируется просто как прямолинейное. Следова¬
тельно, галилеевское расслоение Q должно иметь структуру, которая кодирует «прямизну»
мировых линий. Этого можно добиться, провозгласив Q аффинным пространством (§ 14.1),
в котором аффинная структура, ограниченная отдельными слоями Е3, согласуется с евкли¬
довой аффинной структурой каждого слоя Е3. Другой способ состоит в том. чтобы просто
задать семейство из оо6 прямых линий, которое естественным образом находится в про¬
ЛЭ Почему?
** Й© Объясните причину этого.

336
Глава 17
странстве-времени Е1 х Е3 (соответствующем «аристотелевым» равномерным движениям),
и использовать его для того, чтобы задать «прямолинейную» структуру галилеевского рас¬
слоения, «забыв» о действительной структуре аристотелева пространства-времени Л как
произведения. (Напомним, что оо6 означает шестимерное семейство; см. § 16.7.) Еще один
возможный способ состоит в предположении, что галилеевское пространство-время, рас¬
сматриваемое как многообразие, обладает связностью без кривизны и кручения (что в корне
отличает его от многообразия, обладающего связностью расслоения, которое рассматрива¬
лось как расслоение над Е1).*
Эта третья точка зрения представляется наиболее удовлетворительной, поскольку она
допускает обобщения, которые понадобятся нам в §§ 17.5, 17.9 для описания гравитации
в соответствии с идеями Эйнштейна. Имея связность, определенную на Q, мы приходим
к понятию геодезической (§ 14.5), и такие геодезические (помимо тех, которые представля¬
ют собой просто прямые линии в отдельных пространствах Е3) определяют ньютоновское
инерциальное движение. Можно также рассмотреть мировые линии, не являющиеся гео¬
дезическими. В обычных пространственных терминах они представляют движение частиц
с ускорением. В пространственно-временных терминах величина ускорения измеряется кри-
визной мировой линии . Согласно второму закону Ньютона, это ускорение равно полной
силе, действующей на частицу, деленной на массу частицы. (Это есть ньютоновская фор¬
мула / = та в форме а — //га, где а — ускорение частицы, т — ее масса, / — полная
сила, действующая на частицу.) Таким образом, кривизна мировой линии частицы заданной
массы может служить непосредственной мерой силы, действующей на эту частицу.
В обычной ньютоновской механике полная сила, действующая на частицу, равна (век¬
торной) сумме вкладов от всех других частиц (рис. 17.4 а). В каждом отдельном простран¬
стве Е3 (то есть в каждый момент времени) такой вклад в силу, действующую на одну
частицу со стороны некоторой другой частицы, направлен вдоль прямой, соединяющей эти
две частицы и лежащей в этом пространстве Е3. Другими словами, эта сила действует
одновременно на обе частицы (см. рис. 17.46). Третий закон Ньютона гласит, что сила, дей¬
ствующая на одну из этих частиц со стороны другой, всегда равна по величине (и противопо¬
ложна по направлению) силе, с которой вторая частица действует на первую. В дополнение
к этому для каждого вида сил существует закон силы, определяющий, как зависит величина
силы от пространственного расстояния между частицами и какие параметры необходимо
задать для частиц каждого вида, чтобы найти величину силы. В частном случае гравита¬
ционных сил эта зависимость берется в виде обратного квадрата расстояния, а величина
силы определяется некоторой константой, называемой ньютоновской гравитационной по¬
стоянной G, умноженной на произведение масс двух рассматриваемых частиц. Используя
математические символы, мы получаем известную формулу Ньютона для силы притяже¬
ния, действующей на частицу массы т со стороны другой частицы массы М, находящейся
от нее на расстоянии г:
GmM
г2	*
Замечательно, что на такой простой основе строится теория необычайной силы и уни¬
версальности, которой можно пользоваться для описания с высокой точностью поведения
макроскопических тел (а также, при более внимательном изучении, и субмикроскопиче-
ских частиц), до тех пор, пока их скорости значительно меньше скорости света. В случае
гравитационных сил согласие между теорией и результатами наблюдений особенно очевид¬
но, благодаря очень детальным наблюдениям движения планет нашей Солнечной системы.
* Дайте более подробное объяснение этих трех способов и покажите, что все они приводят к одной и той
же структуре.
**?Ш Попробуйте написать выражение для этой кривизны, выразив ее через связность V. Какое условие
необходимо (если оно действительно необходимо) наложить на касательные векторы?

17.4. Принцип эквивалентности
337
Рис. 17.4. а) Ньютоновская сила. В любой момент времени полная сила, действующая на частицу
(изображается двойной стрелкой), равна векторной сумме отдельных вкладов (притяжения или от¬
талкивания) со стороны всех других частиц, б) Мировые линии двух частиц и сила между ними,
действующая «одновременно» вдоль прямой, соединяющей частицы, в любой момент времени в от¬
дельном пространстве Е3, определяемом этим моментом. Третий закон Ньютона гласит, что сила,
действующая на одну из частиц со стороны другой, равна по величине силе, действующей на вторую
частицу со стороны первой, и имеет противоположное ей направление
В настоящее время точность теории Ньютона оценивается приблизительно в одну десяти¬
миллионную, что является весьма впечатляющим достижением, особенно если учесть, что
точность данных, с которыми вынужден был оперировать Ньютон, была в десять тысяч раз
хуже (одна тысячная).
17.4.	Принцип эквивалентности
Несмотря на такую необычайную точность и на тот факт, что великая теория Ньютона
фактически оставалась неоспоримой в течение двух с половиной веков, мы сейчас знаем, что
эта теория не является абсолютно точной. Чтобы улучшить ньютоновскую схему, потребо¬
вался более глубокий и революционный взгляд Эйнштейна на природу гравитации. В то же
время этот новый взгляд сам по себе не изменил теорию Ньютона во всем, что касалось
наблюдаемых следствий. Изменения появились, только когда этот новый взгляд Эйнштейна
соединился с другими представлениями, связанными с конечной скоростью света и идеями
специальной теории относительности, которые будут изложены в §§ 17.6-17.8. Такое объ¬
единение приводит к общей теории относительности Эйнштейна, качественное изложение
которой будет дано в § 17.9, а более полное — в §§ 19.6-19.8.
В чем же состоит более глубокий взгляд Эйнштейна? Он заключается в принципе экви¬
валентности, имеющем фундаментальное значение. Что такое принцип эквивалентности?
Основная идея восходит (опять!) к великому Галилею (к концу XVI века, хотя у Галилея
были предшественники — Симон Стевин в 1586 году и даже более ранние, например, Иоанн
Филипонский в V или VI веке). Напомним о приписываемом Галилею эксперименте, кото¬
рый состоял в бросании двух камней, большого и маленького, с вершины Падающей башни
в Пизе (рис. 17.5 а). Великое открытие Галилея заключалось в том, что оба камня будут
падать с одинаковой скоростью при условии, что можно пренебречь сопротивлением возду¬
ха. Независимо от того, бросал ли в действительности Галилей камни с Падающей башни,
он определенно проводил другие опыты, которые привели его к этому выводу.
Прежде всего необходимо отметить, что это есть особое свойство гравитационного по¬
ля, и не следует ожидать того же от каких-либо других сил, действующих на тела. Свойство

338
Глава 1
L/
9
\
\
а)
б)
Рис. 17.5. а) Эксперимент, приписываемый Галилею. Два камня, большой и маленький, роняют с вер¬
шины Падающей башни в Пизе. Открытие Галилея состояло в том, что оба камня будут падать
с одинаковой скоростью, если можно пренебречь сопротивлением воздуха, б) Два противоположно
заряженных шарика (с одинаковой малой массой) в электрическом поле, направленном к Земле. Один
заряд будет «падать вниз», другой — подниматься вверх
силы тяжести, подмеченное Галилеем, определяется тем обстоятельством, что сила, действу¬
ющая на тело со стороны некоторого заданного гравитационного поля, пропорциональна
массе этого тела, тогда как величиной, определяющей сопротивление движению (величиной
га, фигурирующей во втором законе Ньютона), также является масса. Полезно разделить эти
два понятия массы, и первую назвать гравитационной массой, а вторую — инертной массой.
(Можно также отличать пассивную инертную массу от активной гравитационной массы.
Пассивная масса — это вклад га в ньютоновскую формулу обратных квадратов GraM/r2.
описывающую гравитационную силу, действующую на частицу га со стороны частицы М.
Если же мы рассматриваем силу, действующую на частицу М со стороны частицы га.
то масса га выступает в активной роли. Но третий закон Ньютона провозглашает равенство
пассивной и активной масс, и потому я не буду здесь делать различие между ними!17*5й)
Таким образом, вывод Галилея основан на равенстве (или, точнее, пропорциональности)
гравитационной и инертной масс.
С точки зрения всей динамической схемы Ньютона, равенство инертной и гравитаци¬
онной масс выглядит как счастливая случайность, игра Природы. Если бы поле было не
гравитационное, а скажем, электрическое, то результат был бы совершенно иным. Элек¬
трическим аналогом пассивной гравитационной массы служит электрический заряд, а роль
инертной массы (сопротивляющейся ускорению) остается такой же, как и в случае грави¬
тационного поля (т. е. ею по-прежнему является га из второго закона Ньютона / = та).
Разница становится особенно очевидной, если по аналогии с галилеевской парой камней
взять пару шариков с одинаковой малой массой, но с зарядами противоположного знака.
Если фоновое электрическое поле направлено в сторону Земли, то один из зарядов будет
«падать» вниз, а другой — подниматься вверх, то есть ускоряться в противоположном на¬
правлении! (См. рис. 17.5 6.) Это становится возможным, поскольку электрический заряд,
находящийся на теле, не имеет никакого отношения к инертной массе тела, вплоть до то¬
го, что он может иметь любой знак. Вывод Галилея не относится к электрическим силам,
а касается лишь такого особого свойства силы тяжести.

17.4. Принцип эквивалентности
339
Почему эта особенность гравитации называется «принципом эквивалентности»? «Эк¬
вивалентность» относится к тому факту, что однородное гравитационное поле эквивалентно
ускорению. Этот эффект хорошо знаком авиапутешественникам, поскольку при движении
самолета с ускорением (которое может менять направление) может возникнуть совершенно
неверное представление о том, где находится «низ». Влияние ускорения и гравитационного
поля Земли нельзя различить на основании того, как они «ощущаются» внутри самолета,
и эти два эффекта могут складываться, действуя в двух разных направлениях, создавая у вас
ощущение того, где «должен быть» низ (возможно, к вашему удивлению, если вы смотрите
в окно), и это кажущееся направление вниз может существенно отличаться от действитель¬
ного.
Чтобы понять, каким образом эквивалентность ускорения воздействию силы тяжести
действительно вытекает из описанного выше открытия Галилея, взглянем снова на его кам¬
ни, падающие вместе с вершины башни. Представим себе, что на одном из камней сидит
какое-то насекомое и смотрит на другой камень. Насекомому должно казаться, что этот
другой камень просто парит в воздухе без движения, как если бы гравитационного поля
вообще не было (см. рис. 17.6 а). Ускорение, которое испытывает насекомое, падая вместе
с камнями, компенсирует действие гравитационного поля, как если бы сила тяжести вообще
отсутствовала (разумеется, так будет лишь до тех пор, пока камни и насекомое не столкнутся
с Землей, так что это впечатление «отсутствия тяжести» внезапно исчезнет^17*6^).
а)
Рис. 17.6. а) Насекомому, сидящему на одном из камней с рис. 17.5 а, другой камень кажется просто
парящим без движения, как если бы гравитационное поле отсутствовало. 6) Аналогично космонавт
на свободной орбите испытывает ощущение невесомости, и космическая станция кажется ему непо¬
движно парящей, несмотря на очевидное присутствие Земли
Известно, что подобное ощущение «невесомости» испытывают также космонавты, од¬
нако, благодаря тому, что они находятся на околоземной орбите (рис. 17.66), они, в отличие
от нашего насекомого (или авиапассажиров в тот момент времени, когда самолет начинает
выходить из пике), избавлены от неприятностей, связанных с внезапным прекращением это¬
го ощущения. Как и то насекомое, космонавты свободно падают, но по более благоприятной
для них замкнутой траектории. Тот факт, что таким образом сила тяжести уничтожается
ускорением (с использованием принципа эквивалентности), есть прямое следствие равен¬
ства (или пропорциональности) пассивной гравитационной массы инертной массе — того
самого факта, который лежит в основе великого открытия Г алилея.
Если подойти к этому принципу эквивалентности серьезно, мы должны пересмотреть
понятие «инерциального движения», введенное в § 17.3. Ранее инерциальное движение вы¬
делялось как такой вид движения, который имеет место, когда полная внешняя сила, действу¬
ющая на частицу, равна нулю. Но в случае силы тяжести мы сталкиваемся с затруднением.

340
Глава 1
В силу принципа эквивалентности не существует локального способа, позволяющего опре¬
делить, действует ли гравитационная сила, или то, что «ощущается» как такая сила, есть все¬
го лишь следствие ускорения. Более того, как в случае нашего насекомого на галилеевском
камне или космонавта на орбите, силу тяжести можно устранить, обеспечив условия свобод¬
ного падения. И поскольку таким путем можно устранить гравитационную силу, нам следует
занять в отношении нее иную позицию. В этом и состоял глубокий новый взгляд Эйнштейна
на «инерциальное движение» как на такое движение, при котором равна нулю сумма всех
действующих на частицу /^гравитационных сил, так что она должна свободно падать в гра¬
витационном поле (при этом эффективная гравитационная сила также обращается в нуль).
Таким образом, падение нашего насекомого и движение космонавтов по орбите вокруг Зем¬
ли должны считаться инерциальными движениями. В то же время человек, просто стоящий
на земле, в этой эйнштейновской схеме не совершает инерциального движения, поскольку
состояние покоя в гравитационном поле не является свободным падением. Согласно Нью¬
тону, движение человека будет инерциальным, поскольку в ньютоновской схеме «состояние
покоя» всегда считается «инерциальным». Гравитационная сила, действующая на человека,
уравновешивается направленной вверх силой со стороны Земли, но по отдельности эти силы
не равны нулю, как требует Эйнштейн. С другой стороны, инерциальное, по Эйнштейну,
движение насекомого или космонавта, согласно Ньютону, не является инерциальным.
17.5.	«Ньютоновское пространство-время» в представлении Картана
Как включить эйнштейновское понятие «инерциального» движения в структуру про¬
странства-времени? В качестве шага в направлении полной теории Эйнштейна будет полез¬
но посмотреть, как следует переформулировать теорию тяготения Ньютона в соответствии
со взглядами Эйнштейна. Как упоминалось в начале § 17.4, в действительности эти взгляды
не изменяют теорию Ньютона, а лишь дают иное ее описание. В этой связи я позволю себе
еще одну вольность с историей и изложу формулировку, предложенную выдающимся гео¬
метром и алгебраистом Эли Картаном (важное влияние которого на теорию непрерывных
групп уже отмечалось в главе 13 (напомним также § 12.5)) спустя шесть лет после того, как
Эйнштейн изложил свои революционные взгляды.
Грубо говоря, в схеме Картана инерциальное движение, которому соответствуют «пря¬
мые» мировые линии, понимается не в ньютоновском, а в эйнштейновском смысле. В то же
время геометрия подобна галилеевской, изложенной в § 17.2. Я назову это ньютоновским
пространством-временем N\ при этом ньютоновское гравитационное поле полностью вклю¬
чено в его структуру. (Возможно, мне следовало назвать его «картановским», но это звучит
довольно неуклюже. В конце концов, и Аристотель ничего не знал о произведении про¬
странств, и Галилей не слыхал о расслоенных пространствах!)
Как и в предыдущем случае галилеевского пространства-времени б, пространство-вре¬
мя N должно быть расслоением с базисным пространством Е1 и слоем Е3. Но теперь
у N не должно быть какой-либо структуры, отличной от структуры Q, поскольку иным
является семейство «прямых» мировых линии, представляющих инерциальные движения
(см. рис. 17.7 а). Оно существенно иное во всех случаях, кроме тех, когда гравитационное
поле нельзя полностью устранить путем выбора некоторой свободно падающей глобальной
системы отсчета. Подобным исключением может служить ньютоновское гравитационное по¬
ле, постоянное (как по величине, так и по направлению) во всем пространстве, но, возможно,
меняющееся во времени. Наблюдателю, свободно падающему в таком поле, должно казать¬
ся, что поля вообще нет!* В таком случае структура ЛГ должна совпадать со структурой Q
Найдите явный вид преобразования координаты х, зависящего от t, которое позволяет устранить поле,
для ньютоновского гравитационного поля F (£), пространственно однородного в любой момент времени, но меня¬
ющегося во времени по величине и направлению.

17.5. «Ньютоновское пространство-время» в представлении Картана
341
(рис. 11.76, в). Однако в большинстве своем гравитационные поля считаются «существенно
отличными» от отсутствующего гравитационного поля. Можно ли понять почему? Можем
ли мы узнать, когда структура М отлична от структуры Q1 К этим вопросам мы сейчас
Рис. 17.7. а) Пространствсг'-время Ньютона - Картана М, как и частный случай галилеевского простран-
ляется семейством движении свооодного падения в поле тяжести, «инерциальных» в эйнштейновском
смысле, б) Частный случай ньютоновского гравитационного поля, однородного во всем простран¬
стве. в) Структура полностью эквивалентна структуре пространства-времени Q, что можно увидеть,
«сдвигая» слои Е3 горизонтально, пока мировые линии свободного падения являются прямыми
Идея состоит в том, что многообразие N должно обладать связностью, как и в частном
случае многообразия Q. Геодезическими этой связности V (см. § 14.5) должны служить «пря¬
мые» мировые линии, представляющие инерциальные движения в эйнштейновском смысле.
Эта связность не содержит кручения (§ 14.4), но в общем случае может обладать кривизной
(§ 14.4). Именно наличие кривизны делает некоторые гравитационные поля «существенно
отличными» от отсутствующего гравитационного поля в противоположность рассмотрен¬
ному случаю пространственно однородного поля. Попробуем понять физический смысл
кривизны.
Представим себе, что некий космонавт Альберт (обозначим его буквой А) свободно
падает в пространстве за пределами земной атмосферы. Полезно рассмотреть А в момент
падения к поверхности Земли, при этом скорость Альберта не имеет значения, интерес
перейдем.
]
а)
ства-времени Q, является расслоением с базисным пространством Е1 и слоем Е3. Его структура опреде-

342
Глава 1
представляет его ускорение и ускорение окружающих его частиц. А может, безопасно нахо¬
диться на орбите, и ему необязательно падать на землю. Представим, что А окружен сферой
из частиц, которые первоначально находятся в покое относительно А. Согласно обычной
ньютоновской схеме, различные частицы из этой сферы будут ускоряться в направлении
центра Земли Е в слегка различных направлениях (потому что направления на центр Е для
разных частиц немного различаются), величина такого ускорения также будет различной
для разных частиц (поскольку различны их расстояния до центра Е). Будем иметь деле
с относительными ускорениями по сравнению с ускорением космонавта А, поскольку на:
интересует, каким будет представляться инерциальному (в эйнштейновском смысле) наблю¬
дателю (в данном случае А) движение соседних инерциальных частиц. Ситуация показана
на рис. 17.8 а. Частицы, смещенные относительно А в горизонтальном направлении, бу¬
дут ускоряться в направлении Е слегка внутрь по отношению к ускорению А, поскольку
расстояние до центра Земли конечно. Те же частицы, которые смещены относительно А
вертикально, будет ускоряться относительно А слегка вовне, потому что гравитационная
сила спадает по мере удаления от Е. В соответствии с этим сфера частиц начнет дефор¬
мироваться. В отношении ближайших частиц эта деформация превратит сферу в вытяну¬
тый эллипсоид вращения, большая ось (ось симметрии) которого направлена по прямой
АЕ. Более того, начальная деформация сферы в эллипсоид такова, что объем последнего
остается равным объему сферы*. Последнее свойство является характерной особенностью
закона обратных квадратов ньютоновской теории тяготения; этот замечательный факт ока¬
жется важным, когда мы приступим собственно к общей теории относительности Эйн-
а)
б)
Рис. 17.8. а) Приливный эффект. Космонавт Альберт (А) окружен сферой из соседних частиц, перво-
v
начально находящихся в покое относительно А. Согласно ньютоновской схеме, они имеют ускорения
в направлении центра Земли Е, слегка различающиеся по направлению и величине (показаны темны¬
ми стрелками). Если вычесть ускорение А, получатся ускорения относительно А (двойные стрелки).
Эти относительные ускорения направлены слегка внутрь для частиц с горизонтальным смещением
относительно А и слегка вовне для вертикально смещенных частиц. В соответствии с этим сфера де¬
формируется в (вытянутый) эллипсоид вращения с осью симметрии в направлении АЕ. Это начальная
деформация сохраняет объем, б) Теперь поместим А в центр Земли Е, а сферой из частиц окружим Е
за пределами земной атмосферы. Ускорение (относительно А = Е) во всей сфере направлено внутрь,
при этом начальный объем уменьшается с ускорением 47tGM, где М — полная окруженная масса
Выведите эти свойства, используя обозначение 0(...), чтобы было ясно, величинам какого порядка
соответствуют сделанные утверждения.

1-7.5. «Ньютоновское пространство-время» в представлении Картана
343
штейна. Следует отметить, что такой эффект сохранения объема имеет место только вна¬
чале, когда частицы стартуют из состояния покоя относительно А. Тем не менее, с ука¬
занной оговоркой, это есть общее свойство ньютоновских гравитационных полей, когда А
находится в безвоздушном пространстве. (В то же время вращательная симметрия эллипсо¬
ида есть случайное обстоятельство, связанное с симметрией рассматриваемой конфигура¬
ции.)
Как понять все это в рамках нашей пространственно-временной картины Ml
На рис. 17.9 а я постарался показать, как должна проявляться эта ситуация в мировых линиях
А и окружающих частиц. (Конечно, я вынужден здесь исключить одно пространственное из¬
мерение, поскольку трудно воспроизвести подлинно четырехмерную конфигурацию! К сча¬
стью, два пространственных измерения здесь оказываются достаточными для того, чтобы
донести основную идею.) Заметим, что деформация сферы, образуемой частицами (здесь
сфера изображается как окружность), возникает из-за отклонения геодезических, соседних
с геодезической мировой линией А. В § 14.5 я объяснил, почему отклонение геодезических
фактически служит мерой кривизны R связности V.
Рис. 17.9. Пространственно-временной вариант рис. 17.7 (в ЛЛпредставлении Ньютона-Картана), вы¬
раженный через относительное отклонение соседних геодезических, а) Отклонение геодезических
в пустом пространстве (кривизна Вейля из § 19.7), проявляющееся в мировых линиях А и окружа¬
ющих частиц (при удалении одного из пространственных измерений), которое может возникать под
действием гравитационного поля соседнего тела Е. 6) Соответствующее ускорение внутрь (кривизна
Риччи), создаваемое распределением плотности массы внутри пучка геодезических
Описанный эффект деформации на ньютоновском физическом языке описывается как
приливный эффект под действием сил тяготения. Происхождение такой терминологии станет
понятным, если позволить Е поменяться ролями с А и рассматривать А как центр Земли,
а Луну (или, возможно, Солнце) расположить в Е. Если рассматривать сферу из частиц
. ✓	• • •
как поверхность земных океанов, мы увидим, что эффект деформации обусловлен неодно¬
родным гравитационным полем Луны (или Солнца)*. Эта деформация является причиной
океанских приливов, поэтому термин «приливный эффект», используемый для такого непо¬
средственного проявления кривизны пространства-времени, вполне удачен.
На самом деле в рассмотренной здесь ситуации влияние Луны (или Солнца) на отно¬
* J0 Покажите, что приливная деформация пропорциональна mr~3, где т — масса тела, создающего гравита¬
ционное поле (и рассматриваемого как точка), а г — расстояние до него. С Земли Луна и Солнце кажутся дисками
почти одинакового углового размера, тем не менее приливное действие Луны на океаны Земли приблизительно
в пять раз сильнее аналогичного действия Солнца. Что это говорит нам об их относительной плотности?

344
Глава Г
сительные ускорения частиц на поверхности Земли есть лишь малая поправка к основному
действию гравитации на эти частицы, а именно к гравитационному притяжению самой
Землей. Оно действует, разумеется, в направлении на центр Земли (при нашем простран¬
ственном описании это теперь точка А, см. рис. 17.8 б), отсчитываемом от положения каждой
отдельной частицы. Если сфера, состоящая из частиц, окружает Землю за пределами зем¬
ной атмосферы (что позволяет не учитывать сопротивление воздуха), то будет иметь место
свободное падение (эйнштейновское инерциальное движение) всех частиц внутрь сферы.
Вместо деформации сферы в эллипсоид первоначально того же объема теперь мы имеем
уменьшение объема. В общем случае могут присутствовать оба эффекта. В пустом простран¬
стве имеет место только деформация и отсутствует эффект уменьшения объема в начальном
состоянии, если же сфера окружает материальное тело, происходит начальное уменьшение
объема, пропорциональное полной окруженной массе. Если эта масса равна М, то начальная
«скорость» уменьшения объема (как мера ускорения внутрь сферы) равна
где G — ньютоновская гравитационная постоянная » .
Фактически, как показал Картан, можно сформулировать ньютоновскую теорию грави¬
тации полностью в виде математических условий, налагаемых на связность V. Эти условия
представляют собой, по существу, уравнения для кривизны R и дают точное математическое
выражение приведенных выше требований, они связывают плотность вещества р (массу на
единицу объема пространства) с «уменьшающей объем» частью кривизны R. Я не буду
приводить здесь подробное описание, данное Картаном, поскольку оно не является необхо¬
димым для дальнейшего изложения, и полная теория Эйнштейна в некотором смысле проще.
Однако сама идея важна для нас не только потому, что она плавно подводит нас к теории
Эйнштейна, но и потому, что она играет роль при изложении главы 30 (§ ЗОЛ 1), касающейся
глубоких загадок, предлагаемых квантовой теорией, и их возможного решения.
17.6.	Фиксированная конечная скорость света
В нашем предыдущем изложении мы рассматривали два фундаментальных аспекта об¬
щей теории относительности Эйнштейна — принцип относительности, который гласит,
что законы физики не чувствительны к разнице между покоем и равномерным движени¬
ем, и принцип эквивалентности, который сообщает нам, как следует модифицировать эти
идеи, чтобы включить в рассмотрение гравитационное поле. Мы должны теперь обратиться
к третьей фундаментальной составляющей теории Эйнштейна — конечной скорости света.
Замечательно, что все эти три фундаментальные составляющие восходят еще к Галилею,
поскольку он был, видимо, первым, кто имел настолько ясное представление о конечной
скорости распространения света, что предпринимал реальные шаги для измерения этой
скорости. Способ, предложенный им в 1638 году, состоял в синхронизации вспышек фона¬
рей, расположенных на удаленных друг до друга холмах, и, как мы теперь понимаем, был
слишком грубым. Галилей не мог предвидеть той необычайно высокой скорости, с которой
действительно распространяется свет.
Галилей и Ньютон, по-видимому, имели сильное подозрение Р7*7^ относительно воз¬
можной глубокой связи между природой света и теми силами, которые связывают материю
воедино. Однако должной реализации этих предчувствий пришлось ждать до двадцатого
• * *
века, когда была вскрыта истинная природа сил химической связи и сил, которые удержи¬
вают вместе отдельные атомы. Сейчас мы знаем, что эти силы имеют фундаментальное
Получите этот результат, предполагая, что масса сосредоточена в центре сферы.
Покажите, что этот результат остается справедливым в общем случае независимо от величины и формы
окружающей оболочки, состоящей из стационарных частиц, и от распределения массы.

17.7. Световые конусы
345
электромагнитное происхождение (они обусловлены взаимодействием электромагнитного
поля с заряженными частицами) и что теория электромагнетизма есть также теория света.
Для понимания атомов и химии необходимы еще дополнительные ингредиенты, предо став-
к*	и
ляемые квантовой теорией, однако основные уравнения, описывающие электромагнетизм
и свет, были сформулированы в 1865 году великим шотландским физиком Джеймсом Клер¬
ком Максвеллом, который был вдохновлен великолепными экспериментальными открыти¬
ями Майкла Фарадея, сделанными 30 годами раньше. Мы подойдем к теории Максвелла
позже (в § 19.2), но сейчас для нас важно, что она требует, чтобы скорость света была опре¬
деленной фиксированной величиной, которая обычно обозначается буквой с и составляет
в обычных единицах 3 • 108 метров в секунду.
Здесь, однако, возникает проблема, если мы хотим сохранить принцип относительности.
Здравый смысл вроде бы говорит нам, что если скорость света, измеряемая одним наблюда¬
телем в своей системе отсчета, равна с, то другой наблюдатель, который движется с очень
высокой скоростью относительно первого, измерит другую скорость распространения света,
большую или меньшую в зависимости от того, как движется второй наблюдатель. Но прин¬
цип относительности требует, чтобы физические законы для второго наблюдателя (которые
определяют, в частности, ту скорость света, которую воспринимает второй наблюдатель)
были точно такими же, как и для первого наблюдателя. Это кажущееся противоречие между
постоянством скорости света и принципом относительности привело Эйнштейна (а также
фактически раньше голландского физика Гендрика Антоона Лоренца и, в более законченной
форме, французского математика Анри Пуанкаре) к замечательной точке зрения, полностью
О
устраняющей это противоречие.
Как это получается? Естественно считать, что имеется неразрешимый конфликт между
требованиями 1) теории максвелловского типа, в которой существует абсолютная скорость
света, и 2) принципа относительности, согласно которому вид физических законов не за¬
висит от скорости движения системы отсчета, используемой для их описания. Потому что
разве нельзя выбрать систему отсчета, движущуюся со скоростью, близкой к скорости све¬
та или даже превышающей ее? И разве скорость света, воспринимаемая в такой системе
отсчета, может оставаться прежней? Это несомненное противоречие не возникает в тео¬
рии, поддерживаемой Ньютоном (и, как я предполагаю, Галилеем), согласно которой свет
ведет себя как частицы, скорость которых зависит, таким образом, от скорости источника.
Поэтому Галилей и Ньютон могли жить в полном согласии с принципом относительности.
Но со временем такой взгляд на природу света вступил в противоречие с наблюдениями
удаленных двойных звезд, показавшими, что скорость света не зависит от скорости его
источника^t17*8!. С другой стороны, набрала силу теория Максвелла — не только из-за мощ¬
ной поддержки со стороны эксперимента (наиболее важными были опыты Генриха Герца
в 1888 году), но и благодаря притягательности и универсальному характеру самой теории,
объединяющей законы, управляющие электрическим полями, магнитными полями и светом,
в единую математическую схему, обладающую замечательным изяществом и существенной
простотой. В теории Максвелла свет представляет собой не частицы, а волны, и мы выну¬
ждены столкнуться с тем фактом, что в этой теории существует фиксированная скорость,
с которой должны распространяться световые волны.
17.7.	Световые конусы
Точка зрения, основанная на геометрии пространства-времени, открывает нам исклю¬
чительно ясный путь к разрешению противоречия, создаваемого конфликтом между теори¬
ей Максвелла и принципом относительности. Как уже отмечалось, эта пространственно-
временная точка зрения первоначально не использовалась Эйнштейном (а также Лоренцем
и, видимо, даже Пуанкаре). Однако в ретроспективе видна мощь этого подхода. Отбросим

346
Глава !
на время гравитацию и все сопутствующие ей тонкости и усложнения, связанные с принци¬
пом эквивалентности. Начнем с чистого листа, то есть с вещественного 4-многообразия без
особенностей. Мы хотим посмотреть, что означает утверждение о существовании фундамен¬
тальной скорости, каковой должна быть скорость света. В любой точке пространства-време¬
ни р (изображающей некоторое «событие») можно рассмотреть семейство всех различных
лучей света, проходящих через эту точку во всевозможных пространственных направле¬
ниях. Пространственно-временное описание дает семейство мировых линий, проходящих
через точку р (см. рис. 17.10 а, б).
а)	б)	в)
Рис. 17.10. Световой конус определяет фундаментальную скорость света. Истории фотонов, прохо¬
дящих через пространственно-временную точку (событие) р. а) В чисто пространственных терминах
световым конусом (конусом будущего) является сфера, расширяющаяся во все стороны от точки р
(волновые фронты), б) В пространственно-временной формулировке истории фотонов, испускаемых
в точке р, образуют световой конус с вершиной в точке р. в) Поскольку далее нам придется рассмат¬
ривать искривленное пространство-время, полезно рассматривать конус (часто называемый нулевым
конусом в точке р) как локальную структуру в пространстве-времени, т. е. в касательном простран¬
стве Тр в точке р
Удобно назвать эти мировые линии «историями фотонов», проходящих через точку р,
хотя теория Максвелла рассматривает свет как волновое явление. По разным причинам
это не приводит к сколько-нибудь существенному конфликту. В теории Максвелла «фотон»
можно рассматривать как очень малый сгусток электромагнитного возмущения очень высо¬
кой частоты, который будет вести себя, вполне адекватно нашим целям, как малая частица,
распространяющаяся со скоростью света. (Вместо этого можно рассматривать «волновые
фронты», то, что математики называют «бихарактеристиками», или же можно предпочесть
обратиться к квантовой теории, согласно которой свет можно также рассматривать состоя¬
щим из «частиц», действительно называемых «фотонами».)
В окрестности точки р семейство историй фотонов, проходящих через точку р, образует
конус в пространстве-времени, называемый «световым конусом» в точке р. Чтобы скорость
света была фундаментальной, в пространственном представлении необходимо придать фун¬
даментальный смысл световым конусам. С точки зрения, принятой в геометрии многообра¬
зий (см. главы 12,14), часто бывает удобнее рассматривать «световой конус» как структуру в
касательном пространстве Тр в точке р (см. рис. 17.10 в). (Нас в конечном счете интересуют
скорости в точке р, а скорость есть объект, определяемый в касательном пространстве.) Эту
структуру в касательном пространстве часто называют нулевым конусом, и я сам предпочи¬
таю использовать этот термин, а термин «световой конус» сохранить для геометрического
места световых лучей, проходящих через точку р в пространстве-времени. Заметим, что све¬
товой конус (или нулевой конус) состоит из двух частей — конуса прошлого и конуса будуще¬
го. Конус прошлого можно рассматривать как историю вспышки света, сходящейся в точку р

17.7. Световые конусы
347
(все световые лучи одновременно приходят в эту пространственно-временную точку); ана¬
логично конус будущего представляет историю вспышки света от взрыва в пространственно
временной точке р (см. рис. 17.11).
Мировая
линия
Времениподобный
касательный
Рис. 17.11. Конус прошлого и конус будущего. Нулевой конус прошлого (или нулевые векторы про¬
шлого) относится к свету, сходящемуся в точку р, подобно тому как конус будущего (нулевые векторы
будущего) относится к свету, возникающему в точке р. Мировая линия любой массивной частицы
в точке р имеет времениподобный касательный вектор (направленный в будущее) и лежит внутри
нулевого конуса будущего в точке р
Как математически описать нулевой конус в точке р! Основа такого описания была
заложена в главах 13 и 14. Потребуем, чтобы в точке р скорость света была одинаковой во
всех направлениях, так чтобы пространственная конфигурация, окружающая эту точку спу¬
стя мгновение после вспышки света, имела сферическую, а не какую-нибудь яйцевидную
форму (форму овоида)[17*91. Говоря «спустя мгновение», я имею в виду, что такое рассмот¬
рение применимо к бесконечно малой временной (а также пространственной) окрестности
точки р; это позволяет считать такие конфигурации структурами в касательном простран¬
стве в точке р. Утверждение, что нулевой конус выглядит «сферическим», означает всего
лишь то, что конус определяется уравнением в касательном пространстве, которое является
квадратичным. Это означает, что уравнение имеет вид
gabvavb = о,
где даь — индексная форма некоторого несингулярного симметричного [^-тензора д с ло-
ренцевой сигнатурой (§ 13.8)*. Термин «нулевой» (конус) указывает на то, что вектор v
имеет нулевую длину (|v|2 = 0) в данной (псевдо)метрике д.
На этой стадии мы касаемся тензора д только в связи с его ролью в определении
нулевых конусов в соответствии с вышеприведенным уравнением. Если умножить д на
какое-либо вещественное число, отличное от нуля, мы получим прежний нулевой конус (см.
также §§ 27.12,33.3). Вскоре мы потребуем, чтобы тензор д играл более важную физическую
роль в определении метрики пространства-времени, поэтому нам понадобится соответству-
Объясните почему.

348
Глава
ющий масштабный множитель, но пока что мы будем иметь дело лишь с семейством нулевых
конусов, по одному в каждой точке пространства-времени. Чтобы можно было утверждать,
что скорость света постоянна, примем, что имеет смысл считать нулевые конусы различных
событий параллельными друг другу, поскольку «скорость» в пространственных терминах со¬
ответствует «наклону» в пространственно-временных терминах. Это приводит нас к картине
пространства-времени, изображенной на рис. 17.12.
Л
>
,4
4
#
Р
♦
■
I
«
►
»
I
Г
«
»«
г
ошв
Рис. 17.12. Пространство Минковского М является плоским, и его нулевые конусы распределены
равномерно; все они изображены параллельными
*
• • • .'
* . • • г '	*
• S	.	*•
• • • •
17.8.	Отказ от абсолютного времени
Теперь можно задать вопрос, уместно ли в дополнение наложить расслоенную струк¬
туру галилеевского пространства-времени Q. Другими словами, можно ли включить в нашу
картину понятие абсолютного времени? Это должно привести нас к картине, показанной на
рис. 17.13. В дополнение к нулевому конусу срезы Е3 в пространстве-времени дают нам
«элемент 3-плоскости» в каждом касательном пространстве Тр (рис. 17.13). Но, как будет
подробнее объяснено в следующей главе, тензор д определяет понятие ортогональности,
которое означает, что для каждого события р теперь имеется выделенное временное направ¬
ление (ортогональное дополнение к этому элементу 3-плоскости относительно тензора д)
и это выделенное временное направление дает нам выделенное состояние покоя для каждого
события. Мы потеряли принцип относительности!
В более прозаических выражениях это рассуждение просто выражает «обыденное»
представление, что если существует абсолютная скорость света, то имеется и выделен¬
ное «состояние покоя», по отношению к которому скорость воспринимается одинаковой
во всех направлениях. Менее очевидно, что этот конфликт возникает, только если мы
попытаемся сохранить понятие абсолютного времени (или, по крайней мере, выделенно¬
го 3-пространства в каждом пространстве Тр). Теперь должно быть ясно, как нам следу¬
ет поступить. Необходимо отказаться от понятия абсолютного времени (и, следовательно,
расслоенной структуры пространств Q и ЛГ). На том уровне сложности, к которому мы
пришли, это не должно нас особенно поразить. Мы уже видели, что от абсолютного про¬
странства необходимо отказаться, коль скоро мы всерьез принимаем принцип относитель¬
ности Галилея (хотя понимание этого распространено не столь широко, как следовало бы).
Поэтому в настоящий момент принятие того факта, что время, как и пространство, не яв¬
ляется абсолютным понятием, не должно выглядеть такой революцией, как можно было
подумать.

17.8. Отказ от абсолютного времени
349
Рис. 17.13. Введенное в пространство М понятие абсолютного времени определяет семейство сре¬
зов ЗЕ3 в этом пространстве и, следовательно, локальный элемент 3-плоскости для каждого события.
Но каждый нулевой конус определяет (с точностью до коэффициента пропорциональности) (псев-
до)метрический тензор д, ортогональность которого определяет состояние покоя
Таким образом, мы должны попрощаться со срезами Е3 в пространстве-времени и со¬
гласиться с тем, что единственной причиной, по которой абсолютное время столь прочно
укоренилось в нашем сознании, является то обстоятельство, что скорость света необы¬
чайно велика по сравнению с привычными нам скоростями. На рис. 17.14 я воспроизвел
часть рис. 17.13 с отношением горизонтального и вертикального масштабов, более близким
к тому, что получается при использовании нормальных единиц, которыми мы стремимся
пользоваться в повседневной жизни. Но более близким лишь в очень малой степени, по¬
скольку мы должны иметь в виду, что при использовании обычных единиц, скажем, секунд
для времени и метров для расстояния, скорость света с имеет следующее значение:
с - 299 792458 м/с
(это есть точное значение!)Е17-101. Поскольку наши пространственно-временные диаграммы
(а также формулы) в обычных единицах выглядят не совсем удобно, в работах по теории
относительности обычно пользуются системой единиц, в которой с = 1. Это значит, что,
выбрав в качестве единицы времени секунду, мы должны в качестве единицы расстояния
пользоваться световой секундой (299 792 458 метров); если же взять за единицу времени год,
то единицей расстояния будет световой год (приблизительно 9,46 ♦ 1010 метров). Если мы
захотим использовать в качестве меры расстояния метр, то единицей времени станет что-то
1
вроде Зтг наносекунды; и т.д.
О
Картина пространства-времени, изображенная на рис. 17.12, впервые была представлена
Германом Минковским (1864-1909), блестящим и оригинальным математиком. По совпа¬
дению, он был также одним из учителей Эйнштейна в Федеральном институте технологии
в Цюрихе в конце 1890-х годов. Фактически сама идея пространства-времени исходила
от Минковского, который написал в 1908 году^17Л1Ь «Отныне и навсегда пространство само
Рис. 17.14. Нулевой конус, воспроизведенный таким образом, чтобы пространственный и временной
масштабы стали несколько ближе к используемым в повседневной практике
Срезы
абсолютного
времени»

350
Глава ;
по себе и время само по себе превращаются лишь в тени, и только некое единство то¬
го и другого сохраняет независимое существование». На мой взгляд, специальная теория
относительности оставалась неполной, несмотря на удивительную физическую интуицию
Эйнштейна и значительный вклад Лоренца и Пуанкаре, пока Минковский не сформулировал
свой фундаментальный революционный вклад на пространство-время.
Чтобы завершить формулировку идей Минковского относительно геометрии, лежашей
в основе специальной теории относительности, и тем самым определить пространство-вре¬
мя Минковского М, необходимо задать нормировку тензора д, определяющую меру «длины-
мировой линии. Это относится к кривым в пространстве М, называемым времениподобны-
ми, касательные к которым всегда лежат внутри нулевых конусов (см. рис. 17.15 а и 17.111.
Согласно теории, такие кривые являются возможными мировыми линиями обычных частиц,
обладающих массой. Такая «длина» в действительности является временем, она измеряет
время т, регистрируемое (идеальными) часами, между двумя точками Л и Б на этой кривой
в соответствии с формулой (см. §§ 14.7, 13.8)
в	г
г — J ds, где ds = (gabdxadxb)2.
А
Для решения указанной задачи выберем сигнатуру метрики пространства-времени g в ви¬
де Н (я предпочитаю такой выбор, в отличие от некоторых других людей, выбирающих.
по разным причинам, сигнатуру 4- + 4—). Фотоны имеют мировые линии, называемые ну¬
левыми (или светоподобными), касательные к ним лежат на нулевых линиях (рис. 17.15 6Т
а)
Рис. 17.15. а) Мировой линией массивной частицы служит времениподобная кривая, касательные
к которой всегда лежат внутри локальных нулевых конусов, это обеспечивает положительность вели-
1
чины ds2 — gabdxadxb. Величина ds = (gabdxadxb)2 измеряет бесконечно малый интервал времени
вдоль кривой, так что «длина» т = / ds есть время, измеряемое идеальными часами, которые пере¬
носятся частицей между двумя событиями на кривой, б) В случае безмассовой частицы (например,
фотона) касательные к мировым линиям лежат на нулевых конусах (нулевые мировые линии), так что
интервал времени т — J ds всегда равен нулю

17.9. Пространство-время общей теории относительности Эйнштейна
351
В соответствии с этим, «время», которое восприни¬
мает фотон (если бы фотон мог что-нибудь воспри¬
нимать), должно быть равно нулю!
Выше подчеркивалось, что структура нулевых
конусов пространства-времени — это больше, чем
его метрика. В некоторых отношениях нулевые ко¬
нусы действительно имеют более фундаментальный
характер, чем метрика. В частности, они опреде¬
ляют свойства причинности пространства-времени.
Как мы только что видели, мировые линии матери¬
альных частиц должны лежать внутри конусов, а ми¬
ровые линии световых лучей — на самих конусах. Ни¬
какая физическая частица не может иметь простран¬
ственноподобную мировую линию (т. е. лежащую вне
соответствующих световых конусов^17Л21). Если мы
будем рассматривать сигналы, переносимые матери¬
альными частицами или фотонами, то окажется, что
никакой сигнал не может выйти за пределы, ограни¬
ченные нулевыми конусами. Если взять некоторую
точку р в пространстве-времени М, то окажется, что
область, лежащая на ее конусе будущего или внутри
него, состоит из всех событий, которые в принципе
могут получить сигнал из р. Аналогично точки про¬
странства-времени М, лежащие на конусе прошлого
точки р или внутри него, — это те события, кото¬
рые в принципе могут послать сигнал в точку р (см.
рис. 17.16). Эта ситуация сохраняется при распро¬
странении полей и даже при учете квантово-механи¬
ческих эффектов (хотя, как будет показано в § 23.10, могут возникать странные ситуации при
так называемом квантовом перепутывании). Таким образом, нулевые конусы действительно
определяют структуру причинности многообразия М.: никакие материальные тела или сиг¬
налы не могут распространяться быстрее света, они с необходимостью должны находиться
внутри световых конусов (или на самих конусах).
Как обстоит дело с принципом относительности? В § 18.2 мы увидим, что замечатель¬
ная геометрия Минковского имеет такую же группу симметрии, что и пространство-время
галилеевой физики Q. На равных основаниях рассматриваются не только все точки про¬
странства М, ко и все возможные скорости (времениподобные и направленные в будущее).
Более подробно это объясняется в § 18.2. Принцип относительности так же выполняется
для М, как и для Q\
17.9.	Пространство-время общей теории относительности Эйнштейна
Перейдем наконец к эйнштейновскому пространству-времени общей теории относи¬
тельности £. По существу, мы проведем такое же обобщение пространства Минковско¬
го М, какое ранее было сделано при переходе от галилеевского пространства-времени Q
к пространству-времени Ньютона(-Картана) Af. Вместо однородного расположения ну¬
левых конусов, изображенного на рис. 17.12, теперь мы имеем менее регулярное распо¬
ложение, подобное показанному на рис. 17.17. Снова используется лоренцева (Н	)
метрика g, физическая интерпретация которой соответствует времени, измеряемому иде¬
альными часами с использованием той же формулы, что и для М, хотя теперь мы имеем
Рис. 17.16. Будущим для точки р являет¬
ся область, в которую мог ут попасть вре¬
мениподобные кривые, исходящие из р
в ее конус будущего. Показан случай ис¬
кривленного пространства-времени (см.
рис. 17.17). Граница этой области (всюду
гладкая) образуется касательными к све¬
товым конусам. Сигналы, переносимые
массивными частицами и безмассовыми
фотонами, достигают точек внутри этой
области или на ее границе. Аналогично
определяется прошлое для точки р
У Будущее для / / У
ч\}А, точки р /, Cl?
^/Прошлое
] для
(у> точки р

Рис. 17.17. Эйнштейновское пространство-времения общей теории относительности S. Это обоб¬
щение пространства Минковского М аналогично переходу от Q к ЛГ (см. соответственн:
рис. 17.12, 17.3, 17.7 а). Как и в случае пространства М, лоренцева (Н	)	псевдометрика д
определяет физическую меру времени
более сложную метрику д, не обладающую однородностью, присущей метрике простран¬
ства М.
Структура нулевых конусов, определяемая этой метрикой д, устанавливает структур)
причинности в пространстве £, как и в случае пространства Минковского М. В локальном
масштабе разница между этими двумя случаями мала, но ситуация может стать гораздо
более запутанной, если рассматривать глобальную структуру причинности более сложно¬
го эйнштейновского пространства-времени £. Экстремальная ситуация возникает, когда мь:
имеем так называемое нарушение причинности, при котором могут появиться «замкнутые
времениподобные кривые» и становится возможным послать сигнал от некоторого события
в прошлое того же самого события! (См. рис. 17.18.) Подобные ситуации обычно отбра¬
сываются как «нефизические», и мое собственное мнение состоит в том, что их следует
отбрасывать для классически приемлемого пространства-времени. Тем не менее некоторые
физики придерживаются значительно менее строгих взглядов на этот предмет[17Л335 допус¬
кая возможность путешествий во времени, которая открывается благодаря таким замкнутым
времениподобным кривым. (См. обсуждение этих вопросов в § 30.6.) С другой стороны, ме¬
нее экстремальные (хотя тоже довольно экзотические) структуры причинности могут возни¬
кать в некоторых интересных моделях пространства-времени, имеющих непосредственное
отношение к современной астрофизике, а именно к физике черных дыр. Этот вопрос будет
рассмотрен в § 27.8,
В § 14.7 мы столкнулись с тем фактом, что (псевдо)метрика д определяет особую связ¬
ность V без кручения, для которой Vg = 0; здесь мы воспользуемся этим. Этот замеча¬
тельный факт означает, что эйнштейновское понятие инерциального движения полностью
определяется метрикой пространства-времени. Это в корне отличается от ситуации с ньюто¬
новским пространством-временем Картана, где связность V должна задаваться в дополнение
к метрике. Здесь имеется то преимущество, что метрика д теперь является невырожденной,
так что связность полностью определяется ею. Времениподобные геодезические (инерци-
альные движения), соответствующие связности V, определяются тем обстоятельством, что
они являются кривыми, которые (локально) обеспечивают максимум так называемого соб¬
ственного времени. Это собственное время представляет собой просто длину, измеряемую
вдоль мировой линии; это время измеряют идеальные часы, которым соответствует данная
мировая линия. (Здесь имеет место забавная «противоположность» понятию «растяжения)-
геодезической на обычной римановой поверхности с положительно определенной метри¬
кой, см. § 14.7. В § 18.3 мы увидим, что максимизация собственного времени на мировой

17.9. Пространство-время общей теории относительности Эйнштейна
353
Рис. 17.18. Структура причинности пространства-времени £ определяется метрикой д (как и в случае
пространства М, см. рис. 17.16). Гипотетически могут возникать экстремальные нефизические ситуа¬
ции с «замкнутыми времениподобными кривыми», позволяющие сигналам, направленным в будущее,
возвращаться из прошлого
линии без ускорения есть, по существу, выражение «парадокса часов» в теории относитель¬
ности.)
Связности V соответствует тензор кривизны R, имеющий такую же физическую интер¬
претацию, как и в случае пространства ЛЛ Локальное отличие пространства Минковского М
в специальной теории относительности от эйнштейновского пространства £ в общей тео¬
рии относительности состоит в том, что в М имеет место равенство R = 0. В следующей
главе мы будем более полно использовать такую лоренцеву геометрию, а в последующей
увидим, как из эйнштейновских уравнений для поля в структуре £ естественным образом
получается «скорость уменьшения объема» 47тGM, упомянутая в конце § 17.5. Мы также
станем свидетелями необычайной мощи, красоты и точности революционной теории Эйн¬
штейна.
Примечания
$17.1.
17.1. Представляется, что Аристотель испытывал затруднения с понятием бесконечного физическо-
Q
го пространства, необходимого при использовании евклидовой геометрии Е для описания
геометрии пространства. Однако его взгляды на время в большей мере согласуются с Е1 в кар¬
тине Е1 х Ш?. См. [532], гл. 2.
§17.2..
17.2. См. [220], стр. 186-187.
17.3. См. [789, 28] и [590], стр. 126.
§ 17.3.
О
17.4. Это содержалось во фрагменте его рукописи De motu corporum in mediis regulariter cedentibus,
написанной в 1684 году и предшествующей его Началам. См. также [607],'стр. 49.
§17.4.
17.5. См., однако, [89].
17.6. В России теперь появился аттракцион для туристов, в котором пассажиры самолета, описыва¬
ющего параболическую траекторию, могут испытать подобные ощущения.

354
Глава :
§17.6.
17.7. См. [219], стр. 278, где содержится замечание Галилея, сделанное им в Assayег. См. также [55~\
вопрос 30, и [607], стр. 23.
17.8. См. [187].
§17.7.
17.9. Различить случаи сферы и эллипсоида в действительности не так просто, поскольку можн:
так определить единицы измерения в разных направлениях, что эллипсоид будет казаться
сферой. Однако никакая (по крайней мере, никакая «гладкая») калибровка не сможет сделать
так, чтобы сферой выглядел неэллипсоидальный овоид. Такие овоиды приводят к финслерое.
пространству, которое не обладает правильной локальной симметрией (псевдо)римановь::.
структур теории относительности.
§17.8.
17.10. Читатель может удивиться тому, что скорость света, измеряемая в метрах в секунду, оказывает¬
ся точным целым числом. Это не случайность, а отражение того обстоятельства, что проводить
очень точные измерения расстояний гораздо труднее, чем соответствующие измерения вре¬
мени. Поэтому наиболее точный стандарт метра удобно определить таким образом, чтобы
за стандартную секунду свет проходил ровно 299 792 458 метров. Это дает для метра величи¬
ну, очень точно согласующуюся со стандартной метровой линейкой в Париже, недостаточна
точной в современных условиях.
17.11. См. [527]. Это перевод адреса, полученного Минковским на 80-й Ассамблее немецких есте¬
ствоиспытателей и физиков (Колон, 21 сентября 1908 года).
17.12. Некоторые физики забавлялись с идеей гипотетических «частиц», именуемых тахионами, ко¬
торые могут иметь пространственноподобные мировые линии (и потому распространяться
быстрее света). См. [81] и несколько более сложное изложение в [752]. В пользу существова¬
ния т ахионов трудно предложить что-то вроде согласованной теории, поэтому обычно считают,
что такие объекты не существуют.	е
§17.9.
17.13. См., например, [563, 178].
•ш

Глава 18
Геометрия Минковского
18.1.	4-пространство Евклида и Минковского
Геометрия евклидова 2-пространства и 3-пространства нам хорошо знакома. Обобщение
на четырехмерную евклидову геометрию Е4 в принципе несложно, хотя оно и не позволяет
обращаться к «зрительной интуиции». Ясно, однако, что существует много красивых четы¬
рехмерных конфигураций, и они действительно были бы красивыми, если бы мы могли их
увидеть! Одной из наиболее простых (!) подобных конфигураций является картина клиф-
фордовых параллелей на 3-сфере, которую мы считаем находящейся в пространстве Е4.
Конечно, здесь можно несколько повысить степень наглядности, поскольку сфера S3 имеет
лишь 3 измерения и ее стереографическая проекция, показанная на рис. 33.15, дает некото¬
рое представление о действительной клиффордовой конфигурации. (Если бы могли реально
«увидеть» эту конфигурацию как часть пространства Е4, мы смогли бы почувствовать, как
«выглядит» структура комплексного векторного 2-пространства С2; см. § 15.4, рис. 15.8.)^18Л1
Пространство Минковского М во многих отношениях подобно пространству Е4, хотя есть
и некоторое важное отличие, к которому мы сейчас перейдем.
В алгебраическом отношении описание пространства Е4 очень близко к координат¬
ному описанию «обычного» 3-пространства Е3. Все, что требуется, — это добавить еще
одну декартову координату гг к обычным ж, у, z. Расстояние s между точками (гг, ж, у, z)
и (гг7, ж7, у7, z’) в пространстве Е4 определяется по теореме Пифагора
s2 = (гг - гг7)2 4- (ж — ж7)2 4- (у - у7)2 4- (z - z)2.
Если принять, что точки (гг, ж, у, z) и (гг7, ж7, у7, z') лишь «бесконечно мало» сме¬
щены относительно одна другой, и формально написать (dw, dx, dy, dz) для разно¬
сти (гг7, ж7, у7, zf) — (гг, ж, у, z), т. eJ18,2l
w' = гг 4- dw, ж7 = ж 4- dx, у' = у 4- dy, z' = z + cfc,
мы получим
ds2 — cfrr2 + с?ж2 + dy2 -f dz2. *
Длина кривой в E4 определяется такой же формулой, что и в Е3, а именно f ds (ds берется
с положительным знаком).
К этому очень близка геометрия пространства-времени Минковского М, различаются
лишь знаки. Многие из работающих в этой области предпочитают псевдометрику с сигна¬
турой (+ + Н—):
d£2 = — dt2 4- dx2 4- dy2 4- dz2,
поскольку это удобно при описании пространственной геометрии, при этом приведенная
выше величина d£2 положительна для пространственноподобных приращений (т. е. таких,
которые не лежат на нулевых конусах будущего и прошлого или внутри них, см. рис. 18.1).
Однако величина ds2, определяемая сигнатурой (4	):
ds2 = dt2 — dx2 — dy2 — dz2,

356
Глава : j
имеет более непосредственный физический смысл, поскольку она положительна вдоль вре-
мениподобных кривых, которые являются допустимыми мировыми линиями частиц, облада¬
ющих массой. Интеграл / ds (с ds > 0) непосредственно интерпретируется как настоящее
физическое время, измеряемое идеальными часами с такой мировой линией. Я буду поль¬
зоваться именно этой сигнатурой (Н	) при выборе (псевдо)метрического тензора g
с индексной формой даь, так что вышеприведенное выражение в индексной форме можж
записать в виде (см. § 13.8)
ds2 = gabdxadyb.
n
Рис. 18.1. В пространстве Минковского М метрика d£ дает меру квадрата пространственного рас-
стояния для пространственноподобных приращений (не лежащих на нулевых конусах будущего или
прошлого либо внутри них). Для времениподобных приращений (лежащих внутри нулевого кону¬
са) ds2 дает меру квадрата временного интервала, при этом J ds есть физическое время, измеряемое
идеальными часами. При нулевом приращении (лежащем на нулевом конусе) обе величины, d£2 и ds2.
равны нулю
Следует, однако, напомнить (см. § 17.8), что, в отличие от случая массивной части¬
цы, интеграл f ds для мировой линии фотона равен нулю (так что не совпадающие между
собой точки на мировой линии могут быть разделены «нулевым расстоянием»). Это бу¬
дет справедливо и. для любой другой частицы, движущейся со скоростью света. Время,
«воспринимаемое» такой частицей, всегда будет равно нулю независимо от того, на сколь
большое расстояние она удалилась! Такое возможно из-за неположительно определенной
(лоренцевой) природы тензора даъ•
На заре теории относительности существовала тенденция подчеркивать близость гео¬
метрии пространства М евклидовой геометрии Е4, считая временную координату t чисто
мнимой:
t — iw;
при этом форма d£2 метрики Минковского выглядит точно так же, как ds2 для Е4. Ко¬
нечно, это сходство несколько иллюзорно из-за неестественно выглядящего условия «ве¬
щественности», при котором время измеряется в чисто мнимых единицах, тогда как для

18.2. Группы симметрии пространства Минковского
357
пространственных координат используются ооычные вещественные единицы, ьолее того,
в движущейся системе отсчета эти условия вещественности усложняются, поскольку ве¬
щественные и мнимые координаты основательно смешиваются между собой. Фактически
существует и современная тенденция, очень близкая к этому, в различных обличьях, под
названием «евклидова квантовая теория поля». Далее, в § 28.9, я объясню, почему я не в
восторге от такого образа действий (по крайней мере, если рассматривать его как основную
составляющую подхода к новой фундаментальной физической теории, как это иногда дела¬
ется; этот прием используется также как некий «трюк» для получения ответов на вопросы
в квантовой теории поля, и в этом случае он действительно играет полезную роль).
Вместо того чтобы принять подобный образ действий, который выглядит (по крайней
мере, на мой взгляд) довольно неестественно, попробуем «пойти до конца», позволив всем
нашим координатам принимать комплексные значения (см. рис. 18.2). При этом исчеза¬
ет различие между разными сигнатурами, наши комплексные координаты ад тд (' теперь
относятся к комплексному пространству С4, которое можно рассматривать как комплекси-
фикацию СЕ4 пространства Е4. По отношению к комплексному аффинному пространству
(см. § 14.1) это есть то же самое, что и комплексификация СМ пространства М. Более то¬
го, оба комплексных 4-пространства СЕ4 и СМ имеют полностью эквивалентную плоскую
(с нулевой кривизной) комплексную метрику Сд. Эту метрику можно взять в виде ds2 =
= dco2 -f d£2 + drf 4- d('2, при этом E4 есть вещественное подпространство пространства СМ,
в котором все величины ид 7Д £ вещественны, а М — пространство, в котором вели¬
чина со вещественна, а гд £ — чисто мнимые величины. Альтернативное вещественное
подпространство Минковского М получается, если взять величину со чисто мнимой, а ве¬
личины £, г/, £ — вещественными; в этом случае ds2 есть вышеприведенный вариант d£2
метрики Минковского, Три подпространства Е4, М и М называются (альтернативными) ее-
_ _	     ..	_	ля	_ _ 	 	/Т
щественными срезами или сечениями пространства СЕ . Мы можем выбрать любое из них,
если ввести в пространстве СЕ4 операцию комплексного сопряжения С, которая является
инволютивной (т. е. обладает свойством С2 = 1) и оставляет точечно-инвариантным только
выбранное вещественное сечение*.
18.2.	Группы симметрии пространства Минковского
Группа симметрии пространства Е4 (т. е. группа евклидовых движений в этом простран¬
стве) 10-мерна, так как 1) группой симметрии, для которой задано начало координат, является
6-мерная группа вращений 0(4) (потому что п(п — 1)/2 — 6 при п — 4; см. § 13.8) и 2) име¬
ется 4-мерная группа симметрии переносов (трансляций) начала координат, см. рис. 18.3 а.
Если взять комплексификацию СЕ4 пространства Е4, получится группа с 10 комплексными
измерениями; ясно, что если мы представим любое из вещественных евклидовых движе¬
ний пространства Е4 в виде алгебраической формулы, содержащей координаты, то все, что
от нас потребуется, — это позволить всем величинам, входящим в формулу (координатам
и коэффициентам), принимать не только вещественные, но и комплексные значения, при
этом мы получим соответствующее комплексное движение пространства СЕ4. Поскольку
первое из этих движении сохраняет метрику, то же относится и ко второму, ьолее того, та¬
кую же природу имеют все непрерывные движения, переводящие пространство СЕ4 в само
себя, которые сохраняют комплексифицированную метрику С д.
Теперь выглядит весьма правдоподобно, хотя на данной стадии и не вполне очевидно,
что группа должна иметь те же 10 измерений (но теперь уже не вещественных измерений),
1.Щ>
Определите операцию С в явном виде для каждого из трех случаев Е , М и М. (.Подсказка. Посмотрите,
как действует операция С на о;, £, 7? и В случаях М и М сопровождайте комплексное сопряжение изменением
знака.)
** Понятно ли, почему это так?

358
Глава 1'
Рис. 18.2. Комплексное евклидово пространство QE4 имеет комплексную (голоморфную) метри¬
ку ds2 — duj2 + d£2 + drf + d(2 в комплексных декартовых координатах (щ, £, 77, С)- Евклидово
4-пространство Е4 является вещественным сечением, в котором все величины £, 77, С, вещественны.
Пространство Минковского М с метрикой Н	ds2	служит другим вещественным сечением, в кото¬
ром величина щ вещественна, а £, 77, £ ~ чисто мнимые величины. Еще одно лоренцево вещественное
сечение М получается, если взять величину и чисто мнимой, а величины £, 77, С ~ вещественными:
О	.о
в этом случае ds~ есть вариант + + 4— d£ метрики Минковского
если мы обратимся к другому «действительному сечению» пространства СЕ4 с координа¬
тами (сд, £, г7, С)? в котором условие вещественности сводится к чисто мнимой величине и;
и действительным величинам £, 77, С (сигнатура +4-4—), или к такому, в котором величина ст
вещественна, а £, 77, ( ~ чисто мнимые величины (сигнатура 4	); см. рис. 18.3. Транс¬
ляционная часть, очевидно, по-прежнему остается четырехмерной. Фактически эта часть
соответствует транзитивности на М; это означает, что любую выбранную точку простран¬
ства М можно перевести в любую другую точку этого пространства с помощью некоторого
элемента группы, как это было в случае пространства Е4. А как обстоит дело с группой Ло¬
ренца (0(3, 1) или 0(1, 3))? Как можно увидеть, что она шестимерна, подобно группе 0(4)?
На самом деле группа Лоренца действительно шестимерна (см. рис. 18.3 б). Наиболее об¬
щий способ состоит в том, чтобы рассмотреть алгебру Ли (см. § 13.6) и убедиться, что она
применима при небольшом изменении знаков . Вскоре (в § 18.5) мы познакомимся с другим
довольно замечательным способом рассмотреть группу 0(1, 3) и убедиться в ее шестимер-
ности, связав ее с группой симметрии сферы Римана.
Полная 10-мерная группа симметрии пространства Минковского М носит название
группы Пуанкаре в знак признания заслуг выдающегося французского математика Анри Пу¬
анкаре (1854-1912) в построении математической структуры специальной теории относи¬
тельности в период с 1898 по 1905 год, независимо от фундаментального вклада Эйнштейна
в 1905 году.^18*3! Группа Пуанкаре играет важную роль в релятивистской физике, особенно
Подтвердите это, рассмотрев в явном виде матрицы алгебры Ли 4 х 4.

18.3. ЛОРЕНЦЕВА ОРТОГОНАЛЬНОСТЬ. «ПАРАДОКС ЧАСОВ»
359
6
а)
б)
Рис. 18.3. а) Группа евклидовых движений пространства Е4 10-мерна, поскольку группой симметрии
при фиксированном начале координат является 6-мерная группа вращений 0(4), а группа переносов
начала координат 4-мерна, б) Симметрия пространства М определяется 6-мерной группой Лорен¬
ца 0(1, 3) (или 0(3, 1)) для фиксированного начала координат и 4 измерениями для переносов, что
дает 10-мерную группу симметрии Пуанкаре
в физике элементарных частиц и квантовой теории поля (главы 25 и 26). Оказывается, что,
согласно правилам квантовой механики, отдельные элементарные частицы соответствуют
представлениям (§§13.6, 13.7) группы Пуанкаре, при этом значения массы и спина частиц
определяют то или иное представление (§22.12).
Ценность этой группы, по существу, заключается в том, что она позволяет утверждать
применимость принципа относительности к пространству М, несмотря на наличие фиксиро¬
ванной скорости света (§§ 17.6, 17.8). Прежде всего, мы видим, что каждая точка простран¬
ства-времени М выступает на равных правах с любой другой точкой вследствие транзитив¬
ного характера подгруппы трансляций. Кроме того, мы имеем полную пространственную
вращательную симметрию (3 измерения). Это оставляет еще 3 измерения для выражения
того факта, что существует полная свобода переходить от одной скорости (< с) к любой
другой, при этом вся структура остается той же самой, — это, в сущности, и означает при¬
менимость принципа относительности к пространству М! В более формальном выражении
принцип относительности утверждает, что группа Пуанкаре действует транзитивно на пучке
времениподобных направлений будущего в пространстве М. ^18'4^ Это те направления, которые
указывают во внутреннюю часть нулевых конусов будущего и являются положительными
направлениями касательных к мировым линиям наблюдателей . Можно отметить, однако,
что все это связано с нашим отказом от семейства «одновременных срезов» в простран¬
стве-времени Галилея или Ньютона. Сохранение их понизило бы симметрию относительно
пространственно-временной точки до трехмерной симметрии 0(3), не оставив никакой сво¬
боды для перехода от одной скорости к другой.
18.3.	Лоренцева ортогональность. «Парадокс часов»
С предложенной точки зрения, пространство М рассматривается как «вещественное се¬
чение» или «срез» комплексного пространства СЕ4 (или С4), но это сечение имеет иной
характер, нежели само пространство Е4. Такая точка зрения весьма удобна, поскольку
дает правильное направление рассуждениям. Например, в евклидовом пространстве Е4
Объясните такое действие группы Пуанкаре более подробно.

360
Глава i;
мы имеем понятие «ортогональный» (что означает «направленный под прямым углом»?.
Это понятие непосредственно переносится на пространство СЕ4 с помощью процесса
«комплексификации»[18 5Г Имеются, однако, свойства иного типа, которые, как следует
ожидать, в результате этой процедуры претерпевают некоторое изменение. Оказывается,
например, что в пространстве СЕ4 направление может быть ортогонально самому себе, что
заведомо невозможно в Е4. Эта особенность, однако, сохраняется при возвращении к нашем)
новому вещественному сечению — лоренцеву пространству М. Таким образом, мы сохра¬
няем в М понятие ортогональности, но обнаруживаем, что теперь имеются вещественные
направления, ортогональные самим себе, — это будут нулевые направления, указывающие
вдоль мировых линий фотонов (см. ниже).
Можно развить далее понятие ортогональности и рассмотреть ортогональное дополне¬
ние Г}х элемента 77 r-плоскоети в точке р. Таковым является элемент г}± (4 — г)-плоскости
во всех направлениях в точке р, которые ортогональны всем направлениям в этой точке эле¬
мента г]. Таким образом, ортогональным дополнением линейного элемента является элемент
3-плоскости, ортогональным дополнением элемента 2-плоскости — элемент другой 2-плос¬
кости, ортогональным дополнением элемента 3-плоскости — линейный элемент. Во всех
случаях, перейдя к ортогональному дополнению повторно, мы получим исходный элемент,
другими словами, (г)^)1- = т/. Напомним, что в §§ 13.9, 14.7 мы рассматривали операции
опускания и поднятия индексов векторных или тензорных величин с помощью тензора gai
или gab. Будучи примененной к простому r-вектору или к простой (4 — г)-форме, пред¬
ставляющей элемент r-поверхности в соответствии с §§ 12.4, 12.7 (например, rjab > г)аЬ =
— Vcd9ac9bdj ??а6 |“> Vab ~ r1cd9ac9bd), эта операция поднятия/опуекания индексов соответ¬
ствует переходу к ортогональному дополнению (см. также § 19.2).
Например, в пространстве Е4 ортогональным дополнением элемента 3-плоскости т?
служит линейный элемент г]1 (нормаль к 77), не содержащийся в 77; см. рис. 18.4. Как и на
рис. 18.2, можно перейти к комплексификации СЕ4, а оттуда — к другому вещественном)
сечению М. Фактически мы уже прибегали к этой процедуре в предыдущей главе (§ 17.8).
когда задавались вопросом об ортогональной компоненте временного среза (элементе про¬
странственноподобной 3-плоскости) в некоторой точке р9 чтобы найти времениподобное
направление («состояние покоя»), при этом мы убедились, что принцип относительности не
может быть сохранен, если мы хотим иметь конечную скорость света и абсолютное время
(см. рис. 17.13)*. Теперь, однако, попробуем прочитать это в обратном направлении. Рас¬
смотрим инерциального наблюдателя в некоторой точке (событии) р пространства М. Пред¬
положим, что мировая линия наблюдателя в точке р имеет некоторое (времениподобное)
направление т. Тогда 3-пространство тх представляет собой семейство «чисто простран¬
ственных» направлений для этого наблюдателя в точке р, т. е. соседних событий, которые
наблюдатель считает одновременными с р.
В мои цели не входит подробное изложение специальной теории относительности и,
в частности, обсуждение разумности такого понимания «одновременности». По этим вопро¬
сам читатель может обратиться к нескольким прекрасным книгам t18-6!. Следует отметить,
однако, что это понятие одновременности действительно зависит от скорости наблюдате¬
ля. В евклидовой геометрии ортогональное дополнение направления в пространстве будет
меняться при изменении этого направления (рис. 18.5а). Соответственно в лоренцевой гео¬
метрии ортогональное дополнение также будет меняться, когда изменяется направление
(т. е. скорость наблюдателя). Единственная разница состоит в том, что такое изменение при¬
водит к наклону ортогонального дополнения в противоположном направлении по сравнению
со случаем евклидовой геометрии (см. рис. 18.5 6); соответственно становится возможной
1) При каких условиях элемент 3-плоскости т)вМ может содержать свою нормаль 2) Покажите,
что существуют два различных семейства 2-плоскостей, которые являются ортогональными дополнениями самих
себя в QE4, но ни одно из них не сохраняется в М (Эти так называемые «самодуальные» и «антисамодуальные»
комплексные 2-плоскости окажутся важными в дальнейшем; см. §§ 32.2, 33.11.)

18.3. ЛОРЕНЦЕВА ОРТОГОНАЛЬНОСТЬ. «ПАРАДОКС ЧАСОВ»
361
Рис. 18.4. В пространстве Е4 элемент г) г-плоскости в точке р имеет ортогональное дополнение ,
которое является элементом (4 — г)-плоскости, при этом г) и гне могут иметь общее направление.
а) В частности, если -ц есть элемент 3-плоскости, то rj± представляет направление нормали к нему.
б) Если т) есть элемент 2-плоскости, то г}^ представляет элемент другой 2-плоскости
ситуация, при которой ортогональное дополнение направления может, как отмечалось выше,
содержать это направление (см. рис. 18.5 в), такое происходит в случае нулевого направле¬
ния (т. е. лежащего на световом конусе).
а)
в)
Рис. 18.5. а) В евклидовой 4-геометрии при вращении направления то же происходит с его ортого¬
нальным дополнением — элементом 3-плоскости, б) Это справедливо также в лоренцевой 4-геомет¬
рии, но в случае времениподобного направления наклон ортогонального дополнения (3-плоскости,
образуемой пространственными направлениями «одновременности») меняется в противоположном
направлении, в) В случае нулевого направления ортогональное дополнение действительно содержит
это направление
При переходе от 1Е к М меняются также некоторые неравенства. Наиоолее драматич¬
ные изменения выражают сущность так называемого «парадокса часов» (или «парадокса
близнецов») в специальной теории относительности. Некоторые читатели, возможно, знако¬
мы с этим «парадоксом». Он касается космического путешественника, который отправляется
в ракетном корабле к далекой планете, движется со скоростью, близкой к скорости света, и,
вернувшись на Землю, обнаруживает, что время здесь ушло на много веков вперед, тогда

362
Глава Н
как сам он постарел лишь на несколько лет. Как подчеркивал Бонди [92, 93], если мь:
примем, что течение времени, регистрируемое движущимися часами, действительно есть
своего рода «длина дуги», измеряемая вдоль мировой линии, то этот эффект оказывается
не более удивительным, чем тот факт, что расстояние между двумя точками в евклидовом
пространстве зависит от пути, вдоль которого измеряется это расстояние. В обоих случаях
длина определяется одной и той же формулой, f ds, но в евклидовом случае прямой путь
представляет минимальное расстояние между двумя фиксированными концевыми точками,
а в случае пространства Минковского оказывается, что прямая, т. е. инерциалъная, траектория
соответствует максимуму измеренного времени между двумя фиксированными концевыми
событиями (см. также § 17.9).
Основное неравенство, из которого все это вытекает, — это так называемое неравенстве
треугольника обычной евклидовой геометрии. Если взять произвольный треугольник ABC
в евклидовом пространстве, то длины его сторон будут удовлетворять неравенству
АВ + ВС > АС.
в котором равенство имеет место только в вырожденном случае, когда точки А, В и С лежат
на одной прямой (см. рис. 18.6 а). Конечно, ситуация вполне симметрична и не зависит
от выбора стороны АС. В лоренцевой геометрии мы имеем согласованное неравенство
треугольника, лишь когда все стороны времениподобны, при этом необходимо следить,
чтобы мировые линии АВ, ВС и АС были направлены в будущее (см. рис. 18.66). Наше
неравенство в этом случае меняет знак:
АВ + ВС < АС,
и равенство опять-таки имеет место, когда все три точки А, В и С лежат на одной прямой —
мировой линии инерциальной частицы. Интерпретация этого неравенства как раз и дает
«парадокс часов». Мировой линией космического путешественника служит ломаная АБС.
тогда как обитателям Земли соответствует мировая линия АС. Видно, что, согласно этому
неравенству, часы путешественника действительно зарегистрируют более короткое полное
время путешествия, чем часы на Земле.
Некоторые могут возразить, что в этом описании не учтено должным образом ускоре¬
ние космического корабля. Действительно, я несколько идеализировал ситуацию, так что на
космонавтов должно действовать импульсное (т. е. бесконечное) ускорение в точке (собы¬
тии) В (которое должно иметь роковые последствия!). Однако положение легко исправить,
просто скруглив углы треугольника, как показано на рис. 18.6 г. На разность времен это силь¬
но не повлияет, что очевидно из соответствующей ситуации для евклидова «скругленного»
треугольника, показанного на рис. 18.6 в. Часто утверждается, что для учета ускорения необ¬
ходим переход к общей теории относительности Эйнштейна, но это совершенно неверно.
В обеих теориях результат измерения времени часами получают с помощью формулы J ds
(при ds > 0). Специальная теория относительности допускает ускорение космонавта точно
так же, как и общая. Разница лишь в метрике, используемой при вычислении величины f ds,
т. е. последняя зависит от вида gij. Мы пользуемся специальной теорией относительности
с плоской метрикой геометрии Минковского М. Физически это означает, что можно пре¬
небречь гравитационными полями. Если потребуется учесть такие поля, мы должны будем
ввести искривленную метрику общей теории относительности Эйнштейна. Подробнее это
будет обсуждено в следующей главе.
18.4.	Гиперболическая геометрия в пространстве Минковского
Рассмотрим некоторые дальнейшие аспекты геометрии Минковского и ее связь с гео¬
метрией Евклида. В евклидовой геометрии геометрическим местом точек, находящихся на

18.4. Гиперболическая геометрия в пространстве Минковского
363
С
В
а)
6)
С
А
В
в)
г)
Рис. 18.6. а) Неравенство треугольника в евклидовой геометрии AB-f ВС ^ АС; равенство имеет место
только в вырожденном случае, когда точки А, В, С лежат на одной прямой, б) В лоренцевой геометрии
с времениподобными мировыми линиями АВ, ВС, АС, направленными в будущее, неравенство меня¬
ет знак: АВ+ВС ^ АС, при этом равенство имеет место, когда точки А, В, С лежат на одной мировой
линии инерциальной частицы. Это иллюстрирует «парадокс часов», в специальной теории относитель¬
ности, состоящий в том, что космический путешественник с мировой линией ABC воспринимает
более короткий временной интервал, нежели обитатели Земли с мировой линией АС. в) «Скругление»
углов евклидова треугольника слабо влияет на длину его сторон, и прямой путь по-прежнему остается
самым коротким, г) Аналогично переход к конечному ускорению (путем «скругления» углов) слабо
влияет на измеряемые времена, и прямая (инерциальная) траектория остается наиболее длинной

364
Глава 18
заданном расстоянии а от некоторой фиксированной точки О, является сфера. В простран¬
стве Е4 это, конечно, 3-сфера §3. Как обстоит дело в М? Здесь нужно рассмотреть две
ситуации в зависимости от того, является ли величина а действительным (в частности,
положительным) числом или чисто мнимым (я использую предпочитаемую мной сигнату¬
ру Н , в обратном случае эти ситуации меняются местами); на рис. 18.7 показаны оба
случая.
Рис. 18.7. «Сферы» в М как геометрические места точек, находящихся на заданном расстоянии Мин¬
ковского а от фиксированной точки О. При а > 0 (и сигнатуре н	) мы имеем два «гипербо¬
лических» куска — «чашевидный» Н+ (внутри светового конуса будущего) и «холмообразный» Н~
(внутри светового конуса прошлого). В случае мнимой величины а (или вещественной величины при
сигнатуре + 4- 4— d£2) получаем однополостной гиперболоид, отделенный от точки О простран¬
ственноподобными интервалами
Случаем мнимого а мы здесь специально заниматься не будем. Предположим а > О
(случай а < 0 эквивалентен рассматриваемому). Тогда наша «сфера» состоит из двух кус¬
ков — «чашевидного» 7Г+, лежащего внутри светового конуса будущего, и «холмообраз¬
ного» Н~, лежащего внутри светового конуса прошлого. Сосредоточим внимание на
(пространство Н~ аналогично). Какова внутренняя метрика на 7i+? Она определенно насле¬
дует метрику, налагаемую на нее при ее погружении в пространство М. (Например, длину
кривой в Н+ определяют, просто считая ее кривой в М.) В этом случае предпочтительной
мерой является величина d£2 (с сигнатурой 4- 4- 4—), поскольку направления вдоль 7i+
пространственноподобны. Можно попробовать угадать метрику пространства 7исходя из
того, что это есть в некотором роде «сфера», но «с измененными знаками». Какой может быть
эта метрика? Вспомним рассуждения Иоганна Ламберта в 1786 году относительно возмож¬
ности построения геометрии, в которой нарушается пятый постулат Евклида. Он показал,
что «сфера» мнимого радиуса позволяет построить такую геометрию при условии, что такой
объект действительно имеет смысл. Фактически приведенное выше построение дает как
раз такое пространство — модель гиперболической геометрии, — но теперь оно трехмерно.

18.4. Гиперболическая геометрия в пространстве Минковского
365
Чтобы получить неевклидову плоскость Ламберта (гиперболическую плоскость), достаточно
в описанном построении освободиться от одного из пространственных измерений. В лю¬
бом случае «гиперболическими прямыми линиями» (геодезическими) служат просто линии
пересечения пространства 7Т+ 2-плоскостями, проходящими через точку О (рис. 18.8).
«Прямая линия»
в геометрической геометрии
пространства Н
Рис. 18.8. «Гиперболической прямой линией» (геодезической) в пространстве является линия пе¬
ресечения этого пространства 2-плоскостью, проходящей через точку О. (Показан двумерный случай,
но он вполне аналогичен трехмерному ТС+.)
Конечно, было бы фантазией предположение, что Ламберт подсознательно подразуме¬
вал что-то похожее на такую конструкцию. Тем не менее она иллюстрирует внутреннюю
согласованность общих идей такого рода, в которых сигнатура может менять знак, так
что вещественные величины становятся мнимыми, а мнимые — вещественными. Ламберт
вполне мог иметь интуитивное представление об этом. Поучительно взглянуть на рис. 18.9.
Там изображен световой конус t2 — х2 - у2 — z2 = 0 (у-измерение опущено) в 4-пространстве
Минковского М с координатами (£, х, у, z) и построено семейство сечений конуса плоско¬
стями
z -\-1 Т* X(t — z) — 2,
проходящими через плоскость t — 1 = z9 при различных значениях Л. Такие сечения дву¬
мерны (сам конус трехмерен), и оказывается, что для каждого положительного значения Л
метрика такой 2-поверхности в точности совпадает с 2-метрикой сферы радиуса А~1//2 —
= 1/>/А. При А = 0 получаем метрику обычной евклидовой плоскости. (Такое сечение
выглядит не «плоским», а «параболоидальным», тем не менее его внутренняя метрика дей¬
ствительно плоская.)* При отрицательных значениях А сечением становится сфера Ламберта
мнимого радиуса (= 1/у/Х). Она имеет внутреннюю метрику гиперболической геометрии
(определяемую из М2). Таким образом, мы видим, что интуитивная догадка Ламберта о том,
что может иметь смысл сфера мнимого радиуса, спустя века оказалась полностью подтвер¬
жденной.
Покажите все это. (Подсказка: удобно использовать координаты х, у и w, где w
= (1 -t-z)/y/X.)
(t — z — 1/А)л/А —

366
Глава 18
Рис. 18.9. Сечения светового конуса t2 — х2 — у2 ~ z2 ~ 0 3-плоскостями z -f t + A(t — z) = 2,
проходящими через 2-плоскость t — 1 — z. Координата у опущена, так что размерности выглядят
на единицу меньшими. При А > 0 сечение S имеет d£2-метрику 2-сферы, которая иллюстрируется
для горизонтального случая А = 1. При А = 0 получаем плоскую евклидову di2-метрику парабо-
лоидального сечения Е. При А < 0 имеем гиперболическую d£2-метрику, которая иллюстрируется
вертикальным гиперболическим сечением Н для случая А = — 1
Построение гиперболической геометрии как «псевдосферы» может быть непосред¬
ственно связано с конформным и проективным представлениями Бельтрами, описанными
(для двумерного случая) в §§2.4, 2.5. На рис. 18.10 показано, каким образом получаются
(0,0,0)
(-1,0,0)
\
М
з
Проективная
модель
Конформная
модель
Рис. 18.10. В 3-пространстве Минковского М3 гиперболическая двумерная геометрии «псевдосфе¬
ры» 7i+, заданной уравнением t2 — х2 — у2 = 1, непосредственно связана с конформным и проектив¬
ным представлениями Бельтрами (показанными соответственно на рис. 2.11 и 2.16 в виде гравюры
Эшера и ее искаженного варианта). Проективная («клейновская») модель Бельтрами получается как
проекция псевдосферы из начала координат (0, 0, 0) на внутреннюю часть единичного круга в
плоскости t = 1. Конформная модель Бельтрами («модель Пуанкаре») получается проектировани¬
ем 7Т+ из точки (—1, 0, 0) на внутреннюю часть единичного круга в плоскости t = 0. (См. также
пример геометрии Бельтрами на рис. 2.17.) Аналогичное построение применимо также к гиперболи¬
ческой 3-геометрии в пространстве М

18.4. Гиперболическая геометрия в пространстве Минковского
367
эти представления из 7Y+, на примере двумерных псевдосфер в 3-пространстве Минков¬
ского М3 (с координатами (t, ж, у)). Задавая 71+ уравнением t2 — ж2 — у2 = 1, получаем
«клейновское» (т. е. проективное) представление Бельтрами путем проектирования из начала
координат (0, 0, 0) на плоскость t — 1 и «представление Пуанкаре» (конформное представле¬
ние Бельтрами) путем проектирования из «южного полюса» (—1, 0, 0) на «экваториальную
плоскость» t = 0 (т. е. используя «стереографическую проекцию», см. § 8.3, рис. 8.7.)*.
Заметим, что точки псевдосферы 71+ представляют времениподобные направления в бу¬
дущее (для определенности я взял а — 1). Это просто возможные скорости частицы, обла¬
дающей массой. Поэтому 7i+ можно рассматривать как пространство скоростей в теории
относительности. (Напомним, что это понятие было введено в конце § 2.7.) Один из результа¬
тов теории относительности, который наиболее часто воспринимается с недоверием, состоит
в том, что нельзя просто складывать скорости обычным образом. Так, например, если кос-
О .
мический корабль, движущийся в некотором направлении со скоростью -с относительно
Земли, выпускает в том же пространственном направлении снаряд со скоростью | с относи¬
тельно корабля, то скорость снаряда относительно Земли будет иметь величину лишь ||с,
ZO
о о	о
а отнюдь не сверхсветовую величину (| + |)с = ~с. (Здесь с есть скорость света, выписы¬
ваемая лишь для большей ясности; обычно единицы измерения выбираются так, что с — 1.)
Этот факт можно понять как результат сложения длин в гиперболической геометрии (см.
рис. 18.11)**.
V
Рис. 18.11. Пространством скоростей в теории относительности служит (единичное) гиперболическое
пространство 7i+, в котором быстрота р (= Arthv) измеряет гиперболическое расстояние вдоль 7L+
(скорость света с = 1 соответствует бесконечному р). Это аналогично (если «обратить» сигнатуру)
расстоянию вдоль единичной окружности, измеряемому центральным углом 0
Чтобы понять это, необходимо дать физическую интерпретацию гиперболической «дли¬
ны». Это есть величина, называемая быстротой, которую я буду обозначать греческой бук¬
вой р\ она связана со скоростью v соотношениями (иллюстрируемыми на рис. 18.12)
1 т 1 + v	ер	—	е~р
р = - log   , т. е. v — -
И 2	ер	+	е~р
Объясните, почему гиперболические прямые линии представляются прямыми в «клейновском» случае
и окружностями, ортогонально пересекающими границу, в «случае Пуанкаре». Используя «обращение сигнатуры»,
покажите, что этот последний случай действительно является конформным представлением.
Применяя рассуждения с «обращением сигнатуры», объясните, почему сложение длин в гиперболической
геометрии должно приводить к используемой здесь формуле (и -f v)c/ (1 4- uv) для «сложения» скоростей ис
и vc, имеющих одно и то же направление в пространстве. Рассмотрите сложение длин дуг окружности или сферы.
«Скорость», соответствующая каждой длине дуги, есть тангенс центрального угла, стягиваемого этой дугой.

368
Глава 18
(правое выражение есть так называемый «гиперболический тангенс» от р, обозначае¬
мый thp). Быстрота есть просто , мера «расстояния» в гиперболическом пространстве Н+
г
(для которого выбран единичный псевдорадиус а = 1 (см. §§2.4, 2.6)). Для скоростей v,
малых по сравнению со скоростью света, быстрота совпадает с v* Заметим, что граница
на рисунке Эшера (рис. 2.11), описывающая бесконечность в гиперболической геометрии
(р = со), представляет недостижимую предельную скорость с (= 1).
Рис. 18.12. График зависимости скорости v (отнесенной к скорости света с =
определяемой соотношением р = — log{(l + v)/(l — г>)}, т. е. v — (ер — е р)/(ер + е р)
Zj
1) от быстроты р,
thp
¥
Векторное сложение скоростей, имеющих одно и то же направление, описывается
просто как сложение их быстрот (т. е. сложение гиперболических длин), см. рис. 18.13 а.
Чтобы складывать скорости различного направления, можно воспользоваться процедурой,
предложенной для обычных поворотов в § 11.4 (см. рис. 11.4), с соответствующим «обра¬
щением сигнатуры». Здесь мы применяем гиперболическое правило треугольника к двум
слагаемым скоростям, каждая из которых представлена гиперболическим отрезком, гипер¬
болическая длина которого равна половине соответствующей быстроты (в согласии с тем
фактом, что длина дуги на рис. 11.4 равна половине соответствующего угла поворота);
см. рис. 18.13 б.
а)
б)
Рис. 18.13. Сложение релятивистских скоростей в гиперболическом пространстве скоростей .
а) При одинаковом направлении скоростей просто складываются соответствующие быстроты.
б) Для сложения скоростей различного направления используется правило треугольника, при этом
гиперболические длины сторон треугольника составляют половину соответствующих быстрот. (Срав¬
ните с рис. 11.46, иллюстрирующим сложение обычных поворотов в 3-пространстве, доказательство
можно провести аналогично.)
Подтвердите это утверждение и докажите эквивалентность двух вышеприведенных формул.

18.5. Небесная сфера как сфера Римана
369
18.5.	Небесная сфера как сфера Римана
Рассмотрим теперь внутреннюю геометрию «границы на бесконечности» в случае ги¬
перболической геометрии Мы должны рассматривать полное четырехмерное простран¬
ство-время Минковского, так что указанной границей будет сфера S2 (а не окружность S1,
которая служила границей гравюры Эшера на рис. 2.11). Каждая точка этой сферы пред¬
ставляет некоторое направление вдоль самого нулевого конуса и соответствует предельной
скорости (скорости света), недостижимой для частиц, обладающих массой. Эта предельная
скорость достижима, однако, для безмассовых частиц, и такая скорость является единствен¬
но возможной для свободно движущихся безмассовых частиц. К счастью для нас, такими
безмассовыми частицами являются фотоны, которые мы способны видеть. Если ясной безоб¬
лачной ночью вы взглянете на небо, то увидите над собой полусферический купол, усеянный
мириадами звезд. На самом деле вы воспринимаете семейство световых лучей, образующих
световой конус с вершиной в пространственно-временной точке (событии) О, где находится
ваш глаз в тот момент, когда вы люоуетесь неоесным сводом, практически вы видите лишь
приблизительно половину лучей светового конуса, но если представить, что вы находитесь
в космическом пространстве и имеете полный обзор окружающей вас небесной сферы, то
вам представится картина сферы лучей, составляющих полный световой конус для точки О.
Вероятно, проще считать, что эта сфера представляет конус прошлого для точки О, посколь¬
ку мы имеем дело с лучами, приходящими в наш глаз, а не выходящими из него. Однако
световые лучи, будучи прямыми на нулевом конусе, протянуты в обе стороны, из прошлого
*
в будущее, поэтому можно считать, что на небесной сфере представлено полное семейство
S световых лучей, проходящих через точку О. (См. также § 33.2.)
Это пространство S определенно обладает топологией 2-сферы, но имеет ли оно какую-
либо структуру? Мы можем снабдить его метрикой и рассматривать как двумерное римано-
во пространство. Наиболее очевидный путь к этому — провести сечение светового конуса,
например, пространственной 3-плоскостью t = — 1 и представить S метрической сферой
единичного радиуса х2 -Ь у2 + z2 = 1 (это следует из уравнения конуса t2 — x2~y2~~z2 = 0),
Вместо этого можно было пересечь конус плоскостью t = 1 и снова получить сферу единич¬
ного радиуса, связанную с первой антиподным отображением (которое сохраняет прежнюю
метрику). Однако указанные способы проведения сечений ничем не выделены, если не за¬
дать мировую линию некоторого определенного наблюдателя, проходящую через точку О,
и не пользоваться t-координатой этого наблюдателя. Для другого наблюдателя, который стал¬
кивается с тем же событием О, но движется с некоторой высокой скоростью относительно
первого, вид небесной сферы может быть несколько искажен по сравнению с тем, что видит
первый
Действительно, существует некоторый вид искажения вследствие эффекта звездной
аберрации, открытого Джеймсом Бредли в 1725 году. Эффект состоит в том, что видимое
положение звезды на небесном своде имеет небольшое сезонное смещение, обусловлен¬
ное различным значением скорости Земли в разных местах ее орбиты вокруг Солнца. Этот
эффект похож на то, что обычно наблюдают автомобилисты при езде с большой скоро¬
стью под дождем. Тем, кто находится в автомобиле, кажется, что дождь падает не сверху,
а почти спереди, тогда как с точки зрения наблюдателя, стоящего на земле, дождь идет прак¬
тически вертикально. Этот эффект связан с тем фактом, что для получения наблюдаемой
относительной скорости необходимо должным образом сложить скорость дождевых капель
со скоростью автомобиля. В данной ситуации скорость автомобиля обычно гораздо больше
скорости дождевых капель, так что основной видимый эффект связан с движением автомо¬
биля. В случае звезды, наоборот, вариации орбитальной скорости Земли намного меньше
корости света, приходящего к нам от звезды. В соответствии с этим сезонные изменения
видимого положения звезды на небесном своде весьма малы (приблизительно 20 угловых

370
Глава 18
секунд). Тем не менее существует такой эффект искажения небесной сферы, зависящий от
скорости, который означает, что эту сферу нельзя считать естественной метрической струк¬
турой, не зависящей от скорости наблюдателя.
Вопрос, который я хочу поставить, состоит в следующем; существует ли у простран¬
ства S какая-либо математическая структура, более слабая, чем метрическая, которая сохра¬
няется при переходе от небесной сферы, воспринимаемой одним наблюдателем, к сфере,
которую видит другой наблюдатель, когда они оба проходят мимо точки О с высокой от¬
носительной скоростью. Фактически здесь имеется такая структура, и, что интересно, это
та самая структура, которую мы изучали в §§8.2, 8.3 при рассмотрении сферы Римана.
Напомним, что сфера Римана обладает конформной структурой. Хотя она и не имеет какой-
либо метрики, так что не определено понятие расстояния между соседними точками, или
длины, приписываемой кривым, тем не менее имеется абсолютное понятие угла между кри¬
выми на сфере. Любое допустимое, т. е. конформное, преобразование сферы Римана в самое
себя должно сохранять это понятие угла. Соответственно при таких преобразованиях со¬
храняется форма (бесконечно) малых структур, хотя размеры могут меняться. Более того,
окружности любого размера на сфере преобразуются опять-таки в окружности. Это именно
та структура, которой обладает небесная сфера 5. Соответственно любая круговая струк¬
тура из звезд, воспринимаемая одним наблюдателем, должна казаться круговой и любому
другому наблюдателю*. Это показывает, что для описания положения звезд на небе было бы
удобно приписать каждой из них некоторое комплексное число (включая оо)! Я не слыхал,
чтобы такое предложение было принято в астрономии, однако такой комплексный параметр,
именуемый «стереографической координатой» и связанный со стандартными сферическими
полярными углами (§22.11, рис, 22.16) формулой** £ = e^ctgQi9j, часто используется
в общей теории относительности^18*7^.
Это свойство может показаться удивительным, особенно в связи с известным сокраще¬
нием Фитцджеральда-Лоренца, из-за которого сфера, быстро движущаяся со скоростью v,
выглядит как сплющенная в направлении движения с коэффициентом 7 — л/(1 — v2/с2);
см. рис. 18.14. (Я не обсуждаю здесь этот эффект сжатия в явном виде. Он возникает при
пространственном описании движущегося объекта, и с ним можно познакомиться в боль¬
шинстве стандартных курсов теории относительности.)^8,8^*** Предположим, что сфера
движется над нами горизонтально со скоростью, близкой к скорости света. Легко предста¬
вить, что наблюдатель, неподвижно стоящий на земле, должен быть способен заметить это
сжатие. Согласно принципу относительности, такой же эффект должен был отмечаться на¬
блюдателем, если бы он двигался со скоростью v в противоположном направлении, а сфера
оставалась в покое. Но для покоящегося наблюдателя, смотрящего на покоящуюся сферу,
последняя воспринимается как объект с круговым контуром. Это утверждение кажется про¬
тиворечащим предыдущему абзацу, согласно которому воспринимаемые окружности преоб¬
разуются также в окружности. На самом деле противоречия здесь нет, поскольку «эффект
сокращения» Фитцджеральда-Лоренца фактически ненаблюдаем непосредственно. Такой
*ДР Попробуйте восстановить детали остроумного доказательства, принадлежащего оригинальному и влия¬
тельному ирландскому теоретику-релятивисту Джону Сингу, которое не требует никаких вычислений! В общих
чертах рассуждение выглядит следующим образом. Рассмотрите геометрическую конфигурацию, состоящую из
светового конуса прошлого С для события О и времениподобной 3-плоскости Р, проходящей через точку О.
Пусть Е есть пересечение множеств С и Р. Напишите «историю» того, что происходит с течением времени с про¬
странственными описаниями множеств С, Р и Е в некоторой выбранной системе отсчета Минковского. Объясните,
почему любой наблюдатель в точке О видит Е как окружность и, кроме того, что такое геометрическое построение
характеризует, независимо от выбранной системы отсчета, те пучки лучей, которые воспринимаются наблюдателем
как окружность.
** Выведите эту формулу.
***Д85 Попробуйте вывести эту формулу, используя изложенные выше идеи пространственно-временной геомет¬
рии.

18.6. Ньютоновская энергия, импульс и момент импульса
371
Рис. 18.14. «Эффект сокращения» Фитцджеральда - Лоренца. Сферическая планета движется вправо
со скоростью v (близкой к скорости света) по отношению к фиксированной системе отсчета. В такой
системе планета должна описываться как сплющенная в направлении ее движения с коэффициен¬
том (1 — v2/c2)
результат получается при детальном рас¬
смотрении длины путей, проходимых светом
на пути к наблюдателю, относительно кото¬
рого движется сфера (см. рис. 18.15). Свет,
приходящий от тыльной стороны сферы, до¬
стигает наблюдателя, пройдя большее рас¬
стояние, чем свет, пришедший от ее передней
стороны ^18'9Ь*.
N
18.6.	Ньютоновская энергия,
импульс и момент импульса
В этой главе я хотел бы обсудить еще
один аспект геометрии Минковского. Это ка¬
сается важных понятий энергии, импульса и
момента импульса в теории относительно¬
сти. Вскоре (в § 18.7) мы этим займемся, но
сначала я должен сделать некоторые замеча¬
ния относительно этих существенных поня¬
тий в ньютоновской теории, поскольку в этой
книге они пока не рассматривались. Важная
роль этих величин состоит в том, что в нью¬
тоновской теории они имеют ясный смысл
сохраняющихся величин в том смысле, что
полные значения энергии, импульса и мо¬
мента импульса системы, на которую не дей¬
ствуют внешние силы, остаются постоянны¬
ми во времени.
Энергию системы можно считать состо¬
ящей из двух частей — кинетической энергии
Рис. 18.15. Сокращение Фитцджеральда-Лоренца
не наблюдается непосредственно, поскольку свет,
приходящий к наблюдателю от тыльной стороны
сферы, проходит более длинный путь, чем свет, ко¬
торый приходит от ее передней стороны (тыльная
часть удаляется от пути распространения света, а
передняя — приближается к нему). В соответствии
с этим видимая задняя сторона соответствует бо¬
лее раннему положению сферы, нежели видимая
передняя часть, что приводит к компенсирующему
растяжению в направлении движения
* ЗВ Разберите это утверждение подробнее и покажите, что сокращение Фитцджеральда - Лоренца точно ком¬
пенсирует эффект, возникающий из-за различия в длине путей, проходимых светом. Покажите, что при малом
угловом диаметре видимым эффектом будет не сжатие, а поворот сферы.

372
Глава 18
(т, е. энергии движения) и потенциальной энергии (т. е. энергии, запасенной в силах, действу¬
ющих между частицами). Кинетическая энергия (бесструктурной) частицы в ньютоновской
теории определяется выражением
\rriv2,
2
где га — масса частицы, a v — ее скорость. Чтобы получить полную кинетическую энер¬
гию, достаточно просто сложить кинетические энергии всех отдельных частиц (хотя, если
имеется множество составляющих частиц, движущихся хаотическим образом, можно счи¬
тать их энергию тепловой энергией, см. §27.3). Чтобы получить полную потенциальную
энергию, мы должны кое-что знать о детальной природе всех участвующих сил. Ни пол¬
ная кинетическая энергия, ни полная потенциальная энергия в отдельности не сохраняют¬
ся, сохраняется лишь полная энергия. (Первый намек на это можно найти в галилеевском
исследовании движения тел в поле тяжести. Когда маятник качается, начиная с верхнего
положения, его гравитационная потенциальная энергия, определяемая высотой над Землей,
переходит в кинетическую энергию, которая затем переходит в потенциальную энергию, та
снова в кинетическую и т. д., и т. п.)
Импульс р нашей частицы есть векторная величина, определяемая соотношением
р = mv,
где v — вектор, описывающий скорость частицы. Чтобы получить полный импульс, мы долж¬
ны взять векторную сумму импульсов всех отдельных частиц. Эта полная величина также
сохраняется во времени*.
Напомним (см. §§ 17.2, 17.3), что в теории Ньютона выполняется принцип относитель¬
ности Галилея. Как в таком случае ухитряются существовать наши законы сохранения, если
ни энергия, ни импульс не остаются неизменными при переходе от одной инерциальной
системы отсчета к другой? Если вторая система равномерно движется относительно первой
со скоростью, определяемой вектором и, то частица, скорость которой в первой системе
равна v, во второй системе будет иметь скорость v — и. Оказывается, что сохранение энер¬
гии и импульса в первой системе приводит к сохранению энергии и импульса во второй
системе, если принять во внимание, что масса также сохраняется (при этом необходимо
также использовать третий закон Ньютона; см. § 17.3, рис. 17.46).
Следует упомянуть, что в ньютоновской механике имеются и другие сохраняющиеся
величины, наиболее важной из которых является момент импульса (или угловой момент) от¬
носительно некоторой точки О, принимаемой за начало координат. Пусть вектор положения
некоторой частицы относительно точки О есть
х = (ж1, ж2, ж3),
где ж1, ж2, ж3 — декартовы координаты этой точки, а импульс частицы равен р. Тогда мо¬
ментом импульса будет величина
М = 2х А р
(относительно смысла символа А см. § 11.6)t1810l. Чтобы найти момент импульса всей
системы, достаточно просто сложить величины М для всех отдельных частиц
* Учитывая сохранение энергии и импульса, покажите, что если на покоящийся бильярдный шар нале¬
тает другой шар той же массы, то они разлетаются под прямым углом друг к другу (предполагается упругое
столкновение, при котором не происходит превращения кинетической энергии в тепло).
Докажите все это.
*** flQ Почему вращающийся конькобежец для увеличения скорости вращения прижимает руки к телу?

18.7. Релятивистская энергия, импульс и момент импульса
373
В ньютоновской теории есть еще одна величина, сохраняющаяся во времени при от¬
сутствии внешних сил, которую упоминают гораздо реже, чем момент импульса. Для одной
частицы это величина
N = tp — тх,
где t — время; полное значение величины N получается сложением значений для отдельных
частиц. Это полное значение имеет тот же вид, что и приведенное выше выражение для N,
но под х теперь следует понимать вектор положения центра масс, а под р — полный импульс.
Постоянство полной величины N отражает тот факт, что центр масс движется равномерно
и прямолинейно (см. рис. 18.16)*.
Рис. 18.16. Равномерное движение центра масс. Величина N = tp — тх, где t — время, ах — вектор
положения центра масс, при таком движении сохраняется. Это выражает тот факт, что центр масс
движется равномерно и прямолинейно со скоростью р/т
Нам придется задать вопрос: как повлиял на всё это переворот, совершенный теорией
относительности? Остаются ли в силе-понятия сохраняющихся энергии, импульса, момента
импульса и скорости движения центра масс? И как обстоит дело с сохранением массы? Ответ
на вопрос относительно перечисленных четырех величин положителен, хотя необходимо
позаботиться о правильном определении этих величин. Что же касается сохранения массы,
то здесь возникает забавная ситуация. Два отдельных ньютоновских закона сохранения
энергии и массы объединяются в один. Масса и энергия в буквальном смысле становятся
полностью эквивалентными одна другой в соответствии с наиболее известной формулой
Эйнштейна
Е ~ тс2,
где Е — полная энергия системы, т — ее полная масса, а с, как и прежде, — скорость света.
В последнем разделе этой главы мы увидим всё это в действии.
18.7.	Релятивистская энергия, импульс и момент импульса
Напомним, каким образом пространство и время в теории относительности объединя¬
ются в единое понятие «пространства-времени». Временная координата t присоединяется
к вектору положения в 3-пространстве х = ( X « X ) X 3), образуя 4-вектор
(.х°, х1, х2, Xs) = (£, х).
Аналогичным образом объединяются импульс и энергия. Любая конечная система в специ¬
альной теории относительности обладает полной энергией Е и 3-вектором полного импуль¬
са р. Они объединяются в так называемый 4-вектор энергии-импульса, пространственные
компоненты которого имеют вид
(р1,р2,р3) = с2р,
Покажите это. (N.B. Вектор положения центра масс есть сумма величин тх, деленная на сумму масс т.)

374
Глава 18
а временная компонента р° определяет не только полную энергию, но и, эквивалентным
образом, полную массу системы т в соответствии с формулой
р° = Е — тс2,
заключающей в себе известное эйнштейновское соотношение между массой и энергией.
В более естественной системе единиц, где с = 1, энергия и масса просто равны
между собой. Однако я явно выписывал скорость света с (т. е. не использовал систему
пространственно-временных единиц, в которой с = 1), чтобы облегчить переход к нереляти¬
вистскому описанию. Здесь используется метрика даь в виде матрицы с отличными от нуля
компонентами (1, —с-2, —с-2, —с~2) на главной диагонали, обратная величина даЬ имеет
на главной диагонали компоненты (1, —с2, —с2, —с2).
Хотя первоначально рассматривался пространственно-временной вектор энергии-им¬
пульса, оказывается, что лучше считать его ковектором (см. §§20.2, 21.2), описывая его
величиной с опущенными индексами ра с компонентами
(Ро, Pi, Р2, Рз) = (Е, -р)-
Здесь содержится непривычный знак минус (хотя скорость света с не выписывается). При ис¬
пользовании любого варианта (ра или ра) 4-импульс удовлетворяет закону сохранения.. Таким
образом, при столкновении двух или более частиц (или систем), или при распаде одной ча¬
стицы (или системы) на две или более, или при захвате частицы другой частицей сумма всех
4-импульсов до столкновения равна сумме всех 4-импульсов после него. При этом законы
сохранения энергии, импульса и массы объединяются в один закон. Причина такого объеди¬
нения состоит в том, что при изменении системы отсчета эти величины преобразуются одна
через другую в соответствии с законами теории относительности, как требует индексная
запись (см. § 12.8).
Заметим, что в теории относительности полная масса системы не является скалярной
величиной, так что ее значение зависит от системы отсчета, в которой она измеряется.
Например, частица, масса которой, измеренная в системе, где она покоится, равна т, бу¬
дет иметь большую массу при измерении в другой системе отсчета, относительно которой
частица движется. Однако чтобы этот эффект был заметен, относительная скорость двух
систем должна быть сравнима со скоростью света .
Эти замечания относятся, однако, лишь к массе, сохраняющейся в только что описан¬
ном аддитивном смысле (для системы, на которую не действуют внешние силы). В теории
относительности имеется другое понятие массы, а именно массы покоя р (^ 0), которая не
зависит от системы отсчета. Она равна массе, измеренной в собственной системе отсчета,
где частица покоится, т. е. в системе, где импульс частицы равен нулю. Масса покоя р равна
энергии покоя (рара)1//2, умноженной на с“2, так что
(с2р)2 = рара = Ё1 - С2р2,
и мы имеем р = с~2(Е2 — с2р2)1//2. Здесь используется трехмерная векторная запись,
в которой для произвольного 3-вектора а вводится определение а2 = а • а = а2 + а2 +
+ а2. Точка означает «скалярное произведение» (обозначение аналогично использованному
в § 12.3):
а • b = a\bi + а2Ь2 + а363,
где а = (ai, а2у аз), b = (bi, b2, &3). (Такая запись окажется удобной в дальнейшем.)
Покажите, что формула, описывающая возрастание массы, имеет вид т( 1 — г>2/с2) 1//2, где v — скорость
частицы во второй системе отсчета; см. ниже.

18.7. Релятивистская энергия, импульс и момент импульса
375
Для одиночной частицы, массивной в том смысле, что р > 0, можно взять 4-импульс
в виде 4-скорости, умноженной на массу покоя р. 4-скорость частицы va есть временипо-
добный (направленный в будущее) касательный вектор к мировой линии частицы, имеющий
длину (в смысле Минковского) с (т. е. это есть единичный вектор, если с = 1):
€ .
ра = pva, где vava = с2
(см. рис. 18.17). Как уже отмечалось, масса покоя массивной частицы есть ее масса (мас¬
са-энергия), измеренная в ее собственной системе покоя. Если взять обычную 3-скорость
частицы v в виде v = (dx1 /dt, dx2/dt, dxs/dt)9 где t = x°, мы получим*5**
p — гаv, m = 7/x, va = 7(c2, v),
где
7 — (1 — v2/c2) 1//2.
Частицы могут быть безмассовыми (т. е. иметь нулевую массу покоя, р = 0), лучшим
примером может служить фотон. В этом случае 4-импульс является нулевым вектором.
Поскольку масса покоя не сохраняется, ничто не мешает массивной частице распасться
на безмассовые или безмассовым частицам объединиться и образовать массивную частицу.
I
#
Рис. 18.17. 4-импульс ра массивной частицы равен 4-скорости va, умноженной на массу покоя р (> 0).
Скорость va есть времениподобный (направленный в будущее) единичный 4-вектор, касательный к
мировой линии частицы (предполагается с = 1)
Почему?
** J$3 Используя ряд Тейлора (§6.4), получите разложение (1 + х)1//2 = 1 + ~х — ^а:2 + ~а;3 — ... Затем
1 о 1о
разложите в степенной ряд энергию Е = [(с2 д)2 + с2р2]частицы с массой покоя д и 3-импульсом р. Покажите,
что главный член разложения есть как раз формула Эйнштейна Е = тс2, примененная к массе покоя д, а
следующий член дает ньютоновскую кинетическую энергию. Выпишите следующие два члена, чтобы получить
улучшенное приближение к полной релятивистской энергии.
4

376
Глава 18
И действительно, массивная частица, именуемая «нейтраль¬
ным пионом» (обозначается 7г°), обычно распадается на два
фотона за время порядка 10“16 секунд.
В любой выбранной системе отсчета полная масса-энер¬
гия {не масса покоя) аддитивно сохраняется, при этом мас¬
са-энергия каждого отдельного фотона отлична от нуля. Спо¬
соб сложения 4-импульсов показан на рис. 18.18.
В заключение посмотрим, как обстоит дело с моментом
импульса в специальной теории относительности. Он опи¬
сывается тензорной величиной Ма6, антисимметричной по
двум индексам:
М
аЪ
м
Ьа
(Относительно МаЬ в квантовой механике см. §22.12.) Для
одиночной бесструктурной точечной частицы имеем (18Л11
М
аЬ
харъ
хъра,
где х
а
Рис. 18.18. Распад массивно¬
го «нейтрального пиона» 7г° на
два безмассовых фотона. 4-век¬
тор массы/энергии аддитивно
сохраняется (хотя масса покоя
не сохраняется)
— 4-вектор положения (в индексной форме) точки на
мировой линии частицы в тот момент, для которого рассмат¬
ривается момент импульса. Если частица движется по инер¬
ции, то величина МаЪ одинакова во всех точках ее мировой
линии*; Чтобы получить полный релятивистский момент им¬
пульса, мы просто складываем тензоры момента импульса
всех отдельных частиц. Для отдельной (невращающейся) ча¬
стицы тремя независимыми чисто пространственными ком¬
понентами М23, М31, М12 служат умноженные на с? ком¬
поненты обычного момента импульса М = 2х А р, рассмот¬
ренного выше в § 18.6, а остальные независимые компонен¬
ты М01, М02, М03 образуют величину N = tp — mx (х с2). (Сохранение полной величи-
ны N соответствует равномерному движению центра масс; см. рис. 18.16.)
Напомним (см. §18.2), что 10-мерная группа Пуанкаре, описывающая симметрию
пространства Минковского, содержит 4 измерения, соответствующие пространственно-
временным трансляциям, а остальные 6 измерений соответствуют (лоренцевым) вращениям.
В § 20.6 мы увидим, как важный принцип классической механики, известный под названи¬
ем теоремы Нётер, связывает симметрию с законами сохранения, а в §§21.1-21.5, 22.8 —
как с этим обстоит дело в квантовой теории. Это вскрывает глубокую причину, лежащую
в основе законов сохранения 4-импульса ра и 6-момента импульса МаЬ и связанную с 4-
трансляционной симметрией и лоренцевой 6-вращательной симметрией пространства Мин¬
ковского. Сохранение величин ра и МаЪ приводит к важным последствиям, рассматривае¬
мым в главе 21 и §§22.8, 22.12, 22.13.
Примечания
I
§18.1.
18.1. Том Банков из Университета Брауна в течение многих лет разрабатывал интерактивные ком¬
пьютерные системы, направленные на развитие четырехмерной интуиции, и, в частности, ви¬
зуализацию комплексных функций как римановых поверхностей в пространстве С2. См, [52].
Почему?
Объясните это подробнее для релятивистского случая.

18.7. Релятивистская энергия, импульс и момент импульса
377
18.2. Величины ds в этом выражении можно рассматривать просто как «бесконечно малые величи¬
ны» (подобно с в § 13.6). Сравните с примечанием 12.2.
§18,2.
18.3. Подробное обсуждение роли Лоренца, Пуанкаре и Эйнштейна в развитии специальной теории
относительности содержится в книге [741], стр. 249-356. По моему мнению, даже Эйнштейн
не завершил создание специальной теории относительности в 1905 году, и для создания полной
картины понадобилась четырехмерная перспектива Минковского, предложенная в 1908 году;
см. § 17.8.
18.4. Существуют также элементы группы Пуанкаре, изменяющие знак времени и превращающие
времениподобные направления в будущее во времениподобные направления в прошлое.
§18.3.
18.5. Я должен подчеркнуть, особенно для тех читателей, которые уже знакомы с квантовой механи¬
кой, что используемое здесь понятие «ортогональности» в комплексной области по необходимо¬
сти является голоморфным (это и означает «комплексификация»), а не эрмитовым (см. § 13.9),
предполагающим комплексное сопряжение, которое используется во многих других областях
математики и физики.
18.6. См., например, [665, 666, 760, 766, 358]. Аксиоматический геометрический подход изложен
в [704].
§18.5.
18.7. См., в частности, [551]; [626], §§1.2-1.4, 4.15; [627], §9.8.
18.8. См., например, [665, 666].
18.9. См., например, [767, 581].
§18.6.
18.10. Некоторых читателей может смутить присутствие множителя 2 в этом выражении, однако им
следуег вспомнить определение операции Л, данное в § 11.6. Компоненты произведения х Л р
r##"J	I	-	I	-	"	♦
имеют вид х[гр3] = “(хУ — х3ръ). Следовательно, М имеет компоненты хгр3 — х3рг.
&
§ 18.7.
18.11. В § 22.8 мы увидим, что большинство (квантовых) частиц обладает также внутренним момен¬
том импульса (<спином), который дает (постоянный) «спиновый» вклад в МаЪ (см. §22.12),
добавляемый к рассмотренному здесь «орбитальному» моменту импульса.

Глава 19
Классические поля Максвелла и Эйнштейна
19.1.	Эволюция ньютоновской динамики
В период между появлением великолепной динамики Ньютона, которое лучше всего
датировать опубликованием его Начал в 1687 году, и появлением специальной теории отно¬
сительности, которое разумно датировать первой публикацией Эйнштейна по этому предме¬
ту в 1905 году, появилось много важных вкладов в картину, создаваемую фундаментальной
физикой. Наибольший скачок, происшедший в этот период, связан с работами Фарадея
и Максвелла в XIX веке, согласно которым понятие физического поля, пронизывающего
пространство, должно сосуществовать с «ньютоновской реальностью» в виде отдельных
частиц, взаимодействующих посредством мгновенных сил^19л^. Позднее такое понятие поля
стало важнейшей составной частью эйнштейновской теории гравитации как искривленного
пространства-времени (1915). То, что сейчас именуется «классическими» полями, — это как
раз электромагнитное поле Максвелла и гравитационное поле Эйнштейна.
Однако сейчас мы знаем, что физический мир не сводится к классической физике.
Еще в 1900 году Макс Планк обнаружил первый намек на необходимость «квантовой те¬
ории», хотя потребовалось более четверти века, чтобы появилась четко сформулированная
и исчерпывающая теория. Следует также подчеркнуть, что помимо всех этих глубоких из¬
менений «ньютоновских» основ физики как до них, так и параллельно с ними появились
мощные математические методы в рамках самой ньютоновской теории. Эти математические
методы будут изложены в главе 20. Они имеют тесную связь с теорией классических по¬
лей и, что еще важнее, образуют основу для правильного понимания квантовой механики,
как будет показано в последующих главах. В качестве следующей важной идеи необходи¬
мо упомянуть термодинамику (или ее дальнейшее развитие — статистическую механику).
Она имеет дело с поведением систем, состоящих из большого числа частиц, при этом по¬
дробности их движения не рассматриваются, что позволяет описывать поведение системы
в терминах средних значений соответствующих величин. Развитие ее с середины XIX века
до начала XX века в наибольшей степени связано с именами Карно, Клаузиуса, Максвел¬
ла, Больцмана, Гиббса и Эйнштейна. Некоторые наиболее фундаментальные и нерешенные
проблемы, поднятые термодинамикой, будут рассмотрены в главе 27.
В этой главе излагается теория физических полей Максвелла и Эйнштейна — «клас¬
сическая физика» электромагнетизма и гравитации. Теория электромагнетизма играет важ¬
ную роль в квантовой теории, предоставляя прототип «поля» для дальнейшего развития
«квантовой теории поля», с которой мы познакомимся в главе 26. В то же время соответ¬
ствующий квантовый подход к гравитационному полю остается противоречивым и полным
загадок. Проблемы квантовой гравитации составят важную часть последующих глав этой
книги (в частности, главы 28). Пока, однако, мы ограничим наше исследование физическими
полями в их классическом понимании.
В начале этой главы я уже упоминал, что значительные изменения в основах ньютонов¬
ской теории появились еще в XIX веке, до той революции, которую совершили в XX веке
теория относительности и квантовая теория. Первый намек на необходимость изменений
появился в результате замечательных экспериментальных исследований Майкла Фарадея

19.2. Максвелловская теория электромагнетизма
379
в 1833 году, для интерпретации которых ему потребовалась новая картина реальности. Наи¬
более фундаментальное изменение состояло в том, что «ньютоновские частицы» и «силы»,
действующие между ними, оказались не единственными обитателями нашей Вселенной.
Появилась и стала серьезно обсуждаться идея «поля», существующего самостоятельно.
В 1864 году великий шотландский физик Джеймс Клерк Максвелл сформулировал урав¬
нения, которым должно удовлетворять это «самостоятельное поле», и показал, что поля
могут переносить энергию из одного места в другое. Эти уравнения описывали единым об¬
разом поведение электрических полей, магнитных полей и даже света, они известны теперь
как уравнения Максвелла, первые релятивистские уравнения поля.
С точки зрения XX века с его замечательными достижениями в разработке математиче¬
ского аппарата (здесь я, в частности, имею в виду математический анализ на многообразиях,
рассмотренный в главах 12-15), уравнения Максвелла обладают неотразимой естественно¬
стью и простотой, так что кажется почти невозможным, чтобы электрические и магнитные
поля подчинялись каким-либо иным законам. Однако такой взгляд на вещи игнорирует
тот факт, что во многом сами уравнения Максвелла способствовали развитию математиче¬
ского аппарата. Именно форма этих уравнений привела Лоренца, Пуанкаре и Эйнштейна
к пространственно-временным преобразованиям специальной теории относительности, ко¬
торые в свою очередь породили концепцию пространства-времени Минковского. В рамках
этой концепции уравнения принимают форму, которая естественно выливается в теорию
дифференциальных форм Картана (§ 12.6). При этом законы сохранения заряда и магнитно¬
го потока в теории Максвелла приводят к интегральным соотношениям, в которых заключена
красивая формула, называемая основной теоремой внешнего анализа (§§ 12.5, 12.6).
Приписывая все эти успехи влиянию уравнений Максвелла, я, возможно, занимаю
слишком крайнюю позицию. Действительно, хотя уравнения Максвелла, несомненно, сыгра¬
ли ключевую роль в этом отношении, важное влияние оказали также их предшественники —
уравнения Лапласа, Даламбера, Гаусса, Грина, Остроградского, Кулона, Ампера и др. Тем не
менее именно необходимость понять природу электрических и магнитных полей оказалась
главной движущей силой, заставившей выйти за рамки этих уравнений; это относится также
к гравитационному полю. Остаток этой главы будет посвящен попыткам понять электромаг¬
нитные и гравитационные поля, а также то, как они вписываются в рамки современной
математики.
19.2.	Максвелловская теория электромагнетизма
Что представляют собой уравнения Максвелла? Это дифференциальные уравнения
в частных производных (см. § 10.2), описывающие временную эволюцию трех компо¬
нент электрического поля Е\, Еъ* Ез и трех компонент магнитного поля В] , 1Г>, £?з, при
этом плотность электрического заряда р и три компоненты плотности электрического то¬
ка Д, j2, j'3 предполагаются заданными величинами. В уравнения могут также входить неко¬
торые другие величины, характеризующие среду, в которой распространяются эти поля. При
изложении фундаментальной физики, которой, собственно, мы здесь занимаемся, обычно
игнорируются те аспекты уравнений Максвелла, которые связаны с такой средой, поскольку
среда в действительности состоит из многих составляющих, каждую из которых в принципе
можно рассматривать на более фундаментальном уровне. Удобно выбрать так называемые
гауссовы единицы и использовать стандартные координаты Минковского (из §18.1) ж0 =
= £, х1 = х, х2 = у, ж3 = z (сигнатура 4	•)	с	пространственно-временными единицами,
в которых скорость света принимается за единицу (с — 1).
Электромагнитное поле и плотности заряда и тока, согласно процедуре, восходящей
к Минковскому, объединяются соответственно в пространственно-временную 2-форму F,
называемую максвелловским тензором поля, и пространственно-временной вектор J, име-

380
Глава 19
нуемый вектором заряда-тока; их компоненты, выраженные в матричной форме, имеют
следующий вид:
£oi
£02
£оз \
(
0
Ег
е2
Е3 \
Fn
£"12
Дз
-Ег
0
-Дз
в2
£21
£22
£23
-£2
Дз
0
-Вг
£31
£32
£33/
V
-£з
-в2
Вг
0 /
/Л
1 j1 '
j2
VW
Заметим, что здесь выполняется условие антисимметрии Fba — —Faь, как и должно быть
для 2-формы. Я буду также использовать так называемые дуальные формы Ходжа для F
и J, которые представляют собой соответственно 2-форму *F и 3-форму * J, определяемые
соотношениями
*
£оо
* ТВ
-^01
* ТВ
02
*F0 3\
До
*Fn
* ТВ
Г12
Тз
£20
* Ег
*21
* ТВ
Г 22
* Гз
До
* ТВ
£ 31
* ТВ
^32
*Тзз/
(*Jl23 \
То 23
*-Л)13
Woi2 )
/о
в1
В2
\S3
-Si
о
Е3
“£2
-£2
-£*з
0
Ег
~Р\
h
~h
7з /
Здесь выполняются необходимые условия антисимметрии *Fab
*F[ab] и *Jabc
J
[abc]
Используя тензор Леви-Чивита е (§ 12.7) с полностью антисимметричными компонента¬
ми eabcd{~ £[abcdj) и нормировкой бот — Д можно представить дуальные формы в виде
*
ЕаЬ
1
2
£abcdE
cd
и
*
Jabc — £abcdJ
d
В соответствии с § 14.7, вариантом формы Fab с поднятыми индексами Fab является вели¬
чина gacgbdFcd• Заметим, что «поднятый» вариант — gapgbqgcrgds£pqrs удовлетворяет
условию е
ем* eabcd =
0123
= — 1, откуда следует, что тензор € из § 12.7 определяется соотношени-
eabcd\ Диаграммная форма этих «дуализированных» операций (а также самих
уравнений Максвелла) показана на рис. 19.1. Мы увидим, что понятие «дуальности», опре¬
деленное таким образом (а также другим сходным образом), окажется важным для нас
в разных ситуациях.
Необходимо сделать замечание относительно геометрического смысла дуальной формы
Ходжа. Напомним (см. § 12.7), что операция перехода от бивектора Н, описываемого анти¬
симметричной величиной НаЬ, к его «дуальной» 2-форме Нопределяемой как ^£abc.dBcdf
не приводит к существенному изменению геометрической интерпретации. Если бы, напри¬
мер, величина Н была простым бивектором, так чтобы 2-форма НЙ тоже была простой
(см. конец § 12.7), то элемент 2-плоскости, определяемый величиной Н$, был бы точно
таким же, как элемент 2-плоскости, определяемый величиной Н (единственная разни¬
ца состоит в том, что НК строго говоря, обладает свойствами плотности, как отмечено
в § 12.7). В то же время поднятие индексов, которое приводит от 2-формы НаЬ к бивек¬
тору Hab(= Hcdgcagdb), производит более значительный геометрический эффект. В случае
Проверьте оба эти утверждения.

19.2. Максвелловская теория электромагнетизма
381
F
1
2
F
лл^
аЬ
lift
*
Fab~*
fMTTS-
*
Кь ~+
1Ш
еа bed
(	^abed)
24
47Г
▼
О
аЬеЛ	~
6
/ аЬсЛ\
(=-£ )
а
*
J
абс
|=-^ lffi
1ТГ =
Рис. 19.1. Диаграммы для дуальных форм Ходжа и уравнений Максвелла. Величины eabcd{~ £[abcd])
0123
1 (в стандартных координатах
аЪ
и eabcd^_ ДabedН0рМИр0ваны таКИМ обраЗОМ, ЧТО 60123 = б
Минковского), и связаны с их «поднятыми» и «опущенными» вариантами (с помощью тензоров д
и д0,ъ) соотношениями eabcd = —tabed и ea6cd = —g.abcd' дИаграммах (на двух нижних строках слева
и в середине рисунка) указанному изменению знака соответствует обращение эффективных индексов.
В правом верхнем углу выписаны уравнения Максвелла, в первом из которых используется тензор
поля F (в «поднятой» форме Fab — gacgbdFcd\ сравните с рис. 14.21), так что уравнения имеют
вид VaFab = 47rJb, V(aFbc] = 0. Ниже приведены уравнения, в которых используется дуальная
форма * F (здесь *Fab
1
2
CabcdF
cd *
Jabc = £abcd.Jd)j так что уравнения имеют вид V[aFbc]
4тг
3
*
Jabc, V*aF
ab
О
простого бивектора элемент 2-плоскости, определяемый величиной Наь9 является орто¬
гональным дополнением элемента 2-плоскости, определяемого величиной НаЪ (см. § 18.3).
Дуальная форма Ходжа, примененная к 2-форме Наь и приводящая к ~еabcdHcd (т. е. к Нй),
использует поднятие индексов Наь НаЬ и, следовательно, включает переход к ортого¬
нальному дополнению (см. рис. 19.2). Соответственно дуальная форма Ходжа, приводящая
нас от F к *F, также включает ортогональное дополнение.
Используя такую запись, можно представить уравнения Максвелла в следующей простой
форме*:
dF -0, d*F — 47г* J.
* *
В полностью индексной записи можно придать уравнениям Максвелла следующий вид:
V(aFbc]=0, VaFab = 4nJb.
0 %
Применяя оператор внешней производной d к обеим частям второго уравнения Максвел¬
ла d*F = 47Г* J и используя тот факт, что d2 = 0 (§ 12.6), получаем, что вектор заряда-тока J
* Выпишите эти уравнения полностью, выразив через компоненты электрического и магнитного полей. По¬
кажите, как описывают эти уравнения временную эволюцию электрических и магнитных полей, с использованием
оператора d/dt.
Покажите их эквивалентность предыдущей паре уравнений.

382
Глава 19
jr
Рис. 19.2. В 4-пространстве простой бивектор Н (На ) представляет тот же элемент 2-плоскости, что
й/1
и его «дуальная» 2-форма	sabcdHcd). Однако вариант Н с опущенными индексами, т. е. простая
1 i. J
форма Наъ> эквивалентная «дуальному бивектору» -еа с Нса, представляет элемент 2-плоскости,
являющийся ортогональным дополнением (см. рис. 18.4). Таким образом, поднятие или опускание
индексов дуальной формы Ходжа соответствует переходу к ортогональному дополнению
удовлетворяет уравнению «отсутствия дивергенции»
d* J = 0 или, что эквивалентно, VaJa = 0.
Здесь уместно сделать небольшое отступление, которое окажется полезным в дальней¬
шем (в §§33.6, 33.8, 33.11; см. §18.3, упражнение 18.5(2)), и обратить внимание на са~
модуальную и антисамодуальную части тензора Максвелла, определяемые соответственно
соотношениями
+
F
1
2
(F — i*F)
И
F
1
2
(F 4- i*F)
(которые являются взаимно комплексно-сопряженными). Оказывается, что в квантовой те¬
ории эти комплексные величины описывают соответственно право- и левополяризованные
фотоны (кванты электромагнитного поля); см. §22.7, 22.12, рис. 22.7. Свойства самодуаль-
, **
ности/антисамодуальности выражаются соотношением
*
i±F)
±i±F.
Учитывая, что величина * J вещественна, можно объединить два уравнения Максвелла (мни¬
мую и вещественную части) в виде
d+F
2т* J.
Фотоны позволяют описывать свет как частицы; в главе 21 мы увидим, как кванто¬
вая теория обеспечивает сосуществование корпускулярного и волнового описания света.
**
Покажите эквивалентность этих двух вариантов условия отсутствия дивергенции.
Подтвердите это, показав предварительно, что двукратная дуализация приводит к изменению знака ис¬
ходной величины. Связан ли этот знак с лоренцевой сигнатурой пространства-времени? Объясните это.

19.3. Законы сохранения и потоки в теории Максвелла
383
Одно из главных открытий Максвелла, сделанных с помощью его уравнений, состояло в до¬
казательстве существования электромагнитных волн, распространяющихся со скоростью
света и обладающих всеми поляризационными свойствами света (они будут рассмотрены
в §22.7). Опираясь на эти замечательные факты, Максвелл предположил, что свет имеет
электромагнитную природу. В 1888 году, почти через четверть века после того, как Макс¬
велл опубликовал свои уравнения, Генрих Герц экспериментально подтвердил замечательное
теоретическое предсказание Максвелла.
В вышеприведенном явном описании в качестве фонового пространства-времени ис¬
пользовалось плоское пространство Минковского М. Последующее обсуждение в §§ 19.3,
19.4 и в первой части § 19.5 также будет проводиться на этой основе. Однако в действитель¬
ности это не обязательно, и все выводы остаются в силе, если пространство-время обладает
кривизной. Для этого указанные выше компоненты следует рассматривать по отношению
к некоторой локальной системе отсчета Минковского, а остальное возьмет на себя индексная
запись1".
19.3. Законы сохранения и потоки в теории Максвелла
Условие отсутствия дивергенции заряда-тока позволяет получить уравнение сохране¬
ния электрического заряда. Причина такого названия связана с тем фактом, что, согласно
основной теореме внешнего анализа (см. § 12.6), / d*J = f * J, так что
71	дП
*
J = О,
где интегрирование проводится по любой замкнутой 3-поверхности в пространстве Мин¬
ковского М. (Всякая замкнутая 3-поверхность Q в М является границей 31Z некоторой
компактной четырехмерной области 1Z в М; см. рис. 19.3.) Величину * J можно интерпре¬
тировать как «поток заряда» через поверхность Q — <97Z. Приведенное выше уравнение
означает, что полный поток электрического заряда через эту поверхность должен быть ра¬
вен нулю, т. е. поток, входящий в 1Z, должен быть в точности равен потоку, выходящему
из 7Z; это означает сохранение электрического заряда**.
Можно также использовать второе уравнение Максвелла d*F = 47г* J, чтобы вывести
так называемый «закон Гаусса». Этот закон частного характера относится к одному задан¬
ному моменту времени t = to, поэтому здесь мы используем трехмерный вариант основной
теоремы внешнего анализа. Закон гласит, что полный заряд, находящийся внутри некоторой
замкнутой 2-поверхности S в момент времени to (см. рис. 19.4), равен интегралу по поверх¬
ности S от дуальной формы тензора Максвелла *F. Это означает, что мы можем получить
полный заряд, окруженный поверхностью S, проинтегрировав полный поток электрического
поля Е через $.
В более общем случае все это применимо, даже если поверхность S не относится
к некоторому фиксированному моменту времени t — to- Предположим, что S есть простран¬
ственноподобная 2-граница некоторой компактной области 3-пространства Л. Тогда полный
Попробуйте проверить это. Каковы будут компоненты тензоров F и * F в криволинейной системе коор¬
динат общего вида? Почему такая модификация не влияет на правильно написанные уравнения Максвелла?
Эти рассуждения несколько поверхностны, хотя и правильны. Проверьте их более внимательно для слу¬
чая, когда 7Z есть пространственно-временной «цилиндр», состоящий из некоторой ограниченной пространствен¬
ной области, постоянной во времени в течение некоторого фиксированного интервала временной координаты t.
Объясните различие в понятиях «потока заряда», используемых для пространственноподобных верхнего и нижнего
«оснований» цилиндра и для времениподобных «боковых поверхностей».
Убедитесь, что это есть именно поток электрического поля.

384
Глава 19
■ ■ l 1Щ
l /У.Щ
w*:*3
•••• 4 »4.a/
а2£:-9!Г
:*>
« +
>?.,
A>...	..
4 W4*‘Vm'♦•vm Я
•	i
v • Ш-ш J
•N • - W;-'* ^
* »V1'< ' .."A
i*A * « * V*v
> A • ■; aC
■	.	%	♦	ir*>*	.	о	.Аг/	<#
Время
Рис. 19.3. Сохранение электрического заряда в пространстве-времени. Замкнутая 3-поверхность Q
представляет собой границу Q = <97?, компактного 4-объема 7?. в пространстве Минковского М, так что,
согласно основной теореме внешнего анализа, f * J = f d*J — 0, поскольку d* J — 0. Величина * J =
Q к
= 0 описывает «поток» заряда через Q, поэтому полный заряд, входящий через поверхность Q, равен
выходящему заряду, что означает сохранение заряда
заряд х в области Л, окруженный поверхностью 5 (или, в пространственно-временных
терминах, «пронизывающий» S,— см. рис. 19.4), определяется соотношением
*
F = 4тгх, где х
J.
л
Аналогичный закон сохранения можно получить также из первого уравнения Максвел¬
ла dF — 0. Он имеет такой же вид, что и полученный из второго уравнения, с той лишь
разницей, что *F заменяется на F, а источник, соответствующий * J, равен нулю. Таким
образом, для любой замкнутой 2-поверхности в пространстве Минковского ^19получается
уравнение для потока:
Г F = 0.
Заметим, что при переходе от *F к F (или от F к *F) мы просто меняем местами
векторы электрического и магнитного полей (с изменением знака у одного из них). Отсут¬
ствие источника в уравнении для F выражает факт отсутствия (насколько нам известно)
в природе магнитных монополей. Магнитный монополь должен представлять собой само-

19.4. Максвелловское поле как калибровочная кривизна
385
Рис. 19.4. Для 3-поверхности постоянного времени t — to уравнение Максвелла d* F = Атт* J дает нам
закон Гаусса, согласно которому интеграл потока электрического поля (интеграл от * F) по замкнутой
пространственной 2-поверхности измеряет полный заряд, окруженный этой поверхностью (согласно
основной теореме внешнего анализа). Фактически закон Гаусса не ограничен 2-поверхностями при
постоянном времени и может быть обобщен
стоятельно существующий северный или южный магнитный полюс, тогда как реально се¬
верный и южный полюсы появляются лишь в паре, как это имеет место в обычном магните.
(Такие полюсы не образуют независимых физических сущностей, а возникают вследствие
циркуляции электрических зарядов.) Представляется, что «магнитный заряд» в чистом виде
(магнитный полюс ненулевой силы) в природе существовать не может. С точки зрения одних
лишь уравнений Максвелла, не видно каких-либо причин отсутствия магнитных монополей,
поскольку можно было бы добавить правую часть в первое уравнение Максвелла dF = 0 без
какой-либо потери согласованности. И действительно, время от времени физики обсужда¬
ют возможность реального существования магнитных монополей и пытаются обнаружить
их. Их существование имело бы важные последствия для физики элементарных частиц
(см. § 28.2), но пока нет никаких указаний на реальное существование таких монополей
в нашей Вселенной.
19А. Максвелловское поле как калибровочная кривизна
Первое уравнение Максвелла dF = 0 можно также представить в виде
F = 2 <L4,
где А — некоторая 1-форма. (Это есть следствие «леммы Пуанкаре», которая утвержда¬
ет, что для всякой r-формы а, удовлетворяющей условию da. = 0, локально существует
(г — 1)-форма /3, для которой а = df3; см. § 12.6.) Более того, в области с евклидовой то¬
пологией этот локальный результат обобщается в глобальный^19'3!. Величина А называется
электромагнитным потенциалом. Он определяется полем F не однозначно, а с точностью
до дополнительного слагаемого dG * где G есть некоторое вещественное скалярное поле:
А I—У А + dG.
* йИ Почему можно добавить такую величину?

386
Глава 19
В индексной форме эти соотношения приобретают вид
Fab ~ VаА-Ъ
причем остается свобода относительно преобразования
Аа Аа -Ь Va0.
Такая «калибровочная свобода» в определении электромагнитного потенциала означа¬
ет, что А не является локально измеримой величиной. Нельзя поставить эксперимент по
измерению «значения потенциала А» в некоторой точке, поскольку A -f dO точно так же
годится для физических целей, как и А. Однако потенциал дает нам математический ключ
к тому, как максвелловское поле взаимодействует с некоторой другой физической сущно¬
стью Ф. Почему так получается? Особая роль потенциала Аа состоит в том, что он дает нам
калибровочную связность (или связность расслоения; см. § 15.8)
Va = д/дха - геАа,
где е есть некоторое вещественное число, измеряющее электрический заряд той сущности,
которая описывается величиной Ф, Такой «сущностью» фактически оказывается некоторая
заряженная квантовая частица, например электрон или протон, тогда величина Ф должна
быть квантово-механической волновой функцией этой частицы. Для полного понимания
этих терминов придется подождать обсуждения в главе 21, где будет объяснено понятие
волновой функции. Пока об этом нам нужно знать лишь то, что Ф можно рассматривать как
сечение расслоения, на котором V действует как связность.
Величины F и А, описывающие электромагнитное поле, не обладают зарядом (для
них е = 0), поэтому все уравнения Максвелла сохраняют свой вид при другом определе¬
нии операции Va, т. е. в этих уравнениях мы по-прежнему имеем Va = д/дха в плоских
координатах Минковского или соответствующее обобщение (см. § 14.3) в случае искрив¬
ленного пространства-времени. Какова геометрическая природа расслоения, на которое дей¬
ствует эта связность? В качестве слоев этого расслоения можно взять окружности S1 над
пространством-временем М, соответствующие фазовому множителю егв для Ф. (Это есть
пример того, что происходит в пространстве Калу цы - Клейна (§ 15.1), но в данном случае
полное расслоение рассматривается как «пространство-время».) Предпочтительнее рассмат¬
ривать это расслоение как векторный пучок значений величины Ф в каждой точке, при этом
свобода выбора фазового множителя делает данное расслоение расслоением U(l) над про¬
странством-временем М. (Понятие такого рода рассматривалось в конце § 15.8.) Чтобы все
это имело смысл, величина Ф должна быть комплексным полем, физическая интерпретация
которого в некотором смысле нечувствительна к замене Ф н* ег9Ф (где 9 есть некоторое
вещественное поле на многообразии М). Эта замена называется электромагнитным ка¬
либровочным преобразованием, а тот факт, что физическая интерпретация нечувствительна
к указанной замене, называется калибровочной инвариантностью. Тогда кривизна нашей
связности расслоения оказывается максвелловским тензором поля Fab.*
Прежде чем развивать эти идеи дальше, уместно сделать некоторые краткие истори¬
ческие комментарии. Вскоре после того как Эйнштейн сформулировал в 1915 году общую
теорию относительности, Вейль в 1918 году предложил ее обобщение, в котором само по¬
нятие длины становилось зависящим от пути перемещения. (Герман Вейль (1885-1955) был
видной фигурой в математике XX века. Из тех математиков, работа которых полностью при¬
шлась на XX век, он был, на мой взгляд, наиболее влиятельным, притом он был не только
чистым математиком, но и физиком.) В теории Вейля нулевые конусы сохраняют такую
Покажите это. (.Подсказка: воспользуйтесь § 15.8.)

19.4. Максвелловское поле как калибровочная кривизна
387
же фундаментальную роль, как и в теории Эйнштейна (например, определяют предель¬
ную скорость частиц, обладающих массой, и локальную «группу Лоренца», действующую в
окрестности каждой точки), поэтому лоренцева метрика д (с сигнатурой, например, Н )
остается локально необходимой для определения этих конусов. Однако в схеме Вейля от¬
сутствует абсолютный масштаб для измерения времени или пространства, так что метрика
определяется лишь с точностью до пропорциональности. Так, допустимы преобразования
вида
а Ад
с некоторой (например, положительной) скалярной функцией Л, заданной на простран¬
стве-времени М., которые не влияют на нулевые конусы в М. (Такие преобразования
называются конформным масштабированием метрики g; в теории Вейля каждый выбор
метрики g дает возможную калибровку, с использованием которой можно измерять расстоя¬
ния и отрезки времени.) Хотя Вейль в основном имел в виду пространственные расстояния,
можно рассматривать и измерения времени (в соответствии с точкой зрения, изложенной
в главе 17). Таким образом, в геометрии Вейля не существует абсолютных «идеальных
часов». Скорость хода часов, измеряющих время, будет зависеть от их истории.
Такая ситуация «еще хуже», чем в случае стандартного «парадокса часов», описанного
в § 18.3 (рис. 18.6г). В геометрии Вейля можно рассматривать космического путешественни¬
ка, который отправляется к далекой звезде, а затем возвращается на Землю. При этом он об¬
наруживает, что не только обитатели Земли постарели гораздо больше, чем он сам, но и часы
на Земле теперь идут с иной скоростью, нежели в его ракетном корабле! См. рис. 19.5 а. Ис¬
пользуя эту поразительную идею, Вейль сумел ввести уравнения электромагнитной теории
Максвелла в геометрию пространства-времени.
Рис. 19.5. В оригинальной калибровочной теории
электромагнетизма Вейля понятие временного (или
пространственного) интервала не абсолютно, а зави¬
сит от пройденного пути, а) Сравнение с «парадок¬
сом часов», иллюстрированным на рис. 18.6. Соглас¬
но теории Вейля, космический путешественник, вер¬
нувшись домой (мировая линия ABC), обнаружит не
только различные показания часов на Земле (прямая
линия АС) и в ракетном корабле, но и различную ско¬
рость хода часов! б) Калибровочная кривизна Вейля
(задающая максвелловское поле F) возникает из это¬
го (конформного) изменения масштаба времени при
обходе бесконечно малой петли (показано различие
между двумя путями от точки р до соседней точки р)
Существенным в теории Вейля является введение электромагнитного потенциала в связ¬
ность расслоения, как мы сделали это выше, но без мнимой единицы % в выражении для V а.
Соответствующее расслоение над ЛЛ можно считать заданным лоренцевой метрикой g с
теми же нулевыми конусами. Таким образом, слой над некоторой точкой х в ЛЛ состо-
I
б)

388
Глава 19
ит из семейства пропорциональных метрик (в котором коэффициенты пропорциональности,
при желании, можно выбрать положительными). Такими коэффициентами являются воз¬
можные множители Л в приведенном выше преобразовании д Ад. При любом выборе
метрики мы получаем калибровку, определяющую расстояния или времена вдоль кривых.
Но выбор калибровки не абсолютен, поэтому не существует предпочтительной метрики д
в классе эквивалентности взаимно пропорциональных метрик. Существует, однако, некото¬
рая структура, дополнительная к структуре нулевых конусов (т. е. к конформной струюуре),
а именно связность расслоения (или калибровочная связность), которую Вейль ввел, чтобы
максвелловское поле F (т. е. Fab) оказалось ее кривизной. Эта кривизна служит мерой рас¬
хождения в ходе часов, показанном на рис. 19.5 а, когда мировые линии различаются лишь
на бесконечно малую величину (см. рис. 19.5 б). (Это можно сравнить с «деформированным
расслоением» Вс над С, рассмотренным в § 15.8 (рис. 15.16 и 15.19), основные понятия
здесь вполне аналогичны.)
Когда Эйнштейн узнал об этой теории, он сообщил Вейлю, что у него есть фундамен¬
тальное физическое возражение против нее, несмотря на несомненное математическое изя¬
щество идей Вейля. Например, спектральные частоты представляются совершенно не зави¬
сящими от истории атома, тогда как теория Вейля предсказывает обратное. Более существен¬
но, что, хотя и не все относящиеся к данному вопросу законы квантовой механики были к то¬
му времени полностью сформулированы (мы рассмотрим их позднее, в §§21.4, 23.7, 23.8),
теория Вейля вступала в конфликт с требованием полной тождественности различных ча¬
стиц одного типа (см. §23.7). В частности, существует прямая связь между ходом часов
и массой частиц. Как мы увидим позже, частица с массой покоя т обладает собственной ча¬
стотой тс2/г”1, где h — постоянная Планка, а с — скорость света. Таким образом, в геометрии
Вейля не только ход часов, но и масса частицы зависит от ее предыстории. В соответствии
с этим, два протона, имеющие разную предысторию, будут, по теории Вейля, почти опреде-
U	\J*
ленно ооладать разной массой, что нарушает один из принципов квантовой механики, соглас¬
но которому частицы одного сорта должны быть точно тождественными (см. §§ 23.7, 23.8).
Несмотря на эти возражения в адрес первоначального варианта теории Вейля, впослед¬
ствии оказалось^19,4J, что эта идея имеет смысл, если под «калибровкой» понимать не веще¬
ственное изменение масштаба (на множитель А), а умножение на комплексное число единич¬
ного модуля егв. Это может показаться странным, однако, как мы увидим в главе 21 и далее
(см. в особенности §§ 21.6, 21.9), правила квантовой механики вынуждают пользоваться
комплексными числами при описании состояния системы. В частности, такое «квантовое
состояние», обозначаемое обычно как волновая функция ф9 можно умножить на комплекс¬
ное число единичного модуля егв без каких-либо локально наблюдаемых последствий. Такое
«ненаблюдаемое» преобразование ф егвф нынче называют «калибровочным преобразова¬
нием», хотя здесь нет никакого изменения масштаба длины, а изменение сводится к повороту
в комплексной плоскости, которая не имеет прямого отношения ни к пространственным, ни к
временному измерениям. В таком странном искаженном виде идея Вейля создает некоторое
физическое обрамление для связности /7(1), рассмотренной в конце главы 15, и образует
основу современной картины взаимодействия с электромагнитным полем. Определенный
выше оператор V с электромагнитным потенциалом (т.е. Va = д/дха — геАа) дает связ¬
ность расслоения /7(1) на расслоении квантовых волновых функций заряженных частиц ф
(см. § 21.9).
Интересно, что зависимость связности от пути (которую можно сравнить с аналогич¬
ной зависимостью, показанной на рис. 19.5) замечательным образом проявляется в неко¬
торой экспериментальной ситуации, иллюстрирующей так называемый эффект Ааронова -
Бома19 5К Поскольку наша связность V действует только на уровне квантовых явлений,
мы не видим проявления этой зависимости от пути в классических экспериментах. Эффект
Ааронова-Бома основан на явлении квантовой интерференции (см. §21.4 и рис. 21.4).
В наиболее известном варианте электроны заставляют проходить через две области, сво¬

19.4. Максвелловское поле как калибровочная кривизна
389
бодные от электромагнитного поля (F = 0), но разделенные длинным цилиндрическим
соленоидом (который содержит магнитные силовые линии), и попадать на расположенный
позади него детектирующий экран (рис. 19.6 а). Ни на какой стадии электроны не стал¬
киваются с каким-либо полем F, отличным от нуля. Однако участвующая в эксперименте
область 7Z (которая начинается от источника электронов, проходит, разделяясь надвое, по
обе стороны соленоида и воссоединяется на экране) не является односвязной. Поэтому для
поля F вне области 1Z не существует такого выбора калибровки, при котором потенци¬
ал А обращается в нуль всюду внутри 7Z. Присутствие такого ненулевого потенциала в
неодносвязной области 1Z (или, точнее, зависимость V от пути в этой области) приводит к
смещению интерференционных полос на экране.
Соленоид
Электронная Расщепитель
пушка
а)	б)
Рис. 19.6. Эффект Ааронова - Бома, а) Пучок электронов расщепляется на два пучка, проходящих по
обе стороны от области, содержащей линии магнитного потока, которая создается с помощью длинного
соленоида. Два пучка снова объединяются на экране. Результирующая квантовая интерференционная
картина на экране (сравните с рис. 21.4) зависит от величины магнитного потока, несмотря на тот факт,
что электроны попадают лишь в ту область, где напряженность поля райна нулю (F = 0). б) Эффект
зависит от величины § А, которая может быть отлична от нуля при интегрировании по топологически
нетривиальному замкнутому пути, несмотря на то что на всем пути поле F равно нулю. Величина $ А
не меняется при непрерывных деформациях пути интегрирования в области, свободной от поля
Фактически эффект сдвига интерференционных полос зависит не от каких-либо локаль¬
ных значений, которые может принимать потенциал А (это и понятно, поскольку, как уже
упоминалось, потенциал А локально не наблюдаем), а от некоторого нелокального интегра¬
ла от А. Это интеграл § А, взятый вдоль некоторой топологически нетривиальной петли
внутри области 7Z (см. рис. 19.66). Так как dA = 0 в области 1Z (поскольку F — 0 в 1Z),
интеграл § А не меняется при непрерывном перемещении нашей замкнутой петли в 7Z*
Отсюда ясно, что ненулевое значение j> А в области, свободной от поля, и, следовательно,
сам эффект Ааронова-Бома связаны с топологической нетривиальностью этой области.
По историческим причинам, связанным с замечательной идеей Вейля (где использова¬
лась «калибровка», зависящая от пути перемещения), мы называем эту электромагнитную
связность V калибровочной связностью; это название принято также для обобщения электро¬
магнетизма, именуемого «теорией Янга-Миллса». Эта теория используется для описания
слабого и сильного взаимодействий в современной теории элементарных частиц. Отметим,
что идея «калибровочной связности», строго говоря, не зависит от существования симмет¬
рии (в случае электромагнетизма это симметрия относительно преобразования ф егвф),
которая предполагается точной и не наблюдаемой непосредственно. Напомним возраже¬
ние Эйнштейна на оригинальную идею Вейля относительно калибровки, состоявшее, по
существу, в том, что масса частицы (и, следовательно, ее собственная частота) является
непосредственно наблюдаемой величиной и потому не может использоваться в качестве
«калибровочного поля». Далее мы увидим, что это понятие становится несколько размытым
в некоторых современных приложениях идеи «калибровки».
Объясните это.

390
Глава 19
19.5.	Тензор энергии-импульса
Прежде чем переключить внимание на другое фундаментальное классическое поле с его
аспектами «калибровочной теории», а именно гравитационное поле, будет полезно сначала
рассмотреть вопрос о плотности энергии поля, которая служит источником гравитации.
Согласно известной формуле Эйнштейна Е — тс2, масса и энергия — это фактически одно
и то же (см. § 18.6), а как сообщил нам еще Ньютон, именно масса является источником
гравитации. Таким образом, нам следует понять, как описывать плотность энергии поля,
подобного максвелловскому, и как она действует в качестве источника гравитации. По Эйн¬
штейну, таким источником является некоторая тензорная величина, известная под названием
тензора энергии-импульса. Это есть симметричный [^-валентный тензор Т (в индексной
форме Таь = Тъа), удовлетворяющий «уравнению сохранения»
VaTab = 0.
*я
(В остальной части этой главы будет использоваться оператор пространственно-временной
ковариантной производной Va вместо д/дха. Поскольку все наши поля здесь не облада¬
ют зарядом, наши прежние соотношения переносятся сюда без изменения; см. также по¬
следний абзац § 19.2, примечание 19.2 и упражнение 19.6.) Можно сравнить приведенное
уравнение с уравнением сохранения электрического заряда Va Ja. Наличие у ТаЬ лишнего
индекса связано с тем, что сохраняющаяся величина, а именно энергия-импульс, являет¬
ся 4-(ко)вектором (4-(ко)вектор ра энергии-импульса рассматривался в § 18.7) в отличие от
скалярного электрического заряда. Для более полного описания физического содержания
тензора ТаЬ удобно перейти к эквивалентной величине Tab — gacTcb, где один из индексов
поднят с помощью метрического тензора даЬ* Величина Таь объединяет различные плот¬
ности и потоки энергии и импульса для полей и частиц, ьолее конкретно, в стандартной
координатной системе Минковского ковектор Т°ь определяет плотность 4-импульса, а три
ковектора Т1^ Т2Ь, Т3Ь ~~ поток 4-импульса в трех независимых пространственных направ¬
лениях. Это вполне аналогично случаю Ja, поскольку J0 есть плотность заряда, а три
величины Ji, J2, J3 — поток заряда (т. е. ток) в трех независимых пространственных на¬
правлениях. Лишний индекс b указывает на то, что наш закон сохранения теперь относится
к (ко)векторной величине. Оказывается, что величина Too служит мерой плотности энергии,
а Тц, Т22, Т33 определяют давление в направлении трех пространственных координатных
осей.
Напомним, что, согласно Максвеллу, сами электромагнитные поля переносят энергию.
*
В индексной записи тензор энергии импульса электромагнитного поля имеет вид
^FacFcb + *Fac*Fcb).
Другие физические поля также имеют свои тензоры энергии-импульса, и необходимо сло¬
жить все такие вклады, чтобы получить полный тензор энергии-импульса Т, удовлетворя¬
ющий уравнению сохранения VaTab — 0.
Однако, как мы сейчас увидим, нечто совсем иное получается с тензором энергии-им¬
пульса самого гравитационного поля. При отсутствии гравитации пространство-время плос¬
кое (т. е. это пространство Минковского), и можно пользоваться плоскими координатами
Как связаны отдельные компоненты Т% с ТаЬ в локальной системе отсчета Минковского, где компоненты
тензора даъ имеют диагональную форму (1,-1,—1,-1)?
** Покажите, что этот тензор удовлетворяет уравнению сохранения VaTa^ = 0, если J = 0. Найдите все
компоненты этого тензора и выразите первоначальную формулу Максвелла для плотности энергии электромагнит¬
ного поля (Е2 + В2)/Stt через компоненты (£1, £2, Ёз) и (£1» ^2, #з)-

19.5. Тензор энергии-импульса
391
Минковского. Тогда каждый из четырех векторов Та0, Таi, Та2, Таз в отдельности подчи¬
няется точно тому же уравнению сохранения, что и вектор Ja (а именно VGTao — 0 и т. п. по
аналогии с Va Ja = 0); отсюда следует, что интегральный закон сохранения для каждой из
четырех компонент энергии-импульса в отдельности вполне аналогичен закону сохранения
заряда J * J — 0. Поэтому сохраняются полная масса и три компоненты полного импуль-
Q
са. Напомним, однако, обсуждение эйнштейновского принципа эквивалентности в главе 17
и то, как он приводит к искривленному пространству-времени. Получается, что при нали¬
чии гравитации мы должны учесть тот факт, что оператор Va теперь не просто д/дха,
а (в соответствии с § 14.3) появляются лишние члены с Тьас, которые меняют сам смысл
выражения VaTao и не позволяют вывести интегральный закон сохранения энергии и им¬
пульса непосредственно из нашего уравнения \/аТаъ = 0. Проблему можно сформулировать
так: лишний индекс b у Таъ не позволяет этой величине быть дуальной по отношению
к некоторой 3-форме, поэтому мы не можем записать это уравнение в виде, не зависящем от
координат (подобно обращению в нуль внешней производной 3-формы * J согласно уравне¬
нию d* J — 0). Создается впечатление, что мы теряем наиболее важные законы сохранения —
законы сохранения энергии и импульса!
В действительности ситуация с сохранением энергии и импульса более удовлетво¬
рительна. Это относится к некоторым видам искривленного пространства-времени, как
и к пространству Минковского, и применимо также к сохранению момента импульса
(см. §§18.6, 22.8, 22.11). Предположим, что мы имеем вектор Киллинга к для многооб¬
разия М (он удовлетворяет уравнению V(акь) — 0; см- § 14.7). Этот вектор описывает неко¬
торую непрерывную симметрию многообразия Л4. В пространстве Минковского имеется
10 таких независимых симметрий — 4 независимые трансляционные симметрии (три про¬
странственные и одна временная) и 6 независимых пространственно-временных вращений
(неотражательная часть группы Лоренца 0(1, 3)); см. рис. 18.3 б. Таким образом, простран¬
ство Минковского имеет 10 независимых векторов Киллинга. Как мы увидим в следующей
главе, лагранжев формализм (теорема Нётер) позволяет вывести закон сохранения из каж¬
дой непрерывной симметрии, которой обладают законы этой системы. Симметрия относи¬
тельно временных трансляций дает закон сохранения энергии, а симметрия относительно
пространственных трансляций — закон сохранения 3-импульса. Вращательная симметрия
обеспечивает сохранение момента импульса. (Обычные пространственные вращения дают
нам три компоненты обычного момента импульса, но есть еще три компоненты, связанные
с преобразованиями Лоренца, позволяющими переходить от одной скорости к другой. Они
дают закон сохранения движения центра масс, см. §§ 18.6, 18.7 и рис. 18.16.) Чтобы по¬
лучить соответствующий закон сохранения из какого-либо вектора Киллинга к, построим
величину, описывающую поток:
La — TabK?,
которая удовлетворяет закону сохранения VaLa — 0, коль скоро симметричный тензор Таь
удовлетворяет условию VaTa& = 0.* Следовательно, как и в § 19.3, существует интегральный
закон сохранения f*L = 0.
Q
Эти законы сохранения имеют место только в пространстве-времени, где имеется со¬
ответствующая симметрия, задаваемая вектором Киллинга к. Физическая причина состоит
в том, что степени свободы в геометрии пространства-времени, т. е. в гравитации, отделены
от полей. Геометрия пространства-времени служит просто фоном, так что оно не дефор-
*/83 Почему? Почему эта процедура применяется к вышеприведенному уравнению VаТао — 0 и ему по¬
добным? Попробуйте найти аналог закона сохранения для непрерывного поля Va(TabKb) = 0, применимый
к дискретной системе частиц, в которой 4-импульс сохраняется при столкновениях. (.Подсказка: найдите величину,
задаваемую вектором Киллинга ка, которая остается постоянной для каждой частицы между столкновениями.)

392
Глава 19
мируется полями внутри него; более того, поля не могут отделить обсуждаемую величину
от фона (или потерять ее в фоне) вследствие симметрии. Эти соображения окажутся важ¬
ными для нас позднее, особенно в главе 30 (§§30.6, 30.7). Тем не менее они не могут
реально помочь нам в понимании судьбы законов сохранения, когда гравитация начинает
играть активную роль. Мы пока не можем вернуть потерянные законы сохранения энергии
и импульса, когда в игру вступает гравитация.
Этот обескураживающий факт вызывал резкие возражения ряда физиков против общей
теории относительности с самого момента ее появленияt19*6). Позднее, в § 19.8, мы увидим,
что на самом деле теория Эйнштейна учитывает сохранение энергии-импульса довольно
разумным образом, во всяком случае в тех условиях, когда такой закон сохранения особен¬
но необходим. Пока же отметим, что в теории Эйнштейна симметричный [^-валентный
тензор Т, фигурирующий в уравнении для поля, должен включать энергию-импульс всех
негравитационных полей (и частиц). При этом какая-либо энергия самого гравитационного
поля никоим образом не должна быть представлена в Т.
Такая точка зрения делается несколько более правдоподобной, если вновь обратиться
к принципу эквивалентности. Представим себе наблюдателя на свободной орбите, например
внутри некоторого космического корабля без окон, которому кажется, что гравитационное
поле, по крайней мере в первом приближении, отсутствует. Такой наблюдатель будет ожи¬
дать, что внутри его корабля энергия сохраняется и, следовательно, выполняется уравне¬
ние VaTab = 0 без какого-либо вклада, вносимого гравитационным полем. Такое «сохране¬
ние», однако, имеет лишь приближенный характер и требует поправок, коль скоро начинают
играть роль эффекты относительного ускорения (приливные эффекты), обусловленные неод¬
нородностью гравитационного поля (см. § 17.5, рис. 17.8 а, б, 17.9). Из всего этого следует,
что величина Т и уравнение для нее VaTab = 0 не должны меняться из-за неоднородности
гравитационного поля, т. е. не должны зависеть от кривизны R пространственно-временной
связности V, и что вклад гравитации в сохранение энергии-импульса должен входить каким-
то нелокальным образом, как поправка при вычислении полной величины энергии-импульса.
(Единственное реальное исключение из этого утверждения может возникнуть, если пона¬
добится рассмотреть поправки на кривизну пространства-времени к тем математическим
выражениям, которые описывают вклад физических полей в Т. Обычно такие поправки
отсутствуют, так что эта тема не играет существенной роли в нашем изложении.) При такой
точке зрения гравитационный вклад в энергию-импульс, в некотором смысле, «проскальзы¬
вает сквозь щель», отделяющую локальное уравнение VaTab = 0 от интегрального закона
сохранения полной величины энергии-импульса.
s
19.6.	Эйнштейновское уравнение поля
Я еще вернусь к этому вопросу в § 19.8, а пока нам следует узнать, какой вид имеет
эйнштейновское уравнение поля. Это уравнение использует термины тензорного форма¬
лизма, который теперь уже не покажется (я надеюсь!) читателю слишком отвлеченным.
Одна из причин привлечения тензоров состоит в том, что кривизна пространства-време¬
ни в 4 измерениях представляет довольно сложное понятие. Вспомним Альберта, нашего
космонавта А из § 17.5, свободно вращающегося на орбите в гравитационном поле Земли.
Вдоль одних направлений относительно А ускорения направлены внутрь, вдоль других —
вовне. Это связано с приливными силами, воспринимаемыми космонавтом. Приливные си¬
лы являются проявлением кривизны пространства-времени. Для того чтобы единым образом
учесть эти сложные эффекты, используется тензорная величина с компонентами Rabcd> ко¬
торая имеет 10 компонент в случае пустого пространства и все 20 при наличии вокруг
некоторой плотности материи. Фактически Rabcd — это просто индексная форма тензора
Римана(-Кристоффеля) R, с которым мы сталкивались в § 14.7.

19.6. ЭЙНШТЕЙНОВСКОЕ УРАВНЕНИЕ ПОЛЯ
393
Однако помимо этих чисто организационных трудностей есть и другая причина, по
которой тензорное исчисление играет столь фундаментальную роль в теории Эйнштейна.
Она восходит к основополагающему принципу эквивалентности, с которого начался весь
ход мыслей Эйнштейна. Гравитация не должна рассматриваться как сила, поскольку для
свободно падающего наблюдателя (того же космонавта А) никакой гравитационной силы не
существует. Вместо этого гравитация проявляется в виде кривизны пространства-времени.
Чтобы эта идея работала, важно, чтобы в теории не существовало каких-то «предпочтитель¬
ных координат»^9*7}. Если бы природа предпочла выбрать некоторый ограниченный класс
координатных систем, то можно было бы ввести «естественные координатные системы на¬
блюдателя», относительно которых можно было бы восстановить понятие «гравитационной
силы»; при этом была бы утрачена центральная роль принципа эквивалентности. Это до¬
вольно тонкий пункт, и многие физики время от времени отступали от этой точки зрения тем
или иным образом. На мой взгляд, для духа эйнштейновской теории существенно поддержа¬
ние этой концепции независимости от выбора координатной системы. Это так называемый
принцип общей ковариантности. Он провозглашает не только отсутствие предпочтительных
координат, но и то, что если мы имеем два различных пространства-времени, представля¬
ющих два физически различных гравитационных поля, то не существует естественного
предпочтительного способа их поточечной идентификации, поэтому мы не можем сказать,
какую из пространственно-временных точек одного из них следует считать той же самой
точкой, что и некоторая выбранная пространственно-временная точка другого! С таким фи¬
лософским подходом мы столкнемся позднее (в §30.11) при рассмотрении вопроса, как
связать эйнштейновскую теорию с принципами квантовой механики. Пока же важная роль
принципа общей ковариантности для нас состоит в том, что он заставляет нас принять
описание физики гравитации, не связанное с определенной системой координат. Имен¬
но в этом состоит основная причина центральной роли тензорного формализма в теории
Эйнштейна.
Теперь посмотрим, что в действительности представляет собой уравнение Эйнштейна.
Вид его определяется в основном двумя требованиями: 1) чтобы (локальным) источником
тяготения был тензор энергии-импульса Т, удовлетворяющий уравнению VaTab = 0, 2) что¬
бы в соответствующем ньютоновском предельном случае (скорости, малые по сравнению со
скоростью света, и слабые гравитационные поля) получалась теория гравитации Ньютона.
Мы должны вернуться к обсуждению в § 17.5, где было показано, что в ньютоновской теории
существует эффект уменьшения объема для геодезических, соседних, а поначалу параллель¬
ных геодезической мировой линии наблюдателя 7. Эти соседние геодезические ускоряются
относительно 7 таким образом, что (бесконечно малый) пространственноподобный 3-объ¬
ем 5V, который они ограничивают, изменяется с полным ускорением —47tG5M, где 5М есть
активная гравитационная масса внутри (бесконечно малого) объема, ограниченного геоде¬
зическими. Знак минус связан с тем фактом, что имеет место уменьшение рассматриваемого
объема; см. рис. 17.86. Это есть полное выражение ньютоновской теории в отношении
активного гравитационного эффекта, создаваемого некоторым распределением массы.
Как перевести это в уравнение, связывающее кривизну пространства-времени R с тен¬
зором энергии-импульса Т? Ключевой геометрический факт состоит в том, что рассмот¬
ренное ускорение объема внутрь в данном случае измеряется [9 ] -валентным симметричным
тензором, называемым тензором Риччи, который определяется соотношением
Rah — Racb i
соотношения
где Rabcd — тензор Римана* (Диаграммное представление этого
на рис. 19.7. Здесь опять-таки имеются бесчисленные различные соглашения относительно
Почему тензор Яаъ симметричен?

394
Глава 19
R
ah
ft
знаков, порядка индексов, сигнатуры и т. д. Как и прежде, я
навязываю читателю мои личные предпочтения; см. § 14.4.)
Более точно, ускорение изменения объема (исходя из состоя¬
ния покоя) определяется формулой*
D2(<5K) = RabtatbSV.
Здесь D представляет собой скорость изменения по отноше¬
нию к собственному времени наблюдателя (см. § 17.9) вдоль
мировой линии наблюдателя 7, так что D2 означает ускоре-
ал.Ъ
Рис. 19.7. Диаграммная запись
определения тензора Риччи
Rab = RacbC (см. рис. 14.21)
ние. Мы имеем
D - taVa
V
t
где ta есть времениподобный, направленный в будущее, единичный касательный вектор к 7
(так что tata — 1).
Плотность массы (которая есть то же, что плотность энергии, если положить с =
= 1 в соотношении Е — тс2; см. § 18.6), измеряемая наблюдателем, есть «00-компонента»
тензора Таь в локальной системе отсчета наблюдателя. Это есть в точности величина Tabtatb,
поэтому масса 8V, ограниченная соседними геодезическими, равна
SM = Tabtatb8V.
Таким образом, «ньютоновское ожидание» —4ttG5M (§ 17.5) для ускорения изменения объ¬
ема равно
4тгGTabtatb5V.
Но мы только что видели, что эффект ускорения изменения объема вследствие кривизны
пространства-времени равен Rabtatb5V. Следовательно, мы приходим к соотношению
Rabtatb5V
4тг GTabtatbSV.
Разделим это равенство на SV и учтем, что оно применимо ко всем наблюдателям, проходя¬
щим через эту мировую точку (событие), и, следовательно, можно убрать tat°. ' В результате
получается искомое уравнение поля
R
а-Ь
47xGTab
которое совпадает с первоначальным уравнением, предложенным Эйнштейном. Оно, одна¬
ко, не вполне удовлетворительно, поскольку из «уравнения сохранения» VaTab = 0 следу
ет Vai?a6, что в свою очередь приводит к неприятностям!
В чем состоят эти неприятности? Напомним (см. § 14.4) тождество Бъянки V [aRbc]de =
0. Свертывая это уравнение, получаем
Va(R
ab
1
2
Rgab) — о?
где скаляр Риччи R (или скалярная кривизна, хотя для положител]
удобнее использовать величину — R) определяется соотношением
R - Raa
*
**
Попробуйте доказать эту формулу, пользуясь тождеством Риччи и свойствами производной Ли.
••
Объясните подробнее, почему можно «отбросить» все множители ta, учитывая роль симметрии тензоров.
Покажите это, используя, при желании, диаграммное представление.

19.7. Дальнейшее развитие. Космологическая постоянная, тензор Вейля
395
(не следует смешивать R с напечатанным жирным шрифтом тензором полной кривизны R).
«Неприятности» с предложенным уравнением Наь — -~4тсОТаь состоят в том, что в со¬
четании со свернутым тождеством Бьянки оно приводит к выводу, что след Т тензора
энергии-импульса, определяемый соотношением
• •
гр 	 гра
1 ~~ 1 а >
должен быть постоянным во всем пространстве-времени*. Это явно несовместимо с обыч¬
ной (негравитационной) физикой. В соответствии с этим Эйнштейн в конечном счете
(в 1915 году) пришел к выводу, что для согласованности следует приравнять (с точностью
до постоянного множителя) друг другу два тензора, удовлетворяющие «уравнению сохра¬
нения» Va(...) = 0, и пришел к ныне известному эйнштейновскому уравнению поля**' ^19 ^
Rab — |Rgab = —S7YGTab.
В частном случае отсутствия какой-либо материи (включая электромагнитное поле)
мы имеем Таь = 0. Это случай вакуума. Уравнение Эйнштейна для этого случая {уравнение
1
вакуума) принимает вид Rab — ~Rgab = 0, что можно переписать в виде
Rab = 0*
Пространство с нулевым тензором Риччи иногда называют плоским пространством Риччи.
19.7.	Дальнейшее развитие. Космологическая постоянная, тензор Вейля
Теперь мы должны рассмотреть дополнительный член, предложенный Эйнштейном
в 1917 году и называемый космологической постоянной. Это чрезвычайно малая величи¬
на Л, необходимость присутствия которой подтверждается современными космологически¬
ми наблюдениями, но которая не может отличаться от нуля более чем на очень малую
величину порядка 10“55 см“2. Она не имела прямого экспериментального подтверждения,
1
пока не были достигнуты космологические масштабы. Величина Rab ~ ту Rgab в вышепри-
выражении заменяется на Каь ~~ ^
также
«уравнению сохранения», поскольку Л является постоянной величиной (и V# = 0). Теперь
уравнение Эйнштейна принимает вид
Rab TjRgcib -д-Qab ~ ^7vGTai).
Первоначально Эйнштейн ввел этот дополнительный член, чтобы обеспечить возмож¬
ность статической пространственно-однородной Вселенной в космологическом масшта-
бе!19‘91. Но когда стало ясно, после наблюдений Эдвина Хаббла в 1929 году, что Вселенная
расширяется, Эйнштейн отказался от космологической постоянной, заявив, что она была
«его самой большой ошибкой» (возможно, потому, что без нее он мог бы предсказать рас¬
ширение Вселенной!). Тем не менее однажды выдвинутая идея не всегда легко уходит.
Космологическая константа с тех пор, как она была предложена Эйнштейном, неизмен¬
но присутствовала в теории, вызывая неудовольствие у одних и чувство удовлетворения
***
Почему?
Объясните, почему — 8ttG, а не —ArcG.
Почему?

396
Глава 19
у других. Совсем недавно результаты наблюдения удаленных сверхновых побудили мно¬
гих теоретиков возродить константу А, связав с ней так называемую «темную энергию»,
чтобы согласовать эти результаты с другими ощущаемыми требованиями f19*10!. я вернусь
к понятию космологической постоянной позже (см., в частности, § 28.10). Что до меня, то,
хотя я, как и большинство теоретиков-релятивистов, обычно и не возражал против воз¬
можного присутствия в уравнениях ненулевой константы Л, мне было довольно трудно
принять, что природа могла бы воспользоваться этим дополнительным членом. Однако,
как мы увидим в §28.10, многие последние данные космологии указывают именно в этом
направлении.
Эйнштейновское уравнение поля (включая космологическую постоянную) можно запи-
сать противоположным образом : Яаь = —87тС{Таь — ~Тдаъ) + Лдаъ. Используя локальную
систему координат с временной осью £°, так что свертка с tatb дает 00-компоненту, мы
получаем для ускорения объема внутрь величину SnG(Tab — 9оо) ~ А что равно 4тгС(р +
-f- Pi + Р2 -Г Рз) —А, где Pi, Р2 и Р3 — значения давления материи в направлении трех
(ортогональных) пространственных осей. Сравнивая это с величиной 47тGSM, которую дает
ньютоновская теория, получаем плотность активной гравитационной массы рс в общей
теории относительности Эйнштейна
PG = Р + Р\ + Р2 + Рз “	’
а не рс — р, как можно было бы ожидать, учитывая соотношение Е' =' тс2. (Выбрана
система единиц, в которой с — 1.) Вклад постоянной А крайне мал, лишние члены (дав¬
ления) также обычно весьма малы по сравнению с энергий, — грубо говоря, потому, что
малые частицы, составляющие рассматриваемое вещество, двигаются медленно по срав¬
нению со скоростью света. Однако в некоторых экстремальных условиях вклад давления
в активную гравитационную массу начинает играть существенную роль. Если звезда очень
большой массы оказывается близка к ситуации, в которой появляется опасность ее кол¬
лапса под действием ее собственного гравитационного притяжения, то оказывается, что
увеличение давления внутри звезды, которое, казалось бы, должно удерживать ее от этого,
в действительности усиливает тенденцию к коллапсу из-за возникновения при этом лишней
гравитационной массы!
Как отмечалось выше (§ 19.5), тензор энергии-импульса Таъ в теории Эйнштейна ана¬
логичен вектору заряда-тока Ja в теории Максвелла. Можно считать, что величина Таъ опи¬
сывает источник гравитации, подобно тому как Ja является источником электромагнитного
поля. Можно задать вопрос: что могло бы служить подходящим аналогом максвелловского
тензора поля Еаь, описывающим гравитационные степени свободы? Таковым не является
метрический тензор д, наиболее близкий к электромагнитному потенциалу А. Можно было
бы рассматривать в качестве аналога тензора F полный тензор кривизны Римана Rabcd,
однако более подходящим выбором является так называемый тензор Вейля (или конформ¬
ный тензор) С abed, похожий на полный тензор Римана, но за вычетом тензорной части
Риччи. Это разумный выбор, поскольку тензор Риччи можно спутать с источником Таь,
так что эти «степени свободы источника» следует исключить, если мы хотим идентифи¬
цировать те степени свободы, которые непосредственно описывают гравитационное поле.
В пустом пространстве, где нет материи (и для простоты предполагается А — 0), тензор
Вейля равен тензору кривизны Римана, однако в общем случае тензор Вейля определяется
довольно сложной формулой, которая исключает тензор Риччи из полного тензора кривизны
(в котором я поднял два индекса, чтобы воспользоваться записью с квадратными скобками
р

19.8. Энергия гравитационного поля
397
из § 11.6):*
cabcd = RabЫ ~ 2R[Jcgb}d] + IRg[ac9b\d-
Ключевая роль тензора Вейля будет показана в §28.8. Обращение этой величины в нуль
является условием конформной гладкости пространства-времени.
19.8.	Энергия гравитационного поля
Вернемся к вопросу о массе/энергии, заключенной в самом гравитационном поле. Хо¬
тя ей нет места в тензоре энергии-импульса Т, тем не менее ясно, что существуют ситуа¬
ции, когда «исключенная» гравитационная энергия действительно играет физическую роль.
Представим себе два массивных тела (например, две планеты). Если они находятся близко
друг от друга (при этом можно предположить, что в данный момент они находятся в покое
относительно друг друга), то будет существовать (отрицательный) вклад гравитационной
потенциальной энергии, уменьшающий полную энергию и, следовательно, полную массу
по сравнению с тем, что было бы при большом расстоянии между телами (см. рис. 19.8).
Игнорируя тонкие эффекты вроде изменения формы каждого из тел гравитационным при¬
ливным полем другого тела, мы видим, что полный вклад энергии, создаваемый тензором
энергии-импульса Т, будет одним и тем же независимо от того, близко или далеко нахо¬
дится одно тело от другого. В то же время полная масса/энергия в этих двух случаях будет
разной, и это различие следует приписать энергии самого гравитационного поля (этот вклад
отрицателен и более заметен, когда тела находятся ближе друг к другу).
а)
€>
б)
Рис. 19.8. Нелокальность гравитационной потенциальной энергии. Рассматриваются две планеты (для
простоты можно считать их покоящимися относительно одна другой в данный момент). Если планеты
находятся вдали одна от другой «), то вклад (ньютоновской) отрицательной потенциальной энергии
будет меньше, чем в случае б), когда расстояние между ними мало. Тогда полная энергия (и, следо¬
вательно, полная масса всей системы) в случае а) будет больше, чем в случае б), несмотря на то что
проинтегрированная полная плотность энергии, определяемая тензором энергии-импульса, в обоих
случаях будет одной и той же
Пусть теперь тела находятся в орбитальном движении относительно друг друга. Из эйн¬
штейновского уравнения поля следует, что система будет излучать гравитационные волны —
«рябь» на ткани пространства-времени, — которые уносят от нее (положительную) энер¬
гию. В обычных условиях эта потеря энергии будет очень мала. Например, наибольший
такой эффект в нашей Солнечной системе создается системой Юпитер-Солнце, при этом
скорость потери энергии примерно соответствует всего лишь мощности 40-ваттной лам¬
почки! Но для более массивных и энергичных систем (примером может служить конечная
стадия слияния двух черных дыр, падающих одна на другую) можно ожидать таких потерь
* Покажите, что все «следы» тензора С обращаются в нуль (т. е. Саъса = 0 и т.д.). При желании, проведите
вычисления в диаграммной форме.

398
Глава 19
энергии, что современные приемники на Земле смогут зарегистрировать присутствие таких
гравитационных волн на расстоянии 15 мегапарсек, или приблизительно 4,6 • 1023 мет¬
ров.
Между этими двумя крайностями находятся гравитационные волны, излучаемые заме¬
чательной системой в виде двойной нейтронной звезды под именем PSR 1913 + 16, изу¬
чавшейся нобелевскими лауреатами Джозефом Тейлором и Расселом Хюлсом; см. рис. 19.9.
— это крайне компактная звезда, состоящая в основном из нейтронов,
сжатых вместе столь плотно, что средняя плотность звезды сравнима с плотностью атомного
ядра. Теннисный мяч, наполненный таким веществом, имел бы массу, сравнимую с массой
марсианской луны Деймоса!) Эта система наблюдается уже в течение 25 лет, и подробности
ее движения прослежены с большой точностью (это оказалось возможным благодаря тому,
что одна из этих звезд представляет собой пульсар, испускающий с большой временной точ¬
ностью электромагнитные сигналы приблизительно 17 раз в секунду). Синхронность этих
сигналов столь велика, а система настолько «чистая», что сравнение результатов
с теоретическими предсказаниями позволяет подтвердить общую теорию относительности
Эйнштейна с точностью 10 ~14, не имеющей прецедента при сравнении с теорией результа¬
тов наблюдения какой-либо системы. Указанная цифра относится к точности синхронности,
наблюдавшейся более 20 лет!19Л11.
PSR 1913+16
9
9
Земля
Рис. 19.9. Система Хюлса-Тейлора в виде двойной нейтронной звезды PSR 1913 + 16. Одной из звезд
системы является пульсар, который посылает точно синхронизованные электромагнитные сигналы,
принимаемые на Земле и позволяющие определить орбиты этих звезд с необычайно высокой точ¬
ностью. Оказалось, что система теряет энергию в точном соответствии с предсказанием Эйнштейна
относительно излучаемых такой системой гравитационных волн, переносящих энергию. Эти волны
представляют собой «рябь» в пространственно-временном вакууме, где тензор энергии-импульса равен
нулю. (Изображено без соблюдения масштаба.)
С наблюдениями такого рода (а также с впечатляющими исследованиями эффекта гра¬
витационной линзы, которые будут рассмотрены в §28.8) экспериментальная общая тео¬
рия относительности прошла долгий путь, начиная со дней ее появления. Однако в пе¬
риод 1915-1969 годов (1969-й год отмечен наблюдениями радиоизлучения удаленных ква-
заров, положившими начало новому семейству экспериментов но проверке
относительности!1912^) существовали лишь известные, но сравнительно мало впечатляющие
«три теста», подтверждающие теорию. Наиболее значительным из них было данное Эйн¬
штейном объяснение «аномального смещения перигелия» планеты Меркурий, наблюдав¬
шегося более полувека!19-131 Отклонение от предсказаний ньютоновской теории тяготения
было очень малым, всего 43 угловых секунды в столетие или один оборот орбиты за 3 мил¬
лиона лет! (См. также §§ ЗОЛ, 34.9.) Другим наблюдательным эффектом было очень малое
искривление света далекой звезды Солнцем, увиденное экспедицией Артура Эддингтона на
острове Принсипе (у берегов западной Африки) во время солнечного затмения 1919 года.
Это пример того же вышеупомянутого «эффекта гравитационной линзы», который сейчас
используется вплоть до ближних космологических расстояний для получения важной инфор¬
мации о распределении массы во Вселенной (см. § 28.8). Наконец, третьим эффектом было

19.8. Энергия гравитационного поля
399
замедление хода часов, предсказанное теорией Эйнштейна. Это, по-видимому, наблюдалось
У. С. Адамсом при изучении белого карлика — спутника звезды Сириуса, — плотность ко¬
торого в тысячи раз больше плотности Солнца. Гораздо более убедительное подтверждение
было получено позднее в тонком эксперименте, проведенном в 1960 году Паундом и Реб-
кой, с использованием собственного гравитационного поля Земли. (Однако наблюдаемый
там эффект следует просто из сохранения энергии и общих квантово-механических сообра¬
жений, поэтому он дает довольно слабое подтверждение теории Эйнштейна.) Существует
также эффект «запаздывания во времени» другого рода, а именно запаздывание сигналов,
приходящих к Земле от объектов, расположенных почти точно позади Солнца. Использовать
такой эффект предложил в 1964 году Ирвин Шапиро [717], он же подтвердил его существо¬
вание в 1968-1971 годах при наблюдениях Меркурия и Венеры; с большей точностью (до
0,1%) это было сделано в 1971 году Ризенбергом и Шапиро путем сравнения сигналов пе¬
редатчика на борту космического корабля «Викинг», находящегося на орбите вокруг Марса,
с сигналами передатчика на поверхности Марса.
Вполне очевидно, что теория Эйнштейна в настоящее время очень хорошо подтвер¬
ждается наблюдениями. Существование гравитационных волн, по-видимому, ясно подтвер¬
ждается наблюдениями Хюлс а-Тейлора, несмотря на то что такие волны пока не были
непосредственно обнаружены. В настоящее время имеется несколько проектов прямого де¬
тектирования гравитационных волн объединенными усилиями для изучения систем высокой
активности (например, столкновения черных дыр) в удаленных областях Вселенной. Такие
объединенные проекты^19-14! предполагают создание гравитационно-волнового телескопа,
в результате чего теория Эйнштейна получит возможность дать нам еще один мощный
способ изучения удаленных частей Вселенной,
Мы видим, что, несмотря на некоторое беспокойство по поводу сохранения энергии,
общая теория относительности замечательно подтверждается наблюдениями. Поэтому вер¬
немся к вопросу о гравитационной энергии. Теория и наблюдения согласны в том пункте,
что «рябь» в пустом пространстве, образующая гравитационные волны, испускаемые си¬
стемой PSR 1913 + 16 и другими подобными системами, действительно уносит энергию.
Тензор энергии-импульса в пустом пространстве равен нулю, так что энергия гравитаци¬
онных волн должна измеряться несколько иным образом, и к ней неприменимо понятие
локальной «плотности» энергии. Гравитационная энергия — это изначально нелокальная
величина. Это, однако, не означает, что гравитационная энергия не допускает математиче¬
ского описания. Хотя, я считаю, следует честно признать, что у нас пока нет полного по¬
нимания гравитационной массы/энергии, тем не менее существует важный класс ситуаций,
в которых можно дать исчерпывающий ответ. Такие ситуации называются асимптотически
плоскими и относятся к гравитирующим системам, которые можно считать изолированными
от остальной Вселенной из-за очень больших расстояний до чего бы то ни было. Таковой
может быть, например, двойная звезда типа двойного пульсара Хюлса-Тейлора, которая
рассматривалась в связи с энергией, теряемой на гравитационное излучение. Работа Герма¬
на Бонди с сотрудниками, обобщенная Райнером Саксом t19-15! (чтобы снять сделанное Бонди
упрощающее предположение относительно аксиальной симметрии), дает четкое математи¬
ческое описание массы/энергии, теряемой такой системой в виде гравитационных волн,
при этом выполняется закон сохранения энергии-импульса^9Л6^; см. рис. 19.10. Этот закон
сохранения не имеет локального характера, как в случае негравитационных полей, где он
проявляется в виде «уравнения сохранения» \7аТаъ. Он применим лишь в предельном слу¬
чае, когда система оказывается полностью пространственно изолированной от окружающего
мира. Есть нечто несколько «сверхъестественное» в том, как все это соединяется вместе,
включая некоторые доказанные позднее теоремы «положительности», которые утверждают,
что полная масса системы (включая рассмотренный выше «отрицательный вклад гравита¬
ционной потенциальной энергии») не может быть отрицательнойI19-17).

400
Глава 19
j - ■
V
Время
Тела
I
Рис. 19.10. В предположении, что пространство-время является асимптотически плоским, для изо¬
лированной системы, излучающей гравитационные волны, существует точная мера полной мас¬
сы/энергии-импульса и потерь на гравитационное излучение, называемая законом сохранения мас¬
сы/энергии Бонди - Сакса. Соответствующие величины нелокальны и определены на «нулевой беско¬
нечности» (это геометрическое понятие будет рассмотрено в §27.12)
Существуют некоторые общие предписания для получения законов сохранения, отно¬
сящихся к системам взаимодействующих полей. Они основаны на использовании лагран¬
жиана, который будет представлен в следующей главе. Метод лагранжиана является очень
мощным, общим и красивым, несмотря на тот факт, что он не может дать (или, по крайней
мере, не может дать непосредственно) все, что нам нужно, в случае гравитации. Этот метод,
а также тесно связанный с ним метод гамильтониана играют центральную роль в современ¬
ной физике, так что стоит узнать о них побольше. Поэтому в следующей главе мы отважимся
проникнуть на эту легендарную территорию.
Примечания
§19,1.
19.1. Кажется сомнительным, чтобы сам Ньютон догматически придерживался картины мира, со¬
стоящей лишь из одних таких частиц (см. главу «Вопросы» в ньютоновской «Оптике» [557]).
Такой «ньютоновский» взгляд был убедительно аргументирован в XVIII веке Р. Дж. Босковичем
(см. [54]).
§19.3.
19.2. Этот результат применим также к искривленному топологически тривиальному простран¬
ству-времени, поэтому, в частности, замкнутая 2-поверхность всегда охватывает некоторый
компактный 3-объем.

19.8. Энергия гравитационного поля
401
§19.4.
19.3. См., например, [266].
19.4. См. [823], стр. 87-88 (в переводе стр. 100-101), а также [824]. Это было также независимо
замечено У. Гордоном и Паули и Гейзенбергом (см. [573], стр. 345).
19.5. См. [9]. Фактически возможность такого эффекта была отмечена 10 годами раньше Эренбергом
и Сайди [235]. Эта возможность была экспериментально подтверждена Чамберсом и более
убедительно Тономурой с сотрудниками [785, 786].
§19.5.
19.6. См. [572].
§19.6.
19.7. Содержащееся в тексте требование отсутствия «предпочтительных координат» не только до¬
вольно расплывчато, но и представляется слишком сильным. Например, в случае плоского
пространства было бы разумно сказать, что выбор «декартовых координат» (такими будут коор¬
динаты Минковского (£, ж, у, z) из § 18.1, для которых метрика принимает особенно простую
форму ds2 — dt2 — dx2 — dy2 — dz2) является «предпочтительным» по сравнению со всеми дру¬
гими системами координат. Космологические модели также используют специальные системы
координат, в которых метрика выглядит наиболее просто (см. § 27.11, упражнение 27.18). Более
тонким пунктом является то, что такие специальные координаты не должны играть физической
роли и уравнения теории должны быть такими, чтобы их наиболее естественное выражение не
зависело от какого-либо определенного выбора координат.
19.8. См. [741], стр. 353-364. Из многих отличных книг по общей теории относительности отме¬
тим [358, 498, 529, 664, 666, 703, 761, 809, 814].
§19.7.
О	-I
19.9. Моделью Эйнштейна было пространство 8 с топологией S х Е , с которым мы встретимся
в §31.16.
19.10. Введение Эйнштейном космологического члена было одной из ряда модификаций первона¬
чального варианта общей теории относительности, предложенных за много лет. Помимо те¬
ории Вейля (§ 19.4) и идей многомерного обобщения в духе Калуцы - Клейна, излагаемых
в §31.4 (и обычно комбинируемых в настоящее время с суперсимметрией; см. §§31.2, 31.3),
имеется модификация Бранса - Дикке, в которой появляется дополнительное скалярное поле,
а также многочисленные попытки самого Эйнштейна создать «единую теорию поля», пред¬
принятые в период между 1925 и 1955 годами. См. [240, 241, 245, 242, 244, 699], а также
более недавнюю работу [23]. Большинство этих предложений было нацелено на включение
электромагнетизма и, возможно, других полей в полную картину общей теории относитель¬
ности. Заслуживает упоминания также схема, именуемая теорией Эйнштейна - Картана - Скья-
мы-Киббла, в которой вводится кручение (§14.4) и описывается прямой гравитационный
эффект плотности спина (§22.8); см. [446, 711], а также обзоры [791], сюда относятся также
работы [122, 123, 124].
§19.8.
19.11. Теория Эйнштейна должна включать в себя теорию Ньютона, поэтому следует под¬
черкнуть, что эта цифра 10“14 не представляет увеличения точности по сравнению
с ньютоновской схемой. Более того, следует иметь в виду, что некоторая часть точ¬
ности синхронизации расходуется на определение неизвестных параметров — масс, на¬
клона орбиты, эксцентриситета и т.д., необходимых для расчета свойств системы. Ве¬
личина 10“14 в действительности является мерой общей согласованности всей карти¬
ны.
19.12. Результаты Д. С. Робинсона с сотрудниками (1991), использующие «интерферометрию со сверх-
длинной базой», подтверждают эффекты искривления световых лучей, предсказываемые общей
теорией относительности, с точностью 10“4.
19.13. Относительно детального учета аномалии перигелия Меркурия см. [671].

402
Глава 19
19Л 4. Проекты поиска гравитационных волн носят звучные названия-акронимы — LIGO, LISA и GEO.
См. [2, 320, 719, 778], а также весьма полезный комментарий Джона Баеца в Интернете по ад¬
ресу: http://math.ucr.edu/home/baez/week 143 .html
19.15. См. [90, 95, 682, 683]. Эти работы были частично предвосхищены Траутманом [787].
19.16. См. также [552, 584, 585, 684, 96] и [627], стр. 423-427.
19.17. [694, 695, 843, 546, 574, 499, 398, 662, 627]; см. также §32.3, особенно примечание
32.11.
1

Глава 20
Лагранжианы и гамильтонианы
20.1.	Магический лагранжев формализм
За те столетия, что прошли после того как Ньютон сформулировал свои законы дина¬
мики, на заложенном им фундаменте был проделан весьма впечатляющий объем теоретиче¬
ской работы. Эйлер, Лаплас, Лагранж, Лежандр, Гаусс, Лиувилль, Остроградский, Пуассон,
Якоби, Гамильтон и другие выступили с идеями, которые привели к переформулировке
ньютоновской теории и созданию замечательной единой картины. Я попробую кратко по¬
знакомить с ней, однако боюсь, что мое изложение даст не вполне адекватное представление
о величии этого достижения. Следует также заметить, что само существование такой мате¬
матически изящной единой картины позволяет глубже судить о математическом фундаменте
нашей физической Вселенной даже на уровне .законов ньютоновской механики, открытых
в XVII веке. Не многие законы, предложенные для описания физической Вселенной, могли
привести к столь впечатляющим математическим структурам.
Что же это за изящная единая теория, появившаяся из ньютоновской механики? Она
проявляется преимущественно в двух различных, но тесно связанных формах, каждая из
которых обладает своими характерными достоинствами. Первую из них можно назвать ла-
гранжевой картиной, другую — гамильтоновой. (Здесь возникает обычная трудность с на¬
званиями. По-видимому, обе картины были известны Лагранжу задолго до Гамильтона,
а лагранжеву картину, по крайней мере частично, предвосхитил Эйлер.) Предположим, что
мы имеем ньютоновскую систему, состоящую из (конечного) числа отдельных частиц и, воз¬
можно, некоторых твердых тел, каждое из которых рассматривается как неделимый объект.
Тогда будет существовать конфигурационное пространство С некоторого большого числа
измерений N, каждая точка которого представляет одно из возможных положений в про¬
странстве всех этих частиц и тел (см. § 12.1). С течением времени одна точка пространства
С, представляющая всю систему в целом, будет двигаться в этом пространстве в соответствии
с некоторым законом, определяющим ньютоновское поведение системы; см. рис. 20.1. За¬
мечательно (и очень ценно в вычислительном отношении), что этот закон можно получить
с помощью некоторой прямой математической процедуры всего лишь из одной функции.
В лагранжевой картине (по крайней мере, в ее наиболее простой и самой распространенной
форме) 120Л1 эта функция, называемая функцией Лагранжа, или лагранжианом, определяется
на касательном расслоении Т(С) конфигурационного пространства С (рис. 20.2 а); см. § 15.5.
В гамильтоновой картине подобная функция, называемая функцией Гамильтона, или га¬
мильтонианом, определяется на кокасательном расслоении Т*(С) (см. § 15.5), называемом
фазовым пространством (рис. 20.2 б). Заметим, что расслоения Т(С) (каждая точка которо¬
го представляет некоторую точку Q пространства С вместе с касательным вектором в этой
точке) и Т*(С) (каждая точка которого представляет некоторую точку Q пространства С
вместе с кокасательным вектором в этой точке) являются 2iV-MepHbiMH многообразиями.
В этом разделе мы займемся лагранжевой картиной, отложив гамильтонову до следу¬
ющего раздела. Координаты лагранжева расслоения Т(С) должны определять положения
всех ньютоновских тел (включая соответствующие углы для описания пространственной
ориентации твердых тел), а также их скорости (включая соответствующие угловые скоро-

404
Глава 20
' *: f -V' '©л -<
'* о -	•	'
*	ар
'♦ . * * • ч * »9	*	«ЭьФ
' / л'*м« ■ -у	t	-	^
Рис. 20.1. Конфигурационное пространство. Каждая точка Q N-мерного многообразия С представляет
все мыслимые конфигурации, например, ньютоновских точечных частиц и твердых тел. При эволюции
системы во времени точка Q описывает в С некоторую кривую
§
Т(С)
с
Рис. 20.2. а) В обычной лагранжевой картине лагранжиан С является гладкой функцией на касательном
расслоении Т(С) конфигурационного пространства С. б) В гамильтоновой картине гамильтониан Л
является гладкой функцией на кокасательном расслоении Т*{С)9 называемом фазовым пространством
сти твердых тел). Координаты q1, ..., qN, определяющие положения и называемые обыч¬
но «обобщенными координатами», приписываются различным точкам q конфигурационного
пространства С (заданного, возможно, в виде «лоскутов», см. § 12.2). Возможна любая (аде¬
кватная) система координат. Она не обязана быть «декартовой» или какой-либо иной систе¬
мой стандартного вида. В этом красота лагранжева (а также гамильтонова) подхода. Выбор
координат определяется исключительно соображениями удобства. Координаты играют та¬
кую же роль, что и в главах 8, 10,12, 14 и 15, где рассматривались различные многообразия
общего вида. Выбранному набору обобщенных координат соответствуют «обобщенные ско¬
рости» q1, ..., qN; точка над буквой означает скорость изменения во времени d/dt:
Q
dq
N
dt

20.1. Магический лагранжев формализм
405
Лагранжиан С записывается в виде функции от всех обобщенных координат и обобщенных
скоростей^20,21
С = Цд1, qN] q1, ... qN).
В этом выражении каждую обобщенную скорость qr следует рассматривать как независимую
переменную (независимую в том числе и от qr). Это одна из озадачивающих поначалу
особенностей лагранжианов, между тем это так^20-3!
Обычная физическая интерпретация истинного смысла функции С состоит в том, что
это есть разность между кинетической энергией системы К и потенциальной энергией V,
обусловленной внешними или внутренними силами и выраженной через обобщенные ко¬
ординаты (см. §18.6). Уравнения движения системы (в которых заложено всё ньютонов¬
ское поведение) представляют собой так называемые уравнения Эйлера-Лагранжа, которые
изумляют своей необычайной широтой охвата и в то же время простотой:
А. р£ — PJL (г — 1 дп
dtdqr dqr 1
Напомним, что каждую величину qr следует считать независимой переменной, так что выра¬
жение d/dqr (которое означает формальное дифференцирование функции С по qr при фик¬
сированных значениях остальных переменных) действительно имеет смысл!
Приведенные уравнения выражают замечательный факт, называемый иногда принципом
Гамильтона или принципом стационарного действия. Смысл этого, возможно, станет яс¬
нее, если рассмотреть движение точки Q в пространстве С, представляющем все возможные
пространственные конфигурации целой системы (т. е. все варианты расположения всех ее
частей). Точка Q, положение которой в любой момент времени описывается координатой qr",
движется вдоль некоторой кривой в С с некоторой скоростью, которая вместе с направлени¬
ем касательной к этой кривой определяется значениями величины qr. Уравнения Эйлера-
Лагранжа утверждают, что движение точки Q в С соответствует минимуму действия. Дей¬
ствие — это интеграл от функции С вдоль кривой, взятый между двумя фиксированными
концевыми точками а и Ъ в конфигурационном пространстве С; см. рис. 20.3.
Рис. 20.3. Принцип Гамильтона. Уравнения Эйлера - Лагранжа утверждают, что движение точки Q в С
соответствует стационарности действия (интеграла от функции С вдоль кривой, взятого между двумя
фиксированными точками а и b в пространстве С) относительно вариаций кривой
Более точно, это не обязательно должен быть минимум, лучше говорить о «стационар¬
ности». Ситуация здесь примерно такая же как, и в обычном анализе (см. § 6.2), где усло¬
вием минимума гладкой вещественной функции f(x) было равенство df/dx = 0, однако
последнее не всегда соответствовало минимуму функции /; это мог быть и максимум,
и, возможно, точка перегиба, или, в случае большего числа измерений, так называемая сед-
ловая точка (рис. 20.46). Все точки, в которых df(x)/dx = 0, называются стационарными
(см. рис. 6.4 и 20.4). Напомним также об аналогичном, по существу, понятии геодезиче¬

406
Глава 20
ской в (псевдо)римановом пространстве, определяемой (см. §§14.7, 17.9, 18.3) как «путь
минимальной длины» в случае (локально) положительно определенной метрики, а иногда
(в случае лоренцевой метрики) как «времениподобная траектория максимальной длины»,
хотя в общем случае это просто «стационарная длина». Таким образом, траектория точки Q
есть в некотором роде «геодезическая» в пространстве С.
/
а)
б)
в)
Рис. 20.4. Стационарные значения гладкой вещественной функции / нескольких переменных. Показан
случай функции двух переменных /(#, у). Функция стационарна в тех точках, где ее график (дву¬
мерная поверхность) горизонтален (df /дх — 0 = df /ду). Так получается, когда функция / имеет
минимум а), но возможны и другие ситуации — седловая точка б) и максимум в). В случае когда
имеет место принцип Гамильтона (рис. 20.3), т. е. когда точки а и Ь соединены геодезической, место
функции / занимает лагранжиан £, однако для описания траектории требуется бесконечно много пара¬
метров, а не просто х и у. Функция С опять-таки может соответствовать не минимуму, а стационарной
точке некоторого вида
Полезно рассмотреть простой пример лагранжиана одной ньютоновской частицы мас¬
сы га, движущейся в некотором заданном внешнем поле, которое описывается потенци¬
алом V, зависящим от положения частицы: V ~ V(x, у, г; t). Величина V определяет
потенциальную энергию частицы во внешнем поле. В случае гравитационного поля Зем¬
ли (вблизи земной поверхности), соответствующего постоянному притяжению вниз, можно
положить V — rngz, где 2 — высота над Землей, a g — направленное вниз ускорение, со¬
здаваемое силой тяжести. Тремя компонентами скорости будут у, z, так что, используя
выражение для кинетической энергии |гаг?2 (см. § 18.6), получаем лагранжиан
Уравнение Эйлера-Лагранжа для переменной 2 дает нам теперь d(mz)/dt = ~mg, откуда
следует галилеевское постоянство ускорения в направлении Земли*.
20.2.	Более симметричная гамильтонова картина
В гамильтоновом представлении мы по-прежнему пользуемся обобщенными коорди¬
натами, но теперь наряду с обобщенными координатами д1, ...qN, описывающими поло¬
жение, мы берем соответствующие им обобщенные импульсы pi, ..., рм (а не скорости).
Для одной свободной частицы импульс есть просто произведение скорости частицы на ее
массу. В общем случае выражение для обобщенного импульса не обязательно будет таким.
* ЙЙ Восстановите подробности рассуждения и получите вывод Галилея относительно параболического дви¬
жения при свободном падении под действием силы тяжести.

20.2. Более симметричная гамильтонова картина
407
Однако его всегда можно получить из лагранжиана, используя определяющую его формулу
р
Pr dqr'
9 *
В любом случае параметры рг дают координаты в кокасателъных пространствах к про¬
странству С, так что можно написать ковектор вида
Padqa
(напомним о соглашении относительно суммирования по повторяющимся индексам (§ 12.7),
хотя это можно рассматривать и как абстрактно-индексную запись (§ 12.8)). Это, разумеется,
есть 1-форма, а ее внешняя производная (§ 12.6)
• •
S = dpa A dqa
представляет собой 2-форму (удовлетворяющую условию dS — 0)*, которая приписыва¬
ет естественную симплектическую структуру фазовому пространству Т*(С) (см. §14.8).
Сила гамильтоновой картины заключена в том факте, что фазовые пространства представ¬
ляют собой симплектические многообразия и эта симплектическая структура не зависит от
конкретного гамильтониана, выбранного для описания динамики. Тем самым классическая
физика оказывается тесно связанной с прекрасной и удивительной геометрией симплекти-
ческих многообразий, к которой мы перейдем в § 20.4.
Прежде чем понять ту роль, которую играет эта геометрия, посмотрим, какой вид имеют
динамические уравнения Гамильтона. Они описывают эволюцию системы во времени как
некоторую траекторию в фазовом пространстве Т*(С) точки Р, представляющей всю нью¬
тоновскую систему в целом. Эта эволюция полностью определяется функцией Гамильтона
(гамильтонианом)	...
ГС	ГС(р 1,	..., PNi q i • • • ? q )>
которая (в рассматриваемом здесь случае, когда лагранжианы и гамильтонианы не зависят
от времени) представляет собой полную энергию системы, выраженную через (обобщен¬
ные) импульсы и координаты. Ее можно получить из лагранжиана с помощью выражения
(с использованием соглашения о суммировании либо абстрактных индексов)
п = Г§-с,
переписав затем результат таким образом, чтобы исключить все обобщенные скорости
в пользу обобщенных импульсов (в общем случае это не такая уж легкая задача!). Буду¬
чи выраженными через такие импульсы и координаты, гамильтоновы уравнения эволюции
приобретают замечательно симметричный вид:
<кг_
dt dqr ’ dt дрг'
* •
 	У
Эти уравнения описывают скорость точки Р в пространстве Т*(С). Эта скорость определяет¬
ся для всех точек Р, так что мы имеем векторное поле на Т*(С), определяемое гамильтони¬
аном ГС. При использовании «оператора частного дифференцирования», введенного в § 12.3,
это векторное поле приобретает вид
дГС д дГС д
дрг dqr dqr дрг ’
**
Почему?
Объясните это.

408
Глава 20
что в §20.4 записывается в форме {'Н, }. Это определяет «поток» на Т*(С), описывающий
ньютоновское поведение системы (рис. 20.5).
Постоянное
значение
Г амильтоново
векторное
поле {Н, }
Рис. 20.5. Гамильтонов поток {Н, }, описывающий ньютоновскую временную эволюцию системы
(см. §20.4), представляет собой векторное поле на фазовом пространстве Т*(С). Для гиперповерхно¬
стей с фиксированными значениями Л (что означает заданную энергию, если Н не зависит от времени)
траектории остаются внутри гиперповерхности с фиксированным значением Н в соответствии с зако¬
ном сохранения энергии. (Относительно термина «гиперповерхность» см. примечание 27.36)
В частном случае частицы, падающей в постоянном гравитационном поле (ее описание
в лагранжевой форме было дано выше в § 20.1), гамильтониан имеет вид
Н
Pl+P2y+P2z
2т
+ mgz
Р
2т
+ mgz,
где Рх, Ру и pz — обычные компоненты пространственного импульса в направлении декар¬
товых осей х, у, г. Это выражение можно написать сразу, зная, какой вид должна иметь
полная энергия частицы, если выразить ее через компоненты импульса и вектора положения
либо получить его из лагранжиана, следуя процедуре, указанной выше.
Здесь я должен признать, что использованная запись была не вполне удобной, и попы¬
таться исправить положение. В § 18.7 мы видели, что пространственные компоненты импуль¬
са pi, р2, Рз в стандартных координатах Минковского для плоского пространства-времени
при выбранной мною сигнатуре (-1	) имеют знак, противоположный знаку обычных
компонент импульса. Так, в вышеприведенном примере мы имеем рх — —pi, ру ~ —Р2, pz =
= —рз. При общем обсуждении гамильтонианов естественно пользоваться «изначальным»
вариантом импульса ра, хотя он не согласуется с обозначением для ра (т. е. pi, Р2, рз) в те¬
ории относительности с сигнатурой (4	).	В	этой	книге я пытаюсь решить проблему
обозначений, излагая общий формализм с использованием комбинации величин qa и ра при
обычном соглашении относительно знаков у р и q безотносительно к тому, какова конкретная
Проделайте это в явном виде. Используя уравнения Гамильтона, получите уравнения Ньютона для дви¬
жения частицы, падающей в постоянном гравитационном поле.

20.3. Малые колебания
409
интерпретация каждой из величин р и q (так что читатель может сделать свой собственный
выбор знаков!). Когда же я использую комбинацию величин ха и ра9 я принимаю запись,
соответствующую § 18.7, так что —рг, ~Рз представляют собой обычные компоненты
обычного пространственного импульса (равные р1, р2, р3 в стандартной системе координат
Минковского). В результате при использовании координат х вместо q уравнения Гамильтона
получаются с противоположным знаком:
ч
Фг = т	dxr	дп
dt	дхТ ’	dt	дрг ’
Тому читателю, который не слишком вникает во все детали излагаемого формализма, я ре¬
комендую просто не принимать во внимание эти различия. (Так же может поступить и боль¬
шинство специалистов — во всяком случае до того момента, когда им самим придется писать
статьи или книги на эту тему!)
20.3,	Малые колебания
Прежде чем перейти в следующем разделе к замечательной геометрии, возникающей
при гамильтоновом описании динамики, полезно рассмотреть сначала важную задачу о ко¬
лебаниях физической системы вокруг положения равновесия. Эта тема имеет отношение
ко многим областям физики, особенно, как мы увидим позже, применительно к квантовой
механике (§22.13). Теория колебаний удобно ошюывается как в лагранжевом, так и в га¬
мильтоновом формализме, каждый из них вполне подходит для этой цели. Здесь я буду
следовать гамильтонову формализму в первую очередь из-за того, что он более непосред¬
ственно приводит к квантово-механическому описанию колебаний, которое будет вкратце
изложено в § 22.13. Теорию колебаний в лагранжевом представлении, которая очень похожа
на ее гамильтонов вариант, я оставляю читателю (см. упражнение 20.10).
Простым примером системы, совершающей колебания, может служить обыкновенный
маятник, качающийся под действием силы тяжести. Если колебания малы, то движение под¬
вешенного груза взад-вперед как функция времени будет иметь вид синусоидальной волны
(см. рис. 20.6). (С поведением такого рода мы сталкивались при рассмотрении отдельных
«фурье-компонент» в §9.1.) Период таких колебаний, если они малы, не зависит от их ам¬
плитуды (т. е. от расстояния, на которое отклоняется груз), что согласуется со знаменитыми
наблюдениями Галилея, проведенными еще в 1583 году. Такой тип движения называется
простым гармоническим движением.
В этом разделе мы увидим, сколь вездесущим является такое движение. Физическая
структура общего вида (если предположить, что эффектом трения можно пренебречь) может
колебаться вокруг положения равновесия лишь весьма специфическим образом. Мы найдем,
что любое малое колебание можно разложить на некоторые определенные моды колебаний,
называемые нормальными колебаниями, при этом вся структура принимает участие в про¬
стом гармоническом движении с некоторой определенной частотой, называемой нормальной
частотой.
Посмотрим сначала, как описывается аналитически простое гармоническое движение.
Пусть q означает взятое по горизонтали расстояние груза нашего маятника от низшей точки
или отклонение любой другой рассматриваемой колеблющейся величины от ее значения
в положении равновесия. Тогда уравнение движения для малых отклонений q будет иметь
вид

410
Глава 20
**• * 9 «*•» — —1
Рис. 20.6. Маятник, качающийся под действием силы тяжести. При малых колебаниях движение груза
приближенно является простым гармоническим движением, при этом смещение груза (изображенное
как функция времени) имеет вид «синусоидальной волны»
положительная постоянная величина со/27г представляет частоту колебаний. Из уравнения
следует, что ускорение d2qfdt2, направленное к положению равновесия, пропорционально
(с коэффициентом и2) отклонению от него. Из § 6.5 следует, что этому уравнению удовле¬
творяют функции q — cos cot и q = sin cot, то же относится и к их линейной комбинации
q — a coscot -f bsincot,
где а и b — постоянные*. Для маятника длины h, качающегося под действием силы тяжести
(в одной плоскости), получается уравнение движения, которое при малых близко к напи¬
санному выше со;2 = g/h; однако при больших значениях q возникают отклонения от этого
уравнения .
Пусть мы имеем гамильтонову систему общего вида, которая находится в равновесии,
когда координаты q принимают значения qa — Будет удобно выбрать это положение
равновесия за начало отсчета наших обобщенных координат, т. е. положить q% — 0. «Рав¬
новесию» соответствует конфигурация, отличающаяся тем, что при отсутствии движения
вначале система остается в стационарном состоянии. Можно поинтересоваться, является
ли это равновесие «устойчивым», устойчивой называется ситуация, при которой система,
будучи выведенной малым возмущением из положения равновесия, не отклоняется от него
еще дальше, а совершает колебания вокруг него. При изучении колебаний мы будем иметь
дело с колебаниями вокруг положения устойчивого равновесия, при этом будут рассмат¬
риваться только малые значения обобщенных координат qa. Более того, поскольку нашим
колебаниям соответствуют только малые возмущения с малыми скоростями, мы будем счи¬
тать малыми и значения импульсов ра.
Предположим, что наш гамильтониан является аналитической функцией переменных q
и р (относительно смысла термина «аналитическая» см. § 6.4), поэтому можно разложить
его в степенной ряд по q и р. В случае устойчивой равновесной конфигурации значения qa
* Подтвердите это, объяснив, почему оо/2тг есть частота. Объясните, почему график этой функции все еще
выглядит как синусоида. Почему это общее решение?
** $5 Покажите это, определив вид полного уравнения. Используйте а) метод Лагранжа; б) метод Гамильтона;
-у
в) непосредственно из законов Ньютона. (Подсказка: покажите, что С = ~mh2q2{h2 — g2)”1 + mg(h2 — g2)1/2.
Заметьте, что в этом простом случае методы Лагранжа и Гамильтона не дают каких-либо преимуществ — их мощь
проявляется при изучении ситуаций более общего характера.)

20.3. Малые колебания
411
должны соответствовать (локальному) минимуму потенциальной энергии . Движение может
лишь увеличивать энергию (кинетическую энергию), так что кинетическая энергия имеет
минимум при ра = 0. Поэтому полная энергия, которая равна значению гамильтониана Н,
имеет локальный минимум при qa = 0 = ра. Отсюда следует, что наше разложение в
степенной ряд должно иметь следующий вид (члены, линейные по переменным q9 р или тем
и другим, отсутствуют):
Н = постоянная + ^Qabqaqb +	%Р+
+ члены третьего и более высоких порядков по переменным q и р.
*
где Qab и РаЪ суть компоненты положительно определенных постоянных симметричных
матриц (так что Qabqaqb > 0, если qa ф 0, и РаЬраръ > 0, если ра ф 0; см. §13.8).
Множители i используются для удобства**.
Отбрасывая члены высоких порядков, рассмотрим природу малых колебаний. Уравне¬
ния Гамильтона дают
pabVh
dt - дРа~ Г ’
откуда, дифференцируя еще раз по £, получаем
d2qa	d pab	pabdpb
dt2	dt Pb	dt
= - pab~T = ~PabQbcqc =
dq
где Wac — PabQbc — произведение матриц Qab и РаЬ (см. § 13.3). Это можно записать в виде
W = PQ,
так что можно переписать приведенное выше уравнение в виде
$ - -w4-
Нас интересуют собственные векторы матрицы W (см. § 13.5); таковыми являются векто¬
ры q, удовлетворяющие уравнению
Wq = u;2q,
где uj2 есть собственное значение матрицы W, соответствующее данному вектору q.
Так как матрицы Р и Q положительно определены, это собственное значение должно быть
^ ^
положительным , поэтому можно записать его в виде квадрата положительной величины со.
Видно, что любой такой собственный вектор q должен удовлетворять уравнению
d2q 2
dt2 ^ q’
описывающему простое гармоническое движение с частотой
*•	•	Vs	Ч
■i t
**
***
Почему?
Объясните все это подробнее. Появятся ли линейные члены, если равновесие неустойчиво?
Попробуйте доказать это утверждение. (Подсказка: покажите, что матрица, обратная положительно опре¬
деленной матрице, тоже положительно определена.)
Попробуйте провести аналогичный анализ в рамках лагранжева, а не гамильтонова формализма.

412
Глава 20
Каждый собственный вектор q представляет собой некоторую комбинацию обобщен¬
ных координат, так что при колебаниях, соответствующих вектору q, все эти координаты
будут колебаться совместно с одной и той же частотой. Такие колебания называются нор¬
мальными модами, а соответствующая частота и/2л — нормальной частотой, соответству¬
ющей этой моде. В наиболее общем случае все эти частоты различны, однако в особых
(«вырожденных») случаях некоторые из этих нормальных частот могут совпадать . Выро¬
жденные собственные значения следует подсчитывать с учетом их кратности, так что пол¬
ное число нормальных мод остается равным числу N обобщенных координат q\ ..., qдг.
Можно заметить, что любые две нормальные моды, соответствующие различным частотам,
взаимно «ортогональны» относительно метрики, определяемой матрицей Q, в том смысле,
что г 1 Qq = 0.**
Что же мы узнали из всего этого? Мы пришли к важному выводу общего характера
относительно того, как классическая система с N степенями свободы может колебаться
вокруг устойчивой равновесной конфигурации. Любое такое колебание строится из нор¬
мальных мод (которые можно считать взаимно независимыми), каждая из которых обладает
своей собственной характерной частотой; общее число таких мод равно N. В этом опи¬
сании мы не учитываем эффекты диссипации, которые на практике приводят к тому, что
колебания в макроскопической системе со временем постепенно затухают, при этом энергия
системы переходит в энергию хаотического движения составляющих ее частиц. Если все
составные части (например, молекулы) системы учитываются явным образом, диссипация
не возникает.
До сих пор мы рассматривали обычную ситуацию, когда число степеней свободы си¬
стемы N конечно, однако изложенная теория применима также к системам, имеющим (хотя
бы в качестве идеализации) бесконечное число степеней свободы. Мы столкнемся с такой
ситуацией, если обратимся к звукам, которые может издавать музыкальный инструмент.
Например, барабан или музыкальный треугольник после удара по ним колеблются с различ¬
ными частотами, и эти частоты определяют тот или иной тембр. Аналогичные звуки издает
духовой инструмент, там они создаются колебаниями столба воздуха внутри него. То же
относится и к колебаниям струны в струнных инструментах и т. д.
Фурье-анализ, изучавшийся в главе 9, позволяет описать колебания струны конечной
длины. Можно предположить, что струна закреплена в концевых точках или, возможно,
замкнута в виде окружности. Фурье-анализ представляет произвольные колебания в виде
линейной комбинации мод, которыми являются чистые тона — синусоидальные или ко¬
синусоидальные волны; число таких мод бесконечно. В этом случае частоты получаются
умножением на все целые числа частоты некоторой первичной моды. К этому стремятся при
конструировании звучного музыкального инструмента. Однако в общем случае (примером
может служить барабан или колокол) нормальные частоты не связаны между собой столь
просто.
В подобных ситуациях гамильтонов или лагранжев формализм можно распространить
на случай N = ос, однако необходима некоторая осторожность. При этом мы, в некотором
смысле, приходим к лагранжевой (или гамильтоновой) теории полей, которая будет рассмот¬
рена в § 20.5. Она находит применение во многих областях современной физики. В частно¬
сти, этот формализм используется в фундаментальной теории Природы, называемой теорией
струн, в которой точечные частицы заменяются петлями малого размера (или «струнами»
с незакрепленными концами). При этом различные поля или частицы Природы возникают
как нормальные моды колебаний «струн» (см. §§ 31.5, 31.7, 31Л4).
В заключение необходимо сделать еще одно замечание. В этом разделе рассматрива¬
лись только колебания вокруг состояния устойчивого равновесия, однако такое обсуждение
Опишите систему собственных векторов в таких вырожденных случаях.
Докажите это. Напомним (см. § 13.7), что символом Т обозначается транспонирование.

20.4. Гамильтонова динамика как симплектическая геометрия
413
также
в том, что наша вещественная симметричная матрица Q теперь не является положительно
определенной (или даже не является отрицательно определенной), так что матричное про¬
изведение W = PQ может иметь отрицательные собственные значения. При этом малые
отклонения от равновесия экспоненциально нарастают*.
20.4.	Гамильтонова динамика как симплектическая геометрия
Вернемся назад, чтобы посмотреть, как связаны уравнения Гамильтона для конечного
числа измерений с симплектической геометрией. Как описано в § 14.8, на любом симплек-
тическом многообразии существует операция, проводимая на паре скалярных полей Ф и Ф,
в результате которой получается другое скалярное поле <9, называемое скобками Пуассона
для этих полей :
в = w ф\ = ММ _ ММ.
’ дра dqa dqa дра
Если оставить пустым «место для Ф», то мы получим дифференциальный оператор {Ф, } —
векторное поле (см. § 12.3), действие которого на Ф.дает {Ф, Ф}. Подставим Н вместо Ф.
Тогда векторное поле {Н, } будет «направлено» вдоль траекторий на Т*(С), определяющих
временную эволюцию; фактически вектор {Н, } описывает такую эволюцию в соответствии
с уравнениями Гамильтона (§20.2). Одна из замечательных особенностей симплектической
геометрии состоит в том, что динамическая эволюция системы может геометрически интер¬
претироваться при помощи одной-единственной скалярной функции (а именно гамильтони¬
ана).
Симплектическая геометрия имеет и многие другие применения. Например, имеется
известный результат, принадлежащий Лиувиллю, согласно которому динамика всегда обес¬
печивает сохранение объема системы в фазовом пространстве; см. рис. 20.7. Элемент объема
в фазовом пространстве дается 2N-формой
£ = SaSA...AS,
в которой А-перемножаются N сомножителей S; напомним, что симплектическая 2-форма S
определяется как S ~ dpa A dqa. Нетрудно проверить, что величина S сама сохраняется
в ходе гамильтоновой эволюции (т. е. что производная Ли от S по векторному полю {7Г, }
равна нулю) . Отсюда немедленно следует, что полный объем U в ходе этой эволюции
также сохраняется. В этом и состоит теорема Лиувилля.
f
Поскольку {7г, Н} — 0, сам гамильтониан сохраняется, т. е. остается постоянным
вдоль траекторий; это отражает тот факт, что полная энергия замкнутой системы посто¬
янна. Таким образом, каждая траектория лежит на (2N — 1)-мерной поверхности, опре¬
деляемой условием Н = const; см. рис. 20.5. Можно считать, что полная история систе¬
мы представлена ее траекторией на Т*(С). Пространство таких траекторий для заданного
значения Н является (2N — 2)-мерным, см. рис. 20.8. (Мы потеряли одно измерение, за¬
фиксировав Н, и еще одно при выделении одномерных траекторий.) Важен тот факт, что
получаемое (2N — 2)-многообразие снова оказывается симплектическим. Эта процедура
(с заменой Ф на 7i) имеет много изящных приложений в классической механике и симплек¬
тической геометрии.
В этой удивительно исчерпывающей картине ньютоновской динамики есть несомнен¬
ная красота. Тем не менее, как мы увидим при рассмотрении более поздних физических
Опишите такое поведение.
**	Подтвердите, что это выра:
***	Покажите это.
Почему?

414
Глава 20
Рис. 20.7. Теорема Лиувилля. Гамильтонов поток сохраняет объем начальной области фазового про¬
странства (представляющей область возможных начальных состояний), хотя форма этой области за вре¬
мя эволюции может сильно измениться
Приведенное фазовое
пространство 27V-2 измерений
Фазовое пространство
2 TV измерений
Рис. 20.8. Фазовое пространство Т*(С) для TV-мерного пространства С представляет собой 27У-мерное
симплектическое многообразие. При заданном значении энергии (постоянном Н, как на рис. 20.5)
имеем (2N — 1)-мерную область, содержащую (2N — 2)-мерное семейство траекторий гамильтонова
потока. Приведенное фазовое пространство, точками которого служат эти траектории, само являет¬
ся 2 (N — 1)-мерным симплектическим многообразием
теорий, важно не дать себе увлечься этой красотой и кажущейся законченностью подобных
вроде бы надежно сработанных математических схем. Природа, как показывает прошлый
опыт, имеет обыкновение сначала приводить нас в состояние благодушной эйфории, являя
нам мощь и изящество математических структур и вынуждая нас принять их как путе¬

20.5. Лагранжева трактовка полей
415
водитель, а затем выталкивать нас время от времени из этого состояния концептуального
оцепенения, наглядно демонстрируя, что сложившиеся у нас представления никак не могут
быть правильными! Тем не менее такие толчки всегда бывают довольно мягкими, так что
построенное здание продолжает стоять, несмотря на полную замену фундамента, на котором
оно было построено.
Гамильтонова картина может служить прекрасным примером этого. Хотя заключенная
в ней классическая механика приходит в противоречие с некоторыми грубыми фактами
квантового мира, гамильтонов подход указывает нам правильную дорогу к квантовой тео¬
рии. Более того, квантовый вариант гамильтониана входит как существенная составная часть
в стандартный квантовый формализм. Должен сказать, что это относится лишь к стандарт¬
ной нерелятивистской квантовой теории, в которой не делается серьезной попытки объеди¬
нить время и пространство в соответствии с принципами теории относительности. Что же
касается релятивистской квантовой теории, то здесь, как оказалось, более естественную от¬
правную точку дает лагранжев формализм. Но куда мы должны отправиться? Именно необ¬
ходимость должного объединения принципов специальной теории относительности с прин¬
ципами квантовой механики вынуждает нас погружаться в пучину квантовой теории поля!
К методам квантовой механики и квантовой теории поля мы придем позже, в гла¬
вах 21-23 и 26. Но прежде чем мы сможем это сделать, следует подготовить почву для
этого. Сам термин «квантовая теория поля» указывает на то, что в рамки законов квантовой
механики необходимо заключить не только частицы, но и поля. Поэтому нам нужно увидеть,
как следует применять к полям методы Лагранжа и Гамильтона.
20.5.	Лагранжева трактовка полей
При обсуждении лагранжианов (и гамильтонианов) мы рассматривали ньютоновские
системы, состоящие из конечного числа частиц и твердых тел. Они обладали большим, но
конечным числом степеней свободы, так что многообразие Л4, описывающее конфигура¬
ционное пространство, и его касательное расслоение Т(Л4) ( а также его кокасательное
расслоение Т*(Л4)) были обычными конечномерными многообразиями. Однако лагранжев
(и гамильтонов) формализм имеет более общий характер и может быть применен также к фи¬
зическим полям. Поле меняется непрерывным образом от точки к точке и потому не может
быть описано конечным числом параметров. Например, конфигурационное пространство
свободных максвелловских полей в некоторой области будет бесконечномерным.
Тем не менее лагранжев (или гамильтонов) формализм можно использовать и в случае
бесконечномерного конфигурационного пространства, и для этого существует стандартная
процедура и в классической, и в квантовой теории поля. Главной новинкой в необходимых
для этого формальных математических процедурах является понятие функционального диф¬
ференцирования. Лагранжиан, вместо того чтобы быть функцией конечного числа обобщен¬
ных координат q1, ..., qN и конечного числа обобщенных скоростей ql, ..., qN, становится
функцией некоторого количества полей Ф, ..., Ф (каждое из которых само является функци¬
ей пространственно-временных координат и, возможно, обладает индексами, указывающими
на его тензорный или спинорный характер) и производных этих полей УаФ,..., (обыч¬
но фигурируют только первые производные, но не исключено и применение производных
более высокого порядка). Заметим, что производные по времени не играют здесь какой-то
особой роли (раньше мы обозначали такую производную точкой над величиной), а учиты¬
ваются на общих основаниях с помощью оператора Va. Тем самым формализм приводится
в согласие с требованиями теории относительности.
В ситуациях такого рода лагранжианы часто называют функционалами, поскольку нас
интересует их функциональная форма, а не конкретные значения их аргументов. Уравнения
Эйлера - Лагранжа теперь содержат «производные по полям» либо «производные по гради¬

416
Глава 20
ентам полей». Формальное проведение таких операций тесно связано с соответствующими
операциями обычного анализа, описанными в главе 6. Часто это сопряжено с некоторыми
математическими тонкостями (если мы хотим быть уверенными в строгой справедливо¬
сти результатов), однако физики обычно не слишком озабочены этим и основное внимание
уделяют правильному применению формальных правил.
В мои цели не входит подробное обсуждение этих понятий, однако необходимо вы¬
писать уравнения Эйлера - Лагранжа с «функциональными производными» (которые будем
обозначать буквой 5 вместо д):
V7	_	§_С	^7	__	5С
5\7аФ ~ 8Ф'"'' а5Х7аФ ~ &Ф'
Как уже упоминалось, поля Ф, ..., Ф могут обладать индексами. При практическом вычис¬
лении функциональной производной применяются, в сущности, те же правила, что и в обыч¬
ном анализе, и широко используется «математический здравый смысл» (например, если С —
=	ФаФьЧаФь, то	6£/5Фс = ФЬХ7СФЬ + ФаУаФс,	= 0,	=	0,	5C/5VcVd
= ФСФЛ).
Для таких лагранжианов выполняется принцип Гамильтона, который, напомним, утвер-
* •
ждает, что уравнения Эйлера - Лагранжа обеспечивают стационарность действия, которое
представляет собой интеграл от лагранжиана вдоль кривой, соединяющей две фиксирован¬
ные точки а и Ъ конфигурационного пространства (см. рис. 20.3). В рассматриваемом здесь
более общем случае две фиксированные концевые точки а и b в пространстве С заменяются
конфигурациями поля в некоторой трехмерной области пространства-времени. Часто они
выбираются в виде двух областей 3-пространства Л и В в пространстве-времени, охваты¬
вающем одно и то же 2-пространство S (которое может находиться на бесконечности); см.
рис. 20.9. Такая картина играет важную роль также в формулировке квантовой теории на
основе инте1ралов по траекториям, к которой мы перейдем позже (§ 26.6). При желании
можно задать области Л и В одновременно (изменив ориентацию одной из них на проти¬
воположную) и построить границу дТ> пространственно-временного 4-объема V (возможно,
компактного, см. § 12.6), рис. 20.10. В любом случае принцип Гамильтона утверждает ста¬
ционарность пространственно-временного интеграла от лагранжиана по области V. Таким
образом, лагранжиан С можно рассматривать как пространственно-временную плотность;
это, строго говоря, означает инвариантность 4-формы Се, где естественная 4-форма е в об¬
щем случае имеет вид^20-4^ е — dx° A dx1 A dx2 A dx3\/(-~ det g). Интеграл действия имеет
вид
S = J Се.
V
Уравнения поля получаются из требования, чтобы величина S была стационарной отно¬
сительно вариаций всех переменных (т. е. аналогична геодезической, см. рис. 20.3); это озна¬
чает, что вариационная производная от лагранжиана С по всем входящим в него полям и их
производным должна обращаться в нуль. Это условие записывается в виде
5S = 0.
Величина S играет центральную роль в формализме интегралов по траекториям примени¬
тельно к квантовой теории поля (это будет рассмотрено в § 26.6).
$
20.6.	Как лагранжианы двигают современную теорию
Теория Лагранжа (как и теория Г амильтона) оказывает сильное влияние на современную
физику благодаря их многочисленным приложениям. Например, имеется важная теорема,

20.6. Как лагранжианы двигают современную теорию
417
5
v
I
Рис. 20.9. Принцип Гамильтона для лагранжиана поля. Две фиксированные концевые точки а и b мно¬
гообразия С с рис. 20.3 представляют некоторые конфигурации поля в двух трехмерных областях про¬
странства-времени, соответственно Ли Б, образуя «пузырь», внутри которого заключена 4-область Х>.
Можно выбрать области Ли В так, чтобы они сходились между собой, оканчиваясь на конечной 2-по¬
верхности S (это не показано на рисунке), либо удалить S на бесконечность, возможно, за пределы
пространственноподобной гиперповерхности, на которой Ли Б совпадают за пределами области Т>
(этот случай показан на рисунке)
Рис. 20.10. При желании можно принять, что области Л и Б иг. рис. 20.9 объединены, но имеют
противоположную ориентацию (см. рис. 12.16), образуя границу дТ> (компактного) пространствен¬
но-временного 4-обьема Т>. Принцип Гамильтона (рис. 20.3) утверждает стационарность величи¬
ны f Се для заданной конфигурации поля на границе дТ>
т>
именуемая теоремой Нётер, которая утверждает, что если обычный лагранжиан обладает
некоторой непрерывной (гладкой) симметрией, то существует некоторый закон сохранения,
связанный с этой симметрией. В частности, если лагранжиан инвариантен относительно вре¬
менной трансляции (т. е он не зависит от времени), то имеет место сохранение энергии; если
он инвариантен относительно пространственной трансляции, то сохраняется импульс. Да¬
лее, если имеется инвариантность относительно поворотов вокруг некоторой оси, то имеет
место сохранение момента импульса относительно этой оси. Можно ожидать, что изолиро¬
ванная система в плоском пространстве-времени обладает всеми этими видами симметрии.
Если выбрать координаты таким образом, чтобы данная симметрия лагранжиана С прояв¬
лялась в независимости С от некоторой обобщенной «координаты» gr, то сохраняющейся
величиной будет «сопряженный импульс» рг, соответствующий этой координате и опреде¬
ляемый, как было указано в §20.2, соотношением pr = d£/dqr. Из уравнений Эйлера-
£
Лагранжа немедленно следует, что этот импульс рг действительно постоянен во времени .
Всё это можно обобщить на функционалы Лагранжа для полей. Например, если суще-
ствует «калибровочная инвариантность», можно надеяться наити соответствующий «сохра¬
няющийся заряд» (например, электрический заряд в случае электромагнитной калибровоч¬
ной инвариантности относительно преобразования Ф i—> егвЩ. Однако в подобных ситуа-
* Й© Объясните почему.

418
Глава 20
днях начинают возникать осложнения. Например, неясно, как применять эти идеи, чтобы
получить сохранение энергии-импульс а в общей теории относительности; строго говоря, в
этом случае метод перестает работать. Кажущимся гравитационным аналогом калибровоч¬
ной симметрии Ф ^ егвФ является «инвариантность относительно общих преобразований
координат» (которая обеспечивается использованием в общей теории относительности урав¬
нений, записываемых с помощью тензорных операций), однако теорема Нётер в этой ситу¬
ации не работает, давая что-то вроде 0 = 0. По-видимому, в общей теории относительности
требуется какой-то совершенно иной способ мышления, несмотря на то что в других обсто¬
ятельствах использование теоремы Нётер может привести к ясному пониманию; примером
может служить эффектный перенос ее на квантовую теорию (см. § 21 Л). В качестве примера
ограничений, налагаемых на теорему Нётер в случае теории гравитации, следует указать, что
в общей теории относительности все еще находится под большим вопросом само понятие
момента импульса, даже в случае асимптотически плоского пространства-времени!20*5!.
Как показал глубокий и разносторонний математик Давид Гильберт (1915), теорию
Эйнштейна можно вывести исходя из лагранжева формализма. Гравитационный лагранжиан
Гильберта представляет собой, по существу, скалярную кривизну R, деленную на постоян¬
ную “16тг<3, которую, однако, нужно превратить в плотность (или 4-форму), умножая ее на
естественную 4-форму в из § 20.5. Полученный лагранжиан нужно добавить к лагранжиану
материи £, в результате полное действие будет иметь вид
S 1 ' £ 16nGR 1 £'
Когда Гильберт предложил это действие, он работал с теорией материи, очень популяр¬
ной в то время, — с теорией Ми, поэтому он сформулировал свой принцип гравитационного
действия только для случая лагранжиана материи, подходящего для теории Ми. Он, по-
видимому, считал, что его полный лагранжиан позволяет построить такую теорию, которую
мы назвали бы нынче «теорией всего». Это было в 1915 году. Кто сегодня помнит о теории
Ми?
Хотя теория Ми содержит отклонения от теории Максвелла, подходящий лагранжи¬
ан для стандартной максвелловской теории электромагнитного поля был известен много
раньше!20*6!; он имеет вид
С — — i F и Fab
CIO1
Однако чтобы воспользоваться им, мы должны быть уверены, что этот лагранжиан выража¬
ется через электромагнитный потенциал Аа. При наличии также заряженных полей требу¬
ются дополнительные члены, учитывающие взаимодействие и тоже содержащие Аа, Все эго
важно проверить на калибровочную инвариантность. Если включить сюда еще и гравитацию,
то должна иметь место «калибровочная инвариантность», соответствующая гравитации,
а именно координатная инвариантность. Это обычно проверяется путем записи уравнений
в тензорной форме (либо путем использования базисных систем координат или подходящего
спинорного формализма в соответствии с другими инвариантными описаниями).
В современной фундаментальной физике при попытке создания новой теории последняя
почти неизменно представляется в виде некоторого лагранжевого функционала. Это имеет
много преимуществ, поскольку дает больше шансов (хотя и не абсолютную уверенность)
на то, что созданная теория будет обладать необходимыми свойствами самосогласованности
и инвариантности и что неявно будет присутствовать некоторая форма «третьего закона Нью¬
тона» (в том смысле, что взаимодействие двух полей носит обоюдный характер: если одно
из них действует на другое, то и второе в той же мере действует на первое). Кроме того, ла¬
гранжианы обладают приятным свойством: если вводится какое-то новое поле, то его вклад

20.6. Как лагранжианы двигают современную теорию
419
обычно можно получить, просто прибавляя его лагранжиан к прежнему и добавляя также
все необходимые члены взаимодействия. Более важна, наверное, возможность непосред¬
ственного подхода к построению квантовой теории с помощью формализма интегрирования
по траекториям, о котором упоминалось выше и к которому мы перейдем в § 26.6.
Однако я должен признать, что не могу представить это как фундаментальный подход.
Мне нелегко сформулировать суть трудностей, поскольку они касаются общности лагран-
жева подхода, который, таким образом, мало помогает в поиске правильных теорий. К тому
же, выбор лагранжиана часто оказывается неоднозначным и иногда требует большой изоб¬
ретательности. Это уводит от действительного понимания физики «на пальцах», особенно
в случае лагранжианов для полей. Даже лагранжиан для максвелловской теории свободного
-'I
поля -FabFab не вполне физически очевиден (в трехмерных обозначениях эта величина
1 *
есть - от разности квадратов длин векторов электрического и магнитного полей) . Более
того, «максвелловский лагранжиан» не работает как лагранжиан, пока он не выражен через
потенциал, хотя значение потенциала не является непосредственно наблюдаемой величи¬
ной. В случае гравитации (в отличие от случая электромагнетизма) лагранжиан для тео¬
рии Эйнштейна тождественно равен нулю, когда выполняются уравнения поля (поскольку
1
из Каъ — ^ Rgab = 0 следует R = 0). С другой стороны, величина R не может служить
лагранжианом, пока она выражается через такие величины (обычно это компоненты мет¬
рического тензора в некоторой координатной системе), которые не имеют инвариантного
смысла. Во многих случаях и сама плотность лагранжиана не имеет ясного физического
смысла; более того, зачастую многие различные лагранжианы приводят к одним и тем же
уравнениям для поля.
Лагранжианы для полей, несомненно, крайне полезны как математический инстру¬
мент, и они позволяют записывать новые формулировки физических теорий. Однако мне
по-прежнему нелегко принять их в качестве надежной опоры при поиске улучшенных фун¬
даментальных физических теорий. Это относится и к понятиям квантовой теории поля,
к которой мы перейдем в § 26.6, но пока достаточно и этого.
Примечания
§20.1.
20.1. Многие лагранжианы общего типа (для неньютоновских систем) могут содержать высшие
производные, и они определяются на так называемых «струйных расслоениях» многообразия С,
однако нам они здесь не понадобятся.
20.2. В своем изложении я упростил обсуждение лагранжианов, предполагая нашу систему голо-
номной. В неголономных системах доступны не все обобщенные скорости, соответствующие
обобщенным координатам. Хорошим примером неголономной системы может служить качение
обруча по горизонтальной плоскости без скольжения, так что точка соприкосновения обруча
с плоскостью в процессе качения может двигаться лишь в направлении касательной к обручу.
Таким образом, для определения положения точки соприкосновения требуются две координаты,
однако имеется лишь одна обобщенная скорость.
Можно предположить, что системы, рассматриваемые на фундаментальном уровне, не могут
быть неголономньши. В нашем случае с обручем ограничение, запрещающее возможность
скольжения, является идеализацией. Коль скоро хотя бы в малой степени допускается сколь¬
жение, система становится голономной.
20.3. Для простоты описания я рассматриваю здесь случай «лагранжиана, не зависящего от време¬
ни». Однако легко включить в рассмотрение силы, зависящие от времени, просто вводя еще
* ГЖ& Покажите это.

420
Глава 20
одну «обобщенную координату» q° = t и формальную величину q°, которой в конечном счете
приписывается значение 1.
§20.5.
20.4.	Другой способ задания величины е состоит в предположении, что компонента £0123 тензора е
в локальной правой ортонормированнои системе координат удовлетворяет условию 60123 =
= 1 (§ 19.2). [4]-тензор е с точностью до знака определяется метрическим тензором с помо¬
щью соотношения eabcd^pqrs9apgbq9°rgds = —24; выбор знака у е определяет ориентацию
пространственно-временного объема .
§20.6.
20.5. См. [603,627,841,667].
20.6. См. [573], стр. 342 и там же ссылки [46-48] на стр. 357
Покажите, что такой способ эквивалентен указанному в основном тексте.

Глава 21
Квантовая частица
21.1.	Некоммутирующие переменные
По всей вероятности, большинство физиков считает те изменения, которые внесла в на¬
шу картину мира квантовая механика, гораздо более революционными, нежели даже вве¬
дение необычного искривленного пространства-времени в общей теории относительности
Эйнштейна. Как мы увидим в этой и двух последующих главах, то, что утверждает квантовая
теория относительно «реальности» на субмикроскопических уровнях атомов или элементар¬
ных частиц, в такой степени не укладывается в привычную нам классическую картину, что
можно просто решить вообще отказаться от квантовой «картины». И действительно, многие
физики, по-видимому, сомневаются в самом существовании истинной «реальности» в кван¬
товом масштабе и вместо этого для получения ответов на свои вопросы просто опираются на
математический формализм квантовой механики. (В главе 29 я вернусь к более подробному
обсуждению противоречивого понятия «квантовой реальности».)
Тем не менее, несмотря на все это, поистине замечательно то, что описанные в главе 20
методы Лагранжа и Гамильтона, которые представляют собой исчерпывающую, но пол¬
ностью классическую схему, выросшую из ньютоновской механики XVII века, образуют
существенную основу квантово-механической теории. Конечно, пришлось внести измене¬
ния в математический формализм. В противном случае новая теория была бы просто копией
старой. Однако дело обстоит так, словно формализм, выросший из ньютоновской схемы, уже
ждал прихода квантовой механики, все детали этой конструкции имели правильные разме¬
ры и формы, так что новые квантовые ингредиенты достаточно было просто поставить
на нужное место.
Ключевым математическим свойством, благодаря которому это стало возможно, оказа¬
лась кажущаяся «странность», замеченная в конце XIX века одним большим оригиналом —
инженером-элекгриком, занимающимся также математической физикой, Оливером Хевисай¬
дом (1850-1925), с которым мы уже встречались в §6.1. Наблюдение Хевисайда состояло
в том, что с дифференциальными операторами часто можно обращаться точно так же, как
и с обычными числами, и этот факт часто оказывается полезным при решении некоторых
типов дифференциальных уравнений. Покажем это на примере. Рассмотрим дифференци¬
альное уравнение^21,1!
d2y 5
dx*=X
(смысл символов см. в § 6.3). Мы хотим найти какую-нибудь функцию у = у(х), удо¬
влетворяющую этому соотношению. Метод Хевисайда состоял в том, чтобы обращаться
с оператором d/dx так, как если бы это было обычное число. Чтобы это выглядело более
«правдоподобным», обозначим этот оператор одной буквой D:
D = d
dx
Тогда символ D2 будет обозначать повторное дифференцирование d2/dx2 — (d/dx)2,
т.е. оператор второй производной; символ D3 означает третью производную d3/dx3 и т.д.

422
Глава 21
Наше уравнение тогда принимает вид у 4~ D2y — х5, что можно представить как
(1 + j02)у = х5
Мы можем «решить» его, формально «разделив» на 1 + D2 и получив в результате у — (1 4-
4~ D2) :1х5. Разлагая (1 -f D2) 1 «в ряд по степеням £>», находим
У
(1 -d2 + d4-d6 + ...)^5-
(Напомним, что в §4.3 мы уже рассматривали этот ряд с х вместо D.) Замечая (§6.5),
что Dx5 = 5х4, D2x5 = 20х3, £)3х5 = 60х2, D4xb = 120х, tD5x5 = 120, D6x5 = 0 и т.д.,
мы находим (правильное!) частное решение
у — х — 20х 4~ 120х.
При внимательном отношении к соответствующим правилам эту формальную процедуру
можно сделать вполне строгой, хотя поначалу левисаид столкнулся с сильным противодей¬
ствием его методу!
Хотя величину D(= d/dx) можно (при должной осмотрительности) подвергать алге¬
браическим операциям, как обычное число, необходима осторожность, когда величины D
и х перемешиваются между собой, поскольку они не коммутируют. Можно рассматривать х
и D как операторы, действующие на некоторую невидимую функцию Ф(х), находящуюся
справа от них. Оператор х просто умножает на х то, что находится справа от него, а опе¬
ратор D дифференцирует это нечто, находящееся справа от него, по х. Тогда мы получаем
перестановочное соотношение
Dx — xD = 1.
Почему так получается? Напомним «правило Лейбница» из §6.5, согласно которо¬
му В(хф) — (В(х))ф + хО(ф)9 т. е. П(хф) — хИ(ф) — (В(х))ф. Принимая во внимание,
что D(x) = 1 (т. е. оператор D, действуя на х, дает 1), получаем соотношение {Dx~~xD)v =
= 1ф9 совпадающее с выписанным вьппе в применении к стоящей справа произвольной
функции ф = ф(х).
Теперь обобщим это на случай многих переменных х1, ..., xN и соответствующих
операторов D\ = д/дх, Ду = d/dxN (теперь это операторы частной производной;
напомним также, что xN — это просто N-я координата, а вовсе не произведение N со¬
множителей х); «невидимой» функцией справа теперь будет некоторая функция всех этих
переменных ф — ф{х1) ..., xN). Мы получаем перестановочные соотношения
DbXa — xaDb — 6%.
(Вспомним дельта-символ Кронекера из § 13.3; в вышеприведенном выражении содержит¬
ся предыдущий коммутатор, если а = Ь, и учитывается тот факт, что х и D коммутиру-
3^%	'4* Г^1
ют , если а Ф Ь.) Можно считать координаты ха обычными пространственными или
пространственно-временными координатами в плоском пространстве, но они могут иметь
Покажите, что (14- D2) cos х — 0 и (1 4- D2) sin х = 0 (в случае необходимости обратитесь в формулам
в § 6.5).
С учетом упражнения 21.1 найдите общее решение уравнения (14- D2)y — ж5 и докажите, что это
решение действительно является наиболее общим.
Попробуйте объяснить, почему при использовании процедуры, изложенной в тексте, теряется болынин-
***
ство решений, полученных в упражнении 21.2. Можете ли вы предложить модифицированную общую процедуру
нахождения всех решений? (Подсказка: в какой степени разложение 1 — D2 4- D4 — D6 4-... удовлетворяет тре¬
бованиям, предъявляемым к обратной величине выражения 14- D2? Попробуйте подействовать этим бесконечным
рядом на (1 4- D2) cos х.)
Почему?

21.2. Квантовые гамильтонианы
423
и более общий характер, например, быть обобщенными координатами qa в формализме Ла¬
гранжа или Гамильтона. Однако возникают значительные трудности, если провести такое
обобщение слишком далеко. Поэтому лучше принять, хотя бы на время, что мы имеем де¬
ло с некоторым плоским JV-пространством EN (не обязательно трех- или четырехмерным).
Тогда операторы ГГ, ..., Dдг описывают бесконечно малые трансляции пространства
в направлении каждой из осей (рис. 21.1), и каждый из них соответствует независимой
симметрии аффинного пространства EN.
Рис. 21.1. В (аффинном) евклидовом iV-пространстве имеются N независимых трансляционных
симметрий, генерируемых операторами (векторными полями) D\ = д/дх1, D2 = д/дх2, ..., Dn —
= d/dxN, удовлетворяющими перестановочным соотношениям Dt>xa - xaDb — &ъ с соответствую¬
щими декартовыми координатами х1, х2, ..., xN. (Показан случай N = 3.)
Напомним (§20.6), что, согласно теореме Нётер, имеется тесная связь между таки¬
ми симметриями пространства и сохранением импульса: если лагранжиан не меняется при
пространственной трансляции в некотором направлении, то импульс в этом направлении
сохраняется. Это изящный и важный факт, совершенно строгий в математическом отноше¬
нии. В квантовой механике делается нечто подобное, однако здесь нет такой математической
законченности. Более того, с математической точки зрения это выглядит совершенно без¬
умным! Тем не менее в этой странной математической процедуре есть несомненное мате¬
матическое изящество. В квантовой механике с каждой такой симметрией не только связан
сохраняющийся импульс, но и сам импульс фактически отождествляется с дифференци¬
альным оператором, который генерирует данную симметрию!
21,2.	Квантовые гамильтонианы
Как, в самом деле, можно отождествить импульс с дифференциальным оператором?
Это действительно звучит дико! Точнее, сюда следует еще добавить множитель h (дираков-
ский вариант постоянной Планка h = hj2тт, где h — обычная постоянная Планка; см. ниже),
а также мнимую единицу г. Тогда получается абсурдно выглядящее определение ра — ihDa,
то есть
ра = гп
дха
для импульса, соответствующего координате ха. Исходя из этого мы придем к закону комму¬
тации, называемому каноническим правилом коммутации, связывающему координату и им¬
пульс:
Рьха — харъ = ihSfr.
Что же надлежит делать с этим диковато выглядящим оператором-импульсом? Роль
этого «квантово-механического импульса» ihd/dxa состоит в том, что он должен занять

424
Глава 21
в классической функции Гамильтона 7i(pi, ..., Pn; ха, • * •, х ) то место, которое зани¬
мает там старый классический импульс ра. Здесь находится ключ к процедуре, именуемой
(каноническим) квантованием. Мы пока не касаемся теории относительности, так что рас¬
сматриваемые «импульсы» являются пространственными импульсами [21*21? а не энергией.
Наше пространство Е должно быть, вероятно, гораздо больше, нежели обычное трех¬
мерное пространство, поскольку рассматриваемая система может содержать большое число
частиц или других структур, и должны быть учтены все компоненты их координат и им¬
пульсов. В соответствии с общим обсуждением в главе 20 я не принимаю во внимание
возможность явной зависимости гамильтониана от времениt21-3!.
При обычной интерпретации считается, что координаты ха задают положения целого
ряда частиц (или, возможно, другие подходящие параметры). В этой главе я буду подробно
рассматривать квантовую механику одной частицы, однако при этом будет использоваться
общий формализм, который пригодится при изучении более сложных систем многих ча¬
стиц в главе 23. В случае одной частицы существует довольно очевидная релятивистская
симметрия между временной компонентой ж0 и тремя пространственными компонента¬
ми ж1, х2, ж3. Скоро мы увидим, что это играет важную роль в определении истинной
временной эволюции в квантовой механике. Тем не менее (каноническое) «квантование»,
особенно при наличии многих частиц, является в своей основе нерелятивистской процеду¬
рой с существенно различной трактовкой пространственных и временных аспектов физики.
Рассмотрим простой пример квантового гамильтониана, чтобы увидеть, как следует
обращаться с упомянутой безумной идеей. Возьмем случай одной ньютоновской частицы
массы га, движущейся в некотором внешнем поле, заданном потенциальной энергией V,
которая может зависеть от координат, V = V(x, у, z). В §20.2 мы уже видели, что клас¬
сический гамильтониан имеет вид Н — (р2 + р\ 4- p2z)/2m + V(x, у, z), где рх, ру, pz —
пространственные импульсы в направлении декартовых осей ж, у, z. Следовательно, кван¬
товый (канонически квантованный) гамильтониан будет иметь иметь вид
^ р2х + р2у+р1
 2то 	' = ~2т	+У(Х’У’2)’
где V2 = (д/дх)2 + (д/ду)2 + (д/дz)2 (это означает д2 / дх2 + д2 / ду2 У-д2 / dz2) представляет
собой лапласиан (уже рассмотренный ранее в § 10.5, но теперь написанный для трехмерного
случая).
В этом примере все идет гладко (а вот куда идет — с этим придется подождать до следу¬
ющего раздела!). В общем случае, однако, замена в гамильтониане классических импульсов
квантовыми не является однозначной процедурой, в основном из-за отсутствия коммутации
между квантово-механическим импульсом р и соответствующей ему координатой ж. Если,
например, в классическом гамильтониане окажется произведение рх, то становится неясно,
должно ли оно появиться в соответствующем квантовом гамильтониане в виде рх, или хр,
или, возможно, |(рж + хр), или в какой-то иной из бесконечного числа возможных форм.
Неоднозначность такого рода называется «проблемой упорядочения множителей». Во мно¬
гих практических ситуациях, эта неоднозначность может не играть серьезной роли, поскольку
часто оказывается, что там существует некоторый «очевидный» выбор. Такой выбор может
определяться некоторым руководящим принципом, например, требованиями симметрии или
инвариантности, или, возможно, некоторыми конкурирующими между собой физическими
или математическими инстинктивными либо эстетическими критериями. Иногда случается,
что разные альтернативы приводят тем не менее к эквивалентным физическим теориям.
И все же сам факт существования, в общем случае, такой неоднозначности означает, что
процесс «квантования» некоторой конкретной классической теории порой может содержать
серьезную проблему выбора.

21.3. Уравнение Шредингера
425
Существует также связанная проблема, касающаяся «общности» выбора коорди¬
нат ж1, ..., xN. Напомним, что в §§20.1, 20.2 допускалась полная свобода выбора обоб¬
щенных координат q1, ..., qN в конфигурационном пространстве С. Можно задать вопрос:
допустима ли такая свобода, когда мы переходим к квантовой теории? Ответ будет отри¬
цательным, если принять, что для каждой координаты qa классический сопряженный им¬
пульс ра должен «квантоваться» просто как ~ihd/dqa. Это очень тонкая проблема, которая
приводит нас в очаровательную область геометрического квантования^21 л\ Она особенно
важна в связи с общей теорией относительности независимо от того, предполагается ли
«квантовать гравитационное поле» или всего лишь рассматривать квантовые поля на фоне
искривленного пространства-времени. (К проблеме квантовой теории на искривленном фоне
я еще вернусь в § 30.4.) Существует, однако, много стандартных ситуаций, в которых, при
должной осторожности, можно успешно применять координаты более общие, чем обычные
плоские координаты. В частности, полезно использовать угловые координаты, когда сопря¬
женными импульсами будут моменты импульса. Моментом импульса мы займемся позднее
(в § 22.8, а также в § 22.12 для релятивистского случая).
21.3.	Уравнение Шредингера
Оставим, хотя бы на время, проблемы упорядочения множителей, обобщенных коор¬
динат и т. п. и предположим, что у нас есть квантово-механический гамильтониан, которым
мы вполне удовлетворены. Какое применение можно ему найти? Ответ таков: он играет
основную роль в фундаментальном уравнении, описывающем эволюцию квантовой систе¬
мы во времени и именуемом уравнением Шредингера. Вид этого уравнения фактически уже
предопределен правилами, сформулированными выше. Как это получается? Прежде всего,
необходимо взглянуть на «невидимую» функцию ф, присутствие которой неявно предпо¬
лагалось на правом краю всех наших перестановочных соотношений. Из-за присутствия
операторов д/дх гамильтониан теперь является оператором, и необходимо иметь что-то
справа от него, на что он мог бы действовать. Поскольку уравнение Шредингера описывает
эволюцию во времени, функция ф должна меняться со временем, так что она должна быть
функцией времени t, а также всех пространственных координат ха:
ф — ф(хг, ..., xN; t).
Однако эта функция не может зависеть от ра, поскольку эти величины теперь не являются
«независимыми переменными», а должны интерпретироваться как операторы дифференци¬
рования по переменным ха. Такая функция ф называется волновой функцией. Она определяет
квантовое состояние системы. Мы обсудим в должное время физическую интерпретацию
волновых функций.
Как приспособить сюда дифференцирование по £? Именно здесь в уравнение Шре¬
дингера входит временная эволюция. Напомним (§ 20.2), что (классический, не зависящий
от времени) гамильтониан представляет полную энергию системы. Отметим также тот факт
(подсказываемый § 21.2), что если нашу квантовую теорию когда-нибудь придется подгонять
под требования теории относительности, то квантовое правило ра = ihd/dxa (для одной
частицы) должно быть распространено на компоненту с а = 0 наряду с тремя простран¬
ственными компонентами (см. § 18.7). В соответствии с этим при процедуре «квантования»
следует заменить энергию дифференцированием по времени (Е = ihd/dt). Уравнение Шре¬
дингера выражает именно такой «квантовый вариант» интерпретации гамильтониана как
полной энергии:
• >-дф

426
Глава 21
где
п = п I in-Ar, ...,гП-^гг; х1
V дх1	дхА
• •
*
Используя в качестве простого примера частный случай квантового гамильтониана, пред¬
ставленного выше в § 21.2, можно написать уравнение Шредингера для одной частицы мае
сы т, движущейся во внешнем поле, которое вносит в энергию вклад V = V(x, у, z):
inft=-£v2*+^-
Конечно, вся эта замена импульса и энергии дифференциальными операторами выгля¬
дит каким-то математическим шаманством, и можно задать законный вопрос: как приме¬
нять подобные упражнения к импульсу, сообщаемому ударом боксера или взмахом игрока
в гольф? Мы можем задать такой вопрос! Но согласно квантовой механике, это все, что мож¬
но сделать. Ключевым свойством импульса является то, что он сохраняется, и действие удара
на того, кому он предназначен, является просто результатом неизбежности его сохранения.
Импульс должен куда-то уйти, он не может просто исчезнуть, потому что он сохраняется.
То же относится и к энергии.
Несомненно, что в классической гамильтоновой теории мы имеем сохранение импульса
и энергии. Однако скептически настроенный читатель может быть недоволен: зачем нужно
это забавное отождествление физической величины с некоторым дифференциальным one-
ратором, даже если это хорошо работает? Чтобы попытаться ответить на этот вопрос
и сделать такую операцию более правдоподобной, приходится обращаться к эксперимен¬
ту. (В противном случае вряд ли удастся придать должный вес этой нелепо выглядящей
манипуляции!) Я не собираюсь входить здесь в подробности экспериментов, однако су¬
щественным фактом, который следует из большого массива опытных данных, оказалась
непосредственная связь между частотой и энергией и аналогичная связь между волновым
числом (обратной величиной длины волны) и импульсом, причем эта связь представляет¬
ся универсальной, проявляющейся во всех явлениях. В §21.5 мы увидим, какое это имеет
отношение к выражению ра = ihd/dxa\ А пока давайте взглянем на некоторые эксперимен¬
тальные факты, дающие основание считать, что энергия и импульс действительно обладают
такими «волновыми» ассоциациями.
21.4.	Экспериментальные основания квантовой теории
Вероятно, наиболее непосредственное проявление ассоциаций такого рода наблюда¬
ется в кристаллических материалах. Такие структуры характеризуются пространственной
периодичностью в расположении атомов. Как было впервые показано в знаменитом опыте
* JШ Найдите явное решение этого уравнения Шредингера для частицы массы т в постоянном ньютоновском
гравитационном поле V = mgz. (Здесь z есть высота над поверхностью Земли, a g — направленное вниз ускорение
под действием силы тяжести.)
Произведя преобразование к свободно падающей системе отсчета с координатами X = х, Y = у, Z =
1
= z— 2 У’ покажите> что уравнение Шредингера из упражнения 21.5 преобразуется в соответствующее уравнение
л	-	а,	~	i(^mt3g2+mtgz)	„
без гравитационного поля с волновой функцией w = е ь	-ф.	Что это говорит об эйнштейновском
принципе эквивалентности в применении к квантовым системам? (См. также § 21.9.)
Покажите, что если квантовый гамильтониан Н обладает трансляционной инвариантностью, будучи,
например, не зависящим от координатной переменной ж3, то соответствующий импульс рз сохраняется в том
смысле, что оператор рз коммутирует с оператором временной эволюции d/dt. В свете данной ниже интерпретации
объясните, почему такая коммутация означает сохранение.

21.4. Экспериментальные основания квантовой теории
427
К.Дж. Дэвиссона и JI.X. Джермера (1927), если в кристалл попадают электроны с доста¬
точным разбросом начального 3-импульса, то они отклоняются (или отражаются) лишь на
вполне определенные углы. Оказалось, что эти направления и углы зависят от входных
и выходных 3-импульсов особым образом, связанным с периодической природой кристал¬
лической решетки. Очевидным следствием этих экспериментальных результатов является
наличие точной обратной пропорциональности между 3-импульсами электронов и перио¬
дом структуры (см. рис. 21.2). То же относится и к частицам другого типа. Из этого следует,
что частица с импульсом р ведет себя как периодический объект типа волны с универ¬
сальной связью между длиной волны Л и величиной импульса р9 описываемой обращенной
формулой (содержащей постоянную Планка h =• 2тгН):
А = hp
-1
2nh
V
Рис. 21.2. Опыт Дэвиссона - Джермера. Пучок электронов с 3-импульсом р попадает в материал с пери¬
одической кристаллической структурой. Рассеяние или отражение происходит, когда атомная структура
согласуется со структурой электронов, рассматриваемых как волны с длиной Л, связанной с величиной
импульса р соотношением Л = h/p, где h — постоянная Планка
Длина волны Л, сопоставляемая частице с импульсом р, называется де-бройлевской
длиной волны этой частицы в честь проницательного французского аристократа и физика
принца Луи де Бройля, который в 1923 году впервые предположил, что все материальные
частицы имеют волновую природу и соответствующая длина волны определяется вышепри¬
веденной формулой. Более того, в соответствии с требованиями теории относительности
(см. § 18.7) частица должна обладать также некоторой частотой и, связанной с энергией Е
формулой Планка
Е — hv — 2тxfw,
которой мы вскоре займемся*. В системе отсчета, где частица покоится, ее энергия описыва¬
ется формулой Эйнштейна Е• = /хс2, где р — ее масса покоя, так что частице сопоставляется
частота рс2/2rch, то есть рс2/h.
Рассуждения такого рода приводят к выводу, что обычная частица проявляет волновое
поведение, связанное с ее массой покоя универсальным образом, определяемым формула¬
ми Планка и де Бройля. Однако двумя десятилетиями раньше уже было сформулировано
обратное утверждение, согласно которому объекты, которым первоначально приписывалась
Попробуйте объяснить, почему требования специальной теории относительности позволяют вывести
формулу Планка Е = hv из формулы де Бройля р = h\~1. {Подсказка: можно предположить, что гиперплоскости
в М, на которых волна сохраняет постоянное значение, лоренц-ортогональны 4-скорости частицы.)

428
Глава 21
чисто волновая природа (в первую очередь максвелловские колебания электрических и маг¬
нитных полей, образующие свет, — вспомним § 19.2), имеют также корпускулярную приро¬
ду, опять-таки согласующуюся с формулами Планка и де Бройля. Наиболее убедительным
проявлением этого стал фотоэлектрический эффект, впервые наблюдавшийся в 1887 го¬
ду Генрихом Герцем. Наиболее загадочные свойства этого эффекта, продемонстрированные
в 1902 году Филиппом Ленардом, были блестяще объяснены Эйнштейном в 1905 году на
основе корпускулярной картины света. (Эйнштейн получил Нобелевскую премию в 1921 го¬
ду именно за это, а не за теорию относительности!) Фотоэлектрический эффект возникает,
когда свет достаточно высокой частоты и, падая на подходящий металл, выбивает из него
электроны. Загадка состоит в том, что энергия выбиваемых электронов совсем не зависит от
интенсивности света (частота v которого поддерживается постоянной). Согласно волновой
картине, следует ожидать, что чем выше интенсивность, тем больше должна быть энергия
испускаемых электронов. Этого не происходит (хотя при повышении интенсивности вы¬
летает больше электронов). Эйнштейн объяснил это, представив свет как поток падающих
частиц (ныне называемых фотонами), энергия каждой из которых определяется формулой
Планка Е — ho, так что испускание каждого электрона является результатом воздействия
такого фотона на отдельный атом. Эйнштейн использовал формулу Планка с большим успе¬
хом, сделав ряд предсказаний, подтвержденных впоследствии, в частности, первоначально
скептически настроенным американским экспериментатором Робертом Милликеном (1916).
На самом деле квантово-механическая корпускулярная природа света начала прояв¬
ляться несколько раньше. Это произошло в 1900 году, когда Макс Планк положил начало
квантовой революции. Он сделал это, проведя замечательный анализ излучения черного
тела, под которым понимается электромагнитное излучение, находящееся в равновесии
с «черным» ^21,5^ материальным окружением, поддерживаемым при некоторой температу¬
ре Т (см. рис. 21.3 а). Планк получил (правильную) формулу, табулированную на рис. 21.3 б:
2 ho3
(phvJkT __ X)-1 ’
которая описывает удельную интенсивность I как функцию частоты о; здесь к есть по¬
стоянная Больцмана (связанная с единицами, в которых измеряется температура; сравните
с §27.3).
Формула Планка оказалась полностью соответствующей результатам наблюдений.
До Планка природа спектра черного излучения оставалась тайной. Полностью волновая кар¬
тина электромагнитного излучения приводила к формуле Рэлея-Джинса I — 2 кТо2, точной
при малых I/, однако при больших о интенсивность расходилась, стремясь к бесконечности.
Кажущимся улучшением была предложенная Вином формула I = 2hv3 e~hl// кТ, точная при
больших v, которую можно обосновать, рассматривая излучение как термостат из класси¬
ческих частиц. Величина h, фигурирующая в формуле Планка, была постулирована им как
новая фундаментальная константа Природы (теперь она называется постоянной Планка);
ее крайне малая величина оказалась равной 6,62 • 10 ~34 Джоуль-секунд. Чтобы получить
свою формулу, Планк был вынужден предположить, что электромагнитные колебания мо¬
гут поглощаться и испускаться лишь в виде сгустков энергии определенной величины Е,
непосредственно связанной с частотой колебаний v соотношением
Е = ho,
Планком был проведен достаточно «безумный» статистический подсчет, поразительным
образом предвосхитивший корректную с точки зрения квантовой механики статистику Бозе-
Эйнштейна, которую мы обсудим в § 23.7.
Здесь была физическая загадка иного рода, нежели в случае электронов, попадающих
в кристалл, поскольку электромагнитные эффекты в то время рассматривались с волновой

21.4. Экспериментальные основания квантовой теории
429
а)
б)
Частота v
Рис. 21.3. Излучение черного тела, а) «Черная» полость обеспечивает тепловое равновесие заклю¬
ченного в ней излучения с окружающей средой при температуре Т. б) При данной температуре Т
интенсивность / на каждой частоте v является вполне определенной функцией от г/. Сплошной кривой
показаны результаты наблюдений, описываемые знаменитой формулой Планка I — 2hi/3 /(ehl/^кТ —
— l)”1, где Ник — соответственно постоянные Планка и Больцмана. Штриховая кривая соответствует
формуле Рэлея-Джинса I — 2 кТи2, которая получается, если рассматривать излучение как клас¬
сические волны; она аппроксимирует формулу Планка для малых г/, но расходится при больших и.
Пунктирная кривая изображает закон Вина I = 2Hy3e~hl/^kT, который трактует излучение как клас¬
сические частицы
точки зрения, а теперь получалось, что в них проявляются корпускулярные свойства! Ис¬
пользуя дираковский вариант постоянной Планка, получаем Е = 2кНи, так что временной
период колебаний у~~г описывается формулой, соответствующей предыдущему соотноше¬
нию (Л — 2irh/p), связывающему длину волны с импульсом. В настоящее время (вслед
за Эйнштейном, Бозе и др.) мы относим соотношение Планка не к «колебаниям электро¬
магнитного поля», а к реальным частицам — квантам максвелловского электромагнетизма,
которые мы называем фотонами, хотя прошло много лет, пока прозрения Эйнштейна по¬
лучили признание. Среди подтверждений, последовавших за успешным объяснением фо¬
тоэлектрического эффекта, был решающий эксперимент Артура Комптона (1923), который
продемонстрировал, что фотоны, сталкиваясь с заряженными частицами, действительно ве¬
дут себя как безмассовые частицы в соответствии с законами релятивистской динамики,
изложенными в § 18.7 (см. §25.4, рис. 25.10). Согласно этим законам, энергия и импульс
обратно пропорциональны периоду (временному для энергии и пространственному для им¬
пульса), измеряемому всегда в единицах 2nh.
Одним из наиболее убедительных (и наиболее известных) фактов, побуждающих нас
признать, что частицы могут вести себя, как волны, а волны — как частицы, является двух¬
щелевой эксперимент J21*6! Здесь мы имеем источник частиц и детектирующий экран, между
которыми расположен барьер с парой близко расположенных параллельных щелей в нем (см.
рис. 21.4а). Предположим, что в направлении экрана поодиночке испускаются электроны.
Если вначале одна щель открыта, а другая закрыта, то на экране появится некоторая картина
из хаотически расположенных точек, создаваемых частицами, столкнувшимися с экраном.
Интенсивность картины (в смысле наибольшей плотности точек), как и следовало ожидать,
максимальна в области центральной полосы, близкой к плоскости, соединяющей источник
со щелью, и равномерно спадает в обе стороны от этой центральной полосы (рис. 21.46).
Аналогичная картина получается, если повторить эксперимент, открыв только вторую щель
(рис. 21.4 в). Здесь пока нет никаких загадок. Но если провести эксперимент еще раз с обе¬
ими открытыми щелями, получится нечто необычное (см. рис. 21.4 г). Частицы одна за
другой по-прежнему оставляют на экране точечные следы, но теперь точки образуют волно¬
вую интерференционную картину в виде параллельных полос повышенной интенсивности.

430
Глава 21
Оказывается даже, что на экране имеются области, не достижимые для частиц, испускаемых
источником, несмотря на тот факт, что частицы могли вполне успешно попадать в эти обла¬
сти, когда была открыта лишь одна из щелей! Хотя пятна появляются на экране по одному
в локализованных положениях и хотя каждой встрече частицы с экраном можно сопоставить
определенный акт испускания частицы источником, поведение частицы между источником
и экраном, включая неоднозначность, связанную с наличием двух щелей в барьере, подоб¬
но поведению волны, при котором волна-частица при столкновении с экраном чувствует
сразу обе щели. Более того (и это особенно важно для наших непосредственных целей),
расстояние между полосами на экране соответствует длине волны Л нашей волны-частицы,
связанной с импульсом частиц р прежней формулой Л —	/р.
Рис. 21.4. а) Схема двухщелевого эксперимента. Электроны поодиночке испускаются в направлении
экрана, находящегося за барьером с парой щелей. 6) Картина на экране при закрытой правой щели.
в) То же при закрытой левой щели, г) Если открыты обе щели, возникает интерференция. Некоторые
области на экране оказываются недостижимыми, несмотря на тот факт, что частицы могли попасть
в них, когда была открыта какая-то одна из щелей
щели
Электронная
пушка
21.5.	Обсуждение дуализма волна-частица
Всё это вполне возможно, скажет трезвомыслящий скептик, но это еще не заставляет
нас проводить такое абсурдно выглядящее отождествление энергии-импульса с каким-то
оператором! Конечно, не заставляет, но должны ли мы отворачиваться от чуда, когда оно
является нам?! В чем же состоит это чудо? Чудом является то, что эта кажущаяся абсурд¬
ность экспериментального факта (волны оказываются частицами, а частицы — волнами)
м*шет быть приведена в систему с помощью красивого математического формализма, в ко¬
тором импульс действительно отождествляется с «дифференцированием по координате»,
а энергия — с «дифференцированием по времени».
Как этот формализм может помочь нам понять загадочную двойственность волна-
частица? Для описания нашей волны-частицы потребуется некий математический объект,
который, с одной стороны, может дать нам четко определенный 4-импульс частицы Ра,
а с другой обладает требуемой пространственной и временной периодичностью волны. (Я те¬
перь пользуюсь прописной буквой Р, поскольку в данном случае имею в виду определен¬
ное «классическое» значение 4-импульса, которым может обладать наша частица. Мы еще
вернемся к «квантовому 4-импульсу», описываемому дифференциальным оператором.) Та¬
ким математическим объектом волнового типа естественным образом оказывается волновая
функция с определенной пространственно-временной зависимостью типа плоской волны
(см. § 5.3)
1р{ха) = e~iPaXa/h.

21.5. Обсуждение дуализма волна-частица
431
Эта величина переходит в самое себя, если увеличить Раха на 2тгh (поскольку это добав¬
ляет —2лг к показателю экспоненты, так что все выражение умножается на е~27гг = 1).
Поэтому она обладает временной периодичностью с периодом 2ттН/Ро и пространственной
периодичностью с периодом 2ттН/Р\ в направлении х\, а также аналогичной периодично¬
стью в остальных пространственных направлениях. Это точно согласуется с требованиями,
выдвинутыми выше.
Что примечательного в этой волновой функции? Это так называемая собственная функ¬
ция нашего квантового оператора импульса
■ р. д
Ра = гп
дх
Последнее означает, что если мы подействуем этим оператором на вышеприведенную функ¬
цию ф(ха), то снова получим функцию ф(ха), умноженную на некоторый постоянный мно¬
житель (см. § 6.5):
ih-^-ip(xb) = ih-^~e~iPbxb fh = Pae-iPbxb/h = Раф{хь).
Отметим, что таким постоянным множителем фактически служит как раз (классиче¬
ский) 4-импульс Ра, обладание которым требовалось от нашего математического объекта.
Итак, если функция ф(ха) имеет правильный вид, показанный выше, то наш загадочный
квантовый импульс ра = ihd/dxa, действуя на нее, превращается в обычный классический
импульс Ра:
РаФ = РаФ\
однако в случае других состояний дело обстоит иначе. Можно сказать, что указанное состоя¬
ние ф обладает определенным значением 4-импульса, и назвать его импульсным состоянием.
Мы должны считать, что свободно движущаяся частица, обладающая определенным клас¬
сически идентифицируемым импульсом Ра, математически описывается такой волновой
функцией ф, которая является собственной функцией квантового оператора ра с собствен¬
ным значением Ра. Единственными волновыми функциями, которым соответствует опреде¬
ленное значение классического импульса, действительно оказываются те, которые являются
собственными функциями квантового оператора импульса.
Напомним, что в § 13.5 было введено понятие собственного вектора линейного опе¬
ратора Т, то есть такого вектора v, для которого Tv = Xv9 где Л — некоторая скалярная
величина, называемая собственным значением этого оператора. Здесь мы имеем точно та¬
кую ситуацию с ihd/dxa в качестве оператора Т и Ра в качестве Л (где индексу а по
очереди приписываются все значения), за исключением того, что в § 13.5 мы рассматри¬
вали в основном конечномерные векторные пространства и их линейные преобразования.
Здесь же мы имеем дело с векторным пространством W всех возможных функций ф(ха),
которое является бесконечномерным векторным пространством. (Это есть именно векторное
пространство, поскольку мы можем складывать функции от ха и умножать такие функции
на числа, получая всякий раз новые функции от ха. Оно бесконечномерно, поскольку, на¬
пример, все функции рассмотренного выше частного вида с величинами Ра, выбираемыми
бесконечно многими различными способами, являются линейно независимыми*.)
Собственные функции (или собственные состояния, как их часто называют в квантовой
механике) играют ключевую роль в квантовом формализме. На языке квантовой механики
различные операторы (такие, как только что рассмотренный оператор ра — Шд/дха, и
другие, например, операторы координаты или момента импульса, которые будут рассмот¬
рены позже) называются динамическими переменными. Наша волновая функция ф, которая
Почему? Здесь линейная зависимость может включать непрерывные суммы, то есть интегралы.

432
Глава 21
первоначально просто играла роль находящейся в тени «невидимой функции», расположен¬
ной справа от всех наших операторов, теперь определенно начинает играть активную роль.
Как упоминалось выше, мы рассматриваем ее как состояние физической системы. Иногда ее
называют вектором состояния (хотя в действительности это более общий термин, не пред¬
полагающий обязательного использования пространственных и временных координат для
описания ф). Как и в рассмотренном выше случае 4-импульса, собственными состояниями
некоторой динамической переменной являются те состояния, в которых данная динамиче¬
ская переменная имеет так называемое «определенное значение», а собственное значение
является действительным «значением», которое принимает динамическая переменная в этом
состоянии.
Здесь необходимо отметить, что до сих пор мы рассматривали наше собственное со¬
стояние импульса в полностью четырехмерном пространственно-временном представлении,
согласованном с требованиями специальной теории относительности. Это более экономный
способ, поскольку выражение"'
^—гРахаjh   ^~iEt/h^i'P--x./h
(где Ра = (Е. —Р) и ха = (£, х), как в § 18.7) содержит как пространственную зависимость,
которая определяет собственное состояние обычного пространственного 3-импульса
р = (~Pi, -Р2, Рз) =
\ааг ох ох*)
с собственным значением Р, так и временную зависимость, определяющую решение урав¬
нения Шредингера с собственным значением энергии Е. Однако формализм Шредингера
в целом не является релятивистской схемой в том смысле, что он рассматривает время от¬
дельно от пространственных переменных, поэтому при последующем обсуждении в этой
главе мне лучше вернуться к нерелятивистскому описанию.
21.6.	Что есть квантовая «реальность»?
••
Отвлечемся на минуту от подробностей и зададимся вопросом: что всё это может ска¬
зать нам о «реальности»? Являются ли динамические переменные «реальными объектами»?
«Реальны» ли квантовые состояния? И должны ли мы считать, что постигли реальность,
лишь получив те «кажущиеся классическими» величины, которые возникают как собствен¬
ные значения динамических переменных (или других операторов)? На самом деле физики,
занимающиеся квантовой теорией, не стремятся к полной ясности в этом вопросе. Многие
из них вообще чувствуют себя явно некомфортабельно при обращении к понятию «реально¬
сти». Они утверждают, что стоят на позициях «позитивизма», и отвергают как «ненаучные»
вопросы о том, как понимать «реальность». Они заявляют, что в отношении нашего форма¬
лизма мы можем задавать вопросы лишь о том, может ли он давать ответы на правильно
поставленные вопросы относительно изучаемой системы и согласуются ли эти ответы с на¬
блюдаемыми фактами.
Если мы считаем, что в квантовом формализме есть нечто «действительно реальное», то
я полагаю, что квантовую реальность должна описывать именно волновая функция (или век¬
тор состояния). (К некоторым другим возможностям я обращусь позже, в главе 29; см. также
конец § 22.4). Моя собственная точка зрения такова, что в квантовой механике должен ста¬
виться вопрос о «реальности», особенно если придерживаться взгляда (разделяемого многи¬
ми физиками), что квантовый формализм универсально применим ко всей физике. Потому
* Почему его можно разложить на множители таким образом?

21.6. Что ЕСТЬ КВАНТОВАЯ «РЕАЛЬНОСТЬ»?
433
что тогда отсутствие квантовой реальности означало бы отсутствие реальности на любом
уровне (поскольку при такой точке зрения все уровни должны быть квантовыми). На мой
взгляд, такой полный отказ от признания реальности не имеет смысла. Нам необходимо
понятие физической реальности, хотя бы предварительное или приближенное, поскольку
без нее наша объективная Вселенная, а значит, и вся наука просто исчезают перед нашим
изумленным взором!
Всё это прекрасно, но как быть с вектором состояния? Что мешает признать, что он
представляет реальность? Почему физики зачастую крайне неохотно принимают такую фи¬
лософскую позицию? Чтобы понять эти трудности, мы должны внимательнее взглянуть
на природу и физическую интерпретацию волновых функций.
Рассмотрим сначала более подробно наше импульсное состояние тр — ег1>*х/й (для удоб¬
ства оно берется в момент времени t — 0). Заметим, что, в отличие от обычной частицы,
оно никоим образом не локализовано, а размазано по всей Вселенной. Его «величина», из¬
меряемая модулем егР‘х/^ , имеет одну и ту же величину 1 во всем пространстве (см. § 5.1).
Читатель вполне может счесть странной такую картину для одной частицы со вполне опре¬
деленным импульсом в некотором пространственном направлении. Как же быть с нашим
обычным представлением о частице как объекте, локализованном (хотя бы приближенно)
в одной точке? Мы могли бы сказать, что импульсное состояние — всего лишь идеализация.
Можно также получить вполне определенный (если и не точно определенный) импульс,
если перейти к похожим состояниям — так называемым «волновым пакетам». Они задаются
волновыми функциями, величина которых имеет резкий пик в некоторой области и которые
в некотором смысле являются «почти-собственными» функциями импульса. В случае одно¬
го измерения такие волновые пакеты можно представить в явном виде, взяв произведение
2
импульсного состояния на гауссову функцию е~х или, еще лучше, на обобщенную гауссову
функцию
Ае-В*(*-С)\
(где А, В и С — вещественные постоянные). Эта «колоколообразная» кривая хорошо из¬
вестна в статистике (в качестве иллюстрации см. рис. 27.5 в § 27.4), «пик» этой функции
находится в точке х — С. Некоторый интерес (а также вычислительные преимущества)
v>	v#
представляет волновой пакет, который получается, если в таком произведении позволить
параметру С быть комплексным числом*. Подобным образом можно построить волновые
т!>2 / 2 2 2\
пакеты в полном трехмерном пространстве, взяв гауссову функцию Ае~в +у с пи¬
ком, смещенным в комплексном направлении. Во всех случаях величина В“1 определя¬
ет меру размытия волнового пакета. Имеется теорема, лежащая в основе так называемо¬
го «принципа неопределенности Гейзенберга», согласно которому существует абсолютный
предел того, насколько малым может быть размытие, связанное с тем, насколько близко
состояние к «почти-собственному» состоянию импульса. В более явном виде мы увидим
это в § 21.11.
А пока попробуем получше представить себе, на что похожи импульсные состояния
и волновые пакеты. Мы должны иметь в виду, что волновая функция — это волна, принима¬
ющая комплексные значения, и ее «волновой» характер не обязательно проявляется в виде
колебаний ее величины (или интенсивности). В случае импульсного состояния аргумент
волновой функции (§ 5.1) ~Раха/Н определен на окружности, т. е. е~гР<хХа!п берется на еди¬
ничной окружности в комплексной плоскости, что дает «волновое» поведение. В квантовой
теории мы рассматриваем аргумент волновой функции как ее фазу. Мы обнаруживаем, что
фаза не столько «колеблется», сколько «закручивается». На рис. 21.5 а я попытался показать
поведение волновой функции в некотором направлении, изобразив это направление вправо
Заменив в вышеприведенном выражении вещественное число С комплексным числом С У W (где С
и D — вещественные числа), найдите частоту волнового пакета и положение его пика.

434
Глава 21
наклоненным на некоторый угол (ось х на рисунке) и взяв плоскость, перпендикулярную
этому направлению, в качестве комплексной плоскости значений, которые может принимать
волновая функция ф (так что на рисунке изображена функция ф = и +' iv на этой плоско¬
сти). Таким образом, направление х на моем рисунке соответствует некоторому реальному
направлению в обычном пространстве, в то же время направления и и v не являются обыч¬
ными пространственными направлениями — они представляют комплексную плоскость воз¬
можных значений волновой функции. Заметим, что волновая функция нашего импульсного
состояния имеет вид штопора (закрученного вправо, если считать положительным импульс
в направлении х на нашем рисунке). На рис. 21.56 представлена соответствующая картина
для волнового пакета. Она похожа на пружину для растягивания (эспандер), и импульс вол¬
нового пакета определен не вполне точно. Здесь спираль затухает в обе стороны, так что за
пределами некоторого интервала волновая функция становится очень малой.
v *
<$>
X
\
■■о
б)
Рис. 21.5. Волновая функция частицы: ф как комплексная функция координаты х. а) Импульсное
состояние е~гРаХ (собственная функция импульса р) изображено в виде штопора. 6) Волновой
пакет е А х2 е гРх!п
\
Разумеется, чтобы получить полную картину этих волн, мы должны попытаться пред¬
ставить себе, что такое происходит сразу во всех трех пространственных измерениях, а это
непросто, потому что нам нужны два дополнительных измерения (то есть всего 5 измерений),
чтобы изобразить комплексную плоскость, а также пространственные измерения! Однако
в случае импульсного состояния дело обстоит не так плохо, если рассматривать просто плос¬
кости постоянной фазы. Таковыми являются параллельные плоскости, перпендикулярные
направлению импульса; расстояние между соседними плоскостями равно 2nh/p, где р — ве¬
личина (пространственного) 3-импульса (см. рис. 21.6). Описание такого рода полезно при
рассмотрении, например, волновой функции фотона, сталкивающегося с кристаллом, как на
рис. 21.2. Можно воспользоваться, таким описанием и в случае двухщелевого эксперимента,
если щели расположены на большом расстоянии от экрана. Тогда можно считать, что вол¬
новая функция каждой частицы, достигающей некоторой локализованной области экрана,
представляет собой сумму двух частей, каждая из которых близка к импульсному состоянию
(будучи, по существу, одночастотной плоской волной из-за удаленности щелей от экрана),
однако направления этих двух компонент несколько различны. В некоторых местах экрана
две волны будут усиливать одна другую, тогда как в других — приводить к взаимному по¬
гашению, в результате возникают описанные выше (рис. 21.4 г) полосы большей и меньшей
интенсивности. Такая конфигурация показана на рис. 21.7, где плоскости представляют об¬
ласти пространства, в которых фаза каждой из волн-компонент имеет постоянное значение.
Полная волновая функция должна быть суммой этих двух компонент. Если предположить,
что обе части в отдельности имеют одинаковую интенсивность, то они будут взаимно пога¬

21.6. ЧТО ЕСТЬ КВАНТОВАЯ «РЕАЛЬНОСТЬ»?
435
шаться в тех местах, где они находятся в противофазе, и усиливаться там, где они находятся
в фазе. Это и дает полосы интенсивности, реально наблюдаемые в двухщелевом экспери¬
менте.
Рис. 21.6. Плоскости заданной фазы для собственного состояния импульса, отстоящие одна от другой
на hp 1, где р — величина пространственного 3-импульса. (Сравните с рис. 21.2)
Рис. 21.7. Волновую функцияю электрона, прибли¬
жающегося к экрану в двухщелевом эксперименте
(см. рис. 21.4), можно рассматривать как суперпо¬
зицию двух из тех плоских волн, что показаны на
рис. 21.6, слегка наклоненных относительно одна
другой. Там, где фазы совпадают (вдоль прерыви¬
стых прямых), две волны усиливают одна другую,
что соответствует максимальной вероятности до¬
стижения экрана. Посредине между максимумами
фазы противоположны, и происходит взаимное по¬
гашение волн, соответствующее нулевой вероятно¬
сти достижения экрана электроном
Да-да, может прервать меня нетерпеливый читатель, но все это о том, как ведут себя
волны. Пока не приведено фактов, доказывающих, что наши волны-частицы — это дей¬
ствительно вошы-частицы\ Помимо внешне не слишком впечатляющего утверждения, что
рассматриваемые волны — это комплексные волны, была лишь описана интерференция волн
вроде той, которую претерпевают обычные морские волны, звуковые волны или максвел¬
ловские волны, создаваемые классическим электромагнитным полем (радиоволны, видимый
свет, рентгеновские лучи и т. п.). Но главный пункт в двухщелевом эксперименте, на чем
следует настаивать, состоит в том, что он выявил конфликт между волновой и корпуску¬
лярной картинами. Действительно, наиболее очевидное проявление природы частиц в этом
эксперименте возникает, когда они оставляют свои следы на экране — причем поодиночке!..

436
Глава 21
21.7.	«Целостная» природа волновой функции
Здесь необходимо кое-что подчеркнуть. Можно представить себе, что маленькое пятно
на экране появляется время от времени, когда локальная интенсивность волны достигает
некоторой критическом величины, или, другими словами, что существует некоторая веро¬
ятность появления пятна на экране, которая повышается с ростом интенсивности волны.
Прекрасно! Однако в описанном выше двухщелевом эксперименте (в идеализированной
форме) все не так просто. Потому что если бы дело было в индивидуальных вероятностях
для отдельных мест, мы могли бы ожидать, что при достаточной интенсивности иногда на
экране будут появляться два пятна на большом расстоянии одно от другого, однако испус¬
кание одной частицы источником описывается одной волновой функцией. Трудность станет
более явной, если предположить, что частицы заряжены, как если бы это были электро¬
ны. Ибо если испускание источником одного электрона могло привести к тому, что экрана,
пусть даже изредка, достигает пара электронов, то это означало бы нарушение закона сохра¬
нения заряда. То же относится и к любому другому сохраняющемуся «квантовому числу»,
характеризующему частицу, например, к сохраняющемуся барионному числу (§ 25.6), если
мы используем нейтроны"'. Такое нарушение законов сохранения находилось бы в резком
противоречии с огромным объемом экспериментальных данных. Тем не менее электроны
и нейтроны проявляют своего рода самоинтерференцию, проявляющуюся в описанных ре¬
зультатах двухщелевого эксперимента!
«Так что мы ничего не достигли в понимании волн/частиц!» — со вполне оправданным
нетерпением возразит сердитый читатель. Но погодите, пожалуйста, мы еще не покончили
с интерпретацией наших волновых функций. Мы должны принять, что вся волна в целом
описывает всего одну частицу (или «является» ею). Хотя она, в некотором смысле, опре¬
деляет вероятность появления пятна в разных местах экрана, эта вероятность относится
лишь к одной частице. Такая интерпретация не годится, если мы рассматриваем волновую
функцию локальным образом, считая, что она определяет вероятность образования пятна
в каждом отдельном месте экрана независимо от других. Мы должны рассматривать волно¬
вую функцию как единое целое. Если она вызывает появление пятна в одном месте, то она
уже выполнила свою работу, и этот видимый акт рождения запрещает ей вызвать появление
пятна где-нибудь еще. В этом отношении волновые функции совершенно отличны от волн
классических частиц. Разные части волны нельзя рассматривать как локальные возмущения,
каждое из которых ведет себя независимо от того, что происходит в какой-то отдаленной
области. Волновые функции имеют сильно нелокальный характер, и в этом смысле они
являются полностью целостными объектами.
Эту точку зрения можно сделать еще более убедительной, взяв несколько иную экс¬
периментальную ситуацию. Она обладает дополнительным преимуществом при разъясне¬
нии того, что представление волны-частицы волновым пакетом само по себе совершенно
неадекватно объясняет частицеподобное квантовое поведение. Представим себе прежний
источник частиц и предположим, что он испускает всего одну частицу. Вместо барьера
с парой щелей поставим на пути частицы так называемый расщепитель луча. Будет понят¬
нее, если считать нашу частицу фотоном, тогда расщепителем луча будет «полупрозрачное
зеркало»^21-7^ которое должно разделить наш фотонный волновой пакет на две части, далеко
отстоящие одна от другой. Чтобы сделать нашу концепцию более ясной, представим, что
наш «эксперимент» проводится в межзвездном пространстве (должен предупредить чита¬
теля, что не предлагаю здесь ничего практического — наш пример призван лишь проявить
некоторые фундаментальные предсказания квантовой механики в особых обстоятельствах).
Покажите, что вероятность появления такого двойного пятна в этой картине должна быть вполне ощу¬
тимой при любой зависимости вероятности появления пятна от интенсивности волновой функции. {Подсказка
разделите экран на две части с равной вероятностью появления пятна на каждой из них.)

21.7. «Целостная» природа волновой функции
437
При желании можно представить себе, что волновая функция фотона выходит из источника
в виде четко очерченного волнового пакета малых размеров, затем, после встречи с рас¬
щепителем луча, она делится на две части, одна из которых отражается от расщепителя,
а другая проходит сквозь него, например, в перпендикулярном направлении (рис. 21.8).
Полная волновая функция является суммой этих двух частей. Мы можем, если захотим,
подождать год, после чего запечатлеть волновую функцию фотона на фотопластинке либо
с помощью какого-то другого приемника. К тому времени две части разойдутся между со¬
бой на очень большое расстояние, но мы можем вообразить, что у меня есть двое коллег
(в двух различных космических лабораториях), разделенных расстоянием в 1,4 световых
года. У каждого из моих коллег есть свой приемник, и, хотя к этому моменту каждая из двух
частей волнового пакета может значительно расплыться в пространстве, каждый из коллег
с помощью имеющегося у него большого параболического зеркала может собрать волновой
пакет, сфокусировав его на своем приемнике. Что скажет нам квантовая механика о том, что
должно произойти? Она скажет, что тот или иной из моих коллег сможет обнаружить фотон,
но они не могут обнаружить его оба. Это не похоже на то, как ведет себя классическая
волна. Напомню, что мои коллеги разделены расстоянием 1,4 световых года. Теория относи¬
тельности утверждает, что никакой сигнал не может пройти это расстояние менее чем за 1,4
года (§ 17.8), тем не менее тот факт, что одна часть волнового пакета воспроизводит фотон,
мешает сделать то же самое другой, отстоящей на 1,4 года, и наоборот. Всего за один год
я смогу узнать у каждого из коллег, что у него там происходит, и окажется, что лишь один
из них зарегистрировал фотон. Та часть волновой функции, с которой имеет дело каждый из
коллег, как будто «знает», что происходит с другой частью! Каждый раз, когда мы проводим
этот эксперимент, оказывается, что фотон зарегистрирован тем или иным из коллег, но не
обоими вместе. Никакой волновой эффект классического типа не мог бы осуществить та¬
кую кажущуюся «мгновенную связь» между двумя частями волновой функции. Квантовые
волновые функции совершенно отличны от классических волн.
I
Приемник
D
£
О I s 1
>&1 I «г
§' \ *
ь.,
811 '%
Ж
Источник
яветовойгод
Расщепитель луча 	—: - Приемник
—	*	\	е
Рис. 21.8. Мысленный космический эксперимент, иллюстрирующий нелокальную природу волновой
функции при измерении. Волновая функция фотона выходит из источника в виде четко очерченного
волнового пакета малых размеров и после прохождения расщепителя луча делится на две части,
которые год спустя достигают приемников D и Е, удаленных от источника на расстояние светового
года. Однако лишь один из этих приемников может зарегистрировать фотон
Однако скептически настроенный читатель, возможно, все еще не убежден, поскольку
не требуется никакой такой связи в том случае, если фотон просто делает выбор, по какому
пути ему идти, в «расщепителе луча». Истинная правда. Все, что обнаруживает описанная
схема эксперимента, — это корпускулярный аспект фотона. Если бы фотон оставался ло¬

438
Глава 21
кализованным и частицеподобным, то его выбор пути прохождения должен был делаться
в расщепителе луча. (Локализованная частица не может одномоментно распространиться на
расстояние светового года!) Если бы фотоны участвовали только в экспериментах такого
рода, то волновая функция была бы не нужна. Но есть и другие эксперименты, проводимые
с фотоном, вышедшим из расщепителя луча. Откуда наш бедный фотон, выходя из расще¬
пителя, может знать, что мои коллеги не уготовили ему иную судьбу? Предположим, что
вместо попыток обнаружить фотон каждому из них в отдельности, они замыслили следу¬
ющий план. Каждый из них в отдельности должен отражать свою часть волновой функции
в какое-то четвертое место, где эти две отраженные части спустя, например, еще год одно¬
временно попадают на второй расщепитель луча (рис. 21.9). Там каждая пришедшая часть
волнового пакета в отдельности должна расщепиться на две, так что одна половина выходит
из этого расщепителя в одном направлении и попадает на приемник А, а другая — в другом
направлении, попадая на приемник В. (Это относится к каждой из двух частей волново¬
го пакета, выходящих соответственно из тех мест, где находятся двое моих коллег.) Если
длины всех путей прохождения точно подобраны должным образом (например, равны меж¬
ду собой), то мы с удивлением обнаружим, что фотон, вышедший из расщепителя, может
воздействовать лишь на один из приемников, например А, и не действовать на В, посколь¬
ку имеет место конструктивная интерференция между двумя частями волновой функции
в том месте, где находится приемник А, и деструктивная интерференция там, где находится
приемник В.
Рис. 21.9. Интерферометр Маха-Цендера в космическом масштабе. Как может фотон, выходящий из
первого расщепителя луча, знать, что, вместо того, что было на рис. 21.8, зеркала D и Е отражают части
волновой функции на второй расщепитель луча? При этом только приемник А может зарегистрировать
фотон
Здесь не может быть получена никакая чисто корпускулярная картина. Волновая функ¬
ция определенно необходима, чтобы объяснить волновой аспект дуализма волна-частица.
Если бы фотон, покидая первый расщепитель луча, уже делал свой выбор, к какому из моих
коллег направиться, то второй вариант был бы исключен. В таком случае фотон, достигаю¬
щий второго расщепителя, приходил бы лишь из одного направления и мог бы идти любым
путем, достигая либо приемника А, либо приемника В. Здесь отсутствует возможность необ¬
ходимой деструктивной интерференции, препятствующей достижению приемника В. По¬
скольку регистрация всегда производится приемником А, получается, что фотон не может
просто делать свой выбор, покидая первый расщепитель луча. Необходимо, чтобы оба аль¬
тернативных пути, доступных для фотона, ощущались им одновременно при прохождении
от одного расщепителя луча до другого ^21,81
/ '
Е

21.8. Таинственные «квантовые скачки»
439
Разумеется, описанные здесь ситуации астрономического масштаба выглядят весьма
фантастически. Ясно, что на подобной основе нельзя провести никакой реальный кванто¬
вый эксперимент! Однако земной вариант эксперимента такого рода (так называемый ин¬
терферометр Маха-Цендера), где расстояния измерялись метрами, а не световыми годами,
осуществлялся неоднократно, при этом предсказания квантовой механики ни разу не были
опровергнуты. Главная загадка состоит в том, что фотон (или другая квантовая частица) как
будто «знает», какой эксперимент предполагают поставить над ним, задолго до реального
проведения эксперимента. Как может он предвидеть, покидая (первый) расщепитель луча,
должен ли он проявлять себя «как частица» или «как волна»?
Способ, которым действует квантовая теория, состоит не в том, чтобы дать частице
какую-то способность «предвидения», а просто в том, чтобы признать нелокальный це¬
лостный характер волновой функции. В обоих описанных экспериментах мы заставляли
волновую функцию разделиться на две части в первом расщепителе луча, а корпускулярный
аспект волны-частицы проявлялся только в приемнике, когда проводилось окончательное
измерение. Измерение заставляет проявиться целостный характер волновой функции в том
V
смысле, что частица всегда обнаруживается лишь в одном месте, и это ее появление в одном
месте запрещает ее одновременное появление где-либо еще.
21.8.	Таинственные «квантовые скачки»
Но теперь возникает другой вопрос. Как нам узнать, каковы те физические условия,
которые соответствуют «измерению»? Почему после того как мы успешно использовали
описание волновой функции частицы как волны, разделенной на две части, распространяю¬
щиеся в совершенно различных направлениях, мы вдруг должны перейти к описанию ее как
локализованной частицы, коль скоро проводится ее детектирование? Та же забавная картина
квантовой частицы возникает при ее регистрации на экране в нашем двухщелевом экспе¬
рименте, точно так же, как в случае «приемников» (неопределенного типа), применяемых
моими далеко заброшенными коллегами. Из моего предыдущего описания следует, что вол¬
новые аспекты должны сохраняться до тех пор, пока мы не решим «провести измерение»,
чтобы обнаружить частицу, после чего мы внезапно переходим к корпускулярному опи¬
санию. Таким образом, возникает скачкообразное (и нелокальное) изменение состояния —
«квантовый скачок», когда мы переходим от картины волновых функций к «реальности»,
представляемой измерением. Почему? Что можно сказать о процессе детектирования, ко¬
торый требует принять для описания события «измерения» иную (и сильно нелокальную)
математическую процедуру, нежели стандартная процедура описания квантовой эволюции
уравнением Шредингера?
Я постараюсь глубже затронуть эту загадочную ситуацию несколько позже, в гла¬
вах 23, 29 и 30. Но даже если мы согласимся принять, хотя бы на уровне формального
математического описания, эту курьезную процедуру со «скачками», остается вопрос: что
это говорит нам о «реальности» волновой функции? Этот «скачок» квантового состояния —
процесс, который, по-видимому, не укладывается в рамки какой-либо непрерывной эволю¬
ции, согласующейся с уравнением Шредингера, — приводил очень многих физиков в со¬
мнение относительно того, может ли эволюция вектора состояния всерьез рассматриваться
в качестве адекватного описания физической реальности. Сам Шредингер испытывал чув¬
ство неудовлетворенности в связи с «квантовыми скачками» и однажды заметил в разговоре
с Нильсом Бором^21
Если мы собираемся сохранить эти проклятые квантовые скачки, то я вообще
сожалею, что имел дело с квантовой теорией!
Давайте пока примем, хотя бы в качестве математической модели квантового мира, это
курьезное описание, согласно которому квантовое состояние эволюционирует какое-то время

440
Глава 21
в виде волновой функции, обычно «размазанной» по всему пространству (но с возможно¬
стью фокусировки в более ограниченной области), а затем, когда проводится измерение, это
состояние превращается в нечто локализованное и вполне определенное. Эта мгновенная ло¬
кализация не зависит от того, в какой мере могла быть «размазана» волновая функция перед
измерением. После этого состояние снова эволюционирует как волна, описываемая уравне¬
нием Шредингера, исходя из указанной определенной локализованной конфигурации, при
этом обычно она снова размывается вплоть до следующего измерения. Из рассмотренных
экспериментальных ситуаций (и «мысленных экспериментов») может возникнуть впечатле¬
ние, что корпускулярные аспекты волны-частицы проявляются при измерении, а волновые
аспекты — в промежутках между измерениями.
Это не так уж далеко от той истины, которую сообщает нам квантовая механика, но есть
две особенности волны-частицы, которые никоим образом не интерпретируются столь про¬
сто. Хотя некоторые физики действительно придерживаются того взгляда, что все измерения
представляют собой в конечном счете измерение положения ^21Л01, я считаю такой взгляд
чрезмерно узким. Действительно, та форма, в которой обычно представляется квантовый
формализм, определенно не требует, чтобы любые измерения были непременно измерения¬
ми положения. Например, измерение импульса частицы (или, скажем, ее момента импульса
относительно некоторой оси) можно провести с тем же успехом, что и измерение положе¬
ния. Я займусь обсуждением связи между измерениями положения и импульса в §21.11,
однако общий вопрос о том, как квантовый формализм трактует измерения, будет отложен
до следующей главы. Математическое описание физического измерения квантовой системы
окажется чем-то совершенно отличным от описания (шредингеровской) квантовой эволю¬
ции. Спорные вопросы, связанные с этим курьезным фактом, будут обсуждены позднее,
наиболее полно в главе 29.
21.9.	Распределение вероятностей в волновой функции
Обратимся к более конкретному вопросу о том, что должна сообщить нам волновая
функция ф относительно положения частицы. Согласно правилам квантовой теории, квад¬
рат модуля этой функции \ф\2{~ фф\ см. § 10.1) должен интерпретироваться как распре¬
деление вероятностей, определяющее возможность обнаружить частицу в том или ином
из возможных мест ее пребывания при измерении координат. Там, где абсолютная величина
волновой функции максимальна, обнаружить частицу всего вероятнее. Там, где она равна
нулю, частица не будет обнаружена. Полная вероятность найти частицу где-нибудь в про¬
странстве должна быть равна 1, следовательно, интеграл от l^]2 по всему пространству^21*11^
\\ф\\ — / \ф(х)\2 dx1 A dx2 A dx3
равен 1:
ф — 1.
Если выполнено это условие, мы говорим, что волновая функция ф нормирована.
Требование нормировки неприятно тем, что оно исключает волновые функции «им¬
пульсного состояния» ф = егГ''к/н, с которых мы начинали, поскольку \ф\2 — 1 во всем
бесконечном пространстве, так что указанный интеграл (равный полному объему всего
пространства) расходится. Поэтому мы должны рассматривать импульсные состояния как
неосуществимую идеализацию. С другой стороны, можно несколько облегчить жизнь им¬
пульсным состояниям, если занять в отношении волновых функций более мягкую позицию.
Можно продолжать называть ф «волновой функцией» даже если она не удовлетворяет этому

21.9. Распределение вероятностей в волновой функции
441
условию нормировки; если же это условие выполняется, мы будем называть ее нормирован¬
ной волновой функцией.
Волновая функция будет нормируемой, если сходится интеграл, определяющий вели¬
чину ||^||. В этом случае можно разделить ф на квадратный корень из ||^|| и получить
нормированную волновую функцию ф\\ф\\~1/2. Только нормируемые волновые функции
имеют шанс быть физически реализованными. Все остальные (такие как импульсные состо¬
яния) представляют собой лишь физическую идеализацию. Комплексным векторным про¬
странством волновых функций (не обязательно нормированных) служит наше пространство
состояний W. По причине, которая вскоре станет ясной, я допускаю также, что некоторые
из наших волновых функций в действительности являются гиперфункциями (§ 9.7).
Что касается физической интерпретации (с учетом нашей смягченной позиции), то мы
считаем, что функция ф, умноженная на некоторое постоянное комплексное число, отличное
от нуля, представляет ту же самую физическую ситуацию, что и до умножения. Во всяком
случае квантовая теория всегда считала физически эквивалентными величины ф и егвф,
где в — некоторая вещественная постоянная. Другими словами, умножение волновой функ¬
ции на произвольный фазовый множитель не вносит изменений в физическое состояние.
(Ясно, что это не влияет на величину \ф(х)\2.) Разумно пойти немного дальше и разре¬
шить умножение на любую отличную от нуля комплексную постоянную к, считая при этом
полученную волновую функцию эквивалентной прежней:
ф = кф.
(Очевидно, что уравнение Шредингера при такой замене также не меняется.) Признание
такой эквивалентности означает переход от комплексного векторного пространства W к со¬
ответствующему проективному пространству PW идеализированных «физических состоя¬
ний». (Относительно понятия проективного пространства см. § 15.6. f21*12]) Умножение на
/,	-	       П/.12
произвольную постоянную ф \-+ кф, разумеется, не сохраняет \ф\ , поэтому мы должны пе¬
реопределить плотность вероятности нахождения частицы таким образом, чтобы она была
применима и тогда, когда функция ф не нормирована. Это мы сделаем, введя измененное
правило, согласно которому плотность вероятности определяется величиной \ф(х)\2, делен¬
ной на интеграл от \ф(х)\2 по всему пространству:
!v(;r)|2
ф
Для некоторых, например импульсных, состояний jj^|[ расходится, так что на этом пути мы
не получим разумного распределения вероятностей (плотность вероятности будет всюду
равна нулю, что естественно для одной частицы в бесконечной Вселенной).
В соответствии с такой интерпретацией вероятности волновую функцию иногда называ¬
ют «волной вероятности». Я думаю, однако, что это крайне неудачное название. Во-первых,
сама функция ф(х) является комплексной и потому не может быть вероятностью. Кроме то¬
го, фаза функции ф (с точностью до общего постоянного множителя) является существенной
составной частью шредингеровской эволюции. Даже считать «волной вероятности» \ф(х)\2
(или \ф(х)\2/11^)1) не кажется мне достаточно разумным. Напомним, что в случае импульсно¬
го состояния модуль \ф\ функции ф сохраняет постоянную величину во всем пространстве.
При этом |^| не дает нам никакой информации даже о направлении движения волны! Только
фаза придает этой волне ее «волнообразный» характер.
Вдобавок вероятности никогда не бывают отрицательными, а тем более комплексными.
Если бы волновая функция была волной вероятности, то никогда не возникало бы пога¬
шение из-за деструктивной интерференции. Такое погашение является характерной чертой
квантовой механики, столь живо проявляющейся (рис. 21.4 г) в двухщелевом эксперименте!

442
Глава 21
Здесь уместно несколько расширить рамки нашего изложения и провести параллель
с обсуждением электромагнитного поля и связанной с ним калибровочной связности V
в § 19.4. Если наша волновая функция описывает заряженную частицу, то можно принять,
что калибровочные преобразования вида ф ь-> ег0ф, где в (= 0(х)) есть произвольная ве¬
щественная функция координат, определяют необходимую «калибровочную симметрию»,
благодаря которой электромагнетизм может играть роль калибровочной связности. Но не
утверждал ли я только что, что шредингеровская временная эволюция существенно зависит
от знания того, как фаза волновой функции меняется от одного места к другому? При¬
менение калибровочного преобразования ф н» егвф должно позволить нам изменять фазу
волновой функции, как мы того пожелаем! Не вступает ли это в противоречие с тем, что
говорилось о важной физической роли того, как изменяются фазы?
Вовсе нет: если изменения непостоянной фазы разрешены, то лишь при условии,
что они сопровождаются компенсирующим изменением операторов д/дха (т. е. импульса).
Это изменение ( д/дха > д/дха — геАа, где Аа — Va# и е = 1) как раз таково, чтобы оста¬
вить неизменным действие связности расслоения V. «Фазовая информация» здесь остается,
но теперь она перемешивается с определением связности V. Нельзя просто применять одно
лишь преобразование ф н-* ег0ф с произвольно меняющейся величиной в и надеяться оста¬
вить неизменной физическую ситуацию. Детали пространственного изменения величины в
(в связи с V) существенны для динамической эволюции системы, и я берусь утверждать,
что ф есть, несомненно, нечто гораздо большее, чем волна вероятности. Во всяком случае,
если ф описывает незаряженную волну-частицу (е = 0), то ситуация остается в точности
такой, как прежде.
21.10.	Координатные состояния
Мне кажется, ясно, что волновая функция должна быть чем-то гораздо более «реаль¬
ным», нежели просто «волной вероятности». Уравнение Шредингера дает нам точное опи¬
сание эволюции этой величины во времени (как при наличии, так и при отсутствии заряда),
причем эта эволюция решающим образом зависит от того, как меняется фаза от одного места
к другому. Но если задать вопрос «где находится частица?» путем проведения измерения
координат, то мы должны быть готовы к потере этой информации о распределении фазы.
Фактически после измерения мы должны начать все сначала с новой волновой функцией.
Если результат измерения показывает, что «частица находится здесь», то наша новая волно¬
вая функция должна иметь резкий максимум в этом месте («здесь»), а затем быстро спадать
в соответствии со шредингеровским законом эволюции. Если бы наше измерение положения
частицы было абсолютно точным, тогда новое состояние должно было иметь в этом месте
«бесконечно высокий максимум», т. е., по существу, описываться дельта-функцией Дирака,
с которой, как с одной из гиперфункций, мы кратко познакомились в §§ 6.6, 9.7.
Посмотрим, как это проявляется в формализме. Для простоты рассмотрим измерение
лишь одной компоненты вектора положения частицы, например, координаты х1. Результа¬
том нашего измерения должно быть состояние с «определенным значением х1», поэтому
в соответствии с тем, что было сказано в отношении импульса, мы потребуем, чтобы волно¬
вая функция ф описывала собственное состояние оператора х1 (т. е. оператора умножения
на хг), а собственным значением было то значение X1 координаты х1, которое было полу¬
чено при измерении. Для того чтобы действие оператора х1
ф ь-» х1ф
давало определенное (вещественное) значение X1 координаты х1, волновая функция должна
удовлетворять уравнению на собственные значения

21.11. Описание в импульсном пространстве
443
(напомним, что х1 есть линейный оператор, а X1 — число). Это условие выполняется при
ф = 5(хг -X1),
где 6(х) — «дельта-функция» Дирака, которая была определена (в качестве гиперфункции)
в §9.7. Поскольку она обладает свойством* х5(х) — 0, откуда (х1 — Х1)5(х1 — X1) = О,
ъе. x1S(x1 — X1) = Х15(х1 — X1), что и требовалось. Эта «волновая функция» не является
функцией в обычном смысле, это обобщенная функция (гиперфункция, или распределение),
как упомянуто выше, она имеет бесконечный пик при собственном значении х1 = X1.
Такое измерение ничего не говорит об остальных пространственных координатах, так
что волновая функция может зависеть от этих координат произвольным образом; это поз¬
воляет умножить дельта-функцию на произвольную функцию от оставшихся координат х2
и ж3, так что для общего вида собственного состояния оператора х1 мы получаем
ф = ф(х2, х3)5(х1 ~ X1).
Можно пойти дальше и задаться вопросом, каково то состояние, которое является соб¬
ственным состоянием одновременно всех трех пространственных координат. (Это закон¬
ное требование, поскольку все операторы ОС «, ОС % ОС 3 коммутируют между собой. Квантово¬
механические наблюдаемые обладают общим свойством: если у нас имеется некоторый на¬
бор наблюдаемых и все они коммутируют между собой, то существует общее собственное
состояние (или состояния) для них всех одновременно; см. §22.13.^21Л31) Ответ таков: для
результата (тройного) измерения пространственных координат {собственного значения) X =
= (X1, X2, X3) должно выполняться требование (с точностью до общего масштабного
множителя)
1 ф = ^(а:1 - Х1)5(х2-	Х2)6(х3 - X3) = <5(х - X);
последняя строка определяется предыдущей!2114!. Так выглядит координатное состояние.
Такие «координатные состояния» представляют собой идеализированные волновые
функции, имеющие характер, противоположный характеру импульсных состояний. В то вре¬
мя как импульсные состояния размазаны по бесконечному объему, координатные состояния
сконцентрированы в бесконечно малом объеме. И те и другие не нормируемы (неприятное
свойство волновой функции ф = <5(х — X) состоит в том, что дельта-функцию нельзя возве¬
сти в квадрат; см. § 9.7). Я закончу эту главу, показав, что между координатой и импульсом
существует дуализм, проливающий свет на эту особенность.
21,11.	Описание в импульсном пространстве
До сих пор я представлял квантовые состояния исключительно в виде функций коор¬
динат (волновых функций). Это означает в конечном счете, что каждое состояние — эле¬
мент пространства W — рассматривается как линейная комбинация собственных состояний
оператора координат х, т. е. координатных состояний (состояний <5(х — X)). Представле¬
ние волновой функции ф в виде функции от координат означает, таким образом, что она
рассматривается как линейная комбинация таких дельта-функций. Это реализуется с по¬
мощью формулы ^(х) — / Ф(Х)6(у: ~ X)d3X, представляющей волновую функцию как
непрерывную комбинацию дельта-функций (где d3X — dXl A dX2 A dX3). В этой формуле
«коэффициентами» в линейной комбинации служат комплексные числа ф(Х).
Существует, однако, много других способов представления квантового состояния ф.
Можно, например, представить его в виде линейной комбинации импульсных состоя-
Проверьте это исходя из определения гиперфункции в § 9.7.

444
Глава 21
ний егРос/й. Теперь «коэффициентами» будут различные комплексные числа, в качестве ко¬
торых мы возьмем величины ф(Р), умноженные на (27г)-3/2, так что мы получаем формулу
гр(х) = (2тг)-3/2 f ф(Р)е1Р'х/л<13Р.
Е3
(Причина, по которой вводится множитель (27г)-3/2, будет вскоре объяснена.) Эта формула
представляет ^(х) в виде преобразования Фурье от некоторой функции ф(Р), как это бы¬
ло сделано в § 9.4, с той лишь разницей, что здесь мы имеем трехмерное преобразование
Фурье, т. е. применяем формулу из § 9.4 трижды.
Тем самым подтверждается, что ф (как функция от Р, но можно считать ее функ¬
цией от р) обеспечивает столь же хорошее представление квантовых состояний частицы,
как и исходная функция ^(х). Действительно, имеется весьма точная симметрия между
координатными и импульсными переменными. Теперь мы можем считать импульсные пере¬
менные первичными, а координатные переменные х представить как «дифференцирование
по р», так что получается обратная интерпретация (обратите внимание на изменение знака):
Ха = -iд
дра
(по крайней мере для пространственных переменных ж1, xz, ж3)\ При этом выполняются
перестановочные соотношения, совпадающие с прежними:
Рьха — харь = ih5%.
«Невидимой» функцией на правом краю теперь должна служить функция от импуль¬
са ра9 а не от координаты ха. Теперь импульсные состояния представляются дельта¬
функциями б(р — Р), а координатные состояния — плоскими волнами е-ш-х/л Представ¬
ление импульсных «волновых функций» через собственные состояния координат е-гр’х/я
дается фактически идентичным (обратным) преобразованием Фурье:
ф{р) = (2тг)~3/2 \ ^(Х)е~ф*х/Гг d3X,
которое отличается лишь знаком в показателе экспоненты. (Теперь видна роль множите¬
ля (27г)-3/2: он нужен «для равновесия», чтобы обратное преобразование Фурье выглядело
так же, как исходное.)
Волновые пакеты в импульсном представлении можно описывать с тем же успехом, что
и в координатном . Можно ввести точное понятие «размытия» (или нарушения локализа¬
ции) волнового пакета как в координатном, так и в импульсном представлении. Обозначим
меру размытия соответственно через Ах и Ар. Соотношение неопределенностей Гейзен¬
берга утверждает, что произведение этих величин не может быть меньше величины порядка
постоянной Планка, так что мы имеем[21.15]
ЛрЛх
Покажите, что замена ф на хгф или Шдф/дх1 означает замену ф соответственно на —гНдф/дрх
и р\ф. Покажите, что замена ф(ха) на ф(ха + Са) соответствует замене ф на е~г°ара^ф (где а пробегает
значения 1, 2, 3).
Используя результаты упражнений 21.11, 21.13 и 21.14, покажите, что фурье-преобразованием волнового
4* 4е
/та Используя
2 /„ ^\2
пакета ф = Ае в (х	eiuJX служит ф — (АегиС / В\/2)е (р А	14В	е гСр (для удобства предполагает¬
ся/1 = 1).

21.11. Описание в импульсном пространстве
445
На рис. 21.10 показаны координатные состояния, импульсные состояния и волновые
пакеты в координатном и импульсном представлении. Видно, что в предельном случае чи¬
сто импульсного состояния неточность в определении импульса равна нулю, так что Ар — 0
(состояние описывается дельта-функцией в импульсном пространстве). Из соотношения Гей¬
зенберга следует, что в этом случае величина Ах бесконечна в соответствии с описанной
выше картиной (см. §21.6), так что волновая функция оказывается равномерно размазан¬
ной по всему координатному пространству. В случае координатного состояния имеет место
противоположная ситуация: Ах — 0, положение определяется совершенно точно, а неточ¬
ность Ар в определении импульса становится бесконечной.
лф
х
/*Ч_/
Ф
Р
Ф
х
'ф
р
Рис. 21.10. Слева показан вид волновых функций ф в координатном пространстве, справа — вид соот-
вететвующих функций ф в импульсном пространстве. Верхняя пара рисунков изображает импульсное
состояние, нижняя — координатное состояние. Две пары рисунков между ними изображают волно¬
вые пакеты. Иллюстрируется соотношение неопределенностей Гейзенберга: увеличение неточности
в определении положения сопровождается уменьшением неопределенности значения импульса и нао¬
борот
Интересно, что здесь мы имеем примеры, ясно иллюстрирующие несовместимость
некоммутирующих измерений в квантовой механике (это общее явление, с которым мы
будем часто сталкиваться в дальнейшем). Измерение импульса частицы переводит ее в им¬
пульсное состояние, соответствующее некоторому классическому значению Р9 и всякое по¬
следующее измерение импульса в этом состоянии будет давать тот же результат Р. Однако
если вместо этого в данном состоянии вслед за начальным измерением импульса проводится
последующее измерение положения частицы, то результат оказывается полностью неопреде¬
ленным и любое из полученных значений, скорее всего, будет отличаться от всякого другого.
Такое измерение дает состояние в виде дельта-функции от координат. В импульсном про¬
странстве это состояние представляет плоскую волну, однородно распределенную по всем
возможным значениям импульса. Последующее измерение импульса тогда должно давать
полностью неопределенный результат. Таким образом, сам акт промежуточного измерения
положения полностью разрушает чистоту исходного импульсного состояния.
Следует также отметить, что в соответствии с теорией относительности (§ 18.7) суще¬
ствует аналогичное соотношение неопределенностей
между энергией и време-

446
Глава 21
нем:
■ >У
АЕ At > \h.
Обычно считается, что оно имеет несколько иной физический статус, нежели более привыч¬
ное соотношение неопределенностей для импульсов и координат, поскольку время в стан¬
дартной квантовой механике обычно трактуется просто как внешний параметр, а не как ди¬
намическая переменная. Обычная интерпретация неопределенности энергия-время состоит
в том, что если энергия квантовой системы определяется в результате некоторого измерения,
проводимого за время At, то неопределенность результата измерения энергии АЕ должна
удовлетворять приведенному соотношению.
Это имеет непосредственное отношение, например, к нестабильным атомным ядрам.
Тот факт, что такое ядро (например, ядро урана) нестабильно, означает, что существует
ограниченный интервал времени (а именно время жизни частицы), в течение которого мож¬
но произвести определение энергии. В соответствии с этим соотношение Гейзенберга дает
нам фундаментальную неопределенность энергии нестабильной частицы или ядра, которая
связана обратной зависимостью с их временем жизни. Вследствие эйнштейновского соот¬
ношения Е — тс2 (см. § 18.7) отсюда следует фундаментальная неопределенность массы
частиц. Например, время жизни ядра урана 238 U составляет приблизительно 109 лет, так
что в этом случае неопределенность энергии будет порядка 10 ~51 Дж и соответствующая
неопределенность массы будет чрезвычайно малой — порядка 10 ~68 кг. (Волновая функция
нестабильной частицы отличается от волновой функции стационарного состояния е~гЕь/п
с некоторым определенным вещественным^21 *16^ значением энергии Е и содержит экспо¬
ненциально затухающий множитель. Поскольку она не описывает собственное состояние
энергии, при измерении энергии получается разброс значений, определяющий неопреде¬
ленность энергии.) Гейзенберговское соотношение неопределенностей энергия-время будет
играть особую роль в § 30.11 в связи с особым подходом к загадке квантовых измерений!
Примечания
§21.1.
21.1. Это пример так называемого обыкновенного дифференциального уравнения (ОДУ), по¬
скольку уравнение содержит лишь обыкновенные дифференциальные операторы, такие
как d/dx, d/dy и т. п., и их степени, например, d3/dx3. Дифференциальное уравнение в част¬
ных производных (УЧП) содержит операторы частных производных: д/дх, д2/дх2, д2/дхду
и т.п., примером могут служить уравнения Максвелла или Эйнштейна из главы 19.
§21.2.
21.2. Однако ради согласованности изложения (см. также §21.3) я придерживаюсь обозначений,
принятых в теории относительности (§ 18.7), так что пространственные компоненты импуль¬
сов в ра имеют обратный знак по сравнению с обычными компонентами импульса (которые
представляют собой пространственные компоненты ра, умноженные на с“2). Такой выбор
совместим с моими замечаниями в § 20.2, поскольку теперь я использую координату х (а не q,
как в общем формализме Лагранжа или Гамильтона).
21.3. Независимость от времени позволяет интерпретировать 7i как сохраняющуюся полную энер¬
гию. Читателя может смутить то обстоятельство, что допускаемая зависимость от простран¬
ственных координат в силу фундаментального принципа релятивистской инвариантности
•	'	ч
означает также возможную зависимость от времени (см. также примечание 20.3). Однако
на фундаментальном уровне естественным будет требование независимости как от времени,
так и от пространственных координат.
21.4. См. [852].

21.11. Описание в импульсном пространстве
447
§21.4.
21.5. Термин «черное» означает здесь полное (по возможности) поглощение излучения окружаю¬
щим его телом. В ранних экспериментах использовалась (почти) сферическая темная полость,
содержащая излучение, с очень узким отверстием, соединяющим внутренний объем с внеш¬
ним миром.
21.6. При описании этого эксперимента я идеализировал ситуацию, опустив все практические
трудности, чтобы донести основную идею.
§21.7.
21.7. В точных экспериментах нецелесообразно применять реальные зеркала с металлическим
напылением, а следует использовать эффекты интерференции между волнами, отражаемыми
от двух сторон тонкой прозрачной пластины.
21.8. При описании квантовой механики в теории де Бройля-Бома [87] одновременно сохраняют¬
ся, по существу, как волновой, так и корпускулярный аспекты. Здесь частица в расщепителе
луча действительно делает выбор, но волна продолжает распространяться, используя одно¬
временно оба пути. При достижении второго расщепителя именно волна определяет, что
частица должна достигнуть приемника А, запрещая ей попасть в приемник В. Я постара¬
юсь представить эту интересную, но «нестандартную» (и по-прежнему нелокальную) точку
зрения в §§29.2, 29.9.
§21Л
21.9. По воспоминаниям Гейзенберга ( [377], стр. 73).
21.10. См. [310, 70].
§21.9.
21.11. Многие авторы определяют «норму» как квадратный корень из того, что я понимаю здесь
под \\ф\\, так что их \\ф\\2 — это моя величина \\ф\\.
21.12. Разные авторы придали квантово-механическому формализму изящную форму на основе
проективной геометрии. См., в частности, [108, 407, 38].
§21.10.
• V
21.13. Это свойство коммутирующих наблюдаемых обсуждается в любой книге по квантовой меха¬
нике, см., например, [716],
21.14. Дельта-функции можно перемножать, если они относятся к разным переменным. Описание
свойств дельта-функций см. в [26].
§21.11.
21.15. См. [716, 349].
21.18.	В физике элементарных частиц часто используют обычную временную зависимость e~lEt/h^
но с комплексным значением величины Е, вещественная часть которой дает среднее значение
энергии, а мнимая — обратное время полураспада, умноженное на — -/Uog2. (См., напри¬
мер, [173].)*
Попробуйте объяснить, откуда берется множитель — -ft log 2, (Временем полураспада называют время,
2
1 ч
за которое частица распадается с вероятностью —

Глава 22
Квантовая алгебра, геометрия и спин
22.1.	Квантовые процедуры U и R
Из-за невозможности наглядной интерпретации квантовой механики (или, скорее, са¬
мой Природы на квантово-механическом уровне) многие исследователи отчаялись постро¬
ить сколько-нибудь правдоподобную картину квантовых явлений. Пока помимо изящной
алгебраической структуры существует лишь красивая геометрия, связанная с квантовой
механикой, и для успешного описания квантово-механических эффектов приходится, к со¬
жалению, опираться на некоторый формализм, не допускающий наглядного истолкования.
Хотя мы видели, что даже одиночная бесструктурная «точечная частица» оказывается за¬
гадочным размазанным объектом волнового характера, такому объекту можно приписать
изящную математическую структуру, в которой начинают проявляться магические свойства
комплексных чисел.
Такая картина позволяет нам перейти к квантовому описанию одиночной точечной ча¬
стицы. Поняв, на что она похожа, мы можем, казалось бы, быть уверены в том, что сумеем
понять и более сложные системы, состоящие из многих различных частиц. К сожалению,
это слишком поспешное заключение, и, чтобы создать исчерпывающую квантовую картину
мира, нам необходим более широкий взгляд. В главе 23 мы увидим, что при рассмотре¬
нии системы из нескольких частиц картина становится гораздо более запутанной. Вместо
совокупности отдельных частиц, каждая из которых характеризуется своим «вектором со¬
стояния», мы обнаружим, что для описания квантовой системы в целом требуется единый
вектор состояния.
Оказывается, однако, что даже отдельные «точечные частицы» имеют более сложную
структуру по сравнению с тем описанием, которое приводилось до сих пор. Дело в том, что
частицы часто обладают так называемым спином, а это приводит к дополнительному услож¬
нению описания. К счастью, как будет показано в этой главе, спин сам по себе представляет
явление, математическое описание которого обладает особым богатством и изяществом,
поскольку в нем проявляются другие стороны геометрии и магии комплексных чисел.
Взглянем на описание в предыдущей главе, где нам пришлось рассматривать (нере¬
лятивистскую) квантовую частицу как объект, описываемый так называемым вектором
состояния (или волновой функцией), эволюция которого точно описывается уравнением
Шредингера, пока над этой системой не производится некоторое измерение. Как мы увидим
в главе 23, то же относится и к векторам состояния, описывающим целую сложную си¬
стему. Математическое описание самого измерения в корне отличается от шредингеровской
эволюции. Намеки на это встречались в §§21.4, 21.7, 21.8. В §§21.10, 21.11 мы рассмат¬
ривали измерение координаты, в процессе которого состояние частицы меняется скачком
и превращается в другое состояние, локализованное в некотором месте, т. е. в состояние,
которое является собственным вектором оператора координаты х (таким собственным век-
• %
тором служит дельта-функция от координаты). Мы рассматривали также результаты изме¬
рения импульса (в §§21.5, 21.6, 21.11), когда состояние частицы скачком превращалось
в собственное состояние оператора импульса р, при этом состояние частицы оказывалось
распределенным в виде волны по некоторой области (в принципе по всему пространству).

22.1. Квантовые процедуры U и R
449
В общем случае измерение соответствует оператору Q некоторого вида (обычно это эрмитов
оператор, см. § 22.5), и результатом воздействия измерения на состояние оказывается скач¬
кообразное превращение этого состояния в некоторое собственное состояние оператора Q.
В какое именно собственное состояние оператора Q приведет такой скачок? Согласно кван¬
товой механике, это полностью дело случая, однако существуют четкие правила вычисления
соответствующих вероятностей (см. § 22.5).
Скачок квантового состояния ^22Л] в одно из собственных состояний оператора Q пред¬
ставляет собой процесс, именуемый редукцией вектора состояния или коллапсом волновой
функции. Это одна из наиболее загадочных черт квантовой теории, и в этой книге мы не
раз будем возвращаться к этому понятию. Мне представляется, что большинство физиков,
занимающихся квантовой теорией, не считают редукцию вектора состояния реальным явле¬
нием физического мира, но это лишь отражает тот факт, что мы не считаем, будто вектор
состояния действительно описывает физическую реальность на квантовом уровне. К этому
спорному вопросу мы вернемся подробнее в главе 29. Тем не менее безотносительно к то¬
му, какой позиции мы придерживаемся относительно физической реальности этого явления,
при практическом применении квантовой механики мы должны считать, что состояние дей¬
ствительно совершает подобный скачок всякий раз, когда производится измерение. Сразу
после измерения опять восстанавливается шредингеровская эволюция, пока над системой
не производится следующее измерение, и так далее.
Я буду обозначать шредингеровскую эволюцию буквой U, а редукцию состояния —
буквой R. Чередование этих двух совершенно различных процессов должно проявлять¬
ся в весьма необычном поведении Вселенной! (См. рис. 22.1). Можно предположить, что
в действительности это есть приближенное описание чего-то пока не известного. Может
быть, существует некоторое более общее математическое уравнение или некоторый прин¬
цип эволюции когерентного типа, по отношению к которому U и R являются предельными
случаями? Мое собственное мнение состоит в том, что подобная модификация квантовой
теории вполне возможна, и она может составить часть новой физики XXI века; в главе 30 бу¬
дут выдвинуты некоторые частные предположения, касающиеся этой возможности. Однако
большинство физиков, по-видимому, не считает, что этот путь окажется плодотворным.
Время
Рис. 22.1. Согласно общепринятой квантовой механике, временная эволюция состояния ф физической
системы состоит в чередовании двух совершенно различных процессов — унитарной (шредингеров-
ской) эволюции U (непрерывной и детерминированной) и редукции состояния R (скачкообразной
и вероятностной)
Причина, по которой не ожидают изменения основного каркаса квантовой механики,
связана, помимо несомненного изящества U-формализма, со впечатляюще высокой степенью
согласия между квантовой теорией и экспериментальными фактами. Не известно ничего, что
говорило бы против квантовой теории (в ее нынешней гибридной форме), в то же время
многие разнообразные результаты подтверждают ее с высокой точностью. В соответствии
с этим большинство физиков склонно принять философскую точку зрения (или, скорее,
одну из альтернативных точек зрения, представленных в §29.1), согласно которой лучше

450
Глава 22
примириться с явным противоречием между процедурами U и R, нежели пытаться изме¬
нить современный квантовый формализм сколько-нибудь существенным образом. Одна из
задач этой и следующей глав состоит в том, чтобы начать изложение этого формализма, не
отклоняясь от стандартной квантовой теории. К проблеме U/R я вернусь позже, в частно¬
сти, в §§ 29.1, 29.2,29.7-29.9 и §§ 30.10-30.13, где более подробно изложу мой собственный
взгляд на нее.
Следует прямо сказать, что наиболее распространенная позиция в «стандартной» кван¬
товой механике состоит в том, что процесс U рассматривается как «основополагающая
истина», а процесс R — всего лишь как некоторое приближение, иллюзия или удобное
соглашение, и такая точка зрения нашла отражение в обширной литературе t22-2!. Даже те
(включая меня), кто придерживается мнения о необходимости некоторого изменения, на
какой-то стадии квантового формализма вынуждены признать, что нынешняя схема может
служить по меньшей мере прекрасным приближением, так что для начала необходимо по¬
нять ее в полной мере, прежде чем пытаться выйти за ее пределы. Поэтому мы должны
постараться глубже понять, как действует процедура U и как она может столь прекрасно
сочетаться с процедурой R, будучи в то же время столь непохожей на нее!
Следует объяснить, почему используется буква U. Она означает унитарную эволюцию.
Нам придется понять, в каком смысле уравнение Шредингера действительно «унитарно»
(см. § 13.9), и мы перейдем к этому вскоре, в §22.4. Существуют и другие (эквивалентные)
способы описания этой «унитарной эволюции», чаще всего применяется так называемое
представление Гейзенберга, которое также будет рассмотрено в § 22.4. Здесь же наиболее
удобным оказывается описание на основе уравнения Шредингера.
22.2.	Линейность U и возникающие в связи с этим проблемы для R
Прежде чем рассматривать в полном объеме проблему унитарности, остановимся на
более простом вопросе о линейности процедуры U. Мы увидим, что это свойство проце¬
дуры U само по себе оказывается плохо совместимым с R. Обратимся снова к уравнению
Шредингера гКдф/дЬ — Нф. Гамильтониан TL будем считать известным (он определяется
природой описываемых им частиц, силами, действующими между ними, а также внешними
консервативными (т. е. сохраняющими энергию) силами, которые могут оказывать влияние
на систему). Существуют определенные следствия, вытекающие непосредственно из общей
формы уравнения и совершенно не зависящие от детальной природы гамильтониана.
Прежде всего отметим, что это детерминированное уравнение (эволюция во времени
полностью определена, коль скоро известно состояние в какой-то один момент времени).
Это может оказаться неожиданным для тех, кто слыхал о «квантовой неопределенности»
и о том, что квантовые системы ведут себя неопределенным образом. Потеря определен¬
ности происходит исключительно в процессе R. Ее нельзя обнаружить во временной (U-)
эволюции квантового состояния, описываемой уравнением Шредингера. Другое очевидное
свойство уравнения Шредингера состоит в том, что это есть комплексное уравнение из-за
явного участия множителя г в его левой части (кроме того, во многих случаях г появляется
и в гамильтониане).
Наконец, видно, что уравнение Шредингера действительно линейно в том смысле, что
если функции ф иф являются решениями уравнений
ih^ = Hip, ih~ = Нф
at	at
(с одним и тем же гамильтонианом Н), то решением будет и любая линейная комбина¬
ция гиф 4- гф, где w и z — комплексные постоянные. Действительно, умножая первое из этих

22.2. Линейность U и возникающие в связи с этим проблемы для R
451
уравнений на w, а второе на г и складывая, получаем (см. § 6.5)
ih~{wф + гф) — Н(п)ф + гф).
Видно, что шредингеровская эволюция сохраняет структуру пространства состояний W
(обычно бесконечномерного) как комплексного векторного пространства.
Гамильтониан Н определяет бесконечно малое ли¬
нейное преобразование пространства W, описывающее
изменение состояния в результате его эволюции за бес¬
конечно малое время. Такое действие гамильтониана
описывается некоторым векторным полем на W (см.
рис. 22.2). За конечное время состояния будут менять¬
ся в соответствии с некоторым конечным линейным
преобразованием, которое получается в результате так
называемого «потенцирования» (помещения под знак
экспоненты) бесконечно малого действия гамильтони¬
ана. Это очень похоже на «потенцирование», с кото¬
рым мы уже сталкивались в § 14.6, описывая процесс,
посредством которого элемент группы Ли получается
как экспонента от элемента соответствующей алгебры
Ли. Однако проводить потенцирование эволюции, про-
изводимои гамильтонианом, может оказаться гораздо
более трудным делом. (Другие трудности возникают
из-за бесконечномерной природы пространства W.)
Однако, независимо от трудностей, существенно
здесь то, что преобразование пространства квантовых
состояний W всегда будет линейным и в случае лю¬
бого конечного времени Т действия гамильтониана.
Это равносильно следующему утверждению (я буду
пользоваться символом для обозначения эволюции
состояния за некоторый отрезок времени Т): если
Рис. 22.2. Поток гамильтониана {77, }
(векторное поле) определяет беско¬
нечно малое линейное преобразование
пространства состояний W, описываю¬
щее изменение состояния за бесконеч¬
но малое время. Чтобы получить (уни¬
тарное) изменение за конечное время,
мы должны «потенцировать» это бес-
конечно малое действие гамильтониа¬
на
ф ^ ф' и ф ^ ф',
то
узф + гф	п)фf	4-	гф'
Здесь ф и ф — два произвольно выбранных состояния (волновые функции), w яг — произ¬
вольные комплексные постоянные*
Этот факт приводит к некоторым любопытным следствиям, если предположить, что U
описывает всю историю системы, а процесс измерения — это лишь удобный способ опи¬
сания ситуации, в которой квантовое состояние оказывается невообразимо сложным из-за
наличия в системе огромного множества «перепутанных» частиц и измерительной установ¬
ки. (Квантово-механическое понятие «перепутывания» будет рассмотрено более подробно
в главе 23. Мы увидим, что квантовые состояния являют собой объекты, «целостные» в го¬
раздо большей степени, чем было представлено в § 21.7: различные части системы не опи¬
сываются отдельными квантовыми состояниями, а являются частями некоторого единого
перепутанного «целого». Это, однако, не сказывается на проводимом здесь обсуждении.)
Объясните, почему действие любой шредингеровской эволюции линейно, несмотря на тот факт, что
гамильтониан 77 может быть сильно нелинейной функцией от импульсов р и координат х.

452
Глава 22
При таком «удобном» взгляде на процедуру R можно считать R некоторым приближением
к «истинной» эволюции, описываемой процедурой U. Однако такая точка зрения приводит
к серьезным парадоксам.
Напомним, например, мысленный эксперимент из §21.7, в котором двое моих коллег
в космическом пространстве имели отдельные приемники, и попробуем представить от¬
клик каждого приемника как результат шредингеровской эволюции, начинающейся с его
взаимодействия с принятой им частью волнового пакета. До регистрации приемником кван¬
товое состояние представляет собой сумму двух отдельных частей волнового пакета, одна из
которых достигает одного приемника, а другая — другого. Отклик каждого приемника в хо¬
де последующей шредингеровской эволюции в силу ее линейности должен сосуществовать
в виде суперпозиции с откликом другого. Шредингеровская эволюция приводит к сложению:
отклик одного приемника плюс отклик другого приемника («плюс» соответствует квантовой
суперпозиции откликов двух приемников), а не к выбору: отклик одного приемника или
отклик другого приемника (это «или» соответствует тому, что всегда происходит на практи¬
ке). Поэтому мне представляется бесперспективным считать, что U описывает всю историю
системы (и «стандартная» квантовая механика в «копенгагенской интерпретации» Нильса
Бора определенно не пытается делать это, рассматривая сами приемники как «классические
объекты»).
Насколько я могу судить, единственный способ принять, что процедура U относит¬
ся ко всем процессам, включая измерение, состоит в том, чтобы перейти к точке зрения
«множественных миров» (см. §29.1), при которой отклики двух детекторов действительно
сосуществуют, но относятся «к разным мирам»t22<33, Но даже в этом случае U не может опи¬
сывать «всю историю», поскольку нам нужна теория, которая объясняла бы, почему должны
восприниматься лишь отклики отдельных приемников и не восприниматься суперпозиции
откликов с отсутствием откликов (мы вернемся к этому вопросу в §§29.1, 29.8). Здесь я дол¬
жен заявить, что не считаю «множественность миров» тем путем, которым следует идти,
и упомянул об этом, чтобы показать, к чему мы придем, предположив, что процедура U
действует «на всех уровнях».
К этой проблеме мы вернемся позднее, в главах 29 и 30, где будет обсужден вопрос,
следует ли рассматривать процедуры U и R как приближения к некоторой более общей
будущей теории. Пока же будем следовать общепринятому формализму. Если потребуется
какая-то улучшенная теория, она в любом случае должна с весьма высокой точностью
согласоваться с предписаниями нынешней теории. Любому читателю, нацеленному на поиск
новой теории (а я уверен, что такие найдутся!), можно посоветовать пользоваться терминами
стандартной теории.
22.3.	Унитарная структура, гильбертово пространство и обозначения
Дирака
Я пока не касался в должной мере «унитарного» аспекта шредингеровской эволюции.
Он связан со свойством «нормировки» волновых функций, рассмотренным в предыдущей
главе. Напомню, что «нормой» волновой функции одной (бесспиновой) частицы называется
величина ||^||, определяемая как интеграл от \ф(х)\2 по всему пространству. Условие норми¬
ровки, налагаемое на функцию ф9 состоит в том, что Ц^Ц = 1 (при выполнении этого усло¬
вия \ф(х)\2 есть плотность вероятности того, что при измерении координаты частица будет
найдена в точке х). В более общей квантово-механической ситуации, когда имеется много
взаимодействующих частиц, обладающих спином (или, возможно, более сложных объектов,
таких, например, как струны), всегда можно ввести некоторое соответствующее понятие
нормы ||^||, которая должна быть положительным вещественным числом\-22Л^ для любого
правильно выбранного квантового состояния ф. Хотя такая норма относится в основном к

22.3. УНИТАРНАЯ СТРУКТУРА, ГИЛЬБЕРТОВО ПРОСТРАНСТВО И ОБОЗНАЧЕНИЯ ДИРАКА
453
U-части квантового формализма, она играет важную роль и в R-части, определяя в конечном
счете все возникающие там вероятности.
В математическом отношении можно рассматривать норму как некоторый квадрат дли¬
ны, который обязан быть конечным для любого «приемлемого» вектора, принадлежащего
пространству состояний W. Прилагательное «унитарная», применяемое к временной эво¬
люции, указывает на то, что эта норма сохраняется в ходе эволюции. Вскоре (в §22.4)
мы увидим, что при шредингеровской эволюции дело обстоит именно так.
Прежде всего будет полезно ввести некоторые обозначения и исследовать свойства
нормируемых квантовых состояний. Имеет смысл рассматривать норму как частный случай
эрмитова скалярного произведения (§ 13.9) двух состояний. Для состояний ф и ф в лите¬
ратуре по квантовой механике обычно используется запись (ф\ф), в таком случае норма
функции ф есть частный случай, в котором ф = ф:
ф\\ = (*/#)•
В случае одной (бесспиновой) частицы скалярное произведение имеет вид
(ф\ф) — J ффйх1 A dx2 A dx3,
Е3
что обобщает выражение для Ц^Ц, данное в §21.9. Здесь мы имеем положительно опре¬
деленное эрмитово скалярное произведение двух произвольных нормируемых волновых
функций ф и ф.
Нормируемые волновые функции образуют комплексное векторное пространство Н
(подпространство векторного пространства W), именуемое гильбертовым пространством
Определение гильбертова пространства выглядит так: это есть комплексное векторное про¬
странство, на котором задана операция скалярного произведения { | ), обладающая следую¬
щими алгебраическими свойствами:
{Ф\Ф + х)	=	(Ф\Ф) + (Ф\х)>
(Ф\аф)	=	а(ф\ф),
{ф\ф)	=	(ф\ф),
{ф\ф)	>	0, если	ф	ф О
*
(для случая приведенного выше одномерного интеграла все эти свойства легко проверяют¬
ся)***. Из этих равенств следует также (ф -I- х\Ф) ~ (Ф\Ф) + (xl^) и (аФ\Ф) — &{Ф\Ф)'
Далее, коль скоро известна норма, через нее можно выразить скалярное произведение
поэтому линейные преобразования, сохраняющие норму, должны также сохранять и ска¬
лярное произведение. Кроме того, гильбертово пространство должно обладать некоторыми
весьма важными свойствами непрерывности[22.5]
... Попробуйте объяснить, почему интеграл {ф\ф) сходится, коль скоро сходятся оба интеграла (ф\ф) и (ф\ф).
(Подсказка: воспользуйтесь тем, что интеграл от \ф — \ф\2 по любой конечной области пространства Е3 неотри¬
цателен. Выведите неравенство, связывающее квадрат модуля интеграла от фф с произведением интегралов от фф
и фф. В качестве промежуточного шага найдите условия на комплексные числа а, 6, с, d, при которых неравен¬
ство а + АЬ -f Ас + A A d ^ 0 выполняется при всех А.)
**ЙИ Следуя предыдущему упражнению, покажите, что нормируемые волновые функции действительно обра¬
зуют комплексное векторное пространство.
***30 Проверьте это, обращая внимание на то, какие именно свойства интеграла при этом используются.
Объясните почему.
***** м Покажите, как можно, зная норму, определить (ф\ф). (Подсказка: воспользуйтесь нормами величин ф + ф
и ф + 1ф.)

454
ГЛАВА 22
Вышеприведенный способ записи представляет собой часть очень полезных и широко
используемых обозначений, введенных в квантовую механику великим физиком XX ве¬
ка Полем Дираком. Как часть этой общей схемы, оказываются удобными выражения
типа
И, I Т), I -*>, I <->, |0>, |7), |+), |Х), |DEAD) или |OFF),
которые представляют различные векторы состояния, принадлежащие гильбертову про¬
странству Н; символом, стоящим внутри скобок |...), служит подходящая (и, возможно,
легко запоминаемая) метка, обозначающая данное состояние. Такие векторы иногда на¬
зывают кет-векторами. Для каждого такого кет-вектора существует определенный элемент
дуального пространства Н* (§ 12.3), называемый соответствующим бра-вектором*, который
эрмитово сопряжен данному состоянию (в смысле § 13.9) и обозначается соответственно
как
(Ф1 (Т I, (— I, <~ I, <0|, (71, <+|, (XI (DEAD! или (OFF).
Поскольку бра-векторы дуальны кет-векторам, они образуют скалярное произведение
в смысле § 12.3. Такое скалярное произведение, или «скобки», бра-вектора (ф\ и кет-
вектора |ф) есть как раз написанное выше эрмитово скалярное произведение (ф\ф). Это
согласуется с тем фактом, что комплексное число (ф\ф) комплексно-сопряжено числу (ф\ф).
Два состояния (ф\ и |ф) называются взаимно ортогональными, если (ф\ф) = 0 (или (ф\ф) =
-0).
Действие некоторого линейного оператора L на |ф) записывается как Ь\ф), а скалярное
произведение бра-вектора (ф\ на вектор Ь\ф) — как
(Ф\т.
Это можно рассматривать также как скалярное произведение некоторого бра-вектора (ф\1>
на вектор |ф). Что означает этот бра-векгор (ф\Ы Это есть величина, комплексно-сопря¬
женная некоторому кет-векгору Х*|ф)9 где X* — оператор, сопряженныйf22,6^ оператору X.
Операция «сопряжения», примененная к линейному оператору X, — это есть как раз опера¬
ция эрмитова сопряжения *, рассмотренная в § 13.9 для случая конечного числа измерений.
Комплексно-сопряженным по отношению к комплексному числу (ф\Цф) будет комплексное
число (ф\Ь*\ф).
22.4.	Унитарная эволюция. Представления Шредингера и Гейзенберга
Теперь у нас есть возможность заняться «унитарной» природой шредингеровской эво¬
люции. Мы уже видели (§ 22.3), что эта эволюция имеет линейный характер, поэтому всё,
что нам нужно, — это убедиться, что она сохраняет скалярное произведение (ф\ф) двух
элементов \ф) и |ф) пространства Н. Другими словами, надо показать, что величина {ф\ф)
остается постоянной во времени: й(ф\ф)/<И = 0. (Согласно сказанному выше, сохранение
нормы и сохранение скалярного произведения являются эквивалентными требованиями.)
От нашего квантового гамильтониана Н требуется, чтобы он 1) действовал в гильбертовом
пространстве, 2) был эрмитовым оператором. Это самые минимальные требования, которые
выполняются при любом разумном выборе гамильтониана. Например, эрмитова природа
гамильтониана — это естественное требование, направленное на то, чтобы собственные зна¬
чения, которые определяют возможные значения энергии системы, были вещественными
величинами. Обычно требуют также, чтобы гамильтониан TL был положительно опреде¬
лен, это означает, что (ф\Н\ф) > 0 для всех ненулевых векторов |ф). Отсюда следует: все
Введенные Дираком названия «бра» (bra) для вектора ( | и «кет» (ket) для вектора | ) представляют собой две
половины английского слова bracket (скобки). Названия связаны с тем, что указанные векторы образуют скалярное
произведение, изображением которого служат скобки ( | ) (см. ниже). — Прим. перев.

22.4. Унитарная эволюция. Представления Шредингера и Гейзенберга
455
собственные значения оператора Н (значения энергии) положительны — хотя это и не тре¬
буется для унитарного характера эволюции. Используя правило Лейбница для производной
произведения (см. § 6.5 и свойства, перечисленные выше), легко получить
Отсюда следует, что скалярное произведение действительно сохраняется, т. е. шрединге-
ровская эволюция унитарна*. Подобные рассуждения применимы также и в отношении
других эрмитовых операторов, например, к генераторам пространственных переносов или
поворотов, которые, таким образом, также соответствуют унитарным преобразованиям про¬
странства Н.
Из приведенного уравнения следует, что скорость изменения скалярного произведе¬
ния (ф\ф) равна нулю. Это означает, что (ф\ф) остается неизменным в течение всего времени,
пока векторы \ф) и \ф) в отдельности претерпевают шредингеровскую эволюцию, опреде¬
ляемую одним и тем же гамильтонианом Н. Пусть мы имеем квантовые состояния |ф) и \ф)
в момент времени t — 0 и предоставляем им возможность эволюционировать в соответ¬
ствии с уравнением Шредингера вплоть до более позднего момента времени Т, когда они
превращаются соответственно в \фт) и \фт)'
Это означает, что линейное действие шредингеровской эволюции на гильбертово простран¬
ство Н от t ~ 0 до некоторого определенного момента t = Т является унитарным в том
смысле, что имеется некоторый оператор Ut, осуществляющий указанное преобразование
таким образом, что
\Фт)=иТ\ф), \фт) = ит\ф) и т. д.,
причем оператор Ut является унитарным в смысле, определенном в § 13.9, а именно,
оператор, обратный данному, равен сопряженному оператору:
Символ I означает здесь тождественный оператор на пространстве Н. (См. демонстрацию
этого свойства оператора Ut в § 13.9.)
Как уже упоминалось в § 22.1, существуют и другие способы описания эволюции кван¬
товой системы, наиболее известной альтернативой является представление Гейзенберга.
В этом представлении «состояние» системы считается постоянным во времени, а временную
эволюцию вместо этого претерпевают динамические переменные. У читателя может воз¬
никнуть законный вопрос: как можно считать квантовое состояние «неизменным», когда
в квантовой системе могут происходить реальные физические изменения?! Все правильно,
но переход от представления Шредингера к представлению Гейзенберга в действительности
сводится лишь к переопределению символов.
* Проверьте эти рассуждения более подробно. Понятно ли, почему мы считаем, что правило Лейбница
выполняется для скалярного произведения в гильбертовом пространстве?
(—ih 1Нф\ф) 4- {ф\ - ih 1Нф) =
ihr1 (ф[Н\ф) — гК~1 (ф[Н\ф) — 0.
Iф) ^ |фт) и \ф) ^ |фт)
(мы используем обозначение, введенное в § 22.2). Тогда
(Ф\Ф) = (Фт\Фт).
т.е. UT Щ = Щит = I.

456
Глава 22
Сначала рассмотрим обычное представление Шредингера, которого мы придержива¬
лись до сих пор. В момент времени t — 0 мы имеем некоторое квантовое состояние \ф},
которое затем эволюционирует в соответствии с уравнением Шредингера, содержащим кван¬
товый гамильтониан Н9 так что в некоторый более поздний момент Т будет иметь место
состояние |фт)-
|ф)	|фт) — 11т\ф).
Напомним, что реально оператор Ut действует линейным образом на все гильбертово про¬
странство Н, так что любое другое состояние должно претерпевать соответствующую эво¬
люцию |ф) ^ |фт) = 11т\ф) с тем же оператором Ut, что и состояние |ф). В представлении
Гейзенберга под состоянием в момент времени Т понимается
| ф) н = Up\ф) = Щ\ф).
Ясно, что такое «гейзенберговское состояние» \ф)н не изменяется с течением времени
(просто по определению!). С другой стороны, для того чтобы в результате проводимых
алгебраических процедур получались те же собственные значения (то есть значения из¬
меряемых физических величин), что и в представлении Шредингера, мы потребуем, чтобы
динамические переменные менялись компенсирующим образом. Для этого любой линейный
оператор Q (на пространстве Н) следует заменить его гейзенберговским вариантом
Qh = UГ1Q Ut = Ut*QUt.
Отсюда сразу следует, что гейзенберговский вариант любого собственного значения или
любого скалярного произведения совпадает со шредингеровским вариантом*. Гейзенбергов¬
скую эволюцию претерпевают операторы Q (которые в представлении Шредингера предпо-
лагаются постоянными) и, в частности, динамические переменные. Мы получаем
ihftQa = nQH- ЯяП,
это есть уравнение движения Гейзенберга. (Заметим, что очевидным следствием его является
сохранение энергии, получаемое, если положить Qh — W.)
Читатель вправе спросить: что дают нам такие переобозначения? В некоторых случаях
представление Гейзенберга обладает преимуществами технического характера, однако оно
не может помочь в отношении загадок, связанных с интерпретацией квантовой механики.
Проблема «квантовых скачков» не исчезает, однако перед нами встает выбор: возложить ли
вину за скачки на состояния, считая, что |^)н в результате R-операции претерпевает «ска¬
чок» куда-то еще, либо принять, что совершают «скачки» гейзенберговские динамические
переменные. По моему мнению, трактовка «скачков» в представлении Гейзенберга лишь
запутывает ситуацию, ничего не решая по существу.
В представлении Шредингера мы по крайней мере имеем эволюционирующий вектор
состояния, который дает нам шанс хотя бы мельком увидеть, на что может быть похожа
«квантовая реальность». Представление Гейзенберга, по-видимому, не дает такой возмож¬
ности, поскольку там вектор состояния остается неподвижным, несмотря на происходящие
физические действия. В то же время эволюция динамических переменных не может пред¬
ставлять изменения какой-либо конкретной физической системы, поскольку эти переменные
вообще не описывают конкретные системы, а в отношении их могут лишь отвечать на во¬
просы типа «Каково положение системы?».
Объясните это подробнее.
** ш Попробуйте доказать это.

22.5. Квантовые «наблюдаемые»
457
Причина, по которой существуют два различных представления, в основном историче¬
ская. Гейзенберг первым предложил свою схему в июле 1925 года, а Шредингер выдвинул
свою теорию полгода спустя, в январе 1926 года; эквивалентность этих двух схем была до¬
казана несколько позже. Это было сделано Максом Борном, который дал вероятностную ин¬
терпретацию квадрата модуля \ф\2 шредингеровской волновой функции (§ 21.9) в июне 1926
года. Сам Шредингер пытался придерживаться «классически-волновой» трактовки функ¬
ции ф. Общая операторная трактовка квантовой механики возникла из работы Гейзенберга,
Борна и Паскуаля Иордана и была полностью сформулирована Дираком, который подробно
изложил ее в своей книге «Принципы квантовой механики», впервые опубликованной в 1930
году!22,7! и оказавшей сильное влияние на дальнейшее развитие.
Возможно, конечно, что, когда в квантовую теорию в конечном счете будут внесе¬
ны какие-то изменения, появится повод предпочесть один из формализмов другому, и их
эквивалентность нарушится. В какой-то мере так обстоит дело в квантовой теории поля
(см. главу 26), которая пытается объединить квантовую механику и (специальную) теорию
относительности в единую согласованную схему. Дирак выдвинул некоторые аргументы
о предпочтительности в данном случае представления Гейзенберга [22*81 Оба представле¬
ния, однако, не являются релятивистски-инвариантными, и потому иногда предпочитают
гибридное «представление взаимодействия»^229^.
22,5.	Квантовые «наблюдаемые»
Посмотрим теперь, как квантовый формализм трактует измерение, производимое над
квантовой системой. Как отмечалось в §22.1, примеры измерения координаты и импуль¬
са, приведенные в главе 21, иллюстрируют происходящее в общем случае квантового из¬
мерения. Некоторое «измеримое» качество квантовой системы представляется некоторым
оператором Q, называемым наблюдаемой (величиной), и этот оператор действует на кван¬
товое состояние. Примером наблюдаемых могут служить такие динамические переменные,
как координата и импульс ^22,101. Теория требует, чтобы наблюдаемая Q была представлена
линейным оператором (как в случае операторов координаты и импульса), так чтобы его
действие на пространство Н было линейным преобразованием этого пространства, хотя,
возможно, и сингулярным (§ 13.3). Говорят, что наблюдаемая Q имеет определенное значе¬
ние в состоянии ф9 если ф есть собственное состояние оператора Q, а соответствующее
собственное значение q является тем самым определенным значением ^22Л11 Это та самая
терминология, с которой мы уже сталкивались в §§21.5, 21.10, 21.11 применительно к ко¬
ординате и импульсу.
В стандартной квантовой механике обычно требуется, чтобы все собственные значения
были вещественными величинами. Это можно обеспечить (в предположении нормируемости
собственных векторов), потребовав, чтобы оператор Q был эрмитовым в том смысле, что
он равен сопряженному ему оператору Q *:
Q* = Q.
На мой взгляд, это требование эрмитовости оператора наблюдаемой Q является неоправ¬
данно жестким, поскольку комплексные числа часто используются в классической физике,
примерами могут служить представление небесной сферы сферой Римана (§ 18.5), стан¬
дартное изложение теории гармонического осциллятора (§22.13) и др. С22*12] Существенное
требование, налагаемое на наблюдаемую, состоит в том, что ее собственные векторы, соот¬
ветствующие различным собственным значениям, должны быть ортогональны друг другу.
* flQ Покажите, что любое собственное значение эрмитова оператора Q является вещественным числом.

458
Глава 22
Операторы, обладающие этим свойством, называются нормальными. Нормальный опера¬
тор Q коммутирует с сопряженным ему оператором:
Q*Q = QQ\
Любые два (нормируемые) собственные вектора нормального оператора Q, соответствую-
щие различным собственным значениям, должны быть взаимно ортогональны . Если до¬
пустить, что результатами измерений (собственными значениями) могут быть комплексные
числа, сохраняя при этом стандартное требование ортогональности альтернативных состоя¬
ний, которые могут быть получены в результате измерений, мы можем потребовать, чтобы
квантовые «наблюдаемые» были нормальными линейными операторами, не налагая более
сильного обычного требования эрмитовости операторов.
Я должен прокомментировать здесь еще одно требование, налагаемое на квантовые
наблюдаемые, — их собственные векторы должны распространяться на все гильбертово
пространство Н (так что любой элемент из Н можно представить в виде линейной ком¬
бинации этих собственных векторов). В случае конечного числа измерений это свойство
является математическим следствием эрмитовой (или нормальной) природы оператора Q.
Однако при бесконечном числе измерений это есть дополнительное допущение в отноше¬
нии любого оператора Q, играющего роль квантовой наблюдаемой. Эрмитов оператор Q,
обладающий таким свойством, называется самосопряженным.
Требование ортогональности, предъявляемое к квантовым наблюдаемым, имеет важ¬
ное значение для квантового процесса измерения. Согласно правилам квантовой механики,
результатом измерения величины, соответствующей некоторому оператору Q, всегда ока¬
зывается одно из его собственных состояний; это и есть результат «скачка» квантового
состояния, происходящего в R-процессе (см. § 22.1). Каково бы ни было состояние системы
до измерения, при измерении она совершает скачок в одно из собственных состояний опе¬
ратора Q в соответствии с R-процедурой. После измерения состояние приобретает опреде¬
ленное значение наблюдаемой Q, а именно соответствующее собственное значение q. Таким
образом, для каждого из различных возможных результатов измерения наблюдаемой Q (то
есть для каждого из различных собственных значений gi, #2, Яз, • • •) мы получаем одно из
множества альтернативных результирующих состояний, каждое из которых ортогонально
всем остальным.
Почему это так важно? Скоро мы узнаем, каковы квантовые правила вычисления ве¬
роятностей каждого из таких альтернативных исходов. Одно из следствий этих правил со¬
стоит в том, что вероятность скачка состояния, в результате измерения, в ортогональное
состояние всегда равна нулю. Соответственно при повторении измерения, определяемого
наблюдаемой Q, второе измерение даст то же собственное значение (т. е. тот же результат
измерения), что и первое измерение. Чтобы результат получился иным, должен произойти
скачок из одного состояния в другое, ортогональное ему, что не допускается правилами
вычисления вероятностей. Такой вывод связан с ортогональностью собственных состояний
оператора Q, соответствующих различным собственным значениям, вот почему мы требуем,
чтобы оператор Q был нормальным.
Теперь перейдем к определению вероятностей различных альтернативных собственных
состояний наблюдаемой Q, когда она представлена состоянием \ф), которое подлежит на¬
блюдению. Замечательная особенность квантового процесса R состоит в том, что квантово¬
механическая вероятность зависит только от квантовых состояний до и после измерения
и не зависит от каких-либо других аспектов наблюдаемой Q (например, величины измерен¬
ного собственного значения). Правило вычисления состоит в том, что вероятность скачка
Попробуйте доказать это. (Подсказка: используя выражение	—	A	I)	(Q — \I)\^), покажите сначала,
что если Q\^) — то Q*\ip) = А|т/>).)

22.5. Квантовые «наблюдаемые»
459
состояния \ф) в собственное состояние |ф) наблюдаемой Q равна
(ФШ2,
при этом предполагается, что состояния \ф) и |ф) нормированы (||-0|| = 1 = \\ф\\). В про¬
тивном случае мы должны разделить указанные состояния соответственно на Ц^Ц и \\ф\\,
прежде чем вычислять вероятность. Для ненормированных состояний лучше записать эту
вероятность в следующем изящном виде:
{ф\ф){^\ф)
(ф\ф){ф\ф)'
Эта вероятность всегда выражается вещественным числом, заключенным межу 0 и 1, причем
значение 1 она принимает лишь в случае, когда одна волновая функция пропорциональна
другой*. Напомним, что, согласно вышеприведенному обсуждению, шредингеровская эво¬
люция сохраняет скалярные произведения (ф\ф). Это устанавливает важную связь между U-
и R-процессами и выражает тот факт, что, несмотря на различие между этими процессами,
они оказываются «плотно пригнанными» друг к другу. Действительно, мы видим, что при
измерении состояние никогда не совершает скачок непосредственно в ортогональное ему
состояние, поскольку равенство {ф\ф) = 0 означает, что вероятность этого должна быть
равна нулю.
При квантовой суперпозиции двух взаимно ортогональных нормированных состояний ф
и ф, например гиф + гф, комплексные весовые множители w и z иногда называют амплиту¬
дами или «амплитудами вероятности». В этом случае эксперимент, поставленный с целью
различить состояния ф и ф, будет давать ф с вероятностью ww — \w\2 и ф с вероятно-
, т. е. вероятности равны квадратам модулей амплитуд. То же относится
и к суперпозициям большего числа таких состояний.
Полезное свойство нормального оператора Q (при условии, что его собственные век¬
торы охватывают все пространство Н) состоит в том, что он всегда обладает семейством
собственных состояний, образующим ортонормированный базис для гильбертова простран¬
ства. Ортонормированным базисом (ср. § 13.9) служит множество элементов е\, е2, ез,
пространства Н, удовлетворяющих условию
стью гг
2
(pij есть дельта-символ Кронекера), причем каждый элемент гр пространства Н можно пред¬
ставить в виде
ф = zid + г2е2 + г3е3 + ...
(коэффициенты гз., г2, гз, ... играют роль комплексных «декартовых координат» в отноше¬
нии ф). Это похоже на представление общей волновой функции одной бесструктурной части¬
цы в виде непрерывной линейной комбинации импульсных состояний (которое получается
при использовании преобразования Фурье) или координатных состояний (что получается
при использовании равенства ф(х) = f ф(Х)6(х — X) d3X) (§ 21.11), поскольку импульс¬
ные и координатные состояния — это собственные состояния соответственно оператора
импульса р и оператора координаты х. Переход от импульсного представления к координат¬
ному эквивалентен изменению базиса в гильбертовом пространстве Н (см. рис. 22.3). Однако
ни импульсные состояния, ни координатные не образуют базиса в практическом отношении,
поскольку они не нормируемы и определенно не принадлежат пространству Н! (Квантовая
Покажите это исходя из алгебраических свойств скобок ( | ). Воспользуйтесь методом, предложенным
в упражнении 22.2.

460
Глава 22
Базис из импульсных
состояний Базис из коор
динатных
состояний
Н
механика полна раздражающих противоречий такого
рода. При нынешнем положении дел приходится либо
пренебрегать подобными математическими тонкостя¬
ми и считать координатные и импульсные состояния
вполне приемлемыми, либо тратить все время на по¬
иски математической строгости. В последнем случае
нас подстерегает противоположного рода опасность
впасть в состояние «математического окостенения».
Я стараюсь выбирать промежуточный путь, но от¬
нюдь не уверен, что он приведет к прогрессу в этой
области!)
Рис. 22.3. Переход от координатного
представления к импульсному сводится
к изменению базиса в гильбертовом про¬
странстве Н (хотя в практическом отно¬
шении ни импульсные состояния, ни ко¬
ординатные, будучи ненормируемыми,
не принадлежат пространству Н)
22.6.	Измерения ДА/НЕТ. Проекторы
В случае операторов, подобных оператору им¬
пульса или координаты, собственные состояния кото¬
рых не нормируемы, вероятность обнаружить части¬
цу в таком состоянии оказывается равной нулю. Это
следует считать «правильным» ответом, поскольку
вероятность того, что координата или импульс име-
ют некоторое точно определенное значение, действительно должна быть равна нулю (так
как координата и импульс являются непрерывными параметрами). От этого не много поль¬
зы, поэтому предпочтительнее использовать наблюдаемые другого рода, которые позволяют
ставить вопрос таким образом: находится ли координата в такой-то области значений? Ана¬
логичный вопрос можно поставить в отношении импульса или любой другой непрерывной
наблюдаемой. Подобные вопросы, на которые дается ответ ДА или НЕТ, можно включить
в квантовый формализм, приписав, например, собственное значение 1 ответу ДА и соб¬
ственное значение 0 ответу НЕТ. Наблюдаемые такого рода описываются так называемыми
проекторами.
Проектор Е обладает следующими свойствами: он самосопряженный, и его квадрат
равен ему самому*:
Е
2
Е = Е*.
Проекторам соответствует наиболее простой вид измерений, и во многих случаях поня¬
тие «измерения» в квантовой механике трактуется в терминах именно таких операторов.
Существует, однако, частный случай, который становится особенно важным, когда прово¬
дятся такие измерения ДА/НЕТ, потому что (при наличии более чем двух измерений) эти
операторы оказываются вырожденными.
Оператор Q называется вырожденным по отношению к некоторому собственному зна¬
чению д, если пространство собственных векторов, соответствующих собственному зна¬
чению q, имеет более одного измерения, т. е. если имеются не пропорциональные друг
другу собственные векторы оператора Q, соответствующие одному и тому же собственно¬
му значению q (§ 13.5). Полное линейное подпространство пространства Н, состоящее из
всех собственных векторов, соответствующих одному и тому же собственному значению q,
называется собственным пространством оператора Q, соответствующим этому собствен¬
ному значению. В подобных случаях получение «результата» измерения (т. е. определение
собственного значения) само по себе ничего не говорит нам, в какое состояние совершает
«скачок» данный вектор состояния. Проблема разрешается так называемым проекционным
Покажите, что если наблюдаемая Q удовлетворяет некоторому полиномиальному уравнению, то каждое
из ее собственных значений удовлетворяет тому же уравнению.

22.7. Нулевые измерения. Спирдльность
461
постулатом, который утверждает, что состояние \ф), будучи подвергнуто измерению, орто¬
гонально проектируется на собственное пространство^2213^ оператора Q7 соответствующее
собственному значению q. Фактически термин «проекционный постулат» часто применяется
к стандартной квантово-механической процедуре, рассмотренной в § 22.1 (и описанной в яв¬
ном виде фон Нейманом^22,14]), согласно которой в результате измерения наблюдаемой Q
состояние скачком переходит в собственное состояние этой наблюдаемой, соответствующее
тому собственному значению, которое дает измерение. В этом и следующем разделах я под¬
черкиваю особо важную роль проекционного аспекта этого постулата в случае вырожденных
собственных значений^22-15].
Эту роль лучше всего выразить, используя подходящий проектор Е, а именно такой,
собственное пространство которого, соответствующее собственному значению 1 (ДА), сов¬
падает с собственным пространством наблюдаемой Q, соответствующим собственному зна¬
чению q. (Это всегда можно сделать, если проектор Е просто задает более общий вопрос,
нежели тот, который ставится измерением наблюдаемой Q, а именно: «является ли q резуль¬
татом измерения Q?») Тогда проекционный постулат утверждает, что результатом измерения
(либо Q с результатом д, либо Е с результатом 1) будет следующее:
ф) совершает скачок в состояние Е\ф).
Здесь я не забочусь о нормировке. Если мы хотим, чтобы результирующее состояние было
нормированным, можно принять, что |ф) совершает скачок в состояние более громоздкого
вида Е\ф)(ф\Е\ф}'~1^2. Здесь, однако, мне представляется более удобным не нормировать
состояния, поскольку формулы при этом имеют более простой вид.
На рис. 22.4 представлена геометрическая природа проекционного постулата приме¬
нительно к гильбертову пространству Н. Заметим, что если заменить проектор Е операто¬
ром I — E (который также является проектором), то получим, что собственные пространства
ДА и НЕТ просто поменялись местами. (Здесь I есть тождественный оператор на Н.) Таким
образом, если при измерении Е получается 0, то состояние |ф) совершает скачок в со¬
стояние (I — Е)\ф) (~ |ф) — Е\ф)). Заметим, что 1*0) есть сумма двух состояний Е\ф)
и (I ~~ Е)\ф), ортогональных друг другу , и измерение Е делает выбор между ДА для
первого состояния и НЕТ для второго:
ф)=Е\ф} + (1-Е)\ф).
Имеется прямой геометрический способ определения вероятностей этих двух альтернатив
как коэффициентов, показывающих, во сколько раз «норма» (квадрат длины) данного состо-
У-*	   V/	**	v>	о	%
яния больше соответствующей проекции . Этот простои геометрический факт затемняется,
если мы требуем, чтобы наши состояния были нормированными!
22.7.	Нулевые измерения. Спиральность
Некоторые физики выражали сомнение в отношении проекционного постулата, при
этом одни считали его бесполезным, другие — ненаблюдаемым. Трудность состоит в том,
что у нас нет способа определить, какое состояние получится после измерения, поскольку
сам процесс измерения приводит к тому, что измеряемый объект «перепутывается» с измери¬
тельной установкой, так что наблюдаемое состояние объекта нельзя считать его собственным
состоянием. Это действительно иногда может оказаться сложной проблемой, однако возмож¬
ны условия, когда проекционный постулат явным образом описывает измерение (в том числе
* Йй Покажите это.
**Й© Почему?

462	Глава	22
Рис. 22.4. Геометрическая природа проекционного постулата применительно к гильбертову простран¬
ству Н. Показаны собственные пространства проектора Е; горизонтальная плоскость представляет
собственное значение 1 (ДА), вертикальная — собственное значение О (НЕТ). Изображено разложе¬
ние |ф) = Е\ф) ~b (I — Е) \ф) состояния jф) на две ортогональные части; здесь Е\ф) есть проекция
состояния |ф) на пространство ДА (т.е. результат измерения, дающего ответ ДА), a (J — Е)\ф) —
проекция на пространство НЕТ (результат измерения, дающего ответ НЕТ). В каждом случае вероят¬
ность дается коэффициентом пропорциональности, так что квадрат (эрмитовой) длины ]|^|| вектора
состояния \ф) при проектировании уменьшается (векторы состояний не нормированы)
и в вырожденном случае). Наиболее очевидным примером такой ситуации может служить
так называемое нулевое измерение (или измерение без взаимодействия). Эта благоприятная
ситуация представляет интерес сама по себе, поскольку она иллюстрирует один из наиболее
странных аспектов квантово-механического поведения. Поэтому имеет смысл проиллюстри¬
ровать ее парой примеров.
Рассмотрим ситуацию такого рода, которая уже обсуждалась в § 21.7. Одиночный фотон
направляется на расщепитель луча, и его состояние частью отражается, частью проходит
дальше. После расщепления состояние фотона представляется суммой двух взаимно орто¬
гональных частей — прошедшей части |т) и отраженной части | р) (чтобы эта сумма имела
более простой вид, мы включили множитель, описывающий относительную фазу, в опреде¬
ление состояний |т) и |р) и не настаиваем на их нормировке);
\Ф) = 1т) +1 р)
ч.
(см. рис. 22.5). Предположим, что приемник помещен на пути прошедшего луча, и положим
для простоты рассуждений, что приемник имеет 100%-ную эффективность детектирования.
(Это очевидная идеализация, в реальном эксперименте приблизиться к такой эффективности
нелегко. Тем не менее разумно прибегнуть к ней, чтобы показать, как работает квантовая
механика.) Если в некоторых случаях мы обнаруживаем, что источник испустил фотон,
а приемник не зафиксировал его, мы можем быть уверены, что в этих случаях фотон «по¬
шел другим путем» и, следовательно, находится в отраженном состоянии | р). Замечательно,
что измерение, не обнаружившее фотон, заставляет состояние фотона совершить кванто¬
вый скачок (из суперпозиции |ф) в отраженное состояние \р))9 несмотря на тот факт, что
фотон вообще не взаимодействовал с измерительной установкой! Это пример нулевого изме¬
рения.
Впечатляющий пример применения подобных понятий был предложен Авшаломом
Элитцуром и Львом Вайдманом^22 161. Будем рассматривать наш расщепитель луча как часть
интерферометра типа Маха - Цендера (вспомните заключительную часть моего мысленного

22.7. Нулевые измерения. Спиральность
463
Рис. 22.5. Нулевое измерение, требующее применения про¬
екционного постулата. Одиночный фотон направляется на
расщепитель луча. Результирующее состояние \ф), будучи
частично отраженным и частично прошедшим, представля¬
ется суммой |ф) ~ |т) + \р) прошедшей части | т) и отра¬
женной части |р) (множитель, описывающий относитель¬
ную фазу, включен в определение состояний, которые не
предполагаются нормированными). Если оказывается, что
источник испустил фотон, а приемник не зафиксировал его,
то мы можем быть уверены, что фотон находится в состоя¬
нии. |р), несмотря на то что он вообще не взаимодействовал
с приемником
А
t
ч
Р)
т)
астрономического эксперимента, описанного в §21.7; см. рис. 21.9), причем мы не знаем,
помещен ли приемник С на пути луча, прошедшего первый расщепитель. Предположим,
что приемник С приводит в действие бомбу, которая взрывается, когда на приемник падает
фотон. На выходе имеются два приемника А и В, и мы знаем (из §21.7), что в отсутствие
приемника С фотон может регистрироваться только приемником А и не может быть зафикси¬
рован приемником В (см. рис. 22.6). Мы хотим убедиться в наличии приемника С (и бомбы)
в условиях, когда он не исчез вследствие взрыва. Так будет в случае, если приемник В реги¬
стрирует фотон, поскольку это может быть лишь при условии, что приемник С производит
измерение, которое не обнаруживает фотон! В этом случае фотон выбирает другой путь,
так что теперь каждый из приемников А и В может зарегистрировать фотон с вероятно¬
стью | (поскольку теперь отсутствует интерференция между двумя лучами). В отсутствие
приемника С зарегистрировать фотон может только приемник А^2217^.
В
*.*.*.*	%	•	.у: у.::
Рис. 22.6. Испытание бомб в примере Элитцура - Вайдмана. Приемник С, прикрепленный к бомбе,
может быть введен либо не введен в интерферометр типа Маха-Цендера (см. рис. 21.9). Светлые тон¬
кие прямоугольники обозначают расщепители луча, темные ■— зеркала. Плечи интерферометра имеют
»
одинаковую длину, так что если приемник С не введен, то фотон, испущенный источником, должен
достигать приемника А. В случае когда фотон регистрируется приемником В (без взрыва бомбы),
мы знаем, что приемник С находится на пути луча, даже если он не взаимодействовал с фотоном
В приведенном примере отсутствует вырождение, поэтому не возникает сделанный
ранее вывод, что измерение не может определить состояние, в которое совершает скачок
данное состояние. Напомним (см. § 22.6), что применение проекционного постулата необхо¬

464
Глава 22
димо для устранения неоднозначности, связанной с вырождением собственных состояний.
В соответствии с этим введем дополнительную степень свободы; это удобно сделать, приняв
во внимание явление поляризации фотонов. Это пример ранее упомянутой физической вели¬
чины — квантово-механического спина. К идеям, связанным со спином, я перейду позднее,
в §§ 22.8-22.11. В данный момент нам понадобится лишь весьма фундаментальное свойство
спина в случае безмассовой частицы. Фотоны представляют собой частицы, обладающие
спином, но поскольку они не имеют массы, их спин ведет себя несколько иначе, нежели
более обычный спин массивной частицы (например, электрона или протона), к изучению
которого мы перейдем в §§ 22.8-22.10. Мы должны считать, что фотон (или другая безмас-
совая частица) вращается вокруг направления своего движения; см. рис. 22.7.
Рис. 22.7. Безмассовая частица, например фотон, может
вращаться только вокруг направления ее движения. Вели¬
чина спина |s| частицы данного типа всегда одна и та же,
однако если спиральность s отлична от нуля (как в случае
фотона), то вращение может происходить либо по часовой
стрелке (s > 0, положительная спиральность) а), либо про¬
тив часовой стрелки (s < 0, отрицательная спиральность)
б). В случае фотона мы имеем \s\ ~ 1 (в единицах Н), что
дает два случая: s — 1 для правой круговой поляризации
и s — — 1 для левой круговой поляризации. В соответствии
с квантовым принципом суперпозиции, можно сформиро¬
вать комплексные линейные комбинации этих вариантов,
создавая все другие возможные состояния поляризации фо¬
тонов, как показано на рис. 22.12 и 22.13
Величина \s\ этого спина для данного типа безмассовой частицы всегда одна и та же, но
вращение относительно направления движения может происходить как по часовой стрелке
(-5 > 0), так и против часовой стрелки (s < 0). В соответствии с общими принципами кванто¬
вой механики, спиновое состояние может быть любой (квантовой) линейной комбинацией
этих двух состояний. Сама величина s называется спиралъностъю безмассовой частицы
(§22.12), и ее значение всегда должно быть целым или полуцелым числом (или, вводя
подходящие единицы, можно сказать, что спиральность равна целому числу, умноженному
1
на -/г). Говорят, что безмассовая частица имеет спин j, если
j (или, в указанных еди¬
ницах, |s| = jh). Фотон имеет спин 1 (так что его спиральность равна ±1), спин гравитона
равен 2 (спиральность ±2). Нейтрино имеет спин ~, так что если существуют безмассовые
нейтрино^22,18!, то они должны иметь спиральность — ~, а соответствующие антинейтрино —
Z
1
спиральность
В случае фотона спиральные состояния (состояния с определенной спиральностью) —
это состояния с круговой поляризацией, правой при s — 1 и левой при s = — 1. Существуют
и другие возможные состояния поляризации фотона, например, плоская (линейная) поля¬
ризация, но это всего лишь линейные комбинации состояний с правой и левой круговой
поляризацией. Вскоре (в конце § 22.9) я перейду ко всей этой геометрии, но пока это не
требуется. Все, что пока нам нужно, — это ответ на один частный вопрос относительно
поведения круговой поляризации при отражении. Предположим, что фотон в состоянии
с круговой поляризацией падает на расщепитель луча (или любой другой отражатель) пер¬
пендикулярно к нему, так что отраженный луч направлен навстречу падающему фотону. Нам
достаточно знать, что состояние поляризации отраженного фотона в этом случае противо¬

22.7. Нулевые измерения. Спиральность
465
положно поляризации фотона, испущенного источником, а поляризация прошедшей части
совпадает с поляризацией падающего фотона*. При желании можно принять, что началь¬
ное направление луча слегка отклонено от перпендикуляра, так что фотон не возвращается
точно к источнику. Это не повлияет сколько-нибудь существенно на наши выводы.
Вернемся к нашему первоначальному эксперименту с «нулевым измерением», пока¬
занному на рис. 22.5, но пусть теперь фотон падает перпендикулярно, как на рис. 22.8.
Предположим, что наш источник устроен таким образом, что он может испускать фото¬
ны как с правой, так и с левой круговой поляризацией. В некотором частном случае он
испускает правополяризованный фотон (и отмечает этот факг). После того как фотон столк¬
нулся с расщепителем луча, состоянием фотона становится линейная комбинация (сумма
с упомянутым выше соглашением относительно фазовых множителей):
\ф+) = |т+) + |р-),
I* *	•
где + и — внутри кет-векторов указывают знак спиральности. Поместим наш приемник, как
и прежде, на пути прошедшего луча (приемник предполагается нечувствительным к поля¬
ризации). Если, как и выше, источник зарегистрировал испускание правополяризованного
фотона, а приемник такого фотона не обнаружил, то приходится сделать вывод, что со¬
стояние совершает скачок (вследствие «необнаружения» источником) в отраженное лево¬
поляризованное состояние |р—) (не отмеченное при испускании фотона источником). Здесь
необходимо отметить, что для установления природы этого результирующего состояния тре¬
буется проекционный постулат в полном объеме (см. рис. 22.9). Мы имеем здесь измерение
типа ДА/НЕТ, поскольку результатом является либо необнаружение (НЕТ), либо обнаруже¬
ние (ДА) фотона. Обе эти альтернативы являются вырожденными, поскольку собственным
пространством ответа НЕТ служит двумерное пространство, натянутое на векторы |р+)
и \р—), а собственным пространством ответа ДА — пространство, натянутое на векторы |т+)
и |т—). Поскольку в данном случае начальное состояние имеет вид |т+) -1- \р—}, проекци¬
онный постулат^22,19] дает нам правильный результат, приводя в случае ответа НЕТ (при
отсутствии факта обнаружения) к состоянию |р—}9 а не к \р+) или |p-f} -j- |р~) (или к любой
другой линейной комбинации состояний |р+) и |р—)).**^22,2°]
ННОнет
т+>
л
Рис. 22.8. Повторение эксперимента, показанного на рис. 22.5, но теперь фотон падает почти перпенди¬
кулярно. Источник испускает правополяризованный фотон. После встречи фотона с расщепителем луча
его состоянием становится линейная комбинация \ф+) — |т+) + \р—), где + и — внутри кет-векторов
указывают знак спиральности. Если приемник (нечувствительный к поляризации) отмечает отсутствие
фотона, мы делаем вывод, что состояние совершает скачок (в результате «необнаружения» источником)
в отраженное левополяризованное состояние \р—). Это требует применения проекционного постулата
(с проекцией в так называемую точку Людерса, см. рис. 22.9), поскольку имеет место вырождение как
0-f) и \р—}), так и в случае ДА (2-пространство,
натянутое на векторы |т-Ь) и \т—)). Реальное исходное состояние |т+) + \р—) необходимо для опре¬
деления того состояния, в которое совершается скачок при измерении (в данном случае это отсутствие
г
обнаружения)
ЛЙ? Попробуйте дать этому простое объяснение.
Объясните подробнее, почему правильный ответ дает «проекция».

466
Глава 22
Рис. 22.9. Описание в проективном гильбертовом пространстве PH4 (см. рис. 15.15) проекционного
постулата (рис. 22.4) для состояний поляризации фотона, показанных на рис. 22.8. Начальным состоя¬
нием служит |т+) + \р~) в пространстве PH2; полное пространство натянуто на состояния |т+), \т—),
р-Ь) и \р—}. Светлая треугольная стрелка указывает проекцию в состояние |р-~) (точку Людерса), она
направлена вдоль прямой, проведенной через начальную точку (|т+)	\р—)) перпендикулярно прямым
ДА и НЕТ. Отсутствие факта обнаружения говорит нам лишь о том, что результирующее состояние
лежит на прямой НЕТ, однако выбор начального состояния снимает это вырождение в соответствии
с полной формой проекционного постулата
22,8.	Спин и спиноры
Описанный эксперимент вряд ли возбудит большой интерес, но он иллюстрирует неко¬
торый важный пункт. В главе 23 мы столкнемся с гораздо более захватывающими фактами.
Но чтобы подготовиться к этому, полезно еще немного поговорить о спйне. В случае мас¬
сивной частицы это имеет отношение к моменту импульса относительно центра масс^22*211
В §§ 21.1-21.5 мы убедились в важной роли законов сохранения массы-энергии и импульса,
являющихся следствием симметрии наших квантовых законов относительно соответственно
временной и пространственной трансляции. Аналогичным образом вращательная симметрия
приводит к сохранению момента импульса (см. также §§ 18.7 и 20.6). В случае массивной
частицы можно представить себе, что мы находимся в системе покоя этой частицы, то¬
гда соответствующие вращения образуют группу вращений 0(3), отнесенную к положению
частицы в этой системе.
По аналогии с тем, что компонента импульса в квантовой механике представляется
как умноженный на ih оператор, генерирующий бесконечно малые трансляции в направ¬
лении соответствующей пространственной координаты (§§21.1, 21.2), компонента момен¬
та импульса представляется умноженным на Ш генератором бесконечно малых поворотов
вокруг соответствующих декартовых пространственных осей. Таким образом, компонен¬
ты момента импульса в квантовой механике имеют непосредственное отношение к алге¬
бре бесконечно малых поворотов (§§ 13.6-13.8), т. е. к алгебре Ли группы вращений 0(3)
или SO(3), что эквивалентно, поскольку алгебра Ли не делает различия между этими двумя
группами.
Поскольку группа SO(3) неабелева, элементы алгебры Ли не коммутируют. Генера¬
торы этой алгебры £\, £2, £3 (бесконечно малые повороты относительно трех декартовых
пространственных осей) удовлетворяют соотношениям*
г*
£\£^ ~ £ъ£\ — £зч £^£з ~ £з£ч — £\>	£з£\	~ £\£ъ — £2•
Проверьте это, используя кватернионы.

22.8. Спин и спиноры
467
Согласно правилам квантовой механики, они связаны с компонентами £i, £2? £3 момента
импульса относительно трех осей:
L\ ~ тг, £2 —	2,	£3	— iM3.
Таким образом, правила коммутации для момента импульса имеют вид^22*22!
£i£2 — L2Li = гй£з, £2£з ~~ £3^2 = ihLi, L3L1 — L\L^ = гй£2.
Как и практически всюду в квантовой механике, компоненты момента импульса £1, £2, £3
должны действовать как линейные операторы в гильбертовом пространстве Н. Таким
образом, квантовые системы, обладающие моментом импульса, реализуют представ-
ление алгебры Ли группы SO(3) в виде линейных преобразований пространства Н
(см. §§13.6-13.8, 13.10, 14.6).
Это приводит к одной из наиболее изящных сторон квантовой механики, послужившей
объектом многочисленных подробных исследований. Здесь не место входить во все детали,
однако я попробую коснуться хотя бы нескольких наиболее важных пунктов. Прежде всего
отметим тот факт, что матрицы
£1 - ~ К : .	£9	-	■	I.	£
именуемые (без множителя Й/2) матрицами Паули, удовлетворяют указанным перестано¬
вочным соотношениям*. Они реализуют простейшее (нетривиальное) представление мо¬
мента импульса; можно считать, что эти матрицы 2x2 действуют на двухкомпонентную
волновую функцию {фо(х), ф\{х)}9 рассматриваемую как вектор-столбец. Если начать вра¬
щать это состояние, то компоненты фо(х) и ф\{х) будут «перемешиваться» в соответствии
с правилами умножения матриц из-за присутствия матриц Паули.
Мы можем записать двухкомпонентную волновую функцию в виде фА с нижним индек¬
сом А, который принимает значения 0 и 1 и может также рассматриваться как абстрактный
индекс при «абстрактно-индексной записи», предложенной в § 12.8. Величина, описываемая
функцией Фа, называется спинором, а индекс А — 2-спинорным индексом. Оказывается,
что фл действительно является спинорным объектом в смысле, описанном в §11.3 (непре¬
рывный поворот на угол 2тг приводит к изменению его знака). Действительно, если «по¬
тенцировать» (см. § 14.6) непрерывным образом одну из матриц Паули, пока не получится
полный оборот на угол 2тг, в результате мы получим оператор — J, который превращает Фа
в —фА‘
Такая запись является частью мощного формализма, которым можно дополнить (или да¬
же заменить t22-23!) формализм тензорного исчисления, вводя «тензороподобные» величины,
построенные из объектов типа Фа• Здесь этот формализм не потребуется в полной мере, его
реальная мощь проявляется при использовании его релятивистского варианта. Там вводятся
«штрихованные» индексы А;, В\ С', ... в дополнение к «нештрихованным» А, В, С, ...;
штрихованные и нештрихованные индексы являются, в определенном смысле, комплекс¬
но-сопряженными по отношению друг к другу; см. § 13.9. Такая запись имеет большое
значение в квантовой теории поля (она, вероятно, получила меньшее признание, чем сле¬
довало бы^22*24!; см. §§25.2, 34.3) и в общей теории относительности^22-25^, а также играет
фундаментальную роль в теории твисторов (см. § 33.6). Углубляться в нее здесь не вполне
уместно (хотя мы и вернемся к ней в §25.2), однако будет полезно позаимствовать кое-что
Проверьте это. Объясните, как связаны правила умножения этих матриц с соответствующими правилами
для кватернионов.
Проделайте это в явном виде.

468
Глава 22
у 2-спинорного формализма. Все, что нам потребуется здесь и в §§22.9-22.11, — это пред¬
ставить общие спиновые состояния в некоторой изящной форме. Поскольку здесь мы име¬
ем дело только с нерелятивистской физикой, штрихованные индексы нам не понадобятся
(вплоть до §§25.2, 25.3, 33.6, 33.8).
Прежде чем перейти к этому, я хотел бы несколько упростить обозначения. В остав¬
шейся части этого раздела, а также до конца §22.11 я буду пользоваться системой единиц,
в которой h — 1. Это всегда возможно; в§27.10(ив§31.1) мы увидим, что можно пойти еще
дальше и пользоваться так называемыми «планковскими единицами», в которых равными
1 положены также скорость света и гравитационная постоянная. Здесь нам нет надобности
заходить так далеко, и в любом случае, если потребуется, нетрудно будет восстановить в пра¬
вах h просто из соображений размерности. (Например, чтобы восстановить h в какой-либо
физической формуле, полученной в предположении Н — 1, мы заменяем каждую величину,
пропорциональную g-й степени массы, этой величиной, умноженной на Н~я, не обращая при
этом внимания на величины с размерностью длины и времени. В частности, массу, энергию,
импульс и момент импульса следует просто разделить на /г.)
Возвращаясь к 2-спинорному формализму, напомним, что унивалентная спинорная ве¬
личина Фа может быть использована для описания частицы со спином ~. Подобную запись
можно применить и к более высоким значениям спина, соответствующим другим представ¬
лениям алгебры Ли группы SO(3). Спин всегда принимает значения, равные неотрицатель¬
ному целому числу, умноженному на i:
(или, если восстановить /г, можно сказать, что эти значения принимает величина с пин/ft).
Волновую функцию может описывать объект Фав..-F («спиновый тензор»), полностью сим¬
метричный по своим п индексам в случае спина ~:
= Ф(АВ...?)
(круглые скобки означают симметризацию по всем п индексам, см. § 12.7). Фактически
все представления группы S0(3) (включая двузначные спинорные представления) можно
построить в виде прямых сумм этих частных неприводимых представлений (см. § 13.7).
Это равносильно утверждению, что представление общего вида можно представить в виде
набора (возможно, бесконечного) волновых функций
{ФаВ...Г, Фен...к, XLM...R, .
т
каждая из которых полностью симметрична по своим спинорным индексам.
Для одной отдельной частицы волновая функция сводится к одному такому симмет¬
ричному полю, например, tPab...f• (Было бы простительной ошибкой считать, что двум
частицам соответствуют по отдельности две такие функции, трем частицам — три, и т.д.
В следующей главе мы увидим, как в действительности описываются системы, состоящие
из более чем одной частицы, — дело обстоит существенно иначе.) Для частицы со спином О,
называемой скалярной частицей (примером может служить тг-мезон), волновая функция со¬
держит 0 индексов; такая ситуация была рассмотрена в главе 21. Наиболее известные части¬
цы — электроны, мюоны, нейтрино, протоны, нейтроны, а также составляющие их кварки —
1
все имеют спин - (всего 1 индекс). Дейтрон (ядро тяжелого водорода) и W-бозон (см. § 25.4)
имеют спин 1 (2 симметричных спиновых индекса). Многие более тяжелые ядра и даже це¬
лые атомы можно рассматривать как единые частицы с более высоким значением спина. В

22.9. Сфера Римана для систем с двумя состояниями
469
случае спина ~п n-индексный объект фab...f имеет п+ 1 независимых1122-261 комплексных
&
компонент*. Хотя спинорный тензор Фав.-.f часто рассматривается как n-индексный спинор,
он является спинорным объектом (§ 11.3) только при нечетных значениях п, т. е. в случае
полуцелого (а не целого) спина. Следует также отметить, что само значение спина j =
= 2П(^ 0) определяет собственное значение j(j -f 1) (и само определяется им) оператора
«полного спина» ^22,271
J2 — X2 -Ь X2 + Х§;
это есть «квадрат длины» 3-векторного оператора J = (Xi, Х2, Х3).
Полный спин J коммутирует ’ с каждой из компонент Xi, Х2, Х3 момента импуль¬
са (несмотря на то что они не коммутируют между собой). Это свойство характеризует J2
как оператор Казимира группы SO(3) (см. §22.12). Чтобы полностью задать квантовые
состояния, обычно строят полный набор коммутирующих операторов (§ 22.12) и отыскива¬
ют состояния, которые одновременно являются собственными состояниями всех операторов
этого набора. В случае момента импульса это можно сделать, взяв в добавление к операто¬
ру J2 оператор Х3 момента импульса относительно направления «вверх» (направления z).
Тогда состояние характеризуется двумя «квантовыми числами» j и га, при этом j (j -f 1)
есть собственное значение оператора J2, ага — собственное значение оператора Х3. Мы бе¬
рем j ^ 0 и — j ^ га < j, где числа j и га либо оба полуцелые (спинорный случай),
либо оба целые. Различным компонентам величины ф'ab...f соответствуют 2j + 1 (= n + 1)
различных возможных значений га.
Выбор направления «вверх», конечно, вполне произволен (он соответствует выбору
базиса вверх/вниз (| Т), | ф)) из §22.9 для спинорных компонент). Вместо направления
«вверх» с тем же успехом можно было выбрать любое другое направление. Поэтому я иногда
буду определять «значение га» относительно какого-либо другого заданного направления
(как, например, в случае описания представления Майораны в §22.10).
22.9.	Сфера Римана для систем с двумя состояниями
Рассмотрим замечательно изящную квантовую геометрию отдельных спиновых со сто-
яний для спина | (т. е. для электронов, протонов, нейтронов и кварков). Это полезно также
для понимания квантовых систем общего вида с двумя состояниями. Такая система описы-
2 ~ 1
вается комплексным двумерным гильбертовым пространством Н , и случай спина - хорошо
иллюстрирует эту геометрию.
При рассмотрении нашей частицы со спином ~ можно ограничиться одной лишь спи¬
новой степенью свободы в системе покоя частицы. Чтобы сделать это более явным, можно
представить себе, что частица находится «в покое» в том смысле, что она находится в соб¬
ственном состоянии с нулевым импульсом, так что это состояние не зависит от простран-
ственной х-координаты' . Тогда величины фо и ф\ будут просто комплексными числами,
**
[ Попробуйте объяснить это, используя приведенную здесь информацию.
SSS Проверьте коммутативность непосредственным вычислением, используя перестановочные соотношения
для момента импульса.
Вычислите коммутаторы операторов L+ = L\ 4- 1L2 и L~ = L\ — iL2 с оператором £3. Выразите J2
через Х± и £3. Покажите, что если \ф) есть собственное состояние оператора L3, то это относится и к каждому из
состояний \ф) при условии, что они отличны от нуля; найдите соответствующее собственное значение, выразив
его через собственное значение для |^>). Покажите, что если \ф) принадлежит конечномерному пространству
неприводимых представлений, натянутому на такие собственные состояния, то размерность пространства равна
целому числу 2j, где j(j + 1) есть собственное значение оператора J2 для всех состояний этого пространства.
уШ Почему?

470
Глава 22
например, фо ~ w к фх ~ z, так что состояние можно обозначить как {гщ z}. Можно при¬
нять, что состояние со «спином вверх» | f) (соответствующее правому вращению вокруг
вертикали, направленной вверх) есть спиновое состояние {1, 0}, а состояние со «спином
вниз» | X) (соответствующее правому вращению вокруг вертикали, направленной вниз) —
спиновое состояние {0, 1}. Эти два базисных состояния взаимно ортогональны:
(Т II) = о.
%
Введем нормировку:
<TIT) = 1 = UU>.
Общее состояние с половинным спином Фа — {щ, z) (общий элемент пространства Н2)
представляется линейной комбинацией этих двух базисных состояний:
{гщ z} = w\ Т) + z| X).
Скалярное произведение другого состояния общего вида {а, Ь} (т. е. а\ t) 4- b\ X)) и {w, z}
равно"
({a, b}\{w, z}) — aw + bz.
Теперь получается, что каждое состояние со спином ~ должно быть чистым состоянием
спина, соответствующим правому вращению вокруг некоторого направления в простран¬
стве, так что можно написать
w\ t) + z\ X) = I
где косой стрелкой /* обозначено некоторое направление в пространстве**. Это дает заме¬
чательное соответствие между проективным пространством PH2 (§ 15.6) и конфигурацией
направлений в пространстве, рассматриваемых как направления спина. Это проективное
пространство содержит физически различные состояния спина ~ (см. §21.9); разным точ-
JLt
С\
кам пространства PH" соответствуют различные отношения
о
Другими словами, PH есть копия нашей старой знакомой — сферы Римана, с которой мы
впервые встретились в § 8,3. Каждой точке сферы Римана соответствует некоторое состояние
1 1
со спином -, которое является собственным состоянием с т = ~ при измерении спина
в направлении на данную точку от центра сферы (рис. 22.10).
Эта геометрическая связь становится более явной, если воспользоваться стереографи¬
ческой проекцией сферы из ее южного полюса на экваториальную плоскость, описанную
в § 8.3 (рис. 8.7 а). Эту плоскость можно рассматривать как комплексную плоскость отно¬
шения и = z/w квантово-механических амплитуд г и го (а не 0, как в § 8.3). Она связывает
выбранную точку на сфере, соответствующую пространственному направлению | /"), непо¬
средственно с отношением z/w.
Воспользуемся проектором Е^ для обозначения измерения, задающего вопрос: «на¬
правлен ли спин в направлении /*?»; при этом получается собственное значение 1 (ДА),
Получите это выражение, используя сказанное выше.
Попробуйте вывести этот результат двумя разными способами: 1) определите в явном виде направление
в некоторой выбранной подходящим образом декартовой системе координат, в которой состояние (а, 6} опреде¬
ляет Ь/а как точку на комплексной плоскости (рис. 8.7 а); 2) не проводя вычислений, воспользуйтесь тем, что,
поскольку Н2 есть пространство представлений группы SO(3), оно включает в себя все направления спина, тогда
как пространство PH2 «недостаточно велико», чтобы содержать еще какие-нибудь состояния.

22.9. Сфера Римана для систем с двумя состояниями
471
Ком плексная
плоскость
Сфера
Римана
Рис. 22.10. Проективное пространство PH2 для системы с двумя состояниями представляет собой
сферу Римана (рис. 8.7). Для спиновых состояний массивной частицы со спином ~ северный полюс
£
соответствует спиновому состоянию | ф) («спин вверх»), а южный полюс — состоянию | ф) («спин
вниз»). Спиновое состояние общего вида | /*} представляется (с соответствующими фазами для | ф)
и ] ф)) точкой на сфере, расположенной в направлении | /*) от центра (т. е. мы получаем достоверный
результат ДА при измерении спина Ер* в этом направлении). Состояние | /*) можно представить
в виде линейной комбинации | /*) == щ| ф) + z\ ф) (комплексные числа z и w как компоненты w —
= 'фо, z = ipi 2-спинора ^а). Точки на сфере соответствуют различным отношениям z : w. Каждую
из них можно представить комплексным числом и — z/w (включая оо) в комплексной плоскости,
которой служит экваториальная плоскость сферы. Точка и является стереографической проекцией из
южного полюса в точку на сфере, представляющую состояние | /*)
если спин оказывается в состоянии | /*) (или проектируется в это состояние), и 0, если
спин проектируется в ортогональное состояние | >/}, противоположно направленное в про¬
странстве (оно соответствует антиподной точке на сфере Римана). (Заметим, что в этом
примере «ортогональности» в гильбертовом пространстве соответствует противоположное
направление в обычном пространстве, а не направление под прямым углом.) Если исходить
из состояния | ф), то вероятность результата ДА при измерении Е у равна |щ|^/(|ц;|2 +
4- И2). Если спин первоначально находился в некотором состоянии | X) и проводится
измерение с целью установить, соответствует ли состояние спина некоторому другому на-
правлению | /*)> то вероятность получения ответа ДА равна
-(1 Н- cos#),
где в есть угол между *\ и у* в обычном евклидовом 3-пространстве. Можно также вы¬
разить эту вероятность непосредственно в геометрических терминах, относящихся к сфере,
сопоставляя направлениям и /* соответственно точки сферы А и В и ортогонально про¬
ектируя точку В в точку С на диаметре, проходящем через точку А (рис. 22.11). Если А'
есть точка, антиподная точке А, то вероятность результата ДА равна длине отрезка А;С,
деленной на диаметр сферы АА .
Заметим, что используемая здесь «сфера Римана» имеет несколько более сложную
структуру, нежели сфера в §8.3 и небесная сфера в § 18.5, в том отношении, что теперь
в эту структуру включена «антиподная точка» (чтобы можно было сказать, какие состояния
**
Покажите это.
Подтвердите это.

472
Глава 22
Рис. 22. 11. Пусть начальное состояние системы с двумя со¬
стояниями (вроде той, что показана на рис. 22.10) представ¬
ляется точкой В на сфере Римана, и мы хотим провести из¬
мерение типа ДА/НЕТ, соответствующее некоторой другой
точке на сфере, при этом результату ДА отвечает состоя¬
ние в точке А, а результату НЕТ — состояние в точке А\
антиподной точке А. Взяв сферу радиуса i и ортогональ-
но проектируя точку В в точку С на оси А/А, мы получим,
что вероятность результата ДА выражается длиной А'С, ко¬
торая равна ~(1 -f cos#), а вероятность результата НЕТ —
2
длиной С А, равной ^(1 — cos в), где в есть угол между ОВ
и ОА (О — центр сферы)
«взаимно ортогональны» в гильбертовом пространстве). Сфера теперь является не «кон¬
формной», а «метрической», так что ее симметрия задается вращениями в обычном смысле,
и пропадают конформные движения, проявляющиеся в явлении аберрации на небесной сфе¬
ре. Тем не менее при нынешнем использовании сферы Римана явно видна непосредственная
связь между отношениями комплексных чисел, которые появляются в квантовой механике,
и обычными направлениями в пространстве. Мы убеждаемся, что комплексные числа, фи¬
гурирующие в квантовом формализме, — это не совсем абстрактные понятия, а они тесно
связаны с геометрией и динамикой систем. (Напомним также о роли комплексных фаз в ди¬
намике импульсного состояния, описанной в § 21.6.)
Следует отметить, что конфигурация, представленная на рис. 22.11 и изображающая
вероятности результатов квантовых измерений, связанные с пространством РН~, не огра¬
ничена случаем спина, а является вполне общей для систем с двумя состояниями. Особен¬
ность случая спина ^ заключается в наличии непосредственной связи между обычными
с\
«пространственными направлениями» и точками сферы Римана PH . Сфера Римана всегда
описывает «квантовое распределение» двух классических альтернатив для системы с двумя
состояниями. Однако во многих физических ситуациях геометрическая роль этой сферы
и соответствующих квантово-механических комплексных чисел (амплитуд) оказывается не
столь явной, и среди физиков существует тенденция считать их полностью «формальными
величинами». Такая позиция вызывается, в частности, тем обстоятельством, что полная фаза
вектора состояния всей физической системы является ненаблюдаемой величиной, и поэтому
часто игнорируют возможное геометрическое богатство внутренних комплексных коэффи¬
циентов. Относительные фазы между различными частями системы определенно играют
роль в наблюдениях. Это проявляется, в частности, в том факте, что комплексная геометрия
полного проективного гильбертова пространства PH имеет физический смысл. Хотя полная
фаза не сказывается на определении этого пространства, все относительные фазы проявля¬
ются в его геометрии. Действительно, существует изящный подход к квантовой механике,
использующий комплексную проективную геометрию пространства PHJ22 281
Существуют и другие ситуации, в которых геометрия сферы Римана непосредственно
связывает комплексные величины квантовой механики с пространственными свойствами
спина. В наибольшей степени это относится к общим спиновым состояниям массивной
частицы с высоким значением спина, которые мы вскоре рассмотрим (§ 22.11).
В заключение этого раздела вернемся к поляризации фотона, с которой мы уже крат¬
ко познакомились в § 22.7. Напомним, что состояние поляризации фотона в общем случае
описывается комплексной линейной комбинацией состояний с положительной спирально-

22.9. Сфера Римана для систем с двумя состояниями
473
стью |+) и отрицательной спиральностью |—):
I	= w| + )	+z\~).
Физическая интерпретация такого состояния описывается как эллиптическая поляризация,
что является обобщением частных случаев плоской и круговой поляризации. В мои цели
не входит излагать это во всех деталях, однако достаточно хорошая картина получается,
если рассмотреть классическую плоскую электромагнитную волну. «Плоскостями» служат
волновые фронты, перпендикулярные направлению движения волны. В каждой точке про¬
странства существуют электрический вектор Е и магнитный вектор В; в случае плоской
волны они всегда перпендикулярны и лежат в плоскости волнового фронта. Если зафикси¬
ровать в пространстве некоторую точку, то при прохождении волны через нее электрический
вектор в этой точке будет вращаться и острие этого вектора будет описывать эллипс в плос¬
кости волнового фронта. Магнитный вектор, следуя ему, будет описывать такой же эллипс,
но повернутый на 90° (см. рис. 22.12). В частном случае эллипс может сплющиваться в от¬
резок прямой — это есть случай плоской (линейной) поляризации. Круговая (циркулярная)
поляризация получается, когда эллипс превращается в окружность. Если волна идет прямо
на нас, то векторы вращаются против часовой стрелки при положительной спиральности
и по часовой стрелке при отрицательной спиральности.
Теперь посмотрим, как приспособить к этому сферу Римана. Пусть северный полюс
представляет состояние с положительной спиральностью |+), а южный — состояние с отри-
Рис. 22.12. Поляризация фотонов (см. рис. 21.7) с точки зрения плоских электромагнитных волн.
а) Плоскополяризованная волна, уходящая от наблюдателя. Электрические векторы (стрелки с тем¬
ным острием) и магнитные векторы (стрелки со светлым острием) колеблются взад-вперед в двух
фиксированных взаимно-перпендикулярных плоскостях, б) В плоской волне с круговой поляризацией
электрические и магнитные векторы вращаются вокруг направления движения волны, всегда оста¬
ваясь перпендикулярными и сохраняя постоянную длину, в) Диаграммы показывают, как вращаются
электрический и магнитный векторы при распространении волны (вид сзади) в случае положительной
спиральности. На нижнем рисунке показана ситуация в случае круговой поляризации, на верхнем —
в общем случае эллиптической поляризации, когда острия двух стрелок описывают конгруэнтные эл¬
липсы с взаимно-перпендикулярными главными осями. Волновая функция одиночного фотона должна
проявлять аналогичное поведение

474
Глава 22
дательной спиральностью |—). Предположим, что фотон распространяется вверх, в направ¬
лении |+). Теперь вместо того чтобы отмечать на сфере отношение z/w, возьмем квадрат¬
ный корень из него q — (z/w)1//2 (неважно, какое именно значение), так что состояниям |+)
и |—) отвечают соответственно значения q = 0 и q = оо. Проведем радиус из центра
сферы в точку q («вектор Стокса») и большую окружность в перпендикулярной этому ра¬
диусу диаметральной плоскости. Придадим окружности правую ориентацию относительно
вектора, указывающего в точку q. Затем ортогонально спроектируем эту окружность на эк¬
ваториальную плоскость сферы. Мы получим требуемый эллипс поляризации с правильной
ориентацией (см. рис. 22.13)*.
q
Вектор Стокса
z\l/2
W )
Экватор
Эллипс
поляризации
Рис. 22.13. Представление состояний поляризации фотона на сфере Римана. Пусть северный полюс
представляет состояние с положительной спиральностью |-Ь), а южный — состояние с отрицательной
спиральностью |—), импульс фотона направлен на север. Состояние поляризации общего вида гу|+) +
+ z\~} изображается точкой q — (z/w)1//2 на сфере. Проведем радиус из центра сферы в точку q,
называемый вектором Стокса, и большую окружность в перпендикулярной этому радиусу диамет¬
ральной плоскости. Придадим окружности правую ориентацию относительно вектора Стокса. Затем
ортогонально спроектируем эту окружность на экваториальную плоскость сферы. Получится требуе¬
мый эллипс поляризации с правильной ориентацией
22.10.	Высокие значения спина. Представление Майораны
В качестве еще одного примера, иллюстрирующего тесную связь между вроде бы аб¬
страктными комплексными числами в квантовой механике и геометрией пространства, рас¬
смотрим спиновые состояния массивной частицы (или атома) со спином j — ~п. Как отмече¬
но выше (в § 22.8), их можно описывать с помощью симметричного n-индексного спинового
тензора Фав...р- Существует теорема, которая гласит, что каждый такой спиновый тензор
допускает «каноническое разложение», посредством которого его можно представить в виде
симметризованного произведения 1-индексных спиноров однозначным образом с точностью
до масштабных множителей и упорядочения :
= &(аРв • • -<PF)\
Проверьте все это. Почему нас не интересует знак величины ql
**Ш% Попробуйте доказать это, используя «основную теорему алгебры», упомянутую в примечании [4.2].
(Подсказка: рассмотрите многочлен iPab...fCaCB ' * * CF с (Г z} в качестве компонент £л.)

22.10. Высокие значения спина. Представление Майораны
475
напомним (см. § 12.7), что круглые скобки вокруг индексов означают симметризацию.
Используя рис. 22.10, на котором одноиндексный спинор фл геометрически представлен
(с точностью до общего комплексного множителя) точкой на сфере Римана (т. е. некоторым
направлением в пространстве), приходим к выводу, что спиновый тензор фab...f можно
представить (с точностью до общего масштабного множителя) неупорядоченным множе¬
ством п точек сферы Римана (т. е. и неупорядоченными направлениями в пространстве);
см. рис. 22.14. Такое представление n-спинового состояния общего вида называется пред¬
ставлением Майораны. Оно первоначально было предложено в 1932 году (в результате
несколько иной процедуры[22-291? которой я вкратце коснусь в §22.11) блестящим итальян¬
ским физиком Этторе Майораной. (В возрасте 31 года он загадочным образом исчез с корабля
в Неаполитанском заливе; возможно, это было самоубийство.)
Рис. 22.14. Описание, предложенное Майораной для описания общего (проективного) спинового
П	Л
состояния массивной частицы со спином —, задаваемого п неупорядоченными точками на сфе¬
ре Римана. В соответствии с показанным на рис. 22.10, можно считать векторы, проведенные из
центра сферы в каждую из этих точек, вкладом от спина ~. Симметризованное произведение
Z
таких спинов дает полное состояние. (В 2-спинорных обозначениях полное спиновое состояние
представляет собой симметричный n-валентный тензор с факторизацией ф’ab...f — <у-(а&в
где а а, (За, • •«, Ра определяют п точек, как показано на рис. 22.10.)
Имеется стандартный базис состояний для спина j =
они реализуются как состояния, которым соответствуют
северном, либо на южном полюсе:
1
-п. В представлении Майораны
Z
точки, расположенные либо на
Т, Т» Т Т>» I и пт,.... Т). II, и Т, •••,?),	11,1,1,..., !>•
Эти п +1 состояний являются собственными состояниями наблюдаемой Хз (ось х3 направ-
лена «вверх»), и, следовательно, все они ортогональны друг другу. Им можно сопоставить
различные собственные значения спина, называемые т-значениями (§22.8), соответствен-
но j, j ~ 1, j — 2, ..., —j. Об этом несколько подробнее будет сказано в § 22.11.
Имеется стандартная измерительная установка, именуемая схемой Штерна-Герлаха,
которая часто используется для измерения такого «m-значения» атомов. Чтобы схема рабо¬
тала, атом должен обладать магнитным моментом (то есть быть маленьким магнитиком),
причем вектор магнитного момента должен быть пропорционален спиновому вектору. Ато¬
мы проходят через сильно неоднородное магнитное поле. Магнитное поле отклоняет траек¬
тории атомов несколько различным образом в зависимости от значения т, так что величи-

476
Глава 22
\Hf>171
Itti) rn
lfit> rn
m
= %
= v2
= -7:
2
2
Рис. 22.15. Схема Штерна-Герлаха для измерения «m-значения» магнитного момента атома (связанно¬
го с его спином). Атомы проходят через сильно неоднородное магнитное поле, при этом их траектории
отклоняются слегка различным образом в зависимости от величины т
на т определяет, как ориентирован вектор магнитного момента каждого атома относительно
неоднородного магнитного поля (см. рис. 22.15).
Хотя состояния с различным значением т ортогональны между собой, условия орто¬
гональности в представлении Майораны в общем случае довольно сложны^22-3°]. Можно
заметить, однако, что состояние Майораны, характеризуемое некоторым направлением У1,
обязательно ортогонально состоянию | У У •.. >/); здесь предполагается, что направле¬
ние ^ диаметрально противоположно направлению Более того, если в представлении
Майораны направление имеет кратность г, то соответствующее состояние ортогонально
к любому другому состоянию со спином iп, описание которого в представлении Майораны
содержит противоположное направление с кратностью хотя бы п ~ г + 1.*
Эти результаты позволяют нам дать физическую интерпретацию направлений Майора¬
ны. Эти направления совпадают с теми, для которых измерения с помощью схемы Штерна-
Герлаха дают нулевую вероятность обнаружить спин в точно противоположном направле¬
нии. Если направление Майораны имеет кратность г, то нулю равна вероятность того, что
значение т для данного направления заключено между —j и — j 4- г — i ^ [22.31]
Следует заметить, что изложенная процедура представления спинового состояния об¬
щего вида для массивной частицы не слишком известна большинству физиков. Вместо этого
они пользуются другой процедурой, которая включает так называемый гармоническии ана¬
лиз. Эта тема оказывается важной и по многим другим причинам, поэтому в следующем
разделе мы кратко обсудим относящиеся к ней идеи.
22.11* Сферические гармоники
В § 20.3 мы познакомились с классической теорией колебаний (в случае малой амплиту¬
ды при отсутствии затухания). Обсуждение в основном касалось систем с конечным числом
степеней свободы. Столь же кратко были рассмотрены системы, у которых число степеней
свободы можно считать бесконечным (колебания барабана или воздушного столба). Во всех
случаях колебания состояли из нормальных мод, каждая из которых имела свою собственную
частоту колебаний, называемую нормальной частотой. Если колеблющийся объект компак¬
тен (смысл этого термина объяснен в § 12.6, рис. 12.12-12.15), то моды колебаний образуют
дискретное семейство с дискретным спектром различных нормальных частот. В частном
случае сферы S2 различные моды колебаний (их можно наблюдать, например, в виде коле¬
баний поверхности мыльного пузыря или сферического воздушного шарика) соответствуют
так называемым сферическим гармоникам.. Какое это имеет отношение к квантовой механике
момента импульса? Вскоре мы получим ответ на этот вопрос.
Чтобы классифицировать эти гармоники, найдем собственные состояния оператора Ла-
О	о
пласа (лапласиана) на сфере S . В § 10.5 мы уже встречались с обычным двумерным
Попробуйте доказать это, воспользовавшись геометрической картиной из § 22.9. Примените этот результат
к вопросу об ортогональности различных собственных состояний наблюдаемой Х3.

22Л1. Сферические гармоники
477
лапласианом V2 — д2/дх2 -f д2/ду2, определенным на евклидовой плоскости. В случае
п
единичной сферы S это выражение следует видоизменить с учетом искривленной метрики.
Эта метрическая форма имеет вид
ds
gabdxadxb = dO2 + sin2 в d(f)
2
в обычных сферических полярных координатах (#, ф)9
приписываемых точкам на сфере S2, декартовы ко¬
ординаты которых (в обычном 3-пространстве) выра¬
жаются через сферические следующим образом: х =
= sin в cos ф, у = sin 9 sin ф, z = cos# (рис. 22 Л 6). Та-
ким образом, ф есть долгота, а -7г ~ # — широта (все
углы выражены в радианах). Лапласиан (с ковариант-
ной производной; см. § 14.3) имеет вид*
V
gahVaVb =
д2 , cos# д ,
и :—~ ттл ~г
1 д2
дв2
sin в дв sin2 Q дф
2 *
Возможными собственными значениями оператора V"
оказываются числа —j(j + 1) (где j = 0, 1, 2, 3, ...)
так что
v2# = -
з(з + 1)Ф,
Рис. 22.16. Стандартные сферические
полярные координаты 0 и ф на сфере
связаны с декартовыми координатами
соотношениями х = sin # cos ф, у =
= sin#sinф, z — cos#. Таким обра¬
зом, ф является мерой долготы (отме-
а|тГ
# — мерой широты
где Ф — соответствующая собственная функция 122‘321. ченной здесь на северном полюсе и на
Этими собственным функциями являются сферические
гармоники. Обычно требуют, чтобы такие гармоники
одновременно были также собственными функциями
оператора д/дф (который коммутирует с V ).
ра д/дф имеют вид im9 где т есть целое число, лежащее
собственные значения операто-
в области ~~j ^ т < j:
дФ
дф
1тФ.
cos#
-0)
Примерами таких собственных функций являются Ф = 1 (для j — т — 0), Ф =
(для j = 1, т = 0), Ф = е±и^ sin # (для j = 1, т = ±1), Ф — 3 cos2 # — 1 (для j — 2, т
И Т. д.[22-33]
От читателя не должно было ускользнуть замечательное сходство этих результатов
с собственными значениями j (j + 1) оператора полного момента импульса J2 — £2 L2 ~f
-f Хз и собственными значениями т оператора компоненты £3, рассмотренными соответ¬
ственно в конце §22.8 и в §22.10. Действительно, угловая зависимость волновой функции
частицы с целочисленным спином j описывается j-й сферической гармоникой. Кроме то¬
го, собственные состояния наблюдаемой £3 соответствуют гармоникам, которые являются
собственными функциями оператора д/дф. Таким образом, можно провести «отождест¬
вление»
д
J
2
г
дф
для описания углового поведения таких волновых функций^22,34!.
Попробуйте вывести это выражение для сферических полярных координат.

478
Глава 22
Сказанное не охватывает «спинорных» случаев, для которых j (а также га) есть полу-
целое число. Чтобы описывать и такие случаи, необходимо обобщение с переходом к так
называемым «сферическим гармоникам, взвешенным по спинам» t22 ■ 351 Это уже не про-
Су
сто функции на сфере S , они зависят также от единичного (спинорного) касательного
вектора в каждой точке сферы S2 (рис. 22.17). (Их можно рассматривать как функции на
сфере S3, которая представляет собой расслоение «спинорных» единичных касательных
векторов к сфере S2, порождаемых клиффордовым расслоением, как описано в § 15.4. t22‘363
Здесь не место входить в подробности, так что читатель отсылается к литературе.)
Рис. 22.17. Сферические гармоники, взвешенные по спинам. Функции, взвешенные по спинам, на
сфере S2 (изображенной справа) не являются просто функциями, заданными на S2, поскольку они
зависят также от единичного (спинорного) касательного вектора к сфере S2 в рассматриваемой точке
(который отмечен здесь «половинкой стрелки», чтобы подчеркнуть его спинорную природу). Такие
функции больше подходят для изображенной слева сферы S3, которая является клиффордовым рассло-
ением спиновых векторов (см. рис. 15.10). (Функция, «взвешенная по спину s», пропорциональна егвх,
где у — угол, на который поворачивается спиновый вектор в плоскости, касательной к S2. При увели¬
чении угла у соответствующая точка на S3 описывает клиффордову окружность.)
На самом деле 2-спинорное описание спиновых состояний, введенное в §22.8 и ис¬
пользованное в § 22.10 применительно к представлению Майораны, тесно связано с теорией
сферических гармоник и сферическими гармониками, взвешенными по спинам. Всякий п-
индексный симметричный спиновый тензор Фав...р явным образом соответствует набору
1
(взвешенных по спинам) сферических гармоник для j = ~п. Чтобы обнаружить это, возьмем
два 2-спинора £л и г]А с компонентами
{£°> Д} — еъ^2 cos е~гФ/2 sin
{тД г]1} — — e*^2sin~, e“^//2cos|,
так что Д и т]А представляют диаметрально противоположные точки на сфере S2.* Чтобы
получить каждую из (взвешенных по спинам) гармоник, возьмем компоненты спинового
тензора	по отношению к спинорам (А и г}А (которые рассматриваются как пере¬
менная спинорная система отсчета). Такими «компонентами» являются величины
^a...cd...f£a • * • £CVD • • • VF-
* £3 Объясните, почему эти точки являются антиподами.

22.11. Сферические гармоники
479
Если число множителей £ в этом выражении равно числу множителей г] (и равно j),
мы получаем обыкновенные (не взвешенные по спинам) гармоники. (В общем случае число
множителей £ и rj равно соответственно j -1- s и j — s, где s — «спиновый вес».) Мы получим
(с точностью до множителя^22,37^) стандартные сферические гармоники, являющиеся соб¬
ственными состояниями оператора д/дф, если в качестве епинорных тензоров фab...f возь¬
мем стандартные базисные состояния, рассмотренные в § 22.10, а именно | | ... || ••• Т)-
(В этом случае отлична от нуля лишь одна из n+1 независимых компонент тензора флв...f)-
Следует иметь в виду, что эти базисные состояния симметризованы. Например, состоя¬
ние | ITT) с точностью до множителя равно состоянию | |}| |)| Т) + | Т)1 1)1 Т) + | T)l Т)| !)•
В данном частном случае все компоненты тензора Фа вс обращаются в нуль за исключени¬
ем одной независимой компоненты фон = фюг = фпо- Хотя мое описание этого предмета
из-за его краткости может быть не слишком понятноl22*383 ? оно дает общий набросок темы,
так что читатель может начать воспринимать спиноры как замечательно эффективный (хотя
и нестандартный) путь к сферическим гармоникам*. Напомним (§22.8, см. также § 13.7),
что епин-тензорные величины ф>ab...f реализуют (и Ч- 1)-мерное пространство неприво¬
димых представлений группы вращений SO(3), то же относится и к пространству j — 2п
(взвешенных по спину) сферических гармоник.
Таким путем легко получить описание в представлении Майораны. Спиноры ад,
Да? • *., Ра в разложении ф'ab...f — &(аРв •••соответствующие нулям (взвешенных
по спинам) сферических гармоник, появляются в вышеприведенном описании, содержащем
только спиноры £ и не содержащем ^.Фактически именно таким путем Майорана впервые
пришел к своему формализму. Используя формализм 2-спиноров, можно получить ряд важ¬
ных сведений о сферических гармониках. Спинорный подход во многих отношениях проще
в применении, однако он недостаточно широко известен.
Сферические гармоники играют важную роль во многих других областях, в частности,
в классической физике, и во многих случаях это не связано непосредственно с моментом
импульса. (В таких ситуациях обычно используют букву £ вместо j, так как последняя
представляется слишком тесно связанной с моментом импульса.) Примером могут служить
малые колебания мыльного пузыря. Другой пример дает анализ распределения по небесной
сфере температуры реликтового СВЧ-излучения (2,7 К), приходящего из глубин Вселен¬
ной, где особый интерес представляют большие значения £, 200 и более. Как мы увидим
в §§ 27.7, 27.10, 27.11, 28.4 и особенно в §28.10, такой анализ имеет большое значение для
космологии.
Контраст между квантовыми и классическими проявлениями сферических гармоник
представляется весьма разительным и не поддающимся воображению. В квантовой системе
координаты 0 и ф имеют обычный смысл пространственных углов, а значение j (или £) всегда
интерпретируется как момент импульса; это далеко от того, что мы имеем в классических
системах. В частности, согласно квантовой механике, система с нулевым моментом импульса
должна быть сферически симметричной, поскольку волновая функция с j — 0 строится
просто из сферических гармоник, постоянных на сфере; в то же время в классической
физике нулевой момент импульса (т. е. «отсутствие вращения») определенно не предполагает
наличия сферической симметрии!
Наоборот, мы видим, что у случайно выбранной квантовой системы с большим мо¬
ментом импульса (большим значением j) есть состояние, определяемое в представлении
су
Майораны как состоящее из 2j точек, рассыпанных по сфере S более или менее случай¬
ным образом. Это никак не похоже на состояние классической системы с большим моментом
импульса, несмотря на распространенное мнение, что квантовая система с большими зна-
Используя этот путь, найдите явные выражения для обыкновенных сферических гармоник (с точностью
до общего множителя) при j = 1, 2, 3. Убедитесь, что они действительно являются собственными состояниями
операторов V2 и д/дф.

480
Глава 22
чениями ее квантовых чисел!22,39! должна аппроксимировать классическую систему! Что¬
бы квантовая система была подобна классической, мы должны потребовать, чтобы точки
Майораны в основном группировались вокруг некоторой прямой, выходящей из центра сфе¬
ры S2, а именно вокруг (положительной) оси классического вращения. Почему же между
этими двумя картинами столь большое расхождение? Ответ состоит в том, что почти все
«большие» квантовые состояния не похожи на классические состояния. Наиболее известным
примером такого рода является гипотетическая кошка Шредингера — квантовая суперпози¬
ция состояний живой и мертвой кошки (см. § 29.7). Почему мы не сталкиваемся с подобным
на классическом уровне? Здесь заключена одна из сторон парадокса измерения, который мы
обсудим в главах 29 и 30.
су
Гармонический анализ пространств более общего вида, чем S , составляет важную
часть многих областей науки. Он особенно полезен при рассмотрении малых возмущений
или колебаний системы. Нелишне, однако, сделать небольшое предупреждение. Если про¬
странство некомпактно, то ситуация может оказаться гораздо сложнее, чем в рассмотренном
О
выше случае сферы S . Нечто подобное мы видели в главе 9 при переходе от анализа Фурье
(на компактной окружности) к преобразованию Фурье (на некомпактной открытой прямой
линии). Иногда считают, что можно переносить результаты анализа с компактной области
на некомпактную (например, со сферы на гиперболическое пространство) простой заменой
знака (а также заменой тригонометрических функций на их гиперболические аналоги в соот¬
ветствии с идеей «изменения сигнатуры», см. § 18.4). К сожалению, истина может оказаться
более гораздо сложной. Такой неполный «гармонический анализ» охватывает лишь исче¬
зающе малую часть функций в гиперболическом пространстве из-за весьма существенной
неполноты системы гармоник.
ч
22.12.	Релятивистский квантовый момент импульса
Обратимся теперь к понятию релятивистского момента импульса. Вспомним класси¬
ческие выражения, описанные в § 18.7. По аналогии с 4-вектором ра, объединяющим мас¬
су/энергию и импульс, существует антисимметричный 6-тензор МаЬ, описывающий момент
импульса и движение центра масс. Как мы должны трактовать это с точки зрения квантовой
механики?!22,40!
В §§21.1-21.3 мы видели, как квантовые понятия энергии и импульса таинственным
образом представляются (или, по существу, являются) генераторами временных и простран¬
ственных трансляций пространства-времени. Аналогично компоненты 6-тензора момента
импульса МаЪ представляются (являются) генераторами (лоренцевых) вращений простран¬
ства Минковского М. Наряду с трансляциями ра такие вращения образуют полную (неотра¬
жательную) группу Пуанкаре (§ 18.2) — аналог движений твердых тел в евклидовой геомет¬
рии, обобщенный на пространство Минковского.
Более подробно, генераторами трансляций Пуанкаре являются компоненты ро, Р\,Р2, Рг
4-импульса ра9 при этом энергия Е = ро = Шд/дх° генерирует временную трансляцию,
а три остальные компоненты (т. е. импульс) аналогичным образом генерируют смещения в
пространстве: pi — ihd/dx\ р2 — ihd/dx2, рз — ihd/dx3 (здесь учтено, что компоненты
3-импульса р имеют вид (— р\) ~Р2, ~Рз); см. § 18.7). Вращения Пуанкаре в 3-пространстве
генерируются компонентами с~2М23 = L\ == гМъ с~2М31 —	~	ih£2, с~2М12 = £3 =
= г%, определяющими квантовое движение обыкновенного момента импульса; мы уже
рассматривали их в §22.8. Это чисто пространственные компоненты 6-тензора момента
импульса МаЪ; три остальные независимые!22,41! компоненты с~2М01, с“2М02, с“2М03
генерируют лоренцевы преобразования скорости, относящиеся к равномерному движению
центра масс в соответствии с §18.7 (см. рис. 18.16). (В этом разделе мы не предпола¬
гаем с — 1).

22.12. Релятивистский квантовый момент импульса
481
Поскольку группа Пуанкаре неабелева, ее генераторы не коммутируют между собой.
Перестановочные соотношения для них совпадают с таковыми для наших квантовых опе¬
раторов ра И МаЬ:
[ра, Pb\ = О,
\Ра, МЬс] = ih(gabpc - дасрЬ),
[МаЬ, Mcd} = ih(gbcMad - gbdMac + gadMbc - gacMbd).
Эти соотношения могут восприниматься как до¬
вольно сложные, однако они играют важную роль
в релятивистской физике, поскольку определяют Ра -<? Р°	|ф
алгебру Ли (§ 14.6) группы Пуанкаре. Они выгля-	>
дят немного проще в диаграммном представлении,	Г1??] = 9 9- 9J? = О
показанном на рис. 22.18.*	И» IJ	I I PS
Напомним, что в случае нерелятивистского мо- Гф Ш =фН-Иф=«14
мента импульса мы могли описывать базис для со- L | » J Т	Т	I
стояний в терминах собственных значений j(j + 1)	гм i i	ми	кл НН
и т двух коммутирующих наблюдаемых J2 и Хз	[ □, □ J = □ □	□
(см. §§22.8, 22.11). Эти операторы образуют пол¬
ный коммутирующий набор (в том смысле, что Рис. 22.18. Диаграммная форма квантовых
любой другой оператор, построенный из генерато- коммутаторов для релятивистского 4-им-
ров L\9 I2 и I3 и коммутирующий с J2 и Хз, не пульса и релятивистского 6-тензора^ мо-
дает ничего нового, поскольку они сами должны мента импульса [р0, рь] — 0, \ра, М с] =
быть функцией этих двух операторов). Определе- =	^(<?а Vе - даср ), [Ма , Мс ]	=
-		 1\/Tad п^ЛТас	A/f^c
ние такого полного коммутирующего набора	для	—	гп\У	1V1	— д ш t 9 т —
г	— пас МЫ\
данной системы в общем случае представляет важ- У ш >
ную часть квантовой механики. Более конкретно,
нам хотелось бы проделать это для операторов, построенных из компонент ра и Ма6,
и использовать их собственные значения для классификации релятивистских частиц или
релятивистских систем.
Почему нас интересуют коммутирующие	наблюдаемые?	Причина состоит в том, что
если А и В являются такими наблюдаемыми	(так	что	А В	— В А), то можно найти та¬
кие состояния \фгз)9 которые одновременно являются собственными состояниями обоих
этих наблюдаемых, и каждое такое состояние можно характеризовать парой соответствую¬
щих собственных значений (ar, bs)S22A2^ Если мы имеем полный набор коммутирующих
наблюдаемых А, В, С, D, ... (собственные состояния которых охватывают рассматривае¬
мое пространство), то у нас есть семейство базисных состояний |фгзьи...} с соответствующим
семейством собственных значений (or, £>s, с*, dUJ .. .)> которое можно использовать для ну-
мерации этих состояний .
При построении полного коммутирующего набора обычно начинают с того, что нахо¬
дят операторы Казимира, которые представляют собой (скалярные) операторы, коммути¬
рующие со всеми операторами рассматриваемой системы. В случае обычного трехмерного
момента импульса (см. §22.8) имеется всего один (независимый^22-43^) оператор Казими¬
ра, а именно J2 — X2 + X2 -f Х§. Возникает важный вопрос: каковы операторы Казимира
для системы, генерируемой величинами ра и МаЬ, удовлетворяющими указанным выше
перестановочным соотношениям?
Покажите, что здесь содержатся коммутаторы для трехмерного момента импульса, приведенные в § 22.8.
Рассмотрите это более подробно, приняв для удобства, что собственные значения образуют дискретную
(а не непрерывную) систему. Сначала предположите, что собственные значения не вырождены, затем покажите,
к чему приводит вырождение. (.Подсказка: выразите каждый собственный вектор наблюдаемой А через собственные
векторы наблюдаемой В и т. д.)

482
Глава 22
Вращение вокруг центра масс определяется так называемым спиновым вектором Пау¬
ли-Луб анского
Sa = \sahcdMbCVd.
Антисимметричный тензор Леви-Чивита £abcd был определен в § 19.2, однако здесь 60123 =
= с-3, поскольку не предполагается с — 1. (В «обозначениях математиков» можно
написать S — *(М А р), где р обозначает 4-импульс, а не 3-импульс, как раньше;
см. §§11.6, 12.7, 19.2.) Мы видели, что в случае одиночной классической бесструктур¬
ной частицы МаЬ — харъ — хьра, где ха — радиус-вектор точки на мировой линии частицы
(см. конец § 18.7). Воспользуемся тем же выражением и в квантовом случае, из него следу¬
ет, что для такой частицы Sa = 0. Однако для полной системы из двух или более частиц
величина Sa не обязательно обращается в нуль. Более того, для одной частицы со спином
момент импульса МаЪ не имеет столь простой формы, а появляется дополнительный спи¬
новый член p~2eabcdScpd\ предполагается р ф 0 (см. примечание 18.11). Мы замечаем, что
вектор Sa всегда ортогонален вектору ра (paSa = 0) и коммутирует с ра (т. е. [5а, рь] = 0),
так что вектор Sa, как и ра, не зависит от выбора начала координат*.
Существуют два независимых оператора Казимира для группы Пуанкаре:
РаРа =	И	SaSa	=	-/i2	J2,
где р — масса покоя всей системы**. Можно убедиться, что оператор J2, определяемый
вторым из этих уравнений, есть J2 = £2 + £2 + X2, где £1, £2, £3 — компоненты момента
импульса относительно центра масс в системе, где он покоится. Для завершения построения
набора коммутирующих операторов можно взять pi, р2, рз и, например, компоненту S3
спинового вектора, так что всего, вместе с рара и SaSa, получаем шесть операторов. (Хотя
существует большое число других возможных вариантов выбора, полное число независимых
операторов всегда равно шести^22'44^.) Это имеет существенное значение для обсуждения
в §§22.13,31.10.
Таким образом, ситуация очень похожа на нерелятивистский случай, где для включения
в рассмотрение трансляций во времени и пространстве мы могли в качестве «оператора
Казимира» выбрать энергию Е в дополнение к величине J2 и три компоненты импульса
в дополнение к £3. Следует отметить, что в релятивистском случае мы получаем не прямо J2,
J2 = ~C4(papay1SaSa,
что дает эквивалентную величину при условии рара ф 0. Действительно, выше мы предпо¬
лагали, что масса покоя р отлична от нуля. При р — 0 представить величину спина таким
образом не удается.
Как поступить в случае нулевой массы, (р = 0)? Вернемся к спиралъности s — вели-
чине, с которой мы уже встречались, применительно к фотону, в §§22.7, 22.9. Она опреде¬
ляется физическим требованием, чтобы вектор Паули-Лубанского Sa был пропорционален
4-импульсу ра:
С : V	Sa	—	Spa.
спиральности соответствует s > 0, левой — s < 0, возможно также 5 = 0. Теперь
... * ^
мИ имеем четыре независимые коммутирующие наблюдаемые, в качестве которых можно
£■•*•*	т в
взять 5, pi, Р2ч Рз- Фактически наиболее изящным подходом к случаю нулевой массы ока¬
зывается теория твисторов. Мы придем к ней в §33.6 (там мы увидим, что «твисторные
Проверьте утверждения, содержащиеся в последних четырех предложениях.
Укажите простую причину, по которой два указанных оператора должны коммутировать с и МаЪ.
{Подсказка. Обратитесь к § 22.13.)
Как могут векторы Sa и ра быть одновременно взаимно ортогональными и пропорциональными?
***

22,13. Общий случай изолированного квантового объекта
483
переменные» Z°, Z1, Z2, Z3 также можно использовать в качестве четырех независимых
коммутирующих операторов).
22.13.	Общий случай изолированного квантового объекта
Как описывает квантовая механика изолированный объект общего вида, например, атом
или молекулу? Предполагается, что на объект не действуют никакие внешние силы и что он
остается локализованным, однако внутри него могут действовать внутренние силы. При опи¬
сании такого объекта важно разделять 1) внешние характеристики объекта как целого и 2) его
внутреннее устройство и геометрическую структуру. Внешние характеристики объекта (1)
г
включают его полную мае су/энергию, импульс, положение и движение центра масс и мо¬
мент импульса. Мы понимаем эти величины в релятивистском смысле и используем для
описания внешних параметров ра и МаЪ из §22.12. Под внутренним устройством (2) по¬
нимается природа частиц, составляющих объект, природа сил, действующих между ними,
и соответствующие геометрические соотношения. Такие соотношения связывают некото¬
рые обобщенные координаты qr (§20.1), имеющие исключительно относительный[22-45] ха¬
рактер (например, расстояние некоторой части объекта от центра масс, угол, образуемый
между собой различными частями, или расстояния между частями). Они не меняются, ес¬
ли весь объект как целое претерпевает пространственные или временные трансляции, или
поворачивается на некоторый угол, или двигается в некотором направлении с постоянной
скоростью.
Вследствие их относительного характера все внутренние координаты не меняются при
любых операциях симметрии группы Пуанкаре. Следовательно, они должны коммутировать
с ра и МаЪ. Почему? Предположим, что некоторый оператор симметрии S действует на
квантовую систему, так что
\Ф) -> S\*l>),
a Q есть некоторый квантовый оператор. Действие оператора симметрии на Q приводит
к преобразованию*
Q ^ SQS-1.
Если Q не меняется под действием S, то SQS~l = Q, откуда
SQ - QS.
Таким образом, действуя оператором S по очереди на компоненты ра и Ма6, мы убеждаемся,
что все внутренние параметры действительно должны коммутировать с ра и МаЬ.
В данном контексте это означает, что мы можем отделить ту часть волновой функции,
которая относится к внутренним степеням свободы, от той, которая относится к внешним
параметрам — 4-вектору импульса и 6-тензору момента импульса. При стандартном подходе
мы считаем, что система находится в собственном состоянии некоторой более общей систе¬
мы внешних наблюдаемых. В частности, энергия и импульс должны задаваться определен¬
ными собственными значениями; обычно выбирают систему отсчета, в которой 3-импульс
равен нулю (Р — 0 в обозначениях § 21.5). В отношении момента импульса можно исполь¬
зовать нерелятивистское описание (§§ 22.8-22.11) и можно принять, что система находится
в собственном состоянии полного момента импульса J2, а также, если угодно, и £3.
Внутренние параметры будут, конечно, зависеть от деталей рассматриваемой систе¬
мы. В некоторых случаях можно с хорошим приближением описывать внутренние степени
Объясните, почему. (Подсказка: может помочь обращение к § 22.4.)

484
Глава 22
свободы как малые колебания вокруг некоторого равновесного положения. Тогда можно
воспользоваться классическим анализом, данным в §20.3. Напомним (см. §20.3), что если
взять гамильтониан вида
П = |Q«mV +
где матрицы Qab и РаЪ симметричны, положительно определены и не зависят от времени,
то в классическом случае каждая нормальная частота и)/2и получается из собственного
значения и/2 матрицы W = PQ (т. е. Wac = PabQbc)•
А как обстоит дело в квантовой механике? Напомним формулу Планка Е = hu =
= 2тгНи, где v — частота. Можно ожидать, что энергия колебаний нормальной моды рав¬
на Е — Ни). Можно также предвидеть возможность больших значений энергии, поскольку
в классической физике амплитуда может становиться сколь угодно большой (пока не на¬
рушится приближение «малых колебаний»), а чем больше амплитуда, тем больше энергия.
Если предположить наличие «высших гармоник» (напомним (§ 9.1), что их частоты кратны
основной частоте и)/2п), то можно представить себе, что разрешенные значения энергии
в квантовых собственных состояниях будут равны
0, Ни), 2Ни\ ЗНсе, 4 Йод ...
На самом деле это не слишком далеко от правильного квантово-механического ответа
на вопрос, однако оказывается, что существует дополнительный вклад в энергию ^Ни,
называемый энергией нулевых колебаний}22 . Разрешенные значения энергии собственных
состояний имеют вид
iftu, 7, Hid, ^Ни), 1пш, ^Hu), ...
Это следует из стандартного квантово-механического обсуждения задачи об одномерном
гармоническом осцилляторе^22*47^, гамильтониан для которого имеет вид Н — (m2u2q2 +
+ р2)/2т. Каждая отдельная мода соответствует одному из этих значений для каждого
из собственных значений и матрицы W.
В случае квантовой системы общего вида эти значения будут лишь приближенными,
поскольку могут оказаться существенными члены более высокого порядка. Однако таким
путем можно успешно аппроксимировать различные системы. Более того, квантовополе¬
вая теория фотонов (или любых других частиц, относящихся к «бозонам», см. §§ 23.7, 26.2),
рассматривает систему бозонов как набор осцилляторов. Это такие же гармонические осцил¬
ляторы, что и рассмотренные выше (при отсутствии в гамильтониане членов более высокого
порядка). Бозоны находятся в стационарном состоянии при отсутствии взаимодействия меж¬
ду ними^22*48!. Такое «представление гармонических осцилляторов» имеет очень широкую
область применения. Тем не менее для дальнейшего продвижения необходимо детальное
знание взаимодействия.
Например, атом водорода состоит из электрона, вращающегося по орбите вокруг про¬
тонного ядра (ядро обычно считают покоящимся, что является хорошим приближением,
поскольку протон почти не движется из-за его большой массы — приблизительно в 1836 раз
большей массы электрона). Однако, согласно правилам квантовой механики, квантово¬
механическая орбита не сводится к единственной классической траектории вокруг ядра,
а представляет квантовую суперпозицию большого числа таких траекторий. Такие «кванто¬
вые орбиты», полученные путем суперпозиции, являются стационарными решениями урав¬
нения Шредингера с гамильтонианом, который имеет в основном тот же вид, что в клас¬
сическом случае, но «канонически квантован» в соответствии с правилами, изложенными
в §§ 21.2, 21.3 (а также § 23.8). Чтобы эти орбиты были собственными состояниями момента
импульса, волновые функции должны иметь угловую зависимость сферических гармоник

22.13. Общий случай изолированного квантового объекта
485
(§22.11). В общем случае в качестве квантовых чисел, нумерующих различные состояния,
можно взять собственное значение энергии Е и собственное значение момента импульса j
(а при необходимости и т). В случае атома водорода (если не учитывать наличие спина
у электрона и протона и использовать нерелятивистскую форму гамильтониана) оказыва¬
ется, что собственное значение энергии Е определяется собственным значением момента
импульса jf, однако значение j не определяется энергией Е. В более точной теории атома
водорода (а также более сложных атомов) j зависит от Е, так что все различные состояния
характеризуются одним лишь собственным значением энергии.
В первоначальной теории атома, выдвинутой Бо¬
ром в 1913 году и более чем на десятилетие опередив¬
шей появление гораздо более точной и полной кван¬
товой механики Гейзенберга, Шредингера и Дирака,
разрешенные значения момента импульса и энергии
вычисляются так, как если бы орбиты были классиче¬
скими эллиптическими орбитами Кеплера-Ньютона,
соответствующими закону обратных квадратов, опи¬
сывающему электростатическое взаимодействие меж¬
ду ядром и электроном на орбите. При этом, однако,
накладывается «квантовое условие», согласно которо¬
му орбитальный момент импульса электрона должен
быть целочисленным кратным постоянной Планка h.
Такие «квантованные орбиты» иногда называют ор¬
биталями (см. рис. 22.19). Эта процедура работает
замечательно f22-49], однако она не опирается на тео¬
ретический фундамент, который был создан появив¬
шейся позже квантовой механикой с ее гораздо более
общими и точными результатами. Более сложные ато¬
мы, простые молекулы, релятивистские эффекты, на¬
личие спина у электронов и ядер и т. д. — все это до¬
ступно квантовому формализму опирающемуся на из¬
ложенные идеи, хотя зачастую приходится надеяться
не столько на точный математический анализ, сколько
на приближенные методы и численные расчеты.
Упомянутое выше применение электростатики
также является приближением, поскольку необходи-
Рис. 22.19. «Атом Бора», в котором
орбиты электронов рассматриваются
как классические эллиптические орби¬
ты Кеплера-Ньютона, соответствую¬
щие закону обратных квадратов, опи¬
сывающему электростатическое взаи¬
модействие. Однако на энергии и мо¬
менты импульса электронов наклады¬
вается «квантовое условие», согласно
которому орбитальный момент импуль¬
са электрона должен быть целочислен¬
ным кратным постоянной Планка К. Эта
идея с наибольшим успехом была при¬
менена к круговым орбитам для един¬
ственного электрона в атоме водорода
мо допустить возможность переходов из одного ста¬
ционарного состояния в другое с испусканием и по¬
глощением фотонов. Это требует применения теории
Максвелла, но в ее квантованной форме, что, строго говоря, нуждается в формализме кван¬
товой теории поля (который будет изложен в главе 26). Для полной точности необходима
также теория релятивистского электрона Дирака из главы 24. Атом, находящийся в состоя¬
нии с наиболее низкой энергией (оно называется основным состоянием), будет оставаться
в этом состоянии (при условии, что он полностью изолирован от внешних возмущений). Ес¬
ли же атом находится в состоянии с более высокой энергией (так называемом возбужденном
состоянии), то, скорее всего J22-50! существует конечная вероятность перехода его в основное
состояние с испусканием одного или нескольких фотонов. По этой причине можно ожидать,
что мы обнаружим свободные атомы или молекулы в их основных состояниях или вблизи от
них. Частота v одиночного фотона, испускаемого атомом или молекулой при их переходе
из одного состояния в другое, определяется, согласно формуле Планка Е — 2ithv (см. § 21.4)
и закону сохранения энергии, разностью Е энергий этих двух состояний.

486
Глава 22
Такие частоты издавна наблюдались в виде спектральных линий, однако проблема объ¬
яснения их долгое время оставалась научной загадкой. Необычайное богатство информации,
заключенной в картине спектральных линий, было успешно объяснено квантовой теорией.
Это стало одним из величайших достижений физики XX века! Классическая физика, опира¬
ющаяся на закон обратных квадратов, описывающий притяжение между положительными
и отрицательными зарядами, и уравнения Максвелла, определяющие излучение электро¬
магнитных волн ускоряющимися электронами, недвусмысленно предсказывала, что орбита
электрона должна закручиваться в спираль вокруг ядра, образуя сингулярное состояние за
очень короткое время. Этот вывод оказался в явном противоречии с наблюдаемыми фак¬
тами. Квантовая механика не только устранила этот парадокс, но и позволила построить
детально разработанную теорию спектральных линий, которая оказалась необычайно мощ¬
ным инструментом во многих областях науки — от криминалистики до ядерной физики
и космологии.
В качестве важного заключительного замечания следует отметить, что существование
дискретных квантовых чисел, например, j и m для момента импульса или собственных
значений энергии для гармонического осциллятора или атома водорода связано в конеч¬
ном счете с компактностью некоторого пространства 122,511 В случае момента импульса это
с\
происходит из-за компактности сферы пространственных направлений S , к которой при¬
меняется гармонический анализ в § 22.11. В отсутствие компактности (или периодичности)
мы будем иметь решения уравнений вроде ЧФ — —кФ, в которых на собственное значение к
не накладываются ограничения. Забавно, что при отсутствии подобной компактности об¬
щий формализм квантовой механики не приводит к дискретности, с которой все началось
и из-за которой появилось само название «квант»!
Примечания
§ 22.1.
22.1. На семинарах квантовые скачки иногда называют «квантовыми прыжками». Это весьма
неудачное выражение, поскольку квантовые скачки, возникающие при редукции квантового
состояния, могут быть крайне тонкими, трудно обнаруживаемыми и, возможно, нереальными
событиями!
22.2. Общее обсуждение разных точек зрения на квантовую механику можно найти в книгах [649,
644, 393, 193].
§22.2.
22.3. См. главу 29, а также [253, 825, 193, 286, 188].
§22.3.
22.4. Как и в случае одной частицы (§21.9), некоторые авторы вместо моего обозначения ||^||
используют \\гр ||2.
22.5. См. удачное изложение теории таких пространств в книгах [137, 655].
♦
22.6. В литературе по квантовой механике часто используется обозначение QT в отличие от боль¬
шей части соответствующей математической литературы, где пользуются обозначением Q*
(см. §13.9).
§22.4.
22.1.	Имеется более поздняя перепечатка [209]. Более современная трактовка содержится в кни¬
ге [716].
22.8.	Аргументацию Дирака о неприменимости представления Шредингера в релятивистской кван¬
товой теории поля см. в книге [208].

22.13. Общий случай изолированного квантового объекта
487
22.9.	Представление взаимодействия часто используется в «нестационарной теории возмущений»,
где гамильтониан зависит от времени. См. [716], гл. 18, [208].
§22.5.
22.10. Я отвлекаюсь здесь от того факта, что собственные состояния ненормируемы, из-за чего
координата или импульс в некоторых формулировках могут не признаваться истинными «на¬
блюдаемыми».
22.11. В более общем случае, независимо от того, является q собственным значением или нет, мы
называем q математическим ожиданием наблюдаемой Q для нормированного состояния |ф)9
если q = {ф\(2\ф).
22.12. См. [209]. Комплексные параметры используются во многих областях физики, см., напри¬
мер, [268].
§22.6.
22.13. Изящную трактовку проекционных измерений можно найти в книгах [461, 561].
22.14. См. [807].
22.15. См. [497], а также [613].
§22.7.
22.16. См. [247].
22.17. Первоначально идея измерений в отсутствие взаимодействия была выдвинута Робертом Дик-
ке [197]. Она нашла некоторые поразительные применения, например, для обнаружения грави¬
тационных волн, см. [100]. Описанный здесь необычный мысленный эксперимент Элитцура-
Вайдмана по «испытанию бомб» (см. также [613]) может привести и к другим применениям.
22.18. Имеются убедительные свидетельства в пользу того, что по крайней мере большинство типов
нейтрино, а возможно, и все их виды обладают массой. Даже если это так, допущение, что
они «безмассовые», может служить хорошим приближением при описании их поведения.
Я вернусь к этому вопросу в § 25.3.
22.19. Проекционный постулат был усовершенствован Людерсом [497], в связи с чем точку \р—)
в пространстве PH4 можно назвать «точкой Людерса».
22.20. В качестве более простого (и более интересного) примера можно рассмотреть несколько
иную ситуацию, при которой расщепителем луча служит поверхность преломляющей среды,
на которую падает луч под углом Брюстера. Тогда отраженный луч характеризуется некото¬
рой линейной поляризацией, а прошедший луч — противоположной линейной поляризацией.
Анализ здесь в основном такой же, что и раньше (только поляризация теперь не круго¬
вая, а линейная), но теперь не обязательно предполагать падающий фотон поляризованным;
сам факт, что он приходит извне среды (под некоторым выбранным углом), а не изнутри,
оказывается достаточным для того, чтобы нулевое измерение приводило к требуемому поля¬
ризованному конечному состоянию. В качестве хороших книг по электромагнетизму можно
рекомендовать [66, 417].
§22.8.
22.21. «Бесструктурная частица» не должна обладать моментом импульса относительно ее центра
масс, поскольку величина М — 2х Л р из § 18.6 обращается в нуль при х = 0. Однако,
как отмечено в примечании 18.11, к моменту импульса должна добавляться величина, опи¬
сывающая «собственный момент импульса» (спин), если существует некоторая «структура»,
определяемая спином частицы. В более явном виде это будет показано в §22.12.
22.22. Внимательный читатель может заинтересоваться, возникают ли здесь какие-то тонкости
со знаками вроде тех, с которыми мы столкнулись в §21.5, где они были связаны с сигнату¬
рой метрики. Ясное и подробное изложение теории момента импульса в квантовой механике
с точки зрения алгебры Ли группы SO(3) читатель сможет найти в книгах [421, 248]. Дру¬
гой, несколько более «физичный» (хотя и более сложный), вывод алгебры момента импульса
имеется в [716].

488
ГЛАВА 22
22.23.
22.24.
22.25.
22.26.
22.27.
§ 22.9.
22.28.
§22.10.
22.29.
22.30.
22.31.
§22.11.
22.32.
22.33.
22.34.
22.35.
22.36.
22.37.
22.38.
22.39.
§22.12.
22.40.
22.41.
22.42.
22.43.
См. [626].
См. [287].
См. [850, 582, 590, 284, 285, 626, 627, 564].
Слово «независимые» (компоненты) используется здесь в том смысле, что все компоненты
спинового тензора §)ab...f можно получить из этого набора независимых волновых функций
и нельзя получить из меньшего набора. В данном случае это следует просто из симметрии,
поэтому полное число компонент 2П сводится к п -f 1 независимым компонентам (напри¬
мер, ”0ооь Фот и фюо не являются независимыми компонентами тривиальным образом,
поскольку фоо1 — ^010 = фюо)-
См. [716].
См. примечание 21.12. Некоторые аспекты квантовой информации с аналогичной точки зрения
обсуждаются также в книге [561].
См. [509].
См. общий обзор в книге [80]. Интересную современную модификацию можно найти в [758].
См. также примечание 22.31.
См. [613, 620, 861].
При работе со сферическими гармониками чаще используется буква а не у, которой я поль¬
зуюсь здесь.
Дальнейшие подробности можно найти в любом учебнике по квантовой механике; см., на¬
пример, [716] или [26].
См. [716].
См. [551, 626].
См. [308].
Сферические гармоники обладают также свойствами ортогональности и нормируемости
(для установления общего масштаба), которые играют важную роль при использовании
их в практических вычислениях. Это, однако, завело бы нас слишком далеко; читатель отсы¬
лается к литературе по теории сферических гармоник [321, 117].
Читателю, желающему подробнее познакомиться с алгеброй и геометрией спиноров, следует
иметь в виду, что спинорные индексы можно «поднимать» или «опускать» по следующей
схеме: £i = £°, £о — —f1. См. [626] и приложение к книге [858].
Термин «квантовое число» обычно относится к возможным дискретным собственным значе¬
ниям некоторых важных квантовых наблюдаемых, — момента импульса, заряда, барионного
числа и т.д., которые используются для классификации частицы или простой квантовой си¬
стемы .
В главах 24-26 мы увидим, что релятивистская квантовая механика требует гораздо больше,
чем изложено в этом разделе, однако это не влияет на проводимое здесь обсуждение.
Напомним примечание 22.6. Независимость учитывает здесь дялшсимметрию МаЬ.
Это связано с явлением «разделения переменных», которое возникает, когда некоторую функ¬
цию f(0, ф) можно представить в виде суммы / (0, ф) = ]ЦГ) Л^д%{0)Нз{ф)9 где д%{0) и hj (ф) —
собственные функции соответствующих (коммутирующих) операторов А и В. Сферические
гармоники обладают этим свойством; см. [321, 117].
Слово «независимый» относится здесь к функциональной независимости (сравните с приме¬
чанием 22.26). Так, хотя 2J2, (J2)3 и cos J2 не совпадают с оператором Казимира J2, они не
являются независимыми от J2.

22.13. Общий случай изолированного квантового объекта
489
22.44. Необходимо проявлять некоторую осторожность в отношении инвариантности «числа незави¬
симых коммутирующих операторов». Строго говоря, это относится к размерности простран¬
ства локальных решений дифференциальных уравнений в частных производных. В квантово¬
механических задачах требования компактности, налагаемые на пространство решений (на-
Л
пример, S из §22.11), устанавливают сильные ограничения на разрешенные собственные
значения и затрудняют подсчет числа степеней свободы.
§22.13.
22.45. Здесь не используются понятия общей теории относительности, так что слово «относитель-
ныи» следует понимать в смысле специальной теории относительности.
22.46. Существует, однако, возможность добавить к гамильтониану постоянную величину соглас¬
но § 20.3. Это приводит лишь к переопределению нуля отсчета энергии (см. упражнение 24.2
1
из § 24.3), поэтому слагаемое -hco иногда считают не имеющим прямого физического смысла.
22.47. См., например, классическую трактовку Дирака в его «Принципах квантовой механики» [209].
22.48. Величины rj — (2imq), появляющиеся в представлении Гейзенберга (§22.4),
играют роль операторов рождения из § 26.2.
22.49. В частности, из нее следует необъяснимая прежде формула Бальмера для частот спектральных
линий водорода и — R(N~2 — М-2), где R — некоторая постоянная (именуемая постоянной
Ридберга - Ритца), М > N > 0 — целые числа.
22.50. Могут вмешаться «правила отбора», обусловленные законами сохранения и запрещающие
некоторые из таких переходов.
22.51. Сравните с примечанием 22.44.

Глава 23
Перепутанный квантовый мир
23.1.	Квантовая механика систем многих частиц
Мы уже видели в двух предыдущих главах, насколько загадочно поведение отдельных
квантовых частиц, со спином или без спина, и какой странный и удивительный формализм
пришлось создать для того, чтобы описывать такое поведение. Естественно ожидать, что,
поскольку наш формализм правильно представляет квантовое поведение отдельных частиц
или других изолированных объектов, он должен позволить нам описывать системы, содер¬
жащие несколько отдельных частиц, которые, возможно, взаимодействуют одна с другой тем
или иным способом. В каком-то смысле это действительно так — до некоторой степени, —
поскольку общий формализм, изложенный в §21.2, имеет достаточно широкий характер,
однако возникают некоторые определенно новые особенности, когда система содержит бо¬
лее одной частицы. Таким новым явлением оказывается квантовое пер впутывание, из-за
которого такая система должна рассматриваться как одно целое, и различные проявления
этого эффекта делают квантовое поведение еще более загадочным, чем то, с которым мы уже
сталкивались. Более того, частицы, тождественные одна другой, всегда автоматически пе¬
репутываются между собой, хотя, как мы увидим, это может происходить двумя совершенно
разными способами в зависимости от природы частиц.
Вернемся к математическому описанию квантовой системы, изложенному в двух пре¬
дыдущих главах. Метод квантового гамильтониана, позволяющий изучать эволюцию кван¬
тового вектора состояния с помощью уравнения Шредингера, применим также к системе
многих частиц, возможно, взаимодействующих и, возможно, обладающих спином, с тем же
успехом, что и в случае одной частицы без спина. Все, что здесь требуется, — это под¬
ходящий гамильтониан, учитывающий все эти особенности. Мы не получим отдельную
волновую функцию для каждой частицы, — вместо этого мы будем иметь один вектор со¬
стояния, описывающий всю систему в целом. В координатном представлении такой единый
вектор состояния можно по-прежнему рассматривать как волновую функцию Ф, но теперь
это будет функция от координат всех частиц, то есть функция, определенная на конфи¬
гурационном пространстве системы частиц (см. § 12.1), которая может также зависеть от
некоторых дискретных параметров, характеризующих спиновые состояния. Так, если мы
описываем частицу со спином 2-спинором &ab...f (см. §22.8), «дискретные параметры»
будут нумеровать различные отдельные компоненты. Уравнение Шредингера показывает,
как функция Ф будет эволюционировать во времени, поэтому она должна зависеть также от
временной переменной t.
Примечательной особенностью стандартной квантовой теории является тот факт, что
О	f
система многих частиц характеризуется всего одной временной координатой, тогда как каж¬
дая из независимых частиц, входящих в квантовую систему, имеет свой собственный неза¬
висимый набор пространственных координат. Это особенность нерелятивистской квантовой
механики, которую можно рассматривать как некоторое предельное приближение к «более
полной» релятивистской теории. В релятивистской схеме пространство и время рассмат¬
риваются на равных правах. Поскольку каждая частица имеет свои собственные простран¬
ственные координаты, она должна также иметь свою собственную временную координату.
В обычной квантовой механике это не так — время одно на все частицы.

23.2. Гигантский объем пространства многочастичных состояний
491
При обычном нереяятивиетском подходе это может выглядеть вполне разумно, посколь¬
ку в нерелятивистской физике время есть нечто внешнее и абсолютное, которое просто
«течет» независимо от того, что содержится во Вселенной в каждый данный момент вре¬
мени. Но с тех пор как появилась теория относительности, мы знаем, что такая картина
может служить лишь некоторым приближением. То, что является «временем» для одного
наблюдателя, для другого есть некоторая смесь пространства и времени и наоборот. Обыч¬
ная квантовая механика требует, чтобы каждая отдельная частица имела свои собственные
пространственные координаты. В соответствии с этим в построенной должным образом ре¬
лятивистской квантовой теории каждой частице следовало бы приписать свою собственную
временную координату. Действительно, такая точка зрения время от времени обсуждается
разными авторами[23л) начиная с 1920-х годов, однако она пока не развилась в полноценную
релятивистскую теорию. Основная трудность здесь в том, что если позволить каждой части¬
це иметь свое собственное время, то каждая из них будет двигаться в отдельном временном
измерении и потребуются немалые усилия, чтобы вернуться к реальности.
В §26.6 будет рассмотрен метод «интегралов по траекториям» применительно к ре¬
лятивистской квантовой теории, основанный не на гамильтоновом, а на релятивистском
лагранжевом формализме. Это позволит обойти проблему «много пространств — одно вре¬
мя», однако при этом, как мы далее увидим, возникают новые серьезные проблемы, и, по-
видимому, таковые будут возникать всегда, какую бы из известных процедур мы ни выбрали.
Более того, как мы вскоре увидим, само уравнение Шредингера не гарантировано от трудно¬
стей «возвращения к реальности». По моему мнению, простая пространственно-временная
асимметрия шредингеровского подхода скрывает нечто глубокое, ускользающее из нашей
квантовой картины мира, но пока мы не будем этим заниматься. Пока будем стоять на точ¬
ке зрения стандартной нерелятивистской квантовой теории, в которой можно пользоваться
понятием универсального внешнего времени. Однако требования теории относительности
остаются, и нам придется вернуться к этому в конце этой главы (в § 23.10).
Как в таком случае описывать многочастичные системы в соответствии со стандарт¬
ным нерелятивистским представлением Шредингера? Как показано в §21.2, мы будем
иметь единый гамильтониан, в котором все импульсные переменные должны относиться
ко всем частицам системы. В координатном (шредингеровском) представлении каждый из
этих импульсов заменяется оператором частной производной по соответствующей коорди¬
нате данной частицы. Все эти операторы должны на что-то действовать, и, чтобы допускать
согласованную интерпретацию, они должны действовать на один и тот же объект. Таким объ¬
ектом является волновая функция. Как установлено выше, мы действительно должны иметь
одну волновую функцию Ф для всей системы, которая должна быть функцией от различных
пространственных координат всех отдельных частиц.
23.2.	Гигантский объем пространства многочастичных состояний
Все это звучит довольно безобидно, но так ли это? Сделаем паузу и попробуем по¬
нять всю сложность этого, казалось бы, простого последнего требования. Если бы каждая
частица обладала своей собственной волновой функцией, то для п скалярных (т. е. бес-
спиновых) частиц мы имели бы п различных комплексных функций координат. Хотя это
предъявляет несколько повышенные требования к нашему воображению, в случае п ча¬
стиц мы, пожалуй, смогли бы с этим справиться. (Я пока не принимаю в расчет время,
рассматривая все в один и тот же момент времени.) Для наглядности можно представить
себе картину поля в пространстве, обладающего п компонентами, и считать, что каждая
компонента описывает отдельное «поле». (Каждое такое отдельное поле можно представить
себе как волновую функцию отдельной частицы.) Возможно, придется рассматривать 2п
компонент, если говорить о вещественных компонентах, поскольку волновые функции ком¬

492
Глава 23
плексны. Электромагнитное поле имеет 6 вещественных компонент, то есть это 6 функций
от 3 переменных (аналогично трем комплексным скалярным волновым функциям), а пред¬
ставить себе поле электрических и магнитных векторов — это не такая уж жуткая нагрузка
на воображение!
Как следует подсчитывать «степени свободы» комплексного скалярного поля, напри¬
мер, волновой функции скалярной частицы в 3-пространстве? Каково «число» различных
возможных таких полей? Напомним, что, согласно обозначениям, введенным в § 16.7, вы-
ражение ооа°° означает свободу, доступную для произвольно выбранного (гладкого) поля
с а вещественными компонентами в пространстве 6 вещественных измерений. Так, для ком¬
плексного скалярного поля а = 2 (поскольку комплексное число засчитывается за два веще-
ственных), так что степеней свободы будет 00	.	Это относится к полю в один момент вре¬
мени (т. е. при постоянном значении £), поэтому мы рассматриваем обычное 3-пространство,
которому соответствует 6 = 3 (а не значение 6 = 4 для пространства-времени). Можно было
бы рассмотреть и пространств о-время, но в этом случае мы имели бы уравнения поля, огра¬
ничивающие свободу. В случае волновой функции таким ограничением является уравнение
Шредингера, которое сводит свободу к той, которая была вначале, при задании начальных
данных в 3-пространстве, то есть оо2°° .
Попутно можно рассмотреть случай свободного максвелловского поля без источников
(зарядов). Здесь мы имеем 6 вещественных компонент в обычном 3-пространстве, так что,
рассматривая поле в некоторый фиксированный момент времени t и игнорируя существо-
вание уравнений Максвелла, мы получили бы оо6°°' степеней свободы. Однако уравнения
Максвелла накладывают два ограничения на любые начальные данные в 3-пространстве,
а именно требуют равенства нулю дивергенции векторов электрического и магнитного по¬
лей* . Это уменьшает на 2 эффективное число свободных компонент при задании начальных
данных в трехмерном пространстве, то есть число степеней свободы в действительности
будет оо4°°3.
Рассмотрим теперь квантово-механическое описание п скалярных частиц. Если бы оно
включало просто п различных волновых функций, то было бы ос2по° степеней свободы,
поскольку была бы свобода выбора п комплексных чисел в каждой точке 3-пространства.
Однако в случае настоящей волновой функции, описывающей п скалярных частиц, мы
имеем одну комплексную функцию от 3п вещественных переменных. Это есть комплексное
скалярное поле в пространстве 3п измерений, поэтому степеней свободы будет сю2ос , что
несравнимо больше!
Непросто, по всей вероятности, представить себе, насколько огромно такое увеличение,
когда оно скрывается за всеми этими знаками бесконечности (оо). Поэтому давайте взглянем
на «игрушечную» Вселенную, состоящую всего из 10 точек. Мы можем пронумеровать эти
точки цифрами О, 1, 2, 3, 4, 5, 6, 7, 8, 9. Волновая функция скалярной частицы в такой
Вселенной будет состоять из комплексного числа, заданного на каждой из этих 10 точек,
т. е. всего будет 10 комплексных чисел: zo, zi, Z2, ■.., z9. Пространством всех таких волно¬
вых функций будет гильбертово пространство с 10 комплексными (или 20 вещественными)
измерениями Н10. Если нормировать волновую функцию таким образом, чтобы сумма квад¬
ратов модулей всех этих чисел г была равна 1, то, например, \zq\2 будет представлять
вероятность того, что измерение обнаружит частицу в точке 6, и т. п.
Эта дискретная модель в действительности не так уж абсурдна. В реальных физических
ситуациях можно иметь, например, набор из 10 ящиков и электрон, который может нахо¬
диться в одном из них (см. рис. 23.1). Экспериментаторы могут создавать нечто подобное
в виде так называемых квантовых точек, и это имеет отношение к теоретической возможно-
Попробуйте объяснить, почему это так. Напомним, что в § 19.3 было дано четырехмерное определение
«дивергенции», здесь же нам потребуется трехмерный вариант. (.Подсказка: см. упражнение 19.2.)

23.3. Квантовое перепутывание. Неравенства Белла
493
Рис. 23.1. Представим себе «игрушечную Вселенную», в которой существует всего 10 возможных
положений для частиц (здесь они показаны в виде 10 ящиков). Показаны две различимые частицы А
и В, каждая их которых, независимо от другой, может находиться в одном из ящиков
сти построения квантовых компьютеров, в которых должна использоваться та обширность
пространства волновых функций, о которой идет речь.
Предположим, что теперь в нашей Вселенной имеются две частицы. По причине, ко-
торой я коснусь позже, будет лучше, если это будут частицы разного сорта. Поэтому бу¬
дем называть их частица А и частица В. Каждая из этих двух частиц может находиться
в 10 различных местах, так что для пары частиц существует 100 возможных вариантов рас¬
положения (если разрешается находиться обеим частицам в одном и том же ящике). Теперь
для того чтобы определить волновую функцию, нам понадобятся 100 различных комплекс¬
ных чисел, скажем zoo, ^оъ ■ ■ •, ^09> ^ю» 2ц> ..., z 19, Z20, .... £99, по одному на каждую
пару положений частиц. Если произвести нормировку так, чтобы сумма квадратов моду¬
лей всех этих чисел z была равна 1, то, например, \z%s\2 будет представлять вероятность
найти частицу А в точке 3, а частицу В — в точке 8. Теперь мы имеем дело с простран¬
ством Н100. Если мы имеем три различные частицы А, В и С, то волновая функция будет
состоять из 1 000 комплексных чисел 2000» ^ооъ - • > z999, и нашим пространством состоя¬
ний будет Н1000. Если же применить эти правила к трем отдельным волновым функциям, то
on
пространством состояний было бы всего лишь Н . Для четырех различных частиц мы по-
м 10000	1	w	и40
лучим Н , тогда как для четырех отдельных волновых функции всего Н , и т. д.
Вернувшись к обозначению ооа°° , отметим тот факт, что верхнее со3 выражает «число
о
точек» в евклидовом 3-пространстве Е . Теперь это число заменяется на 10, настоящее число
точек в нашей игрушечной Вселенной, так что ооаос"п превращается в ооа1°п (что означает
«число точек» в пространстве а х 10п вещественных измерений). Таким образом, вме¬
сто оо2°° 71 степеней свободы п-частичной скалярной волновой функции в пространстве Е3
мы имеем оо2х10 степеней свободы п-частичной волновой функции в нашей игрушечной
Вселенной. Для n-частичной волновой функции в нашей игрушечной Вселенной комплекс-
1 пп
ным скалярным пространством служит И , тогда как для п отдельных одночастичных
комплексных волновых функций — пространство Н10п. Таким образом, наша п-частичная
волновая функция определена в 2 х 10п-мерном пространстве (10п-мерном комплексном
пространстве) вместо 20п-мерного пространства для п отдельных волновых функций. На¬
пример, в случае 8 частиц это будет 200000000 измерений вместо 160.
23.3.	Квантовое перепутывание. Неравенства Белла
Что дает вся эта дополнительная информация? Она выражает так называемое «пере¬
путывание» между частицами. Как следует это понимать? Перепутывание между частица¬
ми, понятие о котором впервые в явном виде сформулировал Шредингер [698], приводит
к крайне загадочным, но уже реально наблюдавшимся явлениям, известным под названи¬
ем эффектов Эйнштейна ~Подольского ~Розена (ЭПР-эффекты)^23,21 Это, однако, довольно
тонкие особенности квантового мира, которые нелегко демонстрировать экспериментально

494
Глава 23
сколько-нибудь убедительным образом. Любопытно, что мы начинаем ощущать присутствие
чего-то таинственного и скрытого от взоров, когда имеем дело с почти полной «информа¬
цией», заключенной в волновой функции многочастичной системы! Это загадка, к которой
я скоро вернусь (§ 23.6). Мне представляется, что эта загадка пытается сообщить нам что-то
о тех новых направлениях, в которых следует развивать нынешний квантовый формализм.
Но в любом случае она говорит нам о потенциальной мощи квантовых вычислений^23,31 —
предмета весьма активных современных исследований, призванных использовать те огром¬
ные «информационнные» ресурсы, которые скрыты в эффекте перепутывания.
Так что же такое квантовое перепутывание? В чем состоят ЭПР-эффекты? Будет по¬
нятнее, если мы рассмотрим ситуацию с конечным числом измерении, что можно сделать,
сосредоточившись на состояниях спина. Простейший пример ЭПР-эффекта был рассмот-
1
рен Дэвидом Бомом [86]. Представим себе пару частиц со спином - (назовем их Рь и Pr),
которые сначала находятся в комбинированном состоянии со спином 0, а затем расходятся
влево и вправо к приемникам соответственно L и R, разнесенным на большое расстояние
(см. рис. 23.2). Предположим, что каждый из приемников способен измерять спин прибли¬
жающейся к нему частицы, и пусть решение о том, с какой стороны проводить измерение,
принимается лишь после того, как частицы разошлись на достаточно большое расстояние.
Задача состоит в том, чтобы понять, оправдываются ли предсказания квантовой механики,
если пользоваться некоторой моделью, согласно которой частицы можно рассматривать как
не связанные между собой независимые объекты классического типа, каждый из которых
теряет связь с другим после их разделения.
Рис. 23.2. Мысленный эксперимент Бома но наблюдению ЭПР-эффекта. Две частицы Рь и Pr первона¬
чально находятся в комбинированном состоянии со спином 0, а затем двигаются в противоположных
направлениях, влево и вправо, к соответствующим приемникам L и R, разнесенным на большое рассто¬
яние. Каждый из приемников может измерить спин пришедшей к нему частицы, однако решение о том,
с какой стороны проводить измерение, принимается, только когда частицы уже находятся в полете.
Теорема Белла утверждает, что невозможно реализовать ожидания квантовой механики, пользуясь мо¬
делью, в которой частицы ведут себя как независимые классические объекты, теряющие связь между
собой после их разделения
Согласно замечательной теореме, выдвинутой физиком из Северной Ирландии Джоном
Беллом, оказывается, что воспроизвести предсказания квантовой теории таким путем невоз¬
можно. Белл вывел неравенства^23,4!, связывающие совместные вероятности результатов
двух физически разделенных измерений, которые противоречат предсказаниям квантовой
механики, хотя согласуются с любой моделью, в которой две частицы ведут себя как неза¬
висимые объекты после их физического разделения. Таким образом, нарушение неравенств
Белла указывает на присутствие существенно квантово-механических эффектов — это и есть
эффекты квантового перепутывания физически разделенных частиц, — которые нельзя объ¬
яснить в рамках любой модели, считающей частицы несвязанными и независимыми.
В литературе имеется много поразительных примеров подобного нарушения неравенств
Белла^23,5!. Некоторые из них, так называемые «неравенства Белла без вероятностей»^23,6!,
особенно примечательны тем, что они включают измерения типа ДА/НЕТ, так что нет на¬
добности связываться с вероятностями, точнее, там мы имеем дело лишь с крайними опре¬
деленными случаями с вероятностями 0 («никогда») и 1 («всегда»). Здесь я приведу лишь два
явных варианта противоречия между квантовыми и отдельными частицами типа неравенств

23.4. ЭПР-ЭКСПЕРИМЕНТЫ по Бому
495
Белла. В обоих фигурирует пара частиц со спином расходящихся к приемнику L слева
и приемнику R справа. Первый, который следует рассуждениям Генри Стаппа [743, 744],
является прямым примером первоначальной версии упомянутого выше ЭПР-эксперимента,
предложенного Бомом, для которого надлежит определить значения вероятности. Второй,
предложенный Люсьен Харди [356, 357], — это «почти» вариант без вероятностей.
Прежде чем перейти к деталям, необходимо добавить кое-что относительно обозна¬
чений Дирака. Пусть мы имеем квантовую систему, состоящую из двух частей \ф) и |ф),
которые можно считать взаимно независимыми. Квантовое состояние такой системы запи¬
шем в виде
ф)\ф).
Это одно целое состояние, и чтобы выразить этот факт, напишем х — \Ф)\Ф)' Произ¬
ведение такого типа алгебраисты называют тензорным произведением, оно подчиняется
правилам (г#»| ф) =	г(\ф)\ф)) = \ф){г\ф))>(|6>) +	=	+ | \Ф){Щ +
+ |ф)) — \ф)\9) + \ф)\ф). В математической литературе операция тензорного произведения
обозначается символом 0 (см. также § 13.7), так что произведение |ф)\ф) можно записать
в виде \ф) 0 |ф).
В любом случае удобно использовать символ 0 для (гильбертовых) пространств, кото¬
рым принадлежат такие произведения. Так, если |ф) принадлежит пространству Нр, а |ф) —
пространству Hq, то \ф)\ф) принадлежит пространству Нр 0 НТ Размерность простран¬
ства Нр 0 Ия равна произведению размерностей перемножаемых пространств, поэтому мож¬
но написать Нр0№ — Нря. Одна из размерностей р и q или они обе могут быть бесконечны¬
ми, в таком случае их произведение тоже можно принять равным оо. Лишь очень малая часть
пространства Нр 0 ЬН состоит из элементов вида \ф)\ф) (предполагается р, q > 1), где 1*0)
принадлежит пространству Нр, а |ф) — пространству Ия. Это неперепутанные состояния.
Произвольный элемент пространства Нр 0 Ия должен быть линейной комбинацией таких
неперепутанных состояний (в случае если р и q бесконечны, это может быть бесконечная
сумма или интеграл)I23*7!. Следует, однако, иметь в виду, что само понятие перепутыва-
ния зависит от конкретного расщепления нашего целого гильбертова пространства Нря на
произведение вида Нр 0 Ня. (Никакое подобное расщепление общего гильбертова простран¬
ства Нря не имеет преимущества перед остальными. В алгебраическом отношении всегда
существует много способов представления Нп в виде тензорного произведения, если п есть
составное число.) В ситуациях, когда нас интересует понятие «перепутывания», расщепле¬
ние, представляющее физический интерес, довольно очевидно, особенно когда «отдельные»
частицы разделены большим расстоянием, что всегда имеет место в ЭПР-эффектах.
Иногда оказывается полезной абстрактно-индексная формулировка операций такого ро¬
да (см. § 12.8). Кет-вектор |ф) можно представить в виде фа с верхним абстрактным индек¬
сом, а соответствующий (комплексно-сопряженный) ему бра-вектор (ф | — в виде фа с ниж¬
ним абстрактным индексом. Полные скобки (ф\ф) примут вид фафа, а выражение (ф\С2\ф)
будет выглядеть как ф^арф^. Тогда тензорное произведение \ф)\ф) векторов фа и ф& мож¬
но записать в виде фафР. Неперепутанные состояния всегда расщепляются подобным об¬
разом. Однако произвольное (возможно, перепутанное) состояние будет объектом вида фа@.
С примерами записи такого рода мы еще встретимся в этой главе.
23.4.	ЭПР-эксперименты по Бому
Вернемся теперь к варианту ЭПР-эксперимента, предложенному Бомом. Рассмотрим
начальное состояние непосредственно перед проводимым измерением. Две отдельные ча-
стицы со спином ~ должны образовать состояние со спином 0. Поскольку момент импульса
&

496
Глава 23
сохраняется, частицы стартуют в комбинированном состоянии со спином 0. Поэтому для
спина каждой частицы нам такая нужна комбинация базисных состояний, для которой пол¬
ный спин равен нулю. Это достигается, если взять состояние | Q) со спином 0, определяемое
следующим образом:
№) =Т Т)| I) - 11)1 Т)
(мы не заботимся здесь о нормировке состояний) 5 . В литературе подобные выражения
часто записываются в виде | f L)| j R) - | | L)| | R), из которого ясно видно, какое
состояние относится к левой частице, а какое — к правой. Мне кажется, что в этом нет
необходимости, поскольку 1) написанное выражение относится только к спиновой части
волновой функции, а не к координате частицы, или к импульсу, или к чему-то еще, поэтому
направление спина само показывает, с чем мы имеем дело; 2) поскольку тензорные произ¬
ведения некоммутативны, мы можем однозначно определить, какая «сторона» произведения
относится к какой частице. Мы договоримся, что левый сомножитель в тензорном произве¬
дении относится к левой частице, а правый — к правой. Читатель, которому это покажется
слишком запутанным, может при желании в ходе всего обсуждения добавлять в кет-векторы
символы L и R.
Это очевидный пример перепутанного состояния, поскольку его нельзя записать в ви¬
де |а)|/3), где \а) относится к L-частице, а \0) — к R-частице***. Попробуем понять, к каким
следствиям приводит такое перепутывание. Предположим, что я нахожусь слева, около при¬
емника L, и намерен произвести измерение спина левой частицы Pl в направлении «вверх» ^
(ответ ДА, если |, и НЕТ, если |). Это означает проектирование полного состояния J2 в со¬
стояние | f)| |), если я получаю ответ ДА, и в состояние (—)| l)\ f) в случае ответа НЕТ.
Результат будет неперепутанным, за исключением стандартной U-эволюции, из-за которой
частица Pl оказывается безнадежно перепутанной с моей измерительной установкой L. Что
можно определенно утверждать, так это то, что если я получаю ответ ДА, то мой коллега,
находящийся возле приемника R, обнаружит частицу Pr в спиновом состоянии | |), если же
результатом моего измерения будет НЕТ, мой коллега получит состояние | "f). При проведе¬
нии последовательности измерений спина частицы Pr в направлении «вверх» мой коллега
будет неизменно получать результат, противоположный полученному мной.
Выбор направлений вверх/вниз здесь ничем не выделен: если я выберу для измерения
какое-то другое направление, скажем то мой коллега, выбрав то же самое направле¬
ние получит результат, противоположный моему. Это должно быть ясно из соображений
вращательной инвариантности состояния со спином 0, однако поучительно провести непо¬
средственное алгебраическое вычисление и проверить, что
Я) <х\ S)\S) - \ S)\S),
где есть направление, противоположное направлению ^ (символ ос означает «пропорци¬
онально», т. е. «равно с точностью до множителя, отличного от нуля», см. § 12.7). (Заметим,
что если | У) — а\ f) 4- b\ |), то | /*) <х 6| Т) — а\ |).)
Из всего этого можно также прийти к заключению о том, каковы будут совместные ве¬
роятности ответов ДД, ДН, НД, НН (Д означает ДА, Н означает НЕТ), если я и мой коллега
выбираем разные направления для измерения спина. Предположим, я выбрал направле¬
ние а мой коллега — направление и угол между этими направлениями равен в. Тогда,
Какой множитель появится у состояния | Q), если состояния | Т ) и j 4) нормированы? (Можно допустить,
4T0J[ |а)[/?>|| = II ИII II |/3)||0
** Jgg Понятно ли, почему это состояние имеет спин 0? (Подсказка: можно воспользоваться индексной записью
и показать, что любая подобная антисимметричная комбинация должна быть скаляром, имея в виду, что спиновое
пространство двумерно.)
Почему нельзя? Найдите способ сделать это, если состояния | а) и | (3) не локализованы подобным образом.
Подтвердите это замечание в скобках и проверьте непосредственным вычислением вышеприведенное
****
выражение для |42). {Подсказка: см. упражнение 22.27.)

23.4, ЭПР-ЭКСПЕРИМЕНТЫ по Бому
497
используя значение вероятности, приведенное в § 22.9 (см. рис. 22.11), получаем совместные
вероятности:
1 1
в случае согласия:	-(1	- cos#), в случае несогласия:	~(1 + cos#)
(«согласие» соответствует результату ДД или НН, «несогласие» — результату ДН или НД).
Обратимся теперь к примеру Стаппа. Пусть конструкция моей установки такова, что
она может измерять спин либо в направлении вертикально вверх (Т), либо в горизонтальном
направлении —■», перпендикулярном направлению t- Установка моего коллеги ориентирована
на измерение спина либо в направлении /*, которое лежит в плоскости направлений t и
под углом 45° к каждому из них, либо в направлении "Х, которое лежит в той же плоскости,
но под углом 45° к | и 135° к —> (см. рис. 23.3). Существуют три возможных варианта,
когда направление моего измерения составляет 45 ° с таковым у моего коллеги, и всего один
вариант, при котором этот угол равен 135°. При угле 45° вероятность согласия немного
меньше 15%, при угле 135° она превышает 85%.
L
R
Возможные варианты	Возможные	варианты
измерений для меня	измерений	для	моего коллеги
Рис. 23.3. Измерение поляризации в варианте Стаппа для ЭПР-эксперимента, предложенного Бомом, —
пример неравенств Белла. Сначала измерения спина проводятся на любой из сторон в направлениях,
показанных сплошными стрелками, однако, в зависимости от настроения, та или другая сторона или
они обе могут изменить эти направления на перпендикулярные, показанные прерывистыми стрелками.
Квантовые совместные вероятности не удается моделировать никакой классической схемой, в кото¬
рой две частицы ведут себя как не связанные между собой независимые объекты без предвидения
направлений, в которых предполагается проводить измерения
Допустим, что решение о том, в каком из двух возможных направлений я буду проводить
измерение, принимается, когда частицы уже находятся в полете, и то же относится к моему
коллеге. Предположим, что мой коллега находится на Титане (это одна из лун Сатурна),
а источник частиц находится где-то между нами, так что даже при световой скорости частиц
мы будем иметь примерно три четверти часа для принятия решений! (См. рис. 23.4.) Частицы
«не имеют понятия», каким образом мой коллега и я собираемся (независимо друг от друга)
ориентировать свои измерительные приборы.
Предположим, я выбираю направление а мой коллега — направление и каждый из
нас принимает поток частиц, ориентированных, по-видим.ому, случайно. Частицы приходят
поодиночке, каждая из них является членом одной и той же пары ЭПР-Бома, испускаемой
источником, расположенным посредине, который посылает одну из частиц ко мне, дру¬
гую — к моему коллеге. Когда мы сравним наши записи (возможно, это произойдет через
несколько лет, когда мой коллега вернется на Землю), мы обнаружим, что между нашими
соответствующими результатами согласие составляет немного меньше 15%, что согласуется
с вышесказанным.
Если частицы не имеют предварительного знания о том, как мы собираемся ориенти¬
ровать наши приборы, и ведут себя как отдельные несвязанные (классические) объекты, то
оезультаты изменений моего коллеги не изменились бы. если бы я в последний момент вне-
намерения
. Если бы я поступил

498
Глава 23
Титан
ЭПР-источник
Рис. 23.4. Автор, находящийся на Земле, принимает одну из компонент последовательности пар частиц
в ЭПР-эксперименте, другую принимает коллега, находящийся на Титане; источник частиц располо¬
жен приблизительно посредине между ними. Даже если частицы движутся со скоростью света, есть
примерно 45 минут для принятия решения относительно ориентации приемника
таким образом, то, поскольку угол между направлениями по-прежнему остается равным 45°,
согласие между результатами моих новых измерений и прежними измерениями моего кол¬
леги составило бы прежние 15%. С другой стороны, допустим, что в последний момент
изменил намерения мой коллега, и он проводил измерения в направлении вместо
тогда как я не менял своих намерений. Изменение выбора моего коллеги не влияет на мои
первоначальные измерения в направлении Мы опять-таки обнаружим, что новые измере¬
ния моего коллеги в направлении дают 15%-ное совпадение с моими первоначальными
измерениями в направлении |.
Допустим, однако, что мы оба в последний момент решили изменить ориентацию наших
установок, так что я стал проводить измерение в направлении —>, а мой коллега — в на¬
правлении Теперь угол между направлениями наших измерений окажется 135°, поэтому,
согласно предсказаниям квантовой механики, совпадение будет иметь место более чем в 85%
случаев. Согласуется ли это с поведением пар частиц, если вычислить совместные вероят¬
ности для каждой возможной комбинации ориентаций приемников? Давайте посмотрим.
Пара частиц должна быть подготовлена к встрече с любой из четырех возможных комбина¬
ций ориентации приемников и в каждом случае давать правильные квантово-механические
вероятности. Напомним, каковы они. Результаты при измененной ориентации —► моего при¬
емника и прежней ориентации приемника коллеги согласуются не более чем в 15%
процентах случаев. То же получается при первоначальной ориентации моего приемника t
и измененной ориентации приемника коллеги Если некоторая пара частиц собирает¬
ся дать согласие результатов измерений в случае —>,	то не может быть несогласия во
всех трех случаях: и —>, /*, и	и	(Три	отрицания дают отрицательный ответ
и не могут дать положительный.) Поэтому по крайней мере в одном из этих трех возмож¬
ных вариантов ориентации приемников должно иметь место согласие результатов. Но такое
случается не более чем в 15% случаев при каждой возможной ориентации. Вариантов ориен¬
тации всего три, поэтому при установке —*\ возможно не более 15%-Е15% Ч~ 15% = 45%
совпадений. (Фактически процент совпадений оказывается немного меньше, поскольку при
нашем подсчете предполагалось, что совпадения имеют место при всех трех вариантах ори¬
ентации.) Но 45% — это никак не 85%, так что налицо вопиющее противоречие с нашими
«классическими» допущениями относительно пары частиц!
Некоторых может смутить тот факт, что в наших рассуждениях фигурируют гипотети¬
ческие измерения, то, что «могло бы случится, но не случилось» (философы называют это
«контрфактуальными действиями»). Но это не столь важно. Главным здесь является допу¬
щение, что частицы ведут себя независимо одна от другой после того, как они покинули
источник, и что реализуются правильные квантовые совместные вероятности при любой
комбинации ориентаций приемников. То есть частицы должны следовать предсказаниям
квантовой механики. Мы видели, что нельзя рассматривать эти предсказания для каждой из
двух частиц по отдельности. Правильный квантово-механический результат соответствует
тому, что частицы как бы «связаны» между собой до того момента, когда та или другая
О
Земля

23.5. ЭПР-ЭКСПЕРИМЕНТ ПО ХАРДИ — ПОЧТИ БЕЗ ВЕРОЯТНОСТЕЙ
499
подвергается измерению. В этой загадочной «связи» между частицами и состоит явление
квантового перепутывания.
Конечно, эксперименты подобного рода не проводились на таких расстояниях. Однако
многие подобные, по существу, ЭПР-эксперименты были реализованы (обычно с исполь¬
зованием поляризации фотонов, а не направлений спина у частиц со спином ~, но это
различие не играет роли). При этом полностью оправдались ожидания квантовой механики
(а не «здравого смысла»)! Хотя квантовое перепутывание такого рода пока заведомо не на¬
блюдалось на расстояниях Земля-Сатурн, некоторыми экспериментами было подтверждено
нарушение неравенств Белла на расстояниях более 15 километровf23-8!.
23.5.	ЭПР-эксперимент
Рассмотрим теперь красивый пример, предложенный Люсьен Харди^23*9^. Мой коллега
и я снова проводим измерения спина. При этом я, как и прежде, выбираю между направ¬
лениями | и (вертикально вверх и горизонтально вправо), однако мой коллега теперь
также выбирает между f и —» совершенно независимо от моего выбора. Существенно новое
здесь в том, что источник пар частиц теперь испускает их не в комбинированном состоянии
со спином 0, а в состоянии со спином 1. Я выбираю это начальное состояние как состояние
в представлении Майораны |	/*) (§22.10, рис. 22.14), причем направление лежит
в квадранте, образуемом взаимно-перпендикулярными направлениями Т и —и имеет на¬
клон у (так что угол в между —» и у75 удовлетворяет условию cos# = |), а направление
О	о
противоположно направлению —► (см. рис. 23.5). Это состояние с точностью до общего
множителя можно представить в виде'
У') = I <->1 У') +1 S)\ <->■
Оно обладает важным свойством: будучи неортогональным к состоянию
i)i I),
(|Х) противоположно |Т))? оно ортогонально каждому из состояний
DI <->, I <->1 i>, I -и ->•
Эти соотношения ортогональности приводят соответственно к следующим свойствам
ДА/НЕТ (0), (1), (2), (3):
(0) иногда я получаю ответ НЕТ при измерении в направлении	когда мой коллега полу¬
чает ответ НЕТ при измерении в направлении Т;
(1) если я получаю ответ НЕТ при измерении в направлении	то мой коллега должен
получить ДА при измерении в направлении
(2) если мой коллега получает ответ НЕТ при измерении в направлении |, то я должен
получить ДА при измерении в направлении
(3) я никогда не получаю ответ ДА при измерении в направлении —», когда мой коллега
получает ДА при измерении в направлении
*
**
Почему?
Попробуйте доказать это. {Подсказка: воспользуйтесь координатным и/или геометрическим описанием
зз §22.9.)

500
Глава 23
В связи со свойством (0) можно отметить, что квантово-механическая вероятность получе¬
ния нами обоими ответа НЕТ, когда мы оба выбираем измерения в направлении Т> точно
равна — .* Заметим, что ^ — 8,33%, тогда как оптимальное значение Харди с некоторыми
поправками близко к 9,017% J23-10]
Спин —
2
Мои возможные
варианты измерения
Спин —
2
 Q
Возможные варианты
измерения у моего коллеги
Рис. 23.5. Вариант ЭПР-эксперимента «почти» без вероятностей, предложенный Харди. Начальное
состояние со спином 1 имеет вид
)\S) + \ /*)\ ч—}, причем направление /* лежит
в квадранте, образуемом вертикальным направлением Т и горизонтальным
, и имеет наклон Каж¬
дый приемник измеряет спин приближающейся частицы либо в вертикальном, либо в горизонтальном
направлении
Я должен объяснить, почему невозможно получить результаты (0),..., (3), если две
частицы являются отдельными не сообщающимися между собой объектами, без предва¬
рительного знания о том, какие эксперименты будут проводиться над ними. Вследствие
свойства (0) две частицы (относительно которых предполагается отсутствие связи и предва¬
рительной информации) должны быть приготовлены таким образом, чтобы время от времени
(фактически часть времени) давать ответ НЕТ при условии, что я и мой коллега одно-
JL Z
временно проводим измерения в направлении Кроме того, при подготовке частиц (пока
они еще находятся вместе) необходимо позаботиться, чтобы в тех случаях, когда они дают
одновременный ответ НЕТ при одновременном измерении в направлении t? они опреде¬
ленно давали ответ ДА при измерении в направлении —проводимом лишь одним из нас,
чтобы не нарушать условия (1) или (2). В то же время само решение подвергает частицы
риску столкнуться с условием (3), поскольку я и мой коллега можем оба решить проводить
измерения в направлении —» и получить при этом запрещенный результат ДА, ДА.
23.6. Две загадки квантового перепутывания
Мне представляется, что с квантовым перепутыванием связаны две совершенно разные
загадки, и я полагаю, что ответ на каждую из них имеет различный (хотя и взаимосвязанный)
характер. Первая загадка — это само явление перепутывания. Как с ним согласиться и выра¬
зить его смысл в виде идей, которые мы в состоянии постигнуть, так чтобы мы были готовы
принять его как нечто, составляющее важную часть поведения нашей реальной Вселен¬
ной? Вторая загадка в некотором смысле дополнительна по отношению к первой. Согласно
квантовой механике, перепутывание представляет собой вездесущее явление (напомним,
что подавляющее большинство квантовых состояний относится именно к перепутанным), —
почему же в таком случае мы так редко встречаемся с ним в нашем непосредственном по¬
стижении мира? Почему с вездесущими эффектами перепутывания мы не сталкиваемся на
Покажите это.

23.6. Две загадки квантового перепутывания
501
каждом шагу? Я не уверен, что эта вторая загадка привлекает такое внимание, какого она
заслуживает, внимание людей почти исключительно концентрируется на первой.
Позвольте мне начать со второй загадки; к первой я вернусь в свое время. Загадка связа¬
на с тем фактом, что перепутывание имеет тенденцию к распространению. Представляется,
что в конечном счете каждая частица во Вселенной должна стать перепутанной с каждой
из остальных. Или они уже и так все перепутаны одна с другой? Почему же мы не испы¬
тываем влияния этой перепутанной мешанины, никак не похожей на (почти) классический
мир, который мы реально воспринимаем? Шредингеровская эволюция системы в этом нам
помочь не может. Она стремится ухудшить положение: с какой бы системы мы ни начали,
с течением времени с ней становятся перепутанными все новые и новые части Вселенной.
На языке гильбертова пространства Н становится особенно очевидным, я полагаю, что урав¬
нение Шредингера (U-процесс) само по себе не может помочь нам в наших затруднениях.
Если даже мы стартуем из относительно неперепутанной части пространства Н, все равно
шредингеровская эволюция обычно немедленно заводит нас в перепутанные глубины и сама
по себе не дает нам какого-либо пути или хотя бы направления выхода из этого заросшего
водорослями огромного океана перепутанных состояний (см. рис. 23.6).
Ир
Нр®Нд
Островок
неперепутанных
^состоянии
Рис. 23.6. Шредингеровская эволюция из начального неперепутанного состояния (островок справа
внизу) почти всегда приводит к увеличению перепутанности (изображенной в виде моря, заросшего
водорослями). Почему же в таком случае обычные объекты нашего повседневного опыта выглядят как
отдельные независимые предметы?
Тем не менее в повседневном быту мы успешно пребываем, не замечая этого перепу¬
тывания. Почему? Если мы не получили помощи от U-процесса квантовой теории, тогда мы
должны обратиться к другому ее ингредиенту — R-процессу. Фактически мы уже встрети¬
лись кое с чем из того, что может помочь нам при рассмотрении ЭПР-эффектов. Напомню,
что я предполагал проведение измерения на ЭПР-паре, один из членов которой приближался
к моему коллеге на Титане. Если я произвожу измерение первым, то сам факт измерения
освобождает частицу моего коллеги от перепутывания с моей частицей, и с этого момента
(до момента ее измерения моим коллегой) она будет обладать собственным вектором состо¬
яния, более не стесненным связью с ее партнером, независимо от того, что я буду делать
дальше. Получается, что именно измерения разрывают эту перепутанность. Так ли это? Дает
ли R-процесс общий ответ на вторую загадку, поставленную самим явлением квантового
перепутывания?
Я полагаю, что ответ должен быть утвердительным, по крайней мере в отношении
практического применения квантовой механики. Имеется в виду постановка любого кван¬
тового эксперимента, подобного только что рассмотренным (мысленным) экспериментам.
Напомним, что в наших ЭПР-экспериментах мы требовали, чтобы пары частиц находились
в определенном квантовом состоянии — со спином 0 в примере Стаппа и со спином 1 в
примере Харди. Как, используя только U-процессы, мы можем быть уверены в том, что

502
ГЛАВА 23
наши частицы уже не перепутаны самым тесным образом со всем вокруг? Мне кажется,
что в природе «измерения» всегда заложена существенная часть постановки квантового
эксперимента, чтобы состояние не было искажено массой нежелательных эффектов перепу-
тывания. Говоря это, я не имею в виду, что экспериментатор преднамеренно производит «из¬
мерение», чтобы достичь такого результата. По моему мнению, сама Природа непрерывно
реализует R-процессы без каких-либо направленных усилий со стороны экспериментатора
или какого-то вмешательства «разумного наблюдателя».
Здесь я вступаю на зыбкую почву, и к моей собственной позиции в этом вопросе я вер¬
нусь позже (в §§ 30.9-30.13). Но как обстоит дело с «обычной» квантовой механикой? Такое
впечатление, что «на практике» физики почти всегда полагают, что этим предполагаемым
перепутыванием с внешним миром можно пренебречь. В противном случае нельзя было бы
доверять ни классической механике, ни стандартной квантовой механике. Похоже, что все
эти эффекты перепутывания как-то «усредняются», так что на практике, в любой реальной
ситуации, их можно не учитывать. Пока я не могу представить сколько-нибудь убедитель¬
ного доказательства, что дело обстоит именно так. Вместо усреднения может оказаться, что
в известной нам Вселенной всё становится меньше и меньше, при этом отдельные объекты
не имеют даже приблизительно определенных положений, поскольку они ничем не выде¬
лены среди множества других положений во Вселенной. Я не вижу какого-либо выхода из
этой головоломной ситуации, если рассматривать ее отдельно от U/R-парадокса, который
находится в центре интерпретации квантовой механики.
Рассматривая это всепроникающее перепутывание с остальной Вселенной, мы не в со¬
стоянии отделить его от более широкой проблемы: почему, с одной стороны, U-процедура
столь хорошо работает в случае достаточно простых систем, а с другой, мы вынуждены
время от времени отказываться от нее и резко, пусть неявно, прерывать ее R-процессом?
Почему, а также когда и как мы должны это делать? Говоря словами Нобелевского лауреата
Тони Леггетта, в этом состоит проблема измерения или (что, на мой взгляд, более точно)
парадокс измерения. К этому вопросу я еще вернусь в главе 29.
Я еще не покончил с другими загадками, которые задает нам перепутывание. Неко¬
торые из них связаны с тем, что измерение перепутанной системы вступает в конфликт
с требованиями теории относительности, поскольку измерение, проводимое на одной части
перепутанной пары, одновременно оказывает влияние на другую, а это, как мы видели в гла¬
ве 17, не должно поощряться, если мы остаемся верны принципам теории относительности.
Прежде чем заняться этой проблемой, я должен обратиться к еще одному аспекту перепу¬
тывания. Эта сторона дела оказывается еще более вездесущей, нежели то, что обсуждалось
в нескольких предыдущих абзацах. Она имеет настолько всеобъемлющий характер, что ее
не загораживает даже проблема измерения, независимо от способа, который мы выберем
при обсуждении парадокса измерения. Более того, это характерная особенность квантовой
механики, которая выглядит не зависящей от других, рассмотренных до сих пор. Я имею
в виду тот замечательный способ, посредством которого квантовая механика описывает
тождественные частицы.
23.7* Бозоны и фермионы
Вспомним о нашей занимательной «игрушечной Вселенной» (§ 23.2), в которой для ча¬
стицы доступны лишь 10 различных положений, нумеруемых цифрами 0, 1, 2, 3, 4, 5, 6, 7,
8, 9. Когда я предполагал, что эту Вселенную может населять более одной частицы, я об¬
ращал внимание на то, чтобы их нельзя было считать частицами «одного и того же сорта»,
и называл их «частица А», «частица В» и т.д., а не, скажем, «два электрона» или как-ни¬
будь еще в этом роде. Причина состоит в том, что квантовая механика трактует частицы,
реально существующие в природе, способом, существенно отличным от того, которого мы

23.7. Бозоны И ФЕРМИОНЫ
503
придерживались в нашем предыдущем обсуждении. Более того, мы должны разделить два
совершенно различных таких способа! Один из них применяется в отношении частиц, на¬
зываемых бозонами, другой — к частицам, именуемым фермионами. Бозонами оказываются
частицы с целым спином (т. е. такие, спин которых, будучи измерен в единицах ft, принима¬
ет одно из значений 0, 1, 2, 3, ...), а фермионами — частицы с полуцелым спином, т. е. со
1 о с 7
значением спина	... Такое сопоставление следует из знаменитой математиче¬
ской теоремы, которая в контексте квантовой теории поля носит название теоремы о связи
спина со статистикой, см. § 26.2. Составные частицы вроде ядер, или целых атомов, или,
скажем, отдельных адронов — протонов или нейтронов (рассматриваемых как составленные
из кварков) — можно с достаточным приближением рассматривать как отдельные бозоны
или отдельные фермионы. Так, бозонами являются фотоны, мезоны (пионы, каоны и др.)
и частицы, ответственные за слабое взаимодействие (W- и Z-частицы) и сильное взаимодей¬
ствие (глюоны). Явно составные а-частицы (2 протона, 2 нейтрона), дейтроны (1 протон, 1
нейтрон) и т. д. также ведут себя почти как бозоны. С другой стороны, электроны, протоны,
нейтроны, составляющие их кварки, нейтрино, мюоны и многие другие частицы являются
фермионами. Можно отметить тот факт, что волновые функции фермионов являются спи-
норными объектами в терминологии § 11.3 (сравните с § 22.8), тогда как волновые функции
бозонов таковыми не являются.
Чтобы понять, чем реально отличаются бозоны от фермионов, вернемся к нашей иг¬
рушечной Вселенной с 10 точками 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Напомним, что приемлемым
аналогом волновой функции может служить просто набор комплексных чисел zq, z\b • * * > z9
ДЛЯ ОДНОЙ частицы, Zoo? • * • j z99 ДЛЯ двух различимых частиц, 2Д00, £(ЮЪ • • * » ^999 ДЛЯ
трех таких частиц и т.д. Однако для пары бозонов выдвигается требование, чтобы набор
комплексных чисел был симметричен по своим индексам:
zij — zjiy
так что, например, z$$ — 2§з. Таким образом, при использовании этой «волновой функ-
ции» безразлично, какая из частиц находится в точке 3, а какая в точке 8. Имеется лишь
пара частиц, занимающая две точки 3 и 8. Заметим, что обе частицы, составляющие пару
бозонов, могут с успехом находиться в одном и том же месте, например, 2:33 есть комплекс¬
ный весовой множитель для двух бозонов, одновременно занимающих точку 3. Видно, что
существует всего ~(10 х 11) = 55 различимых способов разместить (неупорядоченную)
Li
пару частиц на 10 точках, и нам необходимо только это количество комплексных чисел
(т. е Н55 вместо Н100). При трех тождественных бозонах мы имеехм симметрию по всем трем
аргументам:
zijk ~ zjik = zjki ~ zkji zkij ~~ zikji
так что теперь требуется |(Ю х 11 х 12) = 220 комплексных чисел для определения состоя¬
ния, являющегося элементом пространства Н220 вместо Н1000. Для п тождественных бозонов
таким числом будет (9 + п)!/9!п! — оно выражает количество независимых комплексных
чисел	полностью	симметричных но своим индексам (относительно такого способа
обозначения см. §§ 12.4, 12.7, 14.7):
zij...m ~ z(ij...m)‘
Теперь обратимся к фермионам. Отличие от бозонов состоит в том, что волновая функ-
должна
zij —	zji 1
zijk “ ~~zjik “ zjki —	zkji	zkij ~~ zikj

504
Глава 23
так что мы имеем |(10 х 9) = 45 комплексных чисел для двух тождественных фер-
1
мионов, g(10 х 9 х 8) = 120 комплексных чисел для трех тождественных фермионов
и 10!/п!(10 — п)\ для п тождественных фермионов5". Разница в результатах подсчетов про¬
истекает из того факта, что теперь мы не позволяем двум фермионам находиться в одной
и той же точке, поскольку антисимметрия означает, что в этом случае комплексные веса
должны обращаться в нуль: Z33 ~ 0, 2:474 = 0 и т. п.
Заметим, что если в нашей игрушечной Вселенной содержится более 5 фермионов,
то эти числа начинают уменьшаться. Если число фермионов достигает 10, то имеется всего
одно возможное состояние, а больше 10 тождественных фермионов в нашей Вселенной быть
не может. Мы видим, в рамках данной модели, проявление важного принципа квантовой
физики, именуемого принципом запрета Паули. Он гласит, что два тождественных фермиона
не могут находиться в одном и том же состоянии (это просто есть следствие антисимметрии
волновых функций фермионов). Тот факт, что твердые тела не «схлопываются» внутрь себя,
связан в конечном счете именно с этим принципом. Обычное твердое вещество состоит
в основном из фермионов — электронов, протонов, нейтронов. В силу принципа Паули они
должны «избегать друг друга».
В случае бозонов ситуация иная. У бозонов имеется некоторая тенденция «предпочи¬
тать» находиться в одном том же состоянии. (Это чисто статистический эффект, получа¬
ющийся при сравнении результатов подсчета для различных бозонных состояний с соот¬
ветствующими результатами для различных классических состояний.) При очень низких
температурах этот эффект начинает играть важную роль, и становится возможным явление,
называемое конденсацией Бозе - Эйнштейна, когда большинство тождественных частиц со¬
бирается в одном и том же состоянии. Примером такого рода могут служить сверхтекучие
жидкости, и даже лазеры основаны на этом эффекте. В сверхпроводнике электроны находят
способ «спариваться» друг с другом, и такие куперовские пары приобретают способность
вести себя, как отдельные бозоны. Некоторые из этих впечатляющих и противоречащих ин-
туиции практических применении квантовой механики связаны именно с «коллективными»
явлениями такого рода.
23,8.	Квантовые состояния бозонов и фермионов
Хотя я сформулировал требования симметрии и антисимметрии бозонов и фермионов
только в отношении нашей «игрушечной Вселенной», в обычном пространстве условия сим¬
метрии для набора реальных бозонов и фермионов в основном те же самые. Волновая функ¬
ция будет функцией от ряда точек пространства, обозначаемых u, v, ..., у, и различных
дискретных параметров и, г?, ..., у, представляющих спинорные или тензорные индексы
для каждой группы частиц. Зададимся сначала вопросом, как должна выглядеть волновая
функция ф для пары тождественных бозонов. Требование, налагаемое на волновую функ¬
цию ф = ф(и, и; v, v), состоит в том, что она должна быть симметрична относительно
перестановки частиц:
ф(и, и; V, v) — ф{у, у; и, и).
В случае трех тождественных бозонов наша волновая функция должна быть симметрична
относительно перестановок всех трех частиц:
ф{и, и; v, v; w. w) — ^(v, v; и, щ w, w) — ф{х, v; w, w\ u, u) = ...
и т.д.
Объясните, как получаются все эти числа для случаев бозонов и фермионов,

23.8. Квантовые состояния бозонов и фермионов
505
В случае фермионов эти соотношения заменяются условиями антисимметрии относи¬
тельно перестановки частиц:
ф{и, и; v, v)	=	v; и, и),
ф(и, и; v, v:;	w,	w) = —ф(у, v; u, и; w,	id) = i/>(v,	v; w, го; u,	«)	= ...
и т. д. Заметим, что в каждом случае при таких перестановках спиновое состояние (харак¬
теризуемое дискретными переменными щ v, .,.) должно переноситься вместе с частицей.
Из этого следует, что при использовании принципа Паули мы считаем частицы тождествен¬
ными, только если у них одинаковы как координаты, так и спиновые состояния. Это играет
важную роль, например, в химии, где два электрона могут находиться на одной и той же
орбите при условии, что	их	спины противоположны	(см. §24.8,	рис. 24.2).
Здесь может оказаться	удобной (абстрактная)	индексная	запись, упомянутая	выше,
в § 23.3 (а также диаграммное представление, описанное в § 12.8, — см. рис. 26.1). Мы можем
ввести обозначение фа для волновой функции некоторой частицы, отмеченной индексом а,
и ф'в для волновой функции другой частицы, которой приписывается индекс /3, и т. д. Если
частицы не тождественны, то волновая функция пары частиц будет иметь вид (тензорного)
произведения
если же они будут тождественными бозонами, то волновая функция (без учета нормировки)
будет иметь вид
фафР 4- фафР.
(Относительно абстрактно-индексной формулировки: мы имеем коммутативное умножение,
например, фаф& = ф>вфа. Некоммутативность тензорного произведения учитывается по¬
рядком индексов, так что неравенство \ф)\ф) ф |Ф)\Ф) выражается в виде фаф@ ф фаф@.)
Можно записать такое симметризованное состояние (опуская множитель 2) как
ф^фР\
где круглые скобки означают симметризацию (§§ 12.7, 22.8). Здесь имеется то преимуще¬
ство, что можно немедленно представить квантовое состояние п тождественных бозонов
с индивидуальными состояниями фа, фР, ..., хк в виДе симметризованного произведения
ф(а фР ...	•
То же самое можно проделать в отношении фермионов с индивидуальными состояния¬
ми фа, ф@, ..., хп- Набор из п тождественных фермионов будет иметь антисимметризован-
ное состояние (§ 12.4)
Ф^а Фа... хк] ■
f
Заметим, что в математическом отношении все эти многочастичные состояния пере¬
путаны (это видно, например, из того, что пара тождественных фермионов описывается
комбинацией фаф@ — фаф@). Это, однако, довольно «мягкий» вид перепутывания, посколь¬
ку суперпозиция возникает между «физически неразличимыми» состояниями, так как рас¬
сматриваются только тождественные частицы. Состояния ф(аф@ ... хк^ и ф^аф^ ... х^ со¬
ответственно для бозонов и фермионов ближе всего к «неперепутанным» состояниям, и мы
можем занять альтернативную позицию и называть такие состояния «неперепутанными».
(Общее п-частичное бозонное состояние в таком случае будет иметь «нерасщепленный»
вид	Аналогично	будет	выглядеть	общее n-частичное фермионное состо¬
яние	— ijf/N3—'*!,) в записи, использующей кет-векторы, условия симметрии и анти¬
симметрии можно передать^23 Л11 с помощью «V-произведения» \ф) А \ф) А ... А |х); здесь

506
Глава 23
имеется в виду, что сомножители коммутируют или антикоммутируют в зависимости от их
«ранга» (см. § 11.6).
Хотя тот тип «перепутывания», который встречается в случае тождественных бозонов
или фермионов, довольно «безобиден» (и фактически уменьшает, а не увеличивает большое
количество возможностей, открытых для квантовой системы), существует по крайней ме¬
ре одно существенное практическое применение для эффекта распространения на большие
физические расстояния. Бозонная «перепутанная» природа фотонов, приходящих к Земле
с противоположных сторон сравнительно близкой звезды, использовалась для измерения
диаметра таких звезд методом Хэнбери Брауна-Твисса [347, 348]. Когда этот метод был
впервые предложен, он встретил большое сопротивление со стороны многих (в том числе
и выдающихся) специалистов в области квантовой физики, которые утверждали, что «фото¬
ны могут интерферировать только сами с собой, но не с другими фотонами»; при этом они
упускали из виду тот факт, что «другие фотоны» — это часть целой перепутанной бозонной
системы.
23.9.	Квантовая телепортация
В заключение этой главы вернемся к загадкам, связанным с интерпретацией ЭПР-эф¬
фектов. Более конкретно, вспомним о видимом конфликте со специальной теорией относи¬
тельности: «связь» между членами ЭПР-пар как будто не обращает внимания на утверждение
эйнштейновской теории о невозможности распространения сигналов быстрее света. Чтобы
осветить этот вопрос, я рассмотрю здесь еще одно довольно загадочное следствие кван¬
тового перепутывания, известное под названием квантовой телепортации. На мой взгляд,
оно указывает нам путь, которым следует воспользоваться для перехода к описанию ЭПР-
эффектов в общем виде. В то же время этот путь ведет нас в область, войти в которую
большинству людей покажется нелегким делом, — и, как мы увидим, не без оснований!
Что понимается под термином «телепортация»? Это слово вызывает в памяти фильм
«Звездный поход», в котором образы капитана Кирка и его команды были перенесены на
поверхность необитаемой планеты; при этом считалось, что для успешного воспроизвод¬
ства «индивидуальности» личности необходимо точно передать на поверхность планеты
квантовое состояние, а не просто классическое описание положения всех частиц и т.п.
Такая перспектива обладает, с философской точки зрения, тем преимуществом, что про¬
цедура телепортации не может использоваться для «удвоения личности», что могло бы
представить щекотливую проблему — кто из двоих должен считаться продолжателем «по¬
тока сознания» t23*12^? Почему невозможно скопировать неизвестное квантовое состояние?
Этот вопрос широко обсуждался в литературе^23 131. Можно увидеть из общих соображений,
что подобная возможность привела бы к противоречию с принципами стандартной кванто¬
вой механики с U/R-процедурами. Пока мы не готовы разрушить оригинал, мы не сможем
создать точную копию, и поэтому невозможно создать две точные копии неизвестного кван¬
тового состояния.
Почему это невозможно? Если бы это было возможно, то, повторяя процесс, можно
было получить 4 копии, потом 8, затем 16 и т.д. Предположим, что исходное состояние
представляет собой простое спиновое состояние | У) массивной частицы со спином
Тогда после многократного копирования мы получили бы состояние j У)\ У)... | У) —
— | У*/" ... У), которое при достаточно большом моменте импульса можно измерить
классическим образом и таким образом определить пространственное направление | У).
При этом мы получили бы измерение состояния как оно есть (с точностью до коэффициента
пропорциональности). Однако стандартные U/R-процедуры квантовой механики не позво¬
ляют это сделать. Единственные измерения, которые позволяет провести на состоянии | У)

23.9. Квантовая телепортация
507
R-процедура, определяются некоторым эрмитовым (или нормальным) оператором и просто
задают вопросы: «Имеет ли спин направление \,? Да или нет?» После измерения состо¬
яние соответствует либо направлению \,? относительно которого задавался вопрос (ответ
ДА), либо противоположному направлению (ответ НЕТ). Возможны и другие измере¬
ния, которые можно провести, если считать спиновое состояние перепутанным с другими
(вскоре мы увидим, какое значение имеет такой порядок вещей). Если же считать изучаемое
состояние не перепутанным с внешним миром, то мы не можем сделать ничего лучше¬
го, чем провести его прямое измерение. Все, что мы сможем получить, — это единичный
ответ ДА/НЕТ, т. е. ровно один бит (одну двоичную единицу) информации. Можно повер¬
нуть измерительную установку на произвольный угол, но система ничего не скажет нам
о направлении /*, которое имеет спин. Действительно, такое направление выделяется тем
фактом, что это есть единственное направление, для которого достоверно (с вероятностью
1) получается ответ ДА, однако мы не можем заранее знать, каково это направление. (Если
бы тот, кто сконструировал данное квантовое состояние, сообщил нам, что оно соответству¬
ет направлению мы смогли бы скопировать его, однако задача поставлена не так: мы
рассматриваем и предполагаем скопировать первоначально не известное состояние.)
Цель, которой стремится достигнуть квантовая телепортация, — это послать квантовое
состояние из одного места в другое, например, с космического корабля Кирка «Энтерпрайз»
на поверхность необитаемой планеты. Квантовая механика определенно не ставит преград
на пути к этой цели; действительно, мы можем просто физически перенести квантовый объ¬
ект из одного места в другое обычным образом. Но предположим, что в некоторой опреде¬
ленной ситуации условия оказываются неблаго rip иятными для достоверной гранспортации
квантового объекта или передачи квантового сигнала любого рода. Все, что позволяют эти
условия, — это перенос обычной классической информации. Однако при использовании толь¬
ко классических сигналов передать квантовое состояние невозможно. Причина этого должна
быть понятна, поскольку классические сигналы, по самой их природе, допускают копирова¬
ние. Если бы их можно было использовать для передачи квантового состояния, то квантовые
состояния также можно было копировать, а это, как мы видели, не должно быть возможно.
Для этого необходимо сначала «подготовить почву». Поскольку образ «необитаемой пла¬
неты» для этого не вполне подходит, я вместо этого прибегну к помощи моего коллеги на
Титане, которому я намерен переслать не известное ему квантовое состояние со спином ~.
Требуемая «подготовка почвы» состоит в том, что каждый из нас всегда должен обладать
одним из членов ЭПР-пары частиц со спином i Можно предположить, что частицы стар-
туют вместе в состоянии со спином 0, как в первоначальном варианте ЭПР-эксперимента,
предложенном Бомом. Допустим, что сейчас ненадежно пересылать квантовые состояния
через космическое пространство, разделяющее Землю и Титан, Но предположим, что пять
лет назад, когда мой коллега еще не покинул Титан, каждый из нас имел при себе по частице
из вышеупомянутой перепутанной пары, и частицы были полностью изолированы от внеш¬
них воздействий. Если наши частицы останутся невозмущенными ко времени возвращения
моего коллеги, тогда, собрав две частицы вместе, мы восстановим состояние со спином 0.
Предположим теперь, что некоторый мой приятель предъявляет мне другую частицу со
спином i, которая также была изолирована от внешних возмущений. Он просит передать
спиновое состояние этой частицы моему коллеге на Титане. Поскольку нынешние усло¬
вия не допускают надежной передачи квантовых состояний отсюда на Титан, я могу лишь
послать классический радиосигнал. Но прежде чем сделать это, я переношу частицу, пере¬
данную мне приятелем, туда, где хранится моя ЭПР-частица, и собираю их вместе. Каждая
1
из частиц имеет спин -, поэтому их состояния вместе образуют 4-мерную систему (про¬
странство Н4, если нет перепутывания между моей частицей и частицей коллеги на Титане).

508
Глава 23
Теперь я провожу измерение на паре частиц (моей и моего приятеля), которое выделяет
четыре ортогональных состояния (их называют состояниями Белла):
(0)
(1)
1 Т)!
1)-\
1)1
Т),
1Т)|
Т)-|
1)1
1),
1Т>1
Т> + 1
1)1
1),
1Т>|
1} +
11)1
Т).
(2)
(3)
При помощи обычного классического сигнала я сообщаю моему коллеге на Титане резуль¬
таты этого измерения, закодированные, например, цифрами 0, 1,2, 3, соответствующими че¬
тырем указанным состояниям. По получении этого сообщения мой коллега достает вторую
частицу ЭПР-пары (до той поры строго оберегаемую от внешних воздействий) и подвергает
ее поворотам по следующей схеме:
(0)	оставить в покое,
(1)	повернуть на 180°	вокруг	оси х,
(2)	повернуть на 180°	вокруг	оси у,
(3)	повернуть на 180 вокруг оси г.
Можно непосредственно проверить, что этим достигается успешная «телепортация» кван¬
тового состояния частицы моего приятеля моему коллеге на Титане5".
ф
В этой квантовой телепортации особенно удивительно то, что, послав моему коллеге
всего 2 бита классической информации (одно из чисел 0, 1, 2, 3, которые можно закоди¬
ровать соответственно как 00, 01, 10, И), я переправил «информацию» о точке на целой
сфере Римана (см. рис. 22.10). С обычной классической точки зрения, это потребовало бы
информации, содержащейся в ничем не ограниченном выборе одной точки из континуума,
т. е., для полной точности, Ко битов! (См. §§ 16.3,16.4.) Как же нам удался такой трюк? Здесь
я должен упомянуть, что проводились реальные эксперименты, которые подтвердили ожи¬
дания относительно квантовой телепортации (но, конечно, не на дистанции Земля-Сатурн,
а на расстояниях в несколько метров) f2314^, поэтому все это следует принимать всерьез.
На явлениях такого рода основана, в частности, быстро развивающаяся квантовая крипто¬
графия, а также многие идеи квантовых вычислений.
Взглянем на рис. 23.7. Там приведена пространственно-временная диаграмма, на ко¬
торой показаны мировые линии — моя, моего приятеля, моего коллеги и, что важнее, всех
частиц, имеющих отношение к этой истории, вместе с классическим сигналом, который
я послал моему коллеге на Титан. Каким-то образом «информация» о направлении спина
частицы моего приятеля (соответствующая состоянию | у/)) оказалась переданной на Ти¬
тан, несмотря на тот факт, что реально было передано всего 2 бита информации. Как же
попали к моему коллеге все остальные Ко битов?
Некоторые могут прибегнуть к такой точке зрения, что квантовые состояния «нереаль¬
ны», «неизмеряемы» и что-нибудь еще в этом роде. Мне трудно принять такую аргумента¬
цию, поскольку состоянию со спином ~ соответствует вполне определенное направление.
Если кто-то, будучи, например, на Титане, выберет измерение спина в некотором направ¬
лении и только в этом направлении, то определенно получится ответ ДА. Более того, мой
приятель (или приятель моего приятеля) может приготовить исходную частицу в некотором
предписанном направлении и с уверенностью узнать результат измерения, которое должно
быть проведено на Титане в том же (или противоположном) направлении. Это звучит вполне
*®1 Подтвердите это, выбрав соответствующим образом оси координат.

23.10. Квантлеменция
509
реально. (Этому не мешает тот факт, что мои примеры
выглядят несколько экзотически, — дело в принципе!)
Вернемся к рис. 23.7. От моего приятеля к моему
коллеге передано нечто реальное, однако классический
канал (всего 2 бита) слишком узок для передачи осталь¬
ных Но битов. Тем не менее канал связи существует.
Он состоит из малого участка от моего приятеля до ме¬
ня, длинного участка — обратного во времени — от меня
к исходному пункту нашей ЭПР-пары и другого длинно¬
го участка от этого пункта до моего коллеги на Титане.
Это единственный канал связи между нами, позволяю¬
щий передать требуемое количество информации. Дол¬
жен, однако, вызывать беспокойство тот факт, что этот
канал содержит участок, простирающийся на 5 лет в про¬
шлое !
Я сам
Коллега
23.10.	Кванглеменция
Я должен подчеркнуть, что совсем не склонен под¬
держать мысль о возможности распространения обыч¬
ной информации обратно во времени (а также исполь¬
зования ЭПР-эффектов для передачи информации бы¬
стрее света; см. ниже). Это привело бы к парадоксам
разного рода, с которыми мы отнюдь не хотим иметь
дела (я вернусь к этому вопросу позже). Информация
в обычном смысле не может распространяться обратно
во времени. Нечто совершенно противоположное можно
сказать о том, что иногда называют квантовой информа¬
цией. С этим термином связана некоторая трудность из-за
присутствия слова «информация». На мой взгляд, эпитет
«квантовая» недостаточен для того, чтобы смягчить ас¬
социации с обычной информацией, поэтому я предлагаю
~	*	Г2Я	1	'Si
новый термин	—
КВАНГЛЕМЕНЦИЯ.
По крайней мере в рамках этой книги я буду имено¬
вать кванглеменцией то, что обычно называют «кванто¬
вой информацией». Этот термин ассоциируется со слова¬
ми «квантовая механика» (QUANtum mechanics) и «пе¬
репутывание» (entanGLEMENT). Это вполне подходит
Приятель
А
Спин О
Рис. 23.7. «Квантовая телепорга-
ция», демонстрирующая акаузальное
распространение квантовой инфор¬
мации. Пространственно-временная
диаграмма иллюстрирует процесс,
посредством которого неизвестное
квантовое состояние (| ^/)) со спи¬
ном i, переданное мне приятелем,
можно переслать моему коллеге на
Титан посредством всего 2 битов
классической информации при усло¬
вии, что мой коллега и я уже подели¬
ли между собой ЭГГР-пару. Акаузаль-
ная квантовая связь показана пункти¬
ром
и выражает суть понятия. Кванглеменция имеет много
общего с информацией, но это не информация. Не существует способа послать обычный
сигнал с помощью одной лишь кванглеменции. Это ясно из того факга, что каналы квангле-
менции, направленные в прошлое, можно использовать и для переноса в будущее. Если бы
кванглеменция представляла собой передаваемую информацию, то можно было бы посы¬
лать сообщения в прошлое, что на самом деле невозможно. Однако кванглеменцию можно
* Автор предлагает неологизм QUANGLEMENT, составленный из слов QUANtum entanGLEMENT (квантовое
перепутывание). Не найдя подходящего русского эквивалента, мы вынуждены пользоваться английским термином,
снабдив его, однако, окончанием женского рода, чтобы подчеркнуть родство с термином «информация». — Прим.
перев.

510
Глава 23
использовать в сочетании с обычными каналами информации, что позволяет получить ре¬
зультаты, невозможные при использовании обычных сигналов. Это очень тонкий вопрос.
В некотором смысле и квантовые вычисления, и квантовая криптография, и, определенно,
квантовая телепортация критическим образом зависят от свойств кванглеменции и ее связи
с обычной информацией.
Насколько я могу судить, связи, устанавливаемые посредством кванглеменции, всегда
ограничены световыми конусами, как и обычные информационные связи, однако связи,
создаваемые кванглеменцией, обладают новой особенностью — они могут быть зигзагооб¬
разным образом направлены назад и вперед во времени [231б]? как если бы распространение
было «пространственноподобным». Поскольку кванглеменция не является информацией,
это не позволяет посылать реальные сигналы быстрее света. Существует также некоторая
связь между кванглеменцией и обычной пространственной геометрией (из-за связи между
сферой Римана и спином, представленной на рис. 22.10, 22.13, 22.14), так что обращение
времени сопровождается пространственным отражением в приложениях, представляющих
интересf2317^. Их подробное обсуждение завело бы нас слишком далеко.
Одними из наиболее непосредственных применений идеи кванглеменции могут слу¬
жить некоторые эксперименты, в которых пара перепутанных фотонов возникает в процессе
так называемой параметрической даун-конверсии (рис. 23.8). Это происходит, когда фотон,
создаваемый лазером, попадает в кристалл особого типа («нелинейный кристалл»), который
превращает его в пару фотонов. Эти фотоны перепутаны различным образом. Их импульсы
в сумме должны давать импульс падающего фотона, а их поляризации связаны между собой,
как в ЭПР-парах, рассмотренных в приведенных примерах.
Рис. 23.8. Параметрическая даун-конверсия. Фотон, излученный лазером, падая на подходящий «нели¬
нейный кристалл», создает пару перепутанных фотонов. Перепутывание проявляется в ЭПР-природе
коррелированных поляризационных состояний вторичных фотонов, а также в том факте, что сумма их
3-импульсов должна быть равна импульсу падающего фотона
В одном из наиболее поразительных экспериментов один из фотонов (фотон А) прохо¬
дит через отверстие некоторой определенной формы и устремляется к соответствующему
приемнику Da. Другой фотон (фотон В) проходит через линзу, установленную таким об¬
разом, чтобы сфокусировать его на приемник Db- Положение приемника Db несколько
смещается при излучении каждой пары фотонов. Ситуация схематически изображена на
рис. 23.9 а. Положение приемника DB отмечается всякий раз, когда приемник Da регистри¬
рует приход фотона А, и приемник DB также регистрирует приход фотона В. Так повторяется
много раз, и постепенно приемник DB строит изображение, в котором учитываются лишь те
положения фотона В, которые были зарегистрированы одновременно с регистрацией фотона
приемником Da- Форма отверстия, с которым встречается фотон А, постепенно вырисовы¬
вается в месте расположения приемника В, несмотря на то что фотон В никогда напрямую
не сталкивается с отверстием! Это выглядит так, словно приемник DB «видит» форму отвер¬
стия, глядя назад во времени на излучающую точку С в кристалле, а затем вперед во времени
в обличьи фотона А. Это оказывается возможным, поскольку процесс «вйдения» в данной
ситуации обеспечивается благодаря кванглеменции. Такое порхание взад-вперед во време¬
ни вполне в духе того, что допускает кванглеменция. Даже оптическую силу и положение
линзы можно выразить в этих терминах. Чтобы определить положение линзы, представьте

23.10. КВАНГЛЕМЕНЦИЯ
511
Нелинейный
Расщепитель луча
\
С
<х>
б)
Рис. 23.9. Передача изображения посредством квантовых эффектов, а) Перепутанные фотоны А и В
возникают в результате параметрической даун-конверсии в точке С. Фотон А должен проходить че¬
рез отверстие некоторой определенной формы и достигать приемника Da, фотон В проходит через
линзу, установленную таким образом, чтобы сфокусировать его на приемник Db. Положение прием¬
ников слегка варьируется согласованным образом, и положение приемника Db отмечается всякий раз,
когда оба приемника регистрируют фотон. Так повторяется много раз, и постепенно приемник Db
вырисовывает форму отверстия, при этом учитываются лишь те положения фотона В, которые были
зарегистрированы одновременно с регистрацией фотона приемником Da. (Здесь это изображено схе¬
матически: вместо приемника Db установлена в фиксированном положении некоторая фотопластинка,
которая становится активной, только когда происходит регистрация приемником Da.) Кванглеменция
проявляется в положении линзы, определяемом так, как если бы в точке С находилось «зеркало»,
которое отражает фотоны как в пространстве, так и обратно во времени. 6) Альтернативная схема,
использующая адаптированный вариант схемы испытания бомб Элитцура-Вайдмана с рис. 22.6 (от¬
раженная относительно горизонтальной прямой). Фотопластинка В регистрирует фотон, только когда
он «должен был быть остановлен» пластиной С, но в действительности выбрал нижний путь!
себе зеркало, расположенное в излучающей точке С. Линза (собирающая линза) размещает¬
ся таким образом, чтобы изображение отверстия, создаваемое отражением в этом зеркале,
фокусировалось на приемнике Db . На самом деле, конечно, в точке С никакого зеркала нет,
однако связи, устанавливаемые кванглеменцией, действуют наподобие отражения в зеркале,
хотя они соответствуют отражению как во времени, так и в пространстве .
Если читатель сочтет описанный эксперимент надуманным, я должен разъяснить, что
это вполне реальный эффект. Он был успешно подтвержден в экспериментах^2318^, про¬
веденных в Балтиморском университете (штат Мэриленд). Проводились также различные
другие, но родственные эксперименты по параметрической даун-конверсии, которые также
можно понять, пользуясь понятием кванглеменции^23-19^.
С другой стороны, ситуацию общего типа, показанную на рис. 23.9 а, можно не считать
«существенно квантово-механической». Аналогичные результаты можно получить, предпо¬
лагая, что устройство в точке С просто попарно испускает классические частицы в нужных
Попробуйте объяснить это подробнее, пользуясь идеями кванглеменции или иным способом.

512
Глава 23
направлениях безо всякой фокусировки. Это можно сделать, используя модификацию уста¬
новки Элитцура-Вайдмана с рис. 22.6 (отраженную относительно горизонтальной прямой);
см. рис. 23.96. Теперь фотоны испускаются поодиночке. Фотон может регистрироваться фо¬
топластинкой В, только если интерференция разрушается из-за прохождения фотона по
альтернативному пути, минуя отверстие С.
Теперь взглянем снова на обычный ЭПР-эффект вроде рассмотренных выше примеров
Стаппа и Харди. При обычном применении квантовой R-процедуры предполагается наличие
некоторой системы отсчета, в которой существуют временная координата t и параллельные
временные срезы пространства-времени, соответствующие определенным постоянным зна¬
чениям t. Обычно принимается (нерелятивистская) точка зрения, согласно которой при из¬
мерении одного члена ЭПР-пары состояние другого одновременно претерпевает редукцию,
так что последующее измерение производится не над перепутанным, а над редуцированным
(неперепутанным) состоянием. Описание такого рода можно применить, например, к моим
собственным примерам ЭПР-экспериментов. Предположим, что с точки зрения системы от¬
счета, неподвижной относительно Солнца, мой коллега на Титане производит измерение
первым, примерно за 15 минут до моего измерения здесь, на Земле. При таком положении
вещей состояние редуцируется измерением моего коллеги, а я затем провожу измерение на
частице в неперепутанном состоянии. Но вместо этого можно представить себе, что вся
ситуация описывается некоторым посторонним наблюдателем О, пролетающим с большой
2
скоростью (скажем, -с) в направлении от коллеги на Титане ко мне. С точки зрения этого
наблюдателя, первым, кто произвел измерение над ЭПР-парой, был я, а мой коллега прово¬
дил измерение уже на редуцированном неперепутанном состоянии (рис. 23.10) (см. § 18.3,
рис. 18.5 6). Совместные вероятности в обоих случаях получаются одинаковыми, однако
наблюдатель О имеет перед собой иную картину «реальности», нежели имели до того мы
с моим коллегой. Если мы рассматриваем R-процедуру как реальный процесс, тогда мы
оказываемся в конфликте с принципом теории относительности, поскольку возникают два
несовместимых взгляда на то, кто из нас произвел редукцию состояния и кто наблюдал
редуцированное состояние после редукции.
Земля
Рис. 23.10. Конфликт между теорией относительности и объ¬
ективностью редукции состояния? Показана пространственно-
временная диаграмма ЭПР-ситуации с приемниками на Земле и
Титане и источником, расположенным ближе к Титану, чем к Зем¬
ле. С точки зрения инерциальной системы, неподвижной относи¬
тельно Солнца, приемник на Титане производит измерение пер¬
вым (в точке В), что одновременно приводит к редукции состояния
на Земле (в точке В'). На Земле измерение имеет место позже (в
точке А) на уже не перепутанном состоянии (одновременно с со¬
бытием А' на Титане). Однако для наблюдателя О, движущегося
с очень большой скоростью от Титана к Земле, детектирование
имеет место сначала на Земле (в точке А, одновременно с со¬
бытием А" на Титане в соответствии с «наклоненными» линиями
одновременности для наблюдателя О), а Титан получает уже реду¬
цированное неперепутанное состояние (в точке В, одновременной
с В" на Земле)
ЭПР-источник
Отсюда можно сделать вывод, что ЭПР-эффекты, несмотря на их, казалось бы, акау-
зальную природу, не могут быть использованы непосредственным образом для акаузальной

23.10. Кванглеменция
513
передачи обычной информации, которая, как можно вообразить, могла бы повлиять на по¬
ведение ее получателя, отделенного от отправителя пространственноподобным интервалом.
Всегда можно выбрать систему отсчета, в которой сначала происходит «получение» инфор¬
мации, а затем «отправителю» достается лишь редуцированное состояние. К тому времени
оказывается «слишком поздно» использовать перепутывание для посылки сигнала, посколь¬
ку оно уже разрушено редукцией состояния.
Как посмотреть на все это с позиций кванглеменции(23*203? (См. §30.3.) В этом пред¬
ставлении неправильно считать одно измерение (мое или моего коллеги) производящим
редукцию, а другое (соответственно моего коллеги или мое) — проводимым над редуциро¬
ванным состоянием. Оба акта измерения выступают на равных правах, и именно квангле¬
менция обеспечивает связь и корреляцию между ними. При этом не важно, какой из них
считать происходящим раньше другого, поскольку кванглеменцию можно считать в равной
мере распространяющейся как в прошлое, так и в будущее. Не будучи способной непосред¬
ственно переносить информацию, кванглеменция не подчиняется обычным ограничениям
релятивистской причинности. Она лишь налагает ограничения на совместные вероятности
результатов различных измерений.
Хотя кванглеменция относится к разряду обычных идей, «придающих смысл» зага¬
дочным квантовым экспериментам такого рода, я не уверен ни в том, сколь далеко можно
продолжать эти идеи, ни в том, насколько точно можно очертить круг эффектов, связан¬
ных с ними. Идея кванглеменции определенно не решает проблемы квантового измерения,
мало что говоря (если вообще говоря) о том, при каких обстоятельствах U-процесс сменя¬
ется R-процессом. Этот вопрос более полно будет рассмотрен в главах 29 и 30, особенно
в § 30.12, однако точная роль кванглеменции в том или ином явлении пока, на мой взгляд, не
слишком ясна. Более обещающей выглядит связь с некоторыми идеями теории твисторов,
как будет вкратце показано в § 33.2.
Примечания
§ 33. 1-
23.1. См. [231, 534,201].
§ 23.3.
23.2. См. [246, 698], а также [6].
23.3. Более подробное изложение тонкостей квантовых вычислений содержится в препринте [424].
23.4. См. [70]. По-видимому, наиболее четкое и часто цитируемое изложение этого неравенства да¬
но в работе Клаузера и др. [149]. Неравенство имеет вид |Е(А, В) — Е(А, D) | + |Е(С, В) —
— Е(С, D) | ^ 2, где Е(х, у) — ожидаемое значение совпадения результатов альтернативных
измерений А, С для одной компоненты ЭПР-пары и В, D для другой компоненты (Е — 1
соответствует полному согласию результатов, Е — — 1 — полному несогласию). См. так¬
же [304, 453, 654].
23.5. См. [86, 654, 6]. Более позднее необычное экспериментальное подтверждение ЭПР-эффектов
содержится в работе [781].
23.6. См. различные примеры, относящиеся к этому вопросу, в работах [383, 742, 453, 633, 634,
162, 613], раздел 5.3, [620, 861].
23.7. См., например, [349]. Общее обсуждение проблемы перепутывания см. в [561].
§ 33.4.
23.8. См. примечание 23.5.
§23.5.
23.9. См. [356, 357].

514
Глава 23
23.10. См. [357].
§23.8.
23.11. Схема такого рода, но без явного использования V-произведения приводится в моей книге
«Тени разума» [613], § 5.15.
§23.9.
23.12. См. [610].
23.13. См. [854].
23.14. См. [418].
§23.10.
л
23.15. См. [622].
23.16. См. [423, 635].
23.17. См. [617].
23.18. См. [720].
23.19. См. введение в эту важную область [302].
23.20. Сравните с [11, 169, 166, 819].

Глава 24
Электрон Дирака и античастицы
24.1.	Конфликт между квантовой теорией и теорией относительности
В § 23.10 мы лишь слегка коснулись некоторых глубоких проблем связи между принци¬
пами квантовой механики и теории относительности. В самом деле, показывая в предыду¬
щих трех главах, как работает квантовая теория, я придерживался самой что ни на есть нере-
О
лятивистскои точки зрения, игнорируя те важные уроки относительно взаимосвязи между
временем и пространством, которые преподнесли нам Эйнштейн и Минковский (они были
рассмотрены в главе 17). Вообще-то в квантовой теории это вполне обычное дело. При стан¬
дартном подходе принимается «картина реальности», в которой время рассматривается от¬
дельно от пространства. Как отмечалось в главе 22, имеется лишь одна внешняя временная
координата при многих пространственных координатах, поскольку для каждой частицы ну¬
жен свой собственный набор координат. Эту асимметрию обычно считают «временной»
чертой нерелятивистской квантовой теории, которая должна рассматриваться как приближе¬
ние к некоторой более полной релятивистской схеме. В этой и двух последующих главах мы
начнем знакомиться с глубокими проблемами, которые возникают, когда мы всерьез пытаем¬
ся объединить принципы квантовой теории и специальной теории относительности. (Более
фундаментальное объединение с общей теорией относительности Эйнштейна, когда в об¬
щую картину вводятся также гравитация и кривизна пространства-времени, требует чего-то
гораздо большего, и пока еще нет общепринятого мнения относительно наиболее обещаю¬
щих путей развития. Некоторые из этих путей будут рассмотрены в главах 28 и 30-33.)
Теория, которая получается как сочетание квантовой теории со специальной теорией
относительности, оказывается не просто теорией квантовых частиц, но теорией квантовых
полей. Причина состоит в том, что из-за привлечения теории относительности отдельные ча¬
стицы уже не сохраняются, а могут появляться и исчезать в паре со своими античастицами.
Это требует некоторого пояснения. Зачем релятивистской квантовой теории понадобились
«античастицы»? Почему присутствие античастиц приводит нас от квантовой теории частиц
к квантовой теории полей? Эта глава посвящена главным образом ответу на эти два вопроса,
в основном на первый, что приведет нас к удивительному прозрению Дирака в отношении
математического описания электронов.
Сама квантовая теория поля будет обсуждена в главе 26, где мы познакомимся с кон¬
фликтом, который существует между специальной теорией относительности и квантовой
теорией и приводит ко все более сложным математическим схемам. Мы будем вовлечены
в долгое захватывающее путешествие. В конце концов этот конфликт будет приемлемым
образом разрешен в стандартной модели элементарных частиц, рассмотренной в главе 25,
и теория окажется в замечательном согласии с экспериментальными фактами.
Пока, однако, этот конфликт остается и во многих отношениях не разрешен полно¬
стью. Строго говоря, квантовая теория поля (по крайней мере в большинстве известных нам
нетривиальных примеров применения этой теории) является математически несогласован¬
ной, и необходимы различные «трюки» для проведения осмысленных вычислений. Очень
непросто решить, являются ли эти ухищрения просто временной мерой, позволяющей нам
двигаться вперед, используя математические рамки, которые, возможно, дадут трещину на

516
Глава 24
более глубоком уровне, или же эти трюки отражают некую важную истину, хранимую При¬
родой. В большинстве недавних попыток двинуться дальше эти «трюки» рассматриваются
как нечто фундаментальное. В этой и последующих главах мы увидим несколько примеров
таких хитроумных схем. Некоторые из них оказались подлинной разгадкой секретов Приро¬
ды. С другой стороны, может оказаться, что к другим из них Природа относится с гораздо
меньшей симпатией!
4
24.2.	Почему античастицы приводят к квантовым полям?
Теоретическое предвидение существования античастиц, сделанное квантовой теорией
поля, оказалось разгадкой одной из подлинных тайн Природы, теперь уже хорошо под¬
твержденной наблюдениями. В этой главе и особенно в § 24.8 мы поймем кое-что о при¬
чинах введения античастиц в теорию. Пока сосредоточимся на втором из двух поднятых
выше вопросов: почему существование античастиц уводит нас из квантовой теории частиц
в квантовую теорию полей? Пока просто примем, что частица каждого типа имеет свою
античастицу, и постараемся выяснить, к каким следствиям приводит этот замечательный
факт.
Ключевое свойство античастицы (по крайней мере античастицы массивной частицы)
состоит в том, что частица и античастица, сталкиваясь, могут взаимно уничтожаться (анниги¬
лировать), при этом их совместная масса превращается в энергию в соответствии с формулой
Эйнштейна Е — тс2. Если, наоборот, в систему вводится достаточная энергия, локализован¬
ная в достаточно малой области, возникает значительная вероятность того, что эта энергия
пойдет на создание некоторой частицы вместе с ее античастицей. При такой возможности
возникновения античастиц всегда существует вероятность появления все новых частиц вме¬
сте с соответствующими античастицами. Поэтому наша релятивистская теория определенно
не может быть просто теорией ни отдельных частиц, ни какого-то бы ни было фиксиро¬
ванного числа частиц. (Как будет показано в главах 25 и 26, согласно квантовой теории,
если может что-то произойти (например, возникнуть множество пар частица-античастица),
то такая потенциальная возможность вносит реальный вклад в квантовое состояние.) По¬
этому любая теория релятивистских частиц должна предполагать возможность рождения
неограниченного числа частиц.
Это выводит нас за рамки, описанные в главах 21-23, однако в главе 26 мы увидим,
как квантовая теория поля позволяет нам приспособиться к этому. Согласно принятой точке
зрения, первичными объектами в теории являются квантовые поля, а сами частицы воз¬
никают просто как «возбуждения поля». Правда, мы обнаружим, что это не единственный
возможный взгляд на квантовую теорию поля. Метод фейнмановских диаграмм, с которым
мы познакомимся в главах 25 и 26, описывает «частицеподобным» образом основные про¬
цессы квантовой теории поля, в которых может возникать или исчезать неограниченное
число частиц.
Полезно обсудить немного подробнее причины, по которым происходит рождение
частиц, являющееся характерной особенностью релятивистской квантовой теории. По-
прежнему будем предполагать существование античастиц. Причиной, по которой может
ожидаться рождение частиц, является, по существу, знаменитая формула Эйнштейна Е —
— тс2. Происходит взаимообмен между энергией и массой (множитель с2 представляет
просто «коэффициент преобразования» между используемыми единицами энергии и мас¬
сы). Если энергии достаточно, то из этой энергии может возникнуть масса частицы.
Однако наличие условий для создания массы частицы само по себе не достаточно
для рождения самой частицы. Существуют различные сохраняющиеся (аддитивные) кванто¬
вые числа, такие как электрический заряд (или, например, барионное число), которые, как
предполагается, не могут изменяться в ходе физического процесса. Например, чтобы просто

\
24.3. Положительность энергии в квантовой механике
517
создать из одной лишь энергии заряженную части¬
цу, пришлось бы нарушить закон сохранения заряда
(то же относится и к другим сохраняющимся величи¬
нам — барионному числу и др.). Однако если предпо¬
ложить, что для каждого типа частиц существуют со¬
ответствующие античастицы, у которых каждое адди¬
тивное квантовое число имеет противоположный знак,
то частица вместе со своей античастицей может ро¬
диться из одной лишь энергии (см. рис. 24.1). В таком
процессе все аддитивные квантовые числа будут сохра¬
няться.
С другой стороны, масса покоя античастицы (вели¬
чина неаддитивная) совпадает с таковой для исходной ча¬
стицы. Для рождения частицы и античастицы требуется
достаточная энергия — по крайней мере вдвое больше мас¬
сы/энергии покоя самой частицы. Наоборот, при столк-
Частица
Античастица
s
<D
Он
д
Рис. 24.1. Частица и ее античасти¬
ца могут родиться из энергии. Все
сохраняющиеся аддитивные кван¬
товые числа частицы имеют у ан¬
тичастицы противоположный знак,
что обеспечивает сохранение этих
величин в процессе рождения
новении частицы данного типа с античастицей того же
типа они могут уничтожить одна другую с образованием
энергии. Эта энергия опять-таки должна по крайней ме¬
ре вдвое превышать массу/энергию покоя отдельной ча¬
стицы. В процессах рождения или аннигиляции частиц
энергия может быть и больше этого значения, поскольку
частица и античастица, скорее всего, находятся в относительном движении, и остаточная
энергия этого движения (кинетическая энергия) добавляется к полной энергии. В любом слу¬
чае присутствие античастиц вынуждает нас отойти от квантовой теории отдельных частиц,
описанной в главах 21-23.
24.3.	Положительность энергии в квантовой механике
Вернемся на ту дорогу, которая в конечном счете приводит нас к необходимости появле¬
ния античастиц в релятивистской квантовой теории. Нам потребуется несколько более глу¬
бокое, по сравнению с предыдущим, проникновение в основы квантовой механики. Прежде
всего давайте вспомним общий вид уравнения Шредингера:
т= пф.
at
Допустим, что наша квантовая система обладает определенной энергией Е, так что ф есть
собственное энергетическое состояние с собственным значением Е. Поскольку оператор 7i
определяет полную энергию системы, потребуем выполнения уравнения
Пф = Еф.
Согласно квантово-механической R-процедуре (§§22.1, 22.5), такое состояние ф должно
получаться при проведении над системой измерения, задающего ей вопрос о том, какова
ее энергия, и получающего определенный ответ: она равна Е. В этом случае уравнение
Шредингера принимает вид
t

518
Глава 24
Решение этого уравнения имеет вид
ф = Ce~iEt/h,
где С не зависит от t (т. е. это есть комплексная функция только от пространственных
переменных).
Существенно, что значение энергии Е выражается положительным числом. По ряду
причин состояния с отрицательной энергией для квантовой механики нежелательны (их на¬
личие приводит к катастрофической нестабильности ^24Л1)**. Если энергия Е положительна,
то коэффициент —iE/h при t в показателе экспоненты e~lEt/h есть отрицательная вели¬
чина, умноженная на г. Напомним (см. §9.5 и примечание 9.3), что функции ф(£) такой
природы или линейные комбинации таких функций называют (хотя и не вполне обоснован¬
но) положительно-частотными.
Напомним также, что в § 9.3 мы встретились с расщеплением функции f(x) (от ве¬
щественной переменной х) на положительно-частотную и отрицательно-частотную части,
казалось бы, совершенно иным образом, а именно с использованием геометрии сферы
Римана^24'2^. Там это выглядело просто как изящный кусочек чистой математики. Ве¬
щественная ось считалась там обернутой по экватору вокруг сферы Римана, при этом
положительно-частотная часть функции / понималась как часть, голоморфно продолжа¬
емая (см. §7.1) на южное полушарие, а отрицательно-частотная часть — как продолжа¬
емая соответственно на северное полушарие. Но теперь появляется замечательная физи¬
ческая причина, по которой эти понятия оказываются важными. Любая уважающая се¬
бя волновая функция, не будучи непременно собственным состоянием энергии, должна
быть представимой в виде линейной комбинации собственных состояний энергии, и каждое
собственное значение энергии обязано быть положительным. Таким образом, временная
зависимость любой приличной волновой функции должна быть положительно-частотной.
Мне кажется, что эта замечательная связь между существенным физическим требовани¬
ем, с одной стороны, и изящным математическим свойством, с другой стороны, служит
удивительным примером глубокого, тонкого и, по существу, загадочного родства между
изощренными математическими идеями и внутренним устройством нашей реальной Все¬
ленной.
В нерелятивистской квантовой механике это требование положительной частоты вы¬
полняется автоматически, как естественная черта теории, поскольку гамильтониан возни¬
кает из разумной физической задачи, в которой классические энергии положительны. На¬
пример, в случае одной свободной нерелятивистской (бесспиновой) частицы, обладающей
(положительной) массой р9 мы имеем гамильтониан Н = р2/2р (напомним §§20.2, 21.2).
Выражение р2 и, следовательно, сам гамильтониан Н, как говорят, «положительно опреде¬
лены» ^24-31 (см. §§13.8, 13.9). В классическом случае так получается оттого, что р2 есть
сумма квадратов, которая не может быть отрицательной: р2 — р ♦ р = (pi)2 + (Р2)2 + (рз)2*
В квантовой механике мы должны заменить р на —ifiV, где V = (д/дх1, д/дх2, д/дх3).
Теперь утверждение о «положительной определенности» относится к «собственным зна¬
чениям» оператора —V2 (для нормируемых состояний, т. е. элементов соответствующего
гильбертова пространства Н), которые опять-таки не могут быть отрицательными по той же
-jc
самой, в сущности, причине, что и в классическом случае
Проверьте, что это действительно решение.
Объясните, почему добавление к гамильтониану некоторой постоянной К приводит просто к умножению
всех решений уравнения Шредингера на один и тот же множитель. Найдите этот множитель. Оказывает ли это
существенное влияние на квантовую динамику? Предположим, что мы рассматриваем действие силы тяжести на
квантовую систему. Почему в этих условиях мы не можем просто «перенормировать» энергию указанным образом?
В данном случае уравнение Шредингера имеет вид д'ф/дt = (ih/2fi)'V2'ip. Сначала подтвердите, что для
собственного энергетического состояния с энергией Е мы имеем — V2^ = Аф, где А = 2fih~2E. Воспользовав-
***

24.4. Проблемы с релятивистской формулой для энергии
519
24.4.	Проблемы с релятивистской формулой для энергии
Перейдем к рассмотрению релятивистской квантовой частицы. В этом случае гамиль¬
тониан получается из релятивистского выражения для энергии, которое теперь имеет вид
не р2 /2р, а
[(с2М)2 + сУ]1
Это выражение является следствием уравнения (с2р)2 = Е2 - с2р2 из § 18.7, где р — мас¬
са покоя частицы. Читателю, который удивится тому, что это выражение не имеет теперь
привычного вида р2 /2р, следует вернуться к упражнению 18.20. Из разложения в ряд выра-
1
жения \{с2р)2 -f с2р2}2 в качестве первого члена следует эйнштейновское Е = рс2. Это есть
вклад, вносимый в энергию массой покоя частицы и дополняющий кинетическую энергию
движения частицы. Второй член разложения дает нам как раз ньютоновский гамильтониан
(кинетическую энергию) р2 / 2р.
Читатель, возможно, уже согласился с нашим выбором релятивистского гамильтониана.
Этот выбор, однако, оказывается определенно неудобным (и мало что объясняющим), если
пытаться использовать такое разложение нашего гамильтониана в степенной ряд, хотя бы
потому, что классический ряд даже не сходится при р2 > р2с2. Более того, как мы увидим,
1
квадратный корень (половинная степень) в точном выражении [(с2р)2 + с2р2]2 создает
свои собственные трудности, связанные с выполнением условия положительной частоты.
Попробуем понять, насколько это существенно.
Во избежание излишнего усложнения выражений я вернусь к системе единиц, в которой
скорость света принимается за единицу:
с = 1,
так что наш релятивистский гамильтониан (включающий энергию покоя) имеет вид
Н — (р2 -\-р2)2.
Мы должны иметь в виду, что в квантовой механике р2 в действительности есть оператор
частной производной второго порядка —h2V2. Поэтому потребуются значительные матема-
1
тические ухищрения, чтобы придать реальный смысл выражению (/i2~ft2V2)2, которое со¬
держит квадратный корень из оператора частной производной! (Чтобы оценить возникшую
трудность, попробуйте, например, приписать смысл чему-нибудь вроде >/(1 — d?/dx2).)*
С квадратным корнем связана еще более серьезная трудность, поскольку он неявно
содержит неопределенность знака. В классической физике подобное не должно волновать,
так как рассматриваемые величины представляют собой обычные вещественные функции,
и мы представляем себе, как отделить положительные значения от отрицательных. В кван¬
товой механике это не так просто. Одна из причин состоит в том, что квантовые волновые
функции являются комплексными, а два значения квадратного корня из выражения с ком¬
плексными числами отнюдь не стремятся аккуратным и полностью согласованным обра¬
тись теоремой Грина f ф\/2ф d3x = — f ф * У7ф d3x, покажите, что для нормируемого состояния величина А
должна быть положительной. (И наоборот, при положительном значении А существует множество решений уравне¬
ния ~~\72ф = Аф, надлежащим образом спадающих на бесконечности, так что норма |]-0|| остается конечнойf24-4!
и при желании может быть нормирована, чтобы было Ц^Ц = 1.) Покажите, как вывести теорему Грина исходя из
основной теоремы внешнего анализа.
Попробуйте воспользоваться преобразованием Фурье (§9.4), или разложением в степенной ряд, или
контурным интегрированием, или еще чем-нибудь.

520
Глава 24
зом разделиться на «положительное» и «отрицательное» (§ 5.4). Это следует рассматривать
в связи с тем фактом, что квантовая механика имеет дело с операторами, действующими
на комплексные функции, и операции вроде извлечения квадратного корня могут приво¬
дить к существенной неоднозначности, которой нельзя избежать, просто заявив: «Возьмем
положительное значение корня».
Эту трудность можно сформулировать по-другому. В квантовой механике необходимо
учитывать, что в квантовое состояние может дать вклад «всё, что может случиться» в дан¬
ной физической ситуации, и потому все эти альтернативы влияют на то, что происходит
_	-s'	•
на самом деле. Если появляется что-то вроде квадратного корня, то каждое из двух его
значений следует рассматривать как некоторую «возможность», так что даже «нефизиче¬
скую отрицательную энергию» приходится считать одной из «физических возможностей».
Коль скоро появляется возможность такого состояния с отрицательной энергией, возникает
вероятность самопроизвольного перехода из состояния с положительной энергией в состо¬
яние с отрицательной энергией, что может привести к катастрофической нестабильности.
В случае нерелятивистской свободной частицы проблема возможности отрицательной энер¬
гии не возникает, так как положительно определенная величина р2/2 р не содержит этого
1
неприятного квадратного корня. Однако релятивистское выражение (ц2 + р2)2 более про¬
блематично, поскольку обычно у нас нет четкой процедуры отбрасывания отрицательного
значения квадратного корня.
Оказывается, что в случае одиночной свободной частицы (или системы невзаимодей¬
ствующих частиц) это не приводит к реальным трудностям, поскольку мы можем ограни¬
читься суперпозициями решений свободного уравнения Шредингера в виде плоских волн
с положительными энергиями, которые только и рассматривались в §21.5, и отсутствуют
переходы в состояния с отрицательной энергией. Однако при наличии взаимодействия де¬
ло обстоит уже не так. Даже в случае всего одной релятивистской заряженной частицы
в заданном фоновом электромагнитном поле волновая функция в общем случае не может
удовлетворить условию положительной частоты. Здесь мы начинаем ощущать конфликт
между принципами квантовой механики и теории относительности.
В § 24.8 мы увидим, какой путь решения данного конфликта нашел великий физик
Поль Дирак. Однако в качестве первого шага он выдвинул в высшей степени изобрета¬
тельное и проницательное предложение — его знаменитое нынче уравнение для электрона,
которое решило проблему квадратного корня удивительным и неожиданным образом. Это
привело затем к оригинальной точке зрения, которая позволила устранить отрицательные
энергии и сделать поразительное предсказание существования античастиц. Чтобы понять
все это, вернемся к существенной особенности теории относительности, из которой выте¬
кает появление квадратного корня.
24.5.	Неинвариантность оператора d/dt
1
Вспомним, по какой причине у нас возникла необходимость в гамильтониане {ц2 -4- р2)2
для релятивистского случая. Это связано в конечном счете с тем фактом, что в уравне¬
нии Шредингера фигурирует оператор d/dt (т. е. «скорость изменения во времени»), тогда
как в теории относительности этот оператор не является инвариантом, поскольку время
и пространство необходимо рассматривать не раздельно, а в единой комбинации «про¬
странство-время». Таким образом, с «релятивистски-инвариантной» точки зрения нельзя
рассматривать оператор d/dt как нечто фундаментальное. В свою очередь, как отмечалось
в §21.3, оператор d/dt появляется в уравнении Шредингера в результате «фокуса с кван¬
тованием», когда стандартные пространственно-временные 4-импульсы (т. е. энергия Е
и отрицательный 3-импульс —р) заменяются дифференциальными операторами ihd/dxa

24.5. Неинвариантность оператора d/dt
521
(т.е. энергия Е заменяется на ihd/dt, а —р на iftV). Таким образом, «релятивистская
неинвариантность» оператора d/dt тесно связана с неинвариантностью энергии. Энергия
и импульс в теории относительности смешиваются точно так же, как время и пространство
(см. §18.7).
Вспомним также, что эйнштейновская формула Е — тс2 (при сделанном нами согла¬
шении с — 1) говорит нам, что энергия есть масса, а масса есть энергия, поэтому масса тоже
«неинвариантна». Это, однако, относится к понятию аддитивной «массы» т (временной
компоненты 4-вектора энергии-импульса), которая не является собственным свойством са-
мои частицы, а есть масса, измеряемая в некоторой системе отсчета, скорость которой
может отличаться от скорости частицы. Чем больше скорость частицы, тем больше будет
эта «наблюдаемая» масса (именно по этой причине масса т оказывается неинвариантной
величиной). Масса покоя частицы р инвариантна, но с ней связана та трудность, что она
неаддитивна и не сохраняется при превращениях частиц. Это не оставляет большого выбора
при решении вопроса, что следует приравнять к гамильтониану. Кроме того, масса р равна
квадратному корню из выражения, содержащего энергию и импульс (предполагается с = 1):
р2 — рара = га2 — р2, т.е. р = (т2 -р2)2,
что приводит к прежнему выражению с квадратным корнем для массы/энергии: т = (/л2
+ р2)2.
Тем не менее можно попробовать использовать эту инвариантную энергию покоя р или
ее квадрат р2 в уравнении шредингеровского типа вместо неинвариантной энергии т. Про¬
цедура квантования (т. е. замена т на ihd/dt и р на — iW), будучи примененной к квадрату
энергии покоя р2 — т2 — р2, дает нам оператор (с множителем (гй)2)^24*5^
□ =I I -V
в координатах Минковского (£, х, у, z). Это так называемый волновой оператор или опе¬
ратор Даламбера (даламбериан), который имеет вполне инвариантный смысл. (Напомним,
что	означает	оператор второй производной d2/dx2 и т. п.) Хотя стандартное уравне¬
ние Шредингера не позволяет непосредственно использовать этот оператор (по причинам,
3
указанным выше, уравнение Шредингера требует оператора первой производной а не
второй (d/dt)2), тем не менее можно ожидать, что уравнение второго порядка (гК)2Пф —
— р2ф (где (ih)2U получается из р2 в результате процедуры квантования, а р в уравнении
есть сама масса покоя) имеет смысл волнового уравнения для релятивистской частицы.
Это уравнение можно переписать в виде
(□ + М2)ф = о,
<г>
где М — р/Н,н оно действительно играет важную роль в релятивистской квантовой теории.
В настоящее время его часто называют уравнением Клейна-Гордона, хотя впервые это
релятивистски-инвариантное уравнение предложил сам Шредингер, причем раньше, чем он
взялся за свое ныне более известное «уравнение Шредингера» (описанное в §21.3) t24*6!.
В современной квантовой теории поля уравнение Клейна - Гордона при надлежащей ин¬
терпретации можно использовать для описания массивных бесспиновых частиц, в частности

522	Глава	24
•“ а
	1 I	 ' 	 -	 ,	,	 ,	-		 -	,	г	ITT—	—14	-	I	|	|	!■	I I !)■ I ■		 -	•	   |	П	Г I l~r I	г-“ —	■	 	1	1—	I	I		 Т1-*	"	1	I ■ |	II	111НИЧ1И й Г
для частиц, именуемых мезонами (к ним относятся элементарные частицы с промежуточной
величиной массы, такие как пионы и каоны). Однако такая интерпретация требует полно-
стью развитого аппарата квантовой теории поля, которая находилась в зачаточном состоянии
в 1928 году, когда Дирак впервые предложил свое уравнение для электрона, выглядевшее со¬
всем иначе. Дирак сделал выбор в пользу уравнения, в котором производная по времени име¬
ла первый порядок d/dt, как в уравнении Шредингера, а не второй (d/dt)2, как в волновом
операторе □. Он исходил из соображений, указанных выше, но более всего из требования,
чтобы волновая функция частицы давала для плотности вероятности нахождения частицы
в любом выбранной месте выражение, качественно подобное ФФ в стандартной квантовой
механике (§21.9), которое было бы положительно определено, так чтобы эта вероятность
никогда не могла стать отрицательной. Это не то же самое, что и требование положительной
определенности энергии, а столь же важное дополнительное требование ^.
24.6.	Квадратный корень из волнового оператора по
Клиффорду-Дираку
Своим в высшей степени изобретательным и проницательным разрешением казавше¬
гося неразрешимым конфликта между требованиями теории относительности и ощущением
необходимости первой производной d/dt Дирак сумел найти уравнение, которое было пер¬
вого порядка по d/dt; при этом он получил явное выражение для квадратного корня из
волнового оператора □ релятивистки-инвариантным способом. Он сделал это, введя некото¬
рые дополнительные некоммутирующце величины. В квантовой механике такие величины
вполне уместны, поскольку их следует рассматривать как линейные операторы, действую¬
щие на волновую функцию, подобно некоммутирующим операторам координаты и импульса,
с которыми мы уже сталкивались в § 21.2. Как мы вскоре увидим, самое замечательное здесь
то, что эти некоммутирующие операторы, которые пришлось ввести Дираку, описывают фи¬
зические спиновые степени свободы наиболее фундаментальных фермионов (см. §23.7),
существующих в природе, — электронов и протонов, которые были известны во времена
1
Дирака, и нейтронов, мюонов, кварков и многих других частиц со спином ~, известных
ныне.
Введя свои некоммутирующие «спиновые» величины, Дирак фактически переоткрыл
алгебры Клиффорда (один из примеров таких алгебр), с которыми мы встречались в § 11.5.
При этом он не знал ни о более ранней работе Уильяма Кингдона Клиффорда, ни о том, что
Клиффорд (1877), а еще раньше Гамильтон уже отмечали, что элементы этих алгебр можно
использовать для «извлечения квадратного корня» из лапласианов (а волновой оператор □
есть частный случай обобщенного лапласиана для четырех измерений и сигнатуры Н	).
Фактически, как обнаружил сам Клиффорд, Уильям Роуан Гамильтон уже показал прибли¬
зительно в 1840 году, что квадратный корень из обычного трехмерного лапласиана можно
получить, используя кватернионы^24'^:
(^+^+кй)	=~у2
(см. § 11.1). Клиффорд обобщил это на большее число измеренийt24*9l. Неудивительно, что
Дирак не знал об открытиях Клиффорда, сделанных более полувека назад, поскольку эта
работа в 1920-х годах не была известна даже многим специалистам в области алгебры. Даже
если бы Дирак знал об алгебрах Клиффорда, это не уменьшает блеска осознания того, что
подобные математические объекты играют важную роль в квантовой механике электрона
со спином, что составляет главный и неожиданный прорыв в понимании физической кар¬
тины .

24.7. Уравнение Дирака
523
В случае Дирака необходимо извлечь квадратный корень из волнового оператора, кото¬
рый представляет собой четырехмерный (лоренцев) лапласиан, соответствующий геометрии
Минковского:
d=(i)2-v2-
Воспользуемся «лоренцевыми» элементами алгебры Клиффорда 70, ..., 73, удовлетворяю¬
щими условиям
7о = !> li = _1> 72 = -Ь 7з = “!•
*
В стандартной (с сигнатурой + + ... +) алгебре Клиффорда все эти квадраты равны —
—1. Здесь я следую обычному среди физиков соглашению относительно знаков, при кото¬
ром квадраты пространственных элементов 7 остаются отрицательными, как было вначале
у Клиффорда^24 101 Однако временной элемент 7 имеет положительный квадрат. Именно
в этом смысле алгебра Клиффорда в дираковском варианте является «лоренцевой». Для
различных элементов 7 выполняются ютаффордовы соотношения антикоммутации (§ 11.5):
И1] = -1}Ъ
Ключевой факт, которым воспользовался Дирак, состоит в том, что волновой оператор яв¬
ляется квадратом некоторого оператора первого порядка, определяемого с помощью этих
элементов Клиффорда':
□ — (7оd/dt - 71 д/дх - 72д/ду - 'узд/дг)2.
Это можно записать короче, воспользовавшись векторными обозначениями и введя век-
тор 7 = (71, 72, 7з):
□ = (70д/т - 7 • V)2,
или, еще короче,
□ = а2;
величина
д — 7оd/dt - 7 • V
= д/дХа
(где 7а — даЬъ) называется оператором Дирака. Эта удобная запись с помощью «шляп¬
ки» была предложена Ричардом Фейнманом; в более общем случае вектор Аа может быть
представлен элементом алгебры Клиффорда - Дирака
А — 1а,Аа.
24.7.	Уравнение Дирака
Теперь вернемся к нашему «волновому уравнению» (□+М2)ф — 0. Используя оператор
Дирака 9, можно факторизовать фигурирующий там оператор □ + М2:
□+м2 = д2 + м2,
г Проверьте это.

524
Глава 24
/N,
где М = р/К. Тогда получается уравнение Дирака для электрона (д 4- гМ)ф — 0, т. е.
дф — —гМф,
или, если восстановить К путем введения массы покоя р:
Ьдф — —1рф.
Из проведенной факторизации следует, что всякий раз, когда выполняется это уравнение,
должно выполняться также и уравнение (□ -Ь М2)ф = 0. (Это относится и к «антидираков*
скому уравнению» (д—И№)ф — 0, но последнее принято относить к частице с отрицательной
массой —hM.) Таким образом, волновые функции, удовлетворяющие вышеприведенному
уравнению Дирака, должны удовлетворять также «волновому уравнению», которому подчи¬
няются релятивистские частицы с массой покоя КМ.
Уравнение Дирака имеет перед волновым уравнением то преимущество, что оно содер¬
жит оператор d/dt в первой степени. Действительно, уравнение Дирака можно переписать
в форме уравнения Шредингера"5:
ik— = (гЙ7о7 • v + 7омЖ
где г?гуо7 * V + 'Уор играет роль оператора Гамильтона. Оператор d/dt сам по себе, ко¬
нечно, релятивистски-неинвариантен, однако все уравнение Дирака дф = —1Мф в це¬
лом релятивистски-инвариантно. (Чтобы убедиться в этом, необходимо внимательно про¬
следить взаимосвязь между элементами алгебры Клиффорда и преобразованиями Лорен-
ца ".) Для физиков того времени было заметным потрясением узнать, что существуют
релятивистски-инвариантные объекты за рамками стандартного векторного (тензорного)
анализа (см. главы 12 и 14). Дирак инициировал создание мощного нового формализма,
известного теперь под названием спинорного исчисления124Л11? который далеко выходил за
рамки стандартного векторного (тензорного) анализа тех дней.
«Цена», которую приходится платить за такое замечательное устранение неприятного
квадратного корня при сохранении релятивистской инвариантности, — это появление стран¬
ных некоммутирующих элементов алгебры Клиффорда 7а. Что они означают? Мы должны
рассматривать их как операторы, действующие на волновую функцию. Поскольку эти опера¬
торы представляют собой новые объекты, не связанные непосредственно с рассмотренными
ранее (некоммутирующими) квантовыми переменными — координатой и импульсом части¬
цы, они должны относиться к некоторым новым степеням свободы нашей частицы (и дей¬
ствовать именно на них). Мы должны спросить, какой физической цели могут служить эти
новые степени свободы. В ретроспективе, которую предоставляет современная терминоло¬
гия, мы видим ответ в самом названии «спинор»: новые степени свободы описывают спин
электрона^24121 Вспомним, что было сказано в §11.5: «Спинор можно рассматривать как
объект, на который элементы алгебры Клифорда действуют как операторы». В уравнении
Дирака элементы Клиффорда действуют на волновую функцию ф. Тогда сама функция ф
должна быть спинором. Она обладает дополнительными степенями свободы (природу кото¬
рых мы вскоре поймем) помимо зависимости от координат и времени, обычной для скаляр¬
ной волновой функции, и эти дополнительные степени свободы действительно описывают
спин электрона!
Теперь мы начинаем понимать, что цена, которую мы вынуждены были заплатить за
возможность факторизации волнового оператора с помощью элементов Клиффорда, позво¬
лила нам совершить почти невероятную покупку! Мы не только получили теорию, которая
**
Покажите это.
Объясните это. (Подсказка: в этом может помочь упражнение 26.3.)

24.8. Как Дирак пришел к позитрону
525
*
точно описывает спин электрона. Добавив в гамильтониан стандартный член, который опи¬
сывает взаимодействие с фоновым электромагнитным полем и вводит в рассмотрение элек¬
тродинамику в точном соответствии с требованиями «калибровочной инвариантности» [24133
(см. §§ 19.4, § 21.9), мы найдем, что дираковский электрон откликается на электромагнитное
поле точно так, как и подобает заряженному электрону, включая некоторые тонкие эффекты,
обусловленные релятивистским движением электрона.
Но точно описывается не только поведение электрона как заряженной частицы — кроме
того, дираковский электрон ведет себя так, как если бы он обладал магнитным моментом
вполне определенной величины, а именно
h2e/A(ic,
где е — заряд электрона, ад — его масса. Это должно означать, что дираковский электрон
не только имеет электрический заряд, но и ведет себя как маленький магнитик, сила ко¬
торого определяется указанной величиной. Замечательно, что четко определенное Дираком
значение магнитного момента электрона очень близко к экспериментально наблюдаемому
значению, точность достигает одной тысячной. Результат лучшего современного измерения
магнитного момента электрона отличается от указанного первоначального значения Дирака
множителем
1,0011596521188....
В настоящее время получило объяснение с указанной выше явной точностью даже столь
малого расхождения, оно связано с поправочными эффектами квантовой электродинами¬
ки, которая включает уравнение Дирака как одну из важнейших составных частей. Со¬
гласие с Природой у коротенького уравнения Дирака дф — —гМф поистине необычай¬
ное!
24.8.	Как Дирак пришел к позитрону
Однако наша история еще ни в коей мере не окончена, я изложил лишь самое на¬
чало. В продолжение ее отметим кажущуюся аномалию в математике уравнения Дирака,
относящуюся к спину электрона. Эта видимая аномалия связана с числом независимых
компонент, которые можно обнаружить у дираковского спинора ф. Оказывается, что та¬
ких компонент четыре, тогда как при поверхностном рассмотрении мы должны ожидать
1
наличия лишь двух компонент, поскольку частица со спином - имеет всего два незави¬
симых спиновых состояния (см. § 22.8). Попробуем разобраться в этой проблеме немного
подробнее.
В 1925 году, менее чем за три года до того как Дирак опубликовал свое уравнение (эго
произошло в 1928 году), Джордж Уленбек и Сэмюэл Гаудсмит пришли к выводу, что электрон
должен обладать квантово-механическим спином, построенным из двух базисных спиновых
состояний. В 1927 году Вольфганг Паули показал, как можно представить преобразования
этих спинов при поворотах осей координат, используя объекты, которые мы нынче называем
«матрицами Паули» (см. §22.8, а также картину сферы Римана для состояний спина i,
показанную на рис. 22.10). Матрицы Паули (которые, по существу, представляют собой
кватернионы с множителем г) являются также элементами алгебры Клиффорда, но для
группы трехмерных вращений*.
Объясните это замечание, учитывая связь между кватернионами и элементами Клиффорда, рассмотрен¬
ную в § П.5.

526
Глава 24
Фактически в двух спиновых состояниях электрона ощущается настоятельная физиче¬
ская потребность. От этого, по существу, зависит вся химия, как мы ее понимаем. В ато¬
ме электроны, окружающие ядро, вращаются вокруг него, находясь в некоторых опреде¬
ленных состояниях, называемых «орбиталями» (см. §22.13). Согласно принципу запрета
Паули, каждая электронная орбиталь, казалось бы, должна быть занята не более чем од¬
ним электроном, тем не менее мы обнаруживаем, что на каждой орбитали всегда может
находиться и второй электрон. Пара электронов может сосуществовать, не нарушая прин¬
цип запрета, потому что их состояния не одинаковы, а имеют противоположно направ¬
ленные спины. Однако более двух электронов ни на какой орбитали быть не может, по¬
скольку у электрона имеется всего два независимых спиновых состояния. То же явление
лежит в основе химического понятия «ковалентной связи» — там два электрона сосуще¬
ствуют, казалось бы, в одном и том же состоянии, поскольку их спины противоположны
(см.рис. 24.2).
а)
б)
Рис. 24.2. Проявление спина электрона -. а) В атоме одну орбиталь могут занимать два электрона,
но не более. Это возможно, поскольку спиновые состояния электронов противоположны, так что
принцип запрета Паули не нарушается, б) Химическая «ковалентная связь» создается парой электронов
с противоположными спинами, совместно заполняющих орбитали двух отдельных атомов
Предложенное Паули описание электрона как двухкомпонентного объекта Фа —
= (фо, ф\) соответствует тому факту, что матрицы Паули имеют размер 2x2. Однако мы
обнаруживаем, что элементам Клиффорд а-Дирака (70, 71, 72, 73) для реализации клиффор-
довых правил умножения требуются матрицы 4x4.* Таким образом, дираковский электрон
является 4-компонентным объектом, а не просто «спинором Паули» с двумя компонентами,
описывающими два независимых состояний спина, которыми обладает нерелятивистская
1
частица со спином - (см. § 22.8).
Частица, описываемая уравнением Дирака, имеет всего две компоненты спина, несмот¬
ря на то что у волновой функции четыре компоненты. В математическом отношении при¬
чина тесно связана с тем фактом, что уравнение Дирака дф ~ ~гМф является уравнением
первого порядка, так что пространство его решений охватывает лишь половину решений
волнового уравнения второго порядка (□ + М2)ф = 0. (Этому уравнению удовлетворяют
также решения «антидираковского» уравнения дф = -ИМф, которое представляет собой
уравнение Дирака с отрицательной массой покоя —М.) Физически такой «подсчет» f24-14]
решений уравнений Дирака должен учитывать тот факт, что число степеней свободы анти¬
частицы электрона, а именно позитрона, также скрывается в решениях уравнения Дирака.
Однако было бы заблуждением считать, что две компоненты уравнения Дирака относятся
к электрону, а две других — к позитрону (сравните с § 25.2). Как мы увидим, на самом деле
ситуация гораздо сложнее.
Объясните, почему матрицы 2 х 2 не могут удовлетворить всем требуемым условиям, и найдите набор
матриц 4x4, которые им удовлетворяют.

24.8. Как Дирак пришел к позитрону
527
Напомним, что одной из наших главных задач, приведших к уравнению Дирака, бы¬
ло стремление понять, как следует поступать с нежелательными отрицательно-частотными
(т. е. соответствующими отрицательной энергии) решениями уравнения Шредингера. Оказы¬
вается, однако, что решения уравнения Дирака не ограничены положительными частотами,
несмотря на все наши (или, скорее, Дирака) усилия избавиться от квадратного корня в га¬
мильтониане. Что касается описанных выше попыток, то наличие взаимодействия, например,
с фоновым электромагнитным полем приводит к появлению отрицательно-частотной части
у первоначально положительно-частотной волны.
Однако изобретательность Дирака позволила ему не остановиться на этой стадии. Когда
он в конце концов убедился, что отрицательно-частотные решения не устраняются математи¬
ческими ухищрениями, он начал рассуждать примерно следующим образом. В чем, в конце
концов, опасность отрицательно-частотных решений? Проблема состоит в том, что если бы
существовали состояния с отрицательной энергией, то электрон мог бы перейти в такое
состояние с излучением энергии, и если число таких состояний неограниченно велико, то
возникала бы катастрофическая нестабильность: все электроны сваливались бы в состоя¬
ния со все более отрицательной энергией с излучением все большей энергии, и так без
конца. Однако, рассуждал Дирак, электроны подчиняются принципу Паули, а это не позво¬
ляет частице переходить в состояние, которое уже занято. Поэтому он делает поразительное
предположение: все состояния с отрицательной энергией должны быть уже заполнены! Этот
океан заполненных состояний с отрицательной энергией ныне называют «морем Дирака».
Таким образом* согласно «безумной идее» Дирака, мы считаем, что все состояния с отри¬
цательной энергией уже заняты, и в соответствии с принципом Паули электрон не может
перейти в такое состояние.
Но, рассуждал далее Дирак, может случиться, что несколько состояний с отрицатель¬
ной энергией не заполнено. Что в таком случае произойдет? Такая «дырка» в дираковском
море состояний с отрицательной энергией окажется в точности подобной частице с положи¬
тельной энергией (и, следовательно, положительной массой), электрический заряд которой
противоположен заряду электрона. Такое пустое состояние с отрицательной энергией теперь
может быть заполнено обычным электроном, поэтому электрон может «упасть» в это состо¬
яние с излучением энергии (обычно в форме электромагнитного излучения, т. е. фотонов).
Это приведет к взаимному уничтожению (аннигиляции) «дырки» и электрона, которое мы
рассматриваем как взаимную аннигиляцию частицы и ее античастицы (рис. 24.3 а). Наобо¬
рот, если дырки вначале не было, но в систему поступает достаточное количество энергии
а)
^Энергия/*
Энергия
б)
Рис. 24.3. Позитроны как «дырки» в «море Дирака» состояний электрона с отрицательной энергией.
Дирак предположил, что почти все такие состояния заполнены, так что переходу электрона в одно
из таких заполненных состояний препятствует принцип Паули. Незаполненное состояние — «дырка»
в этом море отрицательных энергий — будет проявлять себя как антиэлектрон (позитрон), обладающий
положительной энергией, а) Падение электрона в такую дырку следует интерпретировать как анниги¬
ляцию электрона и позитрона с освобождением энергии — суммы положительных вкладов, вносимых
электроном и позитроном, б) Наоборот, при поступлении в море Дирака достаточной энергии может
ь
возникнуть электрон-позитронная пара. (Изображение схематично, показанная решеточная структура
в действительности морю Дирака не свойственна.)

528
Глава 24
(например, в виде фотонов), тогда электрон может быть вытолкнут из одного состояния с от¬
рицательной энергией с образованием дырки (рис. 24.3 б). Дираковская «дырка» — это и есть
античастица электрона, ныне именуемая позитроном.
Вначале Дирак поостерегся заявить, что его теория действительно предсказывает су¬
ществование у электронов античастиц, полагая тогда (в 1929 году), что «дырками» могут
быть протоны — единственные известные в то время массивные частицы с положительным
зарядом. Но незадолго до того стало ясно^2415^, что масса каждой дырки должна быть равна
массе электрона, а отнюдь не массе протона, которая больше в 1836 раз. В 1931 году Ди¬
рак пришел к выводу, что дырками должны быть «антиэлектроны» — ранее не известные
частицы, которые мы теперь называем позитронами. В следующем году после теоретиче¬
ского предсказания Дирака Карл Андерсон объявил об открытии частицы, обладавшей теми
свойствами, которые предсказал Дирак, — это была открыта первая античастица!
♦
Примечания
§ 24.3.
24.1. В формальном отношении катастрофы можно избежать, приняв, что энергия «ограничена
снизу», то есть превышает некоторое фиксированное значение .Ео, которое может быть отри¬
цательным. В таком случае можно «перенормировать» энергию, добавив — Ео в гамильтониан,
тогда все собственные значения энергии будут положительными.
24.2. Имеется некоторая тонкость, связанная с точкой ос, поскольку функция / там, скорее всего,
сингулярна. Здесь уместен гиперфункциональный подход, описанный в §9.7; см. [51].
24.3. Строго говоря, следовало бы говорить о положительной полуопределенности, так как (непре¬
рывный) спектр собственных значений распространяется до нуля, включая и нуль.
24.4. Относительно применений в квантовой механике см. [716], общее обсуждение можно найти
в книге [26].
§ 24.5.
24.5. Некоторые предпочитают определить этот оператор с противоположным знаком, чтобы полу¬
чить сигнатуру 4-4-4— вместо используемой здесь 4	.
24.6. См. [573, 525, 211].
24.7. Эти два требования, взятые совместно, составляют существенную часть доказательства
СРТ-теоремы, с которой мы встретимся в § 25.4.
§ 24.6.
24.8. Относительно идеи такого «квадратного корня» см. [792].
24.9. См. [152], стр. 778-815, более общее рассмотрение приводится в [496].
24.10. Это соглашение отличается от применяемого математиками (см. [362, 113, 496, 476]), а также
мною самим ([627], приложение). Если принять сигнатуру пространства-времени 4	,
как это сделано здесь, то уравнение, определяющее алгебру Клиффорда общего вида, будет
иметь вид лъ ~ ЪЪ = ~^9г3-
§24.7.
24.11. См. [151, 126, 798, 411, 473, 582, 626, 627, 564]. В 2-спинорных обозначениях из §22.8
это приводит к уравнению Дирака в «зигзагообразной» форме, с которой мы познакомимся
в § 25.2.
24.12. Термин «спинор», по-видимому, был предложен Паулем Эренфестом в письме к Бартелю
В ан-д ер.-В ард ену.
24.13. Дополнительный член имеет вид А, где А = да Аа'уь, а Аа — электромагнитный потенциал;
/S	/Ч.	^
оператор д заменяется на д — геА
* Й© Объясните, почему это есть стандартное требование калибровочной инвариантности.

24.8. Как Дирак пришел к позитрону
529
§24.8.
24.14. Подсчет решений для релятивистских уравнений проще всего проводить методом «точных
наборов», используемым в 2-спинорном исчислении (см. [626], стр. 389, 90).
24.15. Эта работа была проделана Игорем Таммом, Германом Вейлем и Робертом Оппенгеймером;
пример соответствующих рассуждений см. в [566]. В подходе к позитрону существуют некото¬
рые тонкости, которые завели бы нас слишком далеко. Полное, строгое и изящное изложение
можно найти в книге [858].

Глава 2 5
Физика элементарных частиц:
стандартная модель
25.1.	Истоки современной физики элементарных частиц
Уравнение Дирака для электрона стало для физики поворотным пунктом во многих от¬
ношениях. В 1928 году, когда Дирак предложил свое уравнение, из всех элементарных частиц
науке были известны лишь электроны, протоны и фотоны. Свободные уравнения Максвел¬
ла описывают фотоны, предсказанные Эйнштейном в 1905 году Эта ранняя работа была
постепенно развита Эйнштейном, Бозе и другими, и 1927 году Иордан и Паули создали пол¬
ную математическую схему для описания свободных фотонов путем введения квантования
в максвелловскую теорию свободного поля. Казалось также, что протон, как и электрон, до¬
статочно хорошо описывается уравнением Дирака. В теорию Дирака отлично укладывалось
электромагнитное взаимодействие, описывающее, как воздействуют фотоны на электроны
и протоны, благодаря идее калибровки (введенной Вейлем в 1918 году, см. § 19.4). Начало
формулировке полной теории электронов (или протонов), взаимодействующих с фотонами
(т. е. квантовой электродинамике), было положено самим Дираком в 1927 году^25Л1 Таким
образом, казалось, что имеются под руками все более или менее основные средства для опи¬
сания всех частиц, существующих в Природе, а также наиболее очевидных взаимодействий
между ними.
И все же физики того времени в большинстве своем были не настолько глупы, что¬
бы предполагать, что все это вот-вот приведет их к «теории всего». Они сознавали, что
ни силы, удерживающие ядро от распада (ныне это называется сильным взаимодействи¬
ем), ни механизм, ответственный за радиоактивный распад (теперь это называется слабым
взаимодействием), не могут быть объяснены без дальнейшего продвижения вперед. Если
бы единственными составными частями атомов, включая атомные ядра, были дираковские
протоны и электроны, взаимодействующие лишь через электромагнитное поле, тогда все
обычные ядра (за исключением одиночного протона, составляющего ядро атома водорода)
должны были мгновенно распадаться из-за электростатического отталкивания вследствие
преобладания положительных зарядов. Должно было существовать нечто дотоле не извест¬
ное, создающее сильное притяжение между частицами внутри ядра! В 1932 году Чедвик
открыл нейтрон, и это в итоге привело к замене ранее популярной протонно-электронной
модели ядра новой моделью, согласно которой ядро содержит протоны и нейтроны, сильное
взаимодействие между которыми удерживает ядро от распада. Но даже это сильное вза¬
имодействие было еще не все, что ускользало от понимания в то время. Радиоактивность
урана, известная со времени наблюдения Анри Беккереля в 1896 году, оказалась результатом
еще одного — слабого — взаимодействия, отличного и от сильного, и от электромагнитного
взаимодействия. Даже сам нейтрон, будучи предоставлен самому себе, распадается прибли¬
зительно за 15 минут. Одним из загадочных продуктов радиоактивного распада оказалось
неуловимое нейтрино, пробная гипотеза о существовании которого была выдвинута Паули
в 1929 году, но которое не было непосредственно обнаружено вплоть до 1956 года. Именно
изучение радиоактивности в конечном счете принесло физикам неожиданную популярность
и влиятельность к концу Второй мировой войны и после нее...

25.2. Зигзаг-представление электрона
531
Многое изменилось с той поры первоначального проникновения в физику элементар¬
ных частиц в первой трети XX века. Сейчас, в начале XXI века, мы имеем гораздо более
полную картину, известную под названием стандартной модели физики элементарных ча¬
стиц. Эта модель описывает почти все наблюдаемое поведение широкого класса известных
ныне элементарных частиц. К фотону, электрону, протону, позитрону, нейтрону и нейтри¬
но в дальнейшем присоединились разные другие сорта нейтрино, мюон, пионы (эффектно
предсказанные Юкавой в 1934 году), каоны, ламбда- и сигма-частицы, а также омега-минус-
частица, знаменитая благодаря истории ее предсказания. В 1955 году был экспериментально
обнаружен антипротон, в 1956 году — антинейтрон. Существуют объекты нового типа —
кварки, глюоны и W- и Z-бозоны, а также целая стая частиц, существование которых столь
быстротечно, что они никогда не наблюдались непосредственно, их относят к «резонансам».
Формализм современной теории требует также существования нестационарных объектов,
называемых «виртуальными частицами», а также величин, именуемых «духами», относи¬
тельно которых исключается возможность непосредственного наблюдения. Существует так¬
же вызывающее замешательство изобилие гипотетических (и пока не обнаруженных) частиц,
предсказываемых некоторыми теоретическими моделями, но пока не укладывающихся в об¬
щепринятую схему элементарных частиц, — «Х-бозоны», «аксионы», «фотино», «скварки»,
«глюино», «магнитные монополи», «дилатоны» и т. д. Есть еще призрачная частица Хиггса,
не обнаруженная к моменту написания этой книги, существование которой в той или иной
форме (возможно, не в качестве одиночной частицы) существенно для сегодняшней физики
элементарных частиц, в которой связанное с этой частицей поле Хиггса определяет массу
каждой элементарной частицы.
25.2.	Зигзаг-представление электрона
В этой главе предлагается краткий путеводитель по стандартной модели современной
физики элементарных частиц, хотя мой собственный подход к ней местами может оказать¬
ся не вполне стандартным. Начнем несколько нестандартным образом, переформулировав
уравнение Дирака в «2-спинорном представлении», кратко описанном в § 22.8. Как отме-
1
чалось выше, в § 24.8, «спинор Паули», описывающий частицу со спином -, представляет
собой двухкомпонентную величину Фа- (Компонентами служат и Ф\-) При учете тре¬
бований теории относительности в соответствии с § 22.8 нам потребуются также величины
со гитрихованными индексами АВ\ С',..., которые появляются при комплексном сопря¬
жении, применяемом к нештрихованным индексам. Оказывается f25-2 , что описанный выше
дираковский спинор ф с его четырьмя комплексными компонентами можно представить
в виде пары 2-спиноров а а и Дд/, один из которых имеет нештрихованный индекс,
а другой — штрихованный:
ф = (ад, /3А')-
Тогда уравнение Дирака можно записать в виде уравнения, связывающего эти два 2-спинора,
при этом каждый из них играет в отношении другого роль «источника» с «константой
связи» 2‘ -г/2 М, определяющей «силу взаимодействия» между ними:
V%,aA = 2~1/2Мрв,,	= 2^2МаА.
Операторы V^, и Vf представляют собой 2-спинорные трансляции обычного операто¬
ра градиента V. Не следует придавать большого значения всем этим индексам, множите¬
лям 2-1/2 и точной форме этих уравнений, — я привожу их здесь лишь для того, чтобы
показать, как можно ввести уравнение Дирака в общие рамки 2-спинорного анализа и как
это может помочь, коль скоро это сделано, в обретении некоторого нового взгляда на природу
уравнения Дирака^25,4!.

532
Глава 25
Форма этих уравнений показывает, что дираковский электрон можно считать состоя¬
щим из двух ингредиентов — ад и вв' ■ Им можно придать некоторый физический смысл.
Можно представить себе картину, в которой существуют две «частицы», одна из которых
описывается величиной ад, а другая — /Зд/, причем обе они не имеют массы и каждая из
них непрерывно превращается в другую. Дадим этим частицам имена «зиг» и «заг», так
что ад будет описывать частицу «зиг», а /Зд> — частицу «заг». Будучи безмассовыми, они
должны перемещаться со скоростью света, однако вместо этого можно считать, что они
«качаются» взад-вперед, причем движение вперед частицы «зиг» непрерывно превращает¬
ся в движение назад частицы «заг» и наоборот. Фактически это есть реализация явления,
называемого «zitterbewegung» («дрожание») и состоящего в том, что мгновенное движение
электрона из-за участия в таких колебаниях всегда происходит со скоростью света, хо¬
тя полное усредненное движение электрона характеризуется скоростью, меньшей скорости
света^25-5^. Каждый из указанных ингредиентов имеет спин величиной - Гг в направлении дви¬
жения, соответствующий левому вращению в случае частицы «зиг» и правому для частицы
«заг». (Это связано с тем обстоятельством, что частица «зиг» ад имеет нештрихованный ин¬
декс, соответствующий отрицательной спиральности, а частица «заг» (Зв' — штрихованный
индекс, отвечающий положительной спиральности. Все это имеет отношение к обсужде¬
нию в §§33.6-33.8, однако здесь нецелесообразно входить в подробности.) Заметим, что
хотя скорость все время меняется, направление спина в системе покоя электрона остается
постоянным (рис. 25.1). При такой интерпретации частица «зиг» выступает как источник
<^^иг»
$«3аг»
>3
' «Зиг»
<
<
&«3аг»
^^иг»
а)	б)
Рис. 25.1. Зигзаг-представление электрона, а) Электрон (или другую массивную частицу со спином -)
можно рассматривать как осциллирующую в пространстве-времени между безмассовой частицей «зиг»
с левой спиральностью (спиральность — ^ описывается нештрихованным 2-спинором ад или, в обо-
1
значениях, более привычных для физиков, частью, проектируемой оператором - (1 — 75)) и безмассо-
1
вой частицей «заг» с правой спиральностью (спиральность -f- описывается штрихованным 2-спино-
1
ром /Зв' или частью, проектируемой оператором - (1 +75)). Каждая из частиц служит источником для
другой с массой покоя в качестве константы связи, б) С точки зрения 3-пространства, в системе покоя
электрона происходит непрерывное изменение скорости (всегда равной по величине скорости света),
однако направление спина остается постоянным. (Для большей наглядности изображена картина не
вполне в системе покоя электрона — вместо этого электрон медленно смещается вправо.)
Обратившись к уравнению Вейля для нейтрино в §25.3, объясните, почему разумно считать, что ад
и /3Л' описывают безмассовые частицы, связанные взаимодействием, превращающим их одна в другую.

25.2. Зигзаг-представление электрона
533
для частицы «заг», а частица «заг» — как источник в отношении частицы «зиг», сила связи
между ними определяется величиной М.
На рис. 25.2 дано диаграммное представление вклада этого процесса в полный «фейн-
мановский пропагатор» (см. §26.7), подобное фейнмановским диаграммам^25 6!, которыми
мы займемся подробнее в следующей главе. Каждый отдельный зигзаг-процесс имеет ко¬
нечную длину, однако вся их совокупность, включающая зигзаги все нарастающей длины,
дает вклад в полный процесс распространения электрона в соответствии с матрицей 2x2,
изображенной на рис. 25.2. При этом частица «зиг» становится частицей «заг», затем «заг»
превращается в «зиг», та снова в «заг» и так далее на некотором конечном отрезке. Рас¬
сматривая процесс в целом, мы обнаружим, что средняя частота, с которой это происходит,
связана обратным соотношением с параметром связи — массой М; фактически это есть
«де-бройлевская частота» электрона (см. §21.4).
Необходимо, однако, сделать замечание относительно того, как следует интерпретиро¬
вать фейнмановские диаграммы. Изображаемый процесс можно на законных основаниях
рассматривать как пространственно-временное описание происходящего, однако при рас¬
смотрении на квантовом уровне необходимо иметь в виду, что даже в случае одной ча¬
стицы одновременно протекает множество таких процессов. Каждый из них следует рас¬
сматривать как один из вкладов в некоторую квантовую суперпозицию огромного числа
различных процессов. Реальное квантовое состояние определяется всей суперпозицией
в целом. Каждая отдельная фейнмановская диаграмма — это всего лишь одна из ее ком¬
понент.
В таком же духе следует понимать и приведенное выше описание движения электрона
как качания взад-вперед, при котором «зиг» непрерывно превращается в «заг» и наоборот.
Реальное движение слагается из большого (фактически бесконечно большого) числа таких
отдельных процессов, так что наблюдаемое движение электрона можно рассматривать как
результат некоторого их «усреднения» (хотя, строго говоря, здесь имеет место квантовая
суперпозиция). Так обстоит дело в случае всего лишь свободного электрона. В действитель¬
ности электрон непрерывно взаимодействует с другими частицами (например, с фотонами —
квантами электромагнитного поля). Все подобные процессы взаимодействия также должны
быть включены в общую суперпозицию.
Имея все это в виду, зададимся вопросом: насколько «реальны» частицы «зиг» и «заг»?
Или это всего лишь артефакты некоторого математического формализма, которым я вос-
Рис. 25.2. Каждый зигзаг-процесс в отдельности вносит вклад, как часть бесконечной квантовой супер¬
позиции, в полный «пропагатор» наподобие фейнмановских диаграмм. Изображенный слева стандарт¬
ный фейнмановский пропагатор в виде прямой линии представляет целую матрицу из бесконечных
сумм конечных зигзагов, показанную справа

534
Глава 25
пользовался здесь при описании уравнения Дирака для электрона? Возникает вопрос более
общего характера: насколько оправданно с физической точки зрения руководствоваться со¬
ображениями изящества некоторого математического описания, а затем пытаться выдать это
за описание «реальности»? В данном случае следует начать с постановки вопроса о важ¬
ности (а также изяществе) самого 2-спинорного формализма как математического метода.
Я должен предупредить читателя, что этот формализм не относится к числу широко исполь¬
зуемых физиками, которые занимаются уравнением Дирака и его приложениями, в частно¬
сти, квантовой электродинамикой (КЭД) — наиболее успешным разделом квантовой теории
поля^25*7!.
Большинство физиков пользуется формализмом «дираковских спиноров» (или 4-спино¬
ров), в котором спинорные индексы отбрасываются. Вместо 2-спинора ал они используют
4-спинор (1 — 75 )-ф (называя его «левоспиральной частью дираковского электрона» или
как-нибудь в этом роде, вместо моей частицы «зиг»)^25,81 Величина 75 представляет собой
произведение
75 = “Ио 7i727з
и обладает свойством антикоммутировать с каждым из элементов алгебры Клиффорда, при
этом 72 = 1.* Аналогично вместо (За* используется (1 -f 75)^ (правоспиральная часть).
Кто-то может заметить, что это всего лишь вопрос обозначений, и действительно можно
переходить от 2-спинорного формализма к 4-спинорному и обратно. Предложенное мною
зигзаг-представление определенно применимо (хотя и не всегда применяется) к любому
формализму, однако к 2-спинорному формализму оно ближе, чем к 4-спинорному.
Так реальны ли частицы «зиг» и «заг»? Я ответил бы так: они реальны в той же
мере, в какой реален сам «дираковский электрон», — как в высшей степени полезное иде¬
ализированное математическое описание одного из наиболее фундаментальных элементов
Вселенной. Но есть ли это реальная «реальность»? В §§ 1.3, 1.4 я уже касался общего вопро¬
са математической и физической реальности и связи между ними. В конце книги, в § 34.6,
я вернусь к нему снова.
253. Электрослабое взаимодействие. Симметрия относительно
отражения
Каждая из частиц «зиг» и «заг» имеет один и тот же электрический заряд — так должно
быть, поскольку заряд сохраняется, — и каждая частица непрерывно превращается в другую.
На языке фейнмановских диаграмм взаимодействие заряженной частицы с электромагнит¬
ным полем изображается как присоединение линии, представляющей фотон. На рис. 25.3 а
это представлено в стандартной форме с обычным изображением траектории электрона
в виде одной линии дираковского 4-спинора; а на рис. 25.36 — в (не вполне стандартном)
зигзаг-представлении.
Заметим, что в электромагнитном взаимодействии в равной мере участвуют как ле¬
воспиральная часть («зиг»), так и правоспиральная («заг»). Оказывается, однако, что су¬
ществует другое физическое взаимодействие — слабое взаимодействие, — при котором эти
части совершенно неравноправны в том смысле, что в этом взаимодействии принимает
участие только «зиг»-часть электрона, а «заг» не участвует вовсе (см. рис. 25.4). Слабое
взаимодействие переносится аналогами фотона — W- и Z-бозонами. Как уже упоминалось,
слабое взаимодействие ответственно за радиоактивный распад, посредством которого, на¬
пример, ядро урана 238U за время (в среднем) 5 • 109 лет самопроизвольно распадается на
торий и ядро гелия (а-частицу) или свободный нейтрон распадается в среднем за 15 минут
* JSS Проверьте оба эти утверждения.

25.3. ЭЛЕКТРОСЛАБОЕ ВЗАИМОДЕЙСТВИЕ. СИММЕТРИЯ ОТНОСИТЕЛЬНО ОТРАЖЕНИЯ
535
а)
б)
Рис. 25.3. а) Диаграмма Фейнмана (в стандартной форме, без зигзагов) для электрона, взаимодейству¬
ющего с квантом электромагнитного поля (фотоном). Процесс на левом рисунке можно представлять
себе как поглощение фотона, на среднем — как излучение фотона, а на правом — как электростати¬
ческое взаимодействие; все эти процессы можно рассматривать как одно и то же — взаимодействие
с «виртуальным» фотоном, б) То же самое в зигзаг-представлении. Фотон (виртуальный) в равной
мере взаимодействует с частицами «зиг» и «заг». На всех рисунках распространение электрического
заряда показано светлыми треугольными стрелками. Стрелки указывают в прошлое, поскольку мы
рассматриваем электроны, которые заряжены отрицательно
на протон, электрон и антинейтрино (см. рис. 25.5). Эти
процессы именуются «/3-распадом», а электрон в этом
контексте называют (по историческим причинам) «8-
частицей».
В течение многих лет слабое взаимодействие счи¬
талось процессом, происходящим в одной точке, как по¬
казано в виде одной точки распада на рис. 25.5, в со¬
ответствии со схемой, предложенной еще в 1933 го¬
ду выдающимся итальянским физиком Энрико Ферми.
Но впоследствии это стало приводить к трудностям в те¬
ории, которые в конце концов были разрешены в теории
электрослабого взаимодействия Вайнберга, Салама, Уор¬
да и Глэшоу, рассматриваемой вкратце в §25.5. Частью
новых идей была замена точечного взаимодействия Фер¬
ми взаимодействием через промежуточные «калибровоч¬
ные бозоны» (ныне они называются W- и Z-частицами),
переносящие слабое взаимодействие, так что /3-распад,
изображенный на рис. 25.5, теперь интерпретируется,
«Зиг».
«Зиг»
«Заг»
Рис. 25.4. В случае слабого взаи¬
модействия, в отличие от электро¬
магнитного, только «зиг»-часть сла¬
бо взаимодействующей частицы вза¬
имодействует с W- или Z-бозоном.
(В случае «античастицы» в сла¬
бом взаимодействии участвует толь¬
ко «заг»-часть.)
как показано на рис. 25.6. Какую роль играет зиг/заг-
асимметрия? В 1956 году физики испытали сильное потрясение, когда Ли Цзун-дао и Янг
Чжень-нин выдвинули удивительное предположение^25'9^, касающееся /3-распада и вообще
слабого взаимодействия, а именно что оно должно быть неинвариантным относительно от¬
ражения. Вскоре после этого, в январе 1957 года, это предположение было подтверждено
экспериментально By Цзинь-сян и ее группой. Согласно этим результатам, зеркальное отра¬
жение процесса слабого взаимодействия удивительным образом не является в общем случае
разрешенным процессом слабого взаимодействия, то есть слабое взаимодействие проявля¬
ет киральность. В частности, в эксперименте By изучалась структура эмиссии электронов
радиоактивным кобальтом-60, и обнаружилось явно зеркально-асимметричное соотношение
между распределением эмиттируемых электронов и направлениями спинов ядер кобальта
(см. рис. 25.7). Это было поразительно, потому что никогда прежде не наблюдалось явление
зеркальной асимметрии в фундаментальных физических процессах!

536
Глава 25
1Г-бозон
Рис. 25.5. (5-распад нейтрона на протон, элек¬
трон и антинейтрино, который для свободного
нейтрона занимает (в среднем) 15 минут. Обрат¬
ное направление стрелки у антинейтрино пока¬
зывает, что, согласно схеме классификации пеп¬
тонов, оно является «античастицей». Как и на
рис. 25.4, светлые стрелки у электрона и прото¬
на обозначают электрический заряд
Рис. 25.6. Слабое взаимодействие не является
«точечным» подобно показанному на рис. 25.5
(первоначальная теория Ферми), а происходит
при посредничестве «векторного бозона» (W±
или Z0; в данном случае показана W-частица)
dt**
Рис. 25.7. В эксперименте By изучалась структура эмиссии электронов радиоактивным кобальтом-60.
Было обнаружено явно зеркально-асимметричное соотношение между распределением эмиттируемых
электронов и направленияхми спинов ядер кобальта. Здесь показано, что вверх вылетает больше элек¬
тронов, чем вниз
На языке наших частиц «зиг»- и «заг»-киральная асимметрия возникает оттого, что
в зеркале «зиг» выглядит как «заг», а «заг» — как «зиг». Напомним, что «зиг» имеет левую
спиральность. а «заг» — правую. При зеркальном отражении каждая из частиц превраща¬
ется в другую. (В более обычной терминологии 75 при отражении меняет знак, так что
лево- и правоспиральные части волновой функции (1 —75 )ф и (1 + 75) ф меняются места¬
ми.) Таким образом, неинвариантно сть слабого взаимодействия относительно зеркального
отражения выражается в том факте, что только «зиг»-часть электрона принимает участие
в слабом взаимодействии. То же можно сказать о нейтроне, претерпевающем /3-распад,

25.3. ЭЛЕКТРОСЛАБОЕ ВЗАИМОДЕЙСТВИЕ. СИММЕТРИЯ ОТНОСИТЕЛЬНО ОТРАЖЕНИЯ
537
и образующемся протоне. Нейтрон и протон с хорошим приближением также описыва¬
ются уравнением Дирака, так что к ним применимо зигзаг-представление. В процесс сла¬
бого распада здесь опять-таки вовлечены «зиг»-части нейтрона и протона, как показано
на рис. 25.8 а. В соответствии с современной картиной уместнее рассматривать нейтрон
и протон как составные частицы, построенные каждая из трех кварков. Сами кварки, взя¬
тые в отдельности, описываются уравнением Дирака, поэтому для каждого из них также
годится зигзаг-представление. На рис. 25.86 /7-распад нейтрона представлен именно таким
образом.
ч	ч	\	^
а)	б)
Рис. 25.8. Процесс /7-распада, показанный на рис. 25.5, в зигзаг-представлении, а) Нейтрон
и протон с хорошим приближением можно рассматривать как дираковские частицы, так что зиг¬
заг-представление вполне применимо. Как и на рис. 25.4, в процессе слабого распада участвуют
только «зиг»-части нейтрона и протона. Хотя антинейтрино является «заг»-частицей (с левой спираль-
ностью), наличие у него малой массы учитывается наличием небольшой «зиг»-части слева вверху.
б)	Однако нейтрон и протон рассматриваются как составные частицы, построенные каждая из трех
кварков, которые, взятые в отдельности, описываются уравнением Дирака, так что к ним примени¬
мо зигзаг-представление. (Стрелки, обозначающие заряд, и глюоны, соединяющие кварки, здесь не
показаны.)
Особый интерес в этом отношении представляет нейтрино. По крайней мере с очень хо¬
рошим приближением его можно считать безмассовой частицей. (Его масса в любом случае
крайне мала по сравнению с массой электрона и определенно не превышает 6 • 10 ~6 массы
электрона.) Если в 2-спинорном варианте уравнения Дирака положить М = 0, то уравнения
расцепляются:
^B'OLA = 0, Vf /Зв' = 0.
Каждое из них может существовать в отсутствие другого (и каждое можно рассматривать
как «уравнение Вейля»125Л01 для нейтрино). Однако только «зиг»-вариант (определяемый
негитрихо ванным спинором а а, удовлетворяющим уравнению V^/O^ = 0) участвует в сла¬
бом взаимодействии или может возникать в процессах слабого взаимодействия. Таким об¬
разом, нейтрино является частицей с левой спиральностью.
Действительно ли нейтрино обладает массой? В настоящее время имеются убедитель¬
ные экспериментальные свидетельства того, что по крайней мере два из трех типов ней¬
трино должны иметь массу. Эти три типа представляют «электронное нейтрино» ve (оно
участвует в обычном /7-распаде, а его античастица z7e испускается при распаде нейтрона;

538
Глава 25
см. рис. 25.5), «мюонное нейтрино» и «тау-
нейтрино» ит. Наблюдения, сделанные с помо¬
щью японского детектора Superkamiokande, ясно
показывают, что разность масс нейтрино этих трех
типов, хотя и весьма мала (всего около 10 ~7 мас¬
сы электрона), не может быть равной нулю в си¬
лу того факта, что нейтрино разного типа име¬
ют тенденцию превращаться друг в друга, а это
невозможно при нулевой массе. Я допускаю, что
нулевую массу может иметь ve (или некая подхо¬
дящая квантовая «линейная комбинация» трех ти¬
пов), но определенных указаний на этот счет пока
нет. Безмассовое нейтрино определенно должно
быть «зиг»-частицей, но при наличии малой мас¬
сы картина ближе к показанной на рис. 25.9 а, где
«зиг» может на мгновение превратиться в «заг»
и вернуться обратно. Однако в системе отсчета,
движущейся вместе с нейтрино, «зиг»- и «заг»-
аспекты дают равный вклад в полное движение
(см. рис. 25.9б).
Необходимо сказать несколько слов о класси¬
фикации. Когда выше было сказано, что в сла¬
бом взаимодействии участвуют только (левоспиральные) частицы «зиг» и не участву¬
ют частицы «заг», то предполагалось, что мы знаем, как отличить «частицу» от «ан¬
тичастицы». У античастиц все обстоит наоборот. В случае античастицы электрона —
позитрона — можно также ввести «зигзаг-описание», в котором частица «зиг» имеет
левую спиральность, а «заг» — правую, но позитронная частица «зиг» является анти¬
частицей электронной частицы «заг» и наоборот. Таким образом, в случае позитрона
в слабом взаимодействии участвует правоспиральная частица «заг» (античастица элек¬
тронной частицы «зиг») и не участвует «зиг». Такое же замечание можно сделать в от¬
ношении антинейтрона и антипротона, а также, конечно, и антикварка. То же относит¬
ся и к антинейтрино, которое, если оно не имеет массы, полностью является части¬
цей «заг».
Здесь может возникнуть некоторое недоразумение, поскольку не было дано критерия,
позволяющего решить, является ли частицеподобный объект (со спином |) «частицей» или
«античастицей», чтобы узнать, какая его часть, «зиг» или «заг», принимает участие в сла¬
бом взаимодействии. Хотя в предыдущей главе античастица определялась как дираковская
«дырка» в «море состояний с отрицательной энергией», не следует смотреть на античастицу
как на объект совершенного иного рода, нежели частица. В рамках современной квантовой
теории поля нет необходимости следовать первоначальному пути Дирака с его видимой
асимметрией. Античастицы в такой же мере «частицы», в какой и частицы, которые яв¬
ляются в отношении них «античастицами». Более того, понятие античастицы применимо
к бозонам (частицам с целым спином) в той же мере, что и к фермионам, хотя принцип Пау¬
ли распространяется только на фермионы (см. §§ 23.7,23.8) и взгляд на античастицы с точки
зрения «моря Дирака» к бозонам неприменим. Например, положительно заряженный пион
(7г+-мезон), который относится к бозонам, имеет античастицу в виде отрицательно заряжен¬
ного пиона (7г“-мезона). Некоторые бозоны являются своими собственными античастицами.
Примером может служить фотон, а также нейтральный пион (7Г°-мезон). Насколько известно
(и определенно так согласно стандартной теории), каждая частица в природе имеет свою
античастицу.
А «э
«Заг»
«Зиг»,
бЗиг»*
^Загу
\<«3иг»
а)
б)
Рис. 25.9. а) Безмассовое нейтрино долж¬
но быть полностью «зиг»-частицей, одна¬
ко при малой массе мы должны допустить
возможность кратковременного превраще¬
ния в «заг» и обратно. Показана картина
с точки зрения лабораторной системы от¬
счета О. б) С точки зрения системы от¬
счета (У, движущейся вместе с нейтрино,
«зиг»- и «заг»-аспекты дают одинаковый
вклад в полное движение

25.4. Зарядовое сопряжение, четность и обращение времени
539
25,4.	Зарядовое сопряжение, четность и обращение времени
Операция, заменяющая каждую частицу ее античастицей, называется зарядовым сопря¬
жением и обозначается буквой С (от слов charge conjugation). Физическое взаимодействие,
инвариантное относительно замены частиц их античастицами (и наоборот), называется С-
инвариантным. Операция пространственного отражения (отражения в зеркале) обозначает¬
ся буквой Р (от слова parity, т. е. четность). В соответствии с обсуждением, проведенным
в § 25.3, обычное слабое взаимодействие не инвариантно относительно операций Р и С
в отдельности; оказывается, однако, что оно инвариантно относительно комбинированной
операции СР (= PC). Можно рассматривать СР как операцию, производимую необычным
зеркалом, в котором каждая частица отражается в виде ее античастицы. Мы видим, что
операция СР превращает «зиг» частицы в «заг» ее античастицы и наоборот. В связи с этими
операциями обычно обсуждается еще одна, обозначаемая буквой Т, — обращение времени.
Взаимодействие инвариантно относительно операции Т, если оно не меняется, когда мы
рассматриваем его во времени, текущем в направлении, обратном обычному. В квантовой
теории поля имеется знаменитая теорема, именуемая СРТ-теоремой, которая утверждает,
что любое физическое взаимодействие инвариантно относительно действия всех трех опе¬
раций вместе. Конечно, всякая теорема — это всего лишь «кусочек математики», так что ее
физическая применимость зависит от физической справедливости исходных предположе¬
ний. Все это окажется важным для нас в дальнейшем (§ 30.2), где обсуждение приведет нас
к вопросу о справедливости выводов (и, следовательно, исходных допущений) СРТ-теоремы.
Нет, однако, оснований ожидать каких-либо трудностей такого рода в отношении обычно¬
го слабого взаимодействия. В соответствии с этим CP-инвариантность обычного слабого
взаимодействия означает также его инвариантность относительно операции Т (временную
симметрию).
Известно несколько физических эффектов, нарушающих CP-инвариантность. Наиболее
давний эффект («необычный» слабый процесс, впервые наблюдавшийся в 1964 году Фитчем
и Кронином) — это распад частицы, неинвариантный относительно CP-операции. Он также
неинвариантен относительно операции Т (но, насколько известно, инвариантен относительно
СРТ в соответствии с СРТ-теоремой). Таковым является распад К°-мезона (который может
распадаться на 2 или 3 пиона, при этом возникает эффект превращения К0-частицы в ее
античастицу К0 с осцилляциями между ними).
СРТ-теорема дает альтернативный взгляд на античастицы, отличный от использования
понятия «моря Дирака» и более удовлетворительный, так как он применим и к бозонам.
С учетом СРТ-теоремы операцию С — замену частиц античастицами — можно представить
как эквивалент РТ-операции, поэтому античастицу некоторой частицы можно рассматри¬
вать как «пространственно-временное отражение» (РТ) этой частицы. Игнорируя аспект
пространственного отражения, мы получаем интерпретацию античастицы как частицы, пу¬
тешествующей обратно во времени. Именно так Ричард Фейнман предпочитал интерпрети¬
ровать античастицы. Это дает очень удобный и согласованный способ трактовки античастиц
на языке фейнмановских диаграмм. (Эта идея была предложена Фейнману Джоном Уиле¬
ром; еще раньше (1942) и независимо она была выдвинута Штюкельбергом.) По своей
нестандартности это такая же «безумная» идея, как и море Дирака!
Частицы, не являющиеся своими собственными античастицами, на диаграмме Фейн¬
мана изображаются линиями, имеющими определенное направление, как если бы к каждой
линии была присоединена соответствующая стрелка. Можно считать, что такая стрелка на¬
правлена в будущее, когда линия представляет собственно частицу, и в прошлое, когда она
представляет ее античастицу. Такой взгляд на античастицу имеет большое преимущество,
поскольку многие внешне весьма различные процессы с участием частиц оказываются, по
существу, одним и тем же процессом, но рассматриваемым под различным «углом зрения»

540
Глава 25
в пространстве-времени. В качестве примера на
рис. 25.10 показано (без зигзагов), что аннигиляция
электрона и позитрона в пару фотонов — это, «в сущ¬
ности тот же самый» процесс, что и комптонов -
ское рассеяние электрона фотоном, только по-другому
упорядоченный в пространстве-времени. (Вскоре мы
увидим, что линиям частиц следует также приписы¬
вать направление в пространстве-времени, когда они
описывают так называемые «виртуальные частицы»,
но в данный момент это могло бы только запутать!)
Вернемся к вопросу о том, какая часть объекта со
спином ~, «зиг» или «заг», принимает участие в сла¬
бом взаимодействии. Для этого нам нужно иметь чет¬
кое правило, позволяющее определить, что перед на¬
ми — частица или античастица. Действующее правило
гласит, что «частицами» следует считать «лептоны»
(к ним относятся электрон, его более тяжелые род¬
ственники — мюоны и тау-лептоны (тауоны) — и соот¬
ветствующие им нейтрино ие, и гу), а также квар¬
ки, из которых состоят протоны и нейтроны (и другие
адроны). У них в слабом взаимодействии принима¬
ет участие «зиг»-часть. Все эти объекты с приставкой
«анти-» считаются античастицами, у которых в сла¬
бом взаимодействии участвует «заг»-часть. Положение осложняется тем обстоятельством,
что существуют (массивные) объекты со спином 1, W- и Z-бозоны, которые также участвуют
в слабом взаимодействии[25. и] ^ qhh ЯВЛЯются переносчиками слабого взаимодействия, играя
ту же роль, что и фотоны, которые переносят электромагнитное взаимодействие (фотоны яв¬
ляются квантами электромагнитного поля). Такие частицы иногда называют «калибровочны¬
ми квантами», причина этого объясняется ниже. Существуют два различных W-бозона, W+
и W“ (являющихся античастицами друг друга), с зарядом соответственно -f 1 и — 1 (за еди¬
ницу выбран заряд позитрона), и всего один незаряженный Z0-бозон (являющийся своей
собственной античастицей). Каждый из них принимает участие в слабом взаимодействии;
соответствующие им линии на диаграммах Фейнмана присоединяются к концу либо «зиг»~
части лептона или кварка, либо «заг»-части антилептона или антикварка (см. рис. 25.11).
В каждом процессе слабого взаимодействия сохраняется электрический заряд, а также леп-
тонное число. На самом деле существуют три различных вида лептонного числа (электрон¬
ное, мюонное и тау-лептонное (тауонное)), каждое из которых в стандартной модели слабого
взаимодействия сохраняется в отдельности; лептонные числа W±- и Z°-6o3ohob считаются
равными нулю. Чтобы проверить выполнение этих четырех законов сохранения, мы долж¬
ны убедиться, что стрелки всех четырех видов на линиях следуют вдоль всей диаграммы
непрерывным и правильно ориентированным образом.
25.5.	Электрослабая группа симметрии
Всё это, несомненно, выглядит несколько сложным для фундаментальной теории.
Да, она действительно сложна, хотя в основе ее лежит картина, которую я пока не объяснил.
Однако пока я лишь приступил к ее описанию на сугубо качественном уровне и изложил
менее половины того, что называется «стандартной моделью». Более того, мои замечания до
сих имели «ботанический» характер в отношении различных частиц, участвующих в слабом
Рис, 25.10. Перекрестная симметрия.
Процессы, отличающиеся только упо¬
рядочением различных частей во вре¬
мени, не влияющим на топологию диа¬
граммы, по существу математически эк¬
вивалентны (связаны между собой ана¬
литическим продолжением; см. §7.4).
Это иллюстрируется на примере экви¬
валентности показанной слева анниги¬
ляции пары частица-античастица в два
фотона показанному справа процессу
комптоновского рассеяния (изображено
без зигзагов)

25.5. ЭЛЕКТРОСЛАБАЯ ГРУППА СИММЕТРИИ
541
Рис. 25.11. Иллюстрация взаимодействия между «зиг»-частицей и калибровочным бозоном слабого
взаимодействия, а) Заряженные бозоны W+ и W~ (античастицы друг друга) вызывают изменение
электрического заряда «зиг»-части (чтобы обеспечить сохранение электрического заряда), б) Незаря¬
женный бозон Z0 (являющийся своей собственной античастицей) к изменению заряда не приводит.
в)	«Зиг»-часть нейтрино может взаимодействовать с незаряженным бозоном Z0
(и электромагнитном) взаимодействии. В стандартной модели слабое и электромагнитное
взаимодействия объединяются в так называемую электрослабую теорию, где имеет место
особая симметрия, связывающая W+-, W~-, Z0-6o3OHbi и фотон у в соответствии с группой
SU(2) х U(l), или, более точноf2512l? с группой U(2). (Тем, кому необходимо вспомнить,
что это за группы, следует заглянуть в § 13.9.) Это есть (скрытая) симметрия, создающая
упомянутую картину, лежащую в основе.
Роль этой симметрии я объясню несколько подробнее в этой главе попозже. Эта сим¬
метрия связывает также «зиг»-части различных пептонов и кварков. Из этой идеи следует,
что с более примитивной точки зрения все частицы W+, W-, Z° и у могут, в некотором
смысле, «превращаться одна в другую», так что различные наборы (квантовых) линейных
комбинаций выступают на равных правах с самими отдельными частицами!
•
Как отмечалось выше, такая «симметрия» выглядит весьма странной и тонкой матери¬
ей, особенно потому, что чистый электромагнетизм инвариантен относительно отражения,
поскольку «зиг»- и «заг»-части источников входят на равных правах; в то же время слабое
взаимодействие не инвариантно относительно отражения, так как в нем участвуют только
«зиг»-части частиц. Кроме того, фотон явно выделяется из всех бозонов, фигурирующих
в теории, поскольку он является безмассовой частицей. В самом деле, из надежных из¬
мерений следует, что масса фотона если и не равна нулю, то определенно должна быть
меньше 10~20 массы электрона, т. е. меньше 5 • 10~26 измеренной массы W- и Z-бозонов.
Вдобавок W-бозоны электрически заряжены и переносят слабый заряд, а фотон не заряжен.
На рис. 25.12 показаны все возможные треххвостые фейнмановские вершины, содер¬
жащие только калибровочные бозоны (т. е. W+, W~~, Z° или 7). Таковых всего две. Они
являются выражением нелинейности свободного калибровочного поля, которая вытекает из
неабелева характера калибровочной группы U(2) (см. §§ 15.8,19.2). (Чистой электродинами¬
ке соответствует абелева калибровочная группа U(l), поэтому не существует аналогичной
треххвостой фейнмановской диаграммы, содержащей только фотоны. В противном случае
возникла бы нелинейность в максвелловском поле без источников. Аналогичное утвержде¬
ние относится к п-хвостым вершинам с п > 2.) Из ограниченности набора диаграмм на
рис. 25.12 следует, что не может быть полной симметрии между всеми калибровочными
бозонами.
Как примирить эти как будто несомненные отклонения от симметрии с требованиями,
определяемыми целью построения симметричной единой теории? В качестве первого ша¬
га на пути к реализации этой цели отметим, что в фейнмановских диаграммах на самом
деле скрыто больше симметрии, чем кажется на первый взгляд, и при правильном подхо¬
де оказывается, что они обладают симметрией U(2). Рассмотрим сначала две диаграммы

542
Глава 25
на рис. 25.12. Чтобы лучше представить себе симметрию,
лежащую в их основе, возьмем эрмитову матрицу 2x2
(см. § 13.9). Пусть она содержит два вещественных диаго¬
нальных элемента, аналогичных Z0 и 7, и два остальных,
недиагональных, элемента, аналогичных W+ и W“, кото¬
рые являются комплексно-сопряженными по отношению
друг к другу. Вещественность диагональных элементов со¬
ответствует тому, что Z0 и 7 совпадают со своими антича¬
стицами (линии без стрелок на рис. 25.12), а комплексно¬
сопряженный характер недиагональных элементов — то¬
му факту, что W+ и W“ являются античастицами друг
друга (при переходе от одной частицы к другой направле¬
ние стрелки меняется на противоположное). Общее U(2)-
преобразование данной эрмитовой матрицы (которое, на¬
помним, состоит в умножении на матрицу U(2) и после¬
дующем умножении на обратную ей матрицу) «переме¬
шивает» элементы этой эрмитовой матрицы весьма спе¬
цифическим образом, но ее эрмитов характер при этом
сохраняется. Фактически эта аналогия очень близка к тому, как действует преобразова¬
ние U(l) в электрослабой теории (единственное усложнение состоит в том, что при та¬
ком отождествлении линейная комбинация диагональных элементов со следом матрицы
должна быть связана с «углом Вайнберга» (см. §25.7)). Та асимметрия, которую мы вро¬
де бы наблюдаем в отношении этих частиц в реальном мире, вносится в электрослабую
теорию просто потому, что для реализации в качестве свободных частиц Природа выбира¬
ет некоторые определенные комбинации (т. е. определенные квантовые суперпозиции этих
элементов).
Но как быть с другой, наиболее несомненной, асимметрией наших фейнмановских диа¬
грамм, состоящей в том, что Z0 и Wi: могут присоединяться только к «зиг»-линиям частиц,
тогда как 7 присоединяется к «зиг»- и «заг»-линиям, не делая различия между ними? Здесь
опять-таки дело в выборе суперпозиций, которые Природа позволяет нам обнаруживать
в качестве свободных частиц. Например, могла бы существовать некоторая суперпозиция
частиц Z0 и 7 (назовем ее Y), которая замечает только «заг»-часть частицы. (Грубо говоря,
«вычитание» Z0 из 7 устраняет «зиг»-взаимодействие, оставляя только «заг»-часть.) Мож¬
но восстановить нашу прежнюю частицу 7 из Z0 и Y, но возможно и множество других
подобных суперпозиций, которые могли бы с равным успехом играть роль фотона, если бы
Природа сделала какой-то иной выбор.
Ключевой вопрос состоит, таким образом, в следующем: каким критерием руководству¬
ется Природа, позволяя нам обнаруживать в качестве свободных частиц именно данные,
а не какие-то иные суперпозиции? Ответ, в общих чертах, следующий: в случае свободной
частицы нам нужно, чтобы она была собственным состоянием массы, поэтому нам необ¬
ходимо знать, чем вообще определяется масса частиц. Здесь мы не можем ожидать полной
симметрии относительно группы U(2), другими словами, наличие массы предполагает неко¬
торый вид нарушения симметрии. Как это соотносится со стандартной моделью? Идея, по
крайней мере как ее обычно представляют, состоит в следующем: та асимметрия во взаи¬
модействии частиц, которую мы сегодня реально наблюдаем, есть результат спонтанного
нарушения симметрии, которое должно было произойти на ранних стадиях развития Все¬
ленной. До того условия сильно отличались от нынешних, и, как утверждает стандартная
теория электрослабого взаимодействия, при сверхвысоких температурах, господствовавших
в ранней Вселенной, и(2)-симметрия соблюдалась точно, так что W+, W-, Z° и 7 были
полностью эквивалентны множеству других квантовых суперпозиций этих частиц, при этом
Рис. 25.12. Электрослабые трехча¬
стичные вершины с калибровоч¬
ными бозонами, которые теоре¬
тически могут возникнуть вслед¬
ствие неабелевой природы калиб¬
ровочной группы. (Фотон пока¬
зан волнистой линией, Z°-6o3oh —
двойной прямой линией без стрел¬
ки, — двойными прямыми ли¬
ниями со стрелкой.)

25.5. ЭЛЕКТРОСЛАБАЯ ГРУППА СИММЕТРИИ
543
фотон 7 выступал на равных правах со всеми другими комбинациями, которые могли воз¬
никнуть. Но, согласно этой идее, когда температура во Вселенной опустилась ниже 1016 К
(это произошло примерно через 10~12 секунд после Большого взрыва; см. §§28.1-28.3),
наблюдаемые сегодня частицы W+, W~, Z° и 7 были «выморожены» в результате спон¬
танного нарушения симметрии. Таким образом, четыре реальные частицы в этом процессе
выделились из полностью симметричного множества начальных возможностей. Три из них
приобрели массу и стали в дальнейшем называться Wx- и Z0-частицами, четвертая оста¬
лась без массы и ее назвали фотоном. В начальном «чистом» варианте теории, когда имела
место полная, ненарушенная, U(2)-симметрия, все частицы W^, Z° и 7 были эффективно
безмассовыми. В качестве фундаментального аспекта этой концепции нарушения симмет¬
рии требуется ввести еще одну частицу, называемую бозоном. Хиггса, и соответствующее
поле. Поле Хиггса считается ответственным за приобретение массы всеми рассматриваемы¬
ми частицами (включая и сам бозон Хиггса), а также кварками, из которых состоят другие
частицы во Вселенной.
Как это все работает? Все подробности этого заме¬
чательного множества идей, к сожалению, остаются за
рамками этой книги, однако некоторые его части будут
представлены позже, в §§ 26.11, 28.1. Пока, мне кажется,
лучше всего показать (хотя и весьма неполно) роль по¬
ля Хиггса, вернувшись к «зигзаг»-описанию дираковско-
го электрона, представленному на рис. 25.2. Напомним,
что электрон считался совершающим колебания между
левоспиральным «зиг»-состоянием (ад) и правоспираль¬
ным «заг»-с о стоянием фв'), каждое из которых само по
себе не имеет массы. «Перескоки» между ад- и {Зв'-ча¬
стями дираковского спинора определялись «константой
_ 1
связи» 2 2 М. С «хиггсовой» точки зрения, можно рас-
_ 1
сматривать 2 2 М как некоторое поле (по существу, иоле
Хиггса), которое входит в теорию в качестве взаимодей¬
ствия в том месте, где прежде фигурировала константа
_ 1
связи 2 2 М (см. рис. 25.13). Одним из следствий спон¬
танного нарушения симметрии в самой ранней Вселенной
является установление всюду во Вселенной постоянного
значения поля Хиггса. Это значение определяет общий
масштаб для определения масс всех частиц; различные
значения масс определяются некоторым численным ко¬
эффициентом, который зависит от особенностей каждой
отдельной частицы.
Я откладываю изложение коллекции этих необычных идей до §§28.1-28.3, где оно
будет более последовательным. Но что бы мы ни думали об этих идеях, итоговая единая те¬
ория слабого и электромагнитного полей — теория электрослабого взаимодействия^2513^ —
оказалась замечательно успешной. Среди ее предсказаний само существование Z0-бозона
(а также W±-бозонов, однако существование ,W±-частиц уже было предсказано раньше ис¬
ходя из более ранних идей) и некоторые довольно специфические значения массы W^-
и Z°-6o30hob (соответственно 80 и 90 ГэВ)^25,141 и Z0-6o3OHbi были обнаружены в экс¬
периментах, проведенных в ЦЕРНе (Женева, Швейцария) в 1983 году, и предсказанные
значения масс были подтверждены с довольно хорошей точностью, современные экспери¬
ментальные значения составляют соответственно 81,4 и 91,2 ГэВ. Оправдался также ряд
Поле
лапт,!
Хиггса
Поле
Хиггса
Поле
Хиггса
Поле
Хиггса”
Хиггса
Рис. 25.13. В зигзаг-представлении
дираковской частицы вершины
можно рассматривать как взаимо¬
действие с (постоянным) полем
Хиггса

544
Глава 25
других предсказаний, так что в момент написания этой книги теория электрослабого взаи¬
модействия находится в отличной форме.
25.6.	Сильно взаимодействующие частицы
А что представляет собой сильное взаимодействие? Современная теория, которая опи¬
сывает его, составляет другую «половину» стандартной модели, называемую квантовой
хромодинамикощ сокращенно КХД. Это название может показаться странным, поскольку
греческое слово хрома, от которого происходит это название, означает «цвет», и уместно
спросить, какое отношение имеет «цвет» к теории сильного взаимодействия, определяюще¬
го ядерные силы. Ответ таков: понятие «цвета» здесь совершенно условно и не имеет ни
малейшего отношения к обычному цвету, определяемого длиной волны видимого света^25Л51
Чтобы понять, откуда взялось понятие «цвета» в ядерной физике, следует обратиться к зага¬
дочному ряду частиц, именуемых адронами, частным примером которых являются нейтроны
и протоны.
Название «адрон» происходит от греческого адрос, что означает «громоздкий». Адроны
представляют собой наиболее массивные из фундаментальных частиц Природы, и они при¬
нимают участие в сильном взаимодействии (именно сила этого взаимодействия обеспечивает
большой вклад энергии в их массу). Семейство адронов включает в себя фермионы, отно¬
сящиеся к «барионам», а также бозоны, относящиеся к «мезонам». Согласно стандартной
теории, все адроны состоят из кварков, о которых еще будет сказано ниже. В частности, ад¬
роны, относящиеся к барионам, — это обычные «нуклоны» (нейтроны и протоны) и их более
тяжелые собратья, именуемые «гиперонами» (они были обнаружены в ливнях космических
лучей и на ускорителях элементарных частиц). Мезоны первоначально были предсказаны
японским физиком Хидеки Юкавой на основе теоретического анализа ядерных сил; в 1947
году Сесиль Фрэнк Пауэлл обнаружил пионы в следах космических лучей. В настоящее
время известно много других мезонов, родственных пиону.
Термин «барион» происходит от греческого барос, что означает «тяжелый», в проти¬
воположность слову leptos («маленький»), от которого происходит термин «лептон». К пеп¬
тонам относятся электрон и родственные частицы — мюон и тау-лептон (тауон) с соответ¬
ствующими нейтрино; их античастицы называются антилептонами. И лептоны, и барионы
являются фермионами со спином -, однако лептоны отличаются от барионов тем, что они
не участвуют непосредственно в сильном взаимодействии, — и в этом, вероятно, главная
«причина» того, что у лептонов масса намного меньше, чем у барионов (хотя имеется ис¬
ключение — тауон, у которого масса почти вдвое больше, чем у протона или нейтрона).
Начиная с конца 1940-х годов в космических лучах и на ускорителях было открыто
большое число адронов: А°,	Е°, Е_, Е°, Д++, Д1^, Д°, Q", р°, р±, сj°, rf, К^, К0,
а также многочисленные более тяжелые варианты многих из этих частиц с более высоким
спином (обозначаемые путем добавления звездочки к символу, например, Е*~), которые
именуются «повторениями Редже» (см. рис. 31.6). Это могло бы совершенно сбить с толку,
если бы не тот факт, что эти частицы разбиваются на некоторые семейства, называемые
мультиплетами. Успешное объяснение природы этих мультиплетов было дано в 1961 го¬
ду Мюрреем Гелл-Манном и Ювалом Нееманом. В основу было положено то, что эти
мультиплеты реализуют представления группы SU(3) или, точнее, SU(3)/Z3 (относитель¬
но понятия «представление» см. § 13.6; интерпретация понятия «фактор-группа», включая
использование «деления» (знак /), дается в § 13.2); Z3 означает здесь циклическую группу
из 3 элементов, которая возникает естественным образом как нормальная подгруппа груп¬
пы SU(3);* см. также §§5.4, 5.5).
Найдите эту нормальную подгруппу. {Подсказка: рассмотрите определитель матрицы 3 х 3.)

25.6. СИЛЬНО ВЗАИМОДЕЙСТВУЮЩИЕ ЧАСТИЦЫ
545
Лучший способ понять, что заключено в этих представлениях, — это принять гипотезу
(выдвинутую в явном виде Цвейгом и Гелл-Манном в 1963 году), согласно которой каждый
адрон построен из некоторых фундаментальных объектов со спином которые Гелл-Манн
W
окрестил «кварками» (трех видов) и «антикварками» (трех видов). Каждый барион состоит
из трех таких кварков, каждый мезон — из одного кварка и одного антикварка. Кварки трех
видов (о которых говорят как о трех ароматах) были названы (без особой изобретательно¬
сти) «верхним», «нижним» и «странным». Загадочная особенность кварков состоит в том,
что они обладают дробным электрическим зарядом (в единицах заряда протона); верхний,
2	1	1
нижний и странный кварки имеют заряд соответственно — - и —
О	О	О
Вероятно, в первую очередь из-за этих неправдоподобно выглядящих значений элек¬
трического заряда кварков и связанного с этим факта, что кварки сами по себе никогда не
наблюдались (все наблюдавшиеся частицы всегда имели целочисленные значения заряда,
см. § 5.5), кварки первоначально воспринимались не как реальные частицы, а просто как
удобная «бухгалтерия» для различных представлений группы SU(3)/Z3. Эта бухгалтерия
работала, однако, лишь при условии, что кварки рассматриваются как объекты, подчиняю¬
щиеся статистике, «неправильной» для объектов со спином i Для того чтобы получались
£
правильные мультиплеты, необходимо было предположить, что кварки являются бозонами,
а не фермионами, как требует теорема о связи спина со статистикой (см. §§ 23.7, 26.2).
Чтобы понять это последнее утверждение, рассмотрим два примера. Наиболее ярким
Q
из них может служить декуплет из 10 частиц со спином с помощью которого Гелл-Манн
и Нееман в 1962 году предсказали частицу £2“ (остальные частицы этого мультиплета были
уже известны); в 1964 году это предсказание было экспериментально подтверждено. Этот
декуплет имеет следующий вид^25 161;
Д++ Д+	д°	д~
s*~~
77*0	*^7*	—
Vr
Эту схему можно понять, представив каждую частицу состоящей из трех кварков с различ¬
ным ароматом (d означает нижний кварк, и — верхний, s —странный)*:
uuu uud	udd	ddd
uus uds	dds
uss	dss
sss
Эта схема работает лишь потому, что три кварка находятся в симметричном состоянии.
Например, состояние uud неотличимо от состояния udu. Кроме того, состояния с двумя
кварками одного сорта, например uuu или uud, не обращаются тождественно в нуль, как
должно быть в случае антисимметричного состояния, для которого выполняется принцип
О
Паули. Тот факт, что спин равен означает, что спины всех трех кварков (каждый из которых
имеет спин i) направлены в одну и ту же сторону, так что в этом состоянии в отношении
спинов имеет место полная симметрия. Если бы кварки вели себя как фермионы, то мы
имели бы не симметрию, а антисимметрию относительно перестановки кварков, что не
совместимо с данной картиной .
**
рхними индексами в предыдущей таблице.
Объясните это подробнее, используя 2-спинорное индексное описание для спинов кварков (§ 22.8) и вводя
новый трехмерный <<SU(3)-индекс», принимающий 3 значения: u, d, s.

546
Глава 25
Аналогичное (но более запутанное) замечание относится к более сложной ситуации,
~ 1
возникающей в случае октета из 8 частиц со спином -, к которому принадлежат обычные
протон (N+) и нейтрон (№)^25,17^:
N+	№
£+	s\o	S"
О
Здесь можно считать, что Е° и А0 занимают «одну и ту же нишу» в центре нашей шести-
1
угольной таблицы. Такое расположение получается, если учесть, что спин теперь равен
JLj
поэтому можно считать, что спины двух кварков параллельны, а один антипараллелен. Ока¬
зывается, что существуют всего два линейно независимых способа такого расположения
для комбинации кварков uds, расположенной в центре (она соответствует паре Е° и А°),
ни одного для комбинаций шш, ddd и sss (это и объясняет шестиугольную, а не треугольную
форму таблицы) и по одному для каждой из остальных комбинаций*.
25.7,	«Цветные кварки»
Как же можно считать кварки реальными частицами, если у них «неправильная»
связь между спином и статистикой (см. §§23.7, 26.2)? Способ, которым эта проблема
решаетсяt2518^ в стандартной модели, состоит в требовании, чтобы каждый кварк, по¬
мимо аромата, обладал еще одним из трех (так называемых) «цветов» и чтобы любая
реальная частица, состоящая из кварков, была полностью антисимметрична по этой цве¬
товой степени свободы. Это требование антисимметрии не касается состояний самих квар¬
ков, так что антисимметрия между отдельными (фермионными) кварками в трехкварко-
вой частице эффективно превращается в симметрию . Цвета никогда не проявляются
в свободных частицах, так что цвет, по существу, «ненаблюдаем». Любая свободная ча¬
стица должна быть «цветонейтральной». У нас не будет, например, трех различных ва¬
риантов частицы Д+, соответствующих различным цветам d-кварка в комбинации uud.
Это обеспечивается антисимметрией по цветовым степеням свободы в реальных свобод¬
ных частицах***.
«Цвета» иногда называют «красным», «белым» и «синим», что, с одной стороны, приво¬
дит меня в замешательство, так как я не считаю белый цвет подлинным цветом, а с другой
стороны, выглядит как проявление неуместного патриотизма. Иногда их называют «крас¬
ным», «зеленым» и «синим», что уже лучше, но поскольку ассоциация между «цветом
кварка» и цветовыми рецепторами глаза в любом случае не имеет научного оправдания,
я вместо этого буду использовать названия «красный» (R), «желтый» (Y) и «синий» (В). Та¬
кой выбор названий позволяет легче «смешивать» цвета, так что «оранжевый», «зеленый»
и «пурпурный» цвета (которые можно рассматривать как квантовые суперпозиции исходных
R, Y и В) будут вести себя так же, как и исходный набор. Здесь имеется симметрия, ко¬
торая не ограничивается простой перестановкой цветов. Цветовая симметрия соответствует
Попробуйте объяснить всё это подробнее. При желании можно воспользоваться 2-спинорными спино¬
выми индексами. Антисимметрия по паре таких индексов позволяет удалить такую пару (подобно тому, как это
1
делалось при представлении состояния со спином 0 парой частиц со спином - в § 23.4). Имеется также (скрытая)
дополнительная симметрия, связанная с тем, что для каждого кварка существуют лишь два независимых спиновых
состояния.
** ЛШ Объясните это, воспользовавшись индексной записью с новым трехмерным цветовым SU(3)-индексом
в дополнение к трехмерному индексу, определяющему аромат, из упражнения 25.5.
Объясните это.

25.7. «Цветные кварки»
547
полной группе SU(3) с 8 вещественными измерениями, в которой R, Y и В образуют все¬
го лишь один возможный набор базисных элементов векторного пространства, в котором
действуют SU(3)-матрицы (см. § 13.9).
На этой стадии введение таких ненаблюдаемых «цветовых степеней свободы» выглядит
довольно надуманным, поскольку теперь мы имеем девять основных кварков:
dR, dy, dB, UR, Uy, Ub,	Sr, Sy, sb
(с их античастицами и различными квантовыми суперпозициями), ни один из которых нельзя
наблюдать непосредственно. На самом деле ситуация в стандартной модели «вдвое хуже»,
потому что в дальнейшем пришлось ввести еще три аромата кварков, названные (столь же
неизобретательно) «очарованным» (с), «прелестным» (Ь) и «истинным» (t), что дает
cr, Cy, св, 6r, by, bB,	tR, ty, tB.
• •
Всего получается восемнадцать независимых кварков, каждый из которых непосредственно
не наблюдаем.
Если бы единственной пользой от такого размножения гипотетических ненаблюдае¬
мых частиц было выполнение необходимой связи между спином и статистикой, то вся
схема выглядела бы как решительно надуманная. Однако полная ненаблюдаемость «свобод¬
ного» цвета кварков принесла щедрые плоды! Потому что эта ненаблюдаемость (и тес¬
но связанная с ней ненарушенная природа цветовой симметрии SU(3)) позволяет ис¬
пользовать симметрию как непосредственную основу для удивительной идеи калибро¬
вочной связности, как описано в §§15.1, 15.8. Напомним, как обстоит дело с описанием
электромагнитного взаимодействия, в котором использовалась калибровочная группа U(l)
(см. §§ 19.4, 21.9, 24.7). Калибровочная U( 1)-симметрия электромагнетизма рассматривается
как точная и ненарушенная^25Л9а Напомним также, что в самой основе идеи расслоенных
пространств, изложенной в главе 15, лежит существование точной группы симметрии, дей¬
ствующей на расслоения. Адронная «цветовая группа» SU(3) для сильного взаимодействия
определяет столь же точную симметрию, и аналогия с электромагнитной калибровочной
группой U(l) оказывается очень близкой. Обобщение теории электромагнетизма, в основе
которой лежит калибровочная связность для абелевой группы U(l), на соответствующую
теорию, основанную на калибровочной связности для неабелевых групп, например SU(2)
или SU(3), называется теорией Янга-Миллса\2Ъ
Это составляет основу квантовой хромодинамики (КХД). Как и в случае электромаг¬
нетизма, можно использовать величину, аналогичную электромагнитному потенциалу Аа,
для преобразования производной д/дха, действующей на кварковые поля, в подходящее
понятие «оператора ковариантной производной» (подобного д/дха — геАа в случае элек¬
тромагнетизма), который дает связность расслоения (см. §§15.8, 19.4). Поскольку цветовое
пространство трехмерно, ситуация оказывается несколько более сложной, чем в одномерном
случае электромагнетизма, и, чтобы справиться с дополнительными степенями свободы,
удобно ввести индексы. Решающее различие между случаями электромагнитного и силь¬
ного взаимодействий состоит в том, что группа U(l) абелева (т. е. коммутативна, см. 13.1),
а цветовая группа SU(3) неабелева, так что теория сильного взаимодействия является неабе¬
левой калибровочной теорией. Это приводит к специфическим интересным особенностям.
За подробностями я отсылаю читателя к литературеi25-21]? однако основная идея проявления
сильного взаимодействия здесь отражена.
«Калибровочными бозонами» в КХД (SU(3)-аналогом фотонов) служат объекты, на¬
зываемые глюонами. На фейнмановских диаграммах линии глюонов присоединяются к ли¬
ниям кварков так же, как фотонные линии присоединяются к линиям заряженных частиц
(рис. 25.14 а). Неабелева природа группы SU(3) проявляется в том, что сами глюонные
линии обладают «цветовым зарядом», так что возможны фейнмановские диаграммы с тремя

548
Глава 25
Рис. 25.14. «Калибровочными бозонами» в КХД
(811(3)-аналогом фотонов) служат глюоны, а) Обмен
глюонами между кварками (показанный здесь без зиг¬
загов) лежит в основе ядерных сил и удержания квар¬
ков. б) Поскольку калибровочная теория неабелева,
глюонные линии сами обладают «цветовым зарядом»,
поэтому могут возникать фейнмановские диаграммы
с тремя глюонными хвостами (как на рис. 25.12)
б)
(или более) глюонными хвостами (рис. 25.146), отсутствующие в случае абелева электро¬
магнетизма.
Таким образом, главная роль группы SU(3) в стандартной модели сместилась от описа¬
ния «симметрии ароматов» в 1960-70-х годах к описанию «цветовой симметрии» в настоя¬
щее время. В нынешней стандартной модели три аромата d, u, s уже не группируются между
собой. Вместо этого формируются три поколения дублетов (d,u), (s, с), (b, t). Представление
о трех поколениях применимо и к лептонам, такие поколения образуются электроном, мю¬
оном и тауоном (и соответствующими им нейтрино).
В стандартной модели как целом имеется сложная взаимосвязь между сильным и элек-
трослабым взаимодействиями. В частности, существуют некоторые «углы вращения» между
основными объектами, участвующими в сильном взаимодействии, и объектами слабого вза¬
имодействия. Примером может служить К0-мезон, который может рождаться в процессах
протон-протонных столкновений при высоких энергиях. Мы говорим, что К0 есть собствен¬
ное состояние сильного взаимодействия. Однако распадается К0 в процессах слабого вза¬
имодействия, и его следует рассматривать как квантовую линейную комбинацию двух соб¬
ственных состояний слабого взаимодействия — долгоживущего Кь и короткоживущего К s.
(Kl обычно распадается на три пиона за 5 • Ю“10 с, a Kg — на два пиона за гораздо мень¬
шее время 1СГ10 с.) Каждая из частиц Кь и Ks представляет собой линейную комбинацию
из частицы К0 и соответствующей античастицы К , в которую К0 может превратиться по¬
средством не сильного, а слабого взаимодействия. Поворот от базисных состояний сильного
взаимодействия (К0, К ) к базисным состояниям слабого взаимодействия (Kl,Ks) проис¬
ходит на (абстрактный) угол, называемый углом Кабиббо (он составляет 0,26 радиана). Этот
угол определяет взаимосвязь между сильным и слабым взаимодействиями и в общем случае.
Подобно этому существует так называемый угол Вайнберга, или «угол слабого смеши¬
вания» (§25.5), который определяет взаимосвязь между слабым и электромагнитным вза¬
имодействиями и составляет существенную часть теории электрослабого взаимодействия.
Действительно, некоторые из наиболее впечатляющих подтверждений теории электросла¬
бого взаимодействия были получены путем различных (по-видимому, независимых) изме¬
рений этого угла, которые дали близкие результаты. Однако, согласно теории, существует
некоторая разница между углами Кабиббо и Вайнберга. Слабое и электромагнитное взаи¬
модействия рассматриваются с единой точки зрения, и угол Вайнберга «замораживается»,
когда U(2)-симметрия нарушается спустя 10”12 с после Большого взрыва (§28.1). С дру¬
гой стороны, угол Кабиббо не имеет подобного статуса в стандартной модели, посколь¬
ку эта модель не дает указания, каким образом можно объединить электрослабое и силь¬
ное взаимодействия. Базисная группа симметрии^25,22^ полной стандартной модели имеет
вид SU(3) х SU(2) х U(l)/Z6.
25,8.	За пределами стандартной модели
С другой стороны, можно рассматривать угол Кабиббо с тех же позиций, что и угол
Вайнберга, но это потребует выхода за рамки нынешней стандартной модели физики эле¬

25.8. За пределами стандартной модели
549
ментарных частиц. Нам понадобится модель, в которой сильное и слабое взаимодействия
объединены на основе более общей группы симметрии, включающей SU(3) и U(2). Такую
теорию называют моделью Великого Объединения (МВО). В настоящее время не существу¬
ет общепринятой МВО, однако делалось много попыток (наиболее успешные основаны
на SU(5), или SU(10), или на исключительной группе Eg (см. § 13.2)). В §31.14 мы уви¬
дим, что здесь может сказать свое слово также теория струн. Некоторые замечательные
приложения нескольких МВО будут рассмотрены в § 28.2.
В любом случае ясно, что стандартная модель физики элементарных частиц не является
«окончательным ответом», поскольку, несмотря на несомненный успех, она содержит много
необъясненных особенностей и «острых углов». Она содержит 17 параметров, которые при¬
ходится просто брать из результатов наблюдений (углы Кабиббо и Вайнберга, массы кварков
и лептонов и многое другое). Существует также странная асимметрия в роли групп SU(3)
и U(2): в то время как симметрия SU(3) считается точной, симметрия U(2) в сильной степе¬
ни нарушена. Мне представляется действительно несколько странным выбор U(2) в качестве
«калибровочной группы», что, казалось бы, предполагает точную ненарушенную симмет¬
рию (см. главу 15, в частности, заключительный § 15.8).
Здесь уместно обратиться к другому варианту, отличному от идеи МВО, который трак¬
тует этот частный вопрос по-новому. Он особо привлекателен для меня лично, причина
чего станет ясной в § 33.13. Этот вариант был предложен в 2002 году китайско-британской
семейной парой Хань Хонг-мо и Цу Шень-цунь [133]. В их схеме каждая (неабелева) группа
симметрии элементарных частиц имеет соответствующую дуальную группу, которая пред¬
ставляет собой такую же абстрактную группу, что и исходная, но отличается от нее тем,
что играет в некотором смысле противоположную роль. Вспомним тензор *F, дуальный
по отношению к максвелловскому тензору F, который был введен в § 19.2. Можно пред¬
ставить себе «дуальную» калибровочную связность U(l), у которой кривизной связности
(см. § 15.8) служит тензор *F9 а не F. Идея состоит в том, чтобы сделать нечто подобное
для оставшихся групп симметрии стандартной модели SU(2) и SU(3). Однако поскольку
эти группы неабелевы, нельзя просто рассматривать соответствующие дуальные кривизны
как кривизны связности и требуется нечто более изощренное (в частности, рассмотрение
величин, зависящих от траектории).
Одна из привлекательных сторон этой схемы состоит в том, что исходная и дуаль¬
ная группы играют качественно различные роли, при этом одна из них точная, подоб¬
но группе SU(3) в КХД (или U(l) в теории электромагнетизма), а другая — нарушенная,
как SU(2) в теории электрослабого взаимодействия; в отношении точной группы предпо¬
лагается «удержание» (которое в случае SU(3) препятствует кваркам, несущим «цветовой
заряд», выходить во внешний мир). (Это свойство связано с более ранней работой ’т Хооф-
та и Вайнберга^25 23j.) В схеме Ханя-Цу появляется новая точная группа SU(2) (дуальная
к нарушенной группе симметрии, фигурирующей в теории электро слабого взаимодействия),
которая относится к пока не открытой симметрии и определяет аналоги кварков в виде удер¬
живаемых «двухцветных» лептонных образований. (Эти субчастицы должны быть очень
тяжелыми, поэтому они пока не были обнаружены и потому при достижимых сегодня энер¬
гиях лептоны ведут себя как точечные частицы.) В соответствии с этим должна также
существовать нарушенная симметрия SU(3) (дуальная к цветовой SU(3)), и она должна
рассматриваться просто как «группа SU(3)» для трех поколений кварков и лептонов, ко¬
торые выглядят столь загадочно в стандартной модели, как ее обычно понимают. Схема
Ханя - Цу дает также четкие предсказания в отношении 17 (или около того) свободных па¬
раметров стандартной модели, позволяя вычислить 14 из них с помощью трех подгоночных
параметров. Это представляется мне определенным шагом вперед, особенно если учесть,
*Ш$ Понятно ли, в чем состоит трудность? (Подсказка: рассмотрите выражения для калибровочной кривизны,
тождеств Бьянки и т. п.)

550
Глава 25
что предсказания схемы выполняются. На сегодняшний день перспективы выглядят обеща¬
ющими.
Менее ясно, как при современном подходе к стандартной модели можно брать в ка¬
честве калибровочной группы сильно нарушенную группу SU(2). Можно принять, что эта
группа отражает некоторую «скрытую симметрию», в действительности точную и действу¬
ющую в качестве калибровочной группы лишь «потенциально», и что группа SU(2) в тео¬
рии электрослабого взаимодействия есть некоторое внешнее проявление этого. (Возможно,
это не слишком далеко от идеи Ханя-Цу, но пока это не вполне ясно). Обычный взгляд
на SU(2)-симметрию в теории электрослабого взаимодействия состоит в том, что реально
она является (или, скорее, была) точной, но была нарушена в тех экстремальных процессах,
которые имели место в ранней Вселенной. Мы рассмотрим некоторые неприятные послед¬
ствия этого в главе 28. А пока в следующей главе будут изложены некоторые экзотические,
но существенные математические идеи, которые предполагают иное рассмотрение наруше¬
ния симметрии, нежели в нынешней стандартной модели.
Примечания
§25 А.
25.1. См. [573], стр. 334 и 356.
§25,2.
25.2. Я не привел здесь подробностей того, как можно переписать уравнение Дирака, приведенное
в § 24.7, в 2-спинорной форме. Интересующийся читатель отсылается к приложению в книге
Зи [858]. 2-спиноры ввел Вейль [824]. См. также [798, 411] и [626], стр.221-223.
25.3. Это приведенные спиноры (или полуспиноры), рассмотренные в § 11.5.
25.4. См. [411,473,626].
25.5. См. [697, 209, 403], а также интересный современный взгляд в [380].
25.6. Читателя, который уже немного знаком с фейнмановскими диаграммами, может смутить ис¬
пользуемое мной вертикальное упорядочение во времени. В квантовой теории поля обычно
рисуют диаграммы, на которых временная переменная увеличивается слева направо. Мой
выбор, при котором время течет снизу вверх, согласуется с принятым в теории относитель¬
ности, поскольку такое направление времени выбирается для большинства пространственно-
временных диаграмм (см., в частности, главу 17).
✓
25.7. На самом деле применение в КЭД 2-спинорного формализма могло бы значительно облегчить
жизнь таким физикам! См. [287], а также § 34.3.
25.8. Сам я предпочитаю вместо (1 ±75)^ писать (1 ± 275)ф; см. [626] и [627], приложение.
§25.3.
25.9. На это могло в какой-то мере повлиять предположение, выдвинутое Мартином Блоком (и об¬
народованное Ричардом Фейнманом); см. рассказ об этом в замечательной книге Мартина
Гарднера [278], гл. 22.
25.10. Это уравнение было предложено Вейлем и рассматривалось также Дираком еще до того,
как он пришел к своему «уравнению Дирака для электрона» [200, 210]. Паули горячо возра¬
жал против уравнения Вейля на том основании, что оно неинвариантно относительно про¬
странственного отражения. К сожалению, Вейль умер за год до того, как была обнаружена
неинвариантность слабого взаимодействия относительно зеркального отражения и тем са¬
мым оправдано его собственное предположение. См. обсуждение обоих уравнений в книге
Зи [858].
§ 2$- 4-
25.11. Можно принять, что массивные частицы состоят из трех ингредиентов — левоспиральной
части «зиг» (спиральность 1), правоспиральной части «заг» (спиральность —1) и бесспираль-
ной части со спиральностью 0, которую назовем, скажем, «зог». (2-спиноры «зиг» и «заг»

25.8. За пределами стандартной модели
551
имеют соответственно два нештрихованных и штрихованных индекса, а 2-спинор «зог» —
один нештрихованный и один штрихованный.) Можно придерживаться взгляда, что слабое
взаимодействие переносится «зог»-частицами.
§25.5.
25.12. Эту группу можно представить в виде SU(2) х U(l)/Z2, где символ «/Z2» означает переход
к фактор-группе по подгруппе Z2. Поскольку, однако, имеется более одной такой подгруппы,
такая запись оказывается не вполне определенной. Запись U(2) автоматически исправляет
этот недостаток. (Я признателен Флоренс Цоу за это замечание.) Причина того, что элек-
трослабая группа симметрии обычно не обозначается как U(2), состоит в том, что ее нелегко
расширить до симметрии полной стандартной модели, которая включает также сильную груп¬
пу симметрии U(3); полная группа является вариантом группы SU(3) х SU(2) х U(l)/Ze;
см. §25.7.
25.13. Теория слабого взаимодействия была сформулирована Стивеном Вайнбергом, Шелдоном Глэ¬
шоу и Абдусом Саламом в конце 1960-х годов, эта работа принесла всем троим Нобелевскую
премию; см. [813, 688, 303]. Общий обзор теории электрослабого взаимодействия содержится
в [858, 339, 429].
25.14. ГэВ означает гигаэлектрон-вольт. Гига- есть греческая приставка, означающая умножение
на 109; электрон-вольт — это энергия, которую приобретает одиночный свободный электрон
при прохождении между точками с разностью потенциалов в 1 вольт. Электрон-вольт равен
приблизительно 1,6- 10“19 Дж.
§ 25.6.
25.15. Видимый свет охватывает область длин волн Л = 400 — 700 нанометров. Длина волны
и частота v связаны между собой соотношением v ~ cj\.
25.16. См. теорию в [283]; там же (стр. 88-92) содержится статья Бернса о наблюдении -частицы,
первоначально опубликованная в 1964 году.
25.17. В современной физике элементарных частиц N+ и №, обозначающие соответственно про¬
тон и нейтрон, заменяются на р и п. С обозначениями, применяемыми для других частиц,
это согласуется в том, что, согласно схеме классификации SU(3), протон и нейтрон обра¬
зуют дублет (N+, №), подобный (2°, 5“) и другим. Это позволяет говорить о семействе
нуклонов N.
§25.7.
25.18. См. [345].
25.19. См. [816].
25.20. Янг Чжень-нин и P. JI. Миллс сформулировали свою теорию в 1954 году, хотя основная идея
была выдвинута раньше (и была отвергнута, поскольку калибровочные частицы должны бы¬
ли быть безмассовыми) Вольфгангом Паули сразу после Второй мировой войны и Рональдом
Шоу в 1955 году. Исчерпывающая история этого вопроса изложена в Нобелевской лекции
Абдуса Салама [687]. Прием, который ныне используется, чтобы обойти проблему «безмас-
совости», состоит в применении «механизма Хиггса», нарушающего симметрию, о котором
упоминалось в §25.5 и который обсуждается далее в § 26.11.
25.21. Подробности можно найти в [14], т. 2 или [858]. Обзор основных концепций калибровочной
теории см. в [132].
25.22. См. примечание 25.12. Обзор стандартной модели можно найти в любом хорошем учебнике
по квантовой теории поля, например, [858].
§25.8.
25.23. Идея Ханя-Цу изложена в работе [133]; она основана на свойстве, исследованном в работе
’т Хоофта [763].

Глава 26
Квантовая теория поля
26.1.	Фундаментальный статус квантовой теории поля в современной
теоретической физике
В предыдущей главе мы кратко познакомились со стандартной моделью физики элемен¬
тарных частиц, созданной в XX веке. Эта математическая модель замечательно согласуется
с экспериментальными фактами в широком круге явлений и содержит ряд изящных мате¬
матических находок, поэтому она представляется глубоким проникновением в гармонию
Природы. Однако в моем изложении математическая структура этой модели могла показать¬
ся несколько усложненной и произвольной. Конечно, многое в этой структуре появилось
под давлением грубых фактов физики элементарных частиц, и физики вынуждены были со¬
гласиться с этими фактами, коль скоро их представила Природа. Так и должно быть в любой
серьезной научной теории. Но были и серьезные теоретические резоны, обусловившие вы¬
бор конкретной структуры стандартной модели. Предсказательная мощь теории решающим
образом зависит от математической согласованности таких теоретических подпорок.
Теоретической движущей силой служит продолжение истории, начатой в главе 24: как
построить квантовую теорию физики элементарных частиц, которая находилась бы в со¬
гласии с требованиями специальной теории относительности Эйнштейна? Мы видели там,
какую роль сыграло введение Дираком античастиц в релятивистскую квантовую теорию
и как это привело нас к квантовой теории полей. Стандартная модель элементарных частиц
фактически представляет собой частный пример квантовой теории взаимодействующих по¬
лей, и она должна была удовлетворять жестким требованиям согласованности, трудно вы¬
полнимым для теорий такого рода. Для того чтобы увидеть движущие силы за рамками
этих требований согласованности (которые сегодня продолжают двигать более современные
спекулятивные теории вроде теории струн), нам придется рассмотреть кое-что в структуре
квантовой теории поля (КТП). Это поможет нам понять смысл фейнмановских диаграмм,
с которыми мы уже сталкивались в предыдущей главе. Кроме того, мы приобретем новый
взгляд на античастицы, несколько более широкий по сравнению с принятым в главах 24
и 25.
Квантовая теория поля составляет фундамент стандартной модели, а также практически
всех других физических теорий, пытающихся исследовать фундаментальные основы физи¬
ческой реальности. Поэтому нам необходимо увидеть хотя бы мельком тот величественный
и впечатляющий порядок вещей, который возник, в значительной мере, в результате заме¬
чательного прозрения Поля Дирака, с которым мы уже познакомились в главе 24. Следует
отметить, что сам Дирак и был главным инициатором КТП, хотя важный начальный вклад
был также сделан Иорданом, Гейзенбергом и Паули. Однако в ее тогдашнем виде эта тео¬
рия была не способна давать конечные ответы на большинство возникающих вопросов —
вместо этого, казалось, практически всегда появлялась бесконечность. Усилиями Бете, Томо-
наги, Дайсона, Швингера и особенно Фейнмана была построена теория для так называемых
«перенормируемых» вариантов квантовой теории поля. Более поздний вклад Уорда, Вайн-
берга, Салама, Вильсона, Вельтмана и ’т Хоофта, среди прочих, привел к целому классу
перенормируемых теорий и нынешней стандартной модели элементарных частиц (глава 25),

26.2. Операторы рождения и уничтожения
553
способной давать согласованные ответы на возникающие вопросы^261]. (Требования к те¬
ории оказываются настолько жесткими, что кажется невероятным отличное согласие этих
ответов с результатами эксперимента!) Основная проблема всегда состояла в том, чтобы
обойти приемлемым образом проблему бесконечностей, и именно это стремление вместе
с важными результатами, даваемыми экспериментом, направляли теорию по правильному
и плодотворному пути.
Квантовая теория поля лежит в основе практически всех физических теорий, которые
всерьез пытаются построить картину поведения Вселенной на самых глубоких ее уровнях.
Многие физики (возможно, даже большинство из них) придерживаются того взгляда, что
рамки КТП следует сохранить, а вся вина за трудности разного рода (это обычно беско¬
нечности, возникающие из-за расходящихся интегралов, или расходящихся рядов, или того
и другого) лежит не на самом формализме КТП, а на той конкретной схеме, к которой он
применяется. Такие схемы обычно задаются некоторым лагранжианом, удовлетворяющим
определенным принципам симметрии. В §§ 26.6,26.10 мы познакомимся с общим способом
применения идей лагранжиана к КТП.
В большинстве современных попыток устранения бесконечностей в КТП внимание
обращается на гравитацию как возможность изменения пространственно-временного пове¬
дения на самых малых масштабах и введения таким путем «обрезания», которое превратит
нынешние расходящиеся выражения в конечные (см., в частности, §31.1). Пока остается
открытым вопрос, не потребуется ли модификация самой КТП при внесении в нее (гравита¬
ционных) принципов общей теории относительности Эйнштейна (см. главу 30). Однако, судя
по активности подавляющего большинства исследователей в данной области, КТП в ее ны¬
нешнем виде обычно не вызывает у них вопросов, поэтому лучшее, что мы можем сделать, —
это понять и принять ее хитроумные идеи. В своем описании я никак не смогу представить
во всех деталях эту величественную, глубокую, сложную, временами феноменально точную
и зачастую пока еще мучительно противоречивую схему. Однако я постараюсь хотя бы крат¬
ко и неполно донести кое-что от аромата КТП, прежде чем вернусь к тем ее особенностям,
которые служат теоретической движущей силой, лежащей в основе стандартной модели
элементарных частиц.
26.2.	Операторы рождения и уничтожения
Одной из самых ранних идей КТП стала процедура, известная под названием (порой
вводящим в заблуждение) «вторичного квантования». Согласно этой процедуре, мы пыта¬
емся представить дело таким образом, что волновая функция ф некоторой частицы сама
становится «оператором», действующим на некоторый теневой вектор состояния, обознача¬
емый |0), который находится на правом краю (сравните с §21.3 и представлением Гейзен¬
берга в § 22.4). Я буду обозначать эту «операторную волновую функцию» жирной прописной
греческой буквой Ф, соответствующей той греческой букве ф, которая обозначает нашу од¬
ночастичную волновую функцию. Как и в обычной квантовой механике частиц, Ф можно
рассматривать как функцию от трехмерного радиус-вектора частицы х, т. е. Ф — Ф(х), либо
от трехмерного импульса р, т. е. Ф — Ф(р), если предпочтительнее импульсное представле¬
ние.
Как следует интерпретировать эту странную «операторную волновую функцию» Ф
(или Ф)1 Сейчас она не представляет квантовое состояние, а описывает операцию, которая
«рождает» новую частицу, описываемую заданной волновой функцией ^26,21 ф, помещая ее
в состояние, которое существовало раньше; это «предшествующее» состояние представля¬
ется тем, что стоит непосредственно справа от операторного символа Ф (или Ф). Такой
оператор называется оператором рождения.

554
Глава 26
В качестве теневого вектора состояния |0) на правом краю обычно берется «вакуумное
состояние», соответствующее полному отсутствию каких бы то ни было частиц. После¬
довательное применение таких операторов рождения создает последовательность частиц,
добавляемых одна за другой в вакуум, так что
ФФ ...& |0)
есть состояние, которое получается при последовательном введении частиц с волновыми
функциями
..., ф> ф.
Необходимо принимать во внимание, что всякая частица является либо фермионом,
либо бозоном. В частности, следует учитывать принцип Паули, который мешает нам ввести
в одно и то же состояние один за другим два фермиона. В данном формализме принцип
 	А
Паули выражается в виде свойства Ф = 0 (т. е. ФФ = 0), которым должна обладать
волновая функция любого фермиона ф. Это означает, что если мы попробуем ввести эту
фермионную волновую функцию в одно и то же состояние дважды, мы получим нуль, т. е.
такой вектор состояния существовать не может. Это «правило принципа Паули» есть частное
следствие свойства антикоммутации
ФФ = ~ФФ
где Ф и Ф — операторы рождения фермионов одного и того же типа. Для операторов
рождения © и S, описывающих бозоны одного и того же вида, имеем перестановочное
соотношение*
02 = 20.
Таким образом, мы видим, что операторы рождения подчиняются правилам (градуирован¬
ной) алгебры Грассмана, изложенным в §11.6, причем операторы рождения фермионов
имеют нечетный ранг, а операторы рождения бозонов — четный.
В соответствии с обсуждением в.§>24.3 волновые функции, вводимые в некоторое со¬
стояние при рождении частицы, должны быть положительно-частотными. Отрицательно¬
частотные величины также принимают участие в данном формализме в качестве опе¬
раторов уничтожения. Функция ф, комплексно-сопряженная волновой функции ф, есть
отрицательно-частотная величина. Ей соответствует оператор уничтожения Ф*9 эрмитово-
сопряженный^26'3^ оператору рождения Ф (см, § 13.9). Интерпретация оператора Ф* такова:
он описывает удаление частицы из полного состояния (такое полное состояние, как и преж¬
де, есть то, что находится справа от оператора Ф*). Поскольку наше теневое вакуумное
состояние |0), стоящее справа, не содержит каких-либо частиц, действие непосредственно
на него оператора уничтожения должно давать нуль:
Ф*\0) = 0.
Это, разумеется, не означает, что операторы уничтожения всегда дают нуль, поскольку
мы можем с самого начала поместить какие-нибудь частицы в исходное состояние. Напри¬
мер, выражение вида Ф*Ф@ |0) не обязано быть равно нулю. Так будет, даже если ни одно
из состояний Ф и 0 не является тем же состоянием, что и состояние Ф, которое мы удаляем.
Поэтому не следует считать,что оператор Ф* просто удаляет волновую функцию частицы ф
симметрией
в §23.8.

26.2. Операторы рождения и уничтожения
555
из данного состояния^26-4^ В общем случае данная волновая функция ф9 скорее всего, не
является точно частью состояния. Вместо этого оператор Ф* образует скалярное произве¬
дение с той частью состояния, которая относится к удаляемому типу частиц. (На рис. 26.1
приводится
в основном для развлечения специалистов
диаграммное представление
того, что я имею в виду, для случаев фермионов и бозонов; приводятся диаграммы для
процессов рождения и уничтожения.) В соответствии с этим получается, что операторы
рождения и уничтожения (для частиц одного и того же типа) должны подчиняться правилам
(анти)коммутации
ф*ф ± фф* = гк{-ф\ф)1,
где знак «плюс» относится к фермионам, а «минус» — к бозонам; I представляет тож¬
дественный оператор, символом (|) обозначается обычное скалярное произведение в гиль¬
бертовом пространстве для отдельных частиц (в § 22.3 рассматривался случай бесспиновых
частиц; можно провести соответствующее обобщение для частиц со спином I26-5]); %к при¬
нимает одно из значений 1, гу —1, —г в зависимости от спина (я не выбираю здесь между
ними). Мы имеем также правила (анти)коммутации для двух операторов рождения (они при¬
водились и выше) и двух операторов уничтожения (плюс соответствует фермионам, минус —
бозонам):
ФФ±ФФ = О, Ф*Ф*±Ф*Ф* = 0.
Фа= \Ф)
Ф|0) ~w*. I ?
А
Случай бозонов
Рождение Ф:
Случай фермионов
Уничтожение Ф:
Рис. 26.1. Диаграммная запись действия оператора рождения Ф: ф^ф^.-.ф
в случае бозонов и ф^ф^ ... ф^j-	> ф^ф^ф^ • • • Фм в случае фермионов,
чтожения Ф*: ф[аф% • -. ф$ ► ФаФ±аф2 • ■ • Фм в случае бозонов и ф^*ф% .
*0
N
I	^
&а4%ФЪ ...Ф$
а также оператора уни-
• Фи ^	ФаФ[1 44 ■■■Фи
в случае фермионов
Следует отметить, что теорема о связи спина со статистикой, кратко упомянутая в § 23.7,
требует выполнения правил антикоммутации (знака плюс для фермионов в вышеприведен-
-I о г
ных соотношениях) для частиц с полуцелым спином (-, -, -, ...) и правил коммутации
(знака минус для бозонов) для частиц с целым спином (0, 1, 2, 3, .,..)■ Причины этого лежат
за рамками нашего изложения6 Существенным здесь является положительность энер¬
гии (в случае фермионов) и положительность числа частиц (в случае бозонов) в сочетании
с комбинаторными свойствами соответствующих спинорных индексов I26*7!.
Объясните все это (и проверьте перестановочные соотношения для операторов рождения и уничтожения
частиц данного типа), обратившись к индексной записи из § 23.8, или к диаграммному представлению с рис. 12.17,
или к тому и другому и используя выражения типа гф0сФ^а'Ф® ’' *	•	Разберитесь со всеми множителями, содер¬
жащими факториалы, которые обеспечивают нормировку состояний, для случаев фермионов и бозонов.

556
Глава 26
26.3.	Бесконечномерные алгебры
♦
Примечательно, что в случае фермионов указанные правила антикоммутации имеют
точно такую же алгебраическую форму, что и правила, определяющие алгебру Клиффорда,
описанные в § 11.5. * Единственное существенное отличие состоит в том, что обычные алге¬
бры Клиффорда конечномерны, тогда как пространство операторов рождения и уничтожения
для фермионного поля бесконечномерно, поскольку пространство одночастичных волновых
функций имеет бесконечное число измерений. Следует, однако, предупредить читателя, что
бесконечномерные пространства, хотя во многом и аналогичны конечномерным, могут об¬
ладать некоторыми совершенно иными свойствами, и это часто затрудняет работу с ними.
Интересно, что формализм КТП часто содержит бесконечномерные варианты некото¬
рых других типов конечномерных алгебраических структур, рассмотренных ранее в этой
книге. Например, скалярное произведение ( | ) есть бесконечномерный аналог эрмитова
скалярного произведения, рассмотренного в § 13.9 (сравните с § 22.3). В КФТ мы сталкива¬
емся не только с «эрмитовостью» (унитарностью), но и обнаруживаем, что там играют свою
роль также симметричные формы («псевдоортогональность»), антисимметричные (симплек-
тические) формы и комплексные структуры^26*81 Обычные конечномерные варианты псев-
доортогональных и симплектических форм были рассмотрены в §§13.8, 13.10, обычные
конечномерные комплексные структуры — в § 12.9.
Особое значение для КТП имеет возникновение (бесконечномерной) комплексной
структуры. Мы уже видели, что комплексные числа, голоморфные функции и комплексные
векторные пространства играют фундаментальную роль в квантовой теории (и, следователь¬
но, в базисной структуре нашего мира). Однако та бесконечномерная комплексная структу¬
ра, которая возникает в КТП, играет, как кажется, несколько иную (хотя и похожую) роль,
нежели в более ранних примерах магии комплексных чисел. Эта роль не сводится просто
к утверждению, что гильбертовы пространства квантовой теории комплексны (т. е. к тому,
что имеет место квантовая суперпозиция с комплексными коэффициентами). Попробуем
понять, о чем идет речь.
Напомним, как было введено понятие комплексной структуры в § 12.9. Комплексное
векторное пространство п измерений можно рассматривать как вещественное векторное
пространство 2п измерений, в котором задана операция J, удовлетворяющая условию J2 =
= — 1; действие этой операции на вещественное 2п-пространство равносильно «умножению
на г» в комплексном n-пространстве. Бесконечномерный аналог этого, имеющий отношение
к КТП, должен предусмотреть переход от классического поля к квантовому. До сих пор
разговор шел на языке частиц и волновых -функций. Но нам необходимо знать также, как
непосредственно перейти от классического поля к квантовому, поскольку с классическими
полями не связываются классические частицы, которые можно «квантовать» по аналогии
с процедурами, изложенными в главах 21-23.
Полезно в качестве модели рассмотреть частный случай электромагнитного поля. Здесь
положение дел упрощается благодаря линейности уравнений Максвелла (§ 19.2). Простран¬
ство Т решений свободных уравнений Максвелла (при подходящих условиях убывания их на
бесконечности, обеспечивающих сходимость соответствующих интегралов) есть бесконеч-
номерное вещественное векторное пространство . Используя процедуры, подобные описан¬
ным в §§ 9.2, 9.3, 9.5, можно представить каждое решение F уравнений Максвелла^26 в ви¬
де суммы положительно-частотного решения F+ и отрицательно-частотного решения F~:
F =	+	F~.
* Объясните структуру алгебры Клиффорда и проверьте в более явном виде роль скалярного произведения.
(Возьмите определяющие законы для алгебры Клиффорда в виде 7р7<? + 7g7p = —2gpqI.) (Подсказка: тензор
gpq не обязательно диагоналей.)
**ЙИ Объясните, что означают в этом пространстве сложение и умножение на скалярную постоянную.

26.4. Античастицы в КТП
557
Такое расщепление на положительные и отрицательные частоты играет важную роль
при построении подходящей квантовой теории поля (напомним замечания по этому вопросу
в §§ 24.3,26.2). Операция J, примененная к бесконечномерному вещественному векторному
пространству преобразует его в комплексное (бесконечномерное) векторное пространство
и предоставляет, таким образом, способ расщепления на положительные и отрицательные
частоты. Операция J делает это, действуя на каждое свободное максвелловское поле F
следующим образом:
J(F)	-iF-.
Собственными состояниями оператора J с собственным значением i являются
положительно-частотные (комплексные) поля, а аналогичными состояниями с собственным
значением —i — отрицательно-частотные поля . Положительно-частотные поля соответству¬
ют однофотонным волновым функциям, вводимым операторами рождения. Имеется также
явное выражение для скалярного произведения, которое можно использовать, при необхо¬
димости, для нормировки состояний (оно включает интеграл по какой-нибудь простран¬
ственноподобной 3-поверхности от выражения, содержащего компоненты максвелловского
поля, умноженные на компоненты максвелловского потенциала[26. го] (Сравнихе со случаем
скалярного поля в §§ 21.9,22.3)). Другие классические поля можно рассматривать подобным
образом, но в случае, когда «уравнения свободного поля» нелинейны (как, например, в об¬
щей теории относительности), могут возникать значительные трудности. Нелинейные поля
можно рассматривать как «поля с самовзаимодействием», так что трудности можно отнести
за счет проблем, связанных с квантованием в присутствии взаимодействия, к которому мы
вскоре перейдем.
26.4.	Античастицы в КТП
Но прежде чем сделать это, вернемся к понятию античастиц. В главе 24, а также в § 26 Л
я подчеркивал важную роль понятия античастицы в КТП. Как проявляют себя античастицы
в современном формализме КТП? Как отмечалось в §25.3, некоторые элементарные части¬
цы являются своими собственными античастицами, но для большинства частиц это не так.
В математическом отношении вопрос заключается в том, дает ли операция комплексного
сопряжения, будучи примененной непосредственно к величине, описывающей классическое
поле (или к одночастичной волновой функции), величину того же рода. В случае скалярного
поля это обычно (хотя и не вполне обоснованно) сводится к вопросу, является ли данное
классическое поле вещественным. Комплексные поля рассматриваются как заряженные, при
этом комплексный фазовый угол (множитель егв) следует трактовать в соответствии с пред¬
писаниями теории «калибровочного поля» для электромагнитного взаимодействия, как опи¬
сано ⧧15.8, 19.4. Комплексно-сопряженное поле имеет противоположный заряд и потому
это не есть «величина того же рода» (поэтому, например, не имеет смысла сложение поля
с сопряженной ему величиной). В подобных случаях частица и ее античастица определенно
различны. Однако комплексная (или «заряженная») природа классического поля определя¬
ет еще не все. Например, незаряженный К0-мезон отличается от своей античастицы, тогда
как незаряженный 7г°-мезон — это то же самое, что и его античастица. В обоих случаях
классическое поле будет вещественным скаляром.
А как насчет епинорных (или фермионных) полей? В случае дираковского электрона
его заряда достаточно, чтобы считать комплексно-сопряженное поле отличным от исходного
поля. Однако в случае нейтрино, если оно обладает массой, имеется более одной возможно¬
сти^ Например, (массивное) нейтрино, описываемое спинорным полем Майораны, является
своей собственной античастицей. (В описании, приведенном в главе 25, «зиг»-часть ней¬
*Й@ Покажите это. (Можно не заботиться о тонкостях вроде условий убывания.)

558
Глава 26
трино является «заг»-чаетью антинейтрино и наоборот.) В современном же понимании [2611]
все нейтрино отличаются от своих античастиц.
Так как же формализм КТП обращается с античастицами? Рассмотрим случай, ко¬
гда операция комплексного сопряжения в применении к классическому полю (или к од¬
ночастичной волновой функции) дает величину иного характера, так что квантовая ча¬
стица отличается от своей античастицы. (Ситуация, когда частица и античастица — од¬
но и то же, рассматривалась ранее в § 26.2.) Обычная волновая функция ф должна быть
положительно-частотной, однако можно взять некоторую величину ф того же рода, что и ф,
но отрицательно-частотную. Тогда величина ф, комплексно-сопряженная относительно Ф,
будет волновой функцией иного типа, нежели ф, хотя и ф, и ф являются положительно¬
частотными функциями. Величина ф представляет собой одно-античастичную волновую
функцию. Соответствующим оператором рождения для античастицы в этом состоянии бу¬
дет Ф, а оператором уничтожения Ф .
Попробуем установить контакт с первоначальным «морем Дирака» (см. § 24.8), предпо¬
лагая присутствие справа от всех операторов «теневого» состояния, отличного от обычного
вакуумного состояния 10); напомним, что состояние |0) предполагается полностью свобод¬
ным от частиц и античастиц. Вместо |0) возьмем в качестве нового «вакуумного» состояния
само «море Дирака» (обозначив его как |27}), в котором заполнены все состояния с отри¬
цательной энергией (и только они). Рассмотрим одиночный позитрон, который в первона¬
чальной картине Дирака описывается как одиночная «дырка» среди электронных состояний
с отрицательной энергией. Все другие состояния с отрицательной энергией заполнены, кро¬
ме этого, описываемого некоторой отрицательно-частотной функцией ф. Квантово-полевое
описание, использующее этот вакуум |27), получается при действии на \Е) оператора ан¬
нигиляции Ф , поскольку этот оператор удаляет из вакуума состояние с отрицательной
энергией ф и дает в результате полное состояние Ф |27).*
Если бы мы пользовались описанием с более обычным вакуумом |0), то должны были
бы говорить не об удалении электронного состояния с отрицательной энергией Ф, а о добав¬
лении позитронного состояния с волновой функцией_(/>. Это достигается действием на |0)
оператора рождения Ф, что дает полное состояние Ф|0). Это внешне не похоже на выра¬
жение Ф* \£), которое мы получили, пользуясь представлением о «море Дирака», однако
состояния Ф|0) и Ф \Е) в некотором смысле, по сути, эквивалентны. Оба оператора Ф и Ф*
вводят в полное состояние одну и ту же алгебраическую величину — некоторый вектор ф
в гильбертовом пространстве одночастичных волновых функций. Различие между операто-
рами Ф и Ф* заключается лишь в том алгебраическом способе , каким этот вектор гильбер¬
това пространства действует на полное состояние. Поскольку мы всегда можем, пользуясь
правилами антикоммутации, переместить Ф или Ф* на правый край, способ действия ф
на полное состояние приближается к способу действия на выбранное вакуумное состоя¬
ние |0) или \U), расположенное с правого края. Эту информацию можно рассматривать как
часть определения данного вакуумного состояния.
26,5.	Альтернативные вакуумы
Здесь необходимо сделать важные замечания относительно ситуации, в которой по¬
является возможность альтернативного выбора нашего «вакуумного состояния». Мы обна¬
ружим, что в современной КТП важную роль играет понятие «альтернативных вакуумов».
Объясните, почему таким путем можно удалить некоторое определенное состояние, несмотря на мои пре-
рассуждения относительно того, как действует оператор уничтожения. (Подсказка: см. упражнение 26.2.)
Вернувшись к упражнению 26.2 и рис. 12.18, выявите это различие в абстрактно-индексном или диа-
граммном представлении.

26.5. Альтернативные вахуумы
559
Рассмотрим алгебру А, состоящую из всех операторов А, которые можно построить из алге-
выражении или сходящихся степенных рядов, содержащих операторы рождения
и уничтожения. Два возможных «вакуумных состояния», например |0) и |27), могут обладать
тем свойством, что в А нет такого элемента, при действии которого на одно из состояний |0)
или |27) получалось бы другое из них. В таких случаях состояния |0) и \Е) следует счи¬
тать принадлежащими различным гильбертовым пространствам, и мы тогда, скорее всего,
обнаружим, что существуют выражения вида
(27|А|0) или (0|.А|1Д
(где А принадлежит к А), которые либо дают в ответе бесконечность, либо вообще не имеют
смысла. Это обстоятельство не позволяет нам построить согласованную квантовую теорию,
в которой появлялись бы оба состояния |0) и.|27). (Напомним, что, согласно обсуждению
в §22.5, величины типа (27|А|0) представляют собой выражения общего вида, которые
придется использовать при вычислении вероятностей; обозначения см. в § 22.3.)
Введенное здесь понятие играет важную роль в КТП и в современном подходе к физике
элементарных частиц. «Выбор вакуумного состояния» имеет значение, сравнимое с выбором
алгебры А, порождаемой операторами рождения и уничтожения и определяющей, в неко¬
тором смысле, динамику КТП. В случае свободных электронов два рассмотренных нами
вакуума, а именно ]0) (который не содержит частиц и античастиц) и \Е) (в котором заполне¬
ны все состояния частиц с отрицательной энергией), можно рассматривать как, в некотором
смысле, эффективно эквивалентные, несмотря на то что им соответствуют различные гиль¬
бертовы пространства. Мы можем считать, что вакуум | Е) и вакуум |0) отличаются лишь
положением линии, определяющей «нуль отсчета заряда».
В самом деле, можно считать море Дирака физически отличным от истинного вакуума,
поскольку море электронов с отрицательной энергией должно обладать огромным (на самом
деле бесконечно большим) электрическим зарядом. Чтобы придать состоянию \Е) физиче¬
ский смысл, мы должны «перенормировать» заряд таким образом, чтобы бесконечный пол¬
ный заряд «моря» (отрицательный, поскольку отрицателен заряд электрона; считался нулем
отсчета заряда. Аналогичная ситуация возникнет, если нам придется обратиться к мас¬
се моря Дирака, где мы теперь столкнемся с его (активным) гравитационным действием.
Бесконечная полная отрицательная энергия моря Дирака будет давать (в соответствии с со¬
отношением Е — тс2) бесконечную отрицательную массу, которая, как и бесконечный элек¬
трический заряд, не имеет физического смысла. Если рассматривать море Дирака всерьез,
мы опять-таки должны перенормировать массу вакуума, добавив «бесконечную плотность
массы» к плотности массы моря, чтобы в результате получить нулевое значение, которое
должна иметь плотность массы наблюдаемого вакуума.
У читателя может возникнуть впечатление, что вопрос об «альтернативных вакуумах»
и «перенормировке» таких величин, как заряд и масса, путем дооавления оесконечнои по¬
стоянной для получения результатов, имеющих физический смысл, — это всего лишь ар¬
тефакт странной идеи «моря», которую Дирак вынужден был ввести в свою первоначаль¬
ную теорию. Однако мы увидим, что эти две особенности ни в коей мере не специфичны
для необычного «моря» Дирака. Они неизбежно появляются при любом серьезном подходе
к реалистическои теории элементарных частиц — по крайней мере в современной теории.
Перенормировка и альтернативные вакуумы лежат в основе стандартной модели. Не буду¬
чи какой-то аномалией истории, море Дирака представляет собой модель, которую следует
иметь в виду при попытках двигаться вперед, по крайней мере при современном положении
дел. Двойной критерий — согласие с экспериментом и математическая согласованность, —
хотя и не удовлетворяется в полной мере, направляет нас по пути, который, по крайней мере
пока, связан с идеями перенормировки и неоднозначного вакуума.

560
Глава 26
26.6.	Взаимодействия: лагранжианы и интегралы по траекториям
Трудности, с которыми мы сталкиваемся на этом пути, связаны с проблемами, возни¬
кающими при попытке включить взаимодействие в схему КТП. Действительно, до сих пор
мы рассматривали в основном случай свободных полей, и, хотя я не входил во все детали,
читатель, надеюсь, поверит, что при отсутствии взаимодействия никаких опасностей не воз¬
никает. Можно конструировать состояния в виде суперпозиций различного числа частиц и
античастиц и даже с неограниченным числом таких частиц. Эти состояния получаются при
действии на 10) произвольного элемента алгебры Л, т. е, некоторого выражения, содержаще¬
го операторы рождения и уничтожения (в виде многочлена или степенного ряда, в послед¬
нем случае необходимо уделять должное внимание проблеме сходимости). Пространство
таких состояний получило название пространства Фока (в честь русского физика В. А. Фо¬
ка, который одним из первых изучал эти вопросы); его можно рассматривать как прямую
сумму}-26'12} (см. § 13.7) гильбертовых пространств с возрастающим числом частиц. Число
частиц в состоянии может быть неограниченным, как в случае когерентных состояний,
которые в некотором смысле[26лз] МОГуТ рассматриваться как состояния квантовых полей,
наиболее близкие к классическим. Эти состояния имеют вид
е*|0>,
где 3 есть оператор поля, соответствующий некоторой конфигурации поля F (которое мож¬
но рассматривать как свободное вещественное максвелловское поле с подходящим законом
убывания на бесконечности, обеспечивающим существование конечной нормы). Мы опре¬
делим 3 как сумму (ненормированных) операторов рождения и уничтожения, соответству¬
ющих положительно-частотной и отрицательно-частотной частям поля F.
Напомним (§26.2), что операторы рождения и уничтожения подчиняются некоторым
перестановочным соотношениям. Из них следует, что различные компоненты операторов
поля в общем случае не коммутируют между собой. Например, в случае электромагнитного
поля компоненты операторов, определяющих магнитное поле В и электромагнитный по¬
тенциал А (см. §§ 19.2, 19.4), подчиняются каноническим правилам коммутации (подобным
таковым для координат и импульсов частиц, см. § 21-2) [26 141. Эти величины должны удовле¬
творять соотношениям неопределенности Гейзенберга (см. §21.11), определяющим пределы
точности, с которой они могут быть одновременно измерены.
Как в таком случае мы должны поступить с взаимодействием? В общей схеме совре¬
менной КТП решающую роль играет лагражиан (см. §20.1), который во многих отноше-
ниях предпочтительнее гамильтониана, когда мы имеем дело с релятивистской теорией.
Как мы помним из §§21.2, 23.1 и главы 24, стандартная процедура квантования с исполь¬
зованием уравнения Шредингера и гамильтониана плохо согласуется с пространственно-
временной симметрией теории относительности. В отличие от гамильтониана, который
сопряжен с выбором временной координаты, лагранжиан можно выбрать в полностью
релятивистски-инвариантном виде (см. § 20.5). Как же построить КТП исходя из лагран¬
жиана? Основная идея, как и многие другие идеи, лежащие в основе квантовой теории,
восходит к Дираку^2615), хотя ее завершение в качестве основы релятивистской квантовой
теории было осуществлено блестящим американским физиком Ричардом Фейнманом [26л6].
В соответствии с этим ее обычно называют формулировкой в терминах фейнмановских ин¬
тегралов по траекториям или фейнмановских сумм по историям. Она составляет также
основу метода фейнмановских диаграмм, рассмотренных в главе 25.
Эта основная идея представляет собой другой взгляд на фундаментальный квантово¬
механический принцип комплексной линейной суперпозиции, с которым мы уже сталкива¬
лись раньше и который был сформулирован в явном виде в § 22.2. Этот принцип приме¬
няется не к отдельным квантовым состояниям, а к пространственно-временным историям

26.6. Взаимодействия: лагранжианы и интегралы по траекториям
561
в целом. Мы рассматриваем эти истории как «возможные альтернативные классические тра¬
ектории» (в конфигурационном пространстве). Идея состоит в том, что в квантовом мире
вместо одной классической «реальности», представляемой одной траекторией (одной исто¬
рией), существует большая комплексная суперпозиция всех «альтернативных реальностей»
(суперпозиция альтернативных историй). В соответствии с этим, каждой такой истории
сопоставляется некоторый комплексный коэффициент, который называется ее амплитудой
(§ 22.5), если вся суперпозиция нормируется на единичный модуль, так что квадрат моду¬
ля амплитуды дает соответствующую вероятность. Мы обычно интересуемся амплитудами
прохождения из точки а в точку b в конфигурационном пространстве.
Магическая роль лагранжиана состоит в том, что он сообщает нам, какая амплитуда
приписывается каждой такой истории (см. рис. 26.2). Если известен лагранжиан С, мы
можем найти действие S для данной истории (в соответствии с §20.5 (см. рис. 20.3),
действие равно интегралу от С по этой классической истории). Комплексная амплитуда,
приписываемая данной истории, определяется обманчиво-простой формулой
амплитуда ос elS^h.
Обманчивое впечатление простоты этой формулы обусловлено тем фактом, что «ам¬
плитуда» здесь в действительности является не просто (комплексным) числом (которое, как
сказано, должно иметь единичный модуль), а некоторой плотностью. Если бы мы имели
V-/
просто дискретное семейство альтернативных классических истории, нумеруемых, напри¬
мер, 1, 2, 3, 4, ..., то можно было бы приписать п-й истории в качестве амплитуды ком¬
плексное число ап, квадрат модуля которого |ап|2 можно интерпретировать как вероятность
этой истории в соответствии с правилами квантовых измерений (§22.5); мы должны ее нор¬
мировать, чтобы сумма по всем классическим альтернативам дала полную вероятность,
равную 1,	\ап\2	1. Но здесь мы имеем непрерывную бесконечность классических аль¬
тернатив. Тогда «амплитуду» следует понимать как «плотность амплитуды», и требуется
что-то вроде J \а(Х)\2 dX = 1, при этом мы должны интегрировать по всему пространству
классических состояний, чтобы выполнить требование равенства полной вероятности еди¬
нице. Само по себе это не должно особенно беспокоить — мы уже сталкивались с такой
ситуацией в § 21.9 в случае волновой функции точечной частицы в обычной квантовой ме¬
ханике (там величина \ф(х)\2 давала нам плотность вероятности найти частицу в точке х).
Но плохо то, что здесь «пространство классических траекторий» почти неизбежно оказы¬
вается бесконечномерным. Возникает проблема иного порядка величины — придать смысл
различным используемым величинам (и при этом быть уверенным, что в конце получится
конечный результат), определив все необходимые понятия применительно к бесконечномер¬
ному пространству.
Наиболее доступная иллюстрация интеграла по траекториям получается в случае од и-
С/
застицы, движущейся в некотором силовом поле (так что конфигурацион¬
ное пространство в данном случае есть обычное пространство). Рассмотрим все возможные
истории, начинающиеся в некоторой пространственно-временной точке а и оканчивающиеся
в пространственно-временной точке b (рис. 26.3 а). Эти истории берем в виде непрерыв¬
ных пространственно-временных траекторий, проложенных между точками а и Ъ. Мы не
требуем ни того, чтобы траектория была «законной» с точки зрения правил специальной
теории относительности (т. е. лежала внутри светового конуса, см. § 17.8), ни даже того,
чтобы она всюду была направлена в будущее. «История», если ей угодно, может извиваться
взад-вперед во времени (рис. 26.3 6)! Пусть мы имеем некоторый лагранжиан С, равный
(в соответствии с § 20.1) разности кинетической энергии частицы и ее потенциальной энер¬
гии, обусловленной силовым полем. Каждой истории соответствует некоторое действие S —
Дайте «физическую интерпретацию» истории, изображенной на рис. 26.3 б, в терминах рождения и уни¬
чтожения частиц.

562
Глава 26
Полная амплитуда для
квантовой истории ос
*	^	^	jjfc,	&
л?
лС
*
•А
А
А
&°е .2
у
t
•г
Рис. 26.2. При использовании интегралов по траекториям в квантовой механике и КТП рассмат¬
риваются квантовые суперпозиции альтернативных классических историй, которым соответствуют
траектории в конфигурационном пространстве, в данном случае между фиксированными точками а
и 6. Траектории приписывается амплитуда ezS^h (с некоторым постоянным коэффициентом), где дей¬
ствие S есть интеграл от лагранжиана по этой траектории, как в § 20.1 (рис. 20.3). Полная амплитуда
прохождения от а до b равна сумме таких амплитуд
интеграл от лагранжиана, взятый вдоль траектории (см. рис. 20.3). В классической механике,
согласно знакомому нам Жозефу Лагранжу, следует искать историю, для которой интеграл
действия имеет стационарное значение (принцип Гамильтона; см. § 20.1), и она даст нам дей¬
ствительное движение частицы, соответствующее классическому движению под действием
заданной силы. В квантовой механике, использующей представление интегралов по тра¬
екториям, ситуация иная. Предполагается, что в квантовой суперпозиции «сосуществуют»
все истории, каждая со своей амплитудой elS'h. Как совместить это, хотя бы в некотором
приближенном смысле, с требованием Лагранжа выделить некоторую историю, для которой
действие стационарно?
а)	6)
Рис. 26.3. а) Классическая история для одиночной бесструктурной частицы представляет кривую
в пространстве-времени (в данном случае в пространстве Минковского М) между фиксированными
событиями а и 6. 6) Кривая не обязана быть классически разрешенной плавной мировой линией
с времениподобной плавной мировой линией, всегда направленной в будущее, — она может блуждать
взад-вперед во времени
Идея состоит в том, что вклад тех историй в этой суперпозиции, которые далеки от исто¬
рии «стационарного действия», будет уничтожаться вкладом соседних историй (рис. 26.4 а).
Причина заключается в том, что изменения в действии S при варьировании истории создают

26.7. Расходящиеся интегралы по траекториям: ответ Фейнмана
563
фазовые углы егБ!г\ заполняющие всю окружность, и потому в среднем взаимно уничто¬
жаются. (Это относится, в частности, к существенно «нефизическим» вкладам от историй,
резко нарушающих причинность, на рис. 26.3 б.) Только в том случае, если истории очень
близка к такой, для которой действие велико и стационарно (так меняется аргумент), ее вклад
начинает усиливаться вкладами соседних историй, а не погашаться ими (см. рис. 26.4 б), по-
скольку в этом случае фазовые углы группируются вблизи одного и того же значения .
а)
Рис. 26.4. Квантовый «принцип Гамильтона», а) История, для которой действие S не стационарно
(и велико по сравнению с К). Значения ег5^п для соседних историй имеют тенденцию к широкому
разбросу по всей единичной окружности и потому в сумме почти полностью взаимно компенсируются,
б) История, для которой действие S стационарно (и велико). Значения elS‘/h для соседних историй
мало различаются между собой, поэтому взаимная компенсация не возникает
Это действительно очень красивая идея. В соответствии с философией интегралов
по траекториям, мы не только получаем, что классическая история дает основной вклад
в полную амплитуду (и, следовательно, в полную вероятность), но и находим более мелкие
квантовые поправки к классическому поведению, возникающие из-за наличия историй, не
вполне классических и дающих вклады, не вполне погашающие друг друга; такие поправки
часто оказываются экспериментально наблюдаемыми. Хотя в вышеприведенном описании
речь шла о точечной частице, движущейся в силовом поле, эти идеи оказываются совер¬
шенно общими и их можно применять к динамике полей так же, как и к движению частиц.
Здесь опять-таки «истории полей», представляющие классические решения уравнений по¬
ля, дают основной вклад, к которому существуют квантовые поправки, обусловленные не
вполне классическими историями.
26.7.	Расходящиеся интегралы по траекториям: ответ Фейнмана
По крайней мере, так предполагается. Но так ли это? Оправданно ли математически
приведенное выше приближенное описание? Даже если не оправданно и окажется, что
мы лихо промчались, игнорируя математические тонкости, — получим ли мы правильный
физический результат, согласующийся с экспериментом?
На эти вопросы я могу дать лишь весьма уклончивый ответ. Вопрос о математической
обоснованности особенно тонкий, и наилучшим ответом был бы такой: «На сегодняшний
*!Ш Попытайтесь придать этим утверждениям более точный смысл, рассматривая изменения траекторий
первого порядка с использованием символов «О» (как в § 14.5) и связывая их с обсуждением смысла «стационарного
действия» в § 20.1). (Действие S считайте большим по сравнению с /г.)

564
Глава 26
день — нет». Проблемы возникают даже в описанном выше случае одной точечной части¬
цы. Пространство траекторий, несомненно, бесконечномерно* и требует соответствующей
«меры» — бесконечномерного варианта объема. Оказывается, что такая мера имеет наиболь¬
шую величину для историй, даже не гладких, поэтому возникает вопрос, какой смысл имеет
в таких условиях сам лагранжиан. По самому определению, всё расходится.
С математической точки зрения, эти расходимости представляют вполне серьезные
препятствия, и потому предпочтительно прибегнуть к «эйлеровой» философии, которая
в § 4.3 привела нас к рассуждениям о смысле, в котором можно понимать «бессмысленное»
суммирование
1 + 22 + 24 + 26 + 28 + ... = -|,
получающееся при подстановке значения х — 2 в формулу 14- х2 -f х4 4- х6 + Xs +... — (1 —
— х2)-1. Действительно, метод интегралов по траекториям, как кажется, почти полностью
зависит от уверенности в том, что явно расходящиеся выражения (вроде приведенного вы¬
ше расходящегося ряда) в действительности имеют более глубокий «платоновский» смысл,
которого мы, возможно, пока не понимаем в должной мере. Мы вынуждены признать, что
кое-что в этом роде действительно имеет место, поскольку мы нередко получаем результаты
с загадочно-высокой точностью, когда (если мне позволено воспользоваться такой мета¬
форой) мы прокладываем свой путь напролом через математику с высокой точностью! На¬
пример, такие вычислительные процедуры дают поправочный коэффициент 1,001159652188
(см. § 24.7) к первоначальному дираковскому значению для магнитного момента электрона,
обеспечивая тем самым согласие между теорией и экспериментом f26*17) с расхождением
менее 10“п.
Поистине замечательно, что подобные физико-математические упражнения во многих
случаях могут привести нас к отличным результатам. Ценным первым шагом на пути к при¬
данию смысла интегралам по траекториям^2618^ в случае отдельных свободных квантовых
частиц стала замена беспорядочного набора историй так называемым фейнмановским про-
пагаторол^26Л91 Это дает нам математическую интерпретацию одной из линий на фейн-
мановских диаграммах (вроде тех, с которыми мы встречались в главе 25).
Более конкретно, рассмотрим сумму по историям, в которых некоторая свободная ча¬
стица проходит в пространстве-времени путь от начальной точки р до некоторой другой
точки д. В принципе мы должны найти сумму (интеграл) всех величин elS'h для траекторий,
начинающихся в точке р и оканчивающихся в точке д, но это определенно дало бы расхо¬
димость. С другой стороны, мы можем предположить, что такая сумма К(р, q) существует
в некотором «эйлерово-платоновском» смысле, и задаться вопросом, какими формальны¬
ми алгебраическими и дифференциальными свойствами должна обладать эта сумма, если
она существует. Эти свойства (включая условие «положительной частотности», см. § 24.3)
однозначно задают вид функции К (р, q) (если нам повезло с выбором примера), и это да¬
ет нам искомый фейнмановский пропагатор. Фактически более удобно (хотя это ни коей
мере не принципиально I26-20!) пользоваться описанием в импульсном (а не координатном)
пространстве, поскольку оно выглядит значительно проще.
В случае дираковской частицы (электрона) пропагатор в импульсном представлении
имеет вид г(Р — М + гг)-1, где Р = 7аРа (см. §§24.6, 24.7), а Ра есть 4-импульс, кото¬
рым довелось обладать частице на выбранной траектории. В качестве величины г берется
весьма малое положительное вещественное число, предназначенное для обеспечения усло¬
вия положительной или отрицательной частотности фейнмановского пропагатора. В преде¬
ле г —» 0 пропагатор становится сингулярным (принимает бесконечно большое значение),
когда «масса покоя» (PaPa)ljf2, приписываемая частице на выбранной траектории, при-
*$Э Почему?

26.8. Построение фейнмановских диаграмм. S-матрица
565
нимает значение М, соответствующее реальной массе покоя частицы*. Для классической
частицы мы должны потребовать, чтобы эта «масса покоя» принимала указанное значение
(РаРа — М2), однако в случае квантово-механической суммы по историям мы должны
позволить частице принимать и те значения импульса, при которых ее масса покоя оказыва¬
ется «неправильной». Однако вследствие отмеченной сингулярности амплитуда становится
очень большой, когда РаРа приближается к значению М2, так что классическое значение
массы вносит основной вклад. Эта особенность не специфична для дираковской частицы,
а имеет совершенно общий характер.
26.8.	Построение фейнмановских диаграмм. S-матрица
Изложенное в предыдущем разделе составляет первый шаг на пути к построению фейн¬
мановских диаграмм. Это требует некоторого объяснения. То, что мы нашли, есть одна линия
(отрезок) такой диаграммы. Одна такая линия на фейнмановской диаграмме — это обычно
лишь часть более сложного выражения, содержащего другие линии частиц и различные вер¬
шины, в которых эти линии встречаются. Вклад этих вершин в полную амплитуду обычно
сводится^26 2^ к простым множителям, содержащим скалярную константу связи (например,
электрический заряд), которая определяет силу взаимодействия, возможно, член типа
который нужен «для согласования индексов», и дельта-функцию (§9.7), благодаря которой
ненулевой вклад в полную амплитуду получается лишь в том случае, когда в каждой вершине
имеет место сохранение 4-импульса^26*22^. Различным линиям на диаграммах соответствуют
члены разного рода в зависимости от значений спина и массы покоя частиц, представляе¬
мых данными линиями. Бесконечности в таких выражениях (помимо тех, которые связаны
с дельта-функциями и обычно рассматриваются как ограничения, обеспечивающие сохра¬
нение 4-импульса) возникают, когда импульсы Ра принимают значения, соответствующие
классическим траекториям (РаРа — М2). Это имеет смысл, поскольку мы ожидаем, что
классическое поведение должно вносить основной вклад в интеграл по траектории. Присут¬
ствие таких сингулярностей (бесконечностей, не связанных с дельта-функциями) в конечном
счете связано с требованием, чтобы классическое поведение давало, в некотором грубом
смысле, главный вклад в квантово-механическую амплитуду. Хотя, как мы вскоре увидим,
в таких сингулярностях таится некоторая опасность.
Чтобы подчеркнуть необходимость подобных сингулярных выражений, я должен отме¬
тить, что мы не можем рассматривать выражение РаРа = М2 как ограничение (наподобие
сохранения импульса в вершинах) из-за существования фундаментальных процессов вро¬
де показанного на рис. 26.5, в которых два электрона «обмениваются фотоном» (фотон, как
и в §§ 25.3-25.5, обозначается волнистой линией). Это есть основное квантово-механическое
проявление электростатического (кулоновского) отталкивания между двумя отрицательно
заряженными частицами (мёллеровское рассеяние). Две входящие линии (в нижней части
диаграммы) представляют два электрона в их начальном состоянии, а две выходящие ли¬
нии (в верхнейt26 23^ части диаграммы) — электроны в их конечном состоянии. Эти линии
считаются заданными, определяемыми внешними импульсами, и по ним не производится
«интегрирование» при вычислении конечной амплитуды.
Для таких внешних состояний (и только для них) импульсы должны удовлетворять клас¬
сическому соотношению РаРа = М2. Когда это соотношение выполняется, мы говорим, что
масса частицы находится на оболочке; имеется в виду «массовая оболочка», представляющая
собой чашеобразный гиперболоид, подобный изображенному на рис. 18.7, но в простран¬
стве импульсов (см. рис. 26.6). Реальные частицы (те, которые действительно наблюдаются
как свободные частицы) всегда находятся на оболочке. Однако в отношении внутренних
Объясните, как возникает эта сингулярность, представив г(Р — М 4- ге)~1 в виде дроби со знаменате¬
лем РаРа ~ М2 - £2.

566
Глава 26
А
s
<D
Сн
CQ
Рис. 26.5. Мёллеровское рассеяние электронов — наиболее про¬
стое квантовое проявление сил электростатического (кулоновско-
го) взаимодействия. Электростатическое взаимодействие возника¬
ет здесь из-за «обмена» одиночным фотоном (волнистая линия)
между двумя электронами.. Фотон находится «вне оболочки» и
потому должен быть виртуальным, как следует из условия сохра¬
нения 4-импульса в каждой вершине
линий фейнмановской диаграммы уже нельзя ожидать выполнения требования находиться
на оболочке. В частности, фотон, которым обмениваются электроны на рис. 26.5, не мо¬
жет находиться на оболочке (поскольку его 4-импульс не удовлетворяет условию РаРа — 0)
при наличии нетривиального взаимодействия . Такие частицы, расположенные вне оболоч¬
ки, называются виртуальными частицами, они могут появляться только во внутренней части
фейнмановской диаграммы. Обменный фотон на рис. 26.5 является виртуальным, и он не мо¬
жет «убежать» и быть наблюдаемым на больших расстояниях.
Массовая оболочка
Конечная масса
Реальная частица:
Виртуальная частица:
/
t
Нулевая масса
Рис. 26.6. Массовая оболочка в пространстве импульсов. (Сравните рис. 18.7 и 18.17.) Для реальных
(свободных) частиц с массой покоя М 4-импульс ра лежит на массовой оболочке (так что вектор ра
является времениподобным или нулевым и направлен в будущее, при этом РаРа — М2), однако вир¬
туальные частицы во внутренней части фейнмановской диаграммы могут находиться «вне оболочки»
Процесс на рис. 26.5 представляет довольно частный случай в том отношении, что
состояние внутренней линии (виртуального фотона) полностью определяется внешними
линиями. В этом случае необходимое «интегрирование по внутренним состояниям» совер¬
шенно тривиально, поскольку содержит лишь один член. Однако в более сложном процессе,
показанном на рис. 26.7 а, б, где происходит обмен двумя фотонами, имеется некоторая сво-
^ «ft
бода в отношении 4-импульсов внутренних линий . Дело в том, что в подобных случаях
(а также в мириадах еще более сложных, как на рис. 26.7 в) мы предполагаем интегрирова¬
ние по всем возможным значениям импульсов на внутренних линиях, а также суммирование
всех различных вкладов от всех возможных «топологий фейнмановских диаграмм», которые
согласуются с данными внешними линиями, для которых заданы импульсы. (Под «тополо-
►
Почему не может? Объясните, каким образом сохранение 4-импулъса в каждой вершине определяет
4-импульс виртуального фотона. (Подсказка: все электроны имеют одинаковую массу покоя!)
** S3 В чем состоит эта свобода?

26.8. Построение фейнмановских диаграмм. S-матрица	567
а)	б)	в)
Рис. 26.7. Процессы более высокого порядка, определяющие поправки к меллеровскому рассеянию.
На рисунках а) и б) изображен двухфотонный обмен между электронами, на рисунке в) — процесс
гораздо более высокого порядка, включающий внутреннее рождение и уничтожение пар частиц. Каж¬
дая такая фейнмановская диаграмма представляет интеграл; вклады, вносимые всеми диаграммами,
должны суммироваться
гией» понимается просто один из различных способов соединения линий на диаграмме
безотносительно к значениям 4-импульсов, приписываемых линиям на диаграмме.)
Этот процесс должен дать нам полную амплитуду для некоторого набора импульсов «на
входе» и «на выходе», предполагаемых заданными. Набор амплитуд для различных возмож¬
ных состояний на входе и выходе образует некоторую матрицу (хотя и бесконечномерную),
у которой «строки» и «столбцы» соответствуют базису для выходных и входных состояний.
Ее называют матрицей рассеяния или, чаще, просто S-матрицей. Вычисление S-матрицы
можно рассматривать как главную цель КТП-26,241
Описанная процедура представляет, в вычислительном отношении, значительный про¬
гресс по сравнению с первоначальным «суммированием по траекториям», поскольку мы уже,
по существу, нашли бесконечномерные (и, казалось бы, безнадежно расходящиеся) интегра-
О
лы по траекториям, соответствующие каждой от¬
дельной линии диаграммы. Каждый выбор топо¬
логии фейнмановской диаграммы представляет
обычный конечномерный интеграл (вроде рассмот¬
ренного в § 12.6), что является существенным ша¬
гом вперед по сравнению с сильно расходящимися
бесконечномерными интегралами, к которым при¬
водит непосредственная интерпретация интегралов
по траекториям. Более того, к этим конечномерным
интегралам можно применять мощные методы кон¬
турного интегрирования в комплексной плоскости
(§ 7.2). Фейнмановский параметр е, фигурирующий
в пропагаторе (см. последний абзац в § 26.7), указы¬
вает, с какой стороны контур интегрирования дол¬
жен обходить сингулярности, появляющиеся в та¬
ких выражениях.
Пока мы очень далеки от разрешения трудно¬
стей, поскольку конечномерный интеграл для каж¬
дой топологии фейнмановских диаграмм сам ока¬
зывается расходящимся всякий раз, когда диаграм¬
ма содержит замкнутые петли. И это очень плохо,
Рис. 26.8. «Древесная» диаграмма не
содержит петель. Внутренние импульсы
определяются значениями внешних им¬
пульсов, так что интегрирования не тре¬
буется. Такие диаграммы воспроизводят
классическую теорию

568
Глава 26
потому что именно при наличии замкнутых петель мы приходим к необходимости инте¬
грирования. Во всех остальных случаях (для так называемых «древесных» диаграмм, не
содержащих замкнутых петель; см. рис. 26.8) внутренние импульсы просто определяют¬
ся значениями внешних импульсов. Такие диаграммы просто воспроизводят классическую
теорию!
26.9.	Перенормировка
Из этого вроде бы следует, что при всех наших усилиях (или, скорее, усилиях Фейн¬
мана) мы пока еще не в состоянии отделаться от расходимости полной амплитуды любого
подлинно квантового процесса. Утомленный читатель может задать законный вопрос: какая
польза от всего этого? Действительно, со строго математической точки зрения, мы долж¬
ны ответить: «никакой», в том смысле, что все наши выражения остаются «математиче¬
ски бессмысленными» (вроде эйлерова 1 + 22 + 24 + 26 + 28 + ... = -±). Но настоящие
О
физики не сдаются так просто. И правильно делают. Их усилия в конечном счете были
вознаграждены ^26-25^, когда оказалось, что в случае квантовой электродинамики (КЭД) —
теории взаимодействующих электронов, позитронов и фотонов — все расходящиеся части
отдельных фейнмановских диаграмм можно собрать в различные «пакеты», так что беско¬
нечности можно рассматривать просто как «коэффициенты изменения масштабов», которые
можно игнорировать с помощью процесса, называемого перенормировкой (намек на него
уже был сделан в § 26.5).
Бесконечности возникают потому, что фейнмановские диаграммы приводят к интегра¬
лам, которые расходятся, когда значения импульса становятся бесконечно большими или, что
эквивалентно, расстояния становятся бесконечно малыми. (Напомним соотношение неопре¬
деленностей Гейзенберга импульс-координата Ар Ах ^ ifr; см. §21.11.) Такие бесконеч¬
ности называются ультрафиолетовыми расходимостями. Хотя это не единственный вид
расходимостей в КТП, он считается наиболее серьезным. Существуют также инфракрасные
расходимости, которые можно считать происходящими от бесконечно больших расстояний
(т. е. от бесконечно малых импульсов). Они обычно считаются «устранимыми» с помощью
различных методов, часто путем ограничения круга вопросов, задаваемых относительно
изучаемой системы, которые считаются имеющими физический смысл.
Чтобы получить некоторое представление об ультрафиолетовых бесконечностях, вы¬
ясним физический смысл наиболее понятного примера перенормировки. Перенормировка
касается значения электрического заряда электрона. Будем считать электрон точечным заря¬
дом, находящимся в некоторой точке пространства Е. Существует эффект, называемый по¬
ляризацией вакуума, который можно понять следующим образом. Пусть в некоторой точке,
близкой к точке Е, происходит рождение (виртуальной) пары частиц — электрона и позитро¬
на, которые, спустя очень короткое время, аннигилируют между собой. (Мы считаем этот
промежуток времени достаточно коротким, чтобы энергия, требующаяся для рождения пары,
соответствовала неопределенности в соотношении Гейзенберга энергия-время AEAt ^
(§21.11)). Фейнмановская диаграмма для этого процесса показана на рис. 26.9 а. Присут¬
ствие (виртуальной) фотонной линии в начале (а также в конце) процесса должно означать,
что рождение и последующая аннигиляция пары должны происходить во внешнем элек¬
трическом поле, создаваемом электроном, находящимся в точке Е. (Мы могли бы также
рассмотреть полностью несвязные фейнмановские «петли» (см. рис. 26.9 б), в которых про¬
цессы рождения и уничтожения имеют место без участия поля электрона, находящегося
в точке Е, однако такие «полностью несвязные» процессы не создают физически наблюда¬
емых эффектов.) Действие этого внешнего поля состоит в том, что родившийся электрон

26.9. Перенормировка
569
слегка отталкивается электроном в точке Е, тогда как родившийся позитрон слегка притя¬
гивается им, так что имеет место некоторое физическое разделение этих зарядов во время
их кратковременного существования. Такое происходит все время и повсюду вокруг элек¬
трона в точке Е, и результирующий эффект, называемый «поляризацией вакуума», сводится
к уменьшению 126,26^ наблюдаемого значения заряда электрона, измеряемого его действи¬
ем на другие заряды (см. рис. 26.10)*. Вакуум «экранирует» заряд электрона и приводит
к уменьшению его наблюдаемого значения — к так называемому одетому значению заря¬
да — по сравнению с «действительным» голым значением заряда электрона. Именно одетое
значение должно непосредственно измеряться в физических экспериментах.
t
I
а)
• I
4
в)
г)
Рис. 26.9. а) Фейнмановская диаграмма, содержащая перенормировку заряда. Она представляет ро¬
ждение и последующую аннигиляцию электронно-позитронной пары в поле фонового электрона
(см. рис. 26.10). б) Полностью несвязные фейнмановские диаграммы. Они считаются не создающими
непосредственно наблюдаемых эффектов
Все это выглядит вполне разумно. Но беда в том, что вычисленный коэффициент пе¬
рехода от голого значения к одетому, оказывается бесконечным! Эту бесконечность можно
выделить как одну из бесконечностей, возникающих при квантово-электродинамических
расчетах (примером могут служить диаграммы вроде приведенной на рис. 26.9 а и произ¬
водных от нее). Можно придерживаться такого взгляда, что в некоторой будущей теории
расходящиеся интегралы будут заменены конечными величинами, возможно, в результа¬
те некоторого «обрезания» на очень малых расстояниях, т. е. очень больших импульсах
(§21.11), и исправленный таким путем коэффициент перенормировки окажется довольно
Рис. 26.10. Вакуумная поляризация — физическая основа пере¬
нормировки заряда. Электрон в точке Е вызывает небольшое
разделение зарядов в виртуальных электронно-позитронных
парах, рождающихся на короткое время из вакуума. Это
несколько уменьшает эффективный заряд электрона в точке
Е по сравнению с его голым значением, — к сожалению, в бес¬
конечное число раз, согласно непосредственному вычислению
^ \
'7\
4 "1" j
/70.
Е
* Понятно ли, почему это происходит?

570
Глава 26
большим конечным числом, но не бесконечностью. (В «естественных единицах измерения»,
которые мы введем позже, в § 27.10, измеряемый одетый заряд электрона составляет 0,0854,
если принять голое значение заряда за единицу. Это соответствует коэффициенту перенор¬
мировки 11,7062 или приблизительно у/137, вместо оо.) Другая точка зрения состоит в том,
чтобы считать голый заряд не более чем удобной абстракцией, и рассматривать понятие
«голого заряда» как не имеющее реального смысла из-за его «ненаблюдаемости».
Независимо от философской позиции, занимаемой в этом вопросе, перенормировка
представляет существенную деталь современной КТП. Действительно, в настоящее вре¬
мя нет общепринятого способа получения конечных результатов без использования про¬
цедуры «бесконечной перенормировки», применяемой не только по отношению к заряду
или массе, но и к другим величинам. Теории, в которых такая процедура работает, на¬
зываются перенормируемыми. В перенормируемой КТП можно собрать все расходящиеся
части фейнмановских диаграмм в конечное число «пакетов» f26•2т1, которые можно устра¬
нить с помощью перенормировки, все остальные расходящиеся выражения взаимно уни¬
чтожаются в силу некоторых общих принципов (например, принципов симметрии, кото¬
рые играют важную роль в стандартной модели элементарных частиц). Квантовая элек¬
тродинамика является перенормируемой теорией, то же относится к стандартной модели
в целом. С другой стороны, большинство КТП неперенормируемо. Согласно общей точ¬
ке зрения, распространенной среди физиков, занимающихся элементарными частицами,
перенормировка рассматривается как принцип отбора среди предлагаемых теорий. В со¬
ответствии с этим любая неперенормируемая теория должна автоматически отклоняться
как неприемлемая для Природы. Этот принцип сыграл руководящую роль при выборе той
теории, которая стала в XX веке стандартной моделью физики элементарных частиц, рас¬
смотренной нами в главе 25. Таким образом, с этой точки зрения присутствие бесконеч¬
ностей в КТП является вовсе не недостатком, а особенностью, которую можно с успе¬
хом обратить в преимущество f26 28^. Очень немногие теории в состоянии пройти испыта¬
ние на перенормируемость, и только такие теории имеют шанс считаться приемлемыми
для физики.
Однако не все физики разделяют эту позицию. Даже Нобелевский лауреат Герард
’т Хоофт, который внес основной вклад в демонстрацию перенормируемости стандартной
модели, проявил определенную сдержанность в вопросе о приверженности принципу пере-
нормируемости. (В 1971 году, будучи еще студентом Утрехтского университета, ’т Хоофт
потряс физическое сообщество, продемонстрировав перенормируемость теорий, в которых
имеет место «спонтанное нарушение симметрии», ставшее характерной особенностью те¬
ории электрослабого взаимодействия.) Он высказал мне однажды свое мнение, согласно
которому роль перенормируемости в теории зависит от величины константы связи в рас¬
сматриваемом взаимодействии. Он, в частности, имел в виду гравитационное взаимодей¬
ствие, необычайно слабое по сравнению с силами, фигурирующими в физике элементарных
частиц, при том что его квантовая теория оказывается неперенормируемой согласно стан¬
дартному подходу к квантованию уравнения Эйнштейна в общей теории относительности;
см. §§19.6, 31.1. (Гравитационное притяжение между электроном и протоном в атоме во¬
дорода слабее электрического притяжения приблизительно в Ю40 раз, что делает гравита¬
ционное взаимодействие почти невообразимо более слабым по сравнению со «слабым вза¬
имодействием», ответственным за радиоактивный распад.) Замечания ’т Хоофта выражают
так называемый прагматический взгляд на КТП. Даже перенормируемые теории не свобод¬
ны от бесконечностей (к этому вопросу мы вскоре вернемся). Взгляд ’т Хоофта сводился
к вопросу: действительно ли бесконечности, потенциально присутствующие в теории, фи¬
зически существенны при энергиях, лишь отдаленно доступных для эксперимента. В случае
«квантованной гравитации» соответствующие экстремальные энергии лежат невообразимо
далеко за пределами досягаемости, и многие другие неопределенности в физической теории

26.10. Фейнмановские диаграммы из лагранжианов
571
оказываются в поле зрения задолго до того, как начнет проявляться неперенормируемость
гравитационного взаимодействия.
На другом конце шкалы мы имеем сильное взаимодействие с константой связи, на¬
столько большой, что возникает сомнение в целесообразности описания его с помощью
фейнмановских диаграмм, поскольку ряд увеличивающихся членов быстро расходится. Од¬
ной лишь перенормируемости недостаточно для уверенности в том, что квантовая хромо-
динамика может давать конечные результаты. В этом случае имеется преимущество в виде
так называемой асимптотической свободы сильного взаимодействия (за эту работу Гроссу,
Полицеру и Вилчеку в 2004 году была присуждена Нобелевская премия). При очень боль¬
ших импульсах (в квантовой теории это соответствует очень малым расстояниям) сильное
взаимодействие обладает замечательным свойством — оно эффективно исчезает. Это являет
резкий контраст с обычными электрическими и гравитационными силами, действующими
между частицами, которые, согласно закону обратного квадрата, растут при уменьшении
расстояния. Сильное взаимодействие подобно силе натяжения упругой ленты, которая рас¬
тет пропорционально растяжению и спадает до нуля при нулевом растяжении i26-29!. Такой
закон изменения силы обусловлен тем фактом, что кварки не могут по отдельности поки¬
дать адрон (это называется конфайнментом или удержанием); см. §§25.7, 25.8. В отличие
от упругой ленты, сильное взаимодействие не может «лопнуть» при сильном растяжении,
однако в вакуум могут выходить пары кварк-антикварк, что проявляется в виде «струй»
в ускорителях элементарных частиц. Именно это замечательное свойство асимптотической
свободы спасает теорию сильного взаимодействия от полной бесполезности в вычислитель¬
ном отношении, несмотря на ее перенормируем ость. Конкретно, константа сильного взаимо¬
действия приблизительно равна 10, что резко контрастирует с константой электромагнитного
1
взаимодействия (так называемой постоянной тонкой структуры), которая составляет
1о I
и константой слабого взаимодействия, которая, хотя и не допускает непосредственного чис¬
ленного сравнения, гораздо меньше (см. также §31.1).
26.10.	Фейнмановекие диаграммы из лагранжианов
В своем описании фейнмановских диаграмм, перенормировки и т. п. я немного забежал
вперед и не объяснил, как строить эти диаграммы для какой-либо конкретной теории поля.
Описание фейнмановских диаграмм не было связано с общим формализмом КТП, с кото¬
рого началась эта глава. Сейчас я попробую исправить эту оплошность и указать место
фейнмановских диаграмм в общей картине КТП,
Исходной точкой должен быть лагранжиан, соответствующий рассматриваемой теории.
При этом фейнмановекие диаграммы представляют разложение в ряд теории возмущений
квантовой теории при заданном лагранжиане, разложение в ряд теории возмущении — это
просто разложение в ряд по степеням некоторого параметра (или семейства параметров),
обычно предполагаемого малым. Это разложение того же рода, что и в §4.3, где функ¬
ция f(x) разлагается в ряд по степеням х. Аналогом величины ж в случае фейнманов-
ских диаграмм служит обычно некоторая константа связи. Например, в КЭД параметром
разложения служит электрический заряд е. Каждой вершине фейнмановской диаграммы
соответствует множитель е, так что членами ряда будут диаграммы с увеличивающимся
числом вершин, и совокупность диаграмм с п вершинами определяет коэффициент при еп.
В теории с более чем одной константой связи получается более сложный степенной ряд
по нескольким переменным. Примером может служить вариант КЭД, в котором электрон¬
ные линии стандартного представления заменяются зигзагами, как показано на рис. 25.2
и 25.3 6. Двумя «константами связи» при этом служат электрический заряд и масса М
электрона.

572
Глава 26
Я уже отмечал, что перенормируемые теории не обязательно дают конечные результаты.
Даже прототип перенормируемой теории, КЭД, в действительности не является конечной
теорией, даже после перенормировки. Как это возможно? Перенормировка означает устране¬
ние бесконечностей из конечных наборов фейнмановских диаграмм. Это не означает, однако,
что суммирование всех полученных при этом конечных величин действительно будет схо¬
диться. КЭД дает нам степенной ряд типа /о + f\e Т /2е2 + /зе3 + • • •, в котором каждый из
коэффициентов /о, /ь /2, /з> • • • представляет конечную величину, полученную в результа¬
те процедуры перенормировки интегралов, соответствующих фейнмановским диаграммам
разного порядка, 0, 1, 2, 3, ... (Фактически в каждом отдельном случае будут появляться
только четные или только нечетные степени .) Перенормируемость не означает, что сумма
всего ряда конечна. На самом деле она не конечна, а имеет «логарифмическую расходи¬
мость» (подобно ряду 1 + ~ + ^ + 4 + для — log(l — х) при х = 1), которая в КЭД
Z . О 4
начинает проявляться лишь при достижении членов порядка 137 или около того, а это
находится далеко за пределами того, что обычно имеет смысл рассматривать.
В общей квантовой теории поля для получения диаграмм, возникающих в каждом по¬
рядке, приходится обращаться к исходному выражению с интегралами по траекториям, даже
если это приводит к быстрой расходимости при попытке непосредственного суммирования.
При такой процедуре интеграл по траекториям рассматривается как некая чисто формальная
величина, к которой непосредственно, но формально применяется операция функционально¬
го дифференцирования (§ 20.5). При вычислении функциональных производных всё более
высокого порядка получаются фейнмановские графики со всё большим числом вершин.
Я не собираюсь разбирать здесь этот вопрос более подробно, отмечу лишь, что при та¬
кой формальной процедуре появление фейнмановских диаграмм происходит однозначным
образом^26,301 Лагранжианом будет, конечно, полевой лагранжиан общего вида, рассмотрен¬
ный в § 20.5. «Траектория», используемая при вычислении действия с таким лагранжианом,
не будет обычной одномерной кривой в некотором бесконечномерном конфигурационном
пространстве. В полностью релятивистской инвариантной картине «история» должна пред¬
ставлять собой целую четырехмерную конфигурацию поля в некоторой пространственно-
временной области. Интеграл от плотности лагранжиана по такой области дает действие 5,
a e%s!h — амплитуду (плотность), которую следует приписать данной конфигурации.
26.11.	Фейнмановские диаграммы и выбор вакуума
Если теория обладает симметрией относительно некоторой группы преобразований, на¬
пример, симметрией U(2) теории электрослабого взаимодействия, или симметрией SU(3)
квантовой хромодинамики, или ими обеими, то такая симметрия обычно проявляется в ла¬
гранжиане. Наличие такой симметрии играет важную роль в перенормируемости КТП. Грубо
говоря, симметрия используется, чтобы обеспечить взаимное уничтожение некоторых рас¬
ходящихся членов. Такое уничтожение происходит (или так считается, что оно происходит),
потому что расходящееся выражение не могло бы обладать предполагаемой симметрией
данной теории.
Такова, по крайней мере, общая идея. Однако в случае теории электрослабого взаи¬
модействия имеется другая тонкость, поскольку эта теория не обладает в конечном счете
изначально постулируемой симметрией U(2)J26 31^ Потеря симметрии U(2) является след¬
ствием нарушения симметрии, рассмотренного в § 25.5, однако чтобы понять, как это вое-
принимать, нам придется вернуться к общему формализму КТП. Основная идея состоит
в том, что нарушение симметрии объясняется и(2)-асимметричным выбором вакуумного
Понятно ли, почему это так?

26.11. Фейнмановские диаграммы и выбор вакуума
573
стояние
состояния. В соответствии с этим, теневое состояние |0), которое предполагалось сто¬
ящим справа от всех операторов рождения и уничтожения и которое мы, рассматривая
фейнмановские диаграммы, до сих пор в основном игнорировали, теперь должно выйти
из тени.
Прежде всего нам нужно хотя бы в общих чертах понять, как связать элементы алге¬
бры Л в КТП с фейнмановскими диаграммами. Ключевой пункт состоит в том, что фейн¬
мановские пропагаторы, представляемые линиями фейнмановских диаграмм, выражаются
через значения коммутаторов или антикоммутаторов, с которыми мы уже встречались
в § 26.2 (т. е. величины (ф\ф) в приведенных там выражениях). На практике они обычно вы¬
ражаются в виде элементов пространства импульсов, хотя в определении точных фейнманов¬
ских пропагаторов существуют некоторые тонкости, связанные с понятием положительных
и отрицательных частот (которые, вероятно, легче всего понять с позиции гиперфункций,
см. § 9.7). Здесь мы не будем заниматься этими тонкостями.
Предположим, что мы рассматриваем ситуацию, в которой вначале имеется некоторый
набор частиц на входе, а в конце появляется некоторый набор частиц на выходе. Мы исхо¬
дим из вакуумного состояния |0), затем применяем к нему различные операторы рождения,
чтобы создать требуемое состояние входящих частиц. Эта процедура дает начальное со¬
стояние j ). Аналогично можно провести такую же операцию в отношении выходящих
частиц, снова действуя операторами рождения на состояние |0) и создавая конечное со-
^out)- Далее нам необходимо вычислить амплитуду (Vwl^in)» с помощью которой
можно найти вероятность перехода от начального состояния «in» к конечному состоянию
«out», используя стандартную формулу, приведенную в §22.5, а именно KVwl'^m)!2> если
состояния нормированы.
Выражение (V'outlV'm) содержит на левом краю операторы уничтожения (поскольку эр¬
митово сопряжение, используемое для перехода от \ф0их) к (ф0т\, заменяет все операторы
рождения на операторы уничтожения). Все они лежат слева от операторов рождения в \фт)9
так что мы можем «перетащить» все эти операторы уничтожения вправо через операторы
рождения вплоть до состояния |0) на правом краю. Когда это происходит, состояние |0)
«уничтожается» (см. § 26.2), так что в результате получается нуль. Однако всякий раз, ко¬
гда мы перетаскиваем оператор уничтожения через оператор рождения, мы должны учесть
упомянутый коммутатор (и условие положительной или отрицательной частоты), что дает
нам, как уже отмечено, одну линию фейнмановской диаграммы. Каждый раз, когда мы де¬
лаем это, появляется еще одна такая линия. В конце концов мы получаем величину (0|0),
умноженную на набор фейнмановских пропагаторов, представляющих линии фейнманов¬
ской диаграммы, а поскольку для нормированного вакуумного состояния {0(0) = 1, как раз
и получается сама фейнмановская диаграмма.
До сих пор рассматриваемые нами фейнмановские диаграммы были вполне тривиаль¬
ными, не содержащими вершин, — но это потому, что в алгебру операторов Л не было
включено взаимодействие. Чтобы учесть взаимодействие, требуется рассмотреть лагранжи¬
ан, относящийся к данной задаче, и воспользоваться им для генерации правильной алге¬
бры Л. Эта процедура сводится к описанному в § 26.10 процессу генерации фейнмановских
диаграмм с соответствующими вершинными частями.
Пока мы мало что приобрели, однако введение фейнмановских диаграмм в общую схему
КТП имеет то преимущество, что теперь можно заменить вакуумное состояние |0) неэкви¬
валентным ему альтернативным вакуумом |0) (как в случае состояния моря Дирака |27),
рассмотренном в § 26.4). В отношении теории электрослабого взаимодействия и других те¬
орий, существенно зависящих от фундаментального нарушения симметрии, выгода состоит
в том, что, хотя лагранжиан и, следовательно, фейнмановские диаграммы в соответствую¬
щей теории обладают точной симметрией (в случае теории электрослабого взаимодействия
это группа симметрии U(2)), реальные состояния системы будут обладать более низкой сим¬

574
Глава 26
метрией (калибровочной группой электромагнетизма U(l) в указанном случае), поскольку
этой более низкой симметрией обладает вакуумное состояние |0). При этом перенорми-
руемость теории, которой приписывается полная ненарушенная симметрия, остается неиз¬
менной, несмотря на то что теория в целом проявляет лишь более низкую, «нарушенную»
симметрию.
Это замечательный способ построения физических теорий, позволяющий извлекать
пользу из точной симметрии, тогда как в экспериментальной ситуации условия симметрии
отнюдь не выполняются. У физиков появляется сильное искушение использовать его при
поиске более успешных и глубоких схем. И действительно, все современные идеи выхода
за рамки стандартной модели стремятся использовать преимущества такого «нарушения
симметрии». Пока все такие попытки, независимо от степени их популярности (примеры
будут рассмотрены в §§28.1-28.5), следует рассматривать как чисто спекулятивные. Мы
будем придерживаться критического и скептического взгляда на предложения такого рода,
чтобы не увлечься ими слишком легко.
В качестве прелюдии к обсуждению таких предложений нам понадобится получить
в следующей главе некоторое представление о Большом взрыве. Затем в главе 28 мы по¬
пытаемся познакомиться с некоторыми тревожными проблемами, которые могут сопутство¬
вать идее спонтанного нарушения симметрии, в частности, на ранних стадиях развития
Вселенной. Наконец, нам понадобится еще более укрепиться в этой вездесущей идее, когда
в главе 31 мы рассмотрим суперсимметрию, оригинальные идеи теории струн и некоторые
необычные порождения этих идей.
Примечания
§26.1.
26.1. См. [14] или [858].
§26.2.
26.2. Я использую несколько «нестандартное» описание, рассматривая «волновую функцию» об¬
щего вида, — не обязательно нормированное положительно-частотное поле. Соответственно
отсутствие нормировки переносится также на оператор рождения Ф (и оператор уничтоже¬
ния Ф*). При стандартном описании в качестве функции ф часто берется некоторое импульс¬
ное состояние.
26.3. В литературе обычно обозначают символом а оператор уничтожения, а символом а* (это
есть оператор, эрмитово-сопряженный но отношению к а) — соответствующий оператор
рождения. Обычно используется описание в пространстве импульсов (см. [716] и [858]).
26.4. Это может смутить некоторых читателей, знакомых со стандартной литературой, посколь¬
ку используемые там операторы рождения и уничтожения зачастую относятся к различным
импульсным состояниям, образующим ортогональный базис. В этом случае операторы уни¬
чтожения удаляют определенные состояния.
26.5. См. [858, 639].
26.6. Впечатляющую демонстрацию этого требования можно найти в книге [858].
26.7. Существует также несколько интригующих топологических понятий, связывающих обмен
частицами с поворотом на 27т, однако возможность использования этого обстоятельства в КТП
пока остается неясной. См. [265, 259, 79].
§26.3.
26.8. Более глубокое и подробное изложение см. в [469, 37].
26.9. Возможно, выраженное через потенциалы.
26.10.	Общее понятие нормировки состояний представлено, например, в книге [679]. Квантование
электромагнитного поля в несколько более традиционной трактовке дается в [716].

26.11. Фейнмановские диаграммы и выбор вакуума
575
§ 26.4Х
26.11. В книге [722] можно найти последние новости относительно нейтрино — это весьма «горячая»
область современной физики!
§26.6.
26.12. Пространство Фока для простого случая бозонного поля, когда частица является собственной
античастицей, можно записать в виде	..,
где 0 означает операцию нахождения прямой суммы, а символ О — симметризованное тен¬
зорное произведение. Соответствующим образом можно рассмотреть более сложные случаи,
когда присутствуют спин, заряд и т.п. Изложение общей идеи см. в книге [716], может ока¬
заться полезной также книга Давыдова [179].
26.13. Обсуждение когерентных состояний, которые могут иметь много разновидностей (фермион-
ные, спиновые и др.), см. в [349, 716].
26.14. См. [810, 82].
26.15. См. [202, 709].
26.16. См. [257, 258]. Превосходное изложение этой идеи содержится в книге [260]. Альтернатив¬
ный подход к квантовой электродинамике, развитый Швингером (см., например, [708]), был
во многих отношениях более строгим, однако большинство физиков сегодня пользуется более
интуитивной картиной, которую дают интегралы по траекториям и фейнмановские диаграм¬
мы.
§26.7.
26.17. Как отметил Фейнман, такая степень точности соответствует определению расстояния от Лос-
Анджелеса до Нью-Йорка с погрешностью, меньшей толщины человеческого волоса!
26.18. Некоторые другие идеи, достойные внимания, например, так называемую «евклидизацию»,
мы обсудим в § 28.9.
26.19. Это пример так называемой функции Грина (названной в честь замечательного сына мельника,
английского математика-самоучки Джорджа Грина (1793-1841)). Фейнмановский пропагатор
представляет собой частный случай функции Грина К(р, q), удовлетворяющий условию по¬
ложительной частоты в квантовой теории, введенному в §24.3.
26.20. См., например, классический труд Бьёркена и Дрелла [83].
§26.8.
26.21. Существуют величины, называемые «бегущими константами связи», которые зависят от энер¬
гии покоя полной системы входящих частиц для данной вершины фейнмановской диаграммы.
Они играют важную роль во многих современных теориях физики элементарных частиц.
(1) (2)
26.22. Так, если на входе в данную вершину имеются импульсы Ра ,	Ра ,	..., а на выходе	—
импульсы Q^a \ Q^a\ • • -, ТО ПОЯВИТСЯ Член С 8{Р^ + Ра^ + ■ • • — OiX)	— Q(a} “•*')•
26.23. См. примечание 25.6.
26.24. Важное понятие «S-матрицы» (введенное в основном Гейзенбергом и глубоко оригиналь¬
ным американским физиком Дж. А. Уилером) не связано жестко с понятием фейнмановских
диаграмм, так что S-матрицу можно вычислять и другими способами (см. [233]).
§26.9.
26.25. См. [858] или, с большими подробностями, [679].
26.26. Поскольку электрон имеет отрицательный заряд, «уменьшение»	здесь	надо понимать	как
«уменьшение модуля».
26.27. Существуют изящные математические процедуры, предназначенные для систематизации это¬
го метода и использующие понятие «копроизведения», связанное с идеями некоммутативной
геометрии, кратко обсуждаемыми в §33.1 (см. [160]).
26.28. Важную часть метода составляет понятие «ренормализационной группы». Соответствующие
идеи рассматриваются в книгах [858, 679, 639], ее применение в статистической механике
описано в энциклопедическом труде Зинн-Жюстина [862].

576
Глава 26
26.29. Гравитационные силы играют существенную роль (даже в сверхгалактических масштабах к
несмотря на то что они спадают с расстоянием по закону обратного квадрата. Читателя может
удивить, почему в то же время сильное взаимодействие становится совершенно незамет¬
ным на расстояниях, превышающих размер атомного ядра, хотя оно растет с расстоянием.
Причина состоит в том, что гравитационное взаимодействие, будучи всегда притяжением,
накапливается, тогда как сильное взаимодействие является результатом сложения сил притя¬
жения и отталкивания, которые взаимно уничтожаются и не участвуют во взаимодействии
между разделенными ядрами (при этом отдельные ядра являются «цветовыми синглетами»).
§26.10,
26.30. Соответствующий алгоритм изложен в книгах [858, 862]; довольно занимательное и наглядное
изложение можно найти в книге Маттука [520].
§26.11.
26.31.	См. примечание 25.12

Глава 27
Большой взрыв и его термодинамическое
наследие
27.1.	Временная симметрия в динамической эволюции
Какие законы формируют Вселенную со всем ее содержимым? Ответ, который дают
практически все успешные физические теории со времен Галилея, состоит в построении
4
динамики, т. е. описания того, как будет развиваться с течением времени физическая система,
для которой задано ее состояние в некоторый момент времени. Эти теории ничего не говорят
нам о том, на что похож наш мир, вместо этого они утверждают следующее: «если мир был
таким-то в один момент времени, то он будет выглядеть так-то в некоторый более поздний
момент». Подобная теория ничего не скажет нам о том, как устроен мир, если мы не
сообщим ей, как он был устроен раньше.
Из этого порядка вещей есть важные исключения, например, удивительный вывод, сде¬
ланный в 1609 году Кеплером, согласно которому орбиты планет, обращающихся вокруг
Солнца, имеют определенную геометрическую форму — эллипса, в одном из фокусов кото¬
рого находится Солнце, и такие эллипсы описываются планетами со скоростью, подчиняю¬
щейся некоторым определенным правилам. Это утверждение относилось к тому, как устро¬
ена Вселенная, а не к тому, как ее состояние может меняться со временем в соответствии
с некоторым динамическим законом. Однако наш современный взгляд на геометрические
движения, открытые Кеплером, состоит в том, что они всего лишь следствие гравитацион¬
ной динамики XVII века; это было впервые показано Ньютоном в его великих «Принципах
натуральной философии», опубликованных в 1687 году. Так что законы Кеплера не следу¬
ет считать непосредственными фундаментальными законами природы. Можно сказать, что
Кеплеру — и науке в целом — необычайно повезло в том, что закон обратных квадратов
(§17.3), которому подчиняются силы ньютоновского тяготения, обладает тем свойством, что
все орбиты малых тел вокруг центра силы имеют простую и изящную математическую
форму (которая интенсивно изучалась древними греками восемнадцатью веками раньше).
Это есть исключительное свойство, которым не обладают центральные силы, описываемые
другим простым законом. Наш современный взгляд состоит в том, что изящной математи¬
ческой формы следует ожидать от динамических законов, и можно считать удачей, если нам
посчастливится обнаружить простые математические формы как следствие этих законов.
Обычный взгляд на действие этих динамических законов состоит в том, что реализация
той или иной динамики определяется выбором начальных условий. Обычно рассматривает¬
ся эволюция системы в будущем по данным, относящимся к прошлому, при этом эволюция
описывается дифференциальными уравнениями. (В случае динамической эволюции полей
или волновых функций это будут дифференциальные уравнения в частных производных —
уравнения поля; см. §§ 10.2, 19.2, 19.6, 21.3, упражнение 19.2 и примечание 21.1.) С другой
стороны, никто не стремится проследить эволюцию тех же самых уравнений в прошлое,
несмотря на тот факт, что динамические уравнения классической и квантовой механики
симметричны относительно изменения направления течения времени! Пока мы имеем де¬
ло с математикой, мы можем с тем же успехом задавать конечные условия для некоторого

578
ГЛАВА 27
момента времени в отдаленном будущем и рассматривать эволюцию назад в прошлое. В ма¬
тематическом отношении конечные условия при изучении эволюции системы ничем не хуже
начальных.
Напрашиваются некоторые замечания относительно такого динамического детерминиз¬
ма, симметричного во времени. Прежде всего, следует обратить внимание читателя на то,
что такой детерминизм не запрещен ни специальной, ни общей теорией относительно¬
сти. Данные, определяющие состояние системы, задаются для некоторого начального «мо¬
мента времени», которому соответствует некоторая начальная пространственноподобная 3-
поверхность, и это состояние эволюционирует в соответствии с динамическими уравне¬
ниями, определяющими физическое состояние системы как в будущем, так и в прошлом
по отношению к этой 3-поверхности. В общей теории относительности возникают, однако,
некоторые новые аспекты, поскольку сама структура пространства-времени, в котором про¬
текает эволюция, составляет часть определяемого состояния. (Это имеет отношение к про¬
блеме черных дыр, с которой мы столкнемся позже, в §§ 27.8, 27.9, 28.8, 30.4, 30.9.)
В случае квантовой механики детерминизм относится лишь к U-части теории, в кото¬
рой квантовое состояние описывается уравнением Шредингера (или каким-либо его экви¬
валентом). При обращении времени (посредством операции Т, введенной в §25.4) опера¬
тор временной производной ihd/dt в уравнении Шредингера (§21.3) должен быть заменен
на —ihd/dt (поскольку проводится отображение t ~t). Если гамильтониан под дей¬
ствием операции Т переходит сам в себя, то уравнение Шредингера тоже перейдет само
в себя, если сопроводить обращение времени t ^ —t изменением знака у мнимой едини¬
цы: г и-* —i. Именно так понимается действие операции Т в квантовой механике. (Заметим,
что положительно-частотная функция f(t) снова становится положительно-частотной при
комбинированной замене t ь-» — t и i y~> —г, так что в этом отношении тоже все обстоит
как надо*.) Однако поведение редукции квантового состояния R под действием операции Т
совсем иное, и это будет важной темой при обсуждении в главе 30 (§ 30.3).
27.2.	Субмикроскопические составные части
Существуют, однако, и другие вопросы, которые могут возникнуть у осведомленно¬
го читателя, даже в отношении классической механики. В субмикроскопической динамике
отдельных частиц и сопровождающих их полей, описываемой классической механикой,
временная симметрия определенно имеет место. Но на практике мы мало что знаем о по¬
ведении отдельных составных частей системы. Подробное знание координат и импульсов
каждой частицы обычно считается недоступным и ненужным, поскольку поведение всей
системы в целом достаточно хорошо описывается некоторыми подходящими средними зна¬
чениями физических параметров отдельных частиц. Таковыми могут быть распределение
массы, импульса и энергии, положение и скорость центра масс, температура и давление
в разных местах, упругие свойства, моменты инерции, подробная общая форма системы,
ее ориентация в пространстве и т.д. Важный вопрос состоит, следовательно, в том, до¬
статочно ли исходного знания относительно таких усредненных «общих» параметров для
практического определения динамического поведения системы с адекватной степенью точ¬
ности.
Это, определенно, не всегда так. Так называемые хаотические системы обладают тем
свойством, что их конечное поведение критическим образом зависит от начальных усло¬
вий. В качестве примера можно рассмотреть механическую игрушку в виде магнитного
маятника, который качается над набором магнитов, размещенных некоторым образом на ее
основании (рис. 27.1). Динамическое поведение такой системы детерминированным обра-
Почему? Объясните также, почему при такой замене не возникает трудностей и с импульсом.

27.2, Субмикроскопические составные части
579
зом определяется законами Ньютона и законами магни¬
тостатики, а также замедлением из-за сопротивления воз¬
духа. Тем не менее конечное состояние покоя настолько
сильно зависит от начального состояния, что оно ока¬
зывается практически непредсказуемым, хотя при пол¬
ном знании о начальном состоянии всех участвующих
частиц и полей эволюция должна бы быть определена
однозначно 1271^. Известно множество других примеров
подобных «хаотических систем». Изрядная доля неопре¬
деленности в предсказании погоды обычно связывается
Jr
yEbj
N j :
"•■! - 'J
rt%
t Ж|
шш
я
Я
"A
Jf V rtje
* *
% V- “
"г.:
о
с хаотической природой соответствующих динамических
систем. Даже высокоупорядоченное (и хорошо предска¬
зуемое) движение тел в Солнечной системе под действи-
ем ньютоновской гравитации представляет, вероятно, ха¬
отическую систему, только временные масштабы такого
«хаоса» гораздо больше аналогичных масштабов астро¬
номических наблюдений.
Как в этом случае обстоит дело с эволюцией, про-
Рис. 27.1. Хаотическое движение.
Механическая игрушка состоит из
магнитного маятника, который ка¬
чается над набором фиксированных
магнитов. Траектория, описываемая
маятником, весьма чувствительным
образом зависит от его начального
положения и скорости
слеживаемой не в будущее, а в прошлое? Следует прямо
сказать, что такая «хаотическая непредсказуемость» обычно проявляется в гораздо боль¬
шей степени при «предсказании назад» эволюции, направленной в прошлое, нежели при
«предсказании вперед» обычной эволюции в будущее. Это следует из второго закона тер-
модинамики, который в своей простейшей форме гласит:
тепло течет от более горячего тела к более холодному.
В соответствии с этим законом, если соединить горячее тело с холодным некоторым про¬
водником тепла, то горячее тело будет охлаждаться, а холодное нагреваться, пока они не
окажутся при одной и той же температуре^27'2^. Таково «предсказание вперед», и такая
эволюция имеет детерминированный характер. Если же мы взглянем на этот процесс в на¬
правлении, обратном во времени, то увидим, как два тела, первоначально имевшие одну
и iy же температуру, самопроизвольно приобретают разную температуру, и практически
невозможно решить, какое тело станет горячее, а какое холоднее, и на сколько и когда про¬
изойдет изменение температуры. Подобная процедура динамического «предсказания назад»
поведения такой системы, очевидно, практически
Такая трудность «предсказания назад» характерна для почти любой макроскопической
системы, состоящей из большого числа частиц, которая ведет себя в соответствии со вто¬
рым законом. По этой причине физика обычно занимается предсказанием «вперед», а не
«назад»^27‘31 Второй закон рассматривается как существенный элемент предсказательной
способности физики, при этом устраняются из рассмотрения проблемы, требующие «пред¬
сказания назад».
Тем не менее многие физики придерживаются того взгляда, что этот закон не является
«фундаментальным» в том смысле, в каком фундаментальны, например, закон сохранения
энергии, принцип линейной суперпозиции в квантовой механике и, возможно, стандартная
модель физики элементарных частиц. Они заявляют, что второй закон — это почти «очевид¬
ный» необходимый элемент любой разумной физической теории. Они считают этот закон
не вполне определенным и точным, поскольку он не идет ни в какое сравнение по точности
предсказаний с динамическими законами фундаментальной физики. Я придерживаюсь ино¬
го мнения и хочу продемонстрировать «умопомрачительную» точность, скрывающуюся за,
казалось бы, расплывчатым статистическим принципом, который обычно называют вторым
законом термодинамики.

580
Глава 27
27.3.	Энтропия
Уточним, что в действительности утверждает второй закон термодинамики. Прежде все¬
го я должен информировать читателя относительно первого закона термодинамики. Первый
закон — это просто утверждение, что полная энергия сохраняется в любой изолированной
системе. Читатель может возразить, что не такая уж это и новость (§§ 18.6,20.4,21.3). Но ко¬
гда этот закон был провозглашен (это сделал в начале 1820-х годов Сади Карно, хотя он и
не опубликовал свои результаты t27 4l), еще не было очевидно, что теплота — это просто одна
из форм энергии, да и само макроскопическое понятие энергии было не вполне четким.
Из Первого закона следует, что полная энергия не исчезает, когда, например, тело теря¬
ет свою кинетическую энергию (§ 18.6), замедляя движение из-за сопротивления воздуха.
Эта энергия просто расходуется на нагревание воздуха и самого тела. Эта тепловая энергия
понимается (в основном) как кинетическая энергия движения молекул воздуха и колебания
частиц, составляющих тело. При этом температура есть просто мера энергии, приходя¬
щейся на одну степень свободы, так что термодинамические понятия тепловой энергии
и температуры — это фактически те же самые введенные ранее динамические понятия, но
применяемые на уровне отдельных объектов, из которых состоит материал, и трактуемые
статистическим образом. Первый закон обеспечивает привычную нам точность: значение
некоторой величины, а именно полной энергии, остается постоянным, несмотря на то что
могут происходить всевозможные сложные процессы. Полная энергия после протекания
процесса равна полной энергии до его начала.
В то время как Первый закон есть некоторое равенство, Второй закон выражается в виде
неравенства. Он гласит, что некоторая величина, называемая энтропией, после протекания
некоторого процесса имеет большее (или, по крайней мере, не меньшее) значение, чем до его
начала. Грубо говоря, энтропия есть «мера беспорядка» в рассматриваемой системе. Наше
тело, движущееся в воздухе, начинает движение с энергией в организованной форме (в виде
кинетической энергии своего движения), но когда это движение замедляется из-за сопро¬
тивления воздуха, энергия перераспределяется и переходит в энергию случайного движения
частиц воздуха и отдельных частиц тела. При этом происходит «увеличение беспорядка»,
или, в более специальных терминах, рост энтропии.
Понятие энтропии было введено в 1865 году Клаузиусом, однако ясное определе¬
ние энтропии (по крайней мере, настолько ясное, насколько это возможно) дал в 1877
году выдающийся австрийский физик Людвиг Больцман. Чтобы понять идею Больц¬
мана (для классической системы), нам потребуется понятие фазового пространства
(§§ 12.1, 14.1, 14.8, 20.1, 20.2, 20.4). Напомним, что фазовое пространство для классической
системы из п (бесструктурных) частиц — это бп-мерное пространство V, каждая точка кото¬
рого представляет полное семейство координат и импульсов всех п частиц. Чтобы сделать
понятие энтропии более точным, нам понадобится ввести понятие огрубления^7 Это мож¬
но сделать, разделив фазовое пространство V на ряд подобластей, которые будем называть
«ящиками» (см. рис. 27.2). Идея состоит в том, что точки пространства V, представляю¬
щие состояния системы, неразличимые при макроскопическом наблюдении, группируются
в одном ящике, а точки этого пространства, принадлежащие разным ящикам, предполага¬
ются макроскопически различимыми. Больцмановская энтропия S для состояния системы,
представляемого некоторой точкой х пространства V, равна
S = k logV,
где V есть объем ящика V, содержащего точку х (здесь имеется в виду натуральный лога¬
рифм, см. § 5.3), к —постоянная Больцмана^27	имеющая значение
• *
s	*	•	•
к^а.зв-нг^Дж-к-1
(Дж • К-1 означает «джоулей на градус Кельвина»).

27.3. Энтропия
581
Огрубленное фазовое пространство V
Макроскопически
неразличимые
Рис. 27.2. Больцмановская энтропия. Предполагается разбиение фазового пространства V на подобла¬
сти («ящики») — это называется «огрублением пространства» V> — при котором точки, принадлежащие
данному ящику, представляют макроскопически неразличимые физические состояния. Больцмановское
определение энтропии состояния х в ящике V объемом V имеет вид S = к log V, где к — постоянная
Больцмана
Выше я назвал больцмановское определение энтропии «ясным». Однако для того чтобы
вышеприведенная формула Больцмана представляла нечто физически точное, необходимо
иметь четкое предписание относительно огрубления, создаваемого нашим набором «ящи¬
ков». Несомненно, существует некоторый произвол в способе разбиения пространства на
ящики. Представляется, что определение зависит от того, с какой степенью подробности
изучается система. Два состояния, «макроскопически неразличимые» для одного экспери¬
ментатора, могут оказаться вполне различимыми для другого. Более того, произвольным
оказывается способ проведения границы между двумя ящиками, так что двум соседним
точкам пространства Р9 расположенным по разные стороны границы, могут быть припи¬
саны совершенно разные значения энтропии, несмотря на то что эти точки фактически
тождественны. Так что это определение энтропии S остается весьма субъективным, несмот¬
ря на отчетливое преимущество перед более ранними определениями, имеющими более
ограниченную применимость, и несомненную привлекательность идеи энтропии как меры
«беспорядка» в системе.
Моя собственная позиция в вопросе о физическом статусе энтропии состоит в том, что
я не рассматриваю ее как «абсолютное» понятие в современной физической теории, хотя
это понятие, несомненно, весьма полезно. Существует, однако, возможность, что в будущем
оно сможет приобрести более фундаментальный статус. Для этого необходимо привлече¬
ние квантовой физики, и в любом случае именно квантовая механика может предоставить
абсолютную меру для любой конкретной области фазового пространства V, содержащейся
в пространстве V, при этом можно выбрать систему единиц, в которой h = 1 (как в план-
ковской системе единиц, см. §27.10)*, Как бы то ни было, замечательно то, как мало влия¬
ет произвольность огрубления на результаты расчетов в термодинамике. Причина видится
в том, что в большинстве случаев, представляющих интерес, мы имеем дело с совершенно
огромным отношением размеров объемов рассматриваемых ящиков в фазовом пространстве,
и становится безразлично, как проводить границы, если учесть, что огрубление «разумным
образом» отражает интуитивную идею о том, когда следует считать системы макроскопи¬
чески различимыми. Поскольку энтропия определяется как логарифм объема ящика, требу¬
ется весьма кардинально изменить конфигурацию границ, чтобы получить сколько-нибудь
* Й0 Покажите, как можно приписать абсолютную меру объему фазового пространства, выбрав систему еди¬
ниц, в которой Н = 1.

582
Глава 27
заметное изменение энтропии 5. На мой взгляд, в современной теории энтропия имеет
статус не «фундаментального», а «удобного» понятия, хотя имеются указания, что на бо¬
лее глубоком уровне, где становятся существенными квантовые гравитационные эффекты
(особенно это относится к энтропии черной дыры), это понятие может приобрести более
фундаментальный статус. Мы перейдем к этому вопросу позже в этой главе (§ 27.10), а также
в §§30.4-30.8,31.15, 32.6.
27.4.	Прочность концепции энтропии
к
Роль больцмановской формулы для энтропии можно
пояснить на простом примере. Рассмотрим замкнутый кон¬
тейнер, часть которого 71 выделена как особая; это может
быть, например, шарообразный сосуд объемом в одну де¬
сятую объема контейнера, связанный с остальной частью
контейнера через малое отверстие (см. рис. 27.3). Предпо¬
ложим, что газ в этом контейнере состоит из т молекул.
Поставим вопрос об энтропии S в ситуации, когда весь газ
находится в области 71, в сравнении с энтропией в усло¬
виях, когда газ будет распределен случайным образом по
S
всему контейнеру.
Согласно формуле Больцмана, мы имеем
= k log Vn, где Vjz есть объем области фазового простран¬
ства Утг, представляющей все молекулы, находящиеся в 7Z.
Для простоты предполагается статистика Больцмана, ко¬
торая, в отличие от описанных в §23.7 «статистики Бозе-
Эйнштейна» для бозонов и «статистики Ферми - Дирака»
для фермионов, предполагает, что все молекулы газа от-
juf	з(с
личимы (хотя бы в принципе) одна от другой . Если в
качестве газа взять обычный воздух при атмосферном дав¬
лении, то в контейнере объемом в 1 литр мы будем иметь приблизительно т — 1022 молекул.
Отношение объема области фазового пространства Vn к объему всего фазового простран¬
ства V газа в контейнере равно 10~т(—
Рис. 27.3. Замкнутый контейнер,
часть которого в виде шарообраз-
1
ной области 7Z имеет объем в —
объема всего контейнера. Как уве¬
личится энтропия, когда газу, пер¬
воначально заключенному в 7Z, бу¬
дет позволено занять весь объем
контейнера?
10
то есть
10
-10000000000000000000000
так что мы видим действительно замечательное отношение объемов, возникающее в подоб¬
ных ситуациях. На рисунке представлена ситуация, когда вероятность того, что все моле¬
кулы газа чисто случайно окажутся в 7Z, смехотворно мала. Энтропия такой совершенно
неправдоподобной ситуации намного меньше энтропии ситуации, в которой газ равномерно
^
распределен по всему контейнеру, их разность, согласно формуле Больцмана , равна
k log (10
-10000000000000000000000
) = 2,3-10
= 0,32Дж-К
-1.
Какое отношение имеет логарифм в формуле Больцмана к огромной разнице в объемах ящиков?
Объясните, как будут различаться результаты подсчета в указанных трех случаях.
Почему?
Объясните, почему этот результат не изменится существенным образом, если рассматривать фермионы или
бозоны или если учесть вероятное уменьшение импульсов молекул газа, когда они перестают быть заключенными
в области 7Z.
**
***
****

27.4. Прочность концепции энтропии
583
здесь использован тот факт, что натуральный логарифм от 10 равен 2,3. Таким образом,
если предположить, что газ первоначально находился в области 7Z и был отделен (например,
с помощью некоторого вентиля) от остального контейнера и что затем, открыв вентиль, мы
выпустили газ в остальную часть контейнера, то соответствующее увеличение энтропии
будет равно 2,3 • 1022к (в обычных единицах это составляет примерно одну треть джоуля
на кельвин).
Читатель может возразить, что на практике невозможно реализовать контейнер, у кото¬
рого в основной («неособой») части вначале нет ни одной молекулы газа. Поэтому давайте
несколько ослабим наши требования к области Vn и определим ее так, чтобы в 7Z находилось
по крайней мере 99,9% молекул газа. Таким образом, к области Vn теперь предъявляется
требование, чтобы вне 1Z оказалось не более одной тысячной доли всех молекул. Создать
такой вакуум в «неособой» области для современной техники не составляет труда. Оказы-
вается, что такое изменение условии почти не влияет на конечный результат, и увеличение
энтропии после открытия вентиля по-прежнему будет близко к 2,3 • 1022/с.* Это служит
яркой иллюстрацией того факта, что, хотя разбиение на ящики (в частности, выделение
области 71) носило субъективный характер, это не приводит к серьезным проблемам, пока
такое разбиение проводится «разумным образом».
Логарифм в формуле Больцмана имеет важное предназначение, помимо того, что он
позволяет оперировать с огромными числами. Оно состоит в том, что при таком опреде¬
лении энтропии она оказывается аддитивной для взаимно независимых систем. Так, если
двум независимым системам приписываются энтропии Si и S2, то энтропия полной си¬
стемы, состоящей из этих двух систем, будет равна Si + S2. Я предполагаю, что фазовым
пространством полной системы будет V — V\ х Vo, где Vi и V2 — фазовые простран¬
ства двух отдельных систем, и что число ящиков, получающихся при огрублении полной
системы, равно произведению ящиков, огрубляющих V\ и V2', для независимых систем
с энтропиями Si и S2 это вполне естественное предположение**. (См. § 15.2, упражнение
15.1 и рис. 15.3а относительно определения операции х применительно к пространствам.)
Поскольку объемы ящиков перемножаются, соответствующие энтропии будут складываться
(в соответствии со стандартным свойством логарифма, см. § 5.2).
В обычных примерах физических систем (и в хорошо известном случае обычного газа
в обычном сосуде) имеется некоторый ящик £, объем которого Е намного превышает объем
любого из остальных ящиков. Так обстоит дело в состоянии теплового равновесия. Дей¬
ствительно, объем Е обычно практически равен объему Р полного фазового пространства,
и поэтому объем Е значительно превышает объем всех остальных ящиков вместе взятых
(см. рис. 27.4). Для обычного газа, который мы представляем себе состоящим из одинаковых
сферически симметричных шариков, находящихся в тепловом равновесии, распределение
скоростей берется в виде распределения Максвелла (найденного тем самым Джеймсом Клер¬
ком Максвеллом, с которым мы уже встречались в связи с электромагнетизмом). Оно имеет
плотность вероятности вида
(в котором можно узнать гауссово распределение, иногда называемое «колоколообразной
кривой»). Здесь v есть величина 3-скорости рассматриваемой частицы газа, (3 — постоянная,
связанная с температурой, А — постоянная, определяемая таким образом, чтобы интеграл
от вероятности по пространству всех возможных скоростей был равен 1; см. рис. 27.5.
Тепловое равновесие, при котором система имеет наибольшую энтропию, — это состояние,
  ^ Попробуйте объяснить, почему увеличение энтропии меняется очень мало, приблизительно
от 2,30 • 1022/с до 2, 29 • 1022 fc, используя грубые оценки входящих сюда математических величин. (Вы можете
воспользоваться формулой Стирлинга га! (п/е)п(27гп)1/2.)
Почему естественно такое допущение относительно огрубления?

584
Глава 27
S
Тепловое равновесие
Рис. 27.4. Ящик S, представляющий тепловое равновесие, имеет объем Е, который обычно прак¬
тически равен объему Р всего фазового пространства V и потому намного превышает объем всех
%
остальных ящиков вместе взятых
в котором, согласно Второму закону, должна оказаться система, если предоставить ее самой
себе в течение достаточно длительного времени.
Рис. 27.5. Распределение Максвелла для скоростей в газе, находящемся в равновесии, имеет
— В 2
вид Ае , где v — скорость частицы газа, А и /3 — постоянные, причем постоянная /3 связана
с температурой. Пунктиром показано продолжение кривой в область отрицательных значений v, вос¬
производящее известную «колоколообразную» форму гауссова распределения в статистике
Описанное распределение Максвелла относится к газу, состоящему из одинаковых клас¬
сических тел, не имеющих внутренних степеней свободы. Ситуация становится гораздо
более сложной, если газ состоит из частиц многих сортов, имеющих разный размер и раз¬
личные внутренние степени свободы (это могут быть, например, спин или относительные
колебания составных частей). Для таких систем, находящихся в тепловом равновесии, имеет
место принцип равнораспределения энергии, согласно которому энергия системы распределя¬
ется поровну (со статистическим разбросом) между всеми различными степенями свободы
системы.
Другое направление, в котором возможно обобщение распределения Максвелла, — это
уход от точного теплового равновесия и постановка вопроса о том, как будет вести себя
газ в процессе приближения к равновесию (в соответствии со Вторым законом). В таких
условиях эволюция описывается уравнением Больцмана. Читатель, несомненно, чувствует,
что здесь открывается широкий простор для теоретического объяснения поведения класси¬
ческих макроскопических тел, которые состоят из слишком большого числа частиц, чтобы
их можно было рассматривать по отдельности. Это составляет предмет статистической
механики.

27.5. Вывод Второго закона. .. или нет?
585
27.5.	Вывод Второго закона... или нет?
Попробуем понять, что скрывается за Вторым законом. Пусть мы имеем некоторую фи¬
зическую систему, представленную точкой х в некотором подходящем огрубленном фазовом
пространстве V. Предположим, что точка х СЕЙЧАС (см. рис. 27.6 а) находится в некотором
ящике V малого объема V. Точка х будет двигаться в пространстве V некоторым образом
в соответствии с динамическими уравнениями, подходящими для данной физической ситу¬
ации. Имея в виду громадную разницу в размерах различных ящиков и предвидя отсутствие
каких-либо предпочтений в отношении по-разному расположенных ящиков, можно ожидать,
что в процессе динамического движения точка х в подавляющем большинстве случаев будет
проводить время в блуждании по ящикам всё большего объема. Другими словами, с течени¬
ем времени энтропия системы будет становиться всё больше. Коль скоро точка х попадает
в своем движении в ящик с некоторой определенной мерой энтропии, становится весьма
маловероятным, что через некоторый разумный период времени она снова может оказаться в
ящике со значительно меньшей энтропией. Достичь гораздо меньшей энтропии означало бы
оказаться в ящике очень малого объема, а шансы этого ничтожно малы. Из рассмотренного
выше примера и того гигантского уменьшения объема фазового пространства, которое со¬
провождает весьма скромное уменьшение энтропии из-за присутствия логарифма в формуле
Больцмана и малой величины постоянной Больцмана, следует, что, если газ вышел из обла¬
сти Л, вероятность его возвращения обратно в 1Z оказывается ничтожно малой (по крайней
мере, если не рассматривается невообразимо огромный временной масштаб) .
Рис. 27.6. Второй закон в действии. Эволюция физической системы представляется некоторой кривой
в фазовом пространстве, а) Если мы знаем, что в момент времени СЕЙЧАС нашу систему представляет
точка х в ящике V очень малого объема V, и пытаемся понять, каково ее возможное поведение в буду¬
щем, мы приходим к выводу, что из-за огромной разницы в объемах ящиков и отсутствия каких-либо
предпочтений в ее движении она будет почти определенно попадать в ящики всё большего размера
в соответствии со Вторым законом. 6) Предположим, однако, что это рассуждение обращено в про¬
шлое, и зададимся вопросом, каков тот наиболее вероятный путь, пройдя который точка х в первый раз
попала в область V. Рассуждение, подобное предыдущему, приводит к явно абсурдному выводу, что
точка х попала в V из ящиков, которые становятся всё больше по мере удаления в прошлое, в явном
противоречии со Вторым законом
Это рассуждение дает серьезные основания ожидать, что Второй закон будет неуклонно
выполняться. Отметим, что оно совершенно не зависит от конкретной динамики за исклю¬
чением требования, чтобы никакие внешние воздействия не заставляли точку х отыскивать
* Щ Попробуйте оценить, насколько должен быть велик этот масштаб в случаях, когда весь газ возвращается
в7ги когда возвращается 99,9% газа. Требуется ли для этого знать, как быстро движутся молекулы газа?

586
Глава 27
ящики меньшего объема. Действительно ли это всё, что требуется для выполнения Второго
закона? Это условие представляется легко выполнимым, и возможно, именно в универсаль¬
ном характере рассуждений такого рода скрыта причина того, что многие физики не видят
во Втором законе никакой фундаментальной загадки и считают, что ему должна удовле¬
творять любая разумная физическая теория. Здесь уместна любопытная цитата из книги
выдающегося астрофизика сэра Артура Эддингтона^27
Если кто-то скажет вам, что выстраданная вами теория устройства Вселенной
противоречит уравнениям Максвелла, — то можно ответить, что тем хуже для
уравнений Максвелла. Если окажется, что она не согласуется с результатами на¬
блюдений, — ну что ж, и экспериментаторы могут ошибаться. Но если ваша теория
окажется в противоречии со Вторым законом термодинамики, то я не могу оставить
вам никакой надежды, и вашей теории придется признать свое полное поражение.
Однако после краткого размышления вы можете прийти к заключению, что есть нечто
странное в том выводе, к которому привели мои рассуждения, или, возможно, в них упу¬
щено что-то важное. Мы вывели закон, асимметричный относительно обращения времени,
тогда как физика, лежащая в основе вывода, симметрична во времени. Как это может быть?
Мы могли бы попробовать применить то же самое рассуждение к направлению времени
в прошлое (рис. 27.66). Нам придется прийти к выводу, что если мы поместим нашу точ¬
ку фазового пространства х в тот же ящик малого размера, который мы выбрали вначале,
в момент СЕЙЧАС, и будем следить за эволюцией в прошлое, до этого момента, то с подав¬
ляющей вероятностью точка х придет в этот ящик из ящиков, которые будут становиться всё
больше и больше по мере нашего погружения в прошлое! Но это означает, что в прошлом
имел место закон, обратный Второму закону, с возрастанием энтропии, направленным в про¬
шлое, несмотря на наше ожидание, основанное на предыдущем рассуждении, что должен
иметь место обычный вариант Второго закона, направленный в будущее. Такой вывод резко
противоречит результатам наблюдений относительно способа поведения нашей Вселенной
в прошлом (см. рис. 27.7).
Где здесь ошибка? Чтобы попытаться понять это, применим эти рассуждения к пове¬
дению нашего газа в контейнере, предполагая, что в начальный момент времени to весь
газ находится в 7Z, так что точка х лежит в области Vn- Мы можем правильно предсказать
будущее поведение газа после открытия вентиля, когда газ вытекает из области 7Z в осталь¬
ную часть контейнера, при этом энтропия значительно возрастает, поскольку точка х быстро
попадает в область £, представляющую тепловое равновесие. А как обстоит дело с поведе¬
нием в прошлом? Мы должны задаться вопросом: что происходило до момента времени to?
Каким путем газ скорее всего соберется в область 7Z1 Если предположить, что вентиль
открыт непосредственно перед моментом to, то «наиболее вероятная эволюция» будет со¬
стоять в том, что газ несколько раньше момента to был распределен по всему контейнеру
и находился в тепловом равновесии, затем он самопроизвольно всё более концентрировался
в области 7Z и к моменту to весь оказался в 1Z.
/
Этот результат, выглядящий вполне абсурдным, представляет правильный ответ для
проблемы, поставленной подобным образом, в предположении отсутствия какого-либо вме¬
шательства извне. В действительности мы никогда не обнаружим весь газ в области 7Z.
Приведенное рассуждение отвечает на вопрос, как бы вел себя случайно движущийся газ,
если бы он весь самопроизвольно оказался в области 7Z, чего быть не может. Здесь нет ника¬
кого парадокса. Но это рассуждение обходит вопрос, который я хотел задать читателю: как
практически реализовать ситуацию, при которой весь газ окажется в области 7Z7 Здесь нет
конфликта с условиями в нашей реальной Вселенной (можно ослабить требования к обла¬
сти Утг, позволив, чтобы одна тысячная газа находилась вне 7Z). Можно представить себе,
что некий экспериментатор вначале накачал в контейнер десятикратное против требуемого

27.6. Является ли Вселенная в целом «изолированной системой»?
587
Рис. 27.7. Вывод из рис. 27.6, представленный в виде зависимости энтропии S от времени t. Наше
рассуждение приводит нас к правильному выводу относительно поведения, описываемого Вторым
законом, в будущем относительно момента времени СЕЙЧАС, но оно дает явно абсурдный результат —
закон, обратный Второму закону, для поведения в прошлом, который находится в резком противоречии
с реальным опытом
количество газа, затем закрыл вентиль и с помощью вакуумного насоса откачал из основной
части контейнера практически все 90% находящегося там газа. В течение всего процесса эн¬
тропия все время должна возрастать в соответствии со Вторым законом. Разумеется, чтобы
обсуждать это на языке фазового пространства, необходимо фазовое пространство большего
объема, включающее и экспериментатора, а возможно, и какую-то часть Вселенной, про¬
стирающуюся до Солнца, а то и дальше. Энтропия тела экспериментатора сохраняется на
весьма низком уровне, благодаря процессам поглощения пищи и дыхания. Для простоты
предположим, что насос имеет ручной привод, — в противном случае нам пришлось бы
обсуждать причину низкой энтропии источника топлива (что привело бы к рассмотрению
вопросов, не существенных для наших целей). Экспериментатор вместе с газом частично
передает контейнеру свой низкий уровень энтропии, благодаря чему удается загнать газ в 1Z.
Низкая энтропия пищи экспериментатора и воздуха в конечном счете связана с Солнцем.
К особой роли Солнца я вскоре вернусь.
Таким образом, мы смогли получить требуемую ситуацию, при которой весь газ, содер¬
жащийся в контейнере, в конечном счете оказывается в области 1Z без нарушения Второго
закона в его физически приемлемой форме: «энтропия со временем увеличивается». Куда
делось наше явное затруднение с обращением во времени Второго закона при обсуждении
поведения газа в прошлом? Разрешилась ли эта проблема? Нет, отнюдь нет! Тело экспе¬
риментатора должно функционировать (и действительно функционирует) в соответствии
со Вторым законом, коль скоро наше расширенное фазовое пространство описывает так¬
же Солнце и всё вокруг. Но если мы попробуем применить наши рассуждения на языке
фазового пространства (теперь уже нашего расширенного фазового пространства), то по-
прежнему получим физически абсурдный результат: энтропия должна расти в направлении,
обращенном в прошлое, предшествующее любому выбранному моменту времени, если мы
рассматриваем всю систему в целом.
% •
27.6.	Является ли Вселенная в целом «изолированной системой»?
Некоторые теоретики пытаются провести границу между «изолированными» и «откры¬
тыми» системами, утверждая, что в то время как в изолированной системе энтропия воз¬
растает (пока не будет достигнуто равновесие), всегда существует возможность воздействия

588
Глава 27
внешнего мира, которое время от времени может приводить к понижению энтропии (это
может быть вмешательство экспериментатора, приток низкой энтропии от Солнца и т. п.).
Мне представляется, что любая попытка объяснить таким образом временную асимметрию
Второго закона может иметь лишь условный характер, поскольку эти воздействия извне
во всей их совокупности всегда можно включить в рассматриваемую систему. Это означает,
что в качестве такой «системы» придется рассмотреть всю Вселенную в целом. Некоторые
могут возразить на это, но я не вижу никаких оснований для таких возражений. Даже ес¬
ли Вселенная имеет бесконечную протяженность, это не запрещает рассматривать ее как
целое (см. главу 16). Во всяком случае Вселенная может быть конечной в пространстве
(это одна из возможностей, к обсуждению которой мы вскоре перейдем), и было бы стран¬
но доверять рассуждениям относительно Второго закона, справедливость которых зависит
от конечной протяженности Вселенной в пространстве. Как мы увидим дальше, пробле¬
ма конечности/бесконечности Вселенной лишь в очень малой степени связана с вопросом
о происхождении Второго закона. Обсуждение энтропии можно распространить на всю
Вселенную Ы, при этом фазовое пространство Ти (объем которого может быть бесконеч¬
ным) описывает широкую совокупность возможных Вселенных, включающую все варианты
эволюции согласно динамическим уравнениям (соответствующей) классической динамики.
Здесь, однако, мы сталкиваемся с неприятным обстоятельством. Чтобы рассматривать
Вселенную в целом, нам придется войти в царство космологии, что нельзя как следует
сделать, не привлекая общую теорию относительности. Чтобы вести обсуждение в полном
согласии с принципом общей ковариантности общей теории относительности (§ 19.6), необ¬
ходимо пользоваться описанием, при котором нельзя выбрать некоторую особую временную
координату, относительно которой предполагается «эволюция» Вселенной. Картина эволю¬
ции во времени — это способ рассмотрения физической системы, когда мы представляем
ее некоторой точкой ж, движущейся в фазовом пространстве Т. Каждое положение точки ж
дает пространственное описание системы (включая импульсы) в некоторый момент време¬
ни. Но если встать на строго релятивистскую точку зрения, то это приведет к ненужному
усложнению описания, и я не думаю, что это целесообразно делать. На самом деле, как
мы вскоре увидим, стандартные космологические модели включают в себя некоторую вре¬
менную координату, определенную естественным образом, и это с хорошим приближением
дает нам некоторый «временной параметр» • t, по отношению к которому можно описы¬
вать эволюцию всей Вселенной. Каждая точка пространства Ти будет описывать не только
материальное содержимое Вселенной в момент времени t9 но также распределение (и им¬
пульс) непрерывных полей. Одним из таких полей является гравитационное поле, поэтому
пространственная геометрия Вселенной (вместе со скоростью ее изменения, определяе¬
мой соответствующими начальными условиями для гравитационного поля^27'8^) также будет
закодирована положением точки х в пространстве Ти-
Фактически пространство Ти будет бесконечномерным, но это не зависит от того, ко¬
нечна или бесконечна протяженность Вселенной, а характерно и для всех других полей,
например, электромагнитного. Это создает некоторые технические трудности при определе¬
нии энтропии, поскольку каждая область фазового пространства У будет иметь бесконечный
объем. Эту проблему обычно решают, заимствуя у квантовой теории (поля) идею, которая
позволяет получить конечный результат для объемов фазового пространства, относящихся
к системам, у которых должным образом ограничены энергия и пространственные размеры.
Подробные детали этого приема для нас не существенны. Хотя это и не вполне удовле¬
творительный способ решения вопроса в случае гравитационного поля (из-за отсутствия
удовлетворительной теории квантовой гравитации), я склонен считать такие детали не вли¬
яющими на общее обсуждение вопросов, поставленных Вторым законом.
Здесь я должен упомянуть об одном недоразумении, которое часто порождает нераз¬
бериху в отношении Второго закона при космологической постановке вопроса. Существует

27.7. Роль Большого ВЗРЫВА
589
распространенный взгляд, что увеличение энтропии, утверждаемое Вторым законом, есть
в какой-то мере необходимое следствие расширения Вселенной (мы рассмотрим это расши¬
рение в §27.11). Такое мнение, по-видимому, основано на заблуждении, согласно которому
у Вселенной, когда она была «маленькой», было сравнительно мало степеней свободы, что
определяло низкий «потолок» для возможных значений энтропии, а по мере того как Все¬
ленная росла, у нее появлялось всё больше степеней свободы, «потолок» приподнимался,
позволяя ей иметь более высокую энтропию. По мере расширения Вселенной этот допусти¬
мый максимум увеличивается, так что реальная энтропия Вселенной также может расти.
В том, что такая точка зрения не может быть правильной, можно убедиться многими
способами. Например, в моделях Вселенной с фазой коллапса энтропия с необходимостью
должна начать убывать в нарушение Второго закона. По этому поводу можно было бы и не
беспокоитьсяf27*9^, но такая точка зрения встречает фундаментальные трудности, особенно
в связи с существованием черных дыр^2710^.
Черные дыры мы вскоре рассмотрим (в §27.8), однако в действительности нам и не
нужно знать о них, чтобы понять, почему неприемлема изложенная точка зрения, требующая
наличия «потолка» возможных значений энтропии, зависящего от размера Вселенной. Она
не может быть правильным объяснением возрастания энтропии, поскольку степени свобо¬
ды, доступные для Вселенной, описываются полным фазовым пространством Vu- Динамика
общей теории относительности (которая включает и степень свободы, определяющую раз¬
мер Вселенной) описывается движением нашей точки х в той же мере, что и все остальные
физические процессы. Это фазовое пространство уже имеет «готовый вид», оно ни в каком
смысле не «растет со временем», время не является частью пространства Vu- Нет ника¬
кого «потолка», поскольку все состояния, динамически доступные для рассматриваемой
Вселенной (или семейства Вселенных), должны быть представлены в Vu• Можно гово¬
рить о чем-то подобном, пока точка х не достигла большого ящика, двигаясь из заданного
меньшего ящика, но понятие «потолка энтропии» неприемлемо (см. также §27.13).
Вернемся к рассуждению, приведенному выше для демонстрации Второго закона. Будем
использовать фазовое пространство Vu, относящееся ко всей Вселенной, так что эволюция
Вселенной в целом будет описываться точкой ж, движущейся вдоль некоторой кривой £
в пространстве Vu- Кривая £ параметризуется временной координатой t, так что в соответ¬
ствии со Вторым законом можно ожидать, что кривая £ по мере увеличения параметра t
будет входить в ящики всё большего размера. Предположим, что разбиение Vu на ящики
было «разумным», однако если мы хотим получить конечные значения энтропии состояний,
в которые попадает точка ж, ящики должны иметь конечный объем. Может показаться, что
для этого, при физически разумном разбиении, Вселенной необходимо приписать конеч¬
ный размер с ограничением на ее возможную энергию. Как мы вскоре увидим, одна из
трех стандартных космологических моделей действительно предполагает это, поэтому мож¬
но считать, что наше рассуждение относится именно к такой ситуации. Однако указанное
требование не возникает, если не предполагать, что энтропия в какой-то момент времени
принимает бесконечное численное значение. (Мы все же можем придать математический
смысл представлению, что некоторые ящики «существенно больше», чем остальные, даже
если реальные объемы некоторых из них, а следовательно, и их энтропии бесконечны.)
27.7.	Роль Большого взрыва
Как мы должны относиться к тому, что наша параметризованная кривая £, представля¬
ющая возможную историю Вселенной, должна быть помещена в фазовое пространство Vu ?
Если бы кривая £ была просто вброшена в Vu случайным образом, то можно было бы
ожидать, что с подавляющей вероятностью она полностью (или почти полностью) окажется
в наибольшем ящике £, соответствующем тепловому равновесию, и на ее длине не будет

590
Глава 27
заметного «увеличения энтропии» (см. рис. 27.8 а). Такая ситуация находится в полном
противоречии с тем, что в известной нам Вселенной Второй закон не выполняется. То же
относится к ситуации, показанной на рис. 27.8 б, в, где в некоторый момент времени £о(> 0)
(«СЕЙЧАС») точка х на кривой £ заключена в некоторой области V разумного, но не слиш¬
ком большого объема (эта область представляет Вселенную с тем значением энтропии,
которое мы наблюдаем в настоящий момент), но в остальном кривая £ выбирается случай¬
ным образом. Это соответствует Вселенной, энтропия которой растет, начиная с настоящего
момента, при движении в будущее, но она также растет, если двигаться от этого момента
в прошлое, что есть нарушение Второго закона! На рис. 27.8 б, г схематически показано то,
что мы имеем в действительности, — Вселенную, подчиняющуюся Второму закону, при этом
один конец кривой £ (соответствующий некоторому прошлому моменту t = 0) находится
в чрезвычайно малой области В в Vu (что соответствует очень малой энтропии); с ростом
параметра t кривая, следуя динамическим законам, извивается, попадая в ящики всё боль-
шего объема. При t — to («СЕЙЧАС») точка х оказывается в пока еще довольно малом
объеме V, соответствующем наблюдаемой нами Вселенной. Это как раз то, что утверждает
Второй закон, и мы получаем варианты (г), (б) вместо (в), (б).
Рис. 27.8. Различные возможные варианты эволюции Вселенной, описываемые параметризованной
кривой £ в фазовом пространстве Vu возможных состояний Вселенной (например, при фиксирован¬
ном значении полной массы или другой сохраняющейся величины), а) Если кривая £ вброшена в Vu
случайным образом, то она проводит почти всю свою жизнь в области 6 и, с точностью до малых
флуктуаций, состоянием Вселенной будет «тепловое равновесие» (если Вселенная замкнута, это напо¬
минает рис. 27.20 г. 6) Если предположить, что СЕЙЧАС точка х на кривой находится в очень малом
ящике V (затененная область), соответствующем Вселенной, в которой мы сейчас живем, а в осталь¬
ном £ извивается случайным образом, то будущая эволюция -согласуется с тем, что мы продолжаем
наблюдать, — с увеличением энтропии согласно Второму закону, в) Если применить то же рассуждение
к ситуации, при которой вся кривая £ должна пройти через область V в некоторый момент време-
ни In > 0 («СЕЙЧАС»), то мы получим для нашей Вселенной разумное будущее, однако, как и на
рис. 27.6 6, для прошлого поведения мы получаем резкое нарушение Второго закона, г) Это можно
исправить, если предположить, что начальный конец кривой £ (t — 0) лежит в крайне малой обла¬
сти В, из которой Вселенная стартует в момент Большого взрыва, который действительно произошел
в нашей реальной Вселенной
Попробуем несколько перефразировать сказанное. Предположим, что мы рассматриваем
ситуацию с удобной точки в некоторый момент времени £о(> 0) («СЕЙЧАС») и обнаружи¬
ваем в этот момент точку х в некоторой области V разумного размера. Затем мы следим, куда

27.7. Роль Большого взрыва
591
забредет кривая £ в более поздние моменты t, и видим, что с ростом t она попадает в ящики
всё большего размера. Это согласуется со Вторым законом и с принятым выше допущением,
что точка х не испытывает «воздействия извне» в отношении выбора ящиков. Однако при
взгляде назад во времени, начиная с момента t, когда точка х находится в области V, воз¬
никает впечатление, что точка х, двигаясь назад во времени, целенаправленно направляется
к абсурдно малой области фазового пространства, которую мы обозначили как В.
Поведение точки х при взгляде назад во времени, когда она отыскивает ящики всё
меньшего объема, выглядит «навязанным извне». Следует ли понимать это как «целена¬
правленный» поиск всё меньших ящиков под влиянием каких-то потусторонних сил? Нет,
просто область В оказалась окруженной такими ящиками (см. рис. 27.8), поэтому если кри¬
вая £ при t — 0 должна достичь области В, то ей приходится встречать на своем пути
ящики всё меньшего размера. Загадка состоит лишь в том, что один конец кривой £ должен
находиться в области В\ Вот что мы должны понять, если мы хотим найти источник Второго
закона. Область В представляет Большой взрыв в начале Вселенной, и вскоре мы увидим,
сколь непостижимо мала эта область!
Мы должны постараться понять, что всё это значит. В чем состоит особый характер
области В1 Можно ли придать этой «особости» количественную меру? И какие результаты
наблюдений заставляют, в конце концов, верить в Большой взрыв?
Основания для уверенности во взрывном начале Вселенной первоначально появились
при теоретическом изучении уравнения Эйнштейна в космологическом аспекте Алексан¬
дром Фридманом в 1922 году (см. ниже, § 27.11). Позже, в 1929 году, Эдвин Хаббл сделал
замечательное открытие, состоящее в том., что удаленные галактики действительно удаляют¬
ся от нас^27*11^ таким образом, как если бы материя во Вселенной была результатом какого-то
гигантского взрыва. По современным оценкам, этот взрыв (сейчас его называют Большим
взрывом) имел место примерно 1,4* 1010 лет назад. Выводы Хаббла были основаны на том
факте, что свет от быстро удаляющихся объектов претерпевает красное смещение (так что
спектральные линии смещаются к «красному краю спектра», т. е в сторону больших длин
аАв
волн) в соответствии с эффектом Доплера . Хаббл обнаружил, что это красное смещение
систематически растет в тем большей степени, чем дальше от нас находится галактика.
Это означает, что скорость разбегания галактик пропорциональна их расстоянию от нас
в соответствии со «взрывной» картиной.
Однако наиболее впечатляющей наблюдательной поддержкой для картины Большого
взрыва оказалось универсальное присутствие излучения, пронизывающего пространство,
с температурой 2,7К (т.е. 2,7°С выше абсолютного нуля)^2712^. Хотя для такого бурно¬
го события, как взрыв, температура кажется чересчур низкой, это излучение рассматрива¬
ется как «отзвук» того самого Большого взрыва, но после «покраснения» и охлаждения,
связанного с расширением Вселенной. Излучение с температурой 2,7 К играет исклю¬
чительно важную роль в современной космологии. Его часто называют «(космическим)
микроволновым фоном», или иногда «фоновым черным излучением», или «космическим
реликтовым излучением». Оно исключительно однородно (с точностью порядка 10~5),
это означает, что сразу после Большого взрыва сама ранняя Вселенная была крайне од¬
нородной и хорошо описывалась космологическими моделями, которые будут рассмотре¬
ны в § 27.11.
Теперь попытаемся дать физическое объяснение природы необычайно низкой энтро¬
пии, присущей Большому взрыву, что обеспечивает столь малый объем области B.t27*13!
Мы обнаружим, что особый характер Большому взрыву придает именно только что отме¬
ченная высокая однородность. Мы должны постараться понять, почему это соответствует
Выведите формулу специальной теории относительности для доплеровского сдвига частоты при удалении
источника со скоростью v: (а) используя волновое представление для света; (б) используя скалярные произведения
4-векторов и соотношение Е — hv.

592
ГЛАВА 27
очень низкой энтропии и как это приводит ко Второму закону в той форме, к которой мы
привыкли на нашей Земле.
Прежде всего вернемся к роли Солнца как источника низкой энтропии. Существует
распространенное заблуждение, что наше выживание обеспечивается энергией, получаемой
от Солнца. Это ошибочное мнение. Для того чтобы энергия вообще имела для нас какую-то
ценность, она должна быть получена в низкоэнтропийной форме. Например, если бы все
небо однородно светилось с некоторой однородной температурой (с температурой Солн¬
ца или любой другой), то у нас не было бы возможности воспользоваться этой энергией
(независимо от усилий, которые мы приложили бы, пытаясь справиться с этим). Энергия
в состоянии теплового равновесия бесполезна. Нам повезло, однако, в том, что Солнце пред¬
ставляет собой горячее пятно на остальном холодном фоне. В течение дня энергия поступает
на Землю от Солнца, но в течение дня и ночи вся она отдается в окружающее пространство.
Полный баланс энергии (в среднем) состоит просто в том, что мы отправляем обратно всю
полученную нами энергию[27Л4^.
Однако от Солнца мы получаем энергию в виде отдельных фотонов высокой энергии
(из-за высокой температуры Солнца это высокочастотные желтые фотоны), тогда как в окру¬
жающее пространство энергия возвращается в основном в виде фотонов низкой энергии (низ¬
кочастотного инфракрасного излучения). (Энергия фотонов определяется формулой План¬
ка Е = hv и найденным им же законом излучения черного тела, см. §21.4.) Число фото¬
нов, получаемых от Солнца, из-за их более высокой энергии (более высокой температуры)
гораздо меньше числа фотонов, уходящих в окружающее пространство, поэтому полная
энергия, переносимая фотонами, одна и та же для приходящего и уходящего излучения.
Меньшее число фотонов, приходящих от Солнца, означает меньшее число степеней свобо¬
ды и следовательно меньшую область фазового пространства и, соответственно, меньшую
энтропию по сравнению с фотонами, возвращаемыми в космическое пространство. Расте¬
ния могут использовать эту низкоэнтропийную энергию в процессе фотосинтеза, понижая
тем самым свою энтропию. Затем мы используем растения для понижения собственной
энтропии, поедая их (или тех, кто поедает их), а также вдыхая выделяемый ими кислород
(см. рис. 27.9).
Но почему Солнце выглядит горячим пятном на холодном небе? Хотя подробное объ¬
яснение довольно сложно, в конечном счете это связано с тем обстоятельством, что Солнце
(и все другие звезды) возникло в результате гравитационной конденсации из первоначаль¬
но однородного газа (в основном водорода). Независимо от прочих сил (в первую очередь
ядерных) Солнце, не будь гравитации, вообще не могло бы существовать! Низкая энтро¬
пия Солнца (значительная удаленность от состояния теплового равновесия) происходит от
гигантского резервуара низкой энтропии, потенциально заключающегося в однородности
газа, из которого сконденсировалось Солнце под действием гравитации.
Связь гравитации с энтропией выглядит несколько непривычно, поскольку гравита¬
ционное взаимодействие всегда проявляется как притяжение. Мы привыкли иметь дело
с энтропией обычного газа, который, будучи сконцентрирован в малой области, обладает
низкой энтропией (как в случае нашего контейнера на рис. 27.3), а в состоянии теплового
равновесия с высокой энтропией имеет однородное распределение, С гравитацией всё об¬
стоит наоборот. Однородная система гравитирующих тел будет обладать низкой энтропией
(если только скорости этих тел не слишком велики, или/и тела не слишком малы, или/и они
не находятся так далеко друг от друга, что вклад гравитации в энергию становится несуще¬
ственным), тогда как высокая энтропия достигается, когда гравитирующие тела сливаются
воедино (рис. 27.10).
Как обстоит дело с состоянием максимальной энтропии? В случае газа максимальная эн¬
тропия теплового равновесия соответствует равномерному распределению газа в доступной
ему области. В случае больших гравитирующих тел максимальная энтропия достигается,

27.7. Роль Большого ВЗРЫВА
593
Рис. 27.9. Земля возвращает в окружающее пространство такое же количество энергии, какое она
получает от Солнца, но от Солнца она ее получает в форме, характеризуемой гораздо более низкой
энтропией, из-за того, что желтый свет Солнца имеет более высокую частоту, нежели инфракрасное
излучение, возвращаемое Землей. В соответствии с формулой Планка Е = /гг/ солнечные фотоны
несут более высокую энергию (в расчете на один фотон), по сравнению с фотонами, идущими от Зем¬
ли, так что энергия от Солнца переносится меньшим числом фотонов, чем энергия от Земли. Меньшее
число фотонов означает меньшее число степеней свободы и, следовательно, меньший объем соответ¬
ствующей области фазового пространства, а значит, меньшую энтропию по сравнению с фотонами,
уходящими от Земли в окружающее пространство. Растения могут использовать эту низкоэнтропийную
энергию в процессе фотосинтеза, тем самым понижая свою энтропию, а мы понижаем свою энтро¬
пию, поедая растения (или тех, кто поедает растения) и вдыхая выделяемый ими кислород. Всё это
происходит в конечном счете из-за температурного дисбаланса в окружающем нас небе, возникшего
в результате гравитационного сжатия, породившего Солнце
К
В
9
>> а
о- е;
s <Р
н н
к
£•
• *
* •
Возрастание энтропии
Время
а)
* .И
б)
Рис. 27.10. Увеличение энтропии с течением времени (слева направо), (а) Для газа, первоначально со¬
бранного в одном углу ящика, энтропия растет по мере того как газ расширяется, заполняя весь ящик
и достигая в конечном счете однородного состояния теплового равновесия, (б) В случае гравитации
имеет место обратная ситуация. Система гравитирующих тел с изначально однородным распределе¬
нием обладает относительно низкой энтропией, и увеличение энтропии сопровождается сближением
тел. В конце концов возникает черная дыра, проглатывающая большую часть вещества, и энтропия
резко возрастает

.594
Глава 27
когда вся масса оказывается сконцентрированной в одном месте в виде объекта, называемого
черной дырой. Чтобы двигаться дальше, нам необходимо познакомиться с этими странны¬
ми и удивительными объектами, получив при этом замечательно точную оценку энтропии,
потенциально доступной для всей Вселенной в целом. Это позволит нам оценить затем
объемы В и Vu-
27.8.	Черные дыры
Что такое черная дыра? Грубо говоря, это область пространства-времени, которая воз¬
никает в результате гравитационного сжатия (коллапса) вещества, когда гравитационное
притяжение становится настолько сильным, что наружу не может выходить даже свет. Что¬
бы понять на интуитивном уровне, почему может возникнуть подобная ситуация, обратим¬
ся к ньютоновскому понятию скорости убегания (ее называют также второй космической
скоростью). Если швырнуть камень вертикально вверх с некоторой скоростью v, то он,
достигнув некоторой высоты, упадет обратно на землю; при этом высота подъема будет
такой, что кинетическая энергия камня будет полностью израсходована на преодоление гра¬
витационной потенциальной энергии, отсчитываемой от уровня Земли (§§ 17.3, 18.6). Если
пренебречь влиянием сопротивления воздуха, то высота подъема камня над Землей будет
полностью определяться скоростью метания*. Если, однако, эта скорость превышает величи¬
ну (2GM/R)1/2, называемую скоростью убегания, то камень навсегда покинет гравитаци¬
онное поле Земли (здесь М и R — соответственно масса и радиус Земли, G — ньютоновская
гравитационная постоянная). Предположим теперь, что вместо Земли мы имеем гораздо
более массивное и плотное тело. Тогда скорость убегания станет больше (поскольку отно¬
шение М/R растет при увеличении М и уменьшении Д), и мы можем представить, что
масса и плотность станут столь огромными, что скорость убегания превысит даже скорость
света.
Если такое случится, то, согласно ньютоновской теории, при взгляде с большого рас¬
стояния тело покажется совершенно темным, поскольку никакой луч света не сможет его
покинуть. Именно к такому выводу пришел в 1784 году видный английский астроном и свя¬
щенник Джон Мичелл. Позже, в 1799 году, к такому же заключению пришел великий фран¬
цузский математик и физик Пьер Симон Лаплас [27Л51. Однако ситуация представляется мне
не столь очевидной, поскольку в теории Ньютона скорость света не имеет абсолютного ста¬
туса, и вполне можно предположить, что на поверхности такого тела скорость света могла бы
быть значительно больше, чем в пустом пространстве, и потому свет все же мог бы уходить
в бесконечность, как бы ни были велики масса и плотность тела**^27'16^. Так что «темная
звезда» Мичелла, хотя и предвосхищала понятие черной дыры, все же, на мой взгляд, не
может считаться убедительным доказательством возможности существования «невидимых»
гравитирующих объектов в ньютоновской теории.
Такой вывод становится гораздо более убедительным в контексте теории относитель¬
ности, поскольку там скорость света имеет фундаментальный характер и действительно
представляет предельную скорость передачи любого сигнала (§ 17.8). Однако поскольку мы
рассматриваем гравитационный эффект, требуется не просто пространство Минковского,
а пространство-время общей теории относительности. Согласно общей теории относитель¬
ности, действительно можно ожидать возникновения ситуации, в которой скорость убегания
Покажите, что эта высота равна v2 R(2gR—v2)~lf где R есть радиус Земли, а д — ускорение, создаваемое
силой тяжести на поверхности Земли.
Понятно ли, почему это так? (Подсказка: рассматривая свет как поток частиц, представьте, что свет падает
извне на поверхность тела. Что будет, если свет падает на горизонтальное зеркало, находящееся на поверхности
тела?)

27.8. Черные дыры
595
превышает скорость света, в результате чего возникает то, что мы нынче называем черной
дырой.
Возникновения черной дыры можно ожидать, когда большое массивное тело достигает
стадии, на которой сил внутреннего давления оказывается недостаточно, чтобы противо¬
стоять сжатию тела внутрь под влиянием его собственного гравитационного поля. Действи¬
тельно, такой гравитационный коллапс должен возникнуть в ситуации, когда большая звезда
с полной массой, в несколько раз превышающей массу Солнца, например 10М© (1М© есть
масса Солнца), исчерпала все доступные ей внутренние источники энергии, — тогда она
охлаждается и не может поддерживать достаточное давление, чтобы предотвратить кол¬
лапс. Когда такое случается, коллапс становится неудержимым из-за неумолимого действия
гравитационных эффектов.
Подробная картина коллапса может оказаться
весьма сложной, особенно в условиях высокого дав¬
ления; здесь становятся существенными сложные
понятия, касающиеся поведения вещества. Особую
роль играет давление вырождения электронов или
нейтронов. Оно связано с принципом Паули, ко¬
торый, как мы помним из §23.7, запрещает двум
или более фермионам находиться в одном и том же
квантовом состоянии. Белый карлик, который может
иметь массу порядка солнечной, сконцентрирован¬
ную примерно в объеме Земли, удерживает от даль¬
нейшего сжатия давление вырождения электронов;
нейтронная звезда такой же массы представляет со¬
бой тело с поперечником всего 10 км, она удержи¬
вается давлением вырождения нейтронов. (Теннис¬
ным мяч, наполненный веществом нейтронной звез¬
ды, весил бы столько же, сколько марсианская луна
Деймос!) Однако из теории относительности следу¬
ет, что давление вырождения само по себе не может
удержать в равновесии такую звезду, если ее мас¬
са превышает 2М©. Важный результат был получен
в 1931 году Субраманьяном Чандрасекаром, кото¬
рый установил подобный предел 1,4М© для белых
карликов. Более поздние уточнения дали несколько
больший предел для нейтронных звезд’ 127Л71. В ре¬
зультате всего этого оказалось, что не существует
возможной остаточной конфигурации для холодного
объекта с массой, большей примерно 2М© (а воз¬
можно, и с массой более 1,6М©). Такой объект бу¬
дет сжиматься внутрь, и коллапс будет продолжаться
вплоть до размера, при котором вступают в силу рас¬
суждения Мичелла. Что тогда произойдет?
Вернемся к нашей большой звезде массой, ска¬
жем, ЮМ©, предположив, что первоначально она на¬
ходилась при достаточно высокой температуре, так
что тепловое движение могло удерживать ее в рав¬
новесии. Однако при охлаждении звезды ее сжатое
ядро переходит через предел Чандрасекара и начи¬
нает сжиматься. Падение внутрь внешних ее частей
Коллапсирующее
вещество
Рис. 27.11. Пространственно-временная
диаграмма, изображающая коллапс в чер¬
ную дыру (одно пространственное из¬
мерение отброшено). Вещество падает
внутрь через 3-поверхность, которая ста¬
новится (абсолютным) горизонтом собы¬
тий. Коль скоро образовалась черная ды¬
ра, ни вещество, ни информация не мо¬
жет из нее выйти. Нулевые конусы каса¬
ются горизонта событий и позволяют ве¬
ществу или сигналам проходить внутрь
дыры, но не наружу. Внешний наблюда¬
тель не может заглянуть внутрь дыры, он
может видеть лишь вещество, чрезвычай¬
но тусклое из-за красного смещения, по¬
ка оно не оказалось внутри дыры

596
Глава 27
запускает бурный взрыв, в результате возникает сверхновая звезда. Подобные взрываю¬
щиеся звезды часто наблюдались, в основном в других галактиках; в течение нескольких
дней такая звезда может сиять, как целая галактика, в которой она находится. Однако если
при таком взрыве теряется недостаточное количество вещества, — а для звезды с началь¬
ной массой 10М© необходимая большая потеря массы маловероятна, — то можно ожидать,
что звезда будет безостановочно сжиматься, пока не достигнет размера, при котором ста¬
новятся применимыми рассуждения Мичелла. Взглянем на рис. 27.11, где представлена
пространственно-временная диаграмма, изображающая коллапс в черную дыру. (Конечно,
одно из пространственных измерений при этом приходится отбрасывать.) Видно, что веще¬
ство продолжает падать внутрь через поверхность (ее называют (абсолютным) горизонтом
событий), на которой скорость убегания становится равной скорости света. В соответствии
с этим, никакая дальнейшая информация о самой звезде не может достигнуть внешнего
наблюдателя, и возникает черная дыра.
Картина, представленная на рис. 27.11, основана на знаменитом шварцшильдовском ре¬
шении уравнения Эйнштейна, полученном в 1916 году Карлом Шварцшильдом^2718^ вскоре
после опубликования теории Эйнштейна и лишь за несколько месяцев до того, как он
умер от редкой болезни, подхваченной им на восточном фронте Первой мировой войны.
Это решение описывает статическое гравитационное поле, окружающее сферически сим¬
метричное тело, независимо от степени его сжатия. Горизонт расположен на радиальном
расстоянии г — 2MG/c2 (это точно совпадает с критическим значением Мичелла)"5.
Горизонт событий не сделан из какой-то материальной субстанции. Это всего лишь
некоторая (гипер)поверхность в пространстве-времени, отделяющая те места, откуда сигнал
может уйти во внешнюю бесконечность, от тех, где все сигналы будут неминуемо захвачены
черной дырой. Злополучный наблюдатель, который, падая, пролетает снаружи внутрь сквозь
горизонт событий, при пересечении горизонта не заметит ничего особенного. Более того,
сама черная дыра не является каким-то материальным телом — ее следует рассматривать
просто как гравитирующую область пространства-времени, из которой не может вырваться
никакой сигнал. А какова же судьба самой бедной звезды? Мы вернемся к этой загадке
в § 27.9.
Рассмотрим сначала ситуацию, которая вырисовывается из результатов наблюдений.
Замечены ли признаки существования черных дыр? Да, такие признаки имеются. В 1970-х
годах стали известны примеры любопытных систем в виде «двойных звезд», у которых
в видимых лучах наблюдался лишь один из членов пары. Существование, масса и движение
другого партнера угадывались по тонким деталям поведения видимого партнера. Из наблю¬
дений рентгеновского излучения, приходящего из этой области, следовало, что невидимый
партнер должен быть компактным объектом с массой, слишком большой для объектов двух
типов — белых карликов и нейтронных звезд, в форме которых, согласно общепринятым
физическим принципам, могут существовать компактные звезды. Характеристики рентге¬
новского излучения согласовались с предположением, что невидимый объект представляет
собой черную дыру, окруженную так называемым «диском аккреции», состоящим из газа
или пыли, который закручивается вокруг дыры в виде спирали со скоростью, возрастающей
по мере приближения к дыре, и при этом сильно нагревается. Рентгеновское излучение ис¬
*ЯШ Шварцшильд использовал метрику вида ds2 = (l~2M/r.)-efe2-(1 — 2M/r)~~1 dr2 — r2(d02+sm2 9 <3,ф2)\
здесь используется система единиц, в которой G = с ~ I: в ж ф — обычные сферические полярные координаты
(§22.11). Объясните, как задается координата г условием, налагаемым на площадь поверхности сфер, соответ¬
ствующих постоянным значениям г и i. Эта метрическая форма не продолжается непрерывным образом на об¬
ласть г <С 2М, для этого можно воспользоваться метрикой Эддингтона - Финкельштейна ds2 = (1 — 2M/r) dv2 —
— 2 dvdr — r2(d$2 +.sin2 в йф2). Найдите изменение координат в явном виде с помощью этих двух выражений.
Объясните, почему нулевые кривые в каждой плоскости (v, г) должны быть радиальными нулевыми геодезиче¬
скими, и воспользуйтесь этим фактом, чтобы получить их уравнения и построить графики. (Линии постоянного
значения г изобразите вертикальными, а линии постоянного v — наклоненными внутрь справа под углом 45°.)
Определите горизонт событий и сингулярность (см. § 27.9).

27.9. Горизонты событий и пространственно-временные сингулярности
597
пускается перед тем, как вещество непосредственно входит в черную дыру (см. рис. 27.12 а).
Наиболее известным кандидатом на роль черной дыры (и для того времени наиболее убе¬
дительным доказательством существования таких объектов) стал рентгеновский источник
X-1 в созвездии Лебедя, у которого компактный и темный член пары имеет массу приблизи¬
тельно 7М©, что, согласно существующей теории, определенно исключает варианты белого
карлика и нейтронной звезды.
Hi'?
а)
б)
Рис. 27.12. Двойные звездные системы, одним из членов которых является (маленькая) черная ды¬
ра. а) Вещество большей звезды, захватываемое черной дырой, образует вокруг нее диск аккреции,
закручиваясь в виде спирали и нагреваясь, что приводит к испусканию рентгеновского излучения,
пока вещество не попало непосредственно в черную дыру, б) В некоторых случаях диск аккреции
отсутствует, и вещество просто падает «по прямой». Если бы притягивающий компактный объект
имел материальную поверхность, падающее вещество разогревало бы ее, однако никакого свечения не
наблюдается, что подтверждает наличие там черной дыры
Доказательства такого рода всегда оказываются косвенными и не могут считаться
вполне удовлетворительными, поскольку опираются на теорию, согласно которой подобные
массивные компактные объекты не могут существовать в форме протяженных тел. Сей¬
час, однако, имеется более непосредственное и впечатляющее проявление существования
черных дыр. Диски аккреции не являются единственно возможными конфигурациями, об¬
разуемыми веществом, которое падает в черную дыру. В некоторых случаях вещество просто
падает «по прямой», и поведение такого типа в настоящее время, по-видимому, наблюдается
(рис. 27.12 6). Если бы притягивающий компактный объект имел какую-то материальную
поверхность, то падающее вещество должно было разогревать ее, и ее свечение со време¬
нем должно было стать видимым. Но такого свечения не наблюдается. Таким образом, мы
имеем теперь прямое подтверждение того факта, что подобный компактный объект вообще
не имеет поверхности, и это убедительно свидетельствует, что такой объект представляет
собой черную дыру!27Л91.
Всё это относится к «звездным» черным дырам, масса которых лишь в несколько раз
превышает массу Солнца. Существуют также некоторые впечатляющие проявления суще¬
ствования намного больших черных дыр. По-видимому, в центре большинства (а может
быть, и всех) галактик находятся черные дыры очень большого размера. В частности, име¬
ется, видимо, черная дыра с массой 3 • 106М© в центре нашей собственной Галактики —
Млечного Пути, и подробно изученное движение звезд вокруг этого центра вполне согласу-
ется с такой картиной.
27.9.	Горизонты событий и пространственно-временные сингулярности
На рис. 27.11 показаны некоторые нулевые конусы, выражающие в явном виде причин¬
ные свойства пространства-времени. Наиболее существенной чертой является существова¬
ние горизонта событий черной дыры, который представляет собой 3-поверхность Н в про¬
странстве-времени. Как отмечалось в § 27.8, он обладает тем свойством, что никакой сигнал,

598
Глава 27
посылаемый из области внутри Н, не может выйти во внешнюю область. Это, как можно
заметить, связано с наклоном конусов внутрь, так что они могут касаться поверхности Н.
Всякая мировая линия, проведенная из внутренней области поверхности Н во внешнюю,
должна нарушать причинность, определяемую конусами (§ 17.7). Я изобразил случай пол¬
ной сферической симметрии гравитационного коллапса; это именно та ситуация, которую
изучали в 1939 году Роберт Оппенгеймер и Хартлэнд Снайдер с использованием геомет¬
рии Шварцшильда для описания области, внешней по отношению к веществу, попавшему
внутрь.
Хотя горизонт Н обладает странными свойствами, локальная геометрия там не отлича¬
ется от остальной сколько-нибудь значительно. Как уже отмечалось, наблюдатель в космиче¬
ском корабле при пересечении горизонта и переходе из внешней области во внутреннюю не
заметит ничего особенного. Однако, предприняв это опасное путешествие, он уже не смо¬
жет вернуться обратно. Наклон нулевых конусов таков, что возврат невозможен, и наблюда¬
тель будет иметь дело с быстро усиливающимися приливными эффектами, обусловленными
кривизной пространства-времени (см. § 17.5, 19.6); эти эффекты становятся бесконечными
в сингулярности пространства-времени в центре (г = 0). Эти особенности не ограничены
случаем сферической симметрии, а имеют вполне общий характер. Действительно, суще¬
ствуют общие теоремы, утверждающие, что сингулярности неизбежны при любом грави¬
тационном коллапсе при прохождении некоторой «точки невозврата» I27*20]. Некоторые из
связанных с этим вопросов будут освещены несколько подробнее в § 28.8.
Для черной дыры с массой в несколько солнечных масс приливные силы оказываются
вполне достаточными, чтобы привести к гибели человека еще задолго до достижения им
горизонта, не говоря уже о пересечении его. Однако в случае больших черных дыр мас¬
сой 106 М© или более, какие, по-видимому, обитают в центрах галактик, никаких особых
проблем, связанных с приливными эффектами, при пересечении горизонта не возникнет
(в этом случае радиус горизонта составляет миллионы километров). В частности, в нашей
собственной Галактике кривизна пространства-времени в области горизонта ее централь¬
ной черной дыры всего раз в двадцать превышает кривизну на поверхности нашей Земли,
которую мы даже не замечаем! Тем не менее неумолимое втягивание наблюдателя внутрь
к сингулярности в центре вызывает очень быстрое нарастание приливных эффектов вплоть
до бесконечности, и наш наблюдатель будет уничтожен менее чем за минуту! Разрушение
быстро растущими приливными силами ожидает, конечно, любой физический материал,
втягиваемый внутрь к центру черной дыры. Вспомним наше обсуждение судьбы вещества
коллапсирующей звезды с массой ЮМ©. Даже отдельные частицы, из которых оно состоит,
очень скоро подвергнутся действию настолько мощных приливных сил, что будут разорваны
на куски, никто не знает, какого размера!
Мы знаем, по крайней мере, следующее: пока справедлива эйнштейновская модель
классического пространства-времени, действующая в соответствии с уравнением Эйнштей¬
на (при неотрицательной плотности энергии и некоторых других нежестких и «разумных»
допущениях), внутри дыры имеет место пространственно-временная сингулярность t27-2 ^.
Можно ожидать, что, согласно уравнению Эйнштейна, воздействия такой сингулярности не
сможет избежать никакое вещество в черной дыре и что «приливные силы» (т. е. вейлевская
кривизна, см. § 19.7) будут возрастать до бесконечности, — в общем случае, возможно, ква¬
зиосциллирующим образом127,221 Кажется неизбежным появление квантовой гравитации
(возможно и другое название), при этом указанныечожидания классической теории должны
будут принять несколько иную форму. Мы пока не знаем, какой должна быть правильная
«квантово-гравитационная» теория, однако приведенные рассуждения относительно черных
дыр дают нам начальный толчок, который должен вести нас в правильном направлении
при поиске правильной «квантовой гравитации». Эти вопросы окажутся важными для нас
в дальнейшем, особенно в главах 30-32.

27.10. Энтропия черной дыры
599
Обычно считается, что пространственно-временные сингулярности гравитационного
коллапса будут обязательно лежать внутри горизонта событий, поэтому какие физические
явления ни возникали бы в такой сингулярности, они будут скрыты от взора любого внешне¬
го наблюдателя. Это, однако, не является математически обоснованным следствием общей
теории относительности. Предположение, что сингулярности всегда будут скрыты подобным
образом, носит название космической цензуры^-27*23^, мы обсудим эту проблему подробнее
в § 28.8.
С другой стороны, нам не обязательно добираться до сингулярности, чтобы обнаружить
необычные эффекты, связанные с гравитационным коллапсом. Во Вселенной происходят
интенсивные процессы, доступные наблюдению. Например, квазары, обладающие исклю¬
чительно высокой светимостью, как считают, питаются энергией вращающихся черных дыр
в центрах галактик, при этом вращение черной дыры играет роль силовой станции, хотя име¬
ет место выброс вещества из черной дыры (по-видимому, вдоль оси вращения) (см. § 30.7).
Энергия, излучаемая некоторыми квазарами, хотя и выходит через узкую область (порядка
размера Солнечной системы), может превосходить излучение целой галактики в 102-103
и более раз! Такие квазары можно наблюдать на огромных расстояниях, и они играют
важную роль в наблюдательной космологии. Существуют также мощные источники гамма-
излучения (фотонов крайне высокой энергии), которые также приписываются процессам
с участием черных дыр, возможно, их столкновениям^27,24^.
27.10* Энтропия черной дыры
Вернемся к рассмотрению «более безопасных» внешних областей изолированных ста¬
ционарных («мертвых») черных дыр. Мы увидим, сколь аномально велика энтропия, кото¬
рую следует приписать такому объекту. Прежде всего, следует отметить, что существуют
математические теоремы 127,251, неопровержимо доказывающие, что черные дыры общего ви¬
да, которые вначале могут обладать сложными нерегулярностями, обусловленными асиммет¬
ричным коллапсом (возможно, в виде образования спиралей и необратимой катастрофы), бу¬
дут тем не менее быстро принимать замечательно простую и изящную геометрическую фор¬
му (если рассматривать их внешнюю пространственно-временную геометрию). Эта форма
описывается метрикой Керраi27-26] и характеризуется всего двумя физико-геометрическими
параметрами (вещественными числами), обозначаемыми буквами т и aJ27,27l Здесь т озна¬
чает полную массу черной дыры, а а х т — полный момент импульса (в системе единиц,
где G = с = 1). Нобелевский лауреат Субраманьян Чандрасекар (знаменитый результат
которого, полученный в 1931 году, как мы помним из §27.8, повернул астрофизику в на¬
правлении черных дыр) писал:
Черные дыры по своей природе — наиболее совершенные макроскопические объ¬
екты во всей Вселенной, поскольку единственными элементами этих конструкций
служат наши представления о пространстве и времени. А так как общая теория
относительности дает лишь одно-единственное решение для их описания, они яв¬
ляются также простейшими объектами[27,281
Неумолимый характер черной дыры, захватывающей вещество любого вида (которое
может иметь сколь угодно сложную структуру) и превращающей его в простую конфи¬
гурацию, описываемую всего десятью параметрами (к ним относятся a, т, направление
оси вращения, положение центра масс и 3-скорость черной дыры), есть яркое проявление
Второго закона. В этих десяти параметрах заключено всё, что требуется для адекватного
макроскопического описания конечного состояния^27,29^. Хотя черная дыра не похожа на
обычное вещество в тепловом равновесии, у них есть общее ключевое свойство: гигантское
количество микроскопически различных состояний сводится к состоянию, которое можно

600
Глава 27
описать с помощью очень небольшого числа параметров. По этой причине соответству¬
ющий ящик в огрубленном фазовом пространстве имеет огромный объем, и черная дыра
соответственно обладает огромной энтропией.
На самом деле энтропия черной дыры допускает замечательную геометрическую ин¬
терпретацию: она пропорциональна площади горизонта дыры! Согласно знаменитой форму¬
ле Бекенстайна-Хокинга, черной дыре можно приписать вполне определенную энтропию,
равную
с _ fee3 А
вн “ 4Gh ’
где А — площадь поверхности горизонта черной дыры, а индекс ВН есть аббревиатура имен
авторов формулы (Bekenstein-Hawking) или, если угодно, названия объекта (Black Hole).
Присутствие здесь постоянной Планка, а также гравитационной постоянной указывает на
то, что эта энтропия представляет собой «квантово-гравитационный» эффект. Действитель¬
но, здесь мы впервые встречаемся с появлением в одной и той же формуле фундаментальной
постоянной квантовой механики (постоянной Планка h в дираковской форме) и столь же
фундаментальной постоянной общей теории относительности (ньютоновской гравитацион¬
ной постоянной G).
В фундаментальной физике, включающей в себя квантовую механику и общую тео¬
рию относительности, часто бывает удобно пользоваться системой единиц, в которой обе
эти постоянные приняты за единицу. Мы уже видели в §§ 17.8, 19.2, 19.6, 19.7 (а также
в других местах, например, в главе 24), что часто бывает очень удобно принять за единицу
скорость света с. Без потери согласованности можно распространить это соглашение также
на h и G, приняв их за единицы измерения. Это имеет замечательное следствие: все едини¬
цы времени, пространственной длины, массы и электрического заряда теперь оказываются
полностью фиксированными, образуя так называемую платовскую (или естественную, или
абсолютную) систему единиц. Более того, можно положить равной единице также постоян¬
ную Больцмана к (см. § 27.3):
G = c = fi=fc = l,
/
и тогда единица температуры также станет абсолютной.
Эти единицы далеки от практических единиц, используемых в повседневном обиходе,
что видно, если попробовать выразить наши обычные единицы через планковские:
грамм = 4,7 • 104,
метр = 6,3- 1034,
секунда =1,9-10
градус Кельвина = 4 * 10 “~33.
В этих единицах заряд протона (или заряд электрона с обратным знаком) становится
равным приблизительно е —	Д....,	более точно[27.з°]
л/137
е = 0,0854245...
43
Обратив эти соотношения, можно получить:
планковская единица массы = 2,1 • 10 5 г,
планковская единица длины = 1,6-10 35 м,
планковская единица времени = 5,3 • 10 44 с,
■ч.
планковская единица температуры = 2,5* 1032 К,
планковская единица заряда —11,7 заряда протона.
О планковских единицах мы узнаем больше в §31.1.

27.11. Космология
601
Вернувшись к формуле Бекенстайна-Хокинга для энтропии черной дыры, мы найдем,
что в планковских единицах энтропия 5вн черной дыры с площадью поверхности А имеет
простой вид:
5вн =
Для случая керровского решения получаем явные выражения (в обычных единицах):
А = —г~—т(т -Ь у/ т2 — а2),
с
с 2ftGk _
Ьвк = —m
ей
В § 30.4 мы познакомимся с обстоятельствами, лежащими в основе замечательной формулы
Бекенстайна - Хокинга.
Чтобы получить некоторое представление об огромных значениях, которых достига¬
ет энтропия черной дыры, посмотрим сначала, что считалось в 1960-х годах наибольшим
вкладом в энтропию Вселенной. Это была энтропия микроволнового излучения 2,7 К —
«остатка» Большого взрыва. В естественных единицах она составляет 108 или 109 в расче¬
те на один барион. (Грубо говоря, это есть приходящееся на один барион число фотонов,
оставшихся от Большого взрыва.) Сравним эту, казалось бы, огромную цифру с энтропи¬
ей, вносимой во Вселенную черными дырами. Астрономы не имеют ясного представления
ни о количестве существующих черных дыр, ни об их размерах, однако имеются веские
указания на существование в центре нашей собственной Галактики, Млечного Пути, черной
дыры с массой приблизительно 3 • 106М©, которую можно принять в качестве типичной.
Некоторые галактики содержат черные дыры большего размера, и они должны легко компен¬
сировать большое число других галактик с черными дырами меньшего размера, поскольку
именно большие черные дыры дают основной вклад в энтропию*. В качестве грубой (хотя,
возможно, весьма консервативной) оценки будем считать нашу Галактику типичной, тогда
мы получим энтропию 1021 на один барион, что несравнимо велико с соответствующими
цифрами 108 или 109 для микроволнового фона. Более того, какой бы эта величина ни была
сейчас, она неизбежно и в огромной степени вырастет в будущем.
(га + у/т
а
У
27.11. Космология
Прежде чем попытаться оценить ту предположительно колоссальную энтропию, кото¬
рая потенциально доступна для нашей Вселенной (и тем самым почувствовать, насколько
«особой» является наша Вселенная сейчас и насколько «особенно особой» она должна
была быть во времена Большого взрыва), нам необходимо узнать кое-что о космологии.
Мы попробуем применить данные космологии для оценки размера ящика В фазового про¬
странства, представляющего Большой взрыв, и сравнить его с размером всего фазового
пространства Vu, а также с объемом ящика Л/*, представляющего Вселенную в настоящий
момент.
Начнем с краткого описания так называемых стандартных космологических моделей,
которых, в сущности, три. Как мы помним из § 27.7, история начинается с русского физика
Александра Фридмана, который в 1922 году впервые нашел соответствующие космологи¬
ческие решения уравнения Эйнштейна с материальным источником, который можно ис¬
пользовать для аппроксимации полностью однородного крупномасштабного распределения
галактик (называемого иногда «пылью»). Космологические модели общего вида, изучавши¬
еся Фридманом (в том числе и с материальными источниками иного типа, отличными от
Понятно ли, почему это так?

602
Глава 27
фридмановской «пыли»), теперь обычно именуются моделями Фридмана - Леметра - Роберт¬
сона-Уокера (ФЛРУ) с учетом более поздних вкладов, уточнений и обобщений, внесенных
остальными членами этой четверки.
Модель ФЛРУ характеризуется полной пространственной однородностью и изотро¬
пией. Грубо говоря, «изотропия» означает, что Вселенная выглядит одинаково во всех на¬
правлениях и потому обладает симметрией группы вращений 0(3). Аналогично «простран¬
ственная однородность» означает, что Вселенная имеет один и тот же вид во всех точках
пространства в любой момент времени; в соответствии с этим существует группа симметрии,
транзитивная (§ 18.2) по отношению к любому члену семейства пространственноподобных
3-поверхностей, которыми служат 3-поверхности Tt «пространства» при постоянном «вре¬
мени» t (в результате получается шестимерная группа симметрии’"). Эта пара допущений
находится в хорошем согласии с результатами наблюдений распределения вещества в очень
больших масштабах и с природой микроволнового фона. Допущение о пространственной
изотропии оказалось очень хорошим приближением (это показали наблюдения весьма уда¬
ленных источников и прежде всего излучения 2,7 К). Более того, если бы Вселенная была
неоднородной, то она могла бы выглядеть изотропной лишь при взгляде из каких-то опреде¬
ленных мест**, так что мы должны были бы находиться в очень привилегированном положе¬
нии, чтобы Вселенная казалась нам изотропной, не будучи при этом однородной. Разумеется,
наблюдаемая изотропия не вполне точная, поскольку мы видим отдельные галактики, скоп¬
ления галактик и сверхскопления галактик лишь в определенных направлениях. Имеется
неоднородное распределение вещества, не всегда видимого, в умопомрачительных масшта¬
бах, например, так называемый «Большой Аттрактор», который, по-видимому, простирается
не только на нашу Галактику, но и на несколько соседних скоплений галактик. Оказывается,
однако, что относительные отклонения от пространственной однородности становятся тем
меньше, чем дальше мы глядим. Наилучшая информация, которую мы получаем от наиболее
удаленных из доступных нам областей Вселенной, предоставляется нам фоновым черным
излучением 2,7 К. Результаты программ СОВЕ, BOOMERANG, WMAP и других говорят
о том, что хотя и имеют место очень малые вариации температуры порядка 10_5, тем не
менее условие изотропии хорошо выполняется^27*31^.
Представляется, что однородные и изотропные космологические модели ФЛРУ могут
служить отличным приближением для описания структуры реальной Вселенной, по крайней
мере, в пределах наблюдаемой Вселенной, которая охватывает примерно 1011 галактик, со¬
держащих порядка Ю80 барионов (вскоре мы увидим, как следует понимать термин «наблю¬
даемая Вселенная»). Пространственная изотропия и однородность означает^27*32^, что трех¬
мерные пространственные сечения, соответствующие «постоянному времени», Tt, заполня¬
ют всё пространство-время М (не пересекая друг друга), при этом каждая 3-геометрия Tt
обладает симметрией однородного и изотропного пространства-времени М. (см. рис. 27.13).
Для 3-геометрии имеются три существенно различных возможности в зависимости от то¬
го, является ли (постоянная) пространственная кривизна положительной (К > 0), нулевой
(К — 0) или отрицательной (К < 0). В литературе по космологии принято нормировать
радиус кривизны (при К ф 0), полагая просто К = 1 и К = — 1 соответственно для К > 0
и К < 0. Я, однако, не буду этого делать, чтобы обсуждение было более наглядным, пред¬
почитая пользоваться записью К > 0 и К < 0.
На рис. 27.13 а, б, в я попытался изобразить временную эволюцию Вселенной согласно
первоначальному анализу уравнения Эйнштейна, проведенному Фридманом, при различном
выборе пространственной кривизны. Во всех случаях Вселенная начинается с сингулярности
(так называемого Большого взрыва), когда пространственная кривизна становится бесконеч-
"s,^>
* йИ Почему шестимерная?
Приведите общие соображения, объясняющие, почему связное (3-) пространство не может быть изотроп¬
ным относительно двух различных точек, не будучи однородным.

27.11. Космология
603
Рис. 27.13. Пространственно-однородные и изотропные космологические модели Фридмана - Лемет-
ра - Робертсона - Уокера (ФЛРУ). Время направлено вверх, каждая модель'начинается с Большого
взрыва. Каждая из них заполнена однопараметрическим семейством непересекающихся однородных
пространственноподобных 3-поверхностей %, соответствующих «пространству» в момент времени t.
В моделях Фридмана вещество рассматривается как среда без давления («пыль»). Показаны три слу¬
чая: а) К > 0, когда пространства % представляют собой 3-сферы S3 (на рисунках они показаны
в виде ограничивающих окружностей 51), и в конечном счете модель коллапсирует в виде Большого
Q
хлопка; или б) пространства % представляют евклидовы 3-пространства Е*, они показаны в виде
2-плоскости наверху; или в) пространства % представляют гиперболические 3-пространства (пока¬
заны в виде конформного представления наверху). На рисунках г), д) и е) показаны соответственно
случаи а), б), в) с положительной космологической постоянной Л, в которых на конечной стадии
имеет место экспоненциальное расширение, в случае г) предполагается, что постоянная Л достаточно
велика, чтобы предотвратить фазу коллапса
ной, а затем быстро расширяется. Конечное поведение критическим образом зависит от
значения К. При К > 0 (рис. 27 Л За) расширение со временем сменяется сжатием, и Все¬
ленная возвращается к сингулярности, часто называемой Большим хлопком, которая в точной
модели Фридмана является точным отражением во времени начального Большого взрыва.
При К — 0 (рис. 27.13 6) расширение продолжается без конца, и фаза коллапса не насту¬
пает, При К < 0 (рис. 27.13 в) также нет перспектив коллапса, и расширение в конечном
счете происходит с постоянной скоростью. (Здесь имеется аналогия с камнем, брошенным
с Земли вертикально вверх (см. §27.8). Если начальная скорость камня меньше скорости
убегания, то он в конце концов упадет на Землю, подобно Вселенной Фридмана при К > 0,
если скорость камня равна скорости убегания, то он не вернется назад, как при К = 0, если
скорость больше скорости убегания, то скорость камня будет приближаться к предельному
значению, и он не будет замедляться, как в случае К < 0.)
Первоначальная работа Фридмана не содержала космологической постоянной Л, одна¬
ко практически во всем последующем систематическом обсуждении космологии t27-33! до¬
пускалось присутствие космологического члена Лдаь> предложенного Эйнштейном в 1917
году, несмотря на то что сам Эйнштейн после 1929 года (см. § 19.7) предпочитал полагать

604
Глава 27
Л ~ 0. Это оказалось к лучшему, поскольку результаты недавних наблюдений разного ро¬
да начали ясно указывать на существование положительной космологической постоянной
(Л > 0), проявляющейся в поведении нашей Вселенной. Эти проблемы будут обсужде¬
ны позже, в §28.10, а пока я отсылаю читателя к рис. 27ЛЗг9д9е9 которые представляют
аналог рис. 27.13 а, б, в для случая, когда в уравнения Фридмана вводится положительная
(достаточно большая) постоянная Л. Согласно современному балансу наблюдений и мнений
космологов, одна из этих моделей дает хорошее описание истории реальной Вселенной, по
крайней мере, до момента расцепления, когда возраст Вселенной был всего ~ 3 • 105 лет, что
составляет 1/50000 от ее нынешнего возраста ~ 1,5* 1010 лет; под расцеплением понимается
тот момент времени, в который мы «заглядываем», наблюдая микроволновой фон.
До расцепления во Вселенной в основном преобладало излучение, после расцепления —
вещество. Мы не должны ожидать, что фридмановская модель «пыли» применима к фазе
доминирования излучения, более подходящей является предложенная в 1934 году Толме-
ном [784] модель Вселенной, заполненной излучением. Замена модели не приводит к су¬
щественному изменению картины. Она лишь укорачивает отрезок времени между Большим
о
взрывом и расцеплением, добавляя во фридмановский результат множитель как показано
на рис. 27.14.* Сторонники инфляционной космологии предполагают гораздо более ради¬
кальное изменение эволюции — экспоненциальное расширение, увеличивающее масштаб
Вселенной примерно в 1060 раз. Но оно должно было закончиться к моменту, когда возраст
Вселенной составлял всего 10~32 секунд, и потому не вносит заметных изменений в вид
рис. 27.13 или 27.14. Хотя в других отношениях инфляционная картина, если она правильна,
приводит к огромным изменениям. Мы обсудим инфляционную космологию в §§ 28.4, 28.5.
Во всяком случае, я полагаю, что не следует включать инфляцию в так называемую «стан¬
дартную модель», и здесь я не буду это делать^27 341
Рис. 27.14. До «расцепления», которое произошло, когда возраст Вселенной составлял 300000 лет
(приблизительно 1 /50000 ее нынешнего возраста), — это эпоха, в которую мы «заглядываем», наблю¬
дая микроволновой фон, — во Вселенной преобладало излучение, поэтому «пылевое» приближение
Фридмана к ней неприменимо. Вместо этого имеет место более быстрое расширение Толмена, пред¬
ставленное внутренней кривой
Но какая из трех моделей, показанных на рис. 27.13 г, д9е9 наиболее подходит для опи¬
сания реальной Вселенной? Мы обсудим этот вопрос в § 28.10. Пока мы примем, что любая
из них могла бы быть в основном правильной, и рассмотрим каждую из этих различных
пространственных геометрий чуть подробнее.
* &£. Попробуйте получить этот множитель, предполагая, что «пылевая» модель Фридмана предсказывает за¬
висимость вида t = Ai?3/2 при малых t, а «радиационная» модель Толмена — зависимость t = BR2, где R(t) есть
мера «радиуса» Вселенной, А и В — постоянные. (Подсказка: должны ли касательные к кривым соприкасаться?)

27.11. Космология
605
Случай К > 0 обычно представляют в виде 3-сферы. Следует отметить, однако, что
существует также проективное пространство МР3, получаемое при отождествлении анти-
о
йодных точек сферы S (см. §§2.7, 15.4-15.6); трудно представить, чтобы эти два мира были
практически различимы. Возможны и другие способы идентификации отдельных точек сфе-
о
ры S , дающие так называемые линзовые пространства, но ни одно из них не обладает гло¬
бальной изотропиейf27,35l. Случаю К — 0 (изотропному) соответствует обычное евклидово
3-пространство; аналогично случаю К < 0 отвечает гиперболическая 3-геометрия, которую
мы изучали в §§2.4-2.7, 18.4. Пространственные геометрии с К > 0, К = 0 и К <0
изящно и изобретательно представлены (в двумерном варианте) на рисунках М. К. Эшера
(соответственно рис. 2.22 а, б, в). Случай К > 0 обычно называют замкнутой Вселенной,
это означает, что Вселенная замкнута в пространстве (т. е. содержит компактную простран¬
ственноподобную гиперповерхность^7*36^). Случай К < 0 космологи часто называют «от¬
крытой» Вселенной, хотя случай К — 0 на самом деле тоже соответствует пространственной
открытости. Поэтому я не буду здесь пользоваться этой не совсем точной терминологией.
Если отказаться от требования глобальной изотропии, как в упомянутом случае линзовых
пространств с К > 0, то (неизотропные) модели замкнутой Вселенной возможны также
при К — 0 и К < oJ27*37!
Полное 4-пространство М описывается, как мы видели, в терминах временной эво¬
люции пространственной 3-геометрии, полный масштаб которой меняется со временем.
В стандартной картине Вселенная после Большого взрыва очень быстро расширяется, од¬
нако неправильно было бы представлять себе некоторую «центральную точку», в которой
произошел взрыв и из которой всё разбегается. Более правильной будет картина, подоб¬
ная (в двумерном случае) поверхности надуваемого воздушного шарика. Каждая точка его
поверхности с течением времени постепенно удаляется от любой другой точки, и в такой
модели Вселенной нет никакой «центральной точки». Здесь поверхность должна представ¬
лять всю Вселенную в целом. Так что центр нашего воздушного шарика, как и любую
другую точку, не лежащую на его поверхности, нельзя считать частью расширяющейся
Вселенной.
Воспользуемся записью б£2 для обозначения метрической формы одной из указанных
трех геометрий; в случае К ^ 0 мы нормируем метрику таким образом, чтобы получить
единичную 3-сферу или единичное гиперболическое пространство (т. е. полагаем соответ¬
ственно К — 1 или К = —1)*. Тогда 4-метрику всего пространства-времени в целом можно
представить в виде
ds2 = dt2 - R2dl]2,
где t — параметр «космического времени», постоянные значения которого определяют про¬
странство Tt, а
R = R{t)
есть некоторая функция временного параметра t, определяющая пространственный «раз¬
мер» Вселенной «в момент времени t». Таким образом, метрика каждого пространства
описывается выражением R2dTr. На рис. 27.15 а, б, в изображен график функции R = R(t)
соответственно при К = 1, 0, — 1 для первоначальной «пылевой» модели Фридмана (среды
без давления)** при Л — 0. На рис. 27.15 г показано, что будет при положительном значе-
 Попробуйте показать, что выражение d£2 — dr2 + sin2 ip(dip2 У sin2 0 d62) описывает метрику единичной
3-сферы, d£2 = dr2 У sh2 х(Фс2 + sin2#^#2) — единичное гиперболическое пространство. Воспользуйтесь
процедурами, описанными в § 18.1. (Подсказка: напишите сначала формулу для метрики 3-сферы произвольного
радиуса.)
Решение для «пыли» Фридмана при К > 0, А = 0 можно представить в виде R = С( 1 — cos £), t = С(£ —
— sin 4), где С — постоянная, £ — переменный параметр. Покажите, что это есть уравнение цикчоиды — кривой,
которую описывает точка окружности, катящейся по горизонтальной прямой. Попробуйте перейти от случая К > 0
к случаю К < 0, используя прием, аналогичный показанному в §18.1 и упражнении 27.16, и к случаю К — 0
путем подходящего предельного перехода (с соответствующей нормировкой координат).

606
Глава 27
R
\R
t
Л>0
[г)
K>0, Л-0
а)
к= О, Л-0
б)
К< О, Л-0
в)
Рис. 27.15. Графики функции R — R(t) для моделей Фридмана при Л — 0: а) К > 0, б) К — О,
в) К < 0 и г) при Л > 0. График г) показан для случая К — 0, однако остальные случаи дают
очень похожий результат, если постоянная Л достаточно велика по сравнению с пространственной
кривизной
нии Л, когда кривые для всех трех вариантов значений К очень похожи одна на другую (при
условии, что постоянная Л достаточно велика, чтобы в случае К > 0 преодолеть коллапс, ~~
на это указывают результаты наблюдений). Предельная скорость расширения в этом случае
экспоненциально растет.
27.12.	Конформные диаграммы
Чтобы понять, что означают слова «наблюдаемая Вселенная», полезно воспользоваться
так называемой конформной диаграммой^27на которой всё пространство-время (чаще
всего двумерное) изображается таким образом, что нулевые направления образуют с верти¬
калью угол 45°, а бесконечность представлена как часть границы диаграммы. Для обозначе¬
ния бесконечности, в таком понимании, обычно используется рукописная буква У, причем
знаком У+ обозначается будущая (или будущая нулевая) бесконечность, «достигаемая»
в конечном счете выходящими световыми лучами, а знаком У ~ — прошлая бесконечность,
откуда приходят входящие световые лучи. Эти бесконечности обычно оказываются нулевыми
3-поверхностями в стандартной теории Эйнштейна с Л — 0 и пространственноподобными
3-поверхностями, если Л > oJ27,39l
Конформные диаграммы отражают структуру причинности пространства-времени, при
этом здесь нас интересует не полная пространственно-временная метрика, а семейство ну¬
левых конусов. Это есть лоренцев вариант конформной геометрии, с которой мы позна¬
комились в §§2.4, 8.2, 18.4, 18.5 (она определяется классом эквивалентности метрик, при
этом метрика g, эквивалентна Q2 g, где Q — положительная скалярная функция в простран¬
стве-времени, так что Q меняет пространственный масштаб от точки к точке). В § 2.2 мы
видели, каким образом можно получить конформное отображение полной гиперболической
плоскости на конечную область евклидовой плоскости (рис. 2.11,2.12, 2.13). Идея конформ¬
ной пространственно-временной диаграммы в основном та же самая, но теперь конформно
отображается лоренцева (не определенная положительно) метрика пространства-времени.
Главная особенность состоит в том, что в лоренцевой геометрии нулевые конусы сами
определяют конформную геометрию.
В двумерном случае нулевой конус состоит из пары нулевых направлений, и это опре¬
деляет 2-метрику с точностью до локального конформного коэффициента. Такое двумерное
представление особенно полезно, когда полное четырехмерное пространство-время облада¬
ет сферической симметрией. Тогда можно рассматривать такое четырехмерное простран¬
ство-время как результат «вращения» двумерного пространства-времени, при котором каж¬
дая точка 2-пространства представляет сферу S2 в 4-пространстве. Для такого простран¬
ства-времени конформную диаграмму можно сделать совершенно точной, и я буду называть

27.12. Конформные диаграммы
607
такие конформные диаграммы строгими. Остальные конформные диаграммы будем назы¬
вать схематическими. Точки строгой конформной диаграммы действительно представляют
целые (метрические) сферы S . (В случае n-мерного лоренцева «пространства-времени»,
подобного, например, рассматриваемым в теории струн (см. §§ 31.4, 31.7), это будут (п — 2)-
 Г)
сферы S .) Исключение составляют те части границы диаграммы, которые описывают
ось симметрии, — там точки диаграммы представляют единичные точки пространства-вре¬
мени. Эти части изображаются прерывистыми линиями, и можно принять, что диаграмма
вращается вокруг одной из таких линий*. Части границы, представляющие бесконечность,
показаны сплошными линиями, а те части, которые соответствуют сингулярностям, — вол¬
нистыми линиями (см. рис. 27.16). Существуют также угловые точки, в которых встречаются
различные граничные линии конформной диаграммы. Те из них, которые помечены малень¬
кими светлыми кружочками о? следует считать представляющими целые 2-сферы (подобно
границе гиперболического 3-пространства; см. §§ 2.4,18.4); угловые точки, помеченные тем¬
ными кружками •, представляют точки (сферы нулевого радиуса). На рис. 27.166 показана
строгая конформная диаграмма для пространства Минковского, на рис. 27.16 в — гравита¬
ционный коллапс в шварцшильдовскую черную дыру (сферически симметричный коллапс
показан на рис. 27.11). На рис. 27.17 изображены перспективные космологические модели,
соответствующие показанным на рис. 27.13.**
Конформные диаграммы полезны в том отношении, что на них особенно наглядно про¬
являются свойства причинности пространства-времени. Заметим, например, что при сфери¬
чески симметричном коллапсе в черную дыру, показанном на рис. 27.16 в, горизонт черной
дыры образует с вертикалью угол 45°. Мировая линия любой материальной частицы не мо¬
жет быть наклонена относительно вертикали более чем на 45°, поэтому она не может выйти
из внутренней области за горизонтом, коль скоро она попала туда. Более того, оказавшись
в этой области, она вынужденно попадает в сингулярность (рис. 27.18 а). Сингулярность
представляет собой пространственноподобную границу в будущем к внутренней части про¬
странства-времени; этот факт несколько противоречит интуиции при взгляде с более при¬
вычной точки зрения (рис. 27.11). Ситуация, созданная Большим взрывом, играет роль,
аналогичную обращению времени, создавая пространственноподобную границу простран¬
ства-времени в прошлом (рис. 27.186). Это опять-таки противоречит интуиции, поскольку
мы рассматриваем Большой взрыв как (сингулярную) точку^27Л0У
Пространственноподобный характер рассматриваемой начальной границы приводит
нас к понятию горизонта для частиц — важного аспекта Большого взрыва. Взглянем на
рис. 27.186, где наблюдатель находится в точке р, близкой к границе Большого взрыва.
Областью Вселенной, которая может переносить информацию к наблюдателю, является све¬
товой конус прошлого для точки р и область внутри него; заметим, что она пересекается
лишь с частью Р начальной гиперповерхности Большого взрыва[27.41] часхИцЫ) рожден¬
ные Большим взрывом вне области Р, недоступны для наблюдения в точке р. Эти области
находятся за пределами горизонта для частиц точки р. В таком случае говорят, что они
находятся вне наблюдаемой Вселенной для точки р; наблюдаемая часть Вселенной лежит на
2}с ijc dft
световом конусе прошлого для точки р или внутри него
 Попробуйте получить в явном виде 4-пространство Минковского, представленное на рис. 27.16 6, взяв
правую половину полного 2-пространства Минковского (с метрикой ds2 = dt2 — dr2 при г ^ 0) и вращая ее
описанным образом вокруг вертикальной оси. Выразите метрику 4-пространства через подходящие функции от
переменных t, г и сферических полярных углов в, ф (см. упражнение 27.18). (Для большей наглядности попробуйте
сначала получить 3-пространство Минковского, где вращение выглядит более привычно.)
Понятно ли, как согласуются диаграммы, показанные на рис. 27.11 и 27.16 6? Найдите подходящие
конформные коэффициенты для метрик в каждом из примеров на рис. 27.16, 27.17.
Исходя из приведенных конформных диаграмм покажите, что при К = 0 или К < 0 и А = 0 наблюдаемая
Вселенная для частицы, первоначально находившейся в точке р, в будущем увеличивается до всей Вселенной.
В случае К > 0, а также при Л > 0 и любом К (из показанных на рис. 27.17) ситуация будет иной — появляется
«космологический горизонт событий».
***

608
Глава 27
Ось
симметрии
Бесконечность
3
* Сингулярность
Точка
О Сфера S
а)
«)
Рис. 27.16. Конформные диаграммы дают плоские представления пространства-времени, обычно они
изображаются таким образом, что пространственно-временные нулевые линии, лежащие на самой
плоскости, оказываются ориентированными под углом 45°. «Бесконечность» представляют как конеч¬
ную границу картины, при этом конформный коэффициент перехода от физической метрики к метрике
диаграммы на границе стремится к нулю, а) На строгой конформной диаграмме (в отличие от схе¬
матической диаграммы) каждая точка внутренней области диаграммы представляет точную 2-сферу,
однако на оси симметрии (она показана прерывистой линией) 2-сфера стягивается в точку, то же
относится к угловой точке, помеченной темным кружком •; однако в углу, отмеченном светлой точ¬
кой о, граничная точка по-прежнему конформно представляет 2-сферу. Бесконечность изображается
сплошной граничной линией (она часто обозначается знаком J?), сингулярности — волнистыми гра¬
ницами. б) Строгая конформная диаграмма для пространства Минковского М. в) Строгая конформная
диаграмма для рис. 27.11, изображающая сферически симметричный коллапс в черную дыру
Л-0
а)
Л>0
г)
к> о
*
I
I
I
I
I
I
t
6)
д)
к= о
в)
е)
К< О
Рис. 27.17. Строгие конформные диаграммы для перспективных моделей Фридмана, изображенных
на рис. 27.13. а) ТС > 0, Л — 0; б) К — О, Л = 0; в) К < 0, Л = 0; г) К > 0, Л > 0 (Л имеет большую
величину); д) К = О, Л > 0; е) К < 0, Л > 0

27.13. Наш собственный особенный Большой взрыв
609
Сингулярность, или 3
+
/А
/<f
я)
Большой взрыв
б)
Рис. 27.18. Горизонты, а) Горизонты событий возникают, когда граница в будущем на схематической
конформной диаграмме (сингулярность или бесконечность) является пространственноподобной. Ко¬
гда наблюдатель р приближается к границе, всегда остается некоторая часть пространства-времени
(граница которой определяется как горизонт событий), которую р не может видеть; какова эта часть —
зависит от того, как движется частица. (Например, событие q в конечном счете можно будет увидеть,
если р движется по левому пути, а не по правому.) В случае черной дыры более известный «гори¬
зонт событий» (показан пунктирной линией в области будущего) имеет более абсолютный характер
и является общим для всех внешних наблюдателей, б) Горизонты для частиц появляются во всех
стандартных космологических моделях, возникая из пространственноподобной сингулярности в про¬
шлом. Наблюдатель в точке р видит лишь ограниченную часть Р Большого взрыва (или созданных им
частиц), хотя со временем эта часть растет
27.13.	Наш собственный особенный Большой взрыв
Вернемся к «совершенно особенному» характеру Большого взрыва. Тот факт, что он
должен обладать абсурдно низкой энтропией, следует уже из самого существования Вто¬
рого закона термодинамики. Однако низкая энтропия может принимать многие различные
формы. Мы хотим понять, каким именно путем наша Вселенная вначале приобрела особый
характер. Особенно поразительное — и внешне противоречивое — свойство Большого взры¬
ва, прекрасно подтверждаемое наблюдениями, состоит в том, что на самой ранней стадии
Вселенная находилась в состоянии теплового равновесия. Это проявляется, в частности,
в исключительной близости спектра микроволнового фонового излучения 2,7 К к теорети¬
ческой кривой Планка для излучения черного тела (см. §21.4, рис. 21.3 б). Это излучение
действительно представляет сегодня «вспышку» Большого взрыва, хотя и чрезвычайно охла¬
жденную из-за «красного смещения», обусловленного расширением Вселенной (рис. 27.19).
Другим проявлением может служить замечательно точное согласие между предсказаниями
теории и результатами наблюдений, касающимися ядерных процессов в ранней Вселен¬
ной. Результаты теоретических расчетов критическим образом зависят от предположения
о тепловом равновесии вещества в ранней Вселенной с учетом быстрого ее расширения.
Мне представляется, что это видимое тепловое равновесие в ранней Вселенной вве¬
ло в глубокое заблуждение некоторых космологов, которые рассматривают Большой взрыв
как некоторое «хаотическое» (т. е. тепловое) состояние с высокой энтропией, несмотря на
тот факт, что, в силу Второго закона, оно должно быть высокоорганизованным (т. е. низко¬
энтропийным) состоянием. Широко распространена точка зрения, что разрешением этого
парадокса должен служить тот факт, что сразу после Большого взрыва Вселенная была «ма¬
ленькой», так что ей было доступно сравнительно малое число степеней свободы, и это
создавало низкий «потолок» возможных значений энтропии. Однако такая точка зрения,
как было показано в § 27.6, является ошибочной. Корректное разрешение этого кажущегося
парадокса заключено в том факте, что гравитационные степени свободы не были «терма-
лизованы» вместе с теми степенями свободы вещества и электромагнитного поля, которые

610
Глава 27
л
О
*
х
U
• .
сч
н
PQ
00
I
О
Л
е
о
ж
PQ
К
о
Я
(D
Н
К
а
5
4 -
3 -
2 -
1
О
о
200
400
г; ГГц
600
Рис. 27.19. Интенсивность микроволнового фона как функция частоты весьма точно согласуется с план-
ковской кривой для излучения черного тела (рис. 21.3 б). (Заметьте, что величина ошибок, показанная
вертикальными отрезками, преувеличена в 500 раз.)
определяют параметры, описывающие «тепловое состояние» Вселенной после Большого
взрыва. Эти гравитационные степени свободы, представляющие гигантский резервуар эн-
тропии, часто вообще не принимают во внимание!
Напомним (см. рис. 27.10), что коль скоро максимальная энтропия описывается без
учета гравитации, как энтропия обычного «теплового состояния», мы получаем нечто со¬
вершенно отличное от той максимальной энтропии, которая имеет место, когда начинают
доминировать гравитационные эффекты, как в случае черной дыры. При наличии гравита¬
ции сжатию вещества может соответствовать гораздо большая энтропия, нежели обычному
тепловому движению, особенно когда такое гравитационное сжатие приводит к образованию
черных дыр. Это особенно ярко проявляется в случае замкнутой Вселенной. Представим се¬
бе, что Вселенная близка (в соответствии с наблюдениями) к модели ФЛРУ, и предположим,
что К > 0 и А = 0. Присутствие в исходном материале некоторой нерегулярности^27*42^
может привести к гравитационной конденсации; предположим, что этого достаточно для
присутствия галактик, содержащих большие черные дыры (например, с массой 1О6М0),
дающих энтропию порядка 1021 на барион. Если принять, что наша замкнутая Вселенная
содержит Ю80 барионов (примерно такой порядок имеет число барионов в наблюдаемой
Вселенной), то это дает полную энтропию Ю101, что намного больше 1088 — энтропии,
содержавшейся в излучении и веществе в момент расцепления 300000 лет спустя после
Большого взрыва. Галактические черные дыры будут постепенно расти, однако наиболь¬
шее увеличение произойдет на конечной стадии коллапса Вселенной, когда все галактики
соберутся вместе и их черные дыры сольются. Финальный Большой хлопок не выглядит
так изящно, как показано на рис. 27.13 а, где он представлен как временное отражение
Большого взрыва в симметричной модели ФЛРУ, — на самом деле он более похож на
невообразимую мешанину из сливающихся сингулярностей черных дыр (см. рис. 27.20 а).
Пользуясь формулой Бекенстайна- Хокинга, можно оценить энтропию этой мешанины неза¬
долго до финальной стадии Большого хлопка, когда ее еще можно считать состоящей из
реальных черных дыр и приближающейся к конечному агломерату черных дыр, содержа¬
щему все Ю80 барионов. Величина Sbr для такого числа барионов, составляющая 10123,
не должна быть слишком далека от энтропии, приписываемой этой мешанине Большого
хлопка.

27.13. Наш собственный особенный Большой взрыв
611

. \ ч	£t	. *\ t* f '
v* „*	г	v
\л -У	1	/ и
V. #	ъ,)
а)
б)
б)
г)
Рис. 27.20. а) Если для случая К > 0, А = 0, изображенного на рис. 27.13 а, допустить присутствие
нерегулярностей такого типа, какие наблюдаются в нашей реальной Вселенной, то вместо «чистого»
Большого хлопка, описываемого точной моделью Фридмана, мы получим невообразимую мешанину
из сливающихся сингулярностей черных дыр с намного большей энтропией (S 10123). б) Это не
зависит от предположения А — 0, поскольку мы можем аналогично рассмотреть соответствующие
возмущения для рис. 27.13 г (К > 0, А > 0), обращенного во времени, и снова получить подобную
мешанину из сливающихся черных дыр со столь же огромной энтропией (S ~ 10123). в) Большой
взрыв общего вида должен выглядеть как обращение во времени аналогичного коллапса (показано
для К > 0 и А — 0 либо А > 0). г) Наиболее «вероятная» ситуация (соответствующая кривой на
рис. 27.18 а), иллюстрируемая для случая К > 0, А — 0, не похожа на поведение реальной Вселенной
на ее ранней стадии
Здесь читатель может, конечно, резонно возразить, что даже если действительно К > 0,
то современные наблюдения, по-видимому, упорно свидетельствуют против сделанного
мною предположения Л — 0, при этом наблюдаемое положительное значение постоянной Л
(вместе с вытекающим из наблюдений предельным значением пространственной кривиз¬
ны) представляется достаточно большим, чтобы предотвратить появление рассматриваемой
нами фазы коллапса, вместо этого следует ожидать в конечном счете экспоненциально¬
го расширения. Однако предыдущее обсуждение, при правильной формулировке, остается
справедливым, и та же самая величина энтропии (~ 10123) будет иметь место в замкну¬
той Вселенной с Ю80 барионами, невзирая на то что А > 0. Для обращенной во времени
Вселенной с рис. 27.13 г справедливо то же решение динамических уравнений, что и для
исходной Вселенной на рис. 27.13 г (поскольку мы рассматриваем динамические законы,
симметричные относительно обращения времени). Если рассматривать возмущения, возни¬
кающие в такой Вселенной, то можно найти модели, в которых уже сформированные черные
дыры сближаются одна с другой, образуя некоторую «мешанину» из сливающихся черных
дыр, подобную рассмотренной выше (см. рис. 27.20 б). Из тех же рассуждений, что и раньше,
мы опять получаем значение энтропии порядка 10123. (Подобные рассуждения понадобятся
нам снова, когда мы перейдем к рассмотрению инфляционной космологии в § 28.5.)
Итак, мы пришли к разумной оценке для полного объема фазового пространства Vu
(который, по существу, есть то же самое, что и объем Е ящика £ с максимальной энтропией
на рис. 27.4), а именно к экспоненте от полученного значения энтропии:
1П123	1П123
Е = е10	«	Ю10
(это следует из формулы Больцмана S — log У в естественных единицах)*. Как это соотно¬
сится с тем, что мы знаем об объеме N ящика ЛД соответствующего нынешней энтропии,
Почему эти числа (в пределах точности задания числа 123) фактически одни и те же? Почему в ниже-
том заключении не фигурирует реальное значение величины В?

612
Глава 27
и с объемом В ящика В, соответствующего энтропии Большого взрыва (предполагаем пока,
что мы живем во Вселенной с Ю80 барионами)? Используя данные выше оценки для эн¬
тропии черной дыры, нынешней энтропии и энтропии излучения 2,7 К в расчете на один
барион, получаем
1 л88	1П10!	-]	г\123
В : N : Е = Ю10 : Ю10	: Ю10 .
Отсюда следует, что объемы В и N составляют всего лишь
ш123
одну 10 -ю часть
полного объема Е. Более того, объем В составляет всего
in101
одну 10 -ю часть
объема N фазового пространства сегодняшней Вселенной.
Чтобы лучше ощутить проблему, связанную с абсурдно малым объемом фазового про¬
странства В, можно представить себе Создателя, который пытается нащупать тонкой иглой
это крохотное пятнышко в пространстве Ти, чтобы дать Вселенной старт, в результате ко¬
торого она выглядела бы такой, какой мы ее знаем сегодня. На рис. 27.21 я изобразил
фантастическую картину, представляющую это знаменательное событие. Если бы Созда¬
тель чуть-чуть промахнулся мимо этого пятнышка и ткнул своей иголкой куда-то в область
максимальной энтропии £, то получилась бы Вселенная, непригодная для проживания в ней,
вроде показанной на рис. 27.20г для случая А — 0, К > 0, но в остальном подобная вечно
расширяющейся Вселенной на рис. 27.20 в. В такой Вселенной не было бы Второго зако¬
на, определяющего статистическую направленность времени (как на рис. 27.8 а). (Это не
станет намного более понятным, если представить себе, что наш Создатель просто задался
целью построить Вселенную, в которой могли бы существовать разумные существа вроде
нас. Это приводит к «антропному принципу», который мы обсудим в §§28.6, 28.7, 34.7.)
Рис. 27.21. Фантастическое представление: создание Вселенной! Тонкая игла Создателя должна отыс¬
кать крошечный ящик, всего одну 1010 -ю часть полного объема фазового пространства, чтобы
получилась Вселенная с именно таким Большим взрывом, о каком мы знаем
С другой стороны, вполне возможно, что Вселенная бесконечна в пространстве подобно
моделям ФЛРУ с К = 0 или К <0. Это не отменяет предыдущих рассуждений. Мы можем
относить их не ко всей Вселенной, а лишь к ее наблюдаемой (в данный момент) части. Если
принять, что наблюдаемая ныне Вселенная содержит порядка 1080 барионов, то не видно

27.13. Наш собственный особенный Большой взрыв
613
причин, по которым эти рассуждения могли бы серьезно измениться. Если же применить их
ко всей Вселенной в целом (сохраняя модель ФЛРУ в качестве хорошего приближения), это
будет означать требование бесконечной (а не просто крайне высокой) точности со стороны
Создателя. Я не вижу, как это может каким-то образом разрешить загадку необычайно
точной «настройки», присущей Большому взрыву и существенно связанному с ним Второму
закону.
Что получили мы из этих рассуждений? Мы узнали не только об исключительно осо¬
бенной природе Большого взрыва, с которого началась Вселенная, но и нечто важное о ха¬
рактере этой особенности. Пока мы имеем дело с веществом (включая электромагнетизм),
описание «теплового равновесия» в модели расширяющейся Вселенной представляется
вполне подходящим. Картина «горячего Большого взрыва» представляет важную состав¬
ную часть стандартной космологической модели. Спустя 10~п с после взрыва Вселенная,
по-видимому, должна была иметь температуру порядка 1015 К, после 102 с температура
упала до 109 К. Это падение температуры согласуется со скоростью расширения в теории
Толмена - Фридмана, и многие результаты наблюдений (например, наблюдаемые отношения
водород/дейтерий/гелий) находятся в согласии с ядерными процессами, происходящими при
таких температурах.
В то же время при наличии гравитации ситуация совершенно меняется в том отноше¬
нии, что гравитационные степени свободы совсем не «термализуются». Именно высокая од¬
нородность (в соответствии с моделью ФЛРУ) начальной геометрии пространства-времени
была особенностью Большого взрыва. То, что начальное сингулярное состояние Вселенной
«не обязано было быть таким», иллюстрирует рис. 27.20# или обращенный во времени фи¬
зически приемлемый Большой хлопок на рис. 27.20 а. Гравитация имеет совершенно особый
статус, отличный от статуса любого другого поля. Вместо того чтобы участвовать, как все
другие поля, в термализации ранней Вселенной, гравитация остается в стороне, ее степе¬
ни свободы «выжидают в засаде», так что Второй закон вступает в игру, лишь когда эти
степени свободы начинают проявляться. Это дает нам не только Второй закон, но и опре¬
деляет ту частную форму, в которой мы наблюдаем его в Природе. Гравитация играет здесь
совершенно особую роль!
Но почему особую? Пытаясь отвечать на вопросы такого рода, мы вступаем на более
зыбкую почву. В главе 28 мы познакомимся с некоторыми приемами, посредством которых
физики пытаются подойти к этой и связанным с нею загадкам, касающимся происхожде¬
ния Вселенной. На мой взгляд, никакие из этих попыток не приводят к решению загадки,
сформулированной в предыдущем абзаце. Согласно моим собственным воззрениям, нам
придется вернуться к исследованию самих основ квантовой механики, поскольку я глубоко
убежден в существовании глубокой связи между этими проблемами. Мы займемся этим
в главе 29. Далее, в главе 30, я постараюсь изложить свой подход к этим фундаментальным
вопросам.
Примечания
§27.2.
21 Л. Здесь предполагается полностью классическая динамика. В математическом отношении «хао¬
тическая система» — это классическая система, у которой ничтожно малое изменение началь¬
ного состояния может привести к существенному изменению поведения, причем отклонение
со временем растет экспоненциально, а не, например, линейно. Такая «непредсказуемость»
есть, конечно, вопрос меры и степени, а не принципа, как иногда утверждается в отношении
детерминизма.
27.2.	Здесь предполагается, что все теплоемкости положительны, как это обычно и бывает. Однако
в случае черных дыр это допущение обычно не выполняется (см. §31.15).

614
Глава 27
27.3. Существует, однако, забавный «парадокс», состоящий в том, что в обыденной жизни всё как
будто обстоит наоборот! Мы часто делаем точные «предсказания назад», просто вспоминая
то, что произошло в прошлом, тогда как аналогичного доступа в будущее у нас нет. Более того,
геологические и археологические исследования могут распространить подобную «память» на
времена, когда еще не существовало человечество. Однако подобное возвращение назад ни
в каком смысле не включает в себя эволюцию, описываемую динамическими уравнениями,
так что ее детальная связь со Вторым законом пока остается довольно неясной для меня
(см. [600]).
§27.3.
27.4. См. [573].
27.5. См. [297, 236, 572].
27.6. На самом деле сам Больцман этой постоянной никогда не пользовался, так как его не ин-
*
тересовали единицы, которые можно было бы реально применять на практике (см. [131]).
Формула S — к log V, содержащая эту постоянную, впервые, по-видимому, была написана
Планком (см. [572]).
§27.5.
27.7. Из книги [230].
§27.6.
27.8. См. [370, 529, 809, 358].
27.9. См. [307]. В книге [779] эти идеи приводят к	довольно фантастическому выводу.
27.10. См. [600]
• §27.7.
27.11. За несколько лет до Хаббла, в 1917 году, американский астроном Весто Слифер уже обнаружил
некоторые указания на то, что Вселенная расширяется (см. [727]). Этим его наблюдениям
редко доверяют, однако именно он руководил командой, в составе которой Клайд Томбо
открыл Плутон!
27.12. Существование такого излучения впервые было теоретически предсказано в 1946 году Ге¬
оргием Гамовым на основе картины Большого взрыва, в более явном виде Альфером, Бете
и Гамовым в 1948 году и затем независимо	Робертом Дикке в	1964 году. В 1965	году	оно
было (случайно) обнаружено наблюдениями	Арно Пензиаса и	Роберта Вильсона	и	немед¬
ленно интерпретировано Дикке с сотрудниками. См. [17, 198] и, конечно, работу Пензиаса и
Вильсона [630], имеющую, возможно, наиболее скромное название, которое когда-либо было
у научной работы!
27.13. Дальнейшее обсуждение см. в [600, 610].
27.14. Фактически Земля отправляет обратно несколько больше энергии, чем получает. Если прене¬
бречь энергией, получаемой от сжигания людьми ископаемого топлива (при этом фактически
возвращается некоторая энергия, полученная от Солнца и накопленная в недрах Земли много
миллионов лет назад), а также находящимся на обратном конце временной шкалы глобаль¬
ным потеплением из-за «парникового эффекта», в результате которого Земля захватывает
несколько больше солнечной энергии, нежели прежде, то остается разогрев внутренней части
Земли в результате радиоактивного распада; эта энергия постепенно теряется в окружающее
пространство, проникая через атмосферу. См. § 34.10.
§27.8.	•* '• '•
27.15. См. [522, 780].	*
% •
27.16. См. [599].
27.17. Относительно современного состояния этого вопроса см. [801].
27.18. См. [707], а также современное изложение [809].
27.19. См. недавние подтверждения [542].

27.13. Наш собственный особенный Большой взрыв
615
§27.9,
27.20. Одной из характерных особенностей такой «точки невозврата» является появление так назы¬
ваемой «захваченной поверхности». Захваченная поверхность представляет собой компакт¬
ную пространственноподобную 2-поверхность S, обладающую тем свойством, что оба семей¬
ства нулевых нормалей к S сходятся в будущем. (На более обыденном языке это означает, что
если на поверхности S возникает вспышка света, то площади выходной и входной частей этой
вспышки будут становиться всё меньше.) Мы ожидаем обнаружить захваченные поверхности
внутри горизонта Л черной дыры. Эффективность критерия захваченной поверхности обу¬
словлена тем, что он не зависит от каких-либо предположений насчет симметрии и «устойчив»
относительно малых возмущений геометрии. Коль скоро захваченная поверхность сформи¬
ровалась, сингулярности оказываются неизбежными (если наложить очень слабые условия
причинности и положительности энергии в теории Эйнштейна). Аналогичные выводы при¬
менимы также к космологической сингулярности Большого взрыва (см. [587, 372]).
27.21. См. [587, 372]. Более подробное изложение этих теорем содержится в [809].
27.22. См. [592, 618, 69].
27.23. См. [592, 618].
27.24. Наиболее современный взгляд на эти проблемы изложен в [656, 138]. Теория столкновений
содержится в [350].
§27.10.
27.25. См. [416, 129, 364, 668].
27.26. Случай заряженной черной дыры рассмотрен в [444, 553]. Более подробное изложение содер¬
жится в [809].
27.27. Наряду с кеплеровскими эллипсами, упомянутыми в начале этой главы, метрика Керра пред¬
ставляет другой пример исключительной ситуации, когда мы должны благодарить судьбу
за сравнительно простые геометрические конфигурации, которые следуют из динамических
законов.
27.28. См. [135], стр. 1.
27.29. Фактически (как мы увидим в §31.15, см. также примечание 27.26) имеется еще один па-
личиной, см. § 19.3), Но в случае реальных астрофизических черных дыр его влиянием на
геометрию черной дыры можно пренебречь по сравнению с влиянием параметров т и а,
поскольку черная дыра имеет сильную тенденцию к нейтрализации электрического заряда.
27.30. Это число е не следует, конечно, путать с основанием натуральных логарифмов е =
= 2,7182818285 ...; см. § 5.3.
§27.11.
27.31. Относительно результатов программы СОВЕ см. [734], относительно WMAP см. [740].
27.32. Прекрасное введение в космологию содержится в [486]. В книге [809] дается изложение на
более высоком уровне.
27.33. См. [91,666,213].
27.34. Для описания ситуации, когда К — 0, Л > 0 и имеет место инфляция, используется термин
«модель согласия». См. [84, 49]. Моя оценка современного состояния этого вопроса содер¬
жится в §28.10.
27.35. Имеется довольно своеобразная возможность предположить, что древние греки были правы
(рис. 1.1) и наша Вселенная имеет форму додекаэдра (или, скорее, некоторой конструкции,
склеенной из додекаэдров). См. [500].
27.36. Термин гиперповерхность относится к (п — 1)-мерному подмногообразию некоторого п~
многообразия. В данном случае % есть пространственноподобная 3-поверхность.
27.37. См. [449, 851].

616
Глава 27
§27.12.
27.38. Такие диаграммы иногда называют «диаграммами Пенроуза» или «диаграммами Картера-
Пенроуза». Я впервые использовал их в своей лекции в Варшаве [583]; систематическое
понятие строгой конформной диаграммы было введено Картером [127, 128]; см. также [295].
27.39. См. [585, 586, 128] и [627], гл. 9.
27.40. У некоторых теоретиков получили признание определенные гипотетические модели, в ко¬
торых Большой взрыв (или, скорее, Большой хлопок) представляет конформную (т. е. при¬
чинную) точку (так называемую Q-точку); см. [779]. Мне, однако, не известно какое-либо
обсуждение, совместимое с рассуждениями в главе 27, которое сделало бы такие модели
физически правдоподобными.
27.41. Относительно термина «гиперповерхность» см. примечание 27.36. В данном случае мы ви¬
дим, что Большой взрыв в конформном представлении является трехмерным. (Это можно
сопоставить с некоторыми другими представлениями; см. [666].)
§27.13.
27.42. Часто предполагается, что такие нерегулярности в конечном счете обусловлены «квантовыми
флуктуациями» начальной плотности вещества Большого взрыва. (Мы обсудим это в § 30.14.)

Глава 28
Умозрительные теории ранней Вселенной
28.1.	Спонтанное нарушение симметрии в ранней Вселенной
До сих пор наше изложение не выходило за рамки твердо установленной физической
теории, в которой даже порой странно выглядящие идеи имеют мощную поддержку со
стороны впечатляющих результатов наблюдений. Некоторые из моих рассуждений были
изложены в форме, несколько отличной от принятой в литературе, но я не думаю, что в этом
есть что-то предосудительное. В этой главе я начинаю излагать идеи более умозрительного
характера, связанные с особым характером Большого взрыва.
В частности, мы обсудим идеи инфляционной космологии в дополнение к идеям, отно¬
сящимся к спонтанному нарушению симметрии в ранней Вселенной (см. § 25.5), Некоторые
читатели, знакомые с основными идеями космологии, могут удивиться, почему я так уве¬
ренно отношу инфляционную космологию к разряду умозрительных теорий. Действительно,
в популярных обзорах часто преподносится как установленный факт, что на очень ранних
стадиях развития Вселенной имел место период экспоненциального расширения, в ходе ко¬
торого произошло раздувание Вселенной в Ю30 раз, а возможно, даже в 1060 и более раз.
Других осведомленных читателей может еще больше встревожить тот факт, что я рассмат¬
риваю в качестве умозрительной идеи общее явление спонтанного нарушения симметрии
в ранней Вселенной. Тем не менее понятия, которым я собираюсь посвятить эту главу, пока
не получили в полной мере (если получили вообще) достаточное и однозначное подтвер¬
ждение со стороны наблюдений, так что остается вопрос, действительно ли эти идеи имеют
какое-то отношение к Природе.
Начнем с общей идеи спонтанного нарушения симметрии. Вспомним о роли этой идеи
в создании перенормируемой квантовой теории поля (КТП), где перенормируемость предпо¬
лагает наличие более высокой («скрытой») симметрии, нежели та, которая непосредственно
проявляется в наблюдаемом поведении. Потеря части этой полной симметрии во внешних
проявлениях объясняется выбором системой некоторого «вакуумного состояния», не обла¬
дающего полной симметрией динамической теории. Это, в частности, является основной
составляющей той части стандартной модели физики элементарных частиц, которая отно¬
сится к теории электрослабого взаимодействия. Идеи такого рода, содержащие предположе¬
ние о возможности различных «вакуумов», представляют также существенную составную
часть инфляционной теории; понятия спонтанного нарушения симметрии и «ложных вакуу¬
мов» также часто привлекаются теоретиками при поиске схем еще более общего характера.
Однако я должен пояснить, что отнюдь не считаю умозрительной идею спонтанного нару¬
шения симметрии саму по себе. Она принесла несомненную пользу при изучении многих
реально существующих физических явлений (отличным примером может служить сверх¬
проводимость). Она применяется, зачастую весьма изящным и вполне удовлетворительным
образом, к ряду твердо установленных явлений. Мои сомнения относительно нее связаны
с тем, что ее привлекательность может иногда побуждать физиков применять ее слишком
широко и порой в неподходящих условиях.
Идея спонтанного нарушения симметрии часто наглядно иллюстрируется на примере
явления ферромагнетизма. Представим себе сплошной шар из железа. Его атомы можно
представить себе как маленькие магнитики, которые, вследствие действующих на них сил,

618
Глава 28
выстраиваются параллельно своим соседям с одной и той же ориентацией север-юг. При до¬
статочно высокой температуре, а именно некотором критическом значении 770°С (1043 К),
энергетическое тепловое возбуждение атомов пересиливает эту тенденцию к выстраиванию
магнитиков, и материал не проявляет склонности становиться магнитом в макроскопиче¬
ском масштабе, поскольку маленькие атомные магнитики оказываются ориентированными
случайным образом. Однако при температуре ниже 770°С (так называемой «точки Кюри»)
энергетически более выгодна упорядоченная ориентация атомов, так что в идеальной ситу¬
ации железо оказывается намагниченным !28Л1.
Предположим теперь, что наш железный шар первоначально нагрет выше 770 °С
(но не настолько, чтобы он расплавился), так что вначале он не намагничен. Затем окружаю¬
щую среду постепенно охлаждают до температуры ниже критической 770°С. Что при этом
происходит? Естественно, что шар будет переходить в состояние с минимальной энергией,
отдавая энергию внутренних колебаний атомов в более холодную окружающую среду. Из-
за взаимодействия между соседними атомами минимальная энергия получается, когда все
атомы выстроены в одном и том же направлении, так что шар становится намагниченным
с определенным направлением полярности север-юг. Однако никакое из этих направлений
не имеет предпочтения перед любым другим. Имеет место так называемое вырождение со¬
стояний с минимальной энергией (сравните с § 22.6). Если нет выделенного направления в
начальном нагретом ненамагниченном состоянии, то и направление конечной намагниченно¬
сти оказывается случайным. Это есть пример спонтанного нарушения симметрии: начальное
сферически симметричное состояние переходит в состояние с более низкой симметрией, а
именно с симметрией вращения вокруг результирующей магнитной оси север-юг. Состояние
с симметрией SO(3) (исходный горячий ненамагниченный шар) превращается в состояние
с симметрией SO(2) (холодный намагниченный шар); относительно смысла этих символов
см. §§13.1-13.3, 13.8, 13.10.
Ситуацию такого рода можно описать с помощью потенциала в форме мексиканской
шляпы, изображенного на рис. 28.1. «Шляпа» представляет семейство допустимых состоя¬
ний системы (при нулевой температуре окружающей среды), а «высота» - энергию системы.
Мы видим, что существует равновесное состояние (имеющее горизонтальную касательную
плоскость), соответствующее вершине шляпы, которое обладает полной симметрией исход¬
ной группы; на рисунке эта группа представлена вращением вокруг вертикальной оси. (Вра¬
щательная симметрия SO(2) является аналогом полной симметрии железного шара SO(3),
нам пришлось отбросить одно пространственное измерение, чтобы получить наглядную кар¬
тину. Вершина шляпы представляет полное отсутствие намагниченности шара как целого.)
Однако такое равновесие, представляющее ненамагниченное состояние, неустойчиво и не
соответствует минимуму допустимых энергий. Таким минимумам отвечают состояния, пред¬
ставленные горизонтальными частями (по всей окружности) на полях шляпы (различным
точкам на полях соответствуют различные направления полной намагниченности железного
шара).
Исходное состояние на вершине можно рассматривать как состояние находящегося там
шарика, представляющего физическое состояние, оставшееся от предшествующего высо¬
котемпературного состояния. Потеря устойчивости означает, что шарик скатится из этой
точки вниз (предполагается наличие влияния некоторого случайного возмущения) и займет
состояние покоя в некоторой точке на полях шляпы. Каждая точка на полях, в которой мо¬
жет оказаться шарик, представляет некоторое направление намагниченности, которую может
приобрести в конечном счете наш железный шар. Положение шарика представляет конечное
физическое состояние. Однако в силу вращательного вырождения для шарика нет предпо¬
чтительного места, в котором он в конце концов окажется. Все положения равновесия на
полях шляпы одинаково хороши. Выбор шарика есть дело случая, и коль скоро такой выбор
сделан, происходит нарушение симметрии из-за появления некоторого случайно выбранного
направления.

28.1. Спонтанное нарушение симметрии в ранней Вселенной
619
Рис. 28.1. Спонтанное нарушение симметрии в системе с потенциалом в форме мексиканской шляпы,
определяющим допустимые состояния; мерой энергии служит высота. Состояние системы представ¬
лено шариком, движение которого ограничено поверхностью шляпы. Если температура окружающей
среды достаточно высока (точка Кюри), равновесное состояние системы представляется шариком,
покоящимся на вершине шляпы, оно обладает полной вращательной симметрией (в данной упрощен¬
ной картине симметрией SO(2)). При понижении температуры шарик скатывается вниз и достигает
в конечном счете некоторой произвольной точки равновесия на полях шляпы, что нарушает полную
вращательную симметрию
Явление такого рода, когда понижение окружающей температуры приводит к резкому
кардинальному изменению природы устойчивого равновесного состояния вещества, называ¬
ется фазовым переходом. В нашем примере с железным шаром фазовый переход происходит,
когда шар из ненамагниченного состояния (при температуре выше 770° С) переходит в од¬
нородно намагниченное состояние (при температуре ниже 770°С). Более известны явление
замерзания (переход из жидкого состояния в твердое при понижении температуры) и обрат¬
ный процесс кипения (превращение жидкости в пар при повышении температуры). Фазовый
переход при понижении температуры часто сопровождается понижением симметрии, но это
не так существенно.
В КТП фазовый переход часто описывается как выбор нового вакуумного состояния
(вроде \&) в § 26.11), когда состояние «туннелирует»^28*2^ из одного вакуума в другой. Такое
описание следует рассматривать как некоторое приближение, однако, строго говоря, не су¬
ществует (унитарного) квантово-механического процесса, который переводит состояние из
одного сектора в другой (под «сектором» понимаются состояния, которые можно построить
при данном выборе вакуумного состояния 10); состояния различных секторов принадлежат
различным гильбертовым пространствам; см. §§26.5, 26.11). Приближение, в котором си¬
стема предполагается бесконечной, хотя на самом деле она конечна, в практических ситу¬
ациях вполне приемлемо. Например, таким образом трактуется хорошо известное явление
сверхпроводимости (падение электрического сопротивления до нуля при достаточно низкой
температуре): сверхпроводимость рассматривается как фазовый переход, сопровождающий
понижение симметрии, нарушающее обычную U(1)-симметрию электромагнетизма.
В частном примере, представленном на рис. 28.1, симметрия понижается от группы
вращений вокруг оси SO(2) до тривиальной группы SO(l), содержащей всего один элемент
(так что в данном примере в конечном счете теряется вся симметрия, поскольку конечное
положение шарика полностью нарушает симметрию) t28*3!. Однако аналоги этой «шляпы»
с более высокой размерностью иллюстрируют спонтанное понижение симметрии от SO (р)
до SO (р - 1) с р > 2* (Наш железный шар иллюстрирует случай р = 3.) Можно также
использовать картину с «мексиканской шляпой» для иллюстрации понижения симметрии
от U(2) до U(l), что имеет место в стандартной модели физики элементарных частиц ,
Покажите, что «шляпа», форма которой описывается уравнением Е = (ж| Н~ • • ■ + ж2 — I)2, проявляет
такое нарушение симметрии.
Покажите это, рассматривая действие U(2) на С с комплексными координатами (гу, z), в которых «шляпа»
описывается уравнением Е = (\w\2 + \z\2 — I)2. Понятно ли, как выглядит геометрия понижения этой симметрии в
конфигурации клиффордовых параллелей в пространстве S3, описанной в § 15.4 и показанной на рис. 15.8 и 33.15?

620
ч
Глава 28
где электрослабая симметрия U(2) (см. §25.5) понижается до симметрии электромагнетиз¬
ма U(l) при температуре 1016 К, которую имела Вселенная через 10~12 с после Большого
взрыва. В более общих теориях Великого объединения (см. § 25.8) фигурируют другие груп¬
пы, например SU(5), так что можно рассматривать разные стадии нарушения симметрии
при различных температурах. Так, при некоторой температуре, намного большей 1016 К
(т. е. значительно раньше, чем через 10~12 с после Большого взрыва), симметрия SU(5) мо¬
жет нарушиться с понижением до некоторой подходящей t284J симметрии, которая содержит
группу SU(3) для сильного взаимодействия и SU(2) xU(l)/Z2 (т. е. U(2)) для электрослабого
взаимодействия.
28,2.	Космические топологические дефекты
Рис. 28.2. В идеальном случае, при
медленном охлаждении ферромаг¬
нетика ниже точки Кюри, векто¬
ры намагниченности составляю¬
щих его атомов выстраиваются в
одном и том же (произвольном)
направлении. Однако на практике
(или при слишком быстром охла¬
ждении) мы получаем «лоскутную
Мы должны, однако, иметь в виду, что такое наруше¬
ние симметрии редко происходит «сразу повсюду», вместо
этого появляются домены — области, в которых симмет¬
рия нарушается в различных «направлениях». Рассмотрим
снова наш идеализированный железный шар. Можно ожи¬
дать, что случайный начальный выбор направления намаг¬
ниченности будет различным в разных местах шара. Ес¬
ли охлаждение происходит достаточно медленно, то эти
неоднородности «сглаживаются», и получается однород¬
ный магнит^28*5!. Однако при быстром охлаждении может
оказаться, что мы получим «лоскутную» структуру с раз¬
личным направлением намагниченности, подобную пока¬
занной на рис. 28.2. Размер образующихся ячеек и состав¬
ляемая ими картина, помимо всего прочего, могут зависеть
от скорости охлаждения. Они зависят также от того, какова
«связь» между различными областями и в какой мере на¬
правление намагниченности в одной области шара может
«переключаться» под влиянием соседних областей.
Более серьезным и интересным явлением оказывается
возникновение топологических дефектов, которые нельзя
структуру» с различными направ¬
лениями намагниченности
устранить никаким поворотом направлении намагничен¬
ности внутри шара. Таким дефектом является «магнитный
монополь Дирака» (изолированный северный или южный
магнитный полюс). Такой монополь невозможно создать в
обычном пространстве никаким набором магнитов и то¬
ков*. Можно, однако, получить эффективный монополь, позволив магнитному заряду течь
вдоль «дираковской проволоки», как показано на рис. 28.3. Если ввести магнитные заряды
в теорию Максвелла (§ 19.2), то «проволока» появится только в потенциале А (§ 19.4) и ее
можно будет устранить, приняв подходящую «расслоенную» точку зрения (§ 15.4). Монополь
такого рода может существовать также в некоторых неабелевых калибровочных теориях.
Усложнения в картине спонтанного понижения симметрии, частично продемонстриро¬
ванные на «земном» примере железного шара, относятся также и к фундаментальным физи¬
ческим теориям более возвышенного уровня (например, к теории электрослабого взаимодей¬
ствия или теории Великого объединения), в самой основе которых лежит идея спонтанного
нарушения симметрии. Можно ожидать возникновения топологических дефектов в большом
(космологическом) масштабе, если такое спонтанное нарушение симметрии имело место в
Покажите это, воспользовавшись интегральными соотношениями из главы 19.

28.2, Космические топологические дефекты
621
% *
# I
•• ♦
. ^ «Л ^ ^	^	_
♦>	л
^	6	V
✓ * /
* #
♦ S
1 а
*** V
Ф «V
« _
PWi
> •
№
1 л
* А
Аг-
♦ *
»#*
• I
д Север
■ в
ч В
(Юг
Рис, 28.3. Магнитный монополь может возникнуть, если каким-то образом «накачать» в центр сферы
избыточный «южный полюс» по «магнитной проволоке». Если допустить существование магнитных
источников в теории Максвелла, такой полюс можно ввести в центр, и тогда дираковская «проволока»
нужна лишь для создания сбоя потенциала А. Этот сбой можно устранить, приняв «расслоенную»
точку зрения (такие монополи появляются также в некоторых неабелевых калибровочных теориях)
ранней Вселенной. В общем случае (применительно к трехмерному пространству) существу¬
ют три основных вида топологических дефектов в зависимости от размерности той области,
в которой они проявляются. Они носят название (космических) монополей (нулевая про¬
странственная размерность), космических струн (одно пространственное измерение) и до¬
менных стенок (два пространственных измерения). Размерность зависит от топологических
особенностей, совместимых с соответствующей группой симметрии. Важной особенностью
топологических дефектов является невозможность их устранения путем непрерывных из¬
менений «направления» нарушения симметрии (при этом мы считаем, что в самом дефекте
отсутствует определенное направление нарушения симметрии, тогда как в других местах
имеют место непрерывные изменения этого направления). Следует иметь в виду, что поня¬
тие «направления» означает не направление в обычном пространстве, а более абстрактное
«направление», относящееся к рассматриваемой физической модели (например, в теории
электрослабого взаимодействия оно определяет меру смешивания электронов с нейтрино).
В геометрическом смысле можно было бы говорить о векторном расслоении во всем про¬
странстве-времени (если требуется вспомнить это понятие, см. главу 15). Топологические
соображения по-прежнему применимы, и топологические дефекты представляют серьезные
проблемы, от которых нельзя отмахнуться, если нарушение симметрии включается в фун¬
даментальную физическую теорию в качестве составной части.
Действительно, космические струны огромного масштаба (превышающего даже галак¬
тические масштабы) рассматриваются как существенный фактор, определяющий возникно¬
вение в исходном газе тех неоднородностей, которые привели к образованию галактик f28,6^.
Гравитационное поле такой космической струны можно рассматривать как результат приме¬
нения «метода ножниц и клея» к пространству-времени Минковского. Оперируя простран¬
ственными терминами, можно представить себе «сектор», удаленный из 3-пространства,
который ограничен парой полуплоскостей, образующих двугранный утол а, ребром кото¬

622
Глава 28
рого служит сама струна (рис. 28.4). Чтобы построить геометрию космической струны,
следует снова «склеить» вместе две плоские поверхности. (В предложенных моделях угол а
составляет 10~6.)
Рис. 28.4. Гравитационное поле космической струны можно построить, применяя к 4-пространству
Минковского «метод ножниц и клея». В 3-пространстве удаляется сектор, ограниченный двумя полу¬
плоскостями, образующими двугранный угол а, ребром которого служит струна. Поверхности полу¬
плоскостей затем склеиваются
Читателю может не без основания показаться, что это слишком крайние меры для
создания такого «банального» объекта, как обычная галактика. Но в вопросе о происхожде¬
нии галактик пока имеются теоретические загадки, и потому не стоит отметать с порога
подобные экзотические идеи, несмотря на их, казалось бы, неправдоподобный вид. Дей¬
ствительно, одна из наиболее притягательных моделей формирования галактик, получившая
некоторое подтверждение со стороны результатов наблюдений, предполагает, что их «заро¬
дышами» послужили сверхмассивные черные дыры, ныне находящиеся в их центрах f28-7!.
Но черные дыры сегодня следует считать не экзотикой, а стандартными физическими объек¬
тами!
Большинство таких предполагаемых топологических дефектов относится к теориям (на¬
пример, различным теориям Великого объединения), которые пока не имеют существенной
однозначной поддержки со стороны наблюдений. С другой стороны, теория электрослабого
взаимодействия очень хорошо подтверждается наблюдениями, поэтому следует отнестись
со вниманием к результатам применения этой теории к процессам в ранней Вселенной.
Космические монополя, возникающие в результате нарушения симметрии электрослабого
взаимодействия, с топологической точки зрения возможны, но не являются необходимыми.
Они могут возникать при спонтанном понижении симметрии от U(2) до U(l), но лишь при
условии, что в ненарушенной фазе с U (2)-симметрией, которая предполагается существо¬
вавшей до момента 10-12 с, уже присутствуют так называемые «калибровочные монополи».
Такие монополи могут возникать при более раннем нарушении более высокой симметрии
теории Великого объединения, но эти идеи никоим образом не являются необходимой со¬
ставной частью теории электрослабого взаимодействия^288!.
Подобные «калибровочные монополи» являются, в рамках (неабелевой) теории Ян¬
га-Миллса, аналогом «магнитных монополей», впервые предложенных Дираком (в 1931
году) в рамках (абелевой калибровочной) теории электромагнетизма. Путем остроумных
рассуждений Дирак показал, что даже если бы в природе существовал одиночный магнит¬
ный монополь (отдельный северный или южный магнитный полюс), то все электрические
заряды должны были бы иметь значения, кратные некоторой величине, обратно пропор¬

28.3. Проблемы с нарушением симметрии в ранней Вселенной
623
циональной магнитной силе монополя. Фактически современные наблюдения убедительно
свидетельствуют, что все электрические заряды действительно кратны некоторому опре¬
деленному значению (например, заряду анти-б-кварка, составляющему одну треть заряда
протона; см. §§3.5, 25.6). Это можно было бы счесть косвенным подтверждением существо¬
вания магнитных монополей. Тем не менее чтобы такие монополи не оказались в резком кон¬
фликте с наблюдениями, они должны обладать совершенно необычными свойствами i28-93.
(В противном случае они создавали бы эффект «закорачивания» космических магнитных
полей, тогда как такие поля наблюдаются в просторах Вселенной.) Аналогично монополи
Янга-Миллса должны были бы вступать в конфликт с наблюдениями, если бы они присут¬
ствовали в современной Вселенной в достаточном количестве. Как мы скоро увидим, это
понятие играет весьма важную роль в развитии космологии!
28.3.	Проблемы с нарушением симметрии в ранней Вселенной
Прежде чем перейти к этому, полезно вернуться к нарушению симметрии в теории
электрослабого взаимодействия, которое, как предполагается, имело место через 10~12 с
после Большого взрыва. Должны ли мы относиться к этому как к реальному явлению или
это всего лишь артефакт данного способа изложения теории? Насколько я могу судить,
большинство теоретиков в области электрослабого взаимодействия склонно рассматривать
этот процесс как реальный. Тем самым я предупреждаю читателя, что в вопросе о реальности
этого явления я занимаю не вполне стандартную позицию. Тем не менее двинемся дальше
и рассмотрим некоторые трудности, связанные с идеей нарушения симметрии.
Предположим, что, вопреки моему собственному (нестандартному) взгляду на этот
предмет, в ранней истории Вселенной существовал период (предшествующий моменту вре¬
мени 10“12 с после Большого взрыва), когда сохранялась точная симметрия U(2) и все леп-
тоны и кварки имели одинаковую массу, так что «зиг»-электроны и нейтрино можно было
рассматривать на равных основаниях, a W- и Z-бозоны и фотон путем подходящего «поворо¬
та» переводить друг в друга в соответствии с U(2)-симметрией (см. §25.5). Затем, в момент
времени 10“12 с, температура всюду во Вселенной упала чуть ниже критического значения.
В этот момент был сделан случайный выбор (W“, W+, Z°, 7) из полного U(2)-симмет¬
ричного многообразия Q возможных наборов калибровочных бозонов. Мы не ожидаем, что
это произошло совершенно однородным образом во всем пространстве, одновременно во
всей Вселенной. Мы предполагаем, что, как и в случае доменов намагниченности железного
шара, показанных на рис. 28.2, в некоторых областях будет реализован один из возможных
вариантов выбора, а в других местах — другой.
Здесь следует обратиться к вопросу, как понимать в данном контексте слова «тот же са¬
мый» (одинаковый, такой же) и «другой». До момента понижения симметрии пространство Q
возможных калибровочных бозонов в каждой точке пространства-времени обладает полной
симметрией U(2). В понятии расслоения заложено, что не существует предпочтительного
способа установления тождества между пространством Q в одной точке и в какой-то другой
точке. Таким образом, у нас нет априорного правила, определяющего, какой элемент про¬
странства Q в одной точке следует считать «тем же самым» элементом, что и некоторый
элемент пространства Q в другой точке. Это, по-видимому, позволяет нам придерживаться
той точки зрения, что мы можем просто определить понятие «тот же самый», отнеся его
к тому определенному выбору, который делается при спонтанном нарушении симметрии.
Согласно такой точке зрения, тот выбор (W~, W+, Z°, 7), который «замораживается» в од¬
ной точке, должен быть тождествен соответствующему выбору (W“,	Z°, 7) в любой
другой точке, так что мы не можем говорить о каком-то «несоответствии» между наруше¬
ниями симметрии в разных точках при возникновении доменов намагниченности железа,
показанном на рис. 28.2.

624
Глава 28
Однако такая точка зрения сталкивается с общей идеей, лежащей в основе калибро¬
вочной теории, согласно которой не только пространства Q — слои расслоенного простран¬
ства Бд с пространством-временем Л4 в качестве базисного пространства, — но и конкретная
калибровочная теория (в данном случае теория ненарушенного электро слабого взаимодей¬
ствия) определяются в терминах связности на этом расслоении (§§ 15.7, 15.8). Эта связность
определяет локальное отождествление (параллелизм) пространств Q при перемещении вдоль
некоторой замкнутой кривой в пространстве-времени J28ло-1 В общем случае такая иден¬
тификация не является глобально согласованной при обходе замкнутых петель (из-за на¬
личия кривизны связности, определяющей нетривиальное калибровочное поле; см. § 15.8).
В любом случае случайный фактор, вносимый нарушением симметрии в различных точках,
приводит к тому, что локальный параллелизм £-пространств в общем случае не согласуется
с тем выбором, который делается при спонтанном нарушении симметрии, так что картина
на рис. 28.2 может служить неплохой аналогией. Можно представить себе, что, как и в
случае достаточно медленного охлаждения железного шара, неоднородности со временем
будут «сглаживаться», если предположить отсутствие топологических дефектов вроде тех,
что показаны на рис. 28.3 и 28.4. Вопрос, который я хочу задать, состоит в том, найдет¬
ся ли «достаточно времени» в случае спонтанного нарушения симметрии электро слабого
взаимод ействия.
Такая проблема возникает в связи с горизонтом для частиц, рассмотренным в §27.12
(см. рис. 27.186). Рассмотрим схематическую конформную диаграмму на рис. 28.5. На¬
блюдатель, находящийся в точке р, видит квазары (см. §27.9) в двух противоположных
направлениях, которым соответствуют пространственно-временные точки q и г. Согласно
стандартным моделям ФЛРУ, при достаточно большом красном смещении 128Л1] квазаров
(см. § 21 Л) световые конусы прошлого для точек дигне будут пересекаться, так что ни¬
какой связи между этими точками быть не может. Не имея связи между собой, они не
будут иметь времени для согласованного «сглаживания» нарушений симметрии указанным
образом. Вскоре мы рассмотрим «инфляционный сценарий», который отодвигает назад ли¬
нию Большого взрыва на конформной диаграмме, так что точки q и г в конечном счете
оказываются связанными между собой. Но в данном случае это нам не поможет, поскольку
3-поверхность £, на которой имеет место нарушение симметрии электрослабого взаимодей¬
ствия, эффективно играет роль Большого взрыва в этом нашем рассуждении, использующем
соображения причинности, так как спонтанное нарушение симметрии предполагается воз¬
никающим на 3-поверхности £ случайным образом, без эффективного влияния обычных
условий причинности.
Теперь прямые qp и тр представляют нулевые линии, поэтому только фотон может
попасть из точки q в точку р или из г в р, тогда как W- или Z-бозоны этого сделать
не в состоянии, поскольку фотон является единственным безмассовым членом семейства
калибровочных бозонов. Таким образом, в отношении этих двух нулевых линий нам необ¬
ходимо иметь четкое представление о том, что есть фотон. Понятие «фотона» в точке д,
скорее всего, не будет совпадать (в указанном выше смысле) с понятием «фотона» в точке г,
поскольку каждый из них, как предполагалось, выделялся случайным образом без взаим¬
ного причинного влияния и при отсутствии достаточного времени для установления связи
между ними^28Л21. Могут ли фотоны «разного сорта» с течением времени «сглаживаться»,
чтобы избавить принимающего их наблюдателя в точке р от возможного недоразумения,
связанного с объединением W-Z-^y? Я не вижу, как это можно осуществить без значитель¬
ного отступления от прямой нулевой (т. е. «светоподобной») связи точек q и г с точкой р.
Это может привести к резкому конфликту с тем фактом, что удаленные объекты можно
наблюдать с помощью оптических телескопов. Мне представляется, что здесь заключена
опасность несоответствия теории результатам наблюдений, хотя я не встречал обсуждения
этой проблемы в литературе.

28.3. Проблемы с нарушением симметрии в ранней Вселенной
625
Р
Р
а)
Большой взрыв
Большой взрыв
Л
Рис. 28.5. Схематические конформные диаграммы, иллюстрирующие причинную (не)зависимость
в ранней Вселенной, а) Наблюдатель, находящийся в точке р, видит квазары в противоположных
направлениях (точки q и г). Если пунктирная прямая представляет 3-поверхность £ в момент вре-
1 О
мени ~ 10 с, когда предполагается нарушение симметрии электрослабого взаимодействия (связы¬
вавшей фотон у с W- и Z-бозонами), то некоторый «замороженный» выбор фотона 7 в точке q почти
наверняка будет отличаться от выбора в точке г, поскольку пересечения конусов прошлого для этих
точек с поверхностью £ разделены таким образом, что информация о совпадении или различии выбо¬
ров не может достигнуть точки р. Аналогично, если поверхность £ представляет момент расцепления
в момент времени 1013 с, температуры в точках и и v не могут быть выравнены в результате термали-
зации из-за разделения соответствующих конусов прошлого, б) Инфляционное «решение» описанной
«проблемы горизонта». Линия Большого взрыва отодвигается назад, так что конусы прошлого для
точек q и г теперь пересекаются до достижения 3-поверхности Большого взрыва. Однако проблема
остается нерешенной, поскольку пересечение конусов прошлого происходит до «замерзания» в момент
времени ~ 10“12 с
Некоторые читатели, несомненно, могут выразить недовольство (хотя, возможно, и не
вслух) тем, что я как будто игнорирую все весьма впечатляющие подтверждения теории элек¬
трослабого взаимодействия результатами наблюдений. Я вовсе не собираюсь отказываться
от всего этого лишь из-за некоторых затруднений, связанных с явлениями космологиче¬
ского масштаба! Отнюдь нет. Я никоим образом не предлагаю отказаться от прекрасных
достижений теории электрослабого взаимодействия, однако предпочитаю занимать пози¬
цию, несколько отличную от общепринятой, в отношении нарушения U(2)-симметрии этого
взаимодействия. Насколько я понимаю, истинная схема, предложенная Природой в отно¬
шении элементарных частиц, пока скрыта от нас. Такая схема должна быть математически
согласованной и не должна иметь отрицательных черт нашей сегодняшней КТП, которая на
многие разумно поставленные физические вопросы выдает ответ «оо». Каким образом эта
(пока не известная) «правильная» теория даст ответы в виде конечных величин, мы пока
не знаем. Поэтому мы прибегаем к разнообразным «трюкам», благодаря которым наш путь
оказывается сотканным из исторического везения и исключительной человеческой изобре¬
тательности, позволяя нам получать конечные результаты, согласующиеся с наблюдениями.
На нашем нынешнем уровне понимания нам определенно нужна перенормируемая теория,
объединяющая слабое и электромагнитное взаимодействия, которая содержала бы не только
идею нарушенной неабелевой калибровочной симметрии, указывающую способ построения
перенормируемой теории, но и налагаемые при этом ограничения, которые подвели бы нас
ближе к семейству глубоких истин в отношении того пути, на котором эти взаимодействия
объединяются как часть некоторой более широкой картины. Но пока я не вижу, почему спон¬
танно нарушенная симметрия должна быть истинным путем Природы в мире элементарных
частиц. На самом деле существуют и другие пути к пониманию того, как требование пере-

626
Глава 28
нормируемости позволяет получить необходимые соотношения между параметрами теории
электрослабого взаимодействияf28* 131.
Это выдвигает важный вопрос (к которому я еще вернусь в § 34.8): действительно ли
понятие симметрии, столь широко представленное во многих идеях, направленных на рас¬
крытие тайн Природы, играет такую фундаментальную роль, какая ему обычно отводится?
Я не вижу, почему это всегда должно быть так. Я не убежден, что построение физики эле¬
ментарных частиц на основе некоторой большой группы симметрии (а именно это является
составной частью философии Великого объединения) действительно дает «простую» кар¬
тину, коль скоро речь идет о фундаментальной физической теории. На мой взгляд, большие
геометрические группы симметрии не упрощают, а усложняют картину. Вполне может быть,
что законам природы присуща фундаментальная асимметрия, а та симметрия, которую мы
наблюдаем, есть лишь приближенное свойство, которое не сохраняется на более глубоких
••
уровнях. Я вернусь к этому вопросу позже (в § 34.8).
28.4* Инфляционная космология
Вернемся к вопросу о космических монополях, существование которых предполагается
некоторыми вариантами теории Великого объединения. Беда в том, что пока нет никаких
реальных указаний на то, что они действительно существуют. Еще хуже то, что результаты
наблюдений устанавливают жесткие пределы на распространенность таких монополей в кос¬
мосе, причем на уровне, гораздо более низком, чем предсказывает теория. Однако в 1981 году
Алан Гат выдвинул «возмутительную» гипотезу (она была предложена ранее, по существу,
независимо Алексеем Старобинским и Кацуоко Сато), согласно которой в случае если бы
Вселенная расширилась в 1030 или даже в Ю60 и более раз в течение некоторого периода
после ооразования монополеи (однако до нарушения электрослаоои симметрии в момент
времени 10“12 с), то нежелательные монополи сегодня встречались бы столь редко, что
легко могли ускользнуть от обнаружения, что и требуют результаты наблюдений.
Вскоре оказалось, что этот «инфляционный период» экстремального экспоненциально-
го расширения может служить и для других целей, связанных с однородностью
Как подчеркивалось в главе 27, Вселенная действительно крайне однородна и близка к то¬
му, чтобы быть пространственно плоской в очень больших масштабах, и это представляет
загадку для космологов. Например, наблюдаемая температура ранней Вселенной в разных
направлениях почти одинакова (относительные отклонения не превышают 10“°). Это можно
было бы счесть результатом «термализации» на очень ранней стадии развития Вселенной,
но лишь при условии, что разные части Вселенной «имели связь» между собой. (Вспомните,
как Второй закон термодинамики в процессе установления теплового равновесия приводит
к выравниванию температуры в различных частях газа; см. §27.2.) Однако из рис. 28.5 а
следует, что равенство температур в удаленных точках и и ti, наблюдаемое из точки р,
определяющей наше нынешнее положение в пространстве-времени, согласно стандартным
космологическим моделям, не может быть результатом термализации, поскольку точки и
и v (если поверхность Е соответствует моменту «расцепления», когда возникло космиче¬
ское тепловое излучение) находились слишком далеко одна от другой, чтобы между ними
могла существовать какая-либо причинная связь.
Эта невозможность в стандартной модели причинной связи, необходимой для термали¬
зации, носит название проблемы горизонта. Влияние периода инфляции, в этом отношении,
показывает конформная диаграмма на рис. 28.5 б. Пространственноподобная 3-поверхность,
представляющая Большой взрыв, теперь отодвигается в гораздо более «раннее» положение,
так что области прошлого для точек и и v теперь перекрываются, прежде чем будет до¬
стигнута 3-поверхность, описывающая Большой взрыв, поэтому открывается возможность

28.4. Инфляционная космология
627
термализации, и мы можем принять, что равенство температур в точках и и v могло возник¬
нуть именно таким способом.
Другая ощутимая польза от введения пе¬
риода инфляции состоит в том, что появилась
возможность объяснить замечательную однород¬
ность распределения вещества и пространственно-
временной геометрии, что составляло так называе¬
мую «проблему гладкости». Идея состояла в том,
что при наличии инфляции начальное состояние
Вселенной могло быть весьма неоднородным в де¬
талях, однако огромное расширение Вселенной на
стадии инфляции должно было «сгладить» неод¬
нородности, в результате чего получилась Вселен¬
ная, соответствующая модели ФЛРУ. С точки зре¬
ния инфляционной теории, даже исходное состо¬
яние должно выглядеть как гладкое многообразие
в малых масштабах; в течение фазы инфляции та¬
кая гладкая малая часть расширяется до космологи¬
ческих масштабов, обеспечивая пространственную
гладкость (см. рис. 28.6, а также рис. 12.6). Свою
Рис. 28.6. Один из побудительных мо¬
тивов инфляционной теории: экспоненци¬
альное расширение с возможным масшта¬
бом Ю50 (например, между моментами
времени 10”35 с и 10”32 с) может обес¬
печить «сглаживание» исходного состоя¬
ния, что приводит к однородной, простран¬
ственно плоской постинфляционной Все¬
ленной
оценку этой экстравагантной идеи я вскоре изложу.
Пока следует отметить, что в этой картине Вселен¬
ная не только однородна, но и имеет нулевую про¬
странственную кривизну {К = 0). Как мы увидим,
это играет важную роль в историческом развитии
данного предмета. Однако независимо от того, яв¬
ляется ли наблюдаемая Вселенная в среднем пространственно плоской, она, несомненно,
в значительной мере близка к этому, и эта так называемая проблема плоскостности состав¬
ляет загадку для многих космологов.
Не вполне очевидно, как обстоит дело с инфляционной фазой расширения при смеще¬
нии назад 3-поверхности Большого взрыва на конформной диаграмме (рис. 28.5). Поэто¬
му полезно рассмотреть частную космологическую модель, на которой основана эта «ин¬
фляционная фаза». Это «стационарный вариант» пространства де~Ситтера. Проще всего
математически описать пространство де-Ситтера, сказав, что это есть лоренцева 4-сфера
(сигнатура Н	) в 5-пространстве Минковского (сигнатура Н	-). Такое описание
согласуется с идеей «изменения сигнатуры» (§ 18.4), однако геометрически нагляднее пред¬
ставить пространство де-Ситтера в виде гиперболоида (рис. 28.7). Здесь стоит упомянуть
о другой модели — пространстве анти-де-Ситтера, которое представляет собой лоренцеву
4-сферу в 5-пространстве псевдо-Минковского с сигнатурой -f Н	(рис. 28.8) . Заме¬
тим, что, с физической точки зрения, пространство анти-де-Ситтера построено не слишком
разумно, поскольку оно содержит нарушающие причинность замкнутые времениподобные
кривые (т.е. окружности в плоскости, задаваемой осями t и w); см. §17.9 и рис. 17.18.
Иногда пространством анти-де-Ситтера называют «развернутый» вариант, в котором каждая
окружность в плоскости с постоянными значениями (ж, у, z) не образует замкнутой линии,
так что все пространство оказывается односвязным (§ 12.1). Строгая конформная диаграмма
для пространства де-Ситтера, а также для его части, представляющей стационарную модель
Напишите в явном виде уравнения для 4-пространств де-Ситтера и анти-де-Ситтера в фоновом 5-про¬
странстве, используя координаты £, w, ж, у, z, показанные на рис. 28.7 и 28.8. Определите координаты в «поло-
зине» пространства де-Ситтера, так чтобы его собственная метрика имела стационарный вид, указанный далее
з этом разделе.

628
Глава 28
(штриховая граничная линия означает линию разреза), показана на рис, 28.9а, диаграм¬
ма для пространства анти-де-Ситтера с нарушением причинности (верх и низ диаграммы
должны быть отождествлены) — на рис. 28.9 в и 28.9 г, для развернутого (причинного) про¬
странства анти-де-Ситтера — на рис. 28.9 б.
w	Развертывание
Рис. 28.7. Пространство де-Ситтера (изобража¬
емое в виде гиперболоида при отбрасывании
двух пространственных измерений) представ¬
ляет собой лоренцеву «4-сферу» (с мнимым
радиусом и сигнатурой собственной метрики
-|	)	в	5-пространстве Минковского М5
(с метрикой ds2 — dt2~dw2~-dx2—dy2—dz2). Что¬
бы получить стационарную модель, мы «разре¬
заем» гиперболоид пополам по плоскости t —
= w; постоянный момент времени задается по¬
ложительной постоянной величиной t — w
Рис. 28.8. Пространство анти-де-Ситтера
(изображаемое в виде гиперболоида при
отбрасывании двух пространственных измере¬
ний) представляет собой лоренцеву «4-сферу»
(с положительным радиусом и сигнатурой соб¬
ственной метрики Ч	) в 5-пространстве
псевдо-Минковского (с метрикой ds2 = dt2 +
+ dw2 — dx2 — dy2 — dz2). По определению,
времениподобные кривые замыкаются, однако
от этого можно избавиться путем бесконечного
«развертывания» в плоскости (£, w)
Рис. 28.9. Строгие конформные диаграммы (с теми же условными обозначениями, что и на рис. 27.16 а),
а) Пространство де-Ситтера; область над внутренними штриховыми линиями соответствует стацио¬
нарной модели, б) Пространство анти-де-Ситтера (полностью развернутый вариант без нарушения
причинности), в) Пространство анти-де-Ситтера в исходной «гиперболоидной» форме с нарушением
причинности, верхний и нижний края должны быть отождествлены, г) Предыдущий случай с прове¬
денным отождествлением, так что диаграмма имеет вид цилиндра

28.4. Инфляционная космология
629
Чтобы получить стационарную Вселенную в явном виде, «разрежем» пространство де-
Ситтера пополам по плоскости t ~ w 5-пространства Минковского, как показано на рис. 28.7,
и оставим лишь «верхнюю» половину Г28Л41 Любопытно, что, несмотря на «неполноту»
этой модели из-за факта разрезания (разрез показан пунктирной линией на рис. 28.9 а), эта
неполнота обычно не считается дефектом, поскольку никакие реальные частицы не попада¬
ют в пространство-время из «отрезанной» нижней половины. Метрику верхней половины
можно представить в виде
ds2 — dr2 — eAr(dx2 -f dy2 -f dz2),
где A — постоянная. Это есть частный случай метрики ФЛРУ (§27.11) с плоскими про¬
странственными сечениями (К = 0) и экспоненциальным расширением (ему соответствует
множитель еАг)*. (Эта метрика вызывала особый интерес в 1950-х и 60-х годах, когда Гер¬
ман Бонди, Томас Голд и Фред Хойл предложили рассматривать ее как модель реальной
Вселенной — «стационарную» модель, обладающую значительной эстетической привлека¬
тельностью. От этой модели пришлось отказаться в 1960-х годах после того как выяснилось,
что она противоречит результатам наблюдений, в частности, измерениям микроволнового
фона и подсчетам числа отдаленных галактик.)
Тензор Риччи Rab для пространства (анти-)де-Ситтера пропорционален метрике даь**
(По поводу определения этого тензора, а также уравнения Эйнштейна и т. п.; см. § 19.6.) На-
1
помним, что исходное эйнштейновское уравнение поля имеет вид Rab — ~Rgab = —87тСТаь
&
и означает, что тензор энергии-импульса материи равен тензору Риччи с обращенным сле¬
дом, умноженному на — (втгО)™1. Таким образом, для моделей де-Ситтера и анти-де-Ситтера
«тензор материи» Таь сам должен быть пропорционален метрическому тензору. На самом
деле никакая обычная материя не может обладать таким свойством (хотя бы потому, что
энергия-импульс не определяет покоящуюся систему отсчета). Обычная точка зрения состо¬
ит в том, чтобы считать пространства (анти-)де-Ситтера представляющими вакуум без мате¬
рии, при этом уравнение Эйнштейна следует брать в форме, включающей космологическую
постоянную Л, так что уравнение для поля теперь дает нам
Rab “ Адаь>
Здесь А = А2, где А есть постоянная, определяющая коэффициент экспоненциального роста
в вышеприведенном выражении для стационарной метрики. В инфляционной космологии
раздувающееся «вещество» считается «ложным вакуумом», о котором я скажу чуть позже.
Чтобы построить инфляционную модель Вселенной, возьмем часть стационарной Все¬
ленной между двумя 3-поверхностями с постоянными значениями г и наклеим их на две
части стандартной модели ФЛРУ с К =;0. Такая процедура представлена на рис. 28.10.
На рис. 28.10а полное пространство де-Ситтера разрезается, чтобы получить стационарную
модель. На рис. 28.106 отрезается большая часть этой модели, претерпевающая инфля¬
цию. На рис. 28.10 в вырезается кусок модели ФЛРУ с К — 0, и часть, претерпевшая
инфляцию, может быть использована для завершения построения модели на рис. 28.10г.
Введенная стационарная часть фактически «отодвигает назад» момент Большого взрыва
(с конформной, т. е. причинной, точки зрения), так что горизонт для частиц сильно расши¬
ряется; см. рис. 28.56,
Чтобы достичь периода инфляции, необходимо добавить новое скалярное поле <р к на¬
бору известных (и предполагаемых) физических частиц и полей. Насколько мне известно,
это поле р не считают непосредственно связанным с каким-либо другим полем, известным
*гШ Определите вид метрики для пространств де-Ситтера и анти-де-Ситтера типа ФЛРУ ds2 = dt2 —
- (R(t)) dJ22, где dJ22 означает гиперболическую 3-метрику в соответствии со вторым выражением в упраж¬
нении 27.18. Какую часть полного пространства (анти-)де-Ситтера это охватывает?
** ЛИ Понятно ли без вычислений, почему это так?

630
Глава 28
а)
Рис. 28.10. Процедура построения инфляционной модели Вселенной, а) Пространство де-Ситтера
разрезается, чтобы получить стационарную модель, б) Отрезается часть стационарной модели, пре¬
терпевающая инфляцию, между двумя линями, соответствующими постоянным моментам времени.
в) Из модели ФЛРУ с К = 0 удаляется небольшой интервал, соответствующий постоянному моменту
времени, г) Часть, отрезанная на рис. б, вводится вместо удаленной части на рис. в, в результате
получается инфляционная модель Вселенной. При этом момент Большого взрыва отодвигается назад,
как это сделано на рис. 28.5 б
физике, оно вводится лишь для того, чтобы получить фазу инфляции в ранней Вселенной.
Иногда его называют полем Хиггса, однако оно, по-видимому, не является «обычным» по¬
лем, связанным с теорией электрослабого взаимодействия (см. §25.5). Некоторые модели
требуют более одной отдельной фазы инфляции, в этом случае должно существовать отдель¬
ное скалярное поле для каждой фазы. Процесс инфляции описывается с помощью картины,
подобной «мексиканской шляпе» на рис. 28.1, но без начальной симметрии. Часто использу¬
ется диаграмма, подобная показанной на рис. 28.11, где по вертикальной оси откладывается
«эффективная энергия». До периода инфляции состояние («шарик» на рис. 28.1) находит¬
ся на вершине холма, затем оно постепенно скатывается вниз. Инфляция имеет место при
этом спуске и прекращается, когда «шарик» достигает дна. На стадии инфляции мы имеем
область «ложного вакуума», которая представляет квантово-механический фазовый переход
в состояние вакуума, отличного от известного нам сегодня.
Рис. 28.11. Эффективная плотность энергии в ранней Вселенной, согласно инфляционной модели,
определяется в основном эффективным потенциалом У(ф) для скалярного «инфляционного» кванто¬
вого поля ф. На графике показан обычно предполагаемый вид функции У(ф); инфляция возникает,
когда состояние («шарик» на рис. 28.1) «скатывается» с холма, расположенного слева (предполагается
наличие «ложного вакуума»). Инфляция прекращается по достижении дна потенциала
л	'	,
Как упоминалось в § 27.11, в настоящее время имеются четкие указания на существова¬
ние в нынешнюю эпоху положительной величины А, которая по обыденным меркам крайне
мала, — она соответствует плотности, в 1030 раз меньшей плотности воды. В противопо¬
ложность этому, ложный вакуум в фазе инфляции должен был иметь эффективное значение
постоянной Л, которому соответствует плотность, в 1G80 раз превышающая плотность во¬
ды. Эта величина должна была полностью доминировать над тензором энергии-импульса
обычного вещества, и именно по этой причине фазу инфляции можно описывать моделью
де-Ситтера.
На рис. 28.12 изображена некоторая картина истории ранней Вселенной, как ее часто
представляют, так что она стала почти «стандартной». Заметим, что здесь используется ло¬

28,5. Справедливы ли предпосылки инфляционной модели?
631
гарифмический масштаб для времени и расстояний (подобный логарифмической линейке
на рис. 5.6), так что отмечены различные степени 10 для секунд (по горизонтали) и санти¬
метров (по вертикали). «Радиус» означает историю R(t) из §27.11 (не путать со скалярной
кривизной R из § 19.6!). По моему мнению, такую картину следует рассматривать как весь-
1
ма умозрительную вплоть до с (и уж конечно, до 10 30 с), хотя ее часто преподносят как
надежно установленный факт!
A log R
Расцепление
Обычное
толменовское
расширение
Инфляция (?
\
—32
О
К
Я
о
С
ЯГ
о
cd
Рч
ГА
1/А
Ег*
W
О
icf43 ю-35
10
12
СЕЙЧАС
Время
в секундах
ю18 ю18
Рис. 28.12. Обычно описываемая «история Вселенной» (в логарифмическом масштабе), содержащая
фазу инфляции. Показана зависимость log R(t) от logt
28*5. Справедливы ли предпосылки инфляционной модели?
Какие имеются основания считать, что такая инфляционная картина Вселенной близка
к истине? Несмотря на ее очевидную популярность, я хотел бы изложить мои собственные
основания для сомнений во всей этой идее в целом. Как и раньше, я должен официально
предупредить читателя, что инфляционная космология стала важной частью всей современ¬
ной космологической мысли. Даже среди тех, кто пока еще не убежден в необходимости
инфляции, найдется не много таких, кто настроен так же критически, как и я. Если вы
чувствуете необходимость «сбалансировать» мое мнение с мнением тех, кто склоняется
к идее инфляции, советую обратиться ко вполне доступной книге Алана Гата «Раздувающа¬
яся Вселенная»!28'15^. Что касается меня, то я должен представлять положение дел так, как
оно мне видится, и потому считаю, что, поскольку у меня есть веские причины сомневаться
в самих основах инфляционной космологии, мне не следует скрывать их от читателя.
Но прежде чем излагать критические соображения, я должен заявить, что мои замеча¬
ния вовсе не означают, что инфляционная космология ошибочна. Они лишь дают веские
основания для сомнения в большинстве исходных предпосылок, лежащих в основе идеи
инфляции. Можно вспомнить, что многие важные научные идеи прошлого основывались
(частично) на предпосылках, которые не оправдались в ходе дальнейшего развития. Одним
из наиболее важных примеров такого рода было влияние, которое оказал на Эйнштейна

632
Глава 28
принцип Маха, приведя его в конечном счете к созданию общей теории относительности.
Принцип Маха гласит, что физика должна формулироваться исключительно в терминах свя¬
зей одних тел с другими, так что должно быть отброшено само понятие какого-то фонового
пространства^28*16^. Последующий анализ теории Эйнштейна показал, что принцип Маха
в общей теории относительности не содержится^28Л7^, однако это не умаляет значения идеи
Маха как исходной предпосылки^28*18^. Другим примером может служить открытие Дираком
волнового уравнения для электронов, в основе которого лежало его ощущение необходи¬
мости получить уравнение первого порядка (см. §§24.5, 24.6). Дальнейшее развитие КТП
показало, что это требование не является необходимым (§ 26.6).
Аналогично, если бы были убедительным образом подтверждены предсказания инфля¬
ционной космологии в отношении результатов наблюдений, то любые дефекты исходных
предпосылок оказались бы не имеющими значения, и теория могла бы существовать сама
по себе, без тех «строительных лесов», которые позволили Газу и другим ее построить. На
самом деле инфляционисты сделали ряд определенных предсказаний, которые в последние
годы оказались в противоречии с рядом впечатляющих новых наблюдений.
Мне кажется, что космология нуждается в таком предупреждении, особенно в том, что
касается происхождения Вселенной. К вопросу о происхождении Вселенной люди часто от¬
носятся весьма эмоционально, и это зачастую явно или неявно связано с их религиозными
предпочтениями. Это вполне естественно, поскольку речь идет о рождении всего того ми¬
ра, в котором мы живем. Как подчеркивалось в §27.13, в силу Второго закона требовалась
исключительная точность при выборе начального состояния Вселенной в виде Большого
взрыва, и в этом, несомненно, заключена глубокая загадка. Возникает вопрос: найдет ли ее
решение будущая наука, не смотря на то, что пока оно находится за пределами нынешнего
научного знания? (Моя оптимистическая позиция на этот счет изложена в §§30.10-30.14.)
Или мы должны примириться с тем, что это был некий «акт божественного творения»?
Инфляционисты придерживаются иного взгляда, они считают, что их теория в основном
«реишла» эту проблему, и эта уверенность придает силу их позиции. Однако я никогда не
замечал, чтобы глубокая загадка, поставленная Вторым законом, всерьез занимала инфля-
ционистов!
Вместо этого инфляционисты выбрали из стандартной космологической модели три
частные проблемы, имеющие отношение к начальной точности выбора состояния ранней
Вселенной. Они уже упоминались в §28.4 — это проблема горизонта, проблема гладкости
и проблема плоскостности. В стандартной модели эти проблемы трактуются с позиций «тон¬
кой настройки» исходного состояния Большого взрыва, однако инфляционисты называют это
«вздором». Они заявляют, что в картине инфляции такая настройка начального состояния
не требуется, и поэтому такая картина рассматривается как более привлекательная в эсте¬
тическом отношении. Вывод о пространственной плоскостности, достигаемой в результате
инфляции, также считается эстетически привлекательной чертой теории [28Л91.
Мне кажется, что к таким аргументам эстетического характера следует относиться
с большой долей настороженности. В основе инфляционной картины определенно имеются
некоторые элементы с довольно сомнительным эстетическим статусом, например, введение
скалярного поля (или даже нескольких независимых скалярных полей, если рассматривается
более одного периода инфляции), никак не связанного с другими известными физическими
полями и обладающего весьма специфическими свойствами, которое нужно лишь для того,
чтобы инфляция могла иметь место. Весьма спорной является эстетическая привлекатель¬
ность выбора К = 0. Я знаю многих математиков (включая меня самого), которые считают
гиперболический вариант (К < 0) не в пример более привлекательным! Тогда как другие
предпочитают «уют» пространственно конечной Вселенной (с К > 0). Общая проблема
роли красоты как путеводителя в фундаментальной теоретической физике будет обсуждена
в этой книге позже (см. § 34.9), то же относится к дополнительным вопросам, связанным

28.5. Справедливы ли предпосылки инфляционной модели?
633
непосредственно с инфляцией (§34.4), и к влиянию научной моды (§34.3). В среде со¬
временных космологов инфляция, несомненно, очень модна, и важно постараться понять,
насколько оправдан этот модный статус.
Как уже отмечалось, мои главные возражения против идеи космической инфляции
относятся преимущественно к предпосылкам, лежащим в ее основе. Рассмотрим сначала
проблему горизонта и то, как она трактуется в инфляционной космологии, где, например,
почти одинаковая фоновая температура в разных направлениях воспринимается как резуль¬
тат термализации. Инфляция вводится, чтобы устранить горизонты для частиц, которые
в противном случае препятствуют этой термализации.
Существует, однако, какое-то фундаментальное недопонимание в попытках объяснить
однородность ранней Вселенной, будь то однородность фоновой температуры, плотности ве¬
щества или геометрии пространства-времени в целом, как результат процесса термализации
(§ 28.4). В самом деле, непонятно, почему следует объяснять любую однородность Вселен¬
ной, апеллируя к процессу термализации. Если термализация действительно делает что-то
(например, выравнивает температуры в разных местах), это сопровождается определен¬
ным увеличением энтропии (§ 27.2). Поэтому до термализации Вселенная должна обладать
большим разнообразием, нежели после нее. Это лишь усугубляет ту трудность, с которой мы
столкнулись, пытаясь понять совершенно особую исходную природу Вселенной (§27.13).
Есть глубокая загадка, связанная с необычайными ограничениями, налагаемыми на состоя¬
ние ранней Вселенной. Но эти ограничения, как подчеркивалось в главе 27, фундаментально
связаны с самим существованием Второго закона термодинамики. Мы не можем надеять¬
ся объяснить эти ограничения, просто апеллируя к проявлениям Второго закона (одним из
которых является термализация)!
Чтобы развить эту мысль, рассмотрим вопрос о равенстве температур, наблюдаемых
в разных направлениях из некоторой выбранной точки Вселенной. Предположим, что темпе¬
ратуры двух удаленных одна от другой областей действительно оказываются одинаковыми
в некоторый ранний момент космического времени ti, и будем считать эту «особенность»
загадочной. Рассмотрим две возможности. Можно представить себе, что (а) в еще более
раннюю эру (момент времени to) температуры были разными, и они стали одинаковыми
лишь после процесса термализации, который произошел между моментами времени to и ti.
Вместо этого можно предположить, что (б) в более ранний момент to две температуры были
равны между собой и термализация не происходила. В случае (а) в интервале между to и t\
энтропия увеличивается, так что в момент to степень разнообразия выше, чем в момент ti,
и особая природа Вселенной в момент to должна удивлять еще больше, чем таковая в мо¬
мент t\. Ситуация стала еще хуже! В случае (б) проблема особого характера Вселенной
в момент to выглядит по крайней мере не более сложной, чем в момент t±. В обоих случаях
мы не можем ни в каком смысле объяснить загадку особого характера Вселенной, однако
видно, что привлечение к этой проблеме соображений термализации оказывается более чем
бесполезным!
А как обстоит дело с однородностью (и плоскостностью) Вселенной? Здесь основной
аргумент инфляционной теории состоит в следующем. Именно экспоненциальное расши¬
рение в фазе инфляции делает Вселенную однородной (и пространственно плоской). Снова
фундаментальное недоразумение. Идея как будто в том, что если мы стартуем из некото¬
рого «изначального» состояния, то «растягивающее действие» экспоненциального расшире¬
ния в фазе инфляции должно сгладить неоднородности этого начального состояния. Чтобы
узнать, возможен ли такой процесс, мы должны, конечно, иметь некоторую идею отно¬
сительно того, как могла бы выглядеть «изначальная» геометрия. Важное предположение
состоит в том, что такое состояние должно быть гладким в некотором малом масштабе.
Однако, например; фрактальные множества никогда не сглаживаются, независимо от того,
насколько они растянуты. Вспомним множество Мандельброта, части которого показаны на
рис. 1.2. Пожалуй, оно выглядит тем менее гладким, чем больше его увеличить.

634
Глава 28
Однако я слышу ворчание читателя: это же всего лишь увертка — да, возможно, и су¬
ществуют какие-то патологические ситуации, в которых растяжение не приводит к сгла¬
живанию, но в общем реалистическом случае мы не должны ожидать чего-то подобного.
К сожалению, это совсем не очевидно; нечто фрактальное (или что-то похуже) почти на¬
верняка должно присутствовать в исходном состоянии. Какова бы ни была эта начальная
сингулярная структура, мы не можем ожидать, что она сгладится просто в силу того, что
физика допускает процессы инфляции. Почему? Причина совсем не в технических подроб¬
ностях, она заключена в ошибочном предположении, что наша реальная Вселенная начи¬
налась с состоянияf28‘201, которое не могло возникнуть в силу Второго закона (см. §27.7).
Если мы хотим понять, как могло бы выглядеть такое исходное состояние, следует рас¬
смотреть конечные стадии коллапсирующей замкнутой Вселенной вроде той, что показана
на рис. 27.20а, б, а затем обратить поток времени, как на рис. 27.20 в (или рис. 27.20г).
Мешанина в конденсированной сингулярности черной дыры является состоянием, которое,
будучи обращенным во времени, могло бы описывать Большой взрыв.
Разумеется, я не требую, чтобы читатель мгновенно понял и принял такую сложную
геометрию фрактального типа в состоянии Большого хлопка! У меня есть собственная реаль¬
ная концепция на этот счет, и я не думаю, что с ней хорошо знаком кто-нибудь еще^28‘211 Но
нам и не нужно входить в детали этой геометрии. Чтобы понять ее суть, рассмотрим какую-
нибудь модель коллапсирующей Вселенной, которую можно построить исходя из некоторо¬
го сильно неупорядоченного начального расширенного состояния (сравните с рис. 27.206).
Она должна коллапсировать во что-то, и действительно, как следует из .точных матема¬
тических теорем, коллапс приведет к некоторой пространственно-временной сингулярно-
cmu^2S'22\ Если теперь в нашей модели повернуть время вспять (предполагая динамические
законы симметричными во времени), мы получим эволюцию, начинающуюся с сингулярно¬
сти довольно общего вида, и это не зависит от выбора конкретного вида неупорядоченности
Вселенной. Очень может быть, что в такой эволюции не будет никакой инфляции, хотя наши
обращенные во времени физические законы допускают возможность инфляции. Дело в том,
что независимо от того, имеет ли место инфляция, физическая возможность инфляцион¬
ного периода не помогает убедиться, что эволюция из исходной сингулярности приводит
к однородной (или пространственно-плоской) Вселенной.
Попробуем понять, в чем реально состоит проблема. Это подробно обсуждалось в гла¬
ве 27. В момент Большого взрыва Вселенная была в очень специфическом состоянии. Это
следует из Второго закона термодинамики, если пойти назад во времени к самому началу.
Все процессы термализации определяются Вторым законом и потому не могут объяснить ни
причин существования Второго закона, ни весьма особого характера Вселенной в самом на¬
чале. Более того, все процессы спонтанного нарушения симметрии и все фазовые переходы
(которые необходимы для инфляции) имеют место лишь с любезного разрешения Второго
закона. Эти процессы не объясняют Второй закон — они пользуются им. Вдобавок все се¬
рьезные расчеты в инфляционной космологии предполагают пространственно-временного
геометрию типа ФЛРУ, а это не позволяет узнать, что должно было происходить в исходном
состоянии. Если мы хотим понять, почему Вселенная первоначально находилась в весьма
специфическом, необычайно однородном состоянии, мы должны обратиться к совершенно
иным аргументам, нежели те, на которые опирается инфляционная космология.
%
28.6. Антропный принцип
Прежде чем перейти к этим аргументам, мы должны рассмотреть несколько иной во¬
прос, который часто подается как часть точки зрения инфляционной космологии. Это так
называемый антропный принцип, который используют также во многих других рассуждени¬
ях, имеющих целью объяснить, почему Вселенная такая, какой мы ее видим. Грубо говоря,

28.6. Антропный принцип
635
антропный принцип исходит из того факта, что воспринимаемая нами Вселенная вокруг нас
должна быть такой, чтобы в ней могли возникнуть и развиваться существа, способные вос¬
принимать ее. Можно воспользоваться этим аргументом, чтобы объяснить, почему планета,
О
на которой мы живем, предоставляет такие подходящие для жизни условия — интервал
температур, атмосферу, наличие воды и т. д., и т. п. Если бы условия на этой конкретной
планете не были такими подходящими, тогда мы находились бы не здесь, а где-то в другом
месте! i28-23!
Одно из наиболее впечатляющих применений антропному принципу было найдено
в 1957 году Робертом Дикке ив 1973 году Брэндоном Картером [28*24]? которые решили про¬
блему, поставленную в 1937 году Дираком [204] и касающуюся совпадения между возрастом
Вселенной, измеренным в планковских единицах (§27.10), и отношением величин электро¬
магнитных и гравитационных сил^28*25^. Если такое совпадение отражает некоторое фунда¬
ментальное соотношение между параметрами Природы, оно должно сохраняться во всей
истории Вселенной. Но возраст Вселенной есть величина, растущая со временем (это совер¬
шенно очевидно!), и, в соответствии со сказанным, величина гравитационных сил должна
убывать по сравнению с величиной сил электрических. Дирак действительно сделал такое
предположение, однако на сегодняшний день такое изменение гравитационной постоянной
не согласуется с фактами^28 261. Дикке и Картер показали, что дираковское совпадение может
иметь другое объяснение. Проследив роль, которую играют мировые постоянные в опреде¬
лении времени жизни обычной звезды (звезды, как мы знаем, благоприятной для жизни),
они смогли показать, что этот временной масштаб имеет такой порядок величины, при ко¬
тором дираковское совпадение должно хорошо выполняться в отношении существ, которые
возникли (и обитают) на планете, вращающейся вокруг такой звезды. Таким образом, ди¬
раковское совпадение получило антропную интерпретацию. Оно имеет место, потому что
параметры, определяющие возникновение разумной жизни (в данном случае те параметры,
которые определяют возраст звезды), связаны с теми параметрами, которые такие разумные
существа будут видеть в окружающем мире!
Читателю должно быть ясно, что рассуждения, основанные на антропном принципе,
грешат неопределенностью, хотя они и не лишены изящества. Мы не очень много, напри¬
мер, знаем, какие условия действительно необходимы для возникновения разумной жизни.
Тем не менее ситуация не так уж плоха, если, как и в приведенных примерах, мы использу¬
ем известные законы физики и структуру пространства-времени и просто задаем вопросы,
где или когда условия во Вселенной были пригодны для появления разумной жизни. Такой
вариант антропного принципа, следуя Картеру, называют слабым антропным принципом
(рис. 28.13 а).
Гораздо более проблематичны варианты сильного антропного принципа, согласно ко¬
торому соображения антропного характера используются для определения мировых посто¬
янных (например, отношения масс электрона и протона или постоянной тонкой структуры;
см. § § 26.9, 31.1). Может показаться, что сильный антропный принцип приводит к вере в «бо¬
жественное предназначение», посредством которого Создатель Вселенной придал мировым
постоянным такие значения, которые делают возможным возникновение разумной жизни.
Однако мы можем рассматривать сильный принцип как обобщение слабого, при котором
наши вопросы «где» и «когда» относятся уже не к одному-единственному пространству-вре¬
мени, а к целому ансамблю возможных вариантов пространства-времени (рис. 28.13 б)^28 271.
Предполагается, что различным членам этого ансамбля соответствуют разные значения ми-
ровых постоянных. Вопрос «где/когда» теперь включает также выбор Вселенной из этого
ансамбля, при котором мы опять-таки должны ^оказаться в мире, допускающем возникнове¬
ние разума.
Первый пример такого рода, насколько я знаю, был предложен Фредом Хойлом, который
показал, что должен существовать до сих пор не наблюдавшийся ядерный энергетический

636
Глава 28
• у * /У
Слабый
антропный
принцип
I» *
Одна Вселенная
«)
Сильный
антропный
принцип
Альтеда^^:
деленные
б)
Рис. 28.13. Антропный принцип, а) Слабая форма: разумные существа должны оказаться в такой
пространственно-временной области Вселенной, где условия благоприятны для разумной жизни, б)
Сильная форма: вместо одной Вселенной рассматривается ансамбль возможных Вселенных с различ¬
ными значениями фундаментальных постоянных Природы. Разумные существа должны оказаться во
Вселенной с подходящими условиями (помимо благоприятного расположения в пространстве-време¬
ни)
уровень углерода для того, чтобы могли создаваться элементы тяжелее углерода в процессе
звездного нуклеосинтеза. Это есть процесс, посредством которого производятся новые эле¬
менты (сначала они возникают в звездах, а затем, в результате взрыва сверхновых, становятся
материалом для формирования планет; см. § 27.8), от которых зависит и функционирование
наших собственных организмов. Без них мы не могли бы существовать как разумные су¬
щества (в том виде, который нам известен)! Следуя указанию Хойла, Уильям Фаулер и его
сотрудники^28-28! в 1953 году обнаружили этот уровень, подтвердив впечатляющим образом
эту часть предсказания Хойла. Замечательно, что мировые постоянные подогнаны таким
образом, что этот уровень оказался как раз на нужном месте, обеспечивающем возможность
появления жизни в известном нам виде. Другим примером счастливой случайности косми¬
ческого уровня может служить тот факт, что масса нейтрона немного больше массы протона
(соответственно 1 838 и 1 836 электронных масс). Благодаря этому, казалось бы, случайному
факту, существует семейство стабильных ядер, на котором строится почти вся химия.
Моя собственная позиция состоит в необходимости крайней осторожности по отно¬
шению к применению антропного принципа, особенно сильного принципа. У меня такое
впечатление, что сильный антропный принцип зачастую используется в качестве некото¬
рого крайнего средства, когда разумные теоретические соображения кажутся достигшими
своего предела. Мне нередко приходится слышать, как теоретики заявляют примерно сле¬
дующее: «Значения неизвестных постоянных в моей теории определяются в конечном счете
антропным принципом». Разумеется, может оказаться в конечном счете, что в этой «истин¬
ной теории» действительно невозможно определить некоторые параметры математическим
путем и что выбор этих параметров действительно таков, чтобы Вселенная, в которой мы
оказались, допускала существование разумной жизни. Но я должен сознаться, что отнюдь
не в восторге от этой идеи!
Мне кажется, что в пространственно бесконечной и существенно однородной Вселен¬
ной (в стандартной модели это соответствует случаю К ^ 0) сильный антропный принцип
как средство поиска физических параметров почти бесполезен за рамками требования, что¬
бы физические законы допускали возможность разумной жизни (что само по себе в высокой
степени бесполезно, поскольку мы не знаем, что для этого требуется). Ибо если разумная

28.6. Антропный принцип
637
жизнь вообще возможна, то можно ожидать, что в пространственно бесконечной Вселенной
она возникнет. Это произойдет, даже если возникновение условий появления разума в лю¬
бой данной конечной области Вселенной чрезвычайно маловероятно. В пространственно
бесконечной Вселенной, как можно ожидать, разумная жизнь должна возникнуть где-то
на ее бескрайних просторах, как только там случайным образом окажутся в наличии все
необходимые ингредиенты. По воле случая это действительно будет происходить, хотя бы
чрезвычайно редко.
Если окажется, что фундаментальные физические постоянные имеют данные значе¬
ния (возможно, фиксированные математическими критериями), можно задать следующий
вопрос: каковы наиболее благоприятные условия, в которых с наибольшей вероятностью
возникнет разумная жизнь при заданных значениях физических постоянных? В той Вселен-
II-*
ной, которую мы знаем, при известных значениях мировых постоянных, ответ, по-видимому,
может быть следующим: это должна быть планета, похожая на Землю, вблизи звезды, похо¬
жей на Солнце, которая существует примерно 109 или 1010 лет — время, достаточное, чтобы
имела место соответствующая дарвиновская эволюция. Однако для Вселенной с другими
значениями постоянных параметров ответ может оказаться совсем иным.
В заключение этого раздела я должен упомянуть о близкой точке зрения в отноше¬
нии фундаментальных физических постоянных, впервые выдвинутой в 1973 году Джоном
Уилером. Она имеет некоторую связь с антропным принципом. Согласно этой точке зре¬
ния, Вселенная проходит через ряд циклов, содержащих «большие взрывы», следующие
за фазами предшествующего коллапса.
Вспомним о модели Фридмана в случае К > 0, Л — 0. Вселенная расширяется от
начальной сингулярности Большого взрыва, а затем сжимается в другую сингулярность —
финальный Большой хлопок. На заре космологии это называлось осциллирующей моде¬
лью, поскольку кривая, описывающая зависимость R(t) от t, представляет собой цикло¬
иду, которая содержит бесконечное* число циклов расширения и сжатия (см. рис. 27.15 а
и упражнение 27.19). Сейчас, однако, мы лучше, чем раньше, понимаем, что не существу¬
ет способа «сгладить» сингулярность, которая соединяет каждый «хлопок» со следующим
«взрывом» в рамках ограничений, налагаемых стандартной классической общей теорией
относительности^28-29^. Если игнорировать этот факт или предположить, что появится неко¬
торая «квантовая гравитация», допускающая подобный скачок, то можно принять, что фрид-
мановская циклоида представляет правдоподобное приближение к тому, что может произой¬
ти в действительности. Идея Уилера состояла в том, что ультраквантовая физика, которая
должна описывать сингулярный поворот, может приводить к изменению мировых посто¬
янных. В соответствии с этим, «ансамбль» Вселенных, который рассматривается в связи
с сильным антропным принципом, физически реализован в гипотезе Уилера.
Ли Смолин в своей замечательной книге «Жизнь космоса» [28-3°] предлагает любопыт¬
ную модификацию этой идеи. Вместо замкнутой Вселенной, в которой всеобъемлющий
Большой хлопок превращается в Большой взрыв следующей фазы Вселенной, Смолин рас¬
сматривает сингулярности внутри черных дыр как источники новых фаз Вселенной, ггри этом
каждая сингулярность черной дыры в отдельности создает отдельную фазу Вселеннойt28*31^,
и всякий раз происходит небольшое изменение фундаментальных физических постоянных.
Смолин выдвигает остроумную идею о возможности своего рода «естественного отбора»
Вселенных, так что мировые постоянные медленно эволюционируют, создавая «более при¬
способленные» фазы Вселенной, при этом размножение черных дыр рассматривается как
более подходящий индикатор «приспособленности» Вселенной (поскольку она дает боль¬
ше «потомства»), нежели какие-либо соображения антропного характера. Смолин считает,
что имеются некоторые указания на то, что те фундаментальные физические постоянные,
с которыми мы сталкиваемся в нашей Вселенной, имеют как раз такие значения, которые
способствуют размножению черных дыр. Мне кажется, однако, что в этих рассуждениях так¬

638
Глава 28
же играют существенную роль антропные соображения, поскольку мы с вами не оказались
в «мертвой» фазе Вселенной, непригодной для жизни, независимо от количества таких фаз!
Читателя может удивить, каким образом масса-энергия одиночной черной дыры может
превратиться в массу-энергию целой Вселенной, которая может быть в 1022 раз больше.
Всё так, но поскольку, для того чтобы пройти через сингулярность и изменить мировые
постоянные, требуется какая-то не известная нам физика, теряют смысл ссылки на обычные
законы сохранения в традиционной физике. Во всяком случае можно утверждать, что закон
сохранения массы-энергии становится проблематичным в общей теории относительности,
если не предполагать асимптотическую плоскостность (см. § 19.8).
У меня имеются серьезные сомнения в отношении гипотез Уилера и Смолина. Прежде
всего, это относится к основной идее, согласно которой некоторая ныне не известная фи¬
зика может не только превратить пространственно-временную сингулярность в «скачок»,
но и несколько изменить при этом фундаментальные физические постоянные. Я не нахожу
в современной физике оснований для подобной экстраполяции. Однако еще более неправ¬
доподобно, на мой взгляд, в геометрическом отношении волшебное превращение сильно
неупорядоченных сингулярностей, возникших в результате коллапса, в необычайно гладкий
и однородный Большой взрыв, который нужен каждой новой Вселенной, чтобы в ней имел
место Второй закон в известной нам форме (см. § 27.13).
28Л. Особая природа Большого взрыва: антропный ключ?
Можно ли привлечь антропный принцип для объяснения весьма особой природы Боль¬
шого взрыва? Можно ли рассматривать этот принцип как часть инфляционной картины,
в которой изначально хаотическое состояние с максимальной энтропией может привести
 	Ч
в конечном счете к Вселенной, подобной той, в которой мы живем, где выполняется Вто¬
рой закон термодинамики? В качестве общего аргумента можно заявить, что Второй закон
существен для жизни, как мы ее понимаем, кроме того, значения плотности и температуры,
распределение вещества, состав должны быть такими, чтобы способствовать существованию
жизни. Вдобавок Вселенная должна существовать достаточно долго, чтобы могла работать
эволюция, и т.д. Иногда этот аргумент используется в связи с положениями инфляцион¬
ной теории. В соответствии с ними получается, что, хотя исходное состояние может и не
претерпевать инфляцию, чтобы дать нам сглаженную Вселенную вроде той, которую мы
наблюдаем, нам достаточно иметь некоторую малую область начального пространственно-
временного «многообразия» сразу после Большого взрыва, достаточно гладкую, чтобы в ней
имела место инфляция, при этом вся нынешняя наблюдаемая Вселенная возникает как ре¬
зультат инфляции этой малой гладкой области (см. рис. 28.14 а). Рассуждение звучит при¬
близительно так: «Чтобы могла существовать разумная жизнь, нужна большая Вселенная
с временными масштабами, достаточно большими, чтобы могла иметь место эволюция в бла¬
гоприятных условиях, и т. д. Для этого необходима инфляция, начинающаяся из нашей малой
гладкой начальной области, которая, начавшись, дает нам удивительно огромную наблюда¬
емую Вселенную, которую мы знаем».
Эта картина выглядит настолько романтической, что, казалось бы, полностью невос¬
приимчива к какой-либо научной критике. Я так не считаю. Вернемся к той необычайной
степени точности (или к «тонкой настройке»), которая представляется необходимой, что¬
бы получить тот Большой взрыв, последствия которого мы наблюдаем. Как отмечалось
в § 27.13, необходимая точность, относящаяся к объему фазового пространства, составляет
по меньшей мере одну часть на Ю10	. Показатель 10123 соответствует энтропии черной
дыры с массой, равной массе наблюдаемой Вселенной.
Но действительно ли нам нужна вся наблюдаемая Вселенная, чтобы могла возникнуть
разумная жизнь? Это представляется маловероятным. Трудно представить себе, чтобы для

28.7. Особая природа Большого взрыва: антропный ключ?	639
а)	б)	в)
Рис. 28.14. а) Начальное состояние Вселенной совершенно общего вида не претерпевает инфляцию,
но мы можем найти малую начальную область, достаточно гладкую, чтобы в результате инфляции
10123
возникла Вселенная, которую мы наблюдаем (цена 10	).	6)	Насколько	обширная	Вселенная	нужна
в действительности для существования разумной жизни? Неизмеримо «дешевле» обошлось бы появ¬
ление разумной жизни, если бы Создатель произвел Вселенную в одну десятую ее линейного размера
11Т
(цена всего Ю10	).	в)	Чтобы	создать	так	же	много	разумных	существ,	как	и	в	случае а, Создателю
гораздо дешевле просто произвести 103 независимых экземпляров «меньшей» Вселенной (случай б)
1X7	190
(по «дешевой» цене (Ю10	)1000	—	ю10	).	Таким	образом,	антропный	принцип	не объясняет явной
расточительности инфляции
t
этого требовалось что-нибудь даже за пределами нашей Галактики. Хотя и возможно, что
разумная жизнь есть очень редкое явление, и потому для ее надежного появления необходимо
несколько большее пространство. Проявим щедрость и потребуем, чтобы область радиусом
в одну десятую расстояния до края наблюдаемой Вселенной напоминала ту Вселенную,
которую мы знаем, при этом нас не будет заботить, что происходит вне этой области. Область
фазового объема можно вычислить так же, как это было сделано раньше. Мы получим, что
масса этой области составляет 10_3 того, что было раньше; это дает энтропию черной
дыры, составляющую 10~6 от прежней*. Таким образом, точность, требующаяся от нашего
«Создателя» (см. рис. 27.21), чтобы построить эту область меньшего объема, составляет
теперь лишь
одну часть на 10
ю117
Взглянем на рис. 28.146. Наш Создатель теперь требует заметно меныией, чем раньше,
«малой гладкой области» начального «многообразия». Создатель гораздо скорее наткнется
на эту меньшую гладкую область, чем на несколько большую, которую мы рассматрива¬
ли раньше. Предполагая, что в малой области инфляция действует так же, как в большой,
но создает пропорционально меньшую Вселенную, можно оценить, насколько чаще Созда¬
тель наткнется на малую область, нежели на большую. Эта величина не превышает
1П117	I л123	1П123
1(Г10	:	1(Г10	=	Ю10
(в пределах точности, выражаемой наибольшим показателем) . Видно, что для Создате¬
ля было бы крайне расточительно (с точки зрения вероятности) заниматься построением
лишней удаленной части Вселенной, которая в действительности не нужна для нашего су¬
ществования, так что антропный принцип оказывается ненужным!
Некоторых читателей может обеспокоить, что из-за такой «экономии» со стороны Со¬
здателя появится меньшее число разумных существ. Существует такая проблема или нет, это
все равно не объясняет, почему имеет место крайняя «расточительность». Было бы много
**
Почему?
Объясните эти числа.

640
Глава 28
«дешевле», с точки зрения вероятности (оцениваемой по размеру соответствующих ящиков
в фазовом пространстве), а именно в 1010 раз, создать 103 меньших областей Вселенной
с инфляцией (что дает нам то же число разумных существ, что и одна Вселенная большего
ifc
размера), нежели одну область Вселенной большего размера (рис. 28.14 в) .
Чтобы показать, насколько слаб, в указанном отношении, антропный принцип, рас¬
смотрим следующие факты. Жизнь на Земле определенно не нуждается непосредственно
в фоновом СВЧ-излучении. Фактически нам не нужна даже дарвиновская эволюция! Было
бы гораздо «дешевле», в вероятностном смысле, создать разумную жизнь из хаоса, обра¬
зуемого газом и излучением. (Оценки показывают, что вся Солнечная система, включая ее
живых обитателей, могла бы возникнуть путем случайных столкновений частиц и излучения
с вероятностью, не меньшей, чем единица, деленная на 10	.) Число 10iU ничтожно мало
по сравнению с Ю10	, необходимым для Большого взрыва наблюдаемой Вселеннойi28*32).
Нам не требуется, чтобы Большой взрыв имел наблюдаемую однородную конфигурацию.
Нам не нужен Второй закон до момента возникновения жизни. Для Создателя было бы
гораздо «дешевле» не заниматься всем этим. Инфляция здесь не поможет. Кривая «жесткой
экономии» на рис. 27.8, принимаемая Создателем лишь для того чтобы произвести разум¬
ную жизнь, должна быть гораздо ближе к кривой в) б), чем к наблюдаемой кривой г) б),
независимо от инфляции!
Всё это есть просто подтверждение того аргумента, что не стоит предполагать, буд¬
то подходящие условия во Вселенной возникли путем некоторого случайного начального
выбора. В том, с чего начиналась Вселенная, действительно есть что-то весьма особенное.
Мне представляются два возможных подхода к этой проблеме. Выбор между ними есть
вопрос научной позиции. Можно принять, что начальный выбор был «актом божествен¬
ного творения» (чем-то вроде фантастической картины на рис. 27.21). А можно пытаться
построить научную математическую теорию, объясняющую необычайно специфическую
природу Большого взрыва. Сам я определенно склоняюсь к тому, чтобы попробовать по¬
нять, как далеко мы можем продвинуться в рамках второй возможности. Мы пользуемся
весьма точными математическими законами, описывающими поведение физического мира.
Оказывается, однако, что нам требуется еще что-то исключительно точное, а именно за¬
кон, определяющий саму природу Большого взрыва. Но Большой взрыв есть сингулярность
пространства-времени, а наши современные теории не умеют обращаться с такими объек¬
тами. Мы ожидаем, однако, что эта проблема будет решена некоторой квантовой теорией
гравитации^28в которой будут должным образом объединены законы общей теории отно¬
сительности, квантовой механики и, возможно, также некоторых других пока не известных
физических ингредиентов.
28.8.	Гипотеза кривизны Вейля
Свои основные соображения относительно современной деятельности в области кван¬
товой гравитации я изложу в главах 30-33. Пока же попробуем понять, какие геометри¬
ческие ограничения можно наложить на Большой взрыв. Рассмотрим гипотезу Джеймса
Хартла и Стивена Хокинга , которые попытались вывести их из серьезной теории квантовой
гравитации.
Напомним (см. § 19.7), что гравитационные степени свободы описываются конформ¬
ным тензором Вейля Саъс<1• Так, в пустом пространстве (для которого возможная кос¬
мологическая постоянная Л предполагается в любом случае малой в локальных масшта¬
бах и потому пока не учитывается) кривизна пространства-времени совпадает с кри¬
визной Вейля fa кривизна Риччи равна нулю). Действие кривизны Вейля на вещество
Объясните более подробно, откуда берутся эти числа.

28.8. Гипотеза кривизны Вейля
ч
641
носит деформирующий, или приливный характер, в отличие от действия материальных
источников, вызывающего уменьшение объема. Влияние кривизны Вейля иллюстрирует
рис. 17.9 а) (тот факт, что такая картина возникла первоначально на основе ньютонов¬
ских представлений о пространстве-времени, никоим образом не умаляет ее справедли¬
вости). Этой картине противостоит рис. 17.96), на котором показано уменьшение объема
под действием вещества, т. е. тензора Риччи. Возникают, однако, некоторые осложнения,
когда мы рассматриваем (как и здесь) влияние кривизны Вейля и Риччи на времениподоб-
ные геодезические (свободно движущиеся частицы, обладающие массой), поскольку тен¬
зор Риччи, помимо уменьшения объема, также может иногда оказывать деформирующее
влияние.
Это затруднение устраняется, если рассматривать влияние этих видов кривизны на ну¬
левые геодезические (световые лучи). Более того, тогда можно восстановить в правах космо¬
логическую постоянную Л, поскольку член вида Лдаъ не приводит к фокусировке световых
лучей*. Можно рассматривать геодезические на рис. 17.9 как световые лучи, принадлежащие
некоторому световому конусу (как на рис. 17.16). Если считать их относящимися к световому
конусу прошлого некоторого наблюдателя, то эффекты деформации можно представить гра¬
фически как результат действия линзы, помещенной между источником света и наблюдате¬
лем. Влияние тензора Риччиf28*34^, обусловленное распределением вещества, соответствует
действию собирающей линзы, тогда как действие тензора Вейля, обусловленное свобод¬
ным гравитационным полем, эквивалентно чисто астигматической линзе, которая работает
как собирающая в одной плоскости и как рассеивающая в перпендикулярной плоскости
(рис. 28.15). Можно получить довольно точное представление об эффектах (низшего по¬
рядка), создаваемых этими двумя видами кривизны, если представить себе, что мы глядим
Наблюдатель
/
Рис. 28.15. Фокусирующее действие тензора Риччи (с нулевым следом), обусловленное распределе¬
нием вещества, соответствует собирающей линзе. Действие тензора Вейля, обусловленное свободным
гравитационным полем, соответствует чисто астигматической линзе, собирающей в одной плоскости
и в той же мере рассеивающей в перпендикулярной плоскости
сквозь большое прозрачное сферическое массивное твердое тело, имеющее показатель пре¬
ломления вакуума. (Можно считать, что мы «смотрим» сквозь Солнце, используя нейтрино
(предполагаемые безмассовыми частицами), которые свободно проходят сквозь Солнце, за¬
мечая только его гравитационное поле!) В разумном приближении можно принять, что лучи,
проходящие сквозь Солнце, подвергаются в основном действию кривизны Риччи, так что
мы получаем увеличенное изображение (собирающая линза!) звездного поля, находящегося
позади Солнца. С другой стороны, за пределами солнечного диска мы получим чисто астиг-
* Почему не приводит? {Подсказка: см. приложение 28.34.)

642
Глава 28
магическую деформацию, обусловленную кривизной Вейля, так что малая круговая область
звездного неба нашему наблюдателю будет казаться эллиптической (см. рис. 28.16)*. Имен¬
но так, по существу, гравитационное поле Солнца деформирует фон звездного неба, что
впервые наблюдалось экспедицией Эддингтона в 1919 году (см. рис. 19.8).
Рис. 28.16. Можно получить довольно точное представление об эффектах (низшего порядка), создава¬
емых двумя различными видами пространственно-временной кривизны, «взглянув» на звездное небо
сквозь прозрачное непреломляющее Солнце, используя безмассовые нейтрино. В разумном приближе¬
нии можно принять, что лучи, проходящие сквозь Солнце, фокусируются кривизной Риччи, создавая
увеличение (как всякая собирающая линза). За пределами солнечного диска мы получим чисто астиг¬
матическую деформацию, обусловленную кривизной Вейля, так что малая круговая область звездного
неба будет казаться эллиптической
Рассмотрим теперь Вселенную, эволюционирующую таким образом, что изначально
однородное распределение вещества (с некоторыми флуктуациями плотности) постепенно
сжимается под действием гравитации, так что в конечном счете ее части коллапсируют
в черные дыры. Начальная однородность соответствует в основном распределению веще¬
ства с кривизной Риччи, однако по мере того как все больше вещества собирается вместе
под действием гравитационных сил, возрастает роль кривизны Вейля, особенно в областях
деформации пространства-времени, окружающих сжимающееся вещество. Кривизна Вейля
в конце концов обращается в бесконечность, когда возникают сингулярности черных дыр.
Если предположить, что вещество первоначально было выброшено из Большого взрыва по¬
чти однородным образом, то вначале вейлевская кривизна во всех отношениях была равна
нулю. Действительно, характерная особенность моделей ФЛРУ состоит в том, что кривизна
Вейля в них полностью исчезает (в соответствии с этим такие модели являются конформно¬
плоскими, см. § 19.7). Если вначале Вселенная близка к модели ФЛРУ, то можно ожидать,
что кривизна Вейля будет крайне мала по сравнению с кривизной Риччи, которая расходится
в условиях Большого взрыва.
Такая картина предполагает наличие существенной геометрической разницы между
начальной сингулярностью Большого взрыва (с исключительно низкой энтропией) и исход¬
ными сингулярностями черных дыр с весьма высокой энтропией. Кривизна Вейля исчезает
(или, по крайней мере, очень мала (например, конечна) по сравнению с тем, что могло бы
быть) в условиях начальной сингулярности и неограниченно стремится к бесконечности
вблизи конечных сингулярностей. Это есть геометрическое свойство, которое отличает, на¬
пример, рис. 27.20 а от рис. 27.20 г, хотя усмотреть различие в конформных диаграммах
может оказаться нелегко.
Покажите, что при бесконечно малом смещении вовне, изменяющемся обратно пропорционально рассто¬
янию, площади сохраняются.

28.8. Гипотеза кривизны Вейля
643
Этот вывод следует рассматривать в сочетании с другой предполагаемой особенностью
пространственно-временных сингулярностей, называемой космической цензурой. Выдвига¬
ется (пока не доказанное) утверждение, что, грубо говоря, результатом безостановочного
гравитационного коллапса будет черная дыра, а не что-то похуже, получившее название
голой сингулярности. Последняя есть пространственно-временная сингулярность, получа¬
ющаяся в результате гравитационного коллапса, которую могут видеть внешние наблю¬
датели, поскольку она «не одета» горизонтом событий. Существуют и другие, слегка от¬
личные формальные способы определить смысл термина «голая сингулярность», и я не
предполагаю заниматься здесь этими различиями^2835!. Для наших целей достаточно от¬
метить, что голая сингулярность «времениподобна» в том смысле, что сигналы могут вхо¬
дить в сингулярность и покидать ее, как показано на рис. 28.17 а. Космическая цензура
должна подобное запрещать (за исключением, возможно, некоторых умозрительных или
«особых» ситуаций, которые не встречаются в реальных условиях гравитационного кол¬
лапса).
Рис. 28.17. а) Причинные сигналы могут входить в «голую сингулярность» и покидать ее. Если это
исключается (из-за космической цензуры), то остаются б) «будущие сингулярности» (получающиеся
в результате гравитационного коллапса), в которые причинные сигналы могут входить, но из которых
не могут выходить, и в) «прошлые сингулярности» (в условиях Большого взрыва или, возможно,
более локальных актов рождения), из которых причинные сигналы могут выходить, но в которые не
могут входить. Гипотеза кривизны Вейля утверждает, что эта кривизна в исходных сингулярностях
в реальной физической Вселенной должна быть ограничена нулевым (или очень малым) значением
Космическая цензура — это теоретическая гипотеза (пока ни подтвержденная, ни опро¬
вергнутая), касающаяся общих решений уравнения Эйнштейна. Если принять эту гипотезу,
то физические пространственно-временные сингулярности должны быть «пространственно-
подобными» (или, возможно, «нулевыми»), но никак не «времениподобными». Существуют
два вида пространственноподобных (или нулевых) сингулярностей — начальные и конеч¬
ные сингулярности в зависимости от того, могут ли времениподобные кривые выходить из
сингулярности в будущее или входить в нее из прошлого (см. рис. 28.17б,в). Физическая
гипотеза, которую я называю гипотезой кривизны Вейля, гласит, что кривизна Вейля должна
быть нулевой (или, по крайней мере, очень малой) в начальной сингулярности реальной фи¬
зической Вселенной. Рождение Вселенной тем способом, который удовлетворяет гипотезе
кривизны Вейля, должно накладывать невероятные ограничения на выбор Создателя в про-
.*	.	ч
цессе, изображенном на рис. 27.21. Результатом должен быть Второй закон термодинамики,
имеющий известную нам форму. В настоящее время имеется некоторое математическое под¬
тверждение того, что некоторая форма «гипотезы кривизны Вейля» действительно налагает
на Большой взрыв ограничения, в результате чего модель Вселенной напоминает модель
ФЛРУ на ее ранней стадии^28,36!

644
Глава 28
28.9.	Гипотеза отсутствия границ Хартла- Хокинга
Если рассматривать гипотезу кривизны Вейля просто как некоторое утверждение, то
она, вероятно, ближе к варианту «акта божественного творения», нежели к физической те¬
ории. Требуется некоторое теоретическое обоснование положений, лежащих в основе этой
гипотезы. Какого рода теория нам для этого нужна? Обычная точка зрения в отношении
пространственно-временных сингулярностей состоит в том, что это епархия квантовой те¬
ории гравитагщи.
Трудность здесь состоит в том, что, несмотря на более чем полувековые направленные
усилия объединить общую теорию относительности с квантовой механикой, мы пока не
приблизились к согласию в отношении правильного подхода к этой проблеме. Я изложу
некоторые из наиболее популярных схем в главах 31 и 32, однако даже среди них мало се¬
рьезных попыток рассмотреть этот вопрос с учетом особой природы Большого взрыва. Име¬
ется, однако, одно заметное исключение в виде гипотезы, выдвинутой в 1983 году Хартлом
и Хокингом, поэтому уместно сделать несколько замечаний в отношении их основной идеи.
Одной из составных частей гипотезы Хартла - Хокинга является так называемая «ев-
клидизация». Идея, лежащая в ее основе, тесно связана с идеей поворота Вика, при¬
меняемого к пространству Минковского, в результате которого временная координата t
«поворачивается», превращаясь ъ г — it. При этом (пространственная) пространственно- .
временная метрика М2 принимает вид М2 = dr2 + dx2 + dy2 -f dz2 (см. §18.1). Ис¬
ходная идея (Джанкарло Вика)!2837! заключалась в том, что релятивистскую кванто¬
вую теорию поля (использующую специальную теорию относительности) можно по¬
строить, заменив при ее формулировке пространство-время Минковского евклидовым
4-пространством Е4, так что теория теперь будет инвариантной относительно евклидо¬
вой группы симметрии пространства Е4. Предполагая, что величины, полученные в ев¬
клидовом варианте теории, аналитичны по координатам, можно применить непрерыв¬
ный поворот Вика от т обратно к £, при этом получается соответствующая теория,
инвариантная относительно группы Пуанкаре 4-пространства Минковского. Эта процеду¬
ра имеет два существенных преимущества. Во-первых, величины, расходящиеся в про¬
странстве Минковского, в евклидовом варианте теории могут оказаться сходящимися.
(Причина состоит в том, что группа евклидовых вращений 0(4) компактна и потому
имеет конечный объем, тогда как релятивистская лоренцева группа 0(3, 1) некомпакт¬
на и имеет бесконечный объем.) В частности, интегралы по траекториям (см. §26.6)
в евклидовом варианте имеют гораздо больше шансов на математически осмысленное
определение, нежели в варианте Минковского. Другое преимущество состоит в том, что
примененный должным образом поворот Вика обеспечивает условие положительной часто¬
ты (см. §§ 9.3, 9.5, 24.3).
В схеме Хартла- Хокинга используется остроумная модификация идеи Вика, предло¬
женная Хокингом, в которой «повороту» подвергается не пространство, служащее фоном
для траекторий при интегрировании по траекториям, как обычно, а отдельные экземпляры
пространства-времени, которые сами образуют каждую траекторию при интегрировании по
траекториям^28 38!. Эти отдельные экземпляры могут иметь положительно определенную
риманову метрику вместо лоренцевой метрики обычного пространства-времени. (Эти рима-
новы метрики часто ошибочно называют «евклидовыми», хотя обычно так именуют плоское
евклидово пространство Еп!) Следует пояснить, однако, что вариант «евклидизации», пред¬
ложенный Хокингом, содержит «скачок воображения» по сравнению с исходной идеей Вика.
Откроет ли это путь к плодотворному союзу общей теории относительности с квантовой
механикой — еще предстоит понять ^28*391.
Поразительная гипотеза Хартла - Хокинга состоит в том, что такой подход Хокинга
к интегралам по траекториям может описывать квантовую теорию самого Большого взрыва

28.9. Гипотеза отсутствия границ Хартла~ Хокинга
645
и что вместо реального сингулярного пространства-времени используется квантовая супер¬
позиция (т. е. «интеграл по траекториям») «экземпляров пространства-времени», которые
могут иметь риманову, а не лоренцеву метрику. Она была названа гипотезой отсутствия
границ, поскольку вместо сингулярной границы классического пространства-времени, ко¬
торую представляет Большой взрыв, появляется суперпозиция семейства несингулярных
пространств, в которой доминирует риманова метрика. Это просто «закрывает» нижний ко¬
нец, как показано на рис. 28.18, так что сингулярная граница полностью исчезает. Моменты
времени «после» Большого взрыва представляют переход, при котором лоренцева геомет¬
рия начинает доминировать над римановой. (Можно представить это, используя подходящую
комплексную метрику.) Даже в лоренцевой области все же существует суперпозиция «экзем¬
пляров пространства-времени» (некоторые из которых являются римановыми), однако вдали
от Большого взрыва доминирует классическое лоренцево пространство-время, тогда как в
области самого Большого взрыва доминирует «безграничная» риманова метрика. Эта схема
не только обладает подлинным изяществом, намечая путь решения проблемы, казавшейся
неразрешимой, но и непосредственно поддерживает гипотезу «гладкой ранней Вселенной»,
которая может быть совместима с гипотезой кривизны Вейля.
Доминирует
лоренцева
метрика
Доминирует
риманова
метрика
Будущая сингулярность
«закрывается»
только в прошлом
а)
б)
Рис. 28.18. Гипотеза отсутствия границ Хартла-Хокинга предполагает, что а) Большой взрыв можно
рассматривать в рамках квантово-гравитационного подхода, согласно которому риманова (а не лорен¬
цева) геометрия определяет интеграл по траекториям вблизи классической сингулярности и позволяет
закрыть пространство-время несингулярным образом, б) В отношении сингулярностей коллапса такое
«закрытие» представляется необходимым лишь на «дальнем конце» пространства-времени, допуская
таким образом высокоэнтропийные исходные сингулярности, которые, как ожидается, возникают при
гравитационном коллапсе в черные дыры (или Большом хлопке)
Пока всё хорошо. Однако я испытываю значительные затруднения в связи и с этой
гипотезой. Прежде всего, сама идея «евклидизации» проблематична во многих отношениях,
связанных с ее применением. Даже в контексте плоского пространства обычно не может
быть и речи о точном вычислении интеграла по траекториям, и приходится делать много
приближений. Было бы полезно выделить некоторые определенные члены, которые дают
основной вклад в этот интеграл, и отбросить остальные. Это должно бы дать разумное
приближение для «евклидова» интеграла по траекториям, однако напомним, что для полу¬
чения подходящего физического результата требуется процесс аналитического продолжения.
Это весьма ненадежная процедура, поскольку то, что служит приближением голоморфной
функции в одной области, скорее всего, не будет таковым в другой области. Чтобы понять
сущность этой трудности, предположим, что мы имеем некоторую вещественную аналити¬
ческую функцию f(x), известную, но лишь приближенно, в области вещественных значе¬
ний х, и мы хотим определить ее значения при чисто мнимых х. Если прибавить к f(x)
функцию вида е cos( Ах), где ей А — вещественные числа, причем число е очень мало, а А —

646
Глава 28
велико, то на вещественной оси х функция f(x) изменится мало, тогда как ее поведение
вдоль мнимой оси станет совершенно иным. Это демонстрирует крайнюю неустойчивость
процесса аналитического продолжения . Насколько я понимаю, «фокус с евклидизацией»
может оказаться весьма полезным при построении точных моделей КТП, однако возника¬
ют затруднения, когда он, как в данном случае, сочетается с какими-либо приближениями.
(Мне не ясно, однако, в какой мере гипотеза Хартла - Хокинга зависит от особенностей,
связанных с аналитическим продолжением.)
Затруднения технического характера возникают также при обобщении процедуры ев-
клидизации. Насколько я могу понять, это есть ловкий прием для построения согласованных
моделей КТП (и обеспечения условия положительной частоты, см. §§9.3, 9.5), однако бы¬
ло бы крайним оптимизмом ожидать, что таким путем может быть получена какая-либо
конкретная КТП, представляющая интерес. Теории, получаемые в результате евклидизации,
имеют, по существу, скрытую структуру, связанную с группой симметрии, имеющей «непра¬
вильную сигнатуру»; см. §§ 13.8, 18.2. Я не понимаю, почему «правильная» теория должна
иметь такой странный характер.
28.10.	Космологические параметры: согласие с результатами
наблюдений
Существует также проблема связи с результатами наблюдений. Гипотеза отсутствия
границ Хартла - Хокинга, по крайней мере в ее исходной форме, по-видимому, относится
к замкнутой Вселенной (фактически к случаю К > 0), и в течение ряда лет Хокинг ока¬
зывал поддержку именно таким моделям. Однако перед лицом нарастающего количества
космологических свидетельств в пользу гиперболической модели (К < 0) Хокинг в сотруд¬
ничестве с Туроком видоизменил свои рассуждения таким образом, чтобы приспособить
гипотезу отсутствия границ и к гиперболическому случаю I28-40). Здесь имеется любопытная
параллель с ожиданиями инфляционной космологии, которая в течение многих лет заявля¬
ла, что обладает решающими доказательствами в пользу того, что наблюдаемая Вселенная
должна быть пространственно плоской (К — 0). Ряд инфляционистов также в дальнейшем
модифицировали свои аргументы перед давлением впечатляющих космологических данных,
допустив возможность варианта К < oJ28'41!
Каково современное положение дел с результатами наблюдений? В настоящее время
достигнут значительный прогресс и получены свидетельства (причем из более чем одно¬
го источника) в пользу значительной положительной космологической постоянной А. Это
означает, что мы в конце концов можем принять вариант К — 0. А поскольку наблюдения
допускают этот вариант, нельзя исключить возможность малой положительной простран¬
ственной кривизны (Хокинг предпочел К > 0) или малой отрицательной пространственной
кривизны (сам я предпочитаю К < 0), так что опять становятся возможными все варианты!
Какое отношение имеет открытие факта А > 0 к значению кривизны К? Прежде всего
следует упомянуть о тех соображениях, которые лежали в основе прежней уверенности,
что данные космологии указывают на отрицательное значение К. Существенным пунктом
было полное содержание массы-энергии во Вселенной. Если оно слишком мало, то оно не
сможет сделать Вселенную замкнутой с положительной кривизной или (в моделях фрид-
мановского типа) повернуть вспять начальное расширение с образованием фазы коллапса
(см. рис. 27.15 а, б, в). Долгое время считалось, что плотность обычного видимого «бари-
онного» (см. §25.6) вещества в галактиках недостаточна для этого, составляя примерно
лишь одну тридцатую часть критического значения, разделяющего положительные и отри¬
цательные значения кривизны К, так что критическая плотность дает нам К = 0. Обычно
Объясните это, воспользовавшись результатами § 5.3. (.Подсказка: что представляет собой еАгх +е~Агх1)
*

28.10. Космологические параметры: согласие с результатами наблюдений
647
вводится величина fib для обозначения доли критической плотности массы-энергии, обес¬
печиваемой обычным барионным веществом. Так, при fib = 1 барионное вещество обес¬
печивает критическую плотность, и любая дополнительная (положительная) масса-энергия
приводит к Вселенной, у которой К > 0. Однако, как уже упоминалось, мы, по-видимому,
имеем вместо этого что-то вроде fib ~ 0,03, и это создавало уверенность в том, что К < 0.
Здесь, однако, не приняты во внимание убедительные свидетельства, что во Вселенной
имеется гораздо больше материи по сравнению с непосредственно наблюдаемым барион¬
ным веществом звезд. Давно уже стало ясно, что динамику звезд в галактиках не удается
понять в рамках стандартной теории f28*42если не предположить, что в окрестности галак¬
тик находится гораздо больше материи, нежели непосредственно наблюдается в звездах. То
же относится к динамике отдельных галактик в скоплениях. В целом представляется, что
материи примерно в 10 раз больше, чем наблюдается в обычной барионной форме. Это зага-
V#	U	O'
дочная темная материя, относительно действительной природы которой среди астрономов
пока нет согласия и которая может оказаться даже чем-то отличным от того, что определен¬
но известно физикам, изучающим элементарные частицы, однако в настоящее время здесь
большой простор для спекуляций[28.43] Поскольку темная материя содержит массу-энергию
примерно в 10 раз большую, чем обычное барионное вещество, доля критической плотно¬
сти fid, вносимая темной материей, оценивается примерно в fid — 0,3 (неопределенность
этой оценки такова, что в нее, при желании, можно включить и барионную долю fib =
— 0,03). Это значительно меньше, чем требуется для достижения критического значения.
Более того, из наблюдений разного рода (в частности, гравитационного линзового эффекта)
убедительно следует, что во Вселенной не может быть других значительных вкладов массы.
Так что вывод К < 0 в настоящее время кажется надежно подтвержденным, и инфляциони-
сты и последователи Хартла - Хокинга начали искать пути для включения условия К < 0 в
свой взгляд на мир.
Затем пришла сенсация, связанная с космологической постоянной. Напомним (§19.7),
что Эйнштейн относился к введению космологической постоянной Л как к своей «самой
большой ошибке» (возможно, потому, что это помешало ему предсказать расширение Все¬
ленной). Хотя с тех пор такая возможность космологами всегда учитывалась, лишь немногие
из них ожидали, что она может оказаться отличной от нуля в нашей реальной Вселенной.
Дополнительные вопросы принес тот факт, что вычисление «энергии вакуума», проведенное
в рамках квантовой теории поля (по существу, расчет эффекта перенормировки, подобного
рассмотренному в § 26.9), дает абсурдный результат, согласно которому должна существо¬
вать эффективная космологическая постоянная, превышающая наблюдаемую в 10120 раз
(или, по крайней мере, в Ю60 раз при несколько иных допущениях)! Это назвали «пробле¬
мой космологической постоянной». Казалось правдоподобным, что какая-то пока не извест¬
ная компенсация либо новый общий принцип могут привести к тому, что энергия вакуума
окажется равной нулю, однако никоим образом не предполагалось, что обнаружится неко¬
торый малый остаток, имеющий отношение к космологии в современную эпоху. (Следует
упомянуть, что эта «энергия вакуума» в силу требования локальной лоренцевой инвариант¬
ности должна была быть пропорциональна метрическому тензору даь, так что в уравнение
Эйнштейна постоянная Л должна была входить в виде Лдаь, т. е. в точности так, как пред¬
положил Эйнштейн в 1917 году. Беда лишь в том, что значение Л оказывалось совершенно
неверным!)
Тем не менее в 1998 году две группы исследователей, одна в Калифорнии, руково¬
димая Саулом Перельмуттером, другая в Австралии под руководством Брайана Шмидта
и на востоке США во главе с Робертом Киршнером, наблюдая весьма отдаленные сверх¬
новые (см. § 27.8), пришли к замечательному выводу, что расширение Вселенной начало
ускоряться соответственно загибу вверх на рис. 27.15г, а это характерно для положитель¬
ной космологической постоянной! Как велика эта наблюдаемая постоянная Л? Здесь пока

648
Глава 28
нет определенности (и некоторые теоретики считают, что пока нет убедительного подтвер¬
ждения положительного значения yl)I28 44jl, однако замечательно то, что соответствующая
значению Л эффективная плотность массы-энергии отнесенная к критической плотно¬
сти, приблизительно равна — 0,7, так что для полной эффективной плотности как доли
критического значения мы получаем
£2	f2d 4* £2д	~ 0,3 4~ 0,7 — 1.
Другими словами, результаты наблюдений теперь, по-видимому, согласуются с вариан¬
том К — 0.
Инфляционисты (по крайней мере, те из них, кто имел смелость остаться верным своей
прежней позиции), конечно, ликовали, и это действительно можно было считать успехом
их теории, которая, вопреки, казалось бы, убедительным доводам против, предсказывала
значение К = 0. Однако неопределенность пока слишком велика, чтобы можно было с уве¬
ренностью прийти к такому заключению. Существенно, что недавно проводились другие
наблюдения, имеющие отношение к данному вопросу. Как упоминалось в §28.5, измеря¬
лись вариации температуры микроволнового фона, начиная со спутника СОВЕ, запущен¬
ного в 1989 году, и кончая наиболее поздними (ко времени написания книги) данными,
полученными космическим зондом WMAP.
Вариации температуры обычно анализируются путем разложения температуры неба по
сферическим гармоникам в соответствии с процедурой, описанной в §22.11. Напомним,
что различные сферические гармоники нумеруются положительными числами £ и целы¬
ми числами т в области от —£ до £. (В квантовой механике вместо £ обычно пишут j,
причем j и т могут принимать полуцелые значения.) Величина га не так важна, пото¬
му что она зависит от произвольно выбранного направления в небе, так что наибольший
интерес представляет общая интенсивность для каждого значения L Результаты анализа по¬
казаны на рис. 28.19. Отметим, что после прохождения максимума вблизи £ = 200 кривая
начинает осциллировать. Соответствующие локальные максимумы называются «акустиче¬
скими пиками», поскольку они соответствуют предсказанию теории, что на ранней стадии
Вселенной локальные количества вещества начинают падать внутрь и затем либо отража¬
ются обратно, либо проваливаются дальше (этого можно ожидать от темной материи), что
создает своего рода звуковые колебания. Типичный масштаб, на котором возникают эти
колебания, будет определяться «масштабом горизонта» при расцеплении (представьте, что
точки и и v на рис. 28.5 а двигаются по поверхности расцепления, пока их конусы прошлого
не соприкоснутся, — это и будет «масштабом горизонта») t28-45l. Именно этому масштабу
соответствует главный пик.
Возникает, однако, вопрос: какое угловое расстояние на небе соответствует простран¬
ственному расстоянию во Вселенной во времена расцепления? Здесь важную роль играет
пространственная кривизна Вселенной, поскольку акустические пики смещаются тем или
иным образом вдоль оси £ в зависимости от значения кривизны К (в сторону меньших
значений £ при положительных К и больших при отрицательных К). Это, однако, не такой
простой вопрос, поскольку здесь играет роль также скорость расширения Вселенной, по¬
этому необходимы подробные вычисления. Итог таков, что подобный анализ космического
микроволнового фона, вообще говоря, совместим с вариантом К — 0, хотя и остается пока
возможность положительного или отрицательного значения К.
Результаты, соответствующие большим значениям £, как будто согласуются с ожида¬
ниями инфляционной теории (имеет место также масштабная инвариантность флуктуаций
температуры, предсказываемая некоторыми моделями инфляции). А как обстоит дело с ма¬
лыми значениями £1 Значение £ = 0 не слишком информативно, оно описывает Вселенную
в целом. А как насчет значения £ — 1 (описывающего «дипольный момент»)? Оно ничего на
говорит нам об отдаленных областях Вселенной, поскольку движение Земли сквозь микро-

28.10. Космологические параметры: согласие с результатами наблюдений
649
=1
г—. J
см
С'
+
^fwhm [градусы]
10 1
6000	*i	.‘j	.	V	11|"Г'('11"1 '| П''! * Г
5000 г
4000 ‘
3000 г
2000 г
1000 г
10
100
1000
£
Рис. 28.19. Ожидаемые «акустические пики» гармонического анализа космического микроволнового
фона (сплошная линия) и наблюдаемые экспериментальные точки (крестики с указанием погрешно¬
сти измерения). Обратите внимание на весьма значительное расхождение в случае квадрупольной
составляющей (£ = 2), почти скрытое (случайно?) вертикальной осью
волновой фон приводит к асимметричному доплеровскому сдвигу (см. упражнение 27.10),
в результате получается распределение температуры с £ = 1, в котором наблюдаемая темпе¬
ратура слегка повышена в направлении движения и понижена в противоположном направ¬
лении. Первым космологически существенным значением является £ = 2 («квадрупольный
момент»). Здесь имеет место расхождение с масштабно-инвариантными предсказаниями
инфляционной теории, которые подтверждаются в нескольких последующих гармониках.
Это расхождение отнюдь не мало и кажется довольно понятным. Нарушение масштабной
инвариантности можно интерпретировать как следствие отклонения от плоской геометрии
с К — 0 на больших расстояниях, указывающее, возможно, что либо К > 0, либо К < 0,
поскольку такой масштаб задается именно «радиусом кривизны».
Эти рассуждения приводят к интересной, но довольно неопределенной ситуации. Сле¬
дует, однако, иметь в виду, что график на рис. 28.19 использует в действительности лишь
малую часть информации, содержащейся в картах распределения температуры, получен¬
ных в рамках программы WMAP. Для каждого £ существует 2^+1 различных значений т,
каждому из которых соответствует вещественный параметр. Приведенный анализ игнори¬
рует большую часть информации, так что должно существовать еще огромное количество
скрытых данных, которые могли бы сообщить нам нечто, возможно, очень важное о ранней
Вселенной.
Здесь я упомяну лишь об одном альтернативном способе анализа этих данных, предло¬
женном в основном Вахе Гурзадяном с сотрудниками [332, 333, 334, 329, 330, 331], который
приводит к поразительным выводам. В этом подходе гармонический анализ не используется,
вместо этого рассматриваются искажения формы отдаленных областей с различным значени¬
ем температуры, обусловленные влиянием пространственной кривизны. Если принять, что
невозмущенная область имеет круглую форму, то под влиянием кривизны она может стать
эллиптической (вспомним рис. 28.15). На самом деле мы, конечно, не знаем, как выглядит

650
Глава 28
форма области, поскольку возможны статистические эффекты, вынуждающие область с дан¬
ной температурой становиться более (или менее) вытянутой (веретенообразной). Это тонкий
момент статистического анализа; однако вывод, к которому пришли Гурзадян и его коллеги,
состоял в том, что на картах микроволнового излучения (составленных по данным проек¬
тов СОВЕ, затем BOOMERANG, затем WMAP) имеется значительная доля эллиптических
областей. Что это означает? Теоретический анализ ситуации приводит к выводу, что такой
степени эллиптичности можно ожидать лишь при К < 0 (как результат «смешивания геоде¬
зических»). Эти результаты являются новыми, поэтому следует подождать, не появятся ли
существенные возражения против такого замечательного вывода.
Этот анализ дает также независимое подтверждение положительности космологиче¬
ской постоянной примерно такой величины, какая следует из результатов наблюдения за
сверхновыми звездами. Тогда отрицательная кривизна должна быть мала в том смысле, что
сумма Qd + Qa не может сильно отличаться от единицы, имея, например, значение 0,9.
Это придает особое значение загадке, которая не дает покоя многим космологам. Величи¬
ны f2b, Qd и Qa зависят от времени. На ранних стадиях развития Вселенной Qь и будут
гораздо больше, a Qa — гораздо меньше. На поздних стадиях Вселенной J2& и Qd стано¬
вятся пренебрежимо малыми, так что эффективная плотность массы-энергии определяется
величиной Qa . Видимое совпадение порядков величин Qa и Qd именно в нынешнюю эпоху
представляется довольно загадочным.
Забавно, что термин «космологическая постоянная», по-видимому, вышел из моды по¬
чти в тот самый момент, когда величина А проявилась в результатах наблюдений, хотя такая
терминология была стандартной с тех пор, как она была введена Эйнштейном в 1917 году.
Вместо этого величину А называют «темной энергией», или «энергией вакуума», или иногда
«квинтэссенцией», возможно, потому, что сухой термин «космологическая постоянная» не
передает в достаточной мере ощущение чуда, или, более рациональное объяснение, потому
что слово «постоянная» наводит на мысль, что А не может меняться со временем! Многим
космологам было бы приятнее иметь дело с переменной величиной Л, считая нынешнее
значение этой величины связанным с возникновением «новой фазы инфляции» и указывая
тем самым на сходство последней с инфляционной фазой в самой ранней Вселенной. На¬
помним (см. § 28.4), что в такой фазе преобладает «ложный вакуум» с настолько большой
эффективной космологической постоянной, что она полностью доминирует над всем (уже
весьма плотным) обычным веществом. Если бы эффективное значение Л во Вселенной того
времени кардинально отличалось от современного, то мы имели бы переменную величину А
и термин «космологическая постоянная» был бы неподходящим.
Однако эта привлекательная, как может показаться, идея содержит свои математи¬
ческие трудности, так что термин «космологическая постоянная» был введен неспроста.
Постоянство величины А есть прямое следствие условия сохранения энергии УаТаь =
= 0 (§§ 19.5-19.7), поскольку добавление к Таь величины, кратной даъ> может оставить это
условие сохранения ненарушенным лишь в случае постоянного коэффициента при даъ.
Таким образом, всякого рода непостоянство величины А должно сопровождаться компенса¬
цией несохранения массы-энергии вещества. Поэтому с точки зрения теории гораздо удоб¬
нее иметь постоянную величину Л, что действительно согласуется с результатами наблю¬
дений.
Что же мы получаем в итоге? Довольно интересную ситуацию. Я не считаю, что ин¬
фляционная космология «подтверждена» наблюдениями, но даже если бы было так, это не
решило бы космологическую проблему, которая, на мой взгляд, затмевает все прочие, —
совершенно «особую» природу Большого взрыва (с вероятностью не более чем один шанс
22^
из Ю10	), которая лежит в основе Второго закона. Некоторые космологи считают непри¬
емлемой возможность столь тонкой «настройки» (см. рис. 27.21) и пытаются «объяснить»
*
Почему?

28.10. Космологические параметры: согласие с результатами наблюдений
651
всё это в рамках инфляционной теории или антропного принципа (§§ 28.4, 28.6), хотя, как
мы видели, подобный подход не приводит к цели.
Возникает, таким образом, фундаментальная проблема при любой попытке (к тако¬
вым относятся, например, инфляция и гипотеза Хартла - Хокинга) рассматривать проблему
пространственно-временных сингулярностей в рамках физики с временной симметрией.
В инфляционной физике отсутствует временная асимметрия, так же, насколько я пони¬
маю, обстоит дело и с гипотезой Хартла - Хокинга, поэтому она применима как к конечным
сингулярностям типа коллапса (в черных дырах или в условиях Большого хлопка, если та¬
ковой имеет место), так и к Большому взрыву. Хокинг считает, что может происходить,
хотя и весьма экзотическим образом, «замыкание при отсутствии границ» пространства
в окрестности конечной сингулярности с возвращением тем или иным способом к Большо¬
му взрыву, и только там должна проводиться «евклидизация» (рис. 28,18)! По его словам,
гипотеза отсутствия границ просто утверждает, что существует некоторый способ замы¬
кания без границ, и мы определяем «начало» (которое устанавливает направление течения
времени во Вселенной) как конец, в котором происходит замыкание. Я должен сказать,
что это утверждение вызывает у меня серьезные сомнения, как и любые рассуждения, не
предполагающие в явном виде временную асимметрию самих физических законов. (Напри¬
мер, в «экзотических» рассуждениях Хокинга содержится «граница» в условиях конечной
сингулярности коллапса, гладкое замыкание без границы происходит только «на другой сто¬
роне» пространства-времени. Мне кажется, что здесь рассмотрена лишь половина проблемы
устранения границ.)
Должны ли мы рассмотреть возможность построения подлинно асимметричной во вре¬
мени фундаментальной физики, за которую я выступаю? В главе 30 мы рассмотрим именно
этот вопрос. И мы обнаружим, что он связан с некоторой фундаментальной загадкой, кото¬
рую мы оставили нерешенной в главах, посвященных квантовой механике. Поэтому в следу¬
ющей главе я вернусь к этой важной квантово-механической головоломке. Затем в главе 30
я представлю свои собственные идеи относительно правильного подхода к решению вопро¬
са и в конечном счете к решению проблемы временной асимметрии сингулярности. А пока
я должен еще раз официально предупредить читателя, что многие физики не согласятся
с моей позицией.
Примечания
§28.1.
28.1. См., например, [816], стр. 195, где также используется пример ферромагнетизма, почти неиз¬
бежный при популярном изложении вопроса. Все же следует помнить, что здесь имеет место
существенная идеализация куска реального железа, в котором детальное действие сил может
иметь очень сложный характер. Хотя в достаточно малых областях внутри куска железа опи¬
санная тенденция к намагничиванию может служить хорошим приближением, на практике
такие намагниченные области стремятся ориентироваться случайным образом, так что кусок
железа в целом не становится эффективным магнитом. Более того, чтобы железо стало на¬
магниченным в существенной степени, охлаждение ниже точки Кюри должно быть крайне
медленным, и такой идеальной ситуации достигнуть непросто. В нашем теоретическом обсу¬
ждении целесообразно пренебречь этими усложнениями и принять описанную идеализацию.
28.2. Квантово-механическое туннелирование имеет место, когда квантовая система самопроиз¬
вольно переходит из одного состояния в другое состояние с более низкой энергией (с из¬
лучением избытка энергии) при наличии энергетического барьера, препятствующего такому
переходу в классической физике.
Л
28.3. На отсутствие в этом примере симметрии относительно отражения указывает буква S в обо¬
значении SO (2).
28.4. Такой «подходящей группой» представляется SU(3) х SU(2) х

652
Глава 28
§28.2
28.5. См. примечание 28.1.
28.6. См. [805, 277, 686].
28.7. Обещающая теория такого рода излагается в работе [723]. Соответствующий обзор и относя¬
щуюся сюда литературу можно найти в [337].
28.8. См. [133].
28.9. Работы Сотрудничества MACRO установили жесткие ограничения на частоту появления этих
частиц. См. [505].
§28.3.
28.10. Эта связность вначале рассматривалась как калибровочная связность V на меньшем рас¬
слоении Вс над М., слоями которого служат С (2)-симметричные пространства С лептонов
в каждой точке. Но точно так же, как и в обычном тензорном исчислении (§ 14.3), знание
того, как оператор V действует на Вс, полностью определяет его действие на «тензоры»,
заданные на С. Можно задать пространство Q как £* ® С (с одним верхним «индексом»
и одним нижним).
28.11. «Красное смещение» z определяется таким образом, что 1 + z есть коэффициент увеличения
длины волны. Наиболее доступное изложение содержится в [486], более подготовленному
читателю можно рекомендовать книгу [213].
28.12. Можно было бы обсудить возможную роль связности кванглеменции (см. §23.10) между q
и г. Это определенно заслуживает обсуждения, однако выходит за рамки современных идей
«спонтанного нарушения симметрии». На мои взгляды в этом вопросе повлияли беседы
с Джорджем Спарлингом и Бикашем Синха.
28.13. См. [493].
§28.4.
28.14. См. [701].
§28.5.
28.15. См. [335]. Подробности можно найти в книгах [213] или [487]. В качестве вдумчивого кри¬
тического обзора рекомендуется [97].
28.16. См. [54, 56, 57, 59, 710, 732]. Примером полностью «маховского» физического подхода могут
служить спиновые сети, кратко описанные в § 32.6.
28.17. См. [567, 568].
28.18. Существует, однако, и более новый взгляд на этот вопрос, согласно которому теория Эйн¬
штейна в конечном счете является «маховской». См. [58, 59, 650].
28.19. Эстетические критерии особенно подчеркиваются в популярном обзоре Марио Ливио [492].
28.20. Этому взгляду предшествовала так называемая «хаотическая космология», предложенная
независимо Чарльзом Мизнером и Яковом Зельдовичем. Там рассматривалось случайное на¬
чальное состояние (несмотря на, казалось бы, явное противоречие со Вторым законом), при
этом в качестве попытки сгладить Вселенную привлекаются тепловые процессы. См. [528].
28.21. Лучший вариант хаотической структуры этой исходной сингулярности был предложен
в 1970 году Белинским и др. [69].
28.22. См. примечание 27.21, где даются необходимые ссылки на литературу.
§28.6.
28.23. Мне кажется, что впервые я услыхал об этой идее «слабого» антропного принципа из ра¬
диопередачи Би-Би-Си с участием Фреда Хойла в 1950-х годах. О сильной форме антропного
принципа, которая обсуждает «антропную» роль фундаментальных физических постоянных,
я узнал на одной из Кембриджских лекций Хойла «Религия как наука», где кратко описыва¬
лось образование тяжелых элементов в звездах, требующее наличия у углерода определенного
ядерного энергетического уровня.
28.24. См. [196, 130].

28.10. Космологические параметры: согласие с результатами наблюдений
653
28.25. Грубо говоря, кубический корень из возраста Вселенной, выраженного в планковских едини¬
цах, очень близок к квадратному корню из отношения сил электрического и гравитационного
притяжения между протоном и электроном.
28.26. См. [205, 112, 325]. Идее «меняющихся постоянных» посвящена недавняя занимательная
книга [506].
28.27. Используя здесь термин «сильный антропный принцип», я следую Картеру [ 130]. В работе [62]
смысл этого термина отличается в нескольких отношениях.
28.28. Имеется более подробное изложение этой истории [62] и [729], стр. 111. Более глубокое
описание состава нашей Вселенной содержится в статьях [402, 114].
28.29. См. [372].
28.30. См. [729].
28.31. В своем выступлении по случаю присуждения премии Адамса (см. [588, 590]) я выдвинул
подобную идею (но без изменения физических постоянных) в не вполне серьезной форме.
Возможно, кем-то другим это было сделано раньше.
§28,7.	.	•
28.32. См. [610].
28.33. Абхай Аштекар высказал мне альтернативную точку зрения, что совершенно особую природу
Большого взрыва могло бы определить что-то иное, нежели «квантовая гравитация». Может
быть, и так, но я не могу отвлечься от того факта, что именно гравитация и, по-видимому,
только гравитация имела особый характер в условиях Большого взрыва.
§28.8.
28.34. Фактически здесь участвует лишь часть тензора Риччи, имеющая нулевой след, Rab — j Rgab,
и не играет роли космологическая постоянная.
28.35. См. общий обзор проблемы космической цензуры [592, 618].
28.36. См. [555, 148, 782, 783, 22]. Тод выдвинул особенно привлекательную версию гипотезы кри¬
визны Вейля, которая просто утверждает, что при любой начальной сингулярности существует
регулярная конформная геометрия с границей.
§ 28.9.
28.37. Впервые этот подход был применен Виком в работе [831], затем он был с успехом использован
Зинн-Жюстином [862]. •
28.38. См. [360].
28.39. В недавней работе Ренаты Лолл и ее сотрудников предполагается возможность глубокого раз¬
личия между использованием римановой метрики в интегралах по траекториям, как предлагал
Хокинг, и непосредственным применением лоренцевой метрики. См. [18].
§28.10. '
28.40. См. [374].
28.41. См. [111,490].
28.42. Мордехай Милгром [524] выдвинул интригующее предположение, что никакой темной ма¬
терии нет, а необходимо изменить динамику ньютоновской теории тяготения не так, как
это сделал Эйнштейн, а предполагая, что при очень малых ускорениях действие гравитации
усиливается некоторым специфическим образом. Хотя эта идея вроде бы замечательно согла¬
суется с фактами, пока отсутствует цельная теория, имеющая четкий теоретический смысл.
Я считаю, что подобные нестандартные идеи следует не отвергать с порога, а постараться вы¬
яснить, можно ли сделать данную схему частью более широкой согласованной точки зрения.
(Сам я не сумел понять, как это сделать!)
28.43. См. доступное обсуждение проблемы темной материи (а также «темной энергии», возможно,
при переменной величине Л) [462].
v*	•	,	•
28.44. См. [84]. Более распространенную интерпретацию можно найти в [638, 49].
1	■	t
28.45. Доуделсон [213] объясняет, как сделать это и провести аналогичный анализ данных экспери¬
мента СМВ.

Глава 29
Парадокс измерения
29.1.	Традиционные онтологии квантовой теории
Квантовая механика, вне всякого сомнения, стала одним из высших достижений двадца¬
того столетия. Она объясняет огромное множество явлений, которые оставались глубокой
загадкой для физики XIX века. К их числу относятся существование спектральных линий,
стабильность атомов, природа химической связи, прочность и цвет материалов, ферромагне¬
тизм, фазовые переходы между твердым, жидким и газообразным состояниями, цвет нагре¬
того тела, находящегося в равновесии с окружающей средой (излучение черного тела). Даже
некоторые загадочные проблемы биологии, например необычайная надежность наследствен¬
ности, получили объяснение с точки зрения принципов квантовой механики. Эти явления,
а также многие другие, открытые уже в XX веке, — жидкие кристаллы, сверхпроводи¬
мость и сверхтекучесть, поведение лазеров, бозе-эйштейновские конденсаты, любопытная
нелокальность ЭПР-эффектов и квантовая телепортация — теперь хорошо поняты на основе
математического формализма квантовой механики. Этот формализм действительно произвел
революцию в нашей картине реального физического мира, значительно более радикальную,
даже чем это сделала общая теория относительности Эйнштейна с ее искривленным про¬
странством-временем.
Но так ли это? Среди многих физиков сегодня распространен тот взгляд, что квантовая
механика вовсе не дает нам никакой картины «реальности»! Формализм квантовой меха¬
ники, с их точки зрения, следует рассматривать именно как математический формализм.
Этот формализм, как считают многие из занимающихся квантовой теорией, не говорит нам,
в сущности, нечего о действительной квантовой реальности нашего мира, а всего лишь поз¬
воляет вычислять вероятности альтернативных реальностей, которые могли бы возникнуть.
Подобная онтология этих физиков (в той мере, в какой они вообще озабочены вопросами
онтологии) сводится к следующему: (а) квантовый формализм вообще не выражает никакой
реальности. Другая крайность: есть много физиков, которые, по-видимому, придержива¬
ются диаметрально противоположной точки зрения: (б) унитарная эволюция квантового
состояния полностью описывает реальность, при этом подразумевается, что практически
все квантовые альтернативы должны всегда продолжать сосуществовать (в виде суперпози¬
ции). Как уже упоминалось в § 21.8, основная трудность, которая стоит перед теоретиками
в области квантовой физики и которая приводит многих из них к подобным взглядам, — это
конфликт между двумя квантовыми процессами U и R, где (см. § 22.1) U есть детерминиро¬
ванный процесс унитарной эволюции (поскольку он описывается уравнением Шредингера),
a R — редукция квантового состояния, которая имеет место, когда производится «измере¬
ние». U-процесс, когда он был открыт, оказался для физиков чем-то вроде доброго старо¬
го знакомого, поскольку описывал четко очерченную эволюцию определенной физической
величины — вектора состояния \ф), — которая детерминированным образом описывается
некоторым дифференциальным уравнением в частных производных; при этом временная
эволюция, описываемая уравнением Шредингера, не отличалась существенно от таковой
в случае уравнения Максвелла (см. §21.3 и упражнение 19.2). В то же время R-процесс
представлял для физиков нечто совершенно новое — скачкообразное случайное изменение

29.1. Традиционные онтологии квантовой теории
655
этого состояния \ф}9 при котором определению подлежат только вероятности различных ис¬
ходов. Если бы физика наблюдаемого мира описывалась просто величиной | ф), меняющейся
в соответствии с процедурой U самой по себе, то у физиков не возникало бы серьезных со¬
мнений в том, чтобы считать эту процедуру описывающей «физически реальный» процесс
эволюции «физически реальной» величины | ф), Однако наблюдаемый мир ведет себя не так.
Вместо этого перед нами курьезная комбинация, состоящая из U-процессов, прерываемых
время от времени совершенно иным R-процессом! (Вспомним рис. 22.1.) Из-за этого фи¬
зикам гораздо труднее считать, что величина \ф) действительно может служить описанием
физической реальности. Вопрос о том, как R-процесс может возникать в условиях, когда со¬
стояние изменяется в соответствии с U-эволюцией, составляет проблему измерения — или,
как я предпочитаю называть это, парадокс измерения — в квантовой механике (он кратко
обсуждался в §23.6 и, в виде намеков, в §§21.8, 22.1).
Точка зрения (а) выражает онтологию копенгагенской интерпретации, наиболее четко
выраженной Нильсом Бором, который рассматривал величину \ф) не как выражение реаль¬
ности на квантовом уровне, но как нечто, просто описывающее «знание» экспериментатора
о квантовой системе. Тогда скачкообразные R-процессы следует понимать как приобретение
экспериментатором дополнительных знаний о системе, так что скачки претерпевает именно
«знание», а вовсе не физическая система. Согласно точке зрения (а), не следует требовать,
чтобы явлениям на квантово-механическом уровне приписывалась какая-либо «реальность»,
и единственная приемлемая реальность — это реальность того классического мира, в кото¬
ром действует аппаратура экспериментатора. Как возможный вариант этого взгляда мож-
но принять, что «классический мир» появляется не на уровне «макроскопической неживои
природы», частью которой является экспериментальная установка, а. на уровне собственного
сознания наблюдателя. Вскоре я перейду к более подробному обсуждению этих вариантов.
Приверженцы альтернативы (б), напротив, считают, что величина \ф) есть выражение
реальности, но они отказывают R-процессам в праве на существование. Они утверждают,
что при проведении измерения все альтернативные варианты исхода уже реально сосуще¬
ствуют в некоторой большой квантовой суперпозиции альтернативных Вселенных. Эта
большая суперпозиция описывается волновой функцией \ф) для всей Вселенной в целом.
Иногда это называют «множественностью миров» \.29Л\ я же предпочитаю пользоваться тер¬
мином омниум^29^. Несмотря на то что указанная точка зрения обычно представляется
как вера в параллельное сосуществование различных альтернативных миров, здесь налицо
недоразумение. Эта точка зрения не предполагает, что альтернативные миры реально «суще¬
ствуют» по отдельности, — реальной считается лишь ооширная опреоеленная суперпозиция,
выражаемая функцией |^).
Почему, согласно точке зрения (б), омниум не воспринимается экспериментатором как
«реальность»? Идея состоит в том, что состояния разума экспериментатора также сосуще-
ствуют в этой квантовой суперпозиции, при этом различные отдельные состояния разума
перепутаны с различными возможными результатами проводимого измерения. В соответ-
ствии с этим эффективно существует «свои мир» для каждого из возможных результатов
измерения, в каждом из этих миров имеется своя «копия» экспериментатора, и все эти миры
сосуществуют в виде квантовой суперпозиции. Каждая копия экспериментатора получает
свой результат эксперимента, но поскольку эти «копии» обитают в разных мирах, между
которыми нет связи, каждая из них полагает, что существует лишь один результат. При¬
верженцы точки зрения (б) часто утверждают, что «состояние осведомленности», в котором
должен находиться экспериментатор, создает впечатление, что существует всего «один мир»,
в котором как будто имеют место R-процессы. В явном виде такая точка зрения впервые
была высказана в 1957 году Хью Эвереттом Ш^29 3! (хотя я подозреваю, что многие другие,
пусть и не всегда убежденно, высказывали в частных беседах взгляды такого рода и рань¬
ше — как и я сам в середине 1950-х, — не решаясь обнародовать их!).

656
ГЛАВА 29
Точки зрения (а) и (б), несмотря на их диаметрально противоположный характер, име¬
ют, по существу, общий взгляд на то, каким образом, функция \ф) связана с наблюдаемой
нами «реальностью», под которой я понимаю реальный мир, воспринимаемым всеми нами
на макроскопическом уровне. В этом наблюдаемом мире в эксперименте получается лишь
один результат, и дело физиков объяснять или моделировать то, что мы обычно называ¬
ем «реальностью». Ни с одной из этих точек зрения, вектор состояния \ф) не считается
описывающим эту реальность. И в каждом случае приходится вводить понятие о некоем
человеке-экспериментаторе, чтобы придать смысл тому, как формализм связан с наблюда¬
емым реальным миром. В случае (а) вектор состояния |ф) рассматривается как артефакт
восприятия человека-экспериментатора, тогда как в случае (б) в терминах восприятия экс¬
периментатора описывается «обычная реальность», а вектор состояния |ф) представляет
более глубокий уровень реальности (омниум), не наблюдаемый непосредственно. В обоих
случаях «скачок» R не считается физически реальным, а существует, в некотором смысле,
«лишь в сознании».
В свое время я изложу свои затруднения с принятием точек зрения (а) и (б), но преж¬
де я должен указать на еще одну возможность интерпретации традиционной квантовой
механики. Эта точка зрения (в), наиболее распространенная, насколько я понимаю, в со¬
временной квантовой механике, основана на представлении о декогеренции, обусловленной
окружающей средой\ она имеет скорее прагматический, нежели онтологический характер.
Идея варианта (в) состоит в том, что при любом процессе измерения изучаемая квантово¬
механическая система не может рассматриваться изолированно от ее окружения. Так, при
проведении измерения каждый отдельный результат не представляет квантового состояния
самого по себе, а его следует рассматривать как часть перепутанного состояния (§23.3),
О
в котором каждый из альтернативных исходов перепутан с состояниями окружающей сре¬
ды. Окружение будет состоять из большого числа частиц, находящихся в беспорядочном
движении, и все подробности относительно положения и движения частиц должны счи¬
таться полностью ненаблюдаемыми на практике^29 Существует вполне определенная ма¬
тематическая процедура для описания ситуаций такого рода в условиях фундаментальной
потери информации: мы «суммируем» по всем неизвестным состояниям окружающей среды
и получаем математический объект, называемый матрицей плотности и описывающий рас¬
сматриваемую систему. Матрица плотности играет важную роль при обсуждении проблемы
измерения в квантовой механике (а также во многих других случаях), однако ее онтологи¬
ческий статус редко бывает вполне ясным. Что такое матрица плотности, я вскоре объясню
(в § 29.3). Однако мы увидим в дальнейшем, почему для варианта (в) важно, что онтология
матрицы плотности не вполне ясна! Сторонники точки зрения (в) обычно представляют себя
как «позитивисты», которые в любом случае не размениваются на «болтовню» относительно
онтологии и заявляют, что не касаются вопроса о том, что «реально», а что «нереально».
Вот как говорит Стивен Хокингf29*5^:
Я не требую, чтобы теория соответствовала реальности, поскольку не знаю, что это
такое. Реальность — это не то качество, наличие которого можно проверить с помо¬
щью лакмусовой бумажки. Все, что мне нужно, — это чтобы теория предсказывала
результаты измерении.
Я же, напротив, считаю, что онтология имеет для квантовой механики решающее значение,
хотя в настоящее время она ставит вопросы, далекие от разрешения.
29,2.	Нетрадиционные онтологии квантовой теории
Прежде чем углубляться в детали всего этого, я изложу еще три точки зрения общего
характера на квантовую механику. Ни в коем случае не следует считать этот мой список

29.2. Нетрадиционные онтологии квантовой теории
657
исчерпывающим и не следует рассматривать эти новые подходы как полностью независи¬
мые от представленных в предыдущем разделе. Приводимый здесь перечень (а), (б), (в), (г),
■W
(д), (е) дает некоторое представлением различных воззрениях, с которыми можно встре¬
титься в современной литературе, однако я не претендую на полноту или оригинальность
моего списка. Три дополнительные онтологии, которые здесь рассматриваются, представ¬
ляют собой отклонение от обычного квантового формализма, однако две из них, (г) и (д),
не предполагают наличия экспериментально наблюдаемых различий между предлагаемым
формализмом и стандартной квантовой механикой. Вариант (г) — это теория, оперирующая
с «согласованными историями», которая была предложена Гриффитсом, Омнесом и Гелл-
Манном и Хартлом, а (е) — концепция «волны-пилота», сформулированная де Бройлем
и Бомом и ХашиГ29 ^. Последний (по счету) вариант (е) предполагает, что нынешняя кван¬
товая механика — это всего лишь приближение к чему-то лучшему и что в этой улучшенной
теории процессы U и R станут объективно реальными; более того, этот вариант предпола-
C#	Vi	м
гает, в частности, что различия между такой теорией и традиционной квантовой механикой
смогут проявиться в будущих экспериментах.
Коль скоро необходимые предпосылки имеются, я постараюсь дать свою оценку различ¬
ным альтернативам (а),... ,(е). Однако, чтобы читатель смог занять достаточно объектив¬
ную позицию в отношении моих оценок, будет лучше, если я сразу ясно представлю свою
собственную позицию. Я убежден в необходимости движения в направлении (е) для того,
чтобы квантовая механика приобрела полностью согласованный смысл. В следующей главе
я представлю некоторый частный вариант точки зрения (е), который кажется мне наиболее
естественным. После такого предупреждения можно перейти к делу; при этом я сначала
перечислю все варианты, чтобы напомнить их читателю:
а) Копенгагенская интерпретация
б) Множественность миров
в) Декогеренция, вызываемая окружением
г) Согласованные истории
д) Волна-пилот
е) Новая теория с объективными R.
Я буду вынужден сделать несколько замечаний в отношении вариантов (г) и (д), по¬
скольку я не объяснил, в чем их суть. Схема «согласованных историй» (г) предполагает
выход за рамки стандартной квантовой теории. Некоторые ее сторонники предлагают он¬
тологию, которая во многом близка к варианту множественных миров (б), хотя в одном
отношении она еще более экстравагантна; однако, насколько я понимаю, без этой экстра¬
вагантной онтологии можно и обойтись. В обоих вариантах (б) и (г) можно считать, что
в качестве основных ингредиентов мы имеем гильбертово пространство Н, принадлежащее
этому пространству исходное состояние l^o) и гамильтониан 7iJ29 Tl В случае множествен¬
ных миров (б) онтологическая позиция состоит в том, чтобы считать реальность (омниум)
описываемой некоторым непрерывным однопараметрическим семейством состояний (эле¬
ментов пространства Н с временным параметром t), начиная с \фо) в момент t — 0, и пол¬
ностью определяемой при t > 0 уравнением Шредингера с гамильтонианом 77. Здесь нет
никаких процессов R, только U. Вариант (г) с согласованными историями расширяет эту
ситуацию, включая в свою «эволюцию» также и «R-процедуры», несмотря на то что по¬
следние не считаются обязательно связанными каким-то образом с реально проводимыми
измерениями.

658
Глава 29
Чтобы понять математическую природу этих процедур, следует сначала вспомнить
(см. §§22.5, 22.6), что квантово-механическое измерение математически описывается как
результат действия некоторого эрмитова (или нормального, см. § 22.5) оператора Q (хотя
в варианте (г) мы не рассматриваем эти процедуры как измерения). Если непосредствен¬
но перед измерением система находится в состоянии |ф), то сразу после измерения она
«перепрыгнет» в собственное состояние оператора Q, соответствующее тому собственному
значению этого оператора, которое оказывается результатом измерения. Но коль скоро рас¬
сматривается действие этого оператора на \ф)9 мы можем заменить оператор Q «полным
набором ортогональных проекторов» Ei, 25з,, Ег (предполагается, что оператор Q
имеет ровно г различных собственных значений; для удобства мы считаем наше гильбертово
пространство Н конечномерным). Если при этом измерение дает собственное значение qj,
то мы получаем, что состояние \ф) скачком переходит в Е^ф) (постулат проектирования).
Рассмотрим это чуть более подробно. Из § 22.6 мы помним, что проектором называется
эрмитов оператор Е, квадрат которого равен ему самому, т. е.
Е — Е — Е
Утверждение
EiEj = 0, если г ф j,
а их полнота означает, что их сумма равна тождественному оператору в пространстве Н:
Е\ Е% + Е$ 4- ... 4- Ег — I.
Будем называть множество операторов Е, удовлетворяющих всем этим условиям, проек-
торным множеством. Связь между оператором Q и соответствующим ему проекторным
множеством состоит в том, что для каждого собственного значения qj оператора Q со¬
ответствующее пространство собственных векторов состоит из векторов вида Ej\ф). Роль
проектора Ej состоит в том, что он проектирует на пространство собственных векторов,
соответствующее собственному значению qj*
Постулат проектирования для операции R (см. § 22.6) при измерении, представляемом
оператором Q, гласит, что если результатом измерения является величина qj, то состоя¬
ние \ф) скачком переходит в нечто, пропорциональное Ej \ф). Это происходит с вероятно¬
стью
если предположить, что состояние \ф) нормировано, т. е. (ф\ф) — 1. Таким образом, что¬
бы описать действие на квантовое состояния измерения, соответствующего оператору Q,
мы должны лишь рассмотреть проекгорное множество, определенное этим оператором.
Вернемся теперь к онтологии согласованных историй (вариант (г)). Теория оперирует
понятием крупномасштабных историй^29‘8\ каждая из которых сильно напоминает «омни¬
ум» множественных миров (вариант (б)), эволюционирующий согласно уравнению Шре¬
дингера с гамильтонианом Н. Но в случае (г) по ходу эволюции допускается введение
проекторных множеств в различные моменты t.
Объясните, почему Ej\ф) является (с точностью до нормировки) результатом измерения, определяемого
действующим на \ф) оператором Q = q\E\ -f Q2E2 + дз-Ез + . -. + qrEr с собственным значением qj; ве¬
личины qi, <72, <?з > • • • ? Яг являются различными вещественными числами. Попробуйте доказать, что такой вид
имеет любой конечномерный эрмитов оператор. (Вы можете предположить, что любую конечномерную эрмитову
матрицу Q можно привести к диагональному виду с помощью некоторого унитарного преобразования.) Опера¬
торы Е называют главными идемпотентами оператора Q. Какие изменения требуются в случае нормального
оператора Q1

29.2. Нетрадиционные онтологии квантовой теории
659
Онтологический статус введения проекторного множества для меня пока не вполне
ясен, однако приходится придерживаться той позиции, что роль такого множества сводится
к некоторой «очистке» истории, а не к фундаментальному изменению того, что происходит
в мире. Проекторы определенно не должны приписываться онтологическому статусу, опре¬
деляемому некоторым объективным измерением. Правильнее было бы считать, что проек-
торные множества производят очистку или изменение «ящиков», на которое мы разбивали
классическое фазовое пространство (см. §27.3), — и это объясняет использование здесь
термина «крупномасштабная история». В такой крупномасштабной истории при введении
проекторного множества, подобном стандартной процедуре квантового измерения, текущее
состояние \ф) заменяется на величину, пропорциональную Ej \ф)9 где Ej ~ некоторый эле¬
мент проекторного множества. Это можно было бы считать потерей информации, однако
потери не происходит, если мы следим за всем семейством состояний Ej |ф) для всех эле¬
ментов Ej данного множества, поскольку | ф) представляет просто сумму их всех.
В соответствии с желанием иметь что-то напоминающее классический мир, который мы
можем реально воспринимать, некоторые отдельные семейства крупномасштабных историй
выделяют и называют согласованными (или иногда «декогерентными»), если выполняет¬
ся некоторое условие, выражающее тот факт, что вероятности, вычисляемые по правилам
стандартной квантовой механики, подчиняются обычным классическим правилам теории
вероятностейt29 9]. Согласованное множество крупномасштабных историй называется «мак¬
симально очищенным», если нельзя ввести еще одно проекторное множество (не эквива¬
лентное никакому из уже введенных), не нарушая согласованности. История из максимально
очищенного множества представляется мне наиболее подходящим кандидатом на право счи¬
таться онтологически «реальной» в соответствии с точкой зрения (г).
Пока мне не доводилось видеть изложение такой точки зрения в явном виде, и более
близкой к онтологической точке зрения «согласованных историй» представляется совокуп¬
ность историй в максимально очищенном множестве t2910l. Это, возможно, ближе к концеп¬
ции множественных миров (б), однако наличие многих возможных согласованных наборов
проекторных множеств дает нам еще более обширный ансамбль альтернативных «миров».
Напомним, однако, что и в картине множественных миров (б) может возникнуть некото¬
рая онтологическая путаница. Онтологически «реальный» омниум (описываемый величи¬
ной \ф)) представляет собой суперпозицию многочисленных различных миров, и набор всех
этих отдельных миров (а не просто их частная суперпозиция \ф)) не может считаться «ре¬
альным». Поэтому концепция согласованных историй (г) имеет то преимущество, что она
дает правильные квантовые вероятности, тогда как в случае (б) это не имеет места.
В «бомовском» случае (д) (волна-пилот) онтологическая позиция, в подправленном ви¬
де, гораздо «ближе к земле», хотя даже здесь имеются существенные тонкости, поскольку
существуют, в некотором смысле, два уровня реальности, один из которых обладает большей
прочностью. Проще всего рассмотреть этот случай применительно к системе, состоящей все¬
го из одной бесспиновой частицы. Тогда этим более прочным уровнем реальности является
положение частицы. В двухщелевом эксперименте (§21.4, рис. 21.4) положение частицы
онтологически реально, частица проходит либо через одну щель, либо через другую, но
ее движение «управляется» в конечном счете функцией ф, и это придает вторичный, но
все же онтологически «реальный» статус самой функции ф, В этой теории обычно при¬
дается несколько иной смысл модулю и аргументу функции ф (§5.1): модуль используется
для построения «квантового потенциала», а аргумент — для определения так называемой
«волны-пилота». Такое разделение, однако, не является обязательным, и его смысл стано¬
вится менее определенным в случае более сложных систем.
В общем случае можно рассматривать ф как комплексную функцию, определенную
в конфигурационном пространстве С и «управляющую» поведением точки Р в этом про¬
странстве. В качестве более прочной части реальности системы берется классическая кон¬

660
Глава 29
фигурация, определяемая точкой Р, однако некоторая (менее прочная) реальность припи¬
сывается также комплексной функции ф из-за ее роли в управлении поведением точки Р.
Предполагается, что все измерения в конечном счете можно свести к измерениям «поло¬
жения», которые здесь означают измерения конфигурации системы. Квадрат модуля \ф\2
в некоторой точке Q пространства С определяет плотность вероятности обнаружения си¬
стемы в конфигурации, соответствующей точке Q, однако положение Р в пространстве С
определяет то, что считается реальной конфигурацией системы.
Всё это кажется «слишком простым», однако здесь имеются некоторые тонкости. Преж¬
де всего, эта картина в высокой степени нелокальна, поскольку ф является «целостным»
объектом (как и должно быть в соответствии с целостной природой волновых функций,
подчеркнутой в §21.7), Это, однако, кажется неизбежным в квантовой механике. Несколь¬
ко более серьезными представляются важные условия, которые необходимо налагать на
распределение вероятностей для начального состояния |^о), чтобы закон квантовой веро¬
ятности \ф\2 был справедлив и оставался справедливым при последующих измерениях.
Существует еще один пункт, связанный с вопросом о правильности предположения, что все
измерения всегда можно свести в конечном счете к измерениям положения (особенно если
учесть, что точное определение положения не полностью узаконено в квантовой механике,
см. §21.10), и с тем, адекватно ли представление конфигурационного пространства, когда
рассматриваются неклассические параметры, например, спин. Тем не менее ясность онто¬
логической позиции концепции (д) говорит в ее пользу (хотя, как мы увидим в §29.9, здесь
возникают и другие вопросы) [29Л11.
Наконец, имеется много различных предложений в связи с вариантом (е). Я не наме¬
рен подробно описывать их здесь. Можно, однако, сделать некоторые замечания общего
характера. Часть этих предложений принимается (по крайней мере на предварительном
уровне) в качестве онтологически реального статуса для эволюционирующего вектора со¬
стояний \ф). Временная эволюция вектора | ф) в такой теории приближается к чередованию
процессов U и R, принятому в стандартной квантовой механике (см. рис. 22.1). Несмотря
на то что теории, следующие концепции (е), находятся «вне главного потока» квантово¬
механического мышления, было бы правильно сказать, что эта концепция в наибольшей
степени допускает реальность того формализма квантовой механики, который сегодня ис¬
пользуется на практике, поскольку оба процесса квантовой эволюции U и R вполне серьез¬
но считаются описывающими эволюцию реальности! Беда, однако, в том, что процедуры
U не согласованы между собой в математическом отношении, поэтому концепция (е)
требует модификации обычной унитарной эволюции — и именно это отличает ее от тради¬
ционной!
Почему процедура R математически не согласована с U? Наиболее очевидная причина,
вероятно, состоит в том, что R представляет скачкообразное изменение вектора состояния
(за исключением случая, когда состояние перед измерением является собственным состоя¬
нием оператора измерения), тогда как U всегда действует непрерывным образом. Но даже
если принять, что «скачок», создаваемый R-процессом, происходит не абсолютно мгновен¬
но, все равно остается проблема с унитарностью из-за потери детерминизма в процессе R.
Различные возможные исходы могут получаться из одного и того же начального состояния,
что никогда не случается в U-процессе. Более того, теория, которая включает R в реаль¬
ный процесс, не может быть унитарной, если в ней реально происходит (нетривиальный)
квантовый скачок, определяемый R-процессом. Несмотря на это, имеет место замечательное
согласие между процессами U и R, так как «правило квадрата модуля», которое прерывает
U-процесс вероятностным R-процессом, использует саму «унитарность», чтобы обеспечить
закон сохранения вероятности в R-процессах (по существу, тот факт, что скалярные про¬
изведения {ф\ф), используемые при вычислении квантовых вероятностей, сохраняются при
унитарной временной эволюции; см. §§ 22.4, 22.5). Это главное из чудес квантовой меха¬

29.3. Матрица плотности
661
ники и причина того, что многие неохотно обращаются к принципам теории; это частично
объясняет, почему концепция (е) не слишком популярна среди современных физиков.
Тем не менее я считаю, что имеются веские основания ожидать перемен. Такие переме¬
ны, на мой взгляд, должны быть подлинной революцией, а не просто «латанием» нынешней
квантовой механики. В то же время необходимые изменения должны бережно относиться к
основным принципам, лежащим в самой основе современной физики. Основанием для обо¬
их требований служит сама прочность квантового формализма, отмеченная в предыдущем
абзаце. Для сравнения обратимся к ньютоновской физике. Теория относительности и кван¬
товая механика возникли в результате не латания ее прорех, а революционного изменения
взглядов, при котором, однако, было проявлено должное уважение к высокоорганизован-
V/	U	и
нои лагранжево-гамильтоново-симплектическои геометрической структуре ньютоновской
теории. Будут ли перемены в квантовой теории, предлагавшиеся многими людьми[29Л21?
О	Vi
носить такой же революционно-уважительныи характер или дело ограничится мелким ре¬
монтом? Следует сказать, что пока большинство идей такого рода приходится относить к
последней категории, хотя некоторые из них могут оказаться указателем правильного пути
к улучшенной квантовой теории.
29.3.	Матрица плотности
Но почему возникла надобность в «улучшении» квантовой теории? Большинство за¬
нимающихся квантовой физикой вроде бы не видят необходимости в этом, мирясь с ви¬
димыми противоречиями и неясной онтологией той или иной стандартной картины (или с
отсутствием такой картины). Прежде чем обсуждать какие-либо трудности, которые могут
заключаться в любом из стандартных вариантов (а), (б) и (в), следует обратиться к понятию
матрицы плотности, которая играет важную роль не только в концепции (в), но и во многих
других подходах к квантовой механике. Кроме того, она поднимает глубокие и острые во¬
просы относительно того, каким образом реальность должна быть представлена в квантовой
механике.
Предположим, мы имеем некоторую квантовую систему, состояние которой нам не
вполне известно. Это может быть состояние |ф), или \ф), или ..., или |х). Список может
быть бесконечным, однако для наших целей достаточно ограничиться конечным перечнем
возможностей. Каждой из этих возможностей следует приписать некоторую вероятность,
скажем, соответственно р, q. ... s. Перечень возможностей должен быть исчерпывающим,
так что сумма вероятностей — вещественных чисел, заключенных между 0 и 1 (включитель¬
но), — должна быть равна 1:
р ~\~ q	s = 1.
Предположим, что каждое из состояний \ф)9 \ф), ..., |х) нормировано:
М = 1> 11011 = !> •• •>	11x11 =
ф
(Напомним (§22.3), что ||^|| = (ф\ф) и т.д.) Тогда мы определяем матрицу плотности как
следующую величину:
D =р\ф){ф\ + я\Ф){Ф\ + Мх)(х|-
Л
Напомним (
на \ф)(ф\ будет тензорным произведением (или внешним произведением) вектора \ф) на
вектор {ф\ и т.д. В индексной записи (§23.8) можно представить (^{ в виде фа9 при
можно загшсать в виде фафа и т. д. В соответ¬
ствии с этим сама величина D будет иметь индексную структуру Daр. Матрица плотности

662
Глава 29
обладает следующими алгебраическими свойствами: она эрмитова, неотрицательно опреде¬
лена (§§ 13.8, 13.9), и ее след равен единице:
£)*-£>,	<<е|£>|£)>0	для	всех Ю, (D) = 1,
где (D)■ = Tr D = Daa (см. § 13.4) *.
Матрица плотности играет роль, подобную тому, что мы часто имеем в классической
статистической механике, когда нам не известно точное (классическое) состояние системы
и мы вынуждены довольствоваться некоторым распределением вероятностей классических
альтернатив. Проще всего это выразить на языке фазового пространства V возможных клас¬
сических альтернатив. Вместо того чтобы представлять систему точкой Р пространства V,
можно рассматривать распределение вероятностей в этом пространстве. Если у системы
имеется лишь конечное число альтернатив^2913^ с вероятностями р, q-y ..., s, то это можно
представить конечным набором точек Р, Q, ..., S в пространстве Р, каждой из которых
приписывается соответствующее значение вероятности р, q, ..., 5 (см. рис. 29.1). Точно так
же можно рассмотреть аналогичную ситуацию в квантовой физике, где роль фазового про¬
странства V играет гильбертово пространство Н данной квантовой системы, при этом мы
будем иметь некоторое распределение вероятностей в пространстве Н. В связи с тем что мы
только что узнали о матрице плотности, это распределение будет состоять из конечного чис¬
ла точек Р, Q, ..., S в пространстве Н, каждой из которых приписывается соответствующая
Рис. 29.1. Классическое распределение вероятностей, представ¬
ленное в фазовом пространстве V. а) Конечному набору то¬
чек Р, Q, ..., S приписываются соответствующие значения ве¬
роятности р, q, ..., s (вещественные числа, заключенные между
О и 1), причем p + g-K.. + s = 1.6) Непрерывное распределе¬
ние с мерой вероятности (неотрицательной вещественной плот¬
ностью), интеграл от которой равен 1, приписываемое некоторой
области пространства V
вероятность р, q, ..., s.
**
Но использование матрицы плотности отличается от того, что обычно делается в кван¬
товой механике[29Л4^. Почему? Причина состоит в том, что в квантовой механике измере¬
ние, имеющее форму вопроса, поставленного перед квантовой системой (мы ограничимся
вопросом «ДА или НЕТ?»), выражается в виде действия некоторого проектора Е на (нор¬
мированный) вектор состояния |£). При этом вероятность ответа ДА определяется как
вероятность ответа ДА = (£|Е7|£),
откуда следует, что для описанной выше смеси вероятностей возможных альтернативных
состояний \ф), |ф), ..., |х) с матрицей плотности D мы получаем
вероятность ответа ДА = (ED).
Значение этого факта состоит в том, что нам не требуется иметь полную информацию
о распределении вероятностей альтернативных состояний |V>), ..., |х)> чтобы мы могли вы¬
числять вероятности для стандартного вопроса ДА/НЕТ в квантовой механике (или для
ожидаемого значения любой другой квантово-механической наблюдаемой) , — вся необ¬
Выведите эти свойства.
** ЛШ Объясните, почему. Выведите также приведенное ниже выражение с (ED).
*** -шт р[онятно почему должно быть так?

29.4. Матрицы плотности для спина 1 /2. Сфера Блоха
663
ходимая информация содержится в матрице плотности, и мы вскоре увидим, что данную
матрицу плотности можно построить из многих различных распределений вероятности со¬
стояний. Этот замечательный математический объект (введенный в 1932 году выдающимся
венгерско-американским математиком Джоном фон Нейманом) оказывается значительно бо¬
лее экономным и изящным. Он объединяет в одно целое два, казалось бы, совершенно
разных понятия вероятности. С одной стороны, мы имеем числа р, д, ..., s, представля¬
ющие обычные классические вероятности альтернативных состояний \гр), |ф), ..., |х), а с
другой, — квантовые вероятности, полученные по правилу квадрата модуля из § 21.9. Мат¬
рица плотности объединяет их и не отличает непосредственно один вид вероятности от
другого.
29.4.	Матрицы плотности для спина Ч Сфера Блоха
Проиллюстрируем эту точку зрения на простом примере. Пусть мы имеем частицу со
спином о которой мы знаем, что ее спиновое состояние может быть либо | |)? либо | |)
с вероятностью - для каждого из этих вариантов. Если мы решим измерить этот спин в
направлении вверх/вниз, то мы получим ответ «вверх», если спин находится в состоянии | f),
и «вниз» в случае состояния | I). Вероятность каждого случая равна Это обычные
классические вероятности, ничего квантового здесь пока нет. Но предположим, что мы
измеряем спин в направлении влево/вправо. Тогда в случае состояния | t) квантовые правила
1
для R-процесса утверждают, что мы должны получить вероятность - для направления спина
«влево» и такую же вероятность для его направления «вправо». Такой же вывод получается
и для состояния | I). Таким образом, для равновероятной смеси состояний | |) и | I) мы
1
будем иметь вероятность - для направлений «влево» и «вправо». Однако теперь вероятности
получены нами полностью квантово-механическим путем из «закона квадрата модуля». Мы
можем решить измерить спин и в любом другом направлении. Вероятности для каждого из
результатов снова окажутся равными ^ но теперь они, в общем случае, будут некоторой
смесью классической и квантовой вероятностей
Предположим теперь, что мы поворачиваем не измерительную аппаратуру, а смесь
состояний. Тогда равновероятная смесь состояний
и
должна дать те же самые
результаты, что и рассмотренная равновероятная смесь состояний | Т) и I i), то же относится
и к равновероятной смеси | X) и | X) ( в каждом случае состояния предполагаются взаимно
(
) = (Ч I \) = Ои <т | Т)
ортогональными и нормированными, так что (Т I i) ~
= {l|i) — ... = (X I X) — 1). В каждом из этих случаев получаем для матрицы
плотности
D
D
D
\\ Т)(Т I + ^1 i)U 1>
1
2
>{
т
1
2
1
)(
|l Х)(Х I + 7^1 Х)(Х I;
Покажите это для общего случая измерения под произвольным углом в, используя для вероятности
выражение ~ (1 + cos в) из § 22.9.

664
Глава 29
замечательное свойство матрицы плотности состоит в том, что все эти величины D
одинаковы . Все только что рассмотренные вероятности измерений спина можно получить
из приведенной выше формулы с (ED); таким образом, поскольку все величины D одина¬
ковы, то одинаковыми должны быть и соответствующие вероятности, что мы уже и видели.
Но как мы должны относиться к онтологии этих вероятностных смесей состояний?
Если мы приписываем квантовому состоянию физическую реальность некоторого рода, то
указанные три ситуации определенно должны быть онтологически различными. Одно дело
сказать, что одинаковую вероятность имеют (физически реальные) альтернативные состо¬
яния | |) и I I)? другое — что равны вероятности состояний | *\) и | \,). Однако этот
онтологический вопрос в большей части литературы по квантовой механике крайне запутан.
Л
Физики, занимающиеся квантовой теорией, часто придерживаются онтологической позиции,
в корне отличной от описанной, рассматривая матрицу плотности как более точное описание
реальности, нежели отдельные состояния. Они считают, что три как будто различных онто¬
логии для D (т. е три различных набора альтернативных квантовых состояний, взвешенных
с соответствующими вероятностями) физически неразличимы. Соответственно эти физики
(которые часто придерживаются точки зрения (в), основанной на декогеренции, вызывае¬
мой окружением) могут стоять на позитивистской или прагматической позиции, которая не
видит смысла различать эти альтернативы. Эти люди могут принять точку зрения, согласно
которой именно матрица плотности наилучшим образом описывает квантовую реальность.
Действительно, во многих контекстах слово «состояние» часто относят к матрице плот¬
ности, а не к более примитивному понятию, которое я до сих пор называл «квантовым
состоянием», т. е. к величине, описываемой кет-вектором \ф). Если под «состоянием» пони¬
мается матрица плотности, то для матрицы плотности частного вида \ф)(ф\ используется
термин «чистое состояние», а для матрицы плотности общего вида, которую нельзя предста¬
вить в указанной форме, — «смешанное состояние». В этом смысле «чистое состояние» —
это то, что я называл просто «состояние». Лично я не считаю удачным применение термина
«состояние» к матрице плотности (чистой или смешанной) и буду воздерживаться от исполь¬
зования такой терминологии. На мой взгляд, «квантовое состояние» — это вектор квантового
состояния |^), а не матрица плотности. Тем не менее некоторые могут предпочесть различать
термины «квантовое состояние» и «вектор квантового состояния», понимая под последним
кет-вектор \ф), а под первым — класс эквивалентности ненулевых комплексных множителей
при \ф), т. е. элемент проективного гильбертова пространства FH, соответствующий эле¬
менту \ф) пространства Н (см. § 15.6). Если нормировать вектор |ф), полагая (ф\ф) — 1, то
у \ф) (для данной точки в пространстве FH) остается лишь фазовая свобода \ф) i—► егв\ф)
(где в — вещественное число); см. рис. 29.2. Понятие матрицы плотности «чистого со¬
стояния» эквивалентно этому «проективному» понятию, поскольку \ф){ф\ есть инвариант
такой фазовой свободы. Таким образом, разумно считать, что матрица плотности чистого
состояния правильно описывает физическое квантовое состояние.
Тем не менее я ощущаю некоторый дискомфорт, считая «матрицу плотности чистого
состояния» подходящим математическим представлением «физического состояния». Фазо¬
вый множитель ег0 «ненаблюдаем» лишь в том случае, если рассматриваемое состояние
представляет весь интересующий нас объект целиком. Если же рассматривается некоторое
состояние как часть большей системы, то необходимо обращать внимание на такие фа¬
зы. Более того, фундаментальная комплексная линейность базисной структуры гильбертова
пространства кет-векторов становится излишне сложной в математическом отношении, если
всегда оперировать величинами \ф){ф\ вместо математически более простых величин \ф)
(или (ф\) **. Частично по этим причинам я вынужден считать матрицу плотности не «реаль¬
Покажите это путем вычисления в явном виде, используя результаты §§ 22.8, 22.9 и упражнения 22.25.
Попробуйте описать семейство матриц плотности «чистых состояний», которые соответствуют линейным
комбинациям w\ф) + z\<p) для некоторой произвольной пары заданных состояний |^) и |ip).

29.4. Матрицы плотности для спина 1/2. Сфера Блоха
665
Пространство
нормированных
кет-векторов
Комплексная
плоскость
Пространство матриц
плотности
(1<жу»«И+(И)
а)
б)
Рис. 29.2. Как представить чистое квантовое состояние? а) Пространство кет-векторов |ф), нормиро¬
ванных условием (ф\ф) — \. 6) Матрица плотности \ф)(ф\ «эквивалентна» вектору 1^} с точностью
* d
до фазовой свободы \ф) i-* еь |ф) и семейству ненулевых кет-векторов, пропорциональных |ф) (с ком¬
плексными коэффициентами пропорциональности). Однако описание на основе матрицы плотности
затемняет квантовую линейность
ностью», а лишь полезным инструментом. Однако, как мы увидим сейчас и в следующем
разделе, в запутанном онтологическом статусе матрицы плотности имеются некоторые ин¬
тригующие аспекты.
Прежде чем перейти к этому, полезно познакомиться со сферой Блоха, которая пред¬
ставляет собой пространство матриц плотности для системы с двумя состояниями. Это за¬
мкнутая сплошная сфера (или, на языке математики, 3-шар, или 3-диск) В3 в евклидовом
3-пространстве. Она представляет матрицы плотности для спина ~ (или любой другой си-
стемы с двумя состояниями); см. § 22.9. Эрмитову матрицу 2x2 общего вида с единичным
следом можно записать в виде
1 (1 a b -f- ъс\
2 \ Ь — ic 1 — ay
где а, 6, с — вещественные числа. Чтобы это была матрица плотности, она должна быть
неотрицательно определена, это сводится к условию*
а2 + Ь2 + с2 ^ 1.
Это неравенство представляет общую точку сферы Блоха В3, границей которой служит
2-сфера S2, определяемая уравнением а2 + Ь2 + с2 = 1. Здесь S2 представляет чистые
состояния нашей системы с двумя состояниями (например, спина А), и это пространство
можно отождествить со сферой Римана S2, описанной в § 22.9,129Л51
i
В таком случае только что рассмотренная матрица плотности частного вида D = (-/)
будет представлена центром сферы Блоха, и ее неоднозначная онтологическая интерпрета¬
ция довольно очевидным образом следует из симметрии картины (рис. 29.3). Но и любая
точка L внутри сферы В3 представляет матрицу плотности (смешанного состояния), со
столь же неясной онтологической интерпретацией. Чтобы убедиться в этом, просто прове¬
дем через точку L произвольную прямую (хорду) до встречи с границей S2 в точках Р\
* Покажите это. (.Подсказка: как выражается произведение собственных значений через а, Ъ и с? Что озна¬
чает неотрицательность этого произведения?)

666
Глава 29
О	1
Рис. 29.3. Сфера Блоха В с центром -J, представляющая мат¬
рицы плотности системы с двумя состояниями. Любая матрица
плотности (смешанного состояния) имеет неоднозначную онтоло¬
гическую интерпретацию. Произвольная хорда, проходящая через
точку X, встречается с границей S2 в точках Pi и ?2, так что точ¬
ку X можно интерпретировать как вероятностную смесь чистых
состояний Pi И Р2
и Р2. Эти точки представляют два чистых состояния, так что матрицу плотности X мож¬
но интерпретировать как вероятностную смесь этих состояний*. Единственная особенность
центра D сферы Блоха состоит в том, что все такие пары чистых состояний, с помощью
которых можно представить матрицу D, — это пары ортогональных состояний. Однако
в определении матрицы плотности нет ничего такого, что требовало бы взаимной ортого¬
нальности смешиваемых состояний. В §29.5 мы увидим, что вполне возможно появление
и неортогональных смесей.
29.5.	Матрица плотности в условиях ЭПР-эксперимента
Рассмотрим особенно ясную ситуацию, в которой вероятностный набор возможных
векторов состояний возникает естественным образом. Она связана с эффектом Эйнштейна-
Подольского - Розена (ЭПР)-Бома (§23.4). Предположим, что где-то между Землей и одной
из лун Сатурна — Титаном на расстоянии от Земли, примерно вдвое большем расстояния от
Титана, испускается ЭПР-пара частиц со спином | в комбинированном состоянии со спи¬
ном 0. Я предполагаю, что мой коллега на Титане (наш старый знакомый из §§23.4, 23,5)
измеряет спин прибывающей туда частицы в направлении вверх/вниз и получает некото¬
рый результат приблизительно на час раньше, чем я получу свою частицу здесь, на Земле.
Допустим, что к моменту прибытия моей частицы я еще не получил от моего коллеги ника¬
кого сообщения относительно результата его более раннего измерения. (Титан находится на
расстоянии трех световых часов от Земли.) С моей точки зрения, моя частица имеет спин
либо | ф), либо | ф). Это будет ] ф), если мой коллега обнаружил состояние | ф), и | ф),
если у коллеги оказалось состояние | ф). Поскольку я знаю, что у моего коллеги имеются
равные шансы обнаружить состояния j ф) и | ф), я должен считать, что частица, полученная
1
мною (час спустя после измерения моего коллеги), с вероятностью - может находиться
в состоянии | ф) и с такой же вероятностью в состоянии | ф). Таким образом, я пользуюсь
матрицей плотности
я = §|Т)(Т| + §1Ш
(два состояния | ф) и | ф) предполагаются ортогональными и нормированными: (ф | ф) = 0
и (Т | Т) = 1 = Ц 11))-
Но может статься, что мой коллега в последний момент решил измерять спин частицы,
прибывшей на Титан, не в направлении вверх/вниз, а в направлении влево/вправо. Если мой
коллега получил результат | «—), то для моей частицы, пришедшей на Землю, я должен полу¬
чить результат | —»), если же мой коллега получил | —►), то у меня должно получиться | +—).
Объясните, почему это так, показав, что две вероятности в этой смеси относятся так же, как длины двух
отрезков, на которые точка X делит хорду.

29.5. Матрица плотности в условиях ЭПР-эксперимента
667
каждом случае равна ~ , поэтому,
а, я должен считать, что моя часз
1
быть в состоянии | —►} или I <—) с вероятностью ~ для каждого
должен
(при этом (*— | —*) — 0 и (—► | —») = 1 = {<— | <—)). Разумеется, как мы видели,
это та же матрица D, что и прежде. Так и должно быть, поскольку решение моего коллеги
относительно способа измерения спина частицы на Титане не должно влиять на вероятности
здесь, на Земле (в противном случае мы получили бы способ послать сигнал с Титана
на Землю со сверхсветовой скоростью*). Видно, таким образом, что в случаях, подобных
рассмотренному, матрица плотности дает удобное математическое описание физической
ситуации. Спиновое состояние частицы, которую я получаю здесь, на Земле, ничего не зная
о том, что происходит на Титане (ни о направлении, в котором мой коллега решает измерять
спин, ни о результате этого измерения), очень хорошо описывается матрицей плотности D.
Разумеется, всё это выглядит хорошо, только если я не получаю никакой информации
с Титана. Если же я узнаю, измерение какого типа проводит мой коллега, это повлияет на
мою точку зрения относительно онтологии полученного мной спинового состояния, но не
будет влиять на ожидаемые вероятности результатов измерений, которые я мог бы прове¬
сти на Земле1[29Л61. Если я знаю, что мой коллега проводит измерение спина в направлении
вправо/влево, то я могу придерживаться онтологиц, согласно которой спин моей частицы
направлен вправо или влево, но я не знаю, куда именно, — это точка зрения, которой я не мог
бы придерживаться, если бы не знал, в каком направлении проводит измерение мой коллега.
Но такое онтологическое знание не повлияет на мои ожидания в отношении вероятностей
результатов измерения спина, проводимого мной на Земле. Поэтому я мог бы занять аль¬
тернативную позицию, согласно которой «онтология» не имеет существенного значения и,
возможно, вообще не имеет научного смысла, так что матрица плотности — это всё, что
требуется в научном смысле. С другой стороны, если я получаю с Титана сообщение о ре¬
зультатах измерения, проведенного коллегой, то это повлияет на мои ожидания в отношении
вероятностей. Более того, появляются условия согласования, налагающие ограничения на
результаты наших совместных измерений (например, я не могу получить результат
если мой коллега получил результат {*— |). Теперь становится ясно, что описание с по¬
мощью матрицы плотности совершенно неадекватно, и мы должны вернуться к описанию
в терминах реального квантового (вектора) состояния, описывающего всю перепутанную
пару: |f?) = | Т)| I) - | 4}| Т) (= I <-)| -» - I -*>| <-) и т. .д.).
Та матрица плотности, которая получается в данном примере (она уже рассматривалась
в § 29.4), представляет особый случай. В любом ортонормированном базисе она имеет вид
D
Особенность состоит в том, что все ее собственные значения равны между собой (это два
-I
числа ~ на главной диагонали). Отсюда следует, что она имеет один и тот же вид в любом
А
(ортонормированном) базисе, так как она с точностью до множителя представляет собой
просто единичную матрицу. Поэтому невозможно отличить базис вверх/вниз от базиса вле¬
во/вправо или любого другого.
* Объясните это.

668
Глава 29
Важно подчеркнуть, что так получается лишь в простом частном случае, рассмотрен¬
ном в данном примере. В § 29.4 мы уже видели, что частный случай матрицы плотности D
с двумя одинаковыми собственными значениями не содержит ничего особенного в отно¬
шении связанной с ней онтологической путаницы. Путем небольшой модификации этого
примера можно получить любую матрицу 2x2, какую мы пожелаем. Вместо пары ЭПР-ча-
стиц со спином находящейся, как в рассмотренном примере, в состоянии со спином О,
можно взять начальное состояние со спином 1. В качестве частного случая можно рас¬
смотреть пример, предложенный Люсьен Харди (§ 23.5). Начальное состояние здесь имеет
вид | ^~У) — | «—)| У) -Ь | У)\ +—) (в представлении Майораны (§22.10) тангенс угла
между 4— и У равен |), и я предполагаю, что мой коллега на Титане решает проводить
О
измерение спина частицы, прибывающей на Титан, в направлении вправо/влево. Из резуль¬
татов §23.5 следует, что если мой коллега получает результат | —>), то здесь, на Земле,
я получу состояние j «—), если же коллега получит j то я получу | |).* Таким образом,
если мне известно, что мой коллега проводит измерение типа вправо/влево (и при этом
я знаю, что начальным состоянием было | *—У)\ то я делаю вывод, что спиновое состоя¬
ние частицы, принимаемой мною на Земле, имеет вид вероятностной смеси состояний | 4—)
и | |). Заметим, что состояния | +—) и | |) не ортогональны между собой. Ортогональность
не является обязательным требованием для вероятностной смеси состояний, образующих
матрицу плотности, и в данном примере мы наблюдаем это в явном виде.
Какой матрицей плотности я должен пользоваться для описания моей частицы? Ее мож¬
но получить, если известны значения вероятности для двух альтернативных результатов | —>)
и | 4—)9 которые может получить мой коллега. Соответствующие вероятности оказываются
1	Л	-I	с%
равными ~	и	~,	так что у меня имеется вероятность	~	подучить состояние | 4—} и	-	для
О	О	О	о
состояния ||). Следовательно, моя матрица плотности будет иметь вид
-Ь = ||<->1«-) + §1Ш).
В базисе вверх/вниз эта матрица выглядит следующим образом:
L
5
6
1
6
(поскольку | *—) = (| |) — | 1))/у/2). Собственные значения этой матрицы определенно
не одинаковы, они равны ~ + -^5 и |	Однако онтология «| *—) с вероятно-
1	О
стью тг и | |) с вероятностью для этой матрицы плотности отнюдь не единственно
о	О
возможная. Например, из симметрии между ^-и/в начальном состоянии | +—У) с оче¬
видностью следует, что если мой коллега решит проводить измерение в направлении У, г но
влево/вправо (в направлении <—), то моя собственная онтология в отношении матрицы плот¬
ности D должна будет сильно измениться и включать состояние | У) и перпендикулярное
ему состояние. Онтология получается иной при каждом возможном изменении направления
^ ^ ^
измерения, выбираемого моим коллегой на Титане .
Почему?
Выведите эту матричную форму для L, проверьте правильность приведенных собственных значений
и найдите собственные векторы. Точка L в сфере Блоха на рис. 29.3 выбрана в соответствии с этим примером.
Каково ее расстояние от центра сферы?
Покажите, что при такой процедуре можно получить какую угодно матрицу плотности 2x2 для ЭПР-
пары со спином 1. Как связаны спиновые направления собственных векторов матрицы плотности с представлением
Майораны для этого начального состояния?
***

29.5. Матрица плотности в условиях ЭПР-эксперимента
669
Можно получить множество более сложных онтологий для любой конкретной матрицы
плотности, если вероятностная смесь содержит три или более различных состояний. Такая
1
ситуация возникает, если начальное состояние со спином -п при п > 2 распадается на ча-
стицу со спином -, летящую к Земле, и частицу со спином - п — -, прибывающую на Титан,
поскольку измерение спина моим коллегой допускает тогда п различных исходов, каждый
со своей вероятностью (§22.10); см. рис. 29.4. При этом, очевидно, происходит обобщение
ситуации, так что гильбертово пространство состояний, которое я использую для описа¬
ния частицы, прибывающей на Землю, теперь имеет более двух измерений. Всё это имеет
целью подчеркнуть, что не существует единой онтологии «вероятностной смеси альтер¬
нативных состояний», не зависящей от того, какая используется матрица плотностиf29Л7^.
Вскоре мы увидим, что этот факт приводит к затруднениям при использовании концепции
декогеренции, вызываемой окружением (вариант (в)).
Т итан
>•
&
Рис. 29.4. Матрица плотности может представлять вероятностную смесь состояний, число которых
превосходит размерность пространства. Рассматривается следующий пример: в некоторой точке меж¬
ду Землей и Титаном, но ближе к Титану, известное начальное состояние со спином Ц (при п > 2)
Zi
распадается на частицу со спином направляющуюся к Земле, и частицу со спином ~(п — 1),
Z	Z
летящую к Титану. Коллега на Титане измеряет спин последней, и вероятностью каждого из п воз¬
можных результатов измерения является некоторое определенное число, которое можно вычислить
(на Земле), если известно начальное состояние, так что на Земле получается определенная матри¬
ца плотности 2x2, представляющая вероятностную смесь п состояний. (Это, очевидно, приводит
к обобщению гильбертова пространства на случай более чем двух измерений.)
Здесь следует сделать замечание относительно реального вычисления матрицы плотно¬
сти, когда, как в приведенном примере, часть информации в перепутанном состоянии оказы¬
вается скрытой (например, на Титане). Имеется весьма эффективный метод под названием
«суммирование по неизвестным состояниям». Он наиболее просто выглядит в индексной
записи. Запишем наше начальное состояние (нормированный кет-вектор |^)) в виде фар,
Спин
п — 1
Спин
Земля
Спин ~
, v ***>
Г) р
9 а
Рис. 29.5. Диаграммное представление матриц плотности, построенных методом «суммирования по
неизвестным состояням». Нормированный кет-вектор \ф) имеет вид фар, где индексу а соответствует
местонахождение здесь (Земля), а индексу р — местонахождение там (Титан). Эрмитово-сопряженное
состояние (бра-вектор (ф\) имеет вид фар, условие нормировки записывается в виде ф(хрф(Хр = 1.
Матрица плотности, используемая «здесь», представляется в виде D^ — фапфзр, а используемая
«там»
в виде Dp
'Фар'Ф
асг

670
Глава 29
что следует понимать как перепутанное состояние, у которого индексу а соответствует ме¬
стонахождение здесь (например, на Земле), а индексу р — местонахождение там (например,
на Титане); см. §§ 23.4,23.5. Состояние, комплексно-сопряженное данному (бра-вектор (ф|),
будет иметь вид фар. Условие нормировки состояния записывается в виде
ФарГр = 1-
Тогда матрицей плотности, которой я пользуюсь здесь, на Земле, в отсутствие информации
с Титана, будет величина	_
Di = ’Фар-Ф0'3
•	* '
(со сверткой по индексу р). Соответственно матрица плотности моего коллеги будет иметь
вид фарфаа. Соответствующее диаграммное представление показано на рис. 29.5.
29.6.	Практическая философия декогеренции, создаваемой окружением
Приведенные соображения можно рассматривать как «прелюдию» к нашему исследо¬
ванию точки зрения (в), основанной на декогеренции, вызываемой окружением. Согласно
этой позиции, редукция состояния R понимается как результат безнадежного перепутывания
рассматриваемой квантовой системы с ее окружением. Чтобы применять эти идеи, будем
рассматривать саму систему как часть, находящуюся здесь, а окружение — как часть, на¬
ходящуюся там. Окружение мы считаем устроенным крайне сложно и «хаотическим», так
что практически не существует способа извлечь ту часть информации о полном состоянии
системы, которая относится к окружению, находящемуся там. Поэтому мы «суммируем по
неизвестным состояниям» окружения, чтобы получить матрицу плотности, описывающую
ту часть состояния, которая находится здесь. Основная работа здесь состоит в том, чтобы
показать, что при моделировании окружения «разумным» образом матрица плотности, даже
при не слишком «шумящем» окружении, через некоторое очень короткое время с хорошей
степенью приближения становится диагональной
D
(Pi 0
О Р2
\о о
Рп )
если выбрать подходящий базис 11), |2), ..., |п).** Это можно интерпретировать как веро¬
ятностную смесь
D = рх\1){1\ + р2\2)(2\ + ... + р„\п)(п
тех базисных состояний, которые соответствуют диагональным членам. Такая вероятностная
смесь отражает альтернативы, возникающие в процессе редукции состояний R, при этом
вероятностями соответствующих исходов служат числа pi, Р2, - • •, Рп-
Однако мы уже видели, что всякая матрица плотности допускает множество онтологи¬
ческих интерпретаций. Поэтому мы не можем сказать, что какая-то из этих интерпретаций
дает нам представление о «реальном» положении дел. Более того, мы не можем даже утвер-
Объясните, почему это так. (Подсказка: выберите отдельные ортонормированные базисы для двух место¬
положений здесь и там и введите совместные вероятности для различных возможных результатов измерений в двух
12
местах.) Проверьте правильность указанных выше вероятностей - и - для рассмотренного случая \ф) = \ +-/*).
Фактически любая матрица плотности диагональна в некотором базисе! Понятно ли, почему так будет
и в случае, когда все собственные значения различны?

29.7. Кошка Шредингера в «копенгагенской» онтологии
671
ждать, что реальное состояние есть одно из состояний 11), |2), ..., \п) с соответствующими
вероятностями Ръ £>2, • • •, Рп-
При обычных обстоятельствах следует рассматривать матрицу плотности как некото¬
рое приближение к полной квантовой истине, поскольку не существует общего принципа,
налагающего абсолютный запрет на извлечение подробной информации из окружающей
среды. Возможно, будущее развитие техники сможет предоставить возможность подробно
отслеживать квантовые фазовые соотношения, от чего нынешняя техника пока отказывает¬
ся. Создается впечатление, что необходимость в описании с помощью матрицы плотности
определяется уровнем развития техники! По мере ее совершенствования будет расширяться
область, в которой допустимо описание в терминах векторов состояния, а к матрице плотно¬
сти будут обращаться лишь в действительно безнадежно запутанных ситуациях! Представ¬
ляется странным взгляд на физическую реальность как на нечто «реально» описываемое
матрицей плотности. Поэтому такое описание по предложению Джона Белла (прославив¬
шегося неравенствами Белла, см. §23.3) иногда называют «практическим» (в англоязычной
литературе используется аббревиатура FAPP — For All Practical Purposes). Тогда описание на
языке матрицы плотности выбирается из прагматических соображений удобства* как нечто
практически полезное, пусть и не дающее «истинной» картины фундаментальной физиче¬
ской реальности.
Может, однако, существовать уровень, на котором детальные фазовые соотношения дей¬
ствительно теряются, в силу некоторого глубоко спрятанного физического принципа. Идеи,
развиваемые в этом направлении, часто апеллируют к гравитации в надежде прийти таким
путем к этому принципу. Иногда привлекается идея «квантовых флуктуаций гравитационно¬
го поля», согласно которой сама структура пространства-времени в «планковском масштабе»
порядка 10-35 м имеет вид не гладкого многообразия, а напоминает пену (рис. 29.6) t29*18!.
(Я вернусь к этим идеям в §§31.1, 33.1.) Можно вообразить, что в таком масштабе фазо¬
вые соотношения действительно невозвратно «теряются в пене». Другое предположение,
выдвинутое Стивеном Хокингом, состоит в том, что в присутствии черной дыры информа¬
ция о квантовом состоянии «проглатывается» дырой и становится непоправимо потерянной
в принципе. В таком случае можно принять, что квантовая система, перепутанная с той ча¬
стью, которая упала в дыру, действительно должна описываться матрицей плотности, а не
«чистым состоянием»^29,19}. Я вернусь к этим идеям позже, в §§30.4, 30.7, 30.8, 30.14.
Рис. 29.6. Какова природа пространства-времени в план¬
ковском масштабе 10~33 см (или 10-43 с)? Предполага¬
ется, что квантовые флуктуации гравитационного поля
могут приводить к образованию неупорядоченной «пе¬
ны» с многократно меняющейся топологией, в которой
квантовые фазовые соотношения могут действительно
теряться на данном уровне
29.7.	Кошка Шредингера в «копенгагенской» онтологии
Вернемся к проблеме квантового измерения, состоящей в следующем: как будет проис¬
ходить (или выглядеть) R-процесс, если предполагается, что квантовое состояние «реально»
эволюционирует в виде детерминированного U-процееса (§§21.8,22.1,22.2,23.10). Эту про¬
блему часто представляют, весьма схематически, как парадокс кошки Шредингера. Я изложу
его здесь в виде, отличном (хотя и несущественно) от первоначальной версии Шредингера.

672
Глава 29
Пусть имеется источник фотонов S, который испускает одиночный фотон в направлении
расщепителя луча (полупрозрачного зеркала), на котором состояние фотона расщепляется
на две части. В одном из двух получающихся при этом лучей фотон встречает на своем пути
детектор, который связан с некоторым смертоносным устройством, убивающим бедную кош¬
ку; в другом луче фотон уходит прочь, и кошка остается живой (см. рис. 29.7). (Это, конечно,
лишь «мысленный эксперимент». В реальном опыте (например, таком, который будет рас¬
смотрен в § 30.13) нет надобности в участии живого существа. Кошка привлечена здесь лишь
для создания драматического эффекта!) Поскольку эти две альтернативы для фотона должны
сосуществовать в виде квантовой линеинои суперпозиции и так как линейность уравнения
Шредингера (т. е. операции U) требует, чтобы две последовательные временные эволюции
с течением времени продолжали оставаться в постоянной суперпозиции с комплексными
коэффициентами (§ 22.2), квантовое состояние в конечном счете должно представлять по¬
добную комплексную суперпозицию из состояний мертвой кошки и живой кошки, так что
кошка в одно и то же время должна быть мертвой и живой!
*
| W
•V
- *0#°- • ^
S
Рис. 29.7. Кошка Шредингера (в слегка модифицированном варианте). Источник фотонов S испус¬
кает одиночный фотон в направлении расщепителя луча, посредством которого состояние фотона
расщепляется в суперпозицию двух частей. В одной из них фотон попадает в детектор, включающий
смертоносное оружие, которое убивает кошку. В другой части фотон уходит, и кошка остается в живых.
U-эволюция приводит к возникновению суперпозиции мертвой и живой кошки
Конечно, такая ситуация выглядит абсурдом в отношении к поведению объекта раз¬
мером с кошку в реальном физическом мире, известном нам по повседневному опыту.
Как справляются с этим парадоксом различные «стандартные» интерпретации квантовой
механики? Рассмотрим копенгагенскую точку зрения (а). Насколько я понимаю, эта интер¬
претация просто рассматривает детектор фотонов как некоторый «классический измеритель¬
ный прибор», к которому неприменимы правила квантовой суперпозиции. Состояние фотона
между моментами его излучения и детектирования (или недетектирования) прибором опи¬
сывается волновой функцией (вектором состояния), однако последней не приписывается
какой-либо «физической реальности». Волновая функция рассматривается просто как ма¬
тематическое выражение, используемое для вычисления вероятностей. Если расщепитель
луча устроен так, что амплитуда фотона делится ровно пополам, то, согласно вычислениям,
существует 50-процентная вероятность, что детектор зарегистрирует приход фотона, и такая
же вероятность, что этого не произойдет. Следовательно, у кошки есть 50-процентный шанс
погибнуть и такой же шанс остаться в живых.
Это физически правильный ответ, слово «физически» относится к поведению того мира,
с которым мы реально сталкиваемся в повседневном опыте. В то же время такое описание
дает нам весьма неудовлетворительную картину, если мы намерены проследить за физиче¬
скими событиями на более подробном уровне. Что в действительности происходит внутри
детектора? Почему мы рассматриваем его как «классический прибор», хотя он построен
из таких же квантовых объектов (протонов, электронов, нейтронов, виртуальных фотонов
и т. п.), что и любой другой, большой или малый, кусок физического материала? Я пони¬
маю, что на заре квантовой механики воззрения на этот предмет Нильса Бора были почти
вынужденными, необходимыми для того, чтобы теорией можно было пользоваться и был
возможен прогресс в квантовой физике. Однако, насколько я понимаю, такой взгляд мог

29.8. Способны ли разрешить «кошачий» парадокс другие традиционные онтологии?
673
быть лишь временным, поскольку он не позволяет ответить на вопрос, почему и на какой
стадии у больших и сложных систем вроде детектора должно возникать «классическое по¬
ведение». Поскольку интерпретация квантовой механики с точки зрения (а) предполагает
наличие таких «классических структур», эта позиция, вообще не затрагивающая глубоких
вопросов, связанных с измерениями, может быть лишь «временной мерой».
Другой вариант точки зрения (а) предполагает фактически, что «классической изме¬
рительной аппаратурой» служит в конечном счете сознание наблюдателя. В соответствии
с этим вариантом, классическое поведение возникает, только когда кошку наблюдает экс¬
периментатор, обладающий сознанием (если не принимать во внимание сознание самой
кошки). Мне кажется, что если мы опустимся на этот уровень, то окажемся на позиции,
более близкой к точкам зрения (б) или (е). Если принять, что U-правила квантовой линей¬
ной суперпозиции продолжают выполняться на уровне существ, обладающих сознанием, то
мы попадаем в царство со множественными мирами (вариант (б)), если же мы считаем, что
U-правила к таким существам не применимы, то оказываемся на позиции (е), согласно ко¬
торой в отношении существ, обладающих сознанием, в игру вступает некоторый новый тип
поведения за рамками обычных предсказаний квантовой механики. Такое предположение
было выдвинуто в 1961 году выдающимся физиком-теоретиком Юджином Вигнером [29*2°].
Мне кажется, однако, что любая теория, которая для объяснения R-процессов требу¬
ет присутствия наблюдателя, обладающего сознанием, приводит нас к какой-то однобокой
(и, осмелюсь утверждать, крайне неправдоподобной) картине Вселенной. Представим себе
некоторую отдаленную планету, подобную Земле, но лишенную разумной жизни, вокруг
которой на протяжении многих световых лет во всех направлениях разумная жизнь так¬
же отсутствует. На что будет похожа погода на такой планете? Погодные явления обладают
свойством «хаотичности» в том смысле, что они критическим образом зависят от тончайших
деталей того, что было прежде (см. § 27.2). Вполне возможно, что в течение, скажем, месяца
тонкие квантовые эффекты окажутся настолько усиленными, что от них будет зависеть кар¬
тина погоды на всей планете. Согласно обсуждаемой точке зрения (е) (или, возможно, (а)),
отсутствие сознания означает, что на такой планете R-процессы никогда не происходят, так
о
что погода представляет некоторую квантовую суперпозицию в виде какой-то мешанины,
ничем не напоминающую такую погоду, к какой мы привыкли. Пусть теперь эту планету
посещает космический корабль с разумными существами, или зонд, способный передавать
сигналы разумным существам, располагает свои датчики на этой планете. Тогда немедленно
(и только в этом месте) погода внезапно принимает обычный характер, как если бы она
была такой все время! Здесь нет реального противоречия с повседневным опытом, но яв¬
ляется ли такая «вигнеровская реальность» правдоподобной картиной поведения реальной
физической Вселенной? На мой взгляд, — нет, однако я могу понять тех, кто относится к ней
с большим доверием.
29.8.	Способны ли разрешить «кошачий» парадокс другие
традиционные онтологии?
Как же тогда обстоит дело с вариантом многих миров (б)? Здесь «реальность» кванто¬
вой суперпозиции мертвой и живой кошки просто принимается (подобно картине погоды,
создаваемой квантовой суперпозицией, в предыдущем абзаце), но это ничего не говорит нам
о том, что на самом деле «воспринимает» наблюдатель, смотрящий на кошку (или следящий
за погодой). Состояние восприятия наблюдателя считается перепутанным с состоянием кош¬
ки. Состояние восприятия «я вижу живую кошку» сопровождает состояние «живая кошка»,
а состояние восприятия «я вижу мертвую кошку» сопровождает состояние «мертвая кошка»
(см. рис. 29.8). При этом предполагается, что воспринимающее существо всегда находится
в одном из этих двух состояний восприятия; соответственно кошка в этом воспринимаемом

674
Глава 29
\'lp) = WX
Рис. 29.8. Вывод, следующий из рис. 29.7, неприменим при наличии окружения разного рода,
перепутанного с состояниями кошки, или наблюдателя с различными вариантами восприятия.
Состояние при этом имеет вид
\\р) = w х |живая кошка) |окружение живой кошки)[восприятие живой кошки)-f
+z х [мертвая кошка)|окружение мертвой кошки)[восприятие мертвой кошки).
Если U-эволюция должна представлять реальность (вариант многих миров б), то мы должны
принять, что наблюдатель может воспринимать лишь ту или другую альтернативу, так что его
восприятие на этой стадии «расщепляется» между отдельными мирами
мире либо жива, либо мертва. Эти две возможности сосуществуют «в реальности» в виде
перепутанной суперпозиции:
|Ф) — w х [живая кошка) [восприятие живой кошки) -f
+z х [мертвая кошка)[восприятие мертвой кошки).
Я хотел бы отметить, что всё это пока далеко от разрешения «кошачьего» парадок¬
са. В формализме квантовой механики нет ничего, что запрещало бы состоянию сознания
включать в себя одновременное восприятие живой и мертвой кошки. Эта проблема иллю-
стрируется на рис. 29.9, где изображена простая ситуация, в которой амплитуды отражения и
пропускания фотона расщепителем луча z и w равны между собой. Как и в простом примере
1
ЭПР-Бома, где испускаются две частицы со спином - в начальном состоянии со спином О,
результирующее перепутанное состояние можно представить многими способами. В приме¬
ре, изображенном на рис. 29.9, состояние |живая кошка) + [мертвая кошка) сопровождается
состоянием [воспринимаемая живая кошка) + [воспринимаемая мертвая кошка), а состоя¬
ние [живая кошка) — [мертвая кошка) сопровождается состоянием [воспринимаемая живая
кошка) — [воспринимаемая мертвая кошка). Это вполне аналогично записи состояния |Q) =
t)| 1) — I 1)1 Т) в виДе &) — I ~^)1 *—) — I *“)1 как это было сделано в §23.4.
Почему мы не можем допустить такие суперпозиции состояний восприятия? Пока мы не
узнаем точно, каково то квантовое состояние, которое можно рассматривать как «воспри¬
ятие», и соответственно не поймем, что подобные суперпозиции «не разрешены», мы не
сможем объяснить, почему в реальном мире нашего повседневного опыта невозможны су¬
перпозиции живых и мертвых кошек.
Против этого примера иногда возражают на том основании, что равенство амплитуд для
двух альтернатив представляет весьма частный случай и что в общем случае нет возмож¬
ности переопределять перепутанные состояния подобным образом. Если, однако, взглянуть
на эту ситуацию более глубоко, то мы обнаружим, что равенство амплитуд в этом примере
вовсе не существенно. Полезно вспомнить пример ЭПР-пары частиц со спином ~ из § 29.5.
«Равенство амплитуд» (в действительности равенство модулей амплитуд, — \w\) приво¬
дит там к матрице плотности с равными собственными значениями. В §§29.4, 29.5 было
показано в явном виде, что матрицу плотности 2 х 2 с неравными собственными значениями
можно многими способами представить как вероятностную смесь пар состояний, однако со¬
стояния в этих парах в общем случае не будут ортогональны между собой. Ортогональность
имеет место лишь в случае, если два состояния являются собственными векторами данной

29.8. Способны ли разрешить «кошачий» парадокс другие традиционные онтологии?
675
л/8|Ф} =	L*J)	(1®*©} + |®>))
+
ЧГ<ЧД|
Рис. 29.9. Рис. 29.8 можно представить в следующем виде (предполагается z — w = состояние
у 2
окружения включается как составная часть в состояние кошки):
л/8|^) — {[живая кошка) + |мертвая кошка)}{[восприятие живой кошки)-Ь
+ [восприятие мертвой кошки)} + {[живая кошка) —
— [мертвая кошка)}{[восприятие живой кошки) — [восприятие мертвой кошки)}
матрицы плотности . В случае равных амплитуд (точнее, \z\ = [гб?|) состояния
живая кошка
и
мертвая кошка) можно взять взаимно ортогональными, при этом и сопровождающие со¬
стояния [восприятие живой кошки) и [восприятие мертвой кошки) будут ортогональными
(как «собственные векторы»). Однако в случае \z\ ф \w\ пара состояний восприятия, сопро¬
вождающих выбранную пару взаимно ортогональных состояний кошки, которые составляют
суперпозицию, в общем случае не будет ортогональной и пара состояний кошки, сопрово¬
ждающих выбранную пару взаимно ортогональных состояний восприятия, в общем слу¬
чае также не будет ортогональной. Нет ничего плохого в использовании любого из этих
представлений полного состояния \Ф)9 хотя можно придерживаться взгляда, что состояния
восприятия обязаны быть взаимно ортогональными, если это именно те состояния, которые
должны обеспечивать проявления реальности в концепции множественности миров. Однако,
согласно позиции (б), R-процессы в действительности не имеют места, поэтому ортогональ¬
ные альтернативы не имеют какого-то особого статуса (поскольку в любом случае к ним
ничего «не сводится»).
Фактически оказывается, что в общем случае существует единственная пара взаим¬
но ортогональных состояний восприятия, сопровождающих пару взаимно ортогональных
состояний кошки. Это известно под названием разложения Шмидта для перепутанного
состояния^29*21!. Однако этот факт не нашел широкого применения в разрешении парадокса
измерения (несмотря на популярность разложения Шмидта в связи с квантовой теорией
информации^29,22!), поскольку «математически предпочтительная» пара состояний кошки
(собственные состояния матрицы плотности кошки) в общем случае представляет собой
вовсе не искомые состояния [живая кошка) и [мертвая кошка), а лишь некоторые совсем не
нужные нам суперпозиции этих состояний! Вернувшись к примеру Люсьен Харди, рассмот¬
ренному в § 29.5, можно убедиться, что собственные состояния матрицы плотности, которые
появляются в разложении Шмидта, не обязаны быть чем-то «онтологически реальным».
Мы обнаруживаем (см. упражнение 29.12), что собственные векторы матрицы плотности
(для частицы, принимаемой мною здесь, на Земле) совершенно отличны от альтернатив
и | Т), «макроскопически различимых» в соответствии с измерениями, проводимыми моим
коллегой на Титане!
Поскольку математика сама по себе никак не выделяет состояния [живая кошка
и |мертвая кошка) в качестве «предпочтительных», нам необходимо иметь теорию вос¬
приятия, чтобы можно было придать смысл позиции (б). Однако такая теория пока
отсутствует^29*23!. Более того, такая теория должна не только объяснить, почему суперпози¬
ции мертвых и живых кошек (или еще чего-то столь же макроскопического) не встречаются
в наблюдаемом мире, но и ответить на вопрос, почему удивительное и необычайно точное
правило квадрата модуля дает правильные значения вероятностей в квантовой механике!
Покажите это.

676
Глава 29
Теория восприятия, которая могла бы сделать это, сама должна быть такой же точной, как
и квантовая теория. Приверженцы точки зрения (б) пока не приблизились к построению
такой схемы^29,241
Вернемся к попытке разрешить «кошачий» парадокс с позиции декогеренции, вызывае¬
мой окружением (точка зрения (в)). Будем считать начальное испускание фотона онтологиче¬
ски реальным. (Источник можно расположить так, чтобы была возможность регистрировать
это событие макроскопическим образом.) Тогда после встречи фотона с расщепителем луча
мы будем иметь онтологически реальную суперпозицию фотона в двух разделенных лу¬
чах. Прошедшая часть фотонного состояния эволюционирует в состояние мертвой кошки
KJ
вместе с соответствующим окружением, а отраженная часть — в состояние живои кошки
вместе с другим окружением. Пока онтология сводится к суперпозиции этих двух состояний.
Альтернативные окружения «ненаблюдаемы» и по ним проводится суммирование, которое
дает матрицу плотности 2x2. При этом онтологическая позиция плавно смещается, так
что «реальность» теперь описывается самой матрицей плотности. Концепция декогеренции,
вызываемой окружением, утверждает теперь, что эта матрица быстро принимает практи¬
чески диагональный вид в базисе (|живая кошка), |мертвая кошка)). При этом происходит
другой незаметный сдвиг онтологии, и состояние становится вероятностной смесью состоя¬
ний |живая кошка) и |мертвая кошка). Тем самым мы «позволили» перейти от суперпозиции
w\живая кошка)|окружение живой кошки) +
-fz(мертвая кошка)(окружение мертвой кошки)
к альтернативам (живая кошка) или (мертвая кошка)! Напомним, что не существует одно-
значнои онтологической интерпретации матрицы плотности как вероятностной смеси со¬
стояний (независимо от того, одинаковы собственные значения или нет). Действительно,
чтобы перейти к смеси состояний (живая кошка) и (мертвая кошка), необходим (двукрат¬
ный) сдвиг онтологии относительно исходной суперпозиции. Позиция (в) действительно
оказывается «прагматической» и не дает нам никакой согласованной онтологии физической
реальности.
29.9.	Чем могут помочь нетрадиционные онтологии?
Я должен кратко обсудить точки зрения (г) и (д). Если принять «экстравагантную» он¬
тологию согласованных историй (г), то можно выдвинуть возражения, подобные таковым
для концепции множественных миров (б). Как и в случае (б), возникает необходимость в де¬
тальной и точной теории восприятия для того, чтобы с позиции (г) была видна картина,
согласующаяся с тем, что мы знаем о физическом мире. Попытки в этом направлении де¬
лались (примером может служить так называемая программа IGUS — «система накопления
и использования информации»), однако пока они представляются довольно далекими от то¬
го, что требуется^29-25Д Вместо этого можно предпочесть что-то вроде более экономичной
онтологии, намек на которую имеется в § 29.2; при этом один максимально согласованный
набор историй можно рассматривать как подходящий кандидат на роль онтологии «реально¬
го мира». Но это (как и более экстравагантная онтология, рассмотренная выше) зависит от
выбора критерия «согласованной истории», который выделил бы истории, напоминающие
мир, в котором мы живем. Однако, как было показано в 1996 году Даукером и Кентом,
такое условие «согласованности» само по себе отнюдь не дает адекватного описания. По-
видимому, необходимы какие-то дополнительные критерии.
На мой взгляд, главный недостаток позиции (г) состоит в том, что, несмотря на введение
процедур R-типа (путем использования проекторных множеств), она, по-видимому, не при¬
ближает нас к пониманию того, что есть физическое измерение, по сравнению с онтологиями

29,9. Чем могут помочь нетрадиционные онтологии?
677
(а) и (б). Действительно, с точки зрения (г), процедуры R-типа не связаны непосредственно
с реальными физическими измерениями. Я вижу трудность в том, что, устраняя связь меж¬
ду скачками R-типа и физическими измерениями, мы не приходим к пониманию сущности
физического измерения. Почему, согласно точке зрения (г), мы не можем оказаться свиде¬
телями чего-то подобного кошке Шредингера, находящейся в суперпозиции между жизнью
и смертью? Не видно, чтобы теория давала какое-то улучшение стандартной копенгаген¬
ской позиции (а) в попытках объяснить, почему такие системы, как детали аппаратуры или
кошки, должны вести себя классическим образом, а нейтроны или фотоны — нет. Требо¬
вание «согласованности» крупномасштабных историй далеко от того, что необходимо для
построения модели^29*26} наблюдаемой физической реальности.
Положительной чертой позиции (г) является то, что делается серьезная попытка вклю¬
чить процедуры R-типа на фундаментальном уровне, однако те критерии, которые до сих
пор предлагались, недостаточны, чтобы ограничить поведение модели и получить однознач¬
ную картину, напоминающую известный нам мир. Это представляется справедливым как на
макроскопическом уровне «классического типа» (см. комментарии в связи с анализом кри¬
терия «согласованной истории» Даукера-Кента), так и на «квантовом уровне», где можно
надеяться наблюдать невозмущенную унитарную эволюцию. Поскольку парадокс измерения
связан с видимым конфликтом между типами физического поведения на этих двух уровнях,
нелегко понять, как может пролить свет на этот парадокс точка зрения (г), рассматривающая
согласованные истории.
А как обстоит дело с вариантом (д)? Как отмечалось в § 29.2, концепция «волны-пилота»
де Бройля-Бома (д) имеет, по-видимому, наиболее ясную онтологию среди тех, которые на
деле не расходятся с предсказаниями квантовой теории. Тем не менее она, на мой взгляд, не
рассматривает парадокс измерения более удовлетворительным образом, чем остальные кон¬
цепции. Насколько я понимаю, точка зрения (д) может извлечь пользу из двух своих уровней
реальности — первичного «корпускулярного» уровня реальности конфигурации системы,
а также вторичного «волнового» уровня реальности, определяемого волновой функцией гр,
роль которой состоит в том, чтобы управлять поведением на первичном уровне. Мне, од¬
нако, не понятно, можно ли уверенно решить, к какому из уровней обращаться в какой-то
конкретной ситуации реального эксперимента. Трудность состоит в том, что не существу¬
ет параметра, определяющего, какие системы считать «большими» и соответствующими
классической «корпускулярной» или «конфигурационной» картине, а какие — «малыми» на¬
столько, что становится существенным поведение волнового типа, описываемое волновой
функцией (это относится и к позиции (г)). Из §23.4 и последующих разделов мы знаем,
что квантовое поведение может распространяться на расстояния по крайней мере в десятки
километров, так что физическое расстояние само по себе не определяет, когда система пере¬
стает выглядеть как квантово-механическая и начинает вести себя как классический объект.
Тем не менее существует некоторый смысл, в котором большой объект (например, кошка) не
подчиняется унитарным квантовым законам для малых масштабов. (В §30.11 я приступлю
к изложению моих собственных взглядов на то, какого рода «масштабы» нам необходимы.)
Но независимо от того, можно ли считать приемлемым какой-то конкретный масштаб, мне
кажется, что необходим некоторый масштаб, определяющий, когда поведение классического
типа начинает преобладать над мелкомасштабным квантовым поведением. Подобно другим
квантовым онтологиям, не предполагающим заметных отклонений от стандартной кванто¬
вой механики, точка зрения (е) не располагает подобным масштабом, поэтому я не думаю,
что она в состоянии адекватно рассматривать парадокс кошки Шредингера.
В соответствии с этой проблемой может оказаться уместным замечание общего харак¬
тера относительно попыток «вывести» возникновение R-процессов из динамики, например,
U-процессов. Можно заметить, что обычная (детерминированная) динамика сама по себе на
это не способна хотя бы по той причине, что уравнение Шредингера, будучи динамическим,

678
Глава 29
не содержит никаких вероятностей. (Я отсылаю читателя к §27.1.) Необходим некоторый
вероятностный принцип. R-процессы в конечном счете подчиняются вероятностному зако¬
ну. Как отмечалось в § 29.2, существенной чертой позиции (д) является то, что вероятности
для последовательных измерений определяются выбором, например, начального состояния.
В итоге остается лишь позиция (е). Главные трудности, связанные со многими различ¬
ными (зачастую героическими) предложениями относительно «объективных R-процессов»,
состоят в их неестественном появлении, существенно нерелятивистском характере, необхо¬
димости введения произвольных параметров, не вытекающих из известной физики, наруше¬
нии закона сохранения энергии и, в некоторых случаях, прямом конфликте с результатами
наблюдений. В мои планы не входит обсуждать здесь все эти предложения, и было бы
нечестно с моей стороны выделить какие-нибудь из них за счет других. Фактически я ока¬
жусь равно несправедлив ко всем предложениям, выдвинутым другими, всучив читателю
в главе 30 еще одно (минималистское, некоторым образом) предложение, которое я считаю
наиболее близким к истине (приношу извинения многим из моих друзей!). На самом деле
различные предложения, выдвинутые ранее другими авторами, оказали значительное сти¬
мулирующее влияние, и я отмечу их (с соответствующей благодарностью), но лишь в связи
с теми идеями, которые я собираюсь оспаривать.
Примечания
§29.1
29.1. См. [188].
29.2. Этим термином я обязан моему коллеге, специалисту но классической филологии Питеру
Дероу. См. [605].
29.3. См. [253, 825, 193, 188].
29.4. Некоторые физики утверждают, что «нет проблем» в отношении квантовой суперпозиции
макроскопически различных состояний (подобных шредингеровской суперпозиции мертвой
и живой кошки, которую мы рассмотрим в §§ 29.7-29.9), поскольку было бы просто «слишком
дорого» (или практически невозможно) поставить эксперимент по наблюдению интерферен¬
ции между мертвым и живым состояниями. Это опять-таки «прагматическая» позиция, кото¬
рая не касается реально тех онтологических вопросов, которые нас здесь занимают. Я отношу
таких физиков в основном к категории (в).
29.5. См. [373], стр. 121.
§29.2.
29.6. Точка зрения (г) изложена в [282], точка зрения (д) — в [87]. Список (а), (б), (в), (д) имеет обоб¬
щающий характер, внутри каждой из этих точек зрения имеются свои оттенки. В частности,
некоторые придерживаются того взгляда (см., например, [739]), что «квантовую реальность»
лучше всего понять, пользуясь языком интегралов по траекториям и/или фейнмановских диа¬
грамм, с которыми мы познакомились в §§26.6-26.11. Насколько я понимаю, это семейство
онтологий следует отнести к категории (б) (хотя оно и содержит некоторые важные элементы,
общие с позицией (г)), согласно которой статус «реальности» должен быть приписан частной
суперпозиции, определяющей «квантовое состояние» (или «квантовую историю»). Я должен
упомянуть также «компромиссные» онтологии [И, 169, 166, 819], согласно которым в описа¬
нии реальности должны участвовать как волновая функция Шредингера, распространяющаяся
в будущее после последнего измерения, так и другая волновая функция, распространяющаяся
в прошлое от следующего измерения (см. §30.3). Я, однако, не вижу причин, по которым
какая-либо из этих альтернатив способна без введения дополнительных ингредиентов разре¬
шить парадокс измерения лучше, чем точки зрения (а), (б), (в), (г) или (д).
29.7. Формализм (г) допускает также, что «исходным состоянием» может быть матрица плотности
(см. §29.3).

29.9. Чем могут помочь нетрадиционные онтологии?
679
29.8. Иногда их называют просто «историями», однако это может привести к путанице при ис¬
пользовании этого термина применительно к фейнмановскому «суммированию по историям»
(§26.6).
29.9. Это условие состоит в следующем. Пусть мы имеем заданную последовательность проек-
торных множеств (пока предположим 7i = 0). Построим выражение X — (гфо\Е'F'...
К'L'DooLK... FE\ipo), где \фо) — начальное состояние; в качестве «конечного состоя¬
ния» можно взять матрицу плотности Doo (см. примечание 29.7). Проекторы в последо¬
вательных парах (Е, Е'), (F, F'), ..., (НС, К'), (X, L') принадлежат соответственно
данной последовательности проекторных множеств. Условие согласования требует, чтобы ве¬
щественная часть величины X обращалась в нуль всякий раз, когда члены какой-нибудь из
пар (15, Е'), (F, F7), ..., (К, К'), (X, L') не равны между собой. Это строго выполня¬
ется, только когда игнорируется шредингеровская часть эволюции (т.е. мы берем Н = 0),
однако нетривиальная шредингеровская эволюция может быть восстановлена путем введе¬
ния такой эволюции соответствующим образом между моментами действия проекторов. Это
«условие согласования», налагаемое на крупномасштабные истории, можно интерпретировать
как условие «отсутствия интерференции» между сравниваемыми историями.
29.10. На самом деле я не обнаружил какой-либо четко сформулированной «(г)-онтологии» в ли¬
тературе, посвященной согласованным историям. Излагаемое здесь — это всего лишь моя
собственная попытка схватить суть вопроса в продолжительных дискуссиях с Джимом Харт-
лом и особенно в полезной переписке с Феем Даукером. Вполне возможно, что, несмотря на
мои усилия, мне не удалось адекватно представить ту онтологию, которой придерживаются
сторонники точки зрения (г).
29.11. См. [87, 797]. Антоний Валентини написал также книгу о теории де Бройля-Бома, которая,
надеемся, вскоре будет напечатана!
29.12. См. [426, 270, 291, 290, 457, 576, 577, 448, 815, 194, 195, 631, 632, 300, 301, 604, 610, 614, 619,
г
482] (порядок перечисления произвольный).
§293.
29.13. В случае непрерывного распределения вероятностей нам нужна неотрицательная веществен¬
ная функция /, определенная в пространстве V, интеграл от которой равен единице. Про¬
странство V имеет естественную форму объема — 2А/-форму Е из § 20.4, удовлетворяющую
теореме Лиувилля, так что величину fE с полным правом можно интегрировать по всему
пространству V, и наше условие имеет вид J fE — 1.
29.14. См. [107]. Нильсен и Чанг [561] дали исчерпывающий концептуальный анализ матрицы плот¬
ности в действии.
§29.4.	•
29.15. В случае системы с п состояниями (п > 2) картина становится более сложной. Только
часть границы (п2 — 1)-мерного пространства матриц плотности является пространством чи¬
стых состояний, эта часть является комплексным проективным (n — 1)-пространством CFn_1
(см. §§21.9, 22.9).
§ 29.5.
29.16. Читателя может заинтересовать, как влияет на эти онтологические проблемы понятие кван-
глеменции, введенное в §23.10. Это интригующий вопрос, и очень может быть, что само
понятие «онтологии» в квантовом контексте придется в конечном счете рассматривать в но¬
вом свете. Но пока давайте займем «более привычную» позицию по отношению к реальности,
не учитывающую требований теории относительности.
29.17. Этот вопрос обсуждается в работах [561, 408].
§29.6.
29.18. Эта идея (как и многие другие) первоначально была выдвинута Уилером; см. также совре¬
менное изложение в [558].
29.19. См. [368, 647], а также §30.14.

680
Глава 29
§ 29.7.
29.20. Я не уверен, что эта точка зрения выражает действительную позицию Вигнера в отношении
квантового измерения, которая, в конце концов, могла меняться на протяжении его жизни.
Я должен также отметить, что моя собственная позиция фундаментальным образом отлича¬
ется от позиций, подобных изложенной здесь, согласно которым редукция состояния связы¬
вается с сознанием. (Мои взгляды на эту проблему иногда неправильно интерпретируются
другими комментаторами.) См. §§30.9-30.12.
§29.8.
29.21. Разложение Шмидта (или полярное разложение) перепутанного состояния общего вида |^),
принадлежащего пространству Н2 х Н2, выражается (однозначным образом) в виде \Ф) =
= А|а) |/3) 4- р,\р)\<г), где состояния |а) и \р), принадлежащие первому пространству Н2,
будучи нормированными собственными состояниями его матрицы плотности, ортогональ¬
ны состояниям \(3) и |сг), аналогичным образом принадлежащим второму пространству И2.
Здесь АА и Дд представляют собственные значения матрицы плотности. Аналогичное соот¬
ношение имеет место для пространства Нп х Нп; в этом случае |#) представляет сумму п
членов. См. [561].
29.22. См. книгу [561], посвященную квантовой теории информации.
29.23. Обсуждение этих вопросов можно найти в работе Пейджа [569].
29.24. Представление о развитии подобных идей в контексте «согласованных историй» (вариант (г))
за последнее десятилетие можно получить из работ [281, 359].
§ 29.9.
29.25. См. [218].
29.26. Яркий пример, предложенный Адрианом Кентом, ясно показывает, насколько недостаточ¬
но это условие «согласованности» для того, чтобы дать физически правдоподобную карти¬
ну «реальности». В этом примере некоторая частица р может находиться в одном из трех
ящиков А, В, С, что описывается соответственно нормированными ортогональными состо¬
яниями |A), |J3), |С). Пусть гамильтониан равен нулю, что означает постоянную унитарную
эволюцию. Начальное состояние имеет вид |А) + |В) + |С), и предполагается, что измерен¬
ное конечное состояние будет иметь вид | А) + |1?) — | С) (это возможно, поскольку состоя¬
ния \А) + \В) ~\-\С) и \А) + \В) — \С) не ортогональны). Введение между ними проекторного
множества {\А)(А\, 1 — \А){А\} оказывается «согласованным», и мы как будто можем сделать
вывод, что частица р на этой промежуточной стадии должна находиться в ящике А (поскольку
состояния \В) + |С) и \В) — \С) ортогональны). Аналогичные рассуждения с заменой А на В
с тем же успехом приводят к выводу, что на промежуточной стадии частица р должна нахо¬
диться в ящике В\ Этот пример возник из «проблемы короля», сформулированной Якиром
Аароновым (см. [15], стр. 5).

Глава 30
Роль гравитации в редукции квантового
состояния
ЗОЛ. Окончательна ли современная квантовая теория?
В этой главе я представлю читателю веские основания положительного характера (по¬
мимо причин отрицательного характера, приведенных в предыдущей главе) считать, что
законы современной квантовой механики нуждаются в фундаментальном (хотя, вероятно,
и тонком) изменении. Эти ожидания основаны на общепринятых физических принципах
и результатах наблюдений над Вселенной. Хотя сегодня очень немногие физики, занимаю¬
щиеся квантовой теорией, готовы всерьез рассматривать идею реального изменения основ
своей науки. Квантовая механика, несмотря на полную поддержку со стороны эксперимента
и блестяще подтвердившиеся предсказания, все же сравнительно молодая наука, ей всего
три четверти века (если считать от создания Дираком и другими математической теории на
основе схем, предложенных Гейзенбергом и Шредингером, в годы, непосредственно следу¬
ющие за 1925-м). Когда я говорю «сравнительно», я сравниваю квантовую теорию с теорией
Ньютона, которая продержалась почти втрое дольше, прежде чем потребовалась серьезная
модификация в виде специальной, а затем и общей теории относительности и квантовой
механики. Даже если первой модификацией, которой подверглась теория Ньютона, считать
введение максвелловских полей, все равно получается, что эта теория безраздельно господ¬
ствовала в течение почти двух веков!
Кроме того, теория Ньютона не знала «парадокса измерения». В то время как линей¬
ность U-процесеа придает квантовой теории особое изящество, та же самая линейность
(или унитарность) прямым путем приводит к «парадоксу измерения» (см. § 22.2). Так ли уж
неразумно считать, что эта линейность может быть лишь приближением к некоторой более
точной (но более тонкой) нелинейной теории?
У нас есть явный прецедент. Теории тяготения Ньютона присуще особое математиче¬
ское изящество, связанное с тем, что гравитационные силы всегда складываются по линей¬
ному закону, тем не менее в более точной теории Эйнштейна линейность была вытеснена
нелинейностью особого вида, проявляющейся в гравитационных эффектах, создаваемых
совместным действием различных тел. При этом теория Эйнштейна отнюдь не лишилась
изящества, но это изящество совершенно иного рода. Мы видим также, что модификация,
которой ньютоновская теория подверглась в теории Эйнштейна, не имеет ничего общего
с «латанием дыр», о котором упоминалось в § 29.2. В разное время попытки такого латания
ньютоновской теории действительно предпринимались. В 1894 году Аспет Холл предло¬
жил заменить показатель степени 2 в ньютоновском законе обратных квадратов GmM/r2
(см. § 17.3) числом 2,00000016 для того, чтобы объяснить обнаруженные в 1843 году очень
малые отклонения от предсказаний ньютоновской теории в движении Меркурия вокруг
Солнца (как показал Саймон Ньюкомб, предложение Холла хорошо подходит и для других
планет)!301^. Теория Эйнштейна непринужденно объяснила эти отклонения, однако новая
теория получилась не просто путем латания старой, а содержала радикальное изменение
взглядов. Именно такого рода изменений в структуре квантовой механике, мне кажется, еле-

682
Глава 30
дует ожидать, если мы хотим получить необходимую (на мой взгляд) нелинейную теорию
взамен нынешней стандартной квантовой теории.
И действительно, как мне представляется, именно общая теория относительности Эйн¬
штейна дает необходимый ключ к требуемой модификации. XX век принес с собой две фун¬
даментальные революции в физической мысли: я полагаю, что общая теория относительно¬
сти произвела столь же впечатляющий переворот, как и квантовая механика (или квантовая
теория поля). В то же время эти две великие картины мира основаны на принципах, которые
плохо согласуются между собой. Обычный взгляд на возможное объединение этих теорий со¬
стоит в том, что одна из них, а именно общая теория относительности, должна подчиниться
требованиям другой. Распространено мнение, что правила квантовой теории поля не подле¬
жат изменению, а теория Эйнштейна должна принять форму, диктуемую квантовыми закона¬
ми. Не многие полагают, что для обеспечения гармоничного союза двух теорий должны под¬
вергнуться модификации положения квантовой теории. Действительно, уже само название
«квантовая гравитация», которым обычно именуют предполагаемый союз, неявно подразу¬
мевает, что искомая объединенная теория должна иметь вид стандартной квантовой теории
поля. И тем не менее я хотел бы заявить, что имеющиеся результаты наблюдений свидетель¬
ствуют о том, что Природа придерживается иного взгляда на такой союз! Я настаиваю на том,
что ее проект в отношении этого союза может оказаться совершенно неожиданным для нас и
что одной из важных особенностей его должна оказаться объективная редукция состояний.
30.2.	Подсказки со стороны космологической временной асимметрии
Какие же результаты наблюдений имеются в виду? Обратимся сначала к тем случаям,
когда выбор Природы в отношении квантово-гравитационного союза проявляется наиболее
ясно. Я имею в виду пространственно-временные сингулярности Большого взрыва и черных
дыр (а также Большого хлопка, если таковой должен иметь место). В главе 27 отмечалась
исключительно особая природа Большого взрыва, резко отличающаяся от «типичной» при¬
роды сингулярностей коллапса. Несмотря на смелые заявления, сделанные при обсуждении
гипотезы Хартла- Хокинга (§28.9), я не вижу возможности обойти вниманием высокую
степень временной асимметрии как необходимую основу квантового-гравитационного сою¬
за Природы.
Такая временная асимметрия находится в явном противоречии с предсказаниями любой
стандартной квантовой теории поля. Возьмем, например, СРТ-теорему, упомянутую в § 25.4.
(Напомним, что Т означает обращение времени, а Р и С — соответственно пространственное
зеркальное отражение и замену частиц их античастицами.) Если мы верим в то, что СРТ-те-
орема применима к нашему искомому союзу гравитации и квантовой теории, то мы ока¬
зываемся в затруднительном положении. Если мы применим СРТ-операцию к какой-нибудь
допустимой «типичной» финальной сингулярности гравитационного коллапса, то получим
сингулярность начального типа как возможный вариант Большого взрыва (или часть Боль¬
шого взрыва). Вспомним об огромном доступном фазовом пространстве, описанном в § 27.13
(и графически изображенном на рис. 27.21). Коль скоро становятся допустимыми «типич¬
ные» начальные сингулярности, то нет ничего, что привело бы иглу Создателя в ту абсурдно
(и, как следует из «антропного» взгляда (§ 28.6), необязательно) малую область В, которая
представляется реальной стартовой точкой нашей Вселенной. Мне кажется очевидным, что
совершенно особая природа Большого взрыва не может получить объяснение в стандартных
рамках квантовой теории поля.
; Так, по крайней мере, обстоит дело с любой теорией, в применении к которой слово
«стандартная» означает справедливость СРТ-теоремы (§25.4). Строго говоря, эта теорема
неприменима непосредственно к теории, которая полностью принимает основы эйнштей¬
новской общей теории относительности с ее искривленным пространством-временем. Одна

30.3. РОЛЬ ВРЕМЕННОЙ АСИММЕТРИИ В РЕДУКЦИИ КВАНТОВОГО СОСТОЯНИЯ
683
из предпосылок СРТ-теоремы состоит в том, что фоновым пространством-временем слу¬
жит плоское пространство Минковского. Тем не менее я подозреваю, что большинство
физиков относится к этому как к несущественной «технической подробности» и придержи¬
вается взгляда, что при желании можно представить теорию Эйнштейна в форме «Пуанкаре-
инвариантной теории поля» путем введения, для удобства, фонового пространства Минков¬
ского. Сам я отношусь к процедурам такого рода^30*2^ весьма сдержанно, тем не менее я готов
согласиться, что маловероятно, чтобы полностью симметричная во времени классическая
общая теория относительности Эйнштейна стала существенно асимметричной в случае ее
подчинения стандартным симметричным во времени процедурам квантовой теории поля.
С другой стороны, вспомним, что в §§ 25.5,26.5, 26.11 мы столкнулись с ситуацией, ко¬
гда симметрия классической теории нарушается при переходе к квантовой теории. Возможно
ли такое, когда к теории Эйнштейна применяются, должным образом, правила квантовой
теории поля? Я допускаю такую возможность, однако трудно понять, как это может оказать¬
ся подобным нарушению симметрии, которое возникает, например, в теории электрослабого
взаимодействия, где «вакуумное состояние» |0) не обладает симметрией квантовой дина¬
мики. Если принять эту идею, то состояние |0) должно быть «асимметричным во времени».
Я не уверен, что идее такого рода можно придать смысл. Верно, что кет-вектор |0) следу¬
ет размещать справа от всех операторов поля, как показано в § 26.11, и рассматривать как
начальное состояние Вселенной, что в данном случае означает совершенно особое состоя¬
ние Большого взрыва. Однако в стандартной квантовой теории поля должно фигурировать
также состояние, комплексно-сопряженное этому, а именно бра-вектор (0|, необходимый
для получения вероятностей вида (0|Л|0), который играет роль, полностью симметричную
роли |0), но с изменением направления времени. Тогда вектор (0| должен представлять
конечное состояние Вселенной, и это конечное состояние будет иметь такую же структуру,
что и начальное, а это находится в резком противоречии с изложенным в главе 27.
Существуют и другие особенности (аномалии), возникающие в процессе «квантова¬
ния», из-за которых квантовая теория может не обладать симметрией классической теории.
Так обстоит дело, когда классические правила коммутации, определяющие классическую
симметрию (задаваемую скобками Пуассона, см. § 14.8), не могут быть полностью реали¬
зованы квантовыми коммутаторами из-за того, что в квантовой теории сохраняется лишь
некоторая подгруппа полной группы симметрии классической теории. Аномалии обычно
считают подлежащими устранению (мы увидим, к каким вывертам порой вынуждены при¬
бегать теоретики для такого устранения, когда в следующей главе перейдем к изучению
теории струн). Тем не менее возможен и иной взгляд, когда аномалия рассматривается
как нечто положительное, а более высокая симметрия считается нежелательной. Однако
в данном случае должна нарушаться дискретная (СРТ-) симметрия (в дополнение к Т-, СТ-
и РТ-симметриям, также содержащим операцию Т), и трудно понять, насколько пригодна
здесь идея аномалии, которая обычно (но не всегда) относится к непрерывным симметриям,
которые могут быть реализованы с использованием скобок Пуассона.
Однако трудно избежать вывода, что в тех экстремальных условиях, когда должны од¬
новременно возникать квантовые и гравитационные эффекты (это условия пространственно-
временных сингулярностей Большого взрыва и гравитационного коллапса), гравитация ведет
себя иным образом, нежели другие поля. Напомним заключение по этому вопросу, сделан¬
ное в предпоследнем абзаце главы 27. Так или иначе, Природа налагает требование сильной
временной асимметрии на поведение гравитации в таких экстремальных условиях.
30.3.	Роль временной асимметрии в редукции квантового состояния
ч	•
Связано ли это с какими-то другими подсказками относительно возможной взаимо¬
связи между гравитацией и квантовой механикой? Я глубоко верю в это. В то время как

684
Глава 30
мы не замечаем временной асимметрии в той части квантовой теории, которая относится
к U-процессам (§27.1), в R-процессах имеется существенная временная асимметрия. Это
легко понять на примере простого гипотетического эксперимента. Пусть имеется источник
фотонов S, излучающий время от времени одиночные фотоны, и эти события всякий раз
регистрируются[з° 3] Предположим, что фотоны обладают высокой энергией, будучи, на¬
пример, фотонами рентгеновского излучения. Фотоны направляются на расщепитель луча В
(«полупрозрачное зеркало»), расположенный под углом 45° к лучу, так что при прохождении
фотона через него включается детектор D на другой стороне установки; если же фотон отра¬
жается, то он поглощается потолком С (см. рис. 30.1). Предполагается равенство амплитуд
вероятностей этих двух альтернатив, так что детектор будет регистрировать приход фотона
ровно в половине случаев регистрации излучения фотона источником.
с
*
S
D
■; <'
J .... • !
Рис. 30.1. Источник S случайным образом испускает фотоны высокой энергии в сторону расщепителя
луча В,, наклоненного к источнику под углом 45° (каждое такое событие регистрируется). В случае
прохождения через расщепитель фотон включает детектор D (путь SBD), в случае отражения от
поглощается в потолке С (путь SBC). Квантовое правило квадрата модуля правильно
1 1
расщепителя
предсказывает вероятности -, -. С другой стороны, предположим, что детектор регистрирует фотон,
который мог бы прийти от источника S (путь SBD) или от пола F (путь FBD). Тогда правило квадрата
- " 11
времени, используемое с обращением времени, дает неправильные вероятности г-, которые на
*	I	Z
самом деле должны быть 1,0
“ч
Это есть просто непосредственное применение R-процедуры. Имеется амплитуда
1
для истории фотона SBD и амплитуда
1
V2
для истории фотона SBC (мы игнорируем воз¬
можные фазовые множители). Тогда применение правила квадрата модуля для R дает нам
(правильный) ответ, что всякий раз, когда происходит излучение фотона источником, име¬
ется 50%-ная вероятность регистрации этого события детектором и такая же вероятность,
что фотон достигнет потолка С. Это есть просто правильный ответ.
Но предположим теперь, что этот эксперимент рассматривается при обратном направ¬
лении времени. Я не предполагаю, что мы пытаемся построить «обращенный во времени»
источник или детектор. Нет, физические процессы при этом никоим образом не изменяются.
Я просто предлагаю переформулировать мои вопросы относительно этих процессов в форме,
обращенной во времени. Вместо того чтобы задавать вопрос относительно конечных веро¬
ятностей, зададимся вопросом, каковы начальные вероятности при условии регистрации
события детектором D. Рассматриваемые амплитуды теперь относятся к двум альтернатив¬
ным историям SBD и FBD, где F обозначает точку на полу, обладающую тем свойством,
что если бы в ней произошло испускание фотона, то он мог бы, отразившись в расщепителе

30.3. Роль ВРЕМЕННОЙ АСИММЕТРИИ В РЕДУКЦИИ КВАНТОВОГО СОСТОЯНИЯ
685
В, попасть в детектор D. Амплитуда для каждой из этих двух историй снова равна —
л/2
(если пренебречь фазами). Так должно быть, потому что отношение (модулей) амплитуд
для прохождения того или иного пути есть просто свойство расщепителя луча. Здесь нет
никакой временной асимметрии. Если мы теперь применим «правило квадрата модуля»,
чтобы определить вероятности двух указанных альтернатив, то получим вероятность 50%
для излучения источником S и соответственно такую же вероятность прихода фотона от
пола F всякий раз, когда детектор регистрирует очередное событие.
Это, конечно, абсурд. Шанс, что рентгеновский фотон, выпрыгнув из пола, попадет
на расщепитель, фактически нулевой. Всякий раз, когда детектор регистрирует событие,
вероятность прихода фотона, излученного источником S, будет 100%, а вероятность прихода
фотона от пола F будет равна 0%. Правило квадрата модуля, обращенное в прошлое, дает
нам совершенно ошибочный результат! 130 4J
Конечно, это правило не было рассчитано на то, чтобы применять его к прошлому,
но все же поучительно увидеть, к какому ошибочному результату оно приведет, если по¬
ступить с ним подобным образом. Против этого иногда возражают, указывая, что, проводя
обращение времени, я не принял во внимание все сопутствующие обстоятельства, например,
тот факт, что Второй закон термодинамики работает лишь в одном временном направлении
или то, что температура пола намного ниже температуры источника, и т. п. Однако квантово¬
механический закон квадрата модуля имеет ту удивительную особенность, что мы никогда не
должны заботиться о том, в каких условиях его можно применять! Квантово-механические
вероятности, предсказывающие результаты будущего процесса измерения, чудесным обра¬
зом как будто совершенно не зависят от температуры, или конфигурации системы, или еще
чего-то подобной»30'5^. Если нам известны амплитуды, мы можем определить вероятности
будущих процессов. Всё, что нам нужно знать, — это амплитуды. Совсем иначе обстоит дело
с вероятностями процессов в прошлом. Там мы должны знать все подробности сопутству¬
ющих обстоятельств. Амплитуды сами по себе совершенно недостаточны для вычисления
вероятностей прошлых событий.
Существуют, однако, ситуации, когда квантовые вероятности можно вычислять спосо¬
бом, полностью симметричным во времени, и, возможно, поучительно рассмотреть их здесь.
Так происходит, когда квантовое состояние известно как до, так и после некоторого проме¬
жуточного измерения. Для большей конкретности рассмотрим последовательность из трех
измерений, первое из которых проектирует состояние системы в состояние \ф)9 а третье —
в состояние | ф)9 при этом проводится измерение, выбирающее ответ ДА/НЕТ между этими
двумя состояниями и описываемое проектором Е (§ 22.6). Тогда вероятность ответа ДА для
промежуточного измерения равна*
\{ф\Е\ф) |2
(предполагается нормировка ^ф\ф) = 1 = (Ф\Ф)У, эта вероятность очевидным образом сим¬
метрична во времени. (Чтобы создать такую ситуацию, следует повторить последователь¬
ность из этих трех измерений много-много раз, регистрируя лишь те случаи, когда первое
измерение дает состояние \ф)9 а третье — состояние |ф). Тогда приведенная вероятность
определяет долю случаев, когда промежуточное измерение давало ответ ДА.)^0,6! Это по¬
будило некоторых прийти к выводу, что в квантовых измерениях временная асимметрия
отсутствует !30 • 71.
Однако большинство квантовых измерений не относится к данному типу. При нормаль¬
ном применении правила квадрата модуля (вперед во времени) мы не задаем состояния | ф),
а при попытке применения в обратном направлении во времени не задаем состояния |^).
Видно, что мы можем вычислять квантовые вероятности при не заданном состоянии \ф)9 но
Почему? Попробуйте вывести эту формулу.

686
Глава 30
не можем добиться успеха, не задав состояния \ф). Можно принять точку зрения, что успеш¬
ное применение квантовых правил для вычисления будущих вероятностей связано с тем,
что состояние |ф) является, в некотором смысле, «случайным», а это обусловлено Вторым
законом термодинамики. Возможно, в этом что-то есть, но я нахожу это требование, налага¬
емое на | ф), довольно нечетким. Что в данном контексте означает «случайное состояние»?
Тем не менее просматривается определенная связь проблемы измерения со Вторым законом.
Можно отметить, что этот закон стремятся использовать в работе реальных измерительных
приборов. Некоторая связь между R-процессами и Вторым законом составляет часть моего
собственного взгляда на эту проблему. И поскольку мы видели, что Второй закон тесно свя¬
зан с отсутствием союза между квантовой механикоии теорией гравитации, можно ожидать
—_	У'
также наличия связи между R-процессами и этим ожидаемым союзом.
Прежде чем перейти к этому вопросу более конкретно, следует отметить, что другой
аспект R-процессов, а именно «скачки» квантовых состояний как противоположность вы¬
числения вероятностей по правилу квадрата модуля, можно, по-видимому, с равным успехом
представить как в прямом, так и в обратном течении времени. Это схематически показано
на рис. 30.2 а, 6. На рис. 30.2 а представлен «нормальный» взгляд на чередование процес¬
сов ..., U, R, U, R, U, ... (см. рис. 22.1), когда состояние становится собственным со¬
стоянием измерения после того, как было произведено измерение, а на рис. 30.26 показана
картина, «обращенная во времени», когда состояние становится собственным состоянием
измерения до проведения измерения. Результаты вычисления амплитуд в обоих случаях ока-
зываются одинаковыми , однако точка зрения, обращенная во времени, имеет «телеологиче¬
ский» аспект, что может быть сочтено неприемлемым. Существует и «компромиссная» точка
зрения (предложенная независимо друг от друга несколькими теоретиками^30*8^), согласно
которой обе картины должны учитываться одновременно, так что в любой момент времени
одновременно существуют два унитарно эволюционирующих вектора состояния, описыва¬
ющих квантовую систему, при этом эволюция одного из них выглядит, как рис. 30.2 а, а дру¬
гого — как рис. 30.26. Такая точка зрения использовалась в главе 23 при интерпретации
ЭПР-явлений. На мой взгляд, это описание носит несколько избыточный характер, и, может
быть, лучше принять концепцию кванглеменции, в которой направление «распространения»
состояния во времени не имеет значения, поскольку кванглеменция просто устанавливает
связь между состояниями в различные моменты времени (§ 23.10).
30.4.	Хокингова температура черной дыры
Существуют ли какие-нибудь способы связать R с искомым (асимметричным во време¬
ни) квантово-гравитационным союзом, более прямые, нежели просто факт временной асим¬
метрии R-процессов? По моему мнению, такие способы имеются, и я опишу два из них.
Первый вытекает из обсуждения в предыдущем разделе и связан с замечательным явлением
«испарения черных дыр». Аргументация здесь носит несколько спекулятивный и непол¬
ный характер, вдобавок она противоречива в нескольких центральных пунктах. Различные
стороны ее составят содержание настоящего и следующих разделов вплоть до § 30.9 (за
исключением §§30.5, 30.6, которые можно рассматривать как некоторое отступление от те¬
мы). Другой способ более сложный, он основан на фундаментальных противоречиях между
основными принципами общей теории относительности и квантовой механики и приводит к
некоторым ясным количественным предсказаниям. Мы отложим цепочку соответствующих
рассуждений до §§ 30.10-30.13. Однако первый аргумент, касающийся некоторых примене¬
ний понятия энтропии черной дыры, порождает некоторые другие теоретические проблемы,
* ЛЗ Покажите, что это есть, в сущности, выражение «унитарной» природы U-процессов; см. § 22.4.

30.4. ХОКИНГОВА ТЕМПЕРАТУРА ЧЕРНОЙ ДЫРЫ
687
Квантовое состояние
а)
Время
с.с. — собственное состояние
б)
Время
Рис. 30.2. Схематическое изображение чередования ..., U, R, U, R, U, ... двух процессов U и R,
используемого на практике в квантовой механике (сравните с рис. 22.1), согласно а) стандартному
направлению эволюции во времени, когда операторные собственные состояния возникают на «про¬
шлом» конце каждого участка U-эволюции, и б) эволюции, обращенной во времени, при которой такие
состояния возникают на «будущем» конце участка U-эволюции. В «компромиссной» интерпретации
квантовой механики фигурируют два вектора состояния, один из которых эволюционирует по варианту
а, а другой — по варианту б
важные для нас; они упоминаются в современных теоретических дискуссиях, и будет по
лезно получить некоторое представление о них.
Напомним (см. § 27.10) формулу Бекенстайна- Хокинга (в естественных единицах к =
с = G = k — 1) Sbh
1
= ^ А для энтропии 5вн черной дыры, у которой горизонт событий
имеет площадь поверхности А. Хокинг, в частности, показал, что черная дыра должна также
обладать температурой, которая оказывается пропорциональной так называемой «поверх¬
ностной силе тяжести» черной дыры. Для температуры стационарной вращающейся дыры
(керровской геометрии, см. § 27.10) мы имеем
?вн
1
47г т
i + (i
а2/т2
)
1
2
где, как и в § 27.10, т — масса черной дыры, ат — ее момент импульса. Эту температуру
можно получить из стандартной формулы термодинамики
TdS — dE,
в которой при изменении энергии Е сохраняющийся момент импульса предполагается по¬
стоянным*. В соответствии с этим черная дыра будет излучать фотоны, как если бы это
был физический объект, находящийся в тепловом равновесии и излучающий характерный
(планковский) спектр, описанный в §21.4 (см. рис. 21.36), для «черного тела» с темпе¬
ратурой 7 вн • Можно заметить, что хотя энтропия черной дыры, описываемая формулой
Бекенстайна - Хокинга, необычайно высока и приводит к экстраординарным величинам, об¬
суждавшимся в §27.13, температура Хокинга для черной дыры правдоподобного размера
Квантовое состояние
(обращенное)
Получите эту формулу для Твн> предполагая, что площадь горизонта керровской дыры определяется, как
в §27.10.

688
Глава 30
крайне низка. Например, хокингова температура черной дыры с массой Солнца составляет
всего 10“7 К, что не намного выше наинизших температур, искусственно полученных у нас
на Земле (примерно 10”9 К).
Джейкоб Бекенстайн [68] вывел формулу для энтропии черной дыры несколькими года¬
ми раньше из физических соображений, основанных на применении Второго закона термо¬
динамики к ситуации, когда квантовые частицы медленно погружаются в черную дыру, од¬
нако он не получил ни коэффициента |, фигурирующего в этом выражении, ни температуры
черной дыры. Стивен Хокинг впервые получил формулу для температуры и ввел коэффи-
1
циент ~ в выражение для энтропии, применив методы квантовой теории к искривленному
пространственно-временному фону. В данном случае ^трт фон описывает черную дыру,
которая образовалась в отдаленном прошлом в результате коллапса некоторого вещества
(например, звезды). Такая ситуация описывается конформной диаграммой на рис. 21 Лбе
(строгой в случае сферически симметричного коллапса).
На мой взгляд, замечательный расчет энтропии и температуры черной дыры, проведен¬
ный Хокингом (а также связанный с ним «эффект Унру»^30'9^), — это единственный на се¬
годняшний день сколько-нибудь надежный результат квантовой теории гравитации. Причем
выводы Хокинга были получены не из квантовой теории гравитации как таковой, а из кван¬
товой теории поля в искривленном пространстве-времени. В общем случае при попытках
сформулировать квантовую теорию на искривленном фоне возникают серьезные проблемы,
и поразительно, что Хокинг тем не менее сумел прийти к некоторым надежным выводам.
Одна из наиболее серьезных проблем состоит в том, чтобы сформулировать подходящее
понятие «положительной частоты» на искривленном фоне. Как мы видели в §§24.3, 26.2,
это понятие является ключевым пунктом при стандартном подходе к квантовым частицам
и квантовой теории поля. Проблема формулировки его применительно к искривленному про¬
странству-времени общего вида связана с отсутствием определенного естественным образом
«временного параметра», по отношению к которому можно определить понятие «положи¬
тельной частоты».
Бдительный читатель вправе заметить, что такого определенного естественным обра¬
зом временного параметра нет даже в случае плоского пространства Минковского! Однако
здесь имеет место замечательный факт: для решений релятивистских волновых уравнений
(подобных рассмотренным в главах 19,24-26) положительная частота при одном выборе вре¬
менного параметра Минковского t эквивалентна положительной частоте при любом другом
выборе такого параметра, не предполагающем обращения времени. В случае безмассовых
полей можно продвинуться еще дальше и получить то же самое условие положительной ча¬
стоты, используя «временной параметр», который получается из стандартного временного
параметра Минковского в результате конформного преобразования, сохраняющего направ¬
ление времени (это имеет отношение к теории твисторов; см. §§ 33.3, 33.10)I3010!.
В пространстве-времени общего вида отсутствует естественный аналог такого пара¬
метра, поэтому понятие положительной частоты в общем случае оказывается существен¬
но различным для разных вариантов выбора временного параметра. Помимо хокинговой
температуры, наиболее правдоподобные результаты получаются при рассмотрении стацио¬
нарных вариантов пространства-времени, для которых существует непрерывное семейство
временных смещений, сохраняющих геометрию пространства-времени (см. рис. 30.3). Та¬
кие пространственно-временные движения генерируются «времениподобным вектором Кил-
линга» к (см. §§ 14.7, 30.6). Кривые, вдоль которых направлены векторы к (интегральные
кривые векторов к), — это те линии, на которых достаточно естественным образом можно
задать «временной параметр» i, так что

30.4. ХОКИНГОВА ТЕМПЕРАТУРА ЧЕРНОЙ ДЫРЫ
689
Рис. 30.3. Стационарность пространства-времени выражается как существование времениподобного
вектора Киллинга к. Это определяет непрерывное семейство временных смещений, сохраняющих
д
метрику. Если к
dt
, где t — «временной параметр» координатной системы (£, ж, у, z)t то х, у, и z
должны быть постоянными вдоль интегральных кривых векторов к (см. § 14.7)
где три остальные координаты х, у, z остаются постоянными вдоль кривых. При этом по¬
нятие «положительной частоты» можно определить по отношению к этому параметру.
Может возникнуть забавная ситуация, когда имеется более одного времениподобно¬
го вектора Киллинга, поскольку тогда можно ввести более одного понятия «положитель¬
ной частоты». Такая множественность времениподобных векторов Киллинга в пространстве
Минковского
конечно, возможна, однако из сказанного выше следует, что понятие по¬
ложительной частоты сохраняется при переходе от одной инерциальной системы Минков¬
ского к другой. чЭто, однако, не относится к случаю, когда мы переходим от инерциальной
системы отсчета к системе, движущейся е ускорением. В этом случае мы получаем иное
понятие «положительной частоты», и получающаяся в результате квантовая теория поля
оказывается в так называемом тепловом вакууме, при этом ускоряющийся наблюдатель вос¬
принимает ненулевую температуру, хотя и крайне низкую при любой разумной величине
ускорения.
Следует пояснить, что, хотя это и удивительный эффект, такая «температура ускоре¬
ния» — это самая обыкновенная температура, которую можно измерить обычным (хотя
и идеализированным) термометром. Для этого термометр должен двигаться с однородным
ускорением в окружающем вакууме, температура которого, измеряемая неускоренным тер¬
мометром, равна нулю. (Понятие «теплового вакуума» связано с другими понятиями кван¬
товой теории поля — «альтернативными вакуумами» (§§26.5, 26.11) и «ложным вакуумом»
(§§28.1, 28.4).) Это явление называется «эффектом Унру», оно согласуется с хокинговым
тепловым состоянием черной дыры, наолюдатель, находящийся в стационарном состоянии
вблизи очень большой черной дыры, будет, согласно принципу эквивалентности (§ 17.4), ис¬
пытывать эффективное ускорение, и температура Унру, соответствующая этому ускорению,
согласуется с температурой, которая получается из формулы Хокинга.
Трудность, представленную здесь как утрата естественного определения «положитель¬
ной частоты», иногда пытаются обойти, отказавшись от понятия «частица» и сосредото¬
чившись на алгебре квантово-механических операторов^30Л11 На первый взгляд это может
показаться слишком большой жертвой, кроме того, требуется немалая изобретательность,
чтобы сформулировать подобным образом многие вопросы, представляющие интерес. В мо¬
мент написания этой книги я еще не могу оценить в полной мере все преимущества интри¬
гующей и заманчиво выглядящей теории такого рода. Я подозреваю, однако, что она лучше,
чем подходы на основе специфических времениподобных векторных полей. В любом слу¬
чае мне не понятно, почему квантовая теория поля на фиксированном фоне обязательно
должна иметь полный физический смысл. Такая теория есть всего лишь приближение к бо~

690
Глава 30
лее точной схеме, в которой степени свободы гравитационного поля (т. е. геометрии самого
пространства-времени) также должны составлять часть квантовой физики.
При вычислении температуры и энтропии черной дыры Хокинг стремился снять
большую часть таких вопросов, потребовав, чтобы расщепление на положительную и от¬
рицательную частоты проводилось лишь на бесконечности. При этом одно такое понятие
относится к/- (к прошлой нулевой бесконечности), а другое — к (см. § 27.12). Такое
различие приводит к образованию хокингова «теплового состояния», которое проявляется
в так называемом излучении Хокинга. Примечательно, что этот эффект обязан своим суще¬
ствованием тому факту, что некоторая часть информации, определенной на J^_, теряется
в сингулярности и не попадает в (см. рис. 30.4). Важ^гую роль этого факта мы оценим
\
у
Рис. 30.4. При вычислении температуры черной дыры, проведенном Хо¬
кингом, в котором предполагается коллапс некоторого вещества в черную
дыру в отдаленном прошлом. При этом расщепление на положительную
и отрицательную частоты требуется лишь на бесконечностях /+ и/“.
Вакуум черной дыры становится тепловым состоянием (матрицей плот¬
ности), поскольку начальная информация на делится между и
конечной сингулярностью, при этом последняя оказывается потерянной
30.5.	Температура черной дыры и комплексная периодичность
Здесь поучительно рассмотреть остроумный вывод формулы Хокинга для температуры,
предложенный позднее, в 1976 году, Гиббонсом и Перри, хотя это и будет некоторым откло¬
нением от основной линии, которой мы следовали в этой главе (мы вернемся к ней в § 30.8).
Рассуждения Гиббонса-Перри поднимают некоторые интересные вопросы, касающиеся ро¬
ли изящных математических идей в исследовании подлинно физических явлений. Утвержда¬
ется, что если решение уравнения Эйнштейна, описывающее черную дыру в ее конечном
установившемся состоянии (это может быть шварцшильдовское или керровское решение —
см. §§ 27.8, 27.10), подвергнуть «комплексификации» (т. е. продолжить с вещественных зна¬
чений координат на комплексные — см. § 18.1), то из основного условия регулярности, на¬
лагаемого на величины, определенные на этом комплексифицированном пространстве, сле¬
дует, что эти величины с необходимостью приобретают периодичность (см. § 9.1, рис. 9.1 а)
по комплексифицированному времени с чисто мнимым периодом 27ггТвн- Это открывает
замечательно прямой путь к хокинговой температуре черной дыры.
Но можно ли рассматривать такую процедуру как физический вывод? Это, конечно,
замечательно изящный подход, которым можно воспользоваться для непосредственного
определения хокинговой температуры черной дыры в таких различных ситуациях, к ко¬
торым оригинальный подход Хокинга не так легко применить. С другой стороны, мне
трудно считать, что он действительно дает физическое обоснование температуры Хокин¬
га. Это хороший пример красивой математики, которой удается дать правильный ответ
(при этом «правильность» устанавливается на основании согласия с результатом, получен¬
ным из критериев, более приемлемых с физической точки зрения, — в данном случае это
упомянутый выше первоначальный вывод Хокинга), несмотря на то что справедливость
в § 30.8.
Сингулярность
ЦГоризонт
-.4 К
•
' 3 Коллапсирующее
•.,! вещество

30.5. Температура черной дыры и комплексная периодичность
691
некоторых «физических» допущений, используемых в этом новом выводе, может вызывать
сомнения.
Взглянем более внимательно на математические составляющие предлагаемой «комплек-
о
сификации». Удобнее для начала взять обычную двумерную евклидову плоскость Е и ее
стандартную комплексификацию СЕ2(= С2). Вещественное пространство Е2 иногда назы-
О
вают вещественным сечением пространства СЕ (см. рис. 30.5 а, б, а также рис. 18.2). Это
есть евклидово вещественное сечение, поскольку оно обладает обычной евклидовой метри¬
кой. Но пространство СЕ2 содержит также лоренцевы вещественные сечения (см. рис. 18.2
из § 18.2), и мы можем построить одно из них, М2, взяв координату у из обычной пары
декартовых координат (ж, у) в пространстве Е2 (которые являются вещественными пара¬
метрами) и потребовав, чтобы координата у принимала не вещественные, а чисто мнимые
значения. Тогда временной координатой в пространстве М2 будет служить величина t — iy.
(Это есть просто двумерный вариант того, с чем мы уже сталкивались в § 18.1.) Рассмот¬
рим теперь в пространстве Е2 не декартовы координаты (ж, у), а полярные (г, в) (см. § 5.1
и рис. 30.5 а). Неотрицательное вещественное число г измеряет расстояние от начала коорди¬
нат, а вещественный угол в — угол между радиус-вектором и осью ж, отсчитываемый против
часовой стрелки. Как распространить эти координаты на наше лоренцево сечение М2? Если
ГУ
ограничиться правым квадрантом М , как показано на рис. 30.5 б, то величина г остается
вещественной и неотрицательной, но величина в теперь становится чисто мнимой, так что
величина
т = id
вещественна. Координата г теперь измеряет лоренцево пространственное расстояние от на-
чала координат, а т есть «гиперболический угол, отсчитываемый от горизонтали» .
Мы собираемся интерпретировать координату т (умноженную на постоянную го) как
меру «времени» в обычном пространственно-временном смысле для наблюдателя (в данной
двумерной плоской пространственно-временной геометрии), который «однородно ускоряет¬
ся» в направлении от центра; его мировая линия описывается уравнением г = го (так назы¬
ваемые «риндлеровы координаты» t30-12!). В качестве пространства-времени берется полное
2
R
несмотря на то что «время» наолюдателя относится к квадранту ту
Предположим, что наблюдатель имеет дело с аналитическими величинами, определенными
на М2. Такие величины будут иметь голоморфное продолжение на комплексификацию про¬
странства-времени (см. §§ 7.4, 12.9), однако это можно гарантировать только для некоторой
непосредственной окрестности «вещественного сечения», каковым в данном случае является
лоренцево сечение. Но есштакая величина действительно аналитична в начале координат О
этого сечения, то она должна быть также аналитична в начале координат евклидова сечения
(поскольку в обоих случаях это одна и та же точка О). Величина, гладкая в евклидовом
начале координат, должна быть периодична по в с периодом 2тг, так как, если мы увели¬
чим угол в на 27г (при некотором малом значении радиуса г = е), мы просто совершим
один полный оборот вокруг начала координат и вернемся в исходную точку. Таким обра¬
зом, величина т, отнесенная к первоначальным лоренцевым пространственно-временным
координатам, периодична по комплексифицированному т с мнимым периодом 2тгг.
Сказанное составляет основу рассуждений Гиббонса-Перри, если применить его не
к нашему упрощенному двумерному пространству-времени М2, а к полной 4-мерной гео¬
метрии черной дыры. Это будет шварцшильдовская геометрия (для случая невращающейся
сферически симметричной дыры, однако можно также воспользоваться керровской геомет¬
рией для вращающейся дыры). Для проведения рассуждений нам понадобится аналог начала
координат О пространства М2. Это видно из рис. 30.6 а, на котором представлена строго кон¬
формная диаграмма для так называемого «максимально протяженного» шварцшильдовского
Выразите эти координаты (г, т) через лоренцевы декартовы координаты (х, t). Объясните, почему дей
ствительная часть угла в обращается в нуль на М2.

692
Глава 30
а)	6)
Рис. 30.5. Периодичность по мнимому времени, иллюстрируемая на примере двумерного пространства
Минковского М2, комплексификация которого дает пространство СМ2 = СЕ2, а) Евклидова плос¬
кость Е2 представляет собой одно вещественное сечение комплексного пространства СМ2. Вектор
Киллинга д/дв генерирует вращения в плоскости Е2 (используются полярные координаты (г, в)).
Любая функция, однозначная на Е2, должна быть периодична по в с периодом 27г. б) В лоренцевом
вещественном сечении М2 пространства СМ2 «риндлеровой» (соответствующей однородному уско¬
рению) временной координатой будет т = гв (это аналог шварцшильдовского времени, естественного
для черной дыры), и функция, аналитическая в начале координат О, должна быть периодична по т
с мнимым периодом 27гг. (Вектор Киллинга равен к = д/дт = —гд/дв.)
пространства-времени /CJ30*13! Пространство-время К иногда называют «вечной черной ды¬
рой», поскольку такая дыра не возникла в результате гравитационного коллапса, а «была
всегда». Центральная точка О на диаграмме представляет 2-сферу в соответствии с соглаше¬
ниями, принятыми в отношении строго конформных диаграмм. Пространство /С есть аналог
О	о
пространства М~, но нам нужен еще аналог евклидова пространства Е . Такое пространство
имеется, его иногда называют «евклидизированным» шварцшильдовским пространством Q
(а иногда даже просто «еквлидовым пространством», что кажется мне крайне неудачным,
так как приводит к путанице!). Шварцшильдовское «время»[30Л41 т, определенное в про¬
странстве /С, в пространстве Q принимает чисто мнимые значения г = г@в, при этом в есть
угловая координата в б, которая увеличивается на 2тт при каждом обходе вокруг точки О
в положительном направлении (рис. 30.66), а (3 — вещественное число (постоянное при
постоянном г), называемое «поверхностной силой тяжести». Любая величина, регулярная
(т. е. аналитическая, см. §7.4) в точке О пространства /С, должна быть также регулярной
в точке О пространства Q Цюскольку в комплексифицированном шварцшильдовском про¬
странстве это одно и то же место «О» для каждого из двух вещественных сечений /С и Q).
Будучи регулярной в точке О пространства Q, такая величина должна быть периодична
по т с периодом 2nif3, поскольку в есть обычная угловая координата, которая при увели¬
чении на 27Г (= 360°) просто возвращает нас в исходное место в пространстве(-времени).
Такая «мнимая периодичность» характерна для «теплового состояния с температурой /?»
в соответствии с принципами статистической термодинамики.
В мои цели не входит обсуждать здесь эти термодинамические принципы. Это уве¬
ло бы нас слишком далеко. Единственный актуальный вопрос здесь состоит в том, можно
ли доверять рассуждениям относительно комплексной периодичности. Это зависит от то¬
го, насколько серьезно рассматривается область вблизи точки О. Оправданно ли это? Это
никоим образом не ясно. Рассмотренная «вечная» картина никак не соответствует реаль¬
ной физической черной дыре. Физическая дыра должна возникать в результате некото¬
рого гравитационного коллапса (скажем, сверхмассивной звезды или скопления вещества
в центре галактики), если только не имело место «изначальное», в некотором смысле, ро-

30.5. Температура черной дыры и комплексная периодичность
693
а)
б)
Рис. 30.6. Определение температуры Хокинга из периодичности по мнимому времени (доказательство
Гиббонса-Перри), а) Строго конформная диаграмма для «вечной черной дыры», которая представляет
собой «максимально протяженное» шварцшильдовское пространство-время /С со шварцшильдовским
временем т и вектором Киллинга к = д/дт. Центральная точка О представляет 2-сферу, б) «Ев¬
клид изированное» шварцшильдовское пространство Q вблизи точки О имеет вещественную угловую
координату в, так что «время» т принимает чисто мнимые значения т — i/Зв, где постоянное веще-
*
ственное число /3' представляет «поверхностную силу тяжести» для черной дыры. При однократном
обходе вокруг точки О угол в увеличивается на 27т, так что любая определенная на /С функция,
аналитическая в точке О (и тем самым распространяемая на Q), периодична по в с периодом 2д-,
т. е. с периодом 2тггД по т (вблизи точки О), где величину (3 следует интерпретировать как хокингову
температуру черной дыры
ждение самого Большого взрыва. Даже первичная дыра (черная дыра, а не ее обращен¬
ный во времени вариант — белая дыра) все же в некотором смысле представляет «кол¬
лапс» и, будь она черная или белая, не описывается полной моделью, изображенной на
рис. 30.6 а. Некоторая внешняя часть этой модели подходит, однако, для описания коллап¬
са в черную дыру — это часть рис. 30.7, лежащая выше и справа от показанной внеш¬
ней границы вещества, подверженного коллапсу. Пространственно-временная метрика ни¬
же и слева от этой границы — метрика вещества, отличная от метрики «вечной» черной
дыры. Полный коллапс схематически показан на рис. 30.7, который представляет собой
слегка измененный рис. 27.16 в. Заметим, что точка О всегда находится вне области, к
которой применима (обобщенная) метрика Шварцшильда. При этом никак физически не
обосновано предположение, что физические величины, определенные в пространстве-вре¬
мени, регулярны в точке О, и нелегко понять, почему приведенные рассуждения, при всем
их математическом изяществе, должны обеспечить обоснование хокинговой температуры.
(Любая физически реалистическая модель черной дыры будет содержать отклонения от точ¬
ной шварцшильдовской (или керровской) метрики, и можно ожидать, что эти отклонения
будут становиться все больше и больше, стремясь к бесконечности, по мере приближения
к точке О. )
Рис. 30.7. История сферического гравитационного кол¬
лапса (слегка измененный рис. 27.16 в), представленная
с использованием максимально протяженного шварц-
шильдовского пространства-времени /С, изображенного
на рис. 30.6 а. Область с косой штриховкой должна быть
удалена; в области с точечной штриховкой метрика от¬
личается от метрики пространства /С из-за присутствия
вещества. Заметим, что точка О всегда находится вне
области, в которой имеет место метрика пространства К
*/jj3 Попробуйте обосновать это утверждение. (Подсказка: рассмотрите малые линейные возмущения. Можно
ли ожидать их экспоненциального изменения со временем?) (Рассмотрите собственные моды оператора д/дт.)

694
Глава 30
Тем не менее точная стационарная модель черной дыры представляет предельный слу¬
чай реалистического коллапса, где все нерегулярности считаются сглаженными с течением
времени. Именно такое предельное пространство обладает подобной регулярностью и, сле¬
довательно, требуемой комплексной периодичностью, а значит, и требуемой температурой.
Хотя я и не понимаю, почему мы должны рассматривать это рассуждение как какой бы то ни
было реальный физический вывод хокинговой температуры (несмотря на то что его часто
считают таковым), на самом деле оно дает некоторый «убедительный намек» на существо-
вание скрытой внутренней согласованности во всей этой идее «температуры черной дыры».
Здесь я не могу удержаться от сравнения с другим результатом, впервые полученным
Брэндоном Картером, который, в ином контексте, имеет значительное сходство с приве¬
денным рассуждением, хотя никогда не представлялся как «вывод» чего бы то ни было.
Напомним, что стационарная незаряженная черная дыра описывается двумя керровскими
параметрами т и а, где т — массы дыры, а ат — ее момент импульса (для удобства ис¬
пользуется система единиц, в которой, как и в планковской системе (§27.10), c—G — 1).
Обобщение керровской метрики, проведенное Эзроййьюменом!3015] (его обычно называют
метрикой Керра-Ньюмена), описывает электрически заряженную вращающуюся стацио¬
нарную черную дыру. Теперь мы имеем три параметра — га, а и е; помимо массы и мо¬
мента импульса появляется полный электрический заряд е. Возникает также магнитный
момент М — ае, направление которого совпадает с направлением момента импульса. Кар¬
тер заметил, что гиромагнитное отношение (удвоенное произведение массы на магнитный
момент, деленное на произведение заряда на момент импульса; для заряженной черной ды¬
ры это составляет (2т х ае)/(е х ат) = 2) для черной дыры полностью фиксировано (т. е.
не зависит от га, а и е) и имеет в точности то значение, которое Дирак первоначально пред¬
сказал для электрона, а именно 2 (у дираковского электрона момент импульса равен i/i,
а магнитный момент i he/тс, так что для гиромагнитного отношения снова получается
значение 2, если положить с — 1; см. §24.7). Ньюмен интерпретировал это «совпадение»,
пользуясь понятием комплексного направления в пространстве.
Можно ли рассматривать сказанное как вывод гиромагнитного отношения электрона
независимо от оригинального доказательства Дирака? Определенно — нет, при любом обыч¬
ном понимании смысла слова «вывод». Этим результатом можно было бы воспользоваться,
лишь полагая, что электрон можно в каком-то смысле рассматривать как «черную дыру».
На самом деле реальные значения параметров а, т и е для электрона грубо нарушают
неравенство
га2 ^ а2 + е2
необходимое для того, чтобы соответствующая метрика Керра - Ньюмена могла представлять
черную дыру. Таким образом, приведенное рассуждение очень далеко от реального вывода
гиромагнитного отношения дираковского электрона. В то же время оно несколько напомина¬
ет аргументацию Гиббонса-Перри относительно температуры черной дыры тем, что усмат¬
ривает определенную «естественность» полученного значения как результата продолжения
в комплексное пространство^30 16J. Аргументация Гиббонса-Перри имеет дополнительное
очко в свою пользу, поскольку не ограничена лишь семейством пространственно-временных
метрик Шварцшильда-Керра. Тем не менее, по моему убеждению, это едва ли оправдывает
ее общее признание в качестве настоящего вывода.
30.6.	Векторы Киллинга, поток энергии и... путешествие во времени!
«Вечная черная дыра» часто привлекает внимание людей и по другим причинам,
несмотря на тот факт, что она обладает некоторыми забавными глобальными свойствами, ко¬

30.6. Векторы Киллинга, поток энергии и. .. путешествие во времени!
695
торые мешают принять ее всерьез как физически приемлемую модель Вселенной. Хотя неко¬
торые из этих причин относятся скорее к области научной фантастики, вечная черная дыра
имеет для нас некоторое геометрическое значение, поскольку иллюстрирует интересные ма¬
тематические факты, которые понадобятся нам в §§ 30.7,30.10. Мы видим, что она имеет две
различные нулевые бесконечности в прошлом (J^~ и/")и две различные нулевые беско¬
нечности в будущем и ). Часто считают, что это пространство-время представляет
временную эволюцию двух различных Вселенных, соединенных между собой своего рода
«кротовой норой», которая постепенно «стягивается» в сингулярность (см. рис. 30.8).
Что касается двух «внешних» областей, то каждая из этих Вселенных содержит чер¬
ную дыру, но необычную — в том смысле, что она одновременно является «белой дырой».
Сигналы могут уходить в каждую из внешних Вселенных £ и £' из внутренней области
прошлого В~~ («поведение белой дыры»), а также могут распространяться во внутреннюю
область будущего £>+ из каждой внешней Вселенной £ и £’ («поведение черной дыры»). Тот
факт, что пространство-время стационарно, выражается в виде существования вектора Кил¬
линга к (см. §§14.7, 19.5, 30.4). Этот вектор Киллинга схематически показан на рис. 30.9.
Заметим, что вектор Киллинга времениподобен в двух внешних областях £ и £' и простран¬
ственноподобен во внутренних областях В~~ и Времениподобная природа вектора к
во внешних областях означает, что к выражает стационарность черной (или белой) дыры.
Семейство наблюдателей в области £, у которых мировыми линиями служат касательные
к полю векторов Киллинга к, будет воспринимать Вселенную неизменной. То же относится
и к области £'. Однако обладающее этим свойством семейство наблюдателей в области £’
должно относить эти соображения к вектору Киллинга ~к (а не к), поскольку мы хотим
сохранить разделение на будущее и прошлое для всех локальных наблюдателей во всем
«
пространстве-времени. В некотором смысле «направление времени» меняется на противо¬
положное при переходе от £ к £'. Сохраняющаяся плотность энергии (§ 19.5), получаемая
путем свертки тензора энергии-импульса Таъкь с вектором Киллинга к, оказывается поло¬
жительной (для обычного вещества) в области £ и отрицательной для обычного вещества
в области £' (поскольку в области £' вектор к направлен в прошлое, так что обычным векто¬
ром Киллинга, выражающим стационарность, здесь будет —к). Никакого противоречия здесь
нет, это лишь иллюстрация странной природы рассматриваемого пространства-времени.
Сингулярность
Сингулярность
Рис. 30.8. а) Пространство /С, представленное глобально как «эволюционирующее во времени» 3-про¬
странство, которое представляет собой «кротовую нору», соединяющую две асимптотически плоские
области. «Кротовая нора» стягивается в сингулярность при эволюции как в будущее, так и в прошлое.
б) Как видно из конформной диаграммы, никакой космический путешественник, предполагающий
попасть из одной области в другую через «кротовую нору» до того, как она «схлопнется», не сможет
этого сделать, так как для этого потребовалось бы, чтобы мировая линия путешественника содержала
некоторую пространственноподобную (сверхсветовую) часть (показанную пунктиром)

696
Глава 30
***%'] Л *
в s/th л
>• •. ^ У ff И
J ' f f f wf A
, I i .**«. '	' 1 I , £
v 1 .// 4\ M f f
, f .J »* ^	^	л
^^ \ t £ У *•" *~r ^ ^ \ f
\ ?/.</	>чЧ*. <
Рис. 30.9. Вектор Кшитинга « времениподобен в двух
внешних областях £ и £' и пространственноподобен
во внутренних областях В и В'. Сравнивая векторы к
в областях £ и £', находим, что к при переходе из
одной области в другую меняет временную ориента¬
цию, так что сохраняющаяся плотность энергии Таъкь
меняет знак
На самом деле физически реальный наблюдатель не может «переходить» из £ в £',
так как для этого он должен иметь «мировую линию», которая не всюду времениподобна
(рис. 30.8). Тем не менее приходится часто сталкиваться с попытками теоретиков обойти
этот факт путем модификации пространства-времени некоторым вроде бы «минимальным»
образом. Эти попытки идут от намерения (на мой взгляд, основанного на заблуждении)
показать, что какая-то техника будущего позволит совершать фантастические путешествия
между Вселенными через соединяющие их «кротовые норы», либо (при небольшом измене¬
нии картины, показанном на рис. 30.10) из одной области пространства-времени в другую,
весьма отдаленную. Если бы такое предложение было реализовано, это открыло бы возмож¬
ность таких путешествий в пространстве, при которых снимаются обычные ограничения
теории относительности. В лучших традициях фильма «Звездный поход» рассматривается
процедура, позволяющая космическому кораблю проникнуть через «кротовую нору» в отда¬
ленную область, которая может даже относиться к более «раннему» моменту времени, чем
тот, когда корабль вошел в «кротовую нору».
я)
б)
Рис. 30.10. Фантастический проект путешествия в пространстве со сверхсветовой скоростью, основан¬
ный на модифицированном пространстве-времени с «кротовыми норами», а) Путем «отождествления»
далеко отстоящих частей двух внешних пространственных областей, показанных на рис. 30.8, получа¬
ется «кротовая нора», соединяющая отдаленные области одного и того же пространства, но опять-таки
невозможен переход через «нору» из одной области в другую по времениподобной траектории, б) Что¬
бы такое стало возможно, требуется изображенный здесь «растянутый» вариант пространства /С (но
такая модель требует, чтобы плотность энергии была отрицательна)
Может показаться странным, что возможность такого «путешествия во време¬
ни» обсуждают даже некоторые первоклассные специалисты в области общей теории
относительности^3017!. Причина этого (иногда, во всяком случае) отнюдь не в том, что
возможность путешествий во времени якобы признается современной (или предвидимой)
физикой, а в том, что мы можем узнать что-то новое из того факта, что такое физически
невозможно*. При «пространственном описании», изображенном на рис. 30.8, «кротовая
* ЛИ Объясните, почему, согласно принципам специальной теории относительности, возможность путешествия
между событиями pnq, разделенными пространственноподобным интервалом, означает возможность путешествия
из р в некоторую мировую точку, лежащую на времениподобной мировой линии, проходящей через р, и находя¬
щуюся в прошлом относительно р.

30.7. Орбиты с отрицательной энергией и уход энергии с них
697
нора» «охлопывается до нулевого размера», прежде чем путешественник сможет проити
сквозь нее. Согласно современной теории, можно было бы «держать нору открытой» доста¬
точно долго для того, чтобы путешественник мог пройти через нее, если бы была возможна
отрицательная плотность энергии. В классической теории отрицательная плотность энергии
обычно считается невозможной, однако в подходящем варианте квантовой теории поля она
могла бы иметь место в некоторых особых условиях.
Действительно ли физики-релятивисты ожидают, что подобные фантастические проек¬
ты позволят совершать дальние путешествия во Вселенной через «кротовые норы», возмож¬
ность существования которых поддерживается квантовой теорией поля? Думаю, что весьма
ве «теста» для новых идей квантовой теории гравитации. Если такие
идеи допускают подобные путешествия, значит, что-то в этих идеях не так, и надо думать
дальше. Таким образом, появляется некоторый руководящий принцип для оценки степени
правдоподобия предлагаемых теорий квантовой гравитации. (Таково, по крайней мере, мое
собственное отношение к подобным проектам. Возможно, однако, что я ошибаюсь, и гораз¬
до больше теоретиков, чем я думаю, полагают, что возможность таких путешествий следует
рассматривать вполне серьезно!)
30.7.	Орбиты с отрицательной энергией и уход энергии с них
Я слишком далеко отвлекся от своего намерения рассмотреть возможные применения
хокингова понятия температуры черной дыры. Можем ли мы понять из соображений бо¬
лее физического характера, в контексте квантовой механики, почему черная дыра должна
испускать излучение, как если бы она имела ненулевую температуру? Фактически и сам
Хокинг дал «интуитивное» доказательство существования такого излучения. Оно проиллю¬
стрировано на рис. 30.11. Вблизи горизонта черной дыры непрерывно рождаются из вакуума
виртуальные пары частица-античастица, чтобы аннигилировать через очень короткий про¬
межуток времени. (Этот процесс был рассмотрен в §26.9 и показан на рис. 26.9, 26.10.)
Однако присутствие черной дыры модифицирует этот процесс, поскольку время от времени
одна из частиц такой пары падает внутрь дыры, а другая уходит от нее. Такое возможно,
только когда уходящая частица становится реальной (т. е. находится «на оболочке» в отли¬
чие от виртуальной частицы, находящейся «вне оболочки»; см. § 26.8 и рис. 26.6), поэтому
уходящая частица должна обладать положительной энергией, а частица, падающая в дыру,
должна, в силу сохранения энергии, стать реальной частицей с отрицательной энергией
(все энергии отсчитываются от энергии на бесконечности). Фактически реальные частицы
в черной дыре могут обладать отрицательной энергией. Такая возможность появляется из-за
того, что вектор Киллинга ка во внутренней области становится пространственноподоб¬
ным, и времениподобный 4-импульс ра, направленный в будущее, может образовать с ним
отрицательное скалярное произведение рака, которое является (сохраняющейся) энергией
частицы; см. рис. 30.11 б* Процесс Хокинга возникает потому, что реальная (а не виртуаль¬
ная) частица может обладать отрицательной энергией, если она находится внутри горизонта
событий черной дыры. Реальный партнер такой частицы должен иметь положительную
энергию, поэтому от черной дыры может исходить положительная энергия.
Здесь уместно заметить, что очень похожая ситуация возникает в классической теории
черной дыры, когда дыра вращается. В отличие от хокингова излучения, интенсивность
которого, при разумных размерах черной дыры, смехотворно мала и которое представля¬
ет лишь чисто теоретический интерес, классические вращающиеся черные дыры имеют
серьезной представляется возможность использовать приведенные
Объясните, почему пространственноподобный вектор ка может давать отрицательное значение «энер-

698
Глава 30
Рис. ЗОЛ 1. «Интуитивное» доказательство существования
хокингова излучения, данное Хокингом, а) Вдали от черной
дыры из вакуума непрерывно рождаются виртуальные па¬
ры частица-античастица, однако через очень короткое вре¬
мя они аннигилируют (см. рис. 26.9 а), б) Вблизи горизонта
черной дыры одна из частиц пары падает внутрь дыры,
а другая уходит на внешнюю бесконечность. При этом обе
частицы становятся реальными, и закон сохранения энер¬
гии требует, чтобы частицы, входящие в дыру, имели отри¬
цательную энергию. Это возможно, поскольку вектор Кил¬
линга к внутри горизонта становится пространственнопо¬
добным. (В случае пространственноподобного вектора ка,
сохраняющаяся энергия рака, где ра — 4-импульс частицы,
может быть отрицательной.)
&
$
а)
б)
огромное значение для астрофизики. Действительно, наиболее мощные источники энер¬
гии, известные во Вселенной (квазары и радиогалактики), питаются, по-видимому, энергией
вращения крупных черных дыр.
Этот процесс подобен тому, который приводит к появлению хокингова излучения, в том
отношении, что энергия поступает от частиц или полей с отрицательной энергией, захваты¬
ваемых черной дырой, так что от дыры на бесконечность уходит положительная энергия.
Имеется, однако, важное различие, состоящее в том, что в случае вращающейся черной
дыры та часть пространства-времени, в которой вектор Киллинга к становится простран¬
ственноподобным, простирается в область вне горизонта черной дыры. Эту область назы¬
вают эргосферой (рис. 30.12 а). В эргосфере частицы могут иметь отрицательную энергию
(отсчитываемую от энергии на бесконечности), но при этом могут иметь связь с отдален¬
ными частями Вселенной. Становится возможным, например, приход частицы в эргосферу
извне и затем расщепление ее на две частицы, одна из которых имеет отрицательную энер-
®.
Горизонт
Стационарный
предел
а)
Vo*ap«^
б)
Рис. 30.12. Вид «снизу» вдоль временной оси вращающейся (керровской) черной дыры, а) В случае
керровской черной дыры существует область, называемая «эргосферой», внутри которой вектор Кил¬
линга к, определяющий стационарность, становится пространственноподобным вне горизонта черной
дыры. Внутри эргосферы частицы могут иметь отрицательную сохраняющуюся энергию (относитель¬
но энергии на бесконечности), а другие частицы, с которыми они непосредственно сталкиваются,
могут уходить на бесконечность, унося избыток энергии, б) Согласно так называемому «процессу
Пенроуза», этот факт можно использовать для извлечения энергии вращения черной дыры. В простей¬
шем таком процессе частица входит в эргосферу и расщепляется на две частицы, одна из которых
входит в черную дыру, имея отрицательную энергию, а другая уходит на бесконечность, унося с собой
больше энергии, чем принесла исходная частица

30.8. Взрывы Хокинга
699
гию, а другая снова уходит, унося с собой больше энергии, чем принесла первоначальная
частица! t30-19! Результатом будет отток энергии от дыры, немного понижающий энергию ее
вращательного движения (рис. 30.12 б). К аналогичному выводу можно прийти, если вместо
частиц взять (электромагнитные) поля-30'20^.
Следует подчеркнуть, что «частица с отрицательной энергией», падающая в черную ды¬
ру, при ближайшем рассмотрении представляет собой самую обычную частицу (с обычным
времениподобным 4-импульсом такого рода, какой был описан в § 18.7). Просто величи¬
на рака, являющаяся мерой сохраняющейся энергии и отсчитываемая от энергии на бес¬
конечности, оказывается отрицательной, что вполне возможно и для частицы, находящейся
внутри эргосферы. Это замечательная и впечатляющая особенность черных дыр, но здесь
нет ничего математически противоречивого или физически нереального. Однако именно это
обстоятельство приводит к излучению во внешний мир зачастую огромной энергии враще-
ния черной дыры.
Наиболее правдоподобное объяснение огромной энергии, излучаемой квазаром, состоит
в том, что эта энергия берется из вращательной энергии гигантской черной дыры. Огромная
энергия вращения постепенно изымается и выбрасывается в окружающее пространство в ре¬
зультате описанного процесса (см. рис. 30.13). Обычно предполагается, что отрицательная
энергия, поглощаемая черной дырой, первоначально может быть в форме электромагнитно¬
го поля (см., например, [85, 67]), а не реальных частиц (см. [835, 836, 837]). Однако в обоих
случаях основа явления одна и та же.
Ж
Л*
о,
Рис. 30.13. Огромная энергия, излучаемая квазаром, берется, по-
видимому, из энергии вращения огромной черной дыры в центре	у
Галактики. Общий характер процесса подобен изображенному на
рис. 30.12, однако возможно, что черная дыра захватывает не частицы,	4	''''
*л	ч>
а электромагнитные поля с отрицательной энергией
/
Ж
30,8.	Взрывы Хокинга
Вернемся теперь к квантово-механическому процессу Хокинга. Температура черной
дыры с массой Солнца 1М0, как отмечалось выше (§ 30.4), крайне низка (порядка 10“7 К).
Для более крупных черных дыр эта температура может быть еще ниже, поскольку она обрат¬
но пропорциональна массе дыры (при заданном отношении а : т, см. §27.10). Пока нет
астрофизических проявлений существования черных дыр с массой меньше 1М0, так что
температура черных дыр, по-видимому, не представляет непосредственного астрофизиче¬
ского интереса.
Тем не менее, как отметил Хокинг в 1974 году130*211, эта температура представляет
значительный теоретический интерес. Например, если Вселенная относится к тому типу,
которому соответствует бесконечное расширение (см. §§27.11, 28.10), то наступит момент,
когда температура окружающего фона окажется ниже температуры какой-то черной дыры.
(В случае черной дыры массой 1М0 во Вселенной с К = 0 = Л для этого потребуется
порядка 1016 лет, что в 106 раз превышает нынешний возраст Вселенной.) Тогда черная
дыра станет терять на излучение больше энергии, чем она поглощает из окружающего
фона. Теряя энергию, она будет терять и массу, так что ее радиус станет меньше, а тем¬
пература соответственно выше. Пусть вначале масса черной дыры была 1М0. Она будет

700	Глава 30
————	   ■	■	  —	-	    ,	щи—1U__|_J I	I .	.	w	w	_	.	 -	-	 |	 LL U Jl.l ■ I m — ■ ■	I	1	1	ШТ^ШЯЧЧ!	I	J	_	j	I—I——^.
продолжать излучать с очень низкой интенсивностью, постепенно теряя массу, в течение
примерно 1064 лет, при этом ее температура будет повышаться сначала медленно, а затем со
всё возрастающей скоростью, пока не достигнет 109 или Ю10 К (неопределенность связана
с нашим незнанием физики элементарных частиц крайне высоких энергий). В этот момент
возникает неустойчивость со взрывом, при котором оставшаяся масса-энергия черной дыры
почти мгновенно полностью переходит в излучение! (См. рис. 30.14.)
Рис. 30.14. Хокингово испарение черной дыры, а) Черная дыра образуется в результате классическо¬
го гравитационного коллапса. Затем в течение крайне продолжительного периода времени она очень
медленно теряет массу-энергию и столь же медленно нагревается. В конце концов она исчезает в ре¬
зультате взрыва, слабого по астрофизическим масштабам и не зависящего от первоначальной массы
черной дыры. 6) Строго конформная диаграмма этого процесса (для сферически симметричного слу¬
чая). Она дает ясную картину, в соответствии с вариантом ПОТЕРЯ, при котором коллапсирующее
вещество просто падает сквозь горизонт, забирая с собой всю свою «информацию», исчезающую
в сингулярности
Это, по крайней мере, наиболее простое и естественное допущение, выдвинутое Хокин¬
гом. (Хокинг вначале предположил, что взрывы такой природы можно было бы обнаружить
и в наше время, если бы Большой взрыв любезно снабдил нас значительным количеством
«минидыр» массой, например, с гору и диаметром с протон! Однако, по нашим нынешним
воззрениям, это выглядит маловероятным, поскольку никаких подобных взрывов пока не
обнаружено.) Некоторые другие физики[зо.22] счихаюх? что хотя такой финальный взрыв мог
иметь место, дыра могла не исчезнуть полностью, а оставить после себя некий «остаток».
Причина, по которой предпочитают этот вариант, связана с «неудобным» выводом, что вся
«информация», поглощенная черной дырой, оказывается потерянной, более приемлемым
представляется допущение, что она сохраняется в этом «остатке» I30-23]. Проблема, однако,
состоит в том, что нелегко представить, как в таком «остатке» может сохраниться вся по¬
дробная информация о веществе, коллапсировавшем в черную дыру, которая первоначально
могла иметь размер звезды или даже быть галактической черной дырой до того, как почти
вся масса дыры была унесена тепловым излучением, которое фактически не несет никакой

30.8. Взрывы Хокинга
701
информации. В качестве альтернативы некоторые исследователи придерживаются взгляда,
что при финальном взрыве вся информация «в последний момент» возвращается обратно.
Таким образом, имеются три возможных варианта:
ПОТЕРЯ: информация теряется при испарении черной дыры;
СОХРАНЕНИЕ: информация сохраняется в образующемся «остатке»;
ВОЗВРАТ: вся информация возвращается при финальном взрыве.
Читателя может удивить, зачем понадобилось рассматривать варианты СОХРАНЕНИЕ или
ВОЗВРАТ, хотя наиболее очевидной альтернативой представляется ПОТЕРЯ. Причина в том,
что вариант ПОТЕРЯ приводит к нарушению унитарности, т. е. операции U. Если принять
философию квантовой механики, требующую неизменности унитарности, то с этим вариан¬
том возникают трудности. Поэтому среди многих (возможно, даже большинства) физиков,
занимающихся элементарными частицами, варианты СОХРАНЕНИЕ или ВОЗВРАТ пользу¬
ются популярностью, несмотря на их несколько искусственный характер.
Мое собственное мнение таково, что наиболее вероятен вариант ПОТЕРИ информации.
На рис. 30.14 представлена ясная картина того, что коллапсирующее физическое вещество
просто падает внутрь горизонта, унося с собой всю информацию о себе, которая исчезает
в сингулярности. При этом на горизонте не происходит ничего особенного, представляющего
какой-либо физический интерес. Вещество даже «не знает», когда оно пересекает горизонт.
Следует иметь в виду, что мы можем рассматривать изначально очень большую черную
дыру, вроде тех дыр, которые, как полагают, обитают в центре галактик и имеют массу,
в миллион или более раз превышающую массу Солнца. При пересечении горизонта ничего
особенного не происходит. Кривизна пространства-времени и плотность вещества здесь не
слишком велики — того же порядка, что и в нашей Солнечной системе. Даже положение
горизонта не определяется локальными условиями, а зависит от того, какое количество ве¬
щества упадет позднее в черную дыру. Чем больше вещества упадет, тем раньше произойдет
пересечение горизонта! (См. рис. ЗОЛ 5.) Мне представляется невероятным, чтобы «за миг до
пересечения горизонта» во внешний мир излучался какой-то сигнал, уносящий всю деталь¬
ную информацию, содержащуюся в коллапсирующем веществе. Фактически одного лишь
сигнала самого по себе было бы недостаточно, так как само вещество и есть, в некотором
смысле, та «информация», с которой приходится иметь дело. Коль скоро вещество падает
сквозь горизонт, оно захватывается и неизбежно разрушается в самой сингулярности.
Это утверждение, по крайней мере, становится ясным, если принять концепцию косми¬
ческой цензуры (§ 28.8). Я не предвижу, однако, что ситуация существенно изменится, даже
если не сделать этого. Картина будет в основном подобна показанной на рис. 30.14. Согласно
этой картине, вещество при коллапсе разрушается (вместе с заключенной в нем «информа¬
цией»), только когда оно попадает в сингулярность, а не когда пересекает горизонт. Если
принять вариант ВОЗВРАТ!30'24!, согласно которому вся информация коллапсирующего ве¬
щества каким-то образом вновь появляется в момент финального взрыва (на рис. 30.14 этот
момент отмечен словом «ОП!»), то придется как-то объяснить, каким образом эта информа¬
ция ухитряется попасть в нужное место прямо из сингулярности (которая, согласно разум¬
ному варианту космической цензуры, должна быть пространственноподобной, см. §28.8).
Я не могу считать этот вариант правдоподобным.
Ситуация с вариантом СОХРАНЕНИЕ если и лучше, то не намного. Даже если «оста¬
ток» и образуется, этим нельзя реально воспользоваться, поскольку информация навсегда
«запирается внутри», и это, по мне, то же самое, как если бы она терялась. Если единствен¬
ное назначение «остатка» состоит в том, чтобы имела место унитарность, то необходимо
сформулировать соответствующую квантовую теорию поля, что связано со значительными
трудностями^30*25^. Насколько я понимаю, доказательство Хокинга ясно показывает, что,

702
ГЛАВА 30
Окончательный
горизонт
Предполагаемый
начальный
горизонт
в соответствии с вариантом ПОТЕРЯ, можно ожидать наруше¬
ния унитарности в некоторых ситуациях, когда общая теория
относительности вводится в общую картину вместе с кванто¬
во-механическими процессами.
А какова точка зрения на эти проблемы самого Хокинга?
С самого начала он склонялся к варианту ПОТЕРЯ, и мне ка¬
жется, что сегодня оснований для этого не меньше, чем было
тогда, когда выдвинул свои идеи Хокинг. Конечно, испаре¬
ние черных дыр — это чисто теоретическое понятие, и вполне
возможно, что сама Природа имеет иные планы на отдален¬
ное будущее черных дыр. Однако трудно представить, чтобы
любая альтернатива такого рода не была связана с радикаль¬
ными изменениями в структуре либо квантовой теории поля,
либо макроскопической общей теории относительности (либо
их обеих). Позиция Хокинга, по крайней мере на 2003 год,
состоит в том, что унитарность действительно должна нару¬
шаться, но, так сказать, в слабом варианте. Хокинг предпо¬
ложил, что в присутствии черных дыр квантовое состояние
системы должно эволюционировать в состояние, не являюще¬
еся чистым и описываемое матрицей плотности. Эта идея уже
кратко упоминалась в § 29.6, где отмечался тот факт, что если
некоторая часть перепутанного квантового состояния (в дан¬
ном случае это та часть, которая падает в черную дыру) мо¬
жет быть действительно потеряна, в противовес потере лишь на «практическом» уровне,
Рис. 30.15. Точное положение
горизонта черной дыры опре¬
деляется «телеологическим об¬
разом», поскольку оно зависит
от того, сколько вещества упа¬
дет в конечном счете в дыру
О
то представляется разумным придерживаться онтологической позиции, согласно которой
квантовая реальность должна описываться матрицей плотности, а не волновой
чистого состояния. Хокинг рассматривал некоторую «суперунитарную» эволюцию, которой
подвержены матрицы плотности и которая позволяет «чистым состояниям» эволюциониро¬
вать в «смешанные состояния»*’ t30-26l.
30-9. Более радикальный взгляд
Моя собственная точка зрения следующая: коль скоро я согласен с Хокингом в том, что
правильной должна быть некоторая форма варианта ПОТЕРЯ, я полагаю, что необходимо
нечто еще более радикальное. Гипотеза Хокинга, изложенная в предыдущем разделе, не со¬
держит, например, какой-либо временной асимметрии^30-271 Однако при наличии временной
симметрии должна быть допустима картина «белой дыры» (рис. 30.16 а), представляющая
собой обращенную во времени картину на рис. 30.4, а также обращенное во времени ис¬
парение черной дыры, представленное на рис. 30.166. «Общая ситуация, симметричная во
времени», в которой разрушается большое количество информации и в то же время появ¬
ляется много «новой информации», показана на рис. 30.17. Все это противоречит гипотезе
кривизны Вейля (§28.8). «Симметричная» ситуация на рис. 30.17 предполагает рождение
новой белой дыры в момент окончательного испарения исходной черной дыры, при этом
белая дыра растет, пока не достигнет размера прежней черной дыры. Я никогда не видел,
чтобы столь абсурдная модель рассматривалась серьезно! Если допустимы ситуации, подоб¬
ные изображенной на рис. 30.17, то непонятно, почему они не распространяются на Большой
взрыв, приводя к резкому несоответствию с изложенным в главе 27.
Пользуясь индексным представлением (например, фа вместо \ф)), найдите вид преобразования, который
позволяет достигнуть этого. (.Подсказка: посмотрите на рис. 29.5.)

30.9. Более радикальный взгляд
703
а)
Рис. 30.16. Белые дыры, будучи обращенными
во времени черными дырами, нарушают гипо¬
тезу кривизны Вейля, а) Конформная диаграм¬
ма обращенного во времени образования чер¬
ной дыры, показанного на рис. 27.11, 27.16. б)
Конформная диаграмма обращенного во време¬
ни образования черной дыры и последующего
исчезновения в результате хокингова излучения,
показанного на рис. 30.4
Рис, 30.17. а) Ситуация, симметричная во вре¬
мени. В момент окончательного испарения чер¬
ной дыры, образовавшейся в результате грави¬
тационного коллапса, возникает белая дыра. Эта
новая белая дыра растет, пока не достигнет раз¬
мера прежней черной дыры до ее исчезновения
вследствие выброса большого количества веще¬
ства. 6) Соответствующая конформная диаграм¬
ма
Я не предполагаю повторять здесь все свои соображения^30-28^. Грубо говоря, они опира¬
ются на тот факт, что Природа, похоже, указывает на справедливость чего-то напоминающего
гипотезу кривизны Вейля[з°.29] в отношении физической структуры тех пространственно-
временных сингулярностей, которые возможны во Вселенной. Если принять это, то в резуль¬
тате действительно получается необратимая «потеря информации» в сингулярностях черных
дыр. Причина состоит в том, что, согласно указанной гипотезе, окончательные сингулярно¬
сти коллапса могут содержать (и, следовательно, поглощать) огромное число степеней сво¬
боды (которые заключены в кривизне Вейля), тогда как для любой начальной сингулярности
эти степени свободы запрещены.
Попробуем изложить эти соображения в терминах фазового пространства системы,
включив в рассмотрение образование и испарение черных дыр. Строго говоря, чтобы это
было возможно, мы должны рассматривать замкнутую систему, содержащую заданное ко¬
нечное количество энергии. Чтобы помочь нашему воображению, попробуем рассмотреть
большой ящик с размерами больше галактических, стенками которого служат идеальные
зеркала, так что никакая информация и никакие материальные частицы не могут ни вхо¬
дить в ящик, ни покидать его; см. рис. 30.18. С практической точки зрения это, конечно,
нелепость, однако я спешу заверить читателя, что наша система есть всего лишь «мыс¬
ленный эксперимент», а отнюдь не реальность! Она рассматриваетсяf30-30i лишь для того,
чтобы применить формализм фазового пространства к системе, в которой происходит (ви¬
димая) потеря степеней свободы в процессе хокингова излучения. Рассматриваемое фазовое
пространство Р описывает все возможные физические состояния в нашем гипотетическом
ящике при заданной полной энергии. Динамическая эволюция показана на рис. 30.19 при
помощи семейства стрелок по аналогии с рис. 20.5.
В этой («мысленной») ситуации степени свободы с течением времени исчезают, буду¬
чи поглощенными в сингулярностях черных дыр. Гипотеза кривизны Вейля препятствует
восстановлению этих степеней свободы в исходных сингулярностях (в виде белых дыр),
однако я утверждаю, что они могут восстанавливаться благодаря R-процессу. Идея состоит

704
Глава 30
б)
а)
‘ |	•	Г»,
4	.	•	V	*	'	*	»	\	/	.	*	f	Г	•	I	*
-V . ; "•■
•	, Г • -	♦	• *	•	'	*	♦	•
♦ * * * . • * • •
' 'ч » « ' , ' • • *    •
tesSsisksssi
<0
Рис. 30.18. Мысленный эксперимент с «ящиком» Хокинга, а) Представим себе огромный (галактиче¬
ского размера) «ящик» с веществом, стенками которого служат идеальные зеркала, не позволяющие
информации или веществу входить в ящик или выходить из него. б) Один локальный максимум энтро¬
пии в виде черной дыры, содержащей большую часть массы, и небольшое количество окружающего
излучения, находящегося в тепловом равновесии с черной дырой, в) Другой локальный максимум
энтропии представляет просто тепловое излучение (и несколько частиц) при отсутствии черной дыры
Рис. 30.19. Описание ящика Хокинга с использованием фазового пространства. Стрелки изображают
(гамильтонову) эволюцию (для процесса, представленного на рис. 30.18). Области А, В, С относят¬
ся соответственно к случаям а, б, в на рис. 30.18. В соответствии с этим черная дыра присутствует
в области В и отсутствует в области С. Наличие черной дыры приводит к слиянию линий потока
(уменьшению объема фазового пространства) из-за разрушения информации в (будущей) сингулярно¬
сти черной дыры, согласно варианту ПОТЕРЯ. Происходит также компенсирующее рождение линий
потока (увеличение объема фазового пространства), связанное с временной асимметрией R-процесса
(который предполагается объективно реальным); см. рис. 30.1. Предполагается наличие баланса между
этими двумя процессами, нарушающими теорему Лиувилля, который обеспечивает в конечном счете
сохранение объема фазового пространства в потоке
в том, что в целом возможен баланс между асимметричной во времени «потерей информа¬
ции» в черных дырах и асимметричным поведением вероятностей в квантово-механическом
R-процессе, как было показано в § 30.3. Недетерминированная природа R-процесса означает,
что одному и тому же начальному состоянию могут соответствовать несколько различных
конечных состояний, и это должно компенсировать тот факт, что у черных дыр многие
различные начальные условия могут приводить к одному и тому же исходу, поскольку
«информация», которая отличает одно начальное состояние от другого, поглощается в син¬
гулярностях. Напомним, что в мысленном эксперименте из § 30.3 (рис. ЗОЛ) мы имели два
различных исхода (фотон, приходящий в D, и фотон, приходящий в С) для одной и той же
начальной ситуации (фотон, излучаемый в S), тогда как при заданной конечной ситуации
(фотон, приходящий в D) имеется всего одна начальная ситуация (фотон, излучаемый в S).

30.10. ШРЕДИНГЕРОВ ОБЪЕКТ
705
Таким образом, в R-процессе мы имеем эффективное увеличение объема фазового про¬
странства, тогда как асимметрия в структуре пространственно-временной сингулярности
вызывает эффективное уменьшение объема фазового пространства (см. рис. 30.19). Утвер¬
ждение состоит в том, что эти два эффекты должны в среднем уравновешивать друг друга.
Необходимо пояснить, что такая взаимная компенсация физических процессов должна
происходить лишь в общем и целом. Конечно, отнюдь не утверждается, что каждый акт
редукции квантового состояния должен сопровождаться одновременным появлением черной
дыры. Идея состоит в том, что баланс между двумя эффектами имеет место лишь для
всего фазового пространства в целом. В соответствии с этим потенциальная возможность
образования черных дыр с их способностью поглощать информацию должна компенсировать
будущую хаотичность R-процессов.
Можно заметить, что оба этих эффекта нарушают теорему Лиувилля (см. §20.4,
рис. 20.7), согласно которой объем фазового пространства должен сохраняться в ходе дина¬
мической эволюции. Однако в каждом случае мы имеем нечто стоящее за рамками обычной
классической динамики и устанавливающее пределы применимости этой теоремы. Дей¬
ствительно, само понятие классического фазового пространства здесь не вполне пригодно,
поскольку мы рассматриваем совместно квантовые и классические эффекты. В случае чисто
квантовой системы мы вместо этого должны мыслить исключительно в терминах гиль¬
бертова пространства. Для тех, кто признает только U-эволюцию, описание на основе
гильбертова пространства является исчерпывающим. Но тогда возникает серьезная пробле¬
ма с разрушением информации (и, следовательно, унитарности) при испарении черных дыр.
Мое собственное мнение таково, что ни одна из этих картин не является исчерпывающей,
а каждую из них следует рассматривать как некоторое приближение к чему-то такому, что
мы пока не знаем* как описать^30,31!.
Я давно намеревался получить непосредственную численную оценку скорости редук¬
ции квантового состояния путем исследования деталей баланса между двумя процессами,
рассмотренными выше и представленными на рис. 30.19, однако до сих пор я не смог дове¬
сти свои изыскания до завершения. Поэтому можно считать удачей, что имеется совершенно
иная общая линия рассуждения, которую можно использовать для получения соответствую¬
щей оценки. Это составит предмет рассмотрения в остальной части этой главы.
30.10.	Шредингеров объект
Вернемся к ситуации, рассмотренной в §29.7 под названием «кошка Шредингера».
На рис. 29.7 показано, как можно реализовать квантовую суперпозицию живой кошки и мерт¬
вой кошки, используя расщепитель луча, чтобы получить фотонное состояние в виде супер¬
позиции; при этом прошедшая часть фотонного состояния включает устройство, убивающее
кошку, а отраженная часть оставляет кошку в живых. Использовать для этой цели реальную
кошку, конечно, не только негуманно, но и приводит к излишнему усложнению изучаемой
»• ' ,
системы. Поэтому позвольте мне вместо этого считать, что прошедшее фотонное состояние
просто приводит в действие устройство, которое слегка сдвигает некоторый материальный
объект в горизонтальном направлении, тогда как прошедшая часть оставляет его в покое
(см. рис. 30.20). Теперь наш объект играет роль кошки Шредингера — хотя и не в такой
драматической форме!
Вопрос, который я сейчас хочу задать, состоит в следующем: является ли квантовая су¬
перпозиция двух положений объекта стационарным состоянием? В стандартной квантовой
механике дело должно обстоять именно так, если мы считаем, что каждое положение объ-
* »
екта в отдельности соответствует стационарному состоянию и что энергия в каждом случае
имеет одно и то же значение (так что положение покоя смещенного объекта расположено
не выше и не ниже его первоначального положения). Это просто элементарное применение

706
Глава 30
. . • • ♦
Рис. 30.20. «Кошка» Шредингера с рис. 29.7, но теперь квантовая суперпозиция имеет место всего
лишь между двумя немного различающимися положениями материального объекта
тех правил, с которыми познакомились в главе 21 (см. также §24.3). Представляя началь¬
ное положение объекта состоянием \х), а смещенное — состоянием \<р), мы получаем два
уравнения Шредингера, описывающих стационарность для каждого из этих двух положений
объекта:
.*<9|х)	\	.ъд\<р)	р, \
th~of-E 1х)> гН~дГ = Е№>
каждое из этих уравнений дает собственное состояние энергии с собственным значением
энергии Е. Если представить суперпозицию в виде состояния
И =	Мх) +Ф),
то непосредственно получается
при любых значениях (постоянных) амплитуд w и z* Таким образом, каждая суперпози¬
ция \Ф) также является стационарным состоянием. Если каждое из состояний \х) и \р)
в отдельности всегда остается одним и тем же, то же самое относится и к любой их кванто-
•	л'
вой суперпозиции \Ф). Таково предсказание стандартной квантовой механики.
Теперь вспомним урок, который преподнес нам Эйнштейн, создав свою величественную
и ныне блестяще подтвержденную общую теорию относительности. Прежде всего, следует
ввести в рассмотрение гравитационное поле, представляемое в виде геометрии фоново¬
го пространства-времени. Можно представить себе, что эксперимент проводится на Земле
с двумя образцами объекта, расположенными на горизонтальной платформе. Геометрия про¬
странства-времени на Земле не вполне плоская, и мы должны посмотреть, какое влияние
окажет кривизна пространства-времени на приведенные результаты. При этом нам придется
задуматься над самим смыслом оператора d/dt, фигурирующего в уравнении Шредингера.
В общей теории относительности у нас обычно нет выбранной естественным образом систе¬
мы координат, по отношению к которой определяется понятие оператора d/dt. Напомним
(см. §§ 10.3, 12.3 и рис. 10.5), что «инвариантное» понимание оператора частной производ¬
ной (типа .d/dt) предполагает рассматривать его как векторное поле на (пространственно-
временном) многообразии (рис. 30.21). Таким образом, чтобы определить понятие d/dt,
нам понадобится векторное поле, определенное на нашем пространстве-времени.
В данной ситуации мы не испытываем трудностей, поскольку рассматриваем стацио¬
нарные состояния. При этом мы должны, по крайней мере, считать, что стационарно само
фоновое пространство-время. Поле Земли действительно предполагается стационарным.
Как мы видели (§§ 30.4, 30.6, рис. 30.3), стационарное пространство-время характеризуется
существованием некоторого времениподобного вектора Киллинга к. Как выглядит это кон¬
кретное векторное поле в данном обсуждении? Стационарность нашего пространства-време-
Почему? Объясните, какие свойства векторного поля к используются, когда этот вывод распространяется
случай стационарного фонового пространства-времени.

30.10. ШРЕДИНГЕРОВ ОБЪЕКТ
707
Рис. 30.21. Оператор дифференцирования d/dt в урав¬
нении Шредингера следует понимать (инвариантным
образом) как векторное поле к на (пространственно-
временном) многообразии (см. рис. 30.3), при этом ста¬
ционарность пространства-времени выражается в том,
что к(— d/dt) представляет (времениподобное) поле
Киллинга (£g = 0; см. § 14.7)
К,
Уравнение
Шредингера: .
&кЩ=Н\ф)'
f
ни в смысле независимости от t означает, что в предыдущей формуле можно просто сделать
замену (рис. 30.21)
а
dt
к.
Может возникнуть вопрос об общем постоянном масштабном коэффициенте, но это здесь не
так уж важно для нас. Обычно этот коэффициент определяется требованием, чтобы на боль¬
ших расстояниях, где гравитационное поле предполагается спадающим до нуля, вектор к
становился «обычным» сдвигом во времени. Однако локально величина вектора к может
меняться от точки к точке таким образом, чтобы учесть эффект «замедления времени» в гра¬
витационном поле Земли (§ 19.8)*. Поскольку вектор к теперь играет роль оператора d/dt,
наши уравнения Шредингера, определяющие стационарность каждого из отдельных состо¬
яний |х) и | <р), принимают вид
Огк\х) = Е\х) и ihn\ip) = Е\(р),
I
и, как и раньше, мы находим, что для любой суперпозиции \Ф) выполняется уравнение
гПк\Ф) = Е\Ф).
Таким образом, наличие фона в виде стационарного гравитационного поля не отменяет того
факта, что любая квантовая суперпозиция двух стационарных состояний |х) и | <р) сама
является стационарным состоянием.
Но посмотрим, что получится, если принять во внимание гравитационное поле самого
объекта. Если рассматривать состояния |х) и \ф) по отдельности, то реальных проблем
не возникает. Конечно, |х) и | ф) представляют собой квантовые состояния, и в отсутствие
общепринятой квантовой теории гравитации мы не знаем, как описывать соответствующее
им гравитационное поле. Однако это обстоятельство не создает реальной проблемы. Стан¬
дартная точка зрения состоит в том, что правильная квантовая теория гравитации приведет
в конечном счете к чему-то вроде классических материальных объектов, гравитационное по¬
ле которых, пусть и не совершенно точно, но с достаточной точностью, описывается прин¬
ципами классической общей теории относительности Эйнштейна. (На мой взгляд, справед¬
ливость этой «стандартной точки зрения» может быть подвергнута сомнению, однако если
сделать два обычных допущения — что квантовый формализм не нуждается в изменени¬
ях и что к макроскопическим телам должна быть применима классическая общая теория
относительности, — то мы должны принять ее. Целью настоящего рассуждения является
в конечном счете выяснение пределов совместимости этих двух допущений.) В соответ¬
ствии с этим некоторое квантовое состояние |х) и некоторое квантовое состояние \ср) долж¬
ны с хорошей точностью описывать материальный объект, находящийся на горизонтальной
Попробуйте объяснить это, используя закон сохранения, определяемый вектором к., как описано в § 30.6,
и учитывая тот факт, что норма ^ака вблизи гравитирующего тела может отличаться от единицы, даже если она
нормирована на единицу вдали от такого тела. Как это влияет на меру времени?

708
Глава 30
платформе на Земле, в двух его различных положениях, причем каждое появление объек¬
та сопровождается его почти классическим эйнштейновским гравитационным полем I30*32!.
Поскольку состояние объекта в каждом из двух положений предполагается стационарным
в соответствующем пространстве-времени, каждому из положений будет отвечать свой век¬
тор Киллинга^30,33!, соответственно кх и и состояния будут удовлетворять уравнению
Шредингера с собственным значением Е:
ihnx\x) = Е\х)и = Е\ф).
В предыдущей ситуации, когда мы пренебрегали гравитационными полями объектов,
мы могли выписать уравнение Шредингера для любой суперпозиции w\x) + z\ф) и утвер¬
ждать, что все такие суперпозиции стационарны. Однако теперь возникает неприятность,
связанная с тем, что два вектора Киллинга кх и различны. Что в таком случае делать?
Похоже, что мы нуждаемся в инвариантном понятии d/dt, применимом к пространству-
времени суперпозиций, и что ни кх, ни к^ на эту роль не годятся. Как мы увидим в следу¬
ющем разделе, это не частная проблема — она представляет фундаментальную трудность и
приводит к конфликту между фундаментальными принципами квантовой механики и общей
теории относительности.
30.11.	Фундаментальный конфликт с принципами теории Эйнштейна
Следует пристальнее рассмотреть факт различия двух векторов Киллинга. Когда я го¬
ворю, что два вектора Киллинга кх и различны, я вкладываю в это глубокий смысл.
В действительности это векторные поля, определенные в различном пространстве-времени!
Можно попробовать предположить, что два пространства-времени отличаются лишь тем, что
имеют очень слабо различающуюся метрическую структуру. В соответствии с этим можно
попытаться считать их одним и тем же пространством, но с несколько различными полями
метрического тензора, обозначаемыми, например, gx и g^. Но занять такую позицию --
значит вступить в конфликт с одним из наиболее фундаментальных принципов теории Эйн¬
штейна — принципом общей ковариантности (см. § 19.6). Рассматривать множества точек
этих двух пространств как, в некотором смысле, «одни и те же» множества — означает, по су¬
ществу, поточечную идентификацию двух пространств. Это подобно отождествлению точки
в одном пространстве-времени с точкой в другом с теми же координатами. Однако принцип
общей ковариантности отрицает возможность какой-либо зависимости от выбора конкрет¬
ной системы координат. Он утверждает, что между двумя различными пространствами не
должно быть предпочтительной поточечной идентификации.
Почему эта невозможность идентификации пространства-времени двух положений объ¬
екта приводит к трудностям? Мы должны иметь возможность написать уравнение Шредин¬
гера. Но как это сделать, не имея единого вектора к? Проще всего было бы попробовать
идентифицировать векторы кх и к^9 но это было бы нарушением фундаментального прин¬
ципа теории Эйнштейна, поскольку означало бы, что мы считаем эти два вектора Киллинга
относящимися к одному и тому же пространству, а это уже жульничество! Мне кажется, что
в этой ситуации мы действительно становимся свидетелями конфликта между фундамен¬
тальными принципами квантовой механики и общей теории относительности.
Тем не менее мы не должны так просто «сдаваться». Хотя, строго говоря, нам нужна
новая теория, чтобы понять, что делать дальше, мы можем, мне кажется, достигнуть неко¬
торого прогресса, если временно принять этот конфликт как должное и поставить вопрос
о величине той погрешности, которая заключена в нашем «жульничестве». Будем считать,
что Природа готова, в некотором смысле, допустить локальную идентификацию двух про¬
странств при условии, что понятие «свободного падения» в них одно и то же. Это несколько
напоминает принцип эквивалентности (см. § 17.4). Предпринимаемая нами идентификация

ЗОЛ 1. Фундаментальный конфликт с принципами теории Эйнштейна
709
имеет целью добиться того, чтобы понятие геодезической в одном пространстве совпадало
с понятием геодезической в другом из них. Обычно это можно обеспечить лишь в непо¬
средственной окрестности некоторой точки, так что вместо этого мы попытаемся оценить
ту погрешность, которая получается при отождествлении двух пространств. Это нелегко
сделать, оперируя с общей теорией относительности в ее полной форме, однако большин¬
ство используемых идей применимо также к предельной ситуации, когда скорость света с
предполагается бесконечной, но основная философия эйнштейновской теории тем не менее
сохраняется. Это приводит нас к картановской формулировке ньютоновской теории тяготе¬
ния, обсуждавшейся в § 17.5J30*34]
Напомним (см. главу 17), что в теории тяготения Ньютона-Картана пространство-вре¬
мя рассматривается как расслоенное пространство над одномерным евклидовым про¬
странством Е1 различных допустимых значений «времени» t. Слои представляют собой
•	о
различные евклидовы 3-пространства Е , каждое из которых соответствует «пространству»
в некоторый заданный момент времени. Таким образом, мы имеем «абсолютное время», опи¬
сываемое временной координатой t. Читатель вполне резонно может решить, что, поскольку
у нас теперь есть единое понятие времени (измеряемого величиной t) для пространства-вре¬
мени обоих положений объекта, наши проблемы должны исчезнуть. Но горькая правда со¬
стоит в том, что, зная t, мы еще не в состоянии определить djdt. Поскольку оператор d/dt
предполагает, что остальные координатные переменные (например, ж, ?/, z) остаются фик¬
сированными. Это то самое «второе фундаментальное недоразумение анализа», о котором
мы говорили в § 10.3 (см. рис. 10.7). Мы можем пояснить это на примере рассматривае¬
мой геометрии. Зная t9 можно определить, где находятся сечения Е’, а зная d/dt, можно
найти поле векторов Киллинга, которое определяет семейство кривых, пересекающих это
семейство 3-поверхностей (см. рис. 30.22). На самом деле невозможность определить d/dt
в уравнении Шредингера — это глубокая проблема даже при «более стандартном» подходе
к квантовой гравитации. Она связана с так называемой «проблемой времени» в квантовой
космологии [30-351.
Рис. 30.22. Зная t, мы еще не можем определить d/dt («второе фундаментальное недоразумение
анализа» (см. рис. 10.7 в § 10.3). Зная t, можно определить, где находятся сечения Е3, а зная d/dt,
можно найти семейство кривых, пересекающих это семейство 3-поверхностей
В данном контексте я не делаю амбициозной попытки решить все эти проблемы. Всё,
что нам нужно, — это оценить ошибку, которую мы допускаем, пытаясь провести «недозво¬
ленное» отождествление двух различных векторов кх и Мы сделаем это, действительно
отождествив пространства Е3, а затем найдя полную погрешность разности гравитационных
ускорений (различия между свободными падениями, т. е. геодезическими) в двух простран¬
ствах. Пусть гравитационные ускорения описываются соответственно 3-векторами Гх и Г^.
Тогда можно оценить искомую ошибку, взяв квадрат длины их разности (Гх — Г^)2 и про-
Q
интегрировав его по всему пространству Е . Эта интегральная ошибка интерпретируется

710
Глава 30
как мера абсолютной неопределенности в определении оператора d/dt, фигурирующего
в уравнении Шредингера, для момента времени t, соответствующего данному выбору про-
странства Е3. Эта неопределенность дает, согласно уравнению Шредингера, абсолютную
неопределенность Eg энергии, соответствующей суперпозиции рассматриваемых состоя¬
ний. Следующий шаг состоит в том, чтобы придать этому выражению для Eg другую
(эквивалентную) математическую форму, которую можно интерпретировать* следующим
образом:
Eg = гравитационная собственная энергия разности двух распределений масс в
состояниях |х> и |(f).
Гравитационная собственная энергия распределения масс — это выигрыш в энергии, ко¬
торый получается при разбиении этого распределения на отдельные точечные массы, рас¬
сеянные на бесконечности. Указанную разность можно рассматривать как распределение
положительных масс в состоянии |х) и распределение отрицательных масс в состоянии \<р)
(см. рис. 30.23). (Причина, по которой в результате не получается нуль, состоит в том, что
энергия рассматривается с учетом действия гравитационного поля, создаваемого каждым из
распределений масс, на другое распределение.)
Рис. 30.23. Каждое из двух стационарных состояний |х) и |у?), образующих суперпозицию, определя¬
ется как «ожидаемое значение» для соответствующего распределения плотности массы. Разность этих
распределений (т. е. сумма распределений, одно из которых считается положительным, а другое — от¬
рицательным), образует распределение положительной и отрицательной плотности масс, собственная
гравитационная энергия которого дает величину Eg
Всё это несколько трудно для восприятия, особенно из-за присутствия отрицатель¬
ного распределения масс. К счастью, обычно в большинстве рассматриваемых ситуаций,
а именно когда состояние \ф) есть просто результат смещения состояния |х) как целого,
величину Eg можно интерпретировать иным, более непосредственным образом. Рассмот¬
рим энергию, которую необходимо затратить на перемещение одного экземпляра нашего
объекта, первоначально находившегося в положении |х), в положение \(р), находящееся вне
гравитационного поля другого экземпляра, фиксированного в положении [х). При переме-
щении объекта как целого эта энергия оказывается той же энергией Eg, что и прежде ,
но в других условиях это не всегда так.
Можно принять эту другую меру энергии (а именно энергию гравитационного взаимо¬
действия) в качестве альтернативного определения энергии Eg• Первый вариант, осно-
■с
Попробуйте подтвердить это. Доказательство следует линии, намеченной в упражнении 24.3 в §24.3.
Можно воспользоваться уравнением Пуассона У2Ф = —47гр, где Ф — ньютоновский (скалярный) гравитационный
потенциал. Здесь мерой нашей «ошибки» служит интеграл по всему пространству от |V0i ~\7ф2\2.
**Ш$ Понятно ли, почему в данном случае для Eq получается тот же результат, что и прежде? Что произойдет,
если конечное положение смещенного объекта находится несколько выше его первоначального положения? Что
будет в случае сжатия объекта?

30.12. Предпочтительные состояния Шредингера - Ньютона
711
ванный на собственной гравитационной энергии, насколько я понимаю, представляется
лучше обоснованным, однако на современном уровне понимания не следует отвергать
и другие возможности. Диоси [195] рассмотрел оба указанных варианта, поставив ту же
цель, которую я сформулировал выше, но предположив также возможность стохастической
динамики, которая здесь не рассматривалась. Эти различные варианты (а также некото¬
рые другие) должны быть экспериментально различимы при проведении экспериментов,
к описанию которых я вскоре перейду. Следует, однако, подчеркнуть, что даже наиболее
основательные из этих вариантов не вполне мотивированы и не полностью свободны от
противоречий^30*36^.
Итак, что мы должны делать с нашей фундаментальной «неопределенностью энер¬
гии» Eg? Здесь следует привлечь один из вариантов принципа неопределенности Гейзен¬
берга (соотношение неопределенности время-энергия, см. §21.11). Известный факт, обнару¬
женный при изучении нестабильных частиц или ядер (например, ядер урана 238U), состоит
в том, что среднее время жизни Т, соответствующее временной неопределенности, обрат¬
но пропорционально неопределенности энергии, равной Н/2Т. Например, как отмечалось
в §21.11, время жизни ядра 238 U составляет порядка 109 лет, поэтому для каждого ядра
существует фундаментальная неопределенность энергии Ю~51 Дж, что с помощью форму¬
лы Эйнштейна Е = тс2 переводится в неопределенность массы, составляющую 10 ~44 от
полной массы ядра. Теперь взглянем на нашу суперпозицию состояний |^) = w\x) + z\p)
как на аналог этого примера. Будучи нестабильной со временем жизни Тс, она обладает
фундаментальной неопределенностью энергии, определяемой формулой Гейзенберга. Со¬
гласно нашей картине[30*37^, любая суперпозиция вроде \Ф) должна поэтому распадаться на
то или другое из составляющих его состояний |х) или \р) со средним временем распада
Tq ~ h/Ec-
30.12.	Предпочтительные состояния Шредингера-Ньютона
Из приведенных рассуждений вроде бы вытекает, что квантовая суперпозиция двух
состояний должна распадаться на то или иное из этих состояний за время порядка %/Ес•
Однако вдумчивый читатель может возразить, что любое квантовое состояние \ф) можно
представить в виде линейной суперпозиции пары двух состояний (например, \ф) = \а) -f
-г (\ф) — |а)), где |а) — произвольное состояние). Поэтому не имеет смысла считать, что
все такие состояния распадаются на «составные части», особенно если для данного состоя¬
ния \ф) выбрать состояние ja) таким образом, чтобы распределения масс в этих вариантах
различались достаточно сильно и распад происходил почти мгновенно!
Нелепость этого вывода позволяет подвести итог вышеприведенного обсуждения
для случая, когда рассматривается наша суперпозиция \Ф) = w\х) + АФ) всего для одного
электрона. Можно положить \х) = |а), чтобы задать (почти) точное положение электрона.
Распределение масс будет близко к дельта-функции (§21.10), что означает, по существу,
бесконечное значение энергии Ес, соответствующее почти мгновенной редукции состоя¬
ния \Ф) в одно из состояний |х) или \<р). Это относится и к системе, состоящей из точечных
объектов (например, кварков). Ясно, что такое невозможно: если бы было так, то не было
бы никакой квантовой механики.
Нам следует более внимательно посмотреть, какими должны быть наши состояния |х)
и \(р). Напомним, что выше мы предполагали состояния |х) и \ф) стационарными. Электрон
в (почти) фиксированном положении определенно не находится в стационарном состоянии.
Согласно гейзенберговскому принципу неопределенности координата-импульс (§21.11), он
должен обладать очень большим набором импульсов и мгновенно расплываться. С другой

712
Глава 30
стороны, получается, что мы сталкиваемся с трудностями при попытке применить наши рас¬
суждения к отдельным частицам, если требуем точной стационарности обоих состояний |%)
и \(р}9 поскольку не существует стационарных решений обычного уравнения Шредингера
для одной свободной частицы (с положительной массой), спадающих на пространственной
бесконечности*. Разгадка состоит в том, что, выписывая уравнение Шредингера, мы должны
учитывать гравитационное поле частицы. Здесь не требуется, чтобы само гравитационное
поле было квантованным, его действие описывается ньютоновской гравитационной потен¬
циальной функцией Ф, источником которой служит так называемое «математическое ожида¬
ние» распределения масс в волновой функции. В задачи этой книги не входит полное опи¬
сание этой проблемы 130*381 Отметим лишь, что при этом получаются разумные результаты.
Относящиеся сюда подробности составляют предмет активных исследований. Оказывается,
что для одной частицы такое модифицированное уравнение Шредингера (я буду называть
его уравнением Шредингера-Ньютона, поскольку оно учитывает ньютоновское гравита¬
ционное поле) действительно имеет стационарные решения для одной частицы, должным
образом спадающие на бесконечности. (Однако для одиночного электрона протяженность
волновой функции будет превышать размер наблюдаемой Вселенной, для атома водорода
протяженность будет несколько меньше размера Вселенной; протяженность обратно про¬
порциональна кубу массы частицы.)
Теперь мы имеем правдоподобное предположение относительно объективной редук¬
ции состояний, которое применимо, по крайней мере, к ситуациям, в которых квантовое
состояние представляет суперпозицию двух других состояний, каждое из которых стаци¬
онарно (в указанном смысле, связанном с уравнением Шредингера-Ньютона). Согласно
этому допущению, такая суперпозиция будет спонтанно редуцировать в одно из двух со¬
ставляющих ее стационарных состояний за среднее время порядка К/Eg> где Eg — гра¬
витационная собственная энергия разности двух соответствующих распределений массы.
Я назову это предположение гравитационной объективной редукцией (ОР) квантового со¬
стояния. Гравитационная собственная энергия Eq допускает четкое определение для любой
пары стационарных состояний, составляющих суперпозицию. Она относится к разности
двух распределений масс, каждое из которых представляет то «математическое ожидание»,
которое фигурирует в уравнении Шредингера-Ньютона.
Все другие варианты схемы ОР сталкиваются с трудностями, связанными с сохране¬
нием энергии. В частности, остроумное предложение, выдвинутое в 1986 году Джанкар-
ло Жирарди, Альберто Римини и Туллио Вебером, встречает точно такие же трудности,
как и различные другие схемы I30'39!. Общая тенденция состоит в том, чтобы «уживаться»
с этой проблемой, поскольку несохранение энергии можно свести до приемлемо низкого
уровня. Я считаю, что к этой проблеме следует относиться серьезно. Предложенная вы¬
ше схема гравитационной ОР имеет то преимущество, что неопределенность энергии Eq
компенсирует возможное несохранение, так что закон сохранения энергии не нарушается.
Этот вопрос, однако, требует дальнейшего изучения. Дело выглядит так, словно имеет ме¬
сто некоторого рода «обмен» между проблемой с энергией в процессе ОР и существенно
нелокальной природой гравитационной энергии, обсуждавшейся в § 19.8.
Моя точка зрения в отношении редукции квантового состояния состоит в том, что
это есть действительно объективный процесс и что это всегда гравитационное явление.
Так обстоит дело даже в тех случаях, когда имеется существенная декогеренция, создаваемая
окружением, которая приводит к «практической» редукции состояний в системе (например,
в молекуле ДНК), слишком малой для того, чтобы непосредственно применять к ней гра¬
витационную ОР. В таких ситуациях гравитационная ОР определяется полным смещением
массы в окружающей среде. В рассматриваемом частном случае, когда изучаемое состояние
является суперпозицией двух стационарных состояний, этот процесс редукции, по моему
мнению, хорошо аппроксимируется описанной схемой гравитационной ОР.
Почему? (Подсказка: воспользуйтесь еще раз упражнением 24,3.)

30.13. Эксперимент FELIX и другие аналогичные предложения
713
При несомненном отсутствии полной теории я не могу описать реальную динамику
редукции состояния, обусловленную процессом ОР, даже в рассматриваемом случае су¬
перпозиции двух состояний. В этом отношении мое предложение носит «минималистский»
характер, и я не стремлюсь к построению более полной динамики, как это делается в рабо¬
тах [426, 427, 576, 448, 291, 290, 195, 816, 632, 300] [30 4°], Тем не менее мой минималист¬
ский вариант ведет, как мне кажется, к непосредственным экспериментальным проявлениям,
и в заключение этой главы я предложу некоторую идею постановки реальных эксперимен¬
тов, дающих возможность решить, действительно ли схема гравитационной ОР отвечает
замыслам Природы.
30.13.	Эксперимент FELIX и другие аналогичные предложения
Предлагаемая схема состоит в построении «кошки Шредингера», содержащей малень¬
кое зеркало М, положение которого описывается квантовой суперпозицией двух слабо разли¬
чающихся положений в пространстве, разделенных расстоянием порядка диаметра атомного
ядра^30‘411. Разумный размер такого зеркала должен быть сравним с размером пылинки или
примерно с одной десятой толщины человеческого волоса и содержать 1014~1016 ядер (так
что его масса будет примерно 5 * 10~12 кг, а диаметр 10“3 см). Будем считать, что зеркало М
устанавливается в указанной суперпозиции в результате столкновения с одиночным фотоном
рентгеновского излучения, который является суперпозицией двух лучей, один из которых
направлен на зеркало М.
Схема возможной экспериментальной установки показана на рис. 30.24. Фотон, со¬
зданный рентгеновским лазером L, направляется к расщепителю луча В. Прошедшая часть
результирующего состояния фотона направляется к зеркалу М; при столкновении с зерка¬
лом и отражении от него последнему передается некоторый импульс. Зеркало должно быть
весьма высокого качества, достаточно «жестким», чтобы оно реагировало на столкновение
с фотоном как единое целое, без возникновения внутренних колебаний и выбивания атомов.
Зеркало должно быть подвешено таким образом, чтобы оно возвращалось в исходное поло¬
жение, скажем, за одну десятую секунды (или даже за одну секунду, как предполагается на
рис. 30.24). В течение этого времени две части волновой функции фотона каким-то образом
должны поддерживаться когерентными; по истечении этого времени весь процесс должен
быть обращен, чтобы можно было убедиться в потере фазовой когерентности, каковая имеет
место при редукции квантовой суперпозиции положений зеркала в то или иное положение.
Поддержание когерентности рентгеновских фотонов в течение одной десятой секун¬
ды проблемы не составляет. (Рентгеновская область энергии фотона необходима, чтобы
передаваемый импульс был достаточно большим и мог привести зеркало в движение.) Ко¬
герентность в течение такого времени нужна для того, чтобы провести весь эксперимент в
космическом пространстве, где когерентность фотонов обеспечивается отражением между
большими зеркалами на двух космических платформах, разделенных расстоянием порядка
диаметра Земли. Это требует примерно одной десятой секунды для однократного прохо¬
ждения фотона туда и обратно. Та часть волновой функции фотона, которая отразилась от
зеркала М, затем возвращается к нему снова, а часть, отраженная от расщепителя луча В,
возвращается к расщепителю. Соответствующее время должно быть таково, чтобы весь фи¬
зический процесс мог быть полностью обращен. Таким образом, часть волновой функции
фотона, ответственная за движение зеркала М, снова приходит к зеркалу как раз тогда, ко¬
гда зеркало возвращается в исходное положение, поэтому фотон восстанавливает импульс,
который был передан зеркалу, и оставляет зеркало в покое, при этом две части волновой
функции фотона рекомбинируют на расщепителе луча В. При условии отсутствия потери фа¬
зовой когерентности в ходе описанного процесса и надлежащего выбора длин проходимых
путей волновая функция фотона образует одиночный луч, направленный обратно на лазер L.

714
Глава 30
Расстояние
в 10 диаметров
Земли
Параболические
наклонные
зеркала
Плоские
зеркала
Рис. 30.24. Орбитальный эксперимент с лазерной рентгеновской интерферометрией (Free-orbit
Experiment with Laser Interferometry X-rays (FELIX)). Показана схема экспериментальной установки.
Фотон, созданный рентгеновским лазером L, направляется к расщепителю луча В. Прошедшая часть
результирующего состояния фотона направляется к маленькому зеркалу М, представляющему кубик
размером 10 микрон. При отражении фотона зеркалу передается некоторый импульс. Это приводит
зеркало М в состояние квантовой суперпозиции («состояние кошки Шредингера»), которое должно
сохраняться в течение, скажем, одной секунды. В течение этого времени две части волновой функции
фотона должны поддерживаться когерентными (например, путем отражения между двумя платформа¬
ми в космическом пространстве), после чего весь процесс должен быть обращен. В случае идеальной
установки (с одинаковой длиной проходимых путей) стандартная квантовая механика требует, чтобы
детектор реагировал в течение 0% времени. Схема гравитационной ОР предсказывает значение 50%
Такий образом, детектор, помещенный в «альтернативное» положение D, куда фотон может
попасть из расщепителя луча В (см. рис. 30.24), не зарегистрирует ничего. Этот проект полу¬
чил название FELIX (Free-orbit Experiment with Laser Interferometry X-rays — Орбитальный
эксперимент с лазерной рентгеновской интерферометрией).
Заметим, что в течение одной десятой секунды состояние зеркала М будет суперпо¬
зицией смещенного и несмещенного положений, т.е. будет иметь место та же ситуация,
что и в случае описанного выше материального объекта (рис. 30.20). Согласно схеме гра¬
витационной ОР, состояние зеркала М должно спонтанно редуцировать в смещенное или
несмещенное состояние за время порядка одной десятой секунды. Состояние фотона перепу¬
тано с состоянием зеркала, поэтому при редукции состояния зеркала должно редуцировать
и состояние фотона. При этом фотон оказывается в одном или другом луче, так что при
возвращении к расщепителю луча В он будет иметь одинаковую вероятность включить де¬
тектор D либо вернуться к лазеру L. Эта процедура будет повторяться много раз. Эффект,
создаваемый ОР, состоит в том, что детектор реагирует в 50% случаев, тогда как соглас¬
но стандартной квантовой механике (в идеальном эксперименте) фазовая когерентность не
теряется, и детектор вообще не должен реагировать.
Разумеется, в любой реальной ситуации имеется много других возможных причин по¬
тери фазовой когерентности. Чтобы наш эксперимент был успешным, они должны быть по
возможности устранены, так чтобы можно было заметить проявление гравитационной ОР.
Эксперимент следует повторять много раз с зеркалами разного размера, изготовленными
из различных материалов, при изменении временных масштабов (возможно, с использо¬
ванием многократного отражения между космическими платформами). Важным фактором

30.13. Эксперимент FELIX и другие аналогичные предложения
715
в рассматриваемой гравитационной ОР является степень «размытия» распределения мас¬
сы ядер в нашем зеркале. При заданной полной массе более компактно локализованное
распределение масс приводит к уменьшению времени редукции (см. рис. 30.25).
Рис. 30.25. Существенным фактором является степень «размытия» распределения массы ядер в зер¬
кале. При заданной полной массе более компактно локализованное распределение масс соответствует
уменьшению времени редукции
Описанный проект FELIX крайне сложен в техническом отношении по ряду причин.
Главной проблемой является требуемая точность задания направления распространения
рентгеновских фотонов между космическими платформами, разделенными расстоянием по¬
рядка 10000 км. Космические эксперименты в любом случае неизбежно оказываются труд¬
ными и очень дорогостоящими, и если бы существовали наземные варианты, они имели
бы массу преимуществ. К счастью, оказывается, что такая альтернатива практически воз¬
можна. Благодаря остроумному предложению Уильяма Маршалла и столь же ярким идеям
Дика Боумеестера и Кристофа Саймона по его реализации, наземный вариант представля¬
ется вполне возможным и в настоящее время активно обсуждается. Вместо столкновения
с одиночным фотоном, вызывающего необходимое смещение зеркала, предлагается^30*42!
использовать фотон значительно меньшей энергии (в видимой или даже инфракрасной об¬
ласти), который многократно (скажем, 106 раз) отражается, пробегая туда и обратно, так что
зеркало теперь испытывает 106 столкновений с одним и тем же фотоном вместо предпола¬
гавшегося раньше одного соударения с рентгеновским фотоном (см. рис. 30.26). В момент
написания этой книги не видно фундаментальных препятствий для проведения предвари¬
тельного эксперимента такого рода в ближайшие года два. В случае успешного исхода такой
предварительный эксперимент, скорее всего, дал бы величину, на 5-6 порядков меньшую,
чем требуется для уверенного подтверждения схемы гравитационной ОР. Тем не менее ес¬
ли бы можно было поддерживать квантовую когерентность суперпозиции двух положений
зеркала, это дало бы перевес (в терминах массы) над современными вариантами «кош¬
ки Шредингера» (в виде молекул фуллерена С7оУ30‘43! в 1012 раз. Вполне возможно, что,
если будет успешно достигнута эта стадия, на которой «минималистская» схема гравитаци¬
онной ОР, изложенная в §§30.9-30.12, предсказывает согласие со стандартной квантовой
механикой, дальнейшее улучшение, необходимое для проверки новых предсказаний схемы
гравитационной ОР, будет реализовано еще через несколько лет.
Примечательно, что крайне малая неопределенность гравитационной энергии Eg, ко¬
торая фигурирует в экспериментах такого рода (скажем, порядка 10 ~33 Дж) оказывается
достаточной, чтобы дать «разумное» время коллапса — порядка одной десятой секунды или
меньше. Малая величина гравитационных эффектов является причиной, по которой мно¬
гие физики вообще не обращают на них внимания. Тем не менее мы видим, что введение
гравитации в нашу квантовую картину может привести к замечательным наблюдаемым след¬
ствиям. Следует отметить, что временной масштаб H/Eg представляет собой частное от
деления двух малых величин h и G и потому не обязан быть малым по обычным человече¬
ским меркам. Это находится в резком контрасте с крайне малыми величинами, характерными
для квантовой гравитации, — планковской длиной и планковским временем (§§27.10, 31.1),

716
Глава 30
Многократные
отражения
&
Резонатор
Рис. 30.26. Более практический вариант эксперимента FELIX не использует рентгеновские лучи, а тре¬
бует порядка 106 столкновений зеркала с фотоном видимого света вместо одного столкновения с рент¬
геновским фотоном
соответственно 10“33 см и 10~43 с, которые получаются в результате перемножения вели¬
чин Н и G.
Представим себе, что эксперимент по проверке гравитационной ОР успешно проведен.
Если фазовая когерентность не теряется за указанные выше времена, предсказываемые схе¬
мой гравитационной ОР, то от данной схемы придется отказаться или, по крайней мере,
подвергнуть ее серьезной модификации. А как быть в случае, если окажется, что подобные
экспериментыподтверждают эти предсказания схемы гравитационной ОР? Сможем ли мы
тогда утверждать, что редукция квантового состояния действительно есть объективный гра¬
витационный эффект? Я опасаюсь, что и тогда многие предпочтут придерживаться в этом
вопросе одной из более «стандартных» точек зрения. Они могут заявить, например, что
имеет место строгая унитарность (U), тогда как некоторые из состояний становятся недо¬
ступными, возможно, из-за «квантовых флуктуаций метрического поля» (см. §§ 29.6, 30.14).
Лично я не склонен сопротивляться фундаментальным изменениям существующей фи¬
зической теории, поскольку полагаю, что в случае квантовой теории фундаментальные сдви¬
ги действительно необходимы, о чем подробно заявлял выше. Однако, возможно, не будет
чрезмерно смело провести здесь сравнение со взглядами многих весьма уважаемых физиков,
например, Лоренца, предпочитавших рассматривать эффекты специальной теории относи¬
тельности всего лишь как «поправки» к картине мира XIX века, в которой существовало
понятие абсолютного покоя. Несомненно, что точно так же многие уважаемые физики будут
противиться отказу от выстраданной XX веком квантово-механической картины мира, ес¬
ли вдруг окажется, что предсказания схемы гравитационной ОР подтверждаются успешно
проведенным экспериментом типа FELIX. На мой взгляд, это ретроградная точка зрения, от¬
казывающаяся от возможности прогресса на основе новой квантовой картины мира, которая
действительно имеет физический смысл!
Разумеется, те из нас, кто ожидает от гравитационной ОР поддержки нашей не вполне
традиционной точки зрения, должны быть готовы к другому повороту событий, при котором
окажется, что эксперимент опровергает наши ожидания. Моей собственной реакцией на это
было бы значительное замешательство, не смотря на то, что многие физики-теоретики, с ко¬
торыми я обсуждал этот вопрос, выражали твердую уверенность, что стандартная квантовая
механика в очередной раз окажется незыблемой. Мое замешательство связано в основном
с уверенностью в том, что сегодняшняя квантовая механика не обладает онтологией, заслу¬
живающей доверия, поэтому она должна быть существенно модифицирована, чтобы физика
нашего мира приобрела подлинный смысл. Само по себе это не означает ни того, что нам
на выручку должна прийти именно гравитационная ОР, ни того, что выдвинутое здесь
предложение, использующее гравитационный эффект, должно оказаться правильным [30-441.

t
30.14. Природа флуктуаций в ранней Вселенной
717
Тем не менее я чувствую, что прочность современной квантовой теории не позволит так
просто сместить ее с пьедестала. По моему мнению, любое подобное изменение потребует
привлечения чего-то столь же значительного, а в современной физике подобный статус со¬
храняет только общая теория относительности Эйнштейна с ее глубоко мотивированными
принципами. Именно это заставляет меня принять схему гравитационной ОР типа предло¬
женной выше. Каков бы ни был конечный результат подобного обсуждения, я ожидаю, что
в XXI веке будут поставлены и решены многие новые глубокие и интригующих квантово¬
механические проблемы!
30.14.	Природа флуктуаций в ранней Вселенной
Прежде чем закончить эту главу, я хотел бы поставить один из тех многочисленных
важных вопросов, ответ на которые существенно зависит от изменения правил квантовой
теории в соответствии с обсуждением, проведенным в этой главе. В §27.13 я обратил вни¬
мание на необычайно особый характер того состояния, в котором пребывала Вселенная
в самом начале. Главным фактором, который делал это состояние особенным и обладаю¬
щим крайне низкой энтропией, была его очень точная пространственная изотропия и од¬
нородность, и именно поэтому геометрия пространства-времени Вселенной (пока) замеча¬
тельно близка к одной из стандартных космологических моделей ФЛРУ (§27.11). Конечно,
как часто заявляют, Вселенная не может абсолютно точно соответствовать столь симмет¬
ричной модели. Если бы такая высокая симметрия существовала когда-то, то она должна
была бы оставаться таковой и в дальнейшем, поскольку динамика общей теории относи¬
тельности Эйнштейна (и остальной классической физики) обеспечивает точное сохранение
симметрии.
А как насчет квантовой физики? Не приведет ли «хаотичность», присущая процессам
квантовой эволюции, к возникновению отклонений от этой точной симметрии? Здесь часто
привлекается понятие «квантовых флуктуаций» как источника необходимых малых откло¬
нений от точной симметрии. Идея состоит в том, что такие «флуктуации», возникая как
малые отклонения, могут служить источником нерегулярности в распределении масс, кото¬
рые будут постепенно расти в процессе гравитационного сжатия, так что в конечном счете
смогут появиться звезды, галактики и скопления галактик, которые мы наблюдаем сегодня.
Что представляют собой квантовые флуктуации? Из соотношений неопределенности
Гейзенберга (§21.11), применяемых к величинам, описывающим поле (см. §§ 26.2,26.3,26.9),
следует, что при попытке измерить с высокой точностью величину поля в некоторой очень
малой области мы получим очень большую неопределенность значений других, канониче¬
ски связанных, величин и, следовательно, очень быстрое изменение ожидаемого значения
измеряемой величины. Таким образом, сам акт определения точного значения некоторой
величины, характеризующей поле, приводит к сильным флуктуациям этой величины. Такой
величиной может быть некоторая компонента пространственно-временной метрики, поэто¬
му любая попытка точно измерить метрику приводит к огромным изменениям этой метрики.
Соображения такого рода привели в 1950 году Джона Уилера к выводу, что на планковских
масштабах порядка 10-33 см пространство-время будет иметь характер сильно флуктуиру¬
ющей «пены» (см. конец § 29.6 и рис. 29.6).
Чтобы яснее представить эту картину, следует внимательнее разобрать, что действи¬
тельно утверждают соотношения неопределенности Гейзенберга. Они не означают, что име¬
ется некоторая «размытость» или «некогерентность» в поведении Природы на самых малых
масштабах. Гейзенберговская неопределенность налагает ограничения на точность, с кото¬
рой можно провести два некоммутирующих измерения. Напомним, что в случае одиночной
частицы ее координата и импульс в некотором направлении, будучи некоммутирующими ве¬
личинами, не могут быть точно определены в один и тот же момент времени, произведение

718
Глава 30
соответствующих ошибок не может быть меньше -fi, (§21.11). Существует, однако, точно
определенное квантовое состояние, и если никаких измерений не проводится, то состояние
частицы будет эволюционировать в соответствии с уравнением Шредингера (предполагает¬
ся, что справедлива стандартная квантовая механика с U-эволюцией).
Аналогично в стандартной квантовой механике все переменные, определяющие
пространственно-временное состояние, не могут быть определены одновременно. Тем не
менее квантовое описание пространства-времени должно быть вполне определенным. Од¬
нако принцип Гейзенберга утверждает, что такое описание не похоже на (псевдо)риманово
многообразие, поскольку различные величины, описывающие геометрию пространства-вре¬
мени, не коммутируют между собой. Вместо этого, согласно картине, предложенной Уиле¬
ром, состояние должно представлять собой обширную суперпозицию различных геометрий,
большинство которых сильно отклоняется от плоской геометрии, так что мы имеем «пено¬
образную» структуру.
Посмотрим теперь, как применить это к состоянию ранней Вселенной. Можно ли при¬
писать отклонения от точной симметрии «квантовым флуктуациям», если всё начальное
состояние обладает точной космологической симметрией модели ФЛРУ? U-эволюция этого
состояния должна продолжать поддерживать эту точную ФЛРУ-симметрию, независимо от
«квантовых флуктуаций» или любых других проявлений гейзенберговской неопределенно¬
сти* . Как это согласуется с весьма нерегулярной «пенообразной» геометрией, предложенной
Уилером? Здесь нет какого-либо противоречия, поскольку полное состояние представляет
собой суперпозицию таких нерегулярных геометрий, а не отдельную геометрию. Такая су¬
перпозиция сама может обладать симметрией, отсутствующей у составляющих ее отдельных
геометрий. Если вносит свой вклад одна из нерегулярных геометрий, то это относится и ко
всем другим, получающимся из нее применением каждой из ФЛРУ-симметрий^30-451
Как в таком случае эта ФЛРУ-симметричная обширная квантовая суперпозиция нерегу¬
лярных геометрий приводит к чему-то напоминающему «почти ФЛРУ-симметричную» Все¬
ленную, возмущенную лишь в очень слабой степени, совместимой с результатами наблюде¬
ний? Читателю должно быть ясно, что это не может быть обеспечено в рамках U-эволюции
стандартной квантовой механики, так как последняя должна точно сохранять симметрию.
Должно существовать что-то типа R-процесса, переводящего эту обширную суперпозицию
геометрий в одиночную геометрию или хотя бы в некоторую меньшую суперпозицию гео¬
метрий, более близкую к одиночной геометрии. Суть в том, что нерегулярности, создаваемые
«квантовыми флуктуациями», не могут возникать без некоторого процесса R-типа, посред¬
ством которого одиночное начальное квантовое состояние каким-то образом превращается
в вероятностную смесь различных состояний. Это возвращает нас к проблемам, рассмот¬
ренным в главе 29, где обсуждались различные взгляды на «реальность» R-процессов.
Следует иметь в виду, что здесь мы имеем дело с очень ранней стадией Вселенной,
когда ее температура составляла порядка 1032 К. В то время не существовало эксперимен¬
таторов, проводящих «измерения», поэтому не ясно, как следует пользоваться стандартной
«копенгагенской» интерпретацией (вариант (а) в §29.1). А как насчет варианта множе¬
ственности миров (вариант (б) в §29.1)? В этой картине отсутствуют реальные R-процес¬
сы, и ФЛРУ-симметричное состояние Вселенной должно поддерживаться вплоть до сего¬
дняшнего дня. Такое состояние можно представить в виде огромной суперпозиции многих
пространственно-временных геометрий. Согласно этой точке зрения, разложение на аль¬
тернативные пространственно-временные геометрии становится возможным, только когда
разумные наблюдатели пытаются придать смысл миру, при этом существует некоторая супер¬
позиция разумных наблюдателей, каждый из которых воспринимает один из «миров» i30-46i.
С «практической» точки зрения (вариант (в) в §29.1), наличие (достаточной) декогеренции,
Понятно ли, почему поддержание этой симметрии следует просто из детерминированной однозначности
U-эволюции и очень слабого допущения общего характера относительно этой эволюции?

30.14. Природа флуктуаций в ранней Вселенной
719
вызываемой окружением, рассматривается как сигнал, позволяющий трактовать нашу кван¬
товую суперпозицию различных геометрий как вероятностную смесь различных геометрий.
Полезно провести сравнение с примером из обычной квантовой механики[зо.47] пред¬
ставим себе покоящееся радиоактивное ядро в сферически симметричном состоянии (т. е. со
спином 0, см. § 22.11), находящееся в точке О внутри пузырьковой камеры t30-483 (рис. 30.27).
Предположим, что в результате процесса деления ядро распадается на две части А и В, кото¬
рые разлетаются из точки О в противоположных направлениях. Можно предположить, что
части А и В электрически заряжены, так что они оставляют следы в пузырьковой камере.
В этом примере мы исходим из состояния со сферической симметрией относительно центра
О. Тем не менее после распада сферическая симметрия нарушается осью, вдоль которой
разлетаются части А и В. Как это понять на языке U-эволюции исходного состояния? В со¬
ответствии с изложенным выше, ясно, что сферическая симметрия должна быть сохранена,
но это достигается построением линейной суперпозиции всех возможных ситуаций, задава¬
емых различными направлениями оси разлета. Волновая функция имеет вид сферической
волны с центром в точке О, хотя мы должны иметь в виду, что это есть перепутанное
состояние, описывающее части А и В, в котором каждое положение части А коррелирует
с положением части В в антиподном направлении. Поскольку наличие зарядов на А и В
приводит к ионизации вещества в пузырьковой камере и образованию пузырьков, состоя¬
ние становится перепутанным с состоянием этого вещества, поэтому мы обнаружим, что
полное состояние представляет собой суперпозицию, каждая компонента которой содержит
пару следов пузырьков в противоположных направлениях, один из которых соответствует
прохождению части А, а другой — прохождению части В.
Рис. 30.27. Нарушение симметрии объективной редукцией. Ядро (сферически
симметричное) со спином 0 расщепляется на две части, которые наблюдаются
в виде пары с противоположными направлениями распространения. U-эво-
люция начального состояния сохраняет сферическую симметрию, однако мы
имеем (перепутанную) квантовую суперпозицию пары противоположно на¬
правленных путей (Мотт). Процедура R возникает, только если регистрируется
один из них. Этот пример можно рассматривать как модель, показывающую,
что могло бы произойти при возникновении флуктуаций плотности в изна¬
чально высокосимметричном квантовом состоянии ранней Вселенной
Описанная ситуация не отличается существенно от той, что имела место в ранней
Вселенной. Требуется некоторый вариант R-процесса, чтобы можно было заменить симмет¬
ричную квантовую суперпозицию вероятностной смесью менее симметричных состояний.
На практике теоретики, по-видимому, склонны придерживаться некоторой формы «практи¬
ческой» интерпретации (вариант (в) в § 29.1), в которой размер космологического горизонта
произвольным (и не вполне логичным) образом выбирается в качестве некоторого «предела»
квантового перепутывания. Тогда квантовая суперпозиция рассматривается как вероятност¬
ная смесь — хотя это вряд ли делает ситуацию яснее. Видные космологи-инфляционисты
Колб и Тернер пишут в своей книге «Ранняя Вселенная» [456], предназначенной для сту¬
дентов:
По мере того как каждая мода пересекает горизонт, она расстается с микрофизикой
и «замораживается» в виде классической флуктуации.
Слово «мода» означает здесь компоненту квантовой суперпозиции. Мы видим, что авторы
пытаются использовать горизонт как нечто, позволяющее переходить от квантовой амили-

720
Глава 30
туды к некоторой вероятности реальной классической альтернативы. Это, по-видимому, со¬
гласуется с «практическим» вариантом (см. §29.6) и, как уже отмечалось в §§29.6, 29.8,
строго говоря, нелогично t30-49].
Мне представляется ясным, что введение отклонений от точной ФЛРУ-симметрии, обу¬
словленных квантовыми флуктуациями, требует, по необходимости, некоторой теории объ¬
ективной редукции состояний. «Минималистская» схема гравитационной ОР, предложенная
в §§ 30.9-30.12, в данном виде не вполне пригодна для этого. Требуется более исчерпываю¬
щая схема ОР, в которой можно было бы оперировать с квантовыми суперпозициями боль¬
шого числа пространственно-временных геометрий, причем отдельные геометрии не были
бы стационарными, как в §30.10. При наличии такой схемы мы немедленно столкнемся
с впечатляющим массивом данных наблюдений, которые должны подтвердить ее или опро¬
вергнуть. Проекты BOOMERANG, WMAP и другие уже дали огромное количество данных
относительно флуктуаций плотности и температуры в ранней Вселенной, и еще больше
дадут другие эксперименты, находящиеся в стадии подготовки.
Здесь уместно сделать заключительное замечание обо всей этой ситуации. Мы отме¬
тили, что симметричное состояние в нашем предыдущем примере с делением ядра бы¬
ло в высокой степени перепутанным. Это еще более справедливо в отношении редукции
состояний, которая уводит нас от изначально ФЛРУ-симметричного состояния к Вселен¬
ной, подверженной «квантовым флуктуациям». Таким образом, в соответствии с нашим
обсуждением ЭПР-состояний в §§23.3-23.6, мы имеем «нарушение неравенств Белла», что
обеспечивает корреляции между отдаленными событиями, которые выглядят как нарушение
классической причинности. Подобное кажущееся нарушение причинности не обязательно
требует привлечения механизма типа инфляции для приведения таких отдаленных областей
в причинный контакт, а может возникнуть как следствие любой подходящей схемы объек¬
тивной редукции состояний. Однако из проведенного обсуждения следует Е30-50!, что такое
кажущееся «нарушение причинности» становится возможным даже в рамках стандартной
космологии ФЛРУ без всякой инфляции, если начальные флуктуации возникают в некоторой
схеме объективной редукции квантовых состояний.
Ясно, что пока мы далеки от теории, которая смогла бы реально ответить на все эти
вопросы. Но я надеюсь, по крайней мере, что сумел убедить читателя в фундаментальной
необходимости иметь квантовую механику с жизнеспособной онтологией. Эта проблема,
рассмотренная в главах 29 и 30 этой книги, представляет не только философский интерес.
Важность проблемы построения онтологически согласованной (улучшенной) квантовой ме¬
ханики нельзя, на мой взгляд, переоценить. В этой главе я затронул лишь один из фунда¬
ментальных вопросов, существенно зависящих от решения этой проблемы. Таких вопросов
гораздо больше, включая ситуацию в биологии (см. §§34.7, 34.10) , где, как и в случае
ранней Вселенной, «копенгагенская» точка зрения реально не применима, поскольку нет
четкого разделения на квантовую систему и измерительный прибор.
Примечания
§30.1.
30.1. См. [671].
§30.2.
30.2. См. [602].
§30.3.
30.3. Против этого нет теоретических или технических запретов, по крайней мере, если не тре¬
бовать 100%-ной точности. Например, можно устроить так, чтобы начальный фотон всегда
был одним из пары (получаемой, например, в результате параметрической даун-конверсии —
см. §23.10), другой член которой запускал бы измерительное устройство.

30.14. Природа флуктуаций в ранней Вселенной
30.4. Любопытно, что многие испытывают трудности в связи с этими рассуждениями. Вопрос,
' возможно, станет яснее, если рассмотреть различные варианты этого эксперимента, соот¬
ветствующие разным пространственно-временным конфигурациям. Возможны четыре пути
прохождения фотона — SBD, SBC, FBD и FBC. Чтобы оценить различные вероятности, за¬
дадимся вопросом об относительной доле варианта SBD при заданном S (прямое течение
времени) и варианта SBD при заданном D (обратное течение времени). Правило квадрата
модуля дает правильный ответ (50%) в первом случае, но не дает правильного ответа (почти
100%) во втором случае.
30.5. Они, однако, зависят от того, предполагается ли начальное состояние частью некоторого пере¬
путанного состояния (§ 23.3), которое может затрагивать также и детектор. Можно поставить
вопрос, может ли обращение такого перепутывания во времени быть ответственно за то, что
обращенное во времени	правило квадрата модуля дает полностью	неверный ответ.	Но я не ви¬
жу, как можно построить на этой	основе	какое-либо правдоподобное объяснение.	Возможно,
кому-нибудь из предприимчивых читателей это удастся лучше.
30.6. См. [10].
30.7. См. обсуждение этого вопроса в [12].
30.8. См. [11, 169, 166, 819].
§30.4.
30.9. См. [795, 810].
30.10.	См. [591, 606, 51].
30.11.	См. [438, 439, 440, 392,	336].
§30.5.
30.12. См. [809].
30.13. См. [809, 759, 465, 762].
30.14. Имеется несколько смущающее несоответствие между интерпретацией величины т как ре¬
ального времени в рассмотренном здесь шварцшильдовском случае и величиной гот, которая
служит мерой времени ускоряющегося наблюдателя в плоском (риндлеровом) пространстве,
показанном на рис. 30.5 а, б.
30.15. См. [553].
30.16. Это гиромагнитное отношение относится к «чисто дираковской» частице, которая может
служить отличным приближением для электрона, однако реальный электрон подвержен ради¬
ационным поправкам, существование которых предсказывается квантовой теорией поля (см.
конец § 24.7). Протон или нейтрон гораздо меньше похожи на дираковскую частицу, однако
это понятие хорошо применимо к составляющим их кваркам.
§30.6.
30.17. См. [563, 777, 178].
30.18. Занимательное популярное изложение таких возможностей содержится в книге Девиса [178].
§30.7.
30.19. См. [592, 267].
30.20. См. [85, 67, 835, 836, 837].
%
§ 30.8.
30.21. См. [365, 366, 367, 368, 433].
30.22. См. [647].
30.23. См. [647], а также изложение другой точки зрения в [436, 437, 438].
30.24. См. [647, 756].
30.25. См. критику работы [397] в [311]. См. также [755].
30.26. Хокинг предложил обобщение унитарной эволюции, в котором S-матрица обычной квантовой
теории поля (§ 26.8) заменяется так называемым «оператором суперрассеяния» (это не связано
с понятием суперсимметрии; см. § 31.2), обозначаемым символом $. Этот оператор действует

722
Глава 30
не на чистые состояния, как S-матрица, а на состояния, описываемые матрицей плотности
(см. [368]). Следует отметить, что в 2004 году Хокинг отрекся (и напрасно, на мой взгляд!)
от прежней позиции ПОТЕРЯ в пользу позиции ВОЗВРАТ.
§30.9.
30.27. Основное разногласие между Стивеном Хокингом и мною в последние 20 лет заключено
в вопросе временной асимметрии. Хокинг непоколебимо стоит на позициях физики, сим¬
метричной во времени, — либо в форме непреложной квантовой механики U-типа, либо
с указанным выше обобщением (см. примечание 30.26.). Как я отмечал, моя позиция в корне
иная.
30.28. См. [600].
30.29. Гипотеза кривизны Вейля относится к классической геометрии, поэтому она может сообщить
нам кое-что о том, что происходит в точке перехода, где «квантовая геометрия» кристаллизу¬
ется в классическое пространство-время.
30.30. См. [367, 368, 296].
30.31. Возможно, здесь требуется некоторое обобщение понятия гильбертова пространства, кото¬
рое могло бы также описывать некоторые свойства (искривленного) фазового пространства.
См., например, [523, 447, 140, 570, 108].
§30.10.
30.32. Это могут быть когерентные состояния, упомянутые в § 26.6.
30.33. Следует иметь в виду, что индексы у кх и — это просто «ярлыки», а не тензорные индексы
в смысле § 12.8. То же относится к дх и д .
§30.11.
30.34. См. [146].
30.35. См. [414, 467, 672, 728, 55].
30.36. См. список многих работ по теории объективной редукции состояний в примечании 29.12.
В работах Диоси, Персиваля, Киббла, Сквайрса и моих решающую роль играет гравитация.
30.37. Недавно возникла идея более строгого обоснования такого варианта гравитационной OR.
Напомним (см. упражнение 21.6), что для согласования квантовой теории с принципом экви¬
валентности необходимо ввести фазовый множитель, содержащий время в третьей степени,
который описывает переход от свободно падающей системы отсчета к системе, закрепленной
в гравитационном поле. Двум таким системам должны соответствовать два различных вакуу¬
ма (см. § 26.5); это есть проявление того, что остается от эффекта Унру (§ 30.4) в галилеевском
предельном случае. Таким образом, при полном соблюдении принципа эквивалентности су¬
перпозиция двух гравитационных полей будет включать в себя суперпозицию различных
вакуумов и потому должна быть неустойчивой даже в галилеевском пределе. Подробнее эти
соображения будут опубликованы позже.
§30.12.
30.38. См. § 22.5 и [533]. Относительно понятия «математического ожидания» см. примечание 22.11.
30.39. Список наиболее важных работ в этой области приведен в примечании 29.12.
30.40. Я получил очень много от изучения этих работ. Возможно, некоторые из них смогут указать
верный путь к построению более полной теории гравитационной OR. См. примечание 29.12
и работы [301, 301], содержащие некоторые ограничивающие теоремы.
§30.13.
30.41. Многими деталями этой схемы я обязан моим коллегам. Важная часть первоначального замыс¬
ла (предполагавшего столкновение расщепленного фотона с кристаллом «мёссбауэровского
типа») была предложена Иоханнесом Дапричем, некоторые идеи более частного характера,
касающиеся размера зеркала, энергии фотона и много другого, возникли в ходе бесед с Ан¬
тоном Зейлингером и членами его экспериментальной группы, находившейся (в то время)
в Инсбруке. Идея постановки эксперимента FELIX в космическом пространстве появилась
при обсуждении с Андерсом Хансоном. Остроумная идея более реального наземного экспери-
мента была высказана Уильямом Маршаллом, Диком Боумеестером и Кристофом Саймоном.
См. [619, 518].

30.14. Природа флуктуаций в ранней Вселенной
723
30.42. См. [518].
30.43. См. [27].
30.44. Например, первоначальная схема гравитационной OR [426] и более поздний вариант [631]
дают совершенно иные предсказания, нежели высказанные здесь.
§30А 4.
*
30.45. Здесь, однако, имеется некоторая тонкость, поскольку можно предположить, что действие
абстрактной симметрии на геометрию пространства-времени дает ту же самую геометрию
(в силу принципа общей ковариантности, см. § 19.6). В отношении к этому вопросу возможны
разные позиции, однако это не влияет на общую точку зрения, представленную в тексте.
30.46. В варианте множественности миров, предложенном самим Уилером [829], в конечном счете
именно присутствие разумных наблюдателей определяет каким-то (телеологическим) образом
выбор некоторой геометрии пространства-времени, которая имела место в ранней Вселенной.
30.47. Здесь имеется некоторое сходство с обсуждением следов, образуемых а-частицами в камере
Вильсона, в работе Невилла Мотта [534].
30.48. Это стандартная часть измерительной аппаратуры, посредством которой прохождение за¬
ряженной частицы проявляется в виде цепочки мелких пузырьков; см. примечание 30.47
и книгу [256].
• *
30.49. Действительная причина «обрезания» на хаббловском радиусе (где скорость разбегания до¬
стигает скорости света) для данной эпохи не связана непосредственно ни с реальным «раз¬
мером горизонта» (который, согласно инфляционной схеме, в любом случае намного больше
хаббловского радиуса; см. рис. 28.5), ни с переходом от квантовой к классической физи¬
ке. Это чисто классический эффект расширения Вселенной в области действия ограничений
теории относительности.
30.50. Некоторые авторы допускают, что такие «акаузальные» корреляции ЭПР-типа по указанным
причинам могли бы присутствовать во флуктуациях ранней Вселенной. Например, несколько
лет назад предположение такого рода высказал мне Бикаш Синха.

Глава 31
Суперсимметрия, надразмерность и струны
31.1.	Необъяснимые параметры
Ожидания большинства физиков относительно того, что заготовила для нас физика
XXI века, вероятно, в корне отличаются от изложенного в предыдущей главе. Очень немно¬
гие из них ожидают фундаментальных изменений в основах квантовой механики. Вместо
этого они выдвигают странно звучащие идеи вроде необходимости введения лишних из¬
мерений пространства-времени или замены точечных частиц протяженными объектами —
«струнами» либо структурами более высокой размерности, именуемых «мембранами», или
«р-бранами», или просто «бранами»; при этом важную роль играют любопытные допол¬
нительные объекты, называемые «D-бранами». Существуют также загадочные обобщения
идеи симметрии иод названием «суперсимметрия» или «квантовые группы». Имеются также
обобщения самого понятия геометрии, предполагающие некоммутативность, а также кар¬
тины мира, в которых на уровне самых малых масштабов царствует дискретность (вместо
непрерывности) или ткань самого пространства состоит из узлов или петель. Выдвигались
также предложения отказаться от самого понятия пространства-времени либо переопреде¬
лить его через другие понятия.
В чем же состоят эти идеи и как к ним относиться? Более существенный вопрос: что
заставляет столь многих физиков описывать «реальность», слабо напоминающую то, что мы
непосредственно наблюдаем в обычных человеческих масштабах? Несомненно, появление
таких идей частично обусловлено успехами квантовой механики и в меньшей степени общей
теории относительности. Эти достижения XX века показали, до какой степени могут вводить
в заблуждение непосредственные интуитивные соображения, а также то, что «реальность»
может коренным образом отличаться от тех картин, которые были созданы физикой предше¬
ствующих столетий. Тем не менее экзотический и необычный характер предлагаемой схемы
мира еще не дает оснований поверить в нее. Мы должны постараться понять мотивацию, ле¬
жащую в основе исследований современных теоретиков, в их попытках глубже проникнуть
во внутреннее устройство Вселенной.
Мы должны вернуться к рассуждениям, начатым в главе 24 и продолженным в главах 25
и 26, где совместные требования специальной теории относительности и квантовой теории
завели нас в дебри квантовой теории поля. Это в свою очередь привело нас на минное поле
бесконечностей, и потребовалась большая изобретательность, чтобы обойти большинство
из них; это в конечном счете привело к стандартной модели физики элементарных частиц,
которая оказалась в хорошем согласии с измеряемыми проявлениями устройства Природы.
В то же время сама стандартная модель не свободна от бесконечностей, так что это не конеч¬
ная, а «перенормируемая» теория. Перенормируемо сть позволяет проводить определенные
вычисления, получая конечные ответы на большинство интересующих нас вопросов в рам¬
ках этой теории, но ничего не может сказать нам относительно большинства таких важных
параметров, как конкретные значения массы и электрического заряда элементарных частиц,
описываемых этой теорией. Эти значения оказываются «бесконечными» (или, возможно,
«нулевыми»), и процедура перенормировки устраняет эти бесконечности путем переопреде¬
ления используемых терминов, позволяя получить конечные результаты для других искомых

31.1. Необъяснимые параметры
725
структуры
величин. По существу, мы «отмахиваемся» от массы и заряда, значения которых просто
вводятся в теорию как некоторые необъяснимые параметры. На самом деле имеется 17 или
даже больше таких параметров, сюда входят различные константы связи, массы кварков,
лептонов, частицы Хиггса и т. п.
Существует некая тайна, окружающая те странные значения, которые принимают масса
и заряд элементарных частиц, существующих в природе. Например, имеется необъяснимая
«постоянная тонкой структуры» а, задающая величину электромагнитного взаимодействия,
которая определяется формулой
л е2
a=hc’
ч
где — е есть заряд электрона. Обратная величина постоянной тонкой
чение, довольно близкое ка"1 = 137, более точно
г
а-1 = 137,0359...
Многие годы некоторые физики считали, что величина а-1 должна быть равна 137 точно.
В частности, сэр Артур Эддингтон потратил последние годы жизни на попытку создать
«фундаментальную теорию» [232], одним из следствий которой должно было быть равен¬
ство а-1 = 137. Многие из современных физиков настроены менее оптимистично, нежели
их предшественники, в отношении возможности найти непосредственную математическую
«формулу» для а или других «констант Природы». Сегодня физики предпочитают рассмат¬
ривать эти величины не просто как числа, а как функции от энергии частиц, участвующих
во взаимодействии, именуемые «бегущими константами связи» (см. примечание 26.21). На¬
блюдаемые скалярные величины, называемые «константами Природы», оказываются тогда
«низкоэнергетическим пределом» этих «бегущих» значений. Хотя кто-то может продол¬
жать надеяться отыскать чисто математическую причину возникновения этих определенных
предельных значений, тем не менее такие значения кажутся менее «фундаментальными»,
чем было бы в случае их независимости от энергии.
Часто оказывается удобно выражать величины вроде заряда и массы в абсолютных
(планковских) единицах, введенных в § 27.10; в этой системе единиц гравитационная посто¬
янная Ньютона G, скорость света с, постоянная Планка (в дираковской форме) h и постоян¬
ная Больцмана к полагаются равными 1:
G = c = ft = fc = l.
В этих единицах заряд протона (или заряд электрона с обратным знаком) приблизительно
равен е — 1/^137, или, более точной31,^
е = 0,0854246.
Основа заряда кварков (заряд «нижнего» кварка с обратным знаком; см. § 25.6) равна одной
трети этой величины. Абсолютные величины обычно называют платовскими (или ино¬
гда единицами Планка-Уилера), поскольку Макс Планк (прославившийся как создатель
квантовой механики — см. §21.4) выдвинул идею такого рода в статье, опубликованной
в 1906 году. Любопытно, что в качестве основной единицы он использовал не свою соб¬
ственную «постоянную Планка», а электрический заряд, так что в этой схеме мы имеем
просто е — — 1. (Загадка, связанная с зарядом, при этом, конечно, не исчезает, поскольку
в той схеме Н = 137,036.) Важность этих идей позднее (с 1973 года) подчеркивалась во мно¬
гих работах Джона Уилера (который, в отличие от Планка, выбрал не электрический заряд,
а постоянную К).
Если бы на этом всё и кончилось, то планковские единицы правильнее было бы называть
единицами Стони, поскольку ирландский физик Джордж Джонстон Стони (который впервые

726
Глава 31
измерил заряд электрона) выдвинул ту же идею, что и Планк в 1906 году, но опубликовал ее
еще в 1881 году. Имеется, однако, другая статья Планка, опубликованная в 1899 году (то есть
раньше его знаменитой статьи 1900 года, положившей начало квантовой теории), в которой
для определения абсолютных единиц использовалась «постоянная Планка». Поэтому я буду
придерживаться традиционной терминологии, называющей абсолютные единицы «планков-
скими единицами»!
Как обстоит дело со значениями масс элементарных частиц? Проблема массы еще слож¬
нее, чем аналогичная проблема для заряда. Действительно, все частицы в природе имеют
значения заряда, кратные некоторому базисному заряду. В качестве такового можно взять
заряд протона, если мы хотим иметь дело только с такими частицами, которые могут суще¬
ствовать в свободном виде сами по себе, либо заряд «нижнего» кварка (с обратным знаком),
если намерены включить в рассмотрение также внутренние составные части адронов. Хотя
пока нет полного понимания этого факта и определенно непонятен смысл величины 137,036,
проблема все же представляется более доступной пониманию, нежели аналогичный вопрос
о значениях масс, Одна из наиболее загадочных сторон — это крайне малая величина масс
обычных элементарных частиц, если выразить их в абсолютных единицах. Например, масса
электрона те в абсолютных единицах равна
ше - 0,000000000000000000000043,
а масса протона больше этой величины лишь в 1836 раз. Масса электронного нейтрино ve
составляет менее 10~5 указанной величины. Другой способ выразить загадку столь малых
масс — это задаться вопросом, почему естественная «планковская масса», имеющая ма¬
кроскопическую величину 10 “5 г (это масса мелкой мошки), столь велика по сравнению
с массой всех элементарных частиц, встречающихся в природе. Еще один способ перефра¬
зировать эту загадку: почему планковская длина 1,6163 • 10“35 м на 20 порядков меньше
наименьших масштабов, встречающихся в физике элементарных частиц? Эта длина играет
фундаментальную роль в квантовой теории гравитации, будучи масштабом длины, ниже ко¬
торого обычные представления о непрерывном пространстве-времени, по-видимому, теряют
реальный смыслl31'2^.
Один из путей к разгадке состоит в том, чтобы считать малые значения электрическо¬
го заряда или массы результатом некоторого процесса перенормировки, в котором «голое»
значение (§ 26.9) могло быть некоторым математически респектабельным числом вроде 1
или 47Г. При этом малые наблюдаемые значения могли бы появиться из-за просто большо¬
го, а вовсе не бесконечного коэффициента перенормировки. Так было бы, если бы можно
было заменить расходящиеся суммы и интегралы квантовой теории поля чем-то сходящим¬
ся. Расходимости (а именно «ультрафиолетовые» расходимости, см. §26.9) обычно возни¬
кают в результате сложения неограниченно возрастающих импульсов, что соответствует
неограниченно убывающим расстояниям. В соответствии с этим, можно было бы устранить
бесконечности, если обрезать расходящиеся интегралы (или суммы), например, на (грави¬
тационной) планковской длине!31,3^ 10~35 м. Такая идея была выдвинута Оскаром Клейном
в 1935 году. Всё это подтверждает, что должный учет гравитации при квантово-полевых рас¬
четах может привести к конечной теории, а не просто к перенормируемой, и что в рамках
такой конечной теории может найтись место для понимания пока необъяснимых чисел.
Хотя такие надежды появились более полувека назад, сегодня видно, что проблемы,
возникающие при непосредственном внесении гравитации в рассматриваемую картину, ско¬
рее ухудшают, нежели улучшают ситуацию. Применение к теории Эйнштейна стандартных
правил квантования приводит не к конечной теории, а к неперенормируемой. Это побудило
многих исследователей стремиться к чему-то необычному при их поисках, направленных
на построение квантовой теории гравитации. Конечно, и в предыдущих главах этой книги
(особенно в главах 27-30) также звучало, что следует искать нестандартное объединение

31.2. Суперсимметрия
727
квантовой теории (поля) с общей теорией относительности. Но мои доводы в пользу того,
что некоторые изменения должны прийти со стороны квантовой теории, всерьез не вос¬
принимались. Неудовлетворительная неперенормируемая^31-4! квантовая теория гравитации
получается при непосредственном применении к теории Эйнштейна стандартных проце¬
дур квантовой теории поля, и многие предлагали изменить теорию Эйнштейна, не внося
изменений в квантовую теорию поля.	-
/
31.2.	Суперсимметрия
Какие же предлагаются изменения? Одно из направлений такого рода предлагает идею
суперсимметрии, которая при объединении с теорией Эйнштейна (с учетом также кручения;
см. § 14.4 и примечание 19.10) приводит к схеме, получившей название супергравитация.
Что такое суперсимметрия? Почему так много физиков находят ее весьма полезной — до
такой степени, что идеи суперсимметрии кладутся в основу многих современных фунда¬
ментальных теорий (особенно это касается теории струн)? Принципам суперсимметрии
придается огромное значение[зтб], несмоХрЯ на хох факт, что предсказания этих идей пока
имеют слабое отношение к наблюдаемому поведению Природы.
Здесь я должен снова официально предупредить читателя, что выражаю свои личные
пристрастия. Я отнюдь не убежден в высокой физической ценности схемы суперсимметрии,
по крайней мере в той форме, в которой она применяется сегодня в физике элементарных
частиц и теориях, лежащих в ее основе. Пока что претензии суперсимметрии не получили
большой (или вообще какой-либо) поддержки со стороны наблюдений. Притягательность
идей суперсимметрии связана с их математическим изяществом и с несомненной ролью су¬
персимметрии в устранении большой группы бесконечностей в моделях квантовой теории
поля, которые появились благодаря ей. Представим, что вы — физик, стремящийся постро¬
ить квантовую теорию поля, свободную от неконтролируемых бесконечностей. Тогда ваша
задача окажется неизмеримо проще, если вы сделаете вашу теорию суперсимметричной!
Основная идея, лежащая в основе суперсимметрии, состоит в том, что она предоставля¬
ет способ объединять в пары фермионы и бозоны в соответствии с некоторыми правилами
симметрии. Как мы видели в §§25.5-25.8, обычные группы симметрии физики элементар¬
ных частиц просто «вращают» наборы бозонов среди них самих и наборы фермионов также
среди них самих. Они не «поворачивают» бозоны в фермионы или наоборот. Суперсим¬
метрия, в отличие от них, делает именно это. Вспомним (§ 26.2), что бозоны подчиняются
коммутативному закону, а фермионы — антикоммутативному закону. Оператор, который пе¬
реводит одних в другие, сам должен обладать антикоммутативными свойствами. Однако
операторы, образующие обычную непрерывную группу, представляют собой бесконечно
малые генераторы группы, образующие алгебру Ли (см. § 13.6). Обычные элементы алге¬
бры Ли подчиняются коммутативному, а не антикоммутативному закону. Это означает, что
необходимые операторы будут бесконечно малыми генераторами не обычной непрерывной
группы, а более общей супергруппы, для которой законы алгебры Ли обобщаются таким
образом, что некоторые генераторы подчиняются как коммутативным, так и антикоммута-
тивным законам.
В §§ 26.2, 26.3 мы уже встречались с подобным, а именно с уравнениями вида
ab =Ь Ьа — с,
. *
которым могут удовлетворять операторы рождения и уничтожения и полевые операторы
квантовой теории поля (в уравнениях вида Ф*Ф±ФФ* — гк{ф\ф)I из § 26.2). В соответствии
с этим, супер&лгебра Ли строится так же, как обычная алгебра Ли, с той лишь разницей, что
теперь в определяющих ее соотношениях может стоять плюс (+). В § 13.6 отмечалось, что

728
Глава 31
соотношения, определяющие алгебру Ли, имеют вид [Еау Ер] ~ 7 Ех, где 7*^ — струк¬
турные постоянные, [Еа, Ер] = ЕаЕр — ЕрЕа. Эти соотношения имеют тот же вид, что
и приведенное выше, где в обычном варианте между аЪ и Ьа стоит знак минус. В суперал¬
гебре Ли допускается также знак плюс, если оба оператора а и Ь описывают фермионные
величины (в отличие от случая, когда оба описывают бозонные величины либо когда один
из них относится к фермионной величине, а другой — к бозонной). Для антикоммутаторов
используют обозначение [а, Ь]+, т. е. [а, Ь]+ = аЬ + Ьа, в дополнение к обычной записи
скобок Ли [а, Ь] = ab — Ьа. Это требует выхода за рамки обычного понятия алгебры Ли.
Генераторы супергрупп обычно строятся некоторым определенным образом. Вместо
того чтобы исходить из обычных вещественных величин, мы рассматриваем эти генераторы
как элементы грассмановой алгебры, которые, как мы видели в §11.6, обладают как ком¬
мутативными, так и антикоммутативными свойствами. Мы познакомимся с этим несколько
подробнее в § 31.3.
В настоящее время супергруппы представляют вполне респектабельную область чи¬
стой математики. Более того, идеи суперсимметрии могут применяться непосредственно
в математических рассуждениях для получения результатов, которые нелегко было бы по¬
лучить другим способом I31-6!. Это, однако, отнюдь не означает, что суперсимметрия в том
виде, в каком она применяется, имеет какое-то непосредственное отношение к физике.
С другой стороны, известен ряд примеров, когда суперсимметрия оказывается полезной при
постановке задачи и получении результатов, которые имеют непосредственное физическое
содержание^31'7!. Но это опять-таки не означает, на мой взгляд, что супергруппы должны
иметь прямое отношение к физике элементарных частиц или квантовой теории поля.
Какие имеются аргументы в пользу того, что суперсимметрия действительно играет
важную роль в физике элементарных частиц? Вспомним стандартную модель, описанную
в главе 25. Своей перенормируемостью она в высокой степени обязана некоторой «тон¬
кой настройке» ее параметров. Соотношения между параметрами в основном объясняются
требованиями симметрии SU(3) х SU(2) х U(1 )/Zq (§ 25.7). Тем не менее, согласно некото¬
рым утверждениям^31,8!, стандартная модель требует некоторой другой точной «настройки»
помимо упомянутых соотношений. Для этого привлекаются дополнительные симметрии, и
суперсимметрия предлагается как средство для достижения такой точной «настройки». По¬
этому подобные идеи часто используются в теориях Великого объединения. Но есть ли у нас
основания доверять таким теориям? Наблюдения никаких доказательств на этот счет пока
не дали.
Привлекательной чертой суперсимметрии представляется то, что она предлагает способ
установления связи между бозонами и фермионами и что на основе суперсимметричных
квантовых теорий поля получать конечные (нерасходящиеся) результаты гораздо проще,
нежели с помощью теорий, не обладающих сперсимметрией. При суперсимметричном объ¬
единении бозонов с фермионами можно сделать так, чтобы бесконечности одного набора
компенсировались бесконечностями другого набора. Это в большой степени упрощает рабо¬
ту теоретиков, занимающихся построением квантовых теорий поля. Но отсюда не следует,
что таким же образом поступает и сама Природа. Она же может прятать в рукаве и совсем
иные фокусы!
Главная трудность теории суперсимметрии (в ее нынешнем виде) заключается в ее
требовании, чтобы каждая из элементарных частиц, существующих в природе, имела так
называемого «суперпартнера», у которого спин отличался бы от спина исходной частицы
на ~ h. Это требует существования «сэлектрона» со спином 0 как партнера электрона, «сквар-
ка» со спином 0 для каждой разновидности кварков, «фотино» со спином | как партнера
фотона, партнеров «вино» и «зйно» со спином А соответственно для W- и Z-бозонов и т. д.,

31.3, Алгебра и геометрия суперсимметрии
729
и т. п. Беда в том, что ни один из таких «суперпартнеров» пока не обнаружен. Официальное
объяснение этого обстоятельства состоит в том, что из-за наличия некоторого механизма
«нарушения суперсимметрии» (природа которого никогда не была описана должным обра¬
зом) эти предполагаемые суперпартнеры должны иметь намного большую массу, нежели
соответствующие им элементарные частицы. Постулируется, что масса этих ненаблюдав-
шихся частиц должна превышать массу протона в тысячу или более раз. Должен сказать,
что я отнюдь не одинок, считая, что все это выглядит несколько надуманным.
Следует, по-видимому, постулировать, что тот из двух «партнеров», спин которого мень¬
ше (на | ft), обладает гораздо большей массой (за исключением случая, когда оба члена пары
безмассовые). Предполагается, что суперпартнерами обладают только частицы, считающие¬
ся «элементарными» (к таковым относят фотон, гравитон, W- и Z-бозоны, глюоны, лептоны
и кварки). В противном случае возникают трудности с частицами со спином 0, например,
пионами. Если бы существовали элементарные частицы со спином 0, как еще не обнару¬
женный хиггсовский бозон, то их, в данном частном случае, пришлось бы считать более
массивными, чем их суперпартнеры (поскольку исключается отрицательное значение спи¬
на). Но если это верно, то почему не обнаружен суперпартнер хиггсовского бозона? Помимо
этого приверженцам супер симметрии и инфляционной космологии придется объяснить, как
вписывается в картину с «суперпартнерами» скалярная ^-частица (§ 28.4).
Положительной чертой суперсимметрии, которую часто упоминают в ее поддержку,
является идея о том, как свести в единую высокосимметричную схему три взаимодействия
(сильное, слабое и электромагнитное) в физике элементарных частиц, спустя 10 ~39 секунд
(это всего лишь 10000 планковских единиц времени) после Большого взрыва, когда тем¬
пература Вселенной имела огромное значение (1028 К)^31*9!. Идея состоит в том, что для
такого объединения все три взаимодействия должны иметь, при данной температуре, одну
и ту же величину. Следует заметить, что при обычных условиях величины сил, создаваемых
сильным и слабым взаимодействием, различаются примерно в 1013 раз (хотя сравнить их
непосредственно не представляется возможным). При учете эффектов перенормировки (на¬
помним (§26.9), что наблюдаемый заряд частицы может сильно отличаться от ее «голого»
заряда) величины этих взаимодействий при столь высоких температурах могут сравняться,
при том что «голые» значения останутся прежними. (Напомним о понятии «бегущих кон¬
стант связи», введенном в конце §31.1.) Согласно этой схеме, в отсутствие суперсимметрии
константы связи не совпадают (см. рис. 31.1), если же ввести в картину суперсимметрию,
то соответствующие кривые чудесным образом совпадают в одной точке и имеет место
Великое объединение физики элементарных частиц!
Читатель, возможно, чувствует мое отношение к этому. (В §28.3 я уже высказывал
сомнение в отношении теорий, в которых предполагается «восстановление симметрии» при
достаточно высокой температуре Вселенной.) В этих идеях, претендующих на поддержку
суперсимметрии наблюдениями, заключаются гигантские экстраполяции. Одной из таких
м
является допущение, что не возникает ничего существенно нового в огромной щели энергии
(или температур) между 1028 К и приблизительно 1014 К, что доступно для современных
ускорителей. Это само по себе представляется неразумной экстраполяцией, и я не понимаю,
как можно рассматривать изложенные соображения в качестве сколько-нибудь значимой
дополнительной поддержки суперсимметрии.
31.3.	Алгебра и геометрия суперсимметрии
Вернемся к теории супергравитации, с которой начался этот разговор. В соответствии
3
со сказанным, должен существовать суперпартнер гравитона со спином -, который назвали
гравитино. Эта гипотетическая частица, как и сам гравитон, не имеет массы, если только

730
Глава 31
Рис. 31.1. Согласно модели «Великого объединения», константы связи для сильного, слабого и электро¬
магнитного взаимодействий, рассматриваемые как «бегущие константы связи» (см. примечание 26.21
и § 31.1), должны принимать в точности одно и то же значение при достаточно высокой температуре,
порядка 1028 К, которая имела место спустя 10 000 планковсккх единиц времени	10-39 с) после
суперсимметрии
совпали между собой
не имеет место существенное нарушение суперсимметрии. Какое отношение имеет грави-
тино к геометрии? Эйнштейн научил нас тому, что гравитация описывается как кривизна
пространства-времени (§§ 17.9, 19.6). Означает ли это, что гравитино должно играть неко¬
торую соответствующую (супер)геометрическую роль? Стремясь обнаружить такую роль,
многие теоретики, занимающиеся супергравитацией, считают, что обычное понятие много¬
образия (описанное в главах 10 и 30) требует обобщения, и вводят соответствующее понятие
супермногообразия. Его можно определить чисто формальным образом, обобщая обычное
понятие координат путем введения антикоммутирующих элементов. В случае обычного
многообразия координатами служат вещественные числа (или комплексные числа, если рас¬
сматривается комплексное многообразие; см. § 12.9). В случае супермногообразия в качестве
координат выбираются элементы грассмановой алгебры (§ 11.6).
Большинство теоретиков — приверженцев супергравитации не занимают столь строгой
позиции по отношению к природе «многообразия», на котором действуют вводимые ими
суперсимметричные величины, описывающие поля (несмотря на то что «геометрическая»
природа стандартной общей теории относительности должна, казалось бы, требовать это¬
го и от супергравитации). В последующем описании мы не будем строго придерживаться
точки зрения, основанной на супермногообразиях. Идеи «супералгебры» можно изложить
применительно к величинам, определенным на обычном пространственно-временном мно¬
гообразии.
Простейшая алгебра такого рода получается, если мы добавим единственный антиком¬
мутирующий элемент е к системе вещественных чисел R. Величина е должна антикомму-
тировать сама с собой: ее — —ее, откуда следует г2 — 0. Таким образом, каждый элемент
алгебры имеет вид
а Т eb,
где а и Ь — вещественные числа, коммутирующие с е. Сумма и произведение двух таких
элементов определяются следующими формулами:
((2 4~ eb) Т" (с Т ed) — (g 4- с) е{Ъ Т d),
(а 4- eb)(c -f ed) — ас 4- e(ad 4 be).
Заметим, что, если отбросить члены, содержащие умножение на е, мы опять вернемся
к правилам обычной алгебры.

31.3. Алгебра и геометрия суперсимметрии
731
Это остается в силе и в том случае, если мы имеем несколько различных генераторов
суперсимметрии £i, ..., вдг, антикоммутирующих между собой:
2
SiSj — ~6jSi, откуда следует е\ — О,
и общий элемент супералгебры имеет вид
а
+ Ь±£\ + Ь<1£2 4- • * • + ^АГСдг 4- С\2^1^2 4- Cis£iS3 “4 * • • 4" f 12...N^1^2 • • •
Такая алгебра обладает тем свойством, что если взять «обыкновенную» часть а любого
элемента (не содержащую генераторов е\ то получается знакомая нам алгебра обычных
(вещественных или комплексных) чисел. «Суперчасть» алгебры представляет остаток. Она
«нильпотентна» в том смысле, что любой из ее элементов, будучи возведенным в достаточно
высокую степень, дает нуль . Иногда используется довольно причудливая терминология:
«обыкновенную» и «супер»-части именуют соответственно «телом» и «душой».
Будучи одним из тех, кто предпочитает иметь «наглядную картину» обсуждаемого пред¬
мета, я всегда считал такое чисто формальное описание супералгебр и супермногообразий
не вполне удовлетворительным. К счастью, всё это можно представить более наглядным
геометрическим образом. Рассмотрим простейший случай, когда имеется единственный ге¬
нератор суперсимметрии е. Поскольку он должен быть антикоммутирующим объектом, мы
можем рассматривать его как 1-форму е. Однако он не может быть обычной 1-формой,
относящейся к обычному пространству (например, к n-многообразию М), с которым мы
имеем дело. Все обыкновенные дифференциальные формы в М имеют тот же смысл, что
и раньше (§ 12.4). Нам следует считать многообразие Л4 гиперповерхностью, погруженной
в (п 4- 1)-мерное многообразие М! («гиперповерхность» есть подмногообразие с размер¬
ностью, на единицу меньшей размерности окружающего пространства, — см. примечание
27.36). При этом е есть 1-форма, относящаяся к большему многообразию но ограни¬
ченная точками многообразия М. Мы не интересуемся многообразием М' за исключени¬
ем тех точек многообразия М., в которых Л4/ добавляет к М. дополнительное измерение
(см. рис. 31.2 а). (Мы имеем дело только с так называемой окрестностью первого поряд¬
ка М в Мг. Это означает «первые производные» по измерению, не принадлежащему Л4, так
что мы сталкиваемся с понятиями касательных и кокасательных векторов или пространств,
которые имеют «направление» в не принадлежащее М9 но не затрагиваем понятий,
связанных с высшими производными, например кривизны, в направлениях, не принадлежа¬
щих М.) Мы имеем дело с n-мерными объектами в том смысле, что все наши величины
можно представить как функции от п независимых координат в многообразии М. Величи¬
ны, относящиеся к «душе», относятся к направлениям в М\ не принадлежащим Л4, тогда
как величины, соответствующие «телу», относятся к направлениям внутри Л4.
Ситуация не изменится существенным образом, если взять N генераторов суперсиммет¬
рии £д, ..., £дг. Теперь мы считаем наше n-многообразие М погруженным в (п -f ]V)-mho-
гообразие ЛТ и опять интересуемся многообразием М' только в непосредственной
окрестности (первого порядка) многообразия 7И. Здесь нам требуются N различных
1-форм £i, ..., для обозначения N лишних направлений ^31л0^ в М;, не принадлежа¬
щих М. На мой взгляд, эта картина (созданная разными людьми, включая Абхая Аштекара,
что отражено в главе 32)^31Л11 делает идеи, лежащие в основе суперсимметрии и супер¬
многообразий, гораздо более ясными, нежели обычно применяемые формальные (и доволь¬
но загадочно выглядящие) процедуры. Отметим, что «тело» относится к величинам, полно¬
стью принадлежащим многообразию Л4, а «душа» — к величинам с компонентами в Л4;, не
принадлежащими М; см. рис. 31.26.
Выпишите сумму и произведение двух таких величин для N — 3. Какой вид имеет мультипликативный
обратный элемент, соответствующий такому элементу, при о ф О?
Покажите это. В какую степень надо возвести?

732
Глава 31
б)
Рис. 31.2. Геометрическое описание генераторов суперсимметрии, а) Для одиночного генератора е
наше n-многообразие АЛ рассматривается как гиперповерхность в (п+ 1)-мерном многообразии АЛ',
при этом е есть 1-форма в АЛ', определенная в АЛ (е определяет п-плоскость, касательную к АЛ, как
на рис. 12.7 в § 12.3). Многообразие АЛ' интересует нас лишь «в первом порядке» по АЛ, однако АЛ'
содержит дополнительное измерение, не принадлежащее АЛ. б) В случае генераторов суперсиммет¬
рии si, ..., sn n-многообразие АЛ рассматривается как подмногообразие (n + N)-многообразия АЛ' \
здесь мы опять интересуемся многообразием АЛ' лишь в первом порядке по АЛ. N независимых
1-форм е 1, ..., en соответствуют N лишним направлениям в АЛ', не принадлежащим АЛ
Даже при такой ясной геометрической интерпретации имеются некоторые странности,
связанные с использованием «супералгебры», если потребовать согласования с геометриче¬
ской картиной. Обычная р-форма а в АЛ, где р — нечетное число, будет антикоммутировать
с генератором суперсимметрии е, если в качестве произведения £ на а взять V-произведение.
Однако это не является обычным правилом при стандартном подходе к супералгебре, ко¬
гда е предполагается коммутирующим с а. Это в основном вопрос обозначений, и, если
мы рассматриваем произведения генераторов суперсимметрии с формами, можно формаль¬
но использовать симметричное произведение вместо V-произведения. Это хотя и имеет
(формальный) математический смысл, несколько затемняет представленную здесь «ясную»
геометрическую картину.
При использовании суперсимметрии в «обычных» теориях элементарных частиц обыч¬
но рассматривается простейший случай N = 1. Причина, по-видимому, состоит в том, что
при больших N быстро возрастает число суперпартнеров — каждая элементарная частица
должна иметь 27У-плет «партнеров». Это существенно усложняет проблему эксперименталь¬
ного подтверждения! В любом случае соответствующие супергруппы можно рассматривать
как преобразования, содержащие «внутренние симметрии» (которые соответствуют сим¬
метриям слоев некоторого расслоения В над пространством-временем (§ 15.1)) вместе с
«вращениями», которые относятся к продолжению В на непосредственную окрестность В
внутри некоторого пространства В', у которого на N измерений больше.
31.4.	Пространство-время с увеличенным числом измерений
Теперь, когда мы имеем некоторое представление о том, что такое суперсимметрия
и «супергеометрия», вернемся к супергравитации. Первоначальный ажиотаж вокруг этой
идеи в 1970-х годах был связан с надеждой на то, что, в отличие от стандартной общей те¬
ории относительности Эйнштейна, супергравитация окажется перенормируемой. В теории
эйнштейновского вакуума неперенормируемые расходимости появляются «на двухпетлевом
уровне» (имеются в виду «петли», появляющиеся при разложении по фейнмановским диа¬
граммам, при этом «число петель» соответствует числу обрезаний, необходимых для того,

31.4. Пространство-время с увеличенным числом измерений
733
чтобы свести фейнмановскую диаграмму к «древесной» диаграмме (см. § 26.8, особенно по¬
следний параграф, и рис. 26.8, а также §§ 26.9, 26.10)). Однако при наличии вещества такие
расходимости появляются уже на однопетлевом уровне, что можно считать подлинным бед¬
ствием. В теории супергравитации эти однопетлевые расходимости чудесным образом исче¬
зают для вещества такого типа, который допускает теория, и у многих была надежда, что так
будет при любом числе петель. К сожалению, оказалось не так: в теории супергравитации
на двухпетлевом уровне опять-таки появляются неперенормируемые расходимости 131-121.
В дальнейшем было замечено, что, если увеличить число измерений пространства-вре¬
мени с обычных четырех до одиннадцати, ситуация становится гораздо более обещающей.
Несмотря на это, полностью перенормируемого варианта супергравитации пока получить не
удалось и, как показывает недавно проведенное исследование^31*13^, его и нельзя получить.
Как получается, что физики могут всерьез рассматривать возможность размерности
пространства-времени, отличной от непосредственно воспринимаемых четырех измерений
(одного временного и трех пространственных)? В качестве математического упражнения
такие многомерные штучки смотрятся прекрасно, но нам предлагается физическая теория,
в которой «пространство-время» действительно означает комбинацию реальных простран¬
ства и времени. Как мы увидим в § 31.7, теория струн (как ее сегодня понимают) настаивает
на том, что пространство-время действительно должно иметь более четырех измерений.
В более раннем варианте теории было 26 измерений, но последующие нововведения (ис¬
пользующие идеи суперсимметрии — см. § 31.2) привели к тому, что размерность простран¬
ства-времени была уменьшена до 10.
Прежде чем отбросить эту идею как чистую фантастику, мы должны вспомнить
(см. § 15.1) остроумную схему, предложенную в 1919 году малоизвестным (в то время)
немецким математиком Теодором Калуцей и развитую затем шведским физиком и матема¬
тиком Оскаром Клейном, с которым мы уже встречались в этой главе. Если предположить,
что лишние (сверх четырех) измерения в некотором смысле малы, то мы не сможем непо¬
средственно воспринимать их. Что означает в данном контексте эпитет «малые»? Вспомним
аналогию со «шлангом» на рис. 15.1. Если смотреть с большого расстояния, шланг представ¬
ляется одномерным объектом, но если подойти ближе, мы увидим двумерную поверхность.
Идея состоит в том, что некое существо, для которого Вселенной является такой шланг, не
будет «знать» о существовании лишнего измерения, обертывающего шланг, если физические
размеры этого существа велики по сравнению с длиной окружности шланга. Это относится
и к многомерной «шлангоподобной Вселенной» с 4 + d измерениями, у которой d измерений
«малы» и не воспринимаются намного большим существом, обитающим в этой Вселенной
и замечающим лишь 4 «болыних»измерения (см. рис. 31.3).
Рис. 31.3. Шланговая модель пространства-времени с увеличенным числом измерений типа Калуцы-
Клейна (см. рис. 15.1), в которой измерение вдоль шланга представляет обычное 4-пространство-вре-
мя, а измерение вокруг шланга представляет «малые» (возможно, планковского масштаба) лишние
измерения. Изображено обитающее в этом мире «существо», охватывающее эти «малые» лишние
измерения и потому не знающее об их существовании
Какой степени «малости» следует ожидать в модели Калуцы - Клейна или в современ¬
ных вариантах этой идеи с еще большим числом изменений? Сам Клейн пришел к выводу,
D
Лишние
измерения

734
Глава 31
что «масштаб» малого лишнего измерения («длины окружности шланга») должен быть по¬
рядка планковской длины 10~~35 м. Этот (или несколько больший) масштаб, по-видимому,
наиболее часто выбирается и в таких современных схемах, как супергравитация в многомер¬
ном пространстве и теория струн. Ясно, что для существ вроде нас самих такие масштабы
действительно должны считаться «малыми», и вполне можно ожидать, что столь малые
лишние пространственно-временные измерения не должны восприниматься нами.
В некоторых недавних работах (по теории струн) лишние измерения не предполагаются
малыми, а иногда даже могут достигать «большого» размера — миллиметра в диаметре (или,
возможно, вообще быть неограниченными). Идея состоит в том, что такая схема может про¬
являться в виде модификации закона обратного квадрата для гравитационного притяжения
на таких расстояниях. И действительно, недавно были поставлены весьма тонкие экспери¬
менты, чтобы выяснить, можно ли обнаружить такие отклонения от теории Ньютона [31145.
Пока таких отклонений не обнаружено на расстояниях до половины миллиметра.
Как бы ни относились к таким новым идеям, гипотеза пространства-времени с увели¬
ченным числом измерений на данной стадии наших размышлений имеет статус не более
привлекательный, чем просто «остроумная идея», каковой, безусловно, была и исходная
гипотеза Калуцы - Клейна. Какова бы ни была математическая привлекательность идеи, мы
должны поставить вопрос о том, имеются ли физические основания поверить в такую схему.
В случае первоначальной модели Калуцы - Клейна ее следовало принять как попытку «гео¬
метризации» электромагнетизма. Как мы помним из § 25.1, в начале XX века единственными
известными (и понятыми) силами Природы были гравитационные и электромагнитные си¬
лы. Эйнштейн показал, что гравитацию можно описывать как кривизну 4-мерного простран¬
ства-времени. Поэтому казалась весьма привлекательной и естественной идея попытаться
ввести в такие же геометрические рамки и электромагнетизм. Кроме того, было нечто за¬
гадочное в том, что то же самое «уравнение Эйнштейна для вакуума», а именно условие
исчезновения тензора Риччи (Яаъ = 0; см. § 19.6), применимо и к 5-мерной теории Калуцы-
Клейна в той же мере, что и к 4-мерной общей теории относительности. В четырехмерной
теории это уравнение относится к вакуумному состоянию, то есть к случаю отсутствия всех
физических полей за исключением гравитации. В 5-мерной теории это почти относится
к ситуации, в которой действуют только гравитационные и электромагнитные поля — все
физические поля, известные в то время.
Это «почти» звучит здесь, пожалуй, слишком сильно. Поскольку, что более важно, для
классической модели Калуцы - Клейна существенно наличие симметрии в «малом» измере¬
нии, так что здесь нет бесконечно многих степеней свободы. Посмотрим, почему в против¬
ном случае появляются лишние степени свободы. Вспомним обсуждение в § 16.7, касающее¬
ся «размера» бесконечномерного пространства полей на некотором заданном пространстве.
Для поля, которое можно задать к независимыми свободно выбираемыми компонентами
на g-мерной поверхности начальных данных, число степеней свободы составляет оок°°я.
В стандартной общей теории относительности мы имеем (по некоторым причинам более
3
сложного характера)^31*15] к = 4 и q = 3, так что эта величина оказывается равной оо4°° ,
то же получается и в теории Максвелла. В объединенной теории Эйнштейна - Максвелла
эффективное число компонент, приходящихся на одну точку поверхности начальных дан¬
ных, представляет собой сумму значений для каждого из полей в отдельности, так что
мы имеем 4 + 4 — 8 эффективно независимых компонент в расчете на точку начальной
3-поверхности, поэтому правильным значением числа степеней свободы будет
В 5-мерной теории при условии плоской геометрии (нулевого тензора Риччи, Лаь = 0;
см. § 19.6) поверхность начальных условий четырехмерна (q = 4), при этом оказывается к =
= 10. Это дает для поля число степеней свободы оо10°° , намного большее, чем приведенное

31.5. Первоначальная адронная теория струн
735
выше требуемое значение, не потому, что 10 больше 8 (значение к\ а потому, что 4 больше 3
(значение q). Функций от 4 переменных неизмеримо больше, чем функций от 3 переменных!
В модели Калуцы - Клейна мы снова заменяем 4 на 3, налагая условие непрерывной
симметрии (фактически U(l), см. § 13.9) в малом измерении. Эта симметрия должна пред¬
ставляться некоторым вектором Киллинга (§ 14.7), так что 5-пространство Калуцы - Клейна
есть, по существу, S1-расслоение В над обычным четырехмерным пространств ом-време¬
нем М. Это не слишком далеко от обычного описания электромагнетизма в терминах рас¬
слоений (см. §§ 19.4,15.8). Основное отличие в том, что само расслоение В здесь относится к
лоренцевой (псевдо)метрике с нулевым тензором Риччи вместо метрики пространства-вре¬
мени М\31Л^ Примечательная особенность модели Калуцы - Клейна состоит в том, что
наложение на В условия нулевого тензора Риччи (в дополнение к симметрии U(l)) удиви¬
тельно близко к получению полных уравнений теории Эйнштейна-Максвелла^3117^ на Л4.
Все, что для этого нужно, — это добавить условие, чтобы вектор Киллинга имел постоянную
ненулевую (а фактически отрицательную) норму. Это устраняет нежелательное скалярное
поле, и таким образом получается точная 4-мерная теория Эйнштейна-Максвелла!
Будучи изящной сама по себе, теория Калуцы - Клейна в ее отношении к теории Эйн¬
штейна-Максвелла не дает нам убедительной картины реальности. Это определенно не
создает для физиков стимулов принять ее. Например, суперсимметрия физически более
привлекательна из-за ее несомненной роли в решении проблемы бесконечностей в кванто¬
вой теории поля. Почему же в таком случае теории с увеличенным числом измерений типа
теории Калуцы - Клейна так популярны в современных построениях, имеющих целью более
глубокое проникновение в тайны Природы? Основная причина связана с теорией струн,
которая во всех наиболее развитых вариантах активно использует как суперсимметрию, так
и пространства высокой размерности^31,18!.
31.5.	Первоначальная адронная теория струн
Так что же такое теория струн? И почему она имеет такую власть над столь многими
современными теоретиками? Такое положение вещей опять-таки связано со стремлением
изгнать бесконечности из квантовой теории поля. В этом смысле теория струн продолжает
идеи, представленные в главах 24-26. Имеется, однако, и другая важная историческая мо¬
тивация, связанная с некоторыми странностями в физике адронов. Рассмотрим вначале эту
сторону вопроса.
Исходный вопрос связан с некоторыми соотношениями, относящимися к рассеянию
адронов в физике элементарных частиц. В главе 25 упоминалось, что среди адронов есть
много «частиц», у которых время жизни настолько мало (всего лишь 10 "~23 с), что они
едва ли заслуживают этого названия, и их часто именуют резонансами. Вспомним теперь,
что, согласно правилам квантовой теории поля (§§25.2, 26.6, 26.8), в любом физическом
процессе для получения полной квантовой амплитуды необходимо сложить амплитуды всех
возможных элементарных процессов. Таким образом, необходимо учитывать все возможные
частицы и резонансы. Рассмотрим, например, процесс рассеяния адронов, в котором две ча¬
стицы А и В сталкиваются и, спустя короткое время, превращаются в пару частиц С и D.
Одна из возможностей состоит в том, что частицы А и В объединяются в одну частицу
(резонанс) X, которая почти сразу распадается на частицы С и D. Таких промежуточных ча¬
стиц X, X', X", ... может быть много, и вклад каждой из них должен быть учтен в конечном
результате. Фейнмановские диаграммы для таких процессов показаны на рис. 31.4 а. Воз¬
можен и иной способ такого превращения, когда частицы А и В «обмениваются» частицей
Y, в результате чего А превращается в С, а В — в D. Здесь опять-таки имеется целый список
возможных обменных частиц Y, Y', Y", ..., соответствующие фейнмановские диаграммы
показаны на рис. 31.46. Есть и третье семейство процессов, посредством которых может

736
Глава 31
иметь место рассматриваемое превращение, оно отличается иным способом выбора образу¬
ющихся частиц С и D; фейнмановекие диаграммы для этого случая показаны на рис. 31.4 в.
Существуют и более сложные варианты, в которых превращение происходит с участием
замкнутых петель (рис. 31.4 г), но эти процессы «высокого порядка» пока будем считать
несущественными.
Z или ...
X или...
Рис. 31.4. Диаграммы Фейнмана для рассеяния адронов, при котором две частицы А и В превращаются
в пару С, D. а) В одном семействе таких процессов частицы А и В объединяются, образуя одну части¬
цу (резонанс), которая почти сразу распадается на С и D. Это может происходить с участием многих
возможных промежуточных частиц X, Х;, X", ..., и все они вносят вклад в полную амплитуду, б)
Другое семейство процессов, когда происходит «обмен» частицей Y (или Y7, или Y", или ...), пре¬
вращающий А в С, а В в D, и все такие промежуточные участники вносят свой вклад, в) Аналогичный
«обмен» частицей Z (или Z', или Z", или ...), при котором А теперь превращается в D, а В — в С.
Оказывается, что в низшем порядке варианты а), б), в) эквивалентны и не должны складываться, г)
Другие варианты превращения с участием замкнутых петель
Чтобы получить полную амплитуду для процесса превращения пары (А, В) в пару
(С, D), мы должны сложить все такие возможные вклады, однако довольно удивительным
образом оказалось, что каждый из этих трех вариантов дает один и тот же результат,
и каждый из них выглядит как правильный ответ. Если мы сложим эти три результата,
то получим слишком большую величину. Каким-то образом оказывается, что каждый из
трех наборов фейнмановских диаграмм, представленных на рис. 31.4 а, б, в, будучи про¬
суммированным в отдельности, представляет физически одно и то же! При стандартном
взгляде на фейнмановекие диаграммы такая «дуальность»^119^ кажется непонятной, но
в 1970 году японско-американский физик Йоширо Намбу^31'20!, основываясь на замеча¬
тельной формуле^31,21}, полученной в 1968 году молодым итальянцем Габриэле Венециано,
пришел к выводу, что всё это может иметь смысл, если отдельные адроны не рассмат¬
риваются как точечные частицы, а моделируются струнами. История струны описывается
двумерной поверхностью, так что процессы, описываемые соответственно фейнмановскими
диаграммами на рис. 31.4 а, б, в, г, теперь можно представить «трубками», изображенными
соответственно на рис. 31.5 а, б, в, г. Замечательно, что при таком «струнном» представле¬
нии три процесса а, б, в, которые кажутся различными с точки зрения стандартных фей¬
нмановских диаграмм, теперь оказываются топологически эквивалентными, и их можно
рассматривать как три различных способа описания одного и того же процесса. Таким
образом, «струнное» представление дает возможность придать смысл загадочному факту
физики адронов.
Этот комментарий имеет чисто качественный характер, однако струнное представление
содержит также физическую модель с математическим выводом формулы Венециано. Кроме
того, струнная модель, в которой струны ведут себя подобно тонким упругим лентам, сила
натяжения которых растет пропорционально величине растяжения, позволяет объяснить
другой наблюдаемый факт из физики адронов — прямизну траекторий Редже. Траекто¬
рии Редже — это линии, которые получаются, если для данного класса адронов построить
зависимость спина от квадрата массы. Такие линии с замечательной точностью оказываются

31.5. Первоначальная адронная теория струн
737
а)	б)	в)	г)
Рис. 31.5. «Струнное» представление соответствующих процессов на рис. 31.4 позволяет объяснить
эквивалентность процессов а), б), в), так как они, будучи топологически одним и тем же, могут
быть преобразованы друг в друга. Процессы г) более высокого порядка соответствуют более сложной
топологии, при этом топологический род соответствует числу петель (см. рис. 8.9)
прямыми. Пример этого показан на рис. 31.6. Насколько
я знаю, другого исчерпывающего объяснения этот факт по¬
ка не получил ^31*221.
Более того, струнная модель дает обоснованную на¬
дежду на построение конечной теории адронов. Грубо
говоря, она служит для «сглаживания» (ультрафиолето¬
вых) расходимостей в обычных фейнмановских диаграм¬
мах (§ 26.8). Можно считать, что такие расходимости воз¬
никают из-за вклада малых расстояний, когда точечные ча¬
стицы неограниченно сближаются между собой. Струны
не являются точечными объектами, и это дает надежду на
решение проблемы. Трудности с расходимостями фактиче¬
ски связаны с замкнутыми петлями в обычном формализме
фейнмановских диаграмм. В струнной модели замкнутые петли просто заменяются поверх¬
ностями с топологией высокого порядка, подобными показанному на рис. 31.5 г струнному
варианту рис. 31.4 г. Это должно заменить расходящиеся интегралы, соответствующие фейн-
мановским диаграммам, некоторыми конечными величинами. Более того, одна лишь картина
в струнном представлении заключает в себе много различных фейнмановских диаграмм, что
дает больше шансов на получение полного решения физической задачи, которое будет ко¬
нечным, вместо нефизических частей, которые в отдельности могут быть расходящимися;
предполагается, что эти расходимости компенсируют одна другую. Далее, различные се¬
мейства элементарных частиц могут быть включены в эту картину просто как различные
моды колебаний струн. Наконец, двумерные истории струн в пространстве-времени обла¬
дают замечательным дополнительным свойством — их можно рассматривать как римановы
поверхности, которые, как мы помним из главы 8, имеют необычайно богатый набор гео¬
метрических и аналитических свойств (именно этот факт лежит в основе замечательной
формулы Венециано). Здесь мы попадаем в область комплексной магии, которая представ¬
ляется неотъемлемой частью Природы на квантовом уровне реальности.
Это, несомненно, наиболее изящная математическая картина того, что, возможно, имеет
место на некотором более глубоком уровне физического описания, нежели обычная карти¬
на элементарных частиц. Когда я впервые услыхал о ней (где-то в 1970 году от Леонарда
Саскинда — одного из первых исследователей в этой области), я был поражен красотой и по¬
тенциальной мощью этого собрания идей. Мне показалось, что это нечто совершенно новое,
сочетающее математическое изящество и непосредственную причастность к важной обла¬
сти физики элементарных частиц. Мои собственные интересы в то время лежали в области
теории твисторов (к которой мы подойдем в главе 33), и мне казалось, что я обязательно
должен попытаться установить какую-то связь между тем, чем я занимался, и этими заман¬
чиво звучащими идеями. Теория твисторов имеет дело с комплексными (голоморфными)
структурами, а в теории струн такие структуры определяют физическое поведение благода¬
Рис. 31.6. Прямые «траектории Ре¬
дже» для частиц-резонансов с уве¬
личивающимся спином, представ¬
ленным как функция от квадрата
массы. Этот факт получает объяс¬
нение в модели упругих струн

738
Глава 31
ря активному использованию римановых поверхностей, которые, по существу, представляют
собой комплексные кривыеI31*23].
Примечательно, что недавняя работа Виттена [849], возможно, сможет реализовать
некоторые из этих ранних чаяний. Я вернусь к этим перспективным исследованиям, не
прибегающим к пространству-времени высокой размерности, в §31.18. Однако до сих пор
они не привели к новой исчерпывающей теории струн, так что мои комментарии в следую¬
щих разделах относятся к тому, что можно назвать «общепринятой» теорией струн.
ь
31.6.	На пути к струнной теории мира
Как же выдержали испытание временем эти замечательные исходные идеи спустя более
чем 30 лет после их появления? Подтвердили ли последующие изыскания в этой области
возлагавшиеся на них надежды? На эти вопросы разные люди могут дать совершенно раз¬
личные ответы. Теория струн иногда оказывается эмоционально окрашенной в довольно
сильной степени. Для ее бескомпромиссных приверженцев теория струн (с более поздними
уточнениями) — это подлинная физика XXI века, она представляет собой революцию в фи¬
зическом мышлении, сравнимую (если не превосходящую их) с теми, которые совершили
в свое время общая теория относительности или квантовая механика. Для ее крайних про¬
тивников она до сих пор не достигла, в физическом отношении, абсолютно ничего, и она
имеет мало шансов сыграть сколько-нибудь существенную роль в физике будущего.
Для меня совершенно невозможно пытаться беспристрастно оценить развитие этих
идей, но я постараюсь, по крайней мере, быть по возможности справедливым и обосновывать
свои впечатления. Я должен, как бывало и раньше, официально предупредить читателя, что
многие активно работающие и исключительно одаренные физики-теоретики не разделяют
моих взглядов. Однако я не могу сделать ничего, кроме как изложить положение вещей, как
оно мне представляется.
Поскольку мое мнение о многих сторонах современной теории струн не слишком благо¬
желательное, я должен, по крайней мере, дать читателю возможность выправить возможный
крен. Поэтому я сначала представлю точки зрения двух наиболее влиятельных фигур в этой
области. Майкл Грин^31-24^ из Кембриджского университета:
Когда вы знакомитесь с теорией струн и осознаете, что почти все основные дости¬
жения физики последнего столетия можно получить, и притом весьма изящным
образом, из столь простой отправной точки, — вы понимаете, что перед вами неве¬
роятно мощная теория, единственная в своем роде.
Превосходно сказал Эдвард Виттен из Принстонского института высших исследований^31,25^:
Как было замечено (Даниелем Амати), теория струн — это физика двадцать первого
столетия, случайно попавшая в двадцатый век.
В качестве популярного, отнюдь не критического, обзора теории, изложенного очень доступ¬
но, красноречиво и с энтузиазмом, хотя и без глубокого проникновения в математические
идеи, можно рекомендовать книгу Брайана Грина [318][31-2б1.
Чтобы представить согласованный, хотя и не слишком восторженный взгляд на струн¬
ную теорию, я попробую кратко описать в историческом плане, как повлиял обсуждаемый
предмет на мой собственный образ мышления. При этом я постараюсь изложить не только
этапы развития теории, но и мою реакцию на это развитие. Теорию струн трудно оценить
беспристрастно, потому что она получает поддержку и выбирает направления своего раз¬
вития почти исключительно из эстетических соображений, руководимых математическими
предпочтениями. Я считаю необходимым проследить каждый виток теории и показать, что

31.6. НА ПУТИ К СТРУННОЙ ТЕОРИИ МИРА
739
почти всякий раз такой виток уводил нас все дальше от экспериментально установленных
фактов. Хотя теория струн берет начало от экспериментально наблюдаемых особенностей
физики адронов, она затем круто повернула от этих истоков и впоследствии была довольно
слабо связана с данными наблюдений, касающихся физического мира.
Представим себе туриста, который пытается отыскать некоторое здание в большом го¬
роде, совершенно ему незнакомом. Нет ни названий улиц (по крайней мере таких, которые
что-то говорили бы нашему туристу), ни карты города, и по затянутому тучами небу нельзя
определить, где север, где юг. Временами попадаются развилки дорог. Должен ли турист
поворачивать направо или налево или, возможно, стараться держаться той стороны, которая
кажется ему более привлекательной? Улицы часто поворачивают не под прямым углом, и до¬
рога не слишком прямая. Порою дорога оканчивается тупиком, и приходится возвращаться
назад и делать поворот в другую сторону. Иногда при этом на дороге могут оказаться следы,
которых раньше вроде бы не было. Вокруг нет ни души, так что спросить дорогу не у кого,
или же турист не понимает здешнего языка. По крайней мере, турист знает, что здание,
которое он ищет, отличается особым изяществом, и его окружает прекрасный сад. Именно
это в конечном счете и есть главная причина, из-за которой стоит его искать. И некоторые
улицы, выбираемые туристом, эстетически привлекательнее других, с более изысканной ар¬
хитектурой и дворами, украшенными великолепными кустами и цветами (которые, впрочем,
иногда при ближайшем рассмотрении могут оказаться пластиковыми). Много раз туристу
приходится делать выбор, и всякий раз он руководствуется лишь эстетической привлека¬
тельностью местности, а также некоторым своим ощущением общей согласованности стиля
или некоторого воображаемого плана города в целом.
Чтобы аналогия была более полной, предположим, что этот турист — вы, но вы нахо¬
дитесь в составе группы, ведомой экскурсоводом — человеком очень умным, высокообра¬
зованным, обладающим тонким вкусом. Беда лишь в том, что ваш гид ничего не знает об
этом городе и никогда не сталкивался со здешним языком. Вы можете считать, что у гида
эстетическая интуиция лучше, чем у вас, и он способен в таких случаях принимать решения
быстрее, чем вы. Время от времени эстетическое чутье гида позволяет ему отыскать зда¬
ние, отличающееся особым изяществом. Однако критерий выбора при этом, по существу, не
отличается от того, которым руководствовались вы сами. Если вы следуете вместе с груп¬
пой, то у вас по крайней мере есть собеседники, с которыми можно обсуждать особенности
окружающей вас архитектуры и которые могут принять участие в ваших поисках. В этом
случае, даже если вы не ожидаете найти искомую цель, вам может доставить удовольствие
сам процесс поисков. Возможно, однако, что вы предпочтете действовать в одиночку, по¬
скольку стали сомневаться, что ваш гид знает, как найти вашу цель, лучше, чем вы сами.
Каждый последующий выбор направления поворота на пути следования — это бросание
жребия, и при частой смене направлений вам, возможно, покажется более обещающим не
тот поворот, который выорал ваш гид...
Разумеется, в предыдущих главах мы видели примеры того, как великие физики про¬
являли чудеса проницательности, причем часто их озарения были сугубо математического
характера. В качестве одного из наиболее впечатляющих примеров следует, несомненно,
назвать открытие Дираком уравнения для электрона (§ 24.7). Хотя в эстетическом отноше¬
нии это был действительно шаг в неведомое, в основе его лежало тонкое математическое
понимание экспериментальных основ квантовой механики. Другой подобный прорыв — это
предсказание Дираком античастицы электрона. Но оно было сделано с большой осторожно¬
стью и в дальнейшем было подтверждено наблюдениями. Общая теория относительности
Эйнштейна также частично обусловлена эстетическими математическими соображениями,
и сила этой теории в огромной степени связана с ее замечательной математической струк¬
турой. Когда Эйнштейн впервые сформулировал свою теорию, на нее еще не было явных
запросов со стороны эксперимента и наблюдений. Тем не менее вряд ли можно сказать, что

740
Глава 31
Эйнштейн руководствовался лишь соображениями математической эстетики. Им вело его
понимание физики, в первую очередь уверенность, что в основе теории гравитации должен
лежать принцип эквивалентности (§ 17.4).
В противоположность этому, при создании теории струн движущей силой были почти
исключительно математические соображения. Я должен сразу сказать, что само по себе
это не так уж плохо. Все успешные физические теории имели мощный математический
фундамент. Математическая согласованность должна быть обязательным качеством всякой
физической теории, чтобы она вообще имела какой-то смысл. И коль скоро установлены
определенные математические рамки, дальнейшее строгое математическое развитие в этих
рамках может сыграть важнейшую роль в изучении физического мира. (Замечательным
примером этого может служить развитие классической физики в рамках лагранжева и га¬
мильтонова формализмов, описанное в главе 20.) Возникают, однако, трудности, когда для
устранения противоречий необходимо внести изменения в существующую теорию, и спо¬
соб внесения изменений зависит от математических познаний и эстетических предпочтений
конкретного теоретика. Очень часто таким изменением является идея (возможно, даже «бле¬
стящая идея»), которая также имеет дефект в виде математической несогласованности, хотя,
вероятно, и не тот, которым обладает теория, требующая замены. Тогда понадобятся даль¬
нейшие изменения, и так далее. Если таких оказывается слишком много, то шанс каждый
раз угадывать правильно становится исключительно малым.
31.7.	Побудительные мотивы введения лишних измерений
пространства-времени в теории струн
Изначальным противоречием в теории струн было появление серьезной аномалии. На¬
помним (§ 30.2), что аномалии возникают, когда классические правила коммутации, выра¬
жающие классическую симметрию или свойство инвариантности, не могут быть полностью
реализованы квантовыми коммутаторами, так что квантовая теория утрачивает некоторое
качество классической теории, которое считалось весьма существенным. В случае теории
струн такая аномалия касается инвариантности параметризации, используемой при описа¬
нии струны. Наличие аномалии приводит к эффектам, которые трактуются как катастрофа.
Было обнаружено, однако[31,27^, что увеличение числа измерений пространства-времени с 4
до 26 приводит к исчезновению аномалииI31*28]. Таким образом, теория струн согласуется с
квантовой механикой только в пространстве-времени с 26 измерениями.
Моя собственная реакция на это была примерно следующей: «Здесь должен быть и
другой путь», хотя я никогда не занимался этой проблемой в достаточной мере, чтобы оце¬
нить мощь аргументации, стоящей за этим «26-мерным» заключением. Я подозреваю, что
подобным образом реагировали и многие другие, потому что теперь теория теряла изряд¬
ную долю своей былой популярности. Но у меня были и свои дополнительные мотивы
неприятия 26-мерной модели Вселенной, идущие от теории твисторов. Как мы увидим
в §§33.2, 33.4, 33.10, имеются существенные основания для «твисторного» взгляда, соглас¬
но которому непосредственно наблюдаемыми измерениями пространства-времени являются
одно временное и три пространственных измерения (т. е. оно имеет «14-3 измерений»).
Помимо вопроса, что делать с этими лишними измерениями (который ранее уже воз¬
никал в связи с гипотезой Калуцы-Клейна), эта сравнительно просто выглядящая струнная
модель адронов привела и к другим трудностям, в частности, к тахионному поведению (рас¬
пространению быстрее света). Кроме того, нарастающий успех стандартной модели, описан¬
ной в главе 25, заставил физиков меньше, чем прежде, интересоваться такими «далекими
от жизни» материями, как струнные модели. Упомянутые выше загадки физики адронов,
с которых Венециано, Намбу и другие начали свой путь к струнам, нашли альтернативное
(частичное) объяснение в кварк-глюонной картине квантовой хромодинамики.

31.8. Теория струн как квантовая гравитация?
741
«Точечная» природа составных частей адронов начала проявляться в экспериментах,
и это согласовалось с кварковой картиной стандартной модели, но не с тогдашней струн¬
ной моделью. Типичный размер петли струны должен соответствовать величине струнной
константы связи, и для исходных адронных струн (при натяжении струны, согласующемся
с величиной константы связи сильного взаимодействия) это дает величину порядка 10"15
м. В масштабе протона это вряд ли можно считать «точкой», поскольку указанная величина
сравнима с «размером» самого протона.
После почти десятилетия слабого интереса к теории струн в ее развитии произошел
скачок, который иногда называют «первой суперструнной революцией». В 1984 году Майкл
Грин и Джон Шварц предложили схему (в духе более раннего предложения Шварца и Джо-
эля Шерка), вводившую в теорию струн суперсимметрию (чтобы дать нам «суперструны»
вместо просто «струн»), из-за чего размерность пространства-времени[31-29] с 26 сокраща¬
лась до 10. При этом устранялась также упомянутая «тахионная проблема». Более того,
благодаря радикальному изменению масштаба и природы натяжения струн, теорию струн
теперь следовало рассматривать в первую очередь как теорию квантовой гравитации, а не
как теорию сильного взаимодействия. Уже было известно, что должна существовать безмас-
совая частица (с соответствующим полем) со спином 2, возникающая как мода колебаний
струн. Это приводило к затруднениям в первоначальном «адронном» варианте теории струн,
поскольку таких адронов в природе нет. Но в новой теории струн с ее гораздо большей ве¬
личиной натяжения струн эту безмассовую частицу можно отождествить с гравитацией.
Теперь типичный размер петли струны получается порядка (гравитационной) планковской
длины, т. е. на 20 порядков меньше, чем раньше, и в адронных масштабах, безусловно, может
считаться точечным.
Я должен упомянуть еще одно отличие (технического характера) в природе натяжения
струн, которое вносится новыми струнами «гравитационного масштаба» (оно обычно не от¬
мечается в популярных обзорах). Исходные адронные струны напоминали резиновые ленты,
у которых сила натяжения растет пропорционально длине, на которую их растягивают[31.30] ^
Однако новые суперструны гравитационного масштаба имеют постоянное натяжение Не/а'
независимо от степени их растяжения; величина а' (мера площади) очень мала и называется
струнной постоянной. В этом отношении первоначальная адронная струна гораздо больше
похожа на объект, привычный для обычной физики, в которой имеет смысл ее классический
вариант. (Классический вариант новой суперструны с ее постоянным натяжением должен
почти мгновенно сокращаться до сингулярности нулевого размера!)
31.8.	Теория струн как квантовая гравитация?
Такое продвижение вперед полностью изменило общее отношение к теории струн, и
она быстро завоевала популярность. Часто делались заявления, утверждающие, что теория
струн позволяет построить полностью согласованную теорию квантовой гравитации, в кото¬
рой на смену неперенормируемой стандартной общей теории относительности (см. § 31.1)
придет полностью конечная струнная теорияt31-31!. Хотя некоторые сторонники теории струн
могли признать, под давлением аргументов, что не все заявления о конечной теории полно¬
стью обоснованы, этому не придавалось большого значения. Как заметил один выдающийся
физик-теоретик из числа таких сторонников^31,32^:
Конечный характер теории струн настолько очевиден, что, если бы кто-то опубли¬
ковал доказательство этого, я не стал бы его читать.
Более того, теоретики, занимающиеся теорией струн, пытались представить струнную тео¬
рию квантовой гравитации как едва ли не единственное, чем стоит заниматься; примером

742
Глава 31
может служить высказывание Джозефа Полчинского [643] относительно подходов к кванто¬
вой гравитации, отличных от теории струн:
... Здесь нет альтернативы... Все хорошие идеи — это часть теории струн.
Я подозреваю, что именно убеждающий характер ранних заявлений относительно конечного
характера теории (см., однако, §31.13) послужил движущей силой теории. В самом деле,
если бы провозглашаемое открытие — «квантовая гравитация», устанавливающая связь меж¬
ду двумя великими революциями в физике XX века, — действительно подтвердилось, это
сделало бы теорию струн не только главным интеллектуальным достижением столетия, но
и основой будущего прогресса фундаментальной физики.
Мне представляется, что даже многие из сегодняшних теоретиков — сторонников те¬
ории струн могли бы счесть чрезмерно оптимистическими заявления, сделанные в 1980-х
годах, о том, что теория струн «решила» проблему квантовой гравитации. Теперь они могли
бы придерживаться более трезвой позиции, нежели раньше, поскольку теория струн далеко
продвинулась и заметно отличается от схемы 1984 года. Тем не менее они, вероятно, счи¬
тают, что теория струн 1984 года была, как минимум, наиболее заметным шагом на пути
к квантовой теории гравитации.
Каким было мое отношение к этим заявлениям? Боюсь, что весьма отрицательным, как
и у большинства моих близких коллег. Несомненно, что причина такого отношения в зна¬
чительной мере была обусловлена различным культурным фоном у меня и моих коллег, чьи
взгляды сформировались на основе глубокого интереса к общей теории относительности
Эйнштейна, и у тех, кто пришел со стороны квантовой теории поля. Главным следствием
этой разницы во взглядах было то, что мы совершенно по-разному понимали те центральные
проблемы, которые необходимо решить для объединения квантовой теории с теорией гра¬
витации. Пришедшие из квантовой теории поля видели главную цель в перенормируемости
(или, точнее, конечности) теории. Мы же, пришедшие со стороны теории относительности,
такой проблемой считали глубокий концептуальный конфликт между принципами кванто¬
вой механики и общей теории относительности, и именно в его разрешении мы видели путь
к новой физике будущего. Наша негативная реакция на тогдашние громкие заявления сто¬
ронников теории струн возникала не из-за каких-то конкретных деталей или общего неверия
(хотя было, конечно, и это), а из-за того, что сами проблемы, которые мы считали централь¬
ными во всей проблеме квантовой гравитации, казалось, вовсе не замечались теоретиками,
занимавшимися струнами!
Некоторых из этих вопросов мы касалась в §30.11 (и еще коснемся в § 33.2). Следует
отметить, однако, что вопросы, поднятые в этих разделах, лишь скользят по поверхности
того фундаментального конфликта, который возникает при столкновении принципа общей
ковариантности^31'33^ с квантовой теорией поля (§ 19.6). Имеется также фундаментальный
вопрос о том, на что похожа «квантовая геометрия пространства-времени». Теория струн
оперирует просто с гладким «классическим» фоном пространства-времени, на который при¬
сутствие струны даже не оказывает непосредственного влияния, поскольку невозбужденная
струна сама по себе не переносит энергии и не приводит к «искривлению» фонового про¬
странства-времени. Большая часть физиков, занимающихся общей теорией относительности,
ожидает, что истинная «квантовая геометрия» внесет некоторые элементы дискретности или,
по крайней мере, будет коренным образом отличаться от картины классического гладкого
многообразия.
С этими глубокими проблемами мы встретимся более непосредственно в следующих
двух главах (и там же познакомимся с некоторыми подходами к их решению). В частности,
«петли», с которыми мы столкнемся в следующей главе (§ 32.4), хотя внешне и напоминают
струны, совершенно отличны от них в численном отношении. В частности, присутствие та¬
ких петель сильно влияет на геометрию пространства-времени (фактически создает ее), при

31.9. Динамика струн
743
этом пространственная метрика полностью концентрируется вокруг них, обращаясь в нуль
в остальных местах. В то же время в теории струн гладкое пространство-время присутствует
всегда в качестве фона для струн, и ограничения на геометрию его метрики возникают лишь
вследствие косвенного влияния струн, с которым мы познакомимся в недалеком будущем
(в § 31.9). Пока же вопрос о том, рассматривает ли теория струн должным образом важные
стороны проблемы квантовой гравитации, мы отложим в сторону. Вместо этого рассмотрим
утверждения теоретиков, занимающихся струнами, что они имеют конечную квантовую те¬
орию гравитации. Так ли это? Я собираюсь посвятить этому вопросу остаток этого раздела
и пять следующих.
Здесь, вероятно, играет важную роль терминология. Специалисты по струнам заявляют,
что у них есть «квантовая теория гравитации», а не квантовая общая теория относительности
или квантовый аналог теории Эйнштейна. Что они понимают под «гравитацией», если не
блестяще подтвержденную эйнштейновскую общую теорию относительности? Напомним,
что пространство-время теории струн теперь 10-мерно (или, как мы вскоре увидим (§31.14),
приблизительно 10-мерно, но пока это может не волновать вас!). Что такое «гравитация»
в 10 измерениях? Да, тензорный анализ в десяти измерениях работает так же хорошо,
как и в четырех (см. §§ 14.4, 14.8), так что мы можем, как и раньше, построить тензор
Риччи Rab. Как мы видели (§ 19.6), в обычной эйнштейновской теории гравитации ваку¬
ум описывается нулевым тензором Риччи, поэтому можно предположить, что «уравнение
гравитационного вакуума» в теории струн будет иметь такой же вид
Rab — 0>
только теперь мы находимся в 10 измерениях. Можно также ожидать, по аналогии с теорией
Калуцы - Клейна, где «5-вакуум» включает в себя как гравитацию, так и электромагнетизм,
что это уравнение в 10 измерениях, т. е. «10-вакуум», также вбирает в себя, помимо грави¬
тации, все негравитационные поля.
Это есть то, что имеют в виду «струнные» теоретики (хотя бы приближенно). Несколь¬
ко более точно: они рассматривают нулевое значение тензора Риччи лишь как первый член
бесконечного ряда по степеням струнной постоянной а'; следующие члены дают нам «кван¬
товые поправки» к уравнению вакуума. (Коэффициент при (а')г может содержать высшие
производные от тензоров кривизны и полиномы, составленные из таких тензоров.) Более то¬
го, вдобавок к метрике на 10-мерном пространстве-времени здесь могут возникать и другие
поля. Одним из них является антисимметричное тензорное поле, появляется также ска¬
лярное поле, именуемое дилатоном[3L34i (оно связано с установлением общего масштаба),
и это довольно схоже с (нежелательным) скалярным полем в первоначальной теории Калу¬
цы-Клейна. (Напомним, что этот скаляр устраняется путем нормировки вектора Киллинга;
см. предпоследний абзац § 31.4.) Дилатон встретится нам и в дальнейшем (см. § 31.15). На¬
помним, что струнная постоянная очень мала. В настоящее время ее значение выбирается
чуть большим квадрата планковской длины (а’ есть очень малая площадь):
ol« 10-68 м2.
Таким образом, нулевое значение тензора Риччи для 10-мерной пространственно-временной
метрики можно рассматривать как отличное приближение.
31.9.	Динамика струн
Читатель может удивиться, откуда берутся все эти утверждения относительно кривизны
пространства-времени, тогда как в теории струн фигурируют маленькие струны, действую¬
щие в некотором фоновом пространстве-времени (хотя и с 9 пространственными измерения¬

744
Глава 31
ми). Фактически до сих пор не было ничего сказано относительно уравнений, описывающих
динамику струн. Теперь займемся этим.
Как и в обычной теории поля, здесь имеется лагранжиан (§§20.5, 20.6, 26.6), опре¬
деляемый для струн как произведение l/2af на площадь 2-поверхности — следа струны
в пространстве-времени (.мирового листа, описывающего историю струны). Метрика на
мировом листе согласуется с метрикой, диктуемой пространством-временем; в классиче¬
ской физике динамика мирового листа была бы подобна динамике некоторой «мыльной
пленки», или «минимальной поверхности» (с соответствующей сигнатурой метрики) на за¬
данном пространственно-временном фоне. На фон в этом случае не налагается никаких
ограничений. Струна просто совершает разные движения в соответствии с этой динамикой.
Однако в квантовой механике встает во весь рост проблема аномалии, и оказывается, что
недостаточно даже 10 измерений фона с суперсимметрией, и необходимо налагать упомяну¬
тые условия на кривизну 10-пространства, чтобы обеспечить условия согласования метрики
фона для квантовых струн.
В дополнение к этому условию согласования типа уравнения Эйнштейна напомним, что
«низшая мода возбуждений» замкнутой струны, упомянутая в §31.7, считается описываю¬
щей безмассовую частицу со спином 2. Такое значение спина соответствует квадрупольной
структуре моды колебаний (£ = 2) (см. §§22.11, 32.2), а отсутствие массы связано с тем,
что это есть низшая мода очень «жесткой» струны. Хотя эта мода представляла серьезную
проблему для первоначальных адронных струн, в новом, гравитационном, аспекте она, на¬
против, встречается с энтузиазмом, поскольку в обычной (4-мерной) физике гравитон (квант
гравитационного поля) должен быть безмассовой частицей со спином 2. При стандартном
анализе устойчивости этот результат получается путем рассмотрения возмущений метриче¬
ского поля, описываемых симметричным тензором hab, который добавляет к метрическому
тензору даъ бесконечно малое приращение, так что получается даь Л-еЬ,аъ> где в — бесконечно
малая величина; см. также § 32.2. В новой теории струн в связи с упомянутым требованием
согласованности типа уравнения Эйнштейна (но не в четырех, а в десяти измерениях) и этой
«гравитоноподобной» модой возбуждений струны возникла точка зрения, согласно которой
«теория струн включает в себя теорию гравитации». Эдвард Виттен [847] заметил:
Теория струн обладает замечательным свойством: она предсказывает гравитацию.
И далее Виттен продолжает'I31*35):
Тот факт, что гравитация появляется как следствие теории струн, есть одно из
величайших теоретических открытий, сделанных когда-либо.
Следует подчеркнуть, однако, что, помимо вопроса о размерности, подход, основанный на
теории струн, ограничен (пока почти всегда) теорией возмущений, выраженной в виде сте¬
пенного ряда (например, по упомянутой выше величине е, но в большинстве расчетов по
теории струн используется разложение по струнной постоянной 1/2а'). Это обстоятель¬
ство рассматривается как серьезное ограничение большинством специалистов по теории
относительности, которые не считают вышеприведенные соображения достаточными для
построения теории, построенной на основе таких же глубоких принципов, как и общая
теория относительности Эйнштейна.
Одна из версий «струнной философии», о которой мне довелось слышать, состоит
в том, что мы должны рассматривать физику как «реальную» двумерную квантовую теорию
поля, при этом геометрическое понятие 10-мерного пространства-времени оказывается вто¬
ричным по отношению к более примитивной «реальности» самого двумерного струнного
мирового листа. Всё следует описывать в терминах «возбуждений струн», которые надле¬
жит рассматривать просто как функции от двух координат, определенные на мировом листе.
Эти возбуждения «ощущают» десять пространственно-временных измерений, однако всё
выглядит как некоторое «поле на 2-мерном листе».

31.10. Почему мы не видим дополнительных пространственных измерений?
745
Мне трудно принять теорию, которая предлагает описывать гравитацию, предполагая
наличие динамических степеней свободы у геометрии пространства-времени. Напомним
(§ 16.7, а также § § 31.4,31.10-31.12,31.15-31.17), что на пространстве более высокой размер¬
ности можно определить гораздо больше функций или полей, чем на пространстве меньшей
размерности, безотносительно к числу компонент, которое эта функция (или поле) может
иметь в каждой точке, при условии, что число компонент конечно. Кроме того, для обыч¬
ного понятия «возбуждений струны» это число компонент в данной точке должно быть
конечным (поскольку каждая точка мирового листа может смещаться лишь в конечном чис¬
ле направлений окружающего пространства). Такая «струнная философия» представляется
глубоко ошибочным взглядом на вещи. Хотя я сомневаюсь, что ее придерживается много
«струнных» теоретиков, все же тот факт, что некоторые из них готовы принять подобную
точку зрения, иллюстрирует, вероятно, бесцеремонное обращение этих теоретиков с размер¬
ностью пространства-времени. Четырехмерно сть нашего наблюдаемого пространства-вре¬
мени, понимаемая, вероятно, как «низкоэнергетический эффект», часто считается фактом,
не заслуживающим особого внимания!
В любом (даже 10-мерном) случае «эйнтшейновское уравнение для вакуума» в теории
струн рассматривается просто как следствие согласованности двумерного мирового листа.
И получается, что условие нулевого тензора Риччи должно продолжать выполняться даже в
тех областях пространства-времени, где отсутствует сам мировой лист теории струн! Если
бы квантовая теория действительно описывала квантованную динамику соответствующей
классической системы, определяемой
фоновым 9-пространством, содержащим движущуюся струну,
то условие согласованности, налагаемое на кривизну фона, должно выполняться лишь там,
где расположена струна. Поэтому мы должны принять, что квантуется не эта классическая
система. Фактически теория струн, хотя и претендующая быть теорией гравитации, реально
пока не пришла к соглашению с проблемой описания динамических степеней свободы
пространственно-временной метрики. Пространство-время просто служит фиксированным
фоном, на который налагаются ограничения, позволяющие самим струнам иметь полную
свободу.
31.10.	Почему мы не видим дополнительных пространственных
измерений?
Если мы всерьез собираемся рассмотреть полную динамику 10-мерного простран¬
ства-времени, нам придется столкнуться с противоположной проблемой — как свести огром¬
ное число дополнительных функциональных степеней свободы в 10-мерном пространстве
к тому, что свойственно обычной физической теории в четырех пространственно-временных
измерениях. Условие нулевого тензора Риччи в десяти измерениях допускает функциональ¬
ную свободу оо70э° (см. § 16.7), а это неизмеримо больше, чем просто ogNoc , что мы имеем
в обычной теории поля в 4-пространстве с N независимыми компонентами в каждой точке
(§§ 16.7, 31.4). (В 10-мерной теории с нулевым тензором Риччи имеется 70 независимых
функций в качестве свободных данных на 9-мерной поверхности начальных условий]31,361)
Дополнительная огромная величина появляется из-за того, что 9 больше 3. По сравне¬
нию с этим относительная величина чисел 70 и N не дает заметного вклада в столь рез¬
кое увеличение функциональной свободы ^31-37Е Обычная классическая теория в 10-мерном
пространстве-времени (без ограничения, обусловленного симметрией, которое описывается
вектором Киллинга первоначальной теории Калуцы - Клейна; см. §31.4) определенно ока¬
зывается в резком конфликте с нашей наблюдаемой Вселенной из-за такого впечатляющего
избытка функциональной свободы. Мы вернемся к этому вопросу в §§31.12, 31.16.

746
Глава 31
Почему такая избыточная функциональная свобода не особенно беспокоит «струнных»
теоретиков? Это, по-видимому, частично связано с теми значительными надеждами, кото¬
рые они возлагают на то, что в теории струн, квантованной должным образом, могут по¬
явиться дополнительные пространственно-временные ограничения, налагаемые условиями
согласования для квантованных струн, и это приведет к эффективному уменьшению функци¬
ональной свободы струн. Мы кратко обсудим эти надежды в §31.16. Но главный аргумент,
который обычно звучит, связан с ожиданием, что, поскольку шесть «лишних» измерений
исключительно «малы» (имеют, например, планковский масштаб 10-35 м), при энергиях, до¬
ступных сегодня в физическом мире, квантово-механические соображения должны прийти
на помощь и «ликвидировать» степени свободы, связанные с лишними пространственными
измерениями.
Как это все действует? Как уже отмечалось, почти все исследования на основе теории
струн проведены в рамках теории возмущений, где рассматриваются лишь малые откло¬
нения от некоторой исходной базовой модели. В данном случае мы должны рассмотреть
базовое пространство-время в виде произведения М х У обычного 4-пространства Мин¬
ковского на некоторое компактное пространственноподобное риманово 6-пространство У,
полный «размер» которого очень мал, порядка планковского масштаба 10-35 м. Мы должны
рассмотреть малые отклонения от М х У.
Прежде всего, нам следует иметь более яс¬
ное представление о том, что представляет собой
«произведение многообразий» Ах В, в котором га-
пространетво А и гг-пространство В предполага-
ются (псевдо)римановыми многообразиями. Напо¬
мним (см. §15.2 и рис. 15.3 а), что точками про¬
странства А х В служат пары (а, 6), в которых а
принадлежит пространству А, а b — простран¬
ству В, так что размерность пространства А х В
равна га + п (см. упражнение 15.1). Как мы долж¬
ны определить (псевдо)риманову метрику на Ах В?
Это должна быть «прямая сумма» метрик на А
и на В. Для А х В можно воспользоваться ло¬
кальными координатами (ж1, ..., хт, у1, ..., уп),
где (ж1, ..., хт) и (у1, ..., уп) — локальные коор¬
динаты соответственно для А и В. Тогда компонен¬
ты метрического тензора gу для Ах В будут иметь
«блочно-диагональную форму» (подобную показан-
Рис. 31.7. Произведение многообра¬
зий А х В (см. рис. 15.3 а в § 15.2) для
двух (псевдо)римановых пространств А
и В само является (псевдо)римановым.
Если А и В удовлетворяют условию ну¬
левого тензора Риччи, то этому условию
удовлетворяет и Ах В
ной в § 13.7 форме для матриц полностью приводи¬
мого представления), описывающую «прямую сум¬
му» компонент метрических тензоров для А и В\ квадрат метрического расстояния в про¬
странстве Ах В есть сумма таковых для пространств Либпо отдельности (рис. 31.7).
Ключевой факт, существенный для дальнейшего (см. §31.14), состоит в том, что если
метрика А и метрика В обе удовлетворяют условию нулевого тензора Риччи (см. § 19.6), то
«прямая сумма» метрик, соответствующая пространству Ах В, также удовлетворяет этому
условию . Пространство У в нашем произведении М х У выбирается удовлетворяющим
условию нулевого тензора Риччи, этому же условию определенно удовлетворяет плоское
пространство М; следовательно, тем же свойством обладает и произведение ШхУ, что нам
и потребуется.
Чтобы получить полный пространственный объем порядка планковского масштаба (или,
возможно, немного больше), пространство У должно быть компактным (смысл понятия
Почему? (.Подсказка: посмотрите явный вид выражений в упражнениях 14.26 и 14.27 и в § 14.7.)

31.10. Почему мы не видим дополнительных пространственных измерений?
747
компактности объясняется в § 12.6, рис. 12.13). Как можно описать отклонения от ис¬
ходного пространства М х У1 Они задаются (тензорными) полями на этом пространстве
вроде Наь из §31.9, которые дают нам бесконечно малые изменения метрики простран¬
ства МхУ.
Поля на пространстве М х 3^ удобно изучать как задачу с начальными условиями. Пред-
-to	"1
ставим пространство М в виде М = Е х Е , где евклидово 1-пространство ТЕ относится к
временной координате t9 а евклидово 3-пространство Е3 — к пространственным координа-
о
там. Будем анализировать эти поля как нормальные колебания на пространстве Е х У; см.
рис. 31.8 (понятие «нормальных колебаний» в классической физике дается в §20.3, кван¬
товый аспект этого понятия объясняется в §§22.11, 22.13). Как выглядят эти нормальные
Q
колебания? Поскольку Е х У имеет структуру произведения пространств, можно предста¬
вить эти колебательные моды как обычное произведение моды на Е3 и моды на у. Моды
на Е3 — это просто собственные состояния импульса (§21.11), образующие непрерывное се¬
мейство. Что касается нормальных колебаний на пространстве У, то из-за его компактности
они должны образовывать дискретное семейство состояний, каждое из которых характе¬
ризуется некоторым конечным набором собственных значений. (Вспомним обсуждение в
П
конце § 22.13.) Как «возбудить» одну из этих мод, чтобы простая геометрия Е х У превра¬
тилась во что-то другое?
У
Рис. 31.8. Возмущения на пространстве Е3 х У (для уравнения Лапласа) представляют произведения
нормальных мод на Е3 и нормальных мод на У
Обычное утверждение «струнных» теоретиков, что мы можем пренебречь возмущени¬
ями на У, по крайней мере в нынешнюю космологическую эпоху, покоится на ожидании,
что для возбуждения любой из нормальных мод 3^ потребуется огромная энергия, за исклю¬
чением некоторого набора мод с нулевой энергией (в дальнейшем (§31.14) они окажутся
важными для нас), которые мы пока не рассматриваем. Почему эта энергия ожидается столь
большой? Это связано с крайне малым масштабом пространства У. «Стоячей волне» на У
должны соответствовать очень малая длина волны, сравнимая с планковской длиной по¬
рядка 1СГ35 м, и период колебаний, сравнимый с планковским временем порядка 10~43 с.
Энергия, необходимая для возбуждения такой моды, должна быть порядка планковской энер¬
гии ~ 1012 джоулей, что примерно на двадцать порядков больше энергий, определяющих
взаимодействие обычных элементарных частиц! В соответствии с этим утверждается, что
моды, влияющие на геометрию У, остаются невозбужденными в любых процессах с элемен¬
тарными частицами, которые мы можем наблюдать сегодня. Согласно этой картине, на самых
ранних стадиях развития Вселенной шесть из ее измерений образовали конфигурацию У
приблизительно планковского масштаба, а три оставшихся пространственных измерения
расширились в огромной степени, образовав почти плоскую картину 3-мерной Вселенной
в соответствии с данными современной космологии. При этом пространства У остаются

748
Глава 31
в основном невозмущенными, начиная со времени существования Вселенной, измеряемого
планковским масштабом.
Рассмотрим эту аргументацию поближе. Для упрощения изложения ограничимся ситу¬
ацией, в которой, как и в первоначальной теории Калуцы - Клейна из §31.4 и в аналогии
со шлангом (рис. 15.1), пространство У есть просто окружность S1, которой мы припи¬
шем очень малый радиус р. На S1 можно выбрать вещественную координату 9 (при этом 9
отождествляется с 9 4- 2л), так что величина р9 будет мерой расстояния вдоль окружно¬
сти. Собственными модами на У служат просто величины егпв, где п — целое число; они
представляют собой компоненты Фурье, описанные в §9.2. На Е3 можно выбрать обыч¬
ные декартовы координаты (х, у, z). Напомним (§ 22.11), что один из способов определения
«мод» состоит в отыскании собственных состояний соответствующего оператора Лапласа.
В данном контексте это можно рассматривать как некоторое приближение (или, если угодно,
«модель»). Точнее говоря, нам следовало бы заняться собственными состояниями гамиль¬
тониана Н, описывающего эволюцию геометрии. Для 5-пространств с нулевым тензором
Риччи (для требуемых возмущений пространства М х S1) нам необходима соответствующая
гамильтонова формулировка пятимерной общей теории относительности, которая слишком
сложна. Однако главным членом здесь будет именно лапласиан, и для нашего обсуждения
этого вполне достаточно.
Мы уже встречались с 2-мерным лапласианом V2 — д2/дх2 + д2/ду2 в § 10.5. Здесь
нам необходимо провести обобщение на случай четырех измерений, однако метрика нашего
пространства Е3 х S1 по-прежнему остается плоской, так что нам не потребуется более
сложное выражение, вроде того, что фигурировало в §22.11. Всё, что нам нужно, — это
увеличить число переменных до четырех, так что мы можем написать лапласиан в виде*
V2=al+ai + J9i + 1
дх2	ду2	dz2 р2 д92 ’
где четвертой координатой служит величина рв, необходимая для S1. Чтобы найти наши
«моды», необходимо отыскать собственные состояния оператора V2. Точнее, мы должны
1	Q	1	О
провести анализ мод для части S пространства Е х S , считая часть Е обычным полем.
В соответствии с этим, разобьем наши поля на различные составляющие, которым соответ¬
ствуют различные целые значения п, что даст нам зависимость от 9 в виде еъпв, как указано
выше. Тогда для моды n-го порядка в S1 на нашей 4-поверхности начальных условий Е3 х S1
можно написать
Ф = einV,
где ф есть функция обычных пространственных координат х, у, z. Для каждой такой мо¬
ды Ф n-го порядка член р~2д2/д92 в нашем лапласиане можно заменить** просто на —п2/р2:
1 д2 п2
р2 д92 р2
По отношению к остальным переменным х, у, z наш лапласиан теперь превращается
в обычный трехмерный, только добавляется постоянное слагаемое ~-п2/р2.
Вспомним полевое уравнение для обычной (бесспиновой) частицы массы р в обычном
пространстве Минковского М — уравнение Клейна-Гордона (см. §24.5)
п + ^)Ф = 0,
**
Почему?
Почему это можно сделать?
/

31.11. Следует ли принимать аргументацию с точки зрения квантовой стабильности?
749
где □ = д2 /dt2—д2 /дх2 —д2 /ду2 ~д2 /dz2. Можем рассматривать это как «свободную части¬
цу на входе» (как это принято в формализме S-матрицы квантовой теории поля, см. § 26.8).
Однако в случае 5-пространства М х S1 в волновом операторе □ появляется дополнительный
член —р~2д2/дв2. Если эта частица в 5-пространстве является собственным состоянием п-й
моды для S1, то этот член, как и выше, заменяется на п2/р2. В соответствии с этим, с точки
зрения обычного 4-пространства Минковского, наша n-я мода для частицы Клейна-Гордона
в 5-пространстве удовлетворяет следующему уравнению в 4-пространстве:
(°+ь+?) *=
Это есть опять-таки уравнение Клейна-Гордона, но с р2/Н2 + п2/р2 вместо p2/h2. Таким
образом, мы получили уравнение Клейна-Гордона в 4-пространстве для новой частицы
с массой, увеличенной от р до л/ [р2 + h2n2/р2).
Теперь получается, что любая из наблюдаемых элементарных частиц в Природе имеет
массу р, неизмеримо меньшую (см. §31.1) планковского значения, приблизительно равно¬
го h/р (для выбранного нами значения р). Если предположить, что п ^ 0, то указанная новая
частица будет иметь массу, имеющую, по крайней мере, планковский порядок (посколь¬
ку hn/p намного больше р), поэтому она оказывается далеко за пределами возможностей
современных ускорителей элементарных частиц. Это выдвигается «струнными» теорети¬
ками в обоснование того факта, что никакая мода с п ф 0 не проявляется в каких-либо
процессах с участием элементарных частиц в современную космологическую эпоху!
Такие же, по существу, рассуждения применимы и к полному компактному 6-простран¬
ству У планковского размера. В нынешней ситуации с относительно низкими энергиями,
где мы сейчас оказались, моды возбуждений пространства У с п ф 0 экспериментально
недоступны для нас, — так утверждают «струнные» теоретики. Эта означает, следователь¬
но, отсутствие конфликта между гипотезой дополнительных пространственных измерений
и современными наблюдениями и экспериментами.
31.11.	Следует ли принимать аргументацию с точки зрения квантовой
стабильности?
Но так ли уж справедлива приведенная аргументация? Мне кажется, имеются веские
причины усомниться в этом^31*38й Даже если оставить в стороне неразгаданную загадку,
почему три пространственных измерения должны вести себя так непохоже на шесть осталь¬
ных, следует соблюдать осторожность в рассуждениях, касающихся такой «физики элемен¬
тарных частиц», которая опирается на геометрию пространства У, не меняющегося в ходе
последующей эволюции Вселенной.
Прежде чем перейти к вопросу о возмущениях пространства У, обладающих планков-
ской (или несколько большей) энергией, я должен вернуться к модам возмущений с нулевой
энергией, которыми мы пренебрегли в § 31.10. В § 31.14 мы увидим, что эти моды пытаются
рассматривать как аргумент в пользу теории струн, поскольку они дают надежду на установ¬
ление подлинного контакта с группами симметрии стандартной теории элементарных ча¬
стиц (§§ 25.5, 25.7). Тем не менее они приводят к серьезному затруднению математического
характера, известному под названием проблемы модулей. Как и в случае римановой поверх¬
ности (см. § 8.4), имеются некоторые параметры, называемые модулями, которые определяют
конкретный вид рассматриваемого ^-пространства. (В § 31.14 мы увидим, что предпочитае¬
мые ^-пространства представляют собой некоторые комплексные 3-многообразия, называ¬
емые «пространствами Калаби-Яу», модули которых в общем случае образуют семейство
комплексных чисел.) Нулевым модам соответствует изменение этих модулей. Эти изме-

750
Глава 31
Q
нения можно выбрать зависящими от координат Е -пространства, но это дает нам лишь
приемлемое число степеней свободы ocNo°' , где N — число независимых (вещественных)
модулей. Оказывается, однако, что существуют моды, у которых модули быстро убывают
до нуля, что соответствует сингулярному ^-пространству. Эта нестабильность, выглядящая
как катастрофа, и составляет, по существу, «проблему модулей», встающую перед «струн¬
ными» теоретиками (см. также § 31.14)t31-39!. Она остается нерешенной, но на это обычно
не обращают внимания.
Допустим, что мы тоже решили не обращать внимания(!). Будут ли в этом случае моды
колебаний с положительной энергией (планковского масштаба) в шести лишних измерениях
невосприимчивы к возбуждениям? Хотя планковская энергия действительно весьма высока
по сравнению с обычными энергиями в физике элементарных частиц, это не такая уж огром¬
ная энергия — она сравнима с энергией, выделяющейся при взрыве примерно одной тонны
тринитротолуола (тротила). В известной Вселенной встречаются, конечно, неизмеримо бо¬
лее высокие энергии. Например, энергия, получаемая Землей от Солнца за одну секунду,
больше этой энергии примерно в 108 раз! Если иметь в виду одну лишь энергию, то этого
более чем достаточно для возбуждения пространства У во всей Вселенной\
По разумению «струнных» теоретиков, эта энергия освобождается при локальном вза¬
имодействии элементарных частиц в некоторой очень малой области обычного простран¬
ства. Однако моды возбуждения ^-пространства, предполагаемые недосягаемыми, в наших
возбуждениях пространства Е3 х У равномерно распределены по всему пространству Е3.
Напомним, что моды возбуждения пространства Е3 х У — это просто произведения Е -мод
на У-моды. Здесь рассматриваются моды, постоянные во всем пространстве Е3. Это ничего
не говорит о том, что такие моды могут (и тем более должны) инжектироваться в локальную
область обычного физического пространства.
Это само по себе не может, однако, служить аргументом против локальных взаимо¬
действий элементарных частиц, в результате которых могут возбуждаться такие моды.
Их распределенный характер по всему пространству Е не противоречит представлению
об отдельных частицах. Мы помним из обсуждения, касающегося операторов рождения
и уничтожения в §26.2 и фейнмановских диаграмм в §§26.7, 26.8, что частицы и их вза¬
имодействие в квантовой теории поля обычно описываются в импульсном представлении.
Импульсные состояния действительно «распределены» по всему пространству Е3, как особо
подчеркивалось в §21.11. «Квантовые частицы» отнюдь не обязаны быть локализованными
в пространстве. Возможно, это будет понятнее, если говорить не о частицах, а о «кван¬
тах». Вопрос состоит в том, разумно ли ожидать, что одиночный квант планковской энергии
может быть каким-то способом инжектирован в У-моду. Но я не думаю, что мы должны
непременно считать таким «способом» локальное взаимодействие частиц, а не что-то другое
вроде нелинейного возмущения геометрии всего пространства-времени.
Существуют ли какие-то основания верить в существование подобных «других спо¬
собов»? По моему мнению, это стоит обсудить. Вернемся к нашей аналогии со шлангом
(рис. 31.3). Возьмем шланг, прямой в его «большом» измерении (аналогичном Е3) и име¬
ющий постоянное поперечное сечение S1, которое представляет собой окружность малого
радиуса р. Моды возбуждений шланга можно составить из различных волн, распространяю¬
щихся туда и обратно вдоль длины шланга («Е3-моды»), и различных возмущений круговой
формы окружности («У-моды»). Как мы видели, любая из мод этого последнего типа воз¬
никает одновременно по всей длине шланга. С точки зрения квантовой механики, энергия
кванта возбуждения такой моды — экситона — с частотой колебаний v равна 2тгНи (см. § 21.4)
независимо от длины шланга!
При бесконечной длине шланга это дает нулевую плотность энергии для каждого от¬
дельного экситона, поэтому будет понятнее, если предположить, что шланг изогнут в кольцо
очень большого радиуса R, R »р. Рассмотрим некоторую моду колебаний У с частотой и.

31.12. Классическая нестабильность дополнительных измерений
751
Полная энергия этого экситона 2ixhv не зависит от R. Это может показаться странным,
поскольку означает, что чем больше R, тем меньше локальная плотность энергии, которая
пропорциональна 1/R. Здесь нет противоречия: сказанное означает, что амплитуда коле¬
баний в экситоне, соответствующем заданной моде колебаний У, будет тем меньше, чем
больше длина шланга. Если перейти к пределу R —» оо, то локальная энергия, запасенная
в моде, будет стремиться к нулю. Отсюда следует, что при стремлении длины шланга к бес¬
конечности любое локальное колебание будет заключать в себе все большее число квантов,
при этом эффект от каждого кванта будет становиться все меньше, и для описания поведения
шланга более подходит классический, а не квантовый подходt31-40!.
Это ставит вопрос о классическом пределе квантовой системы при больших квантовых
числах и связанную с этим проблему редукции состояний R к такой классической конфигу¬
рации. Мы видели, в частности, в главе 29, что проблема редукции R не решается полностью
в рамках нынешней квантовой теории^31*41!. Тем не менее хороший физик должен знать, ко¬
гда уместнее пользоваться квантовым описанием, а когда имеет больший физический смысл
классический подход. Вспомним ситуацию с обычным моментом импульса (§22.10). Тело
с очень большим моментом импульса лучше рассматривать как классическую систему, при
этом мы получаем хорошо определенную ось вращения. Если трактовать его как квантовую
систему с очень большим значением j, мы получим описание Майораны со многими направ¬
лениями спина, охватывающими обычно все пространство! Практически для систем с очень
большим моментом импульса классическое описание дает правильную картину физической
реальности. В более общей формулировке, классическое описание физически приемлемо,
когда квантовые числа чрезвычайно велики. В случае момента импульса соответствующее
квантовой число j измеряется в единицах h, поэтому можно предложить разумный крите¬
рий того, что мы находимся вдали от квантового режима, — так будет, когда велико отноше¬
ние j/h. В случае шланга мы видим, что малость величины р сама по себе не может служить
подходящей мерой, указывающей на то, что «квантовое» описание более уместно, нежели
классическое. При заданном р описание локальных колебаний шланга должно становиться
все более «классическим» по мере увеличения R, поскольку нам будет нужно учитывать все
большее число экситонов (мод колебаний У) со все большими колебательными квантовыми
числами!31*42!.
В отсутствие такой теории, которая объяснила бы нам, почему «большие» системы хоро¬
шо описываются классической теорией, а малые следуют квантовым правилам (что, на мой
взгляд, требует изменения самой структуры квантовой механики в направлении, указанном
в §§30.9-30.12), мы, по-видимому, не можем прийти к определенному выводу относитель¬
но заявленной недосягаемости возбуждений пространства У. (Соображения, изложенные
в главе 30, пока не дают нам сколько-нибудь однозначного и тем более непротиворечивого
ответа.) Тем не менее из того факта, что возмущения У приводят нас к квантовой картине
с очень большим числом квантов, каждый из которых едва ли способен воздействовать на
геометрию пространства У, и к большим квантовым числам, можно сделать вывод, что
возмущения пространства Мх^с «малым» У ведут себя классическим, а не квантовым
образом. Сейчас мы обсудим это.
31.12.	Классическая нестабильность дополнительных измерений
Что если мы действительно будем считать модель 10-пространства полностью клас¬
сической? Это должно, по крайней мере, дать нам некоторое представление о том, как
будет вести себя полностью квантовая модель. В начале § 31.10 было показано, что в клас¬
сическом (1 + 9)-пространстве-времени (т. е. когда имеется одно временное и девять про¬
странственных измерений) присутствует необъятное море избыточных степеней свободы
9	3
(оом°° оо^00 ). Это весьма серьезно, однако, на мой взгляд, есть кое-что и похуже. Ока¬

752
Глава 31
зывается, что классическая Вселенная М х У с нулевым тензором Риччи сильно неустойчи¬
ва относительно малых возмущений. Если пространство У компактно и имеет иланковский
размер, то можно ожидать возникновения пространственно-временных сингулярностей уже
через малую долю секунды!
Рассмотрим сначала возмущения пространства М х У, которые воздействуют только
на геометрию У и «не просачиваются» в трехмерное пространство Е3. То есть будем рас¬
сматривать (1 + 6)-пространство-время общего вида Z с нулевым тензором Риччи (это есть
возмущенная эволюция пространства У), при этом полное (1 + 9)-пространство-время бу¬
дет иметь вид Z х Е3. Мы считаем, что Z представляет временную эволюцию некоторого
6-пространства, которое в некоторый момент времени «близко» к У, так что Z начинает-
ся вблизи (неизмененной) «временной эволюции» Е х У пространства У, хотя с течением
времени Z может сильно отклониться от Е1 х У (рис. 31.9). Здесь, как и в § 31.10, я представ-
•j	Q	1	Q
ляю М в виде М = Е х Е (Е описывает временное измерение, Е — пространственные),
-1	Q
так что можно рассматривать пространство-время М х У как (Е х У) х Е' (временная
эволюция пространства У стоит в произведении первой); см. рис. 31.9 а.
В конце 1960-х годов Стивен Хокинг и я доказали теорему сингулярности, которая по¬
казывает, что следует ожидать сингулярности пространства Z}31A3^ Мы установили, что эта
теорема применима к (1 + 6)-пространству-времени (и к (1 + 9)-пространству-времени) так
же хорошо, как и к обычному (1 + 3)-пространству-времени, которое мы первоначально рас¬
сматривали. Одно из следствий этой теоремы состоит в том, что любое пространство-время с
нулевым тензором Риччи, которое, подобно Е1 х У или Z, содержит компактную простран¬
ственноподобную гиперповерхность и имеет, в некотором смысле, общий характер f31-44!
(а также не содержит замкнутых времениподобных петель — см. § 17.9 и рис. 17.18), должно
Л
быть сингулярным! Исходное пространство Е х У избегает сингулярной участи, посколь¬
ку в этом случае нарушается условие общности. Однако пространство Z с возмущениями
общего вида должно быть сингулярным.
Следует заметить, что подобные «теоремы сингулярности» не утверждают непосред¬
ственно, что кривизна стремится к бесконечности, а лишь указывают, что существует неко¬
торое препятствие, не позволяющее времениподобным или нулевым геодезическим про¬
стираться на бесконечное расстояние в пространстве-времени (или, в случае нулевых гео¬
дезических, иметь бесконечную аффинную длину — см. § 14.5). Можно думать, что такое
препятствие возникает из-за расходимости кривизны, но прямо теорема об этом не заявляет.
Теорема утверждает, однако, что пространство Z так или иначе становится сингулярным.
Е
1
Рис. 31.9. Теорема сингулярности применяется к возмущениям пространства М х У, где У есть
«малое» пространство Калаби-Яу. а) Несингулярный канонический случай М х У, где использовано
представление М = Е1 хЕ3 (Е1 относится ко времени), б) Возмущение общего вида У' пространства У
О
эволюционирует в сингулярное пространство Z, поэтому возмущения общего вида Е х У, которые
не воздействуют на Е3, эволюционируют в сингулярное пространство Е3 х Z

31.13. Конечна ли струнная квантовая теория поля?
753
Если отклонение от У имеет тот же (планковский) масштаб, что и само пространство У,
то можно ожидать, что сингулярности в Z возникают в сопоставимом временном масштабе
(~ 10~43 с), однако этот временной масштаб становится несколько больше, если возмущения
имеют пропорционально меньший размер, нежели само пространство у.
Мы приходим к выводу, что если мы хотим создать отклонение произвольного вида
от пространства У, чтобы получить несингулярное возмущение полного (1 4- ^-простран¬
ства М х У, мы должны рассматривать возмущения, которые проникают также в часть Мх>’
пространства-времени. Но такие возмущения в определенном смысле еще более опасны
для нашей «обычной» картины пространства-времени, чем те, которые воздействуют толь¬
ко на У 9 поскольку большая кривизна гшанковского масштаба I31-45], которая, по-видимому,
должна иметь место в У, будет распространяться и на обычное пространство (что рез¬
ко противоречит результатам наблюдений) и очень быстро приведет к возникновению
пространственно-временных сингулярностей I31-46!.
Разумеется, неприемлемые сингулярности, присутствующие в классической теории, не
обязательно означают, что такие же пороки сохранятся и в квантовом варианте этой тео¬
рии. Как мы уже видели в § 22.13, квантовая механика устраняет катастрофическую неста¬
бильность обычных классических атомов, согласно которой электроны должны по спирали
приближаться к ядру, испуская электромагнитное излучение. С другой стороны, одно лишь
введение «процедур квантования» не гарантирует устранения классических нестабильно¬
стей. Есть много примеров (например, в большинстве «игрушечных» моделей квантовой
гравитацииf31'47^), когда сингулярности сохраняются и после квантования.
Следует также отметить тот факт (см. §31.8), что нулевое значение (1 + 9)-мерного
Риччи не является точным требованием теории струн. Напомним, что нулевой тензор Риччи
рассматривается всего лишь как отличное приближение к этому требованию, которое полу¬
чается, если пренебречь членами высшего порядка по струнной постоянной аВозможно,
что «точное» требование, учитывающее члены всех порядков по а', ускользнет от действия
упомянутой теоремы сингулярности. Однако если это требование налагает условие нулевого
значения тензора Риччи, при котором выполняется обычное требование положительности
локальной энергии (см. упражнение 27.9 и §28.5), то теорема сингулярности будет все
же иметь место. С другой стороны, нарушение подобных условий для локальной энергии
в квантовой теории поля определенно возможно (§ 24.3), так что подобные проблемы еще
далеки от разрешения.
Более серьезным, на мой взгляд, является тот факт, что полное требование, включающее
члены всех порядков по а', описывается бесконечной системой дифференциальных уравне¬
ний с неограниченно растущим порядком производных. В соответствии с этим, начальные
условия, заданные на 9-поверхности, должны включать производные всех порядков по по¬
левым величинам (а не только первого и второго порядков, как в обычных теориях поля).
Тогда число необходимых параметров, приходящихся на точку этого 9-пространства должно
быть бесконечным, и мы получаем функциональную свободу, большую, нежели оо Мо° , при
любом положительном целом числе М. Это, по-видимому, создает еще худшую, чем преж¬
де, проблему избыточной функциональной свободы! Мне не известно какое-либо серьезное
обсуждение математической формы этого полного требования, а также вопроса о том, какого
рода начальные условия здесь окажутся подходящими.
*
31,13.	Конечна ли струнная квантовая теория поля?
Те доводы, которые я приводил выше, показывают, почему меня трудно убедить в том,
что модели теории струн способны воспроизвести эйнштейновскую (1 4- 3)-мерную об¬
щую теорию относительности в каком бы то ни было разумном «классическом пределе».
Как обстоит дело с другим заявлением теории струн, что она является согласованной ко-

754
Глава 31
печной квантовой теорией поля (безотносительно к физическому смыслу этой теории)? Мне
представляется, что, если бы при заданной топологии струнных мировых листов получа¬
лась конечная амплитуда, это было бы сильнейшим аргументом в пользу теории струн
и соответствовало ее первоначальной идее. Пока, однако, даже в этой части возникают
фундаментальные вопросы.
Прежде всего, имеется серьезное беспокойство, которое я всегда испытывал в отно¬
шении теории струн. Ее представляют как физическую теорию струноподобных структур
с времениподобными мировыми листами, так что создаваемая ими «метрика» представляет
собой (1 4- 1)-мерную лоренцеву метрику. Однако расчеты проводятся для струнных ми¬
ровых листов, обладающих положительно определенной метрикой, так чтобы можно было
привлекать изящные идеи теории римановых поверхностей (как в главе 8); см. рис. 31.10.
В соответствии с этим обычно говорят о модах возмущений, бегущих вдоль мирового листа
влево либо вправо со скоростью света (они распространяются вдоль нулевых кривых на ло-
ренцевом мировом листе). В римановом варианте теории эти «левые» и «правые» моды ста¬
новятся «голоморфными» и «антиголоморфными» функциями на римановой поверхности.
Создается впечатление, что расчеты специально проводятся с использованием положитель¬
но определенной римановой поверхности и последующего «поворота Вика» (§ 28.9), чтобы
в конце концов получить искомую лоренцеву теорию струн. Вполне возможно, что в дан¬
ном случае эта процедура оправданна, но это нельзя просто предположить без должного
обоснования. Справедливость ее сильно зависит, например, от приближений, используемых
при вычислении амплитуд. При наличии таковых возникает серьезный вопрос в отношении
используемой процедуры, аналогичный тому, с которым мы сталкивались при обсужде¬
нии подхода Хокинга к квантовой гравитации и других подходов к квантовой теории поля
на основе аналитического продолжения (см. §28.9). Я понимаю так, что вычисления с ис¬
пользованием римановых поверхностей правильны, поэтому можно надеяться, что оправдан
и поворот Вика. Тем не менее явное обоснование этого поворота опирается на предполо¬
жение о плоском пространственно-временном фоне, которое вполне может не выполняться,
если мы пользуемся серьезной (без применения теории возмущений) общей теорией относи¬
тельности, поэтому остается неясным, как далеко это заведет нас в направлении квантовой
теории гравитации.
Даже если поверить в справедливость такого приближения плоского пространства,
должны ли мы поддерживать сильное утверждение, что для каждой заданной топологии
Рис. 31.10. Математика теории струн использует «истории струн» в виде римановых поверхностей
с римановой (положительно определенной) метрикой. Однако физические истории струн являются
лоренцевыми. Переход от одной метрики к другой имеет вид некоторого «поворота Вика»

31.14. Магические пространства Калаби-Яу; М-теория
755
поверхности Римана (т. е. для поверхности заданного рода д (см. § 8.4), где д соответствует
«числу петель» в обычной фейнмановской диаграмме (см. §§ 26.8,31.5 и рис. 31.5 г)) полная
амплитуда действительно конечна? Фактически это не установлено. Несмотря на повторя¬
ющиеся заверения, никакого математического обоснования декларируемой конечности пока
представлено не было. Утверждения относительности конечности относятся лишь к ультра¬
фиолетовым расходимостям (соответствующим большим импульсам и малым расстояниям),
которые считаются наиболее опасными в квантовой теории поля, но даже такие расходи¬
мости пока были устранены лишь на двухпетлевом уровне. Кроме того, пока, по-видимому,
не было заявлений об устранении инфракрасных расходимостей (при малых импульсах
и больших расстояниях; см. § 26.9). Хотя последние считаются менее серьезными, чем уль¬
трафиолетовые расходимости, их определенно нельзя игнорировать и необходимо учитывать
тем или иным способом в попытках обосновать конечность. Это оставляет нас в некоторой
неопределенности относительно всей программы в целом, поскольку конечность является
краеугольным камнем всей идеи струн ^31,48J.
Возможно, это лишь раздражающие технические трудности, которые будут преодолены
при дальнейшем развитии теории. Но даже если предположить, что мы имеем конечные ам¬
плитуды для каждой заданной топологии, мы все равно оказываемся далеко от финиша. Эти
выражения потом придется суммировать, и проблема в том, что такая сумма, по-видимому,
расходится^31-49^. Предполагаемая конечная теория на деле оказывается вовсе не конечной!
Расходимость такого рода, видимо, не волнует «струнных» теоретиков, но лишь потому,
что они считают такой ряд неадекватным представлением полной амплитуды. Амплитуда
О	vy
считается аналитической величиной, а попытка определить ее с помощью степенного ряда
рассматривается как «разложение вблизи неправильно выбранной точки», т. е. некоторой
точки, в которой амплитуда сингулярна (это напоминает попытку построить степенной ряд
для log z путем разложения вблизи точки z = 0, вместо того чтобы проводить разложение по
степеням z—l (см. § 7.4), — хотя в данном частном случае этот ряд действительно будет иметь
бесконечные коэффициенты). Здесь действительно может быть все в порядке, хотя и было
показано, что возникающая здесь расходимость относится к довольно неуправляемому ти¬
пу («не суммируема в смысле Бореля»). Чтобы придать смысл требуемому рассуждению
«эйлерова типа» (вроде 1 + 22 + 24 + 26 + 2® + • • • = см. §§4.3, 26.9), понадобятся,
по-видимому, какие-то более изощренные процедуры^31-501 Более того, если вычисления
(по теории возмущений) в теории струн действительно представляют собой разложение
«вблизи не той точки», то становится непонятно, как вообще можно доверять каким бы
то ни было результатам, полученным с помощью теории возмущений! Так что мы пока
не знаем, действительно ли струнная квантовая теория поля конечна, не говоря уже о том,
предоставляет ли нам теория струн, при всей ее несомненной привлекательности, квантовую
теорию гравитации.
31.14.	Магические пространства Калаби-Яу; М-теория
Замечания, сделанные мною в §§31.8-31.13 в адрес теории струн, самих «струнных»
теоретиков, похоже, не волнуют. Их занимают другие проблемы, которых я пока не касал¬
ся, в частности, вопрос об однозначности теории. Первоначально большим успехом теории
струн считалась ее способность представить единую схему для всей Вселенной, и этой
предполагаемой однозначности придавалось большое значение. Явная проблема возникала
в связи с компактным 6-многообразием планковского масштаба У, в которое, как предпо¬
лагается, сворачивается 10-мерная Вселенная. Что представляют собой эти 6 измерений?
Почему Вселенная предпочитает свернуться именно в этих, а не в других измерениях? Пер¬
воначально казалось, что жесткие требования суперсимметрии и условие нулевого тензора

756
Глава 3 i
Риччи в сочетании с некоторыми другими фундаментальными требованиями могут привести
к однозначным ответам, однако позже оказалось, что существует широкий набор одинаково
возможных альтернатив.
Вначале предполагалось, что пространство У может быть гипертором S1 х S1 х S1 х
S1 х S1 х S1 с нулевой кривизной (см. примечание 31.45; вспомним понятие тора S1 х S1
и рис. 8.9,8.11 и 15.3). Но позже оказалось, что теория струн на основе гинертора не в состоя¬
нии учесть киральные аспекты^31 стандартной модели (см. § 25.3), и потребовалось что-то
более изощренное. Налагаемые «жесткие требования» привели затем к 6-многообразиям, по¬
лучившим название «пространства Калаби-Яу»^3152^. Эти пространства, представляющие
значительный интерес с точки зрения чистой математики, изучались для этих целей Эудже¬
нио Калаби и Шин-Тун Яу. Это пример так называемых многообразий Келера, обладающих
одновременно вещественной римановой метрикой и комплексной структурой (так что их
можно считать комплексными 3-многообразиями), и эти две структуры совместимы в том
смысле, что метрическая связность сохраняет комплексную структуру, откуда следует, что
они являются также симплектическими многообразиями (см. §§ 12.9, 14.7,14.8). Простран¬
ства Калаби-Яу обладают дополнительными свойствами, которые считаются существенны¬
ми для струнной модели: они обладают метрикой с нулевым тензором Риччи и наделены
спинорными полями, постоянными по отношению к метрической связности. Эти постоян¬
ные спинорные поля играют важную роль в качестве генераторов суперсимметрии. Без них
суперсимметрия была бы невозможна. Различные спинорные поля при заданном выборе
пространства Калаби-Яу могут (формально), «переходить, поворачиваясь, друг в друга»
под действием операций группы симметрии. Эта группа должна играть ту же роль, что
и группы симметрии физики элементарных частиц.
Следует пояснить, что эти операции симметрии не применяются непосредственно к са¬
мим пространствам Калаби-Яу наподобие симметрии, применяемой к слою Т расслоения,
как описано в главе 15. Фактически пространства Калаби- Яу не обладают (непрерывной)
симметрией, и мы не можем рассматривать наше 10-пространство как (нетривиальное) рас¬
слоение 6-пространств Калаби-Яу над обычным четырехмерным пространством-временем.
Вместо этого (внутренняя) симметрия элементарных частиц относится к «поворотам» посто¬
янных спинорных полей между собой. Реальные пространства Калаби-Яу не подвержены
действию операций симметрии[31.53]
Таким образом, теория струн приводит к весьма своеобразной теории Великого объ¬
единения (см. §§25.8, 28.1-28.3). Она предполагает объединить все элементарные частицы
в единую схему. Возникающие при этом группы симметрии оказываются гораздо более
обширными, чем таковые в стандартной модели (§§25.5-25.7), однако, как и в других те-
f	$
ориях Великого объединения (§25.8), предполагается нарушение симметрии, приводящее
к ее понижению до симметрии, имеющей более непосредственное отношение к стандарт¬
ной модели, — хотя эта программа пока не выполнена в должной мере.
Как обстоит дело с проблемой однозначности? К сожалению, существуют десятки ты¬
сяч классов качественно различных возможных вариантов для пространств Калаби-Яу, так
что описанная схема далека от однозначности. Фактически в рамках заданного класса про¬
странства Калаби-Яу существует бесконечно много различных вариантов, отличающихся
друг от друга значениями некоторых параметров, именуемых модулями (см. §31.11), которые
определяют форму пространства (рис. 31.11) так же, как и в случае римановой поверхности
(§8.4, рис. 8.11). Наличие таких модулей рассматривается как полезный факт, поскольку
изменение их создает моды колебаний пространства У с нулевой энергией (упомянутые
в §31.11), которые считаются физически реализуемыми и могут открыть требуемый путь
Понятно ли, почему они обязаны быть симплектическими многообразиями? {Подсказка: постройте Sab
исходя из метрики даъ и комплексной структуры и убедитесь, что dS = 0 (предполагается несингуляр¬
ность Sab).)

31.14. Магические пространства Калаби - Яу; М-теория
757
к физике элементарных частиц и наблюдаемым след-
ствикм теории струн. Однако, как уже отмечалось
в § 31.11, они могут привести к нестабильности.
Существуют, однако, и другие источники неод¬
нозначности, которые поначалу оставляют впечат¬
ление даже более серьезных затруднений, нежели
неоднозначность, связанная с пространствами Кала¬
би -Яу. Оказывается, что существует целых пять со¬
вершенно различных возможных схем связи, уста¬
навливаемой суперсимметрией между «бозонными»
и «фермионными» модами колебаний струны. Соот¬
ветственно имеется пять различных вариантов теории
струн, получивших названия: теория струн типа I, те¬
ория струн типа IIA, теория струн типа IIB, теория
гетеротических струн 0(32) и теория гетеротических струн Eg х Eg. Способ получения групп
0(32) и Eg х Eg описан в предыдущих абзацах этого раздела. (Читатель может узнать здесь
обозначение этих групп в § 13.2; Eg есть наибольшая из исключительных групп Ли.) Теория
типа I пользуется как разомкнутыми струнами, так и замкнутыми петлями, все остальные
оперируют только с замкнутыми струнами. Во всех этих моделях возмущения могут рас¬
пространяться как вправо, так и влево (по и против часовой стрелки)^31*54!. Теории типа ПА
и IIB отличаются тем, как связаны между собой эти правые и левые возмущения. Гетеротиче-
ские струны выглядят особенно странно, поскольку возмущения, распространяющиеся влево
и вправо, принадлежат пространству-времени разной размерности (соответственно 26 и 10).
Этот факт вряд ли имеет какой-либо реальный геометрический смысл (во всяком случае
для меня!), но, по-видимому, ему можно придать некоторый формальный смысл. Считается,
что 10-мерная картина геометрически приемлема, однако левые возмущения ведут себя так
же, как и в случае старых (несуперсимметричных) «бозонных струн» (§§31.5, 31.7), оби¬
тающих в 26-мерном пространстве-времени. Как уже упоминалось, «струнные» теоретики
не слишком обеспокоены явной несогласованностью в размерности пространства-времени,
%*■*
они обычно считают размерность зависящей от энергии (§31.10) и потому не имеющей
фундаментального значения. Мы вернемся к этому в §§31.15, 31.16.
Такое размножение струнных моделей вынудило многих теоретиков усомниться в сво¬
ей способности продолжать заниматься этим дальше. Тем не менее появились некоторые
замечательные работы, указывающие на возможность существования глубокой взаимосвязи
между этими внешне совершенно разными моделями. В 1995 году Эдвард Виттен прочитал
знаменитую лекцию I31*55!, послужившую началом так называемой «второй суперструнной
революции». В этой лекции Виттен изложит программу развития теории струн, которая
полностью изменила взгляд на проблему. Существенно новая черта состояла в том, чтобы
привлечь некоторые загадочно выглядящие «операции симметрии» (их называют «дуально¬
стью сильной и слабой связи», или «зеркальной симметрией» I31-56], иногда S-дуальностями,
а также S-, Т- и U-дуальностями); при этом различные теории струн оказываются настолько
глубоко связанными между собой, что их можно рассматривать как эквивалентные теории.
В предельно малых масштабах некоторые из этих теорий оказываются тождественными,
в некотором определенном смысле, другим теориям в противоположном предельном случае
больших масштабов, и существуют другие типы соотношений симметрии такого рода, воз¬
никающие из-за дуальности теории Янга-Миллса (§ 25.7), аналогичной дуальности между
электричеством и магнетизмом в обычной теории электромагнитного поля. (Сравните это
также с дуальностью в теории Ханя-Цу, кратко изложенной в § 25.8.) Более того, различные
пространства Калаби-Яу также оказываются разным образом дуальными друг другу. До сих
пор, насколько мне известно, не все эти результаты доказаны математическиt31*57!, Одна¬
Рис. 31.11. «Форма» пространства Кала¬
би-Яу У описывается рядом модулей
(сравните с рис. 8.10 и 8.11). Измене¬
ние этих модулей создает моды колеба¬
ний пространства 3^ с нулевой энергией

758
Глава 31
ко оригинальные гипотезы, исходящие от теории струн в качестве впечатляющих выводов,
основанных на «косвенных уликах», стимулировали некоторые весьма значительные иссле¬
дования чисто математического характера, которые привели к более глубокому пониманию
многообразий Калаби-Яу и связей между ними131,58}.
Заслуживает упоминания один особенно яркий пример таких «косвенных улик». Он свя¬
зан со специфической чисто математической проблемой, интересовавшей в течение ряда лет
профессиональных математиков, занимавшихся алгебраической геометрией. Эта проблема
вроде бы не имеет ничего общего с физикой и связана с подсчетом числа рациональных кри¬
вых на некоторых комплексных 3-многообразияхРациональной кривой называется
комплексная кривая (т. е. риманова поверхность — см. главу 8) нулевого рода, то есть с топо-
Су
логией сферы S . Эти комплексные 3-многообразия оказываются пространствами Калаби-
Яу теории струн, которые, в соответствии с завоеваниями «второй суперструнной эволю¬
ции», должны быть связаны зеркальной симметрией с некоторыми другими пространства¬
ми Калаби-Яу. Зеркальная симметрия, в некотором смысле, меняет местами комплексную
и симплектическую структуры; в соответствии с этим задача о подсчете рациональных (го¬
ломорфных) кривых (что представляет очень трудную проблему в техническом отношении)
превращается в гораздо более простую и совершенно иначе выглядящую задачу подсче¬
та в «зеркальном» пространстве Калаби-Яу. Два норвежских математика Гейр Эллингсруд
и Штейн Арилд Штремме разработали методы непосредственного подсчета числа рацио¬
нальных кривых (последовательных порядков1'31-60^ 1, 2, 3,...) в их пространствах, получив
для первых трех случаев последовательные числа
2 875,	609	250,	2	682	549 425.
Предполагая, что выполняются соотношения зеркальной симметрии, так что можно вос¬
пользоваться намного более простой процедурой счета, Филипп Канделас с сотрудниками
смогли получить числа
2 875,	609	250,	317	206 375.
Поскольку зеркальная симметрия в то время была всего лишь недоказанной «гипотезой
физиков», было предположено, что согласие в первых двух случаях было случайным сов¬
падением, и нет оснований принимать число 317206375, полученное Канделасом с колле¬
гами. Но затем оказалось, что из-за ошибки в компьютерной программе число, найденное
норвежскими математиками, получилось неверным, а правильное значение в точности сов¬
падает с полученным из соображений зеркальной симметрии! Впоследствии с использова¬
нием зеркальной симметрии было вычислено много последующих чисел, продолживших
приведенную выше последовательность для рациональных кривых более высокого поряд¬
ка 4, 5, 6, ..., 10):
242467 530000
229 305 888 887625
248 249 742118 022 000
295 091050 570 845 659250
375 632160 937 476 603 550 000
503 840 510 416 985 243 645 106 250
704 288164 978 454 686113 488 249 750
Этот замечательный пример явно указывает на «что-то, происходящее за сценой».
При нынешнем положении вещей это довольно загадочный факт. Эту загадку предстоит раз¬
гадать математике, и некоторые недавние математические разработки наметили возможный

31.14. Магические пространства Калаби-Яу; М-теория
759
у'
р^ть к этому^31‘61i. Однако наиболее важный вопрос связан с физическим смыслом этих
результатов. Имеем ли мы право на основании того несомненного факта, что теория струн
создала глубокий и неожиданный прорыв в области математики, сделать заключение, что
она представляет глубокую физическую истину? Ответ на этот вопрос отнюдь не очевиден.
Виттен провозгласил, что теория струн, как ее сейчас понимают, — это всего лишь вершина
айсберга, или скорее она представляет пять вершин некоторой пока таинственной теории,
которую окрестили «М-теорией» (см. рис. 31.12). Эта новая теория, когда она будет создана,
должна будет заменить собой все другие теории струн, предложенные ранее.
Тип Нв
Тип I
Тип ПА
 	  Гетеротические	Е
Гетеротические О
11 -мерная супергравитация
Рис. 31.12. Загадочная «М-теория» провозглашает, что пять различных типов теории струн, связан¬
ных между собой S-, Т- и U-дуальностями, и 11-мерная супергравитация представляют собой шесть
различных аспектов одной и той же пока не открытой структуры
Эта загадочная М-теория призвана не только объединить все теории струн, но и вклю¬
чить в себя ряд других идей, связанных со струнами и с суперсимметрией. Струны теперь
рассматриваются лишь как частный случай более общего понятия, включающего структуры
большей (и даже меньшей) размерности. Их называют мембранами (или /?-бранами, или
просто бранами), они содержат р пространственных измерений и одно временное, так что
мировой лист становится (1 + р)-мерным (см. рис. 31.13). Могут включаться также род¬
ственные времениподобные структуры, называемые D-бранами, о них будет кое-что сказано
в §31.17.
1 измерение
Время
Струна-1-брана
Рис. 31.13. Мембраны (или р-браны, или просто браны) имеют р пространственных измерений и одно
временное, так что мировой лист оказывается (1 4- р)-мерным. Эти структуры вместе с обычными
струнами (1-бранами) являются составной частью пока еще не сформулированной М-теории
В некоторых вариантах предполагается, что М-теория включает в себя также теорию
11-мерной супергравитации, с которой мы уже встречались в этой главе (§31.4). Фактически
саму М-теорию следует понимать как 11-мерную теорию, поэтому проблема размерностей
кроется скорее в ее связи с различными 10-мерными теориями струн, нежели с 11 -мерной
р-измерений
р-брана

760
Глава 31
супергравитацией. Тот факт, что в согласованной теории струнного типа становятся «раз¬
решенными» 11 измерений, следует из вывода Виттена, согласно которому первоначальные
соображения о том, что 1 + 9 измерений необходимы для устранения струнной аномалии,
рассмотренной в § 31.7, нужно рассматривать как приближение (что частично связано с вве¬
дением этих «бран» повышенной размерности), а правильнее говорить об 11 измерениях
(1 + 10, т.е. 1 временное и 10 пространственных измерений)I31-62). Но «струнным» тео¬
ретикам мало даже 11 измерений. Есть предложение двигаться в сторону все большего
числа измерений, к еще более загадочной (и менее разработанной) «F-теории», в кото¬
рой 12(= 2 + 10) измерений (в том числе 2 временных измерения)! 131-б33
Каким образом теория с 11 -мерным (или, возможно, 12-мерным) «пространством-вре¬
менем» может быть сведена, в предельных случаях низких и высоких энергий, к различным
теориям, в каждой из которых (кроме одной) пространство-время 10-мерно? Это проти¬
воречие, касающееся размерности пространства-времени, опять-таки связывают с тем, что
размерность не является фундаментальным фактором, а зависит от энергии (§31.10). Можно
представить себе, что по мере роста энергии воспринимается все больше пространственно-
временных измерений. Именно так «струнные» теоретики пытаются обосновать свое бесце¬
ремонное обращение с размерностью пространства-времени! Я уже выражал свое неприятие
аргументов такого рода в §§31.11,31.12. На мой взгляд, трудности, связанные с несравнимо
разной функциональной свободой при различном числе измерений I31*64!, далеки от убеди¬
тельного разрешения. Эта проблема вырисовывается также и в других материях, занимаю¬
щих ныне умы многих «струнных» теоретиков, и я сейчас кратко затрону этот вопрос.
31.15.	Струны и энтропия черных дыр
Вспомним (§§27.10, 30.4), что формула Бекенстайна - Хокинга приписывает черной
дыре энтропию, пропорциональную площади ее горизонта. Хотя в поддержку этого вывода
было выдвинуто несколько различных аргументов, ни один из них не доказывал с полной
однозначностью Р1-65!, что энтропия черной дыры в точности равна логарифму объема фа¬
зового пространства, как этого требует формула Больцмана (§ 27.3). Такое доказательство
равносильно непосредственному подсчету степеней свободы, «потерянных в дыре», при¬
чем подсчет должен проводиться в рамках соответствующей квантовой теории гравитации.
В 1996 году Эндрю Строминджер и Кумрун Вафа провели расчет^31,66! с использованием
струн и мембран, который поддержал интерпретацию формулы Бекенстайна-Хокинга для
энтропии как «подсчета числа степеней свободы». «Струнные» теоретики комментировали
это словами: «Решена четвертьвековая загадка!»^16^
Как и в случаях с другими подобными высказываниями этих теоретиков, такое заявле¬
ние представляется чрезмерно громким. Например, первоначальный расчет Строминджера -
Вафы был выполнен лишь для черных дыр в 5-мерном пространстве-времени. Более поздние
результаты относились к обычному 4-мерному пространству-времени, однако начальный
ажиотаж, породивший высказывания, подобные приведенному выше, был вызван именно
первоначальным 5-мерным расчетом. Более того, все эти результаты теории струн относятся
лишь к предельному случаю «экстремальной дыры» (или к возмущениям относительно нее),
для которой температура Хокинга (см. § 30.4) равна нулю и которая включает в себя допол¬
нительные суперсимметричные поля типа Янга-Миллса, не имеющие явного обоснования
в известной физике. Кроме того, вычисления реально проводились для плоского простран¬
ства,, в котором отсутствует горизонт событий, и утверждение, что их можно применять
к сильно искривленной метрике черной дыры, представляет собой явную экстраполяцию.
Несколько слов в пояснение. Мы видели (§27.10), что в обычной обп^ейитебрии от¬
носительности вакуума с четырехмерным пространством-временем стационарная изолиро¬
ванная черная дыра описывается керровской метрикой, характеризуемой значениями всего

31.15. СТРУЙЫ И ЭНТРОПИЯ ЧЕРНЫХ ДЫР
761
двух (неотрицательных) вещественных параметров т и а, где т — масса, а а х т — момент
импульса (в естественных единицах). Чтобы керровская метрика реально описывала черную
дыру, а не просто голую сингулярность (§ 28.8), должно быть т > а. (Отметим, например,
1
что это неравенство должно выполняться для формулы А = 8ттт[т 4- (т2 — а2)2Ю2/с4
из §27.10, определяющей площадь А горизонта керровской дыры.) Для обычной черной
дыры экстремальный случаи возникает при т = а, и это единственная ее характеристика
как «черной дыры». Это есть предельный (астрофизически недостижимый) случай обычной
черной дыры, у которой температура Хокинга равна нулю.
Можно сравнить это с «черной дырой» в теории струн, которая также «экстремаль¬
на» в том смысле, что температура Хокинга для нее обращается в нуль. Однако почти
все расчеты в теории струн относятся к объектам совсем иного сорта! Вместо вращения,
определяемого керровским параметром а, вводятся дополнительные физические поля. В те¬
ории струн «дыра» описывается решением Рейсснера-Нордстрёма уравнения Эйнштейна,
сферически симметричным в отличие от решения Керра. Вместо керровского параметра а
появляется параметр е, который служит мерой полного электрического заряда дыры. Метри¬
ка Рейсснера-Нордстрёма представляет собой решение уравнений Эйнштейна - Максвелла
(§ 31.4), т. е. уравнения Эйнштейна с тензором энергии-импульса максвелловского поля без
источниковf31,68^. Площадь горизонта теперь описывается похожей формулой
А — 87г[т + (га2 — е2)2]2 G2 / с4.
Условием того, что эта метрика представляет черную дыру, а не голую сингулярность,
является неравенство т ^ |е|, а условием экстремальности дыры — равенство т — \е
! •
(Наличие знака модуля (§6.1) учитывает возможность отрицательных значений е).
Тот тип «черной дыры», с которым в основном имеет дело теория струн, есть тот же
случай Рейсснера-Нордстрёма, но с суперсимметричным семейством полей Янга-Миллса
(§25.7), заменяющим максвелловское поле. Полное решение представляет собой частный
пример так называемого состояния Богомольного -Прасада-Соммерфилда (БПС), в кото¬
ром решение определяется требованиями суперсимметрии, стационарности и минимума
энергии. Я не буду подробно объяснять, что это значит. Хотя подобные предметы представ-
ляют несомненный интерес для людей, занимающихся теорией струн и суперсимметриеи,
пока не ясно, имеют ли они отношение к реальному физическому миру (см. § 31.2).
А как быть с тем фактом, что конкретные вычисления струнных степеней свободы
проводятся для плоского пространства, в котором отсутствует горизонт событий? Как и все,
воспитанные на общей теории относительности Эйнштейна, я считаю это одним из наиболее
спорных аспектов заявлений, дедаемых «струнными» теоретиками. Трудно понять, как мож¬
но получить строгие выводы относительно черных дыр, не обращая внимания на сильное
искривление геометрии пространства-времени черной дыры, из-за которого «информация»
о ее образовании не выходит за пределы горизонта событий.
Попробую изложить в общих чертах аргументацию, применяемую в теории струн I31-69).
Для начала оценим число физических степеней свободы путем подсчета числа различных
возможных струнных петель длины I на решетке планковского масштаба, например, в объ¬
еме сферы некоторого заданного радиуса, причем полная масса-энергия струн равна М.
Мы должны предположить, что реальное значение ньютоновской гравитационной посто¬
янной G находится в нашем распоряжении. При достаточно малых значениях G черной
дыры не будет, и в пределе нулевого значения G пространство становится плоским. Но если
мы будем постепенно увеличивать G («управляя ньютоновской постоянной»), то в конце
концов придем к ситуации, в которой, согласно общей теории относительности, образуется
черная дыра (вспомним формулу Мичелла 2MG2/с2 для радиуса «ньютоновской черной
дыры» — см. §27.8). В теории струн G зависит от параметра gs, называемого константой

762
Глава 31
связи струны, и растет при увеличении gs (Gs ~ #2). В пределе малых значений G (ма¬
лых gs) логарифм числа струнных степеней свободы (§ 27.3) дает энтропию, совпадающую
со значением Бекенстайна - Хокинга для черной дыры, несмотря на то что черной дыры нет.
Из соображений подобия следует, что эта связь сохраняется и при увеличении G, так что
формула Бекенстайна - Хокинга действительно имеет место на той стадии, когда появляется
черная дыра.
Это дает лишь качественное согласие между результатом подсчета струнных степеней
свободы и формулой Бекенстайна-XoKiiHra 5вн ~ Ах kc3/Gh, что подтверждает прибли¬
зительную пропорциональность между энтропией струн и площадью поверхности черной
дыры А. Чтобы получить в этой формуле правильное значение Строминджер и Вафа
обратились к состояниям БПС, в которых требования суперсимметрии позволяют выразить
массу через значения различных «зарядов» (для суперсимметричных полей Янга-Миллса),
при этом нумерация струнных конфигураций заменяется подсчетом всех различных состоя¬
ний БПС^31,70!, которые вносят вклад в полную энтропию (это все состояния БПС с данным
набором зарядов). Это можно сделать в довольно явном виде, и логарифм полученного числа
замечательным образом дает ровно ~ А (для экстремального случая). Это еще не всё: как по¬
казали последующие исследования, при малых отклонениях от этого экстремального случая
(т. е. когда температура Хокинга на бесконечно малую величину выше нуля) также получа¬
ется правильное значение энтропии как малой поправки к чисто «чернодырной» природе
излучения Хокинга. Более того, это оказывается справедливым и при наличии вращения,
и для 4-мерного пространства-времени.
Внимательного читателя может удивить, что в теории струн появляется «другая кон¬
станта» gs, тогда как всё должно вроде бы задаваться струнной постоянной а' (§§ 31.8, 31.9),
поскольку в лагранжиане фигурирует только этот параметр. Ответ состоит в том, что ре¬
ально здесь не все фиксировано, поскольку необходимо договориться относительно вели¬
чины дилатонного поля (§31.8). Значение gs определяется средним значением дилатонного
поля^31*71!, которое предполагается постоянной величиной. В общем случае это поле не обя¬
зано быть постоянным, однако для удобства оно, как и в приведенном обсуждении, часто
считается таковым. Значение этого поля зависит от ряда факторов, например, конкретного
выбора пространства У планковского размера или типа теории струн (т. е. струн типа I, IIA,
ИВ, гетеротических 0(32) или гетеротических Eg х Es; см. § 31.14). Фактически такая зави¬
симость лежит в основе дуальности сильной и слабой связи (§31.14), при этом параметр gs
одной теории оказывается обратной величиной аналогичного параметра «дуальной» теории.
Читатель может заметить, что я счел вышеприведенные аргументы весьма далекими от
подлинного вывода формулы для Sbh> несмотря на замечательные совпадения. Мне извест¬
но, что другие специалисты по общей теории относительности также ощущают значитель¬
ный дискомфорт, особенно в связи с тем фактом, что при определении огромной энтропии
черной дыры ее горизонт как будто не играет никакой реальной роли. (Это находится в рез¬
ком противоречии с энтропией черной дыры в представлении петлевых переменных, что
будет кратко обсуждено в § 32.6.) Действительно, в теории струн энтропия вообще вряд ли
увеличивается в точке образования черной дыры, что приводит к точке зрения, совершенно
отличной от обычной (описанной в § 27.10).
В дополнение к этому следует упомянуть специфическую техническую трудность, свя¬
занную с изложенной аргументацией теории струн^31,72!. Она относится к необычному тер¬
модинамическому свойству обычных черных дыр, которые при малых значениях момента
импульса обладают отрицательной теплоемкостью (см. примечание 27.2). Теплоемкость
служит мерой повышения температуры тела при передаче ему некоторок^иадого количе¬
ства тепловой энергии. Для обычного тела эта величина положительна, и наш повседнев¬
ный опыт свидетельствует, что при получении телом тепла его температура повышается.

31.16/«Голографический принцип»	763
—; /■■■■ — —  —— - -  ■■     ■ — —■   ,     —.... -  —
/
i	.
■
■
■
1
Однако в случае черной дыры ее температура понижается. Тепловая энергия придает чер¬
ной дыре некоторую дополнительную массу (согласно формуле Е — тс2), так что дыра
становится более массивной, и, согласно формуле Хокинга для шварцшильдовской дыры
(§30.4) Твн = 1/87Гга, ее температура понижается, так что теплоемкость действительно
оказывается отрицательной. Эта забавная отрицательность теплоемкости черной дыры стал¬
кивается с затруднениями, если применить аргументацию теории струн для энтропии черной
дыры к дырам, которые не близки к экстремальному случаю, поскольку в этой аргументации
предполагается положительная теплоемкость, а теплоемкость черной дыры положительна,
только когда она близка к экстремальной ситуации. Действительно, в керровском случае теп¬
лоемкость положительна лишь при условии т > а > (2д/3 — 3)1//2га, а в случае Рейсснера-
Нордстрёма — при т > е > ту/3/2;,такого же рода результаты получаются для всех других
заряженных полей Янга-Миллса.
Поэтому соотношения, получаемые в расчетах по теории струн, представляются
несколько удивительными. Однако, на мой взгляд, они никак не могут служить незави¬
симым обоснованием формулы Бекенстайна - Хокинга для энтропии. Метод, основанный на
петлевых переменных (§ 32.6), представляется более впечатляющим подходом к проблеме
квантовой гравитации.
31.16.	«Голографический принцип»
Приведенная аргументация теории струн, как и практически все расчеты на основе те¬
ории струн, использует теорию возмущений. Недавно, однако, были предложены некоторые
идеи с целью получения точных результатов. Они основаны на различных примерах так
называемой «голографической гипотезы», которая затем привела к голографическому прин¬
ципу. Идея этого «принципа» состоит в том, что при некоторых обстоятельствах состояния
(квантовой) струнной теории поля, определенной на некотором пространстве-времени М,
могут быть поставлены в одно-однозначное соответствие с состояниями другой квантовой
теории поля, определенной на другом пространстве-времени £ меньшей размерности! Часто
рассматривают £ как (времениподобную) границу пространства АЛ или хотя бы как некото¬
рое конформно-гладкое времениподобное подмногообразие пространства АЛ (см. рис 31.14).
Это, однако, не относится к обычному примеру, с которого мы начнем. Голографический
принцип в некотором смысле аналогичен голограмме, позволяющей создавать впечатление
трехмерного изображения при рассмотрении двумерной поверхности'131<731.
Рис. 31.14. «Голографический принцип». Пространство-время £ пред¬
ставляет собой (времениподобную) границу другого пространства-вре¬
мени АЛ. Выдвигается гипотеза, что подходящая квантовая теория поля,
определенная на £, может быть эквивалентна струнной квантовой тео¬
рии поля на АЛ
Наиболее известная форма этого «голографического принципа» берет начало от ра¬
боты Хуана Малдасены 1998 года, которую иногда называют гипотезой Малдасены или
гипотезой ADS/CFT. Здесь в качестве АЛ берется (1 + 9)-мерное произведение AdSg х S5,
где AdSs — («необернутое») (1 -Ь 4)-мерное пространство анти-де-Ситтера (см. §28.4,
рис. 28.8 и 28.9 б, но здесь мы рассматриваем четыре пространственных измерения). Про¬
странство S5 представляет собой пространственноподобную 5-сферу с радиусом космо¬
логического размера (—А')1/2, где А' есть (отрицательная) космологическая постоянная
пространства AdSs (§ 19.7). Меньшее пространство £ должно быть 4-мерной конформной
бесконечностью (см. §27.12) пространства AdSs; см. рис. 31.15. Заметим, что простран-

764
Глава 31
Ad Sr.
О
s
ство £, будучи 4-мерным, в этом случае определен¬
но не является границей пространства Л4, посколь¬
ку М = AdSs х S5 является 10-мерным простран¬
ством. Вместо этого «границей» пространства £
можно считать £ х S5. Гипотеза Малдасены про¬
возглашает, что теория струн на AdSs х S5 должна
быть эквивалентна некоторой суперсимметричной
теории Янга-Миллса на £.
Здесь нет возможности обратиться к «кван¬
тово-энергетическим» аргументам, предложенным
в §31.10 для объяснения огромной разницы
между функциональной свободой обычного поля
Еоо3
на Л4, оом°°9, и обычного поля на £, ос
Поскольку дополнительные измерения простран¬
ства А4, имея космологический масштаб, никоим
образом не «малы», великое множество дополни¬
тельных степеней свободы вследствие зависимости
полей от части S5 пространства М будет исключать
всякую возможность согласия между двумя теори¬
ями поля. То же относится и к обычной квантовой
теории поля на М и £, поскольку одночастичные
состояния сами описываются просто как «обычные
поля» (см. §26.2). Голографический принцип мо¬
жет быть применим к этим пространствам лишь при условии, что обсуждаемая квантовая
теория поля далека от «обычной».
В случае теории струн на М можно понять, что имеются очень сильные условия согла¬
сования, резко уменьшающие функциональную свободу оом°°' . Однако на первый взгляд
это кажется маловероятным. Вспомним из главы 21 и §§22.8, 16.7, что квантовое состояние
одиночной частицы в (1 + п)-мерном пространстве-времени имеет функциональную свобо-
Р /у4) ^	Т~\
ду ос , где Р — некоторое положительное целое число, описывающее число внутренних
или вращательных степеней свободы частицы (примером может служить спин). Квантовое
состояние одиночной струны будет обладать гораздо большей функциональной свободой, по¬
скольку классическая струна имеет бесконечно много степеней свободы. Если число ооРсс
каким-то способом уменьшить, то это должно быть гигантским ограничением, возможно,
подобным ограничениям, налагаемым на размерность и кривизну пространства-времени
в §31.7, но мне не известно о каких-либо предлагаемых ограничениях такого рода, кото¬
рые в любом случае должны были бы существенно влиять на подсчет струнных состояний,
обсуждавшийся в §31.15.
Остается возможность найти способ значительно увеличить функциональную свободу
в суперсимметричных полях Янга-Миллса на £. Я вижу единственный путь к этому —
взять бесконечное число таких полей, перейдя к пределу Аг —> оо (N — число генераторов
суперсимметрии). Однако в обычном варианте этой гипотезы предполагается N = 4, чтобы
можно было воспользоваться «внутренней группой» SO(6), которая действует на суперсим¬
метричных партнеров, но оставляет неизменными потенциалы Янга - Миллса^31‘74^. Вну-
тренняя симметрия выбирается так, чтобы согласовать симметрию SO(6) пространства SD,
фигурирующего в AdSs х S5. На мой взгляд, принципиально неверно пытаться согласо-
Рис. 31.15. Гипотеза Малдасены (гипотеза
ADS/CFT). Здесь пространство £ должно
быть 4-мерной конформной бесконечно¬
стью (§27.12) анти-де-ситтеровского про¬
странства AdSs (см. рис. 28.9 6), а не
Г
10-мерного пространства ЛЛ — AdSs х S ;
однако теория струн на ЛЛ предполагается
эквивалентной суперсимметричной теории
Янга-Миллса на £
вать «симметрию пространства-времени» с внутренней группой такого рода, если только,
как в случае первоначальной теории Калуцы - Клейна (§31.4), симметрия пространства-вре¬
мени не задается как точная, благодаря существованию полей Киллинга; это относится и ко
всем физическим полям в пространстве-времени. Избыточные степейтювободы в оом°°

31.17. D-браны
 7
765
появляются (ю той причине, что часть S5 пространства Л4 не обладает симметрией, которую
должны иметь поля на ЛЛ.
Мне представляется, что роль такого несоответствия функциональной свободы оценена
недостаточно. «Размеры» пространств Фока (см. §26.6, примечание 26.12) будут совер¬
шенно различными всякий раз, когда существенно различается функциональная свобода
классических полей. Следует отметить, что условие положительной частоты, наложенное
на одночастичные состояния в квантовой теории поля, не меняет свободу осМо° для клас¬
сических полей. Оно просто компенсирует тот факт, что эти классические поля нуждаются
в комплексификации при переходе к описанию на основе квантовой теории поля (см. § 26.3).
Почему гипотеза ADS/CFT воспринимается столь серьезно? Ее поддерживает соответ¬
ствие между состояниями БПС, введенными Малдасеной и рядом других авторов. Это можно
понять как соответствие между группами симметрии SO(2, 4) х SO (б) в различных теориях
поля, однако имеются и другие «совпадения», требующие объяснения. Надежды, возлага¬
емые на гипотезу ADS/CFT, связаны с тем, что она, как предполагается, может позволить
теории струн не прибегать к обычным методам теории возмущений со всеми связанными
с ними ограничениями.
Вычисления с использованием пространства £ упрощаются благодаря тому, что это
пространство является конформно-плоским (его иногда называют «плоским», хотя ему
не приписывается какая-либо реальная метрика, а лишь конформная метрика с сигнату¬
рой Н ). Это универсальное накрывающее пространство (см. примечание 15.9) «ком¬
пактифицированного пространства Минковского», которым мы займемся 131*751 в § 33.3, оно
-1	-f
обладает топологией S х Е . Метрическое пространство S х Е иногда называют «цилиндром
Эйнштейна» или «Вселенной Эйнштейна», поскольку Эйнштейн склонялся к этой космоло¬
гической модели в период 1917-1929 г.г., когда он ввел космологическую постоянную в свое
уравнение поля (§ 19.7)^31'76!.
Гипотеза ADS/CFT возникла как другой способ взглянуть на «вывод» формулы Бекен-
стайна - Хокинга для энтропии черной дыры в теории струн (§31.15). Для этого черную
дыру представляют как «тепловое состояние» на £. Это относится лишь к черным дырам
космологического размера и в лучшем случае представляет собой «гипотезу», основанную
на замечательном согласии между «вычислениями энтропии», сделанными различными спо¬
собами, а вовсе не действительный вывод формулы Бекенстайна - Хокинга.
ч
31.17.	D-браны
В разных местах предыдущего изложения, в частности, в §§31.11, 31.12, 31.15, 31.16,
я высказал свои сомнения в отношении использования пространства-времени высокой раз¬
мерности в теории струн. Одно из моих наиболее фундаментальных затруднений связано
с необычайным увеличением степени функциональной свободы в многомерных теориях
(до оор°° в случае (14- М)-мерного пространства-времени) и с необходимостью найти
какие-то способы «замораживания» лишней свободы. Вспомним «шланговую» аналогию,
изображенную на рис. 15.1 и 31.3. То, что мы воспринимаем как «точку пространства-вре¬
мени», представляет собой полностью динамический объект, в данном случае описываемый
как окружность, но в общем случае более высокой размерности, и именно это создает
огромную дополнительную свободу. Напомним, что Калуца и Клейн устранили эту свободу
волевым образом, постулировав наличие вектора Киллинга, обводящего нас вокруг «шлан¬
га», что в конечном счете приводит к 4-мерному пространству-времени. В математическом
отношении эта процедура вполне законна, но она, по-видимому, никогда серьезно не вы¬
двигалась в теории струн. Вместо этого, как отмечалось в §31.10, «струнные» теоретики
обычно ссылаются на огромную величину энергии, которая необходима для возбуждения

766
ГЛАВА 31
колебаний в этих лишних измерениях. Как мы видели в §§31.11,31.12, имеются основания
сомневаться в весомости этих аргументов.
В то же время природа активности теории струн такова, что на нее нелегко нападать
с аргументами, подобными приведенным в §§31.11, 31.12, 31.16. Поскольку этот объект
в любой момент склонен к превращению в иную форму, при которой эти аргументы оказы¬
ваются не относящимися к делу^31771 Действительно, в соответствии с некоторым новым
взглядом на дополнительные измерения общая философия может быть пересмотрена, как
мне кажется, без уведомления публики о том, что произошли какие-то серьезные измене¬
ния. Именно такой характер носит введение некоторой «D-бранной философии», хотя это
и не обязательно точка зрения большинства «струнных» теоретиков (какой бы она ни была).
Прежде всего, что такое D-браны? Зачем они понадобились теории струн? Ответ на
второй вопрос состоит в том, что они имеют смысл незамкнутых струн, фигурирующих
в теории типа I (§ 31.14), при этом каждый из двух концов открытой струны должен поко¬
иться на некоторой D-бране (рис. 31.16). Ответ на первый вопрос: D-брана (или D-g-брана) —
это времениподобная структура с 1 + q пространственно-временными измерениями (q про¬
странственных измерений и одно временное), представляющая собой устойчивое решение
11-мерной супергравитации. (Воспользовавшись одной из дуальностей М-теории, мы мо¬
жем рассматривать D-брану как решение уравнений некоторого другого варианта струнной
М-теории.) По существу, это есть «брана» (описанная в §31.14) некоторой размерности
(0,1,2,...,9),являющаяся БПС-состоянием (см. §§31.15,31.16)и потому обладающая неко¬
торым суперсимметричным набором «зарядов» Янга-Миллса; этому состоянию соответ¬
ствует минимум энергии. D-браны фигурируют во многих современных работах, посвящен¬
ных теории струн (в частности, энтропии черной дыры — см. §31.15). Их часто пытаются
трактовать как классические объекты, помещенные в полное пространство-время с 1 + 9
(или 1 -j-10) измерениями. Буква D происходит от слова «Дирихле» по аналогии с краевой
задачей, получившей название задача Дирихле, в которой имеется времениподобная граница,
на которой заданы краевые условия (названа в честь выдающегося французского математика
Пьера Лежена Дирихле (1805-1859) — вспомним «ряды Дирихле» из § 7.4).
Рис. 31.16. Два конца открытой струны предполагаются находящими¬
ся на времениподобном (q -j- 1)-мерном подпространстве простран¬
ства-времени, называемом D-браной или D-g-браной. D-брана явля¬
ется существенно классическим объектом (хотя и обладает суперсим-
метричными свойствами), представляющим решение 11-мерной тео¬
рии супергравитации (типа БПС-состояния)
Я не буду пытаться обсуждать здесь D-браны сколько-нибудь подробно. Единствен¬
ный вопрос, который хотелось бы здесь поднять, касается того, что с введением таких
«D-бран» различными теоретиками была выдвинута «струнная революция», представляю¬
щая собой заметный сдвиг по сравнению с тем, что было раньше. Нередко утверждается,
что мы, возможно, «живем» на той или иной D-бране, имея в виду, что воспринимаемое
нами пространство-время в действительности лежит внутри D-браны. При этрм оно может
даже совпадать с D-браной, так что причина, по которой некоторые «лишние» измерения
нами не воспринимаются, объясняется тем, что «наша» D-брана не проникает в эти лишние
измерения.

31.18. Физический статус теории струн	767
Эта последняя возможность должна быть, конечно, наи¬
более экономной позицией, так что «наша» D-брана (D-3-бра-
на) будет иметь 1 + 3 измерений. Это не устраняет степени
свободы в лишних измерениях, но резко уменьшает их чис¬
ло. Почему? Объяснение таково, что мы «не знаем» о степе¬
нях свободы, связанных с внутренней частью пространства
высокой размерности между D-бранами, и это имеет место
там, где проявляется избыточная функциональная свобода.
Мы воспринимаем лишь те дополнительные измерения, ко¬
торые имеют прямое отношение к той D-бране, на которой
мы «живем». Вернемся к нашей аналогии со шлангом. Вме¬
сто «фактор-пространства»^31,78^, картины, которую напоми¬
нает первоначальная аналогия Калуцы - Клейна (рис. 31.3),
наше наблюдаемое пространство-время теперь выглядит как
4-мерное подпространство пространства более высокой раз¬
мерности. Для наглядности представим себе полоску вдоль
нашего шланга, представляющую подпространство D-браны,
которая теперь является «нашей наблюдаемой 4-мерной Все¬
ленной» (рис, 31.17).
Какой же функциональной свободы теперь можно ожи¬
дать? Ситуация подобна геометрической картине, предложен¬
ной в § 31.3, чтобы получить более привычный взгляд на «супергеометрию» (см. рис. 31.2).
Поскольку теперь мы имеем дело с поведением только на D-бране (которая предполагается
обычным (1 + 3)-мерным пространством-временем), можно считать, что наша функциональ¬
ная свобода принимает доступную величину ооМсс , хотя и с некоторым довольно большим
числом М. Но это предполагает, что динамика, ограниченная полным 10-пространством (или
11-пространством), дает нам динамические уравнения обычного типа в «нашей» 4-мерной
D-бране, так что начальные условия, заданные на некотором 3-пространстве, будут доста¬
точны для определения поведения в 4-пространстве. В общем случае это маловероятно, так
что можно ожидать избыточной свободы оом°° . Проблема по-прежнему остается!
При таком подходе к D-бранам делается попытка решить «проблему иерархий», упо¬
мянутую в § 31.1. В частности, это вопрос о том, почему гравитационные силы столь слабы
по сравнению с другими силами, существующими в Природе, или, что эквивалентно, поче¬
му фундаментальная планковская масса, определяемая гравитацией, так мала по сравнению
с массами существующих элементарных частиц (приблизительно в Ю20 раз). D-бранный
подход к этой проблеме требует, по-видимому, существования более чем одной Л-браны,
одна из которых «велика», а остальные «малы». Существует экспоненциальный множитель,
определяющий степень растяжения геометрии при переходе от одной D-браны к другой,
который привлекается для объяснения различия в КЗ40 (или около того) раз между грави¬
тационными и остальными силами^31'79-f. Можно отметить, что такая картина многомерного
пространства-времени, которое протягивается от одной D-бранной границы к другой, пред¬
ставляет один из типов геометрии, предлагаемой для 11 -мерных теорий, подобных М-тео-
рии, где 11 -е измерение имеет вид открытого сегмента, а геометрия каждой границы имеет
топологию 10-пространств, рассмотренных выше (например, ЛЛ х У). В других моделях
11 -е измерение имеет топологию S1.
31.18.	Физический статус теории струн
т
Какой вывод нам следует из всего этого сделать в отношении статуса теории струн как
физической теории будущего? Ситуация поражает сочетанием загадочных и замечательных
Рис. 31.17. Альтернативная по
отношению к рис, 31.3 точ¬
ка зрения, использующая пред¬
ставление D-бран. Она состоит
в том, что «существо» в про¬
странстве высокой размерности
не обязано воспринимать все
лишние измерения, а «живет»
в некотором подпространстве,
возможно, на D-бранной гра¬
нице

768
Глава 31
совпадений и неправдоподобных гипотез, поэтому было бы неверно на данной стадии под¬
ходить к ней с догматической позиции. Пока что многие заявления «струнных» теоретиков
опираются на очевидные совпадения. Несомненно, здесь нужно, как говорится, семь раз
отмерить. Я полагаю, следует прямо сказать, что некоторые из наиболее громких заявле¬
ний (например, о том, что теория струн дает нам законченную и согласованную квантовую
теорию гравитации) можно вообще не принимать во внимание. Но при этом я вынужден при¬
знать, что некоторые аспекты струнной М-теории указывают на что-то несомненно важное,
«происходящее за сценой». Вот что написал мне в электронном письме математик Ричард
Томас из Лондонского Имперского колледжа:
Я не могу выразить в полной мере, насколько глубоки некоторые из этих дуально¬
стей; они постоянно удивляют меня всё новыми предсказаниями. Они выявляют
структуру, которая никогда не считалась возможной. Математики несколько раз
уверенно предсказывали ее невозможность, но такие люди, как Канделас, Де Ла
Олса и другие, показали, что эти предсказания неверны. Каждое их предсказание
после надлежащей математической интерпретации оказывалось правильным. И для
этого вроде нет концептуальных математических оснований, мы понятия не имеем,
почему они правильны, — просто вычисляем независимо обе стороны соотношения
и действительно обнаруживаем в обеих одинаковые структуры, симметрии и ре¬
зультаты. Для математика это не может быть простым совпадением, здесь должна
быть какая-то глубокая причина. И такой причиной является допущение, что эта
большая математическая теория правильно описывает Природу...
Вполне возможно, что здесь есть «нечто», представляющее интерес с точки зрения чистой
математики, однако нет реальных оснований считать, что это сколько-нибудь приближает
нас к тайнам Природы. Я считаю такую позицию наиболее разумной, хотя и готов принять,
что Природа может быть заинтересована в подобных материях (хотя, возможно, и несколько
иным образом, нежели предполагалось до сих пор). Сила доводов теории струн основана на
ряде замечательных математических соотношений, связывающих различные, казалось бы,
«физические ситуации» (хотя эта «физика» обычно кажется довольно удаленной от физики
реального мира Природы). Являются ли такие соотношения «совпадениями» или за ними
действительно стоит какая-то глубокая причина? Мне кажется, что во многих случаях такая
причина имеется, в некоторых из них она пока не найдена, но это все же еще не убеждает
нас, что «струнные» теоретики делают настоящую физику. Или даже если так, то какой
аспект физики они реально изучают?
Я думаю, что оценка этих проблем не может быть сделана без обращения к конкретной
позиции Эдварда Виттена. По общему мнению, именно он является фигурой, определяющей
направление развития теории струн начиная с конца 1980-х годов. Я уже упоминал о его роли
в провозглашении в 1995 году «второй суперструнной революции» (§31.14), но уже к тому
времени он проявил свое превосходство в постановке и развитии нескольких важных на¬
правлений в теории струн и многих других областях, имеющих к ней отношение (не всегда
очевидное). За свою более чем 30-летнюю историю теория струн имела несколько «экскур¬
соводов» (см. §31.6), но Виттен был во многих отношениях наиболее выдающимся. Там,
где прошел Виттен, остальным было двигаться легче. В качестве примера можно отметить,
что оригинальная работа Малдасены, инициировавшая деятельность, описанную в §31.16,
лежала в архивах практически не замеченной теоретиками, пока ее не продолжил Виттен
в 1998 году. После этого она немедленно стала работой, наиболее цитируемой «струнными»
теоретиками^31*80^.
Интересно, что в своей заманчиво выглядящей новойчрабрте^1*81! Виттен вернулся
к рассмотрению стандартного 4-мерного пространства-времени (хотя и с учетом супер¬
симметрии). Комбинируя идеи теории твисторов и теории струн, Виттен сумел получить

31.18: Физический статус теории струн
769
некоторые замечательно красивые результаты, относящиеся к взаимодействию Янга-Милл¬
са для нескоДьких глюонов (§25.7). На мой взгляд, устремленный в сторону твисторов
(см. главу 33), это замечательная работа, которая вполне может привести к новым важным
результатам.
В отношении необычайных интеллектуальных достижений Виттена никаких вопросов
не возникает. Я могу говорить об этом во многом на основании личного опыта. У меня
было много случаев убедиться в этом, когда я посещал семинары по геометрии и анали¬
зу в Математическом институте в Оксфорде, на которых был предложен новый и глубоко
оригинальный подход к некоторой проблеме, и оказалось, что основная плодотворная идея
полностью или, по крайней мере, частично исходит от Виттена. Часто подобные подходы
открывали совсем новую область, и такие непредвиденные озарения проливали яркий свет
на сложные математические проблемы, иногда считавшиеся неразрешимыми. У меня нет
сомнения, что Виттен обладает замечательной математической проницательностью и пони¬
манием высшего порядка. (И действительно, в 1990 году он был удостоен медали Филдса,
которая для математиков имеет такой же статус, что и Нобелевская премия в научном мире.
Для физика это совершенно невероятное достижение.) Тем не менее я полагаю, что сам
Виттен не согласится с тем, что его способности лежат в основном в области математи¬
ки. Насколько я его понимаю, его успехи стали следствием его глубокого проникновения
в замыслы Природы, которое возникло при изучении структуры квантовой теории поля с
интегралами по траекториям и бесконечномерными пространствами функций в сочетании
с идеями суперсимметрии и исследованием самой природы теории струн и ее обобще¬
ний. Если он прав, то это, возможно, один из наиболее подходящих случаев принять его
утверждение, что суперсимметрия и теория струн пользуются глубокой благосклонностью
Природы. С другой стороны, возможно, что он более замечательный математик, чем ему
кажется!
Как я отношусь к тому утверждению, что замечательные математические связи, обна¬
руженные Виттеном и его коллегами, означают некоторую глубокую близость к Природе?
Я не вполне уверен в том, как следует подходить к этому вопросу. Вспомним о заме¬
чательном достижении математика Эндрю Уайлза, доказавшего знаменитую «последнюю
теорему Ферма» после трех с половиной веков безуспешных попыток (§ 1.3). В действи¬
тельности Уайлз установил, что в некотором важном случае два совершенно по-разному
выглядящих вычисления всегда дают один и тот же набор ответов; общая форма этого заме¬
чательного утверждения известна под названием гипотезы Таниямы-Шимуры. (Фактически
доказательство Уайлза подтвердило лишь часть полной гипотезы Таниямы-Шимуры, ко¬
торая достаточна для доказательства утверждения теоремы Ферма, однако использованные
им методы открыли путь для полного доказательства, завершенного впоследствии Брюлом,
Конрадом, Дайемондом и Ричардом Тейлором.)
Существует, возможно, некоторое смутное подобие между этой гипотезой и упомя¬
нутыми выше (§31.14) зеркально-симметричными соотношениями между пространствами
Калаби-Яу. В обоих случаях мы имеем два бесконечных списка чисел, которые загадочным
образом оказываются одинаковыми. В математике такое отнюдь не редкость, и в каждом от¬
дельном случае может пройти много лет, прежде чем станут ясны причины совпадения этих
списков. Как я понимаю, многие соотношения, получаемые при использовании «зеркальной
симметрии», были установлены на основании чисто математической аргументации I31-82!.
Насколько мне известно, подобные загадочные соотношения обычно не выдвигаются для
подтверждения естественнонаучных теорий (в противовес математическим). К этому во¬
просу мы вернемся в § 34.9.
Мы наблюдали «совпадение» такого рода в аргументации теории струн для энтропии
черной дыры, выдвинутой в § 31.15 (и даже еще раньше, вне связи со струнами, в § 30.5). Яв¬
ляется ли это просто математическим совпадением или эти аргументы можно рассматривать

770
Глава 31
как реальный вывод? Позвольте мне закончить эту главу другим примером замечательного
, математического совпадения из физики начала XX века. В 1912 году Вольдемар Фойгт по¬
строил теорию спектральных линий, основанную на неправильной осцилляторной модели.
Пятнадцатью годами позже Гейзенберг и Иордан нашли тот подход к проблеме, который мы
сейчас считаем правильным. Полезно процитировать воспоминания Гейзенберга о работе
Фойгта^31*83!:
Он сумел так подобрать связь осцилляторов друг с другом и с внешним полем,
что оказался правильно воспроизведен эффект Пашена-Бака в слабых магнит¬
ных полях. Для промежуточной области умеренных полей он получил для частот
и интенсивностей длинные комплексные квадратные корни. Эти формулы были
совершенно непонятны, однако они с высокой точностью воспроизводили экспе¬
риментальные результаты. Пятнадцатью годами позже Иордан и я взялись решить
ту же задачу методами квантово-механической теории возмущений. К великому
нашему изумлению, мы получили старые формулы Фойгта для частот и интенсив¬
ностей, в том числе в комплексной области, соответствующей умеренным полям.
Причину этого мы смогли понять позже, и эта причина оказалась чисто формальной
и математической.
В главе 34 я вернусь к этому удивительному свойству математических соотношений как
движущей силе, стоящей за теорией струн и другими направлениями развития фундамен¬
тальной физической теории.
Примечания
§31.1.
*
31.1. Не следует, конечно, путать это с основанием натуральных логарифмов е ~ 2,718281828459 ...
(см. § 5.3).
31.2. Огромную разницу между силами, создаваемыми сильным, электромагнитным, слабым и осо¬
бенно гравитационным взаимодействием, можно приближенно характеризовать относитель¬
ной величиной соответствующих констант связи: 1,	~	10“6, ~ 10“39; иногда ее назы¬
вают «проблемой иерархии». На сайте Университета штата Джорджия есть страничка, разъ¬
ясняющая тонкие моменты, касающиеся сравнения этих констант (см. http://hyperphysics.phy-
astr.gsu.edu/hbase/forces/couple/html).
31.3. Относительно «мягкая» перенормировка заряда связана с логарифмическим характером рас¬
ходимости в электродинамике. Внимательный читатель заметит, конечно, что проблема малых
значений масс элементарных частиц не исчезает лишь от того, что ее переформулируют, ис¬
пользуя крайне малый масштаб длины.
31.4. Вспомним, однако, замечание ’т Хоофта в §26.9.
§31.2.
31.5. См. полезные обзоры истории, персоналий и основных идей суперсимметрии на популяр¬
ном [432] и более продвинутом уровне [431].
31.6. См. [844, 714]. Относительно суперсимметричной теории Янга - Миллса, приводящей к су¬
щественному упрощению теории 4-многообразий Дональдсона, см. [216]. По словам Джона
Баеца, теория Зайберга-Виттена делает некоторые доказательства в теории Дональдсона при¬
мерно в 1 ООО раз короче.	/
31.7. См. доказательство положительности энергии с использованием суиерсимметрии [843, 185].
Интересные неравенства для черных дыр получены в раб^
31.8. См. [318], примечание 5 на стр. 399.
31.9. См. [475] или, гораздо подробнее, [530].

31.18. Физический статус теории струн
771
§313.
31.10. В качестве числа N обычно берут 2 в какой-либо степени, что соответствует числу компо¬
нент некоторого спинора (см. §§ 11.5, 33.4). Не следует путать это с числом 2iV элементов
супереимметричной алгебры. См. обсуждение суперсимметрии одним из ее создателей в кни¬
ге [820].
31.11. Более подробную информацию о супермногообразиях можно найти в [192, 669].
§31.4.
31.12. Более подробное обсуждение всего этого можно найти в обзорной статье [75]. См. также [183,
184].
31.13. Относительно «последней надежды» на перенормируемость супергравитации см. [183, 184],
а также [186].
31.14. См., например, [400], стр. 1418.
31.15. Популярное введение в способ таких подсчетов содержится в [626], стр. 389.
31.16. При обычном описании с использованием расслоений метрика на базисном пространстве М
может при желании быть «поднята» в расслоение В над этим пространством, чтобы получить
каноническую «вырожденную» метрику на В, а также, возможно, невырожденную метрику,
если можно воспользоваться метрической структурой на слоях. Но это не существенно для
структуры расслоения.
31.17. Эта теория содержит уравнения Эйнштейна с максвелловским тензором энергии-импульса
в качестве источника, а также свободные уравнения Максвелла на искривленном простран¬
ственно-временном фоне.
31.18. Однако в некоторых недавних работах нашли применение идеи, комбинирующие теорию
струн с теорией твисторов и использующие стандартное 4-мерное пространство-время
(см. §§31.18, 33.14 и примечание 31.81).
§31.5.
31.19. Сравните с примечанием 12.14.
31.20. Общая история теории струн изложена в обзоре [706]. См. также [804, 541, 754, 560, 306].
31.21. В этой формуле используется бета-функция, введенная в 1777 году великим Эйлером. Первое
представление о дуальности появилось в работе [306].
31.22. Венециано [804] впервые воспользовался этой моделью для объяснения полюсов Редже. Об¬
щее изложение теории Редже можно найти в книге [154], см. также [629].
31.23. Некоторый ограниченный успех был впоследствии достигнут в результате объединения идей
теории твисторов и теории струн, но он имел в основном математическую природу и не
приводил к единой физической точке зрения; см. [718] и примечание 31.76.
§31.6.
31.24. Из интервью Брайана Грина с Майклом Грином 10 декабря 1997 года, цитируется по кни¬
ге [318], стр. 139 (стр. 98 русского перевода).
31.25. См. [847].
31.26. Более подробное и глубокое изложение можно найти в работах [317, 643, 316].
§31.7.
31.27. Аргументация, приводящая к 26 измерениям, содержится в [317, 643, 316].
31.28. Подходящее число, которое аномальным образом появляется в квантовых коммутаторах
(и должно быть положено равным нулю) равно 24 — сг, где а есть число пространственных
измерений минус число временных измерений.
31.29. При наличии суперсимметрии аномалия устраняется, если приравнять нулю 8 — а, где о
имеет тот же смысл, что и в предыдущем примечании.
31.30. Адронная струна немного отличается от обычной резиновой ленты в том отношении, что
последняя имеет конечную естественную длину, при которой натяжение обращается в нуль.
Для адронной струны такая «естественная длина» сама будет равна нулю.

772
Глава 31
§31.8.
31.31. Много подобных заявлений можно найти в книге Брайана Грина [318].
31.32. Цитировалось Абхаем Аштекаром в лекции на совещании по квантовой гравитации в Кали¬
форнийском университете, Санта-Барбара, 1986.
31.33. Хотя не все физики-релятивисты согласны со мной в том, что искомое объединение квантовой
механики и гравитации должно включать в себя изменение правил квантовой теории поля,
я постоянно ощущаю поддержку моей точки зрения. Отношение со стороны специалистов
в области квантовой теории поля куда менее благожелательно!
31.34. Термин «дилатон» (dilaton) — это не опечатка в слове dilation (расширение), а относится
к квантовому варианту этого понятия, связанному со степенями свободы, доступными при
изменении масштаба метрики. Напомним (см. главу 26), что, согласно правилам квантовой
теории поля, квантованные степени свободы могут проявляться как некоторые частицы.
§31.9.
31.35. Из интервью Брайана Грина с Эдвардом Виттеном 11 мая 1998 года, цитируется по книге [318],
стр. 210 (стр. 143 русского перевода).
§31.10.
31.36. Число 70 получается из формулы п(п — 3) для числа независимых компонент в расчете на
одну точку (п — 1)-поверхности начальных условий в n-пространстве с нулевым тензором
Риччи. См. [809, 485, 144].
31.37. См. [623, 110, 294].
§31.11.
31.38. См. [623].
31.39. Относительно проблемы модулей см. [199].
31.40. Можно предпочесть остаться в рамках квантовой теории поля и пользоваться когерентными
состояниями (§ 26.6) вместо классического описания. Это, однако, не снимает возникающих
здесь вопросов.
31.41. Хотя я и сомневаюсь, что многие «струнные» теоретики склонны рассматривать R-процесс
как динамический, имеются все же заметные исключения; см. [249, 250].
31.42. При квантово-полевом описании колебаний шланга (см. §§22.13, 23.8, 26.2) экситоны ведут
себя, как бозоны, поэтому в каждой отдельной З^-моде может содержаться много квантов.
Примером реальной физической системы, к которой применимо такое квантовое описание,
может служить длинный и узкий оптический волновод (например, оптическое волокно).
§31.12.
31.43. См. [372].
31.44. Условие состоит в том, что каждая времениподобная или нулевая геодезическая ощущает
«изначальную» кривизну в том смысле, что вдоль каждой из них где-то выполняется неравен¬
ство k[aRb]cd[ekf]kckd Ф 0, где к° есть нулевой вектор, касательный к геодезической. Простая
непосредственная оценка числа степеней свободы показывает, что это условие определенно
выполняется в любом «изначальном» пространстве-времени. Следует упомянуть, что данная
теорема применима и при ненулевом тензоре Риччи. Требуется лишь, чтобы тензор Риччи
удовлетворял некоторому «условию неотрицательности энергии» (см. §27.9, особенно при¬
мечание 27.20, и §28.5). Относительно термина «компактная гиперповерхность» см. § 12.6
и примечание 27.36.
31.45. Существуют особые случаи пространства У с нулевой кривизной и топологией «гиперто¬
ра» S1 х S1 х S1 х S1 х S1 х S1. Они, однако, не принадлежат к моделям пространства У,
пользующимся сегодня вниманием «струнных» теоретиков (§31.14). Кроме того, возмущения
гипертора, как правило, не являются плоскими.
31.46. Этот вывод получается в результате применения упомянутой теоремы о сингулярности непо¬
средственно ко всему пространству-времени М. В этом случае условие существования неко¬
торой компактной пространственноподобной гиперповерхности заменяется условием суще¬
ствования некоторой точки р, у которой световой конус будущего С «закручивается и пересе¬
кается с самим собой» во всех направлениях. Конус С есть геометрическое место световых

31.18. Физический статус теории струн
773
лучей £ (т.е. нулевых геодезических; см. §28.8), исходящих из точки р в прошлом и неогра¬
ниченно простирающихся в будущее. Реально это условие выполняется, если каждый такой
луч £ содержит некоторую точку q, для которой существует строго времениподобная кривая,'
идущая в будущее из р в q. В описанных точных моделях М х У это условие не выпол¬
няется (как и должно быть, поскольку пространство М х у может быть несингулярным),
однако нарушается только это условие. Из 8-мерного семейства лучей £ лишь очень неболь¬
шое двумерное подсемейство не входит в «3^-часть» пространства-времени (и не выходит из
нее обратно), тем самым закручиваясь внутрь конуса С. Можно показать, что при наличии
малого изначального возмущения этого конуса указанное свойство нарушается, и становится
применимой упомянутая теорема о сингулярности. Подробности этой аргументации будут
представлены в другом месте.
31.47. См., например, [526], где имеются ссылки на другие относящиеся сюда работы.
§31.13,
31.48. См. [733, 559].
31.49. См. [733, 322, 559].
31.50. Ряд 1 + 22 + 24 + 26 -f 28 4- ♦ • • не является суммируемым и в смысле Бореля, несмотря на
1
то что эйлерово значение этой суммы — ~ получается однозначно, в чем можно убедиться,
О
используя аналитическое приближение (§ 7.4). Мне не известно, применялись ли подобные
процедуры к полным струнным амплитудам.
§31.14.
31.51. Это замечание не относится к гетеротическим струнам (мы к ним вскоре перейдем), для
которых всегда используется киральный базис.
31.52. Наиболее современное изложение содержится в [323]. Дополнительно с применением этих
многообразий в теории струн можно познакомиться в работах [733, 643].
31.53. Здесь я испытываю некоторые затруднения, поскольку спинорные поля имеют определен¬
ную геометрическую интерпретацию. Их нельзя «вращать» (и, следовательно, «калибровать»,
строго говоря; см. §§15.2, 15.7), не затрагивая при этом само окружающее пространство;
см. [626].
31.54. Для получения римановой поверхности используется «поворот Вика»; различие между голо¬
морфным и антиголоморфным случаями обсуждается в §31.13.
31.55. В [733, 318] перечисляются фактически все известные дуальности, их статус и даются соот¬
ветствующие ссылки.
31.56. Это понятие «зеркальной симметрии» не имеет ничего общего с операцией зеркального от¬
ражения пространства (четностью), обозначаемой символом Р, которая обсуждалась в § 25.4.
31.57. См. [168], где дается отличное изложение этих идей.
31.58. См., например, [458, 750], более недавние результаты содержатся в [857].
31.59. Эти многообразия представляют собой комплексные 3-поверхности, называемые поверхно¬
стями 5-го порядка. Порядком комплексной поверхности в пространстве СР7П называется
число точек, в которых она пересекает комплексную (га — п)-плоскость общего вида в этом
пространстве.
31.60. Относительно «порядка» комплексной кривой см. предыдущее примечание 31.59. В данном
случае п— 1.
31.61. См. [168, 121, 459].
31.62. См. [733, 846] и популярное изложение в [318], стр. 203.
31.63. См. [796] или [53].
31.64. См. [110] и примечание 31.37.
§31.15.
31.65. См., однако, любопытные аргументы в [776].
31.66. См. [749].
31.67. См. [318], стр. 340.

774
Глава 31
31.68. Читателя может удивить, каким образом поле Максвелла без источников может привести
к ненулевому заряду. Здесь нет противоречия, поскольку черная дыра может возникнуть
в результате коллапса заряженного вещества, при котором все источники заряда исчезают
в дыре.
31.69. См. популярный обзор этих вопросов в [396].
31.70. Такой подсчет использует структуры, называемые «D-бранами», которые мы рассмотрим
в §31.17.
31.71. См. примечание 22.11.
31.72. На это затруднение обратил мое внимание Абхай Аштекар.
§31.16.
31.73. См. обзор по «реальным» голограммам в [434].
31.74. Это довольно сложные идеи. Не боящимся трудностей можно предложить работы [51 1, 848].
31.75. Джери Гиббонс указал на связь этой картины с некоторой интересной геометрией, которая
оказывается связанной даже с теорией твисторов. Различные вопросы, относящиеся к этой
конструкции, можно найти в [590].
31.76. См. [239].
§31.17.
31.77. Пример такого рода можно найти в [33].
31.78. «Фактор-пространство» подобно базисному пространству расслоения; см. §§ 15.1, 15.2.
31.79. Изложение этих вопросов в более общем виде можно найти в [651, 652], стандартное изло¬
жение «D-бранной техники» — в книге [420]. Одним из наиболее фантастических примене¬
ний этой техники стала «экпиротическая» модель происхождения Вселенной, предложенная
Стейнхардом и Туроком [746], в которой предполагается, что Большой взрыв возник из-за
столкновения двух D-бран в предыдущей фазе Вселенной. Несмотря на привлечение столь
экзотических элементов, авторы модели не пытались объяснить главную загадку, связанную
с Большим взрывом, а именно его совершенно особый характер, обсуждавшийся в § 27.13.
§31.18.
31.80. См. примечание 31.74.
31.81. См. [540, 849, 118, 119, 120, 102].
31.82. См. примечания 31.57, 31.58.
31.83. Эта цитата взята из письма Гейзенберга Германскому физическому обществу (1975) «Что такое
элементарная частица?». (Я благодарен Абхаю Аштекару, указавшему мне на него.) См. [378].

Глава 32
Узкая тропа Эйнштейна. Петлевые переменные
32.1.	Каноническая квантовая гравитация
Несмотря на популярность теории струн, было бы абсурдом считать, как делают
некоторыеt321^, что это единственное, чем стоит заниматься (см. §31.8). Было предложе¬
но много других идей, обладающих разными достоинствами и недостатками. К сожалению,
я не в состоянии обсудить здесь множество альтернативных идей, направленных на объ¬
единение квантовой теории со структурой пространства-времени. Вместо этого в данной
и следующей главах я сосредоточусь на некоторых из наиболее активно развивающих¬
ся областей, которые, по моему убеждению, наиболее плодотворны при поиске истинно¬
го союза между квантовой теорией относительности и квантовой механикой. Как можно
понять из моих замечаний в предыдущей главе, я придерживаюсь мнения, что следует
занять более жестко контролируемую позицию, нежели те, кто допускает увеличение раз¬
мерности пространства-времени или решается на введение суперсимметрии (хотя против
\
последнего у меня гораздо меньше возражений, чем против первого, из-за серьезных про¬
блем со стабильностью, с которыми мы столкнулись в §§31.11, 31.12). Соответственно
в этих двух главах мы познакомимся с некоторыми идеями, связанными с 4-мерным лорен-
цевым пространством-временем и предполагающими возможность рассматривать полевое
уравнение Эйнштейна[32.2], ^ез всяксщ суперсимметрии, в некотором подлинно квантовом
контексте. Мы увидим, что даже здесь «картина физической реальности», с которой мы
столкнемся, сильно отличается от знакомой нам — в одних отношениях не до такой сте¬
пени, как в предыдущей главе, в других — в еще большей степени. В этой главе мы по¬
знакомимся с петлевыми переменными Аштекара и спиновыми сетями, в следующей —
получим некоторое представление о теории твисторов. В этих двух главах мы коснемся
также некоторых других идей, получивших распространение, в частности, дискретного про¬
странства-времени, деформированных структур («квантовых групп») и некоммутативной
геометрии.
Один из наиболее прямых путей к квантованию теории Эйнштейна состоит в том, чтобы
привести его к гамильтоновой форме, а затем попытаться применить к нему процедуру ка¬
нонического квантования, описанную в §§ 21.2, 21.3. Здесь имеется много трудностей, и мне
не хотелось бы увязнуть в подробностях. Большинство из этих трудностей связано с «общей
кованиантностью» теории Эйнштейна (§ 19.6), так что выбор координат не имеет значения.
Напомним (§21.2), что стандартный «рецепт квантования», согласно которому импульс ра
заменяется оператором ihd/dxa, где ха — (классически) сопряженная координатная пере¬
менная, не всегда годится даже в случае плоского пространства-времени, если используются
криволинейные координаты. Таким образом, при проведении процедуры квантования такого
рода необходимо проявлять особое внимание.
Другая трудность связана со сложной, неполиномиальной структурой гамильтониана
в общей теории относительности. Следует также отметить, что помимо уравнений эволю¬
ции, описывающих уход от начальной пространственноподобной 3-поверхности S и опре¬
деляемых гамильтонианом, существуют и другие уравнения, действующие внутри этой по¬
верхности и называемые связями^2*3^. Это дает условия согласования для начальных данных

776
Глава 32
на поверхности S, и выполнение условий связи необходимо (и достаточно) для удовлетво¬
рительного (по крайней мере, локального) описания эволюции данных вне поверхности S;
в ходе этой эволюции уравнения связей продолжают удовлетворяться.
Канонический подход к квантованию общей теории относительности имеет длинную
и славную историю, восходящую к Дираку, который в 1932 году разработал новую про¬
цедуру квантования, чтобы учесть сложные ограничения (связи), возникающие в теории
Эйнштейна!32,4!. В течение многих лет этим путем следовал ряд исследователей, делая его
все более сложным!32,5!, однако неполиномиальная природа гамильтониана сильно затруд¬
няла прогресс. Затем в 1986 году индийско-американский физик Абхай Аштекар осуществил
важный прорыв. Путем изобретательного выбора переменных (частично связанного с идея¬
ми, выдвинутыми ранее Амитабхой Сеном!32,6!), приводящего уравнения связи к полиноми¬
альной форме, он сумел существенно упростить структуру уравнений, устранив неприятные
знаменатели в гамильтониане и получив сравнительно простую полиномиальную структуру.
32,2.	Киральность и переменные Аштекара
Одной из интересных особенностей «новых переменных» Аштекара, как их называ¬
ют (до сих пор), является их асимметрия в отношении правой и левой частей гравитона
(кванта гравитации)!32,7!. Из §§ 22.7, 22.9 мы помним, что (нескалярная) безмассовая части¬
ца имеет два спиновых состояния, которые могут быть правыми или левыми относительно
направления движения частицы. Они называются соответственно состояниями частицы с
положительной и отрицательной спиралъностъю. Гравитон должен быть частицей со спи¬
ном 2, поэтому двум его состояниям спиральности будут соответствовать значения s — 2
и s = — 2 (предполагается h = 1, s означает спиральность); см. также §22.12. Подход
Аштекара трактует эти два состояния различным образом. Таким образом, этот формализм
обладает право-левой асимметрией!
Здесь следует пояснить, почему гравитон рассматривается как объект со спином 2, то¬
гда как фотон имеет спин 1 (см. §§22.7, 33.7). Что это значит? Значение спина квантовой
частицы должно быть связано с симметрией (и полевыми уравнениями) описывающих ее
полевых величин (и, как мы видели в § 33.8, это лучше всего проявляется, если уравнения
записаны в 2-спинорной форме). Но хорошо бы иметь прямой геометрический способ уви¬
деть разницу между природой гравитации со спином 2 и природой электромагнетизма со
спином 1. Рассмотрим для этого волны, связанные с каждым из полей, — электромагнитные
волны, образующие свет, и гравитационные волны.
Для случая электромагнетизма геометрическая природа волн показана на рис. 22.12
в § 22.9. Ключевой пункт состоит в том, что векторы электрического и магнитного поля дей¬
ствительно являются векторными величинами, так что поворот волны на угол 7г (т. е. 180°)
вокруг направления ее распространения меняет знак описывающей ее величины на про¬
тивоположный, и, чтобы восстановить ее значение, требуется поворот на 27г. В случае
гравитации волна представляет собой деформацию пространства-времени, как показано на
рис. 17.8а, 17.9а, 28.15, 28.16. Теперь при повороте волны на угол 7г деформация перейдет
в самое себя, а чтобы она изменила знак, требуется поворот на ^7Г. Можно заметить, что так
получается, поскольку кривизна Вейля является квадруполъной величиной в соответствии
с эллипсом деформаций на рис. 28.15, и, как показано в § 31.9, это соответствует объекту со
спином 2. Для значения о поворот на угол тт/а вокруг направления распространения волны
меняет знак полевой величины, а поворот на 2гс/сг восстанавливает прежнее значение. (За¬
метим, что это выполняется и в случае, если а — полуцелое число, так что поле является
спинорным; см. § 11.3.)
В случае безмассового поля, как в рассматриваемой ситуации, можно пойти еще дальше
и считать плоские волны построенными из частей с правой и левой круговой поляризацией

32.2. КИРАЛЬНОСТЬ И ПЕРЕМЕННЫЕ АШТЕКАРА
777
(круговая поляризация электромагнитного поля изображена на рис. 22.12 б). Для квантового
поля соответствующие частицы будут обладать соответственно положительной или отрица¬
тельной спиральностью (рис. 22.13). В случае спина а эти значения спиральности будут ±а
(в описании на рис. 22.13 в этом случае q2 = z/w следует заменить на q2cr — z/w). Таким
образом, для гравитации действительно получаются два возможных значения спирально¬
сти -j-2 и —2.
Чтобы понять, как описываются спиральные состояния, нам придется рассмотреть соот¬
ветствующую математику в несколько более явном виде. Право-левая асимметрия составляет
важную особенность теории твисторов, которую мы рассмотрим в следующей главе, и под¬
ход Аштекара, по-видимому, получил начальный толчок от идей этой теории. Пока всё, что
нам понадобится от этих идей, — это математическое представление право-левой асимметрии
в терминах обычного пространства-времени. Вспомним две тензорные величины, описыва¬
ющие два известных безмассовых поля Природы — электромагнитное и гравитационное.
Такими величинами служат максвелловский тензор поля F — Fab (§ 19.2) и конформный
тензор Вейля С = Cabcd (§ 19.7). Каждый из них имеет так называемый дуальный тензор,
определяемый в индексной записи следующим образом:
*Fab = \sabpqF™И *Cabcd=\sabPqCpqcd,
где Sabpq ~ антисимметричный тензор Леви-Чивиты, выбранный здесь так, что в стандарт¬
ном правом ортонормированном базисе вот = 1 (см. §§ 12.7, 19.2). Мы уже встречались
с тензором *F, дуальным максвелловскому, в § 19.2. Тензор *С, дуальный тензору Вейля,
выглядит аналогично. Можно также проводить «дуализацию» по последней паре индексов cd
тензора Вейля. Но это приводит к тем же результатам, что и дуализация по индексам аЪ. *
Напомним, что элемент 2-плоскости в точке 4-мерного пространства-времени можно
описывать 2-формой / (или бивектором), которая является простой (§ 12.7). Как и в случае
максвелловского тензора (2-формы) F, можно построить дуальную форму */ и принять,
что комплексная форма / может быть самодуалъной (*/ = if) либо антисамодуалъной
(*/ — —if). Аналогично элемент (комплексной) 2-плоскости, соответствующий элементу /,
называется «самодуальным» или «антисамодуальным». Это понятие играет важную роль
в теории твисторов (§ 33.6)**.
В квантовой теории полевые величины могут принимать комплексные значения,
по крайней мере пока их можно интерпретировать как волновые функции. Существуют
различные, но математически эквивалентные способы описания (см. главу 26). Для наших
нынешних целей лучше рассматривать комплексный тензор Максвелла или даже комплекс¬
ный тензор Вейля как некоторую форму волновой функции соответственно фотона или
гравитона. Вместо условия вещественности,. обычного для классической полевой величи¬
ны, наши комплексные волновые функции должны удовлетворить условию положительной
частоты (в соответствии с требованиями, сформулированными в §§24.3, 26.2). Пусть нас
не слишком волнует вопрос о том, что это значит в случае вейлевской кривизны. (Можно
для начала рассмотреть искривленные пространства, которые лишь бесконечно мало отли¬
чаются от плоского, в таком случае С можно трактовать как некоторое поле в пространстве
Минковского, и тогда условие положительной частоты не создает проблем. Оказывается,
однако, что можно сделать еще лучше, как будет показано в §§ 33.10—33.12.)I32 8] Правополя¬
ризованные фотоны и гравитоны описываются (положительно-частотными) само дуальными
величинами +F и + С, где +F — ^(F ~ i*F) и = ~(С — i*C), так что
Z	Z
*(+F) = i+F и *(+C) = i+C;
*tBS Объясните почему. (Вы можете воспользоваться диаграммным предствлением и тождествами в § 12.8.)
Покажите, что если свернуть два индекса самодуалъной формы / = /а& с любой парой индексов антиса-
модуалънош тензора Вейля (или Максвелла), то в результате получится нуль.

778
Глава 32
левополяризованные фотоны и гравитоны описываются (положительно-частотными) анти-
1 1
самодуальными величинами ~~F = -(F 4- г*.Р) и “(7 = ^(С + г* С), так что
и *СС) = -ГС.
В оригинальной работе Аштекара самодуальная и антисамодуальная части кривизны Вейля
играют разную роль.
С физической точки зрения это может показаться странным, поскольку гравитационное
поле не проявляет признаков право-левой асимметрии, и определенно нет ничего подобного
в стандартной общей теории относительности Эйнштейна. Насколько я понимаю, в этом
вопросе возможны две позиции. С одной стороны, можно рассматривать асимметрию как
несущественную особенность используемой математики, которая оказывается полезной для
упрощения гамильтониана. С другой стороны, можно считать, что в Природе глубоко зало¬
жена право-левая асимметрия, и асимметричный формализм каким-то образом ухватывает
это. На самом деле мы знаем, что Природа обладает право-левой асимметрией, и это ясно
проявляется в слабом взаимодействии (см. § 25.3). В некотором смысле электромагнетизм со¬
держит остатки этой асимметрии, но это проявляется лишь косвенно, через его объединение
со слабым взаимодействием в электрослабой теории. В отсутствие (известного) подобно¬
го объединения с гравитацией нет оснований ожидать, что гравитация должна прямо или
косвенно проявлять такую же асимметрию. Что же касается взгляда «струнных» теорети¬
ков на их собственную теорию, то мы можем считать, что квантовая теория гравитации
имеет целью нечто большее, чем построение теории гравитации, она должна лечь в осно¬
ву всей физики, при этом нынешние рамки классического пространства-времени следует
рассматривать как удобную модель или приближение к чему-то более фундаментальному.
Если это «что-то» обладает изначальной киральностью (как гетеротические теории струн
(см. §31.14), формализм Аштекара или теория твисторов), то высокая степень киральной
асимметрии в слабых взаимодействиях становится гораздо более понятной.
32.3.	Вид переменных Аштекара
Каковы же эти киральные переменные Аштекара? Киральность появляется из-за асим¬
метричного выбора одного из двух сортов 2-спинора в применении к лоренцеву 4-про¬
странству. Вспомним такие объекты из §25.2, где было показано, что волновую функцию
электрона ф можно рассматривать как пару объектов с двумя комплексными компонента¬
ми а а и /За а одна из которых имеет нештрихованный индекс, другая — штрихованный.
Отметим, что нештрихованный индекс относится к зиг-части, или левополяризованной (с от¬
рицательной спиральностью) компоненте электрона, а штрихованный индекс — к заг-части,
или правополяризованной (с положительной спиральностью) компоненте. Мы видели также
(§ 25.3), что слабое взаимодействие обращает внимание только на зиг-часть а а и не замечает
заг-часть (За* • Пространственно-временной формализм, который выделяет нештрихованный
или штрихованный спинор как «более фундаментальный», нежели другой, включает в себя,
таким образом, базовую киральность и позволяет различать эти две спиральности на фун¬
даментальном уровне.
Именно это происходит в оригинальном формализме Аштекара (и твисторном форма¬
лизме). У Аштекара каноническими переменными, выбираемыми по отношению к простран¬
ственноподобной 3-поверхности 5, служат компоненты (обратной) 3-метрики 7, внутренней
по отношению к 5, и компоненты (нештрихованной) спиновой связности Г, взятой на по¬
верхности 5. Более точно, они представляют собой компоненты обратного метрического
тензора в локальном спинорном базисе, имеющие вид 2-форм. Спиновая связность Г соот¬

32.3. Вид переменных Аштекара
779
ветствует параллельному переносу спиноров аА, определенных на полном 4-пространстве,
а не «спиноров, внутренних по отношению к поверхности 5>П32*91 Таким образом, Г по¬
казывает, как произвести перенос нештрихованного 2-спинора аА в 4-пространстве парал¬
лельно самому себе по отношению к метрической связности 4-пространства (§§ 14.2, 14.8)
вдоль некоторой кривой, лежащей на 3-поверхности 5132Л°1. Поле компонент (плотностей)
3-метрики 7 играет роль импульсных переменных, поле компонент связности Г — роль со¬
ответствующих сопряженных координат (см. рис. 32.1). В квантовой теории импульс ра
в ^-представлении заменяется на ihd/dxa (§ 21.2); аналогично в Г-представлении мож¬
но заменить поля 7 на ihS/ST (5/ST относится к понятию функциональной производной,
определенной в §20.5). Соответственно в 7-представлении Г заменяется на —ihS/S'y.
Рис. 32.1. Канонические переменные Аштекара, определенные на пространственноподобной 3-по¬
верхности S в пространстве-времени Л4. В качестве «координат» выбираются компоненты спиновой
связности Г в 4-пространстве, ограниченные поверхностью S (для спиноров аЛ, показанных поло¬
винками стрелок). В качестве «импульсов» берутся компоненты (обратной) внутренней метрики 7
поверхности S (представляемые как 2-формы и отнесенные к ортон ормиро ван ному базису в каждой
точке поверхности S)
Связность Г состоит из части Гх, соответствующей внутренней кривизне поверхно¬
сти 5, и другой части Г2, соответствующей внешней кривизне (которая показывает, насколь¬
ко «изогнута» поверхность S в пространстве-времени М; см. рис. 32.2). Полную связность
можно представить в виде
Г = Гх + гГ2
(мы имели бы Гх — гГ2, если бы выбрали формализм с противоположной спирально¬
стью). Величина Г определяет связность расслоения (в смысле § 15.8), в которой базис¬
ным пространством служит поверхность S, а слоем — (нештрихованное) спиновое про¬
странство S (2-мерное комплексное векторное пространство). Слою соответствует груп-
па SL(2, С) (см. §13.3)13211].
Здесь я должен отметить техническую трудность, содержащуюся в оригинальном подхо¬
де Аштекара. Она связана с тем, что группа слоя SL(2, С) некомпактна и имеет нежелатель¬
ные бесконечномерные неприводимые представления, большая часть которых неунитарна
(см. § 13.7). Все это создает серьезные проблемы для строгого построения квантовой теории
гравитации. В соответствии с этим для достижения прогресса использовалась модифициро¬
ванная связность
Tv = Гх + г?Г2,

780
Глава 32
где г] — некоторое вещественное число, отличное от ну¬
ля, называемое параметром Барберо-Мммирци. Это да¬
ет преимущество чисто технического характера, посколь¬
ку группой слоя теперь служит компактная группа SU(2),
все (неприводимые) представления которой конечномер¬
ны и унитарны. Классическая теория, определяемая каж¬
дой связностью Г^, отличается от таковой, определяемой
связностью Г, лишь так называемым «каноническим пре¬
образованием», это означает, что такие классические тео¬
рии эквивалентны (имеют одну и ту же симплектическую
структуру; см. §§14.8, 20.4), хотя и описываются разны¬
ми «обобщенными координатами» в фазовом пространстве
(§20.2). Однако соответствующие квантовые теории уже
не обязаны быть эквивалентными. Эта проблема уже воз¬
никала в § 21.2: процесс квантования обычно не инвариан¬
тен относительно изменения обобщенных координат. По¬
ка остается нерешенным вопрос, как много «нарушений» может создать замена Г на Г^.
В любом случае следует начать с более «легкого» случая, использующего Г^. Хотя можно
возразить, что вместо ожидаемой теории квантовой гравитации в итоге получится некоторая
«игрушечная модель» (в которой значения ??, отличные от =Ы и 0, не имеют геометрическо¬
го обоснования), предполагается, что отличие от ожидаемого квантового варианта теории
Эйнштейна будет не слишком большим.
При использовании жизнь становится относительно проще, поскольку требуемые
различные неприводимые представления группы SU(2) в математическом отношении тожде¬
ственны различным состояниям спина (массивной частицы) в обычной (нерелятивистской)
квантовой механике. Вспомним (§22.8), что эти различные спиновые состояния нумеруют-
1
ся натуральными числами п = 0,1, 2, 3, 4, 5, ..где -nh есть величина спина. В §22.8
мы уже видели, что пространство представлений для каждого значения п состоит из сим¬
метричных спиновых тензоров флв...о с п индексами.) Вскоре мы увидим, как следует
пользоваться этими различными «значениями спина».
32.4.	Петлевые переменные
Как в более явном виде представить общую ковариантность (§ 19.6) хотя бы в пределах
3-поверхности начальных условий S1 Это можно сделать путем описания нашего общего
квантового состояния как некоторого простого семейства базисных состояний квантовой
теории гравитации, которые можно представить как дискретные и для которых условие об¬
щей ковариантности на поверхности S выполняется особенно просто. (Мы займемся этими
базисными состояниями чуть позже.) Состояние общего вида выражается в виде линей¬
ной суперпозиции этих базисных состояний. Чтобы понять, что для этого нужно, возьмем
замкнутую петлю на поверхности и рассмотрим действие нашей связности Г, в результате
которого нештрихованный спинор аЛ переносится «параллельно самому себе» вокруг этой
петли. Когда мы возвращаемся в исходную точку, то обнаруживаем, что имело место линей¬
ное преобразование спинового пространства S. Оно определяется, в компонентной форме,
комплексной матрицей 2x2 Тлв (см. § 13.3), элементы которой зависят от выбора базиса
в S. Однако след ТЛ д этой матрицы представляет собой комплексное число, не зависящее от
базиса*, так что это есть просто свойство спиновой связности Г, соответствующей выбору
петли. (Это пример более общего понятия, называемого петлей Вильсона в честь Кеннета
Рис. 32.2. Можно представить
величину Г в виде Т\ 4- гГг,
где Г1 соответствует внутренней
кривизне, а Г2 ~ внешней кри¬
визне поверхности S (Г2 пока¬
зывает, насколько «изогнута» по¬
верхность S в пространстве-вре¬
мени Л4)
* Й© Попробуйте объяснить почему.

32.4. Петлевые переменные
781
Вильсона, который впервые ввел эту идею в калибровочную теорию.) [32Л21. В 1988 году Кар¬
ло Ровелли, Ли Смолин и Тед Джейкобсон развили эту идею применительно к общей теории
относительности, назвав эти следы, зависящие от выбора петли, петлевыми переменными
для общей теории относительности. Если взять эти петлевые переменные в качестве кван¬
товых операторов, то «базисные состояния», о которых шла речь в начале этого параграфа,
будут их собственными состояниями.
Каков геометрический характер этих базисных квантово-гравитационных постоянных?
Они оказываются весьма необычными с точки зрения знакомой нам обычной метрической
геометрии и очень далекими от «гладкой геометрии» классической общей теории относи¬
тельности. Мы обнаружим, что эти базисные состояния представляют собой сингулярные
геометрические объекты, подобные (дираковским) дельта-функциям, которые были рас¬
смотрены в §§9.7, 21.10. Пусть S есть многообразие без особенностей^32Л31 Рассмотрим
семейство замкнутых петель на этом многообразии. Мы должны считать, что вся геомет¬
рия каждого петлевого состояния каким-то образом концентрируется вокруг петли. Это не
просто кривизна, концентрирующаяся вдоль петли, которая была бы аналогична геометрии
конуса с плоским основанием, показанной на рис. 32.3, где кривизна вдоль края основания
конуса, а также в его вершине ведет себя как дельта-функция (§ 9.7)*; ситуация такого рода
возникает и при другом подходе к квантовой гравитации, известном под названием исчисле¬
ния Редже (см. § 33.1), — вместо этого вся метрика концентрируется вдоль петли наподобие
дельта-функции и полностью исчезает вне петли. «Степень» этой концентрации измеряется
1
значением «спина», приписываемого этой петле, различные значения j — -п соответствуют
разным неприводимым представлениям группы SU(2) (нашу связность мы берем в виде
вместо «более правильной» формы Г).
Кривизна исчезает
Метрика
исчезает
Кривизна в виде
6-функции
Коническая
2-поверхность
а)
Поверхностная
6-функция
Петля
б)
Рис. 32.3. а) Негладкий пример конической 2-поверхности с нулевой кривизной всюду за исключением
вершины и границы основания, где кривизна описывается 6-функциями. (Исчисление Редже, приме¬
няемое к квантовой гравитации, оперирует с аналогичными 4-пространствами с кривизной, описывае¬
мой 6-функцией, на 2-пространствах; см. рис. 33.3.) б) Однако в случае петлевой квантовой гравитации
дело обстоит не так. Здесь фигурирует поверхностная 6-функция вдоль петель, в остальных местах
метрика обращается в нуль
*
Эти утверждения требуют дальнейшего разъяснения. Возникающее здесь понятие «мет¬
рики» приписывает площадь любому пробному элементу 2-поверхности, пересекающему
петлю. Фактически здесь фигурирует дельта-функция, определенная на некоторой площа¬
ди, которая полностью концентрируется вдоль каждой петли семейства. Что это значит?
Представим себе двумерную пробную поверхность Т (не обязательно замкнутую) на 3-
поверхности S. Она может пересекать различные петли в нескольких местах. Всякий раз,
Попробуйте объяснить это. {Подсказка: воспользуйтесь идеями из § 14.5.)

782
Глава 32
когда поверхность Т встречает одну из петель, она приобретает некоторую меру площади,
в остальных местах какой бы то ни было вклад в ее площадь отсутствует. Таким обра¬
зом, «дельтаподобный» характер метрики здесь проявляется в том, что каждой петле при¬
писывается мера площади, только когда поверхность Т пересекает петлю. Каждая точка
пересечения дает значение
8тг Grjh^/j{j + 1),
где j — 2п есть значение «спина» петли (см. рис. 32.4). Мы суммируем эти вклады площади
от всех петель семейства.
Существует интересный контраст между теорией струн и теорией петлевых перемен¬
ных. В то время как подход теории струн к квантовой гравитации почти полностью основан
на теории возмущении, метод петлевых переменных использования теории возмущении
не предполагает. В теории струн вычисления почти всегда проводятся на фоне плоского
пространства-времени, т. е. произведения пространства Минковского М на, скажем, некото¬
рое 6-пространство Калаби-Яу (см. § 31.14), и потому относятся лишь к слабым полям на
этом фоне. При этом рассматриваются возмущения относительно этого предела слабого поля
(т. е. разложение в степенной ряд по некоторому малому параметру); см. §§ 26.10,31.9. В про¬
тивоположность этому, в случае петлевых переменных базисные петлевые состояния (или
состояния спиновых сетей — см. § 32.6) весьма далеки от плоских (или классических), буду¬
чи дельт а-функциями от площади вдоль петли (или линий спиновой сети). Чтобы получить
описание приблизительно классического пространства-времени в формализме петлевых пе¬
ременных, мы должны рассматривать что-то подобное почти однородному распределению
«переплетений», показанному на рис. 32.5.
Рис. 32.4. Двумерная пробная поверхность Т на
3-поверхности S. Каждое пересечение Т с пет¬
лей вносит в площадь вклад StyGrjh^j (j -У 1) (j
есть значение «спина» петли)
Рис. 32.5. Описание приблизительно классиче¬
ского пространства-времени в формализме пет¬
левых переменных можно представить в виде
суперпозиции почти однородных распределений
«переплетений»
Отметим топологический характер этого описания. Оно не обращает внимания на то,
сколь близко одна петля может подходить к другой (поскольку понятие «метрики» не имеет
смысла вне самой петли). Единственное, что имеет значение, — это топологические «связи»
и «узлы» (или пересечения), образуемые петлями, и дискретные значения приписываемого
им «спина». Таким образом, общая ковариантность (внутри поверхности S) учитывается
при условии, что мы остаемся в рамках этой дискретной топологической структуры.
32*5. Математика узлов и связей
Представление квантовой гравитации на основе петлевых переменных вводит нас в об¬
ласть математики, которая имеет дело с топологией узлов и звеньев. Это удивительно слож¬
ный предмет, если принять во внимание простую природу изучаемых объектов — в основном

32.5. Математика узлов и связей
783
перепутанных струн! Нам будет нужен математический критерий, позволяющий решить,
действительно ли замкнутая петля завязана в узел. («Завязана в узел» означает, что петлю
невозможно превратить в обычную окружность посредством гладких движений в обыч¬
ном евклидовом 3-пространстве, при этом не разрешается проносить отрезки петли сквозь
друг друга; см.рис. 32.6). Аналогично можно задаться вопросом о критерии возможности
полного разделения двух или более петель, в этом случае петли называют несвязанными.
Различные хитроумные математические выражения, дающие ответы на этот вопрос (напри¬
мер, так называемый многочлен Александера), известны с начала XX века, однако позднее
были предложены более утонченные процедуры, во многом вдохновленные идеями, при¬
шедшими из физики. Они получили названия «многочлен Джонса», «мнотчлен HOMFLY»,
«многочлен Кауфмана» и др.^32Л4^
сю <в> §Ь
а)	б)	в)	г)	д)
Рис. 32.6. Узлы и связи, а) Трехкратный узел — пример петли, завязанной в узел, б) Пример петли
без узлов (хотя это на первый взгляд и не очевидно), в) Простая связь между двумя петлями, г) Связь
Уайтхеда, при которой две петли не могут быть разделены, хотя они имеют нулевое «число связи» (это
число показывает, сколько раз каждая из нетель встречается с поверхностью, содержащей другую из
них), д) Тройное кольцо, которое не может быть разделено, несмотря на то что никакие два отдельных
кольца не связаны между собой
Один из способов понять эти новые математические структуры состоит в том, что¬
бы рассматривать их как своего рода «диаграммную алгебру» — обобщение диаграммного
описания тензорной алгебры, введенного в § 12.8 (см. рис. 12.17 и 12.18) и широко исполь¬
зуемого в главе 13 (см. рис. 13.6-13.9 и др.). При таком обобщении различаются случаи,
когда «индексная линия» проходит выше или ниже другой подобной линии всякий раз, ко¬
гда они пересекается на диаграмме (см. рис. 32.7). Существуют различные «алгебраические
тождества», подобные показанным на рис. 32.8, которые определяют алгебру Кауфмана.
Это приводит к изящному обобщению комбинаторной схемы, лежащей в основе теории
О	VI	KJ
спиновых сетей, к которой мы вскоре перейдем
У\*а, Х*){
Рис. 32.7. Вариант диаграммной тензорной алгебры, представленной на рис. 12.17, 12.18
и рис. 13.6-13.9 и др., можно обобщить, чтобы построить алгебру узлов и связей. Ее дополнительная
особенность состоит в том, что различаются случаи, когда «индексная линия» проходит выше или
ниже другой подобной линии, которую она пересекает
Величина А на рис. 32.8 представляет собой комплексное число; иногда А выражают
через величину q = А2 = еш/г. (Случай А = — 1 соответствует «бинорному исчисле¬
нию», которое лежит в основе теории спиновых сетей [594, 595].) Имеет место анало¬
гия с симметризаторами и антисимметризаторами на рис. 12.17. Была развита обстоятель¬
ная теория объектов такого рода, иногда называемых q-деформированными структурами.
Часто вместо «^-деформированные» употребляется слово «квантовые», что может ввести

784
Глава 32
Рис. 32.8. Иллюстрируется базовое алгебраическое тож-
дество для алгебры Кауфмана, q = А2 — ег7Г//г определя¬
ет ^^деформированный вариант «бинорной» алгебры, ле-
у^	^	г	\	жащей в основе теории спиновых сетей (для которой Л -
— — 1 и пересечения, показанные на рис. 32.7, не возни¬
кают)
в заблуждение, как и понятие «квантовой группы». Не существует вполне ясной связи между
«квантовой группой» и квантовой теорией, так что широкое применение квантовых групп
в фундаментальной физике хотя в общем и возможно, в настоящее время носит в основном
гипотетический характер.
Попутно стоит заметить, что возможна и другая связь между этими новыми математи¬
ческими структурами (многочленами Джонса и др.) и физикой, которую активно исследовал
Эдвард Виттен^32*15}. Это топологическая квантовая теория поля. В этой теории уравнения
поля полностью исчезают, а информация заключена в глобальной структуре и «склейках»,
которые можно трактовать как «источники» (локально исчезающего) поля. Хорошим приме¬
ром этого может служить общая теория относительности в 1 + 2 измерениях. В 1 -f 2(— 3)
измерениях тензор Вейля тождественно обращается в нуль, так что вся кривизна заключе¬
на в тензоре Риччи. Таким образом, в «пустом пространстве» (с нулевым тензором Риччи)
полная кривизна равна нулю. Однако гравитационное поле «точечного источника» нетриви¬
ально, поскольку источник создает «склейку», которая проявляется в глобальной геометрии.
Эта ситуация изображена на рис. 32.9. Такая геометрия очень похожа на геометрию косми¬
ческой струны, показанной на рис. 28.4, за исключением того, что здесь вместо 3-мерного
пространства фигурирует (1 + 2)-мерное пространство-время. Из него удален некоторый
сегмент с осью вдоль (времениподобной) мировой линии источника, и две образовавшихся
при этом плоских границы склеены между собой. В классической картине мировые ли¬
нии таких источников должны быть прямыми, однако квантовая теория поля, основанная
на этой классической модели, — топологическая квантовая теория поля, — в которой поле
(в данном случае поле кривизны) исчезает, допускает кривые линии источников, образую¬
щие узлы и связи. Именно это позволяет развивать математику узлов и связей на основе
идей топологической квантовой теории поля^32 161. Следует отметить, что петлевым пере¬
менным соответствует система, несколько напоминающая общую схему «топологической
квантовой теории поля», поскольку вклад в меру площади обращается в нуль всюду, кроме
мест «склейки», которыми в данном случае служат петли. Но имеется и различие, поскольку
уравнения поля с петлевыми переменными не исчезают.
Топологические квантовые теории поля представляют интерес как математические
структуры, однако трудно поверить, что они могут играть непосредственную роль моделей
серьезных физических теорий из-за полного исчезновения в них уравнений поля. Большая
часть современной физики опирается на нетривиально сть таких уравнений, описывающих
распространение полей в будущее по определенному закону. Имеется, однако, другая воз¬
можность: идеи топологической квантовой теории поля могут быть использованы в сочета¬
нии с теорией твисторов. Как будет показано в главе 33 (в конце §33.11), при описании
в твисторном пространстве уравнения поля локально исчезают. Применение идей тополо¬
гической квантовой теории поля в теории твисторов пока зашло не слишком далекоt32-17!,
однако было бы интересно понять, чего можно достигнуть на этом пути.
32.6.	Спиновые сети
Интересно, что петлевые состояния, будучи предельными («дельтаобразными») кон¬
фигурациями 3-геометрии, не образуют в ней подходящего базиоа^Иоэтому необходимо

32.6. Спиновые сети
785
Рис. 32.9. «Общая теория относительности» в 2 + 1 измерениях требует, чтобы в отсутствие источ¬
ников пространство-время было плоским (поскольку тензор Риччи там обращается в нуль, а тензор
Вейля в трех измерениях всегда равен нулю). Однако мировая линия источника образует «склейку»
(коническую сингулярность) в плоском пространстве-времени, напоминающую «космическую стру¬
ну», пространственная 3-геометрия которой показана на рис. 28.4 из § 28.2. В классической теории
мировые линии всегда являются прямыми, но в квантовом варианте теории (которая служит примером
топологической квантовой теории поля) это требование снимается
перейти к обобщению, позволяющему петлям пересекаться. Это приводит нас к некоторой
сетке из «пересекающихся петлевых линий», но мы вынуждены спросить: что делать с точ¬
ками пересечения? Ответ оказывается связанным с некоторыми структурами, формально
очень похожими на спиновые сети, которые я сам изучал почти 50 лег назад с иными, но
довольно близкими целями.
Что же такое спиновые сети и почему они заинтересовали меня в 1950-х годах? Моей
целью было попытаться описать физику в терминах дискретных комбинаторных величин,
поскольку в то время я придерживался взгляда, что физика и пространственно-временная
структура должны быть основаны в конечном счете не на непрерывности, а на дискрет¬
ности (см. §3.3). Дополнительной мотивацией служил некоторый вариант принципа Маха
(§28.5)[32181, согласно которому само понятие пространства должно быть выводимым, а не
присутствовать в схеме изначально. Всё должно выражаться через связи между объектами,
а не между объектом и некоторым фоновым пространством.
Я пришел к выводу, что лучший способ удовлетворить этим требованиям — это рас¬
смотреть квантово-механическую величину полного спина системы. «Полный спин» опре¬
деляется как скалярная величина, измеряющая количество спина в целом, а не отдельной
его компоненты в некотором направлении, измеряемой величиной га. (Буквы j и т обычно
используются при рассмотрении квантово-механического момента импульса, выражаемого
в единицах h, при этом га принимает значения, разделенные целочисленными интервалами,
между целыми или полуцелыми числами —j и j; см. §§22.8, 22.10, 22.11). Реальная вели¬
чина полного спина (определяемая как квадратный корень из суммы квадратов значений га
в трех взаимно-перпендикулярных направлениях) равна	+	1),	а это та же самая вели¬
чина, которая раньше фигурировала в формуле для площади. Разрешенные значения п — 2 j
представляют собой просто натуральные числа (четные для бозонов и нечетные для фер¬
мионов; см. §23.7). Более того, будучи не зависящим от направления, число п в конечном
счете оказывается связанным с ориентационными аспектами пространства. Мне казалось,
что полный спин, измеряемый натуральным числом п, представляет идеальную величину,
на которой следует сосредоточить внимание, если мы интересуемся построением некоторой
дискретной комбинаторной структуры, которая приведет к понятию реального физического
пространства. Затем, если мы идем правильным путем, мы сможем представить квантово-

786
Глава 32
механические вероятности как чистые вероятности, не зависящие от того, каким образом
разные части физической установки расположены относительно одна другой.
Как же работает эта схема? Назовем величину полного спина ~nh п-единицей. Что-
Lj.
бы было яснее, можно рассматривать эту «единицу» как некоторую частицу, однако она не
обязательно будет элементарной частицей. Например, это может быть целый атом водоро¬
да. Просто ее полный спин должен иметь вполне определенное значение (в случае атома
водорода он будет равен п — 2 или 0 соответственно для орто- и параводорода) f32 191 Как
получить чистую вероятность? Можно, например, взять пару ЭПР-Бома, состоящую из пар
1-единиц (А, В) и (С, D), каждая из которых вначале находится в состоянии 0-единицы.
(Это есть пара конфигураций, подобных изображенным на рис. 23.3 из § 23.4; см. рис. 32.10.)
Если теперь свести объекты В и D вместе и позволить им объединиться в одну единицу, то
в результате может получиться 0-единица или 2-единица с соответствующими вероятности-
* 1 Я
ми J и Если вместо этого свести вместе А и С, то возможные результаты и вероятности
будут те же самые. Однако эти вероятности отнюдь не независимы одна от другой, так как
если мы получим 0-единицу в одном случае, мы не сможем получить 2-единицу в другом
случае и наоборот.
Рис. 32.10. Спиновые сети. Каждый отрезок прямой, нумеруемый натуральным числом п, представляет
частицу или подсистему с полным спином ~ х Н, именуемую n-единицей. В этом простейшем примере
Л
мы имеем пару ЭПР-Бома, состоящую из пар 1-единиц (А, В) и (С, D), каждая из которых вначале
находится в состоянии 0-единицы (как на рис. 23.2). Если объединить В и D в одну единицу, то в
результате может получиться 0-единица или 2-единица с соответствующими вероятностями - и
Те же вероятности получатся, если вместо этого объединить А и С. Но эти вероятности не являются
взаимно независимыми, поскольку мы не можем иметь 0-единицу в одном случае и 2-единицу в другом
%
*
Вот такого рода идею я собирался применить для вычисления чистых вероятностей,
и я считал, что любая такая вероятность должна выражаться рациональным числом (по¬
скольку Природа делает некоторый случайный выбор между конечным числом дискретных
возможностей). Пример, приведенный выше, весьма прост, но он иллюстрирует общую
идею. Все единицы в данной спиновой сети предполагаются созданными указанным обра¬
зом из начальных 0-единиц (хотя это и не представлено явным образом на диаграмме), так
что нет какого-либо выделенного направления в пространстве. Поэтому различные пары
единиц можно объединять с образованием новых единиц и отмечать значения спина по¬
лученных единиц. Отдельные единицы могут также разделяться на пары единиц. Пример
показан на рис. 32.11. Можно представить себе, что всё это происходит в некотором про¬
странстве-времени. Хотя в начальном варианте теории спиновых сетей никакого фонового
пространства-времени не предполагалось. Идея состояла в том, чтобы все необходимые
пространственные структуры строились просто из сетки спинов и характеризовались веро-
Попробуйте объяснить почему.

32.6. Спиновые сети	787

\
I
I
I
ятностями (вычисляемыми по правилам квантовой механики), с которыми они возникают,
когда две единицы объединяются, образуя третью. Эти спиновые сети обладают тем свой-
ством, что в каждой вершине сходятся ровно три линии. Это приводит к единообразию при
вычислении вероятностей. Всё, что требуется знать, — это топологическая (графическая)
структура спиновой сети и значения спина, соответствующие каждой линии.
Рис. 32.11. Пример спиновой сети, как она первоначально
представлялась. Никакого фонового пространства-време¬
ни не предполагается. Все пространственные структуры
должны возникать из сетки спинов и значений вероятно¬
сти (когда две единицы объединяются, образуя третью).
В каждой вершине сходятся ровно три линии, что одно¬
значно определяет характер связей
Я разработал полностью комбинаторную процедуру («способ подсчета») для вычис¬
ления требуемых вероятностей (которые выражались рациональными числами). В ней ис¬
пользуются правила стандартной квантовой механики спина, однако мы можем «забыть»,
откуда они взялись, и просто рассматривать систему спиновых сетей как некоторую «ком¬
бинаторную Вселенную». При этом становится возможным определить понятия геометрии
(в данном случае обычной евклидовой 3-геометрии), рассматривая спиновые сети, которые
достаточно «велики». В этой картине единица с большим спином может считаться задаю¬
щей некоторое «направление в пространстве» (понимаемое, например, как ось вращения
теннисного мяча). Можно заняться измерением «угла между осями вращения» двух таких
больших единиц, отделяя, например, некоторую 1-единицу от одной из них и присоединяя
ее к другой. При такой операции совместная вероятность того, что один спин увеличивается,
а другой уменьшается, дает меру угла между осями спинов .
Эта схема почти работает и так, но не совсем, и требуется введение новых элементов.
Необходимо иметь еще способ, позволяющий отличать «квантовую вероятность» (связанную
с углом между осями спинов двух больших единиц) от «вероятности, связанной с незна¬
нием», которая может возникать просто из-за неполноты информации относительно связей
между двумя большими единицами. (Напомним о существовании тонкой взаимосвязи меж¬
ду двумя понятиями вероятности, которая обсуждалась в §§29.3, 29.4 в связи с матрицей
плотности.) Оказывается, что этот «фактор незнания» можно устранить, повторяя перенос
1-единицы от одной большой единицы к другой и отбирая лишь те ситуации, когда веро¬
ятности во второй раз получались теми же самыми. Для рассматриваемых здесь семейств
больших единиц можно доказать геометрическую теорему, согласно которой «угловая гео¬
метрия», указанным образом определяемая квантовыми вероятностями, в точности совпада¬
ет с геометрией углов между направлениями в обычном евклидовом 3-пространстве^32-201
Таким образом, из квантовой комбинаторики спиновых сетей возникают понятия обычной
евклидовой геометрии.
Можно заметить, что исходная мотивация, лежавшая в основе исследования спиновых
сетей, была совсем иной, нежели та, что привела к использованию петлевых переменных для
квантования пространства-времени, поскольку в первоначальной версии теории спиновых
сетей не было места для гравитации. Поэтому для меня было большим сюрпризом обна¬
ружить, что спиновые сети играют столь важную роль в этом подходе к квантовой теории
гравитации. Конечно, между этими двумя программами много общего, поскольку в обо¬
их случаях делается попытка свести понятие пространства к чему-то более дискретному
и квантово-механическому. Есть, однако, и существенное отличие, поскольку в формализ-
Что представляет собой этот угол на языке вероятностей?

788
Глава 32
ме петлевых переменных величина п реально есть мера площади, а не мера спина, как
в исходном варианте теории спиновых сетей. Различны и размерности, что выражается
в появлении гравитационной постоянной G в формулах петлевого формализма. Вскоре мы
вернемся к этому факту и обсудим его возможное значение.
Как же выглядят спиновые сети в теории квантовой гравитации с петлевыми перемен¬
ными? Как уже упоминалось, узлы спиновых сетей получаются, по существу, в результате
пересечения пар петель. Это приводит к возможности изменения в этом место значения j
для данной петли. В соответствии с этим мы получаем узлы, в которых сходятся четыре
линии (а возможно, и больше), а не три, как предполагал мой первоначальный вариант
теории спиновых сетей. Это приводит к неоднозначности, поскольку однозначная интер¬
претация получается только для исходных «тройных» узлов. При этом требуется вводить
дополнительное описание («оператор переплетения») для каждого узла. Один из способов
такого описания показан на рис. 32.12, где фигура в виде буквы «X», в которой сходятся
четыре линии, представлена как линейная комбинация пар тройных вершин в виде буквы
«Н». Выбор коэффициентов устраняет неоднозначность.
Рис. 32.12. Все узлы спиновых сетей в теории петлевых переменных содержат четыре (или более)
линии, так что требуется дополнительная информация о «переплетениях». Это можно сделать, пред¬
ставив вершину «Х-типа» как линейную комбинацию пар тройных вершин «Н-типа». При задании
коэффициентов неоднозначность устраняется
Существует и другое, более важное, различие между спиновыми сетями в петлевых
переменных и предложенной мною первоначально моделью на основе полностью комбина¬
торных структур, поскольку сети с петлевыми переменными приобретают дополнительную
топологическую структуру в результате их погружения в многообразие S. Линии сети мо¬
гут, например, образовывать узлы или быть связаны между собой различным образом, и это
дает дополнительную информацию (см. рис. 32.13). Имея чисто топологический характер,
эта информация все еще имеет дискретную комбинаторную природу, однако ее труднее
представить, чем просто указать, что происходит в отдельных узлах.
До сих пор наше описание с использованием петель было, по существу, статическим,
никакая динамика не рассматривалась. Петли и спиновые сети, которые мы рассматривали,
касались решения уравнений связей общей теории относительности, т. е. условий, которые
должны выполняться на поверхности S, при полном соблюдении эйнштейновского прин¬
ципа общей ковариантности. Это немалое достижение, однако пока формализм не решил
более трудную задачу динамической эволюции исходя из поверхности S (иногда называе¬
мую «гамильтоновыми связями»), чтобы можно было воспроизвести уравнения Эйнштейна
(см. §32.1). Работа Томаса Тимана позволила получить одно из возможных решений этой
проблемы гамильтоновой эволюции, но остается некоторое сомнение в том, что оно дей¬
ствительно согласуется с теорией Эйнштейна f32*21!.
В ожидании вполне приемлемого решения этих сложных проблем динамики пока мож¬
но пользоваться формализмом петлевых переменных для получения некоторых впечатля¬
ющих результатов в других направлениях. В частности, идеи спиновых сетей оказались
более полезными для отыскания непосредственного и реалистического подхода к проблеме
энтропии черной дыры, нежели теория струн (см. §31.15). Здесь геометрия черных дыр
описывается непосредственно шварцшильдовским или керровским вакуумным решением

32.7. Статус квантовой гравитации с петлевыми переменными
789
Рис. 32.13. Спиновые сети в стандартном формализме петлевых
переменных теперь уже не являются полностью самостоятель¬
ными объектами, а должны быть погружены в бесструктур¬
ную (но, возможно, аналитическую) 3-поверхность (вроде <S),
при этом приобретают значение топологические свойства свя¬
зей и узлов
4-мерной теории Эйнштейна. Спиновые сети можно использовать для приближенного под¬
счета гравитационных квантовых состояний в явной форме. Если черная дыра становится
достаточно большой, результат для энтропии оказывается в согласии с формулой Бекенстай¬
на-Хокинга 5вн = (где к = с = G = h = 1), но чтобы получить точный хокинговский
1
коэффициент	параметру Барберо - Иммирци приходится придавать курьезное значение
log 2
V= 	7Г-
7Гл/3
Хотя это действительно странное значение, такой выбор дает правильное значение эн¬
тропии Бекенстайна - Хокинга во всех случаях, когда другие методы дают однознач-
ныи ответ с привлечением значении заряда, момента импульса и космологической
постоянной^32*22^.
В связи с этим необходимо отметить различные численные «совпадения», от которых,
по-видимому, зависит теория. Две различные отдельные последовательности, вычисленные
двумя совершенно разными способами, должны согласоваться почленно, что фактически и
имеет место. Это представляется отражением глубокой внутренней согласованности неко-
торых идеи квантовой геометрии.
Тем не менее теория черной дыры может извлечь кое-что из изменения точки зре¬
ния на параметр Барберо-Иммирци. Прежде введение параметра q представлялось спо¬
собом достижения прогресса, при этом казалось, что «геометрически правильная» теория
требует значения q = =Н. Введение реального значения q было лишь вопросом матема¬
тического удобства, чтобы вместо некомпактной группы SL(2, С) появилась компактная
группа SU(2). Впечатляющий успех в получении правильных значений энтропии для очень
широкого класса горизонтов при выборе единого значения параметра Барберо-Иммирци q
(того самого q — log 2/7r>/3) привел ряд приверженцев формализма петлевых переменных к
той точке зрения, что это реальное значение в конечном счете есть «правильный» параметр
квантовой теории гравитации.
Это, конечно, лишь одна из возможностей, хотя мне лично трудно в нее поверить,
поскольку для такого выбора нет четких геометрических оснований. Я должен заметить, что
при любом вещественном значении т/, вроде указанного выше, исчезает тральный аспект
теории, который я подчеркивал в § 32.3 при введении в предмет. Перенос спинора, которому
соответствует связность с вещественным значением ту, представляет собой необычную
смесь внутренней и внешней частей, смысл которой я нахожу особенно темным. Возможно,
будущие исследования прольют свет на эту проблему.
32.7,	Статус квантовой гравитации с петлевыми переменными
Я. должен попробовать дать оценку достижениям формализма петлевых переменных
Аштекара-Ровелли-Смолина применительно к квантовой гравитации и перспективам его
будущего развития в полновесную теорию. Здесь я хотел бы в очередной раз предупредить

790
Глава 32
читателя о возможной необъективности, присущей таким оценкам. В данном случае я вы¬
нужден заявить и о наличии личной заинтересованности, поскольку люди, развивающие
эту программу, являются моими друзьями и, кроме того, я поддерживаю регулярные связи
с двумя американскими университетами (Сиракузским и Пенсильванским), где проводятся
основные исследования в этой области. К этому еще следует добавить мой собственный
интерес к теории спиновых сетей, в силу которого меня должен радовать тот факт, что эти
старые идеи в данном формализме приобретают новое значение. Тем не менее мое участие
в программе построения квантовой теории гравитации на основе петлевых переменных Аш¬
текара лишь слегка касалось основного направления в этой области, поэтому я надеюсь, что
смогу быть достаточно объективным.
Для начала я должен заметить, что как первоначальный вариант формализма петле¬
вых переменных Аштекара, так и дальнейшее его развитие произвели на меня впечатление
существенного продвижения по пути к квантовой теории гравитации. Эта работа прямо
адресуется к общей теории относительности Эйнштейна в контексте квантовой теории по¬
ля и вносит новые идеи в обсуждаемую проблему. Я не решаюсь утверждать, что именно
эти исследования указали наиболее прямой путь к квантовой гравитации, поскольку сама
проблема была поставлена Дираком и другими приблизительно полвека назад. Формализм
петлевых состояний ставит по крайней мере некоторые из важных проблем, связанных с об¬
щей ковариантностью. Более того, эти исследования направили обсуждение по новому и,
возможно, не вполне ожидаемому пути, на котором появляются некоторые элементы дис¬
кретности в структуре пространства-времени. В недавних работах делаются попытки вклю¬
чить другие виды взаимодействия, помимо гравитационного, так что эту теорию теперь
можно рассматривать как подход к фундаментальной физике в целом i32-23].
Против этого можно выдвинуть тот несколько обескураживающий факт, что теория ока¬
залась вынуждена принять связность (с неопределенным значением rf) вместо «геометри¬
чески правильной» Г. На мой взгляд, полностью надежный подход к квантовой гравитации
не будет достигнут, пока не будут преодолены трудности, связанные с переходом к исходной
связности Г. Кроме того, имеется еще одна фундаментальная трудность, поскольку в фор¬
мализм петлевых переменных должен быть однозначным образом введен полный эйнштей¬
новский гамильтониан, несмотря на то что уравнения связи получаются с использованием
спиновых сетей.
Мне представляется, что эти трудности связаны с другой, менее привлекательной чер¬
той теории петлевых переменных Аштекара. Как и при любом другом каноническом подходе
к квантовой гравитации, ее формулировка прямо опирается на описание в 3-пространстве
(т. е. с использованием поверхности S), а не в более глобальном пространстве-времени.
Как мы видели, 3-пространственная часть проблемы «общей ковариантности» тесно свя¬
зана с петлевыми состояниями и спиновыми сетями, однако обобщение на случай общей
ковариантности в 4-пространстве открывает настоящий «ящик Пандоры», полный проблем.
Насколько я могу судить, формализм петлевых переменных пока справляется с ними не луч¬
ше, чем другие канонические подходы ^32*241.
Вопрос состоит в том, как выразить эволюцию во времени, описываемую уравнением
Эйнштейна, в рамках общековариантного 4-мерного формализма. Это связано с так на¬
зываемой «проблемой времени» в квантовой гравитации (иногда ее именуют проблемой
«замороженного времени»). В общей теории относительности нельзя отличить временную
эволюцию от простого изменения координат (т. е. просто замены одной временной коорди¬
наты на другую). Общековариантный формализм должен бьцъ нечувствителен к простой
замене координат, так что понятие временной эволюции оказывается глубоко проблематич¬
ным. Мой собственный взгляд на эту проблему, как отмечалось в § 30.11, состоит в том, что
ее вряд ли удастся решить без удовлетворительного подхода к вопросу о редукции вектора
состояния и что это в свою очередь потребует коренной ревизии общих принципов.

32.7. Статус квантовой гравитации с петлевыми переменными
  1	     -У	—	—«■■■■ —■■■■	—		— ■■■
I
791
С этими вопросами связан и другой аспект, также далекий от разрешения, хотя это
скорее проблема общековариантного описания как такового, нежели метода петлевых пере¬
менных. В некотором смысле этот метод оказался жертвой своего собственного успеха! Хотя
базисные состояния спиновых сетей по отдельности допускают удовлетворительное геомет¬
рическое описание, не зависящее от координат, остается совершенно неясным, как следует
интерпретировать суперпозиции таких базисных состояний. Из-за общей ковариантности от¬
сутствует соответствие между «расположением» одной спиновой сети и другой, с которой
она должна составить суперпозицию. (Это гораздо более серьезный вариант проблемы об¬
основания гравитационной объективной редукции (ОР) состояний, упомянутой в §30.11.)
Как следует понимать возникновение из всего этого почти классического мира?
Как читатель мог понять, в частности, из обсуждения в главе 30, необходимой чертой
корректного объединения квантовой теории с гравитацией я считаю такой отход от стан¬
дартной квантовой механики, при котором R-процедура становится реальным физическим
процессом (ОР). Имеется ли такая возможность в рамках формализма петлевых перемен¬
ных? Возможно, имеется. В петлевых переменных числа п — 2j на краях спиновых сетей
относятся к площади (единицей служит квадрат планковской длины), однако у меня исполь¬
зование спиновых сетей не предполагает ни рассмотрения подобных метрических проблем,
ни фактически гравитации вообще — спиновые числа п относятся к угловым переменным.
Однако первоначально я предполагал, что каждое из этих чисел должно быть, по существу,
результатом отдельного измерения значения полного спина (действия операции R на каждом
из краев), при этом вероятности появляются при объединении двух единиц с образованием
третьей. Если R-процедура представляет объективный гравитационный эффект, то грави¬
тационные процессы необходимо учитывать на этой стадии, как отмечалось в главе 30.
В таком случае невозможно отделить гравитацию от проблемы вероятности в теории спи¬
новых сетей. Возможно, что полное объединение идей петлевых переменных и спиновых
сетей потребует введения в формализм редукции состояний. Если это окажется возможным,
то может открыться путь к построению подходящей схемы гравитационной ОР, как реко¬
мендовано в главе 30. Однако в отсутствие такого формализма подобные идеи остаются
всего лишь умозрительными построениями.
В заключение мне следует прокомментировать другие работы, связанные с теорией
петлевых переменных. В настоящее время она не является чисто гравитационной теорией,
этот формализм применяется^32*25! и к электромагнетизму!32*26!. Существуют и пути, менее
радикальные по сравнению с предложенным в предыдущем абзаце превращением спино¬
вых сетей петлевой квантовой гравитации в нечто «более четырехмерное». Одним из них
является остроумный многомерный вариант спиновых сетей, именуемый спиновой пеной.
Здесь фигурируют 2-поверхности, соответствующие «значениям спина» п = 2j, и такую
спиновую пену можно представить как спиновую сеть, эволюционирующую во времени.
Подобные идеи, выдвинутые Луи Крейном, Джоном Барретом и другими !32*27!, были затем
развиты и модифицированы другими исследователями I32*28!, однако должная связь с идея¬
ми квантовой гравитации пока не установлена. Имеются также возможные связи с теорией
твисторов, и было бы интересно выяснить, можно ли их представить в более полном виде.
В следующей главе мы познакомимся с некоторыми основными понятиями теории твис¬
торов.
Я старался подчеркнуть в этой книге, в частности в главе 30, что проблема редукции
квантового состояния связана в конечном счете со структурой пространственно-временных
сингулярностей и их временной асимметрией. Интересно, что начало этому фактически
уже положено в смысле выяснения той информации, которую может дать метод петле¬
вых переменных относительно влияния квантовых эффектов на пространственно-временные
сингулярности^32*29!. Я не могу комментировать эту работу сколько-нибудь подробно, могу
лишь сказать, что я не вижу, как может возникнуть необходимая временная асимметрия.

792
Глава 32
Примечания
§ 32.1-
32.1. См. [318].
32.2. Некоторая ирония состоит в том, что сам Эйнштейн с его идеей создания единой теории поля,
занимавшей его в более поздние годы, не всегда придерживался упомянутой «узкой тропы».
32.3. Относительно понятия связей и гамильтоновой формулировки см. [207, 32, 809].
32.4. См., например, [206, 207, 641, 73,29]. В [191] приводится уравнение Уилера-Де Витта, которое,
по существу, представляет собой квантово-гравитационное уравнение Шредингера в простран¬
стве компактных 3-геометрий.
32.5. См. [413,466].
32.6. См. [715, 30, 31].
§32.2.
32.7. Как мы вскоре увидим, из-за технических трудностей первоначальный подход Аштекара отли¬
чался от этого явно кирального описания. Однако, насколько я понимаю мотивацию, лежащую
в основе программы Аштекара, это отличие можно трактовать как временное использование
модели, близкой (хотя и не тождественной) предполагаемой квантовой теории гравитации.
32.8. Первоначальное обсуждение линеаризованной гравитации содержится в [263], дальнейшая ин¬
формация — в [685]. Относительно нелинейного гравитона см. [597, 598].
§32.3.
32.9. См. [30, 31], а также обзор [36] и [674] в качестве учебника.
32.10. Тот, кто хочет понять, как работают «индексы», должен учесть, что обратная 3-метрика являет¬
ся величиной 7rs с поднятыми 3-мерными индексами. Образуя дуальную форму s на£ (§ 12.7),
получаем плотность 7rtu, антисимметричную по t, и. Можно рассматривать эти нижние ин¬
дексы как индексы 2-формы в 4-пространстве и взять антисамодуальную часть, которая дает
нам пару нижних симметричных спинорных индексов и величину Jpq или, что эквивалент¬
но, 7rpQ с нулевым следом по Р, Q. Что касается Г, то это есть величина FrPQ, матрица из
1 -форм в спиновом пространстве, которая должна иметь нулевой след (поскольку это есть связ¬
ность SL(2, С)). Заметим, что у Г структура индексов противоположна структуре индексов у 7,
как и должно быть у канонически сопряженных переменных. Подробнее см. [30, 31, 36, 674].
32.11. Именно эту связность ввел в 1981 году Сен, чтобы свести связи общей теории относительно¬
сти к полиномиальной форме. Интересно, что Виттен независимо использовал ту же связность
(тоже в 1981 году) в своем доказательстве положительности полной энергии в общей теории
относительности; см. § 19.8 и [843]. Насколько мне известно, эта связность впервые приме¬
нялась при построении твисторной гиперповерхности для S ([624, 596]); это есть та часть
теории твисторов, которая наиболее тесно связана с переменными Аштекара.
£32.4.
32.12. См. [840]; этот метод квантовой теории поля излагается в [858]. См. также [675].
32.13. Для этого структура многообразия должна быть несколько более сложной, поскольку это усло¬
вие определяет не только его топологию, но и предполагает дифференцируемость или «глад¬
кость» (см. §§ 10.2, 12.3, 33.1). Фактически в целях удобства вычислений поверхности S в фор¬
мализме Аштекара-Левандовского приписывается аналитическая структура [34]; это означает,
что она имеет структуру Сш в смысле § 6.4.
§32.5.
32.14. Очень доступное введение в теорию узлов содержится в [3], более подробное изложение —
в [670, 435].
< .
32.15. См. обзорную статью [468]. Исходный вариант топологической квантовой теории поля излага¬
ется в [845].	/
32.16. Однако топологическая квантовая теория поля не приводит непосредственно к строгим мате¬
матическим теоремам из-за сильных расходимостей.

32.7. Статус квантовой гравитации с петлевыми переменными
793
32.17. См. [608]. Можно отметить, что новые твисторно-струнные идеи, выдвинутые Виттеном [849],
развивают это направление; см. примечание 31.81.
§ 32.6.
32.18. Своим интересом к принципу Маха я во многом обязан дискуссиям с моим коллегой, другом
и учителем Деннисом Скьямой.
32.19. См. [484].
32.20. См. [594, 535].
32.21. См. [769, 770, 771, 772, 773].
32.22. См.	[38, 39]. Недавно, однако,	было	показано,	что	приведенное	значение	для	г]	ошибочно,
и теперь этому параметру приписывается значение более	сложного	вида.	См.	[215, 222]. На по¬
следующую часть моего изложения в §§ 32.6, 32.7 это не повлияет.
§ 32.7.
32.23. См. [772].
32.24. См. [360], а также примечания 32.3-32.5. Я не могу не упомянуть работу Смолина [733],
а также отличную обзорную статью Аштекара и Левандовского [36], из которой взяты многие
из этих ссылок. Я приношу глубокую благодарность Абхаю Аштекару за его помощь в подборе
литературы к этой главе.
32.25. См. [802].
32.26. См. [803].
32.27. См.	[60, 45, 658, 659].
32.28. См.	[61, 45, 660, 661, 637].
32.29. См. [88,41].

Глава 3 3
Более радикальный взгляд. Теория твисторов
33.1.	Геометрия с дискретными элементами
Достаточно ли радикальны теории, изложенные в предыдущих главах, в их попытках
расшифровать действительную схему Природы путем объединения квантовой физики ма¬
лых масштабов с искривленной геометрией пространства в больших масштабах? Возможно,
нам следует искать нечто фундаментально отличное от того пространства-времени в ви¬
де вещественного многообразия, с которым имеют дело теория Эйнштейна и стандартная
квантовая механика. Этот вопрос был поставлен в § 3.3, и теперь мы должны выяснить,
действительно ли пространственно-временной континуум вещественных чисел, почти уни¬
версально используемый физической теорией, представляет собой подходящую математи¬
ческую основу для описания устройства Природы.
Мы уже видели, что подход к квантовой гравитации, реализуемый формализмом пет¬
левых переменных, начинает уводить нас от стандартной картины непрерывного и плавно
меняющегося пространства-времени к чему-то имеющему более дискретный топологиче¬
ский характер. Тем не менее некоторые физики провозглашают необходимость гораздо бо¬
лее радикального пересмотра идей пространства-времени и более глубокого проникновения
в природу «квантового пространства-времени». Первоначальная (хотя и ограниченная) идея
спиновых сетей (§32.6) имеет полностью дискретный характер, однако стандартная кар¬
тина петлевых переменных все еще опирается на непрерывную природу 3-пространства,
в которое должны быть погружены «спиновые сети». В этой последней схеме мы не полу¬
чаем полностью дискретного и явно «комбинаторного» фона, который некоторые считают
необходимым для описания Природы в ее самых малых масштабах.
Предлагались различные идеи, в корне отличные по своему характеру от начальной
схемы спиновых сетей или спиновой пены, целью которых было построение полностью
дискретной комбинаторной картины мира. Одна из наиболее экстравагантных идей такого
рода (уже упомянутая в § 16.1) была выдвинута в 1965 году Ахмаваарой^33Л1 Он пред¬
ложил заменить систему вещественных чисел, являющуюся математическим фундаментом
стандартной физики, некоторым конечным полем Fp, где р — некоторое крайне большое
простое число. Напомним (см. § 16.1), что поле ¥р получается, если взять систему целых
чисел по модулю р. Другие схемы предполагают, что пространств о-время имеет дискрет¬
ную структуру периодической решетки в виде вершин множества кубов, расположенных
регулярным образом один над другим^33-2! (рис. 33.1). Гораздо более правдоподобны в физи¬
ческом отношении схемы, подобные геометрии причинных множеств Рафаэля Соркина^33,3^
(или родственные ей более ранние идеи^33 4^), согласно которым пространство-время состоит
из дискретного, возможно, конечного, множества точек, и вводится4® качестве основопола¬
гающего понятие причинной связи между точками. В обычном клйссическом смысле эта
«причинная связь» означает возможность послать сигнал из одной точки в другую (см.
рис. 33.2). Сугубо случайная природа причинных связей в схеме Соркина допускает по¬
явление чего-то вроде лоренцевой инвариантности специальной теории относительности,
тогда как у структур решеточного типа возникают серьезные проблемы с лоренцевой инва¬
риантностью (хотя решетки вроде показанной на рис. 33.1 могут обладать более высокой

33.1. Геометрия с дискретными элементами
795
симметрией такого рода, чем можно решить с первого взгляда). Другие идеи, приводящие
к экзотическим пространсдвенно-временным структурам, возникают из квантовой теории
множеств или геометрии кратернионов Давида Финкельштейна^33 *5^, октонионной физики
(§§ 11.2, 16.2) Корин Маног и Тевиана Дрея^33,6! и др.
а)
б)
Рис. 33.1. Пространство-время типа Снайдера--
Шильда представляет собой периодическую ре¬
шетку в виде вершин множества кубов, распо¬
ложенных регулярным образом один над дру¬
гим. (Оно может обладать большей лоренцевой
инвариантностью, чем можно ожидать!)
Рис. 33.2. а) Дискретная модель Вселенной,
описываемая геометрией причинных множеств.
б) Связи между точками моделируют лоренцеву
причинность, при которой направления стрелок
лежат внутри световых конусов или на них
Рис. 33.3. В «исчислении Редже» пространство-время аппроксимирует¬
ся 4-мерным многогранником («политопом»), построенным обычно из
4-мерных «тетраэдров» (5-симплексов). Кривизна сосредоточена (в ви¬
де (5-функций) вдоль 2-мерных (обычно треугольных) ребер («скелета»)
Имеется также интересный вариант квантовой теории гравитации, предложенный
в 1959 году Туллио Редже. Пространство-время выбирается в виде неправильного «тет¬
раэдрического» 4-мерного многогранника («политопа»), его кривизна сконцентрирована
в дельта-функции (§9.7) вдоль 2-мерных «ребер» (Редже называл их «скелетом» [33-?]); см.
рис. 33.3 (а также рис. 32.3 а и 32.4). Квантовое состояние берется в виде суммы таких про¬
странств, взвешенных с комплексными коэффициентами, наподобие фейнмановской «суммы
по историям», рассмотренной в § 26.6. Описание самих пространств полностью комбина¬
торное за исключением того факта, что на каждом ребре должен быть задан «угол», опре¬
деляющий величину кривизны. «Космическая струна», описанная в § 28.2 (рис. 28.4), дает
пример геометрии такого рода.
Существуют и другие интригующие радикальные предложения Ричарда Джоссы^33
и Кристофера Ишема^33,9^ использующие теорию топосов. Это разновидность теории
множеств^3310^, возникающая в результате формализации «интуиционистской логики»
(см. примечание 2.6), при которой отрицается правомочность метода «доказательства от про¬
тивного» (§§2.6, 3.1)! Я не обсуждаю здесь какие-либо из этих схем, отсылая интересую-
О
щегося читателя к соответствующей литературе.

796
Глава 33
Другой идеей, которая в один прекрасный день сможет сыграть существенную роль
в физической теории, является теория категорий и ее обобщение на теорию п-категорий.
Теория категорий, сформулированная в 1945 году Самуэлем Эйленбергом и Саундерсом Мак-
Лейном^3311^, представляет собой весьма общий алгебраический формализм, основанный
на весьма примитивных (но запутанных) абстрактных понятиях, изначально вдохновленных
идеями алгебраической топологии. (Процедуры этой теории в разговорах часто называют
«абстрактной бессмыслицей».) Обманчивая мощь этой теории обусловлена крайне элемен¬
тарным характером ее основных ингредиентов в виде «стрелок», соединяющих «объекты»;
она имеет вполне «комбинаторный» вид, как и другие идеи, упомянутые в этом разделе.
Обобщение теории категорий на теорию n-категорий отражает способ, которым «гомото-
пия» улучшает понятие «гомологии», как кратко упоминалось в § 7.2. Теория категорий уже
использовалась как введение в теорию твисторов (в связи с § 33.9), а теория п-категорий
имеет отношение к петлям, связям, спиновой пене (§ 32.7) и к g-деформированным струк¬
турам (§ 32.5)^ЗЗЛ21 Я вообще не удивлюсь, если эти понятия сыграют значительную роль
в вытеснении привычных пространственно-временных понятий из физики XXI века.
Ближе к основному потоку современных исследований стоит понятие некоммутатив¬
ной геометрии, развитое в первую очередь Филдсовским медалистом математиком Аленом
Конном. Что такое некоммутативная геометрия? Чтобы подойти к этой идее, возьмем снача¬
ла обычное гладкое вещественное многообразие Л4. На этом многообразии (которое можно
считать С00-гладким; см. § 6.3) рассмотрим семейство гладких вещественных (скалярных)
функций. Такие функции можно складывать и перемножать между собой, а также умно¬
жать на обычные (постоянные) вещественные числа. Фактически они образуют некоторую
алгебраическую систему Л, называемую коммутативной алгеброй над вещественными чис¬
лами R (см. § 12.2 и примечание 12.5). Оказывается^33'13^, что если мы знаем Л только как
алгебру, не имея информации о том, откуда она взялась, мы можем тем не менее восстано¬
вить многообразие М по алгебре Л. Мы видим тогда, что системы Л4 и А можно строить
одну из другой, так что эти две математические структуры в определенном смысле эквива¬
лентны одна другой.
С другой стороны, в квантовой механике мы часто сталкиваемся с алгебрами, которые
некоммутативны. Примером может служить алгебра величин ха и ра, которые подчиняют¬
ся стандартным правилам коммутации канонически сопряженных величин рьха — харь =
= ih5% (§ 21.2). Если мы попробуем восстановить некоторое «многообразие» по такой алге¬
бре подобно тому, как многообразие М было получено из А, получится то, что называют
некоммутативной геометрией. В качестве еще одного примера можно взять другой част¬
ный случай и исходить из компонент квантово-механического момента импульса £i, £2, £3
из § 22.8 (напомним, что они порождают алгебру при задании перестановочных соотноше¬
ний L1L2-L2L1 ~ ihLs, £2-^3 — £з£г = ihLi, L3L1 — L1L3 — H1L2). Эти операторы можно
рассматривать как генераторы вращений обычной сферы S2. Оказывается, что мы можем
получить из алгебры, порождаемой операторами £1, L2, £3? некоммутативную геометрию,
назвав ее «некоммутативной сферой». Существует много математических тонкостей, краси¬
вых структур и неожиданных применений этой идеи, однако я не смогу здесь коснуться их
всех. Мы вернемся вкратце к некоммутативной геометрии (§33.7) в связи с квантованием
твисторов.
Конн и его коллеги развили идею некоммутативно^ геометрии с целью построить
физическую теорию, которая включала бы стандартную модель физики элементарных
частиц^33,14!. Их модель использует алгебру Л, которая является произведением Л\ х Л2,
где Лг есть (коммутативная) алгебра функций, определенных в пространстве-времени (име¬
ющем положительно определенную метрику), а Л2 — некоммутативная алгебра, получаю¬
щаяся из групп внутренней симметрии стандартной модели физики элементарных частиц
и создающая «две копии» пространства-времени. В таком виде эта модель не содержит

33.2. ТВИСТОРЫ КАК СВЕТОВЫЕ ЛУЧИ
797
лоренцевых идей специальной и тем более общей теории относительности. Более того,
как мне кажется, здесь пока не используется в полной мере потенциальное богатство идеи
*•	4
некоммутативной геометрии. Тем не менее эта модель может служить началом, к тому же,
она обладает некоторыми особенностями, позволяющими делать предсказания относительно
массы хиггсовского бозона^33*15!.
Все эти идеи сосредоточены на построении понятия «пространства-времени», кото¬
рое обладало бы свойством дискретности или какими-то «квантовыми» характеристиками.
В оставшейся части этой главы я опишу совершенно иное семейство идей, а именно те¬
орию твисторов (которой я сам посвятил уже более 40 лет!), где никакой дискретности
на пространство-время специально не налагается. Вместо этого точки пространства-вре¬
мени лишаются той первичной роли, которую они всегда играли в физической теории.
Пространство-время становится (вторичной) конструкцией, построенной из более прими¬
тивных твисторных элементов. Теория твисторов имеет некоторое отношение к теории спи¬
новых сетей и к переменным Аштекара, а возможно, и к некоммутативной геометрии, однако
она не приводит непосредственно к какому-либо понятию «дискретного пространства-вре-
  • /
мени». Ее отход от континуума вещественных чисел происходит в противоположном направ¬
лении — в качестве руководящего принципа для физики она выбирает магию комплексных
чисел. Согласно теории твисторов, комплексным числам принадлежит основополагающая
роль в определении структуры пространства-времени в дополнение к известной фундамен¬
тальной роли таких чисел в квантовой механике. Здесь ощущается возможность присутствия
важной связующей нити между физикой самых больших и самых малых масштабов.
33.2.	Твисторы как световые лучи
Как мы видели в главах 21 и 22, структура комплексных чисел действительно играет
фундаментальную роль в квантовой механике. «Амплитуды», которые появляются в качестве
коэффициентов в законе суперпозиции, основном для квантовой механики, представляют
собой комплексные числа, приводящие к комплексным гильбертовым пространствам. Хотя
эти амплитуды обычно рассматриваются как абстрактные величины, они играют основную
роль при вычислении вероятностей, получающихся в результате измерений, и мы видели
(в § 22.9), что существует тесная взаимосвязь между комплексными числами и геометри¬
ей пространства. Это в наибольшей мере проявляется в квантовой механике частицы со
1
спином где возможные состояния спина сопоставляются различным направлениям в про-
странстве путем введения понятия сферы Римана. Кроме того, в § 22.10 было показано, что
спиновые состояния для более высокого спина можно описать, пользуясь сферой Римана
в представлении Майораны. Однако фундаментальная геометрическая роль сферы Римана
проявляется не только в квантовой механике. Напомним (см. § 18.5), что эта сфера играет
важную пространственно-временную роль в теории относительности, поскольку поле зрения
наблюдателя также можно с полным правом рассматривать как сферу Римана. Как мы скоро
убедимся, этот факт имеет основополагающее значение в теории твисторов.
Другим руководящим принципом, лежащим в основе теории твисторов, является кван¬
товая нелокально сть. Мы обсуждали странные эффекты ЭПР (§§23.3-23.6) и «квантовое
перепутывание», проявляющееся, в частности, в явлении квантовой телеиортации (§23.9),
из которых следует, что физическое поведение нельзя до конца понять, ограничиваясь пол¬
ностью локальными воздействиями обычного «причинного» характера. Это предполагает
необходимость некоторой теории, в которую подобная нелокальность была бы заложена
на самом фундаментальном уровне.
Некоторое указание, как этого достичь, можно получить из теории спиновых сетей. На¬
помним (§ 32.6), что все спиновые сети предполагались построенными из ЭПР-пар. Линии,

798
Глава 33
Время
Рис. 33.4. В спиновых сетях пер¬
воначального типа линии можно
рассматривать как связи кванто¬
вого перепутывания (см. §23.9 и
рис. 23.7). Интерпретация спино¬
вой сети одинаково возможна при
любом выборе направления вре¬
мени — вперед, вбок или назад
образующие сеть, которые затем появлялись, с полным пра¬
вом можно рассматривать как связи квантового перепуты¬
вания. «Квантовая информация», соответствующая перепу-
тыванию, может «распространяться» тем или иным спосо¬
бом вдоль линии перепутывания или линии, входящей в со¬
став спиновой сети. В теорию спиновых сетей не заложено
время (и действительно, спиновые сети в их первоначаль¬
ном варианте можно рассматривать, предполагая любое на¬
правление течения времени — вперед, назад, вбок и т.д.;
см. рис. 33.4). Таким образом, странное «время, текущее
вспять» в условиях квантового перепутывания есть всего
лишь отражение этого безразличия к направлению течения
времени, присущего спиновым сетям.
Теорию твисторов можно рассматривать как продол¬
жение программы, начатой теорией спиновых сетей, с це¬
лью получить релятивистскую схему, в которой идеали¬
зированные световые лучи (или их обобщения, обладаю¬
щие спином) оказываются, в некотором смысле, носителя¬
ми квантового перепутывания. Обычные пространственно-
временные понятия не фигурируют изначально среди ин¬
гредиентов теории твисторов, а должны быть построены из
них. Это во многом сродни философии, лежащей в осно¬
ве моих первоначальных спиновых сетей, согласно которой не спиновые сети населяют
пространство с изначально предписанной геометрией, а пространство должно строиться из
спиновых сетей.
Твисторное описание пространства-времени действительно оказывается нелокальным,
более того, твисторное описание физических полей имеет принципиально «целостный»
характер, что связано с замечательной особенностью комплексной магии (когомологией го¬
ломорфных пучков); с ней мы еще не сталкивались в этой книге, но встретимся в §33.9
(некоторый намек на нее уже содержался в теории гиперфункций, изложенной в §9.7).
С этим связан и другой аспект магии комплексных чисел, а именно голоморфный харак¬
тер условия положительной частоты в квантовой теории поля (§§24.3, 33.10). Мы видим,
таким образом, что нелокальные аспекты теории твисторов тесно связаны с ее основной
мотивацией — со стремлением использовать магию комплексных чисел в надежде, что
сама Природа может пользоваться ею на некотором глубоком уровне. В этом и несколь¬
ких последующих разделах мы увидим, как все эти аспекты комплексной магии начина¬
ют объединяться в рамках теории твисторов. Мы начнем также понимать, каким образом
теория твисторов обнаруживает замечательную и неожиданно глубокую связь с общей те¬
орией относительности, и это открывает заманчивую перспективу для квантовой теории
поля, физики элементарных частиц и возможного нелинейного обобщения квантовой меха¬
ники.
Как же эти идеи начинают объединяться в теории твисторов? В качестве первого шага
к пониманию твисторных идей можно представить себе твистор как световой луч в обычном
пространстве-времени (пространстве Минковскрго) М. Можно рассматривать такой свето¬
вой луч как примитивную «причинную связь»/кежду парой событий (т.е. точек в про¬
странстве-времени). Но сами события следует представлять как вторичные конструкции,
возникающие в результате пересечения световых лучей. Мы можем характеризовать собы¬
тие R (пространственно-временную точку Я), задавая семейство световых лучей, проходя¬
щих через точку R (см. рис. 33.5). В то время как в обычной картине пространства-времени
световой луч Z представляет собой некоторое геометрическое место, а событие R — точку,

33.2. ТВИСТОРЫ КАК СВЕТОВЫЕ ЛУЧИ
799
/
I
Твисторное пространство
т
Рис. 33.5. Луч света Z в пространстве-времени Минковского М представляется одиночной точкой Z
в твисторном пространстве PN (проективном пространстве нулевых твисторов); одиночная точка R
в М представляется сферой Римана в пространстве PN (это есть «небесная сфера» для световых лучей,
приходящих в точку R). (Для полного соответствия требуется компактифицированное пространство
Минковского М^, описанное в § 33.9.)
в твисторном пространстве всё обстоит наоборот: световой луч описывается как точка Z,
а событие — как геометрическое место R.
Упомянутое здесь твисторное пространство, отдельные точки которого представляют
световые лучи в М, обозначаетсяI33 16! символом PN. (Такое обозначение выбрано в целях
согласования с терминологией в §33.5.) Таким образом, точка Z в PN соответствует гео¬
метрическому месту Z (световому лучу) в пространстве М, а точка R в М соответствует
геометрическому месту R (сфере Римана, см. § 18.5) в пространстве PN. Существенная часть
философии теории твисторов состоит в том, что обычные физические понятия, описывае¬
мые обычно в терминах пространства-времени, должны быть приведены к эквивалентному
(но нелокально связанному с прежним) описанию в твисторном пространстве. Мы видим,
что М иШ связаны между собой не точечным преобразованием, а имеет место нелокаль¬
ное соответствие между ними. Однако пространство PN дает лишь начало такого изменения
описания. Подлинное богатство твисторной геометрии (которое оказывается иоистине за¬
мечательным) раскрывается лишь постепенно, по мере того как развиваются дальнейшие
детали соответствия между пространственно-временными понятиями и геометрией твистор-
ного пространства.
Геометрическое место R в пространстве PN описывает «небесную сферу» (полное поле
зрения) для наблюдателя в точке R, которую можно рассматривать как семейство световых
лучей, проходящих через точку R. Как было отмечено, эта сфера представляет собой сферу
Римана, которая есть комплексное 1-мерное пространство (комплексную кривую; см. гла¬
ву 8). Таким образом, пространственно-временные точки рассматриваются как голоморфные
объекты в твисторном пространстве PN в соответствии с философией комплексных чисел,
лежащей в основе теории твисторов. В § § 33.5, 33.6 будет показано в явном виде, как эта
«голоморфная философия» может быть обобщена на более полное твисторное простран¬
ство Т, а в §§33.8-33.12 — как это позволит нам замечательным образом расшифровать
информацию о линейных и нелинейных безмассовых полях.
Пространство световых лучей PN само по себе не согласуется, однако, с «голоморфной
философией», потому что оно не является комплексным пространством. Пространство PN
не может быть комплексным многообразием, поскольку оно имеет пять вещественных из-
Пространство-время М

800
Глава 33
мерений*
а пять — число нечетное, тогда как любое комплексное п-многообразие должно
иметь четное число вещественных измерений 2п (см. § 12.9). Вскоре (в § 33.6) мы увидим,
что если сделать наши «световые лучи» более похожими на безмассовые физические ча¬
стицы, приписав им спин (фактически — спиральность; см. § 22.7) и энергию, то получится
шесишмерное пространство РТ, которое теперь можно интерпретировать как комплекс¬
ное пространство с тремя комплексными измерениями. Пространство PN находится внутри
пространства РТ, разбивая его на два комплексных многообразия РТ+ и РТ~, при этом
можно считать, что РТ4 представляет безмассовые частицы с положительной спирально¬
стью, а РТ- — безмассовые частицы с отрицательной спиральностью (см. рис. 33.6). Однако
было бы неправильно считать твисторы безмассовыми частицами. Твисторы предоставляют
нам переменные, в которых должны выражаться безмассовые частицы. (Это можно срав¬
нить с обычным использованием координатного 3-вектора х для описания положения точки
в пространстве. Хотя частица может занимать точку, положение которой определяется век¬
тором х, было бы неверно отождествлять частицу с этим вектором.)
Рис. 33.6. Вещественное 5-многообразие PN разбивает проективное твисторное пространство РТ на
два комплексных многообразия РТ+ и РТ-, представляющих безмассовые частицы соответственно
с положительной и отрицательной спиральностью
г •
Твисторный формализм приводит нас к совершенно иному взгляду на «квантован¬
ное пространство-время». Существует традиционная точка зрения, согласно которой про¬
цедуры квантовой теории поля должны применяться к метрическому тензору даъ, кото¬
рый рассматривается как тензорное поле на пространственно-временном многообразии.
Такой взгляд приводит к тому, что квантованная метрика оказывается «размытой» из-за
принципа неопределенности Гейзенберга. Мы получаем картину некоторого четырехмер¬
ного пространства, обладающего «размытой метрикой», так что, в частности, нулевые ко¬
нусы (и, следовательно, понятие причинности) оказываются подверженными «квантовым
неопределенностям» (см. рис. 33.7 я). В соответствии с этим исчезает четкое разделение
пространственно-временных векторов на пространственноподобные, времениподобные и
нулевые. Это создает фундаментальные трудности для любой достаточно традиционной
«квантовой теории гравитации», поскольку фундаментальной чертой квантовой теории поля
является требование условия причинности, чтрбы коммутировали операторы поля, соответ¬
ствующие событиям, разделенным пространстр£нно-временным интервалом. Если само по¬
нятие «пространственноподобного интервала» подвержено квантовым неопределенностям
(или само становится квантовым понятием), то неприменимыми становятся стандартные
процедуры квантовой теории поля, которые включают в себя определение перестановоч¬
ных соотношений для операторов поля (§§26.2, 26.3). Теория твисторов предоставляет со-
вепшенно иную каттгину. поскольку тепепь шэопедутэы «квантования», какими бы они ни
* Почему световые лучи имеют пять степеней свободы?

33.2. ТВИСТОРЫ КАК СВЕТОВЫЕ ЛУЧИ
801
были, должны применяться в твисторном пространстве, а не в пространстве-времени (ес¬
ли последнее рассматривать со «стандартной» точки зрения). По аналогии со стандартным
подходом, когда «события» остаются нетронутыми, а «нулевые конусы» становятся размы¬
тыми, твисторный формализм не затрагивает* «Цветовые лучи», делая размытыми «события»
(см. рис. 33.76).
шмшт
*х
а)	б)
Рис. 33.7. а) Согласно обычному взгляду на возможную природу «квантованного пространства-време¬
ни», оно должно иметь «размытую» метрику, что означает «размытие» светового конуса, при котором
разделение направлений в некоторой точке на нулевые, времениподобные и пространственноподоб¬
ные оказывается подверженным квантовым неопределенностям, б) Более «твисторный» взгляд пред¬
полагает, что в твисторном пространстве (в данном случае это PN) некоторые элементы остаются
неизменными (к ним относятся световые лучи), однако условия пересечения лучей подвержены кван¬
товым неопределенностям. В соответствии с этим понятие «пространственно-временной точки» также
становится «размытым»
Теория твисторов, как мы только что видели, с самого начала использует проявление
магии комплексных чисел, отличное от того, которое учитывает квантовая теория, а именно
ту классическую особенность геометрии пространства-времени, что небесную сферу мож¬
но рассматривать как сферу Римана, которая представляет собой 1-мерное комплексное
многообразие. Идея состоит в том, что такой подход дает нам намек на реальную схему
устройства Природы, которая должна в конечном счете связать структуру пространства-вре¬
мени с процедурами квантовой механики. Стоит отметить, что эта особенность геометрии
пространства-времени специфична для определенной размерности и сигнатуры, которыми
насколько мы знаем, обладает физическое пространство-время. Действительно, сфера Ри¬
мана играет важную роль небесной сферы в теории относительности (§ 18.5) при условии,
что пространство-время 4-мерно и лоренцево, а это находится в резком контрасте с идеями,
лежащими в основе теории струн и других схем типа Калуцы - Клейна. Комплексная магия
теории твисторов в полном объеме проявляется в случае 4-мерной геометрии простран¬
ства-времени обычной (специальной) теории относительности и не имеет столь тесной связи
с «пространственно-временной геометрией» более высокой размерности (см. ниже в § 33.4)
Прежде чем двигаться дальше, вернемся к исходной картине спиновых сетей, отметив,
что в ней потеряна какая-либо связь с перемещениями в пространстве. В этой теории ев-
С/
клидовы углы появляются как некоторый «геометрический предел» теории спиновых сетей,
тогда как расстояния в этой теории не фигурируют. В схеме петлевых переменных понятие
«расстояния» определяется числами (п = 2j), приписываемыми линиям и относящимися
не к спину, а к площади. Но это отличается от интерпретации в первоначальной теории
спиновых сетей, в которой отсутствует мера расстояния, поскольку спин представляет со¬
бой момент импульса, связанный лишь с вращениями и углами. Необходимо отвести в этой
теории соответствующую роль импульсу, чтобы можно было ввести в нее трансляционные
перемещения и реальные расстояния. В соответствии с этим получается, что мы должны
переити от группы вращения к полной группе евклидовых движении и, в применении к со¬
ответствующей релятивистской схеме, к группе Пуанкаре (§ 18.2)[33* 173.

802
Глава 33
В конце 1950-х-начале 1960-х годов, когда я активно размышлял над этими проблемами,
теория петлевых переменных еще не была создана, и я намеревался обобщить концепцию
спиновых сетей, включив в нее группу Пуанкаре. Однако я испытывал беспокойство в отно¬
шении неприятной особенности этой группы: она не является полупростой (см. § 13.7), что
затрудняет использование ее представлений. В то время я считал, что расширение группы
Пуанкаре до так называемой конформной группы (которая уже является полупростой) даст
некоторый аналог теории спиновых сетей с более подходящей математической структурой.
Конформная группа обобщает группу Пуанкаре, требуя, чтобы сохранялись лишь световые
конусы, а не вся метрика пространства Минковского. И действительно, оказывается, что
конформная группа занимает важное место в теории твисторов, она является также груп¬
пой симметрии пространства PN (идеализированных) световых лучей. (Неотражательная
часть конформной группы является также группой симметрии каждого из вышеупомянутых
пространств РТ+ и РТ“, описывающих безмассовые частицы, обладающие спиральностью
и энергией.) Роль этих групп в более явном виде будет показана в следующих двух раз¬
делах .
33.3.	Конформная группа. Компактифицированное пространство
Минковского
Выше я упоминал о конформной группе пространства-времени. Попробуем исполь¬
зовать эту группу в более полной мере. Она имеет особое значение в физике безмассовых
полей (например, максвелловского поля), поскольку оказывается, что полевые уравнения для
безмассовых полей инвариантны относительной этой большей группы, будучи неинвариант¬
ными относительно группы Пуанкаре^33 181 Можно предположить, что на фундаментальном,
уровне безмассовые частицы/поля являются основными ингредиентами, а масса появляет¬
ся на более поздней стадии. Действительно, именно такая точка зрения подразумевается
в стандартной модели, описанной в главе 25, где масса вводится посредством хиггсовского
бозона и возникает лишь в результате спонтанного нарушения симметрии (§ 25.5). Как бы то
ни было, одной из наиболее важных мотиваций теории твисторов действительно была вера
в основополагающую роль безмассовых полей и конформной группы. Мы увидим (§33.8),
что теория твисторов дает замечательно краткое описание безмассовых частиц и полей, и это
обстоятельство служит одним из краеугольных камней теории.
Каков точный смысл конформной группы? Строго говоря, эта группа действует не
на пространство Минковского М, а на некоторое его расширение, известное под названием
компактифицированного пространства Минковского М^. Пространство представляет
собой замечательно симметричное замкнутое многообразие, которое обладает геометрией,
во многих отношениях более изящной, нежели само пространство Минковского. Мы не
должны, однако, рассматривать его как «реальное пространство-время» — оно вводится
в целях математического удобства. Это полезное вспомогательное средство для понимания
твисторной геометрии и ее связи с геометрией физического пространства-времени.
Хорошей наглядной иллюстрацией может служить сфера Римана и ее связь с ком¬
плексной плоскостью. Мы помним (из § 8.3), что сфера Римана получается из комплексной
плоскости путем добавления «бесконечного Элемента» — точки, обозначаемой как оо; при
этом мы получаем геометрическую структуру, обладающую более высокой симметрией, чем
исходная плоскость. Аналогично «компактифицированное пространство Минковского»
получается из обычного пространства Минковского М в результате добавления некоторого
«бесконечного элемента», которым в данном случае оказывается полный световой конус на
бесконечности. Возникающее при этом пространство обладает более высокой симметрией,
нежели само пространство Минковского.

33.3. Конформная группа. Компактифицированное пространство Минковского
803
Посмотрим теперь, как всё это работает. Пространство оказывается 4-мерным ве¬
щественным компактным многообразием с дюренцевой конформной метрикой. Напомним
(§27.12), что лоренцева конформная метрика представляет собой, по существу, семейство
нулевых конусов, определенных на данном пространстве. Эту структуру чаще выражают в
терминах класса эквивалентности метрики, при этом метрика д считается эквивалентной
метрике д\ если gf — Q2g для некоторого гладкого скалярного поля 17, которое всюду поло¬
жительно. Такое изменение масштаба сохраняет неизменными нулевые конусы (рис. 33.8).
Чтобы перейти от М (рассматриваемого как конформное многообразие) к компактному кон¬
формному многообразию М^, мы добавляем 3-поверхность J > названную выше «световым
конусом на бесконечности». Вспомним (§ 27.12) 3-пространства и представляющие
прошлую и будущую нулевые бесконечности пространства Минковского (см. рис. 27.166).
Можно построить пространство М^, отождествив и способом, показанным на
рис. 33.9. Точка поверхности считается той же самой точкой, что и соответствующая
точка поверхности , пространственно антиподная ей (на 2-сфере, которую представляют
большинство точек на диаграмме). Световой конус точки а~ на снова фокусируется в
точке а+ на и именно точки а~ и должны быть отождествлены. Кроме того, все три
точки, представляющие временную и пространственные бесконечности, г-, г°, г+, также
отождествляются как одна единая точка г. * Конформное многообразие действитель¬
но обладает более высокой симметрией, чем пространство Минковского, имея 15-мерную
группу симметрии — конформную группу, а не 10-мерную группу Пуанкаре.
С
Рис. 33.8. Структура нулевых конусов лоренцева многообразия М эквивалентна его конформной
структуре. Конформное измерение масштаба действует на метрику этого многообразия, но не влияет на
его свойства причинности. (Метрика g конформно преобразуется в д\ если д’ — Q2д, где 17 — всюду
положительное скалярное поле.) При благоприятных обстоятельствах такие изменения масштаба могут
быть полезными для «введения в поле зрения» сингулярностей и бесконечных областей
Существует изящный способ описания пространства и его группы преобразований.
Рассмотрим «световой конус» /С для точки О в псевдоевклидовом 6-пространстве Е2,4
Попробуйте описать геометрию пространства подробнее, объяснив поточечную идентификацию
поверхностей и/~ в терминах обычного пространства-времени. Понятно ли, почему топологией простран¬
ства является произведение S1 х S3? Понятно ли, что при нечетном числе измерений пространства-времени
ситуация будет существенно иной?

804
Глава 33
• О
Отождествление §
Антиподное
ртождествление
я)
6)
Рис. 33.9. Компактифицированное пространство Минковского получается из обычного простран¬
ства Минковского М добавлением будущей и прошлой нулевых бесконечностей и J?~ с после¬
дующим отождествлением их в виде J. а) Световой конус будущего для любой точки а~ на
снова фокусируется в другую вершину а+ на (этот «световой конус» в обычных терминах есть
просто история плоского волнового фронта, распространяющегося со скоростью света), и точка а~
должна быть отождествлена с а+. Пространственноподобная бесконечность i° и прошлая и будущая
времениподобные бесконечности иг+ — все должны быть отождествлены в одну точку г. 6) Эта
идентификация J? показана в виде строго конформной диаграммы (рис. 27.166), где точка а~ есть
антипод точки а+ на «поверхности вращения S2» для всей диаграммы в целом
с сигнатурой 4- 4-
. Выберем в Е2,4 стандартные координаты w. t, х, у, z, v, в
которых конус /С задается уравнением
2 2 2 2
х — у — Z — V
О,
а метрика ds2 пространства Е2,4 имеет вид
ds
dw2 4- dt2 — dx2 — dy
dz
dv".
Мы имеем 5-мерный «конус» с вершиной О. Я постарался изобразить его на рис. 33.10,
однако эта картинка может ввести в заблуждение из-за того, что конус /С кажется со¬
стоящим из двух отдельных «кусков» («прошлого» и «будущего»), тогда как в действи¬
тельности они соединены в «один кусок»"". Рассмотрим теперь сечение конуса /С нулевой
5-плоскостью w — v = 1. Пересечение плоскости с поверхностью конуса представляет со¬
бой 4-многообразие («параболоид»), внутренняя метрика которого, определяемая простран-
О А	а
ством Е ’ , имеет вид"
= dt2 — dx2 — dy2 — dz2.
ds
Мы узнаем здесь метрическую форму обычного плоского 4-пространства Минковского
(§ 18.1), поэтому можно отождествить его с М, несмотря на то что оно погружено в Е ’
«косым образом» (с образованием параболы на рис. 33.10). Как найти на этой картине М^?
Это есть абстрактное пространство полных образующих конуса К (прямых линий, проходя¬
щих через точку О и лежащих на поверхности конуса, при этом полная прямая, проходящая
через точку О в обоих направлениях, засчитывается за одну образующую). Таким образом,
каждую точку пространства можно рассматривать просто как образующую конуса /С
(рис. 33.10), так что	есть «небесная сфера» для некоторого «наблюдателя», находящегося
в начале координат пространства Е2’4!
Понятно ли, почему это так?
Почему?

33.4. Твисторы как многомерные спиноры
805
Рис. 33.10. Компактифицированное пространство Мин¬
ковского можно определить как пространство образу¬
ющих светового конуса /С в псевдоевклидовом простран¬
стве Е2,4, описываемого уравнением w2 4-t2 — х2 — у2 —
— z2 — v2 = 0. «Параболоидальное» 4-многообразие М,
получающееся в результате пересечения конуса /С нуле¬
вой 5-плоскостью w — V = 1, имеет внутреннюю метрику
Минковского ds2 = dt2 — dx2 — dy2 — dz2. Семейство об¬
разующих конуса JC в плоскости w — v = 1 (на этой диа¬
грамме его не видно, поскольку здесь представлено лишь
одно «временное» измерение) параллельно этой плоско¬
сти и не пересекает пространство М; эти образующие
дают точки поверхности J
Почему эта схема работает? Каждая образующая, не лежащая в 5-плоскости w — v —
— 1, пересекает М в единственной точке, поэтому такое семейство образующих находится
в непрерывном взаимно-однозначном соответствии с М. Но кроме того, имеются образую¬
щие, лежащие в этой 5-плоскости. Они придают пространству М дополнительные точки,
образующие поверхность ^. Определенное таким образом пространство обладает кон¬
формной лоренцевой метрикой, которая локально задается метрикой любого локального
сечения конуса /С.
Псевдоортогональная группа 0(2, 4) (см. §§13.8, 18.1, 18.2), действующая на Е2,4,
состоит из «вращений», сохраняющих метрику ds2. Она переводит образующие конуса К
в другие образующие того же конуса, так что пространство преобразуется само в себя.
Более того, при этом сохраняется конформная структура пространства М^.** Существуют
ровно два элемента группы 0(2, 4), которые действуют на как тождественные, — это
сам тождественный элемент группы 0(2, 4) и тот же элемент, взятый с обратным знаком,
последний просто изменяет направление каждой образующей на противоположное. Если
отвлечься от такого двузначного характера соответствия, возникающего из-за обратимости
направления образующих, 0(2, 4) есть конформная группа. Она включает в себя 10-мерную
подгруппу, сохраняющую 5-плоскость w — v = 1, и это дает группу Пуанкаре простран-
з£с эр
ства М. Эти рассуждения фактически представляют многомерный вариант того, что мы
использовали в § 18.5, показывая, что конформные преобразования обычной сферы (которая
является компактифицированной евклидовой плоскостью) дают реализацию группы Лорен¬
ца 0(1, 3) (см. сечение Е на рис. 18.9).
33.4.	Твисторы как многомерные спиноры
Как ко всему этому пристроить твисторы? Кратчайший (хотя и вряд ли наиболее про¬
зрачный) путь к описанию твистора (в пространстве Минковского) — это объявить его
приведенным спинором (или полуспинором) для группы 0(2, 4). (Пусть вас не пугает мате-
Почему конформная метрика, задаваемая каким-нибудь одним локальным сечением, такая же, как и мет¬
рика, задаваемая любым другим сечением? Почему точки поверхности определенные указанным образом,
согласуются с определением, данным раньше? (Подсказка. см. § 18.4 и рис. 18.9.)
Почему? Можете воспользоваться результатом упражнения 33.5.
Каков явный вид условия, налагаемого на матрицу б х б, чтобы она представляла бесконечно малый
элемент группы 0(2, 4)? Какие из этих матриц дают бесконечно малые преобразования Пуанкаре?
**
***

806
Глава 33
матическая лаконичность такого описания — вскоре я представлю гораздо более разверну¬
тую физическую картину!) О понятии приведенного спинора имеется краткое упоминание
в § 11.5. В случае 2п-мерного пространства, на которое действует псевдоортогональная груп¬
па О(п —г, n-f~r), пространство приведенных спиноров 2п_1-мерно. В данном случае п — 3
(и г — 1), так что мы имеем 4-мерное пространство приведенных спиноров, именуемое
твисторным пространствомt33*19l.
При таком определении мы, к сожалению, не получаем ясного геометрического или
физического представления, на что похож твистор. Кроме того, мы видим, что теория тви¬
сторов должна существовать при любом четном числе пространственно-временных изме¬
рений 2(п — 1) вопреки сказанному в конце §33.2. Мы обобщаем описанное построение
для конуса JC (взяв теперь 2(п — 1) измерений); компактификация 2(п — 1)-мерного про¬
странства-времени Минковского проводится подобно тому, как это было сделано раньше;
как и прежде, мы добавляем две новые координаты у и гг, одной из которых в метри¬
ке соответствует минус, а другой — плюс. «Твисторное пространство» теперь 2п_1-мерно.
При нечетном числе пространственно-временных измерений 2п — 1 также можно это сде¬
лать за исключением того, что теперь у нас нет понятия приведенных спиноров, и нашими
«твисторами» должно считаться все 2п-мерное спиновое пространство в целом. Однако
в нечетномерном случае теряется важная особенность твисторов — их киральная природа
(мы обсудим это полнее в §§33.7, 33.12, 33.14). Лишь при переходе к пространству при¬
веденных спиноров мы получаем истинно киральный формализм (так что объекты с левой
и правой спиральностью получают разное твисторное описание; см. §33.7), и можно на¬
деяться учесть, таким образом, киральные аспекты слабого взаимодействия (§ 25.3). Далее
мы поймем, почему при таком общем n-мерном определении твистора теряются многие из
ключевых физических (и голоморфных) свойств, которые делают теорию твисторов столь
эффективной.
Поскольку твисторы относятся к активной (конформной) группе пространственно-
временных преобразований, при которых одни точки пространства-времени переходят в дру¬
гие его точки, твисторы следует рассматривать как объекты, относящиеся глобально ко всему
пространству-времени, а не к отдельным его точкам. Локальные величины — векторы, тен¬
зоры или обычные спиноры — относятся к группе симметрии, которая действует в одной
точке (§ 14.1), — например, к группе вращений или группе Лоренца (§ 13.8). Хотя это делает
твисторы более трудными в обращении, нежели обычные векторы, тензоры или спиноры,
такая глобальность имеет преимущество, если мы ищем формализм, призванный заменить
пространство-время, а не просто определенный по отношению к некоторому заранее вы¬
бранному пространственно-временному многообразию. Как отмечалось в §33.2, одна из
главных целей теории твисторов состоит в создании такого формализма. Главный недоста¬
ток такого подхода состоит в том, что нелегко понять, как применять его к искривленному
пространству-времени общего вида М, не обладающему симметрией относительно кон¬
формной группы. Далее (в §§ 33.11, 33.12) мы увидим, как теории твисторов замечательным
образом удается справиться с этой трудностью.
Данное выше определение твистора как приведенного спинора для группы 0(2, 4) дает
лишь весьма ограниченное представление об идеях и мотивации теории твисторов. Как толь¬
ко что отмечалось, в этом подходе нет ничего специфически 4-мерного, и потому вроде бы
нет оснований ожидать, что теория твисторов послужит путеводителем в наших поисках
более глубокой теории Природы. Чтобы понять, чем теория твисторов может помочь в этом
отношении, вспомним содержание глав 29 и 30. Коль скоро является общепринятым, что
главной целью поисков принципиально нового взгляда на физику должно стать надлежащее
объединение квантовой механики и гравитации, нам следует искать такой путь, на котором
сами правила квантовой теории (поля) не сохраняются в неприкосновенности как нечто
священное, а подвергают^ изменениям, и то же самое относится к геометрической картине
обычного пространства-времени. Однако квантовые принципы заключают в себе так много

33.5. Элементарная твисторная геометрия и система координат
807
истины и красоты, что от них не так просто отказаться. В теории твисторов, вместо то¬
го чтобы налагать требования квантовой теории поля, мы стараемся отыскать в них черты,
связывающие их с эйнштейновскими концепциями, и скрытую гармонию между теорией от¬
носительности и квантовой механикой. Как уже отмечалось, одним из ключевых направляю¬
щих элементов является магия комплексных чисел, которой в этой книге отведено так много
места. Другим служит особая гармония эйнштейновской теории лоренцева 4-пространства,
отличающая ее от обобщений на большее число измерений или иную сигнатуру.
Что в этом отношении особенного в лоренцевом 4-пространстве? Как подчеркивалось
в §§ 18.5, 33.2, небесная сфера для наблюдателя имеет естественную конформную структу¬
ру, и ее можно рассматривать как сферу Римана. Следует иметь в виду, что нечто подобное
имеет место при любом (ненулевом) числе пространственных и временных измерений, и
небесная сфера всегда имеет структуру конформного многообразия*. Однако особенность
лоренцева 4-мерного случая состоит в том, что такое конформное многообразие можно есте¬
ственным образом интерпретировать как комплексное многообразие (сферу Римана), и это
свойство отсутствует при любом другом числе пространственных и временных измерений.
В чем значение этого факта? В теории твисторов магия комплексных чисел используется в
полной мере. Не только твисторное пространство оказывается комплексным многообразием,
но и это комплексное многообразие допускает непосредственную физическую интерпрета¬
цию. Из общих результатов следует, что «твисторное пространство» оказывается комплекс¬
ным пространством какого-либо вида^33*20^ лишь в тех случаях, когда деление разности
чисел пространственных и временных измерений на 4 дает в остатке 2. Стоит отметить,
что под это условие не подходят ни теория Калу цы - Клейна в ее первоначальной форме, ни
10- или 11 -мерные теории супергравитации, ни 26-мерная первоначальная теория струн, ни
10-мерная теория суперструн, ни 11-мерная супергравитация М-теории, ни даже 12-мерная
F-теория (поскольку в этом последнем случае имеются 2 временных измерения)!
33.5.	Элементарная твисторная геометрия и система координат
Какова физическая или геометрическая интерпретация твистора общего вида для обыч¬
ного 4-пространства Минковского? Проще всего описать положение дел, воспользовавшись
стандартными координатами Минковского С ж, у, z для точки R пространства М, где ско¬
рость света принята за единицу: с = 1. Полное твисторное пространство Т для М представ¬
ляет собой 4-мерное комплексное векторное пространство, в котором можно пользоваться
стандартными комплексными координатами Z°, Z1, Z2, Z3. Будем говорить, что твистор Z
с этими координатами инцидентен пространственно-временной точке R (или наоборот, что
точка R инцидентна твистору Z), если выполняется ключевое матричное соотношение (от¬
носительно матричных обозначений см. § 13.3)
(_ i(t + z Z2\
из которого следует вся геометрия плоского твисторного пространства .
В соответствии с обозначениями, введенными в § 12.8, для представления твистора Z
(с компонентами Z°, Z1, Z2, Z3 в стандартной системе отсчета) иногда будет применяться
(абстрактно-)индексная запись Za. Каждому твистору Z, или Za (элементу пространства Т)
соответствует комплексно-сопряженная величина Z, представляющая собой дуальный тви¬
стор (элемент дуального твисторного пространства Т*). В индексной форме Z записывается
**
Объясните почему.
Запишите это уравнение в обычном алгебраическом виде.

808
Глава 33
как Zc (с нижним индексом), компоненты (в стандартной системе отсчета) будут иметь вид
(Z0, Zi, Z2, Z3) = (Z2, Z3, Z°, Z').
Эта запись, возможно, требует пояснения. Четыре величины (комплексных числа) в левой
части — это просто соответствующие четыре компоненты дуального твистора Z; четыре
величины в правой части — это соответственно ^комплексно-сопряженные величины ком¬
плексных чисел Z2, Z3, Z°. Z1. Так, компонента Zq дуального твистора Z есть комплексно-
сопряженная величина компоненты Z2 твистора Z и т. п. Обратим внимание на перестановку
двух первых компонент с двумя вторыми при операции комплексного сопряжения. Посколь¬
ку Z является дуальным твистором, можно образовать его (эрмитово) скалярное произведе¬
ние (см. §§ 13.9, 22.3) с исходным твистором Z, получив твисторную норму (возведенную
в квадрат)
Z • Z = ~ZaZa = Z0Z0 + Zi^1 + z2z2 + z3z3 =
= ~z^zQ + zrz1 + ~z®z2 + ~zzz2 =
1
2
Z° + Z2 2 + Z1 + Z3 2 - \Z° - z2 2 -	-	z3
последняя строка этой формулы показывает, что эрмитово выражение ZaZa имеет сигнату¬
ру (+ Н ) в соответствии с § 13.9/ (В симметрии твисторного пространства проявляется
локальная эквивалентность (§ 13.10) группы SU(2, 2) группе 0(2, 4) из § 33.3.) Из приведен¬
ного выше ключевого соотношения, определяющего инцидентность, следует, что твистор Za
может быть инцидентен событию в вещественном пространстве Минковского М лишь в том
случае, если его норма обращается в нуль: ZaZa = 0. . Если ZaZa — 0, мы говорим, что
твистор Z нулевой.
Чтобы связать это с обсуждением в § 33.2, нам придется сначала познакомиться с проек¬
тивным твисторным пространством FT, которое представляет собой комплексное проектив-
о
ное 3-пространство (CF'), построенное из комплексного векторного пространства Т. (Отно¬
сительно проективных пространств см. § 15.6.) Большая часть гвисторной геометрии гораздо
проще выглядит при использовании пространства FT вместо Т. Числа Z°, Z1, Z2, Z3 в этом
случае представляют собой однородные координаты в пространстве FT, так что точки этого
пространства определяются тремя независимыми отношениями
Z0 \ Zl : Z2 \Z3.
Нулевые проективные твисторы образуют пространство FN, представляющее собой подпро¬
странство с 5 вещественными измерениями пространства РТ с 6 вещественными измерени¬
ями, для которого твисторная норма обращается в нуль:
= 0.
Это уравнение определяет также 7-мерное вещественное подпространство N нулевых
непроективных твисторов в векторном пространстве Т. При ZaZa > 0 мы имеем простран¬
ство положительных твисторов Т+, при ZaZa < 0 — пространство отрицательных твисто¬
ров Т_. Аналогично определяются проективные пространства FT+ и FT- (см. рис. 33.11
и, для сравнения, рис. 33.6).
Рассмотрим геометрическую связь между FN и М, изображенную на рис. 33.5, как
следствие ключевого соотношения инцидентности, приведенного в начале этого раздела.
**
I ж
Проверьте последнее выражение. Объясните, почему из него следует вывод о сигнатуре.
Покажите это. Докажите и обратное утверждение: такое событие существует, если Zа Za — 0, причем Z2
и Z3 не обращвются в нуль одновременно.

33.5. Элементарная твисторная геометрия и система координат
809
Рис. 33.11, Твисторное пространство Т представляет собой комплексное векторное пространство с
псевдоэрмитовой метрикой. Проективное твисторное пространство FT (или СР3) есть простран¬
ство лучей (1-мерных подпространств) в Т. Таким образом, если твистор Z имеет координа¬
ты Z°, Z1, Z2, Z3, то отношения Z° : Z1 : Z2 : Z3 определяют соответствующую точку в FT.
Подпространство N с 7 вещественными измерениями (пространство нулевых твисторов, удовлетво¬
ряющих условию ZaZa — 0) делит твисторное пространство Т на комплексные 4-пространства
положительных твисторов Т+ и отрицательных Т“, для которых выполняются условия соответствен¬
но ZaZa > 0 и ZaZa < 0. Соответствующими проективными вариантами этих пространств будут
вещественное 5-мерное пространство PN (пространство световых лучей в М#) и два комплексных
3-многообразия: FT4- (которое представляет безмассовые частицы с положительной спиральностью)
и РТ~ (представляет безмассовые частицы с отрицательной спиральностью)
Сразу можно заметить, что две точки Р и R пространства М (два события), инцидентные
одному и тому же твистору с ненулевыми компонентами Z (который с необходимостью
является нулевым твистором), должны быть разделены нулевым интервалом (т. е. каждая
из точек Р и R лежит на световом конусе другой из них). Отсюда следует, что Z опреде¬
ляет световой луч (нулевую прямую линию в М), поскольку все точки в М, инцидентные
твистору Z, должны быть разделены нулевым интервалом (см. рис. 33.12). Более того, тви¬
стор Z будет представлять тот же самый световой луч, если заменить Za на \Za, где А —
любое комплексное число, отличное от нуля. Геометрическое место событий, инцидентных
нулевому проективному твистору (с ненулевыми компонентами) действительно является
световым лучом, однако в частном случае Z2 = Z3 = 0 мы должны дать подходящую
интерпретацию, поскольку в этом случае у нас нет точек в М, инцидентных твистору Za;
тем не менее и в этом случае можно считать, что нулевой твистор описывает световой луч
на бесконечности (образующую поверхности , лежащую не в М, а в М#)\
Поступим теперь наоборот. Зафиксировав событие R с вещественными координата¬
ми t, х, |/, z, мы найдем, что пространство твисторов Z, инцидентных точке R, определяет¬
ся двумя линейными однородными соотношениями в компонентах Z°, Z1, Z2, Z3. Каждое
из этих линейных соотношений определяет плоскость в пространстве FT, и их пересечение
(множество точек в FT, удовлетворяющих обоим соотношениям) дает нам проективную
линию R в FT (CF1), лежащую фактически в PN, которая представляет собой сферу Ри¬
мана, как и требуется (§§ 15.4, 15.6). Таким образом, точки в М (события) представляются
в твисторном пространстве проективными линиями в PN. При Z2 — 0 = Z3 мы получаем
некоторую проективную линию в PN, обозначаемую как I. Эта особая линия представляет
точку г, которая служит вершиной светового конуса на бесконечности. Любая другая
точка Q поверхности У представляется в FN проективной линией Q, пересекающей JP .**
Эта ситуация иллюстрируется на рис. 33.12.
**
Ш Продемо
Почему?

810
Глава 33
Две плоскости в РТ
Рис. 33.12. Геометрия основных геометрических мест в и PN, определяемых соотношением ин¬
цидентности для твисторов. а) Зададим точку (проективный нулевой твистор) Z в пространстве PN.
Точки пространства (например, Р и R), инцидентные твистору Z, составляют некоторый световой
луч, поскольку все такие точки отделены одна от другой нулевым интервалом, б) Зададим точку R
в пространстве М#. Точки пространства PN (например, Z и X), инцидентные точке R (лежащей на
пересечении двух комплексных плоскостей в пространстве РТ), составляют комплексную проектив¬
ную линию, которая представляет собой сферу Римана. Точкам Р и R в М9^, разделенным нулевым
интервалом вдоль светового луча Z, соответствуют сферы Римана Р и R, которые пересекаются в
одной точке Z. (Я изобразил эти сферы Римана сильно вытянутыми как компромисс с тем фактом, что
они являются также проективными прямыми линиями в проективной геометрии пространства РТ!)
Одна из таких сфер Римана I представляет точку г пространства М#. Точка г соответствует про¬
странственноподобной и времениподобной бесконечности, это есть вершина светового конуса J> на
бесконечности. Любая другая точка Q поверхности представлена в PN проективной линией Q,
пересекающей S’
Совершенно замечателен способ, которым эти комплексные структуры представляют
пространство Минковского (со стандартным числом пространственных и временных изме¬
рений). Можно интерпретировать пространство Минковского как пространство комплексных
линий, лежащих в PN (или РМ —	, если нас интересуют только конечные пространственно-
временные точки), рассматривая PN как первичную структуру, а М — как вторичную. Это
означает, что световые лучи считаются более примитивными объектами, нежели сами точки
пространства-времени. Пересечению световых лучей Z и X соответствует существование
проективной линии в PN, содержащей соответствующие точки Z и X пространства PN,
и, как мы видели, условие нулевого интервала между двумя пространственно-временными
точками представляется условием пересечения соответствующих проективных линий Р и R
в PN (рис. 33.12). Таким образом, мы видим, что твисторное пространство дает новый взгляд
на физическую геометрию, совершенно отличный от обычной пространственно-временной
картины. Точки обычного пространства-времени представляются сферами Римана в про¬
странстве PN. Точки пространства PN представляются световыми лучами в простран¬
стве-времени. Оба вида соответствия являются нелокальными. Тем не менее, мы можем
переходить от одной картины к другой, пользуясь точными геометрическими правилами.
&
33.6.	Геометрия твисторов как вращающихся безмассовых частиц
Напомним, что главной идеей, лежащей в основе мотивации теории твисторов, бы¬
ло стремление в полной мере использовать магию комплексных чисел. Пространство PN,
хотя и содержит большую (с 4 вещественными параметрами) систему комплексных про¬

33.6. Геометрия твисторов как вращающихся безмассовых частиц
811
ективных линий, тем не менее не является комплексным многообразием (как отмечалось
в § 33.2, это связано с нечетным числом вещественных измерений). Однако оно становится
таковым (пространством РТ или СР3), если добавить еще одно вещественное измерение.
Можно ли интерпретировать лишние точки пространства РТ физически естественным, ра¬
зумным образом? Оказывается, можно (намек на это содержался в §33.2). Напомним, что
реальные свободные фотоны имеют более сложную структуру, нежели просто световые лучи
в пространстве М. Световой луч описывает точечную частицу, распространяющуюся со ско¬
ростью света в заданном направлении, тогда как реальные фотоны обладают еще энергией
и спином. Пока можно рассматривать ситуацию с классической точки зрения. Фотон может
вращаться по и против часовой стрелки вокруг направления движения (иметь соответствен¬
но положительную и отрицательную спиральность, определяемую правой и левой круговой
поляризацией; см. § 22.7). Мерой этой спиральности в обоих случаях служит величина h.
Оказывается, что классические фотоны с положительной спиральностью можно представить
точками пространства РТ+, а фотоны с отрицательной спиральностью — точками простран¬
ства РТ~, лишнее измерение связано с энергией фотона. Такое описание применимо также
к любой другой безмассовой частице с ненулевым спином ~nh.
Как это всё работает? Здесь не место входить в подробности, но существенные особен¬
ности стоит отметить. В качестве первого шага полезно заметить, что первые две компо¬
ненты Z0 и Z1 твистора Z представляют собой две компоненты 2-спинора со с индексной
формой иА, где о;0 = Z° и ш1 = Z1 (см. §§22.8, 25.2). Остальные две компоненты твисто¬
ра Z, Z2 и Z3 , являются компонентами штрихованного (дуального) спинора 7г с индексной
формой 7ГА', где 7Г(у	и	7Гц	=	Z3.	Это иногда записывают в виде
Z — (со, 7г)
и называют со и 7Г спинорными частями твистора Z. Комплексно-сопряженный твистор Z
имеет свои спинорные части, расположенные в обратном порядке:
Z = (W,w),
так что твисторную норму можно представить в виде
ZaZ° = Z • Z = 7Г •	+	cJ	• 7Г = 7ТА^Л + CUA 7ГА' .
Соотношение инцидентности между твистором Z и пространственно-временной точкой R
с координатами Минковского t\ х, у, z теперь записывается в виде
СО = 2 V 7Г,
irAA\A,; здесь г (или гАА ) имеет матричное представление с компо-
(г00' г01\	1 f t + z х + iy\
yriof riI'J ~ ~Д\х-гу t-z)'
Спинор 7Г связан с импульсом безмассовой частицы в том смысле, что внешнее произве¬
дение 7Г7Г (без свертки — см. § 14.3) описывает ее 4-импульс. Спинор со связан с моментом
импульса частицы в том смысле, что симметризованное произведение спиноров со и W опи¬
сывает антисамодуальную часть 6-момента импульса частицы (§§ 18.7, 19.2, 22.12, 32.2),
а симметризованное произведение спиноров со и 7г — ее самодуальную часть ^33,211 В от¬
личие от импульса, момент импульса зависит от выбора в пространстве-времени начала
координат О, поэтому иногда говорят о моменте импульса относительно точки О. Такая
что означает соА =
нентами

812
Глава 33
независимость от выбора начала в одном случае и зависимость в другом отражается в по¬
ведении епинорных частей 7г и и твистора Z при трансляциях. При перемещении начала
координат О в новую пространственно-временную точку Q с радиус-вектором q (q, как
и прежде, берется в матричной форме) спинорные части претерпевают следующее преобра¬
зование:*
7Г i—> 7Г И 04 из — iqrc.
Существует еще скалярная величина, не зависящая от выбора начала, которую можно по¬
строить из импульса и момента импульса, а именно спиралъность s. Оказывается, что
спирально сть равна половине твисторной нормы:
1 гу	/у а 	 1	rj	ту
2 ol ^	2
(заметим, что это есть просто вещественная часть величины й7 • 7г). Фактически твисто¬
ры дают более компактный формализм для описания безмассовых частиц по сравнению
с обычным 4-векторным/тензорным подходом (§ 22.12). Теперь у нас есть ясная физическая
картина ненулевого твистора (с точностью до фазового сдвига Z ь-► ег9Ъ) как классической
вращающейся безмассовой частицы** (сравните с рис. 33.6).
Мы пока не имеем достаточно ясной геометрической картины ненулевого тви¬
стора. Ее можно получить, построив комплексифицир о ванное пространство Минковско¬
го СМ (или его компактификацию СМ^), в котором пространственно-временные коор¬
динаты ж, у, г теперь считаются комплексными числами. Всегда имеется нетривиальное
двумерное геометрическое место комплексных точек пространства СМ^, инцидентных лю¬
бому твистору Za (с ненулевыми координатами); оно называется а-плоскостъю и явля¬
ется самодуалъным в том смысле, что касательная к нему 2-форма самодуальна (§32.2).
Эта а-плоскость представляет Za с точностью до коэффициента пропорциональности (см.
рис. 33.13). Аналогично дуальный твистор Wa определяет /5-плоскость, которая является
ан/тшеамодуальной комплексной 2-плоскостью в СМ^.
Пока это дает нам геометрическую картину твистора в комплексном пространстве-вре¬
мени. Можно ли получить «вещественную» картину, допускающую наглядное представле¬
ние? Вещественная часть структуры пространства СМ^ содержится в понятии комплекс¬
ного сопряжения (§ 18.1); эта операция меняет местами а- и /3-плоскости в соответствии
с тем фактом, что она меняет местами верхние и нижние индексы (т. е. твисторы и дуаль¬
ные твисторы), а также самодуальные и антисамодуальные объекты. На языке проективной
геометрии пространства FT комплексное сопряжение производит взаимную замену точек
э|с
и плоскостей, так как дуальный твистор определяет плоскость в FT. Это обстоятельство
позволяет представить ненулевой проективный твистор Za в терминах геометрии веще¬
ственного пространства-времени. Для этого прежде всего следует представить твистор Za
комплексно-сопряженным ему твистором Za, который, будучи дуальным твистором, ассо¬
циируется с комплексной плоскостью в FT. Эта плоскость определяется ее пересечением
с вещественным 3-мерным геометрическим местом FN. Это геометрическое место можно
считать задающим 3-параметрическое семейство световых лучей в пространстве М. Та¬
ким образом, это семейство световых лучей геометрически представляет (с точностью до
коэффициента пропорциональности) твистор Za (см. рис. 33.14).
Покажите, что при таком преобразовании сохраняются соотношение инцидентности между твистором
и пространственно-временной точкой, а также твисторная норма.
Объясните, почему имеется такая свобода в выборе фазы и почему для частицы с заданной спирально¬
стью s > 0 энергия частицы определяется положением точки в пространстве РТ+.
***
Покажите это.
Почему?

33.6. Геометрия твисторов как вращающихся безмассовых частиц
813
Рис. 33.13. Описание твисторов (в общем случае ненулевых) и дуальных твисторов в комплексном
пространстве-времени. Для любого твистора Z0" с ненулевыми компонентами всегда существует дву¬
мерное геометрическое место комплексных точек пространства СМ#, инцидентных этому твистору,
называемое а-илоскостью, которая всюду самодуальна. Для любого дуального твистора Wa с нену¬
левыми компонентами инцидентные ему точки пространства СМ# всегда образуют комплексную
2-плоскость, называемую /3-плоскостью, которая антисамодуальна. Вещественными точками этого
геометрического места являются только нулевые твисторы или нулевые дуальные твисторы, так что
эти вещественные точки составляют световой луч в соответствии с рис. 33.12
Конгруэнция Робинсона РТ
Рис. 33.14. Можно получить «вещественное» представление ненулевого твистора перейдя снача¬
ла к комплексно-сопряженной величине Za и определив таким образом комплексную проективную
   •
плоскость в пространстве РТ. Эта плоскость определяется ее пересечением с вещественным 3-мер-
ным геометрическим местом PN, которое задает 3-параметрическое семейство световых лучей в СМ#,
называемое конгруэнцией Робинсона
Световые лучи закручиваются сложным образом, однако можно получить впечатляю-
о
щую картину этой конфигурации. Рассмотрим один момент времени Е (т. е. сечение про¬
странства-времени М обычным евклидовым 3-пространством, соответствующее моменту
«сейчас») Любой световой луч в М (точечная частица, движущаяся в заданном направлении
со скоростью света) представляется в Е3 некоторой точкой с присоединенной к ней «стрел¬
кой», определяющей направление движения. Чтобы представить одиночный твистор Z, мы
должны изобразить 3-параметрическое семейство таких световых лучей — так называемую
конгруэнцию Робинсона. На рис. 33.15 показана система из ориентированных окружностей
(и одной прямой линии), заполняющих все обычное 3-пространство Е3. В каждой точ-
о
ке пространства Е будет находиться одна частица из нашего семейства, движущаяся (со
скоростью света) в направлении, показанном ориентированной касательной к окружности,
проходящей через эту точку. Примечательно, что с течением времени вся эта конфигурация
просто перемещается как целое со скоростью света в (отрицательном) направлении одной
прямой линии на этой картине, и это перемещение представляет движение вращающейся
безмассовой частицы, описываемой твистором. Такая конфигурация с окружностями — это,

814
Глава 33
Направление
движения
Рис. 33.15. Пространственная картина, представляющая «моментальный снимок» конгруэнции Робин¬
сона. (Стереографически спроектированные клиффордовы параллели S3 (рис. 8.7 а и 15.8), которые
представляют 3-параметрическое семейство окружностей (с одной прямой линией), заполняющих все
пространство Е3.) Представлена частица в каждой точке пространства Е3, движущаяся по прямой
линии со скоростью света в направлении (ориентированной) окружности, на которой она находится.
Вся конфигурация распространяется со скоростью света в (отрицательном) направлении прямой ли¬
нии в будущее. Это представляет движение и момент импульса вращающейся безмассовой частицы,
описываемой твистором Za
по существу, стереографическая проекция (§8.3, рис. 8.7 а) на обычное евклидово 3-про¬
странство конфигурации клиффордовых параллелей на S3 (§ 15.4).
Не следует понимать эти «световые лучи» как физические объекты, они всего лишь
представляют геометрическую реализацию (проективного) твистора. Показанная конфигу¬
рация изображает структуру момента импульса (классической) вращающейся безмассовой
частицыJ33'^22^ Это определенно нелокальная структура. На рис. 33.15 имеется самая малень¬
кая окружность, радиус которой равен радиусу спина, деленному на энергию частицы. Центр
этой окружности, грубо говоря, представляет «положение» вращающейся частицы (однако
историю этого центра нельзя рассматривать как световой луч, представляющий историю
безмассовой частицы, потому что она не ведет себя должным образом при преобразованиях
Лоренца)"". Именно этой конфигурации обязано название «твистор»^33*23^
33.7.	Квантовая теория твисторов
Мы представили геометрию теории твисторов в плоском пространстве. Однако у неко-
ЧУ	КУ
торых читателей может возникнуть законный вопрос: чем такая картина, при всей ее гео¬
метрической привлекательности, может помочь нам углубиться в физику? Что может сказать
теория твисторов насчет объединения структуры пространства-времени с принципами кван¬
товой механики? До сих пор мы видели перед собой лишь некоторые хитроумные способы
геометрического и алгебраического описания безмассовых частиц, однако здесь пока не
играли никакой роли ни принципы квантовой механики, ни идеи общей теории относитель¬
ности. Мне следовало бы подумать об этом!
Вернемся к основной идее теории твисторов. Она состоит в том, чтобы рассматривать
все пространственно-временные понятия как вторичные по отношению к соответствующим
понятиям для твисторного пространства Т. Последнее, будучи полностью комплексным про¬
странством, позволяет использовать магию комплексных чисел, применяя способы, которые
нелегко отыскать, оставаясь в рамках стандартного пространства-времени. Поэтому вместо
Найдите этот центр (в координатах, введенных в § 33.5) и покажите, как он преобразуется под действием
лоренцева преобразования скорости общего вида.

33.7. Квантовая теория твисторов
815
того чтобы проводить описание в вещественных пространственно-временных координатах,
мы используем комплексные твисторные переменные Za. Теперь твисторные переменные
оказываются смесью координатных и импульсных переменных, и возникает вопрос: что
приходит на смену стандартному правилу квантования (§ 21.2)
ра «-> ih ^
дха
*
(или ха	~ihd/дра)? Ответ таков: по аналогии с ха и ра, которые являются канонически
сопряженными переменными, что выражается в операторном перестановочном соотноше¬
нии ръха ~ харь = гН5%, в качестве канонически сопряженных операторов следует взять
твисторные переменные Za и Za:
ZaZp-ZpZa = hd^
при этом, как и в случае компонент координат и импульсов, взятых по отдельности, ком¬
поненты твисторов Za_n Z_a, взятых по отдельности, коммутируют между собой: ZaZ& —
- Z^Za = О,	ZaZ0- Z0Za	= 0.
Несколько отвлекаясь, можно заметить, что квантовая некоммутативность твисто¬
ров Za и Za приводит к некоторым любопытным вопросам относительно той «геометрии»,
которая получится, если более серьезно отнестись к тому факту, что фундаментальные «коор¬
динаты» в квантовом твисторном пространстве могут быть подобными некоммутирующими
объектами. В классическом варианте, рассматривая структуру твисторного пространства Т
как вещественное 8-многообразие, мы могли считать Za п Za независимыми коммутирую¬
щими переменными (см. § ЮЛ). Но в квантовой картине твисторы Za и Za не коммутируют.
Попытка использовать такую пару Za и Za, как если бы это были независимые переменные,
завела бы нас в область некоммутативной геометрии, о которой упоминалось в § 33.1. Было
бы интересно проследить эту линию дальше, но мне не известно, чтобы кто-нибудь сделал
это.
Напомним, что в обычной волновой функции частицы V?(x)> записанной в координатном
представлении, импульсные переменные не появляются, вместо этого импульс, как указано
выше, выражается через оператор д/дха. Каков твисторный аналог этого? Мы, по-видимому,
должны потребовать, чтобы наша «твисторная волновая функция» f(Za) была «независи¬
ма от Za» и чтобы твистор Za выражался через оператор djdZa. Это действительно так,
но что на самом деле означает независимость функции / от Za? Формально такую «неза¬
висимость» можно выразить в виде соотношений df/dZa = 0, которые (как мы помним
из § 10.5) представляют собой условия Коши-Римана, из которых следует, что f(Za) есть
голоморфная функция от Za.
Это довольно замечательный факт. Твисторные волновые функции являются голоморф¬
ными объектами и потому тесно связаны с магическим миром комплексных чисел. Кванто¬
вая роль комплексно-сопряженных переменных Za состоит в том, что они появляются как
результат дифференцирования:
-Ту	Р-	д
Za ” ~hoz^'
это есть голоморфный оператор, так что голоморфность сохраняется на квантовом уровне
описания. Этот факт убеждает, что интерпретация твисторов в терминах импульса и мо¬
мента импульса безмассовой частицы согласуется с правилами коммутации твисторов, при
этом получаются правильные выражения для коммутаторов импульса и момента импульса
(§22.12), которые следует добавить к приведенным выше твисторным коммутаторам^33*24^.
Понятно ли, из общих свойств операторов гильбертова пространства, почему в коммутатор твисторов
целесообразно не вводить множитель г?

816
Глава 33
Особый интерес представляет спиральность s, рассматриваемая теперь как оператор,
собственными значениями которого служат всевозможные полуцелые значения (..., —2h,
о	11	Ч
— 2^	“2^’	2^’	2^	^	Д0ПУстимые Д®1 безмассовой частицы. Следует осо¬
бо отметить, что при надлежащем учете некоммутативности оператор спиральности прини¬
мает вид* [33*251
\(ZaZa + ZaZa) ^-hi 2 +za
4У “ 1 ““	'	2	'	1	BZ
д
а
Оператор
Г = Z
а
a
а
называется оператором однородности Эйлера. (Вспомним нашего старого друга Леонарда
Эйлера, с которым мы встречались в главах 5, 6, 7 и особенно 9.) Как показал Эйлер, опера¬
тор Т обладает тем замечательным свойством, что его собственные функции однородны, при
этом собственным значением служит степень однородности. Другими словами, уравнение
Tf =
где и — некоторое число, является условием, при котором имеет место свойство однородно-
сти
f(XZa) = Xuf(Za).
Отсюда следует, что твисторная волновая функция для безмассовой частицы с определен¬
ным значением спиральности S (так что sf — hSj\ где s — оператор спиральности, S —
собственное значение) должна быть однородной функцией степени —2S — 2, притом голо¬
морфной
Так, в частности, твисторная волновая функция фотона (5 = ±1) будет суммой двух
частей, одна из которых, однородная степени 0, описывает левополяризованную компоненту
(S = —1), а другая, степени —4, — правополяризованную компоненту (S = 1). Нейтрино,
рассматриваемое как безмассовая частица, имеет волновую функцию со степенью однород-
1
ности —1 (поскольку спиральность равна — тогда как волновая функция (безмассового)
антинейтрино будет иметь степень однородности —3. Волновая функция безмассовой ска¬
лярной частицы имеет степень однородности —2. Для нашего обсуждения наиболее важен
случай гравитона, который мы предполагаем безмассовой частицей со спином 2 на плос¬
ком фоне пространства Минковского (S = ±2). Его левополяризованной части (S — —2)
соответствует твисторная волновая функция, однородная степени 2, а правополяризованной
части (S ~ 2) — твисторная волновая функция, однородная степени —6.
Такая поразительная асимметрия иллюстрирует существенно киральную природу те¬
ории твисторов. Вскоре мы увидим, что эта асимметрия вырисовывается особенно четко,
когда мы пытаемся подвести общую теорию относительности «под твисторный зонтик».
Пока попытаемся понять, как следует интерпретировать твисторные (линейные) волновые
функции. В этом случае асимметрия не вызывает проблем. Имеется, однако, существенная
тонкость в интерпретации нашей волновой функции f(Z°i), называемой обычно твисторной
функцией. Этим мы займемся в следующем разделе.
33.8.	Твисторное описание безмассовых полей
•
*
Чтобы получить пространственно-временное представление волновой функции сво
бодной безмассовой частицы с произвольным спином, уравнение Шредингера необходи
**
***
Проверьте эквивалентность этих двух выражений для s.
Можете ли вы доказать это?
Откуда берется это значение степени однородности?

33.8. ТВИСТОРНОЕ ОПИСАНИЕ БЕЗМАССОВЫХ ПОЛЕЙ
817
мо преобразовать в некоторое уравнение, называемое уравнением безмассового свободного
поляt33-26 . Примером может служить уравнение для безмассового нейтрино Дирака-Вей¬
ля со спином ~ (§25.3). Здесь не место входить в подробности, однако само уравнение
имеет достаточно простой вид, и его можно записать, используя 2-спинорный формализм
(§§22.8, 25.2). При отрицательной спиральности S = — мы имеем величину Фав...в,
при положительной спиральности — аналогичную величину со штрихованными индекса¬
ми 'Фа'В'...£>'• Каждая из них полностью симметрична по всем п индексам и имеет положи¬
тельную частоту, удовлетворяя соответствующим уравнениям
AA'l	п	уг7АА'
V"" ФАВ...В = О, V— фА'В'...П' = О,
где \/АА' есть просто 2-спинорный аналог обычного оператора градиента Va (записанного
с поднятым индексом; см. § 14.3) . Для спина 0 мы имеем просто волновое уравнение Оф =
— О, где □ — обычный оператор Даламбера, введенный в §24.5. Удобная 2-спинорная
запись этих уравнений выявляет некоторые тонкости. При п = 2 (спин 1) эти два урав¬
нения превращаются просто в свободные уравнения Максвелла соответственно для случая
антисамодуальности и самодуальности**. При п = 4 получается уравнение Эйнштейна для
слабого поля, расщепленное на антисамодуальную и самодуальную части, при этом кривиз¬
на рассматривается как бесконечно малое возмущение плоского пространства М^33,27!
Каковы будут соответствующие уравнения для твисторных функций? Замечательным
образом оказывается^33-28^, что существует явное выражение в виде контурного интеграла
(§ 7.2), которое автоматически дает общее решение положительной частоты для вышеуказан¬
ных уравнений безмассовых свободных полей исходя из твисторной функции f(Za). Факти¬
чески это выражение остается справедливым и без требования положительной частоты, хотя,
как мы увидим в § 33.10, в твисторном формализме выполнение этого требования легко обес¬
печивается. Здесь мы не будем углубляться во все детали, но основная идея состоит в том,
что в случае положительной спиральности функция f(Za) сначала п раз умножается на тт
(§ 33.6), что дает п штрихованных индексов; при отрицательной спиральности сначала п раз
применяется операция д/ди>, что дает и нештрихованных спинорных индексов. Затем произ¬
водится умножение на 2-форму т — di\г<у Admy и интегрирование по подходящему 2-мерному
контуру, при этом вначале используется соотношение инцидентности ш = гг7г, чтобы ис¬
ключить величину и, выразив ее через 7Г и г.-Интегрирование устраняет 7г, и мы получаем в
результате индексированную величину ф... в любой выбранной пространственно-временной
точке R (так что ф,„ зависит только от г). Контур должен лежать внутри геометрическо¬
го места ш = irix (для каждого заданного г), т. е. на линии R (ее непроективном Г33-29]
варианте) в пространстве М, представляющей событие R (см. рис. 33.16).
Условие положительной частоты обеспечивается требованием, чтобы контурный инте¬
грал сохранял смысл, когда линия R полностью попадает в твисторную область РТ+. Линии
в РТ, как мы видели в §33.6, соответствуют «комплексным пространственно-временным
точкам», а линии, полностью лежащие в подобласти РТ+, соответствуют точкам подобла¬
сти М+ пространства СМ, называемой трубой будущего^33,30^. Мы вернемся к этому вопро¬
су в § 33.10. Безмассовые поля с заданной спиральностью, например, плоскополяризованный
фотон, который есть сумма лево- и правополяризованной частей, также можно описывать
Выпишите эти уравнения в явном виде для спиральности — ^п, используя запись фг — фоо...ои...г
с п — г нулями и г единицами; \/АА> получается из Va, подобно тому как величина гАА получается описанным
выше способом из обычных координат Минковского t, х, у, г.
Попробуйте доказать это для фоо — С\ — гС<2, ^01 == ~К?3> фц — —С\ — 1С2, где С = 2Е — 2гВ
(см. § 19.2); для Фа*в' выполняются аналогичные соотношения.

818
Глава 33
i
Рис. 33.16. Основной твисторный контурный интеграл. Твисторная функция / (для спиральности -п),
однородная степени —п — 2,п раз умножается на 7Г (при положительном значении п) или — п раз под¬
вергается действию оператора д/дш (при отрицательном п), что дает индексы, а затем умножается на
2-форму г = dnQf А . Для любой выбранной пространственно-временной точки R с радиус-векто¬
ром г контурный интеграл вычисляется затем по области твисторного пространства R, определяемой
соотношением инцидентности иэ — гт'к. Интегрирование устраняет зависимость от 7Г, и мы получа¬
ем решение уравнений безмассового поля. В случае, изображенном на рисунке, точка R выбрана в
верхней половине твисторного пространства РТ+ (или Т+), а функция / голоморфна в пересечении
открытых множеств Ы\ и Ы2, которые вместе покрывают все пространство РТ+ (или Т+)
в рамках этой схемы, где твисторные функции для двух различных спиральностей просто
складываются.
Само существование такого выражения представляется мне чем-то магическим. Урав¬
нения безмассового поля исчезают из твисторного формализма, давая взамен «чистую гомо-
морфность». Если рассмотреть это выражение более внимательно, обнаруживается важная
тонкость в интерпретации твисторной функции, связанная с расщеплением безмассовых
частей на положительно- и отрицательно-частотные части (§33.10). Эта тонкость прояв¬
ляется также в поведении твисторных функций и в появлении искривленных твисторных
пространств. В чем же состоит эта тонкость? Она в том, что твисторные функции следует
рассматривать не как «функции» в обычном смысле, а как элементы голоморфной когомо¬
логии пучков^33,311.
33.9.	Твисторная когомология пучков
Что такое когомология пучков? Эта идея имеет сложное математическое выражение, но
на самом деле она вполне естественна. Здесь мы будем иметь дело только с так называемой
первой когомологией пучков. Это понятие, вероятно, проще всего себе представить, выяс¬
няя, каким образом можно построить многообразие из ряда координатных лоскутов, как
это делалось в §§ 10.2, 12.2 и изображено на рис. 12.5 а. Для каждого перекрытия пары ло¬
скутов вводится функция перехода (предполагается склеивание лоскутов). Напомним (§12.2,
рис. 12.5 а), что в области тройных перекрытий функции перехода должны удовлетворять
некоторым условиям согласования.
Рассмотрим построенное таким путем многообразие, но будем предполагать, что функ¬
ции перехода отличаются от единицы (тождественного преобразования) лишь на бесконечно
малую величину (см. рис. 33.17). Такой бесконечно малый сдвиг между одним лоскутом Ui
и другим лоскутом Uj описывается векторным полем Fij на той части лоскута Ui, ко¬
торая перекрывается с Uj. Это поле описывает бесконечно малое смещение лоскута Ui
относительно Uj. Точно так же можно считать, что лоскут U3 смещается относительно Ui,
но в противоположном направлении. Это смещение описывается векторным полем Fji на той
части лоскута Uj, которая перекрывается с Ui, так что для этого перекрытия имеет место

33.9. Твисторная когомология пучков
819
Рис. 33.17. Вспомните (см. рис. 12.5 а), как строит¬
ся многообразие из нескольких координатных лоскутов.
(На каждом перекрытии между парой лоскутов определя¬
ется «функция перехода», при этом предполагается «скле¬
ивание» лоскутов.) Здесь рассматриваются функции пере-
г
хода, отличающиеся от единицы (тождественного преоб¬
разования) лишь на бесконечно малую величину, и для
каждого перекрытия лоскутов Ui, U3 вводится векторное
поле Fij, указывающее, на сколько каждый лоскут дол¬
жен «сдвинуться» по отношению к другим, с которыми
он перекрывается. (Лоскуты представляют собой откры¬
тые множества Ui, U2, U-з, ... в плоском координатном
пространстве.)
соотношение
ip ■ • — — р
17 Зг	*	гз
(см. рис. 33.18 а). Для тройного перекрытия между лоскутами Uu	Uk (рис. 33.18 б) должно
выполняться условие согласования
*
Fij + Fji = Fik
Существуют также «тривиальные» бесконечно малые деформации, возникающие про¬
сто из-за (бесконечно малого) изменения координатной системы на каждом лоскуте. Можно
считать, что они создаются на каждом лоскуте Ы{ некоторым векторным полем Щ, которое
просто «приподымает» весь этот лоскут как целое над самим собой. Это дает нам семейство
«тривиальных» полей Fij вида
Fij = Hi — Hj
на перекрытиях между парами лоскутов, которые не изменяют исходного многообразия
(рис. 33.18 в).
Эти идеи устанавливают правила первой когомологии пучков I33-32!. Нам, однако, не
обязательно иметь дело с векторными полями Fij. С тем же успехом можно пользоваться
обычными функциями . Достаточно потребовать, чтобы каждая функция fij, определен¬
ная на пересечении Uj с 1А%, удовлетворяла условию fij — —fji, условию fij -f fji —
для каждого тройного перекрытия и чтобы полный набор {fij} рассматривался как экви¬
валентный другому такому набору {gtj}9 если каждый член набора соответствующих раз¬
ностей {fij — gij} имел «тривиальный» вид {hi — hj}. Можно сказать, что функции fij
представляют собой приведенные по модулю величины вида {hi — hj} в том же смысле,
в каком термин «приведение по модулю» применялся в § 16.1 (см. также понятие «класса
эквивалентности», введенное в предисловии): Фактически тот класс функций, с которым
имеют дело в теории когомологий {fij или /г^), может быть самого общего вида. В тео¬
рии твисторов обычно имеют дело с голоморфными функциями. Это приводит к понятию
«голоморфной когомологии пучков».
Идея такой когомологии применяется, в частности, к твисторным функциям. В самом
деле, мы можем рассматривать «твисторную функцию», в общем случае, не просто как од¬
ну голоморфную функцию /, но как набор голоморфных функций {fij}, в котором каждая
отдельная функция ftJ определяется на перекрытии между парой открытых множеств Ыг
и Uj, при этом fji = — fij, на тройных перекрытиях выполняется условие fij -f fji — Д&,
и весь набор открытых множеств {Ui} покрывает всю рассматриваемую область твисторно¬
го пространства Q. Элемент первой когомологии в области Q (по отношению к покрываю¬
щему набору {Ui}) представляется этим набором {fij}, приведенным по модулю величин
Покажите, что антисимметрия Fij входит в число условий согласования при тройном перекрытии.

820
Глава 33
в)
Рис. 33.18. Векторные поля Fij должны удовлетворять определенным условиям, а) На пересечении
лоскутов Uj и Ыг мы имеем Fji = — Fij. Это показано как движение Ы\ над 24, описываемое век¬
тором jF*i2 на Ы\. Но то же самое относительное перемещение получается при обратном движении
на U2. б) Иллюстрируется условие для тройного перекрытия Fij + Fji = Fik. В области тройного
пересечения лоскутов Ы\,Ыч и Ыз движение Ы\ над 24, описываемое вектором *12, равно сумме
движений Fi3 (24 над Ыз) и *32 (Ыз над 24). в) Если все лоскуты по отдельности сдвигаются как
целое, это ничего не меняет (за исключением изменения координат на каждом лоскуте). Это означает,
что общий сдвиг Fij = Hi — Hj не играет роли и его можно не учитывать
вида hi — hj, с hi, определенным на Ui. Набор функций fij не следует понимать как эле¬
мент когомологии, — он дает лишь способ представления этого таинственного «элемента».
Мы называем функции fij представлениями этого элемента первой когомологии.
Чтобы дать строгое определение когомологии, необходимо рассматривать переход к пре¬
делу все более мелких покрытий области Q, К счастью, существуют теоремы, утверждаю¬
щие, что в случае голоморфных когомологий пучков мы можем остановиться, если множе¬
ства Ui относятся к достаточно простому типу множеств Штейна^*33^. (На любом мно¬
жестве Штейна первая когомология пучков всегда обращается в нуль.) Таким образом, если
ограничиться покрытиями, для которых каждое множество Ui является множеством Штей¬
на, нам не придется произносить слова «по отношению к покрывающему набору {Ui}»,
когда мы имеем дело с элементом когомологии, определенным на Q. Понятие когомологии
не зависит от выбора конкретного покрывающего множества Штейна. Элемент когомоло¬
гии — это объект, определенный на Q, который оказывается одним и тем же независимо
от используемого покрытия !3334!. Этот замечательный факт есть часть магии (голоморфной)
когомологии пучков!
Как всё это применить к твисторным функциям и контурным интегралам, рассмот¬
ренным в §33.8? Наиболее простая ситуация возникает, когда имеются всего два лоску¬
та U\ и 24, которые вместе покрывают рассматриваемую область твисторного пространства.
Тогда приходится рассматривать всего одну функцию, и это есть «твисторная функция»
из § 33.8: f(Za) = /12 — —/21- Согласно приведенным правилам когомологии пучков, мож¬
но сказать, что функция f(Za) эквивалентна функции g(Za), если разность этих функций
тривиальна в указанном выше смысле, т. е. если
/ - g = hi- h2,
где голоморфная функция hi глобально определена на 24, а функция h2 глобально опре¬
делена на U2, Нетрудно показать, что контурный интеграл, примененный к /, совпадает

33.9. Твисторная КОГОМОЛОГИЯ ПУЧКОВ
821
с таковым, примененным к д, коль скоро эти функции эк¬
вивалентны в указанном емысле. Иногда, однако, приходится
рассматривать более сложные системы лоскутов. По существу,
приведенные выше «правила когомологии» для эквивалентно¬
сти между твисторными функциями оставляют в силе резуль¬
таты, получаемые с помощью контурных интегралов, но само
понятие контурного интеграла приходится обобщать, включая
в рассмотрение «ветвящиеся контурные интегралы», в которых
приходится по одной ветви на каждую область перекрытия.
Этот случай показан на рис. 33.19.[33-35]
Важной особенностью когомологии является ее суще¬
ственная нелокальность. Мы можем взять элемент когомоло¬
гии, определенный в некоторой области Q. Рассмотрим ограни¬
чение этого элемента некоторой меньшей областью Q\ содер¬
жащейся в Q. Нелокальность когомологии проявляется в том,
что для любой достаточно малой (открытой) подобласти Q' в Q
этот элемент, будучи ограничен в Q', с необходимостью исче¬
зает в том смысле, что при заданной функции fij в Q' в этой
подобласти всегда найдутся такие функции /г, что fij = }ц — hd.
Такая нелокальность твисторных функций означает, что не следует придавать большого
смысла значению, принимаемому функцией fij в данной точке. В самом деле, можно огра¬
ничиться достаточно малой открытой областью, окружающей эту точку, и обнаружить, что
данный элемент когомологии полностью исчезает (см. рис. 33.20). Эта нелокальность, про¬
являемая твисторными функциями (рассматриваемыми как элементы первой когомологии),
мучительно напоминает нелокальные черты ЭПР-эффектов и квантового перепутывания
(§23.10). На мой взгляд, здесь спрятано нечто важное, что когда-нибудь сможет придать
смысл загадочным нелокальным ЭПР-явлениям, но это «нечто», если оно существует, еще
должно проявиться в полной мере.
Мы должны рассматривать такой «элемент когомологии» как некоторый «объект», опре¬
деленный в пространстве Q, который во всем похож на функцию, определенную в Q, но
обладает существенной не локальностью. Примером «объекта» такого рода может служить
полное (комплексное) векторное расслоение над Q, описанное в §§15.2, 15.5. Напомним,
что, по определению расслоения, его часть, лежащая над достаточно малой областью ба-
Рис. 33.19. «Ветвящийся кон¬
тур» (на сфере Римана), при¬
менимый для пространствен¬
но-временной оценки тви¬
сторных функций, покрытия
которых состоят из более чем
двух множеств
Голоморфный элемент 1-й когомологии ^±0
Рис. 33.20. Элемент когомологии всегда можно заключить в меньшую область. И если эта область
достаточно мала, то этот элемент всегда исчезает. Это иллюстрирует нелокальность когомологии

822
Глава 33
зисного пространства (в данном случае Q), «тривиальна» в том смысле, что она является
(топологическим) произведением (см. § 15.2 и рис. 15.3). Это пример того факта, что при
ограничении элемента первой когомологии некоторой достаточно малой областью он так¬
же становится «тривиальным», т. е. исчезает. Таким образом, «информация», содержащаяся
в элементе когомологии, имеет принципиально нелокальный характер.
Возможно, имеет смысл привести элементарный при¬
мер, наглядно иллюстрирующий эту особенность когомоло¬
гии, хотя и для очень простого случая. На рис. 33.21 изоб¬
ражен «невозможный объект», так называемый трибар!33 36!.
Очевидно, что такой «3-мерный объект» не может существо¬
вать в обычном евклидовом пространстве. Но локально рису¬
нок не содержит ничего невозможного. Невозможность здесь
является нелокальной и исчезает, если рассматривать доста¬
точно малую область рисунка. Фактически понятие «невоз¬
можности» такого рисунка можно представить в виде неко¬
торого элемента когомологии.*,[зз.37] зТ0? однако? довольно
ПрОСТОЙ Пример КОГОМОЛОГИИ, В КОТОРОМ фуНКЦИЯМИ {fij}
служат постоянные величины.
Здесь я лишь слегка коснулся некоторых основных идей
когомологии пучков. Эти идеи находят в математике множе¬
ство приложений, причем не все из них связаны с голоморф¬
ностью. В теории твисторов используются в основном пучки,
описываемые на языке голоморфных функций, и в этом част¬
но малой ооласти рисунка	ном слУчае теории когомологий свойственна особая магия.
(Грубо говоря, термин «пучок» относится к типу функций,
с которыми приходится иметь дело, однако на самом деле
понятие пучка применяется не только к обычным функциям, но и гораздо шире!33,38!.) Кого¬
мология находит много других применений, в частности, она играет важную роль в изучении
пространств Калаби-Яу, которые встречаются, например, в теории струн (§31.14). Имеется
несколько совершенно разных способов определения элементов когомологии пучков, ко¬
торые, как можно показать, математически эквивалентны, несмотря на внешне различную
форму!33 391 На мой взгляд, когомология пучков — это отличный пример платоновской идеи
(§ 1.3), согласно которой она, подобно самой системе комплексных чисел С, «живет соб¬
ственной жизнью» независимо от какого-либо конкретного способа ее представления.
Рис. 33.21. Изображение «невоз¬
можного объекта» («трибара»).
В локальном отношении ни¬
чего невозможного здесь нет.
«Невозможность» определяется
элементом когомологии, кото¬
рый исчезает в любой достаточ-
33.10.	Твисторы и расщепление на положительные и отрицательные
частоты
Как включить в теорию твисторов условие положительной частоты, которое играет
важную роль в квантовой теории поля? Вспомним (§§9.2, 9.3), как разделение сферы Ри¬
мана S2 на южное и северное полушария S" и S+ приводило к расщеплению функции,
определенной на экваторе S1, на положительно-частотную и отрицательно-частотную ча¬
сти (см. рис. 33.22а). Проективное твисторное пространство делает нечто подобное, но
глобальным образом, действуя непосредственно на безмассовые поля во всей их полноте.
Это достигается благодаря тесной аналогии между сферой Римана и проективным твистор-
ным пространством FT, при этом аналогом функции на сфере Римана S2 служит элемент
первой когомологии на РТ. Аналогом экватора S1 будет пространство PN, и можно заме-
Попробуйте разделить этот рисунок на ряд перекрывающихся рисунков	каждый	из	которых
в отдельности представляет согласованную 3-мерную структуру а затем, взяв логарифм расстояния этой 3-мерной
структуры от глаза наблюдателя, вычислить {fij}.

33 Л 0. ТВИСТОРЫ И РАСЩЕПЛЕНИЕ НА ПОЛОЖИТЕЛЬНЫЕ И ОТРИЦАТЕЛЬНЫЕ ЧАСТОТЫ
823
тить, что PN делит пространство РТ (или, что то же самое, СР3) на две половины РТ+
и РТ~“ точно таким же образом, каким S1 делит S2 (или СР1) соответственноf33'40^ на две
полусферы S“ и S+ (рис. 33.226).
г
sCcp1
Положительно-частотная
1 -я когомология
РТ^СР
з
*
У
Отрицательно-частотная
1-я когомология
а)
б)
Рис. 33.22. Аналогия между сферой Римана S2(= СР1) и проективным твисторным простран¬
ством РТ(= СР3). а) Комплексная функция, (т. е. «элемент нулевой когомологии»), определенная
на вещественной оси Ж пространства S2, расщепляется на положительно-частотную часть, голоморф¬
но продолжаемую в изображенное здесь северное полушарие S~, и отрицательно-частотную часть,
продолжаемую в южное полушарие SC (Сфера Римана изображена здесь так, что Ж есть ее экватор,
но точка —г находится на северном полюсе, а г — на южном; сравните с рис. 8.7 и 9.10 в § 9.5.) б) Эле¬
мент 1-й когомологии, определенный на PN (и представляющий безмассовое поле), расщепляется на
положительно-частотную часть, голоморфно продолжаемую в верхнюю половину РТ+ проективного
твисторного пространства, и отрицательно-частотную часть, продолжаемую в нижнюю половину РТ“
Более точно, аналогом обычной (комплексной) функции, определенной на S1, или на S”,
или на S+, является элемент первой когомологии, определенный соответственно на PN, или
на РТ+, или на РТ“. Безмассовые поля на М (точнее, на М^) представляются элементами
первой когомологии на PN. Каждый из них можно представить (по существу, однознач¬
ным образом) в виде суммы элемента, продолжаемого в РТ+, и элемента, продолжаемого
V	.
в РТ~. Первое слагаемое описывает положительно-частотное безмассовое поле, второе —
отрицательно-частотное безмассовое поле^33,411 На языке пространственно-временных тер¬
минов положительно-частотная часть поля при продолжении образует трубу будущего, кото-
+ пространства СМ^, состоящая из точек,
представляемых в твиеторном пространстве проективными линиями в РТ+. В простран¬
стве СМ+ таковыми будут (комплексные) точки, радиус-векторы которых имеют времени-
подобную мнимую часть, направленную в прошлое .
Такая аналогия между пространством РТ и сферой Римана указывает возможный
способ связать идеи теории твисторов с некоторыми идеями теории струн. Напомним
(§§ 31.5, 31.13), что в теории струн римановы поверхности используются для представления
«струнных историй». Сфера Римана (СР1) является простейшей из таких поверхностей, од¬
нако для представления струнных историй более общего вида привлекаются поверхности с
различным числом «ручек» (римановы поверхности более высокого рода — см. § 8.4). Поми¬
мо ручек, эти римановы поверхности могут содержать также «отверстия» (с границами S1);
рой, как мы помним (§33.8), является область
Покажите это. Продемонстрируйте исходя из уравнения инцидентности, что комплексный радиус-
вектор га точки R пространства СМ представляется проективной линией в пространстве РТ+ в том и только
том случае, если мнимая часть вектора та времениподобна и направлена в прошлое.

824
Глава 33
см. рис. 31.5. По аналогии можно рассмотреть[эз.4^] 0б0бщения пространства FT, обла¬
дающие «ручками», а также «отверстиями» (границы которых представляют собой копии
пространства PN). Их называют «крендельными» твисторными пространствами, и можно
построить на их основе вариант квантовой теории поля (см. рис. 33.23). Пока статус этих
идей не вполне ясен.
а)
Рис. 33.23. а) Конформная теория поля (модель типа теории струн) на основе обобщений сферы Ри¬
мана на римановы поверхности более высокого рода, которые могут иметь «отверстия» конечного
размера, а также ручки (см. рис. 31.5; отверстия представляют собой места, откуда поступает внешняя
информация), б) Твисторный вариант, использующий обобщения пространства РТ, обладающие «руч¬
ками» по аналогии с римановыми поверхностями, а также «отверстиями», границами которых служат
копии пространства FN («крендельные» твисторные пространства)
т	I
В историческом отношении требование положительной частоты (и то свойство, что PN
делит РТ на две половины) послужило основным побудительным мотивом при первона¬
чальной формулировке теории твисторов в 1963 году, за 12 с лишним лет до того, как было
обнаружено, что безмассовые поля допускают твисторное описание как голоморфная пер¬
вая когомология пучков^33 43!. Интересно, что здесь мы снова имеем свойство, специфичное
для пространственно-временного четырехмерия с лоренцевой сигнатурой. Примечательно
также, что в этом аспекте твисторной теории играют основную роль не обычные функции
(которые являются элементами «нулевой» когомологии), а элементы первой когомологии
(или даже второй или более высокой когомологии). Понятие когомологии высоких порядков
также существует (и играет определенную роль в теории твистоов), но в первой когомоло¬
гии есть нечто уникальное, фундаментальное для теории твисторов, поскольку именно такие
величины играют основную роль в формировании деформаций твисторного пространства.
Этим мы займемся в следующем разделе.
33.11.	Нелинейный гравитон
Элементы когомологии (твисторные функции) мы пока рассматривали как полностью
«пассивные» в том смысле, что они просто «окрашивают» твисторное пространство. Это со¬
ответствует тому факту, что они описывают поля, которые существуют в пространстве-вре¬
мени, не влияя на другие поля. Чтобы увидеть возможность активного влияния, представим
себе, что «краска», нанесенная на твисторное пространство, «высыхает», и пространство
деформируется (рис. 33.24). Чтобы понять, что при этом происходит, будем считать нашу
прежде пассивную твисторную функцию fij связанной соответствующим образом с век¬
торным полем Fij. Сдвигая один лоскут над другим в направлении векторных полей на
бесконечно малую величину, начинаем «сушить краску», в результате чего получается тви¬
сторное пространство с бесконечно малым искривлением. Можно представить себе, что эта
деформация «потенцируется» (§ 14.6) с возникновением конечной деформации твисторного
пространства (краска полностью высохла!).

33Л1. Нелинейный гравитон
825
а)
б)
Рис. 33.24. Элемент векторного поля первой когомологии «пассивен» (т. е. просто «окрашивает» про¬
странство). Чтобы он оказывал активное влияние, представим себе процесс «высыхания краски» как
результат потенцирования векторного поля на каждом перекрытии. Это приводит к конечному «сдвигу»
одного лоскута над другим с возникновением конечной деформации или «искривленного простран¬
ства»
Первой ситуацией, к которой эта процедура была успешно применена, стал случай
антисамодуальной гравитации^33,441. В случае слабого (бесконечно малого) поля мы име¬
ем безмассовое поле со спиральностью S — —2, так что, используя приведенную выше
формулу —25 — 2 для степени однородности, получаем твисторную функцию /(= fij)
со степенью однородности 2. Здесь мы для простоты предположим, что имеются всего два
лоскута Ы\ и U2, каждый из которых представляет часть плоского твисторного простран¬
ства Т со стандартными координатами из § 33.5. Требуемое векторное поле F, построенное
с использованием функции /, имеет вид
р = ®LJL _ д/ д
дш° дш1 ди>°
Заметим, что степень однородности 2 функции / точно компенсирует степень однородности
двух дифференциальных операторов, так что результирующий оператор, действующий на
проективное твисторное пространство, имеет нулевую степень однородности .
Предположим теперь, что мы потенцируем этот бесконечно малый сдвиг одного ло¬
скута над другим (см. рис. 33.25). Мы получим (локально) искривленное твисторное про¬
странство Т. Отсутствие в вышеприведенном соотношении производных по 7г означает,
что твистор на одном лоскуте должен иметь такую же 7г-часть, что и согласованный с ним
твистор на соседнем лоскуте. Отсюда следует, что операция «проектирования» спинора 7г
из лоскутного пространства Т имеет согласованный характер во всем этом пространстве.
Другими словами, имеет место глобальная проекция пространства Т на пространство спи¬
норов тг. Проигнорируем (а лучше удалим) «нулевые элементы» пространств Т и тт. Тогда
мы обнаружим, что Т представляет собой расслоение над пространством 7г (см. § 15.2). [33-4°]
Каждый слой (отражение данного пространства 7г, т. е. та часть пространства Т, которая ле¬
жит «над» 7г) оказывается комплексным 2-многообразием с симплектической структурой,
как и само пространство тг (см. § 14.8 — в данном случае это означает, что мера площади
определяется на 2-многообразии); этот факт обеспечивается указанным выше специфиче¬
ским выбором лоскутов.
Как от этого искривленного твисторного пространства вернуться к некоторому поня¬
тию «пространства-времени»? Ответ состоит в том, что каждая «пространственно-временная
точка» однозначно соответствует голоморфному сечению расслоения Т. (Понятие голоморф¬
ного сечения было введено в § 15.5; в данном случае это есть отображение ^-пространства
обратно в Т.) Почему это есть разумное определение? В случае плоского пространства Т
это равносильно представлению пространственно-временной точки R (возможно, комплекс¬
ной) с помощью отображения, которое переводит 7Г в Z — (ггтт, тг). В терминах плоского
* Почему нулевая степень однородности означает, что мы имеем векторное поле на некоторой области
в пространстве РТ? (Подсказка: что представляет собой коммутатор величин F и Т (§33.7)?)

826
Глава 33
Т
г * J
♦♦
иг
и,
**
'
■tt’.
1 • ,
1
§т
Т
I *
*
W
-*с
54-
^-пространство
Симплектическое
пространство
Рис. 33.25. Применение идеи, представленной на рис. 33.24, в случае твисторного описания ан-
тисамодуальной гравитации (с двумя лоскутами). Векторное поле имеет вид (Of /ди)°)д/дои1 —
— (df/д(л>г)д/ди;0, где / — однородная функция степени 2. Мы получаем (локально) искривленное
твисторное пространство Т. Имеет место глобальная проекция пространства Т на ^-пространство.
Каждый слой этой проекции представляет собой комплексное симплектическое 2-пространство, как и
само тг-пространство
проективного твисторного пространства FT это сечение есть просто прямая линия R (сфе¬
ра Римана СР1) в пространстве РТ, которая использовалась в §33.5 для представления
точки R * Примечательно, что это определение «пространственно-временной точки» при¬
менимо и в случае искривленного твисторного пространства Т. Оказывается^33'46^, что, как
и в случае плоского пространства, существует 4-параметрическое комплексное семейство
голоморфных сечений. (В проективном пространстве РТ таковым будет 4-параметрическое
комплексное семейство линий СР1.) Таким образом, это семейство представляется 4-мерным
комплексным многообразием Л4. Четырехмерно сть является замечательным фактом — при¬
мером комплексной магии с большим числом комплексных измерений, — который следу¬
ет из теорем японского математика Кунихико Кодаиры^33'47!. (Опыт работы только с ве¬
щественными многообразиями может привести к ожиданию, что существует бесконечно-
параметрическое семейство таких объектов. Но мы уже отмечали в § 15.5, что голоморфные
сечения могут быть весьма ограниченными.)
На рис. 33.26 эта процедура изображена графически (в проективном описании). Начнем
с выбора подходящей области 1Z в комплексном пространстве-времени Минковского СМ.
Для простоты положим, что 1Z есть некоторая (открытая) окрестность точки R в простран¬
стве СМ. Соответствующая область Q проективного пространства РТ есть область, за¬
метаемая семейством линий, каждая из которых представляет точку области 1Z. Это будет
окрестность (называемая трубчатой окрестностью) линии R в РТ, которая представляет 1Z
(рис. 33.266, в). Можно предположить, что область Q имеет топологию S2 х М4, где S2 про¬
исходит от топологии линии R (или, что эквивалентно, проективного 7г-пространства), а!4
описывает поперечную часть непосредственной окрестности каждой точки линии R. Можно
считать, что пространство S2 (в данном случае проективное 7г-пространство) разделено на
две полусферы, слегка растянутые, так что получается некоторый «рукав» перекрытия, а за¬
тем принять, что область Q построена из двух перекрывающихся (открытых) кусков Ы\ и Ы2,
лежащих поверх каждой из этих растянутых полусфер (рис. 33.26г). Можно «сдвинуть» U2
относительно 1Л\ в соответствии с упомянутым выше векторным полем и получить нашу
деформированную область РТ проективного твисторного пространства (рис. 33.266, е).
Объясните, в каком смысле эта линия является «сечением» пространства FT — I.

33.11. Нелинейный гравитон
827
Существует еще глобальная проекция на ^-пространство, результатом которой явля¬
ется расслоенная структура (рис. 33.26эю). Однако исходные «прямые линии» в Ы\ и
теперь разрываются и не могут служить сечениями. Тем не менее, согласно теореме Кода-
иры, имеется новое 4-параметрическое семейство голоморфных кривых в РТ, образующих
голоморфные сечения расслоения. Необходимое пространство М строится таким образом,
что каждая его точка соответствует одному из этих сечений (рис. 33.26 е,ж). Оказывается,
что пространству М. можно естественным образом приписать некоторую метрику р, что
его вейлевская кривизна антисамодуальна и что его тензор Риччи равен нулю. Используя
тот факт, что две точки Р* и Q* пространства М разделены нулевым интервалом в том и
только том случае, если пересекаются соответствующие линии Р* и Q* в пространстве РТ,
можно легко найти нулевые конусы метрики д (конформную структуру) (рис. 33.26 э/с).
/р
М
а)
б)
R
‘тЯЬш цК> ъ'А Гит	кЛу	bf+fi
U
1
и
I
(\
Уг^Ч-fTH
V
9
в)
г)
д)
7г-пространство
Рис. 33.26. Построение левополяризованного нелинейного гравитона, а) При стандартном твистор¬
ном соответствии для плоского пространства точки Р и Q пространства СМ разделены нулевым
интервалом всякий раз, когда пересекаются линии Р и Q в пространстве РТ. б) Мы хотим каким-то
образом деформировать РТ в искривленное твисторное пространство, однако математические теоремы
утверждают, что это нельзя сделать глобально. В соответствии с этим в качестве нашего исходного
«пространства-времени» мы возьмем лишь подходящую (открытую) окрестность 1Z точки R в СМ.
в) Это соответствует трубчатой окрестности Q линии R в РТ. г) Теперь можно применить процеду¬
ру, показанную на рис. 33.25, чтобы деформировать область Q (рассматриваемую как объединение
двух открытых множеств Ui и Ыё). д) Однако исходная линия 7Z теперь разрывается и не может
использоваться для однозначного определения «пространственно-временной точки», ё) На выручку
приходит теорема Кодаиры, из которой следует, что существует 4-параметрическое семейство «ли¬
ний» R* (компактных голоморфных кривых, принадлежащих тому же топологическому классу, что
и наши исходные линии), которое может служить для этой цели, ж) Точки искомого пространства
«нелинейного гравитона» М (комплексного 4-пространства) определяются кривыми Кодаиры R*.
Комплексная конформная метрика пространства М определяется (как и в случае а) условием, что
точки Р* и Q* разделены нулевым интервалом при пересечении соответствующих линий Р* и Q*.
Вейлевская кривизна пространства М автоматически оказывается антисамодуальной, тензор Риччи,
по построению, равен нулю

828
Глава 33
Читатель может поинтересоваться, каков физический смысл этого «пространства-вре¬
мени». Оно оказывается комплексным (и, следовательно, 8-мерным, а не 4-мерным, как
было, когда оно рассматривалось как вещественное многообразие). В случае плоского про¬
странства можно выделить вещественные точки пространства-времени (события в М), взяв
сечения пространства Т, лежащие в N, а затем рассмотреть наше пространство Л4 просто
как комплексификацию СМ пространства Минковского М. Однако в случае искривленно¬
го пространства мы не можем себе этого позволить. В этом случае «пространство-время»,
которое мы получаем при таком построении, с необходимостью оказывается комплексным
многообразием само по себе, и оно не может возникнуть в результате комплексификации
лоренцева вещественного пространств а-времени.
Почему так получается? Лоренцево 4-многообразие с антисамодуальной кривизной
Вейля с необходимостью является плоским по Вейлю (поскольку величина, комплексно-со¬
пряженная нулевой самодуальной части, есть антисамодуальная часть, которая, таким об¬
разом, тоже равна нулю). Если оно обладает также нулевым тензором Риччи, то оно вооб¬
ще плоское. В комплексном случае^33‘48^, с другой стороны, имеется обширное семейство
нетривиальных антисамодуальных 4-многообразий с нулевым тензором Риччи. Замечатель¬
ный факт состоит в том, что все они могут быть получены (по крайней мере, локально) с
помощью вышеупомянутой твисторной процедуры!
Как мы должны относиться к этому комплексному пространству М.1 Физическая ин¬
терпретация комплексного антисамодуального 4-пространств а с нулевым тензором Риччи
(если можно говорить, что оно является «положительно-частотным» в каком-то разумном
смысле) состоит в том, что оно представляет левополяризованный гравитон. Это фактиче¬
ски нелинейный гравитон в том смысле, что, хотя это есть, в некотором роде, «волновая
функция», она теперь является решением нелинейного уравнения Эйнштейна для вакуума
(с нулевым тензором Риччи), а не соответствующим линейным приближением. Последнее
было бы, если бы мы взяли твисторную функцию / в качестве элемента когомологии, а не
позволили «краске высохнуть», деформируя при этом само твисторное пространство. Мы
видим, что теория твисторов, призванная объединить идеи квантовой теории со структу¬
рой пространства-времени, повела нас в любопытном и неожиданном направлении. Наши
твисторные волновые функции оказались нелинейными объектами, так что уже начинают
появляться отклонения от стандартных правил линейной квантовой механики (§§ 22.2-22.4).
Приведенное построение содержит особенность, заслуживающую упоминания. Если
взять какую-либо точку Z искривленного твисторного пространства Т, то окажется, что
любая достаточно малая окрестность этой точки имеет такую же структуру, что и неко¬
торая окрестность произвольно выбранной точки Z7 плоского твисторного пространства Т
(не лежащей в «бесконечно удаленной» области I — см. § 33.5). В соответствии с этим,
твисторное пространство обладает «гибкой» локальной структурой в том смысле, в каком
это слово использовалось в § 14.8. Так, вся информация относительно кривизны и других
свойств пространства М сохраняется в Т не локально, а глобально. Это отражает тот ранее
упомянутый факт, что элемент когомологии, определяемый твисторной функцией, полно¬
стью исчезает, если ограничиться достаточно малой областью. В твисторном пространстве
нет «полевых уравнений». Та информация, которая обычно заключена в пространственно-
временных решениях полевых уравнений (в данном случае антисамодуального уравнения
Эйнштейна), содержится лишь нелокально в построении твисторного пространства^33 49^.
33.12.	Твисторы и общая теория относительности
«Построение нелинейного гравитона» было основным направлением развития теории
твисторов начиная с середины 1970-х годов. Было объявлено о необходимости развития пер¬
воначальной теории в двух разных направлениях. Наиболее очевидным было соответствую¬

33.12. ТВИСТОРЫ И ОБЩАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
829
щее построение /грдвополяризованного нелинейного гравитона, чтобы, образуя комбинации
е левополяризованным гравитоном, можно было получать смешанные поляризационные со¬
стояния (например, плоскополяризованные нелинейные гравитоны). Это было основной ча¬
стью твисторной программы. Как уже отмечалось, понятие «нелинейного гравитона» вполне
в духе поисков теории (см. главу 30), в которой стандартные линейные правила обычной
квантовой U-теории изменились бы таким образом, что позволили бы объединить квантовую
теорию с общей теорией относительности Эйнштейна. Однако тот гравитон, который был
нами сконструирован, — это всего лишь «полгравитона», поскольку допускает лишь одно из
двух возможных состояний спиральности.
Внимательные читатели могут высказать предположение, что если вместо твисторов
использовать для описания дуальные твисторы Wa9 то, повторив предыдущее построение,
можно будет получить нелинейную волновую функцию правоиоляризованного гравитона*.
При этом получился бы правополяризованный гравитон, соответствующий степени одно¬
родности 2 (у Wa), и левополяризованный, соответствующий степени однородности —б.
Но это не избавило бы нас от трудностей, поскольку теперь мы теряем состояния с левой
спиральностью, так что не имеет смысла использовать переменные Wa для правополяризо¬
ванных состояний и Za для левополяризованных, прежде всего потому, что нам необходимо
также описывать состояния смешанной спиральности!33*50!
Проблема, состоящая в том, чтобы, «потенцировав» твисторные функции f(Za) со сте¬
пенью однородности -6, получить правополяризованный нелинейный гравитон, была на¬
звана (гравитационной) goog/y-проблемой (Слово «googly» — это термин игры в крикет,
обозначающий мяч, который совершает правое вращение относительно направления своего
движения, однако внешне ведет себя так, как если бы движение было левым.) Было потра¬
чено почти 25 лет, чтобы найти правдоподобное решение, однако недавние исследования,
по-видимому, дают необходимую конструкцию I33-51!. Пока, в момент написания этой книги,
эти процедуры остаются гипотетическими в некоторых важных аспектах. Я не буду пытать¬
ся описать здесь эти исследования, а назову лишь наиболее существенную особенность,
состоящую в том, что слои проекции нашего искривленного твисторного пространства на
проективное пространство РТ «скручиваются» таким образом, который соответствует тви¬
сторной функции со степенью однородности —6. («Скручивание» вызывается потенцирова¬
нием векторного поля с образованием пары перекрывающихся лоскутов обманчиво простого
вида Cf-QZad/dZa, где С — подходящая константа, /_б — твисторная функция со степе¬
нью однородности —б.) Это позволяет включить в рассмотрение как левополяризованную,
так и правополяризованную часть гравитона.
По крайней мере в случае пространства-времени М с подходящей плоской асимптоти¬
кой существует прямое построение пространства Т в терминах пространства А4. Кроме
того, было предложено получить М по заданному Т, т. е. построить пространственно-
временные точки исходя из чисто твисторной структуры, которая, как предполагается,
обеспечивает нулевое значение тензора Риччи (т. е. выполнение вакуумного уравнения
Эйнштейна). Это предложение существенным образом связано с долгосрочным исследо¬
вательским проектом Эзры Ньюмена и его коллег по интерпретации пространственно-
временных точек в терминах так называемых «срезов световых конусов», которые полу¬
чаются при пересечении световых конусов в пространстве А4 нулевой бесконечно удален¬
ной поверхностью в будущем j^+J33,52! Однако, несмотря на кажущуюся перспективность
проекта, некоторые важные проблемы построения твисторных пространств пока остаются
нерешенными^33,53!.
Другое направление развития первоначальной теории построения левополяризованного
нелинейного гравитона, о котором было объявлено в 1975-1976 годах, состояло в обобщении
* Почему? (Подсказка: почему пространственное зеркальное отражение превращает твисторы в дуальные
твисторы?)

830
Глава 33
результатов теории гравитации на другие калибровочные поля. Вскоре, в 1976-1977 годах,
Ричард Уорд показал, что антисамодуальные калибровочные поля общего вида можно полу¬
чить, используя твисторную конструкцию, подобную использованной в теории гравитации.
Построение Уорда вызвало значительный интерес с математической точки зрения и привело
к исследованиям Уорда и других авторов в области интегрируемых систем (нелинейных
уравнений, которые могут быть решены, в некотором смысле, в общем случае). Здесь те¬
ория твисторов открывает широкий взгляд на проблему в целом I33*54]. Вполне возможно,
что упомянутые успехи на пути к полному решению гравитационной проблемы смешанной
спиральности укажут путь, на котором твисторный формализм окажется применимым также
к калибровочным полям общего вида (со смешанной спиральностью).
33.13.	На пути к твисторной теории элементарных частиц
Всё это приводит к вопросу, каким образом теория твисторов могла бы развиться в пол¬
ноценную физическую теорию, каковой она пока не является. Чтобы это произошло, необ¬
ходимо провести исследования в двух дополнительных областях твисторов. Одна из них
касается исчерпывающего исследования квантовой теории поля. Здесь была развита боль¬
шая активность Эндрю Ходжем и его учениками в Оксфорде (некоторый начальный вклад
был внесен мною и некоторыми другими в начале 1970-х годов), разработавшими для кван¬
товой теории поля метод возмущений, в котором фейнмановские диаграммы были заменены
твисторными диаграммами. Последние включают многомерное контурное интегрирование
и позволяют устранить многие бесконечности, возникающие при использовании обычных
диаграмм Фейнмана^3-551 Пока этот подход выглядит несколько сложнее, чем хотелось бы,
кроме того, ему недостает независимого руководящего принципа, подобного изложенному
в §§26.6-26.8, который позволял бы обращаться с контурными интегралами без необхо¬
димости апеллировать к стандартным фейнмановским выражениям при промежуточных
вычислениях.
Другой из упомянутых областей является теисторная теория элементарных частиц,
первоначально развитая Золтаном Перджесом, Джорджем Спарлингом, Лейном Хьюсто¬
ном, Полом Тодом и Флоренс Цоу (Шэн Цунь) из идей, предложенных мною в середине
1970-х-начале 1980-х годов, но лежавших с тех пор без употребления. Основная идея за¬
ключалась в следующем: в то время как для описания безмассовых частиц достаточно тви-
сторных волновых функций от одной твисторной переменной, например f(Za), частицы,
обладающие массой, требуют большего числа переменных, например, Х(Х. ..., Za. Были
известны выражения для импульса и момента импульса частицы с массой, содержащие
суммирование вкладов всех отдельных твисторов, но теперь появилась внутренняя группа
симметрии, возникающая при преобразованиях этих твисторных переменных и комплекс-
iy	vy
но-сопряженных им, которые не влияют на полный импульс и полный момент импульса.
Следует отметить, что получаются группы, которые включают, несколько обобщая, ipynny
электрослабых взаимодействий U(2) и группу сильных взаимодействий SU(3). Был полу¬
чен ряд интересных соотношений с обычной классификацией элементарных частиц в со¬
ответствии со стандартной моделью, но по некоторым техническим причинам эта схема не
получила развития. Появилась надежда, что недавние работы в области «googly-проблемы»
(особенно если их можно будет применить к калибровочным полям) помогут снова вернуть¬
ся к этому предмету.
Существует, на мой взгляд, возможность, что предложение Хана-Цу в отношении мо¬
дели элементарных частиц, кратко описанное в §25.8, может быть существенным образом
связано с этими исследованиями. Это предложение требует существования дуальной группы
для каждой (неабелевой) группы симметрии элементарных частиц в дополнение к исходной
калибровочной группе. Теория твисторов предполагает, что в соответствии с упомянутым

33.14. Каково будущее теории твисторов?
831
выше построением Уорда (вместе с гипотетическим «googly»-BapHaHTOM) каждая группа
должна проявляться в антисамодуальном и самодуальном вариантах, и это, по-видимому,
требует, чтобы дуальная форма калибровочной группы играла существенную роль помимо
роли исходной калибровочной группы. Таким образом, с использованием идей предложе¬
ния Хана-Цу программа твисторной теории элементарных частиц может сыграть свою роль
в построении будущей физики элементарных частиц. Более того, можно ожидать, что успеш¬
ный прогресс в этой области окажет также существенное влияние на применение теории
твисторных диаграмм к квантовой теории поля.
33.14.	Каково будущее теории твисторов?
В своем изложении теории твисторов я не предупредил читателя, что мои взгляды на
предмет во многом не совпадают с мнением физического сообщества. Поскольку теории
твисторов я отдал в общей сложности более половины жизни, было бы трудно ожидать, что¬
бы мои представления были близки взглядам большинства физиков, не посвятивших себя
этой теории. Следует добавить, что физиков, хорошо знающих этот предмет, довольно мало,
и их, несомненно, гораздо меньше, чем тех, кто знаком с теорией струн или суперсимметри¬
ей. Теорию твисторов никоим образом нельзя считать основным направлением проявления
нынешней активности физиков-теоретиков.
f
Пока что теория твисторов, как и теория струн, оказала значительное влияние на чи¬
стую математику, и это рассматривается как одно из ее достоинств. Теория твисторов оказала
значительное влияние на теорию интегрируемых систем (о чем кратко упоминалось выше),
теорию представлений^33,56^ и дифференциальную геометрию. (В этой последней области
следует отметить работу Сергея Меркулова и JI. Дж. Шваххофера, которым удалось найти
решение так называемой «проблемы голономии», используя методы, развитые при построе¬
нии первоначальной теории нелинейных гравитонов ^33-57L Теория твисторов сыграла также
значительную роль в построении «гиперкэлеровых многообразий», «пространств Цолла»
и т. nJ33'58J) Теория твисторов зачастую руководствовалась соображениями математического
изящества и интересами авторов, и ее успехи во многом связаны с ее математически строгой
структурой.
Всё это хорошо, вправе сказать простодушный читатель, но не отмечал ли сам автор
(в главе 31) в качестве недостатка теории струн тот факт, что она руководствовалась в основ¬
ном математическими соображениями и в гораздо меньшей степени природой физического
мира? Подобная критика во многом справедлива и в отношении теории твисторов. В насто¬
ящее время отсутствуют причины, основанные на данных наблюдений, которые заставили
бы нас считать, что теория твисторов — это тот путь, которым должна следовать современ¬
ная физика. Кроме того, многие могут счесть, что сугубо киральная природа этой теории
приводит к слишком высокой пространственной асимметрии. В конце концов, отсутству¬
ют физические указания на важную роль право-левой асимметрии в физике гравитации.
В главах 27, 28 и 30 я подчеркивал необходимость временной асимметрии в объединении
гравитации с квантовой механикой, однако не видно физических причин существования
пространственной асимметрии (за исключением, возможно, косвенных указаний в виде
СРТ-теоремы в квантовой теории поля; см. §§25.4, 30.2).
Возможно, конечно, что пространственная асимметрия формализма не будет прояв¬
ляться в виде асимметрии физических эффектов. Основанием для таких надежд может
служить тот факт, что алгебры, порождаемые парой (Za, — hd/dZa), с одной стороны,
и (hdjdZa, Za), с другой стороны, формально тождественны. Это наводит на мысль, что
любой результат, полученный с использованием твисторного описания (в переменных Za),
можно получить и при использовании дуальных твисторов (в переменных Wa = Za), и это
подобие оказывается настолько полным, что в результирующей теории 1равитации ника¬

832
Глава 33
кой право-левой асимметрии не появляется. С другой стороны, если формализм должен
отражать Природу, то мы должны потребовать право-левой асимметрии при переходе к опи¬
санию слабого взаимодействия (§ 25.3). Однако при нынешнем состоянии теории твисторов
не видно причин существования такой разницы.
Основной недостаток теории твисторов в ее нынешнем виде состоит в том, что она
не является подлинно физической теорией. Она не делает никаких однозначных физиче¬
ских предсказаний. Мой личный (сверх)оптимистический взгляд состоит в том, что теорию
твисторов следует сравнивать с гамильтоновым формализмом классической физики. Гамиль¬
тонова теория не привела к каким-либо изменениям в физике, но она позволила по-иному
взглянуть на классическую физику, что впоследствии оказалось востребованным новой кван¬
товой теорией Шредингера, как описано в главах 21-23. Аналогично теория твисторов —
это просто другая формулировка, которая не обязательно влечет за собой физические изме¬
нения. При наличии оптимизма можно надеяться, что это создаст точку опоры для развития
физики в будущем.
Никто, конечно, не принуждает скептиков поверить, что такое развитие действительно
состоится, и пока что сила теории твисторов, как и у теории струн (или М-теории), в ее эсте¬
тической и математической привлекательности. Однако эти две теории, в их нынешнем ви¬
де, математически несопоставимы, поскольку оперируют разным числом пространственно-
временных измерений. Кто-то может справедливо (хотя, пожалуй, и слишком самоуверенно)
утверждать, что теория твисторов предсказывает несостоятельность чаяний теории струн
или, наоборот, что из теории струн следует ошибочность теории твисторов! Такая несовме¬
стимость не распространяется на варианты или иные формулировки теории струн (или М-те¬
ории), в которых дополнительные измерения не являются пространственно-временными из¬
мерениями, а рассматриваются как некие «внутренние» измерения особого рода. Хотя такое
изменение формулировки выглядело бы вполне согласованным, оно противоречит движу¬
щим стимулам теории струн в ее обычном представлении.
В этой связи я должен напомнить читателю о недавней работе Эдварда Виттена^33*59^,
упомянутой в § 31.18. В ней показана возможность нового взгляда на амплитуды рассеяния
Янга-Миллса. Идеи теории твисторов комбинируются в ней с некоторыми идеями теории
струн, — но теперь в 4-мерном варианте!
В любом случае теория твисторов требует некоторого нового подхода. Из наиболее важ¬
ных ингредиентов других успешных физических теорий отметим лагранжевы и фейнманов-
ские интегралы по траекториям, определяющие полевые уравнения квантовой теории поля
(см. §26.6). Теория твисторов гордится устранением полевых уравнений (§§33.9, 33.11),
однако требуются, по-видимому, новые идеи для создания полной твисторной квантовой
теории поля^33,60!.
Дает ли теория твисторов какие-либо четкие «предсказания»? Ближе всего к предска¬
занию находится стремление теории объяснить, почему Вселенная имеет отрицательную
пространственную кривизну, К < 0. Чтобы понять причину такого ожидания, вспомним
(см. главы 27 и 28, особенно §27.13), что Большой взрыв имел необычайно однородный
характер, подобный предсказываемому одной из моделей ФЛРУ. Эти модели являются кон¬
формно-плоскими (с нулевой вейлевской кривизной) и допускают простое описание с ис¬
пользованием плоского твисторного пространства (СР3)^33,61^. Для каждого из трех случа¬
ев К >0, А" — 0, К <0 существует точная группа симметрия, но только в случае К < 0
это голоморфная группа. В последнем случае это именно та группа, которая связана с «ком¬
плексной магией» теории твисторов, а именно группа Лоренца 0(1, 3), которая (не учи¬
тывая отражений) представляет собой группу голоморфных преобразований сферы Римана.
Где находится эта сфера Римана? Это «бесконечность» гиперболического 3-пространства,
подобная ограничивающей окружности на рисунке Эшера, воспроизведенном на рис. 2.11, —
это аналог небесной сферы в § 18.5 как границы гиперболического 3-пространства из § 18.4
(см.рис. 18.10).

33.14. Каково будущее теории твисторов?
833
Мы понимаем, что вариант К < О предсказывается не теорией твисторов, а лежащей
в ее основе голоморфной философией. Можно ли пойти дальше и сказать что-то о космологи¬
ческой постоянной Л? Предложенные твисторные конструкции (см. §33.12), по-видимому,
можно естественным образом приспособить к вакуумному уравнению Эйнштейна лишь
в случае А = 0, и трудно понять, как можно модифицировать нынешнюю процедуру, чтобы
включить случай А ф 0. Означает ли это, что теория твисторов предсказывает вариант А =
= 0? Я предпочел бы отрицательный ответ (несмотря на мое личное пристрастие к этому
варианту)! Потому что впечатляющие недавние наблюдения (см. §28.10) дают убедитель¬
ные свидетельства в пользу варианта Л > 0. Это бросает новый вызов теории твисторов.
Ясно, что теории твисторов предстоит сделать гораздо больше, чем сделано, чтобы стать
полноценной физической теорией!
А как насчет правил квантовой теории? Указывает ли теория твисторов какое-то опре¬
деленное направление изменения в соответствии с ожиданиями, сформулированными в гла¬
ве 30? «Нелинейный гравитон» из § 33.11 служит указанием, что твисторный подход в конеч¬
ном счете влечет за собой (нелинейную) модификацию правил квантовой механики. Однако
в твисторном формализме не так уж много такого, что указывало бы на наличие в этой
модификации фундаментальной временной асимметрии, которая требуется согласно обсу¬
ждению в §§30.2, 30.3, 30.9. Однако возможен привлекательный «googly»-BapHaHT, кратко
рассмотренный в §33.12, который, по-видимому, может привести к описанию, асиммет¬
ричному относительно обращения времени. Степень привлекательности этой возможности
оценят будущие исследования, при этой оценке необходимо учитывать замечания, изложен¬
ные в предыдущем абзаце. Так что теория твисторов пока не говорит ничего определенного
относительно редукции квантовых состояний, хотя именно эта проблема сыграла значитель¬
ную роль в исходной мотивации теории.
В заключение рассмотрим вопрос о статусе голоморфной философии, которая служит
одной из главных движущих сил в развитии теории твисторов. Я думаю, следует прямо ска¬
зать, что именно эта философия действительно сыграла такую роль, превзойдя в некоторых
случаях возлагавшиеся на нее ожидания (примером может служить твисторное представле¬
ние безмассовых полей как линейных (§§33.8- 33.10), так и нелинейных (§§33.11, 33.12).
В то же время теории придется что-нибудь сказать о вещественных аспектах физики и него¬
ломорфном поведении, например, появлении значений вероятности (в соответствии с неголо¬
морфной операцией перехода к квадрату модуля 2 н-> \z\2) и вещественных пространственно-
временных точек; при этом мы надеемся суметь описать неаналитическое поведение (не го¬
воря уже о неголоморфном). Что касается этой последней проблемы, то некоторая поддержка
может быть получена со стороны замечательной теории гиперфункций, упомянутой в конце
главы 9 (см. § 9.7); согласно этой теории, неаналитическое поведение можно очень изящным
образом представить в контексте голоморфных операций. В какой степени будущая теория
твисторов окажется способной справиться с такими проблемами, покажет будущее.
Примечания
§33.1.
33.1. См. [13].
33.2. См. [693, 764, 735]
33.3. См. [738, 516]; один из наиболее важных результатов в этой области принадлежит Маркопу-
ло [515].
33.4. См. [464, 289, 369, 538, 764].
33.5. См. [264].
33.6. См. [731, 328, 212, 513, 512].
33.7. См. оригинальную работу [657], а также содержательный неформальный обзор [410].

834
Глава 33
33.8. Джосса развил эти идеи в своей диссертации [422].
33.9. См. [415].
33.10. См. [309].
33.11. См. [237,503,477].
33.12. См. [48,46,47, 136].
33.13. См. [159].
33.14. Имеется и много других приложений некоммутативной геометрии как в чистой математике,
так и применительно к физике; см. [157, 158]. Примером последних может служить изящный
формализм для исчерпывающего исследования перенормировок, развитый с использованием
некоммутативной геометрии; см. §26.9 и книгу Креймера [463].
33.15. См. [159].
§ 33.2.
33.16. Для полной строгости при определении пространства PN следовало бы учесть роль «световых
лучей на бесконечности», принадлежащих сфере Римана; см. §33.3.
33.17. Для группы Пуанкаре понадобятся соответствующие ненаправленные (скалярные) величины
(а именно ее операторы Казимира; см. §22.12). Таковыми являются полный спин и масса покоя
(в квадрате). Однако, насколько известно, масса покоя не слагается из целого числа каких-то
элементарных масс, поэтому комбинаторные аспекты такой схемы не вполне ясны. Тем не
менее такой подход был развит в 1983 году Джоном Муссурисом в его диссертации [535]. Этот
подход предполагает присвоение линиям сети дополнительных индексов, соответствующих
как спинам, так и массам.
33.18. См. [504, 584, 585, 586, 604].
§ 33.4.
33.19. См. [627], в частности, приложение.
33.20. См. [362, 627, 113].
§ 33.6.
33.21. См. [627,405].
33.22. В каждой пространственно-временной точке (событии) х имеются два нулевых направления.
Это направление «светового луча», проходящего через точку х, и направление 4-импульса вра¬
щающейся частицы, представляемой твистором.	Эти два	нулевых	направления	представляют
«главные	нулевые направления», т. е. направления,	определяемые	представлением Майораны
(см. § 22.10) для момента импульса частицы (его самодуальной или антисамодуальной части)
относительно точки х. См. [809, 405].
33.23. См. [589, 596, 606, 627].
§ 33.7.
33.24. См. [591,405].
33.25. См. [405, 627, 406].
§ 33.8.
33.26. См. [203,	261, 262, 586].
33.27. См. [263,	627, 586, 624].
33.28. См. [591,	593, 606, 405, 406, 830, 64, 65].
33.29. Многообразие С2 представляет линию 7Z в пространстве PN (рис. 33.11). Большинству за¬
нимающихся теорией твисторов более привычен проективный вариант этого контурного ин¬
теграла, для которого используется 1-форма i — 7г0' ^l' ~ лд'^тго' вместо 2-формы т =
= с^7г0' Л dir it. В этом случае контурный интеграл становится одномерным, и его связь с дву¬
мерным описанием определяется тем, что одно из контурных измерений (окружность S1)
сводит используемый здесь непроективный вариант к более привычному проективному. Пре¬
имущество используемого варианта в том, что он позволяет описывать состояния со смешан¬
ной спиральностью.

33.14. Каково будущее теории твисторов?
835
33.30. См. [405, 406, 627].
33.31. Теория твисторов многим обязана сэру Майклу Атья за его важный вклад на ранней ста¬
дии ее развития. Первоначальные соображения относительно твисторной когомологии были
сформулированы в работе [601], подробное изложение см. в [229].
§ 33.9.
33.32. Это так называемая когомология Чеха. Существует много других подходов к концепции кого¬
мологии. См. [817, 812, 319].
33.33. См. [326, 812, 817, 627].
33.34. См. [326, 627].
33.35. См. [627].
33.36. См. [580].
33.37. См. [611].
33.38. См. [326,319, 139,817].
33.39. См. ссылки в примечании 33.38, а также [229].
§ 33.10.
33.40. Перестановка знаков -f и — здесь не имеет значения. См. § 9.2.
33.41. Здесь имеются некоторые тонкости технического характера. Если исходное поле неаналитич-
но (не Сш), то поля (на М) могут оказаться гиперфункциональными в смысле § 9.7; см. [51].
33.42. См. [391].
33.43. См. [606].
§33.11.
33.44. См. [597, 598, 811, 625, 627].
33.45. Здесь имеется тонкость: это расслоение не является голоморфным (§ 15.5), хотя все опе¬
рации при его построении были голоморфными, поскольку при локальном рассмотрении
в 7г-пространстве оно не является строго голоморфным произведением пространств. Про¬
странство Т называют голоморфным расслоенным пространством. См. [598].
33.46. Так будет при обычных условиях; см. [405, 812, 625].
33.47. См. [454].
33.48. Или в случае вещественной положительно определенной метрики (+ -f- ++), или в случае
расщепленной сигнатуры (+ Н ). См. [598, 351, 44, 224].
33.49. Здесь, по-видимому, имеется существенная связь с понятием топологической квантовой те¬
ории поля, упомянутым в § 32.5; см. примечание 32.17.
§ 33.12.
33.50. Существует зеркально-симметричный подход к этим проблемам с использованием так называ¬
емых сомбитвисторов, который позволил достигнуть некоторых успехов в этом направлении.
См. [596,478, 479, 412, 842]. См. также [627]. В плоском пространстве амбитвистор представ¬
ляет собой, в сущности, пару (Wa, Za), где WaZa = 0, и описывает комплексный световой
луч. Это, однако, не согласуется с принятой нами философией, согласно которой «твисторные
функции представляют собой волновые функции», поскольку амбитвисторное описание имеет
большее сходство с классическим, при котором появляются как переменная, так и сопряжен¬
ная ей величины (в данном случае Za и Wa), а не та или другая из них, как при описании
с помощью волновой функции. Амбитвисторный подход сталкивается также с некоторыми
математическими трудностями при описании нелинейных полей.
33.51. См. [621].
33.52. См., например, [273, 101, 612].
33.53. См. [621].
33.54. См. [519].

836
Глава 33
§33.13.
33.55. См. ранние работы [624, 596] и более поздние [386, 387, 388, 389, 390].
§33.14.
33.56. Относительно применения твисторов в математике см. [50, 63, 519].
33.57. См. [521].
33.58. См. [298, 299, 480].
33.59. См. примечание 31.81.
33.60. Хотя лагранжианы играют некоторую роль в твисторной теории известных видов физическо¬
го взаимодействия, они пока не получили в этой теории надлежащей общей формулировки.
Есть, возможно, некоторая ирония в том, что именно тот успех, которого достигла теория
твисторов в представлении физических полей путем решения в неявной форме соответству¬
ющих полевых уравнений (с помощью однородных твисторных функций в случае свободных
безмассовых полей), создает трудности с лаграижевой формулировкой этой теории. В стан¬
дартной квантовой формулировке полевые уравнения получаются в результате «суммирова¬
ния по историям» (§ 26.6); чтобы эта идея имела смысл, в данной формулировке должна быть
явная возможность нарушать полевые уравнения, при этом квантовые поправки к класси¬
ческой теории получаются при более подробном рассмотрении интеграла по траекториям.
Всё это теряется, если формулировка не допускает нарушения полевых уравнений! Мне ка¬
жется, необходима некоторая переоценка в отношении того, какой должна быть истинная
«сущность» лагранжианов в теории твисторов и вообще в физической теории. Возможно, это
связано с тем беспокойством, которое я выражал в конце § 26.6, и с действительно серьезной
проблемой вездесущих расходимостей, возникающих при интегрировании по траекториям
(см. §26.6). См., однако, конец §32.5 и примечание 32.17.
33.61. См. [627], §9.5.

Глава 34
Где лежит путь к реальности?
ч.
34.1. Великие физические теории XX века — что дальше?
Давайте попробуем подвести итог и посмотреть, что мы узнали к началу третьего
тысячелетия из наших физических теорий относительно фундаментальной природы этого
замечательного мира, в котором нам довелось жить. Несомненно, что в его понимании были
достигнуты необычайные успехи, обязанные тонким наблюдениям и искусным эксперимен¬
там, глубоким и проницательным размышлениям физического характера и математическим
рассуждениям — как сложным, но рутинным, так и вдохновляющим прорывам на более
высокий уровень. Это привело нас от геометрии древних греков через ньютоновскую меха¬
нику к величественной структуре классической механики, далее к максвелловской теории
электромагнетизма и к термодинамике. XX век принес нам специальную теорию относи¬
тельности, развитие которой привело к эйнштейновской общей теории относительности,
блестяще выдержавшей проверку наблюдениями. Он дал нам также глубоко загадочную, но
тем не менее исключительно точную и универсальную квантовую механику и развившую¬
ся из нее квантовую теорию поля, в частности, мы имеем теперь замечательно успешные
стандартные модели физики элементарных частиц и космологии.
Среди наиболее самонадеянных теоретиков бытует мнение, что мы, возможно, уже
«почти у цели» и что «теория всего» лежит не слишком далеко от направления последова¬
тельного развития достижений конца XX века. Часто такие заявления делались в отношении
какой-либо теории, наиболее модной в то время, например, теории струн. Сейчас стало труд¬
нее поддерживать такую точку зрения, поскольку теория струн трансформировалась в нечто
такое (М- или F-теорию), природа чего в настоящее время совершенно неясна.
На мой взгляд, от «окончательной теории» мы гораздо дальше, чем кажется. Я отнюдь
не уверен, что исследования, описанные в главе 31, вообще имеют правильное направление.
Идеи теории струн (и родственные им) действительно привели к различным замечательным
достижением мателштического характера. Однако я по-прежнему совершенно не убежден,
что они представляют нечто иное, чем просто красивую математику, хотя и с некоторым
притоком глубоких физических идей. Я не вижу причин, по которым теории, в которых раз¬
мерность пространства-времени превышает непосредственно наблюдаемую (а именно 1 + 3)
(см. §§31.11, 31.12), могли бы сами по себе вести нас в направлении более полного физи¬
ческого понимания. Что касается других предложенных схем, изложенных в главах 32 и 33,
с которыми я более согласен, то у меня нет сомнения, что и им не хватает чего-то важ¬
ного. Было бы неразумно предсказывать сколько-нибудь уверенно, что эти теории близки
к тому, чтобы совершить скачок, который вывел бы нас на правильный путь к пониманию
физической реальности.
Тем не менее уже в XX веке человечество, несомненно, достигло на пути понимания
замечательного прогресса, и в этой книге я попытался представить, что достигнуто в этом
направлении. На этом фоне выделяется общая теория относительности Эйнштейна, которая
представляет, на мой взгляд, высшее достижение этого века. Большинство физиков тако¬
вым, по-видимому, считают квантовую механику (и квантовую теорию поля). Я не могу
разделить это мнение. Хотя квантовая теория, несомненно, объяснила несравненно больше,

838
Глава 34
чем общая теория относительности, и в гораздо более широком классе различных явлений,
я считаю, что эта теория пока не достигла той степени согласованности, которая необхо¬
дима для настоящей теории. Проблему составляет, конечно, парадокс измерения, подробно
рассмотренный в главе 29. На мой взгляд, квантовая теория неполна. Когда она достигнет
необходимой полноты (а я надеюсь, что в XXI веке это произойдет), она, несомненно, станет
еще большим достижением, нежели общая теория относительности Эйнштейна. В самом
деле, как подчеркивалось в главе 30, такая полная квантовая механика должна включить
теорию Эйнштейна как предельный случай больших масс и расстояний. (Надеюсь, из моих
замечаний в § 31.8 читателю стало ясно, что я отнюдь не считаю, будто такое объединение
уже достигнуто в теории струн, несмотря на многочисленные заявления такого рода.)
На мой взгляд, общая теория относительности, вероятно, останется теорией простран¬
ства-времени в крупномасштабном пределе (в котором допускается присутствие космоло¬
гической постоянной Л), хотя мы должны ожидать серьезной модификации ее на крайне
малых планковских расстояниях порядка 10“35 м или при плотностях порядка планковского
значения, в 5 • 1093 раз превосходящего плотность воды, которые имеют место в окрестности
некоторых пространственно-временных сингулярностей. Такой взгляд на общую теорию от¬
носительности сегодня является общепринятым. Ее согласие с наблюдениями, по крайней
мере, в довольно больших масштабах, соответствующих вращающимся нейтронным звез¬
дам, эффектам гравитационной линзы и даже черным дырам, следует признать отличным.
Здесь я имею в виду стандартную теорию Эйнштейна без космологической постоянной.
А как насчет космологической постоянной? Наблюдения, сделанные в последние
несколько лет, свидетельствуют в пользу ее положительного значения. Если это действи¬
тельно так, то ее величина должна быть очень мала в обычных локальных масштабах.
Если рассматривать Л как кривизну, то она будет обратно пропорциональна расстоянию,
сравнимому с радиусом наблюдаемой Вселенной, так что постоянная Л несущественна на
всех масштабах, кроме космологических. Если интерпретировать Л как некоторую эффек¬
тивную плотность Qa, то эта плотность не может более чем в 2-3 раза превышать крайне
низкую нынешнюю среднюю плотность вещества в нашей Вселенной, которая составляет
примерно 10“27 кг/м3 — значительно меньше, чем у самого лучшего вакуума, искусственно
получаемого у нас на Земле. Так что опять-таки Л может иметь отношение лишь к космоло¬
гическим масштабам. Тем не менее, с точки зрения многих специалистов в области кванто¬
вой теории поля, Л действительно есть мера эффективной плотности вакуума, создаваемой
«квантовыми вакуумными флуктуациями» (это есть следствие принципа неопределенности
Гейзенберга в квантовой теории поля; см. §§21.11,29.6, 30.14), и соответственно она «долж¬
на» иметь значение (сравнимое с планковским), примерно в 10120 раз (или, по некоторым
оценкам, в Ю60 раз) большее верхнего предела наблюдаемой величины! Это рассматри¬
вается как фундаментальная загадка квантовой теории поля^34-^, не решаемая никакими
стандартными подходами к квантовой гравитации или теорией струн. Меня это тревожит
меньше, чем, видимо, многих теоретиков. Я полагаю (см. §30.14), что само понятие «ва¬
куумных флуктуаций» в целом потребует радикального пересмотра, когда мы будем иметь
лучшую квантовую теорию гравитации и тем более лучшую квантовую теорию поля.
Мы должны, конечно, признать, что существующая квантовая механика и квантовая
теория поля подтверждаются множеством различных явлений. Но я должен пояснить, что
в этом нет противоречия с точкой зрения, выраженной в главе 30, которая предполага¬
ет изменение основ квантовой теории. Пока никакие эксперименты не подвели нас к тому
«квантово-гравитационному» уровню, на котором можно ожидать проявления таких измене¬
ний в виде объективной редукции вектора состояния (гравитационной ОР). Наблюдавшееся
квантовое перепутывание на расстояниях до 15 километров ^34-2^ полностью согласуется с та¬
кими ожидаемыми изменениями, так как в перепутывании участвуют лишь пары фотонов
с энергиями порядка 10“19 Дж, и спонтанная редукция состояний, вызываемая гравита¬
ционной ОР, не может ожидаться, если не проводятся реальные измерения над фотонами

34.1. Великие физические теории XX века — что дальше?
839
(при которых будет иметь место точечная ОР в измерительной установке). Современная
экспериментальная ситуация с применимостью квантовой механики к процессам движения
больших масс лучше всего проявилась в недавних экспериментах Антона Цайлингера и его
коллег в Вене^34-3!. Они провели двухщелевой эксперимент с фуллеренами Сео (а также С70).
Каждая из молекул фуллерена содержит 60 атомов углерода, расположенных в замечательно
симметричном порядке, напоминающем покрышку современного футбольного мяча (или
представляет несколько менее симметричную структуру, содержащую 70 атомов углерода).
Молекулы фуллерена имеют диаметр порядка одного нанометра, и они интерферируют меж¬
ду собой в условиях суперпозищш двух положений, разделенных расстоянием порядка 10 “7
м, которое примерно в 100 раз больше диаметра молекулы фуллерена. Согласно схеме, пред¬
ложенной в § 30.11, такая суперпозиция должна сохраняться несколько сотен тысяч лет или
около того, прежде чем проявится спонтанная редукция, обусловленная гравитационной ОР,
поэтому никакого противоречия с экспериментом Цайлингера не возникает.
Конечно, в некоторых будущих экспериментах ситуация вполне может оказаться иной.
В каком-нибудь космическом эксперименте типа FELIX вроде описанного в §30.13 или,
скорее, в родственном эксперименте, предложенном в работе Дика Бумейстера из Санта-
Барбары, может быть подвергнута проверке схема гравитационной ОР, и вполне возможны
другие эксперименты, которые можно будет провести в начале XXI века. Я считаю такую
перспективу вполне реальной, и возможно, что подобные эксперименты смогут существенно
изменить наш нынешний взгляд на квантовую механику. По крайней мере, они помогут уста¬
новить пределы для спекуляций на тему о том, как должна измениться квантовая механика
в будущей теории.
Это находится в резком противоречии с современной (или предвидимой на ближайшее
будущее) экспериментальной ситуацией в отношении других попыток (подобных рассмот¬
ренным в главах 31-33) объединить квантовую теорию с теорией гравитации. В большин¬
стве проектов экспериментов по обнаружению связи между квантовой механикой и гра¬
витацией фигурируют элементарные частицы, разогнанные до крайне высоких энергий,
лежащих необозримо далеко за пределами возможностей любых существующих (либо
всерьез проектируемых) ускорителей элементарных частиц. (Единственное известное мне
исключение составляют предполагаемые эксперименты по выяснению возможности су¬
ществования «больших» дополнительных измерений пространства-времени (§ 31.4), кото¬
рые могут, например, изменить закон обратного квадрата расстояния для сил тяготения
или тесно связанные с этим эксперименты по проверке возможности нарушения лорен-
цевой ковариантности при высоких энергиях, обусловленного предполагаемыми квантово¬
гравитационными эффектамиL34'4^.) Попытки проверки любой «традиционной» квантово¬
гравитационной схемы наталкиваются на фундаментальные трудности, связанные с пред¬
положением, что квантово-гравитационные эффекты должны модифицировать лишь струк¬
туру пространства-времени (на крайне малых планковских масштабах длины или време¬
ни), оставляя неизменными стандартные процедуры квантовой механики. Мы оказывается
в гораздо лучшем положении, с точки зрения эксперимента, если эффекты общей теории
относительности приводят к изменению правил квантовой механики, как предполагалось
в главе 30, поскольку проверка предполагаемых эффектов находится в рамках современ¬
ных технических возможностей. Если такие эксперименты увенчаются успехом и укажут на
необходимость изменения правил квантовой механики, то мы получим наконец надежные
руководящие указания со стороны физики в дополнение к математическим, в основном,
устремлениям, двигающим сегодня исследования в области квантовой гравитации.
Отсутствие экспериментальных данных, поддерживающих стандартный подход к кван¬
товой гравитации, привело к забавной ситуации в современной фундаментальной теорети¬
ческой физике. Возникло общее мнение, что достижение реального прогресса за рамками
стандартных моделей физики элементарных частиц (и космологии) и, следовательно, более
глубокого понимания устройства Вселенной требует наличия квантовой теории, охватыва¬

840
Глава 34
ющей гравитацию наряду с сильным, слабым и электромагнитным взаимодействием. Ча¬
стично это связано с концепцией (несомненно, физически оправданной), согласно которой
конечная (а не просто перенормируемая) квантовая теория поля потребует, чтобы расходи¬
мости «обрезались» на крайне малых планковских расстояниях, а это с необходимостью
сделает гравитацию частью общей картины (см. §31.1). Но поскольку экспериментов в этой
области нет, усилия теоретиков направлены исключительно во внутренний мир математиче¬
ских устремлений.
34.2* Фундаментальная физика, движимая математикой
Взаимосвязь между математическими идеями и физическим поведением звучала у нас
постоянной темой. Во всей истории физической науки прогресс достигался при нахождении
правильного баланса между структурами, устремлениями и открытиями математической те¬
ории, с одной стороны, и наблюдениями за проявлениями физического мира, обычно путем
тщательно поставленных экспериментов, с другой стороны. При отсутствии руководящих
указаний со стороны эксперимента, как в случае большинства современных фундаменталь¬
ных. исследований, такой баланс нарушается. Математическая последовательностьf34-^ — это
далеко не достаточный критерий того, что мы находимся «на правильном пути» (а зачастую
не выполняется даже это, вроде бы необходимое, требование). Математические эстетиче¬
ские соображения при этом играют гораздо большую роль, чем обычно. Исследователи
часто ссылаются на успехи Дирака, Шредингера, Эйнштейна, Фейнмана и многих других,
которые в значительной мере руководствовались эстетической привлекательностью выдви¬
гаемых ими теоретических идей. Я считаю, что не следует отрицать значение таких эстетиче¬
ских соображений, которые играют чрезвычайно важную роль при отборе правдоподобных
вариантов новых фундаментальных физических теорий.
Эстетические оправдания такого рода иногда просто выражают потребность в мате¬
матически последовательной схеме, поскольку математическая красота и математическая
последовательность, в самом деле, тесно связаны. Мне кажется, что необходимость мате¬
матической последовательности для всякой предложенной физической модели не требует
доказательств. Кроме того, в отличие от множества эстетических критериев, математиче¬
ская последовательность имеет то преимущество, что это есть качество сугубо объективное.
Трудности, связанные с эстетическими обоснованиями, как раз и заложены в их крайне
субъективном характере.
Однако сама математическая последовательность не всегда легко распознается. Те, кто
долго и упорно работает с некоторым набором математических идей, могут лучше вос¬
принимать тонкое и зачастую неожиданное единство, лежащее в основе некоторой схемы.
Те же, кто пришел «со стороны», порой взирают на эту схему с некоторым замешательством,
и им нелегко понять, почему такое-то свойство оказывается полезным и почему некоторые
стороны теории следует рассматривать как более удивительные (и потому, возможно, более
красивые), нежели остальные. Но вполне возможно и обратное, когда составить объектив¬
ное мнение лучше удается именно пришедшему извне, тогда как тот, кто много лет был
сосредоточен на узком круге математических проблем, возникших в рамках некоторого
определенного подхода, приходит к неверным суждениям!
Однако математическая последовательность и изящество математического аппарата фи¬
зической теории, при всем их несомненном значении, все же далеко не достаточны. Обычно
гораздо важнее физические соображения. Но в ситуациях, когда отсутствует направляющее
влияние эксперимента, начинают играть более важную роль математические качества тео¬
рии. Я отнюдь не утверждаю, что на эти вопросы существуют простые ответы. Я полагаю,
что отдельные исследователи вправе следовать своим эстетическим побуждениям. Но им не
следует удивляться, если окажется, что некоторые их коллеги совершенно равнодушны к тем

34.2. Фундаментальная физика, движимая математикой
841
замечательным, по их мнению, выводам, к которым эти побуждения их привели. Я рассмат¬
риваю эстетическую мотивацию как существенную часть развития любых важных новых
идей в теоретической науке. Но без ограничений со стороны эксперимента и наблюдений
такая мотивация порой уводит теорию далеко от физической реальности.
Из истории известно много примеров, когда красивая математическая схема, сулящая
на первый взгляд новый революционный путь к раскрытию тайн Природы, в дальнейшем
этих надежд не оправдывала. Хорошим примером может служить система кватернионов с ее
привлекательным свойством формировать алгебру с делением. Как было описано в § 11.2,
открыв кватернионы в 1846 году, Гамильтон посвятил оставшиеся 22 года жизни попыткам
представить законы Природы исключительно в рамках этой схемы. Однако эта «чисто-
кватернионная» работа (я имею в виду первоначальную систему кватернионов с их свой¬
ством образования алгебры с делением) оказала весьма слабое непосредственное влияние на
дальнейшее развитие основ физической науки. В то же время влияние других работ Гамиль¬
тона было поистине огромным и вполне непосредственным. Его более ранние исследования
того, что мы нынче называем «гамильтонианами», «принципом Гамильтона», «уравнением
Гамильтона-Якоби» и т.д., позволили увидеть аналогию между ньютоновскими частицами
и волнами, что стало поворотным пунктом в развитии квантовой механики и квантовой
теории поля в XX веке (см. §§20.2, 23.1, 21.2). Однако кватернионы оказали на физику кос¬
венное влияние — в виде обобщений, в которых свойство формировать алгебру с делением
никак не использовалось.
В середине XIX века было, наверное, очень легко увлечься прекрасным свойством ква¬
тернионов делиться друг на друга (§ 11.1). Это удивительное свойство, присущее кватерни¬
онам и сравнительно немногим другим алгебрам, оказало значительное влияние на чистую
математику, но не повлияло непосредственно на развитие основной линии физики. Долж¬
но было последовать клиффордово обобщение кватернионов на большее число измерений
с более поздними идеями Паули и особенно Дирака, в которых была использована лоренце¬
ва сигнатура, характерная для пространства-времени, чтобы стало возможным достигнуть
успеха в физической теории (см. §§ 11.5, 24.6, 24.7). Однако красивое свойство делимости,
так привлекавшее Гамильтона, здесь не понадобилось!
К несколько загадочному вопросу о красоте математики, которая приводит к успеху
в физике, я еще вернусь в §§34.9. Но этот вопрос касается важной и интересной пробле¬
мы математического «кругооборота». Даже во времена древних греков теории, начавшись
с описания поведения реального мира, порождали обширную область красивой математи¬
ки, изучаемую сначала ради ее самой, которая затем часто находила применения, далекие
от той физики, из которой она возникла. Иногда эти применения были реализованы через
много столетий (так произошло с теорией конических сечений, созданной Аполлонием за
200 лет до нашей эры, которая сыграла фундаментальную роль в понимании движений пла¬
нет, достигнутом Кеплером и Ньютоном в XVI и XVII веках, и с «малой теоремой» Ферма
1640 года, нашедшей важное применение в криптографии в конце XX века). Математика —
особенно красивая математика — имеет обыкновение находить применение в совершенно
различных областях, и в этом одна из причин ее силы и прочности. Деятельность Приро¬
ды часто оказывается удивительным источником подобных математических идей. Точность
и надежность этих идей, вдохновленных Природой, вероятно, не покажется такой удивитель¬
ной, если принять, что Природа действует в полном согласии с законами математики. Более
замечательна тонкость математики, которая, по-видимому, заключена в законах Природы,
и ее способность находить применение в областях, далеко отстоящих от первоначальной
цели (как было, например, в случае с математическим анализом Ньютона и Лейбница —
см. главу 6).
Но можем ли мы утверждать обратное — что гипотетическая физическая теория, по¬
рождающая множество продуктивных исследований в широко разбросанных областях ма¬

842
Глава 34
тематики, уже в силу этого приобретает физическое правдоподобие? Этот вопрос особенно
актуален в отношении физических схем, изложенных в главах 31, 32 и 33. Мне представля¬
ется, что на него нет простого ответа, однако думать над ним определенно стоит.
В частности, теория струн стимулировала ряд красивых математических работ и приоб¬
рела значительную прочность благодаря своей математической привлекательности. (То же
можно сказать о большей части теории твисторов и о подходах, предложенных Аштека-
ром и Хокингом.) Однако остается неясным, в какой мере это свидетельствует о ее связи
с физической реальностью. Тем не менее я часто слышал, как «чистые» математики выра¬
жали уверенность в том, что некоторый результат, который им удалось получить, должен
найти применение в физике, просто на том основании, что его математическая структура
близка к теории струн! Я вполне могу понять мечтания многих чистых математиков, что
разные аспекты их прекрасной науки найдут важное применение при объяснении устройства
физического мира. Однако следует ясно понимать, что (пока) нет достаточных эксперимен¬
тальных оснований считать, что теория струн (в частности) есть истинная физика, хотя она,
несомненно, порождена мощными физическими устремлениями. Теорией струн занимается
порядочное количество физиков, но делает ли это ее физикой? Здесь возникает вопрос о роли
моды в фундаментальных физических исследованиях, и далее я хотел бы им заняться.
34.3.	Роль моды в физической теории
Начну с исследования, проведенного Карло Ровелли и изложенного в его послании
Международному конгрессу но общей теории относительности и гравитации, проходившему
в Пуне (Индия) в 1997 году^34,61 Ровелли был одним из инициаторов применения метода
петлевых переменных к квантовой гравитации (как описано в §32.4), и он предупредил,
что данное его исследование не является профессиональнььм. Тем не менее полученные
им результаты вполне отражали мои собственные интуитивные ожидания. Он подсчитал
число статей по квантовой гравитации, опубликованных за предыдущие годы, по данным
Лос-Анджелесского архива. Среднее число статей в месяц, распределенных по различным
подходам к проблеме, выглядело следующим образом:
Читатель может почувствовать, что я не слишком следую требованиям моды, по тому
вниманию, которое я уделил в этой книге перечисленным теориям. (Я лишь кратко кос¬
нулся квантовой теории поля в искривленном пространстве в связи с эффектом Хокинга,
обсуждавшимся в § 33.1. Решеточные методы предполагают дискретное (а не непрерывное)
пространство-время —см. §33.1. Особенности евклидовой квантовой гравитации в связи
с подходом Хокинга обсуждались в § 28.9. Квантовая космология использует упрощенные
модели пространства-времени, в которых игнорируется большинство гравитационных степе¬
ней свободы. Другие перечисленные подходы обсуждались в главах 31-33.) Можно заметить,
Теория струн
Квантовая гравитация в петлевых переменных
Квантовая теория поля в искривленном пространстве
Решеточные методы
69
25
8
Евклидова квантовая гравитация
Некоммутативная геометрия
Квантовая космология
Твисторы
Прочее
3
3
1
1
6

34.3. РОЛЬ МОДЫ В ФИЗИЧЕСКОЙ ТЕОРИИ
843
что теории струн посвящено больше статей, чем всем остальным подходам вместе взятым.
По общему мнению, если бы такой подсчет был проведен сегодня, то перевес теории струн
оказался бы еще большим. Если бы в науке мы руководствовались принципами демократии,
то абсолютное большинство голосов, полученных «струнными» теоретиками, позволило бы
им диктовать, какого рода исследования следует проводить! !34,71
К счастью, научные критерии не подчиняются принципам демократии. Результаты ра¬
боты меньшинства исследователей не должны отвергаться только потому, что они в мень¬
шинстве. Куда важнее математическая последовательность и согласие с результатами наблю¬
дений. Но можно ли вообще игнорировать капризы моды? Определенно, нет. В дополнение
ко многим менее правдоподобным идеям, весьма модным в свое время (примером может
служить 11 -мерная супергравитация с семью дополнительными измерениями, образующи¬
ми «сплющенную 7-сферу»!34,8!), я могу вспомнить много модных направлений в прошлом,
которые мне казались (и продолжают казаться) содержащими важные истины (например,
траектории Редже (см. §31.5) и аналитическая S-матрица Джеффри Чу f34*93), но спустя де¬
сятилетия вышли из моды. В некоторой степени популярность теории определяет меру ее
научного правдоподобия — но лишь в некоторой степени.
Верно также, что большое имеет естественную тенденцию становиться еще больше за
счет меньшего (так, например, обстоит дело с бизнес-концернами). Нетрудно понять, почему
это должно относиться и к научной моде, особенно в наш век реактивной авиации и Интер¬
нета, когда новые научные идеи быстро распространяются по всему миру как в устном виде
на научных конференциях, так и почти мгновенно посредством электронных писем и науч¬
ных статей, помещаемых в Интернет (зачастую без всякого рецензирования). Часто жесткая
конкуренция, порождаемая этой легкостью связей, создает у исследователей «эффект ухо¬
дящего поезда», боязнь оказаться отставшим. Мода не оказывает большого влияния там,
где теоретические идеи постоянно проходят проверку экспериментом. Но в отношении тех
идей, которые, подобно квантовой гравитации, далеки от возможности экспериментального
подтверждения или опровержения, мы должны быть особенно бдительны, чтобы не принять
популярность за подтверждение правильности.
Мода играет также определенную роль в таких вопросах, как выбор обозначений и ма¬
тематического формализма. Это, возможно, не такие важные вопросы, как рассмотренные
выше, но они тоже существенны для развития исследований. Укажу один частный пример —
предпочтение, оказываемое 4-компонентному спинорному формализму Дирака перед бо¬
лее поздним 2-компонентным формализмом Ван-дер-Вардена (см. §§22.8, 24.7, 25.2). Здесь
кроется некоторая ирония. В квантовой электродинамике 4-спинорный формализм исполь¬
зуется почти повсеместно, хотя, как было показано Робертом Герочем!34,10!, 2-спинорный
формализм (кратко описанный в §22.8) гораздо проще. Когда Дирак в 1928 году открыл
свое уравнение, он использовал 4-спиноры. Уравнение Дирака возбудило большой интерес
к изучению спиноров, и годом позже выдающийся голландский математик Бартель Ван-
дер-Варден сформулировал мощный аппарат 2-спинорного исчисления!34,11!. Однако возбу¬
ждение, вызванное открытием Дирака, привело к тому, что большинство физиков, следуя
оригинальному подходу Дирака, даже не познакомилось с более гибким и изящным форма¬
лизмом Ван-дер-Вардена. Тем не менее сам Дирак, по-видимому, признал в конечном счете
мощь формализма Ван-дер-Вардена. В начале 1950-х годов я посещал лекции Дирака, в ко¬
торых он дал прекрасное введение в 2-спинорное исчисление, сделав этот предмет в целом
вполне ясным для меня, тогда как в обзорах, которые я видел до того, этот вопрос был
безнадежно запутан.
Сам Дирак воспользовался в 1936 году 2-спинорным формализмом, чтобы обобщить
свое уравнение для электрона на частицы с более высоким спином!34,12!. Однако другие ис¬
следователи, будучи не в ладах с 2-спинорным формализмом, воспроизвели частные случаи
уравнений Дирака для высших спинов, которые ныне известны как уравнение Даффина-

844
Глава 34
Кеммера - Петью (1936-1939) для спинов 0 и 1 и уравнение Рариты - Швингера (1941) для
О
спина И именно их работы в этой области (использующие тензорные и 4-спинорные
методы) обычно цитируются вместо более ранней работы Дирака.
Дирак не был поклонником моды и, по-видимому, не всегда следовал даже той моде,
которую установил он сам! Тем не менее другие иногда оказывались увлечены ею помимо
своего желания. Я столкнулся с примером этого, когда в середине 1970-х годов посетил
ЦЕРН, чтобы побеседовать с Бруно Зумино, одним из авторов некоторых основных идей
суперсимметрии. (Его работа 1974 года (в соавторстве с Юлиусом Вессом)^34-13^ установила
определенную связь с теорией твисторов, и я хотел воспользоваться этим.) Он сказал мне,
что признает мощь 2-спинорного формализма и что однажды написал статью, в которой
использовал 2-спиноры для формулировки некоторой своей идеи. Однако, рассказал он, че¬
рез несколько месяцев после этого уважаемый физик Абдус Салам выдвинул ту же идею,
но с использованием 4-спиноров. И все потом цитировали работу Салама, и никто не ссы¬
лался на него. Зумино заключил, что впредь он не сделает ошибки, используя (технически
более совершенный) 2-спинорный формализм!
С этим связана другая причина, по которой исследователям, особенно молодым, при
всем желании трудно отойти от модного направления. Она состоит в необычайной сложно¬
сти тех математических идей, с которыми приходится сталкиваться в современной математи¬
ческой физике. Довольно трудно выделить небольшую часть некоторого определенного на¬
правления работы и постараться освоить ее. Провести сравнительное изучение преимуществ
того или иного направления большинство молодых исследователей не в состоянии. Если они
должны сделать выбор, им приходится опираться на опыт и предпочтения уже состоявшихся
исследователей, и это лишь поддерживает модные направления за счет менее известных.
Высказанные замечания относились к теоретическим исследованиям, не испытываю¬
щим ограничений со стороны эксперимента, однако элемент моды не чужд и самому экс¬
перименту, хотя и по другой причине. Это связано в основном с огромной стоимостью экс¬
периментов на переднем крае фундаментальной физики. В силу дороговизны большинства
таких экспериментов они обычно требуют финансовой поддержки со стороны правительства
или крупных коммерческих организаций, и потому возникает потребность в многочислен¬
ных комиссиях, призванных решать, следует ли ставить данный эксперимент, или выбирать,
какой из экспериментов лучше поставить в условиях ограниченности фондов. Естественно,
что представителями науки в таких комиссиях оказываются именно те люди, которые при¬
обрели известность, участвуя в разработке тех идей, которые в данный момент считаются
перспективными. Поэтому они будут выступать в поддержку экспериментов, направленных
непосредственно на решение тех вопросов, которые кажутся естественными в рамках этих
идей. Это создает для теории угрозу оказаться «запертой» в узком круге определенных на¬
правлений. По этим причинам всякое существенное изменение направления развития дается
с большим трудом.
34.4.	Можно ли экспериментально опровергнуть неверную теорию?
Кто-нибудь может сказать, что во всем этом нет реальной опасности. Если направ¬
ление развития теории выбрано неверно, то эксперимент опровергнет его, и должно будет
появиться некоторое новое направление. Таково традиционное представление о том, как раз¬
вивается наука. Действительно, широко известный специалист по философии науки Карл
Поппер выдвинул вроде бы разумный критерий[34.14] науЧНОй приемлемости предлагаемой
теории в виде принципа экспериментальной опровергаемости. Однако я боюсь, что это че¬
ресчур строгий критерий и определенно слишком идеалистический взгляд в современном
мире «большой науки».

34.4. МОЖНО ЛИ ЭКСПЕРИМЕНТАЛЬНО ОПРОВЕРГНУТЬ НЕВЕРНУЮ ТЕОРИЮ?
845
Возьмем пример с суперсимметрией в современной физике элементарных частиц.
Эта математически изящная теоретическая идея облегчает жизнь теоретикам, когда речь идет
о построении перенормируемой квантовой теории поля (§31.2). Более важно то, что она яв¬
ляется центральным пунктом теории струн. Ее влияние на теоретиков сегодня столь велико,
что ее рассматривают почти как «стандартную» модель физики элементарных частиц. В то
же время она пока не получила никакой (серьезной) экспериментальной поддержки (§31.2).
Эта теория предсказывает существование «суперпартнеров» для всех наблюдаемых фунда¬
ментальных частиц Природы, но ни один из них до сих пор не наблюдался. По мнению
теоретиков, приверженных суперсимметрии, причина заключена в механизме нарушения
симметрии (неизвестной природы), из-за которого суперпартнеры имеют столь большую
массу, что энергия, необходимая для их образования, пока лежит за рамками возможно¬
стей современных ускорителей частиц. При расширении этих рамок суперпартнеры будут
обнаружены, и это станет поворотным пунктом в развитии физической теории с важными
применениями в будущем. Но предположим, что суперпартнеры так и не будут обнаруже¬
ны. Опровергнет ли это идею суперсимметрии? Вовсе нет. Можно заявить (и скорее всего,
будет заявлено), что был проявлен слишком большой оптимизм в отношении малой степени
нарушения симметрии и что для обнаружения отсутствующих супер партнеров нужны еще
более высокие энергии.
Мы видим, что вытеснить популярную идею, пользуясь традиционным научным ме¬
тодом решающего эксперимента, не так легко, даже если идея ошибочна. Огромная стои¬
мость экспериментов с высокими энергиями также существенно затрудняет проверку тео¬
рии. В физике элементарных частиц есть много других теоретических моделей, в которых
предсказываемые частицы имеют массу-энергию, слишком большую, чтобы было возмож¬
но экспериментальное опровержение. Различные варианты теории Великого объединении
или теории струн содержат много таких «предсказаний», которые по указанной причине
надежно защищены от опровержения.
Приводит ли «непопперовский» характер таких моделей к их неприемлемости в каче¬
стве научных теорий? Я полагаю, что строгий критерий Поппера слишком суров. В качестве
яркого примера напомню утверждение Дирака (§28.2), что если бы где-то в космосе суще¬
ствовал один-единственный магнитный монополь, то это позволило бы объяснить тот факт,
что каждая частица во Вселенной имеет электрический заряд, кратный некоторому фиксиро¬
ванному значению (как это и наблюдается в действительности). Теория, которая утверждает,
что такой монополь существует где-то, является сугубо непопперовской. Эта теория мог¬
ла бы быть подтверждена открытием такой частицы, но она оказывается неопровержимой
с точки зрения критерия Поппера, ибо если теория неверна, то, независимо от того, как дол¬
го продолжались безуспешные поиски экспериментаторов, их неспособность обнаружить
монополь никак не опровергнет теорию! f34 15^ Тем не менее теория определенно является
научной, вполне заслуживающей серьезного рассмотрения.
Аналогичное утверждение можно сделать в отношении космологии. Область Вселен¬
ной за горизонтом для частиц (§ 27.12) недоступна для непосредственного наблюдения. Тем
не менее разумно выглядит предположение, что эта область должна быть в широком мас¬
штабе подобна непосредственно наблюдаемой области. Теория, в которой ненаблюдаемая
область напоминает область, доступную для наблюдения (а это предположение входит со¬
ставной частью в стандартную космологическую модель (§ 27.11) в отличие от большинства
инфляционных схем (§ 28.4)), не может быть опровергнута наблюдениями.
Более того, даже если ограничиться непосредственно наблюдаемой частью Вселенной,
можно задаться вопросом, какую кривизну имеет пространственная геометрия, предполага¬
емая однородной и изотропной в широком масштабе, — положительную, отрицательную или
нулевую (соответственно К > О, К < 0 или К = 0; см. §27.11). Если наша теория утвер¬
ждает, что К — 0, то это может быть опровергнуто наблюдениями, поскольку при любом

846
Глава 34
конечном отклонении от плоской пространственной метрики достаточно точное наблюде¬
ние может (в принципе хотя, возможно, и не на практике) обнаружить такое отклонение, как
бы ни мала была пространственная кривизна. Если же наша теория предполагает К ф О,
то такая теория не может быть опровергнута, если в действительности К = 0, посколь¬
ку при наблюдениях всегда существует некоторая область неопределенности, допускающая
очень малую отрицательную или положительную кривизну пространства. Заметим, что слу¬
чай К > 0 в принципе можно отвергнуть, если в действительности К < 0, а случай К < О
можно исключить, если в действительности К > 0. С другой стороны, модель с К = 0
не может быть (непосредственно) подтверждена^341б1? тогда как случай К ф 0 можно
подтвердить наблюдениями (если Вселенная действительно такова). Таким образом, утвер¬
ждения К > 0 и К < 0 удовлетворяют критерию Поппера в ограниченном смысле: они
могут быть опровергнуты лишь при определенных условиях и не могут быть отвергнуты,
если в действительности К — 0; в то же время они могут быть подтверждены. Заметим, что
модель с К — 0 полностью удовлетворяет в принципе критерию Поппера, но не является
подтверждаемой!
Я не уверен, что критерий Поппера дает нам что-то в отношении этих различных вари¬
антов. Мне представляется очевидным, что каждое из утверждений К > 0, К < 0 я К = 0
«одинаково научно», несмотря на тонкие различия в их отношении к критерию Поппера.
И в любом случае большинство космологов не станет педантично придерживаться той ли¬
нии, согласно которой предполагается, что равенство К = 0 выполняется точно. Правильная
теория будет в лучшем положении, если ей доведется предсказать К > 0 или К < 0, по¬
скольку тогда у нее будет шанс оказаться подтвержденной наблюдениями (и подтверждение
будет вполне научным, несмотря на отрицательное заключение критерия Поппера в отно¬
шении ее научной приемлемости). Теории, предсказывающей К == 0, понадобятся другие
подтверждения, чтобы оказаться приемлемой.
Одно из таких подтверждений может состоять в том, что К = 0 получается как ре¬
зультат некоторой теории, которая получает экспериментальное подтверждение каким-то
иным путем. Такую ситуацию провозглашает весьма модная инфляционная космология,
обсуждавшаяся в § 28.4. Напомним, что подобно тому как суперсимметрия оказалась «по¬
чти» частью стандартной модели физики элементарных частиц, инфляционную космологию
часто рассматривают почти как составную часть современной «стандартной» космологи¬
ческой модели! Попробуем установить статус инфляции по отношению к попперовскому
критерию опровергаемости.
Можно было бы решить, что ситуация ясна и что инфляция — это теория как раз
в духе Поппера. Более десятка лет утверждалось, что вариант К — 0 есть одно из след¬
ствий идеи инфляции^34,17], и я помню многочисленные лекции сторонников инфляцион¬
ной теории, в которых делались такие предсказания^34’18^. Таким образом, если наблюде¬
ния дадут убедительные свидетельства, что К ф 0, то инфляция оказывается вне игры!
Это настолько точно соответствует принципу Поппера, насколько возможно. Делались так¬
же некоторые детальные предсказания относительно фонового микроволнового излучения,
обусловленного инфляцией (вместе с некоторыми другими предположениями), и это, ка¬
залось бы, дает существенную экспериментальную поддержку, в частности, в отношении
наблюдаемой масштабной инвариантности флуктуаций, согласующейся с ожиданиями ин¬
фляционной теории. Однако в середине 1990-х годов начали появляться свидетельства со
стороны различных независимых наблюдений, что средняя плотность материи Qd во Все¬
ленной (барионов плюс темной материи) меньше, чем должно быть в полностью плос¬
ком пространстве, составляя примерно одну треть требуемого значения. (Плотности Qd
и Qa, определяются как доля критической плотности, т. е. плотности при К = 0 в эйн¬
штейновской теории без космологического члена; см. §28.10.) В частности, Qd соответ¬
ствует примерно 0,3. В соответствии с наблюдениями, теоретики-инфляционисты начали

34.4. МОЖНО ЛИ ЭКСПЕРИМЕНТАЛЬНО ОПРОВЕРГНУТЬ НЕВЕРНУЮ ТЕОРИЮ?
847
предлагать инфляционные модели, которые теперь допускали возможность К ф 0, а фак¬
тически К < OJ34*19! Вдобавок можно заметить, что школа Хокинга, которая вроде бы
определенно предсказывала К > 0 (в соответствии с гипотезой «отсутствия границ» Харт-
ла-Хокинга — см. §28.9), также начала пробовать приспособить вариант К < 0 к сво¬
ей схеме ^34,201.
Так продолжалось до 1998 года, когда наблюдения за отдаленной сверхновой (§28.10)
показали, что в уравнение Эйнштейна следует ввести положительную космологическую
постоянную (А > 0). Это вносит дополнительную эффективную плотность Дд, которая
вместе с плотностью материи fid дает критическую полную плотность fid + Дд = 1 (или
вместо этого fla + Дл > 1, как требует первоначальный вариант гипотезы Хартла- Хо¬
кинга). При этом вариант полностью плоского пространства (К = 0) можно согласовать с
результатами наблюдений при Q а «0,7. Перед лицом этого большинство инфляционистов
вернулось к варианту К — 0, предсказываемому инфляционной космологией. Я не уверен,
что Поппер смог бы что-нибудь сказать обо всем этом!
Сейчас появилось экзотическое предложение инфляционистов с введением нового ин¬
гредиента (нового поля), называемого «квинтэссенцией», который определяет некоторую
эффективную космологическую постоянную через динамическую «темную энергию» с от¬
рицательным давлением (см. [746]). Было заявлено, что это может означать наступление но¬
вой фазы инфляции (см. § 28.10)! Остается надеяться, что подобные фантастические предло¬
жения удастся быстро проверить путем наблюдений, хотя на практике так получается далеко
не всегда.
Я считаю, что к заявлениям такого рода следует относиться с исключительной осторож¬
ностью, даже если они вроде бы подтверждаются добротными экспериментами, поскольку
последние зачастую анализируются с точки зрения модной теории. Например, замечатель¬
ные наблюдения микроволнового фона в ходе эксперимента BOOMERANGf34-21] первона¬
чально интерпретировались в основном с позиций инфляционной теории, и делались уве¬
ренные заявления, что результаты соответствуют варианту К — 0 (откуда следует А > 0).
Более того, в некоторых экспериментах (как и в BOOMERANG) с большим массивом данных
и с широким выбором метода анализа необработанные данные могут оставаться неопубли¬
кованными в течение нескольких лет, чтобы люди, причастные к этому, могли первыми
воспользоваться ими (что вполне естественно). В этот период маловероятно, чтобы ре¬
зультаты анализировались с какой-то иной точки зрения, В конкретном случае программы
BOOMERANG реальный доступ к данным имели Ваха Гурзадян и несколько членов его
группы; они применили свой метод анализа эллиптичности (§ 28.10) и получили непосред¬
ственное свидетельство в пользу варианта К < 0 (впоследствии подтвержденное анализом
результатов эксперимента WMAP). Подобно «аномальным» результатам WMAP с £ = 2
(по странности скрытым вертикальной осью на рис. 28.19) это не слишком согласуется с
позицией инфляционистов. Прежде чем делать какой-либо вывод в отношении всего этого,
подождем, пока пыль рассеется!
Мы видим, сколь сильно может влиять научная мода на направление теоретических
исследований, несмотря на традиционные протесты со стороны ученых, объективно под¬
ходящих к предмету. Тем не менее я должен твердо заявить, что кажущаяся потеря объек¬
тивности не присуща самой Природе. Вне нас существует объективный физический мир,
и физики справедливо видят свою задачу в том, чтобы раскрыть его природу и объяснить
его поведение. Кажущаяся субъективность, которую мы видим в описанном выше сильном
влиянии моды, вызвана лишь тем, что в своих попытках понять этот мир мы идем ощупью,
при этом давление со стороны общественности и финансирующих организаций, а также
вполне понятные человеческие слабости и естественные ограничения играют важную роль
в тех хаотических и зачастую взаимно не согласованных картинах, с которыми мы постоянно
сталкиваемся.

848
Глава 34
34.5.	Откуда ожидать следующую физическую революцию?
Я сознаю, что в этой главе мною представлена несколько более пессимистическая кар¬
тина современного прогресса фундаментальной физики, чем это обычно принято в популяр¬
ных изданиях. Но я считаю при этом, что она гораздо более реалистична. Вместе с тем я не
хотел бы утверждать, как некоторые популяризаторы ^34‘22], что мы достигли такой стадии,
когда фундаментальный прогресс уже почти невозможен. Действительно, имеется огромное
количество данных наблюдений, которые необходимо осмыслить, — даже в том случае, если
никаких новых экспериментов больше проводиться не будет.
Данные современных экспериментов часто накапливаются автоматически, и обычно
лишь небольшая часть накопленной информации может представлять интерес для теорети¬
ков и экспериментаторов, непосредственно участвующих в этой работе. Поэтому вся масса
данных будет, скорее всего, анализироваться лишь под определенным углом зрения, чтобы
получить ответ на поставленные вопросы. Вполне возможно, что в таких данных кроется
много ответов на загадки Природы, даже если пока мы и не прочитали их как следует.
Вспомним, что общая теория относительности Эйнштейна основана исключительно на его
умозаключении (принципе эквивалентности; см. § 17.4), которое в неявном виде содержа¬
лось в данных наблюдений, известных со времен Галилея (и даже раньше), но не осмыслен¬
ных должным образом. Очень может быть, что в несравненно более обширных результатах
современных наблюдений скрыты другие разгадки. Не исключено, что они вполне «оче¬
видны», лежат перед самыми нашими глазами, нужно только взглянуть с другой стороны
и под другим углом зрения, чтобы открылась принципиально новая перспектива на природу
физической реальности.
Я убежден, что новый взгляд совершенно необходим и что изменение точки зрения
заставит обратиться к проблеме парадокса измерения в квантовой механике и связанной
с ним нелокально ста, присущей ЭПР-эффектам и «квантовому перепутыванию» (главы 23
и 29). В главе 30 я отмечал, что парадокс измерения должен быть глубоко взаимосвязан
с принципами общей теории относительности (и особенно с только что упомянутым прин¬
ципом эквивалентности Галилея-Эйнштейна). Возможно, новые эксперименты (например,
FELIX или более реалистические наземные варианты; см. §30.13) могут привести к луч¬
шему пониманию квантовой теории. Не исключено, что на природу квантовой гравитации
прольют свет и эксперименты другого типа (например, те, что предлагались для проверки
возможности существования дополнительных измерений пространства-времени). С другой
стороны, нас могут продвинуть вперед и какие-то теоретические соображения.
Содержатся ли уже семена будущего успешного развития теории в некоторых из тех
идей, которые были изложены в предыдущих главах этой книги? Ясно, что здесь возможны
самые разные точки зрения, и любой ответ будет сильно зависеть от личных пристрастий.
У меня лично была (и остается вот уже более 40 лет) надежда, что необходимое изменение
физической точки зрения удастся обрести в рамках теории твисторов. Однако, несмотря на
определенный прогресс (см. главу 33), при нынешнем положении дел нельзя сказать, что
теория твисторов сумела существенно приблизить нас к разрешению парадокса измерения.
Независимо от мнения относительно достоинств тех или иных из описанных теорий,
определенно необходимы новые взгляды и новые прозрения. Как они возникнут? Можно
ли ждать появления «нового Эйнштейна», который, работая в уединении, придет к таким
революционным взглядам исключительно в результате глубоких размышлений? Или мы
снова окажемся вовлеченными в экспериментальные поиски, то и дело заводящие в ту¬
пик? В случае Альберта Эйнштейна его размышления привели в конечном счете к общей
теории относительности, которая в высокой степени является «теорией одного человека»
(несмотря на существенный импульс, полученный Эйнштейном от Лоренца, Пуанкаре, Ма¬
ха, Минковского, Гроссмана и других). Квантовая теория, напротив, была «теорией многих

34.5. Откуда ожидать следующую физическую революцию?
849
людей» и развивалась иод давлением извне, со стороны необычных результатов многих
замечательных экспериментов. При нынешнем климате фундаментальной науки добиться
значительного прогресса отдельной личности намного труднее, чем во времена Эйнштей¬
на. Коллективная работа в общей команде, массивы компьютерных вычислений, погоня за
научной модой — всё это мы видим в современной науке. Можно ли ожидать, что сре¬
ди этой бурной деятельности можно будет разглядеть необходимые фундаментально новые
перспективы? Поживем — увидим, но у меня на этот счет остаются некоторые сомнения.
Возможно, что новые направления появятся в основном под давлением эксперимента, как
в случае квантовой механике в первой трети XX века, и тогда может сработать «многолюд¬
ный» подход. Однако в области квантовой гравитации такое, мне кажется, может произойти,
только если эксперименты обнаружат влияние принципов общей теории относительности
на саму структуру квантовой механики (как об этом говорилось в главе 30). При отсутствии
этого потребуется, скорее, что-то подобное «единоличному» подходу Эйнштейна. Поэтому
я не сомневаюсь, что помимо физической интуиции важной движущей силой должна быть
математическая эстетика.
Моя уверенность основана на том, что по мере углубления в фундамент физического
поведения мы всё больше убеждаемся, что это поведение весьма тонко управляется матема¬
тикой. Более того, математика, как оказывается, имеет характер не просто непосредственных
вычислений, — это есть нечто глубинное, со своими тонкостями и красотами, отсутствующи¬
ми у математики, применяемой на менее фундаментальном уровне физики. В соответствии
с этим, движение к более глубокому физическому пониманию, если оно не может во всех де¬
талях руководствоваться данными эксперимента, должно по возможности прочно опираться
на способность оценивать физическое соответствие и глубину математики и отбирать под¬
ходящие идеи на основе эстетических соображений.
В силу самой природы этой проблемы здесь чрезвычайно трудно предложить сколько-
нибудь надежный критерий. На примере разногласий между подходами, изложенными в по¬
следних хлавах этой книги, мы уже видели, как различные математические разработки,
каждая из которых руководствуется своими собственными эстетическими математическими
и физическим!* критериями, могут увести во взаимно противоположные стороны. Некото¬
рые утверждают, что нам следует искать путь, на котором можно будет объединить все такие
подходы в нечто единое, возможно, соединяя то наиболее ценное, что есть в каждом из них.
С другой стороны, можно резонно возразить, что противоречия между разными подходами
слишком велики, так что выжить может лишь один из них, а остальным суждено быть от¬
брошенными. Сам я подозреваю, что истина лежит где-то посредине и что кое-что важное
может содержаться даже во многих из тех теорий, главные догмы которых со временем
будут отвергнуты.
Некоторые из описанных выше теорий хотя и не вполне согласуются между собой,
имеют некоторую общую основу. В частности, формализм петлевых переменных (глава 32)
имеет много общего с теорией твисторов (глава 33), и я вполне могу представить, что неко¬
торая комбинация идей каждой из них (сюда, вероятно, можно включить спиновые сети,
спиновые пены, теорию п-категорий и даже некоммутативную геометрию) могла бы указать
путь вперед. Однако теория струн в ее нынешнем виде, с ее дополнительными простран¬
ственными измерениями, кажется мне отстоящей слишком далеко от теории твисторов или
теории петлевых переменных, чтобы образовать с ними какой-либо возможный союз. Стру¬
ны сами по себе не причина такой несовместимости (§31.5). Даже суперсимметрия была
объединена с твисторными идеями I34-23!. Однако приверженность теории струн введению
лишних измерений (особенно таких размерностей и сигнатур, которые нарушают голоморф¬
ную философию теории твисторов, — см. последний абзац § 33.4) создает фундаментальный
конфликт с теориями твисторов и петлевых переменных. Вплоть до последнего времени
«струнные» теоретики не проявляли склонности к построению согласованной (1 + 3)-мерной

850
Глава 34
теории. Однако, как упоминалось в §§ 31.18,33.14, недавно это было сделано, и теперь необ¬
ходимо серьезно рассмотреть применение идей теории струн к обычному (1 + 3)-мерному
пространству-времени.
34.6.	Что есть реальность?
Как мог понять из всего изложенного читатель, я считаю, что мы пока не нашли «путь
к реальности», несмотря на необычайный прогресс, достигнутый за более чем два с поло¬
виной тысячелетия, а особенно за последние несколько столетий. Определенно необходимы
некоторые принципиально новые сдвиги в понимании. Некоторые читатели могут даже
считать, что этот путь может оказаться миражом. Действительно, могут они сказать, нам по¬
везло натолкнуться на математические схемы, которые находятся в замечательном согласии
с Природой, однако единство Природы как целого с некоторой математической схемой мо¬
жет оказаться всего лишь пустой фантазией. Другие могут назвать такой фантазией само
понятие «физической реальности» с подлинно объективной Природой, не зависящей от того,
каким образом мы ее рассматриваем.
В самом деле, можно спросить: что такое физическая реальность? Этот вопрос был
поставлен тысячи лет назад, и в течение веков философы по-разному пытались на него
ответить. Сегодня, оглядываясь назад с высот современной науки, мы предпочитаем занять
более трезвую позицию. Вместо того, чтобы пытаться ответить на вопрос «что такое?»,
большинство современных физиков старается обойти его. Эти физики заявляют, что вопрос
неправильно поставлен: следует спрашивать не что есть реальность, а как она проявляется.
«Как?» — вот основной вопрос, с которым мы встречались в этой книге: как описываются
законы, управляющие нашей Вселенной и всем, что в ней находится?
Многие читатели, несомненно, сочтут такой вариант неутешительным. Знание того,
как ведет себя содержимое Вселенной, вроде бы не очень много говорит нам о том, что
заставляет его вести себя таким образом. Этот вопрос «что?» тесно связан с другим глубоким
и древним вопросом —«почему?». Почему объекты в нашей Вселенной ведут себя именно
таким образом? Но не зная, что представляют собой объекты, трудно понять, почему они
должны вести себя так, а не иначе.
Современная наука должна проявлять осторожность в попытках ответить на вопро¬
сы «почему?» и «что?». Тем не менее на эти вопросы часто даются ответы. Это считается
приемлемым, если вопросы не затрагивают реальность на ее самых глубоких уровнях. Мож¬
но надеяться получить ответ на вопросы вроде «Из чего состоит молекула холестерина?»,
«Почему спичка загорается, если быстро чиркнуть ею по подходящей шероховатой поверх¬
ности?», «Почему светит солнце?», «Какие силы удерживают вместе частицы в атоме или
молекуле водорода?» или «Почему нестабильно ядро урана?». В то же время некоторые
другие возможные вопросы оказываются более трудными, например, «Что такое электрон?»
или «Почему пространство имеет именно три измерения?». Однако эти вопросы могут
приобрести смысл в рамках некоторой более фундаментальной картины физической реаль¬
ности.
Мы видели, в частности, из обсуждения в главах 31-33, что современные физики неиз¬
менно описывают объекты с помощью математических моделей. Это не зависит от той
позиции, которой они придерживаются. Всё выглядит так, как если бы они искали «ре¬
альность» в платоновском мире математических идеалов. Такой взгляд представляется след¬
ствием гипотетической «теории всего», поскольку тогда физическая реальность оказывается
просто отражением чисто математических законов. Как я уже отмечал в этой главе, нам еще
далеко до такой теории, и будет ли когда-нибудь найдено что-то напоминающее «теорию
всего», — это предмет спора. Как бы то ни было, остается несомненным, что чем глуб¬
же мы проникаем в тайны Природы, тем в большей степени попытки понять их уводят

34.6. Что ЕСТЬ РЕАЛЬНОСТЬ?
851
Ментальный мир
Физический мир
Рис. 34.1. Повторение диаграммы (рис. 1.3), изображающей «Три мира и три великие загадки», с
другими «Платоновыми абсолютами» Красоты и Морали, добавленными к абсолюту Истины, который
надлежит искать в математике. Красота и Истина переплетаются между собой: красота физической
теории служит признаком ее соответствия физическому миру, тогда как весь мир Морали в конечном
счете определяется ментальным миром
нас в платоновский мир математических идеалов. Почему так происходит? Пока это оста¬
ется загадкой. Это первая из трех великих загадок, упомянутых в § 1.4 и проиллюстри¬
рованных на рис. 1.3, который здесь воспроизводится в несколько приукрашенном виде
(см. рис. 34.1).
Но являются ли математические понятия объектами, реально населяющими собствен¬
ный «мир»? Если это так, то в конечном счете мы обнаружим реальность в ее собствен¬
ном доме, расположенном в этом полностью абстрактном мире. Некоторым трудно счи¬
тать математический мир Платона реальным в каком бы то ни было смысле и встать на
ту точку зрения, что сама физическая реальность строится всего лишь из абстрактных
понятий. Моя собственная позиция в этом вопросе такова: следует рассматривать плато¬
новский мир как своего рода «реальность» математических понятий (я пытался внедрить
эту мысль в § 1.3), но не пытаться отождествить физическую реальность с абстрактной
реальностью платоновского мира. Я думаю, что рис. 34.1 наилучшим образом выражает
мою позицию в этом вопросе: каждый из трех миров — платоновский (математический),
физический и ментальный — обладает своим собственным видом реальности и каждый
глубоким и загадочным образом опирается на предшествующий, так что эти миры обра¬
зуют цикл. Мне хочется думать, что платоновский мир в некотором смысле самый при¬
митивный из всех, поскольку математика по самой своей сущности укладывается в рамки
логики. Так или иначе, существует некоторая загадка (или парадокс) в циклической связи
этих миров, при которой каждый из них, казалось бы, способен вобрать в себя последу-
О
ющии во всей его полноте, тогда как сам он зависит лишь от малой доли своего пред¬
шественника.

852
Глава 34
34.7.	Роль ментальности в физической теории
Мы должны иметь в виду, что каждый из «миров» обладает своим собственным спо¬
собом существования, отличным от двух других. Тем не менее я думаю, что в конечном
счете мы не сможем рассматривать любой из этих миров изолированно от остальных. По¬
скольку один из них есть мир ментальности, возникает вопрос о роли разума в физической
теории, а также о том, как проявляется ментальность в физических структурах, с которы¬
ми она связана (такими, как жизнь, бодрствование, мышление). Я намеренно воздержусь
от сколько-нибудь подробного рассмотрения в этой книге проблем, связанных с сознанием,
хотя в конечном счете они должны сыграть важную роль в нашем стремлении познать физи¬
ческую реальность. (Я подробно обсуждал эти проблемы в другом месте и не хотел бы здесь
связываться с многочисленными спорными вопросами, которые неизбежно возникнут ^34,24^)
Тем не менее избежать проблемы ментальности вовсе мне не удастся. Помимо того, что
в соответствии с рис. 34.1 мир ментальности надлежит рассматривать в сочетании с двумя
другими мирами, в этой книге есть несколько мест, где проблема сознания явно или неявно
играет значительную роль в физической теории.
Одно из таких мест посвящено антропному принципу, упомянутому в §27.13 и по¬
дробнее рассмотренному в §§28.6, 28.7. Любая Вселенная, которую «можно наблюдать»,
с логической необходимостью должна поддерживать существование в ней разумной жиз¬
ни, поскольку именно сознание в конечном счете играет роль «наблюдателя». Это фунда¬
ментальное требование может налагать ограничения на физические законы и физические
параметры Вселенной, чтобы в ней могла существовать (и существовала) разумная жизнь.
В соответствии с этим антропный принцип утверждает, что та Вселенная, которую мы изуча¬
ем в качестве разумных наблюдателей, должна управляться такими законами и иметь такие
параметры, которые согласуются с этими ограничениями. Эти ограничения могут прояв¬
ляться в определенных значениях фундаментальных (безразмерных) констант Природы, как
обсуждалось в §31.1. Сейчас стало вполне обычным делом рассматривать наблюдаемые
значения констант как следствие действия антропного принципа.
К сожалению, даже если значения этих констант действительно определяются антроп¬
ным принципом (а не, скажем, математическими соображениями), этим принципом почти
невозможно воспользоваться, поскольку мы слишком мало знаем об условиях, необходимых
для возникновения и существования разумной жизни. Этот принцип почти не применим
к пространственно бесконечной и существенно однородной Вселенной (с К ^ 0), посколь¬
ку в такой Вселенной любая материальная конфигурация, которая могла бы возникнуть
случайным образом, обязательно где-нибудь да возникнет, так что этот принцип допускает
даже самые неблагоприятные условия для разумной жизни (см. §28.6). На мой взгляд, го¬
раздо оптимистичнее выглядит возможность, что фундаментальные константы — это числа,
определяемые математически. Это не создает серьезных проблем с антропным принципом
в пространственно однородной Вселенной.
Совершенно особую роль играет сознание во многих интерпретациях R-части кванто¬
вой механики (они обсуждались в главе 29, в частности, в §§ 29.7, 29.8). Фактически почти
всякая «стандартная» интерпретация квантовой механики предполагает наличие «восприни¬
мающего существа», а значит, требует, чтобы мы знали, что это за существо! Напомним, что
копенгагенская интерпретация (точка зрения (а) в §29.1) рассматривает волновую функцию
не как реальную физическую сущность, а как нечто, существующее «в сознании наблюдате¬
ля». Более того, по крайней мере в одном из своих проявлений эта интерпретация требует,
чтобы измерение было «наблюдением», т. е. проводилось в конечном счете разумным су-
ществом, хотя на практике оно выполняется «классической» измерительной аппаратурой.
Эта зависимость от классической аппаратуры имеет, однако, лишь преходящее значение,
поскольку любой кусок аппаратуры сделан из квантовых элементов, и в действительности

34.7. РОЛЬ МЕНТАЛЬНОСТИ В ФИЗИЧЕСКОЙ ТЕОРИИ
853
он не будет, даже приближенно, вести себя классическим образом, если он следует стан¬
дартной квантовой U-эволюции. (Это всего лишь та же проблема шредингеровской кошки —
см. §§ 29.7-29.9 и §§ 30.10-30.13.) Проблема декогеренции, вызываемой окружением (точка
зрения (в) в §29.1), также может дать лишь временную позицию, поскольку недоступ¬
ность информации, «потерянной в окружающей среде», не означает, что она действительно
потеряна в объективном смысле. Но чтобы эта потеря была субъективной, нам придется
вернуться к вопросу «субъективное восприятие — кем?», что в свою очередь возвращает нас
к проблеме сознания наблюдателя.
В любом случае, даже при наличии декогеренции, создаваемой окружением, если строго
придерживаться U-эволюции как «истинно» квантового описания Вселенной, мы приходим
к представлению о множественности миров (точка зрения (б) в §29.1). Оно явным обра¬
зом зависит от должного понимания того, что представляет собой «разумный наблюдатель»,
поскольку всякая воспринимаемая «реальность» связывается с некоторым «состоянием на¬
блюдателя», так что мы не знаем, какие допустимы состояния реальности (т. е. «миры»), пока
нам не известно, каковы допустимые состояния наблюдателя. Другими словами, поведение
вроде бы объективного мира, которое реально воспринимается, зависит от того, как чье-
то сознание прокладывает себе путь через мириады альтернатив, образующих квантовую
суперпозицию. При отсутствии адекватной теории разумных наблюдателей интерпретация,
основанная на множественности миров, с необходимостью остается принципиально непол¬
ной (см. § 29.8)^34*251
Вариант с согласованными историями (точка зрения (г) в §29.2) также явным обра¬
зом зависит от того, каким может быть «наблюдатель» (в схеме Гелл-Манна-Хартлаi34*26]
вводится понятие систем сбора и утилизации информации). Точка зрения, поддерживаемая
Вигнером (вариант (е) в § 29.2), согласно которой наличие сознания (или, возможно, вооб¬
ще живых систем) может нарушать U-эволюцию, также явным образом подчеркивает роль
разума (или того, что подразумевается под «наблюдателем») в интерпретации квантовой
механики. Насколько я могу понять, к интерпретациям, не связанным обязательно с неко¬
торым понятием «разумного наблюдателя», относятся лишь точка зрения де-Бройля - Бома
(вариант (д) в § 29.2)^34'27^ и большинства тех (вариант (е) в § 29.2), кто требует некоторого
фундаментального изменения правил квантовой механики, при котором U- и R-процедуры
окажутся приближением к некоторой объективной реальной физической эволюции.
Как отмечалось во многих местах этой книги (особенно в главе 30), я придерживаюсь
этой последней точки зрения, согласно которой гравитационные эффекты обеспечивают
объективную R-процедуру (объективную редукцию, ОР), сменяющую U-процесс. Гравита¬
ционная ОР возникает спонтанно и не требует участия какого-либо разумного наблюдателя.
В обычных условиях происходит частое повторение ОР, и это приводит к классическому
миру, который, в качестве отличного приближения, появляется на больших масштабах. По¬
этому нет необходимости привлекать какого-либо разумного наблюдателя, чтобы обеспечить
редукцию квантового состояния (R) при проведении измерения.
С другой стороны, я считаю, что в явлении сознания (которое я рассматриваю как реаль¬
ный физический процесс, происходящий «где-то» в физическом мире) ОР-процесс использу¬
ется фундаментальным образом. Таким образом, моя позиция противоположна упомянутой
выше, в которой ответственным за R-процесс так или иначе оказывается сознание. По моему
мнению, напротив, физически реальный R-процесс (частично) ответствен за сознание! i34-28)
Может ли эксперимент разрешить этот спор? Я полагаю, что может. Прежде всего,
имеются некоторые предположения относительно структуры мозга, которую можно пред¬
ставить в виде А-решетки нейронных микротрубочек, предложенной первоначально Стюар¬
том Хамероффом^34,29! (возможны и другие структуры типа синаптических клатринов^34*30!,
напоминающие молекулы Сбо)> и существует непосредственная возможность подтвердить
или опровергнуть эти конкретные идеи. Такая схема требует существования некоторой

854
Глава 34
крупномасштабной квантовой когерентности, охватывающей значительные области мозга
(и имеющей общие черты с высокотемпературной сверхпроводимостьюf34-31!; см. §28.1), и
рассматривает А-решетку нейронных микротрубочек в качестве важной составной части,
при этом акт сознания ассоциируется с редукцией некоторого состояния этой квантовой
системы. Этот процесс обычно включает многие области мозга, чтобы достигнуть доста¬
точно когерентного движения в белковых молекулах с гравитационной ОР в соответствии
с изложенным в §§ 30.11, 30.12.
Эндрю Даггинсом было выдвинуто остроумное предложение по проверке таких гипотез
(не только гипотезы с микротрубочками). Оно опирается на тот факт, что за различные аспек¬
ты восприятия (например, визуального восприятия движения, цвета или формы) ответствен¬
ны совершенно различные участки мозга, тогда как при участии сознания все эти аспекты
сочетаются вместе, формируя единый образ. Это иногда называют проблемой связи. Идея
Даггинса состоит в том, чтобы выяснить, имеются ли существенные нарушения неравенств
Белла при формировании образа в сознании, которые указывали бы на присутствие нело¬
кальных эффектов ЭПР-типа (§§23.3-23.5) и означали, что крупномасштабные квантовые
эффекты составляют часть процесса сознательного восприятия. Предварительные результа¬
ты пока далеко не убедительны, однако содержат некоторые ободряющие аспекты I34-32!.
Каков бы ни был статус этих идей, мне представляется, что «фундаментальная» физи¬
ческая теория, претендующая на некоторую полноту на более глубоких уровнях физических
явлений, должна иметь возможность включить в себя разумное сознание. Те, кто стара¬
ется избежать этой проблемы (или ослабить ее влияние), заявляют, что сознание просто
возникает как некоторое «побочное явление». В соответствии с этим можно сказать, что
для возникновения сознания неважно, какого рода физика лежит в основе соответствующих
(не обязательно биологических) процессов. Обычной позицией становится вычислитель¬
ный фунщионализм, в соответствии с которым к разумному сознанию приводит просто
вычислительная активность (некоторой пока не определенной природы). У меня имеются
серьезные возражения (частично основанные на теореме Гёделя и понятии тьюринговой
вычислимости — см. § 16.6), и я полагаю, что сознание зависит от (пока отсутствующей)
теории (гравитационной) ОР^34,33!. Мой подход требует, чтобы эта отсутствующая теория
была невычислимой (т. е. чтобы ее действие не могло быть смоделировано машиной Тью¬
ринга, см. § 16.6). Теоретические идеи, направленные на создание модели ОР такого рода,
пока находятся в весьма предварительном состоянии, но, возможно, здесь содержится ключ
к будущей теории.
34.8.	Наш долгий путь к реальности
Из обсуждения в предыдущих разделах, надеюсь, достаточно ясно, что наш путь к по¬
стижению природы реального мира еще далек от завершения, и мы еще далеки от цели.
Возможно, эта цель никогда и не будет достигнута, но может быть и так, что в конце концов
появится некоторая теория, которая даст нам в принципе понимание того, что мы называем
«реальностью». Если это произойдет, то такая окончательная теория должна будет коренным
образом отличаться от всех существовавших и существующих теорий. Наиболее важное по¬
нимание, достигнутое на нашем пути длиной более чем две с половиной тысячи лет, — это
осознание глубокого единстваf34*34^ между некоторыми областями математики и поведением
физического мира, что составляет «первую загадку», изображенную на рис. 1.3 и 34.1. Если
«дорога к реальности» действительно приведет нас к цели, то, по моему убеждению, в осно¬
ве конечной теории будет лежать глубокая внутренняя простота. Ни в каких существующих
гипотезах такого не наблюдается.
Убеждение древних греков, что в основе физической реальности лежит математика,
исключительно хорошо служит и нам, и я, надеюсь, убедил читателя, что, несмотря на

34.8. Наш долгий путь к реальности
855
расстояние, отделяющее нас от намеченной цели, мы пришли к замечательному пониманию
устройства и поведения Вселенной на самых глубоких из известных нам уровней. Некоторые
математические концепции в прошлом оказались особенно успешными. Среди них система
вещественных чисел и идеи геометрии. Сначала была евклидова геометрия, систематически
изучавшаяся древними греками, затем ее идеи были развиты за ее пределы Ламбертом, Гаус-
сом, Лобачевским, Больяи, Риманом, Бельтрами и другими. Затем Минковский показал, как
объединить время с пространством, а Эйнштейн представил нам величественную геометрию
общей теории относительности с искривленным пространством-временем. Интегральное и
дифференциальное исчисление Архимеда, Ферма, Ньютона, Лейбница, Эйлера, Коши, Кар-
тана и многих других, а также связанные с этим идеи дифференциальных и интегральных
уравнений и вариационных производных оказались абсолютно жизненными и успешными
при описании устройства мира и связанными с геометрией некоторым важным образом.
Фундаментальную роль сыграли также статистические идеи Максвелла, Больцмана, Гиббса,
Эйнштейна и других, позволившие рассматривать большие и сложные физические системы,
состоящие из гигантского количества отдельных элементов. Математика лежит в фундаменте
квантовой теории — от идеи матрицы плотности Гейзенберга до комплексных гильбертовых
пространств, алгебр Клиффорда, теории представлений, бесконечномерного функциональ¬
ного анализа и т. д., восходящих к Дираку, фон Нейману и многим другим.
Я хотел бы выделить два частных аспекта математики, лежащих в основе нашего по¬
нимания устройства мира, обсудив по очереди каждый из них. Я считаю, что они могут по¬
ставить важные, но во многом нерешенные вопросы, связанные с принципами нашей физи¬
ческой теории. Первый из этих аспектов касается роли системы комплексных чисел, которая
оказалась столь фундаментальной при создании квантовой механики, в отличие от системы
вещественных чисел, лежащей в основе всех успешных предшествующих теорий. Другим
аспектом является центральная роль симметрии практически во всех теориях XX века,
особенно в связи с описанием различных взаимодействий на языке калибровочных теорий.
Рассмотрим сначала комплексные числа. В этой книге неоднократно подчеркивалось,
что особая магия этих чисел проявляется не только в математике, но и сама Природа ис¬
пользует эту магию в устройстве Вселенной на самых глубоких уровнях. Можно задаться
вопросом: действительно ли это является особенностью нашего мира, или просто эти числа
настолько полезны в математическом отношении, что находят широкое применение в физи¬
ческой теории. Многие физики, я полагаю, склоняются ко второму варианту. Но тогда им
придется объяснить, почему оказывается столь универсальной роль этих чисел в кванто¬
вой теории, где они лежат в основе фундаментального принципа квантовой суперпозиции
и в несколько ином облике в основе уравнения Шредингера, условия положительной часто¬
ты и бесконечномерной «комплексной структуры» (§ 26.3), которая появляется в квантовой
теории поля. Таким физикам вещественные числа кажутся «естественными», а комплекс¬
ные — «таинственными». Однако с чисто математической точки зрения вещественные числа
ничуть не «естественнее» комплексных. Учитывая несколько магический математический
статус комплексных чисел, вполне можно занять противоположную позицию и считать их
более «естественными» (или, если угодно, «данными Богом»), нежели вещественные числа.
С моей точки зрения, важная роль комплексных чисел или, точнее, роль голоморфности
(комплексной аналитичности), в фундаментальной физике вполне естественна, а загадка со¬
стоит в другом[34.35] ^ак оказалось> чхо столь важную роль в физике играют вещественные
структуры? Следует пояснить, что даже стандартный формализм квантовой механики хотя и
основан на комплексных числах, не является вполне голоморфной теорией. Это проявляется
в обычном требовании, чтобы квантовые наблюдаемые описывались эрмитовыми операто¬
рами (или даже нормальными операторами, как было показано в § 22.5), и в унитарной (а не
просто комплексно-линейной) природе квантовой эволюции, из-за чего появляется поня¬
тие комплексного сопряжения (z н-» z). В связи с этим важное свойство ортогональности

856
Глава 34
различных состояний между собой оказывается неголоморфным понятием. Со свойством
эрмитовости связано обычное (но не вполне обязательное) требование, чтобы результаты
измерений выражались вещественными числами, и унитарность, требование «сохранения
вероятности», т.е. выполнения правила квадрата модуля (также связанного с измерениями),
так что комплексная амплитуда z преобразуется в вероятность в соответствии с неголоморф¬
ной операцией
г гг.
Мы видим, что именно при преобразовании «квантовой информации» (квантового перепу¬
тывания,-- см. §23.10) в «классическую информацию» (вероятность результата измерения)
происходит нарушение квантовой голоморфности. Ортогональность альтернатив опять-таки
является важнейшей чертой процесса измерения. Таким образом, неголоморфность появля¬
ется в тот момент, когда в квантовую теорию вводятся измерения.
Роль вещественных чисел видна, разумеется, также в том фоновом пространстве-вре¬
мени, куда мы помещаем формализм квантовой теории. Если гравитационная ОР действи¬
тельно окажется истинной причиной редукции квантовых состояний, то мы увидим, что
вещественная (неголоморфная) структура реального пространства-времени связана с него-
ломорфностью операции z ь-» zz. Не содержится ли здесь урок для теории твисторов
с ее опорой на голоморфные операции? Или, наоборот, нам следует обдумать роль дискрет¬
ных комбинаторных принципов, появляющихся каким-то образом из комплексной магии,
так что в основе «пространства-времени» будет лежать дискретная структура, а не система
вещественных чисел (как это обсуждалось в §§3.3, 3.5, 32.6, 33.1)? В любом случае, я уве¬
рен, возникают глубокие проблемы, касающиеся самой математической основы физической
реальности.
Теперь обратимся к фундаментальной роли симметрии в физической теории. Полез¬
ность этого понятия не вызывает сомнения. Как теория относительности (в связи с группой
Лоренца), так и квантовая теория широко пользуются им. Но должны ли мы рассматри¬
вать симметрию как фундаментальное свойство Природы или как случайную черту либо
некоторое приближение?
Общий принцип многих современных подходов к физике элементарных частиц состоит
в том, что симметрия рассматривается как нечто действительно фундаментальное, а на¬
блюдаемые отклонения от симметрии считаются следствием нарушения симметрии в ран¬
ней Вселенной. Действительно, как отмечалось в §§13.1, 15.2, 15.4, точная симметрия яв¬
ляется обязательной принадлежностью идеи связности расслоения. Более того, напомним
(§§ 25.5, 25.8), что при стандартном подходе к теории электрослабого взаимодействия U(2)-
симметрия рассматривается как принципиально точная и может играть роль калибровочной
симметрии сил электро слабого взаимодействия (§§ 15.1, 15.8), однако обычно считается, что
симметрия была спонтанно нарушена (спустя 10“12 секунд после Большого взрыва). Напо¬
мним (§28.3), что предположение о необходимом нарушении симметрии в ранней Вселен¬
ной сталкивается с определенными трудностями. Это относится к 11(2)-симметрии теории
элекгрослабого взаимодействия и к более высоким симметриям, используемым в теориях
Великого объединения.
Упрощают ли большие группы симметрии в теориях Великого объединения нашу кар¬
тину физики элементарных частиц? Или было бы проще, если бы многие из этих кажущихся
симметрий были фундаментальным образом нарушены с самого начала? Во втором из этих
вариантов (который действительно согласуется с теорией электрослабого взаимодействия,
см. §28.3) многие из этих симметрий, фигурирующих в наших фундаментальных теори¬
ях, на фундаментальном уровне оказываются лишь приближенными, и необходим более
глубокий поиск, чтобы понять, откуда берутся эти кажущиеся симметрии.
В стандартной квантовой теории присутствуют примеры обоих типов нарушенной сим¬
метрии. Существуют известные ситуации, в которых проявляется спонтанное нарушение

34.9. Красота и чудеса
857
симметрии, например, сверхпроводимость (нарушение и(1)-симметрии) и другие явления.
С другой стороны, имеются примеры, когда идеи симметрии способствуют лучшему пони¬
манию явления, хотя известно, что симметрия лишь приближенная, появляющаяся из более
точной, но менее симметричной теории более глубокого уровня, как в случае классифика¬
ции атомных спектров t34-36!. Остается понять„,ситуация какого из этих двух типов окажется
важнее в более глубокой будущей теории элементарных частиц^34,37^.
Интересно отметить, что существуют условия, когда точная группа симметрии может
возникнуть даже в структурах, первоначально никакой симметрией не обладавших. Мы ви¬
дим это на примере самой сферы Римана, которую можно считать построенной из лоскутов
комплексной плоскости таким образом, который исключает какую-либо симметрию. Од¬
нако поскольку топология образующегося комплексного многообразия имеет вид S2, оно
оказывается эквивалентным сфере Римана как комплексное многообразие (по теореме Ри¬
мана), так что его точной группой симметрии является неотражательная группа Лоренца
(§ 18.5) SL(2, С), независимо от того, насколько нерегулярным образом проводилось по¬
строение сферьг34,38^.
С этим связан вопрос о загадочных числовых константах Природы (§ 31 Л). Не опреде¬
лились ли эти числа на самой ранней стадии развития вселенной (как предполагает гипоте¬
за Уилера-Смолина, рассмотренная в §28.6) по аналогии с идеей нарушения симметрии?
Действительно, некоторым из этих констант, например углам Кабиббо и Вайнберга (§25.7),
обычно приписывают именно такую природу. Или, может быть, эти числа определяются
математическими соотношениями какой-то более фундаментальной теории? Сам я отдаю
предпочтение последнему варианту, но пока мы не приблизились к обретению правдопо¬
добной теории такого рода^34*39!.
В связи с этим интересно поставить вопрос о киралъной асимметрии слабого взаимо¬
действия. При обычном подходе к стандартной модели киральная асимметрия встраивается
в рамки теории. Однако нейтрино (по крайней мере, большинство из них), по нынешним
данным, являются массивными частицами (т. е. обладают ненулевой массой покоя), и уже
этот факт представляет отклонение от первоначальной стандартной модели электрослабо-
го взаимодействия. Мы не можем просто «взвалить всю вину» за киральную асимметрию
слабого взаимодействия на нейтрино с левой спиральностью. Массивное нейтрино — это не
полностью частица «зиг» с отрицательной спиральностью, поскольку, обладая массой, оно
должно содержать также часть «заг» с положительной спиральностью (см. §25.2). Можно
было бы представить себе некоторые варианты стандартной модели (слегка обобщенной
с включением в нее массивных нейтрино), которые получаются в результате спонтанного
нарушения симметрии из первоначальной модели, обладающей право-левой симметрией.
Но в данном примере «общепринятый» взгляд таков, что асимметрия существует с самого
начала, а не появляется как результат спонтанного нарушения симметрии в ранней Вселен¬
ной.
Может возникнуть также вопрос, не следует ли с этих позиций рассмотреть заново
вопрос о временной асимметрии (обсуждавшийся в главах 27 и 28). Однако такая асимметрия
никак не может возникнуть вследствие стандартного «спонтанного нарушения симметрии
в ранней Вселенной». В стандартной картине используется Второй закон термодинамики,
и потому ею нельзя воспользоваться для вывода этого закона.
34.9.	Красота и чудеса
Обратимся теперь к более общим и загадочным аспектам математики, которые обнару¬
живаются в фундаменте физической теории на самых глубоких ее уровнях, — по крайней
мере, тех, которые были до сих пор нам доступны. На направление теоретических исследова¬
ний оказывают сильное влияние две мощные внутренние движущие силы, которые, однако,

858
Глава 34
обычно остаются неназванными в серьезных научных трудах, — вероятно, из страха, что они
могут увести далеко от строгих правил принятой научной процедуры. Одна из них — это
красота, или изящество, и я уже касался этой материи во многих местах этой книги. Другую,
обладающую неодолимым очарованием, часто называют «чудом»; до сих пор я лишь слегка
намекал на нее (в §§ 19.8,21.5, 31.14), однако на основании личного опыта могу поручиться,
что она действительно оказывает мощное влияние на направление исследований.
Прежде чем перейти к вопросу о чудесах, которому в этом разделе отведена основ¬
ная роль, вернемся к теме красоты, поскольку эти два понятия неразделимы. Как отме¬
чалось выше, многие идеи, воспринимаемые как главные достижения физической теории,
в то же время выглядят неотразимо красивыми. Есть несомненная красота в геометрии Ев¬
клида, которая лежит в основе первой точной физической теории — теории пространства,
сформулированной древними греками. Полтора тысячелетия спустя появилась необычай¬
но изящная механика Ньютона с ее глубокой симплектической геометрической структурой,
которая позднее проявилась в лагранжевом и гамильтоновом формализмах (§ 20.4). Матема¬
тическая форма электромагнетизма Максвелла также обладает особой изысканностью, и нет
никакого сомнения в величайшей математической красоте общей теории относительности
Эйнштейна. То же можно сказать о структуре квантовой механики и многих ее специфи¬
ческих особенностях. Следует выделить необычайное математическое изящество понятия
квантово-механического спина, релятивистского волнового уравнения Дирака и формализма
интегралов по траекториям, введенного Фейнманом в квантовую теорию поля.
Однако можно задать вопрос: не является ли несомненная математическая красота этих
схем чем-то независимым, не связанным с устройством нашей Вселенной, просто красотой
чистой математики? В какой мере эти схемы, рассматриваемые просто как математические
структуры, выдерживают сравнение с жемчужинами чистой математики? На мой взгляд,
выдерживают вполне успешно, но не с подавляющим преимуществом. В чистой матема¬
тике есть немало результатов, не имеющих заметной связи с физическим миром, красота
которых не уступает красоте существующих физическР1х теорий (а то и превосходит ее).
(См. также § 16,3.)
Рассмотрим некоторые глубокие и красивые результаты математики, на которые влияние
физики (по крайней мере, до сих пор) было минимальным. В качестве одного из примеров
можно назвать канторову теорию бесконечности. На мой взгляд, это одно из наиболее кра¬
сивых достижений во всей истории математики. Однако к устройству физического мира,
насколько мы его знаем, эта теория имеет крайне малое отношение (см. §§ 16.3, 16.4, 16.7).
Тот же вопрос возникает в связи с другим монументальным достижением математики, по¬
рожденным канторовой теорией бесконечности, а именно со знаменитой теоремой Гёделя
о неполноте (§ 16.6). Универсальные и глубокие идеи теории категорий (§33.1) также пока
кажутся довольно слабо связанными с физикой.
В двух последних случаях существуют правдоподобные указания на возможность их су¬
щественной связи с физикой, которая будет обнаружена в XXI веке (§§ 34.7,33.1), но это умо¬
зрительное заключение. Гораздо менее правдоподобной представляется возможность связи
с физикой большинства других замечательно красивых математических теорий. Возьмем,
например, замечательное достижение XX века — доказанную Эндрю Уайлсом истинность
утверждения, выдвинутого 350 лет назад и известного как «Последняя теорема Ферма».
Насколько мы сейчас понимаем, этот результат очень далек от каких-либо физических за¬
конов, несмотря на заключенные в нем величественные математические идеи. В XX веке
было много других удивительных достижений, например, проведена классификация про¬
стых групп — как непрерывных, так и дискретных. Здесь связь с физикой несомненна, но
это отнюдь не значит, что теория простых групп дает нам «физическую теорию». Это всего
лишь математическая классификация, полезная для физиков тем, что позволяет им видеть
существующие возможности. Рассмотрим другой пример. XIX век дал нам изящную тео¬
7\

34.9. Красота и чудеса
859
рию ^-функции Римана и ее связь с распределением простых чисел. Она кажется почти столь
же далекой от физики, несмотря на несомненную красоту и математическое значение пока
не доказанной гипотезы Римана (§ 7.4). На самом деле здесь имеется некоторая интересная
связь с физикой^34•4°^, однако трудно представить, чтобы теория Римана давала нам что-то
напоминающее модель физического мира.
Должны ли мы ожидать, что физика будущего установит тесную связь с большим
объемом красивых математических результатов? Или нынешние успехи физической теории
создают у нес впечатление о более тесной связи между математикой и физикой, чем она
есть на самом деле? Этот вопрос можно кратко сформулировать, пользуясь рис. 1.3. Какая
часть математического мира Платона лежит на основании стрелки, обозначающей «первое
чудо»?
Можно также спросить: существует ли какой-нибудь способ узнать, какого рода мате¬
матика играет наиболее важную и глубокую роль в управлении поведением физического
мира? Это интригующий вопрос. Возможно, в будущем удастся лучше понять, какие факто¬
ры определяют загадочную связь между математикой и физикой.
Из приведенных соображений читателю, надеюсь, стало ясно, что математическая кра¬
сота сама по себе не может служить надежным проводником. Тем не менее, как я уже
неоднократно отмечал в этой книге, трудно усомниться в той значительной роли, которую
играют доводы эстетического характера, как математические, так и физические, при выбо¬
ре наиболее плодотворных путей развития в теоретической физике. Большинство из них
имеет довольно неуловимый характер, и легко поверить, что выбор одной из нескольких
альтернатив развития является весьма субъективным решением. Однако время от време¬
ни в отношении математических теорий к физическому миру возникает нечто такое, что
оказывает на этот выбор гораздо более мощное влияние, нежели просто математическое
изящество, и именно это я называю «чудом».
Много примеров такого рода можно найти в недавней истории идей «квантовой гра¬
витации». Одной из них была теория суиергравитации (§31.2). В то время как приме¬
нение теории возмущений в квантово-полевом подходе к стандартной общей теории от¬
носительности Эйнштейна приводит во втором порядке к неперенормируемым расходи¬
мостям, при введении суперсимметрии расходящиеся члены чудесным образом взаимно
уничтожаются^34,41^. Эта компенсация затрагивает много членов, и многие из занимающих¬
ся супергравитацией некоторое время считали, что такая «чудесная» компенсация может
служить признаком правильного направления движения теории, которое приведет к пере-
нормируемости во всех порядках, так что скоро появится истинная теория квантовой грави¬
тации! К разочарованию этих людей, когда они сумели закончить расчеты в третьем прибли¬
жении, неперенормируемые расходимости вернулись. Это вызвало поворот к многомерным
пространствам, и развитие супергравитации временно застопорилось. Затем, в конце 1990-
х годов, супергравитация возродилась как часть пути, приведшего к М-теории, описанной
в §§31.4,31.14.
Я убежден, что теория струн и М-теория сами являются порождением многих подобных
чудес. Одним из таких было открытие зеркальной симметрии, благодаря чему загадочный
набор внешне совершенно различных теорий струн, описанных в §31.14, оказался объеди¬
ненным в одну величественную схему под названием «М-теория». Зеркальная симметрия
вела себя, как настоящая магия: числа, которые первоначально казались не имеющими между
собой ничего общего, в дальнейшем оказались одинаковыми, как это произошло в расчетах
Канделаса и его коллег (рассмотрено в §31.14). Это определенно можно назвать чудом в том
смысле, в котором я использую здесь этот термин. Я уверен, что когда число 317206375,
полученное в расчетах Канделаса с использованием зеркальной симметрии, было в кон¬
це концов подтверждено специалистами по алгебраической геометрии, это было объявлено
чудом, убедительно свидетельствующим, что новая М-теория струн находится на верном

860
Глава 34
пути! Так это или нет, но «чудо» оказало замечательную поддержку математическим аспек¬
там идеи зеркальной симметрии. Возник интерес к этой проблеме у «чистых» математиков,
и было достигнуто лучшее понимание используемой теории с чисто математической точки
зрения[34.42]
Подтверждают ли подобные чудеса правильность подхода к физической теории?
Это глубокий и трудный вопрос. Я могу признать, что иногда это так, но здесь необхо¬
димо быть крайне внимательным. Открытие Дираком того факта, что из его релятивистско¬
го волнового уравнения следует существование спина электрона, вполне могло показаться
чудом, так же как и правильный спектр водорода, получающийся из квантования момента
импульса, предложенного Бором. Сюда же относится подход к гравитации как к искривле¬
нию пространства в общей теории относительности Эйнштейна, который дал правильный
ответ на загадку движения перигелия Меркурия, занимавшую астрономов более 70 лет.
Но это были ясные физические следствия предложенных теорий, и чудеса подтверждали
их весьма впечатляющим образом. Менее ясна сила чисто математических чудес, таких как
в случае супергравитации или зеркальной симметрии. Если в конце концов чудо такого ма¬
тематического характера будет понято с чисто математической точки зрения, то это может,
в некоторой степени, «разоблачить» такое чудо. Но даже в этом случае нельзя полностью
исключить психологической силы самого чуда, которое всегда следует рассматривать в его
историческом обрамлении.
Несомненно, однако, одно: подобные математические чудеса не могут всегда быть на¬
дежным проводником. В ходе моих собственных изысканий в области теории твисторов
я несколько раз ощущал поддержку со стороны «чудес», понимаемых в используемом здесь
смысле. Одним из примеров такого рода было обнаружение того факта, что однородные
функции одиночных твисторов порождают общие решения уравнений безмассовых полей
(§ 33.8), другим примером может служить построение нелинейного гравитона (§ 33.11). В ка¬
кой мере это означает, что теория твисторов находится «на верном пути»? Опять-таки сле¬
дует проявлять осторожность. Я не склонен проводить сравнение чудес теории твисторов
с чудесами теории струн. Но они не могут служить путеводными звездами одновременно,
поскольку, как отмечалось в §33.14, эти две теории, в их нынешнем виде, несовместимы
одна с другой!
Однако эти замечания относятся лишь к тому, что мне известно о состоянии этих те¬
орий в данный момент. Некоторые впечатляющие достижения, появившиеся всего лишь
в последние несколько месяцев, смогли полностью изменить тот вывод, к которому я, ка¬
залось бы, должен был прийти в предыдущем абзаце. Намечаются возможные применения
идей теории струн в контексте теории твисторов, обязанные в первую очередь Эдварду
Виттену^34*43} (я упоминал об этом в §§31.18, 33.14). Теория струн применяется здесь к
стандартному четырех мерному пространству-времени и использует взаимодействие типа
Янга-Миллса, которое, по-видимому, имеет непосредственное отношение к реальному вза¬
имодействию между частицами; это означает существенный отход от той формы теории
струн, к которой относились высказывания в предыдущем абзаце. Как это достигнуто? Для
этого «пространство цели», на которое должны отображаться римановы пространства теории
струн, рассматривается не как комплексное 3-многообразие Калаби-Яу (§31.14), которое
привлекается для включения «лишних» пространственных измерений «стандартной» тео¬
рии струн, но как комплексное 3-многообразие, представляющее проективное твисторное
О
пространство FT (или СР ; см. § 33.5). Как мы видели, твисторная геометрия имеет дело
с обычным 4-мерным пространством-временем, и там нет «лишних пространственных изме¬
рений»! В описании этих новых идей еще присутствует в некотором виде суперсимметрия,
и этот суперсимметричный вариант пространства РТ можно рассматривать как некоторую
разновидность «пространства Калаби-Яу». (Это устраняет некоторую «аномалию», однако,
на мой взгляд, необходимость в этом, возможно, преувеличена, так что суперсимметрия на

34.10. Многое понято, еще больше понять предстоит
861
самом деле не требуется.) В нынешнем варианте этих новых идей используются римановы
поверхности рода 0 (см. § 8.4), т. е. сферы Римана\*АЛАУ Это позволяет установить контакт
с ранней теорией твисторов, содержавшей некоторые «струнные» идеи, i34-45]
Если теория струн сможет измениться таким, как мне кажется, весьма существенным
образом, приобретут ли физический смысл «чудеса» этой теории? Мне представляется, что
им можно будет придать такой смысл (хотя, возможно, и косвенный), и будет достигнуто
лучшее понимание того, «что происходит за сценой» (как предполагалось в высказывании
Ричарда Томаса, цитированном в §31.18). Можно ли будет извлечь из теории струн то,
что есть в ней полезного, и устранить ее зависимость от дополнительных размерностей
пространства-времени? Может быть. Что кажется вероятным, так это возможность укреп¬
ления идеи квантовой теории поля на основе отображения сфер Римана (или, возможно,
римановых поверхностей более высокого рода) на комплексные многообразия [34*461? которая
может привести к использованию комплексного многообразия, являющегося (проективным)
твисторным пространством. Что же произойдет на самом деле, пока остается тайной.
34.10.	Многое понято, еще больше понять предстоит
Вопросы, подобные поставленным в нескольких последних разделах, при сегодняш¬
нем понимании физики пока остаются без ответа. Можно надеяться, что на них сможет
пролить свет будущая физика XXI века. Однако, оглядываясь на то, что уже достигнуто
к концу XX века, человечество может испытывать законную гордость. Получены ответы
на многие вопросы, казавшиеся древним глубоко загадочными, а иногда и устрашающими,
и это зачастую позволяет действовать наиболее рациональным образом. Перестали пугать
многие ужасные болезни, благодаря не только современным лекарствам (при создании ко¬
торых научный метод оказался незаменимым), но и методам ранней диагностики на основе
современной техники (рентгеновские лучи, ультразвук, томография и др.) и методам физи¬
ческого воздействия (радиация, лазеры и др.). Эта техника во многих случаях основана на
физических знаниях, которые не были доступны древним. Знания такого рода принесли нам
и многое другое: гидроэлектростанции, электрическое освещение, современные материалы,
защищающие от стихий, такие средства связи, как телевидение и мобильная телефония,
вычислительная техника, Интернет, различные виды транспорта, а также многочисленные
другие стороны современной жизни.
Большинство этих достижений в той или иной форме связано с физикой. Более того,
основные законы химии, как мы сегодня знаем, также в своей основе законы физические
(если не в практическом смысле, то в принципе), возникшие из правил квантовой механики.
Биологию свести к физическим законам гораздо труднее, однако у нас нет причин сомневать¬
ся в том, что в основе биологического поведения лежат известные нам физические законы.
Так что биология в конечном счете также должна подчиняться законам математики.
Возьмем, например, загадочный процесс, при котором из семени развивается целое рас¬
тение, причем сложная структура каждого растения в общих чертах такая же, как и у тех,
что выросли из подобных семян. Здесь заключена глубокая физика, поскольку ДНК, ко¬
торая управляет ростом растения, представляет собой молекулу, сохранение и надежность
структуры которой критическим образом определяются законами квантовой механики (как
убедительно показал в 1944 году Шредингер в своей знаменитой небольшой книге Что та¬
кое жизнь?^34>471). Более того, рост растения в конечном счете определяется теми же фи¬
зическими силами, которые управляют отдельными частицами, из которых оно состоит.
Они в основном имеют электромагнитную природу, однако интенсивные ядерные силы
определяют, какие возможны ядра, а значит, и какого сорта атомы там могут быть.
Слабое взаимодействие также играет свою роль в крупномасштабных явлениях и,
что замечательно, несмотря на свою слабость (оно в 107 слабее сильного взаимодействия

862
Глава 34
ив 105 раз слабее электромагнитного), может проявиться в некоторых событиях из числа
наиболее драматических в истории человечества, поскольку именно слабое взаимодействие,
определяющее радиоактивный распад внутри Земли, ответственно в основном за нагрев маг¬
мы в недрах Земли. Одним из проявлений этого являются извержения вулканов. В истории
Земли был период, длившийся несколько лет, начиная с 535 года нашей эры, когда по всей
Земле был голод и господствовала необычайно холодная погода из-за пыли, выброшенной
при взрыве вулкана. Этим вулканом, вероятно, был Кракатау, расположенный вблизи остро¬
ва Ява, который, по-видимому, катастрофически извергался в 535 году и еще раз (но уже не
столь бурно) в более близкое время, в 1883 году.
Возможно, еще более драматическим для его свидетелей был взрыв вулкана, разру¬
шивший остров Терра (Санторини), который можно было легко видеть с острова Крита,
расположенного на 100 миль южнее (в 1628 году до нашей эры). При этом не только бы¬
ла разрушена цивилизация самого острова Терра, — именно это событие привело, вероятно,
к последующему упадку цивилизации Крита, на котором, по слухам, был расположен знаме¬
нитый лабиринт Дедала1Г34*48!. Вполне возможно, что именно разрушение Терры послужило
источником легенды об Атлантиде f34,49^. Некоторое утешение можно найти в том факте, что
некоторые катаклизмы прошлого могли послужить прогрессу в развитии, которого в против¬
ном случае могло и не быть. (Наиболее ярким примером может служить глобальное исчез¬
новение динозавров, способствовавшее развитию млекопитающих, что привело в конечном
счете к появлению людей; в данном случае причиной катастрофы было, по-видимому, столк¬
новение с астероидом, а не вулканическая деятельность.) Не было ли необычайное развитие
древнегреческой культуры тысячелетие спустя после разрушения Терры в какой-то мере
обязано этому катастрофическому проявлению вулканической активности?
Вероятно, еще более поразительно, что наиболее бурные взрывы, наблюдаемые во Все¬
ленной, вызываются наиболее слабой из всех сил (если ее правильно считать силой) —
гравитационной (в атоме водорода она составляет Ю”40 электрической силы и 10“38 си¬
лы слабого взаимодействия). Черные дыры служат источником неправдоподобно огромной
энергии для квазаров. Но их расстояние от нас столь велико, что самый яркий квазар 3C273,
несмотря на необычайно высокую мощность, с Земли представляется имеющим яркость,
в 106 меньшую яркости соседней звезды Сириуса. Когда тихой ясной ночью мы любуем¬
ся звездами, испытывая благоговение перед необъятностью Вселенной, мы на самом деле
воспринимаем лишь ничтожную часть ее огромного масштаба. Наиболее удаленный объ¬
ект, видимый невооруженным глазом (туманность Андромеды), расположен в 103 раз ближе
квазара 3C273 и в 104 раз ближе края наблюдаемой Вселенной!
Пространственно-временные сингулярности в сердцевине черных дыр принадлежат
к числу известных (или предполагаемых) объектов Вселенной, которые остаются наиболее
загадочными и которые современные теории не в силах описать. Как мы видели, в част¬
ности, в §§34.5, 34.7, 34.8 существуют и другие глубоко загадочные проблемы, пока очень
далекие от разрешения. Вполне возможно, что XXI век принесет еще более удивительные
открытия, чем те, которыми нас порадовал XX век. Но чтобы это произошло, необходимы
глубокие новые идеи, которые направят	нас	по	существенно	иному	пути,	нежели	тот, кото¬
рым мы идем сейчас. Возможно,	главное, что	нам требуется,	это какое-то	тонкое изменение
взгляда на мир — что-то такое, что все мы утратили...
Примечания
§34.1.
34.1. См., например, [536].
34.2. См. [781].
34.3. См. [27].

34.10. Многое понято, еще больше понять предстоит
863
34.4. См. [20, 275, 19, 689]; альтернативный взгляд изложен в [507].
§34.2.
34.5. Я использую здесь слово «последовательность» для обозначения понятия немного более силь¬
ного, нежели согласованность. Это слово должно означать, что в полностью последователь¬
ной математической структуре различные аспекты формализма действуют в полном согласии.
§34.3.
34.6. См. [673].
34.7. Некоторые из моих коллег утверждают, что сегодня так оно и есть!
34.8. Напомним (§ 15.4), что пространство S7 расслаивается пространством S3 по аналогии с клиф-
Q	^
фордовыми параллелями на S . Фактически S есть «параллелизуемое» пространство, это
означает, что каждой его точке можно непрерывным образом сопоставить 7-мерный репер из
касательных векторов. Сплющивание S производится вдоль таких «параллельных» направ¬
лений. См. [419].
34.9. См. [154] относительно траекторий Редже и [143] относительно S-матрицы.
34.10. См. [287].
34.11. См. [798, 411, 626, 627, 564].
34.12. См. [203]; другие варианты уравнений для высших спинов содержатся в [165].
34.13. См. [821].
34.14. См. [645].
34.15. Шутливое использование идеи такого рода можно найти в [16].
34.16. Несмотря на недавние заявления, что эксперимент BOOMERANG подтвердил это. См., на¬
пример, (умеренную) критику этих утверждений в [98].
34.17. Теория стационарной Вселенной, предложенная в начале 1950-х годов Бонди, Голдом и Хой¬
лом (см. [401, 94]), определенно удовлетворяет критерию Поппера, что было явно пока¬
зано Бонди. Эта теория опровергается также тем фактом, что К ф 0. Она была отверг¬
нута и из-за других противоречий с результатами наблюдений, особенно с обнаружением
фона микроволнового излучения с температурой 2,7 К, который представляет собой непо¬
средственное проявление происшедшего когда-то Большого взрыва; см. §§27.7, 27.10, 27.11,
27.13,	28.4, 28.7, 28.10.
34.18. См., например, [489].
34.19. См. [111,490].
34.20. См. [374].
34.21. См. [471].
§34.5.
34.22. См. книгу Джона Гордана Конец науки [395].
34.23. См. [255, 812, 181,409].
§34.7.
34.24. См. [610, 613, 615, 616].
34.25. См. [188,494].
34.26. См. [281, 359].
34.27. Однако тем, кто когда-либо слышал о взглядах Дэвида Бома на этот предмет, придется при¬
знать, что он не рассматривал проблемы сознания в отрыве от проблем квантовой механики.
34.28. См. [610, 613, 615, 616].
34.29. См. [343, 340, 341, 342].
34.30. См. [460].
34.31. См., например, [21].
34.32. Частное сообщение. Насколько мне известно, исследование Даггинса еще не завершено,
и публикаций пока не было.

864
Глава 34
34.33. См.5 например, [605, 613, 342].
§34.8.
34.34. Следует ли считать это единство замечательным и несколько загадочным — это вопрос согла¬
сия между экспертами. В своей знаменитой лекции широко известный специалист в области
математической физики Юджин Вигнер [832] рассуждал «о непостижимой эффективности ма¬
тематики в физических науках». Однако Эндрю Глисон, выдающийся математик, две теоремы
которого упоминались в этой книге (см. примечания 13.4 и 23.4), высказал противоположное
мнение [305], считая, что гармония между математикой и физикой есть просто отражение
того факта, что «математика — это наука о порядке». Сам я склоняюсь скорее к Вигнеру,
чем к Глисону. Не только необычайная точность, но и та тонкость и изощренность, которую
мы обнаруживаем в математических законах, проявляющихся в фундаментальной физике,
представляется мне чем-то гораздо большим, чем просто выражение «порядка» в устройстве
нашего мира.
34.35. Эта философия близка к взглядам Джеффри Чу, который придавал большое значение голо¬
морфным свойствам S-матрицы. См. [143].
34.36. См. вводные замечания Фримена Дайсона в книге [227].
34.37. См. [609].
34.38. Этот факт оказывается существенным при изучении асимптотической симметрии асимптоти¬
чески плоского пространства-времени в общей теории относительности; см. [683, 684, 627].
34.39. Сравните с [232].
§34.9.
34.40. Обсуждение связи гипотезы Римана с физикой проводится в [225, 78]. Другим применением
(эйлеровой) (-функции в физике является так называемая «(-регуляризация». Беглый поиск
в интернетовском архиве LANL дал 142 работы на эту тему.
34.41. См. [820] и примечание 31.13.
34.42. См. примечания 31.57 и 31.58.
34.43. См. примечание 31.81.
34.44. Это само по себе не ограничивает рассмотрение римановыми поверхностями, которые яв¬
ляются линиями твисторного пространства, представляющими точки пространства-времени
(см. § 33.5), — они могут быть также кривыми «более высокого порядка». «Условие рода 0»
означает, что рассматриваются «древесные» процессы Янга-Миллса, не содержащие «за¬
мкнутых петель» (см. § 26.8).
34.45. См. [718, 387, 388, 389].
34.46. Это так называемые «<т-модели»; см. [445].
§34.10.
34.47. Переиздана в 1967 году [702].
34.48. Красочное описание этого события содержится в [177], стр. 89-94 (я воспользовался им при
написании пролога). Старый вариант легенды воспроизведен в [344].
34.49. Современное изложение этой идеи содержится в [272].

Эпилог
Антея, молодой доктор философии в области физики, происходила из маленького город¬
ка на юге Италии. Она обладала замечательными способностями — как художественными,
так и математическими. Сейчас она любовалась ясным ночным небом из большого вос¬
точного окна Института имени Альберта Эйнштейна в Гольме, близ Потсдама в Германии.
Этот престижный исследовательский институт был основан в конце XX века вблизи того
места, где Эйнштейн когда-то приобрел себе дачу. Здесь в основном изучалась волнующая
проблема «квантовой гравитации», направленная на объединение принципов общей теории
относительности Эйнштейна с принципами квантовой механики и затрагивающая самые
глубинные законы нашего мира.
Это было и направление собственных исследований Антеи, но она была новичком в
этой области, и ее нестандартные и не вполне сформировавшиеся идеи порой радикально
отличались от взглядов ее коллег. Этой ночью она продолжала работать в библиотеке на
верхнем этаже института, когда все остальные читатели давно уже отправились спать. Она
изучала старые работы, посвященные явлению выброса гигантской энергии в центре неко¬
торых галактик. Как удачно, думала она, что Земля и Солнечная система не оказались вблизи
одной из них, так как в этом случае они почти мгновенно испарились бы. Общепринятое
объяснение этих гигантских взрывов заключалось в том, что каждый из них питает энергией
черная дыра.
Антея знала, что черная дыра — это область пространства-времени, внутри которой
находится так называемая «пространственно-временная сингулярность», научное описание
которой довольно расплывчато, поскольку для этого необходима отсутствующая пока кван¬
товая теория гравитации. Но Антея реально интересовалась не столько галактическими чер¬
ными дырами, сколько еще более чудовищным взрывом, который положит конец всем взры¬
вам, — или, скорее, был началом всех взрывов, — это известный «Большой взрыв». Она раз¬
мышляла над тем, что это было началом всего хорошего и всего плохого. Пространственно-
временная сингулярность в условиях Большого взрыва представляет еще большую загадку,
нежели черные дыры. Антея знала, что в основе этих загадок лежит вопрос о том, как объ¬
единить крупномасштабную эйнштейновскую теорию пространства, времени и тяготения с
принципами квантовой теории.
Была тихая ночь, и сияли звезды. Какое-то время Антея стояла в задумчивости, опер¬
шись на перила лестницы и глядя на звезды через широкое окно; как долго это продолжалось,
она не знала. Она всегда испытывала благоговение перед этим громадным куполом неба с
мириадами звезд, невообразимо далеких и в то же время близких по сравнению с гораздо
большими космологическим масштабами. Однако, размышляла она, если бы какой-то кос¬
мический взрыв стал бы видимым сейчас, независимо от того, как далеко он расположен,
то фотонам не потребовалось бы времени, чтобы достигнуть ее. То же относится и к гра¬
витонам, порождаемым взрывом, некоторые из которых могли бы быть зарегистрированы
институтским приемником гравитационных волн, расположенным вблизи Ганновера за 250
километров отсюда. Она подумала, что могла бы стать непосредственным свидетелем такого
взрыва...
И вот когда она так стояла и глядела на восток, она внезапно увидела короткую вспыш¬
ку зеленого света, как раз когда должен был наступить рассвет, после чего прорвался

866
Эпилог
глубоко-красный солнечный луч. Она знала о явлении «зеленого луча», и ей было извест¬
но физическое объяснение этого явления, но быть его свидетелем ей никогда раньше не
доводилось, и оно породило в ней странный эмоциональный эффект. Это как-то смеши¬
валось с теми смутными мыслями математического характера, которые занимали ее в эту
ночь.
И тут ее посетила странная мысль...

Предисловие к библиографии
XX век принес не только огромные успехи в понимании физической картины ми¬
ра, достигнутые благодаря тонким экспериментам и изощренной математической теории.
Современная техника неизмеримо расширила возможности распространения и получения
информации в глобальном масштабе. Это относится, в частности, к созданию в Интернете
архива ArXiV.org, где физики и математики, биологи и компьютерщики могут публиковать
препринты (или «Е-принты») своих работ до (а то и вместо!) представления их в журна¬
лы. ArXiV.org предоставляет ученым возможность невероятно быстро обмениваться новыми
идеями, вследствие чего в беспрецедентной (а по мнению некоторых — устрашающей) сте¬
пени возросли темпы научной активности.
Я постарался воспользоваться преимуществами, которые дают эти новые возможности,
при составлении библиографии. Найти статью в ArXiV.org очень просто. С помощью веб¬
браузера, которым вы обычно пользуетесь, вы отправляетесь по адресу www.arxiv.org.
Затем либо ищете нужную статью, либо вводите после команды www. arxiv. огд/ иденти¬
фикационный код, который в нашей библиографии приводится в скобках. Например, чтобы
найти опубликованную в 2003 году статью Ли Смолина «How far are we from the quantum
theory of gravity?» («Насколько далеки мы от квантовой теории гравитации?»), следует ввести
в качестве веб-адреса www. arxiv. org/hep-th/0303185. Это особенно полезно для тех
читателей, кго имеет доступ в Интернет, но находится вдали от университетских библиотек
со специализированными научными журналами. Я надеюсь, что указанная особенность на¬
шей библиографии позволит читателям познакомиться в ArXiV'e со многими прекрасными
работами, независимо от того, цитируются они здесь или нет.
Литература
[1] Abian А. (1965). The theory of sets and transfinite arithmetic. Saunders, Philadelphia.
[2] Abbott B. et ai (2004). Detector Description and Performance for the First Coincidence Observations
between LIGO and GEO. Nucl Instrum. Meth. A517, 154-179. [gr-qc/0308043]
[3] Adams С. C. (2000). The Knot Book. Owl Books, New York.
[4] Adams J.F., Atiyah M. F. A. (1966). On К-theory and Hopf invariant. Quarterly J. Math. 17, 31-38.
[5] Adler S.L. (1995). Quaternionic Quantum Mechanics and Quantum Fields. Oxford University Press,
New York.
[6] Afriat A. (1999). The Einstein, Podolsky, and Rosen Paradox. In Atomic, Nuclear, and Particle Physics.
Plenum Publishing Corp.
[7] Aharonov Y., Albert D. Z. (1981). Can we make sense out of the measurement process in relativistic
quantum mechanics? Phys. Rev. D24, 359-370.
[8] Aharonov Y., Anandan J. (1987). Phase change during a cyclic quantum evolution. Phys. Rev. Lett.
58,1593-1596.
[9] Aharonov Y., Bohm D.J. (1959). Significance of electromagnetic potentials in the quantum theory.
Phys. Rev. 115, 485-491.

868
Литература
[10] Aharonov Y., Vaidman L. (1990). Properties of a quantum system during the time interval between
two measurements. Phys. Rev. A41, 11.
[11] Aharonov Y., Vaidman L. (2001). The Two-State Vector Formalism of Quantum Mechanics. In Time
in Quantum Mechanics (ed. J. G. Muga et al.). Springer-Verlag.
[12] Aharonov Y., Bergmann P., Lebowitz J. L. (1964). Time symmetry in the quantum process of
measurement. In Quantum Theoiy and Measurement (ed. J. A. Wheeler and W. H.Zurek). Princeton
University Press, Princeton, New Jersey, 1983; originally in Phys. Rev. 134B, 1410-1416.
[13] Ahmavaara Y. (1965). The structure of space and the formalism of relativistic quantum theory, I. J.
Math. Phys. 6, 87-93.
[14] Aitchison I., Hey A. (2004). Gauge Theories in Particle Physics: A Practical Introduction, Vols. 1
and 2. Institute of Physics Publishing, Bristol.
[15] Albert D., Aharonov Y, D’Amato S. (1985). Curious New Statistical Prediction of Quantum
Mechanics. Phys. Rev. Lett. 54, 5.
[16] Aldiss B. W., Penrose R, (2000). White Mars. St. Martin’s Press, London.
[17] Alpher Bethe, Gamow (1948). The Origin of Chemical Elements. Phys. Rev. 73, 803.
[18] Ambjom J., Nielsen J. L., Rolf J., Loll R. (1999). Euclidean and Lorentzian Quantum Gravity: Lessons
from Two Dimensions. Chaos Solitons Fractals 10. [hep-th/9805108]
[19] Amelino-Camelia G., Piran T. (2001). Planck-scale deformations of Lorentz symmetry as a solution
to the UHECR and the TeV-MATH-gamma paradoxes. Phys. Rev. D64, 036005. [astro-
ph/0008107]
[20] Amelino-Camelia G., et al. (1998). Potential Sensitivity of Gamma-Ray Burster Observations to Wave
Dispersion in Vacuo. Nature 393, 763-765. [astro-ph/9712103]
[21] Anderson P. W. (1997). The Theory of Superconductivity in the High-Tc Cuprate Superconductors.
Princeton University Press, Princeton, New Jersey.
[22] Anguige К. (1999). Isotropic cosmological singularities 3: The Cauchy problem for the inhomogeneous
«
conformal Einstein-Vlasov equations. Annals Phys. 282, 395-419.
[23] Antoci S. (2001). The origin of the electromagnetic interaction in Einstein’s unified field theory with
sources, [gr-qc/018052 ]
[24] Anton H., Busby R. C. (2003). Contemporary Linear Algebra. John Wiley & Sons, Hoboken, NJ.
[25] Apostol T.M. (1976). Introduction to Analytic Number Theoiy. Springer-Verlag, New York.
%
[26] Arfken G., Weber H. (2000). Mathematical Methods for Physicists. Harcourt/Academic Press.
[27] Arndt M. et. al. (1999). Wave-particle duality of Сбо molecules. Nature 401, 680.
[28] Арнольд В. И. Математические методы классической механики. Наука, М., 1974.
[29] Arnowitt R., Deser S., Misner С. W. (1962). In Gravitation: An Introduction to Current Research (ed.
L. Witten). John Wiley & Sons, Inc. New York.
[30] Ashtekar A. (1986). New variables foi*classical and quantum gravity. Phys. Rev. Lett. 57, 2244-2247.
[31] Ashtekar A. (1987). New Hamiltonian formulation of general relativity. Phys. Rev. D36, 1587-1602.
>
[32] Ashtekar A. (1991). Lectures on Non-Perturbative Canonical Gravity (Appendix). World Scientific,
Singapore.
[33] Ashtekar A., Das S. (2000). Asymptotically anti-de Sitter space-times: Conserved quantities. Classical
and Quantum Gravity 17, L17-L30.
[34] Ashtekar A., Lewandowski J. (1994). Representation theory of analytic holonomy algebras. In Knots
and Quantum Gravity (ed J. C. Baez). Oxford University Press, Oxford.

Литература
869
[35
[36
[37
[38
[39
[40
[41
[42
[43
[44
[45
[46
[47
[48
[49
[50
[51
[52
[53
[54
[55
[56
Ashtekar A., Lewandowski J. (2001). Relation between polymer and Fock excitations. Class. Quant.
Grav. 18, LI 17-L127.
Ashtekar A., Lewandowski J. (2004). Background Independent Quantum Gravity: A Status Report.
[gr-qc/0404018]
Ashtekar A., Magnon A. (1980). A geometric approach to external potential problems in quantum
field theory. General Relativity and Gravity, vol. 12, 205-223.
Ashtekar A., Schilling T. A. (1998). In On Einsteins Path (ed. A. Harvey). Springer-Verlag, Berlin.
Ashtekar A., Baez J. C., Krasnov K. (2000). Quantum geometry of isolated horizons and black hole
entropy. Adv. Theo. Math. Phys. 4, 1-95.
Ashtekar A., Baez J. C., Corichi A., Krasnov K. (1998). Quantum geometry and black hole entropy.
Phys. Rev. Lett. 80, 904-907.
Ashtekar A., Bojowald М., Lewandowski J. (2003). Mathematical structure of loop quantum
cosmology. Adv. Theor. Math. Phys. 7, 233-268.
Atiyah M. F. (1990). The Geometry and Physics of Knots. Cambridge University Press, Cambridge.
Имеется перевод: Атья М. Геометрия и физика узлов. Мир, М., 1995.
Atiyah М. F., Singer I. М. (1963). The Index of Elliptic Operators on Compact Manifolds. Bull. Amer.
Math. Soc. 69, 322-433.
Atiyah M. F., HitchinN. J., Singer I. M. (1978). Self-duality in four-dimensional Riemannian geometry.
Proc. Roy. Soc. bond. A362, 425-461.
Baez J. C. (1998). Spin foam models. Class. Quant. Grav. 15, 1827-1858.
Baez J. C. (2000). An introduction to spin foam models of quantum gravity and BF theory. Lect. Notes
Phvs. 543, 25-94.
*/	У
Baez J. C. (2001). Higher-dimensional algebra and Planck-scale physics. In Physics Meets Philosophy
at the Planck Scale (ed. C. Callender and N. Huggett). Cambridge University Press, Cambridge, [gr-
qc/9902017]
Baez J.C., Dolan D. (1998). Сategorification. In Higher Category Theory (ed. E.Getzler
and M.Kapranov). Contemporary Mathematics, vol. 230. AMS, Providence. RI. [Also see
http://xxx.lanl.gov/abs/math.QA/9802029]
Bahcall N., Ostriker J.P., Perlmutter S., Steinhardt P. J. (1999). The Cosmic Triangle: Revealing the
State of the Universe. Science 284. [astro-ph/99064 63]
Bailey T. N., Baston R. J. (ed.) (1990). Twistors in Mathematics and Physics. LMS Lecture Note Series
156. Cambridge University Press, Cambridge.
Bailey T.N., Ehrenpreis L., Wells R. O., Jr. (1982). Weak solutions of the massless field equations.
Proc. Roy. Soc. bond. A384, 403-425.
Banchoff T. (1990, 1996). Beyond the Third Dimension. Scientific American Library. See also
http://www.faculty.fairfield.edu/jmac/cl/tb4d.htm
Bars I. (2000). Survey of Two-Time Physics, [hep-th/0008164 3
Barbour J. B. (1989). Absolute or Relative Motion, Vol. I: The Discovery of Dynamics. Cambridge
University Press, Cambridge.
Barbour J. B. (1992). Time and the interpretation of quantum gravity. Syracuse University Preprint.
Barbour J. B. (2001). The Discovery of Dynamics: A Study from a Machian Point of View of the
Discovery and the Structure of Dynamical Theories. Oxford University Press, Oxford.
[57]	Barbour J. B. (2001). The End of Time. Oxford University Press, Oxford.

870
Литература
[58] Barbour J. В. (2004). Absolute or Relative Motion: The Deep Structure of General Relativity. Oxford
University Press, Oxford.
[59] Barbour J. B., Foster В., О Murchadha N. (2002). Relativity without relativity. Class. Quant. Grav.
19, 3217-3248. [gr-qc/0012089]
[60] Barrett J. W., Crane L. (1998). Relativistic spin networks and quantum gravity. J. Math. Phys. 39,
3296-3302.
[61
Quant. Grav. 17, 3101-3118.
quantum
[62] Barrow J.D., Tipler F. J. (1988). The Anthropic Cosmological Principle. Oxford University Press,
Oxford.
[63] Baston R. J., Eastwood M. G, (1989). The Penrose transform: its interaction with representation
theory. Oxford University Press, Oxford.
[64] Bateman H. (1904). The solution of partial differential equations by means of definite integrals. Proc.
bond. Math. Soc. (2) 1, 451-458.
[65] Bateman H. (1944). Partial Differential Equations of Mathematical Physics. Dover, New York.
[66] Becker R. (1982). Electromagnetic Fields and Interactions. Dover, New York.
[67] Begelman М. C., Blandford R. D., Rees M. J. (1984). Theory of extragalactic radio sources. Rev. Mod.
Phys. 56, 255.
[68] Bekenstein J. (1972). Black holes and the second law. Lett. Nuovo Cim. 4, 737-740.
[69] Белинский В. А., Халатников И. М., Лифшиц Е.М. (1970). Колебательный режим приближения
к особой точке в релятивистской космологии. Усп. физ. наук 102, 463-500.
[70] Bell J. S. (1987). Speakable and Unspeakable in Quantum Mechanics. Cambridge University Press,
Cambridge.
[71] Beltrami E. (1868). Essay on the interpretation of non-Euclidean geometry. Translated in Stillwell
J. C. (1996). Sources of Hyperbolic Geometry. Hist. Math. 10, AMS Publications.
[72] Bennett C. L. et al. (2003). First Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations:
Preliminary Maps and Basic Results. Astrophys. J. Suppl. 148, 1. [astro-ph/0302207 ]
[73] Bergmann P. G. (1956). Helv. Phys. Acta Suppl. 4, 79.
[74] Bergmann P.G. (1957). Two-component spinors in general relativity. Phys. Rev. 107, 624-629.
[75] Bern Z. (2002). Perturbative Quantum Gravity and its relation to Gauge Theory. Living Rev. Relativity
5.[http://relativity.livingreviews.org/Articles/lrr-2002-5/]
[76] Berry М. V. (1984). Quantal phase factors accompanying adiabatic changes. Proc. Roy. Soc. Lond.
A392, 45-57.
[77] Berry М. V. (1985). Classical adiabatic angles and quantal adiabatic phase. J. Phys. A. Math. Gen. 18,
15-27.
[78] Berry М. V., Keating J. P. (1999). The Riemann Zeros and Eigenvalue Asymptotics. SIAM Review 41,
No. 2, 236-266.
[79] Berry М. V., Robbins J. M. (1997). Indistinguishability for quantum particles: spin, statistics and the
geometric phase. Proc. R. Soc. Lond. A453, 1771-1790.
[80] Biedenham L. C., Louck J. D. (1981). Angular Momentum in Quantum Physics. Addison-Wesley,
London.	*
[81] Bilaniuk O.-M., Sudarshan, G. (1969). Particle beyond the light barrier. Phys. Today 22, 43-51.

Литература
871
[82] Birrell N.D., Davies P.C. W. (1984). Quantum Fields in Curved Space. Cambridge University Press,
Cambridge. Имеется перевод: Биррелл H., Девис П. Квантованные поля в искривленном про¬
странстве-времени. Мир, М., 1984.
[83] Bjorken J. D., Drell S. D. (1965). Relativistic Quantum Mechanics. McGraw Hill, New York & London.
Имеется перевод: Бьёркен Дж. Д., Дрелл С. Д. Релятивистская квантовая теория, т. 1. Реля¬
тивистская квантовая механика. Наука, М., 1978.
[84] Blanchard A., Douspis М., Rowan-Robinson М., Sarkar S. (2003). An alternative to the cosmological
«concordance model». Astron. Astrophys. 412, 35-44.
[85] Blanford R. D., Znajek R. L. (1977). Electromagnetic Extraction of Energy from Kerr Black Holes.
Monthly Notices of the Royal Astronomical Society 179, 433.
[86] Bohm D. (1951). Quantum Theory (Prentice-Hall, Englewood-Cliffs.) Ch. 22, sect. 15-19. Reprinted
as: The Paradox of Einstein, Rosen and Podolsky, in Quantum Theory and Measurement (ed.
J. A. Wheeler, W. H.Zurek) Princeton Univ. Press, Princeton, New Jersey, 1983. Имеется перевод:
Бом Д. Квантовая теория. Физматгиз, М., 1961.
[87] Bohm D., Hiley В. (1994). The Undivided Universe. Routledge, London.
[88] Bojowald M. (2001). Absence of singularity in loop quantum cosmology. Phys. Rev. Lett. 86, 5227-
5230.
e •
[89] Bondi H. (1957). Negative mass in general relativity. Rev. Mod. Phys. 29, 423-428; also in Math.
Rev. 19, 814.
[90] Bondi H. (1960). Gravitational waves in general relativity. Nature (London) 186, 535.
[91] Bondi H. (1961). Cosmology. Cambridge University Press, Cambridge.
[92] Bondi H. (1964). Relativity and Common Sense. Heinemann, London. Имеется перевод: Бонди Г.
Относительность и здравый смысл. Мир, М., 1967.
[93] Bondi Н. (1967). Assumption and Myth in Physical Theory. Cambridge University Press, Cambridge.
Имеется перевод: Бонди Г. Гипотезы и мифы в физической теории. Мир, М., 1972.
[94] Bondi Н., Gold Т. (1948). The Steady-State Theory of the Expanding Universe. Mon. Not. Roy. Astron.
Soc. 108, 252-270.
[95] Bondi H., van der Burg M. G. J., Metzner A.W.K. (1962). Gravitational waves in general relativity,
VII. Waves from axisymmetric isolated systems. Proc. Roy. Soc. Lond. A269, 21-52.
[96] Bonnor W. B., Rotenberg M. A. (1966). Gravitational waves from isolated sources. Proc. Roy. Soc.
Lond. A289, 2 47-274.
[97] Bomer G. (2003). The Early Universe. Springer-Verlag.
[98] Bouchet F. R., Peter P., Riazuelo A., Sakellariadou M. (2002). Evidence against or for topological
defects in the BOOMERANG data? Phys. Rev. D65 (2002), 021301. [astro-ph/0005022]
[99] Boyer С. B. (1968). A History of Mathematics, 2nd ed. John Wiley & Sons, New York.
[100] Braginsky V. (1977). The Detection of Gravitational Waves and Quantum Non-Distributive
Measurements. In Topics in Theoretical and Experimental Gravitation Physics (ed. V. DeSabbata,
J. Weber), 105-122. Plenum Press, New York.
[101] Bramson B.D. (1975). The alignment of frames of reference at null infinity for asymptotically flat
Einstein-Maxwell manifolds. Proc. R. Soc. London, Ser A 341, 451-461.
[102] Brandhuber A., Spence B., Travaglini G. (2004). One-Loop Gauge Theory Amplitudes in N — 4
Super Yang Mills from MHV Vertices, [hep-th/0407214 ]
[103] Brauer R., Weyl H. (1935). Spinors in n dimensions. Am. J. Math. 57, 425-449.
[104] Brekke L., Freund P. G. O. (1993). p-adic numbers in physics. North-Holland, Amsterdam.

872
Литература
[105] Bremermann Н. (1965). Distributions, Complex Variables and Fourier Transforms. Addison Wesley,
Reading, Massachusetts.
[106] Brody D. C., Hugbston L.P. (1998). Geometric models for quantum statistical inference. In The
Geometric Universe; Science, Geometry, and the Work of Roger Penrose (ed. S. A. Huggett,
L. J. Mason, K. P. Tod, S. T. Tsou, N. M. J. Woodhouse). Oxford University Press, Oxford.
[107] Brody D.C., Hughston L.P. (1998). The quantum canonical ensemble. J. Math. Phys. 39(12), 6502-
6508.
[108] Brody D.C., Hughston L.P. (2001). Geometric Quantum Mechanics. J. Geom. and Phys. 38(1),
19-53.
[109] Brown J. W., Churchill R. V. (2004). Complex Variables and Applications. McGraw-Hill, New York
& London.
[110] Bryant R. L., Chem S. S., Gardner R. B., Goldschmidt H. L., Griffiths P. A. (1991). Exterior Differential
Systems. MSRI Publications, 18. Springer-Verlag, New York.
[111] Bucher М., Goldhaber A., Turok N. (1995). An open Universe from Inflation. Phys. Rev. D52.
[hep-ph/9411206]
[112] Buckley P., Peat F. D. (1996). Glimpsing Reality. University of Toronto Press, Toronto.
[113] Budinich P., Trautman A. (1988). The Spinorial Chessboard. Trieste Notes in Physics. Springer-Verlag,
Berlin.
[114] Burbidge G. R., Burbidge E. М., Fowler W. A., Hoyle F. (1957). Synthesis of the Elements in Stars.
Revs. Mod. Phys. 29, 547-650.
[115] Burkert W. (1972). Lore and Science in Ancient Pythagoreanism. Harvard University Press, Harvard.
[116] Burkill J. C. (1962). A First Course in Mathematical Analysis. Cambridge University Press,
Cambridge.
[117] Byerly W. E. (2003). An Elementary? Treatise on Fourier s Series and Spherical', Cylindrical, and
Ellipsoidal Harmonics, with Applications to Problems in Mathematical Physics. Dover, New York.
[118] Cachazo F., Svrcek P., Witten E. (2004). MHV Vertices and Tree Amplitudes in Gauge Theory.
[hep-th/0403047]
[119] Cachazo F., Svrcek P., Witten E. (2004). Twistor Space Structure of One-Loop Amplitudes In Gauge
Theory, [hep-th/0406177]
[120] Cachazo F., Svrcek P., and Witten E. (2004). Gauge Theory Amplitudes In Twistor Space and
Holomorphic Anomaly. [hep-th/0409245]
[121] Candelas P., de la Ossa X. C., Green P. S., Parkes L. (1991). A pair of Calabi-Yau manifolds as an
exactly soluble superconformal theory. Nucl. Phys. B359, 21.
Г
[122] Cartan E. (1923). Sur les varietes a connexion affine et la theorie de la relativite generalisee I. Ann.
Ecole Norm. Sup. 40, 325-412.
/
[123] Cartan E. (1924). Sur les varietes a connexion affine et la theorie de la relativite generalisee (suite).
Ann. Ecole Norm. Sup. 41, 1-45.
Г
[124] Cartan E. (1925). Sur les varietes a connexion affine et la theorie de la relativite generalisee II. Ann.
Ecole Norm. Sup. 42, 17-88.
/
[125] Cartan E. (1945). Les Systemes Differentiels Exterieurs et leurs Applications Geometriques. Hermann,
Paris. Имеется перевод: Картан Э. Внешние дифференциальные системы и их геометрические
применения. — М.: ИЛ, 1962.
/
[126] Cartan Е. (1966). The Theory of Spinors. Hermann, Paris. Имеется перевод: Картан Э. Теория
спиноров. 1997.

Литература
873
[127] Carter В. (1966а). The Complete Analytic Extension of the Reissner-Nordstrom Metric in the Special
Case e2 ~ m2. Phys. Letters. 21, 423^124; Complete Analytic Extension of the Symmetry Axis of
Kerr’s Solution of Einstein’s Equations. Phys. Rev. 141, 1242-1247.
[128] Carter B. (1966b). Cambridge Ph.D. thesis; the relevant pages are accessible on
[http://luth2.obspm.fr/~carter/Thesis/4p25A~25B.html]
[129] Carter B. (1971). Axisymmetric Black Hole Has Only Two Degrees of Freedom. Phys. Rev. Lett. 26,
331-332.
[130] Carter B. (1974). Large Number Coincidences and the Anthropic Principle. In Confrontation of
Cosmological Theory with Astronomical Data (ed. M. S. Longair), 291-298. Reidel, Dordrecht
(Reprinted in [?].)
[131] Cercignani C. (1999). Ludwig Boltzmann: The Man Who Trusted Atoms. Oxford University Press,
Oxford.
[132] Chan H.-M., Tsou S.T. (1993). Some Elementary Gauge Theory Concepts. World Scientific Lecture
Notes in Physics, Vol. 47., London.
[133] Chan H.-M., Tsou S. T. (2002). Fermion Generations and Mixing from Dualized Standard Model. Acta
Physic a Polonica В 12.
[134] Chandrasekhar S. (1981). The maximum mass of ideal white dwarfs. Astrophys. J. 74, 81-82.
[135] Chandrasekhar S. (1983). The Mathematical Theory of Black Holes. Clarendon Press, Oxford.
[136] Chari V., Pressley A. (1994). A Guide to Quantum Groups. Cambridge University Press, Cambridge.
[137] Chen W. W. L. (2002). Linear Functional Analysis. [Available online:
http://www.mauhs.mq.edu.au/~wchen/lnlfafolder/lnlfa.html]
[138]	Cheng K. S., Wang J.	(1999). The formation	and merger of compact objects in central engine	of active
galactic nuclei and quasars: gamma-ray burst and gravitational radiation. Astrophys. J. 521,	502.
[139] Chem S. S. (1979). Complex Manifolds Without Potential Theory. Springer-Verlag, New York.
[140] Chernoff PR., Marsden J. E. (1974). Properties of infinite Hamiltonian systems. Lecture Notes in
Mathematics, vol. 425. Springer-Verlag, Berlin.
[141]	Chevalley C. (1946).	Theory of Lie Groups.	Princeton University Press, Princeton.
[142]	Chevalley C. (1954).	The Algebraic Theory	of Spinors. Columbia University Press, New York,
[143] Chew G. F. (1962). S-Matrix Theory of Strong Interactions. Pearson Benjamin Cummings.
[144] Choquet-Bmhat Y., DeWitt-Morette C. (2000). Analysis, Manifolds, and Physics. Parts I and 11.
North-Holland, Amsterdam.
[145] Christenson J. H., Cronin J. W., Fitch V. L., Turlay R. (1964). Evidence for the 2p decay of the КО
meson. Phys. Rev. Lett. 13, 138-140.
[146] Christian J. (1995). Definite events in Newton-Cartan quantum gravity. Oxford preprint, submitted to
Phys. Rev. D.
4
[147] Church A. (1936). The calculi of lambda-conversion. Annals of Mathematics Studies, No. 6. Princeton
University Press, Princeton, NJ.
[148] Claudel С. М., Newman K. P. (1998). Isotropic Cosmological Singularities I. Polytropic Perfect Fluid
Spacetimes. Proc. R. Soc. Lond. 454, 1073-1107.
[149] Clauser J. F., Home M. A., Shimony A., Holt R. A. (1969). Proposed experiment to test local hidden-
variable theories. Phys. Rev. Lett. 23, 880.
[150] Clifford W. K. (1873). Preliminary Sketch of Biquatemions. Proc. London Math. Soc. 4, 381-395.
[151] Clifford W. K. (1878). Applications of Grassmann’s extensive algebra. Am. J. Math. 1, 350-358.

874
Литература
152] Clifford W. К. (1882). Mathematical papers by William Kingdon Clifford (ed. R. Tucker). London,
153] Cohen R J. (1966). Set Theory and the Continuum Hypothesis. W. A. Benjamin, New York.
154] Collins RD. B. (1977). An Introduction to Regge Theory and High Energy Physics. Cambridge
University Press, Cambridge.
155] Colombeau J. F. (1983). A multiplication of distributions. J. Math. Anal AppL 94, 96-115.
156] Colombeau J. F. (1985). Elementary Introduction to New Generalized Functions. North Holland,
Amsterdam.
157] Connes A. (1990). Essay on physics and non-commutative geometry. In The Interface of Mathematics
and Particle Physics (eds. D. G. Quillen, G. B. Segal, S. T. Tsou). Clarendon Press, Oxford.
158] Connes A. (1998). Noncommutative differential geometry and the structure of space-time. In
The Geometric Universe; Science, Geometry, and the Work of Roger Penrose (eds. S. A. Huggett,
L. J. Mason, K. P. Tod, S. T. Tsou, N. M. J. Woodhouse). Oxford University Press, Oxford.
159] Connes A., Berberian S.K. (1995). Noncommutative Geometry. Academic Press.
r
160] Connes A., Kreimer D. (1998). Hopf Algebras, Renormalization and Noncommutative Geometry,
[hep-th/9808042]
161] Conway J. H. (1976). On Numbers and Games. Academic Press, London.
162] Conway J.H., Kochen S. (2002). The geometry of the quantum paradoxes. In Quantum
[Un]speakables: From Bell to Quantum Information (Eds. R. A. Bertlmann, A. Zeilinger). Springer-
Verlag, Berlin.
163] Conway J.H., Norton S. P. (1979). Monstrous Moonshine. Bull bond. Math. Soc. 11, 308-339.
164] Conway J. H., Smith D.A. (2003). On Quaternions and Octonions. A. K. Peters.
165] Corson E.M. (1953). Introduction to Tensors, Spinors, and Relativistic Wave-equations. Blackie and
Son Ltd., London.
166] Costa de Beauregard, O. (1995). Macroscopic retrocausation. Found. Phy. Lett. 8(3), 287-291.
167] Cotes R. (1714). Logometria. Phil. Trans. Roy. Soc. Lond. (March).
168] Cox D.A., Katz S. (1999). Mirror symmetry and algebraic geometiy. Mathematical Surveys and
Monographs 68. American Mathematical Society, Providence, RI.
169] Cramer J. G. (1988). An overview of the transactional interpretation of quantum mechanics. Int. J.
Theor. Phys. 27(2), 227-236.
170] Crowe M. J. (1967). A History of Vector Analysis: The Evolution of the Idea of a Vectorial System.
University of Notre Dame Press, Toronto. (Reprinted with additions and corrections by Dover, New
York, 1985.)
171] Crumeyrolle A. (1990). Orthogonal and Symplectic Clifford Algebras Abstract: On Spinor Structures.
Kluwer [ISBN 0-7923-0541-8].
172] Cvitanovic P., Kennedy A. D. (1982). Spinors in negative dimensions. Phys. Scripta 26, 5-14.
173] Das A. Ferbel T. (2004). Introduction to Nuclear and Particle Physics. World Scientific Publishing
Company, Singapore.
174] Davenport H. (1952). The Higher Arithmetic: An Introduction to the Theory of Numbers. Hutchinson’s
University Library, London.
175] Davis M. (1978). What is a Computation? In Mathematics Today: Twelve Informal Essays (ed.
L. A. Steen). Springer-Verlag, New York.
176] Davis M. (1988). Mathematical logic and the origin of modem computers. In The Universal Turing
Machine: A Half-Century Survey (ed. R. Herken). Kammerer and Unverzagt, Hamburg.

Литература
875
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
Davies М. (1997). Europe: A History (Oxford University Press, Oxford), 89-94.
Davies P. (2003). How to Build a Time Machine. Penguin, USA.
Давыдов A. C. (1973). Квантовая механика. Наука, Москва.
de Bemardis P., et al. (2000). A Flat Universe from High-Resolution Maps of the Cosmic Microwave
Background Radiation. Nature 404, 955-959.
Delduc F., Galperin A., Howe P., Sokatchev E. (1993). A twistor formulation of the heterotic D =
— 10 superstring with manifest (8,0) worldsheet supersymmetry. Phys. Rev. D47, 578-593. [hep-
th/9207050]
Derbyshire J. (2003). Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in
Mathematics. Joseph Henry Press, Washington, DC.
Deser S. (1999). Nonrenormalizability of D = 11 supergravity, [hep-th/9905017 ]
Deser S. (2000). Infinities in quantum gravities. Annalen Phys. 9, 299-307. [gr-qc/ 9911073]
Deser S., Teitelboim C. (1977). Supergravity Has Positive Energy. Phys. Rev. Lett. 39, 248-252.
Deser S., Zumino B. (1976). Consistent supergravity. Phys. Lett. 62B, 335-337.
de Sitter W. (1913). Phys. Zeitz. 14, 429. (in German).
Deutsch D. (2000). The Fabric of Reality. Penguin, London. Имеется перевод: Дойч Д. Структура
реальности. РХД, Ижевск, 2001.
Devlin К. (1988). Mathematics: The New Golden Age. Penguin Books, London.
Devlin K. (2002). The Millennium Problems: The Seven Greatest Unsolved Mathematical Puzzles of
Our Time. Basic Books, London; Perseus Books, New York.
DeWitt B. S. (1967). Quantum Theory of Gravity. I. The Canonical Theoiy. Phys. Rev. 160, 1113.
DeWitt B. S. (1984). Supermanifolds. Cambridge University Press, Cambridge.
DeWitt B. S., Graham R. D. (eds.) (1973). The Many-Worlds Interpretation of Quantum Mechanics.
Princeton University Press, Princeton.
Diosi L. (1984). Gravitation and quantum mechanical localization of macro-objects. Phys. Lett. 105A,
199-202.
Diosi L. (1989). Models for universal reduction of macroscopic quantum fluctuations. Phys. Rev. A40,
1165-1174.
Dicke R. H. (1961). Dirac’s Cosmology and Mach’s Principle. Nature 192, 440-441.
Dicke R.H. (1981). Interaction-free quantum measurements: A paradox? Am. J. Phys. 49, 925.
Dicke R.H., Peebles P.J. E., Roll P. G., Wilkinson D.T. (1965). Cosmic Black-Body Radiation.
Astrophys. J. 142, 414-419.
Dine M. (2000). Some reflections on Moduli, their Stabilization and Cosmology.
[hep-th/0001157]
Dirac P. A. M . (1928). The quantum theory of the electron. Proc. Roy. Soc. Lond. A117, 610-624; ibid.
part II, A118, 351-361. Имеется перевод: Дирак П. А. М. Квантовая теория электрона. Собрание
научных трудов, т. II. Физматлит, М., 2003, стр. 321-351.
Dirac Р. А. М. (1932). Relativistic Quantum Mechanics. Proc. Roy. Soc.. A136, 453-464. Имеется
перевод: Дирак П. А. М. Релятивистская квантовая механика. Собрание научных трудов, т. II.
Физматлит, М., 2003, стр. 399-408.
[202] Dirac Р. А. М. (1933). The Lagrangian in Quantum Mechanics. Phys. Zs. d. Sowjet.. 3, 64-72. Имеется
перевод: Дирак П. А. М. Лагранжиан в квантовой механике. Собрание научных трудов, т. II.
Физматлит, М., 2003, стр. 573-579.

876
Литература
[203
[204
[205
[206
[207
[208
[209
[210
[211
[212
[213
[214
[215
[216
[217
[218
[219
[220
Dirac Р. A.M. (1936). Relativistic Wave Equations. Proc. Roy. Soc. London A155, 447-^159. Имеется
перевод: Дирак П. А. М. Релятивистские волновые уравнения. Собрание научных трудов, т. II.
Физматлит, М., 2003, стр. 498-510.
Dirac Р. А. М. (1937). The Cosmological Constants. Nature 139, 323. Имеется перевод: Дирак П.
А. М. Космологические постоянные. В сб. статей Альберт Эйнштейн и теория гравитации..
Мир, М., 1979, стр. 538-539.
Dirac Р. А. М. (1938). A new basis for cosmology. Proc. R. Soc. bond. A165, 199.
Dirac P.A.M. (1950). Generalized Hamiltonian dynamics. Can. J. Math. 2, 129-148. Имеется пе¬
ревод: Дирак П. А. М. Обобщенная гамильтонова динамика. Собрание научных трудов, т. III.
Физматлит, М., 2004, стр. 203-223.
Dirac Р. А. М. (1964). Lectures on Quantum Mechanics. Yeshiva University, New York. Имеется
перевод: Дирак П. Лекции по квантовой механике. РХД, Ижевск, 1999.
Dirac Р. А. М. (1966). Lectures in Quantum Field Theory. Имеется перевод: Дирак П. Лекции по
квантовой теории поля. Мир, М., 1971. Academic Press, New York.
Dirac P. A.M. (1982). The Principles of Quantum Mechanics, 4th edn. Clarendon Press, Oxford.
Имеется перевод: Дирак П. Принципы квантовой механики. Наука, М., 1979.
Dirac Р. А. М. (1982). Pretty mathematics. Int. J. Theor. Phys. 21, 603-605. Имеется перевод: Дирак
П. А. М. Очаровательная математика. Собрание научных трудов, т. III. Физматлит, М., 2004,
стр. 372-374.
Dirac Р. А. М. (1983). The Origin of Quantum Field Theory. In The Birth of Particle Physics (ed.
Brown, Hoddeson). Cambridge University Press, New York, pp. 39-55. Имеется перевод: Дирак П.
А.	М. Происхождение квантовой теории поля. Собрание научных трудов, т. III. М.: Физматлит,
2004.-С.629-641.
Dixon G. (1994). Division Algebras, Quaternions, Complex Numbers and the Algebraic Design of
Physics. Kluwer Academic Publishers, Boston.
Dodelson S. (2003). Modern Cosmology. Academic Press, London.
Dolan L. (1996). Superstring twisted conformal field theoiy: Moonshine, the Monster, and related
topics. (South Hadley, MA, 1994). Contemp. Math. 193, 9-24.
Domagala М., Lewandowski J. (2004). Black hole entropy from Quantum Geometry.
[gr-qc/0407041]
Donaldson S. K., Kronheimer P. B. (1990). The Geometry of Four-Manifolds. Oxford University Press,
Oxford.
Douady A., Hubbard J. (1985). On the dynamics of polynomial-like mappings. Ann. Sci. Ecole Norm.
Sup. 18, 287-343.
Dowker F., Kent A. (1996). On the consistent histories approach to quantum mechanics. J. Stat. Phys.
82. [gr-qc/9412067]
Drake S. (1957). Discoveries and Opinions of Galileo. Doubleday, New York.
Drake S. (trans.) (1953). Galileo Galilei: Dialogue Concerning the Two Chief World Systems —
Ptolemaic and Copernican. University of California, Berkeley. Имеется перевод: Галилей Г. Диалог
о двух главнейших системах мира — птолемеевой и коперниковой. В кн.: Галилей Г. Избранные
труды в 2-х т., т. I. М.: Наука, 1964.
[221] Dray Т., Manogue С. А. (1999). The Exceptional Jordan Eigenvalue Problem. Int. J. Theor. Phys. 38,
2901-2916. [math-ph/99110004 ]
[222] Dreyer O., Markopoulou F., Smolin L. (2004). Symmetry and entropy of black hole horizons.
[hep-th/0409056]

Литература
877
[223] Duffin R. J. (1938). On the characteristic matrices of covariant systems. Phys. Rev. 54, 1114.
[224] Dunajski M. (2002). Anti-self-dual four-manifolds with a parallel real spinor. R. Soc. Lond. Proc. Ser.
A Math. Phys. Eng. Sci. 458(2021), 1205-1222.
[225] du Sautoy M. (2003). The Music of the Primes. Perennial, New York.
[226] Dunham W. (1999). Euler: The Master of Us All. Math. Assoc. Amer., Washington, DC.
[227] Dyson F. J. (1966). Symmetry groups in nuclear and particle physics: a lecture-note and reprint
volume. W. A. Benjamin, New York.
[228] Dyson F. J. (1979). Time Without End: Physics and Biology in an Open Universe, Rev. Mod. Phys.
51, 447-460.
[229] Eastwood M. G., Penrose, R., Wells R. O., Jr. (1981). Cohomology and massless fields. Comm. Math.
Phys. 78, 305-351. Имеется перевод: Иствуд М. Дж., Пенроуз Р., Уэллс P.O. Теория когомологий
и безмассовые поля. В сб. статей Твисторы и калибровочные поля. М.: Мир, 1983. — С. 250-308.
[230] Eddington A. S. (1929). The Nature of the Physical World. Cambridge University Press, Cambridge.
[231] Eddington A. S. (1929). A Symmetrical Treatment of the Wave Equation. Proc. R. Soc. Lond. A121,
524-542.
[232] Eddington A. S. (1946). Fundamental Theoty. Cambridge University Press, Cambridge.
[233] Eden R. J., Landshoff P. V., Olive D. L, Polkinghome J. C. (2002). The Analytic S-Matrix. Cambridge
University Press.
[234] Edwards С. H., Penney D. E. (2002). Calculus with Analytic Geometry. Prentice Hall; 6th edition.
[235] Ehrenberg W., Siday R. E. (1949). The refractive index in electron optics and the principles of
dynamics. Proc. Phys. Soc. LXI1B, 8-21.
[236] Ehrenfest P., Ehrenfest T. (1959). The Conceptual Foundations of the Statistical Approach in
Mechanics. Cornell University Press, Ithaca, NY.
[237] Eilenberg S., MacLane S. (1945). General theory of natural equivalences. Trans. Am. Math. Soc. 58,
231-294.
[238] Einstein A. (1914), in [495].
[239] Einstein A. (1917). Kosmologische Betrachtungen zur allgemeinen Relativitatstheorie.
Sitzungsberichte der Preussischen Akademie der Wissenschaften, 142-152. Имеется перевод: Эйн¬
штейн А. Вопросы космологии и общая теория относительности. Собрание научных трудов,
т. I. — М.: Наука, 1965. — С. 601-612.
[240] Einstein А. (1925). Einheitliche Feldtheorie von Gravitation und Elektrizitdt. S. B. Preuss. Akad. Wiss.
22, 414^419. Имеется перевод: Эйнштейн А. Единая полевая теория тяготения и электричества.
Собрание научных трудов, т. II. — М.: Наука, 1966. — С. 171-177.
[241] Einstein А. (1945). A generalization of the relativistic theory of gravitation. Ann. Math. 46, 578-
584. Имеется перевод: Эйнштейн А. Обобщение релятивистской теории гравитации. Собрание
научных трудов, т. II. — М.: Наука, 1966. С. 614-622.
[242] Einstein А. (1948). A generalized theory of gravitation. Rev. Mod. Phys. 20, 35-39. Имеется перевод:
Эйнштейн А. Обобщенная теория тяготения. Собрание научных трудов, т. II. — М.: Наука, 1966.
С.663-673.
[243] Einstein А. (1955). Relativistic theory of the non-symmetric field. In Appendix II: The Meaning of
Relativity, 5th ed., 133-166. Princeton University Press, Princeton, NJ. Имеется перевод: Эйнштейн
А.	Релятивистская теория несимметричного поля. Собрание научных трудов, т. II. — М.: Наука,
1966. С. 849-873.

878
Литература
[244
[245
[246
[247
[248
[249
[250
[251
[252
[253
[254
[255
[256
[257
[258
[259
[260
[261
[262
Einstein A., Kaufman В. (1955). A new form of the general relativistic field equations. Ann. Math.
62, 128-138. Имеется перевод: Эйнштейн А., Кауфман Б. Новая форма уравнений поля в общей
теории относительности. Собрание научных трудов, т. П. — М.: Наука, 1966. — С. 835-848.
Einstein A., Straus Е. G. (1946). A generalization of the relativistic theory of gravitation II. Ann. Math.
47, 731-741. Имеется перевод: Эйнштейн А., Страус Э. Обобщение релятивистской теории
гравитациию Собрание научных трудов, т. II. ~ М.: Наука, 1966. — С. 636-649.
Einstein A., Podolsky P., Rosen N. (1935). Can quantum-mechanical description of physical reality
be considered complete? In Quantum Theory and Measurement (ed. J. A. Wheeler, W. H.Zurek).
Princeton University Press, Princeton, New Jersey, 1983; originally in Phys. Rev. 47, 777-780. Име¬
ется перевод: Эйнштейн А., Подольский П., Розен Н. Можно ли считать квантово-механическое
описание физической реальности полным? Собрание научных трудов, т. Ш. — М.: Наука, 1966.
С. 604-611.
Elitzur А. С., Vaidman L, (1993). Quantum mechanical interaction-free measurements. Found. Phys.
23, 987-997.
Elliott J. P., Dawber P. G. (1984). Symmetry in Physics, Vol. 1. Macmillan, London. Имеется перевод
предыдущего издания: Эллиот Дж., Добер П. Симметрия в физике. Т. 1. — М.: Мир, 1983.
Ellis J., Mavromatos N. Е., Nanopoulos D.V. (1997а). Vacuum fluctuations and decoherence in
mesoscopic and microscopic systems. In Symposium on Flavour-Changing Neutral Currents: Present
and Future Studies. UCLA.
Ellis J., Mavromatos N. E., Nanopoulos D. V. (1997b). Quantum decoherence in a D-foam background.
Mod. Phys. Lett. A12, 2029-2036.
Engelking E. (1968). Outline of General Topology. North-Holland & PWN, Amsterdam.
Euler L. (1748). Introductio in Analysis Infinitorum.
Everett H. (1957). «Relative State» formulation of quantum mechanics. In Quantum Theory and
Measurement (ed. J.A.Wheeler, W.H.Zurek). Princeton University Press, Princeton, New Jersey,
1983; originally in Rev. Mod. Phys. 29, 454-462.
Fauvel J., Gray J. (1987). The History of Mathematics: A Reader. Macmillan, London.
Ferber A. (1978). Supertwistors and conformal supersymmetry. Nucl. Phys. B132, 55- 64.
Femow R. C. (1989). Introduction to Experimental Particle Physics. Cambridge University Press,
Cambridge.
Feynman R. P. (1948). Space-time approach to nonrelativistic quantum mechanics. Rev. Modern Phys.
20, 367-387.
Feynman R. P. (1949). The theory of positrons. Phys. Rev. 76, 749. Имеется перевод: Фейнман P.
Теория позитронов. В сб. статей Новейшее развитие квантовой электродинамики. — М.: ИЛ,
1954, — С. 138-160.
Feynman R.P. (1987). Elementary Particles and the Laws of Physics: The 1986 Dirac Memorial
Lectures. Cambridge University Press, Cambridge.
Feynman R. P., Hibbs A. (1965). Quantum Mechanics and Path Integrals. McGraw-Hill, New York.
Имеется перевод: Фейнман Р., Хибс А. Квантовая механика и интегралы по траекториям. —
М.: Мир, 1968.
Fierz М. (1938). Uber die Relativitische Theorie kraftefreier Teilchen mit beliebigem Spin. Helv.
Phys. Acta 12, 3-37.
Fierz M. (1940). Uber den Drehimpuls von Teilchen mit Ruhemasse null und beliebigem Spin. Helv.
Phys. Acta 13, 45-60.
[263]	Fierz М., Pauli W. (1939). On relativistic wave equations for particles of arbitrary spin in an
electromagnetic field. Proc. Roy. Soc. Lond. A173, 211-232.

Литература
879
[264] Finkeistein D. (1969). Space-time code. Phys. Rev. 184, 1261-1279.
[265] Finkeistein D., Rubinstein J. (1968). Connection between spin, statistics, and kinks. J. Math. Phys. 9,
1972.
[266] Flanders H. (1963). Differential Forms. Academic Press. (Reissued by Dorf, 1989.)
[267] Floyd R. М., Penrose R. (1971). Extraction of Rotational Energy from a Black Hole. Nature Phys.
ScL 229, 177.
[268] Fortney L. R. (1997). Principles of Electronics. Analog and Digital. Harcourt Brace Jovanovich.
[269] Frankel T. (2001). The Geometry of Physics. Cambridge University Press, Cambridge.
[270] Frenkel A. (2000). A Tentative Expression of the Karolyhazy Uncertainty of the Space-time Structure
through Vacuum Spreads in Quantum Gravity. [ quant-ph/0002087 ]
[271] Friedlander F.G. (1982). Introduction to the theory of distributions. Cambridge University Press,
Cambridge.
[272] Friedrich W. L. (2000). Fire in the Sea; The Santorini Volcano: Natural History and the Legend of
Atlantis. (Trans. A. R. McBimey.) Cambridge University Press, Cambridge.
[273] Frittelli S., Kozameh C., Newman E.T. (1997). Dynamics of light cone cuts at null infinity. Phys.
Rev. D56, 8.
[274] Frohlich J., Pedrini B. (2000). New applications of the chiral anomaly. In Mathematical Physics 2000
(eds. A. Fokas, A. Grigoryan, T. Kibble, B. Zegarlinski), 9-47. Imperial College Press, London.
[275] Gambini R., Pullin J. (1999). Nonstandard optics from quantum spacetime. Phys. Rev. D59, 124021.
[276] Gandy R. (1988). The confluence of ideas in 1936. In The Universal Turing Machine: A Half-Century
Survey (ed. R. Herken). Kammerer and Unverzagt, Hamburg.
[277] Gangui A. (2003). Cosmology from Topological Defects. AIP Conf. Proc. 668.
[astro~ph/0303504]
[278] Gardner M. (1990). The New Ambidextrous Universe. W.H. Freeman, New York. Имеется перевод
более раннего издания: Гарднер М. Этот правый, левый мир. — М.: Мир, 1967.
[279] Gauss C.F. (1900). Werke. Vol. VIII, 357-362. Leipzig.
[280] Гельфанд И. М., Шилов Г. Е. Обобщенные функции и действия над ними. — М.: Физматгиз,
1959.
[281] Gell-Mann М. (1994). The Quark and the Jaguar: Adventures in the Simple and the Complex.
W. H. Freeman, New York.
[282] Gell-Mann М., Hartle J.B. (1995). Strong Decoherence. In Proceedings of the 4th Drexel Conference
on Quantum Non-Integrability: The Quantum-Classical Correspondence (eds. D.-H. Feng, B.-L. Hu).
International Press of Boston, Hong Kong (1998). [gr-qc/9509054 ]
[283] Gell-Mann М., Ne’eman Y. (2000). Eightfold Way. Perseus Publishing.
[284] Geroch R. (1968). Spinor structure of space-times in general relativity I. J. Math. Phys. 9, 1739-1744.
[285] Geroch R. (1970). Spinor structure of space-times in general relativity II. J. Math. Phys. 11, 343-348.
[286] Geroch R. (1984). The Everett Interpretation. Nous, 18, 617-633.
[287] Geroch R. (unpublished). Geometrical Quantum. Mechanics. Lecture notes given at University of
Chicago.
[288] Geroch R., Hartle J. (1986)., Computability and physical theories. Found. Phys. 16, 533.
[289] Geroch R., Kronheimer E.H., Penrose R. (1972). Ideal points for space-times. Proc. Roy. Soc. bond..
A347, 545-567.

880
Литература
[290] Ghirardi G. С., Grassi R., Rimini A. (1990). Continuous-spontaneous-reduction model involving
gravity. Phys. Rev. A42, 1057-1064.
[291] Ghirardi G. C., Rimini A., Weber T. (1986). Unified dynamics for microscopic and macroscopic
systems. Phys. Rev. D34, 470.
[292] Gibbons G. W. (1984). The isoperimetric and Bogomolny inequalities for black holes. In Global
Riemannian Geometry (eds. T. Willmore, N. J. Hitchin). Ellis Horwood, Chichester.
[293] Gibbons G. W. (1997). Collapsing Shells and the Isoperimetric Inequality for Black Holes. Class.
Quant. Grav. 14, 2905-2915. [hep-th/9701049]
[294] Gibbons G. W., Hartnoll S. A. (2002). Gravitational instability in higher dimensions.
[hep-th/0206202]
[295] Gibbons G. W. and Hawking S. W. (1977). Cosmological event horizons, thermodynamics, and particle
creation. Phys. Rev. D15, 2738-2751.
[296] Gibbons G. W., Репу M. J. (1978). Black Holes and Thermal Green’s Function. Proc. Roy. Soc. Lond.
A358, 467-494.
[297] Gibbs J. (1960). Elementary Principles in Statistical Mechanics. Dover, New York. Имеется перевод:
Гиббс Дж. В. Основные принципы статистической механики. — Ижевск: РХД, 2002.
[298] Гиндикин С. Г. (1986). Об одном построении гиперкэлеровых метрик. Функциональный анализ
и его приложения. 20, 82-83.
[299] Gindikin S. G. (1990). Between integral geometry and twistors. In Twistors in Mathematics and
Physics (eds. T.N. Bailey, R. J.Baston). LMS Lecture Note Series 156. Cambridge University Press,
Cambridge.
[300] Gisin N. (1989). Stochastic quantum dynamics and relativity. Helv. Phys. Acta 62, 363.
[301] Gisin N. (1990). Weinberg’s non-linear quantum mechanics and supraluminal communications. Phys.
Lett. 143 A, 1-2.
[302] Gisin N., de Riedmatten H., Scarani V., Marcikic I., Acin A., Tittel W., Zbinden H. (2004). Two
independent photon pairs versus four-photon entangled states in parametric down conversion. J. Mod.
Opt. 51, 1637. [quant-ph/0310167]
[303] Glashow S. (1959). The renormalizability of vector meson interactions. Nucl. Phys. 10, 107.
[304] Gleason A.M. (1957). Measures on the Closed Subspaces of a Hilbert Space. J. Math, and Mech. 6,
885-893.
[305] Gleason A. M. (1990). In More Mathematical People (eds. D. J. Albers, G. L. Alexanderson, C. Reid),
94. Harcourt Brace Jovanovich, Boston.
[306] Goddard P., et al. (1973). Quantum dynamics of a massless, relativistic string. Nucl. Phys. B56, 109.
[307] Gold T. (1962). The Arrow of Time. Am. J. Phys. 30, 403.
[308] Goldberg J.N., Macfarlane A. J., Newman E.T., Rohrlich F., Sudarshan E. C. G. (1967). Spin-s
spherical hannonics and eth. J. Math. Phys. 8, 2155-2161.
[309] Goldblatt R. (1979). Topoi: The Categorial Analysis of Logic. North-Holland Publishing Company,
Oxford & New York.
[310] Goldstein S. (1987). Stochastic mechanics and quantum theory. J. Stat. Phys. 47.
[311] Gottesman D., Preskill J. (2003). Comment on «The black hole final state», [hep-th/0311269 ]
[312] Gouvea F. Q. (1993). P-Adic Numbers: An Introduction. Springer-Verlag; 2nd edition (2000), Berlin
& New York.
[313] Grassmann H. G. (1844). Die lineare Ausdehnungslehre, 4th edition, Springer-Verlag.

Литература
881
[314] Grassmann Н. G. (1862). Die lineare Ausdehnungslehre Vollstandig und in strenger Form bearbeitet.
[315] Gray J. (1979). Ideas of Space; Euclidean, Non-Euclidean, and Relativistic. Oxford University Press,
Oxford.
[316] Green М. B. (2000). Superstrings and the unification of physical forces. In Mathematical Physics
2000 (eds. A. Fokas, T. W. B. Kibble, A. Grigouriou, B. Zegarlinski), 59-86. Imperial College Press,
London.
[317] Green M.B., Schwarz J.H., Witten E. (1987). Superstring Theory, Vol. I & II. Cambridge University
Press, Cambridge.
[318] Greene B. (1999). The Elegant Universe; Superstrings, Hidden Dimensions, and the Quest for the
Ultimate Theory. Random House, London. Имеется перевод: Грин Б. Элегантная Вселенная.
Суперструны, скрытые размерности и поиски окончательной теории. УРСС, М., 2004.
[319] Griffiths P., Harris I. (1978), Principles of Algebraic Geometry. John Wiley & Sons, New York.
Имеется перевод: Гриффитс Ф., Харрис Дж. Принципы алгебраической геометрии, т.т. 1, 2. —
М.: Мир, 1982.
[320] Грищук Л. П., Липунов В. М., Постнов К. А., Прохоров М. Е. Сатьяпракаш Б. С. (2001).
Гравитационно-волновая астрономия: в ожидании первого зарегистрированного источника.
Успехи физ. наук 171, 3-60.
[321] Groemer Н. (1996). Geometric Applications of Fourier Series and Spherical Harmonics. Cambridge
University Press, Cambridge.
[322] Gross D. J., Periwal V. (1988). String Perturbation Theory Diverges. Phys. Rev. Lett. 60, 2105.
[323] Gross M. W., Huybrechts D., Joyce D., Winkler G. D. (2003). Calabi~Yau Manifolds and Related
Geometries. Springer-Verlag.
[324] Grosser М., Kunzinger М., Oberguggenberger М., Steinbauer R. (2001). Geometric Theory of
Generalized Functions with Applications to General Relativity. Kluwer Academic Publishers, Boston
and Dordrecht, The Netherlands.
[325] Guenther D. B., Krauss L. М., Demarque P. (1998). Testing the Constancy of the Gravitational Constant
Using Helioseismology. Astrophys. J. 498, 871-876.
[326] Gunning R. C., Rossi H. (1965). Analytic Functions of Several Complex Variables. Prentice-Hall,
Englewood Cliffs, New Jersey. Имеется перевод: Ганнинг P., Росси X. Аналитические функции
многих комплексных переменных. — М.: Мир, 1969.
[327] Gursey F. (1983). Quatemionic and octonionic structures in physics: episodes in the relation between
physics and mathematics. Symm. Phys. (1600-1980), 557-592. San Feliu de Guixols. Univ. Autonoma
Barcelona, Barcelona, 1987.
[328] Gursey F., Tze C.-H. (1996). On the Role of Division, Jordan, and Related Algebras in Particle
Physics. World Scientific, Singapore.
[329] Gurzadyan V. G., et al. (2002). Ellipticity analysis of the BOOMERANG CMB maps. Int. J. Mod.
Phys. D12, 1859-1874. [astro-ph/0210021 ]
[330] Gurzadyan V. G., et al. (2003). Is there a common origin for the WMAP low multipole and for the
ellipticity in BOOMERANG CMB maps? [astro-ph/0312305]
[331] Gurzadyan V. G., et al. (2004). WMAP confirming the ellipticity in BOOMERANG and СОВЕ CMB
maps, [astro-ph/0402399]
[332] Gurzadyan V. G., Kocharyan A. A. (1992). On the problem of isotropization of cosmic background
radiation. Astron. Astrophys. 260, 14.
[333] Gurzadyan V. G., Kocharyan A. A. (1994). Paradigms of the Large-Scale Universe. Gordon and
Breach, Lausanne, Switzerland.

882
Литература
[334] Gurzadyan V. G., Torres S. (1997). Testing the effect of geodesic mixing with СОВЕ data to reveal
the curvature of the universe. Astron. and Astrophys. 321, 19-23. [astro-ph/9610152 ]
[335] Guth A. (1997). The Inflationary Universe. Jonathan Cape, London.
[336] Haag R. (1992). Local Quantum Physics: Fields, Particles, Algebras. Springer-Verlag, Berlin.
[337] Haehnelt M. G. (2003). Joint Formation of Supermassive Black Holes and Galaxies. In Carnegie
Observatories Astrophysics Series, Vol 1: Coevolution of Black Holes and Galaxies (ed. L. C. Ho).
Cambridge University Press, Cambridge. [astro-ph/0307378]
[338] Halverson N. W. (2001). DASI First Results: A Measurement of the Cosmic Microwave Background
Angular Power Spectrum. [ a s t г о~ph / 0104489]
[339] Halzen F., Martin A. D. (1984). Quarks and Leptons: an introductory course in modem particle
physics. John Wiley & Sons, New York.
[340] Hameroff S.R. (1987). Ultimate Computing. Biomolecular Consciousness and Nano-Technology.
North-Holi and, Amsterdam.
[341] Hameroff S.R. (1998). Fundamental geometry: the Penrose-Hameroff «Orch OR» model of
consciousness. In The Geometric Universe; Science, Geometiy, and the Work of Roger Penrose
(eds. S. A. Huggett, L. J. Mason, K. P. Tod, S. T. Tsou, N. M. J. Woodhouse). Oxford University Press,
Oxford.
[342] Hameroff S.R., Penrose R. (1996). Conscious events as orchestrated space-time selections. J. Consc.
Stud. 3, 36-63.
[343] Hameroff S. R., Watt R. С. (1982). Infonnation processing in microtubules. J. Theor. Biol. 98, 549-561.
[344] Hamilton E. (1999). Mythology: Timeless Tales of Gods and Heroes. Warner Books, New York.
[345] Han M. Y., Nambu Y. (1965). Three-Triplet Model with Double 51/(3) Symmetry. Phys. Rev. 139,
B1006-B1010.
[346] Hanany S., et al. (2000). MAXIMA-1: A Measurement of the Cosmic Microwave Background
Anisotropy on angular scales of 10 arcminutes to 5 degrees. Astrophys. J. 545, L5.
[347] Hanbury Brown R., Twiss R. Q. (1954). A new type of interferometer for use in radio astronomy.
Phil. Mag. 45, 663-682.
[348] Hanbury Brown R., Twiss R. Q. (1956). Correlation between photons in 2 coherent beams of light.
Nature 111.
[349] Hannabuss K. (1997). An Introduction to Quantum Theory. Oxford University Press, Oxford.
[350] Hansen В. M. S., Murali C. (1998). Gamma Ray Bursts from Stellar Collisions.
[astro-ph/9806256]
[351] Hansen R. O., Newman E. Т., Penrose R., Tod K. P. (1978). The metric and curvature properties of
//-space. Proc. Roy. Soc. bond. A363, 445-468.
[352] Hardy G. H. (1914). A Course of Pure Mathematics, 2nd edn. Cambridge University Press, Cambridge.
Имеется перевод: Харди Г. X. Курс чистой математики. — М., 1949.
[353] Hardy G.Н. (1940). A Mathematicians Apology. Cambridge University Press, Cambridge. Имеется
перевод: Харди Г. X. Апология математика. — Ижевск: РХД, 2000.
[354] Hardy G. Н. (1949). Divergent Series. Oxford University Press, New York. Имеется перевод: Харди
Г. X. Расходящиеся ряды. — М.: Факториал Пресс, 2006.
[355] Hardy G. Н., Wright Е.М. (1945). An Introduction to the Theory of Numbers (2nd edn.). Clarendon
Press, Oxford.
[356] Hardy L. (1992). Quantum mechanics, local realistic theories, and Lorentz-invariant realistic theories.
Phys. Rev. Lett. 68, 2981. [/abstract/PRL/v68/i20/p2981_l]

Литература
883
[357] Hardy L. (1993). Nonlocality for two particles without inequalities for almost all entangled states.
Phys. Rev. Lett. 71(11), 1665.
[358] Hartle j.B. (2003). Gravity: An Introduction to Einsteins General Relativity. Addison-Wes ley, San
Francisco, CA & London.
[359]	Hartle J.B. (2004). The Physics of «Now», [gr-qc/0403001]
[360]	Hartle J. B., Hawking S. W. (1983). The wave function of the Universe. Phys.	Rev.	D28,	2960.
[361] Harvey F. R. (1966). Hyperfunctions and linear differential equations. Proc. Nat. Acad. Sci. 5, 1042-
1046.
[362] Harvey F. R. (1990). Spinors and Calibrations. Academic Press, San Diego, CA.
[363] Haslehurst L., Penrose R. (2001). The most general (2,2) self-dual vacuum: a googly approach. In
Further Advances in Twistor Theory, Vol. Ill: Curved Twistor Spaces (eds. L. J. Mason, L. P. Hughston,
P. Z. Kobak, K. Pulvere), 345-349.
[364]	Hawking S. W. (1972). Black holes in general relativity. Commun.	Math.	Phys.	25,	152-166.
[365]	Hawking S. W. (1974). Black hole explosions. Nature 248, 30.
[366] Hawking S. W. (1975). Particle creation by black holes. Commun. Math. Phys. 43, 199. Имеется
перевод: Хокинг С. Рождение частиц на черных дырах. В сб. статей Альберт Эйнштейн и
теория гравитации. — М.: Мир, 1979. С. 479-509.
[367] Hawking S. W. (1976). Black holes and thermodynamics. Phys. Rev. D13(2), 191. Имеется перевод:
Хокинг С. Черные дыры и термодинамика. В сб. статей Черные дыры. — М.: Мир, 1979. С. 204-
221.
[368] Hawking S. W. (1976). Breakdown of predictability in gravitational collapse. Phys. Rev. D14, 2460.
[369] Hawking S.W., King A. R., McCarthy P. J. (1976). A new topology for curved space-time which
incorporates the causal, differential, and conformal structures. J. Math. Phys. 17, 174-181.
[370] Hawking S. W., Ellis G. F. R. (1973). The Large-Scale Structure of Space-Time. Cambridge University
Press, Cambridge. Имеется перевод: Хокинг С., Эллис Дж. Крупномасштабная структура про¬
странства-времени. — М.: Мир, 1977.
[371] Hawking S.W., Israel W. (eds.) (1987). 300 Years of Gravitation. Cambridge University Press,
Cambridge.
[372] Hawking S. W., Penrose R. (1970). The singularities of gravitational collapse and cosmology. Proc.
Rov. Soc. Lond. A314, 529-548.
✓ ?
[373] Hawking S.W., Penrose R. (1996). The Nature of Space and Time. Princeton University Press,
Princeton, New Jersey. Имеется перевод: Хокинг С., Пенроуз Р. Природа пространства и време¬
ни. — Ижевск: РХД, 2000.
[374] Hawking S. W., Turok N. (1998). Open Inflation Without False Vacua. Phys. Lett. B425.
[hep-th/9802030]
[375]	Hawkins T.	(1977). Weierstrass and the theory of matrices.	Arch. Hist. Exact Sci. 17, 119-163.
[376]	Hawkins T.	(2000). Emergence of the theory of Lie groups.	Springer-Verlag, New York.
[377]	Heisenberg	W. (1971). Physics and Beyond. Addison Wesley, London.
[378]	Heisenberg	W. (1989). What is an elementary particle?	In Encounters with Einstein.	Princeton
University Press, Princeton.
[379] Helgason S. (2001). Differential Geometry and Symmetric Spaces. AMS Chelsea Publishing,
Providence, RI. Имеется перевод: Хелгасон С. Дифференциальная геометрия и симметриче¬
ские пространства. — М.: Мир, 1964.

884
Литература
[380] Hestenes D. (1990). Thq Zitterbewegung Interpretation of Quantum Mechanics. Found. Physics 20(10),
1213-1232.
[381] Hestenes D., Sobczyk G. (1984). Clifford Algebra to Geometric Calculus: A Unified Language for
Mathematics and Physics. Reidel, Dordrecht, Holland.
[382] Heyting A. (1956). Intuitionism, Studies in Logic and the Foundations of Mathematics. North-Holland,
Amsterdam.
[383] Heywood P., Redhead M. L.G. (1983). Non-locality and the Kochen-Specker paradox. Found. Phys.
13(5), 481-499.
[384] Hicks N.J. (1965). Notes on Differential Geometry. Van Nostrand, Princeton.
[385] Hirschfeld J. W. P. (1998). Projective Geometries over Finite Fields (Second Edition). Clarendon Press,
Oxford.
[386]	Hodges A. P. (1982). Twistor diagrams. Physica 114A, 157-175.
[387]	Hodges A. P. (1985). A twistor approach to the regularization of divergences. Proc. Roy. Soc.	Lond.
A397, 341-374. Mass eigenstates in twistor theory, ibid, 375-396.
[388] Hodges A. P. (1990). String Amplitudes and Twistor Diagrams: An Analogy. In The Interface of
Mathematics and Particle Physics (eds. D. G. Quillen, G. B. Segal, S.T. Tsou). Oxford University
Press, Oxford.
[389]	Hodges A. P. (1990). Twistor diagrams and Feynman diagrams. In	Twistors in	Mathematics and
Physics, LMS Lect. Note Ser. 156 (eds. T. N. Bailey, R. J. Baston).	Cambridge	University	Press,
Cambridge.
[390] Hodges A. P. (1998). The twistor diagram programme. In The Geometric Universe; Science,
Geometry; and the Work of Roger Penrose (eds. S.A.Huggett, L. J.Mason, K.P.Tod, S.T.Tsou,
N. M. J. Woodhouse). Oxford University Press, Oxford.
[391] Hodges A. P, Penrose R., Singer M. A. (1989). A twistor conformal field theory for four space-time
dimensions. Phys. Lett. B216, 48-52.
[392] Hollands S., Wald R. M. (2001). Local Wick Polynomials and Time Ordered Products of Quantum
Fields in Curved Spacetime. Commun. Math. Phys. 223, 289-326. [gr-qc/0103074 ]
[393] Home D. (1997). Conceptual Foundations of Quantum Physics: An Overview from Modern
Perspectives. Plenum Press, New York & London.
• •
[394] Hopf H. (1931). Uber die Abbildungen der dreidimensionalen Sphare auf die Kugelflache. Math. Ann.
104, 637.
[395] Horgan J. (1996). The End of Science. Perseus Publishing, New York.
[396] Horowitz G. T. (1998). Quantum states of black holes. In Black Holes and Relativistic Stars (ed.
R. M. Wald), 241-266. University of Chicago Press, Chicago.
[397] Horowitz G.T., Maldacena J. (2003). The black hole final state, [hep-th/0310281 ]
[398] Horowitz G.T., Репу МЛ. (1982). Gravitational energy cannot become negative. Phys. Rev. Lett. 48,
371-374.
[399] Howie J. (1989). On the SQ-universality of T(6)-groups. Forum Math. 1, 251-272.
[400] Hoyle C. D., et al. (2001). Submillimeter Test of the Gravitational Inverse-Square Law: A Search for
«Large» Extra Dimensions. Phys. Rev. Lett. 86(8), 1418-1421.
[401] Hoyle F. (1948). A New Model for the Expanding Universe. Mon. Not. Roy. Astron. Soc. 108, 372.
[402] Hoyle F., Fowler W. A., Burbidge G.R., Burbidge E. M. (1956). Origin of the elements in stars.
Science 124, 611-614.

Литература
885
[403
[404
[405
[406
[407
[408
[409
[410
[411
[412
[413
[414
[415
[416
[417
[418
[419
[420
[421
[422
[423
[424
[425
[426
Huang К. (1952). On the Zitterbewegung of the Dirac electron. Am. J. Phys. 20, 479-484.
Huggett S. A., Jordon D. (2001). A Topological Aperitif. Springer-Verlag, London.
Huggett S. A., Tod K. P. (2001). An Introduction to Twistor Theory. Cambridge University Press,
Cambridge.
Hughston L.P. (1979). Twistors and Particles. Lecture Notes in Physics, No. 97. Springer-Verlag,
Berlin.
Hughston L.P. (1995). Geometric Aspects of Quantum Mechanics. In Twistor Theory (ed.
S. A. Huggett), 59-79. Marcel Dekker, New York.
Hughston L.P., Jozsa R., Wooters W. K. (1993). A complete classification of quantum ensembles
having a given density matrix. Phys. Letts. A183, 14-18.
Ilyenko K. (1999). Twistor Description of Null Strings. Oxford D. Phil, thesis, unpublished.
л. (1997). Quantum Gravity and Regge Calculus, [gr-qc/97010521
Infeld L., van der Waerden B.L. (1933). Die Wellengleichung des Elektrons in der allgemeinen
Relativitatstheorie. Sitz. Ber. Preuss. Akad. Wiss. Phisik. Math. Kl. 9, 380-401.
Isenberg J., Yasskin P. B., Green P. S. (1978). Non-self-dual gauge fields. Phys. Lett. 78B, 462-464.
Isham C. J. (1975). Quantum Gravity: An Oxford Symposium. Oxford University Press, Oxford.
Isham C. J. (1992). Canonical Quantum Gravity and’ the Problem of Time, [gr-qc/9210011 ]
Quantum
Quantum
Israel W. (1967). Event horizons in static vacuum space-times. Phys. Rev. 164, 1776-1779.
Jackson J.D. (1998). Classical Electrodynamics. John Wiley & Sons, New York & Chichester. Име¬
ется перевод более раннего издания: Джексон Дж. Классическая электродинамика. — М.: Мир,
1965.
Jennewein Т., Weihs G., Pan J., Zeilinger A. (2002). Experimental Non-locality Proof of Quantum
Teleportation and Entanglement Swapping. Phys. Rev. Lett. 88, 017903.
Jensen G. (1973). Einstein Metrics on Principal Fibre Bundles. J. Diff Geom. 8, 599-614.
Johnson C. (2003). D-Branes. Cambridge University Press, Cambridge.
Jones H. F. (2002). Groups, Representations, and Physics. Institute of Physics Publishing, Bristol.
Jozsa R. (1981). Models in Categories and Twistor Theory. Oxford D. Phil, thesis, unpublished.
Jozsa R. O. (1998). Entanglement and quantum computation. In The Geometric Universe (eds.
S. A. Huggett, L.J. Mason, K. P. Tod, S.T. Tsou, N. M. J. Woodhouse), 369-379. Oxford University
Press, Oxford.
[quant-ph/0201143]
quantum
Karolyhazy F. (1966). Gravitation and quantum mechanics of macroscopic bodies. Nuovo Cim. A42,
390.
ф
Karolyhazy F. (1974). Gravitation and Quantum Mechanics of Macroscopic Bodies. Magyar Fizikai
Folyoirat. 22, 23-24. [Thesis, in Hungarian]
[427]	Karolyhazy F., Frenkel A., Lukacs B. (1986). On the possible role of gravity on the reduction of
the wave function. In Quantum. Concepts in Space and Time (eds. R. Penrose, C.J. Isham), 109-128.
• ^
Oxford University Press, Oxford.

886
Литература
[428] Kahn D.W. (1995). Topology’: An Introduction to the Point-Set and Algebraic Areas. Dover
Publications, New York.
[429] Kaku M. (1993). Quantum field theory: a modern introduction. Oxford University Press, Oxford.
%
■
*
[430] Kamberov G., et al. (2002). Quaternions, Spinors, and Surfaces (Contemporary Mathematics
(American Mathematical Society), v. 299.). American Mathematical Society, Providence, RI.
p
[431] Kane G. (ed.) (1999). Perspectives on Supersymmetry (Advanced Series on Directions in High Energy
Physics). World Scientific Pub. Co., Singapore.
[432] Kane G. (2001). Supersymmetry: Unveiling the Ultimate Laws of Nature. Perseus Publishing, New
York.
[433] Kapusta J.I. (2001). Primordial Black Holes and Hot Matter, [astro-ph/0101515]
[434] Kasper J. E., Feller S. A. (2001). The Complete Book of Holograms: How They Work and How to
Make Them. Dover Publications.
[435] Kauffman L.H. (2001). Knots and Physics. World Scientific Publishing, Singapore.
[436] Kay B. S. (1998). Entropy defined, entropy increase and decoherence understood, and some black
hole puzzles solved, [hep-th/9802172 ]
[437] Kay B. S. (1998). Decoherence of Macroscopic Closed Systems within Newtonian Quantum Gravity.
Class. Quant. Grav. 15, L89-L98. [hep-th/9810077]
[438] Kay B. S. (2000). Application of linear hyperbolic PDE to linear quantum in curved space-times:
especially black holes, time machines, and a new semilocal vacuum concept. In Journees Equations
aux Derivees Partielles, Nantes 5-9 Juin 2000. Groupement de Recherche 1151 du CNRS. [gr-
qc/0103056]
[439] Kay B.S., Wald R. M. (1991). Theorems on the uniqueness and thermal properties of stationary,
nonsingular, quasifree states on space-times with a bifurcate Killing horizon. Phys. Kept. 207, 49-136.
[440] Kay B.S., Radzikowski M.J., Wald R.M. (1996). Quantum Field Theory on Spacetimes with
a Compactly Generated Cauchy Horizon. Commun. Math. Phys. 183 (1997), 533-556. [gr-
qc/9603012]
[441] Kelley J. L. (1965), General Topology. Van Nostrand, Princeton, New Jersey.
[442] Kemmer N. (1938). Quantum theory of Einstein-Bose particles and nuclear intonation. Proc. R. Soc.
A166, 127.
[443] Kemmer N. (1939). The particle aspect of meson theory. Proc. R. Soc. A173, 91.
[444] Kerr R. P. (1963). Gravitational field of a spinning mass as an example of algebraically special metrics.
Phys. Rev. Lett. 11, 237-238. Имеется перевод: Керр P. Гравитационное поле вращающейся массы
как пример алгебраически специальной метрики. В сб. статей Альберт Эйнштейн и теория
гравитации.. — М.: Мир, 1979. С.208-211.
[445] Ketov S. V. (2000). Quantum Non-Linear Sigma-Models: From Quantum Field Theory to
Supersymmetry, Conformal Field Theories, Black Holes, and Strings. Springer-Verlag, Berlin, London.
[446] Kibble T. W. B. (1961). Lorentz invariance and the gravitational field. J. Math. Phys. 2, 212-221.
[447] Kibble T. W.B. (1979). Geometrization of quantum mechanics. Commun. Math. Phys. 65, 189.
[448] Kibble T. W.B. (1981). Is a semi-classical theory of gravity viable? In Quantum Gravity 2: A Second
Oxford Symposium (eds. C.J.Isham, R.Penrose, D.W.Sciama), 63-80. Oxford University Press,
Oxford.
[449] Killing W. (1893). Einfuhrung in die Grundlagen der Geometrie. Paderbom.
[450] Klein F. (1898). Uber den Stand der Herausgabe von Gauss’ Werken. Math. Ann. 51, 128-133.

Литература
887
[451] Knott С. G. (1900). Professor Klein’s view of quaternions: A criticism. Proc. Roy. Soc. Edinb. 23,
24-34.
[452] Kobayashi S. Nomizu K. (1963). Foundations of Differential Geometry. Interscience Publishers, New
York & London.
[453] Kochen S., Specker E. P. (1967). The Problem of Hidden Variables in Quantum Mechanics. Journal
of Mathematics and Mechanics. 17, 59-88.
[454] Kodaira K. (1962). A theorem of completeness of characteristic systems for analytic submanifolds of
a complex manifold. Ann. Math. 75, 146-162.
[455] Kodaira K., Spencer D. C. (1958). On deformations of complex analytic structures I, II. Ann. Math.
67, 328-401, 403-66.
[456] Kolb E. W., Turner M. S. (1994). The Early Universe. Perseus Publishing, New York.
[457] Komar A. B. (1964). Undecidability of macroscopically distinguishable states in quantum field theory.
Phys. Rev. 133B, 542-544.
[458] Kontsevich M. (1994). Homological algebra of mirror symmetry. Proceedings of the International
Congress of Mathematicians, Vol. 1, 2. (Zurich, 1994). Birkhauser, Basel.
[459] Kontsevich M. (1995). Enumeration of rational curves via tori с actions. In The Moduli Space of
Curves (eds. R. Dijkgraaf, C. Faber, G. van der Geer). Progress in Math. 129, 335-368. [hep-
th/94050351]
[460] Koruga D., Hameroff S., Withers J., Loutfy R., Sundareshan M. (1993). Fullerene Сбо-‘ History,
physics, nanobiology, nanotechnology\ North-Holland, Amsterdam.
[461] Kraus K. (1983). States, effects and operations: fundamental notions of quantum theory. Lecture Notes
in Physics, Vol. 190. Springer-Verlag, Berlin.
[462] Krauss L. M. (2001). Quintessence: The Mysteiy of the Missing Mass. Basic Books, New York.
[463] Kreimer D. (2000). Knots and Feynman Diagrams. Cambridge University Press, Cambridge.
[464] Kronheimer E. H., Penrose R. (1967). On the structure of causal spaces. Proc. Camb. Phil. Soc. 63,
481-501.
[465] Kruskal M. D. (1960). Maximal Extension of Schwarzschild Metric. Phys. Rev. 119, 1743-1745.
[466] Kuchar K. (1981). Canonical methods of quantization. In Quantum Gravity 2 (eds. D. W. Sciama,
R. Penrose, C. J. Isham). Oxford University Press, Oxford.
[467] Kuchar К. V. (1992). Time and interpretations of quantum gravity. In Proceedings of the 4th Canadian
Conference on General Relativity and Relativistic Astrophysics (eds. G. Kunstatter, D. Vincent,
J. Williams). World Scientific, Singapore.
[468] Labastida J.M. F., Lozano C. (1997). Lectures in Topological Quantum Field Theory, [hep-
th/9709192]
[469] Landsman N.P. (1998). Mathematical Topics Between Classical and Quantum Mechanics. Springer-
Verlag, Berlin.
[470] Lang S. (1972). Differentiable Manifolds. Addison-Wesley, Reading, MA.
[471] Lange A. E., et al. (2001). First Estimations of Cosmological Parameters from BOOMERANG. Phys.
Rev. D63, 042001. [astro-ph/0005004 ]
[472] Laplace P. S. (1799). Allgemeine geographische Ephemeriden herausgegeben von F. von Zach. IV Bd.
1st, 1 Abhandl., Weimar.
[473] Laporte O., Uhlenbeck G. E. (1931). Application of spinor analysis to the Maxwell and Dirac equations.
Phys. Rev. 37, 1380-1552.

888
Литература
[474] Lasenby J., Lasenby A.N., Doran C. J. L. (2000). A unified mathematical language for physics and
engineering in the 21st century. Phil. Trans. Roy. Soc. bond. A358, 21-39.
[475] Lawrie I. (1998). A Unified Grand Tour of Theoretical Physics. Institute of Physics Publishing, Bristol.
[476] Lawson H. B., Michelson M. L. (1990). Spin Geometry. Princeton University Press, Princeton.
[477] Lawvere W., Schanuel S. (1997). Conceptual Mathematics: A First Introduction to Categories.
Cambridge University Press, Cambridge.
[478] LeBrun C. R. (1985). Ambi-twistors and Einstein’s equations. Class, and Quantum Grav. 2, 555-563.
[479] LeBrun C. R. (1990). Twistors, ambitwistors, and conformal gravity. In Twistors in Mathematical
Physics (eds. T.N. Bailey, R. J. Baston). LMS Lecture Note Series 156. Cambridge Univ. Press,
Cambridge.
[480] LeBrun C., Mason L. j. (2002). Zoll manifolds and complex surfaces. J. Diff. Geom. 61(3), 453-535.
[481] Lefshetz J. (1949). Introduction to Topology. Princeton University Press, Princeton, New Jersey.
[482] Leggett A. J. (2002). Testing the limits of quantum mechanics: motivation, state of play, prospects. J.
Phys. CM14,R415-R451.
/V
[483] Lemaitre G. (1933). L’univers en expansion. Ann. Soc. Sci. Bruxelles I A53, 51-85 (see p. 82).
[484] Levitt М. H. (2001). Spin Dynamics: Basics of Nuclear Magnetic Resonance. John Wiley & Sons,
New York.
[485] Lichnerowicz A. (ed.) (1994). Physics on Manifolds: Proceedings of the International Colloquium in
Honour of Yvonne Choquet-Bruhat, Paris, June 3-5, 1992. Kluwer Academic Publishers, Boston and
Dordrecht, The Netherlands.
[486] Liddle A. R. (1999). An Introduction to Modern Cosmology. John Wiley & Sons, New York.
[487] Liddle A.R., Lyth D. H. (2000). Cosmological Inflation and Large-Scale Structure. Cambridge
University Press, Cambridge.
[488] Lifshitz E. М., Khalatnikov I. M. (1963). Investigations in relativistic cosmology. Adv. Phys. 12, 185—
249.
[489] Linde A. (1993). Comments on Inflationary Cosmology, [astro-ph/9309043]
[490] Linde A. (1995). Inflation with Variable Omega. Phys. Lett. B351. [hep-th/9503097 ]
[491] Littlewood J. E. (1949). Littlewoods miscellany. Reprinted in 1986, Cambridge University Press,
Cambridge. Имеется перевод: Литтлвуд Дж. Математическая смесь. — М.: Наука, 1978.
[492] Livio М. (2000). The Accelerating Universe. John Wiley & Sons, New York.
[493] Llewellyn Smith С. H. (1973). High energy behaviour and gauge symmetry. Phys. Lett. B46, 233-236.
[494] Lockwood M. (1989). Mind, Brain and the Quantum; the Compound T. Basil Blackwell, Oxford.
[495] Lorentz H. A., Einstein A., Minkowski H., Weyl H. (1952). The Principle of Relativity: A Collection
of Original Memoirs on the Special and General Theory? of Relativity. Dover, New York. Имеется
перевод: Принцип относительности. — М.: Атомиздат, 1973.
/
[496] Loimesto Р. (2001). Clifford Algebras and Spinors. Cambridge University Press, Cambridge.
[497] Liiders G. (1951). Uber die Zustandsanderung durch den Messprozess. Ann, Physik 8, 322-328.
[498] Ludvigsen M. (1999). General Relativity: A Geometric Approach. Cambridge University Press,
Cambridge.
[499] Ludvigsen М., Vickers J.A. G. (1982). A simple proof of the positivity of the Bondi mass. J. Phys.
A15, L67-L70.

Литература
889
[500]	Luminet J.-P., et al. (2003). Dodecahedral space topology as an explanation for weak wide-angle
temperature correlations in the cosmic microwave background. Nature 425, 593-595.
Lyttleton R. A., Bondi H. (1959). Proc. Roy. Soc. (London) A252, 313.
MacDuffee С. C. (1933). The theory of matrices. Springer-Verlag, Berlin. (Reprinted by Chelsea).
MacLane S. (1988). Categories for the Working Mathematician. Springer-Verlag, Berlin.
McLennan J. A., Jr. (1956). Conformal invariance and conservation laws for relativistic wave equations
for zero rest mass. Nuovo Cim. 3, 1360-1379.
MACRO Collaboration (2002). Search for massive rare particles with MACRO. Nucl Phys. Proc.
Suppl. 110, 186-188. [hep-ex/0009002]
501
502
503
504
505
506
507
508
509
510
511
512
513
514
515
516
517
518
519
520
521
[522
Magueijo J. (2003). Faster Than the Speed of Light: The Story of a Scientific Speculation. Perseus
Publishing, New York.
Magueijo J., Smolin L. (2002). Lorentz invariance with an invariant energy scale.
[gr-qc/0112090]
Mahler (1981). P-Adic Numbers and Functions. Cambridge University Press, Cambridge.
/
Majorana E. (1932). Teoria relativistica di particelle con momento intrinsico arbitrario. Nuovo Cimento
9, 335-344.
Majorana E. (1937). Teoria asimmetriea delP elettrone e del positrone. Nuovo Cimento 14, 171-184.
Maldacena J. (1997). The Large N Limit of Superconformal Field Theories and Supergravity,
[hep-th/9711200]
Manogue C. A., Dray T. (1999). Dimensional Reduction. Mod. Phys. Lett. A14, 93-97.
[hep-th/9807044]
Manogue C. A., Schray J. (1993). Finite Lorentz transformations, automorphisms, and division
algebras. J. Math. Phys. 34, 3746-3767.
Markopoulou F. (1997). Dual formulation of spin network evolution, [gr-qc/970401 ]
Markopoulou F. (1998). The internal description of a causal set: What the universe looks like from
the inside. Commun. Math. Phys. 211, 559-583. [gr-qc/9811053]
Markopoulou F., Smolin L. (1997). Causa! evolution of spin networks. Nucl. Phys. B508, 409-430.
[gr-qc/9702025]
Marsden J. E., Tromba A.J. (1996). Vector Calculus. W. H. Freeman & Co., New York, [new edn.
2004]
Marshall W., Simon C., Penrose R., Bouwmeester D. (2003). Towards Quantum Superpositions of a
Mirror. Phys. Rev. Lett. 91, 13.
Mason L.J., Woodhouse N.M.J. (1996). Integrability, Self-Duality, and Twistor Theoiy. Oxford
University Press, Oxford.
Mattuck R. D. (1976). A Guide to Feynman Diagrams in the Many-Body Problem. Dover, New York.
Имеется перевод более раннего издания: Маттук Р. Д. Фейнмановские диаграммы в проблеме
многих тел. — М.: Мир, 1969.
Merkulov S.A., Schwachhofer L.J. (1998). Twistor solution of the holonomy problem. In The
Geometric Universe: Science, Geometry, and the Work of Roger Penrose (eds. S.A.Huggett,
L. J. Mason, K. P. Tod, S. T. Tsou, N. M. J. Woodhouse). Oxford University Press, Oxford.
Michell J. (1784). On the means of discovering the distance, magnitude, etc., of the fixed stars, in
consequence of the diminution of their light, in case such a diminution should be found to take place in
any of them, and such other data should be procured from observations, as would be further necessary
for that purpose. Phil. Trans. Roy. Soc. Lond. 74, 35-57.

890
Литература
[523] Mielnik В. (1974). Generalized Quantum Mechanics. Cotnmun. Math. Phys. 37, 221.
4
[524] Milgrom М. (1994). Dynamics with a non-standard inertia-acceleration relation: an alternative to dark
matter. Annals Phys. 229. [astro~ph/9303012 ]
[525] Miller A. (2003). Erotica, Aesthetics, and Schroedinger’s Wave Equation. In It Must Be Beautiful (ed.
G. Farmelo). Granta, London.
[526] Minassian E. (2002). Spacetime singularities in (2+l)-dimensional quantum gravity. Class. Quant.
Grav. 19, 5877-5900.
[527] Minkowski H. (1952), in [495].
[528] Misner C. W. (1969). Mixmaster Universe. Phys. Rev. Lett. 22, 1071-1074.
[529] Misner C. W., Thome K. S., Wheeler J. A. (1973). Gravitation. Freeman, San Francisco. Имеется
перевод: Мизнер Ч., Торн К., Уилер Дж. Гравитация. М.: Мир, 1977.
[530] Mohapatra R.N. (2002). Unification and Super symmetry. Springer-Verlag, Berlin & London.
[531] Montgomery D., Zippin L. (1955). Topological Transformation Groups. Interscience, New York &
London.
[532] Moore A. W. (1990). The Infinite. Routledge, London & New York.
[533] Moroz I. М., Penrose R., Tod К. P. (1998). Spherically-symmetric solutions of the Schrodinger-Newton
equations. Class. Quant. Grav. 15, 2733-2742.
[534] Mott N. F. (1929). The wave mechanics of a-ray tracks. Proc. Roy. Soc. Lond. A126, 79-84.
Reprinted in Quantum Theory and Measurement (eds. J. A. Wheeler, W. H.Zurek). Princeton Univ.
Press, Princeton, New Jersey, 1983.
[535] Moussouris J. P. (1983). Quantum models of space-time based on recoupling theory. Oxford D. Phil,
thesis, unpublished.
[536] Mukohyama S., Randall L. (2003). A Dynamical Approach to the Cosmological Constant. Phys. Rev.
Lett. 92 (2004) 211302. [hep-th/0306108]
[537] Munkres J. R. (1954). Elementary Differential Topology. Annals of Mathematics Studies, 54. Princeton
University Press, Princeton, New Jersey.
[538] Myrheim J. (1978). Statistical geometry. CERN preprint, TH-2538, unpublished.
[539] Nahin P. J. (1998). An Imaginary7 Tale: The Story> of Princeton Univ. Press, Princeton.
[540] Nair V. (1988). A Current Algebra For Some Gauge Theory Amplitudes. Phys. Lett. B214, 215.
[541] Nambu Y. (1970). Proceedings of the International Conference on Symmetries and Quark Models.
Wayne State University. Gordon and Breach Publishers.
[542] Narayan R., et al. (2003). Evidence for the Black Hole Event Horizon. Astronomy & Geophysics
44(6), 6.22-6.26.
[543] Nayfeh Ali H. (1993). Methods of Normal Forms, John Wiley & Sons, New York.
[544] Needham T. (1997). Visual Complex Analysis. Clarendon Press, Oxford University Press, Oxford.
[545] Negrepontis S. (2000). The Anthyphairetic Nature of Plato’s Dialectics. In Interdisciplinary Approach
to Mathematics and their Teaching, Volume 5, 15-77. University-Gutenberg, Athens. (In Greek).
[546] Nester J. M. (1981). A new gravitational energy expression, with a simple positivity proof. Phys. Lett.
83A, 241-242.
[547] Netterfield С. B. et al. (2002). A measurement by BOOMERANG of multiple peaks in the angular
power spectrum of the cosmic microwave background. Astrophys.J.. 571, 604-614 [astro-pb/0104460].

Литература
891
[548] Newlander A., Nirenberg L. (1957). Complex Analytic Coordinates in Almost Complex Manifolds.
Ann. of Math. 65, 391^404.
[549] Newman E. T. (2002). On a Classical, Geometric Origin of Magnetic Moments, Spin-Angular
Momentum and the Dirac Gyromagnetic Ratio. Phys. Rev. D65, 104005. [gr-qc/0201055 ]
[550] Newman E. Т., Penrose R. (1962). An approach to gravitational radiation by a method of spin
coefficients. J. Math. Phys. 3, 896-902; errata (1963), 4, 998.
[551] Newman E. Т., Penrose R. (1966). Note on the Вondi-Metzner-Sachs group. J. Math. Phys. 7, 863-
870.
[552] Newman E.T., Unti T. W. J. (1962). Behavior of asymptotically flat empty space. J. Math. Phys. 3,
891-901.
[553] Newman E. Т., Couch E., Chinnapared K., Exton A., Prakash A., Torrence, R. (1965). Metric of a
rotating charged mass. J. Math. Phys. 6, 918-919.
[554] Newman М. H. A. (1942). On a string problem of Dirac. J. Lond. Math. Soc. 17, 173-177.
[555] Newman R. P. A. C. (1993). On the Structure of Confonnal Singularities in Classical General Relativity.
Proc. R. Soc. Lond. A443, 473.
[556] Newton I. (1687). The Principia: Mathematical Principles of Natural Philosophy. Reprinted by
University of California Press, 1999. Имеется перевод: Ньютон И. Математические начала на¬
туральной философии. В кн.: Крылов А. Н. Собрание трудов, т. 7. — М.-Л., 1936.
[557] Newton I. (1730). Opticks. Dover, 1952. Имеется перевод: Ньютон И. Оптика или трактат об
отражениях, претилениях и цветах света. — М.: Гостехиздат, 1954.
[558] Ng Y. J. (2004). Quantum Foam, [gr-qc/0401015]
[559] Nicolai H. (2003). Remarks at AEI Symposium «Strings meet Loops», 29-31 October 2003.
[http://alphaserv3.aei.mpg.de/events/stringloop.html]
[560] Nielsen H. B. (1970). Submitted to Proc. of the XV Int. Conf on High Energy Physics, Kiev
(unpublished).
[561] Nielsen M. A. Chuang I.L. (2000). Quantum Computation and Quantum Information. Cambridge
University Press, Cambridge.
[562] Nomizu K. (1956). Lie Groups and Differential Geometry. The Mathematical Society of Japan, Tokyo.
Имеется перевод: Номидзу К. Группы Ли и дифференциальная геометрия. — М.: ИЛ., 1960.
[563] Новиков И. Д. Куда течет река времени? — М.: Молодая гвардия, 1990.
[564] O’Donnell Р. (2003). Introduction to 2-Spinors in General Relativity. World Scientific, Singapore.
[565] O’Neill B. (1983). Semi-Riemannian Geometry: With Applications to Relativity. Academic Press, New
York.
[566] Oppenheimer J.R. (1930). On the theory of electrons and protons. Phys. Rev. 35, 562-563.
[567] Ozsvath I., Schucking E. (1962). Finite rotating universe. Nature 193, 1168-1169.
[568] Ozsvath I., Schucking E. (1969). The finite rotating universe.Hn/2. Phys. 55, 166-204.
[569] Page D.N. (1995). Sensible Quantum Mechanics: Are Only Perceptions Probabilistic? [quant-
ph/9506010]
[570] Page D. N. (1987). Geometrical description of Berry’s phase. Phys. Rev. A36, 3479-3481.
[571] Page D. N. (1976). Dirac equation around a charged, rotating black hole. Phys. Rev. D 14, 1509-1510.
[572] Pais A. (1982). «Subtle is the Lord»... The Science and the Life of Albert Einstein. Clarendon Press,
Oxford. Имеется перевод: Пайс А. Научная деятатность и жизнь Альберта Эйнштейна. —
М.: Наука, 1989.

892
Литература
[573
[574
[575
[576
[577
[578
[579
[580
[581
[582
[583
[584
[585
[586
[587
[588
Pais А. (1986). Inward Bound: Of Matter and Forces in the Physical World. Clarendon Press, Oxford.
Parker Т., Taubes С. H. (1982). On Witten’s proof of the positive energy theorem. Comm. Math. Phys.
84, 223-238.
Pars L. A. (1968). A Treatise on Analytical Dynamics. Reprinted in 1981, Ox Bow Press.
и
Pearle P. (1985). Models for reduction. In Quantum Concepts in Space and Time (eds. C. J. Isham,
R. Penrose), 84-108. Oxford University Press, Oxford.
Pearle P., Squires E. J. (1995). Gravity, energy conservation and parameter values in collapse models.
Durham University preprint. DTP/95/13.
Peitgen H.-O., Richter P. H. (1986). The Beauty of Fractals: Images of Complex Dynamical Systems.
Springer-Verlag, Berlin & Heidelberg. Имеется перевод: Пайтген X.-O., Рихтер П. X. Красота
фракталов. Образы комплексных динамических систем. — М.: Мир, 1993.
Peitgen H.-O., Saupe D. (1988). The Science of Fractal Images. Springer-Verlag, Berlin.
Penrose L. S., Penrose R. (1958). Impossible Objects: A Special Type of Visual Illusion, Brit. J. Psych.
49, 31-33.
Penrose R. (1959). The apparent shape of relativistically moving sphere. Proc. Camb. Phil. Soc. 55,
137-139.
Penrose R. (1960). A spinor approach to general relativity. Ann. Phys. (New York) 10, 171-201.
Penrose R. (1962). The Light Cone at Infinity. In Proceedings of the 1962 Conference on Relativistic
Theories of Gravitation, Warsaw. Polish Academy of Sciences, Warsaw. (Published 1965.)
Penrose R. (1963). Asymptotic properties of fields and space-times. Phys. Rev. Lett. 10, 66-68.
Penrose R. (1964). Conformal approach to infinity. In Relativity, Groups and Topology: The 1963 Les
Houches Lectures (eds. B. S. DeWitt, C.M. DeWitt). Gordon and Breach, New York. Имеется пере¬
вод: Пенроуз P. Конформный подход к бесконечности. В сб. статей Гравитация и топология. —
М.: Мир, 1966.
Penrose R. (1965). Zero rest-mass fields including gravitation: asymptotic behaviour. Proc. R. Soc.
Lond. A284, 159-203.
Penrose R. (1965). Gravitational collapse and space-time singularities. Phys. Rev. Lett. 14, 57-59.
Имеется перевод: Пенроуз P. Гравитационный коллапс и пространственно-временные сингуляр¬
ности. В сб. статей Альберт Эйнштейн и теория гравитации. — М.: Мир, 1979. — С. 390-395.
Penrose R. (1966). An analysis of the structure of space-time. Adams Prize Essay, Cambridge
University, Cambridge (unpublished; but much of it is in [590]).
[589] Penrose R. (1967). Twistor algebra. J. Math. Phys. 8, 345-366.
[590] Penrose R. (1968). Structure of space-time. In Battelle Rencontres, 1967 (eds. C.M.DeWitt,
J. A. Wheeler). Lectures in Mathematics and Physics. Benjamin, New York. Имеется перевод: Пенро¬
уз P. Структура пространства-времени. — М.: Мир, 1972.
[591] Penrose R. (1968). Twistor quantization and curved space-time. Int. J. Theor. Phys. 1, 61-99.
[592] Penrose R. (1969). Gravitational collapse: the role of general relativity. Rivista del Nuovo Cimento;
Serie I, Vol. 1; Numero speciale, 252-276.
[593] Penrose R. (1969). Solutions of the zero rest-mass equations. J. Math. Phys. 10, 38-39.
[594] Penrose R. (1971). Angular momentum: an approach to combinatorial space-time. In Quantum Theory
and Beyond (ed. T. Bastin). Cambridge University Press, Cambridge.
[595] Penrose R. (1971). Applications of negative dimensional tensors. In Combinatorial Mathematics and
its Applications (ed. D. J. A. Welsh). Academic Press, London.

Литература
893
[596] Penrose R. (1975). Twistor theory: its aims and achievements. In Quantum Gravity, an Oxford
Symposium (eds. C. J. Isham, R. Penrose, D. W. Sciama). Oxford University Press, Oxford.
[597] Penrose R. (1976). The non-linear graviton. Gen. Rel. Grav. 7, 171-176.
[598] Penrose R. (1976). Non-linear gravitons and curved twistor theory. Gen. Rel. Grav. 7, 31-52. Имеется
перевод: Пенроуз P. Нелинейные гравитоны и искривленная теория твисторов. В сб. статей
Твисторы и калибровочные поля. — М.: Мир, 1983. — С. 225-249.
[599] Penrose R. (1978). Gravitational collapse: a Review. In Physics and Astrophysics of Neutron Stars
and Black Holes, LXV Corso, 566-582. Soc. Italiana di Fisica, Bologna, Italy.
[600] Penrose R. (1979). Singularities and time-asymmetry, In General Relativity: An Einstein Centenary
(eds. S. W. Hawking, W. Israel). Cambridge University Press, Cambridge.
[601] Penrose R. (1979). On the twistor description of massless fields. In Complex Manifold Techniques
in Theoretical Physics (eds. D. E. Lemer, P. D. Sommers). Pitman, San Francisco. See also various
articles in L. P. Hughston, R. S. Ward (Editors) (1979) Advances in Twistor Theory. Pitman Advanced
Publishing Program, San Francisco.
[602] Penrose R. (1980). On Schwarzschild causality — a problem for «Lorentz-соvariant» general
relativity. In Essays in General Relativity (A. Taub Festschrift) (ed. F. J. Tipler), 1-12. Academic
Press, New York.
[603] Penrose R. (1982). Quasi-local mass and angular momentum in general relativity. Proc. Roy. Soc.
bond. A381, 53-63.
[604] Penrose R. (1986). Gravity and state-vector reduction. In Quantum Concepts in Space and Time (eds.
R. Penrose, C. J. Isham), 129-146. Oxford University Press, Oxford.
[605] Penrose R. (1987). Quantum physics and conscious thought. In Quantum Implications: Essays in
Honour of David Bohn (eds. B. J. Hi ley, F. D. Peat). Routledge and Kegan Paul, London & New York.
[606] Penrose R. (1987). On the origins of twistor theory. In Gravitation and Geometry?: a volume in honour
of /. Robinson (eds. W. Rindler, A. Trautman). Bibliopolis, Naples.
[607] Penrose R, (1987). Newton, quantum theory, and reality. In 300 years of Gravity (eds. S. W. Hawking,
W. Israel), 17-49. Cambridge University Press, Cambridge.
[608] Penrose R. (1988). Topological QFT and Twistors: Holomorphic Linking; Holomorphic Linking:
Postscript. Twistor Newsletter 27, 1—4.
[609] Penrose R. (1988). Fundamental asymmetry in physical laws. Proceedings of Symposia in Pure
Mathematics 48, 317-328. American Mathematical Society.
[610] Penrose R. (1989). The Emperor s New Mind: Concerning Computers, Minds, and the Laws of Physics.
Oxford University Press, Oxford. Имеется перевод: Пенроуз P. Новый ум короля. — М.: УРСС,
2003.
[611] Penrose R. (1991). On the cohomology of impossible figures [La cohomologie des figures impossibles].
Structural Topology [Topologie structurale] 17, 11-16.
[612] Penrose R. (1992). H-space and Twistors. In Recent Advances in General Relativity. Einstein Studies,
Vol. 4 (eds. A. I. Janis, J. R. Porter), 6-25. Birkhauser, Boston.
[613] Penrose R. (1994). Shadows of the Mind: An Approach to the Missing Science of Consciousness.
Oxford University Press, Oxford. Имеется перевод: Пенроуз P. Тени разума. В поисках науки о
сознании. — Ижевск: РХД, 2003.
[614] Penrose R. (1996). On gravity’s role in quantum state reduction. Gen. Rel. Grav. 28, 581-600.
[615] Penrose R. (1997). The Large, the Small and the Human Mind. Cambridge University Press,
Cambridge. Canto edition (2000).
[616] Penrose R. (1997). On understanding understanding. Internat. Stud. Philos. Sci. 11, 7-20.

894
Литература
[617] Penrose R. (1998). Quantum computation, entanglement and state-reduction, Phil. Trans. Roy. Soc.
Lond. A356, 1927-1939.
[618] Penrose R. (1998). The question of cosmic censorship. In Black Holes and Relativistic Stars (ed.
R. M.Wald). University of Chicago Press, Chicago, Illinois. Reprinted in J. Astrophys. Astr. 20,
233-248 (1999).
[619] Penrose R. (2000). Wavefunction collapse as a real gravitational effect. In Mathematical Physics
2000 (eds. A. Fokas, T. W. B. Kibble, A. Grigouriou, B. Zegarlinski), 266-282. Imperial College Press,
London.
[620] Penrose R. (2000). On Bell non-locality without probabilities: some curious geometry. In Quantum
Reflections (Eds. J. Ellis, D. Amati), 1-27. Cambridge Univ. Press, Cambridge.
[621] Penrose R. (2001). Towards a twistor description of general space-times; introductory comments. In
Further Advances in Twistor Theory; Vol. Ill: Curved Twistor Spaces (eds. L. J. Mason, L. P. Hughston,
P. Z. Kobak, K. Pulverer), 239-255. Chapman & Hall / CRC Research Notes in Mathematics 424,
London.
[622] Penrose R. (2002). John Bell, State Reduction, and Quanglement. In Quantum [Unjspeakables: From
Bell to Quantum Information (eds. R. A. Bertlmann, A. Zeilinger). Springer-Verlag, Berlin.
[623] Penrose R. (2003). On the instability of extra space dimensions. In The Future of Theoretical Physics
and Cosmology, Celebrating Stephen Hawkings 60th Birthday (eds. G. W. Gibbons, E.P. S. Shellard,
S. J. Rankin). Cambridge University Press, Cambridge.
[624] Penrose R., MacCallum М. A. H. (1972). Twistor theory: an approach to the quantization of fields
and space-time. Phys. Repts. 6C, 241-315. Имеется перевод: Пенроуз P., Мак-Каллум М. Л. X..
Теория твисторов: подход к квантованию полей и пространства-времени. В сб. статей Твисторы
и калибровочные поля. — М.: Мир, 1983. С. 131-224.
[625] Penrose R., Ward R. S. (1980). Twistors for flat and curved space-time. In General Relativity and
Gravitation, One Hundred Years after the Birth of Albert Einstein (ed. A. Held), Plenum, New York.
[626] Penrose R., Rindler W. (1984). Spinors and Space-Time, Vol. I: Two-Spinor Calculus and Relativistic
Fields. Cambridge University Press, Cambridge. Имеется перевод: Пенроуз P., Риндлер В. Спиноры
и пространство-время. Т. 1, Два-спинорное исчисление и релятивистские поля. — М.: Мир, 1987.
[627] Penrose R., Rindler W. (1986). Spinors and Space-Time, Vol. II: Spinor and Twistor Methods in Space-
Time Geometry. Cambridge University Press, Cambridge. Имеется перевод: Пенроуз P., Риндлер
В.	Спиноры и пространство-время. Т. 2, Спинорные и твисторные методы в геометрии про¬
странства-времени. — М.: Мир, 1988.
[628] Penrose R., Robinson L, Tafel J. (1997). Andrzej Mariusz Trautman. Class. Quan. Grav. 14, A1-A8.
[629] Penrose R., Sparling G. A. J., Tsou S.T. (1978). Extended Regge Trajectories. J. Phys. A. Math. Gen.
11, L231-L235.
[630] Penzias A. A., Wilson R. W. (1965). A Measurement of Excess Antenna Temperature at 4080 Mc/s.
Astrophys. J. 142, 419.
[631] Percival EC. (1994). Primary state diffusion. Proc. R. Soc. Lond. A447, 189-209.
[632] Percival L C. (1995). Quantum space-time fluctuations and primary state diffusion, [quant-
ph/95080213
[633] Peres A. (1991). Two Simple Proofs of the Kochen-Specker Theorem. Journal of Physics A:
Mathematical and General 24, L175-L178.
[634] Peres A. (1995). Generalized Kochen-Specker Theorem, [quant-ph/9510018]
[635] Peres A. (2000). Delayed choice for entanglement swapping. J. Mod. Opt. 47, 531.
[quant-ph/9904042]

Литература
895
[636] Perez А. (2001). Finiteness of a spin foam model for Euclidean quantum general relativity. Nucl.
Phys. B599, 427-434.
[637] Perez A. (2003). Spin foam models for quantum gravity. Class. Quant. Grav. 20, R43-R104.
[638] Perlmutter S., et al. (1998). Cosmology from Type la Supemovae. Bull. Am. Astron. Soc. 29.
[astro-ph/9812473]
[639] Peskin М. E., Schroder P. V. (1995). Introduction to Quantum Field Theory. Westview Press, Reading,
MA & Wokingham.
[640] Petiau G. (1936) Contribution a la theorie des equations d’onde corpuscuiaires. Acad. Roy. Belgique.
(Cl. Sci. Mem. Collect. 16, No. 2).
[641] Pirani F. A. E., Schild A. (1950). On the Quantization of Einstein’s Gravitational Field Equations.
Phys. Rev. 79, 986-991.
[642] Pitkaenen M. (1994). p-Adic description of Higgs mechanism 1: p-Adic square root and p-adic light
cone, [hep-th/9410058]
[643] Polchinski J. (1998). String Theory. Cambridge University Press, Cambridge.
[644] Polkinghome J. (2002). Quantum Theory, A Very Short Introduction. Oxford University Press, Oxford.
[645] Popper K. (1934). The Logic of Scientific Discovery. Routledge; New edition (March 2002).
[646] Pound R. V., Rebka G. A., Jr. (1960). Apparent weight of photons. Phys. Rev. Lett. 4, 337-341.
[647] Preskill J. (1992). Do black holes destroy information? [hep-th/9209058]
[648] Priestley H. A. (2003). Introduction to Complex Analysis. Oxford University Press, Oxford.
[649] Rae A. I. M. (1994). Quantum Mechanics. Institute of Physics Publishing, 4th edn. 2002.
[650] Raine D. J. (1975). Mach’s principle in General Relativity. Monthly Notices RAS 171, 507-528.
[651] Randall L., Sundrum R. (1999). A Large Mass Hierarchy from a Small Extra Dimension. Phys. Rev.
Lett. 83, 3370-3373. [hep-ph/9905221 ]
[652] Randall L., Sundrum R. (1999). An Alternative to Compactification. Phys. Rev. Lett. 83, 4690-4693.
[hep-th/9906064]
[653] Rarita W., Schwinger J. (1941). On the theory of particles with half-integer spin. Phys. Rev. 60, 61.
[654] Redhead M. L. G. (1987). Incompleteness, Nonlocality, and Realism. Clarendon Press, Oxford.
[655] Reed М., Simon B. (1972). Methods of Mathematical Physics, Vol. 1: Functional Analysis. Academic
Press, New York & London. Имеется перевод: Рид М., Саймон Б. Методы современной матема¬
тической физики. Т. 1, Функциональный анализ. — М.: Мир, 1977.
/
[656] Reeves J. N. et al. (2002). The signature of supernova ejecta in the X-ray afterglow of the gamma-ray
burst 011211. Nature 416, 512-515.
[657] Regge T. (1962). General Relativity without Coordinates. Nuovo Cimento A 19, 558-571.
[658] Reisenberger M. P. (1997). A lattice worldsheet sum for 4-d Euclidean general relativity, [gr-
qc/9711052]
[659] Reisenberger M. P. (1999). On relativistic spin network vertices. J. Math. Phys. 40, 2046-2054.
[660] Reisenberger M. P., Rovelli C. (2001). Spacetime as a Feynman diagram: the connection formulation.
Class. Quant. Grav. 18, 121-140.
[661] Reisenberger M. P., Rovelli C. (2002). Spacetime states and covariant quantum theory. Phys. Rev.
D65, 125016.
[662] Reula O., Tod K. P. (1984). Positivity of the Bondi energy. J. Math. Phys. 25, 1004-1008.

896
Литература
[663] Riemann G.B.F. (1854). Uber die Hypothesen, welche der Geometrie	zu	Grande	liegen
(Habilitationsschrift, Gottingen); see Collected Works of Bernhardt Riemann, Ed.	Heinrich	Weber,
2nd edn. (Dover, New York, 1953), 272-287. Имеется перевод: Риман Б. О гипотезах, лежащих
в основании геометрии. В сб. статей Альберт Эйнштейн и теория гравитации.. — М.: Мир,
1979. С. 18-33.
[664] Rindler W (1977). Essential Relativity. Springer-Verlag, New York.
[665] Rindler W (1982). Introduction to Special Relativity. Clarendon Press, Oxford.
[666] Rindler W (2001). Relativity: Special, General, and Cosmological. Oxford University Press, Oxford.
[667] Rizzi A. (1998). Angular momentum in general relativity: A new definition. Phys. Rev. Lett. 81(6),
1150.
[668] Robinson D. C. (1975). Uniqueness of the Kerr Black Hole. Phys. Rev. Lett. 34, 905-906.
[669] Rogers A. (1980). A global theory of supermanifolds. J. Math. Phys. 21, 1352-1365.
[670] Rolfsen D. (2004). Knots and Links. American Mathematical Society, Providence, RI.
[671] Roseveare N. T. (1982). Mercury s Perihelion from Le Verrier to Einstein. Clarendon Press, Oxford.
[672] Rovelli C. (1991). Quantum mechanics without time: A model. Phys. Rev. D42, 2638.
[673] Rovelli C. (1998). Strings, loops and others: a critical survey of the .present approaches to quantum
gravity. In Gravity and Relativity: At the turn of the Millennium (15th International Conference on
General Relativity and Gravitation, eds. N. Dadhich, J. Narlikar, Inter-University Centre for Astronomy
and Astrophysics, Pune, India), 281-331.
[674] Rovelli С. (2003). Quantum Gravity.
[http: //www. cpt . univ-mrs . fr/'-rovelli/book .pdf 3
[675] Rovelli C., Smolin L. (1990). Loop representation for quantum general relativity. Nucl. Phys. B331,
80-152.
[676] Runde V. (2002). The Banaeh-Tarski paradox — or — What mathematics and religion have in common.
Pi in the Sky 2 (2000), 13-15. [math. GM/0202309 3
[677] Russell B. (1903). Principles of Mathematics. Most recent republication by W. W. Norton & Company,
1996.
[678] Russell B. (1927). The Analysis of Matter. Allen and Unwin; reprinted 1954, Dover, New York.
[679] Ryder L.H. (1996). Quantum Field Theory. Cambridge University Press, Cambridge.
[680] Sabbagh K. (2003). The Riemann Hypothesis: The Greatest Unsolved Problem in Mathematics. Farrar,
Straus and Giroux.
[681] Saccheri G. (1733). Euclides ab Omni Naevo Vindicatus. Translation in Halsted, G. B. (1920). Euclid
Freed from Every Flaw. Open Court, La Salle, Illinois.
[682] Sachs R.K. (1961). Gravitational waves in general relativity, VI: the outgoing radiation condition.
Proc. Roy. Soc. Lond. A264, 309-338.
[683] Sachs R.K. (1962a). Gravitational waves in general relativity, VIII: waves in asymptotically flat
space-time. Proc. Roy. Soc. Lond. A270, 103-126.
[684] Sachs R. K. (1962b). Asymptotic symmetries in gravitational theory. Phys. Rev. 128, 2851-2864.
[685] Sachs R. and Bergmann P.G. (1958). Structure of Particles in Linearized Gravitational Theory. Phys.
Rev. 112, 674-680.
[686] Sakellariadou M. (2002). The role of topological defects in cosmology. Invited lectures in NATO ASI
/ COSLAB (ESF) School «Patterns of Symmetry Breaking», September 2002 (Cracow).
[hep-ph/0212365]

Литература
897
[687] Salam А. (1980). Gauge Unification of Fundamental Forces. Rev. Mod. Phys. 52(3), 515-523.
[688] Salam A., Ward J. C. (1959). Weak and electromagnetic interaction. Nuovo Cimento 11, 568.
[689] Sarkar S. (2002). Possible astrophysical probes of quantum gravity. Mod. Phys. Lett. A17, 1025-1036.
[gr-qc/0204092]
[690]	Sato M.	(1958).	On the generalization of the concept of a function. Proc. Japan Acad. 34,	126-130.
[691]	Sato M.	(1959).	Theory of hyperfunctions I. J. Fac. Scl. Univ. Tokyo, Sect. I, 8, 139-193.
[692]	Sato M.	(1960).	Theory of hyperfunctions II. J. Fac. Sci. Univ. Tolcyo, Sect. I, 8, 387-437.
[693] Schild A. (1949). Discrete space-time and integral Lorentz transformations. Can. J. Math. 1, 29-47.
[694] Schoen R., Yau S.-T. (1979). On the proof of the positive mass conjecture in the general relativity.
Comm. Math. Phys. 65, 45-76.
[695] Schoen R., Yau S.-T. (1982). Proof that Bondi mass is positive. Phys. Rev. Lett. 48, 369-371.
[696] Schouten J. A. (1954). Ricci-Сalcuius. Springer, Berlin.
[697] Schrodinger E. (1930). Sitzungber. Preuss. Akad. Wiss. Phys.-Math. Kl. 24, 418.
[698] Schrodinger E. (1935). Probability relations between separated systems. Proc. Camb. Phil. Soc. 31,
555-563.
[699] Schrodinger E. (1950). Space-Time Structure. Cambridge University Press, Cambridge.
[700] Schrodinger E. (1952) Science and Humanism: Physics in Our Time. Cambridge University Press,
Cambridge.
[701] Schrodinger E. (1956). Expanding Universes. Cambridge University Press, Cambridge.
[702] Schrodinger E. (1967). «What is Life?» and «Mind and Matter». Cambridge Univ. Press, Cambridge.
Имеется перевод более раннего издания: Шредингер Э. Что такое жизнь? Физический аспект
живой клетки. — М.: ИЛ, 1947.
[703] Schutz В. (2003). Gravity from the ground up: an introductory guide to gravity and general relativity.
Cambridge University Press, Cambridge.
[704] Schutz J. W. (1997). Independent Axioms for Minkowski Space-time. Addison-Wesley, Longman Ltd.,
Harlow, Essex.
[705] Schwartz L. (1966). Theorie des distributions. Hermann, Paris.
[706] Schwarz J.H. (2001). String Theory. Curr. Sci. 81(12), 1547-1553.
[707] Schwarzschild K. (1916). Uber das Gravitationsfeld eines Massenpunktes nach der Einsteinschen
Theorie. Sitzber. Deut. Akad. Wiss. Berlin Math.-Phys. Tech. Kl. 189-196. Имеется перевод: Швар-
цшильд К. О гравитационном поле точечной массы в эйнштейновской теории. В сб. статей
Альберт Эйнштейн и теория гравитации.. М.: Мир, 1979. С. 199-207.
[708] Schwinger J. (1951). On the Green’s functions of quantized fields. Proc. Nat. Acad. Sci. 37, 452-455.
[709] Schwinger J. (ed.) (1958). Quantum Electrodynamics. Dover.
[710] Sciama D. W. (1959). The Unity of the Universe. Doubleday & Company, Inc., New York.
[711] Sciama D. W. (1962). On the analogy between charge and spin in general relativity. In Recent
Developments in General Relativity. Pergamon & PWN, Oxford.
[712] Sciama D. W. (1972). The Physical Foundations of General Relativity. Heinemann, London.
[713] Sciama D. W. (1998). Decaying neutrinos and the geometry of the universe. In The Geometric
Universe: Science, Geometry, and the Work of Roger Penrose (eds. S. A. Huggett, L. J. Mason,
K.P.Tod, S.T. Tsou, N. M. J. Woodhouse). Oxford University Press, Oxford.

898
Литература
[714] Seiberg N., Witten E. (1994). Electric-magnetic duality, monopole condensation, and confinement
in N = 2 supersymmetric Yang-Mills theory. Nucl. Phys. B426. [hep-th/9407087 ]
[715] Sen A. (1982). Gravity as a spin system. Phys. Lett. B119, 89-91.
[716] Shankar R. (1994). Principles of Quantum Mechanics, 2nd edn. Plenum Press, New York & London.
[717] Shapiro I.I. (1964). Fourth test of general relativity. Phys. Rev. Lett. 13, 789-791.
[718] Shaw W. Т., Hughston L. P. (1990). Twistors and strings. In Twistors in Mathematics and Physics
(eds. T. N. Bailey, R. J. Baston). London Mathematical Society Lecture Notes Series, 156. Cambridge
University Press, Cambridge.
[719] Shawhan P. (2001). The Search for Gravitational Waves with LIGO: Status and Plans. Intl. J. Mod.
Phys. A 16, supp. 01C, 1028-1030.
[720] Shih Y. H., et al. (1995). Optical Imaging by Means of Two-Photon Entanglement. Phys. Rev. A, Rapid
Comm. 52, R3429.
[721] Shimony A. (1998). Implications of transience for spacetime structures. In The Geometric Universe:
Science, Geometry, and the Work of Roger Penrose (eds. S.A. Huggett, L. J. Mason, K. P. Tod,
S. T. Tsou, N. M. J. Woodhouse). Oxford University Press, Oxford.
[722] Shrock R. (2003). Neutrinos and Implications for Physics Beyond the Standard Model. World Scientific
Pub. Co., Singapore.
[723] Silk J., Rees M. (1998). Quasars and galaxy formation. Astronomy and Astrophysics, 331, L1-L4.
[724] Simon B. (1983). Holonomy, the quantum adiabatic theorem, and Berry’s phase. Phys. Rev. Lett. 51,
2160-2170.
[725] Simmonds J. G., Mann J. E. (1998). A First Look at Perturbation Theory. Dover Publications, New
York.
[726] Singh S. (1997). Fermat’s Last Theorem. Fourth Estate, London.
[727] Slipher V. A. (1917). Nebulae. Proc. Am. Phil. Soc. 56, 403.
[728] Smolin L. (1991). Space and time in the quantum universe. In Conceptual Problems in Quantum
Gravity (eds. A. Ashtekar, J. Stachel). Birkhauser, Boston.
[729]	Smolin L. (1997). The Life of the Cosmos. Oxford University Press, Oxford.
[730]	Smolin L. (1998). The physics of spin networks. In The Geometric Universe: Science, Geometry; and
the Work of Roger Penrose (eds. S. A. Huggett, L. J. Mason, K. P. Tod, S. T. Tsou, N. M. J. Woodhouse).
Oxford University Press, Oxford.
[731]	Smolin L.	(2001).	The exceptional	Jordan algebra and the matrix string, (hep-th/0104050)
[732]	Smolin L.	(2002).	Three Roads To	Quantum Gravity. Basic Books, New York.
[733]	Smolin L.	(2003).	How far are we	from the quantum theory of gravity? [hep-th/0303185 ]
[734]	Smoot G.	F., et al. (1991). Preliminary results from the СОВЕ differential microwave radiometers:
large-angular-scale isotropy of the Cosmic Microwave Background. Astrophys. J. 371, LI.
[735]	Snyder H. S. (1947). Quantized space-time. Physical Review 71, 38-41.
[736]	Sorabji R. J. (1984). Time, Creation, and the Continuum. Cornell University Press.
[737]	Sorabji R. J. (1988). Matter Space and Motion. Duckworth Publishing.
[738] Sorkin R. D. (1991). Spacetime and Causal Sets. In Relativity and Gravitation: Classical and Quantum
(eds. J. C. D’Olivo, et al.). World Scientific, Singapore.
[739] Sorkin R. D. (1994). Quantum. Measure Theory and its Interpretation. In Proceedings of 4th Drexel
Symposium on Quantum Nonintegrability, 8-11 Sep., Philadelphia, PA. [gr-qc/9507057 ]

Литература
899
[740] Spergel D. N. (2003). First Year Wilkinson Microwave Anisotropy Probe Observations: Determination
*
of Cosmological Parameters. Astrophys. J. Suppl. 148, 175.
[741] Stachel J. (1995). History of relativity. In History of 20th Centuiy Physics (eds. L. Brown, A. Pais,
B.	Pippard), Chapter 4, American Institute of Physics (AIP) and British Institute of Physics (BIP).
' . .. •
[742] Stairs A. (1983). Quantum logic, realism and value-definiteness. Phil Sci. 50(4), 578-602.
[743] Stapp H.P. (1971). S-matrix Interpretation of Quantum Mechanics. Phys. Rev. D3, 1303-1320.
*	•	i	t
[744] Stapp H. P. (1979). Whiteheadian Approach to Quantum Theory and the Generalized Bell’s Theorem.
Found. Phys. 9, 1-25.
[745] Steenrod N. E. (1951). The Topology of Fibre Bundles. Princeton University Press, Princeton. Имеется
перевод: Стинрод H. Топология косых произведений. — М.: ИЛ, 1953.
V
[746] Steinhardt P. J., Turok N. (2002). A Cyclic Model of the Universe. Science 296(5572), 1436-1439.
[hep-th/0111030]
[747] Stoney G. J. (1881). On the Physical Units of Nature. Philosophical Magazine, vol. 11, 381.
[748] Strauss W. (1992). Partial Differential Equations: An Introduction. John Wiley and Sons.
[749] Strominger A., Vafa C. (1996). Microscopic Origin of the Bekenstein-Hawking Entropy. Phys. Lett.
B379, 99-104.
[750] Strominger A., Yau S.-Т., Zaslow E. (1996). Mirror symmetry is T-duality. Nucl. Phys. B479, 1-2,
243-259.
[751] Struik D. J. (1954). A Concise Histoiy of Mathematics. Dover, New York.
[752] Sudarshan G., Dhar J. (1968). Quantum Field Theory of Interacting Tachyons. Phys. Rev. 174, 1808.
[753] Sudbery A. (1987). Division algebras, (pseudo) orthogonal groups and spinors. J. Phys. A17, 939-955.
[754] Susskind L. (1970). Structure of Hadrons Implied by Duality. Nuovo Cimento A69, 457.
[755] Susskind L. (2003). Twenty Years of debate with Stephen. In The Future of Theoretical Physics and
Cosmology (eds. G. W. Gibbons, P. Shellard, S. Rankin). Cambridge University Press, Cambridge.
[756] Susskind L., Thorlacius L., Uglum J. (1993). The stretched horizon and black hole complementarity.
Phys. Rev. 48, 3743. [hep-th/9306069]
N
[757] Sutherland W. A. (1975). Introduction to Topology. Oxfrord Uriversity Press, Oxford.
[758] Swain J. (2004). The Majorana representations of spins and the relation between SU(oo)
and SDif f (52). [hep-th/0405004 ]
[759] Synge J. L. (1950). The gravitational field of a particle. Proc. Irish Acad. A53, 83-114.
[760] Synge J. L. (1956). Relativity: The Special Theory. North-Holland, Amsterdam.
[761] Synge J. L. (1960). Relativity: The General Theory. North-Holland Publ. Co., Amsterdam. Имеется
перевод: Синг Дж. Л. Общая теория относительности. — М.: ИЛ, 1963.
[762] Szekeres G. (I960). On the Singularities of a Riemannian Manifold. Publ Mat. Debrecen 7, 285-301.
[763] ’t Hooft G. (1978). On the phase transition towards permanent quark confinement. Nucl. Phys. B138,1.
[764] ’t Hooft G. (1978). Quanlum gravity: a fundamental problem and some radical ideas. In
Developments in Gravitation (eds. M. Levy, S.Deser). Plenum, New York.
> *. *
[765] Tait P. G. (1900). On the claim recently made for Gauss to the invention (not the discovery) of
quaternions. Proc. Roy. Soc. Edinb. 23, 17-23.
•* a
[766] Taylor E. F., Wheeler J. A. (1963). Spacetime Physics. W. H. Freeman, San Francisco. Имеется пере¬
вод: Тейлор Э. Ф., Уилер Дж. А. Физика пространства-времени. — М.: Мир, 1971.

900
Литература
[767] Terrell J. (1959). Invisibility of the Lorentz contraction. Phys. Rev. 116, 1041-1045.
[768] Thiele R. (1982). Leonhard Euler. Leipzig (in German).
[769] Thiemann T. (1996). Anomaly-free formulation of non-perturbative, four-dimensional Lorentzian
quantum gravity. Phys. Lett. B380, 257-264.
[770] Thiemann T. (1998). Quantum spin dynamics (QSD). Class. Quant. Grav. 15, 839-873.
•%
[771] Thiemann T. (1998). QSD III: Quantum constraint algebra and physical scalar product in quantum
general relativity. Class. Quant. Grav. 15, 1207-1247.
[772] Thiemann T. (1998). QSD V: Quantum gravity as the natural regulator of matter quantum field theories.
Class. Quant. Grav. 15, 1281-1314.
[773] Thiemann T. (2001). QSD VII: Symplectic Structures and Continuum Lattice Formulations of Gauge
Field Theories. Class. Quant. Grav. 18, 3293-3338.
[774] Thirring W. E. (1983). A Course in Mathematical Physics: Quantum Mechanics of Large Systems.
Springer-Verlag, Berlin & London.
[775] Thomas I. (1939). Selections Illustrating the History of Greek Mathematics, Vol. I: From Thales to
Euclid. The Loeb Classical Library, Heinemann, London.
[776] Thome K. (1986). Black Holes: The Membrane Paradigm. Yale University Press, New Haven.
[777] Thome K. (1995). Black Holes and Time Warps. W. W. Norton & Company.
[778] Thome K. (1995). Gravitational Waves. [gr-qc/9506086]
[779] Tipler F. J. (1997). The Physics of Immortality. Anchor.
[780] Tipler F. J., Clarke C.J. S., Ellis G. F. R. (1980). Singularities and horizons — a review article. In
General Relativity and Gravitation, Vol. II (ed. A. Held), 97-206. Plenum Press, New York.
[781] Tittel W., Brendel J., Zbinden H., Gisin N. (1998). Violation of Bell Inequalities by Photons More
Than 10 km Apart. Phys. Rev. Lett. 81, 3563.
[782] Tod K. P., Anguige K. (1999). Isotropic cosmological singularities 1: Polytropic perfect fluid
spacetimes. Annals Phys. 276, 257-293. [gr-qc/9903008]
[783] Tod K. P., Anguige K. (1999). Isotropic cosmological singularities 2: The Einstein-Vlasov system.
Annals Phys. 276, 294-320. [gr-qc/9903009]
[784] Tolman R. C. (1934). Relativity, Thermodynamics, and Cosmology. Clarendon Press, Oxford. Имеется
перевод: Толмен P. Относительность, термодинамика и космология. — М.: Наука, 1974.
[785] Tonomura A., Matsuda Т., Suzuki R., Fukuhara A., Osakabe N., Umezaki H., Endo J., Shinagawa K.,
Sugita Y., Fujiwara F. (1982). Observation of Aharonov-Bohm effect with magnetic field completely
shielded from the electronic wave. Phys. Rev. Lett. 48, 1443.
[786] Tonomura A., Osakabe N., Matsuda Т., Kawasaki Т., Endo J., Yano S., Yamada (1986). Evidence for
Aharonov-Bohm effect with magnetic field completely shielded from electron wave. Phys. Rev. Lett.
56, 792-795.
[787] Trautman A. (1958). Radiation and boundary conditions in the theoiy of gravitation. Bull. Acad.
Polon. Sci., Ser. Sci. Math. Astr. Phys. 6, 407-412.
[788] Trautman A. (1962) Conservation laws in general relativity. In Gravitation: An Introduction to Current
Research (ed. L. Witten). Wiley, New York.
[789] Trautman A. (1965) in Trautman A., Pirani F. A. E., Bondi H. (1965). Lectures on General Relativity.
Brandeis 1964 Summer Institute on Theoretical Physics, vol. I. Prentice-Hall, Englewood Cliffs, N.J.
[790] Trautman A. (1970). Fibre bundles associated with space-time. Rep. Math. Phys. (Tomn) 1, 29-34.

Литература
901
[791]	Trautman А. (1972, 1973). On the Einstein-Cartan equations, I-IV. Bull. Acad. Pol Sci., Ser. Sci.
Math. Astron. Phys. 20, 185-190; 503-506; 895-896; 21, 345-346.
[792
[793
[794
[795
[796
[797
[798
[799
[800
[801
[802
[803
[804
[805
[806
[807
[808
[809
[810
[811
[812
[813
[814
[815
[816
Trautman A. (1997). Clifford and the «Square Root» Ideas. In Contemporary Mathematics 203.
Treves F. (1967). Topological Vector Spaces, Distributions and Kernels. Academic Press, New York.
Turing A. M. (1937). On computable numbers, with an application to the Entscheidungsproblem. Proc.
bond. Math. Soc. 42(2). 230-265; a correction (1937), 43, 544-546.
Unruh W. G. (1976). Notes on black hole evaporation. Phys. Rev. D14, 870.
Vafa C. (1996). Evidence for F-theory. Nucl. Phys. B469, 403.
Valentini A. (2002). Signal-Locality and Subquantum Information in Deterministic Hidden-
Variables Theories. In Non-Locality and Modality (eds. T. Placek, J. Butterfield). Kluwer. [quant-
ph/0112151]
van der Waerden B. L. (1929). Spinoranalyse. Nachr. Akad. Wiss. Gotting. Math.-Physik, Kl. 100-109.
van der Waerden B. L. (1985). A History of Algebra: From al-Khwrizmi to Emmy Noether, 166-174.
Springer-Verlag, Berlin.
van Heijenoort J. (ed.) (1967). From Frege to Godel: Source Book in Mathematical Logic, J879-1931.
Harvard University Press, Cambridge, MA.
van Kerkwijk М. H. (2000). Neutron Star Mass Determinations. [astro-ph/0001077 ]
Varadarajan M. (2000). Fock representations from U(l) holonomy algebras. Phys. Rev. D61, 104001.
Varadarajan M. (2001). Photons from quantized electric flux representations. Phys. Rev. D64, 104003.
Veneziano G. (1968). Nuovo Cimento 57A, 190.
Vilenkin A. (2000). Cosmic Strings and Other Topological Defects. Cambridge University Press,
Cambridge.
Vladimirov V. S., Volovich I.V., Zelenov E. I. (1994). P-Adic Analysis and Mathematical Physics.
World Scientific Publishing Company, Inc.
von Neumann J. (1955). Mathematical Foundations of Quantum Mechanics. Princeton University
Press, Princeton, New Jersey. Имеется перевод: фон Нейман И. Математические основы кван¬
товой механики. — М.: Наука, 1964.
Wagon S. (1985). Banach-Tarski Paradox. Cambridge University Press, Cambridge.
Wald R. M. (1984). General Relativity. University of Chicago Press, Chicago.
Wald R. M. (1994). Quantum Field Theory in Curved Spacetime and Black Hole Thermodynamics.
University of Chicago Press, Chicago.
Ward R. S. (1977). On self-dual gauge fields. Phys. Lett. 61 A, 81-82.
Ward R. S., Wells R. O., Jr. (1989). Twistor Geometry and Field Theory. Cambridge University Press,
Cambridge.
Weinberg S. (1967). A model of leptons. Phys. Rev. Lett. 19, 1264-1266.
Weinberg S. (1972). Gravitation and Cosmology: Principles and Applications of the General Theory of
Relativity. Wiley, New York. Имеется перевод: Вайнберг С. Гравитация и космология. Принципы
и применения общей теории относительности. — М.: Мир, 1976.
Weinberg S. (1989). Precision Tests of Quantum Mechanics. Phys. Rev. Lett. 62, 485-488.
Weinberg S. (1992). Dreams of a Final Theory: The Scientists Search for the Ultimate Laws of Nature.
Pantheon Books, New York. Имеется перевод: Вайнберг С. Мечты об окончательной теории. —
М.: УРСС, 2004.

902
Литература
[817] Wells R. О. (1991). Differential analysis on complex manifolds. Prentice Hall, Englewood Cliffs. Име¬
ется перевод более раннего издания: Уэллс Р. Дифференциальное исчисление на комплексных
многообразиях. — М.: Мир, 1976.
[818] Werbos Р. (1989). Bell’s theorem: the forgotten loophole and how to exploit. In Bells Theorem,
Quantum Theory, and Conceptions of the Universe (ed. M. Kafatos). Kluwer, Dordrecht, The
Netherlands.
[819] Werbos P.J., Dolmatova L. (2000). The Backwards-Time Interpretation of Quantum Mechanics:
Revisited With Experiment.
[http://arxiv.org/ftp/quant-ph/papers/0008/0008036.pdf]
[820] Wess J., Bagger J, (1992). Supersymmetry and Supergravity. Princeton University Press, Princeton.
[821] Wess J., Zumino B. (1974). Supergauge transformations in four dimensions. Nucl. Phys. 70, 39-50.
[822] Weyl H. (1918), in [495]. Имеется перевод: Вейль Г. Гравитация и электричество. В сб. статей
Альберт Эйнштейн и теория гравитации.. — М.: Мир, 1979. С. 513-528.
[823] Weyl Н. (1928). Gruppentheorie und Quantenmechanik. Hirzel, Leipzig; English translation of 2nd
edn., The Theory of Groups and Quantum Mechanics. Dover, New York. Имеется перевод: Вейль
Г. Теория групп и квантовая механика. — М.: Наука, 1986.
[824] Weyl Н. (1929). Elektron und Gravitation I. Z Phys. 56, 330-352.
[825] Wheeler J. A. (1957). Assessment of Everett’s «Relative State» Formulation of Quantum Theory. Rev.
Mod. Phys. 29, 463M65.
[826] Wheeler J. A. (1960). Neutrinos, Gravitation and Geometry: contribution to Rendiconti della Scuola
Internazionale di Fisica ’ Enrico Fermi XI, Corso, July 1959. Zanichelli, Bologna. (Reprinted in 1982.)
[827] Wheeler J. A. (1965). Geometrodynamics and the issue of the final state. In Relativity, Groups and
Topology (eds. B. S. DeWitt, С. M. DeWitt). Gordon and Breach, New York.
[828] Wheeler J.A. (1973). From Relativity to Mutability. In The Physicist’s Conception of Nature (ed.
J. Mehra), 202-247. D. Reidel, Boston.
[829] Wheeler J.A. (1983). Law without law, in Quantum Theory and Measurement (eds. J.A.Wheeler,
W.H. Zurek), 182-213. Princeton Univ. Press, Princeton.
[830] Whittaker E.T. (1903). On the partial differential equations of mathematical physics. Math. Ann. 57,
333-355.
[831] Wick G. C. (1956). Spectrum of the Bethe-Salpeter equation. Phys. Rev. 101, 1830.
[832] Wigner E. P. (1960). The Unreasonable Effectiveness of Mathematics in the Physical Sciences.
Commun. Pure Appl. Math. 13, 1-14. Имеется перевод: E. Вигнер, Непостижимая эффективность
математики в физических науках. Усп. физ. наук. 94, 535-546 (1968).
[833] Wilder R, L. (1965). Introduction to the foundations of mathematics. John Wiley & Sons, New York.
[834] Wiles A. (1995). Modular elliptic curves and Fermat’s Last Theorem. Ann. Maths. 142, 443-551.
[835] Williams R. K. (1995). Extracting X-rays, 7-rays, and Relativistic e”e+ Pairs from Supermassive
Kerr Black Holes Using the Penrose Mechanism. Phys. Rev. D51, 5387.
[836] Williams R. K. (2002). Production of the High Energy-Momentum Spectra of Quasars 3C279
and 3C273 Using the Penrose Mechanism, [astro-ph/0306135]. Accepted for publication in
Astrophysical Journal, 2004.
[837] Williams R. K. (2004). Collimated Escaping Vortical Polar e-e+ Jets Intrinsically Produced by
Rotating Black Holes and Penrose Processes, [astro-ph/0404135]
[838] Willmore T. J. (1959). An Introduction to Differential Geometry. Clarendon Press, Oxford.
[839] Wilson K. (1975). Phys. Reps. 23, 331.

Литература
903
[840] Wilson К. (1976). Quarks on a lattice, or the colored string, model. Phys. Rep. 23(3), 331-347.
[841] Winicour J. (1980). Angular momentum in general relativity. In General Relativity and Gravitation
Vol. 2 (ed. A. Held), 71-96. Plenum Press, New York.
*
i
[842] Witten E. (1978). An interpretation of classical Yang-Mills theory. Phys. Lett. 77B, 394-398.
[843] Witten E. (1981). A new proof of the positive energy theorem. Comm. Math. Phys. 80, 381-402.
[844] Witten E. (1982). Supersymmetry and Morse theory. J. Diff. Geom. 17, 661-692.
[845] Witten E. (1988). Topological quantum field theory. Commun. Math. Phys. 118, 411.
[846] Witten E. (1995). String theory in various dimensions. Nucl Phys. B443, 85.
[847] Witten E. (1996). Reflections on the Fate of Spacetime. Phys. Today, April 1996.
[848] Witten E. (1998). Anti de Sitter Space and Holography, [hep-th/9802150]
[849] Witten E. (2003). Perturbative Gauge Theory as a String Theory in Twistor Space, [hep-
th/0312171]
[850] Witten L. (1959). Invariants of general relativity and the classification of spaces. Phys. Rev. 113,
357-362.
[851] Wolf J. (1974). Spaces of Constant Curvature. Publish or Perish Press, Boston, MA.
[852] Woodhouse N. M. J. (1991). Geometric Quantization, 2nd edn., Clarendon Press, Oxford.
[853] Woodin W. H. (2001). The Continuum Hypothesis. Part I: Notices Amer. Math. Soc. 48, 567-576,
Part II: ibid. 681-690; also (Part I) online at: http://www.ams.org/notices/200106/fea”
wooin. pdf and (Part II) ditto, but with /200107/.
[854] Wooters W. K., Zurek W. H. (1982). A single quantum cannot be cloned. Nature 299, 802-803.
[855] Wykes A. (1969). Doctor Cardano: Physician Extraordina/y. Frederick Muller, London.
[856] Yang C.N., Mills R.L. (1954). Conservation of Isotopic Spin and Isotopic Gauge Invariance. Phys.
Rev. 96, 191-195. Имеется перевод: Янг Ч.-Н., Миллс Р. Л. Сохранение изотопического спи¬
на и изотопическая калибровочная инвариантность. В сб. статей Элементарные частицы и
компенсирующие поля. — М.: Наука, 1964. — С. 28-38.
[857] Yui N., Lewis J. D. (2003). Calabi-Yau Varieties and Mirror Symmetry. Fields Institute
Communications, V. 38. American Mathematical Society, Providence, RI.
[858] Zee A. (2003). Quantum Field Theory in a Nutshell. Princeton University Press, Princeton.
[859] Zeilinger A., Gaehler R., Shull C. G., Mampe W. (1988). Single and double slit diffraction of neutrons.
Rev. Mod. Phys. 60, 1067.
[860] Зельдович Я.Б. (1965). Число квантов как инвариант классического электромагнитного поля.
Докл. АН СССР. 163, 1359-1360.
[861] Zimba J., Penrose R. (1993). On Bell non-locality without probabilities: more curious geometry. Stud.
Hist. Phil. Sci. 24, 697-720.
[862] Zinn-Justin J. (1996). Quantum Field Theoty and Critical Phenomena. Oxford University Press,
Oxford.

Предметный указатель
’т Хоофт 552, 570
СРТ-теорема 539
D-браны 759
F-теория 807
М-теория 759
S-матрица 567
W-бозон 468
W-бозоны 531
Х-бозоны 531
Z-бозоны 531
Ааронов, Якир 680
Ааронова - Бома эффект 388
Абелевы группы 224
Абель, Нильс Хенрик 224
Адроны 106, 503, 544
Аксиома выбора 36, 318
Аксионы 531
Алгоритм Евклида 79, 80
Александера многочлен 783
Альфа-распад 534
Амплитуда 409
Амплитуда вероятности 459
Аналитические функции 115
Аналитическое продолжение 128
Андерсон, Карл 528
Антикварки 106, 545
Антилептоны 544
Антинейтрон 531
Антипротон 531
Античастицы 78, 515
Антропный принцип 634
Аполлоний 841
Арган, Жан Робер 89
Аромат кварков 545
Архимед 74, 107, 855
Асимптота 62
Асимптотическая свобода 571
Атья, Майкл 835
Аффинное пространство 257, 259
Аффинный параметр 269
Ахмаваара 311, 794
Аштекар, Абхай 653, 776
Базисное пространство 288
Бальмера формула 489
Банаха-Тарского теорема 318
Барберо - Иммирци параметр 780, 789
Барионы 544
Бекенстайн, Джейкоб 688
Бекенстайна - Хокинга формула 600
Беккерель, Анри 530
Белл, Джон 494
Белла неравенства 494
Белые карлики 399, 595
Бельтрами, Эудженио 61, 855
Бета-распад 535
Бете, Ганс 552
Билинейная форма 250
Блоха сфера 665
Богомольный, Евгений 761
Бозе-Эйнштейна конденсация 504
Бозе-Эйнштейна статистика 428
Бозоны 503
Больцман, Людвиг 378, 580, 855
Больцмана статистика 582
Больцмана уравнение 584
Большой взрыв 591, 601, 609, 616, 626, 774, 832
Большой хлопок 610, 613, 616, 637
Больяи, Янош 61, 855
Бом, Дэвид 494, 657
Бомбелли, Рафаэль 82, 83, 85, 98
Бонди, Герман 399, 629
Бор, Нильс 655
Бора атом 485
Борн, Макс 457
Бра-векгоры 454
Брамагупта 76, 98
Браны 759
Бредли, Джеймс 369
Бройль, Луи де 427, 657
Брюстера угол 487
Бхаскара 76
Быстрота 367
Бьянки тождество 394
Вайдман, Лев 462
Вайнберг, Стивен 552
Вайнберга угол 542, 548
Ван-дер-Варден, Бартель 528, 843

Предметный указатель
905
Вафа, Кумрун 760
Вейль, Герман 386, 529
Вейля тензор 396
Вектор состояния 448
Векторное пространство 203
Векторное расслоение 288
Великое объединение 549, 620, 728, 729, 756
Вельтман 552
Венециано, Габриэле 736
Вессель, Каспар 89, 92
Вещественные числа 72
Вигнер, Юджин 673
Вик, Джанкарло 644
Вильсон, Кеннет 552, 781
Вильсон, Роберт 614
Вина закон 429
Виртуальные частицы 531, 566
Виттен, Эдвард 738, 744, 757, 768
Внешняя производная 204, 210
Возбужденное состояние 485
Волна-пилот 657
Волновая функция 425
Волновой пакет 433
Вполне приводимое представление 244
Вторая космическая скорость 594
Второй закон термодинамики 579
By Цзинь-сян 535
Высшие гармоники 150
Вычислимость 324
Гёдель, Курт 322
Гёделя теорема 326
Галилей, Галилео 74, 316, 333
Галилея принцип относительности 333
Галуа теория 257
Галуа, Эварист 257
Гамильтон, Уильям Роуан 184, 186, 187, 190, 403
Гамильтона принцип 405
Гамильтона уравнения 283
Гамильтона функция 403
Гамильтониан 403
Гамов, Георгий Антонович 614
Гат, Алан 626
Гаудсмит, Сэмюэл 525
Гаусс, Карл Фридрих 61, 89, 209, 403, 855
Гаусса закон 383
Гаусса распределение 583
Гаусса функция 433
Гауссова кривизна 60, 272
Гауссовы единицы 379
Гейзенберг, Вернер 552
Гейзенберга представление 450, 455
Гейзенберга соотношение неопределенностей 444
Гейзенберга уравнение движения 456
Гелл*Манн, Мюррей 544
Геодезическая 268
Герц, Генрих 428
Гиббс, Джозайя Уиллард 378, 855
Гильберт, Давид 418
Гильберта пятая проблема 257
Гильбертово пространство 328, 453
Гиперболический тангенс 368
Гиперкэлеровы многообразия 831
Гипероны 544
Гиперповерхность 408, 731
Гиперфункция 163
Гиромагнитное отношение 694
Глюино 531
Глюоны 78, 531, 547
Голая сингулярность 643
Голд, Томас 629
Голограмма 763
Голографический принцип 763
Голоморфное сечение 297
Гольдбаха гипотеза 327
Гомологические деформации 124
Гомотопические деформации 124
Горизонт событий 596
Гравитационные волны 397
Гравитино 729
Гравитон 744
Грассман, Герман 187
Грассмана алгебра 194
Грейвс, Джон 187
Грин, Брайан 738
Грин, Джордж 209, 575
Грин, Майкл 738, 741
Грина функция 575
Группа расслоения 288
Группа симметрии 223
Группа-монстр 228
Групповое произведение 228
Гурвиц 187
Гурзадян, Вахе 21, 649
Дайсон, Фримен 552
Даламбера оператор (даламбериан) 521
Даламбера уравнение 379
Даукер, Фей 679
Двухщелевой эксперимент 429
Де-бройлевская длина волны 427
Дедекинд, Рихард 72, 73, 76, 77, 83
Дедекинда сечение 73, 316
Дезарг 300
Дезарга теорема 300
Действие 405
Дейтрон 468
Декогеренция, вызываемая окружением 657
Дельта-функция 120
Джермер, Люстер Халберт 427
Джонса многочлен 783
Дикке, Роберт 614, 635
Дилатон 531, 743, 772
Динамические переменные 431
Диофант 35

906
Предметный указатель
Дирак, Поль 74, 78, 121, 454, 520
Дирака монополь 620
Дирака море 527
Дирака оператор 523
Дирака уравнение 193, 524
Дирихле задача 766
Дирихле ряды 131
Дирихле, Пьер Лежен 766
Диск аккреции 596
Диссипация 412
Доказательство от противного 67
Доменные стенки 621
Домены 620
Доплера эффект 591
Дэвиссон, Клинтон Джозеф 427
Дэвиссона - Джермера опыт 427
Евдокс 72, 98
Евклид 67, 71, 74
Евклидова геометрия 72
Жорданова нормальная форма 257
Жуковского преобразование 145
Закрученное расслоение 288
Зарядовое сопряжение 539
Звездная аберрация 369
Зельдович, Яков Борисович 652
Зумино, Бруно 844
Излучение черного тела 428
Импульс 200, 372
Инерциальное движение 335
Интуиционизм 66
Инфляционная космология 626
Иордан, Паскуаль 552
Иррациональные числа 67
Исключительная группа 228
Кабиббо угол 548
Казимира операторы 481
Калаби, Эудженио 756
Калаби-Яу пространства 749, 756
Калибровочная инвариантность 386
Калибровочная связность 223, 286
Калибровочное преобразование 386
Калуца, Теодор 287, 733
Калуцы-Клейна модель 287
Калуцы - Клейна пространство 287
Канделас, Филипп 758
Каноническая проекция 288
Каноническое правило коммутации 423
Кантор, Георг 72, 73, 76
Каоны 522
Кардано, Джироламо 82, 83, 85, 93, 98
Кардинальные числа 317
Карно, Сади 378
Картан, Эли 208, 340, 855
Картер, Брэндон 635
Касательное пространство 260
Касательное расслоение 298, 403
Категорий теория 858
Кауфмана многочлен 783
Квадратичная форма 250
Квадратичные иррациональные числа 71
Квазары 599, 699
Квантование 424
Квантовая гравитация 75
Квантовая интерференция 388
Квантовая информация 798
Квантовая телепортация 506, 654
Квантовая теория поля (КТП) 552
Квантовая хромодинамика (КХД) 544, 740
Квантовая электродинамика (КЭД) 570
Квантовое перепутывание 490, 797
Квантовое состояние 425
Квантовые компьютеры 493
Квантовые точки 492
Квантовые флуктуации 717
Квантовые числа 469
Кварки 78, 106, 468, 531, 544, 545
Кваркность 105
Кватернионы 184
Кеплер, Иоганн 577
Керра - Ньюмена метрика 694
Кет-векторы 454
Киллинг, Вильгельм 228
Киллинга вектор 282
Киллинга форма 244
Кинетическая энергия 371
Киральность 535
Класс эквивалентности 17, 164, 312, 664
Классическая группа 228
Клаузиус, Рудольф Юлиус Эмануэль 378, 580
Клейн, Оскар 287, 726, 733
Клейна-Гордона уравнение 521, 748
Клиффорд, Уильям Кингдон 187, 293
Клиффорда алгебра 194
Клиффорда расслоение 293
Клиффорда - Хопфа расслоение 293
Клиффордовы параллели 295
Ковалентная связь 526
Ковариантная производная 264, 286
Ковекторы 203
Когерентные состояния 560
Когомология пучков 818
Кодаира, Кунихико 826
Кодаиры теоремы 826
Кокасательное расслоение 298, 403
Коллапс волновой функции 449
Кольцо сходимости 153
Комбинированная четность 539
Компактность 211
Комплексификация 245
Комплексная гладкость 136

Предметный указатель
907
Комплексное сопряжение 169, 170, 225
Комплексные числа 82
Комптон, Артур 429
Комптоновское рассеяние 540
Конечное поле 311
Конн, Ален 796
Континуум-гипотеза 322
Контурное интегрирование 122, 830
Конфигурационное пространство 198, 403
Конформная геометрия 136
Конформное отображение 136
Конформные диаграммы 606
Координатная связность 266
Копенгагенская интерпретация 657
Космическая цензура 599, 643
Космические монополи 621
Космические струны 621
Космологическая постоянная 395
Котес, Роджер 106
Коши формула 126, 127
Коши, Огюст 88, 122, 855
Коши- Римана условия 122, 123, 126, 136, 180,
181,217
Кошка Шредингера 480
Коэн, Пол 322
Красное смещение 591
Кристоффель, Элвин 281
Кронекера символ 218
Кротовые норы 696
Куперовские пары 504
Кэли, Артур 187, 232
Кюри точка 618
Лагранж, Жозеф Луи 71, 325, 403, 562
Лагранжа функция 403
Лагранжиан 403
Ламбда-исчисление 120
Ламбда-частица 531
Ламберт, Иоганн Генрих 364, 855
Лаплас, Пьер Симон 403, 594
Лапласа оператор (лапласиан) 476
Лапласа уравнение 379
Леви-Чивита тензор 234
Леви-Чивита, Туллио 281
Лежандр, Адриен Мари 403
Лейбниц, Готфрид 107, 209, 855
Лейбница правило 422, 455
Лейбница формула 116
Ленард, Филипп 428
Лептоны 540
Ли Дзун-дао 535
Ли алгебра 239
Ли группы 225
Ли производная 274
Ли скобки 274
Ли, Софус 239
Линейная комбинация 230
Линейное расслоение 290
Линейные преобразования 229
Лиувилль, Жозеф 403
Лиувилля теорема 413
Лобачевский, Николай Иванович 61, 855
Лобачевского геометрия 51, 61
Логарифмическая линейка 97
Логарифмическая расходимость 572
Логарифмическая спираль 102
Лорана ряды 150, 152-154, 163
Лоренц, Гендрик Антоон 247, 345
Лоренца группа 248
Лоренцева матрица 247
Людерса точка 487
Мёбиуса лента 290
Мебиуса преобразование 138, 139
Мёллеровское рассеяние 565
Магический диск 313
Магнитный монополь 384, 531
Майорана, Этторе 475
Майораны представление 475
Маклореиа ряд 114, 121
Максвелл, Джеймс Клерк 74, 345, 378, 379, 583,
855
Максвелла распределение 583
Максвелла уравнения 379
Малдасена, Хуан 763
Мандельброт, Бенуа 37
Мандельброта множество 37, 92, 93, 633
Масса покоя 374
Математическое доказательство 32
Математическое ожидание 487
Матрица 229
Матрица плотности 656, 661
Матрица рассеяния 567
Маха принцип 632, 785
Маха-Цендера интерферометр 439
Махавира 76
Мезоны 522, 544
Мембраны 759
Метрический тензор 247
Ми теория 418
Мизнер, Чарльз 652
Милгром, Мордехай 653
Милликен, Роберт Эндрю 81, 428
Минковский, Герман 349, 855
Минковского геометрия пространства-времени
355
Мировая линия 335
Мичелл, Джон 594
Мнимая единица 82
Многообразия 134
Множественность миров 657
Момент импульса 371, 372, 468, 480
Мощность множества 316
Муавр, Абрахам де 106
Муавра теорема 106

908
Предметный указатель
Мультиплеты 544
Мюон 468
Нётер теорема 376, 391, 417, 423
Наблюдаемые 457
Намбу, Йоширо 736
Натуральные числа 76
Неабелева калибровочная теория 547
Негрепонтис, Стелиос 80
Нееман, Ювал 544
Нейман, Джон фон 76, 663
Нейтрино 468
Нейтрон 106, 468
Нейтронные звезды 398, 595
Некоммутативная геометрия 796
Неопределенный интеграл 117
Непрерывные дроби 70
Неприводимое представление 244
Норма вектора 253
Нормальная подгруппа 226
Нормальная частота 409
Нормальные колебания 409
Нормальные операторы 458
Нуклоны 544
Нулевое сечение 292
Нулевой конус 346
Нулевые колебания 484
Ньюлендера ~ Ниренберга теорема 220
Ньютон, Исаак 74, 107, 855
Ньютона второй закон 336
Ньютона закон тяготения 336
Ньютона первый закон 335
Ньютона третий закон 336
Обобщенные импульсы 406
Обобщенные координаты 404
Обобщенные скорости 404
Обращение времени 539
Объективная редукция 682
Октонионы 187
Омега-минус частица 531
Омниум 655
Оператор Казимира 469
Операторы рождения 553
Операторы уничтожения 554
Оппенгеймер, Роберт 529, 598
Определенный интеграл 118
Определитель 233
Ортоводород 786
Ортогональное дополнение 360
Ортогональные преобразования 230
Ортонормированный базис 253, 459
Основание натуральных логарифмов 99
Основная теорема алгебры 85
Основная теорема анализа 117
Основная теорема внешнего анализа 211
Основное состояние 485
Остроградский, Михаил Васильевич 209, 403
Относительности теория 74, 259
Отражение 225
Палиндромные последовательности 71
Папп 300
Паппа теорема 300
Параводород 786
Парадокс близнецов 361
Парадокс измерения 480
Парадокс часов 359
Параллельный перенос вектора 262
Параметр Барберо - Иммирци 789
Паули матрицы 467, 525
Паули принцип 504
Паули, Вольфганг 525, 552
Паули - Лубанского спиновый вектор 482
Пауэлл, Сесиль Фрэнк 544
Пашена-Бака эффект 770
Пеано, Джузеппе 76
Пензиас, Арно 614
Первый закон термодинамики 580
Перенормировка 568
Перестановочные соотношения 422
Петлевые переменные 778, 780
Пионы (тг-мезоны) 106, 468, 522, 544
Пифагор 98
Пифагора теорема 67, 68, 71, 97
Пифагорейцы 67
Пифагоров строй 44
Планк, Макс 378, 428
Планка постоянная 428
Планковская длина 74
Планковские единицы 600
Платон 71, 72
Плейфера аксиома 48
Плоскостности проблема 627
Плотность 208
Подгруппа 225
Позитрон 528
Полупростые группы 244
Полчинский, Джозеф 742
Поляризация вакуума 568
Поппер, Карл 844
Поппера критерий 844
Порядок группы 225
Постоянная тонкой структуры 725
Потенциальная энергия 372
Правила отбора 489
Прасад, Манодж 761
Представление взаимодействия 457
Представление группы 238
Приводимое представление 244
Приводимое пространство 243
Приливный эффект 343
Принцип неопределенности 433
Принцип общей ковариантности 393
Принцип стационарного действия 405

Предметный указатель
909
Принцип эквивалентности 337
Проективное пространство 298
Проекторы 460
Произведение пространств 288
Простая группа 228
Простое гармоническое движение 409
Пространственное отражение 539
Протон 106, 468
Прямая сумма представлений 243
Псевдометрика 355
Псевдоортогональная группа 248
Псевдоортонормированный базис 253
Псевдориманово многообразие 279
Псевдоунитарная группа 254
Псевдоунитарное преобразование 253
Пуанкаре группа 358
Пуанкаре диск 136
Пуанкаре лемма 210, 385
Пуанкаре модель 62
Пуанкаре, Анри 345, 358
Пуассон, Симеон Дени 283, 403
Пуассона скобки 283, 413
Пульсары 398
Путешествие во времени 694
Пятый постулат Евклида 67
Равномерно-темперированный строй 44
Радиационные поправки 721
Радиоактивный распад 534
Ранг матрицы 249
Рассел, Бертран 322
Рассела парадокс 322
Расслоенное пространство 286
Расширение Вселенной 395
Рациональные числа 67
Редже траектории 736
Редже, Туллио 795
Редукция вектора состояния 449
Рекурсивно перечислимое множество 326
Рекурсивное множество 325
Ридберга - Ритца постоянная 489
Риман, Бернхард 133, 280, 281, 855
Римана гипотеза 131
Римана дзета-функция 131
Римана сфера 163
Римана тензор 282
Риманова поверхность 133, 134
Риманово многообразие 279
Риччи скаляр 394
Риччи тензор 393
Робинсона конгруэнция 813
Рэлея- Джинса формула 428
Саккери, Джироламо 59, 67
Сакс, Райнер 399
Салам, Абдус 552
Самосопряженный оператор 458
Саскинд, Леонард 737
Сато, Кацуоко 626
Сато, Микио 163
Сверхновые звезды 596
Сверхпроводимость 617, 619
Сверхпроводники 504
Сверхтекучие жидкости 504
Световой конус 345, 607
Связи 783
Связность 264, 286
Связность расслоения 304
Седловая точка 405
Сен, Амитабха 776
Сечение расслоения 291
Сигма-частица 531
Сигнатура матрицы 247
Симплектическая группа 254
Симплектическое многообразие 283
Сингулярное преобразование 232
Скалярное произведение 179
Скалярные частицы 468
Скварки 531
Скорость убегания 594
След матрицы 234
Слифер, Весто 614
Слой 288
Смежные классы 227
Смещение перигелия Меркурия 398
Смолин, Ли 637
Снайдер, Хартлэнд 598
Собственное время 352
Собственное значение 235
Собственный вектор 235
Согласованные истории 657
Соммерфилд, Чарльз 761
Соркин, Рафаэль 794
Спектральные линии 486
Спин 448
Спиновые сети 785
Спиноры 189, 467
Спиральность 464, 482
Спонтанное нарушение симметрии 570
Старобинский, Алексей Александрович 626
Статистическая механика 584
Стационарная точка 405
Стевин, Симон 337
Стереографическая проекция 57, 139
Стокс, Джордж Габриэль 209, 221
Стокса вектор 474
Стони, Джордж Джонстон 81, 725
Строминджер, Эндрю 760
Струнная постоянная 741
Струны 735
Супергравитация 727
Супергруппы 727
Супермногообразие 730
Суперсимметрия 727

910
Предметный указатель
Суперструны 741
Сферические гармоники 476
Сферические координаты 477
Тамм, Игорь Евгеньевич 529
Таниямы-Шимуры гипотеза 769
Тауоны 540
Тахионы 354
Твисторные диаграммы 830
Твисторы 75, 482
Тейлор, Брук 121
Тейлора ряд 122
Темная материя 647
Темная энергия 396
Температура 580
Тензор кривизны 267
Тензор кручения 267
Тензор энергии-импульса 390
Тензорное произведение 495
Теория категорий 796
Тепловое равновесие 583
Теэтет 71
Тождественные частицы 502
Тождественный элемент 805
Томонага, Синьитиро 552
Томсон, Уильям (лорд Кельвин) 209, 221
Топологические дефекты 620
Топология 124
Точка ветвления 134
Точка перегиба 111
Трактриса 62
Транспонированная матрица 241
Тривектор 206
Тривиальное расслоение 288
Труба будущего 817
Тьюринг, Алан 324
Тьюринга машина 324
Уайлз, Эндрю 35
Угловая частота 150
Узлы 783
Уилер, Джон Арчибальд 539, 575, 637, 717
Уленбек, Джордж 525
Унитарная группа 250, 254
Унитарная эволюция 455, 654
Унитарное преобразование 253
Унру эффект 689
Уорд, Джон Клайв 552
Уоррен, Джон 89
Фаза 303
Фазовое пространство 200, 403
Фазовый переход 619
Фактор-группа 228
Фактор-пространство 228, 288
Факториал 99
Фалес Милетский 32
Фано плоскость 313
Фарадей, Майкл 345, 378
Фаулер, Уильям 636
Фейнман, Ричард 523, 552, 560
Фейнмана диаграммы 533, 552
Фейнмана интегралы по траекториям 560
Ферма последняя теорема 35, 327, 769, 858
Ферма, Пьер 35, 107, 855
Ферми, Энрико 535
Фермионы 503
Ферро, Сципион дель 85, 93
Ферромагнетизм 617
Фитцджеральда - Лоренца сокращение 370
Фойгт, Вольдемар 770
Фок, Владимир Александрович 560
Фока пространство 560
Фонтана, Никколо (Тарталья) 85, 93
Фотино 531
Фотон 428
Фотоэлектрический эффект 428
Фреге, Готлиб 317
Фридман, Александр Александрович 591, 601
Фридмана пылевая модель 604
Фридмана - Леметра - Робертсона - Уокера
(ФЛРУ) модель 602
Фробениуса условие 221
Фуллерены 839
Функции перехода 174
Функционал 415
Функциональная производная 416
Функциональное дифференцирование 415
Функция перехода 202
Фурье преобразование 156
Фурье ряды 148
Фурье, Жозеф 148, 150, 161, 163
Хаббл, Эдвин 395, 591
Хаотические системы 578
Хартл, Джеймс 640, 679
Хаусдорфово пространство 202
Хевисайд, Оливер 108, 121, 421
Хевисайда ступенчатая функция 108
Хиггса бозон 543, 797
Хиггса поле 531
Хойл, Фредерик 629, 635
Хокинг, Стивен 640
Хокинга излучение 690
Хопф, Хайнц 293
Хопфа расслоение 293
Хэриот, Томас 60
Цайлингер, Антон 839
Цвейг, Джордж 545
Цвет кварков 546
Цепное правило 175
Цермело - Френкеля аксиомы 44
Циклическая группа 224
Цолла пространства 831

Предметный указатель
911
Цоу, Флоренс (Шэк Цунь) 551, 830
Чандрасекар, Субраманьян 595, 599
Частота колебаний 410
Черные дыры 352, 594
Черч, Алонсо 120
Четность 539
Чеха когомология 835
Шапиро, Ирвин 399
Шварц, Джон 741
Шварцшильд, Карл 596
Швингер, Юлиан 552
Шерк, Джоэль 741
Шмидта разложение 680
Шредингер, Эрвин 74, 75
Шредингера представление 456
Шредингера уравнение 425
Шредингера - Ньютона уравнение 712
Штейна множества 820
Штерна-Герлаха схема 475
Штремме, Штейн Арилд 758
Эддингтон, Артур 398, 586, 725
Эйлер, Леонард 88, 107-113, 115, 120, 122, 148,
158, 161, 167, 403, 816, 855
Эйлера оператор однородности 816
Эйлера формула 101, 103, 106
Эйлера ~ Лагранжа уравнения 405
Эйнштейн, Альберт 72, 74, 75, 215, 378
Эйнштейна уравнение гравитационного поля 395
Эйнштейна формула 374
Эйнштейна - Подольского - Розена эффект 493
Экситон 750
Электрический заряд 78
Электромагнитный потенциал 385
Электрослабое взаимодействие 535
Элитцур, Авшалом 462
Элитцура - Вайдмана мысленный эксперимент
462
Эллингсруд, Гейр 758
Эллипсоид вращения 342
Энтропия 580
Энтропия черной дыры 599
Эргосфера 698
Эрмит, Шарль 250
Эрмитов оператор 252
Эрмитова матрица 252
Эрмитово сопряжение 252
Эшер, Мориц Корнелиус 136
Юкава, Хидеки 531, 544
Якоби тождество 240
Якоби уравнение 273
Якоби, Карл Густав Якоб 403
Янг Чжень-нин 535
Янга-Миллса теория 389, 547
Яу, Шин-Тун 756

Интересующие Вас книги нашего издательства можно заказать почтой или электронной
почтой:
subscribe@rcd.ru
Внимание: дешевле и быстрее всего книги можно приобрести через наш Интернет-
магазин:
http://shop.rcd.ru
Книги также можно приобрести:
1. Москва, ИМАШ, ул. Бардина, д. 4, корп. 3, к. 414, тел. 135-54-37
2. МГУ им. Ломоносова (ГЗ, 1 этаж)
3. Магазины:
Москва: «Дом научно-технической книги» (Ленинский пр., 40)
«Московский дом книги» (ул. Новый Арбат, 8)
«Библиоглобус» (м. «Лубянка», ул. Мясницкая, 6)
Книжный магазин «ФИЗМАТКНИГА» (г. Долгопрудный,
Новый корпус МФТИ, 1 этаж, тел. 409-93-28)
С.-Пб.: «С.-Пб. дом книги» (Невский пр., 28)
Роджер Пенроуз
Путь к реальности, или законы, управляющие Вселенной.
Полный путеводитель
Дизайнер М. В. Ботя
Технический редактор А. В. Широбоков
Компьютерная верстка Д. 77. Вакуленко
Корректор Г Г. Тетерина
Подписано в печать 17.08.2007. Формат 70 х 100У1б.
Печать офсетная. Уся. печ. л. 73,53. Уч. изд. л. 77,32.
Гарнитура Таймс. Бумага офсетная №1. Заказ №30.
Научно-издательский центр «Регулярная и хаотическая динамика»
426034, г. Ижевск, ул. Университетская, 1.
http://shop.rcd.ru E-mail: mail@rcd.ru Тел./факс: (+73412) 500-295
Переплет выполнен в ГУП УР «Ижевский полиграфический комбинат»
426039, г. Ижевск, Боткинское шоссе, 180.